Общий курс физики. Для вузов. В 5 томах. Том IV. Оптика. - Сивухин Д.В.

Автор: Сивухин Д.В.

Теги: оптика физика

ISBN: 5-9221-0228-1

Год: 2005

Похожие

Сборник задач по общему курсу физики. В 5 томах. Книга IV. Оптика

Общий курс физики. Для вузов. В 5 томах. Том V. Атомная и ядерная физика.

Общий курс физики. Учебное пособие: Для вузов. В 5 томах. Том III. Электричество.

Общий курс физики. В 5 томах. Том V. Атомная и ядерная физика

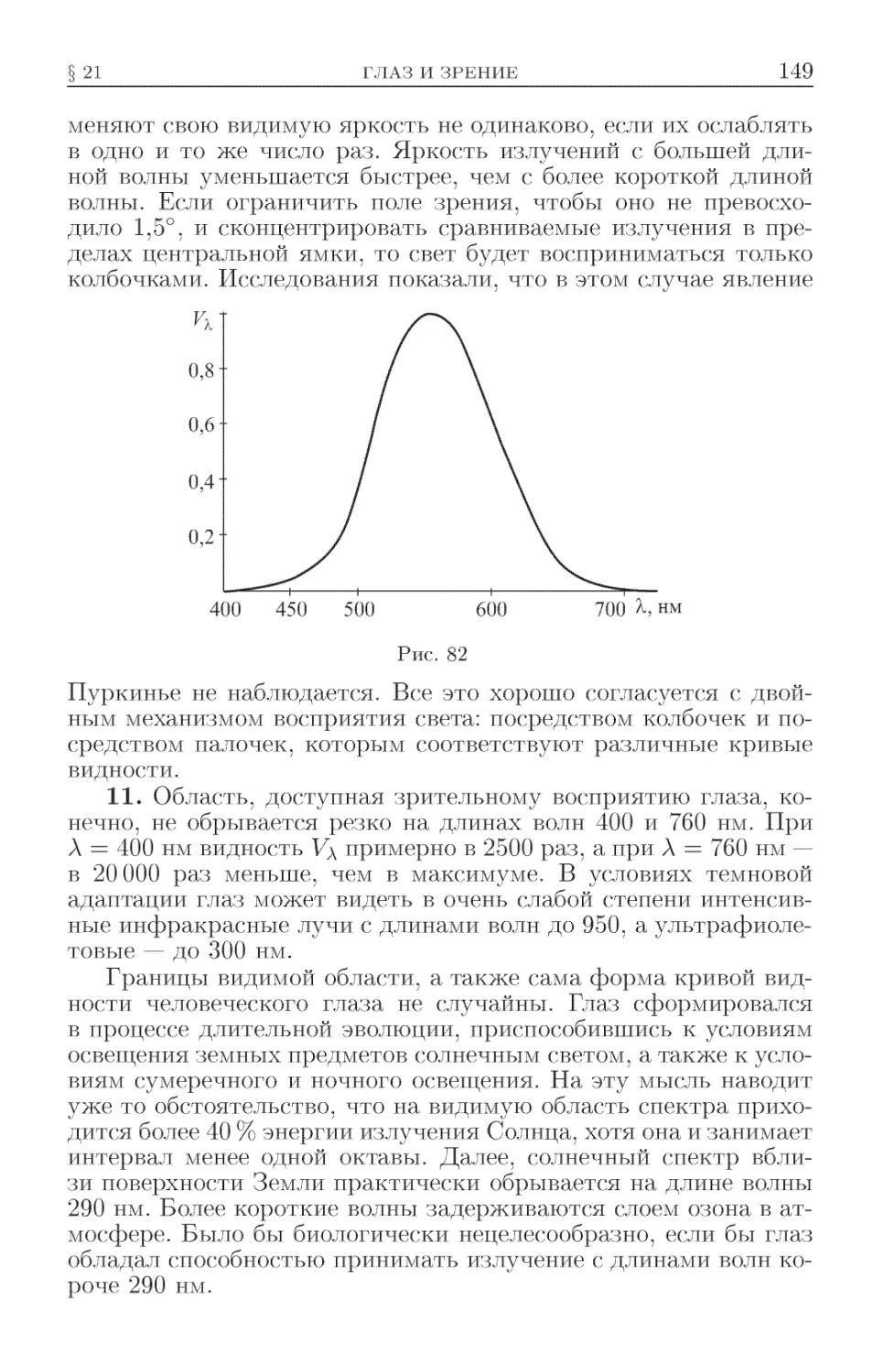
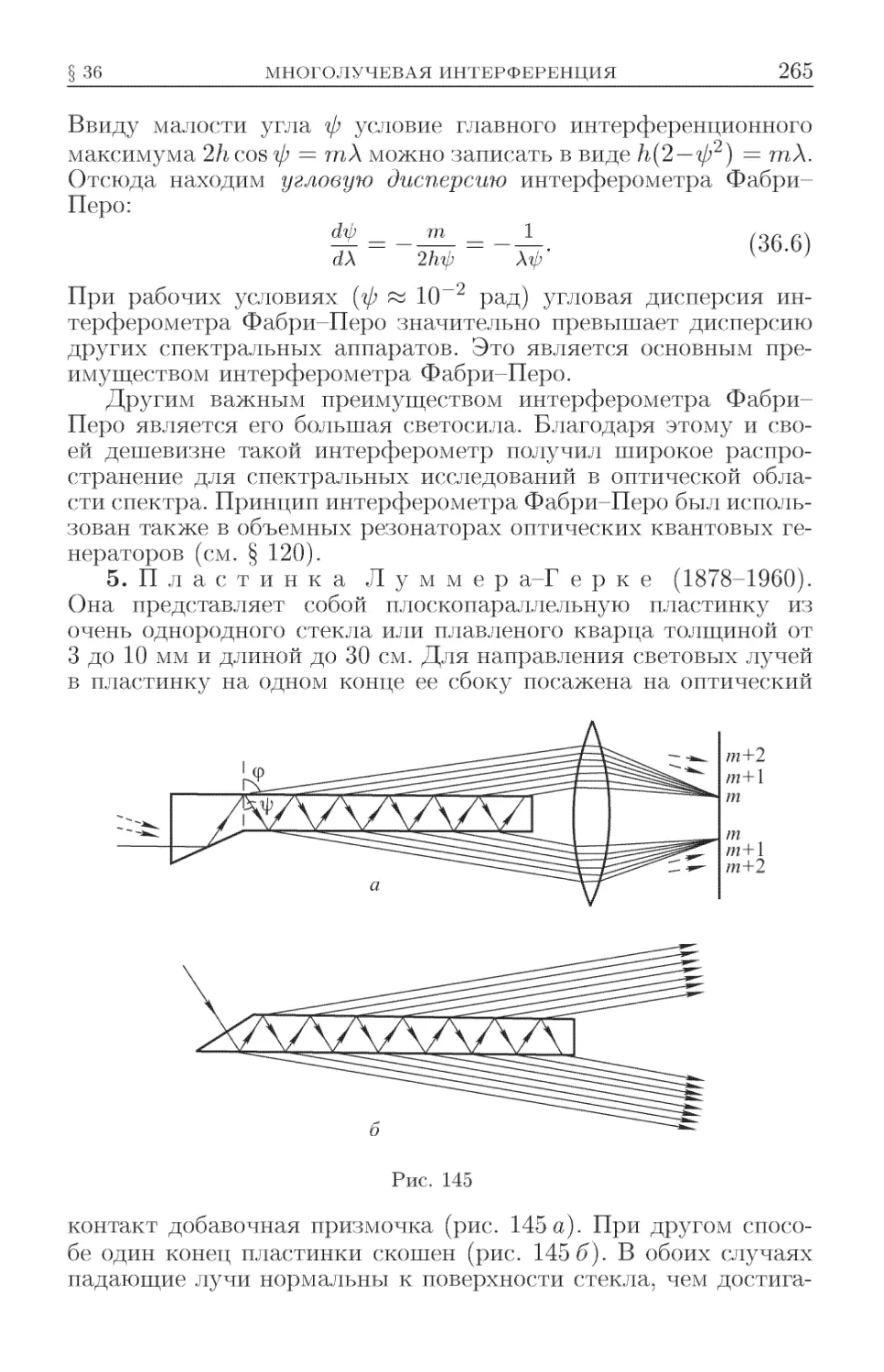
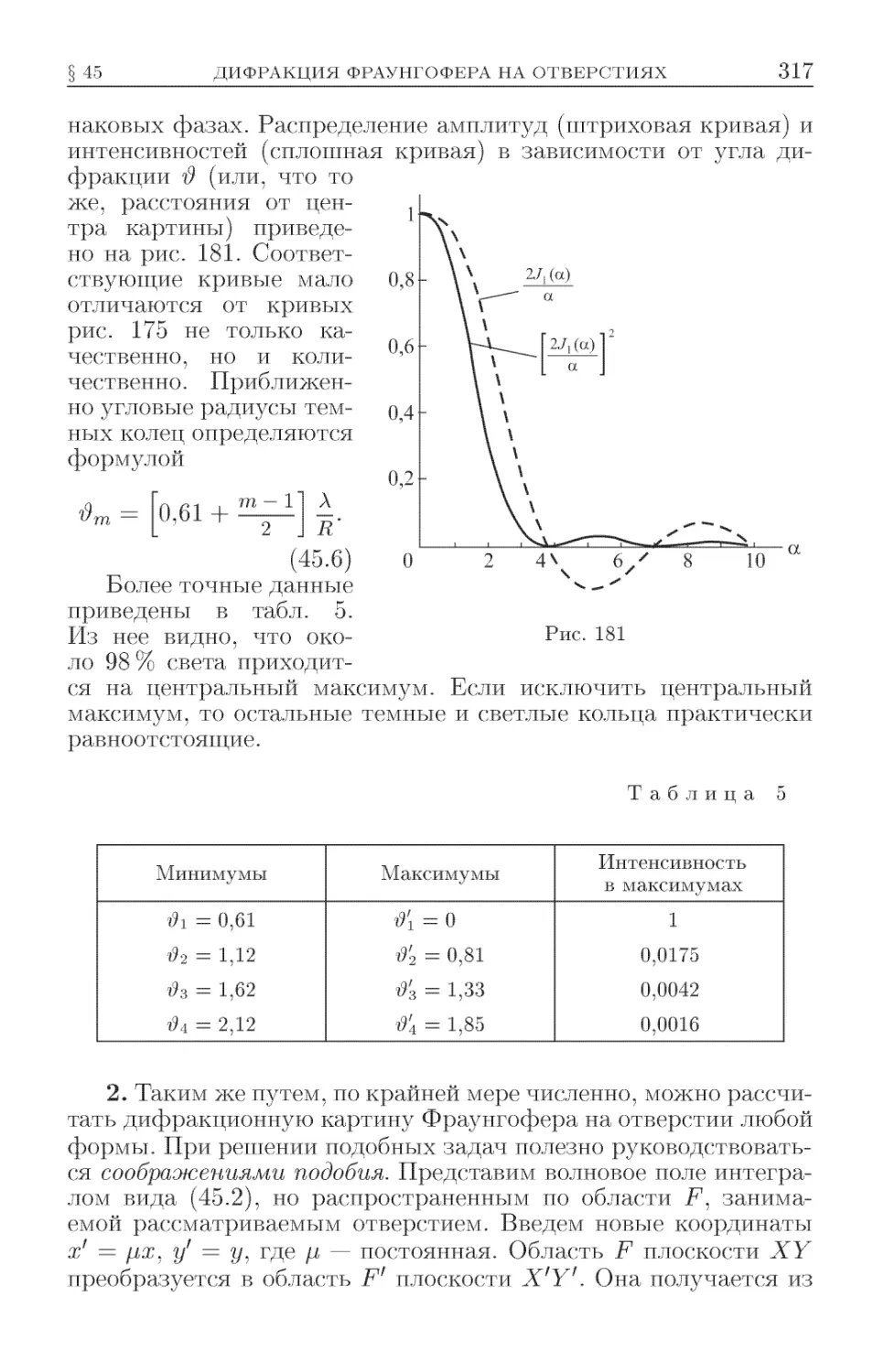
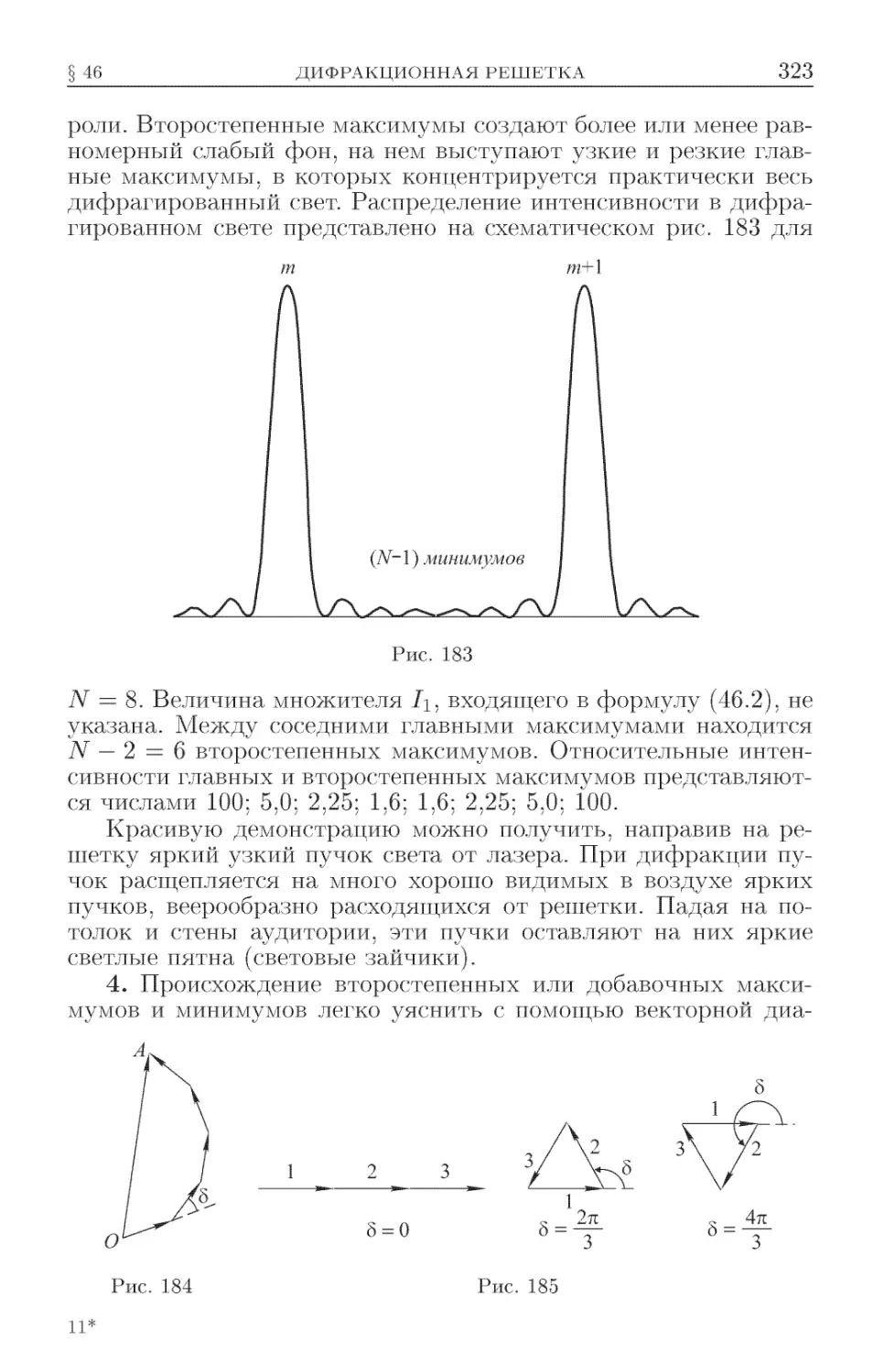
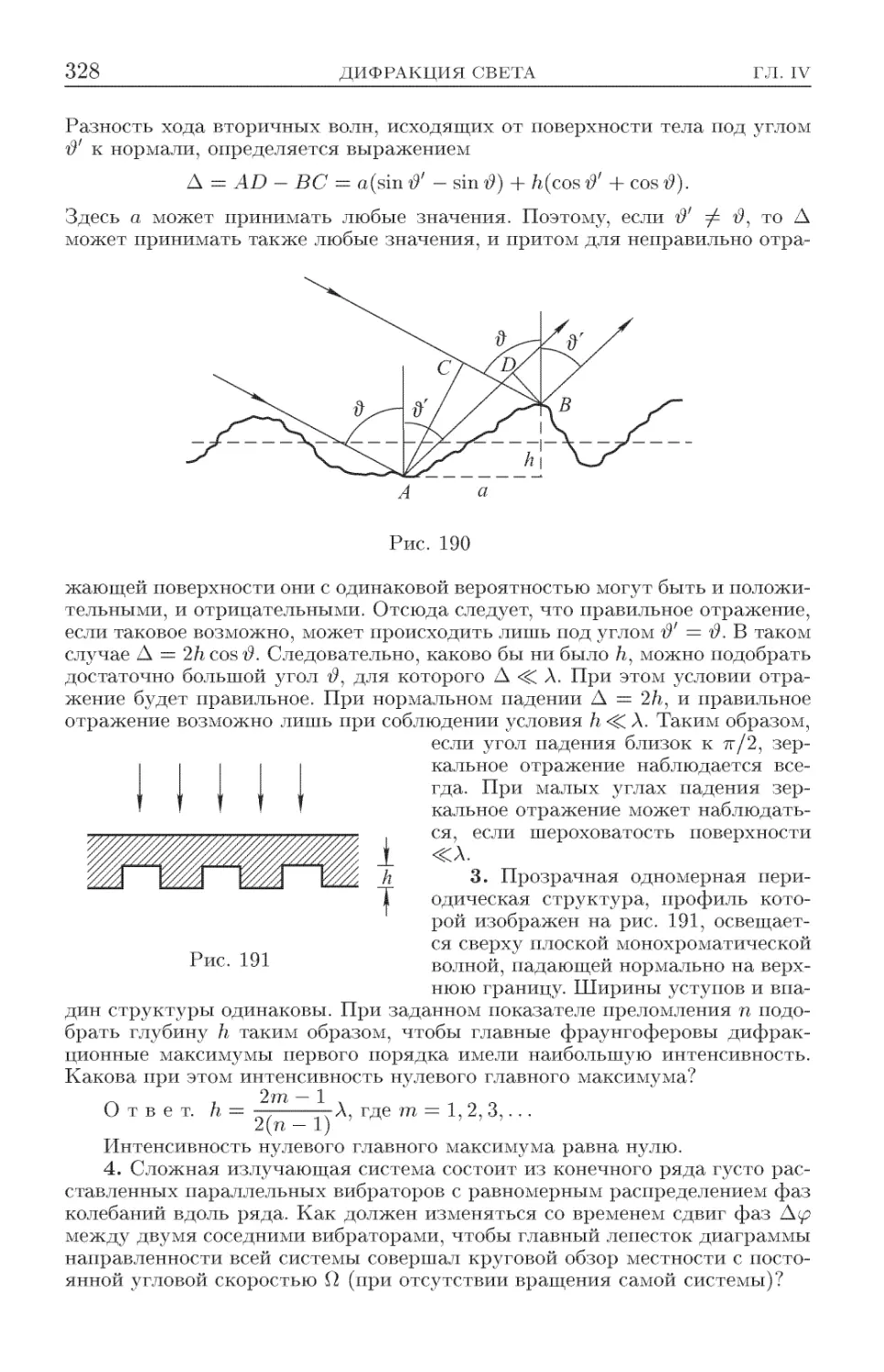
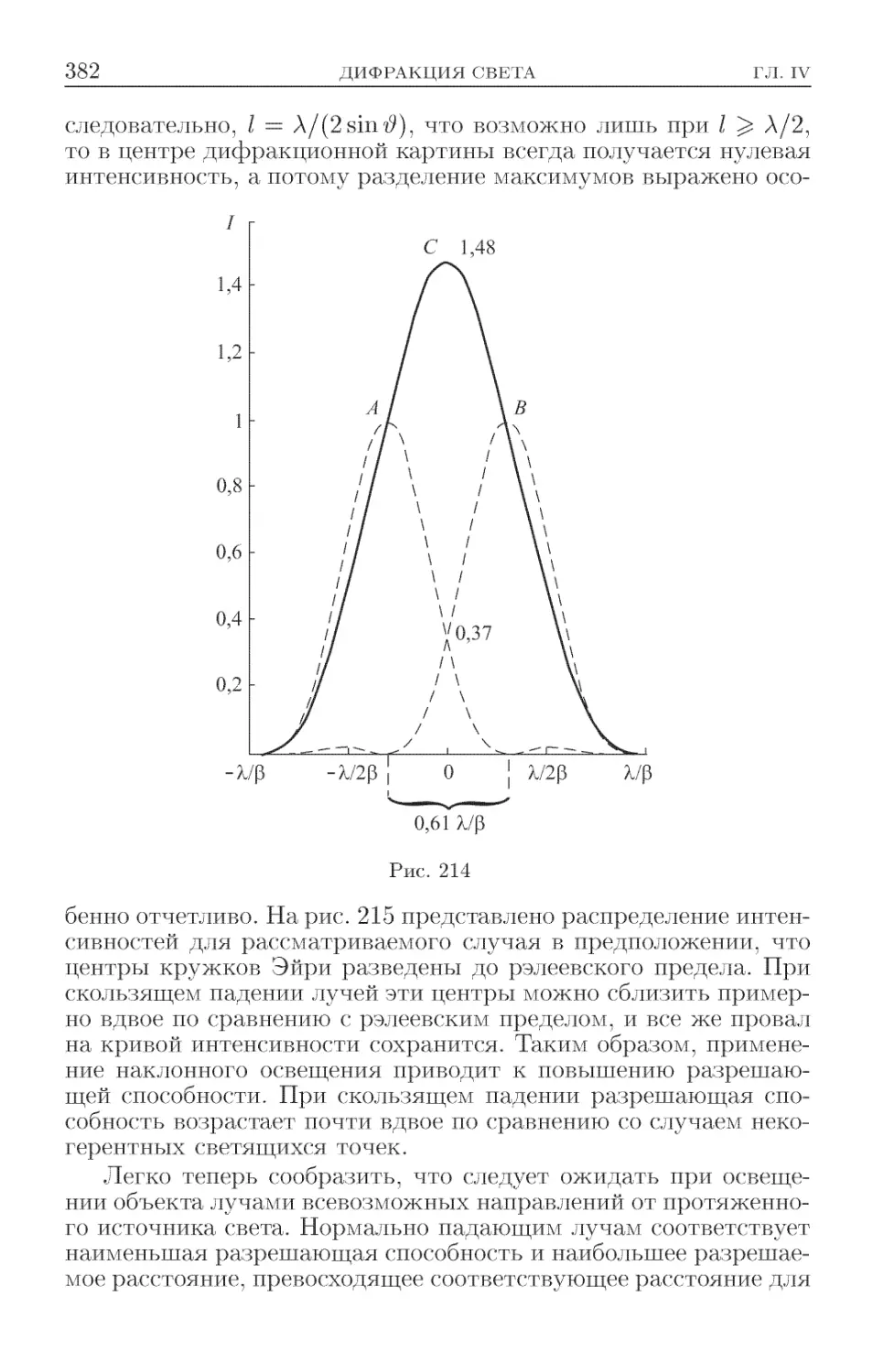
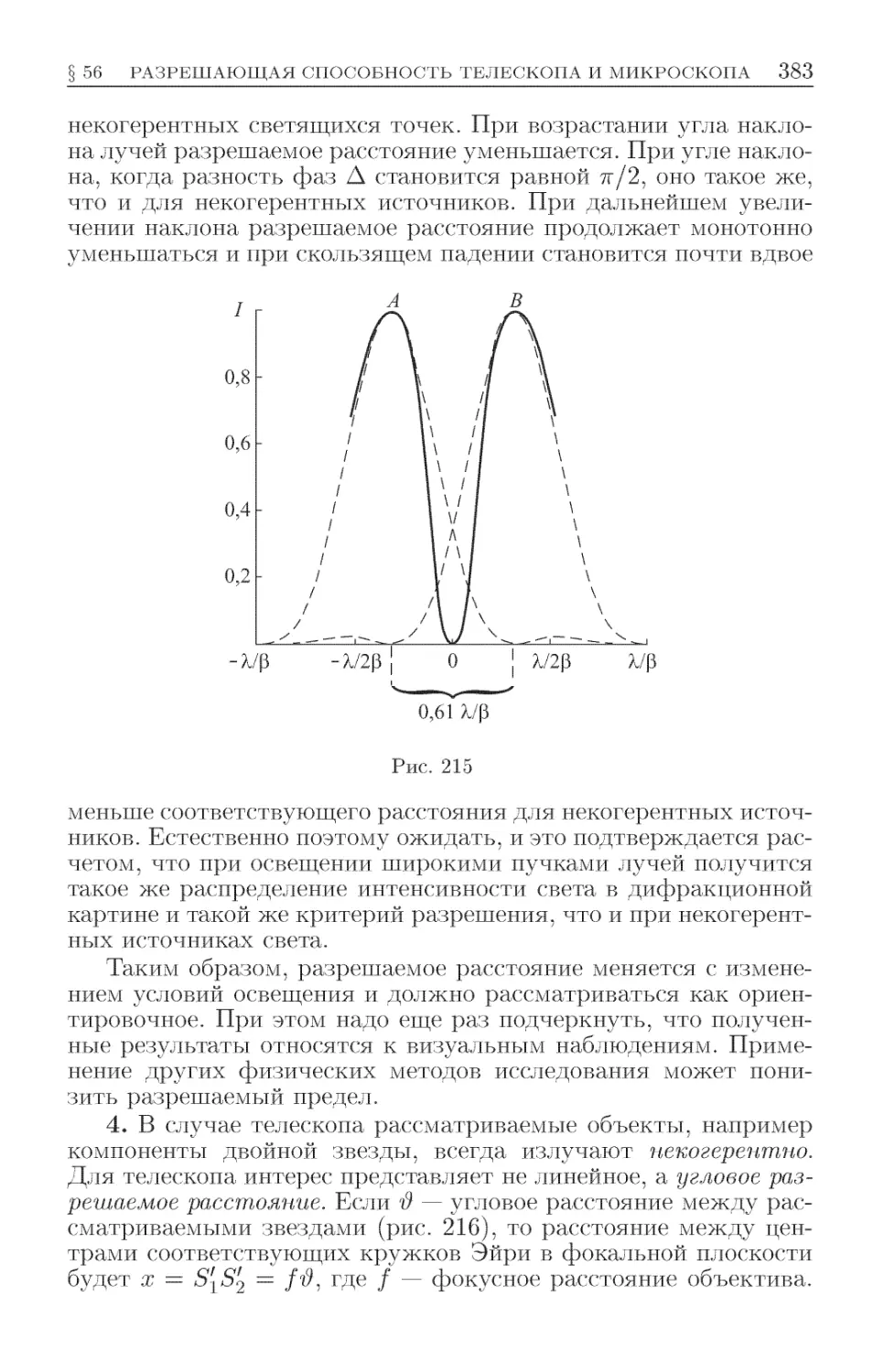
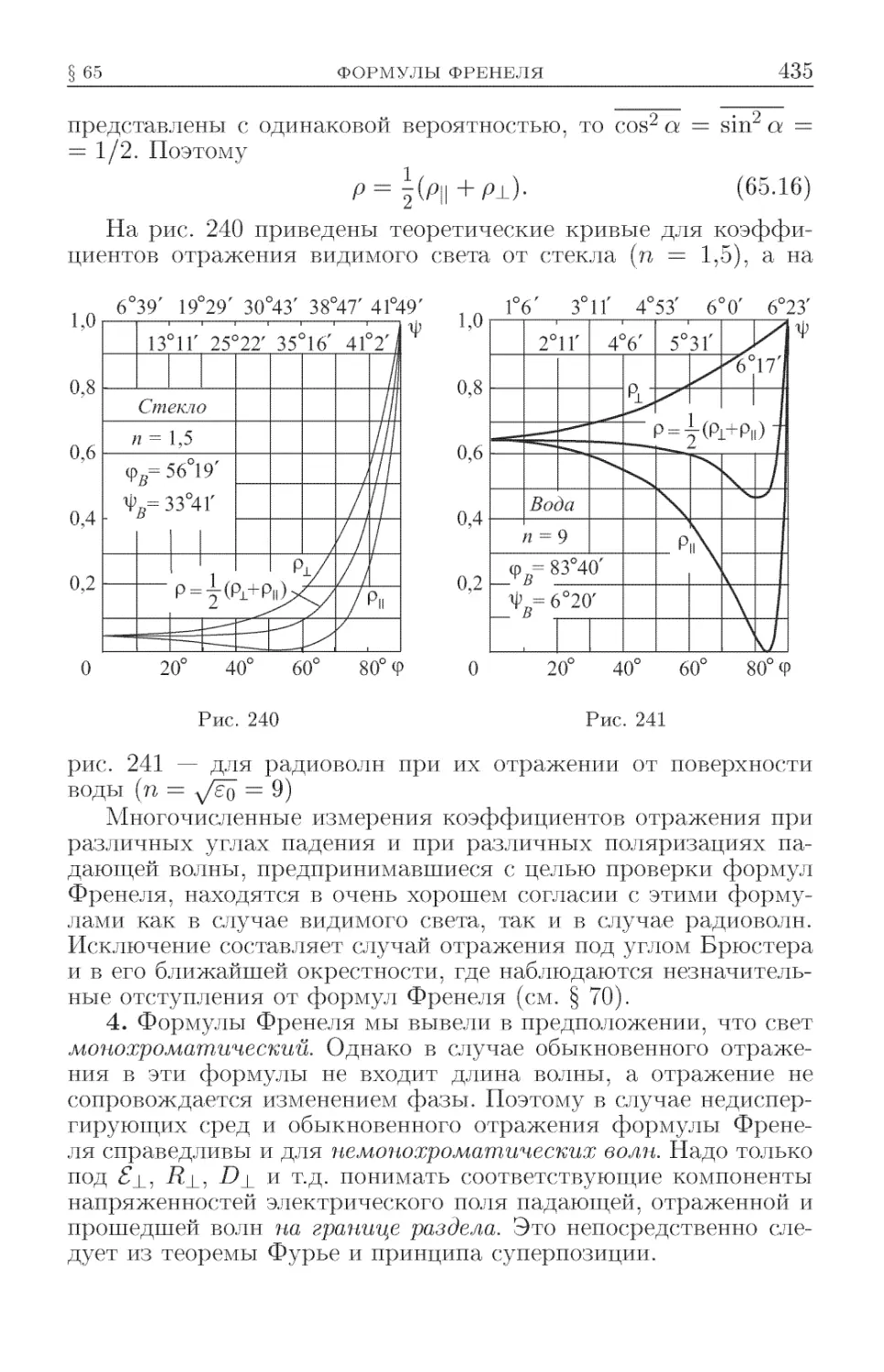
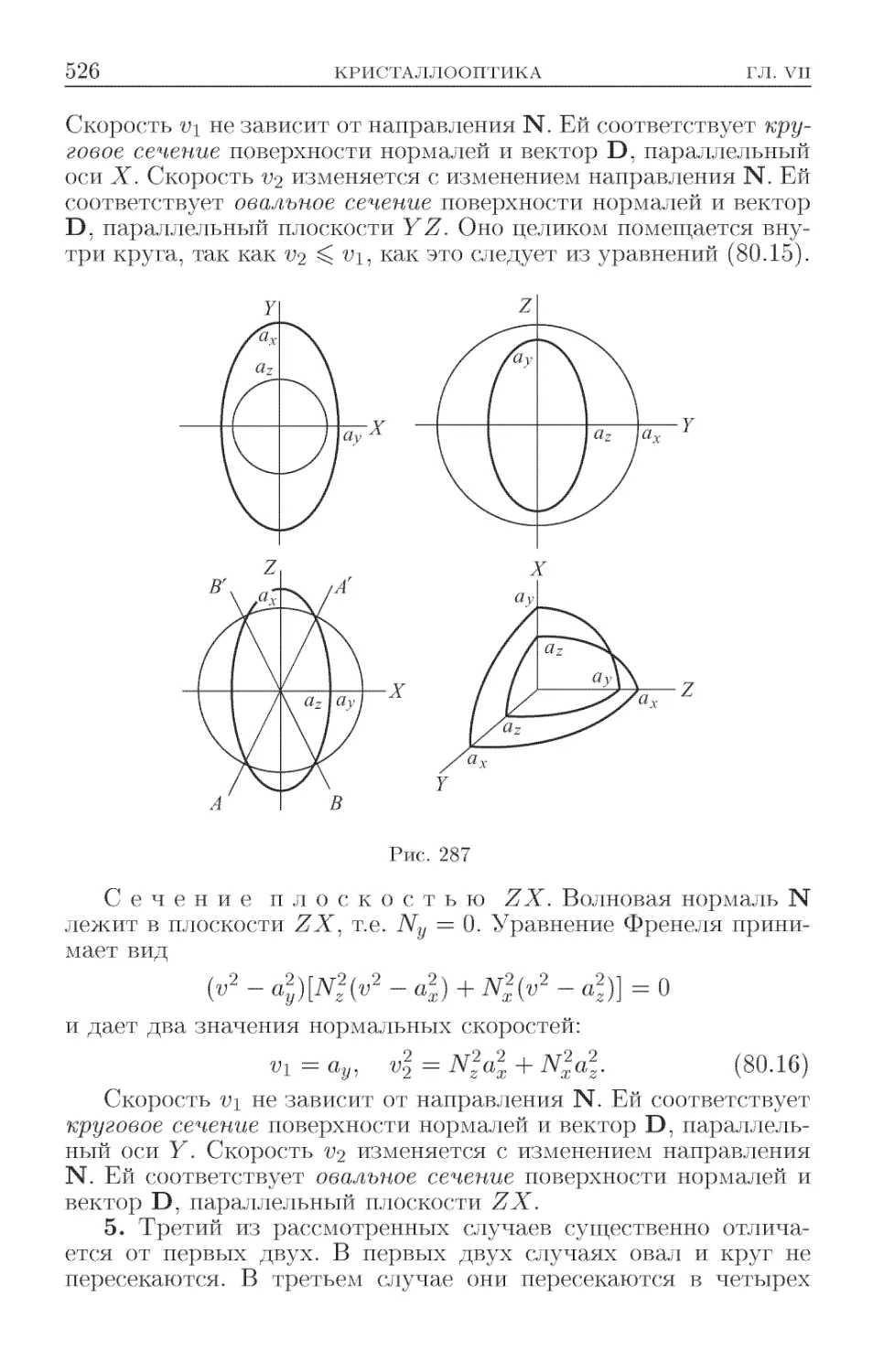
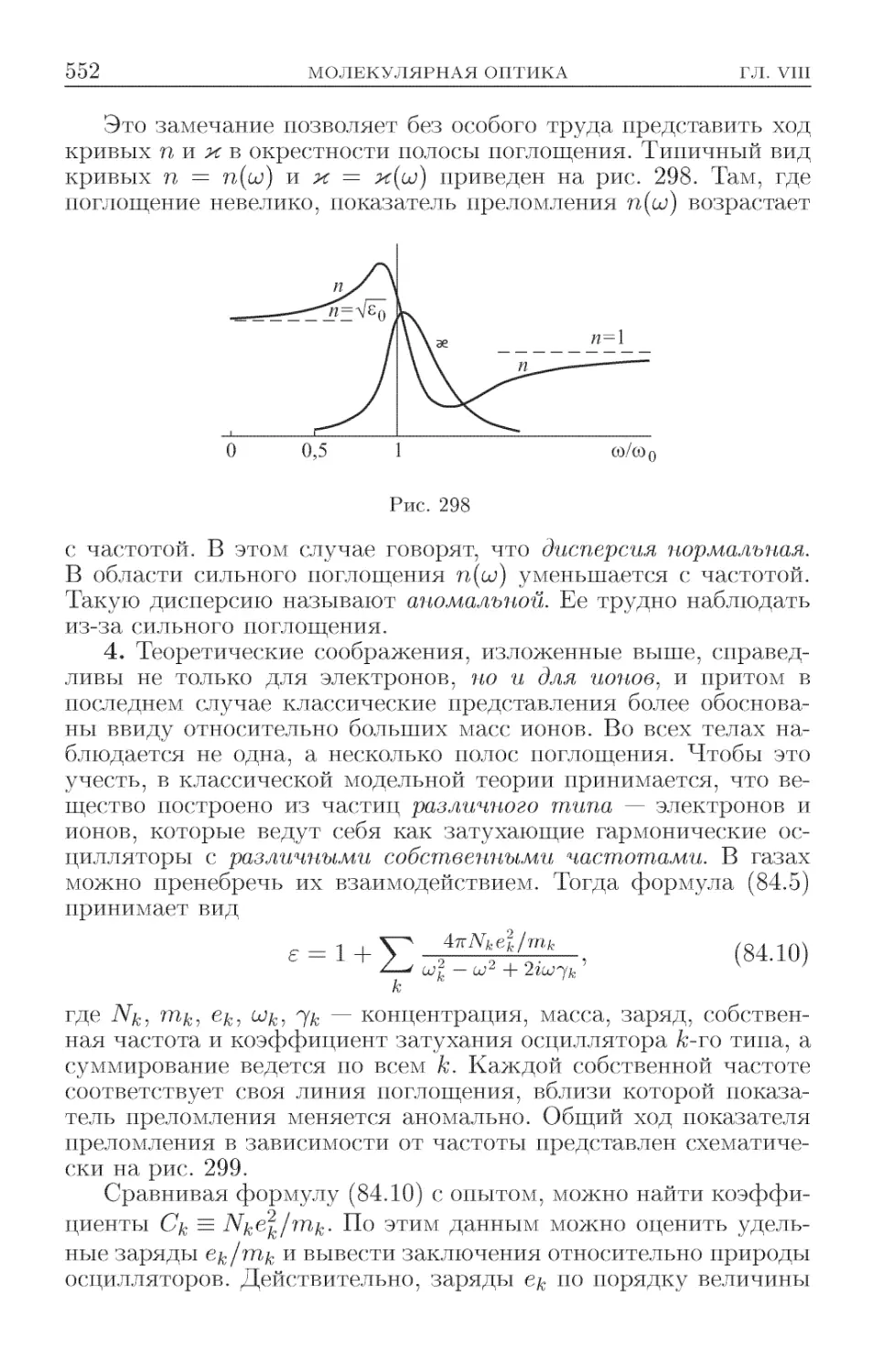
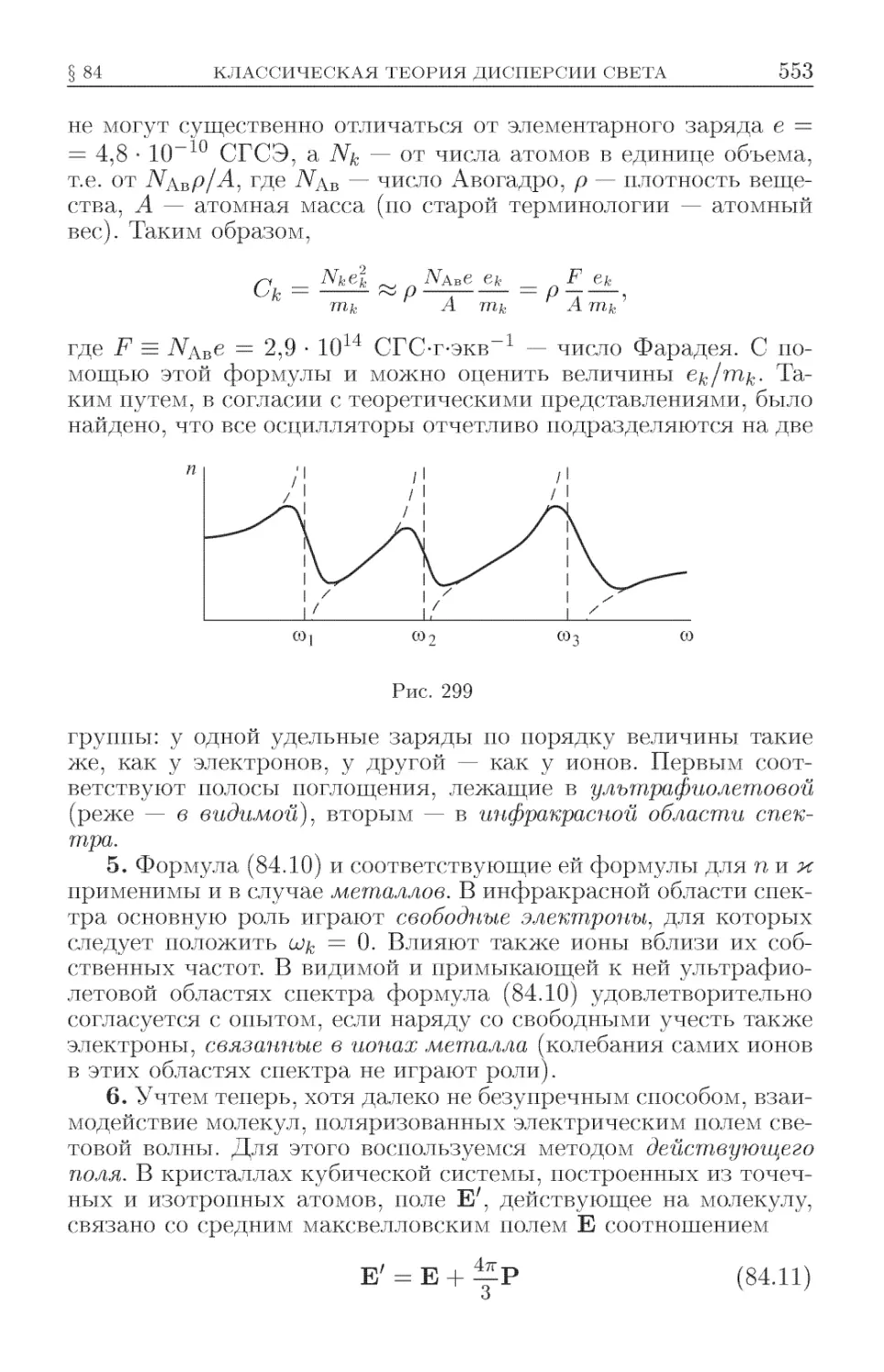
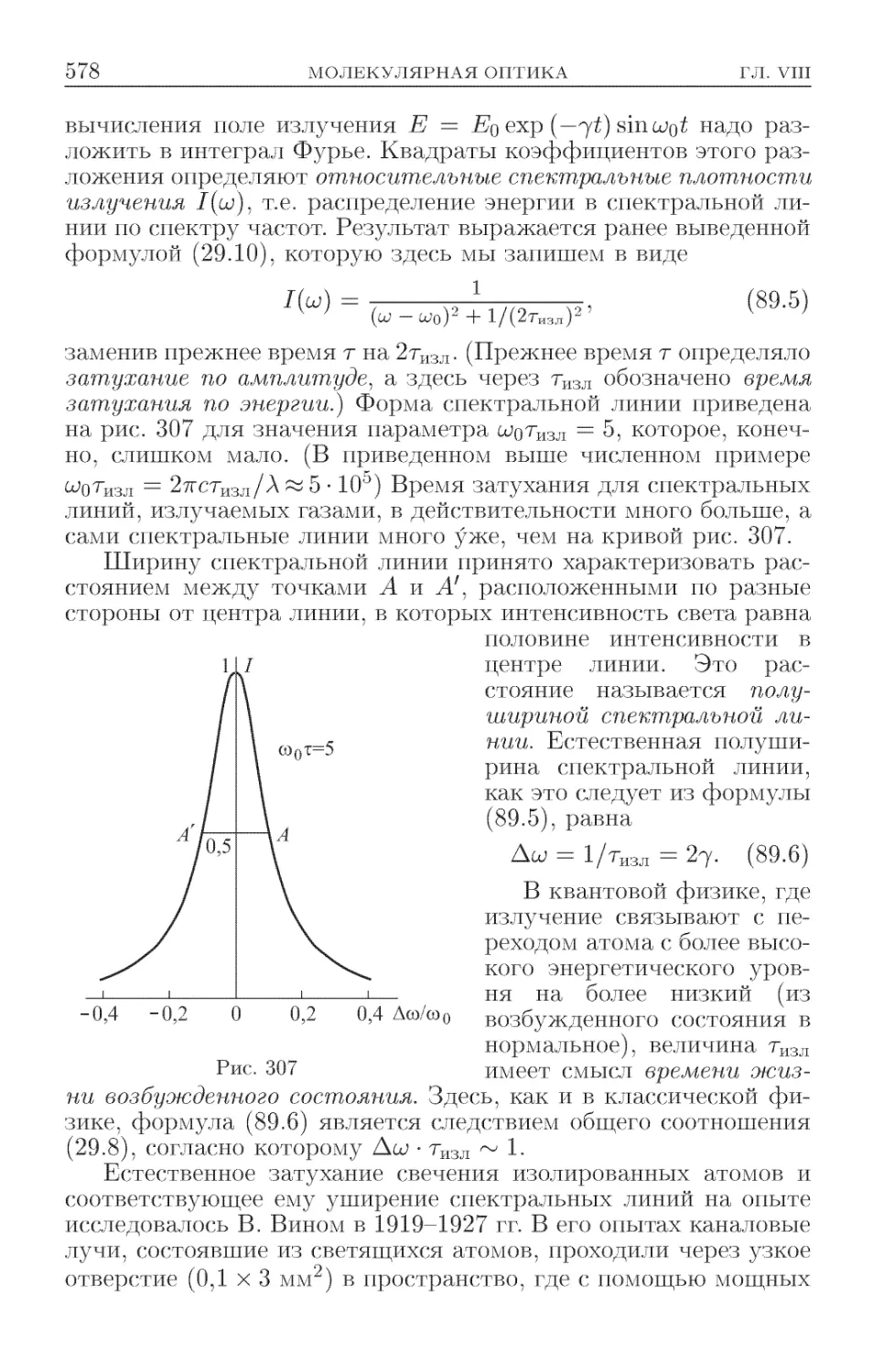
Текст

УДК 535
ББК 22.34
С34
Сивухин Д. В. Общий курс физики. Учеб. пособие: Для
вузов. В 5 т. Т. IV. Оптика. — 3-е изд., стереот. — М.: ФИЗМАТЛИТ,
2005. - 792 с. - ISBN 5-9221-0228-1.
Четвертый том курса физики, широко известного у нас в стране и за
рубежом. Книга написана на основе лекций, которые в течение ряда лет
читались автором студентам Московского физико-технического института.
Основное внимание уделено выяснению физического смысла и содержания
основных законов и понятий оптики, установлению границ применимости
этих законов, развитию у студентов навыков физического мышления и
умения ставить и решать конкретные задачи.
Второе издание четвертого тома вышло в 1985 г.
Для студентов физических и математических факультетов универси-
университетов, физико-технических и инженерно-физических институтов, а также
вузов, где физика является основной дисциплиной.
ISBN 5-9221-0228-1 (Т. IV)
ISBN 5-9221-0229-Х © ФИЗМАТЛИТ, 1985, 2002, 2005

ОГЛАВЛЕНИЕ
Предисловие .................................. 7
ГЛАВА I
ВВЕДЕНИЕ
§ 1. Предмет оптики ............................ 9
§ 2. Геометрическая оптика ........................ 12
§ 3. Эволюция представлений о природе света ............. 20
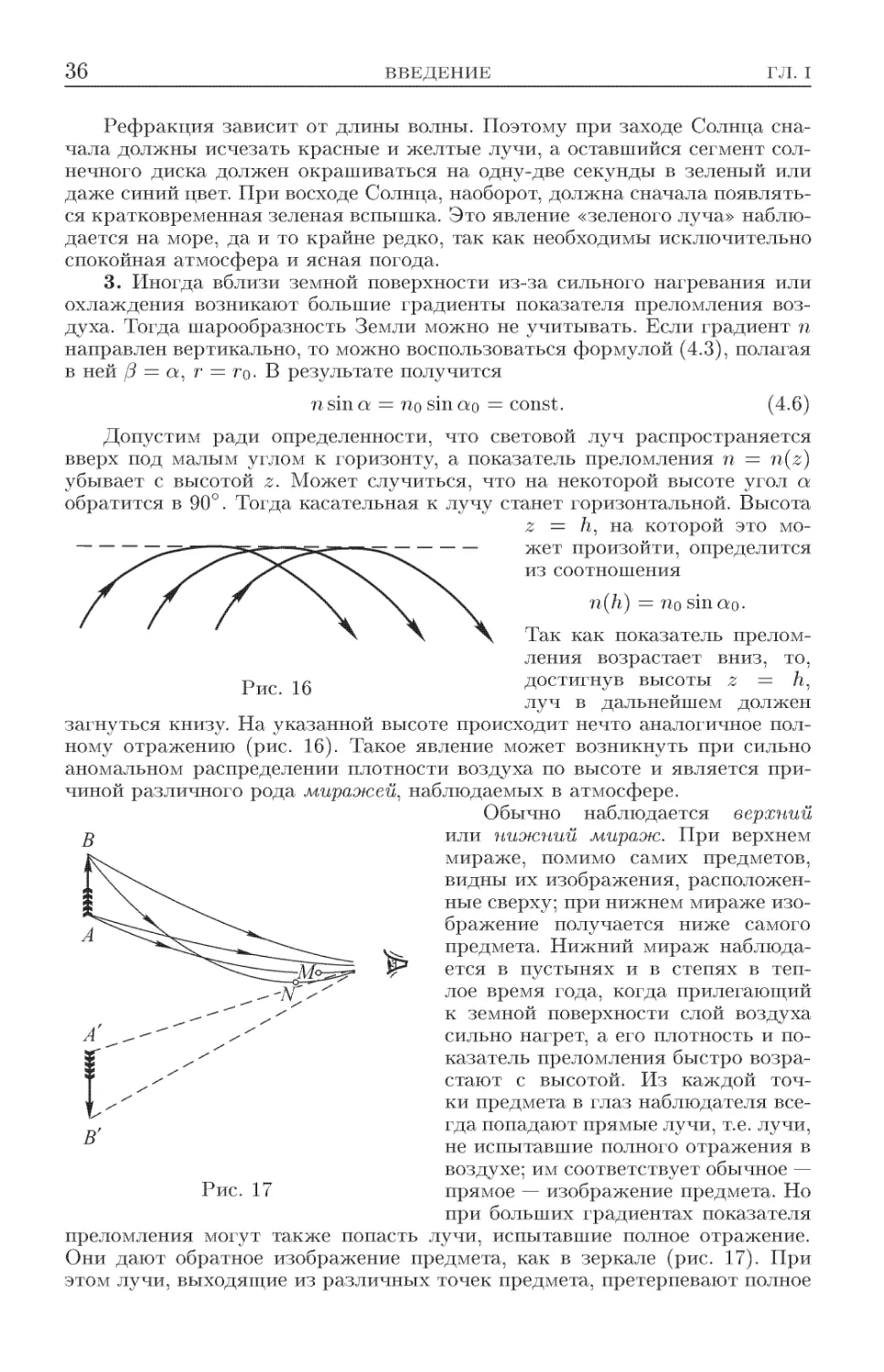
§ 4. Искривление световых лучей в неоднородных сферах ...... 33
§ 5. Плоские электромагнитные волны .................. 37
§ 6. Предельный переход от волновой оптики к геометрической ... 44
§ 7. Принцип Ферма ............................ 49
§ 8. Групповая скорость .......................... 57
ГЛАВА II
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ
ИЗОБРАЖЕНИЙ
§ 9. Понятие оптического изображения ................. 67
§ 10. Преломление на сферической поверхности. Сферические зеркала
и тонкие линзы ............................. 73
§11. Общие свойства центрированных оптических систем ....... 78
§ 12. Сложение центрированных систем. Толстые линзы ........ 89
§ 13. Ограничение лучей при помощи диафрагм ............. 96
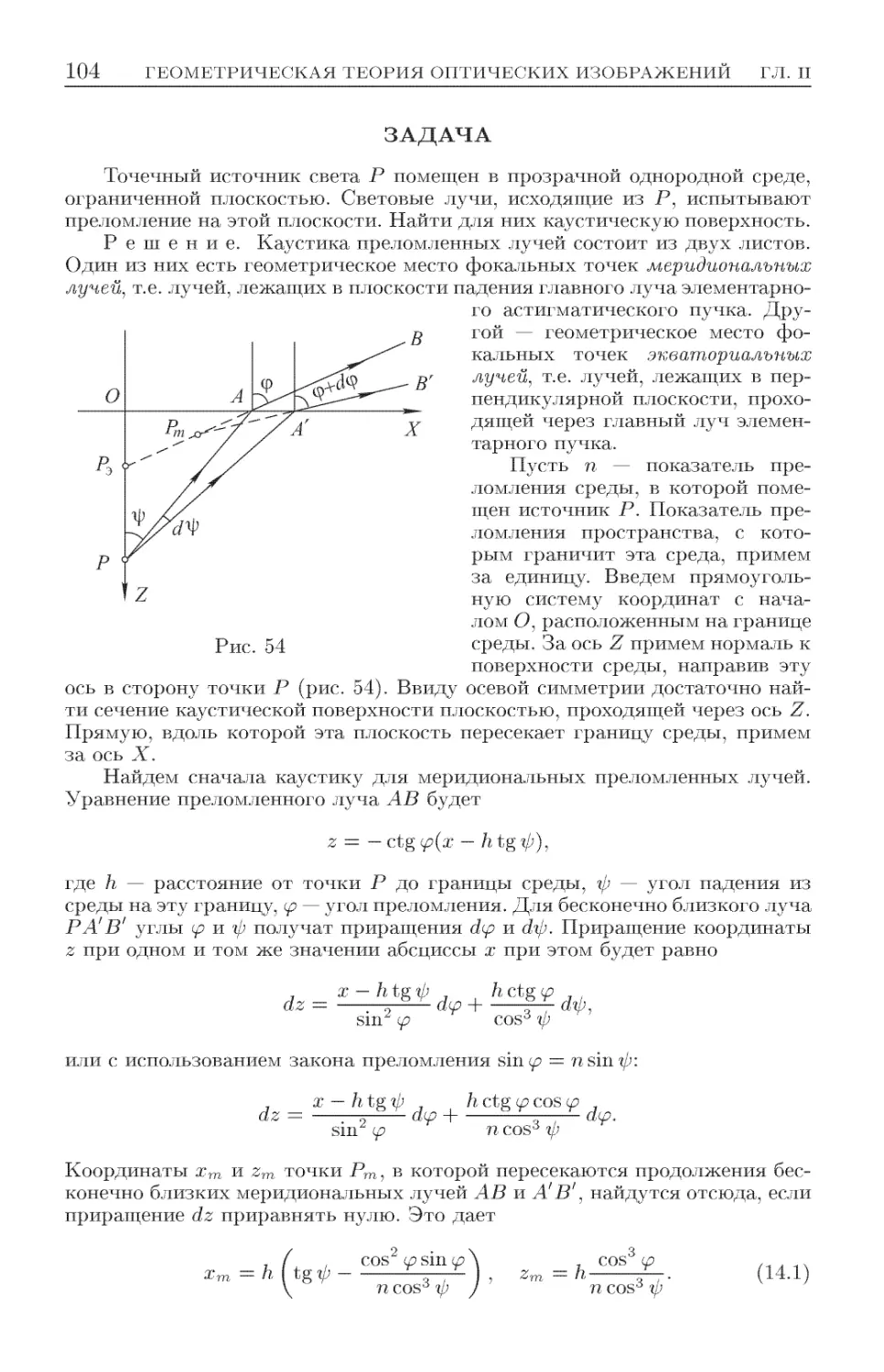
§ 14. Астигматические пучки лучей. Каустика .............. 101
§ 15. Геометрические аберрации центрированных систем ........ 106
§ 16. Хроматическая аберрация ...................... 113
§ 17. Условие отсутствия дисторсии .................... 120
§ 18. Условие синусов Аббе ......................... 122
§ 19. Теорема косинусов. Стигматические изображения широкими
пучками лучей ............................. 129
§ 20. Об абсолютно оптических инструментах .............. 135
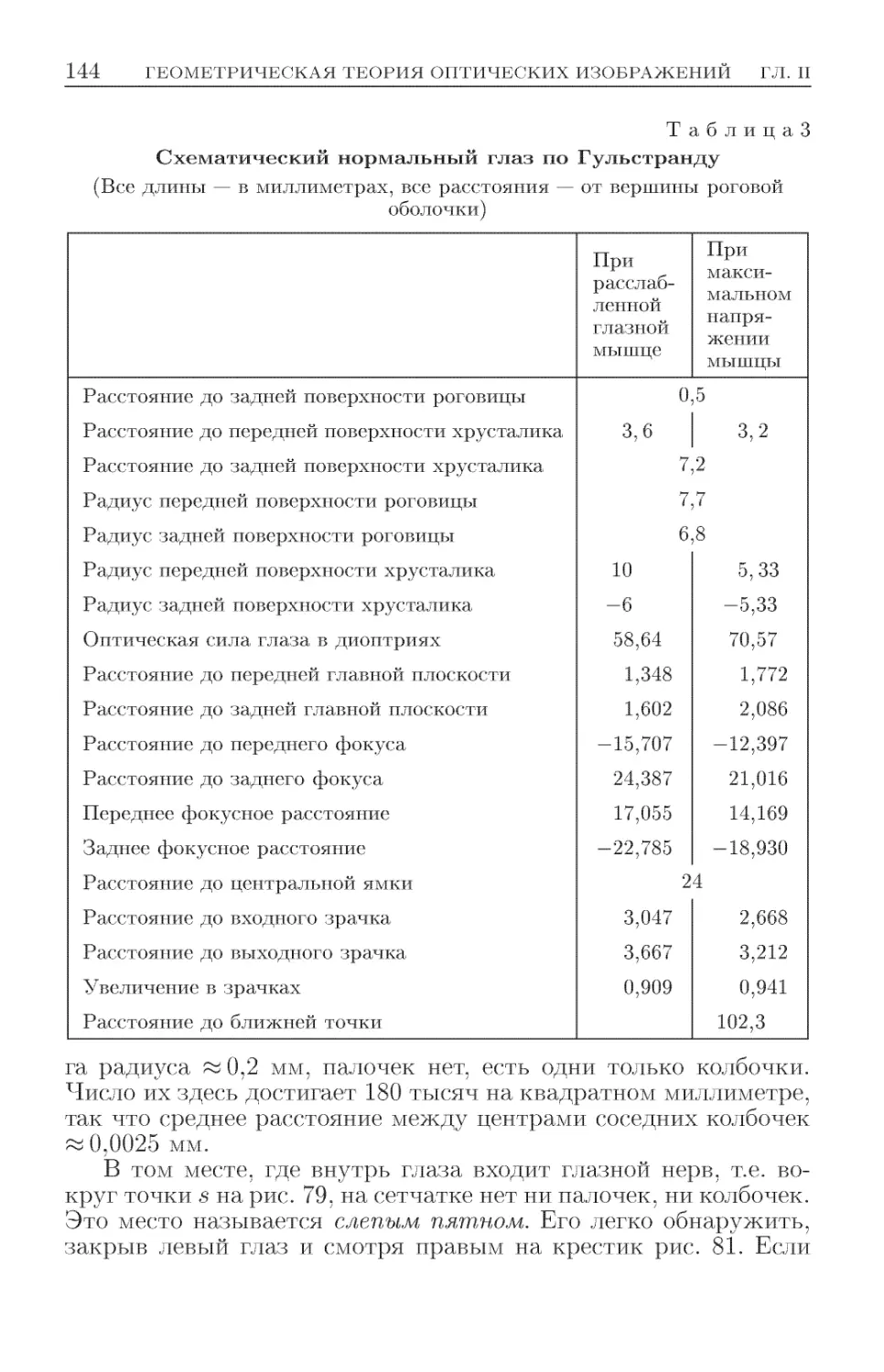
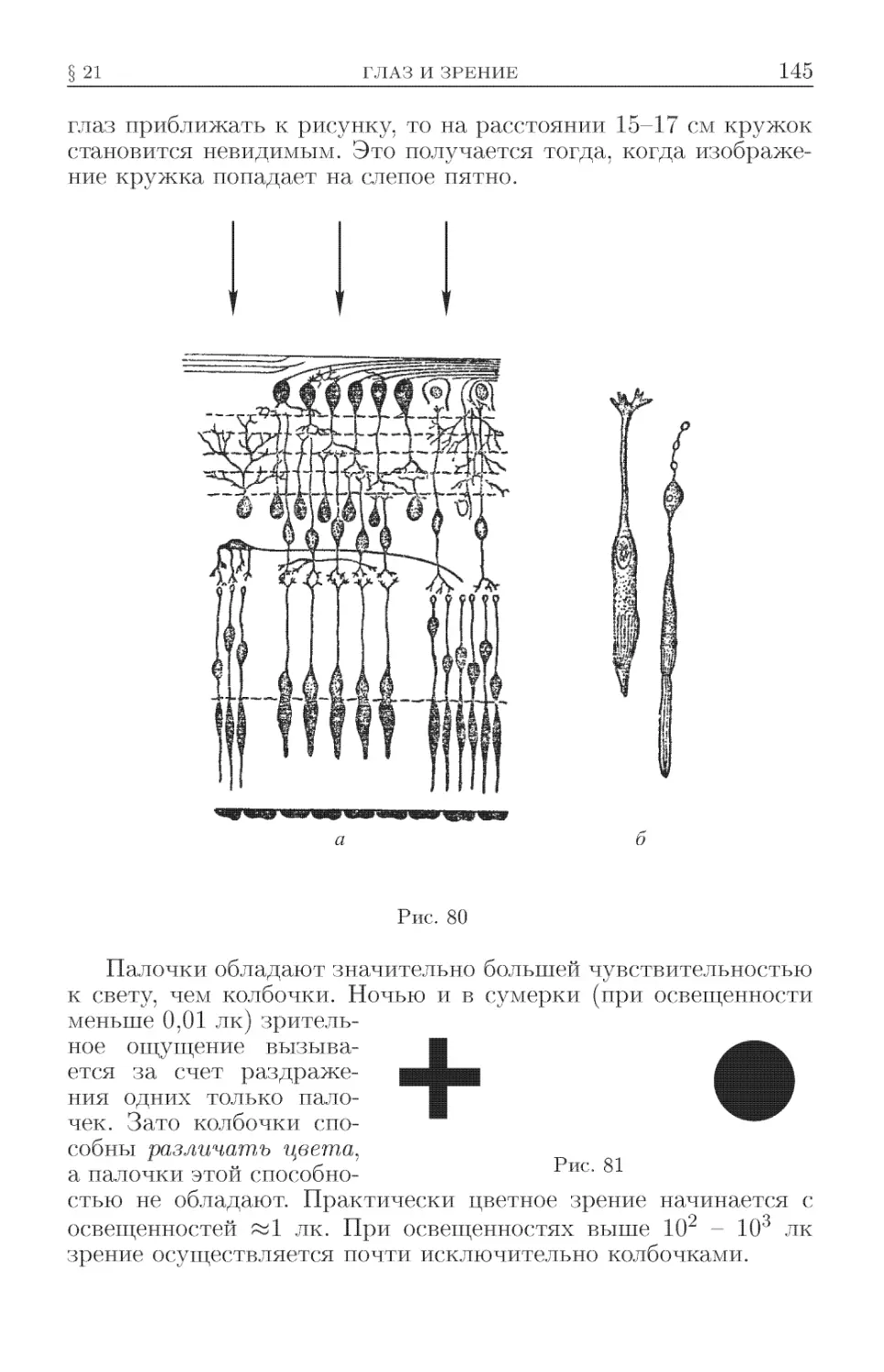
§ 21. Глаз и зрение .............................. 139
§ 22. Фотометрические понятия и единицы ................152
§ 23. Яркость и освещенность оптического изображения. Нормальное
увеличение ............................... 163
§ 24. Оптические инструменты ....................... 172
§ 25. Электрические и магнитные линзы ................. 190

ОГЛАВЛЕНИЕ
ГЛАВА III
ИНТЕРФЕРЕНЦИЯ СВЕТА
26. Общие сведения об интерференции ................. 199
27. Классические интерференционные опыты ............. 210
28. Влияние размеров источника света. Пространственная когерент™
ность ................................... 217
29. Спектральное разложение ...................... 225
30. Влияние немонохроматичности света ................ 230
31. Корреляция и когерентность света ................. 234
32. Теорема Ван™Циттера-Цернике ................... 240
33. Интерференция в пленках и пластинках .............. 242
34. Интерферометр Жамена ....................... 249
35. Интерферометр Майкельсона .................... 256
36. Многолучевая интерференция .................... 258
37. Стоячие световые волны ....................... 267
38. Излучение Вавилова-Черенкова ................... 271
ГЛАВА IV
ДИФРАКЦИЯ СВЕТА
39. Принцип Гюйгенса-Френеля. Зоны Френеля ............ 277
40. Дифракция на оси от круглого отверстия и экрана. Зонная пла-
пластинка .................................. 284
41. Метод Френеля решения дифракционных задач. Дифракция
Фраунгофера и Френеля ....................... 291
42. Зоны Шустера и спираль Корню .................. 298
43. Принцип Гюйгенса в формулировке Кирхгофа .......... 304
44. Дифракция Фраунгофера на щели ................. 309
45. Дифракция Фраунгофера на отверстиях ..............315
46. Дифракционная решетка ....................... 320
47. Дифракционная решетка как спектральный прибор ....... 329
48. Эшелон Майкельсона и интерференционные спектральные при™
боры ................................... 334
49. Разрешающая способность призмы ................. 339
50. Действие спектрального аппарата на световые импульсы .... 344
51. Вогнутая отражательная решетка .................. 350
52. Дифракция на решетке как краевая задача ............ 353
53. Примеры на применение метода Рэлея ............... 359
54. Голография ............................... 363
55. Световое поле вблизи фокуса ..................... 374
56. Разрешающая способность телескопа и микроскопа ....... 378
57. Теория и демонстрационные опыты Аббе .............. 388
58. Телескоп без объектива. Получение изображений с помощью ма-
малых отверстий ............................. 395
59. Фазовый контраст ........................... 399
60. Измерение угловых диаметров звезд ................ 402
61. Дифакция на двумерных и трехмерных решетках. Дифракция
рентгеновских лучей .......................... 407

ОГЛАВЛЕНИЕ
ГЛАВА V
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
62. Поляризованный и естественный свет ................ 420
63. Число независимых граничных условий в электромагнитной те-
теории света ................................ 423
64. Геометрические законы отражения и преломления волн ..... 426
65. Формулы Френеля ........................... 430
66. Полное отражение ........................... 436
67. Прохождение света через плоскопараллельную пластинку. Про-
Просветление оптики ............................ 441
68. Распространение света в среде с точки зрения молекулярной оп-
оптики ................................... 450
69. Вывод формул Френеля в молекулярной оптике ......... 455
70. Отступления от формул Френеля .................. 459
ГЛАВА VI
ОПТИКА МЕТАЛЛОВ
71. Уравнения Максвелла и волны в металлах ............. 466
72. Геометрические законы отражения и преломления света на гра-
границе металла .............................. 469
73. Формулы Френеля. Измерение оптических констант металлов . 472
74. Аномальный скин-эффект и эффективная диэлектрическая про-
проницаемость ............................... 478
ГЛАВА VII
КРИСТАЛЛООПТИКА
75. Плоские волны в кристаллах ..................... 481
76. Оптически одноосные кристаллы .................. 483
77. Поляризационные устройства .................... 491
78. Анализ поляризованного света .................... 499
79. Интерференция поляризованных лучей ............... 508
80. Нормальные скорости и поляризация волн в двуосных кристаллах 520
81. Лучи, волновые нормали и связь между ними ...........528
82. Коническая рефракция ........................ 537
83. Замечания об отражении и преломлении света на границе кри-
кристаллов ................................. 543
ГЛАВА VIII
МОЛЕКУЛЯРНАЯ ОПТИКА
84. Классическая теория дисперсии света ................ 548
85. Понятие о дисперсионной формуле квантовой механики ..... 559
86. Методы экспериментального исследования аномальной дисперсии 564
87. Дисперсия плазмы ........................... 569
88. Средняя плотность электромагнитной энергии в диспергирую-
диспергирующих средах ............................... 573
89. Поглощение света и уширение спектральных линий ....... 576
90. Двойное преломление света в электрическом и магнитном полях 583
91. Линейный электрооптический эффект Поккельса ......... 594

ОГЛАВЛЕНИЕ
§ 92. Эффект Зеемана ............................ 596
§ 93. Понятие об эффекте Штарка ..................... 602
§ 94. Вращение плоскости поляризации .................. 604
§ 95. Магнитное вращение плоскости поляризации ...........611
§ 96. Временная и пространственная дисперсия. Теория естественной
оптической активности ........................ 617
§ 97. О тепловых флуктуациях ....................... 626
§ 98. Рассеяние света ............................. 632
§ 99. Явление Манделыптама-Бриллюэна ................ 643
§ 100. Комбинационное рассеяние света .................. 649
ГЛАВА IX
ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
§ 101. Принцип относительности в ньютоновской и релятивистской ме-
механике .................................. 655
§ 102. Опыт Майкельсона .......................... 659
§ 103. Независимость скорости света от движения источника ...... 665
§ 104. Понятие одновременности ...................... 667
§ 105. Преобразование координат и времени в теории относительности 671
§ 106. Лорентцово сокращение длины и замедление времени ...... 680
§ 107. Эффект Допплера и аберрация света ................ 688
§ 108. Эффект Допплера в акустике и теории эфира ........... 695
§ 109. Замедление хода часов в гравитационном поле .......... 699
§ 110. Сложение скоростей в теории относительности .......... 702
§ 111. Релятивистская механика ....................... 706
ГЛАВА X
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
§ 112. Равновесное излучение в полости .................. 713
§ 113. Закон Кирхгофа ............................ 717
§ 114. Формула Кирхгофа-Клаузиуса ................... 721
§ 115. Закон Стефана-Больцмана ...................... 723
§ 116. Теорема и закон смещения Вина ................... 726
§ 117. Формула Рэлея-Джинса ....................... 731
§ 118. Формула Планка ............................ 737
§ 119. Спонтанное и индуцированное излучение .............. 743
ГЛАВА XI
ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА
§ 120. Принципы работы лазера ....................... 748
§ 121. Рубиновый лазер ............................ 754
§ 122. Гелий^неоновый лазер ......................... 762
§ 123. Нелинейная поляризация среды ................... 765
§ 124. Первое приближение. Оптическое детектирование. Генерация
вторых гармоник, суммарной и разностной частот ........ 768
§ 125. Второе приближение. Самофокусировка .............. 773
§ 126. Параметрическая генерация света .................. 776
Именной указатель .............................. 780
Предметный указатель ............................ 783

ПРЕДИСЛОВИЕ
Этот — четвертый — том общего курса физики посвящен
физической оптике и является естественным продолжением пре-
предыдущего тома, в котором излагается учение об электрических
и магнитных явлениях. Физическая оптика рассматривается в
нем преимущественно с волновой (конечно, электромагнитной)
точки зрения. Вопросы квантовой оптики затрагиваются лишь
частично. Дается представление о фотонах и процессе излуче-
излучения как о квантовом переходе атомных систем из одного энер-
энергетического состояния в другое. Это необходимо для введения
понятия индуцированного излучения и объяснения принципов
работы лазеров. Однако систематическое изложение основ кван-
квантовой оптики, в той мере, в какой это возможно сделать в рам-
рамках общей физики, а также относящихся сюда квантовых явле-
явлений (фотоэффект, эффект Комптона, спектральные закономер-
закономерности, люминесценция, эффект Зеемана, эффект Штарка и пр.),
предполагается дать в пятом томе, где будет излагаться атомная
физика в широком смысле этого слова.
Вопросы геометрической оптики собраны в первых двух гла-
главах курса, чтобы в дальнейшем можно было ссылаться на них
при изложении интерференции, дифракции и других разделов
физической оптики. Геометрическая оптика излагается не как
математическая, а как физическая дисциплина — как прибли-
приближенный предельный случай волновой оптики. Тем самым чет-
четко определяются границы ее применимости. С целью просто-
простоты в основу обоснования геометрической оптики положено ска-
скалярное волновое уравнение. Хотя в общем случае неоднородной
среды оно и неверно, но даже в этом случае при рассмотрении
предельного перехода к геометрической оптике оно приводит к
правильным результатам. Конечно, на основе скалярного урав-
уравнения ничего нельзя сказать относительно вращения плоскости
поляризации луча в неоднородной среде. Для этого надо было
бы положить в основу векторные уравнения Максвелла. Но это,
ничего не меняя в идейном отношении, потребовало бы доволь-
довольно громоздких вычислений. Существенно, что скалярное вол-
волновое уравнение правильно передает основные закономерности
распространения волн не только в однородных, но и в неодно-
неоднородных средах. Геометрическая же оптика получается из него в
предельном случае коротких волн, длины которых пренебрежи-

ПРЕДИСЛОВИЕ
мо малы по сравнению с характерными размерами, определяю-
определяющими распространение света в среде.
Впрочем, обоснование геометрической оптики при всей его
важности может быть опущено при первом чтении книги.
После изложения основ геометрической оптики во второй
главе излагается геометрическая теория оптических изображе-
изображений — главным образом с принципиальной стороны. Большая
часть материала этой главы при первом чтении может быть
также опущена. Достаточно ограничиться минимумом: получе-
получением оптических изображений в параксиальном приближении
и основными понятиями фотометрии. К остальным вопросам
можно обращаться по мере надобности в процессе изучения фи-
физической оптики.
Основное содержание курса составляет физическая оптика,
изложение которой начинается с главы III. В нее входят также
специальная теория относительности, краткое изложение прин-
ципов работы оптических квантовых генераторов (лазеров) и
элементов нелинейной оптики. Как и в предыдущих томах кур-
курса, главное внимание здесь обращено на выяснение физического
смысла и содержания оптических явлений, на связь между ни-
ними и с общими принципами физики. Автор стремился к идейной
простоте изложения, но старался избегать вульгаризации.
Вопросы истории, экспериментальное обоснование законов
оптики, применения ее в технике и других науках затронуты
лишь постольку, поскольку это необходимо для уяснения основ-
основных явлений и принципов оптики. Из-за недостатка места даже
описанию демонстраций в этом томе уделено меньше внимания,
чем в предыдущих томах курса. Впрочем, демонстрации, осу-
осуществленные в Московском физико-техническом институте мо-
моими лекционными ассистентами Е.Н. Морозовым, М.И. Макла-
ковым, В.П. Молчановым, В.А. Кузнецовой, которым я глубоко
благодарен, сыграли немалую роль при написании и этого тома
курса физики.
Рукопись этого тома была тщательно просмотрена рецен-
рецензентами — профессором С.С. Герштейном, профессором И.С.
Горбанем и сотрудниками руководимой им кафедры экспери-
экспериментальной физики Киевского государственного университета
им. Т.Г. Шевченко, а также доктором физико-математических
наук Г.П. Пекой. Их справедливые критические замечания учте-
учтены при окончательном редактировании книги. Всем этим лицам
автор приносит глубокую благодарность.
Д. В. Сивухин

ГЛАВА I
ВВЕДЕНИЕ
§ 1. Предмет оптики
Оптика, точнее — физическая оптика, есть раздел физи-
физики, изучающий свойства и физическую природу света, а также
его взаимодействие с веществом. Под светом понимают не толь-
только видимый свет, но и примыкающие к нему широкие области
спектра электромагнитного излучения — инфракрасную и уль-
ультрафиолетовую. Различные участки спектра электромагнитно-
электромагнитного излучения отличаются друг от друга длиной волны А и часто-
частотой v — величинами, характеризующими не только волновые,
но и квантовые свойства электромагнитного излучения. Элек-
Электромагнитный спектр принято делить на радиоволны, инфра-
инфракрасное, видимое, ультрафиолетовое, рентгеновское и гамма-
излучения. Эти участки спектра различаются не по своей фи-
физической природе, а по способу генерации и приема излучения.
Поэтому между ними нет резких переходов, сами участки пере-
перекрываются, а границы между ними условны.
Радиоволнами называются электромагнитные излучения,
длины волн которых превосходят примерно 0,1 мм. Их принято
делить на: 1) сверхдлинные волны с длиной волны А > 10 км
(частота v < 30 кГц); 2) длинные волны (А = 10 - 1 км, и = 30 -
300 кГц); 3) средние волны (А = 1 км - 100 м, v = 300 кГц -
3 МГц); 4) короткие волны (А = 100 — 10 м, и = 3 — 30 МГц);
5) ультракороткие волны (А < 10 м, и > 30 МГц). Последние
в свою очередь принято подразделять на метровые, децимет-
дециметровые, миллиметровые и субмиллиметровые или микромет-
микрометровые. Волны с длиной А < 1 м {у > 300 МГц) принято так-
также называть микроволнами или волнами сверхвысоких частот
(СВЧ). Из-за больших значений А распространение радиоволн
можно рассматривать феноменологически без учета атомисти-
атомистического строения среды. Исключение составляют только самые

10 ВВЕДЕНИЕ ГЛ. I
короткие радиоволны, примыкающие к инфракрасному участ-
ку спектра. Практически не сказываются и квантовые свойства
радиоизлучения.
Видимое, инфракрасное и ультрафиолетовое излучения со™
ставляют так называемую оптическую область спектра в ши-
широком смысле этого слова. Выделение такой области обусловле-
но не только близостью соответствующих участков спектра, но и
сходством методов и приборов, применяющихся для ее исследо-
исследования и разработанных исторически главным образом при изу-
изучении видимого света (линзы и зеркала для фокусировки излу-
излучения, призмы, дифракционные решетки, интерференционные
приборы для исследования спектрального состава излучения и
пр.). Оптический спектр занимает диапазон от условной гра-
границы инфракрасного излучения (А = 2 мм, v = 1,5 • 1011 Гц)
до условной коротковолновой границы ультрафиолета (А =
= 1СП6см = 10 им, v = 3 • 1016 Гц), что составляет примерно
18 октав1). Видимое излучение занимает приблизительно одну
октаву (А = 400 - 760 им), ультрафиолет — 5 октав (А = 10 -
400 нм), инфракрасное излучение — 11 октав (А = 760 нм —
2 мм). В оптической области спектра частоты и уже перестают
быть малыми по сравнению с собственными частотами атомов
и молекул, а длины волн большими по сравнению с молекуляр-
молекулярными размерами и межмолекулярными расстояниями. Благо-
Благодаря этому в этой области становятся существенными явления,
обусловленные атомистическим строением вещества. По той же
причине, наряду с волновыми, проявляются и квантовые свой-
свойства света. Энергия светового кванта определяется выражением
? = hv, A.1)
где h = 6,63 • 10~27 эрг-с — постоянная Планка. Полезно заме-
заметить, что для длины волны А = 1000 нм энергия соответствую-
соответствующего кванта составляет ? = 1,23 эВ, или приблизительно один
электрон-вольт. На концах видимого спектра (Акр = 760 нм,
^фл = 400 нм) для энергии кванта формула A.1) дает ?кр «
«1,6 эВ, ?фл ^3 эВ.
В области рентгеновского и гамма-излучения на первый план
выступают квантовые свойства излучения. Рентгеновское излу-
излучение возникает при торможении быстрых заряженных частиц
(электронов, протонов и пр.), а также в результате процессов,
происходящих внутри электронных оболочек атомов. Гамма-
излучение появляется в результате процессов, происходящих
1\ г\ «
) Октавой называется интервал частот между произвольной частотой ш
и ее гармоникой 2ш.

ПРЕДМЕТ ОПТИКИ 11
внутри атомных ядер, а также в результате превращения эле™
ментарных частиц. Оно появляется и при торможении быстрых
заряженных частиц. Характерные энергии гамма-квантов — по-
порядка одного или нескольких МэВ. Границы областей рентгенов™
ского и гамма-излучения, в особенности коротковолновые, могут
быть определены лишь весьма условно. Для общей ориентиров-
ориентировки можно принять, что энергия рентгеновских квантов лежит в
пределах 20 эВ - 1 МэВ (Л = 50 - 10~3 нм), а энергия гамма-
квантов — больше 0,1 МэВ (Л < 10^2 нм).
Следует заметить, что волновые и квантовые закономерно-
закономерности являются общими для всего спектра электромагнитного из-
излучения. Только, в зависимости от длины волны, на первый план
выступают разные явления, разные методы исследования и раз-
разные практические применения. Поэтому на оптику нельзя смо-
смотреть как на замкнутую дисциплину, изучающую только оптиче-
оптическую область спектра, отделенную от других областей резкими
границами. Закономерности и результаты, найденные в этих и
других областях, могут оказаться применимыми в оптической
области спектра и обратно.
Практическое значение оптики и ее влияние на другие от-
отрасли знания исключительно велики. Изобретение телескопа и
спектроскопа открыло перед человеком удивительнейший и бо-
богатейший мир явлений, происходящих в необъятной Вселенной.
Изобретение микроскопа произвело революцию в биологии. Фо-
Фотография помогла и продолжает помогать чуть ли не всем отрас-
отраслям науки. Одним из важнейших элементов научной аппарату-
аппаратуры является линза. Без нее не было бы микроскопа, телескопа,
спектроскопа, фотоаппарата, кино, телевидения и т.п. Не бы-
было бы очков, и многие люди, которым перевалило за пятьдесят
лет, были бы лишены возможности читать и выполнять многие
работы, связанные со зрением.
Область явлений, изучаемая физической оптикой, весьма об-
обширна. Оптические явления теснейшим образом связаны с яв-
явлениями, изучаемыми в других разделах физики, а оптические
методы исследования относятся к наиболее тонким и точным.
Поэтому неудивительно, что оптике на протяжении длительно-
длительного времени принадлежала ведущая роль в очень многих фун-
фундаментальных исследованиях и развитии основных физических
воззрений. Достаточно сказать, что обе основные физические
теории текущего столетия — теория относительности и теория
квантов — зародились и в значительной степени развились на
почве оптических исследований. Изобретение лазеров открыло
новые широчайшие возможности не только в оптике, но и ее
приложениях в различных отраслях науки и техники.

12 ВВЕДЕНИЕ ГЛ. I
§ 2. Геометрическая оптика
1. Простейшие оптические явления, например возникновение
теней и получение изображений в оптических приборах, могут
быть поняты в рамках так называемой геометрической оптики.
В основу формального построения последней можно положить
четыре закона, установленных опытным путем: 1) закон пря-
прямолинейного распространения света; 2) закон независимости
световых пучков; 3) закон отражения и 4) закон преломления
света. Для понимания более сложных явлений нужна уже фи-
физическая оптика, рассматривающая эти явления в связи с фи-
зической природой света. Физическая оптика позволяет, в част™
ности, не только вывести все законы геометрической оптики,
но и установить границы их применимости. Без знания этих
границ формальное применение законов геометрической опти™
ки может в конкретных случаях привести к результатам, про-
противоречащим наблюдаемым явлениям. Поэтому нельзя ограни-
ограничиться чисто формальным построением геометрической оптики,
а необходимо смотреть на нее как на раздел физической опти-
оптики. Обоснование геометрической оптики будет дано постепенно
на протяжении нашего курса. Сейчас же ограничимся форму™
лировкой перечисленных четырех опытных законов.
2. Согласно закону прямолинейного распространения, свет в
прозрачной однородной среде распространяется по прямым ли-
линиям. Опытным доказательством этого закона могут служить
резкие тени, отбрасываемые непрозрачными телами, освещае™
мыми точечными источниками света, т.е. источниками, размеры
которых весьма малы по сравнению с размерами освещаемого
тела и расстоянием до него. Непрозрачный предмет АВ (рис. 1),
D
В
'с
Рис. 1 Рис. 2
поставленный на пути светового пучка от точечного источни-
источника Sj не пропускает свет в пространство за этим предметом,
ограниченное боковой поверхностью конуса SCD^ касающейся
краев предмета АВ. Однако на распределение света вне этого

§ 2 ГЕОМЕТРИЧЕСКАЯ ОПТИКА 13
пространства присутствие предмета АВ не оказывает никакого
влияния. Это и значит, что распространение света происходит
вдоль прямых линий 1). Другое доказательство дает общеизвест-
общеизвестный способ получения изображений светящихся предметов в ка-
мере с малым отверстием (камере-обскуре, рис. 2).
Наблюдаются отступления от закона прямолинейного рас™
пространения света. Рассмотрим, например, тень от резкого
края непрозрачного предмета. Если источник света точечный,
то, согласно этому закону, следовало бы ожидать, что на экране
получится совершенно резкий переход от света к тени. На са-
самом деле возникает переходная область, в которой освещенность
меняется непрерывно и не монотонно: в ней наблюдаются «ди™
фракционные полосы». Аналогичное положение имеет место в
камере с малым отверстием. Если отверстие недостаточно мало,
то изображение предмета размыто, так как светящаяся точка
изображается в виде светлого кружка. Можно было бы ожи-
ожидать, что при уменьшении отверстия размеры кружка будут
уменьшаться, а отчетливость изображения увеличиваться, хо-
хотя само изображение и получится менее ярким. На самом деле
это оправдывается лишь до известного предела, а при дальней-
дальнейшем уменьшении отверстия резкость изображения снова начи-
начинает ухудшаться. Когда диаметр отверстия ^ Ю^3 мм, а ис™
точник света точечный, получается практически равномерная
освещенность экрана.
Приведенные примеры показывают, что свет, подобно звуку,
огибает препятствия, стоящие на пути его распространения. Это
явление называется дифракцией.
Если среда мутная, например туман, то из-за дифракции
прямолинейное распространение света сопровождается его рас-
рассеянием в стороны.
3. Закон независимости световых пучков состоит в том, что
распространение всякого светового пучка в среде совершенно не
зависит от того^ есть в ней другие пучки света или нет. Све-
Световой пучок, прошедший через какую-либо область простран-
пространства, выходит из нее одним и тем же, независимо от того, за-
заполнена она другим светом или не заполнена. Так, изображение
на сетчатке глаза не изменится, если свет, образующий это изо-
изображение, будет на своем пути проходить через боковые пуч-
пучки света, не попадающие в глаз. Границы применимости закона
) Протяженный источник ведет себя как совокупность точечных источ-
источников, каждому из которых соответствует свое распределение светового
поля на экране. В результате наложения таких картин наряду с тенями
возникают полутени, т.е. области более или менее плавного перехода от
освещенных частей экрана к менее освещенным и совсем темным.

14 ВВЕДЕНИЕ ГЛ. I
независимости световых пучков лучше рассматривать в связи с
теорией света (см. § 3, 5 и гл. XI).
Закон независимости световых пучков необходимо допол-
нить утверждением, определяющим совместное действие свето-
световых пучков при их наложении друг на друга. Оно состоит в
том, что освещенность экрана, создаваемая несколькими свето-
световыми пучками, равна сумме освещенностей, создаваемых каж-
каждым пучком в отдельности. Нарушения справедливости этого
утверждения имеют место в явлениях интерференции света.
4. На основе законов прямолинейного распространения и
независимости световых пучков сложилось представление о све-
световых лучах. В математическом смысле луч есть линия,
вдоль которой распространяется свет. Это — математическая
абстракция. О существовании луча в таком смысле можно го-
говорить лишь постольку, поскольку он входит в состав свето-
светового пучка, содержащего бесконечное множество лучей. Реаль-
Реальное существование имеют не математические лучи и бесконечно
тонкие пучки света, а пучки конечного поперечного сечения, вы-
вырезаемые, например, диафрагмами. Поэтому под лучом в физи-
физическом смысле этого слова мы будем понимать конечный, но
достаточно узкий световой пучок, который еще может су-
существовать изолированно от других пучков. Луч, выделенный
какой-либо диафрагмой, не может быть бесконечно длинным,
так как из-за дифракции распространение света сопровождается
увеличением поперечных размеров луча, т.е. его боковым уши™
рением и размытием. Чем длиннее луч, тем больше это дифрак-
дифракционное уширение. О луче можно говорить только тогда, когда
уширение мало по сравнению с поперечными размерами самого
луча. Для этого длина луча не должна превышать определен-
определенного предела, величина которого тем больше, чем шире луч (см.
§ 6, формулу F.17)).
5. Когда луч достигает плоской границы раздела двух про-
прозрачных сред, он частично проходит во вторую среду (преломля-
(преломляется), частично возвращается обратно
(отражается). Закон отражения света
был известен еще грекам. Он утвержда-
утверждает, что падающий и отраженный лучи
лежат в одной плоскости с нормалью
к границе раздела в точке падения (эта
'/////////////////// плоскость называется плоскостью па-
падения), причем угол падения (р равен
Рис- 3 углу отражения ipf (рис. 3).
6. Закон преломления был установлен экспериментально в
1621 г. голландским ученым Снеллиусом A580—1626) и опубли-
опубликован только после его смерти. Позднее Декарт A596-1650) в

ГЕОМЕТРИЧЕСКАЯ ОПТИКА
15
1637 г. опубликовал тот же закон, не ссылаясь на Снеллиуса.
Знал ли Декарт работы Снеллиуса — этот вопрос остался откры-
открытым, хотя он и был предметом многочисленных дискуссий. Де-
Декарт получил закон преломления Снеллиуса, пользуясь аналоги-
аналогией между преломлением света и прохождением упругого шара
(мяча) через границу раздела воздуха с водой. Его рассужде-
рассуждения были неубедительны и крайне туманны, но окончательный
результат, к которому он пришел, оказался верным.
Согласно закону преломления Снеллиуса, преломленный луч
лежит в плоскости падения, причем отношение синуса узла
падения (р (рис. 4) к синусу узла пре-
преломления ф для рассматриваемых сред
зависит только от длины световой
волны, но не зависит от узла падения,
т.е.
sin (f
Ф
smw
B.1)
Рис. 4
Постоянная величина п2\ называет-
называется относительным показателем или
коэффициентом преломления второй
среды относительно первой. Показа-
Показатель преломления среды относительно вакуума называют аб-
абсолютным показателем (коэффициентом) преломления этой
среды. Его будем обозначать через п, снабжая эту букву, если
требуется, соответствующими индексами. Например, п\ — по-
показатель преломления первой, а п2 — второй сред. Ради крат™
кости величину п обычно называют просто показателем (коэф-
(коэффициентом) преломления среды,
т.е. опускают прилагательное «аб-
«абсолютный».
Относительный показатель пре- VsV^
ломления п2\ выражается через аб- ^—^—
солютные показатели п\ ж п2 соот-
соотношением
Вакуум
1
«1
B.2) —
Это соотношение молено получить
путем предельного перехода. Пусть
световой луч падает из вакуума на
плоскопараллельную пластинку с
показателем преломления щ, а за-
затем попадает в среду с показателем преломления п2 (рис. 5)
Для преломления на границах пластинки можно написать
Рис. 5

16 ВВЕДЕНИЕ ГЛ. I
Перемножая написанные равенства, получим
^ = пит- B.3)
sin ф
Это соотношение справедливо, какова бы ни была толщина пла-
пластинки. Оно остается верным и в предельном случае, когда тол™
щина пластинки стремится к нулю. Но тогда свет будет пре-
преломляться так, как если бы никакой пластинки вообще не было.
Поэтому должно быть sin (p/sin ^ = П2- Сравнение этого резуль-
результата с предыдущим и приводит к соотношению B.2).
Слабая сторона приведенного рассуждения состоит в сле-
следующем. Показатель преломления есть макроскопическая ха-
характеристика среды. Когда толщина пластинки, разделяющей
среды 1 и 2, становится порядка атомных размеров, ее уже
нельзя рассматривать как непрерывную среду, так что понятие
показателя преломления теряет смысл. Однако окончательный
результат B.2) остается верным. Он подтверждается опытом и
в дальнейшем при рассмотрении теории отражения и преломле-
преломления света будет выведен с различных точек зрения (см. § 3, 64).
С учетом соотношения B.2) закон преломления можно запи-
записать в симметричной форме:
п\ шкр = П2 sint/j. B-4)
Из формулы B.2) следует также:
П21 =
7. Если П21 < 1, то может оказаться, что величина sint/?,
формально вычисленная по формуле B.1), начнет превосходить
единицу, т.е. </?/п21 > 1- Соответствующего угла преломления не
существует. Поэтому преломленный луч не возникает, а свет от-
отражается полностью. Это явление называется полным отраже-
отражением. Угол падения, при котором оно возникает, определяется
условием (р ^ (/9q, причем
sincpo = П2ь B.6)
Величина щ называется предельным углом полного отраже-
отражения. Полное отражение будет исследовано в § 66.
8. Если поверхность тела, на которую падают световые лу-
лучи, не плоская, а кривая, то ее можно мысленно разбить на ма-
малые площадки, считая каждую из них плоской. Тогда ход лучей
можно найти по законам отражения и преломления, изложен-
изложенным выше, а затем выполнить предельный переход к гладкой
поверхности, устремляя к нулю размеры каждой площадки. Од-
Однако этот прием применим только тогда, когда кривизна поверх-
поверхности не превышает некоторого предела, так как в противном
случае начинают проявляться отступления от законов правиль-
правильного отражения и преломления и наступает дифракция.

ГЕОМЕТРИЧЕСКАЯ ОПТИКА
17
Шероховатые поверхности дают не правильное, а рассеянное,
или диффузное^ отражение и преломление света. Только благо-
благодаря этому поверхность тела становится видимой. Абсолютно
зеркальная поверхность невидима, видны только отраженные
от нее лучи, попадающие от источников света, расположенных
вне зеркала, т.е. видны только сами эти источники света.
ЗАДАЧИ
1. Два плоских зеркала 1 is. 2 наклонены друг к другу, образуя двугран-
двугранный угол а (рис. 6). Падающий луч, лежащий в плоскости, перпендику-
перпендикулярной к ребру двугранного угла,
отражается сначала от одного, а
затем от другого зеркала. Пока-
Показать, что в результате этих двух
отражений луч отклоняется на
угол <5, величина которого не за-
зависит от направления падающего
света. Вычислить угол S.
Решение. Как видно из
треугольника ABD, § = 2(cpi +
+ 992), а из треугольника ABC
(рг + (р2 = а. Поэтому ё = 2а. Ре-
Результат справедлив при любом а
и любом направлении падающего
света, если только угол а отсчи-
отсчитывать от зеркала i, вращая его
по кратчайшему пути к зеркалу 2,
а угол 5 — от направления пада-
падающего луча si к направлению выходящего луча S2, производя вращение в
том же направлении.
2. Показать, что луч света, последовательно отражающийся от трех
взаимно перпендикулярных зеркал, меняет свое направление на противо-
противоположное.
Решение. Пусть so, si, S2, S3 — единичные векторы падающего
и отраженных лучей, a Ni, N2, N3 — единичные нормали к отражающим
плоскостям зеркал. Тогда
si -so = -2(Niso)Ni,
S2-S1 = -2(N2si)N2,
рис
Из первого уравнения скалярным умножением на N2 и N3 получаем
(N2si) = (N2s0), (N3si) = (N3so).
Аналогично, скалярное умножение второго уравнения на N3 дает
(N3s2) = (N3si) = (N3so).
Почленно складывая все три уравнения и учитывая найденные соотно-
соотношения, получим
S3 - so = -2(Niso)Ni - 2(N2s0)N2 - 2(N3s0)N3 = -2s0,
откуда s3 = -s0.

18 ВВЕДЕНИЕ ГЛ. I
Полученный результат лежит в основе устройства уголкового отража-
отражателя, применяющегося для изменения направления распространения све-
света на противоположное. Уголковый отражатель можно получить, отсекая
от стеклянного куба с посеребренными гранями трехгранный угол плоско-
плоскостью, перпендикулярной к пространственной диагонали куба. Всякий луч,
вступивший внутрь так полученной пирамиды через ее основание, испытав
отражения от трех ее боковых граней, выйдет через то же основание, изме-
изменив свое направление на противоположное. Действительно, преломление на
основании пирамиды, испытываемое падающим лучом, не играет роли, по-
поскольку оно полностью компенсируется преломлением на том же основании
при выходе луча из пирамиды.
3. Луч света проходит через ряд однородных сред, разграниченных
плоскостями, параллельными между собой. Показать, что направление лу-
луча в последней среде (если луч проникает в нее) зависит только от угла
падения и от показателей преломления первой и последней сред. В частно-
частности, если показатели преломления первой и последней сред одинаковы, то
луч войдет в последнюю среду параллельно тому направлению, которое он
имел в первой среде.
4. В преломляющей призме (рис. 7) ZC = ZD, ZA = a, ZB = 2а. Свето™
вой луч вступает в призму через грань BD, находясь в ее главном сечении,
D
В
Рис. 7
т.е. в плоскости, перпендикулярной к преломляющим ребрам призмы, а за-
затем последовательно отражается от граней АС и AD, выходя наружу через
грань ВС. Показать, что угол 6 отклонения вышедшего луча от исходного
направления не зависит от угла падения. Вычислить угол S.
Ответ. 5 = 2а.
5. Исследовать преломление светового луча в главном сечении трех™
гранной призмы. Определить угол отклонения светового луча S от исход-
исходного направления и его наименьшее значение ^мин.
Решение. Как видно из треугольника CDE (рис. 8),
S = ((fl — ф\) + (<?>2 — fa)-
Далее, из четырехугольника ACFD, у которого углы С и D — прямые,
имеем: А + F = тг, а из треугольника CDF {ф\ + Ф2) + F = тг, так что
= А = const, где А — преломляющий угол призмы. Следовательно,
6 = ipi + <p2-A. B.7)

ГЕОМЕТРИЧЕСКАЯ ОПТИКА
19
Для нахождения минимума угла отклонения 6 удобно за независимую пере™
меыыую принять угол преломления фгу так как при этом будет достигнута
симметрия и упрощение выкладок. Для первой производной получаем
dS dcpi d(f2 d(pi d(f2
или, на основании закона преломления,
dd
dфl \cosy?i
Аналогично, для второй производной
d2§ ( d cost^i d cost
dipt cos cp 1 dtpi cos <f2
COS (f2 J
d cos ф\ d cos %jJ \
B.8)
COS (fi dt[J COS Lp2 J
= »?;
Если n > 1, то d28/d^l > 0, а потому кривая 8 = 8{ф\) во всех точках
обращена выпуклостью вниз. Отсюда следует, что угол 8 достигает мини-
минимума при (fi = (^2, т.е. при
симметричном ходе луча через
призму. Других минимумов (и
вообще экстремумов) быть не
может.
При симметричном ходе лу-
луча (f = 72(^4 +Ямин), Ф = 7зД И
следовательно,
Л B.9)
Рис.
На этой формуле основан удоб-
удобный метод измерения показате-
показателя преломления.
6. Световой луч падает
на боковую грань призмы под
малым углом. Преломляющий
угол призмы А мал (рис. 8). Вычислить угол отклонения луча 5, ограничи-
ограничиваясь членами первой степени по А. Вычислить также угол наименьшего
отклонения <5МИн с точностью до членов порядка А включительно.
Решение. <5 = (ipi — ф\) + ((f2 — Ф2) ~ (пф\ — ф\) + (пф2 ~~ фч) =
= (п — l)('0i + ^2M или, на основании соотношения ф\ + ф2 = -А,
8 = (п-1)А. B.10)
В рассматриваемом приближении угол 8 не зависит от угла падения. В
высших приближениях это уже не так. В третьем приближении из формулы
B.9), разлагая <5МИн в ряд, находим
= (п-1)А 1 +
24
B.11)
7. Удобный метод измерения показателя преломления твердых тел со-
состоит в следующем. Плоскопараллельная пластинка из исследуемого ве-
вещества рассматривается в микроскоп. Сначала микроскоп устанавливается

20 ВВЕДЕНИЕ ГЛ. I
для наблюдения верхней поверхности пластинки. Затем смещают тубус ми™
кроскопа вниз, пока не будет отчетливо видна нижняя поверхность пластин™
ки. (Для удобства наблюдения на поверхностях пластинки можно сделать
метки.) Показать, что если смещение тубуса равно h, а толщина пластинки
I, то показатель преломления пластинки можно найти по формуле
п = l/h.
Метод годится и для измерения показателей преломления жидкостей.
§ 3. Эволюцим представлений о природе света
1. Пифагор (около 580-500 до н.э.) считал, что предметы ста™
новятся видимыми благодаря мельчайшим частицам, испускае-
испускаемым ими и попадающим в глаз наблюдателя. Декарт полагал,
что свет — это сжатие, распространяющееся в идеальной упру-
упругой среде (эфире), заполняющей мировое пространство и проме-
промежутки между частицами тел. Однако последовательно провести
эту точку зрения Декарт не смог, при выводе законов отраже-
отражения и преломления он пользовался представлением о свете как о
потоке частиц. Гук A635-1703) также считал, что свет представ-
представляет собой импульсы сжатия, распространяющиеся мгновенно
или с очень большими скоростями. (Скорость света была опреде-
определена только в 1676 г. Олафом Рёмером A644-1710) из наблюде-
наблюдений затмений спутников Юпитера.) Несколькими годами ранее
Гука чешский монах Марци A595-1667) и итальянский монах
Гримальди A618-1663) также пришли к мысли, что свет пред-
представляет собою быстро распространяющиеся волны. Подобные
отрывочные высказывания о природе света были усовершенство-
усовершенствованы и развиты в более систематические теории Исааком Нью-
Ньютоном A643-1727), с одной стороны, и Христианом Гюйгенсом
A629-1695), с другой.
Основные оптические работы Ньютона докладывались в
Лондонском Королевском обществе A671-1675 гг.) и были напе-
напечатаны в трудах этого общества. Содержание этих сообщений,
наряду с другими оптическими исследованиями Ньютона, было
заимствовано из его «Лекций по оптике» х), которые он читал в
Кембридже в 1669-1671 гг. Спустя много лет (в 1704 г.) вышла
знаменитая книга Ньютона «Оптика» 2). В оптике Ньютон со-
сосредоточил основное внимание на экспериментальных исследо-
исследованиях и стремился при изложении этого, как и других разделов
1) Исаак Ньютон. Лекции по оптике. Перевод, комментарии и редакция
академика СИ. Вавилова. — М.: Издательство АН СССР, 1946.
) И. Ньютон. Оптика или трактат об отражениях, преломлениях, из-
изгибаниях и цветах света. Перевод с примечаниями СИ. Вавилова. — М.:
Гостехиздат, 1954.

§ 3 ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЙ О ПРИРОДЕ СВЕТА 21
физики, отделить достоверные факты от сомнительных гипотез.
Экспериментальные исследования Ньютона по оптике вплоть до
XIX века не имели себе равных. Его «Оптика» служила основ-
основным источником, из которого черпали материал все учебники
того времени («Лекции по оптике» были опубликованы после
смерти Ньютона и по ряду причин остались почти неизвестны-
неизвестными). Что касается природы света, то к этому вопросу Ньютон
подходил значительно более осторожно, чем все остальные уче-
ные, включая Гюйгенса. Он предпочитал с самого начала стро-
строить чисто феноменологическую теорию, освобожденную от про™
извольных гипотез. Все, что относится к физической природе
света, он выделил в особый раздел, содержащий 31 «вопрос»,
которым заканчивается его «Оптика». Здесь после тщательного
рассмотрения различных исключающих друг друга возможно-
возможностей Ньютон пришел к заключению, что факты говорят боль-
больше в пользу корпускулярной теории, чем волновой. Поэтому он,
правда не без колебаний и сомнений, отдал предпочтение кор-
корпускулярной теории.
Гюйгенс в своих высказываниях о природе света не был столь
сдержанным и осторожным, как Ньютон. Он не сомневался в
волновой природе света. Свои воззрения он изложил на заседа-
заседании Парижской Академии наук A678 г.), а затем более полно в
сочинении «Трактат о свете» х), опубликованном в 1690 г. В этом
сочинении впервые в истории оптики была сделана попытка из-
изложить с единой — волновой — точки зрения распространение,
отражение, преломление и двойное лучепреломление света.
2. Перейдем к более подробной характеристике корпускуляр-
корпускулярной и волновой теорий света.
Согласно корпускулярной теории, свет состоит из мельчай-
мельчайших частиц, или корпускул, испускаемых светящимися тела-
телами. С этой точки зрения прямолинейное распространение све-
света сводится к закону инерции. Для истолкования закона неза-
независимости световых пучков надо было ввести предположение,
что средние расстояния между корпускулами в световых пучках
настолько велики, что корпускулы практически не взаимодей-
взаимодействуют между собой; случаи сближения, в которых проявляется
такое взаимодействие, крайне редки и при существующей точ-
точности эксперимента ускользают от наблюдения.
Отражение и преломление света корпускулярная теория объ-
объясняла силами притяжения и отталкивания, действующими на
световые корпускулы в очень тонком приграничном слое вблизи
границы раздела сред, на которую падает свет. Внутри пригра-
приграничного слоя путь световой корпускулы искривляется, по выхо-
X. Гюйгенс. Трактат о свете. — М.; Л.: ОНТИ, 1935.

22
ВВЕДЕНИЕ
ГЛ. I
де из него корпускула движется снова прямолинейно и равно™
мерно, но уже в другом направлении. Если корпускула отража-
отражается, то она возвращается в первую среду с прежним значением
скорости. Если же корпускула проходит во вторую среду, то ве-
личина ее скорости изменяется (рисунки 9 и 10). Ввиду тонкости
Рис. 9
Рис. 10
приграничного слоя явление воспринимается так, как если бы на
границе сред происходил резкий излом траектории корпускулы
(как показано на рисунках 9 и 10 штриховыми линиями).
Для вывода количественных законов отражения и преломле™
ния света надо было ввести предположение, что силы, действую-
действующие на световую корпускулу в приграничном слое, нормальны
к границе раздела сред. Такие силы меняют только нормальные
скорости световой корпускулы, оставляя касательные без изме-
изменения. Рассмотрим, например, преломление света. Обозначим
через v\ скорость световой корпускулы в первой среде, а через
V2 — во второй. В силу равен-
равенства касательных составляющих
Ф j / этих скоростей v\ шар = V2 sin?/>
(рис. 11), или
1 Sin if V<2
Рис. 11
C-1)
S1EL Щ) V\
Эта формула была получена
Ньютоном. Из нее следует, что
в сильнее преломляющих средах
скорость света должна быть
больше^ чем в менее преломляю-
преломляющих. Однако чтобы из формулы
C.1) вывести закон преломления Снеллиуса, необходимо доба-
добавочное предположение, что отношение скоростей света V2 и v\
для световых корпускул одного и того же типа постоянно, т.е.
определяется только свойствами сред 1и2,в которых корпуску-
корпускулы движутся, но не зависит от того, каким путем они туда попа-
попали. Если использовать экспериментальный факт, что в вакууме
скорость света одна и та же, то для выполнения этого условия

§ 3 ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЙ О ПРИРОДЕ СВЕТА 23
необходимо потребовать, чтобы все силы, действующие на све-
товые корпускулы в приграничных слоях, были потенциальны.
(Заметим, что цвета света тогда молено объяснить, например,
различными размерами корпускул.) Однако то обстоятельство,
что скорость световой корпускулы зависит только от среды, в
которую она испускается, но не зависит от способа испускания,
представляется малопонятным с точки зрения классической ме-
механики. В этом отношении корпускулярная теория уступает вол-
волновой теории, поскольку в последней скорость света, естествен-
естественно, есть характеристика только самой среды, в которой он рас-
распространяется .
При справедливости введенных предположений показатель
преломления среды 2 относительно среды 1 определяется выра-
выражением
П21=У2/У1. C.2)
В частности, для абсолютного показателя преломления получа-
получаем
п = v/c, C.3)
где с — скорость света в вакууме. Следовательно, п\ = v\/c,
п2 — V2/Ci a потому
п2\ = n2/ni, C.4)
что совпадает с формулой B.2). Однако это обстоятельство
нельзя рассматривать как аргумент в пользу корпускулярной
теории, так как такое же соотношение следует и из волновой
теории.
3. Согласно волновой теории^ свет представляет собой вол-
ны, распространяющиеся в гипотетической всепроникающей
среде, — мировом или световом эфире — заполняющей все ми-
мировое пространство и промежутки между мельчайшими части-
частицами тел. Если колебания частиц эфира малы, то уравнения,
описывающие распространение волн, будут линейны и однород-
однородны. В этом случае справедлив принцип суперпозиции волн1 явля-
являющийся в волновой теории математическим выражением закона
независимости световых пучков.
Значительно сложнее обстояло дело с объяснением прямоли-
прямолинейного распространения света. Гюйгенс применил к этой про-
проблеме принцип, названный позднее его именем. Если камень бро-
бросить в воду, то от места падения, как из центра, побегут по по-
поверхности воды круговые волны, или возмущения. Этот процесс
продолжается и после того, как камень упадет на дно, т.е. исчез-
исчезнет причина, породившая первоначальное возмущение. Отсюда
следует, что непосредственной причиной распространяющегося
волнового процесса является не камень, а то первоначальное воз-
возмущение движения воды, которое он вызвал. Подобные рассуж-
рассуждения навели Гюйгенса на мысль, что каэюдая точка волнового

24 ВВЕДЕНИЕ ГЛ. I
возмущения является источником сферических волн^ распро-
распространяющихся от нее во все стороны. Они получили название
вторичных или элементарных волн Гюйгенса. Результирующее
волновое возмущение можно рассматривать как наложение вто-
ричных волн. В этом и состоит знаменитый принцип Гюйгенса.
Он справедлив не только для световых, но и для любых волно-
вых процессов и в приведенной формулировке полностью сохра-
сохранил свое значение до настоящего времени. Его значение далеко
выходит за рамки сравнительно узкой задачи о прямолинейном
распространении света. Действительно, принцип Гюйгенса ука-
указывает на принципиальную возможность определения волнового
возмущения во всем пространстве, если известны все вторичные
волны, порожденные в более ранний момент времени.
Но Гюйгенс не рассматривал задачу в столь общей постанов-
постановке. Он дополнил формулировку своего принципа, приведенную
выше, замечанием, что отдельные вторичные волны слишком
слабы и что заметное световое действие они производят толь™
ко на их огибающей. После этого дополнения принцип Гюйгенса
потерял свою общность и превратился лишь в приближенный
геометрический рецепт для построения волновых фронтов, т.е.
поверхностей, до которых дошло световое возмущение. Он стал
непригоден для количественного расчета светового поля, в част-
частности распределения интенсивности последнего в пространстве.
4. Обратимся теперь к объяснению прямолинейного распро-
распространения света, данному Гюйгенсом. Пусть точечный источник
света S (рис. 12), расположенный
перед непрозрачным экраном с от-
отверстием УШ, излучает сферическую
волну. Если в момент времени t вол-
волна дойдет до краев отверстия АВ,
то оно вырежет из волнового фрон-
фронта сферический участок АС В. По-
Построим из каждой точки этого участ-
участка, как из центра, вторичные волны
радиусом cdt. Огибающая всех этих
вторичных волн оборвется на краях
сферического участка A\Bi, за пре-
пределы которого проникнут только от-
Рис- 12 дельные вторичные волны. Действие
таких волн, согласно предположению Гюйгенса, пренебрежи-
пренебрежимо мало, а потому волновой фронт возмущения в момент t+
+ dt ограничится только сферическим участком А\В\. Взяв этот
фронт за исходный, можно таким же построением найти волно-
волновой фронт А2В2 в более поздний момент времени, и т.д. Построе-
Построение показывает, что волновое возмущение будет резко обрывать-
обрываться на поверхности телесного угла с вершиной S, вырезаемого

§ 3 ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЙ О ПРИРОДЕ СВЕТА 25
диафрагмой АВ. А это и означает прямолинейное распростра-
распространение света.
Рассуждение Гюйгенса лишено доказательной силы. В нем
доказывается то, что по существу содержится в исходных пред™
положениях. А само построение Гюйгенса есть только один из
возможных рецептов построения волнового фронта^ согласую™
щийся с представлением о распространении света вдоль лучей.
Непонятно, почему объяснение Гюйгенса применимо к свето-
световым, но не применимо к звуковым волнам, которые, как извест-
известно, огибают препятствия, стоящие на их пути.
Естественно, что такое «объяснение» не могло удовлетворить
Ньютона. Кроме того, Ньютон, как и Гюйгенс, не видел, как
в рамках волновой теории можно объяснить поляризацию све™
та, открытую Гюйгенсом в двойном лучепреломлении. Это дей-
действительно невозможно для продольных волн, какими, согласно
Гюйгенсу, является свет. Только такие волны и были известны в
физике того времени. Представления о поперечных волнах еще
не существовало. Эти трудности казались Ньютону настолько
существенными, что его симпатии оказались на стороне корпус-
корпускулярной теории.
Проблема прямолинейного распространения света есть част-
частный случай проблемы дифракции и может быть решена до кон-
конца только в рамках последней. Дифракция света была откры-
открыта Гримальди и независимо от него несколько позднее Гуком.
Ньютон много занимался экспериментальными исследованиями
дифракции света. Но Гюйгенс в «Трактате о свете» почему-то
полностью обошел молчанием это явление. Кроме того, ему оста-
осталась неизвестной периодичность световых процессов (в отличие
от Ньютона, который первый подметил ее). Гюйгенс писал, что
свет, подобно звуку, распространяется сферическими поверхно-
стями, и именно такие поверхности называл волнами. Он спе-
специально подчеркивал, что удары, возбуждающие световые воз™
мущения в центрах волн, совершаются совершенно беспорядоч-
беспорядочно, а потому не следует думать, что сами волны следуют друг
за другом на равных расстояниях. В этом отношении выска™
зывания Гюйгенса примыкают к более ранним представлениям
Декарта и Гука. Понятие длины волны нигде не встречается в
теории Гюйгенса, а без этого невозможно установить, при ка-
каких условиях (приближенно) справедлив закон прямолинейного
распространения света.
5. Перейдем к вопросу об отражении и преломлении света в
волновой теории Гюйгенса. Пусть плоская волна падает на пло-
плоскую границу раздела двух сред. В некоторый момент в точке А
волновой фронт АВ достигнет границы раздела сред (рис. 13).
В этот момент из А начнут распространяться вторичные волны
Гюйгенса: одна в первую, другая во вторую среду. В точках Е

26
ВВЕДЕНИЕ
ГЛ. I
Рис. 13
и D аналогичные волны возникнут несколько позднее. Согласно
принципу Гюйгенса, от наложения таких вторичных волн в пер-
первой среде образуется отражен-
пая, а во второй — преломленная
волны. Огибающая вторичных
волн во второй среде FGD есть
плоскость, определяющая вол-
волновой фронт преломленной вол-
волны. Аналогично строится волно-
волновой фронт и отраженной волны
(на рис. 13 он не указан). Тако-
Таково объяснение отражения и пре-
преломления света в волновой тео-
теории Гюйгенса. Оно не раскрыва-
раскрывает детальный механизм возник-
возникновения отраженной и прелом-
преломленной волн. Для этого надо бы-
было бы явно использовать физи-
физическую природу световых волн, о которой в эфирной теории
Гюйгенса, в сущности, ничего не говорится.
Геометрические законы отражения и преломления, однако,
совершенно не зависят от физической природы волн и от кон-
конкретного механизма отражения и преломления. Они одинаковы
в любой волновой теории. Действительно, падающая волна воз-
возбуждает возмущение, бегущее вдоль границы раздела со скоро-
скоростью AD = BD/sinp = v\/тар (если воспользоваться надле-
надлежащими единицами), где v\ — скорость света в первой среде.
Но отраженная и преломленная волны порождаются падающей
волной и поэтому бегут вместе с ней вдоль границы раздела с
той же скоростью. Следовательно, можно написать также, что
AD = v\/шкр1 = V2I®шф^ где V2 — скорость света во второй
среде, (р1 — угол наклона фронта отраженной волны к границе
раздела сред (не показанный на рис. 13). В результате получа-
получается
sinLp sins// sin^ /Q .\
Этими соотношениями определяются направления фронтов от-
отраженной и преломленной волн. А так как в плоской волне све-
световые лучи перпендикулярны к волновым фронтам, то те же со-
соотношения определяют также направления отраженных и пре-
преломленных лучей. Легко видеть, что (р есть угол падения, (р1 —
угол отражения, ф — угол преломления. Из C.5) следует, что
р = (р1 (закон отражения) и
—% = — (закон преломления).
smt/; V2
C.6)

§ 3 ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЙ О ПРИРОДЕ СВЕТА 27
В противоположность корпускулярной теории (см. C.1)), вол-
волновая теория приводит к заключению, что скорость света в
более преломляющей среде меньше^ чем в менее преломляющей.
И это заключение справедливо независимо от того, какова фи-
физическая природа световых волн.
Для относительного показателя преломления волновая тео-
рия дает
П21 = Vi/V2j C.7)
а для абсолютного
п = c/v, C.8)
т.е. выражения, обратные соответствующим выражениям в кор-
пускулярной теории C.2) и C.3). Из C.7) и C.8) снова получа-
получается формула C.4), которая, следовательно, справедлива как в
корпускулярной, так и в волновой теориях.
6. В вопросе об отражении и преломлении света между кор-
корпускулярной и волновой теориями имеется и другое различие.
Опыт показывает, что световой пучок, падающий на границу
раздела сред, разделяется на два пучка: отраженный и прелом-
преломленный (исключением является случай полного отражения). В
волновой теории объяснение этого факта не встречает затруд-
затруднений. Но как истолковать его с точки зрения корпускулярной?
Корпускула всегда ведет себя как целое. Она не может раз-
разделиться на две части, из которых одна отражается, а другая
проходит во вторую среду. В противном случае падающий, от-
отраженный и прошедший свет был бы окрашен различно. Для
преодоления этой трудности Ньютон ввел идею о приступах
легкого отражения и легкого прохождения^ в которых периоди-
периодически может находиться световая корпускула. Если корпускула
подходит к границе сред в приступе легкого отражения, то она
отталкивается и отражается. Если же это случится в приступе
легкого прохождения, то произойдет притяжение и прохождение
корпускулы во вторую среду.
Идея «приступов», как заметил Я.И. Френкель A894-1952),
напоминает современные представления о световых квантах —
фотонах. Согласно этим представлениям, отражение и про-
прохождение фотонов через границу раздела сред управляется
статистическими законами: существует определенная вероят-
вероятность, что фотон отразится, и определенная вероятность, что он
пройдет во вторую среду. Сам Ньютон, конечно, не раскрыл фи-
физический механизм приступов легкого отражения и легкого про-
прохождения. Однако он ставил вопрос, не являются ли эти присту-
приступы результатом обратного воздействия каких-то быстрых волн,
возбуждаемых в среде световыми корпускулами. Идея присту-
приступов навязывалась также периодичностью световых процессов^
подмеченной Ньютоном при исследовании интерференционного

28 ВВЕДЕНИЕ ГЛ. I
явления «ньютоновых колец». Эту периодичность Ньютон так™
же пытался объяснить, дополнив корпускулярную теорию вол-
волновыми представлениями.
7. Физики XVIII и начала XIX веков, забыв о колебаниях
и сомнениях Ньютона, приняли корпускулярную теорию света.
Сторонники волновой теории насчитывались единицами. Прав™
да, среди них были Эйлер A707-1783), Ломоносов A711-1765)
и Франклин A706-1790), выдвигавшие возражения против кор-
корпускулярной и приводившие аргументы в пользу волновой тео-
рии света. Эйлер, например, утверждал, что если бы корпуску-
корпускулярная теория была справедлива, то из-за излучения света масса
Солнца заметно уменьшалась бы, а это сказалось бы на движе-
движении планет. Франклин указывал, что по корпускулярной теории
свет должен был бы оказывать давление на освещаемые тела,
тогда как все попытки обнаружить это давление оканчивались
безрезультатно. Слабость этих возражений состояла в том, что
они не содержали количественных оценок ожидаемых эффек-
эффектов. Впрочем, согласно современным представлениям о взаимо-
взаимосвязи между массой и энергией, потеря массы из-за излучения,
а также величина светового давления совершенно не зависят от
того, является ли свет потоком частиц или волновым процессом.
Эти и аналогичные возражения, как показало последующее раз-
развитие физики, не могли решить спор между корпускулярной и
волновой теориями света. Нужны были новые эксперименталь-
экспериментальные факты.
8. Начиная с XIX века, положение стало складываться в
пользу волновой теории благодаря работам Юнга A773-1829)
и в особенности Френеля A788-1827), систематически исследо-
исследовавших явления интерференции и дифракции света. На осно-
основе волновых представлений была создана стройная теория этих
явлений, выводы и предсказания которой полностью согласовы-
согласовывались с экспериментом. Объяснение прямолинейного распро-
распространения света содержалось в этой теории как частный слу-
случай. Были открыты и исследованы новые оптические явления:
поляризация света при отражении (Малюс, 1808) и преломлении
(Малюс и Био, 1811), угол полной поляризации (Брюстер, 1815),
интерференция поляризованных лучей (Френель и Араго, 1816),
количественные законы и теория отражения и преломления све-
света (Френель, 1821), двойное преломление сжатым стеклом (Брю-
(Брюстер, 1815), двуосные кристаллы (Брюстер, 1815), законы и те-
теория распространения света в двуосных кристаллах (Френель,
1821), вращение плоскости поляризации в кварце (Араго, 1811)
и жидкостях (Био, 1815; оба явления исследовались далее Био,
Брюстером и др.). Юнг A807) измерил на опыте длину световой
волны. Оказалось, что волны красного света длиннее, чем сине-
синего и фиолетового. Тем самым в волновой теории было дано экс-

§ 3 ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЙ О ПРИРОДЕ СВЕТА 29
периментально обоснованное объяснение цветов света, которое
связывало это явление с длиной световой волны. (Такое объяс-
объяснение предлагалось еще Эйлером, но он не мог указать, длина
каких волн больше — красных или синих.) Юнг A817) выека-
зал также мысль о поперечности световых волн. К такому же
заключению независимо от него пришел Френель A821) и обос-
новал это заключение путем исследования поляризации света и
интерференции поляризованных лучей. Все эти факты и в осо-
особенности явления интерференции и дифракции света находили
непринужденное объяснение в рамках волновой теории света.
Корпускулярная теория не могла противопоставить ничего эк™
Бивалентного и к началу 30-х годов XIX века была оставлена.
Смертельный удар корпускулярной теории в ее ньютонов-
ньютоновской форме был нанесен в 1850 г. К этому времени Физо
A819-1896) и Фуко A819-1868) впервые измерили скорость све-
света лабораторными методами. Как мы указывали (см. пп. 2 и 5),
по корпускулярной теории скорость света в воде больше, а по
волновой теории меньше, чем в вакууме. В 1850 г. Фуко и неза-
независимо от него Физо и Бреге сравнили обе скорости. Опыт ока-
оказался в согласии с волновой и в противоречии с корпускулярной
теориями света. Физики XIX века восприняли это как решаю-
решающий опыт, окончательно доказавший неправильность корпуску-
корпускулярной теории света.
9. Волновая теория, конечно, не могла считаться полной, по-
пока не была установлена природа световых колебаний^ или ко™
лебаний мирового эфира, как говорили физики девятнадцатого
(и отчасти первой четверти двадцатого) века. Они не сомнева-
сомневались, что эфир подчиняется обычным законам механики Нью-
Ньютона и к нему применимы такие понятия, как плотность, упру-
упругость, пространственное перемещение, скорость, ускорение и пр.
Они пытались вывести строение и свойства эфира из наблюдае-
наблюдаемых явлений и экспериментально установленных законов опти-
оптики. Поперечность световых волн заставила приписать мировому
эфиру свойства твердой среды. Это породило ряд трудностей,
в частности в вопросе об отражении и преломлении света (по-
(подробнее см. § 63). Нет необходимости останавливаться на этих
трудностях и попытках их преодоления в теории эфира. Все это
уже давно потеряло актуальность и сохранило лишь историче-
исторический интерес.
В 60-х годах XIX века Максвеллом были установлены общие
законы электромагнитного поля, которые привели его к заклю-
заключению, что свет — это электромагнитные волны (см. т. III,
гл. IV). Подтверждением такой точки зрения в то время бы-
были открытие Фарадеем в 1846 г. вращения плоскости поляри-
поляризации света в магнитном поле и совпадение скорости света в
вакууме с электродинамической постоянной, установленное на

30 ВВЕДЕНИЕ ГЛ. I
опыте в 1856 г. Вебером и Кольраушем (см. т. III, § 51 и 83).
После известных опытов Герца A887—1888 гг., см. т. III, § 142)
электромагнитная природа света быстро получила признание.
Уже в первом десятилетии XX века она из гипотезы преврати-
превратилась в твердо установленный факт. Световые колебания были
отождествлены с колебаниями электромагнитного поля. Опти-
Оптика превратилась в раздел учения об электрических и магнитных
явлениях.
Электромагнитная теория света устранила трудности, с ко-
которыми столкнулась теория упругого твердого эфира. Однако
физики XIX века считали, что она дала не настоящее, а только
символическое решение вопроса о природе света. Они смотрели
на нее как на формальную схему, уравнения которой правиль-
правильно передают количественные соотношения между различными
величинами и явлениями, но символы, входящие в эти уравне-
уравнения, еще не получили отчетливого физического истолкования.
Считалось, что уравнения Максвелла должны составлять ма-
математический остов будущей более полной физической теории
электромагнитных и световых явлений, но сами по себе они та™
кой физической теории еще не составляют; последняя станет
возможной лишь после того, как будут найдены механические
свойства эфира.
Однако эти надежды не оправдались. Световой (или, луч-
лучше, электромагнитный) эфир упрямо отказывался обнаружить
свои «механические свойства». В частности, потерпели неуда-
неудачу настойчивые попытки обнаружить движение Земли относи-
относительно эфира, начатые Майкельсоном A852-1931) в 1881 г. При
изучении оптических и электродинамических явлений в движу-
движущихся средах обнаружились и другие расхождения теории эфи-
эфира с опытом. Это привело Эйнштейна A879-1955) в 1905 г. к
теории относительности. Гипотеза механического эфира была
оставлена1). Пошатнулась вера в «механическую картину ми™
ра», к построению которой так настойчиво стремились физики
) Необходимо заметить, однако, что в вакууме нет обычного вещества,
как оно понимается в химии. Но вакуум не есть пустота в буквальном смы-
смысле этого слова. Его заполняют физические поля (гравитационное, электро-
электромагнитное, ядерное и пр.). Они, наряду с обычным химическим веществом,
являются различными формами материи. В вакууме могут происходить
различные физические процессы. Примером может служить поляризация
вакуума, т.е. рождение пар электрон—позитрон в сильных электрических
полях. Можно было бы не возражать по существу против употребления тер-
термина «эфир» в смысле носителя этих физических свойств «пустого» про™
странства. Возражение относится к представлению об эфире как о жидкой,
твердой, упругой или какой-либо другой среде, наделенной механическими
свойствами. Однако в современной физике предпочитают не пользоваться
термином «эфир» в указанном смысле, а употребляют термин «вакуум».

§ 3 ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЙ О ПРИРОДЕ СВЕТА 31
XIX века. И все последующее развитие науки привело физиков
к убеждению в невозможности сведения всех явлений природы
к механике. Утверждать противоположное — значит предъяв-
предъявлять к природе необоснованные требования. Поэтому, когда в
современной волновой теории говорят, что свет — это колеба-
колебания электромагнитного поля, то на это уже не смотрят как на
формальное утверждение, а считают, что сами эти колебания не
сводятся к чему-то «более простому и наглядному».
10. Важным этапом в развитии максвелловской электро-
электродинамики было введение в нее атомистических представле-
нищ что было систематически проведено в электронной тео-
теории Г. А. Лорентца A853-1928). В теории Максвелла вещество
характеризовалось феноменологическими постоянными — ди-
диэлектрической и магнитной проницаемостями и удельной элек-
электрической проводимостью. В электронной теории эти макроско-
макроскопические постоянные получили истолкование с атомистической
точки зрения. В результате этого не только получили принци-
принципиальное, хотя и недостаточное, объяснение многие известные
электродинамические и оптические явления (например, диспер-
дисперсия и абсорбция света), но были открыты и объяснены и другие
явления (явления Керра^ Зеемана^ Фарадея^ Коттона-Мутона^
молекулярное рассеяние света и т.д.).
Однако классическая физика и, в частности, электронная
теория оказались недостаточными для истолкования явлений
атомного масштаба. Потребовалось введение квантовых пред-
представлений. Необходимость и плодотворность последних обна-
обнаружилась ранее всего при изучении проблемы распределения
энергии в спектре черного излучения, т.е. температурного из-
излучения абсолютно черного тела. Применение к этой проблеме
принципов классической физики приводило к глубоким проти-
противоречиям с опытом. Планк A858-1947) в конце 1900 г. получил
согласующуюся с опытом формулу для распределения энергии
в спектре черного излучения. При этом он ввел чуждое клас-
классической физике представление, что излучение и поглощение
света осуществляется не непрерывно, а конечными порциями^
или квантами энергии^ причем величина кванта определяется
выражением A.1). Для решения проблемы черного излучения
Планку достаточно было принять, что этот квантовый характер
излучения и поглощения света относится к статистическим
процессам. Через пять лет Эйнштейн показал, что его необходи-
необходимо распространить и на элементарные процессы. Согласно Эйн-
Эйнштейну, не только излучение и поглощение, но и распростране-
распространение света в пространстве происходят конечными порциями —
квантами света, обладающими определенной энергией и опреде-
определенным импульсом. Так возродилось представление о частицах
света, названных позднее фотонами.

32 ВВЕДЕНИЕ ГЛ. I
Гипотеза фотонов позволила прежде всего объяснить зага-
дочные закономерности в явлениях фотоэффекта, совершенно
непонятные с точки зрения классической волновой теории света.
Существование импульса у фотонов было доказано открытием в
1923 г. эффекта Комптона — изменения длины волны при рас-
рассеянии рентгеновского излучения. Гипотеза световых квантов
позволила понять химические действия света и их закономер-
ности. Квантовый характер излучения и поглощения света был
использован Бором A885-1962) для объяснения спектральных
закономерностей.
Но как согласовать корпускулярные представления о свете
с результатами опытов Фуко и Физо (см. п. 8)? Эти опыты вне
всякого сомнения опровергают корпускулярную теорию света в
ее ньютоновской форме. Приходится поэтому признать, что к
световым корпускулам классические представления о движе-
движении неприменимы. Интерференция и дифракция света дока-
доказывают, что в этих явлениях свет ведет себя как волны. Фо™
тоэффект, комптоновское рассеяние рентгеновских лучей и пр.
с неменьшей убедительностью доказывают, что здесь свет дей-
действует как частицы. Вообще, явления распространения света
правильно описываются в рамках волновых теорий, а для опи-
описания взаимодействия света и вещества необходимы корпус-
кулярные представления. Этот «дуализм волн и частиц» надо
рассматривать как экспериментальный факт, и поэтому полная
теория света должна быть не корпускулярной и не волновой, а
корпускулярно-волновой.
Такое парадоксальное положение еще более расширилось
после того, как Дэвиссоном A881-1958) и Джермером A896—
1971) в 1927 г. была открыта дифракция электронов. Оказалось,
что волновые свойства присущи и частицам обычного веще-
ства, — идея, развивавшаяся французским физиком де Врой™
лем (р. 1892) за несколько лет до открытия дифракции элек-
электронов. Развитие квантовой механики позволило частично объ-
объяснить возникшее парадоксальное положение ценой отказа от
основного положения классической физики — принципа при-
причинности в форме детерминизма. А исследования в области
физики высоких энергий (иначе называемой физикой элемен-
элементарных частиц) показали, что если энергия частиц превосходит
их энергию покоя, то частицы могут рождаться, исчезать или
превращаться друг в друга. В этом отношении они ведут се-
себя подобно фотонам, которые могут излучаться или поглощать-
поглощаться. В квантовой электродинамике фотоны рассматриваются как
кванты электромагнитного поля. Поэтому в физике высоких
энергий целесообразно говорить об электронно-позитронном,
мезонном, нуклонном и прочих полях, квантами которых явля-
являются электроны, позитроны, мезоны, протоны, нейтроны и т.д.

§ 4 ИСКРИВЛЕНИЕ СВЕТОВЫХ ЛУЧЕЙ В НЕОДНОРОДНЫХ СРЕДАХ 33
Таким образом, вопрос о природе света стал частью более общей
проблемы строения вещества.
§ 4. Искривление световых лучей в неоднородных
средах
1. В неоднородных средах представление о распространении
света вдоль лучей сохраняется, но сами лучи становятся кри-
криволинейными. Действительно, рассмотрим среду, состоящую из
плоскопараллельных слоев с посто-
постоянными показателями преломления %х^^
(рис. 14), меняющимися скачкообразно ^г~
от слоя к слою. Световой луч, прелом™ л.
ляясь на границах слоев, примет форму
ломаной линии. Будем неограниченно
увеличивать число слоев, устремляя
к нулю их толщины и скачки пока-
зателя преломления. Тогда в пределе
показатель преломления среды станет
меняться в пространстве непрерывно,
а луч перейдет в кривую с непрерывно рИС- 14
изменяющейся касательной. Допустим
теперь, что показатель преломления меняется в пространстве
как угодно, но не слишком резко (см. следующий параграф).
Проведем в среде поверхности равного показателя прелом-
преломления. В пределах каждого достаточно малого объема эти
поверхности можно считать плоскими, а среду плоскослоистой,
к которой применимо рассуждение, приведенное выше.
Из изложенного следует, что геометрическую форму луча
можно однозначно определить из закона Снеллиуса путем пре-
предельного перехода. Но закон Спеллиуса получается не только
в волновой, но и в корпускулярной теории Ньютона. Поэтому
при определении формы светового луча молено рассуждать так,
как если бы свет состоял из ньютоновых корпускул, а показатель
преломления п определялся формулой C.3). Поскольку прелом-
преломление определяется относительным показателем преломления,
абсолютный показатель можно заменить величиной, ему про-
пропорциональной. Ради краткости можно просто положить п = v.
Скорость корпускулы v однозначно определяется уравнением
сохранения энергии, а потому v можно рассматривать как из-
известную функцию координат. Таким образом, траектория кор-
корпускулы в потенциальном поле сил геометрически совпадает
с лучом света в среде^ показатель преломления п которой чис-
численно равен v. Для этого, конечно, необходимо, чтобы исходные
направления этих двух кривых были одинаковы. Эта формаль-
2 Д.В. Сивухин

34 ВВЕДЕНИЕ ГЛ. I
ная аналогия между движением частицы и распространением
светового луча позволяет перенести результаты, полученные в
световой оптике, в электронную микроскопию, где роль свето-
световых лучей выполняют электроны, движущиеся в потенциальных
электрических полях.
Воспользуемся отмеченной аналогией для вычисления ра™
диуса кривизны R светового луча. Нормальное ускорение кор-
корпускулы определяется формулой
™2 „ dU
R
где Fn — составляющая действующей силы F вдоль единичного
вектора главной нормали N, a U — потенциальная энергия кор-
корпускулы. Дифференцируя вдоль нормали N уравнение энергии
1J2imv2 + U = const, получаем Fn = mv dv/dN', а потому
1 — г dv
Заменяя v на п, находим выражение для кривизны луча:
1 1 дп р /-, \ //I 1 \
При этом ускорение корпускулы, а с ним и сила F не име-
имеют составляющей вдоль бинормали b к траектории, т.е. F^ =
= —dU/дЪ = mv dv/db = 0. Отсюда dv/db = 0, а потому так-
также дп/дЬ = 0. Значит, вектор gradn лежит в соприкасающейся
плоскости светового луча. Поэтому из всех направлений, пер-
перпендикулярных к лучу, направление главной нормали N харак-
характеризуется самым быстрым изменением показателя преломле-
преломления среды. Это значит, что в неоднородной среде луч изгиба-
изгибается в сторону наиболее быстрого изменения показателя пре-
преломления. Если среда однородна (п = const), то кривизна 1/1?
обращается в нуль, т.е. световые лучи прямолинейны.
2. Плотность земной атмосферы, а с ней и показатель преломления убы-
убывают с высотой. Этим объясняется ряд явлений, связанных с искривлением
световых лучей. К ним относится, например, астрономическая рефракция,
т.е. кажущееся поднятие небесного светила из™за искривления световых лу™
чей в земной атмосфере. Если светило стоит высоко над горизонтом, то при
расчете этого явления мы не сделаем заметной ошибки, считая поверхность
Земли плоской. Но так поступать нельзя, когда светило находится вблизи
горизонта. В этом случае надо учитывать сферичность земной поверхности.
Пренебрежем малыми боковыми градиентами показателя преломления
воздуха п и будем считать, что п зависит только от высоты над земной
поверхностью или, что то же самое, от расстояния г от центра земного
шара О (рис. 15). Световой луч AM от небесного светила будет лежать в
вертикальной плоскости, проходящей через это светило и глаз наблюдателя.
На основании D.1)
1 da д ,Л \ d(\nn) дг d(\nn)
= = Aпп) = =

4 ИСКРИВЛЕНИЕ СВЕТОВЫХ ЛУЧЕЙ В НЕОДНОРОДНЫХ СРЕДАХ 35
где а — так называемое зенитное расстояние, т.е. переменный угол между
вертикалью места MZ и касательной к лучу, as — длина луча, отсчитыва-
отсчитываемая от глаза наблюдателя М. Как видно
из рис. 15, 7
D.2)
Далее, r dj = ds sin /3, откуда
1 <fo 1 ds . 1
tgp dr r dr r
Вычитая это равенство из D.2) и прини-
принимая во внимание, что а —-7 ~ /3, получим
da
~ds =
а потому
1
tgp
da
Л7
da
dr
ds
=
da
= "*C0S/
--f(lnn).
dr
Рис. 15
dP л dr л ( \
^— = —a In n — — = —a In (nr).
Интегрирование этого уравнения дает
nr sin f3 = тгого sin ao,
D.3)
где нулем обозначены величины n, r, a в точке М (в которой а = /3). Вы-
Вычислив отсюда tg/З и подставив его значение в D.2), найдем
a(X) — ao = —
00
/
dlnn
dr
dr
y/n2r2 —
D.4)
; sin" ao
Здесь ao — видимое зенитное расстояние светила в точке М, а ато — угол
между асимптотой луча и вертикалью в той же точке. Разность аоо — «о
называется рефракцией. Для ее вычисления и служит формула D.4). Зная
зависимость плотности воздуха р от высоты над земной поверхностью, на™
ходят п по формуле (п — 1)/р = const, после чего производят численное
интегрирование в формуле D.4).
Если светило находится не слишком близко от горизонта, то кривиз-
кривизной земной поверхности можно пренебречь. Тогда рефракция не зависит
от характера изменения показателя преломления с высотой и может быть
вычислена по формуле
sin aoo = riosinao D-5)
(см. задачу 3 к § 2). Ошибка, даваемая этой формулой, быстро убывает с
уменьшением а. Уже при ао = 80° она не превосходит 3 %. При ао < 75°
формула D.5) дает достаточную точность.
Если светило находится на горизонте (а = 90 °), то средняя рефракция
при 10° С и 760 мм рт. ст. составляет 35;24/;. Она быстро уменьшается по
мере поднятия светила над горизонтом. Уже при ао = 89° средняя рефрак™
ция уменьшается до 24;37/;. Этим объясняется сплюснутая форма Солнца
при восходе и заходе.
С рефракцией связано некоторое удлинение дня. Для средних широт
оно составляет в среднем 3-4 минуты.

36
ВВЕДЕНИЕ
ГЛ. I
Рефракция зависит от длины волны. Поэтому при заходе Солнца сна™
чала должны исчезать красные и желтые лучи, а оставшийся сегмент сол-
солнечного диска должен окрашиваться на одну-две секунды в зеленый или
даже синий цвет. При восходе Солнца, наоборот, должна сначала появлять-
появляться кратковременная зеленая вспышка. Это явление «зеленого луча» наблю-
наблюдается на море, да и то крайне редко, так как необходимы исключительно
спокойная атмосфера и ясная погода.
3. Иногда вблизи земной поверхности из-за сильного нагревания или
охлаждения возникают большие градиенты показателя преломления воз-
воздуха. Тогда шарообразность Земли можно не учитывать. Если градиент п
направлен вертикально, то можно воспользоваться формулой D.3), полагая
в ней /3 = а, г = го- В результате получится
п sin а = по sin ао = const. D.6)
Допустим ради определенности, что световой луч распространяется
вверх под малым углом к горизонту, а показатель преломления п = n(z)
убывает с высотой z. Может случиться, что на некоторой высоте угол а
обратится в 90°. Тогда касательная к лучу станет горизонтальной. Высота
z = hj на которой это мо-
— жет произойти, определится
из соотношения
n(h) = по sin «о-
Так как показатель прелом-
ления возрастает вниз, то,
рис |g достигнув высоты z = hj
луч в дальнейшем должен
загнуться книзу. На указанной высоте происходит нечто аналогичное пол™
ному отражению (рис. 16). Такое явление может возникнуть при сильно
аномальном распределении плотности воздуха по высоте и является при-
причиной различного рода миражей, наблюдаемых в атмосфере.
Обычно наблюдается верхний
или нижний мираж,. При верхнем
мираже, помимо самих предметов,
видны их изображения, расположен™
ные сверху; при нижнем мираже изо-
изображение получается ниже самого
предмета. Нижний мираж наблюда-
наблюдается в пустынях и в степях в теп-
теплое время года, когда прилегающий
^- -~"""" ^"""" к земной поверхности слой воздуха
X^^^** s' сильно нагрет, а его плотность и по™
[^' казатель преломления быстро возра-
^,// стают с высотой. Из каждой точ™
s' ки предмета в глаз наблюдателя все-
г гда попадают прямые лучи, т.е. лучи,
не испытавшие полного отражения в
воздухе; им соответствует обычное —
Рис. 17 прямое — изображение предмета. Но
при больших градиентах показателя
преломления могут также попасть лучи, испытавшие полное отражение.
Они дают обратное изображение предмета, как в зеркале (рис. 17). При
этом лучи, выходящие из различных точек предмета, претерпевают полное

§ 5 ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 37
отражение на несколько разных высотах; точка М, в которой отражается
луч, выходящий из А, лежит несколько выше точки JV, в которой отража-
отражается луч, выходящий из В. Наблюдатель видит два изображения: прямое и
обратное. Создается иллюзия водной поверхности, в которой, как в зеркале,
видно изображение неба.
Аналогично объясняется и верхний мираж. Он наблюдается зимой в
холодных странах, когда вблизи земной поверхности образуется холодный
слой воздуха, в котором показатель преломления быстро убывает с высо-
высотой. В горах, хотя и очень редко, наблюдается боковой мираж, связанный
с изменением показателя преломления воздуха в боковом направлении. Во-
Вообще, в зависимости от характера распределения показателя преломления
воздуха, мираж проявляется в весьма разнообразных и часто причудливых
формах.
ЗАДАЧИ
1. Показать, что в пренебрежении кривизной земной поверхности спра™
ведлива формула
«оо ™«о = (по - l)tga0. D.7)
2. Определить, при каких градиентах температуры Т воздуха возможен
нижний мираж.
Решение. Показатель преломления, а с ним и плотность возду-
воздуха р должны увеличиваться с высотой h (т.е. dp/dh > 0). Воспользуемся
уравнением состояния р = /jlP/(RT), где Р — давление, /i — относительная
молекулярная масса воздуха, а R — универсальная газовая постоянная. Из
него находим
1 dp _ 1 dP I dT
рЖ ~ ?Ж ~ T~dh'
При механическом равновесии воздуха dP/dh = —pg, где g — ускорение
свободного падения. В результате получаем
f<f-
Используя соотношение ср — cv = R//i, этому условию можно придать вид
dT е-
зг < и -0,025 К/м, D.9)
an ср — cv
где ср и cv — удельные теплоемкости воздуха при постоянном давле™
нии и постоянном объеме. Такое распределение температур конвективно
неустойчиво, так как для конвективной устойчивости необходимо
dT е
^тг > -—и-0,01 К/м
ал ср
(см. т. II, § 121).
§ 5. Плоские электромагнитные волны
1. С электромагнитными волнами мы встречались уже в то™
ме III нашего курса (гл. X). Выведем еще раз основные резуль-
результаты, полученные в § 139 указанного тома, предполагая здесь,

38
ВВЕДЕНИЕ
ГЛ. I
что волны — монохроматические. Будем представлять их в ком-
комплексной форме. В связи с этим полезно еще раз обратиться к
§ 126 того же тома, где введены комплексные обозначения и
изложены правила оперирования с ними. По причинам, кото-
которые выяснятся в ходе изложения, монохроматические волны и
их комплексная форма имеют важнейшее значение в учении о
волнах вообще, а в особенности в оптике.
Допустим, что волны распространяются в однородном неза-
незаряженном диэлектрике. Применим к ним фундаментальные
уравнения Максвелла
, тт 1дТ>
rotH = --^-,
с dt '
с dt
E.1)
и материальные уравнения
D = еЕ, В = /iH. E.2)
Пусть волна — плоская и монохроматическая. Запишем ее в ком-
комплексном виде
Т7\ Aiuit—kr) тт тог „ifctjt-—кг) /г о\
— Л»0е j ¦"¦ — -"-О^ -) \Р*^)
где ш — круговая частота, к — волновой вектор, а амплиту™
ды Ео и Но постоянны. Дифференцируя по времени, получаем
dEi/dt = го;Е, т.е. операция дифференцирования в этом случае
сводится к умножению на ш. Аналогично, дифференцирование
по координатам ж, у, z сводится к умножению на —ikXi —ikyi
^ikz. Заметив это и обозначая координатные орты через еж, eyj
eZj получаем
rotH =
д^
дх
Нх
ду
д
Hz
кх
Нх
Hv Hz
и аналогично для rotE. В результате уравнения E.1) перейдут
в
= -|D, [kE] = |B. E.4)
Введем единичный вектор N нормали к фронту волны и ско-
скорость распространения последнего в направлении этой норма™
ли — так называемую нормальную скорость v. Тогда
и предыдущие соотношения перейдут в
D = --[NH], B = -[NE]. E.6)
V V
Отсюда видно, что векторы Е, Н, v в плоской электромагнит-
электромагнитной волне взаимно перпендикулярны. Их взаимное расположе-

§ 5 ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 39
ние представлено на рис. 18. Перпендикулярность векторов Е и
Н к вектору v, или, что то же, к направлению распростране-
распространения волны, означает, что электромагнитные волны поперечны.
Таким образом, проблема поперечности
световых волн, с которой не могли сира- | Е
виться теории механического эфира, со™
всем не возникает в электромагнитной
теории света.
Следует отметить, что между вза-
имно перпендикулярными составляю-
составляющими, на которые можно разложить
комплексные амплитуды Eg и Но, мо-
может существовать какая-то разность
фаз (р. Если она равна нулю или тг, то
вектор Е во всех точках пространства Рис- 18
и во все моменты времени будет нахо-
находиться в одной и той же плоскости, проходящей через направ-
направление нормали N, а вектор Н — в плоскости, к ней перпенди-
перпендикулярной. Тогда волну называют линейно- или плоскополяри-
зованной. Плоскость (Е, N), в которой лежат векторы Е и N,
называется плоскостью колебаний или плоскостью поляриза-
поляризации волны1). Если (р не равна нулю или тг, то возникает так
называемая эллиптическая поляризация. Исследованием ее мы
займемся в главах V, VI и VII.
Из уравнений E.1) можно определить и скорость электро-
электромагнитной волны v. С этой целью запишем эти уравнения в ска-
скалярной форме:
или
E.8)
V V
Отсюда после почленного перемножения и сокращения на ЕН
получаем для v и показателя преломления п = c/v следующие
выражения:
v = c/y/ejl, E.9)
п = y/iji. E.10)
Последнее соотношение называется законом Максвелла. Для
немагнитных сред (/i = 1) оно переходит в
п = у/ё. E.11)
) Раньше плоскостью поляризации называли плоскость (Н, N), перпен-
перпендикулярную к (Е, N). Но этот термин в таком понимании выходит из упо-
употребления.

40
ВВЕДЕНИЕ
ГЛ. I
В вакууме v = с, т.е. v совпадает с электродинамической
постоянной с. Тем самым раскрывается глубокий физический
смысл открытия В. Вебера A804—1891) и Р. Кольрауша A809—-
1858), впервые измеривших эту постоянную в 1856 г. (см. т. III,
§ 51, 83).
2. Обратимся теперь к экспериментальной проверке соотно™
шения E.11). В табл. 1 сопоставлены экспериментально изме-
измеренные значения п и у/ё для ряда веществ (показатели прелом-
преломления относятся к желтой линии натрия). Для газов, приведен-
приведенных в этой таблице, закон Максвелла E.11) хорошо согласуется
с опытом. Для жидких углеводородов согласие хуже. Для воды
и спиртов, а также для большинства других твердых и жидких
тел наблюдаются резкие нарушения соотношения E.11). Одна-
Однако в этом нет ничего неожиданного. Дело в том, что значения
е, приведенные в табл. 1, относятся к статическим электриче-
электрическим полям, а значения п — к электромагнитным полям све-
световых волн, частоты которых порядка 5 • 1014 Гц. Диэлектриче™
екая проницаемость е обусловлена поляризацией диэлектрика,
т.е. смещением заряженных частиц внутри атомов и молекул
под действием внешнего электрического поля. Для правильного
сопоставления надо брать значения б, измеренные в электриче-
электрических полях тех эюе частот. Действительно, атомы и молеку-
молекулы обладают собственными частотами, так что амплитуды (и
фазы) вынужденных колебаний электронов и ядер, из которых
они состоят, зависят от частоты внешнего электрического поля.
Особенно сильную зависимость следует ожидать в тех случа™
ях, когда частота внешнего поля близка к одной из собственных
частот атомов или молекул (резонанс!). В результате возникает
зависимость показателя преломления вещества от частоты све-
световой волны — так называемая дисперсия света.
Таблица!
Вещество
Воздух
Азот
Кислород
Водород
Углекислота
Гелий
Окись углерода
Аммиак
Закись азота
п
1,000292
1,000299
1,000270
1,000139
1,000499
1,000035
1,000335
1,000385
1,000507
1,000302
1,000307
1,000273
1,000139
1,000485
1,000037
1,000346
1,000385
1,000547
Вещество
Толуол
Четыреххлористый
углерод
Бензол
Сероуглерод
Парафин
Вода
Метиловый спирт
Этиловый спирт
п
1,499
1,461
1,501
1,629
1,422
1,33
1,34
1,36
1,549
1,523
1,511
1,626
1,405
9,00
5,70
5,10

§ 5 ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 41
Аналогично, намагниченность вещества (парамагнетизм и
ферромагнетизм) возникает в результате поворотов магнитных
моментов атомов и молекул под действием внешнего магнит-
магнитного поля. Однако в полях столь высоких частот, которые лежат
в оптической области спектра, атомы и молекулы не успевают
поворачиваться за времена порядка периода световых колеба-
ний. Диамагнитный же эффект, принципиально имеющий место
во всех веществах, пренебрежимо мал. Поэтому в полях указан-
указанных частот намагничивание вещества практически не происхо-
происходит. Вот почему в оптических явлениях, за редкими исключе-
исключениями, магнитные свойства вещества не проявляются, и мож-
можно пользоваться формулой E.11) вместо более общей форму-
формулы E.10).
Таким образом, расхождения закона Максвелла E.10) или
E.11) с опытом происходят за счет нарушения материальных
уравнений E.2). Такие уравнения справедливы не всегда, а
только для монохроматических полей^ причем е и /j, являют-
являются функциями частоты электромагнитного поля^ различными
для различных веществ. Чтобы отметить это обстоятельство,
величины е(ш) и fi(u)) часто называют динамическими диэлек-
диэлектрической и магнитной проницаемостями, в отличие от ста-
статических проницаемостей^ в которые они переходят при ш =
= 0. Лишь в области сравнительно длинных электромагнитных
волн (превышающих примерно 1 см) функции е(ш) и /i(u;) ста-
становятся постоянными для всех веществ. Поэтому в оптике элек-
электромагнитное поле приходится разлагать на монохроматические
составляющие, что всегда возможно, согласно математической
теореме Фурье (см. т. III, § 128). Предполагая, что выполняет-
выполняется принцип суперпозиции, эти монохроматические составляю-
составляющие можно рассматривать независимо друг от друга. Таким
путем можно исследовать распространение электромагнитных
волн любого спектрального состава. Функции можно разлагать
не только по синусам и косинусам, но и по бесконечному мно-
множеству других, «полных систем» функций. Однако выполнение
материальных уравнений E.2) для монохроматических полей,
а также многие другие причины делают в оптике разложение
полей на монохроматические составляющие физически выделен-
выделенным среди множества других математически возможных разло-
разложений. Изложенные соображения, как и соображения, излагае-
излагаемые в следующем пункте, имеют, конечно, общее значение, а не
только для плоских электромагнитных волн.
3. Соблюдение материальных уравнений E.2) (для монохро-
монохроматических полей) предполагает, конечно, что величина е не за-
зависит от Е. Благодаря этому уравнения поля линейны и одно-
однородны. Однако это справедливо только в слабых полях7 т.е. таких
полях, напряженность которых весьма мала по сравнению с на-

42 ВВЕДЕНИЕ ГЛ. I
пряженностями внутриатомных и внутримолекулярных полей
A07~~-108 В/см). В сильных полях, где это условие не соблюдает-
соблюдается, уравнения поля в средах становятся нелинейными, что ведет
к нарушению принципа суперпозиции, а следовательно, и зако-
закона независимости световых пучков. Оптику слабых электромаг-
нитных полей (в указанном выше смысле) называют линейной
оптикой, а оптику сильных полей — нелинейной оптикой.
До недавнего времени источники света, которыми распола-
располагала оптика, позволяли получать световые пучки лишь «сла-
«слабой» интенсивности с максимальными электрическими полями
0,1—10 В/см (см. задачу к этому параграфу). Нелинейные эф-
эффекты (за редкими исключениями) в этих случаях совсем неза-
незаметны. Случай сильных электрических полей в оптике считался
чисто умозрительным и долгое время не исследовался. Начиная
с 1960 г. — года изобретения оптических квантовых генерато-
генераторов (лазеров) — положение изменилось. Эти источники света
позволяют получать световые волны, в которых электрические
поля достигают 105-10 В/см. Такие поля уже не могут считать-
считаться пренебрежимо малыми по сравнению с внутриатомными и
внутримолекулярными полями. В них наблюдаются качественно
новые «нелинейные явления» и притом не как малые поправки к
«линейным эффектам», а как явления крупного масштаба, по-
получившие уже важные практические применения. О нелинейной
оптике мы будем говорить в гл. XI. Во всех остальных главах
излагается линейная оптика.
4. Для некоторых целей требуется более подробное исследо™
вание системы уравнений E.4), которое мы и произведем. Запи-
Запишем эту систему с учетом материальных уравнений E.2):
[кН] = -™ Е, [кЕ] = ^ Н. E.12)
Подставляя Н из второго уравнения в первое, получим
— [к[кЕ]] = - —Е.
UJfl С
Так как векторы к и Е взаимно перпендикулярны, то после рас™
крытия двойного векторного произведения и сокращения на Е
отсюда найдем
к2 = ^?//, E.13)
или, пренебрегая намагничиванием вещества,
к2 = ^е. E.14)
Таково условие совместности уравнений E.12). Так как по само-
самому определению волнового вектора к = ш/v, то из E.13) следует:
v = с/у/ёЦ, т.е. прежний результат E.9).

§ 5 ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 43
Однако условиям E.13) или E.14) можно удовлетворить и в
тех случаях, когда волновой вектор к комплексный, т.е. имеет
вид
к = к; -ik", E.15)
где векторы к; и к." — вещественные. В этом случае волну назы-
называют неоднородной^ в отличие от однородной волны^ у которой
волновой вектор к вещественный. Электрический вектор неод-
неоднородной волны можно представить в виде
Е = Eoe^k//V^k4 E.16)
Это выражение молено рассматривать как волну, амплитуда ко-
которой равна Еде г. Она экспоненциально убывает в направ-
направлении вектора к/;. Для такой волны можно говорить о поверхно-
поверхностях равных амплитуд и поверхностях равных фаз. Поверхно-
Поверхности равных амплитуд суть плоскости, перпендикулярные к век™
тору kff. Поверхности равных фаз также плоскости, но перпен-
перпендикулярные к вектору к'. В непоглощающей изотропной среде
плоскости равных амплитуд и равных фаз взаимно перпендику-
перпендикулярны. Для доказательства подставим выражение E.15) в фор-
формулу E.14). Отделяя вещественную часть от мнимой, найдем
k'2-k = ^?, (k'k") = 0. E.17)
Из второго соотношения видно, что векторы к; и к/;, а следо-
следовательно и плоскости равных амплитуд и фаз, взаимно перпен-
перпендикулярны. Для поглощающих сред это утверждение, вообще
говоря, не справедливо.
Чтобы получить более отчетливое представление о неодно-
неоднородной волне, запишем ее в вещественной форме. Направим ось
X вдоль вектора к;, а ось Z — вдоль вектора к". Кроме того,
положим Eqx = Axex.p(i6x) и аналогично для Е$у и Eqz. Тогда
неоднородную волну E.16) в вещественной форме можно пред-
представить так:
Ех = Axe~k"z cos (out - k'x + 5X),
Ey = Aye~k z cos (u)t — k'x + 5y),
Ez = Aze~kl'z cos (ujt - k'x + 6Z).
Плоскости равных фаз распространяются в направлении оси
X со скоростью v' = uj/k'. Она меньше скорости однородных
волн с/у/ё, поскольку к1 > иол/ejc^ как это следует из E.17).
Амплитуда убывает в направлении оси Z. Когда z —>> ^оо, ам-
амплитуда неоднородной волны возрастает неограниченно. Поэто-
Поэтому плоские неоднородные волны в неограниченной среде суще-
существовать не могут. Но они могут при определенных условиях

44 ВВЕДЕНИЕ ГЛ. I
возникать вблизи границы среды. Так, например, такие волны
возникают в оптически менее плотной среде при полном отра-
отражении света (см. § 66). Поле неоднородной волны заметно лишь
в пограничном слое, толщина которого порядка длины волны.
По этой причине неоднородные волны называют также поверх-
поверхностными волнами.
ЗАДАЧА
Оценить напряженность поля солнечного излучения вблизи зем-
земной поверхности, если величина солнечной постоянной составляет около
2 кал-см^2 мин = 1,39-106 эрг-см^2с^1. Солнечной постоянной называет-
называется количество энергии, попадающей от Солнца (при его среднем удалении
от Земли) за единицу времени на единицу площади земной поверхности,
перпендикулярной к излучению (при отсутствии абсорбции в атмосфере).
Решение. Волну, излучаемую Солнцем, у земной поверхности можно
считать плоской. В такой волне Е = Н, поскольку для вакуума е = /х = 1.
Плотность потока энергии — ЕН = —Е2. Приравнивая среднее значение
4тг 4тг
этой величины значению солнечной постоянной, получим
-S-Ё* = 1,39 • 106, откуда W = 5,85 • 1(Г4, у/Ш = 0,024 СГСЭ = 7,2 В/см.
4тг
§ 6. Предельный переход от волновой оптики к
геометрической
1. Геометрическая оптика является приближенным предель-
предельным случаем, в который переходит волновая оптика, когда дли-
длина световой волны стремится к нулю. Чтобы показать это, надо
было бы исходить из уравнений Максвелла в неоднородных сре-
средах. Однако такой путь приводит к громоздким вычислениям.
Мы поступим иначе. Среду, в которой распространяется свет,
будем считать прозрачной и однородной. Предполагая сначала,
что она изотропна, исключим из уравнений E.1) и E.2) вектор
Н. С этой целью первое уравнение E.1) дифференцируем по t,
а от обеих частей второго возьмем операцию rot, воспользовав-
воспользовавшись при этом векторной формулой
rot rot E = grad dlv E - АЕ х), F.1)
где А — оператор Лапласа в прямоугольной системе координат,
^ ^ ^
г) Эту формулу легко получить, записав левую часть в виде [V[VE]] и
раскрыв по обычному правилу двойное векторное произведение. При этом
надо только помнить, что векторы V и Е нельзя переставлять. Таким путем
получаем: V(VE) — V2E, т.е. правую часть F.1).

§ 6 ПРЕДЕЛЬНЫЙ ПЕРЕХОД К ГЕОМЕТРИЧЕСКОЙ ОПТИКЕ 45
Из полученных таким образом соотношений легко исключить
Н. В результате получится
ДЕ-^ = о> F-3)
где v определяется прежним выражением E.9). Уравнение F.3)
называется волновым. Такому же уравнению удовлетворяет и
вектор Н.
Для неоднородных сред уравнение F.3) усложняется. Одна-
Однако если интересоваться только интенсивностью волн^ отвлека™
ясь от их поляризации, то оказывается, что в предельном случае
геометрической оптики уравнение F.3) приводит к правильным
результатам 1). Поэтому даже в случае неоднородных сред пре-
предельный переход к геометрической оптике можно выполнить на
основе волнового уравнения
АЕ-^ = 0, F.4)
в котором Е означает длину вектора Е, а скорость v считает-
считается известной функцией координат. Хотя такой путь и не вполне
удовлетворителен, но на нем проще уяснить метод, применя-
применяемый при обосновании геометрической оптики. Результаты, к
которым мы придем, применимы не только к световым, но и
ко всем другим волнам^ например акустическим или волнам де
Бройля в квантовой механике.
2. Предполагая волну монохроматической, запишем ее в виде
Е = а(г)е^-коФ\ F.5)
где а (г) и Ф(г) — вещественные функции координат. Волно-
Волновое число в вакууме ко = w/c = 2тг/А введено для удобства,
как большой размерный параметр. Подставим выражение F.5)
в уравнение F.4) и отделим вещественную часть от мнимой. В
результате получим два уравнения:
^ F.6)
аАФ + 2 grad a grad Ф = 0. F.7)
Допустим теперь, что длина волны мала, а амплитуда а меня™
ется в пространстве не очень быстро, так что соблюдается нера-
неравенство
Да
А2
Аа
АО — '" * F^
4тг2 - v
1\ т-г
) Предельный переход к геометрической оптике на основе векторных
уравнений Максвелла подробно исследован в книге: Счвухчн Д.В. Лекции
по физической оптике, ч. П. Ротапринтное издание. — Новосибирск, 1969.

46
ВВЕДЕНИЕ
ГЛ. I
Для этого достаточно, чтобы выполнялись условия
да
л да
л—
ох
«а,
<с
F-9)
для любого направления оси X. Действительно, тогда
2д а
дх2
да
что совпадает с F.8), так как \Аа\ ~
F.6) последним членом, получим
(§гас1ФJ = п2
«а,
' \д2а/дх2\. Пренебрегая в
F.10)
Уравнения F.10) и F.7) и составляют систему уравнений
геометрической оптики. Из их вывода ясно, что условием при-
применимости геометрической оптики является малость изме-
изменения амплитуды волны и ее первых пространственных про-
производных на протяжении длины волны. В противном случае
могут возникать заметные отступления от геометрической оп-
оптики. Это происходит, например, в следующих случаях: 1) на
границе геометрической тени; 2) вблизи фокуса, т.е. геометри-
геометрической точки схождения лучей; 3) при распространении света
в среде с резко меняющимся показателем преломления (напри-
(например, в мутной среде); 4) при распространении света в сильно
поглощающих средах (например, металлах).
3. Величину Ф Клаузиус A822-1888) назвал эйконалом^ а
уравнение F.10) — уравнением эйконала. Его можно записать
в векторной форме:
grad# = rcs, F.11)
где s — единичный вектор нормали к фронту волны
ujt-коФ = const, F.12)
проведенный в сторону ее распространения.
Уравнение эйконала определяет скорость распространения
волнового фронта в направлении нормали s. Действительно, на
основании определения градиента можно записать F.11) в виде
дФ/ds = п. С другой стороны, дифференцирование уравнения
распространения волнового фронта F.12) дает oodt = ко с!Ф, или
7, Ш дФ j Ш
ujdt = — ^— as = —
= —as.
с ds с v
Отсюда для нормальной скорости волнового фронта находим
т.е. эта скорость такая лее, как у плоской волны. Этого и еле™
довало ожидать, так как малый участок волнового фронта в
малых объемах пространства должен вести себя как плоский.

§ 6 ПРЕДЕЛЬНЫЙ ПЕРЕХОД К ГЕОМЕТРИЧЕСКОЙ ОПТИКЕ 47
Полученный результат позволяет построить волновой фронт F^
в момент времени t + dt, если известно его положение Р\ в мо-
момент t. Для этого из каждой точки исходного волнового фронта
F\ (рис. 19) следует отложить в направлении нормали отрезок
t+dt
Рис. 19
длиной v dt. Соединив концы всех таких отрезков, мы и полу-
получим волновой фронт i<2 в момент t + dt. Вместо этого можно
из каждой точки волнового фронта i*\, как из центра, описать
сферы радиусом v dt. Огибающая таких сфер и будет волновым
фронтом ]?2- Оба построения совершенно эквивалентны. Тем са-
мым построение Гюйгенса (см. § 3, п. 4) распространяется и на
волны в неоднородных средах.
4. Второе уравнение геометрической оптики F.7) теперь
можно записать в виде
аДФ + 2п^ = 0. F.14)
Если определить луч как ортогональную траекторию к семей-
ству волновых фронтов^ или семейству равных фаз F.12), то
взятие производной по s можно понимать в смысле дифферен-
дифференцирования по длине луча s. Интегрируя уравнение F.14) вдоль
луча, придем к соотношению
s
^ I —ds), F.15)
где щ — амплитуда в «начальной точке» луча, от которой отсчи™
тывается длина s. Формула F.15) показывает, что для опреде-
определения волнового поля во всех точках луча достаточно знать его
значение в какой-либо одной точке того же луча. Но уравнения
геометрической оптики ничего не могут сказать относительно
изменения амплитуды поля при переходе от одного луча к со-
соседнему. Они допускают любые изменения амплитуды от луча к
лучу. Необходима только достаточная медленность такого изме-
изменения, чтобы волна, формально удовлетворяющая уравнениям
геометрической оптики, могла быть реализована в действитель-
действительности. Таким образом, в приближении геометрической оптики

48 ВВЕДЕНИЕ ГЛ. I
световое поле на всяком луче совершенно не зависит от полей
других лучей.
Отсюда следует основное представление геометрической он-
тики о распространении световой энергии вдоль лучей, точнее —
вдоль «лучевых трубок», образованных лучами. Отсюда так-
также следует, что при нахождении волнового фронта построением
Гюйгенса новый волновой фронт не выходит за пределы огибаю-
огибающей вторичных сферических волн Гюйгенса. Тем самым дано
полное обоснование гипотезы Гюйгенса об огибающей и показа-
показано, что эта гипотеза справедлива только в приближении геомет-
геометрической оптики.
К представлению о распространении света вдоль лучей мож-
можно прийти и другим путем. Умножая уравнение F.7) на а и заме-
замечая, что АФ = div grad<3> = div(ns), перепишем это уравнение
в виде
a2dlv (ns) + 2а grad a(ns) = О,
или
dtv(na2s) =0. F.16)
Полученное соотношение по форме совпадает с уравнением
непрерывности divj = 0 для стационарного течения несжима-
несжимаемой жидкости. Роль линий тока играют световые лучи, а плот™
ности потока жидкости — вектор j = na2s, пропорциональный
плотности потока световой энергии. Свет как бы течет вдоль
узких «световых трубок», т.е. трубок, боковые стенки которых
образованы лучами. Через эти боковые стенки свет не проника-
проникает. Если а — поперечное сечение трубки, то вдоль нее величина
па? а сохраняется неизменной, как это видно из уравнения F.16).
Можно выделить отдельную световую трубку, или физиче-
физический световой луч^ поставив на пути распространяющейся вол-
волны F.5) узкую диафрагму. Только диафрагма не должна быть
особенно узкой, а световая трубка слишком длинной. Дело в
том, что на краях диафрагмы и вблизи боковых границ труб-
трубки амплитуда поля меняется резко, т.е. условия применимости
геометрической оптики не выполняются. Возникает дифракция
света, приводящая к уширению светового пучка. Однако если
диафрагма не слишком мала, а световая трубка не слишком
длинна, эти эффекты малосущественны. Но они всегда скажут-
скажутся на больших расстояниях от диафрагмы. В теории дифракции
будет показано, что необходимым условием, при выполнении ко-
которого можно говорить о физическом световом луче, является
неравенство
KD2/A, F.17)
где D — минимальный линейный размер диафрагмы, а 1 — рас-
расстояние от диафрагмы, измеренное вдоль луча.

ПРИНЦИП ФЕРМА 49
Оптической длиной линии в однородной среде называется
произведение геометрической длины этой линии I на показатель
преломления п. Если среда неоднородна, то оптическая длина
определяется интегралом J ndl, взятым вдоль рассматриваемой
линии. Если ABC — геометрическая длина линии, то оптическая
длина ее обозначается через (ABC), т.е. заключением в круглые
скобки геометрической длины. Из построения Гюйгенса, изло-
изложенного в п. 3 этого параграфа, следует, что оптические длины
всех лучей между двумя положениями волнового фронта равны
между собой.
5. Нетрудно получить из волновых представлений и выражение для
кривизны луча в однородной среде. Для этого через бесконечно малый от™
резок луча АС проведем соприкасающуюся плос-
плоскость (рис. 20). Она пересечет волновые фрон-
фронты, проходящие через концы этого отрезка, вдоль
кривых АВ и CD. Пусть BD — бесконечно близ™
кий луч, лежащий в той же плоскости. Так как
лучи перпендикулярны к волновым фронтам, то
все углы бесконечно малого криволинейного че- В'
тырехугольника ABDC прямые. А так как опти-
оптические длины лучей между любыми двумя поло-
положениями волнового фронта одинаковы, то ril =
= (п + dn)(l + dl), где I и I + dl — длины отрезков
АС и BD, а п и п + dn — соответствующие им
показатели преломления. С точностью до беско-
бесконечно малых высшего порядка отсюда получаем
Idn + ndl = 0. По определению радиуса кривиз-
кривизны I = R(f, где (р — угол между касательными
к лучу АС в точках А ж С, равный углу меж-
между касательными к отрезкам АВ и CD в тех же
точках. Очевидно, dl = —скр^ где а — длина отрез- Рис. 20
ка АВ. Приращение показателя преломления dn
происходит вдоль главной нормали N, так что dn = (dnfdN)a. Учитывая
все это, получаем: Rip(dn/dN)a — пскр = 0, откуда
1 1 On
R n 9N
что совпадает с формулой D.1).
§ 7. Принцип Ферма
1. Пьер Ферма A601—1675) выдвинул принцип, согласно ко-
которому сеет при распространении из одной точки в другую
выбирает путь^ которому соответствует наименьшее вре-
время распространения. Ферма руководствовался телеологически-
телеологическими соображениями, согласно которым природа действует целе-
целенаправленно: она не может быть расточительной и должна до-
достигать своих целей с наименьшей затратой средств. Подобные

50 ВВЕДЕНИЕ ГЛ. I
соображения, конечно, чужды науке и не могут служить обосно-
обоснованием принципа Ферма. Но сам принцип (после введения неко-
некоторых уточнений) верен и может оказаться полезным при реше-
решении отдельных вопросов геометрической оптики. Это было про™
демонстрировано уже самим Ферма, который с помощью своего
принципа вывел закон преломления Снеллиуса и получил такое
лее выражение для показателя преломления, что и в волновой
теории света. В частности, он пришел к заключению, что ско-
скорость света в более преломляющей среде меньше, чем в менее
преломляющей.
2. Для доказательства принципа Ферма допустим сначала,
что показатель преломления среды меняется в пространстве
непрерывно и достаточно медленно, так что условия примени-
применимости геометрической оптики выполнены. Пусть в среде распро™
страняется волна вида F.5), например порожденная точечным
источником. Ей соответствует система лучей, представленная
на рис. 21. Если эйконал Ф —
однозначная функция коор-
координат, то из уравнения F.11)
следует, что циркуляция век-
вектора ns по любому замкнуто-
замкнутому контуру равна нулю, т.е.
fn(sdl) =0, G.1)
где d\ — вектор элементар-
элементарного смещения вдоль этого
Рис. 21 контура. Возьмем две произ-
произвольные точки А и В, лежа-
лежащие на одном из лучей. Соединим их произвольной линией
ADB. В силу G.1)
J n(srfl) = J n(srfl).
АСВ ADB
На луче АСВ векторы s и d\ направлены одинаково, следова-
следовательно, (sdl) = dl. На линии же ADB (sdl) = d/cos(s, dl) ^ dl.
Поэтому
J ndl^ J ndl. G.2)
ACB ADB
Знак равенства относится только к случаю, когда кривая ADB
сама является лучом. Таким образом, если показатель прелом-
преломления меняется в пространстве непрерывно^ то оптическая
длина луча между любыми двумя точками меньше оптиче-
оптической длины всякой друзой линии, соединяющей те же точки.
Но это есть другая формулировка принципа Ферма, так как оп-

ПРИНЦИП ФЕРМА 51
тическая длина луча пропорциональна времени распростране-
распространения света вдоль него.
Приведенная формулировка принципа Ферма нуждается в
уточнении. В некоторых случаях она может оказаться невер-
ной. Рассмотрим, например, среду
со сферически симметричным рас™
пределением показателя преломле-
ния вокруг центра О (рис. 22).
Примером такой среды может слу-
служить планетная атмосфера. Пред-
пол ожим, что показатель прелом-
преломления меняется в пространстве \^ у* в
так, что световой луч, выйдя из
какой-либо точки перпендикуляр-
перпендикулярно к радиусу, описывает окруж- с>
ность с центром в точке О. Пусть свет попадает из точки А в
точку В по большой дуге АС В этой окружности. Но он может
пройти из А в В и по дуге ADB той же окружности, затрачивая
на распространение меньшее время. Меньшее время потребова-
потребовалось бы и в том случае, если бы свет избрал какой-либо другой
путь, бесконечно близкий к дуге ADB. Все это противоречит
принципу Ферма в приведенной выше формулировке.
Причина противоречия состоит в том, что в приведенном
примере эйконал Ф не есть однозначная функция координат, как
это предполагалось при выводе. Действительно, если луч описы-
описывает окружность вокруг центра О, то он вернется в исходную
точку с новым значением эйконала: эйконал Ф получит прира-
приращение п/, где I — длина описанной окружности. Если окруж™
ность описывается т раз, то приращение эйконала будет 2mnl.
Это и значит, что функция Ф неоднозначна. Для справедливости
принципа Ферма необходимо наложить на выбор воображаемых
путей распространения света такие ограничения, чтобы эйконал
Ф вел себя как однозначная функция координат. В приведенном
примере этого молено достигнуть, поставив перегородку вдоль
меридиональной полуплоскости ODE и ограничиваясь только
такими путями, которые не пересекают эту перегородку.
Подобным приемом можно воспользоваться и во всех осталь-
остальных случаях, в которых эйконал Ф оказывается неоднозначным.
Впрочем, в применениях принципа Ферма достаточно ограни-
ограничиться только такими путями, которые проходят бесконечно
близко от действительного пути света. В этом случае надобность
во введении перегородок отпадает.
3. При наличии поверхностей раздела сред, на которых лучи
могут испытывать отражение или преломление, в формулиров-
формулировку и доказательство принципа Ферма надо ввести дополнения.
Пусть луч, выйдя из точки А (рис. 23), после отражений или

52
ВВЕДЕНИЕ
ГЛ. I
С
Рис. 23
преломлений в точках G, D, Е, ... попадает в точку В. Назо-
вем виртуальным путем света любую линию AC'D'E1 В меж-
между крайними точками
А и В, которая полу™
чается из ACDEB в
результате бесконечно
малого бокового сме-
смещения ее и отличается
от нее бесконечно ма-
мало по направлению.
Принцип Ферма утвер-
утверждает, что оптическая
длина действитель-
действительного светового пути
(или пропорциональное
ей время распростра-
распространения) стационарна.
Это значит, что разность оптических длин действительного
и виртуального путей света есть величина более высокого
порядка малости^ чем боковое смещение виртуального пути
относительно действительного. Только эта стационарность, а
не минимальность оптической длины луча и существенна в
приложениях.
При доказательстве достаточно ограничиться преломлением
на одной границе. Случай отражения исследуется так же. Пусть
MN — граница раздела сред 1 и
i?, а АС В — действительный луч,
соединяющий точку А с точкой В
(рис. 24). Вообразим два бесконеч-
бесконечно узких пучка лучей: один в первой
среде, исходящий из точки А7 дру-
другой во второй среде, сходящийся в
точке В. За положительные направ-
направления лучей примем направления от
А к В. Выберем в этих пучках два
луча АС и С'В, пересекающихся на
границе раздела в точке С'. Кривую
АС1 В можно рассматривать как вир-
Рис- 24 туальный путь света, так как луч С В
в общем случае, отнюдь не возникает в результате преломления
луча АС1. Обозначим через Фх и #2 эйконалы рассматриваемых
пучков лучей, отсчитываемые от точек А ж В соответственно.
Тогда
f nds = f nds + f nds = f nds— f nds = Фх(С) —
ACB
AC
CB
AC
ВС

ПРИНЦИП ФЕРМА 53
Вариация интеграла J nds при смещении точки С в произволь-
произвольную бесконечно близкую точку С1 границы раздела будет
S Г nds = 6Ф\ — 6Ф2.
Если Sr = С С1 — вектор смещения, то 5Ф\ = (grad#i^r) =
= ni(siJr) и аналогично 8Ф2 — ^2(s2^r)? так чт0
(f I nds = (niSi — П282)$Г.
В силу закона преломления Снеллиуса вектор (nj_Si — ^82)
перпендикулярен к границе раздела сред в точке падения, а по™
тому и к бесконечно малому смещению вдоль границы 8т. Таким
образом, в первом порядке по дг вариация оптической длины
луча АС В обращается в нуль. При доказательстве предпола-
предполагалось, что виртуальный путь состоит из отрезков лучей АС1 и
С' В. Однако результат не изменится, если эти отрезки заменить
произвольными бесконечно близкими к ним линиями, соединяю™
щими те же точки А и С\ С и В. В самом деле, поскольку АС1
и С1 В — действительные лучи в первой и второй средах, их
оптические длины по доказанному выше минимальны. По этой
причине замена действительных лучей АС и С'В бесконечно
близкими к ним линиями, соединяющими те же крайние точки,
не меняет в первом порядке оптические длины соответствующих
путей. Следовательно, вариация оптической длины луча АС В
останется равной нулю, каков бы
ни был виртуальный путь света.
А к этому в рассматриваемом слу-
случае и сводится содержание прин™
ципа Ферма.
4. В применениях иногда
удобна следующая теорема,
являющаяся непосредственным
следствием принципа Ферма.
Пусть А и В — произвольные
точки луча АС В (рис. 25).
Проведем через точку В произ-
произвольную гладкую поверхность
BE, ортогональную к лучу АС В в точке В. Пусть BD —
бесконечно малое смещение вдоль этой поверхности. Соединим
начальную точку луча А с точкой D произвольной линией
AHD, бесконечно мало отличающейся по направлению от
луча АС В. Тогда вариация оптической длины при переходе
от истинного пути света АСВ к виртуальному AHD будет
равна нулю.
Для доказательства возьмем пучок лучей, исходящих из точ-
точки А. Все эти лучи ортогональны к волновому фронту BF^ а их

54 ВВЕДЕНИЕ ГЛ. I
оптические длины от точки А до волнового фронта одинаковы.
В частности, (АСВ) = (AMК). Но по принципу Ферма с точно-
точностью до бесконечно малых высшего порядка (AMК) = (АНК).
Далее, поскольку поверхности BDE и BKF касаются друг дру-
друга в точке В, длина луча KD будет бесконечно малой высшего
порядка по сравнению с BD. Поэтому оптическая длина AHD
будет отличаться от оптической длины АС В также на величину
высшего порядка малости по сравнению с боковым смещением
BD. Это и требовалось доказать.
5. Если свет распространяется в однородных средах, грани-
граничащих между собой, то в каждой среде путь света будет пря-
прямолинеен. В этом случае задача сводится только к нахождению
точек на поверхностях раздела сред, в которых происходит отра-
отражение и преломление светового луча. Поэтому нет необходимо-
необходимости вводить криволинейные виртуальные пути света. Достаточ-
Достаточно ограничиться ломаными виртуальными путями, состоящими
из отрезков прямых линий, причем изломы таких путей должны
происходить на границах раздела рассматриваемых сред. Да-
Даже при таких ограничениях оптическая длина действительного
светового пути может быть не толь-
только минимальной, но и максимальной
или стационарной.
Чтобы показать это в случае отра-
отражения света, возьмем эллипсоидаль-
эллипсоидальное зеркало, получающееся от враще-
вращения эллипса вокруг его большой оси
FXF2 (рис. 26).
Пусть F\ и F2 — фокусы эллипсо-
рис 26 ида. Если А — точка на его поверхно-
поверхности, то F1A + F2A = 2а, где 2а — дли-
длина большой оси эллипсоида. Поверхность зеркала делит все про-
пространство на две части: внутреннюю^ сумма расстояний каждой
точки которой от фокусов F\ и F2 меньше 2а, и внешнюю, для
которой эта сумма больше 2а. Пусть световой луч выходит из
фокуса F\. Тогда после отражения от эллипсоидального зеркала
в точке А он пройдет через второй фокус F2l так как по извест-
известному свойству эллипса прямые F\A и F2 А образуют одинаковые
углы с нормалью к поверхности зеркала. При смещении вдоль
поверхности зеркала сумма F\A + F2A, а с ней и время распро-
распространения света из F\ в F2 не изменяются. Вариация времени
распространения при таком смещении равна нулю. Однако это
время ни минимально, ни максимально — оно постоянно. Имен-
Именно по этой причине любой луч, вышедший из F\, обязательно
пройдет через F2i в какой бы точке зеркала он ни отразился.
Убедиться в этом молено с помощью таких же рассуждений, ка-
какие были приведены в п. 3.

ПРИНЦИП ФЕРМА 55
Вообразим теперь зеркало S, касающееся эллипсоида в точке
Д обращенное вогнутостью в ту же сторону, что и эллипсоид, но
имеющее большую кривизну. Световой луч F\A после отраже-
отражения от этого зеркала снова попадает в точку F^. Однако при сме-
щении точки А по поверхности зеркала S длина ломаной F\AF^
уменьшается. Следовательно, время распространения света из
F\ в F^ вдоль действительного пути максимально. Наоборот,
если взять зеркало $", имеющее в точке касания меньшую кри-
кривизну, чем эллипсоид, или обращенное вогнутостью в противо-
противоположную сторону, то время распространения света вдоль дей-
действительного пути будет минимально. В частности, оно мини™
мально при отражении от плоского зеркала. Допустим, наконец,
что зеркало SAS' имеет в А точку перегиба. Тогда при смеще-
смещении точки падения луча по поверхности этого зеркала время
распространения либо увеличится, либо уменьшится, либо оста-
останется неизменным, в зависимости от направления смещения.
6. Чтобы разобрать случай преломления, введем понятие
анаберрационной поверхности. Пусть точка Р находится в од-
однородной среде с показателем преломления п, а точка Р1 — в
однородной среде с показателем преломления п! (рис. 27). По-
Поверхность А А1', вдоль кото-
которой среды граничат друг
с другом, называется ана-
анаберрационной, если любая
точка А этой поверхности
удовлетворяет условию
п-РА+п'-АР1 = С = const.
Для случая прелом-
преломления анаберрационная
поверхность имеет форму
так называемого кар-
тезианского овала (см.
задачу 2 к § 9). Он обращен вогнутостью в сторону более
преломляющей среды (р! > п). Анаберрационная поверхность
делит пространство на две части, обладающие следующим
свойством. Если точка М расположена в менее преломляющей
среде, то сумма п • РМ + п1 • МР' больше С] если же она лежит
в более преломляющей среде, то эта сумма меньше С.
Докажем следующую теорему. Луч света, вышедший из
точки Р, после преломления на анаберрационной поверхности
обязательно пройдет через точку Р1. Действительно, пусть
РА — падающий луч, as- единичный вектор, направленный
вдоль него. Соединим точку А с точкой Р1 и обозначим через s;
единичный вектор, направленный вдоль прямой АР1'. По опреде-
определению анаберрационной поверхности вариация оптической дли-

56 ВВЕДЕНИЕ ГЛ. I
ны ломаной РАР1 при смещении точки А по анаберрационной
поверхности будет равна нулю. Поэтому, применяя такие же
рассуждения, какие были проведены в п. 2, найдем, что век™
тор ns — mis1 перпендикулярен к анаберрационной поверхности
в точке А. Отсюда следует, что АР1 дает направление прелом-
преломленного луча.
Доказанной теореме можно дать также следующую форму-
формулировку. Если АА1 — анаберрационная поверхность относи-
относительно пары точек Р и Р1', то каждая из этих точек будет
оптическим изображением другой при преломлении лучей на
этой анаберрационной поверхности. При этом на угловую ши-
ширину пучка лучей не накладывается никаких ограничений.
Вернемся к исследованию характера экстремума оптической
длины луча при преломлении. Наши рассуждения ничем не бу™
дут отличаться от рассуждений, проведенных выше для эллип-
эллипсоидального зеркала. Допустим, например, что среды граничат
друг с другом вдоль поверхности S (рис. 27), касающейся ана-
анаберрационной поверхности в точке А. Тогда падающий луч пос-
после преломления в точке А опять пройдет через точку Р1. Пусть
поверхность S обращена вогнутостью в ту же сторону, что и ана-
анаберрационная поверхность, и имеет в точке касания большую
кривизну. Тогда при смещении точки падения вдоль S она ока-
окажется в менее преломляющей среде. Следовательно, смещенный
путь будет иметь меньшую оптическую длину', чем действитель-
действительный: время распространения света вдоль действительного пути
максимально. Напротив, когда кривизна поверхности S в точке
касания А меньше кривизны анаберрационной поверхности, а
также тогда, когда поверхность S обращена вогнутостью в про-
противоположную сторону, то время распространения вдоль дей-
действительного пути минимально. В частности, оно минимально
при преломлении на плоской поверхности.
ЗАДАЧА
Система лучей называется ортотомной, если все лучи этой системы
ортогональны к одной и той же поверхности. Пользуясь принципом Ферма,
доказать теорему Малюса: ортотомная система лучей остается орто-
томной после произвольного числа отражений и преломлений.
Решение. Пусть все лучи перпендикулярны к поверхности F
(рис. 28). Проведем через каждую точку этой поверхности луч и отложим
на нем отрезок постоянной (но произвольной) оптической длины L. Гео-
Геометрическим местом концов таких отрезков будет какая-то поверхность F .
Докажем, что все лучи рассматриваемой системы перпендикулярны к по™
верхности F', каково бы ни было значение величины L.
Малые отрезки одного из лучей АС и С' А' могут считаться прямоли-
прямолинейными. Возьмем соседний бесконечно близкий луч и притом такой, что
длины АВ и А' В' бесконечно малы по сравнению с АС и С' А'. Соединим В с

ГРУППОВАЯ СКОРОСТЬ 57
С ж С' с В прямолинейными отрезками. По принципу Ферма с точностью до
бесконечно малых второго или высшего порядков (ВЕВ1) = (ВСС!В'), а по
построению (BEBf) = (АС С А1). Таким образом, (ВСС'В') = (АС С А1).
Вычитая отсюда общую часть (СС ),
получим: (АС) + (СА!) = (ВС) +
-\-(С' В'). Так как по условию отрезок
АС перпендикулярен к АВ, то с точ- С С'
ностью до второго порядка малости
АС = ВС', а следовательно, (АС) =
= (ВС). Поэтому с той же точностью
(С'А') = (С В'), или С'А' = С В',
откуда следует, что С' A' _L А! В!. ^ рг
С точки зрения волновой теории
теорема Малюса почти самоочевид-
самоочевидна. Действительно, для ортотомной Рис. 28
системы лучей поверхность jP есть
одна из поверхностей равной фазы (волновой фронт). Распространяясь по
законам геометрической оптики, она продолжает оставаться поверхностью
равной фазы, а совокупность лучей — ортогональной системой. Конечно,
ортогональность может и не соблюдаться. Например, волны вида F.5) при
соблюдении принципа суперпозиции распространяются независимо друг от
друга. Каждой из таких волн соответствует ортотомная система лучей. Од-
Однако совокупность лучей, соответствующих всем волнам^ ортотомную си-
систему, вообще говоря, не образует.
§ 8. Групповая скорость
1. До сих пор при рассмотрении скорости распространения
волн мы предполагали, что соблюдается принцип суперпозиции
и отсутствует дисперсия. При несоблюдении принципа супер-
суперпозиции и наличии дисперсии вопрос о скорости распростра-
распространения волн становится очень сложным. Ниже предполагается,
что принцип суперпозиции соблюдается^ но имеется диспер-
дисперсия. Сначала рассмотрим плоские волны, распространяющиеся
в одном направлении, принимаемом за направление оси X.
Бегущую плоскую монохроматическую волну запишем в ви-
виде
Е = Ео cos (ujt -kx + 5), (8.1)
где Е® ш ё — постоянные. При рассмотрении таких волн дис-
дисперсия не играет роли, поскольку частота ш имеет единствен™
ное значение. Для выяснения смысла скорости распространения
рассмотрим уравнение
ujt - кх + S = const. (8.2)
Это есть уравнение плоскости, перпендикулярной к оси X, на
которой постоянна фаза волны. Дифференцируя его, получим:

58 ВВЕДЕНИЕ ГЛ. I
ujdt — kdx = 0, откуда
Ш
ш к- (8-3)
Таким образом, ш/к есть скорость распространения поверхно-
поверхности постоянной фазы, ранее обозначавшаяся через v. Она на-
называется фазовой скоростью волны. С такой скоростью распро-
распространяется синусоидальная волна типа (8.1) без изменения своей
формы.
Если бы среда не обладала дисперсией, то говорить о какой™
либо другой скорости распространения волны не было бы необ-
необходимости. Действительно, произвольное плоское возмущение,
распространяющееся в направлении оси X, согласно теореме
Фурье можно представить в виде суперпозиции монохроматиче-
монохроматических волн вида (8.1). При отсутствии дисперсии все эти волны
имели бы одну и ту же фазовую скорость, так что форма воз-
возмущения все время оставалась бы одной и той эюе. Возмущение
в целом бежало бы вперед без изменения вида со скоростью,
равной той же фазовой скорости. Не то будет при наличии дис-
дисперсии. Тогда монохроматические волны разных частот будут
распространяться вперед с разными скоростями, вследствие че-
чего форма всего возмущения будет непрерывно деформироваться
(исключение составляют только монохроматические волны, рас-
распространяющиеся по-прежнему без изменения формы). В этих
условиях понятие скорости распространения утрачивает тот яс-
ясный смысл, какой оно имело при отсутствии дисперсии. При
определенных условиях, однако, можно сохранить представле-
представление о скорости распространения немонохроматических волн и
в средах, обладающих дисперсией. Важнейшей после фазовой
скорости является так называемая групповая скорость.
2. Рассмотрим сначала в действительности не существую-
существующую непоглощающую среду, в которой фазовая скорость v вы-
выражается линейной функцией длины волны А:
v = а + ЬЛ, (8.4)
а следовательно, частота ш — линейной функцией волнового чис-
числа к:
ш = ак + 2жЬ. (8.5)
Произвольное плоское возмущение, распространяющееся в
среде, разложим на монохроматические волны. Их число, во-
вообще говоря, будет бесконечно велико. Однако можно ограни-
ограничиться случаем, когда оно равно трем. Это, как будет видно из
дальнейшего, не отразится на общности рассуждений и резуль-
результатов. На рис. 29 представлены эти три синусоиды в какой-то
момент времени. Форма результирующего возмущения зависит
от их взаимного расположения. Не нарушая общности, можно

ГРУППОВАЯ СКОРОСТЬ 59
принять, что в этот момент какие-то три гребня синусоид А, В,
С пространственно совпадают друг с другом.
Л о
Рис. 29
Допустим ради определенности, что фазовая скорость v воз™
растает с возрастанием длины волны Л (если предположить про-
противоположное, то рассуждения и окончательный результат не
изменятся). Таким образом, если Ai > А2 > A3, а г?ь г?2, ^3 —
соответствующие фазовые скорости, то v\ > V2 > v%. При рас-
распространении, например, вправо более длинные волны будут об™
гонять более короткие, что приведет к непрерывному изменению
формы результирующего возмущения. Гребни А, В, С начнут
расходиться, гребни А\, В\, С\ разойдутся еще больше, а гребни
A<i, 1^25 С*2 будут сближаться. Если начало координат поместить
в точку, в которой находились гребни А, В, С в начальный мо-
момент, то координаты гребней А2, ?»2, Сч в произвольный момент
времени t представятся выражениями
XA2(t) = V\t - Ai, XB2(t) = V2t - A2, Xc2(t) = ^3^ - A3.
В момент времени т, определяемый условиями
V\T — Х\ = V2T — \2 = V%T — A3,
т.е.
Ai — Л2 А2 — A3 Ai — A3 dX 1
vi — V2 v2 — V3 vi ™ V3 dv b '
гребни A2i B2l C2 пространственно совпадут, так что первона-
первоначальное взаимное расположение синусоид, а с ним и форма всего
возмущения восстановятся. Только роль гребней А, В, С перей-
перейдет к гребням ^2, ?»2, С*2, что, очевидно, никак не может от™
разиться на форме результирующего возмущения. Полученный
результат при линейном законе дисперсии (8.4) имеет общее зна-
значение, т.е. справедлив для произвольного числа синусоид и про™
извольного начального расположения их.
Таким образом, по истечении времени г = dX/dv^ называе-
называемого временем восстановления^ происходит периодическое вос-
восстановление формы возмущения. Например, в рассмотренном

60 ВВЕДЕНИЕ ГЛ. I
нами случае трех синусоид в начале координат, где наклады-
накладывались гребни А, I?, G, в начальный момент времени был мак-
максимум возмущения. В точности такой же максимум появился
через время т в другом месте пространства, где наложились
гребни ^2, 1?25 С2- Распространение возмущения носит как бы
прыгающий характер, причем от прыжка к прыжку проходит
время т. Естественно определить скорость возмущения как от-
отношение расстояния, проходимого возмущением за один «пры-
«прыжок», к промежутку времени между последовательными прыж-
прыжками. Так определенная величина называется групповой скоро-
скоростью возмущения. В разобранном примере это будет отноше-
отношение расстояния между двумя последовательными положениями
максимума возмущения к времени восстановления т. В момент
времени t = 0 координата максимума жмакс@) = 0. В момент т
координата такого же максимума будет
Жмакс(т) = ViT - Ai = V2T - А2 = V^T - A3 = VT - A.
За время т максимум проходит путь
Жмакс(т) - Жмакс@) =VT-X.
Следовательно, групповая скорость будет и = v — А/т, или
Adv /о гъ\
тг- (8.6)
dX x J
Эта формула впервые была получена Рэлеем A842-1919) и
носит его имя. На рис. 30 приведена графическая интерпретация
этой формулы, принадлежащая П.С. Эренфесту A880-1933). На
нем в координатах A, v представлен гра-
график АВ прямой (8.4). Так как и = v —
— Xdv/dX = а, то эта прямая отсекает на
оси ординат отрезок ?»О, длина которо-
которого равна групповой скорости и. Формулу
(8.6) можно записать в виде
X или
1 dv d f v
Рис. 30 и = d^ (8.7)
Легко также преобразовать (8.6) к виду
u1+
п \ п dX
3. Полученные результаты строго справедливы при линей-
линейном законе дисперсии (8.4) (или (8.5)). Однако если возмущение
занимает небольшую спектральную область, то эти результаты
остаются приближенно верными и в диспергирующих непогло-
щающих средах. Возмущение такого типа называется группой

ГРУППОВАЯ СКОРОСТЬ 61
волн. Точнее, группой волн называется волновое образование^
занимающее столь узкую спектральную область, что в преде-
пределах этой области приращение фазовой скорости v с достаточ-
достаточной точностью может считаться пропорциональным соот-
соответствующему приращению длины волны А, а следовательно^
приращение частоты ш — пропорциональным соответствую-
соответствующему приращению волнового числа к. Это значит, что в пре-
пределах рассматриваемой спектральной области обе зависимости
v = v(X) ж ш = ш(к) могут быть аппроксимированы линейными
функциями А и fc, а именно
(^) (Л-Ло), (8.9)
ал/ Л=Л0
^) (к-к0), (8.10)
ак у k=ko
где Ло — какая-то длина волны, лежащая внутри спектральной
области, занимаемой группой, а ко = 2тг/Ло — соответствую™
щее ей волновое число. При допустимости такой аппроксима-
аппроксимации можно говорить и о времени приближенного восстановления
формы возмущения т = dX/dv7 и о распространении возмуще-
возмущения с групповой скоростью ti, определяемой выражением (8.6)
или (8.7). На диаграмме Эренфеста в случае группы волн игра-
играет роль только малый участок кривой и = 'у(А), который можно
приближенно считать прямолинейным и
заменить соответствующим отрезком ка-
касательной. Групповая скорость и пред-
представится длиной отрезка ОВ, отсекае-
отсекаемого этой касательной на оси ординат
(рис. 31).
4. Учет высших членов в раз ложе™
нии (8.9) или (8.10) приводит к следую-
щему характеру распространения возму-
возмущения. Возмущение идет вперед, но его р ^
форма непрерывно изменяется. Однако
по истечении времени т = dX/dv возмущение принимает фор-
форму, почти совпадающую с исходной, причем за это время оно
продвигается вперед на расстояние х = иг. Можно сказать, что
происходит передача энергии возмущения с групповой скоро-
скоростью и. По истечении последующего промежутка времени той
лее длительности произойдет то же самое, и т.д. Вообще, в лю-
любой момент t + т возмущение воспроизводит с малыми искаже-
искажениями свою форму, какую оно имело в момент t, перемещаясь
за время т на расстояние иг. Но если возмущение распростра-
распространяется достаточно долго, то малые изменения, претерпеваемые
им за следующие друг за другом равные промежутки времени
длительностью т, будут накапливаться и могут настолько силь-

62 ВВЕДЕНИЕ ГЛ. I
но исказить само возмущение, что его форма потеряет всякое
сходство с исходной.
Чтобы оценить требующееся для этого время, дополним раз™
ложеыие (8.10) членом второй степени по (к — ко). С учетом
формулы (8.7) можно написать:
. / ? ? \ i 1 (du \ /1 7 \ 2
ш = ш0 + щ(к - к0) + - ^—J (к - ко) ,
где нулем обозначены значения соответствующих величин при
к = ко- Пусть 5к — максимальное значение разности к—ко- Тогда
соответствующее максимальное изменение фазы, обусловленное
наличием квадратичного члена, будет - — (SkJ. Если это из™
менение мало по сравнению с величиной порядка тг, то оно мало
скажется на относительной разности фаз между синусоидами,
входящими в группу, и тогда форма возмущения будет мало ис-
искажаться наличием квадратичного члена. Таким образом, что™
бы на интервале времени t происходило периодическое восста-
восстановление исходной формы возмущения, необходимо выполнение
условия
* ^ (8U)
Если перейти к длинам волн, то это условие преобразуется к
виду
Если же интервал времени t порядка или больше правой части
этого неравенства, то о восстановлении исходной формы возму-
возмущения говорить не приходится.
5. Выше предполагалось, что плоские монохроматические
волны, входящие в волновое образование, распространяются в
одном и том же направлении. Рассмотрим теперь случай, ко-
когда такие волны занимают по-прежнему узкую область частот,
но распространяются в разных направлениях, лежащих в преде™
лах узкого конуса. Соответствующее волновое образование на-
называется волновым пакетом. Его можно представить тройным
интегралом
кОх + Акх кОу + Аку kOz + Akz
Е(г, t) = J j j a(k)ex(wt~kr) dkx dky dkz,
kox — Akx koy — Аку koz — Akz
или сокращенно
E(r, t) = J a(k)e^~kr) rfk. (8.13)
Частоту ш следует рассматривать как функцию волнового век-
вектора к. Видом этой функции определяется закон дисперсии

ГРУППОВАЯ СКОРОСТЬ 63
волн. Если среда изотропна^ то функция а; (к) может зависеть
только от длины вектора к, но не от его направления. Но в
анизотропных средах, например кристаллах, необходимо учи™
тывать и зависимость ш от направления к. Поэтому ниже вид
функции а;(к) не конкретизируется, а рассуждения проводятся
в общем виде. Полагая ш = ш® + До;, k = kg + Дк, аппроксими-
руем Аш линейным выражением
Асо = §±Акх + ^-Аку + ^-Akz = (u Дк), (8.14)
где через и обозначен вектор с компонентами
дш дш дш /о 1 г\
и^Ж' иУ^Щ> U' = W (8Л5)
Сокращенно его записывают в символической форме:
и = ?. (8.16)
После подстановки соответствующих значений в выражение
(8.13) оно преобразуется в
Е = A(r,i)e^ot~k°r\ (8.17)
где введено обозначение
A(r,t)= J а(к)е*(А"*"Акг) dk = / a(k)e?(ut^Ak rfk.
Отсюда видно, что в точке Ж, движущейся со скоростью и по
закону г = Ы + го (го = const), амплитуда А остается постоян-
постоянной. В такой точке совершаются гармонические колебания
с частотой wo — kgu. По истечении времени т фаза этих коле-
колебаний изменяется на (ujq — kgu)т. Если это изменение равно 2тг,
т.е.
т = — ^ —, (8.18)
шо kou ш — ku
то вектор Е в движущейся точке М в любой момент времени t
примет то же значение, какое он имел в более ранний момент
t — т. Так как это справедливо при любом значении параметра
го, то происходит периодическое восстановление формы возму™
щения с периодом т, причем за это время возмущение перемеща-
перемещается вперед на расстояние иг. В результате мы снова приходим
к представлению о распространении возмущения с групповой
скоростью и, определяемой выражением (8.16).
В изотропных средах векторы и и к параллельны. В этом
случае (8.18) легко преобразовать к прежнему виду т = dX/dv.
Однако в анизотропных средах векторы и и к, вообще говоря,

64 ВВЕДЕНИЕ ГЛ. I
не параллельны, и надо пользоваться более общими выражения-
выражениями (8.16) и (8.18). Конечно, и здесь из-за наличия членов высших
степеней, отброшенных в разложении (8.14), за время т проис-
происходит не точное, а лишь приближенное восстановление формы
возмущения. За это время возмущение претерпевает малые, мо-
может быть едва заметные, искажения. Но на больших интервалах
времени эти искажения накапливаются и исходная форма воз-
возмущения сможет претерпеть существенные изменения.
6. Изложенные соображения позволяют легко решить вопрос
о скорости движения энергии или светового сигнала в диспер-
диспергирующих средах в тех областях спектра, в которых применимо
понятие групповой скорости (т.е. вдали от полос поглощения).
Прежде всего заметим, что фазовая скорость не имеет ниче-
ничего общего со скоростью движения энергии. Фазовой скоростью
устанавливается только связь между фазами колебаний в раз-
различных точках пространства. Связь такого типа в принципе мо-
может существовать и без передачи энергии, как это видно из еле™
дующего примера.
Вообразим длинную цепочку спортсменов, расположенных
вдоль прямой линии на равных расстояниях друг от друга.
Пусть они выполняют одно и то же гимнастическое упражне-
упражнение, например периодическое движение руками, и притом так,
что каждый впереди стоящий спортсмен начинает движение с
некоторым запаздыванием по отношению к спортсмену, стоя-
стоящему за ним. Пусть время запаздывания одно и то же для всех
спортсменов. При наблюдении со стороны будет казаться, что по
цепочке бежит волна с определенной фазовой скоростью, значе-
значение которой зависит от расстояния между соседними спортсме-
нами и от времени запаздывания, о котором говорилось выше.
Наличие такой волны, конечно, не означает, что каждый спортс-
спортсмен приводит в движение впереди стоящего спортсмена. Так и
возможность распространения в среде плоской монохроматиче-
монохроматической волны еще не дает оснований для заключения о переносе
энергии с фазовой скоростью.
Строго плоская монохроматическая волна непригодна для
наблюдения передачи энергии, поскольку она не имеет ни нача-
начала, ни конца во времени и в пространстве. Сама постановка во-
вопроса о передаче энергии требует отказа от такой идеализации.
Необходимо перейти к волновому возмущению, ограниченному
в пространстве по крайней мере с одного конца, т.е. имеющему
передовой фронт, перед которым возмущение отсутствует. Под-
Подходящим волновым образованием может служить группа волн.
Если выполнено условие (8.12), то средняя скорость энергии,
переносимой группой, совпадает с групповой скоростью. Дей-
Действительно, форма группы, какую она имела в момент i, восста-
восстанавливается без заметного искажения в более поздний момент

ГРУППОВАЯ СКОРОСТЬ 65
времени t + т. При этом группа вместе с локализованной в ней
энергией за время т перемещается вперед на расстояние х = ит.
Так как такое восстановление формы имеет место, каков бы ни
был момент времени t, то движение энергии с групповой ско™
ростью будет происходить на протяжении как угодно длинного
промежутка времени, даже если за это время группа существен™
но изменит свою форму.
Итак, в области, далекой от области сильного поглощения,
скорость движения энергии в группе волн совпадает с группо-
вой скоростью. То же самое приближенно справедливо и для
скорости движения энергии в волновом возмущении, занимаю™
щем сравнительно широкую спектральную область, если толь-
только в пределах этой спектральной области групповая скорость
и = и(Х) меняется мало. Если ширина спектральной области
6А, занимаемой группой, стремится к нулю, то группа в преде™
ле переходит в монохроматическую волну. Можно поэтому ска-
сказать, что средняя скорость переноса энергии в монохромати™
ческой волне совпадает с групповой скоростью. Это утвержде-
утверждение следует понимать именно в приведенном смысле, рассма-
рассматривая монохроматическую волну как предельный случай ква-
квазимонохроматической. Нельзя ограничиться идеализированной
плоской строго монохроматической волной, отвлекаясь от пред-
представления ее как предельного случая квазимонохроматической
волны. При такой абстрактной постановке вопроса утрачивается
связь с реальными явлениями, а потому с точки зрения физики
она бессмысленна.
Прямые измерения скорости света сводятся к измерению рас-
расстояния, проходимого световым сигналом за определенный про™
межуток времени. Из изложенного выше следует, что этот метод
практически дает групповую скорость. То же самое, как показы-
показывает подробный анализ, относится ко всем известным косвенным
методам измерения скорости света. Фазовую скорость, точнее —
отношение фазовых скоростей в двух различных средах, можно
определить по отношению показателей преломления, используя
формулу волновой теории C.7), в которую входят фазовые ско-
рости света в рассматриваемых средах (см. § 64).
7. Остановимся еще на вопросе о скорости распространения
передового фронта волнового возмущения. Речь идет о волне,
резко ограниченной передовым фронтом, перед которым пика™
кого возмущения нет. Скорость такого фронта точно совпадает
со скоростью света в вакууме с. В этом легко убедиться, исхо-
исходя из основных представлений электронной теории. Согласно
этой теории, всякую среду следует рассматривать как вакуум, в
который вкраплены молекулы и атомы вещества. Свет распро-
распространяется в вакууме между атомами и молекулами вещества,
т.е. всегда со скоростью с. Когда световое возмущение дости™
3 Д.В. Сивухин

66 ВВЕДЕНИЕ ГЛ. I
гает какого-либо атома, электроны и атомные ядра приходят в
колебания и сами становятся центрами излучения новых элек-
электромагнитных волн. Эти вторичные волны накладываются на
первичную волну и тем самым определяют все волновое поле в
среде. Но из-за инерции электроны и ядра не сразу приходят в
колебания. Пока электроны и ядра не пришли в колебания, они
не излучают вторичные волны, а потому не оказывают влияния
на распространение возмущения. Поэтому ясно, что передовой
фронт должен распространяться в среде с той же скоростью,
что и в вакууме. Но почему же при измерении скорости света
получается не с, а другая величина? Дело в том, что передовой
фронт несет слишком малую энергию, а приемники света недо-
недостаточно чувствительны, чтобы ее обнаружить. Количественные
расчеты, выполненные впервые Зоммерфельдом A868—1951) и
более подробно Л. Бриллюэном A889-1969), показали, что это
действительно так.

ГЛАВА II
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ
ИЗОБРАЖЕНИЙ
§ 9. Понятие оптического изображения
1. Если пучок световых лучей, исходящий из какой-либо точ-
точки F, в результате отражений, преломлений или изгибаний в
неоднородной среде сходится в точке Р;, то Р1 называется оп-
оптическим изображением или просто изображением точки Р.
Точку Р1 называют также фокусом геометрического схождения
лучей. Изображение Р1 называется действительным^ если све-
световые лучи действительно пересекаются в точке Р1'. Если же
в Р' пересекаются продолжения лучей, проведенные в направ™
лении, обратном распространению света, то изображение назы-
называется мнимым. При помощи оптических приспособлений мни-
мнимые изображения могут быть преобразованы в действительные.
Например, в нашем глазу мнимое изображение преобразуется в
действительное, получающееся на сетчатке глаза.
Если в некоторый момент времени изменить на противопо-
противоположное направление магнитного или электрического вектора,
то, согласно принципу обратимости (см. т. III, § 83, п. 8), фор-
форма лучей остается без изменения, но направление распростране-
распространения света изменится на противоположное. Точка Р1 будет играть
роль источника света^ а Р — его изображения. Поэтому Р и Р1
называются сопряженными или взаимно сопряженными точ-
точками. Аналогично, две линии или две поверхности называются
сопряженными^ если одна из них является оптическим изобра™
жением другой.
Если желают подчеркнуть, что лучи строго пересекаются в
точке Р;, то изображение называют стигматическим. Пучок же
лучей, исходящих из одной точки или сходящихся в одной точке,
называется гомоцентрическим. Примером может служить от™
ражение от эллипсоидального зеркала. По свойству эллипсоида

68
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
вращения прямые FA и F'А (рис. 32), соединяющие его фокусы
F и F1 с произвольной точкой А поверхности эллипсоида, накло-
наклонены под одинаковыми углами к этой поверхности. Поэтому все
лучи, вышедшие из одного фокуса, пос-
после отражения от поверхности эллипсои-
эллипсоида пересекутся в другом фокусе. Практи-
Практически более важен случай параболоидаль-
ного зеркала, используемого в астрономи-
астрономических телескопах-рефлекторах. Парабо-
лоидальное зеркало есть частный случай
эллипсоидального, когда один из фоку-
фокусов F1 удален в бесконечность. В силу из-
известного свойства параболы все лучи, па-
параллельные оси параболоида, после отражения от его вогнутой
поверхности пересекутся в фокусе параболоида F (рис. 33). Если
лее такие лучи отразятся от выпуклой поверхности параболои-
параболоида, то в фокусе F пересекутся продолжения отраженных лучей
(рис. 34). Стигматическое изображение точки Р в виде точки
Р1 получается также при преломлении на поверхности, являю-
являющейся анаберрационной для этой пары точек (см. § 7 и задачи к
настоящему параграфу).
Рис. 32
у
Рис. 33
Рис. 34
На практике случаи стигматических изображений, как пра-
правило, бывают исключениями. Обычно лучи пересекаются не
строго в одной точке, а в некоторой окрестности ее. Изображе-
Изображением светящейся точки на экране будет в этих случаях не мате-
математическая точка, а светлое пятнышко. Это снижает качество
изображения. Однако строго точечное изображение светящейся
точки не получается даже в тех случаях, когда по законам гео-
геометрической оптики лучи должны точно пересекаться в одной
точке. Из-за дифракции света изображение светящейся точки

§ 9 ПОНЯТИЕ ОПТИЧЕСКОГО ИЗОБРАЖЕНИЯ 69
получается в виде светлого кружка, окруженного темными и
светлыми кольцами.
Полная — физическая — теория оптических изображений
должна учитывать волновые свойства света. Но начинать с та™
кой теории, из-за ее сложности, было бы нецелесообразно. Сна-
Сначала надо уяснить получение изображений с простейшей — гео-
геометрической — точки зрения, а затем ввести поправки, учиты-
учитывающие волновую природу света. Геометрическая теория стро-
строится на основе одних только законов отражения и преломления
света, полностью отвлекаясь от его физической природы. Таким
путем, конечно, нельзя установить границы применимости гео-
геометрической теории. Это молено сделать только на основе вол-
волновой теории. Но значение последней этим не исчерпывается.
Более существенно, что волновая теория позволяет определить,
что принципиально возможно в оптике, и указать, как этого
достигнуть.
2. Непрерывная совокупность точек, изображаемых оптиче-
ской системой, называется пространством предметов. Непре-
Непрерывная же совокупность точек, являющихся их изображениями,
называется пространством изображений. Одна и та же точка
может принадлежать к пространству предметов и к простран-
пространству изображений, в зависимости от того, рассматривается ли
она как предмет или как изображение. Показатель преломле-
преломления пространства предметов будем обозначать через п, а про-
пространства изображений — через п1. В оптических приборах све-
световой оптики величины п ж п1 всегда постоянны, т.е. не меняют-
меняются от точки к точке. Когда изображение действительное, под п!
следует понимать показатель преломления среды в той точке,
где получилось это изображение. В случае мнимого изображе-
изображения пг не всегда совпадает с показателем преломления среды в
месте нахождения точки Р!. Значение п1 относится к той среде,
через которую проходят действительные лучи, продолжения
которых пересекаются в точке Р1.
Мы будем исследовать и такие случаи, когда показатель пре-
преломления среды меняется непрерывно от точки к точке, а пото-
потому лучи криволинейны. Такой случай практически реализуется
в электронной оптике. Здесь роль линз выполняют электриче-
электрические и магнитные поля, а показателя преломления — скорость
электрона (см. § 4).
8. С математической точки зрения задача геометрической
теории оптических изображений сводится к определению поло-
положения изображения при любом заданном положении предмета.
При этом общие свойства оптических систем удобно исследовать
с помощью следующего положения. Оптические длины всех лу-
лучей, соединяющих сопряженные точки Р и Р', одинаковы. Это
непосредственно очевидно, когда изображение Р1 действитель-

70 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ное, так как тогда сферическая волна, вышедшая из Р, превра-
превращается в сферическую волну, сходящуюся в Р1. Оптические же
длины всех лучей от одного положения волнового фронта до
другого одинаковы. Но это положение можно распространить и
на мнимые изображения. В этом случае не существует лучей,
соединяющих Р с Р1. Роль луча играет прямолинейное продол™
жение его в сторону изображения Р1. По аналогии с мнимым
изображением такое продолжение можно назвать мнимым лу~
чом.
Оптическую длину луча следует считать положительной,
когда он проходится в направлении распространения света, и
отрицательной в противоположном случае. Чтобы в случае
мнимых изображений избежать неопределенности, будем пред-
предполагать, что пространство изображений однородно, т.е. свето™
вые лучи в нем прямолинейны. Это не значит, что изображение
Р1 должно обязательно получаться
в том месте, где среда однородна.
Требуется только, чтобы действи-
действительные световые лучи, продолже-
продолжения которых сходятся в Р1, были
прямолинейны.
После этих замечаний обратим™
ся к доказательству нашего утвер-
утверждения. Пусть лучи РАС и PBD
(рис. 35), вышедшие из точки Р,
Рис 35 на участках АС и BD прямолиней-
прямолинейны. Их продолжения пересекаются
в точке Р1, являющейся мнимым изображением точки Р. Волно-
Волновой фронт в однородном пространстве изображений будет иметь
форму сферы CD с центром в Pf. Очевидно,
(РАС) = (PBD), (Р'АС) = (P'BD).
Почленное вычитание дает
(РА) - (Р'А) = (РВ) - (PfB).
Но, согласно нашему правилу знаков,
(РА) - (PfA) = (РА) + (APf) = (PAPf),
(РВ) - (PfB) = (РВ) + (BPf) = (PBPf),
Следовательно, (PAP1) = (РВР1)^ что и требовалось доказать.
Доказанное свойство оптических длин эквивалентно утвер-
утверждению, что сеет затрачивает одно и то же время, распро-
распространяясь вдоль различных лучей от точечного источника до
его изображения. В таком виде это утверждение называется
принципом таутохронизма (равенства времен распространен

ПОНЯТИЕ ОПТИЧЕСКОГО ИЗОБРАЖЕНИЯ
71
ния). Принципом таутохронизма мы воспользуемся при изуче™
нии явлений интерференции.
Наряду с мнимыми изображениями, следует ввести и мни-
мнимые источники света^ или мнимые объекты. Точечный объект
называется мнимым^ если он является точкой пересечения про-
продолжений действительных лучей, проведенных в обратных на™
правлениях. Мнимый объект можно рассматривать как источ-
источник мнимых лучей. Из множества точечных мнимых объектов
составляются мнимые объекты конечных размеров.
Введение мнимых объектов и мнимых лучей освобождает
теорию от необходимости раздельного рассмотрения действи-
действительных и мнимых изображений.
Отпадает также необходимость в
раздельном рассмотрении прелом-
преломления и отражения света, что име-
имеет большое значение в теории опти-
оптических систем, содержащих боль™
шое количество преломляющих и
отражающих поверхностей. Дей-
Действительно, пусть Р! — мнимое
изображение точки Р, полученное
в результате отражения света от
зеркала (рис. 36). Согласно приня-
тому нами правилу знаков, оптиче-
оптическая длина мнимого луча АР1 отрицательна. Поэтому для оп-
оптической длины пути РАР' можно написать:
{РАР') = п\РА\ - n\APf\ = п\РА\ + п'|АР'|,
где п' = —п. Поэтому отражение формально математиче-
математически моэюно рассматривать как преломление, если только по-
показателю преломления п1 приписать отрицательное значение
(п'/п = -1).
ЗАДАЧИ
1. Две однородные среды с показателями преломления п и п граничат
друг с другом вдоль поверхности S (рис. 37), являющейся поверхностью
вращения вокруг оси ОР1 (оптической оси). Найти форму поверхности S,
при которой она будет анаберрационной для пары точек Ри?', лежащих
на оптической оси, из которых точка Р удалена в бесконечность, а Р1 может
занимать любое положение на оптической оси.
Решение. Примем оптическую ось за координатную ось X, начало
координат поместим в точке пересечения ее с поверхностью 5, ось Y напра-
направим вверх перпендикулярно к оптической оси. Так как оптические длины
лучей от бесконечно удаленной точки Р до плоскости О А одинаковы, то
условие анаберрационности поверхности S будет (ABPf) = (OP')j шли
рис. зб
пх
+ п' л/(х — qJ + у2 = nq,

72
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
где х и у — текущие координаты точек поверхности S, a q — абсцисса точ-
ки Pf. Перенеся пх в правую часть и возведя в квадрат, находим уравнение
искомой поверхности:
(п2 - п2)х2 + п2у2 - 2п(п - n)qx = 0. (9Л)
Допустим сначала, что п —п > 0. Тогда уравнение (9.1) представляет
эллипсоид вращения с полуосями
а =
п
п' +п" у п1 +п
Эллипсоид вытянут в направлении оси X. Его эксцентриситет равен
е =
71
Изображение Pf действительное.
Пусть теперь п2 — п2 < 0. Тогда (9.1) есть уравнение двуполостного
гиперболоида вращения с полуосями
Y
П , \7Х — 7Х
а = — д,
п1 +п
и эксцентриситетом
X
Рис. 37
а п'
Изображение Р' мнимое (рис. 38).
Рассмотрим, наконец, случай, ко-
когда п'2 — п2 =0. Это может быть либо
при п' — п = 0, либо при п! + п = 0.
Первая возможность не представляет
интереса, поскольку она соответству-
соответствует тривиальному случаю, когда обе граничащие среды в оптическом от™
ношении тождественны. Вторая возможность п' = —п может быть ре-
реализована при отражении света. В этом
случае уравнение (9.1) переходит в
у2 = Aqx (9.2)
и представляет параболоид вращения с
параметром р = 2q (параболоидальное
зеркало). Если q > 0 (см. рис. 34), то
фокус Р1 (на рис. 34 — точка F) мни-
мнимый. Если q < 0 (см. рис. 33), то он
действительный. Эти случаи уже были
рассмотрены в тексте.
Результаты решения этой задачи
указывают способ построения идеаль-
идеальной линзы для пары сопряженных
точек, из которых одна бесконечно
удаленная. Рассмотрим сначала линзу,
ограниченную поверхностью эллипсои-
эллипсоида вращения ОВ и сферической поверх-
Рис. 38

§ 10 ПРЕЛОМЛЕНИЕ НА СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ 73
ностью с центром в Р' (на рис. 37 эта поверхность изображена штриховой
линией). Эксцентриситет эллипсоида должен быть равен 1/п, где п — пока-
показатель преломления линзы относительно окружающей среды. Параллель-
Параллельный пучок лучей, падая на поверхность эллипсоида, после преломления на
ней превращается в пучок, сходящийся в точке Р''. Задняя — сферическая —
поверхность линзы не меняет направления лучей, поскольку ее центр нахо-
находится в точке схождения пучка Р . Таким образом, рассматриваемая линза
собирает параллельный пучок лучей строго в одной точке Р . Если точеч-
точечный источник поместить в Р;, то после прохождения через линзу пучок
лучей станет строго параллельным оптической оси.
Рассмотрим далее линзу, ограниченную плоской поверхностью (на
рис. 38 она изображена штриховой линией) и гиперболоидом вращения с
эксцентриситетом п. Параллельный пучок лучей, падающих на плоскую
поверхность линзы, после прохождения через эту поверхность не изменит
направления, а после преломления на поверхности гиперболоида превра-
превратится в расходящийся пучок лучей, продолжения которых пересекаются
строго в одной точке Р'.
2. Найти уравнение картезианского овала (см. § 7, п. 6).
Решение. Пусть P(q, 0) и Pf (q*, 0) — сопряженные точки, для кото-
рых поверхность, получающаяся от вращения картезианского овала отно-
относительно оси симметрии РР , анаберрационна. Поместим начало координат
в точку перечения овала с прямой РР . Тогда по определению анаберраци-
онной поверхности
п-\/(х — qJ + у2 + п д/(ж — q'J + у2 = п q — nq.
Освобождаясь от радикалов, получим уравнение картезианского овала:
/ 2 /2\/ 2 , 2\ , л/ 2 /2\/ /2 / 2 \/ 2 . 2\ ,
(п — п )(х + у ) + 4(п — п )(п q — п q)(x + у )х +
+ Ann {nq ~~ n q){nq — nq)(x + у ) + 4(п' q ~~ n q) x +
+ 8пп (п — n)(nq — п q)qq х = 0. (9.3)
При определенных значениях параметров n, n , g, q картезианской овал вы-
вырождается в поверхности второго порядка. Тогда получаются, в частности,
уже разобранные ранее случаи, изображенные на рисунках 32, 33, 34, 37 и 38.
§ 10. Преломление на сферической поверхности.
Сферические зеркала и тонкие линзы
1. Важнейшие из оптических инструментов или их составные
части относятся к так называемым центрированным оптиче-
оптическим системам. Они представляют собой оптически однород™
ные преломляющие или отражающие среды, отделенные одна
от другой сферическими поверхностями, центры кривизны ко-
которых расположены на одной прямой, называемой главной оп-
оптической осью системы. Обычно если это не может привести к
недоразумениям, прилагательное «главная» мы будем опускать.
2. Начнем с простейшего случая одной сферической прелом-
преломляющей поверхности, разграничивающей однородные среды с

74
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
показателями преломления п и п!. Можно предполагать (хотя
это и не обязательно), что эта поверхность обладает симмет-
симметрией вращения относительно одной из прямых 0G, проходящих
через центр кривизны сферической поверхности (рис. 39). Та™
кая прямая и будет главной оптической осью. Примем ее за
координатную ось X. Начало координат поместим в точке О,
в которой главная оп-
оптическая ось пересе-
пересекает сферическую по™
верхность.
Ввиду симметрии
вращения достаточно
ограничиться рассмо-
рассмотрением хода лучей в
координатной плоско-
плоскости XY. Совместим ее
Рис. 39 с плоскостью рисунка.
Абсциссы и ординаты
будем отсчитывать от начала координат О. Если направление
отсчета совпадает с направлением распространения света
вдоль оптической оси, то соответствующая абсцисса считается
положительной] в противоположном случае она считается
отрицательной. То же относится и ко всем другим направ-
направленным отрезкам. Например, на рис. 39 абсцисса точки Р
отрищательна, а точка Р1 положительна. Ордината считается
положительной, если соответствующая точка лежит выше
оптической оси, и отрицательной, когда она расположена ниже.
Допустим, что точечный источник света Р находится на оп-
оптической оси системы (рис. 39). Произвольный луч РА после
преломления на сферической поверхности пойдет по пути АР1.
Обозначим длины АР и АР1 через и и и1 соответственно. Эти
длины отсчитываются от точки А и считаются положительны-
положительными, если направление отсчета совпадает с направлением распро-
распространения света, и отрицательными в противоположном случае.
Из рисунка видно, что
пл. РАС + пл. САР1 = пл. РАР1»
Так как и < 0, и1 > 0, то для этих площадей молено написать:
пл. РАС = \\РА\ • |AC|sin</? = -i
пл.САР' = ^
пл.РАР' = —- ии sin (</? — ф) = — - ии (sin cp cos ф — sin ф cos ср).
Здесь R — радиус кривизны преломляющей поверхности. Он от-
считывается от сферической поверхности к ее центру (на рис. 39

§ 10 ПРЕЛОМЛЕНИЕ НА СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ 75
радиус R положителен). Таким образом,
—uR sin if + и R sin ф = —uv! (sin <p cos ф — sin ф cos </?).
По закону преломления sin ip/ sin t/? = n'/n, а потому
—u'Rn' + i/i?n = !1^; (n cos (p — nf cos t/^).
Отсюда
тг n' тгcos<p — n cos^ fin "П
и и' R '
Положение точки Pf зависит от угла наклона а падающего
луча к оптической оси. Ограничимся, однако, малыми углами
а и допустим, что углы (р и ф также малы. Лучи, удовлетво-
удовлетворяющие таким условиям, называются параксиальными (приосе™
выми) лучами. Для них можно принять
СО8(р = соБф = 1, АР « ОР = х, АР' « OF' = х«
В этом приближении формула A0.1) переходит в
п п
, ^- (Ю.2)
х х1 R
Отсюда видно, что в рассматриваемом приближении положе™
ние точки Р! не зависит от угла а. Следовательно, все паракси-
параксиальные лучи, выходящие из одной точки оптической оси, после
преломления на сферической поверхности пересекутся прибли-
приближенно в одной точке, лежащей также на оптической оси. Точка
Р1 будет поэтому оптическим
изображением точки Р в парак-
параксиальных лучах. Во всем даль-
дальнейшем предполагается, что все
лучи, проходящие через центри™
рованные системы, параксиаль-
параксиальны.
При выводе предполагалось,
что источник света Р действи-
действительный. Однако все сказанное
справедливо и для мнимого ис-
источника, т.е. тогда, когда источ-
источником служит точка схождения Рис. 40
продолжений падающих лучей. В этом легко убедиться, повто™
рив рассуждения применительно к рис. 40.
Полагая формально п! = —п, из A0.2) получаем формулу
для сферического зеркала:
1 + 1 = |. (ю.з)
х х' R х /
3. Рассмотрим теперь случай, когда точечный источник Р
не лежит на главной оптической оси (рис. 41). Проведем пря-

76
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
мую PC, соединяющую точку Р с центром кривизны прелом-
преломляющей поверхности. Такую прямую можно рассматривать как
оптическую ось, сведя тем самым разбираемый случай к пре-
предыдущему. Для параксиальных лучей О'Р ~ OQ, О1 Р' ~ OQ1
Рис. 41
(здесь Q и Q1 — проекции точек Р и Р1 на главную оптическую
ось). Абсцисса ж' точки Р1 определится из уравнения A0.2), а
ордината у — из соотношения
У- =
у
CQ1
CQ
х' - R
ж-Я '
которое следует из подобия треугольников PCQ и P'CQ1. В ре-
результате находим
n'Rx , = nRy ,10 4ч
/ =
Проведем через точку Q произвольный параксиальный луч
QA, образующий с главной оптической осью какой-то угол а.
Угол наклона преломленного луча AQ1 с той же осью обозначим
через а'. Отсчет углов производится в направлении от главной
оптической оси к лучу. Если это направление противоположно
направлению вращения часовой стрелки, то угол считается по™
ложительным; в противоположном случае его следует считать
отрицательным (на рис. 41 угол а положительный, угол а1 от-
отрицательный) . Опустим из точки А перпендикуляр АА1 на глав-
главную оптическую ось. В приближении параксиальной оптики его
длину можно представить в виде \АА'\ = —ха = —х'а1. Следо-
Следовательно, ха = х'а1. Но из формул A0.4) следует
а потому
х п у
х пу
пуа = пу'а .
A0.5)
A0.6)
Таким образом, величина пуа не изменяется при преломлении

§ 10 ПРЕЛОМЛЕНИЕ НА СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ 77
параксиального луча на сферической поверхности. Эта величи-
величина называется инвариантом Лагранэюа-Гельмгольца^ а равен-
равенство A0.6) — теоремой Лагранэюа-Гельмгольца. Теорема, оче-
очевидно, справедлива для центрированных систем, состоящих из
какого угодно числа преломляющих и отражающих сфериче-
сферических поверхностей.
Формулы A0.4) можно положить в основу геометрической
теории любых центрированных систем в параксиальных лучах.
Применяя их к первой преломляющей поверхности сложной си-
системы, найдем положение изображения, возникающее от пре-
преломления на этой поверхности. Полученное промежуточное изо-
изображение играет роль предмета для преломления на второй сфе-
сферической поверхности. С помощью тех же формул A0.4) можно
найти положение второго промежуточного изображения, возни-
возникающего от преломления на второй сферической поверхности, и
т.д. В конце концов путем последовательного применения фор-
формул A0.4) к каждой из преломляющих поверхностей можно най-
ти положение окончательного изображения, даваемого всей си-
системой.
4. В качестве примера рассмотрим тонкую линзу, ограничен-
ограниченную сферическими поверхностями с радиусами кривизны R\ и
i?2- Относительный показатель преломления линзы обозначим
через п, приняв за единицу показатель преломления окружа-
окружающего пространства. Пусть точечный предмет Р находится на
главной оптической оси линзы. Толщиной линзы будем прене-
пренебрегать и поместим начало координат в ее центре. Обозначим
через х абсциссу точки Р, через х\ — абсциссу ее промежуточ-
промежуточного изображения Pi, возникающего от преломления лучей на
первой поверхности линзы. Абсциссу х\ можно найти с помо-
помощью формулы A0.2), если в ней сделать замену п —>• 1, п1 —>• п,
х1 -Л #i, R —>> R\. Это дает
1 п 1 — п
х х\ R\
Промежуточное изображение Pi будем рассматривать как пред-
предмет при преломлении света на второй сферической поверхности
линзы. Изображение точки Р, возникающее при таком прелом-
преломлении, и будет окончательным изображением Р;, которое дает
линза. Абсцисса х' точки Р1 найдется из формулы A0.2), если
в ней сделать замену п1 —± 1, х —)> х\, R —Ь i?2- Таким путем
находим
п 1 п — 1
Х\ Х! R.2
Складывая это равенство с предыдущим, получим

78 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Это хорошо известная формула тонкой линзы
i-i7 = - A0-8)
X X1 f V 7
Фокусное расстояние / определяется формулой
И"-
Эта формула справедлива для всяких тонких линз: двояко-
двояковыпуклых, двояковогнутых, плоско-выпуклых и т.д. Надо толь-
только придерживаться правила знаков, сформулированного в п. 2
настоящего параграфа. Так, для двояковыпуклой линзы R\ > О,
i?2 < 0, а потому фокусное расстояние / положительно. Для
двояковогнутой линзы R\ < 0, i?2 > 0, и фокусное расстояние /
отрицательно. (В обоих случаях предполагается, что п > 1.)
§ 11. Общие свойства центрированных оптических
систем
1. Свойства центрированных оптических систем в парак-
параксиальных лучах были систематически исследованы Гауссом
A777—-1855) в 1841 г. Поэтому оптику параксиальных лучей ча-
часто называют гауссовой оптикой. При изложении относящихся
сюда вопросов мы применим аналитический метод. Он менее
нагляден, чем геометрический метод. Зато аналитический метод
отличается большей простотой и систематичностью.
В случае одной преломляющей поверхности координаты
ж, у точки-предмета связаны с координатами ж;, у1 точки-
изображения формулами A0.4). В этих формулах используется
одна и та же координатная система в пространствах предметов
и изображений. Выберем теперь в этих пространствах разные
системы координат, получающиеся из исходной системы парал-
параллельным переносом вдоль главной оптической оси. Начала ко-
координат этих систем лежат на главной оптической оси, но могут
и не совпадать друг с другом. При новом выборе координатных
систем формулы A0.4) преобразуются в
/
ах + b
х = , у = у,
cx + d' y cx + d^"
где а, Ь, с, d, e — постоянные. Их легко вычислить, если из-
известны положения начал координат и параметры преломляю-
преломляющей сферической поверхности. Этими формулами устанавли-
устанавливается соответствие между точками пространства предметов и
пространства изображений. Оно называется коллинеарным со-

§ 11 ОБЩИЕ СВОЙСТВА ЦЕНТРИРОВАННЫХ СИСТЕМ 79
ответствием (точнее — коллинеарным соответствием с осе-
осевой симметрией).
Допустим теперь, что после прохождения через первую пре-
преломляющую поверхность лучи испытывают преломление на вто™
рой сферической поверхности. Тогда получится второе изобра-
изображение — точка Pff с координатами ж/;, у". Они связаны с ж;, у'
формулами такого же вида, т.е.
и а х + о и е /
Х У ~ с'х1 +й'У
Х ~ с'х1 + d>'
с новыми коэффициентами а;, 6;, с;, d!, ef. Исключим из этих
и предыдущих соотношений координаты ж;, у1 промежуточного
изображения Р1. Нетрудно убедиться, что таким путем снова
получатся формулы коллинеарного соответствия:
// а"х + Ъ" „ е"
<Т- == у = у
d'x + d y c"x + d" yi
причем коэффициенты а/;, Ь/;, с/;, d/;, efl могут быть выраже™
ны через десять коэффициентов а, Ь, ..., d;, e1. Таким обра-
образом, два или несколько последовательно выполненных коллине-
арных соответствий эквивалентны одному коллинеарному со-
соответствию. Следовательно, любая центрированная система
в параксиальных лучах устанавливает коллинеарное соответ-
соответствие между точками пространства предметов и простран-
пространства изображений. Его можно выразить формулами
/ ах + Ь / е / е /iii\
X = -, у = у, Z = ; Z. A1.1)
cx + d1 y cx + d^' cx + d v ;
Здесь добавлена формула для координат z и z1. Ввиду осевой
симметрии, она совпадает с соответствующей формулой для у
и у1.
Коллинеарное соответствие определяется четырьмя пара-
метрами, за которые можно принять отношения четырех из
коэффициентов а, Ь, с, d, e к пятому. Поэтому и произвольная
центрированная система характеризуется также четырьмя па-
параметрами.
Разрешая уравнения A1.1) относительно ж, у, z, получим
а'х1 +У е1 i e! i /i i о\
Ж = ^Т^' у = ^Т*у' * = ^т^' AL2)
причем
rii/ i I if i be — ad /-, 1 o\
6=6, с = c^ a = —a, a = —a, e = . (H-*>)
Обратное преобразование, таким образом, выралсается таклее
формулами коллинеарного соответствия, что, очевидно, являет-
является следствием обратимости светового пути (см. § 10, п. 1).

80 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
2. Из формул коллинеарного соответствия вв1текают следую™
щие свойства оптических изображений в центрированных систе-
системах.
1. Каждая плоскость пространства предметов изобража-
изображается в виде плоскости. Действительно, уравнение плоскости в
пространстве предметов
Ах + By + Cz + D = 0
после замены координат ж, у, z их выражениями через х\ у\ z1
по формулам A1.2) переходит в уравнение вида
Afxf + В'у' + Cz' + D' = 0,
которое представляет плоскость в пространстве изображений.
2. Каждая прямая пространства предметов изображается
в виде прямой, так как прямую можно рассматривать как линию
пересечения двух плоскостей.
3. Каждая точка пространства предметов изображается
в виде точки, так как всякую точку можно рассматривать как
точку пересечения трех плоскостей.
3. Из формул A1.1) следует, что конечным значениям х,у, z
соответствуют, вообще говоря, конечные значения х!, у\ z'. Ис-
ключение составляют точки плоскости
сж + d = 0. A1.4)
Каждая точка такой плоскости изображается бесконечно уда-
удаленной точкой. Это означает, что все лучи, вышедшие из одной и
той же точки плоскости A1.4), после прохождения через оптиче-
оптическую систему становятся параллельными. Плоскость A1.4) на™
зывается фокальной плоскостью пространства предметов, или
передней фокальной плоскостью оптической системы. Анало-
Аналогично, плоскость
c'x' + d' = 0 A1.5)
называется фокальной плоскостью пространства изображе-
ний, или задней фокальной плоскостью оптической системы.
Параллельные лучи после прохождения через оптическую си-
систему пересекаются в одной из точек этой плоскости.
Точки пересечения фокальных плоскостей с главной опти-
оптической осью называются фокальными точками, или главными
фокусами оптической системы. Главный фокус пространства
предметов (передний главный фокус) будем обозначать через F,
а главный фокус пространства изображений (задний главный
фокус) — через F'. Согласно формулам A1.4), A1.5) и A1.3),
абсциссы главных фокусов системы определяются выражения-
выражениями:
d i da /л а п\
Хр = —-, Хр, = — — = -. A1.6)

§ 11 ОБЩИЕ СВОЙСТВА ЦЕНТРИРОВАННЫХ СИСТЕМ 81
Система может и не иметь фокальных плоскостей. Это будет,
когда с = 0, и следовательно, с1 = 0. Такие системы называются
афокальными, или телескопическими. Они являются предель-
предельными случаями обычных систем, когда обе фокальные плоско-
плоскости сдвинуты в бесконечность. После прохождения через афо-
кальную систему всякий параллельный пучок лучей остается
параллельным, могут изменяться лишь ширина и направление
пучка. Примером афокальной системы может служить зритель-
зрительная труба (телескоп), установленная на бесконечность. В этом
случае задняя фокальная плоскость объектива совмещается с
передней фокальной плоскостью окуляра.
Рассмотрим сначала системы с конечными фокусными рас-
расстояниями.
4. Отношение у'/у называется поперечным увеличением, или
просто увеличением системы. Согласно формулам A1.1) или
A1.2), оно не зависит от у и z. Отсюда следует, что из обра-
жение плоского предмета, перпендикулярного к главной опти-
оптической оси, подобно самому предмету. Если увеличение поло-
положительное, то изображение прямое. В противоположном случае
изображение обратное.
Две сопряженные плоскости, отображающиеся друг в дру-
друга с поперечным увеличением у' /у = +1, называются главными
плоскостями оптической системы. Уравнения таких плоско-
плоскостей можно получить, полагая в формулах A1.1) и A1.2) у1 = у.
Это дает
сж + с!-е = 0, cV + d'-e' = 0. A1.7)
Первая плоскость называется главной плоскостью простран-
пространства предметов (передней главной плоскостью), вторая — глав-
главной плоскостью пространства изображений (задней главной
плоскостью). Точки пересечения главных плоскостей с главной
оптической осью называются главными точками центрирован-
ной системы. Главную точку в пространстве предметов будем
обозначать через Н, а в пространстве изображений — через Н'.
Полагая в формулах A1.1) и A1.2) у = у'', находим абсциссы
главных точек:
е — d i е — df bc + a(e — d) /11 о\
5. Главные и фокальные точки центрированной системы на-
называются ее кардинальными точками. Так как коллинеарное
соответствие определяется четырьмя параметрами, то положе-
положение четырех кардинальных точек полностью определяет колли-
коллинеарное соответствие. Фокальные и главные точки полностью
характеризуют оптическую систему в том смысле, что, зная по™
ложение этих точек, можно найти изображение любого предме-
предмета, даваемое оптической системой.

82
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Допустим сначала, что предмет Р точечный и не лежит на
главной оптической оси системы (рис. 42). Опустим из точки Р
В
Рис. 42
перпендикуляр PQ на эту ось. Луч РА, параллельный главной
оптической оси, или его продолжение в сторону пространства
изображений встретит главные плоскости в сопряженных точ-
точках А и А'. Поэтому после прохождения через оптическую систе-
му этот луч или его продолжение пройдет через точку А1. Кроме
того, он должен пройти через задний фокус F1'. Двумя точками
А' и F1 положение луча в пространстве изображений определя-
определяется полностью. Проведем теперь второй луч PF', проходящий
через передний фокус F. Он или его продолжение встретит пе-
реднюю главную плоскость в точке В. Проведя через В прямую
ВВ'Р1', параллельную главной оптической оси, найдем положе-
положение луча В'Р' в пространстве изображений. Точка Р;, в которой
пересекаются лучи А'Р1 и В'Р1', и будет изображением точки
Р. При этом проекция Q точки Р на главную оптическую ось
изобразится проекцией точки Р! на ту же ось. Это дает пра-
правило построения изображения точки и в том случае, когда она
лежит на главной оптической оси. Отрезок QP изображается
отрезком Q'P'.
Расстояния главных точек от соответствующих фокальных
точек называются главными фокусными расстояниями систе-
мы. Фокусное расстояние в пространстве предметов будем обо-
обозначать через /, в пространстве изображений — через /;. В со-
соответствии с принятым нами правилом знаков фокусное рас-
расстояние считается положительным, если падающий свет идет
в направлении от главного фокуса к соответствующей главной
плоскости. Фокусные расстояния определяются формулами
-жр/ = -- =
be — ао
A1.9)
Надлежащим выбором начал координат молено упростить
формулы A1.1) и A1.2). Рассмотрим два важнейших случая.

§ 11 ОБЩИЕ СВОЙСТВА ЦЕНТРИРОВАННЫХ СИСТЕМ 83
6. Случай 1. Начала координат помещены в главные
точки Н и Н1. Абсциссы в этих координатных системах будем
обозначать через ? и ?', а ординаты — через г/ и rf. Очевидно,
г\ = у, rf = у\ а по самому выбору начал координат ?я — Ся; =
= 0. Поэтому из A1.8) следует: е = d, Ь = 0. Формулы A1.1)
преобразуются в
Абсциссы фокальных точек, ввиду соотношений A1.6), будут
?f — —d/c, ?^v = а/с, а фокусные расстояния / = d/c, /; =
= —а/с. Исключая с помощью этих соотношений коэффициенты
а, с, d, получим
Первую из этих формул мо]«но записать также в виде
f + ? = -i. (п.")
Как видно из рис. 42, НА = ^?о, Д"'^ = —?'а'. Так как
A = Н1 А'^ то ^а = ^;а;. Далее, из уравнений A1.10) находим:
= ^fffif^,j так что
/^ = -/V«'- A1.12)
Но по теореме Лагранжа^Гельмгольца тща. = n'r}1 a1 ^ а потому
^ = -4- (и.13)
Такова связь между фокусными расстояниями / и /;.
Допустим, как это обычно бывает, что среда по обе стороны
оптической системы одна и та же. Если система содержит четное
число отражений (такая система называется диоптрической), то
п = п;, и следовательно, / = ^f. В этом случае формула A1.11)
переходит в формулу линзы:
Если же система содержит нечетное число отражающих поверх-
поверхностей (такая система называется катоптрической), то п =
= ^п;, и следовательно, / = /;. Тогда формула A1.11) пере™
ходит в формулу зеркала:
В диоптрических системах направления распространения па™
дающего и прошедшего света одинаковы, а в катоптрических
противоположны.

84
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
7. Случай 2. Начала координатных систем помеще-
ны в главные фокусы F и F1'. Абсциссы в этих системах будем
обозначать через X и Х\ а ординаты через Y ш Yf. Очевидно,
Y = у = f]^ Yf = yf = f]f. Кроме того, по самому выбору начал
координат Хр = X'Fi = 0. Следовательно, должно быть а =
= d = 0, Ъ/с = //', е/с = /, как в этом нетрудно убедиться с
помощью формул A1.6) и A1.9). В результате формулы A1.1)
переходят в
XX1 = //', A1.16)
Эти простые формулы были известны еще Ньютону, — правда,
для частных случаев.
8. К кардинальным точкам, наряду с главными и фокаль-
фокальными, относят еще узловые точки. Они естественно появляются
при рассмотрении углового увеличения системы. Угловое увели-
увеличение есть отношение а'/а углов а' и о, образуемых с главной
оптической осью проходящим и падающим лучами. Узловыми
точками называются две сопряженные точки К и К'', лежа-
лежащие на главной оптической оси^ которые отображаются друг в
друга с угловым увеличением +1. Это значит, что всякий луч,
проходящий через узловую точку К, после прохождения через
оптическую систему остается параллельным своему исходному
направлению и проходит через вторую узловую точку систе-
системы К1. Для доказательства существования и определения по-
положения узловых точек положим в формуле A0.6) а = о!. Это
дает пу = n'f/, или на основании формулы A1.13) у1 /у = —///'.
Сравнивая этот результат с формулами A1.17), находим абсцис-
абсциссы узловых точек относительно фокальных точек:
Хк = -/', Х'к, = -/, A1.18)
или на основании определения фокусных расстояний
FK = H'F1, F'K1 = HF. A1.19)
Это приводит к следу-
следующему правилу для на-
нахождения узловых то-
точек. Отрезки HF и HfF'
надо перенести парал-
параллельно самим себе, что-
чтобы их начальные точки
г, „о Н и Н1 совпали с фо-
Рис. 43 . ^
кусами г ж г соответ-
соответственно. Тогда другие концы этих отрезков F и F1 укажут поло-
положение узловых точек К' ж К (рис. 43). Если п1 = п, то /; = —/.

§ 11 ОБЩИЕ СВОЙСТВА ЦЕНТРИРОВАННЫХ СИСТЕМ 85
В этом случае узловые точки совпадают с главными. Узловые
точки также могут быть использованы для построения оптиче-
оптических изображений в центрированных системах.
Иногда к числу кардинальных точек относят обратные глав-
главные и обратные узловые точки. Первые характеризуются ли-
линейным увеличением, равным минус единице; вторые — угло™
вым увеличением, равным так лее минус единице. Доказатель-
Доказательство существования и определение положения таких пар точек
не представляют затруднений.
9. Отношение длины 8Х' изображения бесконечно малого
отрезка, параллельного главной оптической оси, к длине SX са-
самого отрезка, называется осевым или продольным увеличением.
Для этого увеличения из формулы A1.16) находим
sx " х ~ х* ~ //'• {11°щ
Сравнение этих формул с формулами A1.17) показывает, что
осевое увеличение в общем случае не равно поперечному уве-
увеличению. Отсюда следует, что изображение бесконечно мало-
малого объемного предмета в центрированной оптической систе-
системе, вообще говоря^ не подобно самому предмету. Исключение
составляет случай^ когда предмет помещен в одной из узло-
узловых или в одной из обратных узловых точек системы. В самом
деле, для изображения бесконечно малого объемного предмета
с сохранением подобия необходимо и достаточно, чтобы осевое
увеличение по абсолютной величине было равно поперечному
увеличению, т.е.
X2 X'
Отсюда X = ±/;. Формулы A1.17) и A1.13) дают
? = 4 = *"-
Y f п1
После этого из теоремы Лагранжа—Гельмгольца A0.6) получаем
а = =Ьс/, что и требовалось доказать.
Если система диоптрическая (см. п. 6), то знаки / и /; про-
противоположны. В этом случае, как видно из A1.17), SX и 8Х'
имеют одинаковые знаки. Отсюда следует, что при перемещении
предмета вдоль оптической оси его изображение перемещается
в том же направлении. Напротив, если система катоптриче-
катоптрическая, то при перемещении предмета вдоль оптической оси его
изображение перемещается в противоположном направлении.
А так как в диоптрических системах направления распростра-
распространения света в пространствах предметов и изображений одина-
одинаковы, а в катоптрических противоположны, то для всех систем
справедливо такое правило:

86 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Если предмет перемещается вдоль оптической оси в на-
направлении распространения падающего света, то его изображе-
изображение перемещается в направлении распространения прошедшего
света, и наоборот.
10. В случае телескопической системы с = 0. Но коэффи-
коэффициент d в нуль обращаться не должен, иначе формулы A1.1)
потеряли бы смысл. Не должны обращаться в нуль также коэф-
коэффициенты а и е, так как в противном случае из формул A1.1)
мы получили бы х1 = const, у1 = 0, z1 = 0, т.е. любая точка изо-
изображалась бы всегда одной и той же точкой. Такой случай в оп-
оптических системах не встречается, он имеет только формально-
математический характер. Итак, для телескопической системы
с = 0, d Ф 0, а ф 0, е ф 0. Следовательно, должно быть также
с' = 0, d1 ф 0, а1 ф 0, е1 ф 0, как это видно из формул A1.3). Те-
Телескопическую систему можно рассматривать как предельный
случай фокальной системы, обе фокальные точки которой уда-
удалены в бесконечность (хр = =Ьоо, x'F, = ±oo). Оба фокусных
расстояния / и /; телескопической системы бесконечно велики,
хотя их отношение ///' = —п/п1 и остается конечным.
Формулы A1.1) для телескопической системы принимают
вид
х' = Ах + С, у' = Ву, A1.21)
где А = a/d, В = e/d, С = b/d — постоянные. Отсюда вид-
видно, что всякий параллельный пучок света после прохождения
через телескопическую систему остается параллельным. По-
Постоянные А и В не независимы. Действительно, формулы A1.9)
для телескопических систем дают
f ad A1
или на основании A1.13)
^ = J* AL22)
Если за начала координатных систем принять любую пару
сопряженных точек оптической оси, то формулы A1.21) упро-
упростятся и перейдут в
х' = Ах, у' = By. A1.23)
Таким образом, поперечное и осевое увеличения телескопиче-
телескопической системы постоянны, т.е. не зависят от положения пред-
предмета. Постоянно также и угловое увеличение, так как по фор-
формуле A0.6)
2L = 3L = JL = Е. Mi 24)
а п'у1 Вп' А' \ • )

11
ОБЩИЕ СВОЙСТВА ЦЕНТРИРОВАННЫХ СИСТЕМ
87
Для зрительных труб и любых систем, у которых п = nf,
= У.
у'
A1.25)
В этом случае угловое увеличение называют просто увеличе-
увеличением трубы, опуская прилагательное «угловое». Эта величина
показывает, во сколько раз угол, под которым виден бесконечно
удаленный малый предмет в трубу, больше угла, под которым
он был бы виден невооруженным глазом. Согласно A1.25), угло-
угловое увеличение зрительной трубы равно обратному значению ее
поперечного увеличения. Отсюда следует, что увеличение зри-
зрительной трубы численно равно отношению ширины падающего
пучка лучей к ширине соответствующего выходящего пучка.
Поясним последнее утверждение на примере кеплеровой тру-
трубы, состоящей из двух тонких собирающих линз — объектива О
и окуляра О; (рис. 44). Задняя фокальная плоскость объектива
совпадает с передней фокальной плоскостью окуляра. Пусть в
трубу рассматривается бесконечно удаленный предмет. Объек-
Объектив дает изображение FC этого предмета в общей фокальной
плоскости объектива и окуляра. Допустим для простоты, что
один из крайних лучей (луч AF) идет вдоль оптической оси
трубы, а другой (луч ВС) — под углом а к ней. Проходя через
оптический центр объектива, луч ВС не испытывает преломле-
преломления. Угол а есть угол, под которым бесконечно удаленный пред-
предмет виден невооруженным глазом; угол о! — угол, под которым
тот же предмет виден в зрительную трубу. Угловое увеличение
а'/а, согласно рис. 44, численно равно отношению фокусного
расстояния объектива к фокусному расстоянию окуляра. Но это
отношение в свою очередь равно отношению ширины падающего
Рис. 44
Рис. 45
параллельного пучка лучей к ширине соответствующего выхо-
выходящего пучка (рис. 45).
11. Более общий подход к вопросу об угловом увеличении те-
телескопической системы дает принцип Ферма. Этот подход при-
применим и к телескопическим системам, не обладающим осевой
симметрией. Телескопической системой в общем случае называ-
называют любую оптическую систему, при прохождении через кото-
которую каждый параллельный пучок света остается параллель-

ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ним. Пусть АВ (рис. 46) — плоский участок волнового фрон-
фронта перед телескопической системой. После прохождения через
В
D
D"
С
С
вг
I ,
Е
I
аг/Е
'А"
Рис. 46
эту систему (не изображенную на рисунке) он переходит в штос-
кий участок А1 В1. Продолжением луча АС является луч С1 А1,
а луча BD — луч D'B1. Таким образом, {АСС'А1) = (BDD'B').
Возьмем другой плоский участок волнового фронта АЕ, накло-
наклоненный к АВ под бесконечно малым углом а. За оптической
системой волновой фронт АЕ перейдет в волновой фронт А"Е1 ^
образующий с прежним волновым фронтом А1 В1 угол а1'. Угло-
Угловое увеличение системы будет N = а'/а. Возьмем тот волновой
фронт АПЕ'', который проходит через точку А1. На основании
следствия принципа Ферма, доказанного в п. 4 § 7, оптические
длины лучей АА" и ЕЕ1 при смещении вдоль волнового фронта
А"Е1 будут меняться во втором или высшем порядке малости.
В этом порядке указанные оптические длины останутся неиз-
неизменными, если заменить их оптическими длинами {АССА1) и
(EDD'B'K). Таким образом, (АСС'А') = (EDDfBfK). Срав-
Сравнивая это соотношение с предыдущим, получим (BEDDrBf) =
= (EDD'B'K), откуда (BE) = (BfK), или
nha = n'tia', A1.26)
где п — показатель преломления среды перед телескопической
системой, п1 — за этой системой, h — поперечное сечение падаю-
падающего пучка лучей, a hf — выходящего. Если, как обычно бывает,
г
пг = п, то
т.е. увеличение телескопической системы равно отношению
ширин пучков света до и после прохождения через эту систе-
систему. Полученные результаты имеют общий характер и не зависят
от конкретного устройства телескопической системы.
Увеличение может и не быть одинаковым по всем направле-
направлениям. Рассмотрим, например, призму, преломляющее ребро ко-

12
СЛОЖЕНИЕ ЦЕНТРИРОВАННЫХ СИСТЕМ
89
торой вертикально. Вертикальные размеры параллельного све-
тового пучка после прохождения через призму не изменяются,
тогда как горизонтальные размеры, вообще говоря, меняются.
Призма будет давать увеличение в горизонтальном направле-
направлении, но не будет увеличивать в вертикальном направлении. Изо-
Изображение, даваемое призмой, получится вытянутым или сплюс™
нутым в горизонтальном направлении, в зависимости от того,
уменьшаются или увеличиваются поперечные размеры свето-
светового пучка в этом направлении. Искажения не получится, ее™
ли держать призму под углом наименьшего отклонения, но в
этом случае не будет и увеличения. Комбинацией двух призм,
преломляющие ребра которых взаимно перпендикулярны, моле-
молено произвольно увеличивать или уменьшать поперечное сечение
светового пучка и притом одинаково по всем направлениям. Та™
кая комбинация действует как обыкновенная зрительная труба.
Вращая каждую из призм вокруг своего преломляющего ребра,
можно получить произвольное увеличение. Недостатками такого
оптического прибора являются большие геометрические и хро-
хроматические аберрации, вносимые им. Практического значения
он не имеет.
§ 12. Сложение центрированных систем. Толстые
линзы
1. Пусть две центрированные системы соединены вместе та-
таким образом, что их оптические оси совпадают. Если известны
параметры каждой системы, а также их взаимное расположе-
расположение, то геометрическим построением или аналитическим рас-
расчетом можно определить положение всех кардинальных точек
сложной оптической системы, состоящей из этих двух систем.
Обозначим фокусные расстояния первой системы через f\ и
/{, а второй системы — через /2 и /^ Пусть А означает расстоя-
расстояние передней фокальной точки F2 второй системы от задней
фокальной точки F[ первой системы (рис. 47). Это расстояние
F, Я,
H{F{
Fj Hj Hj
Рис. 47
называется оптическим интервалом двух систем и в соответ-
соответствии с принятым правилом знаков считается положительным,

90 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
если падающий свет идет в направлении от фокуса F[ к фокусу
i*2, в противоположном случае оптический интервал считает-
считается отрицательным. Заданием оптического интервала полностью
определяется взаимное расположение складываемых систем. С
целью упрощения вычислений начала координат для каждой из
складываемых систем поместим в ее фокальные точки. Фокус
F\ примем за начало координат в пространстре предметов всей
сложной системы, а фокус F^ — за начало координат в про-
пространстве изображений той же системы. Пусть ж, у — координа-
координаты предмета, a #i, yi — его изображения, даваемого первой из
складываемых систем. Тогда
Примем это промежуточное изображение за «предмет» для вто™
рой из складываемых систем. Координаты этого предмета в ко-
координатной системе с началом в точке F<i будут ж 2 = х\ — А,
1/2 = Ш- Если х\ у1 — координаты изображения, даваемого вто-
второй системой (а следовательно, и всей сложной системой) отно-
относительно начала F^ то
Исключая промежуточные координаты #i, yi, #2, 1/2, получим
Х "Д/1А-х"' У ~ hf[^xV' [12Л
Это — формулы коллинеарного соответствия с коэффициентами
Из них по формулам A1.6) и A1.9) находим координаты фо-
фокальных точек и фокусные расстояния сложной системы:
xF = i?, x'F, = -b&, A2.2)
A2-3)
Координаты главных точек определяются выражениями
Следовательно,
Г f A2.4)
xHi — xFi -f- j — j2 ^
= f A2.5)
«/2

§ 12 СЛОЖЕНИЕ ЦЕНТРИРОВАННЫХ СИСТЕМ 91
Если оптический интервал А обращается в нуль, то фокусные
расстояния / и /; обращаются в бесконечность, т.е. система бу-
будет телескопической. (Такой случай осуществляется, например,
в зрительной трубе.) В этом случае уравнения A2.1) переходят
в A1.23), причем
л _ hf'2 о _ h
nli /i
Угловое увеличение сложной системы будет
? = ! = ?¦ A2б)
В частности, при п = п1
- = -?. A2.7)
Это согласуется с результатом, полученным выше для кеплеро™
вой трубы.
Если обе складываемые системы телескопические, то со-
составная система также телескопическая, причем ее угловое
увеличение равно произведению узловых увеличений складывае-
складываемых систем. Наконец, соединение телескопической системы и
системы с конечными фокусными расстояниями образует си-
систему с конечными фокусными расстояниями при всякой по-
следовательности расположения обеих систем.
2. Величина, обратная главному фокусному расстоянию /;
пространства изображений, взятая с противоположным знаком,
т.е. — 1//', называется оптической силой системы. Оптическая
сила измеряется диоптриями. Диоптрия есть оптическая сила
такой системы, фокусное расстояние |/;| которой равно одному
метру. Для собирательных тонких линз оптическая сила поло-
положительна, для рассеивающих отрицательна.
Определим оптическую силу сложной системы, зная опти-
ческие силы составляющих систем и их взаимное расположе-
расположение. Будем предполагать, что показатели преломления всех про™
странств предметов и изображений одинаковы. Обозначим че™
рез 1\2 расстояние Н[Н2 передней главной плоскости Н^ второй
системы от задней главной плоскости Н[ первой системы. Оп-
Оптический интервал между рассматриваемыми системами будет
А = F[F2 = F[H[ + H[H2 + H2F2 = f[ + l12 - f2 = f[ + ll2 + f!2.
Подставляя это значение в формулу A2.3), получим
1 1 , 1 . Il2 /19 О\
/ /1 /2 /1/2
В частности, когда задняя главная плоскость первой системы

92 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
совпадает с передней главной плоскостью второй системы, то
? = т + i, A2.9)
т.е. оптическая сила сложной системы равна сумме оптиче-
оптических сил составляющих систем. Это имеет место, например,
для двух тонких линз, прижатых вплотную одна к другой.
Применим полученные результаты к системе двух центрированных тон-
тонких линз: собирательной и рассеивающей, поставленных друг за другом.
Пусть фокусные расстояния линз по абсолютной величине одинаковы: f\ =
= —/2, а потому fi = —/2- Оптический интервал между линзами А = Д +
+ 1\2 + /2 :=: ^12, т.е. положителен (Ii2 > 0). Из формулы A2.6) получаем
J J I 1 7
l>12 ь12 fcl2
Далее, по формулам A2.2) и A2.4) находим хн = х'н, = 0, т.е. главные
плоскости Н ш Н' системы проходят соответственно через фокусы F\ и F[
и находятся на расстоянии 1\2 друг от друга. Абсцисса главного фокуса F'
системы:
/2 Л Л'
Xpl = = ,
^12 ^12
абсцисса линзы L/2'.
Таким образом,
Хр, - XL = -^ - /i.
112
Для того чтобы система линз собирала лучи, параллельные главной опти-
оптической оси, в действительном фокусе, т.е. была собирающей, необходимо,
чтобы эта разность была положительна. Если первая линза рассеивающая,
то указанное условие соблюдается всегда, так как в этом случае /i < 0. Если
же первая линза собирательная, то это условие сводится к 1\2 < /ь Эти ре-
результаты легче получить непосредственным геометрическим построением,
что и рекомендуется сделать читателю.
Системы линз, аналогичные рассмотренной, применяются в современ-
современных ускорителях для фокусировки заряженных частиц. На них основан
принцип так называемой жесткой фокусировки.
3. Каждая центрированная система может рассматривать-
рассматриваться как сложная система, состоящая из нескольких подсистем. В
качестве подсистем можно взять сферические границы раздела
сред, на которых световые лучи испытывают преломление или
отражение. Для сферической границы раздела коллинеарное со™
ответствие выражается формулами A0.4). Из них и из формул
A1.8) находим прежде всего: хн = х'н, = 0, т.е. обе главные
плоскости совпадают между собой и проходят через точку пере-
пересечения рассматриваемой преломляющей поверхности с главной
оптической осью системы. Для фокусных расстояний / и /; под-
подсистем формулы A0.4) и A1.9) дают
j = ^_^ jf = _Jir^^ A2.10)

12
СЛОЖЕНИЕ ЦЕНТРИРОВАННЫХ СИСТЕМ
93
Используя эти формулы, а также формулы A2.2), A2.3) и A2.4),
можно рассчитать параметры любой центрированной системы.
4. В качестве примера проведем расчет параметров толстой
линзы. Пусть R\ и i?2 означают радиусы кривизны преломляю-
преломляющих сферических поверхностей линзы, ni, П2, Щ — показате-
показатели преломления первой среды, вещества линзы и второй среды
Fj
О
I
Н
-д
Н'
О Fr
пъ
F{
Рис. 48
(рис. 48), /i и /{ — фокусные расстояния при преломлении на
передней поверхности линзы, /2 и/^ — на задней. В таком случае
n2Ri
~~ П\
/2 =
p/
Л = ~
pf _
/2 —
П2 — П\
— П2 Пз — П2
Будем рассматривать преломляющие поверхности линзы как
центрированные подсистемы, а саму линзу — как сложную си-
систему. Если d — толщина линзы, то А = /{ + d — /2, или после
подстановки значений /{ и f!2
А A2Л1)
где введено обозначение
D = rf(ni - n2)(n2 - п3) + n2[Ri(n2 - п3) + Д2(п1 - п2)]. A2.12)
Для фокусных расстояний / и /; линзы из формул A2.3) полу-
получаем
R1R2 p/ R1R2
= -
A2.13)
Координаты фокальных точек линзы F и F' мо^но вычислить
по формулам A2.2), которые дают
П2 —
П1 — П2
^г^^ ^^3^- A2Л4)
При этом за начало координат в пространстве предметов линзы
принят фокус Fi, ав пространстве изображений — фокус F^.

94
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Найдем расстояния h и h! главных плоскостей линзы от то™
чек О ж О1. По определению
FH = -Д + xF + /,
'F,
h = ОН = i
ft' = QfHf = O'F^
x'F,
Отсюда
h =
- ^з)^г, h' = -n3(ni - rc2)-^-.
A2.15)
Обычно показатели преломления крайних сред п\ и пз оди-
одинаковы. Полагая в этом случае п\ = щ = 1, П2 = п, получим
/ = -/' = -п
R1R2
e =
i2i-i22)-rf(n-l)],
1 = d — h + h!:
A2.16)
A2.17)
A2.18)
A2.19)
через е здесь обозначено расстояние главной плоскости Н' от
главной плоскости Н (см. рис. 48).
Рис. 49
Если линза не очень толстая, а разность R\ — R2 не слиш-
слишком мала, то в выражении A2.18) слагаемым d(n — 1) можно

§ 12 СЛОЖЕНИЕ ЦЕНТРИРОВАННЫХ СИСТЕМ 95
пренебречь. В этом приближении
I = Ь ^
е = ^—irf. A2.23)
На рис. 49 изображены типичные линзы с указанием поло-
положений их главных плоскостей (п = 1,5).
ЗАДАЧИ
1. Для определения углового увеличения зрительной трубы методом
Рамсдена A735-1800) трубу устанавливают на бесконечность. Вывернув
объектив, устанавливают на его место предмет определенной величины
(экран с вырезом). Окуляр трубы дает действительное изображение взятого
предмета. Пусть L — величина предмета, а I — величина его изображения.
Показать, что угловое увеличение зрительной трубы равно L/1.
Решение. Примем за начала координатных систем фокальные точки
окуляра. Тогда в формуле A1.17) следует положить X = /l5 / = /2. Это
дает L/1 = /{//г, т.е. увеличение трубы (см. § 11, п. 10).
2. Для определения фокусного расстояния собирательной линзы Бес-
Бессель A784—1846) предложил следующий метод.
С помощью линзы на экране получается действительное изображение
предмета. Пусть А — расстояние от предмета до его изображения. Тогда А =
= (;' + е — ?. Исключая с помощью этого соотношения (;' из A1.14), получим
f + (А - е)С + (А - e)f = 0. A2.24)
Если
А^е>4/, A2.25)
то уравнение A2.24) имеет два вещественных корня ?i и ?г- В этом слу-
случае существуют два положения линзы, при которых на экране получаются
действительные изображения предмета (при неизменном расстоянии между
предметом и экраном). Чтобы перейти от одного изображения к другому,
надо сместить линзу на расстояние а = ?i — ^2 = у/(А — еJ — 4/(А — е),
откуда
/ = -/'= iA~?:f- A2-26)
Величины А ж а можно измерить. Величина же е — расстояние меж-
между главными плоскостями — неизвестна. Для ее определения можно взять
другое расстояние А\ между предметом и экраном и измерить соответству-
соответствующее смещение линзы а\. Получится выражение вида A2.26), в котором А
и а заменены на А\ и а\. Сравнивая эти два выражения, можно вычис-
вычислить е. Для упрощения расчета можно пренебречь е2 по сравнению с А2.
Это дает

96
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
§ 13. Ограничение лучей при помощи диафрагм
1. Четкие изображения, как правило, получаются только
в параксиальных лучах. Непараксиальные лучи на практике
устраняются диафрагмами. Роль диафрагм могут играть также
оправы линз или зеркал.
D
Рис. 50
Пусть D (рис. 50) — какая-либо диафрагма, a D\ — ее изо-
изображение в параксиальных лучах впереди стоящими линзами.
Если диафрагму D заменить диафрагмой D\, то D\ будет так
же ограничивать параксиальные лучи, как и D. В самом деле,
в приближении параксиальной оптики всякий луч, проходящий
через край отверстия диафрагмы D\, проходит и через край от-
отверстия диафрагмы D. Следовательно, в этом приближении все
реальные диафрагмы можно заменить их изображениями, по-
получаемыми с помощью впереди стоящих линз. Тем самым все
диафрагмы мысленно как бы переносятся в пространство пред-
предметов. Этим достигается то упрощение, что при исследовании
действия диафрагм можно отвлечься от преломления лучей.
Точно так же все реальные диафрагмы можно мысленно пере-
перенести в пространство изображений, заменив эти диафрагмы их
изображениями, получаемыми с помощью позади стоящих линз.
2. Указанным способом мысленно перенесем все диафрагмы
в пространство предметов (рис. 51). Воображаемая диафрагма
DD1', которая видна под наименьшим углом из точки предме-
предмета Р, лежащей на главной оптической оси системы, всего более
ограничивает лучи, исходящие из Р. Она называется входным
зрачком или входным отверстием системы. Реальная диафраг-
диафрагма, изображением которой является входной зрачок, носит на-
название апертурной или действующей диафрагмы. Если апертур-
ная диафрагма находится перед передней линзой, то она совпа-
совпадает с входным зрачком. Таким образом, апертурная диафрагма
всего более диафрагмирует лучи^ исходящие из точки предме-
та, лежащей на главной оптической оси системы. Поэтому от

13
ОГРАНИЧЕНИЕ ЛУЧЕЙ ПРИ ПОМОЩИ ДИАФРАГМ
97
с
вг
А"
F<
A
В
С
~~ ~~ —
,—-—'T—
-—¦—•—_^____
^——__
- — —¦"" "^.
1
\
______—X
M
У
1
у
\
\
\
D
Рис. 51
размеров апертурной диафрагмы зависит яркость изображе-
изображения. При изменении апертурной диафрагмы меняется свето-
светосила прибора. Угол
2и, под которым ви-
ден входной зрачок
из точки предмета
Р, называется апер-
турным углом со
стороны предмета^
или узлом раскрытия.
Его называют также
апертурой системы.
Изображение апертур-
апертурной диафрагмы в па™
раксиальных лучах,
получаемое с помо-
помощью позади стоящих
линз, называется вы-
выходным зрачком или
выходным отверстием системы. Очевидно, выходной зрачок
есть изображение входного зрачка в параксиальных лучах,
даваемое всей системой. Выходной зрачок всего более диа-
диафрагмирует лучи, проведенные из точки Р;, являющейся
изображением точки предмета Р, которая лежит на главной
оптической оси. Угол 2г/, под которым выходной зрачок виден
из Р;, называется апертурным углом со стороны изображения^
или углом проекции системы (см. рис. 52).
В зрительных трубах апертурной диафрагмой часто служит
край объектива. В таком случае этот край играет роль и вход-
входного зрачка, а его параксиальное изображение, даваемое оку-
окуляром, будет выходным зрачком. Если держать трубу на неко-
некотором расстоянии от глаза против светлого фона, то выходной
зрачок будет виден как действительное или мнимое изображе-
изображение.
В некоторых случаях апертурной диафрагмой может слу-
служить радужная оболочка глаза. Ее параксиальное изображение,
даваемое роговой оболочкой и водянистым телом глаза, называ-
называется зрачком глаза.
Лучи, проходящие через центр апертурной диафрагмы, на™
зываются главными лучами. В приближении параксиальной оп-
оптики главный луч проходит также через центры входного и вы-
выходного зрачков.
Если предмет находится на бесконечности, то входным зрач-
зрачком служит изображение той диафрагмы в пространстве пред-
предметов, которое имеет наименьший диаметр. Аналогично, если
изображение получается в бесконечности, то выходным зрачком
4 Д.В. Сивухин

98 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
служит изображение той диафрагмы в пространстве изображе-
изображений, которое имеет наименьший диаметр.
3. Если точка предмета лежит на главной оптической оси си-
системы, то всякий луч, проходящий через входной зрачок, прой™
дет и через оптическую систему. Но если луч исходит из точ-
точки предмета, не лежащей на главной оптической оси, то этот
луч может и не пройти через оптическую систему далее в том
случае, когда он прошел через входной зрачок. Он может быть
задержан другими диафрагмами. Чтобы разобрать этот вопрос,
рассмотрим сначала только главные лучи.
Та диафрагма, которая всего больше ограничивает главные
лучи, называется диафрагмой поля зрения. Если бы входной зра-
зрачок был бесконечно малым, то все лучи, проходящие через си-
систему, могли бы считаться главными. Поэтому при бесконечно
малом входном зрачке поле зрения было бы резко ограничено
и определялось размерами диафрагмы поля зрения. Изображе-
Изображение диафрагмы поля зрения, даваемое впереди стоящими лин™
зами, называется входным окном^ или входным люком системы.
Изображение диафрагмы поля зрения, даваемое сзади стоящи-
стоящими линзами, называется выходным окном, или выходным лю-
люком. Очевидно, выходной люк есть изображение входного лю-
люка, даваемое всей системой. На рис. 51 входной люк изображен
диафрагмой D\D[. При бесконечно малом входном зрачке угол
поля зрения со стороны предмета равен углу 2 го, под которым
входной люк виден из центра входного зрачка. Аналогично опре-
определяется угол поля зрения 2wr со стороны изображения.
В действительности входной зрачок имеет конечные разме-
размеры. Это может повести к нарушению резкости границы поля
зрения. В самом деле, из рис. 51 видно, что любой луч, исходя™
щий из точек, лежащих между А и А1, и прошедший через вход-
входной зрачок, пройдет и через оптическую систему. Лучи из точки
В1 пройдут через оптическую систему, если они направлены в
нижнюю половину входного зрачка; лучи, направленные в верх-
верхнюю половину входного зрачка, задерживаются диафрагмой по-
поля зрения и через оптическую систему не проходят. Для лучей,
выходящих из В1, верхняя половина входного зрачка оказыва-
оказывается как бы закрытой диафрагмой поля зрения. Наконец, лучи,
исходящие из точек, лежащих дальше С и С\ через оптическую
систему вообще не пройдут. Таким образом, на краю поля зре-
зрения будет наблюдаться непрерывное ослабление освещенности.
Оно называется затенением или виньетированием. При нали-
наличии виньетирования поле зрения ограничено не резко. Чтобы
виньетирования не было, необходимо, чтобы входной люк си-
системы лежал в плоскости предмета. Поэтому почти во всех
визуальных оптических системах для устранения виньетиро-

§ 13 ОГРАНИЧЕНИЕ ЛУЧЕЙ ПРИ ПОМОЩИ ДИАФРАГМ 99
вания применяют диафрагмы поля зрения, помещаемые обычно
в передней фокальной плоскости окуляра.
4. В оптических инструментах изображение обычно воспри-
воспринимается на какую-нибудь поверхность, например матовое стек-
стекло, фотографическую пластинку, сетчатку глаза и т.п. Эта по™
верхность перпендикулярна к главной оптической оси системы и
в первом приближении может быть принята за плоскость {плос-
{плоскость изображения). Между тем в большинстве случаев пред™
мет, изображение которого надо получить, бывает простран-
ственным, а не представляет собой плоскости или какой-либо
простой поверхности. Чему же соответствует картина, получае-
получаемая в плоскости изображения оптической системы?
Для ответа на этот вопрос найдем в пространстве предмета
плоскость, оптически сопряженную с плоскостью изображения.
Она называется плоскостью установки или плоскостью навод-
наводки. Спроецируем предмет из центра входного зрачка на плос-
плоскость установки. Эта проекция и будет тем объектом, изобра-
изображение которого более или менее резко передает оптическая си™
стема. Действительно, главный луч, исходящий из любой точки
предмета, проходит также через ее проекцию на плоскость уста-
установки. Он является центром пучка лучей, исходящих из этой
точки. Если точка предмета лежит в плоскости установки, т.е.
совпадает со своей проекцией, то ее изображение получится рез™
ким. Если же она не лежит в плоскости установки, то ее изо-
изображение получится в виде кружка рассеяния^ центр которо-
которого является изображением проекции этой точки на плоскость
установки. Чем больше апертурная диафрагма, тем шире пуч-
пучки, исходящие из точек предмета, а следовательно, тем больше
размеры соответствующих кружков рассеяния. Если бы пучки
совсем не были ограничены диафрагмами или краями линз, то
кружки рассеяния занимали бы всю плоскость изображения и
изображение не могло бы вообще быть получено. Отсюда ясно,
насколько важную роль играет диафрагмирование при получе-
получении изображений объемных предметов.
5. Для резкости изображения необходимо, чтобы диаметр
кружка рассеяния d не превосходил известного предела (напри-
(например, 0,1 мм). Этим определяется глубина резко изображаемого
пространства. Найдем выражение для этой глубины в прибли-
приближении параксиальной оптики. Пусть DD1 (рис. 52) — входной,
а В\В[ — выходной зрачки, Р — точка предмета на оптической
оси, Р' — ее изображение, ЕЕ1 — плоскость изображения. Опи-
Опишем из Р;, как из центра, кружок диаметром d. Соединим диа-
диаметрально противоположные крайние точки А и А1 этого круж-
кружка с краями D\ и D^ выходного зрачка. В пересечении с опти-
оптической осью получатся точки Р[ и?[ Пусть Р\ ж Р2 — сопря-

100
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
женные им точки в пространстве предметов. Расстояние \SX\ =
= Р1Р2 и определит глубину резко изображаемого пространства.
Пусть X и X1 — координаты сопряженных точек Р и Р1 отно™
Е'
D
Рис. 52
сительно главных фокусов системы. Из уравнения A1.16) с точ™
ностью до членов второго порядка получаем X1 SX + X ёХг = 0.
С той же точностью, как видно из рис. 52, 8Х1 = d/igu' « d/u'.
Следовательно,
X
X7
d
v/'
Комбинация этой формулы с формулами A1.12) и A1.17) при-
приводит к результату
\5Х\ = №. A3.1)
Если р — расстояние от предмета до входного зрачка, а г —
радиус последнего, то и = г/р. Для объектива фотоаппарата
можно принять \Х\ = р. Тогда
\SX\ = ^-d. A3.2)
Каждому фотографу известно, что при недостатке глубины изо™
бражения надо либо уменьшить апертурную диафрагму, либо
удалиться от фотографируемого объекта.
6. Положение входного зрачка по отношению к плоскости
установки определяет перспективу^ в которой виден предмет.
Если входной зрачок расположен за предметом в направлении
лучей, то при проецировании предмета из центра входного зрач-
зрачка на плоскость установки ближние к оптической системе ча-
части предмета получат большее увеличение, чем дальние. При
таком расположении близкие предметы на изображении будут
получаться большими, чем равные им более далекие предметы
(нормальная или энтоцентрическая перспектива). Напротив,
если входной зрачок лежит перед предметом, то на изображе-

§ 14 АСТИГМАТИЧЕСКИЕ ПУЧКИ ЛУЧЕЙ. КАУСТИКА 101
нии близкие предметы получатся меньшими, чем равные им бо-
лее далекие предметы {гиперцентрическая перспектива). На-
Наконец, в промежуточном случае, когда входной зрачок удален в
бесконечность, величина изображения не зависит от расстояния
предмета до оптической системы (телецентрическая перспек-
перспектива). Изменение расстояния до предмета сказывается в этом
случае не на величине изображения1 а на его резкости. Поэто-
Поэтому такая перспектива применяется в измерительных микроско-
пах, так как результат измерения при этом не зависит от точной
установки измеряемого предмета. Чтобы ее осуществить, доста-
достаточно поместить апертурную диафрагму в задний фокус линзы
L\ (см. рис. 50).
В зрительных трубах, когда предмет практически находит-
находится в бесконечности, необходимо, чтобы величина изображения,
проецирующегося на шкалу с делениями, не зависела от точной
установки шкалы. Этого можно достигнуть, поместив апертур-
апертурную диафрагму в передний фокус линзы L2 (рис. 50). Тогда вы™
ходной зрачок удалится в бесконечность, главный луч будет па-
параллелен оптической оси и встретит плоскость шкалы на одном
и том же удалении от оптической оси. Следовательно, величина
изображения на шкале не будет зависеть от ее положения.
§ 14. Астигматические пучки лучей. Каустика
1. При наличии непараксиальных лучей, а также при от™
сутствии осевой симметрии оптической системы (примером мо-
может служить цилиндрическая линза) сферическая волна, исхо-
дящая из светящейся точки, после прохождения через оптиче-
оптическую систему перестает быть сферической. В результате светя-
светящаяся точка уже не будет изображаться оптической системой в
виде точки. Связанные с этим искажения оптических изображе-
изображений называются геометрическими или лучевыми аберрациями
оптических систем. Помимо лучевых существуют еще хрома-
хроматическая аберрация^ т.е. появление окрашенных каемок в изо-
изображении, когда оно получается в белом свете, а так лее волно-
волновые или дифракционные аберрации, обусловленные дифракцией
света. Учет последних необходим при рассмотрении разрешаю-
разрешающей способности оптических и спектральных приборов, а также
других тонких вопросов, связанных с получением оптических
изображений. Однако сначала мы отвлечемся от хроматической
и дифракционных аберраций, предполагая, что световые пуч-
пучки, формирующие изображение, — монохроматические и к ним
применима геометрическая оптика.
2. Напомним сначала необходимые сведения из дифферен-
дифференциальной геометрии. Пусть S — какая-то гладкая поверхность,

102
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Рис. 53 а
а О — произвольная точка на ней (рис. 53 а). Нормаль к по™
верхности S в точке О обозначим через N. Проведем через
N плоскость П, пересекающую поверхность S вдоль некоторой
кривой L. Если плоскость П вращать вокруг нормали N в преде™
лах 180°, то кривизна кривой L, вообще говоря, будет изменять-
изменяться, достигая в каком-то положении L\ максимума, а в другом
положении L2 — минимума. В диффе™
ренциальной геометрии доказывается,
что нормальные сечения поверхности S
максимальной и минимальной кривиз-
кривизны взаимно перпендикулярны. Эти се™
чения называются главными нормаль-
нормальными сечениями поверхности 5, про-
проходящими через точку О. Линии, по ко™
торым они пересекают поверхность S в
окрестности точки О, называются ли-
линиями кривизны, а радиусы кривизны
последних ]?i и Й2 - главными ради-
радиусами кривизны поверхности S. Если
знаки R\ и i?2 одинаковы, то линии кривизны обращены вогну™
тостями в одну и ту эюе сторону; если разные, то в проти-
противоположные стороны. Если в точке О R\ = i?2, то эта точка
называется точкой закругления поверхности.
3. Пусть теперь поверхность S является волновым фронтом.
Возьмем на ней какую-то элементарную площадку dS. Беско-
Бесконечно узкий пучок лучей волнового фронта, проходящий через
эту площадку, называется астигматическим^ если главные ра-
диусы кривизны R\ и i?2 не совпадают между собой. Луч, про™
ходящий через центр площадки dS, называется главным 1).
Вообще говоря, две нормали к поверхности S не пересекают™
ся в одной точке. Однако нормали, восстановленные в бесконеч-
бесконечно близких точках, лежащих на одной и той же линии кривизны,
пересекаются в одной точке (если пренебречь величинами выс-
высших порядков малости). Заметив это, возьмем в качестве эле™
мента dS бесконечно малую площадку ABDC', имеющую форму
криволинейного четырехугольника, сторонами которого служат
линии кривизны поверхности S (рис. 53 6). Лучи, лежащие в
главных сечениях элемента волнового фронта dS, проходящих
через его центр, сходятся в различных точках F\ и i^, называв™
мых фокальными точками; расстояние F1F2 называется астиг-
астигматической разностью элементарного пучка. Лучи, проходя™
г) При отсутствии симметрии площадки понятие ее центра, строго говоря,
теряет смысл. Однако и в этом случае можно указать какую-то, хотя и не
совсем четко определенную, точку в середине площадки, которую можно
рассматривать как центр последней.

14
АСТИГМАТИЧЕСКИЕ ПУЧКИ ЛУЧЕЙ. КАУСТИКА
103
щие через противоположные стороны АВ и CD, пересекутся
в точках Mi и N\ соответственно. Лучи, исходящие из всякой
промежуточной линии кривизны между сторонами АВ и CD,
сойдутся в какой-то промежуточной точке бесконечно малого
отрезка M\N\, проходящего через фокальную точку F\. Днало-
Рис. 535
гично, лучи, исходящие из линий кривизны между сторонами
BD и АС, пересекутся в какой-то точке другого бесконечно ма-
малого отрезка M2N2, проходящего через вторую фокальную точ-
ку F2.
Отрезки M\N\ и M2N2 называются фокальными отрезка-
отрезками элементарного астигматического пучка лучей, исходящих от
элемента волнового фронта ABCD. Если элементарный астиг™
матический пучок лучей исходит из светящейся точки, то фо-
фокальные отрезки M\N\ и M2N2 принято называть изобраэюе-
ниями этой точки, даваемыми астигматическим пучком^ хотя
точечного изображения в этом случае и не существует. Если эле-
элемент ABCD обладает симметрией прямоугольника, то отрезки
M\N\ и M2N2 будут перпендикулярны между собой, а также
к главному лучу пучка. В общем случае это может быть и не
так. При бесконечном уменьшении поперечных размеров пучка
лучей отрезки M\N\ и M2N2 стягиваются в фокальные точки
Fx и F2.
Таким образом, в отличие от гомоцентрического пучка, бес-
бесконечно узкий астигматический пучок дает не одно, а два точен-
них изображения F\ и F2 светящейся точки. Конечный пучок
лучей можно разложить на элементарные астигматические пуч-
пучки, каждому из которых соответствует пара фокальных точек.
Геометрическое место этих точек есть двухлистная поверхность,
называемая каустической поверхностью^ или каустикой.

104
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
О
Ф
Рт
X
ЗАДАЧА
Точечный источник света Р помещен в прозрачной однородной среде,
ограниченной плоскостью. Световые лучи, исходящие из Р, испытывают
преломление на этой плоскости. Найти для них каустическую поверхность.
Решение. Каустика преломленных лучей состоит из двух листов.
Один из них есть геометрическое место фокальных точек меридиональных
лучей, т.е. лучей, лежащих в плоскости падения главного луча элементарно-
элементарного астигматического пучка. Дру-
Другой — геометрическое место фо-
фокальных точек экваториальных
лучей, т.е. лучей, лежащих в пер-
перпендикулярной плоскости, прохо-
проходящей через главный луч элемен-
тарного пучка.
Пусть п — показатель пре-
преломления среды, в которой поме-
помещен источник Р. Показатель пре-
преломления пространства, с кото-
которым граничит эта среда, примем
за единицу. Введем прямоуголь-
прямоугольную систему координат с нача-
началом О, расположенным на границе
среды. За ось Z примем нормаль к
поверхности среды, направив эту
ось в сторону точки Р (рис. 54). Ввиду осевой симметрии достаточно най-
найти сечение каустической поверхности плоскостью, проходящей через ось Z.
Прямую, вдоль которой эта плоскость пересекает границу среды, примем
за ось X.
Найдем сначала каустику для меридиональных преломленных лучей.
Уравнение преломленного луча АВ будет
z = -ctg(p(x-htgi/;),
где h — расстояние от точки Р до границы среды, ф — угол падения из
среды на эту границу, (р — угол преломления. Для бесконечно близкого луча
РА В углы ср и ф получат приращения dtp и ёф. Приращение координаты
z при одном и том же значении абсциссы ж при этом будет равно
Рис. 54
sin" (p ' cos3 ф
или с использованием закона преломления sin cp =
х ~~ h tg ф h ctg (p cos (p
dz = 9 a op + a<z?.
sin (p псоБ6ф
Координаты хт и zm точки Fm, в которой пересекаются продолжения бес-
бесконечно близких меридиональных лучей АВ и А В , найдутся отсюда, если
приращение dz приравнять нулю. Это дает
cos (p sin (p \
пcos3 ф J
Zm = h
n cos3 ф'
A4.1)

14
АСТИГМАТИЧЕСКИЕ ПУЧКИ ЛУЧЕЙ. КАУСТИКА
105
Это и есть уравнение каустики для меридиональных лучей. Используя его,
нетрудно вывести формулу
2
(T\G (Г)
1т =1-
„ fr, A4.2)
где I — расстояние от предмета Р до точки выхода А преломленного луча,
а 1т — расстояние меридионального изображения Рт до той же точки.
Еще проще находится каустика для экваториальных лучей. Пусть
РАВ — один из лучей, исходящих из точки Р (см. рис. 54). Если этот
луч вращать вокруг перпендикуляра ОР к преломляющей поверхности, то
получится конус падающих и соответствующий ему конус преломленных
лучей. Вершиной второго конуса будет точка РЭ1 в которой продолжение
преломленного луча АВ пересекает перпендикуляр РО. Бесконечно ма-
малые пучки падающих и преломленных лучей, лежащих на поверхностях
указанных конусов, для которых луч РАВ является главным, будут, оче-
очевидно, расположены в плоскостях, перпендикулярных к плоскости падения
луча РАВ. Значит, лучи этих пучков будут экваториальными, а точка Рэ —
изображением в этих лучах. Таким образом, все фокальные точки эквато™
риальных лучей расположатся на перпендикуляре РО, т.е. каустика таких
лучей выродится в отрезок этого перпендикуляра. Расстояние 1Э точки Рэ
от точки выхода преломленного луча АВ будет РЭА = I sin ф/ sin 99, т.е.
h = -¦ A4.3)
п
Результаты вычислений представлены на рис. 55 для п = 1,5 (стекло).
Каустика экваториальных лучей представляется вертикальным отрезком
ОР , длина которого равна h/n. Сечение каустики меридиональных лучей
плоскостью рисунка есть кривая BPfA, для которой Р' является точкой
возврата. Продолжения преломленных лучей, изображенные на рисунке
штриховыми прямыми, касаются кривой ВР А. Таким образом, если на-
начертить еще сечение волнового фронта вышедших преломленных лучей, то

106 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
для этого сечения кривая ВР'А будет эволютой. Сама каустика меридио-
нальных лучей получится от вращения этой эволюты вокруг вертикальной
прямой РО. Для параксиальных пучков фокальные точки меридиональных
и экваториальных лучей совпадают и получаются в Р . Крайние точки А и
В каустики меридиональных лучей получаются от пересечения предельных
лучей полного отражения РА и РВ с границей среды. Предлагаем читателю
начертить каустику меридиональных и экваториальных лучей для случая
п < 1.
§ 15. Геометрические аберрации центрированных
систем
1. Геометрические аберрации в центрированных системах,
т.е. отступления от параксиальной оптики, вызываются непарак-
непараксиальными пучками лучей^ участвующими в образовании опти-
оптических изображений. Дадим классификацию таких аберраций.
Произвольный луч в пространстве предметов можно задать,
указав прямоугольные координаты ж, z и г/, ? точек его пере-
пересечения с предметной плоскостью (т.е. плоскостью, проходящей
через изображаемую точку Р перпендикулярно к главной опти-
оптической оси) и плоскостью входного зрачка. После прохождения
через оптическую систему луч пересечет плоскость параксиаль™
ного изображения в точке с координатами f/, z1. Координаты са-
самого параксиального изображения (называемого в дальнейшем
также параксиальным фокусом) обозначим через f/g, z'o. Тогда
разности Ayf = у1 — yfQi Azf = z1 — zfQ и можно принять за меру
отступлений оптики реальной системы от предельного случая
параксиальной оптики.
Координаты у', z1 будут функциями аргументов у, z, r/, (:
У = h(y,z,V,O, z' = f2(y,z,V,0-
Для классификации геометрических аберраций разложим эти
функции в степенные ряды по своим аргументам. Линейные чле-
члены этих разложений, пропорциональные у и z, соответствуют
параксиальной оптике. Линейные члены по г/ и ( не войдут, так
как в параксиальном приближении у1 и z' не зависят от наклона
лучей, выходящих из точки Р. Не могут войти и члены четных
степеней ввиду осевой симметрии оптической системы. Из все™
го этого следует, что разложения в степенные ряды отклонений
Ayf = у1 — f/g и Azf = z1 — zf0 могут содержать только члены
нечетных степеней по у, z, r/, (*, причем эти разложения могут
начаться с членов, степень которых не ниже трех. Считая аргу-
аргументы у, z1 r/, ( малыми, сохраним в разложениях только члены
третьей степени. Аберрации, вычисленные в этом приближении,
называются первичными, или аберрациями третьего порядка.

§ 15 ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ 107
Члены пятой степени вызывают аберрации пятого порядка, и
т.д. Мы ограничимся только аберрациями третьего порядка.
Переходя к векторным обозначениям, введем три вектора,
перпендикулярных к главной оптической оси системы:
г = yj + zk, r; = y'j + z% 0 = 77J + Ck,
где j и k — единичные векторы, указывающие направления ко™
ординатных осей Y и Z. Вектор г определяет положение точки™
предмета Р в предметной плоскости, вектор т1 — точки пересе-
пересечения выходящего луча с параксиальной плоскостью изображе-
ния, вектор 0 — точки пересечения падающего луча с плоско-
плоскостью входного зрачка. Вектор Аг; = Af/j + Az;k можно разло-
разложить по векторам 0 и г. Ввиду осевой симметрии коэффици-
коэффициенты этих разложений могут зависеть только от «инвариантов
вращения» а , (от) и г . Поэтому с точностью до членов третьей
степени включительно
Аг; = [Аа2 + В (or) + Cr2]o + [Dg2 + E(pr) + Fr2}r, A5.1)
где А, I?, О, D, E, F — постоянные коэффициенты, зависящие
от устройства оптической системы и от положения предметной
плоскости.
В дальнейшем будем понимать под а радиус входного зрач-
зрачка, выделяя тем самым падающие лучи (или их продолжения),
проходящие через точки окружности входного зрачка. Тогда
вектор Аг; окажется разложенным по степеням радиуса вход-
входного зрачка. Назовем аберрационной кривой кривую, по кото-
которой плоскость параксиального изображения пересекает пучок
лучей, проведенных из точки-объекта Р через окружность вход-
входного зрачка. Изображением точки Р в параксиальной плоско-
плоскости изображения будет не точка, а какое-то пятнышко, ограни-
ограниченное аберрационной кривой. Для наглядности можно пред-
представить, что в качестве апертурной взята ирисовая диафрагма,
радиус которой молено непрерывно менять. Тогда разложение
A5.1) определит, как в рассматриваемом приближении будет ме-
меняться аберрационная кривая при изменении радиуса этой диа-
диафрагмы. Отступления от параксиальной оптики определяются,
конечно, суммой A5.1) в целом, а не отдельными слагаемыми,
из которых она состоит. Однако при классификации аберраций
имеет смысл рассматривать каждое слагаемое в отдельности и
рассуждать так, как если бы остальных слагаемых не было со-
совсем. Тогда, в зависимости от степени а, все аберрации третьего
порядка можно разбить на четыре группы, которые мы и рас-
рассмотрим.
2. Сферическая аберрация. Эта аберрация
вызывается членом третьей степени Аст20, так что при нали-
наличии одной только сферической аберрации |Аг;| = Аа3 = const.

108
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Следовательно, аберрационной кривой будет окружность с цен™
тром в параксиальном фокусе и с радиусом Аа^. Каждая точка
будет изображаться в виде кружка рассеяния, радиус которого
пропорционален кубу радиуса входного зрачка и не зависит от
положения этой точки. Освещенность кружка рассеяния быстро
убывает от центра к краям.
Происхождение сферической аберрации наглядно пояснено
на рис. 56. Пусть точечный объект лежит на главной оптической
оси системы. Выходящие из
него параксиальные лучи
встречают плоскость парак-
параксиальных изображений в
точке G. Лучи, проходящие
через окружность выходного
зрачка DD', сойдутся на
оптической оси в точке Ж,
которая может лежать как
ближе, так и дальше G.
Лучи, проходящие через
какую-либо окружность в
плоскости выходного зрачка,
концентрическую с окруж-
окружностью DD1', сойдутся на
Рис. 56
оптической оси между точками М и G. Расстояние MG назы-
называется продольной сферической аберрацией. Если в плоскости
параксиальных изображений А А' поместить экран, то на нем
получится светлый кружок радиуса GA. Радиус GA называется
поперечной сферической аберрацией. С точностью до членов
третьего порядка включительно поперечная аберрация пропор-
пропорциональна кубу апертуры 2и. Отсюда следует, что продольная
аберрация пропорциональна квадрату апертуры.
Если экран перемещать от плоскости АА! по направлению
к М, то радиус кружка рассеяния сначала будет уменьшать-
уменьшаться, а затем начнет увеличиваться. Нетрудно показать, что наи-
наименьший кружок рассеяния получится, когда экран займет по-
положение В В1 на расстоянии ^/^MG от плоскости параксиаль-
параксиальных изображений АА'. Однако плоскость ВВ*, строго говоря, не
будет плоскостью наилучшей отчетливости изображения. При
нахождении последней необходимо учитывать не только разме-
размеры кружка рассеяния, но и распределение освещенности внутри
этого кружка. Исходя из дифракционных соображений, можно
показать, что при наличии одной только сферической аберра-
аберрации плоскость наилучшей отчетливости изображения проходит
посередине между точками М и G.
Сферическая аберрация есть единственная из геометриче-
геометрических аберраций, остающаяся и в том случае, когда точка-объект

15
ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ
109
находится на главной оптической оси системы. Все прочие гео-
метрические аберрации в этом случае исчезают. Это верно в лю-
любом приближении, а не только для аберраций третьего порядка.
8. К о м а. Если в разложении A5.1) отличны от нуля только
коэффициенты В и D, то соответствующая аберрация называ-
называется комой. В этом случае
Отсюда легко получить
^|a2r
В
Следовательно, аберрационной кривой будет окружность ра-
радиуса У21?cr2r, центр которой смещен от параксиального фокуса
в направлении вектора г на расстояние (D + lJ2B)a2r. Теперь
легко получить представление о характере изображения точеч-
точечного объекта при наличии одной только комы в отсутствие дру-
других аберраций. Для этого проведем в плоскости входного зрачка
произвольную окружность, центр которой совпадает с центром
зрачка. Лучи, исходящие из точечного объекта и проходящие
через эту окружность, пересекут плоскость параксиального изо-
изображения также по окружности. Совокупность таких окружно™
стей и даст изображение рассматри-
г ваемого точечного объекта в этой
плоскости. Окружности имеют две
прямолинейные огибающие, пересе-
пересекающиеся в параксиальном фокусе
Рис. 57
Рис. 58
и составляющие между собой угол а, определяемый соотноше-
соотношением sin (а/2) = В /(В + 2D). Более подробное исследование,
которое мы не приводим, показывает, что В = 2D, а потому
а = 60°. Направление вектора г является биссектрисой угла
между огибающими (рис. 57). Изображение точки, таким обра-
образом, напоминает комету. Отсюда и произошло название «кома».

110 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Происхождение комы ясно из рис. 58. Она обусловлена ко™
сыми пучками лучей.
4. Астигматизм косых пучков и искривление
плоскости изображения. Эти аберрации удобно
рассматривать совместно, так как обе они обусловлены членами
первой степени по 0 и второй степени по г. Они возникают, когда
оба коэффициента С ш Е или один из них отличны от нуля.
Если все прочие коэффициенты равны нулю, то формула A5.1)
переходит в
Ar; = Cr2o + E(or)r. A5.2)
Для определения формы аберрационной кривой ось Y прове-
проведем через точку-объект Р. Тогда г = yj. Уравнение окружности
входного зрачка запишем в параметрической форме r\ = a cos 99,
? = ашир^ где (р — центральный угол, рассматриваемый как
параметр. Таким путем из предыдущего соотношения получаем
уравнение аберрационной кривой:
Ау' = (С + Е)у2г} = (С + Е)ау2 cos <p,
A5. о)
Az1 = Cy2( = Cay2 i
Это — эллипс, центр которого находится в параксиальном фо-
фокусе, оси параллельны координатным осям 7 и Z, а их длины
пропорциональны радиусу входного зрачка и квадрату расстоя-
расстояния изображаемой точки от главной оптической оси. Изображе™
нием точки будет светлое пятнышко, ограниченное аберраци-
аберрационной кривой. Это указывает на то, что пучок лучей, дающий
изображение, — астигматический. При параллельном смещении
экрана, на котором получается изображение, вдоль оптической
оси оно по-прежнему сохраняет форму эллипса, но форма и раз-
размеры эллипса изменяются. При двух положениях экрана эллипс
вырождается в прямолинейные отрезки, один из которых парал™
лелен оси У, а другой — оси Z.
Для доказательства поместим начало координат в центре
выходного зрачка и будем характеризовать луч в пространстве
изображений точками пересечения его с плоскостью выходного
зрачка и с плоскостью параксиального изображения. Координа-
Координаты первой точки будут @,rj', (;), второй — (ж;, у'+Ау7, Az1). Если
X, У, Z — текущие координаты, то уравнение рассматриваемого
луча запишется в виде
Полагая здесь rjf = (' = Ayf = Azf = 0, найдем поперечные
координаты параксиального фокуса: Yq = у'Х/х1', Z® = 0 (про-

§15 ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ 111
дольная координата того же фокуса равна х!). Таким образом,
, х , A5)
В последних слагаемых в окрестности параксиального фокуса
можно считать X = ж;, так как это вносит ошибки высшего
порядка малости, не учитываемые в рассматриваемом прибли-
приближении. По той же причине в формулах A5.3) можно положить
У = 2/7^Ь z = я7/3ь г] = 7///З2, С = С7Аь где /5i и ^2 — линейные
поперечные увеличения для объектов, лежащих соответственно
в предметной плоскости и в плоскости входного зрачка, как они
выражаются в параксиальном приближении. Учтя еще, что у и
Y являются лишь различными обозначениями одной и той же
ординаты, можем записать A5.3) в виде
где С и Е1 — новые постоянные, а абсцисса х' введена в знаме-
знаменатели для удобства. В результате всего этого формулы A5.4)
в окрестности параксиального фокуса преобразуются в
Если
X ^xf = [С1 + E')Y2, A5.6)
то Y ~~ Y® = 0, т.е. эллипс вырождается в прямолинейный отре-
отрезок, параллельный оси Z. Это есть фокальный отрезок, образо-
образованный меридиональными лучами. Аналогично, если
X ^х' = CfY2, A5.7)
то Z — Zq = 0, и эллипс переходит в другой фокальный отрезок,
параллельный оси Y. Он образуется экваториальными лучами.
От вращения кривых A5.6) и A5.7) вокруг главной оптической
оси получаются две поверхности, касающиеся друг друга в об-
общей точке пересечения их с главной оптической осью. Эти две
поверхности и образуют каустику лучей, прошедших через оп-
оптическую систему. Вообще говоря, они имеют только одну об™
щую точку. Каустика и есть та поверхность, в которую перехо-
переходит плоскость изображения параксиальной оптики. Таким об™
разом, имеет место не только астигматизм, но и искривление
поверхности изображения.

112
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
1
5. Дисторсия. Коэффициент F не равен нулю, все
прочие коэффициенты равны нулю. Поэтому из A5.1) получаем
дг/ = Fr^m
Отсюда видно, что при наличии только рассматриваемой абер™
рации каждая точка изображается резко в виде точки, како-
каковы бы ни были размеры диафрагмы. Однако отклонение изо™
бражения точки от соответствующего параксиального фокуса
пропорционально кубу ее расстояния г от главной оптической
оси. Поэтому происходит искажение (дисторсия) изображения.
Прямые линии, проходящие через главную оптическую ось, изо-
изображаются в виде прямых. Все прочие прямые при изображе™
нии искривляются. При положительном F изображения точек
смещаются относительно соответствующих параксиальных фо-
фокусов наружу¦, т.е. от главной оптической оси. Такая дисторсия
называется подушкообразной (рис. 59 6). При отрицательном F
смещения происходят внутрь — к главной оптической оси. Со-
Соответствующая дистор™
сия называется бочкооб-
бочкообразной (рис. 59 в).
Все эти выводы со™
храняются в силе и для
аберраций высших по-
порядков. В общем слу-
случае дисторсия обуслов-
обусловлена всеми членами раз-
разложения Аг;, не содержащими степеней радиуса входного зрач-
зрачка а. В любом приближении при наличии одной только дистор™
сии точка всегда изображается в виде точки, каковы бы ни были
размеры диафрагмы.
6. Устранение (точнее — ослабление) геометрических абер-
аберраций на практике достигается комбинацией различных линз
(и зеркал), изготовляемых из оптического стекла с различными
оптическими характеристиками. Полное устранение всех абер-
аберраций невозможно. На практике речь может идти только об
определенном оптимуме, зависящем от задач, которые должен
решать оптический прибор. Наиболее вредными из всех абер™
раций третьего порядка являются обычно сферическая аберра-
аберрация и кома. В большинстве случаев их надо как можно больше
ослабить. Уменьшая диафрагму, можно практически полностью
устранить обе эти аберрации. После этого подбором линз надо
устранить дисторсию, а затем астигматизм и изгиб поверхности
изображения. Но уменьшение диафрагмы уменьшает яркость
изображения и увеличивает дифракционные ошибки. Дистор-
Дисторсия вредна в фотографических объективах. В астрономических
приборах ее можно допускать, так как она не влияет на резкость
Рис. 59

§16 ХРОМАТИЧЕСКАЯ АБЕРРАЦИЯ 113
изображения, а вызывает толвко искажение его, которое можно
учесть вычислением.
§ 16. Хроматическая аберрация
1. Если используется белый свет, то в изображении возника-
возникают дополнительные аберрации. Действительно, показатель пре-
преломления зависит от длины волны (дисперсия света). Поэтому
оптическая система дает не одно, а множество монохроматиче-
монохроматических изображений, отличающихся друг от друга по величине и
положению. В этом молено убедиться, разложив белый свет на
монохроматические составляющие и воспользовавшись принци-
принципом суперпозиции. Результирующее изображение, получающее-
получающееся от наложения таких монохроматических изображений, ока-
оказывается нерезким и с окрашенными краями. Это явление на-
называется хроматической аберрацией^ или хроматизмом.
Хроматическая аберрация устраняется путем комбинации
линз, изготовленных из стекла с различными оптическими свой-
свойствами. Устранение ее для всех лучей спектра невозможно.
Обычно совмещают изображения только для каких-либо двух
лучей с различными длинами волн. Тогда говорят, что оптиче-
оптическая система ахроматизована или исправлена в хроматическом
отношении. Оставшаяся хроматическая аберрация называется
вторичным спектром. В большинстве случаев на практике она
уже не сказывается существенно на качестве изображения. Вы-
Выбор лучей, для которых должна быть ахроматизована оптиче-
оптическая система, определяется ее назначением. В случае визуаль-
ных приборов эти лучи надо выбирать по разные стороны вбли-
вблизи желто-зеленой области спектра, к которой наиболее чувстви-
чувствителен человеческий глаз. Обычно в таких приборах ахроматиза-
ция производится для фраунгоферовых линий с длинами волн
Хс = 656,3 им и Ар = 486,1 нм. В фотографических аппара-
аппаратах ахроматизация осуществляется для лучей, лежащих ближе
к синему концу спектра, так как эти лучи сильнее действуют
на фотографическую пластинку. Здесь обычно ахроматизация
выполняется для фраунгоферовых линий с длинами волн X® =
= 589,3 нм и XG = 434,0 нм.
Для полной ахроматизации, т.е. совмещения изображений
двух цветов (например, красных и синих), необходимо, чтобы
были равны не только фокусные расстояния для этих цветов,
но и совпадали соответствующие им главные плоскости. Одна-
Однако во многих случаях достаточна уже частичная ахроматиза-
ахроматизация^ т.е. либо равенство только фокусных расстояний без точ-
точного совмещения главных плоскостей, либо совмещение только
главных плоскостей без точного равенства фокусных расстоя-

114 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ний. Это зависит от назначения прибора и определяется тем,
что в его работе важнее — увеличение изображения или его ме-
местоположение. Так, в окулярах зрительных труб и микроскопов
главный интерес представляют углы, под которыми глаз видит
различные окрашенные изображения предмета. Для равенства
этих углов необходимо, чтобы окуляры были ахроматизованы в
смысле одинаковости фокусных расстояний (см. § 24, п. 4).
Подробное рассмотрение ахроматизации дается в руковод-
руководствах по расчету оптических систем. Здесь мы можем остано-
остановиться только на простейших принципиальных вопросах и при-
притом только в параксиальном приближении. В высших прибли-
приближениях также возникает хроматическая аберрация, устранение
которой требует выполнения особых условий. Но мы не будем
их рассматривать.
2. Ахроматизацию фокусного расстояния можно получить
с помощью уже одной толстой линзы (см. задачу 2). Однако
этот способ не имеет практического значения. Практически бо-
более важной является монохроматизация тонкой линзы или си-
системы тонких линз.
Рассмотрим сначала одиночную тонкую линзу или систему
тонких линз и подсчитаем, как меняется ее фокусное расстояние
при малых изменениях показателя преломления. Взяв логариф-
логарифмическую производную от выражения A0.9), получим
Так как показатель преломления уменьшается с увеличением
длины волны, то из этой формулы следует, что фокусное рас-
расстояние / по абсолютной величине больше для красных лучей,
чем для синих.
По сравнению с изменением фокусного расстояния положе-
положения главных плоскостей линзы меняются ничтожно. Рассмо-
Рассмотрим, например, это изменение для главной плоскости простран-
пространства предметов. Для не слишком толстой линзы можно восполь-
воспользоваться формулой A2.21), из которой находим: Shjh = —с
и следовательно,
Sh /г ii, — 1 d
If ~ / п ~ ^Ж
Так как даже для сравнительно толстой линзы, как правило,
d <C i?2 и? кроме того, п — 1 < п, то Sh <C Sf. Поэтому тон-
тонкая линза будет практически полностью ахроматизована, когда
ахроматизовано ее фокусное расстояние.
В практических расчетах принимается, что формула A6.1)
приближенно справедлива и для конечных изменений показате-
показателя преломления. В случае визуальных приборов полагают Sn =

16
ХРОМАТИЧЕСКАЯ АБЕРРАЦИЯ
115
— пС — nF и вводят величину
и = ^^-, A6.2)
где пр — показатель преломления для желтой D-линии натрия
А = 589,3 нм. Эта величина называется коэффициентом дис~
персии^ или числом Аббе. (Вместо пи в числителе молено взять
показатель преломления для любой другой длины волны из ви-
видимой области спектра, так как от этого v изменится самое боль-
большее на 2%) В результате формула A6.1) преобразуется к виду
Ц- = i, A6.3)
откуда
8) = -±.
A6.4)
В табл. 2 приведены оптические характеристики некоторых
марок оптического стекла. Разность показателей преломления
Таблица2
Марка
стекла
ЛК 6
К 1
КЗ
К 14
БК 4
БК 6
ТК 2
ТК 21
ЛФ 1
ЛФ 7
Ф 6
Ф 8
БФ 1
БФ 28
ТФ 1
ТФ 5
по
1,4704
1,4982
1,5100
1,5147
1,5302
1,5399
1,5724
1,6568
1,5406
1,5783
1,6031
1,6248
1,5247
1,6641
1,6475
1,7550
Пр — ПС
0,00704
0,00765
0,00805
0,00849
0,00877
0,00905
0,00996
0,01285
0,01145
0,01407
0,01590
0,01757
0,00955
0,01874
0,01912
0,02743
Пр — По
0,00493
0,00535
0,00565
0,00597
0,00617
0,00637
0,00702
0,00910
0,00812
0,01002
0,01135
0,1260
0,00674
0,01342
0,01369
0,01972
по — пр
0,00339
0,00423
0,00451
0,00477
0,00495
0,00513
0,00567
0,00745
0,00673
0,00843
0,00903
0,01088
0,00547
0,01145
0,01172
0,01728
V
66,8
65,1
63,4
60,6
60,5
59,7
57,5
51,1
47,2
41,1
37,9
35,6
54,9
35,4
33,9
27,5
Обозначения: ЛК — легкий крон, К — крон, БК — баритовый крон,
ТК — тяжелый крон, ЛФ — легкий флинт, Ф — флинт, БФ — баритовый
флинт, ТФ — тяжелый флинт.

116 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
пр — пс называется средней дисперсией^ отношения
(nF - nD)/{nF - пс), (nG - nF)/(nF - пс)
и аналогичные им — относительными или частными диспер-
дисперсиями.
3. Рассмотрим теперь ахроматизацию тонкой линзы, сложен-
сложенной из двух тонких линз, прижатых вплотную друг к другу.
Обозначим через п\ и /i показатель преломления и фокусное
расстояние первой линзы, а через П2 и /2 — второй. Фокусное
расстояние составной линзы находится по формуле
Оно будет одно и то же для длин волн XF и Ас, если выполнено
условие
или
/2^2 = 0. A6.7)
Это и есть условие ахроматизации составной линзы. Так как
коэффициенты дисперсии для всех оптических стекол положи-
положительны, то из равенства A6.6) следует, что фокусные расстояния
/i и /2 должны иметь противоположные знаки. Из уравнений
A6.5) и A6.6) находим
— — 1 щ — — -1 U2 A6 8)
/l / У\ - У2 ' /2 / У\ - V2 '
Если общее фокусное расстояние / положительно, то линза с
большим коэффициентом дисперсии будет иметь положитель-
положительное, а линза с меньшим коэффициентом дисперсии — отрица-
отрицательное фокусное расстояние. В частности, собирательная лин™
за должна делаться из крона, а рассеивающая — из флинта (см.
табл. 2).
Если задано фокусное расстояние / составной линзы, а также
указаны сорта стекол, из которых изготовлены первая и вторая
линзы, то фокусные расстояния Д и /2 определятся из уравне™
ний A6.8). Тем самым по формуле A0.9) определятся разности
1111 o(i) o(i) ,
— - — и — - —, где Щ J и Щ; — радиусы сферических
1ъ-^ 1L2 -^1 -^2
поверхностей первой, а К\ и Щ — второй линз. Два из этих
радиусов можно выбрать произвольно. Если линзы 1 и 2 должны
склеиваться, то надо положить Щ = R\ . Остается еще один
радиус (или, в общем случае, один свободный параметр). Им
целесообразно распорядиться так, чтобы сделать сферическую
аберрацию возможно меньше (см. задачу 1).

§16 ХРОМАТИЧЕСКАЯ АБЕРРАЦИЯ 117
Ахроматические пары тонких склеенных линз широко при™
меняются в объективах микроскопов. Каждая пара состоит из
двояковыпуклой линзы из крона, склеенной с плоско-вогнутой
линзой из флинта, плоская поверхность которой обращена в сто™
рону падающего света.
4. Если составные части (подсистемы) сложной оптической
системы полностью ахроматизованы, то будет полностью ахро-
матчзована и система в целом. Действительно, так как первая
подсистема полностью ахроматизована, то изображения, давае-
даваемые ею, совмещаются в двух цветах. Рассматривая совмещенные
изображения как предмет для второй подсистемы, найдем, что
изображения, даваемые и этой подсистемой, также совмещают™
ся для тех же двух цветов. Применив это рассуждение для всех
подсистем, найдем, что совмещение изображений будет иметь
место и для системы в целом.
Обратное утверждение не справедливо. Система может быть
полностью ахроматизована без того, чтобы были полностью
ахроматизованы ее составные части. Однако если система со™
стоит из двух тонких линз, находящихся на некотором рассто-
расстоянии друг от друга, то справедливо и обратное утверждение.
Действительно, пусть х\, х\ и ух, у[ — абсциссы и ординаты
точки-предмета и ее промежуточного изображения, даваемого
первой линзой, причем за начало координат принят центр этой
ЛИНЗЫ. ПуСТЬ Х2, У2 и x2j У2 имеют тот же СМЫСЛ ДЛЯ ВТОрОЙ ЛИН-
ЛИНЗЫ, причем роль предмета в этом случае играет промежуточное
изображение. Очевидно, ординаты промежуточного изображе™
ния у[ и у2 одинаковы, а абсциссы х\ и Х2 связаны соотношени-
соотношением х[ = Х2 + /, где I — расстояние между линзами. Поперечные
увеличения первой и второй линз равны соответственно
Ш_ _ Х± 2/2 _ Х^
У\ XI ' |/2 Х2 '
Отсюда с учетом соотношения у[ = f/2 находим
2/2 = ^4 A6J)
2/i xi х2
т.е. поперечное увеличение всей системы. По условию сложная
система полностью ахроматизована, а потому увеличение долж-
должно быть одно и то же для обоих рассматриваемых нами цве™
тов. Значит, вариация левой, а с ней и правой части равенства
A6.9) обращается в нуль. Но абсцисса предмета х\ постоянна,
а абсцисса окончательного изображения х'2 одинакова для обо-
обоих цветов. Поэтому, взяв вариацию логарифма от правой части
A6.9), получим: —^ — —- = 0. Кроме того, из соотношения х^ =
Х^ Х'2
= Х2 + /, ввиду постоянства расстояния I между линзами, еле™

118 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
дует: 8х\ = 8хо. Таким образом, ( — — — ) 8х\ = 0. Если — —
— — Ф 0, т.е. I ф 0, то 8х[ = 0, т.е. промежуточные изображения
Х2
совмещаются в обоих цветах. Но это означает, что первая линза
полностью ахроматизована. Учтя свойство обратимости свето™
вых лучей, убедимся, что полностью ахроматизована и вторая
линза. Исключение составляет случай, когда — — — = 0. В
Х^ Х2
этом случае линзы вплотную прижаты друг к другу A = 0), и
ахроматизация возможна даже тогда, когда каждая из линз не
ахроматизована. Такой случай был разобран выше.
5. Таким образом, чтобы система из двух тонких линз, рас-
расстояние I между которыми не равно нулю, была полностью
ахроматизована, необходимо, чтобы были в отдельности пол-
полностью ахроматизованы обе составляющие ее линзы. Однако
если не требовать полной ахроматизации системы, а ограни-
читься только ахроматизацией ее фокусных расстояний, то
такая ахроматизация моэюет быть получена и с неахромати-
зованными линзами.
Действительно, фокусное расстояние системы из двух тон-
тонких линз определяется формулой A2.8). Из нее находим условие
ахроматизации фокусного расстояния:
rl A I \ ёт { 1 I \ ёп2 п (лалп\
0-= = [-г — т^ 1 + ( т - ТТ" 1 = °5 A6.10)
/ V/i /1/2/wi-i I/2 /1/2/712-1
где п\ — показатель преломления первой линзы, ап2~™ второй.
Если п\ ж П2 одинаковы, то это условие переходит в
i = \{h + h)- A6-11)
Таким образом, система из двух тонких линз, изготовленных
из одного и того лее стекла, будет ахроматизована в отношении
фокусного расстояния и притом для всех цветов спектра, если
расстояние между линзами равно полусумме их фокусных рас™
стояний. Такой способ ахроматизации применяется в окулярах
зрительных труб (см. § 24).
6. Объективы, в которых ахроматизация выполнена для
двух цветов спектра, называются ахроматами. В некоторых оп-
оптических системах (в объективах микроскопов, длиннофокус™
ных астрономических труб и спектральных аппаратов) нали-
наличие вторичного спектра (см. п. 1) существенно ухудшает каче-
качество изображения. Аббе ввел в микроскопию апохроматы, т.е.
объективы, в которых ахроматизация выполнена для трех цве-
цветов спектра и, кроме того, удовлетворено условие синусов (см.
§ 18). Остающаяся при этом хроматическая аберрация называ-
называется третичным спектром.

16
ХРОМАТИЧЕСКАЯ АБЕРРАЦИЯ
119
7. В заключение упомянем о сложных призмах^ изготовля-
изготовляемых из стекол различных сортов. На рис. 60 изображена ахро-
ахроматическая призма. Первая призма, из крона, отклоняет и рас-
рассеивает лучи. Вторая призма, из флинта, отклоняет их в про-
противоположную сторону. Рассеивающая способность (дисперсия)
флинта больше, чем крона. Поэтому вторую призму можно по-
подобрать так, чтобы компенсировать рассеивающую способность
первой призмы, т.е. добиться одинаковости направлений каких-
либо двух лучей (например, красного и фиолетового) при их
выходе из рассматриваемой системы.
Однако отклонение лучей, вызываемое
первой призмой, компенсируется лишь
частично. В результате белый луч про-
проходит через сложную призму без замет-
заметной дисперсии, но испытывает отклоне-
отклонение в сторону.
На рис. 61 а изображена дисперси-
дисперсионная призма^ применяемая в спектро-
спектрографах. У нее дисперсия очень зна-
значительна благодаря большому прелом-
преломляющему углу внутренней призмы из флинта. Боковые призмы
из крона мало влияют на общую дисперсию призмы, но сильно
уменьшают отклонение лучей, так как угол между их наруж-
наружными гранями сравнительно невелик. Кроме того, эти призмы
позволяют увеличить преломляющий угол внутренней призмы,
Рис. 60
Рис. 61
величина которого лимитируется полным отражением. Наконец,
на рис. 61 б изображена призма прямого зрения. Она произ-
производит спектральное разложение, но оставляет неотклоненным
средний луч пучка света.
ЗАДАЧИ
1. Рассчитать ахроматический объектив с фокусным расстоянием / =
= 50 см, склеенный из двух линз. Передняя линза изготовлена из крона
К 1, задняя — из флинта Ф 8. Задняя линза — выпукло-вогнутая, обращена
выпуклой поверхностью наружу, радиус кривизны этой поверхности равен
100 см.

120 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Решение. Из табл. 2 находим для первой линзы: v\ = 65,1, пв =
= 1,4982; для второй линзы V2 = 35,6, пв = 1,6248. По формулам A6.8)
вычисляем фокусные расстояния линз:
, tvi-V2 ,n 65,1-35,6
/ = / = 5° = 2266см
=
65,1
65,1-35,6
50 41>43 ^
/2 35,6
По условию задачи Щ = —100 см. По формуле A0.9) находим щ2^:
B) _ (п - 1)/2Д<2) _ 0,6248-41,43-100 _ _
Kl -(п_1)/2 + дB)- 0,6248-41,43-100" 34'93 СМ'
Той же величине равен радиус щ , так что
(D = (n-l)/ii^1} = 0,4982 ¦ 22,66 • 20,56 =
1 (п - l)/i + Я<1} 0,4982 • 22,66 - 20,56
Вид рассчитанного объектива изображен на рис. 62.
2. Возможна ли ахроматизация толстой одиночной
линзы относительно фокусных расстояний для двух
длин волн?
Ответ. Ахроматизация возможна потому, что в
формулу для фокусного расстояния толстой линзы вхо-
входит п . Следовательно, для заданного фокусного рас-
расстояния могут существовать два значения показателя
преломления тц и пг, которым соответствует это фо-
фокусное расстояние. Толщина линзы должна быть равна
2
Рис. 62 d= J1^ l {Ri - R2),
где п = л/п\П2 — среднее геометрическое из п\ и П2. Так как толщина d су-
существенно положительна, то для возможности ахроматизации необходимо,
чтобы Ri — В.2 > 0. Этому условию удовлетворяют только двояковыпук-
двояковыпуклые и плоско-вогнутые линзы. Все прочие толстые линзы не могут быть
ахроматизованы.
3. Написать условие ахроматизации преломляющей призмы для двух
близких цветов. Призма состоит из двух призм с малыми преломляющими
углами, изготовленных из стекол с коэффициентами дисперсии щ и^.
Ответ. Призмы должны быть обращены преломляющими углами в
противоположные стороны. Условие ахроматизации: —— — —— = и, где ср± —
V\ V2
угол отклонения луча, даваемый первой призмой, а^>2 — второй. Если v\ ф
Ф i/2 j то результирующее отклонение (fi ~~ tp2 отлично от нуля.
§ 17. Условие отсутствия дисторсии
1. В фотографическом объективе особо важное значение
имеет устранение изгиба плоскости изображения и дистор-
дисторсии. Найдем условие отсутствия дисторсии. Пусть РРр

17
УСЛОВИЕ ОТСУТСТВИЯ ДИСТОРОИИ
121
(рис. 63) — плоскость предмета, Р1 Р[Р2 — сопряженная ей плос-
кость изображения, О и О' — центры входного и выходного зрач-
ков. Проведем главные лучи Pi О и Р2О от точек предметной
плоскости через центр входного зрачка. Сопряженные им лучи
P{Of и P^Of пройдут через центр О' выходного зрачка. Обозна-
Обозначим через и ж и1 углы
наклона этих лучей к
главной оптической оси.
Тогда РРг = POtguu
PfP{ = P'O'tgu'i, PP2 =
= POigu2l PfP2 =
= PfOftguf2i и следова-
следовательно,
P'P[_tgUf1 P'P^_tgu'2
P
РРг tgV PP2 tgu2
Отсутствие дисторсии
означает, что поперечные
увеличения PfP{/PPi и
PfP2/PP2 одинаковы при
любых положениях точек Pi и Р2. Следовательно, для устра-
устранения дисторсии необходимо и достаточно, чтобы соблюдалось
равенство
Рис. 63
каковы бы ни были значения углов щ и и2. Это равенство на™
зывается условием тангенсов^ или условием ортоскопии. Точки
О и О' главной оптической оси, удовлетворяющие этому усло-
условию, называются ортоскопическими точками. Центры входного
и выходного зрачков являются центрами перспективы предме-
предмета и его изображения. Таким образом, условие отсутствия дис-
дисторсии сводится к требованию, чтобы эти центры перспективы
были ортоскопическими точками.
2. Простейшим примером, где выполнено условие ортоско-
ортоскопии, может служить симметричный фотографический объек-
объектив, изображенный на рис. 64. Он состоит из двух совершенно
одинаковых ахроматизованных двойных линз, обращенных друг
к другу вогнутыми поверхностями. Апертурная диафрагма по-
помещена посередине между этими линзами. Так как она распо-
расположена близко к обеим линзам, то оба изображения ее мнимые,
прямые и лежат обычно внутри объектива недалеко от диафраг-
диафрагмы А\А2. Изображение D\D2i даваемое передней линзой, лежит
справа от диафрагмы А\А2 и служит входным зрачком системы;
изображение D^D^ даваемое задней линзой, лежит левее диа-
диафрагмы А\А2 и служит выходным зрачком. Выходной зрачок

122
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Dr2 A2 D2
D[Df2 есть изображение входного зрачка Z?]_Z?2, даваемое всей
оптической системой.
Как видно из рис. 64, это изображение производится с попе™
речным увеличением +1. Поэтому плоскости входного и выход-
выходного зрачков являются главными плоскостями, а центры этих
зрачков — главными точка™
ми объектива. Возьмем теперь
любой падающий луч, продол™
жение которого проходит че-
рез центр входного зрачка. То™
гда, ввиду симметрии, продол-
продолжение выходящего луча прой-
пройдет через центр выходного
зрачка, а самый луч внутри
системы — через центр апер™
турной диафрагмы. Следова-
Следовательно, углы наклона и и и' этих главных лучей к главной он™
тической оси будут всегда одинаковы, каковы бы ни были зна-
значения самих углов и ж и1. Это значит, что в рассматриваемой
системе соблюдено условие ортоскопии.
Рис. 64
§ 18. Условие синусов Аббе
1. В микроскопах изучаемые объекты малы и помещаются
перед объективом вблизи главной оптической оси. Апертуры лу-
лучей, формирующих изображение в микроскопе, должны быть
как можно шире (в лучших объективах микроскопов апертуры
практически доведены до своего теоретического предела 180°).
От этого увеличивается яркость изображения, а главное повы-
повышается разрешающая сила объектива, т.е. его способность раз-
различать мелкие детали (см. § 56). Поэтому сопряженные точки
главной оптической оси, в первой из которых помещается объ-
объект, а во второй получается его изображение, даваемое объек-
объективом, должны быть анаберрационными^ т.е. точка Р должна
изображаться в виде точки Р1 широкими пучками лучей (см.
§ 9). Однако этого условия еще недостаточно. Необходимо, что™
бы без аберраций изображались все точки малого участка пред-
предметной плоскости, проходящей через точку Р перпендикулярно
к главной оптической оси. Практически речь идет об устранении
сферической аберрации и комы. Анаберрационные точки глав-
главной оптической оси Р и Р', удовлетворяющие этому условию,
называются апланатическими.
Значение апланатизма было выяснено немецким физиком
Аббе A840-1905). Аббе был оптиком-теоретиком. Он не толь-
только глубоко понимал теорию оптических приборов, но и указал

§ 18 УСЛОВИЕ СИНУСОВ АББЕ 123
пути их совершенствования. Особое внимание он уделил тео-
рии и совершенствованию микроскопа. Его многолетнее плодо-
плодотворное сотрудничество с известной оптической фирмой Цейсса
A816—1888) в Иене (Германия) привело к созданию и массовому
производству лучших в мире оптических приборов, в которв1х
практически было достигнуто то, что принципиально возможно
с точки зрения волновой теории света. Аббе вывел необходимое
и достаточное условие апланатизма, получившее название уело-
вия синусов. К выводу этого условия мы и перейдем.
2. Ввиду осевой симметрии оптической системы, при выводе
достаточно ограничиться рассмотрением изображений не штос™
ких площадок, а прямо-
прямолинейных отрезков ма- ^ / \
О
лои, но произвольной ^
длины, перпендикуляр-
перпендикуляр\ /
Рг
ных к главной оптиче-
оптической оси. Пусть один
из таких отрезков, PQ,
изображается широкими
пучками лучей в виде
отрезка P'Q1', также пер-
перпендикулярного к главной оптической оси (рис. 65). Оптические
длины всех лучей, соединяющих сопряженные точки РиР',
одинаковы. То же справедливо для лучей, соединяющих сопря-
сопряженные точки Q и Q1'.
Докажем, что оптическая длина (РР') любого луча, соеди-
соединяющего апланатические точки Р и Р;, равна оптической длине
(QQf) любого луча, соединяющего сопряженные точки Q ж Q'.
Иными словами, оптические длины лучей между сопряженны-
сопряженными точками отрезка PQ и его изображения P'Q1 одинаковы для
всех пар сопряженных точек. Ввиду отмеченного выше свойства
оптических длин лучей, соединяющих сопряженные точки, до™
статочно доказать это утверждение для параксиальных лучей,
выходящих из точек объекта PQ параллельно главной оптиче-
оптической оси. Волновой фронт, соответствующий таким лучам, по™
еле прохождения через объектив становится сферическим, ма-
малый участок которого можно считать плоским. Таким образом,
объект PQ целиком лежит в плоскости падающего, а его изо™
бражение P'Q1 — в плоскости прошедшего волновых фронтов.
Но оптические длины всех лучей между двумя положениями
волнового фронта одинаковы. Отсюда и следует доказываемое
утверждение.
Проведем теперь через точки отрезка PQ пучок параллель-
параллельных лучей под произвольным углом и к главной оптической оси
(рис. 66). Так как лучи лежат в одной плоскости, то соответству-

124
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ющий им волновой фронт представится прямолинейнвш отрез™
ком QA, перпендикулярным к лучам. После прохождения через
объектив параллельность лучей нарушится. Однако ввиду ма-
малости объекта PQ будет мал и угол расхождения прошедших
лучей. Пренебрегая им, можно считать, что все прошедшие лу-
лучи наклонены к оптической оси практически под одним и тем же
Рис. 66
углом и1'. Соответствующий участок волнового фронта предста-
представится прямолинейным отрезком Q1 А'. Ввиду одинаковости опти-
оптических длин всех лучей между волновыми фронтами [АР'А') =
— iQQ1)- По доказанной только что теореме (PAP1) = (QQ1)^ и
предыдущее соотношение переходит в (РАР1) = [АР1 А1). Вы-
Вычитая из обеих частей этого равенства общую часть (APf), по-
получим: (РА) = (Р'А1), или
nl sinu = nlf sin г/,
A8.1)
где I и I1 — длины отрезков PQ и P'Q1', а п и п' — показатели
преломления пространств предметов и изображений. Равенство
A8.1) и выражает условие синусов Аббе. Оно должно выпол-
выполняться для любых значений угла и и для любых малых значе-
значений длины отрезка I. Для параксиальных лучей условие синусов
A8.1) переходит в теорему Лагранжа^Гельмгольца A0.6) и, сле-
следовательно, выполняется для любой пары сопряженных точек
на главной оптической оси.
В следующем параграфе приводится более строгий вывод
условия синусов, основанный на теореме косинусов.
3. К важному примеру аплапатических точек приводит по-
построение преломленного луча на поверхности шара, указан-
указанное Вейерштрассом A815—1897). Пусть R — радиус шара, п —
его показатель преломления относительно окружающей среды
(рис. 67). Построим две концентрические с шаровой поверхно-
поверхностью сферы S ш Sf с радиусами nR и R/n. Продолжим падаю-

18
УСЛОВИЕ СИНУСОВ АББЕ
125
щий луч АВ до пересечения в точке Р со сферой S и соединим
точку Р с центром шара О. Прямая ОР пересечет сферу S' в
точке Р1'. Прямая, соединяющая точку падения В с точкой Р;,
дает направление проломленного луча. Действительно, из подо-
подобия треугольников ОВР и ОВР1 следует, что угол ОР1 В равен
углу падения </?, а потому
sin (р
sint/; ~
OB
= га,
что и доказывает наше утверждение.
Из построения видно, что падающий пучок лучей, сходящий-
сходящийся в точке Р, после преломления на шаровой поверхности будет
сходиться в точке Р1. Обратно, если точечный источник поме™
стить в Р;, то после преломления получится пучок лучей, расхо-
расходящихся из Р. Следовательно, Р и Р1 являются сопряженными
анаберрационными точками и притом аи л апатическими.
Действительно, ввиду шаровой симметрии не только точки
Р и Р;, но и сферы S и S' отображаются друг в друга широкими
пучками лучей. Так как обе сферы нормальны к прямой РР;, то
точки Р и Р1 должны удовлетворять условию синусов, в чем лег-
легко убедиться и непосредственно. Точки Q и Q7, очевидно, также
аил апатические. Наконец, центр сферы О можно рассматривать
как пару совпадающих апланатических точек, являющихся од-
одновременно узловыми точками системы.
Рис. 67
Итак, на оптической оси QP имеется три пары изолирован-
изолированных апланатических точек: Р и Р;, Q и Q1 и двойная апланати-
ческая точка О.
4. Апланатические точки шара используются для построе-
построения иммерсионных объективов микроскопов с очень большими
увеличениями. Иммерсионным называют такой объектив, когда

126 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
между покровным стеклом и фронтальной линзой объектива на™
ходится слой жидкости (иммерсия). Иммерсия была предложе-
предложена Амичи A786—1863) в 1840 г. С целью уменьшения вредного
для качества изображения преломления на поверхности покров-
покровного стекла он заполнял водой промежуток между покровным
стеклом и фронтальной линзой объектива. Аббе в 1878 г. стал
применять однородную иммерсию с показателем преломления,
почти равным показателю преломления покровного стекла и
фронтальной линзы. В такой системе лучи, исходящие из каж-
дой точки предмета, распространяются практически прямоли-
прямолинейно до выхода из фронтальной линзы объектива. В качестве
однородной иммерсии приме™
няется кедровое масло (п =
= 1,515). В однородной иммер-
иммерсионной системе Аббе фрон-
фронтальная линза объектива со™
гС X р( 1^—Н—I стоит из стеклянного полуша-
v ^ ' ' ' рия, плоская сторона которого
обращена к предмету (рис. 68).
Предмет помещается на рас-
расстоянии OP = R/n от центра
(R — радиус полушария). Так
Рис. 68 как лучи до выхода из фрон-
фронтальной линзы не испытывают
преломления, то Р будет апланатической точкой. Изображение
предмета получается в сопряженной апланатической точке Р1
на расстоянии OP' = Rn от центра О. Как видно из построе-
построения Вейерштрасса, линейное увеличение равно п2. Поэтому из
A8.1) следует sin и* = (sin^)/n, так что угол наклона луча к
оптической оси уменьшается.
Амичи для получения большего увеличения и дальнейше-
дальнейшего уменьшения углов наклона лучей к оптической оси предло-
предложил помещать за фронтальной линзой вогнуто-выпуклую лин-
линзу. Точка Рг должна находиться в центре кривизны вогнутой по-
поверхности линзы. По отношению к преломлению на этой поверх-
поверхности Pf будет апланатической точкой, совпадающей со своей
сопряженной точкой. Точка Р1 должна одновременно находить-
находиться на расстоянии R\jn\ от центра кривизны выпуклой поверх-
поверхности второй линзы (п\ — показатель преломления этой лин-
линзы, R\ — радиус кривизны ее выпуклой поверхности). Тогда по
отношению к преломлению на этой поверхности Р! будет апла-
апланатической точкой; ее изображение получится в сопряженной
апланатической точке Р".
Применив метод Амичи несколько раз, можно добиться ка-
какого угодно уменьшения углов наклона лучей к оптической оси.

18
УСЛОВИЕ СИНУСОВ АББЕ
127
При этом для всей системы в целом будет выполнено условие
синусов. Метод Амичи часто применяют при конструкции объ-
объективов микроскопов. Однако таким методом конструируются
в лучшем случае первые две линзы, так как иначе возникает
сильная, ничем не компенсируемая хроматическая аберрация.
5. Аббе принадлежит простой способ испытания объективов на выпол-
выполнение условия синусов. Допустим, что во второй апланатической точке объ-
объектива Р (рис. 69) помещена малая диафрагма, через которую произво-
производится наблюдение. Ее сильно уменьшенное изображение, получающееся в
сопряженной апланатической точке Р, будет входным зрачком системы.
В (у, z)
F А
Рис. 69
Рассмотрим изображение конечного участка плоскости АВ, даваемое объ-
объективом, когда расстояние q этой плоскости от точки Р очень велико по
сравнению с диаметром входного зрачка. Так как при перемещении объек-
объекта влево от апланатической точки Р его изображение перемещается также
влево (см. § 11, п. 6), то изображение плоскости АВ получится левее вто-
второй апланатической точки Р . Когда расстояние q достаточно велико, то
изображение А1 В1 плоскости АВ можно увидеть невооруженным глазом,
если смотреть через диафрагму. Изображение получится сильно искажен-
искаженным из-за использования косых пучков лучей, наклоненных под большими
углами к главной оптической оси. Однако, ввиду исключительной малости
входного зрачка, в разложении аберраций в степенные ряды можно пре-
пренебречь всеми степенями радиуса входного зрачка а, сохранив лишь член
нулевой степени, не содержащий а. Иными словами, достаточно ограни-
ограничиться учетом одной только дчсторсчч. В этом приближении изображение
А'В' будет расположено в плоскости параксиальных изображений.
Поставим задачу найти в предметной плоскости АВ такое семейство
кривых, чтобы его изображение в плоскости А В получилось в форме ква-
квадратной сетки.
Возьмем в предметной плоскости произвольную точку В с координата-
координатами г/, z на расстоянии у у2 + z2 от главной оптической оси. Проведем луч
ВР через центр входного зрачка. Сопряженный луч В' Р1 однозначно опре-
определится условием синусов sin г//sin n = А, где А = nl/(n'l'), т.е. для рас-
рассматриваемого объектива А — величина постоянная, и и и — углы накло-
наклона падающего и прошедшего лучей к главной оптической оси. Положение
изображения В' определится точкой пересечения луча В1 Р' с плоскостью
параксиальных изображений. Подставим вместо sin и и sin и их значения
V2 + z2
q12 + у1'

128
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
где q1 — расстояние плоскости А'В' от апланатической точки Р'. Учтем
при этом, что точки В ж В' лежат в одной плоскости, проходящей через
главную оптическую ось, так что z /у' = z/y. Тогда получим
Возьмем теперь в плоскости А В семейство прямых, параллельных оси
Z: у' = О, где С — параметр, который может принимать произвольные
значения. Уравнение кривых в предметной плоскости АВ, изображением
которых является это семейство, найдется из предыдущего соотношения,
если в нем у1 заменить на С. Таким путем получим
2- - — = 1
а2 Ь2
где
а2 =
Ь2 =
A8.2)
A8.3)
aw — новый параметр, связанный с параметром С соотношением
ш = C/Aq. A8.4)
Для объективов микроскопов всегда А2 < 1, так что при ш2 < 1/A — А2)
величина а существенно положительна. В этом случае A8.2) представляет
семейство гипербол, осью которого является координатная ось Y. При ш =
= 0 уравнение A8.2) переходит в у2 = 0 и изображает ось Z. Значения
ш > 1/A — Л ) надо исключить, так как в этом случае уравнение A8.2)
представляет семейство мни-
мнимых эллипсов и никакого
оптического изображения не
получается. Аналогично, се-
семейство прямых z1 = С при
тех же значениях параметра
uj является оптическим изо-
изображением семейства гипер-
гипербол
z2 v2
а2 о2
получающегося из семейства
A8.2) поворотом на 90°
вокруг начала координат О.
Оба семейства гипербол
A8.2) и A8.5) пересекают-
пересекаются между собой, образуя
криволинейную сетку, пред-
представленную на рис. 70. При
переходе от одной гиперболы
к соседней параметр ш дол-
должен получать одинаковые
приращения. Тогда и приращения параметра С, как это видно из A8.4),
также будут одинаковыми. Следовательно, если рис. 70 поместить на
расстоянии q перед передней апланатической точкой jP, to гиперболы
изобразятся в виде квадратной сетки прямых. При ш = A —¦ А )/2 урав-
уравнение A8.2) переходит в у2 — z2 = Ь2, а уравнение A8.5) — в z2 — у2 = Ь2.
Рис. 70

§ 19 ТЕОРЕМА КОСИНУСОВ 129
Обе эти гиперболы имеют асимптотами биссектрисы координатных углов.
Следовательно, Ь есть расстояние от начала координат до вершины той из
гипербол, асимптоты которой совпадают с биссектрисами координатных
углов. Для объективов микроскопов А — величина малая, квадратом
которой по сравнению с единицей можно пренебречь. В этом приближении
Ь = q. Это дает простой способ определения расстояния д, на котором
следует поместить рис. 70, чтобы его изображение получилось в виде
квадратной сетки.
Теперь становится понятным метод Аббе испытания объективов микро-
микроскопов на выполнение условия синусов. Аббе пользовался шаблоном, вос-
воспроизведенным на рис. 71. Удалив
окуляр микроскопа, следует поме-
поместить такой шаблон на расстоянии q
перед передней апланатической точ-
точкой. Глаз наблюдателя помещается
во вторую апланатическую точку.
Зрачок глаза играет роль выходного,
а его изображение, даваемое объек-
объективом, — входного зрачка системы.
Если изображение шаблона получа-
получается в виде сетки квадратов, то объ- рис ^1
ектив удовлетворяет условию сину-
синусов. Если изображение получается слишком мелким, то можно применить
вспомогательный микроскоп небольшого увеличения, перед объективом ко-
которого помещена малая диафрагма, расположенная во второй апланатиче-
апланатической точке Р'. При испытании описанным способом большого числа объек-
объективов микроскопов, ранее изготовленных лучшими мастерами без всяких
расчетов путем последовательных проб и подбора линз, Аббе обнаружил,
что все хорошие объективы всегда удовлетворяли условию синусов.
§ 19. Теорема косинусов. Стигматические изображения
широкими пучками лучей
1. Обобщим результаты предыдущего параграфа на случай произволь-
произвольных оптических систем. Среды, в которых распространяются световые лу-
лучи, здесь предполагаются изотропными, но могут быть неоднородными. Та-
Таким образом, в общем случае световые лучи будут криволинейными. Пусть
Р и Pf — две точки с радиусами-векторами г и г;, лежащие на одном лу-
луче. Оптическая длина луча, соединяющего эти точки, рассматриваемая как
функция их координат, называется точечным эйконалом, или характери-
характеристической функцией оптической системы. Она была введена Гамильто-
Гамильтоном A805-1865) и оказалась весьма полезной при исследовании оптических
изображений. Характеристическую функцию будем обозначать через Н =
= Я(г,г').
Фиксировав положение начальной точки Р, будем перемещать конеч-
конечную точку Р . Вместе с точкой Р будет перемещаться и луч РР , соеди-
соединяющий ее с точкой Р. В результате получится пучок лучей, исходящих
в различных направлениях из точки Р, как если бы она была источни-
источником света (рис. 72). Пусть F F — волновой фронт, соответствующий этому
пучку, проходящий через начальное положение точки Р . При смещении
Р' в точку Q'', лежащую на луче PA'Q', функция Н получает приращение
5 Д.В. Сивухин

130
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
АН = (PA'Q1) ~~ (РР'), или, ввиду равенства оптических длин РР' и
АЯ = (PA'Q') - (РА') = (A'Qf).
Если смещение dr' = P'Q' бесконечно мало, то АН переходит в
dH = n\dv
cos a = п (s
.'dr'),
где af — угол между вектором dr1 и единичным вектором луча sf в точке
Р;, а п — показатель преломления среды в этой точке. Аналогично най-
найдется бесконечно малое приращение функции Н', когда конечная точка Р'
остается неподвижной, а начальная точка Р перемещается на dr. В этом
случае при вычислении надо воспользоваться пучком лучей, сходящихся в
точке Р' (рис. 73). В результате получится dH = —n(sdr), где n, s и dr име-
имеют такой же смысл, что и в предыдущем случае, но относятся к начальной
точке Р. При изменении обоих аргументов г и г; получим
dH = n (s; dr') — n(s dr).
A9.1)
Q'
Рис. 72
Рис. 73
Докажем теперь следующую теорему, называемую теоремой косинусов:
Пусть точка Р' (рис. 74) является стигматическим изображением
точки Р. Соединим эти точки произвольным лучом, направления кото-
которого в Р и Р' определяются единичными векторами s и s;. Пусть Q и
Qf — две точки, бесконечно близкие к Р и Pf. Для того чтобы точка Q'
была стигматическим изображением точки Q в широких пучках лучей,
необходимо и достаточно, чтобы разность
ns d\ — п s d\ ,
A9.2)
где d\ = PQ, dlf = P Q , не вависела от направления луча, соединяющего
Р с Pf.
Для доказательства необходимости теоремы допустим, что Qf является
стигматическим изображением точки Q. Обозначим через Н оптическую
длину какого-либо луча, соединяющего сопряженные точки РиР,а через
Н' — оптическую длину луча, соединяющего сопряженные точки Q и Q'. В
силу известного свойства сопряженных точек величины if и if', ас ними
и разность dH = Н' — Н = n's1 dlf — ns d\ не зависят от направлений лучей,
соединяющих Р с Р , a Q с Q . Таким образом, выражение A9.2) не может
зависеть от s, и необходимость теоремы доказана.

19
ТЕОРЕМА КОСИНУСОВ
131
Рис. 74
Докажем теперь ее достаточность. Соединим точки Q и Q' лучом QQ'.
Кроме того, через Q проведем произвольный луч QQ" и отметим на нем
такую точку Q , чтобы оптическая длина (QQ ) была равна оптической
длине (QQ ). Так как по условию теоремы Р является стигматическим изо-
изображением точки Р, то из сообра-
соображений непрерывности следует, что
вектор Р1 Q" = dl" бесконечно мал.
В таком случае по формуле A9.1)
(QQl - (PPf) = n's df - nsdl
По той же формуле
(QQf) - (PPf) = n's dlf - nsdl
Так как по построению {QQ1) =
= {QQ11), то s'dl" = sdV, причем
по условию теоремы это соотноше-
соотношение должно выполняться для всех
направлений вектора s . Это возможно тогда и только тогда, когда d\ = dl ,
т.е. когда точка Q" совпадает с Q1'. Таким образом, любой луч, исходящий
из Qj пройдет через Q', что и доказывает достаточность теоремы.
Чтобы конечная кривая изображалась стигматически широкими пуч-
пучками лучей, необходимо и достаточно, чтобы условия теоремы косинусов
выполнялись для каждой пары сопряженных бесконечно малых отрезков
этих кривых.
2. Условие синусов является следствием теоремы косинусов. Действи-
Действительно, согласно этой теореме разность nls — n'l's' = nlsinu ~~ n'l' sinu не
должна зависеть от направ-
направления луча, соединяющего д
сопряженные точки Р и Р'
(рис. 75). Но если луч идет
вдоль оптической оси, то
указанная разность обраща-
обращается в нуль. В результате
снова получается соотноше-
соотношение A8.1), и притом не толь-
только как необходимое, но и как
достаточное условие.
Допустим теперь, что от-
отрезок I = РВ лежит на опти-
оптической оси. Найдем условие,
при котором он изображается стигматически широкими пучками лучей в
виде отрезка I' = Р1 В1, также лежащего на оптической оси. В рассматри-
рассматриваемом случае при и = О
nls — n'l's' = nl cos и — nl' cos и = nl — nl'.
Поэтому на основании теоремы косинусов должно быть
nl cos и — n'l' cos и = nl — nl',
или
nl sin2 (и/2) = nl'sin2 (и/2), A9.3)
каковы бы ни были значения углов и и и . Это соотношение называется
условием Гершеля.
Рис. 75

132 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Пусть Р и Р' — сопряженные апланатические точки. Если в бесконеч-
но малых окрестностях этих точек существует другая пара апланатиче-
ских точек Q и Q (а следовательно, и бесконечное множество таких пар),
то оптическая длина бесконечно малого линейного объекта, лежащего в
окрестности точки Р, будет равна оптической длине его изображения, по™
лучающегося в окрестности точки Р'. Действительно, так как Р ш Р1 —
апланатические точки, то по условию синусов отношение
sin и cos(ii,/2) sm(ii,/2)
sin u' cos(u' /2) sin(tt;/2)
не должно зависеть от и. С другой стороны, так как Q и Q' — также апла-
апланатические точки, то бесконечно малый отрезок PQ оптической оси изо-
изображается в виде отрезка Р1 Q' той же оси. Поэтому должно соблюдаться и
условие Гершеля: отношение
sin2(ti/2)
sin2(t//2)
не должно зависеть от угла и. Оба условия могут быть выполнены одно™
временно тогда и только тогда, когда и = =Ьг/, т.е. когда апланатические
точки Р и Р являются узловыми или обратными узловыми точками си-
системы. Но в таком случае, если отрезок I перпендикулярен к оптической
оси, из A8.1) следует: \nl\ = \п'1'\. Если же отрезок I лежит на оптической
оси, то из A9.3) также следует \nl\ = \п'1'\. Таким образом, теорема дока-
доказана для двух частных случаев: когда отрезок I лежит на оптической оси
и когда он перпендикулярен к ней. Тем самым она доказана для отрезка I
произвольного направления.
Во всех центрированных системах, применяющихся на практике, ли-
линейное увеличение, как правило, отлично от п/п'. Поэтому из доказанной
теоремы следует, что для таких систем апланатические пары точек, если
они существуют, могут быть лишь изолированными точками оптической
оси. Это значит, что для каждой пары апланатических точек можно ука-
указать конечные интервалы оптической оси, содержащие эти точки, внутри
которых нет другой пары апланатических точек.
В приближении параксиальной оптики условие синусов и условие Гер-
Гершеля выполняются всегда. Первое из них в указанном приближении пе-
переходит в теорему Лагранжа-Гельмгольца. Для доказательства второго из
соотношений A1.20), A1.17), A1.13), A0.6) находим
ёХ^ _ V___f_f_ ^ IL|/!^ w_^l
ёХ ~ I ~ X2 f ~ п у2 ~ п1 и12'
а это при малых углах и и и совпадает с условием Гершеля A9.3). Таким
образом, равенство углов и и и , а следовательно, и равенство оптических
длин nl и n'V не обязательны. Благодаря этому в параксиальной оптике
поперечное и продольное увеличения могут принимать любые значения, не
обязательно равные п/п .
3. Пусть Р' является стигматическим изображением точки Р. Для
того чтобы бесконечно малый элемент плоскости S, проходящий через Р,
изображался стигматически в виде бесконечно малого элемента плоско-
плоскости S , проходящей через Р , необходимо и достаточно^ чтобы выполня-
выполнялось условие косинусов для двух бесконечно малых непараллельных отрез-
отрезков^ лежащих в плоскости S и проходящих через точку Р.

§ 19 ТЕОРЕМА КОСИНУСОВ 133
Необходимость теоремы очевидна. Для доказательства ее достаточно™
сти соединим Р и Р1 произвольным лучом. Пусть d\\ и dh — два бесконечно
малых неколлинеарных вектора, проходящих через точку jP, для которых
удовлетворяется условие теоремы косинусов. Таким образом, по условию
разности
п s d\\ ~~ ns dl\ = dHi,
A9 4)
=dH2
не зависят от направления луча, соединяющего Р с Р'. Но они могут зави-
зависеть от направлений векторов d\\ и dh- Произвольный вектор dl, проходя-
проходящий через точку Р и лежащий в плоскости предмета, можно разложить по
векторам d\\ и dh:
d\ = adh + bdhj
причем коэффициенты а и Ь не зависят от s. Введем вектор
<й' =а<й'1+Ь<ПГ2,
умножим соотношения A9.4) на а и b и сложим. Получим
ris'dl' -nsdl = dHJ A9.5)
где dH = adH\ +bdH'2. Отсюда видно, что разность A9.5) не зависит от s,
т.е. условие теоремы косинусов выполняется для произвольного вектора cfl,
проходящего через точку Р и лежащего в плоскости предмета. Следова-
Следовательно, предмет изобразится оптической системой стигматически. Вообще
говоря, изображение не будет подобно самому предмету.
Направления произвольных неколлинеарных векторов d\\ и dh можно
принять за координатные оси У и Z в плоскости предмета, направления
оптически сопряженных с ними отрезков d\\ и dl2 — за координатные оси Y
hZ'b плоскости изображения, а сами точки Р и Р' — за начала координат
соответствующих координатных систем. Тогда в окрестностях точек Р и Р'
координатные оси Y и Z изобразятся оптической системой координатными
осями Y и Z . Координаты сопряженных точек, бесконечно близких к Р и
Р', будут связаны линейными соотношениями
у' = Ay, z = Вг. A9.6)
Координатная система У Z , вообще говоря, будет косоугольной, даже
в том случае, когда система YZ прямоугольная. Однако если в плоскостях
предмета и его изображения ввести прямоугольные системы координат, то
из соотношений A9.6) и из формул преобразования координат непосред-
непосредственно следует, что прямоугольные координаты сопряженных точек будут
связаны формулами линейного преобразования
у^Аиу + А^г, z=A2iy + A22Z. A9.7)
Из свойств линейного преобразования следует, что в плоскости предмета
существует пара взаимно перпендикулярных прямых, которой в плоскости
изображения соответствует пара также взаимно перпендикулярных пря-
прямых. Если эти четыре прямые принять за координатные оси, то формулы
преобразования снова примут вид A9.6), с тем отличием, что теперь обе ко-
координатные системы прямоугольны. Вообще говоря, А ф В. Поэтому изо-
изображение бесконечно малой площадки происходит с нарушением подобия:
бесконечно малый круг изображается в виде эллипса. Только в частном слу-
случае, когда А = В, система дает подобные изображения бесконечно малых
площадок, находящихся в окрестности точки Р.

134 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
4. Следуя Каратеодори A873—1950), говорят, что световой луч лежит
в поле инструмента, если он действительно проходит через диафрагмы
из пространства предметов в пространство изображений. Говорят также,
что отрезок кривой лежит тангенциально в поле инструмента, если все
лучи, касающиеся этого отрезка, лежат в поле инструмента.
Пусть бесконечно малая площадка изображается оптической систе-
системой стигматически. Пусть, далее, d\\ и d\2 — бесконечно малые не парал-
параллельные отрезки, пересекающиеся в пределах площадки и лежащие в ее
плоскости. Если эти отрезки лежат тангенциально в поле инструмен-
инструмента, то рассматриваемая площадка изображается оптической системой с
сохранением подобия. При этом оптическая длина любого отрезка, лежа-
лежащего на площадке, равна оптической длине сопряженного с ним отрезка.
По условию теоремы лучи, выходящие из Р (рис. 76) в направлениях d\\
и d\2, лежат в поле инструмента. В пространстве изображений они пройдут
d\x
Рис. 76
в направлениях оптически сопряженных отрезков dl'i и dl2. Рассмотрим
сначала изображение отрезка d\\. Возьмем два луча, исходящих из Р в
направлениях d\2 и d\\. На основании теоремы косинусов
п dl\ cos a — п dl'i cos а = п dl\ — п dl[. A9.8)
Аналогично, рассматривая изображение отрезка dl'2,
ndh cos a — п dl2 cose/ = ndh — n dl'2. A9.9)
Допустим, что dl\ = dl2- Докажем, что тогда dl\ = dl2- В самом деле,
почленное вычитание A9.9) из A9.8) дает
п dl'^l-cosa) = n dlf2(l-cosa). A9.10)
Разность 1 — cqsq/ не может обращаться в нуль. Действительно, по
предположению угол а не равен нулю. Но заданием направления в какой-
либо точке луч определяется однозначно. Если бы а = 0, т.е. направления
обоих рассматриваемых нами лучей в точке Р1 совпадали, то они совпадали
бы и во всех других точках, в частности в начальной точке Р. Значит, было
бы а = 0, вопреки предположению. Поэтому, сокращая на п A — cos с/), из
A9.10) находим dl\ = dl2, что и требовалось доказать.
Из доказанного следует, что отрезки d\\ и d\2 изображаются оптической
системой с одинаковым увеличением. Следовательно, в рассматриваемом
случае в формулах A9.6) А = В, т.е. увеличение любого отрезка в плоскости
предмета не зависит от его направления. Отсюда следует, что изображение
происходит с сохранением подобия, т.е. является конф

§ 20 ОБ АБСОЛЮТНЫХ ОПТИЧЕСКИХ ИНСТРУМЕНТАХ 135
Но изображение с сохранением подобия характеризуется также сохра™
нением углов. Следовательно, а = а', и формула A9.8) дает ndl\ = п' dl[.
Вообще, для всякого отрезка dl, лежащего в плоскости предмета, ndl =
= п dl1, dl1 /dl = п/п , и вторая часть теоремы доказана.
Итак, стигматические изображения площадок, тангенциально лежа-
лежащих в поле инструмента, могут происходить только с вполне определен-
определенным увеличением п/п . В частности, когда показатели преломления про™
странств предметов и изображений одинаковы, увеличение равно единице.
Это утверждение перестает быть справедливым для площадок, не лежащих
тангенциально в поле инструмента.
Примером может служить преломление на сферической поверхности
(см. рис. 67). Сфера S отображается на сферу S' стигматически широки™
ми пучками лучей. Однако линейное увеличение, как видно из построения,
равно отношению квадратов показателей преломления, а не их первых сте-
степеней. Причина этого в том, что ни одна из сфер S и S не лежит танген-
тангенциально в поле инструмента. Напротив, если линейный объект поместить в
точку О, то, поскольку последняя является парой совпадающих узловых то-
точек, линейное увеличение будет равно просто отношению показателей пре-
преломления в согласии с обсуждаемой нами общей теоремой. Действительно,
ввиду шаровой симметрии любой линейный объект, помещенный в центре
О, лежит тангенциально в поле инструмента.
Бесконечно малую часть конечной поверхности можно рассматривать
как бесконечно малую плоскую площадку. Поэтому для стигматическо-
стигматического изображения конечной поверхности необходимо и достаточно, чтобы
стигматически изображались все бесконечно малые площадки, на кото-
которые можно разбить эту поверхность.
5. Рассмотрим, наконец, стигматические изображения объемных объек™
тов широкими пучками лучей. Этот вопрос может быть исследован в точ-
точности так же, как и аналогичный вопрос для поверхностных объектов. В
частности, может быть доказана следующая теорема:
Пусть точка Р является стигматическим изображением точки Р.
Для того чтобы бесконечно малый элемент объема в окрестности точки
Р изображался стигматически, необходимо и достаточно, чтобы выпол-
выполнялось условие теоремы косинусов для трех бесконечно малых отрезков,
проходящих через точку Р и не лежащих в одной плоскости.
Новым по сравнению с изображениями элементов поверхностей являет-
является то, что в случае стигматического изображения элементов объема всегда
существуют три отрезка dli, dh, Лз, не находящиеся в одной плоскости и
лежащие тангенциально в поле инструмента. Поэтому, повторяя рассужде-
рассуждения, приведенные применительно к изображениям элементов поверхности,
приходим к заключению, что эти три отрезка изображаются с одним и тем
же увеличением. Как следствие этого, получаем следующую теорему:
Стигматическое изображение элементов объема, если оно осуще-
осуществляется широкими пучками лучей, всегда конформно, т.е. происходит с
сохранением подобия. При этом линейное увеличение равно п/п , так что
оптическая длина предмета всегда равна оптической длине изображения.
§ 20. Об абсолютных оптических инструментах
1. С точки зрения геометрической оптики идеалом был бы оптический
инструмент, изображающий стигматически широкими пучками лучей каж-

136 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
дую точку пространства предметов в виде точки пространства изображе-
изображений. Такой инструмент называется абсолютным. Обсудим вопрос о принци-
пиальной возможности абсолютных оптических инструментов и исследуем
их свойства.
Как доказано в предыдущем параграфе, изображения бесконечно ма-
малых объектов, даваемые абсолютным оптическим инструментом, всегда
конформны. При этом оптическая длина любой линии равна оптической
длине ее изображения. Отсюда следует, что в абсолютном оптическом ин-
инструменте оптическая длина луча метсду двумя сопряженными точка-
ми одинакова для всех пар сопряженных точек. Это положение называется
теоремой Каратеодори.
Для доказательства возьмем две пары сопряженных точек: jP, P и Q,
Q (рис. 76). Через точку Р проведем пучок лучей во всевозможных на-
направлениях. Все эти лучи пересекутся в точке Pf. Один из них пройдет
через точку Q. Возьмем другой произвольный луч РАР'. В силу свойства
сопряженных точек (PAPf) = (PQPf). Луч PQP', поскольку он проходит
через точку Q, должен пройти и через сопряженную ей точку Q'. При этом
кривая P'Q' будет оптическим изображением кривой PQ, а потому (PQ) =
= (PfQ!). Отсюда следует (QPfQf) = (PQPf). Сравнивая это равенство с
предыдущим, получаем: (РАР ) = (QP Q ), что и требовалось доказать.
2. Допустим теперь, что пространства предметов и изображений одно-
родны^ т.е. показатели преломления п и п' не зависят от координат. В этом
случае любая прямая пространства предметов изобразится абсолютным
инструментом в виде прямой пространства изображений. В самом де-
деле, проведем через произвольную точку О пространства предметов три лу-
ча, лежащих в поле инструмента и не находящихся в одной плоскости. В
пространстве изображений сопряженные с ними лучи пересекутся в сопря-
сопряженной точке О . Примем эти лучи за координатные оси в пространствах
предметов и изображений. Ясно, что координатные оси одной координатной
системы будут изображаться координатными осями другой координатной
системы. При этом без потери общности можно принять, что одноименные
оси являются сопряженными. Так как изображение происходит с постоян-
постоянным увеличением п/п , то при надлежащем выборе положительных направ-
направлений координатных осей координаты сопряженных точек будут связаны
соотношениями
х =^х> у =^у' z =^z> B0Л)
справедливыми для всех точек пространства предметов и пространства изо-
изображений, а не только для окрестностей сопряженных точек О и О . Из них
непосредственно следует, что любая прямая изображается прямой. Таким
образом, при постоянных nun абсолютный инструмент является те-
телескопической системой.
Докажем теперь, что при постоянных nun абсолютный оптический
инструмент возможен только при п = п . Для доказательства заметим,
что линейное увеличение п/п не зависит от положения объекта. Чтобы
определить это увеличение, поместим бесконечно малый объект тангенци-
тангенциально на границе раздела сред. Тогда его изображение, возникающее как
при преломлении, так и при отражении, совместится с самим объектом.
Отсюда следует, что п/п = 1, и наше утверждение доказано. Таким об-
образом, показатели преломления сред должны быть одинаковы, и никакого
преломления не будет.
Остается исследовать только отражение. По теореме Каратеодори оп-
оптическая длина луча между сопряженными точками не зависит от поло-

20
ОБ АБСОЛЮТНЫХ ОПТИЧЕСКИХ ИНСТРУМЕНТАХ
137
жения объекта. Поместим точечный объект на границе раздела сред. Его
изображение получится в той же точке. Поэтому оптическая длина луча
между объектом и его изображением должна равняться нулю, независимо
от положения объекта. При преломлении, когда оптические длины лучей
на всех участках сохраняют знаки, это было бы возможно только тогда,
когда изображение совпадает с самим объектом. Но в этом случае, как мы
видели, никакого преломления нет, и об изображении можно говорить лишь
условно. Однако при отражении, если изображение получается мнимым, оп-
оптические длины лучей на разных участках могут иметь противоположные
знаки. Тогда возможен и нетривиальный случай, когда объект и его изо-
изображение находятся в разных местах, хотя оптические длины лучей между
ними и обращаются в нуль. При этом формулы B0.1) переходят в
х' = х, у' = у, z=z. B0.2)
Такой случай осуществляется в плоском зеркале или в системе плоских
зеркал. Это единственный абсолютный оптический инструмент, возможный
при постоянных п и п .
3. Нетривиальные абсолютные оптические инструменты^ дающие
изображения с увеличением^ отличным от единицы, возможны только с
использованием неоднородных сред и криволинейных лучей. Первый пример
такого инструмента был приведен Максвеллом. В дальнейшем были приве-
приведены и другие примеры. Максвелл назвал свой инструмент «рыбьим гла-
глазом», хотя никакого сходства с глазом рыбы у него нет. Более того, «рыбий
глаз» Максвелла вообще трудно назвать инструментом в обычном смысле
этого слова. Действительно, он представляет собой неограниченную неод-
неоднородную среду, показатель преломления которой меняется в пространстве
таким образом, что любой луч в этой среде имеет форму окружности. К
идее «рыбьего глаза» естественнее всего прийти с помощью геометрическо-
геометрического построения, называемого стереографической проекцией.
Такая проекция осуществляется следующим образом. Возьмем сферу S,
через центр которой проведем координатную плоскость XY (рис. 77). Пусть
Рис. 77
N — точка пересечения этой сферы с осью Z. Соединим точку N с точкой К
сферы прямой NK и продолжим эту прямую до пересечения с плоскостью
XY в точке Р. Точка Р и называется стереографической проекцией точки К
на плоскость XY. Легко показать, что координаты ж, г/, z точки К связаны

138
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
с координатами ?, rj соотношениями
х
С = а , 4 = а-
,е
¦ 1] —а
B0.3)
B0.4)
ж = Za 79Н—Г^—9' У = ^а ——¦———-, 5
где а — радиус сферы S.
Каждая окружность сферы S при стереографической проекции преоб-
преобразуется в окружность плоскости XY и обратно. В самом деле, плоскость
Ах + By + Cz + D = 0 пересекает сферу S по окружности. Если в уравнение
этой плоскости подставить значения координат B0.4), то получится урав-
уравнение второй степени, в котором будет отсутствовать член с произведением
, р уд у
?ту, а квадраты ? и tj войдут только в комбинации ?
есть уравнение окружности.
. Такое уравнение
Пусть da = л/dx2 + dy2 + dz2 — элемент длины на сфере S. При стерео-
стереографической проекции он отобразится элементом длины ds = л/d^2 + df]2
на плоскости XY. Пользуясь формулами B0.4), нетрудно показать, что эти
элементы связаны соотношением
da = 2 ds, B0.5)
1 +(г/аJ
где г = ? -\- г] . Кривая кратчайшей длины, проведенная на какой-либо
поверхности между двумя точками, называется геодезической линией этой
поверхности. Для сферы геодези™
ческими линиями являются дуги
больших кругов. Возьмем на сфе-
сфере S любые диаметрально про-
противоположные точки K(xo,yo,zo)
и К1 (—жо, —г/о, —zo). Пусть Р и
Р' — их стереографические проек-
проекции на плоскость XY. Через пря-
прямую, соединяющую точки К и К\
можно провести бесконечное мно-
множество плоскостей, пересекающих
сферу S вдоль больших кругов,
проходящих через эти точки. При
стереографической проекции эти
большие круги изобразятся окруж-
окружностями, соединяющими точки Р
и Р1 (рис. 78). Вдоль этих окруж-
окружностей интеграл J ds/{l + г2/а2)
принимает одно и то же значение,
Рис. 78 Как это непосредственно видно из
соотношения B0.5).
Вообразим теперь сферически симметричную среду с центром в начале
координат О, показатель преломления которой определяется выражением
где по — постоянная, а г — расстояние от начала координат. Тогда опти-
оптические длины всех окружностей между точками РиР, изображенных на
рис. 78, будут одинаковыми. Отсюда следует, что все эти окружности будут
совпадать со световыми лучами, исходящими из точки Р и сходящимися в

§ 21 ГЛАЗ И ЗРЕНИЕ 139
точке Р'. Одна из этих окружностей вырождается в прямую, соединяющую
точки Р и Р!. Она получается в результате стереографической проекции
большого круга, лежащего в плоскости NKK . Начало координат О лежит
в той же плоскости, а следовательно, и на прямой РР . Вообще говоря, его
положение не совпадает с серединой отрезка РР'. Исключение составляет
только случай, когда диаметрально противоположные точки К ш К1 сферы
S лежат в координатной плоскости XY. В этом случае большой круг, лежа-
лежащий в той же плоскости, совпадает со своей стереографической проекцией,
а потому радиус кривизны светового луча будет равен радиусу сферы S,
т.е. а.
Ввиду шаровой симметрии все плоскости, проходящие через центр О,
эквивалентны. Поэтому луч, исходящий из точки Р, пройдет через сопря-
сопряженную точку Р;, независимо от того, лежит он в координатной плоскости
XY или не лежит. Кроме того, приведенные нами рассуждения применимы
для любой пары диаметрально противоположных точек К и К и соответ-
соответствующей им пары сопряженных точек Р и Pf.
Таким образом, получается следующий результат. Все лучи, выходя™
щие из любой точки среды Р, описав окружности, собираются в другой
точке Р , т.е. точка Р является стигматическим изображением точки Р в
широких пучках лучей. Иными словами, среда с показателем преломления
B0.6) обладает свойствами абсолютного оптического инструмента. Она и
была названа Максвеллом «рыбьим глазом».
§ 21. Глаз и зрение
1. На рис. 79 приведен горизонтальный разрез правого гла-
глаза человека (вид сверху). Глазное яблоко заключено в плотную
белую непрозрачную оболочку ww, называемую склерой. Через
заднюю стенку склеры проходит глазной нерв е и кровеносные
сосуды. Передняя часть склеры переходит в прозрачную рого-
роговую оболочку, или роговицу h, более выпуклую, чем склера. Тол-
Толщина склеры от 0,4 до 1,1 мм, роговицы — около 0,5 мм. За рого-
роговицей следуют передняя глазная камера а, хрусталик I, задняя
глазная камера gl. Эти части вместе с роговицей составляют
оптическую систему глаза, дающую при преломлении лучей
оптические изображения предметов. Толщина передней глазной
камеры, а также хрусталика около 3,6 мм. Передняя глазная
камера заполнена прозрачной жидкостью, называемой водяни-
водянистой влагой, задняя — прозрачным студенистым веществом, на™
зываемым стекловидным телом. Показатели преломления обе-
обеих этих сред практически одинаковы и равны 1,336. Показатель
преломления роговой оболочки равен 1,376.
Внутренняя поверхность склеры покрыта сосудистой обо-
лочкой (толщиной около 0,4 мм), содержащей разветвления кро™
веносных сосудов, питающих глаз. Спереди она переходит в
утолщенную часть si, содержащую кольцевидную ресничную
мышцу ии, и далее в радужную оболочку И, не одинаково окра™
шенную у различных людей и определяющую «цвет глаз». По-

140 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
середине радужной оболочки имеется круглое отверстие, назы-
называемое зрачком глаза^ которое выполняет ролв апертурной диа-
диафрагмы. Изображение этого отверстия, даваемое расположен-
расположенными перед ним водянистой влагой и роговицей, играет роль
входного, а изображение, даваемое хрусталиком и стекловид-
стекловидным телом, — выходного зрачков глаза. Оба они практически
совпадают с настоящим зрачком. В зависимости от яркости све-
света зрачок может рефлекторно сужаться и расширяться посред-
посредством мышцы гш, с которой связана радужная оболочка. Диа-
Диаметр его может меняться примерно от 2 до 8 мм. Этим достига-
достигается ограничение поперечных размеров пучков света, поступаю-
поступающих в глаз.
Рис. 79
2. На внутренней поверхности сосудистой оболочки располо-
расположена светочувствительная сетчатая оболочка^ или сетчатка
(ретина), состоящая главным образом из радиально расходя-
расходящихся разветвлений зрительного нерва е, входящего во внутрен-
внутреннюю полость глаза несколько сбоку от линии прямого зрения
АВ, ближе к носовой полости. Около точки s толщина сетчатки
составляет 0,24),22 мм; к периферии она непрерывно уменьша-
уменьшается. Оптическая система глаза дает изображение предметов на
сетчатке, где оно вызывает зрительные раздражения, передава-
передаваемые в мозг по нервным волокнам.
Недалеко от точки s, где начинаются разветвления зритель-
зрительного нерва, со стороны виска, находится так называемое эюел-
тое пятно / (горизонтальный поперечник 1—3 мм, вертикаль-
вертикальный 0,8 мм). В его центральной части (размером ^0,3 мм по
горизонтали и ^0,2 мм по вертикали) имеется углубление, на-

§ 21 ГЛАЗ И ЗРЕНИЕ 141
зываемое центральной ямкой. Здесь толщина сетчатки не пре-
вышает 0,08-0,1 мм. Желтое пятно и в особенности централь-
центральная ямка являются наиболее чувствительными местами сетчат-
сетчатки (при дневном зрении). Изображение рассматриваемой точки
пространства всегда приводится к середине центральной ямки.
Прямая, проходящая через эту точку и заднюю узловую точку
глаза, вместе с параллельной ей прямой, проходящей через пе-
переднюю узловую точку, определяет так называемую линию пря~
мого зрения. Она не совсем совпадает с осью симметрии гла-
глаза^ так как преломляющие поверхности глаза не вполне симмет-
симметричны и центрированы. Ось симметрии глаза можно провести
в некотором смысле только условно. Обычно ее проводят через
крайнюю, наиболее выступающую точку выпуклой поверхности
роговицы (несколько выше точки А на рис. 79) и через центр
зрачка. Она встречает заднюю стенку глаза где-то между точ-
точками / и s, образуя с линией прямого зрения АВ угол около 5°.
3. Хрусталик I представляет собой прозрачное бесцветное
тело, напоминающее двояковыпуклую линзу, передняя поверх-
поверхность которой менее выпукла, чем задняя. Он состоит из сло-
слоев различной плотности, имеющих волокнистое строение. На-
Наружный слой мягкий и почти студенистый; ядро же более твер-
твердое и вполне упругое. Показатель преломления наружного слоя
хрусталика 1,405, средних слоев — около 1,429, ядра — 1,454.
Мышца гш, рефлекторно напрягаясь или расслабляясь, может
менять кривизну его поверхностей, главным образом передней.
Этим осуществляется аккомодация, т.е. изменение оптической
силы глаза, позволяющее фокусировать изображения на сетчат-
сетчатке. Так как деформация хрусталика может происходить толь-
только в определенных пределах, то для всякого глаза существуют
определенные границы, в пределах которых глаз может отчет-
отчетливо видеть предметы. Эти границы определяют так называе-
называемую область аккомодации глаза. Наиболее отдаленная грани-
граница, которую глаз может видеть отчетливо при вполне ослаблен-
ослабленной мышце, называется дальней, а ближайшая граница, кото-
которую он способен отчетливо видеть при максимальном напряже-
напряжении мышцы, — ближней точкой ясного видения. В ненапряжен-
ненапряженном состоянии нормальный глаз аккомодирован на рассмотре-
рассмотрение бесконечно удаленных предметов, т.е. он собирает парал-
параллельные лучи в точке сетчатки. Таким образом, дальняя точка
ясного видения для нормального глаза находится в бесконечно-
бесконечности. В возрасте до десяти лет ближняя точка нормального глаза
лежит впереди на расстоянии 7-8 см от глаза. К 30 годам это
расстояние увеличивается примерно до 15 см, к 40-45 годам —
до 25 см.
Приближая рассматриваемый предмет к глазу, мы увели-
увеличиваем угол зрения, а с ним и размеры изображения на сет-

142 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
чатке. Это позволяет рассмотреть более мелкие детали. Однако
при максимально возможном приближении усиливается напря-
напряжение мышцы, деформирующей хрусталик. Работа глаза стано-
становится утомительной. В случае нормального глаза оптимальное
расстояние для чтения и письма составляет около 25 см. Это
расстояние для нормального глаза и принимается условно за
расстояние ясного зрения. При необходимости рассмотреть (в
течение ограниченного времени) более мелкие детали его можно
уменьшить, оставаясь в пределах области аккомодации глаза.
4. У близорукого глаза оба предела ясного видения находят-
находятся ближе, а ближний предел дальнозоркого глаза — дальше, чем
у нормального глаза. Дальний предел дальнозоркого глаза все-
всегда отрицателен, т.е. дальняя точка ясного видения находится не
спереди, а позади глаза. Такой глаз в ненапряженном состоянии
может собирать на сетчатке только сходящиеся пучки лучей.
При сильной дальнозоркости и ближний предел ясного зрения
может сделаться отрицательным. У близорукого глаза в нена-
ненапряженном состоянии параллельные лучи сходятся перед, а у
дальнозоркого — за сетчаткой.
Близорукость может быть обусловлена большей, а дально-
дальнозоркость — меньшей длиной глаза по сравнению с длиной нор-
нормального глаза. Отступления длины глаза от нормальной да™
лее в пределах одного миллиметра уже могут приводить к за-
заметной близорукости или дальнозоркости. Эти, а также другие
недостатки глаза могут возникать из-за неправильных значе™
ний кривизны преломляющих поверхностей хрусталика и рого-
роговицы, несимметричности этих поверхностей, неправильного по-
положения хрусталика и пр.
Термин «дальнозоркий» очень неудачен, так как с ним ас-
ассоциируется ошибочное представление, что дальнозоркость яко-
якобы способствует отчетливо видеть далекие предметы. Никакими
преимуществами перед нормальным глазом дальнозоркий глаз
не обладает, так как вся область перед глазом, отчетливо ви-
видимая дальнозорким глазом, отчетливо видна и нормальным
глазом. Но область между ближними точками ясного видения
дальнозоркого и нормального глаза недоступна для отчетливого
рассматривания дальнозорким глазом. Близорукому глазу, на™
против, недоступна область, лежащая за дальней точкой ясного
видения нормального глаза1).
) У близорукого глаза есть по крайней мере то преимущество, что он
может выявить более мелкие детали, приближая рассматриваемый пред™
мет на меньшие расстояния, чем это возможно для нормального глаза. У
дальнозоркого глаза аналогичное преимущество появилось бы, если бы воз-
возникла необходимость рассматривать мнимые изображения, образующиеся
с задней стороны глаза.

§ 21 ГЛАЗ И ЗРЕНИЕ 143
Как уже отмечено выше, с возрастом (в основном из™
за уплотнения хрусталика, теряющего способность достаточно
сжиматься) ближняя точка ясного видения удаляется от глаза.
Для нормального глаза это удаление к 50 годам составляет око™
ло 50 см. Читать на таком расстоянии уже трудно. В дальней-
дальнейшем указанная точка уходит еще дальше, удаляется в бесконеч-
ность и к 60-65 годам перескакивает на противоположную сто-
сторону глаза. Затем она начинает приближаться к нему, но уже с
противоположной стороны. Это явление называется старческой
дальнозоркостью.
Дальнозоркость устраняется применением очков с положи-
положительными (т.е. собирающими), а близорукость — с отрицатель-
отрицательными (т.е. рассеивающими) стеклами. Положительные стекла
приближают, а отрицательные отдаляют ближнюю точку ясно-
ясного видения.
5. Систематические измерения привели к установлению
средних значений всех параметров нормального глаза. Сово-
Совокупность этих значений определяет так называемый схемати-
ческий глаз.
В табл. 3 приведены эти параметры, как они были определе-
определены Гульстрандом. Так как показатели преломления пространств
предметов [п = 1) и изображений (nf = 1,336) различны, то
переднее / и заднее /; фокусные расстояния не совпадают по
величине (/'// — —1,336). Задняя узловая точка К1 расположе-
расположена внутри глаза на расстоянии / от заднего фокуса F1', т.е. от
сетчатой оболочки (см. рис. 43). Если линейный размер предме-
предмета равен I, то он виден из точки нахождения глаза под углом
зрения а = 1/L. Поэтому линейный размер изображения на сет-
сетчатке будет I1 = fa = fl/L, или при рассматривании удаленных
предметов «17'а мм.
6. Сетчатка глаза имеет весьма сложное строение. Схемати-
Схематический разрез ее приведен на рис. 80 а (предполагается, что свет
падает сверху). Сетчатка состоит из нескольких слоев нервных
клеток различного типа и назначения. В последнем слое нахо-
находятся светочувствительные рецепторные клетки — палочки
и колбочки (рис. 80 6"). В них свет вызывает первичные раздра-
раздражения, превращающиеся в электрические импульсы, которые
по волокнам зрительного нерва передаются в кору головного
мозга. Общая длина палочки 0,06—0,08 мм, колбочки — около
0,035 мм. Число колбочек в глазу достигает 7 миллионов, пало-
палочек — до 130 миллионов. Периферия сетчатки заполнена почти
исключительно палочками. Число колбочек на единицу площа-
площади возрастает по мере приближения к желтому пятну, достигая
максимума в его середине. Число колбочек на площади желтого
пятна 13-15 тысяч. В его центральной части, в пределах кру-

144
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ТаблицаЗ
Схематический нормальный глаз по Гульстранду
(Все длины — в миллиметрах, все расстояния — от вершины роговой
оболочки)
Расстояние до задней поверхности роговицы
Расстояние до передней поверхности хрусталика
Расстояние до задней поверхности хрусталика
Радиус передней поверхности роговицы
Радиус задней поверхности роговицы
Радиус передней поверхности хрусталика
Радиус задней поверхности хрусталика
Оптическая сила глаза в диоптриях
Расстояние до передней главной плоскости
Расстояние до задней главной плоскости
Расстояние до переднего фокуса
Расстояние до заднего фокуса
Переднее фокусное расстояние
Заднее фокусное расстояние
Расстояние до центральной ямки
Расстояние до входного зрачка
Расстояние до выходного зрачка
Увеличение в зрачках
Расстояние до ближней точки
При
расслаб-
расслабленной
глазной
мышце
При
макси™
мальном
напря-
напряжении
мышцы
0,5
3,6
3,2
7,2
7,7
6,8
10
-6
58,64
1,348
1,602
-15,707
24,387
17,055
-22,785
5,33
-5,33
70,57
1,772
2,086
-12,397
21,016
14,169
-18,930
24
3,047
3,667
0,909
2,668
3,212
0,941
102,3
га радиуса ^0,2 мм, палочек нет, есть одни только колбочки.
Число их здесь достигает 180 тысяч на квадратном миллиметре,
так что среднее расстояние между центрами соседних колбочек
^0,0025 мм.
В том месте, где внутрь глаза входит глазной нерв, т.е. во™
круг точки s на рис. 79, на сетчатке нет ни палочек, ни колбочек.
Это место называется слепым пятном. Его легко обнаружить,
закрыв левый глаз и смотря правым на крестик рис. 81. Если

21
ГЛАЗ И ЗРЕНИЕ
145
глаз приближать к рисунку, то на расстоянии 15-17 см кружок
становится невидимым. Это получается тогда, когда изображе-
изображение кружка попадает на слепое пятно.
Рис. 80
Палочки обладают значительно большей чувствительностью
к свету, чем колбочки. Ночью и в сумерки (при освещенности
меньше 0,01 лк) зритель™
ное ощущение вызыва™
ется за счет раздраже™ _
ния одних только пало™
чек. Зато колбочки спо™ ""
собны различать цвета^
а палочки этой способно™
Рис. 81
стью не обладают. Практически цветное зрение начинается с
освещенностей «1 лк. При освещенностях выше ID2 — ID3 лк
зрение осуществляется почти исключительно колбочками.

146 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Детали предмета различаются наиболее отчетливо, когда его
изображение получается на желтом пятне и в особенности на
центральной ямке сетчатки. Это — так называемое фовеальное
зрение, в отличие от периферического зрения, при котором изо™
бражение предмета получается вдали от центральной ямки. При
периферическом зрении человек видит предметы значительно
менее четко, различая в них мало деталей. Благодаря наличию
на периферии в небольшом количестве колбочек, при перифе-
периферическом зрении ощущение цветов имеет место, но только при
условии, что яркость света достаточно велика, чтобы его вос-
воспринимали колбочки.
7. Две близкие светящиеся точки глаз воспринимает раздель-
раздельно, а не как одну слившуюся точку только при условии, что уг-
угловое расстояние между этими точками не меньше определен-
определенного предела. Этот предел называется разрешаемым угловым
расстоянием^ а его обратная величина — разрешающей способ-
способностью или остротой зрения глаза. За единицу остроты зрения
врачи принимают остроту зрения такого глаза, который разре-
разрешает угол в одну угловую минуту. Это — в среднем острота
зрения нормального глаза.
Острота зрения максимальна, когда изображение приходит-
приходится на центральную ямку сетчатки. Здесь плотность расположе-
расположения колбочек максимальна, а каждая колбочка соединена с от-
отдельным волокном зрительного нерва (число этих волокон —
несколько миллионов). Мозг реагирует на раздражение каждой
колбочки. Когда изображения двух близких светящихся точек
приходятся на одну и ту же колбочку, эти точки действуют как
одна светящаяся точка. В этом случае разрешения не получает-
получается. Для разрешения необходимо, чтобы изображения этих двух
точек приходились на разные колбочки. На периферии плот-
плотность распределения светочувствительных рецепторов — колбо-
колбочек и палочек — меньше, а каждое волокно зрительного нерва
соединено с большим числом этих рецепторов. Вот почему мак-
максимальная разрешающая способность глаза получается при фо-
веальном зрении, когда изображение получается на центральной
ямке сетчатки. Зрение же при помощи палочек предназначено
не для повышения разрешающей способности глаза, а для уве-
увеличения его чувствительности в условиях работы при слабой
освещенности. Для этого выгодно, как это и есть на самом деле,
чтобы с каждым волокном зрительного нерва была соединена не
одна палочка, а большая группа их. От этого усилится сигнал,
передаваемый по этому волокну.
С изложенной точки зрения разрешаемое угловое расстоя-
расстояние глаза д'в равно углу, под которым видно из задней узловой
точки глаза среднее расстояние ёх между двумя соседними кол-
колбочками на центральной ямке, т.е. 5$ = Sx/f, где / — переднее

§ 21 ГЛАЗ И ЗРЕНИЕ 147
фокусное расстояние. Подставив числа, приведенные выше, по™
лучим 5$ « 30/;. И действительно, наблюдения показали, что
для нормального глаза 6$ несколько меньше одной угловой ми™
нуты. Приведенная оценка совпадает с той, какая получается на
основе дифракционных соображений (см. § 56).
Поле зрения, соответствующее желтому пятну, невелико. На
это пятно одновременно может проектироваться картина с уг™
ловыми размерами около 6° по горизонтальному направлению и
около 4° по вертикальному. Поле зрения центральной ямки еще
меньше — около 1° по горизонтали и вертикали. Такая огра-
ограниченность поля ясного зрения компенсируется, однако, тем,
что живой глаз обладает способностью быстро поворачивать-
поворачиваться в глазной впадине, за очень короткое время обегая все точ-
точки видимой поверхности рассматриваемого большого предмета.
Благодаря этому поле ясного зрения глаза расширяется прибли-
приблизительно до 150° по горизонтали и 120° по вертикали. Вместе с
тем отмеченная подвижность глаза позволяет быстро концен-
трировать внимание на наиболее важных деталях предмета.
8. Глазу присущи все аберрации обычных оптических систем:
и геометрические, и хроматические, и дифракционные. Одна™
ко геометрические и хроматические аберрации очень мало за-
заметны, так как глаз использует особые средства снижения их
вредного действия. Теперь выяснено, что колбочки имеют фор-
форму волноводов. Устройство каждого волновода таково, что лу-
лучи, проходящие через периферийную зону зрачка, воздействуют
на колбочку слабее центральных лучей. В глазу используются
асферические преломляющие поверхности, а хрусталик пред™
ставляет собой линзу, показатель преломления которой непре™
рывно возрастает к центру. Это приводит к концентрации света
преимущественно вблизи центров кружков рассеяния. Поэтому
при не очень ярком освещении края кружков рассеяния мало ин™
тенсивны. При ярком же освещении зрачок глаза сильно сужен,
а от этого кружок рассеяния уменьшается еще сильнее. Все это
ослабляет сферическую аберрацию и кому. Астигматизм косых
пучков и дисторсия почти незаметны, так как при подвижно-
подвижности глаза изображение каждой точки бессознательно приводит™
ся в наиболее выгодное место сетчатки — центральную ямку.
Искривление поверхности изображения компенсируется сфери™
ческой формой сетчатки. Хроматическая аберрация почти неза™
метна, ввиду чувствительности сетчатки только к сравнительно
узкой части спектра.
9. Остановимся теперь схематически на теории цветного зре-
зрения Юнга-Гельмгольца A821-1894), которая лучше других тео-
теорий согласуется с наблюдаемыми фактами. Она исходит из того
экспериментально установленного факта, что ощущение любого
цвета можно получить смешением спектрально чистых излуче-

148 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ний красного, зеленого и сине-голубого цветов. На этом осно-
основании теория предполагает, что в глазу есть только три ти-
типа светочувствительных приемников. Они отличаются друг от
друга областями спектральной чувствительности. Красный свет
воздействует преимущественно на приемники первого типа, зе-
зеленый — второго, сине-голубой — третьего. Сложением из луче™
ний таких трех цветов в различных количествах можно полу-
получить любую комбинацию возбуждений всех трех приемников, а
это физиологически эквивалентно получению любого цветово-
цветового ощущения. Еще не установлено, имеются ли приемники всех
трех типов в каждой колбочке или существуют три различных
типа колбочек.
Встречаются люди (более 1% среди мужчин и около 0,1%
среди женщин), зрение которых характеризуется отсутствием
приемников одного из трех указанных типов. Они называют-
называются дихроматами. Дихромат не различает цвета всех излучений,
которые для людей с нормальным зрением различаются по сте-
пени возбуждения приемника, недостающего у дихромата. Еще
реже (примерно раз на миллион людей) встречаются монохро-
маты, у которых есть приемники только одного типа. Такие
люди совсем не различают цвета.
10. Чувствительность глаза к излучениям различных длин
волн характеризуется кривой видности. На этой кривой по оси
абсцисс откладывается длина волны, а по оси ординат — вид-
ность Ух, т.е. величина, обратная энергетической мощности из-
излучений, которые при оценке глазом воспринимаются как оди-
наково яркие. Визуальное сравнение яркостей излучений да-
далеких друг от друга длин волн затруднительно. Поэтому для
построения кривой видности обычно применяют метод малых
ступеней, т.е. сравнивают попарно по видимой яркости излуче-
излучения столь близких длин волн, что разница в цвете не затруд-
затрудняет такое сравнение. Несмотря на субъективность этого мето-
метода, воспроизводимость результатов достаточно хороша, а кри-
кривые видности для различных людей не сильно отличаются друг
от друга.
Кривая видности среднего нормального глаза при дневном
зрении, утвержденная Международной осветительной комисси-
комиссией, приведена на рис. 82. Она имеет максимум в желто-зеленой
части спектра при А = 555 нм, условно принимаемый за едини™
цу. При сумеречном зрении, когда работает только палочковый
аппарат, кривая видности сохраняет свой общий вид, но смеща-
смещается в сторону коротких волн с максимумом около 510 нм. При
этом область максимальной чувствительности сетчатки смеща-
смещается на 10—-20 ° в сторону от центральной ямки.
Еще в 1825 г. Пуркинье A787-1869) наблюдал, что излучения
различного цвета, воспринимаемые глазом как одинаково яркие,

21
ГЛАЗ И ЗРЕНИЕ
149
меняют свою видимую яркость не одинаково, если их ослаблять
в одно и то же число раз. Яркость излучений с большей дли-
длиной волны уменьшается быстрее, чем с более короткой длиной
волны. Если ограничить поле зрения, чтобы оно не превосхо-
превосходило 1,5°, и сконцентрировать сравниваемые излучения в пре-
пределах центральной ямки, то свет будет восприниматься только
колбочками. Исследования показали, что в этом случае явление
400 450
600
700 К нм
Рис. 82
Пуркинье не наблюдается. Все это хорошо согласуется с двой-
двойным механизмом восприятия света: посредством колбочек и по™
средством палочек, которым соответствуют различные кривые
видности.
11. Область, доступная зрительному восприятию глаза, ко™
нечно, не обрывается резко на длинах волн 400 и 760 нм. При
А = 400 нм видность Fa примерно в 2500 раз, а при А = 760 нм —
в 20 000 раз меньше, чем в максимуме. В условиях темновой
адаптации глаз может видеть в очень слабой степени интенсив™
ные инфракрасные лучи с длинами волн до 950, а ультрафиоле-
ультрафиолетовые — до 300 нм.
Границы видимой области, а также сама форма кривой вид™
ности человеческого глаза не случайны. Глаз сформировался
в процессе длительной эволюции, приспособившись к условиям
освещения земных предметов солнечным светом, а также к усло-
условиям сумеречного и ночного освещения. На эту мысль наводит
уже то обстоятельство, что на видимую область спектра прихо-
приходится более 40 % энергии излучения Солнца, хотя она и занимает
интервал менее одной октавы. Далее, солнечный спектр вбли™
зи поверхности Земли практически обрывается на длине волны
290 нм. Более короткие волны задерживаются слоем озона в ат™
мосфере. Было бы биологически нецелесообразно, если бы глаз
обладал способностью принимать излучение с длинами волн ко™
роче 290 нм.

150 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Более того, глаз должен защитить себя от ультрафиолето-
ультрафиолетовых лучей. Они в большинстве случаев химически разлагают
органические вещества и могут убивать живые микроорганизмы
и клетки. Особенно вредно попадание ультрафиолетовых лучей
на сетчатку глаза. Чувствительность сетчатки к ультрафиолето-
ультрафиолетовым лучам довольно велика и, как показал СИ. Вавилов, имеет
резкий максимум при А = 380 нм. Однако от длинноволновых
ультрафиолетовых лучей B90 < А < 400 нм), пропускаемых
земной атмосферой, глаз защищен собственными средствами.
Такие лучи сильно поглощаются внутри глаза, особенно в хру-
хрусталике, и лишь ничтожная доля их доходит до сетчатки. С этим
и связан сильный спад кривой чувствительности глаза на гра-
границе и в области ультрафиолета. При хирургическом удалении
хрусталика, если только глаз продолжает функционировать, его
чувствительность к ультрафиолетовым лучам заметно повыша-
повышается х).
Высокая чувствительность к инфракрасному излучению, ес-
если бы глаз обладал таковой, была бы не только нецелесообразна,
но и сделала бы невозможной работу глаза в условиях солнеч-
солнечного освещения. Причина этого — в тепловом излучении гла-
глаза. При низкой температуре глаза C10 К) все его тепловое из-
излучение приходится на инфракрасную область. Мощность, из-
излучаемую 1 см2 стенки глаза внутрь глазной полости, нетруд-
нетрудно оценить, пользуясь законом Стефана—Больцмана (см. § 115).
Она составляет около 0,105 Вт/см2. Общая внутренняя поверх-
поверхность глазной полости «17 см , так что полная мощность из-
излучения глаза внутрь глазной полости будет «1,7 Вт. Оценим
теперь мощность прямого солнечного излучения, попадающего
через зрачок глаза, пользуясь значением солнечной постоянной
@,139 Вт/см2), приведенным в задаче к § 5. Получим ОДЗЭтгг2^
« 0,017 Вт (радиус г зрачка глаза принят равным 2 мм). Эта
величина примерно в 100 раз меньше мощности собственного
теплового излучения глаза. Если бы чувствительность глаза в
инфракрасной области спектра была столь же велика, что и в
желто-зеленой, то собственное тепловое инфракрасное излуче-
излучение глаза затмило бы не только рассеянное излучение неба, но
и прямой солнечный свет. Работа глаза как органа зрения стала
х) Ультрафиолетовые лучи, попадая в глаз, вызывают его флуоресцен-
флуоресценцию, преобразуясь в синеватый свет, воспринимаемый сетчаткой. Такое
косвенное воздействие ультрафиолета проявляется, например, в следующем
опыте. Если посмотреть на мощную ртутную кварцевую лампу, излучаю-
излучающую ультрафиолет, через специальное темное стекло, задерживающее ви-
видимые, но пропускающее ультрафиолетовые лучи, то благодаря флуорес-
флуоресценции внутри глаза окружающий воздух покажется наполненным синева-
синеватым туманом, напоминающим табачный дым.

§ 21 ГЛАЗ И ЗРЕНИЕ 151
бы абсолютно невозможной. В этом, по мнению СИ. Вавилова
A891-1951), одна из причин, почему нет зрения в инфракрасных
лучах. Другая причина заключается в малости энергии инфра-
инфракрасных квантов света. Процесс зрения должен начинаться либо
химическими, либо фотоэлектрическими действиями, а они вы-
вызываются отдельными квантами света и не могут происходить,
если энергия кванта меньше некоторого минимального предела.
12. Для возбуждения светочувствительных рецепторов необ-
необходимо, чтобы они поглощали свет. Как правило, чувствитель-
чувствительность рецептора к свету определенной длины волны должна
быть тем выше, чем сильнее поглощает он свет той же дли™
ны волны. Это обстоятельство уже давно побудило исследова-
исследователей искать в сетчатке глаза светочувствительные пигмен-
пигменты. Такой пигмент (родопсин^ или зрительный пурпур) был об-
обнаружен в палочках человеческого глаза. Это — вещество ро-
розоватого цвета, разлагающееся (выцветающее) на свету и снова
восстанавливающееся в темноте. Спектральная кривая поглоще-
поглощения родопсина близка к сумеречной кривой видности. Извлечь
светочувствительные пигменты из колбочек сетчатки человека
пока не удалось, хотя наблюдения живого глаза через зрачок,
по-видимому, подтверждают, что в центральной части сетчатки
имеются пигменты, выцветающие на свету.
Глаз человека обладает способностью приспосабливаться к
освещенностям, меняющимся в необычайно широких пределах.
Прямые солнечные лучи создают освещенности ~ 105 лк, а в
полной темноте глаз способен отличать от темноты предметы
с освещенностью 10~6 лк. Глаз способен воспринимать свето-
световые потоки в интервале 10^17-10^5 Вт. Процесс приспособле-
приспособления глаза к тому или иному уровню яркости света называется
адаптацией. При повышении яркости происходит световая^ при
понижении — темновая адаптация. При переходе от яркости
~ 1000 кд/м2 к темноте чувствительность глаза возрастает в
течение часа примерно в 10 миллионов раз. Сначала чувстви-
чувствительность возрастает очень быстро, затем ее рост замедляет-
замедляется и после часа пребывания в темноте уровень чувствительно™
сти почти не меняется. Световая адаптация происходит много
быстрее. При средних яркостях она продолжается 1-3 минуты.
Изменение чувствительности к световому восприятию в столь
широких пределах свойственно палочкам. Темновая адаптация
колбочек происходит значительно быстрее, причем чувствитель-
чувствительность колбочек возрастает всего в 10-100 раз. В состоянии мак-
максимальной световой адаптации глаз может без вреда переносить
сравнительно большие яркости (например, яркости белых ма-
матовых поверхностей, освещаемых прямым солнечным светом).
При больших яркостях необходима искусственная защита гла-

152 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
за. Так, наблюдение солнечного затмения можно вести только
через закопченное стекло пли другой сильно ослабляющий све-
светофильтр. При пребывании на ледниках и в горах на большой
высоте необходимо пользоваться темными или цветными очка™
ми. Здесь очки необходимы также для защиты от ультрафиоле-
ультрафиолетовых лучей, достигающих на больших высотах значительных
интенсивностей и вредно действующих на глаз.
Адаптация глаза происходит автоматически, но механизм ее
выяснен не совсем. При резком увеличении яркости света по™
чти мгновенно сужается зрачок. При уменьшении яркости до
прежнего уровня зрачок вновь расширяется. Происходит так лее
изменение чувствительности самих рецепторов. Долгое время
считалось, что такое изменение чувствительности связано с из-
изменением количества родопсина в палочках. Когда яркость све-
света повышается, родопсин выцветает, и чувствительность глаза
понижается. При уменьшении яркости происходит восстановле-
восстановление родопсина и связанное с этим повышение чувствительно™
сти. Однако работы последнего времени поставили под сомне-
сомнение эту точку зрения. Наблюдения показали, что чувствитель-
чувствительность глаза к свету меняется всего сильнее, когда уменьшение
родопсина еще очень невелико. Наоборот, когда концентрация
родопсина резко уменьшается, чувствительность уменьшается
незначительно. С изложенной точки зрения это понять трудно.
Возможно, играет роль перестройка корковых центров головно-
головного мозга, воспринимающих свет, т.е. повышение и понижение их
чувствительности.
§ 22. Фотометрические понмтим и единицы
1. Излучение в пространстве или в прозрачной однородной
среде можно характеризовать интенсивностью, спектральным
составом и поляризацией. При этом надо иметь в виду, что пуч-
пучки строго параллельных лучей являются идеализацией и нико-
никогда не встречаются в действительности. Конечной энергией мо-
могут обладать лучи, направления которых заполняют конечные
телесные углы, хотя величина этих углов и может быть очень
малой.
Заметив это, возьмем в поле излучения произвольную малую
площадку ds. Она должна быть настолько мала, чтобы харак-
характеристики излучения практически не изменялись при переходе
от одной точки площадки к другой. В то же время линейные
размеры площадки ds должны быть велики по сравнению с дли-
длинами волн излучения, чтобы к излучению можно было приме-
применять понятия и законы геометрической оптики. Проведем че-
через площадку ds лучи, заполняющие какой-то телесный угол О.

§ 22 ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ЕДИНИЦЫ 153
Энергия, переносимая этими лучами в единицу времени, назы-
называется лучистым потоком Ф, проходящим через площадку ds в
телесный угол О. Если телесный угол cffi бесконечно мал, а пло-
площадка ds перпендикулярна к его оси, то лучистый поток можно
представить в виде dФ = IdsdQ. Величина / есть лучистый
поток, отнесенный к единичной площадке, перпендикулярной к
излучению, и к единице телесного угла. Она называется интен-
интенсивностью лучистого потока, или лучистостью излучения в
направлении оси телесного угла сШ. Если нормаль к площадке
ds образует с направлением излучения угол #, то
d<S> = I ds cos fidu,
так как лучистые потоки через площадку ds и ее проекцию
ds± = ds cos #, перпендикулярную к излучению, одинаковы. Для
краткости проекцию ds cos $ называют видимой величиной пло-
площадки ds, если ее рассматривать под углом t? к нормали. При вы-
выполнении принципа суперпозиции лучи, проходящие в данный
момент времени через определенную точку среды, совершенно
независимы друг от друга. Поэтому для полной характеристики
состояния излучения необходимо указать интенсивность лучи™
стого потока по любому из бесчисленного множества направле-
направлений, проходящих через каждую точку пространства. При этом
надо учитывать отдельно каждое из двух прямо противополож™
ных направлений, поскольку независимость лучей имеет место
и для этих направлений.
Энергия, проходящая за время dt через площадку ds в те™
лесный угол d?l, представится выражением I ds dtldt cos t?. При
этом время dt, хотя оно и входит в виде дифференциала, долж-
должно быть все же велико по сравнению с периодами колебаний
волн, входящих в излучение. Иначе значение мощности, напри™
мер, монохроматического излучения, как энергии, отнесенной к
единице времени, при малом интервале dt, в течение которого
измеряется энергия, зависело бы от фазы колебаний в момент
начала измерения. Независимость имела бы место только тогда,
когда время dt случайно содержало бы целое число колебаний.
Если же dt велико по сравнению с периодами колебаний любых
волн, входящих в излучение, то измеренная мощность из луче™
ния практически не будет зависеть от выбора dt.
2. Объемной плотностью лучистой энергии называется
энергия, содержащаяся в единице объема пространства. Чтобы
выразить ее через интенсивность излучения /, возьмем сначала
малый конус лучей с телесным углом dQ при вершине (рис. 83).
Через площадку ds, перпендикулярную к излучению, за вре-
время dt проходит энергия Idsdudt. Если v — скорость распро-
распространения излучения, то за время dt эта энергия распростра™

154 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
нится на расстояние v dt и заполнит объем dsv dt, заштрихо-
заштрихованный на рис. 83. (Предполагается, что дисперсии нет, так что
скорость распространения энергии
совпадает с фазовой скоростью v.)
Разделив предыдущее выражение
на этот объем, найдем (I/v) dft —
плотность лучистой энергии, созда-
создаваемую рассматриваемым элемен™
рис> 83 тарным пучком лучей. Полная плот-
плотность лучистой энергии и найдется
интегрированием этого выражения по всем телесным углам:
и = - [ Idu, B2.1)
причем величина I может зависеть от направления лучей. Когда
/ одинакова по всем направлениям, то
и = Ш/v. B2.2)
3. Величины Ф, /, и можно подвергнуть спектральному раз-
разложению по частотам или длинам волн. Строго монохромати-
монохроматическое излучение, как и параллельные пучки лучей, никогда не
реализуется в действительности. Каждое излучение, обладаю™
щее конечной энергией, занимает конечный интервал частот
или длин волн. Например, величину и можно представить в виде
и
= juIJ(u)du= JUuj(uj)duj= fux(\)d\. B2.3)
Подынтегральные выражения u^du, u^jdu)^ u\d\ имеют смысл
объемной плотности лучистой энергии в спектральных интерва-
интервалах {y,v-\-dv), (cj, oj + do;), (A, A + dA) соответственно. Ради крат-
краткости эти термины обычно применяют к самим функциям uv{y),
иш(и)), и, опуская дифференциалы dz/, do;, d\, хотя это и не
совсем логично. При установлении связи между этими функци-
функциями надо, конечно, приравнивать друг другу дифференциалы
Ujjdu, uUJduj) uxdX^ поскольку они представляют в различных
формах одну и ту же величину, если только соответствие меж™
ду A, v и и) устанавливается соотношениями А = с/и = 2ттс/ш.
Таким путем находим
и„ = (Х2/с)их. B2.4)
Говоря о спектральном распределении, надо указывать, идет ли
речь о функции ии (распределение по частотам) или о функции
и\ (распределение по длинам волн). Так, в спектре излучения
Солнца функция uv имеет максимум в инфракрасной области
приблизительно при А = 880 нм, а функция и\ — в желто-
зеленой части приблизительно при А = 500 нм.

§ 22 ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ЕДИНИЦЫ 155
Далее, интенсивность излучения / в каждой точке простран-
пространства можно представить в виде суммы интенсивностей двух из-
излучений, линейно поляризованных во взаимно перпендикуляр-
перпендикулярных плоскостях. Однако для наших целей в этом пока нет необ™
ходимости.
4. Все приведенные энергетические характеристики излуче-
излучения измеряются в механических единицах, например по произ™
водимому ими тепловому действию. Так, в системе СИ лучистый
поток измеряется в ваттах (Вт), интенсивность излучения —
в ваттах на стерадиан-квадратный метр (Вт/ср-м2), объем-
объемная плотность лучистой энергии — в джоулях на кубический
метр (Дж/м3). Такие единицы применяются, например, в те-
теории теплового излучения. Однако в видимой области спектра
представляет интерес характеризовать излучение по зрительно-
зрительному или световому ощущению, оцениваемому по действию света
на глаз человека. Соответствующие характеристики и их едини-
единицы называются световыми, или фотометрическими, в отличие
от энергетических величин и единиц, о которых говорилось вы-
выше.
Световые измерения, конечно, содержат немалый элемент
субъективизма, поскольку световые впечатления, получаемые
различными людьми от одного и того же светового потока, не
совсем совпадают между собой. Когда указывают количествен-
количественные соотношения световых единиц с энергетическими, то при
этом имеют в виду не индивидуальный, а какой-то средний че-
человеческий глаз. Сами названия величин, характеризующих из-
излучение, при световых измерениях несколько изменяют. Вместо
лучистой энергии говорят о световой энергии, вместо лучисто-
лучистого потока — о световом потоке, вместо интенсивности излуче™
ния — об интенсивности света и т.п. Вообще, вместо энерге™
тических величин и единиц вводят световые или фотометри-
фотометрические величины и единицы. Мы не будем вводить для энерге™
тических и фотометрических величин различные обозначения,
так как в каждом отдельном случае будет ясно, в каком смысле
следует понимать ту или иную величину.
5. Силой света источника Jf в заданном направлении на-
называют световой поток, посылаемый им в этом направлении и
отнесенный к единице телесного угла. (Когда пользуются энер-
энергетическими единицами, то говорят об энергетической силе ис-
источника, измеряя эту величину в Вт/ср.) Обычно это понятие
относят к точечному источнику света, т.е. характеризуют им
источник на расстояниях, больших по сравнению с его линейны-
линейными размерами. Вообще говоря, величина Jf зависит от направле-
направления излучения. Световой поток, посылаемый точечным источ-
источником в телесный угол du, определяется выражением ёФ du

156
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Полный световой поток, исходящий от источника,
ф = /jfdfi,
причем интеграл берется по полному телесному углу 4тг. Вели-
Величина J"o = Ф/Dтг) называется средней сферической силой света
источника.
Единицей силы света источника в системе СИ служит кан-
дела (старое название — свеча). Это — основная фотометриче-
фотометрическая единица. Она осуществляется с помощью светового эталона
в виде абсолютно черно™
го тела при температуре
затвердевания чистой пла-
платины B046,6 К) и давлении
101325 Па. Устройство эта-
эталона показано на рис. 84
A — платина, 2 — трубочка
из плавленой окиси тория,
8 — сосуд из плавленой оки-
си тория, 4 — засыпка из
окиси тория, 5 — сосуд из
кварца). Нагрев и расплав-
расплавление платины производятся
токами высокой частоты.
Излучателем света служит
трубочка 2, стенки которой
по всей длине имеют одну и
ту же температуру, равную
температуре окружающей на-
нагретой платины. Кандела (кд)
есть сила света, излучаемого
Рис. 84
в направлении нормали с
1/60 см2 излучающей поверх-
поверхности указанного светового
эталона. До введения этого
эталона (он был введен с 1 января 1948 г.) единицей силы
света источника служила международная свеча (м. св.), равная
1,005 кд. Она осуществлялась специально изготовленными
электрическими лампочками.
Единица светового потока есть люмен (лм) — световой поток,
посылаемый источником в 1 канделу внутрь телесного угла в
1 стерадиан.
Лучистый поток, измеренный в ваттах, можно рассматри-
рассматривать и как световой поток, измеряя его в люменах. Световая
эффективность лучистого потока, или просто световая эффек-
эффективность, есть число люменов, соответствующее мощности в

§ 22 ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ЕДИНИЦЫ 157
один ватт (лм/Вт). Обратная величина (Вт/лм) называется ме-
механическим эквивалентом света. Из-за различной чувствитель-
чувствительности глаза к различным участкам спектра обе эти величины
зависят от длины волны Л. Принято приводить их значения для
Л = 555 нм, где чувствительность глаза максимальна. Для та-
такой длины волны эти величины по новейшим измерениям равны
соответственно:
625 лм/Вт и 0,00160 Вт/лм.
Пользуясь кривой видности среднего человеческого глаза, при-
приведенной на рис. 82, нетрудно найти значения этих величин для
любой длины волны видимого спектра излучения.
6. Из закона сохранения энергии следует, что полный све-
световой поток, посылаемый источником, не может быть увеличен
никакими отражающими и преломляющими устройствами, по
крайней мере пока они остаются неподвижными. Такие устрой-
устройства могут только перераспределять световые потоки по раз-
различным направлениям, что и осуществляется, например, про-
прожекторами. Если точечный источник света помещен в прозрач-
прозрачной однородной среде, то на любых расстояниях от него остается
постоянным не только полный поток Ф, испущенный источником
в какой-либо момент времени, но и световой поток dФ = jfdO в
пределах любого телесного угла dQ, исходящего из источника.
Ввиду того, что телесный угол dVt никак не связан с расстояни-
расстоянием г до источника, не будет зависеть от г и сила света источника
Jf. Интенсивность света / на расстоянии г найдется делением dФ
на площадь ds = r2 dQ перпендикулярного сечения рассматри-
рассматриваемого элементарного пучка лучей. Это дает
/=//г2, B2.5)
т.е. интенсивность света обратно пропорциональна квадрату
расстояния до точечного источника.
7. Световой поток, приходящийся на единицу площади осве-
освещаемой поверхности, называется освещенностью Е этой поверх-
поверхности. (При энергетических измерениях вместо этого термина
пользуются термином энергетическая освещенность, или облу-
облученность, единицей которой служит Вт/м2.) Пусть источник
точечный, а лучи падают под углом # к нормали к освещае-
освещаемой поверхности. Тогда dФ =j[dQ = jfdscos^/r2. Разделив на
площадь поверхности ds, получим
Е = 4 cost?. B2.6)
Таким образом, освещенность, создаваемая точечным источ-
источником в отсутствие поглощения, обратно пропорциональна
квадрату расстояния до него и прямо пропорциональна коси-
косинусу угла между направлением падающих лучей и нормалью к

158 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
освещаемой поверхности. Первая часть этого утверждения, а
также формула B2.5) называются законом обратных квадра-
квадратов. Единица освещенности есть люкс (лк) — освещенность,
создаваемая световым потоком в 1 люмен, равномерно распре-
распределенным по площади в 1м2. Освещенность в 1 лк создается
точечным источником силою в 1 кд на внутренней поверхно-
поверхности шара радиуса 1 м, если он помещен в центре этого шара и
излучает равномерно по всем направлениям.
Чтобы составить конкретное представление о величине люк-
люкса, приведем некоторые цифры. Освещенность от Солнца вне
земной атмосферы на среднем расстоянии Земли от Солнца
1,35-ID5 лк. Освещенность в одну™две десятых люкса создает но™
чью при безоблачном небе полная Луна. Освещенность, создава-
создаваемая молодой Луной или Луной на ущербе, порядка нескольких
сотых люкса. Безоблачное звездное небо создает ночью осве-
освещенность в тысячные доли люкса. Освещенность в десятиты-
десятитысячные доли люкса позволяет с трудом ориентироваться ночью.
При освещенности порядка одного люкса можно с трудом чи-
читать. Скорость чтения быстро нарастает при увеличении осве-
освещенности до 50 лк. При дальнейшем увеличении освещенности
до 100-150 лк она растет более медленно, а дальше этого предела
возрастание скорости чтения становится малоощутимым. Осве-
Освещенность 50 лк уже удовлетворительна для чтения и письма.
Инструкциями по охране труда установлены определенные нор-
нормы минимальной освещенности рабочих помещений. Освещен-
Освещенность рабочей поверхности (стола) ни для каких видов работ не
должна быть меньше 10 лк. При очень тонкой работе, связанной
с различением мелких деталей, черточек, букв, рисунков (угол
зрения меньше 2;), требуется освещенность не менее 200 лк. В
классах и аудиториях на столах учащихся и черных досках осве-
освещенность должна быть не менее 75 лк.
8. Для протяженных (не точечных) источников света вво-
вводится понятие поверхностной яркости, или просто яркости В.
(При энергетических измерениях вместо этого термина употреб-
употребляют термин энергетическая яркость и для нее вводят единицу
Вт/(ср-м2).) Понятие поверхностной яркости неприменимо для
точечных источников, т.е. источников, угловые размеры кото-
которых лежат за пределами разрешающей способности глаза или
оптического инструмента, которым он вооружен. Возьмем на
поверхности излучающего источника малую площадку ds и про-
проведем от нее световой луч под углом t? к ее нормали. При рас-
рассмотрении излучения в этом направлении более существенна не
сама площадка ds, а ее видимая величина, т.е. ds cose (см. п. 1).
Яркостью поверхности в рассматриваемом направлении назы-
называется световой поток dФJ исходящий из площадки ds в этом
направлении, отнесенный к единице телесного угла и к единице

§ 22 ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ЕДИНИЦЫ 159
ее видимой величины:
В = аФ = d% B2 7)
dQ ds cos •& ds cos #'
где djjf = с?Ф/бШ — сила света площадки ds в том же направле-
направлении (рис. 85). Буква В снабжена индексом t?, так как яркость,
вообще говоря, зависит от угла i9, под кото™
рым рассматривается площадка ds.
Источники света, поверхностная яркость
которых В не зависит от направления излу-
излучения, называются источниками, подчиняю-
подчиняющимися закону Ламберта A728--1777). Для
таких источников, как видно из B2.7), си-
сила света djf элементарной площадки ds про-
пропорциональна cost?. Однородный светящий™
ся шар, подчиняющийся закону Ламберта,
кажется одинаково ярким в середине и по
краям. Такие наблюдения и привели Лам™ Рис- 85
берта к формулировке своего закона. В действительности от за-
закона Ламберта наблюдаются большие отступления.
В § 113 будет показано, что при температурном излучении
поверхность непрозрачного тела излучала бы по закону Лам™
берта, если бы коэффициент отражения света от этой поверх-
поверхности для каждой длины волны не зависел от угла падения.
Для гладких поверхностей, отражающих зеркально, это условие
не выполняется (см. § 65). Но для матовых поверхностей, от-
отражающих диффузно, оно может выполняться с той или иной
степенью приближения. Для таких поверхностей при темпера-
температурном излучении приближенно соблюдается закон Ламберта.
Он строго справедлив при температурном излучении абсолютно
черного тела. Матовые поверхности, например освещенная бе-
белая поверхность тела, покрытая окисью магния, или наружная
поверхность колпака из хорошего молочного стекла, освещенно™
го изнутри, являются источниками, довольно хорошо подчиняю-
подчиняющимися закону Ламберта. Однако к этим случаям вывод закона
Ламберта, приводимый в § 113, неприменим, так как в них речь
идет не о самосветящихся телах и температурном излучении, а
о телах, рассеивающих свет от посторонних источников.
Единицей яркости является кандела на квадратный метр
(кд/м2). Это — яркость плоской поверхности, сила света кото-
которой в перпендикулярном направлении составляет одну канделу
с каждого квадратного метра. Если при тех же условиях сила
света равна одной канделе с каждого квадратного сантиметра,
то соответствующая единица называется стильб (сб). Очевид-
Очевидно, 1 сб = 1 кд/см2 = 10 кд/м2. В табл. 4 приведены значения
яркости некоторых светящихся поверхностей.

160
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Таблица4
Источник света
Ночное безлунное небо
Полная Луна, видимая
сквозь атмосферу
Пламя обычной стеари-
стеариновой свечи
Ясное дневное небо
Газосветная лампа
Спираль газонаполнен-
газонаполненной лампы накаливания
Яркость,
кд/м
Около
Ы4
1 -103
2,5 • 103
1,5-104
5-Ю4
5-Ю6
Источник света
Кратер обычной электри-
электрической угольной дуги
Шаровая ртутная лампа
сверхвысокого давления
(СВДШ)
Солнце
Импульсная стробоско-
стробоскопическая лампа (ИСШ)
Яркость,
кд/м
1,5-108
1,2-1G9
1,5-109
МО11
9. Светимостью К называется полный световой поток, по™
сылаемый единицей светящейся поверхности в одну сторону, т.е.
в телесный угол Q = 2тг. Ее единица такая же, что и едини-
единица освещенности, т.е. лм/м . (При энергетическом рассмотре-
рассмотрении вместо этого термина употребляется энергетическая свети-
мостъ^ или излучателъностъ, а единицей служит Вт/м2.) Так
как световой поток с единицы поверхности в телесный угол dft
равен с1Ф = B§ cos i? dO, то
тг/2
К = J Вф cos # dU = 2тг J B^ cos i? sin i? dti. B2.8)
о
Для поверхностей, излучающих по закону Ламберта, яркость
В§ = В не зависит от угла i?, а потому в этом случае
К = жВ» B2.9)
10. Рассчитаем теперь освещенность, создаваемую протя-
протяженным источником света с известной поверхностной яркостью
Bv. Возьмем на поверхности источника бесконечно малую пло-
площадку ds (рис. 86). Пусть dsf — освещаемая площадка, г —
расстояние между площадками, # и §' — углы, составляемые
нормалями к площадкам с прямой MN, соединяющей их. Те-
Телесный угол, под которым из площадки ds видна площадка dsf,
равен ds1 cost?'/r2. В него площадка ds посылает световой поток
йф = B^ ds cos t? ds' cos $''/r2, или dФ = B§ du cos t9; ds'', где du =
= ds cos #/r2 — телесный угол, под которым из освещаемой пло-
площадки ds1 видна излучающая площадка ds. Разделив на ds1, най-
найдем освещенность dE площадки ds\ создаваемую потоком d^.

22
ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ЕДИНИЦЫ
161
Полная освещенность Е найдется интегрированием полученного
выражения по всей видимой поверхности источника:
E= I B^cos^' du. B2.10)
В качестве примера возьмем источник в виде равномерно све-
светящегося диска с поверхностной яркостью В§ = I?, не зависящей
от угла #. Освещаемую площадку dsf расположим на геометри™
ds
Рис. 86
Рис. 87
ческой оси диска перпендикулярно к ней (рис. 87). Полагая в
B2.10) dft = 2тг sin??'б?т?' и интегрируя, получим
Е = ттВ sin2 0,
B2.10)
где в — угол, составляемый крайним лучом MN с геометри-
геометрической осью диска. Формула B2.11) справедлива и для шара,
а также для источника произвольной формы, видимая граница
которого имеет форму окружности.
11. В нашу задачу не входит изложение методов измерения и
описание приборов, применяемых в фотометрии. Ограничимся
только схематическим описанием одного из наиболее совершен-
совершенных фотометров, построенных Луммером A860—1925) и Брод™
хуном. Наиболее существенной частью этого фотометра являет™
ся стеклянный кубик, состоящий из двух прямоугольных стек-
стеклянных призм А ж В (рис. 88). Гипотенузная плоскость приз™
мы А сошлифовывается под шаровую поверхность, так что от
этой плоскости остается только резко очерченный участок в ви™
де плоского круга. Затем призмы гипотенузными плоскостями
плотно прикладываются друг к другу (на оптический контакт).
Между сравниваемыми источниками света L\ и L^ ставится бе-
белый экран S, обе поверхности которого одинаково диффузно
рассеивают свет. Рассеянный свет отражается двумя одинако-
одинаковыми зеркалами S\ и *$2 на кубик фотометра. На призму А
попадает свет от источника Li, на призму В — от источника
L2. Из призмы А свет может попасть в зрительную трубу толь-
6 Д.В. Сивухин

162
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ко через плоский круг на ее гипотенузной плоскости. Наоборот,
свет из призмы В может попасть в ту же трубу только после
полного отражения от гипо-
гипотенузной поверхности этой
призмы, внешней по отноше-
отношению к тому же кругу. Тру™
ба сфокусирована для на-
наблюдения плоскости указан-
указанного круга. Наблюдатель ви-
видит два поля зрения раз-
различной яркости, граничащие
друг с другом вдоль окруж-
окружности этого круга. Передви-
Передвигая один из источников L\
или 1^2, добиваются исчезно-
исчезновения видимой границы меж-
между обоими полями, чтобы все
поле зрения получилось рав-
равномерно освещенным. Это
произойдет тогда, когда осве-
освещенности обеих сторон экра-
экрана S станут одинаковыми. Если г\ и г2 — расстояния (точечных)
источников L\ и L2 до экрана в этом положении, то для отно-
отношения сил света jfi и jfe этих источников по закону обратных
квадратов можно написать
(f 2
ф1 ri
Рис. 88
ЗАДАЧИ
1. Найти освещенность Е площадки, создаваемую бесконечной плоско-
плоскостью, излучающей свет по закону Ламберта с постоянной поверхностной
яркостью В. Площадка и плоскость параллельны между собой.
Ответ. Е = тгВ.
2. Вычислить освещенность Е на горизонтальной площадке, освещае-
освещаемой небесной полусферой, в предположении, что яркость неба В постоянна.
Ответ. Е = тгВ.
3. Найти освещенность, создаваемую однородным светящимся шаром
радиуса а на расстоянии R от его центра, если освещаемая площадка пер-
перпендикулярна к радиусу, а поверхность шара излучает по закону Ламбер-
та с поверхностной яркостью В. Показать, что в этих условиях на любых
расстояниях от центра шара строго выполняется закон обратных квадра-
квадратов, т.е. освещенность площадки меняется обратно пропорционально ква-
квадрату R.
Ответ. Е = тгВа2/112.
4. Найти освещенность, создаваемую равномерно светящимся диском
радиуса а на его геометрической оси, перпендикулярной к плоскости дис-
диска, если освещаемая поверхность перпендикулярна к этой оси и находится

§ 23 ЯРКОСТЬ И ОСВЕЩЕННОСТЬ ИЗОБРАЖЕНИЯ 163
на расстоянии R от центра диска. Диск излучает по закону Ламберта с по™
верхностной яркостью В. С какой относительной точностью будет выпол-
выполняться закон обратных квадратов, если диск рассматривать как точечный
источник света, помещенный в его центре?
Ответ. Е = тгВа2/(К2 + а2). Если a/R < 1, то
2 la2
Закон обратных квадратов выполняется с относительной точностью
a2/{2R2). При а/R ~ 1/10 эта точность будет около 1 %.
5. Предполагая, что излучение Солнца подчиняется закону Ламбер-
Ламберта, определить его поверхностную яркость В при наблюдении с поверх-
поверхности Земли (т.е. с учетом поглощения и рассеяния света земной атмосфе-
атмосферой), если освещенность поверхности Земли, создаваемая солнечными лу-
лучами при перпендикулярном падении в тех же условиях, — Е и 105 лк.
Средний телесный угол, под которым солнечный диск виден с Земли, О =
= б,8-1СГ5 ср.
Ответ. В = Е/п и 1,5 • 109 кд/м2.
§ 23. Мркость и освещенность оптического
изображения. Нормальное увеличение
1. Во всех дальнейших расчетах, если нет специальной ого-
оговорки, не будем учитывать потери света при отражении на гра-
ницах линз, призм и других отражающих поверхностях. Будем
также пренебрегать поглощением и рассеянием света. Потери
света на отражение довольно значительны. Так, для призмати-
ческого бинокля они составляют около 50% (см. § 67). С учетом
всех этих потерь яркость и освещенность изображения получи-
получились бы несколько меньше вычисленных. Сначала рассмотрим
случай, когда размеры предмета заметно превосходят предел
разрешения оптической системы. Тогда система дает геометри-
геометрически подобные изображе-
изображения, и можно ограничиться _
точностью геометрической ¦ ¦
оптики.
Допустим, что предмет
помещен на главной оптиче-
оптической оси центрированной си-
системы и имеет форму малой
площадки 5, перпендикуляр- Рис. 89 а
ной к этой оси (рис. 89 а).
Изображением площадки s будет какая-то другая площадка s1.
Обозначим через В§ яркость площадки s под углом $ к ее нор-
нормали, или (что то же) к главной оптической оси системы. Соот-
Соответствующую яркость изображения обозначим через В'^,. Соот-

164 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ветствие означает, что угол #, составляемый падающим лучом
с оптической осью системы, после выхода из нее переходит в #'.
Будем предполагать, что в образовании изображения участвуют
не только параксиальные, но и широкие пучки лучей, так что
должно выполняться условие синусов A8.1). Из него следует
sn2 sin2 & = s'n12 sin2 §'« B3.1)
Если условие синусов не выполняется, то все результаты, полу™
чаемые ниже, также сохраняют силу, но только для паракси-
параксиальных лучей. Возьмем теперь два конуса с общей вершиной на
площадке s, образующие которых составляют с главной оптиче™
ской осью углы $ и id + d'&. (На рис. 89 а указаны только сечения
этих конусов плоскостью рисунка.) Величина телесного угла, за-
заключенного между этими конусами, будет dVt = 27rsin#d#. Све-
товой поток, посылаемый площадкой s внутрь телесного угла
сШ, равен
ёФ = B§s cos # du = 2ttB^s sin & cos # M.
В пространстве изображений световой поток d<S> перейдет в по-
поток
пронизывающий площадку sf. При отсутствии потерь света
d<^> = dФr, т.е.
B§s sin $ cos # di9 = Вфг sf sin #; cos #; cfa?'.
Учтем теперь соотношение B3.1), дифференцирование которого
дает
sn2 sin # cos 1? d# = s;n/2 sin i?; cos i?; cfa?'.
В результате получим
чем и определяется яркость изобра^кения. Если показатели пре-
преломления пространств предметов и изображений одинаковы
(п = п;), то Вф, = 1?^, т.е. яркость изображения равна яркости
предмета. Как видно из вывода, одинаковость яркостей обуслов-
обусловлена тем, что увеличение площади изображения сопровождает-
сопровождается уменьшением в такое же число раз телесного угла, в котором
распространяется световой поток. Для источников света, под-
подчиняющихся закону Ламберта, В$ не зависит от угла $. В этом
случае нет смысла сохранять индексы i? и #;, так что можно
написать
Bf = (n'fnfB. B3.3)
2. Иначе ведет себя освещенность изображения, проеци-
проецирующегося на экран. В этом случае величина телесного угла,
в котором распространяются лучи после выхода из оптического

§ 23 ЯРКОСТЬ И ОСВЕЩЕННОСТЬ ИЗОБРАЖЕНИЯ 165
прибора, не играет роли. Существенны только площади изобра-
изображения и полный световой поток, концентрирующийся на этой
площади. При неизменном световом потоке освещенность будет
тем больше, чем меньше площадь изображения.
При количественном исследовании этого вопроса будем пред-
предполагать, что изображаемая площадка s имеет форму диска,
плоскость которого перпендикулярна к главной оптической оси,
и излучает свет по закону Ламберта. Если бы оптического при-
прибора не было, то освещенность экрана, согласно формуле B2.11),
была бы равна Eq = тгI? sin2 f9, где 20 — угол зрения, т.е. угол
между лучами, исходящими из диаметрально противоположных
точек площадки s и направленными к центру площадки s'. При
наличии оптического прибора угол схождения крайних лучей
с вершиной на площадке sf меняется и становится равным 26'.
Это есть угол между крайними лучами, идущими к центру пло-
площадки s' от диаметрально противоположных точек выходного
зрачка прибора. Полный световой поток через площадку s;, как
было показано выше, представляется интегралом
Ф; = 2tlBV J sin# cos §' d§' = tlBV sin2 в1\
а освещенность площадки sf будет Ф;/s', т.е.
Е = жВ1 sin2 9' = жВ {^Л sin2 0'. B3.4)
Если п = п;, то
А(^J. B3.5)
Ео
Эта формула показывает, что влияние оптического прибора на
освещенность изображения сводится к изменению угла меж-
между крайними лучами, исходящими из противоположных точек
предмета. Например, действие лупы как зажигательного стекла
(в отсутствие потерь света) эквивалентно приближению источ-
источника (Солнца) на такое расстояние, чтобы он был виден невоору-
невооруженным глазом под тем же углом зрения, как и входной зрачок
(свободное отверстие) лупы из ее главного фокуса.
Если изображение получается в главной фокальной плоско-
плоскости объектива (как в фотоаппарате), то в параксиальном при-
приближении sin б7 = D//B//), где D1 — диаметр выходного зрачка,
а /; — заднее фокусное расстояние объектива. Освещенность
изображения будет пропорциональна квадрату этого отноше-
отношения, а с ним и отношению Dfff, где D — диаметр входного зрач-
зрачка. Отношение D/f называется относительным отверстием^
а его квадрат (D/f) , определяющий освещенность изображе-
изображения, — светосилой объектива.

166 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
В иммерсионных микроскопах (см. § 18, п. 4) свет от конден-
конденсора, помещенного перед объективом, попадает в пространство,
заполненное жидкостью (иммерсией) с показателем преломле-
преломления п, в которой помещается предмет. Пусть 2i9q — угол (апер-
тура) между крайними направлениями лучей в конденсоре, ко-
которые попадают в микроскоп. Так как сам конденсор находится
в воздухе, то по закону преломления sIii^q = nsin#. Световой
поток пропорционален sin2 <9q, т.е. (n sin l9J. При одной и той же
апертуре 2в световой поток, попадающий в объектив, а с ним
и освещенность изображения пропорциональны квадрату пока™
зателя преломления п. Величину в sin 19, следуя Аббе, называ-
называют числовой апертурой. Таким образом, применение иммерсии
увеличивает освещенность изображения. Так как, однако, окон-
окончательное изображение получается в воздухе, то и при наличии
иммерсии его яркость может быть самое большее равна яркости
источника света.
3. Перейдем теперь к зрительной оценке поверхностной яр-
яркости предметов, т.е. оценке при наблюдении их глазом.
Отдельные элементы сетчатки — колбочки и группы пало-
палочек, соединенные с одним и тем же волокном зрительного нер-
нерва, — реагируют на световое раздражение независимо друг от
друга. Увеличение освещаемой поверхности сетчатки при сохра-
сохранении неизменной ее освещенности не усиливает интенсивно-
интенсивности светового раздражения отдельного элемента, а увеличивает
лишь число освещенных элементов. Если отвлечься от трудно
поддающихся учету различных физиологических и психологи-
психологических факторов, с которыми связаны, например, многочислен-
многочисленные обманы зрения, то следует сказать, что глаз судит о яркости
предмета не по общему световому потоку, попадающему в него,
а прежде всего по потоку, приходящемуся на единицу площади
сетчатки, т.е. по освещенности последней. Поэтому, если исклю-
исключить все субъективные факторы, то вопрос о зрительной оценке
яркости сведется к вопросу об освещенности сетчатки.
Освещенность сетчатки невооруженного глаза называется
естественной освещенностью. Она найдется по формуле B3.4),
в которой следует положить п = 1, если, как это обычно и бы-
бывает, рассматриваемый предмет находится в воздухе. Таким об-
образом,
E = 7rB(nfmn0fJ. B3.6)
Угол в1 есть угол, под которым из заднего фокуса глаза ви-
виден диаметр его выходного зрачка. В формулу B3.6) совсем не
входит расстояние до предмета. При неизменном зрачке глаза
освещенность сетчатки Е не зависит от этого расстояния, а
определяется только поверхностной яркостью предмета. Вот
почему одинаковые фонари, находящиеся на разных расстояни-

§ 23 ЯРКОСТЬ И ОСВЕЩЕННОСТЬ ИЗОБРАЖЕНИЯ 167
ях от нас, кажутся нам одинаково яркими (если, конечно, прене-
брежимо малы потери света при распространении его от фонаря
до глаза).
Допустим теперь, что глаз вооружен, т.е. наблюдение ведется
через зрительную трубу (телескоп) или микроскоп. В этом слу-
чае оптический прибор и глаз следует рассматривать как еди-
единую оптическую систему, к которой применимы формулы B3.5)
и B3.6). Однако величина угла вг может измениться. Смотреть
в оптический прибор следует так, чтобы плоскость выходного
зрачка прибора совмещалась с плоскостью входного зрачка гла-
глаза. Только тогда поле зрения будет резко очерчено. Угол в1 опре-
определяется тем из зрачков, который сильнее диафрагмирует свето-
вые лучи. Если входной зрачок глаза меньше выходного зрачка
прибора, то угол в1 определяется зрачком глаза. В этом случае
получается естественная освещенность сетчатки, т.е. сетчатка
будет освещена так же, как и при отсутствии прибора (если, ко-
конечно, пренебречь дополнительными потерями света, вносимы-
вносимыми оптическим прибором). Если же входной зрачок глаза боль™
ше выходного зрачка прибора, то угол в1 определится зрачком
прибора. В этом случае освещенность сетчатки будет меньше
естественной. Будем непрерывно увеличивать выходной зрачок
прибора, начиная с очень малых размеров. Сначала освещен-
освещенность сетчатки будет возрастать пропорционально площади вы-
выходного (а, следовательно, и входного) зрачка (в параксиальном
приближении). Когда выходной зрачок прибора сделается рав-
равным входному зрачку глаза, освещенность Е достигнет макси-
максимума, а затем будет оставаться постоянной.
4. Изложенными соображениями руководствуются при вы-
выборе рационального увеличения зрительных труб, телескопов,
биноклей и микроскопов. Нормальным или равнозрачковым уве-
увеличением таких приборов называют такое увеличение, когда вы-
выходной зрачок прибора равен входному зрачку глаза.
В телескопе, как и во всякой зрительной трубе, апертурной
диафрагмой и входным зрачком служит свободное отверстие
объектива. Объектив дает изображение в своей задней фокаль-
фокальной плоскости, которая одновременно является передней фо-
фокальной плоскостью окуляра. При этом условии изображение
в телескопе получается на бесконечности, и его отчетливо бу-
будет видеть нормальный глаз в ненапряженном состоянии. Все
параллельные пучки лучей после прохождения через телескоп
остаются параллельными, т.е. телескоп является телескопиче-
телескопической оптической системой. Меняется только ширина пучков. Ес-
Если падающие лучи параллельны главной оптической оси, то ши-
ширина пучка равна диаметру объектива D. Увеличение телескопа
N есть отношение угла, под которым виден малый предмет в

168 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
телескоп, к углу, под которым он был бы виден, если бы рас™
сматривался невооруженным глазом. Как было показано в § 11
(п. 10), для телескопических систем такое увеличение равно от™
ношению ширины падающего пучка параллельных лучей к ши-
ширине выходящего пучка. В телескопе ширина выходящего пучка
равна диаметру выходного зрачка D1. При нормальном увели™
чении D1 = d, где d — диаметр входного зрачка глаза. Таким
образом, нормальное увеличение телескопа определяется выра-
выражением
iVH0PM = D/d. B3.7)
Диаметр d зрачка глаза не остается постоянным, а зависит от яр™
кости. Увеличение, равнозрачковое в дневных условиях, оказы™
вается слишком большим при наблюдении в сумерки и ночью. В
последних случаях требуются трубы с большим выходным зрач™
ком, т.е. либо с малым увеличением, либо, что гораздо лучше, с
большим объективом.
Освещенность изображения не зависит от увеличения, ее™
ли оно меньше нормального. Увеличения меньше нормально™
го нецелесообразны, так как при этом используется только цен™
тральная часть объектива; периферийные лучи, достаточно уда™
ленные от оптической оси, задерживаются радужной оболочкой
и не попадают в зрачок глаза. Нормальное увеличение есть мак™
симальное увеличение, при котором освещенность изображения
еще максимальна. При таком увеличении объектив используется
полностью. Поэтому окуляры к зрительным трубам подбирают
так, чтобы они давали нормальное увеличение.
В некоторых случаях имеет смысл применять увеличения,
превосходящие нормальное в 2-4 раза, несмотря на то, что это
связано с значительным уменьшением освещенности изображе™
ния (соответственно в 4-—16 раз). Дело в том, что разрешаемый
предел глаза 30-60/; соответствует случаю, когда изображение
получается на центральной ямке желтого пятна. На периферии
разрешаемый предел больше. Он увеличивается также при дли-
длительной работе и усталости глаза. В этих условиях выгоднее
пойти на некоторое уменьшение освещенности, чтобы получить
большие увеличения и возможность различать более мелкие де™
тали предметов. Однако далеко идти в этом направлении неце™
лесообразно из-за уменьшения освещенности и поля зрения.
При JV-кратном увеличении угловые размеры поля зрения
на местности уменьшаются в JV, а его площадь в N2 раз. Поэто-
Поэтому в биноклях предпочитают увеличение меньше нормального.
Этим достигается большее поле зрения и облегчается нахожде-
нахождение нужного объекта на местности. Бинокли рассчитывают для
сравнительно широких выходных зрачков (в пределах 3-5 мм).
Так, полевые бинокли с диаметром объектива 3 см имеют 6- или

§ 23 ЯРКОСТЬ И ОСВЕЩЕННОСТЬ ИЗОБРАЖЕНИЯ 169
8-кратные увеличения (диаметр выходного зрачка соответствен-
соответственно 5 и 3,75 мм).
5. Зрительные трубы, как обнаружил еще М.В. Ломоносов
A711-1765), улучшают видимость изображений предметов при
слабых освещенностях, например ночью. Конечно, освещенность
изображений при этом не только не увеличивается, но даже
уменьшается из-за неизбежных потерь света на отражение от
поверхностей линз и поглощение в стекле. Однако при слабых
освещенностях сильно уменьшается разрешающая способность
глаза. Ночью, когда освещенность падает до десятитысячных
долей люкса, угол, разрешаемый глазом, возрастает с ~ V до
~ 1°. Зрительные трубы увеличивают угол зрения, а потому их
применение способствует различению контуров и крупных де™
талей предметов, даже если они неразличимы невооруженным
глазом.
В трубах, предназначенных для ночных наблюдений, число
линз должно быть минимальным, а сами линзы должны быть
простыми, чтобы максимально уменьшить потери света на от™
ражение. Увеличение трубы должно быть как можно ближе к
нормальному, чтобы использовать весь световой поток, падаю-
падающий на объектив. Конечно, нормальное увеличение определяет™
ся размерами зрачка глаза в ночных условиях F—8 мм).
6. Найдем теперь нормальное увеличение микроскопа. Уве-
Увеличением микроскопа N называется отношение угла <р', под ко-
которым виден малый объект в микроскоп, к углу (/?, под которым
он был бы виден невооруженным глазом, если бы был помещен
от него на расстоянии ясного зрения L (см. § 21, п. 3). Если
у — линейный размер рассматриваемого объекта, то ip = y/L.
Поместим этот объект у = АВ в передней апланатической точке
В
Рис. 896"
объектива (рис. 89 6); для упрощения рисунка сложные объек-
объектив и окуляр изображены тонкими линзами, это не отражается
на общности выводов и результатов). Его изображение А1 В1 =
= у1 получится в задней апланатической точке. Так как угол в'
всегда мал, то его синус молено заменить самим углом, записав
условие синусов в виде nysinO = у'в'. Так же, как и в телескопе,
изображение у1 должно получаться в передней фокальной плос-

170 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
кости окуляра. Если / — фокусное расстояние окуляра, то 2/<9;
будет шириной выходящего пучка лучей. При нормальном уве-
увеличении эта ширина должна быть равна диаметру d входного
зрачка глаза, т.е.
2f.
Но у = Lip, у1 = /У, так что у/у1 = L(p/(f(pf) = L/(Nf). Под-
Подставляя это в предыдущее соотношение, получим г)
iVHOpM = 2Ln^. B3.8)
Нормальное увеличение для микроскопа еще в большей сте-
степени есть величина субъективная, чем для телескопа, так как
оно зависит от двух параметров глаза: диаметра зрачка d и рас-
расстояния ясного зрения L. Характеризуя увеличение микроско-
микроскопа, обычно полагают d = 2 мм, L = 250 мм. Для сухих систем
(п = 1) верхний предел числовой апертуры n sin 19 составляет 1,
для иммерсионных 1,5. Соответствующие нормальные увеличе-
увеличения будут N = 250 и N = 375. По тем же соображениям, что
и для телескопа, от этих значений можно несколько отступать
в большую сторону, но не более чем в 2-4 раза. Таким обра-
образом, в лучших безиммерсионных микроскопах верхний предел
увеличения можно принять равным 1000, а в иммерсионных —
1500. Большие увеличения не только бесполезны, но и вредны.
К этому вопросу, а также к вопросу об увеличении телескопа мы
вернемся в § 56 и разберем его с новой точки зрения — в свя-
связи с разрешающей способностью этих приборов, определяемой
волновой природой света.
7. В заключение рассмотрим случай, когда размеры объекта
меньше предела разрешения оптической системы. Такой случай
типичен при наблюдении звезд невооруженным глазом и в теле-
телескоп. В этом случае оптическое изображение не передает формы
предмета, а представляет собой дифракционный кружок, окру-
окруженный темными и светлыми кольцами (см. рис. 180, с. 316),
причем почти весь свет сконцентрирован в центральном круж-
кружке. Назначение телескопа при наблюдении звезд состоит не в
том, чтобы различать детали рассматриваемого объекта (они на-
находятся за пределами его разрешающей способности), а в том,
чтобы увеличить световой поток^ попадающий в глаз наблю-
) Очень часто при выводе формулы B3.8) вводят ненужное предполо-
предположение, что изображение в микроскопе получается на расстоянии ясного
зрения L от глаза. На самом деле это может быть и не так. Справедливость
формулы B3.8) никак не связана с тем, на каком расстоянии от глаза по-
получается изображение в микроскопе. Величина L входит в формулу B3.8)
совсем по другой причине, как это видно из нашего вывода.

§ 23 ЯРКОСТЬ И ОСВЕЩЕННОСТЬ ИЗОБРАЖЕНИЯ 171
дателя, и тем самым обнаруживать все более и более слабые
звезды.
Применять увеличение меньше нормального не имеет смыс-
смысла, так как при этом будет использоваться не весь объектив.
Поэтому в дальнейшем достаточно ограничиться случаем, когда
диаметр выходного зрачка телескопа D1 меньше или равен диа™
метру входного зрачка глаза d (Df ^ d). Тогда размер дифрак-
дифракционного кружка будет определяться величиной D'. Как будет
показано в теории дифракции (см. § 55), диаметр дифракцион-
дифракционного кружка будет обратно пропорционален D;, а его площадь
обратно пропорциональна D12. Световой поток, попадающий в
глаз, Ф ~ D2, где D — диаметр объектива, а освещенность ди-
дифракционного кружка на сетчатке
Е? №
Вводя увеличение телескопа N = D/D1, получим
Е - DA/N2,
Видимость звезды определяется не только освещенностью
дифракционного кружка на сетчатке, но и освещенностью окру-
окружающего фона. Освещенность фона Ефоп определяется ярко-
яркостью В неба. Ее можно найти по формуле B3.6), в которой под
в1 теперь следует понимать угол, под которым из заднего фоку-
фокуса глаза виден диаметр D1 выходного зрачка телескопа. Таким
образом, Ефош ~ BD'2 = BD2/N2, и следовательно,
Е/Ефош - ЖJ. B3.9)
Эта формула объясняет, почему в телескоп звезды видны и
днем.
ЗАДАЧА
С помощью собирательной линзы можно зажечь папиросу, фокусируя
на ней прямой солнечный свет. Можно ли, взяв линзу достаточных размеров
(например, объектив большого астрономического телескопа), сделать то же
самое, используя свет полной Луны?
Решение. Для простоты будем считать, что излучение Солнца
подчиняется закону Ламберта. Прямые солнечные лучи, падающие на Зем-
Землю перпендикулярно, создают на ней освещенность Ее = 7i\Bsin2#c, где
В — поверхностная яркость Солнца, а §с — угловой размер его. Из по-
повседневного опыта известно, что такой освещенности для воспламенения
папиросы недостаточно. Средняя освещенность поверхности Земли будет
в тг раз меньше, т.е. Ее = В$т2 §с- Если пренебречь поглощением и рас-
рассеянием света, то действие линзы сводится просто к увеличению видимых
угловых размеров Солнца. Однако максимальная освещенность не может
быть больше ж В.

172 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
Так как диаметр лунной орбиты пренебрежимо мал по сравнению с
расстоянием до Солнца, то средняя освещенность поверхности Луны бу-
будет такой же, как и у Земли, т.е. Ее = В sin $c- Если Луна как источ-
источник света подчиняется закону Ламберта, то ее поверхностная яркость будет
В sin2 #c- Лучи от Луны, падая на поверхность Земли перпендикулярно, со-
создают освещенность В sin2 #c sin2 $л, где #л — угловой радиус Луны. Эта
освещенность много меньше, чем Bsm2$c- Поэтому, каковы бы ни были
размеры линзы, с помощью лунного света воспламенить папиросу нельзя.
§ 24. Оптические инструменты
1. Л у п а. Лупа, как и микроскоп, дает увеличенные изобра-
изображения предметов, находящихся на небольших расстояниях от
глаза. Увеличение N лупы (и микроскопа) определяется как от-
отношение угла, под которым виден (малый) предмет через лупу,
к углу, под которым он был бы виден невооруженным глазом,
если бы был помещен от глаза на расстоянии ясного зрения L
(см. § 23, п. 6). Можно также сказать, что увеличение лупы (и
микроскопа) есть отношение линейных размеров изображения
предмета на сетчатке при рассматривании его в лупу к линей-
линейным размерам изображения того же предмета на сетчатке, когда
он рассматривается невооруженным глазом с расстояния ясного
зрения. При увеличениях, не превосходящих 5, в качестве лупы
обычно применяется простая собирательная линза, при больших
увеличениях — система, состоящая из таких линз.
При вычислении увеличения лупы будем для общности рас™
сматривать ее как сложную центрированную систему и восполь-
воспользуемся уравнениями такой системы в форме Ньютона A1.16) и
A1.17). Предмет помещается между передним главным фокусом
и передней главной плоскостью лупы. Лупа дает прямое мнимое
изображение его. Пусть X, Y — координаты точки предмета
относительно переднего главного фокуса, X1', Y1 — координа-
координаты соответствующей точки изображения относительно заднего
главного фокуса, а — координата глаза (точнее — его передней
узловой точки) относительно того же заднего главного фокуса.
Расстояние глаза от изображения будет а — X1. Глаз через лупу
видит отрезок Y1 под углом ipr = Y1 /(а ~~ Xf). Соответствую-
Соответствующий отрезок предмета Y был бы виден невооруженным глазом
с расстояния ясного зрения под углом (р = Y/L. Отсюда
Ч> Y a-X"
или на основании A1.17)
N _ / L _X' L
Ха-Х' f а-Х1'

§ 24 ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ 173
Для лупы п = в;, а потому /' = —/. Следовательно, с учетом
(иле)
N = 7TS77- B41)
Если глаз помещен в заднем главном фокусе лупы (а = 0),
то N = L//. То же самое увеличение получится, если предмет
поместить в переднем главном фокусе лупы. В этом случае глаз
должен быть аккомодирован на бесконечность, т.е. для нормаль-
нормального глаза аккомодирующая мышца должна находиться в рас™
слабленном состоянии. Однако многие наблюдатели ведут на-
наблюдение с напряжением аккомодирующей мышцы, чтобы изо™
бражение получалось на привычном для них расстоянии ясного
зрения. В этом случае а — X1 = L, так что
jyj X а — L L — а
Если лупой является тонкая линза, вплотную придвинутая к
глазу, то а = —/, так что N = (L/f) + 1. Рассматриваемый
предмет всегда помещается вблизи переднего главного фокуса,
т.е. a/f <С 1. Величина аХ/'f также меньше единицы. Поэтому,
независимо от способа наблюдения, увеличение лупы практиче-
практически всегда определяется формулой
N = L/f. B4.2)
Подставляя сюда N = ipf/ip = {(p1 /Y)L1 получим Lp1 = Y/f.
Размер изображения предмета на сетчатке глаза равен fTJI(pf =
= (/гл/f)Y, где /гл — переднее фокусное расстояние глаза (см.
§ 21, п. 5). Этот размер определяется практически только фо-
фокусным расстоянием лупы /, так как от глаза к глазу величина
/гл меняется незначительно. Таким образом, действие лупы эк-
эквивалентно уменьшению расстояния ясного зрения с величины
L до /; лупа как бы приближает рассматриваемый предмет к
глазу на фокусное расстояние /.
Теоретически увеличение лупы ничем не ограничено. Так,
лупа с фокусным расстоянием / = 0,25 мм имела бы увеличе-
увеличение N = 1000. Изготовление луп со столь малыми значениями
/, а следовательно и с малыми диаметрами линз, очень затруд™
нительно, а пользование ими крайне неудобно. Кроме того, для
таких луп очень велики геометрические и хроматические абер™
рации. Поэтому увеличение луп, применяемых в действительно-
действительности, в настоящее время не превосходит 40. Большие увеличения
получаются с помощью микроскопа.
Изображение в лупе формируется с помощью сравнительно
тонких пучков лучей, выделяемых зрачком глаза. Поэтому тре-
требования к лупам в отношении исправления аберраций не очень

174 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
жесткие. Хроматическая аберрация положения при малых уве-
увеличениях не исправляется вовсе. При более значительных увели-
увеличениях и необходимости иметь большое поле зрения надо испра-
исправить кому и астигматизм, а также хроматическую разность уве-
увеличений. Астигматизм исправляется для главных лучей, прохо-
проходящих через центр вращения глаза.
Простая плоско-выпуклая линза дает хорошие изображения
вплоть до восьмикратного увеличения (т.е. когда ее фокусное
расстояние / не менее 3 см). Линза должна быть обращена к
глазу плоской стороной. В этом случае, так как предмет поме-
помещен вблизи фокуса лупы, преломление лучей происходит прак-
практически только на выпуклой поверхности лупы, а не распреде-
распределяется между обеими поверхностями ее. Это несколько увеличи-
увеличивает сферическую аберрацию. Зато в противоположном случае,
когда к глазу обращена выпуклая сторона лупы, значительно
увеличиваются аберрации изображений периферийных частей
предмета.
2.Микроскоп. Микроскоп состоит из двух собирающих
систем линз — объектива и окуляра^ расположенных на большом
расстоянии друг от друга. Они помещаются на концах трубки
(тубуса), которая обычно укрепляется вертикально на штативе
микроскопа, объектив ввинчивается в нее снизу, а окуляр встав™
ляется сверху. Предмет помещается на малом расстоянии перед
передним фокусом объектива. Объектив дает его действитель-
действительное обратное увеличенное изображение, которое рассматривает-
рассматривается через окуляр, действующий как лупа. Пусть Д и /{ — главные
фокусные расстояния объектива, /2 и f2 — окуляра. Тогда фо-
фокусные расстояния / и /; всей оптической системы микроскопа
определятся формулами A2.3), т.е.
/ = -^, /' = ^, B4.3)
где А — оптический интервал между объективом и окуляром.
В применении к микроскопу величину А называют оптической
длиной тубуса. Ее следует отличать от механической длины ту-
буса Т. Последняя обычно составляет 160 или 190 мм; величина
А зависит от объектива и окуляра и, как правило, больше Т.
Для безиммерсионного микроскопа его увеличение, согласно
формуле B4.2), будет
n=7=-jj <244)
(при наличии иммерсии с показателем преломления п это вы-
выражение надо умножить на п). Величину N можно представить
в виде N = N\N2j где N\ = L/fi — увеличение объектива как
лупы, N2 = A//2 — добавочное увеличение, обусловленное оку-

§ 24 ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ 175
ляром. При заданном общем увеличении N для устранения оши-
ошибок в изображении осевых точек выгоднее делать большим iVi,
а для уменьшения ошибок всего поля зрения выгоднее приме™
нять большие N2. По этой причине, а также по соображениям,
указанным в п. 1, требуемое общее увеличение N не получают
с помощью одних только сильных объективов или одних только
сильных окуляров, а идут на компромисс, комбинируя и те и
другие.
В микроскопе величина А, а также фокусные расстояния Д
и /2 положительны. Фокусное расстояние / всей системы, а с
ним и увеличение N отрицательны. Это значит, что изображе-
изображение, получаемое в микроскопе, обратное. Говоря в дальнейшем
об увеличении микроскопа, мы обычно будем иметь в виду аб-
абсолютное значение N.
Величина А обычно лежит в пределах 150—200 мм. Фокусное
расстояние f\ объектива при самых больших увеличениях его
A00-120) не меньше 1,5 мм, а окуляра — не меньше 8-10 мм. При
достаточно больших значениях А можно получить увеличение
до 2500-3000 раз без чрезмерного уменьшения f\ и /2. (Впрочем,
столь большие увеличения бесполезны, как это будет подробно
разобрано в § 56.)
Штатив микроскопа обычно имеет револьверное приспособ-
приспособление для смены объективов. Такое же приспособление может
применяться для смены окуляров. Это позволяет варьировать
увеличение микроскопа в широких пределах.
Со стороны предмета в микроскопе велики углы раскрытия,
а со стороны изображения — углы наклона лучей. Вследствие
этого у объектива особенно велики сферическая аберрация и ко™
ма, а у окуляра — астигматизм. Поэтому к объективу и окуляру
предъявляются различные требования.
3. Основные требования, предъявляемые к объективу микро-
микроскопа: 1) высокая числовая апертура; 2) исправление сфериче-
сферической аберрации для всего очень широкого пучка лучей; 3) вы-
выполнение условия синусов для того же пучка; 4) ахроматизация.
Ахроматизация состоит в выполнении условия синусов по мень-
меньшей мере для двух цветов, а также в получении через объектив
ахроматических действительных изображений предмета.
Всем этим требованиям в той или иной мере удается удо-
удовлетворить применением довольно сложных конструкций объ™
ективов, особенно при больших увеличениях. Наиболее совер-
совершенными объективами до настоящего времени являются апо-
апохроматы, разработанные и рассчитанные Аббе. Впервые апо-
апохромат Аббе был выпущен фирмой Цейсса в 1886 г. Это — им-
иммерсионный объектив, состоящий из 10 линз. Он изображен на
рис. 90 в увеличенном виде (примерно вдвое). Роль нижней (по-
(полусферической) линзы была выяснена в § 18 (п. 4). Поверхность

176
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
этой линзы погружена в масло, в котором помещен и предмет.
Эта линза обладает весьма сильной хроматической аберрацией,
уничтожаемой остальными линзами. Из этих остальных линз
рассеивающие изготовлены из различных сортов флинта, соби-
рающие — из крона. Аббе нашел, что, перемещая слегка неко-
некоторые из этих линз относительно других, можно достигнуть
почти полного уничтожения хроматической аберрации. Апохро-
Апохромат ахроматизован для трех и удовлетворяет условию синусов
для двух цветов спектра. Фокусное расстояние апохромата Аббе
/ = 2 мм, числовая апертура п slnf9 = 1,4, а геометро-оптические
качества таковы, что можно
считать фактически достиг-
достигнутыми границы разреша-
разрешающей способности микро-
микроскопа, определяемые вол™
новой природой света (см.
§ 56). Апохроматы применя-
ются во всех наиболее от-
Рис. 90
ветственных микроскопиче™
ских и микрофотографиче-
микрофотографических исследованиях.
Менее совершенными,
но более распространенны-
распространенными являются ахроматы,
т.е. объективы, ахрома-
тизованные для двух
~\ цветов спектра. Если удо-
удовлетвориться частичной
ахроматизацией объектива,
то надо совместить положе™
ния передних фокальных
точек для двух цветов (ахромативация положения). Иначе
положение изображения предмета, помещенного вблизи перед-
передней фокальной точки объектива, очень сильно менялось бы с
изменением цвета. Фокусные расстояния при этом остаются
неахроматизованными, т.е. неравными. Поэтому хроматическая
разность увеличений остается. Она исправляется применени-
применением особых окуляров, называемых компенсационными. Такие
окуляры всегда применяются и в апохроматах, так как у них
разность увеличений для лучей различного цвета исправлена
не вполне.
Вообще, ахроматизация положения, т.е. совмещение фоку-
фокусов, или точек схождения лучей различного цвета, должна про-
производиться во всех оптических системах, предназначенных для
получения действительных изображений объектов с малыми
угловыми размерами. Например, объективы зрительных труб

§ 24 ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ 177
должны быть ахроматизованы в смысле совмещения задних фо-
фокальных точек для лучей разного цвета.
Свет от объекта попадает в объектив, проходя через покров-
покровное стекло. В сухих объективах толщина покровного стекла
влияет на сферическую аберрацию. Поэтому все расчеты объ-
объективов производят в предположении, что толщина покровного
стекла равна 0,17 мм @,15Ч},20 мм). Все сильные сухие объ-
объективы в настоящее время снабжены коррекционной оправой,
с помощью которой можно немного менять расстояние между
верхней и нижней линзами объектива и тем самым уничтожать
сферическую аберрацию, вносимую покровным стеклом несоот-
несоответствующей толщины. В объективах с однородной иммерсией,
когда показатели преломления покровного стекла, иммерсион-
иммерсионной жидкости и фронтальной линзы объектива одинаковы, тол-
толщина покровного стекла не имеет значения, так как ее можно
компенсировать слоем иммерсионной жидкости между покров-
покровным стеклом и объективом.
4. Основные требования, предъявляемые к окуляру:
1) устранение астигматизма в косых пучках; 2) устранение дис-
торсии; 3) ахроматизация.
Кривизна поверхности изображения обычно невелика и су-
существенно не мешает визуальным наблюдениям. Если объектив
дает изображение, свободное от хроматической аберрации, то
достаточна уже частичная ахроматизация окуляра. Однако те-
теперь существенна не ахроматизация положения, а ахромати-
ахроматизация увеличения, т.е. равенство фокусных расстояний для лу-
лучей различного цвета. Действительно, благодаря значительной
длине тубуса микроскопа лучи попадают на окуляр под малыми
углами наклона к главной оптической оси микроскопа. В этом
случае угловое увеличение, даваемое окуляром, определяется
формулой B4.2), независимо от того, как аккомодирован глаз:
на бесконечность или на расстояние ясного зрения. Если фокус-
фокусные расстояния окуляра ахроматизованы, то угловое увеличение
будет одинаковым для всех цветов. Поэтому изображения пред-
предмета на сетчатке глаза во всех цветах совместятся между собой,
т.е. окончательное изображение получится неокрашенным, далее
если положения главных фокусов и главных плоскостей окуля-
окуляра не ахроматизованы. Если же изображение, даваемое объек-
объективом, не свободно от хроматической аберрации, то ее можно
компенсировать хроматической аберрацией противоположного
знака, которую дает окуляр. Так, апохроматы дают хромати-
хроматическую разность увеличений: синее изображение увеличивается
сильнее красного. Аббе комбинирует их с такими компенсиро-
компенсированными окулярами, у которых фокусное расстояние для си-
синих лучей больше, а следовательно, увеличение меньше, чем для
красных лучей.

178
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
В § 16 (п. 5) было показано, что фокусное расстояние си-
системы из двух тонких линз, изготовленных из стекла одного
и того лее сорта, будет одним и тем лее для всех цветов спек-
спектра, если расстояние I между линзами равно полусумме ее фо-
фокусных расстояний: I = VsC/i + /2)- Составлением окуляров из
двух линз одновременно молено достигнуть устранения астиг-
астигматизма косых пучков, а потому окуляры и конструируются по
этому принципу. Линза, обращенная к объективу, называется
коллективом^ или собирательной линзой, а обращенная к гла-
глазу — глазной линзой. Коллектив выполняет ту лее роль, что и
конденсор проекционного аппарата; он собирает все лучи, участ-
участвующие в образовании изображения, направляя их в зрачок гла-
глаза наблюдателя. При отсутствии специальной диафрагмы поля
зрения роль этой диафрагмы выполняет оправа коллектива. Вот
почему коллектив часто называют таклее полевой линзой. Уве-
Увеличение окуляра определяется главным образом глазной лин-
зой. Простейшими окулярами описанного типа, применяемыми
в микроскопах и телескопах, являются окуляр Гюйгенса и оку-
ляр Рамсдена A735-1800).
5. Окуляр Гюйгенса состоит из двух плоско-выпуклых или
двояковыпуклых линз, обращенных более выпуклыми поверх-
поверхностями в сторону падающих лучей (рис. 91). Для уменьшения
сферической аберра-
аберрации Гюйгенс выбрал
фокусные расстояния
и взаимное располо-
расположение линз так, что-
чтобы отклонение луча,
первоначально направ™
ленного параллельно
главной оптической
оси, при преломлении
распределялось по-
поровну между обеими
линзами. Нетрудно
подсчитать (что ре-
рекомендуется сделать
читателю), что в па-
параксиальном приблилеении это будет достигнуто при условии
I = /i — /2, где /i — фокусное расстояние собирательной, а
/2 — глазной линзы. Комбинируя это уравнение с условием
I = 1k(fi + /2), находим: Д = З/2, I = 2/2. Таким образом,
в окуляре самого Гюйгенса f'2'l'fi — 1:2:3 (в современных
конструкциях окуляра Гюйгенса чаще пользуются отношением
2:3:4). Оптический интервал меледу линзами окуляра А =
= —2/2. По формулам A2.2), A2.3) и A2.4) нетрудно рассчитать
(
А
1
\
\
С 1
-^
F2
я-
н
FVF2
Н
Рис. 91

24
ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ
179
положение главных фокусов, главных плоскостей и фокусные
расстояния окуляра Гюйгенса. Результаты расчета приведены
на рис. 91 (положение переднего фокуса F\ коллектива не
показано).
На рис. 92 приведен ход лучей в окуляре Гюйгенса. Пред-
Предположим, что глаз аккомодирован на бесконечность, а потому
окончательное изображение, даваемое микроскопом, должно по-
получаться в бесконечности. Значит, объектив должен давать пе-
перевернутое изображение АВ предмета в передней фокальной
плоскости окуляра. Этого можно добиться, перемещая весь ми-
Рис. 92
кроскоп вверх или вниз под предметным столиком. Изображение
АВ для коллектива О\ играет роль мнимого предмета. Коллек-
Коллектив даст его действительное уменьшенное изображение А'В1 в
передней фокальной плоскости глазной линзы О2, так как окон-
окончательное изображение должно получиться в бесконечности (в
этом можно убедиться и непосредственным расчетом). Изобра-
Изображение А1 В1 увеличивается глазной линзой 02, действующей как
лупа. Угол А1 С В1 определяет поле зрения. Его можно изменить,
поместив в фокальной плоскости F<i глазной линзы диафрагму
поля зрения.
Окуляр Гюйгенса мало пригоден для точных измерений.
Действительно, в этом окуляре шкалу микрометра следовало бы
располагать между линзами окуляра. Но тогда шкала микромет-
микрометра сравнивалась бы с изображением предмета, даваемым объек-
объективом микроскопа, которое искажено первой линзой окуляра.
Аберрации этой линзы, и прежде всего ее дисторсия, вносили
бы в измерения значительные ошибки, не поддающиеся точному
учету. Окуляр Гюйгенса не может быть использован и в каче-
качестве обыкновенной лупы, предназначенной для непосредствен-
непосредственного рассматривания мелких предметов, так как рассматрива-

180
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
емый предмет надо было бы опять помещать между линзами
окуляра. Окуляр Гюйгенса применяется в качестве компенса-
компенсационного окуляра в комбинации с объективами-ахроматами. В
этом случае, однако, глазную линзу изготовляют из двух скле™
енных сферических стекол различного сорта.
6. Окуляр Рамсдена состоит из двух плоско-выпуклых линз с
одинаковыми фокусными расстояниями (Д = /2), обращенных
выпуклыми поверхностями одна к другой (рис. 93). В первона™
чальном варианте окуляра расстояние между линзами I = /i =
= /2, что обеспечивает ахроматизацию фокусного расстояния /
всего окуляра. Но в таком варианте собирательная линза нахо-
находится в передней фокальной плоскости глазной линзы. Поэтому
глазная линза отчетливо изображает каждую пылинку, грязь и
F7F
f'f;
Рис. 93
царапину на поверхности собирательной линзы, что, конечно,
портит изображение предмета. Чтобы это устранить, расстоя-
расстояние между линзами уменьшают, выбирая обычно I = 2/з/ь Это,
конечно, нарушает ахроматизацию окуляра. Однако возникаю-
возникающие хроматические явления мало заметны. Их можно устра™
нить, применяя ахроматическую глазную линзу, склеенную из
собирательной (крон) и рассеивающей (флинт) линз. Это дела-
делается в окулярах типа Кельнера. Рассеивающая линза должна
быть обращена к глазу. Желательно также ахроматизовать и
коллектив окуляра, но этого почти никогда не делают.
Положение фокальных точек и главных плоскостей в окуля-
окуляре Рамсдена показано на рис. 93, а на рис. 94 приведен ход лучей
в этом окуляре. Сравнивая их с рисунками 91 и 92, видим невы-
невыгоду окуляра Рамсдена: он удлиняет всю систему микроскопа,
так как передняя фокальная плоскость окуляра, в которой объ™
ектив должен давать действительное изображение АВ, лежит
перед передней линзой окуляра на расстоянии У4/1 (а не между
линзами окуляра, как в случае окуляра Гюйгенса).
Но в этой особенности окуляра Рамсдена есть и его преиму™
щество. В фокальной плоскости F можно поместить микрометр

24
ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ
181
(шкалу на стеклянной пластинке или нити, перемещаемые ми-
микрометрическим винтом) и таким путем измерить размеры дей-
действительного изображения, даваемого объективом микроскопа.
При этом микрометр и действительное изображение, даваемое
объективом, оба находятся перед окуляром, и аберрации поле-
полевой линзы окуляра искажают их одинаково. Тем самым в окуля-
окуляре Рамсдена устраняется основной недостаток окуляра Гюйгенса
как измерительного прибора. Зная линейное увеличение объек-
Рис. 94
тива микроскопа, легко вычислить и размеры самого предмета.
Поэтому в микроскопах, служащих для измерения длин и углов,
применяются окуляры Рамсдена с окулярными микрометрами.
В зависимости от назначения применяются и более сложные
окуляры, состоящие не из двух, а из большего количества линз.
7. На рис. 95 изображен ход лучей в микроскопе с окуля-
окуляром Гюйгенса. Главные лучи, исходящие из крайних точек пред-
предмета АВ, начерчены толстыми, а крайние лучи, исходящие из
тех же точек, — тонкими линиями. Если увеличение меньше
нормального, то зрачок глаза наблюдателя служит апертурной
диафрагмой, а его изображение, даваемое всем микроскопом, —
входным зрачком этого прибора. Если же увеличение больше
нормального, то апертурной диафрагмой и входным зрачком яв-
является диафрагма или края полушаровой линзы CD. Ее изобра-
изображение CD1 будет выходным зрачком микроскопа. Диафрагма
поля зрения дол лена быть помещена в том месте, где получается
изображение А'В', даваемое объективом и собирательной лин-
линзой окуляра. Изображение А"В" 1 которое видит наблюдатель,
можно получить на любом расстоянии, что достигается неболь-
небольшим поднятием или опусканием всего микроскопа. Обычно его
получают на расстоянии ясного зрения B5 см для нормального
глаза) или в бесконечности. Перемещая окуляр, можно менять
оптическую длину тубуса, а с ней и увеличение микроскопа.
Из рисунка видно главное преимущество микроскопа перед
лупой. Оно состоит в том, что в микроскопе задача получения
изображения распадается на две части, из которых одна реша-

182
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ется объективом, другая окуляром. Объектив дает изображение
предмета при максимально возможной числовой апертуре. Оку-
Окуляр, как и лупа, при большом поле зрения дает изображение то™
чек предмета с помощью узких пучков лучей, так как эти пучки
ограничены выходным зрачком микроскопа.
в
Рис. 95
Объекты, рассматриваемые в микроскоп, обычно не самосве-
самосветящиеся, а освещаются посторонним источником. Для этой це-
цели употребляется конденсор^ состоящий из одной или нескольких
короткофокусных линз, помещаемый под предметным столиком
микроскопа. Чтобы полностью использовать высокую числовую
апертуру объектива микроскопа, наклон освещающих лучей к
оптической оси должен быть большим. Вот почему для кон-
конденсора берут короткофокусные линзы. Конечно, конденсор не
может повысить поверхностную яркость источника света, его
действие эквивалентно приближению источника к освещаемому
объекту.
8. Зрительные трубы и телескопы. Глав-
Главными частями зрительной трубы являются объектив и окуляр.
Объектив дает в задней фокальной плоскости обратное умень-
уменьшенное изображение АВ удаленного предмета, рассматриваемое
в окуляр как в лупу (рис. 96). Для нормального глаза, аккомо™
дированного на бесконечность, задний фокус объектива должен
быть совмещен с передним фокусом окуляра. Это совмещение
нарушается, но незначительно, для близорукого и дальнозорко™

24
ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ
183
го глаза. Таким образом, параллельный пучок лучей после про™
хождения через трубу, установленную на бесконечность, остает-
остается параллельным, т.е. зрительная труба является телескопиче-
телескопической оптической системой. Увеличение (угловое) таких систем
равно отношению ширины падающего пучка лучей к ширине со-
соответствующего выходящего пучка, или отношению фокусного
расстояния объектива f\ к фокусному расстоянию окуляра /2
(см.§ 11, п. 10). О нормальном увеличении подробно говорилось
в п. 4 предыдущего параграфа.
Рис. 96
Лучи, падающие на объектив зрительной трубы, наклонены
под малыми углами к главной оптической оси. Поэтому нет на™
добности в тщательном исправлении аберраций, зависящих от
этих углов. Объективом служит ахроматическая двойная линза,
исправленная на сферическую аберрацию. Кома, т.е. отступле-
ние от условия синусов, может быть исправлена не столь тща-
тщательно. Ахроматизация окуляра должна удовлетворять тем же
условиям, что и в случае микроскопа: если главный луч пада-
падает на окуляр под небольшим углом к главной оптической оси,
то можно ограничиться ахроматизацией только фокусного рас-
расстояния. Поэтому для микроскопов и зрительных труб мож-
можно пользоваться одними и теми же окулярами. Если требуют-
требуются микрометрические измерения изображения (как в астроно-
мических трубах), то предпочтительнее пользоваться окуляром
Рамсдена, а не Гюйгенса.
На рис. 96 изображен ход лучей в зрительной трубе Кепле-
Кеплера (для простоты сложный окуляр заменен простой собиратель™
ной линзой). Эта труба дает перевернутое изображение. Чтобы
устранить этот недостаток, за изображением АВ, даваемым объ-
объективом, на двойном фокусном расстоянии помещают добавоч-
добавочную ахроматизованную собирательную линзу, которая перево-
переворачивает изображение АВ, не меняя его величины. Полученное
изображение и рассматривается в окуляр. Окончательное изо-
изображение, которое видит глаз, получается прямым.

184
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
В трубе Галилея окончательное изображение получается
прямым без введения промежуточной линзы. Это достигается
тем, что в качестве окуляра применяется простая двояковогну-
двояковогнутая линза, передний фокус которой F^ совпадает с задним фоку-
фокусом объектива F[ (рис. 97). Поле зрения галилеевой трубы неве-
Рис. 97
лико. Зато при том же объективе галилеева труба значительно
короче кеплеровой. Поэтому труба с отрицательным окуляром
применяется только в театральных биноклях.
В обыкновенном бинокле, состоящем из двух зрительных
труб, переворачивание изображения, даваемого объективом, до™
стигается в каждой тру-
трубе с помощью четырех™
кратного полного отра-
отражения от гипотенузных
поверхностей двух пря-
моугольных стеклянных
призм А и В, распо-
расположенных, как показано
на рис. 98. Луч выхо™
дит из призмы В парал-
параллельно падающему лу-
лучу, но получает боко-
Рис- 98 вое смещение. В осталь-
остальном устройство зритель-
зрительной трубы не отличается от устройства трубы Кеплера. Так как
луч проходит расстояние между призмами трижды, то мож-
можно значительно уменьшить длину трубы, раздвигая призмы А
и В друг относительно друга. При несколько иной конструк-
конструкции молено получить бинокулярную трубу, у которой расстояние
между объективами во много раз превышает расстояние между
глазами наблюдателя. В такой «стереотрубе» сильно увеличива-
увеличивается стереоскопический эффект, обусловленный зрением двумя
глазами.

§ 24 ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ 185
9. Астрономические трубы, или телескопы^ бывают двух
типов: преломляющие (рефракторы) и отражающие (рефлекто-
(рефлекторы). В преломляющих объективом служит линза, в отражаю-
отражающих — вогнутое зеркало, называемое главным зеркалом.
Изготовление объективов для телескопов-рефракторов пред™
ставляет большие трудности, быстро возрастающие с увеличе-
нием размеров объектива. Главная трудность состоит в получе-
получении большого диска стекла с вполне однородным показателем
преломления и отсутствием натяжений. Последние снимаются
медленным отжигом стекла, длящимся месяцами. Необходима
большая точность в изготовлении сферических поверхностей, в
центровке и сборке линз. Влияние неизбежных небольших слу-
случайных отклонений от полной однородности показателя прелом-
преломления стекла устраняется деформацией точных сферических по-
поверхностей объектива путем местной полировки — ретуши. Из-
Изготовление объектива для рефракторов больших обсерваторий
тянется годами. Самым крупным рефрактором в настоящее вре-
время является телескоп Иеркской обсерватории в США. Диаметр
его объектива составляет 40 дюймов Aм). Диаметр объектива
рефрактора Главной астрономической обсерватории АН СССР
в Пулкове равен 30 дюймов G5 см).
Значительно легче изготовить главное зеркало телескопа,
так как свет не проходит сквозь стекло, и последнее может быть
менее высокого качества, но должно быть лишь хорошо отожже-
отожжено. Такое стекло может быть отлито в диски огромного разме-
размера. Поэтому крупнейшими являются отражательные телескопы
(рефлекторы). Самый крупный телескоп с диаметром главно-
главного зеркала 6 м недавно установлен в СССР на северных отро-
отрогах Кавказского хребта вблизи станицы Зеленчукской. До этого
самым крупным был телескоп в обсерватории Маунт Паломар
(Калифорния, США) с диаметром главного зеркала 5 м.
Отражающая поверхность главного зеркала телескопа-
рефлектора шлифуется на стекле. Ей придают форму параболо-
параболоида, чтобы лучи, параллельные главной оптической оси, собира-
собирались в фокусе параболоида. При изготовлении поверхности зер-
зеркала сначала придают форму сферы, радиус которой R почти в
точности равен удвоенному фокусному расстоянию F параболо-
параболоида. Затем производят параболизацию этой поверхности путем
снятия шлифовкой (ретушью) тонкого слоя стекла на централь-
центральной части зеркала. В наиболее толстом месте, как нетрудно под-
подсчитать, толщина слоя должна составлять l/g(r/RL:R1 где г —
радиус кривизны зеркала. При г = 50 см, F = 5 м для этой тол-
толщины получаем 7,8 • 10™4 см, т.е. примерно 15 длин волн желто-
зеленого света. Отражающая поверхность зеркала покрывается
тонким слоем серебра, алюминия или родия. С течением време-

186
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
ни под действием воздуха отражатедвная способность металли-
металлического слоя постепенно уменьшается. Серебряный слой должен
обновляться примерно каждые полгода. Алюминиевый слой бо-
более устойчив и держится годами. Еще лучшие результаты дает
покрытие зеркала слоем родия.
Важное преимущество зеркального телескопа перед рефрак™
тором состоит в том, что этот телескоп абсолютно ахроматичен.
Это позволяет не только работать со светом любой окраски, но и
значительно повысить светосилу телескопа с соответствующим
уменьшением его длины.
Свет должен дважды пройти трубу рефлектора, прежде чем
он соберется в фокусе. Поэтому требуется небольшое вспомога-
вспомогательное зеркало (или призма), чтобы сместить фокальную плос-
плоскость в более удобное положение для наблюдения глазом или по™
мещения фотографической пластинки. В зеркальном телескопе
Ньютона плоское вспомогательное зеркало s смещало фокус F
вбок, как указано на рис. 99 (на этом и последующих рисунках
Рис. 99
окуляр не изображен, указано только смещенное положение F
фокуса оптической системы).
В телескопе Вильяма Гершеля (рис. 100) вспомогательного
зеркала нет, главный фокус F смещается вбок трубы путем
небольшого наклона главного зеркала S. За несколько лет до
Гершеля такой телескоп был изобретен Ломоносовым, но его
Рис. 100
изобретение оставалось неизвестным вплоть до начала XX ве™
ка. Недостаток системы Ломоносова—Гершеля состоит в том,

24
ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ
187
что изображение получается не на главной оптической оси. Это
ухудшает качество изображения. Впрочем, сам Гершель поль-
пользовался столь длиннофокусными зеркалами, что требовались
лишь небольшие углы наклона, и ухудшение изображения было
незначительным.
В системе Кассегрена (рис. 101) применяется выпуклое ги-
перболическое зеркало s, располагающееся на главной оптиче-
оптической оси несколько ближе фокуса главного зеркала S. Фокус
гиперболической поверхности вспомогательного зеркала s сов-
Рис. 101
падает с фокусом главного зеркала S. После отражения лучей от
зеркала образуется новый фокус F оптической системы, совпа™
дающий со вторым фокусом гиперболической поверхности зер-
зеркала s. Лучи выходят из системы через отверстие в центре глав-
главного зеркала S и попадают в окуляр или на фотопластинку.
Сходное устройство имеет телескоп Грегори (рис. 102). Здесь
вспомогательным зеркалом s служит вогнутое эллиптическое
зеркало, располагающееся на главной оптической оси несколько
дальше фокуса главного зеркала S. Фокус зеркала S совмеща-
Рис. 102
ется с первым фокусом эллиптического зеркала s. Смещенный
фокус F всей оптической системы получается в точке нахожде-
нахождения второго фокуса эллиптической поверхности зеркала s. Лу-
Лучи также выходят из системы через отверстие в центре главно-
главного зеркала S и попадают в окуляр или на фотопластинку. По
качеству изображения телескоп Грегори несколько превосходит
телескоп Кассегрена. Но для него требуется гораздо более длин-
длинная труба. По этой причине система Грегори почти никогда не
применяется.

188 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
10. Камера Шмидта и менисковые системы
Максутова. Придание отражающей поверхности главно-
главного зеркала телескопа параболической формы, а также исполь-
использование в качестве вспомогательных эллиптических и гипербо-
гиперболических зеркал устраняет сферическую аберрацию, но сохра-
сохраняет все прочие геометрические аберрации, так как геометри-
ческие фокусы параболоида, эллипсоида и гиперболоида явля-
являются только анаберрационными, но не апланатическими точ~
тми. Зеркальным объективам телескопов всегда свойственны
значительные аберрации комы и астигматизма. Вследствие это-
этого поле зрения, где получаются четкие изображения, у этих при™
боров невелико и измеряется минутами, а в лучших случаях —
десятками минут. В 1930 г. Б. Шмидт, сотрудник Гамбургской
обсерватории в Бергедорфе, предложил новый тип телескопа,
получивший название камеры Шмидта. Короткофокусная каме-
камера Шмидта с относительным отверстием D/ f = 1 может давать
резкие изображения при поле зрения ^25°. Параболическое же
зеркало при таком же относительном отверстии может иметь по-
полезное поле зрения, измеряемое только несколькими дуговыми
минутами.
Рисунок 103 поясняет основную идею камеры Шмидта. На
этом рисунке S1S2 — вогнутое сферическое зеркало с центром
в точке G, a D\D2 — отверстие диафрагмы с центром в той же
точке, введенной только для
лучшего уяснения указанной
идеи. Пучок лучей А, парал-
лельных главной оптической
оси зеркала, после отражения
пройдет через кружок с центром
в главном фокусе F. Размеры
кружка определяются сфериче-
сферической аберрацией. Параллельный
пучок А\, падающий наклонно,
пройдет через аналогичный
кружок с центром в побочном
фокусе F\. Геометрическим ме-
р стом всех таких фокусов будет
сфера, радиус которой вдвое
меньше радиуса зеркала S1S2. Она изображена штриховой ли-
линией. Таким образом, бесконечно удаленные точки в результате
отражения света от сферического зеркала S1S2 изобразятся
кружками, расположенными на этой штриховой сфере.
Размеры кружков почти одинаковы, так как они образуют-
образуются параллельными пучками лучей практически одинакового по-
поперечного сечения. Наклон пучков влияет лишь на положение
кружков на штриховой сфере, но не на их величину. Впрочем,

§ 24 ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ 189
полная одинаковость кружков несущественна. Существенно, что
единственными геометрическими аберрациями будут сфериче-
сферическая аберрация и искривление поверхности изображения. Комы,
астигматизма и дисторсии не будет.
В обычных зеркальных телескопах сферическая аберрация
устраняется параболизацией отражающей поверхности зеркала.
Но такой способ годится только для точек, лежащих на главной
оптической оси зеркала. Шмидт предложил устранять сфери-
сферическую аберрацию коррекционной стеклянной пластинкой, по™
мещаемой перед сферическим зеркалом S\S2- Одна поверхность
пластинки плоская, вторая — поверхность вращения надлежа-
надлежащей формы, мало отклоняющаяся от плоскости. Это отклонение
настолько мало, что оно совершенно незаметно невооруженному
глазу.
Сечение коррекционной пластинки Р1Р2 представлено на ехе-
матическом рис. 104 в преувеличенном виде. Центральная часть
пластинки более толстая — действует как собирательная линза,
приближая фокус центральных лу-
лучей к зеркалу. Края пластинки бо „
лее тонкие и, подобно рассеивающей —*- 2
линзе, удаляют от зеркала фокусы
наклонных пучков лучей.
Помещение коррекционной пла-
пластинки вплотную к зеркалу не мо- ~
жет дать никаких преимуществ по 1
сравнению с параболизацией его по-
поверхности. Однако коррекционная Рис. 104
пластинка, если правильно рассчи-
тать ее форму, помещенная на определенном расстоянии от зер-
зеркала, устраняет сферическую аберрацию не только для пучков
лучей, параллельных главной оптической оси, но и для пучков,
наклоненных к ней. Обычно коррекционную пластинку помеща-
помещают в центре сферического зеркала и для этого положения рас-
рассчитывают ее форму. При этом другие аберрации практически
не возникают. Изготовление коррекционных пластинок Шмид-
Шмидта — очень трудная задача.
В 1941 г. Д.Д. Максутов A896-1964) для исправления абер-
аберраций сферического зеркала предложил применять мениски^
значительно более легкие в изготовлении, чем коррекционные
пластинки Шмидта с несферическими поверхностями. Систе-
Системы Максутова быстро получили широкое распространение. При
определенном соотношении между радиусами кривизны сфери-
сферических поверхностей мениска и его толщиной мениск ахромати-
зован (для двух требуемых цветов спектра).
На рис. 105 а приведена простейшая система Максутова, со-
состоящая из сферического зеркала S и мениска ?», обращенно-

190
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
го к нему выпуклой стороной. Если мениск ахроматизован, то
в фокусе F образуется ахроматическое изображение. Сфериче-
Сферическая аберрация мениска подбирается так, чтобы компенсировать
сферическую аберрацию зеркала S. При правильно выбранном
расстоянии I между мениском и зеркалом оказывается исправ-
исправленной и кома, т.е. система становится апланатической. Если
при том же расстоянии I мениск повернуть к зеркалу вогнутой
стороной, то апланатизм нарушается. Его можно восстановить,
увеличивая расстояние I (рис. 105 б). Первая ориентация менис™
Рис. 105
ка более выгодна, так как при ней телескоп получается вдвое
короче, чем при второй. Однако для некоторых целей предпоч™
тительнее вторая ориентация.
Астигматизм менисковой системы может быть сделан нич™
тожно малым, а в частных случаях и вполне устранен. Искрив-
Искривление поверхности изображения остается. Но из всех аберраций
эта аберрация является наименее вредной, и существуют спосо™
бы ее устранения. Соединение камеры Шмидта или менисковых
систем Максутова с окуляром производится так же, как в теле™
скопах Ньютона, Кассегрена и Грегори.
§ 25. Электрические и магнитные линзы
1. Допустим, что показатель преломления п меняется в пространстве
непрерывно. Проведем поверхности равного показателя преломления и при-
притом настолько часто, что показатели преломления между каждыми сосед™
ними поверхностями можно будет считать величинами постоянными. Тогда
непрерывное изменение величины п заменится скачкообразным, происходя-
происходящим на границах между слоями. Если среда обладает осевой симметрией,
то эти границы будут поверхностями вращения, вершины которых лежат
на оси симметрии системы. В малой окрестности вокруг оси симметрии их
можно аппроксимировать сферами, центры которых также лежат на той
же оси. Таким путем мы приходим к центрированной системе тонких сфе-
сферических линз, у которой ось симметрии служит главной оптической осью
и к которой применимы все результаты оптики параксиальных лучей. Уве-
Увеличивая число слоев бесконечно и одновременно устремляя к нулю их тол-
толщины, мы восстановим в пределе первоначальное непрерывное распределе-

§ 25 ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЛИНЗЫ 191
ние показателя преломления. Отсюда следует, что осесимметричную среду
с непрерывно изменяющимся в пространстве показателем преломления
можно рассматривать как предельный случай центрированной системы
линз и применять к ней законы и методы оптики параксиальных лучей.
Такая среда обладает способностью давать оптические изображения.
Оптические системы с непрерывно изменяющимися показателями пре-
преломления принципиально возможны, но из-за трудностей их изготовления
в световой оптике они не встречаются. (Исключение составляет хрусталик
глаза, показатель преломления которого возрастает от периферии к цен™
тру.) Аналогом таких систем являются электронные и ионные приборы
(электронный микроскоп, электронный осциллограф, электронно™лучевая
трубка в телевидении и пр.), в которых роль лучей играют электроны или
ионы, движущиеся в электростатических или магнитных полях, создавае-
создаваемых заряженными электродами или катушками, по которым текут элек-
электрические токи. Эти электроды называются электрическими^ а катушки —
магнитными линзами. Получение изображений в таких системах изучает™
ся в электронной и ионной оптике.
2. Возможность фокусировки заряженных частиц и получения изо-
изображений в осесимметричных системах электростатических линз непосред-
непосредственно следует из формальной аналогии между геометрической оптикой
и классической механикой, отмеченной нами в п. 1 § 4. Действительно, со-
согласно этой аналогии, траектория частицы в потенциальном силовом поле
совпадает со световым лучом в непрерывной среде, показатель преломления
которой пропорционален скорости (а в релятивистской механике — импуль-
импульсу) частицы, однозначно определяющейся ее положением в пространстве.
Например, можно положить
- eV), B5.1)
где W — полная энергия частицы, е — ее заряд, V — потенциал электро-
электростатического поля.
3. Несколько труднее понять действие магнитных линз и комбинаций
таких линз с электростатическими линзами. Для исследования вопроса рас-
рассмотрим статическое электромагнитное поле, обладающее симметрией вра-
вращения вокруг некоторой оси. Эту ось примем за ось X цилиндрической
системы координат. Расстояние до оси X будем обозначать через г, а ази-
азимутальный угол — через ip. Ввиду симметрии вращения, электрическое и
магнитное поля не могут зависеть от <р. Предположим кроме того, что вся-
всякая плоскость, проходящая через ось X, является плоскостью симметрии
поля. Тогда не будет (^-составляющих электрического и магнитного полей
(Ер = Вр = 0). Оставшиеся ж- и r-составляющие этих полей будут функ-
функциями только координат жиг. Уравнение div В = 0 после умножения на г
запишется в виде
(гВх) + (гВг) = 0. B5.2)
ох иг
Введем потенциальную функцию А(х,г), определяемую условием гВх =
= —дА/дг. Тогда предыдущее уравнение преобразуется в
д д (дА\ д (дА
— (гВг) = о- т =f T
or их \ог J or \ их
откуда гВг = дА/дх, причем «постоянную интегрирования» (точнее —
функцию ж) мы без ущерба для общности положили равной нулю. Таким

192 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
образом,
гВх = - — , гВг = —. B5.3)
дг дх
Отсюда
А(х, г) = J r(Br dx - Вх dr). B5.4)
В силу B5.2) входящий сюда интеграл не зависит от пути интегрирования, а
только от его начальной и конечной точек. Условимся помещать начальную
точку на оси системы. На оси системы в силу симметрии Вг = 0. Поэтому
не имеет значения, в каком месте этой оси выбрать начальную точку. От
этого значение интеграла B5.4) не зависит, и он может быть представлен в
виде
г
А{х,г) = - J Bxrdr. B5.5)
о
Обратимся теперь к исследованию движения частицы с массой т и
зарядом е, ограничиваясь ради простоты нерелятивистским приближением.
Угловую скорость ф частицы можно найти из уравнения моментов
d , 2-х я м-
— (гаг (р) = Мх,
dt
где Мх — момент сил, действующих на частицу, относительно оси X. Элек-
трическое поле не влияет на момент Мх. Он создается только силой F =
= — [vB], действующей со стороны магнитного поля. Вычисляя этот мо-
момент, находим
ег,_ _ ч е / дА дА
Мх = — (Вr vx — Вх vr) = — I vx — + vr —
с с \ дх дг
Если под ж, г и (р понимать координаты движущейся частицы, то А(х,г)
станет функцией времени t. Производная этой функции равна
dA _ дА dx дА dr _ дА дА
dt дх dt дг dt х дх г дг '
Следовательно,
,, е d A d , 2 • х е d A
МТ = , —imr ф) = .
с dt' dV r) с dt
Отсюда
е л С
Постоянная С должна обращаться в нуль. Иначе (так как на оси системы
функция А равна нулю) при г = 0 мы получили бы гф = оо. А это невоз-
невозможно, так как гф есть линейная скорость частицы в ее вращении вокруг
оси X. Таким образом,
^ B5.6)
тег2
Возьмем теперь уравнение движения частицы
ma = e(E+ -[vB] ) , B5.7)
Vе/
где а — ускорение. При проецировании его на ось X и направление радиуса
г слева получим соответственно тах = тх и гпаг. Радиальное ускорение в

§ 25 ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЛИНЗЫ 193
цилиндрической системе координат определяется выражением аг = г — ш2г
(см. т. I, § 46). Введем еще электрический потенциал V и учтем соотношения
B5.3) и B5.6). Тогда после недлинных преобразований из B5.7) получим
тх = -е— [V + С ) , тг = -е— (V + в ) . B5.8)
дх \ 2тс2г2) дг \ 2тс2г2)
Задача о движении частицы распалась на две независимые задачи:
определение угловой координаты (р и определение координат жиг. Для
решения первой задачи имеется уравнение B5.6), а для второй — урав-
уравнения B5.8). Формально вторая задача идентична с задачей определения
траектории заряженной частицы в плоском электростатическом поле с по-
потенциалом
Ее формальным аналогом в оптике служит задача о распространении све-
светового луча в неоднородной изотропной среде с показателем преломления
п = \l2m(W - eV) - -=-? = Jn* - —^, B5.10)
где по = у 2m(W -— eV) — «показатель преломления» в отсутствие магнит-
магнитного поля. Для получения окончательной формы траектории частицы надо
наложить на этот «луч» дополнительное вращение, выражаемое формулой
B5.6).
Учтем теперь условие параксиальности. Для этого разложим Вх(х1г)
в ряд по степеням г. Ввиду осевой симметрии, это разложение может со-
содержать только четные степени г. Оборвем разложение на члене нулевой
степени — в этом приближении поле Вх не зависит от г. Вынося Вх из-под
знака интеграла B5.5) и выполнив интегрирование, получим
А = ^\вхг\ B5.11)
а после подстановки в формулу B5.6)
ф = -еВх/Bтс). B5.12)
Отсюда
dip = <hpdt_ = _]_eB^ B5 13)
dx dt dx vx 2mc
В параксиальном приближении скорость vx также не зависит от рас-
расстояния г до оси X и равна скорости частицы, движущейся вдоль этой
оси. Поэтому производные dip/dx имеют одинаковые значения для всех ча-
частиц, независимо от наклона их траекторий к оси X. Если I — расстояние
от предметной плоскости до плоскости изображения, то на этом расстоя-
расстоянии в параксиальном приближении все частицы поворачивают вокруг оси
симметрии системы на один и тот же угол
I
^ Г ^-dx. B5.14)
2тс J vx
x
0
Следовательно, в смысле получения изображений система будет вести
себя так^ как если бы магнитного поля не было, а электростатическое
7 Д.В. Сивухин

194
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
определялось потенциалом B5.9). Магнитное поле приводит еще к несу-
щественному повороту всего изображения вокруг оси симметрии систе-
системы на угол, определяемый формулой B5.14). В высших приближениях угол
поворота зависит от наклона траектории к оси системы. Это ведет к по-
появлению дополнительных аберраций, обусловленных наличием магнитного
поля.
4. Отметим еще одно обстоятельство. Если электрического поля нет, а
магнитное поле однородно, то частица движется по спирали, вращаясь с
циклотронной частотой ш = -—еВ/тс (см. т. III, § 86). Между тем формула
B5.12) для этого случая дает угловую скорость, вдвое меньшую ш. Недр-
разумение легко разъясняется, если заметить,
что ш есть угловая скорость вращения частицы
вокруг оси спирали, тогда как формула B5.12)
определяет ее вращение вокруг одной из образу-
образующих той же спирали. Допустим, например, что
магнитное поле перпендикулярно к плоскости ри-
рисунка (рис. 106), а частица вращается по окруж-
ности в той же плоскости. За ось X можно, конеч-
конечно, принять любую прямую, направленную вдоль
поля В. Поэтому можно считать, что частица
выходит из какой-то точки М этой оси. Описав
окружность, она снова возвращается в исходную
точку. Ее вращение вокруг точки М описывает-
описывается формулой B5.12), тогда как вращение вокруг
центра О окружности происходит с циклотронной частотой ш. За время dt
частица повернется вокруг центра О на угол о; dt, а вокруг точки М — на
угол dip = lJ2U0 dt, так что ф = 1/2W.
5. Выше фокусировка частиц в электрических линзах была объяснена с
помощью аналогии со световой оптикой. Сделаем теперь то же самое, рас-
рассматривая силы, действующие на частицу. На рис. 107 представлена линза,
состоящая из трех соосных металлических цилиндров одинакового диамет-
Рис. 106
т
Рис. 107
ра. Крайние цилиндры заземлены, на средний подан положительный или
отрицательный потенциал. Линзы такого типа используются в электронно-
электроннолучевых трубках и некоторых электронных микроскопах. На рисунке изо-
изображены электрические силовые линии с указанием направлений сил, дей-
действующих на частицу.

§ 25 ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЛИНЗЫ 195
Допустим, что частица влетает в линзу, двигаясь параллельно ее оси. В
области А действующая на нее сила имеет составляющую, направленную
вверх. Эта сила будет смещать частицу вверх. В области В направление
вертикальной составляющей силы изменится на противоположное. Однако,
так как под действием электрического поля скорость частицы непрерывно
возрастает, на прохождение области В частица затрачивает меньше време-
времени, чем на прохождение области А. Поэтому поперечная скорость, приобре-
приобретенная частицей в области А, не может быть скомпенсирована скоростью
противоположного направления, которую она получает в области В. В ре-
результате в областях А и В и по выходе из них частица будет двигаться вверх,
приближаясь к оси линзы. Аналогично, в области С на частицу действует
сила, стремящаяся удалить ее от оси линзы, а в области D — приблизить.
Но в этих областях частица замедляется, а потому проводит в области D
большее время, чем в С. Поэтому при прохождении обеих областей С и D
вертикальная скорость частицы, направленная вверх, возрастет.
Эти разъяснения объясняют, почему частицы приближаются к оси лип™
зы. Конечно, из них не следует, что все частицы пучка соберутся в одной и
той же точке на оси линзы. Для доказательства этого требуется уже количе-
количественное рассмотрение, которое и было проведено выше на основе аналогии
со световой оптикой.
ЗАДАЧИ
1. Вычислить фокусное расстояние тонкой оптической линзы, показа-
показатель преломления которой в пространстве меняется непрерывно.
Решение. Сначала не будем вводить предположение о тонко™
сти линзы, а рассмотрим среду, обладающую симметрией вращения вокруг
оси X. Уравнение луча в меридиональной плоскости представится в виде
г = г(х). Обозначим через и угол, образуемый касательной к лучу с осью X
(рис. 108). В параксиальном приближении
квадратом этого угла пренебрегают. В этом
приближении кривизна луча определяется
выражением 1/R = —du/dx, причем ради-
радиус кривизны R мы считаем положительным,
когда луч обращен вогнутостью к главной
оптической оси X, и отрицательным в про™
тивоположном случае. Воспользуемся фор-
формулой D.1). В пределах точности парак-
параксиальной оптики dr/dN = — cos и и — 1, у
dxjdN = sin u^ и, так что
дп дп дг дп дх ^ дп дп Рис. 108
Так как на луче г = г(ж), то п(х,г) можно рассматривать как сложную
функцию от ж, т.е. п(х) = ?г[ж,г(ж)]. Ее производная по ж определяется
выражением
dn дп дп дг дп дп
dx дх дг дх дх дг'
т.е. отличается от частной производной дп/дх на величину первого порядка
малости по и. Поэтому замена дп/дх на dn/dx в предыдущем выражении
вносит ошибку второго порядка, которой мы пренебрегаем. Сделав эту за-

196
ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
мену и воспользовавшись формулой D.1), получим
1 du 1 дп
R dx n dN
или
1 дп dn
п дт dx
дп
B5.15)
Разложим п = п(х,г) в ряд по степеням г и оборвем разложение на
члене второй степени. Член первой степени должен отсутствовать, ввиду
осевой симметрии системы. Таким образом,
1/ <л2
, , , (длп
а потому
дп
д2п
дг2
Здесь нуль в индексе означает, что величина с таким индексом берется при
г = 0, т.е. на главной оптической оси системы. В результате уравнение
B5.15) переходит в
Допустим теперь, что линза тонкая. Пусть Р и Р1 — оптически сопря-
сопряженные точки на ее оси (рис. 109). Отрезки соединяющего их луча вне лин-
линзы прямолинейны. Проинтегрируем уравнение B5.16) по х в пределах от
\
Рис. 109
^оо до +оо. Фактически это сводится к интегрированию по отрезку АВ, так
как вне этого отрезка д2п/дг2 = 0. Внутри линзы, поскольку она тонкая,
радиус г можно считать постоянным и вынести его из-под знака интеграла.
Это дает
П2П2 — П\П\ = Г
дг2
CLX,
где п\ — показатель преломления в пространстве предметов, а П2 — в про™
странстве изображений. Обозначим, как и раньше, через ? и ^f расстояния
предмета Р и его изображения Р от центра линзы. С учетом правила зна-
знаков и\ = —r/?, U2 = —г/^\ так что предыдущее уравнение переходит в
B5.17)

25
ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЛИНЗЫ
197
где
+ ОО
+ ОО
1_ _ J_ r (<rn\ ]__J_ г fd2n
dx.
B5.18)
2. Вычислить фокусные расстояния тонкой электростатической линзы
(примером такой линзы может служить «одиночная линза», представлен™
ная на рис. 110).
Решение. Потенциал поля V определим по формуле Дти =
= е| V. При таком определении V — существенно положительная величина.
Рис. 110
В формулах B5.18) делаем замену п —> yV. Учитывая, что на оси системы
dV/dr = 0, получаем
[д2п
[дг2
—»¦
д2У
дг2
При отсутствии свободных зарядов V2F = 0. На оси d'2V/dy2 = d2V/dz2 =
= 02V/dr21 так что V2F = d2V/dx2 + 2(d2V/dr2) = 0. В результате из
B5.18) находим
7
Проинтегрировав по частям и приняв во внимание, что на пределах инте-
интеграла dV/dx = 0, получим
1 1 +о°
f 8VW ¦'
7
1
7
1 +о°
L_ f v
' ?^ж с?ж,
B5.20)
где Vi — потенциал пространства предметов, Vb — потенциал пространства
изображ:ений, Ех = -—dV/dx — напряженность электрического поля на оси.
Если Vi = F2, то / = —/ .
Так как V > 0, то для тонких электростатических линз / > 0, /; < 0. Та-
Такие линзы всегда будут собирательными. Оптические линзы, даже тонкие,
могут быть и собирательными, и рассеивающими. Это различие связано
с тем, что функция п(г) может быть какой угодно, тогда как потенциал

198 ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЛ. II
V(г) при отсутствии свободных зарядов должен удовлетворять уравнению
Лапласа V2F = 0. Толстые электростатические линзы могут быть и соби-
собирательными, и рассеивающими. В этом нетрудно убедиться на примере си-
системы, состоящей из двух тонких электростатических линз. Формулы A2.3)
показывают, что такая система будет собирательной, когда оптический ин-
тервал А отрицателен, и рассеивающей, когда он положителен.
еА
3. Предполагая, что по ^>
, вычислить фокусное расстояние тонкой
er
магнитной линзы.
Решение. Разлагая B5.10) в ряд и отбрасывая члены высших
степеней, получим
2 л 2 2 2
е А е г „9
П = По ~~ ^^7 = ^0 —
откуда
"дг2
Следовательно,
Как и электростатическая, тонкая магнитная линза всегда будет собира-
собирательной.
4. Вычислить фокусное расстояние кругового витка радиуса а тонкой
проволоки, по которой течет ток /.
Ответ. В гауссовой системе единиц
1. eVa4!2 +f° dx 3^3е2 I
f dx = 3^3е2 I2
J (ж2+а2K 16mc4W a ' { ' }
f Smc4W J (ж2+а2K 16mc4W
— оо
Выражая энергию W в электрон-вольтах, полагаем W = |e|Vo и переходим
к практическим единицам (сантиметры, вольты, амперы). Тогда получаем
для электронов
/ = -/'= 98^. B5.23)
Для короткой катушки с числом витков N
/ = -/'=98^. B5.24)
5. Показать, что формула B5.18) для / в предельном случае тонкой
линзы с резкими краями переходит в формулу A0.9). Считать, что показа-
показатели преломления тц и П2 по обе стороны линзы одинаковы.
Указание. Принять, что показатель преломления п меняется только
в бесконечно тонких слоях вблизи каждой сферической границы линзы. На
всякой сферической поверхности, проведенной внутри этих слоев парал-
параллельно ближайшей поверхности линзы, функция п постоянна. Пользуясь
этим, дифференцирование по г можно заменить дифференцированием по
ж, а затем вычислить интеграл в формулах B5.18).

ГЛАВА III
ИНТЕРФЕРЕНЦИЯ СВЕТА
§ 26. Общие сведения об интерференции
1. В интерференции и дифракции проявляются волновые
свойства света. После открытия этих явлений на них смо-
смотрели сначала как на доказательство исключительно волновой
природы света. Такая точка зрения оказалась недостаточной.
В XX веке были открыты корпускулярные свойства света, а
затем волновые свойства обыкновенных частиц: электронов,
протонов, нейтронов, атомов, молекул и пр. Как это ни пара-
парадоксально, природа света и вещества оказалась двойственной:
корпускулярно-волновой. С открытием этого факта связан ко™
репной пересмотр физических воззрений, приведший к построе-
построению квантовой механики. От этого, однако, значение интерфе-
интерференционных и дифракционных явлений не уменьшилось. В на™
ши дни интерференция и дифракция света имеют важные прак-
практические применения, например в спектроскопии и метрологии.
2. С помощью различных приспособлений, например отра-
отражений, преломлений или как-либо иначе, можно наложить один
световой пучок на другой. Если выполняется принцип суперпо-
суперпозиции (а это предполагается всюду в настоящей главе), то каж-
каждый пучок будет проходить через область перекрытия так, как
если бы другого пучка не было совсем. Пусть Ei — напряжен-
напряженность электрического поля, создаваемая первым пучком в про-
произвольной точке А области перекрытия, а Е2 — вторым. Соглас-
Согласно принципу суперпозиции, результирующая напряженность по-
поля в той лее точке А, создаваемая обоими пучками, будет пред-
представляться векторной суммой Е = Ei + E2. Так же ведут себя
любые скалярные или векторные волны, какова бы ни была их
физическая природа. Требуется только, чтобы они подчинялись
принципу суперпозиции. Однако частота световых волн совсем
иного порядка, чем частота, скажем, звуковых волн или волн на

200 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
поверхности воды. Это ограничивает возможности приемников
света.
Всем приемникам света присуща определенная инерцион-
инерционность. Ее молено характеризовать временем установления или
разрешения приемника т. Так, для глаза т~0,1 с. Это есть вре-
мя, в течение которого глаз сохраняет зрительное впечатление,
т.е. «видит свет» даже тогда, когда излучение уже перестало
в него попадать. Глаз не замечает, например, быстрых миганий
света, если они следуют друг за другом через времена, малые по
сравнению с т (кино, телевидение). У фотоматериалов г (время
экспозиции) обычно порядка 10"~2—-10" с. Существуют прием-
приемники, для которых время разрешения может быть сделано го-
гораздо меньше. В ячейках Керра это время может быть доведено
до 10~™8—-10""9. Наиболее быстродействующие современные фо-
фотоэлектрические приемники имеют время разрешения порядка
1СГ10 с, но оно может быть сделано еще меньше.
Однако даже такие времена очень велики по сравнению с
периодами оптических колебаний. Средний период колебаний Т
электромагнитного поля в видимой области спектра составляет
около 10~15 с. Поэтому ни один приемник света не позволяет
измерить мгновенное значение напряженности электрического
или магнитного поля в световой волне. Для этого время раз™
решения приемника должно было бы быть мало по сравнению
с периодом световых колебаний Т. Все приемники могут изме-
измерять только величины, квадратичные по полю, усредненные за
времена, не меньшие времени разрешения приемника. Сюда от-
относятся энергетические и фотометрические величины: лучистый
и световой поток, яркость, освещенность и пр.
В явлениях интерференции, дифракции и пр. представля-
представляют интерес не абсолютные, а только относительные значения
этих величин. Например, нас может интересовать относитель-
относительное распределение освещенности на экране, куда попадает свет.
При такой постановке вопроса нет смысла точно указывать, о
какой именно энергетической или фотометрической величине
идет речь в том или ином конкретном случае. Заключения бу-
будут относиться к любой усредненной по времени величине, ква-
квадратичной по напряженности электрического поля. Эту нечет-
нечетко определенную величину принято называть интенсивностью
света или интенсивностью колебаний. Ниже она обозначается
через /. За / мы будем обычно принимать усредненное по време-
времени значение квадрата напряженности электрического поля, т.е.
i = W.
3. Найдем теперь интенсивность света в какой-либо точке
пространства, где перекрываются два пучка света. Возведя ра-
равенство Е = Ei + Е2 в квадрат и произведя усреднение по вре-

§ 26 ОБЩИЕ СВЕДЕНИЯ ОБ ИНТЕРФЕРЕНЦИИ 201
мени, получим
I = h+l2 + h2, B6.1)
где 1\ — интенсивность света первого пучка, а /2 — второго.
Последнее слагаемое
/12 = 2(EiE2), B6.2)
учитывающее взаимодействие пучков, называется интерферен-
интерференционным членом. Если взять независимые источники света, на-
например две электрические лампочки, то повседневный опыт по™
казывает, что I = 1\ + /2, т.е. результирующая интенсивность
равна сумме интенсивностей налагающихся пучков, а потому ин-
интерференционный член обращается в нуль. Тогда говорят, что
пучки не коррелированны или не когерентны между собой. Од-
Однако, если накладывающиеся пучки не независимы, например
один получается отражением другого от зеркала, то в некоторых
случаях интерференционный член 1\2 не обращается в нуль, а
потому I ф I\ + h- В одних точках пространства результирукь
щая интенсивность / больше, в других меньше суммы интенсив-
интенсивностей 1\ и I<i. Это явление называется интерференцией волн,
или интерференцией колебаний. Говорят, что источники света
и соответствующие им пучки, дающие интерференцию, корре-
лированы или когерентны между собой, т.е. колебательные и
волновые процессы в них протекают во времени согласованно.
Говорят также, что когерентные пучки интерферируют^ а неко-
некогерентные не интерферируют между собой.
Все сказанное о двух пучках относится и к случаю наложе-
наложения нескольких пучков. Интерференция двух пучков называется
двухлучевой^ многих пучков — многолучевой.
4. Начнем с идеализированного случая, когда обе волны
строго монохроматические и имеют одну и ту же частоту. Мо-
Монохроматическая волна — это строго синусоидальная волна с
постоянными во времени частотой cj, амплитудой а и начальной
фазой (р. Амплитуда и фаза колебаний могут меняться от одной
точки пространства к другой, частота одна и та же для колеба-
колебательного процесса во всем пространстве. Монохроматическое
колебание в каждой точке пространства длится бесконечно дол-
долго^ не имея ни начала, ни конца во времени. Поэтому строго
монохроматические колебания и волны никогда не могут быть
точно реализованы в действительности. Однако эти идеализа-
идеализации играют громадную роль в учении о колебаниях и волнах, в
чем мы уже убедились в гл. X третьего тома и еще в большей
степени убедимся в дальнейшем.
Допустим сначала, что в рассматриваемой точке наблюдения
оба вектора Ei и Е2 параллельны или антипараллельны. Тогда
можно отвлечься от векторного характера колебаний, считая их

202
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
скалярными. Представим эти колебания в вещественной форме:
Е\ = а\ cos (out + <pi), Е2 = «2 cos (ujt + (p2)^ B6.3)
где ai и ci2, ^1 и (^2 - амплитуды и начальные фазы колебаний.
Если ввести комплексные амплитуды А\ = а\ег(р1 и А2 = a2elLp2 ^
то в комплексной форме те же колебания представятся так:
Ег = Агегш\ Е2 = А2ешК B6.4)
Результирующее колебание будет
Е = Ег + Е2 = {А1+А2)еш\
Это — также монохроматическое колебание с той же частотой
ш и комплексной амплитудой А = А\ + А2. Чтобы найти веще™
ственную амплитуду а и начальную фазу (р результирующего
колебания, запишем последнее соотношение так:
aeitp =
а2е
г{р\
Умножая его на комплексно-сопряженное, получим
а2 = а\ + а2 + 2а\а2 cos (ip2 — </?i),
а после отделения вещественной части от мнимой
a cos (р = ai cos </?i + а2 cos ^2 5 tt sin <p = o>i sin c/?i +
Отсюда
B6.5)
, a\ sin <z?i
tg(p=
2 sin y?2
B6.6)
ai COS (/9i + tt2 COS (f2
На рис. Ill приведена векторная диаграмма сложения рас™
сматриваемых колебаний, из которой также нетрудно получить
результаты B6.5) и B6.6).
Вводя интенсивности колебаний, ре™
зультат B6.5) можно записать в виде
I = h+h+2^hh cos((p2-ipi). B6.7)
Если колебания синфазны, т.е. фазы щ
и (р2 одинаковы или отличаются на чет-
четное число тг, то интенсивность / макси-
максимальна и равна
J-ы
= К//1 +
{26Л
РИС-
Если колебания противофазны, т.е. фа-
фазы if\ и ip2 отличаются на нечетное чис™
ло тг, то получается минимальная интенсивность:
су
/мин=
B6.9)
Если колебания совершаются в квадратуре, т.е. их фазы отли-
отличаются на тж ± тг/2 (т — целое число), то I = 1\ + 12. В этом

§ 26 ОБЩИЕ СВЕДЕНИЯ ОБ ИНТЕРФЕРЕНЦИИ 203
случае интенсивность результирующего колебания равна сумме
интенсивностей складываемых колебаний.
5. Не представляет труда написать интерференционный член
и для общего случая, когда складываются векторные колеба-
колебания, причем между декартовыми компонентами каждого век-
вектора могут существовать произвольные разности фаз. Предо™
ставляя это сделать читателю, заметим, что Френель и Араго
обнаружили на опыте, что две световые волны, распространяю-
щиеся в одном направлении, никогда не интерферируют между
собой, если они линейно поляризованы во взаимно перпендику-
перпендикулярных плоскостях. На этом основании Френель пришел к за™
ключению, что световые волны поперечны.
Покажем это, не вводя никаких специальных предположений
о физической природе «светового вектора» Е, совершающего ко™
лебания в световой волне. Допустим, что вдоль оси Z распро-
страняются две волны, плоскости колебаний которых взаимно
перпендикулярны. В одной волне колебания происходят в ко™
ординатной плоскости 1Z, в другой — в координатной плоско-
плоскости YZ. Представим световые векторы этих волн в виде Ei =
= Eix + Eiz и Е2 = E2|/ + E2Z, где координатные индексы указы™
вают, какой из координатных осей параллелен соответствующий
вектор. Перемножая скалярно и усредняя по времени, находим
интерференционный член:
E2z) = 2aiza2z cos (ip2z - <piz),
где a\Z) d2z — амплитуды, a (fiz, (f2z — фазы соответствующих
продольных колебаний. Опыты Френеля и Араго показали, что
интерференционный член обращается в нуль, каковы бы ни бы™
ли фазы колебаний. Отсюда следует, что по крайней мере одна
из амплитуд, например a\z, равна нулю, т.е. первая волна попе™
речна. Но тогда и вторая волна должна быть поперечной, так
как нет никаких оснований предпочесть первую волну второй.
6. Допустим теперь, что перекрываются две плоские волны:
Е\ = а\ cos (out — kir + Ji), E2 = fl2 cos (u>t — k2r + S2). B6.10)
Снова предположим, что векторы Ei и Е2 параллельны или
антипараллельны, так что от векторного характера колебаний
можно отвлечься. Сравнивая эти выражения с B6.3), видим,
что в рассматриваемом случае
^2-V?i=Kr + E2-5i), B6.11)
где введен новый вектор К = ki — k2. Он параллелен биссектри-
биссектрисе угла, внешнего по отношению к углу а, который составляют
между собой волновые векторы ki и к2 (рис. 112). Поверхно-
Поверхности равных разностей фаз (р2 — (fi = const суть параллельные
плоскости, перпендикулярные к вектору К. Они обозначены на

204
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
рис. 112 штриховыми прямыми. Вдоль каждой из этих плоско-
плоскостей, следовательно, интенсивность результирующего колебания
будет постоянна. Она максимальна,
когда разность фаз (р2 — (fi содержит
ж четное число раз, и минимальна, ко-
когда тг содержится нечетное число раз.
В частности, если складываются вол-
^ ны с одной и той же интенсивностью
X /, то интенсивность в максимуме бу-
будет 41, а в минимуме — нуль. Расстоя-
Расстояние Ах между двумя соседними плос-
плоскостями максимальной или минималь-
Рис. 112 ной интенсивности найдется из усло-
условия К Ах = 2тг. Так как длины обоих
одинаковы и равны к = 2тг/А, то
А
B6.12)
волновых векторов ki и
К = 2А; sin (а/2), и следовательно,
Ат = — =
К к sin (a/2) 2 sin (а/2)*
Для малых углов а
Ах^Х/а. B6.13)
Если поставить плоский экран, то он пересечет плоскости
равной интенсивности вдоль параллельных прямых; на экране
появятся светлые и темные «интерференционные полосы». Рас-
Расстояние между серединами соседних светлых или темных полос
называется шириной интерференционной полосы. Если плос-
плоскость экрана параллельна плоскости (ki,k2), в которой лежат
волновые векторы ki и k2, то ширина интерференционной поло-
полосы равна Дж, т.е. определяется выражением B6.12). То же самое
получится, если экран установлен в перпенди-
перпендикулярной плоскости перпендикулярно к бис-
биссектрисе угла между волновыми векторами ki
и к2. Если же, оставляя экран перпендику-
перпендикулярным к плоскости (ki,k2), повернуть его на
угол <р, то ширина интерференционной полосы
сделается равной А^х = Ах/ cos (p.
7. Разберем теперь случай, когда перекры-
перекрываются сферические монохроматические вол-
волны от двух точечных источников света Si и
$2 (рис. 113). В этом случае амплитуды а\ и «2
складываемых колебаний обратно пропорцио-
пропорциональны расстояниям г\ и Г2 от точки наблю-
наблюдения до источников Si и *$2. Поэтому интен-
интенсивность света будет меняться вдоль каждой
интерференционной полосы. Однако это изменение медленное,
и от него можно отвлечься. Основное значение для результи-
Рис. 113

§ 26 ОБЩИЕ СВЕДЕНИЯ ОБ ИНТЕРФЕРЕНЦИИ 205
рующей интенсивности имеет разность фаз складываемых ко™
лебаний. Поверхности равных разностей фаз г\ ~~ г 2 = const бу-
будут двухполостными гиперболоидами вращения с фокусами Si
и $2- На экране, перпендикулярном к линии источников S1S2,
получатся интерференционные полосы в виде концентрических
колец с центром в точке пересечения экрана с указанной линией.
Если же экран параллелен линии источников Si$2, то интерфе-
интерференционные полосы будут гиперболами с фокусами S\ и S2. В
последнем случае в небольшой центральной части интерферен-
интерференционная картина практически будет состоять из равноотстоя-
равноотстоящих параллельных светлых и темных полос.
Если фазы колебаний обоих источников света одинаковы, то
разность фаз складываемых колебаний будет
А<р = Цг2 - П) = Bтг/Л)(г2 - п).
Когда она равна 2гатг (га — целое число, положительное или
отрицательное), то получается максимум интенсивности коле-
колебаний (светлая интерференционная полоса). Если же А(р =
= 2тг(т + х/2), то интерференционная полоса будет темной. Усло-
Условия максимума и минимума можно также записать в виде
[ тпХ (светлая полоса),
Ar = r2-r1 = { v ;' B6.14)
I (га + /2)А (темная полоса).
Величина г 2 —П. называется разностью хода интерферирую™
щих лучей. Если интерферирующие лучи проходят через среды
с различными показателями преломления, то величину г 2 — г\
надо заменить на
А = J П2(И — I
т.е. на оптическую разность хода интерферирующих лучей.
Для светлых интерференционных полос оптическая разность хо-
хода составляет целое, для темных — полуцелое число длин волн
(в вакууме). Целое число т называется порядком интерферен-
интерференции. Порядок интерференции есть округленная до целого числа
оптическая разность хода интерферирующих лучей, выражен-
выраженная в длинах волн (в вакууме).
8. Основные результаты, найденные выше, можно также по-
получить на следующем простом примере. Пусть Si и S2 — близко
расположенные точечные монохроматические источники света
(рис. 114). Для увеличения интенсивности интерференционных
полос вместо них можно взять два коротких линейных источни-
источника, например две узкие ярко освещенные щели. Плоскость экра-
экрана Э предполагается параллельной плоскости, в которой лежат
линейные источники Si и S2. Пусть СО — перпендикуляр к этой
плоскости, проходящий через середину между источниками Si

206
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
и *$2, D — длина этого перпендикуляра, d — расстояние между
источниками Si и S2. Предполагается, что не только расстоя-
расстояние d, но также длины источников и линейные размеры экрана
малы по сравнению с расстоянием D. Тогда интерференцион-
интерференционные полосы на экране будут прямолинейны и перпендикулярны
к линии, соединяющей источники Si и S2. Начало координат
поместим в точке О на экране, ось X направим параллельно
линии источников S\S2- Если х — абсцисса точки наблюдения
А, то
Г2 _ D2 , (т I d/2J г2 - П2 4- (т - d/2\2
так что rf — г2 = 2xd, и следовательно, ri — Г2 = 2xd/{г\ + Г2).
Так как ж<1), то без существенной ошибки знаменатель ri +Г2
моясно заменить на 2D. Тогда
xd
П - г2 = — = ах
B6.15)
где а ^ d/D — угол схождения интерферирующих лучей, т.е.
угол, под которым из точки О (или в рассматриваемом прибли™
жении из любой точки экрана) видно расстояние d между ис-
источниками Si и S2. Интенсив-
Интенсивность света найдется по форму-
формулам B6.7) и B6.11). Если источ-
источники Si и S2 одинаковы и син™
фазны, то эти формулы дают
= 2L
/
B6.16)
Рис. 114
Интенсивность I периодически
меняется вдоль оси X от нуля до
максимального значения /макс =
= 4/х. Пространственный пе-
период изменения интенсивности
Ах = А/а есть ширина интерфе-
интерференционной полосы.
Если на пути одного из лучей, например 52^4, ввести прозрач-
прозрачную плоскопараллельную пластинку Р с толщиной I и показате-
показателем преломления п, то оптическая длина этого луча увеличится
на (п — 1)/, а разность хода между лучами Si А и S2A умень-
уменьшится на такую же величину. Прежнее значение разности хода
получится в какой-то другой точке А1', отстоящей от S\ и S2 на
х) Если пренебречь членами третьей степени по d, то п — Г2 =
= xdj\fD2 + ж2. Пренебрегая далее пятыми степенями x/D, отсюда полу-
получим
r1-r2 = g(l-^)*ox(l-^). B6.15a)

§ 26 ОБЩИЕ СВЕДЕНИЯ ОБ ИНТЕРФЕРЕНЦИИ 207
расстояниях г[ иг^. Положение точки А1 найдется из условия
ИЛИ (Г1!—Г2) = (ri — 7
Это значит, что произойдет смещение всей рфр
картины на N = (п — 1I/Ах полос в ту сторону, с какой бы-
была введена пластинка Р. На этом основаны интерференционные
методы измерения малых изменений показателя преломления,
обладающие высокой чувствительностью. Для таких измерений
надо пользоваться белым светом (см. § 30). В монохроматиче-
монохроматическом свете все полосы одинаковы, и их смещение трудно изме-
измерить — для этого толщину пластинки 1 надо было бы увеличи-
увеличивать непрерывно от нуля до окончательной величины.
9. Наличие интерференционных максимумов и минимумов в
волновом поле, конечно, не может привести к противоречию с
принципом сохранения энергии. Обсудим этот вопрос для толь-
только что исследованного случая двух одинаковых синфазных мо-
нохроматических точечных источников Si и $2.
Максимумы интенсивности находятся на гиперболах Г].—Г2 =
= га А, минимумы — на гиперболах г\ — г 2 = (га- + У2)А. Макси-
Максимальное значение, которое может принимать разность г\ — Г2,
равно расстоянию между источниками d, а максимальное зна-
значение га — целой части, содержащейся в числе d/X. Когда d >>
^>А, число интерференционных полос в волновом поле велико. В
этом случае интерференция приводит только к пространствен-
пространственному перераспределению лучистой энергии, в результате чего в
одних местах пространства (в максимумах) плотность лучистой
энергии увеличивается, в других (в минимумах) уменьшается, а
общий запас энергии в пространстве остается неизменным.
Полный поток лучистой энергии через любую замкнутую по-
поверхность, окружающую источники Si и *$2, равен сумме пото-
потоков через ту же поверхность, которые излучались бы каждым
из этих источников в отсутствие другого. Однако это равенство
не точное^ а только приближенное и в среднем выполняется
тем точнее, чем больше d/X. Когда d < А, в волновом поле уже
нет линии нулевой интенсивности. Когда лее d<CA, то во всех
точках пространства складываются колебания, фазы которых
практически одинаковы. В этом случае интенсивность резуль-
результирующего колебания, а с ним и поток результирующего излу-
излучения, исходящий от обоих источников, в четыре раза больше со-
соответствующих величин для одного из источников в отсутствие
другого. Таким образом, если расстояние между источниками
Si и ,$2 меньше длины волны А, то поток лучистой энергии че-
через замкнутую поверхность, окружающую эти источники, боль-
больше суммы потоков, которые излучали бы те же, но уединенные
источники.

208 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
Однако принцип сохранения энергии и не требует равенства
этих величин. Источники вместе действителвно болвше излуча-
излучают энергии, чем в том случае, когда они находятся далеко друг
от друга. Но это увеличение излучения происходит не за счет
нарушения сохранения энергии, а за счет работы генератора^
который должен поддерживатв постояннвши амплитудв! коле™
баний в источниках. Если же колебания в источниках свободные,
то увеличение излучения приводит просто к более быстрому за-
затуханию этих колебаний.
Рассмотренный случай трудно реализовать в оптическом
диапазоне спектра из-за малости длин световых волн. Но в обла-
области радиоволн это не только возможно, но и практически ис-
полвзуется для получения направленных излучений и увеличе-
увеличения их мощности. Конечно, возможен и такой случай, когда
совместное действие двух источников приводит не к увеличе-
увеличению, а к уменьшению общего излучения. Это будет, например,
когда колебания в источниках происходят в противоположных
фазах.
10. Строго монохроматические волны одной и той же ча-
частоты, даже от двух различных точечных источников, всегда
интерферируют между собой^ т.е. когерентны. Интерференци-
Интерференционная картина от таких источников устойчива в том смысле,
что распределение интенсивности волнового поля в простран-
пространстве остается неизменным во времени. Интерференция излу-
излучений от независимых источников света, например от элек-
электрических лампочек, недоступна наблюдению глазом. Глаз не
наблюдает интерференцию даже при наложении излучений от
двух независимых самых узких спектральных линий, излуча-
излучаемых разреженными газами. Это служит лучшим доказатель-
доказательством того, что излучения реальных источников света никогда
не бывают строго монохроматичными.
Невозможность визуального наблюдения интерференцион-
интерференционных полос от независимых источников света можно пояснить на
примере идеализированных источников, излучающих квазимо-
квазимонохроматический свет. Такой свет представляется колебания-
колебаниями вида B6.3), в которых, однако, амплитуды ai, «2 и фазы <pi,
(f2 медленно и хаотически меняются во времени, т.е. испыты-
испытывают заметные изменения за времена, очень большие по срав-
сравнению с периодом Т самих световых колебаний. Примером мо-
может служить излучение изолированного атома. Возбужденный
атом испускает ряд или, как принято говорить, цуг волн в тече-
течение времени тИЗЛ5 характерная длительность которого порядка
10~8 с (см. § 89). В таком цуге содержится 106^108 волн. За
время тизл атом «высвечивается» и переходит в невозбужденное
состояние. В результате различных процессов, например столк-

§ 26 ОБЩИЕ СВЕДЕНИЯ ОБ ИНТЕРФЕРЕНЦИИ 209
новений с другими атомами или ударов электронов, атом может
снова вернуться в возбужденное состояние, а затем начать излу-
излучать новый цуг волн. Таким образом, получится последователь-
последовательность цугов, испускаемых атомом через малые и нерегулярно
меняющиеся промежутки времени. Пусть теперь на экран попа-
попадают излучения от двух независимых атомов. При наложении
двух цугов, излучаемых этими атомами, на экране получится
какая-то картина интерференционных полос. Положение полос
определяется разностью фаз между колебаниями обоих цугов.
А такая разность фаз быстро и беспорядочно меняется от одной
пары цугов к следующей. В течение секунды десятки и сотни
миллионов раз или чаще одна система интерференционных по-
полос будет сменяться другой. Глаз или другой приемник света
не в состоянии следить за этой быстрой сменой интерференци-
интерференционных картин и фиксирует только равномерную освещенность
экрана.
Смещение интерференционных полос при замене одной пары
цугов другой происходить не будет, если у этих цугов начальные
фазы 5\ и <?2 хотя и меняются нерегулярно во времени, но оди-
одинаково. Действительно, в этом случае ^2 — ^1 = 0 и, как видно из
B6.11), разность фаз складываемых колебаний ip2 — ipi содер-
содержит только слагаемое Кг, регулярно меняющееся в простран-
пространстве. Чтобы этого достигнуть, надо излучение от одного и того
эюе источника расщепить на два или несколько пучков и заста-
заставить их попадать на экран различными путями. Если при этом
будут накладываться пучки, полученные из одного и того же
цуга, то интерференционные полосы на экране будут сохранять
свое положение и глаз зафиксирует устойчивую (неподвижную)
интерференционную картину. Некоторые опыты, основанные на
таком принципе, будут описаны в следующем параграфе.
11. Отметим, что нет принципиальных запретов на возмож-
возможность получения интерференции от двух независимых источни-
источников света. Такая возможность определяется уровнем техники
генерирования и приема излучения. Еще в 1947 г. Г.С. Горелик
A906-1957) предлагал осуществить гетеродинирование, или де-
демодуляцию видимого света. В видимом свете можно выделить
дублеты или мультиплеты, т.е. сложные спектральные линии,
состоящие из двух или нескольких одиночных спектральных ли-
линий с разностями частот v\ — V2 порядка 109-~1010 Гц. По идее
Горелика такой свет должен падать на катод фотоэлемента (а
еще лучше фотоумножителя). Если верно предположение, что
мгновенный фототок пропорционален квадрату напряженности
результирующего электрического поля, то его можно предста-
представить в виде
3 = A(Ei + Е2J = А{Е\ + Е| + 2EiE2),

210 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
где Ei и Е2 — напряженности электрического поля, соответ-
соответствующие частотам ^ и i/2, a i - постоянная прибора. В этом
выражении слагаемое 2/ЦЕ1Е2) содержит составляющую с раз-
разностной частотой У\ — V2- Частоте v\ — V2 ^ Ю10 Гц соответ-
соответствует длина волны А ~ 3 см, лежащая в микроволновой области
радиоволн. Ее можно усилить радиотехническими средствами и
сделать доступной наблюдению. Тем самым биения интенсивно™
сти, возникающие при наложении пучков света от двух источ-
источников, превратятся в колебания электрического тока.
Для осуществления опыта в принципе безразлично, испус-
испускаются ли волны с частотами v\ и щ одним источником или
двумя независимыми источниками света. Трудность опыта со-
состоит в том, что на выделяемый сигнал разностной частоты
и\ — V2 накладывается «шум», интенсивность которого превос-
превосходит интенсивность сигнала примерно в 104 раз. Эта трудность
была преодолена в 1955 г. Форрестором и его сотрудниками. Ис-
Источником света служила яркая одиночная зеленая линия рту-
ртути А = 546,1 нм, расщеплявшаяся в магнитном поле (эффект
Зеемана). Применялся фотоэлемент с сурьмяно-цезиевым като-
катодом. Положительный результат опыта доказывает, что если и
существует запаздывание выхода электронов с поверхности фо-
фотокатода по сравнению с попаданием на нее фотонов, то оно
значительно меньше 10~10 с.
С изобретением лазеров техника эксперимента получила ис-
источники света столь высокой степени монохроматичности, что
наблюдение интерференционных максимумов и минимумов от
двух независимых лазеров с помощью надлежащих приемни-
приемников света (например, тех же фотоэлементов) стало сравнительно
легко осуществимой экспериментальной работой.
§ 27. Классические интерференционные опыты
1. Опыт Юнга. Юнг получал полосы интерференции
по способу, описанному им в публичных лекциях 1807 г. Яр-
Яркий пучок света от Солнца падал на экран с малым отверстием
или узкой щелью S (рис. 115). Дифрагированный свет шел ко
второму экрану с двумя узкими отверстиями или щелями Si и
$2. На этих щелях свет также претерпевал дифракцию, в ре-
результате чего получались два перекрывающихся расходящихся
пучка света с вершинами в Si и 5*2. Ввиду общности происхо-
происхождения эти пучки когерентны. На экране в месте перекрытия
пучков наблюдались параллельные интерференционные полосы
(см. предыдущий параграф, п. 8). Расстояние между щелями S\
и S2 должно быть велико по сравнению с шириной каждой щели.

§ 27 КЛАССИЧЕСКИЕ ИНТЕРФЕРЕНЦИОННЫЕ ОПЫТЫ 211
Удобный способ получения нужных щелей был указан Рэлеем.
Стеклянные пластинки покрываются тонким слоем серебра и
тем самым становятся непрозрачными. На серебряном слое од™
ной из пластинок лезвием
бритвы проводится одна, а
на другой две близко рас™
положенные параллельные
линии, которые и использу-
используются в качестве щелей.
Оценим по формуле
B6.13) ширину Ах ин-
интерференционной полосы.
Допустим, что расстояние
d между щелями S\ и *$2
составляет 1 мм, а расстоя» рис. 115
ние от щелей до экрана
D = 1 м. Тогда а = d/D = 0,001 рад. Для красного света
(А = 600 им) получаем Ах = А/а = 6 • 10 им = 0,6 мм. В синем
свете ширина полосы будет порядка 0,4 мм. Таким путем впер™
вые Юнг измерил длины световых волн, хотя эти измерения и
не могли быть точными. В опыте Юнга из-за дифракции свет
распространяется от щелей Si и $2 в различных направлениях
неравномерно. Влияние этого осложняющего обстоятельства
будет выяснено в гл. IV.
Задолго до Юнга, в 1665 г., аналогичный опыт был поставлен
Гримальди. Однако в опыте Гримальди свет от Солнца падал
непосредственно на щели Si и $2- Дополнительной щели S не
было. При такой постановке опыта интерференционные поло™
сы получаться не могли, ввиду значительных угловых размеров
Солнца (см. § 28, п. 7).
При использовании лазеров, генерирующих практически па™
раллельные пучки лучей, щель S в опыте Юнга не нужна.
2. Зеркала Френеля. В 1816 г. Френель осу™
ществил следующий интерференционный опыт. Свет от узкой
ярко освещенной щели S (рис. 116) падал на два плоских зер™
кала CD и СЕ^ наклоненных друг к другу под углом, близким
к 180°. Щель S устанавливалась параллельно линии С пересече-
пересечения плоскостей зеркал. При отражении падающий пучок разде-
лялся на два когерентных пучка, как бы исходивших от прямых
Si и $2, являющихся мнимыми изображениями щели S в зерка-
зеркалах. Прямой свет от источника S загораживался непрозрачной
ширмой MN. На экран Э попадали только отраженные пуч-
пучки. В области АВ, где пучки перекрывались, наблюдались па™
раллельные интерференционные полосы. Для расчета ширины
интерференционной полосы Ах введем следующие обозначения:

212
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
СО = a, CS = Ь, AHCD = <р. Так как точки S, Si и *$2 лежат
на одной окружности радиуса Ь, то, предполагая угол <р малым,
можем написать d = S1S2 = 2b(p. Угол а, под которым из точки
О видно расстояние S1S2, равен а = d/(a + Ь) = 2Ь(р/(а + 6), а
потому
о; 2Ь<^?
Угол а молено просто измерить по шкале зрительной трубы.
Для этого трубу следует поместить в точке О и установить ее на
отчетливое видение изображений Si и S2 щели S. Тогда можно
Рис. 116
найти А по формуле А = а Ах. Ширина области перекрытия
АВ = 2аср7 а потому число полос, которые могут наблюдаться
на экране, равно
пт 2аш 2аша АаЬ 2
1V "^ _______________ (П
Ах X Х(а + Ь)
В опыте Френеля интерференционная картина искажается
дифракцией на ребре С, вдоль которого пересекаются плоскости
зеркал.
3. Бипризма Френеля. Бипризма Френеля
состоит из двух стеклянных призм с малыми преломляющими
углами, сложенных своими основаниями (рис. 117). Практиче-
Практически она изготовляется из целого куска стекла. Источником света
служит ярко освещенная щель S, устанавливаемая параллельно
ребру бипризмы. После преломления в бипризме падающий пу™
чок света разделяется на два когерентных пучка с вершинами
в мнимых изображениях Si и S2 щели S. В области АВ экрана
пучки перекрываются и дают систему параллельных интерфе-
интерференционных полос. Пусть /3 — преломляющий угол бипризмы,
п — ее показатель преломления, а ж Ь — длины отрезков СО
и SC. Каждая половина бипризмы отклоняет параксиальный

27
КЛАССИЧЕСКИЕ ИНТЕРФЕРЕНЦИОННЫЕ ОПЫТЫ
213
луч на угол (п — 1)/5. Расстояние d между изображениями S\ и
Й2 равно d = SiS2 — 2Ь(п — 1)/3, а угловое расстояние между
ними а = d/(a + Ъ). Ширина полосы
= А = Л(о + Ь)
дт = А =
B7.3)
Искажения интерференционной картины, вносимые дифрак-
цией на ребре С бипризмы, более существенны, чем в опыте с
зеркалами Френеля. Однако осуществить опыт с бипризмой зна-
значительно легче.
Рис. 117
Рис. 118
4. Билинза Бийе. Собирательная линза разрезает-
разрезается пополам, и обе половинки ее раздвигаются. Образовавшаяся
система называется бчлипзоп. На билинзу направляется свет от
щели S, параллельной плоскости разреза (рис. 118). В Si и S^
получаются действительные изображения щели S. Пучки света,
проходящие через Si и S2, перекрываются. В местах перекры-
перекрытия наблюдается интерференция. Если щель S поместить между
билинзой и ее фокальной плоскостью, то изображения Si и S2
будут мнимыми. В этом случае интерференция невозможна, так
как световые пучки не перекрываются. Чтобы получить интер-
интерференцию и при таком расположении щели S, надо из централь-
центральной части линзы вырезать плоскопа-
плоскопараллельный кусок стекла и обе поло-
половинки линзы сблизить между собой.
Тогда пучки будут перекрываться, и
интерференция станет возможной.
5. Зеркало Ллойда A800—
1881). Свет, исходящий из узкой яр-
ярко освещенной щели Si (рис. 119),
отражается от полированной плос-
плоской поверхности черного стекла. На
участке АВ экрана, где перекрываются прямой и отраженный
свет, наблюдаются полосы интерференции.
Рис. 119

214 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
6. Во всех описанных опытах полосы интерференции можно
наблюдать на белом матовом экране. Можно пользоваться так-
также матовым стеклом, наблюдая полосы интерференции на его
задней стороне через лупу или микроскоп малого увеличения.
Такой объективный способ наблюдения применял и Френель в
первых опытах. Но он заметил, что полосы интерференции не
исчезали, а становились более яркими, когда матовое стекло
убиралось. Поэтому в дальнейших исследованиях Френель пе-
перешел к субъективному методу наблюдения интерференцион-
интерференционных (и дифракционных) полос. Идея, на которой основан субъ-
субъективный способ наблюдения полос, весьма проста. Допустим,
что интерференционные полосы получены на задней плоско-
плоскости П матового стекла. Интенсивность света в какой-либо точке
Р плоскости П определяется разностью фаз интерферирующих
лучей, приходящих в эту точку. Отобразим теперь с помощью
линзы плоскость П на сопряженную плоскость П7. Лучи, вы-
вышедшие из точки Р, снова соберутся теперь в точке Р1'. Но так
как оптические длины всех лучей между сопряженными точка-
точками одинаковы, то интерферирующие лучи придут в точку Р1 с
той же разностью фаз, какой они обладали в точке Р. Поэто-
Поэтому в плоскости П; получится изображение не только плоскости
П, но и всей системы интерференционных полос на ней. Линза
как бы переносит интерференционную картину с плоскости П
на плоскость П;. Так же действует и оптическая система глаза,
с помощью которой интерференционные полосы получаются на
сетчатке. Если пользоваться зрительной трубой, установленной
на бесконечность, то таким путем будет наблюдаться интерфе-
интерференционная картина, получающаяся на бесконечном (т.е. очень
далеком) расстоянии от глаза.
7. Интерференционный опыт Поля A884—
1976). Описанные выше установки отличаются малой светоси-
светосилой, а потому мало пригодны для
демонстрации интерференции света в
большой аудитории. Опыт Поля свобо-
свободен от этого недостатка. Здесь источ-
источник света S (рис. 120), которым мо-
может служить небольшая, но достаточ-
достаточно яркая ртутная лампа, помещается
перед пластинкой слюды, толщина ко-
которой порядка нескольких сотых долей
миллиметра. Свет отражается от перед-
передней и задней поверхностей пластинки с
Рис- 120 образованием двух мнимых изображе-
изображений Si и S2 источника S. Прямой свет от источника S загора-
загораживается ширмой. Получаются два широких когерентных пучка
света с вершинами в точках Si и $2- Падая на экран, потолок или

§ 27 КЛАССИЧЕСКИЕ ИНТЕРФЕРЕНЦИОННЫЕ ОПЫТЫ 215
стены аудитории, они дают при интерференции систему светлых
и темных колец (см. п. 6 предыдущего параграфа). Благодаря
большому количеству света кольца хорошо видны во всей ауди-
аудитории. Преимущества метода Поля будут выяснены в § 28.
8. Опыт Меслина. Этот опыт является видоизменени-
видоизменением опыта Бийе. Только в нем половинки разрезанной линзы не
раздвигаются перпендику-
перпендикулярно к оптической оси,
а смещаются вдоль нее,
и притом на значитель-
значительное расстояние (рис. 121).
Половинки билинзы дают
действительные изображе- рис> 121
ния точечного источника S
в точках Si и ^2 на главной оптической оси. Интерференцион-
Интерференционные полосы наблюдаются в заштрихованной области, где накла-
накладываются соответствующие пучки света, т.е. между изображе-
изображениями S\ и S2- В плоскости, перпендикулярной к главной опти-
оптической оси, интерференционные полосы имеют вид концентри-
концентрических полуколец с общим центром на этой оси.
Интересно, что центр колец темный. Явление связано с тем,
что один пучок, прежде чем интерферировать со вторым, про-
проходит через свой фокус Si, тогда как другой пучок проходит
через свой фокус S2 позже. На этом основании можно прийти к
заключению, что прохождение волны через фокус сопровожда-
сопровождается изменением фазы на тт.
Это легко понять на примере скалярной сферической волны,
сходящейся к своему центру О и заполняющей полный телесный
1 / г \
угол 4тг. Представим поле этой волны в виде Е\ = -Д f ? + - 1,
где г — расстояние от центра О, a v — скорость распространения
волны. Когда волна проходит через центр О, начинает образо-
образовываться расходящаяся сферическая волна Е^ = -f2\t—-
Волновое поле в пространстве теперь представится в виде
Г \ V
Но напряженность поля Е нигде не может обращаться в беско-
бесконечность, в частности и при г = 0. Поэтому необходимо, что-
чтобы в любой момент времени выполнялось соотношение /2^) =
= —/i(t), т.е. функция /2 может отличаться от функции f\ толь-
только знаком. Если колебания f\ и /2 синусоидальны, то в точке О
их фазы будут противоположны. А это и значит, что при про-
прохождении через фокус фаза волны меняется на тг.

216
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
Из приведенного рассуждения следует, что на передовом
фронте функция f\ должна оставаться непрерывной. Если бы
здесь она испытывала разрыв, то при подходе передового фрон-
фронта к центру О напряженность поля Е возрастала бы неогра-
неограниченно. То же самое относится и к заднему фронту волны, а
также к функции /2.
ЗАДАЧИ
1. Как надо поместить собирательную линзу в опыте с бипризмой (см.
рис. 117), чтобы ширина интерференционной полосы Ах не зависела от
положения экрана? Найти Ах. Найти максимальное число N полос, которое
может наблюдаться в этой установке, если оно получается при удалении
экрана от бипризмы на расстояние L.
А
Ответ. Ах =
N =
2(п-1)/Г" А
2. При каком расстоянии L экрана от бипризмы в предыдущей задаче
число интерференционных полос N будет максимальным, если расстояние
между вершинами бипризмы равно I? Найти N. При каком положении экра-
экрана полосы пропадут?
Ответ. N = 1{п — 1)/3/А; L = Если экран удалить от
бипризмы на расстояние L или больше, то полосы пропадут.
3. Найти число полос интерференции N в установке с бипризмой (см.
рис. 117).
_ жт 4ab (п — 1Jв2
Ответ. N = г г^ •
а + b A
4. В опыте с бипризмой Френеля экран для наблюдения интерференци-
интерференционных полос расположен перпендикулярно к оси установки. Нулевая полоса
получается в центре экрана в
g вертикальной плоскости, прохо-
проходящей через ребро бипризмы
и ось установки. В какую сто-
сторону и на какую величину х
сместится нулевая полоса, ес-
если освещающую щель немного
сместить в сторону на величину
h перпендикулярно к оси уста-
установки?
Решение. При смеще-
смещении источника из положения S
в положение S' (рис. 122) дей-
С ствие бипризмы CAB сведет-
сведется к действию ее части DEB
Рис. 122 и плоскопараллельной пластин-
пластинки CAED. Суммируя смеще-
смещения, вызываемые этими частями в отдельности, найдем, что центр интер-
интерференционной картины из прежнего положения О сместится вверх на рас-
расстояние х = hb/a.
h
о а А
S Л \
ог
ъ
о
D

28
ВЛИЯНИЕ РАЗМЕРОВ ИСТОЧНИКА СВЕТА
217
§ 28. Влимние размеров источника света.
Пространственная когерентность
1. Увеличение размеров источника света приводит к ухуд-
ухудшению контрастности интерференционных полос и даже к их
полному исчезновению. Допустим сначала, что источник состо-
состоит из двух одинаковых некогерентных светящихся точек А ж В,
находящихся на малом расстоянии I друг от друга (рис. 123).
Как было выяснено в § 26 (п. 10),
для получения интерференции
от одного источника А надо рас-
расщепить свет, исходящий от это™
го источника, на два пучка, по-
попадающих на экран различными
путями. То же самое надо сде-
сделать со светом от источника В.
Конкретный способ расщепле-
расщепления пучка лучей на два в после™
дующих рассуждениях не имеет
никакого значения. На рис. 123
один пучок света попадает к ме-
месту интерференции Р непосред-
непосредственно от источников А и В,
другой — после отражения от
зеркала M2N2. Последующие рассуждения применимы и к кри-
криволинейным лучам. Однако, во избежание ненужных усложне-
усложнений в написании формул, показатели преломления сред в точках
А и В, & также в месте нахождения экрана, на котором наблю-
наблюдается интерференция, предполагаются равными единице.
Пусть АМ\Р и АМ2Р — два луча, исходящие из точки А
под углами /Зх и /?2 к линии АВ и сходящиеся в точке Р, где они
и интерферируют. Аналогичные лучи, исходящие из точки В,
пусть будут BN\P и BN2P. Если расстояние I = АВ достаточ-
достаточно мало, то для разности оптических длин лучей АМ\Р и BN\P
можно написать: (АМ\Р) — (BN\P) = (АС) = I cos fa. Анало-
Аналогично для АМ2Р и BN2P: (AM2P) - (BN2P) = (AD) = lcos/32.
Следовательно,
Рис. 123
[(АМгР) - (АМ2Р)] ~~
~~ (BN2P)] = I (cos fa - cos fa).
В первой квадратной скобке стоит оптическая разность хода лу-
лучей, исходящих из точки А. Она определяет характер интерфе-
интерференции этих лучей в точке Р: максимум, минимум или какой-
либо промежуточный случай. Аналогично, во второй квадрат-
квадратной скобке стоит оптическая разность хода лучей, исходящих
из точки I?, от которой зависит характер интерференции этих

218 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
лучей. Разность этих величин
Д = 11 cos /3i — cos /321
характеризует фазовый сдвиг интерференционной картины от
точечного источника А относительно интерференционной кар-
картины от точечного источника В. Она определяет результат на™
ложения одной из этих картин на другую. Если величина А рав-
равна нулю или мала по сравнению с длиной волны А, то макси-
максимумы одной картины накладываются на максимумы другой, а
минимумы — на минимумы. Тогда происходит усиление интер-
интерференционных картин, а полосы интерференции наиболее кон-
контрастны: наблюдается плавный переход от яркой освещенности
в максимумах к полной темноте в минимумах. При возрастании
А контрастность полос сначала ухудшается. Когда А = А/2, т.е.
/|cos/3i -cos/32| = A/2, B8.1)
максимумы одной картины накладываются на минимумы дру-
другой, и полосы интерференции исчезают. При дальнейшем воз-
возрастании А полосы интерференции появляются вновь, причем
интерференционная картина периодически повторяется от наи-
наибольшей контрастности до их полного исчезновения. При
A = l|cos/3i -cos/32| =m\ B8.2)
(т — целое число) полосы столь же контрастны, что и при А =
= 0. При
( |) А B8.3)
полосы пропадают, а экран освещается равномерно. Если А не
превышает примерно А/4, то контрастность полос лишь немного
уступает контрастности при А = 0. То же самое бу-
будет при А = (га + а)А, где а — правильная дробь, не
превышающая примерно 1/4. Это несколько произ-
д"'\ ±- вольное условие в дальнейшем мы будем рассматри-
рассматривать как условие хорошей контрастности интер-
интерференционных полос. Заметим еще, что в пределах
принятой точности расчета угол /32 можно отожде-
отождествить с углом /?2? что и делается в дальнейшем без
особых оговорок.
2. Допустим теперь, что источник света протя-
протяженный и имеет форму равномерно светящейся ли-
линии АВ длины 1, все точки которой излучают свет
Рис. 124 некогерентно (рис. 124). Разобьем ее мысленно на
бесконечное множество пар некогерентных точеч-
точечных источников (Aj ?»;), (Atf^B/t)J ..., находящихся на расстоя-
расстоянии 1/2 друг от друга. Применим к таким парам точечных ис-
источников результаты, полученные выше. Для этого надо рас-
расстояние 1 заменить на 1/2. Если — = -|cos/?i — cos/32| = -, то
в'
А'"\
А'
А

§ 28 ВЛИЯНИЕ РАЗМЕРОВ ИСТОЧНИКА СВЕТА 219
интерференционных полос от каждой пары точечных источни-
источников не получится, они создадут на экране только светлый фон.
То же самое будет, если размеры источника I = АВ увеличить
в 2, 3, ... раз. Итак, если выполнено условие
A = l|cos/?i -cos/32| = гаА, B8.4)
то протяженный источник создает на экране только освещенный
фон без интерференционных полос (в противоположность тому,
что было в случае пары точечных источников, когда при том
же условии получалась наилучшая контрастность полос). Если
А = (га + о) А, где а — правильная дробь, то протяженный ис-
точник можно мысленно разбить на две части, длины которых
относятся как га : а. Меньшая часть источника даст интерфе-
интерференционные полосы на светлом фоне, создаваемом большей ча-
частью того же источника. От этого контрастность полос умень-
уменьшается. Чем больше га, тем хуже контрастность. При больших
га интерференционные полосы практически наблюдаться не бу-
будут. Условие хорошей контрастности интерференционных полос
в случае протяженного источника света можно ориентировочно
представить в виде
l|cos/3i -cos/321 ^ А/2, B8.5)
Если крайние интерферирующие лучи выходят из какой-
либо точки протяженного источника симметрично по отноше-
отношению к перпендикуляру к линии АВ, проведенному из этой точ-
точки, т.е. /?2 = тг — /?i, то cos 02 = — cos/?i, и предыдущее условие
можно представить в виде
ls!n(O/2) ^ А/4, B8.6)
где ft — угол между этими крайними лучами. Его часто назы-
называют узлом интерференции. Следует, однако, иметь в виду, что
условие B8.6) можно применять только при наличии той сим™
метрии^ которая была использована при его выводе. Задания
только одного угла интерференции (вопреки распространенно-
распространенному противоположному утверждению) совершенно недостаточно,
чтобы в общем виде записать условие хорошей контрастности
интерференционных полос. Для этого надо ввести два угла {5\ и
/?2? как эт° и было сделано выше.
Результаты, полученные выше для точечных источников, без
всяких затруднений распространяются на источники света, име-
имеющие форму коротких параллельных прямолинейных отрезков,
смещенных один относительно другого в поперечном направле-
направлении на расстояние I и параллельных плоскости экрана, в сред-
средней части которого наблюдается интерференция. (Под средней
частью здесь понимается малая окрестность экрана вблизи ли-
линии, вдоль которой экран пересекается с плоскостью, проведен-
проведенной через середину источников перпендикулярно к их длине.)

220
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
При том же расположении справедливы и результаты B8.4) и
B8.5) для некогерентных протяженных источников, имеющих
форму прямоугольных полосок, если только под I понимать те-
теперь их ширину. Такими источниками в оптике обычно служат
прямоугольные щели, ярко освещаемые широкими пучками лу-
лучей. Если выполнено условие
11 cos /?i — cos /?21 <С А,
то щель действует как бесконечно тонкий линейный источник
света.
3. Таким образом, для получения интерференционных полос
от двух источников света недостаточно, чтобы эти источники со™
стояли из попарно когерентных точечных источников. (Приме-
(Примером могут служить источник и его оптическое изображение или
два оптических изображения одного и того же источника.) Да™
же в случае строго монохроматического света необходимо еще,
чтобы размеры источников не превосходили определенного пре™
дела, зависящего от взаимного расположения и расстояния меж-
между ними, а также от положения экрана, предназначенного для
наблюдения интерференционных полос.
Два источника, размеры и взаимное расположение которых
позволяют наблюдать интерференционные полосы (при необ-
необходимой степени монохроматичности света), называются про-
пространственно когерентными. Если же интерференционных по-
полос (даже при идеальной монохроматичности
. Р света) получить нельзя, то источники назы-
называются пространственно некогерентными
(см. далее п. 8).
4. Посмотрим теперь, при каких условиях будет
соблюдаться пространственная когерентность в клас-
классических интерференционных опытах, описанных в
предыдущем параграфе. Во всех опытах источники
света линейные (за исключением опыта Меслина, где
они точечные, так что вопрос о пространственной ко™
герентности здесь практически не возникает). При
этом в опытах с зеркалами и бипризмой Френеля,
а также в установках Бийе и Поля взаимное распо-
расположение когерентных источников АВ и А'В' «пря™
мое», т.е. соответствует рис. 125, а в опыте с зеркалом
Ллойда — «обратное», как представлено на рис. 126
(стр. 221). На этих рисунках соответствующие коге™
рентные пары точечных источников обозначены че-
через (А, А ), (jB, В ) и т.д. При этом в установках Фре-
Френеля, Ллойда и Бийе, где источниками служат освещаемые щели, послед-
последние предполагаются перпендикулярными к плоскости рисунка, а I = АВ
означает ширину щели. В установке Поля линейные источники АВ и А'В'
(например, изображение ртутной лампы, имеющей форму небольшого ци-
цилиндра) ориентированы вертикально, так что здесь АВ означает длину I
источника света.
П
Рис. 125

§ 28 ВЛИЯНИЕ РАЗМЕРОВ ИСТОЧНИКА СВЕТА 221
5. Начнем с прямого расположения (см. рис. 125). В этом случае
02 — /3i = а. Ввиду малости угла а схождения интерферирующих лучей мо-
можем написать
cos/3i — cos/32 = sin /ЗД/3 = asin/3,
где с принятой точностью расчета под /3 можно понимать любой из углов
/3\ и /?2 или любое промежуточное значение между ними. "Условие B8.5)
хорошей контрастности интерференционных полос принимает вид
I ^ A/Basin/3), B8.7)
или, ввиду B6.13),
I ^ Ax/Bsin/3). B8.8)
В установках Френеля и Бийе углы /3i и /З2 практически не отличаются
от тг/2, так что в этом случае I ^ Аж/2, т.е. ширина щели не должна пре-
превосходить примерно половину ширины интерференционной полосы (пред™
полагается, что плоскость экрана перпендикулярна к оси установки СО, см.
рис. 116).
В интерференционном опыте Поля (см. рис. 120), напротив, углы /3
составляют 20-50 °, а интерференционные полосы, если они наблюдаются на
потолке аудитории, имеют форму колец. Для упрощения вычислений заме-
заменим пластинку слюды двумя отражающими параллельными плоскостями,
расстояние между которыми равно толщине h этой пластинки. Тогда рас™
стояние между соответствующими точками источников (например, между
А и А или В ж В) будет 2/г, так что 2/isin/3 = га, где г в нашем прибли-
приближении равно п или Г2 либо любой промежуточной величине между п иг2.
Подставляя отсюда значение а в B8.7), получаем условие пространственной
когерентности:
I <; г A/D/i sin2/3). B8.9)
В опыте Поля толщина пластинки слюды h должна быть очень мала,
так что мнимые источники АВ и А' В' сдвинуты один относительно другого
на ничтожную величину 2/г, во много раз меньшую длины I самого источни-
источника. Допустим, например, что А = 500 нм = 5 • 10~5 см, h = 0,05 мм, г = 8 м,
/3 = 30°. Тогда, согласно формуле B8.9), должно быть I ^ 8 см. Таким об-
образом, для получения хорошей контрастности полос источник света может
иметь сравнительно большие размеры, а потому его
можно взять светосильным. В этом основное пре-
преимущество установки Поля при демонстрации явле- Гг}
ний интерференции. Другое преимущество — боль-
большие апертуры интерферирующих пучков, позволяю-
щие получать полосы интерференции на большой
площади.
6. Перейдем теперь к обратному расположению
когерентных источников АВ и А'В' (рис. 126), реа-
реализующемуся в опыте Ллойда. В этом случае в сере-
середине экрана О условие B8.5) выполняется при любой
ширине щели I. При другом расположении точки на-
наблюдения Р
cos/3i = (AC + OP)/ru cosft = -(
Так как АС = А'С^ то, пренебрегая в знаменателях Рис. 126
различием между г\ и f2, отсюда получим: cos/3i —
— cos/32 = 2ж/г, где х = ОР — координата точки Р. Поскольку интерфери-
интерферирующие лучи почти перпендикулярны к плоскости экрана, условие хорошей

222
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
контрастности интерференционных полос запишется в виде 2lx/r ^ А/2, т.е.
х ^ гА/D!). B8.10)
На вдвое болвшем расстоянии интерференционные полосвх пропадут. Пол-
Полное число N полос, которые будут наблюдаться до такого расстояния, най-
найдется делением 2х на ширину полосы Аж = А/а. Это дает
га d
21 V
B8.11)
где 2d = га — расстояние между источниками света. Это выражение дает
оценку наивысшего порядка интерференции в монохроматическом свете в
установках типа опыта Ллойда.
7. Рассмотрим, наконец, интерференционный опыт Юнга (рис. 127). Ис™
точником света служит прямоугольная полоска ширины I (например, ярко
освещенная щель). Из каждой точки этой полоски, например, точки А, лучи
идут к щелям Si и S2 экрана под углами C\ и /?2 •
Если опять пренебречь в знаменателях различи-
различием между п и Г2, то можно написать: cos/3i —
— cos/?2 = d/r, где d — расстояние между середи-
серединами щелей Si и S2. Тогда условие B8.5) перехо-
переходит в Id/г ^ А/2, или
(р <; A/Bd), B8.12)
где (р = 1/г — угловой размер источника АВ, ес-
если его рассматривать с места расположения ще-
щелей Si и 5г (так как в опыте Юнга углы /3± и
02 почти не отличались от тг/2). Когда <р = А/с!,
интерференционные полосы пропадают.
Допустим, что свет направляется к щелям Si
и S2 непосредственно от Солнца, как это было в
опыте Гримальди (см. § 27, п. 1; в опыте Гри-
и 5г служили два рядом расположенных неболь-
небольших отверстия). Угловой размер Солнца (р ~ 30 = 0,0087 рад, длину вол-
волны примем равной А = 550 нм. Тогда для получения каких бы то ни бы-
было интерференционных полос необходимо выполнение условия d < А/92 ~
~ 6 • 10 нм = 0,06 мм. Такое условие в опытах Гримальди, конечно, не мог-
могло соблюдаться, а потому не могла наблюдаться и интерференция света.
8. Более важным является следующее обобщение. Допустим, что свет,
освещающий отверстия Si и S25 монохроматичен. Будет или не будет в этих
условиях наблюдаться интерференция пучков света, прошедших через ма-
малые отверстия Si и S2, при заданном расстоянии d между ними, зависит от
степени углового расхождения лучей, освещающих эти отверстия. Пусть,
например, источник имеет форму диска, плоскость которого параллельна
плоскости экрана, на котором сделаны отверстия Si и S2. Если ср — угловой
диаметр диска, то интерференция будет наблюдаться, когда отверстия Si
и S2 можно покрыть кругом с диаметром d < А/(р. Если же этого сделать
нельзя, то интерференции не будет. В первом случае говорят, что световые
пучки, прошедшие через отверстия Si и S2, пространственно когерент-
ны, а во втором — пространственно некогерентны. Минимальная площадь
поперечного сечения пучка
Рис. 127
мальди источниками S\
B8.13)

§ 28 ВЛИЯНИЕ РАЗМЕРОВ ИСТОЧНИКА СВЕТА 223
обладающая этим свойством, называется площадью пространственной ко-
герентности освещающего света. Когда свет строго монохроматичен, то все
нарушения когерентности носят чисто пространственный характер, т.е. свя-
связаны с различием направлений световых лучей. Для строго плоских волн
все направления лучей одинаковы ip = 0), так что площадь когерентности
а становится бесконечной. По мере удаления от источника угловое расхож-
расхождение лучей, попадающих в прибор, уменьшается, а их пространственная
когерентность повышается. Примером могут служить звезды. Несмотря на
громадные линейные размеры звезд, свет от них доходит до нас с высо-
высокой степенью пространственной когерентности. Световые лучи от лазеров
характеризуются высокой направленностью, недоступной никаким другим
земным источникам света. Именно эту особенность лазерного излучения
имеют в виду, когда говорят о его высокой пространственной когерентно-
когерентности.
ЗАДАЧИ
1. Для характеристики контрастности интерференционных полос Май™
кельсон ввел функцию
V = 1макс ~ 1мин , B8.14)
-*макс i -*мин
называемую видностью (или видимостью) их. Определить видность V в
случае интерференции двух одинаково интенсивных монохроматических
пучков света, попадающих на экран по различным путям от точечного ис-
источника света.
Решение. Согласно B6.7), интенсивность света на экране при осве-
освещении обоими источниками дается выражением I = 2/i(l + cos S), где 1\ —
интенсивность, создаваемая одним из них. При смещении точки наблюде-
наблюдения по экрану из-за изменения разности фаз 8 между интерферирующими
пучками интенсивность I меняется от /Макс :=: 4/i до /Мин = 0, так что V = 1.
2. Решить ту же задачу для источника света, состоящего из двух одина-
одинаковых некогерентных светящихся точек А и JB, расположенных на расстоя-
расстоянии I друг от друга (см. рис. 123). Интерференционные полосы наблюдаются
на удаленном экране.
Решение. Интенсивности света в интерференционных картинах
на экране, создаваемые в отдельности светящимися точками А и J3, равны
соответственно Ia = 2ii(l + cos?i), 1в = 2ii(l + cos(b), где <5i, 82 и I имеют
такой же смысл, что и в предыдущей задаче. Результирующая интенсив-
интенсивность
г г i г лт (л . Ь\ — 0^2 Si +
I = 1а + 1в = 4/i I + c
2 2
Величина 8\ ~~ 82 есть разность фаз между обеими интерференционными
картинами. Согласно вычислениям, приведенным в п. 1,
8 = \8\ — 82] = к А = Ы\ cos/3i — cos/32|,
где к = 2тг/Л — волновое число. При перемещении по экрану точки на-
наблюдения изменения фаз 8\ и 82 происходят быстро и определяют ширину
интерференционных полос. Напротив, разность фаз 8=\8\ ^<Ь| изменяется
медленно, оставаясь практически постоянной на протяжении многих интер-
интерференционных полос. Она определяет видность, т.е. контрастность полос.

224
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
Максимальные и минимальные интенсивности будут
/макс = 4/i
а потому
1 +
F =
ее
4)'
cosfe —
/мин = 4/l
=
тгА
cos ~—
л
(l-
8
cos-
B8.15)
При изменении А, т.е. расстояния I между светящимися точками А и J5,
видность У" периодически изменяется от 1 до 0 (рис. 128).
3. Найти видность интер™
V
2%
871
кА
Рис. 128
ференционных полос, когда ис-
источником света является пря-
прямолинейный отрезок длины I,
все точки которого излучают
некогерентно (см. рис. 124).
Решение. Направим ось
Y вдоль излучающего отрезка,
поместив начало координат О
в его середине. Пусть ср — раз-
разность фаз между двумя лучами, исходящими из точки О и попадающими
в точку наблюдения Р по различным путям. Разность фаз между такими
же лучами, исходящими из другой точки отрезка с координатой у и прихо-
приходящими в ту же точку Р, будет
8 = b/(cos/3i - cos ^2) + if = (kA/l)y + ср.
Лучи, исходящие по различным путям из отрезка с/г/, при интерференции
на экране создают интенсивность
dl = A + cos<f) dy
(в условных единицах). Так как точки источника излучают некогерентно,
то полная интенсивность будет
+1/2
I =
/[¦
¦ cos
-1/2
X1
ч>
кА
sm
кА
sm
кА
При смещении вдоль экрана будет меняться фаза ср. Значения фазы
которых интенсивность I экстремальна, найдутся из условия
'кА
при
откуда ср = ттг, где т — целое число;
sin (fcA/2)
~ к А/2
Т^1 _ sin (кА/2)
кА/2
при четном т,
при нечетном ггг.
Следовательно,
_, , ,sin(fcA/2) _ sm(fcA/2)
-iмакс — ь ~г fc т л /г» 5 ^мин — «> t '
fcA/2
кА/2 '
sin (fcA/2)
feA/2 "
B8.16)

29
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ
225
1
Кривая видности представлена на рис. 129. Из рисунка видно, как
быстро с увеличением длины I
источника уменьшаются макси™ у
мумы на кривой видности. Той
же кривой представляется вид™
ность интерференционных полос
в опытах типа зеркал и биприз-
бипризмы Френеля (если только точки
щелевого источника света излу-
излучают некогерентно). В этом слу™
О
Ътг
кА
чае I означает ширину щели.
4. Решить предыдущую за™ Рис. 129
дачу в предположении, что все
точки источника излучают когерентно и притом в одинаковых фазах.
Ответ.
о sin(*A/2)
V =
кА/2
B8.17)
кА/2
§ 29. Спектральное разложение
1. До сих пор интерференция исследовалась только в идеаль-
идеальном случае монохроматического света. Интерференцию в немо™
нохроматическом свете можно исследовать, разлагая свет по
теореме Фурье на монохроматические составляющие. Если вол™
новое поле в точке наблюдения описывается периодической
функцией Е = E(i) с основным периодом т и основной частотой
п = 2тг/т, то его можно представить в виде вещественной части
ряда Фурье:
E(t) =
B9.1)
п=0
коэффициенты которого определяются выражением
г/2
ап = - Г E(t)e-inQtdt B9.2)
Т *J
-т/2
(см. т. III, § 128; конечно, в случае света постоянного слагаемо-
слагаемого с коэффициентом uq не будет). Средняя за период объемная
плотность энергии колебаний (в условных единицах) будет
т/2
W = - I
т J
-т/2
B9.3)
п=0
п=0
Д.В. Сивухин

226 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
Она равна сумме средних плотностей энергии монохроматиче-
монохроматических колебаний, из которых складывается результирующее ко-
колебание. То же заключение справедливо и для интенсивности
колебаний, если понимать под интенсивностью усредненную по
периоду т любую энергетическую величину, характеризующую
поле излучения в рассматриваемой точке пространства.
Полученный результат остается приближенно верным и для
случая, когда функция E(t) не периодична, а представляется су-
суперпозицией монохроматических колебаний, частоты которых
распределены по спектру совершенно произвольно. Только в
этом случае усреднение надо производить не по периоду т (ко™
торого теперь не существует), а по времени, весьма большому
по сравнению с периодами всех монохроматических колебаний,
входящих в суперпозицию. Результат приближенно верен и в
случае суперпозиции почти гармонических колебаний с произ-
произвольными частотами, например для света, состоящего из узких
спектральных линий.
2. Если функция E(t) не периодична, то она представляется
не рядом, а интегралом Фурье. Для возможности такого пред-
представления на функцию E(t) приходится накладывать различ-
различные (достаточные) ограничения, например требовать, чтобы она
была абсолютно интегрируема во всем бесконечном интервале
(), т.е. чтобы сходился интеграл
+ ОО
/ \E(t)\dt.
Это обстоятельство, однако, в физике не создает никаких суще-
существенных затруднений, даже в тех случаях, когда вводят функ-
функции, не обращающиеся в нуль на бесконечности, т.е. не удовлет-
удовлетворяющие требованию абсолютной интегрируемости.
Действительно, пусть E(t) — такая функция. Разделим t на
интервалы времени, достаточно длительные по сравнению с не-
риодами световых колебаний. Световое поле на каждом из таких
интервалов (to, to + т) и его воздействие на приемник при любом
значении to практически совсем не зависят от полей на соседних
интервалах. Поэтому при рассмотрении света только на интер-
интервале (to, to + т) функцию E(t) вне рассматриваемого интервала
можно заменить любой другой функцией. В частности, ее моле-
молено периодически продолжить за пределы интервала (to, to + т) с
периодом т. Но тогда для представления функции E(t) в интер-
интервале (to,to + r) можно воспользоваться рядом Фурье B9.1). При
этом, ввиду малости частоты П = 2тг/т, целесообразно ввести
обозначения Аш = f), шп = пп. Тогда
E(t) =

§ 29 СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ 227
После аппроксимации суммы интегралом получаем
E{t) = J a{co)eiajt dco, B9.4)
о
где а(ш) = an/Q,, или с учетом B9.2)
г/2 г/2
a(uj) = -L Г E(t)e-iujt dt = -L Г E(t)e-iujt dt. B9.5)
^т/2 ^t/2
Интеграл Фурье получается из этих формул, если в послед-
последнем выражении конечные пределы заменить на бесконечные ^оо
и +оо (см. т. III, § 128). Однако здесь мы не будем делать этого,
оставляя время т неопределенным. При физической постановке
задач всегда молено достигнуть необходимой точности, выбирая
т достаточно большим. Таким путем достигается то преимуще-
преимущество, что формулу B9.4) в каждом интервале длительностью т
можно будет применять и для функций E(t), не интегрируемых
абсолютно, например к плоским волнам постоянной интенсивно-
интенсивности, не ограниченным во времени. При этом выражения B9.4)
на разных интервалах времени т (если т выбрать достаточно
большим), вообще говоря, не будут когерентны.
В случае интеграла Фурье формула B9.3) заменится на
т/2
Если аппроксимировать сумму интегралом и учесть, что тп =
= 2тг, то получится
т/2 оо
J \E\2dt = 27i J \a(uj)\2dD, B9.6)
^т/2 О
О физическом смысле этого соотношения говорится ниже в п. 5.
3. Приведем пример спектрального разложения, приводя™
щий к важным обобщениям. Бесконечно длящееся синусоидаль-
синусоидальное колебание является идеализацией ограниченного ряда, или
цуга синусоидальных волн, представленного на рис. 130 а «обор™
ванной синусоидой». Пусть Tq — «период», а ш® — «частота»
этой «синусоиды». Тогда в комплексной форме
т/2
2тг и % iri [ш — шо)т/2
-т/2

228
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
В вещественной форме
о
(ш — шо)т/2
где
а = (ш^ш°)т
приведен на
рис
График функции , .^ _
а 2
130 б. Таким образом, оборванный цуг волн, изображен-
изображенный на рис. 130 а, может быть представлен суперпозицией бес-
бесконечного множества синусоид, частоты которых непрерывно
sin а (ш-ш0)т
2% Ъ%
б
Рис. 130
заполняют бесконечный интервал 0 < ш < +оо. Впрочем, основ-
основное значение имеет только интервал ^— < а < + —, или ин-
тервал cdQ^^ <cj<o;o + ^, где амплитуды колебаний велики.
На всех остальных участках амплитуды малы. Если ими прене-
пренебречь, то можно сказать, что весь спектр частот практически
сосредоточен в пределах интервала шириной Да;, который удо-
удовлетворяет условию
Аш>т> 2тг. B9.8)
Если ввести обычную частоту v = о;/Bтг), то
Avt>1. B9.8а)
Это важное соотношение между шириной спектра Да; (или
Аи) и длительностью цуга т имеет общий характер. Его мож-
можно также уяснить на следующем простом примере. Рассмотрим
множество синусоид с одинаковыми амплитудами, но различны-
различными частотами, непрерывно и равномерно заполняющими интер™
вал Да;. Пусть в точке t = 0 фазы всех синусоид совпадают, а
следовательно, амплитуда колебаний максимальна. При t = т/2
разность фаз между крайними синусоидами будет Да; • т/2. Ес-
Если она сделается равной 2тг, то в точке t = т/2 наложатся си-
синусоиды со всевозможными фазами, непрерывно и равномерно
заполняющими интервал шириной 2тг. При таком наложении,
как легко уяснить с помощью векторной диаграммы, синусоиды

§ 29 СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ 229
погасят друг друга. При том же условии произойдет взаимное
гашение синусоид и в точке t = —т/2. Таким образом, выделится
интервал времени (—т/2,+т/2), на обоих концах которого вол™
новое поле обратится в нуль. На этом участке время т связано
с шириной спектра Да; соотношением Аы • т = 4тг, которое по
существу совпадает с B9.8).
4. Формула, аналогичная B9.8), имеет место и для простран-
пространственного распределения волнового поля, когда оно рассматри-
рассматривается в какой-либо фиксированный момент времени. Примером
может служить «оборванная синусоида» на рис. 130 а, если по
оси абсцисс откладывать координату х в направлении распро-
распространения волны. При таком рассмотрении снова можно поль-
пользоваться формулой B9.4), заменив в ней время t на координату
ж, а частоту ш на волновое число к = ш/v. Поступив так, лег-
легко найти, что длина цуга волн Ах связана с соответствующим
интервалом волновых чисел Ак соотношением
Ак • Ах > 2ж« B9.9)
Этот результат будет обобщен в § 44 на случай трех измере-
измерений. Соотношения B9.8) и B9.9) играют важную роль в кванто-
вой механике, где они при несколько иной интерпретации выра-
выражают так называемый принцип неопределенности Гайзенберга
A901-1976).
5. Когда ширина спектра Да; достаточно мала (До; <С а;),
то соответствующий свет называют квазимонохроматическим.
Часто пользуются также «спектроскопическим волновым чис-
числом» к = к/Bтг). Для него
Ак°Ах> 1. B9.9а)
Примером могут служить спектральные линии, излучаемые раз-
разреженными газами. Квазимонохроматический свет можно вы-
выделить из непрерывного спектра излучения (например, Солн-
Солнца) призмой, дифракционной решеткой или другими приборами,
осуществляющими спектральное разложение. За меру монохро-
монохроматичности света можно принять отношение |а;/Да;| или рав-
равное ему отношение |А/ДА|. Наибольшей монохроматичностью
обладает свет, излучаемый газовыми лазерами. Нельзя, однако,
упускать из виду, что цуг волн или световой пучок, занимающий
спектральную область Да;, должен обладать конечной длитель-
длительностью, не меньшей т « 2тт/Аш. В частности, не имеет смысла
говорить о мгновенной объемной плотности энергии излучения в
интервале do;, т.е. о величине ^ \dE\ = \а(ш) dw\ . Вместо мгно-
мгновенной надо пользоваться средней плотностью энергии излуче-
излучения за время порядка т ~ 2ж/duo. Это значит, что интенсивность
излучения в спектральном интервале {oo^oo + doo) должна опреде-
определяться величиной, пропорциональной t|qLEJ|2, т.е. \а(ш)\2 duo. Be-

230 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
личину |«(о;)|2 называют спектральной плотностью излучения.
Именно такую величину имеют в виду, говоря о распределении
интенсивности или энергии излучения в спектре. Вместо часто-
частоты можно, конечно, пользоваться длинами волн, представляя ту
же величину в виде |ад(А)|2с1А. Очевидно, а(ш) = 2тгса\(Х)/ш2.
ЗАДАЧА
Разложить в интеграл Фурье и найти спектральную плотность излу-
излучения для затухающего осциллятора, волновое поле которого определяется
выражением
E(t) = е^г'т sinwot (t ^ 0).
Ответ. а(ш) =
2тг (ш - ш0) - t/
т
а(^)|2 = 4^^-с0J1+A/г)^ B910)
Если ш — шо = 1/г, т.е. Аш • т = 1, то спектральная плотность излучения
уменьшается в два раза.
Этот пример снова подтверждает общее соотношение B9.8). В примере,
рассмотренном в тексте (см. рис. 130 б), спектральная плотность излучения
|а(а;)|2 на краях интервала < а < — убывает в (тг/2J и 2,5 раза по
сравнению с той же величиной при а = 0.
§ 30. Влияние немонохроматичности света
1. Как и увеличение размеров источников, немонохроматич-
немонохроматичность света ведет сначала к ухудшению контрастности (види-
(видимости) интерференционных полос, а затем к полному исчезно-
исчезновению их. Чтобы не усложнять исследование учетом конечных
размеров источника, будем предполагать, что источник света S
точечный. Пусть S\ и S2 (см. рис. 113) — когерентные источни-
источники, являющиеся действительными или мнимыми изображения-
изображениями источника S. Допустим сначала, что излучение источника S
состоит из двух близких одинаково интенсивных спектральных
линий с длинами волн А и А; = А + SX. Точка или линия экрана,
где оптическая разность хода А интерферирующих лучей равна
нулю, называется центром интерференционной картины.
Если начальные фазы источников Si и S2 одинаковы, то в
центр картины лучи с длинами волн А и X1 придут в одинаковых
фазах. Для обеих волн там получится светлая полоса. В дру-
другой точке экрана А1 в которой А = NX1', где N — целое число
(номер полосы или порядок интерференции), для длины волны
X1 получится также светлая интерференционная полоса. Если
А = (N + х/2) А, то в ту же точку А интерферирующие лучи

§ 30 ВЛИЯНИЕ НЕМОНОХРОМАТИЧНОСТИ СВЕТА 231
с другой длиной волны А придут уже в противоположных фа-
зах^ и для такой длины волны интерференционная полоса будет
темной. При этом условии в окрестности точки А светлые по™
лосы с длиной волны А; наложатся на темные полосы с длиной
волны А. Интерференционные полосы в указанной окрестности
исчезнут. Условие первого исчезновения полос, таким образом,
есть NX' = (N + г/2)\ или
N = - = — C0 1)
2(А'-А) 2ё\° { }
Все изложенное остается верным и в том случае, когда фазы
лучей, приходящих в центр интерференционной картины, про™
тивоположны. Только в этом случае центральная полоса будет
темной.
Когда номер полосы мал по сравнению с величиной N, опре-
деляемой выражением C0.1), интерференционные полосы будут
почти столь же отчетливы, что и в случае света с одной длиной
волны. Когда номер полосы для длины волны X1 достигнет зна-
чения 2JV, номер соответствующей полосы для длины волны А;
сделается равным BN + 1). Тогда полосы интерференции еде™
лаются столь же резкими, что и в центре интерференционной
картины. При дальнейшем возрастании порядка интерференции
будет наблюдаться периодическая смена резкости интерферен-
ционных полос от наибольшей отчетливости их до полного ис-
исчезновения.
Например, когда источником света является пламя натрия,
то излучаются две узкие спектральные линии с длинами волн
А = 589 и А; = 589,6 им. При N « А/[2(А; - А)] = 490 интер™
ференционные полосы становятся очень неясными или совсем
ненаблюдаемыми. При Ж, равном 980 или кратном этому числу,
полосы опять становятся отчетливыми. При дальнейшем воз™
растании порядка интерференции полосы периодически меняют
свой вид, становясь попеременно то отчетливыми, то размыты-
размытыми. И так продолжается до тех пор, пока из-за конечной ширины
обеих спектральных линий интерференционная картина не про-
пропадет совсем.
2. Перейдем теперь к случаю, когда свет от источника S
непрерывно и равномерно заполняет спектральный интервал
(А, А + SX). В этом случае можно поступить так же, как мы
поступали в § 28 (п. 2) при рассмотрении интерференционных
полос от протяженного источника света. Весь спектральный ин-
интервал (А, А + SX) разобьем на множество пар бесконечно узких
спектральных линий, находящихся на расстоянии SX/2 друг от
друга (на шкале длин волн). К каждой такой паре применима
формула C0.1), если в ней сделать замену SX —>* SX/2. Поэтому
первое исчезновение интерференционных полос произойдет для

232 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
порядка интерференции
N = Х/ёХ, C0.2)
вдвое большего, чем в предыдущем случае. При дальнейшем
возрастании порядка интерференции интерференционные поло-
полосы появятся вновь, но уже на светлом фоне, аналогично тому,
как это было в случае протяженного монохроматического источ-
источника света (§ 28, п. 2, а также задача 3). Их контрастность будет
незначительна, а при дальнейшем возрастании порядка интер-
интерференции и совсем исчезнет. Практически наблюдение интерфе-
ренционных полос ограничится порядками интерференции, не
превосходящими C0.2).
Формула C0.2) как оценочная остается верной и в случае
произвольного распределения интенсивности света по длинам
волн в интервале ёХ. Таким образом, эта формула дает оценку
максимально возможного порядка интерференции при заданной
степени монохроматичности Х/ёХ используемого света. Два ква-
квазимонохроматических пучка света, когерентные при низких по™
рядках интерференции, перестают быть таковыми при высоких
порядках, превышающих примерно величину C0.2).
8. Максимально возможный порядок интерференции мож-
можно также найти из следующих соображений. Пусть используе-
мый свет состоит из одинаковых цугов волн, следующих друг
за другом через беспорядочно меняющиеся промежутки време-
времени. Один из возможных цугов изображен на рис. 130 а (здесь
показано колебание волнового поля во времени в фиксирован-
фиксированной точке пространства; совершенно аналогично выглядит цуг в
пространстве в фиксированный момент времени). Интерферен™
ционный прибор разделяет пучок света на два пучка, идущие к
месту схождения по разным путям, так что между пучками воз-
возникает разность хода. Для когерентности пучков необходимо,
чтобы разность хода между ними не превосходила длину цуга
L = ст. В противоположном случае будет происходить нало-
наложение независимых цугов волн, испущенных в разные моменты
времени, и интерференция не возникнет. Максимальный поря-
порядок интерференции не может превышать величину
iVMaKC = j = т-. C0.3)
Разумеется, это условие должно согласовываться с условием
C0.2), а потому должно быть
L т А ш
А ~ Т ~ J\ ~ J^j'
Если учесть, что А = 2ж/к и Т = 2тг/о;, то отсюда получится
т • 5ш = 2тг и L • 6к = 2тг.

§ 30 ВЛИЯНИЕ НЕМОНОХРОМАТИЧНОСТИ СВЕТА 233
К таким соотношениям мы уже пришли в предыдущем парагра-
параграфе из других соображений.
С изложенной точки зрения нарушения когерентности свя™
заны с запаздыванием одного цуга волн по сравнению с другим.
Поэтому здесь, в отличие от пространственной, говорят о вре-
менной когерентности^ а длительность цуга т называют време-
временем когерентности. Временная когерентность — это то же са-
самое, что и когерентность, связанная с узостью спектрального
интервала До;, занимаемого светом. В силу B9.8) время коге-
когерентности тког связано с шириной спектрального интервала Да;
соотношением
Чем меньше Дг/, тем больше время когерентности и тем вы-
выше порядок интерференции, который может наблюдаться при
заданном и. Максимальная разность хода, при которой еще воз™
можна интерференция, определяется соотношением
т — \ v - д2
Ь^Стког^А-^-.
Она называется длиной когерентности. Ей соответствует мак-
максимальный порядок интерференции
Значения параметров 8v, г и L очень резко различаются для
света тепловых источников и света, генерируемого газовыми ла-
лазерами. Ширина спектральной линии 8и лучших «монохрома-
«монохроматических» тепловых источников, которые могут быть созданы в
лаборатории, порядка 108 Гц, тогда как в случае лазеров можно
получить 6и ^ 102 Гц или даже еще меньше. Соответствую-
Соответствующие времена когерентности будут 10~8 и 10~2 с, а длины ко™
герентности 1 и 106 м. Лазерные источники света позволяют
наблюдать интерференцию при разности хода в несколько ки-
километров. Здесь максимальный порядок интерференции, кото™
рый можно наблюдать, ограничивается не степенью монохрома-
монохроматичности лазерного излучения, а неоднородностью земной атмо™
сферы и трудностями создания стабильной интерференционной
схемы столь больших размеров.
4. Для белого света SX ~ А, т.е. N ~ 1. Казалось бы, что в бе-
белом свете интерференционные полосы наблюдаться не должны.
Это действительно так, если пользоваться такими приемника-
приемниками света, как фотоэлемент, болометр или термостолбик, кото™
рые обладают примерно одинаковой чувствительностью в раз-
различных участках спектра. Но глаз — селективный приемник^
т.е. его чувствительность к различным длинам волн разная (см.

234 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
кривую видности человеческого глаза на рис. 82). Именно по™
этому в белом свете глаз видит около десятка интерференцион-
интерференционных полос. Полосы цветные, так как из-за различия в длинах
волн полосы разного цвета имеют разную ширину и сдвинуты
относительно друг друга. Только в центре картины, куда волны
от обоих источников приходят в одинаковых фазах, соблюда™
ется условие максимума для всех длин волн. Там получается
ахроматическая, т.е. неокрашенная, светлая интерференцион-
интерференционная полоса. В опыте с зеркалом Ллойда ахроматическая полоса
темная. Это доказывает, что отражение света от зеркала сопро-
сопровождается изменением фазы волны на тг (см. § 33, 65). Конечно,
при обычной постановке опыта (см. рис. 119) ахроматическую
полосу увидеть нельзя, так как луч, отражающийся от зерка-
зеркала, проходит больший путь, чем прямой луч. Чтобы получить
эту полосу, надо на пути прямого луча поставить плоскопарал-
плоскопараллельную пластинку, смещающую вверх всю интерференционную
картину.
§ 31. Корреляция и когерентность света
1. При точном количественном определении понятия когерентности на-
надо учесть, что реальные световые колебания не синусоидальны. Напряжен™
ность поля в каждой точке пространства может быть представлена инте-
интегралом Фурье B9.4), т.е. в виде суперпозиции синусоидальных колебаний
различных частот. Если область Аш, заполняемая этими частотами, мала
по сравнению с самими частотами ш, входящими в суперпозицию, то ре™
зультирующее колебание и представляемый им свет называются квазимо-
квазимонохроматическими. Выбрав внутри интервала Аш произвольную частоту
шо, запишем квазимонохроматическое колебание в виде
E(t) =a(t)eluJ0\ C1.1)
где a(t) — комплексная амплитуда, медленно меняющаяся по сравнению
с быстро осциллирующей функцией еги}° . Она, конечно, определена не со-
совсем однозначно, поскольку ее значение зависит от выбора частоты ujq. Про
колебание, представленное формулой C1.1), говорят, что оно модулировано.
При модуляции может медленно меняться (вещественная) амплитуда,
колебания или его (начальная) фаза. В первом случае говорят об амплитуд-
амплитудной, во втором — о фазовой модуляции. Могут также одновременно менять™
ся и амплитуда, и фаза. В случае квазимонохроматического света, излуча-
излучаемого реальными источниками, такие изменения происходят хаотически —
амплитуда и фаза являются случайными функциями времени. Поэтому при
изучении реального света, в том числе и квазимонохроматического, нельзя
обойтись без использования статистических методов. Для простоты мы
отвлечемся от векторного характера колебаний, считая их скалярными.
Важно отметить, что из-за очень высоких оптических частот все суще™
ствующие приемники света не позволяют регистрировать быстрые измене-
изменения напряженности световых полей за времена порядка периода световых
колебаний. Обычно они не позволяют следить и за быстрыми изменения-
изменениями световых потоков, обусловленных случайными изменениями амплитуд и

§ 31 КОРРЕЛЯЦИЯ И КОГЕРЕНТНОСТЬ СВЕТА 235
фаз колебаний. Удается измерять только квадраты напрятсенностей све-
товых полей, усредненные по промежуткам времени, весьма большим не
только по сравнению с периодами световых колебаний, по и по сравнению с
временами, в течение которых происходят случайные изменения амплитуд
и фаз этих колебаний. Ниже предполагается, что световые потоки регистри-
регистрируются именно такими «инерционными» приемниками.
Более того, мы будем предполагать, что световые потоки в среднем ста-
стационарны, т.е. значение среднего квадрата поля в каждой точке простран-
пространства одинаково для всех моментов времени и не зависит от положения на
шкале времени временного интервала, по которому производится усредне-
усреднение. Квадрат поля можно представить в виде
(Re Ь) - I I - -{Ь + Ь ) + -ЬЬ .
Если положить а = ao(t)etS^\ где ao(t) и S(t) — медленно меняющиеся
вещественная амплитуда и фаза, то
Е2 + Е*2 = a2[e2^°t+S) + e-2i^°t+s)] = 2а2 cos [2(wot + 6)].
Эта величина осциллирует во времени очень быстро и при усреднении про-
пропадает. Результат усреднения величины (Re Е)' определяется только по-
последним членом /2 ЕЕ*. Поэтому за меру интенсивности колебаний можно
принять величину ЕЕ*.
2. Допустим теперь, что в точку наблюдения Р в момент времени t
приходят два колебания от источников света Si и 5г (см. рис. 113). Чтобы
прийти в Р в момент ?, эти колебания должны выйти из Si и & в более
ранние моменты времени t — в\ и ? — 02, где 0\ и 02 — времена, затрачи-
затрачиваемые светом на распространение от Si и S2 до точки Р. Чтобы отметить
это, рассматриваемые колебания в точке Р обозначим через E$t — 9$ и
E2(t ^02) соответственно. При их сложении в точке Р получится резуль-
результирующее колебание
Е = Е(Р71) = Ег(г- 0i) + E2(t - 62).
Для нахождения его интенсивности в точке Р умножим это равенство на
комплексно-сопряженное и произведем усреднение по времени. В результа-
результате получим
- 0i)E{{t - 0i) + E2(t -
+ #i(t - 0i)E*(t - 02) + E{(t - 9i)E2(t - 02).
В силу предположения о стационарности (в среднем) световых потоков пер-
первое слагаемое справа не зависит от 0\ и t. Оно представляет просто интен-
интенсивность 1\ первого колебания, пришедшего в точку Р:
г/2 г/2
, г/2 г/
= - f E1{t-e1)El{t-e1)dt=- f
/ /
-г/2
где т — ширина временного интервала, по которому производится усред-
усреднение. Аналогично, второе слагаемое есть интенсивность 12 второго коле-
колебания. По той же причине последнее слагаемое (интерференционный член)
не зависит от t, а также от 0\ и 02 в отдельности. Оно есть функция только

236 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
разности 0 = 02 ~~ 01, т.е. времени запаздывания второго колебания относи™
тельно первого. Поэтому можно положить
t -в) = Fl2{9), C1.2)
где Fi2{0) — комплексная функция, характеризующая степень согласован-
согласованности рассматриваемых колебаний в точке Р. Она называется корреляци-
корреляционной функцией колебаний E$t — 0$ и E2(t — О2) или взаимной корреляци-
корреляционной функцией.
В частном случае функции E\(t) и E2(t) могут оказаться тождествен-
тождественными. Это будет, например, когда оба колебания выходят из одного и того
же источника, но приходят в точку Р по различным путям. Тогда F\2(9) на™
зывают автокорреляционной функцией. Ее можно обозначать через jFn@),
но мы чаще будем применять обозначение F(9). При 0 = 0 автокорреляци-
автокорреляционная функция переходит в \E\(t ~~ 0i)|2, т.е. в интенсивность колебания 1\
в точке Р.
Функция Fi2(9) зависит от 1\ и /г, т.е. от интенсивностей складываемых
колебаний в точке Р. Если положить
F12@) = V^2/i2№, C1.3)
то получится нормированная корреляционная функция, которая зависит
только от времени запаздывания 0, но уже не зависит от 1\ и /г- Через эту
функцию результирующая интенсивность в точке Р представляется выра-
выражением ^___
I = h + /2 + 2л/ьТ2 Re [fi2(9)l C1.4)
Для квазимонохроматического света E\(t) = ai{t)e%UJQt, E>2(t) =
= a2(t)etuJot, так что
ai(t)a*(t - 0)егшов = y/hl2~fi2F). C1.5)
Как видно из этой формулы, величина fi2(9) есть быстро меняющаяся
функция времени запаздывания 9. Разделив ее на столь же быстро меняю-
меняющуюся осциллирующую функцию еги}° , получим уже медленно меняющу-
меняющуюся функцию
712F) = /12(в)е-шов, C1.6)
которая называется комплексной степенью когерентности колебаний^ а ее
модуль |7i2@)| = |/i2@)| — просто степенью когерентности колебаний в
точке Р. Таким образом,
2@), C1.7)
т.е. 712@) есть нормированная взаимная корреляционная функция для ам-
амплитуд a\(t) и a,2(t). Далее,
I = I1+I2 + 2VhhRe[j(e)eiwo(>}. C1.8)
Полагая 712@) = \'Ji2(9)\e%s, запишем последний результат в веществен-
вещественной форме:
I = h + /2 + 2л/Ш2~ |7i2@)| cos (ujo9 + S). C1.9)
Эта формула отличается от аналогичной формулы B6.7) для строго сину-
синусоидальных колебаний добавочным множителем |7i2@)| в интерференцион-
интерференционном члене и добавочным, медленно меняющимся слагаемым 6(9) в разности

31
КОРРЕЛЯЦИЯ И КОГЕРЕНТНОСТЬ СВЕТА
237
фаз. Значения вещественных амплитуд |ai| и \аъ\ и соответствующих ин-
тенсивностей 1\ и /з не зависят от выбора промежуточной частоты ш® в
спектральном интервале До; квазимонохроматического света. Не может за-
зависеть от выбора со»о и полная фаза ujqO + ё, входящая в формулу C1.9).
Но добавочная фаза <5, конечно, будет другой при другом выборе шо. Фаза
ш®9 + S определяет наиболее быстрые изменения в пространстве интенсив-
интенсивности светового поля, т.е. изменения при переходе от одной интерференци-
интерференционной полосы к другой. Ввиду медленности изменения функции |7i2@)|? ее
изменениями при таком переходе можно пренебречь. Тогда в максимумах
cos (шов + 5) будет равен +1, а в минимумах — 1. Поэтому
1макс =Il+I2+ 2л/ТТ2 |712 @)|, /мин = /i + /2 - 2л/Д/2 |712 @)|.
Отсюда для видности интерференционных полос находим
v =
/макс + /мин /l + /2
C1.10)
Когда интенсивности складываемых колебаний одинаковы A\ = /2), то
V :=: |7i2@)|- По самому определению видность V не может быть больше
единицы, а функция 712@) от интенсивностей пучков не зависит. Поэтому
всегда |7i2@)| ^ 1- Когда |7i2@)| = 0, то V = 0, т.е. интерференционных по-
полос не получается. В этом случае колебания называются некогерентными.
Если при этом функция 712@) обращается в нуль при любых значениях 0,
то некогерентность называется полной. Тогда всюду / = 1\ + /г, т.е. имеет
место закон фотометрического сложения интенсивностей. Такой случай
осуществляется при наложении световых пучков от независимых источни-
источников света.
Если же 712@) ф 0, то наблюдается интерференция, и колебания назы-
называются когерентными. Когерентность называется полной^ когда величина
|7i2@)| ВСЮДУ достигает своего предельного значения 1. В этом случае ин-
интерференционные полосы наиболее контрастны, т.е. при заданных 1\ и /2
видность V максимальна. Такой случай реализуется при наложении строго
периодических, в частности монохроматических, пучков одинаковых пери-
периодов. Во всех остальных случаях (когда 0 < |7i2@)| < 1) говорят о частич-
частичной когерентности. При перемещении точки наблюдения степень когерент-
когерентности |7i2@)| медленно изменяется.
Вследствие этого медленно изменяется и
видность интерференционных полос.
3. До сих пор речь шла о когерентно-
когерентности двух колебаний, происходящих в од-
одной и той мсе точке пространства. Но
можно говорить о когерентности одного и
того мсе волнового поля в двух различ-
различных пространственно-временных точках
RiiQi^ti) и ^2(^2,^2). Этот вопрос сво-
сводится к предыдущему.
Пусть Q\ и Q2 — какие-либо две
точки пространства, находящиеся в рас-
рассматриваемом поле излучения (рис. 131).
Пусть они являются центрами двух бес-
бесконечно малых отверстий в непрозрачном экране, поставленном на пути
распространения света. Экран всюду загородит падающий свет, но пропу-
пропустит свет через отверстия. Через отверстия пройдет не только прямой, но
Рис. 131

238 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
и дифрагированный свет. Бесконечно малые отверстия в силу принципа
Гюйгенса могут рассматриваться как точечные вторичные источники, по-
посылающие свет за экран во всех направлениях. Возьмем за экраном удален-
удаленную точку наблюдения Р. Пусть колебания, вышедшие из точек Q\ и Q2
в моменты времени t\ и ?2, приходят в точку Р одновременно. Тогда мож-
можно говорить о когерентности этих колебаний в том смысле, как это было
разъяснено выше.
По определению мы называем колебания в точках Q\ и Q2 в моменты
времени t\ и fo (т.е. в пространственно-временных точках R\ ж R2) коге-
когерентными или некогерентными, если когерентны или некогерентны соот-
соответствующие колебания в точке Р. При этом степень когерентности ^(9) мы
определяем той же величиной, что и для колебаний в точке наблюдения.
В частности, если пространственные точки Qi ш Q2 совпадают, но свет
попадает в Р различными путями, то пространственно-временные точки
Ri(Qijti) и -^2(^2,^2) отличаются только моментами времени t\ и t2- В
этом случае говорят о временной когерентности. При t\ = ?2 степень вре-
временной когерентности равна единице. С увеличением разности этих времен
степень когерентности убывает. Максимальное значение \t\ — fel, при кото-
котором когерентность еще сохраняется, называется временем когерентности.
Расстояние v\t\ — ?2!, проходимое светом эа это время, называется длиной
когерентности.
В другом крайнем случае времена t\ и fe одинаковы, но пространствен-
пространственные точки Q\ и Q2 не совпадают. Тогда говорят о пространственной ко-
герентности. Сохраняя точку Q\ неподвижной, будем поворачивать во-
вокруг нее экран вместе с точкой Q2. Тогда точка Q2 будет перемещаться
вокруг Qi, а степень когерентности I712I будет меняться. Геометрическое
место точек, где 712 обращается в нуль, есть некоторая поверхность, окру-
окружающая точку Q\. Объем, который она ограничивает, называется объемом
когерентности вокруг точки Р\.
Вычисление степени временной когерентности может быть системати-
систематически использовано при определении допустимой ширины спектральной
области, а пространственной когерентности — допустимых размеров источ-
источников света для возможности наблюдения интерференции.
4. Иллюстрируем понятие и свойства автокорреляционной функции и
степени когерентности на простейшем примере, когда оба колебания пред-
представляются «оборванной синусоидой»: E(t) = sincuot в интервале 0 < t < т
и E(t) = 0 вне этого интервала. Перейдем к комплексной форме E{t) =
= — егш°ь и примем т за промежуток времени, по которому производится
г
усреднение. Тогда 1\ = /2 = 1. Произведение E(t)E*(t — 9) отлично от нуля
только в интервале 9 < t < т. Поэтому только при 9 < т функция ^(9)
может отличаться от нуля. При 9 > т она обращается в нуль. В первом
случае
E(t)E*(t-0) = - Г ешов dt = l^Le1^ = F(9) = f{9).
r J 7™
о
Следовательно,
0 при в > т.
К тому же результату мы пришли бы, если бы предположили, что ис-
источник света излучает цуги волн одинаковой длительности г, беспорядочно

§ 31 КОРРЕЛЯЦИЯ И КОГЕРЕНТНОСТЬ СВЕТА 239
следующие друг за другом, причем каждый цуг разделяется на две части,
идущие к точке наблюдения различными путями. Это непосредственно сле-
следует из того, что различные цуги, испускаемые источником, статистиче-
статистически независимы и поэтому не интерферируют между собой. Из формулы
C1.11) следует физически очевидный результат, что колебания когерент-
когерентны, если время запаздывания в меньше длины цуга т. В противоположном
случае они некогерентны. Значит, т есть время когерентности колебаний.
5. Модуль функции |7i2@)| легко вычислить по формуле C1.10), из-
измерив предварительно видность полос V и интенсивности 1\ и 1% накла-
дывающихся пучков в точке наблюдения. Значительно труднее измерить
добавочную фазу <5, входящую в формулу C1.9). Особенно трудно это сде-
сделать, когда источниками света являются узкие спектральные линии. Для
этого надо сравнить в одном и том же месте интерференционной карти-
картины номера интерференционных полос от рассматриваемого источника света
с номерами полос от источника с частотой ujq. Для номера максимума JV-й
интерференционной полосы от первого источника можно написать ш^О+ё =
= 2ttN. В том же месте второй источник, вообще говоря, не даст максиму-
максимума. Этому месту будет соответствовать уже дробное число интерференци-
интерференционных полос, определяемое условием ujqO = 2жЩ. Отсюда S = 2tt(N — N0).
Таким путем в принципе можно экспериментально определить не только
модуль, но и аргумент комплексной степени когерентности 712 @). Вместе с
тем можно определить и корреляционную функцию F\2@).
6. Автокорреляционная функция F{9) связана важным соотношением
со спектральной плотностью 1ш{и)) излучения. Для установления этой связи
пишем на основании определения автокорреляционной функции:
1 г/2
= E(t)E*(t-6) = - f E(t)E*(t-6)dt. C1.12)
Подставим сюда
со
E*(t-0)= f a*(uj)e~zu}(t~e)duj
о
и поменяем порядок интегрирования по t и ш. Использовав при этом фор-
формулу B9.5), получим
= — f а*(ш)а(ш)егш
т J
О
Но Bтт/т)а* (ш)а(ш) есть спектральная плотность излучения 1ш{и) (см. § 29,
п. 5). Следовательно,
со
F@) = J 1^(ш)ешв duo. C1.13)
о
Эта формула представляет фурье-разложение функции F@), а потому
1 +оо
Iu(w) = -±- f F@)e-lue d9. C1.14)
— со

240
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
Формулу C1.14) можно привести к другому виду. Для этого заме-
заметим, что, ввиду стационарности светового потока, в формуле C1.12) пре-
пределы интегрирования можно заменить любыми другими, сохраняя только
неизменной ширину интервала интегрирования. Используя это, нетрудно
доказать, что автокорреляционная функция удовлетворяет соотношению
F(—9) = F*(9). После этого формула C1.14) приводится к виду
Uu) = :т-
C1.15)
Это соотношение можно записать в символическом виде
1 °°
C1.16)
понимая его в том смысле, что левая часть равенства равна веществен-
вещественной части правой. Соотношение C1.13) позволяет найти корреляционную
функцию F(9) по экспериментально измеренной спектральной плотности
излучения 1ш(ш). С помощью обратного соотношения C1.16) можно опре-
определить спектральную плотность 1ш(и), если экспериментально определить
корреляционную функцию F@).
Именно так поступал Майкельсон, используя свой интерферометр для
исследования структуры спектральных линий. Он измерял видность ин-
интерференционных полос в интерферометре и фазу 6, входящую в форму™
лу C1.9), и по этим данным вычислял спектральную плотность излучения
Iuj(uj). В свое время из всех методов этот метод был наиболее точным. Позд-
Позднее метод Майкельсона был вытеснен более простыми методами многолу-
многолучевой интерферометрии.
§ 32. Теорема Ван-Циттера—Цернике
Определим комплексную степень пространственной когерентности 712
для точек Qi ш Q2 экрана Э, освещаемого протяженным квазимонохрома-
квазимонохроматическим самосветящимся источником све-
света (рис. 132). Сами точки Q\ и Q2 должны
рассматриваться как вторичные источни-
источники волн в том смысле, как это было ука-
указано в п. 3 предыдущего параграфа. Бу-
Будем предполагать, что точка наблюдения Р
равноудалена от Q\ ш Q2. При этом усло-
условии вместо волн, накладывающихся в точке
Р, можно брать волновые поля, создавае-
создаваемые первичным источником в точках Qi и
Q2, что и будет делаться в дальнейшем. На-
Наши вычисления, следовательно, проводятся
в предположении, что время запаздывания
в равно нулю. Однако, ввиду медленности
изменения функции 712@M вычисленным значением ее можно пользоваться
не только при 0 = 0, но и при малых значениях аргумента 0, пока видность
интерференционных полос не претерпит существенных изменений.
Рис. 132

§ 32 ТЕОРЕМА ВАН-ЦИТТЕРА-ЦЕРНИКЕ 241
Для простоты в качестве источника света возьмем малую площадку а,
плоскость которой параллельна плоскости экрана Э. Среда между источ-
источником <т и экраном «9 предполагается однородной, а скорость света в ней
обозначается через у. Линейные размеры площадки а должны быть малы
по сравнению с расстоянием ее до экрана. Предполагается также, что малы
углы между «средней линией» ОО' и прямыми, соединяющими произволь-
произвольную точку S источника с точками Q\ и Q>2-
Разобьем источник а на малые площадки, линейные размеры которых
малы по сравнению с длиной волны А. Будем рассматривать их как некоге-
некогерентные точечные источники, излучающие сферические волны. Волновые
поля, создаваемые таким источником в точках Q\ и Q2, представятся вы-
выражениями
Am(t - Г1т/v) i(wot-krlm) Am(t - Г'2т/у) ci(ujot^kr2m)
Tim T2m
где Пт и г 2т — расстояния тв~го источника до точек Qi и Q2 соответствен-
соответственно. Амплитуды результирующих колебаний в точках Q\ и Q2 будут
^ rim
т
U\ ^^ Am(t-r2m/v) ^ikr2m
0,2 (t) = / e .
^ Г2т
m
Вычислим теперь взаимную корреляционную функцию амплитуд а\ и
tt2, т.е. среднее по времени от произведения ai(?)a\(t — в), в предположе-
предположении, что 9 = 0. Перемножив почленно предыдущие суммы, заметим, что
все слагаемые с различными т при усреднении обратятся в нуль, ввиду
статистической независимости соответствующих элементарных источников
света. В результате получим
а а* _ у^ Arn(t - rim/v)Afn(t - Г2т/У) ^к(г2т^г1т)
т
(Усреднению подвергается только числитель, так как все прочие величины
от времени не зависят.) Если предположить, что для всех т разности г2т —
— rim малы по сравнению с длиной когерентности, то различие аргументов
t — fim/v и t-—r2m/v можно не учитывать. Следовательно, в силу предпола-
предполагаемой однородности световых потоков можно опустить и сами аргументы,
т.е.
Am(t - rlm/v)Am(t - Г2т/У) = АтАт.
Во всех практически интересных случаях число элементарных излуча™
телей света очень велико, так что их можно считать непрерывно распреде-
распределенными по площадке а с определенной поверхностной плотностью. Тогда
от суммы можно перейти к интегралу. Если I(S) — интенсивность света, соз-
создаваемая единицей площади источника на единичном расстоянии от него,
то АтАт = I(S)dS. В точках Q\ и Q2 соответственно
Г I^dS г - Tin \ Г T^dS
h=I(Qi)= J —j3—, h = I(Q2)= J —j3—.
Введя еще нормирующий множитель 1/\/1\12, получим окончательно
712@) = ^L= f ^1 егк{г^Г1) dS. C2.1)
\/Тл То J Г-1Г2

242
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
Для наглядной интерпретации полученного результата воспользуемся
следующей аналогией. Пусть точка Q2 неподвижна, а точка Q\ может зани-
занимать различные положения на экране «9. Заменим площадку а отверстием
а той же формы в непрозрачном экране. Допустим, что на него падает сфе-
сферическая волна, сходящаяся в центре Q2, волновое поле которой в точках
отверстия представляется выражением
Пусть каждый элемент dS площади отверстия излучает по принципу Гюй-
Гюйгенса вторичную сферическую волну, поле которой в точке Pi определя-
определяется выражением — фоеъ^ш°г^кГ1 \ Тогда в результате суперпозиции таких
вторичных волн получится волна, комплексная амплитуда которой опреде-
определяется формулой C2.1). Но именно так по принципу Гюйгенса решается
задача о дифракции сферической волны на отверстии а1 (см. § 39). Следо-
Следовательно, комплексная степень взаимной когерентности в точках Qi и
Q>2 ровна комплексный амплитуде в точке Q\ соответствующей дифра-
дифрагированной волны.
В этом состоит теорема Ван-Циттера-Цернике. Она сводит вычисле-
вычисление степени взаимной когерентности 712 к соответствующей задаче дифрак-
дифракции.
§ 33. Интерференция в пленках и пластинках
1. При освещении тонкой пленки происходит наложение волн
от одного и того же источника, отразившихся от передней и
задней поверхностей пленки. При этом может возникнуть ин-
интерференция. Если свет белый, то интерференционные полосы
окрашены. Поэтому явление получило название цветов тонких
пленок. Оно легко наблюдается на стенках мыльных пузырей,
на тонких пленках масла или нефти, плавающих на поверхно-
сти воды, на пленках, возни-
возникающих на поверхности ме-
металлов при закалке (цвета по™
бежалости), и т.д.
2. Рассмотрим сначала
плоскопараллельную пла-
пластинку толщины d с показа-
7
С
Рис. 133 а
телем преломления п, осве-
освещаемую точечным источни-
источником света S (рис. 133 а). При
отражении от поверхностей
пластинки возникает оптиче-
оптическая разность хода между со-
соответствующими отраженными волнами. Вычислим ее в какой-
либо произвольно выбранной точке Р.

§ 33 ИНТЕРФЕРЕНЦИЯ В ПЛЕНКАХ И ПЛАСТИНКАХ 243
Пусть SACBP и SDP — отраженные лучи, пересекающиеся
в этой точке. Через точку D проведем плоскости DA и DB^ пер-
перпендикулярные к соответствующим преломленным лучам в пла-
пластинке. Если пластинка тонкая, то для вычисляемой оптической
разности хода можно написать: А = (SACBP) — (SDP). Через
точку О, симметрично расположенную на верхней поверхности
пластинки между точками i и В, проведем плоскости О А1 и
О В1 (начерченные штриховыми линиями), параллельные плос-
плоскостям DA и DB. Тогда А = {А1 С В1) = 2(А'С) = 2nd cos ф, где
ф — угол преломления.
Сюда необходимо, однако, ввести поправку. В пределе, ко-
когда толщина пластинки стремится к нулю, наша формула да-
дает А = 0. Поэтому в точке Р должно было бы в этом случае
происходить усиление колебаний. Но это невозможно, так как
бесконечно тонкая пластинка вообще не может оказывать влия-
влияния на распространение света, так что никакого отражения воз-
возникнуть не может. Для этого волны, отраженные от передней
и задней поверхностей пластинки, должны при интерференции
гасить друг друга. Их фазы должны быть противоположны, т.е.
оптическая разность хода А при d —> 0 должна стремиться к
А/2. Поэтому к прежнему выражению для А надо прибавить
или отнять А/2 (что совершенно безразлично). После этого по-
получим 1)
Д = 2rfncos^ + ^. C3.1)
Введение такой поправки, как будет показано в § 65, обусловле-
обусловлено изменением фазы на тг, которое претерпевает волна при отра-
отражении на одной из поверхностей пластинки. Экспериментально
это явление подтверждается наблюдением интерференции бело-
белого света в установке Ллойда (см. конец § 30).
Все рассуждения и результаты остаются в силе и для случая,
когда точка Р лежит по другую сторону пластинки (рис. 133 б).
В этом случае отраженные лучи расходящиеся, в точке Р пе-
пересекаются не сами лучи, а их продолжения за пластинку. Для
наблюдения интерференции в точке Р надо отраженные лучи
сделать сходящимися с помощью собирающей линзы или вогну-
вогнутого зеркала. Тогда интерференцию следует наблюдать в точке
Р;, оптически сопряженной с точкой Р.
Формула C3.1) справедлива и для тонких пластинок пере-
переменной толщины. Только в этом случае под d надо понимать
толщину пластинки в том ее месте, где происходит отражение
лучей, пересекающихся в точке Р. Но в точку Р от точечного
) Неудовлетворительность приведенной аргументации была отмечена
при выводе формулы B.2).

244
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
источника света могут попадать, вообще говоря, только два лу-
луча. Отсюда следует, что в случае точечного монохроматическо-
монохроматического источника света каждая точка пространства характеризуется
вполне определенной разностью хода приходящих в нее отра-
Рис.
женных лучей. Поэтому устойчивая интерференция должна на™
блюдаться в каждой точке пространства. Про соответствую-
соответствующие полосы интерференции говорят, что они не локализованы
(или локализованы всюду).
3. Положение существенно изменится, если источник света
протяженный. Тогда в точку Р будут попадать, вообще гово-
ря, два отраженных луча от каждой точки источника. Место
отражения на пластинке, углы падения и отражения, а следова-
тельно, и разность хода для каждой пары лучей будут разными.
Поэтому никакой устойчивой интерференции в точке Р наблю-
наблюдаться не будет.
Допустим, однако, что точка Р находится близко от пластин-
пластинки, например совпадает с точкой В. Тогда при малой толщине
пластинки отражение будет происходить практически в одном
и том же месте, т.е. при одной и той же толщине d, независи-
независимо от того, из какой точки источника исходят лучи. Если при
этом лучи падают на пластинку почти нормально (так что cos ф
изменяется мало), то оптическая разность хода А будет зави-
сеть только от толщины пластинки d в точке падения лучей.
Линии на поверхности пластинки, где толщина d постоянна, бу-
будут также линиями постоянной разности фаз. На поверхности
пластинки, если только степень монохроматичности света до-
достаточна, появятся интерференционные полосы, каждая из ко-
которых характеризуется условием d = const. Они называются по-
полосами или линиями равной толщины. Такие полосы как бы

§ 33 ИНТЕРФЕРЕНЦИЯ В ПЛЕНКАХ И ПЛАСТИНКАХ 245
нарисованы на самой пластинке. Про них говорят, что они лока-
локализованы на пластинке. Конечно, интерференционные полосы
должны наблюдаться не только на пластинке, но и с обеих сто™
рон вблизи от нее. Однако максимальной видностью обладают
интерференционные полосы на самой пластинке.
Для наблюдения таких полос удобно воспользоваться соби™
рательной линзой, с помощью которой можно получить изобра-
изображение пластинки на экране. Так как линза не вносит дополни™
тельной разности хода, то при этом на экране получается изо-
изображение и интерференционных полос. Линза как бы переносит
место локализации интерференционной картины с поверхности
пластинки на экран. При визуальном наблюдении полос равной
толщины глаз надо аккомодировать на пластинку. Роль линзы
выполняет хрусталик, а экрана — сетчатая оболочка глаза. Оп-
Оптический прибор или глаз выполняет также и другую полезную
функцию. Диафрагма прибора или зрачок глаза вырезают из
отраженных лучей узкие пучки, в пределах которых угол ф ые-
няется незначительно. Тем самым создаются условия, благопри-
благоприятные для получения полос равной толщины.
При наблюдении в белом свете полосы интерференции окра-
1 4тг dn cos ф . \ т% г
шены, так как разность фаз — +тг зависит от А. Б белом
А
свете возможна интерференция только низкого порядка. Поэто-
Поэтому пленка должна быть тонкой — ее толщина не должна превы-
превышать примерно одной-двух длин волн. Когда толщина пленки
составляет доли длины волны, то разность фаз приближается к
тг, и пленка становится темной.
Если обе поверхности пленки плоские, то интерференцион-
интерференционные полосы прямолинейны и параллельны линии пересечения
соответствующих плоскостей. Такие полосы наблюдаются, на™
пример, в клине, т.е. тонкой воздушной прослойке между пло-
плоскопараллельными стеклянными пластинками, когда с одного
края между ними проложен, например, тонкий лист бумаги. Но
если поверхности сложенных стеклянных пластинок неровные,
то полосы равной толщины принимают неправильную, причуд-
причудливую форму. На этом основан чувствительный интерференци-
интерференционный метод контроля поверхности на плоскопараллельность.
В этом методе испытуемая поверхность прижимается к плоской
и наблюдаются полосы интерференции в образовавшейся про-
прослойке. Метод применяется и для контроля сферических или
параболических поверхностей при шлифовке оптических зеркал
и линз.
4. Интерференция в тонких пленках рассматривалась вы-
выше как двухлучевая интерференция. Мы ограничились интерфе™
ренцией только двух волн, одна из которых получилась при од-

246
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
некратном отражении от верхней, а другая — от нижней поверх-
поверхностей пленки. Многократными отражениями мы пренебрегли.
Это можно делать, когда коэффициент отражения невелик. Ее™
ли же коэффициент отражения близок к единице, то так посту™
пать нельзя. Допустим, например, что при каждом отражении
отражается 5 % падающего света, а остальные 95 % проходят.
Примем интенсивность падающего света за единицу. Тогда, как
нетрудно подсчитать, интенсивности отраженных и прошедших
лучей (рис. 134) представятся следующей таблицей:
Лучи
Интенсивности
1
1
2
0,05
3
0,0451
4
0,00011
г
0,9025
21
0,00226
Рис. 134
Из таблицы видно, что интенсивности отраженных лучей 2 и 8
почти одинаковы, а интенсивность луча 4 более чем в 100 раз
меньше. Поэтому луч 4 и все отражения высших порядков мож-
можно не принимать во внимание. Из
прошедших лучей интенсивность
луча 21 примерно в 400 раз мень-
меньше интенсивности луча tf. Поэто-
Поэтому интерференционные полосы в
проходящем свете получаются на
светлом фоне и по этой причине
очень мало контрастны.
5. Допустим теперь, что пла-
пластинка толстая и строго плоскопа-
плоскопараллельная. Пусть она освещается
параллельным пучком света. Формально это соответствует слу-
случаю точечного бесконечно удаленного источника S (см. рисунки
133 а и 133 6). Отраженные лучи будут также параллельными,
т.е. точка наблюдения Р удалится в бесконечность. При посто-
постоянной толщине пластинки d оптическая разность хода между
отраженными лучами 2dпcoнф + А/2 зависит только от угла
наклона падающих лучей. Угол ф может принимать всевозмож-
всевозможные значения, если источник света протяженный и имеет ко-
конечные угловые размеры. Практически это можно осуществить,
поместив протяженный источник света в фокальной плоскости
линзы, которая как бы удаляет источник света в бесконечность.
Интерференционную картину следует наблюдать на бесконечно
(т.е. достаточно) удаленном экране или в фокальной плоскости
линзы, поставленной на пути отраженных лучей. Каждая интер-
интерференционная полоса на бесконечно удаленном экране характе-
характеризуется постоянством косинуса угла ф. Поэтому интерферен-
интерференционные полосы при описанном способе наблюдения называют

33
ИНТЕРФЕРЕНЦИЯ В ПЛЕНКАХ И ПЛАСТИНКАХ
247
полосами или линиями равного наклона 1). Они локализованы в
бесконечности.
Линза переносит область локализации из бесконечности в
фокальную плоскость, оптически сопряженную с бесконечно
удаленной плоскостью. Роль линзы может играть глаз, акко-
аккомодированный на бесконечность. В этом случае полосы равного
наклона локализуются на сетчатке глаза. При наблюдении в
зрительную трубу последняя должа быть установлена на беско-
бесконечность.
Для толстых пластинок оптическая разность хода А вели-
велика, т.е. содержит тысячи и десятки тысяч длин волн. Интерфе-
Интерференционные полосы будут высокого порядка. Для их получения
требуется высокая степень монохроматичности X/SX падающего
света.
6. Ньютон наблюдал интерференционные полосы равной
толщины в воздушной прослойке между плоской поверхностью
стеклянной пластинки и плоско-выпуклой линзой, прижатой
к пластинке выпуклой стороной. Интерференционные полосы
имели форму концентрических колец. Они получили название
колец Ньютона. При постановке опыта радиус кривизны вы-
выпуклой поверхности линзы надо брать не менее приблизитель-
приблизительно одного метра. Кольца удобно наблюдать в длиннофокусный
микроскоп, сфокусированный на воздушную прослойку. Более
контрастные кольца наблю-
наблюдаются, конечно, в отражен-
отраженном, а не в проходящем свете.
Чтобы наблюдалось много
колец, надо пользоваться све-
светом сравнительно высокой
монохроматичности. Подхо-
Подходящим может быть желтый
свет натровой горелки или
свет ртутной лампы. Вид ко-
колец показан на рис. 135.
Для вычисления радиу-
радиусов колец дополним выпук-
выпуклую поверхность линзы до
полной сферы (рис. 136). Ес-
Если BD — диаметр, то по из-
известной геометрической тео-
теореме АВ • AD = АО2 = ж2. Ввиду малости кривизны сферы и
угла ОСА, отрезок АВ можно принять за толщину d воздушной
Рис. 135
) Этот общепринятый термин не совсем точно передает существо де-
дела. Лучам одинакового наклона соответствует не линия, а точка — фокус
линзы, в котором они собираются.

248 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
прослойки в точке А. Пренебрегая еще различием между AD и
диаметром сферы 21?, получим
Светлые кольца получатся при А = т\, где т — целое число.
Из этого условия находим радиус хт т-то светлого кольца:
хт = V(m - lJ2)XR = у/ХЕЦЪу/Ъп-Л. C3.2)
Аналогично для радиуса т-го темного кольца
Таким образом, радиусы последовательных светлых колец
пропорциональны квадратным корням из нечетных чисел 1,3,
5, ..., а радиусы темных колец — квадратным корням из после-
последовательных четных чисел 0, 2, 4, ... Эти закономерности экс™
периментально были установлены Ньютоном. Как указывалось
в § 3 (п. 6), в интерференции Ньютон видел проявление пери-
периодичности световых процессов. Из наблюдения интерференци-
интерференционных колец Ньютон даже довольно точно вычислил величину,
являющуюся количественной мерой ука-
Z>^. —^ занной периодичности. В переводе на
//^х \ язык волновой теории вычисленная Нью-
Ньютоном величина есть половина длины све-
световой волны.
Центр колец в отраженном свете тем-
темный, а в проходящем светлый. Это дока™
зывает, что при отражении на одной из
границ воздушной прослойки фаза отра™
женной волны меняется на ж. Как будет
показано в § 65, электрический вектор ме-
меняет фазу на тг при отражении от среды с
большим показателем преломления. В противоположном случае
изменения фазы не наблюдается. Это подтверждается следую-
следующим опытом Юнга. Он взял пластинку из флинта (п = 1,7),
прижал к ней линзу из крона [п = 1,5), а прослойку между ни™
ми заполнил сассафрасовым маслом, показатель преломления
которого имел промежуточное значение. Тогда фаза волны ме™
нялась на ж при отражении как от верхней, так и от нижней
поверхностей масляной прослойки. Благодаря этому центр ньк>
тоновых колец получался светлым в отраженном и темным в
проходящем свете.
7. Если в установке Ньютона линзу перемещать вверх парал-
параллельно самой себе, то из™за увеличения толщины воздушной про™
слойки каждая окружность постоянной (фиксированной) разно-
разности хода будет стягиваться к центру картины. Интерференци-
Интерференционные кольца также станут стягиваться к центру, так как вдоль
/
1
\
\
\
\
\
V
Риг,
\ (^
\\
I \
1 \
О х А
136
\
/
\
\
}

§ 34 ИНТЕРФЕРОМЕТР ЖАМЕНА 249
каждого кольца оптическая разность хода остается постоянной.
Достигнув центра, каждое кольцо превратится в кружок, исче-
исчезающий при дальнейшем перемещении линзы. Таким образом,
центр картины будет становиться попеременно то светлым, то
темным. Одновременно на периферии поля зрения будут заро-
зарождаться и перемещаться к центру новые интерференционные
кольца, пока каждое из них не исчезнет в центре картины. Моле-
Молено сказать, что при перемещении линзы непрерывно вверх про-
пропадают кольца самых низких порядков интерференции и заро-
зарождаются кольца более высоких порядков. Таким путем удается
наблюдать интерференцию все более и более высокого порядка.
Понятно, что для этого требуется свет высокой степени моно-
монохроматичности.
Физо, впервые осуществивший подобный опыт, пользовался
желтым светом натровой горелки (в опыте Физо интерференци-
интерференционные полосы получались между двумя плоскопараллельными
пластинками). Физо заметил, что при увеличении числа полос
JV, прошедших в поле зрения, ухудшалась видимость полос. При
N = 490 видимость достигала минимума, затем она опять улуч-
улучшалась; при N = 980 полосы приобретали прежнюю отчетли-
отчетливость. Ближайший минимум наступал при N = 1470, следую-
следующий максимум при N = 1960 и т.д. Физо сумел заметить 52
таких максимума. На этом основании он пришел к заключению,
что желтая линия натрия — двойная, т.е. состоит из двух близко
расположенных спектральных линий с длинами волн Аи А' > А.
Легко найти расстояние между этими линиями А; — А. Как
было показано в § 30, первое исчезновение видимости интер-
интерференционных полос происходит при условии А; — А = X/2N.
По наблюдениям Физо N = 490. Средняя длина волны желтой
спектральной линии натрия « 589,3 нм. Поэтому У — А ^ 0,6 нм.
Этот пример показывает, как интерференция высокого поряд-
порядка может быть использована для разрешения сложных спектраль-
спектральных линий, состоящих из двух близко расположенных линий.
§ 34. Интерферометр Жамена
1. Интерферометрами называют оптические измерительные
приборы, основанные на интерференции света. Они позволяют с
высокой степенью точности измерять линейные и угловые рас-
расстояния, малые разности показателей преломления, исследовать
структуру спектральных линий и т.п. Принцип действия интер-
интерферометров в основном один и тот же. Но в зависимости от
предназначения им придают различные конструкции.
2. Интерферометр Жамена A818-1886) состоит из двух тол-
толстых (толщина не менее 20 мм) плоскопараллельных пластин Pi

250
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
С
F
НЕГЕНГ
'U1
Рис. 137
и F2) изготовленных из весьма однородного стекла и смонтиро-
смонтированных на массивной плите (рис. 137). Для исследований в дале-
далекой ультрафиолетовой
' s области спектра пла-
пластины изготовляются из
кварца или флюорита.
Чтобы обе пластины
имели строго одина-
одинаковую толщину, они
вырезаются из одной и
той же пластины. Пла-
Пластины устанавливаются
приблизительно под
углом 45° к линии, со-
соединяющей их центры.
Угол между пласти-
пластинами можно менять с
помощью специальных
установочных винтов,
поворачивающих пла-
пластины вокруг вертикальной и горизонтальной осей. Чем меньше
этот угол, тем шире интерференционные полосы. Задние от-
отражающие поверхности пластин посеребрены. Луч света SA,
отразившись от передней и задней поверхностей пластины Pi,
разделяется на два параллельных луча АВ и C'D11 между
которыми возникает разность хода. Каждый из этих лучей в
свою очередь раздваивается при отражении от пластины Р2.
Между средними лучами DE и DfE' возникает разность хода
А = 2dn(cost/J - cos^i), C4.1)
где d — толщина пластин, ф\ и ф2 — углы преломления в них,
п — показатель преломления пластин относительно окружаю-
окружающего воздуха. Таким образом, на величину А пластины влияют
противоположно. Потери фаз при отражении в формулу C4.1)
не входят, так как они одинаковы для обоих интерферирующих
лучей и компенсируют друг друга. Если ф\ = ф21 то А = 0. Если
же угол между пластинами мал, то и разность хода невелика.
Это позволяет наблюдать интерференцию низкого порядка, ис-
используя белый свет. Лучи DE и D1 Е' будут интерферировать
так же, как и соответствующие лучи в случае только одной, но
тонкой плоскопараллельной пластинки.
Назначение двух толстых пластин состоит в том, чтобы да-
далеко развести лучи АВ и C'D', что позволяет ставить на пу-
пути этих лучей трубки с исследуемыми газами. Разность хода
между средними и крайними лучами, а также между самими
крайними лучами очень велика, и интерференцию в белом свете

§ 34 ИНТЕРФЕРОМЕТР ЖАМЕНА 251
от этих лучей получить невозможно. Источником света обычно
служит освещаемая вертикальная щель шириной около одно-
одного или нескольких миллиметров, прикрываемая матовым стек™
лом. Невооруженным глазом видны три изображения щели. Са-
мое яркое (справа) дают лучи, дважды отразившиеся от задних
посеребренных поверхностей пластин. Среднее, промежуточной
яркости, образуется лучами DE и D'E'. Наименее яркое (сле-
(слева) соответствует лучам, дважды отразившимся от передних по-
поверхностей пластин. Если фиксировать глаз на среднем изобра-
изображении и вращением установочных винтов менять разность хода,
то в белом свете можно получить цветные интерференционные
полосы низкого порядка. Центральная ахроматическая полоса,
т.е. полоса, которой соответствует разность хода А = 0, получа-
получается белой. Наблюдая эту полосу, можно легко следить за сме-
смещением интерференционной картины.
Так как разность хода А зависит от направления падаю-
падающих лучей, то в интерферометре Жамена получаются полосы
равного наклона. Для их наблюдения удобно воспользоваться
зрительной трубой небольшого увеличения, но большого поля
зрения, установленной на бесконечность. Применение трубы не
только увеличивает ширину полос, но и обладает еще тем пре-
преимуществом, что в трубу не попадают крайние лучи GH1 и ВН,
создающие светлый фон и сильно уменьшающие контрастность
интерференционных полос. В лекционных демонстрациях ин-
интерференционные полосы можно получать без дополнительных
оптических приспособлений, направив лучи DE и D1 Е1 непо-
непосредственно на белый экран. Крайние лучи при этом должны
быть экранированы.
3. Интерферометр Жамена предназначен для измерения
небольших изменений показателей преломления. Поэтому его
называют также интерференционным рефрактометром. Для
уяснения принципа действия такого рефрактометра вообразим,
что на пути одного из интерферирующих лучей АВ или C'D'
(см. рис. 137) помещен плоскопараллельный слой какого-либо
вещества толщины I с показателем преломления n<i- Тогда раз-
разность хода между интерферирующими лучами изменится на ве-
величину (n2 — Tii)l, где п\ — показатель преломления окружающе-
окружающего воздуха. В результате интерференционная картина сместится
на т полос, причем га = (п2 — щI /А. Число т (вообще говоря,
дробное) можно найти, наблюдая интерференционные полосы в
белом свете до и после внесения исследуемого вещества. Опыт
показывает, что смещение на 1/10 полосы (га = 1/10) наблюда-
наблюдается вполне уверенно и без труда.
Разность показателей преломления можно вычислить по
формуле П2 — п\ = гаЛ/1. Если толщина слоя вещества I = 10 см,

252 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
а А = 500 нм, то при т = 1/10 получаем П2^п\ = 5-10" ~ 10^6.
В специальных установках измерялись гораздо меньшие измене-
изменения показателя преломления. Интерферометр Жамена позволя-
позволяет, таким образом, измерять ничтожные изменения показателя
преломления, например, при изменении температуры газа или
при добавлении к нему посторонних примесей. Измерение самих
абсолютных значений показателя преломления этим прибором
затруднительно. Обычно его используют для измерения разно-
разности показателей преломления исследуемого и хорошо изученно-
го газа, например воздуха.
При практических измерениях на пути лучей АВ и С1 D1 ста™
вятся по возможности одинаковые трубки. Сначала наблюдают-
наблюдаются интерференционные полосы, когда обе трубки наполнены воз-
воздухом. Затем измеряется смещение полос интерференции, когда
одна из трубок наполняется исследуемым газом. Для компен-
компенсации значительной разности хода между интерферирующими
лучами служит компенсатор. Он состоит из двух совершенно
одинаковых стеклянных пластинок, насаженных на общую ось,
причем угол наклона между пластинками можно плавно ме-
менять. Одна из пластинок ставится на пути одного, вторая — на
пути другого лучей. Вращая компенсатор при неизменном уг-
угле наклона между пластинками, можно привести в поле зрения
центральную ахроматическую полосу, а затем по углу поворота
определить число полос, прошедших через поле зрения.
4. Не так просто разобраться в вопросе о форме интерферен-
интерференционных полос, наблюдаемых в интерферометре Жамена. Для
упрощения исследования этого вопроса введем несущественное
предположение, что п = 1. Такому предположению соответству-
соответствует замена каждой пластины парой бесконечно тонких парал-
параллельных отражающих плоскостей (из которых одна посеребре-
посеребрена). Тогда вместо C4.1) получится более простое выражение:
А = 2d(cos гр2 — cos Ф\) •
Перейдем к векторной форме записи, обозначив через Ni и
N2 единичные нормали к отражающим плоскостям, как это по-
показано на рис. 137. Обозначим через Sj_, s^, s единичные векторы
лучей SA, АВ и ВЫ соответственно (те же векторы определяют
направления и всех параллельных им лучей). Тогда
cos^i = (Nisi) = -(Nisi), cos ^2 = (N2s).
По закону отражения s^ = s — 2(N2s)N2, а потому
cos^i = -(Nis) + 2(N2s)(NiN2).
Следовательно,
A = 2rf(Ni + N2)s - 4

§ 34 ИНТЕРФЕРОМЕТР ЖАМЕНА 253
Введем новые векторв!
N = i(Ni
Из них первый направлен по биссектрисе угла между норма™
лями Ni и N2, а второй перпендикулярен к этой биссектрисе.
Очевидно,
Ni =N-v, N2 = N + v.
После подстановки этих выражений в формулу для А получим
А = -4rf(l ^v2)(vs) + 4dv2. C4.2)
При работе с прибором угол между пластинами, а следователь-
следовательно, и длина вектора v всегда малы. Поэтому квадратичными
членами, содержащими v2, в формуле C4.2) обычно можно пре-
пренебречь.
5. Для светлых полос А = га А, для темных А = (га+1/2)А, где
т — целое число (порядок интерференции). Если для наблюде-
ния используется труба, то она сводит параллельные лучи в фо-
кальной плоскости объектива, где и получается первичная ин-
интерференционная картина. Поле зрения трубы ограничено, так
что используется лишь небольшой участок фокальной плоско-
плоскости. При повороте трубы вокруг оптического центра объектива
поворачивается и фокальная плоскость вместе с выделенным
участком. Если последний мал, то без заметной ошибки мож-
можно принять все такие участки за элементы неподвижной сферы,
центр которой совпадает с оптическим центром объектива. На-
Назовем для краткости такую вспомогательную сферу фокальной
сферой объектива. (Если объектив не является тонкой линзой,
то все это можно повторить, заменив только оптический центр
второй узловой точкой объектива.) Можно сказать, что первич-
первичная интерференционная картина как бы создается на неподвиж-
неподвижной фокальной сфере, а наблюдатель рассматривает эту карти-
картину через окуляр трубы. Поворачивая трубу, он видит на фо-
фокальной сфере различные участки интерференционной карти-
картины. Разумеется, вид картины совершенно не зависит от того,
вокруг какой точки вращалась труба, он определяется только
направлением последней.
Таким образом, вопрос о форме видимых полос интерферен-
интерференции сводится к вопросу о форме их на вспомогательной фокаль-
фокальной сфере. Практически, однако, вращение трубы всегда произ-
производится вокруг вертикальной оси. Поэтому наблюдению досту-
доступен только узкий экваториальный поясок на фокальной сфере.
Его приближенно можно считать поверхностью цилиндра с вер-
вертикальной осью, проходящей через оптический центр объектива.
В дальнейшем ограничимся рассмотрением интерференционных
полос только на таком «цилиндрическом фокальном пояске».

254
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
Фиксировав положение пластин интерферометра, отложим
векторы N и v, а также единичный вектор луча s из общего
начала О, помещенного в оптическом центре объектива. На™
правления этих векторов будут играть роль координатных осей,
перпендикулярную к ним прямую примем за ось Z. Различные
единичные векторы лучей s будем откладывать из того же на™
чала О. Как видно из C4.2), на поверхностях равных фаз (vs) =
= const, т.е. эти поверхности представляют собой параллельные
плоскости, перпендикулярные к вектору V. Среди этих плоско-
плоскостей находятся и равноотстоящие плоскости, на которых раз-
разность хода А содержит целое или полуцелое число длин волн.
Они пересекают фокальную сферу вдоль некоторых кривых, ко™
торые и представляют собой интерференционные полосы, на-
наблюдаемые в трубу. Ввиду малости поля зрения, при каждом по™
ложении трубы наблюдается лишь незначительный участок фо-
фокальной сферы, на котором интерференционные полосы прак-
тически неотличимы от прямолинейных.
В интерферометре Жамена первая пластина обычно непо-
неподвижна и установлена вертикально. Вторую пластину можно
немного поворачивать вокруг вертикальной и горизонтальной
осей, параллельных отражающим плоскостям. Если пластины
строго параллельны друг другу, то v = 0 и А = 0. Следова-
Следовательно, никаких интерференционных полос нет, все поле зрения
освещено равномерно. В этом положении нормали Ni и N2, a
следовательно, и вектор N лежат в горизонтальной плоскости.
Повернем теперь вторую пластину на малый угол вокруг
вертикальной оси. Тогда вектор v расположится в той же го-
Рис. 138
ризонтальной плоскости (рис. 138 а). Перпендикулярные к нему
плоскости равных фаз вертикальны. Одна из таких плоскостей
BCEF изображена на рис. 138 а. Она пересекает экваториаль-
экваториальный цилиндрический поясок вдоль вертикального отрезка EF.
Следовательно, интерференционные полосы, лежащие на этом
пояске, будут вертикальны. На схематическом рис. 138 а они
представлены жирными отрезками. Ширина интерференцион-

§ 34 ИНТЕРФЕРОМЕТР ЖАМЕНА 255
ных полос минимальна при наблюдении вдоль N и максималь-
максимальна при наблюдении вдоль v. Однако фактически ось трубы OF
бывает направлена под углом ^45° к нормали N. Тогда верти™
кальные интерференционные полосы могут наблюдаться толь-
только в монохроматическом (квазимонохроматическом) свете, так
как им соответствуют высокие порядки интерференции. Дей-
Действительно, если наблюдение ведется вдоль N, то (sv) = 0, и
формула C4.2) дает А = 4rfv2. Ввиду малости v порядок ин-
интерференции получается низким. Нулевая полоса практически
проходит через точку А.
Когда труба направлена вдоль N или близко к этому направ-
направлению, вертикальные интерференционные полосы можно уви-
увидеть и в белом свете. Но при удалении от этого направления
скалярное произведение (vs), а с ним и порядок интерференции
возрастают. При повороте на угол ~ 45° порядок интерференции
становится столь высоким, что вертикальные интерференцион-
интерференционные полосы в белом свете наблюдаться уже не могут. Исклю-
Исключение было бы только в случае очень малых v, когда порядок
интерференции при любых положениях трубы низкий. Но то-
тогда интерференционная полоса была бы столь широка, что не
уместилась бы в поле зрения трубы. Поэтому этот случай не
представляет никакого интереса.
Совсем иное положение возникнет, если вторую пластину из
исходного положения повернуть вокруг горизонтальной оси. То-
Тогда вектор v встанет вертикально (рис. 138 5), а перпендцкуляр-
ные к нему плоскости равных фаз сделаются горизонтальными.
Интерференционные полосы определятся, если пересечь таки-
такими плоскостями поверхность экваториального цилиндрического
пояска. На рис. 138 б они изображены жирными дугами окруж-
окружностей, плоскости которых горизонтальны. При этом все они бу-
будут низкого порядка, а потому могут наблюдаться в белом свете,
так как наблюдение ведется практически перпендикулярно к v,
когда (vs) ~ 0. В поле зрения трубы будут видны практически
прямолинейные горизонтальные полосы. Легко сообразить, что
при наклоне вектора v интерференционные полосы сделаются
также наклонными к горизонту. Но в белом свете могут наблю-
наблюдаться только интерференционные полосы малого наклона. Для
получения полос с большим наклоном надо пользоваться моно-
монохроматическим (квазимонохроматическим) светом.
Все приведенные рассуждения можно повторить по той же
схеме и не вводя предположения, что п = 1. Для избежания гро-
громоздкости вычислений надо только всюду ограничиться члена-
членами, линейными по V, отбрасывая все члены более высоких степе-
степеней. При этом окончательные результаты не претерпят никаких
существенных изменений.

256 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
6. Интерферометр Жамена обладает рядом недостатков, де-
лающих его непригодным в некоторых особенно тонких оптиче-
оптических исследованиях. Изготовить пластины толще 5 см из вполне
однородного стекла с точно параллельными плоскостями прак™
тически невозможно. Поэтому и интерферирующие лучи АВ и
CD' невозможно развести на расстояние больше ^ 4 см. Но
главный недостаток интерферометра Жамена состоит в том, что
толстые пластины при освещении медленно прогреваются и мед-
медленно приходят в состояние теплового равновесия. Это приводит
к тому, что интерференционные полосы часами медленно ползут
в поле зрения трубы. Крайне затруднена работа в ультрафиоле-
ультрафиолетовой области, требующая уникальных пластин из кварца или
флуорита. Указанные недостатки устранены в интерферометре
Д.С. Рождественского A876—-1940).
Интерферометр Рождественского принципиально не отлича-
отличается от интерферометра Жамена. Каждая пластина в нем заме-
заменена комбинацией из двух парал™
лельно установленных тонких пла-
пластинок Mi, Pi и М2, F2 (рис. 139).
Пластинки Mi и М2 посеребрены
и выполняют роль зеркал. Пластин-
Пластинки Pi и Р2, также посеребрены, по-
полупрозрачны, они пропускают по-
половину падающего света, а осталь-
НУЮ половину отражают. Комбина-
ция параллельных пластинок М2,
Р2 может поворачиваться на малый
Рис- 139 угол относительно другой комбина™
ции также параллельных пластинок Mi, Pi. Ход лучей в интер-
интерферометре показан на схематическом рис. 139. Прибор действу-
действует так же, как и интерферометр Жамена. В нем наблюдаются
интерференционные полосы равного наклона.
Аналогично устроен построенный несколько раньше интер-
интерферометр Маха-Цендера. Отличие от интерферометра Рожде-
Рождественского состоит в том, что параллельно устанавливаются
между собой зеркала Mi и М2, а также полупрозрачные пла-
пластинки Pi и Р2. Одна пара пластин может поворачиваться на
малый угол относительно другой пары.
§ 35. Интерферометр Майкельеона
С помощью интерферометра Майкельеона A852-1931) впер-
впервые было проведено систематическое изучение тонкой структу-
структуры спектральных линий и выполнено первое прямое сравнение
эталонного метра с длиной световой волны. Знаменитый опыт

35
ИНТЕРФЕРОМЕТР МАЙКЕЛЬСОНА
257
Майкельсона-Морли, целью которого было обнаружение дви-
жения Земли относительно эфира (см. § 102), был выполнен
также с помощью интерферометра Майкельсона. В настоящее
время интерферометр Майкельсона устарел. Однако историче-
историческое значение указанных выше исследований, в особенности по-
последнего, слишком велико. Поэтому необходимо хотя бы кратко
остановиться на описании устройства и работы интерферометра
Майкельсона.
Схема интерферометра приведена на рис. 140. Свет от про-
протяженного источника S попадает на плоскопараллельную раз™
ж s
Рис. 140
делительную пластинку Pi, покрытую полупрозрачным тонким
слоем серебра или алюминия. Эта пластинка частично пропус-
кает, частично отражает свет, разделяя падающий пучок на два
взаимно перпендикулярных пучка. Первый пучок, пройдя через
пластинку Pi, отражается обратно зеркалом М\, а затем частич-
частично отражается от пластинки Pi в направлении АО. Второй пу-
пучок, отразившись от покрытой металлом поверхности пластинки
Pi, направляется к зеркалу М2, отражается от него, снова про-
проходит через пластинку Pi и далее идет в направлении АО, как
и первый пучок.
Таким образом, от одного и того же источника получаются
два пучка лучей одинаковой интенсивности, идущих в зритель-
зрительную трубу, где и наблюдаются интерференционные полосы.
На пути первого пучка лучей ставится пластинка Р2, тожде-
тождественная пластинке Pi. Она компенсирует разность хода между
пучками, возникающую из-за того, что второй пучок пересекает
разделительную пластинку Pi три, а первый только один раз.
Так как стекло обладает дисперсией, то без такой компенсации
наблюдение интерференции в белом свете было бы невозможно.
Зеркало М\ неподвижно, а Л#2 с помощью микрометрическо-
микрометрического винта может перемещаться на специальных салазках строго
9 Д.В. Сивухин

258 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
параллельно самому себе. В больших интерферометрах такое
перемещение должно происходить на десятки сантиметров. По-
Поэтому к механической части прибора предъявляются исключи™
тельно высокие требования. Зеркала интерферометра снабже-
снабжены также установочными винтами, позволяющими придавать им
правильное положение.
Пусть М[ — изображение поверхности зеркала М\ в отра-
отражающей плоскости разделительной пластинки Pi. Тогда интер-
интерференция будет происходить так же, как и в воздушном слое
между двумя отражающими плоскостями М.^ и М[. Разность
хода между отраженными лучами А = 2dcos </?, где d — толщина
слоя, a if — угол падения. Если слой плоскопараллелен, то будут
получаться интерференционные полосы равного наклона, лока-
локализованные в бесконечности. Их можно наблюдать глазом, ак-
аккомодированным на бесконечность, или в трубу, установленную
также на бесконечность. Получатся интерференционные кольца
с центром в точке схождения лучей, нормально отраженных от
поверхностей М~2 и М[. Этому направлению соответствует мак-
максимальная разность хода А = 2d. Поэтому максимальный поря-
порядок интерференции будет наблюдаться в центре картины. Отсю-
Отсюда следует, что при увеличении толщины d воздушного зазора
полосы интерференции будут перемещаться в направлении от
центра (в противоположность тому, что было с кольцами Нью-
Ньютона, см. § 33, п. 7).
При увеличении зазора d на А/2 разность хода увеличится
на А, так что произойдет смещение на одну полосу (т.е. на ме-
место каждой светлой полосы станет такая же светлая соседняя
полоса). При изменении угла падения на Аср разность хода из-
изменится на 2dsin(p A(p. Отсюда видно, что полосы интерферен-
интерференции получатся тем шире, чем меньше d. При d = 0 они стали
бы бесконечно широкими, т.е. поле зрения было бы освещено
равномерно.
При больших зазорах и высокой степени монохроматичности
света с интерферометром Майкельсона наблюдалась интерфе-
интерференция очень высокого порядка (около 106). Если М~2 и М[ близ-
близки друг к другу и образуют воздушный клин с небольшим углом,
то полосы интерференции локализуются либо на поверхности
клина, либо вблизи нее. Это — полосы равной толщины, имею-
имеющие вид равноотстоящих прямых, параллельных ребру клина.
§ 36. Многолучевам интерференция
1. Вернемся к исследованию интерференции в плоскопарал-
плоскопараллельных пластинках и учтем лучи, претерпевшие в них много-

§ 36 МНОГОЛУЧЕВАЯ ИНТЕРФЕРЕНЦИЯ 259
кратные отражения (см. рис. 134). Обозначим через R коэффи-
коэффициент отражения света от границы раздела пластинки с возду-
воздухом, т.е. долю энергии падающего света, которая возвращается
обратно при каждом отражении. При отсутствии поглощения
оставшаяся доля A — R) приходит через эту границу. Если сре-
дв! по обе стороны пластинки одинаковы (воздух), то, как будет
показано в § 65, коэффициентв! отражения на обеих поверхно-
поверхностях пластинки будут одинаковы. Допустим, что падающий свет
монохроматический. Обозначим через 1$ его интенсивность. То-
Тогда интенсивности прошедших пучков 1;, 2;, 3;, ... будут
Iv = {l- Rfh, h> = ^2A ~~ Rflo, h = R\l - R2)h,...,
а соответствующие (вещественные) амплитуды
пу = A —
где «о — амплитуда падающего света. Разность хода между
двумя соседними интерферирующими пучками составляет А =
= 2dncostp1 а разность фаз Ф = к А = Dтт/A) dn cos ф. Амплиту-
Амплитуда прошедшей волны представится убывающей геометрической
прогрессией
ad = аоA - Д)[1 + Re^ + R2e^ + ...].
Если пластинка достаточно длинная, то прогрессию молено счи-
считать бесконечной. Тогда
1-R
Интенсивность прошедшей волны будет
т _ С1™^J 2 _ A-^J г схал\
Рассчитаем теперь интенсивность 1Г отраж:енной волны. Ин-
Интенсивности отраженных пучков 1, 2, 3, ... будут
h=RI0, h = R{l-R?h, /3 = i?3(l-i?J/0,...,
а соответствующие (вещественные) амплитуды
«з = —
Знак минус в выра^кениях для амплитуд учитывает потерю по-
полуволны при отражении на одной из поверхностей пластинки.
Такую потерю полуволны не надо было учитывать при расчете
амплитуды прошедшей волны, так как там все отражения про-
происходят на границе стекло^воздух. В случае же отражения от
пластинки луч 2 претерпевает отражение на границе воздух^
стекло, а все остальные лучи — на границе стекло^воздух. Ре-
Результирующая амплитуда отраженной волны представится гео™
метрической прогрессией
аг = VRа0 - VM A - Л)аое-'Ф[1 + Re~i<s> + R2e~2iq> + ...].

260 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
Поступая, как раньше, найдем для интенсивности
_ 4Д8ш2(Ф/2) , ,
2. Из C6.1) и C6.2) видно, что 1^ + Ir = Iq, как это и
должно быть при отсутствии поглощения. Таким образом, кар-
картины распределения интенсивностей в прошедшем и отражен-
отраженном свете — взаимно дополнительные: светлым местам и мак™
симумам одной картины соответствуют темные места и мини-
минимумы другой. Для получения интерференционных полос, конеч-
конечно, надо пользоваться протяженными источниками света. Поло-
Полосы интерференции будут полосами равного наклона. Их можно
спроецировать линзой на экран, помещенный в ее фокальной
плоскости. Можно также пользоваться зрительной трубой, уста™
нов ленной на бесконечность. Интерференционные полосы будут
иметь форму концентрических колец, центр которых находится
в точке схождения лучей, нормальных к поверхности пластин-
пластинки. Максимумы в проходящем свете получаются при Ф/2 = гатг,
т.е. при 2dncosi/? = гаА, где т — целое число. В отраженном
свете этим местам соответствуют минимумы.
Таким образом, положения максимумов и минимумов опре-
определяются в точности теми же условиями, что и в случае простой
двухлучевой интерференции. То же относится и к распределе-
распределению интенсивностей, но при том существенном условии, что ко™
эффициент отражения мал (!?<С1). Тогда в C6.1) и C6.2) можно
пренебречь квадратами R и произвести разложение по R. В пер™
вом порядке получится
Id = 1-41? sin2 (Ф/2) = 1-2ДA-со8Ф),
Ir =4i?sIn2(#/2) = 2ДA-со8Ф).
Но к тому же результату мы пришли бы, если бы и не учитывали
многократные отражения.
Однако распределение интенсивности существенно изменя-
изменяется при увеличении коэффициента отражения I?, в особенности
когда этот коэффициент приближается к единице. На рис. 141
приведены кривые интенсивности прошедшего света для трех
значений R. Интенсивность падающего света принята за едини-
единицу. По оси абсцисс отложена разность фаз Ф = D7rdncos^)/A.
При Ф = 2гатг (га — целое) получаются максимумы. Когда R <С
<С1, максимумы пологие. Но уже при R = 0,75 они очень резкие.
При приближении R к единице весь свет практически сосредото-
сосредоточивается в очень узких интерференционных полосах на темном
фоне. В отраженном свете получаются столь же резкие, но тем-
темные интерференционные полосы на светлом фоне. Числитель в
формуле C6.1) — величина постоянная. В максимуме (Ф = 2тптт)
-*м

36
МНОГОЛУЧЕВАЯ ИНТЕРФЕРЕНЦИЯ
261
Резкость интерференционных полос характеризуется их по-
полушириной. Для полос в проходящем свете полушириной назы-
называется расстояние между точками, лежащими по обе сторо-
стороны максимума, в которых интенсивность составляет поло-
вину максимальной величины /Макс- В окрестности максимума
/и-1/2
т-\ {An ndcos
Рис. 141
тп-то порядка Ф представим в виде Ф = тж + (р. Тогда в формуле
C6.1) Ф молено заменить на (р. Ввиду малости ср ту же формулу
можно переписать так:
т 1макс /о/'» о\
h = 1 + ду2/A-ДJ' C6'3)
Если Rip2/A — RJ = 1, то Id = Уг/макс- Следовательно, полу™
ширина определится выра^кением
= 2(р = 2-
C6.4)
3. В применениях многолучевая интерференция всегда осу-
осуществляется в толстых пластинках, так что приходится иметь
дело с интерференцией высоких порядков. Поэтому для получе-
получения интерференционных полос требуется высокая монохрома-
монохроматичность света (Х/8Х > га). В интерференционной спектро-
спектроскопии, где многолучевая интерференция применяется для изу™
чения спектров, исследуемый свет, если он не обладает достаточ-
достаточной монохроматичностью, должен быть предварительно моно-
хроматизован, например с помощью призменного спектрометра
или другого монохроматора.
Обычно методами интерференционной спектроскопии иссле-
исследуется структура тонких спектральных линий. Достоинством
интерференционных спектроскопов является их высокая разре-

262
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
шающая способность при большой светосиле, простоте устрой-
устройства, дешевизне и удобстве в обращении. Разрешающая спо-
способность определяет наименьшее расстояние между близкими
спектральными линиями^ которые изображаются в виде раз-
раздельных спектральных линий.
Для уяснения понятия разрешающей способности допустим,
что применяемый свет состоит из двух близких, одинаково ин™
тенсивных спектральных линий с длинами волн А и А1 = А +
+ 6Х. Интерференционная картина будет состоять из двух си™
стем интерференционных полос (максимумов) с теми же длина™
ми волн. Одна система максимумов окажется сдвинутой относи™
тельно другой. Если сдвиг недостаточен, максимумы наложатся
друг на друга, получится распределение с единственным мак™
симумом, которое для глаза неотличимо от распределения, со-
соответствующего одной спектральной линии. Тогда говорят, что
рассматриваемая двойная линия не разрешается спектральным
прибором.
Допустим теперь, что сдвиг равен полуширине интерферен™
ционной полосы. Соответствующее распределение интенсивно-
интенсивности показано на рис. 142.
Кривые Аи А1 изобража-
изображают контуры спектраль™
ных линий, как они бы™
ли бы видны в спектраль-
спектральном приборе в отдельно™
сти. В центре картины,
где контуры пересекают-
пересекаются, интенсивность спек™
тральных линий состав™
ляет У^/макс- При сложе-
нии интенсивностей ин™
тенсивность в центре по-
получится равной /Макс- В точке А интенсивность первой линии
равна /макс5 а второй Уз/макс? как эт0 видно из формулы C6.3).
Таким образом, полная интенсивность в точке А будет /макс +
+ Уб/макс = 1,2/макс. Такая же интенсивность получится в точке
А1. Кривая результирующей интенсивности будет состоять из
двух максимумов с провалом в центре между ними. Интенсив™
ность в месте провала будет составлять 1/1,2 = 83% от интен-
интенсивности одного из максимумов на результирующей кривой.
Будет ли разрешаться спектральная линия при таком прова-
провале — это зависит от индивидуальных особенностей глаза. Опыт
показывает, что нормальный глаз такие провалы обычно замеча-
замечает без особого труда. Поэтому расстояние между максимумами
спектральных линий, равное или большее полуширины интер™
Рис. 142

36
МНОГОЛУЧЕВАЯ ИНТЕРФЕРЕНЦИЯ
263
ференционной полосы, мы примем (до некоторой степени услов-
условно) за условие спектрального разрешения.
Определим теперь минимальную разность длин волн SX =
= А; — А, соответствующую такому критерию разрешения. Все
величины, относящиеся к свету с длиной волны А, будем обозна-
обозначать нештрихованными, а к длине волны А; — штрихованными
буквами. Показатель преломления п будем считать одним и тем
же для обеих длин волн. (Это строго выполняется только в ин-
интерферометре Фабри-Перо.) Тогда, независимо от длины волны,
всем падающим лучам одного и того же направления будут со-
соответствовать преломленные лучи также одного направления.
В точке А' для длины волны А; получается интерференционный
максимум m-го порядка, а потому Ф; = 2тж. В той же точке вол-
волна с длиной А максимума уже не дает. Для такой волны разность
фаз имеет значение Ф = 2ттг + A — Д)/\/Д, т.е. в рассматрива-
рассматриваемой точке Ф; — Ф = <5Ф = A — R)/y/~R. Но ввиду одинаковости
п и ф для обеих волн из формулы Ф = D7rdncos^)/A следу-
следует: EФ/Ф = |$А/А|. Учтя, что в максимуме Ф = 2жт1 поэтому
находим
SX
1-Я
т.
^36.5)
Величина Х/6Х называется разрешающей способностью
спектрального прибора.
Интерференционные спектральные аппараты осуществлены
в виде двух приборов, которые мы и рассмотрим.
4. Интерферометр или эталон Фабр и^П е р о.
Этот прибор, изобретенный Фабри A867-1945) и Перо A863—
1925), является наиболее распространенным из интерференци-
интерференционных спектральных приборов. Он состоит из двух стеклянных
или кварцевых пластинок Pi и Р25 между которыми обычно
Рис. 143
находится воздух (рис. 143). Плоские поверхности пластинок,
обращенные друг к другу, тщательно отшлифованы и покрыты
высокоотражающими слоями (серебро, алюминий, многослой-

264
ИНТЕРФЕРЕНЦИЯ СВЕТА
ГЛ. III
ные диэлектрические покрытия). В хороших приборах отступ™
ления внутренних поверхностей пластинок от идеальных плос-
плоскостей не превышают 0,01 А. Отражательная способность зер-
зеркальных поверхностей пластинок при металлическом покрытии
может быть доведена до 95 %, а при диэлектрических — до 98 %.
Параллельность зеркальных поверхностей достигается с по™
мощью распорного кольца из инвара или плавленого кварца,
помещаемого между пластинками. Кольцо снабжено тремя вы-
выступами с каждой стороны, к которым пластинки прижимаются
при помощи трех пружин. Выступы подшлифованы так, что зер-
зеркальные поверхности устанавливаются параллельно друг другу.
Небольшие отступления от параллельности устраняются нажи-
нажимом соответствующей пружины.
Интерферометр, в котором используются распорные кольца,
называется эталоном Фабри-Перо. Располагая набором этало-
эталонов с кольцами разной толщины, можно производить измерения
при различных расстояниях между зеркальными поверхностя-
поверхностями. В прежних моделях интерферометра Фабри^Перо можно
было с помощью специаль-
специальных микрометрических вин-
винтов менять расстояние меж-
между зеркалами. Но таким пу-
путем не удается достигнуть
той высокой точности, кото-
которую можно получить с помо-
помощью эталона. Наружные по-
поверхности пластинок обыч-
обычно образуют небольшие углы
с внутренними, чтобы отра-
отраженный от них светлый блик
не мешал наблюдению основ-
основной интерференционной кар-
картины. Таким образом, интер-
интерферометр Фабри-Перо мож-
можно рассматривать как плос-
плоскопараллельную воздушную
пластинку, на которой происходят многократные отражения
световых лучей и последующая интерференция их.
Интерференционная картина состоит из концентрических
колец равного наклона. Она приведена на рис. 144 в проходящем
свете. Интерференционные максимумы тем уже, чем больше от-
отражательная способность зеркальных поверхностей пластинок
интерферометра.
Расстояние между зеркалами h обычно составляет 1—100 мм,
а в специальных эталонах доходит до 1 м. Поэтому порядки ин-
интерференции т « 2h/X очень высоки (при h = 5 мм т « 20 000).
Рис. 144

36
МНОГОЛУЧЕВАЯ ИНТЕРФЕРЕНЦИЯ
265
Ввиду малости угла ф условие главного интерференционного
максимума 2h cos ф = га А можно записать в виде кB^ф2) = га А.
Отсюда находим угловую дисперсию интерферометра Фабри-
Перо:
йф т 1 (оа ^ч
Ж = ~2Нф = ~Хф- ^36-6)
При рабочих условиях (ф « 10^2 рад) угловая дисперсия ин-
интерферометра Фабри-Перо значительно превышает дисперсию
других спектральных аппаратов. Это является основным пре-
преимуществом интерферометра ФабриЧПеро.
Другим важным преимуществом интерферометра Фабри^
Перо является его большая светосила. Благодаря этому и сво™
ей дешевизне такой интерферометр получил широкое распро-
распространение для спектральных исследований в оптической обла-
области спектра. Принцип интерферометра Фабри-Перо был исполь-
использован также в объемных резонаторах оптических квантовых ге-
генераторов (см. § 120).
5. Пластинка Луммер а-Г е р к е A878-1960).
Она представляет собой плоскопараллельную пластинку из
очень однородного стекла или плавленого кварца толщиной от
3 до 10 мм и длиной до 30 см. Для направления световых лучей
в пластинку на одном конце ее сбоку посажена на оптический
т+2
ЛУ\/\/\/\/\/1
Рис. 145
контакт добавочная призмочка (рис. 145 а). При другом спосо-
способе один конец пластинки скошен (рис. 145 6"). В обоих случаях
падающие лучи нормальны к поверхности стекла, чем достига-

266 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
ется уменьшение потерь света на отражение. Направление пада-
ющих лучей подбирается таким, чтобы угол падения на границе
стекло^воздух был близок к предельному углу полного отраже-
отражения. Тогда коэффициент отражения мало отличается от едини™
цы. Пучки испытывают многократные отражения от плоскостей
пластинки и выходят из нее с почти одинаковыми интенсивно™
стями. Можно получить до 10—15 таких пучков с каждой сторо-
стороны пластинки.
В пластинке Луммера-Герке наблюдаются интерференцион-
интерференционные полосы равного наклона. Условие интерференционного мак-
максимума га-го порядка имеет вид
2кпсозф = т\, C6.7)
где h — толщина пластинки, а ф — угол преломления. Здесь не
учтено изменение фазы при отражении, так как оно произво-
производит только несущественное смещение всей интерференционной
картины. Число интерферирующих пучков по одну сторону пла-
стинки равно N = L/Bhtgф)J где L — длина пластинки. А так
как свет падает почти под предельным углом, то
C6.8)
Вопрос о разрешающей способности пластинки Луммера-
Герке будет разобран в § 48.
6. Затронем еще два вопроса, имеющих отношение к много™
лучевой интерференции. Рассмотрим сначала много равноотсто-
равноотстоящих параллельных отражающих плоскостей с малыми коэф-
фициентами отражения (рис. 146). Почти весь свет, падающий
на каждую плоскость, проходит через нее без потерь. В резуль-
результате получится много параллельных
12 3 4 отраженных лучей 1, 2, 5, ... по-
почти одинаковой интенсивности. Раз-
Разность хода между соседними лучами
составляет 2dcos(/?, где d — рассто-
расстояние между соседними плоскостями.
Если выполнено условие
2dcoscp = raA C6.9)
(га — целое число), то все лучи будут
рис> 246 находиться в фазе. Возникнет силь-
ное отражение, называемое интерфе-
интерференционным отражением. При заданном т условие C6.9) мо-
может выполняться только для определенных длин волн. Поэто-
Поэтому при освещении рассматриваемой системы плоскостей белым
светом интерференционное отражение будет наблюдаться лишь
для некоторых (а при d < А — для одной) сравнительно узких
спектральных линий. Система плоскостей, таким образом, при-

37
СТОЯЧИЕ СВЕТОВЫЕ ВОЛНЫ
267
обретает свойство избирательного отражения. При этом, так
как разность хода зависит от угла падения, цвет избирательно
отраженного света будет меняться с изменением угла падения.
Отметим так лее, не входя ни в какие подробности, что над™
лежащей комбинацией диэлектрических слоев с различными по-
показателями преломления удается осуществить на поверхности
стекла многослойные покрытия (пленки) с высокими коэффи-
коэффициентами отражения (до 98-99% для определенных длин волн).
Такие покрытия применяются, например, в зеркалах интерфе-
интерферометров Фабри-Перо. Следует, однако, иметь в виду, что отра-
отражающие многослойные пленки в белом свете окрашены, так как
интерференционное условие сильного отражения точно выпол-
выполняется только для какой-либо одной длины волны.
§ 37. Стомчие световые волны
1. При интерференции монохроматических волн, распро-
распространяющихся навстречу друг другу, образуются стоячие вол-
волны (см. т. III, § 140). В этом случае, как видно из формулы
B6.12), ширина полосы Ах равна Л/2, т.е. расстоянию между
соседними пучностями или узлами. В случае электромагнит-
электромагнитных волн пучности (узлы) электрического вектора Е совпада-
совпадают с узлами (пучностями) магнитного вектора В. Таким обра-
образом, в стоячей волне электрическое и магнитное поля можно
пространственно разделить и исследовать свойства и действия
этих полей в отдельности. Моменты прохождения электрическо-
электрического и магнитного полей через максимум в стоячей волне не совпа-
совпадают, а сдвинуты относительно
друг друга на половину перио-
периода световых колебаний. Полу-
Получение стоячих световых волн
наталкивается на трудности,
связанные с малостью длины
волны. Эти трудности впервые
были преодолены О. Винером
A862-1927) в 1890 г.
Стеклянная пластинка F
(рис. 147), покрытая тонким
фоточувствительным слоем
А А
толщиной
шим металлическим зеркалом М, образуя с ним очень малый
угол а (порядка 1; или меньше). Пластинка освещалась моно-
монохроматическими лучами, нормальными к поверхности зеркала.
Рис. 147
— — —, приводилась в соприкосновение с хоро-

268 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
В результате отражения от зеркала в воздушном клине между
зеркалом и фотослоем образовывались стоячие световые волны.
Их пучности обнаруживались в фотослое после его проявления
в виде равноотстоящих почерневших полос, параллельных ре™
бру воздушного клина. Расстояние между этими полосами равно
A/Bsina). Полосы молено видеть глазом, если угол а взять до™
статочно малым. В опытах Винера расстояние между полосами
составляло 1—2 мм. По этим данным можно было оценить дли-
длину световой волны. Удадось также показать, что для красного
света длина волны примерно вдвое больше, чем для синего.
Выдвигалось возражение, что при интерпретации опыта не
было учтено обратное отражение света от фотослоя. Чтобы
снять это возражение, Винер заполнял пространство между фо-
фотослоем и металлическим зеркалом бензолом, показатель пре™
ломления которого близок к показателю преломления желатины
фотослоя. Тем самым устранялось влияние отражения от фото™
слоя. Оказалось, что при этом вид интерференционных полос не
менялся.
Главное значение опытов Винера состоит в том, что они
позволили установить, какой вектор производит фотохимиче-
фотохимическое действие: электрический или магнитный. Опыты показали,
что первый слой почернения получается на расстоянии А/4 от
поверхности металлического зеркала. Здесь поэтому находится
пучность вектора, вызывающего фотографическое действие. Но
при отражении электромагнитной волны от металла на его по-
поверхности получается узел электрического вектора (см. т. III,
§ 45). Первая пучность электрического вектора находится на
расстоянии А/4 от поверхности металлического зеркала — там
же, где наблюдается почернение фотографического слоя. От™
сюда следует, что фотографическое (и вообще фотохимическое)
действие производится электрическим, а не магнитным полем
световой волны.
Позднее, в 1892 г., Друде A863^1906) и Пернет A864-1941)
повторили опыт Винера, заменив фотографический слой тонкой
пленкой флуоресцирующего вещества. Айве в 1933 г. сделал то
же самое с фотоэлектрическим слоем. Оказалось, что флуорес-
флуоресценция и фотоэффект вызываются также электрическим полем.
Этого и следовало ожидать с точки зрения электронных пред-
представлений о строении вещества.
Действительно, действие света на вещество сводится к си-
силам, с которыми на электроны действуют электрические и маг™
нитные поля. Первая сила равна еЕ, вторая - [vB], где v — ско-
скорость электрона. Магнитная сила много меньше электрической,
так как v <C с. Таким образом, во всех действиях электрический

§ 37 СТОЯЧИЕ СВЕТОВЫЕ ВОЛНЫ 269
вектор световой волны является более важным, чем магнитный.
Поэтому его нередко называют световым вектором.
2. Винер исследовал также стоячие световые волнв! в по-
поляризованном свете. При отражении от прозрачной среды под
определенным углом отраженный свет оказывается линейно по™
ляризованнвш (см. § 65). Про такой свет теперь говорят, что он
поляризован перпендикулярно к плоскости падения. Со времен
Френеля A821 г.) до конца XIX века во всех эфирных теориях
света обсуждался вопрос, как направлен световой вектор: па™
раллельно плоскости поляризации или перпендикулярно к ней.
Опыт Винера и должен был решить этот вопрос.
Винер изменил постановку своего предыдущего опыта, за-
заставив линейно поляризованный свет отражаться от металличе-
металлического зеркала под углом 45°. Тогда угол между направлениями
распространения падающей и отраженной волн будет 90°. По™
этому при интерференции этих волн расстояние между сосед™
ними пучностями или узлами стоячей волны окажется равным
А/у2, как это видно из формулы B6.12). Если световой вектор
перпендикулярен к плоскости падения, то колебания в падаю™
щей и отраженной волнах будут параллельными. Тогда возник-
возникнет интерференция этих волн и на фотографической пластинке,
наклоненной к поверхности металлического зеркала, получатся
такие же темные и светлые полосы, как и в первом опыте Вине™
ра. Если же световой вектор параллелен плоскости падения, то
интерференция невозможна, так как в этом случае колебания в
падающем и отраженном свете будут взаимно перпендикулярны
(см. § 26, п. 5).
Опыт показал, что полосы получаются, когда свет поляризо-
поляризован перпендикулярно к плоскости падения. Если же он поляри-
поляризован в плоскости падения, то получается равномерное почер™
нение пленки. Отсюда следует, что световой вектор лежит в
плоскости поляризации. А так как предыдущими опытами до-
доказано, что он является электрическим вектором, то последний
также лежит в плоскости поляризации.
8. На явлении стоячих волн основан метод цветной фотогра-
фии, разработанный Липпманом A845-1922) в 1891 г. Стеклян-
Стеклянная пластинка покрыта с одной стороны толстым слоем мелко-
мелкозернистой сухой фотографической эмульсии высокой чувстви-
чувствительности. Пластинка составляет стенку сосуда, в который на-
наливается ртуть. Эмульсией пластинка должна быть обращена
внутрь сосуда, чтобы фотографический слой находился в кон™
такте с ртутью. Пластинка освещается снаружи нормально па-
падающими лучами определенной длины волны. При отражении
света от поверхности ртути в толще эмульсии образуются стоя™
чие волны, которые и экспонируют фотопластинку. После это™

270 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
го пластинка вынимается, проявляется и фиксируется. В ме-
стах пучностей электрического вектора выделяются тонкие слои
металлического серебра, находящиеся на расстоянии А/2 друг
от друга. Получается плоскослоистая среда из отражающих па™
раллельных плоскостей, подобная той, которая изображена на
рис. 146.
Осветим теперь со стороны эмульсии так обработанную пла-
пластинку нормально падающим светом. Малая часть света отра-
отразится от слоя /, остальная часть пройдет прямо. От второго
слоя отразится столь же малая часть, и т.д. Получится столько
лее отраженных пучков, сколько металлических слоев отложи-
отложилось в толще эмульсии. Интенсивность каждого пучка мала, но
их число велико. Если длины волн освещающего света и света,
применявшегося при экспонировании, в точности одинаковы, то
каждый последующий отраженный пучок будет запаздывать по
фазе относительно предыдущего на 2тг. В этом случае произой-
произойдет интерференционное усиление пучков, так что результирую-
результирующая интенсивность отраженного света окажется большой. Если
же каждый пучок будет сдвинут по фазе относительно предыду-
предыдущего на ±27r/JV, где N — общее число пучков, то произойдет их
взаимное гашение. Вообще, интенсивно будут отражаться толь-
только такие длины волн, которые равны длине волны света, приме-
применявшегося при экспонировании, или очень близки к ней. Поэто-
Поэтому при освещении пластинки белым светом она в отраженном
свете будет казаться окрашенной в соответствующий цвет.
Спектральная область SX отраженного света тем уже, чем
толще слой эмульсии, чем больше число отложившихся слоев
металлического серебра. Если на эмульсию подышать, то она
немного разбухнет, расстояния между металлическими слоями
увеличатся, что вызовет смещение цвета в красную сторону. При
увеличении угла падения ср условие интерференционного усиле-
усиления 2dsiinp = А будет выполняться для более коротких волн.
Поэтому при наклоне пластинки ее цвет меняется в сторону
фиолетового конца спектра.
Для получения цветных фотографий предметов при экспо-
экспонировании пластинки надо получать цветное изображение фо-
фотографируемого предмета на светочувствительном слое, как во
всяком фотоаппарате. Липпмановские цветные фотографии по-
получаются высокого качества в чистых спектральных цветах, на-
например при фотографировании спектров. Смешанные цвета, как
правило, дают плохие результаты. Метод Липпмана не полу-
получил распространения. Современная техническая цветная фото-
фотография основана на принципе светофильтров — использовании
соответствующих красящих пигментов, вводимых в эмульсию
фотопластинок.

§ 38 ИЗЛУЧЕНИЕ ВАВИЛОВА-ЧЕРЕНКОВА 271
Нейхаусс в конце ЭО-х годов прошлого века на опыте убе-
убедился в слоистой структуре пленок Липпмана. Была получена
по методу Липпмана фотография в красном свете. После этого
пленка была отделена от стекла и произведен поперечный разрез
ее. Затем была получена микрофотография одного из разрезов
пленки с увеличением в 1000 раз. На микрофотографии было
видно около десяти темных полос, чередовавшихся со светлыми.
Темные полосы получились в местах отложения металлического
серебра. Расстояние между серединами темных полос получи-
получилось «350 им. Необходимо заметить, что никакой микроскоп
не позволяет различить детали предмета, много меньшие дли™
ны световой волны. Успех опыта отчасти определялся тем, что
пленка заметно разбухла при обработке до ее разрезания. Кроме
того, разрез производился в косом направлении.
§ 38. Излучение Вавилова^Черенкова
1. Интерференция света — отнюдь не редкое явление, как
это может показаться с первого взгляда. По существу все, что
связано с распространением света в веществе, относится к клас-
классу явлений интерференции. Действительно, световая волна, па™
дая на среду, возбуждает электрические колебания в атомах и
молекулах. Вследствие этого эти частицы начинают излучать
вторичные электромагнитные волны, также воздействующие на
атомы и молекулы среды. Падающая волна и возбужденные ею
вторичные волны интерферируют, и этой интерференцией опре-
определяются все особенности распространения света в среде.
Действие линзы и вогнутого зеркала можно рассматривать
также как интерференционный эффект. Действительно, возму-
возмущения от точечного источника, если они попадают на различные
участки линзы, в дальнейшем распространяются по различным
путям вдоль лучей к фокусу. Так как оптические длины всех
лучей от источника до фокуса одинаковы, то возмущения при™
ходят в фокус в одинаковых фазах и при наложении усиливают
друг друга. Этим интерференционным эффектом и объясняется
фокусирующее действие линзы. Если бы при своем распростра-
распространении световые возмущения строго следовали законам лучевой
(геометрической) оптики, то в фокусе получилась бы бесконеч-
бесконечная интенсивность светового поля. То обстоятельство, что этого
не происходит, связано с отступлениями от геометрической оп-
оптики и прежде всего с дифракцией.
2. Рассмотрим более интересный пример. Допустим, что в
прозрачной однородной среде движется электрон или какая™
либо другая заряженная частица с постоянной скоростью V.
Своим полем движущийся электрон возбуждает атомы и моле-

272 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
кулы среды, и они становятся центрами излучения электромаг-
электромагнитных волн. При равномерном движении электрона эти волны
когерентны и могут интерферировать между собой. Если ско-
скорость электрона V больше фазовой
А V В скорости света в среде г?, то волны,
исходящие от электрона в различ™
ные моменты времени, при опреде-
ленных условиях могут приходить в
точку наблюдения одновременно.
Действительно, пусть А и В
(рис. 148) — точки, через которые
электрон проходил в моменты вре™
мени t\ и #2 соответственно. На про-
Рис. 148 хождение расстояния АВ электрон
затратил время t2 — t\ = АВ/V. В точку наблюдения Р волны
из А и В придут в моменты времени i\ + AP/v и ?2 + BP/v.
Разность этих времен равна
д, /, , ч АР^ВР АВ АР^ВР
Если точка Р удалена достаточно далеко, то АР ~~ ВР « АС =
= АВ cos #, так что At = АВ (— — ^^). Так как по предполо-
предположению v < F, то существует угол #, удовлетворяющий условию
cosi? = - = \, C8.1)
V пр
где /3 = V/c, а п = с/г? — показатель преломления среды. Если
это условие выполнено, то все волны придут в точку Р одно-
одновременно¦, какова бы ни была длина отрезка АВ. В этом случае
при интерференции произойдет взаимное усиление их. Во всех
других случаях путь электрона молено разбить на такие отрез™
ки, чтобы от крайних точек каждого из них волны приходили в
точку Р с разностью хода А. Волны, приходящие от всех точек
каждого из таких отрезков, полностью погасят друг друга из-за
интерференции. Следовательно, то же произойдет с волнами,
приходящими от всех точек среды, лежащих на пути движения
электрона. Таким образом, в направлениях, определяемых усло-
условием C8.1), электрон (точнее — среда, в которой он движется)
будет излучать электромагнитные волны, а в остальных направ™
лениях излучения не будет.
Такое излучение экспериментально было обнаружено в
1934 г., а затем подробно исследовано Ф.А. Черенковым
(р. 1904), в то время аспирантом СИ. Вавилова A891-1951).
Черенков показал, что все без исключения жидкие и твердые
тела при прохождении через них быстрых электронов, помимо
флуоресценции, имеющей место в некоторых случаях, всегда не-

§ 38 ИЗЛУЧЕНИЕ ВАВИЛОВА-ЧЕРЕНКОВА 273
пускают слабый видимый свет с непрерывным спектром. Свече™
ние частично поляризовано, причем электрический вектор ле-
лежит преимущественно в плоскости, образованной световым лу-
лучом излучения и направлением движения электрона. Излучение
направлено главным образом вперед и максимально вдоль обра-
образующих конуса, ось которого задается направлением движения
электрона, а угол при вершине 2$ определяется формулой C8.1).
Свечение не удается потушить ни температурным воздействием,
ни прибавлением к светящейся среде веществ, тушащих флуо-
флуоресценцию. Попытки определения времени нахождения излуча-
излучающих атомов и молекул в возбужденном состоянии показали,
что это время равно нулю: свечение прекращается одновременно
с прекращением прохождения электронов через среду. Эти осо-
особенности свечения привели СИ. Вавилова к заключению, что
оно не является люминесценцией, для которой характерна ко-
конечная длительность свечения.
Ввиду очень слабой яркости свечения, Черенков при коли-
количественных измерениях в большинстве случаев применял метод
Вавилова фотометрирования по порогу зрения.
В дальнейшем было показано, что свечение вызывается так-
также протонами, мезонами и другими быстрыми заряженными ча-
частицами. Свечение, вызываемое радиоактивными излучениями,
было известно и ранее, но оно во всех случаях неправильно счи-
считалось одним из видов люминесценции.
3. Ведущая роль в руководстве экспериментальными иссле-
исследованиями, направленными на выяснение природы свечения,
принадлежит СИ. Вавилову. Качественное объяснение явления
излучения Вавилова-Черенкова, приведенное выше, было дано
И.Е. Таммом A895-1971) и И.М. Франком (р. 1908) в 1934 г.
Тогда же ими была создана и количественная теория, согласую-
согласующаяся с наблюдаемыми фактами. Несколько позднее, в 1940 г.,
В.Л. Гинзбург (р. 1916) построил квантовую теорию, основан-
основанную на законах сохранения энергии и импульса.
Из рассуждений, приведенных выше, ясно, что в формулу
C8.1) должна входить фазовая^ а не какая-либо другая скорость
света, так как именно она определяет фазы колебаний, а с ни-
ними и условие интерференционного усиления волн. Из форму-
формулы C8.1) видно, что излучение на частотах о;, для которых
п(ш) < 1//3, невозможно. Поэтому спектр излучения Вавилова-
Черенкова должен обрываться на коротких волнах, где условие
C8.1) перестает выполняться из-за дисперсии света. В частно-
частности, невозможно излучение Вавилова-Черенкова рентгеновских
волн, так как для них п < 1.
Если бы электрон двигался в среде строго равномерно, то
излучение было бы точно сосредоточено на поверхности конуса,
определяемого условием C8.1). Из-за неравномерности движе-

274 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
ния появляется размытие этой поверхности. Но далее и при на™
личии такого размытия направленность излучения указывает на
то, что молекулы и атомы среды, возбуждаемые электроном, из™
лучают когерентно если и не на всем пути движения электрона,
то во всяком случае на его части порядка длины световой волны.
Следовательно, рассматриваемое явление практически не зави-
зависит от атомного строения среды и может быть рассмотрено
в рамках макроскопической электромагнитной теории. Это и
было сделано Таммом и Франком. Ограничимся приведением
основного результата. Полная энергия, излучаемая электроном
в единицу времени на единице его пути, определяется формулой
/
/Зп > 1
Интегрирование производится по частотам, для которых
j3n{(jj) > 1. Той же формулой очевидным образом определяется
и распределение излучаемой энергии по спектру частот. Форму-
Формула справедлива при выполнении условия
у(и;), C8.3)
т.е. когда скорость электрона V за период световых колебаний
Т = 2ж/и меняется мало по сравнению с фазовой скоростью
v(uj). По оценке Тамма и Франка полная потеря энергии элек™
трона на излучение Вавилова^Черенкова в жидкостях и твер-
твердых телах по порядку величины составляет несколько тысяч
электрон-вольт на сантиметр пути, т.е. пренебрежимо мала по
сравнению с потерями энергии по другим причинам.
Излучение электрона, конечно, приводит к его торможению.
Само по себе ускоренное движение электрона вызывает излуче™
ние. Однако из изложенного выше следует, что это излучение не
имеет ничего общего с интерференцией, определяющей из луче™
ние Вавилова^Черенкова. Если бы к электрону приложить силу,
уравновешивающую все тормозящие силы, то ускорение исчез™
ло бы, а излучение Вавилова-Черенкова осталось бы. Именно
так надо понимать утверждение, что электрон, равномерно дви™
жущийся в среде, излучает, если его скорость больше фазовой
скорости света в этой среде.
4. Явления, аналогичные излучению Вавилова-Черенкова,
давно известны в гидро™ и аэродинамике. Например, если ско™
рость судна превышает минимальную фазовую скорость на по-
поверхности воды, то оно начинает непрерывно генерировать вол™
новые цуги, даже когда его скорость остается постоянной. В
этом причина так называемого волнового сопротивления^ ветре™
чаемого судами при движении по поверхности воды. То же са™
мое происходит при полете снарядов и самолетов в воздухе. Они

§ 38 ИЗЛУЧЕНИЕ ВАВИЛОВА-ЧЕРЕНКОВА 275
начинают излучать ударные волны, называемые волнами Маха
A838-1916), если движутся со сверхзвуковыми скоростями. По-
Потери энергии на это излучение столь значительны, что они обу-
обусловливают основное сопротивление, испытываемое снарядами
и самолетами при сверхзвуковых движениях. Указанные явле-
явления сложнее излучения Вавилова-Черепкова из-за нелинейно-
нелинейности гидродинамических уравнений.
5. Излучение Вавилова-Черепкова может вызываться не
только движущимися частицами, но и каким-либо возбуждени-
ем, распространяющимся со скоростью, превышающей фазовую
скорость света в среде. Допустим, например, что на границу раз-
раздела двух сред падает волна с плоским фронтом АВ (рис. 149).
Вдоль границы раздела побежит
возмущение со скоростью V =
= v\/simp, где v\ — фазовая ско-
скорость света в первой среде. Оно воз-
возбудит во второй среде излучение
Вавилова-Черенкова под углом $ к
границе раздела. Угол # определя-
ется формулой C8.1), т.е. cost? =
= V2/V, где V2 — фазовая ско-
скорость во второй среде. Замечая,
что cost? = smt/^, отсюда нахо-
находим sinф/ sin if = V2/v\. Это — за- Рис. 149
кон преломления Снеллиуса. Таким
образом, преломление света можно трактовать как эффект
Вавилова-Черенкова, возбуждаемый во второй среде падающей
волной. Так же можно рассматривать и отражение света. Рас-
Распространение света в однородной среде тоже подчиняется закону
C8.1). В этом случае скорость волнового фронта V совпадает с
фазовой скоростью -у, так что формула C8.1) дает # = 0, т.е.
волновой фронт распространяется без изменения направления.
6. Излучение Вавилова-Черенкова нашло широкое примене-
применение в ядерной физике и физике высоких энергий. На нем осно-
основано действие так называемых черепковских счетчиков^ т.е. де-
детекторов релятивистских заряженных частиц, излучение кото-
которых регистрируется с помощью фотоумножителей. Основное на-
назначение черепковских счетчиков — разделение релятивистских
частиц с одинаковыми импульсами, но различными скоростя-
скоростями. Пусть, например, пучок, состоящий из релятивистских про-
протонов и тг-мезонов, проходит через однородное поперечное маг-
магнитное поле. Направления траекторий прошедших частиц будут
определяться только их импульсами, но не будут зависеть от их
скоростей. С помощью диафрагм можно выделить протоны и
тг-мезоны с одинаковыми импульсами. Из-за различия масс ско-
скорости тг-мезонов vw окажутся несколько больше скоростей про-

276 ИНТЕРФЕРЕНЦИЯ СВЕТА ГЛ. III
тонов vp. Если полученный пучок направить в газ и подобрать
с
показатель преломления п газа так, чтобы было vn > — > vpi то
п
тг-мезоны будут давать излучение Вавилова^Черенкова, а прото-
протоны — нет. Таким образом, счетчик будет регистрировать только
тг-мезоны, но не будет регистрировать протоны. Показатель пре-
преломления газа в камере счетчика п молено менять, изменяя его
давление.
7. В заключение остановимся на вопросе, может ли возник-
возникнуть электромагнитное излучение, когда заряженная частица
движется равномерно в среде с досветовой скоростью, т.е. со
скоростью, меньшей фазовой скорости света в рассматриваемой
среде. Если среда однородна, то ответ будет отрицательным.
Действительно, движущаяся заряженная частица на своем пу-
ти, конечно, будет возбуждать атомы и молекулы среды. По-
Последние начнут излучать. Однако эти излучения в результате
интерференции погасят друг друга, так как при равномерном
движении частицы и однородности среды их амплитуды одина-
одинаковы, а фазы возрастают линейно с расстоянием, пройденным
частицей. Но если среда неоднородна, то гашения не будет и
появится излучение. Такое излучение, на существование кото-
которого было указано В.Л. Гинзбургом и И.М. Франком в 1944 г.,
называется переходным излучением.
Особенно наглядно происхождение переходного излучения
молено понять на следующем примере. Если электрон (или дру-
гая заряженная частица) находится перед плоской границей иде-
идеального металла, то электрическое поле вне металла молено рас™
сматривать как поле диполя, состоящего из электрона и его
«электрического изображения» в поверхности металла (см. т. III,
§ 23). Если электрон приближается к металлу, то электрическое
изображение движется к нему навстречу. При этом электриче-
электрический момент диполя уменьшается. Вследствие этого и возникает
излучение. В момент, когда электрон пересекает границу метал-
металла, происходит как бы аннигиляция электрона и его электри-
электрического изображения. Так лее возникает переходное излучение,
когда электрон выходит из металла в вакуум.
Аналогично объясняется возникновение переходного излуче-
излучения, когда зарялеенная частица переходит через границу двух
диэлектриков. В этом случае также применим метод электриче-
электрических изображений, хотя и в несколько измененной форме (см.
т. III, § 24).
Переходное излучение наблюдалось уже давно в виде свече-
свечения анодов рентгеновских трубок. Конечно, природа этого све-
свечения была выяснена много позднее.
Переходное излучение также используется в счетчиках реля-
релятивистских частиц для определения их скоростей.

ГЛАВА IV
ДИФРАКЦИЯ СВЕТА
§ 39. Принцип Гюйгенса—Френелм. Зоны Френелм
1. Под дифракцией света понимают всякое уклонение от пря-
молинейного распространения света, если оно не может бытв
истолковано как результат отражения, преломления или изги-
изгибания световых лучей в средах с непрерывно меняющимся пока™
зателем преломления. Если в среде имеются мельчайшие части-
частицы постороннего вещества (туман) или показатель преломления
заметно меняется на расстояниях порядка длины волны, то в
этих случаях говорят о рассеянии света и термин «дифракция»
не употребляется. Явления дифракции для своего истолкова-
истолкования и количественного рассмотрения не требуют никаких новых
принципов. Всякая дифракционная задача, если ее рассматри-
рассматривать строго, сводится к нахождению решения уравнений Макс-
Максвелла, удовлетворяющего соответствующим граничным услови-
условиям. Однако в такой строгой постановке дифракционные задачи,
ввиду их сложности, допускают аналитические решения лишь в
простейших идеализированных случаях. В оптике значительно
большее значение имеют нестрогие методы решения дифракци-
дифракционных задач, основанные на принципе Гюйгенса в обобщенной
формулировке Френеля или Кирхгофа.
2. В § 3 мы указывали, что принцип Гюйгенса в том виде, в
каком он был сформулирован самим Гюйгенсом, есть не более
чем геометрический рецепт для построения волновых фронтов.
Во всех применениях вторичные волны Гюйгенса выступают не
как реальные волны, а как вспомогательные сферы, использу-
используемые для такого построения. Эти сферы, построенные из то-
точек волнового фронта как из центров, проявляют свое действие
только на огибающей, которая и дает новое положение волно-
волнового фронта. При этом оставалось необъясненным, почему при
распространении волны не возникает обратная волна.

278
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
Искусственную гипотезу об огибающей вторичных волн Фре-
нель заменил физически ясным положением, согласно которому
вторичные волны при наложении интерферируют друг с дру-
другом. Свет должен наблюдаться во всех местах пространства, где
при интерференции вторичные волны усиливаются; в тех же ме-
местах, где они взаимно гасят друг друга, должна наблюдаться
темнота. Тем самым выясняется и физический смысл огибаю-
огибающей. К огибающей все вторичные волны приходят в одинаковых
фазах, и их интерференция приводит к большой интенсивности
света. Становится ясным, по крайней мере качественно, и отсут-
отсутствие обратной волны. Вторичные волны, идущие от волнового
фронта вперед, вступают в свободное от возмущений простран-
пространство. Они интерферируют только друг с другом. Напротив, вто-
вторичные волны, идущие назад, вступают в пространство, где уже
есть волновое возмущение — прямая волна. При интерференции
вторичные волны гасят прямую волну, так что после прохожде-
прохождения волны пространство за ней оказывается невозмущенным.
Френель дал следующую формулировку принципа Гюйген-
Гюйгенса, несколько обобщенную Рэлеем A842—1919). Окружим все
источники света Si, S2, S%, ...
произвольной замкнутой поверх-
поверхностью F (рис. 150). Каждую
точку такой поверхности мож-
можно рассматривать как источник
вторичных волн, распространяю-
распространяющихся во всех направлениях. Эти
волны когерентны, поскольку все
они возбуждаются одними и те-
теми же первичными источника-
источниками. Световое поле, возникающее
в результате их интерференции, в пространстве вне поверх-
поверхности F совпадает с полем реальных источников света.
Таким образом, действительные источники света молено как
бы заменить окружающей их светящейся поверхностью F с
непрерывно распределенными по ней когерентными вторичны-
вторичными источниками. Отличие этой поверхности от реальной поверх-
поверхности излучающего тела состоит в том, что она абсолютно про-
прозрачна для всякого излучения. В такой формулировке принцип
Гюйгенса-Френеля выражает весьма общее положение. Он озна-
чает, что волна, отделившаяся от своих источников, в дальней-
дальнейшем ведет автономное существование, совершенно не завися-
зависящее от наличия источников.
3. При математической формулировке принципа Гюйгенса-
Френеля будем предполагать, что источники света — монохро-
монохроматические с одной и той же частотой ио. По предположению
Френеля каждый элемент площади dF поверхности F (рис. 150)
Рис. 150

39
ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. ЗОНЫ ФРЕНЕЛЯ
279
испускает вторичную сферическую волну, а волновое поле в точ-
ке наблюдения Р представляется суперпозицией таких волн в
виде интеграла
Е= Г Z*Lj№-bp) C9.1)
J р
по всей (замкнутой) поверхности F. Френель предположил, что
амплитуда вторичной волны пропорциональна амплитуде пер™
вичной волны, приходящей к элементу dF', а так лее площади
самого элемента dF. Кроме того, она убывает с возрастанием
угла между нормалью к поверхности F и направлением излу-
чения вторичной волны. Конкретного выражения для амплиту-
амплитуды вторичной волны Френель не дал. Это было сделано толь-
только в 1883 г. Кирхгофом A824-—1887) при строгой формулировке
принципа Гюйгенса-Френеля (см. § 43). Несмотря на это, Фре-
Френелю удалось получить правильные решения многих дифракци-
онных задач, пользуясь простыми интуитивными соображения-
соображениями и нестрогими методами расчета. Эти простые и наглядные
методы, приводящие быстро к цели, до сих пор используются
при элементарном изложении теории дифракции. Они взяты за
основу и в настоящей книге. Мы изменим только те (не вли-
влияющие на окончательный результат) предположения Френеля,
которые оказались неверными.
4. Рассмотрим сначала свободное распространение сфериче-
сферической волны
го
C9.2)
в однородной среде (рис. 151). Перед этим выражением мож-
можно было бы поставить какую-то постоянную амплитуду Aq. Мы
не делаем этого, выбирая еди-
единицы измерения так, чтобы бы-
было Aq = 1. В качестве вспо-
вспомогательной поверхности F в
формуле C9.1) выберем сфери-
сферический волновой фронт радиу-
радиуса го- Согласно гипотезе Фре-
Френеля, а = K(a)e~lkr° /Vq, где
функция К (а), помимо длины
волны, зависит только от угла
между нормалью к волновому р -._..
фронту и направлением излу-
излучения вторичной волны Гюйгенса. Полное поле в точке наблю-
наблюдения Р представится интегралом
/
D /
\ О
/
\
\
с
р
\
г
= [
J
rop
Если за элемент площади dF принять площадь кольца, выре-

280 ДИФРАКЦИЯ СВЕТА ГЛ. IV
заемого из волнового фронта двумя бесконечно близкими кон-
концентрическими сферами с центрами в точке наблюдения Р, то
dF = 2тггд sini?di?. Примем за переменную интегрирования рас-
расстояние р. Дифференцируя соотношение р2 = Гд + (го + гJ —
— 2го(го + r)cosi? при постоянных го и г, находим sin # cfa?, a
затем и элемент площади dF. В результате получим
Гмакс
Е = ^^ ei(ut-kr0) Г К{р)е^гкр dp, C9.3)
Го + Г J
г
где прежняя функция К (а) теперь рассматривается как функ-
функция р. Верхний предел интеграла равен гмакс = г + 2г®. Однако,
имея в виду дальнейшие применения, мы не будем его конкрети-
конкретизировать. Точное вычисление интеграла C9.3), конечно, невоз-
невозможно без знания вида функ-
функции К(р). Однако Френель, ис-
используя малость длины свето-
световой волны, дал метод прибли-
приближенного вычисления подобных
интегралов при весьма общих
предположениях относительно
функции К(р). Опишем из точ-
точки Р, как из центра, концентри-
концентрические сферы с радиусами г, г+
+ Л/2, г + 2(Л/2), г + 3(Л/2), ...
Рис. 152 (рис. 152). Они разобьют вол-
волновой фронт F на кольцевые
области, получившие название зон Френеля. Ввиду малости дли-
длины волны, аргумент р, а с ним и функция К(р) в пределах одной
зоны могут считаться постоянными. В этом приближении инте-
интеграл C9.3) по n-й зоне будет равен
г + п\/2
./Л. 77, I ^ UfJ I X J —7"J— С' ч
г + (п - 1)А/2
где через Кп обозначено среднее значение функции К(р) для в-й
зоны. Если N — общее число зон, посылающих вторичные волны
в точку наблюдения, то поле Е представится знакопеременной
суммой
тр тр _|_ тр _|_ тр _|_ _|_ тр if4Q A.\
Общий член ее имеет вид
То обстоятельство, что знаки рядом стоящих слагаемых в сум-
сумме C9.4) противоположны, означает, что колебания, вносимые

§ 39 ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. ЗОНЫ ФРЕНЕЛЯ 281
соседними зонами Френеля, противоположны по фазе. Этого и
следовало ожидать, так как из самого построения зон Френеля
видно, что одно из этих двух колебаний запаздывает относитель-
относительно другого на полволны. По предположению Френеля абсолют-
абсолютные значения множителей Кп, а с ними и членов суммы C9.4)
медленно убывают с возрастанием номера п. Уберем в сумме
C9.4) слагаемое Е\ и добавим слагаемое Е^+\- Ввиду медлен-
медленности убывания членов суммы C9.4), интуитивно можно ожи-
ожидать, что от этого абсолютное значение суммы C9.4) почти не
изменится, а ее знак заменится на противоположный. Приняв
это, наряду с C9.4) молено также написать:
Е = —Е^ — Е% — ... — En —
Тогда 2Е = Е\ — En+i- Но в том же приближении En = —
и следовательно,
Е = \{Е1+Еп). C9.6)
Таким образом, волновое возмущение, создаваемое N первыми
зонами Френеля, равно полусумме возмущений, вносимых край-
крайними зонами.
Возьмем теперь все зоны на сферическом волновом фрон-
фронте F (см. рис. 151). Введем предположение (обосновываемое
при строгой формулировке принципа Гюйгенса, данной Кирхго-
Кирхгофом), что при а = тг, т.е. в точке D волнового фронта, функция
К (а) обращается в нуль. Тогда Е^ = 0, и из формулы C9.6)
получаем
E=lEl= 2^ e*M-*(ro+r)] C9.7)
т.е. при свободном распространении волны волновое возмущение
от всего волнового фронта составляет половину возмущения^
даваемого одной только первой зоной Френеля. Дело происхо-
происходит так, как если бы из всего волнового фронта действующей
осталась только часть первой зоны Френеля х).
5. Формула C9.7) интересна также в том отношении, что
она позволяет точно определить множитель К\. Действитель-
Действительно, при свободном распространении сферической волны C9.2)
г) В полученном результате авторы многих книг видят доказательство
прямолинейного распространения света, утверждая, что свет распростра-
распространяется как бы в узком прямолинейном канале, поперечное сечение которого
порядка размеров первой френелевой зоны. Однако не надо забывать, что
этот вывод относится к свободному распространению волны, когда пробле™
ма прямолинейного распространения света вообще не возникает. Она возни-
возникает лишь при наличии препятствий на пути распространения света. Это
есть проблема теней, являющаяся частным случаем проблемы дифракции
света.

282
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
напряженность поля заранее известна в любой точке простран-
пространства. В частности, в точке наблюдения
Е =
J[ut-k(ro+r)]
го + г
Сравнивая это выражение с C9.7), находим
/3Э.
2тг 2тг
Таким образом, множитель К\, а также все остальные множи-
тели i^2? ^з? • • •? — чисто мнимые. Значит, вторичные волны
Гюйгенса опережают по фазе колебания поля в точках волно-
волнового фронта на тг/2. Если бы такого опережения не было, то
вторичные волны из центра первой френелевой зоны приходи-
приходили бы в точку наблюдения с фазой ujt — k(r® + г), а от ее краев —
с меньшей фазой uot — к(го + г) — тт. Фаза результирующего ко-
колебания, возбуждаемого всей первой зоной, была бы равна по-
полусумме этих значений, т.е. оказалась бы меньше правильного
значения на тг/2.
Рис. 153
6. Результаты C9.6) и C9.7) имеют основное значение в ме-
методе зон Френеля. Для лучшего уяснения интерпретируем их на
векторной диаграмме (см. т. III, § 126). Разобьем каждую зону
Френеля на т кольцевых подзон (на рис. 153 а построение вы-
выполнено для т = 6). Колебания, возбуждаемые в точке наблк>
дения такими подзонами, на векторной диаграмме изобразят-
изобразятся векторами AqAi, A\A2j A2A3 и т.д., образующими ломаную
линию. Колебание, возбуждаемое несколькими соседними под-
подзонами, представится геометрической суммой таких векторов.
Например, вектор ApAg представляет «действие» первой фре-
френелевой зоны, вектор AoAi2 — совместное действие двух первых
френелевых зон, и т.п. Если число подзон N устремить к бес-
бесконечности, то в пределе ломаная перейдет в непрерывную спи-

§ 39 ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. ЗОНЫ ФРЕНЕЛЯ 283
раль, вьющуюся вокруг фокуса F (рис. 153 5). На этой спира™
ли действие первой френелевой зоны представляется вектором
AqAq^ а всего волнового фронта — вектором AqF, который почти
точно вдвое короче предыдущего. Действие центральной поло™
вины первой зоны представляется наклонным вектором AqA^, и
т.п.
7. В § 27 (п. 8) указывалось, что прохождение сходящейся сферической
волны через фокус (т.е. ее центр) сопровождается изменением фазы на тг.
Приведем новое истолкование этого явления, используя метод зон Френеля.
Как всегда, зоны Френеля надо строить с той стороны волнового фрон-
фронта, куда он распространяется. В рассматриваемом случае это будет вогну™
тая сторона. Конечно, и здесь вторичные волны будут опережать по фазе
колебания поля на волновом фронте, так как это есть свойство самих эле-
элементарных источников вторичных волн, не зависящее от формы волново-
волнового фронта, на котором они находятся. Действие же всего волнового фронта
в точке наблюдения при свободном распространении волны по-прежнему
будет равно половине действия первой френелевой зоны. В частности, вто-
вторичные волны, исходящие от этой зоны, при интерференции всегда дают
правильную фазу, независимо от положения
точки наблюдения. Если точка наблюдения Р
лежит перед центром (фокусом) О сходящейся
сферической волны (рис. 154), то в наших пре-
предыдущих рассуждениях ничего не изменится,
так как в этом случае колебания от краев А и
В первой френелевой зоны приходят в Р поз™
же, чем от ее середины С. Но положение изме-
изменится, когда точка наблюдения Р будет нахо-
находиться по другую сторону от центра О (тогда,
конечно, и первая зона AfBf будет другой). Те-
Теперь края первой зоны Af и В' окажутся ближе А'
на полволны к точке Р , чем ее центр С. Вслед-
Вследствие этого, помимо обычного опережения по Рис 154
фазе на тг/2, вторичные волны, приходящие в
Р' от краев А! и В1 первой зоны, получат дополнительное приращение фа-
фазы на тг, так что полное опережение по фазе вследствие указанных двух
1 /тг Зтг\
причин составит — I 1 1 = тг. Его надо добавить к фазе волны uot ~~
— kr, прошедшей через точку О. В результате мы и приходим к явлению
изменения фазы сходящейся сферической волны при ее прохождении через
фокус.
Когда точка наблюдения Р приближается к фокусу О, френелевы зо-
зоны расширяются. В некотором положении Лз этой точки первая френелева
зона охватывает всю сферу. При дальнейшем приближении к О построение
зон Френеля становится невозможным. Можно сказать, что вся сфера ста-
становится как бы частью первой зоны Френеля. Применяя к этому случаю
наши предыдущие рассуждения, нетрудно убедиться, что появляется опе-
опережение по фазе, заключенное между нулем и тг/2, когда точка наблюдения
находится между Ро и О. В точке О оно составляет тг/2, а при переходе че-
через нее возрастает до тг. Таким образом, изменение фазы волны на тг при
переходе через фокус совершается не скачком, а непрерывно.

284 ДИФРАКЦИЯ СВЕТА ГЛ. IV
§ 40. Дифракцим на оси от круглого отверстия и
экрана. Зоннам пластинка
1. Поставим между точечным источником S и точкой наблк>
дения Р непрозрачный экран с круглым отверстием, плоскость
которого перпендикулярна к оси
SP, а центр О расположен на той
же оси (рис. 155). Согласно Фре-
Френелю, действие такого препятствия
сводится к тому, что экран как
бы устраняет ту часть волнового
фронта, которую он прикрывает.
На открытой же части волнового
фронта световое поле не изменяет-
изменяется. Такое предположение соответ-
соответствует приближению геометриче-
геометрической оптики, а потому оно может
быть приближенно верным толь™
Рис- 155 ко тогда, когда радиус отверстия
очень велик по сравнению с дли™
ной световой волны. Это и предполагается в дальнейшем. Бу-
Будем предполагать, кроме того, что размеры отверстия можно
менять, что дает возможность открывать любое число зон Фре-
не ля.
Пусть ао и /q означают амплитуду и интенсивность света в
точке Р при свободном распространении волны, т.е. в отсутствие
экрана. Общий световой поток, поступающий через отверстие,
строго пропорционален его площади. Но он будет распределять-
распределяться по-разному по освещаемой поверхности, в зависимости от то™
го, сколько, зон Френеля укладывается в отверстии. В одних ме™
стах может получиться интенсивность меньше, в других больше
Iq . Никакого противоречия с законом сохранения энергии в этом
нет.
Если открыть первую зону Френеля, то амплитуда и интен-
интенсивность света в той же точке будут а\ = 2ад, I\ — Bflo) = 4/q.
Таким образом, интенсивность в центре Р дифракционной кар-
картины получится в четыре раза большей, чем было бы при свобод™
ном распространении волны. При удалении от центра Р интен-
интенсивность будет монотонно убывать. При расширении отверстия
в точку Р начнут приходить вторичные волны. Их интерферен-
интерференция с ранее пришедшими волнами вызовет уменьшение интен™
сивности в той же точке. При определенных размерах отверстия
центр Р перестанет быть точкой максимальной интенсивности.
Вокруг точки Р начнет образовываться светлое кольцо, к ко™
торому и переместится максимум интенсивности. Когда отвер-

40
ДИФРАКЦИЯ ОТ КРУГЛОГО ОТВЕРСТИЯ И ЭКРАНА
285
стие откроет две первые зоны Френеля, то их действия в точке
Р практически полностью уничтожат друг друга из-за интер-
интерференции. В точке Р получится темный кружок, окруженный
светлым кольцом.
При дальнейшем увеличении размеров отверстия действия
двух первых зон Френеля в точке Р остаются компенсированны-
компенсированными. Все поле в Р создается только частью третьей зоны Френеля.
В центре картины появляется светлое пятнышко, а централь-
центральный темный кружок расширяется и переходит в темное кольцо,
окружающее это пятнышко. Когда число N открытых зон рав-
равно трем, интенсивность света в точке Р будет такой же, какая
получилась бы, если бы была открыта только одна третья зона.
Центр картины будет практически столь же светлым, что и при
одной открытой первой зоне Френеля. При N = 4 светлый центр
сменится темным. Вообще, при нечетном N центр дифракцион-
дифракционных колец светлый, а при четном — темный. На схематическом
рис. 156 для различных N показано распределение интенсив-
У\ Л/\
N=1
N=2
N=3
N=4
Рис. 156
ности света в зависимости от расстояния до центра картины, а
рис. 157 воспроизводит фотографии наблюдаемой картины ко-
колец при нечетном (а) и четном (б) N.
Рис. 157
2. Определим теперь размеры и число т зон Френеля, укла-
укладывающихся в отверстии АВ (см. рис. 155). Пусть D — диаметр
отверстия, а а и Ъ — расстояния от его центра до точек S и Р.
Из точек S ш Р как из центров опишем сферы, проходящие че-

286
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
рез край отверстия АВ. Пренебрегая квадратами отрезков ОЕ
и OF, по известной геометрической теореме можем написать:
(D/2J « OF • 2а, (D/2J = ОЕ • 2L
Отсюда
SF = FO + OF = — f i + i) .
8 \a о/
Число га найдется делением этого отрезка на А/2. Оно равно
D0Л)
Если 777. целое, то D будет диаметром, а Rm = D/2 — радиусом
га-й зоны, точнее — ее внешнего края. Следовательно,
Rm —
ab
тХ.
D0.2)
J 0,55,
Например, если а = Ь=1м, А = 600 им, то R\
Rs ^ 0,95 мм и т.д.
3. Интенсивность света в точке наблюдения Р мож:но во
много раз усилить, прикрыв все четные или все нечетные зо~
ны Френеля. Оставшиеся неприкрытыми зоны будут усиливать
действие друг друга. Прикрытие молено осуществить, поместив
в плоскости отверстия так
называемую зонную пла-
пластинку (рис. 158). Ее мож-
можно изготовить, начертив на
листе бумаги темные коль-
кольца, а затем сфотографи™
ровав их в уменьшенном
масштабе. Внутренние ра-
радиусы колец должны быть
II пропорциональны квадрат-
ш/ ным корням из последо-
¦:f вательных нечетных чисел,
а внешние — из четных.
Тогда получится пластин-
пластинка, центр которой светлый.
Можно изготовить анало-
аналогичную пластинку с тем™
ным центром. Ширина всех
колец должна быть велика по сравнению с длиной волны. Тогда
при надлежащих размерах колец пластинка со светлым центром
будет удалять из волнового фронта все четные, а пластинка с
темным центром — все нечетные зоны Френеля.
Усиление интенсивности света зонной пластинкой аналогич-
аналогично фокусирующему действию линзы. Более того, расстояния от
Рис. 158

§ 40 ДИФРАКЦИЯ ОТ КРУГЛОГО ОТВЕРСТИЯ И ЭКРАНА 287
пластинки до источника S и «изображения» Р связаны тем же
соотношением, что и соответствующие величины для линзы. Это
видно, если формулу D0.1) переписать в виде
I + \ = у, D0.3)
где «фокусное расстояние» определяется формулой
I = 4шЛ = т\ (т 4х
f О2 I?2 * \^\j-^j
Если центр зонной пластинки светлый, то число т — нечетное,
в этом случае в формулу D0.4) входит (внешний) радиус свет-
светлого кольца пластинки. Если же центр пластинки темный, то
число т — четное и под Rm следует понимать (внешний) ради-
радиус темного кольца. Какой номер брать при вычислении / — это,
конечно, не имеет значения.
С помощью зонной пластинки можно даже получать оптиче-
ские изображения, хотя и весьма низкого качества.
В отличие от линзы, зонная пластинка имеет несколько фо~
кусов. Действительло, найдем положение точки наблюдения Р,
при котором в центральном круге пластинки уместятся первые
три зоны Френеля. Тогда в следующее кольцо пластинки попа-
попадут четвертая, пятая и шестая зоны и т.д. Если центр зонной
пластинки светлый, то поле в точке Р представится суммой
Е = (Ei + Еъ + Е%) + (Е7 + Ея + Eg) + (Е\3 + Ей + Ei§) + ...,
или Е = Ei + Е^ + I?i3 + • • •, так как действия соседних зон прак-
практически уничтожают друг друга. Таким образом в Р получится
максимум (фокус). Фокусное расстояние найдется по формуле
/i = ^i/CA) = //3. Аналогично находятся фокусы высших по™
рядков:
In = 5^7. D0-5)
где п — целые числа, которым можно придавать не только поло-
положительные, но и отрицательные значения. Отрицательным зна-
значениям соответствуют расходящиеся волны и мнимые фокусы.
Рэлей указал, что интенсивность света в точке наблюдения Р
увеличится в четыре раза, если изменить на тг фазы вторичных
волн, исходящих от всех зон Френеля с четными (или нечетны-
нечетными) номерами. Такая «зонная пластинка с обращением фазы»
была изготовлена Вудом A868-—1955) путем травления поверх-
поверхности стеклянной пластинки. Ее действие вполне эквивалентно
действию линзы, поскольку в обоих случаях вторичные волны
от всех точек волнового фронта приходят в Р в одинаковых фа-
фазах.
4. Поставим теперь между источником S и точкой наблюде-
наблюдения Р непрозрачный круглый экран АВ (рис. 159), плоскость

288
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
которого перпендикулярна к оси SP. Пусть DA и BE — непри-
крытые части волнового фронта сферической волны, исходящей
из источника S. Разобьем ее на
кольцевые зоны Френеля, начав их
построение от края экрана. Рас-
Рассуждая как и раньше, предста™
вим напряженность поля излуче-
излучения в точке Р в виде половины на-
напряженности, создаваемой в этой
точке вторичными волнами первой
кольцевой зоны Френеля. Следова-
Следовательно, каков бы ни был диаметр
диска, в центре Р его геометри-
геометрической тени должно наблюдаться
светлое пятнышко. Такой вывод
был сделан Пуассоном A781-1840)
Рис. 159
и показался последнему столь абсурдным, что он выдвинул его
в качестве возражения против волновой теории света Френеля.
Араго A786-—1853) немедленно поставил опыт и обнаружил пят-
пятнышко в соответствии с выводом Пуассона1). Явление получи-
получило название пятна Ара-
го-Пуассона. Наблюдае-
Наблюдаемая картина дифракции
от круглого экрана при-
приведена на рис. 160.
Если точка наблю-
наблюдения Р не находится
в центре картины, то
кольцевые зоны Фре-
Френеля, конечно, можно
построить и для нее.
Однако зоны, располо-
расположенные ближе к центру,
окажутся неприкрыты-
неприкрытыми лишь частично. Это
сильно усложняет вы-
Рис. 160 числение интенсивности
света. Можно только
сказать, что дифракционная картина должна обладать осевой
симметрией. Вне геометрической тени получается система
концентрических светлых и темных колец. Внутри самой
г) Маральди наблюдал такое пятнышко еще в 1723 г. Вероятно, еще рань-
раньше A715 г.) оно наблюдалось Делилем, хотя указания последнего недоста-
недостаточно ясны. Однако эти наблюдения остались незамеченными и были за-
забыты, поскольку природа явления не была понята.

§ 40 ДИФРАКЦИЯ ОТ КРУГЛОГО ОТВЕРСТИЯ И ЭКРАНА 289
геометрической тени также могут получиться дифракционные
кольца, в особенности когда экран прикрывает небольшое число
зон Френеля. Но эти кольца мало контраст™
ны, а распределение света в них сложное.
Демонстрацией явления пятна Араго^
Пуассона может служить опыт Поля. Поль
сфотографировал ярко освещенный ша-
шаблон, заменив объектив гладким металли-
металлическим шаром. Эта фотография воспроиз-
воспроизведена на рис. 161, а параметры установки
приведены в задаче в конце этого парагра-
параграфа. Ангерер сфотографировал изображе-
изображение человеческого лица, заменив шар ме-
таллическим диском. ис"
5. Применим метод зон Френеля к объяснению теней, т.е.
прямолинейного распространения света. Поскольку речь идет
о законе, от которого принципиально должны наблюдаться от™
ступления, наши рассуждения не могут претендовать на стро-
строгость.
Пусть на пути распространяющейся волны поставлен экран
или отверстие произвольной формы. Их размеры должны быть
велики по сравнению с длиной волны. Разобьем волновой фронт
на кольцевые зоны Френеля. Некоторые зоны могут оказаться
открытыми полностью, другие частично, третьи совсем закры-
закрытыми.
Допустим сначала, что точка наблюдения лежит вне геомет-
геометрической тени, далеко от ее границы. Первые члены ряда C9.4)
получатся такими же, как и при свободном распространении
волны. Последующие члены начнут изменяться из-за частич-
частичного экранирования соответствующих им зон. В зависимости от
формы края экрана эти изменения будут носить более или менее
нерегулярный характер. Если обнаружится тенденция убывания
их по абсолютной величине, то правдоподобно допустить, что
напряженность поля в точке наблюдения окажется равной поло-
половине напряженности, создаваемой центральной зоной. В случае
точечного источника и ровного края экрана это может оказать-
оказаться и не совсем так. Однако если источник не совсем точечный, а
края экрана не совсем ровные, то произойдет статистическое
сглаживание при наложении дифракционных картин от точеч-
ных источников, на которые можно разложить протяженный
источник. Тогда вдали от края экрана получится такая же осве-
освещенность, какая получилась бы при свободном распространении
волны.
Допустим теперь, что точка наблюдения лежит внутри гео-
геометрической тени, опять далеко от ее границы. Первые зоны
Френеля будут полностью закрыты. Нумерацию зон начнем с
10 Д.В. Сивухин

290 ДИФРАКЦИЯ СВЕТА ГЛ. IV
первой (частично) открытой зоны. Представим поле рядом
Е = (Ег + Е2 + ... + EN) + (EN+i + EN+2 + ...)>
в котором N+1 означает номер первой целиком открытой зоны.
Ко второй скобке применимы рассуждения, применявшиеся вы-
выше в случае свободного распространения волны. Поэтому вторая
скобка приближенно равна 1/2^v+i- В первой скобке слагаемые
меняются более или менее нерегулярно, обнаруживая в среднем
тенденцию возрастания по абсолютной величине. При статисти-
статистическом усреднении (с учетом неполной точечности источника и
неровностей краев экрана) эти нерегулярности сглаживаются,
так что первую скобку можно принять равной lJ2{E\ + En), или
l/2 En1 поскольку величина Е\ дол лена считаться близкой к ну-
нулю из-за малости открытой части соответствующей зоны. Таким
образом, Е = 1/2{En -\~En-\-i) ^0, так как для соседних зон En~
~—En+i- Итак, при погружении в область геометрической тени
интенсивность света обращается в нуль.
Если источник точечный, а края экрана резкие, то граница
геометрической тени расщепляется в дифракционные полосы,
как это мы видели при рассмотрении дифракции на круглых от™
верстии и экране. Однако если края экрана неровные, то полосы
начинают размываться, а при увеличении размеров источника
переходят в полутень.
ЗАДАЧИ
1. В опыте Поля, описанном в тексте, диаметр шара D = 40 мм, рас-
расстояние от фотографируемого шаблона до шара а = 12 м, расстояние от
шара до изображения b = 18 м, размер шаблона у = 7 мм. Определить
размер его изображения у1. При каких условиях опвхт удастся с шаром,
поверхность которого испещрена множеством неправильных царапин?
Ответ. 2/' = — 2/ = 10,5 мм. Для удачи опыта необходимо, чтобы
а
глубина царапин h не превосходила ширины крайней френелевой зоны:
= A^L = 180A = 0,1 мм.
Da + 6
2. Оценить максимальные угловые размеры а предмета, который мож-
можно сфотографировать с помощью непрозрачного диска с идеально гладкими
краями.
Решение. При смещении точечного объекта в сторону с главной
оптической оси диск представится эллипсом. Малая полуось эллипса бу™
дет отличаться от радиуса диска на г ( 1 — cos — 1. Это отличие не должно
превышать ширины крайней френелевой зоны. Из этого условия для мак-
максимально допустимых угловых размеров предмета находим
, ,jO,2 рад и 10°,
а + о
где использованы обозначения и численные данные из предыдущей задачи.

41
ДИФРАКЦИЯ ФРАУНГОФЕРА И ФРЕНЕЛЯ
291
3. Зонная пластинка применяется для фотографирования предмета, ко™
торый виден из места нахождения пластинки под углом а = 0,1 рад. Оце-
Оценить оптимальное число зон пластинки для
получения наибольшей яркости и отчетли-
отчетливости изображения.
Решение. Допустим сначала, что
источник света 5* точечный, а зонная пла-
пластинка CD наклонена к оптической оси под
углом (ж —а)/2 (рис. 162). Из рисунка вид-
¦ R + 2aR sin —, и аналогично
для у. Извлекая квадратные корни и пре-
пренебрегая всеми степенями радиуса R, начи-
начиная с третьей, получим для разности хода
между лучами SCP и SOP:
1°
I
I
I D
Рис. 162
А = (х + у) - (а + Ъ) =
R cos2 (a/2)
a b
шли А = А о — S А. Здесь А о — значение А при отсутствии наклона зонной
пластинки, а <5А — приращение величины А, обусловленное наклоном:
SA = Ао A -cos -) = До sin - и -
Если ()Д <С А, то наклон пластинки не скажется существенно на работе
зон, расположенных в пределах круга радиуса R. Если же (!) А и А/2, то все
зоны, расположенные выше этого круга, становятся бесполезными и даже
вредными. Из этого условия находится предельное значение разности хода:
Ао ~ 2А/а . Соответствующее число зон Френеля будет
Ао _ 4
А/2 ~ а2 -
Допустим теперь, что фотографируемый предмет не точечный, причем
его центр расположен на оси зонной пластинки. Для периферийных точек
предмета, не лежащих на оси пластинки, последняя действует как накло-
наклоненная под углом а/2. Поэтому предельное число зон Френеля, при котором
должно получиться наиболее отчетливое изображение, будет
N;
N - 4/а2
'400.
§ 41. Метод Френелм решеним дифракционных задач.
Дифракция Фраунгофера и Френелм
1. Принципа Гюйгенса еще недостаточно для решения ди-
дифракционных задач, если даже пользоваться точной формули™
ровкой его, данной Кирхгофом (см. § 43). Этот принцип сводит
только любую дифракционную задачу к определению волнового
поля на произвольной замкнутой поверхности F, окружающей
все источники света (см. рис. 150). Но точное определение поля
на поверхности F возможно лишь после нахождения его во всем
ю*

292 ДИФРАКЦИЯ СВЕТА ГЛ. IV
пространстве. Эту трудность Френель преодолел введением спе-
циальной гипотезы, которой мы, в сущности, уже пользовались
в предыдущем параграфе. Сформулируем ее на примере непро-
непрозрачного плоского экрана с отверстиями, поставленного на пути
распространяющейся волны.
Выберем в качестве вспомогательной поверхности F заднюю
(т.е. неосвещаемую) сторону экрана. Примем, что на всех участ-
участках этой поверхности, которые прикрыты экраном, волновое по-
поле равно нулю, а на отверстиях оно определяется приближенны-
приближенными законами геометрической оптики, т.е. поле такое, какое по-
получилось бы в отсутствие экрана. Тем самым интегрирование в
C9.1) распространяется только на отверстия, где волновое поле
считается известным. Отметим недостатки введенной гипотезы.
1) Распространение гипотезы на неплоские экраны неодно-
неоднозначно, так как в этом случае неясно, как провести вспомога-
вспомогательную поверхность через отверстия экрана.
2) Гипотеза противоречива. Если с помощью принципа Гюй-
Гюйгенса вычислить волновое поле во всем пространстве, то на по-
поверхности F оно не совпадает с исходным полем, принятым при
вычислении. На задних сторонах экранов вычисленное поле не
обратится в нуль, а на отверстиях не будет совпадать с полем
свободно распространяющейся волны.
3) Гипотеза допускает разрыв волнового поля на краях от™
верстий, что противоречит граничным условиям электродина-
электродинамики Максвелла.
4) Гипотеза противоречит поперечности световых волн. Это
противоречие не устраняется заменой скалярных колебаний век-
векторными. Колебания, как и при изучении явлений интерферен-
ции, мы считали скалярными лишь ради простоты. При пере-
переходе к векторным колебаниям математическая формулировка
принципа Гюйгенса и полученные из него результаты по суще-
существу не изменятся. Как строго показал Кирхгоф, для этого до-
достаточно только скаляр Е всюду заменить вектором Е.
Допустим теперь, что на непрозрачный экран с отверсти-
отверстием нормально падает плоская линейно поляризованная электро-
электромагнитная волна. На вспомогательной поверхности F вектор Е
будет иметь одно и то же направление, параллельное плоско-
плоскости экрана. Принцип Гюйгенса сводит задачу о дифракции к
суперпозиции коллинеарных векторных колебаний того же на-
направления. Поэтому следует ожидать, что в дифрагированной
волне вектор Е всюду будет параллелен плоскости экрана. Это
будет так и вдали от экрана, где дифрагированные волны раз-
разных направлений расходятся и перестают накладываться друг
на друга. Так будет и в волне, дифрагировавшей косо к плоско-
плоскости экрана. Но в действительности вектор Е перпендикулярен

41
ДИФРАКЦИЯ ФРАУНГОФЕРА И ФРЕНЕЛЯ
293
Рис. 163
к дифрагирующим лучам и образует с вычисленным направле-
направлением угол, равный «углу дифракции» # (рис. 163).
Метод Френеля решения дифракционных задач может быть
оправдан, когда размеры отверстий и непрозрачных промежут-
промежутков между ними велики по срав-
сравнению с длиной световой волны,
а потому заметная интенсивность
света наблюдается лишь при ма-
малых углах дифракции. Действи-
Действительно, в отверстиях законы гео-
геометрической оптики нарушаются
лишь в непосредственной близи от
их краев. Применяя гипотезу Фре-
Френеля, мы при вычислении интегра-
интеграла C9.1) пользуемся неправильны-
неправильными значениями подынтегральной
функции только внутри узких по-
полосок вблизи краев отверстий. Ширина этих полосок поряд-
порядка длины световой волны. В основной области интегрирования
используются правильные значения подынтегрального выраже-
выражения. Автоматически снимается и возражение D), связанное с
поперечностью световых колебаний, так как различием направ-
направлений вычисленного и действительного полей при малых углах
дифракции можно пренебречь. Все это в основном подтвержда-
подтверждается совпадением результатов теоретических расчетов с опытом.
Но для малых препятствий, сравнимых с длиной волны, и, сле-
следовательно, для больших углов дифракции гипотезой Френеля
уже нельзя пользоваться.
Отметим еще, что гипотеза Френеля приводит к выводу о
независимости дифрагированной волны от материала экрана.
Этот вывод в основном также подтверждается опытом. Только
более точные опыты обнаруживают и влияние материала экрана
на дифракцию света.
2. Явления дифракции принято классифицировать в зави-
зависимости от расстояний источника и точки наблюдения (экрана)
от препятствия, поставленного на пути распространения света.
Если эти расстояния очень велики (бесконечно велики), то ди-
дифракция называется дифракцией в параллельных лучах или ди-
дифракцией Фраунгофера A787-1826). В противоположном случае
говорят о дифракции в непараллельных лучах или дифракции
Френеля. Практически для осуществления дифракции Фраунго-
Фраунгофера точечный источник света помещают в фокусе собиратель-
собирательной линзы. Получающийся параллельный пучок света дифра-
дифрагирует на каком-то препятствии. Дифракционная картина на-
наблюдается в фокальной плоскости линзы, поставленной на пути
дифрагированного света, или в зрительную трубу, установлен-

294
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
ную на бесконечность. Ясно, что между фраунгоферовой и фре-
нелевой дифракциями нет принципиального различия и резкой
границы. Одна непрерывно переходит в другую.
Для лучшего уяснения приведенной классификации начнем
с примера. Рассмотрим круглое отверстие и точечный источ-
источник на его оси. Пусть сначала точка наблюдения так лее нахо-
дится на оси. Если в отверстии укладывается небольшая часть
первой зоны Френеля, то дифракция будет фраунгоферовой. В
этом случае все колебания в плоскости отверстия совершают™
ся и приходят в точку наблюдения практически в одинаковых
фазах. При смещении точки наблюдения вбок появляются раз™
ности фаз между вторичными волнами, приходящими в точку
наблюдения от различных точек отверстия. Этим и обусловле-
обусловлено появление дифракционных колец. Если отверстие заменить
непрозрачным экраном, то этот случай, по соображениям, кото-
которые выяснятся в п. 4, также относят к дифракции Фраунгофера.
Если же в отверстии или экране (для точки наблюдения, лежа-
лежащей на оси системы) укладывается заметная часть первой зоны
или несколько зон Френеля, то дифракция считается френеле-
вой.
3. Рассмотрим теперь общий случай. Пусть препятствием яв-
является непрозрачный экран с отверстием (рис. 164), S — то-
точечный источник монохроматическо-
монохроматического света, Р — точка наблюдения. За
начало координат примем произволь-
произвольную точку О в плоскости отверстия.
По принципу Гюйгенса^Френеля вол-
волновое поле в точке Р представляется
интегралом
ЕР=
D1.1)
где Ф = tot — к (г + г;). Ввиду малости
углов дифракции в подынтегральном
выражении D1.1) опущен множитель
К (а), определяющий зависимость по-
поля вторичной волны от направления
ее излучения. Знаменатель г г1 можно
считать постоянным, так как размеры
отверстия предполагаются очень ма-
малыми как по сравнению с г, так и по сравнению с г1. Но за-
зависимость фазы Ф от радиуса-вектора R, определяющего поло-
положение элемента площади dF, конечно, должна быть учтена, так
как фаза быстро меняется уже на малых расстояниях (поряд-
(порядка ширины френелевой зоны). Интегрирование в D1.1) во всех
случаях выполняется по практически небольшому числу (не бо™
Рис. 164

§ 41 ДИФРАКЦИЯ ФРАУНГОФЕРА И ФРЕНЕЛЯ 295
лее нескольких десятков) полных или неполных зон Френеля
(см., например, следующий параграф). Если расстояния г® и Гд
настолько велики, что разложение фазы Ф(Н) по степеням R,
можно оборвать на членах первой степени, то такие расстояния
можно считать бесконечно большими. В этом случае имеет место
дифракция Фраунгофера. Если же такая точность недостаточна,
то дифракция будет френелевой. Обычно в случае френелевой
дифракции разложение фазы Ф(Н) по степеням R, достаточно
оборвать на членах второй степени.
Найдем количественный критерий, при выполнении которого
в фазе Ф можно пренебречь квадратичными членами и, следо-
следовательно, считать дифракцию фраунгоферовой. Как видно из
рис. 164, г = го + R, откуда
г2 = rg + 2(r0R)+i?2.
Извлекая квадратный корень с точностью до квадратичных чле-
членов включительно, получим
где через s обозначен единичный вектор s = tq/г®. Аналогично
вычисляется расстояние г'. В результате получаем
Ф = о;* - к(г0 + го) + fc(s - s;)R +
1
. D1.2)
В отличие от постоянного вектора s, единичный вектор s; =
= Fq/Vq меняется при изменении положения точки наблюдения.
Этим и обусловлено появление дифракционных картин, т.е. из-
изменение интенсивности светового поля от точки к точке. Слагае-
Слагаемое ^к(го + Гд) не играет роли. Оно вносит в выражение для Ер
только постоянный фазовый множитель е™^Го+го^, не влияю-
влияющий на интенсивность светового поля в точке Р. Квадратичные
члены имеют порядки
kR2/r0 = 2жЕ2/(\г0) и kR2/rf0 = 2жЕ2 /(\г'о).
Максимальные значения эти величины принимают при R = D,
где D — диаметр отверстия. Практически этими членами мож-
можно пренебречь, если они меньше тг/2. Действительно, характер™
ной величиной для фазы является тг/2, так как при изменении
углов на такую величину синусы и косинусы претерпевают су-
существенные изменения. Все слагаемые в фазе, много меньшие
тг/2, не играют роли и могут быть отброшены без особого ущер-
ущерба для точности. Для максимальных изменений, обусловленных
квадратичными членами, мы (несколько условно) заменим тре-
требование «много меньше» более слабым требованием «меньше».

296 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Таким путем получим
г0 > —, г0 > —. D1.3)
Этими условиями и определяется область фраунгоферовой ди-
дифракции. Например, если D = 1 мм, А = 500 нм, то фраунгофе-
рова дифракция наступает при го, rfQ > 4D2/A = 8 м.
Легко также написать условия, при которых разложение фа™
зы Ф(И) можно оборвать на членах второй степени:
г0 > лДЩх, rf0 > лДЩх* D1.4)
В приведенном примере они удовлетворяются при r*o, Tq > 9 см.
Впрочем, квадратичным приближением D1.2) пользуются далее
тогда, когда условия D1.4) не выполняются. Это делается при
вычислении интеграла D1.1) в несущественных частях области
интегрирования, где точное знание фазы Ф не имеет значения.
Пример такого рода будет приведен в следующем параграфе при
рассмотрении дифракции на прямолинейном крае экрана.
Теперь становится качественно ясным, как ведет себя свето-
световой пучок, прошедший через диафрагму, на различных расстоя-
расстояниях г от нее. Для определенности будем считать, что диафраг-
диафрагма освещается параллельным пучком света. На малых расстоя-
расстояниях г <С D2/А приближенно применима геометрическая опти-
оптика (прямолинейное распространение света). Затем с увеличени-
увеличением расстояния г наблюдается сложная картина френелевой ди-
дифракции. На больших расстояниях г ^> D2/A дифракционная
картина упрощается и переходит в дифракцию Фраунгофера.
4. Следствием гипотезы Френеля является полезная теорема
Бабине A794-1872) о свойствах так называемых дополнитель-
дополнительных экранов. Возьмем плоский экран, освещаемый каким-либо
источником света. Пусть Евх — поле падающей волны, какое по-
получилось бы в точке (ж, у) на передней поверхности экрана при
отсутствии последнего, а Евъш — поле в той же точке на задней
поверхности экрана (экран предполагается тонким, и его тол-
толщина не играет роли). Пусть эти поля связаны соотношением
?вых = а\Евх. Коэффициент а\ называется пропускаемостью
экрана. Он может зависеть от координат ж, у, структуры экрана
и длины волны, но не зависит от напряженности волнового по-
поля. Для другого экрана той же геометрической формы Евых =
= о^^вх- Эти два экрана называются дополнительными, если
а\ + «2 = 1- Примером могут служить два непрозрачных экра-
экрана с отверстиями, причем отверстия одного экрана совпадают
с непрозрачными частями другого. Согласно D1.1), волновые
поля в точке наблюдения при использовании дополнительных

§ 41 ДИФРАКЦИЯ ФРАУНГОФЕРА И ФРЕНЕЛЯ 297
экранов могут быть записаны в виде
ЬР -
_ f «I el гФ ip трB) _ Г
причем в обоих случаях интегрирование распространяется по
всей поверхности экрана. (Для определенности источник све-
света предполагается точечным, что не имеет никакого значения.)
Сложив эти два выражения и учтя, что а\ + «2 = 1, получим
= S h1
Но последний интеграл есть поле Ер в точке Р, которое получи-
получилось бы при свободном распространении волны. Таким образом,
4Х)+42) = яр- D1-5)
Эта формула и выражает теорему Бабине в ее наиболее общей
форме.
Обычно теорема Бабине понимается в более узком смысле —
применительно к случаю фраунгоферовой дифракции. Пусть
фраунгоферова дифракционная картина наблюдается в фокаль-
фокальной плоскости линзы. Если бы на пути параллельных лучей не
было препятствий, то световое поле в этой плоскости было бы
всюду равно нулю, за исключением фокуса линзы. Таким обра-
образом, согласно D1.5), во всякой точке фокальной плоскости, за
исключением фокуса, должно быть Ер + Ер = 0. Так как ин-
интенсивность света I пропорциональна \Ер\2^ то отсюда получаем
h = h- D1.6)
Следовательно, поскольку наблюдению доступна только интен-
интенсивность светового поля, а не его фаза, фраунгоферовы дифрак-
дифракционные картины от дополнительных экранов, получаемые в
фокальной плоскости линзы, всюду одинаковы, за исключением
самого фокуса.
ЗАДАЧА
На черный экран падает плоская световая волна. Из-за дифракции за
экраном, наряду с неотклоненной волной, появятся волны всевозможных
направлений (рассеянный свет). Показать, что количество рассеянной энер-
энергии равно количеству энергии, поглощенному экраном.
Решение. Заменим экран дополнительным, т.е. отверстием той
же величины и формы. От этого по теореме Бабине интенсивность свето-
светового поля в бесконечности сохранится неизменной во всех направлениях,
за исключением направления первичной волны. Но на любое строго фик™
сированное направление за отверстием приходится нулевая интенсивность
света, так как отверстие рассеивает весь падающий на него свет. С другой
стороны, экран по предположению полностью поглощает весь падающий

298
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
свет. Отсюда непосредственно получается требуемый результат. Разумеет™
ся, он применим только в тех случаях, когда размеры экрана очень велики
по сравнению с длиной волны.
§ 42. Зоны Шустера и спираль Корню
1. В одномерных задачах, например при рассмотрении ди-
дифракции на прямоугольной щели, разбиение волнового фронта
на кольцевые зоны нецелесообразно. Лучше разбивать волновой
фронт на полосатые зоны,
называемые зонами Шу-
Шустера A851-1934). Огра-
Ограничимся случаем, когда
В
Рис. 165
О
волновой фронт плоский,
хотя обобщение на слу-
случай сферического фрон-
фронта и не встречает ника-
никаких затруднений. Пусть
плоскость волнового фрон-
фронта АВ перпендикулярна к
плоскости рис. 165. Обо-
Обозначим через Ь длину пер-
перпендикуляра РО^ опущенного из точки наблюдения на волно-
волновой фронт. Проведем цилиндрические коаксиальные поверхно-
поверхности, ось которых проходит через точку Р перпендикулярно к
плоскости рисунка, а радиусы равны Ь, Ъ + А/2, Ъ + 2(А/2), ...
Тогда волновой фронт разобьется на прямоугольные полосы, ко-
которые и называются зонами Шустера. Центральную зону усло-
условимся считать за две зоны: одна расположена справа, а другая
слева от точки О. Тогда г^ = Ь2 + х2п1 т\_х = Ъ2 + х2п_ъ а потому
т\ — г^ь_1 = х2п — xfl_1. Приближенно
т2п - т\_х = (гп + rn_i)(rn - rn_i) = 2Ь(А/2) = ЬА.
Таким образом, получаем рекуррентное соотношение
Хп Xn_i — UAj Y11)
из которого могут быть найдены все хп. Так как х® = 0, то
xi = л/bX, х2 = л/2ЬХ, ..., хп = л/пЬХ. D2.2)
Ширины последовательных зон Шустера будут
л/ЬА, (у/2-1)у/Ь\, (у/3 - у/2)у/Ь\,... D2.3)
Они монотонно убывают и в пределе, когда г —>- оо, стремятся к
А/2, как это ясно из их построения. (Впрочем, высшие зоны не

42
ЗОНЫ ШУСТЕРА И СПИРАЛЬ КОРНЮ
299
играют роли. Имеют значение только несколько десятков пер™
вых зон Шустера.)
Как и в случае зон Френеля, применим теперь графический
метод (см. рис. 153). Каждую зону Шустера разобьем на уз™
кие полоски и будем изображать колебание в точке Р, вно-
вносимое отдельной полоской, вектором на векторной диаграмме.
Затем перейдем к пределу, устремляя к нулю ширину каждой
полоски. В результате получится плавная кривая, называемая
спиралью Корню A841-1902) (рис. 166). Она состоит из двух
симметричных ветвей, бесконечное число раз обвивающихся во™
Рис. 166
круг «фокусов» F и F1 и неограниченно приближающихся к
ним. Верхняя ветвь представляет действие правой половины
волнового фронта, нижняя — левой. Отличие каждой из вет-
ветвей от соответствующей спирали на рис. 153 обусловлено более
быстрым убыванием начальных зон Шустера, чем зон Френеля.
Колебание, возбуждаемое первой правой зоной Шустера, изо-
изображается вектором ОА, второй правой — вектором Zz, двумя
первыми правыми зонами вместе — вектором 02 и т.д. (все эти
векторы на рис. 166 не проведены). Колебание, возбуждаемое
всем волновым фронтом, представляется вектором FrF, соеди-
соединяющим фокусы спирали Корню. По мере приближения к фо-
фокусам амплитуды колебаний становятся все меньше и меньше и
в пределе обращаются в нуль.
2. При нахождении уравнения спирали Корню надо учесть,
что реально всегда приходится иметь дело не с бесконечными, а

300 ДИФРАКЦИЯ СВЕТА ГЛ. IV
с ограниченными волновыми фронтами, причем заметная интен™
сивность наблюдается лишь при малых углах дифракции. По-
Поэтому в формуле D1.1) изменения знаменателей г и г' (а также
уже отброшенных ранее ослабляющих множителей К (а)) моле-
молено не принимать во внимание. Если нас интересует только от-
относительное распределение интенсивности, то можно положить
rrf = 1. В плоскости волнового фронта фазу можно предста-
представить в виде Ф = out — кг (здесь произведено переобозначение: в
формуле D1.1) расстояние г обозначалось через г1).
Примем волновой фронт за координатную плоскость XY, а
начало координат поместим в точке О. Тогда г2 = Ь2 + (х2 +
+ у2), а следовательно, r^b= (ж2+у2)/BЬ) + ... Члены высших
степеней можно отбросить, если даже они добавляют в фазу ела™
гаемые порядка тг и больше. Дело в том, что такие члены, как
это видно из формы спирали Корню, не меняя общего характе-
характера дифракционной картины, производят в ней только практиче-
практически незаметные смещения высших дифракционных максимумов
и минимумов. Кроме того, высшие дифракционные максимумы
и минимумы следуют друг за другом столь часто, что для их
реального осуществления требуются точечные источники света
высокой степени монохроматичности. В противном случае все
дифракционные полосы высших порядков размываются и пе-
переходят в равномерно освещенный фон. Отбросим все фазовые
множители, не влияющие на относительное распределение ин-
интенсивности светового поля. Тогда поле в точке наблюдения Р
представится интегралом
ЕР=
Интегрирование должно быть выполнено по всей открытой
поверхности волнового фронта. Допустим, что в направлении
оси Y она простирается достаточно далеко в обе стороны. То-
Тогда интегрирование по у можно выполнить в пределах от ^оо
до +оо, в результате чего появится постоянный множитель, не
представляющий интереса. Интегрирование по х произведем от
нуля, считая верхний предел х переменным (он может быть и
положительным, и отрицательным). Вместо ж, как это принято,
введем новую переменную s по формуле кх2 /Ь = ns2. Тогда
2ds, D2.4)
ds. D2.5)
ЕР =
Ер =
J
0
s
С " ^

§ 42 ЗОНЫ ШУСТЕРА И СПИРАЛЬ КОРНЮ 301
При изображении колебаний молено пользоваться как вы™
ражением D2.4), так и комплексно сопряженным с ним D2.5).
При построении спирали Корню обычно применяют выражение
D2.5). Оно и представляет уравнение спирали Корню в ком-
комплексной форме. Если координатные оси выбраны так, как ука-
указано на рис. 166, то в прямоугольных координатах уравнение
спирали Корню запишется в виде
S S
X(s) = J cos ^ds, Y(s) = J sln^ ds. D2.6)
о о
Входящие сюда интегралы называются интегралами Френеля.
Очевидно,
X(s) = -X(-s), Y(s) = -Y(-s),
т.е. кривая D2.6) симметрична относительно начала координат.
Полагая s = oo, находим координаты фокусов спирали Кор-
Корню:
XF = YF = 1/2, XF> = YF> = -1/2.
Впрочем, для многих целей проще пользоваться непосред-
непосредственно комплексной формой D2.5). В частности, для диффе-
дифференциала дуги спирали Корню из D2.5) находим: \ems /2 ds\ =
= \ds\. Отсюда следует, что параметр s есть длина дуги спирали,
отсчитываемая от начала координат О.
Если т — угол между касательной к спирали Корню и осью
X, то tgr = dYjdX = tg (тгл2/2), а потому
г = its2:/2. D2.7)
При s = 0 угол т = 0, т.е. в начале координат кривая каса-
касается оси X. При 5 = 1 касательная вертикальна и идет вверх.
При s = \/2, т = тг касательная снова горизонтальна, но идет
в отрицательном направлении оси X. При s = V3, т = 3/27г она
вертикальна и идет вниз. При s = 2, т = 2тг касательная прини-
принимает исходное — горизонтальное — направление. Формула D2.7)
позволяет наглядно проследить, как кривая обвивается вокруг
фокусов F и F1', делая при этом бесконечное число оборотов. Эта
формула особенно полезна в том отношении, что она позволя-
позволяет по заданному параметру s легко находить соответствующую
точку на спирали Корню.
Из формулы D2.7) получаем формулу для кривизны спира-
спирали Корню:
s=?=«• <42-8»
Длина всей спирали Корню бесконечна, а потому при прибли-
приближении к фокусам ее кривизна стремится к бесконечности.

302
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
3. При работе со спиралью Корню надо знать значение па™
раметра s. Его легко найти, зная на экране расстояние х точки
наблюдения от центра картины О (см. рис. 165). Вычислив ши-
ширину первой зоны Шустера vA65 находим далее s = жу2/(АЬ).
Рассмотрим в качестве примера дифракционную картину от
прямолинейного края экрана (рис. 167). Где бы ни находилась
точка наблюдения Р, для нее всегда будет открыт правый край
волнового фронта. На векторной диаграмме (см. рис. 166) ко™
лебание в точке наблюдения представится вектором MnF', ко-
конечная точка которого всегда находится в верхнем фокусе F,
а начальная Мп лежит где-то на спирали Корню. Если, сохра-
сохраняя неизменным положение конечной точки F, перемещать на-
начальную точку Мп вдоль спирали Корню (положения Mi, M.2,
М"з, ...), то таким путем молено получить распределение ампли-
амплитуд и интенсивности колебаний света по всему экрану.
Обозначим через а® = |i^F'| и I® = Oq амплитуду и интен-
интенсивность волны, когда открыт весь волновой фронт. Когда точ-
точка наблюдения Р находится на границе геометрической тени,
то колебание представится вектором OF = 1^Р1г. Ему соответ-
соответствует амплитуда а®/2 и интенсивность I®/4. При перемещении
точки Р в освещенную область экрана изображающая точка Мп
начнет перемещаться по нижней ветви спирали Корню, а ампли-
амплитуда и интенсивность колебаний будут последовательно прохо-
проходить через максимумы и минимумы. Максимальная амплитуда,
как видно из рис. 166, составляет 1,12ао, а интенсивность 1,25/q ;
минимальные значения их соответственно О,89ао и 0,78/q. При
дальнейшем продвижении в
освещенную область интен-
интенсивность асимптотически при-
приближается к I®. При погруже-
погружении точки Р в область гео-
геометрической тени изображаю-
изображающая точка Мп перемещает-
- ся по верхней ветви спира-
спирали Корню. При этом по ме-
мере погружения в указанную
область интенсивность света
монотонно убывает и асимпто-
асимптотически стремится к нулю.
Распределение интенсив-
интенсивности графически представ-
представлено на рис. 167. Таким обра-
образом, нет резкой границы между светом и тенью: в области
геометрической тени интенсивность света убывает непрерывно
О
Рис. 167

42
ЗОНЫ ШУСТЕРА И СПИРАЛЬ КОРНЮ
303
и монотонно, а освещенная область расщепляется в дифракци-
дифракционные полосы. На рис. 168 показана дифракционная картина,
наблюдаемая при дифракции света на крае экрана. Таким же
путем можно рассчитать дифракционную картину на щели или
длинном прямоугольном экране. На рис. 169 показана тень
проволоки от точечного (или линейного) источника.
ц ]
Рис. 168
Рис. 169
ЗАДАЧИ
1. Положение светлых и темных полос при дифракции плоской волны
на крае экрана можно приближенно (но с достаточной точностью) опреде-
определить по точкам пересечения нижней ветви спирали Корню с прямой jP jF,
соединяющей ее фокусы, приняв во внимание, что в этих точках прямая
FF' практически перпендикулярна к спирали Корню. Найти таким путем
координаты указанных полос.
Ответ.
хп = /'2л/Хг(8п — 5) (светлые полосы),
хп = />2л/\г(8п ~~ 1) (темные полосы),
где п = 1, 2, 3,...
2. Когда звезда проходит мимо края Луны, получаются дифракцион-
дифракционные полосы. Определить скорость их движения v по земной поверхности и
оценить порядок их ширины Ах. Для наблюдения полос можно воспользо-
воспользоваться телескопом, в фокусе которого помещен фотоэлемент. Полосы, про-
проходя перед объективом телескопа, возбуждают переменные электрические
токи, которые могут быть усилены и с помощью осциллографа записаны
на движущейся ленте. Оценить длительность t прохождения полос перед
объективом.
Принимая звезду за равномерно светящийся диск, можно теоретически
рассчитать распределение освещенности в дифракционной картине. Срав-
Сравнивая его с распределением освещенности, найденным экспериментально,
можно определить угловой диаметр звезды, что и было фактически выпол-
выполнено в 1946 г. Уайтфордом для четырех звезд на стодюймовом рефлекторе
Маунт-Вильсоновской обсерватории. Оценить угловые размеры звезд, для
которых может быть пригоден этот метод.

304 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Ответ, г; и 500 м/с; Ах ~ у ЬХ и 10 м, где Ь = 3,8 • 10 км — среднее
расстояние до Луны. Метод пригоден, когда угловые размерв! звезд лежат
примерно в интервале от 10"" до 10"" угловой секунды.
3. Для получения фотографий дифракционных картин в тех случаях,
когда источник света и экран расположены очень далеко, В.К. Аркадьевым
A884-1953) был применен метод подобия^ в котором вместо действитель-
действительных препятствий, стоящих на пути лучей, используются их уменьшенные
и подобные модели, но длина волны сохраняется неизменной.
Требуется получить фотографию дифракционной картины от диска
диаметром D = 50 см, когда на его оси расположен точечный источник
света на расстоянии А = 25 км, а экран удален от него на В = 50 км (плос-
(плоскость экрана перпендикулярна к оси диска). С этой целью диск заменили
уменьшенной моделью с диаметром d = 1 см. Пользуясь методом зон Фре-
Френеля, определить, на каких расстояниях а и b следует поместить источник
света и экран, чтобы получилась подобная и уменьшенная в п = 50 раз
дифракционная картина.
Ответ, а = А/п2 = 10 м, Ь = В/п2 = 20 м.
§ 43. Принцип Гюйгенса в формулировке Кирхгофа
1. До Кирхгофа принцип Гюйгенса—Френеля оставался гипотезой.
Кирхгоф в 1883 г. вывел формулу, которую можно рассматривать как уточ-
ненную формулировку указанного принципа. Приведем вывод формулы
Кирхгофа, хотя в дальнейшем и не будем ею пользоваться. Читатель может
опустить его без ущерба для понимания дальнейшего.
Допустим, что среда, в которой распро-
распространяется свет, однородна. Будем характери-
характеризовать световое поле какой-то величиной Е.
Под Е можно понимать либо вектор Е, либо
вектор В, либо одну из их проекций на декар-
декартовы оси координат. Эта величина удовлетво-
удовлетворяет волновому уравнению
которое в случае монохроматического поля пе-
переходит в
Рис- 170 АЕ + к2Е = 0. D3.1)
Найдем значение Е в произвольной точке пространства Р (рис. 170). Обо-
Обозначим через г переменное расстояние какой-либо точки А от Р. Величина
X=\e-lkr, D3.2)
рассматриваемая как функция точки А, также удовлетворяет уравнению
Дх + ^2х = 0. D3.3)
Окружим точку Р произвольной замкнутой поверхностью F, и притом
такой, что в окружаемом ею пространстве нет источников света. Функция
X обращается в бесконечность в точке Р. Исключим эту точку, окружив
ее сферой / достаточно малого радиуса R с центром в Р. Тогда во всем

§ 43 ПРИНЦИП ГЮЙГЕНСА В ФОРМУЛИРОВКЕ КИРХГОФА 305
пространстве между сферой / и поверхностью F функции Е и х, а также
их производные будут конечны и непрерывны. К ним можно применить
формулу Грина A793-1841)
D3.4)
где V — объем пространства между поверхностями / и F, an — внутрен-
внутренняя нормаль по отношению к этому пространству. Так как в указанном
пространстве источников света нет, то в нем справедливы уравнения D3.1)
и D3.3), Следовательно,
= -к\Ех - ХЕ) = 0,
а потому
/
Перейдем в этом равенстве к пределу, устремляя радиус сферы / к нулю.
Правая часть равенства при этом не будет меняться. Что касается левой,
то, взяв радиус R настолько малым, чтобы lcR<C 1, можно заменить экспо-
экспоненциальный множитель е^гкК единицей. Тогда левая часть примет вид
Так как величины Е и —— в окрестности точки Р конечны, то интеграл от
oR
BF1
второго слагаемого будет порядка ^4тгД—;? т-е- ПРИ Я ^ 0 он обратится
ом
в нуль. Интеграл же от первого слагаемого в пределе перейдет в —4
Окончательно имеем
где Ер — значение функции Е в точке Р.
2. Формула D3.5) по виду напоминает принцип Гюйгенса-Френеля. И
тут и там поле в точке Р выражается интегралом по замкнутой поверхности
F. Однако у Френеля источники света лежат внутри замкнутой поверхно-
поверхности F, а точка Р вне этой поверхности. Формула же D3.5), наоборот, пред-
предполагает, что точка Р лежит внутри поверхности F, а источники вне ее.
Легко, однако, преобразовать формулу D3.5), чтобы указанное различие
исчезло. Для этого предположим, что все источники света Si, 5*2, S3, •••
лежат в конечной области пространства. Окружим эту область замкнутой
поверхностью JF (рис. 171). Пусть точка Р находится в пространстве вне
поверхности F. Опишем из Р как из центра сферу / настолько большого
радиуса, чтобы она целиком окружала поверхность F. Тогда в пространстве

306
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
между / и F не будет источников света, а потому можно для вычисления
Е в точке Р применить формулу D3.5):
4тг J \ дп дп
F + f
Докажем, что интеграл по сфере / стремится к нулю, когда ее радиус стре-
стремится к бесконечности. Для этого необходимо выяснить поведение функции
Е на бесконечности. Предположим, что в
пространстве, ограниченном F, находится
один или несколько точечных источников
света: Si, S2, S3, ... Тогда поле этих источ-
источников представится в виде
„ v^ е~гкгт
где Ст — постоянные коэффициенты. Если
г стремится к оо, то гт также стремится к
оо, однако разность гт—г будет оставаться
конечной. Представим Е в виде
o~ik{r+am)
А
Рис. 171
где Ат — новые постоянные. Разлагая выражение под знаком суммы в ряд
по степеням 1/г, получим
Е =
где С — постоянная, а Ф стремится к нулю по крайней мере как 1/г. Под-
Подставляя это значение Е в интеграл по сфере /, получим
Подынтегральное выражение в последнем интеграле стремится к нулю по
крайней мере как 1/г3, тогда как поверхность сферы обращается в беско-
бесконечность как г2. Поэтому при г —>• оо весь интеграл стремится к нулю.
Таким образом, если сферу / удалить в бесконечность, то получится
Ер = — ф \Е —
-. — ikr
дп
D3.6)
Эти рассуждения приводят также к следующему важному результату. Ес-
Если некоторый участок поверхности F удаляется в бесконечность, то часть

§ 43 ПРИНЦИП ГЮЙГЕНСА В ФОРМУЛИРОВКЕ КИРХГОФА 307
интеграла D3.6) по этому участку стремится к нулю. При этом предполагав
ется, что все источники света находятся в конечной области пространства.
3. Формулы D3.5) и D3.6) и выражают принцип Гюйгенса в форму-
формулировке Кирхгофа. В обеих формулах п означает внутреннюю нормаль по
отношению к тому пространству, в котором находится точка наблюдения Р.
Выполнив дифференцирование по п и приняв во внимание, что дг/дп =
= —cosа, где а — угол между нормалью п и направлением из площадки
dF на точку Р, получим
ЕР= ? К (а, г) ^—^ dF. D3.7)
Здесь введено обозначение
К (a, r) = ^-\(ik + -}E cos a - |^1 . D3.8)
4тг [ \ т J on J
Тем самым установлена связь формулы Кирхгофа с принципом Гюйгенса:
подынтегральное выражение в формуле D3.8) может рассматриваться как
вторичная волна^ распространяющаяся от площадки dF к точке Р. Мно-
Множитель Ж", однако, зависит не только от угла а, как предполагал Френель,
но также и от расстояния г. В противном случае вторичная волна не могла
бы удовлетворять волновому уравнению. Таким образом, вторичные волны
не обладают шаровой симметрией. Они сферические только в том смысле,
что их волновые фронты имеют форму сфер. Амплитуды же зависят от
направления распространения и меняются с расстоянием иначе, чем 1/г.
Только в «волновой зоне», когда расстояние точки Р от излучающего цен-
центра dF очень велико по сравнению с длиной волны, можно в выражении
D3.8) пренебречь 1/г по сравнению с гк. Тогда
S ( ^) ^^
ер = т- S (гкЕ cos а - ^) ^—^ dF. D3.9)
4тг J \ дп J r
Благодаря малости длин световых волн такой упрощенной формой принци-
принципа Гюйгенса в оптике можно пользоваться при решении всех конкретных
задач.
4. Чтобы составить на примере бо™
лее конкретное представление о вторич-
вторичных волнах, рассмотрим свободное рас-
пространение сферической волны от то™
чечного источника. В качестве поверхно-
поверхности F возьмем сферу радиуса го с цен-
центром в источнике О (рис. 172). Поле на
поверхности F представим выражением
Ео =
ГО
Предполагая, что радиус г о очень велик Рис. 172
по сравнению с длиной волны, отсюда
найдем дЕ/дп = дЕо/дго = ^ikEo. Подставляя это значение в формулу
D3.9), получим
Ер = — ф (l + cosa)#o dF. D3.10)
4тг J r

308 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Сравнение этой формулы с формулой D3.7) дает
К (а) = ^A+cosa). D3.11)
Это и есть «ослабляющий множитель» К (а), введенный в § 39 ad hoc. Из
теории автоматически получается, что он чисто мнимый и с возрастани-
возрастанием а монотонно убывает по абсолютной величине. Он обращается в нуль
при а = тг, т.е. в точке D сферы, диаметрально противоположной точке
наблюдения Р.
Интеграл D3.10) теперь можно вычислить, поскольку он не содержит
никаких неизвестных функций. Произведем это вычисление, так как таким
путем можно получить строгое обоснование метода зон Френеля и резуль-
результатов, полученных этим методом. Взяв за переменную интегрирования г и
использовав значение Ео, преобразуем интеграл D3.10) к виду
Ер = j А(г)е^гкг dr, D3.12)
где введено обозначение
!*(l±cosa)(wt_fcP0)
а через п и г2 обозначены наибольшее и наименьшее значения, принимае-
принимаемые г. Интегрируя D3.12) по частям, получим
Г2
НА
^V'*r dr. D3.14)
ik
Здесь единственной величиной, зависящей от г, является cos а. Найдем ее
производную. Из рис. 172 следует, что (р + гоJ = г2 +г*о +2rro cos а, откуда
dcosa /I coscA _ ,лП«п\ i
— = — I 1 1. Взяв от D3.13) логарифмическую производную
dr \го г J
по г и воспользовавшись предыдущей формулой, найдем
1 dA г /1 cosa\ л/ ,
^^ = ^^-^^ ^^ + — А(г).
ik dr 1 + cos а \ кго кг J
Такой величиной, а следовательно, и интегралом в формуле D3.14) следует
пренебречь, так как это уже было сделано при выводе исходной формулы
D3.9). Таким образом, в формуле D3.14) остается только первое слагаемое,
т.е.
ЕР = A(n)e l ^ ^А^е Ъ Г\ D3.15)
гк
Существенно, что величина Ер представляется разностью одной и той же
функции, но при различных значениях аргумента г, причем при изменении
г на Л/2 знак этой функции меняется на противоположный. Этого доста™
точно для обоснования основного результата C9.6), на котором основан ме-
метод зон Френеля. Действительно, применив формулу D3.15) к первой зоне
Френеля, найдем, что действие этой зоны может быть представлено в виде
Е\ = {и\ +11,2), действие второй зоны — в виде Еч = —{и^ +^з), и т.д. Явный

44
ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ
309
вид выражений щ для доказательства не имеет значения. Действие первых
N зон выразится суммой
Е = (иг +и2) - (г*2 +г*3) + ... + {-
,
= (—1)n+1un =
Так как по величине действия двух соседних зон почти одинаковы, то
un+i = un- С той же степенью точности Уг-Ео. = щ, 1 n+1
= (—1) un+i- Следовательно,
Е= i(
§ 44. Дифракция Фраунгофера на щели
1. Дифракционные явления Фраунгофера имеют в оптике
значительно большее практическое значение, чем дифракцион-
дифракционные явления Френеля. При практическом осуществлении ди-
дифракции Фраунгофера источник света S помещается в фокусе
линзы (рис. 173). (Линза L\ не нужна, если источником све-
света служит лазер, поскольку от него исходит уже параллельный
пучок света.) Дифракция возника-
возникает на каком-либо препятствии АВ,
поставленном на пути световых лу-
лучей, прошедших через линзу L\. Ди-
Дифракционная картина наблюдается
в фокальной плоскости другой лин-
линзы i/2- Ее молено также наблюдать
в зрительную трубу, установленную
на бесконечность. Но в теоретиче™
ских рассуждениях удобнее от всех
этих вспомогательных приспособле-
приспособлений отвлечься, предполагая, что на
препятствие АВ падает параллель-
параллельный пучок лучей, а дифракция на-
наблюдается «в бесконечности».
Простейшим для расчета и прак-
практически очень важным случаем яв-
является фраунгоферова дифракция
на длинной прямоугольной щели.
Ширину щели обозначим через Ь, ее длину будем считать бес-
бесконечной. Пусть на щель нормально падает плоская монохро-
монохроматическая волна (рис. 174). Световое поле за щелью найдется
по принципу Гюйгенса как результат интерференции когерент-
когерентных вторичных волн, исходящих из различных точек волнового
Рис. 173

310
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
фронта на щели. Вторичные волны, излучаемые полоской вол-
волнового фронта ширины dx, параллельной щели, складываясь,
дают цилиндрическую волну, осью которой является эта полос-
полоска. Зависимость этой волны от направления ее распространения,
определяемого углом i?, мож-
можно не учитывать, так как за-
задача решается методом Фре-
Френеля, а потому угол дифрак-
дифракции 1? должен предполагать-
предполагаться малым. Однако необходи-
необходимо учесть разности фаз между
волнами, исходящими из раз-
различных полосок. Разумеется,
речь идет о фазах колебаний
на бесконечном расстоянии от
щели. Волна, исходящая из dx
под углом #, опережает по фа-
фазе волну того лее направления, исходящую из середины щели О,
на kxsin'&. Поэтому результирующее поле в бесконечности, со-
создаваемое всей щелью, представится интегралом
Рис. 174
+Ь/
Е= J
Здесь опущены все множители, не влияющие на относительное
распределение волнового поля по направлениям. Вычислив ин-
интеграл, получим
?7 = Ь*|?, D4.1)
где введено обозначение
kbsine Trbsint? /д. ~ч
а - 2 ^ Л ' ( }
Отсюда для распределения интенсивности света по направлени-
направлениям найдем
= i0 I
I
\ а
I
у
D4.3)
где /q — интенсивность в направлении падающей волны. На
1Г7Г т -, „ sin a /
рис. 175 представлены графики функции (штриховая кри-
кри\ / sin а \ / \ гхГ 1 г
вая) и I ^^ 1 (сплошная кривая). Обе функции обращаются в
максимум, равный единице, при а = 0. При а = ттг, где т =
= ±1, ±2,..., они равны нулю, т.е. в этих точках наблюдаются
минимумы интенсивности. Между двумя соседними минимума-
минимумами располагаются максимумы различных порядков. Их положе-

44
ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ
311
ния определяются трансцендентным уравнением a cos a—sin a =
= 0. Практически можно считать, что максимумы располагают-
располагаются посередине между соседними минимумами.
ft
//
//
j
/10,6
;; /
/ / 0,4
/
/ /
// ОД
/ х ч
v
\\
\\
" V
\
_
-
\
V-
\
\\
\
\
\
^-—-
\
\
\
\
\ \
\\
sin a
а
/sinaj2
7 \
0 п \
/
V/
Рис. 175
2. Условие минимума а = гптг можно также записать в виде
6stni? = mA. D4.4)
Оно означает, что разность хода между волнами, исходящими
от крайних точек щели, должна содержать целое число волн.
Этот результат легко уяснить без всяких вычислений. Допустим
сначала, что bslnt? = А. Разобьем щель на две части одинаковой
ширины. Тогда волны от этих частей придут в (удаленную) точ-
точку наблюдения в противоположных фазах и погасят друг друга
при интерференции, — получится минимум интенсивности. Если
bsint? = га А, то разбиение щели надо произвести на 2га частей
одинаковой ширины. Волны от частей с нечетными номерами
придут в фазах, противоположных фазам волн, пришедших от
частей с четными номерами. А так как, ввиду симметрии, части
щели, равноудаленные от противоположных краев ее, совершен-
совершенно равноправны, то ясно, что эффект, вызванный нечетными
частями, погасится при интерференции эффектом, вызванным
четными частями.
Приведенное обоснование формулы D4.4) не только проще
предыдущего, но, что особенно важно, и обладает большей общ™
ностью. Действительно, в предыдущем выводе щель должна
предполагаться широкой (Ь^> А), чтобы молено было применять
приближенный метод Френеля. Последний же вывод использу-
использует только свойства симметрии щели и применим не только при

312
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
малых, но и при любых углах дифракции #. Требуется только,
чтобы было b > А. В противном случае из условия D4.4) мы по-
получили бы sin 1? > 1, и все дифракционные минимумы с нулевой
интенсивностью были бы невозможны.
3. Когда падающая волна плоская, то все дифрагированные
лучи перпендикулярны к оси щели. Если на их пути поставить
линзу, то каждый дифрагированный пучок параллельных лучей
соберется в маленькое пятнышко. Такие пятнышки — максиму™
мы и минимумы интенсивности — расположатся вдоль прямой,
перпендикулярной к оси щели и лежащей в фокальной плоско-
плоскости линзы. В этой плоскости и надо поместить экран для на™
блюдения.
Если в качестве источника света взять светящуюся линию
или узкую освещаемую коллиматорную щель, параллельную
щели, на которой происходит дифракция, то каждая точка ис-
источника даст на экране дифракционную картину, описанную
выше. В результате наложения таких картин каждое дифрак-
дифракционное пятнышко вытянется в полоску. Образуется система
дифракционных полос, показанная на рис. 176. Центральная
полоса светлая и примерно вдвое шире остальных светлых и тем-
Рис. 176
пых полос. Максимальный порядок минимума, который может
наблюдаться, определяется условием slnt? < 1, т.е. т < Ь/А, как
это видно из формулы D4.4). Чем ши-
шире щель, тем ярче картина, тем уже
дифракционные полосы, а число са-
самих полос больше. При сужении ще-
щели картина расширяется, а ее яркость
уменьшается. Когда b = А, минимумы
первого порядка получаются при $ =
= тг/2 и исчезают при дальнейшем су-
сужении щели.
4. При наклонном падении света
под углом $о (рис. 177) разность хода
между крайними интерферирующими
лучами АВ — CD составляет 6(sint? — sin#o)- Поэтому условие
дифракционного минимума D4.4) переходит в
Рис. 177
b (slni? — si
D4.5)

44 ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ 313
Если углы # и $о малы, то Ь(# — #о) ~ w^- Основная доля
света сосредоточена в центральной дифракционной полосе, т.е.
между минимумами первого и минус первого порядков. Этим
можно воспользоваться для оценки дифракционной расходимо-
расходимости световых пучков, выделяемых тем или иным способом, на-
например в результате прохождения плоской волны через диа-
фрагму. Световые лучи, прошедшие через диафрагму, откло-
отклоняются от своего исходного направления на угол
&? - А/А D4.6)
где D — поперечное сечение пучка (в направлении, где оно ми™
нимально). Такое дифракционное уширение пучка обусловлено
волновой природой света и принципиально не может быть устра-
устранено при заданной ширине пучка. Поэтому не существует строго
параллельных пучков лучей. Это — идеализация, предполагаю-
предполагающая, что поперечное сечение пучка бесконечно велико. Если пу-
пучок проходит путь I, то на этом пути он претерпевает дифрак-
ционное уширение ~ I 6$ = IX/D. Таким уширением можно пре-
пренебрегать только тогда, когда оно мало по сравнению с шириной
самого пучка, т.е. когда f A/D<CD, или 1<^D2/X. Только на таких
расстояниях пучок может рассматриваться как луч геометриче-
геометрической оптики (см. § 41, п. 3).
5. Допустим, что источником света является бесконечно уда-
удаленная светящаяся точка или линия, параллельная длине щели.
Угол t? на дифракционный минимум га-го порядка определяется
условием D4.5). Ближайший к нему максимум сдвинут на угол
5$, причем
Ь [sin(# + 8$) - smi?0] = m\ + ^.
Вычитая отсюда D4.5) и заменяя разности дифференциалами,
получим 6cost? • 6§ = А/2. Пусть другой такой же (некогерент-
(некогерентный) источник света сдвинут относительно первого как раз на
угол 8$. Тогда дифракционные максимумы от одного из этих
источников належатся на минимумы от другого. В результате
дифракционные полосы пропадут. Угловое расстояние 8$ между
точечными (или линейными) источниками, когда это произой-
произойдет, определяется формулой
6& = Х/2Ь D4.7)
(при условии, что угол $ мал).
Допустим теперь, что источник света протяженный и имеет
форму равномерно светящейся полосы с угловой шириной 8&.
Разобьем ее на две одинаковые части. Каждую часть в свою оче-
очередь разобьем на бесконечно узкие полоски одинаковой ширины.
Скомбинируем их в пары полосок, сдвинутых относительно друг
друга на угол 8Q/2. Если 80/2 = &?, то, очевидно, дифракцион-
дифракционных полос не получится. Таким образом, условие исчезновения

314 ДИФРАКЦИЯ СВЕТА ГЛ. IV
дифракционных полос от протяженного источника рассматри-
рассматриваемой формы будет
80 = \/Ь. D4.8)
От угловв1х размеров 80 источника легко перейти к его ли-
линейным поперечным размерам 81. Если источник помещен в
главном фокусе коллиматорной линзв! с фокусным расстоянием
/, то 81 = f $0, т.е.
61 = /?. D4.9)
6. Когда ширина щели становится меньше или порядка дли™
ны волны, приближенный метод Френеля, которым мы пользо-
пользовались выше, становится неприменимым. Тогда волновое поле
в плоскости щели уже нельзя отождествлять с неискаженным
полем падающей волны, как это делается в методе Френеля. За™
дачу надо решать математически строго с использованием урав-
уравнений Максвелла и соответствующих им граничных условий.
Впервые такой метод был осуществлен в 1896 г. Зоммер-
фельдом A868—1951) в задаче о дифракции плоской волны на
прямолинейном крае экрана. Зоммерфельд рассмотрел идеаль-
идеально проводящий (а потому непрозрачный) экран, толщина ко-
которого пренебрежимо мала по сравнению с длиной волны. Хо-
Хотя в оптике такой случай и невозможно осуществить, решение
Зоммерфельда имеет большое значение, так как оно позволя-
позволяет судить о точности и границах применимости приближенных
методов. В 1897 г. Рэлей решил задачу о дифракции на узкой
щели (Ь<СА) в бесконечно тонком идеально проводящем экране.
В курсе общей физики нет возможности приводить эти реше™
ния1). Сравним только их результаты с тем, что дает простой
метод Френеля, чтобы составить более конкретное представле-
представление о границах применимости этого метода.
Предположим, что электрический вектор падающей волны
параллелен щели. Как показывает строгий расчет, ход амплиту-
амплитуды дифрагированной волны качественно сохраняется, но выра-
выражается через функции Бесселя. Амплитудная кривая с ростом #
спадает круче прежней функции (sin а)/а. В максимуме значе-
значение амплитуды в 4А/(Ътг2) раз меньше значения, определяемого
формулой D4.1). Так, при Ь = УюА, амплитуда уменьшается в
четыре раза2). Расхождение с приближенной теорией уменьша-
уменьшается при дальнейшем увеличении Ь.
1) Интересующихся отсылаем к книге: А. Зоммерфельд. Оптика. — М.:
ИЛ, 1953.
) Если электрический вектор падающей волны перпендикулярен к длине
щели, то амплитуда уменьшается слабее. Это легко понять, обратившись к
соответствующему опыту Герца с проволочной решеткой (см. т. III, § 142,
п. 7).

§ 45 ДИФРАКЦИЯ ФРАУНГОФЕРА НА ОТВЕРСТИЯХ 315
Численные расчеты, выполненные Морзе и Рубинштейном
A938), показали, что при ширине щели около Л или больше ре-
результаты, полученные по приближенному методу Френеля, мо-
могут считаться достаточно удовлетворительными. Таким обра™
зом, даже в случае наиболее тонких современных дифракцион-
дифракционных решеток (при щелях порядка 1000-2000 нм) приближенный
метод Френеля не ведет еще к заметным ошибкам.
§ 45. Дифракцим Фраунгофера на отверстиях
1. Допустим, что свет падает перпендикулярно к плоскости
непрозрачного экрана с отверстиями. (Обобщение на случай на-
наклонного падения не встреча™
ет никаких затруднений.) Ко™
ординатную плоскость XY сов™
местим с плоскостью экра-
экрана, через dF обозначим эле-
элемент площади в этой плоско™
сти. Направление дифрагиро-
дифрагированного света будем характери-
характеризовать единичным вектором s
(рис. 178). Разность хода меж-
между лучами, вышедшими в этом
направлении из элемента пло™
щади dF и из начала координат Рис. 178
О, т.е. длина отрезка О А, равна
(rs), где г (ж, у) — радиус-вектор элемента dF. Соответствующая
разность фаз будет fc(rs). Результирующее поле в фраунгоферо™
вой дифракционной картине представится интегралом
Е = J eik(sr^ dF, D5.1)
распространенным по всем отверстиям.
В случае прямоугольного отверстия удобно перейти к пря™
моугольным координатам, предполагая, что координатные оси
параллельны сторонам отверстия. Если а ш Ъ — длины этих сто™
рон, то
+а/2 +5/2
Е= J J etk^xX+syyUxdy. D5.2)
^а/2 ^Ъ/2
Это — в точности такие же интегралы, которые встречались нам
при рассмотрении дифракции на щели. Выполнив интегрирова-
интегрирование, получим
^^, D5.3)

316
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
где
1 i 7rasx
a = - kasx = —^
/3 = 77 kbsv =
D5.4)
2 у X
Заменив в одном из интегралов пределы интегрирования беско-
бесконечными, получим предельный случай бесконечно длинной ще-
щели. Интенсивность определяется формулой
.
/sin/
D5.5)
Дифракционную картину молено получить, если наложить друг
на друга две взаимно перпендикулярные дифракционные карти™
ны, одна из которых получена при дифракции на щели ширины
а, а другая — на щели ширины Ь (рис. 179). Картина вытянута
в направлении более короткой стороны прямоугольного отвер-
отверстия.
Случай круглого отверстия на практике представляет боль-
большой интерес, так как все оправы линз и объективов имеют обыч-
обычно круглую форму. В этом случае при вычислении интеграла
D5.1) естественно перейти к
;Ы\: KOOjYUi ПГП'Я М .. ТТрП
Рис. 179
Рис. 180
теграл выражается через бесселеву функцию первого порядка
Ji(a), где а = kRe = 2ttjRi9/A (R — радиус отверстия, # — угол
дифракции). Опуская вычисления, приведем окончательные ре-
результаты. Дифракционная картина, естественно, имеет вид кон-
концентрических светлых и темных колец (рис. 180). Центр карти-
картины светлый, так как в него все вторичные волны приходят в оди-

45
ДИФРАКЦИЯ ФРАУНГОФЕРА НА ОТВЕРСТИЯХ
317
наковых фазах. Распределение амплитуд (штриховая кривая) и
интенсивностей (сплошная кривая) в зависимости от угла ди-
дифракции 1? (или, что то
же, расстояния от цен-
центра картины) приведе-
приведено на рис. 181. Соответ-
ствующие кривые мало
отличаются от кривых
рис. 175 не только ка-
качественно, но и коли-
количественно. Приближен-
Приближенно угловые радиусы тем-
0,8
0,6
ных колец определяются
формулой
= [0,
= 0,61 +
Л
0,4
0,2
0
D5.6)
Более точные данные
приведены в табл. 5.
Из нее видно, что око- Рис. 181
л о 98 % света приходит-
приходится на центральный максимум. Если исключить центральный
максимум, то остальные темные и светлые кольца практически
равноотстоящие.
Таблица 5
Минимумы
•&1 =0,61
02 = 1,12
&з = 1,62
#4 = 2,12
Максимумы
tf'i = 0
#2 = 0,81
#з = 1,33
•&'А = 1,85
Интенсивность
в максимумах
1
0,0175
0,0042
0,0016
2. Таким же путем, по крайней мере численно, молено рассчи-
рассчитать дифракционную картину Фраунгофера на отверстии любой
формы. При решении подобных задач полезно руководствовать-
руководствоваться соображениями подобия. Представим волновое поле интегра-
интегралом вида D5.2), но распространенным по области F, занима-
занимаемой рассматриваемым отверстием. Введем новые координаты
х1 = /jLXj yf = у, где /i — постоянная. Область F плоскости XY
преобразуется в область Ff плоскости X'Y'. Она получается из

318 ДИФРАКЦИЯ СВЕТА ГЛ. IV
F равномерным растяжением в /i раз в направлении оси X. Ин-
теграл D5.2) преобразуется в
где единичный вектор s; определяется своими проекциями s'x =
= sx/11, Sy = sy. (Постоянная /i должна быть такой, чтобы s'x +
+ s'y < 1.) Но последний интеграл представляет волновое поле
Ef(sf) (в штрихованной системе координат) в направлении еди-
единичного вектора s; при фраунгоферовой дифракции на отвер-
отверстии F1, а потому
E'(sr) =ijlE(s). D5.7)
Таким образом, по известной дифракционной картине на
каком-либо отверстии можно без новых вычислений получить
новые дифракционные картины. Для этого надо отверстие рав-
равномерно вытянуть (сжать) в каком-либо направлении. Тогда,
как видно из формул х1 = fix, sx = <sx/jti, дифракционная кар-
картина сожмется (вытянется) в том же направлении. Так, при ра-
растяжении круглого отверстия оно переходит в эллиптическое, а
дифракционные кольца сжимаются, также принимая эллипти-
эллиптическую форму. Конечно, отверстие можно вытянуть или сжать
и вдоль каких-либо двух направлений.
8. Рассмотрим теперь случай, когда в экране имеется боль-
большое число N одинаковых и одинаково ориентированных отвер-
отверстий. Волновое поле в бесконечности представится суммой Е =
= *Y^Ei, где Ei — поле, которое возникло бы при дифракции
при наличии одного только г-го отверстия. Для интенсивности
получим
При фраунгоферовой дифракции распределение интенсивности
в дифракционной картине определяется только направлением
лучей^ а не положением световых пучков. При боковом смеще-
смещении последних интенсивность не меняется. Распределение ин~
тенсивности не изменится^ если отверстие в плоскости экра-
экрана сместить в сторону без изменения его ориентации. Поэто-
Поэтому в последней сумме все интенсивности одинаковы: Ц = 1\.
Рассмотрим особо два случая: 1) отверстия расположены ха-
хаотически; 2) отверстия расположены «правильно», в определен-
определенном порядке. В первом случае среди членов двойной суммы с
г Ф j в среднем найдется столько же положительных членов,
сколько и отрицательных. При сложении таких членов в сред-

§ 45 ДИФРАКЦИЯ ФРАУНГОФЕРА НА ОТВЕРСТИЯХ 319
нем получится нуль. Поэтому / = NI\. Получается такая же
дифракционная картина, что и от одного отверстия, но усилен-
усиленная по интенсивности в N раз. Интенсивности отдельных кар™
тин арифметически складываются, но сами картины не интер-
ферируют между собой. Во втором случае, напротив, члены с
г Ф j не компенсируются. Они могут интерферировать и суще-
существенно влиять на дифракционную картину. Этот случай будет
рассмотрен в следующем параграфе на примере дифракционной
решетки.
Первый случай легко демонстрировать на стеклянной пла-
стинке, запыленной спорами ликоподия. Последние имеют фор-
форму шариков практически одинаковых размеров. При освещении
пластинки параллельным пучком лучей на удаленном экране
появляется дифракционная картина, состоящая из концентри-
концентрических колец. При освещении белым светом внешние края колец
окрашены в красный, а внутренние — в фиолетовый цвет. Это
указывает на дифракционную природу явления, так как длины
волн красных лучей больше, чем фиолетовых.
4. Описанное явление наблюдается в природе в виде венцов.
Так называются светлые туманные кольца на небесном своде
вокруг Солнца или Луны. Иногда венцы наблюдаются вокруг
ярких звезд или планет, а также вокруг земных источников све-
света. Венцы возникают в результате дифракции света на водяных
капельках (или кристалликах льда), когда перед светилом про™
ходит полупрозрачное облако (чаще всего высококучевое) или
туман. Угловые радиусы венцов обычно не превосходят 5°. Ди-
Дифракционная природа колец в явлении венцов подтверждается
тем, что наружные края колец имеют красноватый цвет, а вну-
внутренние — синеватый. При наличии в атмосфере капель всевоз-
всевозможных размеров кольца венцов налагаются друг на друга и
образуют общее белое сияние вокруг диска светила, называемое
в случае Солнца околосолнечным ореолом.
От венцов следует отличать гало. Так называется группа оп-
оптических явлений в атмосфере, возникающая при преломлении
или отражении лучей Солнца или Луны на плавающих в возду-
воздухе кристалликах льда, образующих перистые облака. Угловые
радиусы гало значительно больше угловых радиусов венцов и
составляют 22° или 46°. Наружный край колец гало имеет си-
синеватую, а. внутренний — красноватую окраску. Это указывает
на рефракционную природу явления (дисперсия). В отличие от
венцов, угловые размеры которых могут меняться с изменением
радиусов водяных капелек, угловые размеры колец гало строго
постоянны, так как они зависят только от углов между граня-
гранями кристалликов, которые при изменении размеров последних
остаются неизменными.

320
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
§ 46. Дифракционная решетка
1. Дифракционная решетка — важнейший спектральный
прибор, предназначенный для разложения света в спектр и из-
измерения длин волн. Она представляет собой плоскую стеклян-
стеклянную или металлическую поверхность, на которой делительной
машиной нарезано очень много (до сотен тысяч) прямых равно-
равноотстоящих штрихов. На стеклянных решетках наблюдения мож-
можно производить как в проходящем, так и в отраженном свете,
на металлических — только в отраженном. Применяются во™
гнутые металлические решетки, в которых штрихи наносятся
на вогнутой сферической поверхности.
Сначала рассмотрим простейшую идеализированную решет™
ку, состоящую из одинаковых равноотстоящих параллельных
щелей, сделанных в непрозрачном экране. Ширину щели обозна-
обозначим через Ь, ширину непрозрачной части экрана между двумя
соседними щелями — через а. Величина d = а + Ь называется пе-
периодом решетки. В решетке осуществляется многолучевая ин-
интерференция когерентных дифрагированных пучков света, ис™
ходящих от щелей решетки при ее освещении. Дифракционная
картина наблюдается по методу Фраунгофера, т.е. либо на бес-
бесконечно удаленном экране, либо в фокальной плоскости линзы,
поставленной на пути дифрагированного света.
Пусть на решетку перпендикулярно к ее поверхности пада-
падает плоская монохроматическая волна (рис. 182). Разность хода
/yd sin ft
Рис. 182
между вторичными волнами, исходящими из соседних щелей ре-
решетки, будет dsint?, а разность фаз 6 = kdsin# = —dsin#, где
А
# — угол дифракции. Обозначим через Е\ поле в точке наблю-
наблюдения, излучаемое первой щелью. Оно определяется формулой

§ 46 ДИФРАКЦИОННАЯ РЕШЕТКА 321
!-, i sin а у-,-
Ь\ = о . Поля, излучаемые остальными щелями, предста-
вляются выражениями:
Е2 = Ехе-г\ Еъ = Eie~2iS, ...,EN = ^е"^^
где N — общее число щелей. Полное поле, излучаемое всеми
щелями, представляется суммой
Е = ?i[l + e~iS + e~2iS + ... + e~i{N-1)s] = E1 1~f^x >
откуда
1
sin F/2) G
_л sm(N6/2)
лл 461
A~Al SmF/2) ' ^4b"ij
где A\ — вещественная амплитуда волны от одной щели, А —
от всей решетки. Для интенсивностей получаем
Dб-2)
Формулы D6.1) и D6.2) — основные в теории дифракционной
решетки.
2. Когда i? = 0, то<5 = 0. В этом случае выражения D6.1) и
D6.2) принимают неопределенный вид 0/0. Раскрыв неопреде-
неопределенность, получим
ATa = NAx, ITa = N2h. D6.3)
Тот же результат получается в случае 8/2 = ттг, т.е. при
dsintf = mA (m = 0,±1,±2,...). D6.4)
В направлениях, определяемых этим условием, получаются мак-
максимумы, интенсивность которых в N2 раз превосходит интенсив-
интенсивность волны от одной щели в том же направлении. Они называ-
называются главными максимумами. Целое число т называют поряд-
порядком главного максимума или порядком спектра. Условие D6.4)
определяет направления, в которых излучения от всех щелей ре-
решетки приходят в точку наблюдения в одинаковых фазах, а по™
тому усиливают друг друга. В таких направлениях при отдель-
отдельных значениях т могут и не возникнуть максимумы. Это будет,
когда 1\ = 0, т.е. в направлениях на дифракционные минимумы
от одной щели. Например, если а = Ь, то все главные максимумы
четных порядков не появятся. Действительно, условие появле-
появления главного максимума порядка 2в имеет вид dsint? = 2пХ.
При d = 2b оно переходит в bsin# = пА, т.е. в условие дифрак-
дифракционного минимума на щели. Таким образом, в рассматривае-
рассматриваемом направлении ни одна щель, а потому и решетка в целом не
излучают.
11 Д.В. Сивухин

322 ДИФРАКЦИЯ СВЕТА ГЛ. IV
3. Выражения D6.1) и D6.2) обращаются в нуль, если
sin (N8/2) = О, но sin (8/2) ф 0, т.е. при N8/2 = (JVm + р)тг,
или
(p=l,2,...,JV-l). D6.5)
В соответствующих направлениях получаются дифракционные
минимумы, в которых интенсивность света равна нулю. Меж-
Между двумя соседними минимумами получается максимум. Такие
максимумы называются второстепенными или добавочными.
Между двумя соседними главными максимумами располагается
(N — 1) минимумов и (N — 2) добавочных максимумов. На эти
максимумы и минимумы накладываются минимумы, возникаю-
возникающие при дифракции от отдельной щели, в которых функция Е\
обращается в нуль.
Второстепенные максимумы находятся примерно посередине
между соответствующими дифракционными минимумами. Ве-
Величину E, определяющую направление на какой-либо из второ™
степенных максимумов, можно поэтому вычислить по прибли-
приближенной формуле
N5_=(Nm + P) + (Nm+p+l)n^
ИЛИ
1 - ( + 2р + ]
2 ^ \ 2JV
Пользуясь этой формулой, найдем приближенное выражение
для интенсивности второстепенных максимумов в окрестности
соответствующего главного максимума (т.е. при малых р). В
положениях второстепенных максимумов числители в форму™
ле D6.2) равны единице. Если число щелей решетки N очень
велико, а номер второстепенного максимума р невелик, то угол
8/2 будет мал, и можно положить
. 6 , . 2р + 1 1 2р + 1
Это дает
2iV \2 4 ,ло ^
Таким образом, интенсивности главного максимума и ближай™
ших к нему второстепенных максимумов находятся в отношени-
отношениях
1:А:*ГТ:ЖТ:-" = 1: °'045 : °'016 : °'0083 : • • •
9тг2 25тг2 49тН
Второстепенные максимумы слабы по сравнению с главными
максимумами. При большом числе щелей они обычно не играют

46
ДИФРАКЦИОННАЯ РЕШЕТКА
323
роли. Второстепенные максимумы создают более или менее рав-
номерный слабый фон, на нем выступают узкие и резкие глав-
главные максимумы, в которых концентрируется практически весь
дифрагированный свет. Распределение интенсивности в дифра-
дифрагированном свете представлено на схематическом рис. 183 для
т+1
(iV~l) минимумов
Рис. 183
N = 8. Величина множителя Д, входящего в формулу D6.2), не
указана. Между соседними главными максимумами находится
N — 2 = 6 второстепенных максимумов. Относительные интен-
интенсивности главных и второстепенных максимумов представляют-
представляются числами 100; 5,0; 2,25; 1,6; 1,6; 2,25; 5,0; 100.
Красивую демонстрацию можно получить, направив на ре-
решетку яркий узкий пучок света от лазера. При дифракции пу-
пучок расщепляется на много хорошо видимых в воздухе ярких
пучков, веерообразно расходящихся от решетки. Падая на по-
потолок и стены аудитории, эти пучки оставляют на них яркие
светлые пятна (световые зайчики).
4. Происхождение второстепенных или добавочных макси-
максимумов и минимумов легко уяснить с помощью векторной диа-
2тг_
3
Рис. 184
Рис. 185
11*

324
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
граммы. На векторной диаграмме колебания от отдельных ще-
щелей решетки представляются векторами равной длины. Из-за
сдвига фаз такие векторы повернуты один относительно друго-
другого на один и тот же угол 6 = — dslnt? (рис. 184), образуя звенья
л
правильной ломаной линии. Замыкающая этой ломаной О А изо-
изображает колебание, возбуждаемое всей решеткой. Если ломаная
замкнутая, то Е = 0, т.е. получается дифракционный минимум.
Первый раз это произойдет при 5 = 2тг/Ж, второй — при 5 =
= 4тг/N и т.д. Легко видеть, что таким путем получается условие
дифракционного минимума D6.5). Все это проиллюстрировано
на рис. 185 для N = 3 и на рис. 186 для N = 4.
8=0
3
4 2
1
4 2
3
Рис. 186
5. Если волна падает на решетку наклонно под углом i?q
(рис. 187), то разность хода между соседними пучками стано™
вится равной AD — СВ =
= d(sin# — sin#o)- Харак-
Характер дифракционной картины
в основном сохраняется. По-
Положение главных максимумов
определяется условием
d(sin# - sm#o) = m\, D6.8)
а дифракционных миниму™
мов — условием
( v\
d(sin i? — sin #o) = ( тп + -j- ) A
(p=l,2,...,JVr-l). D6.9)
Зная положение главных максимумов, можно вычислить
длину волны по формуле D6.4) или D6.8). Решетка есть прибор
для измерения именно длины волны, а не частоты колебаний,
как это иногда неверно утверждают.
6. Форма штрихов, нанесенных на решетку, материал, из ко-
которого она изготовлена, и т.п. сказываются лишь на виде волны
Рис. 187

§ 46 ДИФРАКЦИОННАЯ РЕШЕТКА 325
Е\ от отдельного штриха. Положение же главных максимумов
определяется исключительно периодом решетки, а дифракци-
дифракционных минимумов — кроме того еще числом штрихов N. При
выводе формул D6.4), D6.8) и D6.9) из принципа Гюйгенса^
Френеля нет необходимости применять приближенные методы.
Из рассуждений п. 4 ясно, что существенна только периодич-
периодичность светового поля на выходе (т.е. задней стороне) решет-
ки, обусловленная в свою очередь периодичностью структуры
последней. Ничего другого о поле на выходе решетки знать не
надо. Поэтому перечисленные формулы совершенно точны.
Под дифракционной решеткой в широком смысле слова по™
нимается всякая структура, обладающая пространственной пе-
периодичностью. Если свойства структуры периодически меняют-
меняются только в одном направлении, то решетка называется одномер-
одномерной или линейной. Если же периодичность решетки имеет место
в двух или трех направлениях, то решетка называется соответ-
соответственно двух- или трехмерной. В последнем случае ее называют
также пространственной. В этом и следующих параграфах рас-
рассматриваются только линейные решетки.
Не обязательно, чтобы при прохождении через решетку ме-
менялась амплитуда волны. Существенно только, чтобы на выходе
решетки периодически менялось волновое поле в целом. Моле-
Молено различать два крайних идеализованных случая: 1) решетка
вносит периодические изменения в амплитуду волны, не влияя
на ее фазу; такая решетка называется амплитудной; 2) решетка
вносит периодические изменения в фазу волны, но не влияет на
ее амплитуду; такую решетку называют фазовой.
Всякая реальная решетка, строго говоря, не является чи™
сто амплитудной или чисто фазовой. Она периодически ме-
меняет на выходе как амплитуду, так и фазу волнового поля.
Приблизительно амплитудной решеткой является рассмотрен-
рассмотренная выше совокупность равноотстоящих щелей в непрозрачном
экране (рис. 187). Приближением фазовой решетки может слу-
служить стеклянная пластинка, представленная на рис. 188. В обо-
обоих случаях период решетки должен быть велик по сравнению с
длиной волны. Примером фазовой отражательной решетки мо-
может служить решетка, изготовленная СМ. Рытовым (р. 1908) и
И.Л. Фабелинским (р. 1911). Она представляет собой равнобоч-
равнобочную стеклянную призму с преломляющим углом 90° (рис. 189).
На гипотенузной поверхности АВ напылены узкие равноотсто-
равноотстоящие полоски серебра, параллельные преломляющему ребру
призмы. Свет падает нормально на одну из боковых граней
призмы. Попадая на гипотенузную грань АВ, он испытает либо
полное отражение от непосеребренных полосок, либо отразит-
отразится от посеребренных полосок. В последнем случае отражение
также практически полное благодаря высокому коэффициенту

326 ДИФРАКЦИЯ СВЕТА ГЛ. IV
отражения серебра. В обоих случаях отражение сопровождает-
сопровождается изменением фазы, но эти изменения разные (см. § 66 и 73).
Таким образом, амплитуда волны при отражении не меняется,
а в фазу вносятся периодические изменения.
Рис. 188 Рис. 189
7. Не все целые числа га, входящие в формулы D6.4) и D6.8),
допустимы. Так как | sint?| < 1, то на га должно быть наложено
ограничение
1. D6.10)
га - + sin#o
а
В частности, при нормальном падении
т\ ^ rf/A. D6.11)
При d < X может возникнуть только главный максимум нуле-
нулевого порядка. Плоская волна после прохождения через решет™
ку продолжает оставаться плоской, и никаких боковых волн не
возникает. Решетка ведет себя подобно плоскопараллельной пла-
пластинке. Но это справедливо только вдали от решетки. В тонком
поверхностном слое вблизи решетки существуют неоднородные
волны, быстро затухающие при удалении от нее (см. § 52).
8. Допустим, что решетка грубая (d^>A), а свет падает на нее
под небольшим углом i?q. Тогда углы дифракции будут малы,
так что вместо D6.8) можно написать приближенно
d.(tf-tf0) =m\. D6.12)
На очень грубых решетках обнаружить дифракцию трудно из™
за малости углов дифракции (# —#о)- Но этого можно добиться,
применяя скользящее падение света, когда угол падения близок
к 90°. При малой разности (# —#о) формулу D6.8) можно пере-
переписать в виде
dcosi?o • (# ~~ #о) = гп\. D6.13)
По виду формула D6.13) совпадает с формулой D6.12). Роль
периода d играет величина d cos #q , которая может быть еде™
лана очень малой. Следовательно, скользящее падение как бы
уменьшает период решетки и увеличивает углы дифракции. Та™
ким путем удается получать отчетливые дифракционные спек™
тры даже от очень грубых решеток, например от граммофонных

§ 46 ДИФРАКЦИОННАЯ РЕШЕТКА 327
пластинок. Последние позволяют в демонстрационной аудито-
аудитории получать в белом свете даже довольно красивые дифракци-
дифракционные спектры разных порядков.
Большое значение метод скользящего падения имеет в рент-
рентгеновской спектроскопии. Изготовление дифракционной решет-
решетки для рентгеновской области спектра встречает большие труд™
ности из-за исключительной малости длин рентгеновских волн
(порядка ОД нм и меньше). Но метод скользящего падения
позволяет получать великолепные дифракционные картины в
рентгеновском свете от обычных отражательных оптических ре-
решеток. Задача облегчается тем, что показатель преломления
рентгеновских лучей меньше единицы. Это позволяет приме-
применять такие углы падения, при которых рентгеновские лучи ис-
испытывают полное отражение. Таким образом, с помощью опти-
оптической дифракционной решетки можно точно измерить длину
волны монохроматического рентгеновского излучения. Изучая
далее дифракцию этого излучения на естественном кристалле,
можно измерить в абсолютных единицах постоянную решетки
этого кристалла. После этого такой кристалл может быть ис-
использован в рентгеновском спектрографе для измерения длин
волн рентгеновских лучей в абсолютных единицах (см. § 61).
ЗАДАЧИ
1. Показать, что для обычной щелевой дифракционной решетки /диф ^
^ У^пад, где 1Пад — интенсивность падающего, а /диф — дифрагированного
света, приходящегося на все дифракционные максимумы, кроме максиму-
максимума нулевого порядка. Максимальное значение интенсивности дифрагиро™
ванного света достигается, когда ширина щелей решетки равна половине ее
периода.
Решение. Если Jo — интенсивность света, сосредоточенного в
максимуме нулевого порядка, а /диф — дифрагированного света, то 1прош =
= Jo + /диф, где Jnpoin — интенсивность прошедшего света. Аналогично, для
дополнительной решетки JnpOm = ^о +^диф- По теореме Бабине /диф = ^диф-
Кроме того,
Jnpoiii _ Ь Jo _ / Ь
1крош d-b' Го \d-b
С учетом этого получаем
т -bd~bT
-*диф — , , -*пад-
а а
Максимум этого выражения достигается при Ь = ^cf, а потому /диф ^
2. При каком условии можно наблюдать зеркальное отражение от ше-
шероховатой поверхности при малых и больших углах падения?
Решение. Обозначим через $ угол, который падающие лучи образу-
образуют с нормалью к плоскости, изображенной на рис. 190 штриховой линией.

328
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
Разность хода вторичных волн, исходящих от поверхности тела под углом
#' к нормали, определяется выражением
А = AD - ВС = a(sintf' - sintf) + h(cosef + costf).
Здесь а может пр н ать любые значения. Поэтому, если $ / if, то А
может принимать также любые значения, и притом для неправильно отра-
Рис. 190
жающей поверхности они с одинаковой вероятностью могут быть и положи-
положительными, и отрицательными. Отсюда следует, что правильное отражение,
если таковое возможно, может происходить лишь под углом $ = $. В таком
случае А = 2/&cos#. Следовательно, каково бы ни было h, можно подобрать
достаточно большой угол $, для которого А <С А. При этом условии отра-
отражение будет правильное. При нормальном падении А = 2/г, и правильное
отражение возможно лишь при соблюдении условия Л<А. Таким образом,
если угол падения близок к тг/2, зер-
зеркальное отражение наблюдается все-
всегда. При малых углах падения зер-
зеркальное отражение может наблюдать-
наблюдаться, если шероховатость поверхности
3. Прозрачная одномерная пери-
периодическая структура, профиль кото-
которой изображен на рис. 191, освещает-
освещается сверху плоской монохроматической
Рис. 191 волной, падающей нормально на верх-
верхнюю границу. Ширины уступов и впа-
впадин структуры одинаковы. При заданном показателе преломления п подо-
подобрать глубину h таким образом, чтобы главные фраунгоферовы дифрак-
дифракционные максимумы первого порядка имели наибольшую интенсивность.
Какова при этом интенсивность нулевого главного максимума?
Ответ, h = А, где т = 1, 2, 3,...
Интенсивность нулевого главного максимума равна нулю.
4. Сложная излучающая система состоит из конечного ряда густо рас-
расставленных параллельных вибраторов с равномерным распределением фаз
колебаний вдоль ряда. Как должен изменяться со временем сдвиг фаз А<р
между двумя соседними вибраторами, чтобы главный лепесток диаграммы
направленности всей системы совершал круговой обзор местности с посто-
постоянной угловой скоростью Q (при отсутствии вращения самой системы)?

47 ДИФРАКЦИОННАЯ РЕШЕТКА КАК СПЕКТРАЛЬНЫЙ ПРИБОР 329
Ответ. Если угол между нормалью к ряду вибраторов и направлением
на главный лепесток i^ = Ot + <5, то
2тг
А(р = —- sin (Ot + 8) + 2штг,
А
где
m = 0,±l,±2,...
5. Над центром граммофонной пластинки Oi помещен точечный не™
точник монохроматического света на высоте hi = 1 см. Глаз наблюдателя
расположен на высоте /г 2 = 10 см на расстоянии а = 110 см от оси пластин-
пластинки. Помимо геометрического изобра-
изображения источника глаз видит систему
дифракционных полос на поверхно-
поверхности пластинки. Определить расстоя-
расстояние Аж между ними, если расстояние
между бороздками d = 0,5 мм. Длина
световой волны Л = 550 нм.
Решение. "Условие максиму-
максимума га-го порядка (рис. 192) d(sin#i —
— sin #2) = ттгА, а максимума (га +
+ 1)-го порядка <i(sini5>i — sin $2) :=:
= (га + 1)Л. При переходе от одно-
одного максимума к другому углы #i и
$2 получают приращения Ai7*i и Ai^,
связанные соотношением <i(cosi^i Ai7*i — cos #2 А 1^2) = А. Кроме того, жх =
= /&itg#i, Ж2 = /&2tg#2, причем Ж1 + Ж2 = а = const. Из этого условия
получается второе соотношение
COS2 17i COS2 172
Из этих двух соотношений находим Ai?i и Ai?2, а после этого — расстояние
между максимумами:
Л-i * п h'2 * п
Рис. 192
Аж = Аж1 = Аж2 =
S2
COS2 1^1 COS2
Результат можно упростить, заметив, что углы $i и $2 мало отличаются
от угла падения $о, соответствующего зеркальному отраж:ению. Заменив
эти углы на #о, находим
A
Аж =
hi + /1,2 dcos3 1
При этом
Q Л,1 hi
cos 1/0 и — ~ —,
Ж1 Ж2
или cos #0 =
Л-2
Ж1 + Ж2
Подстановка числовых значений дает А ж = 1 см.
10'
§ 47. Дифракцмоннам решетка как спектральный
прибор
1. Положение главных максимумов в дифракционной решет™
ке зависит от длины волны. Исключение составляют только

330 ДИФРАКЦИЯ СВЕТА ГЛ. IV
главные максимумы нулевого порядка (га = 0), положения ко™
торых от длины волны не зависят. Белый и всякий сложный
свет можно рассматривать как суперпозицию монохроматиче-
монохроматических волн с различными длинами. Эти волны при дифракции
на решетке ведут себя независимо. Поэтому решетка в каждом
порядке т ф 0 разложит падающий свет в спектр, в котором
отдельные монохроматические компоненты окажутся простран-
пространственно разделенными. Главные дифракционные максимумы,
соответствующие т = 1, образуют спектр первого порядка. За
ним идет спектр второго (т = 2), третьего (га = 3) и высших
порядков. Если падающий свет белый, то спектр каждого поряд-
порядка имеет вид цветной полосы, в которой встречаются все цвета
радуги. В такой полосе наиболее отклоненными будут красные
лучи, наименее отклоненными — фиолетовые.
Положение спектральных линий в спектрах дифракцион-
дифракционной решетки определяется простыми соотношениями D6.4) или
D6.8). В этом отношении дифракционные спектры выгодно
отличаются, например, от спектров призматических, получае-
получаемых разложением света дисперсионными призмами. В призма-
призматических спектрах положение спектральной линии определяет-
определяется сложной зависимостью показателя преломления материала
призмы от длины волны. Спектр называется нормальным^ если
координата ж, характеризующая положение спектральной линии
в спектре, линейно меняется с длиной волны. При малых углах
дифракции, когда изменением косинуса угла $ можно прене-
пренебречь, дифракционная решетка дает нормальный спектр.
Важными характеристиками дифракционной решетки и дру-
других спектральных аппаратов являются угловая дисперсия^ дис-
дисперсионная область и разрешающая способность.
2. Угловая дисперсия. Угловой дисперсией на-
называется производная dfi/dX. Чем больше угловая дисперсия,
тем больше расстояние в спектре между двумя спектральны-
спектральными линиями с фиксированными длинами волн. Дифференцируя
формулу D6.8) при постоянном #q, находим для решетки
d'd т sinё — sin#o /лгу -i \
Следовательно, угловая дисперсия не зависит от параметров
решетки, а определяется^ помимо длины волны^ только углами
t? и t?0. При заданных ёшт она возрастает с увеличением угла i?.
Наличие косинуса в знаменателе объясняет выгоду скользящего
падения (см. конец предыдущего параграфа).
3. Дисперсионная область. Если спектры соседних
порядков перекрываются, то спектральный аппарат становится
непригодным для исследования соответствующего участка спек-
спектра. Максимальная ширина спектрального интервала АЛ, при

§ 47 ДИФРАКЦИОННАЯ РЕШЕТКА КАК СПЕКТРАЛЬНЫЙ ПРИБОР 331
которой еще нет перекрытия^ называется дисперсионной обла-
областью спектрального аппарата. Найдем дисперсионную область
для дифракционной решетки. Пусть длины волн падающего из™
лучения лежат в спектральном интервале от А до А; = А + А А.
Пусть правый конец спектра (га + 1)-го порядка для длины вол-
волны А совпадает по своему положению с левым концом спектра
га-го порядка для длины волны А; (см. рис. 182). Тогда
— sin#o) — ^
sIii^q) = (га
Отсюда mXf = (га + 1)A, а следовательно,
A; - A = ДА = A/m. D7.2)
Это и есть дисперсионная область дифракционной решетки в
рассматриваемом участке спектра. При заданной длине волны
она определяется только порядком спектра га. Чем больше га,
тем уже дисперсионная область. В дифракционных решетках
используются спектры низких порядков (обычно второго или
третьего). Поэтому дифракционные решетки характеризуются
широкими областями дисперсии и пригодны для исследования
широких участков спектра. В этом основное преимущество ди-
дифракционных решеток перед интерференционными спектраль-
спектральными аппаратами, у которых из-за высоких порядков га диспер-
дисперсионные области очень узкие.
4. Разрешающая способность. Большая дис-
дисперсия еще не означает, что две спектральные линии с близкими
длинами волн А и X1 = А + ёХ разрешаются спектральным аппа-
аппаратом, т.е. при их наблюдении воспринимаются как раздельные
спектральные линии. Каждая спектральная линия, как бы узка
она ни была, изображается спектральным аппаратом не в виде
линии, а в виде более или менее размытой дифракционной кар-
картины с максимумами и минимумами интенсивности. Дисперсия
определяет расстояние, на которое спектральный аппарат раз-
разводит центры дифракционных картин, возникающих от двух
спектральных линий с различными длинами волн. Если сами
картины размыты и имеют значительную ширину, то далее при
сравнительно большом разведении их результирующая картина,
возникающая от их наложения, неотличима от дифракционной
картины, возникающей от одиночной спектральной линии. Чем
уже дифракционные картины от двух близких спектральных
линий, тем на меньшее расстояние требуется развести их цен-
центры, чтобы разрешить эти спектральные линии. Наименьшая
разность длин волн двух спектральных линий <5А, при кото-
которой спектральный аппарат разрешает эти линии^ называет-
называется спектральным разрешаемым расстоянием^ а величина R =
= Х/5Х — разрешающей способностью аппарата.

332 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Разрешаемое спектральное расстояние SX относится к числу
не вполне точно определенных понятий и может быть указа-
указано лишь ориентировочно. Для дифракционной решетки Рэлей
предложил следующий критерий спектрального разрешения.
Спектральные линии с близкими длинами волн X и У счита-
считаются разрешенными, если главный максимум дифракционной
картины для одной длины волны совпадает по своему положе-
положению с первым дифракционным минимумом в том же порядке
для другой длины волны. Если такой критерий выполняется, то
на основании формулы D6.9) можно написать
d(sin# — sin#o) = f m, 4- ^-jr J A,
Отсюда (га + 1/N)X = mXf, и следовательно, SX = X1 — X =
= X/(NmI
R=^r = Nm. D7.3)
д А
С целью обоснования критерия Рэлея начертим распределе-
распределение интенсивности для спектральных линий А и А;, сдвинутых
одна относительно другой на расстояние 5Х (рис. 193). Так как
спектральные линии с различными
X X длинами волн некогерентны, то ре™
зультирующая интенсивность най-
найдется простым сложением интен™
сивностей обеих линий. Она пред-
представлена на рис. 193 сплошной
кривой, когда интенсивности обе-
обеих спектральных линий одинако™
вы, а расстояние между ними SX
соответствует критерию Рэлея. В
центре кривой получился провал
Рис. 193 или минимум, интенсивность в ко™
тором, как легко подсчитать, со™
ставляет около 80 % максимальной. При наличии такого провала
нормальный глаз обычно воспринимает получившуюся картину
как «двойную спектральную линию».
5. Для повышения разрешающей способности можно либо
увеличивать число штрихов Ж, либо повышать порядок ин-
интерференции га. Первый путь используется в дифракционных
решетках, второй — в интерференционных спектральных при-
приборах. В Советском Союзе изготовляются плоские и вогну™
тые дифракционные решетки различных размеров и с раз-
различным числом штрихов на миллиметр. Для ультрафиолето™
вой и видимой областей изготовляются дифракционные решет™
ки, имеющие 1200 и 600 штрихов на миллиметр при размерах

§ 47 ДИФРАКЦИОННАЯ РЕШЕТКА КАК СПЕКТРАЛЬНЫЙ ПРИБОР 333
100 х 100 мм2 и 150 х 150 мм2, а для инфракрасной области — от
300 до 1 штриха на миллиметр при размерах от 150 х 150 мм2 до
300x300 мм2 Таким образом, общее число штрихов доходит при-
приблизительно до 200 000, а разрешающая способность во втором
порядке — до 400 000. Важным достоинством дифракционной
решетки является малый порядок спектра га. Благодаря этому
дифракционные решетки обладают широкими дисперсионными
областями АЛ = А/га и пригодны для исследования широких ин-
интервалов спектра. Недостатками дифракционных решеток яв-
являются малая светосила и сложность в обращении.
В интерференционных спектральных приборах число интер-
интерференционных пучков N относительно невелико (несколько де-
десятков, в интерферометре Майкельсона п = 2), тогда как поряд-
порядки спектров га очень высоки (около 10 000 и больше). Поэтому
интерференционные спектральные приборы имеют малые дис-
дисперсионные области. Они могут применяться для исследования
только очень узких участков спектра^ например для изучения
структуры отдельных спектральных линий, выделенных каким-
либо другим спектральным аппаратом с большей дисперсионной
областью, но с недостаточной разрешающей способностью. Од-
Однако эти приборы более просты в обращении и имеют большую
светосилу, чем дифракционные решетки.
6. К решетке, как точному спектральному прибору, предъявляются
очень высокие требования. Надо нанести десятки или сотни тысяч совер-
совершенно идентичных штрихов с идеальной периодичностью. Поэтому техника
изготовления дифракционных решеток совершенствовалась довольно мед-
медленно. Первая дифракционная решетка, по-видимому, была изготовлена в
1785 г. американским астрономом Риттенгаузом. Но ни самим Риттенгаузом
и никем другим она не использовалась для получения и изучения спектров.
Решетка была вновь открыта в 1821 г. Фраунгофером, который заложил
основы дифракции в параллельных лучах и выполнил первые исследова-
исследования с помощью дифракционного спектроскопа (в частности, открыл темные
линии в спектре солнечного излучения). Фраунгофер построил решетки с
числом штрихов от 15 до 130 на сантиметр, наматывая тонкую проволоку на
два параллельных винта. До недавнего времени подобные проволочные ре-
решетки применялись в области длинных (инфракрасных) волн. Затем Фра-
Фраунгофер стал изготовлять более совершенные решетки штриховкой слоя
золота на поверхности стекла и, наконец, штриховкой самого стекла ал-
алмазным острием. Наилучшие решетки были получены последним методом.
Лучшая решетка имела ширину около 12 мм и период 3 • 10~ мм C300
штрихов на сантиметр).
После Фраунгофера многие искусные механики уделяли много вни-
внимания штриховке решеток. Особо следует отметить астронома-любителя
Л.М. Резерфорда, большая часть решеток которого была изготовлена в
1880 г. Его решетки значительно превосходили все предшествующие. Ре-
зерфорд ввел в практику отражательные решетки, нанося делительной ма-
машиной штрихи на зеркальной поверхности металла. Металл более мягок,
чем стекло, и поэтому значительно меньше изнашивает алмазное острие,
от постоянства которого так сильно зависит качество решетки.

334 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Но наиболее значительные усовершенствования были сделаны Роулэн™
дом A848-1901). Он усовершенствовал способы изготовления винтов для
делительной машины и первый стал изготовлять вогнутые отражатель-
отражательные решетки, выполняющие одновременно функции решетки и собираю-
собирающей линзы. Решетки Роулэнда имели до 8000 штрихов на сантиметр при
ширине до 10 см и превосходном качестве. Они сделали возможным выпол-
выполнение важнейших спектроскопических исследований в конце XIX и начале
XX веков.
Дальнейшие улучшения в машины Роулэнда ввели Андерсон и Вуд,
которые после смерти Роулэнда заменили его в его лаборатории. Из этой
лаборатории и поныне выходят наиболее совершенные решетки, имеющие
до 12 000 штрихов на сантиметр. С таких гравированных решеток получа-
получают дешевые копии (реплики) путем изготовления отпечатков на желатине
или специальных пластмассах. В СССР налажено производство дифрак-
дифракционных решеток, а также реплик высокого качества. Их параметры были
указаны выше.
§ 48. Эшелон Майкельсона и интерференционные
спектральные приборы
1. Дифракционная решетка, как уже указывалось, есть спек-
спектральный прибор, в котором осуществляется многолучевая ин-
терференция идентичных световых пучков, из которых каждый
сдвинут по фазе относительно предыдущего на одну и ту же
величину. Ко всем приборам, работающим по этому принци-
пу, применимы общие результаты, изложенные в двух преды-
предыдущих параграфах. В частности, их спектральная разрешаю-
разрешающая способность выражается формулой \/8\ = Nm, т.е. равна
разности хода между крайними интерферирующими лучами^
выраженной в длинах волн. Высокая разрешающая способность
достигается как увеличением числа интерферирующих пучков
JV, так и повышением порядка интерференции га. В дифракци-
онных решетках число интерферирующих пучков очень велико
(до 200 000 и больше), а порядки интерференции т низкие (не
выше 3). В так называемых интерференционных спектральных
приборах^ наоборот, порядки интерференции т очень высокие
(до 10 и выше), а число интерферирующих пучков сравнитель-
сравнительно невелико B0-40). Одним из таких приборов является ступен-
ступенчатая решетка, или эшелон Майкельсона.
2. Эшелон Майкельсона состоит из нескольких C0-40) пла-
пластин из очень однородного стекла, толщина h которых порядка
1-3 см. Толщина пластин должна быть совершенно одинакова с
точностью до сотой длины волны. Поэтому их вырезают из од-
одной и той же плоскопараллельной пластины, постоянство тол-
толщины которой контролируется интерференционными методами.
Пластины сложены в виде ступенчатой лестницы (рис. 194).

48
ИНТЕРФЕРЕНЦИОННЫЕ СПЕКТРАЛЬНЫЕ ПРИБОРЫ
335
Ширина ступеньки а должна быть одной и той же на протя-
протяжении всей «лестницы». Получается как бы сплошной кусок од-
однородного стекла, ступенчатая поверхность которого действу™
ет как дифракционная решетка. Пусть на эшелон нормально
падает пучок параллельных лучей. Разность хода между вто-
вторичными волнами Гюйгенса, исходящими под углом # от сосед™
них ступенек эшелона и приходящими в соответствующую точ-
Рис. 194
Рис. 195
ку фраунгоферовой дифракционной картины, будет (BDF) —
— АЕ = nh + a suit? — /icosi? (рис. 195). Положения главных
максимумов определяются условием
nh + asin# — /icosi? = гаА, D8.1)
где т — целое число.
Из D8.1) дифференцированием находим угловую дисперсию
D8.2)
D8.3)
dX a cos # + h sin $'
или, ввиду малости угла #, d§/d\ = т/а, или
М _ h(n-l)
dX aX
Так как h ~ а, то угловая дисперсия эшелона относительно ве™
лика. Поэтому при незначительных изменениях А получаются
заметные изменения угла дифракции #.
Дисперсионная область эшелона определяется выражением
А
Л2
АЛ _ А _
т h(n — 1)
D8.4)
Она очень мала, и это является недостатком эшелона. Напри™
мер, при h = 1 см, п = 1,5, А = 600 нм получаем АА « 0,07 нм,

336 ДИФРАКЦИЯ СВЕТА ГЛ. IV
что примерно в 10 раз меньше расстояния между компонентами
желтой D-линии натрия.
Разрешающая способность дается формулой
± = Nm= iVft("-1), D8.5)
где N — число пластин. При N = 40 в предыдущем примере
получим X/SX ~ 3,3 • 105. Со штриховой решеткой в спектре пер-
первого порядка такой разрешающей способности молено было бы
достигнуть при числе штрихов порядка 300 000.
Уточним формулу D8.5), приняв во внимание дисперсию по™
казателя преломления стекла. Пусть при угле дифракции i? по™
лучается дифракционный максимум га-го порядка для длины
волны А; = А + 6Х. Тогда
hn + asini? — hcosfl = га А' = га(А + JA),
где п1 — показатель преломления стекла для той же длины вол-
волны. Согласно Рэлею, SX будет равна разрешаемому спектрально™
му расстоянию, если для длины волны А в том же направлении
получится первый дифракционный минимум, т.е.
hn + a sin $ — h cos $ = гаА + X/N.
Вычитая это соотношение из предыдущего, получим
или после подстановки т = h(n — 1)/Х
Так как в прозрачной области спектра dn/dX < 0 (нормаль™
ная дисперсия), то дисперсия показателя преломления повыша-
повышает разрешающую способность эшелона.
Рассуждая аналогично, легко получить следующие выраже-
выражения для дисперсионной области и угловой дисперсии эшелона:
АЛ = j^-jjtt, D8.
т — h(dn/d\)
т
— h(dn/d\) /до q\
d\ a cos •& + h sin §'
Дисперсия показателя преломления увеличивает угловую дис-
дисперсию эшелона, но уменьшает его дисперсионную область.
Интенсивность света в дифракционной картине, разумеется,
определяется общей формулой D6.2). В ней /i(#) означает ин™
тенсивность, которая получилась бы при дифракции на отдель-
отдельной ступеньке эшелона ширины а. Функция /i(#) такая же, что
и при дифракции на щели. Поэтому весь дифрагированный свет

§ 48 ИНТЕРФЕРЕНЦИОННЫЕ СПЕКТРАЛЬНЫЕ ПРИБОРЫ 337
практически концентрируется в интервале углов $ между t?i =
= —А/а и i?2 = +А/а. Заметную интенсивность будут иметь
только такие главные максимумы, которые попадают в указан™
ный интервал. Ввиду малости угла i? можно пренебречь его ква-
дратами, представив формулу D8.1) в виде (п — l)h + at? = гаА,
или
1? = wA"(aW)fe. D8.10)
Допустим, что показатель преломления таков, что для опре-
деленного га числитель в этой формуле обращается в нуль. То-
Тогда в указанный интервал попадут только три главных максиму-
максимума, порядки которых равны (га — 1), га, (га + 1). Крайние из них
приходятся на концы интервала, их интенсивность равна нулю.
Поэтому дифрагированный свет будет состоять только из спек™
тра одного порядка га. Если же числитель в формуле D8.10) не
равен нулю, то будут видны спектры двух соседних порядков,
вообще говоря, разной интенсивности. Их интенсивности будут
одинаковы, когда числитель в формуле D8.10) по абсолютной
величине равен А/2. Таким образом, возможны такие установки
эшелона, при одной из которых получается только один дифрак-
дифракционный максимум, а при другой — два одинаковых симметрии™
ных максимума. Чтобы перейти от одной установки к другой,
эшелон обычно помещают в герметическую камеру и изменяют
в ней давление, а с ним и относительный показатель преломле-
преломления п, пока не будут достигнуты требуемые для работы условия.
Майкельсону принадлежит также идея использования эше-
эшелона как отражательной решетки. Такой эшелон был построен
Вильямсом в 1933 г. из пластин плавленого кварца. Тщательно
очищенные пластины кварца сажались на оптический контакт и
нагревались до температуры, значительно меньшей температу-
температуры плавления кварца. В результате пластины прилипали друг
к другу настолько прочно, что после охлаждения их удавалось
отделить одна от другой только при значительном усилии. От-
Отражающие ступеньки эшелона покрывались алюминием, напы-
напыленным в вакууме.
3. В эшелоне Майкельсона интерферирующие пучки возни-
возникают в результате дифракции на ступеньках. В чисто интер-
интерференционных спектроскопах — интерферометре Фабри-Перо
и пластинке Луммера-Герке — они образуются в результате от-
отражений света. Эти приборы уже были рассмотрены в § 36.
Получаемый в них спектр определенного порядка есть не что
иное, как интерференционная полоса равного наклона. Диспер-
Дисперсионная область, конечно, определяется общей формулой D7.2).
Для интерферометра Фабри-Перо порядок спектра га можно
вычислить по формуле га = 2/i/A, где h — расстояние между
отражающими поверхностями интерферометра. Для пластинки

338 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Луммера-Герке то же самое молено сделать по формуле C6.7),
заменяя в ней ф предельным углом полного отражения. Это да-
дает
m=2W~1. D8.11)
А
Остановимся еще на разрешающей способности интерферо-
метра Фабри-Перо и пластинки Луммера-Герке. В них интерфе-
интерферируют пучки, интенсивность которых медленно убывает с воз™
растанием номера пучка. Если бы число пучков было бесконеч-
бесконечно, как предполагалось при вычислениях в § 36, то спектр содер-
содержал бы только одни главные максимумы (см. рис. 141) и никаких
добавочных максимумов и минимумов1). В этом случае крите-
рий спектрального разрешения Рэлея теряет смысл. Поэтому
в § 36 был дан другой критерий. Для разрешающей способно-
способности интерферометра Фабри-Перо он приводит к формуле C6.5),
имеющей тот же вид, что и формула D7.3). Роль числа интерфе-
интерферирующих пучков N играет величина N = 2тгу/В,/A — Д), прак-
практически равная 2тг/A — R). В этом нет ничего неожиданного,
так как интуитивно следует ожидать, что убывание интенсив-
интенсивности эквивалентно ограничению числа эффективно действую-
действующих пучков без учета их ослабления. Число таких эффективных
пучков, очевидно, пропорционально 1/A — R).
Что касается пластинки Луммера-Герке, то для нее в фор-
формулу C6.5) необходимо ввести поправку на зависимость пока-
показателя преломления стекла от длины волны А, а также на ко-
конечное число интерферирующих пучков. Поэтому мы повторим
вывод формулы C6.5) с этим уточнением, считая сначала число
интерферирующих пучков бесконечным. Сохраняя обозначения
прежнего вывода, пишем, как и раньше, <5Ф = A — R)/\fR1 при-
причем в максимуме m-го порядка Ф = 2жт1 а во всех остальных
точках Ф = Dтг'dn cos ф)/\. Однако теперь величины п и ф име-
имеют разные значения для А и А;. Общим для них является только
угол падения (так как свет исследуется вне пластинки), а потому
пБтф = п1 ш\ф' = шар. Следовательно, должно быть
8Ф дп simp S ф 6\
Ф п costp X
при условии
— + ^f &Ф = 0.
п simp
Исключив 5ф^ получим
М> _ 1 8п _ ^А
Ф cos2 ф п X
) Реально они, конечно, есть из-за ограниченности числа интерфери-
интерферирующих пучков.

§ 49 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ПРИЗМЫ 339
Подставим сюда значения 5Ф,Ф = 2ттг, а также 5п = (dn/d\)8X.
Тогда
Л 2тгл/Кт Л _ 1 \dn\ /,o in\
<5Л 1 — R\ cos2 фпdX/
Эта формула выведена в предположении бесконечного числа
интерферирующих пучков. Она была бы применима к интерфе-
интерферометру Фабри-Перо, если бы в нем пространство между отра-
отражающими зеркалами было заполнено однородной средой, пока-
показатель преломления п которой отличен от единицы (для такого
интерферометра можно было бы положить cose/? = l). Для пла-
пластинки Луммера-Герке формула неприменима из-за ограничен-
ограниченного числа интерферирующих пучков. В этом случае, как ясно
из изложенного выше, формулу надо заменить на
D8.13)
Xdn
cos2 ф п
После подстановки значений N', т и cos ф получаем
Jx=L i^Y^ ~ п ж) ' D8.14)
Аналогично, для дисперсионной области
АЛ = -г^ ,-. D8.15)
\ п2 — 1 dXJ
Из-за дисперсии показателя преломления стекла разрешающая
способность пластинки Луммера-Герке возрастает, а дисперси-
дисперсионная область уменьшается.
§ 49. Разрешающая способность призмы
1. Действие призмы как спектрального прибора основано на
зависимости показателя преломления вещества от длины вол-
волны. Для определения разрешающей способности призмы необ-
необходимо учесть дифракцию света на краях диафрагмы или са-
самой призмы, ограничивающих ширину падающего светового
пучка. Допустим сначала, что на призму падает монохромати-
монохроматический параллельный пучок лучей, ограниченный диафрагмой
АА1 (рис. 196). Пусть волновой фронт падающей волны совпа-
совпадает с плоскостью диафрагмы АА1. Возьмем за призмой произ-
произвольный волновой фронт ВВ1. По определению волнового фрон-
фронта оптические длины (ACDB) и (A'C'D'B') одинаковы:
АС + па + DB = А1 С + nb + D'B1, D9.1)
где а и Ъ — геометрические длины CD и С1'D1', проходимые све-
светом в веществе призмы.

340
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
Рис. 196
Если крайние точки В ж В1 сместить бесконечно мало вдоль
плоскости В В' и соединить их с А и А' бесконечно близкими
виртуальными лучами, то в силу принципа Ферма равенство
D9.1) сохранится с точностью до членов высших порядков от™
носительно этих боковых смещений. Это приводит к следующе-
следующему правилу построения волнового фронта. Надо от точек исход-
исходного волнового фронта
провести действитель-
действительные или бесконечно
близкие к ним вирту-
виртуальные лучи и отложить
на них отрезки одинако-
одинаковой оптической длины.
Геометрическое место
концов таких отрезков
и даст новое положение
волнового фронта. В
случае плоских волно-
волновых фронтов достаточно ограничиться построением крайних лу-
лучей ACDB и A'C'D'B1'. При построении волновых фронтов,
отличающихся бесконечно мало своими направлениями, можно
пользоваться одними и теми же световыми путями, хотя истин-
истинные пути света и отличаются друг от друга. То же справедливо
для световых пучков, бесконечно мало отличающихся длинами
волн. Это используется ниже для упрощения вычислений.
Учтем теперь дифракцию света на краях диафрагмы АЛ! и
определим за призмой направления на нулевой дифракционный
максимум и дифракционные минимумы. Проведем крайние лу-
лучи ACDB и A'C'D'B1', которые могут быть либо действительны-
действительными, либо бесконечно близкими к ним виртуальными, и пересечем
их произвольной плоскостью ВВ'. (Мы не предполагаем теперь,
что плоскость В В1 перпендикулярна к световым лучам.) Если
разность оптических длин (ACDB) и (A'C'D'B') равна нулю,
то плоскость В В' будет одним из волновых фронтов. Нормаль
к ней укажет направление на главный максимум, т.е. максимум
нулевого порядка. Если же эти оптические длины отличаются на
целое число длин волн, то, как и при дифракции на щели, нор™
маль к плоскости В В' укажет направление на дифракционный
минимум соответствующего порядка. В частности, если опти-
оптические длины отличаются на А, то получится дифракционный
минимум первого порядка.
2. Теперь нетрудно вывести формулу для разрешающей спо-
способности призмы. Предположим, что на диафрагму падает па-
параллельный пучок света с двумя длинами волн А и А'. Пусть
плоскость В В' есть волновой фронт для длины волны А;. Нор-

§ 49 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ПРИЗМЫ 341
маль к ней определяет направление на нулевой максимум для
длины волны X1'. Пусть то же направление есть направление на
дифракционный минимум первого порядка для длины волны А.
Согласно критерию Рэлея разность 6Х = А; — А есть минималь-
минимальное расстояние, разрешаемое призмой. На основании сказанного
выше
АС + n(Xf)a + DB = AfCf + n(X')b + D'B\
AC + n(X)a + DB = А'С + n(X)b + DfBf + A.
Вычитая почленно, получим
(a - b)[n(Xf) - n(X)] = -A,
или
/ i \ dfl с л л
(a — Ъ)—оХ = —A.
Отсюда для разрешающей способности призмы получаем
*. = -(а-Ъ)?х. D9.2)
Из вывода ясно, что под А следует понимать длину волны в
вакууме. Предполагается, что дисперсия стекла нормальная, т.е.
dn/dX < 0.
Разрешающая способность призмы зависит только от дис-
дисперсии показателя преломления dn/dX и разности путей а и
Ь, проходимых в призме крайними лучами пучка. Поэтому для
полного использования разрешающей способности необходимо,
чтобы световой пучок покрывал всю боковую поверхность приз™
мы, на которую он падает. В этом случае Ъ = 0, а а означает
длину основания призмы. Например, для стеклянной призмы из
тяжелого флинта в желтой области спектра dn/dX^ ^956 см.
Разрешающая способность призмы при а = 1 см в указанной
области спектра будет Х/ёХ^956. Это минимальная разрешаю™
щая способность, при которой может быть разрешена двойная
D-линия натрия (А = 589,0 нм, X1 = 589,6 нм).
Для сложной призмы, состоящей из нескольких простых
призм, поставленных одна за другой, формула D9.2) должна
быть заменена на
? -fc)?. D9.3)
Здесь суммирование производится по всем призмам, составляю-
составляющим систему.
3. Призму можно рассматривать как предельный случай
эшелона Майкельсона (см. рисунки 194 и 195). Допустим, что
ширина и высота ступеньки эшелона стремятся к нулю, а об™
щее число ступенек — к бесконечности. При этом последова-
последовательно будут исчезать спектры высших порядков, пока не оста-

342 ДИФРАКЦИЯ СВЕТА ГЛ. IV
нется только спектр нулевого порядка. Начиная с этого момен™
та, эшелон будет действовать как призма. При т = 0 формула
D8.6) перейдет в формулу D9.2), так как Nh есть длина основа-
основания призмы. Для дисперсионной области в этом случае формула
D8.8) дает АЛ = оо. Этого и следовало ожидать, так как весь
свет, выходящий из призмы, концентрируется в спектре нуле™
вого порядка, а потому вопрос о наложении спектров разных
порядков не возникает.
ЗАДАЧИ
1. Какую разрешающую силу должен иметь спектральный аппарат для
разрешения дублета D-линии натрия (Ai = 589,0 нм, Аг = 589,6 нм)? Под-
Подсчитать минимальное число штрихов решетки, которая может разрешить
его в спектре первого порядка. При каком наименьшем основании а можно
сделать то же самое с помощью призмы, изготовленной из стекла с диспер-
дисперсией dn/dX = —956 см™1?
Ответ. 1) Х/8Х > 1000; 2) N ~ 1000; 3) а и 1 см.
2. Изменяется ли разрешающая сила решетки при изменении наклона
первичного пучка, падающего на нее?
Ответ. Нет.
3. Изменится ли разрешающая способность и дисперсионная область
дифракционной решетки, если, закрепив неподвижно трубу, в которую на-
наблюдаются дифракционные спектры, закрыть через одну щели решетки?
Ответ. Разрешающая способность не изменится. Дисперсионная
область уменьшится вдвое.
4. На плоскую отражательную решетку, содержащую N = 50 000 штри-
штрихов, нормально падает свет от двойной линии натрия (Ai = 589,0 нм, Аг =
= 589,6 нм). Число штрихов, приходящееся на 1 см длины решетки, равно
п = 5000. Какой максимальный порядок спектра т можно получить от та-
такой решетки и каково минимальное расстояние 8X между спектральными
линиями, которое способна разрешить решетка в указанной области спек-
спектра? Спектр максимального порядка фотографируется на фотопластинке с
помощью объектива с фокусным расстоянием / = 50 см. Какое расстояние
Аж между спектральными линиями Ai и А 2 получится на фотопластинке?
*6
Ответ, т = 3; SX = -?- = 0,004 нм; Ах = . *т6Х = 1 мм.
Nm л/d2 -т2Х2
5. Как изменится разрешающая способность и дисперсионная область
пластинки Луммера-Герке, если 1) ее толщину увеличить вдвое, а длину
оставить без изменения; 2) длину увеличить вдвое, а толщину оставить без
изменения?
Ответ. 1) Разрешающая способность не изменится, дисперсионная
область уменьшится вдвое. 2) Разрешающая способность увеличится вдвое,
дисперсионная область не изменится.
6. Какую минимальную длину должна иметь пластинка Луммера-Герке
(п = 1,5), чтобы разрешить дублетную структуру водородной линии Ша
(А = 656,3 нм)? Разность длин волн линий дублета равна 0,014 нм. Прене-
Пренебречь величиной dn/dX.
X2
Ответ. L = -г— г-—— = 2,5 см.
(п2 — 1) оХ

§ 49 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ПРИЗМЫ 343
7. Какая интерференционная картина будет наблюдаться при осве-
освещении монохроматическим светом двух скрещенных пластинок Луммера™
Герке, т.е. двух пластинок, расположенных одна за другой вдоль прямой
линии, но повернутых друг относительно друга на 90°?
Ответ. Будет наблюдаться система пятен, расположенных в узлах
прямоугольной сетки.
8. Какой должна быть длина а основания стеклянной призмы, чтобы
она имела такую же разрешающую способность, как и пластинка Луммера—
Герке длиной L = 20 см? Показатель преломления пластинки п = 1,5; дис-
дисперсия показателя преломления призмы drinp/dX = ^956 см~~ ; Л = 600 нм.
гл L(n-l) ..
Ответ, а = —--- т— = 44 м.
/
/
9. Эшелон Майкельсона состоит из N = 30 стеклянных пластинок с
показателем преломления п = 1,5; толщина каждой из них h = 1 см. Како-
Какова должна быть длина а основания стеклянной призмы, чтобы она имела
такую же разрешающую способность, что и рассматриваемый эшелон? Дис-
Дисперсия показателя преломления призмы dnUp/d\ = 956 см"" ; Л = 600 нм.
„ Nh(n - 1)
Ответ, а = Л т . ' = 2,6 м.
ап/ал
10. Стеклянная призма с основанием а = 10 см изготовлена из тя-
тяжелого флинта, дисперсия которого в окрестности Л = 600 нм равна
dn/dX = 1000 см™1. Какую максимальную разрешающую способность мо-
может иметь дифракционная решетка, ширина заштрихованной части кото-
которой равна длине основания этой призмы? Сравнить разрешающую способ-
способность такой решетки с разрешающей способностью призмы.
Решение. Из формулы решетки d{sm§ — sin#o) = fnX следует
тХ ^ 2d. Отсюда умножением на N = a/d получаем для максимальной
разрешающей способности решетки
Дреш = Nm = -^ = 3 • 105 и —^ = ' = 33.
Л Япр dn/dX
Из этого примера видно, что при одних и тех же геометрических разме-
размерах разрешающая способность решетки, вообще говоря, много больше, чем
призмы.
11. Оценить ширину коллиматорной щели, при которой практически
полностью используется теоретическая разрешающая способность призмы.
Решение. Предельная разрешаю-
разрешающая способность призмы найдется из фор-
формулы D9.2), если положить 6 = 0. Пусть
на призму падает плоская волна, содержа-
содержащая длины волн Л и Л , расстояние между
которыми ^Л равно минимальному расстоя-
расстоянию, разрешаемому призмой. Разность по-
показателей преломления для этих длин волн
$п = (dn/dX)SX. Подставляя сюда <5А =
\ К dn\ л А тт
= Л / I а —— I, получим on = —. По выхо-
/ \ аХ) а
де из призмы первоначально параллельный Рис. 197
пучок света из-за дисперсии сделается рас-
расходящимся. Рассчитаем угловое расхождение вышедшего пучка. Как видно
из рис. 197, sin (pi = 7isin ^i. Дифференцируя при постоянном (pi, находим:
f n cos ф\ • ёф\ = 0. Так как ф\ + гр2 = А = const и, следовательно,

344 ДИФРАКЦИЯ СВЕТА ГЛ. IV
8ф\ + Stp2 = 0, то 8п sin фг = псоъф\ • 8ф2. Из закона преломления sin if 2 =
= п sin Ф2 находим искомое угловое расхождение вышедшего пучка:
sinФ2 _ пcosФ2 r , /sin^2 ncos 1^2
0W + 0^2 = +
0W + 0^2 + T
COS Lp2 COS у?2 \C0S(^2 COS (^2 ПСОБф\
При работе призма должна быть установлена на угол наименьшего откло-
отклонения, а потому (fi = (f2 = <р, ф\ — фч — фу
sin t^ sin ф А
д(р2 = 2 on = 2 .
cos у? cos (f a
Если h — ширина щели, / — фокусное расстояние коллиматора, то угловая
ширина щели будет а = h/f. Для полного использования разрешающей
способности призмы угол а должен быть мал по сравнению с углом Stp2-
Практически достаточно, чтобы угол а был меньше приблизительно поло-
половины угла 5(f2- Это дает
^^ D9.4)
cos Lp a
Так как ф = А/2, то
h < , Sia^2) !±. D9.5)
у/1 -п2 sin2'(A/2) a
При а = 10 см, А = 60°, п = 1,73, / = 25 см, Л = 500 нм последняя формула
дает h < 1,2 • 1Q~3 мм.
§ 50. Действие спектрального аппарата на световые
импульсы
1. В предыдущих параграфах спектральный аппарат рассма™
тривался как анализатор^ пространственно разделяющий моно-
монохроматические волны, уже имеющиеся (согласно теореме Фу-
Фурье) в световом возмущении, попадающем в этот прибор. Но на
него можно также смотреть как на генератор, который под дей-
действием непериодических возмущений (импульсов) вырабатыва-
вырабатывает периодические возмущения и пространственно разделяет их.
Проще всего такой подход разъяснить на примере дифракцион-
дифракционной решетки.
Предположим, что решетка состоит из бесконечного числа
равноотстоящих щелей в непрозрачном экране. Пусть на нее
нормально падает какое™либо плоское непериодическое возму™
щение. Его форма для последующих рассуждений не имеет зна-
значения. Для наглядности будем изображать его в виде бесконеч-
бесконечно короткого прямоугольного импульса (рис. 198). Достигнув в
момент to всех точек решетки, импульс возбудит вторичные ци-
цилиндрические волны, исходящие от щелей решетки. Вместо оди-
одиночного импульса за решеткой получится бесконечное множе-
множество следующих друг за другом пространственно разделенных

50
СПЕКТРАЛЬНЫЙ АППАРАТ И СВЕТОВЫЕ ИМПУЛЬСЫ
345
импульсов с цилиндрическими волновыми фронтами (рис. 199).
Сечения волновых фронтов плоскостью чертежа в любой фик-
фиксированный момент времени t 6vhvt окпчжяостямм ояного и то™
Рис. 198
Рис. 199
го же радиуса c(t ~~ to), описанными из щелей решетки как из
центров (рис. 200). На больших расстояниях от решетки малые
участки волновых фронтов могут рассматриваться как плоские
и следующие друг за другом через равные промежутки времени
т = ^. E0.1)
На таких расстояниях возмущение представляется периодиче-
ской функцией E(t), период которой т зависит от угла #, т.е.
от направления излучения. Вместо непериодического импульса
решетка создает пространственно разделенные периодические
возмущения различных
периодов. Исключение
составляют импульсы, _
которые за решеткой
распространяются под
углом § = 0. В этом слу-
случае разложения не бу-
будет. Эти периодические
возмущения, вообще го-
говоря, не синусоидаль-
синусоидальны. Но, как и всякие пе-
периодические функции,
они могут быть разло-
разложены в ряд Фурье с
основным периодом т.
Для понимания действия решетки такое разложение не обяза-
обязательно. Но оно целесообразно, когда приемниками излучения в
спектроскопах и спектрографах являются глаз, фотографиче-
фотографическая пластинка и другие селективные приемники. Они действу-
действуют подобно набору гармонических осцилляторов с различными
собственными частотами.
Ряд Фурье, в который может быть разложено периодическое
возмущение E(t), вообще говоря, будет содержать монохромати-
монохроматическую волну с основным периодом т. Наряду с ней могут войти
гармоники с периодами т/2, т/3, .... Не все эти гармоники вос-
воспринимаются приемником. В простейшем случае только одна из
Рис. 200

346 ДИФРАКЦИЯ СВЕТА ГЛ. IV
них, например гармоника с периодом т/т, действует на прием™
ник. Обозначим ее период через Т. Тогда Т = — = , или
т cm
dsin^ = m\. E0.2)
Это — основная формула дифракционной решетки. Но могут
быть и такие случаи, когда разложение Фурье содержит две
или больше гармоник, действующих на приемник. Тогда име-
имеет место перекрытие спектров разных порядков. Это, однако,
возможно только тогда, когда падающее излучение заполняет
спектральный интервал, ширина которого превосходит диспер-
дисперсионную область решетки.
Рассмотрим теперь воздействие на решетку единичной мо-
монохроматической волны с периодом Т. Вторичные волны, выхо™
дящие в этом случае из щелей решетки, а потому и их суперпо-
суперпозиция будут монохроматическими с тем же периодом Т. Значит,
монохроматическая волна после прохождения через спектраль™
ный аппарат остается монохроматической без изменения перио-
периода. Отсюда и из принципа суперпозиции следует, что в спектре
решетки не могут появиться монохроматические составляю-
составляющие с частотами, отсутствующими в спектре падающего из-
излучения. Если спектральная область, занимаемая падающим из-
излучением, не превосходит дисперсионную область, перекрытия
спектров различных порядков совсем не будет. При этом в слу-
случае неограниченной решетки в спектре каждого порядка каждо™
му направлению луча будет соответствовать строго определен-
определенная длина волны А. Наложения волн различных частот не будет.
Это значит, что разрешающая способность неограниченной ре™
шетки бесконечно велика.
2. Допустим теперь, что длина решетки L и число штрихов
N конечны. Тогда периодические возмущения, формирующиеся
решеткой, будут состоять из N импульсов, следующих один за
другим через время т = (dsine)/с. Время
@ = Nt= Ndsme = Lsml E0>3)
С С
приблизительно равно времени от момента появления первого
до момента появления N-vo импульсов. Оно называется време-
временем затягивания импульса, так как за решеткой вместо одиноч-
одиночного короткого импульса получается волновой процесс длитель-
длительностью в. Время в называют также временем установления
спектрального аппарата, так как по прошествии такого времени
начинают действовать все N штрихов решетки. Волновое возму-
возмущение в точке наблюдения может быть представлено в виде
где слагаемые в правой части представляют импульсы, приходя-
приходящие от отдельных штрихов. Так как эти импульсы запаздывают

§ 50 СПЕКТРАЛЬНЫЙ АППАРАТ И СВЕТОВЫЕ ИМПУЛЬСЫ 347
один относительно другого на время т, а в остальном совершен-
совершенно тождественны, то f2{t) = /i(t — т), /з(?) = fi{t — 2т) и т.д.
Результирующее возмущение представится в виде
E(t) = /i(t) + /i(*-r) + ... + h[t -(N- 1)т].
Разложим его в интеграл Фурье
E(t) = J A(co)eiujt dco, где А(ш) = ± J E(t)e~iujt dt.
0 -оо
Подставив сюда выражение для E(t) и учтя, что f\{t — r) = /i(t),
получим
+ ОО
А(ш) = J-[l + e^WT + ... + е"^^^] Г h{t)e-™1 dt =
— оо
= FHsin(JV^/2), E0.4)
где введено обозначение
+ ОО
Г
J
Величина ^(о;)!2 do; с точностью до постоянного множите-
множителя представляет интенсивность падающего импульса, приходя-
приходящуюся на интервал частот (uj^uj + duo). Такой же смысл имеет
величина |A(c«j)|2 da; для излучения, выходящего из решетки под
углом 1?. Теперь дифрагированное излучение, распространяю™
щееся от решетки в определенном направлении, состоит не из
одной монохроматической волны, как было в случае неограни-
неограниченной решетки, а непрерывно распределено по спектру частот.
Главные максимумы в этом распределении приходятся на ча-
частоты, при которых знаменатель в выражении E0.4) обращает-
обращается в нуль, т.е. got/2 = тж. Это приводит к соотношению E0.2).
Главные максимумы не появятся, если Р(ш) = 0, т.е. когда в
падающем импульсе не представлено излучение соответствую-
соответствующей частоты. Ближайший минимум в распределении интенсив-
интенсивности по частотам приходится на частоту, определяемую усло-
условием Nujt/2 = Nmr + тг, так как при такой частоте числитель
в формуле E0.4) обращается в нуль. Величина
*- = ш = I <5»-5>
определяет порядок ширины спектральной области, которую за-
заполняют волны, выходящие из решетки в одном и том же на-
направлении. По своему содержанию соотношение E0.5), очевид-

348 ДИФРАКЦИЯ СВЕТА ГЛ. IV
но, совпадает с ранее выведенной и подробно проанализирован-
проанализированной формулой B9.8).
Допустим теперь, что возмущение, падающее на решетку, со™
стоит из одной только неограниченной синусоиды. Тогда частота
ш в формуле E0.4) будет фиксирована. Но угол $ может менять-
меняться, а формула E0.4) определит зависимость амплитуды дифра-
дифрагированного света от этого угла. Так как шт = B7r/A)dsint?, то
эта зависимость представится формулой
sin JV
ndsi^ , E0.6)
тождественной с формулой D6.1). Поэтому отпадает надобность
в дальнейших рассуждениях. Заметим только, что разрешаю™
щая способность R связана с временем установления в соотно-
соотношением
R = в/Т. E0.7)
3. По описанной схеме действует всякий спектральный при™
бор. Это совершенно очевидно для интерференционных спек-
спектральных приборов, но не столь очевидно для призмы. В случае
призмы время распространения света от волнового фронта АВ
(рис. 201) до другого волнового фронта А1 В' одно и то же для
В
Рис. 201
всех лучей. Однако это заключение относится к фазе волны и
из него не следует, что световой импульс придет в точку на-
наблюдения целиком (что было бы, если бы вещество призмы не
обладало дисперсией), а не разобьется на ряд следующих друг
за другом тождественных импульсов. В диспергирующей среде
импульсы, вышедшие одновременно от различных точек волно-
волнового фронта АВ, придут в соответствующие точки волнового
фронта А1 В1 не одновременно. Импульс растянется во времени,
и можно говорить о времени затягивания в.

§ 51 СПЕКТРАЛЬНЫЙ АППАРАТ И СВЕТОВЫЕ ИМПУЛЬСЫ 349
Наиболее просто работу призмы молено проанализировать,
когда падающий на нее импульс представляет группу волн, т.е.
заполняет узкую область частот. Этого предположения доста-
достаточно для анализа наиболее важного вопроса — о разрешающей
способности призмы. Как известно (см. § 8), при распростране-
распространении в диспергирующей среде группа непрерывно деформирует™
ся, периодически восстанавливая свою форму через время вос-
восстановления т = dX/dv. Разобьем падающий пучок на ряд пуч-
пучков I, II, III, ... равноотстоящими плоскостями, параллельными
лучам самого пучка. Разбиение произведем так, чтобы каждый
пучок приходил в фокус F с запаздыванием т по отношению
к предыдущему пучку. Тогда волновые импульсы, связанные с
рассматриваемыми пучками, по выходе из призмы будут иметь
одну и ту же форму. Через фокус F последовательно будут про-
проходить тождественные световые импульсы, следующие друг за
другом через одно и то же время т. Призма преобразовала па-
падающий на нее импульс в последовательность равноотстоящих
импульсов, т.е. в периодическое возмущение, а это и требуется
от спектрального аппарата. Время затягивания, очевидно, рав-
равно в = АА1 /и — ВСЁ'/с. По определению волнового фронта
ВС В11 с = АА1 /v = a/v. Здесь v означает фазовую, а и — груп-
групповую скорости света в веществе призмы. Таким образом,
г\ /1 1\ v — и
о = й ¦- - - 1 = а ,
\и v у uv
или на основании формулы (8.8)
Л dn
r\ n Н\ a Xdn /rr% o\
( Xdn\ v d(nX) x 7
\ п dXj
Поделив это выражение на Т, найдем разрешающую способ-
способность призмы:
R = -a-^r. E0.9)
Здесь А означает длину волны в призме, тогда как в формуле
D9.2) той же буквой обозначена длина волны в вакууме. Обо-
Обозначив последнюю через Aq, получим
R=^a^, E0.10)
что по содержанию совпадает с формулой D9.2). С изложен™
ной точки зрения особенно ясно действие системы призм, разре-
разрешающая способность которой выражается формулой D9.3).

350
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
§ 51. Вогнутам отражательная решетка
1. Свет, дифрагировавший на обычной плоской решетке с равноотсто-
равноотстоящими штрихами, должен направляться на линзу или другое фокусирую-
фокусирующее устройство, чтобы в фокальной плоскости получилась картина резких
спектральных линий. Однако можно обойтись и без линзы, если штрихи
на плоской поверхности нанести неравномерно, надлежащим образом мо-
монотонно уменьшая или увеличивая расстояние между ними. Можно также
придать поверхности решетки вогнутую сферическую форму и нанести на
нее равноотстоящие штрихи.
Фокусирующее действие многих решеток было замечено давно, но до
работ Роулэнда оно рассматривалось как недостаток решетки. Роулэнд пре-
превратил его в достоинство решетки, построив вогнутые отражательные ре-
решетки. Наряду с интерферометром Фабри-Перо такие решетки до насто-
настоящего времени являются основными спектральными аппаратами, широко
используемыми в точных спектроскопических исследованиях. Спектраль-
Спектральные линии, получаемые с помощью вогнутых отражательных решеток, по
своей резкости значительно превосходят те же линии в решетках, где фо-
фокусировка осуществляется с помощью линз.
2. Пусть GqG (рис. 202) — отражающая сферическая поверхность ради-
радиуса р с центром в точке G, на которой нанесены штрихи равноотстоящими
плоскостями, перпендикулярными к плоскости рисунка и параллельными
диаметру ОС, ad — расстояние между этими плоскостями (период решет-
решетки). Поместив источник света в точке Ао, выясним, при каких условиях
спектр m-го порядка можно сфоку-
Y
а,Ь)
сировать в заданной точке А, лежа-
лежащей в плоскости AqOC. При иссле-
исследовании ограничимся рассмотрени-
рассмотрением лучей, лежащих в той же плос-
плоскости, приняв ее за координатную
плоскость XY. Начало координат по-
местим в центре решетки О, ось X
направим вдоль диаметра ОС, ось
Y — по касательной к сфере, лежа-
лежащей в рассматриваемой плоскости.
Пусть Р(х,у) — точка на поверхно-
поверхности решетки, находящаяся у какого-
либо штриха. Введем обозначения:
А0О = г0, АО = г, А0Р = и0, АР =
= и. Для фокусировки в точке А
спектра т-го порядка необходимо и достаточно, чтобы разность хода между
лучами, приходящими от соседних штрихов, составляла га А. Предполагая
(что не влияет на результат), что начало О находится также у штриха, за-
запишем это условие в виде ио + и = г о + г ± птХ, где п — номер штриха Р.
При описанном выше способе нанесения штрихов п = =Ьг//с/, а потому при
любом у должно быть
Рис. 202
+ и = го + г ±
E1-1)
Обозначим через ао, Ьо координаты точки А®] а, Ь — координаты точки А.
Тогда
= (у - boJ + (ж - а0J = го + ж2 + у2 - 2Ьоу - 2аож.
E1.2)

§ 51 ВОГНУТАЯ ОТРАЖАТЕЛЬНАЯ РЕШЕТКА 351
Уравнение окружности, по которой поверхность решетки пересекается с
плоскостью рисунка, имеет вид
х2 +у2 = 2рх. E1.3)
Подставив отсюда 2х в предыдущее уравнение и использовав соотношение
ro ~ bo = flo? найдем
E1.4)
Второй член — величина второго, а последний — четвертого порядка мало-
малости по у. Сохраняя только члены второго порядка, получим
_ boy 1 /ао 1
го 2ro \Tq р
Аналогично,
tt = r_*«?+ I D-1W. E1.6)
г 2г \г2 р/
Подставим эти выражения в формулу E1.1) и приравняем нулю члены с
первыми и вторыми степенями у. Тогда получим два условия:
*+*=*?> E1-7)
E1.8)
при выполнении которых, по крайней мере с рассматриваемой степенью
точности, решетка будет обладать требуемыми фокусирующими свойства-
свойствами.
3. Условие E1.7) определяет направления на дифракционные максиму-
максимумы m-го порядка. Действительно, если #о — угол падения центрального
луча на решетку, а $ — угол между соответствующим дифрагированным
лучом и нормалью к ней (рис. 202), то sin^o = bo/ro, sin# = b/r, и уравне-
уравнение E1.7) принимает вид
d(sin $ + sin #o) = ±т\, E1.9)
такой же, что и при дифракции на плоской отражательной решетке.
Второе условие, E1.8), определяет расстояние г точки А от центра ре-
решетки О. Вместе с уравнением E1.9) оно, таким образом, однозначно опре™
деляет положение этой точки, если известно положение источника света Ао.
Используя соотношения ао = ro cos^o и а = г cos#, уравнение E1.8) можно
представить в виде
cos2 #0 cos21? cos #0 + cos # . ч
ro г р
При малых углах $о и $ получается общеизвестное уравнение вогнутого зер-
зеркала радиуса р. Таким образом, каково бы ни было положение источника
света Ао, всегда существует такая точка А, в которой приближенно соби-
собираются дифрагированные лучи. Однако можно достигнуть большей точно-
точности и простоты в установке решетки, а также лучшей резкости спектраль-
спектральных линий, если распорядиться выбором точки Ао так, чтобы в выражении

352 ДИФРАКЦИЯ СВЕТА ГЛ. IV
E1.4) исчезли члены второго порядка. Для этого должно быть —^ =0.
го Р
Тогда, ввиду E1.8), будет — — — = 0. Эти соотношения можно записать в
rz р
виде
г0 = аор, или ro=pcosi5>o, E1.11)
г2 = ар, или г = pease. E1.12)
Соотношение E1.11) означает, что источник света должен лежать на окруж-
окружности диаметра р, касающейся поверхности решетки в точке О. Из E1.12)
тогда следует, что дифрагированные лучи соберутся в точке А, лежащей
на той же окружности. Эта окружность называется кругом Роулэнда. На
рис. 202 она изображена штриховой линией.
Угловая дисперсия решетки dejdX = m/(dcose) не будет зависеть от
угла #, если спектры получаются при малых д- вблизи § = 0. Тогда cos #« 1,
угол $ будет линейной функцией длины волны, т.е. получится нормальный
спектр. Поэтому в обычных условиях решетка устанавливается так, чтобы
изучаемый спектр получался вблизи ее главной оптической оси.
Большие решетки в первом порядке имеют разрешающую способность
около 200 000. Угловое расстояние между спектральными линиями, еще раз-
разрешаемыми решеткой, составляет mSX/(d cos #) = mX/(Rd cos #), а линей-
ное
E11)
R ~ d Я' E 6)
Для эффективного использования разрешающей способности решетки
необходимо, чтобы величина Дж была не меньше определенного предела.
Положим Ах = 0,01 мм, т = 1, R = 200 000, Л = 500 нм, d = 1/600 мм.
Тогда по предыдущей формуле найдем, что радиус кривизны решетки р
должен быть не меньше и 7 м, т.е. очень велик.
4. Вычисления, приведенные выше, применимы только к лучам, лежа-
лежащим в плоскости рисунка. Более подробное исследование показывает, что
лучи, выходящие из этой плоскости, дают астигматические изображения:
точечный источник, помещенный в Ао, изображается в виде отрезка, пер-
перпендикулярного к плоскости рисунка и проходящего через точку А. Астиг-
Астигматизм увеличивается по мере возрастания угла падения #о, т.е. с увели™
чением порядка спектра. Когда источником света является щель, то нали-
наличие астигматизма ведет к уменьшению резкости изображения и понижению
разрешающей способности, если щель установлена не совсем параллельно
штрихам решетки. Поэтому необходимо добиваться тщательной установки
щели на параллельность штрихам решетки. По той же причине нельзя де-
делать штрихи решетки очень длинными. Обычно наносят короткие штрихи
вдоль широких участков, а не стремятся покрыть ими большую площадь,
как в случае плоской решетки, не обладающей астигматизмом.
5. Роулэнду принадлежит и теоретически наиболее совершенный способ
установки дифракционной решетки, показанный на схематическом рис. 203.
Решетка GqG и фотографическая камера устанавливаются на противопо-
противоположных концах твердого стержня ОА, длина которого равна радиусу кри-
кривизны решетки р. Они могут скользить вдоль взаимно перпендикулярных
рельсов AqO и AqA на салазках, шарнирно соединенных со стержнем О А.
Для достижения лучшей отчетливости изображения фотопластинку PqP
изгибают по окружности, совпадающей с кругом Роулэнда. Щель помеща-
помещается в точке пересечения Ао направляющих рельсов. При фотографирова-
фотографировании спектров разных порядков, а также различных участков одного и того

§ 52 ДИФРАКЦИЯ НА РЕШЕТКЕ КАК КРАЕВАЯ ЗАДАЧА 353
же спектра щель Ао и источник света L остаются неподвижными. Так как
точки О, Ао, А лежат на круге Роулэнда, то при надлежащем положении
стержня О А изображение щели Ао получится в точке А. При перемеще-
перемещении концов стержня вдоль направляющих рельсов через точку А будут
последовательно проходить фокусы раз™
личных длин волн в спектре рассматри-
рассматриваемого порядка. Так как в установке Ро-
Роулэнда # = 0, то d sin #o = тпХ. С другой
стороны, OAq = р sin #о- Комбинируя эти
две формулы, находим
О А = &. E1.14)
а
На стержне, связанном с рельсом
О.До, можно нанести равномерную шка-
шкалу длин волн. Тогда длина волны, попа-
попадающей в центр поля зрения А, может
быть отсчитана непосредственно по этой
шкале.
При установке решетки по способу
Роулэнда объем, занимаемый приборами, Рис. 203
настолько велик, что в нем трудно под-
поддерживать постоянство температуры, необходимое при длительных экспо-
экспозициях. Кроме того, установка Роулэнда довольно дорога. По этим и по
ряду других причин она применяется редко. Пашеном, Иглом и др. были
разработаны другие способы; с ними можно ознакомиться по специальным
руководствам по технике спектроскопии.
§ 52. Дифракция на решетке как краевам задача
1. В предыдущих параграфах волновое поле за решеткой вы™
числялось путем суммирования волн^ исходящих от штрихов ре-
решетки. Для некоторых целей более предпочтителен другой спо-
способ. Допустим сначала, что решетка бесконечна. Переднюю по™
верхность ее будем называть входом^ заднюю — выходом. Эта
терминология применима и для отражательной решетки. Для
нее входом и выходом служит одна и та же (передняя) поверх-
поверхность. Без потери общности можно рассуждать так, как если
бы решетка была бесконечно тонкой. Примем плоскость решет™
ки за координатную плоскость XY. Ось X направим перпен-
перпендикулярно к штрихам, а ось Z — в сторону распространения
дифрагированного света (рис. 204). Как и раньше, отвлечемся
от векторного характера волнового поля, считая его скалярным.
Это всегда можно сделать, если электрический или магнитный
вектор падающей волны параллелен штрихам решетки. Надо
только в первом случае световое поле характеризовать электри-
электрическим, а во втором — магнитным вектором. В общем случае
падающую волну можно разложить на две составляющие, из
которых одна поляризована в плоскости падения, а другая пер-
12 Д.В. Сивухин

354
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
пендикулярно к ней. Тогда задача о дифракции волны сведется
к двум независимым задачам, отличающимся состоянием поля-
поляризации падающего света.
Z
Рис. 204
Падающую волну представим в виде
Е0 = Ае^-кгК E2.1)
Полагая здесь z = 0, найдем поле Евх на входе решетки. В си-
силу линейности уравнений, определяющих распространение волн,
суммарное поле прошедшей (отраженной) и дифрагированных
волн на выходе молено представить в виде Евых = DEB^. Ко™
эффициент D, вообще говоря, зависит от длины волны и назы-
называется пропускаемостью или амплитудной прозрачностью ре-
решетки. Это есть характеристика только самой решетки. Для
двумерной решетки величина D = D(x^y) есть функция двух
координат, для одномерной — одной координаты: D = D(x).
Задача о дифракции на всякой решетке сводится к нахожде-
нахождению амплитудной прозрачности последней. Действительно, зна-
знание этой величины позволяет определить поле на выходе решет™
ки, а этого достаточно, чтобы по принципу Гюйгенса^Френеля
вычислить поле дифрагированной волны. Для нахождения са-
самого решения, конечно, не обязательно пользоваться принципом
Гюйгенса^Френеля. Достаточно найти решение волнового урав-
уравнения
АЕ + к?Е = 0,
E2.2)
которое в плоскости z = 0 переходило бы в функцию
EBbI^(xjy) = D(х,у)Ев^(х,у) и удовлетворяло некоторым допол-
дополнительным требованиям, определяющимся физическими усло-
условиями задачи. Такой метод в литературе известен под названи-
названием метода Рэлея, хотя он и является только частным случаем
общего метода краевых задач математической физики. Здесь
этот метод применяется к одномерной дифракционной решетке.

§ 52 ДИФРАКЦИЯ НА РЕШЕТКЕ КАК КРАЕВАЯ ЗАДАЧА 355
2. Поскольку для решетки D есть периодическая функция х
с периодом d, ее можно представить рядом Фурье
+ ОО
D=
Поэтому
га= —оо
На это соотношение надо смотреть как на граничное условие^ ко-
которому должно удовлетворять за решеткой решение уравнения
E2.2). Частным решением этого уравнения является плоская
волна Е = ае^ш^чт\ волновой вектор q которой удовлетворяет
условию q2 = к2. Он может быть и вещественным (однородная
волна), и комплексным (неоднородная волна). Суперпозицией
таких решений можно получить общее решение:
+ СО
Е= J2 аше|И~9гоГ). E2.5)
Чтобы при этом удовлетворить граничному условию E2.4),
необходимо положить
Чтх = кх+ тр, qmy = 0. E2.6)
Тогда qmz = у к2 — Ятх- Двузначность квадратного корня
устраняется физическими соображениями. Вещественным зна-
значениям qmz соответствуют однородные волны, которые могут
только уходить от решетки, а не приходить к ней. Этому усло-
условию удовлетворяют только положительные значения qmz. Мни-
Мнимым соответствуют неоднородные волны. При удалении от ре-
решетки они могут только затухать. Поэтому коэффициент при
мнимой части должен быть отрицательным. Таким образом, со-
соотношение E2.6) надо пополнить условиями
-?L и 4mz = -iy/k2 -(ёпХ, E2.6а)
в которых квадратные корни понимаются в арифметическом
смысле. После этого волновые векторы qTO определяются одно-
однозначно, а для поля на выходе можно написать
+ ОО
Т? —
^вых —
\ п
— со
Сравнение этого выраясения с E2.4) дает
am = ADmi E2.7)
чем и завершается решение задачи.
12*

356 ДИФРАКЦИЯ СВЕТА ГЛ. IV
3. Полагая в E2.6) кх = Bтг/А) slnf9, qmx = Bтг/А) sin#m,
р = 2тг/й, получим
rf(sin i?TO - sin в) = гаА, E2.8)
т.е. основную формулу дифракционной решетки. Однако в по-
полученном решении содержатся и новые результаты. Во-первых,
весь спектр за решеткой состоит из одних только главных мак-
максимумов , никаких второстепенных максимумов нет. Это, конеч-
конечно, объясняется тем, что полученные результаты относятся к
неограниченной решетке. Во-вторых, в формулу E2.5), наря-
наряду с однородными, входят и неоднородные волны, а потому она
определяет волновое поле на любых расстояниях от решетки^
а не только в волновой зоне, как было в случае формулы D6.2).
При нормальном падении света наивысший порядок однород-
однородных волн т определяется условием т ^ d/X. При га > d/X со™
ставляющая qmz мнимая. Соответствующая неоднородная волна
экспоненциально затухает по закону ехр (—xmz), где
= f \/m2 ~~ [d/X)\ E2.9)
жт = лД2 -
На расстоянии z = \/ кш амплитуда волны убывает в е раз, ее
квадрат -ве2 раз. Наибольшее из этих расстояний порядка d.
Поэтому при z^> d поле за решеткой состоит только из однород-
однородных волн.
В частности, если d < А, то при нормальном падении по-
поле вдали от решетки состоит только из одной плоской волны
нулевого порядка (га = 0). Никаких боковых дифракционных
максимумов не появляется. Исследование прошедшей или отра™
Ad
женнои волны при z ^> ^^^^, или практически на расстоя™
2ттл/Х2 — d2
ниях z >» А, не даст никакой информации о структуре решетки.
Рассматривая решетку в микроскоп, мы не обнаружим на ней
штрихов. По той же причине свет, распространяющийся в про-
прозрачной среде, например в кристалле, не отклоняется в стороны,
хотя среда и построена из дискретных атомов или молекул —
кристалл является периодической структурой и в этом смысле
может рассматриваться как дифракционная решетка (фактиче-
(фактически наблюдаемое рассеяние света вызывается неоднородностями
среды и тепловыми флуктуациями). В оптическом отношении
кристалл ведет себя как однородная сплошная среда. Причи-
Причина этого в том, что период молекулярной структуры кристалла
меньше длины волны. Но как только нарушится это условие,
появятся дифракционные максимумы. Возникнет интерферен-
интерференционное рассеяние волн. Такой случай реализуется в рентгенов-
рентгеновской области спектра.

§ 52 ДИФРАКЦИЯ НА РЕШЕТКЕ КАК КРАЕВАЯ ЗАДАЧА 357
4. В непосредственной близи от решетки волновое поле имеет
очень сложный вид. На расстояниях z ^> 1/кт поле становится
более простым, поскольку из него выпадают неоднородные вол™
ны. Однако картина поля все еще довольно сложна, так как од™
нородные волны, из которых оно состоит, накладываются друг
на друга. При удалении от решетки на некоторое минималь-
ное расстояние плоские волны различных порядков простран-
пространственно разделяются. На сравнительно малых расстояниях от
решетки к пространственно разделенным волнам различных по™
рядков можно применять геометрическую оптику. Направления
на главные максимумы излучения определяются требованием,
чтобы все волны, исходящие из различных щелей решетки, при
интерференции усиливали друг друга. При этом явно или неяв-
неявно всегда имеется в виду, что интерференция происходит либо в
фокусе собирающей линзы, либо на бесконечном расстоянии от
решетки. Однако поскольку дифрагированное поле всюду пред™
ставляется суперпозицией плоских волн, условие интерференци-
интерференционного усиления определяет также направление распространен
ния таких плоских волн на любых расстояниях от решетки.
5. Если в разложении пропускаемости D в ряд Фурье отсут-
отсутствует какой™либо член, то будет отсутствовать и главный мак™
симум соответствующего порядка в волновом поле за решеткой.
Рассмотрим в качестве примера синусоидальную решетку, пазы™
ваемую также решеткой Рэлея. Ее пропускаемость определяется
выражением
D = а + /3cospx = а + ? (егрх + е~грх)
с постоянными а, /3 и р. В этом случае световое поле за решеткой
состоит из трех плоских однородных волн: неотклоненной волны
(максимум нулевого порядка) с амплитудой а® = а.А и двух бо-
боковых максимумов первого порядка с амплитудами а\ = a_i =
= ^-/2/ЗА. Других главных максимумов не будет. Если поверхно™
сти тела придать форму синусоиды, амплитуда которой мала по
сравнению с длиной волны, то такая поверхность приближенно
будет вести себя как решетка Рэлея. Это удалось сделать Вуду
путем травления (примерно в течение 10 с) поверхности стек™
лянной дифракционной решетки слабым раствором фтористо-
фтористоводородной кислоты. Обычные стеклянные решетки дают очень
слабые спектры, так как штрихи, нанесенные алмазом, узки по
сравнению со светлыми промежутками между ними. Если штри™
хи расширить, смочив поверхность решетки слабой фтористово™
дородной кислотой, то удается достигнуть увеличения интенсив™
ности спектров в несколько раз (до десяти).
Возможны и такие структуры, которые формально могут
рассматриваться как дифракционные решетки, дающие только

358 ДИФРАКЦИЯ СВЕТА ГЛ. IV
один максимум. Примером может служить призма. Если на одну
из боковых граней призмы падает плоская монохроматическая
волна, то фаза волнового поля на выходе (на второй грани приз™
мы) будет меняться с координатой по линейному закону. Соот™
ветствующее граничное условие удовлетворяется только одной
уходящей плоской волной. Это и есть волна, прошедшая через
призму и отклоненная ею. Проблема отражения и преломления
света на плоской границе раздела двух сред может решаться
как краевая задача по методу Рэлея. При таком подходе плос™
кая граница, раздела ведет себя как дифракционная решетка,
дающая только один максимум.
6. Ограниченная решетка может быть рассмотрена также методом
Рэлея. В пределах решетки ее пропускаемость периодична, а вне обраща-
обращается в нуль. Разложение пропускаемости в интеграл Фурье имеет вид
+ OG
D(x)= J C(f)e^tfxdf. E2.10)
Поле на выходе решетки представится выражением
Е^ = А J CU)e~nkm
m+f)x
Решение, удовлетворяющее этому и всем прочим условиям задачи, имеет
вид
+ ОО
G{f)e~l4rdf, E2.11)
— оо
гДе Я.х :=: кх + /, % =0, a qz определяется прежними формулами E2.6а).
Зададим теперь пропускаемость решетки выражением
0, если — оо < х < —L,
D(x) = { Ё Dme~imipx, если - L < х < +L, E2.12)
П = -— ОО
0, если + L < х < +оо.
Вычисляя коэффициент Фурье C(f), получим
CU) = iz \ D(*)e<"d*=± g Dm**W-m™rt.
— oo
m = — oo
В результате поле за решеткой представится в вида
E = J2Enn E2.13)

53 ПРИМЕРЫ НА ПРИМЕНЕНИЕ МЕТОДА РЭЛЕЯ 359
где
+ ОО
Dm e *qF df =
/ — mp
+00
А Г
тг J
м г
7Г J
fd — 2ттг
2_
По-прежнему волновое поле за решеткой складывается из волн различных
порядков т. Однако волна Ет уже не сводится к единственной плоской
волне определенного направления, а состоит из суперпозиции непрерывно-
непрерывного множества плоских волн различных направлений. Распределение ин-
интенсивности по направлениям в отдельной волне Ет определяется той же
кривой, что и в волне, дифрагированной на щели (см. рис. 175). Интен-
Интенсивность достигает максимума, когда знаменатель обращается в нуль, т.е.
когда qx = кх + тр = 0. Это условие определяет направление на главный
максимум m-го порядка. В рассматриваемом случае
sin[(iV/2)(/ri-277i7r)] _ N_
fd - 2ттг ~ У'
а потому интенсивность волны Ет в главном максимуме пропорциональна
N2. Когда sin [(N/2)(fd — 2ттг)] = 0, но fd — 2ттг ф 0, интенсивность волны
обращается в нуль. Этим определяются направления на дифракционные
минимумы, число которых между двумя соседними главными максимумами
равно N — 1. Таким образом, получаются все результаты, найденные выше
методом суммирования волн.
§ 53. Примеры на применение метода Рэлем
Ниже предполагается, что период решетки значительно больше длины
световой волны, так что пропускасмость D(x) можно вычислить в прибли-
приближении геометрической оптики.
1. Начнем с плоской амплитудной решетки, состоящей из прозрачных
щелей ширины Ь и непрозрачных промежутков между ними ширины а. В
приближении геометрической оптики пропускаемость D(x) равна единице
на щели и нулю в промежутках между ними. Начало координат поместим
в середине щели. Тогда коэффициент Фурье Dm представится выражением
+6/2
Dm=11 f D{X)e—dX = \ f e^pXdx=b sin (^mb/d)^
d J d J d umb d
-d/2 -6/2
При вычислении интенсивности дифрагированного пучка в принципе
следовало бы учесть изменение его поперечного сечения из™за наклона к
плоскости решетки. Однако это было бы превышением точности, так как
наши вычисления применимы лишь при малых углах дифракции, когда
cos $ ~ 1. В этом приближении относительная интенсивность m-го дифрак-
дифракционного пучка 1Ш = Dm- (Интенсивность падающей волны принята за

360 ДИФРАКЦИЯ СВЕТА ГЛ. IV
единицу.) Для спектра нулевого порядка Do = b/d, /о = (b/dJ. Полная ин-
интенсивность, пропускаемая решеткой, 1прОш = b/d. Разность этих величин
дает суммарную интенсивность света, приходящуюся на спектры прочих
порядков:
Ь Ь 2 y^ 1 . 2 тгтЬ , .
d d2 тг2 ^—' т2 d
т = 1
(Это — чисто математическое соотношение, доказываемое в теории рядов
Фурье.)
Относительная доля дифрагированного света будет
/прош — 1о_ _ . _ b_ C53 31
-*про
Она максимальна и стремится к единице, когда b/d —>¦ 0. Однако в этом
случае сама интенсивность 1прОш также стремится к нулю. Интенсивность
m-го дифракционного пучка равна
1Ш = Dm = /о гп— • E3.4)
[ тгтЬ/d J
Когда b/d —>• 0, интенсивности всех дифракционных пучков становятся оди-
одинаковыми и равными /о. Однако, как уже отмечено выше, в этом случае
каждая из этих интенслвностей сама стремится к нулю.
Если жтЬ/d = птг, т.е. b/d = п/тп, где п — целое число, меньшее тп и
взаимно простое с ним, то обращаются в нуль интенсивности спектров с
порядками т, 2т, Зт, ... Так, при b/d =1/2 пропадают все спектры чет-
четных порядков. Смысл этого результата, как уже отмечалось в § 46, станет
очевидным, если заметить, что условие m-го главного максимума dsiwd =
= тпХ умножением на b/d = п/тп преобразуется в bsiwd = пЛ, т.е. в условие
тг-го дифракционного минимума при дифракции на отдельной щели. Таким
образом, под углом § каждая щель, а потому и решетка в целом света не
посылают.
2. Рассмотрим более общий случай. Допустим, что на участках длины
Ь пропускаемость решетки равна /5, а на участках длины а она равна а.
Величины а и /3 постоянны, но могут быть комплексными. Таким образом,
решетка является амплитудно-фазовой. Когда а и /3 — числа вещественные,
то решетка будет амплитудной. Если же они — числа вида егр (р веществен-
вещественно), то решетка становится чисто фазовой. Рассматриваемая амплитудно-
фазовая решетка эквивалентна плоскопараллельной пластинке с пропуска™
емостью а и наложенной на нее дифракционной решетке. Пропускаемость
последней на участках b равна (/3 — а), а на участках а — нулю. Разумеется,
величины а ш /3, а шЬ можно поменять местами и получить вторую эквива™
лентную систему. Математически обе системы отличаются одна от другой
только обозначениями, а потому достаточно рассмотреть лишь одну из них,
например, первую.
Вычисление коэффициентов Фурье Dm сводится к предыдущей задаче.
Для плоскопараллельной пластинки все коэффициенты Фурье обращают-
обращаются в нуль, за исключением нулевого, который равен а. Поэтому, поместив
начало координат в центре одного из отрезков Ь и воспользовавшись фор-
формулой E3.1), получим
_ / ч b sin (nmb/d) ( гЧ
Dm = (Р-а)- ,,' +Qtem, E3.5)
а ттто/а

§ 53 ПРИМЕРЫ НА ПРИМЕНЕНИЕ МЕТОДА РЭЛЕЯ 361
где ёт = 1 при т = 0 и 8т = 0 при т ф 0. При а = 0, /3 = 1 получаются
результаты предыдущей задачи.
3. Рассмотрим теперь частные случаи чисто амплитудной и чисто фа-
фазовой решеток. Для амплитудной решетки величины а и /3 вещественны
и положительны. Все коэффициенты Dm также вещественны. Знаки этих
коэффициентов, начиная с т = =Ы, чередуются. Коэффициенты нулевого
и первого порядков могут иметь одинаковые или противоположные знаки
в зависимости от соотношения между пропускаемостями а и /3. В случае
чисто фазовой решетки пропускасмости а и C имеют вид егр. Так как су™
щественна только разность фаз между волнами, исходящими из участков
а и Ь, то без ущерба для общности можно положить а = 1, /3 = егр. Тогда
из формулы E3.5) находим
( ip л b sin (mnb/d) ( ч ( ч
An = (е р - 1) ,/ (то Ф 0), E3.6)
а тпо/а
Do = (eip - 1) ^ + I- E3.7)
Как и в случае амплитудной решетки, коэффициенты Фурье Dmj начиная
с т = ±1, попеременно меняют знаки. Никакого дополнительного сдвига
фаз между этими коэффициентами нет.
Качественное отличие фазовой решетки от амплитудной состоит в том,
что в случае фазовой решетки имеется дополнительный сдвиг фаз (р между
спектром нулевого и спектрами всех прочих порядков. Чтобы его вычис-
вычислить, найдем из формул E3.6) и E3.7) комплексное отношение Dm/Do.
Аргумент этого комплексного числа и будет (р. Простое вычисление дает
6 + a snip ( л
о — а 1 — cos p
Сдвиг фаз ср один и тот же для всех порядков т. Так как после дифракции
на решетке спектры различных порядков пространственно разделяются на
независимые пучки, то можно оказывать воздействие на каждый из них, не
меняя при этом амплитуды и фазы всех остальных пучков. Например, если
на пути нулевого пучка поставить прозрачную пластинку, которая измени-
ла бы его фазу на <р, то фазовые соотношения между дифрагированными
пучками будут такими же, как и у амплитудной решетки. С введением такой
пластинки фазовая решетка действует как амплитудная. На этом основан
метод фазового контраста^ используемый в микроскопии (см. § 59).
Отметим два частных случая. Во-первых, случай а = Ь. Тогда формула
E3.8) дает tgy? = сю, т.е. (р = тг/2. Во-вторых, случай малых значений р.
Тогда
т.е. tg (p очень велик, а самый угол ip практически равен тг/2. В обоих слу-
случаях для превращения фазовой решетки в амплитудную на пути нулевого
пучка или на пути всех прочих дифрагированных пучков достаточно ввести
пластинку, вносящую дополнительную разность фаз ±тг/2.
4. В качестве последнего примера рассмотрим фазовую решетку, про-
профиль штрихов которой показан на рис. 205. Поперечное сечение штриха
имеет форму треугольника, одна сторона которого длинная и пологая, а
другая — короткая и крутая. Такая решетка интересна тем, что при опреде-
определенных условиях она может концентрировать основную часть света в спек-
спектре одного порядка. Решетка может действовать и как пропускающая, и как

362
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
отражательная. Ради определенности разберем действие пропускающей ре™
шетки.
Поместим начало координат О в середине длинной стороны АВ. Пусть
а — длина проекции длинной, a b — короткой стороны на направление оси
X. Если &<а, то в интеграле E3.1) можно пренебречь вкладом, вноси™
мым короткой стороной. В этом приближении можно положить а = d и
вычислить пропускаемость решетки только на участке а. Влияние пропус-
¦z=h
Рис. 205
каемости участка Ь практически не отразится на результатах. Пусть волна
падает перпендикулярно к плоскости XY и в воздухе представляется вы-
выражением Е = Еое~~~г 'z. На входе, т.е. в плоскости z = —/&, поле предста-
представляется выражением Евх = Еоегк1г. Чтобы вычислить поле на выходе при
z = +/i, можно, ввиду малости угла наклона а, пренебречь преломлением.
Если zq — текущая координата точки на прямой АВ, то поле на выходе в
лежащей под ней точкой будет равно
где S — некоторая постоянная. Постоянный фазовый множитель ег не игра-
играет роли и может быть отброшен. Таким образом, пропускаемость решетки
D = егЛ;(Г1-1)го? или после подстановки zq = xtga и ах
D(x) = eife(n)ax.
Коэффициенты Фурье Dm вычисляем по формуле E3.1) и находим
sin7r[m + (е//А)(п —
т = [
E3.9)
Если знаменатель этого выраж;ения обращается в нуль, то почти весь
свет сконцентрируется в спектре порядка т. Для этого должно быть т +
+ (d/X)(n — l)a = 0. С другой стороны, dsiwd = mA, или, ввиду малости
угла дифракции, d • Ф = тХ. Исключая т, получаем
§ = -(n-l)a.
E3.10)
Эта формула показывает, что угол § равен углу отклонения луча при пре-
преломлении в призме с малым преломляющим углом а. Таким образом, по-
почти весь свет может сконцентрироваться в одном направлении, если это
направление совпадает с направлением преломленных лучей. Для концен-
концентрации необходимо, чтобы разность хода между пучками, преломленными
на соседних ступеньках решетки, составляла целое число волн. С подоб-
подобной концентрацией дифрагированного света в спектре одного порядка мы
столкнулись также в § 48 при изучении эшелона Майкельсона.

§ 54 ГОЛОГРАФИЯ 363
§ 54. Голография
1. Применим метод Рэлея для уяснения идеи голографии^
т.е. без линзового получения оптических изображений путем так
называемого восстановления волнового фронта. В принципе
идея голографии была выдвинута и экспериментально прове™
рена польским физиком М. Вольфке A883—1947). Его работа
была опубликована еще в 1920 г., но была забыта. Эту идею
независимо от Вольфке вновь предложил и обосновал в 1947 г.
английский инженер и физик Габор (р. 1900), который по пра-
праву считается изобретателем голографии. Однако понадобилось
15 лет, чтобы стало возможно практическое осуществление го™
лографии. Причина столь длительной задержки заключается в
том, что в голографии требуются источники света, обладающие
высокой степенью временной и пространственной когерентно-
когерентности. Таких источников в 1947 г. еще не существовало. Положе-
Положение изменилось в 1960 г. с изобретением лазеров и проникнове-
нием их в лабораторную технику. Первые изображения по ме-
методу голографии были получены американцами Лейтом и Упат-
ниексом в 1962 г.
При освещении или просвечивании предмета от него распро-
распространяется рассеянная или прошедшая волна. (Для определен-
определенности в дальнейшем предполагается, что предмет освещается,
а не просвечивается, хотя принципиального различия между
этими случаями при нашем рассмотрении нет.) Отделившись
от предмета, рассеянная волна сохраняет в дальнейшем неза-
независимое существование и несет полную информацию о форме
и прочих свойствах предмета, какая может быть получена путем
освещения его световыми лучами. Попадая в глаз или объектив
фотоаппарата, эта волна образует на сетчатке или на фотопла-
фотопластинке изображение предмета. Если любым путем создать такую
же волну, то, очевидно, она сможет вызвать в точности такие же
эффекты, что и исходная волна, рассеянная предметом. На этом
замечании и основана идея голографии.
Процесс получения изображения в голографии распадается
на две стадии. На первой стадии изготовляется голограмма, т.е.
фотопластинка, с помощью которой можно восстанавливать свето-
световую волну, рассеянную телом. Вторую стадию составляет само вос-
восстановление этой волны и получение оптического изображения.
2. Пусть какой-то предмет А (рис. 206) освещается пучком
паралелльных лучей от лазера. Рассеянные лучи попадают на
фотопластинку Г. По степени почернения пластинки после про-
проявления можно судить об амплитуде рассеянной волны во всех
местах пластинки, которых эта волна достигла. В этом смысле
экспонированная и проявленная пластинка сохраняет информа-
информацию об амплитуде волнового поля. Для восстановления волново-

364
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
Рис. 206
го поля такой информации, конечно, недостаточно. Нужна еще
дополнительная информация о фазе, которой пластинка не со-
содержит, так как степень почернения зависит только от интен-
интенсивности, но не от фазы вол™
ны. Габор указал, что необходи-
необходимую информацию о фазе мож-
можно получить и записать на той
же фотопластинке J1, если осве-
осветить ее вторым пучком от того
же лазера и заставить его ин-
интерферировать с пучком, рассе-
рассеянным предметом. Практически
этого можно достигнуть, расши-
расширив предварительно пучок от ла-
лазера, а затем разделив его на два
пучка. Один из них (предмет-
(предметный) направляется на предмет
Д другой (опорный) отражается
от плоского зеркала S. Оба пучка направляются на фотопла-
фотопластинку Г и там интерферируют между собой. Интерференцион-
Интерференционная картина фотографируется. Так полученная фотография и
называется голограммой.
Поскольку волна, рассеянная предметом, возникает при от-
отражении и дифракции на макроскопических деталях предмета
со сложной формой и взаимным расположением, реальная го-
голограмма представляет собой очень сложную и запутанную ин-
интерференционную картину с очень мелкими деталями, которые
невозможно различить невооруженным глазом. (На ней обычно
видны и крупные дифракционные кольца. Но они не имеют ни-
никакого отношения к делу, так как возникают при дифракции на
случайных пылинках, встретившихся на пути распространения
света.)
Дифракционная картина на голограмме не имеет ни малей-
малейшего сходства с предметом. При рассматривании ее в микроскоп
в ней трудно усмотреть следы каких-либо закономерностей. И
тем не менее расположение, форма и интенсивность дифракци-
дифракционных пятен голограммы полностью определяются геометриче-
геометрической формой и физическими свойствами отражающей поверх-
поверхности объекта. Голограмма в закодированной форме содержит
полную информацию об амплитудах и фазах рассеянной волны,
которая достаточна для ее восстановления и получения оптиче-
оптического изображения. Само название «голография» происходит от
греческих слов «голог» — полный и «графе» — пишу и может
быть переведено как «полная запись».
3. Разность хода между опорной волной и волнами, рассе-
рассеянными предметом, очень велика и может составлять несколь-

§ 54 ГОЛОГРАФИЯ 365
ко метров. Поэтому при изготовлении голограммы время коге-
когерентности света должно бвхть очень велико (не меньше 1СР5^
10^7 с). Длина когерентности также должна быть очень боль-
большой (не меньше НО м). Никакие источники света, кроме ла-
лазеров, не могут обеспечить столь высокую степень временной и
пространственной когерентности. Кроме того, необходима непо-
неподвижность (с точностью до долей длины световой волны) и вы-
высокая контрастность интерференционной картины, образую™
щейся в области перекрытия предметного и опорного пучков во
время экспозиции. Для этого также требуется высокая когерент-
когерентность света, а также механическая жесткость всех элементов
голографической установки.
Необходимая степень монохроматичности света определяет™
ся по общей формуле Х/81 > га, где т — максимальный по-
порядок интерференции, наблюдающейся при голографировании.
При рациональном расположении источника света и прочей ап-
паратуры его можно оценить по формуле т ~ L/X, где L —
линейные размеры предмета. Таким образом, должно быть SX <
< X2/L. Уже при небольших размерах предмета ~ 10 см и А =
= 500 нм эта формула дает SX < 10~3 нм. Между тем спектраль-
спектральные линии ртутной лампы, даже с низким давлением ртутных
паров, имеют ширину ~ 30 нм. Требования к размерам источ-
источника света, пожалуй, еще более жесткие. Для получения высо-
высокой контрастности интерференционной картины на голограмме
поперечные размеры Ах источника света (т.е. размеры парал-
параллельно плоскости голограммы) должны быть малы по сравне-
сравнению с шириной интерференционной полосы А/а, где а — угол
схождения крайних интерферирующих лучей (см. § 28). По по-
порядку величины а = h/l, где h — ширина опорного пучка, а I —
расстояние между предметом и голограммой. Если h = 3 см, а
I = 30 см, то должно быть Ах < XI/h = 5 мкм.
С нелазерными источниками (например, ртутной дуговой
лампой) этим требованиям пытались удовлетворить стандарт-
стандартными приемами, пропуская свет через различные монохрома-
торы, а затем фокусируя его на малом отверстии. При этом че-
через отверстие проходила и достигала освещаемого объекта лишь
ничтожная часть светового потока. Требующееся время экспо-
экспозиции при этом будет достигать порядка года. Поэтому Габору
удалось получить голограммы только простейших микроскопи-
микроскопических объектов при экспозициях в несколько часов. Лазеры
сделали описанные операции ненужными, а идея голографии
получила практическое осуществление.
4. Представим поле волны, рассеянной предметом А, в виде
и = а{г)е1^-ф^\ E4.1)

366 ДИФРАКЦИЯ СВЕТА ГЛ. IV
а поле волны, отраженной плоским зеркалом S, — в виде
v = Ье*М~кг) E4.2)
(Ъ и к — постоянные). Оба поля записаны в скалярной форме.
Это упрощение не существенно, так как изменения поляризации
волн в интересующих нас процессах не играют заметной роли.
При таком упрощении величины а (г), Ф(г) и Ъ могут считатвся
вещественными. Интенсивность результирующего поля на пла-
пластинке Г и перед ней представится выражением
I = (и + v)(u* + v*) = v*u + vu* + v*v + и* и.
Начало координат поместим в какой-либо точке О в плоскости
пластинки Г. С той же плоскостью совместим координатную
плоскость XY, направив ось Y перпендикулярно к направле-
направлению опорного пучка, отраженного зеркалом S (ку = 0). Тогда
ось Z будет нормальна к плоскости пластинки Г. Направим ее
в сторону распространения опорного пучка. Интенсивность 1ц
светового поля в плоскости пластинки найдется из предыдуще-
предыдущего выражения, если все входящие в него функции заменить их
значениями при z = 0:
/0 = Ьа{х, у, 0)e*^#^'°)] + Ьа{х, у, 0)e^k*x^x^^ +
+ Ь2 + а2(ж,|/,0). E4.3)
Допустим теперь, что контактным способом изготовлен по™
зитив голограммы при таком режиме проявления, что ампли-
амплитудная прозрачность (пропускаемость) D позитива оказалась
пропорциональной Iq. Для краткости коэффициент пропорци-
пропорциональности можно принять равным единице, т.е. положить D =
= /о. Этого всегда молено достигнуть надлежащим выбором еди-
единиц. Такая позитивная голограмма может быть использована
для восстановления рассеянной волны u(r,t). Для этого, убрав
предмет А, голограмму просвечивают таким же опорным пуч-
пучком г>(г, ?), какой применялся при ее изготовлении. Этот пучок
будет испытывать дифракцию на голограмме подобно тому, как
дифрагирует свет на дифракционной решетке. Задача сводится
к расчету дифракционной картины за голограммой. Для ее ре-
решения можно применить метод Рэлея. Обозначим через E(r,t)
волновое поле за голограммой. На выходе голограммы оно пред-
представится выражением
Евых = Dv(x, у, 0) = 10Ъе«ш*-к*х\ E4.4)
Надо найти решение волнового уравнения
0 + 0 + 0 + ^ = 0, E4.5)
дх2 ду2 dz2 x 7

§ 54 ГОЛОГРАФИЯ 367
удовлетворяющее краевому условию E4.4). Ввиду линейности
и однородности такого уравнения и условия E4.4), эту задачу
можно расчленить на четыре независимые задачи. Представим
функцию Е в виде суммы
Е = Ег + Е2 + ^з + ЕА E4.6)
и потребуем, чтобы слагаемые Е\, E2i ^з5 ^4 были решениями
уравнения E4.5) и удовлетворяли следующим граничным усло-
условиям:
Ег ВЬ1Х = Ъ2а(х,у,0)ег^ф^У^\ E4.7)
Е2 вых = Ь2а(х,у,0)ег^ф^У^2к*х\ E4.8)
^Звых = Ь3е^^ж), E4.9)
ЕА вых = Ы2{х,у,ъу^-к*х\ E4.10)
Сюда необходимо добавить физическое условие, чтобы волны,
дифрагированные на голограмме, были уходящими. Этим обес-
обеспечивается единственность решения.
5. Проще всего найти функцию E3j т.е. решение задачи, удо-
удовлетворяющее граничному условию E4.9). Ввиду постоянства Ь
таким решением, очевидно, будет
Е3 = bV^kr) = b2v(r, t). E4.9a)
Если отвлечься от амплитудного множителя Ь2, то это есть
просвечивающая (опорная) волна, распространившаяся за го-
голограмму.
6. Основной интерес в голографии представляет решение Е\,
удовлетворяющее граничному условию E4.7). Ввиду постоян-
постоянства Ь, его можно также сразу указать. Именно:
Ег = Ъ2а[х, у, г)<?№-ф(*>У>*)] = Ъ2и[т, t). E4.7а)
Действительно, функция Е\ удовлетворяет волновому уравне™
нию E4.5) и представляет волну, уходящую от голограммы, ко™
торая при z = 0 переходит в выражение E4.7). Но эта волна с
точностью до несущественного постоянного множителя тожде™
ственна с волной и, рассеянной объектом. Она, таким образом,
точно воспроизводит рассеянную волну и дает мнимое изобра-
эюение (МИ) объекта, в том же самом месте, в каком он нахо™
дился во время получения голограммы (рис. 207 а). Тем самым
разъяснен основной принцип голографии.
7. Для нахождения волны E2j т.е. решения волнового уравне™
ния, удовлетворяющего граничному условию E4.8), рассмотрим
сначала частный случай, когда опорный, а следовательно, и про™
свечивающий пучки перпендикулярны к плоскости голограммы.
Тогда кх = 0, и граничное условие E4.8) переходит в

368
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
Волна _
E2(x,y,z) = Ъ2а(х,у,г)ег^+ф(^\ E4.12)
очевидно, удовлетворяет этому граничному условию. Это еств
волна, получающаяся из волны E4.7а) обращением направле™
ния ее распространения, а потому она также удовлетворяет и
волновому уравнению E4.5). Она давала бы мнимое изображе-
изображение предмета перед голограммой в точности в том же месте, где
Рис. 207
находился сам предмет при получении голограммы (рис. 207^).
Однако волна Ез(г, ?) распространяется к голограмме, а не от
нее, и по этой причине не может служить решением рассматри-
рассматриваемой нами задачи. Для нахождения нужного решения заме-
заметим, что волновое уравнение E4.5) не изменится, если изменить
на противоположные знаки одной или нескольких координат.
Так, при изменении знака у z уравнение E4.5) переходит в
д2Е . д2Е . д2Е . j2t? а /кл к \
¦-— + -—¦ + ——— + к Е = 0. E4.5а)
Это уравнение, очевидно, имеет решение Е2{х1у1 —z). А так как
оно тождественно с уравнением E4.5), то последнее имеет такое
же решение, т.е.
Е2 = Ь2а(ж,у,-^е*["*+ф(ж'^-*)]. E4.11а)
Решение это, очевидно, удовлетворяет граничному условию
E4.11). Оно получится из E4.12), если пространства перед и
за голограммой поменять местами. Решение E4.11а) представ-
представляет волну, идущую от голограммы, а потому оно и будет ис™
комым решением задачи. Полученная волна сходится за голо-
голограммой и дает там действительное изображение (ДИ) пред™
мета. Положение его зеркально симметрично с положением са-
самого предмета относительно плоскости голограммы (рис. 207 в).
Однако глаз может видеть действительное изображение только
тогда, когда оно рассматривается с задней стороны, т.е. когда
изображение находится между голограммой и глазом. Поэто-
Поэтому действительное изображение будет псевдоскопическим, или
вывернутым. На нем выпуклые места предмета глаз видит как

54
ГОЛОГРАФИЯ
369
вогнутые и наоборот. (Псевдоскопичпость не будет проявлять-
проявляться, если действительное изображение спроецировать на экран.)
Если смотреть на голограмму перпендикулярно к ее поверхно-
поверхности, то действительное изображение будет мешать рассматри-
рассматриванию мнимого изображения, так как оба изображения лежат
на одной линии зрения. Такое же вредное влияние оказывают
прямые лучи просвечивающего пучка, поскольку они также по-
попадают в глаз. Эти недостатки устраняются применением на-
наклонных опорных (а следовательно, и просвечивающих) пучков
света.
В случае наклонных пучков кх ф О, и надо найти решение
^2 5 удовлетворяющее общему граничному условию E4.8). Но
этот случай легко сводится к частному случаю нормального па-
падения, разобранному выше. Действительно, если бы граничное
условие имело частный вид E4.11), то молено было бы перейти
к общему граничному условию E4.8), наложив на голограмму
дополнительную дифракционную решетку с амплитудной про-
прозрачностью D = е^ хХ. Это — фазовая решетка, дающая толь-
только спектр минус первого порядка (см. § 52, п. 5). Она действует
как призма, т.е. только изменяет направление падающего пуч™
ка света. В результате действительное изображение смещается в
Действительное
изображение
а
Y Действительное
х Мнимое изображение
изображение
Рис. 208
сторону, как указано на рис. 208 а. Такое смещение, конечно, ис™
кажает изображение совершенно так лее, как это происходит при
рассматривании предмета через призму. При большом наклоне
опорного (а следовательно, и просвечивающего) пучка действи-
действительного изображения может и не получиться.
8. Искажения действительного изображения можно избе™
жать, если просвечивающий пучок направить на голограмму под
тем же углом и в той же плоскости падения, что и опорный, но
с другой стороны от нормали к плоскости голограммы. Тогда
и вместо граничных условий E4.7) и E4.8) мы получим соответ-

370 ДИФРАКЦИЯ СВЕТА ГЛ. IV
ственно
Ег вых = Ь2а(х,у,0)ег^ф^У^2к^\ E4.76)
Е2 вых = Ь2а(х, у, 0)е^+ф^'°)]. E4.86)
Теперь действительное изображение будет расположено зер-
кально симметрично (относительно плоскости голограммы) с са-
самим предметом в том положении, какое он занимал при изготов-
изготовлении голограммы. Оно по-прежнему будет псевдоскопическим,
но не искаженным. Зато мнимое изображение сместится в сто-
сторону (рис. 208 б) и будет искажено, как при рассматривании
предмета через призму.
9. Остается выяснить влияние волны Е±, удовлетворяющей
граничному условию E4.10). Найти решение в этом случае без
конкретизации вида функции а(ж,у, 0) невозможно, так как
в условие E4.10) входит не сама эта функция, а ее квадрат.
Для отыскания Е± в общем случае следует разложить функ-
функцию а (ж, у, 0) в интеграл Фурье, а затем стандартным способом
(см. § 52) представить волну Е± в виде суперпозиции плоских
волн, распространяющихся в различных направлениях. Таким
образом, за голограммой возникает волновое поле, создающее
фон, на котором получаются мнимое и действительное изобра-
изображения. Интенсивность этого фона зависит от квадрата ампли-
амплитуды a(x^y^z) волны, рассеянной предметом при изготовлении
голограммы. Поэтому для ослабления вредного влияния такого
фона интенсивность опорной волны берут значительно большей
интенсивности предметной волны.
Так как фотослой, на котором записана голограмма, тонкий,
то при восстановлении изображения не возникает интерферен-
интерференция столь же высоких порядков, что и при изготовлении го-
голограммы. По этой причине удовлетворительное изображение
предмета можно получить с голограммой, освещаемой при вос-
восстановлении светом от ртутной лампы.
10. Чем больше углы, под которыми сходятся интерфериру-
интерферирующие лучи на голограмме, а следовательно, чем мельче детали
интерференционной картины, тем выше разрешающая способ-
способность голограммы (см. § 57). При предельно возможном раз-
разрешении эти детали порядка длины световой волны. Но и при
углах схождения в несколько градусов интерференционная кар-
картина на голограмме получается все же довольно тонкой. Что-
Чтобы ее зафиксировать на фотопластинке, требуется фотографи-
фотографическая эмульсия весьма высокого качества. Наиболее высокие
требования к фотопластинкам предъявляются в цветной фото-
фотографии Денисюка, где предметная и опорная волны идут на-
навстречу друг к другу (см. п. 13). Современные мелкозернистые
фотопластинки, применяемые в голографии, разрешают 1000-

§ 54 ГОЛОГРАФИЯ 371
10 000 линий на миллиметр (расстояние между разрешаемыми
линиями 1000-100 нм). Следует, однако, заметить, что повыше-
повышение разрешающей способности фотоэмульсии, как правило, со™
провождается падением ее чувствительности.
11. Для получения изображения нет необходимости изгото-
изготовлять позитивную голограмму; негатив столь же хорош, что и
позитив. Это непосредственно следует из теоремы Бабине. Раз-
Различие в дифракционных картинах касается только просвечиваю-
просвечивающего пучка, проникшего за голограмму, и совсем не затрагива-
затрагивает волновые поля Е\ и E<i, дающие мнимое и действительное
изображения. В обоих случаях при восстановлении волнового
фронта получаются одинаковые изображения.
Конечно, при изготовлении голограммы условие D ~ IQi со-
соблюдение которого предполагалось при нашем изложении, не
может быть выполнено вполне точно. Его невыполнение при-
приводит к появлению дополнительных изображений. Это проще
всего пояснить на примере, в котором предметная и опорная
волны обе плоские и падают на фотопластинку под разными
углами (предметом является бесконечно удаленная светящаяся
точка). Тогда при соблюдении условия D ^ Iq голограмма будет
представлять собой дифракционную решетку с синусоидальной
амплитудной прозрачностью. При ее просвечивании, наряду со
спектром нулевого порядка (т.е. прямого просвечивающего пуч-
пучка, проникшего за голограмму), появятся спектры первого и ми-
минус первого порядков, один из которых будет мнимым, а дру-
другой действительным изображениями предмета. Если же условие
D ~ Jo не соблюдается, то разложение функции D(x) в ряд
Фурье будет содержать гармоники высших порядков. При про™
свечивании голограммы, наряду со спектрами первых порядков,
появятся спектры высших порядков, т.е. дополнительные мни-
мнимые и действительные изображения предмета. Однако если та-
такие дополнительные изображения слабы и получаются в стороне
от основного изображения, то они не причиняют существенного
вреда.
Для получения большей яркости изображения применяют
так называемые отбеленные голограммы. Они получаются из
обычных голограмм путем обработки их специальными отбели-
отбеливающими растворами, образующими прозрачные соединения с
серебром, отложившимся в эмульсии голограммы. Получается
прозрачная фазовая голограмма, пропускаемость которой ва-
варьируется как за счет толщины, так и за счет показателя пре-
преломления отбеленного слоя. Такая голограмма сохраняет спо-
способность давать оптические изображения. В какой степени от-
отбелка голограммы и отступления от условия D ~ Iq сказыва-
сказываются на получаемых изображениях, эти вопросы представля-
представляют громадный интерес в практической голографии. Однако они

372 ДИФРАКЦИЯ СВЕТА ГЛ. IV
трудно поддаются теоретическому изучению и по своему содер-
содержанию не могут быть включены в курс общей физики.
12. По сравнению с обычными фотографиями изображения,
получаемые по методу голографии, обладают тем преимуще-
преимуществом, что они трехмерны. Мнимые изображения полностью
воспроизводят без каких бы то ни было искажений взаимное
расположение реальных предметов в пространстве. Если при
рассматривании голограммы одни предметы заслоняются дру-
гими, то достаточно сместить в сторону глаз, чтобы увидеть и
заслоненные предметы. Часть голограммы действует как целая
голограмма. Например, для воспроизведения изображения го™
дится каждый кусочек разбитой голограммы. По мере уменьше-
уменьшения размеров голограммы ослабевают лишь четкость изображе-
изображения (разрешающая способность) и ощущение объемности. Эта
особенность голографического метода связана с тем, что при
экспонировании, как правило, все части фотопластинки подвер-
подвергаются действию света, рассеянного всеми точками предмета.
Поэтому в каждой части голограммы хранится в закодирован-
закодированной форме изображение всего предмета. Вопрос о разрешающей
способности голограмм будет разобран в § 57 (п. 5), как частный
случай общего вопроса о разрешающей способности оптических
приборов.
На одной фотопластинке можно последовательно зареги-
зарегистрировать несколько изображений, причем каждое из них моле-
молено восстановить без помех со стороны других изображений.
Можно, например, произвести несколько экспозиций при одном
и том же опорном пучке, голографируя каждый раз только один
предмет. Во избежание наложения восстановленных изображе-
изображений друг на друга голографируемые объекты должны распола-
располагаться в различных местах. Можно так лее объекты помещать
в одно и то же место, но менять направление опорного пучка.
Можно получать цветные изображения, освещая предмет тремя
источниками света с различными длинами волн, подобранными
так, чтобы наиболее полно передать цвет предмета. От тех же
трех источников формируются опорные пучки, создающие вме-
вместе с волнами, рассеянными предметом, единую голограмму на
черно-белой фотопластинке. Для восстановления изображения
такая «трехкомпонентная голограмма» помещается в то же ме-
место, какое она занимала при экспонировании, и одновременно
освещается тремя просвечивающими пучками, тождественными
с опорными. При просвечивании голограммы каждый из этих
пучков создает три действительных и три мнимых изображе-
изображения. Три из этих мнимых изображений, и притом разноцвет-
разноцветных, пространственно совпадут друг с другом, образуя цветное
изображение. Остальные изображения расположатся в разных
местах, не мешая основному изображению.

Стекло
Фотослой
§ 54 ГОЛОГРАФИЯ 373
13. Голограммы, о которых шла речь выше, молено назвать
двумерными^ так как в них применяются фотопластинки с тон-
тонкими слоями эмульсии. В 1962 г. советский физик Ю.Н. Де-
нисюк (р. 1927) стал получать трехмерные^ объемные голограм-
голограммы на фотопластинках с толстослойной эмульсией. В его ме-
методе удачно сочетаются принципы голографии и цветной фото™
графии Липпмана. Толщина фотографического слоя составляет
15—-20 мкм, т.е. 30—40 длин волн зеле-
зеленого цвета. Фотослой настолько прозра-
чей, что через него можно освещать го-
голографируемый объект. Опорная плос-
плоская монохроматическая волна от лазе-
лазера падает на фотопластинку со сто-
стороны стекла (рис. 209). Пройдя через
фотопластинку, она освещает гологра-
голографируемый предмет. Волна, рассеянная
предметом, распространяется навстре-
чу опорной волне, интерферируя с ней
в толще фотоэмульсии. Интерференци-
Интерференционная картина представляет стоячие
волны^ на которые наложен довольно
причудливый узор мелких деталей из Рис. 209
максимумов и минимумов, так как сре-
среди интерферирующих волн только опорная волна является плос-
плоской. Проявленная и отфиксированная фотопластинка и бу-
будет объемной голограммой Денисюка. Она состоит как бы из
нескольких десятков поверхностных голограмм, расположенных
в толще эмульсии.
Восстановление предметной волны производится расходя-
расходящимся пучком белого света. Каждый слой выделившегося сере-
серебра, действуя подобно двумерной голограмме, дает слабые мни-
мнимое и действительное изображения предмета. При многолучевой
интерференции происходит усиление тех волн, длина которых
равна длине волны излучения лазера, в тех направлениях, в ко-
которых разность фаз между волнами от соседних слоев серебра
равна 2тг. В результате возникают изображения того же цвета,
что и цвет луча лазера. Остальные изображения гасят друг дру-
друга при интерференции.
Таким образом, голограмма производит монохроматизацию
белого света, которым она освещается. Конечно, такая моно-
хроматизация сравнительно невысокая, из-за незначительного
числа отложившихся слоев серебра и связанной с этим неболь-
небольшой спектральной разрешающей способности голограммы. Кро-
Кроме того, цвет изображения может существенно отличаться от
цвета излучения лазера. Это связано с изменением расстояний

374
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
между слоями почернения при проявлении, фиксировании и
сушке фотопластинки.
Метод Денисюка, подобно трехцветной фотографии, позво-
ляет получать изображения предметов в натуральных цветах.
Для этого на одной и той же фотопластинке получают голограм-
голограмму предмета с помощью трех лазеров, излучения которых имеют
различные длины волн. Последние подбираются так, чтобы при
смешении они наиболее совершенно воспроизводили цвет пред™
мета. Такая голограмма действует как три голограммы, дающие
при освещении белым светом совмещенные изображения пред-
предмета в трех цветах. При этом цвет изображения кажется глазу
таким лее, как и цвет самого предмета.
Голография в настоящее время представляет самостоятель-
самостоятельный, быстро развивающийся раздел науки, техники и искусства,
возможно с большим будущим. Ей посвящены специальные ру-
руководства, к которым и следует обратиться всем, кто пожелает
глубже и детальнее изучить голографию.
§ 55. Световое поле вблизи фокуса
1. Согласно геометрической оптике, волновое поле в центре
сферической сходящейся волны (фокусе) обращается в бесконеч-
бесконечность. Это указывает на неприменимость геометрической опти-
оптики в фокусе и его ближайшей окрест-
окрестности.
Рассмотрим задачу о волновом
поле в окрестности фокуса с точки
зрения волновой оптики. Пусть на
пути сходящейся сферической волны
поставлена диафрагма с отверстием
АВ (рис. 210). Неприкрытую часть
волнового фронта F примем за вспо-
вспомогательную поверхность, из кото-
которой исходят вторичные волны Гюй-
Гюйгенса. Следуя приближенному мето-
методу Френеля (§ 41), поле на поверхно-
поверхности F запишем в виде
Рис. 210
EF = -ё
го
Если пренебречь зависимостью амплитуд вторичных волн от
(малого) угла 7? т0 поле в точке наблюдения Р представится
интегралом
Aujt
I
¦dF,

§ 55 СВЕТОВОЕ ПОЛЕ ВБЛИЗИ ФОКУСА 375
распространенным по всей неприкрытой поверхности волново-
волнового фронта. Если точка Р лежит в малой окрестности фокуса
О, то расстояния го и г в знаменателе подынтегрального вы™
ражения могут считаться постоянными. Различие между ними
надо учесть только в фазовом множителе е^г°~гК Как видно из
рис. 210, г = го + Ж. Возведем это равенство в квадрат, учтем,
что R <С го, а затем приближенно извлечем квадратный корень
с точностью до квадратичных членов по R включительно. По™
лучим
(r0R) , R2 (roRJ / -оч , В2 . 2(ту \
г - го = ^ L + — - ^—з^- = (nR) + Т^ siir (R, п),
го 2ro rg 2r0
где п = го/го — единичный вектор нормали к поверхности F,
направленный к фокусу О. В дальнейшем в этом выражении
сохраним только линейный член. Это молено делать, если по™
правка в фазе, вносимая квадратичным членом, много меньше
тг, т.е. когда
Д2/П)<А. E5.1)
С учетом всего изложенного для волнового поля (в условных
единицах) в точке Р получим
ЕР = / e*M^nR) dU, E5.2)
где du = dF/rQ — телесный угол, под которым из точки О видна
площадка dF.
Когда диафрагма удалена в бесконечность, а расстояние R
остается конечным, то R2/r® = 0. Тем самым ограничение E5.1)
снимается, а E5.2) переходит в точное решение задачи. Это
видно и из самой структуры выражения E5.2). Действительно,
сШ ечш^кпЩ есть плоская волна, распространяющаяся в направ-
направлении волнового вектора k = fcn, а потому она удовлетворяет
волновому уравнению D3.1). Интеграл E5.2) есть суперпозиция
таких плоских волн различных направлений, а следовательно,
является точным решением того же уравнения. Такое решение
позволяет точно исследовать все явления, связанные с прохож™
дением сферической волны через фокус.
2. Если точка Р находится в фокусе О, т.е. R = 0, то все
вторичные волны приходят в О в одинаковых фазах, а потому
интенсивность света в этой точке максимальна. Формула E5.2) в
этом случае дает Eq = fteiujt. Наибольший интерес представля-
представляет распределение интенсивности света в фокальной плоскости,
т.е. в плоскости, проходящей через фокус О перпендикулярно
к оси пучка МО. Чтобы интегрирование в E5.2) выполнялось
элементарно, будем предполагать телесный угол О небольшим,
так что при вычислении интеграла неприкрытую часть сфери-

376 ДИФРАКЦИЯ СВЕТА ГЛ. IV
ческого волнового фронта молено заменить плоской. Саму диа-
фрагму возьмем прямоугольной формы со сторонами 2а и 2Ь.
Угловые размеры этих сторон при наблюдении из точки О бу-
будут 2а = 2а/го и 2/3 = 2b/ro соответственно. Начало координат
поместим в точке О, направив оси X и Y параллельно сторонам
прямоугольной диафрагмы. Координаты точки наблюдения Р
обозначим через X и Y ^ текущие координаты в плоскости диа-
диафрагмы — через х ж у. Тогда dF = dxdy = Гд dip eft/?, du = dip d^,
где ip-aif; — углы, под которыми из точки О видны отрезки х и у.
Далее, (nR) = nxX + nyY = ^(x/ro)X^(y/ro)Y = -{ )
В результате интеграл E5.2) перейдет в
ЕР = еш J
Это в точности такой же интеграл, какой встречался в § 45
при рассмотрении фраунгоферовой дифракции на прямоуголь-
прямоугольном отверстии. Поэтому распределение интенсивности света в
фокальной плоскости в окрестности фокуса можно представить
формулой
22
= 7
кха J \ кур J
В фокальной плоскости получается система светлых пятен
прямоугольной формы со светлым центром (см. рис. 179). Рас-
Расстояния между двумя соседними минимумами, а также от цен™
тра центрального максимума до первого минимума равны
Остается проверить, выполняется ли условие E5.1). Так как
заметная интенсивность по формуле E5.3) получается при R
порядка Аж, то формула E5.1) переходит в
/3 > \/Щ^° E5.5)
В оптических приборах под tq следует понимать расстояние от
линзы (или сферического зеркала) до точки геометрического
схождения лучей. Например, если лучи сходятся в главном фо-
фокусе, то го равно фокусному расстоянию / линзы или зеркала.
Ввиду малости длины волны, условие E5.5) очень хорошо вы-
выполняется во всех оптических приборах. Так, при / = 10 см,
А = 500 нм из E5.5) получаем /3 > 4 • 10~3 рад ~ 15'. Поэтому
применимость выведенных здесь формул к оптическим прибо-
приборам с линзами и зеркалами не вызывает сомнений.
Для теории оптических приборов наибольшее значение имеет
случай круглой диафрагмы. Исследование этого случая, конеч-
конечно, не встречает каких-либо затруднений. Качественно ясно, что

§ 55 СВЕТОВОЕ ПОЛЕ ВБЛИЗИ ФОКУСА 377
дифракционная картина в фокальной плоскости должна иметь
вид светлых и темных концентрических кругов со светлым цен-
центром (см. рис. 180). Для определения размеров дифракцион-
дифракционных кругов надо вычислить интеграл E5.2). В случае круглой
диафрагмы результат вычисления выражается через бесселеву
функцию первого порядка. Радиусы темных колец имеют еле™
дующие значения:
R = О,61А//3; 1Д2А//3; 1,62А//3;..., E5.6)
где /3 — угловой размер радиуса диафрагмы, если его рассма™
тривать из точки О.
3. Найдем теперь распределение интенсивности света на оси
МО^ предполагая, что пучок лучей ограничен круглой диа™
фрагмой. В этом случае в E5.2) можно взять dft = 2тг sin$ dti
(см. рис. 210). Если точка Р лежит перед фокусом, то пИ =
= —Rcos'i}. Если же она лежит за фокусом, то nR = i? cos#. По
формуле E5.2)
Ер = 2neiLOt j
±ikR
где верхний знак относится к случаю, когда точка наблюдения
расположена левее, а нижний — правее фокуса. Вычислив мо-
модуль этого выражения, находим амплитуду колебаний поля на
оси пучка:
а - - sin —К— ^. E5.7)
Во всякой плоскости, перпендикулярной к оси пучка, дифрак-
дифракционная картина имеет вид концентрических колец. Однако в
зависимости от положения этой плоскости центр пучка может
быть и светлым, и темным. Амплитуда на оси обращается в
нуль, когда kR(l — cos/3) = ттг, т.е.
В этом случае, как легко убедиться, в неприкрытой части сфе-
сферического волнового фронта содержится четное число зон Фре-
Френеля, а потому центр колец и получается темным. Расстояние
между ближайшими минимумами интенсивности, расположен-
расположенными по разные стороны от фокуса, равно
S = « -ш. E5.9)
1 — cos f3 f32
Эта величина может служить мерой продольных размеров обла-
области, в которой концентрируется свет вблизи фокуса. Объем этой
г 4А /А\2 4А3
области порядка — . I - 1 = —.

378 ДИФРАКЦИЯ СВЕТА ГЛ. IV
§ 56. Разрешающая способность телескопа и
микроскопа
1. Будем предполагать, что оптические системы идеальны в
смысле геометрической оптики, т.е. дают строго точечные изо-
изображения каждой точки объекта. По волновой оптике это не так.
Как показано в предыдущем параграфе, изображением светя-
светящейся точки в сопряженной плоскости является дифракционная
картина, состоящая из концентрических колец, окружающих
центральный светлый дифракционный кружок. Распределение
интенсивности в такой картине представлено сплошной кривой
на рис. 181. Основная доля энергии света (около 84%) прихо-
приходится на центральный дифракционный кружок. Этот кружок и
будет изображением светящейся точки, если пренебречь энерги-
энергией, приходящейся на окружающие его дифракционные кольца.
Он называется кружком Эйри по имени ученого, впервые рас-
рассчитавшего дифракционную картину Фраунгофера от круглого
отверстия.
Конечный объект можно рассматривать как совокупность
точечных источников, каждый из которых изображается круж-
кружком Эйри A801-1892) с окружающими его дифракционными
кольцами. Изображение объекта есть наложение таких крулеков
и дифракционных колец. Задача теории сводится к расчету рас-
распределения интенсивности света в такой картине. Следует раз-
различать два предельных случая: 1) точечные источники некоге-
некогерентны; 2) точечные источники когерентны. В первом случае
складываются интенсивности волновых полей, во втором — их
напряженности. Приближенно первый случай реализуется для
самосветящихся^ второй — для освещаемых объектов. Первый
случай имеет основное значение в теории телескопа, а второй —
микроскопа.
В простейшем случае сложный объект состоит из двух то-
точечных источников Si и ^2 (рис. 211). Если расстояние между
центрами кружков Эйри от этих то-
точечных источников мало по срав-
сравнению с размерами самих круж-
кружков, то распределение интенсивно-
интенсивности света в изображении будет мало
отличаться от того, которое получи-
лось бы только от одного точечного
источника. Глаз не сможет решить,
является ли объект точечным или
Рис> 211 состоит из нескольких близко рас-
расположенных светящихся точек. Говорят, что в этом случае све-
светящиеся точки не разрешаются оптическим прибором. При уве-
увеличении расстояния между Si и S2 будет увеличиваться и рас-

§ 56 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ТЕЛЕСКОПА И МИКРОСКОПА 379
стояние между центрами соответствующих им кружков Эйри S[
и $2, тогда как размеры самих кружков останутся неизменны™
ми. Начиная с некоторого минимального расстояния I = 1МИН на
кривой распределения интенсивности в ее центре появится про-
провал, который сможет зарегистрировать глаз или другой прием™
ник света. Тогда говорят, что светящиеся точки Si и S2 разре-
разрешаются оптическим прибором. Величина 1МИН называется раз-
решаемым расстоянием прибора (объектива), а обратная ему
величина 1//Мин ~~ разрешающей способностью.
Точно указать величину 1МИН невозможно. Она в значитель-
значительной степени зависит от индивидуальных особенностей глаза или
другого приемника излучения. Речь может идти только о ра-
рациональной оценке /Мин- Согласно Рэлею, за 1МИН принимается
такое расстояние между светящимися точками Si и $2, при ко™
тором расстояние между центрами кружков Эйри равно радиу-
радиусу одного кружка. В этом случае центр дифракционной карти™
ны от одной светящейся точки будет накладываться на первый
дифракционный минимум дифракционной картины от второй
светящейся точки. Такой критерий аналогичен критерию спек™
трального разрешения, предложенному также Рэлеем (см. § 47).
2. Для исследования вопроса о применимости критерия
Рэлея к различным условиям наблюдения надо рассчитать рас-
распределение интенсивности света в плоскости изображения двух
точечных источников света S\ и *$2. С этой целью можно вое™
пользоваться формулами предыдущего параграфа. Если источ-
источники Si и S2 некогерентны, то надо сложить интенсивности
создаваемых ими дифракционных картин. Если же они коге™
рентны, то надо складывать волновые поля, а затем вычислять
интенсивность результирующего волнового поля. Распределение
интенсивности света в плоскости изображения в случае одной
светящейся точки представлено сплошной кривой на рис. 181.
Для нахождения распределения интенсивности света в случае
двух одинаковых светящихся точек Si и *$2 применим графиче-
графический метод.
Рассмотрим сначала случай, когда источники Si и *$2 неко™
герентны. На рис. 212 штриховые кривые представляют распре-
распределение интенсивности в плоскости изображения для каждого
из точечных источников. Расстояние между центрами дифрак-
дифракционных картин предполагается равным 0,61А//3, т.е. радиусу
кружка Эйри, как этого требует критерий Рэлея на пределе раз™
решения (угол /5 имеет тот же смысл, что и в предыдущем пара-
параграфе). Результирующая интенсивность получается сложением
ординат обеих штриховых кривых и изображена сплошной ли-
линией. В центре С она имеет провал, где интенсивность состав-
составляет 74 % от максимальной интенсивности. Между тем средний

380
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
глаз уверенно обнаруживает наличие провала уже тогда, когда
интенсивность в центре составляет около 85%. Таким образом,
можно считать, что при выбранном расстоянии между светящи-
светящимися точками получится разрешение. С другой стороны, сбли™
жая штриховые кривые, легко установить, что провал исчезает,
когда расстояние между центрами кружков Эйри уменьшает™
0,2-
-А/р -АУ2р ] 0 ! А/2р АУР
0,61 Щ
Рис. 212
ся до А//3, что очень мало отличается от рэлеевского предела
0,61 А//?. В этом случае разрешения нет. Таким образом, в слу-
чае некогерентных точечных источников света при визуальном
наблюдении критерий Рэлея дает практически необходимое и
достаточное условие для их разрешения.
3. Рассмотрим теперь случай, когда источники S\ и $2 коге-
когерентны. В качестве таких источников можно взять, например,
два малых отверстия в непрозрачном экране, освещаемые ко™
герентным светом (рис. 213). Такие отверстия ведут себя как
точечные когерентные источники, излучающие вторичные вол™
ны Гюйгенса. Пусть отверстия освещаются пучком параллель-
параллельных лучей, наклоненных под углом t? к нормали к плоскости

§ 56 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ТЕЛЕСКОПА И МИКРОСКОПА 381
экрана. Если I — расстояние между центрами отверстий, то раз™
ность фаз между волнами, приходящими в эти отверстия, будет
А = Bтг/АI slnt?. Такова же будет и разность фаз между ко™
лебаниями, приходящими в центр дифрак-
дифракционной картины, т.е. в точку, расположен™
ную посередине между центрами кружков
Эйри от источников Si и $2- Интенсивность
света в этой точке представится выраже-
нием
1С = 1г + /2 + 2^/hh cos A =
= 2Ji(l + cos A) = Ah cos2 у.
Принципиальное отличие от случая
некогерентных источников света состоит в
появлении дополнительного — интерферен- рИс. 213
ционного — члена. Это сказывается на кри™
терии разрешения и на разрешающей способности объектива.
Меняя угол наклона #, можно повысить разрешающую способ-
способность объектива.
Если свет, освещающий отверстия Si и $2, падает нормаль-
нормально к плоскости экрана, то А = 0 и, следовательно, Iq = 4Д.
Допустим, что в этом случае расстояние между центрами ди-
дифракционных кружков Эйри равно радиусу одного кружка, т.е.
наименьшему расстоянию, которое требуется критерием Рэлея
для разрешения светящихся точек. Тогда, как мы видели, ин™
тенсивность J\ составляет 37 % от максимальной интенсивно-
интенсивности, которую создает в центре кружка Эйри только один ис™
точник света. Поэтому результирующая интенсивность в цен-
центре дифракционной картины будет равна 4 • 37 = 148 % от той
же максимальной интенсивности. Распределение интенсивности
света для рассматриваемого случая представлено на рис. 214.
Штриховые кривые по-прежнему представляют интенсивности
от каждого из источников Si и S2 в отдельности, а сплошная
кривая — результирующую интенсивность. На кривой результи-
результирующей интенсивности имеется всего лишь один максимум С.
Поэтому никакого раздельного изображения светящихся точек в
рассматриваемом случае получиться не может. Для этого необ-
необходимо развести центры кружков Эйри на расстояние, превы-
превышающее рэлеевский предел примерно в 1,2 раза.
Перейдем теперь к рассмотрению наклонного освещения. Ес-
Если А = тг/2, т.е. разность хода между лучами, освещающими от-
отверстия Si и Й2, равна А/4, то cos A = 0. Интерференционный
член пропадает, и получается в точности такое же распределе-
распределение интенсивности света, а с ним и тот же критерий разрешения,
что и в случае некогерентных светящихся точек. Если А = тг, а

382
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
следовательно, I = А/Bsin??), что возможно лишь при I ^ А/2,
то в центре дифракционной картины всегда получается нулевая
интенсивность, а потому разделение максимумов выражено осо-
1,4 ¦
1,2 -
1
0,8
0,6
0,4
0,2
-Щ -АУ2р ] 0 ! Шр Щ
/
1
1 j
11
¦ /
ll
/
A
/
1
I
I
/
/
I
С 1,48
A
/\
\ 1
\ 1
\ 1
\ 1
\ 1
\ I
\ 1
\ 1
\ 1
\ 1
V0,37
/ \
/ \
/ \
/ \
/ \
/ ( \
[B
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\
\\
\
\
\
0,61 Щ
Рис. 214
бенно отчетливо. На рис. 215 представлено распределение интен-
сивностей для рассматриваемого случая в предположении, что
центры кружков Эйри разведены до рэлеевского предела. При
скользящем падении лучей эти центры можно сблизить пример-
примерно вдвое по сравнению с рэлеевским пределом, и все же провал
на кривой интенсивности сохранится. Таким образом, примене-
применение наклонного освещения приводит к повышению разрешаю™
щей способности. При скользящем падении разрешающая спо-
способность возрастает почти вдвое по сравнению со случаем неко-
некогерентных светящихся точек.
Легко теперь сообразить, что следует ожидать при освеще-
освещении объекта лучами всевозможных направлений от протяженно-
протяженного источника света. Нормально падающим лучам соответствует
наименьшая разрешающая способность и наибольшее разрешае-
разрешаемое расстояние, превосходящее соответствующее расстояние для

§ 56 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ТЕЛЕСКОПА И МИКРОСКОПА 383
некогерентных светящихся точек. При возрастании угла накло-
на лучей разрешаемое расстояние уменьшается. При угле накло-
наклона, когда разность фаз А становится равной тг/2, оно такое же,
что и для некогерентных источников. При дальнейшем увели™
чении наклона разрешаемое расстояние продолжает монотонно
уменьшаться и при скользящем падении становится почти вдвое
/
0,8
0,6
0,4
0,2
/
/
_ У . —
А
Л
/ \
/ V
1 \\
1
г
1 \
/
1/
д
/
/
/
/
\|
\/
/\
/
/
//
'/
В
/Л
\
\\
\\
л
\
\
\
\
\
\
\
\
\
\
\
\
>. . --,— — . \ _
Рис. 215
меньше соответствующего расстояния для некогерентных источ-
источников. Естественно поэтому ожидать, и это подтверждается рас™
четом, что при освещении широкими пучками лучей получится
такое же распределение интенсивности света в дифракционной
картине и такой же критерий разрешения, что и при некогерент-
некогерентных источниках света.
Таким образом, разрешаемое расстояние меняется с измене-
изменением условий освещения и должно рассматриваться как ориен-
ориентировочное. При этом надо еще раз подчеркнуть, что получен-
полученные результаты относятся к визуальным наблюдениям. Приме™
нение других физических методов исследования может пони-
понизить разрешаемый предел.
4. В случае телескопа рассматриваемые объекты, например
компоненты двойной звезды, всегда излучают некогерентно.
Для телескопа интерес представляет не линейное, а угловое раз-
разрешаемое расстояние. Если # — угловое расстояние между рас-
рассматриваемыми звездами (рис. 216), то расстояние между цен-
центрами соответствующих кружков Эйри в фокальной плоскости
будет х = S[Sr2 = /#, где / — фокусное расстояние объектива.

384 ДИФРАКЦИЯ СВЕТА ГЛ. IV
Согласно критерию Рэлея, для разрешения звезд это расстояние
должно быть не меньше 0,61А//5, т.е. /t? ^ 0,61А//3. Учитывая,
что для небольших углов //3 = D /21
где D — диаметр объектива, отсюда
получим
1
л > 1 99 (^п 1\
^ ^ ' 1У (оо.ij
Разрешаемое угловое расстояние
равно
^мин = 1,22^. E6.2)
рис 216 Глаз при рассматривании удален-
удаленных предметов действует принципи-
принципиально так же, как объектив телескопа. Поэтому формулы E6.1)
и E6.2) применимы и к глазу. Роль D играет диаметр зрачка
глаза d. Полагая d = 4 мм, А = 550 нм, находим для разрешае-
разрешаемого расстояния человеческого глаза
#гл = 1,22^ = 1,67 • 10~4 рад = 35/;. E6.3)
Этот результат удивительно хорошо согласуется с физиологи-
физиологической оценкой разрешающей способности глаза (см. § 21, п. 7).
Достойна восхищения способность живого организма приспосаб-
приспосабливаться к окружающим условиям и в процессе эволюции дости-
достигать максимума того, что принципиально допускается законами
природы.
Таким образом, разрешающая способность телескопа про-
пропорциональна диаметру его объектива. Крупнейший в мире дей™
ствующий телескоп-рефлектор (см. § 24) имеет диаметр пара-
параболического зеркала D = 6 м. Теоретическая разрешающая
сила его превосходит разрешающую силу глаза в 6000/4 =
= 1500 раз. Теоретическое разрешаемое расстояние составля-
составляет 35/;/1500 = 0,023/;. Для второго по величине телескопа-
рефлектора Маунт-Паломарской обсерватории с диаметром зер-
зеркала 5 м теоретическое разрешаемое расстояние равно 0,028/;.
Разрешающей способности таких гигантских телескопов доста-
достаточно, чтобы изображения звезд с наибольшими угловыми раз-
размерами получались уже в виде дисков, подобно изображениям
планет.
Однако наличие земной атмосферы не позволяет полностью
использовать разрешающую способность телескопа. Нерегуляр-
Нерегулярные процессы в атмосфере, сопровождающиеся изменениями по-
показателя преломления на пути световых лучей, портят изобра-
изображения и снижают реальную разрешающую способность теле-
телескопов до величин порядка 1" — 0,5/;, причем особенно сильно
это снижение сказывается на больших телескопах. Такая разре-

§ 56 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ТЕЛЕСКОПА И МИКРОСКОПА 385
шающая способность может быть достигнута с помощью много
меньших объективов. Большие телескопы строятся не с целью
повышения разрешающей способности, а для увеличения коли-
чества света, поступающего в телескоп от наблюдаемых небес™
пых объектов. Оно пропорционально площади отверстия объек-
объектива. Поэтому с помощью больших телескопов можно обнару-
жить и сфотографировать более слабые небесные объекты, чем
с помощью малых. Для повышения же разрешающей способно-
способности астрономических телескопов необходимо исключить вред™
ное влияние атмосферы. Большие перспективы открываются пе-
перед телескопами, устанавливаемыми на космических кораблях,
а еще лучше — на Луне.
5. Увеличение телескопа должно быть согласовано с разре-
разрешающей способностью его объектива. Допустим, что угловой
размер предмета равен минимальному углу !?мин, разрешаемо-
разрешаемому объективом телескопа. Если угловое увеличение телескопа
равно Ж, то в телескоп предмет будет виден под углом N§MWM.
Для полного использования разрешающей способности телеско-
телескопа необходимо, чтобы этот угол разрешался глазом, т.е. должно
быть iVt?MHH ^ 1?гл. Подставляя сюда значения 1?Мин и ^гл из
формул E6.2) и E6.3), получим
Ж>^ = Жнорм, E6.4)
где iVHOpM — нормальное увеличение телескопа (см. § 23, п. 4).
В § 11 (п. 10) было показано, что N = D/h, т.е. увеличение те-
телескопа равно отношению ширины D падающего параллельного
пучка лучей к ширине h выходящего пучка. Когда увеличение
меньше нормального, т.е. D/H < D/d, то h > d. Значит, не весь
пучок параллельных лучей, падающий на объектив, попадает в
зрачок глаза, а только часть его. Действующей является толь™
ко центральная часть объектива, диаметр которой меньше D.
Телескоп действует так, как если бы его объектив и разреша-
разрешающая способность уменьшились. При нормальном увеличении
h = d, разрешающая способность объектива согласована с раз-
разрешающей способностью глаза. Наконец, когда увеличение боль-
больше нормального, т.е. D/h > D/d, то h < d. В этом случае глаз
действует так, как если бы его зрачок сузился, а разрешающая
способность понизилась.
Применение увеличений больше нормального не может вы-
выявить новые детали рассматриваемого объекта. Увеличения,
значительно превосходящие нормальное, приносят только вред,
поскольку чрезмерное сужение выходящего пучка может внести
в изображение значительные дифракционные искажения. Одна-
Однако по физиологическим причинам иногда бывает полезно брать
увеличения, превосходящие нормальное в 2-4 раза. Рассматри-
13 Д.В. Сивухин

386 ДИФРАКЦИЯ СВЕТА ГЛ. IV
вая детали на пределе разрешающей способности, глаз работа-
работает с напряжением и быстро утомляется, его чувствительность
и разрешающая способность понижаются. Применение увеличе-
увеличений, несколько превышающих нормальное, не выявляет новых
подробностей в строении рассматриваемых объектов, но позво-
позволяет рассматривать их с меньшим напряжением. К таким же
выводам мы пришли в § 23 из фотометрических соображений.
6. Вопрос о разрешающей способности микроскопа решается
так же, как и для телескопа. Критерий разрешения Рэлея в этом
случае требует
lf > 0,61^, E6.5)
где V — расстояние между центрами кружков Эйри для рассма-
рассматриваемых двух светящихся точек (предполагается, что апер-
турный угол со стороны изо-
бражения 2/3 мал). Чтобы пе-
перейти к линейным размерам са-
самого объекта, следует восполь-
воспользоваться условием синусов Аб-
бе, которое должно выполнять-
выполняться для объектива всякого ми™
кроскопа. При малых углах /3
Рис- 217 (рис. 217) оно может быть на™
писано в виде In sin а = 1;/3, где п — показатель преломления
пространства объектов, а 2а — апертурный угол со стороны это™
го пространства. Исключая /3 и 1;, приходим к соотношению
1 > 0,61—^—, E6.6)
в sin a x 7
которое и определяет предел разрешения микроскопа. Мини-
Минимальное разрешаемое расстояние (с точностью до небольшого
численного коэффициента) равно
Uh = 0,61—^—. E6.7)
п sin a
Этот предел разрешения определяется волновой природой све-
света и не может быть превзойден никакими техническими усо-
усовершенствованиями микроскопа. При прочих равных условиях
предел разрешения тем меньше, чем короче длина волны. Нали-
Наличие в знаменателе показателя преломления п объясняется тем,
что разрешаемое расстояние может непосредственно зависеть от
длины волны не в вакууме, а в той среде, где находится объект^
т.е. от величины А/в.
Нетрудно проверить, что при малых апертурах формула
E6.7) переходит в формулу E6.2), определяющую разрешаю-
разрешающую способность телескопа. В этом случае обе формулы от-
отличаются одна от другой только по форме. В формуле E6.7)

§ 56 РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ТЕЛЕСКОПА И МИКРОСКОПА 387
разрешаемое расстояние выражено в линейных единицах, а в
формуле E6.2) — в угловых.
Для повышения разрешающей способности микроскопа мож-
можно идти двумя путями: 1) уменьшать длину волны (переход к
ультрафиолету); 2) увеличивать числовую апертуру объектива
микроскопа nsina. Таким образом, угол а дол леей быть как
можно больше. В лучших современных объективах он практи-
практически достиг своего теоретического предела а = тг/2. Для по™
вышения числовой апертуры применяют также иммерсию, т.е.
жидкость с возможно высоким показателем преломления, за-
заполняющую пространство между покровным стеклом и фрон-
фронтальной линзой объектива (см. § 18, п. 4). Если принять п« 1,5,
то максимальное значение числовой апертуры будет nsina«1,5.
Применение иммерсии, таким образом, позволяет снизить раз-
разрешаемый предел примерно в полтора раза, т.е. довести его до
величины /«0,61 А/1,5«0,4А. Детали объекта, размеры которых
меньше примерно 0,4А, принципиально не могут быть выявле-
ны с помощью микроскопа. Ни при каком увеличении нельзя
определить форму объекта, рассматривая его в микроскоп, если
размеры самого объекта меньше приблизительно 0,4А. Разумеет-
Разумеется, с помощью микроскопа можно обнаружить объекты и много
меньших размеров, если только они светятся достаточно ярко
(ультрамикроскоп). Нельзя определить только их форму.
Радикальное повышение разрешающей способности достига-
достигается в электронном микроскопе, где роль световых лучей выпол-
выполняют электроны, фокусируемые электрическими и магнитными
линзами. Электроны ведут себя подобно волнам с длиной волны
л h h
А — — — _,
Р
где h — постоянная Планка, т — масса, р — импульс, ? —
энергия электрона. Эти волны называются волнами де Бройля
(р. 1892). При ? = 10 000 эВ приведенная формула дает А =
= 0,0122 им. Такая длина волны на порядок меньше размеров
атома. Однако такое разрешение в электронном микроскопе не
достигается, так как для уменьшения геометрических аберра-
аберраций в электронных микроскопах приходится пользоваться узки™
ми параксиальными пучками с малыми апертурами. Но даже в
таких пучках электронный микроскоп позволяет разрешать де™
тали, превосходящие размеры атомов всего в несколько раз.
7. Рассмотрим в заключение вопрос о рациональном увели-
увеличении микроскопа. Напомним, что увеличением микроскопа (лу-
(лупы) называется отношение угла, под которым виден объект в
микроскоп, к тому углу, под которым он был бы виден нево-
невооруженным глазом, если бы был помещен на расстоянии ясного
зрения. Пусть 1МИН — минимальное расстояние, разрешаемое ми-
13*

388 ДИФРАКЦИЯ СВЕТА ГЛ. IV
кроскопом. Невооруженным глазом с расстояния ясного зрения
оно видно под углом 1? = 1МШШ/Ь. В микроскоп то же расстояние
видно под углом §' = Nfi. Для разрешения необходимо, чтобы
угол #' был не меньше минимального угла, разрешаемого гла-
глазом, т.е. 1?' = N§ ^ 1?гл. Отсюда, используя выражения E6.3) и
E6.7), найдем
N > 2Ln^a. E6.8)
Знаку равенства соответствует нормальное увеличение
^норм = d E6.9)
Как и в случае телескопа, нормальное увеличение микроскопа
есть наименьшее увеличение, при котором может быть использо-
использована вся разрешающая способность объектива. О целесообраз-
целесообразности работать при увеличениях больше нормального для ми™
кроскопа можно повторить без всяких изменений все, что выше
было сказано относительно телескопа.
Максимальная числовая апертура, как указывалось выше,
для сухих систем имеет своим пределом единицу. Для иммерси-
иммерсионных систем этот предел равен примерно 1,5. Диаметр зрачка
глаза d примем равным 2 мм. Тогда для нормального глаза (L =
= 25 см) получатся следующие предельные значения нормаль-
нормальных увеличений:
для сухих систем Жнорм = 250,
для иммерсионных систем iV"HOpM = 375.
По физиологическим соображениям имеет смысл переходить
к несколько большим увеличениям. Однако бессмысленно стро-
строить микроскопы с увеличением больше, чем в 1000-1500 раз.
§ 57. Теорим и демонстрационные опыты Аббе
1. Впервые предел разрешения объектива микроскопа был
найден Гельмгольцем в 1874 г. Гельмгольц рассматривал само-
самосветящиеся объекты. Примерно в то же время и независимо
от Гельмгольца вопрос о разрешающей способности микроскопа
был разобран Аббе, но для случая освещаемых объектов. Имен-
Именно этот случай встречается в практике микроскопии. От освеще-
освещения очень сильно зависит качество изображения в микроскопе.
Этот вопрос подвергся глубокому изучению Д.С. Рождествен-
Рождественским A876—1940) в последние годы его жизни. Ниже излагается
метод Аббе с некоторыми изменениями и затрагиваются допол-
дополнительные вопросы, связанные с этим методом.

§ 57 ТЕОРИЯ И ДЕМОНСТРАЦИОННЫЕ ОПЫТЫ АББЕ 389
Допустим сначала, что объектом является достаточно боль-
большая (бесконечная) плоская дифракционная решетка, освеща-
освещаемая параллельным пучком монохроматических лучей. Свет,
прошедший через решетку, будет состоять из дискретного ряда
плоских волн (дифракционных пучков или спектров различных
порядков), распространяющихся от решетки в различных на™
правлениях. Пучки низких порядков будут однородными волна-
волнами, а пучки, порядок которых превосходит определенное значе-
значение, — неоднородными (см. § 52). Неоднородные волны, затухая
на расстояниях порядка длины волны, в объектив не попадают
и потому не влияют на изображение, даваемое им.
2. Допустим, что перед объективом поставлена диафрагма,
пропускающая спектры определенных порядков. Если диафраг-
диафрагма пропускает пучок одного лишь нулевого порядка, то прошед-
прошедший свет будет состоять только из одной однородной плоской
волны, как если бы на месте дифракционной решетки стояла
прозрачная идеально плоскопараллельная пластинка. Никакой
информации о структуре объекта такой свет не несет. В плос-
плоскости изображения, сопряженной с плоскостью решетки, полу-
получится равномерно освещенное поле.
Возьмем теперь такую диафрагму, чтобы она пропускала
только два спектра соседних порядков, например m-го и (т + 1)-
го (рис. 218). За решеткой эффек-
эффективными останутся только две одно-
однородные волны, распространяющие-
распространяющиеся в различных направлениях:
Ет = ат cos (u)t - kmr),
Em+i = am+i cos (ujt — km+ir),
интерферирующие между собой.
Плоскость решетки примем за коор- РИС- 218
динатную плоскость ХУ, направив
ось X перпендикулярно к ее штрихам, а ось Z — в сторону рас-
распространения падающего света. Интерференционные полосы во
всякой плоскости z = const, параллельной плоскости решетки,
будут параллельны ее штрихам. Найдем расстояние Ах между
ними. Разность фаз между рассматриваемыми волнами в ука-
указанной плоскости представляется выражением
При изменении х на Ах она изменится на Aip =
— kmjX)Ax. Интенсивность света будет периодически повторять-
повторяться, когда Аср = 2тг, 4тг,... Ширина интерференционной полосы
Ах найдется, если положить Aip = 2тг. Направления на дифрак-
дифракционные максимумы рассматриваемых порядков определяются

390 ДИФРАКЦИЯ СВЕТА ГЛ. IV
формулами
d(sin#m — sin б) = га A, d(sin#TO+i — sin0) = (га + 1)А,
где 0 — угол, под которым свет падает на решетку. Отсюда
d(sin#m+i - sin#m) = А. Но ктх = Bтг/А) sini?TO, km+ijX =
= Bтг/А) sini?TO+i, так что
&т+1,ж - ктх = B7r/A)(sm#TO+i - sin#m) = 2n/d.
Следовательно, ширина интерференционной полосы будет Ах =
= 2тг : {2жId) = d, независимо от направления освещающе™
го пучка лучей. В частности, такая система интерференцион-
интерференционных полос возникнет на выходе самой решетки, т.е. в плоскости
z = 0. Объектив даст изображение этой системы полос в плос-
плоскости изображения, сопряженной с плоскостью решетки (см.
§ 27, п. 6). Такое изображение передает основной характер
структуры решетки — ее периодичность с основным периодом
d. Распределение интенсивности в плоскости изображения будет
синусоидальным, т.е. таким же, какое получилось бы от синусо-
синусоидальной решетки Рэлея. Чтобы изображение передавало более
мелкие детали структуры объекта, необходимо расширить диа™
фрагму. Тогда за решеткой появятся плоские дифрагированные
волны, порядки которых отличаются друг от друга не только
на единицу, но также на 2, 3, ... Рассуждая как выше, нетрудно
показать, что интерференция двух волн, порядки которых от-
отличаются на Ага, даст интерференционные полосы с шириной
Ах = d/Ara.
Структуру решетки можно характеризовать разложением ее
пропускаемости в ряд Фурье. Полностью подобное изображение
со всеми деталями получилось бы, если бы интенсивность света
в плоскости изображения представлялась рядом Фурье с теми
же коэффициентами. Однако этого никогда не бывает. Из ря™
да Фурье выпадают компоненты, соответствующие неоднород-
неоднородным волнам и тем однородным волнам, которые задерживаются
диафрагмой. Чем больше дифрагированных волн различных по-
порядков проходит через диафрагму, тем совершеннее получается
изображение.
3. Если при определении разрешающей способности доволь-
довольствоваться наименее совершенным изображением, которое пра-
правильно передавало бы только периодическую структуру решет™
ки с периодом d, то разрешающую способность объектива ми-
микроскопа можно определять следующим образом. Пусть решет-
решетка освещается нормально падающими лучами света (рис. 219 а).
Тогда для разрешения необходимо, чтобы наряду с прямо про-
прошедшим пучком света в объектив попали также дифракционные
пучки первого и минус первого порядков. Если объектив иммер-
иммерсионный с показателем иммерсии п, то минимальный период

57
ТЕОРИЯ И ДЕМОНСТРАЦИОННЫЕ ОПЫТЫ АББЕ
391
решетки, при котором выполняется это условие, будет ds'ma =
= Л/n, где Л — длина волны в вакууме. Отсюда и находится
минимальное расстояние, разрешаемое объективом микроскопа:
Полученный результат отличается от E6.7) только несуществен™
ным числовым коэффициентом. Различие в коэффициентах
связано с некоторым различием критериев разрешения, кото-
Рис. 219
рые использовались при выводе формул E6.7) и E7.1), а также
с тем, что формула E6.7) относится к разрешению точечных, а
E7.1) — линейных объектов.
Разрешаемый предел E7.1) можно понизить за счет примене-
ния наклонного освещения. При нормальном падении освещаю-
освещающего пучка за решеткой интерферируют три пучка. При интер-
интерференции пучков нулевого и одного из первых порядков в изо™
бражении выявляется структура с основным периодом d. Такая
лее картина интерференции получается при наложении нулевого
пучка с другим пучком первого порядка. Второй пучок первого
порядка просто усиливает действие другого пучка того же по-
порядка. Кроме того, оба пучка первого порядка интерферируют
между собой, в результате чего на интерференционную картину
накладываются новые, более слабые, интерференционные поло-
полосы, расстояние между которыми вдвое меньше, т.е. равно d/2. В
этом проявляется действие первых гармоник в разложении про-
пускаемости решетки в ряд Фурье. Не меняя основного периода
в изображении решетки, они несколько усиливают его контраст.
Но для выявления структуры с основным периодом d, как выяс-
выяснено выше, достаточно двух соседних пучков, например, нуле-
нулевого и одного из пучков первого порядка. Максимально возмож-
возможное разрешение получится, если освещающий пучок направить

392 ДИФРАКЦИЯ СВЕТА ГЛ. IV
под углом а к решетке, как указано на рис. 219 б. Тогда будет
2dsina = Х/п и, следовательно,
1мин= 2^Р E7'2)
что вдвое меньше величины E7.1).
4. Таким образом, разрешающую способность микроскопа
можно повысить изменением направления освещающих лучей.
Однако влияние способа освещения на изображение в микро-
скопе этим не ограничивается. Оно более существенно. Если
бы освещение производилось пучком параллельных лучей, то,
как было выяснено выше, интерференционная картина за ре™
шеткой в каждой параллельной ей плоскости П имела бы вид
параллельных полос с расстоянием между ними d. Такие поло-
полосы не локализованы. Изображение, видимое в микроскоп, имело
бы один и тот же вид независимо от того, куда сфокусирован
микроскоп: на плоскость решетки или на любую плоскость, ей
параллельную. Для устранения этого вредного обстоятельства
в микроскопе объекты освещаются пучками лучей различных
направлений с широкими апертурами. Интерференционные по™
лосы, даваемые параллельными пучками различных направле-
направлений, смещены относительно друг друга вдоль оси X. Поэтому
во всех плоскостях П происходит гашение интерференционных
полос. Исключение составляет только случай, когда плоскость
П совпадает с плоскостью самой решетки. В этом случае все
интерференционные полосы, создаваемые освещающими пучка™
ми различных направлений, пространственно совпадают между
собой. Поэтому изображение объекта в микроскопе может воз™
никнуть только тогда, когда он сфокусирован на плоскость са-
самого объекта. В этом основная причина использования широких
апертур при освещении объектов в микроскопе.
5. В качестве объекта была взята дифракционная решетка
лишь с целью упрощения рассуждений. Это упрощение не прин-
принципиальное. Если взять объект произвольной формы и осветить
его параллельным пучком лучей, то за объектом возникнут ди-
дифрагированные пучки различных направлений с максимумами
и минимумами. Угол дифракционной расходимости #, определя-
определяющий направление на первый дифракционный минимум, опре-
определяется формулой n/sin# ~ А, где I — линейный размер объ-
объекта. Если диафрагма пропускает лишь незначительную часть
центрального дифракционного пучка, то изображение в микро-
микроскопе получится таким лее, как и в случае точечного объекта,
излучающего сферические волны равномерно по всем направ-
направлениям. Это был бы дифракционный кружок Эйри, совершенно
не зависящий от формы объекта, и никакого разрешения не по-
получилось бы. Минимальные размеры объекта 1МИН, при которых

57
ТЕОРИЯ И ДЕМОНСТРАЦИОННЫЕ ОПЫТЫ АББЕ
393
возможно разрешение, определяются условием
1мин ~ ^ь^-
а, т.е.
E7-3)
Мы снова пришли к формуле вида E7.1) или E7.2).
В приведенном рассуждении не столь существенно, куда по™
падает свет после рассеяния на объекте. Вместо объектива мож-
можно, например, взять фотопластинку и произвести на ней го™
лографическую запись предмета. Из предыдущих рассуждений
следует, что минимальный размер объекта, который может быть
записан таким способом, определяется формулой
1МИН - Л/а, E7.4)
где а — угловой размер голограммы, если ее рассматривать из
точки нахождения предмета во время голографирования (пред™
полагается, что он невелик).
6. Сам Аббе представил изложенную теорию в следующей
форме. Каждый пучок параллельных лучей, получившийся в
результате дифракции на объекте АВ (например, дифракцион-
ной решетке), собирается объективом в точке фокальной плос-
плоскости (рис. 220). Ди-
Дифракционную картину %В ^^ |F
в фокальной плоскости,
состоящую из совокуп-
совокупности таких точек: Со,
Ci, C_i, Сг, С^2, •••,
Аббе назвал первичным
изображением объекта.
Если известно первич™
ное изображение, то
с помощью принципа
Гюйгенса- Френеля мож-
можно рассчитать световое поле во всем пространстве за фокальной
плоскостью. В частности, изображение объекта есть не что
иное, как интерференционная картина, получающаяся в плос-
плоскости изображения в результате интерференции вторичных
волн Гюйгенса, исходящих из различных точек первичного
изображения. Эту интерференционную картину Аббе назвал
вторичным изображением.
Если диафрагма объектива пропускает один только цен™
тральный дифрагированный пучок, то первичное изображение
будет состоять только из одного центрального точечного мак-
максимума. Получится лишь одна вторичная сферическая волна,
исходящая из этого центрального максимума, которой не с чем
будет интерферировать. Вторичное изображение получится бес-
бесструктурным и будет представлять собой более или менее равно-
равномерно освещенное поле. Для появления какой-то структуры во
Рис. 220

394
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
вторичном изображении необходимо, чтобы первичное изобра-
изображение состояло по крайней мере из двух точечных дифракци-
дифракционных максимумов. Но это условие лишь по форме отличается
от того условия, из которого были выведены формулы E7.1) и
E7.2).
Если закрыть некоторые дифракционные максимумы в фо-
кальной плоскости, то вторичное изображение будет искажено.
Характер искажения часто можно предсказать. Этим восполь™
зовался Аббе для экспериментального подтверждения своей те-
теории. Объектом служила грубая дифракционная решетка. Аббе
помещал в фокальной плоскости другую решетку из проволок,
которые закрывали дифракционные максимумы через один. То-
Тогда расстояния между действующими (открытыми) максиму-
максимумами возрастали вдвое. В изображении решетки наблюдалось
удвоение штрихов. Все происходило так, как если бы экраниро-
экранирования не было, а объект был заменен более мелкой решеткой,
расстояния между штрихами которой вдвое меньше.
Еще более интересные искажения наблюдаются в случае дву™
мерной решетки, например, квадратной проволочной сетки. В
этом случае дифракционная картина в фокальной плоскости
состоит из светлых пятен, расположенных в узлах так лее ква-
квадратной сетки. Поместим в фокальной плоскости узкую щель,
с помощью которой можно открывать прямолинейные ряды из
таких пятен, а остальные пятна закрывать. Если щель гори-
горизонтальна и достаточно узка, то она выделит прямолинейный
ряд максимумов, расположенных вдоль горизонтальной прямой
Рис. 221
(рис. 221а). Такой ряд максимумов аналогичен дифракцион-
дифракционной картине от одномерной решетки с вертикальными щелями.
Поэтому оптическое изображение квадратной сетки при вве-

§ 58 ТЕЛЕСКОП БЕЗ ОБЪЕКТИВА 395
дении горизонтальной щели перейдет в систему вертикальных
полос. Если щель повернуть на 90° в вертикальное положение
(рис. 221 б"), то полосы сделаются горизонтальными. Если щель
повернуть параллельно диагонали сетки (рис. 221 в и г), то она
выделит прямолинейный ряд максимумов, параллельный той же
диагонали, причем расстояния между максимумами увеличатся
в л/2 раз. В результате оптическое изображение сетки перейдет
в систему наклонных полос, перпендикулярных к щели, а сами
полосы сделаются в у/2 раз уже.
Д.С. Рождественский указал, что непосредственной причи-
причиной появления ложных структур в опытах Аббе является ди-
дифракция света на экранирующей сетке. В отсутствие последней
объектив дает геометрически подобное изображение объекта.
Например, сетка из параллельных проволок изображается в ви-
виде системы параллельных полос. При введении экранирующей
сетки эти полосы остаются на прежних местах. Но на них накла-
накладывается дифракционная картина, возникающая при дифрак-
дифракции света на экранирующей сетке. Если экранирующая сетка
состоит из проволок, параллельных проволокам сетки-объекта,
то возникнут дифракционные полосы, параллельные полосам в
прежнем изображении сетки-объекта. При надлежащем перио-
периоде экранирующей сетки дифракционные полосы расположатся
посередине между прежними полосами. Произойдет удвоение
полос в изображении, как если бы проволоки в сетке-объекте
были натянуты вдвое чаще. Так лее, хотя и не столь просто,
объясняется и появление диагоналей, когда объектом является
квадратная проволочная сетка.
Дифракция на экранирующей сетке происходит независимо
от того, освещается ли объект посторонним светом или явля-
является самосветящимся. Поэтому и в случае самосвечения долж-
должны появляться такие же ложные структуры, как и при освеще-
освещении. Это было теоретически предсказано Л.И. Мандельштамом
A879^1944) еще в 1911 г. Опыты с накаленными сетками, постав-
поставленные самим Мандельштамом, подтвердили это предсказание.
§ 58. Телескоп без объектива. Получение изображений
с помощью малых отверстий
1. В принципе можно построить телескоп без объектива сколь угодно
высокой разрешающей способности. Роль объектива может играть круг-
круглое отверстие. Следующее рассуждение, принадлежащее Рэлею, разъяс™
няет идею такого телескопа. Допустим сначала, что в отверстие вставлен
объектив. Лучи, идущие от какой-либо точки объекта к ее изображению
вдоль оптической оси и по периферии, имеют различные геометрические
длины. При отсутствии объектива различны и их оптические длины. Объ™

396 ДИФРАКЦИЯ СВЕТА ГЛ. IV
ектив должен скомпенсировать своей толщиной различие оптических длин
всех лучей, чтобы они приходили в точку-изображение в одинаковых фазах.
Но небольшое расхождение в фазах лучей мало сказывается на результате
их интерференции. Например, если интерферируют два одинаковых луча в
одинаковых фазах, то результирующая интенсивность превосходит интен-
интенсивность отдельного луча в 4 раза. Если же разность фаз составляет тг/4, то
она будет превосходить в 2 + у/2 = 3,42 раза, т.е. изменится незначительно.
Поэтому разности фаз в тг/4 или меньше можно не принимать во внима-
внимание. Допустим теперь, что фокусное расстояние объектива увеличивается
все больше и больше. Различие в геометрических длинах центрального и
крайнего периферийного лучей будет становиться все меньше и меньше. Ко-
Когда это различие достигнет примерно А/8, надобность в объективе отпадет.
Действительно, в этом случае максимальная разность фаз между лучами,
приходящими в точку-изображение от различных точек плоскости отвер-
отверстия, не будет превышать тг/4, и компенсация различия оптических длин
становится практически не нужной. Отверстие будет действовать как объ-
объектив телескопа. При увеличении фокусного расстояния / разрешающая
способность объектива не меняется и все время определяется формулой
E6.2). Она останется неизменной и в предельном случае, когда / = оо, т.е.
когда объектив совсем удален.
Разность геометрических длин крайнего периферийного и центрального
лучей составляет D /(81), где D — диаметр отверстия, а I — длина телеско-
телескопа, которую можно считать равной фокусному расстоянию. Для оценки I
приравняем эту разность А/8 и получим
l = D2/\. E8.1)
Эта формула показывает, что о практической реализации телескопа без
объектива не может быть и речи ввиду колоссальных размеров, которые
должен был бы иметь такой телескоп. Например, при D = 1 м, А = 500 нм =
= 5 • 10^7 м формула E8.1) дает 1 = 2- 106 м = 2000 км. При гигантских
размерах телескоп обладал бы ничтожной светосилой: (D//J = IX/ f2 =
= A/f^lQ3.
2. К идее безлинзового телескопа примыкает способ получения изо-
изображений и фотографирования при помощи камеры с малым отверстием
(камеры-обскуры). Она отличается от безлинзового телескопа только мас-
масштабами и возможностью практического осуществления. Поэтому приводи-
приводимые ниже рассуждения относятся не только к камере с малым отверстием,
но дополняют и уточняют идею безлинзового телескопа.
При уменьшении размеров отверстия четкость изображения в камере
сначала улучшается, а затем начинает ухудшаться из-за дифракции. Ди-
Дифракция несущественна при больших отверстиях, а при малых отверстиях
становится основным фактором, определяющим четкость изображения. Оп-
Оптимальные размеры отверстия, при которых достигается наибольшая чет-
четкость, легко оценить с помощью следующих соображений. Пусть отверстие
имеет форму круга радиуса R. Расстояние до фотографируемого объекта
может считаться бесконечно большим по сравнению с глубиной камеры I.
Если бы была применима геометрическая оптика, то светящаяся точка изо-
изобразилась бы кружком того же радиуса R. Из-за дифракции точка изоб-
изобразится дифракционным кружком, радиус которого порядка XI/R. Умень-
Уменьшать размеры отверстия имеет смысл лишь до тех пор, пока дифракцион-
дифракционные ошибки не превзойдут геометрические. Наилучшая четкость изображе-
изображения достигается при таких размерах отверстия, когда эти ошибки примерно

§ 58 ТЕЛЕСКОП БЕЗ ОБЪЕКТИВА 397
одинаковы, т.е. при выполнении условия XI/R и Д, или R и л/ГХ. Это зна-
чит, что размер отверстия должен быть порядка центральной френелевой
зоны. Рэлей, более подробно исследовавший вопрос как теоретически, так
и экспериментально, нашел для наивыгоднейшего радиуса отверстия:
E8-2)
где а и b — расстояния предмета и его изображения от отверстия.
ЗАДАЧИ
1. При наблюдении в телескоп с нормальным увеличением освещен-
освещенность изображения звезды на сетчатке глаза в а = 10 раз меньше осве-
освещенности дневного неба, рассматриваемого в тот же телескоп. Во сколько
раз надо увеличить диаметр объектива для того, чтобы освещенность изо-
изображения звезды на сетчатке стала в /3 = 10 раз больше освещенности
изображения неба, если вместе с объективом телескопа заменен и окуляр
таким образом, что увеличение телескопа осталось нормальным?
Ответ. В у/а/3 = 10 раз.
2. В фокальной плоскости объектива телескопа помещена фотопластин™
ка. Освещенность изображения звезды на фотопластинке в а = 10 раз мень-
меньше освещенности дневного неба. Во сколько раз надо увеличить диаметр
объектива, чтобы освещенность изображения звезды на фотопластинке ста-
ла в /3 = 10 раз больше освещенности изображения неба?
Ответ. В \/оф = 10 раз.
3. Ракету, удаляющуюся от Земли, фотографируют, помещая фото-
фотопленку в фокальной плоскости объектива астрономического телескопа. При
диаметре объектива D\ = 80 мм дифракционное изображение ракеты ста-
становится неразличимым на фоне изображения неба, когда ракета находится
на расстоянии 1\ = 2 • 104 км от Земли. На каком расстоянии от Земли h
удастся заметить ракету на фотографии, полученной с помощью объекти-
объектива с диаметром J92 = 200 мм при той же контрастной чувствительности
пленки?
Ответ, h = hD2/Di = 5 • 104 км.
4. Как изменится разрешающая способность объектива телескопа, если
его центральную часть закрыть круглым экраном, диаметр которого мало
отличается от диаметра самого объектива?
Указание. При решении задачи круглые объектив и экран можно
заменить квадратными.
Ответ. Разрешающая способность увеличится приблизительно в два
раза.
5. Производится фотографирование удаленных предметов с помощью
объектива телескопа на фотопластинке, помещенной в его фокальной плос-
плоскости. Полученный снимок с помощью окуляра того же телескопа проеци-
проецируется на удаленный экран. Каково должно быть угловое увеличение те-
телескопа, чтобы при этом была использована полностью разрешающая спо-
способность объектива телескопа? Изображение на экране рассматривается с
того места, где установлен проекционный аппарат.
Ответ. N ^ D/dj где D — диаметр объектива, ad — зрачка глаза.
6. С какого расстояния г можно увидеть невооруженным глазом свет
лазера, генерирующего в непрерывном режиме Р = 10 кВт на частоте ш =
= 4 • 1015 с^1, если для формирования луча используется параболическое

398 ДИФРАКЦИЯ СВЕТА ГЛ. IV
зеркало с диаметром D = 5 м? Глаз видит источник, если в зрачок диамет-
ром d = 5 мм попадает в 1 с п = 60 квантов излучения, лежащего в зеленой
части спектра.
Ответ, г ~ \/ ~ 0,1 светового года (h — постоянная Планка.)
2 V hcXn
7. Излучение лазера непрерывного действия на волне Л = 500 нм мощ-
мощностью Р = 1 Вт направляется на спутник с помощью телескопа, диаметр
объектива которого равен D = 30 см. Свет, рассеянный спутником, улав-
улавливается другим таким же телескопом и фокусируется на фотоумножитель
с пороговой чувствительностью -РПор = 10~ Вт. При каких расстояниях I
до спутника отраженный сигнал может быть обнаружен, если поверхность
спутника равномерно рассеивает падающий на него свет (по закону Лам-
Ламберта)? Диаметр спутника d = 20 см.
Ответ. l<— tl— — и 250 км.
L у ZJrnOpA
8. В § 40 был описан способ Поля фотографирования предметов с по™
мощью непрозрачного гладкого шара. Оценить минимальное угловое разре-
разрешаемое расстояние Sip при фотографировании удаленных предметов этим
способом.
"Указание. Размер светлого кружка в центре геометрической тени от
точечного источника можно оценить из условия, что первый дифракцион-
дифракционный минимум получается, когда разность хода лучей от противоположных
точек шара порядка длины волны.
Ответ. Scp и X/D.
9. Существующие радиотелескопы и радиоустановки, предназначенные
для изучения радиоизлучения Солнца и Галактики, обладают малой раз-
разрешающей способностью из-за больших длин волн радиоизлучения.
1) Найти минимальное разрешаемое угловое расстояние S(p радиотеле-
радиотелескопа с диаметром зеркала d = 50 м для длин волн А = 1 ми А=10 см.
2) Для увеличения разрешающей способности предлагалось использо-
использовать дифракцию радиоволн от края Луны (см. задачу 2 к § 42). Оценить
разрешающую способность этого метода для тех же волн в предположении,
что край Луны действует как тонкий непрозрачный экран, ограниченный
прямолинейным краем.
3) Оценить, каковы должны быть высоты h неровностей лунной поверх-
поверхности, чтобы можно было пользоваться этим методом. Расстояние до Луны
Ь = 380 000 км.
Ответ. 1) ёср и X/d. При Л = 1 м Sip и 1°; при Л = 10 см ёср и 7".
2) Sip и л/Xjb. При A = 1m^^2;; при Л = 10 см Sip и 40/;.
3) h < л/ЬХ. При Л = 1 м л/ЬХ = 19,5 км; при Л = 10 см л/bX = 6,2 км.
10. Один из принципиально возможных (но практически не осуществи-
осуществимых) способов повышения разрешающей способности радиоустановок для
изучения радиоизлучения космических масс состоит в том, чтобы исполь-
использовать дифракционный максимум интенсивности радиоизлучения, получа-
получающийся в центре геометрической тени Луны от точечного источника. Оце-
Оценить разрешающую способность этого метода, найти минимальное угловое
разрешаемое расстояние для тех же длин волн, что и в предыдущей задаче.

§ 59 ФАЗОВЫЙ КОНТРАСТ 399
Обсудить возможности использования рассматриваемого метода. Диаметр
Луны D = 3470 км.
Ответ. SipaX/D. При А = 1 м^^0,06/;. При А = 10 см <fy>« 0,00б/;.
Метод требует, чтобы источник радиоизлучения находился на прямой,
соединяющей точку наблюдения с центром Луны. Кроме того, он предъ-
предъявляет весьма жесткие требования к гладкости лунной поверхности и к
отступлениям формы Луны от сферической. Высота неровностей поверх-
поверхности по всей границе лунного диска должна быть мала по сравнению с
h = ЬХ/D. Разность наибольшего и наименьшего диаметров лунного дис™
ка также не должна превышать этой величины. При А = 1 м /i и 100 м;
при А = 10 см /г й 10 м. Эти жесткие требования исключают возможность
использования рассматриваемого метода по крайней мере для радиоволн с
длиной волны А < 100 м.
11. С помощью объектива микроскопа получена микрофотография ма-
малого объекта (например, растительных клеток или бактерий) с линейным
увеличением N. Тот же объектив был использован для проецирования по-
полученной микрофотографии на удаленный экран. Каково должно быть ми-
минимальное значение увеличения JV, чтобы полностью была использована
разрешающая способность микроскопа? Диаметр апертурной диафрагмы
объектива равен D, диаметр зрачка глаза d. Изображение на экране рас™
сматривается с места нахождения объектива.
Ответ. N ^ D/d.
12. Каково должно быть фокусное расстояние /2 окуляра микроскопа,
чтобы была полностью использована разрешающая способность объектива?
Числовая апертура объектива равна и-sin а, фокусное расстояние объекти-
объектива /i, длина тубуса (трубы микроскопа) I. Длину тубуса можно считать
равной расстоянию между объективом и плоскостью первого изображения
(т.е. изображения, даваемого объективом).
r\ j, ^ Id
Ответ. /2 ^ , , где а — диаметр зрачка глаза.
2 fin sm a
13. С помощью объектива телескопа с диаметром D и фокусным рас-
расстоянием / производится фотографирование удаленных объектов на мел™
козернистой пластинке, помещенной в фокальной плоскости объектива. По-
Полученное изображение рассматривается в микроскоп с числовой апертурой
п sin а и увеличением N. Каким условиям должны удовлетворять числовая
апертура и увеличение микроскопа, чтобы полностью использовать разре-
разрешающую способность объектива телескопа?
Ответ, nsina ^ D/B/), N ^ DLf(fd), где L — расстояние ясного
зрения, d — диаметр зрачка глаза.
14. Современные фотопластинки способны разрешать до z = 104 ли™
ний на сантиметр. Какую светосилу (т.е. отношение квадратов диаметра D
и фокусного расстояния /) должен иметь объектив фотоаппарата, чтобы
полностью использовать разрешающую способность пленки?
Ответ. {D/ff > ^2А2^0,25.
§ 59. Фазовый контраст
1. В зависимости от вида изучаемых объектов при работе микроско-
микроскопа следует различать два предельных случая. Одни объекты, называемые
абсорбционными^ в различных местах обладают различной прозрачностью.
Такие объекты в основном влияют на амплитуду проходящего света. Дру™

400 ДИФРАКЦИЯ СВЕТА ГЛ. IV
гие объекты, называемые рефракционными, практически не поглощают све-
та. Имея в различных местах различные толщины и показатели преломле-
преломления, они влияют не на интенсивность, а на фазу проходящего света. Типич-
Типичными примерами абсорбционного и рефракционного объектов могут слу-
служить амплитудная и фазовая дифракционные решетки.
Абсорбционные объекты дают контрастные изображения с хорошо вы™
раженными границами между темными и светлыми частями. На них можно
обнаружить все детали, которые способен разрешить микроскоп при за-
заданной разрешающей способности. Напротив, изображения рефракцион-
рефракционных объектов почти лишены контраста. В таких изображениях трудно,
а часто и практически невозможно разрешить детали изучаемого объекта,
хотя бы разрешающей способности микроскопа и было достаточно для этой
цели. Причина такого различия между абсорбционными и рефракционны-
рефракционными структурами состоит в том, что объектив микроскопа воспроизводит в
плоскости изображения, а следовательно и на сетчатке глаза, то же рас-
распределение интенсивности светового поля, которое существует в плоскости
объекта, а светочувствительные нервные окончания сетчатки реагируют
именно на интенсивность световой волны, а не на ее фазу.
С рефракционными объектами постоянно приходится иметь дело в био-
биологии при изучении хотя бы микроорганизмов. Биологические объекты в
подавляющем большинстве случаев практически совершенно прозрачны в
видимой области спектра. Отсутствие контраста в изображении затрудняет
изучение таких объектов. Поэтому проблема контрастности изображения
стоит в биологии особенно остро. Один из методов ее решения состоит в
превращении рефракционных объектов в абсорбционные путем дифферен-
дифференциального окрашивания объекта. Однако такой метод не всегда возможен.
Кроме того, он убивает живые организмы или по крайней мере нарушает их
нормальную жизнедеятельность. Единственный метод изучения биологиче-
биологических объектов в естественных условиях состоит в том, чтобы воздейство-
воздействовать не на самый объект, а на его изображение. Это достигается в методе
фазового контраста, предложенном Цернике A888-1966) в 1934 г.
2. Идею метода фазового контраста проще всего выяснить на примере
периодической структуры — одномерной дифракционной решетки. Разли-
Различие между амплитудной и фазовой решетками с интересующей нас точки
зрения по существу уже было выяснено в § 53. Остановимся на этом вопросе
более подробно.
Отвлекаясь от поляризации, будем рассматривать свет как скалярное
волновое поле и представлять световые колебания векторами на векторной
диаграмме. Пусть свет падает нормально на поверхность решетки. Допу-
Допустим сначала, что решетка амплитудная и состоит из чередующихся участ-
участков различной прозрачности, причем на участках I прозрачность больше,
а на участках II — меньше. Для простоты (это несущественно для выяс-
выяснения существа вопроса) предположим, что участки I и II имеют одина-
одинаковую ширину. Колебание на выходе участка I изобразится более длинной
стрелкой а, чем колебание на выходе участка II, представляемое стрелкой
b (рис. 222). Так как амплитудная решетка не вносит разности фаз между
волнами, прошедшими через различные участки ее, то обе стрелки а и b
будут направлены одинаково.
Допустим теперь, что решетка фазовая и геометрически подобна ампли-
амплитудной, т.е. состоит из чередующихся участков той же ширины, влияющих
на фазу, но не на амплитуду волны. Колебания на выходе всех участков
изобразятся стрелками А и В одинаковой длины, но различно направлен-
направленными (рис. 222, положение а). Поскольку существенна лишь относительная

59
ФАЗОВЫЙ КОНТРАСТ
401
разность фаз между обоими колебаниями, стрелки А и В можно повернуть
на один и тот же угол, ничего не меняя в физических условиях задачи. По-
Поэтому, не нарушая общности, можно предположить, что биссектриса угла
между векторами А и В горизонтальна, т.е. параллельна поверхности ре-
решетки. Разложим каждый из векторов А и В на горизонтальную и верти-
кальную составляющие: A = D + c,B = D^c (рис. 222, положение б).
Допустим теперь, что оба вектора с и —с повернуты на 90° в одном и том
Участок I
Участок II
Амплитудная решетка
a b
Фазовая решетка
D
D
D
¦ -с'
В
D
-с
D
D
- с
¦ь
Рис. 222
же направлении в положении с; и ^с (рис. 222, положение в). Тогда на
выходе участков I и II колебания представятся векторами a = D + c;nb =
= D — с , параллельными поверхности решетки. Поле на выходе фазовой
решетки будет иметь такой же вид, что и на выходе амплитудной решет™
ки. Поворот на 90° означает изменение фаз соответствующих колебаний на
такой же угол. Таким образом, изменением фазы колебания на 90° можно
превратить фазовую решетку в амплитудную. В этом и состоит идея метода
фазового контраста.

402 ДИФРАКЦИЯ СВЕТА ГЛ. IV
При рассмотренном повороте по часовой стрелке вектор а получается
длиннее вектора Ь. Это значит, что светлым местам в изображении ампли-
амплитудной решетки будут соответствовать светлые же места в изображении
фазовой решетки, а темным — темные (позитивный фазовый контраст).
Если же векторы си-с повернуть на 90° в противоположном направлении
(рис. 222, положение г), то соотношение между длинами векторов аиЬ,
а с ним и соответствие между светлыми и темными частями заменятся на
противоположные (негативный фазовый контраст).
3. Чтобы повернуть векторы с и —с, сохраняя неизменным направле-
направление вектора D, надо прежде всего пространственно разделить волновые
поля, представляемые этими векторами. Полное колебание на выходе ре-
решетки можно разложить на два колебания. Одно колебание имеет постоян-
постоянную амплитуду на протяжении всей решетки и изображается постоянным
вектором D. Оно дает в фокальной плоскости объектива центральный мак-
максимум нулевого порядка и не влияет на все остальные максимумы. Другое
колебание представляется периодической функцией, которая равна +с на
одних участках решетки и-сна соседних участках. Так как среднее по пе-
периоду решетки значение такой функции равно нулю, то такое колебание бу-
будет возбуждать только боковые максимумы, не оказывая никакого влияния
на центральный максимум нулевого порядка. Таким образом, в фокальной
плоскости объектива оба колебания окажутся пространственно разделен-
разделенными. Одно концентрируется в центральном максимуме, другое распреде-
распределяется по всем остальным — боковым — максимумам. Поставив на пути
либо центрального максимума, либо всех боковых максимумов прозрачную
плоскопараллельную пластинку надлежащей толщины, можно внести необ-
необходимую разность фаз в 90° и тем самым осуществить фазовый контраст.
Такая пластинка называется фазовой.
4. До внесения фазовой пластинки энергия на участке I в условных
единицах представляется выражением А2 = D2 + с . Такова же энергия
на участке П. Полная энергия на обоих участках равна 2(D + с ). После
поворота векторов с и —с на 90° энергии на участках I и II будут равны
соответственно (D + сJ и (D — сJ, а их сумма 2(D2 + с2). Таким обра-
образом, энергия не изменяется, а лишь перераспределяется между участками
I и П. Этим перераспределением и объясняется просветление участков I и
потемнение участков П.
§ 60. Измерение угловых диаметров звезд
1. Пусть перед объективом телескопа помещен экран с двумя круглыми
отверстиями, расстояние между центрами которых равно D (рис. 223). На™
правив телескоп на звезду, закроем сначала правое отверстие. В результате
дифракции на открытом левом отверстии в фокальной плоскости объектива
получится система дифракционных колец. Их положение и размеры будут
зависеть только от диаметра отверстия, но не от его положения в плоскости
экрана. Поэтому, если закрыть левое отверстие и открыть правое, то ди-
дифракционная картина в фокальной плоскости объектива, видимая глазом,
не изменится. Если затем открыть оба отверстия, то одна система дифрак™
ционных колец точно совместится с другой. При этом не получится, однако,
простого усиления яркости дифракционных колец. Дифракционные кольца
будут пересечены параллельными интерференционными полосами, перпен-
перпендикулярными к линии, соединяющей центры отверстий О\ и О2 (рис. 224).

60
ИЗМЕРЕНИЕ УГЛОВЫХ ДИАМЕТРОВ ЗВЕЗД
403
Как и в опыте Юнга, эти полосы возникают из-за интерференции дифрак™
ционных пучков света, исходящих из первого и второго отверстий. Направ-
Направления на соседние интерференционные максимумы (или минимумы) отли-
отличаются на угол $ = X/D. Это и есть угловое расстояние между соседними
интерференционными полосами, если смотреть на фокальную плоскость из
центра объектива.
D
Рис. 223
Рис. 224
Допустим, что звезда — двойная с угловым расстоянием между ее ком™
понентами 6(р = ё/2. Тогда максимумы интерференционных полос от одной
звезды наложатся на минимумы другой: интерференционные полосы либо
пропадут, либо их видимость сделается наименьшей. На этом основан ин-
интерференционный метод измерения угловых расстояний между компонен-
компонентами двойных звезд, идея которого была предложена Физо. Надо менять
расстояние между отверстиями О\ и Ог, пока не пропадут интерференцион-
интерференционные полосы или их видимость сделается наименьшей. Если D — расстояние
между отверстиями в этот момент, то угловое расстояние между компонен-
компонентами двойной звезды найдется по формуле
6(р = X/BD).
F0.1)
Тот же метод применим и для измерения угловых диаметров одиночных
звезд. Допустим для простоты вычислений, что звезда излучает как рав™
номерно светящийся квадрат, плоскость которого параллельна фокальной
плоскости объектива, а одна пара противоположных сторон параллельна
прямой OiO'2j соединяющей центры отверстий О\ и Ог« Пусть угловой раз-
размер стороны квадрата будет 6(р' = X/D. Тогда можно мысленно разбить
весь квадрат на пары узких одинаковых полосок, угловое расстояние меж-
между которыми равно X/BD). Согласно формуле F0.1), каждая пара таких
полосок не даст интерференционных полос. Следовательно, интерференци-
интерференционные полосы не получатся и от всей звезды. Таким образом, увеличивая
расстояние между отверстиями О\ и Ог, можно в этом случае добиться
исчезновения интерференционных полос. Если D — расстояние между от-
отверстиями в момент исчезновения, то угловой размер звезды найдется по
формуле
S(pf = X/D. F0.2)
Если предположить, что звезда излучает как равномерно светящийся
диск (что ближе соответствует действительности), то идейно простые, но

404
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
громоздкие вычисления показывают, что интерференционные полосы про-
пропадут, когда
Sip' = 1,22-^. F0.3)
2. Угловые размеры 5ср', даваемые формулами F0.2) и F0.3), совпа-
совпадают с разрешаемым расстоянием телескопа. Однако если угловой размер
звезды порядка F0.2) или F0.3), то ее изображение в телескопе настолько
мало отличается от изображения точечного источника, что непосредствен-
непосредственное измерение диаметра звезд с помощью телескопа становится практиче-
практически непригодным. Интерференционный же метод дает в этом случае еще
хорошую точность. Однако чтобы ин-
интерференционные полосы исчезли, а это
необходимо по идее самого интерфе-
интерференционного метода, нужен телескоп с
^^ большим диаметром объектива. Физо
q указал способ, как преодолеть эту труд-
трудность. Идея Физо была использована
Майкельсоном, соединившим телескоп
с интерферометром.
Принципиальная схема звездного
интерферометра Майкельсона показа-
показана на рис 225. Лучи от звезды падают
на два круглых отверстия О\ и О2 и
после отражения от зеркал Mi, M3 и
Мг, М4 попадают в объектив телеско-
телескопа. Если закрыть отверстие Ог, то из-
за дифракции на краях отверстия О\ в
телескоп будут видны дифракционные
кольца. Если открыть О2 и закрыть О\,
Рис. 225 то получится такая же система колец,
но сдвинутая относительно первой. По-
Поворотом зеркала Мг ее можно совместить с первой системой. Тогда дифрак-
дифракционные кольца снова будут пересечены интерференционными полосами
(рис. 224). Изменяя расстояние между отверстиями О\ и О2 с одновремен-
одновременным перемещением зеркал Mi и Мг, можно добиться либо полного исчез-
исчезновения полос (в случае одиночной звезды), либо их наименьшей видимо-
видимости (в случае двойной звезды, состоящей из двух различных компонентов).
Зная расстояние между центрами отверстий О\ и Ог в этот момент, можно
вычислить угловой размер звезды по формулам F0.1) или F0.3).
3. Для уяснения действия установки Майкельсона отвлечемся от на-
наличия звезды. Ее действие эквивалентно действию вторичных источников
Гюйгенса, распределенных в плоскостях отверстий О\ и Ог. Не теряя общ-
общности, можно для простоты рассуждений взять отверстия Ог и О2 бес-
бесконечно малыми. Тогда действие звезды сведется к действию вторичных
точечных источников ft и ft, помещенных в центрах отверстий О\ и Ог
(рисунки 226 и 225). Если от звезды идет пучок параллельных лучей, пер-
перпендикулярных к плоскости экрана O1O2, то фазы вторичных источников
Si и S2 будут одинаковы. То же справедливо и для мнимых вторичных ис-
источников S[, Sf2 и Si , S'2 , являющихся изображениями ft и ft в плоских
зеркалах. Таким образом, зеркала как бы сближают источники ft и ft и
тем самым делают интерференционные полосы шире.
Допустим теперь, что вблизи первой звезды на угловом расстоянии 8(р
находится вторая звезда. Волновой фронт от второй звезды будет дости-

60
ИЗМЕРЕНИЕ УГЛОВЫХ ДИАМЕТРОВ ЗВЕЗД
405
гать отверстий Oi и Ог не одновременно. Разность хода между лучами,
приходящими от второй звезды в Si и ?2, будет D • S(fj где D — расстояние
между Si и S2- Если эта разность хода равна А/2, то вторичные источ-
источники Si и S'2, заменяющие действие второй звезды, будут находиться в
противоположных фазах. Следовательно, максимумы интерференционных
полос, даваемые второй звездой, наложатся на минимумы интерференци-
интерференционных полос от первой звезды. Интерференционные полосы либо пропадут,
либо их видимость станет наименьшей. Это произойдет, когда D • 6<р = А/2.
Таким образом, мы снова приходим к формуле F0.1), причем D означает
расстояние между центрами отверстий Oi и Ог- Аналогично, в случае оди-
одиночной звезды, излучающей как равномерно светящийся квадрат или диск,
получаются формулы F0.2) и F0.3).
/
:- М
\
л
I
I
I
I
\^
a '
i »¦—1
1
4
\
\
\s2
I D
X /
Рис. 226
Таким образом, нет надобности в телескопе с большим объективом. (Ин-
(Интерферометр Майкельсона был смонтирован на большом рефлекторе с диа-
диаметром зеркала 2,5 м обсерватории Маунт Вильсон, выбранном только из-за
прочности своей механической конструкции. При расстоянии между зерка-
зеркалами Ms и М± 114 см расстояние между интерференционными полосами в
фокальной плоскости составляло около 0,02 мм.) Необходимо только иметь
возможность достаточно далеко раздвигать отверстия Oi и Ог с зеркала-
зеркалами Mi и Мч- Это предъявляет весьма жесткие требования к механическим
качествам установки. Случайные колебания зеркал с амплитудами, соста-
составляющими незначительные доли длины волны, сделали бы измерения по
этому методу невозможными. Допустим ради простоты, что центр зеркала
все время остается неподвижным, а его концы испытывают беспорядочные
смещения порядка h. Если бы зеркало было абсолютно твердым, то такие
смещения вызвали бы беспорядочные вращения плоскости зеркала на углы
порядка 2h/d, где d — диаметр зеркала. Благодаря этому отраженные от
зеркала лучи беспорядочно меняли бы свое направление на углы порядка
4h/d. Это повело бы к дрожанию дифракционных колец. Для устойчивости
интерференционных полос необходимо, чтобы угол Ah/d был мал по срав-

406 ДИФРАКЦИЯ СВЕТА ГЛ. IV
нению с угловым расстоянием между звездами A/BD), т.е. должно быть
h<^.d\/(8D). Хотя действительные беспорядочные колебания зеркал слож-
сложнее рассмотренных беспорядочных вращений, приведенный пример дает
правильное представление о трудностях, которые должны быть преодоле-
преодолены при конструировании прибора. Майкельсон успешно справился с этой
задачей.
4. В интерферометре Маикельсона зеркала М\ и М.2 могли быть раз-
раздвинуты до расстояния D = 6,1 метра. Интерференционные полосы от звез-
звезды Бетельгейзе исчезали при D = 306,5 см, хотя при том же расстоянии
интерференция от других звезд прекрасно наблюдалась. Считая эффек-
эффективную длину волны для Бетельгейзе равной А = 5,75 • 10"" см, получим
Sip' = 0,047/;. Параллакс для этой звезды составляет 0,003/;. Это дает для
линейного диаметра звезды около 9 • 108 км, что превосходит диаметр ор-
орбиты Марса.
Измерения Маикельсона были выполнены в двадцатых годах нашего
столетия, когда астрофизика в современном ее понимании еще только заро-
зарождалась. Результаты этих измерений произвели сильное впечатление на
современников. Майкельсон начал строить интерферометр с базой D =
= 15,24 м, но смерть помешала ему осуществить это намерение.
Звездным интерферометром Маикельсона были измерены угловые диа-
диаметры только нескольких звезд. Все они, как и Бетельгейзе, — гиганты,
линейные диаметры которых во много раз превосходят диаметр Солнца.
Одна из причин небольшого числа измеренных диаметров звезд связана с
вредным влиянием турбулентности атмосферы. Правда, это влияние зна-
значительно сильнее проявляется при наблюдении в телескоп, чем при работе
с интерферометром. В случае интерферометра изменение показателя пре-
преломления воздуха перед небольшими отверстиями зеркал лишь смещает
интерференционную картину в целом, так что интерференционные полосы
остаются различимыми, если только это смещение происходит достаточно
медленно. При наблюдении же в тех же условиях в телескоп с недиафраг™
мированным объективом нерегулярные изменения показателя преломления
воздуха сильно искажают изображение звезды.
Другая причина заключается в том, что линейные диаметры подавля-
подавляющего большинства звезд мало отличаются от диаметра Солнца. На рас™
стоянии же ближайшей звезды диск Солнца был бы виден под углом всего
0,007/;. Для измерения таких углов расстояние между внешними зеркалами
интерферометра М\ и Мч (база) должно быть не меньше примерно 20 м.
Постройка такого большого интерферометра трудна из-за высоких требо-
требований к механическим параметрам конструкции всей установки, о которых
говорилось выше.
5. Принципы, изложенные выше, применимы, конечно, и в радиодиапа-
радиодиапазоне. Радиотелескопы, благодаря большим значениям длин радиоволн, ха-
характеризуются низкой разрешающей способностью. Даже для самых круп-
крупных из них с диаметром зеркала D <**» 100 м, работающих на длине волны
А ~ 10 см, разрешаемое угловое расстояние ~ А/?)?^10^3 рад, т.е. всего око™
ло 3;. Иное дело — радиоинтерферометр, работающий по принципу звезд-
звездного интерферометра Маикельсона. Он состоит из двух антенн, установ-
установленных в разных местах, сигналы с которых подаются на общий детектор.
Высокая разрешающая способность достигается за счет увеличения рассто-
расстояния D между антеннами (базы радиоинтерферометра). Рекордное угловое
разрешение достигается, когда антенны удалены друг от друга на меж-
межконтинентальные расстояния. Были осуществлены радиоинтерферометры

§ 61 ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ 407
с базой Крым-США, США-Австралия. На самой короткой длине волны
было достигнуто угловое разрешение ~ Ю~4 угловой секунды, т.е. разре-
разрешающая способность была примерно в 100 раз больше, чем у звездного
интерферометра Майкельсона.
Надо отметить, что с увеличением базы возрастают технические труд™
ности, обусловленные внесением нерегулярно меняющейся разности фаз на
пути от антенн к детектору. Для устранения этого недостатка в радиоинтер-
радиоинтерферометре Брауна и Твисса сигналы, принятые антеннами, детектируются
независимо. Измеряется корреляция флуктуирующих интенсивностей этих
сигналов в зависимости от расстояния между антеннами. По этим данным
находятся угловые размеры источника. Браун и Твисс показали, что ана™
логичное устройство может работать также и в видимой области спектра.
Свет от звезды фокусируется двумя вогнутыми зеркалами на два фото-
фотоэлемента. Измеряется корреляция флуктуирующих фототоков, возбужда-
возбуждающихся в фотоэлементах, в зависимости от расстояния между зеркалами.
Без особых осложнений расстояние между зеркалами может быть сделано
большим и достигнута высокая разрешающая способность прибора.
§ 61. Дифракция на двумерных и трехмерных
решетках. Дифракцим рентгеновских лучей
1. Двумерной решеткой называется всякая структура, свой™
ства которой периодически меняются в двух различных направ-
направлениях. Примером могут служить две скрещенные одномерные
решетки, т.е. решетки, наложенные одна на другую таким об™
разом, что штрихи одной решетки пересекаются со штрихами
другой под некоторым углом. Дифракционная картина от та™
кой структуры, как нетрудно показать, может быть получена
путем наложения дифракционных картин от соответствующих
одномерных решеток.
Трехмерные, пространственные решетки обладают перио-
периодичностью в трех различных направлениях. Они играют важ-
ную роль в физике рентгеновских лучей. Долгое время не уда-
удавалось получить дифракцию рентгеновских лучей, так как ди-
дифракционные решетки, применявшиеся в оптической области
спектра, были слишком грубыми для рентгеновских лучей с дли-
длиной волны порядка 0,1 нм и меньше (см., впрочем, § 46, п. 8).
Лауэ A879-—1960) в 1912 г. предложил для этой цели восполь-
воспользоваться кристаллом, который можно рассматривать как есте-
естественную периодическую пространственную решетку^ постро™
енную из атомов или ионов. По указанию Лауэ его сотрудники
Фридрих A883—-1968) и Книппинг A883-—1935) направили узкий
пучок сплошного рентгеновского излучения на монокристалл
и получили на фотопластинке картину дискретных, правиль-
правильно расположенных пятен, возникших в результате дифракции
рентгеновских лучей на кристаллической решетке. Этот осново-
основополагающий опыт установил волновую природу рентгеновского

408
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
излучения и заложил начала современной физики твердого те-
тела. Он впервые принес экспериментальное доказательство давно
высказывавшейся кристаллографами гипотезы о структуре кри-
кристаллов из частиц, правильно и периодически расположенных в
пространстве.
Из этого опыта возникли два направления в физике: рентге-
рентгеновская спектроскопия и рентгеноструктурный анализ. Рент-
Рентгеновская спектроскопия использует естественные кристаллы
известной кристаллической структуры для анализа рентгенов-
рентгеновского излучения и измерения длин волн. Рентгеноструктурный
анализ, напротив, использует рентгеновское излучение извест-
известной длины волны для выяснения кристаллической структуры
кристаллов и измерения параметров этой структуры. По сравне-
сравнению с оптической дифракцией дифракция рентгеновских лучей
обладает той особенностью, что она осуществляется без линз и
зеркал, ввиду отсутствия материалов, из которых можно было
бы изготовить эти приспособления.
2. Качественное рассмотрение дифракции рентгеновских лу-
лучей удобно начать с дифракции на прямолинейной цепочке, со-
состоящей из одинаковых равноотстоящих частиц (атомов). Рас-
Расстояние между сосед-
соседними частицами обо-
обозначим через а. Пусть
на такую цепочку под
углом скольжения «о
падает параллельный
пучок рентгеновских лу-
лучей (рис. 227). Разность
хода между лучами,
рассеянными соседними
Рис. 227
атомами под углом о, будет AD — С В = a(cosa —
Условие интерференционного усиления этих лучей имеет вид
a(cos a — cos ао) = тХ F1.1)
(га = 0, ±1, ±2,...). Оно определяет положения дифракционных
максимумов в фраунгоферовой дифракционной картине, т.е. на
бесконечных расстояниях от цепочки. Бесконечными могут счи-
считаться расстояния г, удовлетворяющие условию:
r^f/X, F1.2)
где I — длина цепочки. Ввиду малости длин рентгеновских волн,
эти расстояния всегда очень велики. Так, при 1 = 1 мм, А =
= ОД нм = 1СП7 мм условие F1.2) дает г >> 107 мм = 10 км.
Таким образом, для осуществления фраунгоферовой дифрак-
дифракции потребовались бы очень большие расстояния. В реальных
опытах фотографическая пластинка, регистрирующая дифрак-

§ 61 ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ 409
ционную картину, ставится на расстоянии в несколвко десятков
сантиметров от рассеивающего кристалла или меньше, т.е. не в
волновой зоне, а в десятки и сотни тысяч раз ближе. Это заме™
чание относится, конечно, не только к линейным цепочкам, но
и к поверхностным и объемным решеткам.
Однако, как было выяснено в § 52, волновое поле^ возникаю-
возникающее при дифракции на плоской решетке^ представляется на
всех расстояниях суперпозицией плоских волн различных на-
правлений. В эту суперпозицию входят и неоднородные волны.
Но на расстояниях от решетки, превышающих ее период, неод-
неоднородные волны не играют роли, так как на таких расстояни-
расстояниях они практически полностью затухают. Так же обстоит дело
и в случае дифракции на кристаллической решетке. (В случае
линейной цепочки вместо плоских удобнее пользоваться цилин-
цилиндрическими волнами.) Фотопластинка ставится на малых рас-
расстояниях от кристалла, где применима геометрическая оптика,
но все же достаточно далеко, чтобы различные плоские вол-
волны, исходящие от кристалла, успели разделиться пространствен-
пространственно. Для определения положения максимумов интенсивности на
фотопластинке достаточно знать направления распространения
этих волн. Но эти направления не зависят от расстояния до кри-
кристалла. В области применимости геометрической оптики они та-
такие же, что и в волновой зоне, а потому для определения по™
ложения максимумов интенсивности на фотопластинке можно
пользоваться формулой F1.1). Однако такие максимумы отли-
отличаются от интерференционных максимумов в волновой зоне. В
каждый максимум в волновой зоне колебания от всех атомов
решетки приходят либо в одинаковых фазах, либо в фазах^ от-
отличающихся на 2тж (га — целые числа). Для максимумов же
интенсивности в области применимости геометрической оптики
это не имеет места.
При фиксированном угле а® условие F1.1) определяет дис-
кретный набор углов о, удовлетворяющих этому условию. Оно
выделяет в пространстве дискретное семейство конусов^ вдоль
образующих которых могут распространяться дифрагирован-
дифрагированные пучки лучей. В сечении таких конусов плоскостью фотопла-
фотопластинки получается дискретное семейство эллипсов или гипер-
гипербол в зависимости от направления этой плоскости. В частности,
когда плоскость пластинки перпендикулярна к направлению це-
цепочки, возникает семейство концентрических кругов.
3. Двумерные и трехмерные решетки могут быть просты-
простыми (примитивными) и составными (см. т. II, § 130). Решетка
называется простой, если она построена из одинаковых атомов,
причем элементарная ячейка решетки состоит из восьми ато-
атомов, расположенных в вершинах параллелепипедов. Все осталь-
остальные решетки называются составными. Составная решетка состо-

410 ДИФРАКЦИЯ СВЕТА ГЛ. IV
ит из нескольких простых решеток, вставленных друг в друга.
Дифракционная картина, возникающая при дифракции рент-
рентгеновских волн на составной решетке, получается в результате
интерференции дифракционных картин от простых решеток, из
которых она состоит. Поэтому достаточно ограничиться рассмо-
рассмотрением дифракции на простых решетках.
Если какие-либо два атома простой решетки соединить пря-
прямой линией, то, ввиду периодичности распределения атомов в
пространстве, на этой прямой окажется бесконечно много ато-
атомов, находящихся на одинаковых расстояниях друг от друга.
Такие прямые мы будем называть атомными прямыми^ а плос-
плоскости, в которых располагаются атомы, — атомными плоско-
плоскостями. Всю неограниченную решетку можно рассматривать
как бесконечную двоякопериодическую систему параллельных
атомных прямых или как бесконечную однократно периодиче-
периодическую систему параллельных атомных плоскостей. Оба эти пред-
представления не единственны, а могут быть выполнены бесконеч-
бесконечным множеством способов. Три произвольные атомные прямые,
не лежащие в одной плоскости и пересекающиеся в каком-либо
атоме, можно принять за координатные оси X, У, Z прямоли-
прямолинейной (вообще говоря, косоугольной) системы координат. Тогда
координаты атомов простой решетки представятся выражения-
выражениями
Щтп = la>u Vlmn = ша2, zimn = na3 (ал о,
(ol.J)
(J,m,n = 0,±l,±,2,...),
где ai, «2, «з — постоянные, называемые периодами решетки.
Элементарной ячейкой такой решетки является параллелепипед
с ребрами «i, u2j «з5 в вершинах которого находятся атомы.
Пусть на простую решетку падает параллельный пучок рент-
рентгеновских лучей, образующий углы «о, /?о5 7о с координатными
осями X, У, Z. Чтобы волны, рассеянные всеми атомами в на-
направлении прямой, составляющей углы а, /3, 7 c координатными
осями, при интерференции в волновой зоне усиливали друг дру™
га, должны выполняться условия
ai(cos a — cos «о) = mi А,
a2(cos^ - cos A)) = ш2А,
(о1.4)
аз (cos 7 — COS70) = шз^
G711,7712,7713 = 0, ±1, ±2, . . .),
называемые условиями Лауэ. Необходимость первого условия
станет очевидной, если заметить, что оно является условием ин-
интерференционного усиления волн, рассеянных под углом а к оси
X атомами каждой атомной прямой, параллельной этой оси.
Аналогичный смысл имеют и остальные два условия.

§ 61 ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ 411
Но условия F1.4) являются и достаточнвши для интерфе-
ренционного усиления волн, рассеянных в рассматриваемом на-
направлении всеми атомами решетки. Действительно, проведем
через произвольный атом 1 атомную прямую, параллельную оси
X. При выполнении первого условия F1.4) в направлении под
углом а к этой прямой получится интерференционный макси™
мум. Проведем теперь через тот же атом 1 атомную прямую,
параллельную оси Y. При выполнении второго условия F1.4)
все атомы этой прямой рассеивают волны в рассматриваемом
направлении в той же фазе, что и атом 1. Значит, все атомы
обеих атомных прямых, а с ними и все атомы, лежащие в их
плоскости, будут посылать волны в том же направлении также
в одинаковых фазах. Таким образом, выполнение первых двух
условий F1.4) приводит к интерференционному усилению волн,
рассеиваемых в рассматриваемом направлении всеми атомами
любой атомной плоскости, параллельной координатной плоско-
плоскости XY. Аналогично убедимся, что при выполнении еще тре™
тьего условия F1.4) будет иметь место интерференционное уси-
усиление волн, рассеянных всеми такими атомными плоскостями.
Тем самым достаточность условий F1.4) доказана.
4. Дифракционная картина, возникающая на фотопластин-
фотопластинке, поставленной на пути рентгеновских пучков, рассеянных мо-
монокристаллом в опытах типа Лауэ, называется лауэграммой. Об
использовании условий Лауэ в области применимости геомет-
геометрической оптики можно повторить все, что было сказано вы-
выше в связи с формулой F1.1). Формулы Лауэ F1.4) указывают
направления пучков^ возникающих при дифракции на кристал-
кристалле. Физический смысл лауэграммы хорошо иллюстрируется ана™
логией с отражением светового пучка от многогранного зерка-
зеркала. Здесь возникают отраженные пучки, распространяющиеся в
различных направлениях. При падении на экран они дают си-
систему правильно расположенных светлых пятен, аналогичную
лауэграмме, возникающей при дифракции рентгеновских лучей.
Рассмотрим сначала лауэграмму от плоской двумерной кри-
кристаллической решетки. В этом случае три условия Лауэ F1.4)
сводятся к двум. Если плоскость решетки принять за атомную
плоскость XY, то останутся только два первых условия F1.4).
Первое условие F1.4) означает, что максимумы лежат на по-
поверхности конуса, образующего угол а с осью X, а второе —
на поверхности другого конуса, образующего угол /3 с осью Y.
Прямые, по которым пересекаются поверхности обоих конусов,
указывают направления дифрагированных пучков. При пересе-
пересечении таких пучков плоскостью фотопластинки возникают дис-
дискретные дифракционные точечные максимумы, расположенные
вдоль эллипсов, гипербол или кругов в зависимости от направ-
направления этой плоскости. Максимумы могут и не получиться, если

412 ДИФРАКЦИЯ СВЕТА ГЛ. IV
cos а или cos/5, или обе эти величины, вычисленные по формуле
F1.4), окажутся по модулю больше единицы.
Рассмотрим теперь трехмерную решетку. К двум конусам,
выделяемым первыми двумя условиями F1.4), теперь добавля-
добавляется еще третий конус, образующие которого составляют угол
7 с осью Z. Дифрагированные пучки должны одновременно ле-
жать на поверхности всех трех конусов. Но три конуса, вообще
говоря, не пересекаются вдоль общей прямой. Отсюда следует,
что при падении на монокристалл монохроматического рентге-
рентгеновского луча дискретные пучки рассеянного излучения, вооб-
вообще говоря, не возникают, а рассеяние происходит более или ме-
менее равномерно во все стороны. Исключение составляет только
прямой луч, проходящий через кристалл без изменения направ-
направления. Но для избранных длин волн три конуса могут иметь об™
щие образующие. Поэтому для получения лауэграмм от трех-
трехмерных решеток необходимо сплошное рентгеновское излуче-
ние, так как в таком излучении могут присутствовать такие дли-
длины волн, для которых выполняются все три условия Лауэ F1.4).
Таким образом, если бы
глаз обладал способностью
воспринимать рентгенов-
рентгеновские лучи и различать
их цвета, то лауэграмма,
наблюдаемая на экране,
представлялась бы для
него цветной, т.е. состоя-
состоящей из пятен разного
цвета.
Подтвердим получен-
полученные результаты простым
вычислением. Предполо-
Предположим, что простая крис-
кристаллическая решетка при-
принадлежит к ромбической
Рис. 228 системе, так что эле-
элементарная ячейка будет
прямоугольным параллелепипедом. Пусть для некоторой дли-
длины волны А условия Лауэ F1.4) выполняются. Разрешим их
относительно cos a, cos/3, cos7, возведем в квадрат и сложим
почленно. Тогда, принимая во внимание соотношения cos2 a +
+ cos2 /3 + cos2 7 — 1 > cos2 ao + cos2 /3q + cos2 70 = 1, после простых
преобразований получим
л _ 2G7li COStto + ГП2 COS/3o + W3COS70) //^-1 г\
\

61
ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
413
Только при этом условии уравнения F1.4) совместны. Оно одно-
однозначно определяет длину волны, при которой может получиться
дифракционный максимум, выделяемый целыми числами rai,
т2•) чпз и углами а, /3, j.
Ha рис. 228 приведена лауэграмма для монокристалла квар-
кварца. Закономерное расположение пятен на фотопластинке указы™
вает на правильность расположения атомов, из которых постро-
построен кристалл.
5. Дифракцию рентгеновских лучей в кристаллах можно
трактовать несколько иначе. Такая трактовка была дана ан-
английским физиком Лоуренсом Брэггом A890—1971) и незави-
независимо от него русским кристаллографом Ю.В. Вульфом A863—
1925). Проведем в кристалле произвольную атомную плоскость
АВ, достаточно густо усеянную атомами (рис. 229 а). Если на
м
Рис. 229
нее падает рентгеновский луч МО, то под тем же углом воз-
возникнет отраженный луч ON. В том же направлении возник-
возникнут лучи, отраженные атомными плоскостями, параллельны-
параллельными плоскости АВ. Интенсивность луча, отраженного отдельной
атомной плоскостью, слишком мала, чтобы произвести замет-
заметное действие. Последнее может возникнуть лишь в результате
интерференционного усиления всех лучей, отраженных рассма-
рассматриваемыми атомными плоскостями. Разность хода PO'Q меж-
между лучами, отраженными соседними плоскостями, равна 2dsin#,
где d — расстояние между этими плоскостями. Для интерферен-
интерференционного усиления должно выполняться условие
F1.6)
называемое условием Брэгга-Вульфа (га = 0, ±1, ±2,...). Каков
бы ни был угол скольжения t? и порядок отражения га, всегда
найдутся длины волн А, удовлетворяющие условию F1.6). Толь-

414 ДИФРАКЦИЯ СВЕТА ГЛ. IV
ко волны с такими длинами могут отражаться от рассматрива-
рассматриваемых атомных плоскостей.
В кристалле можно провести бесконечное множество систем
параллельных атомных плоскостей в различных направлениях.
Таковы, например, плоскости, параллельные атомной плоскости
АА1 или атомной плоскости В В1 (рис. 229 б). Эффективными
являются только такие плоскости, на которых атомы располо-
расположены достаточно часто. От всех этих плоскостей возможно ин-
интерференционное отражение. И дифракционную картину можно
рассматривать как совокупность рентгеновских пучков, претер-
претерпевших отражения на таких атомных плоскостях.
Против последнего заключения можно, однако, выдвинуть
следующее возражение. Рентгеновский пучок МО, падающий
на атомную плоскость АВ (рис. 229 а), дает не только отражен-
отраженный пучок ON, но и боковые дифрагированные пучки, кото-
которые при определенных условиях могут усиливаться пучками то-
того же направления, дифрагировавшими на параллельных атом-
атомных плоскостях. Такие пучки в наших рассуждениях не были
учтены. Поэтому может показаться, что метод Брэгга^Вульфа
дает не все возможные дифракционные пучки в дифракцион-
дифракционной картине. Следующее простое рассуждение, устанавливаю-
устанавливающее эквивалентность условий Лауэ и условия Брэгга-Вульфа^
показывает, что это не так.
6. Примем векторы ai, a2, аз, являющиеся ребрами элемен-
элементарного параллелепипеда кристаллической решетки, за базис-
базисные векторы косоугольной системы координат. Тогда радиус-
вектор каждого атома решетки
представится выражением
г = Х3.1 + ув.2 + 2:аз, F1-7)
в котором координаты ж, у, z
принимают целочисленные зна-
значения. Пусть Sq — единичный
вектор, проведенный в направ-
направлении падающего луча, as —
р 2зо единичный вектор, указываю-
указывающий направление одного из ди-
дифрагированных пучков (рис. 230). Тогда условия Лауэ F1.4)
можно записать в следующей векторной форме:
(s - so)ai = mi A,
(s — So)a2 = m2A, F1.8)
(s — 8о)аз = т%\.
Вектор N = s — Sq направлен параллельно биссектрисе угла, об-
образованного падающим и отраженным лучами. Введя этот век-

§ 61 ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ 415
тор,получим
(Nai) = mi A, (Na2) = m2A, (Na3) = m3X. F1.9)
Через атом, находящийся в начале координат О, проведем плос-
плоскость, перпендикулярную к вектору N. Докажем, что она яв™
ляется атомной плоскостью. Уравнение рассматриваемой плос-
плоскости имеет вид (Nr) = 0. Чтобы атом с координатами F1.7)
лежал в этой плоскости, необходимо и достаточно, чтобы его
координаты удовлетворяли уравнению
(Nai)x + (Na2)y + (Na3)z = 0,
или, ввиду соотношений F1.9), mix + ТП2У + m%z = 0. Каковы
бы ни были целые числа mi, W2, тз, существует двухпарамет-
рическое семейство целочисленных решений этого уравнения.
Тем самым доказано, что плоскость (Nr) = 0 является атомной
плоскостью.
Из доказанного следует, что для любого дифрагированного
луча s можно указать атомную плоскость, а следовательно, и
бесконечное семейство параллельных ей атомных плоскостей,
при зеркальном отражении от которых возникают лучи того
же направления, что и рассматриваемый дифрагированный луч.
Тем самым доказано, что условием Брэгга-Вульфа охватывают-
охватываются все направления, по которым могут распространяться дифра-
дифрагированные рентгеновские пучки. Значит, каждый боковой ди-
дифракционный пучок, возникший при дифракции на той или иной
атомной плоскости, совпадает по направлению с пучком, зер-
зеркально отразившимся какой-то другой атомной плоскостью.
Направлениями зеркально отраженных лучей исчерпываются
все возможные направления на дифракционные максимумы.
Конечно, не всякие атомные плоскости эффективно отража-
отражают и дают максимумы, действительно наблюдающиеся на опы-
опыте. Необходимо, чтобы атомные плоскости были усеяны атома-
атомами достаточно густо. Иначе интенсивность отраженных лучей
может оказаться настолько малой, что они не проявят никакого
действия на опыте.
7. В связи с изложенным уточним смысл условия Брэгга-
Вульфа. Выделим какое-либо семейство параллельных атомных
плоскостей и рассмотрим лучи, возникшие при зеркальном от™
ражении от каждой из этих плоскостей в отсутствие остальных.
Условие Брэгга-Вульфа вовсе не означает, что при интерферен™
ции таких лучей между собой и с падающим лучом возникнет
истинная картина распределения волнового поля в кристалле.
Действительно, луч, который при выводе и интерпретации усло-
условия Брэгга-Вульфа принято называть лучом, отраженным от-
отдельной атомной плоскостью, в действительности не является
таковым. Он возникает в результате сложного процесса, в ко-
котором участвуют атомы всего кристалла, а не только атомы

416 ДИФРАКЦИЯ СВЕТА ГЛ. IV
рассматриваемой атомной плоскости. В частности, в формиро-
вании этого луча участвуют боковые пучки того же направле-
направления, возникающие при дифракции на других атомных плоско-
плоскостях. Однако окончательная дифракционная картина будет та™
кой, как если бы отдельные атомные плоскости только зеркально
отражали рентгеновские лучи с некоторыми надлежаще выбран™
ными эффективными коэффициентами отражения и не давали
никаких боковых дифракционных пучков.
8. Изложенным по существу завершается доказательство эк™
вивалентности методов Лауэ и Брэгга-Вульфа. Не лишено, од-
однако, интереса показать, что из формул Лауэ без привлечения
каких бы то ни было дополнительных соображений вытекает
условие Брэгга—Вульфа. Вычислим прежде всего длину вектора
N = s — Sq, нормального к плоскости, от которой происходит
рассматриваемое брэгговское отражение. Угол между единич-
единичными векторами Sq и s равен 2$, т.е. удвоенному углу скольже™
ния. Следовательно, N2 = 2 — 2(ssq) = 2A — cos2t?) = 4sin2#,
а потому N = 2sin#. Примем атомную плоскость, от которой
происходит рассматриваемое брэгговское отражение, за коор-
координатную плоскость XY. Тогда межплоскостное расстояние d
представится выражением
Используя последнее соотношение F1.9), получим
d = m3A/Bsin#),
что совпадает с условием Брэгга-Вульфа F1.6).
9. Рассмотрим два примера на применение условия F1.6).
а) Рентгеновский спектрограф с
вращающимся кристаллом (рис. 231). Рент-
Рентгеновский пучок после диафрагмирования на щелях направля-
направляется на монокристалл К известной кристаллической структуры.
Кристалл может вращаться вокруг оси, перпендикулярной к па-
падающему лучу, или совершать вращательные колебания вокруг
этой оси. Дифрагированный пучок попадает на фотопластинку
FF1 или в ионизационную камеру. Таким образом, направления
падающего и дифрагированного пучков, а с ними и величина
угла скольжения ё фиксированы. Если падающий пучок моно™
хроматичен или состоит из отдельных монохроматических ли-
линий, то при произвольном положении кристалла условие Брэгга^
Вульфа, вообще говоря, не будет выполняться. Однако при пово-
повороте кристалл может занять такое положение, при котором это
условие выполняется. Тогда возникнет отраженный максимум,
регистрируемый по почернению фотопластинки или по току в
ионизационной камере. Найдя такое положение, можно опреде-

61
ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
417
лить угол скольжения #, а затем по формуле F1.6) вычислить
длину волны А.
Разумеется, такой метод дает не абсолютное значение дли™
ны волны, а только ее отношение к постоянной решетки d. Для
абсолютных измерений надо знать величину d. Для нахожде-
Рис. 231
ния d достаточно независимым способом измерить длину вол™
ны какой-либо строго определенной спектральной линии. Это
можно сделать, например, с помощью обычной отражательной
дифракционной решетки с известным периодом, измерив угол
дифракции при скользящем падении луча (см. § 46, п. 8).
б) Метод Деба я-Ш е р е р а-Х е л л а. Этот ме™
тод применяется в рентгеноструктурном анализе для исследо-
исследования кристаллической структуры металлов и других кристал-
кристаллических материалов в порошкообразном состоянии. Исследуе™
мый образец (поликристалл) обычно имеет форму цилиндрика
и состоит из множества мельчайших кристалликов, беспорядоч-
но ориентированных во всевозможных направлениях. Установка
аналогична приведенной на рис. 231. Однако столик, на котором
помещается исследуемый образец, неподвижен. На образец на-
направляется монохроматический рентгеновский луч с известной
длиной волны А. Дифракционная картина, называемая дебае-
граммой, фотографируется.
Происхождение этой картины объясняется следующим обра-
образом. Среди множества беспорядочно ориентированных кристал-
кристалликов найдется еще очень много кристалликов с такими ори™
ентациями, что при заданной длине волны А будет выполнено
14 Д.В. Сивухин

418
ДИФРАКЦИЯ СВЕТА
ГЛ. IV
условие Брэгга-Вульфа. Лучи, испытавшие брэгговские отраже-
отражения от таких кристалликов, образуют поверхность конуса, ось
которого направлена вдоль падающего луча, а угол раствора
определяется межплоскостным расстоянием d (см. рис. 232, на
котором показано отражение от отдельного микрокристаллика;
сам микрокристаллик изображен
в виде зеркальца). Так как эти
А расстояния образуют дискретный
набор, то за образцом возникнет
дискретное семейство конусов с
q общими вершиной и осью.
Если бы фотопластинка бы™
ла установлена перпендикулярно
к этой общей оси, то дебаеграм™
ма состояла бы из концентриче-
концентрических кругов. Измерив радиусы
Рис 232 этих кругов, можно определить
возможные значения угла #, а за-
затем по формуле Брэгга-Вульфа вычислить соответствующие
межплоскостные расстояния и воспользоваться этими данны-
данными для воспроизведения кристаллической структуры образца.
Чтобы получить действительно все межплоскостные расстоя-
расстояния, фотопластинке придают форму полоски, опоясывающей по
окружности исследуемый образец. Дебаеграмма, полученная на
кристаллическом порошке NaCl, приведена на рис. 233.
Рис. 233
Нелишне подчеркнуть, что, в отличие от лауэграмм, для по-
получения которых требуется сплошное рентгеновское излучение,
дебаеграммы получаются в монохроматическом свете. В белом
свете никаких дебаеграмм с резкими дифракционными кольца™
ми получиться не может.
10. Остановимся в заключение на вопросе о разрешающей
способности дифракционной решетки (одномерной) в рентгенов-
рентгеновской области спектра. Формула D7.3) для разрешающей способ-
способности решетки относится к случаю, когда решетка дает фраун-
гоферову дифракционную картину. Как было выяснено выше,
в рентгеноскопии реализуется противоположный случай. Фоку™
сирующего устройства нет, а фотопластинка ставится на ма-
малых расстояниях от решетки. В таких условиях дифракционные
пучки подчиняются геометрической оптике, и формулой D7.3)
пользоваться нельзя.

§ 61 ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ 419
Пусть на решетку падает пучок параллельных лучей с дли™
ной волны А под углом скольжения а$. Направление распро-
распространения дифрагированного пучка га~го порядка определится
из условия d(cos a® ~~ cos а) = га А. Для такого же пучка с близ™
кой длиной волны А;: d(cos щ — cos af) = га А7. Отсюда d(cos а1 —
— cos а) = га(А ~~ А;), или
dsina • 5а = т5\
где введены обозначения: 5а = \а' — а|, 5Х = |А; — А|. Для спек-
спектрального разрешения необходимо, чтобы оба пучка простран-
пространственно разделились. Если L — расстояние до фотопластинки,
измеренное вдоль направления дифрагированного луча, то бо-
боковое смещение одного пучка относительно другого равно х =
= LSa. Условие разрешения состоит в том, чтобы это смещение
было не меньше ширины дифрагированного пучка: х ^ h. По-
Последняя определяется выражением h = Dsliia, где D — длина
дифракционной решетки. В результате условие разрешения при-
примет вид
LmSX >. т^ .
1 . ^ U sin а.
asm a
Минимальному разрешаемому расстоянию соответствует знак
равенства. Для него получаем
SX = ^^, F1.10)
а для разрешающей способности
Запишем эту формулу в виде
Tx
ИЛИ
A LmX ,ал л о\
TV = ТТ^ ' F1.13)
о л да sin a
Для повышения разрешающей способности надо применять
узкие пучки, а фотопластинку помещать как можно дальше. По
сравнению с рэлеевской формулой формула F1.12) дает мень-
меньшее значение для разрешающей способности, поскольку она от™
носится к области, в которой L <C h2/X.
14*

ГЛАВА V
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
§ 62. Поляризованный и естественный свет
1. При изучении интерференции и дифракции мы отвле™
клись от поперечности световых колебаний, предполагая, что
складываемые колебания совершаются в одном направлении.
Обратимся теперь к изучению явлений поляризации света7 ти-
пичных именно для поперечных колебаний. Плоская волна на-
называется линейно поляризованной или плоскополяризованной^
если электрический вектор Е все время лежит в одной плоско-
плоскости, в которой расположена также нор™
Ei маль N к фронту волны (рис. 234).
Эта плоскость называется плоскостью
колебаний или плоскостью поляриза-
^ -^ ции1). От поляризованного света еле™
дует отличать естественный свет. В
нем в каждый момент времени векторы
Е, Н, N, хотя и остаются взаимно пер™
р 2^4 пендикулярными, но направления век-
векторов Е и Н беспорядочно изменяют™
ся с течением времени. Поэтому естественный свет обладает
(статистически) осевой симметрией относительно направления
его распространения. Для линейно поляризованного света такой
симметрии нет. Его свойства в различных плоскостях, проходя-
проходящих через направление нормали N, различны. Среди этих плос™
костей есть две избранные плоскости, в одной из которых лежит
вектор Е, а в другой — вектор Н. Осевая асимметрия сохраняет™
ся и для смеси естественного света с линейно поляризованным.
Такой свет называется частично поляризованным.
1Л тт
) По старой терминологии плоскостью поляризации называлась плос-
плоскость (N, Н), содержащая магнитный вектор Н.

62
ПОЛЯРИЗОВАННЫЙ И ЕСТЕСТВЕННЫЙ СВЕТ
421
2. Линейно поляризованный свет легко получить, пропустив
естественный свет через пластинку турмалина, вырезанную па-
параллельно его кристаллографической (оптической) оси. Турма-
Турмалин сильно поглощает световые лучи, в которых электрический
вектор перпендикулярен к оптической оси. Если же электри-
электрический вектор параллелен оси, то такие лучи проходят через
турмалин почти без поглощения. Поэтому естественный свет,
пройдя через пластинку турмалина, наполовину поглощается и
становится линейно поляризованным с электрическим вектором,
ориентированным параллельно оптической оси турмалина.
Таким лее свойством обладают поляроиды^ более удобные в
обращении. Они представляют собой искусственно приготовляе-
приготовляемые коллоидные пленки, служащие для получения поляризован-
поляризованного света. Наиболее распространенным материалом для при-
приготовления поляроидов является герапатит^ представляющий
собой соединение йода с хинином. Этот материал вводят в цел-
целлулоидную или желатиновую пленку. В ней ультрамикроско-
пические кристаллики герапатита каким-либо способом (обыч-
(обычно механически, например протаскиванием вязкой массы через
узкую щель) ориентируются своими осями в одном и том же
направлении. Полученная масса, подобно турмалину, действует
как один кристалл и поглощает световые колебания, электри-
электрический вектор которых перпендикулярен к оптической оси. С
другими способами получения поляризованного света мы позна-
познакомимся в дальнейшем.
Всякий прибор, служащий для получения поляризованно-
поляризованного света, называется поляризатором. Тот же прибор, применя-
применяемый для исследования поляризации све-
света, называется анализатором. Таким об-
образом, кристаллы турмалина или поляро-
поляроиды могут служить и поляризаторами, и
анализаторами.
3. Допустим, что два кристалла тур-
турмалина или два поляроида поставлены
друг за другом, так что их оси ОА\ и ОА2
образуют между собой некоторый угол а
(рис. 235). Первый поляроид пропустит
свет, электрический вектор Eq которого па-
параллелен его оси ОА\. Обозначим через Iq
интенсивность этого света. Разложим Eq на вектор Ец, парал-
параллельный оси ОА2 второго поляроида, и вектор Ej_, перпендику-
перпендикулярный к ней (Ео =Ец+E_l). Составляющая E_l будет задер-
задержана вторым поляроидом. Через оба поляроида пройдет свет с
электрическим вектором Е = Ец, длина которого Е = Eqcosol.
Интенсивность света, прошедшего через оба поляроида, будет
1 = /0 cos2 a. F2.1)
Рис. 235

422
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
Такое соотношение справедливо для любого поляризатора и ана-
лизатора. Оно называется законом Малюса A775-1812).
4. Важные состояния поляризации возникают при наложе-
наложении монохроматических волн. Их общий характер одинаков для
векторных волн любой физической природы. Для наглядности
начнем с механического примера, когда частица совершает два
гармонических колебания с одной и той же частотой ш: одно
колебание происходит вдоль оси X, другое — вдоль оси Y. Ко-
Координаты частицы представляются выражениями
х = acoscdi, у = Ь cos (cot + S) (а, Ь>0). F2.2)
Исключив из этих выражений время t, найдем уравнение тра-
траектории частицы:
^ _ ^l CoS S + ^ = sin2 S. F2.3)
а2 аЬ Ь2
Это — кривая второго порядка, а именно эллипс1 так как коор-
координаты жну, как это видно из F2.2), не могут обращаться в
бесконечность. Таким образом, от сложения двух взаимно пер-
перпендикулярных колебаний одной и той же частоты возникает
движение по эллипсу.
Для определения направления движения частицы по эллип-
эллипсу заметим, что начальную фазу 6 всегда молено выбрать так,
чтобы она была заключена между ^тг и +тг. Тогда колебание с
большей фазой называют опережающим, а с меньшей фазой —
запаздывающим. Напишем далее компоненты скорости частицы
вдоль осей X и Y:
х = —ша sin cj?, у = —шЬ sin (cot + 5).
При t = 0 получим х = а, у = —cobsinS. Таким образом, при
t = 0 частица находится на вертикальной прямой х = а. Если
^тг < 6 < 0, то у > 0, т.е. частица
движется вверх, описывая эллипс
против часовой стрелки. Если же
О < 6 < тг, то у < 0, частица дви-
движется вниз, описывая эллипс по
часовой стрелке (рис. 236). В обо-
обоих случаях движение по эллипсу
совершается от положительного
конца оси опережающего колеба-
колебания к положительному концу оси
запаздывающего колебания.
В зависимости от значений па-
параметров а, Ь, S эллипс может вы-
вырождаться в отрезки прямой или в окружность. Из F2.3) вид-
видно, что для движения по окружности должны выполняться два
условия: 1) cos 5 = 0, т.е. 5 = ±тг/2; 2) а = Ь.
Y

§ 63 НЕЗАВИСИМЫЕ ГРАНИЧНЫЕ УСЛОВИЯ 423
5. Все изложенное относится и к сложению любых векторных
колебаний, в частности электромагнитных. Две электромагнит-
электромагнитные волны, линейно поляризованные во взаимно перпендику-
перпендикулярных плоскостях, при сложении в общем случае дают волну,
поляризованную эллиптически. В такой волне конец электри-
электрического (и магнитного) вектора в каждой точке пространства
движется по эллипсу. Если эллипс вырождается в круг, то гово-
говорят, что волна поляризована по кругу.
Монохроматическое векторное поле всегда поляризовано^ в
общем случае эллиптически. Векторное поле называется моно-
монохроматическим, если все три его проекции на координатные оси
совершают гармонические колебания с одной и той же частотой,
т.е. представляются формулами вида
Ej = Cj(r) cos[w< + ej(r)} (j = x, у, z). F2.4)
Умножая эти выражения на координатные орты ej и суммируя
по всем j, запишем монохроматическое поле в векторной форме:
Е = Ai(r) cos cut + A2(r) sincjt. F2.5)
Если векторв! Ai(r) и А2(г) везде или в некоторвгх точках кол™
линеарны, то в таких точках вектор Е параллелен этим векто-
векторам, т.е. поле Е поляризовано линейно. Если же А]_ и Л 2 не кол-
линеарны, то, как видно из формулы F2.5), вектор Е в любой
момент времени лежит в плоскости векторов А]_(г) и А2(г). Сле-
Следовательно, конец вектора Е описывает плоскую кривую. Чтобы
найти ее форму, примем направление Ai за ось X, а перпенди-
перпендикулярное к нему направление, лежащее в плоскости (Ai, A2), —
за ось Y. Тогда проекции Ех и Еу представятся в виде
Ех = «ш(г) cos (out + ?ж), Еу = %(r) cos (ujt + 5У).
Задача свелась к сложению двух взаимно перпендикулярных
гармонических колебаний одной и той же частоты, сдвинутых
по фазе относительно друг друга. От такого сложения получа-
получается движение по эллипсу.
Свет, испускаемый реальными источниками, всегда не поля-
поляризован или поляризован частично. Это является лучшим до-
доказательством того, что он не монохроматичен.
§ 63. Число независимых граничных условий в
электромагнитной теории света
1. Формальная теория отражения и преломления света
строится на основе граничных условий^ которым удовлетворя-
удовлетворяют векторы электромагнитного поля на границе раздела двух
сред. Она определяет величины, характеризующие отраженную

424
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
и преломленную волны, но ничего не говорит о механизме воз™
никновения этих волн. На последний вопрос, а также на более
тонкие вопросы дает ответ молекулярная теория. Сначала мы
изложим формальную, а затем дадим краткое представление о
молекулярной теории отражения и преломления света.
Будем рассматривать все тела как сплошные среды и пред™
положим, что на границах раздела таких сред нет (в сущности,
искусственно вводимых) поверхностных зарядов и токов. Тогда
на границах раздела должны быть непрерывны тангенциальные
составляющие векторов ЕиНи нормальные составляющие век-
векторов D и В:
ТГ71 \-•-/ ШР\ ) У"УV / тт~\ —'J /jf?*3 I \
?Lft — ?Lrt , tlt — ?lt , (OO.IJ
Z)W = дBM #W = в@)а F3.2)
Все эти условия являются следствиями макроскопических урав™
нений Максвелла в интегральной форме, а потому они вер-
верны для всяких сред^ пока последние можно рассматривать как
сплошные. Условия F3.1) вытекают из уравнений
1 г "
ф Hdl= - lT>dF + —J,
J с J с
а условия F3.2) — из уравнений
^DdP = 0, ^BdF = 0 F3.4)
(см. т. III, § 82).
2. Уравнения F3.1) и F3.2) не совсем независимы. Для ис™
следования этого вопроса построим бесконечно короткий ци-
цилиндр, образующие которого перпендикулярны к границе раз™
дела, а основания F\ и F2 лежат по разные стороны от нее
(рис. 237). На основании тео™
L2 ремы о циркуляции вектора Н
~~^ получим
L2
Рис. 237
В пределе, когда высота ци-
цилиндра обратится в нуль, кон™
туры L\ и L2 сольются в общий контур L, а основания F\ и
F2 — в общую площадку F, ограниченную контуром L. При

§ 64 ГЕОМЕТРИЧЕСКИЕ ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ 425
этом, ввиду непрерывности тангенциальных составляющих век™
тора Н, контурные интегралы совпадут между собой, а потому
Z)W dF= J D& dF.
F F
Аналогично,
Отсюда, ввиду произвольности области интегрирования,
D^=dM, bV=bW. F3.5)
Таким образом, граничные условия F3.5), как видно из их
вывода, являются следствиями граничных условий F3.1) и урав-
уравнений Максвелла для циркуляции векторов Е и Н. В случае
монохроматического поля D = гсЛЗ, В = го;В, так что усло-
условия F3.5) переходят в F3.2). Отсюда следует, что для монохро-
монохроматических полей граничные условия F3.2) выполняются авто™
матически, если только выполняются условия F3.1). Поэтому
в дальнейшем молено пользоваться только условиями F3.1), не
заботясь о выполнении условий F3.2).
Если условия F3.1) записать в координатной форме, то по™
лучатся четыре уравнения, так как каждый из векторов Е или
Н можно разложить на две тангенциальные и одну нормаль-
нормальную составляющие. Таким образом, электродинамика приводит
к четырем независимым граничным условиям.
В старых теориях упругого эфира число независимых гра-
граничных условий было шесть: равенство трех составляющих сме-
смещений и трех составляющих сил упругих напряжений по обе
стороны границы раздела. Чтобы удовлетворить этим шести
граничным условиям, вообще говоря, необходимо, чтобы кроме
поперечных волн существовали также и продольные. Но опыт
говорил против существования продольных волн. Возникшую
трудность теория пыталась устранить, наделяя эфир такими
свойствами, чтобы продольные волны в нем никогда не возни™
кали (несжимаемый или бесконечно сжимаемый эфир). Однако
удовлетворительного решения проблемы таким путем получе-
получено не было. Электромагнитная теория не знает этой трудности,
поскольку число независимых граничных условий в ней равно
четырем. Им молено удовлетворить с помощью двух попереч-
поперечных составляющих отраженной и двух поперечных составляю-
составляющих преломленной волн.

426 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
§ 64. Геометрические законы отражения и
преломления волн
1. Необходимость отражения и преломления света на грани™
це раздела двух сред следует уже из граничных условий. Дей-
Действительно, как будет видно из дальнейшего, граничные уело™
вия могут быть удовлетворены, вообще говоря, лишь при нали-
наличии отраженной и преломленной волн. Будем обозначать пада-
падающую волну индексом е (entfallende), отраженную — индексом
г (reflektierte), проходящую — индексом d (durchgehende).
Пусть на плоскую неподвижную границу раздела падает
плоская монохроматическая волна
Е(е) =?е»И-к1г)в F41)
Из соображений симметрии следует, что отраженная и прошед-
прошедшая волны
Е^) =Re*<a;*-kir), F4.2)
E(d) = DeiH-k2r) F43)
будут также плоскими и притом той же частоты ш. Равенство
частот следует из линейности и однородности граничных уело™
вий. Если среды неподвижны, то коэффициенты при напряжен-
ностях полей в граничных условиях могут зависеть от коорди™
пат, но не от времени. Пусть шг и ш^ — частоты отраженной
и прошедшей волн. Тогда любое из граничных условий F3.1)
принимает вид
А(г)еш + B(r)etuJrt + C(r)eluJdt = 0.
Коэффициенты А (г), -В (г), С (г) отличны от нуля, если толь-
только отраженная и прошедшая волны действительно существуют.
Следовательно, функции etujt, elUrt, eluJdt линейно зависимы, а
это возможно лишь при ш = шг = ujd- Если граница движется,
то А, В и С зависят не только от г, но и от времени. Тогда имеет
место изменение частоты (эффект Доплера). В этой главе всюду
предполагается, что среды неподвижны.
2. Найдем теперь волновые векторы отраженной и прошед-
прошедшей волн. Формулы, определяющие эти векторы, называются
геометрическими законами отражения и преломления волн.
Они определяют направления распространения отраженной и
прошедшей волн^ а в случае их неоднородности также и зату-
затухание в пространстве.
Примем границу раздела сред за координатную плоскость
XY. За ось X возьмем линию пересечения плоскости раздела
сред с плоскостью падения. Ось Z направим вниз, т.е. в сторону
второй среды. Тогда ось Y окажется перпендикулярной к плос-
плоскости падения и будет лежать в плоскости раздела сред. Так как

§ 64 ГЕОМЕТРИЧЕСКИЕ ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ 427
по доказанному частоты падающей, отраженной и прошедшей
волн одинаковы, то любое из граничных условий F3.1) примет
вид
у) _ q
где А,В,С — постоянные и притом отличные от нуля, если толь-
только отраженная и прошедшая волны действительно существуют.
Полагая у = 0, получаем линейную зависимость между функ-
функциями е~гк1хХ, е~гк1хх^ е~гк2х% и ПОЭТОМу заключаем, что
hx = к'1х = к2х. F4.4)
Аналогично,
hy = к[у = к2у. F4.5)
Таким образом, тангенциальные составляющие волновых век-
векторов отраженной и прошедшей волн равны тангенциальной
составляющей волнового вектора падающей волны. Остается
найти нормальные составляющие этих векторов. Согласно со-
соотношению E.14),
*i2 = *i = ^i, F4.6)
к\ = ^е2, F4.7)
где е\ и е2 — диэлектрические проницаемости первой и второй
сред. Далее
! - к%х, F4.8)
k2z = yjk% - к\х. F4.9)
Знак минус перед корнем в формуле F4.8) взят потому, что
плюс соответствует падающей волне. Что касается знака перед
корнем в F4.9), то он будет определен в дальнейшем из физи-
физических соображений.
Если падающая волна однородна, то из F4.4), F4.5) и F4.8)
следует, что отраженная волна также однородна. Ее волновая
нормаль лежит в плоскости падения, а угол отражения равен
углу падения. Для проходящей волны надо различать два слу-
случая.
Первый случай. Щ > к\х, т.е. преломленная вол-
волна однородна. Определим, какой знак следует выбрать в этом
случае перед квадратным корнем в F4.9). Знаку плюс соответ-
соответствует волна, распространяющаяся от границы раздела, — на-
направление ее распространения обозначено на рис. 238 сплошной
стрелкой. Знаку минус соответствует волна, идущая к грани-
границе раздела, — ее направление обозначено штриховой стрелкой.

428
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
Эти стрелки указывают направления распространения волно-
волновых фронтов, т.е. плоскостей равных фаз. Ясно, что отражен-
отраженная и преломленная волны
должны быть уходящими от
границы раздела. Этим тре-
требованием обеспечивается одно™
значность решения задачи. Од-
Однако требование ухода относит-
относится не к фазе, а к энергии вол-
волны. Можно показать, что в слу-
случае электромагнитных волн в
изотропных средах направле-
направления распространения фазы и
Рис. 238 энергии волны совпадают. По-
Поэтому знак минус перед корнем
в F4.9) следует отбросить; условиям задачи удовлетворяет толь-
только знак плюс.
Как видно из F4.4), нормали к падающей и преломленной
волнам лежат в плоскости падения. Если ip — угол падения, а
ф — угол преломления, то
= к\ sinip = —
Vi
откуда на основании F4.4)
= — sin
Sill if Vi П2
2 п\
sin^ v
Второй случай. Щ <
к2
ИЛИ Ш2
F4.10)
9
sir
откуда sin ip > v\/v2 = п. Здесь п — относительный показатель
преломления второй среды относительно первой. Так как simp <
< 1, то рассматриваемый случай возможен только при п < 1.
Составляющая k2Z чисто мнимая, а волна во второй среде, если
она существует, неоднородная. Знак корня в F4.9) определится
из требования, чтобы при удалении от границы раздела ампли-
амплитуда волны затухала. Этому требованию удовлетворяет только
выражение
В самом деле, тогда F4.3) принимает вид
= De-*/2^-*1-*), F4.12)
т.е. волна во второй среде будет затухать в направлении оси Z,
чего не получилось бы, если бы в F4.11) вместо минуса взять
плюс.
Плоскости равных фаз волны F4.12) перпендикулярны к оси
X и распространяются вдоль нее с фазовой скоростью vx =

§ 64 ГЕОМЕТРИЧЕСКИЕ ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ 429
— ш/kix- Плоскости равных амплитуд параллельны границе раз™
дела. При смещении вглубь среды на h интенсивность волны
(пропорциональная квадрату амплитуды) убывает в е раз. Be™
личина h называется глубиной проникновения волны во вторую
среду. Она равна
h = . 1 = . Al F4.13)
/kf h\ 4/I2 2
4tti/sIii2 (p ~~ n2
где Ai — длина волны в первой среде.
Из F4.12) видно, что на больших (по сравнению с глуби™
ной проникновения) расстояниях от границы раздела волна во
второй среде практически полностью затухает. А так как по™
глощения света нет, то энергия падающей волны, проникшая
во вторую среду, должна снова целиком возвратиться в первую
среду. Иными словами, при sin^ > n отражение света должно
быть полным. Угол (/9q, определяемый соотношением sinc^o = п,
называется предельным узлом полного отражения.
8. В случае обыкновенного отражения
smt/? = &2ж/&25 cost/? = k2Z/k2-
В случае полного отражения не существует вещественного угла
t/?, удовлетворяющего соотношениям F4.14), так как они дают
для sint/? значения, превосходящие единицу, а для cost/? — мни™
мые значения. Однако в целях сохранения единой формы записи
при обыкновенном и полном отражениях целесообразно сохра™
нить формулы F4.14) как простые определения smt/? и cost/?.
Поскольку эти величины удовлетворяют соотношению sin2 ф +
+ cos ф = 1, они могут рассматриваться как синус и косинус
комплексного аргумента ф в смысле теории функций комплекс™
ного переменного:
е1ф _ е^{ф ^ф _|_ е-ъф
suit/? = , cost/? =
2г 2
Если sint/? и cost/? известны, то этими формулами аргумент ф
определяется с точностью до целого кратного от 2тг. Это не мо™
жет сказаться на однозначности физических выводов, так как во
все формулы будет входить не сам комплексный угол ф, а его
синус и косинус. К так определенным функциям sint/? и cost/?
применимы все формальные соотношения обычной тригономет-
тригонометрии. Поэтому над комплексными suit/? и cost/? можно выполнять
все преобразования, как если бы они были обыкновенными си™
нусом и косинусом.
Заметим, наконец, что вместо F4.14) можно написать
в'тф = sin</?/n, cost/? = ^ — у sin2 cp — в2. F4.15)

430 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
§ 65. Формулы Френелм
1. При выводе геометрических законов отражения и прелом-
преломления волн явный вид граничных условий не использовался. Для
определения амплитуд отраженной и проходящей волн необхо-
необходимо использовать граничные условия в явном виде.
Разложим электрическое поле каждой волны на две состав-
составляющие. Одна из них лежит в плоскости падения, другая пер-
перпендикулярна к этой плоскости. Часто эти составляющие на-
называют главными составляющими соответствующих волн. Они
обозначаются значками || и _L соответственно. Пусть еж, eyi ez —
единичные векторы вдоль координатных осей, a ei, e;l5 е2 — еди-
единичные векторы, лежащие в плоскости падения и перпендику-
перпендикулярные соответственно к падающему, отраженному и прелом-
преломленному лучам (рис. 238). Тогда
ЬМ е'1 = ЬМ1, е2 = ЬМ. F5.1)
кг L k\ fe
В случае полного отражения вектор е2 — комплексный, его
геометрическая интерпретация как единичного вектора, перпен-
перпендикулярного к преломленному лучу, теряет смысл. Поэтому,
чтобы охватить не только обыкновенное, но и полное отраже-
отражение, дальнейшие вычисления проводятся чисто аналитически,
не прибегая к чертежу. Введем разложения
? = ?±еу + ?цв1,
В. = R±ey + Ще[, F5.2)
D = D±ey + 1)це2
и определим амплитуды i?j_, Дц, D±^ ?)ц. Умножая скалярно
первое из уравнений F5.2) на еж, находим
р f p
^(e^ki]) = ^([e^ki) = -^(ezki)=?\\ cos (p.
Аналогично, ?у = ?±, ?z = —<?"ц sin</9. Таким образом, ж™, у™,
z-составляющие электрического поля на границе раздела сред
(т.е. при z = 0) будут
Е^ = cos ip • ?ц, 4е) = ?^ Eze) = ^sin(P ' ^||- F5-3)
При этом мы всюду опустили фазовые множители, так как в лю-
любой точке границы раздела они одинаковы для всех трех волн:
падающей, отраженной и прошедшей. Магнитные свойства сред
учитывать не будем, считая, что Н = В. Магнитное поле вычис-
вычисляем по формуле E.6) и находим
HJfJ = —n\ cos (р • ?±^ Н^ = ni?||, H^ = п\ simp • ?±.
F5.3а)

§ 65 ФОРМУЛЫ ФРЕНЕЛЯ 431
Для отраженной волны:
х 'II' У ' ^ 'II'
Нхг = п\ costp • Д^, Ну = П]_Дц, Щг = п\ шар • R±.
F5.4)
Для прошедшей волны:
(d) (d) (d)
ttW _ _ / n /r(d) _ n ir(d) _ n • /
F5.5)
Для определения четырех неизвестных i?x5 -Rm , -Dj_, -Dii элек-
электродинамика дает четыре независимых граничных условия:
XIX X 5 У 1 У У 1 /?jr |-\
гг(е) , гг(г) _ tr«» гт(е) , ff(r) _ IjW lOO.OJ
х'ж Х7 У У У
Подставляя в них найденные выше значения, получим
cos (р • (?п — Д11) = cos ф • Z)||, ?± + Д^ = Z?j_,
Tii c°s ^ * (^j_ ~ R±.)
Отсюда
R± m cos y? — ri2 cos t/; ^ D^ 2rii cos <p
7li COS (f + Tl2 COS ^j_ Til COS ^9 + П2 COS
Щ П2 COS y? — m COS c/y , x^||
B2 COS if + П1 COS -0 'I S\\ П2 COS (fi + П\ COS ф
F5.7)
Отношения R±/?±, D±/?±, ... называются коэффициентами
Френеля. С помощью соотношений F4.10) формулы F5.7) легко
привести к виду
R± sin {tp ~~ ф) D± 2 cos if sin tp
?±_ sin ((р + ф)' Е±_ sin (ip + фI
• (oo.o)
Щ\ tg (ip ~~ ф) JJ\\ 2 cos (p sin (p
S\\ tg (cp + ф)' «6*|| sin (y? + ^?) cos (у? — ф)
Эти формулы и решают поставленную задачу. Они были
впервые получены в 1821 г. Френелем из механической теории
упругого эфира с помощью весьма простых, но нестрогих и про-
противоречивых рассуждений. Последующие попытки строгого ре-
решения задачи с помощью уравнений упругости ухудшили дело:
в случае волн, поляризованных в плоскости падения, они при-
приводили к формулам, не согласующимся с опытом. Только элек-
электромагнитная теория света впервые дала строгое и удовлетво-
удовлетворительное решение задачи.

432 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
2. При обыкновенном отражении угол f, ас ним и все ко-
коэффициенты Френеля вещественны. Отсюда следует, что отра-
отражение и преломление не сопровождаются изменением фаз^ за
исключением, быть может, изменения фазы отраженной волны
на 180°. Если падающая волна была линейно поляризована^ то
отраженная и преломленная волны будут также линейно по-
поляризованы.
При нормальном падении волны формулы F5.7) дают
В этом случае исчезает разница между волнами, поляризован™
ными в плоскости падения и перпендикулярно к ней. Различие в
знаках коэффициентов Френеля R±/?± и Дц/?ц связано с услов-
условным выбором положительных направлений, в которых проведе-
проведены векторы ei и е^: в предельном случае нормального падения
эти векторы направлены прямо противоположно (см. рис. 238).
Если п\ < П2, то R±/?± < 0; если щ > П2, то R±/?± > 0. В
первом случае отражение света сопровождается скачкообраз-
скачкообразным изменением фазы на 180°. Во втором оно происходит без
изменения фазы.
При скользящем падении, когда угол (р близок к 90°,
т.е. отражение практически полное. С этим связано происхожде-
происхождение ярких и красивых изображений противоположных берегов
в спокойных водоемах. Этим же объясняется, почему изображе-
изображение заходящего солнца в тех же условиях по яркости почти не
уступает самому солнцу.
Как видно из формул F5.7) или F5.8), отношение R±/?± ни-
никогда не обращается в нуль, за исключением тривиального слу-
случая п\ = П2. Напротив, при (р + ф = тг/2 знаменатель tg ((p + ф)
обращается в бесконечность. В этом случае Дм = 0, т.е. отра-
отражение отсутствует. Таким образом, если электрический вектор
падающей волны лежит в плоскости падения, то при некотором
угле падения отражение света исчезает. В этом состоит закон
Брюстера A781—1868), открытый им экспериментально в 1815 г.
Соответствующий угол падения (рв называется углом Брюсте-
Брюстера. Для его вычисления заметим, что при (р + ф = тг/2 направ-
направления прошедшего и отраженного лучей взаимно перпендику-
перпендикулярны (рис. 239). Следовательно, cosc/^ = sin^ = -slncp^,
т.е. п
tgipB = n, F5.10)
Если неполяризованный свет падает под узлом Брюстера, то

65
ФОРМУЛЫ ФРЕНЕЛЯ
433
составляющая с электрическим вектором Ец отражаться не
будет. Отраженный свет окажется линейно поляризованным
и притом перпендикулярно к плоскости падения 1).
Отражение под углом Брюстера дает простейший способ по™
лучения поляризованного света. Недостаток этого способа — ма-
малая интенсивность отраженного све™
та. Для его устранения применя-
применяют несколько стеклянных пласти-
нок, сложенных в стопу (стопу Сто-
Столетова). При большом числе пла-
пластинок отражается почти полови-
половина падающего света. Если свет па-
падает под углом Брюстера, то от-
отраженный свет оказывается полно-
полностью поляризованным перпендику-
перпендикулярно к плоскости падения. Про-
Прошедший свет поляризован в плоско-
плоскости падения, но эта поляризация не
совсем полная. В настоящее время
стопа для получения поляризованного света почти не употреб-
употребляется, так как существуют более удобные и совершенные спо-
способы (поляризационные призмы, поляроиды).
3. Отношение отраженной энергии к энергии падающей на-
называется коэффициентом отражения. Так как энергия пропор-
пропорциональна квадрату амплитуды, то формулы F5.7) дают для
коэффициентов отражения главных составляющих падающей
волны следующие выражения:
2
Рис. 239
/ COS if — П COS ф
\ COS if + П COS ф
11
ncosip + costp
Коэффициент отражения при нормальном падении R назы-
называется отражательной способностью:
. F5.12)
Для стекла (п = 1,5) R = 0,04 = 4%; для воды (п = 1,33)
R = 2%. При отражении от воды длинных электромагнитных
волн (п = у/г = 9) R = 64%. Эти цифры показывают, что ни
вода, ни стекло при нормальном падении не могут служить зер-
зеркалом. Обычные зеркала используют отражение света от метал™
лических поверхностей. Стекло служит только для защиты их
г) Малюс, открывший поляризацию света при отражении, назвал плос-
плоскость падения плоскостью поляризации отраженного света. Здесь под плос-
плоскостью поляризации понимается плоскость, перпендикулярная к плоскости
поляризации Малюса.

434 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
задних посеребренных поверхностей. Однако наличие далее сла-
слабого отражения от передней стороны стекла делает такие посе-
посеребренные с задней стороны зеркала непригодными для опти-
оптических целей. Для этих целей необходимо покрывать металлом
(лучше всего родием) переднюю поверхность стекла.
Отношение Ь прошедшей энергии к энергии падающей на-
называется коэффициентом пропускания. Коэффициент пропуска-
пропускания можно также определить как отношение нормальных ком-
компонент усредненного по времени вектора Пойнтинга прошедшей
и падающей волн. На основании F5.3) и F5.3а) находим для па-
падающей волны
sie) = ^[Е^Н<е^ - Е^Н^Щ +компл. сопр. =
а для прошедшей
Предполагая сначала, что вектор Е перпендикулярен к плоско-
плоскости падения, а затем параллелен ей, находим
, п costb ( 2 cos у? \2 , ncosip ( 2собш \2
и± = I I , Oil = I I .
cosy? V cos if + n cos ф / " cosy? \ncos (p + cost/? у
F5.13)
Нетрудно проверить, что p± + b± = рц + Ьц = 1, как и должно
быть согласно закону сохранения энергии.
Коэффициент пропускания при нормальном падении
в = JjTir F54)
называется поверхностной прозрачностью. Измерения отража-
отражательной способности и поверхностной прозрачности дают удоб-
удобный метод измерения показателей преломления в инфракрасной
части спектра.
Найдем теперь коэффициент отражения для случая, когда
плоскость поляризации падающей волны составляет с плоско-
плоскостью падения угол а. Этот угол называется азимутом поляри-
зации падающей волны. Очевидно, ?ц = ylcosa, ?± = A sin a,
где А — амплитуда падающей волны. Полная отраженная энер-
энергия пропорциональна Р\\??\ + Р^?\ — ^42(рц cos2 a + p±sin2 а).
Следовательно, коэффициент отражения равен
Ра = Р\\ cos2 а + р± sin2 a. F5.15)
Коэффициент отражения неполяризованного света р получает-
получается отсюда путем усреднения по а. Так как в неполяризованном
свете все направления электрического (и магнитного) вектора

65
ФОРМУЛЫ ФРЕНЕЛЯ
435
представлены с одинаковой вероятностью, то cos2 a = sin a =
= 1/2. Поэтому
Р = 9 (Р|| "^ Р-^' F5.16)
На рис. 240 приведены теоретические кривые для коэффи-
коэффициентов отражения видимого света от стекла (п = 1,5), а на
1 Л б°39' 19°29' 30°43' 38°47' 41°49' 1 л 1°6' 3°lf 4°53' 6°0' 6°23'
1,U i 1 . . . . . . . j-i, 1,0
0,8 I " 1 1 1 1 \-li 0,8
Стекло Jjj
0,61 " = !i_,| 1 I И 0,6
0Л[ 'в " '" I 1—| \/ hi I О.4
од I—\—'o=Up.+o^y У L 1 0,2 h'
13°1Г 25°22'
Стекло
n = 1,5
Ф5=56°19'
35°16'
,v
о /¦ j
у
/,
//
//
1
//
'//
/
/p.
i
2°
1Г
—-—-
Вода
n = 9
3°4
»°20
4C
6'
5°31'
\
P
1 ,
—J
5-(Pl+P|
\
\
V
\
\
1
\
20°
40°
60°
80° Ф
20°
40°
60°
80° Ф
Рис. 240
Рис. 241
рис. 241 — для радиоволн при их отражении от поверхности
воды (п = у/во = 9)
Многочисленные измерения коэффициентов отражения при
различных углах падения и при различных поляризациях па-
падающей волны, предпринимавшиеся с целью проверки формул
Френеля, находятся в очень хорошем согласии с этими форму-
формулами как в случае видимого света, так и в случае радиоволн.
Исключение составляет случай отражения под углом Брюстера
и в его ближайшей окрестности, где наблюдаются незначитель-
незначительные отступления от формул Френеля (см. § 70).
4. Формулы Френеля мы вывели в предположении, что свет
монохроматический. Однако в случае обыкновенного отраже-
отражения в эти формулы не входит длина волны, а отражение не
сопровождается изменением фазы. Поэтому в случае недиспер™
гирующих сред и обыкновенного отражения формулы Френе-
Френеля справедливы и для немонохроматических волн. Надо только
под ?j_, i?j_, D± и т.д. понимать соответствующие компоненты
напряженностей электрического поля падающей, отраженной и
прошедшей волн на границе раздела. Это непосредственно сле-
следует из теоремы Фурье и принципа суперпозиции.

436 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
§ 66. Полное отражение
1. В случае полного отражения созф — чисто мнимая вели™
чина, при этом формулы Френеля удобно записать в виде
R± _ cos ер + i\/sin2 ер — n'2 D± _ 2 cos cp
cos (f — i у sin2 (p — n2 ^-L cos (p — i у sin2 ip — n2

R\\ n2 cos ip + i^/sin2 ip — n2 D\\ 2ncosip
?\\ n2 cos (p — i\/sln2 (p — n2 ?\\ n2 cos (p — i^sin2 ip — n2
Из этих формул видно, что \R_\_\ = \S_\_\ и |Дц| = |?ц|, т.е. отра-
отражение действительно является «полным». В то же время неод-
неоднородная волна во второй среде, вообще говоря, не исчезает.
Например, если (р = щ = arcslrm, то D± = 2?±. Здесь нет на-
нарушения закона сохранения энергии. Дело в том, что формулы
Френеля относятся к монохроматическому полю7 т.е. к некото-
некоторому установившемуся процессу. А в этом случае закон сохра-
сохранения энергии требует только, чтобы количество энергии во вто-
второй среде менялось во времени периодически. Иными словами,
среднее за период изменение энергии во второй среде должно
быть равно нулю. Что это условие действительно выполняется,
показывает следующее простое вычисление.
Вычислим усредненную по времени нормальную составляю-
составляющую вектора Пойнтинга во второй среде. Пусть электрический
вектор лежит в плоскости падения. Тогда
Sz = ^—Е^Ну + компл. сопр.
Поле во второй среде определяется формулами F5.5). Так как
cos^ — величина чисто мнимая, то из F5.5) видно, что между
электрическим и магнитным полями существует сдвиг фаз в 90°.
При этом величина Е*Ну также чисто мнимая, а потому Sz =
= 0. То же справедливо и в случае, когда электрический вектор
перпендикулярен к плоскости падения. Этим наше утверждение
доказано.
Вычисление остальных компонент усредненного вектора
Пойнтинга дает
!/h, 5^ = 0, F6.2)
где h — глубина проникновения, определяемая выражением
F4.13). Таким образом, во второй среде действительно имеет-
имеется энергия, средний запас которой со временем не изменяется, а
средний поток параллелен оси X. Существование такой энергии
при установившемся режиме, очевидно, не противоречит полно-
полному отражению падающей волны.

§ 66 ПОЛНОЕ ОТРАЖЕНИЕ 437
Чтобы ответить на вопрос, как появилась энергия во второй
среде, надо было бы исследовать процесс установления колеба-
колебаний. Молено, например, рассмотреть квазимонохроматическую
волну с передовым фронтом, перед которым нет никакого волно-
волнового возмущения. Пока фронт волны не достиг границы раздела,
во второй среде нет поля. Как только волна дойдет до границы
раздела, она сначала будет почти целиком проникать во вто-
вторую среду и лишь частично отражаться. По мере установления
колебаний коэффициент отражения будет быстро нарастать и
стремиться к своему предельному значению — единице. Полное
отражение имеет место лишь для установившегося режима. По-
Пока процесс не установился, отражение всегда частичное.
2. Пусть две одинаковые среды разделены тонким воз-
воздушным промежутком, на который падает волна под углом,
большим предельного. Можно ожидать (см. § 67), что она про-
проникнет в воздушный зазор в виде неоднородной волны. При до-
достаточно малой толщине зазора неоднородная волна достигнет
его второй границы еще не очень сильно ослабленной. Вступив
из воздушного зазора во вторую среду, волна снова превратится
в однородную и может быть обнаружена обычными средствами.
Опыт такого рода был выполнен еще
Ньютоном и рассматривался как экспе- |
риментальное доказательство проникно- —L
вения света в оптически менее плотную —
среду при полном отражении. (Строго __
говоря, здесь нет полного отражения:
оно возмущено наличием второй среды.) _^_
Ньютон прижимал к гипотенузной грани
прямоугольной призмы другую призму,
сошлифованную сферически (рис. 242).
Оказалось, что свет проходит во вторую
призму не только в месте соприкоснове- Рис 242
ния (оптический контакт), но и в неболь-
небольшом кольце вокруг него — там, где толщина воздушного про-
промежутка сравнима с длиной волны. При наблюдении в белом
свете внешний край кольца имел красноватую окраску. Этого и
следовало ожидать, так как глубина проникновения пропорци-
пропорциональна длине волны: для красных лучей она больше, чем для
синих.
Меняя толщину воздушного зазора, можно изменять интен-
интенсивность проходящего света. На этом основано устройство све-
тового телефона^ запатентованного фирмой Цейсе. Роль одной
из сред играет прозрачная мембрана, колеблющаяся под дей-
действием падающего на нее звука. Свет, прошедший через зазор,
меняет интенсивность в такт с изменениями силы звука. Падая
на фотоэлемент, он возбуждает переменный ток, сила которо-

438 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
го изменяется также в соответствии с изменениями силы звука.
Этот ток усиливается и используется в дальнейшем.
Явления прохождения волн через тонкие зазоры, аналогич-
аналогичные описанному, не специфичны для оптики. Они имеют место
для волн любой природы и могут происходить, когда фазовая
скорость в зазоре превосходит фазовую скорость в окружаю™
щих средах. Легче всего они реализуются для длинных волн
(радиотехника, акустика). Особо важное значение эти явления
приобрели в ядерной и атомной физике, а так лее в теории твер™
дого тела. Об этом будет говориться в пятом томе нашего курса.
3. При обыкновенном отражении оба отношения R±/?± и
||/?ц всегда вещественны. При полном отражении они, вооб™
ще говоря, комплексны. Это значит, что при полном отражении
фаза волны испытывает скачок, и притом, как правило, отлич-
отличный от нуля или ж. Пусть волна поляризована перпендикулярно
к плоскости падения. Можно написать
cos (р + г у sin2 ip — п2 =
где А и 5± — величины вещественные. Тогда
cos if - i\fsin(pn Ae, ^
Отсюда видно, что 5± и есть интересующий нас скачок фазы.
Приравнивая вещественные и мнимые части, получим
Отсюда
A cos — = cos </?, A sin — = ^/sln2 ip — n2.
i 0\ \/S1H Ю — Tl (nn o\
tg -± = -? ? . F6.3)
2 cos^
Аналогично, для волны, поляризованной в плоскости падения,
tg*jL= Vsm^-n^ F64)
2 в2 cos у?
Скачки фаз 5± и Eц не одинаковы. Если падающая волна по™
ляризована линейно, то в отраженной волне между Ец и Е^ воз™
никнет определенная разность фаз. Поэтому отраженная волна
будет, вообще говоря, поляризована эллиптически. Допустим,
что между Ец и Е^ в падающей волне нет разности фаз. Тогда
разность фаз между ними в отраженной волне будет 5 = <5ц —д±.
С помощью формул F6.3) и F6.4) найдем
, § COS (Z>vSin Ф — W2 (nn г\
tg - = — .о 66.5
2 V
Отсюда видно, что tg (S/2) > 0, т.е. S лежит в пределах от нуля
до тг. Значит, колебание Ем опережает по фазе колебание Е^5

§ 66 ПОЛНОЕ ОТРАЖЕНИЕ 439
и эллиптическая поляризация отраженного света будет левой.
Наоборот, если разность фаз между такими же колебаниями в
падающей волне равна тг, то эллиптическая поляризация отра-
отраженной волны будет правой.
Величина д обращается в нуль при ip = ipo и ip = тг/2. Между
этими пределами она должна достигать максимума. Максимум
достигается при cosip = у A ^п2)/A+п2), максимальная раз™
ность фаз 6т определяется уравнением
tg = ii F66)
Для получения круговой поляризации отраженного света
необходимо выполнение двух условий: 1) ?ц = ±?±; 2) 6 = тг/2
(см. § 62, п. 4). Чтобы получить 5т = тг/2, нужен показатель пре~
ломления, удовлетворяющий уравнению 1 = A^п2)/2п. Отсюда
п = у/2 — 1 = 0,414. Показатель преломления оптически более
плотной среды относительно менее плотной будет пг = 1/п =
= 2,41. Если пг не меньше этого значения, то при однократном
отражении можно получить разность фаз 6 = 90°. В этом слу-
случае при ?± = ?ц поляризация отраженного света будет круговая
и притом левая. В видимой области спектра такой большой по-
показатель преломления имеет только алмаз (nf = 2,42). Для всех
прочих сред nf < 2,41. Поэтому для видимого света получить
разность фаз S = 90° при однократном отражении невозможно.
Но это возможно для коротких радиоволн. Для воды, напри™
мер, п' = ^/е® = 9, п = 1/9; круговая поляризация, согласно
F6.6), должна получиться при ip = 6°29' и ср = 44°38'. Опыт
подтвердил это предсказание.
Для стекла (nf = 1,51) максимальная разность фаз дости-
достигается при (р = 51°20/ и составляет 45°36;. Разность фаз 5 в
точности равна 45° при (р = 48°37; и при (р = 54°37;. Если
применить двукратное отражение под одним из этих углов, то
возникнет относительная раз-
разность фаз 90°. Этим восполь™ S В N С
зовался Френель для получе™ ^ / ^^ /
ния круговой поляризации. Он о
изготовил стеклянный парал™ /\ VV /
лелепипед с углом А = 54°37; AM D
(рис. 243). Луч SM, падающий
перпендикулярно на грань АВ, Рис. 243
претерпевает двукратное пол-
полное отражение на гранях AD и ВС', после чего выходит из па™
раллелепипеда в направлении NQ. При каждом из отражений
колебание Ем опережает по фазе колебание Е^ на 45°. Если па-

440 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
дающий свет поляризован линейно и ?ц = ?j_, то выходящий
свет будет поляризован по левому кругу. Если его заставить вто-
вторично пройти через параллелепипед Френеля, то он снова пре-
превратится в линейно поляризованный, но плоскость поляризации
повернется на 90° относительно своего исходного положения.
4. Возникновение скачка фазы при полном отражении мож-
можно понять, не обращаясь к формулам Френеля. Допустим ра-
ради определенности, что электрический вектор лежит в плоско-
плоскости падения. Если угол падения строго равен предельному углу
полного отражения <ро, то волна во второй
среде будет еще однородной. Она долж-
должна распространяться параллельно границе
раздела. Так как однородные волны попе-
поперечны, то отсюда следует, что электриче-
электрический вектор во второй, а следовательно, в
Рис 244 силу граничных условий, и в первой сре-
среде нормален к границе раздела. При том
выборе положительного направления электрического поля, ко-
которого мы придерживаемся (рис. 244), это означает, что фазы
падающей и отраженной волн на границе раздела совпадают.
Напротив, при (р = 90° полное отражение сопровождается
изменением фазы на 180°. В этом случае падающая и отражен-
отраженная волны распространяются в одном и том же направлении —
параллельно границе раздела. Граничные условия будут удо-
удовлетворены, если положить Дм = —?\\- Падающая и отраженная
волны гасят друг друга, в результате чего как в первой, так и
во второй средах не будет никакого светового поля, и гранич-
граничные условия выполняются тривиально. Но равенство Дц = —?\\
означает, что при отражении появляется скачок фазы в 180°.
Следует заметить, что говорить об отражении света, когда
угол падения точно равен 90°, не имеет смысла. Приведенное
рассуждение показывает только, к какому пределу стремится
амплитуда Дц, когда угол падения приближается к 90°. Если
отражение полное, то в первой среде образуются стоячие волны
с узловыми плоскостями, параллельными границе раздела. По
мере приближения угла падения к 90° расстояние между узло-
узловыми плоскостями увеличивается и стремится к бесконечности.
При этом ближайшая узловая плоскость в пределе сливается с
границей раздела. Одновременно исчезает поле во второй (оп-
(оптически менее плотной) среде.
Итак, при if = (fo скачок фазы при отражении равен нулю,
а при (р = 90° он составляет 180°. При этом во всем интерва-
интервале изменения угла (р от щ до 90° отражение должно оставать-
оставаться полным (§ 64). Изобразим колебание электрического поля в
отраженной волне на векторной диаграмме. При ip = щ ам-

§ 67 ПРОСВЕТЛЕНИЕ ОПТИКИ 441
плитуда изобразится вектором А(<^о) (рис. 245), а само коле-
колебание — его проекцией на ось X (если заставить вектор А(</?о)
равномерно вращаться вокруг О
с угловой скоростью ш). При (р =
= тг/2 амплитуда изобразится
вектором А(тг/2), равным век™
тору А(<ро), но противополож-
противоположно направленным. Для проме- A(f) I ^ ^/ ^ ^ 1 А(Ф0)
жуточного угла падения ср ам-
амплитуду, представляющую коле-
бание, обозначим через А(<р).
При возрастании <р от <ро до тг/2 длина вектора А(<р) не мо-
может изменяться, так как отражение полное. С другой стороны,
вектор А(у>), изменяясь непрерывно, должен из исходного поло-
положения А(<ро) перейти в конечное положение А(тг/2). Это можно
осуществить только поворотом его вокруг точки О. Значит, ес-
если угол падения (р лежит между щ и 90°, то вектор А(</?) должен
быть наклонен к оси X. Угол наклона <5ц и есть скачок фазы при
отражении.
5. Относительно перехода частичного отражения в полное
сделаем следующее замечание. В области частичного отраже-
отражения коэффициенты отражения р±_ и рм меняются непрерывно и
при (р —>• щ приближаются к единице. При ip = cpo они не испы-
испытывают разрыва. Однако их производные по (р претерпевают в
этом месте разрыв. Вычислим производные по (р от коэффици-
коэффициентов Френеля r± = R±/?± и гц = Дц/?ц в окрестности угла щ
в предположении, что (р < (р®. Простое вычисление дает
dr± _ 2 drj_ _ 2 /gg ^ч
dtp cos ф1 dip n2 cos ф
При ip = щ совф = О, и обе производные обращаются в беско-
бесконечность. Обращаются в бесконечность также dp±/dip и dp^/dip
(р± = r\i Р\\ = гп)- Поэтому вблизи предельного угла ^о коэф-
коэффициенты частичного отражения р± и рц должны очень резко
меняться с изменением угла падения. Этим объясняется проис-
происхождение резкой границы между областями частичного и пол-
полного отражений, которая бывает видна в рефрактометрах, осно-
основанных на полном отражении света.
§ 67. Прохождение света через плоскопараллельную
пластинку. Просветление оптики
1. Допустим, что на поверхность отражающего тела нанесе-
нанесена пленка толщины I с показателем преломления п (рис. 246).

442
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
Показатель преломления первой среды обозначим через ni, a
второй — через П2- Пусть все показатели преломления ni, П2 и п
постоянны (т.е. среды од™
нородны), а падающая
волна поляризована ли-
бо в плоскости падения,
либо перпендикулярно к
ней. Падающая волна
Е{е) =?ег(шг~к1г) ^67Л^
(начало координат в О)
претерпевает многократ-
многократные отражения на грани-
цах ПЛенки. В результате
интерференции в первой среде возникает отраженная волна
??(*•) = Де*(а;*-к/1г). F7.2)
Поле внутри пленки будет состоять из двух плоских волн:
Е = Ае*^*-^, Е1 = А! е1^1-*1 *}. F7.3)
Наконец, во второй среде возникнет преломленная волна
E{d) = Dei(ut-b2T)
R
Ввиду граничных условий, тангенциальные компоненты всех
волновых векторов должны быть одинаковы. Этим однозначно
определяются направления всех
волн (см. § 64). Для определения
неизвестных амплитуд I?, А, у!',
D электромагнитная теория дает
четыре независимых граничных
условия (два на верхней поверх-
поверхности пленки и два на нижней),
из которых эти неизвестные могут
быть найдены.
Однако мы предпочитаем ре™
шить задачу более коротким спосо™
бом. На верхней границе сходятся
четыре волны (рис. 247), из которых
две приходящие, а две другие — уходящие. При написании со-
соотношений между их комплексными амплитудами можно от-
влечься от наличия нижней границы. Тогда формально можно
рассуждать так, как если бы многократных отражений не бы-
было. Все приходящие волны можно рассматривать как падающие,
в результате (однократных) отражений и преломлений которых
возникают уходящие волны. Падающая волна с амплитудой ?,
Рис. 247

§ 67 ПРОСВЕТЛЕНИЕ ОПТИКИ 443
отражаясь от верхней границы, дает волну, идущую в направ-
направлении вектора Ц. Волна с амплитудой А1', преломляясь на той
лее границе, дает волну, идущую в том же направлении. Резуль-
Результатом интерференции этих волн и является отраженная волна с
амплитудой R. Это дает
d'lAf> F7.5)
Аналогично,
A = d1? + r'1A!. F7.6)
Здесь г\ и d\ означают коэффициенты Френеля на верхней гра-
границе пленки, а г2 и (?2 ™~ такие же коэффициенты на ее ниж-
нижней границе (предполагается, что свет пересекает эти границы
сверху вниз). Коэффициенты Френеля при обратном ходе лу-
лучей обозначаются теми же буквами, но со штрихами. С помо-
помощью формул Френеля нетрудно проверить, что эти величины
удовлетворяют соотношениям
rf = -r, r2 + dd' = l> F7.7)
Такое же рассуждение можно провести и для нижней гра-
границы пленки. Надо только перенести начало координат в точку
О;, находящуюся на нижней поверхности пленки (см. рис. 246).
Тогда волна F7.1) запишется в виде
^(е) _ ge-ikizlei(ut-kirf)
откуда видно, что роль комплексной амплитуды будет играть
величина ?' = ?e^iklzl. Аналогично преобразуются комплексные
амплитуды и остальных волн. В результате получим
A'E~ik'zl = r2Ae-ikzl, De~lk2zl = d2Ae~lkzl. F7.8)
Из полученных уравнений найдем
R г\+ Г2 exp (—2ikonl cos ф)
? 1 + г\Г2 exp (^2ikonl cos (pf)
D d\d2 exp [ikol(n2 cos ф — n cos (p)]
? 1 + Г1Г2 exp (^2ifconf cos^')
где fcg — волновое число в вакууме, а^и^ — углы преломления
на первой и второй границах. Для наглядности при выводе мы
ссылались на чертеж, относящийся к однородным волнам. Но,
очевидно, результаты F7.9) справедливы и в том случае, когда
волны в пленке или во второй среде неоднородны.
2. При нормальном падении первая формула F7.9) перехо-
переходит в
R- * + ™-™?7. F7.10)

444 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
Это выражение обращается в нуль, если выполняются два усло-
условия:
г\ + Г2 cos BnfcoO = 0, sin Bnkol) = 0.
Из второго условия получаем: 2пк®1 = Жтг, или
f = лф = N^ F7.11)
где Ж — целое число, а А — длина волны в пленке. Теперь первое
условие можно записать в виде: r\ + (—l)Nr2 = 0. Если N —
нечетное, то г\ = Г2] если же N четное, то г\ = ^Г2- Однако
последнее равенство не может быть выполнено. Действительно,
П — П\ П'2 — П
П = ——, г2 = ——.
П + П\ П2 + П
Если бы г\ = ^Г2, то мы получили бы п(п2 — щ) = 0, откуда
либо п = 0, что невозможно, либо П2 = п\, что не представляет
интереса. Это показывает, что число N должно быть нечетным,
а следовательно, г\ = г%. Отсюда
П = л/п\П2. F7.12)
Таким образом, если п = ^/щп2^ а толщина пленки равна
iVA/4, где N — нечетное число, то отражательная способность
обращается в нуль.
На этом результате основан один из методов увеличения
поверхностной прозрачности стекол, применяемый в оптиче-
оптической промышленности (так называемое просветление оптики).
Для стекла (п = 1,5) отражательная способность равна R =
= (п — 1J/(п + IJ = 0,04 = 4%, т.е. совсем невелика. Однако
оптические приборы состоят из многих деталей, изготовленных
из стекла. Отражение на границах их соприкосновения явля™
ется главной причиной ослабления света при его прохождении
через оптический прибор. Так, например, потери света в приз™
менном бинокле составляют свыше 50%, причем они почти це~
ликом происходят за счет отражения света. Значительная доля
отраженного света, благодаря последующим отражениям, дохо-
доходит до глаза наблюдателя и, будучи в лучшем случае равномер-
равномерно рассеянной, дает освещенный фон, ослабляющий контраст
света и тени в изображении. Особенно вреден этот рассеянный
свет в фотографических приборах. В лучшем случае он создает
общую вуаль на эмульсии. При некоторых же неблагоприятных
расположениях источников света могут получиться блики и до™
полнительные изображения.
Для увеличения поверхностной прозрачности стекла на его
поверхности создается пленка с показателем преломления п =
= ^Jn\n2 и толщиной А/4. Применение более толстых пленок (со-

§ 67 ПРОСВЕТЛЕНИЕ ОПТИКИ 445
ответствующих N = 3, 5 и т.д.) нецелесообразно, так как условие
полного исчезновения отражения может быть точно выполнено
только для одной определенной длины волны и одного опреде-
определенного угла падения. При N = 1 возрастание коэффициента
отражения с изменением длины волны, а также с изменением
угла падения получается наиболее медленным. Поэтому в этом
случае можно добиться почти полного исчезновения отражения
для сравнительно большого участка спектра и сравнительно ши-
широкого интервала углов падения.
Просветляющие пленки создаются либо путем выщелачива-
выщелачивания из поверхности стекла его компонентов, либо, что лучше,
путем напыления на поверхность стекла слоя посторонних ве-
ществ. При этом возникают трудности, связанные с тем, что по-
показатель преломления пленки должен быть значительно меньше
показателя преломления стекла. Например, если П2 = 1,52, п\ =
= 1, то п = 1,23. Твердых веществ с таким малым показателем
преломления в природе не встречается. Поэтому пленку прихо-
дится делать пористой, причем, во избежание заметного рассея-
рассеяния света, размеры пор должны быть весьма малы по сравнению
с длиной волны. Но пористая пленка не обладает достаточной
механической прочностью. Трудности могут быть преодолены
путем применения двуслойных покрытий. Сначала просветляе-
просветляемая поверхность покрывается пленкой, показатель преломления
которой значительно превосходит показатель преломления стек-
стекла, а затем пленкой с меньшим показателем преломления.
8. Условия отсутствия отражения F7.11) и F7.12) могут
быть также получены из простых интерференционных сообра-
соображений.
При малых коэффициентах отражения можно пренебречь
волнами, претерпевшими многократные отражения на границах
пленки. Тогда останутся две отраженные волны, из которых од-
одна отразилась от передней, а другая от задней поверхности плен-
пленки. Чтобы эти волны гасили друг друга, должны соблюдаться
два условия: 1) фазы их должны быть противоположны; 2) ин-
интенсивности их должны быть равны. Первое условие при нор-
нормальном падении приводит к соотношению F7.11). Второе усло-
условие, если пренебречь ослаблением волны за счет отражения от
передней поверхности пленки, сводится к т\ = т^- Отсюда, как
показано выше, получается формула F7.12). Недостаток приве-
приведенного доказательства в том, что оно не учитывает многократ-
многократные отражения.
ЗАДАЧИ
1. Вывести формулы для отражения и преломления электромагнитных
волн в предположении, что магнитная проницаемость отлична от единицы.

446
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
Ответ.
D±
COS ^ + л/Е21^2 COS ^ '
621^2 cosy™ \fsijiii cost/;
^21/12 COSt[)
F7.13)
/61//11 cosy
/62//12 cos у + л/si/fn cos 1/?
2. Какой вид принимают формулы F7.13), если ei =82 = 1?
Ответ.
^2 COS у — Wi COS У>
712 COS у + Щ COS У? '
П1 COS у — П2 COS ^
П\ COS у + П2 COS ^ '
2П2 COS у
П2 COS у + m COS ф
2П2 COS у
711 COS у + П2 COS ^ '
F7.14)
Формулы для отражения в точности совпадают с формулами Френеля, если
только поменять местами X и |^составляющие. Этот факт был отмечен
Ге льмгольцем.
3. Показать, что отражательная способность среды для радиоволн обра-
обращается в нуль, если е = /л.
4. Останется ли справедливым закон Брюстера для радиоволн, если
магнитные проницаемости сред /л\ и /12 отличны от единицы?
Ответ. Если закон Брюстера имеет место, то угол Брюстера, при ко-
котором не отражается составляющая Е\\ электрического поля, определяется
выражением
' -61/12
F7.15)
61 62fl2 — 61/JLl
Возможен случай, когда не будет отражаться составляющая Е±. Угол, при
котором это имеет место, находится из уравнения
Е1Е1Ё1^11Ё1. F7.16)
/11 61/I1 - ?2/i2
Оба случая взаимно исключают друг друга, так как знаки подкоренных
выражений в F7.15) и F7.16) противоположны. (Предполагается, что б и /х
существенно положительны.) Таким образом, всегда существует угол, при
котором не отражается либо составляющая Е\\, либо составляющая Е±.
5. Проверить, что коэффициенты Френеля удовлетворяют соотношени-
соотношениям F7.7).
6. Пользуясь формулами Френеля, показать, что линейно поляризован-
поляризованный свет остается линейно поляризованным после отражения на границе
раздела двух прозрачных изотропных сред во всех случаях, за исключени-
исключением случаев полного отражения.
7. Угол между плоскостью колебаний поляризованного света и плоско-
плоскостью падения называется азимутом колебания. Найти азимут преломлен-
преломленной волны 7 и азимут отраженной волны /3, если азимут падающей волны
а, а угол падения у.
Ответ, tg 7 = cos (у — ф) tg a, tg /3 = — , . tg a.
8. 1) Найти угол Брюстера для света, отраженного от стекла с показа-
показателем преломления п = 1,5; 2) найти для этого угла степень поляризации

§ 67 ПРОСВЕТЛЕНИЕ ОПТИКИ 447
преломленного света, т.е. величину А = ~^, где In и 1± — интенсивно™
1± + 1\\
сти отраженных волн, поляризованных соответственно в плоскости падения
и перпендикулярно к ней. Падающий свет — естественный.
4п2 _ (п2 + IJ
Ответ, if в = 56°19;, А = ^ ,\ 19 = -0,08.
An2 + (п2 + IJ
9. Естественный свет падает под углом Брюстера из воздуха на поверх-
поверхность стекла с показателем преломления п = 1,5. Найти интенсивность 1Г
отраженного света, зная интенсивность падающего света 1е.
2
10. Естественный свет падает под углом Брюстера из воздуха на по-
поверхность диэлектрика с показателем преломления п. Найти амплитуду D\\
преломленной волны, если амплитуда падающей волны той же поляризации
равна ?ц.
Ответ. D\\ = ?\\/n.
11. На боковую грань призмы, изготовленной из стекла с показателем
преломления п = 1,5, падает под углом Брюстера срв световой пучок, элек™
трический вектор которого лежит в плоскости падения. Каким должен быть
преломляющий угол А призмы, чтобы свет прошел через нее, не испытав
потерь на отражение?
Ответ. А = ж - 2(рв = 68°.
12. При каких условиях луч света, падающий на боковую грань про-
прозрачной изотропной призмы с преломляющим углом А = 60°, проходит
через нее без потерь на отражение?
Ответ. Электрический вектор должен лежать в плоскости падения.
Показатель преломления призмы должен быть равен
n = tgj = >/3 = l,73.
13. Свет падает из среды 1 на среду 2 под углом (р и преломляется под
углом ф. Доказать, что коэффициент отражения не изменится, если свет
будет падать из среды 2 на среду 1 под углом ф.
14. Пользуясь формулами Френеля, показать, что при отражении плос-
плоской электромагнитной волны от идеального зеркала, покрытого сверху сло-
слоем прозрачного диэлектрика, амплитуда отраженной волны равна ампли™
туде падающей. Изменяется лишь фаза волны, как это и должно быть со-
согласно закону сохранения энергии.
Решение. При отражении от идеального зеркала может меняться
только фаза, но не амплитуда волны. Поэтому коэффициент Френеля г2 в
формуле F7.10) должен иметь вид г2 = ега. Вводя еще обозначение «5 =
= 2коп17 получим из той же формулы
R _ п+ег{а~6)
? ~ 1 + пе*(а-6У
Отсюда |Д| = \?\.
15. Свет, частично отражаясь, проходит через две параллельные полу-
полупрозрачные плоскости. Коэффициенты отражения и пропускания первой
из них равны pi и fei, а второй р2 и Ьг соответственно. Степень монохрома-
монохроматичности падающего света невелика, так что интерференции не возникает,
а имеет место сложение интенсивностей света. Найти коэффициенты отра-
отражения р и пропускания Ь для системы обеих плоскостей.

448
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
Решение.
p = pi
b = -
= Pi
- P1P2
bib2
1 - P1P2'
Используя соотношения pi + Ь\ = 1, рг + &2 = 1, полученные результаты
можно записать в виде
Р =
р\ + р2 ~
- Р1р2
Ь =
- Р1Р2
При pi = p2 отсюда получаем
Р =
2pi
ь =
1-Р1
1 + рГ
F7.17)
F7.18)
16. Свет, частично отражаясь, проходит через систему ж параллель-
параллельных полупрозрачных плоскостей. Коэффициенты отражения и пропускания
каждой из них равны р и Ь. Найти коэффициент отражения рт и коэффици-
коэффициент пропускания bm всей системы ж плоскостей. (Относительно падающего
света см. предыдущую задачу.)
Решение. Присоединим к системе ж плоскостей одну такую же
(ж + 1)-ю плоскость. Первые ж плоскостей можно заменить одной плоско-
плоскостью с коэффициентом отражения рт. Тогда задача будет сведена к преды-
предыдущей, и мы получим для
100% г коэффициентов отражения и
пропускания (ж + 1) плоско-
плоскостей
_ Рт + Р — 2ртр
рт + 1 — 1 ,
80
60
40
20
Ьт + 1 =
-ртр
Отсюда методом доказатель-
• 1 нетрудно
ства от ж к ж
получить
рт =
тр
1-р
10
20
30
40
N
Рис. 248
т 1 + (ш-1)р'
F7.19)
17. Стопа Столетова
A839-1896) состоит из плос-
плоскопараллельных стеклянных
пластинок с показателем преломления п = 1,5. На нее под углом Брюстера
падает свет, поляризованный перпендикулярно к плоскости падения.
Найти выражения и начертить график для коэффициентов отражения и
пропускания стопы в зависимости от числа N пластинок.
2N 5 76
Ответ. pN = ———-, bN = ^гт^^ (рис. 248).

§ 67 ПРОСВЕТЛЕНИЕ ОПТИКИ 449
18. Естественный свет падает под углом ip на стопу Столетова, состо-
ящую из N стеклянных пластинок с показателем преломления п. Найти
степени поляризации А и А прошедшего и отраженного света, а также
отношение интенсивностей /_|_//ц главных компонент прошедшего света.
Ответ.
д=
BJV - 1)р±рц -(N- 1)(р± + рн) - 1'
д, = Р±. - Р\\ 1±_ = 1-р± BJV — 1)/оп Ч-
2(iV-l)p±pn + (p±+p||)' /|| 1-pn
где р|| и p± — коэффициенты отражения волн, поляризованных в плоскости
падения и перпендикулярно к ней, для одной отражающей поверхности:
/ / \ 2 / / \ 2
/ cos ш — п cos w \ ( п cos ш ~~ cos 1
р± = , , р|| =
\COS<^ + HCOStp) " \WCOS<^ + COS1
19. Падающий свет поляризован линейно с азимутом колебаний, рав-
равным +45° 1). Можно ли путем однократного отражения превратить его в
свет, поляризованный по правому кругу?
Ответ. Нельзя.
20. Какой должен быть минимальный показатель преломления парал-
параллелепипеда Френеля, чтобы при азимуте колебаний падающего света в +45°
выходящий свет был поляризован по правому кругу?
Ответ, п = - —— = 5,028. В оптическом диапазоне спектра
cos (Зтг/8)
этот случай осуществить нельзя. Его можно было бы осуществить с более
длинными электромагнитными волнами.
21. Линейно поляризованная электромагнитная волна с азимутом ко-
колебаний, равным +135°, отражается на границе вода-воздух. Диэлектри-
Диэлектрическая проницаемость воды е = 81. Под каким углом должна падать эта
волна, чтобы отраженная волна получилась поляризованной по кругу? Ка-
Какая при этом будет поляризация: правая
или левая?
Ответ. 6°29; или 44°38;. Правая.
22. Линейно поляризованный луч с
азимутом колебаний +135° падает пер-
перпендикулярно на грань АВ стеклянной
призмы ABCD (рис. 249) и, испытав три
раза полное отражение, выходит из нее. Рис. 249
Каков должен быть преломляющий угол
А призмы, чтобы вышедший свет был поляризован по кругу, если показа-
показатель преломления стекла призмы равен 1,52? Какая получится поляризация
вышедшего света: правая или левая?
Ответ. 69°21; или 42°46;. Правая.
23. Каким должен быть минимальный показатель преломления приз-
призмы, описанной в предыдущей задаче, чтобы при азимуте колебаний падаю-
падающего света, равном +45°, выходящий свет был поляризован по правому
кругу? Какой при этом должен быть угол А?
х) Азимут колебаний падающей волны может изменяться от ™тг/2 до
+тг/2. Он считается положительным, если ?\\/?± > 0, и отрицательным,
если ?\\/?± < 0.
15 Д.В. Сивухин

450 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
Ответ, п = 1/(л/2 - 1) = 2,4143; А = 35°34;.
24. С помощью векторной диаграммы показать, что скачок фазы при
полном отражении превосходит вдвое скачок фазы, испытываемый прелом-
преломленной (поверхностной) волной.
§ 68. Распространение света в среде с точки зреним
молекулярной оптики
1. С точки зрения атомистических представлений всякую
среду следует рассматривать как вакуум, в который вкрапле-
вкраплены атомы вещества. (Молекулы можно рассматривать тоже как
атомы.) Под действием падающей волны, а также излучений со™
седних атомов внутри каждого атома возбуждаются колебания
электронов и атомных ядер. Вследствие этого атомы становятся
источниками вторичных сферических волн, распространяющих-
распространяющихся между этими частицами со скоростью света в вакууме с. Эти
волны когерентны, поскольку они возбуждаются одной и той же
падающей волной. Их интерференция между собой и с падаю-
падающей волной определяет волновое поле во всем пространстве. В
частности, отраженная волна возникает в результате интерфе-
интерференции вторичных волн, вышедших из среды в вакуум, с кото-
которым она граничит.
Почему же в среде свет распространяется с иной скоростью,
чем в вакууме? Вопрос этот надо уточнить, указав, о какой
скорости идет речь. В теории отражения и преломления све™
та основной интерес представляет фазовая скорость^ поскольку
она определяет показатель преломления среды, а следователь™
но, и законы отражения и преломления волн на границе разде-
раздела сред. Отличие фазовой скорости света в среде от скорости
света в вакууме вкратце объясняется тем, что в каждую точку
пространства вторичные волны приходят не только от атомов,
расположенных вдоль луча, проходящего через рассматривае-
рассматриваемую точку, но и от множества других атомов, расположенных в
стороне от него.
Более подробное рассмотрение приводится ниже для точеч-
точечных атомов. В поле световой волны атомы приобретают меняю-
меняющиеся во времени дипольные моменты и излучают как точечные
диполи Герца. Для наших целей достаточно знать поле излуче-
излучения такого диполя в волновой зоне. Оно определяется только
составляющей дипольного момента p_L, перпендикулярной к на™
правлению излучения. Параллельная составляющая рм в волно-
волновой зоне на излучение диполя Герца не влияет.
2. Допустим, что в вакууме вдоль оси X распространяется
плоская монохроматическая волна Л,ъеъ^1~к°х\ на пути которой
перпендикулярно к оси X поставлен бесконечно тонкий плоско-

РАСПРОСТРАНЕНИЕ СВЕТА В МОЛЕКУЛЯРНОЙ ОПТИКЕ
451
параллельный слой толщины d?, состоящий из точечных непо-
движных атомов, равномерно распределенных по объему слоя
(рис. 250). Следуя Рэлею, выясним влияние такого слоя на фа-
фазу колебаний в какой-то удаленной точке А(х), расположенной
впереди слоя. Дипольные моменты атомов слоя, возбужденные
падающей волной, можно представить в виде р =
где ? — абсцисса слоя. Предполо-
Предположим, что точка А расположена в
волновой зоне ближайшего, а сле-
следовательно, и всех остальных ди-
диполей слоя. Тогда электрическое
поле каждого диполя в точке А
будет
F8.1)
А(х)
Рис. 250
где г — расстояние от диполя
(см. т. III, § 141). Такие выраже-
выражения надо просуммировать по всем
диполям слоя. Применим для это-
этого метод кольцевых зон Френеля. Из теории таких зон известно,
что результирующая напряженность dM\ всех диполей слоя в
точке А будет равна половине напряженности поля, возбуждае-
возбуждаемого в той же точке диполями одной только центральной зоны.
Таким образом, для нахождения dM\ надо просуммировать вы-
выражение F8.1) по всем диполям центральной зоны и результат
разделить на два. Вторичные волны, исходящие от края цен-
центральной зоны, отстают по фазе на тг от волны, исходящей из
ее центра О, а следовательно, и от падающей волны. Отстава-
Отставание по фазе вторичных волн, исходящих от остальных точек той
же зоны, будет промежуточным. Таким образом, возникнет за-
замедление скорости распространения фазы волны в результате
прохождения ее через слой вещества.
Для фактического выполнения расчета заменим суммирова-
суммирование интегрированием. Возьмем кольцо с внутренним радиусом
р и наружным р + dp, заштрихованное на рис. 250. В элемен-
элементарном объеме dV = 2rrpdpd^ находится N dV диполей (N —
число диполей в единице объема). Для возможности аппрокси-
аппроксимации сумм интегралами и применимости метода зон Френеля
предположим, что число N dV еще достаточно велико. На это
число надо умножить выражение F8.1), проинтегрировать по
центральной зоне и результат разделить на два. Из соотноше-
соотношения р2 = г2 — (х — ?J при постоянном ? получаем pdp = rdr
и вводим в качестве переменной интегрирования расстояние г.
В пределах центральной зоны величину р®± можно считать по-
15*

452 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
стоянной и равной ро. Тогда интегрирование сведется к
х - g + л/2
Г p-ikor j _ _ 2 •
а после введения коэффициента перед интегралом получится
rfEi = -г - 2nkoNpo d^ el(ut^k®x).
Интегрированием по остальным зонам убеждаемся, что из-за
убывания ро^ их действия медленно убывают с возрастанием
номера зоны п и при п —> оо стремятся к нулю. Это может слу-
служить обоснованием применимости метода зон Френеля к рас-
рассматриваемому случаю.
Добавив dE\ к падающей волне, найдем полное поле в точ-
точке А:
Е = (Ео - г
где введено обозначение
йФ = 2nkfpo <%.
Таким образом, наличие слоя вносит дополнительное отставание
по фазе б?Ф. Если толщина слоя I конечна, то отставание по фазе
будет равно
Ф =
В этой формуле содержится принципиальное объяснение замед™
ления фазовой скорости световой волны при ее распространении
в веществе.
Для завершения расчета надо было бы найти связь между
амплитудами ро и Eq. В общем случае это весьма сложная за-
задача, так как дипольный момент атома р определяется не сред-
средним макроскопическим полем Е, а микроскопическим полем,
действующим на атомы среды. Только для не очень плотных
газов (когда п - 1 <С1) оба поля практически совпадают. То-
Тогда ро = /3Eq, где Р — поляризуемость атома, связанная с ди-
диэлектрической проницаемостью е и показателем преломления п
соотношением
е = п2 = 1 + 4тгЖ/5 = 1 + 4жМро/Ео.
Используя это соотношение, из F8.2) найдем
Ф коЫ(п1)ко1,
что совпадает с результатом феноменологического рассмотре-
рассмотрения.

§ 68 РАСПРОСТРАНЕНИЕ СВЕТА В МОЛЕКУЛЯРНОЙ ОПТИКЕ 453
3. В феноменологической теории показатель преломления
вводится с помощью макроскопических уравнений Максвелла.
Последние предполагают, что в каждом элементарном объеме,
линейные размеры которого малы по сравнению с длиной вол™
ны, содержится еще очень много атомов. Молекулярное рас-
рассмотрение, приведенное выше, показывает, что это условие не
обязательно. Показатель преломления можно определить через
сдвиг фазы, который вносит вещество, стоящее на пути световой
волны. Такой сдвиг был вычислен выше в предположении, что
велико число атомов во всяком элементе объема порядка dV =
= 2npdpd^. А этому условию молено удовлетворить для сколь
угодно разреженной среды, если только точку наблюдения А
отодвинуть от слоя d^ достаточно далеко. Так, можно говорить
о показателе преломления рентгеновских лучей, хотя макроско-
макроскопические уравнения Максвелла на них не распространяются. Не
лишено смысла говорить о показателе преломления межпла-
четного и межзвездного пространства, хотя плотность веще™
ства в нем и ничтожна (не превышает примерно одного атома в
кубическом сантиметре).
4. Если бы точку наблюдения А поместить перед слоем, то
наше вычисление привело бы к волне, распространяющейся в
противоположном направлении, т.е. к отраженной волне. Если
средние межатомные расстояния меньше длины волны и ато-
атомы распределены в пространстве равномерно, то не возникнет
никаких волн помимо прошедшей прямо и отраженной.
Не так будет, когда межатомные расстояния больше длины
волны. Если атомы в среде распределены регулярно, например
находятся в узлах кристаллической решетки, то вторичные вол™
ны, излучаемые атомами, когерентны, и будут складываться
напряженности волновых полей. Условия интерференционного
усиления вторичных волн могут выполняться не только в на-
направлениях падающего и отраженного света, но и для некоторых
других направлений. Возникнет дискретный ряд плоских волн,
распространяющихся в различных направлениях (интерферен-
(интерференционное рассеяние). Такой случай реализуется при дифракции
коротких рентгеновских волн на кристаллической решетке. Ес-
Если же атомы среды распределены в пространстве хаотически,
то вторичные волны при рассмотрении бокового рассеяния ве-
ведут себя как некогерентные: складываются их интенсивности.
5. До сих пор не учитывалось тепловое движение атомов.
Объясним теперь, как при наличии такового в среде может рас-
распространяться регулярная волна и как может возникнуть пра-
правильное отражение от зеркальных поверхностей твердых и жид™
ких тел.
Рассмотрим сначала газы. Между столкновениями атомы га-
газа движутся прямолинейно и равномерно. Из™за эффекта До™

454 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
плера атомы, движущиеся с различными скоростями, излучают
свет с различивши частотами. Казалось бы, что никакой интер-
интерференции при таких условиях возникнуть не может. На самом
деле изменение частоты не имеет места, когда речь идет о вто-
ричнв1х волнах, идущих в направлении распространения света.
Действительно, пусть в газе распространяется плоская монохро-
матическая волна с частотой ш. Речь идет о частоте в системе
отсчета S, в которой газ покоится. Рассмотрим какой-либо дви-
движущийся атом. Перейдем в систему отсчета 5", в которой атом
неподвижен. В системе Sf частота распространяющейся плоской
волны изменится и будет равна, скажем, о/. С той же частотой в
системе Sf возбудятся колебания атома и будут излучаться вто-
ричные сферические волны. При обратном переходе в систему
S частота а/ излучаемой сферической волны изменится и бу-
будет зависеть от направления излучения. Только для излучения,
идущего в направлении первичной волны, получится прежняя
частота а;, независимо от того, с какой скоростью и в каком на-
направлении двигался атом.
Таким образом, в направлении распространения первичной
волны все атомы будут излучать волны с одной и той же ча-
частотой ш. С этим и связана возможность регулярного распро-
распространения света в газах. Во всех других направлениях движу™
щиеся атомы будут посылать волны с различными частотами.
Например, если атом движется в направлении света, то в обрат-
обратном направлении он будет излучать волны с меньшей частотой.
Если же он движется навстречу свету, то частота излучаемой
волны в направлении его движения увеличится.
В твердых и жидких телах тепловое движение носит иной ха-
характер. В этих случаях атомы движутся ускоренно¦, и рассужде-
рассуждение с переходом к движущейся системе отсчета здесь непримени-
неприменимо. Атомы совершают колебания около положений равновесия
и тем самым модулируют поле световой волны. В результате не
только сохраняются вторичные волны с прежней частотой, но
возникают и волны с новыми частотами. К излучениям с преж-
прежними частотами применимо все сказанное выше. С ними свя-
связана возможность регулярного распространения световых волн
в твердых и жидких средах, а также правильного отражения и
преломления их на зеркальных поверхностях тел. Излучения же
с изменившимися частотами приводят к появлению в рассеян-
рассеянном свете новых частот.
6. Закончим этот параграф замечанием, которое понадобит-
понадобится нам при выводе формул Френеля с атомистической точки
зрения. Если среда однородна и неограниченна, то в ней могут
распространяться дипольные колебания в виде бегущей волны
р = Рое^~кг), F8.3)

69
ВЫВОД ФОРМУЛ ФРЕНЕЛЯ В МОЛЕКУЛЯРНОЙ ОПТИКЕ
455
где р — диподьный момент атома с радиусом-вектором г. Каж-
дый диполь, излучая, теряет энергию. Но эта убыль энергии
восполняется за счет энергии, приходящей от других диполей.
Излучение других диполей создает в месте нахождения рассма-
рассматриваемого диполя электрическое поле, которое поддерживает
установившиеся гармонические колебания этого диполя. Таким
образом, вся среда ведет себя как замкнутая система^ совер-
совершающая свободные, а не вынужденные колебания без каких бы
то ни было внешних воздействий. Если длина волны велика по
сравнению с межатомными расстояниями, то среду можно счи-
считать сплошной и характеризовать ее состояние вектором поля™
ризации
Р = ЛГр = Рое*И-кг), F8.4)
где N — число атомов в единице объема.
§ 69. Вывод формул Френелм в молекулярной оптике
1. Допустим, что однородная изотропная среда граничит с
вакуумом вдоль плоскости. Падающая на нее плоская электро-
электромагнитная волна возбудит в среде диполъную волну F8.3), кото-
которую при усреднении по физически бесконечно малым объемам
можно рассматривать как волну поляризации F8.4). Направле-
Направления распространения этой и отраженной волн найдутся из усло-
условия равенства фазовых скоростей всех волн параллельно грани-
границе раздела. Это приводит к равен-
равенству тангенциальных слагающих
волновых векторов kg, kg и к па-
падающей, отраженной и прошедшей
волн. Кроме того, должны выпол-
няться соотношения
)
= fcg2 =
О
Р
= (ujI'с) , так как волна падает на
среду из вакуума.
Пусть теперь электрический
вектор падающей волны лежит в
плоскости падения (рис. 251). Ес-
Если волна падает под углом Брюсте-
ра, то преломленный луч ОС бу-
будет перпендикулярен к направле-
направлению отраженного луча ОВ. Ввиду поперечности световых волн
электрический вектор в среде перпендикулярен к преломленно-
преломленному лучу ОС. Возбуждаемые им дипольные моменты атомов бу-
будут также перпендикулярны к 0G, а следовательно, параллель-
параллельны ОВ. Но вдоль колебаний дипольного момента диполь Герца
не излучает. Значит, в направлении ОВ атомы среды не излу-
Рис. 251

456
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
чают и отраженная волна возникнуть не может. Так просто
объясняется закон Брюстера. (См. также задачу 4 к следующе-
следующему параграфу.)
2. При выводе формул Френеля для отраженного света сре-
среду можно считать сплошной, так как межатомные расстояния
пренебрежимо малы по сравнению с расстояниями от границы
среды до точки наблюдения, где определяется поле отраженной
волны. При такой идеализации излучающими центрами будут
не отдельные атомы, а элемен-
элементы объема среды, малые по
сравнению с Л3, но содержащие
еще очень много атомов.
Выберем координатные оси
так же, как это было сдела-
сделано на рис. 238. Разобьем сре-
среду на плоскопараллельные слои
I, II, III, ... одинаковой тол-
толщины, называемые в дальней-
дальнейшем зонами, по аналогии с
кольцевыми зонами Френеля
(рис. 252). Каждая плоскопа-
плоскопараллельная зона будет излучать в верхнее полупространство
плоскую волну с волновым вектором kg.
Толщину зоны L1 подберем так, чтобы каждая последующая
волна запаздывала по фазе на тг относительно предыдущей вол™
ны. В момент t = 0 фаза дипольных колебаний в точке О рав-
равна нулю, в точку О1 дипольные колебания приходят с фазой
(^kzLf). Волна же, излученная в О1, приходит в О с дополни-
дополнительным запаздыванием по фазе на k®zL'. Результирующее за-
запаздывание по фазе (kz + koz)Lf по условию должно быть равно
тг, откуда и находится требуемое значение L1 = ж/{kz + k®z).
Теперь ясно, что электрическое поле Е^ отраженной волны
представится знакопеременным рядом
Рис. 252
— Ех — Е2 -Ь Е3 — • • • •)
F9.1)
члены которого представляют поля излучения соответствующих
зон. При строгой однородности волны поляризации F8.4) чле-
члены ряда F9.1) одинаковы по абсолютной величине. Частичные
суммы ряда колеблются между нулем и Е]_, а сумма самого ряда
не имеет определенного значения.
В действительности реальная волна поляризации не однород-
однородна. Она имеет передовой фронт, перед которым волнового воз-
возмущения нет. На самом деле ряд F9.1) содержит конечное число
членов, а потому сходится. Для нахождения его суммы мыслен-
мысленно удалим первую зону вместе с излучаемым ею полем и сдвинем

§ 69 ВЫВОД ФОРМУЛ ФРЕНЕЛЯ В МОЛЕКУЛЯРНОЙ ОПТИКЕ 457
оставшуюся среду вверх на расстояние V'. Изменим далее фазы
всех диполей среды на одну и ту же величину и притом такую,
чтобы диполи, оказавшиеся после смещения на границе раздела,
получили те же фазы, какие имели бы в тот же момент времени
удаленные с этой границы диполи первой зоны. Ввиду медлен-
медленности изменения членов ряда F9.1) и тождественности зон, поле
излучения среды в верхнем полупространстве в результате этих
операций практически останется без изменения. Но теперь оно
может быть представлено рядом
Е(г) = Е2 ~~ Е3 + Е4 - ... F9.2)
Складывая его с предыдущим, найдем
EW = iEi. F9.3)
Таким образом, напряженность поля излучения среды в
верхнем полупространстве равна половине напряженности по-
ля, излучаемого в то же полупространство первой зоной. Мы
пришли к тому же конечному результату, что и в теории коль-
кольцевых зон Френеля (см. § 39). Однако здесь наши результаты
более убедительны, поскольку соотношение F9.2) для плоских
зон лучше обосновано, чем аналогичное соотношение для коль-
кольцевых зон Френеля.
8. Прежде чем идти дальше, необходимо сделать следую-
следующее замечание. Отраженная волна, излучаемая сплошной сре-
средой с непрерывно распределенным вектором поляризации F8.4),
в верхнем полупространстве будет всюду плоской и однородной.
В случае реальной среды, построенной из дискретных атомов,
на плавно меняющееся поле волны вблизи границы среды накла-
дывается «молекулярная рябь», т.е. дополнительное поле, резко
меняющееся на расстояниях порядка межатомных расстояний.
Это поле может быть представлено в виде суперпозиции волн,
быстро затухающих при удалении от границы среды. Простран-
Пространственный период вдоль оси X таких неоднородных или поверх™
ностных волн порядка расстояния а между атомами. Соответ-
Соответствующая составляющая волнового вектора будет порядка Кх «
~ 2жjа. А так как длина самого вектора К должна быть равна
и)/с, то для его z-составляющей получится Kz = у/(ш/сJ — К^ «
~ г • 2жIа. Отсюда видно, что при удалении от границы раздела
на расстояние а поле неоднородных волн убывает приблизитель-
но в е2ж ^ 500 раз.
Выше указывалось, что замена дискретных излучающих цен-
центров (атомов) непрерывно распределенными источниками го-
годится при вычислении поля излучения в верхнем полупростран-
полупространстве на таких расстояниях от границы, которые очень велики по
сравнению с а. Приведенная оценка показывает, что это ограни-

458
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
ГЛ. V
чение в действительности должно быть сильно ослаблено. Поле
излучения реальной среды не отличается от соответствующего
поля ее идеализированной сплошной модели уже на расстояниях
от границы порядка а.
4. Дальше при выводе формул Френеля можно было бы пой-
пойти двумя путями. Молено было бы рассчитать поле излучения
диполей среды в занимаемом ею полупространстве. Это сложно.
Мы обойдем вычисления, использовав замечание в конце преды-
предыдущего параграфа.
Представим падающую волну как результат излучения
некоторой среды. Вообразим, что верхнее полупространство на
рис. 252 заполнено такой же средой, что и нижнее, а во всем
бесконечном пространстве распространяется однородная волна
поляризации F8.4) Воображаемая среда оказывает влияние на
среду в нижнем полупространстве посредством своего поля из-
излучения. А так как в нижнем
полупространстве ничего не из™
менилось, то поле, излучаемое
воображаемой средой в нижнее
полупространство, тождествен-
тождественно с полем падающей волны.
Разобьем воображаемую
среду на плоскопараллель-
плоскопараллельные зоны I', IF, III', толщина
каждой из которых равна
L = n/(kz - kOz) (рис. 253).
Рассуждая, как и раньше,
Рис. 253 легко показать, что напря-
напряженность поля, излучаемого
воображаемой средой в нижнее полупространство, равна по-
половине напряженности поля излучения зоны /;. Вычисление
отношения амплитуд отраженной и падающей волн R и ?
свелось, таким образом, к сравнению полей излучения зон / и
/; на границе раздела z = 0.
Если вектор Р перпендикулярен к плоскости падения, то от™
ношение амплитуд R и ? будет просто равно отношению толщин
зон / и /;, взятому со знаком минус, поскольку фазы волн, из™
лучаемых этими зонами, на границе раздела противоположны.
Это дает первую формулу Френеля:
X
R±
' L
kz — koz
sin
— ф)
_ F9 4)
kz + kOz sin {ер + ф)' V • /
Если же вектор Р параллелен плоскости падения, то необхо-
необходимо еще учесть зависимость поля излучения диполя от угла
между дипольным моментом и направлением излучения. Из™
лучение дает только поперечная слагающая дипольного момен-

§ 70 ОТСТУПЛЕНИЯ ОТ ФОРМУЛ ФРЕНЕЛЯ 459
та. Поэтому величину —V'/'L необходимо умножить на отноше™
ние проекций вектора Р на направления единичных векторов
е'ие, перпендикулярных к направлениям распространения от™
раженной и падающей волн. С учетом поперечности прелом-
преломленной волны (кР = 0) для этого отношения нетрудно найти
— cos ((р + ф)/ cos (ip — ф) (см. рисунки 252 и 253), а для отноше™
ния самих амплитуд Дц и ?ц
Щ_ _ R± cos (if + ф) _ tg (ip-ф) /gg 5x
?\\ ^± cos ((f -ф) tgfa + tp)'
Это — вторая формула Френеля.
Таким же путем может быть разобран случай обратного па™
дения, когда волна падает из среды на ее границу с вакуумом,
а также общий случай отражения на границе раздела двух ма-
материальных сред.
§ 70. Отступления от формул Френелм
1. Отражение и преломление света на чистой границе разде-
раздела двух прозрачных изотропных сред хорошо описывается фор-
формулами Френеля. Небольшие отступления от них заметны лишь
при отражении под углом Брюстера и вблизи него. С особой от™
четливостью они проявляются в существовании следующих двух
явлений:
а) при отражении света, поляризованного в плоскости па™
дения, закон Брюстера соблюдается не строго; коэффициент
отражения не обращается в нуль ни для какого угла падения,
хотя при угле Брюстера он и очень мал;
б) свет, линейно поляризованный под углом к плоскости па-
падения, при отражении в малой окрестности угла Брюстера ста™
новится поляризованным эллиптически, тогда как при строгой
справедливости формул Френеля он должен был бы оставать™
ся поляризованным линейно во всех случаях, за исключением
случаев полного отражения.
Эти два отступления не независимы, а взаимно обусловливав
ют друг друга. Действительно, при точной справедливости фор-
формул Френеля
R± _ sin (у? - Ф) Щ _ Ч((р-ф) /~,q jx
отношение R±/?± сохраняло бы знак при всех углах падения,
тогда как знак отношения -йц/?ц менялся бы при переходе через
угол Брюстера. Это значит, что во втором случае при переходе
через угол Брюстера фаза отражающейся волны скачкообразно
менялась бы на тт. Никакого нарушения непрерывности Дм, как

460 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
функции угла падения (/?, при этом не произошло бы, так как,
согласно второй формуле G0.1), эта функция при (р = (рв обра-
обращается в нуль. Однако функция R\\(ip) сделалась бы разрывной
при ср = срв, если бы, как это действительно имеет место, она
при этом угле не была равна нулю. Для такого разрыва нет фи-
физических оснований. Поэтому следует заключить, что изменение
фазы, претерпеваемое Дц(<р), происходит не скачкообразно при
угле (р = фв, а в какой-то малой окрестности вокруг угла Брю-
стера. В пределах этой окрестности фаза меняется непрерывно
от 0 до тг. В той же окрестности возникает сдвиг фаз между со-
составляющими Ец и Ej_, а потому отраженный свет будет поля-
поляризован эллиптически, если только падающий был поляризован
линейно. Это показывает, что второе отступление является
следствием первого.
Обратное также справедливо: первое отступление вытека-
вытекает из второго^ если только среды не вращают плоскость по-
поляризации. Это непосредственно очевидно, если заметить, что
при соблюдении указанного условия волны Ец и Е^ сохраня-
сохраняют характер своей поляризации и в соответствии с принципом
суперпозиции распространяются независимо друг от друга.
2. Такие отступления от формул Френеля можно объяснить
наличием на поверхности отражающей среды тонкого переход-
переходного слоя^ оптические свойства которого отличны от оптических
свойств самой среды. В правильности такого объяснения не при-
приходится сомневаться, по крайней мере когда среда свободна от
внутренних напряжений. Но на вопрос, как эти слои возникают
и каковы их свойства, еще нельзя ответить с полной определен-
определенностью.
Простейшим является случай, когда на поверхности отра-
отражающей среды существует тонкая пленка постороннего веще-
вещества, нанесенная искусственно или возникшая в результате обра-
обработки и загрязнения поверхности. Когда толщина пленки велика
по сравнению с межатомными расстояниями, ее молено харак-
характеризовать макроскопическими величинами — толщиной I и по-
показателем преломления п. Пленки с толщиной порядка А искус-
искусственно наносятся на отражающие поверхности для увеличения
их поверхностной прозрачности, а также для изготовления ин-
интерференционных светофильтров. Если пленка однородна, т.е.
величина п одинакова по всей толщине ее, то отражение и пре-
преломление света описывается формулами F7.9).
Нас, однако, сейчас интересуют тонкие пленки^ толщина ко-
которых мала по сравнению с А. В этом случае формулы F7.9)
можно упростить, разложив их по степеням //Аи сохранив толь-
только члены первой степени. Для таких пленок вычисление можно
обобщить, не вводя предположения об однородности пленки, а

§ 70 ОТСТУПЛЕНИЯ ОТ ФОРМУЛ ФРЕНЕЛЯ 461
предполагая, что при переходе через пленку показатель прелом-
преломления меняется непрерывно. Так поступили Друде A863-1906) и
многие другие авторы. Однако оценка толщин переходных слоев
на поверхностях чистых жидкостей и свежих сколов кристаллов
показала, что эти толщины того же порядка, что и атомные
размеры или межатомные расстояния. Применять внутри таких
слоев макроскопические уравнения Максвелла и характеризо-
характеризовать их показателем преломления не корректно. Мы получим
нужные результаты методами молекулярной оптики, изложен-
изложенными в предыдущем параграфе.
3. Допустим сначала, что никакого переходного слоя на отражающей
поверхности нет. Как выяснено в предыдущем параграфе, для определения
поля отраженной волны достаточно рассмотреть излучение первой зоны
I (см. рис. 252). Разобьем эту зону на бесконечно тонкие слои толщины
d? (рис. 254). Вектор поляризации в точке О определяется выражением
Рое1^ ~ z^ . На единицу площади слоя dC, приходится дипольный момент
Ро d( ei(a!t^fczC). Колебания из О' приходят в
О с запаздыванием по фазе на kozC- При вы-
вычислениях слой dC, можно мысленно перене- q
сти на границу среды, введя соответствую- X
щий сдвиг фаз. Дипольный момент, прихо™
дящийся на единицу площади так мысленно
передвинутого слоя, будет
,^
Проинтегрируем это выражение по тол™
щине первой зоны I и результат разделим Р с 254
на два. Тогда найдем, что отраженная волна
может быть моделирована полем излучения
«эквивалентной плоскости», расположенной на границе среды, на которой
совершаются дипольные колебания с поверхностной плотностью амплиту-
ды
V
А (г) _^0 f ^i(kOz+kz)C j> _ • Р0 r-i(kOz+kz)L' -,-.
~" ~™2~" J ~~ 2(к + к )
О
или, с учетом соотношения (koz + ^2)Ь; = тг,
А^г) = -« ° G0.2а)
Рассуждая так же применительно к зоне 1; (см. рис. 253), найдем, что
падающая волна может быть моделирована полем излучения другой «экви-
«эквивалентной плоскости», расположенной также на границе среды. На единицу
площади такой плоскости приходится дипольный момент с амплитудой
Аоб) = ^ Р% • G0.26)
4. Учтем теперь наличие переходного слоя. Так как толщина слоя пред-
предполагается малой по сравнению с А, его можно моделировать математиче-

462 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
ской плоскостью. Обозначим через т = тоеъ^шЬ~к°хХ^ дополнительный ди-
польный момент, вносимый переходным слоем на единицу его площади. Хо-
Хотя т — величина макроскопическая, ею допустимо пользоваться для сколь
угодно тонких переходных слоев (в том числе и мономолекулярных). Это
связано с тем, что введение т предполагает усреднение не по малым объ-
емам среды, а по малым площадкам отражающей поверхности. Последние
же можно выбрать малыми по сравнению с длиной волны, но еще большими
по сравнению с межатомными расстояниями.
Величину то надо добавить к амплитуде Ад , чтобы моделировать поле
отраженной волны с учетом излучения переходного слоя. Для моделирова-
моделирования падающей волны ту же величину т® надо добавить к амплитуде Ад ,
но с противоположным знаком. Действительно, после такого добавления
волна, проникающая извне внутрь среды и воздействующая на нее, будет
моделирована излучением двух плоскостей, расположенных на границе сре-
среды: плоскости с амплитудой дипольных колебаний (Ад — то) и плоскости с
амплитудой таких же колебаний то- Амплитуды то и ™то компенсируются.
Остается только одна амплитуда Ао , как если бы переходный слой не
оказывал никакого влияния на среду вдали от ее границы. Но это как раз
и необходимо, чтобы поляризация среды вне переходного слоя представля-
представлялась однородной волной F8.4).
Таким образом, вместо G0.2а) и G0.26) получаются выражения
А^ = -г-^— + то, A^=i-^—-T0, G0.3)
которыми и надо пользоваться при вычислении поля падающей и отражен-
отраженной волн. При этом, разумеется, надо учесть, что для излучения существен-
существенны не сами амплитуды G0.3), а только их составляющие, перпендикулярные
к направлению излучения. Коэффициенты Френеля R±/?± и R\\/?\\ найдут-
найдутся как отношения таких составляющих. Ограничиваясь линейными членами
по ко, в результате простых, но несколько длинных вычислений получим
R± sin ((f-ф)
—^ = у- l-i(i + 2ikojx cos <z?), G0.4)
с± sin ((f + ф)
R\\ tg(<p-ip) f jxcos2 ф-jzsin2 ip\
1 + 2ikocos(p - —^ '— -I. G0.5)
t\\ tg (if + tfj) \ COS2 ф — Sin (f
Здесь введены обозначения:
TQX _ Toy TQz /7Пм
7ж = ^ = ^, ъ = —. G0.6)
¦M)cc JOj/ -* Oz
Параметры 7Ж и 7^ имеют размерность длины. В изложенной теории
ими и характеризуются свойства переходного слоя. Теория справедлива при
выполнении условий
Квадратичные члены (jx/X) и (jz/X) в ней отброшены. В этом при-
приближении все коэффициенты при малых величинах jx/X и jz/X не зависят
от А. Это значит, что вычисление параметров jx и jz есть чисто электро-
электростатическая задача. Для фактического вычисления самих параметров в
молекулярной теории необходимо знать молекулярную структуру среды и
переходного слоя.

70
ОТСТУПЛЕНИЯ ОТ ФОРМУЛ ФРЕНЕЛЯ
463
5. Состояние поляризации отраженного света полностью характеризую
ется комплексным отношением R\\/R±. Если 8± = 8\\, то
lko{
| =
#_i_ cos (ip — ip)
При угле Брюстера это отношение чисто мнимое, т.е. отраженный свет
поляризован эллиптически. Одна из главных осей эллипса колебаний пер™
пендикулярна к плоскости падения, а другая лежит в этой плоскости. Отно-
Отношение этих осей называется коэффициентом эллиптичности света, отра-
отраженного под углом Брюстера. Он может быть и положительным, и отрица-
отрицательным, так как разность фаз S между составляющими R\\ и R± при угле
Брюстера принято считать равной +тг/2. При таком соглашении R\\/R±_ =
= регж^2 = ip. Для р из формулы G0.7) нетрудно получить
G0.8)
где А означает длину волны в вакууме. Положительному коэффициенту
эллиптичности соответствует левая эллиптическая поляризация отражен-
отраженного света, отрицательному — правая (предполагается, что падающий свет
линейно поляризован под углом 45° к плоскости падения, т.е. 8\\ = 8±). Эл-
Эллиптическая поляризация называется правой, если для глаза, смотрящего
против распространения света, движение по эллипсу совершается по часо-
часовой стрелке. В противоположном случае она называется левой.
Для всех исследованных жидкостей с чистой отражающей поверхно-
поверхностью коэффициент р положителен. Для обыкновенной воды он отрицате-
отрицателен. Однако, как показал Рэлей, при очищении поверхности воды величи-
величина р меняет знак, обращаясь в нуль при некоторой промежуточной степе-
степени очищения. Для предельно чистой поверхности воды Рэлей нашел р =
= +0,00042. В табл. 6 приведены значения р для различных жидкостей
(при А = 546 нм).
Таблицаб
Вещество
Вода
Метиловый спирт
Этиловый спирт
Четыреххлористый углерод
Бензол
Толуол
Ортоксилол
/}-105
42
46
92
107
135
144
137
п
1,33
1,33
1,33
1,46
1,51
1,50
1,51
чин/ А
0,00057
0,00062
0,00124
0,00103
0,00117
0,00101
0,00119
В последнем столбце табл. 6 приведены значения минимальной толщи-
толщины 1Мин переходного слоя, которые по теории Друде достаточны для получе-
получения наблюдаемой эллиптичности отраженного света (см. задачу 3 к этому
параграфу). Хотя эта теория и макроскопическая, приведенная оценка да-
дает правильный порядок величины 1Ш1Ш. Из нее видно, что переходные слои
порядка одного или нескольких межатомных расстояний уже достаточны,
чтобы вызвать наблюдаемые отступления от формул Френеля. Это с несо-
несомненностью указывает на то, что, наряду с переходными слоями, вызванны-
вызванными загрязнением, обработкой, абсорбцией газов и пр., существуют и пере-

464 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА ГЛ. V
ходные слои, обусловленные молекулярной структурой самой отражающей
среды вблизи ее поверхности.
Трудно указать причины возникновения таких переходных слоев. Вот
некоторые из возможных причин. 1. Электрическое поле световой волны,
действующее на приграничные молекулы среды, может отличаться от дей-
действующего поля для остальных молекул. 2. Анизотропные молекулы, если
среда построена из таковых, могут ориентироваться вблизи поверхности в
некоторых преимущественных направлениях. 3. Плотность среды в тонком
приграничном слое может отличаться от плотности остальной среды.
ЗАДАЧИ
1. Считая переходный слой сплошным, вычислить для него параметры
Решение. Задача сводится к нахождению вектора поляризации
~P(z) среды и переходного слоя в однородном электрическом поле Е. Среду
будем характеризовать диэлектрическими проницаемостями ех (z) и ez (z) в
направлениях параллельно и перпендикулярно к слою. Координатные оси
можно выбрать так, чтобы Еу = Dy = 0. В силу симметрии векторы Е и
D не могут зависеть от х и у. Поэтому уравнения rot Е = 0 и dlvD = 0
переходят в
dEx _ d?z_
dz dz
Отсюда следует, что во всем пространстве Ех и Dz постоянны, т.е. не зави-
зависят от z. Вектор поляризации в переходном слое будет
4тг 4тг 4
Чтобы выделить дополнительную поляризацию АР переходного слоя,
вычтем отсюда вектор поляризации самой однородной среды:
4тг гтг
где е — диэлектрическая проницаемость этой среды. Для нахождения tqx и
Toz полученные выражения надо проинтегрировать по толщине I переход-
переходного слоя. Выполнив это и введя обозначения
I I
Р= I ex(z)dz, q= I —^т,
?z \Z I
О О
найдем
1х = ^=^j, ъ = l-^j- G0-9)
Если подставить эти значения в G0.4) и G0.5), то получатся формулы Друде.
2. Считая переходный слой макроскопическим и однородным, получить
выражение для коэффициента эллиптичности при угле Брюстера.
Ответ.
^^^ " " G0.10)
где п' — показатель преломления переходного слоя.

§ 70 ОТСТУПЛЕНИЯ ОТ ФОРМУЛ ФРЕНЕЛЯ 465
3. Считая эллиптичность р положительной, найти значение п', чтобы
при заданных п и I величина р получилась максимальной. Найти минималь-
минимальное значение для I, чтобы при заданном п получилось заданное значение р.
Ответ.
?±Ц G0.11)
4. Изотропная среда построена из анизотропных молекул. Ее макро-
макроскопическая изотропия обусловлена беспорядочными изменениями направ-
направлений молекул в результате теплового движения. Дипольный момент ани-
анизотропной молекулы, возбуждаемый полем световой волны, вообще говоря,
не совпадает по направлению с электрическим полем. Пусть электрический
вектор падающей волны лежит в плоскости падения, а сама волна падает
под углом Брюстера. Электрический вектор в среде хотя и перпендикуля-
перпендикулярен к преломленному лучу, но дипольные моменты молекул, вообще говоря,
имеют составляющие вдоль луча. Такие молекулы, очевидно, будут излу-
излучать в направлении отраженного луча. Будет ли в этом случае выполняться
закон Брюстера? (См. § 69, п. 1.)
Решение. Закон Брюстера останется справедливым. Для макро-
макроскопически изотропной среды составляющие дипольных моментов молекул,
параллельные преломленному лучу, меняются хаотически во времени. В си-
силу этого излучения отдельных молекул в направлении отраженного луча
некогерентны. Они не могут привести к правильному отражению, а только
к диффузному рассеянию света. Но если в тонком поверхностном слое ани-
анизотропные молекулы преимущественно ориентированы в некотором направ-
направлении, то излучения таких молекул становятся частично когерентными, и
появляется отраженный свет (см. § 69).

ГЛАВА VI
ОПТИКА МЕТАЛЛОВ
§ 71. Уравнения Максвелла и волны в металлах
1. Как и в диэлектриках, распространение электромагнит-
электромагнитных волн в металлах описывается уравнениями Максвелла:
rotH = - D + —j,
с с
, (пл)
div D = 4тгр,
dlvB = 0.
По сравнению с диэлектриками добавляется член с током про™
водимости j. В статических и низкочастотных полях ток обу-
обусловлен движением практически одних только свободных элек-
электронов. Движение связанных электронов, а тем более атомных
ядер в этой области спектра не играет никакой роли. Но уже в
инфракрасной области, где лежат собственные частоты колеба-
колебаний атомных ядер, движения последних начинают существенно
влиять на оптическое поведение металлов (резонанс). В даль-
дальнейшем, в видимой и ультрафиолетовой областях спектра, в ко™
лебания вовлекаются и связанные электроны.
Смещения связанных зарядов вызывают поляризацию ме-
металлов , аналогичную поляризации диэлектриков. Появляется
ток поляризации. Однако в высокочастотных полях нет суще-
существенной разницы между движениями свободных и связанных
частиц. Нерационально связывать ток проводимости с движе-
движением только свободных, а ток поляризации — только связанных
электронов. Этим понятиям надо дать точные определения, в
соответствии с тем, как они используются в теории.
Молено поступить следующим образом. Вынужденное коле-
колебание заряженной частицы (электрона или атомного ядра) в по™

§ 71 УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНВ1 В МЕТАЛЛАХ 467
ле световой волны молено разложить на колебание, происходя-
происходящее в фазе (или противофазе) с электрическим полем, и коле-
колебание, сдвинутое относительно него по фазе на 90°. Ток, обу-
обусловленный первыми колебаниями, условимся называть током
проводимости и обозначать его плотность через j. Токи прово-
проводимости вызывают поглощение электромагнитных волн. Токи
же, обусловленные колебаниями, сдвинутыми по фазе на 90°,
назовем токами поляризации. С ними не связано поглощение
волн. Плотность тока поляризации можно представить в виде
jirnn = Р? где Р — вектор поляризации. На последнее соотноше-
соотношение можно смотреть как на определение вектора Р. Тем самым в
металлах раскрывается и точный смысл вектора индукции D =
= Е + 4тгР, который входит в уравнения G1.1).
Магнитные свойства вещества, не играющие существенной
роли в оптической области спектра, мы учитывать не будем.
Металлы будем считать оптически изотропными^ хотя все ме-
металлы (за исключением, конечно, жидких) и имеют кристалли-
кристаллическую структуру. Однако кристаллы кубической системы оп-
оптически изотропны. Другие металлы, как правило, макроскопи-
макроскопически изотропны, так как они состоят из множества хаотиче-
хаотически ориентированных кристалликов, размеры которых малы по
сравнению с длиной волны. Для изотропных металлов матери-
материальные уравнения имеют вид
D = е'Е, G1.2)
j = <тЕ. G1.3)
Величина а называется электрической проводимостью, а
е1 — диэлектрической проницаемостью металла. (Мы пользу-
пользуемся обозначением е;, сохраняя е для обозначения комплексной
величины, вводимой ниже.) Обе величины е1 и а являются функ-
функциями частоты ш. Поэтому в уравнениях G1.2) и G1.3) поле Е
должно предполагаться монохроматическим. Немонохроматиче-
Немонохроматические поля надо разлагать на монохроматические составляющие
и применять принцип суперпозиции.
С наличием проводимости а связано поглощение света в ме-
металлах. С точки зрения излагаемой здесь формальной теории
поглощение света есть не что иное, как превращение электро-
электромагнитной энергии в джоулево тепло.
Материальные уравнения G1.2) и G1.3) дают лишь грубое
описание оптических свойств металлов (см. § 74). В ряде вопро-
вопросов, в особенности для коротких волн (ультрафиолетовые, види-
видимые и короткие инфракрасные лучи), они приводят к выводам,
не совсем согласующимся с опытом. Более удовлетворительная
теория должна основываться на квантовой теории металлов.

468 ОПТИКА МЕТАЛЛОВ ГЛ. VI
Однако изложение такой теории далеко выходит за рамки этой
книги.
2. Для монохроматических полей D = iujD = icj^'E, так что
правая часть первого уравнения G1.1) преобразуется в - {iooe1 +
+ 4тга)Е. Если ввести величину
e'-ie", G1.4)
называемую комплексной диэлектрической проницаемостью,
то система уравнений G1.1) примет вид
rot Н = — еЕ, rot Е = -^ Н, G1.5)
с с
т.е. формально совпадет с соответствующими уравнениями для
диэлектриков. Граничные условия также имеют одинаковый
вид: они требуют непрерывности тангенциальных компонент
векторов Е и Н на границе раздела сред. Как следствие та™
ких граничных условий и уравнений G1.5), получается непре-
рывность нормальных компонент вектора еЕ (см. § 63). Поэто-
Поэтому любое соотношение оптики прозрачных сред^ полученное из
уравнений G1.5) и граничных условий с помощью линейных ве-
вещественных операций^ может быть формально перенесено в
оптику металлов и других поглощающих сред простой заменой
вещественной величины е на комплексную. Требуется только
дополнительное исследование физического содержания и смы-
смысла полученного соотношения.
Для характеристики оптических свойств металлов применя-
применяется также комплексный показатель преломления и. Он опре-
определяется соотношением
u2 = s = e'-ie". G1.6)
Полагая
v = п — гх, G1.7)
где п и к вещественны и существенно положительны, получим
п2 - к2 = е\ 2пк = е". G1.8)
Величина п называется главным показателем преломления
металла. Величину к называют главным показателем зату-
затухания. Этот термин надо предпочесть обычно употребляемому
термину «показатель поглощения», так как затухание волны
моэюет происходить и без поглощения. Примером может слу-
служить плазма, когда частота ш меньше так называемой плазмен-
плазменной частоты (см. § 87). Для нее величина е вещественна, но
отрицательна^ т.е. е" = 0. В этом случае поглощения нет, но
есть затухание, так как л/е — величина чисто мнимая, а потому
ж ^0.

72
ГЕОМЕТРИЧЕСКИЕ ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ
469
Если среда однородна, то в ней могут распространяться плос-
кие монохроматические волны вида E.3). Для них должны вы-
выполняться соотношения
Е = ^— [кВ], В = Sl [kE], G1.9)
с
ше
ш
G1.10)
В поглощающей среде волновой вектор к всегда комплексный,
а соответствующая плоская волна всегда неоднородна. Это есте-
естественно, так как при наличии поглощения плоская волна не мо-
может распространяться без затухания. Положим
k = k/-ik//, G1.11)
где к; и к/; — вещественные векторы. Тогда на основании G1.10)
к'2 - к112 = ^
2(k'k") = ^
G1-12)
Вектор к; указывает направление распространения плоскостей
равных фаз. В направлении вектора к/; убывает амплитуда вол-
волны. В общем случае плоскости равных фаз и плоскости равных
амплитуд не перпендикулярны между собой. Перпендикуляр-
Перпендикулярность всегда имеет место только для непоглощающих сред, ко-
когда е11 = 0.
§ 72. Геометрические законы отражения и
преломления света на границе металла
1. Пусть из вакуума на плоскую границу металла падает
плоская монохроматическая однородная волна, распространяю-
распространяющаяся вдоль волнового век-
вектора ki (рис. 255). При этом
возникнет однородная отра-
отраженная волна с волновым
вектором Ц и неоднородная
волна, прошедшая в металл.
Комплексный волновой век-
вектор прошедшей волны обо-
обозначим через к (без индекса).
Как было показано ранее, из
граничных условий получа-
получаются соотношения
Плоскость равных амплитуд
Рис
Из них следует, что геомет-
рические законы отражения
света от металлов такие же, что и для непоглощающих сред.
Различие есть лишь в законах преломления.

470 ОПТИКА МЕТАЛЛОВ ГЛ. VI
Прежде всего отметим, что плоскости равных амплитуд про™
шедшей волны параллельны границе металла. Действительно,
представим комплексный вектор к в виде G1.11). Из G2.1) еле™
дует, что тангенциальная составляющая вектора к вещественна,
а потому вектор к/; перпендикулярен к поверхности металла.
Это и доказывает наше утверждение. Прошедшая волна затуха-
ет в направлении вектора к/;. Поэтому вектор к/; надо направить
вниз, т.е. в сторону металла, так как затухание волны в металле
должно идти в этом, а не в противоположном направлении. В
сторону металла должен быть направлен и вектор к;, посколь-
поскольку угол между векторами к; и к/; острый, как это следует из
второго соотношения G1.12).
Вектор к; перпендикулярен к плоскости равных фаз прошед-
прошедшей волны. Угол х, образуемый этим вектором с положитель-
положительным направлением оси /?, называется вещественным узлом пре-
преломления. Отношение
^ = п„, G2.2)
sinx
вообще говоря, зависит от угла падения ср. Оно положительно
и называется показателем преломления. Так как кх = к'х =
'x, то из соотношения G2.1) следует
fc, sin^u, G23)
По аналогии с G2.3) введем другую положительную величи-
величину х<р, определяемую соотношением
к" = |>v G2.4)
Ее называют показателем затухания. Физический смысл пока-
показателя затухания легко установить, рассмотрев выражение для
поля прошедшей волны. Таким путем не представляет труда
установить, что на глубине
* = *„ = -?-, G2.5)
где Ао — длина волны в вакууме, интенсивность света (пропор-
(пропорциональная квадрату амплитуды) убывает в е раз. Величина
h(p называется глубиной проникновения света в металл. Таким
образом, показатель затухания к^ можно определить как от-
отношение длины световой волны в вакууме к умноженной на 4тг
глубине проникновения света в металл.
Для металлов показатель затухания в видимой области спек-
спектра обычно порядка единицы. Например, для золота при нор-
нормальном падении к^ = 2,82, h^ = Ао/Dтгх^) = Aq/35,4. Отсюда
находим, что на протяжении длины волны интенсивность света
в золоте убывает в exp (Xo/h^) « 2,4 • 1015 раз.

§ 72 ГЕОМЕТРИЧЕСКИЕ ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ 471
Пленки металлов с толщиной порядка длины волны, как пра™
вило, практически непрозрачны для света. Об оптических свой-
свойствах металлов обычно судят по отраженному свету. Тем не
менее необходимо изучить законы проникновения света в ме™
талл, так как без этого нельзя понять и законы отражения. Свет,
отраженный от металла (как и от диэлектрика), возникает в ре™
зультате интерференции когерентных вторичных волн, излуча-
излучаемых электронами и атомными ядрами металла. Но вторичные
волны, очевидно, возбуждаются падающей волной, проникшей
в металл. Если бы поле в металл совсем не проникало, то отра-
отражение света было бы невозможно.
2. Выразим теперь п^ и к^ через оптические константы ме-
металла п, ж и угол падения (р. Подставляя выражения G2.3) и
G2.4) в формулы G1.12), получим
п2 ~~ ж2 = е1\ 2п(рж(р cos x = ^'• G2.6)
Сравнивая эти выражения с G1.8), находим
п2 - ж2 = п2 - ж2, п^ж^ cosх = пк. G2.7)
Кеттелер A839-1900), впервые получивший эти соотношения,
назвал их главными уравнениями распространения световых
волн в металлах и поглощающих средах. Они показывают, что
величины
а = п2^- м^, Ь = 2п(рк(рсоБх G2.8)
не зависят от угла падения <р, а только от рода металла, его
физического состояния и от длины световой волны. Величины а
и Ъ называются инвариантами Кеттелера и могут служить для
характеристики оптических свойств металлов (вместо п и к).
Если (р = 0, то х = 0, и уравнения G2.7) дают п^ = ±п,
Кф = ±х. Здесь надо взять знак плюс, так как по определению
величины Пф и к^ существенно положительны. Таким образом,
при нормальном падении показатели преломления и затухания
п^р и к^р принимают свои главные значения п и ж.
Для нахождения п^ж к^ как функций угла падения if пере™
пишем второе уравнение G2.7) в виде
п2^ cos2 х = п1"%>{1 ~ si»2 X) = ^%^% ~ ^1 si»2 Ч> = | &2-
Решая его совместно с первым уравнением, найдем
п% = \ [±^/(a-sm2ipJ + b2 + (a + sin2 9?)] ,
= [±A/(«smV) + b(a - sin2
1
tp)\ .
G2«9)
Знаки перед квадратными корнями должны быть одинаковы в
г2 -к2
д
обеих формулах, чтобы разность т? — ж2 была равна а. Кроме

472 ОПТИКА МЕТАЛЛОВ ГЛ. VI
того, П(р и к^ должны быть непрерывными функциями угла (р.
Для действительно поглощающих сред инвариант b не равен ну-
нулю, как это видно из выражения b = 2пж = е". Поэтому ква-
квадратный корень в формулах G2.9) не может обращаться в нуль
и менять знак при изменении угла (р. Но при ip = 0 величины
п2 и к2 могут быть существенно положительными тогда и толь-
только тогда, когда оба квадратных корня в G2.9) взяты со знаком
плюс. Значит, знак плюс следует брать и при любых значениях
угла (р. Таким образом, для дейсвительно поглощающих сред
п\ = i У (а - sinVJ + Ь2 + (а + sin2 ф)] ,
\ г J, G2.10)
х2 = - у (а - sin2 рJ + Ь2 - (а - sin2 Щ .
В частности, при </? = 0
п2 = I(^/a2 + 62 + a), к2 = -(л/а2 + Ь2-а). G2.11)
Zi Zi
Особые случаи в выборе знака могут иметь место только при
Ъ = 2пк = 0, т.е. либо при п = 0, к ф 0, либо при п ф 0, ж = 0.
В обоих случаях диэлектрическая проницаемость вещественна,
т.е. среда непоглощающая. Однако величины п^ и к^ сохраняют
смысл и для таких случаев. Например, теорию полного отраже-
отражения на границе прозрачных сред (см. § 66) молено представить
как частный случай теории, изложенной в этом параграфе.
§ 73. Формулы Френеля. Измерение оптических
констант металлов
1. Формулы Френеля F5.7) или F5.8) применимы и для ме-
металлов, если под тиф и cost/? понимать комплексные величины
cost/? = -у и2 — sin2 (р. G3.1)
Здесь надо взять то значение квадратного корня, которое име-
имеет отрицательную мнимую часть — только тогда неоднородная
волна, проникшая в поглощающую среду, будет затухать при
удалении от границы раздела.
При нормальном падении
G3.2)
Для отражательной способности металла получаем

§ 73 ИЗМЕРЕНИЕ ОПТИЧЕСКИХ КОНСТАНТ МЕТАЛЛОВ 473
2. При отражении от металла оба отношения R±/?± и Дц/?ц,
вообще говоря, комплексны, т.е. появляются скачки фаз. Они,
как правило, различны для составляющих Ец и Ej_. Если падаю-
падающий свет поляризован линейно под углом к плоскости паде-
ния, то отраженный свет будет поляризован эллиптически.
Исследуя эллиптическую поляризацию
отраженного света, можно определить оп-
оптические константы металла п и к. На
этом основан метод Друде, излагаемый
ни лее.
Световой луч, пройдя через поляриза-
поляризатор Р (рис. 256), поляризуется линейно.
Для простоты расчета предположим, что
азимут поляризации равен 45° (?± = ?\\). р 0_л
'' i ИС. ZOu
Обобщение на случай произвольного ази-
азимута не встречает затруднений. Отраженный луч сначала прохо-
проходит через компенсатор К^ а затем через анализатор А. Изменяя
установку компенсатора и вращая анализатор вокруг направле-
направления отраженного луча, можно погасить отраженный луч. В этом
случае после прохождения через компенсатор свет становится
поляризованным линейно. Азимут его поляризации называется
азимутом восстановленной линейной поляризации отраженно™
го света. Компенсатором К молено измерить разность фаз А
между Ец и Е^ отраженной волны, а анализатором А — азимут
/3 ее восстановленной линейной поляризации. По этим данным
можно вычислить оптические константы металла п и к.
Действительно, из формул Френеля F5.8) при ?± = ?ц полу-
получаем
Щ_ = cos (tp + ф)
R± cos (ip — ф)
Очевидно,
/ill j/\ j/O
—lL — re , r = tgp.
Отсюда
1 — гегА cos ip cos ф \/v2 — sin2 ip
1 + гегА sin Lp sin ф igtp sin (p
Далее,
v — sin (p = [n — ik) — sin cp = n — к — 2тк — sin (p.
На основании G2.7) и G2.2)
и2 — sin2 if = n2 — к2 —2in(pMlfcosx^nisin2x = (n

474 ОПТИКА МЕТАЛЛОВ ГЛ. VI
Следовательно,
v cos ф = yi/2- sin (p = n^ cos x — «>fy, G3.4)
1 — геъА n^ cos x — ^м(р
1 + гегЛ tg (f sin 99
Умножая числитель и знаменатель левой части на 1 + ге~ ,
получим
1 — г2 — 2ir sin A n<p cos x — «ж^
1 + г2 + 2r cos A tg ip sin if '
а отделяя вещественную часть от мнимой и используя соотно-
соотношение г = tg/3,
cos х = tg у sin у х
ts /3 sin A
или
, . cos 2/3
Пш COS Y = tg Ш Sill Ш A ,
^ A &Y^ ^1+sin 2^ cos A' G4 K\
sin 2/3 sin A ^^
^ 1 + sin 2/3 cos A
Из этих формул можно определить n^cosx и к^. После этого
легко вычислить инварианты Кеттелера по формулам
a = n%-rf> = n% cos2 X + sin2 if - ж2,
Ь = n^^cosx-
Наконец, с помощью формул G2.11) по инвариантам Кеттелера
мозсно вычислить главные показатели преломления и затухания
п и ж.
Для упрощения расчетов измерения можно производить при
таком угле падения </?, когда А = тг/2. Такой угол называется
главным углом падения, а соответствующий ему азимут /3 —
главным азимутом. При <р = 7р формулы G3.5) принимают вид
n^cosx = tg(^sm(^cos2/3, ж-^ = tglps'mTps'm2/3. G3.7)
Наиболее трудным моментом при экспериментальном опре-
определении п и ж является приготовление металлических поверх-
поверхностей. При обработке отражающих поверхностей на них воз™
никают переходные слои, свойства которых зависят от способа
обработки. Если толщина переходного слоя того же порядка, что
и глубина проникновения света в металл, то измерения дают оп-
оптические постоянные не цельного металла, а переходного слоя

73
ИЗМЕРЕНИЕ ОПТИЧЕСКИХ КОНСТАНТ МЕТАЛЛОВ
475
на его поверхности. В табл. 7 приведены для ориентировки зна-
чения ж и п некоторых металлов, полученные по методу Друде
(Л = 589,3 им). Отражательная способность R вычислена по
формуле G3.3).
3. Запишем формулу G3.3) в виде
_ (п2 + ж2 + 1) ~~ 2п
R =
(п2
G3.S
Как видно из табл. 7, почти для всех металлов 2п мало по срав-
сравнению с п2 + х2 + 1. Благодаря этому отражательная способность
металлов очень велика — для многих металлов она близка к еди-
единице. «Металлический блеск», присущий металлам, объясняется
их большой отражательной способностью. Так как к и п изме-
изменяются в зависимости от длины волны, некоторые металлы —
в особенности медь и золото — обладают резко выраженным
цветом. Металл кажется нам, например, красным, если он силь-
сильнее всего отражает красные лучи. Поэтому, грубо говоря, по™
верхностная окраска металла является дополнительной к цвету
лучей, проходящих через тонкие металлические пленки. Напри-
Например, очень тонкие золотые пленки в проходящем свете кажутся
зелеными.
Таблица7
Металл
Натрий
Серебро, цельное
Магний, цельный
Золото, цельное
Золото, электролитическое
Ртуть
Медь, цельная
Никель, цельный
Никель, электролитический
Никель, гальванически распыленный
^Железо, гальванически распыленное
ж
2,61
3,64
4,42
2,82
2,83
4,41
2,62
3,32
3,48
1,97
1,63
п
0,05
0,18
0,37
0,37
0,47
1,62
0,64
1,79
2,01
1,30
1,51
Д, %
97,5
95,1
93,1
84,9
81,5
75,4
73,2
62,0
62,0
43,3
32,6
Для слабо поглощающих тел отражательная способность
определяется почти исключительно главным показателем пре™
ломления п и практически не зависит от к. К таким телам отно-
относятся красящие вещества. В этом случае поверхностная окраска
тел обусловлена не избирательным отражением, а избиратель-
избирательным поглощением в слое красящего вещества. Поэтому окрас-
окраска тел кажется одинаковой в отраженном и проходящем све-
свете. Слои лаковых красок свободны от неоднородностей, кото-
которые сделали бы эти слои мутными. Сквозь слои таких красок

476 ОПТИКА МЕТАЛЛОВ ГЛ. VI
видны детали поверхности тела. Свет от источника попадает на
поверхность тела и на ней рассеивается. Таким образом, на пу-
пути к глазу он дважды проходит через поглощающий слой крас™
ки, претерпевая при этом избирательное поглощение. Свет, от™
раженный от передней поверхности лака, может дать слабый
беловатый оттенок. Если поверхность слоя лака гладкая, то та™
кой беловатый оттенок практически ограничивается областью
зеркального отражения. Клеевые краски искусственно делают-
делаются мутными путем введения в них различных неоднородностей.
Свет, падающий на слой краски, рассеивается на этих неодно™
родностях, не достигая поверхности тела. Таким образом, зна-
значительная доля света рассеивается верхними слоями краски, не
претерпевая избирательного поглощения. Благодаря этому по™
является заметный беловатый оттенок.
Различие в происхождении поверхностной окраски слабо и
сильно поглощающих сред можно иллюстрировать и следую-
следующим примером. Покроем поверхность прозрачной стеклянной
пластинки слоем фиолетовых чернил. Чернила, пока они не
засохли, являются «слабо поглощающей средой». Они кажут™
ся фиолетовыми как в отраженном, так и в проходящем свете:
окраска обусловлена избирательным поглощением света, прохо™
дящего через слой чернил и испытывающего рассеяние в нем.
Когда чернила засохнут, они превращаются в «сильно поглоща-
поглощающую среду». В проходящем свете они по™прежнему кажутся
фиолетовыми — окраска обусловлена избирательным поглоще-
поглощением. В отраженном же свете засохший слой чернил приобре™
тает дополнительный желтовато-зеленый металлический блеск,
вызванный избирательным отражением.
Зависимость оптических констант многих металлов от длины
волны выражена весьма резко. Так, серебро, характеризующееся
в видимой области большим коэффициентом отражения (около
95%), имеет в ультрафиолете резко выраженную область пло™
хого отражения и большой прозрачности — вблизи А = 316 нм
отражательная способность серебра снижается до 4,2 %, т.е. ста-
становится такой же, как у стекла. Вуд показал, что тонкие пленки
щелочных металлов прозрачны в ультрафиолетовой части спек-
спектра, но совершенно не пропускают видимых лучей. Ему удалось
даже обнаружить угол Брюстера при отражении ультрафиоле-
ультрафиолетовых лучей от этих металлов.
Для многих поглощающих тел отражательная способность
имеет резко выраженный максимум в некоторой, иногда весьма
узкой, области спектра. Путем многократных отражений от та-
таких тел можно получить лучи с довольно высокой степенью мо™
нохроматичности. Такие лучи называются остаточными. Этот
метод применяли Рубенс A865-1922) и его сотрудники для по-
получения монохроматических инфракрасных лучей.

§ 73 ИЗМЕРЕНИЕ ОПТИЧЕСКИХ КОНСТАНТ МЕТАЛЛОВ 477
4. В заключение остановимся на отражательной способности
металлов для длинных волн (радиоволны, инфракрасные лучи).
В этой области проводимость а практически не зависит от ча-
частоты ш и равна своему статическому значению gq. Как пока™
зывает формула G1.4), мнимая часть е" диэлектрической про-
проницаемости с уменьшением частоты растет. Для длинных волн
вещественной частью е1 можно пренебречь, полагая
е{и) = -i*EZl. G3.9)
UJ
Тогда из соотношений G1.8) получаем
/ Ad /i-yr» 1Л\
G3.10)
где Т — период колебаний, Л — длина волны в вакууме.
Соотношения G3.10) впервые были получены Друде. Для
видимого света они не оправдываются. Так, для меди а® =
= 5,14 • 1017 с. Полагая А = 589,3 нм = 5,893 • 10 см, из
формул G3.10) найдем п = ж « 33, тогда как опыт дает п =
= 0,64, ж = 2,62. Соотношениями G3.10) можно пользоваться
только для длинных волн. В этом случае G3.8) переходит в
R 2п2 - 2п +
или
/ 1 \
G3.11)
Эта формула проверялась Гагеном и Рубенсом для инфракрас-
инфракрасных лучей (Л = 4; 8; 12; 25,5 мкм). Они нашли, что при Л >
> 5 мкм формула G3.11) начинает оправдываться количествен-
количественно. Для радиоволн величина 1/л/а®Т очень близка к нулю, а
отражательная способность — к единице: металлы отражают ра-
радиоволны практически полностью.
ЗАДАЧА
В каких случаях возможно полное отражение света от среды?
Решение. Если свет поляризован перпендикулярно к плоскости
падения, то условие полного отражения будет
COS (f — V COS ф COS (f — V* COS* ф
cos 99 + 1/ cos ф cos (p + v* cos* ф
или cos ip(y cos (p + 1/* cos* ф) = О. Пользуясь формулой G3.4), ему можно
придать вид
п<р cos if cos x = 0. G3.12)
Такое же условие получится и в случае света, поляризованного в плоско-
плоскости падения. Полное отражение может наступить в одном из трех случаев:

R±
s±
COS if
COSLp
-1/1-
+ гжсовф
— гжсоъф'
sin2 ф у.
щ
. 2
и2
гжсоБ ip
° 4/1 4-
¦ V
+ COSi/)
¦) + cos ф
f sin (/? ^
478 ОПТИКА МЕТАЛЛОВ ГЛ. VI
1) cosy? = 0; 2) п^ = 0; 3) cos% = 0. Первый случай соответствует скользя™
щему падению. Во втором случае п^ =0, а потому, ввиду G2.7), пж = 0.
В третьем случае cos \ = 0 и, следовательно, пж также равно нулю. Итак,
если Lp ф тг/2, то для полного отражения необходимо, чтобы пж = 0. Это
условие может осуществиться в двух случаях: 1) п = 0, ж/0;2)в^0,
>е = 0.
Случай 1. п = 0j ж ф 0. Отражение будет полным при любом угле
падения. Действительно, в рассматриваемом случае v = п — 1ж = —%>с, и
формулы Френеля принимают вид
В НИХ
откуда видно, что cos ф — величина всегда вещественная. В знаменателях
формул Френеля стоят величины, комплексно-сопряженные с числителя-
числителями. Следовательно, \R±/S±\2 = |-Кц/?ц|2 = 1. В рассматриваемом случае
е = 1/ = —-ж < 0, т.е. среда непоглощающая с отрицательной диэлек-
диэлектрической проницаемостью. Такой случай осуществляется при отражении
радиоволн от плазмы (см. § 87).
Случай 2. п ф 0, ж = 0. В этом случае v = 71, е = п2 > 0, т.е.
среда прозрачна. Полное отражение будет иметь место при п < 1, если (р
превосходит предельный угол (fo = arcsinn, (см. § 66).
§ 74. Аномальный скин-эффект и эффективная
диэлектрическая проницаемость
1. Проникновение электромагнитной волны в тонкий поверх-
поверхностный слой металла есть частный случай скин-эффекта^ рас-
рассмотренного нами в т. III, § 144. Самый слой, в который про™
никает электромагнитное поле, называется скин-слоем. Толщи-
Толщина скин-слоя определяется формулой G2.5). Она выводится на
основе макроскопических уравнений Максвелла G1.5). Из тех
же уравнений следует, что напряженность поля в скин-слое убы-
убывает экспоненциально. Такой скин-слой называется нормаль-
нормальным.
Для применимости макроскопических уравнений Максвел-
Максвелла необходимо, чтобы межатомные расстояния были малы по
сравнению не только с длиной волны^ но и с толщиной скин-
слоя. Это условие можно считать выполненным для всех ме-
металлов. Более жестким является условие применимости поня-
понятия диэлектрической проницаемости е(о;), как оно было введено
в § 71. Там было учтено, что электроны и ионы, движением
которых создаются токи проводимости и поляризации, движут-
движутся в электрическом поле, которое меняется во времени, но не

§ 74 АНОМАЛЬНЫЙ СКИН-ЭФФЕКТ 479
было принято во внимание его изменение в пространстве. Это
допустимо, когда средняя длина свободного пробега электронов
мала по сравнению с расстояниями, на которых заметно ме-
меняется напряженность электрического поля, т.е. по сравне-
сравнению с длиной волны и толщиной скин-слоя. Только тогда элек-
электрон от столкновения до столкновения движется практически
в однородном поле. Если же средняя длина свободного пробега
электрона порядка или больше толщины скин™слоя или длины
волны, то результаты § 71 требуют пересмотра. Понятие диэлек-
диэлектрической проницаемости е(ш) может потерять смысл. Тогда на-
напряженность поля и ток будут убывать в глубь металла не экс-
экспоненциально, а по более сложному закону. Соответствующий
скин-эффект называется аномальным.
Если воспользоваться значениями ж из табл. 7, то легко убе-
диться, что у всех металлов, приведенных в этой таблице, ве-
величина h = А/Dтгх) для видимого света порядка 10^6 см. То-
Того же порядка при комнатных температурах и средняя длина
свободного пробега электронов. Это указывает на аномальный
характер скин-эффекта. Только для плохих проводников, у ко-
которых длина свободного пробега меньше, скин-эффект при ком-
комнатных температурах нормальный. В области же низких тем-
температур, где средняя длина свободного пробега достигает для
очень чистых образцов значений порядка 10~2 — 1СГ3 см, об
использовании теории нормального скин-эффекта, основанной
на понятии диэлектрической проницаемости, не может быть и
речи. Поскольку характер скин-эффекта определяется соотно-
соотношением между средней длиной свободного пробега электрона и
толщиной скин-слоя, полная теория аномального скин-эффекта
должна строиться на основе кинетики электронов, в ее кванто-
квантовой форме.
2. Однако независимо от того, является ли скин-эффект нор-
нормальным или аномальным, отражение света возникает в резуль-
результате излучения электромагнитных волн токами, текущими в по-
поверхностном слое металла и возбуждаемыми падающей волной.
Механизм отражения света от металлов вполне аналогичен со-
соответствующему механизму для диэлектриков, разобранному в
§ 68 и 69.
В случае нормального скин-эффекта плотность полного тока
убывает в глубь металла по экспоненциальному закону. В слу-
случае аномального скин-эффекта это не так. Однако если толщина
скин-слоя много меньше длины волны, конкретный закон изме-
изменения плотности тока в поверхностном слое может лишь сла-
слабо сказаться на отражении света, так как в этом случае фазы
источников вторичных волн, распределенных в поверхностном
слое, практически одинаковы по всей его толщине. Поэтому при
вычислении поля отраженной волны действительное распреде-

480 ОПТИКА МЕТАЛЛОВ ГЛ. VI
ление полного тока в скин-слое может быть заменено распре-
распределением, в котором плотность тока убывает экспоненциально.
Такая замена эквивалентна введению вместо е эффективной ди-
диэлектрической проницаемости металла еэф.
Пользуясь величиной еэф, можно вычислять поле отражен-
отраженной волны так, как если бы скин-эффект был нормальным, а ые-
талл имел диэлектрическую проницаемость е = бэф. Однако ес-
если скин-эффект аномальный, пользоваться бэф для вычисления
поля внутри металла нельзя: термин «эффективная» понимает-
понимается в смысле: эффективная в отношении отражения. Эффек-
Эффективная диэлектрическая проницаемость, очевидно, может быть
введена и в случае более толстых скин-слоев. Однако в этих
случаях она, вообще говоря, зависит от состояния поляризации
падающей волны и от угла падения. Для теоретического вы-
вычисления еэф надо было бы решить задачу об отражении света
методами кинетики и статистики, что далеко выходит за рамки
этой книги.

ГЛАВА VII
КРИСТАЛЛООПТИКА
§ 75. Плоские волны в кристаллах
1. Большинство кристаллов оптически анизотропны^ т.е. их
оптические свойства в разных направлениях не одинаковы. Наи™
более важным проявлением этой анизотропии является двойное
лучепреломление в кристаллах. Изучение этого явления и свя™
занной с ним поляризации света составит основное содержание
настоящей главы.
Фундаментальные уравнения Максвелла справедливы без
всяких изменений и в кристаллических средах. В отсутствие
электрических зарядов и токов они имеют вид
rot Н = - D, rot Е = -- Н. G5.1)
с с
Но материальные уравнения усложняются. Изотропные среды
характеризуются скалярной диэлектрической проницаемостью
е(ш). Для характеристики оптических свойств кристаллов тре-
требуются девять величин б^(о;), образующих тензор диэлектри-
диэлектрической проницаемости^ или диэлектрический тензор. Он вво™
дится посредством соотношений
Di =
Для прозрачных кристаллов, как можно показать, исходя из за™
кона сохранения энергии, диэлектрический тензор симметри-
симметричен, т.е. Sij = 6ji (см. § 80). Разумеется, в различных системах
координат компоненты диэлектрического тензора имеют разные
значения. При переходе от одной системы координат к другой
они преобразуются как компоненты всякого тензора. Благода-
Благодаря тензорной связи между D и Е направления этих векторов в
кристаллах, вообще говоря, не совпадают.

482 КРИСТАЛЛООПТИКА ГЛ. VII
2. Если среды прозрачны и однородны, то в них могут рас™
пространяться плоские монохроматические волны. Каждую из
них молено записать в виде
Е = Eoe^~kr), Н = Ное^~кг), D = Бое^~кг1 G5.3)
Рассмотрим сначала свойства таких волн, которые вытекают
из одних только фундаментальных уравнений G5.1) без исполь-
использования материальных уравнений G5.2). Как и в случае изо™
тропных сред,
rot Н = -г [kH], D = -гоШ,... G5.4)
Подставив эти выражения в G5.1) и вводя единичный вектор
волновой нормали N по формуле к = — N, получим
V
D = -^[NH], H = ^[NE], G5.5)
где v — нормальная скорость волны, т.е. фазовая скорость, с ко-
которой распространяется волновой фронт в направлении волно-
волновой нормали N. Присоединим к этим формулам еще выражение
для вектора Пойнтинга
S = ?[EH]. G5.6)
Фундаментальное значение этого вектора в кристаллооптике со-
состоит в том, что он определяет направление световых лучей^ т.е.
линий, вдоль которых происходит распространение энергии све-
света. Чтобы убедиться в этом, достаточно показать, что направ-
направление S совпадает с направлением вектора групповой скорости
u = doo/dk. (см. § 8). Это будет сделано в § 81. В кристаллах
векторы S и N, вообще говоря^ не совпадают по направлению.
Именно с этим связано двойное лучепреломление, а также ко-
коническая рефракция.
Из формул G5.5) видно, что векторы DwH взаимно перпен-
перпендикулярны. Кроме того, они перпендикулярны к волновой норма-
нормали N, т.е. параллельны фронту волны.
Значит, плоские волны в кристалле по-
поперечны в отношении векторов DuH.
Однако в общем случае они не попе-
поперечны в отношении вектора Е. Четы-
Четыре вектора Е, D, N, S лежат в одной
плоскости^ перпендикулярной к векто-
вектору Н. Взаимное расположение этих век-
векторов показано на рис. 257. Из него вид-
Рис, 257 н05 чт0 заданием в кристалле направ-
направления вектора Е (или D) однозначно
определяется направление вектора D (или Е) и с точностью
до 180° — направления всех остальных векторов Н, N, S. Опре-

§ 76 ОПТИЧЕСКИ ОДНООСНЫЕ КРИСТАЛЛЫ 483
деляется также величина нормальной скорости волны v. Дей™
ствительно, если задано направление вектора Е, то уравнение
G5.2) однозначно определит направление вектора D, а с ним
и плоскость (Е, D), к которой перпендикулярен вектор Н. Тем
самым с точностью до 180° определится направление Н, а следо-
следовательно, и направления векторов N и S. Исключение состав ля™
ет случай, когда направления векторов Е и D совпадают. Тогда
всякая прямая, перпендикулярная к вектору Е, может служить
направлением магнитного поля. Те же рассуждения применимы
и к случаю, когда задано направление вектора D. Для опреде-
определения v исключим из G5.5) вектор Н:
D = 4е - 4(NE)N- G5J)
V2 V2
Так как (DN) = 0, то отсюда скалярным умножением на D
находим
2 2(DE) (rjr оч
v = с i-^. G5.8)
Таким образом, электрический вектор (Е или D) в кристал-
кристалле в известном смысле является главным. Это и понятно, так
как именно он определяет электрическую поляризацию среды,
а возбуждение последней составляет сущность процесса распро-
распространения электромагнитных волн в материальных средах.
§ 76. Оптически одноосные кристаллы
1. Простейшими оптическими свойствами обладают оптиче-
ски одноосные кристаллы^ которые к тому же имеют наибольшее
практическое значение. Поэтому имеет смысл особо выделить
этот простейший частный случай. Оптически одноосными на™
зываются кристаллы, свойства которых обладают симметрией
вращения относительно некоторого направления, называемого
оптической осью кристалла.
Разложим электрические векторы Е и D на составляющие
Ец, D|| вдоль оптической оси и составляющие Ej_, Dj_, перпен-
перпендикулярные к ней. Тогда
D||=<-||E||, D± = e±E±, G6.1)
где ?м и е± — постоянные, называемые продольной и поперечной
диэлектрическими проницаемостями кристалла. К этим двум
величинам и сводится диэлектрический тензор одноосного кри™
сталла. К оптически одноосным кристаллам относятся все кри-
кристаллы тетрагональной, гексагональной и ромбоэдрической си™
стем. Кристаллы кубической системы являются вырожденным
случаем их. Для них ец = е±. Поэтому кристаллы кубической
16*

484 КРИСТАЛЛООПТИКА ГЛ. VII
системы в оптическом отношении ведут себя как оптически
изотропные тела. Плоскость, в которой лежат оптическая ось
кристалла и нормаль N к фронту волны, называется главным
сечением кристалла. Главное сечение — это не какая-то опреде-
определенная плоскость, а целое семейство параллельных плоскостей.
Рассмотрим теперь два частных случая.
Случай 1. Вектор D перпендикулярен к главному се-
сечению кристалла. В этом случае D = Dj_, а потому D = е±Е.
Кристалл ведет себя как изотропная среда с диэлектрической
проницаемостью е±. Для нее
D = е±Е, G6.2)
и из уравнений G5.5) получаем
D = ^H, Н = -Е, G6.3)
V V
или
8±Е =^Н, Н= ±Е, G6.4)
откуда
v = v± = v0 = -^=. G6.5)
Таким образом, если электрический вектор перпендикулярен к
главному сечению, то скорость волны не зависит от направле-
направления ее распространения. Такая волна называется обыкновенной.
Случай 2. Вектор D лежит в главном сечении. Так как
вектор Е лежит также в главном сечении (см. рис. 257), то Е =
= Едг + Ed, где Едг — составляющая этого вектора вдоль N, а
Ed — вдоль D. Из векторного произведения [NE] составляющая
Ejv выпадает. Поэтому вторую формулу G5.5) можно записать
в виде
Н = I [NED].
Очевидно,
„ ED EllDll+E±D± (Dl/?ll) (l/)
E
Ed^ DD
ИЛИ
ED = () (
V ? ? J ?\\
где а — угол между оптической осью и волновой нормалью
(рис. 258). Если ввести обозначение
1 = ^ + ^, G6.6)
е е\\ е±

§ 76 ОПТИЧЕСКИ ОДНООСНЫЕ КРИСТАЛЛЫ 485
то получится D = eEjj, и мы придем к соотношениям
eED = ^Я, Я = C-ED, G6.7)
формально тождественным с соотношениями G6.4). Роль вели™
чины е± теперь играет величина е, определяемая выражением
G6.6). Поэтому нормальная скорость волны будет определяться
выражением
с InI . Щ (па оч
v = -= = с\ — + —U- = ш. G6.8)
Она меняется с изменением направления волновой нормали N.
По этой причине волну, электрический вектор которой лежит
в главном сечении кристалла, называют необыкновенной. Зави-
Зависимость ее скорости г?ц от направле-
ния распространения обусловлена тем,
что с изменением направления волно-
волновой нормали N меняется угол меж-
ду электрическим вектором и оптиче™ /а\ Оптическая осъ
ской осью кристалла. Когда N± = О,
т.е. необыкновенная волна распростра™
няется вдоль оптической оси кристал-
кристалла, то из формулы G6.8) получаем v =
= с/л/^1 = v± = v0. В этом случае, Рис> 258
как это очевидно заранее, нет разницы
между обыкновенной и необыкновенной волнами. Если же N\\ =
= 0, т.е. необыкновенная волна распространяется перпендику™
лярно к оптической оси, то скорость волны будет равна
v = Ve = c/ /щт G6.9)
Термин «оптическая ось» был введен для обозначения такой
прямой, вдоль которой обе волны в кристалле распространяют-
распространяются с одинаковыми скоростями. Таких прямых в общем случае
две (см. § 80 и 81). Поэтому в этом случае кристалл называется
оптически двуосным. В рассматриваемом нами частном случае
оптические оси совпадают между собой, сливаясь в одну пря-
прямую, а потому кристалл и называется оптически одноосным.
2. Так как уравнения Максвелла в кристаллах линейны и од-
однородны, то в общем случае волна, вступающая в кристалл из
изотропной среды, разделяется внутри кристалла на две ли-
линейно поляризованные волны: обыкновенную, вектор электри-
ческой индукции которой перпендикулярен к главному сечению,
и необыкновенную с вектором электрической индукции, леэюа-
щим в главном сечении. Эти волны распространяются в кри-
кристалле в различных направлениях и с различными скоростями
v± и г;ц. В направлении оптической оси скорости обеих волн сов-

486 КРИСТАЛЛООПТИКА ГЛ. VII
падают, так что в этом направлении может распространяться
волна любой поляризации.
К обеим волнам применимы все рассуждения, которыми мы
пользовались при выводе геометрических законов отражения и
преломления (см. § 64). Но в кристаллах они относятся к вол-
новым нормалям, а не к световым лучам. Волновые нормали
отраженной и обеих преломленных волн лежат в плоскости па-
падения. Их направления формально подчиняются закону Онел-
лиуса
simp simp (r?a 1 пч
^^=п±, —2L=nn G6.10)
sm^i sin ^|| п
где п± и пц — показатели преломления обыкновенной и необык-
необыкновенной волн, т.е.
Из них п± = п0 не зависит, а пц зависит от угла падения. Посто-
Постоянная п0 называется обыкновенным показателем преломления
кристалла. Когда необыкновенная волна распространяется пер-
перпендикулярно к оптической оси (N± = 1, Щ = 0),
п _ /?~ = п Gа 19)
\\ — л/ — в • i I UiiZi i
Величину пе называют необыкновенным показателем прелом-
преломления кристалла. Ее нельзя смешивать с показателем прелом-
преломления пц необыкновенной волны. Величина пе есть постоянная,
а пц — функция направления распространения волны. Обе ве™
личины совпадают только тогда, когда волна распространяется
перпендикулярно к оптической оси.
3. Теперь легко понять происхождение двойного лучепрелом-
лучепреломления. Допустим, что плоская волна падает на плоскопараллель-
плоскопараллельную пластинку из одноосного кристалла. При преломлении на
первой поверхности пластинки волна внутри кристалла разде-
разделится на обыкновенную и необыкновенную. Эти волны поляри-
поляризованы во взаимно перпендикулярных плоскостях и распростра-
распространяются внутри пластинки в разных направлениях и с разными
скоростями. Волновые нормали обеих волн лежат в плоскости
падения. Обыкновенный луч, поскольку его направление совпа™
дает с направлением волновой нормали, также лежит в плос-
плоскости падения. Но необыкновенный луч, вообще говоря, выхо-
выходит из этой плоскости. (В случае двуосных кристаллов деление
на обыкновенную и необыкновенную волны теряет смысл — вну-
внутри кристалла обе волны «необыкновенные». При преломлении
волновые нормали обеих волн, конечно, остаются в плоскости
падения, однако оба луча, вообще говоря, выходят из нее.)

76
ОПТИЧЕСКИ ОДНООСНЫЕ КРИСТАЛЛЫ
487
Рис. 259
Если падающая волна ограничена диафрагмой, то в пластин-
пластинке получатся два пучка света, которые при достаточной толщине
пластинки окажутся разделенными пространственно. При пре-
преломлении на второй границе пластинки из нее выйдут два пуч-
пучка света^ параллельные падающему лучу. Они будут линейно
поляризованы во взаимно перпендикулярных плоскостях. Если
падающий свет естественный, то всегда выйдут два пучка. Если
же падающий свет линейно поляризован в плоскости главного
сечения или перпендикулярно к ней,
то двойного преломления не получит-
получится — из пластинки выйдет только
один пучок с сохранением исходной
поляризации.
Двойное преломление возникает и
при нормальном падении света на пла-
пластинку. В этом случае преломление ис-
испытывает необыкновенный луч, хотя
волновые нормали и волновые фронты
не преломляются. Примером может
служить кристаллическая пластинка,
вырезанная параллельно оптической
оси кристалла (рис. 259). Параллель-
Параллельный пучок света, ограниченный диафрагмой, падает нормально
к поверхности пластинки. Волновые фронты, обозначенные на
рисунке тонкими горизонтальными линиями, всюду параллель-
параллельны той же поверхности. Обыкновенный пучок лучей о преломле-
преломления не испытывает. Необыкновенный е в пластинке отклоняется
вбок, но по выходе из нее снова идет в первоначальном направ-
направлении.
4. Двойное лучепреломление было открыто в 1669 г. Барто-
линусом A625-1698) на кристаллах исландского (известкового)
шпата. Гюйгенс дал объяснение этого явления, введя гипотезу,
что элементарная (вторичная) волна в кристалле распадается
на две волны: сферическую (обыкновенную) и эллипсоидаль-
эллипсоидальную (необыкновенную). Гюйгенс же открыл и поляризацию све-
света при двойном лучепреломлении.
Исландский шпат есть разновидность углекислого кальция
(СаСОз). Он встречается в природе в виде довольно больших
и оптически чистых кристаллов. Его обыкновенный показатель
преломления п0 = 1,6585, необыкновенный пе = 1,4863 (для
желтой линии). Благодаря большому различию п0 и пе двойное
преломление в исландском шпате выражено очень отчетливо. И
до сих пор кристаллы исландского шпата наиболее удобны для
демонстрации двойного лучепреломления и являются наилуч-
наилучшим материалом для изготовления поляризационных призм и
других поляризационных приборов, хотя теперь известно мно-

488 КРИСТАЛЛООПТИКА ГЛ. VII
го естественных и искусственных кристаллов с аналогичными
свойствами.
Кристаллы исландского шпата принадлежат к гексагональ-
гексагональной системе, но встречаются в различных формах. Каждый
кристалл раскалыванием легко при-
В вести к форме ромбоэдра, ограни-
ограниченного шестью подобными парал-
параллелограммами с углами 78°08' и
101°52/ (рис. 260). В двух противо-
противоположных вершинах А и В сходятся
стороны трех тупых углов, в осталь-
остальных — стороны одного тупого и двух
острых. Прямая, проходящая через
Рис 260 точку А или В и одинаково накло-
наклоненная к ребрам, сходящимся в этих
точках, а также всякая прямая, ей параллельная, есть оптиче-
оптическая ось кристалла. Если отшлифовать кристалл так, чтобы все
ребра его имели одинаковую длину, то линия АВ и будет опти-
оптической осью.
5. Для демонстрации двойного преломления берут ромбо-
ромбоэдр исландского шпата, вставленный в круглую вращающую-
вращающуюся оправу, устанавливаемую на подставке оптической скамьи.
Луч света должен проходить перпендикулярно к противополож-
противоположным граням ромбоэдра. Перед конденсором проекционного фо-
фонаря на той же оптической скамье устанавливают ирисовую
диафрагму. В отсутствие исландского шпата длиннофокусный
объектив фонаря дает изображение отверстия диафрагмы на
удаленном экране. При введении непосредственно за диафраг-
диафрагмой исландского шпата изображение раздваивается. Уменьшая
диаметр диафрагмы, можно добиться, чтобы оба изображения
не накладывались друг на друга. При освещении естественным
светом изображения получаются одинаково яркими. Если вра-
вращать исландский шпат вокруг главной оптической оси установ-
установки, то при правильной юстировке одно изображение остается
неподвижным, а другое движется вокруг него по кругу. Когда
кристалл исландского шпата делает полоборота, второе изобра-
изображение совершает полный оборот. С помощью поляроида, постав-
поставленного за объективом, легко убедиться, что оба пучка света ли-
линейно поляризованы во взаимно перпендикулярных плоскостях.
Неподвижное изображение дает обыкновенный, а вращающее-
вращающееся — необыкновенный пучок света. Увеличив диафрагму, можно
частично наложить одно изображение на другое. При вращении
поляроида неперекрывающиеся части изображения периодиче-
периодически становятся светлыми и темными: когда максимальна осве-
освещенность одной части, освещенность другой обращается в нуль.
Освещенность же перекрывающейся части при вращении поля-

§ 76 ОПТИЧЕСКИ ОДНООСНЫЕ КРИСТАЛЛЫ 489
роида все время остается неизменной — эта частв освещается
неполяризованным светом.
ЗАДАЧИ
1. Если пластинку исландского шпата положить на страницу печатно-
печатного текста, то происходит раздвоение букв. Будет ли происходить удвоение
изображения, если через ту же пластинку смотреть на удаленный предмет?
Ответ. Не будет.
2. Показатели преломления кристалла можно измерить с помощью
кристалл-рефрактометра, действующего по следующему принципу. Пла-
Пластинка исследуемого кристалла кладется на плоскую поверхность стеклян-
ного полушария с очень высоким (до 2) показателем преломления N. Свет
падает со стороны стеклянного полушария вдоль его радиуса и отражается
от пластинки. Показатель преломления п исследуемого вещества вычисля-
вычисляется по предельному углу полного отражения по формуле п = N sin ср. В
случае отражения от кристалла существуют два предельных угла, соответ-
соответствующих двум преломленным лучам в кристалле.
Как надо ориентировать на кристалл-рефрактометре плоскопараллель-
ную пластинку, вырезанную произвольным образом из одноосного кристал-
кристалла, чтобы получить оба главных показателя преломления кристалла по
ИПе?
Решение. Для определения обыкновенного показателя преломления
по пластинка, очевидно, может быть ориентирована как угодно. Чтобы по-
получить необыкновенный показатель преломления пе (т.е. максимальное или
минимальное значение пц), пластинку надо ориентировать так, чтобы плос-
кость, проходящая через оптическую ось кристалла и нормаль к границе
раздела пластинки со стеклом кристалл-рефрактометра, была перпендику-
перпендикулярна к плоскости падения.
Действительно, при полном отражении световое поле проникает во
«вторую» среду, вообще говоря, в виде неоднородной (поверхностной) вол-
волны. Но если свет падает строго под предельным углом полного отражения,
то волна во второй среде будет еще однородна. Ее волновая нормаль парал-
параллельна линии пересечения плоскости падения с плоскостью раздела сред.
Повернем кристалл так, чтобы его оптическая ось стала перпендикулярна к
этой линии. Тогда волна в кристалле будет распространяться перпендику-
перпендикулярно к оптической оси. При такой ориентировке кристалла электрический
вектор необыкновенной волны будет параллелен оптической оси. Значит, на
кристалл-рефрактометре в этом случае будет измерен главный показатель
преломления необыкновенной волны, т.е. величина пе.
3. При измерении показателей преломления кристаллической пластин-
пластинки на кристалл-рефрактометре оказалось, что один показатель преломле-
преломления сохраняет постоянное значение по при всех поворотах стеклянного по-
полушария. Другой показатель преломления изменяется так, что значение
по для него 1) максимально; 2) минимально. Определить оптический знак
кристалла ) и ориентировку пластинки относительно оптической оси.
Ответ. Пластинка вырезана параллельно оптической оси. 1) Кристалл
отрицателен. 2) Кристалл положителен.
) Одноосный кристалл называется положительным, если обыкновен-
обыкновенный показатель преломления по меньше необыкновенного пе (по < пе). В
противоположном случае (по > пе) кристалл называется отрицательным.

490 КРИСТАЛЛООПТИКА ГЛ. VII
4. Как будут меняться при вращении полушария кристалл™
рефрактометра оба показателя преломления пластинки, если она
вырезана перпендикулярно к оптической оси?
Ответ. Оба показателя преломления будут оставаться постоянными
и равными соответственно по и пе.
5. Как надо вырезать призму из одноосного кристалла, чтобы методом
наименьшего отклонения преломленного луча измерить обыкновенный по
и необыкновенный пе показатели преломления кристалла?
Ответ. Оптическая ось должна быть параллельна преломляющему
ребру призмы.
6. Узкий параллельный пучок неполяризованного света падает нор-
нормально на пластинку исландского шпата, вырезанную не перпендикулярно
к оптической оси. После этого пучок падает на вторую такую же пластинку,
параллельную первой, а затем попадает на экран. Главные сечения пласти-
пластинок образуют между собой угол 30°. Какая картина будет наблюдаться на
экране?
Ответ. На экране образуются четыре пятна, интенсивности которых
относятся как 1:3:1:3. Два из них с интенсивностями 1 : 3 поляризованы
линейно, два других с такими же интенсивностями поляризованы также
линейно, но в перпендикулярной плоскости.
7. Ветровое стекло и фары автомашины прикрыты поляроидами, глав-
главные сечения которых параллельны между собой и составляют угол 45° с
горизонтом. У всех машин они должны быть повернуты в одну и ту же
сторону (считая по ходу машины). Показать, что при таком устройстве во-
водитель машины будет видеть дорогу, освещенную светом его фар, но ему
не будет мешать слепящее действие фар встречных машин.
8. Определить максимальный угол <5Макс между направлениями луча и
волновой нормали в кристалле исландского шпата.
Решение. Векторы N, S, D, Е в необыкновенной волне лежат в
одной плоскости, причем угол 6 между N и S равен углу между D и Е.
Обозначим через /3 угол между D и оптической осью кристалла, а через
7 — между Е и той же осью. Тогда
D|| = Dcos/3 = е\\Е\\ =
D± = Dsin/3 = e±E± =
Отсюда tg/5 = (e±/e\\)igj = (no/neJ tgj. Искомый угол <5 = /3 — 7. Поэтому
Максимум достигается, когда tg/3 = no/ne = 1,1157, т.е. при f3 = 48°7/53//.
Максимальный угол ?)Макс определяется формулой
2 2
*8<5макс = ^^ = 0,1097. G6.14)
Из нее находим <5макс = 6°15/46//.
9. Определить показатель преломления пц необыкновенной волны в
ромбоэдре исландского шпата, если волновая нормаль параллельна боково-
боковому ребру кристалла. Для исландского шпата угол между боковым ребром
и оптической осью равен а = 64°. Найти для этого случая угол S между
направлениями луча и волновой нормали в кристалле.
Ответ, пц = у/'(sinа/пеJ + (cosа/поJ = 1,515; 8 = 4°36/20//.

§ 77 ПОЛЯРИЗАЦИОННЫЕ УСТРОЙСТВА 491
§ 77. Поляризационные устройства
1. Двупреломляющие кристаллы (лучше всего исландско-
исландского шпата) можно использовать для получения поляризованного
света. Для этого в опыте типа рис. 259 достаточно задержать
один из двух линейно поляризованных пучков света, вышедших
из кристалла. Однако гораздо удобнее пользоваться не просты™
ми кристаллами, а их комбинациями, называемыми поляризаци-
поляризационными призмами. Обычно для изготовления поляризационных
призм применяется исландский шпат, иногда кварц и натронная
селитра, что значительно удешевляет стоимость поляризацион-
поляризационных приборов.
Поляризационная призма состоит из двух или более трех™
гранных призм из одноосного кристалла с одинаковой или раз™
личной ориентацией оптических осей, склеенных между собой
прозрачными веществами или разделенных воздушной прослой™
кой. Для склейки применяются канадский бальзам (пр = 1,550),
льняное масло (пр = 1,49), глицерин (пр = 1,474) и другие ма-
материалы. Для работы в ультрафиолетовой части спектра при™
меняют призмы, склеенные глицерином, касторовым маслом, а
также призмы с воздушной прослойкой.
Различают однолучевые поляризационные призмы^ из кото™
рых выходит только один пучок линейно поляризованного света,
и двухлучевые поляризационные призмы, из которых выходят
два пучка света, поляризованных во взаимно перпендикуляр-
перпендикулярных плоскостях. Призмы первого типа действуют по принци-
принципу полного отражения. Падающий пучок естественного света,
проникая в призму, расщепляется в ней на два пучка, поляри-
поляризованных линейно во взаимно перпендикулярных плоскостях.
Один из этих пучков претерпевает полное отражение на грани-
границе склейки призм и отклоняется вбок, другой проходит прямо и
используется в дальнейшем.
2. Первая поляризационная призма была изобретена в 1828 г.
шотландским физиком Николем A768-1851). Ее сокращенно на-
называют николем. То лее название часто применяют и для других
призм, действующих по тому же принципу. Для изготовления
призмы Николя у продолговатого ромбоэдра, полученного ска-
скалыванием из куска исландского шпата, сошлифовывают основа-
основания так, чтобы новые основания составляли с боковыми ребрами
угол 68° (вместо 71° у естественного кристалла). Затем кристалл
разрезают вдоль плоскости, перпендикулярной к новым основа-
основаниям и к главному сечению кристалла (последнее нормально к
этим основаниям и проходит через оптическую ось кристалла).
Отполировав плоскости разреза, оба куска склеивают в прежнем
положении тонким слоем канадского бальзама.

492 КРИСТАЛЛООПТИКА ГЛ. VII
Сечение призмы Николя плоскостью главного сечения пока™
зано на рис. 261. Двойная стрелка, наклоненная под углом 64° к
длинному ребру, указывает направление оптической оси. Такое
обозначение применяется в дальнейшем и для других призм.
Луч света, падая на искус-
искусственное основание кри-
сталла, разделяется вну-
внутри кристалла на обыкно-
обыкновенный АО и необыкновен-
необыкновенный АЕ. Показатель пре-
преломления канадского баль-
бальзама A,550) имеет проме-
Рис. 261 жуточное значение меж-
между обыкновенным (п0 =
= 1,658) и необыкновенным (пе = 1,486) показателями прелом-
преломления исландского шпата. Углы в призме Николя рассчитаны
так, чтобы необыкновенный луч прошел через слой канадского
бальзама, а обыкновенный претерпел на нем полное отражение
и поглотился зачерненной боковой гранью. (В больших призмах
во избежание их нагревания обыкновенный луч выводится на-
наружу специальной призмочкой, наклеенной на боковую грань и
изображенной на рис. 261 штриховой линией.) В результате свет,
вышедший из призмы, окажется линейно поляризованным.
В пучке лучей, падающих на входную грань призмы Нико-
Николя, обычно встречаются лучи разных направлений. Если луч
падает на плоскость разреза слишком наклонно, то претерпит
полное отражение не только обыкновенный луч, но и необыкно-
необыкновенный. Если же наклон недостаточен, то через призму пройдет
и обыкновенный луч. Через призму может пройти один толь-
только необыкновенный луч тогда и только тогда, когда углы па-
падения на входную грань лежат в определенных пределах. Раз-
Разность углов наклона между крайними лучами падающего пучка,
удовлетворяющими этому условию, определяет так называемую
апертуру полной поляризации призмы. Для призмы Николя она
составляет 29°, а отношение длины призмы к ее ширине — 3,28
(см. задачу 1 к этому параграфу).
В призме Фуко (рис. 262), устроенной как и николь, канад-
канадский бальзам заменен тонким слоем воздуха. Благодаря этому
она может применяться для ультрафиолета, тогда как призма
Николя непригодна для этой цели, так как канадский бальзам
поглощает ультрафиолетовый свет. От николя призма Фуко от-
отличается еще тем, что показатель преломления воздушной про-
прослойки меньше обоих показателей п0 и пе, а не равен промежу-
промежуточному значению между ними, как это было в случае канад-
канадского бальзама. Поэтому полное отражение от плоскости разре-
разреза в призме Фуко осуществляется под меньшими углами, а сама

77
ПОЛЯРИЗАЦИОННЫЕ УСТРОЙСТВА
493
призма Фуко (при заданном поперечном сечении) гораздо ко™
роче и, следовательно, дешевле николя. Зато апертура полной
поляризации ее составляет всего 8°.
/59'
V
Рис. 262
Рис. 263
3. Призмы Николя и Фуко имеют скошенные основания.
Это вызывает параллельное боковое смещение падающего луча
при прохождении его через призму. Следствием этого являет™
ся кругообразное перемещение выходящего луча при вращении
призмы вокруг ее оси. От этого недостатка свободны призмы,
имеющие форму прямоугольного параллелепипеда: Глазебру™
ка (рис. 263), Глана, Глана—Томпсона, Гартнака-Празмовского,
Франка-Риттера (рис. 264), Аренса (рис. 265) и др. Сечение
склеенной поляризационной призмы Глазебрука показано на
Рис. 264
Рис. 265
рис. 263. Оптическая ось перпендикулярна к плоскости рисун™
ка, что отмечено точками. Аналогично устроены призмы Гла-
Глана, Глана—Томпсона и Гартнака-Празмовского. Их отличия от
призмы Глазебрука заключаются в следующем. Призма Глана —
воздушная. Призмы Глана—Томпсона имеют другие параметры.
В призме Гартнака^Празмовского оптическая ось нормальна к
плоскости распила, а в призме Франка-Риттера (рис. 264) она
параллельна одной из диагоналей основания призмы. Призма
Аренса — тройная призма, устройство и действие которой по™
нятно из рис. 265. Параметры поляризационных призм указаны
в табл. 8.

494
КРИСТАЛЛООПТИКА
ГЛ. VII
Таблица
Вид призмы
Призма Николя
Укороченная призма Николя, склеенная:
а) канадским бальзамом,
б) копайским бальзамом
Призма Фуко
Призма Глазебрука, склеенная:
а) канадским бальзамом,
б) льняным маслом,
в) глицерином
Призма Глана с воздушной прослойкой
Призма Глана—Томпсона, склеенная:
а) канадским бальзамом,
б) льняным маслом
Призма Гартнака—Празмовского
Призма Франка-Риттера, склеенная ка™
надским бальзамом
Призма Аренса, склеенная канадским
бальзамом
Апертур-
ный угол
полной
поляриза-
поляризации
29°
13°
24°
8°
35°
42°
32,1°
7,9°
27,5°
41°
41,9°
19°
35°
Угол
плоскости
разреза с
боковой
гранью
22°
25°
25°
40°
12,1°
14°
17,3°
50,3°
13,5°
13,5°
13,9°
17,5°
12,1°
Отно-
Отношение
длины к
ширине
3,28
2,83
2,83
1,53
4,65
4,02
3,2
0,83
4,15
4,15
4,04
3 17
2,32
4. Различные типы двухлучевых поляризационных призм
представлены на рис. 266. Первая призма состоит из комби-
Рис. 266
нации стеклянной призмы с кристаллической из исландского
шпата, оптическая ось которой параллельна преломляющему
ребру. Призмы соприкасаются или склеиваются, как показано
на рис. 266 а. Показатель преломления стекла A,49) почти точ™
но совпадает с необыкновенным показателем преломления пе

§ 77 ПОЛЯРИЗАЦИОННЫЕ УСТРОЙСТВА 495
исландского шпата. Падающий пучок неполяризованного све™
та в кристаллической призме разделяется на обыкновенный и
необыкновенный. Необыкновенный проходит без преломления.
Обыкновенный сильно отклоняется к основанию кристалличе-
кристаллической призмы в результате двукратного преломления на ее гра-
гранях. Аналогично действуют призмы Ротона (рис. 266 б) и Се-
нармона (рис. 266 в). В призме Волластона (рис. 266 г) выходя-
выходящие лучи линейно поляризованного света отклоняются в разные
стороны.
5. У многих кристаллов поглощение света зависит от направ-
направления электрического вектора в световой волне. Это явление
также используется для получения линейно поляризованного
света в так называемых дихроичных пластинках. К ним отно-
относятся, например, пластинки турмалина и поляроиды. В турма-
турмалине обыкновенный луч поглощается сильнее необыкновенного.
Поэтому после прохождения через пластинку турмалина есте-
естественный свет становится частично поляризованным в плоско-
плоскости главного сечения. Если пластинка достаточно толстая (около
1 мм), то в области видимого света обыкновенный луч поглоща-
поглощается практически полностью, так что прошедший свет окажется
полностью линейно поляризованным. Для некоторых участков
видимого спектра и необыкновенный луч испытывает заметное
поглощение. Турмалин при надлежащей толщине действует не
только как поляризатор, но и как светофильтр, пропускающий
преимущественно желто-зеленую область спектра. Это — суще-
существенный недостаток турмалина как поляризатора. Зато аперту-
апертура полной поляризации у него очень велика и ограничена одними
только конструктивными условиями.
Заметим еще, что с изменением направления волновой нор-
нормали меняется и направление электрического вектора в обе-
обеих линейно поляризованных волнах, на которые разделяется
естественный свет, распространяющийся вдоль этой нормали.
Вследствие этого меняется и поглощение таких волн, которое к
тому лее обычно зависит от длины волны. Это приводит к за-
зависимости окраски кристалла от направления распространения
света. Такое явление называется дихроизмом (двуцветностью)
или, лучше, плеохроизмом (многоцветностью) и в большей или
меньшей степени присуще большинству двупреломляющих кри-
кристаллов.
ЗАДАЧИ
1. В поляризационной призме Николя плоскость разреза ВС (рис. 267)
перпендикулярна к основаниям АВ и CD. Разрез произведен по диагонали
призмы. Определить предельные углы полного отражения от слоя канад-
канадского бальзама для обыкновенной и необыкновенной волн. Найти соответ™

496
КРИСТАЛЛООПТИКА
ГЛ. VII
ствующие им углы падения на основание АВ и апертуру полной поляри-
зации призмы. Найти показатель преломления пц необыкновенной волны в
кристалле. Найти также отношение длины I призмы к ширине h ее попе-
поперечного сечения. Вычисления произвести для двух случаев: 1) основания
призмы сошлифованы G = 68°); 2) для естественного кристалла G = 71°).
В
Рис. 267
Решение. Проведем расчет для необыкновенной волны в предполо-
предположении, что 7 = 68°. Пусть /3 = 64° — угол между оптической осью кристал-
кристалла и продольным ребром АС, ОМ — волновая нормаль для предельного
случая полного отражения, <ре — соответствующий угол падения на слой
канадского бальзама ВС. Тогда sin (ре = п/п\\, где п — показатель прелом-
преломления канадского бальзама. Показатель преломления щ необыкновенной
волны в кристалле для рассматриваемого направления волновой нормали
определяется уравнением
1 sin2 a cos2 a
Как видно из рис. 267, а = /3 + 7 ~~ (fie- Подставив числовые значения в
предыдущее соотношение, придем к уравнению
tg2 (р - 7,046608 tg ip - 32,84593 = 0.
Из него находим
tg ip = 10,250829,
ip = 84,422825°
= n/ sin y?e = 1,5573726.
Угол преломления на основании АВ равен ф = тг/2 — Lpe = 5,5771175°.
По закону Снеллиуса находим угол падения
sin ip = щ sin ф = 0,1513532, (р = 8,705349°.
Чтобы необыкновенная волна не испытывала полного отражения, угол па-
падения (р должен удовлетворять условию Lp > 8,705349°.
Аналогичный расчет для обыкновенной волны, разумеется, проще, так
как показатель преломления такой волны не зависит от направления ее рас-
распространения. Для предельного угла полного отражения в этом случае по-
получаем ipo = 69,20573°, а для соответствующего угла падения ср = 36,05854°.
Чтобы обыкновенная волна испытывала полное отражение, угол падения
должен быть меньше этого значения. При угле падения, удовлетворяющем
условию 8,705349° < (р < 36,05854°, прошедший свет будет поляризован
полностью. Апертура полной поляризации е = 36,06 — 8,71 и 27,35°. (При

77
ПОЛЯРИЗАЦИОННЫЕ УСТРОЙСТВА
497
вычислениях использовано неточное значение угла /3. Десятичные знаки
сохранялись для того, чтобы не потерять точность во время расчета.)
Для отношения l/h получаем
1
h
sin 7 cos 7 sin 27
Практически призму Николя распиливают не по диагонали, а как указано
на рис. 261, чтобы легче монтировать ее. В этом случае отношение l/h
несколько больше.
Рассмотрим теперь случай естественного кристалла, когда 7 = 71°. Вы-
Вычисления для обыкновенной волны остаются без всяких изменений. Вычис-
Вычисления же для необыкновенной волны сильно упрощаются благодаря случай-
случайному соотношению: /3 + 7 = 135°, и следовательно, sin (/3 + 7) =— cos (/3 + 7)-
Приводим окончательные результаты: щ = 1,564955, (ре = 82,0728°, <р =
= 12,46454°, е = 23,59°, l/h = 3,25. По сравнению с предыдущим случаем
параметры поляризационной призмы ухудшились.
2. Призма Волластона (рис. 266 г) сделана из исландского шпата. Угол
а = 15°. На какой угол S будут разведены обыкновенный и необыкновенный
лучи?
Ответ. S = 5° 17 .
3. Две поляризационные призмы с воздушной прослойкой изготовлены
из исландского шпата. В одной призме оптическая ось перпендикулярна,
в другой — параллельна плоскости падения (рис. 268). Опишите действие
Рис. 268
каждой призмы. Как будет поляризован проходящий свет? Какая призма
будет пропускать больше света? В каких пределах должен быть заключен
угол а, чтобы из призмы выходил линейно поляризованный свет? Свет па-
падает на грань призмы перпендикулярно.
Ответ. Через призмы проходит необыкновенный луч. Вторая призма
пропускает больше света. В обоих случаях должно выполняться условие
1/по < sina < 1/пе, т.е. 37°6; < а < 42°18;.
4. В призме Глазебрука (рис. 263) склеивающим веществом является
либо канадский бальзам (п = 1,550), либо льняное масло (п = 1,494). Пай™
ти наивыгоднейшую апертуру полной поляризации призмы и соответствую-
соответствующее ей отношение длины а к ширине Ь для обоих склеивающих материалов.
Пучок падающих лучей, дающих полную поляризацию, должен быть сим™
метричен относительно оси, параллельной боковому ребру призмы.
Решение. В рассматриваемом случае электрический вектор необык-
необыкновенной волны всегда параллелен оптической оси, а обыкновенной — пер-
перпендикулярен к ней. Поэтому направления лучей и волновых нормалей
совпадают между собой. Необыкновенный луч не может претерпеть пол-
полное отражение от плоскости разреза призмы, так как пе меньше показа-
показателя преломления склеивающего вещества. Наибольший наклон необык-
необыкновенного луча, идущего сверху вниз направо (рис. 269), определяется

498
КРИСТАЛЛООПТИКА
ГЛ. VII
направлением диагонали ВС. Угол преломления для такого луча фе =
= arcsin (
(а/ЬJ), а угол падения
G7.1)
Если угол падения превышает это значение, то необыкновенный луч на
плоскость разреза не попадет, а поглотится боковой гранью АС. Подберем
теперь отношение а/Ь так, чтобы обыкновенный луч SO, падающий под
углом <р в направлении снизу вверх направо, встретил плоскость разреза
ВС под предельным углом полного отражения /3 = arcsin (n/по). Тогда
всякий обыкновенный луч, падающий снизу вверх под меньшим углом, а
Рис. 269
также приходящий сверху вниз полностью отразится от плоскости разреза
ВС. Апертура полной поляризации будет е = 2<р. Как видно из рис. 269,
/3 = — — (фе + фо), и следовательно, cos (фе + фо) = п/по. Добавив сюда
закон преломления sin (р = по sin фо = пе sin фе, получим полную систему
уравнений для нахождения искомых величин: отношения а/Ь и апертуры
2ср. Из нее находим удобные расчетные формулы:
2 \ 2 2
ТТ] + [^о - тае - 2w(w + We)] 73- ~ (П + ПеJ = О,
G7.2)
G7.3)
Они дают для канадского бальзама а/Ь = 5,32, е = 31°51 , для льняного
масла а/Ь = 4,25, е = 39°50;.
5. Решить предыдущую задачу в предположении, что слой склеиваю™
щего вещества заменен прослойкой воздуха.
Решение. Для того чтобы обыкновенный луч, падающий на грань
АВ под углом (р снизу вверх направо (рис. 270), испытал полное отражение
от плоскости разреза ВС, необходимо, чтобы угол падения на эту плоскость
превосходил предельный угол полного отражения:
а — фо
sin/3o = 1/по.
G7.4)
Для того чтобы необыкновенный луч, падающий на грань АВ под углом Lp'
сверху вниз направо, прошел через плоскость разреза ВС, необходимо, что-
чтобы он падал на ВС под углом, не превосходящим предельного угла полного
отражения:
о^ + ф'е^Ре, smf3e = ljne. G7.5)

78
АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА
499
Наибольшей апертуре призмы соответствуют в G7.4) и G7.5) знаки ра-
венства. В этом случае угол (р + (pf равен апертуре е полной поляризации
призмы. Потребовав дополнительно tp = tp , будем иметь
G7.6)
причем
simp =
: по sin фо
tga
= Пе Sin ф'е
= a/b.
, G7
G7
•7)
.8)
Отсюда могут быть найдены все
интересующие нас величины. Из
G7.6) получаем
Таким образом, углы фо, ф!е1 <р малы
и их синусы можно заменить сами-
самими углами. Это дает для апертуры
2попе ( , о ,
? = 2ш = ———————— {р — р ) = о У
G7.10)
и для отношения сторон
В
- = tg (Д, + фо) = tg
Рис. 270
2- = 0,826.
G7.11)
§ 78. Анализ поляризованного света
1. В линейной поляризации света можно убедиться с помо™
щью поляризационной призмы (николя) или любого поляризато™
ра, способного давать полностью линейно поляризованный свет.
(С целью сокращения всякий поляризатор в дальнейшем назы-
называется николем.) Для этого николь ставят на пути исследуемого
света. При вращении николя вокруг направления луча интен-
интенсивность проходящего света, вообще говоря, будет изменяться.
Если при некотором положении николя проходящий свет полно-
полностью гасится, то падающий свет был поляризован линейно.
Если падающий свет естественный или поляризован по кру-
кругу, то при вращении николя интенсивность проходящего све-
света меняться не будет. Для отличия одного случая от другого
применяется пластинка в четверть волны (короче, А/4) или
компенсатор. Пластинка в четверть волны есть кристалличе™
екая пластинка, которая вносит дополнительную разность фаз
в тг/2 между проходящими через нее лучами, поляризованны-
поляризованными во взаимно перпендикулярных плоскостях. Эти плоскости
определяют в плоскости пластинки два направления, называ-
называемые главными направлениями пластинки. Обычно пластинка

500
КРИСТАЛЛООПТИКА
ГЛ. VII
А/4 вырезается из одноосного кристалла (например, кварца) па™
раллельно его оптической оси. Тогда дополнительная разность
фаз в тг/2 вносится между обыкновенным и необыкновенным
лучами. Но пластинку А/4 можно изготовить и из двуосного
кристалла, например слюды. В дальнейшем для определенности
предполагается, что пластинка А/4 вырезана из одноосного кри-
сталла. В свете, поляризованном по кругу, разность фаз между
любыми двумя взаимно перпендикулярными колебаниями рав-
равна ±тг/2. Если на пути такого света поставить пластинку А/4,
то она внесет дополнительную разность фаз =Ьтг/2. Результи-
Результирующая разность фаз получится 0 или тг, и свет станет поляри-
поляризованным линейно. Его молено полностью погасить поворотом
николя. Если же падающий свет естественный, то он останет-
останется таковым и после прохождения через пластинку А/4. В этом
случае гашения не будет.
2. Для отличия правой круговой поляризации от левой мож-
можно воспользоваться тем же приспособлением. Допустим, что свет
распространяется вдоль оси Z по направлению к читателю, а оп-
оптическая ось пластинки А/4 ориентирована вдоль оси Y. Тогда
вектор Е в необыкновенной волне будет параллелен оси У, а в
обыкновенной — оси X. Для определенности допустим, что по-
В
N
N-
В
N
Рис. 271
ляризация правая (рис. 271), т.е. вращение вектора Е совершает-
совершается по часовой стрелке. В этом случае перед пластинкой необык-
необыкновенная волна опережает по фазе обыкновенную на тг/2 (см.
§ 62, п. 4). Если z — толщина пластинки, то после прохожде-
прохождения через нее между этими волнами возникнет дополнительная
разность фаз
Ддоп = (шг — knez) — (out ~~ knoz) = k(n0 — ne)z,
где к — волновое число в вакууме. Для отрицательного кри-
кристалла (п0 > пе, исландский шпат) Адоп = +тг/2, для поло-
положительного (п0 < пе, кварц) Адоп = ^тг/2. В первом случае

§ 78 АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА 501
полная разность хода равна А = тг, и плоскость колебаний про™
шедшего света на рис. 271 а будет направлена вдоль штриховой
биссектрисы АВ. Если первоначально главное сечение николя
проходило через оптическую ось Y пластинки А/4, то его надо
повернуть в положение NN в направлении штриховой стрелки,
т.е. в ту эюе сторону, куда вращается вектор Е в падающей
волне, чтобы полностью погасить проходящий свет. Во втором
случае А = 0 (рис. 271 б) и николь надо повернуть в противо-
противоположную сторону, т.е. против направления вращения вектора
Е в падающей волне. Если поляризация падающей волны левая,
то все вращения николя надо производить в противоположную
сторону.
Результаты можно резюмировать в виде следующего прави-
правила. Пусть в исходном положении плоскость главного сечения
николя проходит через оптическую ось пластинки А/4. Поло-
Положительным считается вращение николя вправо, отрицатель-
отрицательным — влево (если смотреть против направления распростра-
распространения света, выходящего из николя). Тогда если знаки кристал-
кристаллической пластинки А/4 и вращения николя одинаковы, то кру-
круговая поляризация левая, если эюе они разные, то правая.
8. Рассмотрим более общий вопрос: как отличить естествен-
естественный свет от света, поляризованного по кругу, и от смеси есте-
естественного света с поляризованным по кругу? Для этого поста™
вим снова на пути света пластинку в четверть волны и николь.
Если при вращении николя при любом положении пластинки
интенсивность не меняется, то свет естественный. Если ин-
интенсивность меняется и падает до нуля, то он поляризован
по кругу. Если эюе интенсивность меняется, но не падает до
нуля, то падающий свет состоит из смеси естественного с
поляризованным по кругу.
4. Допустим теперь, что падающая волна поляризована эл-
эллиптически. Если поставить николь, то при его вращении интен™
сивность проходящего света в двух положениях (отличающихся
друг от друга на 180°) будет максимальна, а в перпендикуляр-
перпендикулярных к ним положениях минимальна. Эти положения определят
направления главных осей эллипса колебаний. После этого на
пути падающего света поставим пластинку А/4, оптическая ось
которой ориентирована параллельно одной из главных осей эл-
эллипса. Тогда после прохождения через пластинку свет станет
поляризован линейно и может быть погашен поворотом николя.
При этом николь надо будет повернуть на некоторый угол от-
относительно исходного положения, когда интенсивность проходя™
щего через него света была минимальна или максимальна. Дей-
Действительно, в исходном положении главное сечение николя было
ориентировано параллельно одной из главных осей эллипса ко™
лебаний. После же прохождения через пластинку А/4 плоскость

502
КРИСТАЛЛООПТИКА
ГЛ. VII
колебаний линейно поляризованного света будет проходить че-
рез одну из диагоналей прямоугольника на рис. 236.
5. Нетрудно сообразить, как поступить, чтобы отличить друг
от друга: 1) эллиптически поляризованный свет; 2) смесь есте-
ственного света с линейно поляризованным светом (отчасти
линейно поляризованный свет); 3) смесь естественного света с
эллиптически поляризованным светом (отчасти эллиптически
поляризованный свет). Опять надо поместить на пути распро-
распространения света пластинку в четверть волны, а за ней николь.
Если вращением пластинки вокруг направления луча можно
найти такое положение, при котором свет, прошедший через нее,
можно погасить последующим вращением николя, то падающий
свет был эллиптически поляризован. Если это сделать не уда-
удается, то мы имеем дело либо со смесью естественного света с
линейно поляризованным, либо со смесью естественного света с
эллиптически поляризованным. Чтобы отличить друг от друга
эти два последних случая, на пути света ставят сначала толь™
ко один николь и устанавливают его на минимум интенсивности
проходящего света. Затем перед николем помещают пластинку
в четверть волны. Вращением пластинки и николя снова доби-
ваются минимума интенсивности. Если этот минимум интенсив-
интенсивности получается при прежнем положении николя (или при по™
вороте его на 180°), то мы имеем смесь естественного света
с линейно поляризованным. Если же для получения миниму-
минимума требуется повернуть николь на некоторый угол, — то смесь
естественного света с эллиптически поляризованным.
6. Вместо пластинки А/4 (а также пластинки А/2, внося-
вносящей дополнительную разность хода в полволны) применяются
более совершенные приспособления, называе-
называемые компенсаторами. Они также могут слу-
служить для анализа поляризации света.
Компенсатор Бабине (рис. 272) состоит из
двух слабо скошенных кварцевых клиньев I и
II, оптические оси которых взаимно перпенди-
перпендикулярны, что показано на рисунках точками и
направлением штриховки. Клин I неподвижен,
клин II может относительно него перемещать-
перемещаться вверх и вниз с помощью микрометрическо-
микрометрического винта. При таких перемещениях обращен-
обращенные друг к другу поверхности клиньев оста-
остаются параллельными. Пусть луч падает на компенсатор слева
направо перпендикулярно к его поверхности. В компенсаторе он
разделяется на обыкновенный и необыкновенный лучи, идущие
в одном направлении. Обыкновенный луч в первом клине при
вступлении во второй, очевидно, становится необыкновенным и
наоборот. В результате между колебаниями, параллельными и
Рис. 272

78
АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА
503
перпендикулярными к плоскости рисунка, возникнет дополни-
дополнительная разность фаз
Адоп = (cot — kned\ — knod,2) — (cot — knod\ — kned2) =
= k(ne — no)(d2 - rfi),
где d\ и ^2 — толщины первого и второго клиньев вдоль пересе-
кающего их луча, а к = 2тг/А — волновое число в вакууме.
Для кварца (положительный кристалл) пе > п0. В том ме-
месте, где d\ = б?2? дополнительная разность фаз Адоп равна ну-
нулю. Выше этого места величина Адоп положительна, ниже — от-
отрицательна, причем она линейно возрастает с расстоянием при
смещении луча вверх. Если на компенсатор падает параллель-
параллельный пучок линейно или эллиптически поляризованного света,
то на выходе компенсатора в разных местах полная разность
фаз А будет разной. Линии равной разности фаз имеют форму
прямых, параллельных ребрам клиньев. Выходящий свет оста-
останется поляризованным эллиптически, но форма эллипса коле-
колебаний будет другой, меняясь при переходе от одной линии рав-
равной разности фаз к другой. Когда полная разность фаз рав-
равна А = 2ттт (га = 0,1,2,...), свет будет поляризован линейно.
Если его рассматривать через надлежаще ориентированный ни-
коль, то на поверхности компенсатора появятся равноотстоящие
параллельные темные полосы. Если николь повернуть на 90°,
то полосы сместятся на полполосы, т.е. появятся там, где А =
= Bга + 1)тг. Если микрометрическим винтом перемещать клин
II, то при неизменном положении луча будет меняться и допол-
дополнительная разность фаз Адоп. Шкалу на барабане микромет-
микрометрического винта можно проградуировать таким образом, чтобы
сразу получить значение величины Адоп.
Разность фаз Адоп, вносимая компенсатором Бабине, зави-
зависит от точки вхождения падающего луча. В усовершенствован-
усовершенствованной форме, приданной компенсато-
компенсатору Солейлем A798-1878), этот недо-
недостаток устранен: все падающие лу-
лучи приобретают одну и ту же до-
дополнительную разность фаз. Как и —•
компенсатор Бабине, компенсатор
Бабине-Солейля состоит из таких
же кварцевых клиньев, но ориенти-
ориентированных оптическими осями парал-
параллельно друг другу (рис. 273). Перед
клиньями располагается плоско-параллельная кварцевая пла-
пластинка, оптическая ось которой перпендикулярна к оптической
оси клиньев. Толщина пластинки равна сумме толщин клиньев
в нулевом положении, когда они по высоте не смещены отно-
относительно друг друга. Оба клина вместе действуют как пло-
Рис. 273

504 КРИСТАЛЛООПТИКА ГЛ. VII
скопараллельная пластинка, толщину которой можно менять
микрометрическим винтом. Тем самым действие компенсатора
Бабине^Солейля сведено к действию двух кристаллических пла-
пластинок с взаимно перпендикулярными оптическими осями.
ЗАДАЧИ
1. Определить наименьшую толщину d пластинки слюды, чтобы она
могла служить пластинкой в четверть волны для желтого света натрия.
Для такого света показатели преломления волн, идущих внутри пластинки
перпендикулярно к ней, соответственно равны тц = 1,5941, П2 = 1,5887.
Сделать то же самое для кварца (по = 1,5442, пе = 1,5533).
Ответ. 1) d = ™77 г = 27 мкм: 2) d = —, г = 16,2 мкм.
4(П1 — П2) Цпе — По)
2. Смесь света, поляризованного по кругу, и естественного рассматри™
вается через кристаллическую пластинку в четверть волны и николь. При
вращении николя вокруг оси светового пучка найдено, что максимальная
интенсивность света, прошедшего через систему, в m = 3 раза превосхо-
превосходит минимальную интенсивность. Найти отношение интенсивности света
/к, поляризованного по кругу, к интенсивности естественного света 1е.
Ответ. IK/Ie = 1/2(m - 1) = 1.
3. На пути линейно поляризованного света поставлена пластинка в пол™
волны. Плоскость колебаний падающего света составляет угол а с оптиче-
оптической осью пластинки. Определить поляризацию света, прошедшего через
пластинку.
Ответ. Линейная поляризация сохранится, но плоскость колебаний
будет наклонена к оптической оси под углом /3 = —а, т.е. повернется на угол
2а. В частности, когда а = 45°, плоскость колебаний повернется на 90°.
4. Параллельный пучок монохроматического света, поляризованный по
правому кругу, падает нормально на пластинку в полволны. Найти состоя™
ние поляризации света, прошедшего через эту пластинку.
Ответ. Свет будет поляризован по левому кругу.
5. Параллельный пучок монохроматического света падает нормально
на поляроид, а затем на пластинку в полволны. Главная плоскость поля-
роида (в которой лежит электрический вектор пропускаемой им волны)
составляет угол а с осью этой пластинки. Найти состояние поляризации
прошедшего света на выходе из пластинки в полволны.
Ответ. Свет останется линейно поляризованным, но плоскость коле™
баний электрического вектора повернется на угол 2а и станет симметрично
расположенной со своим исходным положением относительно оси пластин-
пластинки в полволны.
6. Параллельный пучок монохроматического света проходит через два
николя, главные сечения которых повернуты друг относительно друга на
угол а = 20°. Между николями ставится пластинка в полволны из одно-
одноосного кристалла, вырезанная параллельно оптической оси. Какой угол /3
должна составлять оптическая ось пластинки с главным направлением пер™
вого николя, чтобы свет через эту систему не прошел?
Решение. Свет не пройдет через второй николь, если электрический
вектор перпендикулярен к главному сечению этого николя, т.е. параллелен

78
АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА
505
Рис. 274
прямой АВ, перпендикулярной к тому же сечению (рис. 274). Ось пластин™
ки должна быть ориентирована по биссектрисе угла AON\ или угла NiOB,
ему дополнительного до тг (см. предыдущую
задачу). Это дает два значения угла /3:
А = _^ + ^ = -35°, & = ? + ? =+55°.
4 2 4 2
7. Линейно поляризованная волна про™
ходит через кристаллическую пластинку,
одно из главных направлений которой со-
составляет с главным сечением поляризатора
угол (р. Разность фаз, сообщаемая пластин-
пластинкой, равна S. Найти: 1) отношение полуосей
эллипса колебаний полученного эллиптиче-
эллиптически поляризованного света; 2) угол между
главными направлениями пластинки и по-
полуосями эллипса.
Решение. Линейно поляризованный
луч по выходе из пластинки превращается в эллиптически поляризованный:
х = acos cut, у = 5 cos (out + <5),
где х и у — составляющие электрического вектора вдоль координатных
осей, совпадающих с главными направлениями пластинки. Для определе-
определения полуосей полученного эллипса найдем проекции светового вектора х
и у1 на оси координат, повернутые на угол 0 относительно первоначальной
системы:
х = a cos 0 cos out + b sin 0 cos (out + S) = A cos (out + a),
yf = —a sin 0 cos out + b cos 0 cos (out + S) = В cos (out + f3),
где А ж В — полуоси эллипса, определяющиеся уравнениями
A cos a = a cos 0 + 6 sin 0 cos 5, A sin a = b sin 0 sin <5,
В cos f3 = —a sin 0 + 6 cos 0 cos S, В sin C = b cos 0 sin S.
Отсюда
A2 = a2 cos2 0 + 62 sin2 0 + ab sin 20 cos S,
B2 = a2 sin2 0 + ft2 cos2 0 — ab sin 20 cos <f.
Складывая и вычитая эти соотношения, получим
А2 + В2=а2 + Ь2 = Д2,
А2 - В2 = (а2 - Ь2) cos 20 + 2ab sin 20 cos S,
где Д — амплитуда волны, прошедшей через поляризатор. Чтобы амплиту™
ды А и В соответствовали колебаниям вдоль осей эллипса, надо выбрать 0
так, чтобы разность А — В' была максимальной или минимальной. При-
Приравнивая ее производную нулю, из этого условия найдем
G8.1)
G8.2)
G8.3)
G8.4)
tg 29 =
'-Ъ2
cos S.
Из G8.1) находим
АВ sin (a — /3) = ^ab sin 5,
AB cos (a — /3) = ab cos 20 cos 6 —
a2 - b2
sin 26»,
G8.5)
G8.6)

506 КРИСТАЛЛООПТИКА ГЛ. VII
ABcos(a-l3) =1 a2-62
ab cos 20 cos ё 2abcos8
тт х ал (па г\ А В COS (а — /3)
Подставляя вместо tg26> его значение из G8.5), получаем =
ab cos 2$ cos о
= 0, откуда cos (а — /3) = 0, (а — /3) = =Ьтг/2. Следовательно, из первого
уравнения G8.6) имеем /Ш = zLab sine. Так как Ь/a = tg(f, то
а2 ~~ Ь2 п 2аЬ
Таким образом, уравнение G8.5) получит следующий вид:
tff 26» = 1
Этим уравнением и определяется угол в между главными направлениями
пластинки и осями эллипса. Для второго неизвестного введем обозначение
В/А = tgl и воспользуемся формулой sin 21 = 2tg 1/A + tg2 I). Тогда по™
лучим
2АВ 2absinS
8. На кристаллическую пластинку, вырезанную параллельно оптиче-
оптической оси, падает нормально свет, поляризованный по кругу. Прошедший
свет рассматривается через анализатор.
1) Пренебрегая потерями света на отражение, определить интенсив™
ность прошедшего света, если главное сечение анализатора составляет угол
а с одним из главных направлений пластинки. 2) Под каким углом надо
поставить анализатор, чтобы получить максимальную и минимальную ин-
интенсивности?
Решение. 1) Если свет поляризован по кругу, то слагающие коле-
колебания по координатным осям могут быть представлены в виде
х = a cos wt, у = a sin uot.
После прохождения через кристаллическую пластинку, сообщающую раз-
разность фаз 5, уравнения колебаний перейдут в
x = acosoutJ у = a sin (uot + 6).
При выходе из анализатора результирующее колебание будет
? = a cos a cos out + a sin a sin (ut + S) =
= a(cos a + sin a sin S) cos out + a sin a cos 5 sin out.
Отсюда получаем для интенсивности
I = a {(cos a + sin a sin S) +(sinacos«5) } = a A + sin 2a sin S).
2) При постоянном 6 интенсивность достигает максимума или мини-
минимума, когда cos 2а = 0, т.е. при а = 1/47Г53А7Г- Если sin^ > 0, то первому
значению соответствует максимум, а второму — минимум; при sin^ < 0 —
наоборот.
9. Клин из двоякопреломляющего вещества помещен на пути монохро-
монохроматического света, поляризованного по кругу. Оптическая ось параллель-
параллельна ребру клина. Описать картину, наблюдаемую через николь, когда клин

§ 78 АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА 507
неподвижен и когда он поворачивается вокруг направления распространен
ния света.
Решение. Согласно предыдущей задаче интенсивность света, про-
прошедшего через анализатор,
I = а A + sin 2а sin 6).
Если sin 2а > 0, то при постоянном а интенсивность минимальна, когда
sin <5 = — 1, т.е. при <5 = Зтг/2, 7тг/2,...,
и максимальна, когда
sin? = l, т.е. при ? = тг/2, 5тг/2, 9тг/2,...
Если же sin 2а < 0, то в первом случае будет максимум, а во втором —
минимум интенсивности. Во всех случаях в поле зрения будут видны чере-
чередующиеся светлые и темные полосы. При вращении клина будет меняться
угол а, а с ним и интенсивность в каждой точке клина. При углах а = 90,
180 и 270° весь клин будет освещен равномерно, а при углах а = 45, 135,
225, 315° будет наблюдаться наибольший контраст темных и светлых полос.
При переходе через углы а = 90, 180, 270° темные полосы будут переходить
в светлые, а светлые — в темные.
10. Два когерентных пучка квазимонохроматического ыеполяризоваы-
ного света равной интенсивности дают на экране интерференционные по-
полосы. Какой толщины кристаллическую пластинку надо ввести на пути од-
одного из этих пучков, чтобы интерференционные полосы исчезли и притом
так, чтобы их нельзя было восстановить никакой стеклянной пластинкой,
вводимой в другой пучок? Как изменится картина, если за кристаллической
пластинкой поставить поляроид? При каком положении поляроида интер-
интерференционных полос не будет?
Решение. Разложим мысленно световую волну на две составляющие,
электрические векторы которых взаимно перпендикулярны и параллельны
главным осям пластинки. При введении пластинки интерференционные по-
полосы от каждой составляющей сместятся. Если введенная пластинка явля-
является пластинкой в полволны, то разность смещений составит половину ши-
ширины полосы. В этом случае при введении пластинки интерференционные
полосы пропадут. При введении поляроида они появятся вновь. Исключе-
Исключение составляет случай, когда оси поляроида наклонены под углом 45° к
осям пластинки. В этом случае интерференционные полосы наблюдаться
не будут.
11. Плоская световая волна эллиптически поляризована. Длины полу-
полуосей эллипса колебаний равны соответственно а и Ь. Какую кристалличе-
кристаллическую пластинку надо поставить на пути распространения волны и как на-
надо ориентировать эту пластинку, чтобы получить свет, поляризованный по
кругу: 1) с тем же направлением вращения; 2) с противоположным направ-
направлением вращения?
Решение. В системе главных осей X, У" эллиптическое колебание
представляется уравнениями Ex = a cos cut, Еу = b sin out (рис. 275). Перей-
Перейдем к новой системе ?, rj, оси которой являются биссектрисами прежних
координатных углов. В этой системе то же колебание представится в виде
Е% = —=. (a cos out + Ь sin out) = у о cos (out —
л/2
Ev = —={—а cos out + 6sina;t) = \j ——l—^— cos [out — (тг —
2

508
КРИСТАЛЛООПТИКА
ГЛ. VII
где (р — острый угол, определяемый уравнением tg 99 = Ь/а. Колебания
вдоль осей ? и 77 совершаются с одинаковыми амплитудами у (а2 +Ь2)/2,
причем колебание вдоль оси ? опережает по фазе колебание вдоль оси rj на
угол S = тг — 2(р. Внесем кристалли-
кристаллическую пластинку, чтобы ее оси были
ориентированы вдоль ? и 7] и чтобы
она изменила разность фаз до ±тг/2.
Для этого должно быть выполнено со-
соотношение
(U)t-(p-ksl)-(ujt-7r + (p-kr,l) = ±7г/2,
откуда
l = 2у?-7Г±7г/2 = лУ?/7Г-72±74
ft г? ft,
Тогда волна перейдет в волну, поляри-
гис. 2@ зованную по кругу. Знаку плюс соот-
соответствует то же направление вращения, что и в исходной эллиптически
поляризованной волне, а знаку минус — противоположное. Такой же ре-
результат получится, если толщину пластинки изменить на т\/(п^ —щ), где
т — целое число.
§ 79. Интерференция поляризованных лучей
1. Явления интерференции поляризованных лучей в истории
оптики имели большое значение для выяснения фундаменталь-
фундаментального вопроса о природе световых колебаний. Они исследовались
в классических опытах Френеля и Араго A816 г.). Конечно, лу-
лучи от независимых источников света интерферировать не бу™
дут, даже если они предварительно пропущены через поляри-
поляризационное приспособление. Для интерференции необходима ко-
зерентность. Однако, как видно из формулы B6.2), результат
интерференции линейно поляризованных лучей зависит от угла
между плоскостями световых колебаний. Интерференционные
полосы наиболее контрастны, когда плоскости колебаний парал-
параллельны. Интерференция никогда не наблюдается, если волны
поляризованы во взаимно перпендикулярных плоскостях. Это
впервые было установлено в упомянутых выше опытах Френеля
и Араго. Отсюда Френель пришел к заключению о поперечно-
сти световых колебаний (см. § 26, п. 5).
2. Одна из возможных схем для исследования интерферен-
интерференции поляризованных лучей изображена на рис. 276. Лучи от
первичного источника света S проходят через поляроид П или
другое поляризационное приспособление. Вторичные когерент-
когерентные источники S\ и S2 получаются одним из способов, приме-
применяемых для осуществления двухлучевой интерференции. Исхо-
Исходящие из них пучки поляризованы в параллельных плоскостях.

79
ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ
509
На пути одного из пучков вводится полуволновая кристалличе-
кристаллическая пластинка К. В другом пучке для компенсации возникшей
разности хода помещается стеклянная пластинка Р надлежащей
толщины. Стеклянная пластинка, конечно, не меняет направле-
направления колебаний проходящей через нее линейно поляризованной
волны. Кристаллическая пластинка действует так же только в
том случае, когда ее оптическая ось параллельна или перпенди-
перпендикулярна к плоскости колебаний. В этом случае из пластинок К и
Р выходят одинаково поляризованные когерентные пучки света.
Направления колебаний в этих пучках изображены на рис. 276
совпадающими векторами Ei и Е2.
Рис. 276
Если повернуть пластинку К вокруг ее нормали на угол а,
то вектор Ei повернется на угол 2а и перейдет в положение
Е]_ (см. задачу 5 к предыдущему параграфу). Таким образом,
можно исследовать интерференцию при различных значениях
угла 2а между плоскостями колебаний интерферирующих волн.
Интерференционную картину можно получать на экране Э,
а также наблюдать без экрана с помощью лупы или зрительной
трубы. В дальнейших пояснениях плоскость экрана принима-
принимается за координатную плоскость XY1 направление оптической
оси пластинки К — за ось У, а нормаль к экрану, проведенная в
сторону распространения света, — за ось Z. Следовательно, при
повороте пластинки К будет поворачиваться и ось Y.
От наложения линейно поляризованных монохроматических
волн везде, в том числе и на экране Э, возникнет эллиптическая
поляризация света. При неизменном угле между плоскостями
колебаний форма и ориентация эллипса колебаний будут изме-
изменяться с изменением разности хода между интерферирующими
лучами. При определенных значениях разности хода эллипти-

510 КРИСТАЛЛООПТИКА ГЛ. VII
ческие колебания могут вырождаться в линейные. Поверхности
(а на экране — линии) равной разности хода являются в то же
время поверхностями (линиями) одинаковых и одинаково ори™
ентированных эллипсов колебаний.
Разложим, например, в описанной выше установке все ко-
колебания по осям X и Y. В центре экрана О ^составляющие
векторов Е^ и Е2 направлены в одну сторону, т.е. колебания
вдоль оси Y совершаются в фазе. Составляющие тех же векто-
векторов вдоль оси X направлены противоположно — вдоль этой оси
колебания противофазны и взаимно гасят друг друга. В резуль-
результате в точке О, а также во всякой точке оси X получится линей™
ное колебание параллельно оси Y. Если сместиться параллельно
оси Y на половину ширины интерференционной полосы, то х-
колебание станет синфазным, а у-колебание противофазным. Ре-
Результирующее колебание также будет линейным, но уже вдоль
оси X. В промежуточных точках из-за разности хода между лу-
лучами полного гашения не будет ни для ж-, ни для у-колебания.
Однако одно из этих колебаний всегда будет сдвинуто относи-
относительно другого по фазе на тг/2: результирующее колебание —
эллиптическое с главными осями эллипса, параллельными ко-
координатным осям X и Y.
3. Эллиптический характер поляризации проявляется при
наблюдении через николь. Если николь пропускает колебания,
параллельные оси У, то на экране получаются интерференци-
интерференционные полосы, параллельные оси X. Центральная полоса, про-
проходящая через центр О экрана (где разность хода равна нулю),
будет светлой. При повороте николя на 90° эти полосы гасят-
гасятся. Зато появляется другая система интерференционных полос,
сдвинутая относительно предыдущей на половину ширины по-
полосы. В ней, следовательно, центральная полоса будет темной.
Таким образом, поворот николя на 90° из указанного исходного
положения приводит к замене светлых полос темными и наобо-
наоборот.
То же, в частности, будет, когда поляризация круговая (т.е.
когда в нашей интерференционной установке кристаллическая
пластинка К повернута из своего исходного положения на угол
а = 45°). Тогда интерференционные полосы, как они воспри-
воспринимаются глазом, будут иметь один и тот же вид при любой
ориентации николя. При вращении николя полосы непрерывно
перемещаются параллельно самим себе. При повороте на 90°
это перемещение составляет половину ширины полосы. Направ-
Направление колебаний изменяется также на 90°. Если убрать николь,
то произойдет наложение двух сдвинутых на полполосы неко-
некогерентных интерференционных картин со взаимно перпенди-
перпендикулярными колебаниями. Это даст равномерную освещенность
экрана, в соответствии с тем, что волны со взаимно перпенди-

§ 79 ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ 511
кулярными колебаниями никогда не интерферируют. Таким об™
разом, поворот плоскости колебаний одного из линейно поляри-
поляризованных лучей на 90° (осуществляемый, например, вращением
кристаллической пластинки К) существенно меняет распреде-
распределение освещенности на экране. При отсутствии такого поворота
на экране видны полосы интерференции. При наблюдении через
николь их интенсивность изменяется; полосы пропадают, когда
колебания перпендикулярны к главному сечению николя. При
наличии же поворота плоскости колебаний одного из лучей на
90° и отсутствии николя никаких интерференционных полос не
наблюдается. Зато они появляются при наблюдении через ни™
коль и непрерывно перемещаются параллельно самим себе при
его вращении, причем при повороте николя на 90° это переме-
перемещение равно половине ширины полосы.
Если опыт производить в неполяризованном свете (т.е. уб-
убрать поляроид П), то введение кристаллической пластинки, по™
верну той на любой угол, конечно, оставляет естественным свет,
проходящий через нее. Однако, как указал и подтвердил свое за™
ключение на опыте СИ. Вавилов, при этом также должна пре-
претерпеть изменения интерференционная картина на экране. Это
объясняется тем, что и после введения кристаллической пла-
пластинки лучи не остаются независимыми, а определенным обра™
зом скоррелированы между собой.
В самом деле, падающий естественный свет можно предста-
представить в виде суперпозиции линейно поляризованных некогерент™
пых волн с всевозможными направлениями плоскости колеба-
колебаний. Возьмем одну из таких волн. При наличии кристалличе™
ской пластинки К и при наблюдении через николь N на экране
получатся интерференционные полосы, описанные выше. Суще™
ственно, что положение полос не зависит от угла между плоско-
плоскостями колебаний интерферирующих волн. Значит, все линейно
поляризованные компоненты, на которые разложена падающая
волна, дадут совпадающие по положению интерференционные
картины. А так как эти картины некогерентны, то их наложе-
наложение приведет только к взаимному усилению интерференционных
полос. При вращении николя, ввиду статистической изотропии
естественного света относительно всех направлений, перпенди-
перпендикулярных к лучу, вид интерференционных полос изменяться не
будет. Будет происходить лишь перемещение полос параллель-
параллельно самим себе, как при круговой поляризации, описанной выше.
При повороте николя на 90° светлые полосы заменятся темными
и наоборот. Не то будет, когда нет кристаллической пластинки.
В этом случае в отсутствие николя интерференционные полосы
наблюдаться будут. Однако при введении николя интенсивность
полос уменьшится вдвое. Вращение же николя вообще не сказы™
вается на положении и интенсивности полос.

512
КРИСТАЛЛООПТИКА
ГЛ. VII
Рис. 277
4. Важный случай интерференции осуществляется при про™
хождении через кристалл поляризованного света. Пусть на пло-
плоскопараллельную кристалличе-
кристаллическую пластинку падает волна под
углом ip (рис. 277). В кристалле
она разделяется на две волны,
распространяющиеся в разных
направлениях и с различными
скоростями. Пусть АВ и АС —
волновые нормали этих волн,
а ф\ и ф2 — соответствующие
им углы преломления. В кри-
кристалле направления волновых
нормалей не совпадают. Вне
кристалла различие между этими
направлениями пропадает. Из
кристалла выходят два луча 1
и 2, параллельные падающему
и поляризованные в перпенди-
перпендикулярных плоскостях. Оптическая разность хода между ними
представляется выражением
А = (ACD) - (АВ) =n2-AC + CD-m- AB,
где ni и П2 — показатели преломления рассматриваемых волн,
a D — основание перпендикуляра, опущенного из точки В на
луч 2. Если h — толщина пластинки, то
АС = /г/cos ^25 АВ = h/ cos ф\, CD = h(tgt/ji — tgt/^) sin ср.
По закону преломления sine/? = щтпфх = r^slni/^- Используя
эти выражения, получим
А = h(ri2 cost/^ — n\ cost/^i). G9.1)
Разность хода А между лучами 1 и 2 обусловлена двумя обсто-
обстоятельствами: 1) различием показателей преломления п\ и п2] 2)
различием углов преломления ф\ и ф2. Второе обстоятельство
играет малую роль. В большинстве случаев им можно прене-
пренебречь и пользоваться приближенным выражением
А = НсоБф(п2 -ni), G9.2)
где угол ф имеет любое промежуточное значение между углами
преломления ф\ и ф2.
5. Разность хода А можно использовать для получения ин-
интерференции лучей t ж 2. Если бы свет, падавший на кристал-
кристаллическую пластинку, был естественный, то интерференция бы-
была бы невозможна, так как в этом случае лучи 1 и 2 не были
бы коррелированы между собой. Для получения коррелирован-
коррелированных лучей 1 ж 2 падающий свет должен быть поляризован —

79
ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ
513
линейно или эллиптически. Но и в этом случае при наложении
лучей 1 ж 2 интерференция все же не возникнет, так как лучи
1 и 2 поляризованы во взаимно перпендикулярных плоскостях.
Нужно свести колебания в этих лучах к одному направлению,
т.е. предварительно пропустить их через николь. В случае пло-
плоскопараллельных пластинок лучи сводятся вместе в фокальной
плоскости линзы — получаются полосы равного наклона. В слу-
случае тонких пластинок переменной толщины наблюдаются поло-
полосы равной толщины, локализованные на самих пластинках.
Схема для получения так называемой интерференции в па~
раллельных лучах приведена на рис. 278. Кристаллическая пла-
пластинка К вводится между поляризатором Р и анализатором А.
Линейно поляризованный свет, выйдя из поляризатора Р, после
р
к
А
Рис. 278
прохождения через кристаллическую пластинку К превраща-
превращается в поляризованный эллиптически, а затем проходит через
анализатор А, превращаясь снова в линейно поляризованный.
Интенсивность проходящего света зависит от ориентации ана™
лизатора. При вращении последнего интенсивность / будет ме-
меняться.
Разность фаз, возникающая при прохождении света через
кристаллическую пластинку, равна 2тгА/А, т.е. зависит от дли™
ны волны А. При неподвижном анализаторе она различна для
разных длин волн. По этой причине интерференционная карти-
картина получается окрашенной. При вращении анализатора окраска
меняется. При повороте анализатора на 90° окраска меняется
на дополнительную — светлые места становятся темными и на-
наоборот. Если главные сечения поляризатора и пластинки парал-
параллельны или перпендикулярны между собой, то через пластинку
проходит только один луч. Ему не с чем интерферировать, и
окрашивание пропадает. Все эти явления получили физически
не совсем удачное название хроматической поляризации. Она
была открыта Араго в 1911 г.
Обычно главные сечения поляризатора и анализатора уста-
устанавливаются параллельно (николи параллельны) или перпенди™
кулярно (николи скрещены) друг к другу. В последнем случае
установка весьма чувствительна к обнаружению анизотропии.
Через два скрещенных николя свет не проходит (поле зрения
темное). Если же между ними ввести какое-либо анизотропное
17 Д.В. Сивухин

514 КРИСТАЛЛООПТИКА ГЛ. VII
тело, то далее при наличии слабой анизотропии система начина-
начинает пропускать свет (поле зрения просветляется).
Для количественного расчета примем главные направле™
ния кристаллической пластинки за координатные оси X и Y
(рис. 279). Пусть поляризатор пропускает колебания только в
направлении Р, а анализатор — толь™
ко в направлении А. Углы между эти-
этими направлениями и осью X обозначим
соответственно через а и /3. Амплиту-
Амплитуду света, вышедшего из поляризатора,
примем за единицу. Тогда по выходе из
пластинки амплитуда световых колеба-
колебаний вдоль оси X будет cos a, a вдоль оси
— Y — sin а. Из этих колебаний анализа™
тор пропустит колебания с амплитуда™
Рис 279 ми ai = cos a cos/3 и «2 = sin а sin/3 со-
соответственно, причем в результате про™
хождения через пластинку между обоими колебаниями возник-
возникнет разность фаз 6. От сложения обоих колебаний получится
колебание, амплитуда а которого определяется соотношением
2 2 2 г* с / \2 л 2 $
а = a-i + «о + ^tt]tt2 cos о = [ал + ао) ~~ шшо sin -.
2
После подстановки значений «i и «2, приведенных выше, для
интенсивности света, проходящего через анализатор, получим
I = cos2(/3 - а) - sin 2a sin 2/3 sin2 i. G9.3)
В этой формуле в сочетании с формулой G9.1) содержит™
ся объяснение всех особенностей интерференции поляризован-
поляризованного света в параллельных лучах. Пока свет монохроматичен,
а толщина пластинки всюду одинакова, все величины в G9.3)
постоянны, так что получается равномерная освещенность пла-
пластинки. При повороте поляризатора или анализатора на 90° вы-
выражение G9.3) переходит в
/' = sin (/3 — а) + sin 2a sin 2/3 sin -.
Следовательно, I + I1 = 1. Это очевидно и из общих соображе-
соображений, так как при указанном повороте весь свет, пропускавшийся
ранее, будет задержан, а задержавшийся начнет проходить. В
частном случае, когда николи параллельны (а = /3),
I = 1 _ sin2 2a sin2 ^, G9.4)
а когда скрещены —
' I G9.5)

79
ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ
515
В белом свете, если его разложить на спектральные состав™
ляющие, первое слагаемое в G9.3) остается постоянным, а вто-
второе зависит от длины волны и приводит к окрашиванию поля
зрения. Если направление Р совпадает с одним из главных на™
правлений пластинки (а = 0 или а = тг/2), то I = cos2(/3 — о),
т.е. интенсивность / постоянна и не зависит от длины волны. В
этом случае, как было уже отмечено выше, интерференции нет,
и в белом свете получается равномерно освещенное неокрашен-
неокрашенное поле. Интенсивность его можно менять поворотом николя-
анализатора А, но оно все время остается белым.
6. Более сложные явления наблюдаются при интерференции
сходящихся поляризованных лучей. Обычно применяемая схема
для наблюдения таких явлений представлена на рис. 280. Парал™
Lj F
Рис. 280
о
лельный пучок линейно поляризованного света линзой L\ пре-
превращается в сходящийся и концентрируется на кристаллической
пластинке К. После прохождения через пластинку К каждый
луч разделяется на два параллельных луча, между которыми
возникает разность хода. При наложении таких лучей свет ста-
становится поляризованным эллиптически, причем разность хода
между лучами, а с ней и характер эллиптической поляризации
зависят от угла наклона падающего луча. Линза L2, одинаковая
с Li, делает лучи снова параллельными. Распределение светово™
го поля в фокальной плоскости FF линзы проецируется объек-
объективом О и николем-анализатором А на экран, где и наблюдается
интерференционная картина.
Чтобы составить представление о форме получающихся ин-
интерференционных полос, введем понятие изохроматической по-
поверхности (поверхности одинакового цвета). Возьмем в неогра-
неограниченной кристаллической среде произвольную точку О и пред-
представим, что через нее во всевозможных направлениях и притом
в одинаковых фазах проходят плоские волны. В каждом направ-
направлении волновой нормали распространяются две волны, линейно
поляризованные во взаимно перпендикулярных плоскостях. На
расстоянии г от точки О между ними возникнет разность хо-
хода А = (п2 — п{)г, где п\ ж П2 — показатели преломления этих
волн. Фиксировав А, будем откладывать на волновых нормалях
отрезки с длиной г = А/(п2 —п\). Геометрическое место концов
17*

516
КРИСТАЛЛООПТИКА
ГЛ. VII
Рис. 281
таких отрезков есть поверхность равной разности фаз между
волнами, которые могут распространяться вдоль одной и той
лее волновой нормали. Она и называется изохроматической по-
поверхностью. Придавая А всевозможные значения, получим се-
семейство изохроматических поверхностей с общим центром О.
Линии, получающиеся от сечения такого семейства плоскостя-
ми, называются изохроматическими линиями, или изохрома-
тами. Очевидно, изохроматы есть линии постоянной разности
фаз между соответствующими вол™
нами, могущими распространять-
распространяться вдоль одной и той же волновой
нормали.
Для одноосного кристалла изо-
изохроматическая поверхность есть
поверхность вращения вокруг оп-
оптической оси (рис. 281). В направ-
направлении оптической оси она уходит в бесконечность, так как для
этого направления оба показателя преломления п\ и П2 совпа-
совпадают. В двуосных кристаллах таких направлений два (рис. 282).
Это есть оптические оси, точнее —
оси нормалей (см. § 80). Мы не
будем заниматься выводом уравне-
уравнения изохроматической поверхности,
а ограничимся качественными со-
соображениями .
Напомним, что интерферирую-
интерферирующие волны возникают при двойном
преломлении одной и той же пада-
падающей волны. Волновые нормали по-
получившихся двух волн внутри кри-
кристаллической пластинки несколько
отличаются друг от друга по на-
направлению. Однако таким различи-
различием мы пренебрежем, как это уже де-
делалось при замене точной формулы
G9.1) приближенной G9.2). В этом приближении, как показы-
показывается ниже, интерференционные полосы можно отождествить
с определенным семейством изохромат. В самом деле, предста-
представим, что на передней плоскости кристаллической пластинки К
(см. рис. 280) помещена маленькая диафрагма. (В такой диа-
диафрагме нет надобности, если задний фокус линзы L\ находится
на передней поверхности пластинки.) Примем центр этой диа-
диафрагмы за центр О семейства изохроматических поверхностей.
Задняя плоскость пластинки К пересечет это семейство вдоль
изохроматических линий. Последние в указанном выше прибли-
приближении будут совпадать с интерференционными линиями на зад-
Рис. 282

§ 79 ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ 517
ней поверхности пластинки К. Если оптическая система дает
изображение этой поверхности на экране, то при этом получит-
получится и подобное изображение рассматриваемой системы интерфе-
интерференционных линий. При иной фокусировке, из™за преломления
волновых нормалей при выходе из пластинки К^ полного по-
подобия между изохроматами и интерференционными линиями
на экране не будет. Однако это обстоятельство не сказывает-
сказывается существенно на виде интерференционных полос. Изохроматы
практически всегда качественно верно передают форму интер-
интерференционных полос.
Форма изохромат и интерференционных полос определяет-
определяется симметрией кристалла и ориентацией его оптических осей.
На рис. 283 показаны интерференционные полосы в случае пла-
пластинки одноосного кристалла, вырезанной перпендикулярно к
оптической оси. В соответствии с осевой симметрией они име-
имеют форму концентрических кругов. Картина получена в скре-
скрещенных николях. Кольца пересечены темным крестом. Проис-
Происхождение его весьма простое. На пластинку К падает линейно
поляризованный свет. Рассмотрим плоскость главного сечения и
Рис. 283 Рис. 284
плоскость, перпендикулярную к ней. Пусть обе плоскости пере-
пересекаются вдоль оси вращения системы. Лучи в этих плоскостях
не испытывают двойного преломления, интерференции в таких
лучах не возникает. После прохождения через пластинку обе си™
стемы лучей остаются линейно поляризованными с сохранени-
сохранением прежнего направления колебаний. Лучи с такими колебания™
ми гасятся николем-анализатором. Вокруг прямых, по которым
рассматриваемые плоскости пересекаются с плоскостью экрана,
и формируется темный крест. Если николи перевести в парал-
параллельное положение, то вся картина сменяется дополнительной,
в частности, черный крест заменяется белым.

518
КРИСТАЛЛООПТИКА
ГЛ. VII
Если в предыдущем опыте пластинку К заменить двумя ело™
женными вместе пластинками из правого и левого кварца, вы-
вырезанными перпендикулярно к оптической оси, то получают-
получаются спиралеобразные интерференционные картины, называемые
спиралями Эйри (рис. 284). Их происхождение связано с тем,
что кварц вращает плоскость поляризации. Для правого квар-
ца это вращение происходит в одну сторону, а для левого — в
противоположную.
На рис. 285 показан вид изохромат для пластинки одноос-
одноосного кристалла, вырезанной параллельно оптической оси, а на
рис. 286 — для пластинки двуосного кристалла, вырезанной пер™
пендикулярно к биссектрисе угла между оптическими осями.
И-...»-
Рис. 285
Рис. 286
7. Интерференция поляризованных лучей дает удобный и
чувствительный метод обнаружения и исследования оптической
анизотропии тел во всех случаях, когда она мала. Для этого
обычно применяется установка в параллельных лучах с скре-
щенными николями, схематически изображенная на рис. 278.
Вместо кристаллической пластинки ставится исследуемый об-
образец. В отсутствие образца свет через систему не проходит.
При введении образца, обладающего анизотропией, поле зрения
просветляется и в случае белого света становится окрашенным.
Таким методом исследуются различные случаи искусственной
анизотропии.
Брюстером в 1815 г. было открыто двойное преломление при
механических деформациях изотропных тел. Среда может со-
состоять из анизотропных молекул. В отсутствие деформаций они
ориентированы хаотически, вследствие чего среда макроскопи-
макроскопически изотропна. При деформациях может возникнуть преиму-
преимущественная ориентация и изменение расположения молекул в
пространстве. Это и ведет к возникновению двойного преломле-

§ 79 ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ 519
ния. В простейшем случае одностороннего растяжения или сжа-
сжатия тело ведет себя как одноосный кристалл с оптической осью
вдоль растяжения или сжатия. Как показали опыты, разность
по — пе между обыкновенным и необыкновенным показателя-
показателями преломления пропорциональна приложенному напряжению,
а коэффициент пропорциональности зависит от длины волны.
Эффект сохраняется и при остаточных деформациях. Он при-
применяется для исследования упругих напряжений и остаточных
деформаций в телах. Двойное преломление возникает при тече-
течении жидкостей с анизотропными молекулами (эффект Максвел-
Максвелла), а также при внесении тел в электрическое или магнитное
поля (см. § 90 и 91).
ЗАДАЧИ
1. Почему никогда не может получиться интерференция обыкновенного
и необыкновенного лучей, вышедших из пластинки двоякопреломляющего
кристалла, настолько тонкой, что она не дает заметного разделения лучей?
2. Почему демонстрационные опыты по интерференции поляризован™
ных лучей удобнее делать с тонкими, а не с толстыми пластинками? По-
Почему даже с тонкими пластинками из исландского шпата трудно получить
интерференционную картину в белом свете?
Ответ. У исландского шпата очень велика разность обыкновенного
и необыкновенного показателей преломления, так что даже в тонких пла-
пластинках получаются большие разности хода, при которых интерференция
в белом свете невозможна.
3. Две толстые пластинки одноосного кристалла, одинаково ориентиро-
ориентированные и весьма мало отличающиеся по толщине, в скрещенных николях
дают порознь белый свет. Почему в тех же условиях может получиться
окрашивание, если повернуть одну пластинку относительно другой на 90°?
Решение. Когда пластинки одинаково ориентированы, вносимая
ими разность хода велика, т.е. соответствует высокому порядку интерфе-
интерференции. В таких условиях интерференция в белом свете наблюдаться не
может. Если одну из пластинок повернуть относительно другой на 90°, то
вносимая ими разность хода будет такая же, какая вносится пластинкой с
толщиной, равной разности толщин рассматриваемых пластинок. При ма-
малой разности толщин разность хода может сделаться настолько малой, что
станет возможна интерференция в белом свете.
4. Кварцевая пластинка толщиной в 1 мм вырезана перпендикулярно
к оптической оси. Как определить, из право- или левовращающего кварца
сделана пластинка, имея в своем распоряжении два николя и источник:
1) монохроматического света; 2) белого света?
Ответ. 1) Если поместить пластинку кварца, вырезанную перпенди-
перпендикулярно к оптической оси, между скрещенными николями и осветить си-
систему монохроматическим светом, то она будет пропускать свет; повернув
анализатор на угол, меньший 90°, можно снова погасить свет. Если при этом
наблюдатель должен вращать анализатор по направлению часовой стрел-
стрелки, то кварц будет правовращающий, если же против часовой стрелки, то
левовращающий.
2) Если осветить систему белым светом, то пластинка будет казать-
казаться окрашенной. Вращательная способность увеличивается с уменьшением

520 КРИСТАЛЛООПТИКА ГЛ. VII
длины волны. Поэтому если вращать анализатор по часовой стрелке, то
для правовращающего кварца окраска будет меняться в сторону коротких
длин волн спектра. Для левовращающего кварца порядок изменения окрас-
окраски будет обратный.
§ 80. Нормальные скорости и поляризация волн
в двуосных кристаллах
1. Перейдем теперь к исследованию распространения волн в
оптически двуосных кристаллах. В общем случае вектор D мо-
может зависеть не только от вектора Е, но и от его пространствен™
ных производных. Это явление называется пространственной
дисперсией (см. § 96). В слабых полях такая зависимость, ко-
конечно, может считаться линейной. Для плоских монохромати™
ческих волн дифференцирование Е по координатам ж, у, z сво-
сводится к умножению его проекций на —ikXi —ikyi —ikz. В этом
случае зависимость от пространственных производных можно
учесть прежней формулой G5.2), если диэлектрический тензор
Ещ считать комплексным. Формально так можно поступать и в
случае неплоских волн. Однако волны должны предполагаться
монохроматическими.
Для непоглощающих сред диэлектрический тензор должен
быть эрмитовым, т.е. ещ = ?%. Действительно, для производ-
производной плотности электромагнитной энергии и по времени электро-
электродинамика дает
? = -L(Ei>+HB)
(см. т. III, § 84). В случае монохроматического поля в непогло™
щающей среде среднее значение этой производной, согласно за-
закону сохранения энергии, должно равняться нулю. Если поль-
пользоваться комплексной формой монохроматического поля, то это
условие запишется в виде (ED* + НВ*) + компл. сопр. = 0. А
так как мы пренебрегаем различием между В и Н, то ED* +
+ компл. сопр. = 0. Отсюда с учетом соотношений D =
D* = -гсЛЭ* получаем: ED* - E*D = 0, или
Заменим в первой сумме немой индекс а на /5 и наоборот. Тогда
а/? - 4а)ВД = 0.
Это соотношение должно выполняться для любого поля Е, что
возможно тогда и только тогда, когда Еар = eL. Действитель-
Действительно, пусть все компоненты вектора Е, за исключением одной Еа,

§ 80 ВОЛНЫ В ДВУОСНЫХ КРИСТАЛЛАХ 521
равны нулю. Тогда предыдущее соотношение переходит в (еаа —
— е^а)ЕаЕ^ = 0, откуда еаа = е*а. Пусть теперь отличны от ну-
нуля две компоненты Еа и Ер, а третья компонента равна нулю.
Тогда
(еар - е}а)Е*аЕр + (ера - е*ар)ЕаЩ = 0.
Полагая здесь Еа = Ер, получим
Полагая лее Ер = гЕа, найдем
(?аC — ?*ра) — (?/За ~ ?*ар) = 0.
Из этого и предыдущего соотношений следует: еар = Йа. Таким
образом, соотношение еар = 6L справедливо как для одинако-
одинаковых, так и для разных индексов а и /3, т.е. для непоглощающих
кристаллов тензор еар эрмитов. Для поглощающих кристаллов
он не эрмитов.
Допустим теперь, что среда не обладает пространственной
дисперсией или этим явлением, ввиду его малости, можно пре-
пренебречь. Тогда величины еар вещественны, а потому еар = вра1
т.е. тензор еар будет симметричен. В дальнейшем мы ограни-
ограничимся этим случаем. Кроме того, будем предполагать, что все
диагональные элементы еаа положительны. Только тогда сре-
среда будет прозрачной^ т.е. плоские волны в ней будут распро-
распространяться без затухания. В противном случае возникнет зату-
затухание без поглощения, как это имеет место, например, в плазме
(см. § 87).
Всякий симметричный тензор можно привести к так назы-
называемому диагональному виду, т.е. найти такую систему пря-
прямоугольных координат, в которой недиагональные компоненты
тензора обращаются в нуль. Диагональные компоненты тензо-
тензора в этой системе координат условимся обозначать через еХ1 еу1
eZj т.е. характеризовать их не двойными, а только единичными
индексами ж, у, z. В рассматриваемой системе материальные
уравнения имеют вид
Da = eaEa. (80.1)
Координатные оси, относительно которых тензор еар диа-
диагоналей, называются главными осями тензора или диэлектри-
диэлектрическими осями кристалла, а величины еж, еу, ez — главными
диэлектрическими проницаемостями. Эти оси мы и примем за
координатные оси, причем названия осей X, У, Z установим так,
чтобы соблюдались неравенства
ex^sy^ez. (80.2)
Так как компоненты тензора еар могут зависеть от дли-
длины волны А, могут зависеть от А и направления диэлектри-

522 КРИСТАЛЛООПТИКА ГЛ. VII
ческих осей. Это явление, называемое дисперсией диэлектри-
диэлектрических осей^ действительно встречается в триклинных и моно-
моноклинных кристаллах, характеризующихся наиболее низкой сим™
метрией.
Отметим, наконец, что угол а между векторами Е и D все-
всегда острый. Это вытекает из того, что скалярное произведение
(ED) = ED cos а пропорционально плотности электрической
энергии, а она существенно положительна.
2. Обратимся теперь к исследованию плоских волн G5.3) в
прозрачных кристаллах в общем виде. Фиксируем направление
волновой нормали N и определим, какие плоские волны могут
распространяться в этом направлении. Используя материаль-
материальные уравнения (80.1), перепишем соотношение G5.7) в следую-
следующем виде:
(v2-al)Da = -c2(TSl-E)Na, (80.3)
где введено обозначение
аа = с/у/ё^. (80.4)
Разделив на v2 — a^, получим
^ (80.5)
Умножим обе части этого соотношения на Na и просуммируем
по а. Тогда
Y, DaNa = (DN) = -c2(NE) Y, ^г = 0,
а а
так как (DN) = 0. Скалярное произведение (NE), вообще гово™
ря, отлично от нуля. Поэтому
(80.6)
В развернутом виде
= 0, (80.7)
v2 —a2 v2 — a2 v2 — ai
а после освобождения от знаменателей
F(v2) = N2x{v2 - a2y)(v2 - a2z) + N2(v2 - a2z)(v2 - a2x) +
+ N2(v2 - a2x)(v2 - a2y) = 0. (80.8)
Хотя уравнение (80.8) мы и получили преобразованием урав™
нения (80.7), в действительности оно обладает большей общно-
общностью. Как видно из вывода, при получении (80.7) надо было
вводить предположение, что v2 — а2а ф 0 и (NE) ф 0. Уравнение
(80.7) теряет смысл, когда по крайней мере одна из разностей

§ 80 ВОЛНЫ В ДВУОСНЫХ КРИСТАЛЛАХ 523
v2 — а2а обращается в нуль Уравнение же (80.8) остается спра-
ведливым и в этом случае, как показывает несложное матема-
математическое исследование, которое мы опускаем.
8. Уравнение (80.6), или (80.8), называется законом Френе-
Френеля для нормальной скорости распространения световых волн в
кристалле. Если задать направление N, то из этих уравнений
можно определить нормальную скорость v. Уравнение (80.8)
второй степени относительно v2. Докажем, что оно имеет ве-
вещественные и притом положительные корни. Для прозрачных
кристаллов главные диэлектрические проницаемости, а с ними и
величины а^, существенно положительны. При этом ввиду усло-
условия (80.2)
«ж ^ ®у ^ Q>z- (80.9)
Придавая в функции F(v2) аргументу v2 значения а^, a2, a2zl
придем к неравенствам:
F(al) = N2(a2x - а2у)(а2х - a2z) > 0,
Из них видно, что функция F(v2) дважды меняет знак: один
раз между а%. и а2^ другой — между а2 и а2. Следовательно,
уравнение F(v2) = 0 имеет два вещественных положительных
корня: v\ и v|, причем
ах > vi ^ ау > v2 > az. (80.10)
Отсюда следует, что в направлении N могут распространяться
две волны: одна с нормальной скоростью v\, а другая с V2- В
частных случаях скорости v\ и V2 могут совпадать.
Если скорости v\ и V2 различны, то каждая из волн будет
поляризована линейно. Это следует из соотношения
Dx:Dy:Dz = ^Ц : ^^ : -^Ц, (80.11)
у v2 — а?х v2 — а\ v2 — а%
которое получается из (80.5) и в котором под v следует пони-
понимать либо г?х, либо V2- Все величины, стоящие в правой части
(80.11), вещественны. Значит, между компонентами DXJ Dyj Dz
нет сдвигов фаз, отличающихся от 0 или тт, а потому волна по-
поляризована линейно.
Докажем, что если скорости v\ и V2 различны, то векторы D
обеих волн, которые могут распространяться в направлении N,
взаимно перпендикулярны. Отмечая величины, относящиеся к
одной из волн, индексом 1, а к другой — индексом 2, из G5.7)

524 КРИСТАЛЛООПТИКА ГЛ. VII
получим
- с2Е2 = -
Умножим первое уравнение скалярно на D2, второе на Di и
вычтем одно уравнение из другого. Так как (D]_N) = (D2N) =
= 0, то в результате получим
(vf - v|)DiD2 = c2(EiD2 - E2Di).
Но, очевидно, EiD2 = E2Di, так как каждое из этих скалярных
произведений равно Y2saEiaE2a- Следовательно,
Отсюда при v\ 7^ ^2 следует (DiD2) = 0, что и требовалось
доказать. Аналогично докажем, что (Bj_B2) = 0.
Итак, в каждом направлении в кристалле могут распро-
страняться две линейно поляризованные волны^ скорости ко-
mopuXj вообще говоря^ различны. Обе волны поперечны относи-
относительно векторов D и В. Векторы D (а такэюе В) в этих вол-
нах взаимно перпендикулярны. Относительно вектора Е обе
волны в кристалле не поперечны, за исключением тех случа-
ев, когда вектор Е параллелен одной из диэлектрических осей
кристалла. Однако деление волн на обыкновенную и необыкно-
необыкновенную возможно только для одноосных кристаллов. В общем
случае такое деление смысла не имеет — обе волны в кристалле
ведут себя как «необыкновенные».
Чтобы выяснить физический смысл постоянных aaj напра-
направим вектор Е вдоль диэлектрической оси а. Тогда D = eftE, и
уравнение G5.8) перейдет в
V2 _ С2 еаЕ* _ с" _ 2
откуда v = аа. Таким образом, величина аа есть нормаль-
нормальная скорость распространения волны, у которой электриче-
электрический вектор параллелен диэлектрической оси а. Это утвер-
утверждение становится очевидным, если заметить, что в частном
случае, когда электрическое поле параллельно диэлектрической
оси, уравнения распространения волн в кристалле не отличают™
ся от уравнений в изотропных средах.
Величины аа называются главными скоростями распро-
распространения света в кристалле. Наряду с главными скоростями,
для характеристики оптических свойств кристаллов пользуются
также главными показателями преломления^ которые опреде-
определяются выражениями
па = с/аа = у/е^. (80.12)

§ 80 ВОЛНЫ В ДВУОСНЫХ КРИСТАЛЛАХ 525
Для волны произвольного направления показатель прелом-
преломления кристалла определяется выражением
п = ф. (80.13)
Его значение, как видно из G5.8), однозначно определяется на-
направлением вектора D или Е. Каждому направлению нормали
N соответствуют два значения показателя преломления в соот-
соответствии с двумя возможными поляризациями волны.
4. Для исследования уравнения Френеля применим геомет-
геометрический метод. Из какой-то точки О в различных направлени-
направлениях будем проводить прямые и на них откладывать отрезки, дли-
длины которых равны значениям нормальных скоростей в этих на-
направлениях. Геометрическое место концов таких отрезков назы-
называется поверхностью нормалей. В кристалле каждому направ-
направлению нормали соответствуют два значения скорости. Поэто-
Поэтому поверхность нормалей в кристалле будет двойной поверхно-
поверхностью , т.е. состоит из двух слоев. Она представляет собой по-
поверхность шестого порядка и имеет очень сложный вид. Чтобы
составить представление о поверхности нормалей электромаг-
электромагнитных волн в кристалле, рассмотрим сечения ее координатны-
координатными плоскостями XY, YZ, ZX.
Сечение плоскостью XY. Волновая нормаль
лежит в плоскости XY, т.е. Nz = 0. Уравнение Френеля (80.8)
принимает вид
(v2 - a2z)[N2(v2 - а2у) + N2(v2 - а2х)} = 0.
Из него получаем два значения нормальных скоростей:
v2 = aZl v\ = Nla2y + Ща2х. (80.14)
Скорость V2 не зависит от направления N. Ей соответствует кру-
круговое сечение поверхности нормалей (рис. 287). Скорость v\ из-
изменяется с изменением направления N. Ей соответствует сече-
сечение поверхности нормалей, имеющее форму овала. Из уравне-
уравнений (80.14) следует: v\ ^ ^2, так что круг находится целиком
внутри овала. Вектор D должен быть перпендикулярен к N. Из
соображений симметрии ясно, что вектор D одной волны парал-
параллелен оси Z, а вектор D другой волны параллелен плоскости
XY. Первому направлению вектора D соответствует круговое
сечение поверхности нормалей, второму — овальное.
Сечение плоскостью YZ. Волновая нормаль N ле-
лежит в плоскости YZ, т.е. Nx = 0. Уравнение Френеля принимает
вид
Оно дает два значения нормальных скоростей:
Vl=ax, v2 = N2a2 + N2a2 (80.15)

526
КРИСТАЛЛООПТИКА
ГЛ. VII
Скорость v\ не зависит от направления N. Ей соответствует кру-
круговое сечение поверхности нормалей и вектор D, параллельный
оси X. Скорость V2 изменяется с изменением направления N. Ей
соответствует овальное сечение поверхности нормалей и вектор
D, параллельный плоскости YZ. Оно целиком помещается вну-
внутри круга, так как V2 ^ г?х, как это следует из уравнений (80.15).
([
X
А
Z
?2-
/
"X /А'
А)
\ az I ay\
в
Рис. 287
Сечение плоскостью ZX. Волновая нормаль N
лежит в плоскости ZX, т.е. Ny = 0. Уравнение Френеля прини-
принимает вид
(v2 _ a2)\N2(v2 ~~ а2) + N2(v2 — а2)} = 0
и дает два значения нормальных скоростей:
vi = ay, v\ = N2a2x + N2a2z. (80.16)
Скорость v\ не зависит от направления N. Ей соответствует
круговое сечение поверхности нормалей и вектор D, параллель-
параллельный оси Y. Скорость V2 изменяется с изменением направления
N. Ей соответствует овальное сечение поверхности нормалей и
вектор D, параллельный плоскости ZX.
5. Третий из рассмотренных случаев существенно отлича-
отличается от первых двух. В первых двух случаях овал и круг не
пересекаются. В третьем случае они пересекаются в четырех

§ 80 ВОЛНЫ В ДВУОСНЫХ КРИСТАЛЛАХ 527
точках (рис. 287). Это означает, что в плоскости ZX имеются
два направления А А1 и ВВ1, симметричные относительно оси Z,
вдоль которых обе волны распространяются с одной и той же
нормальной скоростью. Направления, вдоль которых совпада-
совпадают нормальные скорости волн, называются оптическими ося-
осями второго рода, осями нормалей или бинормалями.
Если в кристалле все три главные скорости ах, ау, az раз-
различны, то в нем существуют две и только две оптические оси
второго рода. Действительно, если вектор N направлен вдоль
оптической оси второго рода, то должно быть v\ = V2- Ввиду со™
отношений (80.10), это возможно только тогда, когда ^1=^2 =
= ау. Но тогда уравнение (80.8) дает N2(a2 — а%)(а% — а^) = 0.
Так как по предположению ах ф ау ф az, то отсюда следует, что
Ny = 0. Это значит, что оптические оси лежат в плоскости ZX.
Но в этой плоскости, как показано выше, имеются две и только
две оптические оси второго рода. Они симметрично расположе-
расположены относительно оси Z и наклонены к ней под некоторым углом
/3. Для нахождения /3 в уравнение v\ = V2 подставим значения
v\ и V2 из формул (80.16). Получим
а2у = N2za2x + N2a2z, или a2y(N2 + N2) = N2a2x + N2a2z,
откуда
(80Л7)
Теперь оправдан термин «оптически двуосный кристалл», кото-
которым мы уже пользовались.
Если две из трех главных скоростей совпадают между собой
(ах = ау или ау = az), то оптические оси сливаются в одну ось,
параллельную оси Z (когда ах = ау) или оси X (когда ау = az).
Кристалл становится оптически одноосным. Наконец, если все
три главные скорости одинаковы, то любое направление в кри-
кристалле обладает свойством оптической оси. В таких кристаллах
плоские волны, независимо от их поляризации и направления,
распространяются с одной и той же скоростью — кристаллы в
оптическом отношении ведут себя как изотропные среды. К ним
относятся кристаллы кубической системы 1).
) Необходимо, однако, отметить, что при наличии пространственной
дисперсии кристаллы кубической системы могут быть оптически анизо™
тронными. На эту возможность указывал еще Г.А. Лорентц. Только в 1960 г.
Е.Ф. Гросс и А.А. Каплянский, исследуя спектры поглощения на моно-
монокристаллических образцах СщО, экспериментально обнаружили необыч-
необычное для кубических кристаллов явление анизотропного поглощения света.

528 КРИСТАЛЛООПТИКА ГЛ. VII
ЗАДАЧИ
1. Как надо ориентировать пластинку из двуосного кристалла, чтобы
получить на кристалл-рефрактометре три главных показателя преломле-
преломления?
Ответ. Перпендикулярно к любой из диэлектрических осей кристал-
кристалла.
2. Исходя из соображений симметрии, показать, что все кристаллы три-,
тетра™ и гексагональной систем оптически одноосны.
§ 81. Лучи, волновые нормали и свмзь между ними
1. Распространение света в кристаллах, как и любых волн
в анизотропных средах, характеризуется замечательной двой-
двойственностью, или взаимностью. Она обусловлена тем, что в
анизотропных средах каждой волновой нормали соответству-
соответствует луч, т.е. прямая, вдоль которой происходит распространение
энергии волны. Поскольку энергия распространяется с группо-
групповой скоростью, для исследования свойств лучей и обоснования
самого понятия луча надо вычислить групповую скорость в ани-
анизотропной среде. В этом случае такую скорость называют также
лучевой скоростью. Для ее вычисления воспользуемся форму-
формулой (8.16), подставив в нее ш = kv(k). Дифференцируя по ki и
учитывая, что dk/dki = ki/k, получим
дш ki . ? dv
Отсюда для вектора групповой скорости находим
u = vN + ^, (81.1)
где N = k/fc — единичный вектор волновой нормали, a v —
нормальная скорость^ т.е. скорость распространения фазы в на-
направлении волновой нормали.
Групповая скорость и в анизотропной среде отличается от
нормальной скорости v добавочным слагаемым k dv/dh. Это
слагаемое в свою очередь содержит составляющую вдоль норма-
нормали N. Чтобы определить ее, заметим, что k = fcN, а потому ука-
указанная составляющая равна hdv/dh. Поэтому для самой груп-
групповой скорости Ujv в направлении волновой нормали N можно
написать
" , i dv
Этот результат совпадает с формулой Рэлея (8.6) для группо-
групповой скорости в изотропной среде. Этого и следовало ожидать,
так как он относится не ко всему вектору групповой скорости,

§ 81 ЛУЧИ И ВОЛНОВЫЕ НОРМАЛИ 529
а только к его проекции на направление волновой нормали. А
вычисление такой проекции можно провести в точности так же,
как и вычисление групповой скорости в изотропной среде.
Отличие им от v обусловлено дисперсией волн, т.е. зависи-
зависимостью нормальной скорости v от частоты ш. Дисперсия в рав-
равной мере свойственна и изотропным, и анизотропным средам.
Специфика распространения световых волн в кристаллах обу-
обусловлена не столько дисперсией, сколько отличием направлений
волновых нормалей и лучей. Чтобы не вводить излишних услож-
усложнений, пренебрежем совсем дисперсией, т.е. будем считать кри-
кристаллы недиспергирующими. Тогда dv/dX = 0, а потому п^ =
= vN, или un = v. Но им = (uN), так что
(uN) = v. (81.3)
2. Наряду с поверхностью нормалей, введенной в предыду-
предыдущем параграфе, введем еще лучевую поверхность, называемую
иногда также волновой поверхностью. Для этого из произволь-
произвольной точки О во всевозможных направлениях будем проводить
лучи и откладывать на них величины лучевой скорости в этих
направлениях. Геометрическое место концов отложенных отрез-
отрезков есть замкнутая поверхность, которая и называется лучевой
поверхностью.
Если лучевую поверхность и поверхность нормалей строить
из общего центра О, то между этими двумя поверхностями су-
существует простая и важная связь. Для установления этой связи
умножим формулу (81.3) на к и придадим ей вид
(uk) = и). (81.4)
Отсюда следует, что бесконечно малые изменения величин и, к,
ш связаны соотношением (u$k) + (k<5u) = ёш. По определению
групповой скорости (u$k) = 6ш. Следовательно, (k$u) = 0, или
(NSu) = 0. (81.5)
Но и есть радиус-вектор лучевой поверхности, а потому всякий
бесконечно малый вектор 5п лежит в плоскости, касательной к
этой поверхности в соответствующей точке касания. Поэтому из
формул (81.5) и (81.3) следует, что касательная плоскость к лу-
лучевой поверхности перпендикулярна к соответствующей вол-
волновой нормали и отсекает на ней отрезок, равный нормальной
скорости волны. Отсюда в свою очередь следует, что лучевая по-
поверхность есть огибающая плоских волн, распространившихся
из ее центра за единицу времени в различных направлениях.
Этими теоремами и устанавливается искомая геометрическая
связь между лучевой поверхностью и поверхностью нормалей.

530 КРИСТАЛЛООПТИКА ГЛ. VII
Молено также сказать, что касательная плоскость к луче-
лучевой поверхности есть фронт волны, соответствующий лучу,
проведенному в точку касания. В таком виде теорема допус-
допускает простую интерпретацию. Действительно, лучевая поверх-
поверхность есть поверхность равных фаз, до которой световое возму-
возмущение от точечного источника доходит в течение одной секунды.
Малый участок такой поверхности может рассматриваться как
плоский. Если размеры участка очень велики по сравнению с
длиной волны, то его распространение в течение ближайшего
времени будет с достаточной точностью подчиняться законам
геометрической оптики. Согласно этим законам, участок дол-
должен распространяться как безграничная плоская волна в на™
правлении луча, причем лучевая и нормальная скорости будут
связаны соотношением (81.3). Отсюда непосредственно следу-
следует, что волновой фронт есть касательная плоскость к лучевой
поверхности.
Эта простая интерпретация не может, однако, заменить стро-
строгое доказательство. В ее основе лежит утверждение, что расхо-
расходящийся пучок, исходящий из точечного источника, ведет се-
себя совершенно так же, как система не зависящих друг от дру-
друга плоских волн, распространение которых чисто геометриче™
ски представляется с помощью лучевой поверхности. Впервые
A852 г.) Ламе A795-1870) указал, что здесь необходимо решить
сложную математическую задачу: точно представить волновой
комплекс, исходящий в анизотропной среде из одного точечно-
точечного центра (аналог шаровой волны в изотропной среде). Ламе
решил эту задачу для упругой анизотропной среды. При этом
он действительно (при исключении продольных волн) пришел
к френелевой форме лучевой поверхности. В электромагнитной
теории аналогичный вопрос сводится к решению задачи о поле
точечного диполя Герца, помещенного в однородную анизотроп-
анизотропную среду.
3. Все изложенное выше справедливо для любых волн в ани-
анизотропных средах. Специфичность электромагнитных волн в
кристаллах состоит в том, что для них направление луча совпа-
совпадает с направлением вектора Пойнтинга. Докажем это утвер-
утверждение для рассматриваемого нами случая недиспергирующих
кристаллов. В этом случае лучевая скорость вдоль волновой
нормали равна Ujv = ^N = /y2N/v, или на основании форму-
формулы G5.8)
Найдем теперь составляющую лучевой скорости u^ = k dv/dh,
перпендикулярную к волновой нормали. Умножая формулу

§ 81 ЛУЧИ И ВОЛНОВЫЕ НОРМАЛИ 531
(80.6) на к21 представим ее в виде
2 2
v2 ~~ а2а
а
Дифференцируя это соотношение по к\, получим
v~^ кадка/дкг _ V" к^ dv _ ~
2^ v2-al ~ 2^ {v*-aiyV~dki ~ '
а а
или, с учетом соотношений dkajdki = 6ai и hi =
J
a
Из формулы (80.5) находим
u2-a2aJ c4(NEJ'
о
После подстановки этих значений в предыдущее соотношение и
перехода к векторной форме получим
Следователвно,
u = uN + и± = ^ {(DE)N - (NE)D} = -^ [E[ND]].
Согласно первой формуле G5.5),
а по формуле G5.8) v2D2 = c2(DE) = c2H2, так что
VD = cH« (81.
В резулвтате получим
Таким образом, лучевая скорость и, а с ней и самый луч дей-
ствителвно направленв! вдоль вектора Пойнтинга. Так как век™
торы ЕиН взаимно перпендикулярны, то [EH] = EHs^ где s —
единичный вектор в направлении луча. С учетом этого
u = us = ^s. (81.9)
При доказательстве предполагалось, что скалярное произве-
произведение (NE) не равно нулю. Если (NE) = 0, то вектор Е парал-
параллелен одной из диэлектрических осей кристалла. В этом случае
теорема очевидна.

532 КРИСТАЛЛООПТИКА ГЛ. VII
4. Обоснование понятия луча и определение его направле-
направления были даны выше через групповую скорость в анизотропной
среде. Мы не воспользовались сразу теоремой Пойнтинга, чтобы
показать, что это понятие и его общие свойства не специфичны
для электромагнитных волн, а относятся к волнам любой физи-
физической природы. Кроме того, теорема Умова-Пойнтинга строго
доказана для потоков энергии только через замкнутые поверх-
поверхности. Локализация потока энергии в пространстве требует до-
дополнительных соображений. Такая локализация не вызывает за™
труднений в рамках применимости геометрической оптики, т.е.
в той же области, к которой относится понятие луча. Тогда тео-
теорема Умова-Пойнтинга открывает наиболее простой и общий
метод для решения всех вопросов, связанных с понятием луча.
Пусть, например, АВ — участок плоского волнового фронта,
вырезаемый диафрагмой, поставленной на пути распростране-
распространения электромагнитной волны (рис. 288). Если размеры участка
велики по сравнению с длиной волны, то справедлива геомет-
геометрическая оптика. Надо только опре-
делить направление световых лучей.
С этой целью построим на основа™
нии АВ цилиндр ABA*В', образую-
образующие которого совпадают с направле-
направлениями вектора Пойнтинга. Тогда по-
поток электромагнитной энергии через
С # V боковую поверхность цилиндра будет
тождественно равен нулю. Останутся
Рис 288 только потоки через основания АВ и
А1 В1. Энергия, втекающая через АВ,
целиком выйдет через А1 В'. Но так же ведут себя и световые лу-
лучи геометрической оптики. Поэтому направления лучей и век-
вектора Пойнтинга должны совпадать и притом не только в случае
недиспергирующих сред (как предполагалось в доказательстве,
приведенном выше), но и в случае сред^ обладающих дисперсией.
5. Двойственность, характерная для кристаллооптики, о ко™
торой говорилось в начале этого параграфа, в электромагнит-
электромагнитной теории выражается общим положением, называемом теоре-
теоремой обращения. Эта важная теорема помогает ориентироваться
в обилии сложных формул кристаллооптики, давая руководя-
руководящую нить при установлении внутренних связей между ними.
Выражаясь упрощенно, можно сказать, что теорема обращения
сокращает вдвое число формул и теорем кристаллооптики, под-
подлежащих запоминанию. Для вывода этой теоремы умножим пер-
первое уравнение G5.5) векторно на s. Получим
[sD] = -с- [s[NH]] = с- {(Ns)H - (sH)N} = с- (Ns)H.

§ 81 ЛУЧИ И ВОЛНОВЫЕ НОРМАЛИ 533
Из (81.3) следует ti(Ns) =v. Исключая (Ns), найдем Н = - [sD].
Таким же путем можно получить Е = — — [sH]. Таким образом,
получаются два ряда формул:
(81.10)
Н = - [NE], Н = - [sD],
" с
с
Ea = —
S
Все результаты, относящиеся к распространению плоских
волн в однородных кристаллах, были получены нами как след-
следствия первого ряда формул. Но формулы второго ряда можно
формально получить из формул первого ряда заменой всех ве-
величин по следующей схеме:
D Н N с , еа
Е Н s 1/е 1/и 1/еа
Следовательно, любое соотношение между величинами^ харак-
характеризующими распространение плоских волн в однородных кри-
сталлах, останется справедливым^ если все входящие в него ве-
величины заменить на соответствующие согласно схеме (81.11).
Соответствующими считаются величины, стоящие друг под дру-
другом в рядах (81.11). Этот результат и называется теоремой обра-
обращения.
6. Применяя теорему обращения, легко найти лучевую ско-
рость в кристалле, если известно направление луча s. Для этого
в уравнении (80.6) или (80.7) заменяем N на s, v на 1/и, аа на
1/аа и получаем
пзт4ттг^ = 0, (81.12)
ИЛИ
V-Д = 0. (81.13)
^ и2 - ag v ;
а
Это уравнение называется законом Френеля для лучевой скоро-
сти в кристалле. Оно вполне аналогично закону Френеля для
нормальной скорости и может быть исследовано теми же спо-
способами. Но в этом нет необходимости, так как все результаты
получаются непосредственно из теоремы обращения. Достаточ-
Достаточно перечислить их.

534 КРИСТАЛЛООПТИКА ГЛ. VII
Уравнение (81.13) второй степени относительно и2. Для
каждого направления s оно имеет два положительных веще-
вещественных корня и\ и и^, причем
ах ^ Щ > ау > г/2 ^ «z- (81.14)
В каждом направлении в кристалле могут распространяться
два линейно поляризованных луча^ вообще говоря^ с различными
лучевыми скоростями щ и щ. Электрические векторы в этих
двух лучах взаимно перпендикулярны.
Лучевая поверхность, как и поверхность нормалей, состоит
из двух слоев. Это есть поверхность четвертого порядка. Рас-
Рассмотрим ее сечения координатными плоскостями ХУ, YZ и ZX.
При этом можно воспользоваться прежним рис. 287, так как ка-
качественно сечения лучевой поверхности координатными плоско-
плоскостями не отличаются от соответствующих сечений поверхности
нормалей. Отличия, трудно передаваемые чертежом, лучше вы-
выразить словами или математическими формулами. При сечении
поверхности нормалей получаются круги и овалы. Сечениями
лучевой поверхности будут круги и эллипсы.
Сечение плоскостью XY. Луч s лежит в плоскости
XY, т.е. sz = 0. Лучевая скорость может иметь два значения:
u2 = az, 4 = 4 + 4- (8L15)
щ пу а%
Скорость ii2 не зависит от направления луча. Ей соответствует
круговое сечение лучевой поверхности. Скорость щ меняется с
изменением направления луча. Соответствующее сечение имеет
форму эллипса. Действительно, уравнение рассматриваемого се-
сечения в векторной форме имеет вид г = щб^ откуда sx = xju\,
sy = у/щ. Подставляя эти значения в (81.15), получаем
т.е. уравнение эллипса с полуосями ау и ах. Ввиду соотношений
(81.14) щ ^ щ, так что круг находится целиком внутри эллипса.
Вектор Е должен быть перпендикулярен к s. Из соображений
симметрии ясно, что вектор Е одной волны параллелен оси Z,
а вектор Е другой волны параллелен плоскости XY. Первому
направлению вектора Е соответствует круговое, второму — эл™
липтическое сечение лучевой поверхности.
Сечение плоскостью YZ. В этой плоскости
лучевые скорости могут иметь два значения:
Щ = ах, 4 = 4 + 4- (8L17)
«2 az uy
Скорость щ не зависит от направления луча. Ей соответствует
круговое сечение лучевой поверхности и вектор Е, параллель-

§ 81 ЛУЧИ И ВОЛНОВЫЕ НОРМАЛИ 535
ный оси X. Скорость U2 меняется с изменением направления
луча. Соответствующее сечение есть эллипс
4 + 4 = 1> (81Л8)
az ay
а вектор Е лежит в плоскости ZX. Согласно (81.14) щ ^ г^2,
так что эллипс целиком помещается внутри круга.
Сечение плоскостью ZX. Скорость луча
определяется двумя выражениями:
Скорости tii соответствует круговое сечение лучевой поверхно-
поверхности и вектор Е, параллельный оси Y. Для u<i получается эллипс
4 + 4 = 1, (81.20)
а вектор Е лежит в плоскости ZX. Эллипс и круг пересекают-
пересекаются друг с другом в четырех точках (рис. 287). В соответствии
с этим в плоскости ZX имеются два направления А А' и ВВ1,
симметричные относительно оси Z, вдоль которых оба луча рас-
распространяются с одинаковыми лучевыми скоростями. Такие на™
правления называются оптическими осями первого рода^ луче-
лучевыми осями или бирадиалями.
Если в кристалле все три главные скорости аХ1 ayi az раз-
личны, то в нем существуют две и только две оптические оси
первого рода. Они лежат в плоскости ZX и симметрично рас-
расположены относительно оси Z. Угол 7, образуемый одной из
оптических осей первого рода с осью Z, определяется форму-
формулой
- A/dy) _ az I ax - «^ /g^ 2]_\
Сравнение этой формулы с формулой (80.17) приводит к соот-
соотношению
= — tg/3, (81.22)
из которого следует: j < /3, т.е. оптические оси первого рода
расположены ближе к оси Z, чем оптические оси второго ро-
рода. Обычно ах и az не очень сильно отличаются друг от друга.
Поэтому угол между оптическими осями первого и второго рода,
как правило, мал и при рассмотрении многих явлений может не
приниматься во внимание. Для слюды он составляет около 4(У.
Если две из трех главных скоростей равны между собой, то
оптические оси второго рода сливаются в одну ось, направлен-
направленную либо параллельно оси Z (когда ах = ау), либо параллельно

536 КРИСТАЛЛООПТИКА ГЛ. VII
оси X (когда ау = az). В этом случае оптическая ось первого
рода совпадает с оптической осью второго рода. Наконец, когда
все три главные скорости равны между собой, любое направле-
направление в кристалле обладает свойствами оптической оси.
По числу оптических осей первого рода кристаллы разделя-
разделяются на: 1) двуосные, 2) одноосные и 3) оптически изотропные.
Эта классификация совпадает с классификацией, основанной на
числе оптических осей второго рода.
7. Отметим еще одно следствие теоремы обращения, которое
понадобится нам в следующем параграфе. Умножая скалярно
уравнение G5.7) на s и принимая во внимание, что (Es) = О,
получим
(Ds) = ~ (NE)(Ns) = ~ (NE). (81.23)
Преобразуем (80.3) с помощью теоремы обращения:
\и2 а
или на основании (81.23)
Ц
2 а
Умножим и разделим левую часть этого соотношения на еа и
учтем, что Da = eaEai а2аеа = с2. Тогда
D - u2)Da = ^ (NEMa. (81.24)
Сравнение этого соотношения с (80.3) дает
и(а2а - v2)sa = v(a2a - u2)Na, (81.25)
откуда
Умножая это соотношение на Nai суммируя по а и принимая во
внимание (80.6), получим
^=^ = 0' (81-27)
ИЛИ
Nxsx(a2y - u2)(a2z - и2) + Nysy(a2z - и2)(а2х - и2) +
+ Nzsz(a2x - u2){a2y - и2) = 0
— соотношение более общее, чем (81.27), так как справедливость
его, как легко показать, не связана с предположением, что а^ —
- и2 ф 0.

82
КОНИЧЕСКАЯ РЕФРАКЦИЯ
537
8. Теорема о связи между лучевой поверхностью и поверхно-
поверхностью нормалей (см. п. 2) позволяет геометрически построить од-
одну из этих поверхностей, если известна другая. Пусть, например,
АС В — участок лучевой поверхности с центром О (рис. 289).
В каждой точке этой лучевой поверхности проведем касатель-
касательную плоскость и опустим на нее перпендикуляр из центра О.
Геометрическое место оснований таких перпендикуляров будет
поверхностью нормалей. Наоборот, чтобы
по заданной поверхности нормалей постро-
построить лучевую поверхность, надо из центра
О провести во всевозможных направлени-
направлениях радиусы-векторы и в точках пересече-
пересечения их с поверхностью нормалей построить
плоскости, перпендикулярные к ним. Оги-
Огибающая таких плоскостей и будет лучевой
поверхностью.
Допустим, что в некоторый момент вре-
времени t в кристалле известно положение
плоского волнового фронта. Для того что-
чтобы построить волновой фронт в более позд-
поздний момент времени t;, можно на осно- О В
вании доказанной теоремы поступить сле-
следующим образом. Из каждой точки исход- Рис. 289
ного волнового фронта опишем элементар-
элементарную волну, радиусы-векторы которой получаются умножением
на (tf — t) соответствующих радиусов-векторов лучевой поверх-
поверхности. Плоскость, касательная ко всем элементарным волнам, и
даст положение волнового фронта в момент времени tf. Из двух
возможных касательных плоскостей следует выбрать ту, кото-
которой соответствует волна требуемой поляризации. Направление
луча найдется соединением центра элементарной волны с соот-
соответствующей точкой касания.
Это построение является обобщением построения Гюйген-
Гюйгенса для изотропных сред. Оно было впервые введено Гюйген-
Гюйгенсом для объяснения двойного преломления. Гюйгенс постули-
постулировал, что элементарная волна в кристаллах состоит из двух
волн: сферической и эллипсоидальной. Сферические волны по-
порождают обыкновенную^ а эллипсоидальные — необыкновенную
волны. Это предположение Гюйгенса оправдалось, но оно верно
только для оптически одноосных кристаллов.
§ 82. Коническая рефракцим
1. Когда волновая нормаль N параллельна одной из оптических осей
второго рода, нормальные скорости обеих волн v\ и V2 совпадают между
собой, а направления векторов D становятся неопределенными. Значит, в

538 КРИСТАЛЛООПТИКА ГЛ. VII
направлении оптической оси второго рода может распространяться плоская
волна любой поляризации, причем скорость распространения не зависит от
характера поляризации. В этом отношении рассматриваемый случай ана-
аналогичен распространению волн в изотропной среде. Однако если кристалл
двуосный, между ними имеется существенное различие.
В изотропной среде направления векторов D и Е, а также N и S всегда
совпадают. Для волны, распространяющейся вдоль оптической оси двуос™
ного кристалла, положение меняется. В этом случае вектор D может при-
принимать любое направление, перпендикулярное к N. Так как N лежит в
плоскости ZX, то одним из возможных направлений вектора D будет ось
У. Тогда и только тогда вектор D будет совпадать по направлению с век-
вектором Е, а нормаль N — с лучом s. Во всех остальных случаях направ-
направления луча и волновой нормали отличаются друг от друга. Придавая D
всевозможные направления, перпендикулярные к оптической оси, получим
бесчисленное множество направлений луча s. Направление вектора s стано-
становится неопределенным. Докажем, что в рассматриваемом случае все лучи
лежат на поверхности конуса.
Для доказательства воспользуемся соотношением (81.27), которое спра-
справедливо при любом направлении волновой нормали. Так как волновая нор-
нормаль N направлена вдоль оптической оси, то Ny = 0, и соотношение (81.27)
принимает вид
Nxsx Nzsz
Отсюда
a2zNxsx + a2xNzsz = u'2(Ns).
Ввиду соотношения (81.3), u(Ns) = v = ау. Следовательно,
(a2zNxsx + a2yNzsz){Nxsx + Nzsz) = a2y.
Рассмотрим произвольную точку на луче s с радиусом-вектором
r(x,y,z). Очевидно, ха = rsaj и предыдущее соотношение переходит в
(a2zNxx + a2yNzz)(Nxx + Nzz) = а2у(х2 + у2 + z2). (82.1)
Это однородное уравнение второго порядка представляет конус. Образую-
Образующими конуса являются лучи, соответствующие волновой нормали N, парал-
параллельной одной из двух оптических осей второго рода. Конус (82.1) назы-
называется конусом внутренней конической рефракции. Волновая нормаль есть
одна из образующих конуса (82.1). Это следует из того, что направления s
и N совпадают, когда вектор D параллелен диэлектрической оси Y.
2. Конус внутренней конической рефракции пересекается фронтом вол-
волны
Nr = Nxx + Nzz = ау (82.2)
по кругу. В самом деле, линия пересечения определяется системой уравне-
уравнений (82.1) и (82.2), равносильной системе
azNxx + ayNzz = ау(х +у +z),
(82.3)
Nr = ау.
Первое уравнение есть уравнение сферы, второе — уравнение плоскости.
Их пересечение есть круг, и наше утверждение доказано.

82
КОНИЧЕСКАЯ РЕФРАКЦИЯ
539
Определим угол раствора конуса внутренней конической рефракции,
точнее — угол х? получающийся от пересечения этого конуса плоскостью
ZXj проходящей через оптическую
ось кристалла (рис. 290). Когда век™
тор D направлен вдоль диэлектриче™
ской оси У, векторы s и N, а также
оптическая ось второго рода совпада-
совпадают по направлению. Если же вектор
D лежит в плоскости ZX, то в той
же плоскости будет лежать и луч s,
так как четыре вектора Е, D, s, N
всегда должны лежать в одной плос-
плоскости (см. § 75). Искомый угол \ бу-
будет равен углу между векторами D
и Е, поскольку стороны этих углов
взаимно перпендикулярны. Его легко определить из формулы G5.8), так
как в рассматриваемом случае нормальная скорость v равна ау. Формула
G5.8) дает
D /ау\2
Рис. 290
Как видно из рис. 290, Dx = ^Dcos/3, Dz = Dsin/З, где /3 — угол между
оптической осью второго рода и осью Z. Поэтому
Dx

Dcos/3 2
5— ax,
2
Dz Dsin/3 2
bz = — = — az.
2
Подставляя эти значения в выражение для cos%, получим
2
а?.
у/а% cos2 /3 + а\ sin2 /3
откуда
tgx = — Jai
Qiy
cos2
ai sin2 /3 - a\.
Использовав формулу (80.17), после несложных преобразований найдем
tg X = 4 л/(а§-а2)(а!-а§). (82.4)
ау
Конус внутренней конической рефракции пересекает лучевую поверх-
ность по кругу^ вдоль которого ее касается фронт волны. Это непосред-
непосредственно следует из теоремы, доказанной в § 81 (п. 2).
3. Теорема обращения распространяет полученные результаты на лу-
лучи. Если луч в двуосном кристалле направлен вдоль одной из оптических
осей первого рода, то ему соответствует бесконечное множество волновых
нормалей, образующих конус. Этот конус называется конусом внешней ко-
конической рефракции. Луч есть одна из образующих этого конуса. Сечение
конуса внешней конической рефракции плоскостью, перпендикулярной лу-
лучу, есть круг. Угол раствора конуса определяется уравнением
(82'5)

540
КРИСТАЛЛООПТИКА
ГЛ. VII
О
X
Рис. 291
Проведем касательную плоскость к лучевой поверхности в точке S пе-
ресечения ее с лучевой осью. Такая плоскость будет перпендикулярна к
волновой нормали. А так как волновых
нормалей, соответствующих лучу, направ-
направленному вдоль лучевой оси, бесконечно
много, то в точке S можно провести беско-
нечное множество касательных плоскостей
к лучевой поверхности. Это означает, что
в окрестности такой точки лучевая поверх-
ность имеет воронкообразную форму.
На рис. 291 представлено сечение по™
верхности нормалей и лучевой поверхно-
сти плоскостью ZX. Точка N есть двой-
двойная точка поверхности нормалей, ON — оп-
оптическая ось второго рода. Перпендикуляр
NA к этой оси дает сечение фронта волны
плоскостью рисунка. Прямая NA касается
лучевой поверхности в точке А, угол \ =
= ZNOA есть угол раствора конуса вну-
внутренней конической рефракции, S — двои™
ная точка лучевой поверхности, OS — лу-
лучевая ось. Касательная к лучевой поверхности в точке S пересекает поверх-
поверхность нормалей в точке В\ прямая О В будет одной из волновых нормалей,
принадлежащих лучу OS. Сам луч OS является нормалью плоской волны,
которая касается кругового сечения лучевой поверхности и = ау в точке S.
"Угол ф = Z.SOB есть угол раствора конуса внешней конической рефракции.
Каждому лучу, принадлежащему конусу внутренней конической ре-
рефракции, например лучу О А (рис. 291), соответствует вполне определенная
линейная поляризация. В самом деле, в направлении О А могут распро-
распространяться два луча, электрические векторы которых взаимно перпенди-
перпендикулярны. Однако только один из них соответствует волне, распространяю-
распространяющейся вдоль волновой нормали ON. Другому лучу соответствует лучевая
скорость OL и, следовательно, иное направление волновой нормали. Ана-
Аналогично, каждой волновой нормали, принадлежащей конусу внешней ко-
конической рефракции, также соответствует вполне определенная линейная
поляризация.
4. Волновой фронт AN, распространяющийся в направлении оптиче-
оптической оси второго рода ON, как было показано, касается лучевой поверх-
поверхности по кругу, вдоль которого эта поверх-
поверхность пересекается конусом внутренней ко-
конической рефракции. Такой волновой фронт
не может пересекать лучевую поверхность. В
самом деле, пересечем лучевую поверхность
плоскостью ANOj проходящей через оптиче-
оптическую ось ON (рис. 292). В сечении получится
кривая С В А. Если бы фронт AN пересекал лу-
лучевую поверхность, то, ввиду конечности лу-
лучевой скорости, на кривой СВА нашлись бы
такие точки JB, С, что проекции радиусов-
векторов ОВ, ОС на направление ON были
бы минимальны или максимальны. Если плоскость AN О проводить во все-
всевозможных направлениях, проходящих через оптическую ось ON', то точки
С
А
N
Рис. 292

§ 82 КОНИЧЕСКАЯ РЕФРАКЦИЯ 541
В, С опишут замкнутые кривые. На этих кривых в свою очередь найдут™
ся точки, проекции радиусов-векторов которых на направление бинорма-
бинормали ON будут максимальны или минимальны. Пусть JE» — одна из таких
точек. Тогда касательная плоскость BN к лучевой поверхности в точке
В будет параллельна волновому фронту AN, т.е. перпендикулярна к би-
нормали ON. Значит, плоскость BNf сама является волновым фронтом,
распространяющимся в направлении бинормали ON.
Таким образом, если бы волновой фронт N А мог пересекать лучевую
поверхность, то вдоль бинормали могли бы распространяться две волны с
различными нормальными скоростями v = ON и v' = ON', что противоре-
противоречит определению бинормали. Поскольку волновой фронт касается лучевой
поверхности по кругу (в точках А), из доказанного следует, что лучевая по™
верхность целиком лежит с той стороны волнового фронта AN, с которой
находится ее центр О (рис. 291). Значит, в точке S лучевая поверхность
имеет не просто воронкообразную форму, как было отмечено выше, но во-
воронкообразное углубление.
5. После выяснения этих геометрических соотношений обратимся к рас-
рассмотрению внутренней конической рефракции, теоретически предсказан-
предсказанной Гамильтоном A805—1865) в 1832 г. Примерный ход рассуждений Га-
Гамильтона был следующий. Пусть плоскопараллельная пластинка из двуое-
ного кристалла прикрыта с одной стороны непрозрачным экраном с малым
отверстием О (рис. 293). Осветим пластинку
параллельным пучком неполяризованных лу-
чей таким образом, чтобы после преломления
на передней поверхности пластинки волновая
нормаль оказалась направленной вдоль одной
из оптических осей второго рода О А. Волно-
вой нормали О А соответствует конус лучей.
Энергия распространяется вдоль лучей, поэто-
поэтому при достаточно малых размерах отверстия
О световой пучок внутри пластинки развер-
развернется в конус ОАВ. После преломления на зад-
задней поверхности пластинки волновая нормаль
примет свое исходное направление. А так как в р ~д„
изотропных средах направления лучей и вол-
волновых нормалей совпадают, то все лучи выйдут из пластинки параллель-
параллельным пучком и расположатся по поверхности цилиндра. Если на их пути
поместить экран, то на нем должно получиться светлое кольцо. По пред-
предложению Гамильтона отысканием этого явления занялся Ллойд, который
и обнаружил его в 1833 г. на кристалле арагонита: на экране наблюдалось
светлое эллиптическое кольцо. (Угол \ для арагонита равен 1°52;.)
Хотя Гамильтон и предсказал коническую рефракцию, его объяснение
неправильно. При более детальном изучении оказалось, что явление выгля-
выглядит иначе, чем предсказывал Гамильтон. Применяя более узкие отверстия
в экране, Поггендорф A796-1877) нашел, что кольцо в действительности
двойное. Объяснение было дано Фохтом A850-1919). Гамильтон рассма-
рассматривал строго плоскую волну, распространяющуюся в кристалле точно в
направлении оптической оси. Физически это реализовать невозможно. Ес-
Если бы даже можно было осветить отверстие О строго плоской волной, то
после прохождения через него волна перестала бы быть плоской из-за ди-
дифракции. Такая волна распадается на бесконечное множество плоских волн,
направления распространения которых близки к направлению оптической
оси. Нельзя ограничиться рассмотрением поведения только одной волны,

542
КРИСТАЛЛООПТИКА
ГЛ. VII
Рис. 294
распространяющейся строго в направлении оптической оси. Это ясно уже
из того, что на ее долю приходится исчезающе малая энергия, и физиче-
физически ничего не изменится, если эту волну даже совсем удалить из волнового
комплекса. Необходимо рассмотреть бесконечное множество плоских волн,
волновые нормали которых группируются вблизи оптической оси. Это и
было сделано Фохтом.
Если строго плоская волна распространяется в направлении оптической
оси второго рода, то, как было показано, волновой фронт касается лучевой
поверхности по кругу. Примем плоскость такого круга за плоскость рис. 294.
Пусть N — точка пересечения плоскости ри-
сунка с оптической осью. Допустим, что име-
имеется бесконечная совокупность плоских волн,
волновые нормали которых лежат в преде-
пределах небольшого конуса, ось которого совпада-
совпадает с оптической осью. Этот конус пересекает-
ся плоскостью рисунка по кругу к. Каждой
волновой нормали соответствует точка внутри
или на границе круга к. Найдем, где распо-
расположатся соответствующие ей лучи. Волновой
нормали N соответствует конус лучей, пере-
пересекающих плоскость рисунка по окружности
К. Лучевая поверхность касается плоскости
рисунка вдоль этой окружности, а поэтому
кривизна лучевой поверхности в направлении
окружности К равна нулю. Кроме того, лучевая поверхность должна ле-
лежать по одну сторону от плоскости рисунка. Ради определенности примем,
что все волны распространяются к читателю. Тогда лучевая поверхность
будет лежать за плоскостью рисунка, и следовательно, ее окрестность вбли-
вблизи окружности К будет обращена к читателю своей выпуклостью. В такой
окрестности лучевая поверхность имеет баранкообразную форму.
Пересечем лучевую поверхность двумя параллельными плоскостями
РаРв и АВ, перпендикулярными к плоскости рисунка и проходящими че-
через центры окружностей К ж к. Бесконечно малые отрезки РаРв и Р'аР'в
перпендикулярны к окружности К, поэтому в направлениях этих отрезков
кривизна лучевой поверхности будет максимальна, а в перпендикулярных
направлениях равна нулю. Следовательно, перпендикуляры к этим беско-
бесконечно малым отрезкам должны лежать в плоскости PaPbj T-e- они будут
параллельны волновым нормалям, лежащим в плоскости АВ. Значит, каса-
касательная плоскость к лучевой поверхности в какой-либо точке отрезка РаР
или отрезка РаР будет перпендикулярна к соответствующей волновой нор-
нормали, проходящей через отрезок AN. Касательная же плоскость к лучевой
поверхности в какой-либо точке отрезков РРв в Р'' Р'в будет перпендикуляр-
перпендикулярна к волновой нормали, проходящей через отрезок NB. Это означает, что
каждой волновой нормали, проходящей через отрезок AN, соответствуют
два луча, из которых один проходит через отрезок РаР, а другой — через
отрезок Р'аР'• Каждой же волновой нормали, проходящей через отрезок
NB, соответствуют два луча, проходящие через отрезки РРв и Р1 Р'в- Та-
Таким образом, каждой волновой нормали, наклоненной под малым углом
к оптической оси второго рода, соответствуют два луча, один из которых
проходит внутри конуса внутренней конической рефракции, а другой вне
этого конуса.
Теперь ясно происхождение двойного светлого кольца Поггендорфа.
Волновым нормалям, пересекающим плоскость рисунка внутри малого кру-

§ 83 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ГРАНИЦЕ КРИСТАЛЛОВ 543
га радиуса dr с центром в JV, соответствует малая доля энергии, которая
должна распределиться по сравнительно большой площади dS кольца по
обе стороны от окружности К. Если же взять волновые нормали, пересе-
пересекающие плоскость рисунка внутри кольца со средним радиусом г и той же
толщиной dr, то таким волновым нормалям будет соответствовать значи-
значительно большая энергия, поскольку она пропорциональна площади кольца
2ттт dr. Эта энергия должна распределиться по площади двух колец, одно
из которых лежит внутри, а другое вне окружности К. Площади обоих ко-
колец с точностью до бесконечно малых высшего порядка по-прежнему равны
dS. Поэтому освещенность обоих колец будет много больше освещенности
центрального кольца в окрестности окружности К. Освещенность долж-
должна равняться нулю вдоль окружности К и непрерывно возрастать по мере
удаления от этой окружности как в на-
наружную, так и во внутреннюю стороны.
Таким образом, там, где по Гамильто-
Гамильтону должна была бы получаться макси-
максимальная освещенность, в действительно-
действительности наблюдается темнота.
6. Гамильтоном была предсказа-
предсказана еще внешняя коническая рефракция^
экспериментально обнаруженная также
Ллойдом в 1833 г. Она связана с тем,
что световому лучу, идущему вдоль лу-
чевой оси двуосного кристалла, соответ-
ствует бесконечная совокупность волно-
волновых нормалей, лежащих на конической
поверхности. Нет необходимости входить
в теорию этого явления. Достаточно со-
сослаться на теорему обращения и описать Рис. 295
явление, как оно наблюдалось в установ-
установке Ллойда. Обе поверхности плоскопараллельной арагонитовой пластинки
были покрыты экранами с малыми отверстиями О и О1 (рис. 295), центры
которых лежали на оптической оси первого рода. Линза L концентриро-
концентрировала на О сходящийся пучок лучей. Диафрагмы О ж О' выделяли только
те лучи, которые шли вдоль оптической оси ОО'. По выходе из пластинки
лучи развертывались в конус, и на экране Э наблюдалось светлое кольцо.
Разумеется, при достаточно малых размерах отверстий О и О кольцо будет
двойное.
§ 83. Замечания об отражении и преломлении света
на границе кристаллов
1. Как и в оптике изотропных сред, задача об отражении и
преломлении в кристаллооптике может быть полностью реше-
решена на основе граничных условий, которым должны удовлетво-
удовлетворять векторы электромагнитного поля: по обе стороны границы
раздела тангенциальные компоненты векторов Ей Н должны
быть равны. Задача распадается на две части: геометрическую,
в которой определяются направления распространения, поляри-

544
КРИСТАЛЛООПТИКА
ГЛ. VII
зация и скорости отраженных и преломленных волн, а в случае
их неоднородности также и затухание волн в пространстве, и
физическую^ в которой определяются амплитуды волн (вообще
говоря, комплексные). Остановимся кратко только на геометри-
геометрической стороне вопроса. Формулы для амплитуд, из-за их гро-
громоздкости, выводить не будем, хотя сам вывод и не встречает
принципиальных затруднений.
Пусть на плоскую границу раздела падает плоская монохро-
монохроматическая волна с волновым вектором ki. В случае изотропных
сред получается только одна отраженная и только одна прелом-
преломленная волна. Для анизотропных сред это, вообще говоря, не
так. Однако, каково бы ни было число отраженных и прелом-
преломленных волн, из линейности и однородности граничных условий
непосредственно следует, что тангенциальные компоненты вол-
волновых векторов падающей, отраженных и преломленных волн
должны быть одинаковы (см. § 69). Следовательно, нормали па~
дающей^ отраженных и преломленных волн^ а также нормаль
к границе раздела все лежат в одной плоскости. Кроме того,
преломление волновых нормалей подчиняется закону прелом-
преломления Снеллиуса: отношение синуса угла падения к синусу угла
преломления равно отношению соответствующих нормальных
скоростей волн. Практически от этого закона мало пользы. Его
недостаточно для нахождения направления волновой нормали
преломленной волны, так как нормальная скорость преломлен-
преломленной волны неизвестна. Она зависит от направления падающей
волны и сама подлежит определению. Проще всего это можно
сделать графическим методом.
2. Рассмотрим одну из преломленных волн. Пусть к = О А
или к = ОЁ означает ее волновой вектор. Ввиду граничных
условий, тангенциальную составляющую этого вектора kj моле-
молено считать известной: k^ = kit.
Она лежит в плоскости паде-
падения. Остается найти нормаль-
нормальную составляющую kn. Прежде
всего, она должна быть направ-
направлена вниз, в сторону второй
среды, так как преломленная
волна должна уходить от гра-
границы раздела. Для решения за-
задачи можно применить следу-
следующее геометрическое построе-
рис> 296 ние- Будем проводить из точ-
точки О (рис. 296) во вторую среду
прямые по всевозможным направлениям и на них откладывать
длины волнового вектора к. Поскольку направления к и N сов-
совпадают, а каждому направлению N соответствуют два значе-
С D

§ 83 ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ГРАНИЦЕ КРИСТАЛЛОВ 545
ния нормальной скорости, молено сказать также, что каждому
направлению нормали N соответствуют два значения волново-
волнового числа к. Поэтому в результате построения получится слож-
сложная поверхность, состоящая из двух слоев. Будем называть ее
поверхностью волновых векторов1). Она просто связана с по-
поверхностью нормалей. Поскольку к = ш/v, поверхность волно-
волновых векторов по отношению к поверхности нормалей являет-
является обратной: длины ее радиусов-векторов обратно пропорцио-
пропорциональны длинам параллельных им радиусов-векторов поверхно-
сти нормалей.
Пересечем поверхность волновых векторов плоскостью паде-
ния — в сечении получатся две кривые (рис. 296). Отложим от
точки О вдоль границы раздела тангенциальную составляющую
ht = kit волнового вектора к и из конца этой составляющей вое™
становим перпендикуляр к границе раздела. Он пересечет ука-
указанные две кривые, вообще говоря, в двух точках А и В. Со-
Соединив эти точки с точкой О, получим два вектора О А и 015,
каждый из которых может быть волновым вектором преломлен-
преломленной волны.
Тем самым определятся направления волновых нормалей N
и соответствующие им значения нормальных скоростей. Поверх-
Поверхность волновых векторов позволяет построить поверхность нор-
нормалей, а затем лучевую поверхность и найти направления соот-
соответствующих лучей и лучевые скорости. Векторы N и s опреде-
определят направление магнитного поля Н, поскольку оно перпендику-
перпендикулярно к плоскости (N, s). Определятся и направления векторов
D и Е, т.е. поляризация обеих волн в кристалле. В общем случае
направления лучей и волновых нормалей не совпадают. В опти-
оптически двуосных кристаллах оба луча, как правило, выходят из
плоскости падения.
Если волна падает на кристалл из изотропной среды, то она
может быть поляризована как угодно. В кристалл она вступит в
виде двух линейно поляризованных волн. Если же первая среда
также кристаллическая, то в направлении ki могут распростра-
распространяться две волны с различными поляризациями и с различными
нормальными скоростями. Их надо рассматривать как незави-
независимые волны. Каждая из них в кристалле расщепится на две
линейно поляризованные волны. Во второй среде получится все-
всего четыре волны.
) Если вместо величины к = uj/v откладыватв величину с/г;, т.е. по-
показатель преломления п, то получится поверхность, подобная поверхно-
сти волновых векторов. В кристаллооптике ее называют индикатрисой или
поверхностью показателей преломления. Радиус-вектор этой поверхности
дает значение показателя преломления для плоской волны, нормаль кото-
которой совпадает по направлению с этим радиусом-вектором.
18 Д.В. Сивухин

546 КРИСТАЛЛООПТИКА ГЛ. VII
Может случиться, что длина вектора ~кц окажется больше
длины одного или обоих отрезков ОС и OD^ отсекаемых на оси
X поверхностью волновых векторов. Тогда построение, выпол-
выполненное на рис. 296, станет невозможным. Возникнет либо одна
преломленная волна, либо ни одной. Одна из волн или обе волны
испытают полное отражение.
8. Таким же способом может быть решен вопрос о направле-
направлении и поляризации отраженного света. Надо только построить
поверхность волновых векторов не во второй, а в первой среде.
Если первая среда изотропна, то поверхность волновых векто-
векторов будет сферой. Возникнет только одна отраженная волна,
причем угол падения будет равен углу отражения. Если же пер-
первая среда анизотропна, то при отражении волна расщепится на
две линейно поляризованные волны, идущие в разных направ-
направлениях.

ГЛАВА VIII
МОЛЕКУЛЯРНАЯ ОПТИКА
§ 84. Классическая теормм дисперсии света
1. Все среды, за исключением абсолютного вакуума, облада-
обладают дисперсией^ т.е. зависимостью показателя преломления элек-
электромагнитных волн от их частоты. Наилучшим приближени-
приближением к вакууму является межпланетное и межзвездное простран-
пространство. По астрофизическим данным средняя плотность вещества
в межпланетном пространстве составляет около одного атома
(иона) на 1 см3. В межзвездном пространстве нашей Галактики
средняя концентрация вещества — около 10~2 атомов на 1 см3,
а в межгалактическом пространстве еще меньше. В лучших же
вакуумных приборах она не меньше 10 атомов на 1 см3, а обыч-
обычно гораздо больше.
Отсутствие дисперсии у межзвездного пространства доказы-
доказывается астрономическими наблюдениями над затмениями двой-
двойных звезд. Допустим, например, что красные лучи в межзвезд-
межзвездном пространстве распространяются быстрее синих. Тогда при
начале затмения должно было бы наблюдаться изменение цвета
звезды от нормального к синему, а при окончании — от крас-
красного к нормальному. При колоссальных расстояниях до звезд
этот эффект не мог бы ускользнуть от наблюдения, далее если
бы разница в скоростях красных и синих лучей оказалась ни-
ничтожно малой. В действительности в видимой области спектра
он обнаружен не был. Еще Араго на основании своих наблюде-
наблюдений над двойной звездой Альголь пришел к заключению, что
разность между скоростями красных и синих лучей во всяком
случае не может превышать одной стотысячной скорости света.
Конечно, отсутствие дисперсии видимого света в межзвезд-
межзвездном пространстве экспериментально доказано лишь с той точно-
точностью, которую может обеспечить эксперимент. Наблюдения над
пульсарами с помощью современных радиоприемных устройств

548 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
позволили установить наличие дисперсии межзвездного про™
странства в области радиодиапазона (см. § 87).
2. Феноменологическая теория Максвелла, не содержащая
никаких атомно™молекулярных констант, не давала объяснения
дисперсии света. Для этого необходимы атомистические пред-
представления. Дисперсия света возникает в результате вынужден-
вынужденных колебаний заряженных частиц — электронов и ионов — под
действием переменного поля электромагнитной волны.
В классической теории Г.А. Лорентца строение колеблющих-
колеблющихся систем — атомов и молекул — и их колебания описываются на
основе классических представлений о движении и законов Нью-
Ньютона. В нашем курсе мы можем в основном ограничиться толь-
только такой классической теорией. Теоретическому рассмотрению
проще всего поддается дисперсия в газах^ так как в этом слу-
чае в первом приближении молено не учитывать сложное вза-
взаимодействие атомов и молекул среды. Для не очень плотных
газов основные предположения теории выполняются с меньшей
натяжкой, чем в случае конденсированных сред. Поэтому экспе-
экспериментальную проверку этих предположений лучше всего про™
изводить именно на газах, для которых и теория разработана
лучше. В дальнейшем мы в основном ограничимся этим про™
стейшим случаем.
Все электроны, входящие в атом, можно разделить на пери-
ферийные, или оптические, и электроны внутренних оболочек.
На излучение и поглощение света в оптической области спек™
тра оказывают влияние практически одни только оптические
электроны. Собственные частоты электронов внутренних оболо-
оболочек слишком велики, так что их колебания в поле световой вол™
ны практически не возбуждаются. Поэтому в теории дисперсии
молено ограничиться рассмотрением одних только оптических
электронов.
Для простоты предположим сначала, что в атоме есть всего
один оптический электрон. В классической теории дисперсии
оптический электрон рассматривается как затухающий гармо-
гармонический осциллятор^ колебания которого в поле световой вол-
волны описываются уравнением
тт = —кт — gr + еЕ;,
где га — масса, е — заряд электрона, —кг — квазиупругая воз-
возвращающая сила^ стремящаяся вернуть электрон в положение
равновесия, —gr — сила, аналогичная силе трения и введенная
для учета поглощения света^ Е; — напряженность электриче™
ского поля, действующего на электрон. Поле Е;, вообще говоря,
отличается от среднего макроскопического поля Е, входящего
в уравнения Максвелла (см. т. III, § 35), но в случае неплот™
пых газов этим различием можно пренебречь. Разделив на га,

§ 84 КЛАССИЧЕСКАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА 549
приведем предыдущее уравнение к виду
г + 27Г + Шпг = — Е;, (84.1)
и т v /
где ujq = к/т, 2j = g/m. Магнитной силой - [vH], действую-
действующей на электрон, мы пренебрегли, так как скорость электрона v
пренебрежимо мала по сравнению со скоростью света с. Эта си-
сила проявляется лишь в световом давлении, которое в обычных
условиях мало и в разбираемом нами вопросе не играет суще-
существенной роли (см. задачу 2 к этому параграфу).
Все силы, действующие внутри атомов и молекул, имеют
электрическую природу. Такими силами определяется и вну-
внутренняя структура этих частиц. Однако объяснить этими си-
силами существование и структуру атомов и молекул на основе
классических представлений оказалось невозможным. Это бы-
было сделано только в рамках квантовой физики. Никаких ква-
квазиупругих сил и сил трения, пропорциональных скорости заря-
заряженных частиц, в атомах и молекулах нет. Правильная теория
дисперсии должна принимать во внимание только реально су-
существующие силы и основываться на квантовых законах. Та-
Такую теорию дает квантовая механика. Однако она приводит к
поразительному результату, что в отношении дисперсии и по-
поглощения света атомы и молекулы ведут себя так, как если
бы среда представляла собой набор осцилляторов с различны-
различными собственными частотами и коэффициентами затухания,
подчиняющихся классическим уравнениям движения Ньютона.
Собственные частоты и коэффициенты затухания не могут
быть вычислены на основе классической модели. В классической
теории на них надо смотреть как на формально введенные по-
постоянные. Вычисление этих постоянных и раскрытие их истин-
истинного физического смысла возможно только в рамках квантовой
теории. На классическую же теорию надо смотреть как на тео-
теорию, даюшую модель диспергирующей среды, которая приводит
к правильным окончательным результатам, если к ней приме-
применять законы классической механики.
После этого замечания можно перейти к изложению класси-
классической теории дисперсии, не опасаясь, что смысл этой теории
будет понят неправильно.
3. Предположим, что поле Е представляется плоской вол-
волной Е = Аег^*~кг) = Eo(r)exwt. Амплитуда поля Eq = Ae^lhr
меняется от точки к точке. Значит, в различных точках траек-
траектории электрон подвергается действию поля различной ампли-
амплитуды. (Указанное обстоятельство приводит к явлению так назы-
называемой пространственной дисперсии.) Однако мы пренебрежем
этим обстоятельством, предполагая, что амплитуда колебаний
электрона г о мала по сравнению с длиной волны А. Для теории

550 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
дисперсии имеет значение не общее, а только частное решение
уравнения (84.1), представляющее вынужденные колебания ос-
осциллятора г = r®etut. Амплитуда го найдется подстановкой это™
го выражения в (84.1). Если пренебречь различием между Е и
Е;, то получится
г = 2 е{™ . Е. (84.2)
uJq — ш2 + 2iu)j
Атом в электрическом поле приобретает дипольный момент р =
= ег = /ЗЕ, где /5 — поляризуемость атома, определяемая фор-
формулой
Р = 2 е>" . (84.3)
Если N — число атомов в единице объема, то вектор поляриза-
поляризации среды будет Р = JVp = JV/3E, а индукция
D = Е + 4тгР = еЕ, (84.4)
где
6 = 1+ **Nf/m • (84.5)
Материальное уравнение D = бЕ принимает такой же вид,
как и в формальной теории Максвелла, с тем существенным от™
личием, что диэлектрическая проницаемость е теперь зависит
от частоты ш. Поэтому сохраняют силу все ранее полученные
результаты, если в них постоянную е заменить функцией е(ш).
Функция e(uj) получилась комплексной. Этого и следовало ожи-
ожидать, так как в нашей модели учтено поглощение света. Введем
комплексный показатель преломления по формуле
у/? = п-Ы, (84.6)
где п — вещественный показатель преломления, а к — показа-
показатель затухания среды. Обе функции п(ш) и к(ш) зависят от ча-
частоты. Таким образом, получают принципиальное, хотя и фор-
формальное объяснение не только дисперсия, но и абсорбция света.
Возведем (84.6) в квадрат и сравним вещественные и мнимые
части полученного соотношения и соотношения (84.5). Тогда по™
лучим
С помощью этих формул показатели преломления и затухания
п и к можно выразить через частоту ш и молекулярные пара-
параметры N и е2/га.

КЛАССИЧЕСКАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА
551
Вдали от собственной частоты cjq, где 2(^7^ |ojq —oj2|, мнимой
частью в (84.5) можно пренебречь и получить приближенную
формулу:
Р — 17 —
(84.9)
Формула для п такого вида впервые была получена Зель-
мейером в 1871 г.х) в механической теории эфира. Конечно, в
формуле самого Зельмейера нет никакого намека на связь по™
казателя преломления с диэлектрической проницаемостью е и
вообще со всякими величинами, характеризующими электриче-
ские свойства среды.
На рис. 297 сплошной линией представлен график функции
е = е(со). При переходе через точку со = ш® эта функция пре-
терпевает скачок от +оо до ^оо. Показатель преломления п
представлен штриховой, а показатель затухания ж — штрих-
пунктирной линией. Величина п обращается в нуль на участке,
где е(со) < 0. Показатель затухания ж, наоборот, на этом участке
отличен от нуля, обращаясь
в нуль при всех остальных
частотах. Величина к опи-
описывает именно затухание,
а не поглощение волн^ так
как кривые рис. 297 отно-
относятся к модели непоглоща-
ющей среды (диэлектриче-
(диэлектрическая проницаемость е всюду
вещественна).
Впрочем, эти выводы
имеют формальный харак-
характер, так как вблизи соб-
собственной частоты ш® соот-
соотношение 2ujj <C \u)q — oj2 | не Рис. 297
выполняется, а потому фор-
формула (84.9) неприменима. В действительности при переходе че-
через точку ш = ш® величины 6, п, к должны меняться непре-
непрерывно', нигде не обращаясь в бесконечность. В частности, под-
поднимающаяся ветвь кривой е = s(co) левее точки ш = ш® должна
переходить в опускающуюся, чтобы сомкнуться с другой подни™
мающейся ветвью, расположенной правее той же точки.
0,5
©/(Of
г) Как отметил Рэлей, формула (84.9) была получена двумя годами рань-
раньше Максвеллом, который еще в 1869 г. изложил основы механической тео-
теории дисперсии в виде экзаменационной задачи. Формулы Максвелла содер-
содержали также члены с затуханием.

552
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
Это замечание позволяет без особого труда представить ход
кривых п и ж в окрестности полосы поглощения. Типичный вид
кривых п = п(ш) и к = м(ш) приведен на рис. 298. Там, где
поглощение невелико, показатель преломления п(ш) возрастает
п=\
0,5
Рис. 298
с частотой. В этом случае говорят, что дисперсия нормальная.
В области сильного поглощения п(ш) уменьшается с частотой.
Такую дисперсию называют аномальной. Ее трудно наблюдать
из-за сильного поглощения.
4. Теоретические соображения, изложенные выше, справед-
справедливы не только для электронов, но и для ионов, и притом в
последнем случае классические представления более обоснова-
обоснованы ввиду относительно больших масс ионов. Во всех телах на-
наблюдается не одна, а несколько полос поглощения. Чтобы это
учесть, в классической модельной теории принимается, что ве-
вещество построено из частиц различного типа — электронов и
ионов, которые ведут себя как затухающие гармонические ос™
цилляторы с различными собственными частотами. В газах
можно пренебречь их взаимодействием. Тогда формула (84.5)
принимает вид
е =
Е47Г
(84.10)
где TVfc, m&, e^, cj^, 7^ — концентрация, масса, заряд, собствен-
собственная частота и коэффициент затухания осциллятора fc-ro типа, а
суммирование ведется по всем к. Каждой собственной частоте
соответствует своя линия поглощения, вблизи которой показа-
показатель преломления меняется аномально. Общий ход показателя
преломления в зависимости от частоты представлен схематиче-
схематически на рис. 299.
Сравнивая формулу (84.10) с опытом, можно найти коэффи-
коэффициенты С к = iV^e^/m^. По этим данным можно оценить удель-
удельные заряды е^/т^ и вывести заключения относительно природы
осцилляторов. Действительно, заряды е^ по порядку величины

КЛАССИЧЕСКАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА
553
не могут существенно отличаться от элементарного заряда е =
= 4,8 • 1СР10 СГСЭ, a N^ — от числа атомов в единице объема,
т.е. от JVabP/^4, где N^B — число Авогадро, р — плотность веще™
ства, А — атомная масса (по старой терминологии — атомный
вес). Таким образом,
ск =
ек
тк
А
тк А тк
где F = МАве = 2,9 • 10м СГСт-экв^1 — число Фарадея. С по™
мощью этой формулы и можно оценить величины е^/т^. Та™
ким путем, в согласии с теоретическими представлениями, было
найдено, что все осцилляторы отчетливо подразделяются на две
/
/
^^ X
\
\\ у
1 \-У^
I /
\f
/1
/ I
/ 1
Ух
I /
\(
/1
/ I
/Ч
/ |\
у i \
i \
i /"^
i '
Ш3
ш
Рис. 299
группы: у одной удельные заряды по порядку величины такие
же, как у электронов, у другой — как у ионов. Первым соот™
ветствуют полосы поглощения, лежащие в ультрафиолетовой
(реже — в видимой), вторым — в инфракрасной области спек-
тра.
5. Формула (84.10) и соответствующие ей формулы для п и к
применимы и в случае металлов. В инфракрасной области спек-
спектра основную роль играют свободные электроны^ для которых
следует положить ш^ = 0. Влияют также ионы вблизи их соб-
собственных частот. В видимой и примыкающей к ней ультрафио-
ультрафиолетовой областях спектра формула (84.10) удовлетворительно
согласуется с опытом, если наряду со свободными учесть так лее
электроны, связанные в ионах металла (колебания самих ионов
в этих областях спектра не играют роли).
6. Учтем теперь, хотя далеко не безупречным способом, взаи-
взаимодействие молекул, поляризованных электрическим полем све-
световой волны. Для этого воспользуемся методом действующего
поля. В кристаллах кубической системы, построенных из точеч-
точечных и изотропных атомов, поле Е;, действующее на молекулу,
связано со средним максвелловским полем Е соотношением
Е' = Е
(84.11)

554 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
(см. т. III, § 35). То же соотношение приближенно справедливо
для изотропных газов и жидкостей, построенных из изотропных
молекул, если под Е; понимать действующее поле, усредненное
по положениям центров молекул в физически бесконечно ма-
лом объеме среды. Формула (84.11) выведена в электростатике,
но ею можно приближенно пользоваться и в случае переменных
полей, когда длина волны велика по сравнению с межмолеку-
межмолекулярными расстояниями.
Будем предполагать, что все молекулы одинаковы и каждая
из них содержит только один оптический электрон. Кроме того,
пренебрежем затуханием, предполагая, что частота ш далека от
полосы поглощения. В этих предположениях все, что нужно еде™
лать, — это заменить в уравнении (84.1) Е; выражением (84.11).
Последующие вычисления крайне элементарны, но мы опустим
их, так как они уже были выполнены в электростатике (см. т. III,
§ 35). Там по методу, в точности совпадающему с излагаемым
здесь, была получена формула Мосотти-Клаузиуса:
|^| = f N15. (84.12)
Подставив сюда е = п2 и выражение для /3 из формулы (84.3),
придем к соотношению
п2 — 1 4тг Ne2/т (ОА л о\
Эта формула была одновременно A880 г.) получена в электрон™
ной теории голландским физиком Г.А. Лорентцом и датским
физиком Л. Лоренцом A829—1891) еще из домаксвелловских
представлений о свете. Она называется формулой Лорентца-
Лоренца. Из нее следует, что для данного вещества при неиз-
неизменной частоте ш должно выполняться соотношение
г. 1^1 = const, (84.14)
поскольку концентрация N молекул пропорциональна плотно-
плотности вещества р. Величина, стоящая в левой части этого соотно-
соотношения, называется удельной рефракцией. Таким образом, соглас-
согласно формуле Лорентца^Лоренца удельная рефракция вещества
не должна изменяться при изменении плотности.
В ряде случаев формула (84.14) хорошо выполняется. Так,
для воздуха при изменении давления от 1 до 200 атм постоянство
удельной рефракции выполняется с ошибкой, не превышающей
0,1 %. Нередко удельная рефракция остается приблизительно
постоянной даже при переходе вещества из парообразного со-
состояния в жидкое. Так, при ожижении газообразного кислорода
(изменение плотности в 800 раз) или конденсации водяного пара
(изменение плотности в 1200 раз) удельная рефракция остает-

§ 84 КЛАССИЧЕСКАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА 555
ся постоянной с точностью до 2-3%. Эти факты удивительны,
так как в приведенных примерах предположения, в которых вы-
выведена формула (84.11), несомненно, не выполняются. Имеется,
однако, много случаев отступлений от формулы (84.14).
7. Еще более удивительно эмпирическое правило, по кото-
которому молено приближенно вычислять рефракцию смеси или хи-
химического соединения. Если вещество состоит из одинаковых
частиц (атомов или молекул), то д = Nm^ где т — масса одной
частицы. Поэтому из формулы (84.12) с учетом соотношения
/3 = ^шг (84.15)
е = п получаем
Поляризуемость частицы /3, а с ней и величина тг есть свой-
свойство только самой частицы. Правило, которое было упомянуто
выше, состоит в том, что поляризуемость частицы аддитивна^
т.е. поляризуемость сложной частицы равна сумме поляри-
зуемостей части% из которых она состоит. Следовательно,
тг = 2,miri-) (84.16)
где т и nii — массы составной и составляющих частиц, а г и
ri — удельные рефракции соответствующих им химических ве-
веществ. Удивительно, что правило это относится не только к ме-
механическим смесям, ноик химическим соединениям. Возьмем в
качестве составляющих частиц атомы, а составных — молекулы.
Тогда mi = А^тн, тп = Мтн, где шн — масса атома водорода,
а М и Ai — соответствующие молекулярная и атомные массы.
Поэтому формула (84.16) переходит в
iTi. (84.17)
Произведение удельной рефракции на атомную массу называет-
называется атомной, а на молекулярную массу — молекулярной рефрак-
рефракцией. Таким образом, молекулярная рефракция химического
соединения равна сумме атомных рефракций.
В книге Борна1) приведены обширные таблицы, подтвер-
подтверждающие формулу Лорентца-Лоренца и аддитивность атомной
рефракции. Там же приведены примеры и значительных отступ-
отступлений от этих правил.
8. Помимо дисперсии, связанной с вынужденными колеба-
колебаниями электронов и ионов, существует другой вид дисперсии,
на который обратил внимание Дебай. Она проявляется в ере™
г) Макс Борн. Оптика.— Харьков; Киев: Гос. научно-техн. изд-во Украи-
Украины. 1937.

556 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
дах с полярными молекулами, главным образом в жидкостях.
Полярные — это такие молекулы, которые обладают «тверды-
«твердыми» дипольными моментами, обусловленными несимметричным
распределением зарядов внутри молекулы. Полярные молекулы
могут обладать и «индуцированными» дипольными моментами,
возбуждаемыми внешним электрическим полем. Как правило,
индуцированные моменты полярных молекул малы по сравне-
сравнению с твердыми.
В отсутствие электрического поля дипольные моменты по™
лярных молекул изотропной среды ориентируются в простран-
пространстве по всем направлениям и притом хаотически. В этом случае
среда никакой электрической поляризацией не обладает. При на™
ложении электрического поля оно стремится ориентировать ди-
дипольные моменты молекул вдоль поля, причем эта ориентация
постоянно нарушается из-за теплового движения. В результате
в среде возникает электрическая поляризация (см. т. III, § 36).
Если электрическое поле меняется во времени с частотой о;, то с
той же частотой будет меняться эта «ориентационная» поляри-
поляризация и обусловленная ею диэлектрическая проницаемость сре-
среды. Амплитуды вынужденных вращений полярных молекул за™
висят от частоты а; приложенного электрического поля. С этим
связана дисперсия вращательной части диэлектрической про™
ницаемости и показателя преломления.
Не входя в подробное количественное рассмотрение, ограни-
ограничимся качественными замечаниями.
В полях низких частот успевает установиться такая же мгно-
мгновенная поляризация среды, как и в статических полях. В такой
области частот величины е и п практически постоянны, т.е. не
зависят от ш. Если дипольные моменты полярных молекул ве™
лики, как, например, у воды и спиртов, то в этой области частот
значения е и п велики. Так, в случае воды е = 81, п = л/е = 9.
В другом предельном случае очень высоких частот диполь-
дипольные молекулы не успевают заметно поворачиваться за време™
на порядка периода световых колебаний. В этой области частот
практически нет вынужденных вращений молекул, т.е. враща-
вращательные части е и п выпадают. Поэтому должна существовать
промежуточная область частот, в которой величины е и п ано-
аномально сильно уменьшаются до тех значений, которые они при™
нимают в оптической области спектра. Такая область частот у
воды и спиртов лежит в диапазоне сантиметровых радиоволн.
За пределами этой области (со стороны высоких частот) молеку-
молекулы начинают вести себя так, как если бы они не были полярны™
ми. Этим объясняется резкое расхождение между показателем
преломления воды п в оптической области спектра и значением
л/е в электростатике и области низкочастотных электромагнит-
электромагнитных волн.

§ 84 КЛАССИЧЕСКАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА 557
Этим же объясняется, почему в оптике магнитную проница-
проницаемость /i почти всегда можно считать равной единице для всех
веществ. Действительно, механизм намагничивания — такой лее,
как и поляризации полярных диэлектриков. Он состоит в ориен™
тации магнитных моментов атомов и молекул во внешнем маг-
магнитном поле. Но этот эффект не имеет места в высокочастотных
полях, видимой и примыкающих к ней областях спектра.
9. Подводя итоги, дадим схематический обзор дисперсии во
всем диапазоне частот электромагнитных волн. В области ра-
радиоволн длиннее примерно 1 см существенна только одна соб-
собственная частота ш® = 0, которой обладают свободные электро-
электроны или ионы. В указанном радиодиапазопе дисперсией прак-
практически могут обладать только ионизованные газы (см. § 86).
Если свободных электронов или ионов нет, то в этом диапазоне
нет и дисперсии.
В полярных диэлектриках дисперсия появляется примерно с
сантиметрового диапазона радиоволн. Показатель преломления
убывает с частотой, т.е. дисперсия аномальна, а поглощение ве-
велико.
По мере приближения к собственным частотам ионов диспер-
дисперсия становится нормальной, а внутри самой полосы поглощения,
обусловленной колебаниями ионов, — аномальной. После про-
прохождения через инфракрасную область поглощения вдали от
нее вынужденные колебания ионов практически прекращаются.
Здесь, а также в видимой и ультрафиолетовой областях спектра
дисперсия вызывается колебаниями только связанных оптиче-
оптических электронов. В прозрачной области (точнее, области сла-
слабого поглощения) она имеет нормальный, а в области сильного
поглощения — аномальный характер. Полоса поглощения лежит
обычно в области ультрафиолета, а иногда в видимой области.
При переходе через полосу поглощения, т.е. область ано-
аномальной дисперсии, сбусловленную колебаниями электронов,
дисперсия снова становится нормальной. Если частота ш велика
по сравнению со всеми собственными частотами электронов, то в
формуле (84.10) величинами ш^ можно пренебречь по сравнению
с ш2. Мы вступили в область мягкого рентгеновского излучения.
Если не учитывать поглощение и заметить, что в колебаниях при-
принимают участие одни только электроны, то дисперсионной фор-
формуле (84.10) в указанной области спектра можно придать вид
nl = x_Nl_ (84Л8)
та;2
Показатель преломления здесь меньше единицы, хотя и очень
мало отличается от нее. Его удалось измерить, наблюдая откло-
отклонение рентгеновских лучей в призме из различных материалов,
хотя этот метод и не может дать большой точности.

558 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Более падежные результаты дают измерения предельного
угла полного отражения, испытываемого рентгеновскими луча-
лучами при переходе из воздуха в твердое тело (п < 1). Оказалось,
что показатель преломления рентгеновских лучей меньше еди™
ницы на величину порядка AСП5 — 10~6)р, где р — плотность
вещества. Так, в случае стекла (крон с плотностью 2,52) для
А = 0,1279 нм он оказался равным п = 0,999995 = 1 - 5 • 10~6.
При увеличении жесткости рентгеновского излучения резо-
нансные явления могут проявляться на электронах внутренних
оболочек атомов, связанных с ними более сильно, чем оптиче-
оптические электроны. Действительно, удалось наблюдать аномаль-
аномальную дисперсию рентгеновских лучей вблизи частот их истин-
истинного фотоэлектрического поглощения.
ЗАДАЧИ
1. Найти максимальную скорость вынужденных колебаний свободно-
свободного электрона в поле солнечного излучения вблизи земной поверхности (см.
задачу к § 5). Определить также отношение максимальной силы Fb, дей-
действующей на такой электрон со стороны магнитного поля, к максимальной
силе Fe, действующей со стороны электрического поля. Поле солнечного
излучения заменить монохроматическим Е = Ео cos out с длиной волны А =
= 550 нм.
Решение. В уравнении движения свободного электрона mv =
= е I Е Н— [vB] 1 пренебрежем действием магнитного поля. Тогда
тл -п . е тл • е^о ei?oA
mv = еЕ = еЕо cos cut, v = ^^Ео sj^ •
Eosino;?, ^макс п
тш тш 2тттс
Так как Е2 = -Е$ = 5,85 • 10 , то Ео = л/2Е2 = 0,034 СГСЭ. Подставляя
это значение, получим
^макс = 5,3 см/с, —- = —— = 0,9 • 10
Fe 2с
2. Определить среднюю силу светового давления на гармонический за-
затухающий осциллятор, колеблющийся в поле монохроматической однород-
однородной световой волны. Рассчитать также среднюю энергию г, поглощаемую
осциллятором в одну секунду, и выразить через нее среднюю силу светово-
светового давления. Показать, что если бы поглощения света не было, то средняя
сила светового давления равнялась бы нулю.
Решение. В месте нахождения осциллятора электромагнитное поле
имеет вид Е = Аеегш*, В = Ahelujt, где еиЬ — взаимно перпендикуляр™
ные единичные векторы. Пренебрегая сначала действием магнитного поля,
дифференцированием (84.2) находим
„ _ гше/т Е
)q — ш2)

§ 85 ДИСПЕРСИОННАЯ ФОРМУЛА КВАНТОВОЙ МЕХАНИКИ 559
Сила, действующая на электрон со стороны магнитного поля, F = - [vB].
Поскольку, однако, вычисления ведутся в комплексной форме, следует за-
заменить это выражение на
Для средней силы получаем
F =
или после простых преобразований
F = ± {[v-B] + [vB-]},
Fw[eb].
Отсюда видно, что средняя сила светового давления направлена в сторону
векторного произведения [eb], т.е. в сторону распространения волны.
Энергия, поглощаемая в единицу времени:
а ее среднее значение
1
е = I ш/yvv* dt = rwyw* •
о
Таким образом,
~F = e/c. (84.19)
Эта формула может быть получена из простых соображений. Излуче-
Излучение, поглощаемое атомом вещества, передает ему не только энергию е, но и
связанный с ней импульс g = е/с, который проявляется в силах светового
давления.
Если свет распространяется через поглощающий газ, то, согласно изло-
изложенному, он должен производить на него давление. Впервые такое предпо-
предположение высказал Кеплер, изучая формы кометных хвостов. Эксперимент
тальное доказательство существования светового давления на газы было
дано П.Н. Лебедевым A910 г.).
§ 85. Понятие о дисперсионной формуле
квантовой механики
1. Классическая дисперсионная формула (84.10) для газов
с большой точностью описывает фактически наблюдаемый ход
показателя преломления вблизи отдельных линий поглощения
а;&, но лишь при том условии, если коэффициенты JV"^, а так™
же собственные частоты ш^ и коэффициенты затухания j^ Р&с-
сматриваются как эмпирические постоянные^ определяемые из
самой кривой дисперсии и фактического положения спектраль-
спектральных линий в спектре излучения или поглощения вещества. В

560 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
частности, для согласования с опытом оказалось необходимым
в этой формуле величины N^ заменить на /fc-ZVfc, где /& — посто-
постоянные коэффициенты, меньшие единицы, называемые силами
осцилляторов.
Теорию дисперсии в квантовой механике можно строить по
той же схеме, что и в классической физике. Задача сводит™
ся к вычислению поляризуемости атомов и молекул в элек-
электрическом поле световой волны. Но при решении этой задачи
надо пользоваться не классическими, а квантомеханическими
уравнениями движения, например, в форме волнового уравнения
Шредингера A887—1961). Поскольку в данной книге квантовая
механика не предполагается известной, систематическое из ложе™
ние квантовой теории дисперсии в ней невозможно. Можно дать
только общую характеристику и некоторые результаты этой те-
теории.
2. Квантовая теория дисперсии (и в этом одно из преиму-
преимуществ ее перед классической) не пользуется моделью квазиупру-
го связанного электрона и не вводит никаких в действительно-
действительности не существующих сил. Квантовая механика объясняет стро-
строение и устойчивость атомных систем с помощью одних только
электрических сил. Для простоты будем предполагать, что в
атоме есть всего только один валентный электрон^ определяю-
определяющий его химические и оптические свойства. Остальные элек-
электроны прочно удерживаются на внутренних оболочках, обладая
значительно большими энергиями связи. Состояния таких элек-
электронов практически не возмущаются слабым электрическим по-
полем световой волны. Их роль сводится только к изменению элек-
электрического поля атомного ядра, в котором движется валентный
электрон. Именно по этой причине атом может рассматриваться
как одноэлектронный. Такая модель атома весьма близко соот-
соответствует действительности.
В отсутствие внешних полей атом может находиться только
во вполне определенных стационарных состояниях, в которых
его энергия может принимать также вполне определенные дис-
дискретные значения W\j W2, Ws, • • • (уровни энергии). Их принято
нумеровать в порядке возрастания энергии. При переходе атома
с высшего энергетического уровня к на более низкий уровень п
происходит излучение света с испусканием кванта энергии
Пюкп = hvkn ^Wk- Wn. (85.1)
При обратном переходе атома с низшего энергетического уров-
уровня п на более высокий уровень к происходит возбуждение атома
с поглощением такого же кванта. Таким образом, в отличие от
классического гармонического осциллятора, атом, далее если он
одноэлектронный, излучает не одну частоту cjq, а целый спектр

85 ДИСПЕРСИОННАЯ ФОРМУЛА КВАНТОВОЙ МЕХАНИКИ 561
частот ujfcnj которые в квантовой теории дисперсии и играют
ролв собственных частот атома. Если переход происходит с бо-
более низкого уровня к на более высокий уровень п (поглощение),
то для сохранения без изменения соотношения (84.10) удобно
ввести отрицательные частоты ш^п. Если нет внешних возму-
возмущений (отсутствие силовых полей, невысокие температуры), то
в результате процессов излучения все атомы перейдут на низ-
низший или основной энергетический уровень, т.е. в так называемое
основное или нормальное состояние. На основном уровне изо™
лированный атом будет находиться неограниченно долго, пока
в результате внешнего воздействия он не перейдет на другой
уровень.
При включении внешнего поля атом выйдет из исходного
основного стационарного состояния. Возникшее состояние, со™
гласно квантовой механике, можно характеризовать как супер-
суперпозицию стационарных состояний, каждому из которых припи-
приписывается определенная вероятность. Если электрическое поле
слабое и гармонически меняется во времени с частотой о;, то
эти вероятности также будут меняться во времени с той же ча™
стотой. Появится переменный дипольный момент атома, инду-
цированный электрическим полем световой волны. Его можно
представить в виде р = /ЗЕ. В общем случае поляризуемость
атома /3 есть тензор^ но мы ограничимся простейшим случаем,
когда он скаляр. Если не учитывать поглощения (что допусти-
допустимо вдали от собственных частот о;^), то квантовая механика
приводит к результату
т
5.2)
f
к
!
пк
где fnk — постоянные. Формула предполагает, что до включения
электрического поля атом находился в стационарном состоянии
п. Суммирование ведется по всем возможным значениям fc, как
большим, так и меньшим п.
Для выяснения физического смысла постоянных /пд. заме-
заметим, что существует определенная вероятность, что за опре-
определенное время (например, равное единице) атом в отсутствие
внешних полей самопроизвольно перейдет из высшего стацио-
стационарного состояния к в более низкое стационарное состояние п.
Постоянная fn^ пропорциональна этой вероятности. Самопро-
Самопроизвольный переход из низшего состояния п в высшее состояние
fc, конечно, невозможен. В этом случае /&п определяется соот-
соотношением fkn = —fnk- Следовательно, при п = к величины /пд.
равны нулю, так что суммирование в (85.2) производится толь-
только по к Ф п. Величина /п& и называется силой осциллятора с
частотой

562 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Используя выражения (85.2), приходим к следующей диспер-
дисперсионной формуле для атомов с одним валентным электроном:
п2 = 1 + 4тгЖ^ V Jnk .. (85.3)
кфп
Сравнение этой формулы с классической формулой (84.10) (без
учета поглощения) приводит к следующей наглядной аналогии.
Все атомы, находящиеся в одном и том же исходном состоянии
п, как бы разбиваются на группы, нумеруемые индексом к. Ато-
мы одной и той же группы ведут себя как классические гармо-
гармонические осцилляторы с собственной частотой о;п&. Если к > п,
то частота шп^ считается положительной, а при к < п — отри-
отрицательной. Число атомов fc-й группы в единице объема опреде-
определяется выражением N^ = fnkN. Так как ]Р N^ = -/V, то должно
быть
?/** = !. (85.4)
к
Если в атоме Z валентных электронов, то это соотношение пе-
переходит в соотношение
Y,fnh = Z. (85.5)
к
Полученные формулы выражают так называемое правило
сумм^ найденное независимо друг от друга Томасом и Рейхе, с
одной стороны, и Куном, с другой A925 г.). Приведенные наво-
наводящие рассуждения не могут служить доказательством формул
(85.4) и (85.5). Это видно уже из того, что при к < п силы осцил-
осцилляторов /пд., а потому и числа атомов N^ отрицательны. Однако
сами формулы (85.4) и (85.5) могут быть строго доказаны мето-
методами квантовой механики.
8. Если до включения электрического поля атомы газа не
находились в одном и том же стационарном состоянии, а были
распределены по таким состояниям, то формулу (85.3) следует
заменить на формулу
п2 = 1 + AttN^- У У -ф^. (85.6)
п I
Таким же путем должны быть обобщены и правила сумм (85.4)
и (85.5) — в них суммирование надо производить не только по
всем значениям fc, но и по всем значениям п.
Принципиально новое явление, предсказанное квантовой ме-
механикой, состоит в том, что в формулу (85.6) могут входить
слагаемые не только с положительными fn^ (когда к > п), но

п+
§ 86 ДИСПЕРСИОННАЯ ФОРМУЛА КВАНТОВОЙ МЕХАНИКИ 563
и с отрицательными (когда к < п). Так как uj^k = cj|n, то в
ДИСПерСИОННуЮ формулу ВОЙДУТ ТОЛЬКО СуММЫ (fnk + fkn)j а не
каждое слагаемое в отдельности. Если на нижнем энергетиче-
ском уровне находится больше атомов, чем на верхнем, то {fnkJr
+ fkn) > 0, в противоположном случае (fnk + fkn) < 0. В первом
случае собственная частота \шп^\ внесет в дисперсионную фор-
формулу (85.6) слагаемое того же знака, что и в классическую фор-
формулу, во втором — противоположного. В соответствии с этим
различают положительную и от-
отрицательную дисперсию. Ход по™
казателя преломления п(ш) вблизи
собственной частоты wq = \шп^\ в
обоих случаях представлен схема-
схематически на рис. 300 (п_|_ для поло-
положительной, п— для отрицательной \
дисперсии). Что касается коэффи- ~\
циента затухания 7, то в случае от-
отрицательной дисперсии он также
отрицателен, т.е. при распростра- рис 300
нении света имеет место его усиле-
усиление, а не ослабление. Это происходит, конечно, за счет переходов
атомов с более высокого энергетического уровня на более низ-
низкий с испусканием квантов света (индуцированное излучение,
см. § 119).
В обычных условиях до включения внешнего поля атомы
среды находятся на самом низком — основном — энергетическом
уровне. В этом случае световая волна будет переводить атомы
только на более высокие уровни, так что все fnk окажутся по-
положительными. То же самое будет происходить и при тепловом
возбуждении в случае термодинамического равновесия, так как,
в соответствии с формулой Больцмана, число атомов в исходном
состоянии будет убывать с возрастанием номера энергетическо-
энергетического уровня. Однако, применяя нетепловые методы возбуждения,
например, пропуская через вещество сильные электрические то-
токи, можно создавать термодинамически неравновесные метаста-
бильные состояния вещества с инверсной заселенностью энер-
энергетических уровней, как это в действительности и делается в
лазерах. Под инверсной заселенностью двух различных энерге-
энергетических уровней понимают такое состояние, когда на верхнем
уровне находится больше атомов, чем на нижнем. В этом случае
можно получать и действительно получают среду с отрицатель-
отрицательной дисперсией. Влияние отрицательных слагаемых в дисперси-
дисперсионной формуле впервые A930 г.) наблюдал Ладенбург в газе при
прохождении через него сильного электрического разряда, хотя
дисперсия в целом в его опытах и оставалась положительной.

564 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
§ 86. Методы экспериментального исследования
аномальной дисперсии
1. Аномальная дисперсия впервые наблюдалась Л еру A832—-
1907) в 1861 г. Он обнаружил, что в призме, наполненной пара-
парами йода, синие лучи преломляются меньше красных (промежу-
точные лучи парами йода сильно поглощаются и ускользают от
наблюдения). Отсюда следует, что при переходе от красных к
синим лучам показатель преломления паров йода должен убы-
убывать, т.е. в указанной области спектра дисперсия паров йода
аномальна.
Открытие Л еру не обратило на себя должного внимания, по™
ка Христиансен A848-1917) в 1870 г. не обнаружил и деталь-
детально изучил аномальную дисперсию в растворе фуксина в спир-
спирте. Здесь показатель преломления наименьший (п = 1,285) для
фиолетовых и наибольший (п = 1,561) для желтых лучей, зеле-
зеленые лучи поглощаются.
Систематические экспериментальные исследования аномаль-
аномальной дисперсии были выполнены Кундтом A839—-1894). Он уста-
установил важный экспериментальный результат, что аномальный
ход дисперсии всегда сопровождается поглощением. После экс-
экспериментальных работ Кундта и разработки теории дисперсии
стало ясно, что аномальная дисперсия не есть какое-то редкое
явление природы, а должна наблюдаться у всех веществ в тех
областях спектра, где имеется сильное поглощение.
При изучении аномальной дисперсии Кундт пользовался ме-
методом скрещенных призм, который применялся еще Ньютоном
в его исследованиях по дисперсии света. Идея метода состоит
в следующем. Берутся две призмы, из которых первая изго-
изготовлена из вещества с нормальной дисперсией (обычно из стек-
стекла), вторая — из исследуемого вещества. Источником света, как
во всяком спектроскопе, служит освещаемая щель, помещаемая
в фокальной плоскости коллиматорной линзы. Первая призма,
ребро которой устанавливается вертикально, разлагает падаю-
падающий свет в цветную горизонтальную полоску (спектр). Вторая
призма, преломляющее ребро которой горизонтально, помеща-
помещается за первой призмой. Она смещает каждую точку полоски
вверх или вниз, в зависимости от того, куда обращена эта приз-
призма своим основанием: вверх или вниз. Смещение зависит от дли™
ны волны. Вследствие этого полоска искривляется и становится
наклонной. Если дисперсия второй призмы нормальная, то по-
полоска монотонно поднимается или опускается (рис. 301 а). Если
же она аномальная, то в результате поглощения лучей с ано-
аномальной преломляемостью полоска разрывается на две части,
края которых, примыкающие к полосе поглощения, загибаются
в противоположные стороны (рис. 3016"). Разумеется, для по-

86
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ДИСПЕРСИИ
565
лучения описанной картины должна применяться система линз,
дающая на экране изображение освещаемой щели в различных
цветах спектра.
В изящной лекционной демонстрации Кундта, широко при-
применяющейся до настоящего времени, роль второй призмы игра™
ло конусообразное пламя горелки, в которое вводился метал-
металлический натрий. В результате прохождения света через пламя
горелки в спектре наблюдалась не только темная полоска, соот-
Кр
ф
Кр
ф
Рис. 301
Рис. 302
ветствующая желтой линии поглощения паров натрия, но и за™
гиб в противоположные стороны разорванных частей спектра,
примыкающих к области поглощения (рис. 301 б). D-линия по-
поглощения паров натрия в желтой части спектра состоит из двух
близко расположенных тонких линий с длинами волн А^ =
= 589,0 и Xd2 = 589,6 нм. В описанной демонстрации плотность
паров натрия была настолько велика, что обе линии сливались в
одну полоску, и детали явления не разрешались. Их можно раз-
разрешить, уменьшая плотность паров натрия и улучшая условия
опыта. Тогда молено наблюдать две области аномальной диспер-
дисперсии, соответствующие линиям поглощения с длинами волн А^
и Ad2 (рис. 302).
2. Как уже указывалось в п. 2 § 84, проверку теории лучше
всего производить на газах малой плотности, характеризующих-
характеризующихся тонкими и резкими линиями поглощения. Однако при малой
плотности, необходимой для работы вблизи линии поглощения,
показатели преломления газов малы. Для их измерения наилуч™
шим является интерференционный метод, предложенный Пуч-
чианти A901 г.) и усовершенствованный Д.С. Рождественским
в его классических работах по аномальной дисперсии в парах
натрия A912 г.).
В этом методе интерферометр (например, Жамена) скрещи-
скрещивается со спектрографом (дифракционной решеткой или приз-
призмой с большой дисперсией). Интерферометр устанавливают так,
что он дает в белом свете горизонтальные интерференцион-

566 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
ные полосы на щели спектрографа, установленной вертикаль-
вертикально. Цветную интерференционную картину, полученную на ще-
щели, спектрограф развертывает в горизонтальном направлении.
Спектр оказывается пересеченным в продольном направлении
интерференционными полосами, каждая из которых характери-
характеризуется одним и тем же порядком интерференции. Цвет полосы
меняется вдоль ее длины от красного к фиолетовому, а рас-
расстояния между полосами при этом уменьшаются из-за умень-
уменьшения длины волны. Интерференционным минимумам соответ-
соответствуют темные линии. Таким образом, спектр будет пересечен
в продольном направлении темными линиями, сужающимися от
красного конца спектра к фиолетовому.
Перед измерением прибор регулируется так, чтобы нулевая
интерференционная полоса была прямолинейной и горизонталь-
горизонтальной. Примем ее за ось X с направлением от красного конца к
фиолетовому, а ось Y направим параллельно щели спектрогра-
спектрографа. Ширина интерференционной полосы пропорциональна А и
может быть представлена в виде Ау = аА(ж), где а — постоян-
постоянная прибора, практически не зависящая от номера полосы (по-
(порядка интерференции) к. Поэтому ордината к-й полосы будет
Ук = к Ау = акХ(х). Это есть уравнение кривой, определяющей
форму рассматриваемой полосы.
Введем теперь в одно из плеч интерферометра слой иссле-
исследуемого вещества толщины I с показателем преломления п(А).
Тогда добавится разность хода (п —1I, в результате чего полосы
интерференции сместятся вверх или вниз на (п — 1I/Х полос, т.е.
на расстояние (п — 1I/А(Ду). Уравнение, определяющее форму
к-й полосы, примет вид
Ук = a[k\(x) ± (п - 1I] (86.1)
(знак определяется тем, в какое из плеч интерферометра введен
слой исследуемого вещества). В частности, при к = 0 получаем
у о = а(п — 1I. Отсюда видно, что нулевая интерференционная
полоса вычерчивает в определенном масштабе график зависимо-
зависимости показателя преломления п от абсциссы ж, а следовательно,
и от длины волны А, т.е. определяет дисперсию исследуемого
вещества. Полосы ненулевого порядка имеют дополнительный
наклон, изменяющийся с изменением к (см. рис. 303, заимство-
заимствованный из работ Рождественского).
8. Небольшое изменение метода позволило Рождественскому
значительно повысить точность измерений в окрестности поло-
полосы поглощения. Измененный метод получил название метода
крюков. Допустим, что в одно из плеч интерферометра введено
исследуемое вещество (газ или пар), а в другое — стеклянная
пластинка толщины 1СТ с показателем преломления пСТ. Пла-
Пластинка вносит между интерферирующими пучками разность хо-

86
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ДИСПЕРСИИ
567
да (пст — 1)/ст? смещая интерференционную картину вверх или
вниз на расстояние (пст ~~ 1I ста. Теперь ордината fc-й полосы
будет определяться выражением
ук = а[к\(х) ± (п - 1I т (пст ^ 1IСТ]. (86.2)
Интерференционная полоса нулевого порядка уйдет из поля зре-
зрения. Ее место в поле зрения займет другая интерференционная
Рис. 303
полоса, порядок к которой найдется, если в (86.2) положить уд. =
= 0. Это дает
к = ±?*LZ± lCT T Hl-L I (86.3)
А А
Из-за близости к единице показателей преломления газов по™
следнее слагаемое мало и при вычислении к может не учиты-
учитываться. Таким путем для пластинки с 1СТ = 1 мм, пст = 1,5
при длине волны А = 600 нм получаем к ~ 104. В белом свете
интерференция столь высокого порядка невозможна. Интерфе-
Интерференция в белом свете становится возможной благодаря наличию
спектроскопа, играющего роль монохроматора, пространствен-
пространственно разлагающего белый свет на квазимонохроматические состав™
ляющие. Поэтому длина волны А вдоль каждой интерференци-
интерференционной полосы изменяется, т.е. является функцией координаты х.

568 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Дифференцируя у д. по х при постоянном к7 находим наклон
к-й интерференционной полосы:
Благодаря малой дисперсии стекла последнее слагаемое мало и
может быть отброшено. Если в отсутствие стеклянной пластин™
ки и исследуемого вещества нулевая интерференционная полоса
горизонтальна, то внесение одной только пластинки делает ин-
интерференционные полосы наклонными. Наклон полосы опреде-
определяется производной -^ = ка—, т.е. он тем больше, чем боль-
dx dx
ше порядок интерференции к. Наклон, вызываемый стеклянной
пластинкой, происходит в одну и ту же сторону во всей исследуе-
исследуемой области спектра. При перенесении пластинки в другое плечо
интерферометра знак fc, а с ним и наклон интерференционных
полос меняются на противоположные. Поместим пластинку в то
плечо интерферометра, чтобы было к > 0, т.е.
к^!^±1стт (86.5)
А
Тогда при нашем выборе положительного направления оси X
(dX/dx < 0) получится dy^/dx < 0, т.е. полосы интерферен-
ции будут наклонены сверху (от положительного конца оси Y)
вниз направо (в сторону положительного — фиолетового — кон-
конца оси X).
Допустим теперь, что во второе плечо интерферометра вве-
введен исследуемый газ. Показатель преломления газа вдали от
линии поглощения очень близок к единице и на наклон полос
практически не оказывает никакого влияния. Зато вблизи ли-
линии поглощения велика производная dn/dX, вызывающая силь-
сильный загиб интерференционных полос. В отсутствие пластинки
наклон будет определяться производной
dyk _ _ jdX dn
dx dx dX
Следовательно, в области нормальной дисперсии (dn/dX < 0)
получится dyk/dx > 0, т.е. в этом случае интерференционные
полосы пойдут сверху вниз налево.
Таким образом, в области нормальной дисперсии стеклянная
пластинка и исследуемый газ вызывают наклон полос в проти-
противоположные стороны. При одновременном действии газа и стек-
стеклянной пластинки с надлежаще подобранной толщиной эти дей-
действия в определенной точке интерференционной полосы могут
компенсировать друг друга. В такой точке касательная к ин-
интерференционной полосе станет горизонтальной, т.е. на полосе
получится крюк, по выражению Рождественского. Вблизи линии

87
ДИСПЕРСИЯ ПЛАЗМЫ
569
поглощения таких крюков получится два. Оба они расположены
в области нормальной дисперсии. Слева (со стороны длинных
волн) крюк будет обращен вершиною
вниз, а справа (со стороны коротких ™™*-**^—^«^m..»---«-
волн) — вверх (рис. 304). В вершине .
крюка должно быть dy^/dx = 0, или ^мШг
dyk/d\ = 0, т.е. ( ¦¦' ;¦
или
и
jdn
1
ал
ал
dnCT
= 0,
(86.6)
рис> 304
Последнее слагаемое, как уже указы™ ^
валось, пренебрежимо мало, а пер-
первое может быть вычислено по форму™
ле (86.5). Таким образом, по формуле
(86.6) можно вычислить значения дисперсии газа dn/dX для тех
значений А, которые соответствуют вершинам крюков, т.е. точ-
точкам загиба интерференционных полос.
У лее в начале своих исследований Рождественский убедился,
что вдали от линии поглощения формула Зельмейера правильно
передает ход показателя преломления в зависимости от длины
волны. Эту формулу следует писать в виде
= 1 +
= 1 +
(86.7)
где / — сила осциллятора. Обозначим через ДА расстояние вер™
шины одного из крюков от линии поглощения Aq (тогда рас-
расстояние между вершинами обоих крюков будет 2ДА). Вычислим
по формуле (86.7) производную dn/dX7 учитывая при этом, что
|ДА| С Ао и п ~ 1 <С 1. Тогда из формулы (86.6), пренебрегая
последним слагаемым, найдем
/ =
Таким образом, силу осциллятора молено найти по расстоянию
между вершинами крюков.
§ 87. Дисперсия плазмы
1. Плазма есть ионизованный газ, в котором электроны и
ионы могут рассматриваться как свободные частицы с собствен™
ными частотами, равными нулю (см. т. III, § 121). Диэлектриче-
Диэлектрическая проницаемость плазмы определяется в основном свободны-
свободными электронами. Влиянием ионов можно пренебречь, так как

570 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
их массы практически бесконечно велики по сравнению с мае™
сами легких электронов. Полагая в формуле (84.5) ш® = 0 и
пренебрегая затуханием, получим для плазмы
+ |
I Е
I *"*~
+ 1
+1
+ 1
+ |
_|
I
I
-I
-1
_|
, (87.1)
где введено обозначение
ш2р = 4тгЖе2/^, (87.2)
а N означает концентрацию свободных электронов. Величина шр
называется плазменной или ленгмюровской частотой. Частота
шр играет для плазмы роль собственной частоты. Однако она
характеризует не отдельные частицы, а весь коллектив заря-
заряженных частиц, из которых состоит плазма.
Чтобы понять, как может появиться такая «собственная ча™
стота» у коллектива частиц, каждая из которых в отдельности
собственными частотами не обладает, рассмотрим следующий
пример. Допустим, что нейтральная
плазма занимает пространство меж-
между бесконечными плоскостями, пер™
пендикулярными к оси X. Среднее
электрическое поле в такой нейтраль-
нейтральной плазме равно нулю. Сместим все
электроны плазмы параллельно оси X
на малое расстояние х (рис. 305), а ио-
Рис 305 ны °ставим несмещенными. Тогда на
границах плазмы возникнут электри-
электрические заряды с поверхностной плотностью а = Nex1 и в плазме
возникнет электрическое поле Е = 4тга = 4тгЖеж. На каждый
электрон будет действовать квазиупругая сила F = 4тгМе2х.
Если плазму предоставить самой себе, то возникнет свобод-
свободное гармоническое колебание электронов с собственной частотой
д/4тгЖе2/т. Но это и есть плазменная частота.
2. Для плазменной частоты ш = шр диэлектрическая про™
ницаемость е обращается в нуль. При ш > шр величина ? (ас
ней и показатель преломления п = л/е) положительна, но мень-
меньше единицы. При ш < шр диэлектрическая проницаемость е от™
рицательна, а показатель преломления чисто мнимый, т.е. п =
= —гн. Поэтому длинные электромагнитные волны (частота ко-
которых ш < Шр) в плазме распространяться не могут. Они могут
проникать только в тонкий поверхностный слой плазмы, испы-
испытывая от него полное отражение. Действительно, предположим,
что падающая волна поляризована перпендикулярно к плоско-
плоскости падения. (Случай другой поляризации разбирается так же.)

§ 87 ДИСПЕРСИЯ ПЛАЗМЫ 571
Тогда по формуле Френеля
R cos ер — \fe cos ф cos ip + %ж cos ф
E cos if + л/ё cost/; cos Lp — гмcosф '
причем simp/ sin 1/; = ^e = -ix. Следовательно, costjj =
= д/l ~ sin2 V> — лА + sin2 (f/^2. Таким образом, сонф — вели-
величина вещественная, а потому \R/S\ = 1, что и доказывает наше
утверждение.
Изложенное играет исключительно важную роль в осуще-
осуществлении на Земле дальней радиосвязи. В земной атмосфере име-
ется ионизованная область, называемая ионосферой. Она начи-
начинается примерно с высоты 60 км и простирается, по-видимому,
до высот ^ 20 000 км. Основными источниками ионизации ионо-
ионосферы являются ультрафиолетовое излучение Солнца и мягкое
(от 0,8 до 30 нм) рентгеновское излучение солнечной короны.
Другим источником служит корпускулярное излучение Солн-
Солнца. Концентрация электронов N меняется с высотой неравно-
неравномерно. Имеется несколько относительных максимумов иониза-
ионизации, расположенных на различных высотах. Область ионосфе-
ионосферы, содержащая один из таких максимумов, условно называется
ионосферным слоем. Слои, расположенные в порядке возраста-
возрастания высоты, обозначаются через D, Е\, 1?2, ^ъ ^2- Максимумы
электронной концентрации в них меняются примерно в преде™
л ах 104 — 106 электронов на 1 см3. Концентрация электронов
зависит от географической широты места и испытывает регу-
регулярные суточные и годичные изменения. Летом она больше, чем
зимой, днем больше, чем ночью. Кроме того, наблюдаются спо~
радические изменения концентрации, вызванные вспышками на
Солнце и пр.
Посмотрим теперь, как радиоволны, излученные какой-либо
радиостанцией А, находящейся на земной поверхности, могут
достигнуть приемника В1 расположенного также на земной по-
поверхности на расстоянии нескольких тысяч километров. Прямой
путь через землю исключен, так как радиоволны в земле силь-
сильно поглощаются из-за ее высокой электрической проводимости.
Показатель преломления неионизованного воздуха очень мало
отличается от единицы, так что рефракция радиоволн практи-
практически не играет роли. Если бы не было ионосферы, то единствен-
единственным способом достигнуть приемника В была бы дифракция. Но
приемник В расположен глубоко в области геометрической те-
тени на расстоянии в тысячи или десятки тысяч длин волн от
ее границы. При таких условиях интенсивность дифрагирован-
дифрагированной волны в точке нахождения приемника В будет ничтожно
мала, и никакой приемник практически не сможет обнаружить
эту волну. Положение меняется при наличии ионосферы, так

572 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
как радиоволна может отразиться от ионосферы и таким пу-
путем достигнуть приемника. Только благодаря такому отраже-
отражению возможна передача радиосигналов на земной поверхности
на многие тысячи километров.
3. Найдем связь между фазовой v и групповой и скоростями
электромагнитных волн в плазме при шр > ш. Используя выра™
жение (87.1), для волнового числа к получаем
с2к2 = ш2е = иJ -ш2.
Дифференцирование этого соотношения дает: c2kdk = ouduj^ т.е.
(u)jk)(du)jdk) = с2, или
vu = с2. (87.3)
Фазовая скорость в плазме
всегда больше скорости света в вакууме. Для групповой скоро-
скорости соотношение (87.3) дает
и = c2/v = су/1 - ш%/ш2. (87.5)
Она всегда меньше с, как это и должно быть.
Отметим интересное астрофизическое применение формулы
(87.5). После открытия Хьюишем в 1967 г. пульсаров (нейтрон-
ных звезд) сразу же было обнаружено, что длинноволновые сиг-
сигналы доходят от пульсаров до Земли медленнее коротковолно-
коротковолновых. (В этом можно убедиться, принимая один и тот же сигнал
с помощью двух радиоприемников, настроенных на разные ча-
частоты.) Это было объяснено влиянием межзвездной плазмы^ че-
через которую проходит сигнал. Квазимонохроматический сигнал
распространяется в межзвездной плазме с групповой скоростью
(87.5). Время распространения сигнала от пульсара до Земли
определяется интегралом t = J dx/u по всему пути сигнала.
Концентрация свободных электронов Ж, а с ней и плазменная
частота шр имеют разные значения в разных точках пути. Од-
Однако всюду Шр^ш^ так что можно ограничиться первым членом
разложения подынтегрального выражения по степеням отноше™
ния ш2/ш2. Это дает
По сравнению с вакуумом время распространения сигнала уве-
увеличивается на
At = -1^ Г ol dx =
2сш2 J p
1
2ттстс2

§ 88 ЭЛЕКТРОМАГНИТНАЯ ЭНЕРГИЯ В ДИСПЕРГИРУЮЩИХ СРЕДАХ 573
где г = е2/(тс2) « 2,8 • 1СП13 см — классический радиус электро-
электрона.
1. Интеграл J N dx имеет смысл полного числа электронов
в цилиндрическом канале, поперечное сечение которого равно
1 см , а длина — пути, пройденному сигналом от пульсара до
Земли. Он является одной из интегральных характеристик меж-
межзвездной плазмы на пути распространения сигнала. Несмотря на
ничтожную концентрацию такой плазмы, из™за колоссальности
расстояний до пульсаров величина этого интеграла оказалась
достаточной, чтобы обнаружить запаздывание (в области санти™
метровых волн) длинноволновых сигналов относительно корот-
коротковолновых. Таким путем впервые были оценены расстояния до
пульсаров. В предположении, что на пути от пульсаров к Земле
около 10 % атомов водорода ионизовано, было найдено, что рас-
расстояния до большинства зарегистрированных пульсаров лежат
между 200 и 7000 световых лет.
§ 88. Среднмм плотность электромагнитной энергии в
диспергирующих средах
1. Выражение для плотности электромагнитной энергии w = (sE +
+ fiH )/(8тг) получается в предположении, что е и /i постоянны, т.е. не
зависят от частоты ш (см. т. III, § 84). В случае диспергирующих сред это
выражение неприменимо. Не разбирая этот вопрос в общем виде, выве™
дем выражение для средней плотности электромагнитной энергии в непо-
глощающей диспергирующей среде на частном примере, принадлежащем
М.Л. Левину.
Пусть вещество с диэлектрической проницаемостью е(ш) и магнитной
проницаемостью /л(и)) заполняет плоский конденсатор с емкостью С =
= е(ш)Со и тонкий соленоид с индуктивностью L = /i(u;)Lo, соединенные
в колебательный контур (рис. 306). Здесь Со и Lq —
значения емкости и индуктивности для того случая,
когда в пространстве между обкладками конденсато-
конденсатора и внутри соленоида вакуум. При отсутствии со™
R
противления в контуре будут совершаться свобод-
свободные гармонические колебания с циклической часто™ '—
С
той ш = 1/у Ь(ш)С(ш). Если в некоторый момент
времени ввести в контур малое сопротивление R, то, Рис. 306
начиная с этого момента, колебания сделаются зату-
затухающими и первоначально запасенная электромагнитная энергия будет пе-
реходть в джоулево тепло, выделяющееся в сопротивлении R. Полное коли™
чество тепла, выделившееся в сопротивлении R за время, когда колебания
прекратятся, будет равно электромагнитной энергии, запасенной в контуре
до введения сопротивления. Поэтому задача сводится к вычислению джо-
улева тепла.
Пусть при t < 0 в контуре совершаются свободные колебания:
= Joe , V = Voe ,

574 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
где I — сила тока в контуре, а V — напряжение на обкладках конденсатора,
связанные между собой соотношением Ы + V = 0, или iujLI + V = 0. Если в
момент t = 0 в контур ввести сопротивление R, то, начиная с этого момента,
колебания будут описываться уравнением
откуда
где ш — комплексная частота, определяемая уравнением
Если R исчезающе мало, то ш должна отличаться от ш также на исчезающе
малую величину. Но ш удовлетворяет уравнению
± = 0.
шЦш)
шС(ш)
Вычитая его из предыдущего соотношения и заменяя все разности диффе™
ренциалами, получим
откуда ш = ш + гд, причем
R d(ujL) I d(u)C) d(ujL) L d(ujC)
5 duo uj2C2 duj duo С duo
Для определения джоулева тепла надо проинтегрировать выражение
RI' по времени. Поскольку возведение в квадрат — нелинейная операция,
необходимо перейти к вещественной форме, т.е. сделать замену
/ ^ Re (/) = (/ +Г )/2.
Энергия, первоначально запасенная в колебательном контуре, равна
сю
8 1
о
или в пределе при ё -^ О
4 8'
Подставляя сюда значение для R/8 и пользуясь соотношением ujL\Iq\ = |Vo|,
получим
w= Lq\Iq\2 djujfi) [ GolFol2cl(a;g)
4 duj 4 duj
Если бы между обкладками конденсатора и внутри соленоида был ваку-
вакуум, то для средних по времени значений магнитной и электрической энер-
энергий можно было бы написать
О7Г 4 О7Г

§ 88 ЭЛЕКТРОМАГНИТНАЯ ЭНЕРГИЯ В ДИСПЕРГИРУЮЩИХ СРЕДАХ 575
где тт ж те — объемы соленоида и конденсатора, аЕиН — напряженно™
сти электрического и магнитного полей, когда амплитуды напряжения на
конденсаторе и тока в соленоиде равны Vo и /о- Но при заданных Vo и /о
поля ЕиНне зависят от среды, заполняющей конденсатор и соленоид. По-
Поэтому предыдущие соотношения остаются справедливыми и в том случае,
когда конденсатор и соленоид заполнены веществом. Используя их, полу-
получаем следующие выражения для средних по времени значений плотностей
электрической и магнитной энергий:
W
Принципиальный недостаток приведенного вывода состоит в том, что
в нем дифференцирование функций шL и шС производится вдоль мнимой
оси (так как разность частот ш — ш = iR — величина чисто мнимая), а в
окончательном выражении (88.1) производится подмена дифференцирова-
дифференцированием по вещественной переменной ш. Так можно поступать, когда функ™
ции ujL шшС аналитичны. Поэтому для полноты доказательства надо было
бы доказать аналитичность этих функций, чего в выводе Левина нет. Это
можно сделать в общей теории дисперсии, исследуя аналитические свой-
свойства функций е(ш) и /л(и). Однако рассмотрение этого вопроса выходит за
рамки нашей книги.
2. Смысл формулы (88.1) полезно уяснить на примере газа классиче-
классических гармонических осцилляторов в монохроматическом электрическом по™
ле с частотой ш. Вдали от собственной частоты шо осциллятора можно пре-
пренебречь затуханием. Тогда смещение осциллятора из положения равновесия
выразится формулой
_ еЕ
/2 9 \ *
7JI{UJq — 0JZ)
В этом случае энергия слагается из энергии самого электромагнитного по-
ля (т.е. поля в вакууме) и из энергии частиц, находящихся в поле. Послед-
Последняя энергия в свою очередь состоит из кинетической и потенциальной
энергии колеблющихся осцилляторов. В статических полях кинетической
энергии нет. Это приводит к формуле w = еЕ2 /(8тг). В переменных полях
кинетическую энергию надо учитывать, что и делается ниже.
Плотность собственно энергии электрического поля равна
+ Е* \ 2 Е2 ЕЕ*
Плотность потенциальной энергии:
NmujQ /r + r\ Nmujl 2 . *ч .
w>2 = = (г + rr ) + компл. сопр.
2 \ 2 J 8
Плотность кинетической энергии:
Nm /r + r*\ Nmuj2, 2 *ч
W3 = I 1 = (г — rr ) + компл. сопр.
2 \ 2 J 8
Подставляя сюда выражение для г и замечая, что из формулы Зельмейера
следует
d{ue) _л , (eg2
аш

576 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
получим для плотности электрической энергии:
We = :r— + -— ^^(ЕЕ ) + компл. сопр.
32тг 32тг аш
Усредняя по времени, получаем первую формулу (88.1). Для плотности маг™
нитной энергии имеем обычное выражение, как в недиспергирующей среде.
ЗАДАЧИ
1. Рэлей предложил определять среднюю скорость движения энергии и
в плоской бегущей волне как отношение средней плотности потока энергии
к средней плотности самой энергии. Пользуясь выражением для вектора
Пойнтинга, показать, что так определенная скорость в случае монохрома-
монохроматической электромагнитной волны совпадает с групповой скоростью.
Решение. Для средних плотностей энергии и ее потока нетрудно
получить
w = —лД —(ЕЕ*), 5= —.Д
откуда и следует требуемый результат.
2. Показать, что если е(ш) и /л(и) положительны, то фазовая и группо-
групповая скорости в электромагнитной волне направлены в одну сторону.
Решение. Средняя плотность электромагнитной энергии
w=±d{^ ±d{u^
8тг duo к } 8тг 8тг v ;
— существенно положительная величина. В плоской волне е(ЕЕ*) =
= //(НН*). Поэтому
d{ue) | fidjujfi) ^ Q
dou e duj
Это неравенство должно соблюдаться для любых сред, у которых знаки
е и [л совпадают, поскольку оно выведено в предположении, что в среде
может распространяться однородная монохроматическая волна, для кото-
которой k2 = efiuj2/с2 > 0. В этом же предположении имеет смысл говорить о
групповой скорости. Преобразовав предыдущее неравенство к виду
ш duj
»kdk>0
легко получить требуемый результат.
§ 89. Поглощение света и ушмрение спектральных
линий
1. В классической теории дисперсии поглощение (затухание)
излучения учитывается формально с помощью тормозящей си™
лы ^gr = ^2m/yv в уравнении (84.1). Благодаря этому ампли™
туда колебаний убывает во времени экспоненциально по закону
ехр (—7^)> а энергия колебаний — по закону
? = ?ое-2ч* = ?ое^Т. (89.1)

§ 89 ПОГЛОЩЕНИЕ СВЕТА И УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ 577
Физическая природа тормозящей силы ^g"v при этом остается
нераскрытой.
Планк развил теорию дисперсии и поглощения света в пред™
положении, что колеблющийся осциллятор (электрон), двигаясь
ускоренно, непрерывно теряет энергию на излучение. Эта убыль
энергии на излучение определяется формулой
-I = S*2 <89-2»
(см. т. III, § 141). Применим эту формулу к осциллятору. Если
потеря энергии осциллятора за период колебаний относительно
мала, то колебания будут отличаться от гармонических мало.
Тогда можно считать, что средние за период колебаний значения
кинетической и потенциальной энергий осциллятора одинаковы,
а потому среднее значение его полной энергии равно удвоенному
среднему значению кинетической энергии. Но полная энергия 8
слабо затухающего осциллятора в течение периода колебаний
остается почти постоянной, так что ? ~ ?. В случае слабо за-
затухающих колебаний v « vq sin (u)®t + #), v = ujqVq cos (ujt + 8).
Возведя последнее соотношение в квадрат и усреднив по перио-
периоду колебаний, получим
(v2)=oo2(v2)=oo2S/m.
Усреднив теперь по времени формулу (89.2), найдем
_д?_ _ 2е2ш1 а
dt Зтс3
Отсюда снова получается формула вида (89.1). Таким образом,
излучение проявляется так, как если бы на колеблющийся заряд
действовала тормозящая сила —2?тгрг, причем
7 = i^f. (89.3)
3 тс3
Затухание, обусловленное излучением, называется есте-
естественным затуханием. Время естественного затухания тизл, в
течение которого энергия убывает в е раз, равно
1 Зтс3 Зтс Х2 3 (\\ f X\ fQU Ax
^изл = ^- = tty^ = ^^ТЛ = Б~2 I " J \ ~ Ь (89.4)
27 2e2uj %7T2e2 Ы2 \rj\cj
где г = е2/(тс2) = 2,8 • 1СГ13 см — классический радиус элек-
электрона. Для длины волны Л = 600 нм эта формула дает тизл —
= 1,63 • 10"8 с.
2. Затухание делает колебания немонохроматическими. Это
приводит к уширению спектральных линий. Ширина спектраль-
спектральной линии, обусловленная затуханием вследствие излучения, на™
зывается естественной шириной спектральной линии. Для ее
19 Д.В. Сивухин

578
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
вычисления поле излучения Е = Eq ехр (—7^) sincjot надо раз™
ложить в интеграл Фурье. Квадраты коэффициентов этого раз-
разложения определяют относительные спектральные плотности
излучения /(cj), т.е. распределение энергии в спектральной ли™
нии по спектру частот. Результат выражается ранее выведенной
формулой B9.10), которую здесь мы запишем в виде
ш0т=5
заменив прежнее время т на 2тизл. (Прежнее время т определяло
затухание по амплитуде^ а здесь через тизл обозначено время
затухания по энергии.) Форма спектральной линии приведена
на рис. 307 для значения параметра б^отизл = 5, которое, конеч-
конечно, слишком мало. (В приведенном выше численном примере
^отизл = 2тгстизл/А ^ 5 • 105) Время затухания для спектральных
линий, излучаемых газами, в действительности много больше, а
сами спектральные линии много уже, чем на кривой рис. 307.
Ширину спектральной линии принято характеризовать рас-
расстоянием между точками А и А', расположенными по разные
стороны от центра линии, в которых интенсивность света равна
половине интенсивности в
центре линии. Это рас™
стояние называется полу-
полушириной спектральной ли-
линии. Естественная полуши-
полуширина спектральной линии,
как это следует из формулы
(89.5), равна
Да; = 1/тизл = 27. (89.6)
В квантовой физике, где
излучение связывают с пе-
переходом атома с более высо-
высокого энергетического уров-
уровня на более низкий (из
возбужденного состояния в
нормальное), величина тизл
Рис. 307 имеет смысл времени жиз-
жизни возбужденного состояния. Здесь, как и в классической фи-
физике, формула (89.6) является следствием общего соотношения
B9.8), согласно которому Да; • тизл ~ 1.
Естественное затухание свечения изолированных атомов и
соответствующее ему уширение спектральных линий на опыте
исследовалось В. Вином в 1919-1927 гг. В его опытах каналовые
лучи, состоявшие из светящихся атомов, проходили через узкое
отверстие (ОД х 3 мм2) в пространство, где с помощью мощных
-0,4 -0,2
0
0,2 0,4

§ 89 ПОГЛОЩЕНИЕ СВЕТА И УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ 579
насосов поддерживался высокий вакуум (< 0,001 мм рт. ст.). В
этом пространстве атомы двигались без столкновений, но их све-
свечение постепенно затухало по мере удаления от входного от™
верстия. По затуханию свечения можно было оценить время
естественного затухания. Для этого надо было знать среднюю
скорость движения атомов каналовых лучей. Она измерялась
по доплеровскому смещению спектральных линий при наблюде-
наблюдении вдоль направления каналовых лучей и оказалась порядка
5 • 107 см/с (для атомов водорода). Из своих опытов Вин нашел
для времени затухания т около 10~8 с. Эта величина несколько
менялась от одного вещества к другому и от одной спектраль-
спектральной линии к другой. Полученные результаты совпадали с пред-
предсказаниями теории, но только по порядку величины, а простая
зависимость (89.4) времени затухания от длины волны (т ~ А )
не подтвердилась. Впрочем, полного количественного согласия
и нельзя было ожидать от простой классической теории, осно-
основанной на модели гармонического осциллятора.
3. Все изложенное относится к излучению изолированного
атома. В случае среды, состоящей из атомов, надо принять во
внимание, что атом не только теряет энергию на излучение, но и
получает энергию, излучаемую другими атомами. Если бы среда
была оптически однородна, то, как показал Л.И. Мандельштам,
эти два процесса в точности компенсировали бы друг друга. В
отсутствие других причин затухания колебания атома были бы
незатухающими. Плоская бегущая волна распространялась бы
в среде без ослабления.
Дело меняется при нарушении оптической однородности сре-
среды. Однородность может нарушиться либо за счет включения
посторонних частиц (например, пыли или капелек тумана в
воздухе), либо за счет тепловых флуктуации, возникающих в
среде. В этом случае потеря энергии атомами на излучение при
распространении волны будет приводить к ее ослаблению. Од-
Однако это не есть истинное поглощение света с переходом элек-
электромагнитной энергии волны в другие формы энергии (тепло),
а рассеяние света, где такого превращения нет. Истинное по-
поглощение, когда энергия волны превращается в другие формы
(тепло), вызывается другими причинами. Кроме того, ослабле-
ослабление волны, обусловленное излучением, слишком мало по сравне-
сравнению с тем ослаблением, которое во многих случаях наблюдается
в действительности.
4. Одна из причин поглощения света состоит в том, что ато-
атомы, внутри которых происходят колебания, совершая тепловое
движение, претерпевают столкновения друг с другом. При каж-
каждом столкновении резко и неправильно меняются амплитуды
и фазы гармонических колебаний, происходит переход в тепло
19*

580 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
энергии регулярных колебаний, т.е. поглощение света. Исходя
из этих представлений, Г.А. Лорентц развил теорию уширения
спектральных линий, обусловленного столкновениями между
атомами (молекулами) газа. Такое уширение называется удар-
ним уширением. Лорентц показал, что в газах столкновения
между молекулами при тепловом движении статистически при™
водят также к экспоненциальному закону затухания интенсив-
интенсивности волны и к форме спектральных линий такого же вида, что
и при естественном затухании.
Мы не будем проводить детальные вычисления, как это сде-
сделал сам Лорентц. При таких вычислениях надо было бы вводить
специальные предположения относительно характера наруше-
нарушения регулярности амплитуд и фаз колебаний при столкновени-
столкновениях, так что результат оказался бы верным все равно с точностью
до числового коэффициента. А в пределах такой точности его
можно получить из общих соображений без всяких вычислений,
если воспользоваться общей формулой B9.8).
Обозначим через туд среднее время свободного пробега ато-
атома от одного столкновения до следующего. Можно считать, что
между двумя последовательными столкновениями колебания
внутри атома происходят гармонически, а при каждом столк-
столкновении обрываются. Затем они опять возобновляются, но уже
с новыми значениями амплитуд и фаз, никак не связанными
с амплитудами и фазами до столкновения. Но такие обрываю-
обрывающиеся во времени колебания при разложении в спектр будут
заполнять интервал частот Да;, подчиняющийся соотношению
Аи) • Туд ~ 1. Отсюда следует, что ударное уширение спектраль-
спектральных линий определяется формулой
Аш - 1/туд. (89.7)
Число столкновений, претерпеваемых атомом в единицу вре-
времени, определяется формулой кинетической теории газов z =
= NaVj где N — число атомов в единице объема, а — газоки-
газокинетическое поперечное сечение атома, v « ^/кТ/т — средняя
скорость теплового движения атома (см. т. II, § 86). Следова-
Следовательно,
Ударные затухание и уширение спектральных линий особен-
особенно существенны в плотных газах и при высоких температурах.
Для уменьшения влияния столкновений надо уменьшать плот-
плотность газа. Вот почему в опытах Вина при изучении естествен-
естественного затухания свечения атомов каналовые лучи направлялись в
высокий вакуум. В обычных условиях столкновения значитель-
значительно сильнее влияют на затухание волны, чем излучение. Однако
формула (89.8) дает для времени затухания все же большие, а

§ 89 ПОГЛОЩЕНИЕ СВЕТА И УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ 581
следовательно, для уширения спектральных линий — меньшие
значения, чем наблюдаются на опыте. Следовательно, должны
существовать другие причины поглощения света и уширения
спектральных линий.
Такими причинами могут быть воздействия на излучающий
атом различных силовых полей^ в первую очередь электриче-
электрических полей, создаваемых окружающими атомами. В постоян-
постоянных электрических полях спектральные линии претерпевают
расщепление (эффект Штарка). В переменных полях измене-
изменение спектральных линий носит более сложный характер. Это —
одна из основных причин уширения спектральных линий.
5. Другой причиной уширения спектральных линий являет-
является изменение частоты излучаемого света из-за эффекта Доплера.
Пусть и® — частота волны, излучаемой неподвижной молекулой
(атомом). Если молекула равномерно движется, то частота вол-
волны, излучаемой ею в направлении оси Х1 в лабораторной си™
стеме отсчета изменяется и в нерелятивистском приближении
определяется формулой
cj = ljoA + vx/c), (89.9)
где vx — скорость молекулы в направлении оси X.
Согласно закону распределения скоростей Максвелла, веро-
вероятность того, что ж-составляющая скорости молекулы газа ле-
лежит в интервале (vx,vx + dvx), равна
7 л (
dw = Аг exp y—
где m — масса молекулы, aii - постоянная нормировки (см.
т. II, § 72). Заменив в этом выражении переменную vx на w по
формуле (89.9), получим
1 л с тс (ш — шо\
dw = A1—exp\-—
шо Y Ikl
Так как излучения различных молекул газа некогерентны^ то
эта величина определяет вероятность излучения в спектральный
интервал {оо^оо + dui). Интенсивность света 1(ш) dw, приходяща-
приходящаяся на этот интервал, будет пропорциональна dw. В результате
получится
[^(J] (89.10)
где /о — новая постоянная. Очевидно, I® = /(cjq), т.е. Iq есть
спектральная интенсивность в середине линии. По обе стороны
от середины линии спектральная интенсивность убывает экспо-
экспоненциально по закону (89.10). Полуширина спектральной линии,

582 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
как нетрудно вычислить, определяется формулой
0 = 2л/Ы2 —а;0 = 1,67 — ш0, (89.11)
с с
где vm = л/2кТ/т — наиболее вероятная скорость молекулы.
Эффект Доплера является основной причиной уширения
спектральных линий в разреженных газах при высоких тем-
температурах.
6. В основе теории дисперсии и абсорбции света, как она из-
изложена в этой главе, лежат линейные уравнения. По этой при™
чине показатели преломления п и затухания к в этой теории по-
постоянны, т.е. не зависят от интенсивности света. Амплитуда
монохроматической волны при ее распространении убывает по
закону А = Aq exp (^2ттмх/ХI а интенсивность — по закону
1 = 10е-ах, (89.12)
где а = Аттк/Х — коэффициент затухания (поглощения), за-
зависящий, вообще говоря, от длины волны. Формула (89.12) вы™
ражает так называемый закон Бугера A698-1758), постулиро-
постулированный им в 1729 г. Сущность этого закона состоит в том, что
для монохроматического света коэффициент затухания (погло-
щения) а не зависит от интенсивности света. СИ. Вавилов, ис-
исследуя на опыте поглощение света в некоторых растворах, уста-
установил, что постоянство коэффициента поглощения а соблюда-
соблюдается с точностью не менее 5 % в крайне широком интервале из-
изменения интенсивности света — от 20 до 2,5-10~19 Вт/см2, т.е. от
интенсивности прямых солнечных лучей, сконцентрированных в
фокусе линзы, до ничтожных интенсивностей, соответствующих
порогу зрительного восприятия глаза.
Интерпретируем эти результаты с точки зрения квантовых
представлений о поглощении света. При поглощении световая
волна переводит молекулу (атом) с основного энергетического
уровня Wq на возбужденный уровень Wni увеличивая тем са-
самым запас поглощенной энергии. Способность молекулы погло-
поглощать свет в возбужденном состоянии иная, чем в основном. Если
в опытах Вавилова коэффициент поглощения оставался одним
и тем же при всех интенсивностях, то отсюда следует, что в
этих опытах число возбужденных молекул было пренебрежимо
мало по сравнению с числом невозбужденных, т.е. было отно-
относительно мало среднее время жизни молекулы в возбужденном
состоянии. И действительно, для веществ, с которыми имел дело
Вавилов в своих опытах, это время не превышало 1СП8 с. Мож-
Можно было бы ожидать, что при больших временах жизни и боль-
больших интенсивностях света число молекул в основном состоянии
(которые практически только и поглощают свет) уменьшится и

§ 90 ЭФФЕКТ КЕРРА 583
закон Бугера перестанет выполняться. Выбрав специально веще™
ства с большими временами жизни в возбужденном состоянии,
Вавилов наблюдал уменьшение коэффициента поглощения при
увеличении интенсивности света. Это было первым примером,
где наблюдалось нарушение принципа суперпозиции в оптике.
После открытия лазеров, сделавших возможным получение
световых волн с напряженностями электрических полей, сравни-
сравнимыми с внутримолекулярными и внутриатомными, класс подоб-
подобных «нелинейных» оптических явлений быстро расширился. Их
изучением занимается нелинейная оптика — самостоятельная
обширная и быстро развивающаяся наука. Краткое представле-
представление об этих явлениях будет дано в последней (XI) главе этого
тома.
§ 90. Двойное преломление в электрическом и
магнитном полмх
1. Электромагнитная природа света и вещества заставляет
ожидать, что оптические свойства вещества должны изменять-
изменяться при его внесении в электрическое и магнитное поле. Действи-
Действительно, такие изменения были обнаружены на опыте. Сначала
Фарадей в 1846 г. открыл магнитооптическое явление — ера-
щение плоскости поляризации света в магнитном поле. Затем
Керр A824—1907) в 1875 г. открыл «электрооптическое явление»,
названное его именем. В 1877 г. тот же Керр нашел, что намагни-
намагниченное железное зеркало иначе отражает поляризованный свет,
чем ненамагниченное. В дальнейшем были открыты и другие
электрооптические и магнитооптические явления.
Электрооптический эффект Керра состоит в том, что
многие изотропные тела при введении в постоянное электри-
электрическое поле становятся оптически анизотропными. Они на-
начинают вести себя подобно одноосным двупреломляющим кри-
кристаллам, оптическая ось которых параллельна приложенному
электрическому полю.
Сам Керр наблюдал это явление сначала на стекле, вводи-
вводимом в электрическое поле. В этом случае, а также в случае всех
других твердых тел оптическая анизотропия может быть вто-
вторичным явлением, а именно может возникать в результате ме-
ханических деформаций, производимых электрическим полем.
Однако последующие исследования самого Керра и других уче-
ученых показали, что явление наблюдается так лее в жидкостях и
даже газах, где механическая анизотропия исключена. Кроме
того, «чистый эффект Керра» можно отделить от эффекта, вы-
вызванного механическими деформациями, исследуя явление в пе-
переменных полях: при внезапном включении или выключении

584
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
к
электрического поля механические деформации возникают и ис™
чезают не сразу, а с некоторой задержкой, тогда как явление
Керра в чистом виде (наблюдаемое в жидкостях и газах) пропс™
ходит практически безынерционно (см. п. 5).
Как и всякое двойное преломление, эффект Керра мож-
можно обнаружить, помещая между скрещенными николями N\ и
N2 плоский конденсатор, заполненный исследуемым веществом
(рис. 308, ср. с рис. 278). В
отсутствие внешнего элек-
электрического поля свет че-
-— рез систему не проходит.
При наложении электриче-
электрического поля возникает двой-
двойное преломление, вслед™
Рис. 308 ствие чего свет по выходе
из конденсатора становит™
ся поляризованным эллиптически и частично проходит через
николь JV2, — поле зрения просветляется. Вводя компенсатор К,
можно измерить разность фаз между обоими лучами, возник-
возникшими при двойном преломлении, и таким образом найти раз™
ность пе ~~ п0 между необыкновенным пе и обыкновенным п0
показателями преломления исследуемого вещества в электриче™
ском поле. Ввиду малых значений указанной разности ее изме-
измерение возможно только интерференционными методами, анало-
аналогичными изложенному.
Небольшим изменением описанного опыта можно для жид™
костей найти обе разности пе — п и п0 — п. Для этого по предло-
предложению Л.И. Мандельштама можно воспользоваться, например,
интерферометром Жамена. Исследу-
Исследуемая жидкость наливается в кювету,
а конденсатор погружается в нее це-
целиком (рис. 309). Один из интерфе-
интерферирующих лучей проходит внутри,
а другой — снаружи конденсатора.
Николь-поляризатор N устанавлива-
устанавливается так, чтобы свет был поляризован
либо в плоскости рисунка, либо пер™
пендикулярно к ней. При наложении
электрического поля показатель пре-
преломления п наружного луча не из™
меняется, тогда как луч, проходящий
между пластинами конденсатора, становится либо необыкновен™
ным, либо обыкновенным (в зависимости от установки нико-
ля). По смещению интерференционных полос можно вычислить
пе — п и п0 — п.
Рис. 309

90
ЭФФЕКТ КЕРРА
585
2. В дальнейшем предполагается, что внешнее электриче-
электрическое поле однородно^ а луч распространяется перпендикулярно
к нему. Внешнее поле обозначается через Eq, в отличие от поля
Е самой волны. Очевидно, разность пе — п0 является функцией
компонент поля Е®Х1 E®yi E®z. Если (свободная от поля) среда
изотропна, то эта функция не может зависеть от направления
вектора Eg. В частности, она не должна изменяться при измене-
изменении знаков своих аргументов, т.е. быть четной по отношению к
каждому из них. Поэтому ее разложение в степенной ряд долж-
должно содержать только четные степени. В слабых электрических
полях, какими являются все поля, применяемые на опыте, мож-
можно сохранить только первые — квадратичные — члены этого
разложения. В силу уже отмеченной изотропии среды они вой-
войдут только в виде квадратов Eqx1 Eq , Eqz и притом с одним и
тем лее коэффициентом. Поэтому их можно объединить, напи-
написав
ne-n0 = qE$, (ЭОЛ)
где коэффициент q зависит только от рода вещества и его состо-
состояния, а также от длины световой волны А. Опыт действительно
подтвердил формулу (90.1). Разность фаз между необыкновен-
необыкновенным и обыкновенным лучами после прохождения через конден-
конденсатор будет
<р = ^(пе - поI =
А
А
(90.2)
где I — толщина проходимого слоя вещества, a Be q/X — так
называемая постоянная Керра. Она увеличивается при умень-
уменьшении длины волны (дисперсия) и сильно уменьшается с повы-
повышением температуры.
ТаблицаЭ
Вещество
Жидкости
Нитробензол
Нитротолуол
Хлорбензол
Вода
Сероуглерод
Бензол
Хлороформ
Тем-
Темпера™
тура,
°С
20
20
20
20
20
20
20
Постоян-
Постоянная
Керра В,
СГСЭ-ед.
2,2- 10^5
1,2- 10^5
1-10^6
4,7- 10~7
3,2- Ю^7
6-10~8
-3,5- 10^8
Вещество
Газы
Этиловый спирт
Ацетон
Сероуглерод
Этиловый эфир
Этиленовый
спирт
Тем-
пера-
пература,
°С
18
83
57
63
20
Постоян-
Постоянная
Керра В,
СГСЭ-ед.
9,2-Ю^10
5,4- МП10
3,6-Ю^10
—0,66 • 10"0
-1,7- Ю-10

586 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
В табл. 9 приведены значения постоянной Керра для неко-
некоторых жидкостей и газов (А = 589 нм, давление в случае газов
760 мм рт. ст.). Для большинства веществ пе > п0, т.е. посто-
постоянная Керра положительна. Это соответствует анизотропии по-
положительного кристалла. Значительно реже встречаются слу-
случаи, когда В < 0 (этиловый эфир, многие масла и спирты). Мак™
симальным значением В из всех исследованных веществ обла-
обладает нитробензол.
Чтобы составить представление о порядке величины эффек-
эффекта Керра, приведем следующий пример. Пусть расстояние меж-
между пластинами «конденсатора Керра» равно 1 мм, а напряжение
между ними 1500 В, так что Ео = 15000 В/см = 50 СГСЭ-ед.
Если конденсатор заполнен жидким нитробензолом, то при I =
= 5 см возникшая разность фаз будет ip = тг/2. Такой конден-
конденсатор может служить пластинкой А/4. Нетрудно обнаружить и
значительно меньшие разности фаз. Поэтому эффект Керра в
нитробензоле находит широкие технические применения.
3. Эффект Керра — явление более простое и теоретически
лучше изучено, чем искусственная анизотропия при механиче-
механических деформациях. Это и понятно. В последнем случае прояв-
проявляется воздействие сложных молекулярных полей на молекулы
тела, подвергшегося деформации. Оно плохо изучено и значи-
значительно сложнее соответствующего сравнительно простого воз-
воздействия постоянного однородного электрического поля. Кроме
того, явление Керра удалось наблюдать в газах, для которых
теория развита наиболее глубоко и подробно. Изучение явле-
явления Керра в газах совместно с рефракцией и деполяризацией
рассеянного света позволяет определить тензор поляризуемости
молекул.
Явление Керра объясняется анизотропией самих молекул.
Количественная теория для газов была развита Данжевеном
A872-1946) в 1910 г. В ней анизотропия молекулы характери-
характеризовалась только тензором поляризуемости. В отсутствие элек-
электрического поля анизотропные молекулы ориентированы в про-
пространстве хаотически, так что среда в целом макроскопически
изотропна. При наложении внешнего электрического поля моле-
молекулы преимущественно ориентируются осями наибольшей поля-
поляризуемости вдоль поля, вследствие чего среда становится ани-
анизотропной. В общем случае произвольного тензора поляризуе-
поляризуемости вычисления очень громоздки. Однако сущность теории и
ее основные результаты, по крайней мере качественно, можно
передать, предполагая, что молекулы полностью анизотропны^
что очень сильно упрощает вычисления. Это и делается ниже.
Полностью анизотропной называется такая молекула, внутри
которой электрические заряды могут смещаться только в опре-
определенном направлении, называемом осью молекулы. Моделью

§ 90 ЭФФЕКТ КЕРРА 587
такой молекулы может служить палочка, вдоль которой и мо-
жет происходить смещение зарядов г).
При проведении расчета (подчеркнем это еще раз) надо со™
блюдать осторожность, чтобы не спутать внешнее поле Eg с по™
лем Е электромагнитной волны, которое предполагается моно-
монохроматическим. Роль постоянного поля Eg сводится к созданию
в среде определенного распределения молекул по их направле-
направлениям в пространстве. Переменное же поле Е создает в ней пере-
переменную электрическую поляризацию Р, определяющую показа-
показатели преломления электромагнитной волны.
Переменный дипольный момент р полностью анизотропной
молекулы создается только составляющей поля Е, параллель-
параллельной ее оси. Он равен р = /3Ess = /3(Es)s, где s — единичный
вектор в направлении оси молекулы, а /3 — ее поляризуемость
в том же направлении. Очевидно, р можно представить в виде
р = CEse^- Направление внешнего поля Eq примем за ось X, а
направление распространения волны — за ось Z. Допустим сна™
чала, что электрический вектор Е волны направлен по оси X.
Тогда se = sXj и следовательно,
рх = fiEsl, py = pEsxsy, pz =
Все направления, перпендикулярные к оси X, для распределе-
распределения молекул равновероятны. Усредняя по этим направлениям,
найдем: sxsy = sxsz = 0. Следовательно, для средних значений
проекций дипольного момента получится
а для вектора поляризации
Рх = NpE4, Py = Pz = 0.
Вектор поляризации среды, таким образом, направлен по Е и
равен
Р = Ж/ЗЕ^
Соответствующая поляризуемость среды
ах = N04.
Показатель преломления будет необыкновенным. Для него и ди™
электрической поляризуемости получаем
ех = п2е = 1
1) Полностью анизотропных молекул, конечно, не существует. Поляризу™
емость реальной молекулы можно характеризовать главными значениями
CXl /3yj /3Z тензора поляризуемости. Если одно из этих главных значений
очень велико по сравнению с остальными двумя, то такая молекула может
служить хорошим приближением к полной анизотропии.

588 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Так как показатель преломления газа близок к единице, то
пе « 1 + 2жИрЩ. = 1 + 2жЫ^шЧ}1 (90.3)
где # — угол между осью молекулы и внешним полем Eg (т.е.
осью X). Если распределение молекул изотропно (т.е. внешнего
поля нет), то s2, = s2 = s2. Но <s2+s2 + s2 = 1, а потому s2, = 1/3.
Значит, среда будет оптически изотропна, причем
п = 1 + Щ-Np. (90.4)
О
Если поле Е направлено вдоль оси У, то se = <%• В этом
случае показатель преломления будет обыкновенным. Для него
расчет, аналогичный приведенному выше, дает
п0 = 1
Чтобы вычислить s2 представим проекции единичного век-
вектора s в полярной системе координат с полярной осью вдоль
поля Е:
sx = cos#, sy = sin т? cos (p^ sz = sin t? sin y?,
где (p — соответствующий азимут. Он с равной вероятностью
может принимать все значения от 0 до 2тг. Поэтому
s2 = sin2 # cos2 (p = sin2 # cos2 ер = - sin2 #.
Следовательно,
n0 = 1 + 7riV/3sIn2 i?. (90.5)
Прежде чем проводить дальнейшие вычисления, отметим од-
одно следствие теории. Вычитая соотношение (90.4) из соотноше-
соотношений (90.3) и (90.5), получим
пе - п = 2
п0 — ть = ( sin2 # — - ] nN/3 = f - — cos2
Отсюда
^~—^ = -2. (90.6)
По — П
Это соотношение, как показали тщательные измерения, хорошо
выполняется для большинства веществ.
Найдем теперь постоянную Керра В. Из (90.3) и (90.5) полу™
чаем
пР — по = 2жНв (cos2 # — - sin # ) = ЗтгМв (cos2 '
или на основании (90.4)
пе-п0 = 9^ (cos2^-^j. (90.7)

§ 90 ЭФФЕКТ КЕРРА 589
Для дальнейших вычислений воспользуемся формулой
Больцмана
dw = const • е~и/кт dft, (90.8)
которая определяет вероятность dw направления оси молекулы
в пределах телесного угла dft. Потенциальная энергия молекулы
в электрическом поле Eg равна U = р2/B/3) ^рЕ® cost?. Первый
член есть энергия, затраченная на создание диполя с диполь™
ным моментом р = /JE^cost?, второй — потенциальная энергия
этого диполя в электрическом поле Eg. Сумма обоих членов U =
= — - /3Eq cos2 #. Поскольку она зависит только от угла #, в ка~
честве телесного угла dft удобно взять 2тг sin # dti и переписать
формулу Больцмана в виде
dw = Ce^u/kTsin<&d<&, (90.9)
где С — постоянная нормировки. Предполагая, что выполнено
условие \U/kT\ <С 1, разложим экспоненциальную функцию в
ряд и оборвем его на линейном члене:
Постоянную С определим из условия нормировки:
о
Следовательно,
, 1
dw=2
1 f
о J
2
45
= 0
После подстановки в формулу (90.7) получим
п — п — п ~ ^ ^Е° (Quid)
ос/ г ТсНП
а для постоянной Керра
'. (90.11)
4. Таким образом, разность пе — п0 пропорциональна квас
ту внешнего поля Е®, как этого и следовало ожидать из сообра-
соображений симметрии. Но в теории Данжевена постоянная Керра
всегда положительна и притом не только для полностью анизо™
тропных молекул, но и для молекул с произвольным тензором

590 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
поляризуемости. Борн A882-1971) в 1916 г. устранил этот недо-
статок теории, распространив ее на полярные молекулы со зна-
значительными постоянными дипольными моментами ро, направ-
направления которых могут не совпадать с направлениями наиболь-
наибольшей поляризуемости молекул. Если ро велико по сравнению с
дипольным моментом молекулы, индуцированным внешним по™
лем Eq, to ориентация молекул в таком поле будет определяться
преимущественно постоянными моментами. Постоянные момен-
моменты ро будут стремиться ориентироваться вдоль поля Eq, опре-
деляющего в среде направление оптической оси. Направление
лее наибольшей поляризуемости среды может составлять с ним
заметный угол. Если эти два направления совпадают, то посто-
янная Керра В будет положительна. Если они взаимно перпен-
перпендикулярны, то В < 0. В промежуточных случаях может полу™
читься и тот и другой знак.
Конечно, наличие постоянного дипольного момента заметно
усложняет вычисления, далее если молекулы полностью анизо-
тропны. Ограничимся простейшим случаем, когда направления
вектора ро и наибольшей поляризуемости полностью анизотроп-
анизотропной молекулы совпадают между собой. Тогда единственное от™
личие от случая, разобранного выше, состоит в том, что теперь
потенциальная энергия молекулы в электрическом поле Eq бу-
будет U = ^(pqEq) = ^pqEq cost?, и в разложении соответствую-
соответствующего экспоненциального множителя появится линейный член
по Е®:
-U/kT _ 1 i po^ocos^ pJEl cos2 <&
~ кТ "^ 2FT2
Но этот член не сказывается на вычислении cos2 #, так как ин-
интегралы от cost?sini? и cos3 #sin# обращаются в нуль. Таким
образом, чтобы получить окончательный результат, достаточно
в формуле (90.11) поляризуемость /5 заменить на р^/кТ. Это
дает
Формула (90.12) показывает, что и в случае полярных молекул
разность пе ~~ п0 пропорциональна квадрату поля Eq.
5. Поскольку процессы поляризации молекул и их ориента-
ориентация в электрическом поле происходят за очень короткие вре™
мена, следует ожидать, что и время возникновения и уничто-
уничтожения эффекта Керра при наложении и снятии электрическо-
электрического поля должно быть такого же порядка. Действительно, опы-
опыты Абрагама и Лемуана, начатые еще в 1899 г. и неоднократно
продолженные другими исследователями, показали, что это вре-
время меньше 10~8 с, а в некоторых случаях даже меньше 10~9 с.

90
ЭФФЕКТ КЕРРА
591
Точность всех этих опытов была недостаточна, чтобы высказать
более определенные суждения. Это удалось только в результа-
результате развития лазерной техники, позволившей получать короткие
импульсы (с длительностью порядка 10~12 с) мощного лазерно-
лазерного излучения (со средней напряженностью электрического поля
в несколько десятков кВ/см).
Такие световые поля, хотя они и не являются статически™
ми, способны вызывать двойное преломление в ячейках Керра.
Принципиальная схема опыта приведена на рис. 310. Справа на-
ФЭУ
Рис. 310
лево через ячейку Керра К проходит луч 1 голубого света, пре-
терпевающий затем отражение от полупрозрачной пластинки S
и попадающий в фотоумножитель ФЭУ. Если николи N\ и N2
скрещены, то свет в фотоумножитель не попадет. Однако если
через ячейку Керра слева направо пропустить мощный импульс
света от лазера L, то при прохождении через ячейку он вызовет
в исследуемой жидкости двойное преломление луча 1, и свет в
фотоумножитель начнет поступать. Если на ту же ячейку на-
наложить статическое электрическое поле и подобрать его напря-
напряженность так, чтобы возникла такая же разность фаз между
необыкновенным и обыкновенным лучами, что и в предыду-
предыдущем случае, то можно сравнить постоянные Керра в статиче-
ском и переменном полях лазерного излучения. Оказалось, что
в недипольных жидкостях постоянные Керра в обоих случаях
практически совпадают. В дипольных жидкостях при переходе
от статического поля к переменному полю лазерного излучения
постоянная Керра уменьшается. Так, в случае нитробензола она
уменьшается приблизительно в 100 раз.
Уже описанный опыт позволяет оценить длительность суще-
существования эффекта Керра. Более точные результаты дают из-
измерения по схеме, приведенной на рис. 311. Мощный инфра-
инфракрасный импульс от лазера с длительностью порядка 10~12 с
и длиной волны А = 1060 нм проходит через кристалл дигид-

592
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
рофосфата калия (KDP). Из-за нелинейного эффекта удвоения
частоты (см. § 124) незначительная часть света превращается в
зеленый свет с длиной волны А = 530 нм. Зеркало Si пропускает
инфракрасный луч и отражает зеленый. Зеркало *$2, наоборот,
пропускает зеленый луч, но отражает инфракрасный. Оба луча
проходят через ячейку Керра К с исследуемой жидкостью, рас-
расположенную между скрещенными николями iVi и^. За нико
лем N2 поставлен светофильтр F, задерживающий инфракрас-
инфракрасное излучение и пропускающий на фотоумножитель ФЭУ зеле-
зеленое. Если после зеркала S2 импульс зеленого излучения идет
впереди мощного инфракрасного импульса, не перекрываясь с
F ФЭУ
Рис. 311
ним, то, разумеется, зеленый свет не сможет достигнуть фо-
фотоумножителя. Помещая на пути зеленого луча пластинку Р,
можно задержать зеленый импульс относительно инфракрасно-
инфракрасного и по толщине пластинки измерить время задержки т. Распо-
Располагая набором пластинок разной толщины, можно менять вре-
мя т. Опыты показали, что в простейшем случае интенсивность
проходящего света, регистрируемая фотоумножителем, меняет-
меняется экспоненциально по закону I = I® exp (—т/то). Постоянная т®
имеет смысл времени релаксации анизотропии жидкости, выз-
вызванной инфракрасным импульсом. Она и является мерой дли-
длительности эффекта Керра. Измерения дали для сероуглерода
то = 2 • 1СП12 с, а для нитробензола т® = 5 • 1СП11 с.
6. Рассмотрим теперь механизм возникновения двойного
преломления в переменных полях. Если молекулы полярные, то
в одну половину периода их постоянные дипольные моменты
стремятся ориентироваться в направлении внешнего электриче-
электрического поля. В следующую половину периода, когда внешнее поле
изменит направление на противоположное, возникнет такая же,
но противоположно направленная ориентация. Эффекты ориен-
ориентации, вызванные такими полями, вычитаются. В низкочастот-
низкочастотных полях (в радиодиапазоне) в каждый момент времени уста-
устанавливается ориентация, соответствующая мгновенному значе-

§ 90 ЭФФЕКТ КЕРРА 593
нию электрического поля. В этом случае явление протекает так
же, как в статических полях.
Однако в высокочастотных полях (с длинами волн короче
примерно 1 см) ориентация постоянных дипольных моментов
практически прекращается. В таких полях постоянные диполь-
ные моменты ро не могут играть роли в возникновении анизо-
анизотропии, а с ней и двойного преломления среды. Ориентация обу-
обусловлена только индуцированными дипольными моментами. В
одну половину периода, когда электрическое поле направлено в
определенную сторону, индуцированные дипольные моменты со™
здают моменты сил, стремящиеся приблизить оси наибольшей
поляризуемости молекул к направлению электрического поля. В
следующую половину периода направления всех моментов ме-
меняются на противоположные. Однако они также будут прибли-
приближать оси наибольшей поляризуемости молекул к тому же на-
направлению внешнего поля. Действительно, в отличие от векто-
вектора, у оси наибольшей поляризуемости нет одностороннего на-
направления, оба направления ее совершенно эквивалентны. Не
имеет никакого значения, каким концом эта ось приближается к
направлению вектора Eq. Таким образом, эффекты ориентации
осей наибольшей поляризуемости в соседние половины перио-
да, несмотря на противоположные направления векторов Eg в
эти полупериоды, будут складываться, а не вычитаться. Хотя
за каждый полупериод ориентация и ничтожна, благодаря та-
такому сложению за время релаксации анизотропии tq возникает
достаточная ориентация, чтобы вызвать двойное преломление.
Таким образом, механизм возникновения двойного прелом-
преломления в переменных полях высокой частоты — такой же, какой
принимается в теории Ланжевена.
7. Благодаря чрезвычайной быстроте установления и исчез-
исчезновения явления Керра оно нашло широкие научные и техни-
технические применения в качестве быстродействующих затворов и
модуляторов света. Керровский модулятор света представляет
собой ячейку Керра, конденсатор которой питается электриче-
электрическим полем высокой частоты. Он позволяет осуществить гро-
громадное число (до 109) прерываний в секунду, недостижимое дру-
другими (например, механическими) средствами. Ячейка Керра, на
которую подается кратковременный импульс электрического по-
поля, может служить фотографическим затвором, время действия
которого определяется длительностью этого импульса. Если в
качестве электрического импульса взять мощный световой им-
импульс от лазера, то время экспозиции можно довести до 10~12 с.
Керровские затворы и модуляторы света применяются в лазер-
лазерной технике для управления режимом работы лазеров.
8. Аналогом эффекта Керра является эффект Коттона-
Мутона, открытый в 1910 г. Если молекулы среды анизотропны

594 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
и обладают постоянными магнитными моментами, то они могут
преимущественно ориентироваться постоянным магнитным по-
полем. В достаточно сильных магнитных полях возникает анизо-
анизотропия и связанное с ней двойное лучепреломление среды. Это
и есть эффект Коттона^Мутона. Среда ведет себя подобно од-
одноосному кристаллу, оптическая ось которого параллельна маг™
нитному полю В.
Двойное преломление можно обнаружить и измерить так же,
как это делается при изучении явления Керра. И законы обоих
явлений совершенно аналогичны. Разность необыкновенного и
обыкновенного показателей преломления определяется выраже-
выражением пе ~~ п0 = DB2^ а соответствующая разность фаз
<р = ^(пе - поI = 2ттС1В2, (90.13)
А
где D и С = D/X — постоянные, зависящие от свойств среды и
ее физического состояния. Для «постоянной Коттона-Мутона»
в нитробензоле измерения дают С = 2,23 • 1СП12 СГСМ. В маг-
магнитном поле В = 20 000 Гс на пути I = 10 см возникает разность
фаз (р = 0,056 рад, т.е. всего 3,2 градуса.
§ 91. Линейный электрооптический эффект Поккельса
1. Свободные колебания гармонического осциллятора опи-
описываются уравнением г + 2jr + ujqT = 0. Они происходят около
положения равновесия г = 0. Допустим теперь, что осциллятор
находится в постоянном электрическом поле Е$. Тогда в отсут-
отсутствие других внешних сил будет
г + 2^г + ш1г = -—Ео.
Теперь положение равновесия сместится от начала координат
на расстояние г о = —еЕо/(тш^). Обозначим через q расстояние
колеблющейся частицы от нового положения равновесия. Тогда
г = го + д, и после подстановки в предыдущее уравнение имеем
q + 2jq + ouoq = 0.
Отсюда видно, что в постоянном внешнем электрическом поле
колебания осциллятора останутся гармоническими с прежней
частотой cjq, но они будут происходить около нового положе-
положения равновесия. Таким образом, постоянное электрическое поле
не изменяет собственную частоту гармонического осциллятора,
а только смещает положение равновесия, около которого совер-
совершаются свободные колебания.
В случае колебаний с большой амплитудой модель гармони-
гармонического осциллятора может оказаться непригодной. В простей-

§ 91 ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ ПОККЕЛЬСА 595
шем случае к квазиупругой силе тш^г надо добавить член, про™
порциональный квадрату смещения частицы из положения рав-
равновесия (начала координат). Свободные колебания такого ангар-
тонического осциллятора описываются уравнением г +
2
+ ш®г + /3r2 = 0, где /3 — постоянная. При наличии внешнего
постоянного электрического поля Eq уравнение колебаний пере-
переходит в
г + 2jr + ш^г + j3r2 = -—Eq.
Теперь положение равновесия г = г® определится из уравнения
Ц)П) + C4 = -еЕо/т.
Из двух корней этого квадратного уравнения надо взять тот,
который мало отличается от ранее найденного значения г® =
= —еЕ®/(тш^) без учета ангармоничности (так как последняя
предполагается малой). Пусть по-прежнему q означает откло-
отклонение колеблющейся частицы от нового положения равновесия,
так что г = го+g. Предполагая колебания малыми, пренебрежем
квадратами q. Тогда
q + 27q + (ul + 2f3rQ)q = 0.
Отсюда видно, что во внешнем постоянном электрическом по-
поле малые колебания ангармонического осциллятора в рассма-
рассматриваемом приближении опять будут гармоническими. Однако
при наличии ангармоничности внешнее поле Eq не только сме-
смещает положение равновесия, но и изменяет собственную ча-
частоту осциллятора. Изменение квадрата собственной частоты
осциллятора приближенно равно Aojq = 2/Зго, или в том же при-
приближении
IIIUJq
2. Смещение собственных частот меняет кривую дисперсии,
т.е. показатель преломления п среды. В простейшем случае, ко-
когда собственная частота ш® одна, величина п вдали от линии
поглощения зависит только от разности ш2 ~~ uJq, как это видно
из формулы (84.9). Тогда изменение п в статическом электриче-
электрическом поле Eq определяется выражением
л дп д 2 дп 2е/3 -р,
dujQ dujQ tyiuJq
Это выражение можно преобразовать, заметив, что df /дш^ =
= ^df/дш2. Тогда
Л дп 2е/3 w дп е{3 „ /01 9^
WIUJq ОШ WIUJUJq

596 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
При фиксированном направлении внешнего поля Eg величи-
величина An зависит от направления распространения света. Это ска-
сказывается на двойном преломлении среды. Изменение двойного
преломления вещества из-за смещения собственной частоты
во внешнем электрическом поле называется электрооптиче-
электрооптическим эффектом Поккельса. В этом эффекте изменения показа™
телей преломления пропорциональны первой степени внешнего
поля Eqj в отличие от эффекта Керра, где они пропорциональны
квадрату поля.
Эффект Поккельса может наблюдаться только в кристал-
кристаллах, не обладающих центром симметрии. Дело в том, что он
линеен относительно внешнего поля Eq. Поэтому при изменении
направления поля Eq на противоположное должен меняться на
противоположный и знак изменения An показателя преломле-
преломления. Но в кристаллах с центром симметрии это невозможно, так
как оба взаимно противоположных направления внешнего поля
физически совершенно эквивалентны.
Из механизма явления ясно, что эффект Поккельса по край-
крайней мере столь же безынерционен, что и эффект Керра. Поэто-
Поэтому он, наряду с эффектом Керра, нашел применение (например,
в технике лазеров) в качестве оптических затворов и высоко-
высокочастотных модуляторов света. Соответствующее устройство
называется ячейкой Поккельса. Она представляет собой кри-
кристалл, помещаемый между двумя скрещенными николями. Та-
Такое устройство действует так же, как и ячейка Керра. Николи
не пропускают свет, когда нет внешнего электрического поля,
но при наложении такого поля пропускание появляется. Необхо-
Необходимо, чтобы кристалл до наложения внешнего электрического
поля не давал двойного преломления. Этого можно достигнуть,
если взять оптически одноосный кристалл, вырезанный перпен-
перпендикулярно к оптической оси, а свет направить вдоль этой оси.
Внешнее поле Eq может быть направлено либо перпендикулярно
(поперечный модулятор света), либо параллельно распростра-
распространению света (продольный модулятор).
§ 92. Эффект Зеемана
1. В 1896 г. Зееман A865-1943) обнаружил, что спектраль-
спектральные линии определенным образом расщепляются, если источник
света поместить в магнитное поле. В опыте Зеемана исследова-
исследовалась очень узкая зелено-голубая линия кадмия и применялись
магнитные поля с напряженностью 10 000-15 000 Гс. Г.А. Ло-
рентц, развивавший в то время электронную теорию, сразу же
объяснил явление Зеемана и тем самым придал дальнейшим
исследованиям планомерный и целенаправленный характер.

92
ЭФФЕКТ ЗЕЕМАНА
597
Применяемая схема для наблюдения и исследования явления
приведена на рис. 312. Источник света с линейчатым спектром
(например, газоразрядная трубка или вакуумная дуга) помеща-
помещается между полюсами электромагнита, создающего достаточно
однородное магнитное поле. Исследуемый свет попадает на щелв
Рис. 312
спектроскопа или спектрографа Sp с разрешающей силой около
100 000 или выше (дифракционную решетку или интерференци-
интерференционный спектральный аппарат). Николи JVj_, N2 и пластинка А/4
служат для исследования поляризации излучаемого света. При
фотографировании наблюдаемой картины применяются иногда
многочасовые экспозиции. В течение всего этого времени долж-
должно быть обеспечено с достаточной точностью постоянство маг-
магнитного поля и температуры источника, чтобы картина остава-
оставалась неизменной во времени и можно было использовать спек-
спектральный аппарат высокой разрешающей силы.
В первых опытах Зееман обнаружил, что при наблюдении по-
поперек поля спектральная линия расщепляется на три линейно
поляризованные компоненты. Средняя компонента не смещена,
крайние смещены в противоположные стороны на одинаковые
расстояния (в шкале частот). Смещение пропорционально на-
напряженности внешнего магнитного поля В. В средней компо-
компоненте электрический вектор направлен параллельно магнитно-
магнитному полю (такие компоненты называются ж-компонентами), в
крайних — перпендикулярно к нему (такие компоненты назы-
называются а-компонентами). Интенсивность тг-компоненты вдвое,
а каждой из ст-компонент в четыре раза меньше интенсивности
исходной линии.
При наблюдении вдоль магнитного поля получается такое
же смещение (при одинаковой напряженности магнитного по-
поля), что и в предыдущем случае, но несмещенная компонента
отсутствует. Интенсивность каждой компоненты вдвое мень-

598
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
В
ов
Без поля
\ С полем
г
ш0-О
ш0-О
Рис. 313
ше интенсивности исходной спектральной линии. Обе компонен-
компоненты поляризованы по кругу в противоположных направлениях
(их принято называть также ст-компонентами). Если свет рас™
пространяется в направлении магнитного поля, то (т-компонента
с меньшей частотой поляри-
поляризована по правому, а с боль™
шей — по левому кругу. При
изменении направления маг-
магнитного поля на противопо-
противоположное меняется на противо-
противоположную и круговая поляри-
поляризация обеих компонент.
Картина, наблюдаемая по-
поперек и вдоль магнитного по-
поля, представлена схематиче-
схематически на рис. 313. Предполага-
Предполагается, что в случае продольного
эффекта свет распространяет-
распространяется вдоль магнитного поля, на-
направленного к читателю. От-
Относительные интенсивности линий показаны их толщиной, по-
поляризация тг-компоненты — штрихами, параллельными магнит-
магнитному полю, а а-компонент — кружочками.
2. Описанная картина расщепления спектральных линий
объясняется классической теорией Лорентца. Как и классиче-
классическая теория дисперсии, это есть модельная теория, в простей-
простейшей форме которой излучающими центрами являются гармони-
гармонические осцилляторы в виде квазиупруго связанных электронов.
В отсутствие внешнего магнитного поля уравнение движения
такого электрона имеет вид г + uj^t = 0, где ш® — собствен-
собственная частота электрона. При наличии постоянного магнитного
поля на электрон действует еще сила Лорентца — - [гВ] (заряд
электрона обозначен через —е). Уравнение движения электрона
принимает вид
g = -—[гВ],
mc L П
(92.1)
где т — масса электрона. Введя ларморовскую частоту
2тс
приведем его к виду
r + 2[rO]+a^r = 0 (92.2)
(см. т. III, § 86). Классическая теория сводится к решению этого
уравнения. Для решения уравнения (92.2) перейдем к коорди-
координатной форме. Направим ось Z прямоугольной системы коор-
координат вдоль магнитного поля В. Тогда предыдущее уравнение

92
ЭФФЕКТ ЗЕЕМАНА
599
сведется к системе трех скалярных уравнений
х + 2пу + и%х = О,
у- 2пх + ы1у = О, (92.3)
z^^z = о.
Из последнего уравнения видно, что магнитное поле не влияет
на движение электрона вдоль магнитного поля. Это и понятно,
так как при таком движении не возникает силы, действующей со
стороны магнитного поля. Интегрирование первых двух уравне-
уравнений (92.3) удобно провести в комплексной форме. Объединим х
и у в комплексную координату ? = х + гу. Она определяет поло-
положение электрона в координатной плоскости (X, Y) совершенно
так лее, как это делается с помощью двумерного вектора (^ с со™
ставляющими хжу. Заметив, что —г? = у — ii, умножим второе
уравнение (92.3) на г и сложим с первым. Тогда
С - г • 2п( + ш^( = 0.
Ищем решение этого уравнения в виде ( = eiu3t. Постоянная ш
найдется из квадратного уравнения
-и? + 2пы ¦
которое дает
"о = 0,
] + &.
Даже в очень сильных магнитных полях квадратом ларморов™
ской частоты можно пренебречь по сравнению с ojq. Например,
если В = 104 Гс, то формула (92.1) дает п « 1011 с, тогда
как для видимого света (А = 500 нм) о;~4-1015 с^1, а потому
(O/cjJ ^ 10~9. Максимальное магнитное поле, в котором изме-
измерялось зеемановское расщепление спектральных линий, получе-
получено в 1938 г. П.Л. Капицей A894-1984). Оно было 3,2 • 105 Гс.
Даже в этом случае п/ш® ~ 1,4
образом, с большой точно-
точностью ш = ±а;о + ft. Что™
бы не пользоваться отри™
дательными частотами, вве-
введем переобозначение, поло™
ЖИВ U)i = UJQ + О, UJ2 = UJQ —
— О. Тогда полученные два
решения запишутся в виде
ИГ3, (п/ш0J - 2 • ИГ6. Таким
— о ¦ — о РИС' 314
Первое решение представляет круговое движение, в котором
электрон вращается против часовой стрелки с угловой часто™
той cji, второе — также круговое движение, но по часовой стрел-

600 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
ке ж с частотой Ш2 (рис. 314). Общее решение соответствует на™
ложению таких двух вращений и представляется в виде ( =
— CiCi + C2C2J где С\ и С2 — произвольные постоянные.
3. Чтобы нагляднее уяснить полученные результаты, разло™
жим первоначальное движение электрона (т.е. движение в от-
отсутствие магнитного поля) на два движения: на гармоническое
колебание в направлении оси Z и на движение в плоскости XY.
Второе движение в свою очередь разложим на два круговых
вращения с одной и той же угловой частотой cjq, но соверша-
ющиеся в противоположных направлениях. Тогда в постоянном
магнитном поле колебание вдоль оси Z остается неизменным.
Частоты же обоих круговых вращений изменяются на одну и
ту же величину О: если вращение совершается против часовой
стрелки, то частота увеличивается, а если по часовой стрелке,
то уменьшается.
Для изменения частоты при вращении по кругу можно при-
привести простое объяснение. Центростремительная сила, действу™
ющая на вращающийся электрон в отсутствие магнитного поля,
равна тш^г. В магнитном поле к ней добавляется сила ±- vB =
в ^
= ±- шгВ. так что новая центростремительная сила становится
с
равной
Выбор знака зависит от направления вращения. Приравнивая
это выражение ma;2r, приходим к уравнению о;2 = ojq =Ь 2ilcj, из
которого для положительных корней находим ш « ш® =Ь П. Это
совпадает с результатами, полученными выше.
При включении магнитного поля кинетическая энергия вра-
вращения электрона изменяется. Возникает вопрос, как это может
происходить, если сила, действующая со стороны магнитного
поля, перпендикулярна к скорости электрона v и, следователь-
следовательно, работы не совершает? Ответ состоит в том, что последнее
утверждение относится к постоянным магнитным полям, ко-
которые только и учитываются уравнением (92.2). Но при вклю-
включении магнитного поля оно нарастает во времени от нуля до
максимального значения, а в дальнейшем вплоть до выключе™
ния остается постоянным. Во время же нарастания магнитного
поля, согласно закону индукции Фарадея, возбуждается вихре-
вихревое электрическое поле^ которое и совершает работу над элек-
электроном, меняя его кинетическую энергию. Когда магнитное поле
становится постоянным, электрическое поле пропадает и даль™
нейшее изменение кинетической энергии вращения электрона
прекращается, пока не будет выключено магнитное поле. К этим
установившимся вращениям и относятся движения, найденные
выше. Подробное рассмотрение механизма изменения кинетиче™

§ 92 ЭФФЕКТ ЗЕЕМАНА 601
ской энергии вращения электрона было приведено в учении об
электричестве (см. т. III, § 88).
4. Перейдем теперь к объяснению расщепления спектраль-
спектральных линий в магнитном поле. Колеблющийся электрон излучает
электромагнитные волны. Излучение максимально в направле-
направлении, перпендикулярном к ускорению электрона, а в направле-
направлении ускорения отсутствует. Согласно классической теории, ча-
частота излучаемого света совпадает с частотой колебания элек-
электрона. Но последняя меняется при включении магнитного по-
поля. Поэтому должна измениться и частота излучаемого света.
При наблюдении вдоль магнитного поля колебание в том же
направлении излучения не дает. Излучение создается только
круговыми вращениями электрона. В результате наблюдаются
две сг-компоненты с круговой поляризацией и частотами ujq +
+ О и ш® — п. Если свет идет в направлении вектора В, то по™
ляризация первой линии будет левой^ а второй — правой. При
изменении направления магнитного поля на противоположное
меняется на противоположную и круговая поляризация каждой
линии. При наблюдении поперек магнитного поля В колебания
электрона, параллельные В, дают максимум излучения. Им со-
соответствует несмещенная тг-компонента, в которой электриче-
электрический вектор параллелен В. Оба круговых движения соверша-
совершаются в плоскости, перпендикулярной к В. Разложим каждое из
них на гармоническое колебание вдоль линии наблюдения и пер-
перпендикулярное к нему. Только колебания, перпендикулярные к
линии наблюдения, сопровождаются излучением и дают две а-
компоненты с частотами а; + Л и oj^O, в которых электриче-
электрические векторы перпендикулярны к В.
Таково объяснение расщепления спектральных линий, на-
наблюдавшееся в первых опытах Зеемана. Если учесть, что в от-
отсутствие магнитного поля все направления движения электрона
равновероятны, то нетрудно объяснить и относительные интен-
интенсивности спектральных линий в этих опытах.
Как видно из численного примера, приведенного выше (В =
= 104 Гс), п/ujq « 2 • 10~5. Для разрешения такого расщепления
требуются спектральные приборы с разрешающей силой ujq/u
не менее 5 • 10 , т.е. дифракционные решетки или интерференци-
интерференционные спектроскопы. Но в опытах П.Л. Капицы (В = 3,2 • 105 Гс)
были уже достаточны призменные спектроскопы.
Исследуя характер круговой поляризации линий в продоль-
продольном эффекте Зеемана, можно определить знак зарядов, вы-
вызывающих этот эффект. Он оказался отрицательным. Изме-
Измеряя лее величину расщепления, можно определить удельный за-
заряд е/т. Он оказался таким же, как и при измерениях по от-
отклонениям катодных лучей в электрических и магнитных полях

602 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
(е/т = 1,759 • 107 СГСМ). Это не оставляет сомнений в том, что
заряженные частицы, определяющие оптическое поведение ато-
атомов, действительно являются электронами.
5. Дальнейшие опыты показали, что явление Зеемана в том
виде, в каком оно наблюдалось сначала и нашло объяснение в
теории Лорентца — лорентцовский триплет, состоящий из од™
ной тг-компоненты и двух сг-компонент, а также дублет из двух
а-компонент, поляризованных по кругу, — наблюдается крайне
редко. Такое расщепление называется нормальным или про-
простым эффектом Зеемана. Простой эффект дают так называ-
называемые синглетные^ т.е. одиночные, практически монохромати-
монохроматические спектральные линии. Подавляющее большинство спек™
тральных линий являются мультиплетами (дублетами^ три-
триплетами^ квартетами и т.д.), т.е. состоят из нескольких тесно
расположенных спектральных линий.
Простейшим примером мультиплета (дублета) может слу-
служить двойная D-линия натрия. Она состоит из двух близко рас™
положенных линий с длинами волн Xd1 = 589,5930 нм и А^2 =
= 588,96963 нм, причем интенсивность линии Z?2 вдвое больше
интенсивности линии D\.
Мультиплеты в магнитных полях дают значительно бо-
более сложную картину расщепления, чем расщепление в про™
стом эффекте Зеемана. Так, линия D\ натрия расщепляется
на четыре линии: средние из них являются тг-, а крайние —
<т-компонентами. Линия же D2 расщепляется на шесть ком-
компонент: две средние являются тг-, а четыре крайние —
^-компонентами. Таким образом, весь дублет расщепляется на
10 линий. Наблюдаются и значительно более сложные карти™
ны расщепления мультиплетов. Такие расщепления называются
аномальным или сложным эффектом Зеемана. Предпочтите-
Предпочтителен термин «сложный эффект», так как именно сложный^ а не
простой эффект является правилом^ а не исключением.
Объяснение сложного эффекта Зеемана дала квантовая те-
ория, да и то после того, как был открыт спин (т.е. собственный
момент количества движения) и связанный с ним магнитный
момент электрона. В случае синглетных спектральных линий
квантовая теория приводит к тем же результатам, что и простая
теория Лорентца. Мы вернемся ко всем этим вопросам в пятом
томе нашего курса.
§ 93. Понятие об эффекте Штарка
Как было показано в § 91, однородное электрическое поле
не меняет собственную частоту ш® гармонического осциллято-
осциллятора. Однако при учете ангармоничности такое изменение должно
происходить. Если ограничиться линейными членами по внеш-

§ 93 ПОНЯТИЕ ОБ ЭФФЕКТЕ ШТАРКА 603
нему полю Eq, to оно будет выражаться формулой (91.1), из ко-
которой следует Acjq = —^eEQ/(mujQ). В этом приближении внеш-
внешнее поле Eq не вызывает расщепления спектральных линий, а
только производит небольшое смещение их в сторону, пропор-
пропорциональное напряженности поля Eq. При учете членов высших
степеней можно ожидать расщепления спектральных линий с
расстояниями между компонентами, пропорциональными ква-
квадрату поля Eq, а именно
8ш0 - [е/(тш1)]Е1
На возможность такого расщепления указывал Фохт A850—-
1919). Однако из-за экспериментальных трудностей ему не уда-
удалось наблюдать ожидаемое явление. Трудность состояла в том,
что для наблюдения эффекта требуются электрические поля Eq
порядка 100 000 В/см. В обычных же газоразрядных трубках,
излучающих узкие спектральные линии (например, водородной
серии Бальмера), такие сильные поля создавать и поддерживать
невозможно из™за сильной ионизации газа в трубках.
Штарк A874—-1957) в 1913 г. преодолел эту трудность, соз-
создавая сильное электрическое поле за катодом в узком зазоре
(~ 1 мм) между F и К (рис. 315), в котором непрерывной откач-
откачкой поддерживалея вы™
сокий вакуум, так что ^ 10000В^ _ 5000-10000В
в этом зазоре практи- ~*
чески не происходило
ионизации частиц из-за
столкновений между ни™
ми. Возбуждение свече-
свечения атомов газа про™ ^ ¦_
исходило в другой ча- JzT Катодные
сти трубки, как в обыч™
ной газоразрядной труб- Направление наблюдения
ке. Светящиеся атомы
(каналовые лучи) про™ РИС- 315
никали через отверстия
(каналы) в катоде и попадали в пространство между F ж К,
где и подвергались воздействию внешнего электрического поля.
С помощью такой установки Штарку удалось наблюдать рас™
щепление спектральных линий в электрическом поле. Это явле-
явление было названо его именем. Оно оказалось совсем не похожим
на то, что ожидал Фохт. Штарк исследовал расщепление спек-
спектральных линий водородной серии Бальмера. В видимой обла™
сти спектра она содержит четыре линии: Но (А = 656,285 нм),
Нд (А = 486,132 нм), Н7 (А = 434,046 нм), Яё (А = 410,173 нм).
Расщепление в водороде, а также в случае всех одноэлектронных
ионов оказалось пропорциональным не второй степени элек-
Каналовые
лучи
лучи

604 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
трического поля, а первой, т.е. значительно более сильным. По
этой причине такое расщепление стали называть линейным эф-
эффектом Штарка.
Картина расщепления оказалась довольно сложной и различ-
различной для различных спектральных линий. Каждая спектральная
линия водорода расщеплялась на несколько компонент. Для ли™
нии Ша было найдено расщепление на 15 компонент, для Нд на
20, для Н7 на 27 и для Л§ на 32 компоненты. В электрическом
поле Eq = 104 000 В/см для расстояния между крайними компо-
компонентами Штарк нашел 2,3; 3,88; 5,88 и 7,5 нм для линий На, Н^,
Ы7, Hj соответственно. Эти расстояния довольно велики по срав™
нению с соответствующими расстояниями между крайними ком-
компонентами простого триплета Зеемана. (В поле В = 104 000 Гс
для указанных линий зеемановские расщепления составляли бы
соответственно 0,42; 0,23; 0,18 и 0,16 нм.)
При наблюдении поперек поля Eq компоненты поляризованы
линейно, причем часть из них является ^компонентами (у ко™
торых электрическое поле параллельно внешнему полю Eq), a
часть (^компонентами (у которых электрическое поле перпенди™
кулярно к внешнему полю Eq). При наблюдении вдоль поля Eq
тг-компоыенты не появляются, а ст-компоненты не поляризованы.
Более сильные тг-компоненты в общем случае лежат снаружи, а
более сильные а-компоненты — внутри. Расщепление и поля-
поляризация у водорода по обе стороны от первоначальной линии
симметричны; у других атомов часто встречается несимметрич-
несимметричное расположение. Расстояния (в шкале частот) компонент от
первоначальной линии оказались кратными наименьшему воз-
возможному расстоянию между компонентами, причем опыты по-
показали, что последнее одно и то же для всех линий бальмеров-
ской серии водорода. В сильных полях (превосходящих пример™
но 100 000 В/см) были обнаружены отступления от линейной
зависимости между расщеплением и напряженностью внешне-
внешнего поля Eq. Линии атомов или ионов, содержащих более одного
электрона, дают не линейный, а квадратичный эффект Штар-
Штарка, в котором расщепление пропорционально квадрату электри-
электрического поля Eq.
Классическая теория не дает объяснения эффекта Штарка,
как и всякого явления, связанного с излучением и поглощением
спектральных линий. Его теория — существенно квантовая и не
может быть изложена в этом томе.
§ 94. Вращение плоскости поляризации
1. Если линейно поляризованный свет проходит через плос-
плоскопараллельный слой вещества, то в некоторых случаях плос-

§ 94 ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ 605
кость поляризации света оказывается повернутой относительно
своего исходного положения. Это явление называется вращени-
вращением плоскости поляризации или оптической активностью. Если
вещество не находится во внешнем магнитном поле, то оптиче-
оптическая активность и вращение плоскости поляризации называются
естественными. В противоположном случае говорят о магнит-
магнитном вращении плоскости поляризации или эффекте Фарадея.
Естественная активность была открыта в 1811 г. Араго на
пластинках кварца, вырезанных перпендикулярно к оптической
оси. В 1815 г. Био подробно исследовал это явление, а также
обнаруженное им вращение плоскости поляризации в раство-
растворах сахара. Затем естественное вращение плоскости поляриза-
поляризации было найдено у многих других тел. К концу прошлого века
число известных естественно-активных веществ превышало 700.
Теперь их известно гораздо больше, хотя для большинства ве-
ществ, где обнаружено это явление, оно выражено очень слабо.
Для наблюдения явления можно установить на оптической
скамье два скрещенных николя. Такая система не пропускает
свет. Однако, если между николями ввести пластинку квар-
кварца, вырезанную перпендикулярно к оптической оси, или слой
какого-либо другого оптически активного вещества, то свет че-
через систему будет проходить. Но его можно погасить враще-
вращением одного из николей. Отсюда следует, что после прохожде-
прохождения через активное вещество свет остается линейно поляризо-
поляризованным, но его плоскость поляризации оказывается повернутой.
Для успеха опыта падающий свет, если он белый, необходимо мо-
нохроматизировать, пропустив его через светофильтр, так как
угол поворота плоскости поляризации зависит от длины вол-
волны. Кварц — одноосный кристалл. В описанном опыте свет рас-
распространяется вдоль оптической оси, когда кварц ведет себя как
изотропное тело, не давая обычного (линейного) двойного луче-
лучепреломления.
В зависимости от взятого вещества естественное вращение
плоскости поляризации может происходить вправо или влево,
причем эти два направления условились относить к наблюдате-
наблюдателю, к которому свет приближается. В соответствии с этим раз-
различают право- и левовращающие вещества. Вращение вправо
считается положительным, а влево — отрицательным.
2. Явление вращения плоскости поляризации указывает на
определенную дисимметрию^ свойственную оптически актив-
активным средам. Она выражается в том, что в таких средах на-
направления вращения по и против часовой стрелки физически не
эквивалентны. Поэтому в среде не может быть плоскости сим-
симметрии, проходящей через направление нормали к фронту вол-
волны. Иначе, как это следует из общих соображений симметрии,
плоскость поляризации света не могла бы вращаться, если бы

606 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
она совпадала с любой из плоскостей симметрии. В то же время
естественно-активные среды, если они жидкие, полностью изо-
изотропны , т.е. все направления в них совершенно эквивалентны.
Это проявляется, в частности, в том, что естественно-активная
жидкость вращает плоскость поляризации в одну и ту же сто-
сторону, независимо от направления распространения света. По™
этому естественно-активную жидкость можно охарактеризовать
как дисимметрично-изотропную среду. В кристаллах нет изо-
изотропии, но в одноосных кристаллах всякие два взаимно проти-
противоположные направления оптической оси также эквивалентны,
по крайней мере в оптическом отношении.
Отмеченная дисимметрия напоминает дисимметрию винто-
винтовой спирали. Будем смотреть на один из торцов спирали. Пусть
по спирали движется точка, вращаясь по часовой стрелке. Если
при этом точка удаляется от нас, то спираль называется правой
(в противоположном случае она называется левой). Если посмо-
посмотреть на спираль с противоположного торца, то вращение той
лее точки будет происходить против часовой стрелки, но в этом
случае точка будет приближаться к нам. Чтобы она удалялась,
надо направление вращения изменить на противоположное. Та-
Таким образом, свойство спирали быть правой или левой не за-
зависит от того, с какого торца на нее смотреть. Так и свойство
естественно-активной среды быть право- или левовращающей
не зависит от того, в каком из двух прямо противоположных
направлений распространяется свет.
Таким образом, если плоскость поляризации в естественно-
активной среде вращается, например, вправо, то при измене-
изменении направления распространения света на противоположное
она по-прежнему будет вращаться вправо. Однако направления
вращения «вправо» и «влево» относятся к разным наблюдате-
наблюдателям: к каждому из них свет должен приближаться. Объек-
Объективно, независимо от выбора наблюдателя, вращения проис-
происходят в противоположные стороны, если лучи распространя-
распространяются навстречу друз другу. Если свет заставить пройти туда
и обратно через естественно-активное вещество, отразив его от
зеркала, то плоскость поляризации возвратится к своему исход-
исходному направлению.
3. Кварц встречается в природе в виде двух модификаций:
правовращающего и левовращающего (короче — правого и лево-
левого). Это явление называется энантиоморфизмом и встречает-
встречается у кристаллов, не содержащих центров и плоскостей симмет-
симметрии. Обе энантиоморфные модификации кристалла отличаются
друг от друга внешней формой и внутренней кристаллической
структурой. По своей симметрии они отличаются друг от друга
примерно так же, как правая спираль отличается от левой или
правая рука от левой. Таким образом, обе модификации не кон-

§ 94 ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ 607
груэнтны, т.е. правая не может быть наложена на левую и нао-
борот. Но зеркальное изображение одной из этих модификаций
может быть совмещено с другой. По-видимому, все естественно-
активные кристаллы существуют в двух энантиоморфных моди-
модификациях, хотя не во всех случаях известны обе модификации.
Некоторые жидкости, например винная кислота, могут ветре™
чаться также в виде двух модификаций, вращающих плоскость
поляризации в противоположных направлениях.
4. Био установил на опыте, что угол поворота х плоскости
поляризации пропорционален толщине I оптически активного
вещества: х = al, где коэффициент а называется вращением на
единицу длины. Он зависит от длины волны, природы вещества
и температуры. Для кварца при температуре 20 °С и желтого
света натрия (А = 589,3 нм) а = ±21,728, для хлорноватисто-
кислого натрия (NaClOa) a = 3,170 угловых градуса на мил-
миллиметр. Для некоторых жидких кристаллов а может достигать
40 000 градусов на миллиметр. Для правых и левых модифи-
модификаций кварца и всех остальных кристаллов значения вращения
а одинаковы по величине^ но противоположны по знаку. Вра-
щение а увеличивается с уменьшением длины волны. Био на-
нашел, что величина а обратно пропорциональна квадрату длины
волны А2. Но такая зависимость грубо приближенна. В области
прозрачности и малого поглощения хорошо согласуется с опы-
опытом формула Друде
Вг
где Bi — постоянные, a Aj — длины волн, соответствующие соб-
собственным частотам рассматриваемого вещества.
Оптическую активность жидкостей принято характеризо-
характеризовать удельным вращением [а]. В случае химически чистых жид-
жидкостей это есть отношение вращения а к плотности жидкости р,
т.е. [а] = а/р. В случае растворов речь идет обычно о раство-
растворах активного вещества в неактивном растворителе. В этом
случае при определении удельного вращения [а] под р понима-
понимают плотность активного вещества, т.е. массу его в единице
объема раствора. Молекулярным вращением жидкости или рас-
раствора называют произведение удельного вращения [а] на моле-
молекулярную массу активного вещества [М] = Ж [а]. Зависимость
вращения плоскости поляризации от концентрации активного
вещества используется в сахарометрии для определения содер-
содержания сахара в растворе.
Вращение плоскости поляризации в одноосных кристаллах
имеет место и в тех случаях, когда свет распространяется под
углом к оптической оси. Но в этих случаях явление осложняется

608 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
обычным двойным лучепреломлением. Еще больше усложнение
в оптически двуосных кристаллах, так как вращение может быть
разным вдоль каждой из оптических осей. Наконец, встреча-
встречаются естественно™активные кристаллы кубической системы, не
обнаруживающие обычного двойного лучепреломления (хлор-
новатистокислый натрий NaC103, бромноватистокислый натрий
МаВгОз)- Для них вращение а не зависит от ориентации кри-
кристалла.
5. Согласно Френелю, вращение плоскости поляризации, ка-
какова бы ни была его физическая природа, есть проявление осо-
особого, так называемого кругового двойного лучепреломления. Од-
Однако две волны, которые могут распространяться в оптически
активной среде с определенными, но различными скоростями,
поляризованы не линейно, как при обычном (линейном) двои™
ном лучепреломлении, а по кругу: одна по левому, другая по
правому.
Для обоснования достаточности такого предположения до-
допустим, что плоская волна с вращающейся плоскостью поляри-
зации распространяется в положительном направлении оси Z.
Так как волна поперечна, ее электрический вектор Е будет со-
содержать только две компоненты Ех и Еу. Если А — амплитуда
колебаний, то Ех = A cos х cos (wt — kz), Ey = A sin x cos (wt — kz),
где х — угол между направлением электрического вектора Е и
осью X. Этот угол может зависеть от координаты z, так что
можно положить х — —olz, где а — введенный ранее коэффици-
ент, определяющий вращение плоскости поляризации. Когда ко-
коэффициент а положителен, то при распространении волны угол
X уменьшается, т.е. вращение происходит по часовой стрелке
(вправо). При отрицательном а плоскость поляризации враща-
ется против часовой стрелки (влево). Подставив значение х =
= ^az в выражения для Ех и Еу и воспользовавшись известны-
известными формулами тригонометрии, представим их в виде
А А
Ех = — cos (out — hz + az) + — cos (out — hz — oz),
Ey = — cos f ujt — kz + az + ^ 1 + — cos f oot — kz — az — ^
Разложим полученную волну на две: Е = Еп + Ел, где ком-
компоненты векторов Еп и Ел определяются выражениями
E% = j cos (out - kuz), E^ = | cos Lot - knz + |) , (94.1)
E^ = | cos (out - hPz), E^ = | cos Lot - k^z - |) (94.2)
и введены обозначения
ku = k - о, кл = к + а. (94.3)

§ 94 ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ 609
В волне (94.1) компонента Еу опережает по фазе компоненту Ех
на тг/2, а в волне (94.2) отстает на такую же величину. Обе вол™
ны поляризованы по кругу: в волне (94.1) электрический вектор
вращается от положительного конца оси Y к положительному
концу оси X, в волне (94.2) вращение происходит в противопо-
противоположном направлении (см. рис. 314). Иначе говоря, волна (94.1)
поляризована по правому, а волна (94.2) — по левому кругу.
Таким образом, кинематически волну с вращающейся плоско-
стью поляризации можно рассматривать как наложение двух
волн, поляризованных по кругу: правому и левому. Скорости
этих волн определяются выражениями
v11 = ----, Vя = -----, (94.4)
а показатели преломления — выражениями
п11 = — = -(к - а), пл = — = -(А; + а). (94.5)
Отсюда
пл - п11 = ^ а, а=^(пл^ п11). (94.6)
UJ ZC
Если пл^пп > 0, то а > 0, т.е. вращение плоскости поляризации
происходит вправо. Если же пл — п11 < 0, то плоскость поляри-
поляризации вращается влево. Иначе говоря, плоскость поляризации
вращается в ту же сторону, что и электрический вектор по-
поляризованной по кругу волны с меньшим показателем прелом-
ления, т.е. с большей фазовой скоростью.
6. Приведенное рассуждение отнюдь не доказывает, что каж-
каждая из поляризованных по кругу волн (94.1) и (94.2) может в от™
дельности существовать в среде. Мы исходили из опытного фак™
та, что в оптически активной среде может реально существовать
волна с вращающейся плоскостью поляризации. Такая волна,
конечно, должна быть решением системы фундаментальных
уравнений Максвелла^ дополненной материальными уравнения™
ми в оптически активной среде. Должна удовлетворять этой си™
стеме уравнений и суперпозиция поляризованных по кругу волн
(94.1) и (94.2), так как мы доказали, что такая суперпозиция да™
ет волну с вращающейся плоскостью поляризации. Но любое ре™
шение всякой системы уравнений можно представить (и притом
бесконечным числом способов) в виде суммы нескольких слага™
емых, которые вовсе не обязательно должны быть решениями
той же системы. Поэтому из того факта, что в оптически ак-
активной среде возможна волна с вращающейся плоскостью поля™
ризации, еще не следует, что в ней возможны и одиночные волны
с круговой поляризацией. Однако Френель предположил, что
поляризованные по кругу волны со скоростями (94.4) действи-
действительно могут распространяться в оптически активной среде.

610 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Их можно назвать нормальными волнами^ т.е. такими волнами,
которые распространяются в среде с сохранением своей формы
и характера поляризации. Это предположение есть гипотеза^
которую теоретически Френель доказать не мог, так как для
этого необходимо было бы располагать полной системой урав-
уравнений волновой теории света в оптически активных средах. Но
Френель подтвердил свою гипотезу экспериментально.
Френель изготовил сложную призму, состоящую из трех
кварцевых призм: двух призм АВМ и DCM из правовращаю-
правовращающего кварца и одной AMD из левовращающего с тупым углом
М = 152° (рис. 316). Оптические оси всех трех призм были
параллельны основанию
В М С AD. Падающий луч, парал-
лельный оптической оси,
на грани АВ не испытывал
преломления, но разлагался
внутри призмы АВМ на
два луча, поляризованные
по кругу. Луч с правой
поляризацией, как показы™
рис 316 вают формулы (94.5), имел
меньший, а луч с левой
поляризацией — больший
показатель преломления (п11 < пл). В левовращающей призме
AMD соотношение между этими показателями преломления
было обратным (п11 > пл). Поэтому на грани AM лучи ис-
пытывали разное преломление: правый луч приближался к
основанию AD, а левый удалялся. Угол расхождения между
лучами еще больше увеличивался при преломлении на гранях
DM и CD. В результате из призмы выходили два луча: один
отклонялся вниз, а другой вверх, угол расхождения между
которыми составлял около 4; (см. задачу к этому парагра-
параграфу). Исследование с помощью параллелепипеда Френеля или
пластинки А/4 показало, что луч, отклонившийся вниз, был
поляризован по правому, а вверх — по левому кругу.
Френель предлагал проверить свою гипотезу и для жидко-
жидкостей путем комбинации большого ряда призм, попеременно на™
полненных жидкостями, вращающими плоскость поляризации
вправо и влево. Позднее такой опыт был осуществлен и показал,
что и в оптически активных жидкостях также могут существо-
существовать две волны с различной круговой поляризацией: правой и
левой.
Существование двойного кругового лучепреломления в квар-
кварце можно обнаружить и с помощью одной призмы, вырезанной
так, что ее оптическая ось перпендикулярна к плоскости, де-
делящей пополам двугранный преломляющий угол. При наимень-

§ 95 МАГНИТНОЕ ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ 611
шем отклонении луч внутри призмы идет параллельно оптиче-
оптической оси, не испытывая обычного двойного преломления. Если
падающий свет естественный или поляризован линейно и содер-
содержит только одну спектральную линию, то в минимуме отклоне-
отклонения при выходе из призмы спектральная линия расщепляется на
две линии, из которых одна поляризована по правому, а другая
по левому кругу.
Таким образом, Френель доказал экспериментально, что при
вступлении в оптически активную среду луч света испытыва-
испытывает двойное круговое лучепреломление: лучи^ поляризованные по
правому и левому кругу^ идут внутри оптически активной сре-
среды с различными фазовыми скоростями. Если падающий свет
был поляризован линейно^ то при выходе из такой среды эти
волны складываются снова в линейно поляризованную волну1
но с повернутой плоскостью поляризации. Тем самым задача
объяснения вращения плоскости поляризации была сведена к
задаче объяснения кругового двойного лучепреломления.
Поляризованные по кругу в противоположных направлениях
волны в окрестности полос или линий поглощения могут отли-
отличаться не только скоростями распространения, но и коэффици-
коэффициентами поглощения. Тогда они выйдут с различными амплиту-
амплитудами. Если падающий свет был поляризован линейно, то выхо-
выходящий будет поляризован эллиптически. Это явление называ-
называется круговым дихроизмом. Оно впервые A847 г.) было заме-
замечено Гайдингером A795—1871) на аметисте и подробно изучено
A895 г.) Коттоном A869—1951) на растворах солей винной кис-
кислоты.
ЗАДАЧА
Пользуясь данными, приведенными в тексте, вычислить угол расхожде-
расхождения S(f между лучами, поляризованными по правому и левому кругу, вы-
вышедшими из призмы ABCD в опыте Френеля (рис. 316). Зная обыкновен-
обыкновенный показатель преломления кварца (по = 1,544 для Л = 589,3 нм), найти
угловое расхождение между теми же лучами 6\ip после преломления на
плоскости AM и §2^р после последующего преломления на плоскости MD.
Ответ. «V = — tg ^ = 3,92'; SlV = ^-= 1,27'; 52<р = ^ = 2,54'.
§ 95. Магнитное вращение плоскости поляризации
1. В 1846 г. Фарадей обнаружил, что естественно-неактивное
вещество, помещенное в постоянное сильное магнитное поле,
вращает плоскость поляризации, когда свет распространяет-
распространяется вдоль магнитного поля. Для наблюдения явления можно
воспользоваться электромагнитом, вдоль оси которого просвер™

612
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
лен цилиндрический канал, как это показано схематически на
рис. 312. Электромагнит помещается между скрещенными нико-
лями, исследуемое вещество вводится между полюсами электро-
электромагнита. Если наблюдатель смотрит в направлении магнитного
поля, то вращение вправо условились считать положительным,
а влево — отрицательным. В первом случае вращение происхо™
дит в ту лее сторону, куда течет ток по виткам электромагнита,
во втором — в противоположную сторону. Фарадей наблюдал
только положительное вращение. Таким вращением обладает
большинство веществ. Из диамагнитных веществ единственным
исключением является хлористый титан. Среди парамагнитных
веществ встречается значительное число отрицательно вращаю™
щих, например соли железа и редких земель, К2СГ2О7, КОЮ4
и др.
Опыты самого Фарадея, а затем более точные опыты Верде
A824-1866) показали, что угол поворота плоскости поляриза-
поляризации пропорционален длине пути I света в веществе и напря-
напряженности внешнего магнитного поля^ т.е. магнитной индук-
индукции В в веществе:
Х = ШВ, (95.1)
где коэффициент R называется постоянной Верде или магнит-
магнитной вращательной способностью. Этот коэффициент зависит
от рода вещества, его физического состояния и длины волны. В
табл. 10 приведены характеристики магнитного вращения для
некоторых веществ.
Таблица 10
Вещество
Вода B5 °С)
Сероуглерод B5 °С)
Кварц
Кислород
Водород
Углекислота
Железо
Никель
X
А = 656 им
0,0102'
0,0319'
0,0186'
0,484'
0,430'
0,691'
217°
92°
А = 589 нм
0,0130'
0,0415'
0,0166'
0,559'
0,537'
0,862'
195°
75°
А = 486 нм
0,0197'
0,0667'
0,0250'
0,721'
0,805'
0,286'
145°
64°
На 1 см дли-
длины луча в по-
поле 1 Гс
При дав л.
1 ат на 1 см
длины луча в
поле 105 Гс
На 10~3 см в
поле 15 000 Гс
В ферромагнитных металлах угол поворота х не пропорцио-
пропорционален В, но в сильных магнитных полях с возрастанием В воз™
растает очень медленно, приближаясь асимптотически к пре™
дельному значению. Согласно Кундту, угол х пропорционален

§ 95 МАГНИТНОЕ ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ 613
намагниченности магнетика / = (/i — 1M/Dтф), где /i — маг™
нитная проницаемость. Этот угол определяется выражением
X = KII, (95.2)
где К — так называемая постоянная Кундта. При В = 15 000 Гс
ферромагнетик можно считать намагниченным до насыщения.
2. Физическая природа магнитного вращения плоскости по™
ляризации была выяснена после открытия явления Зеемана и
объяснения его, данного Лорентцом. Допустим для простоты,
что в отсутствие магнитного поля вещество испускает только
одну спектральную линию^ т.е. обладает одной собственной (ре-
(резонансной) частотой ш®. При внесении в магнитное поле В у
осцилляторов вещества появляются две новые резонансные ча-
стоты ш® + п и ш® — п (где п — ларморовская частота), соответ-
соответствующие круговым вращениям электрона (см. § 92). Эти соб-
собственные частоты проявляются не только в испускании (прямой
эффект Зеемана), но и в поглощении света (обратный эффект
Зеемана). Прежняя резонансная частота ш® проявляется толь-
только при распространении света поперек магнитного поля и под
углом к нему. Нормальные волны, которые могут распростра-
распространяться вдоль магнитного поля, поляризованы по кругу. Когда
направления распространения света и магнитного поля совпа-
совпадают, большей собственной частоте ш^ = cjq + Q соответствует
вращение по, а меньшей ш^ = ш® — О — против часовой стрелки,
если смотреть в направлении магнитного поля (см. рис. 313).
Поскольку собственные частоты ш+ и ш- различны, скорости
распространения обеих поляризованных по кругу волн также
различны. Этим принципиально дано объяснение магнитного
вращения плоскости поляризации, так как, согласно Френелю,
при сложении таких поляризованных по кругу волн получается
волна с вращающейся плоскостью поляризации. Угол поворота
плоскости поляризации найдется из формулы (94.6). Она дает
X = YSn~ ~ П+^ = У ^ ~ П+^ ^95*3^
где через п+ и п^ обозначены показатели преломления соответ-
соответственно для волн с собственными частотами ш+ и ш-. При выбо-
выборе знака учтено, что положительные вращения плоскости поля™
ризации в случае естественного и магнитного вращения в рас-
рассмотренном нами случае принято выбирать противоположно.
Формулу (95.3) удобно исследовать графически. На рис. 317
штриховыми линиями представлены графики для показателей
преломления п_ и п+ как функций частоты света ш. Их раз-
разность представлена сплошной линией. Как видно из рисунка,
вне интервала (о;_,а;+) разность п_ — п+, а с ней и вращение
плоскости поляризации положительны^ а внутри этого интер-
интервала — отрицательны.

614
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
Во всех случаях направления ларморовского вращения О,
а следовательно, и вращения плоскости поляризации определя-
определяются только направлением магнитного поля В и не зависят
от направления распространения света. При изменении на про™
тивоположное направления распространения света направление
вращения плоскости поляризации не изменяется^ в противо™
Рис. 317
Рис. 318
положность тому, что происходит при естественном вращении.
Этим воспользовался Фарадей для усиления магнитного враще™
ния плоскости поляризации. Он увеличил расстояние I, проходи-
проходимое светом в веществе, заставив луч многократно отразиться от
концов исследуемого образца (рис. 318). Для этого концы образ™
ца серебрились (за исключением мест входа и выхода светового
луча).
3. Вне интервала (о;_,а;-|_) вдали от резонансных частот ш^
и ш+ поглощением можно пренебречь и воспользоваться для по™
казателей преломления п^ и п+ формулой Зельмейера (84.9),
заменив в ней ш® на ш^ и оо+ для показателей преломления п^ и
п+ соответственно. Согласно этой формуле, п^ и п+ являются
одной и той же функцией аргументов (а;2 — u?l) и (ш2 —uj\).
Такой же функцией, но от аргумента (а;2 — <-^о) выражается и
показатель преломления п вещества в отсутствие магнитного
поля. Следовательно,
^ — в+ = п(ш2 —
— п(ш2 —
2 \ dn
— ш~) dn
Вращение плоскости поляризации имеет заметную величину
только не очень далеко от полосы поглощения, а потому мож-
можно принять, что ш+ + ш^ = 2ш. Кроме того, cj+ — ш^ = 20 =
= еВ/(тс). Следовательно,
еВ dn
——
тс аш
eB
2жтс2 ал
Подстановка этого значения в (95.3) приводит к формуле (95.1),

§ 95 МАГНИТНОЕ ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ 615
причем для постоянной Верде получается выражение
д = _ « А^. (95.4)
2тс2 dX
Нелишне напомнить, что здесь е означает заряд электрона по
абсолютной величине. Формулу (95.4) обычно называют фор-
формулой Беккереля A852—1908),
4. Перейдем теперь к исследованию магнитного вращения
плоскости поляризации в области полосы поглощения веще-
ства. Здесь показатель преломления, а так лее коэффициент по™
глощения меняются с частотой быстро и аномально. Поэтому
магнитное вращение плоскости поляризации велико и носит так-
также аномальный характер. Кроме того, внутри самой полосы по™
глощения между резонансными частотами ш^ и а;+ знак враще-
вращения отрицателен^ как это видно из рис. 317. Такое аномальное
поведение плоскости поляризации называется эффектом Мака-
люзо и Корбино. Эти итальянские физики открыли его экспери™
ментально в 1898 г., а затем Фохт дал теорию явления.
Макалюзо и Корбино показали, что пары натрия в магнит-
магнитном поле вызывают очень сильное вращение плоскости поля™
ризации в непосредственной близости к желтым линиям D\ и
Z?2- Знак вращения одинаков по обе стороны этой двойной ли™
нии. Между полюсами электромагнита помещалось небольшое
натровое пламя, через которое проходил пучок линейно поляри™
зованного белого света в направлении магнитного поля. На пути
лучей ставился николь™анализатор, который при выключенном
магнитном поле полностью тушил свет. При включении тока в
обмотке электромагнита поле зрения становилось освещенным
ярким желтым светом: в спектроскопе были видны две желтые
линии, симметрично расположенные по обе стороны линии D.
Дело в том, что свет с такими длинами волн испытывал в маг™
нитном поле поворот плоскости поляризации на 90° и потому
проходил через скрещенные поляризатор и анализатор. Повора™
чивая николь-анализатор сначала в одном направлении, а затем
в другом, можно было убедиться, что по обе стороны полосы
поглощения знак вращения был один и тот же.
Вуд усовершенствовал установку Макалюзо и Корбино, про-
произведя опыты с парами натрия, заключенными в стальной тру™
бе. В его опытах плотность паров натрия можно было варьиро-
варьировать в значительных пределах. При сравнительно малой плот™
ности наблюдалась такая же картина, как и в опытах Макалюзо
и Корбино. Разница состояла в том, что в опытах Макалюзо
и Корбино двойная D-линия натрия не разрешалась, а в опы-
опытах Вуда разрешалась. Желтые линии появлялись по обе сторо™
ны как компоненты Di, так и компоненты Z?2- При увеличении
плотности паров натрия расстояние между наружными желты-

616
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
ми линиями увеличивалось и между ними появлялись новые ли™
нии, соответствующие вращению на 270°, 450°, 630° и т.д. Центр
между линиями D\ и D2 последовательно становился то тем™
ным, то светлым. В некоторых случаях Вуд наблюдал до восьми
таких перемен, что соответствует вращению на 1440°.
5. Изложенная теория основана на классической теории^ т.е.
на простом эффекте Зеемана. Полная теория должна учиты-
учитывать сложный эффект Зеемана, т.е. быть квантовой. Кроме
того, для объяснения отрицательного вращения плоскости по™
ляризации необходимо учитывать парамагнетизм атомов. На
этих вопросах мы останавливаться не можем.
ЗАДАЧИ
1. Между двумя николями N\ и N2 (рис. 319), главные сечения которых
повернуты относительно друг друга на 45°, в продольном магнитном поле
помещен слой вещества, вращающий плоскость поляризации. На какой угол
Рис. 319
этот слой должен вращать плоскость поляризации, чтобы система была
оптическим вентилем, т.е. свет проходил бы через нее только в одном
направлении (например, от тела А к телу JB), а в обратном направлении не
проходил?
Ответ. На угол 45° + 180°т (га — целое число).
2. Как будет вести себя оптический вентиль, описанный в предыдущей
задаче, если направление магнитного поля изменить на противоположное,
оставляя без изменения взаимное расположение николей и величину напря-
напряженности магнитного поля?
Ответ. Направление, в котором пропускается свет, изменится на
противоположное.
3. Может ли установка, описанная в задаче 1, быть оптическим венти-
вентилем, если между николями поместить слой естественно-активного веще-
вещества без магнитного поля?
Ответ. Нет.
4. Разъяснить парадокс Вина, заключающийся в следующем. В адиаба-
адиабатической оболочке помещены два одинаково нагретых тела А и В (рис. 319),
а между ними световой вентиль. Свет, излученный телом А, падает на ни-
коль N\. Половина падающей энергии I, т.е. 1/2, проходит через николь,

§ 96 ВРЕМЕННАЯ И ПРОСТРАНСТВЕННАЯ ДИСПЕРСИЯ 617
а другая половина, испытав полное отражение в николе, возвращается зер™
калом Si к телу А (применяя зеркало, можно не учитывать нагревание
николя). Другая половина энергии 1/2, пройдя через николь JVi, полностью
пройдет через николь N2 и поглотится телом В. Свет же от тела В не прой-
пройдет через вентиль. Половина излученной этим телом энергии I, равная 1/2,
испытает полное отражение в николе N2 и после отражения от зеркала S2
вернется к телу В. Другая половина энергии, пройдя через николь N\ и вра-
вращающую среду, испытает поворот плоскости поляризации на 45° и поэтому
не сможет пройти через николь ]Vi, а претерпит в нем полное отражение.
Добавочным зеркалом 5з эта часть энергии будет отражена обратно и после
полного отражения в николе N\ вернется к телу В. Таким образом, тело
А получит энергию 1/2, а тело В — энергию 31/2 и будет нагреваться в
противоречии со вторым началом термодинамики.
Решение. Свет, излученный телом В (см. рис. 319) и возвра-
возвращающийся к нему обратно после отражения от николя JVi, испытает при
прохождении через вращающее вещество дополнительный поворот плоско™
сти поляризации на 45° и поэтому не пройдет через николь N2. Испытав в
николе N2 полное отражение, этот свет вернется (если поставить еще одно
зеркало напротив 5г) к телу А. Приведенное решение парадокса Вина было
дано Рэлеем.
§ 96. Временнам и пространственная дисперсия.
Теорим естественной оптической активности
1. Многие оптические явления находят удовлетворительное
объяснение в предположении, что связь между векторами D и
Е (а также между В и Н) локальна во времени и простран-
пространстве. Это значит, что вектор D в любой точке пространства г
и в любой момент времени t определяется значением вектора
Е в той же точке и в тот же момент времени. (То же от™
носится к векторам В и Н. В целях сокращения подобные за-
замечания в дальнейшем подразумеваются, а все изложение ве™
дется для векторов D и Е.) Однако для истолкования некото-
некоторых явлений предположения о локальной связи недостаточно.
Пространственно-временную нелокальность молено разбить на
чисто пространственную и чисто временную. Отвлечемся сна™
чала от чисто пространственной нелокальности и учтем нело™
кальность временную. Среда во всем дальнейшем предполага-
предполагается однородной.
2. Временная нелокальность проявляется в оптической дис-
дисперсии среды. Действительно, для истолкования дисперсии необ™
ходимо учитывать инерционные свойства электронов, атомных
ядер и ионов вещества. А такая инерционность и приводит к
нелокальной связи по времени между D и Е. Пренебрегая про™
странственной нелокальностью, будем рассуждать так, как ее™
ли бы во всем пространстве электромагнитное поле было од-
породно и менялось только во времени. Действием магнитно-

618 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
го поля будем пренебрегать. Рассмотрим сначала импульсные
воздействия на среду. Допустим, что от момента t = 0 в тече-
течение времени dt среда подверглась воздействию электрического
поля Е, а по истечении этого промежутка поле в среде снова
обратилось в нуль. Такое воздействие может рассматриваться
как электрический толчок^ возбуждающий регулярные колеба-
ния электронов, атомных ядер и ионов среды. Эти колебания
не прекращаются после прекращения действия поля, но продол™
жаются дальше в силу конечности масс колеблющихся частиц.
В этом и проявляется временная нелокальность связи между
отклонением частиц из положений равновесия и электрическим
полем, а следовательно, между поляризацией Р или индукци-
индукцией D среды и полем Е.
В рамках линейной электродинамики поляризация ере™
ды dP, вызванная электрическим толчком, пропорциональна
Edt. Предполагая, что среда однородна и изотропна^ для век™
тора dP в момент времени t можно написать
dP(t) = /(t)E(O)dt, (96.1)
где функция f(t) зависит только от свойств среды и от времени
t, которое прошло с момента действия толчка до момента наблю-
наблюдения. Функция f(t) должна обращаться в нуль при t = 0, так
как из-за своей инерционности электроны, атомные ядра и ионы
не могут мгновенно получить конечные смещения. Она должна
обращаться в нуль и при t = оо, так как все реальные среды дис-
сипативны^ так что всякое свободное колебание в них должно в
конце концов затухнуть.
Если поле Е действует в течение длительного промежутка
времени, то этот промежуток можно разбить на бесконечно ма-
малые промежутки и таким путем свести воздействие электри-
электрического поля на среду к действию последовательных толчков.
Вклад в поляризацию среды в момент времени t, внесенный
более ранним электрическим толчком E(t;) dt1, будет dP(t) =
= f(t — t;)E(t;) dtf. В линейной электродинамике справедлив
принцип суперпозиции^ а потому полный вектор поляризации
в момент времени t будет
t
P(t)= J f(t-t')E(t')dt', (96.2)
или, вводя новую переменную интегрирования # = t — i\
оо
P(t) = J /(t?)E(t - i?) dt?. (96.3)

§ 96 ВРЕМЕННАЯ И ПРОСТРАНСТВЕННАЯ ДИСПЕРСИЯ 619
Следовательно,
с©
D(t) = E(i) + 4тг J /(#)E(t - #) dti. (96.4)
о
Интегрирование производится по времени, предшествующему
рассматриваемому моменту t. Этого требует принцип причинно-
причинности. В своей нерелятивистской форме он означает, что каждое
событие определяется только прошедшими событиями, но не
может зависеть от будущих.
Если Е = Eq exp (iujt), то после подстановки этого выраже-
выражения в (96.4) получится
D(t) =e(o;)E(t), (96.5)
где
со
е(ш) = 1 + 4тг J f{§)e~luJ§ d&. (96.6)
о
Таким образом, для монохроматического поля связь между D и
Е формально может быть записана в локальной форме с помо-
помощью диэлектрической проницаемости как функции частоты ш.
Оптическая дисперсия, т.е. зависимость е от ш, эквивалентна
нелокальной связи по времени между D(t) и E(t). Поэтому та™
кую дисперсию называют временной или частотной дисперси-
дисперсией, в отличие от пространственной дисперсии, о которой гово-
говорится ниже.
3. Учтем теперь пространственную нелокальность. Если
электрическое поле неоднородно, то для нахождения индуциро-
индуцированного дипольного момента молекулы недостаточно знать век™
тор Е в одной точке пространства, а требуется знание функции
Е(г) во всем объеме, занимаемом молекулой. Это эквивалентно
знанию поля Е и его пространственных производных всех поряд-
порядков в какой-то одной точке внутри молекулы (которую условно
можно назвать центром молекулы), так как тогда функция Е(г)
представится рядом Тэйлора по координатам х\, Х2, %з векто-
вектора г.
Легко оценить порядок последовательных членов этого ря-
ряда в монохроматическом поле световой волны. Производная
dEijdxm будет порядка Е/Х, а координата хт — порядка раз-
размеров молекулы а, так что член хт • dEijdxm будет порядка
(а/Х)Е. Так же оцениваются и порядки членов, содержащих
высшие производные. Если нулевой член ряда принять за еди-
единицу, то члены, содержащие первые, вторые и последующие про-
производные, будут порядка а/А, (а/АJ, (а/АK и т.д.
Как видно, в неоднородном поле связь между индуцирован-
индуцированным дипольным моментом молекулы и электрическим полем Е

620 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
пространственно нелокальна. Это ведет к пространственной
нелокальности связи между Р и Е, а также между D и Е.
При этом в слабых электрических полях, с которыми имеют дело
линейная электродинамика и оптика, можно пренебречь влияни™
ем квадратов и высших степеней поля Е и его пространственных
производных. В этом «линейном приближении» в монохромати™
ческом поле световой волны молено написать
Dj = ejlEl + №? + ^тп^г + • • • (96.7)
Для общности предполагается, что среда анизотропна. Ее опти-
оптические свойства характеризуются тензорами Sji, Jjimj • • •? являю-
являющимися функциями частоты ш. В соответствии с общепринятой
тензорной символикой по дважды встречающимся координат™
ным индексам подразумевается суммирование. Как выяснено
выше, если нулевой член ряда (96.7) принять за единицу, то
последующие члены будут порядка а/Л, (а/ЛJ и т.д.
В случае плоской монохроматической волны
Е = Ео exp [i(u)t — kr)]
дифференцирование по координате хт сводится к умножению
на ^ikm. Поэтому соотношение (96.7) можно записать в виде
DJ(r,t) = ejl(co,k)El(r,t), (96.8)
где введено обозначение
?ji(w,k) = Sji{u)) - ikmjjim + (-ikm)(-ikn)ajimn + ... (96.9)
Таким образом, в поле плоской монохроматической волны связь
между D и Е опять принимает формально локальный харак-
характер. Однако тензор диэлектрической проницаемости 6ji(a;,k)
теперь зависит не только от w, но и от к. Зависимость этого
тензора от волнового вектора к называется пространственной
дисперсией.
4. Ввиду малости параметра а/Л эффекты пространствен-
пространственной дисперсии в оптике малы и трудно наблюдаемы. Долгое
время единственно известным из таких эффектов было есте-
естественное вращение плоскости поляризации. Оно наблюдается
в таких средах, у которых тензор jjim отличен от нуля.
Найдем вид тензора 7jfm Для дисимметрично изотропных
сред — жидкостей и кристаллов кубической системы, у кото-
которых тензор Sji{uj) вырождается в скаляр. Отбросив в выраже-
выражении (96.7) все члены, содержащие тензоры четвертого и высших
порядков, напишем
Dj{T,t) = еЕ3(г,г)+Ъ1т^. (96.10)

§ 96 ВРЕМЕННАЯ И ПРОСТРАНСТВЕННАЯ ДИСПЕРСИЯ 621
В развернутом виде для ^-составляющей вектора D это соотно-
соотношение гласит
дЕ дЕ дЕ дЕу +
о ~г 7ж|/2 ^ т- 7жгж ^ж т- Jxzy q
Повернем теперь координатную систему вокруг оси X на угол
90° (рис. 320). Ввиду изотропии среды, все коэффициенты в пре™
дыдущем соотношении останутся неизменными. Однако у и Еу
перейдут в ^z и ^EZJ a z и Ez — в у и Еу. Остальные коор-
координаты и компоненты векторов Е и D останутся неизменными.
Произведя в (96.11) соответствующую замену, получим
п _ тр , 9ЕХ дЕх дЕх dEz
Пх - 6^х + Ъхх^ Ъху-fa- + Ixxz-Qj- 7х2/х^^ +
dEz dEz . дЕу дЕу . дЕу Г(ла 11 ч
-^ ^ Jxyz-Qj- + -Yxzx-q? ~ Ixzy^ + Jxzz^« (96.11a)
Но в силу определения тензора jjim в повернутой системе коор-
координат соотношение между Dx и компонентами вектора Е можно
записать в прежней форме
(96.11). Сравнение обоих со- Zh
отношений дает jxxy = jxxz,
Ixxz = -Ixxyi откуда jxxy =
— Ixxz = 0 и т.д. Кроме того,
Ixyz = Ixzy И Т.Д.
Что касается коэффици-
коэффициента jXXXj то он равен нулю.
Действительно, в силу сим™
метрии <уххх = 7щ/ = Izzz-
Повернем исходную систему координат вокруг оси Z на угол
90°, чтобы ось Y приняла отрицательное направление прежней
оси X. Тогда в (96.11), оставляя коэффициенты неизменными,
следует сделать замену х —>> —у, Dx —>• ^Dyj Ex —>• ^Eyj что
дает
-Уу = ?-*^у ' Тжжж~™Б | • • •
С другой стороны, на основании определения тензора 7jfm в
вернутой системе можно сразу написать
Отсюда, ввиду равенства jxxx = 72/2/2/' получаем 7жжж = 0.
Таким образом, все компоненты тензора jjim обращаются в
нуль, если какие-либо два из индексов j, I, m одинаковы, неза-
независимо от значения третьего индекса. Отличны от нуля только

622 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
компоненты, у которых все три индекса различны. При этом
при перестановке любых соседних индексов составляющая тен-
тензора jjim меняет знак. Следовательно, молено написать
Ixyz = ^lyxz = ^yzx — ^^zyx = Izxy =
В результате (96.11) перейдет в
или в векторной форме
D = eE + grotE. (96.13)
Если каждая точка среды является центром симметрии^ то
при отражении в этом центре среда переходит сама в себя, а по™
тому тензор jjim при таком отражении должен оставаться неиз-
неизменным. Но при этом правая система координат переходит в
левую, а знаки координат ж, у, z и компонент полярных век™
торов Е и D меняются на противоположные, так что (96.10)
переходит в
Следовательно, 7jfm — 0, т.е. вращение плоскости поляризации
невозможно. Для возможности вращения необходимо, чтобы мо-
молекулы жидкости или кристаллов кубической системы не имели
центров симметрии.
Заметим еще, что в случае изотропной естественно-активной
среды величина g есть псевдоскаляр¦, а не истинный скаляр (см.
т. I, § 7). При переходе от правой системы координат к левой
или наоборот знак этой величины меняется на противополож-
противоположный. Это непосредственно видно из соотношения (96.12), кото-
которое показывает, что 7jfm есть полностью антисимметричный
псевдотензор.
5. По аналогии с формулой (96.13) можно написать
B = H + g/rotH, (96.14)
где gf — новый псевдоскаляр. Магнитную проницаемость /i мы
при этом приняли равной единице. Введение добавочного члена
g'rot H необходимо для выполнения закона сохранения энергии.
Действительно, используя уравнения Максвелла, приведем со™
отношения (96.13) и (96.14) к виду
Эти уравнения молено упростить. Для этого подставим второе
выражение в первое, а первое во второе и отбросим при этом

§ 96 ВРЕМЕННАЯ И ПРОСТРАНСТВЕННАЯ ДИСПЕРСИЯ 623
произведение gg1, как величину более высокого порядка мало-
малости. Тогда получим
D = бЕ — — —, В = Н + — . (96.15)
с dt с dt
Теперь воспользуемся результатом электродинамики, согласно
которому величина ED + НВ равна производной по времени от
(умноженной на 8тг) плотности электромагнитной энергии (см.
т. III, § 84). Используя (96.15), преобразуем это выражение к
виду
ED + НВ = (еЕЁ + НН) + * (eg'EE - gHH).
Первый член справа есть производная от 1/2{еЕр1 + Н2). Следо™
вательно, и второй член должен быть производной по времени
от некоторой функции. Это будет действительно так, если вы-
выполняется соотношение eg' = g, так как тогда
_ „'тглтп! „т.ттт ~, " /тглТТ1 тттт\
С И Pj IPi — Р ?1Ц. — М I Fj "i — jrUTj. I.
Тем самым доказана необходимость введения второго члена в
формуле (96.14), а формулы (96.15) приводятся к окончатель-
окончательному виду
с dt с dt
6. Теперь мы располагаем полной системой уравнений для
монохроматических волн в однородной естественно-активной
среде. Из уравнений divD = 0 и divB = 0 следует, что плоские
волны в такой среде поперечны относительно векторов Dt/B.
Они поперечны также относительно векторов EwH, так как
из уравнений (96.13) и (96.14) следует, что divE = divH = 0.
Подставив далее выражения (96.16) в уравнения Максвелла
rotH= I^H, rotE = —i^,
с dt с dt
получим
.^2 ' (96.17)
с dt
1 дШ
Допустим, что волна плоская и распространяется в положи-
положительном направлении оси Z. Тогда отличными от нуля будут
только компоненты Ех и Eyi Hx и Ну1 причем эти величины за™
висят только от одной координаты z. С учетом этого запишем

624 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
уравнения (96.17) в координатной форме
дЕх = _1^ _ g д2Еу
dz с dt с2 dt2 ' /Qfi 1 оч
и аналогично для производных дНх/дг и дНу/дг. Здесь все
величины вещественные. Для упрощения рассуждений удобно
ввести комплексные комбинации
Ел. = Ет -\- iEq,. Е— = Ет — iEq,.
+ х у, у, (96.19)
Я U I ATI TJ TJ A U Х '
+ = пх + шУ1 а^ = пх — гиу.
Вещественная часть комплексного числа Е+ дает компонен-
ту Ех, а коэффициент при мнимой части — компоненту Еу, и
т.д. Однако при исследовании явлений круговой поляризации
удобнее оперировать непосредственно с самими комплексными
комбинациями, не переходя к вещественной форме. Например,
если совершаются гармонические колебания Ех = Acoscjt, Ey =
= Asincdt, то Е+ = Aetujt. Точка, изображающая комплексное
число ?7_|_, дви^кется в комплексной плоскости по кругу в на™
правлении от оси X к оси Y, т.е. представляет волну, поляризо-
поляризованную по левому кругу. Аналогично, комплексная комбинация
?L описывает волну^ поляризованную по правому кругу.
Умножив второе уравнение (96.18) на г, почленным сложени-
сложением и вычитанием этих уравнений найдем выражения для произ-
производных dE+jdz и dE^/dz. Аналогично поступаем с магнитным
полем. В результате получим
dE+ % dH+ , is d2E+
dz
dH+
dz
dE^
dz
с
is
с
i
с
dt
¦dE+
dt
dH^
dt
c2
1 ig
c2
ig
c2
ig
dt2 '
¦ d2H+
dt2
d2E^
dt2 '
(96.21)
~dz~ ~ 7^T ~& dt2 '
Уравнения разделились на две группы независимых уравне-
уравнений. В одну группу входят комбинации Е+ и Д"+, описывающие
волны с левой круговой поляризацией, в другую — комбинации
EL и i/_, которым соответствует правая круговая поляризация.
Ввиду однотипности обеих групп достаточно исследовать одну
из них, например группу (96.20). Исключим из нее стандартным
способом величину И+. Отбрасывая члены, содержащие g2, по-

§ 96 ВРЕМЕННАЯ И ПРОСТРАНСТВЕННАЯ ДИСПЕРСИЯ 625
лучим
д2Е+ _ е д2Е+ 2ig д3Е+
+
dz2 с2 dt2 с2 dt2dz
и такое же уравнение для JJ+. В монохроматической плоской
волне Е+ = Gехр [i(ujt ~~ kz)} дифференцирование по z эквива-
эквивалентно умножению на —гк. Поэтому
д2Е+ _ е д2Е+ 2gk д2Е+
dz2 с2 dt2 с2 dt2
Здесь в последнем члене вместо к можно подставить волновое
число в нулевом приближении, т.е. к = uj^fejc. Тогда получится
волновое уравнение
(96.22)
dz2 v\ dt2 '
в котором
С 1 С gUJ
или
Ул. ^^ — — 7 (9o.ZOj
п п
где п — показатель преломления среды. Аналогично, для волны
с левой круговой поляризацией
„_ = ? + Щ. (96.24)
п п2
Скорости v+ и v^ различны. Поэтому должно существовать кру-
круговое двойное лучепреломление^ а следовательно, и вращение
плоскости поляризации.
Убедимся еще, что в каждой поляризованной по кругу плос-
плоской волне электрический и магнитный векторы взаимно перпен™
дикулярны. Для этого в уравнениях (96.20) достаточно произ-
произвести замену д/dt —>• icj, д/dz —>• —ik. Тогда первое уравнение
перейдет в
—Нл. = г Ik — s— Ел..
с ^ \ с ) ^
Отсюда видно, что отношение Ел./'Нл. чисто мнимое^ а это экви-
эквивалентно утверждению, что векторы ЕиНв рассматриваемой
волне взаимно перпендикулярны.
7. В средах, обладающих центром симметрии^ разложе™
ние (96.9) тензора ?^(о;,к) не может содержать линейных чле-
членов по к. В таких случаях пространственная дисперсия может
быть обусловлена квадратичными членами. С ней связана сла-
слабая зависимость поглощения кубических кристаллов закиси ме-
меди O112O от поляризации света (Гросс и Каплянский, 1960 г.), а
также слабая анизотропия показателя преломления кубических
кристаллов кремния (Пастернак и Ведам, 1971 г.). Эффекты

626 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
очень малы, так как они определяются квадратом (а/АJ, т.е.
величиной порядка 10"~6—-10™ (а — размер молекулы или по-
постоянная кристаллической решетки). Существуют и другие эф-
эффекты пространственной дисперсии, в обсуждение которых мы
входить не будем.
§ 97. О тепловых флуктуацимх
В этом вспомогательном параграфе сообщаются краткие сведения о
тепловых флуктуациях, необходимые для изложения вопросов молекуляр-
молекулярного рассеяния света.
1. Пусть / — любая флуктуирующая величина. Флуктуацией этой ве-
величины называется отклонение А/ = f — f мгновенного значения этой ве-
величины от ее среднего значения. Обычно пользуются средним квадратом
флуктуации, т.е. величиной (А/J. Квадратный корень из этой величины
i (AfJ называется среднеквадратичной флуктуацией, а ее отношение к
среднему значению /, т.е. у (А/J//, — среднеквадратичной относитель-
относительной флуктуацией.
Усредняя выражение (А/J = (/ — /J = /2 — 2// + (/J, получим
Но / — величина постоянная, а потому // = // = (/J. Следовательно,
7F = F-GJ- (97.1)
Усредним теперь произведение двух флуктуирующих величин:
fg = (f + Af)(-g+Ag) = fg+jAf + jAg+A
Так как /ng — величины постоянные, а А/ = Ag = 0, то
fg = fg + AfAg. (97.2)
Формула (97.1) содержится здесь как частный случай, если взять / = g.
Величины fug называются статистически независимыми, если
A/ Ag" = 0. Для таких величин
7g=fg- (97.3)
2. Рассмотрим теперь любую физическую систему, состоящую из N
независимых одинаковых частей. Примером такой системы может служить
идеальный газ, а составных частей — отдельные молекулы. Пусть fi — про™
извольная аддитивная величина, характеризующая г-ю подсистему, напри-
например в приведенном примере — кинетическая энергия г-й молекулы. Тогда
в силу предполагаемой аддитивности соответствующая величина для всей
системы будет F = Yl fi- Выразим средний квадрат флуктуации величины
F через аналогичный квадрат для величины fi. Очевидно, F = ^ f i = iV/,
где опущен индекс г, так как предполагается, что все составные части си-

§ 97 О ТЕПЛОВЫХ ФЛУКТУАЦИЯХ 627
стемы тождественны. Далее,
= (?/«)'=
А так как эти части независимы, то fifj = f if ¦ = (/J. Следовательно,
Подставляя эти значения в формулу (97.1), получим
?2\
(AFJ = F2 - (FJ = N(P - / ). (97.4)
Отсюда на основании (97.1)
(97.5)
f
Таким образом, относительная флуктуация величины F обратно про-
пропорциональна квадратному корню из N. При больших N относительные
флуктуации ничтожны. Этот вывод верен и для неаддитивных величин. С
ним связана достоверность термодинамических результатов для макро-
макроскопических систем.
3. Применим формулу (97.4) к вычислению флуктуации числа молекул
в фиксированном объеме V идеального газа. Пусть в большом закрытом
сосуде объема V в отсутствие силовых полей находятся N молекул иде-
идеального газа. Разделим объем V на z = V/v одинаковых объемчиков v%
величиной v каждый. Если щ — число молекул в объемчике Vi, a N — в
большом объеме V, то ЛГ = ^щ. Среднее число молекул щ в объемчике
Vi будет rii = п = Nv/V, т.е. одно и то же во всех объемчиках. Представим
его в виде п = Np, где р = v/V — вероятность нахождения молекулы в
объемчике v. Возьмем теперь в качестве fi следующие величины: fi = 1,
если г-я молекула находится внутри объемчика v, и fi = 0, если она нахо-
находится в оставшемся объеме V — v. Тогда число молекул п в объемчике v
можно представить в виде п = ]Г) /^, предполагая, что суммирование ведет-
ведется по всем N молекулам объема V. Ясно, что fi = ff = ff = ..., а потому
fi = f? = f^ = ... = р. Следовательно, по формуле (97.1)
A/f = f?~(fi) =P-P =РA-Р)-
А так как в случае идеального газа величины /i, /2, /3, ... статистически
независимы, то по формуле (97.4)
An2 = Np(l - р) = A - р)п. (97.6)
Если объем V бесконечно велик, то р —»¦ 0, а следовательно,
Ат? = п. (97.7)
Отсюда получаем для относительной флуктуации плотности газа
(97.8)
4. Более общий метод вычисления флуктуации плотности, применимый
также к жидкостям и твердым телам, основан на теореме о равномерном

628 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
распределении кинетической энергии по степеням свободы. Рассмотрим ма-
малую часть жидкости или газа, окруженную такой же жидкой или газооб-
газообразной средой, температура которой Т поддерживается постоянной (термо-
(термостатом). С целью упрощения и наглядности вычислений предположим, что
эта малая часть жидкости или газа заключена в цилиндр с поршнем. Стен-
ки цилиндра идеально проводят тепло, а поршень может ходить в нем без
трения. Тогда наличие стенок цилиндра и поршня не будет препятствовать
обмену энергией и выравниванию давлений между веществом в цилиндре
и термостатом. Благодаря тепловому движению поршень будет совершать
броуновское движение. К нему мы и применим теорему о равномерном рас-
распределении кинетической энергии по степеням свободы.
Поршень можно рассматривать как гармонический осциллятор, совер-
совершающий тепловые колебания. Среднее значение его потенциальной энергии
при смещении на ж из положения равновесия ж = 0 равно г/2жх2 = 1/2~кТ1
где ж — коэффициент упругости, соответствующий такому смещению. Если
S — площадь поршня, а А У — изменение объема системы, то AV = Sx.
Таким образом, (AFJ = S2x2 = Б2кТ/ж. Сила, возвращающая поршень в
дР
положение равновесия, будет F = S^^x. где Р — давление газа или жид™
дх
кости. Поэтому ж = —SdP/дх = —S2dP/dV. В результате получим
Значок Т указывает, что в выводе предполагалось постоянство темпера-
температуры окружающей среды (термостата). Если бы вещество внутри объема
V было адиабатически изолировано, то Т следовало бы заменить на S (по-
(постоянство энтропии), т.е.
(AV2)S = -kT(dV/dP)s. (97.10)
Формулы (97.9) и (97.10) выражают флуктуации объема одной и той
шее массы вещества^ находящейся в термодинамическом равновесии с окру-
жающей средой. Для идеального газа при постоянстве температуры PV =
= const, так что (дУ/дР)т = —V/P. А так как PV = пкТ, где п — число
молекул в объеме V, то из формулы (97.9) получаем (AFJ = V2/п. Пусть
теперь объем V фиксирован, а число молекул в нем п меняется из-за теп-
тепловых флуктуации. Если бы объем V увеличился на А У, то число молекул
в прежнем объеме V уменьшилось бы на An = п АV/V. Отсюда
(AnJ = (nlVf(AVJ = n = n,
что совпадает с прежним результатом (97.7). В окончательном результате
различием между п шп можно пренебречь, что мы и сделали.
5. Перейдем теперь к вычислению флуктуации энергии. С целью луч-
лучшего уяснения метода начнем с вычисления флуктуации кинетической энер-
энергии 8 молекулы одноатомного идеального газа. Согласно максвелловскому
закону распределения скоростей,
7= — J 8e^a? dY, (97.11)
где а = 1/(/гТ), dY — элемент объема пространства скоростей, a Z опреде-
определяется условием нормировки:
J
с1Г. (97.12)

§ 97 О ТЕПЛОВЫХ ФЛУКТУАЦИЯХ 629
Дифференцируя это соотношение по параметру а, получим
da
и формула (97.11) перейдет в
?=_!^. (97.13)
Отсюда
da^ Z da2 Z2 \da) ~ Z da2
Аналогично,
?2 = 1 Г ?2e-a? dv = 1 ^Z^ (g7 M)
Сравнение этой формулы с предыдущей дает
d?_
daJ
шли после подстановки значения параметра а = 1/(кТ)
(АЕJ = кТ2^. (97.15)
Так как для идеального одноатомного газа Е = 3/'2кТ, то
^ " (97.16)
6. Приведенный метод вычисления (А^J может быть распространен
практически без изменений на более общие и важные случаи. Выделим, на™
пример, малую часть (подсистему) изотропной среды (жидкости или газа),
находящуюся в статистическом равновесии со всей средой, температура Т
которой поддерживается постоянной. По отношению к выделенной подси-
подсистеме окружающая среда играет роль термостата. Из-за обмена энергией
между термостатом и подсистемой энергия последней будет непрерывно
флуктуировать. Беспорядочные изменения энергии подсистемы подчиня-
подчиняются статистическому закону, вполне аналогичному максвелловскому за™
кону распределения кинетической энергии между молекулами. Поэтому
среднее значение энергии подсистемы будет выражаться прежней форму-
формулой (97.13), где а имеет прежнее значение, а интегрирование в выражении
(97.12) производится по многомерному пространству координат и импуль-
импульсов подсистемы. В этом единственное отличие рассматриваемого случая от
предыдущего. Но оно совсем не отражается на последующих выкладках.
Поэтому окончательный результат (97.15) применим к рассматриваемой
подсистеме без всяких изменений.
Результат (97.15) остается верным и в квантовой статистике. Чтобы
убедиться в этом, достаточно заменить интеграл (97.12) суммой
где Si — энергии квантовых уровней подсистемы, a gi — кратности этих
уровней. Суммирование производится по всем квантовым состояниям под-
подсистемы (см. т. II, § 85).

630 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
В случае макроскопической подсистемы, объем которой поддерживает™
ся постоянным, Е имеет смысл внутренней энергии подсистемы, a d?/dT —
ее теплоемкости Су при постоянном объеме. Тогда из формулы (97.15) по-
получается
(Шу =kT2Gy (97.17)
Значок V слева указывает на то, что величина (А,?2)у есть средний квадрат
флуктуации энергии подсистемы при сохранении ее объема V постоянным.
7. Рассмотрим теперь флуктуации энтальпии I подсистемы. Для это-
этого воспользуемся следующим искусственным приемом. Предположим, что
подсистема заключена в оболочку с идеально проводящими подвижными
стенками, так что объем подсистемы не сохраняется постоянным. Пусть
оболочка снаружи подвергается действию постоянных внешних сил, под-
держивающих внешнее давление Р постоянным. Эти силы увеличивают
потенциальную энергию подсистемы на величину PV. Если под ? понимать
ту же энергию, что и в предыдущем выводе, то с учетом дополнительной
потенциальной энергии PV среднее значение полной энергии подсистемы
будет ?-\-РУ. Но это есть энтальпия подсистемы I. Все предыдущие рассуж-
рассуждения можно повторить без изменений, заменив Е на Е + PV. В результате
вместо формулы (97.15) получится
§. (97.18)
а!
Но при Р = const производная dl/dT есть теплоемкость Ср подсистемы
при постоянном давлении, а потому
(АР)р =кТ2СР. (97.19)
8. Распространим теперь термодинамический метод вычисления флук-
флуктуации, изложенный вьше, на любые величины, характеризующие макро-
макроскопические свойства подсистем. Ограничимся при этом изотропными те-
телами. Для них любая термодинамическая величина в состоянии термоди-
термодинамического равновесия есть функция двух других термодинамических ве-
величин, которые могут быть приняты за независимые переменные. Термо-
Термодинамические величины макроскопических подсистем хотя и испытывают
флуктуации, но в случае малости таких подсистем их мгновенные состоя-
состояния практически равновесны. Они также определяются двумя независимы-
независимыми переменными. Поэтому задача сводится к вычислению тепловых флук-
флуктуации таких двух независимых переменных. В окончательном результате,
определяющем значение среднего квадрата той или иной флуктуации, необ-
необходимо указывать, какая из двух величин, выбранных для характеристики
состояния подсистемы, поддерживается постоянной. Иначе самый резуль-
результат будет неопределенным, а потому и бессмысленным.
Покажем на примерах, как применяется изложенный метод к вычисле-
вычислению флуктуации различных физических величин.
Начнем с флуктуации температуры, предполагая, что рассматриваемая
макроскопическая подсистема находится в тепловом контакте с термоста-
термостатом. Считая температуру подсистемы функцией независимых переменных
V и ?, напишем
(§) (§) AS.
В силу независимости V и ? имеем: AV-AE = 0, а потому
2/дал2

§ 98 РАССЕЯНИЕ СВЕТА 631
При постоянном объеме производная {дЕ/дТ)у есть теплоемкость подси-
стемы Су • Тогда из формулы (97.17) находим
___ 1 ^-^ kT2
(ДТ> = ^(Л?2)у = —. (97.20)
Вычислим теперь флуктуации энтропии S подсистемы. В качестве неза-
независимых переменных выберем V и S. Рассуждая как в предыдущем приме-
примере, напишем
AV-A8 = 0,
Так как dS/dS = 1/Т, то с учетом (97.17)
(AS2)V =kCv. (97.21)
Если бы за независимые переменные были приняты Р и 1, то получилось
бы
(AS2~)p=kGP. (97.22)
Рассмотрим теперь флуктуации давления Р. Примем за независимые
переменные V ш Т. Тогда
т = ( -~Т7 )
dVJ
AV-AT = O, ч„. ;1 - ,
v /т
или на основании формулы (97.9)
/ЯР\
(97.23)
Приняв за независимые переменные Р и 5, мы получили бы
jT> (97.24)
где 7 = Ср/Су. При этом было использовано термодинамическое соотно™
—; ] / | — ) =7 (см.т. II, § 47).
Вычислим, наконец, флуктуации плотности вещества р в объеме V.
Задача сводится просто к преобразованию формулы (97.9). Прежде всего
заметим, что величина V дР/дУ не зависит от величины объема V. Поэто-
Поэтому в таком выражении V можно заменить удельным объемом вещества v.
Тогда
Так как масса вещества Vр в объеме V остается постоянной, то V Ар +
+ р AV = 0. Следовательно, (АрJ = (тт) (AFJ, а потому
;- (97-25)
Чем меньше объем V, тем больше относительные флуктуации плотности в
нем.

632 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
§ 98. Рассемние света
1. В прозрачной однородной среде бегущая плоская волна
распространяется только в прямом направлении, не испытывая
рассеяния в стороны. (Мы отвлекаемся от дифракции, предпо-
предполагая, что ширина фронта волны достаточно велика, а следова™
тельно, угол дифракционной расходимости мал.) Допустим те-
теперь, что оптическая однородность среды нарушена, например
множеством мельчайших частиц постороннего вещества, беспо-
беспорядочно распределенных по объему среды. Примерами могут
служить пыльный воздух, туман, дым, эмульсии и суспензии с
взвешенными в них посторонними частицами. Тогда показатель
преломления будет меняться в пространстве весьма нерегуляр-
нерегулярно, но среднее значение его во всяком малом объеме, содержа-
содержащем еще очень много макроскопических неоднородностей, будет
оставаться одним и тем же во всей среде. Такую среду называют
оптически мутной. В оптически мутных средах свет распро™
страняется не только в прямом направлении, но и рассеивается
в стороны. Рассеяние света в мутных средах на частицах посто-
постороннего вещества экспериментально впервые исследовал Тин-
даль A820-1893) в 1869 г. Поэтому это явление получило назва-
название тиндалевского рассеяния пли эффекта Тиндаля. Его теория
была дана Рэлеем.
2. В неоднородной неподвижной изотропной среде распро-
распространение света описывается уравнениями Максвелла
rotE = -i^p,
с at
где диэлектрическая проницаемость е является функцией коор™
динат. Выделим из нее постоянную часть ?q, полагая е = е® + 8е.
В проблеме рассеяния света интерес представляет случай, когда
бе мало по сравнению с ?q, но пока мы не будем вводить этого
ограничения. Более того, постоянное слагаемое во в принципе
можно было бы выбрать произвольно. От этого, если вычисле-
вычисления производить точно, окончательный результат зависеть не
может. Однако удобно и естественно понимать под во диэлек-
диэлектрическую проницаемость среды, из которой удалены частицы
постороннего вещества.
Представим электромагнитное поле в виде Е = Eq + Е;, Н =
= Н + Н;, где Ео, Но удовлетворяют уравнениям Максвелла в
однородной среде
divH0 = 0.

§ 98 РАССЕЯНИЕ СВЕТА 633
В задаче о рассеянии света это есть падающая волна^ которая
распространялась бы в среде, если бы в ней не было оптических
неоднородностей, а Е;, Н; — поле рассеянного света. Вычитая
предыдущие уравнения из (98.1), получим
гоШ' - ^ = ^, div(eoE') = -div(feE),
С 01 С 01
С
= 0, divH' = 0.
rotE^
с dt
Таким образом, для поля Е;, Н; получились такие же уравне-
ния Максвелла, как в однородной среде с диэлектрической про-
проницаемостью в®. Только первые два из этих уравнений содержат
правые части, которые можно рассматривать как дополнитель-
дополнительные источники электромагнитных волн. Если ввести обозначе-
обозначение
5Р = |1Е, (98.3)
то эти два уравнения перейдут в
rot Н; - ^^ = — ? JP, div (б0Е;) = -47rdiv (SP). (98.4)
С 0ь С 0~Ь
Из них видно, что в среде появляется дополнительная поля-
поляризация ()Р, определяемая выражением (98.3), так что каждый
малый элемент объема среды SV получает дополнительный ди™
польный момент SV-SP. Меняясь во времени, он излучает элек-
электромагнитные волны как колеблющийся диполь Герца. Это и
есть свет, рассеянный элементом объема 5V.
3. Допустим теперь, что оптическая неоднородность созда-
создается одинаковыми шариками радиуса а, беспорядочно распреде™
ленными по объему, занятому средой. Пусть среднее расстояние
между шариками велико по сравнению с а, а сами шарики ма-
малы по сравнению с длиной волны. Тогда при вычислении элек-
электрического поля Е внутри шарика можно считать внешнее поле
Eg световой волны однородным. Как показано в электростатике
(см. т. III, § 16), поле Е также однородно и определяется выра-
выражением
Е = 77ГТ?Ео = 7^ГЕо' (98-5)
где 6 — диэлектрическая проницаемость шарика, a eq — окру™
жающей среды. Дополнительная поляризация, согласно форму-
формуле (98.3), будет отлична от нуля только внутри шариков, где она
равна
^р = ?^?оЕ=в-во 3?0
4тг 4тг е + 2ео
а дополнительный дипольный момент шарика
Р = -^- (е - ео)а3Во. (98.6)

634 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Предположим сначала, что падающая волна поляризована
линейно. Тогда векторы р и Е все время будут параллельны
одному и тому же неизменному направлению. Электрическое
поле диполя р на больших расстояниях г от него (в волновой
зоне) определяется выражением
!-, sin#r..n ш2 sinter I /AO rj\
^i = -&r\p\t-r/v = —^r-\p\t-r/v, (98.7)
где v = с/у/е = с/п — скорость света в рассматриваемой среде,
а $ — угол между осью диполя р и направлением рассеянно-
рассеянного излучения (см. т. III, § 141). Рассеянный свет поляризован
линейно^ причем электрический вектор лежит в плоскости, про-
проходящей через ось диполя р и направление излучения. Под ин~
тенсивностью света здесь и в дальнейшем будем понимать
усредненное по времени численное значение вектора Пойнтин-
га. Для интенсивности света, рассеянного одним шариком, элек-
электродинамика дает
. 2 о 4 • 2 о
Т Sin U ~^п Ш Sin 17 ~~о /АО о\
h = - гтР =й гтР (98-8)
2 4жеоУЛг2
(см. т. Ill, § 141). Интенсивность прямой волны равна
" (98.9)
Воспользовавшись выражением (98.6), получим
или
где А — длина волны в вакууме, a V\ = /з^го3 — объем ша-
шарика. Энергия Pi, рассеиваемая шариком в единицу времени
по всем направлениям, найдется интегрированием величины
(98.11) по сфере радиуса г. Взяв в качестве элемента поверх-
поверхности 2тгг2 smi?di?, получим
(^J^10. (98.12)
Допустим теперь, что падающий свет естественный. На-
Направление его распространения примем за ось Z. Пусть рассе-
рассеянный свет наблюдается в направлении О А под углом 6^ к оси Z.
Угол 6^ называется углом рассеяния (рис. 321). Направим ось X
перпендикулярно к О А и OZ. Так как р и Eg коллинеарны, то
вектор р параллелен плоскости XY. Разложим его по осям X и
Y. Интенсивности излучений дипольных моментов рх и р^ най-
найдутся по формуле (98.8), если в ней положить сначала # = тг/2,

§ 98 РАССЕЯНИЕ СВЕТА 635
а затем $ = ~~ — в. Так как падающий свет естественный, то эти
z
излучения некогерентны, так что для нахождения J\ надо сло-
сложить их интенсивности. В результате формула (98.8) перейдет
в
Л = 1 гткРх + pi cos в) = ——-—рг,
2
так как в случае естественного света р^ = рН = 1/2Р2- Следова-
Следовательно, вместо формулы (98.11) получится
Формула (98.12), очевидно, останется без изменения.
Теперь рассеянный свет будет поляризован частично. Полная
линейная поляризация будет наблюдаться только в тех слу~
чаях, когда линия наблюдения О А перпендикулярна к направле-
направлению распространения падающе-
падающего света^ так как в этом случае
дипольный момент р^ излучения
не дает.
Найдем теперь интенсив-
интенсивность / света, рассеиваемого
объемом F, содержащим очень
много шариков. Их среднее
число в этом объеме равно NV,
где N — среднее число шариков
в единице объема. Так как
расстояния между шариками
велики по сравнению с а и они распределены по объему V
беспорядочно, то для нахождения / надо сложить интенсив-
интенсивности, рассеиваемые отдельными шариками. Предположим,
что расстояние от объема V до точки наблюдения велико по
сравнению с линейными размерами самого объема V. Тогда в
формуле (98.13) все расстояния г можно считать одинаковыми
и написать
{У^^Ч^1 (98Л4)
4. Рассчитаем убывание интенсивности Iq падающего света
из-за рассеяния. Выделим в среде произвольный цилиндр, пло-
площадь поперечного сечения которого равна единице, а образую-
образующие параллельны оси Z. Вырежем из него бесконечно короткий
цилиндрик, ограниченный плоскостями z = const и z + dz =
= const. Через первое основание такого цилиндрика ежесекунд-
ежесекундно вступает энергия /о(^)? а через второе выходит Iq(z + dz).
Разность этих энергий —dl® есть рассеянная энергия V\Ndz.

636 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
Приравнивая оба выражения, получим
dIQ = -jlodz, (98.15)
где в соответствии с формулой (98.12)
?J^ <98Л6>
Таким образом, из-за рассеяния интенсивность падающей волны
убывает экспоненциально:
/0 = const *e~lz. (98.17)
Величина j называется коэффициентом рассеяния.
5. Согласно формуле (98.14), впервые полученной Рэле-
ем, интенсивность рассеянного света обратно пропорциональна
четвертой степени длины волны. Этот результат называется
законом Рэлея. Он справедлив для рассеивающих частиц, ли-
линейные размеры которых малы по сравнению с длиной волны.
Закон Рэлея качественно подтверждается уже ранними ис™
следованиями Тиндаля, который наблюдал, что белый свет при
рассеянии становится синеватым. На основе этих наблюдений
Тиндаль высказал мысль, что синий цвет и поляризация неба
определяются рассеянием солнечного света на мелких частицах
пыли, всегда имеющихся в достаточном количестве в земной ат™
мосфере.
Количественная теория была развита Рэлеем. Если бы рас™
сеяния света не было, то небо было бы совершенно черным. На
этом черном фоне звезды и другие небесные светила выделялись
бы более ярко и контрастно. Именно таким видят небо космо-
космонавты из космических кораблей. При наличии же атмосферы
значительная доля прямого солнечного излучения рассеивается
в стороны. Она тем больше, чем короче длина волны. Поэто™
му рассеянный свет обогащен короткими волнами, чем и объяс-
объясняется синий цвет неба. При восходе и заходе Солнца прямой
солнечный свет проходит через большую толщу атмосферы, и
при этом большая часть коротковолнового излучения теряется
на рассеяние. Из прямого света до поверхности Земли доходят
преимущественно красные лучи. Вот почему при восходе и за™
ходе Солнце красное. Так же объясняется красный цвет зари.
По мере поднятия над земной поверхностью содержание пы-
пыли и других посторонних частиц в воздухе уменьшается. Каза-
Казалось бы, что при этом насыщенность рассеянного света синими
лучами должна так лее уменьшаться. Однако наблюдения в вы-
высокогорных обсерваториях показали, что дело обстоит как раз
наоборот. Чем чище воздух, чем меньше в нем содержится по-
посторонних частиц, тем насыщеннее излучение неба синими лу-
лучами и тем полнее его поляризация. На этом основании Рэлей

§ 98 РАССЕЯНИЕ СВЕТА 637
пришел к заключению, подтвержденному всеми последующи-
последующими экспериментальными и теоретическими исследованиями, что
здесь рассеяние вызывается не посторонними частицами, а са-
самими молекулами воздуха. Такое рассеяние света называется
рэлеевским или молекулярным рассеянием. Однако физическая
природа молекулярного рассеяния была понята только в 1908 г.
М. Омолуховским A872-1917). Молекулярное рассеяние вызыва-
вызывается тепловыми флуктуациями показателя преломления, ко-
которые и делают среду оптически мутной. Теория рассеяния све-
света в жидкостях и газах, построенная на этой основе, была созда-
создана в 1910 г. Эйнштейном. Она применима в тех случаях, когда
длина световой волны настолько велика, что среду молено раз-
разбить на объемчики, малые по сравнению с кубом длины волны,
каждый из которых содержит, однако, еще очень много молекул.
К таким объемчикам еще можно применять макроскопические
уравнения Максвелла, не учитывая явно молекулярную струк-
структуру вещества. Флуктуации показателя преломления в таких
объемчиках и играют роль макроскопических неоднородностей^
вызывающих рассеяние света, подобно шарикам в предыдущем
рассмотрении.
Поле Е;, Н; рассеянного излучения в общем случае можно
рассчитать с помощью уравнений (98.2). В них теперь во озна-
означает среднее значение диэлектрической проницаемости среды, а
бе — ее флуктуацию. Решение можно получить методом после-
последовательных приближений. В нулевом приближении в уравне-
уравнениях (98.2) пренебрегаем неоднородностями среды, т.е. правыми
частями. Тогда рассеянного излучения Е;, Н; не будет — оста-
останется только падающая волна Eg, Но. Для нахождения первого
приближения в правых частях (98.2) заменяем поле Е его зна-
значением Ео в нулевом приближении. Решая полученные уравне-
уравнения, находим Е; и Н;, а затем Е и Н в первом приближении.
Используя полученное решение, уточняем правые части уравне-
уравнений (98.2) и находим Е и Н во втором приближении, и т.д.
Практически достаточно ограничиться первым приближени-
приближением, полагая SP = #?Ео/Dтг). Разделим среду на элементарные
объемчики SiV, малые по сравнению с кубом длины волны, но
содержащие еще очень много молекул. Дополнительный диполь-
ный момент объемчика <^V, обусловленный флуктуациями ди-
диэлектрической проницаемости, будет
Р = —1^Ео'
Это выражение отличается от (98.6) только коэффициентом при
Eq. Поэтому, предполагая падающий свет естественным, для
средней интенсивности света, рассеиваемого объемчиком 8iV,

638 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
можно сразу написать
2
к = ^^§г^ШУJEгбУ, (98.18)
Соответствующее электрическое поле будет пропорционально
SiV и 6ге.
6. Рассмотрим сначала молекулярное рассеяние в идеальных
газах. В этом случае
где /3 — поляризуемость молекулы, a Ni — число молекул в
объемчике SiV. Поскольку объемчик SiV фиксирован в про-
пространстве, т.е. не флуктуирует, из последней формулы получаем
SiVSei = AnfSSNi^ т.е. рассеяние света вызывается флуктуация-
ми числа молекул в объемчиках SiV. Согласно (97.7),
= Ni = NSiV, где N — число молекул в единице объема. Таким
образом,
Для газов п — 1 = 4?riV/3, причем показатель преломления п
близок к единице. Поэтому вместо этой формулы можно взять
п — 1 = 2тгN/3. Исключив /3, найдем
Чтобы найти интенсивность / света, рассеянного конечным
объемом F, заметим, что различные объемчики SiV ж SjV рас™
сеивают некогерентно. Действительно, возьмем все объемчики
SiV одинаковыми по величине. Тогда электрические поля рассе-
рассеянных ими волн представятся в виде Е^ = A SNi, где коэффици™
ент А одинаков для всех объемчиков. Полное поле рассеянной
волны будет J^ Е^, а интенсивность
Но в идеальных газах числа молекул в различных объемчиках
флуктуируют независимо. Поэтому двойная сумма в предыду-
предыдущей формуле обращается в нуль, что и доказывает наше утвер-
утверждение. Значит, для нахождения / надо /^ умножить на число
элементарных объемчиков в объеме V, т.е. на V/SiV. Это дает
Т_ 2л2{п1JУ1 + соБ2в
Если свет линейно поляризован, то множитель A + cos2 в)/2 еле™
дует заменить на sin2 $.

§ 98 РАССЕЯНИЕ СВЕТА 639
Формула (98.19) была впервые получена Рэлеем в 1899 г., но
недостаточно обоснована им. Рэлей вывел ее в предположении,
что рассеяние происходит на отдельных молекулах газа, кото-
которые ведут себя совершенно аналогично независимым шарикам,
о которых шла речь при выводе формулы (98.14). Результирую-
Результирующую интенсивность рассеянного света он вычислял, складывая
интенсивности рассеянных волн от отдельных молекул, как ес-
если бы эти волны были некогерентны. Он полагал, что некоге-
некогерентность возникает из-за теплового движения молекул, но не
учитывал явно флуктуации числа частиц в рассеивающих объ-
емчиках.
Л.И. Мандельштам в 1907 г. указал, что если бы все (оди-
(одинаковые) малые пространственно неподвижные объемчики SiV
содержали одинаковое число молекул, то излучаемые ими вто-
вторичные волны были бы когерентны, независимо от того, дви-
движутся в них молекулы или нет. При сложении напряженно-
стей полей таких волн происходило бы интерференционное га-
гашение их во всех направлениях, за исключением направления
падающей волны.
Полного гашения на самом деле не будет, так как (на что
в 1908 г. указал Смолуховский) числа молекул в элементар-
элементарных объемчиках испытывают флуктуации. Из-за таких флукту-
флуктуации излучения объемчиков можно разложить на когерентную
и некогерентную части. Когерентная часть влияет на падаю-
падающую волну, изменяя ее фазовую скорость (см. § 68). Некогерент-
Некогерентные излучения появляются из-за флуктуации числа частиц. С
ними и связано рассеяние света. Только благодаря случайному
соотношению (97.7) окончательный результат (98.19) в случае
идеальных газов получается таким же, как если бы молекулы
рассеивали свет некогерентно.
7. Формула (98.19) хорошо согласуется с опытом во всех слу-
случаях, когда молекулы газа обладают сферической симметрией,
т.е. изотропны. Таковы, например, молекулы инертных газов.
Первое количественное подтверждение эта формула получила
при исследовании рассеяния солнечного света в земной атмо-
атмосфере (синевы неба). Измерив коэффициент рассеяния, можно
с помощью формулы (98.19) вычислить число Лошмидта N', т.е.
число молекул воздуха в единице объема. Полученное таким пу-
путем значение N прекрасно согласуется со значениями этого чис-
числа, определенными другими методами.
Если молекулы газа анизотропны, например СО2, то наблю-
наблюдаются отступления от изложенной теории. Прежде всего, если
падающий свет поляризован линейно, то рассеянный свет поля-
поляризован только частично, а не полностью, как требует эта тео-
теория. Такая деполяризация рассеянного света вызывается имен-
именно анизотропией молекул. Пусть электрический вектор Eq па-

640 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
дающей волны параллелен оси X. Если бы молекула была изо™
тропна, то ее индуцированный дипольный момент р = /3Eq имел
бы то лее направление. Свет, рассеянный молекулой, получился
бы поляризованным линейно, с плоскостью колебаний, проходя-
проходящей через ось диполя р и линию наблюдения. Но если молекула
анизотропна, то параллельности между р и Е, вообще говоря,
уже не будет. Появятся составляющие вектора р вдоль осей Y
и Z. А так как при тепловом движении ориентация молекулы
в пространстве непрерывно и беспорядочно меняется, то поля™
ризуемости молекулы вдоль координатных осей X, У, Z будут
также флуктуировать. Составляющие р^ и pz дают рассеянные
волны, поляризация которых отлична от поляризации излуче™
ния, даваемого составляющей рх. Это и приводит к деполяри-
деполяризации рассеянного света.
Флуктуации в ориентации анизотропных молекул вызывают
не только деполяризацию, но и влияют на интенсивность рас-
рассеянного света. Однако в такие детали теории мы входить не
можем.
8. Перейдем теперь к молекулярному рассеянию в неидеаль-
неидеальных газах и жидкостях, когда они находятся в состоянии, не
очень близком к критической точке. Исходной будет формула
(98.18). Диэлектрическая проницаемость е является функцией
плотности р и температуры Т среды. От температуры она зави™
сит слабо. Этой зависимостью можно пренебречь. Тогда
S — de S
dp г '
где Sip — флуктуация плотности в объеме SiV. Полагая в фор-
формуле (97.25) V = SiV, можем написать
Следовательно, формула (98.18) переходит в
fde\2 kT
Предположим теперь, что рассеивающий объем V не мал. В
газах и жидкостях вдали от критической точки линейные раз-
размеры элементарных объемчиков SiV можно взять малыми по
сравнению с А, но большими по сравнению с радиусом действия
молекулярных сил (порядка 10 см). В таком случае различные
элементарные объемчики будут рассеивать свет некогерентно.
Для нахождения результирующей интенсивности света, рассеи-
рассеиваемого всем объемом V, надо Ц умножить на число этих объ-
объемчиков, т.е. на V/SiV. (Мы берем объемчики SiV одинаковой
величины, что, очевидно, несущественно и не может влиять на

§ 98 РАССЕЯНИЕ СВЕТА 641
окончательный результат.) Таким путем получаем
т 7г2 1 + cos2 вт/т (^de\2 kT (QQ 9п\
1У1ЛР (9820)
(-vdP/dv)T- (98-20)
Эта формула была выведена Эйнштейном в 1910 г. Формула
Рэлея (98.19) содержится в ней как частный случай.
Флуктуации плотности становятся очень большими при при-
приближении к критической точке рассматриваемого вещества,
так как при этом производная dP/dv стремится к нулю. Этим
объясняется так называемая критическая опалесценция^ т.е.
очень сильное рассеяние света в окрестности критической точки.
Явление это было известно задолго до создания Смолуховским
и Эйнштейном теории флуктуации, но его причина оставалась
неясной вплоть до появления работ этих ученых. В самой кри-
критической точке формула Эйнштейна (98.20) дает для интенсив-
интенсивности рассеянного света бесконечное значение. Отсюда следует,
что в окрестности критической точки эта формула непримени™
ма. Причина заключается в том, что флуктуации плотности в
малых объемчиках SiV в окрестности критической точки уже
нельзя считать статистически независимыми. Орнштейн и
Цернике обобщили формулу Эйнштейна на случай рассеяния
света вблизи критической точки. Так как здесь линейные разме-
размеры неоднородностей, на которых рассеивается свет, уже не малы
по сравнению с А, то интенсивность рассеянного света не пропор-
пропорциональна четвертой степени частоты, а возрастает с частотой
более медленно. Кроме того, рассеяние перестает быть симмет-
симметричным относительно плоскости, перпендикулярной к падаю-
падающим лучам: вперед рассеивается больше света, чем назад. На
всех этих вопросах мы не можем останавливаться.
Формула Эйнштейна учитывает не все причины рассеяния
света. В частности, она не учитывает флуктуации анизотро-
анизотропии в случае жидкостей, состоящих из анизотропных молекул.
Учет этого обстоятельства увеличивает интенсивность рассеян-
рассеянного света и объясняет его деполяризацию. В случае жидкостей
соответствующие теоретические расчеты, конечно, не столь на-
надежны, а их согласие с опытом не такое хорошее, как в случае
газов.
9. Молекулярное рассеяние света может вызываться не толь-
только флуктуациями плотности, но и другими причинами. Инте-
ресным примером может служить рассеяние света в раство-
растворах. В обычных условиях молекулы растворенного вещества на-
настолько равномерно перемешаны с молекулами растворителя,
что весь раствор в оптическом отношении представляет собой
почти столь лее однородную среду, что и чистый растворитель.
Флуктуации концентрации растворенного вещества в раство-
растворителе могут быть причиной рассеяния света. В обычных уело-

642 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
виях флуктуации концентрации и обусловленное ими рассея-
ние света малы. Однако существует много комбинаций веществ,
которые ниже определенной температуры Тк, называемой кри-
критической температурой смешения, растворяются друг в дру-
друге только частично, а выше этой температуры смешиваются в
любых пропорциях (см. т. II, § 123). При критической темпе™
ратуре смешения две жидкости полностью смешиваются друг с
другом только при вполне определенных весовых отношениях.
Такова, например, смесь 20 частей по весу сероуглерода и 80 ча-
стей метилового спирта при температуре Тк = 40 °С. При крити-
критической температуре смешения надо ожидать особенно больших
флуктуации концентрации, подобно тому, что имеет место для
флуктуации плотности вблизи критической точки. Действитель-
Действительно, при критической температуре смешения наблюдается очень
сильное рассеяние света, аналогичное критической опалесцен-
ции.
10. Вторым примером может служить рассеяние света на
границе раздела двух несмешивающихся жидкостей или на сво-
свободной поверхности жидкости. Из-за теплового движения по-
поверхность жидкости не бывает абсолютно гладкой. Она всегда
неровная. На этих неровностях свет претерпевает дифракцию,
т.е. происходит поверхностное молекулярное рассеяние. Если
высота неровностей мала по сравнению с длиной волны, как это
имеет место в обычных условиях, то амплитуда рассеянного све-
света обратно пропорциональна первой, а его интенсивность вто~
рой степени длины волны. Поверхностное натяжение сглажива-
сглаживает неровности, появившиеся из-за тепловых флуктуации. Поэто-
Поэтому молекулярное поверхностное рассеяние света наиболее интен-
интенсивно на границе двух несмешивающихся жидкостей с близким
коэффициентом поверхностного натяжения.
11. Молекулярное рассеяние света в кристаллах впервые бы-
было надежно установлено Г.С. Ландсбергом в 1926-1927 гг. Труд-
Трудность состояла не только в том, что интенсивность рассеянного
света в хороших кристаллах по предварительной оценке должна
составлять всего около 10~8 от интенсивности падающего света.
В то время вообще было не ясно, существуют ли кристаллы, в
которых основную долю рассеянного света составляет свет мо-
молекулярного рассеяния, а не паразитный свет, возникающий при
рассеянии на различных вкраплениях, микротрещинах и других
дефектах кристалла. Метод, с помощью которого удалось отде-
отделить одно рассеяние от другого, состоял в исследовании темпе-
температурной зависимости интенсивности рассеянного света. Ин-
Интенсивность паразитно рассеянного света не должна зависеть
от температуры, а молекулярно рассеянного — возрастать с
температурой. Г.С. Ландсберг нашел, что в лучших кристал-
кристаллах кварца только 25 % рассеянного света не зависит от темпе-

§ 99 ЯВЛЕНИЕ МАНДЕЛЬШТАМА-БРИЛЛЮЭНА 643
ратуры и, следовательно, вызвано посторонними включениями,
а остальные 75 % зависят от температуры линейно, что и указы-
указывает на их молекулярное происхождение.
§ 99. Явление Мандельштама^Бриллюэна
1. Как показано в предыдущем параграфе, электромагнит™
ное поле в оптически неоднородной среде с диэлектрической
проницаемостью е = ?q + бе может быть представлено в виде
Е = Ео + Е;, Н = Но + Н;, где Ео, Но — поле падающей, а
Е;, Н; — рассеянной волн. При слабой неоднородности можно
ограничиться линейным приближением и написать
rotH'- ^^ = -JUP, div(eoE') = -47rdiv(<5P),
с ot с at
с ot с
rotE'-i^ = 0, divH' = O,
с ot
где
*P = ijE0. (99.2)
Эти уравнения показывают, что среда может рассматриваться
как однородная с диэлектрической проницаемостью sq. Влия™
ние фактически имеющихся неоднородностей эквивалентно на-
наличию в среде дополнительных источников волн: каждый эле-
элемент объема среды dV дает дополнительное излучение как ди-
диполь Герца с дипольным моментом 6Р dV. Это дополнительное
излучение и есть рассеянный свет.
Уравнения (99.1) линейны и однородны как относительно по™
лей Е;, Н;, так и относительно бе. Отсюда следует, что если
представить бе в виде бе = ^ б^е^ то в линейном приближении
рассеянное излучение может быть получено простой суперпози-
суперпозицией полей, рассеянных на неоднородностях Si6. Таким образом,
можно рассмотреть задачу о рассеянии падающей волны снача-
сначала для случая, когда в среде имеется всего одна неоднородность
5iE какого-либо специального вида. При этом неоднородности
6i6j суперпозицией которых представляется fe, можно выбирать
произвольно. Рассмотрим сначала случай, когда бе состоит всего
из одного слагаемого бе = аехр (—гКг), где а и К — постоянные.
Пусть падающая волна плоская и представляется выражениями
Ео = Ae^~kr\ Но = Ве^").
Посмотрим, при каких длинах волн А = 2ж/к и в каких направ-
направлениях будет наблюдаться рассеянное излучение.
Разобьем среду равноотстоящими плоскостями, перпендику-
перпендикулярными к вектору К (рис. 322). Выберем расстояние между

644
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
III
плоскостями равным Л = 2тт/К. Тогда, согласно (99.2), фазы
вторичных источников на этих равноотстоящих плоскостях бу-
будут одинаковы. Если бы неоднородность была только в слое I,
а дальше среда была одно-
однородна, то падающая волна
претерпела бы отражение от
этого слоя и частично про-
прошла бы дальше. При нали-
наличии неоднородности только в
слое II мы получили бы дру-
другую отраженную волну с той
же амплитудой, но иной фа-
фазой. При наличии неоднород-
неоднородности в слое III получилась
бы третья отраженная волна,
Рис. 322 и т.д. В линейном приближе-
приближении поле рассеяния всей сре-
среды равно простой суперпозиции этих отраженных волн. Чтобы
они не гасили, а усиливали друг друга, необходимо выполнение
условия Брэгга-Вульфа: 2Д sin F^/2) = гаА, где в — угол рассе-
рассеяния, т.е. угол между направлениями падающего и рассеянного
излучений, а га — целое число (порядок дифракционного спек-
спектра).
Покажем, что га = 1. Все плоские волны, отраженные
различными слоями, складываясь, дают волну вида Е; =
= А;е^ш*~ ', где волновой вектор к; определяет направление
распространения отраженных волн. С другой стороны, допол-
дополнительная поляризация среды
4тг 4тг
Подставляя эти выражения во второе уравнение (99.1) и срав-
сравнивая показатели, легко получить к; — к = К, откуда
2AsinF>/2) = A. (99.3)
Таким образом, при дифракции волны на синусоидальной неод-
неоднородности диэлектрической проницаемости в линейном при-
приближении получается дифракционный спектр только первого
порядка.
Любую неоднородность в среде можно по теореме Фурье
представить в виде суперпозиции плоских синусоидальных неод-
нородностей различных направлений. Согласно доказанному
выше такие синусоидальные неоднородности рассеивают свет
независимо друг от друга. Но при фиксированном направле-
направлении рассеянного излучения эффективны не все синусоидальные
неоднородности, а только такие, волновой вектор К которых

§ 99 ЯВЛЕНИЕ МАНДЕЛЬШТАМА-БРИЛЛЮЭНА 645
направлен по биссектрисе угла, дополнительного к в до 180°
(рис. 322). Остальные синусоидальные неоднородности для рас-
рассеяния в рассматриваемом направлении не играют роли. Мы ви-
видим, что механизм рассеяния света на неоднородностях диэлек-
диэлектрической проницаемости вполне аналогичен механизму рассея-
рассеяния рентгеновских лучей в кристаллах в той форме, в какой он
был представлен Вульфом и Брэггом (см. § 61).
2. До сих пор мы принимали во внимание изменения функ-
функции 8е в пространстве^ но не учитывали ее изменения во вре-
времени. Учет последнего обстоятельства приводит к новому явле-
явлению в рассеянии света. Считая, как и в предыдущем парагра-
параграфе, е функцией только плотности р, напишем в линейном при-
приближении Ае = (de/dp)Ap. Всякая неоднородность плотности,
возникшая в среде, является источником звуковых волн. Разло-
Разложим Ар в интеграл или ряд Фурье и возьмем в этом разложении
только те звуковые волны, которые существенны для рассеяния
волн в рассматриваемом направлении. Их волновой вектор К
был определен выше. Этому значению К соответствует опреде-
определенная звуковая частота О и два направления распространения
звуковой волны: вдоль К и против К. Неоднородность fe, вызы-
вызывающая рассеяние света в рассматриваемом направлении, пред-
представится суммой де = 8е\ +8б21 где 8е\ и 8в2 имеют вид плоских
звуковых волн:
S?l = а!е«ш-Кг> и 8е2 =
Им соответствуют векторы дополнительной поляризации среды:
АР, - ^? XF,
gp = O2Aei[(
4тг
Таким образом, источники рассеянного излучения, а значит
и само рассеянное излучение, будут меняться во времени с ча-
частотами ш + Оио)-0 (модуляция световой волны акустиче-
акустической волной). В спектре рассеянного излучения должен наблю-
наблюдаться дублет с теми же частотами. Это явление называется
тонкой структурой линий рэлеевского рассеяния или рассеяни-
рассеянием Мандельштама-Бриллюэна. Смещение частоты равно ft =
= Kv = Btt/A)vj где v — скорость звука, а Л — длина звуковой
волны. На основании (99.3)
И = —г- sin - = 2шп- sin -, (99.4)
л 2 с Z
где с — скорость света в вакууме, ап~ показатель преломления
среды.
Дублет Манделынтама-Бриллюэна молено трактовать как
доплеровское изменение частоты света при отражении от аку-

646 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
стической волны. Когда акустическая волна распространяется
навстречу световой, происходит увеличение частоты света, в
противоположном случае — уменьшение. Доплеровское измене-
изменение частоты определяется формулой
О _ 2ц sin 0/2
ш с/п
откуда и получается формула (99.4).
Представление о тепловом движении как о звуковых волнах
всевозможных частот и направлений распространения было вве-
введено Дебаем A884—1966) в его теории теплоемкости твердых
тел. К ним Дебай применял методы статистической физики.
Это — те же волны, которые вызывают рассеяние света и ду-
дублет Мандельштама-Бриллюэна.
3. Тонкая структура линий рэлеевского рассеяния была
предсказана независимо друг от друга Л.И. Мандельштамом и
Л. Бриллюэном. По свидетельству Г.С. Ландсберга, Л.И. Ман-
Мандельштам выполнил свою работу еще в 1918 г., хотя краткая
заметка о ней появилась значительно позже, в 1926 г., когда
часть найденных Д.И. Мандельштамом результатов была уже
опубликована Бриллюэном A922 г.). Мандельштам и Ландсберг
пытались на опыте обнаружить предсказанное явление при рас™
сеянии света в кварце. Качественно им удалось констатировать
существование явления. Однако недостаточная разрешающая
способность их спектральной аппаратуры не позволяла иссле-
исследовать его количественно. Кроме того, эти опыты привели их к
открытию комбинационного рассеяния света (см. § 100). Есте-
Естественно, что их внимание переключилось на исследование этого
более важного явления. По их предложению исследованием тон-
тонкой структуры рэлеевского рассеяния занялся Е.Ф. Гросс A897—
1972) в Ленинграде.
Гросс обнаружил явление при рассеянии света в эюидко-
стях1). Однако оказалось, что в жидкостях, наряду с двумя
смещенными компонентами, наблюдается также и несмещен-
несмещенная компонента. Происхождение несмещенной компоненты бы-
было объяснено Ландау A908-1968) и Плачеком A905-1955).
х) Это было неожиданно, так как, согласно гидродинамической теории,
поглощение звука в жидкостях пропорционально квадрату частоты ш. Ес-
Если бы гидродинамическая теория была верна без ограничений, то звуковые
волны оптических частот в жидкостях распространяться не могли бы. Об™
наружение тонкой структуры в жидкостях послужило поводом Л.И. Ман-
Мандельштаму и М.А. Леонтовичу (р. 1903) к разработке релаксационной мо-
молекулярной теории вязкости жидкостей и основанной на ней теории погло-
поглощения звука.

§ 99 ЯВЛЕНИЕ МАНДЕЛЬШТАМА-БРИЛЛЮЭНА 647
Рассматривая удельный объем жидкости V как функцию
давления и энтропии, можно написать
SV = (dV/dP)s SP + (dV/dS)P SS. (99.5)
Отсюда видно, что существует два вида флуктуации удельно-
удельного объема: одни вызваны флуктуациями давления при посто-
постоянной энтропии, другие — флуктуациями энтропии при по™
стоянном давлении. Флуктуации первого типа распространяют-
распространяются в виде акустических волн и ведут к появлению смещенных
компонент. Флуктуационные неоднородности второго типа вы-
выравниваются посредством теплопроводности, а следовательно,
распространяются значительно более медленно, — они и ведут
к появлению в рассеянном свете несмещенной компоненты.
Для количественного исследования заметим, что процессы
рассеяния света на флуктуациях давления и энтропии некоге-
некогерентны. Поэтому интегральные интенсивности несмещенной 1Ш
и смещенных 1и_$ш, 1ш+$ш компонент связаны соотношением
1Ш
1Ш-6ш + Iuj+Suj {dV/dP){EP^ \dsjp \dTjp \dV
ds\
j
где использованы выражения (97.22) и (97.24), а также фор-
формула ср = T(ds/dT)p1 причем малой буквой s обозначена
удельная энтропия. Так как дифференциал удельной энталь-
энтальпии di = Т ds + V dP — полный дифференциал, то (dT/dP)s =
= (dV/ds)p. Поэтому
dPJs \dVJs \дз)р \дт)Р ~ \dV
или, на основании тождества (дТ/dV)s(dV/ds)T(ds/дТ)у = — 1,
ds\ fdT\ _ (дУ/дТ)Р(дз/дУ)т
)
дт)р \dV)T \ds)y^ {ds/dT)v
Рассматривая энтропию s как функцию Ти7, получим
dTjy \дУ)т\дТ)р'
Окончательно:
1с _ {ds/dT)P - {ds/dT)y _ cP^c
(99.6)
Iuj^Sw + 1ш+5ш (ds/dT)v cv
Эта формула была получена Ландау и Плачеком.
В аморфных твердых телах звуковые волны могут быть про-
продольными и поперечными. Они распространяются с различны-
различными скоростями. Поэтому в рассеянном свете спектральная линия
должна расщепляться на пять компонент: одну несмещенную
и две пары смещенных компонент, из которых одна пара по-
получается от рассеяния на продольных акустических волнах, а
другая — на поперечных.

648 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
В.В. Владимирский (р. 1915) указал, что в кристаллах в об-
щем случае спектральная линия неполяризованного света долж-
должна расщепляться на 25 компонент: одну несмещенную и 24 сме-
смещенные. Дело в том, что в кристалле в каждом направлении мо™
гут распространяться одна продольная акустическая волна и две
поперечные. В том же направлении могут распространяться две
световые волны, поляризованные во взаимно перпендикулярных
плоскостях. Каждая из этих световых волн в свою очередь рас-
расщепляется на две волны при отражении от акустических волн
соответствующих направлений распространения. Это и приво-
приводит к появлению в рассеянном свете 24 смещенных компонент.
Однако из-за слабой анизотропии всех исследованных кристал-
кристаллов эти 24 компоненты обычно группируются в шесть групп по
четыре линии в каждой и не разрешаются спектральными при-
приборами. На опыте наблюдаются шесть смещенных компонент.
4. С изобретением лазеров стала возможной генерация мощ-
мощных (так называемых гигантских) световых импульсов, оказы-
оказывающих существенное воздействие на среду, в которой распро-
распространяется свет. В переменном электрическом поле Е возникает
электрострикционное давление
d?> (99.7)
(см. т. III, § 32). Величина pde/dp порядка единицы. В слабых
световых полях, с которыми имеет дело линейная оптика, дав-
давление V ничтожно и его влиянием на среду можно полностью
пренебречь. Но в световом поле гигантского лазерного импуль-
импульса это давление может достигать сотни тысяч атмосфер. Тогда
световые и акустические волны в среде надо рассматривать сов-
совместно. Они описываются сложной системой взаимосвязанных
нелинейных уравнений электродинамики и акустики. Это при-
приводит к ряду нелинейных оптических явлений. Одним из них
является вынужденное рассеяние Мандельштама-Бриллюэна.
Хотя нелинейные оптические явления будут разбираться в гла™
ве XI, возникновение вынужденного рассеяния Мандельштама^
Бриллюэна удобнее разобрать уже здесь.
Пусть Ео = A0cos(cdt — кг), Ei = Ai cos [(ш + u)t — k'r],
E2 = A2 cos [(и) ~~ u)t ~~ k'r], E3 = A3 cos [out ~~ k'r] — напряжен-
напряженности электрического поля падающей и трех рассеянных волн
Мандельштама^Бриллюэна. Последние три волны возникают
при рассеянии на тепловых флуктуациях. Интенсивности их
сначала малы, но в дальнейшем могут усилиться за счет взаи-
взаимодействия с падающей волной. Электрострикционное давление
V определяется квадратом суммы всех полей, т.е. (Ео + Е]_ +
+ Е2 + ЕзJ. При возведении в квадрат представим по известным
формулам тригонометрии квадраты и произведения косинусов в

§ 100 КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА 649
виде сумм постоянных членов и косинусов суммарных и разност-
разностных аргументов. Постоянные члены для возбуждения звуковых
волн не играют роли. Не имеют значения и члены с косинусами
от суммарных аргументов. Это — высокочастотные члены,
меняющиеся во времени с оптическими частотами, а звуковые
волны быстро затухают с увеличением частоты. Возбуждение
звуковых волн связано только с низкочастотными членами^ со-
содержащими косинусы разностных аргументов. Выпишем все эти
члены, опуская при этом числовые коэффициенты и принимая
во внимание соотношение К = к; — к (см. рис. 322). Получим
AqAi cos (Ш — Кг), А0Л2 cos (Ot + Кг), А0А3 cos Кг,
Из этих членов имеет значение только первый. Он пред-
представляет волну, распространяющуюся в том же направлении и
с той же фазой, что и первичная звуковая волна, возникшая
из-за тепловых флуктуации. Поэтому будет происходить пара-
метрическое усиление этой акустической волны и всех световых
волн, рассеянных на ней. Такой процесс усиления будет про-
продолжаться до тех пор, пока интенсивность рассеянного света не
станет сравнимой с интенсивностью падающего. Это действи-
действительно и наблюдается на опыте. В отличие от некогерентного
рассеяния на тепловых флуктуациях, вынужденное рассеяние
Мандельштама-Бриллюэна когерентно.
ЗАДАЧА
При рассеянии света резонансной линии ртутной лампы (А = 253,65 нм)
в кристалле алмаза под углом в = 90° к направлению падающего пучка бы-
были найдены две пары смещенных компонент с SX = 0,052 нм и<5А = 0,032 нм.
(Речь идет о смещении относительно центральной — несмещенной — компо-
компоненты.) Определить скорости продольной и поперечной акустических волн
в алмазе. Показатель преломления алмаза п = 2,42.
Ответ, v = -—. Гп/п\~г\ ^прод = 18000 м/с; -Ушшереч = 11 000 м/с.
Zn sin \uIzj А
Благодаря большой скорости звука в алмазе тонкую структуру линий
рэлеевского рассеяния удается исследовать даже с помощью призменных
спектрографов.
§ 100. Комбинационное рассемние света
1. При спектральных исследованиях рассеяния света в квар-
кварце и исландском шпате (февраль 1928 г.) Мандельштам и Ланд™
сберг обнаружили, что каждая спектральная линия падающего
света сопровождается появлением системы линий измененной

650
МОЛЕКУЛЯРНАЯ ОПТИКА
ГЛ. VIII
частоты, называемых сателлитами (спутниками). Практиче-
Практически одновременно то же явление было открыто в Индии Ра-
маном A888-1970) и Кришнаном A898-1961) при исследовании
рассеяния света в жидкостях. Изменение длины волны оказа™
лось значительно больше, чем при рассеянии Мандельштама-
Бриллюэна. Это явление называется комбинационным рассея-
нием света или эффектом Рамана (который раньше послал в
печать сообщение о своем открытии). Приведем основные за-
законы комбинационного рассеяния, установленные эксперимент
тально.
1) Частоты сателлитов отличаются от частоты возбуждаю-
возбуждающей их линии на Д^комб' где J ~ номеР сателлита, так что раз-
различным сателлитам соответствуют различные Аа;комб. При пе-
переходе от одной спектральной линии первичного пучка к другой
совокупность значений Аш3ком6 остается одной и той эюе. Она
характерна для рассматриваемого вещества и меняется только
при переходе от одного вещества к другому. Это обстоятельство
используется в спектральном анализе методом комбинационно-
комбинационного рассеяния света. Обычно частоты спектральных линий и их
изменения принято характеризовать числом волн, укладываю-
укладывающихся в 1 см. Их мы будем обозначать через v и Ai/, полагая
v = 1/А. Таблица 11 показывает, насколько хорошо по измерени-
ТаблицаП
Частота
основной
ЛИНИИ I/,
см™1
33 692
33 086
31985
31923
29 917
27 388
27 354
27 290
24 705
24 515
23 034
22 994
22 938
Среднее
Бензол
СбНб
А1/Красн
992,9
991,3
992,9
992,3
—
991,2
991,3
991,1
992,2
—
992,9
992,1
992,3
992,0
Хлороформ
СНС13
Ai/KpaCH
—
667,7
667,7
667,3
668,1
666,6
666,8
—
669,2
667,5
667,3
670,8
669,4
668,0
А^фиол
—
—
669,3
669,5
670,5
—
669,9
669,8
669,5
—
—
—
667,1
669,4
Четыреххлористь й
углерод ССЦ
Ai/KpaCH
—
459,7
458,3
457,8
458,7
458,4
459,4
459,1
457,9
457,8
—
457,8
459,6
458,5
Az/ф о.
—
—
459,4
460,4
458,8
461,2
461,8
461,8
459,7
—
—
—
457,8
460,2

§ 100 КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА 651
ям Г.С. Ландсберга соблюдается постоянство Аи для различных
длин волн в комбинационном рассеянии света.
2) Каждому сателлиту с частотой ш — Да;комб, смещенной
в красную сторону спектра, соответствует сателлит с частотой
ш + Ао;комб, смещенной в фиолетовую сторону. Первые сателли-
сателлиты называются красными или стоксовыми^ вторые — фиолето-
фиолетовыми или антистоксовыми.
3) Число различных сателлитов (т.е. число значений индек-
индекса j) и их относительная интенсивность при одной и той же тем™
пературе также зависят от рассеивающего вещества. Но интен-
интенсивности фиолетовых сателлитов значительно меньше ин-
тенсивностей соответствующих им красных сателлитов и
проявляют общую тенденцию к ослаблению по мере увеличе-
увеличения А^комб-
4) Постоянные Аа;комб, характерные для рассматриваемого
вещества^ совпадают с собственными частотами Оинфр ин-
инфракрасных колебаний того же вещества^ хотя не всем извест-
ным Оинфр находятся соответствующие Аа;комб, и наоборот. Кро-
Кроме того, нередко интенсивной линии комбинационного рассея-
рассеяния соответствует слабая линия инфракрасного поглощения и
наоборот.
5) Линии комбинационного рассеяния света более или менее
поляризованы. Степень поляризации различных сателлитов од-
одной и той же линии не одинакова и не находится в прямой свя-
связи с поляризацией основной линии рассеянного света. Характер
поляризации красных и фиолетовых сателлитов, соответствую-
соответствующих данному значению Ао;комб, всегда одинаков и не зависит
от частоты основной линии.
2. Явление комбинационного рассеяния света было объясне-
объяснено сразу же Мандельштамом и Ландсбергом, когда они открыли
это явление.
В поле световой волны Е электроны внутри молекулы прихо-
приходят в колебания, и молекула приобретает индуцированный ди-
польный момент р = /ЗЕ. С классической точки зрения тензор
поляризуемости молекулы /3 определяется мгновенными поло-
положениями ее атомных ядер. Но сами ядра не находятся в покое,
а совершают беспорядочное тепловое движение. По этой при-
причине поляризуемость /3 не остается постоянной, а меняется во
времени. Ее можно представить наложением гармонических ко-
колебаний, частоты которых определяются колебаниями атомных
ядер, т.е. совпадают с собственными частотами инфракрасных
колебаний молекулы. Возникает модуляция колебаний индуци-
индуцированных дипольных моментов р.
Если внешнее электрическое поле Е меняется во времени гар-
гармонически с частотой w5 то в колебаниях дипольного момента р
появятся комбинационные частоты а; =Ь Оинфр. Такие же частоты

652 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
появятся и в излучении этих дипольных моментов, т.е. в рассеян™
ном свете. Таково с классической точки зрения происхождение
комбинационного рассеяния.
Изложенные соображения можно облечь в математическую
форму. Если число ядер в молекуле равно s, то они обладают
3s степенями свободы. Из них три степени свободы посту па-
тельные^ а три вращательные. Остальные / = 3s — 6 степеней
свободы приходятся на внутреннее движение ядер молекулы.
Для описания внутреннего движения ядер требуется / коорди-
координат gi, #25 •••? Qj- Выбор координат произволен. Удобнее всего
взять нормальные обобщенные координаты.
В положении равновесия ядер все координаты равны нулю.
При малых отклонениях из положений равновесия каждая ко-
координата qm при тепловом движении совершает свободное гар-
гармоническое колебание qm = am cos (OTOt + 8т) с инфракрасной
частотой Ош и хаотически меняющейся фазой 6т. В силу мало-
малости колебаний тензор /3 можно разложить в ряд и ограничиться
первыми степенями по q. Считая для простоты /3 скаляром, по-
получим
или после подстановки значении
¦т COS (ftmt +
2 2^ Ugm/ ttw6
Падающую волну запишем в комплексной форме Е =
Тогда
р = A)Eoe
iart+
V(Mn Pi[(w+nm)t+tfm] , Ео v^ / dp \ A[(u>-nm)t-6m]
2 ^^ \oqmj 2 ^^ \dqmj
Отсюда видно, что в рассеянном излучении появляется свет не
только с исходной частотой а;, но и с комбинированными ча-
частотами ш =Ь Ош. Ясно, что волны, рассеиваемые отдельными
молекулами, некогерентны^ так как при тепловом возбуждении
колебаний ядер фазы 6т меняются нерегулярно при переходе от
одной молекулы к другой и от одного колебания к другому.
3. Классическая теория комбинационного рассеяния, как и
всякого явления, связанного с излучением и поглощением све-
света, конечно, недостаточна. Успехи этой теории связаны с от-
относительно большими массами атомных ядер, благодаря чему
многие особенности их колебаний правильно передаются урав-
уравнениями классической механики. Однако классическая теория

§ 100 КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА 653
объясняет не все закономерности комбинационного рассеяния
света. В частности, она не может объяснить соотношения меж-
между интенсивностями соответственных красных и фиолетовых са-
сателлитов. По классической теории эти интенсивности должны
быть практически одинаковы. Опыт же показывает, что интен-
интенсивность красных сателлитов всегда больше интенсивности
соответственных фиолетовых сателлитов.
Квантовая теория дает естественное объяснение этой законо-
закономерности. Согласно квантовой механике энергетические уровни
молекулы образуют дискретный ряд Е\, <?25 <?з5 ••• Рассеяние
фотона на молекуле аналогично процессу столкновения его с
молекулой, к которому применим закон сохранения энергии. В
таком процессе фотон может либо передать часть своей энергии
молекуле, либо, наоборот, получить энергию от возбужденной
молекулы. Согласно соотношению <?*фот = ^? изменение энергии
фотона проявляется в изменении его частоты. Пусть фотон с
энергией Нш рассеивается на молекуле с энергией ?п. В резуль-
результате получается рассеянный фотон с энергией /га/, а молекула
переходит на энергетический уровень ?т. По закону сохранения
энергии tvuj + ?п = tvuj1 + ?т, откуда
J =и + Ппт, A00.1)
где
Ппт = (?п-?т)/Ь. (Ю0.2)
Если ?п > ?т1 то частота рассеянного фотона больше, чем
падающего, т.е. в рассеянном свете появляется фиолетовый са-
сателлит. Если же ?п < ?mj то при рассеянии возникает красный
сателлит.
Пусть ?п < ?т. Тогда красный сателлит появится, когда ис-
исходным уровнем является уровень ?П1 а фиолетовый — когда
исходным будет уровень ?т. Для отношения интенсивностей са-
теллитов можно написать /КрДфиол — Nn/Nm, где Nn — число
молекул на уровне ?nj a Nm — на уровне ?т. Согласно формуле
Больцмана, при тепловом равновесии
— = exp I -
а потому
A00.3)
Эта формула вполне объясняет наблюдаемое соотношение ин-
интенсивностей.
4. В мощных импульсах лазерного излучения наблюдает-
наблюдается нелинейное явление, называемое вынужденным комбинаци-
комбинационным рассеянием света. Оно возникает из-за обратного воз-
воздействия световой волны на молекулы среды. В неоднородном

654 МОЛЕКУЛЯРНАЯ ОПТИКА ГЛ. VIII
электрическом поле Е на молекулу с дипольным моментом р
действует сила F = (pV)E. Силы такого рода действуют и
на части молекулы^ так как всякая электрически нейтраль-
нейтральная часть молекулы, состоящая, например, из ядра и электро-
электрона, обладает дипольным моментом. Индуцированные дипольные
моменты р пропорциональны полю Е, так что все эти силы ква-
квадратично зависят от поля. Поле Е слагается из поля падаю-
падающей волны Eg и поля рассеянных волн Е;. Первоначально поле
Е; слабое, так как оно возникает из-за тепловых флуктуации в
среде. Но затем оно может усиливаться из-за взаимодействия с
падающей волной. Среди слагающих сил
[(Eo + E')V](Eo + E')
присутствуют члены с произведением полей Eq и Е;, частоты
которых совпадают с соответствующими частотами инфракрас-
инфракрасных колебаний молекулы. Они вызовут резонансное усиление та™
ких инфракрасных колебаний, что поведет к увеличению интен-
интенсивности соответствующих линий комбинационного рассеяния.
Вынужденные колебания ядер молекулы происходят в фазе с
падающей волной, а потому, в отличие от обычного (теплово-
(теплового) комбинационного рассеяния, вынужденное комбинационное
рассеяние когерентно с падающей волной.

ГЛАВА IX
ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
§ 101. Принцип относительности в ньютоновской и
релятивистской механике
1. Теория относительности — фундаментальная физиче-
екая теория, охватывающая всю физику. Она возникла в нача-
начале XX века в результате преодоления принципиальных трудно-
трудностей, с которыми столкнулась электродинамика и оптика дви™
жущихся тел. Настойчивые и мучительные попытки преодолеть
эти трудности на основе гипотезы мирового эфира окончились
неудачей. Теория относительности отказалась от использования
гипотезы эфира. В ее основе лежат не гипотезы, а принципы или
постулаты^ твердо установленные экспериментально. В этом
сила теории относительности, причина ее успехов. В нашу зада-
задачу не входит подробное изложение истории теории относитель-
относительности и экспериментального обоснования ее постулатов. Мы кос™
немея этих вопросов предельно кратко, чтобы лучше оттенить
принципиальные моменты, глубже уяснить смысл постулатов и
содержание теории относительности.
Творцом теории относительности является Альберт Эйн-
Эйнштейн. Теория относительности была изложена им в 1905 г.
в основополагающей работе «К электродинамике движущихся
тел». Многие результаты этой работы были получены ранее
Лармором A857—1942), Лорентцом и Пуанкаре A854-1912). Од-
Однако и Лармор и Лорентц принципиально стояли на точке зре-
зрения неподвижного эфира, с которым связывалась преимуще-
преимущественная система отсчета. Ближе всего к теории относительно™
сти был Пуанкаре, который еще в 1898 г. дал критику понятия
одновременности пространственно разделенных событий, повто™
ренную в дальнейшем Эйнштейном. Пуанкаре заполнил также
математические пробелы и устранил ошибки, допущенные Л о™
рентцом. Однако принципиально новое и глубокое физическое
понимание всей проблемы и последовательное построение тео-

656 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
рии относительности с единой точки зрения содержится лишь в
упомянутой выше работе Эйнштейна, написанной к тому же без
всякого влияния своих предшественников.
2. Начнем с повторения того, что было сказано в первом томе
о принципе относительности в ньютоновской механике. Основ-
Основной закон ньютоновской механики выражается уравнением
тг = Р, A01.1)
где F — сила, действующая на материальную точку, а г —
радиус-вектор, определяющий положение последней относи-
относительно какой-либо инерциальной системы отсчета. Возьмем две
инерциальные системы отсчета, одну из которых будем обозна-
обозначать через S и называть неподвижной (или нештрихованной),
а другую — через S", называя ее движущейся (или штрихован-
штрихованной). Пусть система S1 движется относительно системы S рав-
равномерно и прямолинейно со скоростью V. Если гиг' — радиусы-
векторы, определяющие положения движущейся материальной
точки относительно этих систем отсчета в момент времени t, то
они связаны между собой преобразованием Галилея
r = r' + Vt. A01.2)
При этом в ньютоновской механике предполагается, что время t
абсолютно, т.е. одинаково во всех системах отсчета. Для просто™
ты отсчет времени ведется с того момента, когда начала коорди-
координат систем S и Sr совмещаются между собой. Это не отражается
на общности рассуждений.
Дважды дифференцируя соотношение A01.2) по времени,
находим формулы преобразования скорости и ускорения:
v = v; + V, a = a;. A01.3)
Таким образом, ускорение инвариантно относительно преобра-
преобразования Галилея, т.е. одинаково в обеих системах отсчета S и S1.
Радиусы-векторы гиг', скорости v и v' не одинаковы. Однако
разности радиусов-векторов^ а также скоростей двух любых
материальных точек одни и те же, поскольку они определя-
определяют относительные положения и скорость одной точки относи-
относительно другой. Сила F в ньютоновской механике зависит толь-
только от разностей радиусов-векторов и скоростей взаимодейству-
взаимодействующих материальных точек. Поэтому она, а с ней и уравнение
Ньютона A01.1) не меняются при преобразовании Галилея. То
же относится и к дифференциальным уравнениям движения си-
систем материальных точек в механике Ньютона. Таким образом,
получается следующий результат:
Уравнения механики Ньютона^ определяющие изменения
состояния движения механических систем^ инвариантны от-
относительно преобразования Галилея.

§ 101 ПРИНЦИП ОТНОСИТЕЛЬНОСТИ 657
Это положение называется принципом относительности
Галилея. Ему можно дать также следующую формулировку:
Законы природы, определяющие изменения состояния дви-
движения механических систем, не зависят от того, к какой из
двух инерциальных систем отсчета, движущихся одна отно-
относительно друзой прямолинейно и равномерно, они относятся.
Дорелятивистская физика считала обе формулировки то-
тождественными, поскольку при равномерном поступательном
движении инерциальных систем отсчета относительно друг дру-
друга она не допускала никакого другого преобразования г и t, кро-
кроме преобразования Галилея. На самом деле вторая формулиров-
формулировка более общая, чем предыдущая, так как в ней не конкретизиро-
конкретизирован вид того преобразования координат и времени, относительно
которого инвариантны уравнения механики. В дальнейшем, ес-
если не сделано специальной оговорки, принцип относительности
понимается во второй формулировке.
3. Принцип относительности отнюдь не утверждает, что одно
и то же физическое явление выглядит одинаково в различных
инерциальных системах отсчета. Дело в том, что одни только
дифференциальные уравнения механики не определяют движе-
движение системы. К ним необходимо присоединить еще начальные
условия, например задать координаты и скорости всех взаимо-
взаимодействующих частиц в определенный момент времени. А эти
начальные условия меняются при переходе от одной системы
отсчета к другой. Именно из-за различия начальных условий
движение предмета, свалившегося с полки равномерно движу™
щегося вагона, происходит вниз по прямой линии, если его рас-
рассматривать относительно самого вагона, тогда как относитель™
но полотна железной дороги то же движение совершается по
параболе. Вот почему в формулировке принципа относительно™
сти говорится не об одинаковости явлений, а об одинаковости
законов, определяющих изменение состояний движения механи™
ческих систем.
Смысл принципа относительности молено также уяснить на
следующем примере. Возьмем замкнутую систему тел А и за™
дадим их начальные положения и скорости относительно инер-
циальной системы отсчета S. Пусть имеется тождественная с А
другая замкнутая система тел А1, в которой созданы в точности
такие же начальные условия, но уже относительно инерциаль™
ной системы отсчета S1. Тогда движение в системе тел А отно-
относительно S будет тождественным с движением в системе тел А1
относительно 5". В этом и состоит равноправие инерциальных
систем отсчета, устанавливаемое принципом относительности.
Принципиально взаимодействие имеет место между любыми
телами Вселенной. Поэтому, если бы и существовали замкнутые
системы, то единственной из таких систем могла бы быть, строго

658 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
говоря, только вся Вселенная. Но тогда принцип относительно-
относительности в том смысле, какой ему придан в последнем примере, был
бы бессодержательным, так как двух Вселенных не существует.
Принцип относительности только потому сохраняет содержание,
что многими взаимодействиями, ввиду их слабости, можно пре-
пренебречь и таким путем выделить практически бесконечное шло-
жество ограниченных систем тел, каждая из которых прибли-
приближенно ведет себя как замкнутая. В какой степени та или иная
система удовлетворяет этому условию, зависит от исследуемого
вопроса и от точности, какая предъявляется при его изучении.
Достаточно ли для (приближенной) замкнутости системы отда-
отдаленности всех масс, не входящих в рассматриваемую систему?
Ответ в соответствии с опытом гласит, что в случае равномер-
равномерного и прямолинейного движения (относительно инерциальной
системы отсчета) этого достаточно, а для всех остальных видов
движения недостаточно.
4. Явления природы не представляется возможным разде™
лить на чисто «механические» и «немеханические». Если бы да-
даже это и можно было сделать, то принцип относительности не
мог бы относиться к одним только «механическим» явлениям.
Действительно, всякое «механическое» явление связано с мно-
множеством «физических» явлений и обусловлено ими. И если бы
принцип относительности не был справедлив для этих «физи-
«физических» явлений, то он не мог бы оставаться справедливым и
для «чисто механических» явлений. Поэтому принцип относи-
относительности необходимо распространить на все явления природы
и дать ему следующую формулировку:
Законы природы, определяющие изменение состояний физи-
физических систем, не зависят от того, к какой из двух инерциаль-
ных систем отсчета, движущихся одна относительно другой
прямолинейно и равномерно, они относятся.
Это положение называется частным, или специальным,
принципом относительности Эйнштейна. Он устанавливает
равноправие только инерциальных систем отсчета. На основе
этого принципа Эйнштейн создал в 1905 г. частную, или спе-
специальную, теорию относительности. Через 10 лет он обобщил
принцип относительности на случай произвольных неинерциаль-
ных систем отсчета и создал общую теорию относительно-
относительности, иначе называемую релятивистской теорией тяготения.
Эта фундаментальная теория приобрела особое значение в свя-
связи с астрофизическими открытиями последнего времени. Общая
теория относительности стала основной теорией в астрофизи-
астрофизике, в частности в космологии. Однако в нашем курсе мы можем
ограничиться изложением только специальной теории относи-
относительности.

§ 102 ОПЫТ МАЙКЕЛЬСОНА 659
§ 102. Опыт Майкельсона
1. Основные уравнения электродинамики Максвелла-
Лорентца не инвариантны относительно преобразования Гали-
Галилея. Действительно, скорость света в вакууме, вычисленная из
этих уравнений, равна постоянной с. Такой результат оставал-
оставался бы верным во всех инерциальных системах отсчета, если бы
в них уравнения Максвелла имели один и тот же вид. Но это
несовместимо с законом сложения скоростей A01.3), который
является следствием преобразования Галилея.
Неинвариантность уравнений Максвелла относительно пре-
образования Галилея, как думали физики конца XIX и начала
XX веков, не противоречит, однако, принципу относительности.
Дело в том, что во всех электродинамических явлениях, помп-
мо обыкновенного вещества, по господствовавшим в то время
воззрениям, участвует еще мировой эфир. Уравнения Максвел-
Максвелла принимают обычный вид только в системе отсчета, в кото-
которой эфир покоится. Такая система является преимущественной
или выделенной среди всех прочих инерциальных систем отсче-
отсчета. Во всех остальных системах должно наблюдаться движение
эфира — эфирный ветер. Его обнаружение считалось в XIX и
начале XX веков одной из центральных проблем физики. Опыт
привел к результату, что гипотеза эфира, как она понималась
в физике XIX века, несостоятельна, а эфирного ветра не суще-
существует. Однако опыты по его обнаружению не совсем потеряли
свое значение. Не вводя представления об эфире, можно поста™
вить вопрос о существовании преимущественной инерциальной
системы отсчета. На этот вопрос и отвечают опыты по обна-
обнаружению эфирного ветра.
2. Если принять гипотезу о существовании преимуществен-
преимущественной системы отсчета, то прежде всего возникает вопрос, как дви-
движется Земля относительно этой системы? Обозначим скорость
такого движения через V. Тогда, согласно дорелятивистской ки-
кинематике, в направлении вектора V скорость света относительно
Земли будет с — V, а в прямо противоположном направлении —
с + V, где с — скорость света относительно преимущественной
системы отсчета.
Этот результат можно подвергнуть экспериментальной про-
проверке. Для этого, казалось бы, можно воспользоваться двумя
одинаково идущими часами, установленными на Земле в раз-
различных точках А и В на расстоянии I = АВ друг от друга
(рис. 323). Если прямая АВ ориентирована вдоль скорости V,
то время, затрачиваемое светом на прохождение расстояния АВ,
будет Iab = l/(c^^)i а на возвращение обратно гва — l/(c + V).
Разность этих времен, если ограничиться точностью до первого

660 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
порядка относительно We, равна tAB ~ tsA ^2 —. Если прямая
с с
АВ составляет с направлением скорости V угол а, то
^ IV
2-^cosa.
с с
Время tAB находится по разности показаний часов в моменты
прихода светового сигнала в В и его отправления из А. Таким
же путем находится время tsA-
С /л С
^ В А/Т *" В
О О О О
Рис. 323
Не было недостатка в предложениях, часто остроумных, как
фактически осуществить опыт. Но в принципиальном отноше-
нии все они не отличались от схемы опыта, описанной выше.
Предложения такого рода были оставлены после следующего
замечания Майкельсона. Времена tAB и tBA измеряются с по™
мощью двух часов^ находящихся в различных точках простран-
пространства. Для измерения необходимо эти часы синхронизовать, что
практически невозможно сделать с требуемой точностью. (Эйн-
(Эйнштейн позднее заметил, что эта трудность принципиальная, а
не только практическая, см. § 104.) Для осуществления опыта
надо обойтись без синхронизации, т.е. все измерения произво-
производить с помощью только одних часов. Для этого из точки А, где
помещены часы, надо послать световой сигнал и отразить его
обратно в А с помощью зеркала, помещенного в В. Полное вре-
время распространения света t вдоль прямой АВ туда и обратно
можно измерить с помощью лишь одних часов. Делением удво™
енного расстояния между точками А и В на это время можно
найти скорость света с. Но это бу™
дет не скорость света в каком-либо
одном определенном направлении,
а средняя скорость в двух пря-
прямо противоположных направлени-
направлениях. Майкельсон исследовал зависи™
Рис 324 мость полного времени t от ориента-
ориентации прямой АВ.
Как видно из рис. 324, с2 = с'2 + V2 + 2Fc;cosof, где с и
V — скорости света и Земли относительно преимущественной
системы отсчета, с; — скорость света относительно Земли, а а —
угол между скоростями Уис'. Решая полученное квадратное

§ 102 ОПЫТ МАЙКЕЛЬСОНА 661
уравнение относительно с;, найдем
с = —V cos а + су 1 — /32 sin2 a,
где введено обозначение /3 = V/c. Ограничиваясь квадратами /3,
получим
cf = с И - f3 cos a - i /32 sin2 i
3. Майкельсон воспользовался сконструированным им ин-
интерферометром, описанным в § 35 (см. рис. 140). Пластинка Р2
была введена для уравнивания оптических длин плеч интерфе-
интерферометра. Без этого интерференция в белом свете была бы невоз-
невозможна. В принципиальных рассуждениях от наличия пластин-
пластинки Р2 можно отвлечься и считать разделительную пластинку Pi
бесконечно тонкой. Пусть плечо интерферометра 2 составляет
с направлением скорости V угол а. Тогда на прохождение рас-
расстояния от А до зеркала М~2 и обратно свет затратит время
_ 1 г i l г _
с 1 — /3 cos а — У2/З2 sin2 а с 1 + C cos а ~~ г/2р2 sin2 a
_ 21 1 - У2/32 sin2 а _ 21 1 - 1/2f32 sin2 a
Найдем теперь время ti, которое требуется свету, чтобы пройти
туда и обратно перпендикулярное плечо интерферометра. Оно
найдется из предыдущего выражения заменой угла а на угол
а ± —. Это дает
_211- г/2р2 cos2 a
Таким образом,
cos 2a^ - В2 cos 2a.
с
t2 t\ по cos 2a^
d — р1 с
Этой разности времен соответствует разность фаз интерфери-
интерферирующих лучей
?>2 - ?>1 = — (*2 - *i) = — Р cos 2a.
При вращении интерферометра угол а будет меняться, а ин-
интерференционные полосы должны смещаться. Этот эффект и
пытался обнаружить Майкельсон.
Если за единицу принять ширину интерференционной поло-
полосы, то смещение полос при повороте интерферометра будет
2Ж ДГ — у----^;. A1У.1)
Максимального значения
A02.2)

662 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
оно достигает, когда при повороте интерферометра cos 2а ые-
няется от ±1 до =pl. Отсюда видно, что ожидаемое смещение
очень мало, так как оно второго порядка по /3 = V/c. Точно оце-
оценить его невозможно, поскольку скорость Земли относительно
преимущественной инерциальной системы отсчета неизвестна.
Можно, однако, оценить нижний предел АЖмакс. Действитель-
но, допустим сначала, что Солнце покоится относительно пре-
преимущественной системы отсчета. Тогда под V надо понимать
скорость движения Земли по своей орбите, которая равна около
30 км/с, так что /3 = 1СР4, /З2 = 1СР8. В первом опыте Майкель™
сона A881 г.) длина плеча интерферометра была I = 1,2 м. Если
взять А = 600 нм, то получится АЛГмакс = 0,04 полосы.
При учете движения Солнца можно ожидать и большего сме-
щения. Действительно, разложим скорость движения Солнца на
составляющую V|| в плоскости земной орбиты и составляющую
V_l, перпендикулярную к этой плоскости. Полная скорость Зем-
ли будет V = Vop6 + V|| +Vx, где Vop6 — скорость орбитального
движения Земли. Если опыт производится в момент, когда на-
направления скоростей Vop6 и V|| совпадают между собой, то для
полной скорости Земли можно написать
так что V получится больше Кэрб- Следовательно, и ожидаемое
смещение полос будет больше вычисленного выше.
Конечно, минимальное ожидаемое смещение в 0,04 полосы,
вычисленное выше, могло бы наблюдаться только два раза в год,
когда направление эфирного ветра совпадает или прямо проти-
противоположно направлению движения Земли. Поэтому необходимо
производить наблюдения в течение по крайней мере полугода,
что фактически и делалось Майкельсоном и всеми физиками,
повторявшими его опыт.
Опыт был поставлен настолько тщательно, что позволял об-
обнаружить смещение на 0,01 интерференционной полосы. Ожи-
Ожидаемое смещение на 0,04 полосы могло быть уверенно обнару-
обнаружено на фоне неизбежных случайных ошибок измерений. Ока-
Оказалось, что смещения нет. Точнее, результат опыта позволял
утверждать, что скорость эфирного ветра, если бы он существо-
существовал, не может превышать 18 км/с.
4. В 1887 г. Майкельсон повторил свой опыт совместно с
Морли A837—1925). Для того чтобы при вращении интерферо-
интерферометра не возникали деформации, вызывавшие небольшое смеще™
ние интерференционных полос, интерферометр вместе с осталь-
остальной аппаратурой монтировался на тяжелой цементной плите,
которая плавала в сосуде со ртутью. С той же целью прибор все
время находился в медленном вращении, даже в моменты на-

102
ОПЫТ МАЙКЕЛЬСОНА
663
блюдения. Путем применения многократных отражений от 16
зеркал, установленных на той же плите, эффективная длина
плеча интерферометра была доведена до 11 м. Ожидаемое сме-
смещение из-за орбитального движения Земли составляло уже 0,4
интерференционной полосы. Максимально наблюдавшееся сме-
смещение (из-за неизбежных случайных помех) составляло 0,02, а
среднее — много меньше 0,01 интерференционной полосы. Опыт
позволил утверждать, что скорость эфирного ветра не сможет
превышать 7 км/с. Сам Майкельсон пришел к заключению, что
результат опыта определенно отрицательный — эфирного ветра
не существует.
Опыт Майкельсона неоднократно повторялся другими физи-
физиками с улучшенной аппаратурой и улучшенными методами на-
наблюдения. Не останавливаясь на истории вопроса, укажем толь-
только, что к началу 30-х годов было с достоверностью установлено,
что скорость эфирного ветра, если он и существует, не может
превышать 1—1,5 км/с.
5. Изобретение лазеров, благодаря исключительно высокой
степени монохроматичности и пространственной когерентности
этих источников света, позволило
чрезвычайно упростить схему опыта
Майкельсона и повысить его точность.
Опыт был поставлен в 1964 г. амери-
американскими физиками Джасея, Джава-
ном, Мурреем и Таунсом. Идея опыта
заключалась в следующем.
Если скорость света зависит от на-
направления его распространения отно-
относительно Земли, то частота, на кото-
которой генерирует лазер, должна изме-
изменяться при его повороте. Это изме-
изменение пропорционально /З2, т.е. вто-
второго порядка по /3. Два одинаковых
гелий-неоновых лазера были установ-
установлены на поворотной платформе пер-
перпендикулярно друг к другу (рис. 325).
Световой пучок от одного из лазеров
проходил полупосеребренное зеркало
S, а пучок от другого лазера отражал-
ся от того же зеркала. Далее пучки шли в одном и том же на-
направлении и попадали в фотоэлектронный умножитель, уста-
установленный на той же поворотной платформе. Если бы частоты
этих пучков немного отличались друг от друга, то должны были
бы возникнуть биения фототока с частотой, лежащей в области
радиодиапазона, которые можно было бы наблюдать обычными
о d
Газовый
лазер
\ \фэу
Рис-

664 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
радиотехническими приемами с помощью анализатора А. Ча-
стота биений должна была бы меняться при вращении прибора.
Если в исходном положении один лазер был ориентирован вдоль,
а другой — перпендикулярно к направлению движения Земли,
то при повороте прибора на 90°, согласно теории неподвижно-
неподвижного эфира, из-за орбитального движения Земли должно было бы
наблюдаться изменение разности частот лазеров примерно на
3 МГц, тогда как возможная ошибка опыта не превосходила
нескольких герц. На опыте такое смещение обнаружено не бы™
ло. На основании своих наблюдений экспериментаторы пришли
к заключению, что скорость эфирного ветра, если бы таковой
существовал, не может превышать 30 м/с. По сравнению с пре-
предыдущими результатами точность была повышена примерно в
50 раз.
6. Отрицательный результат опыта Майкельсона доказыва-
доказывает, что в земной системе отсчета скорость света в вакууме изо-
изотропна, т.е. не зависит от направления его распространения.
Под скоростью света здесь понимается средняя скорость в двух
прямо противоположных направлениях — она и только она опре-
определяет результат опыта с «одними часами». Обобщая этот ре-
результат, можно сказать, что он справедлив во всех инерциаль-
них системах отсчета.
Остается выяснить, одинаковы ли числовые значения скоро-
скорости света в различных системах отсчета? Утвердительный ответ
можно дать на основании опыта Кеннеди и Торндайка, которые
в 1932 г. изменили опыт Майкельсона. В их опыте использовал-
использовался интерферометр Майкельсона, в котором длины плеч были
разными и отличались на 16 см. Они наблюдали интерференци-
интерференционные полосы (при неподвижном относительно Земли интерфе-
интерферометре) в течение шести месяцев. За это время Земля из своего
исходного положения непрерывно перемещалась в диаметраль-
диаметрально противоположную точку своей орбиты, участвуя вместе с тем
в движении Солнца. Тем самым реализовалось множество си-
систем отсчета, отличающихся друг от друга положением и ори-
ориентацией в пространстве. Если бы в них скорость света была
разной, то должно было бы наблюдаться регулярное смещение
интерференционных полос. На самом деле смещение носило слу-
случайный характер и не превосходило 3/1000 ширины полосы. На
этом основании можно прийти к заключению, что с точностью
примерно 2 м/с скорость света в вакууме относительно Земли
одинакова во всех ее положениях в пространстве.
Все это подтверждает равноправие различных инерциаль-
ных систем отсчета по отношению ко всем физическим явлени-
явлениям — преимущественной инерциальной системы отсчета не
существует.

§ 103 ПОСТОЯНСТВО СКОРОСТИ СВЕТА 665
§ 103. Независимость скорости света от движения
источника
1. Помимо принципа или постулата относительности, Эйн-
штейн положил в основу теории относительности постулат о
независимости скорости света в вакууме от движения источ-
источника. Его обычно называют принципом «постоянства скорости
света», хотя, как заметил еще Паули A900—1958), такое назва-
название может привести к недоразумениям. Об универсальности по™
стоянства скорости света в вакууме не может быть речи уже
потому, что эта скорость постоянна только в инерциальных си-
системах отсчета, а независимость скорости света от движения
источника сохраняется и в общей теории относительности, где
на выбор систем отсчета не накладывается никаких ограниче-
ограничений.
Независимость скорости света от движения источника можно
было бы не выдвигать в качестве самостоятельного постулата,
если с самого начала принять волновую теорию света. Однако
столь фундаментальную теорию, какой является теория относи-
относительности, лучше строить, не связывая ее ни с какими гипоте-
гипотетическими представлениями о природе и механизме физических
явлений.
2. Предположение о зависимости скорости света от движе-
движения источника ввел Ритц A878-1909). Согласно этому предпо-
предположению скорость света в вакууме постоянна и равна с только
относительно источника. Если же источник света движется со
скоростью v относительно какой-либо системы отсчета, то ско-
скорость света с; в этой системе векторно складывается из с и v, т.е.
с; = c + v, как это происходит со скоростью снаряда при стрель-
стрельбе из движущегося орудия. Такая гипотеза получила название
баллистической. Ритц перестроил электродинамику Максвелла,
приведя ее в соответствие с этой гипотезой. Ясно, что балли-
баллистическая гипотеза объясняет отрицательный результат опыта
Майкельсона, если только источник света неподвижен относи-
относительно интерферометра.
Но баллистическая гипотеза, как и любое предположение о
зависимости скорости света от движения источника, не согла-
согласуется с молекулярным объяснением отражения и преломления
света (см. § 68 и 69). В основе такого объяснения лежит пред™
ставление, что отраженная и преломленная волны возникают в
результате интерференции падающей волны с вторичными вол-
волнами, излучаемыми молекулами и атомами среды. Действитель-
Действительно, если среду считать неподвижной, а источник света взять дви-
движущимся, то волны, излучаемые источником, будут распростра-
распространяться с иными скоростями, чем волны, излучаемые молекулами
н атомами среды. Интерференция между ними невозможна. Од-

666 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
нако это замечание есть аргументация, основанная на волновой
теории света, а не экспериментальное доказательство, свободное
от гипотетических представлений о природе света.
Убедительное доказательство несостоятельности баллисти-
баллистической гипотезы, как показал в 1913 г. голландский астроном
де Ситтер A872-1934), дают астрономические наблюдения над
движением двойных звезд. Действительно, допустим, что бал-
баллистическая гипотеза верна. Предположим для простоты, что
компоненты двойной звезды вращаются вокруг их центра масс
по круговым орбитам в той же плоскости, в которой располо-
расположена Земля. Рассмотрим движение одной из этих двух звезд.
Пусть v — скорость движения ее по круговой орбите. В положе-
положении звезды, когда она удаляется от Земли вдоль соединяющей
их прямой, скорость света равна (с — г?), а в положении, когда
звезда приближается, равна [c + v). Если отсчитывать время от
момента, когда звезда находилась в первом положении, то свет
из этого положения дойдет до Земли в момент t\ = L/(c — v), a
из второго положения — в момент t<i = Т/2 + L/(c + v), где Т —
период обращения звезды, ai- расстояние до нее. При гро™
мадных расстояниях до звезд наблюдаемые движения звезды
могли бы заметно отступать от законов Кеплера. В частности,
при очень больших L могло бы случиться, что ?2 ^ ^ъ т-е- звезда
одновременно была бы видна в двух (и даже нескольких) поло-
положениях или обращалась бы в противоположном направлении.
Ничего подобного, как показали астрономические наблюдения,
не происходит.
Если бы баллистическая гипотеза была верна, то опыт Май-
кельсона должен был бы дать положительный результат, если
его произвести не с земным источником света, а со светом от
звезд. Томашек в 1926 г. так и поступил, но получил отрица™
тельный результат.
A.M. Бонч-Бруевич и В.А. Молчанов в 1956 г., применив со-
современные методы измерения скорости света, сравнили скорости
света от правого и левого краев Солнца. Из-за осевого враще-
вращения Солнца один из этих краев приближался к нам со скоростью
2,3 км/с, а другой удалялся с той же скоростью. Обе скорости
света с достаточной точностью совпали между собой.
Наконец, ставились специальные опыты, в которых сравни-
сравнивались скорости 7™квантов5 испускаемых движущимися возбу™
жденными ядрами углерода (*С12) и неподвижными возбужден-
возбужденными ядрами кислорода (*О16). Ставились также опыты по ан-
аннигиляции электрона с позитроном, специально приспособлен-
приспособленные для проверки независимости скорости света от движения
источника. По сравнению с астрономическими опытами, в кото-
которых используются космические источники света со сравнитель-

§ 104 ПОНЯТИЕ ОДНОВРЕМЕННОСТИ 667
но малыми скоростями, в опытах с атомными ядрами и элемен-
элементарными частицами скорость источников гораздо выше (сравни-
(сравнима со скоростью самого света). Опыты подтвердили, что с точ-
точностью около 10 % скорость 7™квантов не зависит от движения
источников.
Все приведенные опыты подтверждают постулат о независи-
мости скорости света в вакууме от движения источника.
3. Заметим в заключение, что теория относительности во™
обще была бы невозможна, если бы не был установлен фунда-
фундаментальный факт конечности скорости распространения све-
света. Изучение методов и результатов измерения скорости све-
света представляет громадный, не только исторический интерес. В
частности, уточнение числового значения этой постоянной необ-
необходимо для точных измерений астрономических расстояний ме-
тодами радиолокации. Это в свою очередь необходимо для це-
целей космонавтики. Однако мы не можем касаться этих вопро-
вопросов. Ограничимся замечанием, что в 1972 г. скорость света была
определена на основе независимых измерений длины волны Л и
частоты света и. Источником света служил гелий-неоновый ла-
лазер, генерировавший излучение с длиной волны 3,39 мкм. Длина
волны измерялась интерферометрически сравнением ее с этало-
эталоном длины, т.е. с длиной волны в вакууме оранжевой линии изо-
изотопа криптона-86. Ошибка таких измерений ^ Ю^5 нм. Часто-
Частота лазерного излучения измерялась путем сравнения ее с атом-
атомным стандартом частоты, т.е. с частотой перехода между двумя
сверхтонкими квантовыми уровнями атома цезия-133 в нулевом
магнитном поле. При этом использовались методы нелинейной
оптики — генерация излучений с суммарной и разностной часто-
частотами. В итоге для скорости света с = Хи было найдено значение
с = 299 792 458 ±1,2 м/с,
превосходящее по точности все ранее полученные значения бо-
более чем на два порядка.
§ 104. Понятие одновременности
1. До теории относительности считалось, что принцип отно-
относительности и принцип независимости скорости света от движе-
движения источника противоречат друг другу. Действительно, соглас-
согласно принципу относительности скорость света в вакууме во всех
инерциальных системах отсчета должна быть одной и той же.
Обозначим ее, как всегда, через с. Возьмем две инерциальные
системы отсчета S и S11 движущиеся относительно друг друга
прямолинейно и равномерно. Пусть О ж О1 — какие-либо две
точки, неподвижные в системах S и S' соответственно и про-

668 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
странственно совпадающие в момент времени t = 0. Произве-
Произведем в этих точках в тот же момент времени кратковременную
световую вспышку. Рассмотрим распространение этой вспышки
сначала в системе S. Так как свет во всех направлениях распро-
распространяется с одной и той же скоростью с, то к моменту времени
t вспышка достигнет сферы И радиуса ct с центром в точке О.
Рассмотрим теперь распространение той же вспышки в систе-
системе S1. Обе системы совершенно равноправны. Они отличают-
отличаются друг от друга только тем, что источник света относительно
них движется по-разному. Но это в рассматриваемом вопросе не
имеет никакого значения, так как скорость света не зависит от
движения источника. Поэтому можно утверждать, что к момен-
моменту t та же вспышка достигнет сферы Е; с тем же радиусом ct^ но
с центром в точке Of. Сферы S и S; разные, так как к моменту
t их центры О и О' разойдутся. Таким образом, одна и та же
световая вспышка одновременно должна находиться и на сфере
X, и на сфере Е;, что, очевидно, невозможно.
2. Однако приведенное рассуждение несостоятельно, так как
в его основе лежит интуитивное представление об одновремен-
одновременности. Если два события происходят в одном и том же месте
пространства, то не возникает трудностей при суждении о том,
одновременны эти события или нет. Но если события происходят
в разных местах пространства^ то без дальнейших разъясне-
разъяснений утверждение об их одновременности или неодновременно-
неодновременности просто бессодержательно, так как никакой априорной одно-
одновременности пространственно разделенных событий не суще-
существует.
В принципе пространственно-временное описание явлений
природы молено дать и без использования понятия одновре-
одновременности. Действительно, возьмем какую-либо инерциальную
систему отсчета. Для определения положения точки в ней бу-
будем пользоваться координатными осями, реализованными, на-
например, с помощью трех взаимно перпендикулярных твердых
стержней. Расстояние между двумя точками будем измерять
путем откладывания неподвижного масштабного стержня, т.е.
твердого стержня определенной длины, разделенного на метры
и более мелкие единицы. Для измерения больших расстояний
этот способ непригоден. Тогда надо применять косвенные мето-
методы измерения длин, о которых говорилось в § 1 первого тома.
Для определения времени расставим в нашей координатной си-
системе достаточно часто какие-либо одинаково устроенные часы.
Стрелки часов в различных точках пространства установим со-
совершенно произвольно и независимо друг от друга. После этого
получится пространственно-временная система отсчета. Всякое
событие в такой системе можно характеризовать местом, где оно
произошло, и показаниями часов в том же месте.

§ 104 ПОНЯТИЕ ОДНОВРЕМЕННОСТИ 669
Пока что введено толвко местное время, т.е. время в каждой
точке пространства, причем времена в различных точках никак
не связанв! между собой. Это обстоятелвство делает нашу систе-
систему практически совершенно непригодной для пространственно-
временного описания явлений природы. Практической может
бытв только система с единым временем^ в которой показания
часов в различных точках не независимы, а определеннвш обра-
образом связаны или синхронизированы друг с другом. Способ син-
синхронизации в принципе произволен. Требуется толвко, чтобв! он
был внутренне непротиворечив. Однако соображения целесооб-
целесообразности, основанные на принципе относителвности и независи-
независимости скорости света от движения источника, почти однознач-
однозначно вынуждают принять способ синхронизации, предложенный
Эйнштейном, и основанное на нем определение одновременности.
3. Эйнштейн предложил устанавливатв синхронизацию про-
пространственно разделенных часов с помощью световых сигналов
в вакууме. Пока синхронизация часов не установлена, не имеет
смысла говоритв о скорости в любом определенном направле-
направлении. Имеет смысл говорить лишь о средней скорости света в
двух прямо противоположных направлениях, так как эту вели-
величину можно измерить с помощью только одних часов. Для этого
из неподвижной точки А в момент времени tf пошлем световой
сигнал к неподвижному зеркалу, установленному на расстоянии
I от А. Пусть отраженный сигнал вернется в А в момент щ.
Время отсчитывается по одним и тем же часам, так что ника-
никакой синхронизации не требуется. Разделив пройденное расстоя™
ние 21 на затраченное время t^ — tf, найдем искомую среднюю
скорость света с = 21/ {Щ — tf). Опыт Майкельсона и другие
опытв! показали, что эта величина еств универсальная посто-
постоянная. Теперь полазаем по определению^ что скорости света
во всяких двух взаимно противоположных направлениях оди-
одинаковы. Тем самым постулативно будет установлена синхрони-
синхронизация часов и введено понятие одновременности. После этого
уже имеет смысл говорить о скорости любого движения в одном
направлении^ так как время, затрачиваемое на такое движение,
можно измеритв по двум
пространственно разде- А с С В
ленным часам, синхро- • ' ^ —•
низованным между собой. tf/T\ c t
Сформулируем теперв \\) а
окончательно правило f2
Эйнштейна синхрониза-
синхронизации часов. Пусть в непо- Рис. 326
двиэюных точках А и В (рис. 326) установлены одинаковые ча-
часы. Из точки А в момент tf no часам А пошлем световой сиг-

670 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
нал к зеркалу? установленному в точке В. Пусть отраженный
сигнал возвращается в А в момент Щ (по часам А). В момент
прихода сигнала в В поставим на часах в В время tB = Y2 (tf +
+ t?). Тогда по определению часы в А и В будут синхронизова-
синхронизованы между собой.
Можно дать другой, эквивалентный, способ синхронизации.
В середине отрезка АВ произведем световую вспышку. В мо-
момент прихода света от вспышки к часам А и В поставим их
одинаково. Тогда часы будут синхронизованы.
Но часы А и В можно синхронизовать между собой не только
непосредственно, но также посредством третьих часов С. Син-
Синхронизуем сначала одним из указанных способов часы А и С, за™
тем часы В жС. Мы утверждаем и рассматриваем это утвержде-
утверждение как постулат, что при этом часы А и В окажутся синхрони-
синхронизованными. Такое утверждение, как показывают все следствия
из него, не приводит к противоречиям и согласуется с опытом.
Таким образом, получается пространственно-временная систе-
система отсчета с единым временем, в которой часы синхронизова-
синхронизованы между собой по правилу Эйнштейна. Два пространственно
разделенных события в этой системе отсчета называются од-
повременными, если часы, находящиеся в тех точках, где про-
происходят эти события, показывают одно и то же время.
4. Одновременность есть понятие относительное, т.е. два
события, одновременные в одной инерциальной системе отсчета,
могут оказаться не одновременными в другой системе. Поясним
это на следующем мысленном опы-
—^V те. По поверхности Земли равно™
мерно и прямолинейно со скоростью
V движется поезд А1 В' (рис. 327).
^ С • В Примем его за движущуюся систе-
систему отсчета Sf. Неподвижной систе-
Рис. 327 моц g будем считать полотно желез-
железной дороги. Пусть в концы поезда А1 и В1 ударяют две молнии,
оставляющие следы А и В на полотне железной дороги. Отме-
Отметим в поезде среднюю точку С1, а на полотне — среднюю точку
С между А и В. Пусть в точку С вспышки от молний приходят
одновременно. Тогда с точки зрения системы S удары молний в
концы поезда будут событиями одновременными. Но в момент
встречи обеих вспышек точка С окажется правее С. В этот мо-
мент вспышка от В1 уже прошла через С, а от А1 еще не дошла.
Значит, с точки зрения системы S' удар молнии в В1 произошел
раньше удара в А1'.
Теперь ясно, как разрешается парадокс, о котором говори-
говорилось в п. 1. Свет доходит до сферы S одновременно в систе-
системе отсчета S, но не одновременно в системе S1. Аналогично, до

§ 105 ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА 671
сферы S; свет доходит одновременно с точки зрения системв!
отсчета S", но не одновременно с точки зрения системы S.
Дорелятивистская физика развивалась, и вполне успешно,
считая время и одновременность абсолютными^ т.е. одинаковы™
ми во всех системах отсчета. Но так происходило лишь до тех
пор, пока рассматривались медленные движения. А распростра-
распространение света есть быстрый процесс. Вот почему именно в оптике
физика встретилась раньше всего с принципиальными трудно-
трудностями, преодоленными теорией относительности.
§ 105. Преобразование координат и времени в теории
относительности
1. Рассмотрим две инерциальные системы отсчета S и 5;, из
которых вторая движется относительно первой прямолинейно и
равномерно со скоростью V, а следовательно, первая движется
относительно второй со скоростью — V. В каждой системе отсче-
отсчета расставлены достаточно часто одинаковые часы, неподвиж-
неподвижные в этой системе и синхронизованные по правилу Эйнштейна.
Пусть ж, у, z, t — координаты и время какого-либо события (на™
пример, столкновения двух шаров) в системе отсчета Я, а х\
у', z1, t' — координаты и время того же события в системе от-
отсчета S1. Возникает вопрос, как по значениям ж, у, z, t найти
значения ж;, f/, zf, tf и наоборот. Решение этого вопроса основа-
основано на предположении, что пространство однородно и изотроп™
но, а время однородно1). Однородность пространства и времени
означает, что все точки пространства и все моменты времени,
как в системе S, так и в системе S", абсолютно эквивалентны.
Изотропия же пространства означает полную эквивалентность
всех пространственных направлений в системе *S, а также в си™
стеме S'. В силу указанной однородности и изотропии простран-
пространства и времени связь между ж, у, z, t и ж;, f/, z\ if должна быть
линейной.
Вопрос о чисто пространственных преобразованиях коорди-
координат в этих предположениях решается в аналитической геомет-
геометрии. Поэтому можно отвлечься от этого вопроса и сосредоточить
все внимание на том, что нового вносит в преобразование коор-
координат и времени равномерное движение одной системы отсче-
отсчета относительно другой. Для этой цели достаточно рассмотреть
частный случай, когда начала О и О' координатных систем S
) Эти свойства нельзя рассматривать как априорные. Они установле-
установлены и проверены экспериментально. Их объяснение, по-видимому, должна
дать космология при рассмотрении происхождения и эволюции Вселенной
в целом.

672
ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
ГЛ. IX
и Sf в некоторый момент времени совмещаются. Этот момент
мы примем за начало отсчета времени как в системе S, так и в
системе Sf. Тогда связь между ж, у, z, t и ж;, у1, z;, ? будет не
только линейной, но и однородной, так как нулевым значениям
нештрихованных параметров соответствуют также нулевые зна-
значения штрихованных. Кроме того, оси Х\ Y1, Z1 координатной
системы S1 молено выбрать так, чтобы они были параллельны
осям X, Y, Z координат-
координатной системы S и, следо-
следовательно, ось X1 все вре™
мя совмещалась с осью X
(рис. 328).
2. Предположим, что
относительная скорость
V координатных систем
S и S1 меньше скорости
света с (V < с). Пусть
при этом условии из
начала координат О в
момент времени t\ > 0 (по часам системы S) послан световой
сигнал в положительном направлении оси X. Пусть этот сигнал
приходит в точку О1 в момент времени i1 (по часам системы S1).
Тогда, ввиду линейности связи между координатами и временем
в системах S и S', время t1 должно выражаться также линейно
через t\. При этом нулевому значению t\ соответствует нулевое
значение t;, так как в момент t = tf начала координат О и О'
совмещаются между собой. Следовательно, должно быть
? = Ыъ A05.1)
где к — некоторый коэффициент. В силу изотропии простран-
пространства он может зависеть только от абсолютного значения скоро-
скорости V, но не от ее направления.
Выразим коэффициент к через скорость V. Пусть в точке
О1 световой сигнал отражается и, распространяясь в обратном
направлении, возвращается в точку О в момент #2 (по часам си™
стемы S). Тогда, ввиду полной эквивалентности систем отсчета
ис"
t2 = ktf, A05.2)
где к имеет то лее значение, что и в формуле A05.1). Исключив
t;, получим
^^ к t\.
A05.3)
Согласно эйнштейновскому правилу синхронизации часов сиг-
сигнал, посланный из О в момент t\ и возвратившийся обратно в

§ 105 ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА 673
момент #2, отражается в точке О1 в момент времени
t = *! + *! = i±*!tl (Ю5.4)
(по часам системы S). Расстояние ж, проходимое точкой О1 за
время i, равно ж = Ft. То же расстояние свет проходит за вре-
время t — t\, и следовательно, х = c(t — t\). Таким образом, Vt =
= c(t ~~ t\). Подставив сюда значение t из предыдущей формулы,
получим
V(k2 + 1) =c(jfc2-l), A05.5)
откуда
Извлекая из последнего выражения квадратный корень, най-
найдем к. После этого получаем две вспомогательные формулы:
fc + i= , 2 => fc-l= y 2F/C =, (Ю5.8)
Л Vl-(V/cJ * V1 ^ (WeJ
которые понадобятся нам в дальнейшем. Все эти соотношения,
разумеется, имеют смысл только при условии V < с.
Отметим, в частности, что из формул A05.1) и A05.4) еле™
дует
I = WTT = лЛ-07сJ, (Ю5.9)
откуда t; < t. Величина t есть время движения точки О' из
неподвижного начала О до точки, в которой его догонит све-
световой сигнал, измеренное по «неподвижным часам», т.е. часам
системы S. Величина tf имеет смысл того же времени, но изме-
измеренного уже по «движущимся часам», т.е. часам системы Sf. Та-
Таким образом, величины t и tf представляют собой времена меле™
ду одними и теми же событиями, измеренные соответственно в
«неподвижной» S и «движущейся» S1 системах отсчета. Фор-
Формула A05.9) показывает, что движущиеся часы идут медленнее
неподвижных. Это явление будет обсуждено ниже с различных
точек зрения, а сейчас мы вернемся к вопросу о преобразовании
координат и времени.
8. Пусть на оси X произошло какое-то событие А, напри-
например столкновение двух шаров (рис. 329). В системе отсчета S
это событие характеризуется абсциссой х и моментом времени
t. В системе отсчета S1 абсцисса и время того же события будут
ж;, tf. Рассмотрим световой сигнал, отправляющийся из начала
координат О к месту события А (рис. 329 а). На прохождение
расстояния О А сигнал затрачивает время х/с. Чтобы он пришел

674 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
в А в момент t, его надо отправить из О в момент t\ = t — x/c. На
прохождение расстояния О1 А тот же сигнал затрачивает время
ж'/с, так что он проходит че-
О —»- О' —»- Л x,t рез точку О; в момент t\ =
а • • • ., // гг
г-х/с t'-x'/c x',t' = t — х Iс. Но определению
коэффициента к t\ = kt\
или tf — xf /с = k(t — x/c). От™
О —— О' -•— ^4 х,!1 разим теперь световой сиг-
t+x/c t'+x'/c x',tr нал в А в обратном направ-
направлении (рис. 329 б"). Через
Рис. 329 точку О1 он пройдет в мо-
момент времени tf2 = t1 + ж;/с,
а через точку О — в момент t<i = t + ж/с. Теперь роли штрихо-
штрихованных и нештрихованных величин поменялись местами, и на
основании того же определения коэффициента к можно напи-
написать #2 — kt^j или t + х/с = fc(t; + х1 /с). Таким образом,
tf - х/с = fc(t - х/с), k(tf + ж;/с) = t + ж/с. A05.10)
Полученные соотношения справедливы, в каком бы месте оси
X ни произошло событие А. Пусть, например, оно произошло
левее точек ОиО', как указано на рис. 330 а. Отправим от места
события световой сигнал вправо. Так как теперь жиж' отри-
отрицательны, то сигнал достиг-
достигнет точек О и О1 в более позд-
ние моменты t — х/с и t'-
— х1 /с. На основании опре-
определения коэффициента к на-
напишем f — х1/с = k(t —
— ж/с), а это есть первое со-
отношение A05.10). Возьмем
теперь световой сигнал, рас-
распространяющийся справа на-
лево (рис. 330 б). Пусть он достигает точки А в моменты t и tr
по часам в системах S и S1 соответственно. Через точки О и О1
сигнал пройдет в моменты времени t + х/с и t1 + ж;/с, а пото-
потому t1 + х1 /с = kit1 — ж'/с), т.е. получается и второе соотношение
A05.10).
Очень полезно рассмотреть все случаи взаимного расположе-
расположения точек А, О, О1 и убедиться, что во всех случаях справедливы
соотношения A05.10).
Из соотношений A05.10) находим
*'=К*-4) * - К* - *
, 1
2
x,t
x',t'
x,t
x'J'
A
•—
A
ф
—— О ——
t-x/c
—— о ——
t+x/c
O'
t'-x',
Or
t'+x',

105
ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА
675
или на основании A05.?
х - Vt
х =
У =У,
A05.12)
A05.13)
z, которые показыва™
V А
Рис-
где введено обозначение
/3 = V/c.
Мы добавили формулы у1 = у, z1
ют, что поперечные координаты события у ж z не преобразу-
преобразуются. Для доказательства последнего утверждения изготовим
в системах отсчета S и Sf одним и тем же способом два оди-
одинаковых твердых стержня, каждый из которых неподвижен в
своей системе отсчета. Устано™
вим их своими концами на оси
X параллельно осям Y и Y1
(рис. 331). Длины стержней у и
f/, измеренные соответственно в
системах S и S1, конечно, бу-
будут одинаковы. Но это еще не
означает, что справедливо вто-
второе уравнение A05.12). Надо еще
показать, что ужу1 молено рас-
рассматривать как координаты од-
одного и того эюе события. Для доказательства этого к свободным
концам стержней прикрепим маленькие шарики А ж А1. Пусть
сначала щарик А1 расположен левее шарика А. Мы утверждаем,
что при движении шарик А1 обязательно столкнется с шариком
А. Действительно, если бы движущийся шарик прошел выше
или ни лее неподвижного, то системы отсчета S и S1 не были бы
эквивалентны. Но если шарики столкнутся, то у ж у1 становятся
координатами одного и того же события — столкновения шари-
шариков, и второе уравнение A05.12) может считаться доказанным.
Так же доказывается и третье уравнение A05.12).
Формулы A05.12) и решают задачу о преобразовании коор-
координат и времени при переходе от одной системы отсчета к дру-
другой. Они называются преобразованием Лорентца (этот термин
был введен Пуанкаре). Лорентц получил их в 1904 г. К тем же
формулам несколько раньше (в 1900 г.) пришел Лармор. И Л ар-
мор, и Лорентц, однако, принципиально стояли на точке зрения
неподвижного эфира. У них истинным было только время t в
системе отсчета, в которой эфир покоится. Величина же tf лишь
формально играла роль времени — это была математическая
переменная, вводимая таким образом, чтобы соблюдалась инва-
инвариантность уравнений электродинамики при переходе от пере-
переменных ж, у, z, t к переменным ж;, f/, z\ t1. Настоящий вывод
формул преобразования Лорентца и установление их истинного

676 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
смысла дал Эйнштейн в 1905 г. В его теории все инерциальные
системы отсчета совершенно эквивалентны, a tf является таким
лее «истинным временем», как и t. Это проявляется, в частно-
частности, если уравнения A05.12) разрешить относительно ж, у, z, t.
Таким путем получатся формулы «обратного преобразования»
х = . , у = у , z = z , t = —. ' , A05.14)
имеющие тот же вид, что и формулы «прямого преобразования»
A05.12). Как и следовало ожидать, они получаются из формул
A05.12) простой заменой V на —V.
Формулы A05.12) и A05.14) при /3 > 1 дали бы мнимые зна-
значения для координат и времени. Поэтому нет смысла говорить
о движении одной системы отсчета со скоростью F, превышаю™
щей скорость света с. Отсюда следует, что скорость любого тела
не может превышать с, так как с каждым телом можно связать
систему отсчета.
При медленных движениях, когда (V/cJ < 1 и Vv/c2 <C 1
(v — скорость движения тела), преобразование Лорентца, как и
следовало ожидать, в пределе переходит в преобразование Га™
ли лея.
4. В дорелятивистской физике пространство и время счи-
считались независимыми друг от друга. Расстояния между двумя
пространственными точками (точнее, расстояния между двумя
материальными точками в один и тот же момент времени), а
также промежутки времени между двумя событиями считались
одинаковыми во всех системах отсчета. Иными словами, обе
эта величины считались инвариантными при переходе от одной
системы отсчета к другой. В теории относительности такая ин-
инвариантность была утрачена. Вместо двух инвариантов — про™
странственного и временного — в ней сохранился только один,
пространственно-временной^ инвариант. Его легко найти, не-
ремножая почленно уравнения A05.11). Это дает
A05.15)
Для удобства запишем этот инвариант через новые временные
переменные
т = с?, г = с?, A05.16)
имеющие размерность длины. Введение таких переменных озна™
чает, что промежутки времени теперь измеряются теми же еди-
единицами, что и пространственные расстояния: за единицу време™
ни принимается время, в течение которого свет проходит едини-
единицу расстояния. В новых переменных
г2 _ х2 = г2 - х12 = Inv . A05.17)

§ 105 ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА 677
Учтем теперь, что при выбранной нами ориентации коорди-
координатных осей у' = у, z1 = z. Поэтому
т2 - (х2 + у2 + z2) = т12 - {х12 + у12 + z12) = Inv . A05.18)
В этом виде пространственно-временной инвариант A05.18) уже
не зависит от ориентации систем отсчета S ш Sf относительно
друг друга, а также от направления скорости V. Однако в фор-
формуле A05.18) предполагается, что одно из событий фиксировано.
Таким событием является совмещение начал координат О и О1.
Чтобы освободиться от этого ограничения, запишем A05.18) в
виде
Ат2 - (Ах2 + Ау2 + Az2) = At12 - [Ах12 + Ay2 + Az12) = Inv,
A05.19)
где At, Аж, ..., Ат;, Аж;, ... означают разности между време-
временами и пространственными координатами двух событий 1 и 2 в
системах отсчета S и Sr:
Квадратный корень из инварианта A05.19) называется ин-
интервалом между рассматриваемыми событиями и в дальней-
дальнейшем обозначается через s\2 или As. Очевидно, квадрат интер-
интервала между событиями 1 и 2 можно представить в виде
s\2 = (т2 - пJ - 1\2 = {т'2 - т[J - 1% A05.20)
где 1\2 и 1^2 — расстояния между точками, в которых произошли
события, в системах S и S1 соответственно.
Мозсно также в формулы преобразования Лорентца ввести
параметры гит' вместо t и tf. Ограничиваясь частным случа-
случаем, представленным на рис. 328, перепишем формулы A05.12) в
виде
xf= XZ^, rf= TZ^. A05.21)
Величина /3 имеет смысл скорости движущейся системы коор-
координат, если за единицу принять скорость света.
Минковский A864-—1909) для описания пространственно-
временных событий ввел геометрическую терминологию. Сово-
Совокупность значений т, ж, у, z, характеризующую время и место
события, он назвал мировой точкой. Многообразие мировых то-
точек есть четырехмерное пространство, называемое миром или
пространством Минковского. Линия в пространстве Минков-
ского называется мировой линией. Интервал между двумя со-
событиями принимается за инвариантное расстояние между со-
соответствующими мировыми точками. На основе таких представ-

678 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
лений было создано тензорное исчисление в пространстве Мин™
ковского, аналогичное тензорному исчислению обычной эвкли-
эвклидовой геометрии. Оно является адекватным математическим ап-
аппаратом специальной теории относительности.
5. Интервалы между событиями можно разделить на веще-
вещественные и чисто мнимые. Ввиду инвариантности интервала,
это деление не зависит от выбора системы отсчета.
Поставим вопрос, можно ли выбрать такую систему отсчета,
в которой события 1 и 2 были бы одноместны^ т.е. происходи™
ли бы в одной и той же точке пространства? Если Sf — такая
система, то в ней 1'12 = 0, и на основании A05.20) квадрат ин-
интервала может быть представлен в виде s\2 — (Т2 ^TiJ- Отсюда
видно, что s\_2 > 0, т.е. необходимо, чтобы интервал s\2 был ве-
вещественным. Для доказательства достаточности этого условия
можно без нарушения общности ограничиться частным преоб-
преобразованием Лорентца A05.21). Чтобы рассматриваемые собы-
события в системе S' пространственно совпадали, достаточно, чтобы
выполнялось условие Ах1 = 0, т.е. Ах = /ЗАт. Отсюда вид-
видно, что система Sf должна двигаться со скоростью /3 = Аж/Ат.
Но для вещественных интервалов \Ах\ < Ат, так что |/3| < 1.
Значит, система Sf должна двигаться со скоростью, меньшей
скорости света, а потому ее можно реализовать. Промежуток
времени между одноместными событиями в системе отсчета S1
будет равен Атг = |si2|? или в обычных единицах At1 = |si2|/c.
Вещественные интервалы называются времениподобными.
Поставим теперь вопрос о существовании системы отсчета, в
которой события 1 и 2 были бы одновременны. Если Sf — такая
система, то т2 — т[ = 0 и, следовательно, на основании A05.20)
должно быть s\2 = ~1'\2- Значит, необходимо, чтобы интервал
s\2 был чисто мнимым. Достаточность этого условия доказыва-
доказывается совершенно так же, как в предыдущем случае. Расстояние
между точками, в которых произошли одновременные события
1 и 2, в системе S1 равно 1'12 = |si2|- Чисто мнимые интервалы
называются пространственноподобными.
Рассмотрим, наконец, особый случай, когда интервал между
событиями равен нулю. В этом случае, чтобы сделать события
одноместными, надо перейти к системе отсчета, движущейся со
скоростью света. То же требуется, чтобы события стали одновре-
одновременными. И то и другое невозможно. Нулевые интервалы назы-
называются световыми. Такими интервалами связаны отправление
светового сигнала из некоторой точки и приход его в другую
точку пространства.
6. В случае частного преобразования Лорентца A05.21), со-
соответствующего рис. 328, все изложенное можно наглядно ин-

105
ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА
679
терпретировать графически. Это возможно потому, что доста-
точно ограничиться рассмотрением преобразования только од-
одной пространственной координаты х и времени т, т.е. рассуж-
рассуждать так, как если бы пространство Минковского было двумер-
двумерной плоскостью (ж,т). Произвольное событие (мировую точку)
О в этой плоскости примем за начало прямоугольной системы
координат (рис. 332). Проведем через О взаимно перпендику-
перпендикулярные оси, одну из которых примем за пространственную ось ж,
а другую — за временную ось т в системе отсчета S. Штриховые
прямые т = ж и т = -ж будут мировыми линиями световых сиг-
сигналов, распространяющихся соответственно в положительном и
отрицательном направлениях оси X. Пусть А — произвольное
событие. Соединим точки А и О прямой мировой линией т =
= х tg а, описывающей равномерное движение какого-то тела
вдоль оси X со скоростью /3. Если /3 < 1, то с этим телом можно
связать систему отсчета S1', а прямую О А принять за простран-
пространственную ось X1. Ось времени т1 найдется из условия, что на ней
х1 = 0. Как видно из A05.21), это будет мировая линия х = /Зт,
т.е. прямая ОВ, наклоненная под тем же углом а = arctg/З, но
уже к временной оси т. В новой системе отсчета события О и А
будут одновременными, но не одноместными. События же О и
В одноместны, но не одновременны.
\
Абсолютно
\ будущие
Абс. удал.
0s
Абс. удал.
Абсолютно \
прошедшие
Рис. 332
Рис. 333
Вообще, все события по отношению к событию О молено раз-
разделить на абсолютно удаленные и абсолютно неодновременные
(т.е. абсолютно прошедшие и абсолютно будущие), как это по-
показано на рис. 333. Для первых интервал между событиями чи-
чисто мнимый, для вторых — вещественный. Границей между та-
такими событиями служат штриховые мировые линии световых
сигналов, распространяющихся в положительном и отрицатель-
отрицательном направлениях пространственной оси. В четырехмерном про-

680 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
странстве Минковского такой границей будет трехмерное мно-
гообразие, а именно конус т2 — х2 — у2 — z2 = 0, осью которого
является ось времени т. Он называется световым конусом.
Причинно связанными могут быть только события, ин-
интервал между которыми времениподобный. Например, событие
О (см. рис. 332) могло бы быть причиной события В, так как в
любой системе отсчета событие В наступает позлее события О.
Но события не могут быть причинно связанными, когда интер-
интервал между ними пространственноподобный. Таковы, например,
события О и А (рис. 332). В неподвижной системе отсчета S
событие А происходит позже события О. В штрихованной си-
системе (х',тг) оба эти события одновременны. Если же взять си™
стему отсчета, движущуюся быстрее системы (V,r;), но все еще
медленнее света, то ее пространственная ось будет на рис. 332
наклонена круче оси X'. В такой системе отсчета событие А
произойдет раньше события О. Таким образом, нельзя удовле-
удовлетворить требованию, чтобы в любой системе отсчета «причина»
предшествовала «следствию». Это и доказывает наше утвержде-
утверждение.
Прямая О А с уравнением т = /Зх есть мировая линия неко-
некоторого движения, происходящего со скоростью х/т = 1//3, т.е.
со сверхсветовой скоростью. Существование сверхсветовых ско™
ростей не противоречит теории относительности. Последняя до-
допускает любые скорости. Однако в случае распространения со™
стояний со сверхсветовыми скоростями интервал между любы-
любыми двумя состояниями будет пространственноподобным, а по-
потому каждое из этих состояний не может быть причиной дру™
того. Такие процессы не могут служить «сигналами» для пе-
передачи информации. Все тела и сигналы, передающие воздей-
ствие, не могут распространяться со скоростью, превышаю-
превышающей скорость света в вакууме. Скорость света в вакууме
есть максимально возможная скорость распространения вза-
взаимодействий 1).
§ 106. Лорентцово сокращение длины и замедление
времени
1. Если твердый стержень покоится в какой-то системе от-
отсчета, то его длина Iq определяется сравнением с масштабным
х) За последние примерно 10 лет обсуждается вопрос о существовании
гипотетических сверхсветовых частиц — тахионов. Ясно, что если бы та-
такие частицы существовали, то они не могли бы служить «сигналами» для
передачи взаимодействий. Подробнее см. Угаров В.А. Специальная теория
относительности.—М.: Наука, 1977.

§ 106 СОКРАЩЕНИЕ ДЛИНЫ И ЗАМЕДЛЕНИЕ ВРЕМЕНИ 681
стержнем, покоящимся в той же системе отсчета. Величину !q
можно назвать собственной длиной стержня, поскольку она не
зависит от выбора системы отсчета, в которой покоится стер™
жень. Но если стержень движется, то необходимо условиться,
что понимать под его длиной в покоящейся системе отсчета. Во
избежание недоразумений специально подчеркнем, что все из™
мерения расстояний и промежутков времени во всякой системе
отсчета должны производиться с помощью масштабных стерж-
стержней и часов, неподвижных в этой системе.
Длиной I движущегося стержня в покоящейся системе от-
отсчета называется расстояние между двумя точками в этой
системе, мимо которых концы стержня проходят одновремен-
одновременно. Для нахождения связи между I и Iq воспользуемся частной
формой преобразования Лорентца A05.12). Пусть стержень по™
коится в системе S1 и лежит на оси X1. Тогда разность коорди-
координат его концов Axf в системе Sr и будет длиной I® покоящегося
стержня. Разность же координат тех же концов Ах в системе S,
взятая в один и тот же момент t, будет длиной I движущегося
стержня. Но из первой формулы A05.12) при t = const следует
Ах' = Axj \/\ — /З2, а потому
1 = !0\/1-/32. A06.1)
Таким образом, длина движущегося стержня короче, чем
покоящегося. Это явление называется лорентцовым сокращени-
сокращением длины. Первоначально оно было введено независимо друг от
друга Фицжеральдом A851—1901) и Лорентцом. Но у них это
была гипотеза ad hoc, специально придуманная для объяснения
отрицательного результата опыта Майкельсона, хотя Лорентц и
пытался обосновать ее с точки зрения электронной теории. В
теории относительности лорентцово сокращение получается, а
его истинный физический смысл устанавливается без каких бы
то ни было добавочных предположений. Это, конечно, не ис-
исключает возможности атомистического объяснения лорентцова
сокращения, а также явления замедления хода движущихся ча-
часов, о котором говорится дальше. Но для этого надо располагать
не только уравнениями электродинамики, но и пока еще не из™
вестными законами, определяющими строение вещества. Когда
такие законы будут установлены, можно на их основе рассмо™
треть и вопрос об изменении длин и времен. Однако если те-
теория относительности верна, то результат такого рассмотрения
заранее известен. Правильные законы природы должны быть
инвариантны относительно преобразования Лорентца, а пото-
потому в вопросе о сокращении длин и замедлении времени они не
могут привести к иным результатам, чем теория относительно-
относительности.

682 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
2. Рассмотрим теперь какие-либо два события, интервал
между которыми времениподобный. Промежутки времени At
и Aif между этими событиями, измеренные в «неподвижной» S
и «движущейся» Sf системах отсчета, вообще говоря, будут раз™
ными. Конечно, обе системы S и Sf совершенно равноправны,
так что между At и At; может существовать любое соотношение
At ^ At;. Допустим теперь, что в качестве движущейся систе-
системы S1 взята такая, в которой оба события происходят в одном
и том же месте пространства. (В случае времениподобных
интервалов такая система существует, см. п. 5 предыдущего па-
параграфа.) Тогда система Sf становится выделенной среди всех
прочих инерциальных систем отсчета. Время, измеренное в та-
такой системе, будем обозначать через to, а в «неподвижной» си-
системе S — по-прежнему через t. Для нахождения соотношения
между At и A to будем предполагать, что в A05.14) координа-
координата х1 постоянна, т.е. одна и та же для обоих событий. Тогда из
последней формулы A05.14) получим At = At'/л/1 — /З2. Но,
согласно нашему определению, At; и есть A to- Следовательно,
A06.2)
Из A06.2) видно, что Ato < At, т.е. промежуток времени
между двумя событиями минимален в той системе отсчета,
в которой эти события одноместны. Это явление называется
замедлением хода движущихся часов. Причина такого назва-
названия заключается в следующем. Допустим, что взяты какие-то
одни часы, помещенные в одну из точек системы Sf. Такие часы
называются «движущимися», поскольку они движутся вместе с
системой Sf. Все же часы, покоящиеся в системе S, называются
«неподвижными». Ясно, что в системе S1 любые два события,
происходящие в месте нахождения «движущихся» часов, будут
одноместны, так что эти часы измерят промежуток времени Ato.
Здесь моменты наступления обоих событий отмечаются по од-
одним и тем же («движущимся») часам, так что никакой син-
синхронизации не требуется. Напротив, в «неподвижной» системе
S моменты наступления событий отмечаются по часам, находя-
находящимся в различных местах пространства. Для измерения At
необходимо иметь двое часов^ синхронизованных между собой
по правилу Эйнштейна. С этим и связана асимметрия при из-
измерении времени по «неподвижным» и «движущимся» часам,
проявляющаяся в неравенстве Ato < ^t.
3. Допустим теперь, что какая-либо частица движется от-
относительно «неподвижной» системы отсчета S по криволиней-
криволинейной траектории с переменной по величине скоростью у. В спе-
специальной теории относительности допускаются только такие
пространственно-временные системы отсчета, которые движут-

§ 106 СОКРАЩЕНИЕ ДЛИНЫ И ЗАМЕДЛЕНИЕ ВРЕМЕНИ 683
ся относительно S равномерно и прямолинейно. Возьмем беско-
бесконечное множество таких систем, движущихся со всевозможными
скоростями и во всевозможных направлениях. Система отсчета,
относительно которой мгновенная скорость частицы равна ну-
нулю, и связанные с ней часы называются сопутствующими. При
движении частица непрерывно переходит из одной сопутствую™
щей системы отсчета в другую. Разобьем траекторию частицы
в системе S на бесконечно короткие отрезки. Пусть dt — вре-
время, затрачиваемое в системе S на прохождение одного из таких
отрезков. Согласно A06.2), по сопутствующим часам на то же
движение потребуется время dto = dty/l — v2/c2. Конечный про™
межуток времени, измеренный по неподвижным часам, предста-
представится интегралом
h-h= f-zJt=, (Юб.з)
J у 1 — v2 /с2
взятым по всей траектории движения.
Если часы движутся вместе с частицей, то возникает вопрос,
как связана длительность, измеренная по таким часам, с дли-
длительностью, измеренной по сопутствующим часам? На этот во-
вопрос нельзя ответить без рассмотрения конкретного устрой-
ства часов^ так как при ускоренном движении появляются силы
инерции, влияющие на ход часов. Например, в случае движения
пружинных часов силы инерции могут деформировать балан-
балансир или другие части их. Деформации могут быть настолько
большими, что часы остановятся или сломаются. Маятниковые
часы вообще станут непригодными для измерения времени в
отсутствие поля тяготения. Сердце живого организма (а оно в
принципе может рассматриваться тоже как «часы») перестанет
биться, а сам организм погибнет, если ему сообщить достаточно
большое ускорение, и т.д. Однако в принципе допустимы и такие
часы, на ход которых сила тяжести и силы инерции оказывают
ничтожное влияние, в пределе совсем исчезающее. Такие часы
условимся называть идеальными. Измеряемая ими длительность
совпадает с длительностью, измеренной по сопутствующим ча-
часам. Этот признак в принципе позволяет экспериментально про-
проверить, являются ли те или иные конкретные часы идеальными
или не являются. Ясно, что в формуле A06.3) под to можно по-
понимать время, отсчитываемое по идеальным часам^ движущим-
движущимся вместе с частицей. Это время называется собственным вре~
менем, поскольку оно инвариантно, т.е. не зависит от движения
частицы. Из A06.3) видно, что длительности по «неподвижным»
и «движущимся» идеальным часам связаны соотношением
*2-*1>*02-*01. (Юб.4)
В частности, если часы вернутся в исходное положение (относи-

684 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
тельно системы S), то они покажут время, меньшее времени по
«неподвижным» часам.
4. Наилучшим приближением к идеальным часам являют™
ся атомные и в особенности ядерные часы. Силы инерции по
своему действию эквивалентны гравитационным силам (см. т. I,
§ 71). В обычных условиях как те, так и другие силы пренебре-
пренебрежимо малы по сравнению с электрическими и еще более мощны-
мощными ядерными силами, определяющими процессы в электронных
оболочках и ядрах атомов. В таких процессах гравитационные
силы и силы инерции практически не играют никакой роли.
Рассмотрим, например, атом цезия™ 133 в цезиевых эталон-
эталонных часах^ с помощью которых устанавливается эталон вре-
времени — секунда. По принятому соглашению электромагнитное
излучение такого атома в отсутствие внешних полей соверша-
ет v = 9192 631770 ~ 1010 колебаний в секунду. Радиус ато-
атома ~ 10^8 см. Если атом уподобить гармоническому осцилля-
осциллятору, то при колебаниях будут развиваться громадные уско-
рения ^ BтшJг ^ ID13 см/с2. Если часам сообщить ускорение
~ 1 см/с2, то для этого потребуются силы в 1013 раз слабее.
Ясно, что никакого существенного действия на процессы вну-
внутри атома они оказать не могут. Только при измерениях време-
времени с относительной точностью ~ 1СП12-1СП13 такие ускорения
и соответствующие им гравитационные поля, возможно, могут
сказаться на ходе часов и результатах измерений. Тогда их на-
надо учитывать. Из сказанного ясно, что из всех часов атомные
и ядерные часы являются, пожалуй, единственными, которые
пригодны для обнаружения и исследования релятивистского за-
замедления времени, по крайней мере при скоростях, малых по
сравнению со скоростью света.
Явление радиоактивного распада атомов или других неста-
нестабильных частиц может выполнять роль идеальных часов. Ра-
Радиоактивный распад подчиняется закону
п = пое"*/т, A06.5)
где по — начальное число частиц, an — число их через вре-
время t. Постоянная т называется временем эюизни рассматривае-
рассматриваемой нестабильной частицы. О времени t можно судить по отно-
отношению п/щ. Релятивистское замедление времени было подтвер-
подтверждено в явлении распада мюонов (/i-мезонов). Так называют-
называются нестабильные заряженные частицы, масса которых в 207 раз
превышает массу электрона. Заряд мюона равен заряду электро-
электрона, но может быть и положительным, и отрицательным. Мюоны
образуются в космических лучах в верхних слоях атмосферы (на
высотах порядка 10 км). Сравнение интенсивностей потока мю-
мюонов в космических лучах на горе и у ее основания показало,

§ 106 СОКРАЩЕНИЕ ДЛИНЫ И ЗАМЕДЛЕНИЕ ВРЕМЕНИ 685
что среднее время жизни мюона в лабораторной системе отсче-
отсчета т ^ 10^5 с. С другой стороны, космические мюоны можно
было замедлить в свинцовом блоке и с помощью специального
устройства отфильтровать медленные мюоны. Измерения пока-
показали, что время жизни медленного (покоящегося) мюона tq «
~ 2,20 • 1СР6 с. Если бы не было релятивистского замедления
времени, то поток космических мюонов, даже если бы они дви-
двигались со скоростью света, уменьшался бы в е раз при прохо™
ждении расстояния ^ 600 м. На расстоянии уже 5 км их интен™
сивность уменьшилась бы в е50/6 ~ 4000 раз, т.е. мюоны вообще
не могли бы достигать поверхности земли. В действительности
их интенсивность при прохождении такого расстояния умень™
шается примерно в е5/3 ~ 5 раз. Учет релятивистского замедле-
замедления времени устраняет это противоречие. Действительно, время
жизни мюона в лабораторной системе отсчета т связано с соб-
собственным временем жизни соотношением т = то/у 1 ~~ /З2- Из-
Измерение средней кинетической энергии космических мюонов по™
казало, что она « 109 эВ. По этой энергии нетрудно рассчитать
у/1 — /З2 «0,1. Поэтому следует ожидать, что т^2,2 • 10~6/0,1«
^2 • 10~5 с. Это по порядку величины согласуется со значением,
полученным на опыте.
5. С построением мощных ускорителей заряженных частиц
опыты подобного рода производились в более определенных и
лучше контролируемых условиях. Наиболее подходящими ча-
частицами для таких опытов оказались заряженные пионы (иначе
называемые тг-мезонами). Их масса в 273 раза больше массы
электрона, а заряд равен заряду электрона. Пионы во множе-
множестве образуются при взаимодействии протонов высоких энергий
с веществом. Среднее время жизни пиона в системе отсчета, где
он покоится, то = 2,60 • 10^8 с. На циклотроне Колумбийского
университета был получен пучок пионов со скоростью v = 0,75 с
(/3 = 0,75). Если бы не было релятивистского замедления време™
ни, то за время tq пучок проходил бы расстояние 0,75 • 3 • 1010 х
х 2,60 • 10^8 = 5,85 м. На самом деле, как показали измерения,
расстояние, на котором интенсивность пучка уменьшается в е
раз, равно 8,5 =Ь 0,6 м, т.е. в лабораторной системе время жизни
пиона т в 1,45 ±0,11 раза больше собственного времени жиз-
жизни то. Но это хорошо согласуется с формулой t/tq = lj\Jl — /З2,
которая дает t/tq = 1,51.
Результат опыта можно интерпретировать и как проявление
релятивистского сокращения длины. Действительно, в системе
отсчета, где пион покоится, его время жизни равно tq. Лабора-
Лаборатория движется относительно пиона со скоростью v. За время

686 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
то она проходит в системе пиона расстояние I = vtq. Если то же
расстояние измерять масштабным стержнем, который покоится
в лаборатории, то оно окажется равным 1ц = I/ у 1 — /З2 = 8,8 м,
что согласуется с опытом.
6. Хафель и Китинг поставили опыт для обнаружения ре-
релятивистского замедления хода часов уже в макроскопических
условиях. В этом опыте четыре экземпляра цезиевых часов в ок-
тябре 1971 г. были помещены на реактивных самолетах, облетев-
облетевших вокруг земного шара в восточном и западном направлени-
направлениях. Временные интервалы tB0CT и t3an? измеренные по часам, дви-
двигавшимся соответственно на восток и на запад, сравнивались с
интервалами tHen, измеренными эталонными неподвижными ча-
сами, находившимися в Морской обсерватории в Вашингтоне.
После усреднения по четырем движущимся часам получились
такие результаты:
Wt - tHen = (-59 ± 10) • Ю-9 с, t3an - W = B73 ± 7) ¦ Ю-9 с.
Посмотрим, что следует ожидать согласно теории относи-
относительности. Ускорение центра Земли, вызванное гравитационным
притяжением Солнца, составляет примерно 0,18 ускорения, ко™
торое получают точки земного экватора из-за осевого вращения
Земли. Хотя это ускорение и немало, его можно не принимать
во внимание, ввиду принципа эквивалентности сил тяготения
и сил инерции (см. т. I, § 71). Если не учитывать неоднород-
неоднородность гравитационного поля Солнца, то это поле будет полно-
полностью компенсировано центробежной силой инерции, обусловлен-
обусловленной вращением центра Земли вокруг Солнца. Таким образом,
можно считать, что относительно инерциальной системы отсче-
отсчета центр Земли движется прямолинейно и равномерно. Поэтому
невращающаяся система отсчета с началом координат в центре
Земли практически будет также инерциальной системой отсче-
отсчета. Ее мы и используем в последующих рассуждениях. Пусть
самолеты облетают земной шар по параллели со скоростью v
относительно Земли на постоянной высоте h. Их скорости отно-
относительно инерциальной системы отсчета будут FB0CT = V® + v,
^4ап — Vq — vj гДе Vq — скорость наземной лаборатории в той
же системе. Сначала будем считать, что h = 0. Тогда, если to —
собственное время, то
Аналогично,
0' зап ^ 0 9™^
Вычтем отсюда предыдущие выражения и учтем, что в оконча-
окончательных формулах в пределах точности расчета время to можно

106 СОКРАЩЕНИЕ ДЛИНЫ И ЗАМЕДЛЕНИЕ ВРЕМЕНИ 687
заменить на tHen. Тогда получим
_ 2Vqv + v2 _ 2Уоу - у'2
^вост 6неп — п 2 ^неп? 6зап ^неп — « 2 ^неп
Естественно, под tHen надо понимать время нахождения само™
летов в воздухе без учета времени остановок, так как время
остановок не влияет на величину разностей tB0CT — tHen и i3an ~~
Допустим, что самолет облетает земной шар в течение суток.
Тогда для широты Вашингтона потребуется скорость v = V® ^
^1000 км/ч « 300 м/с. По формулам A06.6) найдем tB0CT^tHen^
« -130 • 10"9 с, t3an - tnen « +43 • 10^9 с.
В приведенном вычислении не учтено влияние гравитацион-
гравитационного потенциала Земли на течение времени (см. § 109, а также
т. I, § 72). С учетом этого обстоятельства оба выражения A06.6)
надо увеличить на
AtrpaB = |JtHen, A06.7)
где h — высота полета, ag - ускорение свободного падения на
поверхности Земли. Если положить h = 10 км, то в приведенном
выше примере получится AtrpaB = 94 • 10™9 с, т.е. «гравитаци-
«гравитационный эффект» того же порядка, что и учтенный выше «кине-
«кинематический эффект». Хафель и Китинг провели вычисление с
учетом этой поправки, выполнив интегрирование по фактически
совершенным маршрутам самолетов. Они получили теоретиче™
ские значения:
Wt - tHen = (-40 ± 23) • 1(Г9 С, t3an - tHen = B75 ± 21) • 1(Г9 С,
удовлетворительно согласующиеся с полученными на опыте. За-
Заметим, что из разности (i3an ^^вост) поправка AtrpaB исключает-
исключается. Эта разность обусловлена только «кинематическим эффек™
том» замедления времени. Совпадение теоретических результа-
результатов с измеренными на опыте рассматривается как доказатель-
доказательство не вызывающего сомнения релятивистского замедления хо-
хода движущихся часов.
7. Остановимся в заключение на так называемом парадоксе
близнецов. Из двух братьев-близнецов А остается на Земле, а В
отправляется в кругосветное путешествие на межзвездном ко-
корабле, двигаясь со скоростью, близкой к скорости света. Через 5
лет по своим часам брат В возвращается обратно и находит бра-
брата А глубоким стариком. Оказалось, что за время путешествия
по часам на Земле прошло 50 лет. Таким образом, открывается
возможность за время человеческой жизни совершать не толь-
только путешествия к далеким звездным мирам, но и путешествия
в будущее. Если отвлечься от технической и практической сто-
стороны вопроса, то такие путешествия принципиально возможны.

ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
В самом деле, биологические процессы не представляют собой
какую-то обособленную группу явлений природы. Как и прочие
явления природы, они подчиняются законам физики. Если на
межзвездном корабле создать условия, близкие к условиям на
Земле, то и жизненные процессы на нем будут протекать прак-
практически так же, как и на Земле. Биения сердца в человеческом
организме выполняют роль часов. Если за время жизни сердце
человека на Земле совершает 2-Ю9 ударов, то столько лее ударов
оно совершит и на корабле. Но движущиеся часы идут медлен-
медленнее неподвижных. Если за время путешествия сердце брата В
совершит 1,5 • 108 ударов, то на Земле к моменту встречи сердце
брата А успеет совершить ударов в 10 раз больше. Но это и есть
«парадокс близнецов».
В 1974 г. парадокс близнецов был подтвержден эксперимент
тально на ускорителе в ЦЕРНе (Европейский центр по ядерным
исследованиям, Швейцария). Ускоренные мю-мезоны удержива-
удерживались магнитным полем на круговой орбите радиуса 5 м в течение
свыше 150 мкс. За это время они совершали более 105 оборотов.
Энергия мезонов превышала энергию покоя примерно в 12 раз,
так что 1/у 1 — /З2 = 12. Поэтому ожидаемое время жизни мезо™
на в лабораторной системе должно составлять 2,2-12 = 26,4 мкс.
Опыт дал для этого времени 26,37 =Ь 0,05 мкс.
§ 107. Эффект Доплера и аберрацмм света
1. Если в «неподвижной» системе S распространяется моно-
монохроматическая волна с определенной частотой шив определен-
определенном направлении, то в «движущейся» системе S1 та же волна
будет иметь другую частоту а/ и распространяться в другом
направлении. Изменение частоты волны при переходе от одной
системы отсчета к другой называется эффектом Доплера A803—
1853), а изменение направления — аберрацией света. При изло-
изложении теории этих явлений мы ограничимся случаем, когда све-
световая волна распространяется в вакууме. Тогда в обеих систе-
системах отсчета пространство, в котором распространяется волна,
будет изотропным. При наличии же среды изотропия сохра-
сохранится только в той системе отсчета, в которой среда покоится.
В системе отсчета, относительно которой среда движется, появ-
появляется анизотропия, вносящая осложнения в теорию эффекта
Доплера и аберрации в материальных средах.
В релятивистской теории изменение частоты и направления
распространения волны проще всего можно определить из усло-
условия равенства фаз одной и той же волны в обеих системах отсче™
та. Предполагая, что волна плоская, это условие можно записать

§ 107 ЭФФЕКТ ДОПЛЕРА И АБЕРРАЦИЯ СВЕТА 689
в виде
о;* - кг = о/t'- к'г', A07.1)
где г, t и r;, tf — координаты и время одного и того же события в
рассматриваемых системах отсчета, причем начало отсчета вре-
мени выбрано так, что в момент совмещения начал координат
обеих систем t = tf = 0.
Для доказательства сформулированного условия предполо-
предположим, что в началах координат в момент t = f = 0 на волне
сделана метка, переносимая волной с фазовой скоростью, так
что фаза колебания в месте нахождения метки в обеих систе-
системах отсчета будет (р\ = (fi =0. Вообразим теперь произвольно
движущихся наблюдателей i и i', из которых А для опреде-
определения своего положения в пространстве и времени пользуется
координатами и часами системы 5, а А1 — координатами и часа-
часами системы S'. Можно, например, не нарушая общности, пред-
предположить, что наблюдатель А покоится в системе отсчета 5,
а наблюдатель А1 — в системе отсчета S''. Однако это предпо-
предположение в такой специальной форме не обязательно. (Обычно
при рассмотрении эффекта Доплера систему S связывают с ис-
точником, а систему Sf — с наблюдателем.) Оба наблюдателя
начинают счет проходящих мимо них волн с того момента, ко-
когда мимо них проходит сделанная метка. Пусть оба наблюдателя
встречаются друг с другом. Обозначим через г, t координаты и
время этого события в системе Я, а через r;, tf — в системе Sf.
Наблюдатель А найдет, что к моменту встречи фаза пришедше-
пришедшего к нему колебания будет ср2 = uji — kr, и сосчитает к этому
моменту
^ _ у?2 - pi _ ut - kr
~~ 2тг ~~ 2тг
волн. Наблюдатель А1 найдет, что к моменту встречи мимо него
прошло
N, = ш? - kY
2тг
волн. Но число прошедших волн не может зависеть от того, кто
их считает, а потому
N = Nf, или ujt - kr = uj'i1 - kV,
что и требовалось доказать.
Для нахождения формул, определяющих преобразование ча-
частоты и направления распространения волны в релятивистской
теории, достаточно в формуле A07.1) выразить переменные
г(ж, |/, z) и t через переменные г;(ж;, у1\ z1) и t;, воспользовавшись
для этого формулами преобразования Лорентца A05.14). Сде-
Сделав это и сравнив коэффициенты при одинаковых переменных,

690 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
получим
, = ш-кхУ (Ж 2)
^х' /i _ R2 ' ^у' ^у> ^z' ^z'
Аналогично получаются формулы обратного преобразования:
ш = ш' + к*'У', A07.4)
Формулы A07.2) и A07.4) описывают эффект Доплера, а фор-
формулы A07.3) и A07.5) — аберрацию света.
2. Рассмотрим частный случай, когда волна распространя-
распространяется вдоль оси X. В этом случае полагаем в формуле A07.2)
кх = ш/с и получаем
Изменение частоты в этом случае называется продольным эф-
эффектом Доплера. Понятно, что результат A07.6) можно полу-
получить и из общей формулы A07.4). Частота волны при наблю-
наблюдении из системы Sf уменьшается, когда эта система движется
в направлении распространения волны, и увеличивается, когда
она движется навстречу волне. При медленных движениях, ко™
гда можно пренебречь квадратами отношения /3 = F/c, формула
A07.6) переходит в
а/ « шA -Р)= шA - V/c). A07.7)
3. Рассмотрим теперь второй частный случай, когда наблю-
наблюдение ведется в системе отсчета S1 и притом перпендикулярно
к направлению распространяющейся в ней волны. В этом слу-
случае удобнее воспользоваться формулой A07.4), полагая в ней
к'х! =0. Это дает
о/ = шл/l-P2 « шA - f/2). A07.8)
Происходит смещение частоты в длинноволновую область спек-
спектра во втором порядке по /3. Это — чисто релятивистский эф-
эффект, невозможный в классической (дорелятивистской) теории.
Он называется поперечным эффектом Доплера.
Для установления физического смысла поперечного эффекта
Доплера предположим, что мимо наблюдателя прошел цуг из N
волн. Наблюдатель измерил по своим часам время прохождения
этого цуга и нашел для него значение t'. Очевидно, а/ = 2/jrN/t/.

§ 107 ЭФФЕКТ ДОПЛЕРА И АБЕРРАЦИЯ СВЕТА 691
Найдем длительность того же процесса по часам системы S. Для
этого надо отметить показания таких часов в моменты прохо-
прохождения начала и конца цуга мимо наблюдателя. Разность этих
показаний и определит длительность цуга t по часам системы S.
Опять можно написать а; = 2тгNjt и, следовательно, uof/ш = t/t1.
В этих измерениях время f измеряется с помощью одних и тех
же часов, неподвижных относительно наблюдателя, а для изме-
измерения времени t надо пользоваться различными часами системы
S, синхронизованными между собой. Поэтому часы наблюдате-
наблюдателя надо рассматривать как «неподвижные», а все часы системы
S — как «движущиеся» (см. § 106, п. 2). Но движущиеся часы
идут медленнее неподвижных, причем t/tf = у 1 — /З2, а потому
и/ = шл/l — /З2. Таким образом, поперечный эффект Доплера
есть не что иное, как проявление релятивистского эффекта за-
замедления хода движущихся часов. Тем же эффектом объясня-
объясняется появление квадратного корня д/l — /З2 в формулах A07.2)
и A07.4).
4. Поперечный эффект Доплера впервые удалось наблюдать
Айвсу и Стилуэллу в 1938 г., а затем в 1941 г. Источником
света служил пучок каналовых лучей атомов водорода, несу™
щихся со значительной скоростью v ~ 108 см/с. Специальная
конструкция трубки обеспечивала высокую однородность кана-
ловых лучей по скоростям. Скорость v вычислялась по прило-
приложенному к электродам напряжению и по величине продольного
доплеровского эффекта. Свет, испущенный движущимися ато-
атомами перпендикулярно к направлению их движения, попадал
в спектрограф. По оценке авторов спектрограф давал возмож-
ность измерять длину волны с точностью 0,00025 нм. Главная
трудность опыта состояла в том, что при отклонении направле-
направления пучка каналовых лучей от строгой перпендикулярности к
линии наблюдения поперечное доплеровское смещение, пропор-
пропорциональное (v/cJ, могло оказаться перекрытым более сильным
продольным эффектом Доплера, поскольку этот эффект — пер-
первого порядка по (vcost?)/с (i? — угол между скоростью атома и
линией наблюдения). При скорости атома v « 108 см/с оба эф-
эффекта сравнимы между собой уже при $ ~ 5;. Эта трудность
была преодолена тем, что ось спектрографа устанавливалась
перпендикулярно к плоскости зеркала. В спектрограф попадал
не только свет, непосредственно излученный атомом, но и свет,
отраженный от зеркала. Последний можно рассматривать как
свет, излученный движущимся изображением атома. Если атом
движется под углом $ к линии наблюдения, то его изображение
в зеркале будет двигаться под углом тг — #. Доплеровские сме-
смещения первого порядка для атома и его изображения в зеркале

692 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
будут равны по величине, но противоположны по знаку. Если бы
не было смещения второго порядка, то в спектрографе наблю-
наблюдались бы две линии Ai = А — А А и А2 = А + А А, симметрично
расположенные относительно исходной линии А. Эта симметрия
будет нарушена поперечным доплеровским смещением 8А, ко-
которое происходит всегда в длинноволновую сторону спектра. С
учетом этого Ai = А — АА + 8\, А2 = А + АА + SX. Отсюда
Г\ Al + А2 л
= 2 ~
Таким путем удается отделить квадратичный (поперечный) эф-
эффект Доплера от линейного (продольного). Согласно A07.8), из™
менение длины волны при поперечном эффекте Доплера опре-
определяется выражением
6Х = ^А/52. A07.9)
В одном из опытов при напряжении на трубке 6788 В ожидае-
ожидаемое смещение, вычисленное по напряжению, должно было быть
SX = 0,00116 нм, а вычисленное по линейному доплеровскому
смещению 0,00109 нм. Опыт дал SX = 0,0011 нм. Подобное со-
согласие получалось и при других напряжениях на трубке.
Результаты Айвса и Стилуэлла были подтверждены и дру-
гими учеными. Это были первые опыты, на которых впервые
было экспериментально доказано релятивистское замедление
времени, хотя сами Айве и Стилуэлл, ничего не говоря о теории
относительности, пытались интерпретировать их с точки зрения
старой теории эфира.
5. Перейдем теперь к аберрации света. Введем единичные
векторы N и N7 в направлении распространения волны в систе-
системах отсчета S ш Sf. Тогда k = cjN/c, k; = o/N'/c, и из формул
A07.2) и A07.3) получим
Аберрация света была открыта в 1727 г. королевским астро-
астрономом Брадлеем A692-—1762) при наблюдении звезд в телескоп.
По этой причине ее называют также астрономической аберраци-
аберрацией. При описании этого явления в качестве «неподвижной» си-
системы отсчета S возьмем систему Коперника (в которой Солнце
считается неподвижным), а в качестве «движущейся» системы
Sr — систему, связанную с Землей. При этом мы полностью от-
отвлечемся от вращения Земли вокруг собственной оси и будем
рассуждать так, как если бы этого вращения совсем не было.
Оси X и X1 выберем в направлении орбитального движения Зем-
Земли, скорость которого обозначим через V. Ось Y направим про™
извольно, но перпендикулярно к направлению движения Земли.

107
ЭФФЕКТ ДОПЛЕРА И АБЕРРАЦИЯ СВЕТА
693
Обозначим далее через а угол между направлением на звезду
(направлением оси телескопа) в системе S и положительным на-
направлением оси Y (рис. 334). Тогда
Nx = ^slno, Ny = ^coso, Nz = 0.
Соответствующие величины в системе
S' обозначим теми же буквами, но со
штрихами. После подстановки в первую
формулу A07.10) получим
Y, Y'
sin a =
1 + /3 sin a '
или
sin а =
sin с/ — В
A07.11)
A07.12)
х,х
Рис. 334
1 — /3 sin af'
Формулами A07.11) и A07.12) и опре-
деляется направление распространения
волны в одной из систем отсчета, если известно это направление
в другой системе отсчета.
Рассмотрим частный случай, когда свет в системе S распро-
распространяется вдоль оси Y. В этом случае а = 0, и следовательно,
slW = /3. A07.13)
Для того чтобы увидеть звезду в телескоп, его необходимо из
перпендикулярного положения наклонить вперед на угол а;,
определяемый формулой A07.13). Угол а' называется углом
аберрации. В аналогичном случае, когда свет в системе S1 рас™
пространяется вдоль оси Y1', т.е. когда а' = 0, получим
sfno = -/3. A07.14)
Телескоп надо наклонить на такой же угол, но уже назад. Ско-
Скорость орбитального движения Земли V « 30 км/с, так что а «
^F/c^lO^4 рад ^20,5/;.
Если бы скорость V оставалась постоянной по величине и на™
правлению, то видимое положение звезд на небесном своде оста™
валось бы неизменным и заметить аберрацию было бы нельзя.
В действительности направление движения Земли по ее орбите
непрерывно изменяется. Вследствие этого из-за аберрации будет
изменяться и видимое положение звезд на небесном своде. Через
полгода направление движения Земли изменится на противопо-
противоположное, а угол аберрации изменит знак. Если звезда находится
в плоскости земной орбиты, то ее видимое положение будет со-
совершать в той же плоскости прямолинейное колебание с угло-
угловой амплитудой а = V/c = 20,5/; и периодом в один год. Если
направление на звезду (в системе S) перпендикулярно к плоско-
плоскости земной орбиты, то видимое положение ее на небесном своде
будет описывать окружность с угловым радиусом 20,5/;. Во вся-

694 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
ком промежуточном положении траекторией видимого положе-
положения звезды будет эллипс, большая полуось которого имеет такие
лее угловые размеры. Так выглядело бы явление аберрации света
в воображаемом идеальном случае, если бы единственным дви™
жением Земли было только ее движение по круговой орбите во-
вокруг Солнца. В действительности аберрация света есть ничтож™
ный эффект, накладывающийся на движение звезд по небесно-
небесному своду, обусловленное вращением Земли вокруг собственной
оси. Требовалась исключительная наблюдательность и экспери-
экспериментальное искусство, чтобы выделить и измерить этот эффект.
Это и было сделано Брадлеем.
Подчеркнем особо, что явление аберрации света не имеет ни™
какого отношения к самой скорости движения звезд относитель-
относительно Земли. Оно отражает только изменение скорости этого от™
носительного движения, обусловленное движением Земли. Вот
почему аберрация света одна и та же для всех звезду хотя их
скорости относительно Земли весьма различны.
6. Брадлей видел в явлении аберрации доказательство конеч-
конечности скорости распространения света. Измерив угол аберрации
а, он вычислил эту скорость но формуле а = V/с. По времени
это было второе (после Рёмера) измерение скорости света. Сам
Брадлей истолковал открытое им явление с точки зрения ньюто™
новской корпускулярной теории света. В нерелятивистской ки-
кинематике скорости световой корпускулы v и v; в системах от-
отсчета S и S' связаны соотношением v = v; + V. Ограничимся
случаем, когда в системе S световая корпускула движется по
оси Y со скоростью у у = —с. В системе S1 появляется составля-
составляющая скорости корпускулы в перпендикулярном направлении
vx = vx — Vx = —V. Из-за этого траектория корпускулы в си-
системе 5" будет наклонена к оси Y под углом а7, определяемым
формулой
tga' = vf = ^=p. A07.15)
У
Этой формулой в ньютоновской корпускулярной теории и опре-
определяется угол аберрации. При малых углах а1 она совпадает с
релятивистской формулой A07.13), если пренебречь квадратич-
квадратичными членами по /5. Если бы к движению световой корпускулы
применить релятивистский закон сложения скоростей (с учетом
того, что скорость корпускулы по абсолютной величине равна
с), то получились бы в точности прежние релятивистские фор-
формулы A07.10). Наблюдение аберрации света не позволяет, еле™
довательно, сделать выбор между волновой и корпускулярной
теориями света.
7. Истолкование аберрации в волновых теориях света, да-
даже в их электромагнитной форме, встретило большие трудно-

§ 108 ЭФФЕКТ ДОПЛЕРА В АКУСТИКЕ И ТЕОРИИ ЭФИРА 695
сти, пока эти теории оставались механистическими. Все они бы-
ли неудовлетворительны уже по той причине, что вводили про-
произвольные предположения относительно механических свойств
эфира и его движения относительно Земли. Впервые безупреч™
ная и в идейном отношении необычайно простая теория аберра-
аберрации света (и оптического эффекта Доплера) была дана только
в теории относительности.
В связи с этим затронем один вопрос, поставленный в эфир™
ной теории света. Что будет с углом аберрации, если телескоп
для его измерения заполнить водой? На этот вопрос эфирные
теории света давали различный ответ, в зависимости от того,
какие предположения вводили они о движении эфира относи-
относительно Земли и т.п. Опыт был поставлен Эйри в 1871 г. Ока™
залось, что при заполнении телескопа водой угол аберрации не
изменяется. Объяснение этого результата в теории относитель-
ности не представляет затруднений. Для простоты рассуждений
обратим направление распространения света, предположив, что
источник света помещен в главном фокусе объектива телескопа.
Поскольку нет никакого эфира, в системе отсчета, где телескоп
покоится, вода или воздух, заполняющие его, а также стекло са-
мого объектива телескопа оптически изотропны. В этой системе
отсчета лучи выйдут из телескопа параллельно главной оптиче-
оптической оси, независимо от того, заполнен ли телескоп водой или не
заполнен. Для определения угла аберрации надо выполнить пе-
переход к движущейся системе отсчета S1. Но это можно сделать
для волны, уже вышедшей из телескопа. Направление этой вол-
волны совершенно не зависит от того, какой средой заполнен сам
телескоп. Наличие телескопа и этой среды на таком переходе
никак не отразится. Следовательно, и угол аберрации не будет
зависеть от среды, заполняющей телескоп.
§ 108. Эффект Доплера в акустике и теории эфира
Эффект Доплера был открыт самим Доплером в 1842 г. на акусти-
ческих волнах. В дальнейшем теория этого эффекта была перенесена без
всяких изменений в оптику. При этом предполагаласв справедливоств вол-
волновой эфирной теории света. Место воздуха, в котором распространяются
звуковые волны, в оптике занял световой эфир. В осталвном все рассужде-
рассуждения в акустике и оптике бвши абсолютно тождественны. Эфирная теория
безвозвратно ушла в область истории. Но акустический эффект Доплера
полностью сохранил свое значение. Поэтому имеет смысл изложить здесь
теорию этого эффекта. Поскольку, однако, этот том посвящен оптике, мы
по-прежнему будем говорить о световых волнах в эфире. Для перехода к
акустике слово «эфир» надо заменить словом «воздух», а световые волны —
звуковыми.
В эфирной теории, помимо источника и наблюдателя, в явлении при-
нимает участие промежуточная среда — световой эфир. С этим связаны

696 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
усложнение и неопределенность эфирной теории эффекта Доплера, по™
скольку в каждом конкретном случае мы не можем сказать, как движутся
источник и наблюдатель относительно «неуловимого» эфира. Различные
теории эфира отличались друг от друга прежде всего тем, как они выбира-
выбирали систему отсчета, в которой эфир покоится и, следовательно, ведет себя
как оптически изотропная среда. Пусть в эфире распространяется плоская
монохроматическая волна. Ее частоту в системе отсчета, в которой эфир
покоится, обозначим через ш, а волновой вектор — через k = ojN/c, где
N — единичный вектор, в направлении которого волна распространяется.
Фаза волны в указанной системе отсчета представится выражением tp =
= cut ~~ kr. Пусть относительно эфира равномерно движутся источник со
скоростью VH и наблюдатель со скоростью VH. Их радиусы-векторы будут
соответственно ги = VHt и гн = VHt. Фазы колебаний в этих движущих-
движущихся точках определятся выражениями (рш = (to — kVH)t и ipH = (cj — kVH)t.
Отсюда следует, что источник в системе отсчета, где он покоится, излучает
волны с частотой ши = ш ~~ kVM, а частота, воспринимаемая наблюдателем,
определяется выражением шш = ш — kVH. Почленным делением с учетом
соотношения k = ojN/c исключаем промежуточную частоту ш и находим
цн _ 1 - (NVH)/c
» ~ l-(NVH)/c-
Это и есть основная формула, определяющая доплеровское изменение
частоты в теории эфира и в акустике. Мы видим, что в этой теории часто-
частота ши определяется движением как источника, так и наблюдателя относи-
относительно эфира, а также направлением распространения N волны в самом
«неподвижном» эфире. В этом ее отличие от теории относительности, в
которой эфира нет, а потому эффект Доплера зависит только от скорости
источника относительно наблюдателя (VH — VH). В частности, при одной
и той же относительной скорости (VH — VH) формула A08.1) приводит к
разным результатам, в зависимости от того, что движется: источник или
наблюдатель. Когда движется источник, а наблюдатель неподвижен, она
дает
ш с A08-2)
Если же движется наблюдатель, а источник остается в покое, то
Wh=WhA-NVh/c). A08.3)
В линейном приближении, когда в формуле A08.1) можно пренебречь ква-
квадратами обоих отношений VM/c и V^/c, она переходит в
^1 = 1 + ^(VH^VH). A08.4)
шИ с
В эту формулу входит лишь относительная скорость (VH — VH), а не скоро-
скорости VM и VH в отдельности. Однако формула еще не определяет изменения
частоты, поскольку в нее входит также направление распространения вол-
волны N в «неподвижном» эфире. Действительно, хотя волна и посылается ис-
источником к наблюдателю, ее направление из-за аберрации будет изменяться
с изменением движения эфира. Только в частном случае, когда источник
или наблюдатель покоятся относительно эфира, эта неопределенность исче-
исчезает, а формула A08.4) совпадает с тем, что дает в первом порядке теория
относительности. Тогда ей можно придать вид
Шн = (\ + VN/c), A08.5)

108
ЭФФЕКТ ДОПЛЕРА В АКУСТИКЕ И ТЕОРИИ ЭФИРА
697
где Vn — скорость источника относительно наблюдателя по лучу зрения.
Она считается положительной, когда источник приближается к наблюдате-
наблюдателю, и отрицательной, когда он удаляется.
Все изложенное показывает, какие существенные упрощения и опре-
определенность внесла теория относительности в теорию эффекта Доплера и
аберрации света.
ЗАДАЧА
На рис. 335 приведена схема опыта Фуко по определению скорости света
в материальной среде. Лучи от источника 5*, пройдя через стеклянную пла-
пластинку М и линзу L, отражаются от плоского зеркала R, которое может
вращаться вокруг оси, перпендикулярной к плоскости чертежа. Линза L
дает изображение источника S на поверхности вогнутого зеркала G, центр
кривизны которого совпадает с осью вращения зеркала R. Сосуд Р напол-
наполняют исследуемым веществом, в котором измеряется скорость света. Если
зеркало R неподвижно, то лучи, отраженные от С и R, снова сойдутся в
точке S. Зеркало М отклонит часть лучей в сторону и даст действительное
изображение источника в Si. При вращении зеркала R изображение Si сме-
смещается в S[. По величине смещения SiS[ можно вычислить скорость света
в исследуемом веществе. При отражении от движущегося зеркала проис-
происходит доплеровское изменение частоты света. Учитывая это, показать, что
метод Фуко дает групповую скорость света.
Si S[
С
Рис. 335
Решение. Не теряя общности, воздушные зазоры между R и Р, а
также между Р ш С можно считать бесконечно тонкими и во всех расчетах
пренебречь толщиной этих зазоров.
Обычный расчет проводится следующим образом. На прохождение рас-
расстояния от R до С и обратно волновой фронт, распространяющийся с фазо-
фазовой скоростью v, затрачивает время Т = 2D/v, где D — расстояние между
зеркалами R и С. За это время R повернется на угол (р = ТО, если О —
угловая скорость вращения зеркала. Луч, отраженный от зеркала R, вра-
вращается с вдвое большей скоростью. За то же время он повернется на угол

698 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
а = 2(р = 2ТО = DD/v)Q. Угол а легко рассчитать по величине смещения
SiS[. Таким образом,
v = ADQ/a. A08.6)
В этом рассуждении не принято во внимание доплеровское изменение ча-
частоты при отражении света от вращающегося зеркала R. Поэтому оно не
дает ответа, что за скорость вычисляется по формуле A08.6).
Поместим начало координат на оси вращающегося зеркала jR и напра-
направим ось У по линии пересечения плоскости этого зеркала с плоскостью
чертежа. Так как линейные скорости различных точек вращающегося зер-
кала различны, то и изменение частоты волны при ее отражении от зеркала
будет разным в зависимости от того, в каком месте зеркала произошло от-
отражение. Благодаря этому различные точки волнового фронта будут рас-
распространяться в среде с различными фазовыми скоростями. Это поведет
к вращению волнового фронта в среде. Если за направление положитель-
положительного вращения принять направление вращения зеркала R, то для угловой
скорости вращения волнового фронта в среде можно написать
, 1 dv I dv duo
cos <p dy cos <p dou dyJ
где if — угол падения светового луча на зеркало R. Так как v = ш/к7 то
dv 1 ш dk v v
duo к к2 duj ш ши1
где и — групповая скорость. Остается определить dcu/dy. Если ш — часто-
частота волны, отраженной от зеркала в точке с координатой у, а ш + duj — с
2
координатой у + dy, то в первом порядке duo/uj = О cos ipdy, откуда
с
cos (f dy с nv1
где n — показатель преломления. Таким образом,
Отраженный от зеркала С волновой фронт будет также поворачиваться
при распространении в веществе с угловой скоростью О и притом, как
легко сообразить, в том же направлении, что и падающий волновой фронт.
С другой стороны, на прохождение слоя вещества толщиной 2D волновой
фронт затрачивает время Т = 2D/v. За это время он повернется в среде
4DQ (v \
на угол О!Т = ( 1). По выходе из сосуда Р в вакуум волновой
nv \и /
фронт преломляется, вследствие чего угол поворота увеличивается в п раз
и становится равным
пп'Т =
\и ) и v
V
Этот поворот надо прибавить к повороту 4DQ/v, найденному ранее без
учета эффекта Доплера. Таким образом, измеряемый угол поворота а в
действительности равен
4DQ /4DQ 4Ш\ 4DU
а = + = ,
V \ U V J U

§ 109 ЗАМЕДЛЕНИЕ ХОДА ЧАСОВ В ГРАВИТАЦИОННОМ ПОЛЕ 699
так что вместо формулы A08.6) получится
и = 4DQ/a. A08.7)
Следовательно, метод вращающегося зеркала Фуко дает групповую ско-
скорость.
§ 109. Замедление хода часов в гравитационном поле
1. Вопросы релятивистской теории тяготения относятся к
компетенции общей теории относительности^ излагать кото-
которую мы не предполагаем. Затронем лишь кратко вопрос о вли-
влиянии поля тяготения на течение времени. Будем исходить из
принципа эквивалентности гравитационных сил и сил инер-
инерции. Он был подробно изложен в § 71 первого тома. Гравитаци™
онное поле будем предполагать слабым (критерий слабости поля
указывается ниже).
Возьмем какую-либо инерциальную систему отсчета S, в раз™
личных точках которой установлены неподвижные часы, син-
синхронизованные по правилу Эйнштейна. Как всегда, время, опре-
определяемое по таким синхронизованным часам, будем обозначать
через t. Пусть относительно S ускоренно движутся какие-то од-
одни часы А. Время, отмечаемое часами А в точках, через кото-
которые они проходят, условимся обозначать через to- Часы А пред-
предполагаются идеальными, так что ускорение их само по себе не
оказывает никакого влияния на физические процессы в часах.
Такие часы идут одинаково быстро с часами в сопутствующих
инерциальных системах отсчета. Промежутки времени по непо-
неподвижным и движущимся часам связаны соотношением
dt = dto/y/l-(v/cJ, A09.1)
где v — скорость часов А относительно системы S. В инерци™
альной системе отсчета S нет никакого гравитационного поля.
Единственной причиной замедления времени to по сравнению с
t может быть только движение часов А относительно инерци-
альной системы отсчета S.
2. Однако возможна и другая точка зрения. Допустим сна-
сначала, что часы А относительно системы S движутся с постоян-
постоянным ускорением а. Будем отсчитывать время i от того момента,
когда скорость v была равна нулю. Тогда v = у/2ах, где х —
расстояние, которое прошли часы А за время t. Следовательно,
dt = dto/y/l-2ax/c2» A09.2)
Теперь введем ускоренную систему отсчета So, движущуюся
вместе с часами А. В этой системе часы А неподвижны, зато есть
силы инерции. Если все явления описывать, приняв Sq за систе-
систему отсчета, то причиной замедления времени t® следует считать

700 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
силы инерции. Сила инерции, отнесенная к единице массы дви-
жущегося тела, равна —а. Но, согласно принципу эквивалентно-
эквивалентности, силы инерции по своим физическим действиям неотличимы
от гравитационного поля, напряженность которого в рассматри-
рассматриваемом нами случае равна g = —а. Введем еще гравитационный
потенциал (р = =Ь^ж. Тогда предыдущая формула примет вид
dt = dto/л/1 — 2w/c2 « dto | 1 — -^ ) , A09.3)
V с1 у
или
dt-dto = _^_ A094)
За нуль гравитационного потенциала принят потенциал такой
точки, в которой движущиеся и неподвижные часы идут оди-
одинаково быстро. Поэтому в формулах A09.3) и A09.4) интервал
времени dt можно отсчитывать не по часам инерциальной си-
системы 5, а по тем часам, покоящимся в системе So, которые
находятся в точке В с нулевым потенциалом. Можно вообще
начало отсчета гравитационного потенциала поместить в любой
точке, если формулу A09.4) записать в виде
где интервалы времени cHqa и dtos отсчитываются по двум ча-
часам, покоящимся в ускоренной системе отсчета S® и помещен-
помещенным в точках А и В с гравитационными потенциалами ip^ и (рв •
При этом на потенциалы должно быть наложено ограничение
«слабого поля»:
|1, A09.6)
так как только при этом условии приближенно справедлива нью-
ньютоновская теория тяготения и имеет смысл понятие гравитаци-
гравитационного потенциала. (На поверхности Земли (р/с2 ^ —7- Ю~10, на
поверхности Солнца (р/с2 « —2,12 • 10^6, если за нуль принять
потенциал в бесконечности.) Поэтому в формуле A09.5) безраз-
безразлично, писать ли в знаменателе dto а или dt®B-
Формула A09.5) имеет следующий смысл. Пусть в точках А
и В гравитационного поля помещены тождественные часы, по-
покоящиеся в системе отсчета S®. Для сравнения темпа хода этих
часов будем после каждого удара часов А посылать световые
сигналы к часам В. Пусть Na — число посланных сигналов. За
время прихода сигналов часы в В совершат Nb ударов, причем
Если pa < Рв (световой сигнал распространяется против на-
направления гравитационного поля), то Na > Nb^ т.е. часы В идут

§ 109 ЗАМЕДЛЕНИЕ ХОДА ЧАСОВ В ГРАВИТАЦИОННОМ ПОЛЕ 701
медленнее часов А. В противоположном случае, когда срв < ^а?
медленнее будут идти часы А. Вообще, часы в гравитацион-
гравитационном поле идут тем медленнее^ чем выше гравитационный по-
потенциал в том месте^ где они находятся. Этот эффект, как
и замедление хода движущихся часов, следует рассматриватв
как свойство пространства-времени^ а не как влияние грави-
тационного поля на ход физических процессов в часах. Такое
влияние, как уже указывалось в § 106, в случае реальных ча-
часов несомненно существует, но оно существенно зависит от того,
какие физические явления положены в основу устройства ча-
часов. Для идеальных часов такого влияния нет — в этом случае
эффект гравитационного замедления хода часов проявляется в
чистом виде. Отмеченное обстоятельство проявляется и в фор-
формуле A09.5): гравитационное замедление времени есть взаимное
свойство двух часов^ определяющееся разностью гравитацией-
hbix потенциалов между ними, тогда как для физических про-
процессов в часах, очевидно, существен не потенциал, а напряжен-
напряженность гравитационного поля.
Конечно, формула A09.5) верна независимо от того, явля-
является ли гравитационное поле «фиктивным» полем сил инерции
или «истинным» гравитационным полем, создаваемым массами
вещества. Но эта формула была получена для однородного гра-
гравитационного поля. Применяя обычный прием, распространим
ее на случай произвольного неоднородного гравитационного по-
поля. Для этого вообразим, что в системе отсчета S® вдоль про™
извольной кривой АВ, соединяющей часы А и J?, расставлены
достаточно часто тождественные чаев! 1, 2, 3, ..., п. Гравитаци-
Гравитационное поле между каждыми соседними часами можно считать
однородным и применить к ним формулу A09.5). Перемножив
почленно все эти формулы и учтя, что в пределах их точности
различием знаменателей можно пренебречь, мы снова придем к
результату A09.5) и тем самым докажем его справедливость и
для неоднородного поля.
Так как при наличии гравитационного поля темп хода даже
тождественных часов в разных точках пространства разный, то
теряет смысл тот способ синхронизации часов и установления
одновременности пространственно разделенных событий, кото-
который применялся в инерциалвных системах отсчета, т.е. при от-
отсутствии гравитационного поля. При наличии гравитационного
поля сохраняет смысл лишь местное время^ устанавливаемое
по тождественным часам в каждой точке пространства. Следу-
Следует говорить не о синхронизации пространственно разделенных
часов, а только о сравнении темпа их хода^ как это описано
выше.
В свете изложенного парадокс близнецов можно рассматри-
рассматривать с иной точки зрения. Часы брата А все время находятся в

702 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
инерциальной системе отсчета, а часы брата В испытывают вме-
сте с ним ускорение, что эквивалентно тому, что они неподвиж-
неподвижны, но находятся в гравитационном поле. Это поле замедляет
ход часов В. При возвращении к А часы В будут показывать
меньшее время, чем А.
В последнее время A976 г.) гравитационное замедление вре-
мени было подтверждено группой американских физиков Мери-
Мерилендского университета. Измерялась разность показаний атом™
ных часов на самолете и в наземной лаборатории. Самолет кур-
курсировал на высоте 10 км с небольшой скоростью, чтобы умень-
уменьшить кинематический эффект замедления времени. Время по-
полета было около 15 часов. Ожидаемый гравитационный эффект
составлял примерно +50 не, кинематический ^7 не. Летающие
часы сравнивались с наземными до, после и во время полета. Та-
Таким образом, можно было следить за монотонным возрастанием
разности показаний сравниваемых часов. Опыт подтвердил тео-
теорию с точностью до 1,6%.
3. Применим полученные результаты к излучению света.
Пусть два тождественных неподвижных атома находятся в точ-
точках А и В гравитационного поля. Каждый из них в том месте,
где он находится, излучает свет с одной и той же частотой ujq.
Рассматривая излучающие атомы как часы и применяя к ним
формулу A09.5) или A09.7), получим
шо^ = <рв-<рА
шо с2
где ш — частота света, приходящего от А в точку наблюдения В.
Если свет распространяется от низшего потенциала (рл к выс-
высшему if в (т.е. против гравитационного поля), то наблюдается
изменение частоты в красную сторону. Для света, приходящего
от поверхности Солнца к Земле, это изменение частоты состав-
составляет (ш® — оо)/ш® = 2,12 • 10~6. Напротив, если свет распростра-
распространяется от высшего гравитационного потенциала к низшему (т.е.
в направлении гравитационного поля), то наблюдаемая часто-
частота света увеличивается. Это явление, называемое гравитацион-
гравитационным смещением спектральных линий, было теоретически пред-
предсказано Эйнштейном, а затем подтверждено экспериментально.
Несколько иначе описанное явление было рассмотрено в § 72 т. I.
§ 110. Сложение скоростей в теории относительности
1. Задача (физического) сложения скоростей формулируется
следующим образом (см. т. I, § 7). Пусть скорость движущейся
частицы в системе отсчета Sf равна v;, причем сама система
S1 равномерно движется относительно «неподвижной» системы

§ 110 СЛОЖЕНИЕ СКОРОСТЕЙ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 703
S со скоростью V в направлении оси X. Требуется определить
скорость v той же частицы в системе отсчета S. Обозначим коор-
координаты частицы в системе S в момент времени t через ж, у, z. Те
же величины в системе Sf обозначим штрихованными буквами
t;, ж;, у\ z1. Так как обе эти группы переменных характеризуют
одно и то же событие (прохождение частицы через одну и ту
лее пространственно-временную точку), то они связаны между
собой формулами преобразования Лорентца A05.12). Поскольку
V = const, координаты и время при движении частицы получа-
получают приращения
i / i т /¦ jjl jjl/ i л г I I 2
dx = -, dy = dy , dz = dz , dt = ;^.
Разделив первые три соотношения на последнее и замечая, что
dx/dt = vXj dx1 /dt' = vx, получим
x " 1 + v'xV/c* ' y " 1 + v'xV/c* ' z "
Эти формулы и выражают правило сложения скоростей в ре~
лятивистской кинематике. При медленных движениях, когда
можно пренебречь квадратичными величинами V2/с2 и v^V/c2^
они переходят в нерелятивистские формулы
vx = v'x + V, vy = vfy1 vz=vfz1
получающиеся из преобразования Галилея.
2. Для исследования формул A10.1) удобно принять за еди™
ницу скорость света с, введя безразмерные величины (Зх = vx/c,
Р'х = v'x/c, ... Тогда
то 2)
Все скорости по величине не могут превосходить с, а соот-
соответствующие им безразмерные величины /3, /Зх, ... — единицы.
Возникает, однако, вопрос, не может ли в результате (физиче-
(физического) сложения двух скоростей получиться скорость, превосхо-
превосходящая с? Ответ на этот вопрос должен быть отрицательным.
Для доказательства рассмотрим сначала случай сложения
параллельных скоростей, когда направления векторов v; и V
совпадают или прямо противоположны. Результирующая сю>
рость в этом случае полностью определяется первой формулой
A10.1) или эквивалентной ей первой формулой A10.2). Так как
/3 и /Зх не превосходят единицы, то их можно представить в виде
/3 = tht?, fi'x = thi9^, где аргументы гиперболических тангенсов
t? и $х могут принимать любые вещественные значения. Тогда

704 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
первая формула A10.2) запишется в виде
о _ th &'x + thtf
Р
Сравнивая ее с формулой сложения гиперболических тангенсов
видим, что результирующую безразмерную скорость также
можно представить гиперболическим тангенсом /Зх = tht?x, при™
чем
#ж = #'х + #т A10.3)
Это значит, что (физическое) сложение параллельных ско-
ростей сводится к алгебраическому сложению аргументов
соответствующих им гиперболических тангенсов. Но при любых
значениях аргументов гиперболический тангенс по абсолютной
величине не может превосходить единицы. Следовательно, како-
каковы бы ни были (параллельные) скорости составляющих движе-
движений, при их (физическом) сложении не может получиться ско-
скорость, превосходящая с. Если одна из складываемых скоростей
равна с, то при сложении ее с любой другой скоростью получит-
получится также с. В этом и проявляется специфичность скорости света
как предельной скорости, которую нельзя превзойти, сколько
бы ни ускорять движение тела.
Для завершения доказательства остается исследовать слу-
случай, когда складываемые скорости взаимно перпендикулярны.
Без ограничения общности молено считать, что скорость v; на-
направлена вдоль оси Y1. Тогда, полагая в формуле A10.2) /Зх =
= f3'z =0, получим
Квадрат (безразмерной) скорости в системе S будет
Придав /3 постоянное, но произвольное значение, будем рассма-
рассматривать величину (у/сJ как функцию аргумента /З^2. Производ-
Производная этой величины A ^/З2) ^ 0, а потому функция (v/cJ возра-
возрастает с возрастанием /З^2. Она достигает максимума при /З^2 = 1,
который равен 1. При всех остальных значениях /3' отношение
(у/сJ не может превосходить единицы. Это и доказывает, что
при сложении перпендикулярных скоростей также не может по-
получиться скорость, превосходящая с.

110 СЛОЖЕНИЕ СКОРОСТЕЙ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
705
3. Когда складываемые скорости параллельны, то индекс х
можно опустить и написать
Если V <С с, то в этой формуле можно ограничиться первыми
степенями по V. В этом приближении
V^(V> + V) (l - ?f
Применим последнюю формулу к распространению света в
жидкости, равномерно движущейся со скоростью V. Скорость
света относительно неподвижной жидкости будет vf = с/в, где
п — показатель преломления жидкости. Предполагая, что свет
распространяется в направлении течения жидкости, найдем его
скорость v относительно «неподвижной» системы отсчета. Для
этого подставляем в формулу A10.5) vf/с = 1/в и находим
С
V = —
п
-4 к
A10.6)
Формула A10.6) была получена еще Френелем в 1818 г. Он
исходил из представления, что эфир увлекается движущимися
телами, однако не полностью, а частично. Лорентц в электрон-
электронной теории вновь пришел к формуле A10.6). Но истинный смысл
ее был установлен только в теории относительности.
Формула A10.6) была экспериментально подтверждена Фи-
зо в 1851 г. Схема его опыта в усовершенствованном виде, какой
ему придал Майкельсон в 1886 г., показана на рис. 336. Луч
ж S
Рис. 336
от источника S раздваивается разделительной пластинкой Р.
Один луч на рис. 336 изображен сплошной, а другой — штри™
ховой линией. Затем лучи проходят через трубки, в которых
течет вода. Один луч идет в направлении, а другой против тече-
течения воды. Из-за различия скоростей лучей относительно непо-
неподвижных стенок трубки между ними при выходе из прибора

706 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
возникает разность хода, изменяющаяся с изменением скорости
течения V. Сначала наблюдается интерференция между луча-
лучами при неподвижной, а затем при текущей воде. По смещению
интерференционных полос можно измерить разность хода, воз™
никающую при течении, а по ней и разность скоростей v — с/п.
4. Лорентц в электронной теории обобщил формулу A10.6), учтя дис-
дисперсию света. Формулу Лорентца легко получить и в теории относитель-
относительности. Надо только учесть доплеровское изменение длины волны, возни-
возникающее при течении воды. Обозначим через А длину световой волны (в
вакууме) в «неподвижной» системе отсчета S, а через А + ёХ — в системе
S , относительно которой вода неподвижна. Доплеровское изменение длины
волны SА в первом порядке по V определяется выражением
ёХ _ V _ Vn
A v1 с '
Следовательно,
/(A + 5A) '(A) + ^ A,
с
Xdn
--—V.
Х
v (А + 5Х) = v (А) + — ( - 1 ^^ = —- --—
ал \п/ с п(Х) п аХ
В формуле A10.5) под г/ надо понимать, конечно, не t/(A), a v' {Х + ёХ). При
этом второе слагаемое в правой части A10.5) в рассматриваемом прибли™
жении следует оставить без изменения. В результате получим
с (. 1 A dn\ тг /ллп „ч
v = - + 1 - — - ^— У. A10.7)
п \ п2 ndXJ
Наличие добавочного члена, обусловленного дисперсией, было экспери-
экспериментально подтверждено Зееманом в 1914 г.
Нелишне подчеркнуть, что доплеровское изменение длины волны отно-
относится к системе отсчета S', в которой вода неподвижна. Течение воды не
сказывается на длине волны в «неподвижной» системе S, так что оба ин-
интерферирующих луча при выходе из прибора (см. рис. 336) имеют одну и
ту тсе длину волны. Только благодаря этому и возможна интерференция.
§ 111. Релмтмвистскам механика
1. Если какой-либо закон природы представлен в виде А =
= В^ причем при переходе от одной системы отсчета к другой
величины А ж В остаются неизменными^ то эти величины и са™
мый закон называются инвариантными относительно этого пе-
перехода. Более общим является понятие ковариантности. Если
при переходе от одной системы отсчета к другой величины А и
В хотя и не остаются неизменными, но преобразуются одина-
ково^ то закон А = В сохраняется и в новой системе отсчета.
В этом случае говорят, что закон А = В ковариантен относи-
относительно рассматриваемого преобразования систем отсчета. Часто
термин «инвариантность закона» употребляют в смысле его ко™
вариантности.

§ 111 РЕЛЯТИВИСТСКАЯ МЕХАНИКА 707
До теории относительности допустимыми считались только
галилеевы преобразования координат. Относительно этих преоб-
преобразований уравнения механики Ньютона были ковариантны (ин-
(инвариантны) , тогда как уравнения электродинамики Максвелла^
Лорентца — не ковариантны. Теория относительности показала,
что от галилеева преобразования надо отказаться и заменить
его преобразованием Лорентца. Тогда принцип относительно-
относительности требует, чтобы законы природы были ковариантны отно-
сительно преобразования Лорентца. Этому требованию урав-
нения электродинамики удовлетворяют, а уравнения механики
Ньютона не удовлетворяют. Поэтому механика Ньютона должна
быть изменена.
В ньютоновской механике сила, действующая на тело в
какой-то момент времени, определяется положением всех вза-
взаимодействующих тел в тот же момент. Но в теории от™
носительности понятие «тот же момент времени» зависит от
выбора системы отсчета. Невозможно автоматически преобра-
зовать каждый закон сил ньютоновской механики в лорентц-
ковариантную форму. Допустимы только такие теории, из кото-
которых может быть исключено понятие действия на расстоянии.
Такая возможность существует в теории столкновений. Послед-
Последняя исходит из идеализированного представления, что взаимо-
взаимодействие имеет место только в продолжение того промежутка
времени, когда расстояние между телами или точечными ча-
частицами бесконечно мало по сравнению с размерами самих тел
или другими характерными расстояниями, определяющими ха-
характер процессов столкновения. До и после этого бесконечно ма-
малого промежутка времени тела движутся свободно. К процессам
столкновений применимы законы сохранения импульса и энер-
энергии, но им надо придать лорентц-ковариантную форму. Это и
является целью настоящего параграфа. Дальнодействие моле-
молено исключить также при рассмотрении движения электрически
заряженных частиц в электромагнитных полях. Однако изложе-
изложение относящихся сюда вопросов электродинамики потребовало
бы слишком много места, а потому мы ограничимся только рас-
рассмотрением процессов столкновения.
2. Для решения поставленной задачи проще и логичнее всего
воспользоваться понятием четырехмерного вектора (или, коро-
короче, 4швектоРа) в пространстве Минковского. Каждое «точечное»
событие в таком пространстве характеризуется совокупностью
четырех координат ж, у, z, т = ct. При переходе от системы от-
отсчета S к системе отсчета S1 разности координат двух точек
преобразуются по формулам

708 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
как это следует из A05.12). Напомним, что квадрат интервала
между рассматриваемыми точками есть инвариант:
Ат2 - Ах2 - Ay2 - Az2 = Inv . A1L2)
Мы воспользовались частным преобразованием Лорентца
A05.12), в котором предполагается, что координатные оси
X, Y, Z параллельны осям Х\ Y\ Z\ а система S1 движет-
движется относительно S вдоль оси X. Можно было бы взять любую
ориентацию осей и любое направление движения, но это только
усложнило бы запись, ничего не меняя по существу.
Назовем четырехмерным вектором совокупность четырех
величин Ар, Ау, Az, АТ, которые при переходе от одной си-
системы отсчета к другой преобразуются так же, как разности
координат двух точек в пространстве Минковского^ т.е.
а1 а а1 а
A11.3)
Величины Ах, Ау, Az называются пространственными^ а АТ —
временной составляющей четырехмерного вектора. Простран-
Пространственные составляющие мы объединим в обычный трехмер-
трехмерный вектор А и будем обозначать четырехмерный вектор через
(А,Ат-). Из тождественности законов преобразования A11.1) и
A11.3) следует, что четырехмерный вектор (А, Ат-) обладает ин-
инвариантом:
А2Т -A2 = Inv . A11.4)
Если какой-либо закон природы записан в четырехмер-
четырехмерной векторной форме (А,АТ) = (В,ВТ), то он лорентц-
ковариантен^ так как обе части написанного равенства при
преобразовании Лорентца преобразуются одинаково. Четырех-
Четырехмерная векторная форма эквивалентна двум уравнениям: А =
= В и АТ = Вт. Этим замечанием мы и воспользуемся для реше-
решения поставленной задачи. Именно, мы постулируем, что закон
сохранения импульса и энергии моэюно записать в виде равен-
равенства четырехмерных векторов. Задача состоит в том, чтобы
найти вид этих векторов.
3. Рассмотрим частицу, движущуюся со скоростью v отно-
относительно неподвижной системы отсчета S. Пусть dr — ее пере-
перемещение за время dt = dr/с. Эти величины образуют четырех-
четырехмерный вектор (dr,cdt). Очевидно, он останется четырехмер-
четырехмерным вектором и после умножения его составляющих на одну
и ту же постоянную. Возьмем в качестве таковой mo/dto, где
то — некоторая постоянная, a dt® = dty/\ — v2/с2 — собствен-
собственное время, которое, как известно, является инвариантом. Тогда

§ 111 РЕЛЯТИВИСТСКАЯ МЕХАНИКА 709
получим четырехмерный вектор
где введено обозначение
т= , то =. A11.6)
у 1 — v2 /с2
Допустим теперь, что частица движется медленно, так что ве-
личиной v2/с2 можно пренебречь. Возьмем в качестве т® массу
частицы, как она определяется в нерелятивистской механике.
Тогда пространственная составляющая четырехмерного векто-
вектора A11.5) будет mgv. Вектор mgv в ньютоновской механике на™
зывается импульсом. Поэтому в релятивистской механике есте-
естественно определить импульс выражением
P = mv = —g?^ (Ш.7)
/1 9 / 9
/1 V2/C2
поскольку в пределе при малых скоростях оно переходит в нере-
нерелятивистское выражение m®w. Величина т® называется массой
покоя^ am — массой движения или релятивистской массой.
Таким образом, (Р,тс) есть четырехмерный вектор, а величи-
величина (тсJ ^Р2 — его инвариант. Значение этого инварианта легко
найти: при v = 0 он обращается в (гадеJ, а потому
(тсJ -Р2 = (т0сJ. A11.8)
Остается выяснить физический смысл временной части че-
четырехмерного вектора A11.5). Для этого замечаем, что dP/dt
есть сила, действующая на частицу. Работа этой силы на пе-
перемещении v db равна dA = vdP = PdP/ra или на основании
A11.8) dA = с2 dm. Энергия частицы найдется интегрированием
этого выражения по га. Если постоянную интегрирования поло-
положить равной нулю, то получится формула
A11.9)
Величина ? называется полной энергией частицы. Для покоя-
покоящейся частицы т = гао, так что A11.9) переходит в
So = m0c2, A11.10)
Величина ?® называется энергией покоя частицы.
Формула A11.9), впервые в общем виде полученная Эйн-
Эйнштейном, устанавливает взаимосвязь между массой и энергией.
Кинетическая энергия частицы определяется выражением
K = S-S0 = (m- m®)c2. A11.11)
При медленных движениях это выражение переходит в обычную
формулу К = г/2

710 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
Импульс и энергия теперь объединены в четырехмерный век™
тор
(Р,тс) = (Р,?/с), A11.12)
называемый вектором импульса-энергии. Его инвариантом от™
носительно преобразования Лорентца является
|) - Р2 = (т0сJ = Inv . A11.13)
Тем самым в теории относительности законы сохранения им™
пульса и энергии перестают быть независимыми законами, а
объединяются в единый закон сохранения четырехмерного век-
тора импульса-энергии. Его называют также законом сохране-
сохранения импульса-энергии.
Остается ответить на два вопроса. Во-первых, почему при
вычислении работы сила была определена так же, как в нереля-
нерелятивистской механике, т.е. как производная dP/dt? Во-вторых,
почему энергия всегда определяется с точностью до несуще™
ственной произвольной постоянной, здесь же она определена од-
однозначно? Ответ на оба вопроса, в сущности, один и тот же.
Он состоит в том, что на величину ?*, вычисленную выше и на™
званную полной энергией, было наложено требование, чтобы она
(после деления на с) была временной компонентой четырехмер-
четырехмерного вектора A11.5). Если энергию не определить однозначно,
то она этому требованию удовлетворять не будет.
Для системы невзаимодействующих частиц, а также частиц,
взаимодействующих только при столкновениях, четырехмерный
вектор импульса-энергии определяется как сумма четырехмер-
ных векторов импульса^энергии этих частиц. При этом в теории
относительности достигается однообразная трактовка упругих
и неупругих столкновений. Независимо от характера столкно-
столкновения сохраняется трехмерный вектор импульса системы. Сле-
довательно, должна сохраняться и энергия, как (умноженная
на с) временная компонента четырехмерного вектора. Вместе с
энергией сохраняется и релятивистская масса. Только при упру-
упругих и неупругих столкновениях она по-разному распределяется
между массой покоя и массой, связанной с кинетической энерги-
энергией макроскопического движения. Например, при столкновении
двух одинаковых неупругих шаров, движущихся с одинаковыми
скоростями навстречу друг другу, исчезновение кинетической
энергии макроскопического движения (т.е. переход его во вну-
внутреннее молекулярное движение) проявляется в эквивалентном
увеличении массы покоя системы: масса нагретого шара больше,
чем масса такого же холодного шара. При упругих же столкно-
столкновениях остаются неизменными и масса покоя, в масса, связанная
с кинетической энергией макроскопического движения.

§111 РЕЛЯТИВИСТСКАЯ МЕХАНИКА 711
Существуют частицы (фотоны^ нейтрино), для которых
масса покоя равна нулю. Для них связв A11.13) между энер-
энергией и импульсом имеет вид
Р = ?/с« A11.14)
Такие частицы всегда движутся со скоростью с. Иначе, как вид™
но из формул A11.7) и A11.9), импулвс и энергия таких частиц
обращались бы в нуль.
ЗАДАЧИ
1. Две одинаковые частицы движутся в лабораторной системе навстре-
навстречу друг другу с одной и той же скоростью v. Найти относительную скорость
V каждой из них относительно другой. Какой энергией Е' в лаборатор-
лабораторной системе отсчета должна обладать одна из частиц, чтобы получить ту
же относительную скорость, если вторая частица (мишень) неподвижна?
(Принцип действия ускорителя на встречных пучках.)
Решение. По теореме сложения скоростей
v = 2v
l+V2/c2'
Искомая полная энергия, которую надо было бы сообщить одной частице,
равна
ci _ ^0
~ у/1 - V*l<? '
где So — энергия покоя частицы. Фактическая энергия, которой обладает
частица, Е = So/y/l — v2/с2. Отсюда нетрудно получить
?' = 2|--?о, A11.15)
со
а для кинетической энергии
(Другое решение см. в т. I, § 28.)
2. Вывести формулу, являющуюся релятивистским обобщением фор-
формулы Циолковского (см. т. I, § 21) для движения ракеты. Считать, что
скорости ракеты и газовой струи направлены вдоль одной прямой.
Решение. На основании законов сохранения импульса и энергии
ГПУ + Шгаз^газ = COIlSt, ГП + Шгаз = COIlSt,
где т и тгаз — релятивистские массы ракеты и газов, a v и vr8h3 — их сю>
рости в произвольный момент времени. Газы, уже покинувшие ракету, не
влияют на ее движение. Поэтому можно считать, что в рассматриваемый
момент времени тгаз = 0. Тогда не возникает неопределенности, что еле™
дует понимать под г;газ- Однако, поскольку газы непрерывно образуются,
с1тг8ьз ф 0. Дифференцируя предыдущие уравнения, получим
mdv + (v — ^газ) dm = 0.

712 ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ГЛ. IX
По релятивистскому закону сложения скоростей
v — и
^газ — i 1 о 1
1 — vu/c2
где и — скорость газовой струи относительно ракеты. Исключение t;ra3 при™
водит к уравнению
1 - v2/с2 dm
dv + и- '-г-г = 0.
1 — vu/c2 m
Воспользовавшись формулой A11.6), после несложных преобразований
найдем
dv и dmo
v2 ~~ с2 с2 то
Предполагая скорость и газовой струи постоянной и интегрируя, получим
искомый результат:
l-v/cj

ГЛАВА X
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
§ 112. Равновесное излучение в полости
1. Излучение света происходит в результате переходов ато-
атомов, молекул и других атомных систем из состояний с большей
в состояния с меньшей энергией. Так называемое тепловое или
температурное излучение отличается от других видов излуче-
излучения (люминесценции) только способом перехода излучающих си™
стем в возбужденные состояния. В явлениях теплового излуче-
излучения такой переход осуществляется в результате теплового дви-
движения атомов и молекул.
В проблемах теплового излучения особо важное значение
имеет понятие так называемого равновесного излучения. Для
установления этого понятия рассмотрим полость с неподвижны-
неподвижными и непрозрачными стенками, температура которых поддер-
поддерживается постоянной. Атомы и молекулы стенок переходят в
возбужденные состояния за счет энергии теплового движения и
при обратных переходах в невозбужденные состояния дают из-
излучение, заполняющее полость. Падая на стенки полости, лучи-
лучистая энергия частично отражается, частично поглощается. Про-
Происходит изменение направления распространения, спектрально-
спектрального состава, поляризации, интенсивности излучения. В результате
всех этих процессов, как это следует из общего начала термоди-
термодинамики, в полости в конце концов устанавливается макроскопи-
макроскопически вполне определенное состояние излучения, при котором за
каждый промежуток времени количество излученной лучистой
энергии определенного цвета, направления распространения и
поляризации в среднем равно количеству поглощенной энергии
того же цвета, направления распространения и поляризации.
Как и всякое равновесное состояние, оно характеризуется тем,
что каждому микропроцессу, происходящему в системе, с той же
вероятностью соответствует микропроцесс, идущий в обратном
направлении (принцип детального равновесия). Благодаря это-

714 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
му состояние излучения в полости и остается макроскопически
неизменным во времени. Переход в равновесное состояние, как
и всякий статистический процесс, управляется вероятностны-
ми законами. В полости устанавливается хаотическое состояние
излучения, которому соответствует наибольшая вероятность.
Оно и называется равновесным излучением.
Свойства равновесного излучения: плотность лучистой энер-
энергии, ее распределение по спектру частот и направлениям рас-
распространения, а также поляризация излучения совершенно не
зависят от формы и материала стенок полости. Эти свойства,
подобно состоянию газа в сосуде, определяются только темпе-
температурой стенок полости. Равновесное излучение однородно, т.е.
его плотность одна и та же во всех точках внутри полости. Оно
изотропно и неполяризовано: все возможные направления рас™
пространения излучения представлены с одинаковой вероятно-
вероятностью, а направления векторов Е и В и каждой точке простран-
пространства хаотически меняются во времени. Поскольку излучение на™
ходится в тепловом равновесии со стенками, молено говорить о
температуре не только стенок, но и о температуре самого излу-
чения, считая по определению обе температуры равными. Надо,
однако, подчеркнуть, что температура равновесного излучения
есть свойство самого излучения, а не стенки, с которой оно на™
ходится в тепловом равновесии. О ней имеет смысл говорить и
тогда, когда вообще нет никакой стенки. В частности, например,
плотность энергии равновесного излучения однозначно опреде-
определяет и его температуру (см. § 115).
Если стенки полости совершенно непоглощающие, например
идеально зеркальные, то в такой полости не будет поглощения
и испускания света. В полость можно ввести излучение произ-
произвольного спектрального состава. Отражаясь от стенок, излуче-
излучение меняет направление распространения, но его спектральный
состав сохраняется неизменным. При надлежащей геометриче-
геометрической форме полости с зеркальными стенками возможны и такие
случаи, когда сохраняются так лее направление распространения
и поляризация излучения. Так будет, например, когда полость
имеет форму прямого цилиндра с абсолютно зеркальными осно-
основаниями. Тогда луч света произвольной частоты и поляризации
может распространяться туда и обратно параллельно оси ци-
цилиндра, последовательно отражаясь от зеркальных оснований.
Но все подобные случаи являются идеальными и никогда точно
не реализуются в действительности. Излучение в полости в этих
случаях неравновесно и неустойчиво. Уже при сколь угодно ма-
малых отклонениях от идеальности, если только подождать доста-
достаточно долго, в полости обязательно установится равновесное из-
излучение. Идеальные системы, однако, имеют большое значение
в теоретических рассуждениях. Можно брать стенки абсолют-

§ 112 РАВНОВЕСНОЕ ИЗЛУЧЕНИЕ В ПОЛОСТИ 715
но зеркальными и в то же время считать, что в полости всегда
устанавливается равновесное излучение. Для этого достаточно,
например, ввести в полость сколь угодно малое поглощающее и
излучающее тельце — пылинку, по выражению Планка. Такая
пылинка, практически не играя никакой роли в энергетическом
балансе системы, переводит, однако, любое неравновесное состо-
яние, возникшее в полости, в равновесное.
2. Введем теперь некоторые величины, характеризующие со-
состояние излучения в пространстве. Эти величины имеют смысл
для произвольного излучения, а не только для равновесного.
Обозначим через и плотность энергии излучения, т.е. коли™
чество такой энергии в единице объема пространства. Ее можно
разложить по частотам или длинам волн, т.е. представить в виде
со со
и= I иш duj = I u\d\. A12.1)
о о
Величины иш duj и и\ dX имеют смысл объемной плотности лучи™
стой энергии, приходящейся на интервал частот cj, ш + duo или
интервал длин волн А, А + dX. Коэффициенты иш и ч\ назы-
называются спектральными плотностями лучистой энергии. Если
речь идет об одном и том же спектральном интервале, но пред-
представленном в различных формах, то иш duj = u\dX. При этом
А = 2тгс/ш7 и следовательно, dX/X = ^duojuj. Знак минус мы
опустим — он означает только, что с возрастанием частоты дли-
длина волны убывает. Таким образом, считая величины duj и dX
существенно положительными, можно написать
и\ = y иш, иш = - их. A12.2)
В теоретической физике обычно пользуются величиной иш, в
экспериментальной отдают предпочтение и\. В случае равно-
равновесного излучения функции иш и и\ зависят только от частоты
ш (или длины волны А) и от температуры излучения Т, но не
зависят от формы и материала стенок полости. Они зависят от
среды, занимающей полость. Эта зависимость будет установле-
установлена в § 114. Пока же будем предполагать, что в полости вакуум.
В этом случае иш будет универсальной функцией только ш и Т,
aw — универсальной функцией только Т. Нахождение функции
иш(и),Т) является основной задачей теории теплового излуче-
излучения.
Поток лучистой энергии, проходящей за время dt через ма-
малую площадку ds в пределах телесного угла dO, ось которого
перпендикулярна к площадке ds, можно представить выраже-
выражением
dФ = IdsdПdt, A12.3)

716 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
Величина / называется удельной интенсивностью излучения.
Если ее разложить в спектр, т.е. представить интегралом
оо
1= / 1шAш, A12.4)
о
то величину 1Ш называют удельной интенсивностью излучения
частоты ш.
Найдем связь между и и / (а также между иш и 1Ш) для
поля излучения в вакууме. Возьмем в пространстве бесконеч-
бесконечно малый прямоугольный параллелепипед с площадью основа-
основания ds и высотой dl (рис. 337). Выделим пучок лучей, вступаю™
щих через площадку ds внутрь параллелепипеда, направления
которых лежат в пределах телесно-
телесного угла сШ, а ось телесного угла
нормальна к основанию ds. Каждый
из этих лучей доходит до второго
основания параллелепипеда за вре-
мя dt = dl/c. За это время из выде-
выделенного пучка лучей через площад-
рис 337 ку ds внутрь параллелепипеда всту-
вступает лучистая энергия / ds dQ, dt =
= (I/c)dVtdV1 где dV = dl ds — объем параллелепипеда. Раз-
Разделив на dV, найдем (I/с) dU. Эта величина есть плотность du
лучистой энергии, распространяющейся в пределах телесного
угла сШ. По своему смыслу она может быть функцией точки в
пространстве, но не может зависеть от формы параллелепипеда.
Поэтому для нахождения полной плотности и лучистой энергии
в рассматриваемой точке пространства надо проинтегрировать
выражение du по всем направлениям в пространстве. В общем
случае при таком интегрировании надо принять во внимание,
что удельная интенсивность I зависит от направления излуче-
излучения. Но в случае изотропного излучения, каким, в частности,
является равновесное излучение, такой зависимости нет. В этом
случае интегрирование сводится к простой замене элементарно-
элементарного телесного угла dVt на полный телесный угол ft = 4тг. Тогда
получится
и = Ц-1. A12.5)
Аналогично,
иш = ^1Ш. A12.6)
Такие же соотношения справедливы и в том случае, когда по-
полость заполнена однородной изотропной непоглощающей сре-
средой. Надо только величину с заменить групповой скоростью све-
света в рассматриваемой среде.

§ 113 ЗАКОН КИРХГОФА 717
§ 113. Закон Кирхгофа
1. Перейдем теперь к рассмотрению законов теплового излу-
излучения и поглощения тел. Ограничимся частным случаем, когда
излучающее и поглощающее тело непрозрачно. Этому условию
можно удовлетворить, если толщина тела достаточна, чтобы
всякий луч, вступивший в него, успел поглотиться, не достиг-
достигнув противоположной границы тела. Поток лучистой энергии
с частотами между ш и ш + do;, излучаемый за время dt пло-
площадкой ds поверхности тела внутрь телесного угла сШ, можно
представить выражением
dФ = Еш ds cos cp dU duo dt, A13.1)
где if — угол между направлением излучения и нормалью к
площадке ds. Здесь введен множитель cosc/9, так как из луче™
ние удобнее относить не к величине полной площади ds, а к ее
«видимой» части, т.е. проекции площадки ds на плоскость, пер-
перпендикулярную к направлению излучения (см. § 22). Величина
Еш называется излучательной способностью поверхности тела
в направлении, определяемом углом (р 1).
Поглощательной способностью Аш поверхности для излуче™
ния той же частоты, направления распространения и поляриза-
поляризации называется безразмерная величина, показывающая, какая
доля энергии падающего излучения поглощается рассматривае-
рассматриваемой поверхностью.
Речь идет, конечно, только о чисто температурном излу-
чении^ когда все свойства излучающего и поглощающего те-
тела определяются только температурой тела. Исключаются из
рассмотрения все случаи «холодного» или неравновесного свече-
свечения, когда светящееся тело излучает не потому, что оно нагре-
нагрето, а потому, что определенные уровни энергии его возбужде-
возбуждены и тело постепенно «высвечивается», переходя в нормальное,
невозбужденное состояние.
Что касается зависимости излучательной способности тела
от окружающей однородной среды, то к этому вопросу мож-
можно подходить с двух точек зрения. Молено определить Еш че-
через полный поток лучистой энергии выделенного направления
и частоты, исходящий от поверхности тела в окружающую сре~
ду. При такой точке зрения излучательная способность характе-
характеризует свойства двух сред, граничащих между собой вдоль рас-
х) Здесь мы отступаем от традиции. По историческим причинам излучаю-
излучающую способность тела принято характеризовать полным потоком лучистой
энергии, посылаемым излучающей площадкой ds наружу по всем направле-
направлениям, т.е. в пределах телесного угла 2тг. При более детальном рассмотрении
надо разложить ее по разным направлениям и частотам, что мы и делам.

718 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
сматриваемой поверхности. Но можно встать на другую точку
зрения, развивавшуюся Прево A751-1839) в начале прошлого
века. Согласно этой точке зрения, результирующий поток лу-
лучистой энергии через поверхность тела есть разность двух по-
потоков , которые оба излучаются в вакуум: потока, излучаемо-
излучаемого телом в окружающее пространство, и потока, излучаемого
средой в пространство, занятое телом. Первый поток определя-
определяет излучательную способность тела, второй — излучательную
способность среды. Мы будем придерживаться второй точки зре-
зрения, так как тогда величины Еш и Аш будут характеристиками
только самого тела^ не зависящими от окружающей среды. При
прочих равных условиях они определяются только температу-
температурой тела.
2. Установим связь между излучательной и поглощательной
способностью тела. Так как эти величины характеризуют только
поверхность самого тела и совершенно не зависят от окружаю-
окружающего излучения, то в рассуждениях относительно этого излуче-
излучения можно вводить любые предположения. Предположим, что
излучающее тело со всех сторон
окружено равновесным излучени-
излучением, температура которого равна
температуре тела. Это, например,
можно осуществить, если в ка-
качестве рассматриваемого участ-
участка поверхности тела взять часть
внутренней поверхности замкну-
замкнутой полости, температура стенок
которой поддерживается постоян-
Рис. 338 ной. Выделим из всего излуче-
излучения часть, заполняющую интер-
интервал частот ио, ш + duj, и рассмотрим превращения ее при излу-
излучении и отражении от стенок полости. На площадку ds стенки
(рис. 338) за время dt в пределах телесного угла du падает лу-
лучистый поток
1Ш ds cos (p duj du dt.
Часть его
A — АШIШ ds cos (f duj du dt
отражается, остальная часть поглощается. На отраженный по-
поток накладывается поток
Еш ds cos ip duj dQ dt
собственного излучения площадки. Таким образом, от площадки
ds внутрь полости исходит лучистый поток
[A — АШIШ + Еш] ds cos <p duo du dt.

§ 113 ЗАКОН КИРХГОФА 719
Но в состоянии равновесия тот же поток может быть представ-
представлен выражением
1Ш ds cos (p duj dft dt.
Приравнивая оба выражения, получим
Т- = Ъ- (Н3.2)
Доказательство проведено в предположении, что площад-
площадка ds отражает свет зеркально. Но это предположение несуще™
ственно. Если отражение диффузное, то происходит рассеяние
падающего лучистого потока по всем направлениям. Однако в
состоянии равновесия это приводит только к замене одних лучей
другими. Общий поток рассеянной энергии, исходящий от пло-
площадки ds в любой фиксированный в пространстве телесный угол
сШ, остается неизменным. Остаются неизменными и все количе-
ственные соотношения, использованные при доказательстве, а с
ними и окончательный результат A13.2).
Величина 1Ш не зависит от вещества стенок полости, а явля-
является универсальной функцией только частоты ш и температуры
тела Т. Таким образом, отношение лучеиспускательной способ-
ности тела к его поглощательной способности одинаково для
всех тел и является универсальной функцией только частоты
и температуры. Этот закон был установлен в 1859 г. Кирхгофом
и носит его имя. Он является точным количественным обобще-
обобщением правила, эмпирически установленного Прево в 1809 г. Со™
гласно этому правилу, если поглощательные способности тел
различны, то будут различными и их лучеиспускательные спо-
способности.
3. Тело называется абсолютно черным, если его поглоща™
тельная способность Аш равна единице для излучений всех ча-
частот. Излучательную способность абсолютно черного тела будем
обозначать через еш. Очевидно, еш = 1Ш. Поэтому равновесное
излучение называют также черным излучением. Закону Кирхго-
Кирхгофа можно теперь дать следующую формулировку: отношение
лучеиспускательной способности тела к его поглощательной
способности есть универсальная функция частоты и темпера-
температуры тела, равная лучеиспускательной способности абсолют-
абсолютно черного тела. Излучательная способность тела тем больше,
чем больше его поглощательная способность. Так как величи-
величина Аш не может быть больше единицы, то из всех тел при од~
ной и той же температуре абсолютно черное тело обладает
наибольшей излучательной способностью. Из закона Кирхгофа
следует также, что всякое тело при данной температуре излу-
излучает преимущественно лучи таких длин волн, которые оно при
той же температуре сильнее всего поглощает.

720 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
Абсолютно черных тел, как и других идеализированных объ-
объектов, в природе не существует. Наилучшим приближением к
абсолютно черному телу является замкнутая полость, в стенке
которой сделано малое отверстие, через которое излучение из
полости может выходить наружу. Если стенки полости непро-
непрозрачны, то при достаточно малых размерах отверстия в полости
установится излучение, лишь бесконечно мало отличающееся от
равновесного. Через отверстие будет выхо-
выходить практически такое же излучение, ка-
кое испускалось бы абсолютно черной пло-
площадкой той же формы и размеров.
Убедиться в этом молено и другим спо-
собом. Луч света, вступивший снаружи в
полость через ее отверстие, будет претер-
претерпевать многократные отражения от стенок
полости (рис. 339) При каждом отражении
часть лучистой энергии поглощается. По™
еле многократных отражений луч либо со-
Рис 339 всем не выйдет наружу через отверстие,
либо выйдет лишь ничтожная часть лучи-
лучистой энергии, вступившей в полость. Почти вся энергия погло-
поглотится стенками полости. Это значит, что полость с малым отвер-
отверстием в отношении поглощения, а потому по закону Кирхгофа и
в отношении испускания, ведет себя практически как абсолютно
черное тело. Изложенный способ всегда применяется при точ-
точных количественных измерениях излучения абсолютно черного
тела.
Поясним изложенное примером. Если стенки полости с ма-
малым отверстием ярко осветить снаружи, то отверстие будет вы-
выделяться своей чернотой на светлом фоне освещенных стенок.
Таким представляется, например, открытое окно здания. Так
будет происходить даже в том случае, когда наружная поверх-
поверхность стенок полости закрашена черной краской. Если же рас-
раскалить стенки полости, сделанные из материала с малой погло-
щательной способностью (например, из белого фарфора), то от-
отверстие будет ярко светиться на более тусклом фоне прямого
излучения самих стенок. При закрашивании стенок снаружи в
черный цвет стенки светятся ярче, но все же их яркость оста-
остается меньше яркости отверстия. Закрашивание стенок изнутри
совсем не сказывается на яркости отверстия.
4. Так как для абсолютно черного тела еш = /ш, а равновесное
излучение изотропно, то излучательная способность абсолютно
черного тела одинакова по всем направлениям. При тепловом
излучении она, очевидно, совпадает с поверхностной яркостью
тела (см. § 22). Значит, излучательная способность абсолютно
черного тела подчиняется закону Ламберта (см. § 22).

§ 114 ФОРМУЛА КИРХГОФА-КЛАУЗИУСА 721
Обратное, конечно, не справедливо. Закон Ламберта может
выполняться и для не абсолютно черных тел. Закон Кирхгофа
позволяет полнее исследовать этот вопрос. Согласно этому зако-
закону, Еш = Ашеш, а потому тело будет излучать по закону Ламбер-
Ламберта, если его поглощательная способность не зависит от направ-
направления поглощаемого излучения. Так как для непрозрачного тела
энергия падающего света равна сумме энергий поглощенного и
рассеянного света, то, очевидно, закону Ламберта будет подчи-
подчиняться излучение всяких тел, равномерно рассеивающих падаю™
щий свет во все стороны, независимо от его направления. Такие
тела называются абсолютно матовыми. Итак, тепловое излуче-
излучение абсолютно матовых тел следует закону Ламберта. На эту
связь закона Ламберта с законом Кирхгофа указал В.А. Улья-
нин A863—1930) в 1897 г., хотя его рассуждения и были несколь-
несколько сложнее приведенных здесь.
§ 114. Формула Кирхгофа^Клаузмуса
Найдем теперь плотность энергии и удельную интенсивность
равновесного излучения в прозрачной однородной изотропной
среде с показателем преломления п. Такое излучение устанав-
устанавливается в замкнутой полости, заполненной рассматриваемой
средой, стенки которой поддерживаются при постоянной тем-
температуре. В точности такое же излучение установится в среде и
в том случае, когда она заполняет только часть полости. Пред-
Предположим, что часть полости заполнена рассматриваемой средой,
а в другой находится вакуум. Равновесное излучение как в сре-
среде, так и в вакууме совершенно не зависит от формы и свойств
поверхности, вдоль которой среда граничит с вакуумом. Не ме-
меняя окончательного результата, можно принять, что эта граница
плоская и гладкая.
Излучение в среде не зависит и от ее размеров. Поэтому
среду можно считать настолько протяженной, чтобы при сколь
угодно малом коэффициенте поглощения световой луч, вступив-
вступивший в среду, успел полностью поглотиться, не достигнув стенок
полости. Тогда обмен энергией между средой и вакуумом будет
происходить только в результате отражения и преломления из-
излучения на рассматриваемой границе. Такой обмен подчиняется
принципу детального равновесия и не может нарушить состоя-
состояние равновесия излучения как в среде, так и в вакууме. Из этого
условия и можно найти соотношение между плотностью энергии
и0 и удельной интенсивностью 1° излучения в вакууме с такими
лее величинами и и / в среде. (В этом параграфе все величи-
величины, относящиеся к вакууму, снабжены нулем в индексе, а все
величины в среде оставлены без индекса.)

722
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
ГЛ. X
п=\
Рис. 340
Ввиду выполнения принципа деталвного равновесия, рас™
суждение достаточно провести не для всего излучения, а только
для произвольной части его, заполняющей интервал частот а;,
ш + duj. Через единичную площадку границы раздела в едини™
цу времени из вакуума в пре-
пределах телесного угла Qq па™
дает лучистый поток Фх =
= I® dU0 duj cos (pOj где щ —
угол падения (рис. 340). Со™
гласно принципу детального
равновесия, должен существо™
вать такой же лучистый поток,
распространяющийся в обрат™
ном направлении. Он состоит
из двух потоков. Первый по™
ток возникает в результате от™
ражения потока <3>2 и равен
A — Аш) 1^ duo duj cos (fQ. Вто™
рой поток возникает в резуль™
тате преломления потока Фз, приходящего снизу из среды. Так
как в силу формул Френеля коэффициенты отражения на гра™
нице раздела при прямом и обратном ходе лучей одинаковы, то
второй поток будет АШ1Ш du duj cos </?, где (р — угол преломления,
а сШ — телесный угол в среде, переходящий при преломлении в
dOo- Сокращая на duj^ запишем условие детального равновесия
в виде
A ~~ АшI® cos щ dU0 + АШ1Ш cos (pdU = I® cos щ dO0,
или
1Ш cos ipdu = I^ cos щ duo-
В качестве duo возьмем (не изображенный на рис. 340) телес™
ный угол, заключенный между коническими поверхностями, об™
разующие которых составляют с нормалью к границе раздела
углы (fo и ^о + d(fo7 т.е. dQo = 2тг sin ipo dcpo. Аналогично, dQ =
= 2тг sin (p dip. Тогда
1Ш cos ip sin if dip = I^j cos (po sin щ dipo.
В силу закона преломления slnc^o = rising, так что cosc^o dipo =
= n cos ip dip. Поэтому
1Ш sin (p = nl^ sin (fo •
Отсюда в силу того же закона преломления
1ш = п2С A14.1)
Эта формула и решает поставленную задачу. Она была получена
Кирхгофом в 1860 г. и независимо от него Клаузиусом в 1864 г.
Ее называют формулой Кирхгофа-Клаузиуса.

§ 115 ЗАКОН СТЕФАНА-БОЛЬЦМАНА 723
В вакууме величины /^ и г^ связаны соотношением A12.6),
т.е. си^ = 47г1^. В среде оно заменяется на угриш = 4,ж1ш, где
vTp — групповая скорость. Следовательно,
ии = и°шп2^-. A14.2)
Для недиспергирующих сред
иш = п3и° . A14.3)
Соотношениям A14.1) и A14.3) молено придать другую, лег-
легче запоминаемую форму, глубокий смысл которой выяснится
при рассмотрении проблемы методами статистической физики
(см § 117). Для этого заметим, что п = Ао/А. Тогда A14.1) и
A14.3) преобразуются в
Х21Ш = Х20С A14.4)
Х3иш = Х3ои°ш. A14.5)
Соотношение A14.4) означает, что в равновесном излучении по-
потоки лучистой энергии через квадратную площадку со сторо-
стороной, равной длине волны А (в рассматриваемой среде), отнесен-
отнесенные к единице телесного угла, в направлении нормали к площад-
площадке одинаковы для всех сред и зависят только от их темпера-
температуры. Это утверждение справедливо как для полного потока,
так и для его монохроматических составляющих. Аналогично,
соотношение A14.5) утверждает, что энергия равновесного из-
излучения, локализованная в кубике с ребром, равным длине вол-
волны А, одинакова во всех изотропных недиспергирующих средах
и определяется только температурой среды. Это утверждение
относится также не только к полной плотности энергии, но и к
ее монохроматическим составляющим.
§ 115. Закон Стефана^Больцмана
1. В XIX веке производились многочисленные исследова-
исследования зависимости интегральной лучеиспускательной способно-
способности нагретых тел от температуры, т.е. величины, которая опре™
деляет суммарную энергию всех длин волн, излучаемых тела-
телами. Эти исследования приводили к противоречивым результа™
там. Основная причина расхождений была окончательно выяс-
выяснена после установления закона Кирхгофа, так как излучение
определяется не только температурой, но также составом тела
и физическими свойствами излучающей поверхности. А на эту
сторону дела в экспериментальных исследованиях не обраща-
обращалось должного внимания. Из эмпирически установленных за-
законов следует отметить только результат, найденный в 1879 г.

724 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
Стефаном A835-1898). Он нашел, что для черных тел излу-
нательная способность пропорциональна четвертой степени
температуры. Через пять лет Больцман получил этот резуль-
результат теоретически из термодинамических соображений и показал,
что он абсолютно верен для абсолютно черных тел. Этот ре-
результат, получивший название закона Стефана-Больцмана^ был
подтвержден последующими опытами по излучению абсолютно
черного тела.
Вывод Больцмана и все последующие работы по теории теп™
лового излучения существенно используют результаты Максвел-
Максвелла, предсказавшего и рассчитавшего давление света (см. т. II,
§ 61; т. III, § 145, а также задачу 2 к § 84 этого тома). Для изо™
тройного излучения это давление равно V = Уз^, где и — ин-
интегральная плотность лучистой энергии. К такому выражению
должна приводить всякая релятивистская теория света, незави-
независимо от того, является ли она корпускулярной или волновой.
До теории относительности этот результат, разумеется, не был
известен, а результаты Максвелла не считались общепризнан-
общепризнанными. В частности, согласно нерелятивистской корпускулярной
теории должно было бы быть V = 2/%и^ как это предсказыва-
предсказывает кинетическая теория газов (см. т. II, § 59). Поэтому опыты
П.Н. Лебедева, впервые измерившего в 1900 г. световое давле-
ние, подтвердившие результаты Максвелла, имели основопола-
основополагающее значение для всей термодинамики лучистой энергии.
2. Доказательство закона Стефана-Больцмана мы проведем
методом циклов^ так как таким путем попутно будут получены
важные соотношения, используемые в дальнейшем. Допустим,
что изотропное излучение произвольного спектрального соста-
состава заключено в адиабатическую оболочку с абсолютно зеркаль-
зеркальными стенками. Произведем над ним адиабатический квазиста-
квазистатический процесс, при котором объем V, ограниченный оболоч-
оболочкой, меняется бесконечно медленно. Чтобы быть уверенным, что
во время этого процесса излучение все время остается изотроп-
изотропным, можно взять оболочку сферической формы (в следующем
параграфе будет показано, что эта предосторожность является
лишней). Внутренняя энергия излучения в оболочке равна uV.
При увеличении объема оболочки на dV за счет этой энергии
совершается работа VdV, так что V dV = —d(uV). А так как
для изотропного излучения V = 1/%и, то этому уравнению мож-
можно придать вид ^feudV' + V du = 0. Отсюда следует, что во время
процесса
uV4/3 = const, A15.1)
или
4/3 = const. A15.2)

§ 115 ЗАКОН СТЕФАНА-БОЛЬЦМАНА 725
Это — уравнение адиабаты для изотропного излучения, совер-
шенно аналогичное уравнению адиабаты Пуассона для идеаль-
идеального газа. Постоянная адиабаты равна 7 = 4/з-
В силу эффекта Доплера при адиабатическом сжатии или
расширении излучения должен меняться его спектральный со™
став. Допустим, например, что изотропное излучение занимает
спектральный интервал cj, uj + duj. В результате отражения от
движущейся стенки частота ио и ширина интервала duj изменят-
изменятся и сделаются равными и/ и duj'. При этом будет выполняться
соотношение
иш duj • F4/3 = и'ш, du' • F/4/3 = const, A15.3)
где Vf и игш, — объем и спектральная плотность энергии излуче-
излучения частоты а/ в конце процесса.
8. Докажем теперь закон Стефана-Больцмана. Для этого
произведем над черным излучением цикл Карно. Допустим, что
излучение заключено в цилиндре, боковые стенки и поршень
которого идеально отражающие, а дно черное и может приво-
приводиться в тепловой контакт с нагревателем температуры Т\ и
холодильником температуры Т2. Излучение молено адиабатиче-
адиабатически изолировать с помощью идеально отражающей задвижки,
вводимой сбоку для прикрытия черного дна цилиндра. В отсут-
отсутствие задвижки, когда черное дно
цилиндра приведено в тепловой р
контакт с нагревателем или хо™
лодильником, излучение в цилин-
цилиндре, конечно, будет равновесным.
Чтобы быть уверенным, что оно
сохранится равновесным и во вре-
время адиабатического процесса, ко-
когда задвижка вставлена, введем
внутрь цилиндра черную пылин- V
ку, роль которой была выяснена
в п. 1 § 112. На изотерме 1-2 Рис- 341
(рис. 341) дно цилиндра контактирует с нагревателем. Количе-
Количество тепла, переданное нагревателем на этой изотерме, равно
Qi = иг(У2 - Fi) + Pi(F2 - Fi) = | Ul(V2 - Vi).
Количество тепла, отданное холодильнику на изотерме 3-^
Q2 = 4/3^2(F3 — F4). По теореме Карно
I
\
4
Ту
ш
т2
2
\\
\
3
Q2 U2IV3-V4) Т2'
На адиабатах 2-3 и-|-] в силу A15.1) выполняются соотноше-
соотношения
3/4Т/ 3/4ТЛ 3/4Т. 3/4Т/
u{ F2 = u2f V3, и{ Vi = u^ F4.

726 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
Отсюда
vL-vL = (М3/4
Уз — Уа \ui /
а потому щ/Tf = U2T2 = const. Следовательно,
и = аТ4, A15.4)
где а — универсальная постоянная. Но это есть иная форма за-
закона Стефана^Больцмана.
Результат A15.4) молено получить короче, если к равновесно-
равновесному излучению применить общую термодинамическую формулу
Подставив сюда U = Vu^)^ V = 1/%и{ТI придем к тому же
дифференциальному уравнению, интегрированием которого бы-
была получена формула A15.4). Однако мы не хотели пользоваться
формулой A15.5).
§ 116. Теорема и закон смещения Вина
1. Важные результаты в термодинамике излучения были по™
лучены Вильгельмом Вином A864-1928) в 1893-1894 гг. Вин
доказал, что равновесное излучение, заключенное в оболочке с
идеально отражающими стенками, будет оставаться равно-
равновесным при квазистатическом сжатии или расширении обо-
лочки.
Для наших целей при доказательстве теоремы Вина доста™
точно ограничиться оболочкой сферической формы. В этом слу-
случае, ввиду сферической симметрии системы, отпадает необхо-
необходимость специально доказывать, что в ходе процесса изотропия
излучения все время сохраняется. Сожмем излучение квазиста-
тически от начального объема V\ до конечного V2. При этом бу-
будет совершена работа против сил светового давления, и энергия
излучения в оболочке увеличится. Спектральный состав излуче-
излучения также изменится, из-за эффекта Доплера. Допустим, что в
результате этого излучение перестанет быть равновесным. Вве™
дем внутрь оболочки в конечном состоянии бесконечно малую
черную пылинку, поглощающую и излучающую свет. По исте™
чении достаточно длительного времени она превратит неравно-
неравновесное излучение в оболочке в равновесное. Это — необратимый
процесс, идущий самопроизвольно. Обратный процесс превра-
превращения равновесного излучения в неравновесное, разумеется, сам
собою идти не может.
Когда излучение внутри оболочки станет равновесным, не
убирая пылинку, начнем бесконечно медленно адиабатически

§ 116 ТЕОРЕМА И ЗАКОН СМЕЩЕНИЯ ВИНА 727
расширять оболочку, доведя объем излучения до исходного зна-
чения V\. После этого удалим пылинку. Энергия пылинки бес-
бесконечно мала, а потому ее наличие может сказаться на общей
энергии излучения в полости также бесконечно мало. С дру-
другой стороны, давление изотропного излучения зависит только
от интегральной плотности энергии излучения к, но не от его
спектрального состава Поэтому работа, которую совершит све-
световое давление при расширении оболочки, будет с точностью
до бесконечно малой величины равна внешней работе, совер-
совершенной над излучением при его сжатии. Отсюда следует, что в
результате сжатия и последующего расширения энергия, а с ней
и температура излучения не изменятся.
Система совершила круговой процесс, в ходе которого она
не получала и не отдавала тепло, а общая работа, произведен-
произведенная ею, равна нулю. Значит, в окружающих телах не произо-
произошло никаких изменений, а потому рассматриваемый круговой
процесс обратим. Но это невозможно, так как одна из стадий
этого кругового процесса по нашему предположению необрати-
необратима. Следовательно, это предположение неверно, и теорема Вина
доказана.
2. Значение теоремы Вина — методическое. Действительно,
адиабатически и квазистатически меняя объем равновесного из-
излучения в оболочке с идеально зеркальными стенками, можно
получить равновесное излучение произвольной плотности, а сле-
следовательно, и температуры. Энергию (и температуру) этого из-
излучения можно найти, вычислив работу, совершенную над ним
в этом процессе. Его спектральный состав найдется, если вы-
вычислить доплеровское изменение частоты излучения при его от™
ражении от движущейся оболочки. Тем самым будет установ-
установлено определенное соответствие между параметрами равновес-
равновесного излучения в начале процесса и на
любой стадии его.
Применим этот метод к равновес-
равновесному излучению в сферической обо-
оболочке с идеально зеркальными стенка-
стенками. При бесконечно медленном адиа-
адиабатическом расширении или сжатии
оболочки излучение в ней все вре-
время будет оставаться равновесным, так
что его можно в любой момент вре-
времени характеризовать определенной
температурой Т. Выделим внутри обо-
оболочки произвольный луч, падающий Рис. 342
на оболочку под углом $ (рис. 342).
Время между двумя последовательными отражениями этого лу-
луча равно At = Br/c) cos i9. За это время радиус оболочки г полу-

728 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
чает приращение Ar = r At. При каждом отражении происходит
доплеровское изменение частоты, определяемое формулой
Аш _ 2fcos^ _ 2Arcos$ _ Ar
ш с с At r '
если пренебречь квадратом бесконечно малой радиальной ско-
скорости г расширения оболочки. Относительное изменение часто™
ты Аш/ш определяется только относительным изменением Аг/г
радиуса оболочки. Такая же формула получится и в том случае,
когда за время изменения радиуса оболочки на Аг произойдет
не одно, а много отражений светового луча. Требуется только,
чтобы выполнялось условие Аг<Сг. При бесконечно медленном
расширении величины Аг и Да; можно заменить их дифферен-
дифференциалами, т.е. написать
— + ^ = 0. A16.1)
и г
Это означает, что реальный процесс, в котором последователь™
ные отражения отделены друг от друга малыми, но все же
конечными промежутками времени, при расчетах заменяется
идеализированной схемой, в которой эти отражения следуют
друг за другом непрерывно во времени. Интегрируя уравнение
A16.1), получим
шг = const. A16.2)
Так как г ~ У1/3, то этот результат можно записать также в
виде
uj3V = const. A16.3)
В таком виде он справедлив для полости произвольной формы.
А поскольку он получен для бесконечно медленного процесса,
величина d3V является адиабатическим инвариантом. Комби™
нируя его с ранее полученными адиабатическими инвариантами
A15.1) и A15.3), получим новые адиабатические инварианты.
Так, из формул A15.1) и A16.3) следует
— = const, A16.4)
и
или на основании закона Стефана^Больцмана
— = const. A16.5)
Аналогично, формулы A15.3) и A16.3) дают
^^ = const. A16.6)
Таким образом, при квазистатическом расширении или ежа™
тип равновесного излучения в полости с зеркальными стенками
каждая квазимонохроматическая составляющая излучения ве~
дет себя независимо от остальных составляющих и меняется

§ 116 ТЕОРЕМА И ЗАКОН СМЕЩЕНИЯ ВИНА 729
так, что величины ш^У', и/ш и иш dш/ш остаются постоянными,
т.е. являются адиабатическими инвариантами. По теореме Вина
при таком процессе излучение все время остается равновесным.
Такое же излучение можно было бы получить в неподвижной
оболочке, нагревая или охлаждая ее стенки. Поэтому получен-
полученные результаты можно представить как свойства только само-
самого равновесного излучения^ не связывая их ни с каким конкрет-
конкретным процессом. Сформулируем их следующим образом. Изме-
Изменим любым способом температуру равновесного излучения от
Т до Т1', чтобы излучение оставалось равновесным. Каэюдой
частоте ш излучения в начальном состоянии приведем в со-
соответствие такую частоту ш' в конечном состоянии^ чтобы
ш/Т = ш1 /Т' и, следовательно^ dш/T = dшl/Т'. Тогда плотно-
плотности лучистой энергии в этих состояниях будут связаны соот-
соотношениями
V^ = <L^L. (И6.8)
Эти результаты составляют содержание так называемого закона
смещения Вина в его наиболее общей форме.
8. Из формулы A16.8) получаем
ш4 duj' Т3
и/4 duj ш Т/3 ш
Это соотношение справедливо при любом значении температу-
температуры Т;, а потому величина справа от Т1 не зависит. Величине Т1
можно придать любое значение^ представив полученное соотно™
шение в виде
иш(ш,Т) =Т3(^(|) , A16.9)
где (р(ш/Т) — универсальная функция аргумента ш/Т. Ввиду
соотношения ш/Т = ш1 /Т\ тот же результат можно записать в
виде
A16.10)
где /(ш/Т) = (Т1/шгK(р(ш/Т) — новая универсальная функция
того же аргумента ш/Т. Тем самым определение универсальной
функции иш(ш1Т) двух аргументов сведено к задаче нахожде-
нахождения универсальной функции (р(ш^Т) или /(ш/Т) только одного
аргумента ш/Т. Отсюда следует, что если известно спектраль-
спектральное распределение в равновесном излучении при какой-либо про-
произвольной температуре Т;, то с помощью формулы A16.9) или
A16.10) можно найти это распределение при всякой другой
температуре Т.

730 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
В переменных А, Т, как это следует из соотношения A12.2),
формулам A16.9) и A16.10) можно придать вид
A16.11)
A5^V— /> A16.12)
где ipi(XT) и fi(XT) — новые универсальные функции. При фик-
фиксированной температуре Т величина и\ становится функцией
только длины волны А. Эта функция не может возрастать мо-
монотонно, а должна иметь максимум. В противном случае инте-
интегральная плотность излучения
оо
и= I (u\)T=constdX A16.13)
не могла бы оставаться конечной. Длину волны в максимуме
обозначим через Лш. Если ввести обозначение х = AT, то для
определения положения максимума получится уравнение
d(fi/d\ = Т difi/dx = 0, т.е. dipi/dx = 0.
Таким образом, при всех температурах максимум получается
при одном и том же значении аргумента х. Отсюда следует,
что при повышении температуры максимум функции tiA,T=const
смещается в сторону более коротких волн и притом так, что
выполняется соотношение
\тТ = Ъ = const. A16.14)
Измерения дают: Ъ = 0,2898 см-К. Этот результат, определяю-
определяющий смещение максимума излучения при изменении темпера-
температуры Т, называют законом Вина в его специальной форме. В
точках максимума функции и\(Т) и u\f(Tf) относятся как пя-
тые степени абсолютных температур Т и Т1.
Функция иш(и),Т) при постоянной температуре Т также
обращается в максимум при какой-то частоте ш = шт. Частота
шт не равна 2тгс/Лш, так как речь идет о максимумах различных
функций иш(ш) и и\(Х). При изменении температуры излучения
положение максимума смещается, но при этом имеет место со-
соотношение
^ = const, A16.15)
которое является другой формой закона смещения Вина
A16.14).
4. Выведенный ранее закон Стефана-Больцмана является
следствием общей формулы A16.9). Действительно, вводя обо-

§ 117 ФОРМУЛА РЭЛЕЯ-ДЖИНСА 731
значение х = ш/Т, из этой формулы при постоянной Т находим
и= j Uujduj = T3 j Ч>{^) duj = T4 j ф) dx = aTA,
0 0 0
где a = J <p(x) dx — универсальная постоянная,
о
§ 117. Формула Рэлем—Джинса
1. Результатами, изложенными в предыдущих параграфах,
исчерпывается все, что могла дать феноменологическая термо™
динамика в проблеме теплового излучения. Ее оказалось недо-
недостаточно для решения основной проблемы теории теплового из-
излучения: определения функции иш(ш^Т) или функции /ш(о;,Т),
связанной с ней соотношением A12.6). Для этого оказалось необ-
необходимым привлечь статистические методы и учесть кванто-
вые свойства вещества и излучения. Первая попытка теоре-
теоретического решения указанной проблемы была предпринята в
1887 г. В.А. Михельсоном A860—1927). В то время, как показало
последующее развитие физики, правильное решение рассматри-
рассматриваемой проблемы было, конечно, невозможно. Заслуга Михель-
сона состоит в том, что он привлек внимание физиков к одной из
важнейших проблем, решение который положило начало кван-
квантовой физики.
Общий метод теоретического определения функции иш(ш^Т)
в рамках классической физики, не связанный с модельными
представлениями, был указан в 1900 г. Рэлеем и через пять лет
более подробно развит Джинсом A877-1946). Рэлей и Джине
применили к равновесному излучению в полости теорему клас-
классической статистической механики о равномерном распределе-
распределении кинетической энергии по степеням свободы. Согласно этой
теореме, в состоянии статистического равновесия на каждую
степень свободы приходится в среднем кинетическая энергия
l^kT^ где к = 1,38 • 10~16 эрг/К — постоянная Больцмана.
Если степень свободы колебательная, то надо учесть еще по-
тенциальную энергию. В случае гармонических колебаний сред-
среднее значение потенциальной энергии равно также l/2~kT (см. т. II,
§ 63). Таким образом, в состоянии статистического равновесия
на каждую колебательную степень свободы приходится сред-
средняя энергия^ равная кТ.
Эта теорема сводит задачу нахождения функции иш(ш,Т)
к определению числа степеней свободы излучения в полости.
Поскольку равновесное излучение в полости не зависит от ее

732 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
формы и материала стенок, можно предположить, что полость
имеет форму куба с идеально отражающими стенками. А что-
чтобы излучение в полости было равновесным, можно ввести в нее
бесконечно малую черную пылинку, как это делалось в преды-
предыдущем параграфе при доказательстве теоремы Вина.
2. Чтобы лучше уяснить метод определения числа степеней
свободы, рассмотрим этот вопрос сначала не для векторного
электромагнитного поля, а для скалярного волнового поля^ на-
например для продольных акустических волн. В такой постанов-
постановке этот вопрос имеет и самостоятельный интерес, например в
теории теплоемкости твердых тел Дебая. Волновое поле будем
характеризовать какой-то функцией V(r, ?), удовлетворяющей
волновому уравнению
дх2 ^ ду2 ^ QZ2 C2 df2 U'
Предположим, что на стенках полости функция V обращается
в нуль. Тогда (а также и при других граничных условиях) по
теореме Фурье функция V(r,t) может быть представлена су™
перпозицией стоячих волн. Координатные оси X, Y, Z напра-
направим параллельно ребрам кубической полости. Так как гранич-
граничные условия должны удовлетворяться на гранях х = 0, у = О,
z = 0 и на параллельных им гранях полости, то каждая стоя-
стоячая волна должна представляться функцией с разделяющимися
переменными^ т.е.
V = X(x)Y(y)Z(z) exp {iut).
Отсюда
1 d2V _ 1 d2X I d2V _ ш2
Fa? - х^"''11']/"^ ~ ~&'
Подставив эти выражения в уравнение A17.1), получим
X dx2 Y dy2 Z dz2 c2 '
Левая часть этого уравнения есть сумма функций от ж, у, z
соответственно, т.е. от различных переменных. Она равна по-
постоянной ш2/с2. Это может быть тогда и только тогда, когда
каждая из этих функций сама постоянна, т.е.
1 d2X _ 2 1 d2Y _ 2 1 d2Z _ 2
где qX7 qyj qz — постоянные, удовлетворяющие условию
ql + ql + q2z = q2 = ^. A17.2)
Решение первого уравнения запишем в виде X = mn{qxx + 8ХI
где 5х — постоянная интегрирования. Второй постоянной инте-
интегрирования служит амплитуда, которую без потери общности

§ 117 ФОРМУЛА РЭЛЕЯ-ДЖИНСА 733
можно опустить. На грани полости х = 0 функция X должна
обращаться в нуль, т.е. sln^ = 0. Также не теряя общности,
можно положить дх = 0. На противоположной грани х = 1, где
I — длина ребра кубической полости, функция X также должна
обращаться в нуль, а потому sinkxl = 0. Такие же результаты
получаются и для координат у и z. Следовательно,
V = sinqxx sinqyy sinqzzelujt^ A17.3)
где
qxl = тжтг, qyl = туж^ qzl = т2тг, A17.4)
а тж, ту, mz — целые числа. Все их можно считать положи™
тельными, так как введение отрицательных чисел не приводит
к новым, линейно независимым решениям. В выражение A17.3)
можно было бы ввести еще постоянную амплитуду, зависящую
от тХ1 ту, mZi но для наших целей в этом нет надобности. Это
выражение и представляет общий вид стоячей волны в поло-
полости. Каждой тройке целых положительных чисел mXj myj mZj
удовлетворяющей условиям A17.4), соответствует одна стоячая
волна. Число возможных стоячих волн бесконечно велико.
Будем рассматривать qXj qyj qz как прямоугольные коорди™
паты точки трехмерного «пространства волновых векторов» q.
Эти «изображающие точки» расположатся в узлах кубической
решетки, элементарная ячейка которой есть кубик с длиной сто™
роны Aqx = (тг/1)Атх = ж/1 и объемом (тг/1K. Решетка заполня-
заполняет только положительный октант пространства волновых векто™
ров, так как все координаты qXj qyj qz положительны. Объем ча™
сти шара радиуса д, лежащей в этом октанте, равен 1/%{Аж/3)д3 =
= (тг/6)д3. Число изображающих точек в нем и будет равно чис-
числу Z стоячих волн, волновые числа которых не превосходят q =
= 2тг/А. Подавляющее число волн очень короткие, для них вели™
чина q очень велика по сравнению с длиной ж/1 ребра элементар-
элементарного кубика. Поэтому число стоячих волн в указанном октанте
шара найдется делением его объема на объем элементарного ку-
кубика. Таким путем получается асимптотическая формула
7 _ (тг/6)д3 _ V з _ V ш3 П17 ^
А — о /?о — -^ч Q — ^ч^ч {lit.о
ж3/!3 6ж2 бтг2 с3
где V = I3 — объем полости. Она справедлива, когда сторона
кубической полости очень велика по сравнению с длиной волны
А = 2тг/д. Можно доказать, что формула A17.5) остается верной
и для полости произвольной формы, хотя в этом случае стоячие
волны и не будут представляться выражениями вида A17.3).
Дифференцируя A17.5), получим
^ ^?duJ. A17.6)

734 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
Эта асимптотическая формула дает число стоячих волн в ин-
тервале частот а;, ш + duj. Она, разумеется, справедлива только
для достаточно широких интервалов da;, когда dZ ^> 1.
3. Рассуждения существенно не изменятся и в случае вектор-
векторного (электромагнитного) поля. В этом случае вектор Е и его
прямоугольные составляющие Ех, Еу, Ez удовлетворяют преж™
нему волновому уравнению A17.1). Для полости с идеально зер-
зеркальными стенками граничные условия требуют обращения в
нуль тангенциальных составляющих вектора Е на стенках по-
полости. Для этого необходимо и достаточно, чтобы выполнялись
следующие условия:
Еу = Ez = 0 при х = 0 и х = I,
Ez = Ех = 0 при у = 0 и у = I,
Ех = Еу = 0 при z = 0 и z = I.
Стоячая волна, удовлетворяющая этим условиям, имеет вид
Ех = sin (qxx + (px) sin qyy sin qzz elujt,
E^ = slng^ sm(g2/y + ^) smqzze%ujt^
Ez = slng^x singly sin (gzz + (рг) e2Ct;t,
где qXj qyj qz определяются прежними формулами A17.4). Что
касается фаз срх, (pyj ipZj то их можно было бы найти из гранич-
граничных условий, которым на стенках полости удовлетворяют нор™
мальные составляющие электрического вектора Е. Но для на-
наших целей в этом нет необходимости, так как для определения
величин Z и dZ достаточно знать только значения, которые мо-
могут принимать составляющие qx, qy, qz. Однако по сравнению с
предыдущим случаем выражения A17.5) и A17.6) надо удвоить,
так как электромагнитные волны векторные и притом попереч-
ные. Каждому направлению распространения соответствуют две
волны^ поляризованные во взаимно перпендикулярных плоско-
плоскостях, в результате суперпозиции которых может быть получена
волна любой поляризации, распространяющаяся в том же на-
направлении. Итак, для электромагнитного поля
dZ = ^—uj2dou. A17.7)
7г2е3 v '
На каждую стоячую волну в состоянии статистического рав-
равновесия приходится в среднем энергия ? = кТ: одна половина
ее — электрическая, другая — магнитная. Записав энергию рав™
новесного излучения в полости в спектральном интервале duj в
виде VuUJduj^ из формулы A17.7) получим

§ 117 ФОРМУЛА РЭЛЕЯ-ДЖИНСА 735
Этот результат известен под названием формулы Рэлея-
Джинса, хотя он независимо и практически одновременно с
Рэлеем был получен также Планком из столь же общих, но
несколько других соображений (см. п. 6).
4. Прежде чем обсуждать формулу Рэлея^Джинса, заметим,
что в случае полости, заполненной изотропной средой, число
стоячих волн будет определяться прежними формулами A17.5)
и A17.6), если только в них величину с заменить скоростью све-
света v в рассматриваемой среде (предполагается, что среда изо™
тройная). Отсюда следует, что числа Z и dZ в одном и том же
интервале частоты, а с ними и функция иш пропорциональны
с3/г?3, т.е. кубу показателя преломления среды п. Но это есть
закон Кирхгофа-Клаузиуса^ доказанный в § 114. Вывод справед-
справедлив при более общих предположениях, чем это сделано в тексте.
Нет необходимости ссылаться на классическую теорему о равно-
равномерном распределении энергии по степеням свободы. Достаточ™
но, чтобы средняя энергия гармонического осциллятора была
функцией только частоты а;, как это имеет место в квантовой
теории.
5. Формула Рэлея-Джинса согласуется с общей термодина-
термодинамической формулой Вина A16.9) или A16.10). Более того, вид
этой формулы может быть непосредственно установлен на осно™
ве одной только формулы Вина, если ограничиться предель-
предельным случаем низких частот. Для этого заметим, что в формуле
A16.10) функция f(u)/T) должна быть возрастающей функцией
температуры Т и обращаться в нуль при Т = 0. Ее удобнее рас-
рассматривать как функцию аргумента Т/ш и разложить в ряд по
степеням этого аргумента. Если ограничиться первым членом
этого ряда, то получится
иш(ш,Т) = СТш2. A17.9)
Но по своему виду этот результат совпадает с формулой A17.8).
Только коэффициент С остается неопределенным. Зато форму-
формула A17.9) выведена в более общих предположениях, чем A17.8).
Таким образом, в предельном случае низких частот нет сомне-
сомнений в правильности вида формулы A17.9). И действительно, для
достаточно длинных волн (точный критерий приводится в сле-
следующем параграфе) формула Рэлея^Джинса прекрасно согла-
согласуется с опытом. Она с успехом применяется в длинноволновой
инфракрасной области спектра и в радиодиапазоне.
Но классическая статистика требует, чтобы формула Рэлея^
Джинса A17.8) была верна при любых частотах. Однако это
невозможно, так как тогда для интегральной плотности энергии

736 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
получилось бы бесконечное значение:
оо
кТ
кТ г 2 i
= —— I ш аш = оо.
7Г2С3 J
и
7TZCO
О
Отсюда следует, что по теории Рэлея-Джчнса тепловое рав-
равновесие между веществом и излучением невозможно. Этот вы-
вывод противоречит опыту. П.С. Эренфест назвал его ультрафио-
ультрафиолетовой катастрофой. Причина ультрафиолетовой катастрофы
заключается в том, что в теории Рэлея-Джинса излучение в по-
полости имеет бесконечное, а вещество конечное число степеней
свободы. Поэтому, если бы было справедливо равномерное рас-
распределение энергии по степеням свободы, то при тепловом рав-
равновесии вся энергия должна была бы сосредоточиться в излуче-
излучении.
6. Можно было бы возразить, что классическая статистиче-
статистическая механика, следствием которой является теорема о равно-
равномерном распределении кинетической энергии по степеням сво-
свободы, неприменима к системам с бесконечным числом степеней
свободы. Но такое возражение неубедительно. В основе класси-
классической статистической механики лежат уравнения классической
механики в форме Гамильтона A805-—1865). Хотя они и были
установлены для механических систем с конечным числом сте-
степеней свободы, но можно показать, что излучение в полости
можно описывать бесконечным, но счетным числом обобщен-
обобщенных координат, также подчиняющихся уравнениям Гамильто-
Гамильтона. Следовательно, и вся система, состоящая из вещества и из-
излучения, будет описываться уравнениями Гамильтона.
Поэтому было бы непонятно, почему теорема о равномерном
распределении энергии справедлива для одних и не имеет места
для других степеней свободы.
Кроме того, к формуле Рэлея^Джинса независимо пришел
также Планк, применивший эту теорему только к веществу, но
не к излучению. Он провел рассуждение для одномерного гар-
гармонического осциллятора, например, квазиупруго-связанного
электрона, помещенного в полость с равновесным излучением.
Под действием хаотически меняющегося электромагнитного по-
поля излучения осциллятор будет совершать колебания с хаотиче-
хаотически меняющимися амплитудами и фазами, излучая и поглощая
при этом электромагнитные волны. Энергия осциллятора будет
совершать беспорядочные флуктуации вокруг среднего значе-
значения ?. В результате идейно-простых, но несколько длинных вы-
вычислений Планк пришел к формуле
иш = 4г^ь?« A17.10)

§ 118 ФОРМУЛА ПЛАНКА 737
Если в этой формуле применить к осциллятору (вещество!) тео-
рему о равномерном распределении кинетической энергии по
степеням свободы, то получится формула Рэлея-Джинса.
§ 118. Формула Планка
1. Правильная формула для спектральной плотности энер-
энергии равновесного излучения, подтвержденная всеми экспери-
экспериментальными исследованиями, была найдена Планком сначала
полуэмпирическим путем. Спустя короткое время, Планк на™
шел теоретический вывод этой формулы, изложенный им 14 де-
декабря 1900 г. на заседании Немецкого физического Общества.
Этот день считается днем рождения новой — квантовой — фи-
физики. Идея о квантах, осторожно формулированная Планком,
развилась в стройное и глубокое учение, покорившее всю фи-
физику. Решение проблемы равновесного излучения Планком бы-
было бы невозможно, если бы в своих исследованиях он не нахо-
находился в тесном контакте с экспериментаторами. Из эксперимент
тальных работ по излучению абсолютно черного тела особенно
следует отметить исследования Лэнглея A834-1906), Рубенса
A865-1922), Пашена A865-1947), Вина, Луммера A860-1925),
Э. Принсхейма A859-1917), Курльбаума.
2. Гипотеза Планка состоит в том, что излучение и поглоще-
поглощение света веществом происходит не непрерывно, а конечными
порциями, называемыми квантами света или квантами энер-
энергии. Получим формулу Планка тем же методом, который при-
применялся при выводе формулы Рэлея-Джинса. Тогда гипотезу
Планка удобно взять в следующей форме: энергия гармониче-
гармонического осциллятора может принимать не произвольные, а только
избранные значения, образующие дискретный ряд: 0, <?q, 2?о>
З^о? • • -> где So — определенная величина, зависящая только от
собственной частоты ш осциллятора. Здесь под осциллятором
понимается не только частица, могущая совершать гармониче-
гармонические свободные колебания, но, например, и стоячая волна опре-
определенной частоты в полости.
Если осциллятор изолирован, то по истечении достаточно
длительного времени он потеряет всю свою энергию на излу-
излучение и перейдет на наинизший энергетический уровень с энер™
гией S = 0. Но если осциллятор находится в полости, стенки ко-
которой поддерживаются при постоянной температуре, то наряду
с излучением будут происходить и акты поглощения, в резуль-
результате которых возбуждаются и высшие энергетические уровни.
Установится вполне определенное состояние детального равно-
равновесия, в котором число актов излучения в среднем равно числу
обратных актов поглощения. В этом состоянии будут возбужде-

738 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
ны все энергетические уровни, но с различными вероятностями.
И все, что требуется для нахождения функции иш(и),Т), — это
определить среднюю энергию ? осциллятора в этом состоянии
статистического равновесия. Такая задача уже была решена на™
ми (см. т. II, § 85). Приведем еще раз это решение в несколько
измененной форме. По теореме Больцмана вероятности возбуж-
возбуждения энергетических уровней осциллятора пропорциональны
величинам
Поэтому
Е
п?ое-п?о/кт
где введено обозначение х = ?®/кТ. Значение знаменателя опре-
определяется формулой
е-пх =
п=0
Числитель находится дифференцированием этой формулы по х:
со
A-е-J'
п=1
и следовательно,
Подставив это значение в формулу A17.8), найдем
Перейдем в этой формуле к пределу ?q —>> 0. Тогда
« 1 + ?о/кТ^ а потому ? = кТ. Получается классическое вы™
ражение для средней энергии осциллятора. Формула A18.2) в
рассматриваемом предельном случае переходит, следовательно,
в формулу Рэлея-Джинса. Этого и следовало ожидать, так как
переход к пределу ? о —>> 0 фактически означает возвращение к
классическому рассмотрению, когда энергия осциллятора меня-
меняется не дискретными порциями, а непрерывно. Однако Планк,
и это привело его к великому открытию, поставил вопрос, что
получится, если предельный переход ?q —> 0 не производить.
Величину ?q он определил из требования, чтобы выражение
A18.2) удовлетворяло общей термодинамической формуле Вина

§ 118 ФОРМУЛА ПЛАНКА 739
A16.10). Приравняв A18.2) и A16.10), видим, что это требова-
требование сводится к выполнению соотношения
Т^2СЪ е?0/кТ _ I
Но ?® есть характеристика только самого осциллятора, а по-
потому не может зависеть от температуры Т — макроскопическо-
макроскопического параметра, определяющего состояние вещества и излучения.
Величина ?q может зависеть только от собственной частоты
ш осциллятора. В таком случае, чтобы левая часть равенства
A18.3) была функцией только аргумента с^/Т, необходимо и до-
достаточно, чтобы
So = huj, A18.4)
где h — постоянная. Она универсальна, поскольку в правой части
A18.3) стоит универсальная функция f(u/T) аргумента ио/Т.
Величина h называется постоянной Планка. Ее числовое значе-
значение по современным данным равно
П = A,0545887 ± 0,0000057) • 1(Г27 эрг • с =
= A,0545887 ± 0,0000057) • 104 Дж • с, A18.5)
Сам Планк пользовался постоянной
h = 2nh = F,626176 ± 0,000036) • 107 эрг • с =
= F,626176 ± 0,000036) • 104 Дж • с. A18.5а)
Если теперь выражение A18.4) подставить в A18.2), то и
получится формула Планка
7Г С g/гш/й! — 2
Формулу Планка обычно пишут в переменных v, Т:
3 1
(П8.6)
" сз ew*
а также в переменных А, Т:
Swhc 1
/11 о
(П8-
ца= Д5 ehc/XkT_1-
При низких частотах, когда
Пш/kT^l, A18.9)
формула A18.6) переходит в формулу Рэлея-Джинса A17.8). В
другом предельном случае высоких частот, когда
Пш/kT^l, A18.10)
получается формула

740
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
ГЛ. X
К формуле такого вида в 1896 г. пришел Вин на основе некото-
некоторых произвольных допущений.
Для высоких частот (ультрафиолет) формула Вина прекрас-
прекрасно согласуется с опытом. Однако в области низких частот (ин-
(инфракрасная область спектра) она дает совершенно неверные ре-
результаты, здесь применима формула Рэлея-Джинса. Первона-
чально Планк и искал эмпи-
1,5 - i рическую формулу, которая
бы при низких частотах сов-
совпадала с формулой Рэлея-
Джинса и непрерывно пере-
переходила в формулу Вина в
области высоких частот.
in_ri // д Если ввести безразмер-
' >=*' '• •* ную переменную х = Нш/кТ^
то формулу A18.6) можно
записать в виде
0,5
При введении другой без-
безразмерной переменной х =
= АкТ/he получится
Q. 7Г/€ I 1/X
Графики функций
10
kT
Уш =
1/ж5
Рис. 343
представлены на рисунках
343 и 344. Штриховые линии
на тех же рисунках предста-
представляют те же функции, если их аппроксимировать по формулам
Вина и Рэлея-Джинса.
3. Пользуясь формулой Планка, уточним значения постоян-
постоянных в законах Стефана-Больцмана A15.4) и Вина A16.14), а
также A16.15). Очевидно, что эти законы должны быть след-
следствиями формулы Планка, так как последняя является частным
случаем общей термодинамической формулы Вина A16.9). Со™
гласно формуле Планка, интегральная плотность энергии рав-
равновесного излучения в вакууме равна
и =
h
;=
ш3 duo
ехр (Нш/кТ) - .
1 -I
о о
(введена безразмерная переменная интегрирования х = Нш/кТ).

118
ФОРМУЛА ПЛАНКА
741
Разложив знаменатель последнего интеграла 1 — е х в ряд и
интегрируя, получим для последнего интеграла
+
так как по известной формуле сумма последнего ряда в скобках
равна тг4/90. Таким образом,
и =
15с3 Я3
-т4 О 7Г л грА
A18.12)
т.е. получается закон Стефана^Больцмана A15.4), в котором по™
стоянная а выражена через одни только фундаментальные по-
постоянные с, h и к.
20
16
12
1/х5
Рис. 344
На практике более удобна формула для энергетической све™
тимости S излучающей абсолютно черной поверхности. Это есть
интегральный лучистый поток, излучаемый наружу во всех на™
правлениях (т.е. в телесный угол 2тг) единицей площади такой
поверхности в единицу времени. Она связана с яркостью В из-
излучающей поверхности соотношением S = ж В = тг/ (см. § 22)
или, ввиду формулы A12.5), S = си/4. (Эта формула вполне
аналогична выражению для среднего числа молекул газа, уда™
ряющихся в единицу времени об единицу площади стенки со™
суда, в который газ заключен, см. т. II, § 75.) Подставив сюда

742 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
выражения A18.12), получим
S = аТ4, A18.13)
где
а = *^L- = ^4й = E,67032 ± 0,00071) • 10 4
60с2 Я3 15с2/г3
A18.14)
Величина а называется постоянной Стефана-Больцмана.
4. Найдем теперь постоянную b в законе смещения Вина
A16.14). Для этого надо найти значение А = Ато, для которо-
которого функция A18.8) при постоянном Т обращается в максимум.
Введем безразмерную переменную /3 = hc/XkT и выразим через
нее функцию A18.8). Тогда, как легко убедиться, задача сводит-
сводится к отысканию минимума функции (е^-~1)//35. Приравняв нулю
первую производную этой функции по /3, получим уравнение
e^ + f-l = 0, A18.15)
5
корень которого /3 = 4,9651142. Поэтому
b = XmT = ксЦкр) = B,897790 ± 0,000090) • 10~3 м-К. A18.16)
Если вместо А пользоваться частотой о;, то закон Вина надо
писать в виде A16.15). Тогда положение максимума, как нетруд-
нетрудно убедиться, будет определяться уравнением
C -/З^ - 3 = 0, A18.17)
где /3 = huj/kT = hc/(XkT), т.е. /3 имеет тот же смысл, что и
в предыдущем случае. Корень этого уравнения /3; = 2,8214393.
Если снова перейти к длинам волн, то максимуму функции иш
соответствует длина волны А^, определяемая условием
\'mT = hc/(kpr). A18.18)
Таким образом, максимум на кривой частот сдвинут в длин-
длинноволновую сторону относительно максимума на кривой длин
волн и притом так, что Xfm/Xm = /3//3; ~ 1,76.
Заметим еще, что, измерив на опыте величины с, а и Ь, мож-
можно по формулам A18.14) и A18.16) вычислить универсальные
постоянные к и /i, что и было впервые сделано Планком. После
этого можно найти число Авогадро N = R/k и элементарный
заряд е = F/N, где R — универсальная газовая постоянная, а
F — число Фарадея. Когда Планк производил эти вычисления,
величины fc, N и е были известны с малой точностью. Планк
получил для них, а также для постоянной h значения, мало от™
личающиеся от современных.
5. Формулу Планка можно также получить, рассматривая
равновесное излучение в полости как фотонный газ, к которо-
которому применима статистика Бозе-Эйнштейна (см. т. II, § 82).

§ 119 СПОНТАННОЕ И ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ 743
Особенность этого газа состоит в том, что в результате взаимо-
взаимодействия с веществом фотоны могут рождаться и уничтожаться.
Число их N в полости не остается постоянным. При равновесии
оно устанавливается таким, что свободная энергия F(T^V^N)
при заданных Т nV обращается в минимум, а потому dF/dN =
= 0. Но dF/dN есть химический потенциал /л газа. Таким обра™
зом, для фотонов должно быть /i = 0. Поэтому общая формула
Бозе^Эйнштейна
\v A18Л9)
определяющая среднее число частиц в г-м квантовом состоянии,
в случае фотонов переходит в формулу
Число квантовых состояний в интервале частот (ш^ш + duj) опре-
определяется выражением A17.7). Умножив п на это число, на энер™
гию фотона Ни) и разделив на объем полости V, получим фор™
мулу Планка A18.6).
§ 119. Спонтанное и индуцированное излучение
1. В 1916 г. Эйнштейн дал новый вывод формулы Планка,
основанный на представлениях Бора о механизме излучения.
В этой работе было введено понятие индуцированного излуче-
излучения — явления, на котором основан принцип действия лазера.
Пусть <?i, <?25 ?з? • • • — значения энергии, которые может при™
нимать атом или вообще любая атомная система. Атом может
самопроизвольно перейти из высшего энергетического состоя-
состояния ?п в низшее ?т с испусканием света. Такое излучение на™
зывается спонтанным. Если атом находится в световом поле, то
последнее может вызывать переходы как с высшего уровня ?п на
низший ?т, так и обратно с низшего ?т на высший ?п. Первые
переходы сопровождаются излучением света. Оно и называется
индуцированным (вынужденным) излучением. Обратные пере™
ходы сопровождаются поглощением света атомом.
Имеются аналоги описанных явлений и в классической фи-
физике. Если атом рассматривать как колебательную систему, то
в поле световой волны она будет совершать вынужденные коле™
бания. В зависимости от соотношения фаз между колебаниями
этой системы и светового поля амплитуда колебаний атома мо-
может как увеличиваться (поглощение света), так и уменьшаться
(вынужденное излучение).
Эйнштейн применил к описанию процессов спонтанного и
вынужденного излучения вероятностные методы. При этом

744 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
для проблемы равновесного излучения не имеет значения, при™
суща ли вероятность ансамблю физических объектов или самим
элементарным законам, управляющим их поведением.
Рассмотрим теперь много одинаковых атомов в световом по™
ле. Последнее будем предполагать изотропным и неполяризован-
ным. Тогда отпадает вопрос о зависимости коэффициентов, вво-
димых ни лее, от поляризации и направления излучения. Пусть
Nm и Nn — числа атомов в состояниях ?т и ?П1 причем состоя-
состояния ?т и ?п могут быть взяты какими угодно из ряда допусти-
допустимых состояний Е\, «?2, <?з5 • • • Среднее число переходов атомов из
состояния ?п в состояние ?т в единицу времени из-за спонтан-
спонтанного излучения будет пропорционально исходному числу атомов
Nn. Представим его в виде A™Nn. Эйнштейн постулировал, что
из-за индуцированного излучения среднее число переходов меж-
между теми же уровнями будет по-прежнему пропорционально Nni
а также спектральной плотности излучения и(штп) при часто-
частоте испускаемого света, соответствующей рассматриваемому пе-
переходу. Обозначим это число через В™Nnu(ujmn). Аналогично,
среднее число переходов с уровня ?т на уровень ?п из-за по-
поглощения света представится как B1l^lNmu(u)mn). Величины А7^^
В™, В7^ называются коэффициентами Эйнштейна. Они явля-
являются характеристиками только самого атома и могут зависеть
лишь от частоты штп.
2. Допустим теперь, что поле излучения, в котором нахо-
находятся атомы, равновесное и имеет температуру Т. Тогда имеет
место детальное равновесие, а потому
A™Nn + B™Nnu(comn) = B^Nmu{umn). A19.1)
Если уровни энергии ?т и ?п простые^ а не кратные, то ко-
коэффициенты Эйнштейна связаны соотношением
Впт = В™. A19.2)
Действительно, будем повышать температуру системы. Коэф-
Коэффициенты Эйнштейна при этом меняться не будут, так как они
от температуры не зависят. Спонтанное же излучение будет
играть все меньшую и меньшую роль по сравнению с индуциро-
индуцированным. Если им пренебречь, то условие детального равновесия
примет вид B™Nn = B^Nm. Но, согласно формуле Больцмана,
при Т —>> оо населенности уровней Nn и Nm должны сравняться.
Отсюда и следует, что В^ = В™.
Допустим теперь, что уровень ?т состоит из gm, а уровень
?п — из gn слившихся простых энергетических подуровней. Та-
Такие уровни называются кратными, а целые числа gm ж gn —
их кратностями. Вероятность перехода атома с уровня ?т на
каждый простой подуровень ?п меньше вероятности перехода на
кратный уровень ?п в gn раз, т.е. она равна иВ7^/gn. Аналогич-
Аналогично, вероятность перехода с уровня ?п на простой подуровень ?т

§ 119 СПОНТАННОЕ И ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ 745
будет иВ™ /gm. Но по доказанному эти вероятности равны меж™
ду собой. Поэтому для кратных уровней соотношение A19.2)
заменится на В^/'gn = В™/gm или
gmBl = gnB™. A19.3)
Так как спектральная плотность излучения и(ш) не зависит
от того, какие атомы использованы для ее вычисления, то для
простоты расчета энергетические уровни ?П1 ?т молено считать
простыми. Тогда с учетом формулы Больцмана
Nn еХР кТ
из A19.1) получим
где а(штп) = А™/В™. Сравнение этого выражения с формулой
Вина A16.10) показывает, что разность ?п — ?т должна быть
линейной функцией частоты, т.е.
?п -?т = fwmn. A19.5)
В предельном случае низких частот (или высоких температур)
Но в этом случае применима формула Рэлея-Джинса, так что
а^шп) = ^f- (И9.6)
Подставим теперь выражения A19.5) и A19.6) в формулу
A19.4). При этом индексы т и п можно опустить, так как в
нашем выводе уровни энергии ?т и ?п молено взять произволь-
произвольными. Тогда получится формула Планка A18.6).
Из универсальности функции A18.6) следует, что и постоян-
постоянная Я, введенная посредством соотношения A19.5), также уни™
версальна. Формула A19.5), определяющая частоту излучаемо-
излучаемого света при квантовых переходах между энергетическими уров-
уровнями, называется правилом частот Бора.
Заметим еще, что если бы не учитывать индуцированное
излучение, т.е. положить В™и(штп) = 0, то вместо формулы
Планка получился бы ее предельный случай — формула Ви™
на A18.11). Отсюда следует, что формула Планка с неизбеж-
неизбежностью приводит к заключению о существовании индуциро-
индуцированного излучения. При низких температурах индуцированное
излучение, очевидно, несущественно по сравнению со спонтан-
спонтанным. Вот почему в области низких температур, когда Н/k
справедлива формула Вина.

746 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГЛ. X
ЗАДАЧИ
1. Определить среднее число фотонов п в единице объема полости, за-
полненной равновесным (черным) излучением, при температуре Т.
Ответ.
с©
к^Т^
п = ^о о о I ™ "'о_х dx =
J 1-е^ж
- 20 5Г3
- 20'5Г '
где Т — температура в Кельвинах.
2. В полости с зеркальными стенками находится изотропное излучение
с средней плотностью п фотонов в единице объема. Определить среднее
число фотонов z, ежесекундно ударяющихся об единицу площади стенки.
Ответ. ^ = т пс.
3. Решить предыдущую задачу в предположении, что излучение рав-
равновесное, а температура стенок полости равна Т. Какое среднее число фо-
фотонов N будет выходить ежесекундно из полости через отверстие в стенке
полости площадью s = 1 см , если Т = 1000 К?
jL,3rp3 k^T^
Ответ, п и 2,404 _ . ., N = 0,6—^— и 1,5 • 1020.
ПЛ7Т2С6 П67Г2С2
4. В какой области спектра равновесного (черного) излучения при тем™
пературе Т = 300 К интенсивность индуцированного излучения превосхо-
превосходит интенсивность спонтанного?
Ответ. Если Л ^ hc/(kT In 2), то интенсивность индуцированного
излучения становится равной или большей интенсивности спонтанного. При
Т = 300 К получаем Л ^ 692 мкм.
5. При какой температуре равновесного (черного) излучения индуциро-
индуцированное излучение в видимой области (Л = 550 нм) превосходит спонтанное?
Ответ. Т > hc/(k\ In 2) и 3,8 • 104 К.
6. Среднее число фотонов в единице объема равновесного (черного)
излучения, приходящееся на интервал частот (ш,ш + duj) или на соответ-
соответствующий ему интервал длин волн (Л, Л + d\), можно представить в виде
dN = f(ujjT)duj = (f(X^T) dXj где Т — температура излучения. Найти по-
положение максимумов функций f(uj, T) и <р(ш, Т) при фиксированной темпе-
температуре Т.
Ответ. Для функции /(cu, T) максимум получается при huj/(kT) = ж,
где х — корень уравнения (ж — 2)еж + 2 = 0, т.е. х = 1,593624. Соответствую-
Соответствующая длина волны Ai находится из соотношения
AlT = ^ = ^ = 0,902867 см-К.
кх кх
he
Для функции <р(Х,Т) максимум получается при А = Аг, причем
Xkl
= ?, где ? — корень уравнения (? — 4)е^ +4 = 0, т.е. ? = 3,920690. Таким
образом, Х2Т = 0,368967 см-К. Следовательно, Аг < Аь
7. Равновесное излучение заключено в полости, стенки которой поддер-
поддерживаются при постоянной (абсолютной) температуре Т. Вычислить флук-
флуктуации энергии S такого излучения в объеме V в спектральном интервале

§ 119 СПОНТАННОЕ И ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ 747
(ш,ш -\-du), пользуясь формулами 1) Вина, 2) Рэлея™ Джинса, 3) Планка, и
интерпретировать полученные результаты с точки зрения корпускулярных
и волновых представлений о свете.
Решение. Применяя к (97.15) формулы Вина, Рэлея—Джинса и
Планка, получим
= Shw (Вин), A19.7)
AS2 = SkT = тг о , S2 (Рэлей- Джине), A19.S
Vujz аш
AS2 = ЕПш + ' о , Е2 (Планк). A19.9)
V ш1 аш
Формула A19.7) имеет такой же вид, что и формула (97.7) для флукту-
флуктуации числа частиц идеального газа. Ее можно было бы получить из корпус-
корпускулярных представлений, рассматривая излучение как газ независимых ча-
частиц. Напротив, формула A19.8) соответствует волновым представлениям
о свете. Здесь флуктуации возникают из-за суперпозиции волн различных
частот. Формула A19.9) соответствует синтезу обоих представлений.
8. Освещенность Е, создаваемая звездой первой величины на поверхно-
поверхности Земли при нормальном падении света, составляет около 10~ лк. Можно
ли объяснить мерцание звезд квантовыми флуктуациями света?
Решение. Среднее число фотонов, попадающее от звезды в зрачок
глаза в одну секунду,
hX/c
где А — механический эквивалент света, площадь зрачка глаза s принята
равной 0,5 см , а длина волны А = 550 нм. В рассматриваемой области
спектра с хорошим приближением можно пользоваться формулой Вина, а
потому
Отсюда видно, что квантовые флуктуации света к мерцанию звезд не имеют
отношения.

ГЛАВА XI
ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТМКА
§ 120. Принципы работы лазера
1. Спонтанное излучение некогерентно. В этом случае атомы
источника излучают свет независимо друг от друга. Фазы волн,
испускаемых различными атомами, их поляризация и направле-
направления распространения никак не связаны между собой. Обычные
источники света — пламена, лампы накаливания, газоразряд-
газоразрядные трубки, люминесцентные лампы ипр. - излучают некоге-
некогерентно. В них свечение вызывается либо столкновениями между
атомами, совершающими тепловое движение, либо электронны-
электронными ударами. Правда, в таких источниках наряду со спонтаннвш
происходит и индуцированное излучение. Однако оно возбужда™
ется некогерентным спонтаннвш излучением, а потому и само
некогерентно. Испускаемый свет характеризуется большей или
меньшей степенью беспорядка. Максимальный беспорядок до™
стигается в равновесном излучении в полости. В нем представле-
представлены всевозможные фазы и частоты, всевозможные направления
колебаний, всевозможные направления распространения света.
Если заимствовать терминологию из акустики и радиотехники,
то можно сказать, что указанные источники света генерируют
не правильные или упорядоченные волны, а шумы, пригодные
только для освещения, грубой сигнализации, получения изобра-
изображений, фотографирования и пр., но не для передачи речи, теле™
видения и т.д., осуществляющихся посредством радиоволн, из-
излучаемых радиостанциями.
Однако можно создать и когерентно излучающие источни-
источники света, в которых бы различные атомы излучали волны со-
согласованно, подобно радиостанциям, т.е. с одинаковыми часто-
частотами, фазами, поляризацией и направлением распространения.
Такие источники открыли широкие возможности для разнооб-
разнообразных научных и технических применений. Они называются
оптическими квантовыми генераторами или лазерами. Слово

§ 120 ПРИНЦИПЫ РАБОТЫ ЛАЗЕРА 749
«лазер» образовалось из первых букв полного английского на™
звания «Light amplification by stimulated emission of radiation»,
что в переводе означает: усиление света посредством индуциро-
индуцированного излучения. Созданию лазеров предшествовало изобре-
изобретение мазеров, т.е. усилителей микроволн, работающих также на
принципе индуцированного излучения. Поэтому первоначально
лазеры назывались оптическими мазерами. Подробное рассмо-
рассмотрение устройства и работы лазеров и мазеров дается в кванто-
квантовой электронике. Здесь, в оптике, мы ограничимся только крат-
кратким изложением принципов работы лазеров.
Лазер работает на принципе индуцированного излучения. До-
Допустим, что на атом падает фотон с энергией Ни) = ?2 — ?i, где ?\
и ?2 — какие-либо два энергетических уровня атома. Если атом
находится на нижнем уровне ?\, то падающий фотон может по-
поглотиться. Если же атом находится на верхнем уровне <?2, то
может произойти вынужденный переход на нижний уровень ?\
с испусканием второго фотона. Индуцированно излученный фо-
фотон характеризуется не только той же частотой ш (как и при
спонтанном излучении), но также теми же фазой^ поляризаци-
поляризацией и направлением распространения. Вместо одного падающего
фотона получается два тождественных фотона. Эта особен-
особенность индуцированного излучения и используется в лазерах.
2. Рассмотрим теперь не единичный атом, а среду из ато-
атомов. Обозначим через N\ и N2 числа атомов в единице объема
на уровнях ?\ и ?% соответственно. Допустим, что в среде рас-
распространяется плоская монохроматическая волна, частота кото-
которой определяется условием Ни) = ?2 — ?\- За время dt = dx/v,
где v — скорость распространения, a dx — расстояние, пройден-
пройденное волной, с нижнего уровня на верхний переходит в среднем
u(uj)BfNi dt атомов и такое же число фотонов поглощается. Из-
за индуцированного излучения с верхнего уровня на пилений
перейдет ti(a;)I?2^2 dt атомов и родится такое же число фотонов
той же поляризации и направления распространения, что и у
рассматриваемой волны. Фотоны, излученные спонтанно, а так-
также фотоны, индуцированные другими волнами, можно не учи-
учитывать, так как среди них только ничтожная часть распростра-
распространяется в нужном направлении и обладает нужной поляризацией.
Увеличение числа фотонов в единице объема при прохождении
волной расстояния dx = v dt представится выражением
ёЫф0Т = {B\N2 - BlN{)u(u)^.
Коэффициенты Эйнштейна В\ и В\ связаны соотношением
«?2^2 = ё\В\ •> гДе ё\ и Я2 ~~ кратности уровней ?\ и ?2. Ис-
Используя это соотношение, перепишем предыдущее уравнение в

750 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
виде
A20.1)
2 61
Чтобы при распространении в среде волна усиливалась, необхо-
необходимо выполнение условия
— > —. A20.2)
Его молено записать в виде
п2 > пъ A20.3)
где п\ = N\jgi и п2 = N2/g2 — числа атомов на каждом из
простых уровней, из которых состоят сложные уровни ?\ и ?2.
В обычных условиях, когда среда находится в термодинами-
песком равновесии, п2 < п\, т.е. на каждом простом верхнем
уровне находится меньше атомов, чем на нижнем. Это непо-
непосредственно следует из формулы Больцмана
п = ще-?1кТ.
Можно искусственно получить термодинамически неравно-
весную среду, у которой выполняется соотношение, обратное
A20.3) или A20.2). Такая среда называется активной или средой
с инверсной заселенностью по отношению к энергетическим
уровням ?\ и ?2. Следовательно, для усиления световой волны
необходимо, чтобы среда, в которой волна распространяется,
была активной. Идея использования индуцированного излуче-
излучения для усиления волны была впервые высказана в 1939 г. в
докторской диссертации В.А. Фабрикантом (р. 1907) и впослед-
впоследствии (в 1951 г.) на нее было выдано авторское свидетельство.
В то время на идею Фабриканта не было обращено должного
внимания. Казалось, что создание систем с инверсной заселен-
заселенностью энергетических уровней — дело бесперспективное.
3. Усиление света в активной среде обычно сравнивают с на-
нарастанием лавины, изображая фотоны в виде шариков. Летящий
фотон-шарик порождает второй фотон-шарик с переходом ато-
атома с верхнего уровня на нижний. Получаются два одинаковых
шарика, летящих в прежнем направлении, затем четыре шарика
и т.д. Но эта грубая иллюстрация не объясняет, как в результа-
результате наложения фотонов формируется монохроматическая волна
строго определенного направления. Эта сторона дела становит-
становится понятной, если сравнить изучаемое нами явление с класси-
классической картиной распространения плоской монохроматической
волны в однородной среде. Волна вызывает колебания в атомах
и молекулах среды. Последние переизлучают шаровые волны,
когерентные друг с другом и с падающей волной. Эти шаровые
волны, интерферируя между собой, создают снова плоский вол-

120
ПРИНЦИПЫ РАБОТЫ ЛАЗЕРА
751
новой фронт, распространяющийся в среде. Они влияют толь-
только на фазовую скорость волны. Если среда абсолютно прозрач-
прозрачна, то амплитуда волны должна оставаться постоянной, как то-
того требует закон сохранения энергии. В поглощающих средах
энергия волны частично переходит в тепло — амплитуда вол-
волны убывает. Но в активной среде молекулы и атомы находят-
находятся в возбужденных состояниях. За счет энергии возбуждения
вторичные световые волны, излучаемые молекулами и атомами,
усиливаются. Однако их фазы и поляризация остаются прежни-
прежними. Поэтому остаются прежними поляризация и фаза также и
результирующей волны, возникающей в результате интерферен-
интерференции таких вторичных волн. Усиливается только ее амплитуда.
4. Индуцированное излучение было использовано для гене-
генерации когерентных световых волн. Идея этого впервые была
высказана в 1957 г. A.M. Прохоровым (р. 1916) и П.Г. Басо-
Басовым (р. 1922) и независимо от них Ч. Таунсом (р. 1915). Что-
Чтобы активное вещество превратить в генератор световых коле-
колебаний, надо осуществить обратную связь. Необходимо, чтобы
часть излученного света все время находилась в зоне активно-
активного вещества и вызывала вынужденное излучение все новых и
новых атомов. Для этого активное вещество помещают между
двумя параллельными зеркалами. Допустим, например, что оно
представляет собой цилиндр, а плоскости зеркал S\ и $2 пер-
перпендикулярны к оси этого цилиндра (рис. 345). Тогда луч света,
претерпевая многократные отражения от зеркал S\ и $2? будет
Рис. 345
проходить много раз через активное вещество, усиливаясь при
этом в результате вынужденных переходов атомов с высшего
энергетического уровня ?2 на более низкий уровень ?\. Получа-
Получается открытый резонатор^ представляющий собой в сущности
интерферометр Фабри^Перо, только заполненный активной сре-
средой.
Такой резонатор будет не только усиливать свеш, но так-
также коллимировать и монохроматизировать его. Для просто-
простоты предположим сначала, что зеркала S\ и *$2 идеальные. Тогда
лучи, параллельные оси цилиндра, будут проходить через ак-
активное вещество туда и обратно неограниченное число раз. Все
же лучи, идущие наклонно, в конце концов попадут на боковую
стенку цилиндра, где они рассеются или выйдут наружу. Ясно

752 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
поэтому, что максимально усилятся лучи, распространяющие-
распространяющиеся параллельно оси цилиндра. Этим и объясняется коллимация
лучей. Конечно, строго параллельные лучи получить нельзя.
Этому препятствует дифракция света. Угол расхождения лучей
принципиально не может быть меньше дифракционного предела
S$ « A/D, где D — ширина пучка. Однако в лучших газовых
лазерах такой предел практически достигнут.
5. Объясним теперь, как происходит монохроматизация
света. Для простоты проведем рассуждение применительно к
рис. 345 а, когда роль зеркал Si и S2 выполняют отполированные
и посеребренные торцы цилиндра активного вещества, перпен-
перпендикулярные к его геометрической оси. Пусть L — длина цилин-
цилиндра. Если 2L = гаА, т.е. на длине L укладывается целое число
полуволн га, то световая волна, выйдя от $i, после прохожде-
прохождения через цилиндр туда и обратно вернется к Si в той же фазе.
Такая волна усилится при втором и всех следующих прохож-
прохождениях через активное вещество в прямом и обратном направ-
лениях. Ближайшая длина волны А =Ь А А, для которой долж-
должно происходить такое же усиление, найдется из условия 2L =
= (га ± 1)(А =F АА). Следовательно, АА = А/га, т.е. АА, как и
следовало ожидать, совпадает со спектральной областью интер-
интерферометра Фабри-Перо.
Учтем теперь, что энергетические уровни Е\ и ?2 и спек-
спектральные линии, возникающие при переходах между ними, не
бесконечно тонкие, а имеют конечную ширину. Предположим
сначала, что ширина спектральной линии, излучаемой атома™
ми, меньше дисперсионной области прибора. Тогда из всех длин
волн, излучаемых атомами, условию 2L = тХ может удовлетво-
рять только одна длина волны А. Такая волна усилится макси-
максимально. Это и ведет к сужению спектральных линий, генериру-
генерируемых лазером, т.е. к монохроматизации света.
Степень монохроматизации нетрудно определить. Пусть свет
проходит через активное вещество туда и обратно N раз. Для
длины волны А имеем 2LN = NmX. Возьмем ближайшую длину
волны А;, удовлетворяющую условию 2LN = (Nm =Ь 1)А;. Для
такой длины волны каждый цуг волн, возникший при прохожде-
прохождении через активное вещество туда и обратно, будет отличаться
по фазе от предыдущего и последующего цугов на =Ь2тг/]\Г. В ре-
результате все N цугов погасят друг друга — получится минимум
интенсивности для А;. Отсюда ясно, что ширина спектральной
линии, усиливаемой лазером, будет SX = |А — А' ~ A/(JVra), т.е.
она определяется разрешающей силой прибора. При N —>> оо по-
получится 5Х —> 0, т.е. бесконечно тонкая спектральная линия. В
действительности из-за неидеальности отражающих поверхно-
поверхностей зеркал SX остается конечной. Однако при хороших отража-
отражающих поверхностях лазер дает очень тонкую, практически мо-

§ 120 ПРИНЦИПЫ РАБОТЫ ЛАЗЕРА 753
нохроматическую линию. Допустим теперь, что спектральные
линии, излучаемые атомами активной среды, шире дисперсион-
дисперсионной области прибора АЛ. В этом случае вместо усиления одной
спектральной линии может возникнуть усиление нескольких ли™
ний. Свет лазера будет состоять из близких, практически моно-
монохроматических линий.
6. В приведенных рассуждениях не принято во внимание,
что в резонаторе Фабри^Перо могут усиливаться волны, распро-
распространяющиеся не только параллельно его оси, но и под малыми
узлами (р к ней. Условие усиления имеет вид 2L cos (p = га А. Это,
как и во всяком объемном резонаторе, создает систему стоячих
волн с узлами и пучностями. Каждой такой волне соответствует
определенный тип или, как принято говорить, мода колебаний.
Это обстоятельство отражается на распределении интенсивно-
интенсивности в поперечном сечении пучка лучей, генерируемых лазером.
Здесь наблюдается система светлых пятен, разделенных темны-
темными узловыми линиями. Это, конечно, усложняет дело. Но мы
не будем входить в подробное обсуждение этого вопроса. Заме-
Заметим только, что наряду с плоскими зеркалами в резонаторах
употребляются длиннофокусные сферические зеркала. Они мо-
могут быть, например, вогнутыми конфокальными зеркалами, т.е.
зеркалами, у которых главные фокусы совпадают и находятся
в середине системы. Применение подобных зеркал, как показы-
показывают опыт и численные расчеты, позволяет значительно умень-
уменьшить потери света в лазерах и упрощает их юстировку.
7. Учтем теперь, что в реальном лазере часть света, чтобы ее
можно было использовать, должна быть выпущена из активной
среды наружу. С этой целью одно из зеркал, например $2, де™
лается полупрозрачным. Кроме того, и зеркало Si лишь частич-
частично отражает свет, хотя коэффициент отражения его и близок к
100 %. Это приводит к ослаблению светового пучка. Чтобы лазер
был генератором света, необходимо, чтобы усиление светового
пучка в активной среде превосходило некоторое минимальное —
пороговое — значение. Именно, должно быть выполнено следую-
следующее условие. Световой пучок, вышедший от Si, после прохож-
прохождения туда и обратно через активную среду и отражения от
S\ должен вернуться в исходное положение с неменьшей интен-
интенсивностью. Иначе в результате последовательного повторения
этих процессов интенсивность пучка будет непрерывно убывать
и лазер перестанет генерировать. Поэтому для генерации недо-
недостаточно выполнения простого неравенства A20.3). Оно должно
быть выполнено с некоторым запасом, т.е. число атомов N2 на
верхнем уровне в единице объема активной среды должно пре-
превышать некоторое минимальное — пороговое — значение.
Конечно, нарастание интенсивности волны в активной сре-
среде не может продолжаться беспредельно, так как заселенность

754
ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА
ГЛ. XI
верхнего энергетического уровня ограничена. По мере обедне-
обеднения атомами верхнего уровня ?2 скорость нарастания интенсив-
интенсивности волны будет уменьшаться и волна начнет затухать еще до
того, как перестанет выполняться условие A20.3).
§ 121. Рубиновый лазер
1. Существует много материалов, применяемых в качестве
активных сред в лазерах. Сюда относятся различные диэлектри-
диэлектрические кристаллы, стекла, газы, полупроводники и даже плазма.
Эта сторона дела подробно изучается в квантовой электронике.
Мы ограничимся описанием устройства и принципа действия
толвко двух лазеров: рубинового и гелий-неонового.
Первый квантовый генератор света был создан в 1961 г. Мей-
маном (р. 1927) на рубине. Рубин — это твердый кристалл, осно-
основой которого является корунд, т.е. кристалл окиси алюминия
(AI2O3), в котором небольшая часть атомов алюминия (около
0,05%) замещена ионами хрома Сг+++ 1). Ионы хрома игра-
играют основную роль в работе квантового генератора. Корунд —
это диэлектрик с широкой за™
$ прещенной энергетической зоной
-^2
hv
26
между валентной зоной и зо-
зоной проводимости (см. т. III,
§ 100). Энергетические уровни
хрома в корунде лежат в этой за-
запрещенной зоне. Они были изу-
чены задолго до создания ла-
лазеров. Основным (невозбужден™
1=694,3 нм ным) уровнем является уровень
?\ (рис. 346). Он имеет слож-
сложную структуру, которая, однако,
не играет роли в работе квантово-
квантового генератора. Выше лежат близ-
близкие возбужденные уровни <?2а и
<?2б- Это — узкие уровни. При переходе с них на основной уро-
уровень ?\ излучается красный свет с длинами волн А = 694,3 и
692,9 нм. Он-то и придает рубину характерную розовую или
¦hv
¦ hv
¦#i
Рис. 346
) Для лазеров монокристаллы рубина выращивают искусственно. Смесь
AI2O3 и СггОз в виде пудры сыплется сверху на выращиваемый кристалл
рубина, верхняя кромка которого находится в кислородно-водородном пла™
мени горелки с температурой 2050 °С, достаточной для плавления рубина.
При медленном опускании кристалла расплавленный слой смеси выходит из
пламени и кристаллизуется. Таким путем удается получать монокристаллы
рубина в виде стержней длиной до 0,5 м и диаметром до 5 см.

121
РУБИНОВЫЙ ЛАЗЕР
755
красную окраску (в зависимости от концентрации ионов хрома).
Более интенсивна линия А = 694,3 нм. По этой причине только
она и усиливается при работе лазера. Вторая линия не играет
роли. Выше уровней <5*2а и <?2б расположены две сравнительно
широкие полосы энергий ?% и ?±. Переходы между уровнями
этих полос и основным уровнем ?\ сопровождаются излучением
зеленого и голубого света соответственно.
2. Инверсная заселенность создается между уровнями ?\
и ?2. Для этого используется так называемая оптическая на-
качка, т.е. освещение кристалла рубина мощной вспышкой све-
света. Рубину придают форму цилиндрического стержня с диа-
диаметром 0,1-2 см и длиной от 2 до 20 см и больше. Концы
стержня тщательно отполированы. Они могут служить зерка-
зеркалами. Тогда их серебрят, как показано на рис. 345 а. Зеркала
могут быть и внешними (рис. 345 6"), тогда серебрение не нуж-
нужно. Для освещения рубинового стержня применяют импульсные
ксеноновые газоразрядные лампы-вспышки, через которые раз™
ряжаются батареи высоковольтных конденсаторов (напряжение
2^3 кВ). Длительность вспышки по-
порядка одной миллисекунды. Лампа-
вспышка имеет форму спиральной
трубки, обвивающейся вокруг руби-
рубинового стержня (рис. 347). Она мо-
может быть и прямолинейной. Тогда
применяют зеркальные осветите-
осветители, имеющие форму эллиптических
цилиндров с внутренними отра-
отражающими поверхностями. Лампа-
вспышка располагается вдоль одной
из фокальных линий цилиндра; отраженный свет концентриру-
концентрируется на рубиновом стержне, помещаемом вдоль другой фокаль-
фокальной линии.
Если бы энергетический спектр состоял только из двух уров-
уровней ?\ и ?2, то с помощью оптической накачки создать инверс-
инверсную заселенность их было бы невозможно. Действительно, как
видно из A19.2), индуцированные переходы атомов с нижнего
уровня на верхний и обратно идут с одинаковыми скоростями.
Поэтому лампа-вспышка самое большее могла бы лишь урав-
уравнять заселенности обоих уровней. Наличие же спонтанного из-
излучения приводило бы к обеднению (атомами) верхнего уровня
по сравнению с нижним.
Положение меняется благодаря наличию третьего, широко-
широкого энергетического уровня, состоящего из полос ?% и ?^. Лампа-
вспышка переводит атомы хрома из невозбужденного состояния
в возбужденное, т.е. в энергетические полосы ?% ж?^. Значитель-
Значительная ширина этих полос имеет большое практическое значение.
Рис. 347

756 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
Лампа-вспышка излучает свет, близкий к белому. Если бы уров-
уровни 8з и <?4 были очень узкими, то лишь ничтожная часть энергии
лампы-вспышки могла бы быть использована на их возбужде-
возбуждение. Благодаря же значительной ширине полос 8% и 8± на их
возбуждение уходит 10—15 % лучистой энергии лампы-вспышки.
На уровнях 8s и 8± возбужденные атомы хрома живут очень ко™
роткое время (~ 10~8 с). За это время они переходят на один
из уровней «?2- При таком переходе атомы хрома не излучают, а
расходуют свою энергию на возбуждение колебаний кристалли-
кристаллической решетки. Возможность обратного возвращения атома из
полос 8s и 8^ на уровень 8\, хотя и существует, но вероятность
такого процесса пренебрежимо мала по сравнению с вероятно-
вероятностью перехода на уровни 8^- Уровни ?2 метастабильны. Время
жизни атома на них ~ Ю~3 с, что по атомным масштабам очень
велико. Это позволяет накапливать атомы на уровнях 82- Ес-
Если переводить атомы с уровня 8\ на уровни 8s и <?4 достаточно
быстро, то на уровни ?2 можно перевести больше половины ато-
атомов хрома. Тогда на уровнях ?2 окажется больше атомов, чем на
уровне 8\, т.е. возникнет инверсная заселенность этих уровней.
3. Подсчитаем мощность лампы-вспышки, необходимую для
создания инверсной заселенности уровней ?\ и 82- Средняя дли-
длина волны, излучаемая при переходе из полос <5*з и <?4 на уровень
<?1, порядка 450 нм. Поэтому для перевода одного атома хрома
с уровня ?\ на уровни ?% и ?^ требуется в среднем энергия hv =
= hc/X « 4,4 • 10^12 эрг. В рубине, обычно употребляемом для
лазеров, на каждый см3 приходится около 1019 атомов хрома.
Не менее половины из них надо перевести в полосы 8s и <?4- На
это требуется энергия ^2,2 • 107 эрг = 2,2 Дж. Атомы долж™
ны быть переведены на возбужденные уровни 8s и 8± за вре-
время, не превышающее времени жизни атома хрома на уровне ?2
(~ 2-10~3 с). В противном случае инверсная заселенность полу-
получиться не может. Таким образом, минимальная мощность, иду-
идущая на возбуждение атомов, должна быть порядка 2,2/10" =
= 2200 Вт/см3 = 2,2 кВт/см3. Если коэффициент использова-
использования лучистой энергии лампы принять равным 10—15%, то по-
потребляемая мощность лампы должна быть ~ 20 кВт/см3. Для
рубинового стержня с объемом 10 см3 получится ~ 200 кВт.
Это достигается сравнительно легко. Нетрудно подсчитать, что
при напряжении 2000 В емкость батареи конденсаторов долж-
должна быть не меньше 100 мкФ. Обычно употребляются батареи с
емкостью ^ 1000 мкФ.
Значительная доля лучистой энергии (более 50 %), поглощен-
поглощенной рубиновым стержнем, тратится на его нагревание. Но при
температурах, превышающих примерно 1000 К, рубиновый ла-

§ 121 РУБИНОВЫЙ ЛАЗЕР 757
зер перестает генерировать. Поэтому в некоторых конструкциях
лазеров предусмотрено охлаждение рубина проточной водой и
даже жидким азотом.
4. Рубин — одноосный кристалл. Обыкновенный и необык-
необыкновенный показатели преломления светло-красного рубина, упо-
употребляемого в лазерах, равны соответственно п0 = 1,7653 и пе =
= 1,7573 (для А = 656 нм). Рубиновый лазер может давать поля-
поляризованный свет без каких-либо специальных поляризационных
приспособлений. Для этого оптическая ось рубинового стержня
не должна совпадать с его геометрической осью. Возникновение
линейной поляризации нельзя объяснить различием коэффици-
коэффициентов отражения обыкновенного и необыкновенного лучей, так
как разность п0 — пе слишком мала. Поляризация возникает по-
потому, что в обыкновенной волне направления волновой нормали
и луча совпадают между собой, а в необыкновенной не совпа-
совпадают. Чтобы зеркала лазера действовали эффективно, как ре-
резонатор, необходимо, чтобы волновые нормали были к ним пер-
перпендикулярны. Но тогда в рубине только обыкновенный луч бу-
будет распространяться параллельно геометрической оси стерж-
стержня, а необыкновенный пойдет под углом к ней, попадая на бо-
боковую поверхность стержня. Поэтому резонатор будет эффек-
эффективнее усиливать обыкновенные лучи, чем необыкновенные. Из
лазера будут преимущественно выходить обыкновенные лучи, в
которых электрический вектор перпендикулярен к оптической
и геометрической осям кристалла. Если эти оси совпадают, то
поляризация не возникает. Если же, как показали наблюдения,
угол между ними заключен в пределах от 60 до 90°, то линейная
поляризация полная.
5. Наиболее распространенным является импульсный ре-
режим работы рубинового лазера. Лампа-вспышка дает импульс
света длительностью ^ 10^3 с. Длительность когерентного им-
импульса, излучаемого лазером, несколько короче. Это связано,
во-первых, с тем, что требуется некоторое время, чтобы засе-
заселенность уровня <5*2 достигла порогового значения, после чего
лазер начинает генерировать. Во-вторых, с тем, что генерация
лазера прекращается, когда интенсивность вспышки лампы по-
пони жается настолько, что ее становится уже недостаточно для
поддержания заселенности выше пороговой. Сам лазерный им-
импульс имеет сложную структуру и состоит из множества отдель-
отдельных импульсов длительностью до 10^6 с, следующих друг за
другом с интервалом ~ 3 • 10~~6—-10" с. Мощность рубиново-
рубинового лазера в импульсе может достигать десятков кВт при длине
стержня в 20-30 см и диаметре 1,5 см.
Эта мощность может быть повышена до нескольких десят-
десятков мегаватт за счет уменьшения длительности генерируемого

758 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
импульса. Для этого на уровень ?2 надо перевести не половину,
а большую часть атомов хрома, оставив уровень ?\ практически
незаполненным. Тогда при длине рубинового стержня 10—-20 см
импульс генерируемого света, как показывает расчет, может раз™
виться за время ~ 10~8 с. Лампа-вспышка легко могла бы про™
извести такой переход, если бы в рубине не возникала генера-
генерация, возвращающая атомы хрома снова на исходный уровень
?\. А генерация начинается сразу же, как только заселенность
уровня ?2 станет выше пороговой. Задачу можно решить, если
на короткое время выключить обратную связь, осуществляемую
зеркалами. За это время молено перевести все атомы хрома на
возбужденный уровень ?2. При выключенных зеркалах среднее
время жизни атома хрома на уровне ?2 составляет около 0,002 с.
Если в течение этого времени на мгновение снова включить зер-
зеркала, то происходит почти мгновенный вынужденный переход
атомов на невозбужденный уровень ?\ и связанная с ним мощ-
мощная вспышка лазерного излучения.
6. Быстрое включение и выключение обратной связи, а так-
также вообще изменение добротности резонатора можно осуще-
осуществить, заменив одно из зеркал призмой Р полного отражения
(рис. 348), вращающейся с угловой скоростью ~ 500 об/с. Лазер
может генерировать только в положении призмы, изображенном
на рис. 348, или очень
близком к нему. Во всех
остальных положениях
обратной связи нет и
лазер не генерирует. В
это время происходит
оптическая накачка ру-
рубинового стержня R.
Когда призма займет
Рис. 348 положение, указанное на
рис. 348, происходит излучение мощного лазерного импульса.
Хотя при этом призма и продолжает быстро вращаться, но за
короткое время ~ 10~8 с, требующееся для развития лазерного
импульса, она не успевает сколько-нибудь заметно сместиться
из указанного положения. После высвечивания запасенной
энергии при дальнейшем вращении призмы снова начинается
оптическая накачка, пока при повороте на 360° не произойдет
излучение нового лазерного импульса. Однако при прохожде-
прохождении через стержень мощного импульса выключение призмы не
всегда достаточно для прекращения действия обратной связи,
так как она может сохраняться из-за отражения света от концов
рубинового стержня (для рубина коэффициент отражения
(п — IJ1(п + IJ « 7,6 %). Во избежание этого концы рубинового

т
§ 121 РУБИНОВЫЙ ЛАЗЕР 759
стержня делают скошенными под углом к его геометрической
оси. Обычно угол падения берут равным углу Брюстера (на
границе рубин^воздух (рв ~ 30°). Тогда генерируется линейно
поляризованный свет, электрический вектор которого лежит в
плоскости падения.
7. Более быстрое включение и выключение обратной связи
производится с помощью оптического затвора — ячейки Керра с
нитробензолом или ячейки Поккельса с анизотропным кристал-
кристаллом (рис. 349). Ячейка вместе со своим конденсатором повернута
вокруг оси установки на угол 45° (это на рис. 349 не показано).
Поляризатор Р (поля-
(поляроид или поляризацией™
ная призма) ориентире™
ван так, чтобы полно- 1 II К
стью пропускать линей-
линейно поляризованное излу™
чение рубинового стерж-
стержня, когда он генери™ 5?
рует. Перед включени-
включением лампы-вспышки на рис ^49
ячейку К подается такое
напряжение, чтобы она поворачивала плоскость поляризации
излучения лазера на угол 90°. Тогда свет через поляризатор Р
не пройдет, т.е. обратная связь будет выключена. В то время,
когда лампа дает вспышку, происходит оптическая накачка ру-
рубинового стержня. Если затем быстро снять напряжение с кон™
денсатора ячейки, то линейно поляризованное излучение рубина
начнет свободно распространяться между зеркалами S\ и $2 и
возникает мощный импульс индуцированного излучения лазера
длительностью порядка 10^8 с.
8. Большое распространение в качестве оптических затворов
получили также просветляющиеся фильтры^ помещаемые вме-
сто ячейки Керра или Поккельса. (Поляризатор Р в этом слу-
случае не нужен.) Их действие основано на увеличении прозрачно-
прозрачности вещества, когда интенсивность света становится достаточно
большой, как это имеет место в случае излучения лазеров (см.
§ 89, п. 6). При малой интенсивности света фильтр поглощает
свет, почти полностью устраняя обратную связь. С увеличением
заселенности верхнего уровня возникает слабая генерация руби-
рубинового стержня, несколько уменьшающая поглощение фильтра.
Это приводит к усилению обратной связи и вызывает лавину
лазерного излучения. Последняя по мере нарастания все более
и более просветляет фильтр. Когда интенсивность излучения
начнет уменьшаться, поглощение фильтра будет быстро возра-
возрастать, а обратная связь ослабляться. Поскольку вся система ра~
ботает автоматически, лазер с просветляющимися фильтрами

760 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
во время вспышки лампы накачки может генерировать серию
импульсов, следующих друг за другом.
9. Быстрое включение обратной связи позволяет сократить
длительность импульса лазерного излучения до 10"™7-—10""8 с.
Так как энергия импульса, снимаемая с рубинового стержня
длиной 20 см и диаметром 1,5 см, составляет 1-2 Дж, то при
этом развивается мощность 10-200 МВт. Дальнейшее повыше-
повышение мощности лазерного импульса может быть достигнуто пу-
путем усиления света в каскаде из нескольких последовательно
расположенных лазеров. Первый лазер в таком каскаде должен
служить генератором, остальные — усилителями света. Если
мощность генерируемого импульса достаточно велика, то уже
небольшой его части вблизи передового фронта достаточно, что™
бы вызвать вынужденные переходы в ыевозбуждеыыое состояние
всех возбужденных атомов хрома в рубине усилителей. Это со-
сокращает длительность импульса и повышает его мощность. Та™
ким путем удалось получить гигантские импульсы света дли-
длительностью в 2 • 10^9 с при полной энергии импульса ~ 20 Дж.
Это соответствует мощности ^ 104 МВт. Но и такая мощность
еще не предел. Лазер с просветляющимся фильтром дает им-
импульс длительностью ~ 10^8 с, состоящий из последовательно-
последовательности импульсов, длительность которых может составлять 10™1-
10~12 с. Выделение одного такого импульса с последующим уси-
усилением его позволяет достигнуть мощности ~ 107 МВт.
10. Из других твердых материалов, употребляемых в лазе-
лазерах, надо упомянуть прежде всего неодимовое стекло и флю-
флюорит кальция (CaF2) с небольшой примесью атомов редкозе-
редкоземельных элементов: диспрозия (Dy), самария (Sm) и пр. Ак-
Активность среды создается ионами неодима Nd+++, диспрозия
Dy++, самария Sm++ и т.д. Неодимовое стекло генерирует ин-
инфракрасное излучение с длиной волны А = 1,06 мкм, а флюорит
кальция с диспрозием — еще более длинноволновое излучение с
А = 2,36 мкм. Стержни из неодимового стекла изготовить лег-
легче, чем из рубина. Стеклянные стержни могут достигать дли-
длины 0,5—1 м при диаметре до 5 см. Ширина полос у неодимово-
неодимового стекла больше, чем у рубина, что позволяет получить боль-
больший КПД. Зато у рубина более высокая прочность. При дли-
длительности импульса 10~"8~-10"~9 с рубин выдерживает мощности
C-)-103 МВт на каждый см2 поперечного сечения стержня, а
неодимовое стекло — только (И,5)-103 МВт.
В отличие от рубинового лазера, работающего по трехуров-
трехуровневой схеме, лазер на флюорите кальция с примесью диспро-
диспрозия работает по четырехуровневой схеме. Это позволяет созда-
создавать достаточно мощные лазеры, работающие не импульсами, а

121
РУБИНОВЫЙ ЛАЗЕР
761
непрерывно¦, что для некоторых применений очень существенно.
Между основным уровнем ?\ диспрозия в кристалле и энерге-
энергетической полосой <?2 расположены два промежуточных уровня
<?з и ?а (рис. 350). Между ними и созда-
создается инверсная заселенность атомов дис-
диспрозия. Лампа-вспышка переводит ато-
атомы диспрозия через широкую энергети-
энергетическую полосу &2 на уровень ?%. Уро-
Уровень ?4 по энергии приподнят над уров-
уровнем ?\ настолько высоко, что при тем-
температуре жидкого азота его заселенность
N4 практически равна нулю. Поэтому нет
необходимости переводить на уровень ?$
больше половины атомов диспрозия. До-
Достаточно лишь, чтобы разность заселен-
ностей N% — N± уровней ?% и ?4 превы-
превысила пороговое значение. Оно составляет
лишь небольшую долю атомов диспрозия.
Рис-
Достаточна сравнительно небольшая мощность лампы-накачки
(«15-20 Вт), чтобы осуществить непрерывную работу лазера.
Кроме того, непрерывная накачка позволяет генерировать ги-
гигантские импульсы с большой частотой повторения (до несколь-
нескольких кГц). Мощности света, получаемые при этом в каждом им-
импульсе, около 1-2 МВт.
ЗАДАЧИ
1. Мощность рубинового лазера в импульсе равна W = 100 МВт. Пло-
Площадь поперечного сечения рубинового стержня S = 1 см . Оценить напря-
напряженность Е электрического поля и давление света в лазерном пучке, считая
его строго плоскопараллельным (А = 694,3 нм). Как изменятся эти величи-
величины, если пучок сфокусировать идеальной линзой с фокусным расстоянием
/ = 5 см?
Решение. Напряженность электрического поля Е® в несфокусиро™
ванном пучке оценим по формуле
W = — 'EHS = — WS,
4тг 4тг
а давление излучения То — по формуле То = W/(cS). Таким путем находим
= 647 СГСЭ = 1,94 • 105 В/см,
То'
cS
i 3,3 • 104 дин/см2
j 0,033 атм.
Для расчета соответствующих величин в фокусе можно пользоваться
теми же формулами, вычислив предварительно ширину пучка. Для оцен™
ки будем считать, что весь свет концентрируется в пределах центрального
светлого кружка с радиусом R = 0,61/А/г и площадью
ttR2 = тг@,61/А/гJ = (О,б1тг/АJ/5;

762 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
где г — радиус поперечного сечения падающего пучка. Эту площадь и надо
подставить в предыдущие формулы вместо S. В результате получим
E0 = 1,5 • 103#0 = 2,9 • 108 В/см,
0,617г/А
V = (nJ ,Л То = 2,25 • 106Ро и 7,4 • 104 атм.
Такое давление было бы, если бы пучок лазерного света фокусировался
в вакууме. Если же он падает на вещество, то из-за большой концентра-
концентрации энергии вблизи фокуса происходит практически мгновенное испарение
вещества (с превращением его в плазму). С этим связано еще большее по-
повышение давления.
2. Эффективной температурой Тэф лазерного излучения называется та-
такая температура абсолютно черного тела, при которой оно дает излучение
той же удельной интенсивности 1и частоты i/, что и лазер. Оценить эффек-
эффективную температуру гелий-неонового лазера, генерирующего в непрерыв-
непрерывном режиме свет с длиной волны А = 632,8 нм (у и 5 • 1014 Гц.) Ширина
спектральной линии генерируемого света 5и и 104 Гц, расходимость свето-
светового пучка 6$ ~ 1' ~ 3 • 10"" рад, мощность излучения W = 10 мВт.
Решение. Удельная интенсивность лазерного излучения равна 1и =
= W/Fv • <Ш), где 5Q = (<5i9J рп 10~~7 ср — телесный угол, определяющий
расходимость светового пучка. По формуле Рэлея—Джинса
Приравнивая это предыдущему выражению, получим
что примерно в 1011 раз превосходит температуру Солнца.
§ 122. Гелий-неоновый лазер
1. Энергетический спектр газов, во всяком случае при тех
давлениях, которые применяются в рекламных трубках и лазе™
pax, весьма точно совпадает с энергетическим спектром изоли-
изолированных атомов и молекул, из которых состоит газ. Поэтому
спектральные линии газов более узкие, чем линии примесей в
твердых телах. Газы отличаются высокой оптической однород-
однородностью и малой плотностью, а поэтому слабо рассеивают и
искажают волны, распространяющиеся в них. Все это позволя-
позволяет использовать в газовых лазерах большие расстояния между
зеркалами и получать острую направленность, высокую моно-
хроматичность и стабильность частоты излучения. Так, в
гелий-неоновом лазере реально получаемая расходимость пуч-
пучка лучей обычно составляет 1^2;, а в лучших случаях достигает
теоретического предела 5$ ~ X/D ~ 20/;. Относительная шири™

122
ГЕЛИЙ-НЕОНОВЫЙ ЛАЗЕР
763
на спектральной линии в излучении такого лазера будет равна
ёш/ш ^ 10"1—-10"2, а сама частота ш в оптимальных услови-
условиях поддерживается с относительной точностью ^ 10~14 (хотя в
обычных условиях относительная точность не выше 10~10).
Однако при малой плотности газов в них нельзя получить
столь же большие концентрации возбужденных атомов, а пото-
потому и столь же большие импульсные мощности излучения, как в
твердых телах. Так, выходная мощность гелий-неонового лазера
в непрерывном режиме обычно составляет от десяти до несколь™
ких сот милливат. Однако, ввиду высокой монохроматичности
и направленности излучения, эта величина все же громадна по
сравнению с тем, что могут дать тепловые источники света. Она
соответствует эффективной температуре излучения, превышаю-
превышающей температуру Солнца примерно в 1011—-1012 раз (см. задачу
2 к предыдущему параграфу). Впрочем, в непрерывном режиме
инфракрасный лазер на СО2 может генерировать до 10 кВт, а
ионный аргоновый лазер в видимой области — до ^ 1 кВт. В
импульсном режиме мощность этих лазеров может составлять
несколько сот киловатт.
2. Первым газовым лазером был гелий-неоновый лазер, соз™
данный в конце 1960 г. Джаваном (р. 1926), Беннетом (р. 1903)
и Эрриотом. Принципиальная схема гелий-неонового лазера в
ее современном виде приведена на рис. 351. Лазер состоит из
Рис. 351
газоразрядной трубки Т длиной от нескольких десятков сан-
сантиметров до 1,5-2 м и внутренним диаметром 7-10 мм. Труб-
Трубка наполнена смесью гелия (давление ~ 1 мм рт. ст.) и неона
(^ ОД мм рт. ст.). Концы трубки закрыты плоскопараллельны-
плоскопараллельными стеклянными или кварцевыми пластинками Pi и Р2, установ-
установленными под углом Брюстера к ее оси. Это создает линейную
поляризацию лазерного излучения с электрическим вектором,
параллельным плоскости падения. Зеркала S\ и $2, между ко™
торыми помещается трубка, делаются обычно сферическими с
многослойными диэлектрическими покрытиями. Они имеют вы-
высокие коэффициенты отражения и практически не поглощают
свет. Пропускаемость зеркала, через которое преимущественно

764
ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА
ГЛ. XI
Гелий
Неон
3390
выходит излучение лазера, составляет обычно 2 %, другого — ме-
менее 1%. Между электродами трубки прикладывается постоян-
постоянное напряжение 1—2 кВ. Катод К трубки может быть холодным,
но для увеличения разрядного тока применяют также трубки с
пустотелым цилиндрическим анодом, катод которых нагревает-
нагревается низковольтным источником тока. Разрядный ток в трубке
составляет несколько десятков миллиампер. В первом варианте
гелий-неонового лазера, построенном Мейманом, применялась
безэлектродная трубка, в которой возбуждался высокочастот-
высокочастотный разряд. Лазер может работать и в непрерывном, и в им-
импульсном режиме. Он генерирует красный свет с длиной волны
632,8 нм и может генерировать также инфракрасное излучение
с длинами волн 1,150 и 3,390 мкм. Но тогда необходимо иметь
торцевые окна, прозрачные для инфракрасного света, и зеркала
с высокими коэффициентами отражения в инфракрасной обла-
области спектра.
3. Рассмотрим теперь, как возникает инверсная заселенность
атомов неона. Упрощенная схема уровней неона приведена спра-
справа на рис. 352. Выше уровня ?± у неона имеется еще 28 уровней
с энергией, меньшей ?%1 но
они для нас не имеют зна-
значения и на рисунке не изо-
изображены. Возбуждение ато-
атомов неона происходит в ре-
результате столкновений их с
электронами газоразрядной
плазмы. При определенном
режиме разряда этот про-
процесс может привести к ин-
инверсной заселенности уров-
уровней ?\ и <?2- Однако засе-
заселенность уровней ?\ и ?3? a
также уровней ?± и ?% оста-
остается неинверсной. Инверс-
Инверсной заселенности препят-
препятствует долгоживущий мета-
стабильный уровень «?55 ле-
лежащий немного ниже ко-
роткоживущего уровня ?\.
Заселенность уровня ?$ велика, за счет этого происходит по-
пополнение быстро опустошающегося уровня ?\, и инверсии засе-
заселенности между уровнями ?\ и ?% не возникает.
Добавление гелия меняет дело. Из всех уровней гелия, по-
помимо нормального ?q, для работы лазера имеют значение мета-
стабильные уровни ?'2 и ?f3 с энергиями 19,82 и 20,61 эВ соответ-
соответственно. Спонтанный радиационный переход с этих уровней на
Рис. 352

§ 123 НЕЛИНЕЙНАЯ ПОЛЯРИЗАЦИЯ СРЕДЫ 765
основной уровень ?q «запрещен», т.е. происходит с очень малой
вероятностью. Поэтому время жизни атома на уровнях ?'2 и ^з
очень велико. В результате электронных ударов на этих метаста-
бильных уровнях накапливается очень много атомов гелия. Но
уровни гелия ?2 и ?% почти совпадают с уровнями ?2 и ?% нео-
на. Благодаря этому при столкновениях возбужденных атомов
гелия с невозбужденными атомами неона интенсивно происхо-
происходят безызлучательные переходы атомов гелия в невозбужден-
невозбужденное состояние с резонансной передачей энергии атомам неона.
Этот процесс возбуждения атомов неона на рис. 352 символиче-
символически изображен горизонтальными штриховыми стрелками. В ре™
зультате концентрации атомов неона на уровнях ?2 и ?% сильно
возрастают, и возникает инверсная заселенность по отношению
к уровням ?\ и ?3? a разность заселенностей уровней ?2 и ?\
увеличивается в несколько раз.
Выясним в заключение влияние столкновений атомов неона
со стенками трубки. Такие столкновения практически не влия™
ют на заселенность уровней ?2 и ?*з и непосредственно уровня
?i, так как все эти уровни короткоживущие. За время жизни в
возбужденных состояниях на этих уровнях атомы неона практи-
практически не успевают доходить до стенок трубки. Указанные уров-
уровни разрушаются значительно раньше. Напротив, на уровне ?§
возбужденные атомы живут долго, претерпевая в этих состоя™
ниях многочисленные столкновения со стенками трубки. Столк-
Столкновения разгружают уровень ?5? B результате чего атомы нео-
неона переходят с уровня ?\ на уровень ?$. Опустошение уровня
?\ происходит быстрее, чем при заселенном уровне ?§. Разни-
Разница заселенностей уровней ?% и ?\ увеличивается, что повышает
эффективность работы лазера. Процесс опустошения уровня ?\
происходит наиболее эффективно при некотором оптимальном
диаметре трубки. Опыты показали, что максимальная мощ-
мощность гелий-неонового лазера достигается при диаметре трубки
~ 7 мм. При больших диаметрах мощность лазера падает, несмо-
несмотря на сильное увеличение объема рабочего газа (объем трубки
пропорционален квадрату ее диаметра). Это связано с тем, что
эффективное опустошение уровня ?\ происходит у атомов, нахо™
дящихся вблизи стенок трубки^ а атомы, находящиеся вблизи
ее центра, практически выключаются из процесса генерации.
§ 123. Нелинейная полмризацим среды
1. Изобретение лазеров сделало возможным эксперименти-
экспериментировать с интенсивными световыми пучками, в которых напря-
напряженность электрического поля не пренебрежимо мала по срав-

766 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
нению с внутриатомными и внутримолекулярными полями (см.
§ 5, п. 3). В таких пучках возникают уже нелинейные оптические
явления, и притом не только как малые поправки к линейным,
но также и как явления крупного масштаба, нашедшие важ-
ные практические применения. О некоторых нелинейных явле-
явлениях в оптике (увеличение прозрачности среды с увеличением
интенсивности света, вынужденное рассеяние Мандельштама^
Бриллюэна, вынужденное комбинационное рассеяние) уже го-
говорилось в гл. VIII (см. § 91, 99, 100).
При распространении света в среде все такие явления связа-
связаны прежде всего с нелинейной зависимостью вектора поляриза-
поляризации среды Р от напряженности электрического поля Е световой
волны. Среду мы будем предполагать однородной, не будем учи-
учитывать ее магнитные свойства и пространственную дисперсию.
Если поле Е еще не очень сильное, то вектор Р можно раз-
разложить по степеням составляющих вектора Е и оборвать такое
разложение на нескольких первых членах. Тогда в общем слу-
случае, когда среда анизотропна, можно написать
Pj = ajkEk + ajklEkEt + ajkimEkEiEm + ..., A23.1)
где в соответствии с общепринятой тензорной символикой под-
подразумевается, что по дважды повторяющимся индексам произ-
производится суммирование. Здесь тензор оу& есть обычная или ли-
линейная поляризуемость среды, а тензоры высших порядков ода,
ajklmi • • • называются соответственно квадратичной, кубичной
и пр. поляризуемостями. Поле Е предполагается монохрома-
тическим, а поляризуемости а — функциями частоты ш. Для
изотропной среды все тензоры ода ода, ... вырождаются в ска-
скаляры.
Если каждая точка среды является центром симметрии,
то все поляризуемости четных порядков обращаются в нуль.
(Четность определяется числом индексов без первого.) Действи-
Действительно, изменим на противоположные направления всех коорди-
координатных осей. Тогда изменятся знаки у Е\* и Ei, но ада останется
неизменным, так как начало координат, как и всякая точка сре-
среды, есть ее центр симметрии. Не изменится и весь квадратич-
квадратичный член ajkiEfcEi. Но знак Pj изменится на противоположный.
Чтобы соотношение A23.1) осталось справедливым и в новой
системе координат, должно быть ода = 0. Так же докажем, что
должны обращаться в нуль и остальные поляризуемости четных
порядков.
С наличием квадратичной поляризуемости связаны многие
нелинейные оптические явления. Из доказанного выше следу-
следует, что в изотропных средах нелинейные квадратичные явления
невозможны. Тем не менее и при рассмотрении таких явлений

§ 123 НЕЛИНЕЙНАЯ ПОЛЯРИЗАЦИЯ СРЕДЫ 767
можно пользоваться моделью изотропной среды, полагая
Р = аЕ + а2ЕЕ + а3Е2Е, + ..., A23.2)
где поляризуемости а, a2j аз, • • • являются уже скалярами. Та™
кое упрощение вполне допустимо при качественном рассмотре-
рассмотрении возможных нелинейных оптических явлений. Надо только
иметь в виду, что в кристаллах в выбранном направлении могут
распространяться волны не всех, а только избранных поляриза-
ций. Соотношение A23.2) приближенно применимо к каждой
из таких волн, причем для различных волн поляризуемости о,
«2, ... имеют разные значения. Кроме того, волны разных по™
ляризаций могут нелинейно взаимодействовать, обмениваясь
энергией друг с другом. Такое взаимодействие должно иметь
место при тензорной связи A23.1) между Р и Е. Но оно было бы
невозможно, если бы эта связь была скалярной типа A23.2). По™
пятно, что при нашем подходе влияние такого взаимодействия
может быть учтено только качественно.
2. Разобьем поляризацию Р на линейную и нелинейную ча-
части: Р = Рл+Рнл. Нелинейная часть определяется выражением
рнл = а2ЕВ + «3^2Е + ..., A23.3)
а линейная Рл = аЕ. В соответствии с этим и индукция D =
= Е + 4тгР представится суммой линейной части Ол = Е + 4тгРл
и нелинейной DHJ1 = 4тгРнл. Линейная часть, очевидно, равна
Ол = бЕ, где в — обычная диэлектрическая проницаемость
среды, как она определяется в линейной электродинамике. После
этого запишем систему фундаментальных уравнений Максвелла
в следующем виде:
"" cdt с dt '
rotE^c^ = 0' A23.4)
div(eE) = -4ячИуРНЛ5
d!vH = O.
Для решения такой системы применяем метод последова-
последовательных приближений. В нулевом приближении в уравнении
A23.4) отбрасываем правые части. Получатся обычные уравне-
уравнения линейной электродинамики. В качестве нулевого прибли™
жения возьмем плоскую волну
Е = Ео = A cos (out - kr), A23.5)
где волновой вектор к удовлетворяет обычному соотношению
к2 = еш21с2. Для нахождения первого приближения в A23.3)
отбросим кубичные и высшие члены, а в квадратичном члене

768 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
поле Е заменим его выражением A23.5) в нулевом при™
ближении. После этого снова получатся линейные уравнения, но
уже неоднородные, с известными правыми частями. Эти правые
части могут быть истолкованы как добавочные источники волн,
обусловленные нелинейной частью поляризации среды. Каждый
элемент объема dV среды переизлучает волны как диполь Гер™
ца с добавочным дипольным моментом Рнл dV. Эти излучения,
накладываясь на волну A23.5), и создают волновое поле Eq + Ei
в первом приближении. Второе приближение находится так же.
Для этого выражение A23.3) обрываем на членах третьей сте-
степени, заменяя в оборванном выражении вектор Е на Eq + Ei,
после чего вычисляем поле Eg + Ei + Е2 во втором приближе-
нии, и т.д.
К изложенному надо еще добавить, что следует понимать
под е в уравнениях A23.4), когда среда обладает дисперсией.
Ответ заключается в следующем. Если взять какое-либо при-
приближение, то в правой части уравнений A23.4) появятся ела™
гаемые не только с исходной частотой а;, но и с частотами 2ш,
За;,... Могут появиться и другие частоты, как, например, при
параметрической генерации света (см. § 126). Надо ЕиН искать
в виде суммы монохроматических полей с теми же частота-
частотами. Уравнение A23.4) следует написать для каждой частоты
в отдельности, сохранив в правой части только члены той же
частоты и понимая под е значение функции е также при той
же частоте. Именно такой символический смысл имеет систе-
система уравнений A23.4).
§ 124. Первое приближение. Оптическое
детектирование. Генерация вторых гармоник,
суммарной и разностной частот
1. Нелинейная добавка A23.3) к поляризации среды, вычис™
ленная в нулевом приближении, равна
Рнл = a2El = ^f- + ^f- cos [2M - кг)]. A24.1)
Первое слагаемое в этом выражении не зависит от времени.
С ним связано так называемое оптическое детектирование,
т.е. возникновение в нелинейной среде постоянной электриче™
ской поляризации при прохождении через нее мощной световой
волны. Это явление аналогично выпрямлению синусоидального
электрического тока. Его можно наблюдать, если между об-
обкладками конденсатора, одна из которых заземлена через боль-
большое сопротивление, поместить кристалл (например, кварца) и
пропустить через него световой пучок от рубинового лазера.

§ 124 ГЕНЕРАЦИЯ ВТОРЫХ ГАРМОНИК 769
Вследствие детектирования световой пучок возбуждает в це-
пи конденсатора импульс электрического тока, который можно
обнаружить с помощью осциллографа.
2. Второе слагаемое в A24.1) гармонически меняется во вре™
мени. С ним связана генерация в нелинейной среде второй гар-
моники, т.е. волны с удвоенной частотой иJ = 2cj. Для нахожде™
ния поля этой гармоники поступаем так, как изложено в пре-
предыдущем параграфе. Переходя к комплексной форме, получаем
систему уравнений
rotH - ?
с at
rotE-If?=0, A24.2)
с dt
Найдем сначала частное решение этой системы
соответствующее вынужденным колебаниям с частотой 2ш. Из
второго уравнения обычным путем находим, что векторы Е и
Н взаимно перпендикулярны. Аналогично, из последних двух
уравнений следует, что (kAi) = (kBi) = 0, т.е. рассматриваемая
плоская волна поперечна как в отношении вектора Е, так и в
отношении вектора Н. Учтя это, а также соотношение к2с2 =
= uJe({jj)J из первых двух уравнений получим
Ai = . ч , ЧЛА.
е(ш) - е{2ш)
Надо еще удовлетворить условию, чтобы на входе в нелинейную
среду (где мы поместим начало координат) интенсивность вто™
рой гармоники обращалась в нуль. Для этого к частному реше-
решению, найденному выше, надо добавить общее решение соответ-
соответствующей однородной системы уравнений и подобрать амплиту-
амплитуду его так, чтобы указанное условие выполнялось. Возвращаясь
снова к вещественной форме записи, таким путем получим
™AA[cos (aj2t - 2kr) - cos (uj2t - k2r)], A24.3)
Ei = , ,
?{UJ) —
где
к2 = qj2s(laJ)/c2.
3. Таким образом, вторая гармоника представляет собой на-
наложение двух волн одной и той же частоты Ш2 = 2ш: вынужден-
вынужденной волны cos (о;2^^2кг) и свободно распространяющейся волны
— cos (uj2i^^2T)- Обе волны распространяются в одном и том же
направлении, но с различными фазовыми скоростями. Поэтому
по мере распространения будет меняться разность фаз между

770 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
ними и возникнет характерное в таких случаях явление бие-
биений. Интенсивность 1\ второй гармоники найдется возведением
в квадрат и последующим усреднением по времени выражения
A24.3). Опуская числовые коэффициенты и обозначая через I
интенсивность исходной волны, таким путем найдем
где х — расстояние, пройденное волной, и введено обозначение
о _ Bk^k2)r _ Bк-к2)х
А А
При этом в знаменателе формулы A24.4) мы пренебрегли раз-
различием между показателями преломления п(ш) и пBш).
Когда /5 = 0, тг, 2тг, ..., интенсивность первой гармоники
обращается в нуль. Максимумы интенсивности получаются при-
примерно посередине между минимумами. Таким образом, с возра-
возрастанием х интенсивность второй гармоники возрастает, когда
/5 лежит приблизительно между нулем и тг/2, между тг и Зтг/2
и т.д. В этих случаях энергия переходит от исходной волны
ко второй гармонике. Если же /3 лежит приблизительно между
тг/2 и тг, между Зтг/2 и 2тг и т.д., то с возрастанием х интенсив-
интенсивность второй гармоники убывает. В этих случаях энергия снова
возвращается от второй гармоники к исходной волне. Такой
процесс перекачки энергии периодически повторяется по мере
распространения исходной волны.
Условие /3 = тг/2 определяет расстояние ж, до которого про-
происходит перекачка энергии от исходной волны ко второй гармо-
гармонике с последующим возвращением ее опять в исходную волну.
Это расстояние называется когерентной длиной. Для нее из ука-
указанного условия нетрудно получить
'ког = ,„,,./-л, л.» A24.6)
4\п(ш) -n(
где А — длина исходной волны, п(ш) — ее показатель прелом-
преломления, а пBш) — показатель преломления второй гармоники.
Чем больше когерентная длина^ тем интенсивнее происходит
перекачка энергии от исходной волны во вторую гармонику.
Когда
п(ш) = nBcj), а потому 2к = к2, A24.7)
то длина когерентности 1КОГ обращается в бесконечность. В этом
случае переход энергии особенно интенсивен и должен проис-
происходить от исходной волны к ее второй гармонике. Обе волны
cos (uJt — 2kr) и — cos (uJt — k2f) распространяются с одина-
одинаковыми фазовыми скоростями, а потому фазовое соотношение
между ними сохраняется все время при их распространении. С

§ 124 ГЕНЕРАЦИЯ ВТОРЫХ ГАРМОНИК 771
этим, как и при всяком резонансе, и связана эффективность об™
мена энергией между взаимодействующими волнами. Поэтому
условие A24.7) называется фазовым синхронизмом между рас™
сматриваемыми волнами. В этом случае /3 = 0 при любом ж, и
из A24.4) предельным переходом /3 —>> 0 получаем
= ?ЩЦ. A24.8)
п2с2
Конечно, при достаточно больших х формула A24.8) перестает
быть верной, так как при х —> сю она дает 1\ —> оо, а интенсив-
интенсивность второй гармоники не может превосходить интенсивности
/ исходной волны. В этом случае метод последовательных при™
ближений, с помощью которого была получена формула A24.8),
неприменим.
Когерентную длину 1КОГ моэюно определить как максималь-
ное расстояние^ на котором приближенно сохраняется фазо-
фазовый синхронизм между падающей и переизлученной волнами,
т.е. расстояние^ на котором набег фазы одной из этих волн
относительно другой не превышает ж.
4. Генерация второй гармоники впервые была обнаружена
Франкеном в 1961 г. Излучение рубинового лазера фокусирова™
лось на кристалле кварца, расположенном между двумя филь-
трамп, прозрачными только в узких окрестностях длин волн
Ai = 694,3 нм и А2 = Ai/2 = 347,0 нм. Из кристалла, помимо
исходного красного излучения лазера (Ai = 694,3 нм), выходило
также ультрафиолетовое излучение с половинной длиной волны
347,0 нм. В первых опытах Франкена в энергию второй гармо-
гармоники превращалось ~ 10™8 энергии первичного излучения.
Почему лишь столь ничтожная доля энергии переходила
ко второй гармонике? Это объясняется малостью когерентной
длины 1КОГ в кварце. Для интенсивного обмена энергией надо
удовлетворить условию фазового синхронизма п(ш) = пBш).
Но это невозможно сделать для изотропных сред в прозрачной
области спектра, так как в этой области показатель преломле-
преломления п(ш) монотонно возрастает с частотой. Равенство п(ш) =
= пBш) может удовлетворяться только тогда, когда частота ш
взята в прозрачной области, а 2ш — в области сильного погло-
поглощения или наоборот.
Однако, как указали в 1962 г. Джордмейн и Терхьюн и под™
твердили это указание на опыте, фазовый синхронизм на ча-
частотах ш и 2uj моэюно осуществить между обыкновенной и
необыкновенной волнами в некоторых кристаллах. На рис. 353
представлены обыкновенный п° и необыкновенный пе показа-
показатели преломления одноосного кристалла в зависимости от на-
направления волновой нормали. Сплошные кривые относятся к
частоте cj, штриховые — к удвоенной частоте 2ш. На первом из

772
ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА
ГЛ. XI
этих двух рисунков кривые п°(ш) и пеBш) пересекаются меж™
ду собой. Точкам их пересечения соответствуют направления,
для которых между обыкновенной волной с частотой о; и ее гар-
гармоникой с частотой 2ш выполняется фазовый синхронизм. Эти
направления называются направлениями синхронизма^ а угол $
между ними и оптической осью кристалла — узлом синхрониз-
синхронизма.
пеBш)
я°Bсо)
пе(т)
Рис. 353
Хотя обе волны и поляризованы в различных плоскостях, но
они могут нелинейно взаимодействовать между собой, посколь™
ку в кристаллах квадратичная поляризуемость есть не скаляр
«2, а тензор {oi.2)jkh Поэтому при наличии фазового синхрониз-
синхронизма должна происходить перекачка энергии от исходной волны к
ее второй гармонике, что и наблюдается на самом деле. Таким
путем удается более половины падающего света превратить во
вторую гармонику. Понятно, что при таких больших интенсив™
ностях второй гармоники метод последовательных приближений
может оказаться неточным и даже неприменимым. Однако ка™
чественное заключение о влиянии фазового синхронизма оста-
остается в силе.
Подходящим кристаллом может быть одноосный кристалл
дигидрофосфата калия КН2РО4 (сокращенно KDP). Для этого
кристалла при А = 1,15 мкм, как показывает расчет, подтвер-
подтверждаемый наблюдениями, угол синхронизма равен 41°35;. Суще™
ствует красивый демонстрационный опыт. Кристалл KDP, вы™
резанный параллельно оптической оси, кладется на столик, ко™
торый может вращаться вокруг вертикальной оси. Оптическая
ось кристалла должна быть горизонтальна. На кристалл напра™
вляется мощный инфракрасный луч от лазера на неодимовом
стекле (А = 1060 нм). Луч лазера невидим, но его можно об™
наружить с помощью листа черной бумаги. Бумага загорается,
если ее поместить на пути луча. При произвольной ориентации

§ 125 САМОФОКУСИРОВКА 773
кристалла никакого видимого света не возникает. Но если кри-
сталл медленно поворачивать, то из него выходит ослепитель-
ослепительно яркий зеленый луч (А = 530 нм), когда станет выполняться
условие синхронизма.
Не всякий одноосный кристалл годится для опыта такого ти-
типа. Не годится, например, кристалл кварца, в котором, как вид™
но из рис. 353 6j условие фазового синхронизма не выполняется
ни для какого направления.
5. Остановимся теперь на генерации волн с суммарной и
разностной частотами. Природа этого явления в точности та-
такая же, что и генерация второй гармоники. Поэтому достаточно
только указать, в чем состоит явление. Если на нелинейную сре-
среду направить два мощных пучка света с различными частотами
oji и ^2, то из нее будет выходить свет не только с первона-
первоначальными частотами ш\ и иJ и их гармониками 2uj\ и 2oj2, но
и свет с суммарной ш\ + Ш2 и разностной ш\ — Ш2 частотами.
Подобными методами генерации волн разных частот удается да™
леко проникнуть в инфракрасную и ультрафиолетовую области
спектра. Например, удалось получить ультрафиолетовое излу-
излучение с длиной волны « 80 нм.
§ 125. Второе приближение. Самофокусировка
1. Для нахождения второго приближения надо использо-
использовать вектор Рнл в первом приближении, т.е.
Рнл = «2(^о + Si)(E0 + Ei) + а3^Е0.
Однако мы ограничимся только изотропными средами или
кристаллами, обладающими центром симметрии. Для них,
как было показано в § 123, «2 = 0, и следовательно, в нуж-
нужном приближении Рнл = (x^EqEi®. Подставив сюда выражение
A23.5), получим
Рнл = :^j!1acos (ut - кг) + 5^Д cos [3(wt - кг)], A25.1)
Слагаемое с тройной частотой оо% = За;, очевидно, приводит
к генерации третьей гармоники. Разность показателей прелом-
преломления пCш)—п(ш) здесь еще больше, чем в случае второй гармо™
ники. Это ограничивает выбор кристаллов, для которых можно
удовлетворить условию фазового синхронизма. Основная труд-
трудность опыта связана с малыми значениями кубичной поляри-
поляризуемости «з5 ч™ вынуждает применять большие кристаллы и
большие освещенности, часто приводящие к разрушению кри-
кристаллов. Несмотря на это, генерация третьей гармоники наблю-
наблюдалась еще в 1962 г. группой американских физиков на кри-

774 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
сталле исландского шпата при освещении его светом рубинового
лазера. На выходе кристалла удалось зарегистрировать излуче-
излучение с длиной волны 231,3 нм. Позднее генерация наблюдалась
в некоторых оптически изотропных кристаллах (например, LiF,
NaCl), жидкостях и газах.
В третьем приближении, помимо гармоник более низкого по™
рядка, очевидно, должна появиться четвертая^ а в следующем
приближении — пятая гармоники и т.д. Экспериментально чет-
четвертая гармоника наблюдалась С.А. Ахмановым в 1974 г., а пя-
тая — Харрисом в 1973 г.
2. Посмотрим теперь, какие явления связаны с первым ела™
гаемым в выражении A25.1). Множитель A cos (ujt^hr) есть ис-
ходная падающая волна Eq. Ясно, что в рассматриваемом при-
приближении его можно заменить на Е, так как такая замена сказы™
вается лишь на членах более высокого порядка малости, не учи-
учитываемых в рассматриваемом приближении. После этого A23.4)
запишется в виде
rot Н - ±[е(ш) + Зпа3(ш)А2]^ = 0.
Отсюда видно, что влияние рассматриваемого слагаемого экви-
эквивалентно изменению диэлектрической проницаемости или по-
показателя преломления среды. Учитывая малость поправки к
е(а;), для показателя преломления п в поле интенсивной све-
товой волны можно написать
п = п0 + П2А2, A25.2)
где по — значение показателя преломления среды в линейной оп-
оптике, а П2(ш) — некоторый коэффициент, зависящий от свойств
среды.
Помимо рассмотренной, есть и другие причины изменения
показателя преломления в электрическом поле. В нелинейной
среде из-за электрострикции световая волна вызывает появле-
появление постоянного давления^ аналогично тому как появляется по™
стоянное слагаемое в формуле A24.1). Это приводит к измене-
изменению плотности и показателя преломления среды. В жидкостях
с анизотропными молекулами показатель преломления изменя-
изменяется из-за высокочастотного эффекта Керра (см. § 90). Пока-
Показатель преломления всегда изменяется из-за нагревания среды
световой волной. Во всех этих случаях изменение показателя
преломления пропорционально квадрату амплитуды^ а потому
может быть также представлено формулой A25.2).
Постоянная П2 может быть и отрицательной, и положитель-
положительной. Она особенно велика у нитробензола и имеет для него по-
положительный знак.
3. Из изложенного следует, что если через однородную среду
проходит интенсивный пучок света, то среда становится оптиче-

\
§ 125 САМОФОКУСИРОВКА 775
ски неоднородной. Луч света в такой среде загибается в сторону
большего показателя преломления. С этим связано явление са-
самофокусировки (когда П2 > 0) и дефокусировки (когда П2 < 0)
света, предсказанное теоретически Г.А. Аскарьяном в 1962 г. и
впервые наблюдавшееся Н.Ф. Пилипецким и А.Р. Рустамовым в
1965 г. Затем самофокусировка наблюдалась для многих газов,
жидкостей и твердых тел.
Чтобы простейшим путем понять сущность явления самофо-
самофокусировки, предположим, что в однородную среду с показате-
показателем преломления щ вступает плоскопараллельный пучок лучей
кругового поперечного сече-
сечения с диаметром D (рис. 354).
Допустим сначала, что ампли-
амплитуда пучка постоянна по все-
всему сечению. Показатель пре- D
ломления в пространстве, за- п=по+п2^
нятом пучком, сделается рав- Т~
ным п = по + П2А2, причем мы '
предположим, что в 2 > 0. Из-
за дифракции пучок расширя- Рис. 354
ется. Практически все направ-
направления лучей сосредоточатся в пределах конуса с углом при вер-
вершине 21?диф, где 1?дИф = l,22A/(Dno), а А- длина волны в ва-
вакууме. (Направления лучей относятся к пространству внутри
цилиндра.) Предельный угол скольжения t?o для полного отра-
отражения от боковой стенки цилиндра определяется соотношением
cost?o = щ/(п® +п2А2).
Ввиду малости этого угла отсюда находим: 1 — cqs#q :
и, следовательно,
Если ^диф > t?o? то часть дифрагированных лучей будет вы-
выходить из цилиндра — пучок будет расширяться. При обратном
соотношении 1?дИф < i?o все дифрагированные лучи будут ис-
испытывать полное отражение от боковой поверхности цилиндра.
А так как в реальных условиях интенсивность света и показа-
показатель преломления возрастают к оси пучка, то из-за искривления
лучей пучок начнет сжиматься и может стянуться в тонкий
шнур. Это и есть самофокусировка.
В промежуточном случае, когда 1?диф ^^сь пучок будет про-
проходить через нелинейную среду практически без изменения по-
поперечных размеров. Он создает для себя как бы волновод, в
котором и распространяется без рассеяния в стороны. Такой ре-
режим распространения называется самоканализацией светового
пучка. Таким образом, самоканализация имеет место при уело-

776 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
вии ^о^^диф- Подставив сюда значения углов $о и ^диф? а также
выражение амплитуды А через мощность пучка
р _ споА2 7iD2 _ cnoD2 Л2
получим так называемую пороговую мощность^ выше которой
начинается сжатие пучка. Она определяется соотношением
±\ПОРОГ ^ С 1Д_ A25.3)
,@,61АJ
ШП2
Расстояние от края среды, на котором фокусируются край-
крайние лучи пучка, легко оценить из следующих соображений. В
пучке угловое расхождение лучей из-за дифракции равно 21?диф.
При критической мощности в результате отражения от боковой
поверхности пучка крайние лучи делаются параллельными. Это
произойдет на расстоянии
f D 2
Оно играет при самофокусировке роль эффективного фокусного
расстояния для крайних лучей пучка. Если вместо расходящих-
расходящихся лучей взять лучи, параллельные оси пучка, то они сфокуси-
сфокусируются на том же расстоянии /эф.
Для сероуглерода OS2, обладающего сравнительно большим
значением П2 = 2-101 СГСЭ, при освещении рубиновым лазе™
ром (А = 694,3 нм) пороговая мощность, вычисленная по форму-
формуле A25.3), равна РпОрот ~ 17 кВт. Если диаметр пучка D = 1 мм,
то формула A25.4) в этом случае дает /эф « 96 см (по = 1,62).
В некоторых сортах оптического стекла Рпорот ^ 1 Вт. В этих
случаях явление самофокусировки можно наблюдать не только
в мощных пучках импульсных лазеров, но и в малоинтенсивных
пучках лазеров непрерывного действия.
§ 126. Параметрическая генерация света
1. Нелинейные оптические явления в кристаллах позволя-
позволяют преобразовывать излучение лазера не только в излучения
гармоник, суммарных и разностных частот, но и в излучения
с плавно перестраиваемой частотой. Принцип такого преобра-
преобразования был указан в 1962 г. С.А. Ахмановым и Р.В. Хохло-
вым A926-1977). Он заключается в следующем. Пусть на среду,
нелинейная поляризация которой с точностью до квадратичных
членов определяется выражением Рнл = о^^ЕЕ, падает мощная
«волна накачки» Ен = Ан cos (wHt — kHr) и Две слабые волны
Ei = Ai cos (uj\t — kir) и Е2 = A2 cos (o^t — k2r), частоты кото-

§ 126 ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ СВЕТА 777
рых связаны соотношением
шш = оо\ +OJ2- A26.1)
Считая для простоты, что направления амплитуд всех волн сов-
совпадают, перейдем к скалярной форме записи. В первом прибли-
жении нелинейная поляризация среды будет равна a2(EH + Ei +
+ Е2) . Возведя в квадрат, рассмотрим член 2а2Е\ЕЪ) представ-
представляющий собой произведение двух косинусов. Преобразуем его в
сумму двух косинусов и возьмем слагаемое с разностной часто-
частотой (а;н —cji), которая, ввиду A26.1), равна а^. Так же поступим
с произведением 2а2^2^н- В результате из нелинейной поляри-
поляризации Ршл выделятся два члена с частотами и)\ и Ш2".
Ршл(шг) = а2А2Аш cos [u)it - (kH - k2)r],
cos [u2t - (kH - ki)r].
Следовательно, возникнет переизлучение волн с теми же часто-
частотами u)i и Ш2. Это может привести к усилению волн таких ча-
частот за счет энергии волны накачки. Такое явление называется
параметрическим усилением света, так как его можно рассма-
рассматривать как результат модуляции параметров среды (показате-
(показателя преломления) при ее взаимодействии с волной накачки. Оно
было открыто в 1965 г. Ахмановым и Хохловым с сотрудниками
в СССР, а также Джордмейном и Миллером в США и использо-
использовано ими для создания когерентных генераторов света с плав-
плавно перестраиваемой частотой. Взаимодействие с волной накач-
накачки будет особенно сильным, когда фазы волн A26.2) длительно
совпадают с фазами обеих волн Е\ и Е2, т.е. когда соблюдается
условие
к1(ш1)+к2(ш2) = кн(о;н). A26.3)
Это условие называется условием фазового синхронизма между
волной накачки и обеими волнами с частотами ио\ и ио2- Полу™
ченное ранее условие A24.7) является частным случаем условия
A26.3). Чтобы в этом убедиться, достаточно записать A24.7) в
виде
к(ш) +к(и) =к2Bо;)
и применить его к процессу образования волны с частотой ш из
ее второй гармоники.
Если условие синхронизма выполнено, то энергия от волны
накачки будет в нелинейной среде передаваться волнам с часто-
частотами ш\ и Ш2- Для эффективного усиления этих волн надо вол-
волну накачки заставить многократно проходить через нелинейную
среду (кристалл). Для этого последнюю, как в лазерах, поме-
помещают в оптический резонатор меэюду двумя зеркалами. Оба
зеркала должны иметь достаточно высокие коэффициенты от™
ражения для волн обеих частот ио\ и Ы2 и в то же время одно

778 ЛАЗЕРЫ И НЕЛИНЕЙНАЯ ОПТИКА ГЛ. XI
из них, через которое входит волна накачки, должно бв1ть в до™
статочной степени прозрачным для этой волны. При достаточно
высоких коэффициентах отражения зеркал и большой мощно™
сти волны накачки возникает генерация на частотах ш\ и бс?2,
удовлетворяющих условиям A26.1) и A26.3).
Нет необходимости специально посылать в резонатор вол™
ны с частотами ш\ и о^. Они сами возникают либо из-за всегда
имеющихся шумов, либо из-за тепловых флуктуации. Проис-
Происходит самовозбуждение генератора с последующим усилением
генерируемых волн при нелинейном взаимодействии их с волной
накачки. В качестве волны накачки обычно используется вторая
(или третья) гармоника рубинового или неодимового лазера.
2. В изотропных средах в области нормальной дисперсии
нельзя удовлетворить одновременно обоим условиям A26.1) и
A26.3). Действительно, допустим сначала, что все три волны с
частотами а;н, cji, Ш2 распространяются в одном направлении.
В этом случае условие A26.3) можно записать в виде GJj.ni +
+ ^2^2 = ^н^н, где ni, П2, пн — показатели преломления для
соответствующих частот. С учетом условия A26.1) отсюда по-
получаем (пн — п\)ий1 + (пн — П2)иJ = 0, а это невозможно, так как
(пн — ^i) > 0 и (пн ^^2) > 0. Из приведенного рассуждения еле™
дует, что волновое число кш всегда больше суммы волновых чи™
сел к\ и &2? независимо от направления волн. Поэтому условию
A26.3) нельзя удовлетворить и при различных направлениях
векторов ki, k2, kH. Иначе получился бы векторный треуголь-
треугольник, одна сторона которого длиннее суммы длин двух других
сторон.
Однако синхронизм можно получить в некоторых кри-
кристаллах между обыкновенной и необыкновенной волнами. Толь-
Только теперь, когда частоты ш\ и Ш2 могут не совпадать, для осу-
осуществления синхронизма имеется больше возможностей, чем в
аналогичном случае при генерации второй или третьей гармо™
ник (см. § 124). В принципе синхронизм мог бы осуществляться
в четырех случаях:
1)К = К + Щ, 2)к = К + Ч, A2б4)
где индексы one относятся к обыкновенной и необыкновенной
волнам. Разумеется, не всем этим условиям, и далее хотя бы од™
ному из них, можно удовлетворить в реальных кристаллах. Так,
в случае одноосного кристалла дифосфата калия КН2РО4 моле-
молено удовлетворить первым двум условиям. В первом случае в
«направлении синхронизма» необыкновенная волна накачки бу™
дет генерировать в кристалле обыкновенную и необыкновенную
волны с частотами ш\ и Ш2^ а во втором случае обе генерируемые

§ 126 ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ СВЕТА 779
волны будут обыкновенными. Для одноосного кристалла ниоба-
та лития ЬИЧЬОз, обладающего очень большой нелинейностью,
можно удовлетворить только второму из условий A26.4).
Поворачивая кристалл (или изменяя его температуру, а так™
же накладывая постоянное электрическое поле), можно изме-
изменять частоты ш\ и cd2, для которых направление, перпендику-
лярное к зеркалам, является направлением синхронизма. Имен-
Именно так действуют параметрические генераторы когерентного
света, позволяющие плавно перестраивать частоту. КПД та-
таких генераторов, определяемый как отношение мощностей па-
параметрически генерируемых волн к мощности волны накач-
накачки, достигает нескольких процентов при выходной мощности
в несколько десятков и сотен киловатт. Ясно, что генерируе-
генерируемые частоты ш\ и иJ всегда меньше частоты шш волны накачки.
Плавно перестраивая параметрический генератор света, можно
пройти весь диапазон видимого света от красного до фиолето-
фиолетового, а также далеко проникнуть и в инфракрасную область
спектра.
3. Если A26.1) умножить на постоянную Планка /г, то полу-
получится
Ншш = h(jj\ + НиJ- A26.5)
Это соотношение в квантовой физике интерпретируется как про™
цесс распада фотона Ншн на два фотона hu)\ и Нш2, причем
уравнение A26.5) выражает закон сохранения энергии для этого
элементарного акта. Аналогично, генерация второй гармоники с
квантовой точки зрения есть процесс взаимодействия двух фо-
фотонов с энергией Нш каждый, в результате которого рождается
фотон huJ с удвоенной частотой Ш2 = 2ш. Точно так же мож-
можно интерпретировать генерацию третьей и высших гармоник,
а также генерацию волн с суммарной и разностной частотами.
Однако сейчас мы не будем входить в обсуждение всех этих во™
просов, так как квантовые явления предполагается рассмотреть
в пятом томе нашего курса.

ИМЕННОМ УКАЗАТЕЛЬ
Аббе 115, 118, 122-124, 126, 127, 129,
166, 175-177, 386, 388, 393-395
Абрагам 590
Авогадро 553, 742
Айве 268, 691, 692
Амичи 126, 127
Ангерер 289
Андерсон 334
Араго 28, 203, 288, 289, 508, 513, 547,
605
Арене 493, 494
Аркадьев 304
Аскарьян 775
Ахманов 774, 776, 777
Бабине 296, 297, 327, 371, 502-504
Бальмер 603
Бартолинус 487
Басов 751
Беккерель 615
Беннет 763
Бессель 95, 314
Бийе 213, 215, 220, 221
Био 28, 605, 607
Бозе 742, 743
Больцман 150, 563, 589, 723-726, 728,
730, 731, 738, 740-742, 744, 745
Бонч—Бруевич 666
Бор 32, 743, 745
Борн 555, 590
Брадлей 692, 694
Браун 407
Бреге 29
Бриллюэн 66, 643, 645, 646, 648-650,
766
Бродхун 161
Бройль де 32, 45, 387
Брэгг 413-416, 418, 644, 645
Брюстер 28, 432, 433, 435, 446-448,
455, 456, 459, 460, 463-465, 476,
518, 759
Бугер 582, 583
Вавилов 151, 271-276, 511, 582, 583
Ван-Циттер 240, 242
Вебер 30, 40
Ведам 625
Вейерштрасс 124, 126
Верде 612, 615
Вильяме 337
Вин 578-580, 616, 617, 726, 727, 729,
730, 732, 735, 737, 738, 740, 742,
745, 747
Винер 267-269
Владимирский 648
Воллаетон 495, 497
Вольфке 363
Вуд 287, 334, 357, 476, 616
Вульф 413-416, 418, 644, 645
Габор 363-365
Гаген 477
Гайдингер 611
Гайзенберг 229
Галилей 184, 656, 657, 659, 676, 703
Гамильтон 129, 541, 543, 736
Гартнак 493, 494
Гаусс 78
Гельмгольц 77, 83, 85, 124, 132, 147,
388, 446
Герке 265, 266, 337-339, 342, 343
Герц 30, 314, 450, 455, 530, 633, 643,
768
Гершель 131, 132, 186-187
Гинзбург 273, 276
Глазебрук 493, 494, 497
Глан 493, 494
Горелик 209
Грегори 187, 190
Гримальди 20, 25, 211, 222
Грин 305
Гросс 527, 625, 646
Гук 20, 25
Гульстранд 143, 144
Гюйгенс 20, 21, 23-26, 47-49, 178-181,
183, 238, 242, 277-279, 281, 282,
291, 292, 294, 304, 305, 307, 309,
325, 335, 354, 374, 380, 393, 404,
487, 537
Дебай 417, 555, 646, 732
Декарт 14, 15, 20, 25
Делиль 288
Денисюк 370, 373, 374
Джаван 663, 763
Джасея 663
Джермер 32
Джине 731, 735-740, 745, 747, 762

ИМЕННОЙ УКАЗАТЕЛЬ
781
Джордмейы 771, 777
Доплер 426, 453, 582, 688-692, 695,
696, 698, 725, 726
Друде 268, 461, 463, 464, 473, 475,
477, 607
Дэвиссон 32
Жамен 249, 251, 252, 254, 256, 565,
584
Зееман 31, 210, 596, 597, 601, 602,
604, 613, 616, 706
Зельмейер 551, 569, 575, 614
Зоммерфельд 66, 314
Мнгл 353
Капица 599, 601
Каплянский 527, 625
Каратеодори 134, 136
Карно 725
Кассегрен 187, 190
Кельнер 180
Кеннеди 664
Кеплер 183, 184, 559, 666
Керр 31, 200, 583-586, 588-594, 596,
759, 774
Кеттелер 471, 474
Кирхгоф 277, 279, 281, 292, 304, 307,
717, 719-723, 735
Китинг 686
Клаузиус 46, 554, 721, 722, 735
Книппинг 407
Кольрауш 31, 40
Комптон 32
Коперник 692
Корбино 615
Корню 298-303
Коттон 31, 593, 594, 611
Кришнан 650
Кун 562
Кундт 564, 565, 612, 613
Курльбаум 737
Лагранж 77, 83, 85, 124, 132
Ладенбург 563
Ламберт 159, 160, 162, 163, 165, 398,
720, 721
Ламе 530
Ландау 646, 647
Ландсберг 642, 646, 649, 651
Ланжевен 586, 589, 593
Лаплас 44
Лармор 655, 675
Лауэ 407, 410-412, 414, 416
Лебедев 559, 724
Левин 573, 575
Лейт 363
Лемуан 590
Леонтович 646
Леру 564
Липпман 269-271, 373
Ллойд 213, 220-222, 234, 243, 541, 543
Ломоносов 28, 169, 186
Лорентц 31, 527, 548, 554, 555, 580,
596, 598, 602, 613, 655, 659, 675-
678, 680, 681, 689, 703, 705-708, 710
Лоренц 554, 555
Лошмидт 639
Луммер 161, 265, 266, 337-339, 342,
343, 737
Лэнглей 737
Майкельсон 30, 223, 240, 256-258,
333, 334, 337, 341, 362, 404-407,
659-664, 669, 681, 705
Макалюзо 615
Максвелл 29, 30, 38, 39-41, 44, 45,
137, 139, 292, 314, 424, 425, 453,
461, 466, 478, 481, 485, 519, 548,
551, 581, 609, 622, 632, 633, 637,
659, 665, 707, 724, 767
Максутов 188-190
Малюс 28, 56, 57, 422, 433
Мандельштам 395, 579, 584, 639, 643,
645, 646, 648-651, 766
Маральди 288
Марци 20
Мах 256, 275
Мейман 754, 764
Меслин 215, 220
Миллер 777
Минковский 677-680, 707, 708
Михельсон 731
Молчанов 666
Морзе 315
Морли 257, 662
Мосотти 554
Муррей 663
Мутон 31, 593, 594
Нейхаусс 271
Нернст 268
Николь 491-495, 497
Ньютон 20, 21, 25, 27-29, 33, 84, 172,
186, 190, 247, 248, 437, 548, 549,
564, 656, 707
Орнштейн 641
Пастернак 625
Паули 665
Пашен 353, 737

782
ИМЕННОЙ УКАЗАТЕЛЬ
Перо 263-265, 267, 337-339, 350, 751™
753
Пилипецкий 775
Пифагор 20
Планк 10, 31, 387, 577, 715, 736-740,
742, 743, 745, 747, 779
Плачек 646, 647
Поггендорф 541
Пойнтинг 434, 436, 482, 501-503, 530,
532, 576, 634
Поккельс 594, 596, 759
Поль 214, 215, 220, 221, 289, 290, 398
Празмовский 493, 494
Прево 718, 719
Принсхейм 737
Прохоров 751
Пуанкаре 655, 675
Пуассон 288, 289, 725
Пуркинье 148
Пуччианти 565
Раман 650
Рамсден 95, 178, 180, 181, 183
Резерфорд 333
Рейхе 562
Рёмер 20, 694
Риттенгауз 333
Риттер 493, 494
Ритц 665
Рождественский 256, 388, 395, 565,
566, 569
Роулэнд 334, 350, 352, 353
Рошон 495
Рубенс 476, 477, 737
Рубинштейн 315
Рустамов 775
Рытов 325
Рэлей 60, 211, 278, 287, 314, 332, 336,
338, 341, 354, 357-359, 363, 366,
379-381, 384, 386, 390, 395, 451,
463, 528, 551, 576, 617, 632, 636,
639, 641, 731, 735-740, 745, 747, 762
Сенармон 495
Сивухин 45
Ситтер де 666
Смолуховский 637, 639, 641
Снеллиус 14, 15, 22, 33, 50, 53, 275,
486, 496, 544
Солейль 503, 504
Стефан 150, 723-726, 728, 730, 740-
742
Стилуэлл 691, 692
Столетов 433, 448, 449
Тамм 273, 274
Таунс 663, 751
Твисс 407
Терхьюн 771
Тиндаль 632, 636
Томас 562
Томашек 666
Томпсон 493, 494
Торндайк 664
Уайтфорд 303
Угаров 680
Ульянин 721
Умов 532
Упатинекс 363
Фабелинский 325
Фабри 263-265, 267, 337-339, 350,
751-753
Фабрикант 750
Фарадей 29, 31, 553, 583, 600, 605,
611, 612, 614, 742
Ферма 49-54, 56-57, 87, 88, 340
Физо 29, 32, 249, 403, 404, 705
Фицжеральд 681
Форрестор 210
Фохт 541, 542, 603, 615
Франк И.М. 273, 274, 276
Франк (поляризационная призма)
493, 494
Франкен 771
Франклин 28
Фраунгофер 291, 293-296, 309, 315,
317, 320, 333, 378
Френель 28, 29, 203, 211-214, 216,
220, 221, 225, 269, 277-289, 291-
294, 296, 299, 304, 307-311, 314,
315, 325, 354, 374, 393, 430-432,
434-436, 439, 440, 443, 446, 447,
449, 451, 454-460, 462, 463, 472,
473, 478, 508, 523, 525, 526, 533,
571, 608-611, 613, 705
Френкель 27
Фридрих 407
Фуко 29, 32, 492-494, 697, 699
Фурье 41, 58, 225-227, 230, 234, 239,
344-346, 355, 357-362, 370, 371,
390, 391, 435, 578, 644, 645, 732
Харрис 774
Хафель 686
Хелл 417
Хохлов 776, 777
Христиансен 564
Хьюиш 572
Цейсе 123, 175, 438
Цендер 256

ИМЕННОЙ УКАЗАТЕЛЬ
783
Цернике 240, 242, 400, 641
Циолковский 711
Черенков 271-276
Шерер 417
Шмидт 188-190
Шредингер 560
Штарк 581, 602-604
Шустер 298, 299, 302
Эйлер 28, 29
Эйнштейн 30, 31, 637, 641, 655, 656,
658, 660, 665, 669, 670, 672, 676,
682, 699, 702, 709, 742-744, 749
Эйри 378-383, 386, 392, 518, 695
Эренфест 60, 61, 736
Эрриот 763
Юнг 28, 29, 147, 210, 211, 222, 248,
403

ПРЕДМЕТНЫМ УКАЗАТЕЛЬ
Аббе способ испытания объективов
127
— число 115
Аберрации оптических систем 101,
106, 113
Аберрационная кривая 107
Аберрация света 688, 692
Абсолютно матовое тело 721
— черное тело 719
Абсолютный оптический инстру-
инструмент 136
Адаптация 151
Адиабатические инварианты 725,
728, 729
Аккомодация 141
—, область 141
Активная (инверсно заселенная)
среда 750
Анаберрационная поверхность 55
Анализатор 421
Апертура 96
— полной поляризации 492
— числовая 166
Апертурный угол 97
Апохромат 118, 175
Астигматизм 101, 110
Астигматическая разность 102
Астрономическая рефракция 34
Атомные плоскости 410
— прямые 410
Ахромат 118, 176
Ахроматизм положения 176
— увеличения 177
Бабине компенсатор 502
— теорема 297
Бабине—Солейля компенсатор 503
Баллистическая гипотеза 665
Беккереля формула 615
Бийе билинза 213
Бинокль 184
Бора правило частот 745
Брэгга-Вульфа условие 413
Брюстера закон 432, 456, 459, 465
— угол 432
Бугера закон 582
Вектор импульса-энергии 710
Венцы 319
Верде постоянная 612
Видимая величина площадки 153
Видности кривая 148
Вина закон смещения 729, 730
— парадокс 616
— постоянная 742
— теорема 726
Виньетирование 98
Водянистая влага 139
Волна де Бройля 387
— дипольная 455
— монохроматическая 201
— необыкновенная 485
— неоднородная 43
— нормальная 610
— обыкновенная 484
— однородная 43
— поверхностная 43
— поляризации 455
— стоячая световая 267
Волновое сопротивление 274
— уравнение 45
— число спектроскопическое 229
Время восстановления 59, 63
— жизни 578
— затягивания 346
— установления 200
Вторичные волны Гюйгенса 24
Вторичный спектр 113
Входной зрачок 96
— люк 98
Выходной зрачок 97
— люк 98
Галилея преобразование 656
— принцип относительности 657
Гало 319
Гамма-излучение 9, 10
Генерация волн суммарной и раз-
разностной частот 773
— гармоник 769, 773
Геометрические законы отражения и
преломления 426, 543
на границе металла 469
Гигантские импульсы 760
Главная оптическая ось 73
Главное зеркало 185
— сечение кристалла 484
Главные нормальные сечения 102

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
785
Главные плоскости 81
— показатели преломления кристал-
кристалла 524
— радиусы кривизны 102
— скорости света в кристалле 524
Главный азимут 474
— угол падения 474
Глаз близорукий 142
— дальнозоркий 142
— схематический 143
—, камера задняя 139
—, — передняя 139
—, область аккомодации 141
—, оптическая система 139
—, острота зрения 146
Глазная линза 178
Глубина проникновения 429, 470
— резкости 99
Голограмма 363
Голография 363
Гравитационное смещение спек-
спектральных линий 702
Группа волн 61
Гюйгенса принцип 24, 537
в формулировке Кирхгофа 304,
307
Френеля 278
Двойное лучепреломление 486
круговое 608
при механических деформациях
518
течении жидкостей 519
Дебаеграмма 417
Дебая-Шерера-Хелла метод 417
Демодуляция света 209
Денисюка метод в голографии 373
Диафрагма апертурная 96
— поля зрения 98
Диоптрия 91
Дисперсионная область 330
Дисперсия аномальная 552
— временная 619
— диэлектрических осей 522
— нормальная 552
— относительная 116
— отрицательная 563
— плазмы 569
— положительная 563
— пространственная 520, 526, 527,
619
— света 40
— средняя 116
— угловая 330
— коэффициент 115
Дисторсия 112
Дисторсия, условие отсутствия 120
Дифракционная решетка 320, 325
амплитудная 325
Дифракционная решетка вогнутая
отражательная 350
двумерная 407
Рэлея 357
трехмерная (пространственная)
407
— —, второстепенные максимумы
321
, главные максимумы 321
, дисперсионная область 330
, метод скользящего падения 326
, период 320, 410
, порядок спектра 321
, пропускаемость (амплитудная
прозрачность) 354
, разрешаемое расстояние 331
, разрешающая способность 331,
339^349, 379
, в рентгеновской области
418, 419
Дифракция 13, 277
— рентгеновских лучей 407
— Фраунгофера 293
на двумерной решетке 407
круглом отверстии 316
отверстиях 315
трехмерной решетке 407
— Френеля 293
от края Луны 303
экрана 302
, метод подобия 304
Дихроизм 495
— круговой 611
Диэлектрическая проницаемость ди-
динамическая 41
комплексная 468
металла 467
поперечная 483
продольная 483
статическая 41
эффективная 478
Диэлектрические оси 521
Диэлектрический тензор 481, 520
Длина тубуса механическая 174
оптическая 174
Дополнительные экраны 297
Доплера эффект 688, 690, 691, 695
Друде метод 473
Дуализм волн и частиц 32
Естественная ширина спектральных
линий 577
Естественное затухание 577

786
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Желтое пятно 140
Жесткая фокусировка 92
Закон дисперсии волн 62
— независимости световых пучков
12, 13
— обратных квадратов 158
— отражения света 12, 14
— преломления света 12, 14
— прямолинейного распространения
света 12, 24
— сохранения импульса—энергии 710
— фотометрического сложения 237
Замедление хода движущихся часов
682
часов гравитационное 701
Зеемана эффект 596
простой (нормальный) 602
сложный (аномальный) 602
, классическая теория 598
, пи-компоненты 597
, сигма-компоненты 597
Зеленый луч 36
Зельмейера формула 551
Зенитное расстояние 35
Зонная пластинка 286
Зрачок глаза 97, 140
Зрение периферическое 146
— фовеальное 146
Зрительные трубы и телескопы 182
Избирательное отражение 475
— поглощение 475
Излучательная способность 717
Излучение Вавилова-Черенкова 271
— видимое 9, 10
— вынужденное (индуцированное)
743
— инфракрасное 9, 10
— переходное 276
— равновесное (черное) 713, 719
— рентгеновское 9, 10
— спонтанное 743
— температурное 717
— ультрафиолетовое 9, 10
—, спектральная плотность 230
Измерение угловых диаметров звезд
303, 402
Изображение вторичное 393
— действительное 67
— мнимое 67
— обратное 81
— оптическое 67, 103
— первичное 393
— прямое 81
— стигматическое 67
Изохроматические линии (изохрома-
ты) 516
— поверхности 516
Иммерсия 387
Инвариантность 706
Инверсная заселенность 563
Индикатриса 545
Интенсивность излучения 716
удельная 716
— колебаний (света) 155, 200
Интервал 677
— времениподобный 678
— пространственноподобный 678
— световой 678
Интерференционное отражение 266
— рассеяние 453
Интерференционные полосы 204
равного наклона 247
равной толщины 244
, видность 223, 237
, локализация 245, 247
, полуширина 261
— —, способ наблюдения объектив-
объективный 214
, субъективный 214
, ширина 204
, условие контрастности 218, 219
Интерференционный член 201
Интерференция 14, 201
— в пленках 242
— многолучевая 258
— поляризованных лучей 508, 515
—, порядок 231
—, угол 219
Интерферометр Жамена 249
— Майкельсона 256
звездный 404
— Маха-Цендера 256
— Рождественского 256
— Фабри-Перо 263, 339
Ионосфера 571
Искривление плоскости изображе-
изображения 110
Источники света мнимые 67
Камера-обскура 13, 394
Кандела 156
Каратеодори теорема 136
Кардинальные точки 81
Картезианский овал 55
Каустика 103
Квант света 737
Керра постоянная 585
— электрооптический эффект 583
, теория Борна 590

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
787
Керра электрооптический эффект,
теория Лаыжевеыа 586
Кеттелера инварианты 471
Кирхгофа закон 719
Кирхгофа-Клаузиуса формула 722
Ковариантность 706
Когерентность 201, 237
— временная 233, 238
— полная 237
— пространственная 220, 222, 238
— частичная 237
—, время 233, 238
—, длина 233, 238
—, объем 238
—, площадь 223
—, степень 236
—, — комплексная 236
Колбочки 143
Колебание квазимонохроматическое
234
— модулированное 234
Коллектив (полевая линза) 178
Коллинеарное соответствие 79
Кома 109
Компенсатор 499
Конденсор 182
Коническая рефракция 541, 543
, конус 538, 539
Корню спираль 299, 302
Коррекционная оправа 177
— пластинка 189
Косинусов теорема 130
Коттона-Мутона постоянная 594
эффект 593
Коэффициент затухания (поглоще-
(поглощения) 582
— отражения 433
— преломления 15
— пропускания 434
— рассеяния 636
— эллиптичности 463
Кристаллическая решетка 410
Кристалл-рефрактометр 489
Кристаллы двуосные 485, 527, 536
— одноосные 483, 485, 527, 536
— отрицательные 489
— положительные 489
Критическая опалесценция 641
— температура смешения 642
Кундта постоянная 613
Лагранжа—Гельмгольца инвариант
77
теорема 77, 124
Лазер 748
Лазер гелий-неоновый 762
— рубиновый 754
—, трехуровневая схема 760
—, четырехуровневая схема 760
Ламберта закон 159
Ландау и Плачека формула 647
Лауэ условия 410
Лауэграмма 411
Линза магнитная 191
— одиночная 197
— с непрерывным показателем пре-
преломления 195
— толстая 93
— тонкая 77
—, фокусное расстояние 78, 198
—, формула 78, 83
Линии кривизны 102
Линия прямого зрения 141
Ллойда зеркало 213
Локальная связь 617
Лорентца-Лоренца формула 554
Лорентца преобразование 675
— сокращение длины 681
Луммера-Бродхуна фотометр 161
Луммера—Герке пластинка 266
Лупа 172
Луч 14, 47, 528
— главный 97, 102
— мнимый 70
— необыкновенный 486
— обыкновенный 486
— параксиальный 75
Лучи остаточные 476
Лучистый поток 153
— —, интенсивность (лучистость)
153
Люкс 158
Люмен 156
Магнитная проницаемость динами-
динамическая 41
статическая 41
Мазер 749
Майкельсона опыт 659
— эшелон 334
Макалюзо-Корбино эффект 615
Максвелла закон 39
— эффект 519
Малюса закон 422
— теорема 56
Малых ступеней метод 148
Мандельштама—Бриллюэна явление
643
вынужденное 648
Масса покоя 709

788
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Масса релятивистская 709
Маха волны 275
Менисковые системы Максутова 188
Меслина опыт 220
Метод крюков Рождественского 566
Механика релятивистская 706
Механический эквивалент света 157
Микроволны 9
Микроскоп 174, 182, 387
Мировая линия 677
— точка 677
Многослойные покрытия 267
Модуляция амплитудная 234
— фазовая 234
Молекулы полностью анизотропные
586
— полярные 556
Монохроматическое векторное поле
423
Монохроматы 148
Мосотти-Клаузиуса формула 554
Мутная среда 632
Направления синхронизма 772
Некогерентность 201, 237
Нелокальность временная 617
— пространственная 617
Ньютона кольца 247
Обратная связь 751
Объектив иммерсионный 125
Объекты абсорбционные 399
— рефракционные 400
Одновременность 667
Окуляр Гюйгенса 178
— Кельнера 180
— компенсационный 176
— Рамсдена 178, 180
Оптика 9
— геометрическая 12, 44
— ионная 191
— линейная 42
— нелинейная 42, 748
— параксиальная (гауссова) 78
— физическая 9
— электронная 69, 191
Оптическая накачка 755
— область спектра 10
— сила 91
Оптические оси 483
второго рода (бинормали) 527
первого рода (бирадиали) 535
Оптический интервал 89
Оптическое детектирование 768
Ортотомная система 56
Освещенность 157
Освещенность естественная 166
Освещенность энергетическая (облу-
(облученность) 157
Относительное отверстие 165
Отражение диффузное 17
— избирательное 267
— интерференционное 266
— правильное 16
Очки 143
Палочки 143
Парадокс близнецов 687
Параметрическая генерация света
776
Параметрическое усиление света 777
Перспектива 100
Плазменная (ленгмюровская) часто-
частота 570
Планка постоянная 10, 739
— формула 739
Пластинка в четверть волны 499
, главные направления 499
Плеохроизм 495
Плоскость поляризации (колебаний)
38, 420, 433
, вращение естественное 605, 620
— —, — магнитное (эффект Фара-
дея) 605, 611
— установки (наводки) 99
Плотность лучистой энергии 153,
715
спектральная 715
Поверхностная прозрачность 434
Поверхность волновых векторов 545
— лучевая (волновая) 529
— нормалей 525
— показателей преломления 545
— равных амплитуд 43
фаз 43
Поглощательная способность 717
Показатель затухания 470
главный 468
— преломления 470
главный 468
комплексный 468
межпланетного и межзвездного
пространств 453
необыкновенный 486
обыкновенный 486
рентгеновских лучей 453
Поккельса линейный электроопти-
электрооптический эффект 594
Покровное стекло 177
Полное отражение 16, 429, 436, 546
, предельный угол 16, 429

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
789
Полуширина спектральной линии
578
Поля опыт 214
Поляризатор 421
Поляризация вакуума 30
Поляризация света круговая 423
линейная 39, 420
эллиптическая 422, 473
при полном отражении 438
Поляризуемость 766
Поляроиды 421, 495
Правило сумм 562
Прево правило 719
Призма дисперсионная 119
прямого зрения 119
сложная 119
разрешающая способность 339,
349
— поляризационная Аренса 493
Волластона 495
Глазебрука 493
Глана 493
Глана-Томпсона 493
Николя (николь) 491
Рошона 495
Сенармона 495
Франка-Риттера 493
Фуко 493
Призмы поляризационные двухлу-
чевые 491
однолучевые 491
Принцип детального равновесия 713
— неопределенности 229
— суперпозиции 199
— таутохронизма 70
Просветление оптики 444
Просветляющие фильтры 759
Пространство изображений 69
— предметов 69
Пуркинье явление 149
Пучок лучей астигматический 103
гомоцентрический 67
опорный 364
предметный 364
Радиоволны 9
Радужная оболочка 139
Разность хода 205
оптическая 205
Разрешаемое расстояние 146, 379,
383, 386, 391, 393
Разрешающая способность 146
глаза 384
голограммы 393
микроскопа 386, 391, 393
объектива 378
Разрешающая способность спек-
спектральная 230, 263, 348
телескопа 383
, критерий Рэлея 332
Рассеяние света 13, 277, 632
молекулярное (рэлеевское) 637
, деполяризация 639
, тонкая структура 641
комбинационное 650
вынужденное 653
поверхностное 642
тиндалевское 632
Расстояние ясного зрения 142
Рефлектор 185
Рефрактометр интерференционный
251
Рефрактор 185
Рефракция 34
Рефракция атомная 555
— молекулярная 555
— удельная 554
Роговица 139
Родопсин 151
Рождение пар 30
Роулэнда круг 352
«Рыбий глаз» 139
Рэлея-Джинса формула 735
Рэлея закон 636
— формула 639
Самоканализация 775
Самофокусировка 775
Сателлиты 650
— красные (стоксовы) 651
— фиолетовые (антистоксовы) 651
Свет естественный 420
— квазимонохроматический 208, 234
— поляризованный 420
частично 420
Светимость 160
— энергетическая (излучаемость)
160
Световая эффективность 156
Световое давление 558
— поле вблизи фокуса 374
Световой вектор 269
— конус 680
— поток 155
Световые (фотометрические) вели-
величины 155
Светосила 165
Свеча международная 156
Связь массы с энергией 709
Сетчатка (ретина) 140, 143

790
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Сила осциллятора 561
— света источника 155
средняя сферическая 156
Система афокальная (телескопиче-
(телескопическая) 81, 84
— диоптрическая 83
— катоптрическая 83
Скачок фазы при отражении 234,
243, 432
полном 438
Скин-эффект аномальный 479
Скин-эффект нормальный 478
Склера 139
Скорость групповая 57, 60, 63, 528
— движения энергии 64
— лучевая 528
— нормальная 55, 528
— передового фронта 65
— света в вакууме 667
— фазовая 58
Слепое пятно 144
Сложение скоростей релятивистское
703
Собственная длина 681
Собственное время 683
События абсолютно будущие 679
прошедшие 679
удаленные 679
Сопряженные точки 67
Сопутствующая система отсчета 683
Сопутствующие часы 683
Сосудистая оболочка 139
Спектр нормальный 330
— призматический 330
Статистически независимые величи-
величины 626
Стационарные состояния 89
Стекловидное тело 139
Степень поляризации 446
Стереографическая проекция 137
Стереотруба 184
Стефана-Больцмана закон 724
Стефана-Больцмана постоянная 742
Стильб 159
Столетова стопа 433
Сферическая аберрация 107
поперечная 108
продольная 108
Тахионы 680
Телескоп Гершеля-Ломоносова 186
— Грегори 187
— Кассегрена 187
— Ньютона 186
Телефон световой 437
Тени 13
Теорема Ван-Циттера—Цернике 242
— обращения 532
Теория света волновая 23
Теория света корпускулярная 21
электромагнитная 29
Ток поляризации 467
— проводимости 467
Точка ясного видения ближняя 141
дальняя 141
Точки апланатические 122
— главные 81
обратные 85
— закругления 102
— ортоскопические 121
— узловые 84
обратные 85
— фокальные 80, 102
Третичный спектр 118
Труба Галилея 184
— Кеплера 183
Турмалин 495
"Увеличение зрительной трубы 87
— лупы 173, 388
Увеличение микроскопа 170, 172, 388
— нормальное 167
— осевое (продольное) 85
— поперечное 81
— угловое 84
Угол аберрации 693
— зрения 141
— преломления вещественный 470
— проекции 97
— раскрытия 97
— рассеяния 634
— синхронизма 772
Уголковый отражатель 18
Ультрамикроскоп 387
Ультрафиолетовая катастрофа 736
Уравнение адиабаты для излучения
725
Ускоритель на встречных пучках 711
Условие Гершеля 131
— синусов 122, 131
— тангенсов (ортоскопии) 121
Уширение спектральных линий до-
плеровское 581
естественное 577
ударное 580
штарковское 581
Фазовая пластинка 402
Фазовый контраст 399
негативный 402

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
791
Фазовый контраст позитивный 402
— синхронизм 771, 777, 778
Ферма принцип 49
Флуктуация 626
— относительная 626
— среднеквадратичная 626
Фокальные отрезки 103
— плоскости 80
Фокус 67
— главный 80
— параксиальный 106
Формула зеркала 75, 83
Фотон 32
Френеля бипризма 212
— закон лучевых скоростей света в
кристалле 533
нормальных скоростей света в
кристалле 523
— зеркала 211
— коэффициенты 431
— параллелепипед 439
— формулы 431, 472
Функция автокорреляционная 236
— корреляционная 236
взаимная 236
Фурье интеграл 226
Фурье ряд 225
Характеристическая функция 129
Хроматическая поляризация 513
Хрусталик 139, 141
Цветная фотография 270
Липпмана 269
Цветного зрения теория 147
Центр интерференционной картины
230
Центральная ямка 141
Центрированная оптическая систе-
система 73
Часы идеальные 683
Черепковские счетчики 275
Четырехмерный вектор 707
Шмидта камера 188
Штарка эффект 602
Шустера зоны 298
Эйконал 46
— точечный 129
—, уравнение 46
Эйнштейна коэффициенты 744
— принцип относительности 658
— формула 641
Эйри кружок 378
— спирали 518
Электроны оптические 548
Энантиоморфизм 606
Энергетическая сила источника 155
Энергетические величины 155
Энергия кинетическая релятивист-
релятивистская 709
— покоя 709
— полная 709
Эрмитов тензор 520
Эфир световой (мировой) 23
Эффективная температура излуче-
излучения 762
Юнга опыт 210
Яркость 158
— энергетическая 158

Учебное издание
СИВУХИН Дмитрий Васильевич
ОБЩИЙ КУРС ФИЗИКИ
Том IV
ОПТИКА
Редактор Д. А. Миртова
Оригинал-макет: О. Б. Широкова
Оформление переплета: А. А. Логунов
ЛР №071930 от 06.07.99
Подписано в печать 14.01.05. Формат 60x90/16
Бумага офсетная № 1. Печать офсетная
Усл. печ. л. 49,5. Уч.-изд. л. 51,17. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117864 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru; http://www.fml.ru
Отпечатано с диапозитивов
в РГУП «Чебоксарская типография № 1»
428019 Чебоксары, пр. И. Яковлева, 15
БВМ 5-9221-0228-1
9 785922 102285