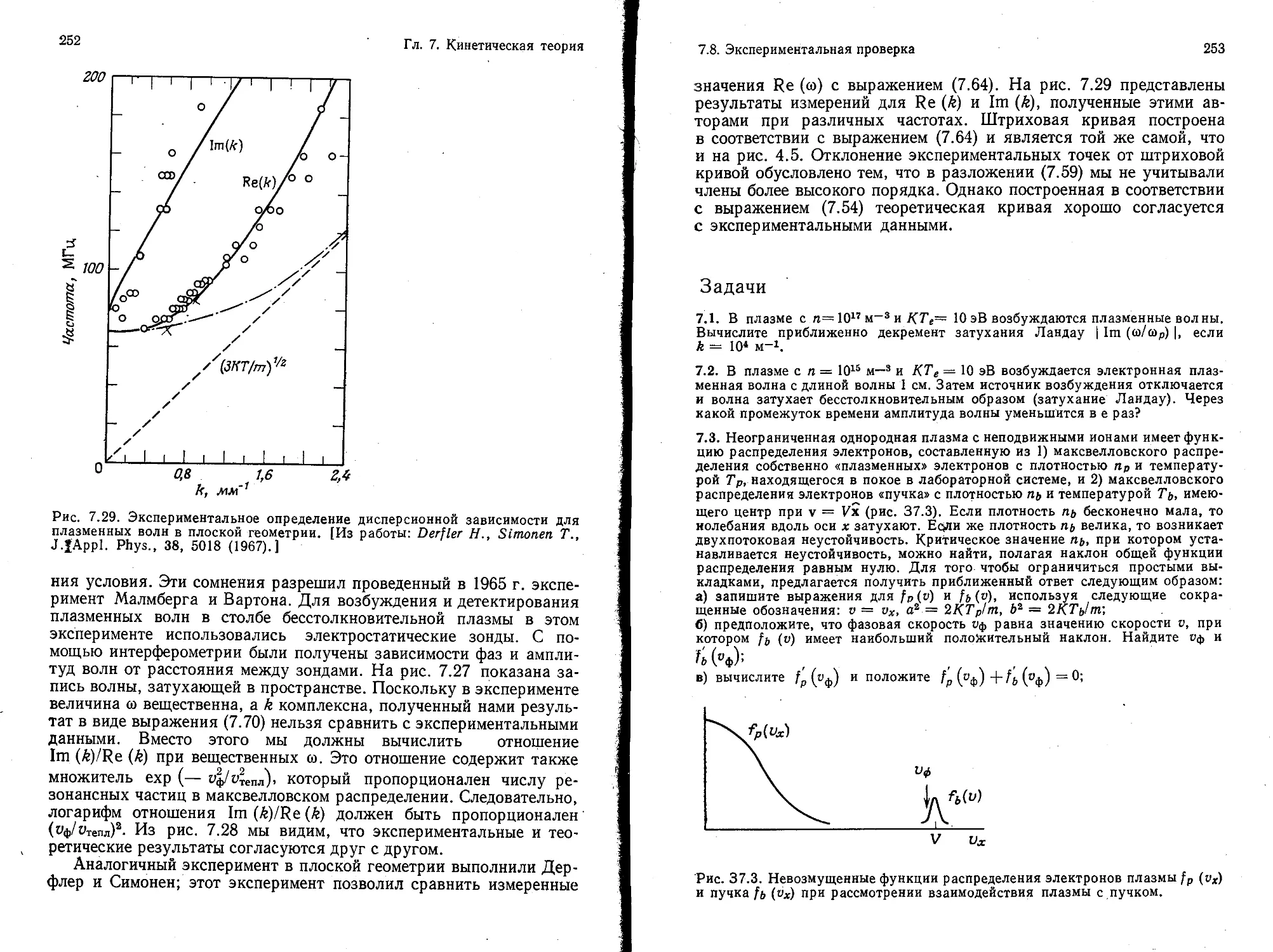
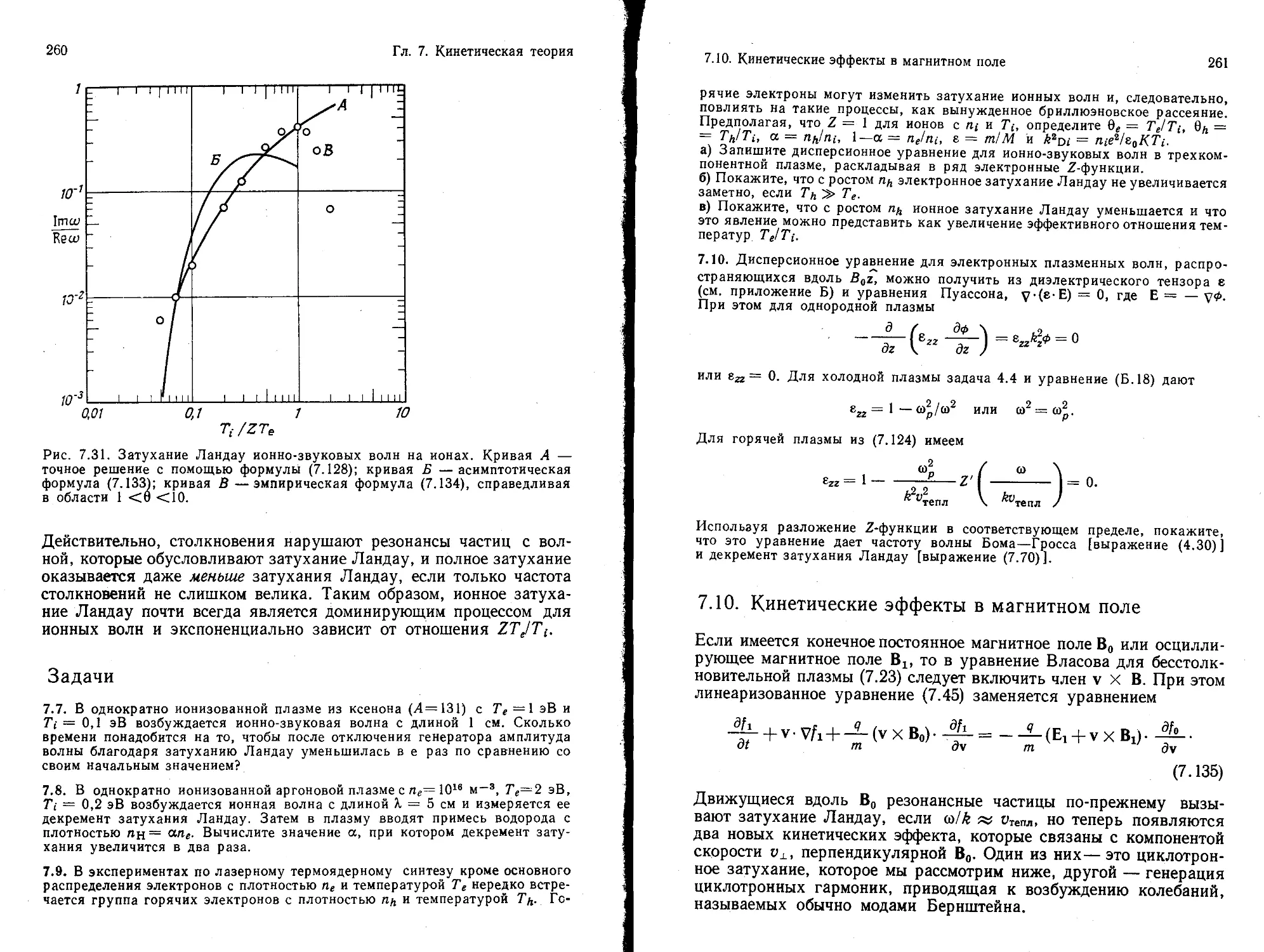
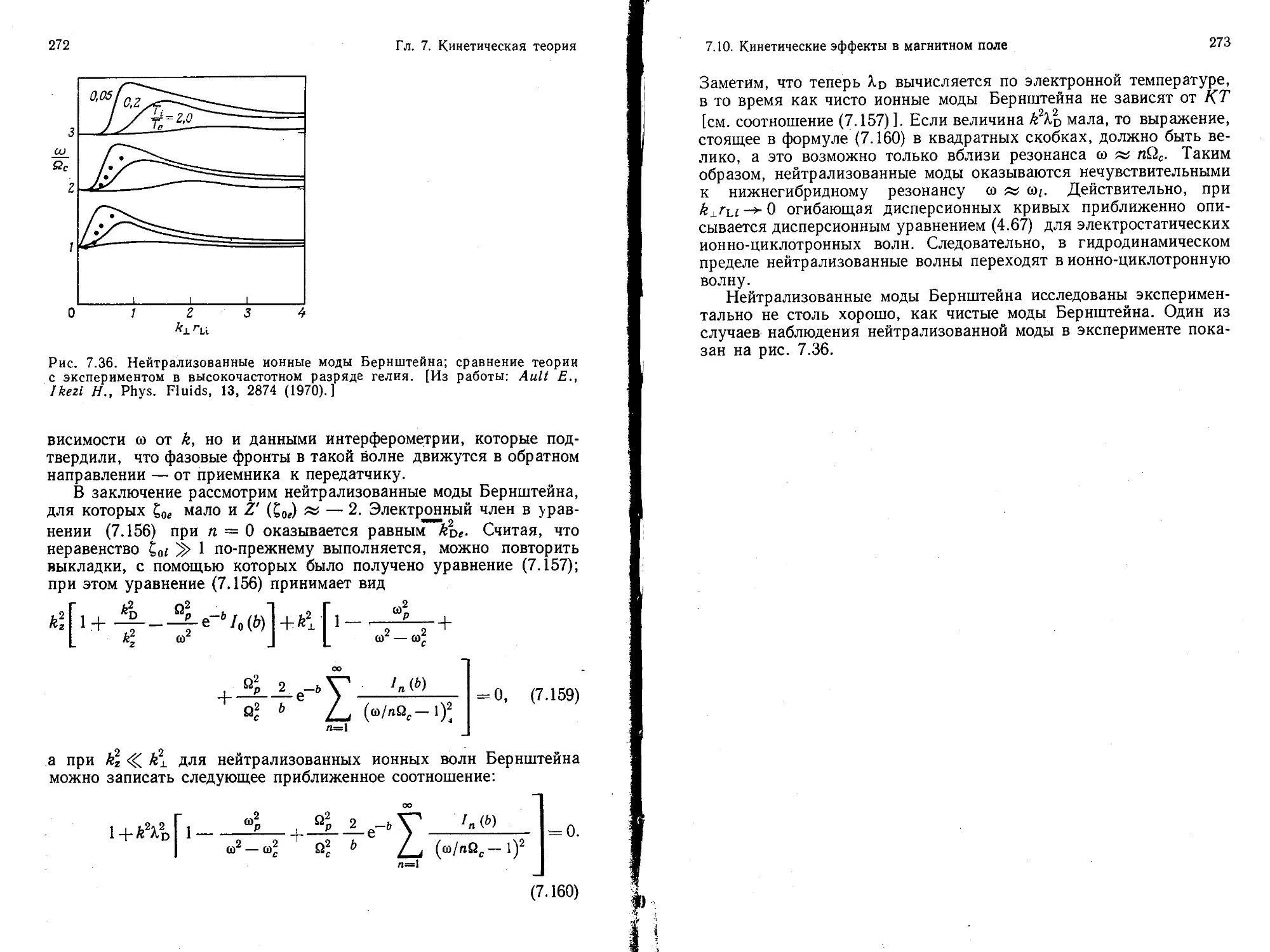
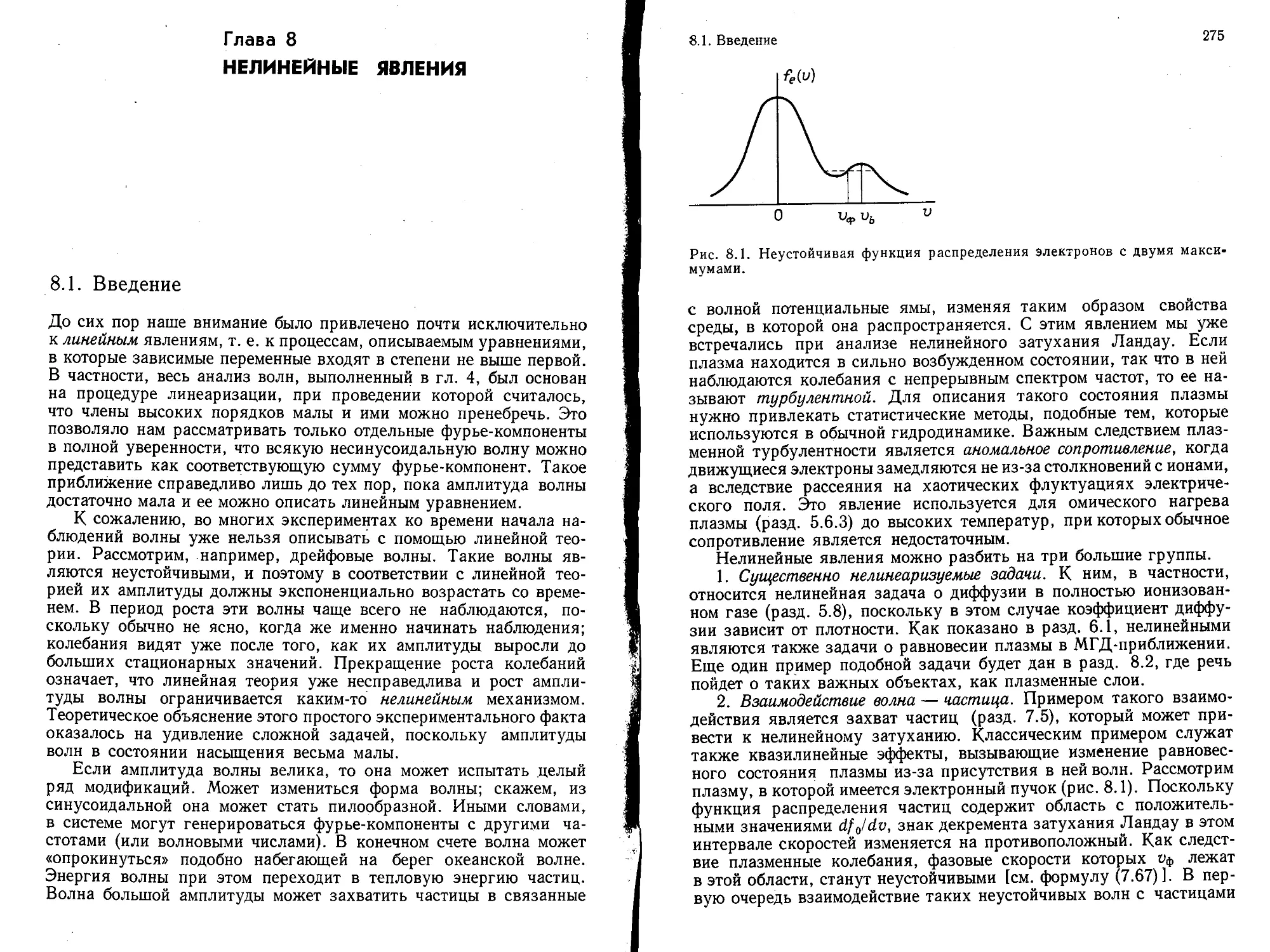
Текст
Introduction to Plasma Physics
and Controlled Fusion
Second Edition
Volume 1: Plasma Physics
Francis F. Chen
Electrical Engineering Department
School of Engineering and Applied Science
University of California, Los Angeles
Los Angeles, California
Plenum Press
New York and London
Ф.Чен
Введение
в физику плазмы
Перевод с английского
канд. физ.-мат. наук
Е. Н. Кручины
под редакцией
д-ра физ.-мат. наук
В. И. Шевченко
Москва «Мир» 1987
ББК 22.835
443
УДК 533.9
Чен Ф.
443 Введение в физику плазмы: Пер. с англ.— М.: Мир, 1987.—
398 с., ил.
В книге американского физика Ф. Чена, вышедшей в США вторым изданием,
представлены практически все проблемы современной физики плазмы, начиная
с «классических», таких, как движение отдельных заряженных частиц, гидроди-
намическое описание плазмы, теория волновых движений плазмы, и кончая та-
кими современными вопросами, как ударные волны, плазменное эхо, параметри-
ческие неустойчивости плазмы и др. Книга написана ясным языком, содержит
много рисунков и схем, а также большое число задач. Ее можно использовать в ка-
честве учебного пособия.
Для студентов, аспирантов, а также в качестве справочного пособия Для
специалистов по физике плазмы и работающих в смежных областях физики.
„ 1704040000—331 65__87 ч t
041(01)—87
ББК 22.835
Редакция литературы по физике и астрономии
81984, Plenum Press, New York
Перевод на русский язык, «Мир», 1987
Предисловие
редактора перевода
Книга написана известным американским специалистом по физике
высокотемпературной плазмы, работы которого в области диагно-
стики, аномальных явлений переноса, параметрических неустойчи-
востей, физики лазер-плазменного взаимодействия и др. снискали
заслуженное признание. Она представляет собой курс физики
плазмы, который проф. Ф. Чен уже много лет читает в Калифорний-
ском университете в Лос-Анджелесе.
Автор дает достаточно полное изложение основ физики плазмы,
рассматривая при этом не только классические результаты, но и
современные проблемы, которые в настоящее время интенсивно
изучаются. Большим достоинством книги являются ясность и про-
стота изложения материала, отсутствие утомительных алгебраи-
ческих расчетов и вместе с тем достаточная строгость доказательств.
Любой результат автор стремится пояснить «на пальцах», исполь-
зует различные физические аналогии.
Материал, преподносимый в книге, иллюстрируется многочис-
ленными рисунками и схемами, что дает наглядное представление
о физических принципах, обсуждаемых в тексте. По наглядности,
ясности и простоте подачи материала настоящее издание, пожалуй,
не имеет аналогов среди многочисленной литературы по физике
плазмы.
В первой, вводной главе автор дает определение плазмы, под-
робно рассматривает одну из фундаментальных ее характеристик —
дебаевское экранирование вносимых в нее электрических полей —
и приводит условия, при которых ионизованный газ является плаз-
мой. Здесь же кратко обсуждаются характеристики (плотность и
температура) различных плазм, начиная с плазмы газового раз-
ряда и кончая твердотельной плазмой. Приводится краткая сводка
основных применений плазмы.
Вторая глава посвящена динамике отдельной заряженной ча-
стицы в электрическом и магнитном полях (постоянных и медленно
меняющихся в пространстве и во времени) и приводится таблица
всех возможных дрейфов ведущих центров. Автор вводит понятие
6
Предисловие редактора перевода
об адиабатических инвариантах, обсуждая при этом достаточно
подробно три адиабатических инварианта.
В третьей главе обсуждается гидродинамическое описание
плазмы. Автор приводит полный набор уравнений, описывающих
плазму в двухжидкостном приближении, и рассматривает проблему
плазменного дрейфа в магнитном поле.
Четвертая глава одна из самых больших по объему. Достаточно
подробное рассмотрение распространения электромагнитных волн
в плазме сопровождается приведением схем экспериментов и наи-
более характерных результатов волновых измерений, что делает
стиль изложения живым и интересным. Определенное внимание
уделено диагностике; обсуждаются методы интерферометрии.
Подробно изучаются свисты, волны Альфвена, магнитный звук.
Главу завершает весьма наглядная диаграмма Клеммова — Мул-
лали — Эллиса.
В пятой главе рассматриваются вопросы распада слабоионизо-
ванной плазмы вследствие диффузии. Автор приводит выражения
для коэффициентов диффузии полностью ионизованного газа, а
также обсуждает механизмы аномального переноса (бомовская
диффузия, неоклассическая диффузия).
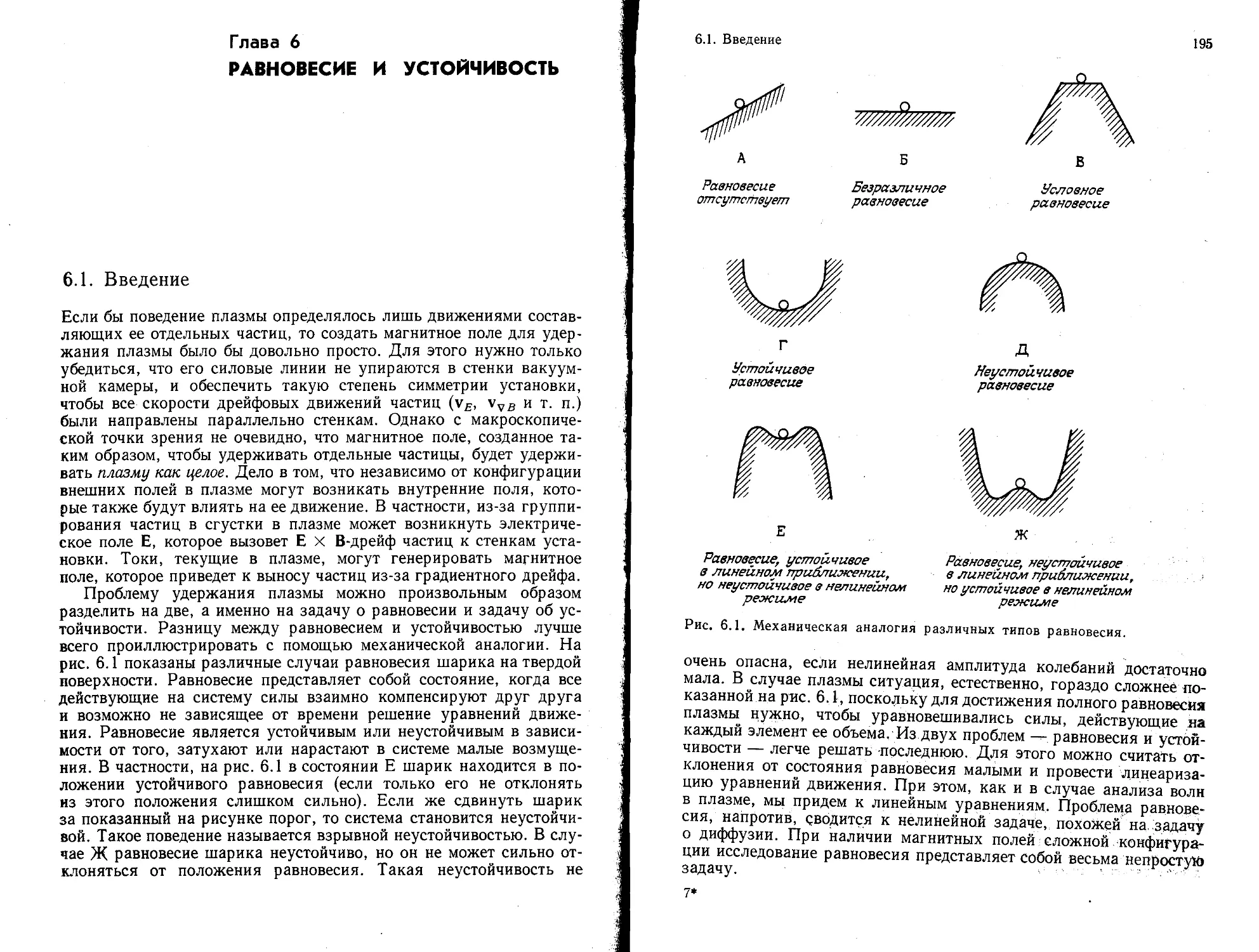
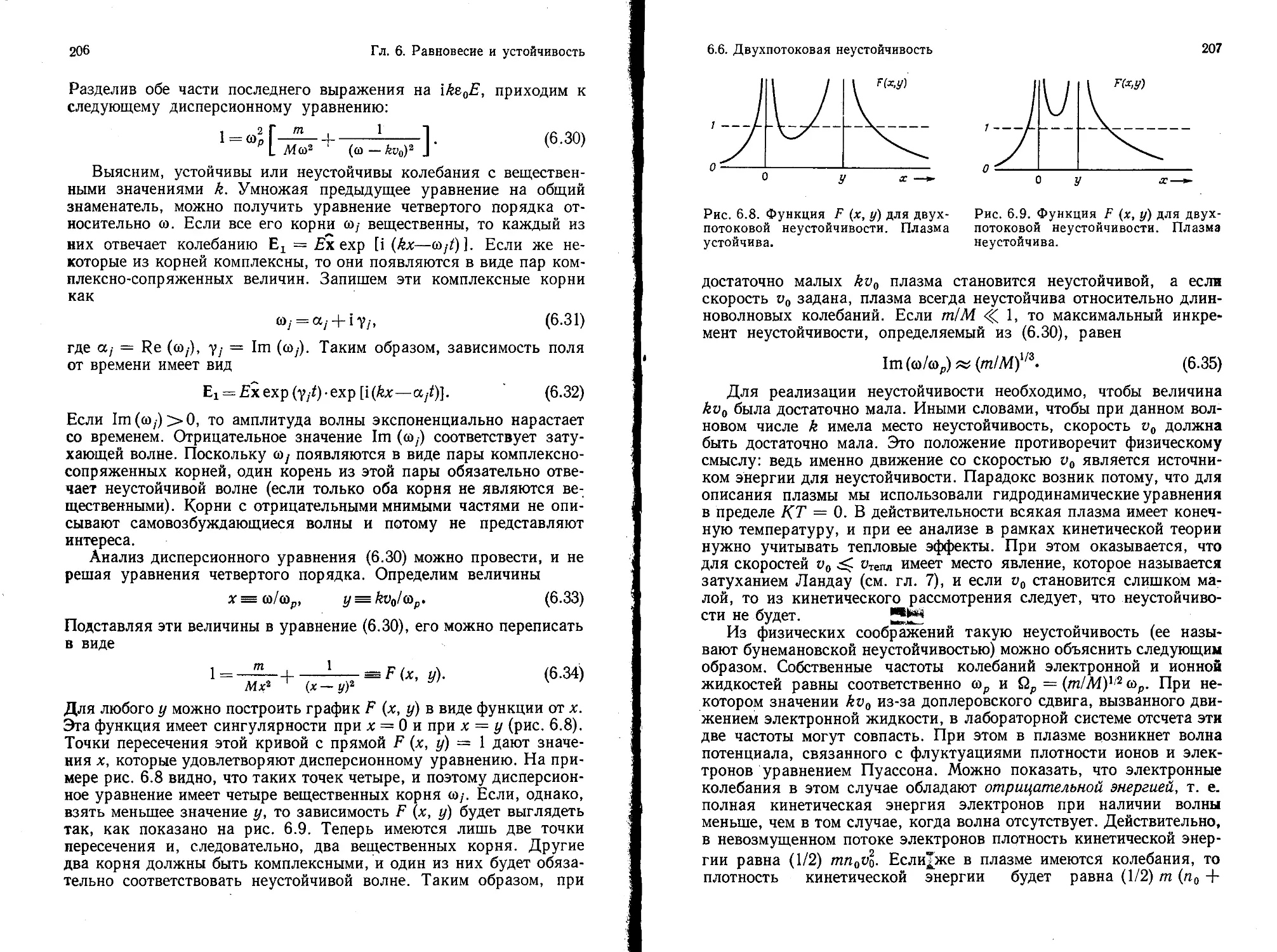
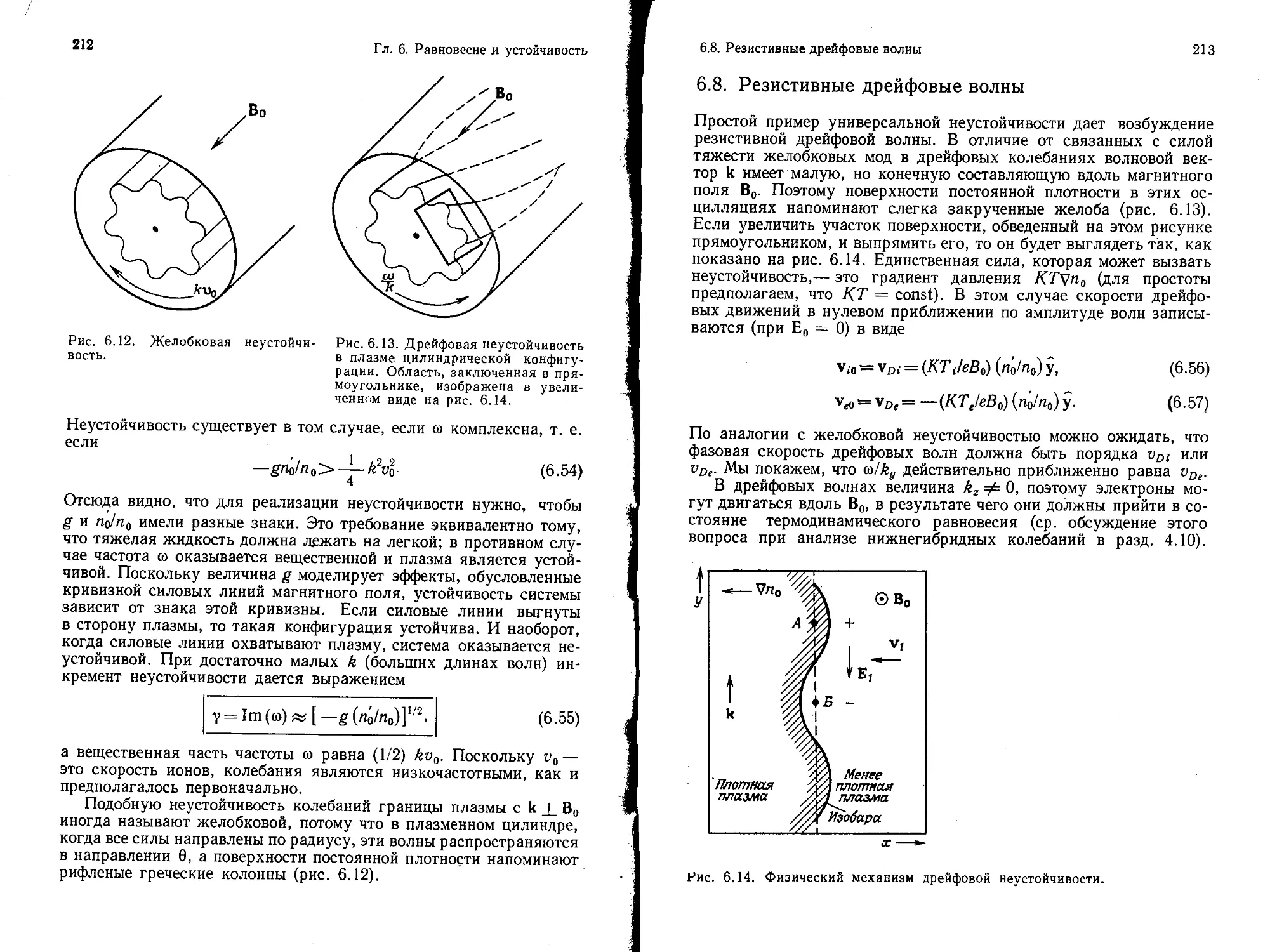
Значительное место в книге уделено рассмотрению устойчивости
плазмы (гл. 6). В зависимости от типа свободной энергии, приводя-
щей к неустойчивости, автор разбивает их на четыре категории:
потоковые, неустойчивости Рэлея—Тейлора, универсальные и ки-
нетические неустойчивости.
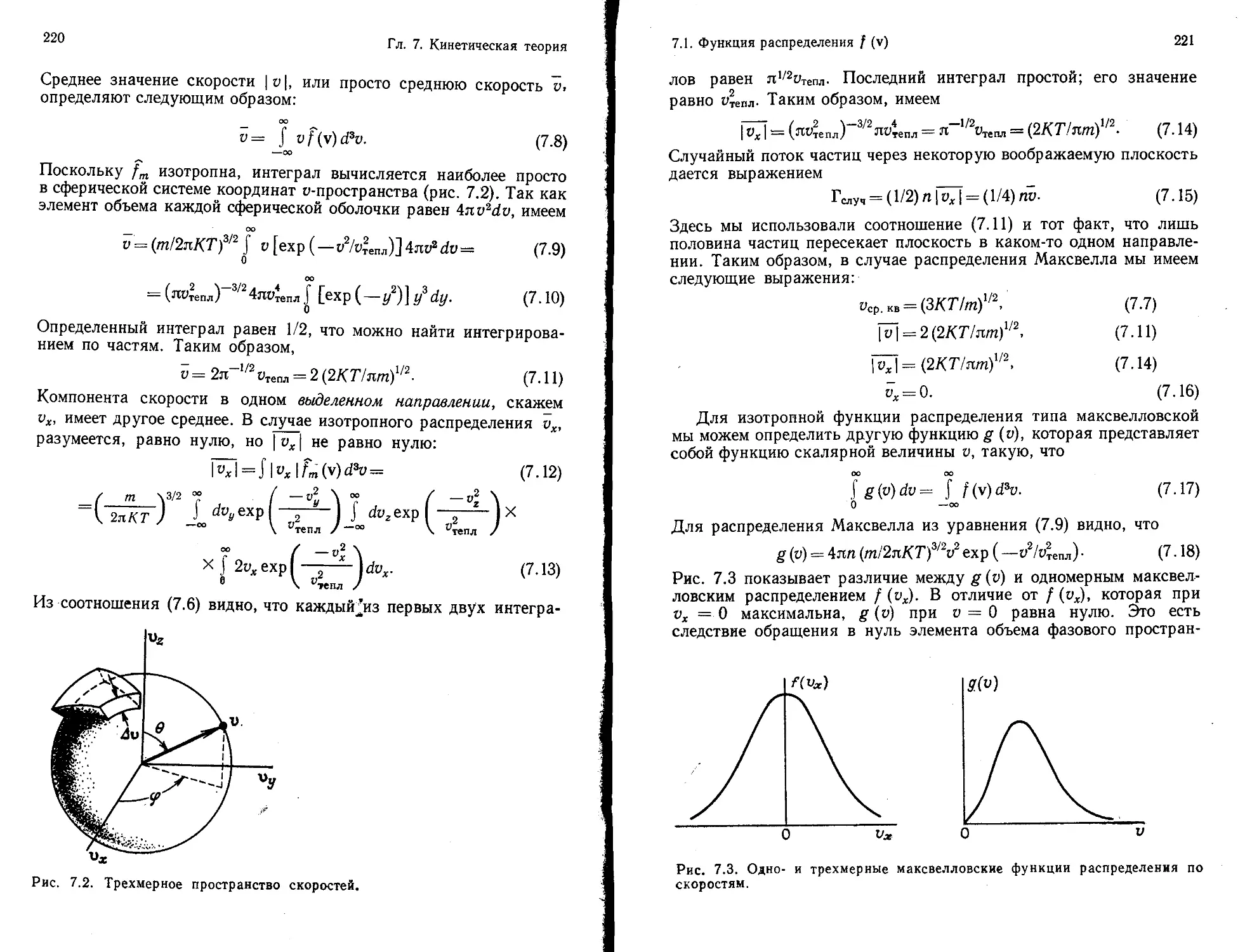
Весьма интересным представляется изложение вопросов бес-
столкновительного поглощения волн в плазме (гл. 7). Автор под-
робно рассматривает физические механизмы такого затухания и
приводит наиболее важные экспериментальные результаты.
Заключительная восьмая глава посвящена нелинейным эффек-
там в плазме. На примере ионно-звуковых колебаний приводятся
различные нелинейные решения (солитоны, ударные волны). Боль-
шое внимание автор уделяет актуальной проблеме приповерхност-
ных слоев, а также зондовым измерениям. Описываются нелиней-
ные эффекты в связи с различного рода параметрическими неустой-
чивостями. Глава завершается рассмотрением двух нелинейных
уравнений, играющих важную роль в современной физике плазмы,
а именно уравнения Кортевега—де Вриза и нелинейного уравне-
ния Шредингера.
В конце книги помещен ряд приложений, которые принесут не-
сомненную пользу как справочный материал, а преподавателям
физики помогут в подготовке экзаменационных вопросов для сту-
дентов.
Мы надеемся, что книга в целом будет весьма интересна и по-
лезна как студентам и преподавателям университетов и техниче-
ских вузов, так и специалистам, имеющим дело с плазмой.
В. И. Шевченко
Поэту и вечной студентке . . .
М. Конрад Чен
Эвелин Чен
Предисловие
ко второму изданию
За девять лет, которые прошли с тех пор, как эта книга была напи-
сана, научные достижения в области ядерного синтеза, космиче-
ской физики и нелинейной теории плазмы шагнули далеко вперед.
В то же время проблема истощения энергетических запасов, с од-
ной стороны, и исследования Юпитера и Сатурна, с другой, при-
вели к осознанию в широких масштабах того, сколь важную роль
играет физика плазмы в производстве энергии и в понимании нашего
космического окружения.
За этот период в области магнитного удержания плазмы для
термоядерного синтеза на токамаках Алкатор в Массачусетском
технологическом институте было достигнуто лоусоновское число
тЕ = 2-1013 см-3-с, на токамаке PLT Принстонской лаборатории
был осуществлен нагрев плазмы с помощью нейтрального пучка
до KTi = 6,5 кэВ, увеличено среднее значение |3 до 3—5 % на то-
камаках Ок-Риджской лаборатории и фирмы «Дженерал Атомик»,
в Ливерморской лаборатории получена стабилизация удерживае-
мой магнитными ловушками плазмы на установке 2XIIB, осущест-
влена инжекция ионного тока почти в условиях обращенного поля.
Благодаря изобретению сдвоенного зеркала в области магнитного
удержания достигнуты впечатляющие успехи. Предложены новые
конструкции, такие, как компактные торы, установки поверхност-
ного поля и ЕВТ — гибрид тора с магнитными ловушками. Воз-
рождены некоторые старые принципы удержания плазмы, напри-
мер, в стеллараторе или с помощью пинча в обращенном поле. Но-
вой яркой звездой вспыхнула идея о радиочастотном нагреве, обе-
щающем генерацию постоянного тока. Может быть, самое важ-
ное — это то, что мы существенно продвинулись в понимании
МГД-поведения плазмы тороидальной конфигурации: тиринг-мод,
магнитных островов и разрывов. Вместе с тем впервые привлекли
пристальное внимание проблемы конструирования реакторов, тех-
нологии синтеза, а также гибридных установок, использующих
синтез и расщепление ядер.
Вышел из младенческого возраста управляемый термоядерный
синтез с инерционным удержанием; сейчас на него направлена при-
мерно одна четверть исследовательских усилий, приходящихся на
8 Предисловие ко второму изданию
долю магнитного удержания. В Ливерморской лаборатории на ла-
зерной установке «Шива» мощностью 25 ТВт при направленном
взрыве одной крупинки горючего получено 3-1010 термоядерных
нейтронов, достигнуто сжатие горючего до плотности, в сотню раз
превышающей плотность жидкого водорода. Пристальное внима-
ние привлекли нелинейные плазменные процессы при взаимодейст-
вии лазерного излучения с веществом. Мы также находимся на
пути к пониманию таких важных процессов, как резонансное по-
глощение, вынужденное рамановское и бриллюэновское рассеяние
и спонтанное возбуждение магнитного поля. В качестве возмож-
ной альтернативы лазерам предложено использование ускоренных
частиц, а именно электронных пучков, пучков легких или тяжелых
ионов, что привело к целому ряду новых проблем в физике плазмы.
В физике космической плазмы мы имеем четко разработанное
представление о магнитосфере, которое подтверждается наблюде-
нием вистлеров в магнитосфере Юпитера, предсказанных соответст-
вующей теорией. Теперь хорошо известна структура солнечной
короны и объяснена ее связь с магнитными полями в солнечных
пятнах и с образованием солнечного ветра. В удовлетворительном
состоянии находится теория полярных сияний.
Все возрастающий интерес к термоядерному синтезу привел
к тому, что гл. 9 первого издания вылилась в отдельную обстоя-
тельную книгу по физике термоядерного синтеза и будет опублико-
вана в виде второго тома а). Его содержание основано на конспекте
моих лекций по магнитному удержанию плазмы для студентов стар-
ших курсов. При написании книги я заменил утомительные мате-
матические расчеты на короткие выкладки, основанные на физиче-
ской картине поведения плазмы. Решение последней задачи и при-
вело к тому, что выпуск второго издания был задержан почти на
три года.
В том 1 включены первые восемь глав первого издания книги.
Он сохранил первоначальную простоту, но был исправлен и допол-
нен. Устранено несколько мелких ошибок, обнаруженных студен-
тами и преподавателями. В ответ на их просьбы система единиц
была с неохотой заменена на СИ (МКС). Приношу извинения фи-
зикам моего поколения; утешайтесь мыслью, что первое издание
книги стало библиографической редкостью.
В настоящий том помещен вывод тензора диэлектрической про-
ницаемости для холодной плазмы; чтобы не усложнять и без того
длинную и трудную для начинающего главу, данный вывод при-
водится в приложении Б, которое можно использовать как готовый
справочный материал. Излагаемая в соответствующей главе кине-
тическая теория дополнена изучением вопросов, связанных с зату-
ханием Ландау звуковых волн, дисперсионной [функцией плазмы
х) В переводе на русский язык книга выходит в одном томе, посвящен»-
ном физике плазмы. — Прим. ред.
Предисловие ко второму изданию
9
и волнами Бернштейна, Глава, посвященная нелинейным явлениям,
в новом издании включает рассмотрение солитонов в рамках урав-
нения Кортевега—де Вриза и нелинейного уравнения Шредингера.
Материал здесь излагается более подробно, чем в остальной части
первого тома, что сделано специально для того, чтобы разжечь ин-
терес у более подготовленных студентов. Здесь заслуживают при-
знания полезные советы, которые мне дали Дж. Моралес и К. Ни-
шикава.
Специально для преподавателей в книгу добавлены новые за-
дачи, предлагавшиеся на экзаменах последнего десятилетия, и при-
ведены решения задач, помещенных в первом издании. В приложе-
нии В приводится пример трехчасового заключительного экзамена
для старшекурсников. Ответы к задачам проверял Дэвид Брауер;
если там есть ошибки, то это его ошибки, а не мои.
Наконец, о помещенном мною в начале книги загадочном посвя-
щении. Дело в том, что у меня есть хорошие и плохие новости. Пло-
хие новости — это то, что поэт (мой отец) отправился в страну
вечной песни. Хорошие новости — вечная студентка (моя мать)
достигла наконец своей цели, получив степень доктора философии,
когда ей исполнилось 72 года. Поистине процесс познания беско-
нечен.
Франсис Ф. Чен
Лос-Анджелес, 1983
Предисловие
к первому изданию
Эта книга выросла из конспекта лекций по физике плазмы, которые
в течение ряда лет читались старшекурсникам Калифорнийского
университета в Лос-Анджелесе. При нынешнем росте интереса
к управляемому термоядерному синтезу и широком применении
физики плазмы в космических исследованиях и в релятивистской
астрофизике имеет смысл сделать изучение плазмы на старших кур-
сах частью основного учебного процесса наряду с такими предме-
тами, как термодинамика или квантовая механика. Хотя вначале
целью этой книги было удовлетворение потребностей в учебнике,
в котором материал излагался бы в форме, доступной для студен-
тов как старших, так и младших курсов, я надеюсь, что с помощью
этой книги и ученые других специальностей, скажем, имеющие
дело с физикой твердого тела или лазерной физикой, смогут без осо-
бого труда познакомиться с плазмой.
Здесь я следовал двум основным принципам: не оставлять алге-
браических выкладок в качестве упражнений для читателя и не
позволять алгебраическим преобразованиям затемнять физику.
Удовлетворить этим двум противоречивым целям стало возможным
благодаря рассмотрению плазмы в виде двух взаимопроникающих
жидкостей. Двухжидкостную модель легче понять, и она оказы-
вается более точной, чем одножидкостное приближение, по крайней
мере для процессов, протекающих в плазме низкой плотности.
Первые главы не требуют от студента особой подготовки, однако
последние соответствуют его возросшему опыту. За учебную чет-
верть, состоящую из девяти или десяти недель, можно изучить пер-
вые шесть с половиной глав. Материал этих глав прошел тщатель-
ный отбор и содержит только то, что действительно существенно.
Последние две с половиной главы можно использовать в семестро-
вом курсе для дополнительной работы. Значительные усилия ав-
тора были направлены на то, чтобы сделать более понятным зату-
хание Ландау. Объяснение, даваемое в этой книге, не предполагает
знания контурного интегрирования. За помощь в упрощении фи-
зической картины затухания Ландау, которую сформулировал
Джон Даусон, я многим обязан Тому О’Нейлу и Джорджу
Шмидту.
Предисловие к первому изданию
11
Некоторые читатели будут испытывать неудобства из-за того,
что в книге используется электростатическая система СГС. Естест-
венно, аргументировать выбор системы единиц бессмысленно; каж-
дый квалифицированный физик с помощью ораторского искусства
и безупречной логики будет защищать свою любимую систему.
Используемая здесь система единиц объясняется в приложении 1.
Она была выбрана потому, что позволяет избежать ненужного вы-
писывания постоянных с, fx0 и е0, а также потому, что согласуется
с большинством научных статей по физике плазмы.
Я хотел бы поблагодарить г-жу Лайзу Тартар и г-жу Бетти Рей
Браун, которые проявили большую интуицию, расшифровывая
мой почерк, г-на Тима Ламберта за аналогичное понимание при
подготовке рисунков, а более всего Анди Чен за то, что она смири-
лась со многими вечерами, проведенными в одиночестве.
Франсис Ф. Чен
Лос-Анджелес, 1974
Глава 1
ВВЕДЕНИЕ
1.1. Распространенность плазмы в природе
Нередко можно слышать, что 99 % вещества во Вселенной нахо-
дится в состоянии плазмы, т. е. в виде ионизованного газа, в кото-
ром атомы диссоциированы на положительные ионы и отрицатель-
ные электроны. Эта оценка, возможно, и не является точной, но
она, конечно, вполне обоснованна, если учесть тот факт, что звезды
и их атмосферы, газовые туманности и значительная часть меж-
звездного газа представляют собой плазму. Что касается непосредст-
венного окружения нашей Земли, то, как только мы выходим за
пределы земной атмосферы, мы сталкиваемся с плазмой радиа-
ционных поясов и солнечного ветра. Однако в повседневной жизни
наши встречи с плазмой ограничиваются всего лишь несколькими
примерами: вспышка молнии, мягкое свечение северного сияния,
проводящий газ внутри флуоресцентной трубки или неоновой рек-
ламы и слабоионизованная плазма ракетных факелов. По-видимому,
мы живем в той части Вселенной, составляющей один процент ее,
где плазма естественным путем не возникает.
Причину этого можно понять с помощью уравнения Саха, ко-
торое позволяет вычислить степень ионизации газа, находящегося
в тепловом равновесии:
7*3/2
— да 2,4-1021-----е-£/</кг. (1.1)
пп п{
Здесь щ и пп — плотность (число в 1 м3) ионизованных и нейтраль-
ных атомов соответственно, Т — температура газа в кельвинах,
К — постоянная Больцмана, Ut — энергия ионизации газа, т. е.
количество энергии, необходимое для удаления электрона с внеш-
ней электронной оболочки атома. (В этой книге мы будем исполь-
зовать систему единиц измерения СИ.) В обычной воздушной среде
при комнатной температуре можно принять, что п„ « 3- 1025 м~3
(см. задачу 1.1), Т » 300 К и Ut = 14,5 эВ (для азота); 1 эВ =
= 1,6-10-19 Дж. Относительная ионизация, определяемая урав-
нением (1.1), ничтожно мала:
1Q—122 е
Лд
1.1. Распространенность плазмы в природе
13
С ростом температуры степень ионизации остается низкой, до
тех пор пока КТ не станет всего лишь в несколько раз меньше Ut.
После этого п//п„ резко возрастает и газ переходит в плазменное
состояние. При дальнейшем возрастании температуры плотность
нейтралов пп становится меньше tit и плазма в конечном счете ока-
зывается полностью ионизованной. Именно поэтому плазма су-
ществует в астрономических телах с температурой в миллионы гра-
дусов и отсутствует на Земле. Вряд ли можно представить себе
спокойное сосуществование биологической жизни и плазмы, по
крайней мере той плазмы, о которой идет речь в данной книге. Вот
почему плазма, естественным образом существующая при высоких
температурах, называется «четвертым состоянием вещества».
Мы не собираемся подробно изучать уравнение Саха, однако
необходимо пояснить его физический смысл. В газе атомы имеют
разброс по тепловым энергиям, и вследствие соударений между
ними может произойти ионизация атома в том случае, когда он ис-
пытывает столкновение со скоростью, достаточной для выбивания
из него электрона. В холодном газе такие энергичные столкнове-
ния встречаются редко, поскольку для этого атом серией «благо-
приятных» столкновений нужно ускорить до энергий, во много
раз превышающих среднюю энергию. Экспоненциальный множи-
тель в уравнении (1.1) отражает тот факт, что число быстрых ато-
мов экспоненциально уменьшается с увеличением отношения UJKT.
Если атом стал ионизованным, то это его состояние сохраняется
до тех пор, пока он не столкнется с электроном; при этом весьма
вероятно, что произойдет рекомбинация с электроном и атом снова
станет нейтральным. Скорость рекомбинации, очевидно, зависит
от плотности электронов, которую можно принять равной плотно-
сти ионов п.{. Следовательно, равновесная плотность ионов должна
уменьшаться с ростом п{-, именно поэтому в правой части уравне-
ния (1.1) возникает множитель и”1. Плазма в межзвездной среде
обязана своим существованием малому значению гц (~ 1 см-3)
и, следовательно, низкой скорости рекомбинации.
1.2. Определение плазмы
Разумеется, не всякий ионизованный газ можно называть плазмой:
какой бы газ мы ни взяли, в любом случае он имеет некоторую не-
большую степень ионизации. Удовлетворительным определением
плазмы является следующее:
Плазма — это квазинейтральный газ заряженных и нейтраль-
ных частиц, который проявляет коллективные свойства.
Понятия «квазинейтральный» и «коллективные свойства» тре-
буют разъяснения. Что такое квазинейтральность, мы покажем
в разд. 1.4. Понятие «коллективные свойства» поясним на следую-
щем примере.
14
Гл. 1. Введение
Рис. 1.1. Иллюстрация дальнодействующих электромагнитных сил в плазме-
Рассмотрим силы, действующие на молекулу, скажем, в обыч-
ном воздухе. Поскольку молекула нейтральна, на нее не действует
электромагнитная сила, а сила тяжести пренебрежимо мала. Моле-
кула движется свободно до тех пор, пока она не испытает столк-
новение с другой молекулой; следовательно, движение частицы
в воздухе определяется этими столкновениями. Действие макро-
скопической силы, приложенной к нейтральному газу, например
от громкоговорителя, генерирующего звуковые волны, передается
отдельным атомам благодаря столкновениям. В случае же плазмы,
которая содержит заряженные частицы, ситуация становится сов-
сем иной. Во время движения заряженные частицы изменяют ло-
кальные концентрации положительного и отрицательного зарядов,
что приводит к возникновению электрических полей. С движением
зарядов связаны также токи и, следовательно, магнитные поля.
Эти поля на больших расстояниях могут влиять на движение
других заряженных частиц.
Каково же влияние, которое оказывают друг на друга две слабо
заряженные области плазмы А и В, находящиеся на расстоянии
г друг от друга (рис. 1.1)? Сила кулоновского взаимодействия убы-
вает с г как 1/г2. Однако при данном телесном угле (т. е. при Ar/г =
= const) объем плазмы в области В, который может воздействовать
на область А, увеличивается с г как г3. Следовательно, элементы
плазмы действуют друг на друга с силой, которая проявляется
даже на больших расстояниях. Именно эта дальнодействующая ку-
лоновская сила приводит к огромному разнообразию возможных
движений плазмы и делает столь богатой область исследований,
называемую физикой плазмы. Действительно, наиболее интерес-
ные результаты относятся к так называемой бесстолкновительной
плазме, в которой дальнодействующие электромагнитные силы
1.3. Понятие температуры
15
настолько больше сил, обусловленных обычными локальными
столкновениями, что последними можно полностью пренебречь.
Таким образом, понятие «коллективные свойства» означает, что
в плазме движение частиц определяется не только локальными ус-
ловиями, но и ее состоянием в удаленных областях.
По-видимому, сам термин «плазма» выбран по ошибке. Это на-
звание происходит от греческого лАастра, — ато£, то, что означает
нечто сформированное или вылепленное. Однако плазма, напротив,
из-за коллективного поведения составляющих ее частиц не стре-
мится подчиняться внешним воздействиям, скорее наоборот, во
многих случаях она ведет себя так, как будто сама наделена ра-
зумом.
1.3. Понятие температуры
Прежде всего полезно рассмотреть и обобщить наши физические
представления о температуре. Газ в тепловом равновесии состоит
из частиц, которые имеют всевозможные скорости, и наиболее ве-
Рис. 1.2. Максвелловская функция распределения по скоростям.
рентным распределением по этим скоростям является максвеллов-
ское. Для простоты рассмотрим газ, в котором частицы могут совер-
шать только одномерное движение. (Этот пример не является чисто
надуманным; в частности, электроны в сильном магнитном поле
могут двигаться только вдоль магнитных силовых линий.) Одно-
мерная максвелловская функция распределения имеет вид
f (и) = Л ехр(—(1/2) тиЖГ), (1.2)
где f du — число частиц в единице объема (1 м3), скорости которых
лежат в интервале и -4- и + du\ тиЧ2 — кинетическая энергия,
а К — постоянная Больцмана (= 1,38-10-23 Дж/К). Плотность п,
16
Гл. 1. Введение
т. е. число частиц в одном кубическом метре, дается выражением
(см. рис. 1.2)
4-00
п — f f (и) du. (1.3)
Постоянная А связана с плотностью п соотношением (см. за-
дачу 1.2)
A = n(tn/2nK.T)ii2. (1.4)
Ширина распределения по скоростям определяется величиной Т,
которую мы называем температурой. Чтобы понять точный смысл
этой величины, вычислим среднюю кинетическую энергию частиц
с такой функцией распределения:
+°° 1 i/+°° А
fcp = f —mu2[ (и) dull J f(u)duj-
Вводя обозначения
^тепл = (2/(77/7l)''2, у~и1итепЛ9
функцию (1.2) можно записать в виде
/ (и) = A exp ( U /Утепл)1
При этом выражение (1.5) принимает вид
+°°
(1/2)тА^епл J [exp ( — t/2)] t? dy
F “°0
сСр —
Л^тепл J exp(— y2)dy
—00
В числителе интеграл берется по частям:
J у- [ехр (—г/2)] ydy= {— (1/2) [exp (— z/2)] y]t“ ~
—00
-|-00 -]-oo
- f (—1/2)exp(—y2)dy = (]/2) J exp(—y*)dy.
—00 —oo
Сокращая интегралы, имеем
(1/2) тЛ»Зепл (1/2) i _
(1-5)
(1.6)
(1-7)
Таким образом, средняя кинетическая энергия равна KTI2.
Полученный нами результат нетрудно обобщить на трехмерный
случай. При этом максвелловская функция распределения за-
пишется в виде
f(u, v, иО=Л3ехр[(—1/2)щ(г?4-о2 + иЯ)//(Т], (1.8)
1.3. Понятие температуры
17
где
A3s= п (т/2лКТ)312. (1.9)
Средняя кинетическая энергия определяется выражением
+»
£ср = Щ Аз (V2) т (и* + о2 + ш2) ехр [ - (1/2) т (и* + о2 + а>2)/КГ] X
—00
X dudvdw/\§\ А3 ехр [ — (1/2) т (и* 4- ь*+ w^IKT] du dvdw.
—00
Следует заметить, что благодаря изотропности максвелловского
распределения последнее выражение является симметричным от-
носительно и, v и w. Таким образом, в числителе все три слагаемых
равны друг Другу. Для получения ответа достаточно вычислить
только первый член и умножить его на три:
Еср = ЗА3$ (1/2) mu4 ехр [ — (1/2) тиг/КТ] du $$ ехр [( — 1/2) т (о4 4- w^IKT] х
X dvdwt{A3 $ ехр [ — (1/2) тиЧКТ] du\\ ехр [ — (1/2) т (о2 4- w^/KT] dvdw}.
Используя предыдущий результат, имеем
Дср=уЛТ. (1.10)
Общий результат состоит в том, что средняя энергия Еср, приходя-
щаяся на одну степень свободы, равна КТ/2.
Поскольку величины Т и Дер столь тесно взаимосвязаны, в фи-
зике плазмы принято измерять температуру в единицах энергии.
Чтобы избежать путаницы из-за зависимости £Ср от размерности
задачи, для определения температуры используется не £ср, а энер-
гия, соответствующая КТ. Если КТ — 1 эВ = 1,6-10-19 Дж, то
Т = -L’.6' 10L- . = Ц600.
1,38-Ю-23
Таким образом,
1 эВ = 11 600 К. (1.11)
Под плазмой с температурой 2 эВ мы понимаем такую плазму, у ко-
торой КТ = 2 эВ, а в трех измерениях Еср = 3 эВ.
Интересно отметить, что плазма в одно и то же время может ха-
рактеризоваться несколькими температурами. Это имеет место
в тех случаях, когда ионы и электроны характеризуются собствен-
ными максвелловскими распределениями с различными температу-
рами Т( и Те. Такая ситуация может возникнуть вследствие того,
что частоты столкновений ионов с ионами или электронов с элек-
тронами больше частоты электрон-ионных столкновений. При этом
каждая компонента сама по себе может находиться в тепловом рав-
новесии, но плазма в целом не будет равновесной в течение доста-
точно долгого времени, необходимого для выравнивания двух тем-
18
Гл. 1. Введение
ператур. При наличии магнитного поля даже одна компонента,
например ионная, может иметь две температуры. Это объясняется
тем, что силы, действующие на ионы в направлении поля В, отли-
чаются от сил, действующих в поперечном направлении (сил Ло-
ренца). В таком случае распределения по скоростям, перпендику-
лярным В и параллельным В, могут описываться различными макс-
велловскими функциями — одна из них с температурой 7\, а другая
с температурой Тц .
Прежде чем закончить наше знакомство с понятием темпера-
туры, необходимо рассеять достаточно распространенное недора-
зумение, что высокая температура непременно связана с большим
количеством тепла. Многие обычно поражаются, узнав, что темпе-
ратура электронов внутри лампы дневного света равна примерно
20 000 К: «По-моему, она не кажется столь горячей!» Конечно,
нужно учитывать и теплоемкость. Дело в том, что плотность элек-
тронов внутри лампы дневного света гораздо меньше плотности
газа при атмосферном давлении, и полное количество энергии,
передаваемой стенке при столкновениях с ней тепловых электронов,
не так велико. Каждому случалось ронять на ладонь сигаретный пе-
пел, не ощущая при этом боли. Хотя температура пепла достаточно
высока, чтобы вызвать ожог, полное количество тепла невелико.
Во многих лабораторных устройствах плазма имеет температуру
порядка 1 000 000 К (100 эВ), но при плотностях 1018—1019 м~3
стенки не испытывают значительного нагрева.
Задачи
1.1. Вычислите плотность идеального газа (в единицах м-8) при следующих
условиях:
а) При температуре 0 °C и давлении 760 мм рт. ст: Эта величина называется
числом Лошмидта.
б) При ^комнатной температуре (20 °C) и давлении 10-8 мм рт. ст. Экспери-
ментатору полезно запомнить это число.
1.2. Найдите постоянную А для одномерной функции распределения Мак-
свелла
f(u) = А ехр (— ти2/2КТ),
нормированной следующим образом:
+~ ~
J f (и) du = 1.
1.4. Дебаевское экранирование
Фундаментальной особенностью поведения плазмы является ее
способность экранировать действующие на нее электрические поля.
Предположим, что мы попытались создать электрическое поле
внутри плазмы, поместив в нее два заряженных шарика, соединен-
1.4. Дебаевское экранирование
19
ные с электрический батарейкой (рис. 1.3). Шарики будут притяги-
вать частицы противоположного заряда, и почти сразу отрица-
тельно заряженный шарик будет окружен облаком ионов, а поло-
жительно заряженный — облаком электронов. (Мы предполагаем,
что слой диэлектрика не позволяет плазме рекомбинировать на
поверхности шарика или что емкость электрической батареи до-
статочно велика, чтобы поддерживать постоянной разность потен-
циалов.) Если плазма холодная и тепловое движение в ней отсутст-
вует, то в облаке должно быть столько же зарядов, сколько и на
шарике; при этом имеет место полное экранирование и вне облака
электрическое поле в плазме равно нулю. Если же температура
плазмы конечная, то частицы, которые находятся на краях облака,
где электрическое поле слабое, имеют достаточно большую тепло-
вую энергию и могут покинуть электростатическую потенциаль-
ную яму. Таким образом, «граница» облака расположена на таком
расстоянии от центра, на котором потенциальная энергия примерно
равна тепловой энергии частиц КТ, и в этом случае экранирование
не является полным. Потенциалы порядка КТ/е могут проникать
в плазму и создавать в ней конечные электрические поля.
Вычислим приближенно толщину такого заряженного облака.
Пусть в плоскости х = 0 расположена полностью прозрачная
сетка, находящаяся под потенциалом Ф — ф0 (рис. 1.4). Нам нужно
найти распределение потенциала ф (х). Для простоты предположим,
что отношение масс иона и электрона М/tn бесконечно велико;
иными словами, ионы неподвижны и создают однородный фон по-
ложительного заряда. Точнее говоря, отношение М/т достаточно
велико, так что за счет своей инерции ионы не могут существенно
изменить своего положения за характерное время эксперимента.
Запишем уравнение Пуассона для одномерного случая:
e0v2^-e0(d2^/t/x2)^—e(nf—ne), (Z= 1). (1.12)
Если плотность плазмы вдали от сетки равна ««,, то гц—пх. При
20
Гл. 1. Введение
наличии потенциальной энергии q<j> функция распределения элек-
тронов имеет вид
f (и) = А ехр £ — (у- mu2 + q<ty
Мы не будем здесь терять время на то, чтобы доказывать это выра-
жение. Физический смысл данного распределения интуитивно по-
нятен: там, где потенциальная энергия велика, частиц меньше,
поскольку не все частицы имеют достаточную энергию, чтобы про-
никнуть в такую область. Интегрируя f (и) по и, полагая q — — е
и замечая, что пе (</>->- 0) = находим
пе — Поо ехр (е$1КТ^-
В разд. 3.5 мы получим это выражение, основываясь на более фи-
зическом представлении. Подставляя в уравнение Пуассона (1.12)
вместо tit величину п«>, а вместо пе последнее выражение, имеем
80 (d2</>/dx2) = епх [ехр (еф/КТе)— 1].
В области, где \е$1КТе\ < 1, экспоненту можно разложить в ряд
Тейлора:
е0(^х2) = епте[(^/КТе)-|-(1/2)(^/КЛ)2Н- . . . (1.13)
Такое упрощение невозможно для области вблизи сетки, где вели-
чина \e<f>iKTe\ может быть очень большой. К счастью, эта область
не дает значительного вклада в толщину облака (называемого
также слоем), поскольку в ней потенциал очень быстро уменьшается.
Удерживая в уравнении (1.13) только линейные члены, имеем
е0(^/^2) = (поое2/ЛТг) ф. (1-14)
Определим следующую величину:
\D^(e0KTe/ne2)^ (1.15)
где мы обозначили пж через п. Тогда решение уравнения (1.14)
можно записать в виде
<£ = ^>eexp(—|x|/XD). (1.16)
Величина %D, называемая дебаевской длиной, является характер-
ным масштабом экранирования или толщины слоя.
Заметим, что с увеличением плотности величина XD уменьшается,
поскольку теперь каждый слой плазмы будет содержать больше
электронов и экранировка будет более эффективной. Кроме того,
%D увеличивается с ростом КТе. В отсутствие теплового движения
облако зарядов сжалось бы в бесконечно тонкий слой. Наконец,
надо отметить, что при определении дебаевской длины используется
именно электронная температура, поскольку экранирование осу- -
ществляется главным образом электронами, которые, будучи более
1.5. Плазменный параметр 21
подвижными, смещаются таким образом, чтобы образовать избыток
или дефицит отрицательного заряда. Лишь в некоторых частных
случаях это происходит иным образом (см. задачу 1.5).
Полезно запомнить следующие записи выражения (1.15):
XD = 69 (7/п)1'2 м,
XD = 7430 (КТtri)™ м. (1Л7>
Здесь в первом выражении температура Т измеряется в кельвинах,
а во втором выражении величина КТ измеряется в электрон-воль-
тах.
Теперь можно дать определение «квазинейтральности». Если
размеры системы L намного больше, чем XD, то возникающие в ней
локальные концентрации зарядов или вносимые в систему внешние
потенциалы экранируются на расстояниях, малых по сравнению
с L, так что основной объем плазмы не содержит значительных
электрических потенциалов или полей. Вне слоя на стенке или на
каком-либо препятствии величина v2<p очень мала и с точностью
выше 10“6 плотность ионов п£ равна плотности электронов пе. Для
создания потенциалов порядка КТ/е требуется только незначитель-
ный зарядовый разбаланс. Плазма является «квазинейтральной»;
иными словами, она достаточно нейтральна в том смысле, что можно
положить та пе « п (где п — общая плотность, называемая
плотностью плазмы), но не настолько нейтральна, чтобы исчезли
абсолютно все электромагнитные силы.
Ионизованный газ является плазмой только тогда, когда его
плотность достаточно велика, т. е. XD много меньше L.
Явление дебаевского экранирования возникает также (в модифи-
цированном виде) в одно компонентных системах, таких, как 'элек-
тронные потоки в клистронах и магнетронах или протонные пучки
в циклотроне. В этих случаях любая локальная группировка ча-
стиц приводит к возникновению значительного неэкранированного
электрического поля, если только плотность частиц не является
очень низкой (что часто встречается на практике). Потенциал, при-
ложенный к такой системе извне, например от проволочного зонда,
будет экранироваться из-за перераспределения плотности вблизи
электрода. Заряженная плазма, т. е. система, состоящая из частиц,
одного сорта, не является плазмой в точном смысле этого слова,
но для изучения таких систем можно применять математический
аппарат физики плазмы.
1.5. Плазменный параметр
Дебаевское экранирование, которое мы рассмотрели выше, имеет
место только в том случае, когда в заряженном облаке находится
достаточно много частиц. Очевидно, если слой состоит только из.
1
л
i i 22 Гл. 1. Введение
U одной или двух частиц, то дебаевское экранирование нельзя считать
статистически правильным понятием.
i Используя выражения (1.17), можно вычислить число частиц 2VD
i в «дебаевской сфере»:
[ = nA.D= 1,38-106Т32/п1/2. (1.18)
3
Здесь температура измеряется в кельвинах. Для того чтобы плазма
? имела «коллективные свойства», помимо неравенства XD<^ L должно
i выполняться условие
’ М>» 1. (1.19)
1.6. Критерии существования плазмы
Выше мы привели два условия, которым должен удовлетворять
ионизованный газ, чтобы его можно было считать плазмой. Третье
условие связано со столкновениями. Слабоионизованный газ, на-
пример в струе реактивного двигателя, не может считаться плаз-
мой, поскольку заряженные частицы сталкиваются с нейтральными
атомами столь часто, что их движение определяется обычными гид-
родинамическими, а не электромагнитными силами. Если со — ха-
рактерная частота плазменных колебаний, ат — среднее время
между столкновениями с нейтральными атомами, то, для того чтобы
ионизованный газ обладал свойствами плазмы, а не обычного газа,
должно выполняться условие сот >1.
Таким образом, плазма должна удовлетворять следующим трем
условиям:
1) Xd«L; 2) TVD»> 1; 3) сот > 1.
? Задачи
J 1.3. Нарисуйте линии Xd= const и Wd= const в системе координат пе
| и КТе, считая, что масштаб для обеих осей логарифмический, плотность пе
изменяется от 106 до 1025 м-3, а температура КТе — от 0,01 до 105 эВ. От-
метьте на этом графике следующие точки (пе в м—3, КТе в эВ), типичные для
;; . различных видов плазмы:
| 1) плазма термоядерного реактора (пе = 1021, КТе = 10 000);
) 2) плазма в типичных экспериментах по управляемому термоядерному син-
тезу [пе = 1019, КТе — 100 (тороидальная ловушка), пе — 1023, КТе =
; = 1000 (пинч)];
j 3) ионосфера (пе = 1011, КТе = 0,05);
s 4) тлеющий разряд (пе — 1015, КТе ~ 2);
j 5) пламя (пе = 1014, КТе = 0,1);
! В) цезиевая плазма (пе = 10х7, КТе = 0,2);
। 7) межпланетное пространство (пе ~ 10е, КТе = 0,01).
J Докажите, что все ионизованные газы с такими параметрами являются плаз-
! мой.
1.7. Применения физики плазмы
23
1.4. Вычислите давление (в атмосферах и тоннах/ма), оказываемое термо-
ядерной плазмой на стенки ловушки. Предположите, что КТе — /("А' =
= 20 кэВ, пе = 1021 м-8, ар — пКТ, где Т = Ti + Те.
1.5. В строго равновесном состоянии плотность ионов и электронов опреде-
ляется уравнением Больцмана
п/ = По exp (— qj<t>!KТ/).
Покажите, что в случае бесконечной прозрачной сетки, заряженной до по-
тенциала Ф, длина экранирования приближенно описывается формулой
Хр2 = (пе2/ео)(1/ЛТв+1/К^).
Покажите, что %d определяется температурой более холодной компоненты.
1.6. Другой возможный способ вывода выражения для дебаевского радиуса
экранирования Id позволит лучше понять его физический смысл. Рассмот-
рим две бесконечные параллельные пластины, расположенные в точках
х = которые находятся под потенциалом Ф = 0. Пространство между
ними заполнено однородным газом частиц с зарядом q и плотностью п.
а) Используя уравнение Пуассона, покажите, что распределение потенциала
между пластинами записывается в виде
Ф — (np/2e0) (d2 — х2).
б) Покажите, что при энергия, необходимая для передвижения ча-
стицы от пластины к центральной плоскости, больше средней кинетической
энергии частиц.
1.7. Вычислите %d и Wd в следующих случаях:
а) тлеющий разряд (п — 101в м“3, КТе = 2 эВ);
б) ионосфера Земли (n = 1012 м-3, КТе = 0,1 эВ);
в) 6-пинч (и = Ю23 м-3, КТе = 800 эВ).
1.7. Применения физики плазмы
Плазму можно характеризовать следующими двумя параметрами:
п и В различных приложениях параметры плазмы п и КТе
меняются в чрезвычайно широких пределах: п меняется на 28 по-
рядков величины (от 106 до 1034 м~3), а КТе — на семь порядков
(от 0,1 до 10еэВ). Некоторые из этих применений плазмы мы кратко
обсудим ниже. Огромный диапазон плотностей плазмы можно оце-
нить по достоинству, если представить себе, что воздух и вода раз-
личаются по плотности только в 103 раз, а плотности воды и веще-
ства белых карликов различаются в 105 раз. Даже нейтронные
звезды лишь в 1016 раз плотнее, чем вода. Тем не менее различные
типы газовой плазмы во всем диапазоне плотностей, различающихся
на 28 порядков, можно описать одним и тем же набором уравнений,
поскольку при этом нужны только классические (а не квантовомеха-
нические) законы физики.
24
Гл. 1. Введение
1,7.1. Газовый разряд (газоразрядные электронные
приборы)
Первая работа по физике плазмы была выполнена Ленгмюром, Тонк-
сом и их сотрудниками в 1920-х гг. Это исследование было вызвано
необходимостью разработать вакуумные электронные лампы, ко-
торые могли бы пропускать большие токи, а для этого их нужно
было наполнять ионизованным газом. Были проведены исследова-
ния слабоионизованного тлеющего разряда и положительного
столба с КТе « 2 эВ и 10м < п <1018 м-3. Именно в этой работе
было открыто явление экранирования; оболочку, окружавшую
электрод, можно было непосредственно наблюдать в виде темного
слоя. В настоящее время мы сталкивается с газовым разрядом
в ртутных выпрямителях, водородных тиратронах, игнитронах,
разрядниках, сварочных дугах, неоновых лампах и лампах днев-
ного света, в грозовых разрядах.
1.7.2. Управляемый термоядерный синтез
Началом современной физики плазмы можно считать 1952 г., когда
была выдвинута идея создания термоядерного реактора на основе
управления реакцией синтеза, протекающей при взрыве водород-
ной бомбы. Главными реакциями синтеза с участием атомов дейте-
рия (D) и трития (Т) являются следующие:
D + D->®He + n-H3,2 МэВ,
D-f-D->T + p + 4,0 МэВ,
D + T->4He + n+17,6 МэВ.
Сечения этих реакций синтеза значительны, только если энергии
взаимодействующих атомов превышают 5 кэВ. Использование пучка
ускоренных атомов дейтерия для бомбардировки мишени не решает
проблему, так как вследствие рассеяния большинство атомов те-
ряют свою энергию еще до того, как они вступят в реакцию синтеза.
Поэтому для осуществления термоядерной реакции необходимо
•создать плазму с тепловыми энергиями частиц порядка 10 кэВ.
Проблема нагрева и удержания такой плазмы и явилась причиной
быстрого роста научных исследований в области физики плазмы
начиная с 1952 г. Эта задача до сих пор не решена, и большинство
активных исследований в физике плазмы ведутся в направлении
преодоления данной проблемы.
1.7.3. Космическая физика
Другим важным применением физики плазмы является изучение
космического окружения Земли. Непрерывный поток заряженных
частиц, называемый солнечным ветром, сталкивается с земной маг-
1.7. Применения физики плазмы 25
нитосферой, которая деформируется под его воздействием и защи-
щает нас от этого потока частиц. Характерные параметры солнеч-
ного ветра следующие: п = 5- 10е м-3, КТ{ = 10 эВ, КТе = 50 эВ,
В = 5-10-9 Тл, скорость солнечного ветра— 300 км/с. Ионосфера,,
простирающаяся по высоте от 50 км до 10 земных радиусов, заполнена
слабоионизованной плазмой, плотность которой изменяется с вы-
сотой До п — 1012 м~3. Температура ионосферной плазмы состав-
ляет всего 0,1 эВ. Радиационные пояса ван Аллена состоят из зах-
ваченных магнитным полем Земли заряженных частиц с парамет-
рами п =S 10е м-3, КТе < 1 кэВ, KTi^ 1 эВ, В « 500-10-9 Тл.
Кроме того, имеется горячая компонента с n'= 103 м-3 и КТе —
— 40 кэВ.
1.7.4. Современная астрофизика
Звезды и их атмосферы настолько горячи, что находятся в плазмен-
ном состоянии. Например, согласно оценкам, температура в центре
Солнца равна 2 кэВ; солнечное излучение обусловлено термоядер-
ными реакциями, протекающими при этой температуре. Солнечная
корона представляет собой разреженную плазму с температурой
до 200 эВ. Межзвездная среда содержит ионизованный водород
с плотностью п « 10е м~3. Для объяснения процесса ускорения
космических лучей использовались различные теории плазмы.
Хотя звезды в галактиках не являются заряженными, они ведут
себя подобно частицам в плазме; поэтому для предсказания хода
эволюции галактик применялась кинетическая теория плазмы.
Радиоастрономия открыла многочисленные источники излучения;
весьма вероятно, что это излучение создается плазмой. Богатым
источником плазменных явлений служит Крабовидная туманность,
поскольку она, как известно, имеет магнитное поле. В ней нахо-
дится также видимый пульсар. Согласно современным теориям,
пульсары — это быстро вращающиеся нейтронные звезды, на по-
верхности которых (в плазме) генерируется синхротронное излу-
чение.
1.7.5. МГД-преобразование энергии
и ионные двигатели
Возвращаясь с небес на Землю, рассмотрим два практических при»
менения физики плазмы. Для генерации электричества используется
магнитогидродинамическое (МГД) преобразование энергии плот-
ной плазменной струи, движущейся поперек внешнего магнитного
поля (рис. 1.5). Под действием силы Лоренца q [v X В], где v —
скорость струи, ионы движутся вверх, а электроны — вниз, что
создает разность потенциалов между двумя электродами. При
этом с электродов можно снимать электрический ток, минуя не-
эффективный тепловой цикл.
26
Гл. 1. Введение
© v * -етхв
Рис. 1.5. Принцип действия МГД-генератора.
Такой же принцип, но действующий в обратном направлении,
применяется в разработках двигателей для межпланетных полетов.
Как показано на рис. 1.6, к электродам прикладывается потенциал,
вызывающий протекание тока через плазму. Под действием силы
[j X В] плазма выбрасывается из ракеты, а возникающая при этом
сила реакции ускоряет аппарат. Выбрасываемая плазма должна
быть обязательно нейтральной; в противном случае космический
корабль зарядится до высокого потенциала.
Рис. 1.6. Принцип действия плазменного реактивного двигателя для косми-
ческого аппарата.
1.7.6. Плазма твердого тела
В полупроводниках свободные электроны и дырки образуют плазму,
в которой наблюдаются такие же колебания и неустойчивости, как
и в газовой плазме. Для изучения этих явлений особенно полезной
оказалась плазма в полупроводнике InSb. Было показано, что из-
за влияния кристаллической решетки частота столкновений значи-
тельно меньше, чем следовало бы ожидать в твердом теле с плот-
ностью частиц п « 1029 м~3. Кроме того, поскольку в полупровод-
нике эффективная масса дырок может быть очень небольшой (по-
рядка 0,01 те), даже в умеренных магнитных полях мы имеем очень
высокую циклотронную частоту. Вычисление 2VD для плазмы твер-
1.7. Применения физики плазмы 27
дого тела показало бы, что вследствие низкой температуры и высо-
кой плотности эта величина меньше единицы. Однако благодаря
квантовомеханическим эффектам (принципу неопределенности) эф-
фективная температура плазмы оказывается достаточно высокой,
так что Nd становится весьма большой величиной. Обнаружено,
что некоторые жидкости, например раствор натрия в аммиаке,
ведут себя также аналогично плазме.
1.7.7. Газовые лазеры
Наиболее широко распространенным методом накачки газового ла-
зера, т. е. его перевода в инвертированное состояние, которое мо-
жет привести к усилению излучения, является применение газо-
вого разряда. Это может быть тлеющий разряд при низком давле-
нии для непрерывного лазера или же лавинный разряд высокого
давления для импульсного лазера. Примерами непрерывных га-
зовых лазеров являются Не—Ne-лазеры, используемые для юсти-
ровки и топографических съемок, а также Аг- и Кг-лазеры, при-
меняемые в лазерных шоу. Мощный СО2-лазер нашел применение
в промышленности как режущий инструмент. Молекулярные ла-
зеры сделали возможным исследование недоступной до этого дале-
кой инфракрасной области электромагнитного спектра. Накачку
этих лазеров можно непосредственно осуществлять электрическим
разрядом как в лазере на синильной кислоте (HCN) или, как в случае
лазеров на метилфториде CH3F или метиловом спирте (СН3ОН),
использовать оптическую накачку с помощью СО2-лазера. Даже
действие твердотельных лазеров, таких, как лазер на неодимо-
вом стекле, определяется плазмой, поскольку для накачки этого
лазера применяется лампа-вспышка с газовым разрядом.
Задачи
1.8. В лазерном термоядерном синтезе сердцевина крошечной таблетки из
смеси дейтерия с тритием сжимается до плотности 103® м—8 при температуре
50 000 000 К. Оцените для такой плазмы число частиц в дебаевской сфере.
1.9. Далекая галактика состоит из облака протонов и антипротонов с одина-
ковыми плотностями п = 10е м~3 и температурой 100 К. Чему равен дебаев-
ский радиус экранирования?
1.10. Сферический проводник радиусом а погружен в плазму и заряжен до
потенциала Фй. Электроны имеют максвелловское распределение по скоро-
стям и движутся таким образом, чтобы образовать дебаевский слой; ионы
же за время эксперимента остаются неподвижными. Предполагая, что
С КТе!е, найдите, как зависит потенциал Ф от координаты г и величин а,
0О и %d. (Указание: решение следует искать в виде ехр (— kr)lr.)
1.11. Полевой транзистор представляет собой по существу электронную
лампу, в основе принципа действия которой лежит эффект конечного деба-
евского радиуса. Схема такого транзистора представлена на рис. 31.11. Элек-
28
Гл. 1. Введение
троны проводимости текут от источника S к стоку D при наличии разности
потенциалов между ними. Если приложить отрицательный потенциал к изо-
лированному от полупроводника затвору G, то ток через G течь не сможет,
поскольку приложенный потенциал проникает внутрь полупроводника н от-
рб
oG
Рис. 31.11.
ражает электроны. С ростом потенциала затвора ширина канала, по кото-
рому могут течь электроны, сужается и электронный поток уменьшается.
Если толщина прибора слишком велика, то происходит дебаевское экрани-
рование потенциала затвора. Оцените максимальную толщину проводящего
участка в n-слое полевого транзистора при комнатной температуре, если его
уровень легирования (плотность плазмы) составляет 1022 м-®, а толщина
прибора не превышает десяти дебаевских радиусов экранирования (см.
рис. 3.1.11).
Глава 2
ДВИЖЕНИЕ ОТДЕЛЬНЫХ ЧАСТИЦ
2.1. Введение
Исследование плазмы представляет собой особенно трудную задачу
вследствие того, что она является средой, плотность которой имеет
промежуточное значение. Жидкости, такие, как вода, характери-
зуются настолько высокой плотностью, что движение отдельных
молекул в них рассматривать не нужно. В этом случае главную
роль играют столкновения, и для описания жидкости достаточно
простых уравнений гидродинамики. В другом пределе, когда мы
имеем дело с очень малой плотностью вещества, например в таких
устройствах, как синхротрон с переменным градиентом, необходимо
рассматривать траектории отдельных частиц; коллективные эф-
фекты часто несущественны. Плазма же в некоторых случаях ве-
дет себя как жидкость, а в некоторых — как скопление отдельных
частиц. И первый шаг, для того чтобы понять, как иметь дело с этой
сумасбродной особой,— это изучить поведение отдельных частиц
в электрических и магнитных полях. Данная глава отличается от
последующих тем, что поля Е и В в ней предполагаются заданными
и считается, что заряженные частицы не влияют на эти поля.
2.2. Постоянные поля Е и В
2.2.1. Е = О
В этом случае заряженная частица совершает простое циклотрон-
ное вращение. Уравнение ее движения записывается в виде
/n-^=<?vxB. (2.1)
Направляя z по В (В = Bz), мы имеем
mvx = qBvy, mVy=—qBvx, mvz = Q,
vx^^v vx, (2.2)
tn \ tn /
30
Гл. 2. Движение отдельных частиц
Ч/ =
Эти уравнения описывают простой гармонический осциллятор на
циклотронной частоте, которую мы определяем следующим об-
разом:
т
(2-3)
В соответствии с принятым нами соглашением ас всегда неотрица-
тельна. Величина В измеряется в теслах (Тл), или в веберах на
квадратный метр (Вб/м2), причем 1 Тл = 104 Гс. При этом решение
уравнения (2.2) можно записать в виде
vx, y = v± ехр (± i ad + i 6Х, у),
где ± относятся к знаку заряда q. Мы можем выбрать фазу S так,
чтобы
е10^ & х, (2.4а)
где — положительная постоянная, обозначающая скорость в
плоскости, перпендикулярной вектору В. Следовательно,
= р*=± — vx= ± ii)±e‘“^ ^у. (2.46)
qB <ос
Интегрируя выражения (2.4а) и (2.46), получаем
х—х0= — i—— е101^,
<ос
у—у0= ± — е‘“Л
<£>с
Определим ларморовский радиус как
v mv.
Г, =-----=--------
сос | q | В
(2.5)
(2-6)
Взяв вещественную часть уравнений (2.5), получим
х—x0 = rLsin<M, у—уо = ± rL cos (2.7)
Эти формулы описывают круговую орбиту вокруг фиксированного
ведущего центра (х0, z/0) (рис. 2.1). Направление вращения частицы
всегда таково, что создаваемое при этом магнитное поле направ-
лено противоположно внешнему магнитному полю. Следовательно,
частицы плазмы стремятся уменьшить магнитное поле, и плазма
является диамагнетиком. Помимо этого движения имеет место еще
движение с произвольной скоростью vz вдоль В, на которое В не
2.2. Постоянные поля Е и В
31
Рис. 2.1. Ларморовские орбиты в магнитном поле.
влияет. Таким образом, заряженная частица в магнитном поле дви-
жется в пространстве по траектории, которая в общем случае яв-
ляется спиралью.
2.2.2. Конечное Е
Если мы теперь допустим, что помимо магнитного поля имеется
и электрическое, то движение частицы будет суммой двух движений:
обычного ларморовского вращения и дрейфа ведущего центра. Вы-
берем направление поля Е таким образом, чтобы оно располага-
лось в плоскости xz, т. е. мы имеем Еу — 0. Как и прежде, z-ком-
понента скорости не связана с поперечными движениями и ее можно
рассматривать отдельно. Уравнение движения теперь принимает
вид
m^.=q(E + vxB). (2.8)
at
Записывая z-проекцию этого уравнения
&'2 ? Е
dt т г’
находим
uz = -^+^. (2.9)
т
Это соотношение описывает движение с постоянным ускорением
вдоль поля В. Поперечные проекции уравнения (2.8) запишутся
в виде
-^-=-Я-Ех± <i>cvy, А = (2.10)
dt т dt
32
Гл. 2. Движение отдельных частиц
Дифференцируя, получаем (при постоянном Е):
vx = — a>2cvx,
vy = т (-3- Ejt± G>cVy^ = —(£ + fy) •
Последнее уравнение можно переписать в виде
Таким образом, если во втором уравнении (2.11) заменить
Vy + (Ех/В) на vy, то оно сведется к последнему из уравнений (2.2).
При этом уравнения (2.4) принимают вид
их = v± ехр (i act), vy = ± i v± exp (i act)—(Ex/B). (2.12)
Ларморовское движение — такое же, как и раньше, но на него при
Ех>0 накладывается дрейф ведущего центра vgc в направлении
— У (рис. 2.2).
Чтобы получить общую формулу для Vgc, нужно решить урав-
нение (2.8) в векторном виде. В этом уравнении член т dv/dt можно
опустить, поскольку он описывает только круговое движение с ча-
стотой <ос, которое нам уже известно. Таким образом, уравнение
(2.8) принимает вид
E + vxB = 0. (2.13)
Умножая векторно на В, имеем
Е х В = В х (v х B) = vB2— B(v.-B). (2.14)
Поперечные компоненты этого уравнения запишутся в виде
v±gC —Ex ,В/В2 = v£, (2.15)
где v£ — скорость дрейфа ведущего центра в электрическом поле.
Величина этой скорости определяется выражением
v м/с. (2.16)
ь В (Тл)
Е --*-
0В
Ион
Электрон
Рис. 2.2. Дрейф частиц в скрещенных электрическом и магнитном полях.
2.2. Постоянные поля Е и В
33
ЕхВ
Рис. 2.3. Реальная орбита частицы в пространстве.
Важно заметить, что v£ не зависит от q, т и п±. Это очевидно
из следующей физической картины. На первом полуобороте своей
орбиты (рис. 2.2) положительно заряженный ион получает энергию
от электрического поля, увеличивается v± и, следовательно, rL-
На втором полуобороте ион теряет энергию и rL уменьшается. Эта
разница в rL на левой и правой частях орбиты и вызывает дрейф со
скоростью vE. Отрицательно заряженный электрон вращается в
противоположном направлении (рис. 2.2), но и энергию от поля он
получает при движении в направлении, противоположном тому,
в котором движется ион. Следовательно, дрейф электрона проис-
ходит в том же направлении, что и дрейф иона. Из частиц, имею-
щих разные массы, но одинаковые скорости, у более легких будет
меньше rL и, следовательно, меньше дрейф за один оборот. Однако
у более легких частиц выше частота вращения, и два эффекта в точ-
ности компенсируют друг друга. Две частицы с одинаковыми мас-
сами, но с разными энергиями должны иметь одну и ту же частоту
Более медленная заряженная частица будет иметь меньший rL
и поэтому за один оборот получит от электрического поля меньше
энергии. Однако для менее энергичных частиц относительное изме-
нение в rL при данном изменении энергии будет больше, и эти
два эффекта также взаимно компенсируются (задача 2.2).
Таким образом, трехмерная орбита частицы в пространстве
представляет собой раскручивающуюся спираль с изменяющимся
шагом (рис. 2.3).
2.2.3. Гравитационное поле
Заменив в уравнении движения (2.8) величину qE на общее обозна-
чение силы F, можно применить полученный выше результат и к
другим видам силы. Скорость дрейфа ведущего центра, вызванного
силой F, в общем случае равна
2 Заказ 3170
34
Гл. 2. Движение отдельных частиц
В частности, если F — сила тяжести mg, то скорость дрейфа
„ _ т g X В
vg — ”
q В2
(2-18)
Этот вид дрейфа похож на дрейф в электрическом поле (v^) тем, что
его направление перпендикулярно как приложенной силе, так и
вектору В; но он имеет и одно важное отличие: скорость vg меняет
направление в зависимости от знака заряда частицы. Таким обра-
зом, под действием силы тяжести ионы и электроны дрейфуют в
противоположных направлениях, что приводит к возникновению
в плазме тока, плотность которого
(2.19)
Физически возникновение этого дрейфа (рис. 2.4), как и рассматри-
ваемых ранее, объясняется тем, что при движении частицы меняется
ларморовский радиус ее орбиты, поскольку она отдает или полу-
чает энергию от поля силы тяжести. Но теперь, хотя электроны
и ионы вращаются в разные стороны, силы, действующие на них,
направлены в одну сторону, поэтому дрейфуют эти частицы в про-
тивоположных направлениях. Величина vg, связанная с обычной
силой тяжести, в большинстве случаев пренебрежимо мала (за-
дача 2.4), но если силовые линии магнитного поля изогнуты, то
из-за наличия центробежной силы возникает эффективная сила
тяжести, пренебречь которой уже нельзя. Эта сила не зависит от
массы, поэтому мы и не упоминали, что в общее выражение (2.18)
входит т. Отметим, что центробежная сила является причиной
так называемой «гравитационной» неустойчивости плазмы, кото-
рая также с реальной гравитацией ничего общего не имеет.
Mqh
9
Злектрон
®Б
Рис. 2.4. Дрейф частиц в поле силы тяжести.
2.2. Постоянные поля Е и В
35
Задачи
2.1. Пусть мала. Вычислите rL в следующих случаях:
а) для электрона с энергией 10 кэВ, находящегося в магнитном поле Земли
В = 5-10-5 Тл;
б) для протона из потока солнечного ветра, скорость движения которого в
межпланетном магнитном поле В = 5-10~9 Тл составляет 300 км/с;
в) для иона Не+ с энергией 1 кэВ, находящегося в атмосфере Солнца вблизи
пятна, где В = 5-10"2 Тл;
г) для частицы примеси Не++ с энергией 3,5 МэВ в дейтериево-тритиевом
реакторе синтеза с магнитным полем В = 8 Тл.
2.2. На установке TFTR (Tokamak Fusion Test Reactor) в Принстоне плазма
будет нагреваться посредством инжекции нейтральных атомов дейтерия с
энергией 200 кэВ, которые, войдя в магнитное поле, из-за перезарядки пре-
вратятся в ионы дейтерия с атомным номером А = 2 и с той же энергией.
Такие ионы могут удерживаться в ловушке, только если rL <С а, где а =
= 0,6 м — меньший радиус плазменного тора. Проверьте, выполняется ли
это условие, вычислив максимальный ларморовский радиус иона в магнит-
ном поле В = 5 Тл.
Рис. 32.7.
2.3. В ионном двигателе (см. рис. 1.6) создается магнитное поле величиной
1 Тл, а водородная плазма вследствие Е X В-дрейфа выталкивается из него
со скоростью 1000 км/с. Насколько велико должно быть для этого электри-
ческое поле внутри плазмы?
2.4. Воспользовавшись картиной движения заряженных частиц (рис. 2.2),
покажите, что для двух ионов с одинаковыми массами и зарядами, но с раз-
ными энергиями дрейфа vE равны между собой. Для этого аппроксимируйте
правую половину орбиты полуокружностью, соответствующей энергии иона
после ускорения в поле Е, а левую половину — полуокружностью, соот-
ветствующей энергии после замедления. Можете предположить, что поле Е
слабое, так что относительное изменение мало.
2.5. Предположим, что в симметричном цилиндрическом столбе плазмы
плотность п (г) меняется на характерной длине X, т. е. дп!дг « — n/Х, а рас-
пределение электронов удовлетворяет уравнению Больцмана (задача 1.5).
а) Используя соотношение Е=—V0, вычислите при данной длине X ра-
диальное распределение электрического поля.
б) Покажите, что при ve ж у-гепл существенны эффекты, связанные с ко-
нечной величиной ларморовского радиуса электронов. В частности, покажите,
что при VE = Цтепл
в) Справедливо ли утверждение в п. б для ионов?
Указание: Не пользуйтесь уравнением Пуассона.
2.6. Предположим, что в так называемой Q-машине с постоянным магнит-
ным полем 0,2 Тл помещен плазменный цилиндр с температурой KTg =
2*
2.3. Неоднородное поле В
37
36 Гл. 2. Движение отдельных частиц
= ДТ/ = 0,2 эВ. Экспериментальным путем установлено, что профиль плот-
ности плазмы имеет вид
п = п0 ехр [ехр (—г2/а2) — 1].
Пусть плотность электронов удовлетворяет уравнению Больцмана,
а) Вычислите максимальную скорость дрейфа V£, если а = 1 см.
б) Сравните ее со скоростью дрейфа vg, обусловленного магнитным полем
Земли.
в) До какой величины нужно понизить напряженность магнитного поля В,
чтобы ионы калия (Л = 39, Z = 1) имели ларморовский радиус, равный а?
2.7. Заряженный пучок электронов плотностью пе = 10м м~3 и радиусом
а — 1 см движется вдоль магнитного поля 2 Тл. Вычислите скорость и на-
правление Е X В-дрейфа при г = а, если В направлено по z, а Е — электро-
статическое поле, связанное с зарядом пучка (см. рис, 32.7).
2.3. Неоднородное поле В
Теперь, когда понятие о дрейфе ведущего центра твердо нами ус-
воено, мы можем рассмотреть движение частиц в неоднородных
полях, т. е. в полях Е и В, которые изменяются в пространстве и во
времени. В случае постоянных полей нам удалось получить точные
выражения для скорости дрейфа ведущего центра, но как только
мы вводим в задачу неоднородность, проблема становится слиш-
ком сложной для точного решения. Чтобы получить приближен-
ный ответ, обычно проводят разложение по малому отношению
rJL, где L — масштаб неоднородности. Вычисления в рамках та-
кой теории (она называется теорией орбит) могут быть сложными,
поэтому мы рассмотрим лишь простейшие случаи, когда в системе
существует неоднородность только одного вида.
2.3.1. Градиентный дрейф\ V5J_B
В данном разделе мы будем считать, что силовые линии х) магнит-
ного поля представляют собой прямые, а их плотность возрастает,
например в направлении у (рис. 2.5). Пользуясь разработанной
нами простой физической моделью, можно заранее предвидеть,
как будут вести себя в таком поле заряженные частицы. Из-за на-
личия градиента поля |В| ларморовский радиус в нижней части
орбиты движущейся частицы будет больше, чем в верхней, а это
должно приводить к дрейфу ионов и электронов в противополож-
ных направлениях, перпендикулярных как В, так и Оче-
видно, что величина скорости дрейфа должна быть пропорциональна
rL/L и Vj_.
Для вычисления скорости дрейфа рассмотрим силу Лоренца
F = qv X В, усредненную по периоду вращения частицы. Ясно,
х) Линии магнитного поля часто называют силовыми линиями. Они,
однако, не являются линиями действия силы в точном смысле этого слова.
Неправильный термин увековечен здесь, чтобы подготовить студента к веро-
ломству избранной им специальности.
Рис. 2.5. Дрейф частиц, совершающих вращение в неоднородном магнитном
поле.
что Fx = 0, поскольку частица движется вверх столько же времени,
сколько и вниз. Теперь приближенно вычислим Fy, используя ус-
реднение по невозмущенной орбите частицы. Невозмущенная ор-
бита в постоянном магнитном поле В описывается уравнениями
(2.4) и (2.7). Взяв вещественную часть уравнения (2.46), получаем
Fy = —qvxBz (у) = — qv± (cos to./) Гв0 ± rL (cos act) —1 • (2.20)
L fy J
Здесь мы разложили поле В в ряд Тейлора вблизи точки х0 = 0,
Уо — 0 и воспользовались выражениями (2.7):
В = Во + (г-V) В 4- . . . ,
B2 = B04-z/(dBz/fy)+ .... (2.21)
Такое разложение, конечно, можно провести только в том случае-
если выполняется неравенство rJL < 1, где L — масштаб изме-
нения dBjdy. Первый член в уравнении (2.20) после усредне-
ния по периоду вращения дает нуль, а среднее от cos2wc/ равно
1/2, так что
~Fy~ -L(dB/dy). (2.22)
При этом скорость дрейфа ведущего центра дается выражением
V - 1 FxB - 1 Fy ~ v±rL ! дв ~
gC q В2 q | В | Х В 2 ду Х’ (2.23).
при выводе которого мы использовали формулу (2.17). Поскольку
выбор оси у был произволен, последнее соотношение можно обоб-
щить:
v _и 1 „ г в х VB
VVB = ± — uxrL -----------
2 В2
(2.24)
Данная формула включает все зависимости, которые мы предви-
дели исходя из физической картины процесса; не был предсказан
только множитель 1/2, возникший из-за усреднения. Заметим, что
знаки ± соответствуют знаку заряда, а светлая буква В отвечает
38
Гл. 2. Движение отдельных частиц
|В|. Величина vvb называется скоростью градиентного дрейфа.
Дрейф имеет противоположные направления для ионов и электро-
нов и создает ток, перпендикулярный В. Заметим также, что по-
лученное выражение для скорости дрейфа является приближенным;
для точного вычисления нужно при усреднении пользоваться
точной орбитой частицы с учетом дрейфа.
2.3.2. Центробежный дрейф-, искривленные силовые
линии поля В
Предположим, что силовые линии магнитного поля изогнуты и
имеют постоянный радиус кривизны Цс, а |В] = const (рис. 2.6).
Такое поле не удовлетворяет в вакууме уравнениям Максвелла,
Рис. 2.6. Магнитное поле с искривленными силовыми линиями.
поэтому на практике к изучаемому здесь эффекту всегда будет до-
бавляться градиентный дрейф. В рассматриваемом же случае дрейф
ведущего центра возникает из-за центробежной силы, действующей
на частицы, перемещающиеся вдоль силовых линий вследствие
теплового движения. Пусть обозначает средний квадрат ско-
рости хаотического движения вдоль В, тогда средняя центробежная
сила
FCf^-^l-r = ffW|| (2.25)
Rc R2C
В соответствии с соотношением (2.17) она приводит к дрейфу
, F‘'XB (2.26)
к V в2 ,в2 п2
Дрейф со скоростью vR называется центробежным дрейфом.
Вычислим скорость градиентного дрейфа, который сопровождает
2.3. Неоднородное поле В
39
дрейф со скоростью vR, если принять во внимание уменьшение | В|
с радиусом. Обратимся к рис. 2.6. Как известно, в вакууме
V х В = 0. В цилиндрических координатах, показанных на ри-
сунке, V X В имеет только z-компоненту, поскольку В имеет лишь
0-компоненту, a VB — лишь r-компоненту. В этом случае
(V X В)2 =ХЛ_(гВе) = 0, Ве----(2.27)
Таким образом,
|В,___________________viBl ___________
’ |В| /?2 '
(2.28)
Используя уравнение (2.24), получаем
VvB= T_L2^k.BxiB|A 1
2 в2 R2
v2± Rc X В
2 R2cb
1 т 2 Rc X В
------V , --------
2 q р2в2
(2.29)
Прибавляя скорость дрейфа vvb к получаем общее выражение
для дрейфа частицы в магнитном поле с изогнутыми силовыми ли-
ниями:
vvb + v^
(2.30)
т
q
К сожалению, скорости обоих дрейфов направлены в одну сторону.
Поэтому если попытаться удержать термоядерную плазму, свер-
нув магнитное поле в тор, то частицы будут дрейфовать из этого тора
независимо от того, как мы будем менять температуры и магнитные
поля.
В случае максвелловского распределения из уравнений (1.7)
и (1.10) ясно, что v\ =(1/2) v\ — КТ/т, поскольку отвечают
две степени свободы. Уравнения (2.3) и (1.6) позволяют записать
в этом случае среднюю скорость дрейфа в поле с искривленными
силовыми линиями в виде
- v21 - +"
Vfl-1-v.B = ± —---у = --------ПтеплУ. (2.30а)
К с® с
где у— единичный вектор в направлении RCX В. Отсюда следует,
что v#+v.b зависит от заряда ионов, но не от их массы.
2.3.3. || В; магнитные зеркала (пробкотрон)
Рассмотрим теперь магнитное поле, направленное в основном вдоль
оси z. Пусть поле осесимметричное, Ве = 0, 0/00 = 0, а напряжен-
ность его зависит от z. Поскольку силовые линии такого поля схо-
42
Гл. 2. Движение отдельных частиц
Здесь dBldt — это изменение величины В, которое «видит» частица;
само поле В постоянно. Поскольку энергия частицы должна сохра-
няться, мы имеем
~(4_/7гу''+1“/"и2±)==’^_(т/”у'|+иВ)=0- (2-41)
uA X / СИ’ х. ~ /
С учетом соотношения (2.40) условие (2.41) принимает вид
-р—+ — (ИВ)=0,
dt dt
откуда следует, что
dp,/ttt = O. (2.42)
На инвариантности магнитного момента р основана одна из
первых схем удержания плазмы — магнитное зеркало {магнитная
пробка}. Идея метода состоит в следующем. Пусть вследствие теп-
лового движения частица перемещается из области слабого поля В
в область, где оно сильнее. Частица «видит», что В увеличивается;
следовательно, для того чтобы сохранялся р, поперечная скорость
тоже должна увеличиваться. Поскольку полная энергия частицы
должна сохраняться постоянной, »ц при этом должна уменьшаться.
Если поле В в «горловине» достаточно велико, то v ц в конце кон-
цов обратится в нуль и частица «отразится» назад в область более
слабого поля. К такому отражению приводит, несомненно, сущест-
вование силы Ясно, что неоднородное магнитное поле, созда-
ваемое парой катушек, образует два магнитных зеркала, между
которыми можно запереть плазму (рис. 2.8). Заметим, что этот ме-
ханизм работает как для ионов, так и для электронов.
К сожалению, такая ловушка несовершенна. В частности, ча-
стица с = 0, не имеющая магнитного момента, вообще не по-
чувствует никакой силы, действующей вдоль В. Кроме того, если
максимальное значение Вт поля недостаточно велико, из ловушки
убегут также и те частицы, у которых в центральной плоскости
(В — Во) мало отношение vjv$. Какие частицы будут покидать
ловушку при данных Во и Вт? Для ответа на этот вопрос рассмот-
рим частицу, которая в центральной плоскости ловушки имеет
= Oj-o и f|| = цц0, в точке поворота она будет иметь некото-
Рис. 2.8. Плазма, захваченная между магнитными зеркалами
2.3. Неоднородное поле В
43
рую v± = v'j, и о и = 0. Если поле в точке поворота равно В', то
из инвариантности магнитного момента р. следует, что
~ то\й!Вй = -~ mo'll В’. (2.43)
Рис. 2.9. Конус потерь.
Закон сохранения энергии требует, чтобы выполнялось равенство
Ох = Wj.0 + v || о v0. (2.44)
Из соотношений (2.43) и (2.44) находим
d _.2 _,2
—— = sin20, (2.45)
В' v'l Oq
где 6 — питч-угол орбиты в области слабого поля. Частицы с мень-
шими 0 будут отражаться от областей с большими В. Если 0 слиш-
ком мал, то В' превышает Вт и частица вообще не отразится. За-
меняя в уравнении (2.45) В' на Вт, мы увидим, что наименьший
угол 0 у захваченной частицы определяется равенством
sin90m = Bo/Bm^l/^m. (2.46)
Величина Rm называется пробочным (зеркальным) отношением.
Условие (2.46) определяет в пространстве скоростей границу об-
ласти в виде конуса, называемого конусом потерь (рис. 2.9). Ча-
стицы, скорости которых лежат внутри конуса, не удерживаются
магнитными пробками, поэтому плазма в такой ловушке никогда
не будет изотропной. Заметим, что форма конуса потерь не зависит
от q и т и при отсутствии столкновений ловушка будет удерживать
как ионы, так и электроны При наличии в системе столкновений
частицы могут уходить из ловушки. Это происходит в том случае,
когда при столкновениях питч-углы частиц меняются таким обра-
44
Гл. 2. Движение отдельных частиц
зом, что они рассеиваются в конус потерь. Обычно электроны ухо-
дят из ловушки быстрее, чем ионы, поскольку частота столкнове-
ний у них выше.
Магнитное зеркало впервые было предложено Энрико Ферми
для объяснения механизма ускорения космических лучей. Он за-
метил, что протоны, осциллирующие между двумя сближающи-
мися с большой скоростью магнитными зеркалами, могут при каж-
дом пролете между ними увеличивать свою энергию. Как возни-
кают эти зеркала — это уже другой вопрос. Еще один пример
«зеркальных» эффектов — это захват частиц в радиационные пояса
ван Аллена. Поскольку магнитное поле Земли велико у полюсов
и мало у экватора, оно образует естественную ловушку с довольно
большим пробочным отношением.
Задачи
2.8. Предположим, что магнитное поле Земли на экваторе равно 3-Ю"8 Тл
и спадает с расстоянием по закону 1/г3, как в случае идеального диполя.
Пусть на расстоянии г = 5/?3 от центра Земли в экваториальной плоскости
имеются изотропные распределения протонов с энергией 1 эВ и электронов
с энергией 30 кэВ, плотностью п = 10’ м-3 каждое.
а) Вычислите скорости градиентных (уВ) дрейфов ионов и электронов.
б) На запад или на восток дрейфуют электроны?
в) Сколько времени потребуется электрону, чтобы обойти вокруг Земли?
г) Вычислите плотность возникающего из-за дрейфа кольцевого тока в А/м2.
Указание: Дрейфом из-за искривленности силовых линий магнитного поля
пренебречь нельзя— он будет влиять на числа в ответе, но все-таки прене-
брегите им.
2.9. Электрон покоится в магнитном поле, которое создается током I, теку-
щим по бесконечному прямому проводу. В момент t = 0 при неизменном I
провод внезапно заряжается до потенциала Ф. Электрон получает от электри-
ческого поля энергию и начинает двигаться.
а) Нарисуйте схему, показывающую орбиту электрона и направления век-
торов I, В, v£, vvB и vR.
6) Вычислите скорости различных типов дрейфа на расстоянии 1 см от центра
провода, если / = 500 А, Ф = 460 В, а радиус провода 1 мм. Предположите,
что на стенках вакуумной камеры, расположенных в 10 см от провода, под-
держивается Ф=0. Указание: Нужно не только знать формулы, приведен-
ные в тексте, но еще и хорошо представлять себе картину движения.
2.10. Ядро атома дейтерия с энергией 20 кэВ движется под питч-углом 0 =
= 45° в центральной плоскости большой установки для синтеза с В= 0,7 Тл.
Вычислите ларморовский радиус частицы.
2.11. Плазма с изотропным распределением по скоростям помещена в маг-
нитную зеркальную ловушку с пробочным отношением Rm = 4. Столкно-
вений нет, так что частицы, попавшие в конус потерь, просто убегают, а
захваченные остаются в ловушке. Какая доля частиц будет захвачена?
2.12. Протон из космических лучей захвачен в ловушке между двумя дви-
жущимися магнитными пробками. Пробочное отношение равно 5. В началь-
ный момент в центральной плоскости энергия частицы IT = 1 кэВ, причем
Цц = ох. Каждая из пробок движется к центру системы со скоростью vm=
= 10 км/с (рис. 2.10).
2.4. Неоднородное поле Е
45
а) Пользуясь формулой, описывающей конус потерь, и инвариантностью
магнитного момента р, найдите энергию, до которой будет ускорен протон,
прежде чем он покинет систему.
б) Сколько времени потребуется на то, чтобы набрать эту энергию?
Рис. 2.10. Ускорение космических лучей.
Указания:
1. Считая пробки плоскими поршнями, покажите, что за каждый период
осцилляций между ними скорость протона увеличивается на 2 vm.
2. Рассчитайте необходимое количество осцилляций.
3. Вычислите время Т, необходимое для того, чтобы столько раз пройти рас-
стояние L. Достаточно получить ответ с точностью до множителя 2.
2.4. Неоднородное поле Е
Пусть теперь магнитное поле в системе однородно, а электри-
ческое — неоднородно. Для простоты предположим, что Е направ-
лено по оси х и меняется с х синусоидально (рис. 2.11):
Е=Ео (coskx) х. (2.47)
Это распределение поля с длиной волны Л = 2л//г создается сину-
соидальным распределением заряда, на анализе которого мы оста-
навливаться не будем. На практике такое распределение заряда
Рис. 2.11. Дрейф вращающейся частицы в неоднородном электрическом поле.
46
Гл. 2. Движение отдельных частиц
может возникнуть в плазме во время распространения в ней волны.
Уравнение движения частицы в поле Е(х) имеет вид
т (dv/dt) = q [Е (х) + v х В]; (2.48)
поперечные составляющие этого уравнения запишутся следующим
образом:
(*),. (2.49)
tTl tn tn
vy = — (Oc^—Юс (2.51)
Здесь Ex (x) — электрическое поле в точке, где находится частица.
Чтобы вычислить его, нам нужно знать траекторию частицы, ко-
торую мы и попытаемся в первую очередь найти. Если электриче-
ское поле слабое, то для приближенного вычисления Ех (х) мы мо-
жем использовать невозмущенную орбиту, т. е. орбиту частицы
в отсутствие поля Е. Она определяется выражением (2.7):
x = x04-rLsin<oci. (2.52)
Из уравнений (2.51) и (2.47) получаем
vy = — ofay—©с cos k (х0 + rL sin (ОсО. (2.53)
В
Предугадывая результат, будем искать решение в виде суперпо-
зиции вращения с частотой сос и дрейфа с постоянной скоростью vE.
Поскольку нас интересует только выражение для и£, избавимся
от членов, описывающих вращение, путем усреднения по периоду.
Из уравнения (2.50) тогда следует, что ох = 0. В уравнении (2.53)
осциллирующий член vu, очевидно, тоже при усреднении обра-
щается в нуль, и мы получаем
1^ = 0— —со^—cos k (х0 + г, sinatct). (2.54)
В
Преобразовывая косинус, имеем
cos k (х0 + rL sin = cos (fex0) cos (krL sin (oci)—sin(fex0)sin(ferL sin .
(2.55)
Достаточно рассмотреть случай малого ларморовского радиуса,
< 1. Разложения в ряды Тейлора
cose=l-(l/2)*a+ • • (256)
sine = e-|- . . .
2.4. Неоднородное поле Е
47
позволяют записать следующие соотношения:
cos k (х0 + rL sin act) « (cos kx0) (1 — (1/2) k2rl sin2 act) —
— (sin kxo) krt sin act.
Последний член при усреднении по времени исчезает, и уравнение
(2.54) принимает вид
Ьу= --^(cosfcx0)(l--U2r2L) = -^^(1-^W)-
(2.57)
Следовательно, в неоднородном поле обычный Е X В-дрейф изме-
няется таким образом, что его скорость принимает вид
Нетрудно понять физическую причину этого изменения. Дело
в том, что ион, ведущий центр которого расположен в точке макси-
мума поля, в действительности большую часть времени проводит
в областях, где поле Е слабее. Следовательно, средняя скорость
его дрейфа будет меньше, чем скорость vE, рассчитанная по полю
в точке, где расположен ведущий центр. В линейно меняющемся
поле Е ион на одной стороне своей орбиты должен находиться в бо-
лее сильном поле, а на другой стороне — в настолько же более
слабом, и поправки к v£ должны компенсировать друг друга. Из
этого ясно, что поправочный член зависит от второй производной
поля Е. У синусоидального распределения, которое мы рассматри-
вали, вторая производная по отношению к Е всегда имеет противо-
положный знак, что и объясняет «минус» в формуле (2.58). Чтобы
обобщить эту формулу на случай произвольного распределения
поля Е, нам достаточно лишь заменить k на — iv и записать ее в
виде
v£=(l + 4-r2LV2)-^- (2.59)
\ 4 J В2
Второй член в скобках описывает эффект, связанный с конечной,
величиной ларморовского радиуса частицы. Какова роль этой по-
правки? Поскольку для ионов rL гораздо больше, чем для электро-
нов, v£ теперь зависит от вида частиц. Допустим, что в плазме воз-
ник сгусток плотности, тогда электрическое поле Е может вызвать
разделение ионов и электронов, поскольку они дрейфуют с раз-
ными скоростями; это приведет к появлению нового электрического
поля. Если существует механизм обратной связи, позволяющий
вторичному электрическому полю усиливать первичное, то Е бу-
дет расти до бесконечности и плазма станет неустойчивой. Такую
неустойчивость, называемую дрейфовой, мы обсудим в одной из
48
Гл. 2. Движение отдельных частиц
последующих глав. Градиентный дрейф, разумеется, также свя-
зан с конечностью величины ларморовского радиуса и тоже вызы-
вает разделение зарядов, однако, согласно (2.24), скорость vvB
пропорциональна krL, а поправочный член в соотношении (2.58)
пропорционален k2rt. Следовательно, неоднородность поля Е играет
важную роль при относительно больших k, или малых масштабах
неоднородности. Вследствие этого дрейфовые неустойчивости от-
носят к более широкому классу микронеустойчивоапей.
2.5. Нестационарное поле Е
Перейдем теперь к анализу движения заряженных частиц в одно
родных, но нестационарных полях Е и В. Для начала рассмотрим
случай, когда В постоянно, а поле Е синусоидально меняется со
временем. Пусть электрическое поле направлено по оси х:
E = Eoeiiaix. (2.60)
Поскольку Ех = ia>Ex, мы можем записать уравнение движения
(2.50) в виде
S.= -^(^=F^-4). (2-6»
Введем определения:
5е=-А.. (2.62)
LJ D
Здесь тильда добавлена лишь для того, чтобы подчеркнуть, что
дрейф является осциллирующим. Верхний (нижний) знак, как
обычно, относится к положительному (отрицательному) заряду q.
Уравнения (2.50) и (2.51) в этих обозначениях принимают вид
= —о>? (vx — Vp), vy — —©с (fy —»£). (2.63)
По аналогии с соотношениями (2.12) попытаемся найти решение,
которое является суперпозицией дрейфа и вращения:
vx = v± eia>ct +?р, vy = ± i Oj. е^ + vE; (2.64)
Если мы дважды продифференцируем эти соотношения по времени,
то получим
Vx — — ©X + ((Ос — “2) V„,
х сх-гч с ) р, (2.65)
Vy = — ofay + (©С— (О2) VE.
Эти уравнения совпадают с соотношениями (2.63) только в том слу-
чае, когда ©2 мало по сравнению с ©2. Если теперь предположить,
2.5. Нестационарное поле Е
49
что Е действительно меняется медленно, т. е. что со2 < ©2, то (2.64)
будут приближенными решениями уравнений (2.63).
Из соотношений (2.64) следует, что движение ведущего центра
теперь более сложное, скорость движения имеет две составляющие;
^-компонента скорости перпендикулярна Е й В — это обычный
Е х В-дрейф, за исключением лишь того, что vE теперь медленно
осциллирует с частотой <о; х-составляющая скорости отвечает но-
вому типу дрейфа вдоль направления Е, который называется поля-
ризационным дрейфом. Заменяя со на — d!dt, мы можем обобщить
соотношение (2.62) и записать скорость поляризационного дрейфа
в виде
(2.66)
в>сВ dt
Поскольку скорости vp у ионов и электронов направлены в разные
стороны, возникает поляризационный ток. При Z — 1 он равен
j„ = ne(Vip — vw) = -^-(A4 4- tri) , (2.67)
Jp v ‘Р ер> eBi V । > dt В* dt
гд.е р — массовая плотность.
Е ----*-
Рис. 2.12. Поляризационный дрейф.
Физическая причина возникновения поляризационного тока
проста (рис. 2.12). Рассмотрим ион, покоящийся в магнитном поле.
Если к нему внезапно приложить электрическое поле Е, то прежде
всего он начнет двигаться вдоль Е. Только после того как ион на-
берет скорость v, он почувствует силу Лоренца и начнет повора-
чивать вниз, как показано на рис. 2.12. Если теперь поддерживать
Е постоянным, то дрейф со скоростью ур прекратится, а будет на-
блюдаться лишь движение со скоростью v£. Однако если Е сменит
направление, то снова возникает мгновенный дрейф, на этот раз
влево. Таким образом, поляризационный дрейф со скоростью vp —
это дрейф «стартерного» типа. Он связан с инерцией частицы и
имеет место только на первом полупериоде каждого оборота, во
время которого поле Е меняет направление на противоположное.
Следовательно, vp стремится к нулю вместе с
50
Гл. 2. Движение отдельных частиц
Явление поляризации в плазме аналогично тому, которое имеет
место в твердом диэлектрике, где D = е0Е + Р. В плазме диполи—
это ионы и электроны, разнесенные на расстояние rL. Несмотря
на это, в ней нельзя создать поляризационное поле Р при помощи
постоянного поля Е, поскольку ионы и электроны могут смещаться
и восстанавливать квазинейтральность плазмы. Однако если поле Е
колеблется, то из-за запаздывания, вызванного инерцией ионов,
возникает осциллирующий ток jp.
2.6. Нестационарное поле В
Пусть теперь магнитное поле изменяется во времени. Поскольку
сила Лоренца всегда перпендикулярна В, магнитное поле не может
передать энергию заряженной частице. Однако при изменении В-
возникает электрическое поле Е:
VXE=—В, (2.68)
которое уже может ускорять частицы. Рассмотрим этот процесс
детальнее. Ясно, что теперь нельзя предполагать, будто поля со-
вершенно однородны. Пусть 1 — элемент дуги вдоль траектории
частицы, Vj. = dX/dt— ее поперечная скорость (скоростью рц пре-
небрегаем). Умножив скалярно уравнение движения (2.8) на v±,
мы получим
= ?Е• v± = qE• -£- (2.69>
at \ 2. j at
Интегрирование по периоду позволяет вычислить изменение энер-
гии частицы за один оборот:
, 1 ч 2Л(ЙС Л
6 ?E--^-d/.
Если поле меняется медленно, то интеграл по времени можно за-
менить интегралом вдоль невозмущенной орбиты:
6 (— = f <7E.dl = <7,f(VxE)-dS= — q$ В dS. (2.70>
\ 2 J s s
Здесь S — ориентированная поверхность, окруженная ларморов-
ской орбитой; направление нормали к ней определяется по правилу
правой руки (пальцы указывают направление скорости v). По-
скольку плазма является диамагнетиком, то для ионов произведе-
ние B-dS меньше нуля, а для электронов — больше нуля. С уче-
том этого уравнение (2.70) принимает вид
о / 1 2 \ , А 2 , А А т (1/2) 2лВ
о (— mv_: 1 = ± qBarL = ± qnB---------------------------
I 2 ) 4 4 <ос (±qB) В <йс
(2.71
2.6. Нестационарное поле В
Величина 2лВ/(о1. = B/fc равна изменению 6В за период вращения.
Таким образом,
6^2_mv2) = p6B. (2.72)
Поскольку левая часть этого равенства тождественна б(рВ), мы
получаем искомый результат:
бр=О. (2.73)
В медленноменяющемся магнитном поле магнитный момент ос-
тается постоянным.
Рис. 2.13. Двухступенчатое адиабатическое сжатие плазмы.
При изменении напряженности магнитного поля В ларморов-
ские орбиты сжимаются или расширяются, а поперечная энергия
частиц уменьшается или увеличивается. Этот обмен энергией ме-
жду полем и частицами очень просто описывается соотношением
(2.73). Инвариантность величины р позволяет без особого труда до-
казать следующую теорему:
Магнитный поток через поверхность, ограниченную ларморов-
ской орбитой, постоянен.
Магнитный поток Ф = BS, где S = лг[, поэтому
ЛЧ О о у2хт2 2лт (U2)mv2± 2ят
<?2В2 f В f
Таким образом, если р = const, то и Ф = const.
Это свойство используется в методе нагрева плазмы,
как адиабатическое сжатие. На рис. 2.13 схематически
как это происходит. Плазма инжектируется в область между проб-
ками 1 и 2, затем с помощью импульса тока в обмотках катушек 1
и 2 в системе увеличивается магнитное поле В и, следовательно,
v\. Следующим импульсом в 1 можно увеличить пробочное отно-
шение и переправить нагретую плазму в область 3—4. Подавая
известном
показано,
52
Гл. 2. Движение отдельных частиц
затем импульсы в 3 и 4, можно еще раз сжать и нагреть плазму-
Этот тип нагрева использовался в первых установках управляв'
мого термоядерного синтеза. Адиабатическое сжатие успешно при-
менялось также в плазменных торах, оно является основным эле-
ментом в схемах лазерного синтеза с использованием как магнит-
ного, так и инерциального удержания.
2.7. Сводка формул для скоростей дрейфа
ведущего центра
Дрейф под действием произвольной силы F:
_L_fx^_.
’ q В*
В электрическом поле:
В гравитационном поле:
т g X В
Ver — *
q В*
В неоднородном поле Е:
У£=(1 + Аг^)ЛАВ
В неоднородном поле В:
Градиентный дрейф:
Центробежный дрейф:
mv\ R. X В
Vo =----Я-------- •
4
Дрейф из-за искривленности силовых линий в вакууме:
। т / 2 , 1 2 \ Rc X В
Vj?+vVH = —(ра+ —•
4 \ 2 7 /?2д2
Поляризационный дрейф:
р асВ dt
(2-17)
(2.15)
(2.18))
(2.59)
(2.24)
(2.26):
(2.30)
(2.66)
2.8. Адиабатические инварианты
53
2.8. Адиабатические инварианты
Из классической механики хорошо известно, что если в системе
есть периодическое движение, то действие ф р dq, где интеграл
берется по периоду, является интегралом движения. Здесь р и q —
периодические обобщенный импульс и обобщенная координата.
Если в системе происходят медленные изменения и движение не
является чисто периодическим, то интеграл движения остается
неизменным и поэтому его называют адиабатическим инвариантом.
Под «медленными» мы понимаем величины, медленно меняющиеся
по сравнению с периодом движения, так что интеграл § р dq имеет
смысл, хотя он и не является уже интегралом по замкнутому кон-
туру. Адиабатические инварианты играют важную роль в физике
плазмы; они позволяют получить простые ответы во многих слу-
чаях сложных движений частиц. Существует три адиабатических
инварианта, которые соответствуют различным типам периодиче-
ских движений.
2.8.1. Первый адиабатический инвариант (р)
Мы уже имели дело с величиной
p = mw2±/2B
и показали, что в нестационарных и неоднородных магнитных по-
лях она сохраняется. Периодическим движением, соответствующим
этому инварианту, является, конечно, ларморовское вращение.
В самом деле, если в общей формуле для адиабатического инвари-
анта в качестве р выбрать момент количества движения то±г, а ко-
ординатой q считать 6, то действие запишется в виде
2
/ПСГ ffi
фрdq = jmv^r^dQ = 2nrj_mv_ = 2л----= 4л —р р- (2.75)
Таким образом, при постоянном отношении qlm величина р яв-
ляется интегралом движения. Мы доказали постоянство р, неявно
предполагая, что (<о/сос) < 1, где со — частота, характеризующая
изменение В с точки зрения частицы. Можно, однако, показать,
что р — инвариант даже при со < сос. На языке теоретиков р ин-
вариантен «во всех порядках разложения по со/со£». На практике
это значит, что за один период вращения величина р оказывается
значительно ближе к константе, чем В.
Одинаково важно знать, в каких случаях существует адиаба-
тический инвариант, а в каких его нет. Инвариантность величины р
нарушается, если со не мала по сравнению с <ос. Приведем три при-
мера такого нарушения.
54
Гл. 2. Движение отдельных частиц
А. Магнитная накачка. Пусть величина В в ловушке с маг-
нитными зеркалами синусоидально меняется во времени; тогда vr
у частиц будет осциллировать, но их энергия за большой промежу-
ток времени не увеличится. Однако если частицы сталкиваются
между собой, то инвариантность величины р нарушается и плазма
может быть нагрета. В частности, у частицы, которая сталкивается
с другой частицей на стадии сжатия, часть энергии вращательного
движения может преобразоваться в энергию, связанную с v й. На
стадии расширения эту энергию забрать обратно уже нельзя.
Б. Циклотронный нагрев. Представим себе, что поле В осцилли-
рует с частотой (i)c. Индуцированное электрическое поле будет тогда
вращаться в фазе с некоторыми частицами и непрерывно ускорять
их ларморовское вращение. В этом случае условие со сос нару-
шается, р, не сохраняется и плазму можно нагреть.
В. Магнитные каспы. Если изменить направление тока в одной
из катушек обычной системы с магнитными зеркалами (пробкотрона),
то образуется магнитный касп (рис. 2.14). Эта конфигурация, кроме
обычных магнитных зеркал, имеет еще круговое зеркало в виде
каспа, занимающее по азимуту угол 360°. Считается, что плазма,
запертая в такой установке, более устойчива, чем в обычной зер-
кальной ловушке. К сожалению, потери частиц в этом случае
больше, поскольку кроме конуса существует еще одна область по-
терь. Движение частицы в этой системе не является адиабатиче-
ским, поскольку в центре симметрии поле В обращается в нуль,
там тоже равна нулю и р при движении не сохраняется. Лармо-
ровский радиус вблизи центра системы становится больше, чем
размер установки. Из-за этого нельзя гарантировать, что частицы,
которые были вне конуса потерь, останутся там после прохожде-
ние. 2.14. Удержание плазмы в магнитном поле с каспом.
2.8. Адиабатические инварианты
55
ния области неадиабатичности. К счастью, в этом случае сущест-
вует другой инвариант — канонический момент импульса ре =
= mrve —егАв. В бесстолкновительном случае это гарантирует,
что в системе будут бесконечно долго существовать захваченные
ловушкой частицы.
2.8.2. Второй адиабатический инвариант (J)
Рассмотрим частицу, удерживаемую между двумя магнитными
зеркалами. Она колеблется между ними, совершая периодическое
движение с так называемой «баунс-частотой». Интеграл этого дви-.
жения записывается в виде $>тиц ds, где ds — элемент длины при
движении ведущего центра вдоль силовой линии. Вследствие того
что ведущий центр дрейфует поперек силовых линий, движение не
является чисто периодическим и интеграл движения оказывается
адиабатическим инвариантом. Он называется продольным инва-
Рис. 2.15. Частица, совершающая в магнитном поле колебаниям между точ-
ками поворота а и Ь.
Рис. 2.16. Движение заряженной частицы в магнитном поле Земли.
риантом J и вычисляется для половины цикла движения между
двумя точками поворота (рис. 2.15):
ь
J=$vnds.
(2.76)
Мы докажем, что J инвариантен в статическом неоднородном поле В.
Этот результат справедлив также и в том случае, когда поле мед-
ленно меняется со временем.
56
Гл. 2. Движение отдельных частиц
Прежде чем начать довольно длинное доказательство, рассмот-
рим пример в виде задачи, в которой будет полезна теорема об ин-
вариантности J. Как мы уже упоминали, магнитное поле Земли
захватывает заряженные частицы, которые затем медленно дрей-
фуют вокруг Земли в широтном направлении (задача 2.8; см. также
рис. 2.16). Если бы магнитное поле было совершенно симметричным,
то частица в конце концов вернулась бы на исходную силовую ли-
нию. Однако в действительности магнитное поле Земли деформи-
Рис. 2.17. К доказательству инвариантности величины J.
руется, например под действием солнечного ветра. Вернется ли в
таком случае частица на ту же силовую линию? Вследствие того
что энергия частицы сохраняется и равна (1/2) mv\ в точке пово-
рота, из сохранения первого адиабатического инварианта ц следует,
что и величина | В | в точке поворота останется прежней. Однако,
придя в результате дрейфа на исходную долготу, частица может
оказаться на другой силовой линии и на другой высоте. Этого не
случится, если J сохраняется. Величина J определяет длину си-
ловой линии между точками поворота, и не существует двух ли-
ний, которые имели бы одну и ту же длину между точками с оди-
наковыми | В|. Следовательно, даже в слегка асимметричном поле
частица все равно вернется на исходную силовую линию.
Чтобы доказать инвариантность величины J, рассмотрим сна-
чала вопрос об инвариантности v л 6s, где 6s — отрезок пути вдоль В
(рис. 2.17). Из-за дрейфа ведущего центра через время Д/ частица
сместится с линии 6s на линию 6s'. Длину 6s' можно определить,
если через концы отрезка 6s провести плоскости, перпендикуляр-
ные В. Длина 6s, очевидно, пропорциональна радиусу кривизны:
6s _ 6s' .
/?с ” ’
следовательно, можно написать
6s’ — 6s R' — R.
----- =_£ L. (2.77)
Д/ 6s MRC-----------------------------4
Радиальная компонента скорости vgc имеет такое
выполняется равенство
Rc
vgc • ———-----•
значение, что
(2.78)
2.8. Адиабатические инварианты
57
Из уравнений (2.24) и (2.26) получаем
, ,1 в х VB , mv || Rc х в
Vgc = Vvb + Vn — ± — v j. rL---------s---------
g i Л 2 52 g R2B2
(2.79)
Заметим, что последний член не имеет составляющей, направленной
вдоль Rc . Используя равенства (2.78) и (2.79), выражение (2.77)
можно записать в виде
1
6s
d
dt
6s = Vgc •
Re
R2
B3
p
(BXVB)- -f •
я2
(2.80)
2
m
q
Такова скорость изменения 6s с точки зрения частицы. Теперь мы
должны получить скорость изменения величины v ц в системе коорди-
нат частицы. Введем определения продольной и поперечной энергий
с помощью равенства
J-Wu+y +рВ==№|| + (2.81)
Таким образом, мы имеем
=1(2//тг)(№—цВ)]1'2. (2.82)
Здесь (Тир. постоянны, а изменяется только В. Следовательно,
^11______1 ____1 цВ (2.83)
V „ 2 W — цВ 2 W |( mv2tl
Поскольку В предполагается стационарным, В не равна нулю
только из-за движения ведущего центра:
(2.84)
dr dt q Я2В2
Теперь мы можем написать:
и (RCXB).V2? (2.85)
Я R2cB2 2 q В
Относительное изменение величины оц 6s равно
—!----—(o„6s) = — — + — (2.86)
v и 6s dt 6s dt t>|| dt
Как видно из соотношений (2.80) и (2.85), эти последние два члена
взаимно уничтожаются; следовательно,
v у 6s = const. (2.87)
58
Гл. 2. Движение отдельных частиц
Отсюда, однако, не следует, что J = const. При вычислении интег-
рала от v к 6s между точками поворота может случиться так, что
точки поворота на 6s' не совпадут с концами отрезка, полученного
сечением 6s перпендикулярными плоскостями (рис. 2.17). Погреш-
ность в вычислении J из-за этого расхождения будет, однако, пре-
небрежимо мала, поскольку вблизи точек поворота цц почти равна
нулю. Следовательно, мы доказали, что
ь
J= jt>uds = const. (2.88)
а
Пример нарушения инвариантности J дает схема нагрева
плазмы, называемая времяпролетной магнитной накачкой. Пред-
положим, что к катушкам пробкотрона подводятся переменные
токи, так что пробки попеременно приближаются и отдаляются
друг от друга с частотой, близкой к баунс-частоте. Частицы, ко-
торые колеблются с этой баунс-частотой, всегда будут видеть сбли-
жающиеся пробки и, следовательно, их скорость Оц будет увели-
чиваться. В этом случае I не сохраняется, поскольку изменение
поля В происходит на временных масштабах, которые нельзя счи-
тать большими по сравнению с временем колебания частиц между
зеркалами.
2.8.3. Третий адиабатический инвариант (Ф)
Возвращаясь вновь к рис. 2.16,. мы видим, что медленный дрейф
ведущего центра вокруг Земли представляет собой третий тип пе-
риодического движения. Оказывается, что адиабатический инва-
риант, связанный с этим движением, есть полный магнитный поток,
охватываемый дрейфовой поверхностью. Почти очевидно, что при
изменении В частица остается на такой поверхности, для которой
полное число охватываемых ею силовых линий остается постоян-
ным. Инвариант Ф применяется редко, поскольку большинство
флуктуаций магнитного поля В происходит на временных масшта-
бах, которые малы по сравнению с периодом дрейфа, отвечающим
этому инварианту. Как пример нарушения инвариантности Ф
можно привести недавние исследования по возбуждению МГД-волн
в ионосфере. Эти волны имеют большой период, сравнимый со вре-
менем перемещения частицы вокруг Земли. Следовательно, частицы
после одного оборота могут встретить волну в той же самой фазе.
Если это происходит, то передача энергии от дрейфующих частиц
к волне может привести к ее раскачке. Инвариант Ф в этом случае
не сохраняется.
2.8. Адиабатические инварианты
59
Задачи
2.13. Решите задачу 2.126, пользуясь инвариантностью величины J.
а) Положив J v л ds » V\\L, выполните дифференцирование по времени.
б) Исходя из этого, получите выражение для времени Т через dLldt. По-
ложив dLldt = — 2vm, вы получите ответ.
2.14. При нагреве плазмы путем адиабатического сжатия из инвариантности
величины ц следует, что с увеличением В должна расти и КТ±. Немагнит-
ное поле не может ускорять частицы, поскольку сила Лоренца qv X В всегда
перпендикулярна скорости. Как же частицы получают энергию?
2.15. Выражение для скорости поляризационного дрейфа можно получить
и из закона сохранения энергии. Пусть Е осциллирует, тогда скорость ЕХВ-
дрейфа тоже осциллирует и с движением ведущего центра связана энергия
(1/2) mv2E. Поскольку энергию от электрического поля можно отобрать только
при движении вдоль Е, должен существовать дрейф со скоростью vp в направ-
лении Е. Найдите vp, приравнивая скорость изменения величины (1/2) mv^
к скорости прироста энергии у частицы vp-E.
2.16. Водородная плазма нагревается волной радиодиапазона (<в= 109 рад/с),
в которой Е перпендикулярно В; плазма удерживается магнитным полем
1 Тл. Являются ли адиабатическими движения а) электронов и б) ионов,
взаимодействующих с этой волной?
2.17. Протон с энергией 1 кэВ и 0ц= 0 находится в однородном магнитном
поле В = 0,1 Тл. Поле медленно возрастает до величины 1 Тл, и протон уско-
ряется. После этого он упруго сталкивается с тяжелой частицей и меняет
направление движения, так что теперь = Оц. Поле В снова уменьшается
до 0,1 Тл. Какова теперь энергия протона?
2.18. Бесстолкновительная водородная плазма удерживается в торе, внешние
обмотки которого создают магнитное поле, почти целиком направленное
по <р (рис. 32.18). Плазма в начальный момент максвелловская, ее температура
КТ = 1 кэВ. Начиная с t = 0, магнитное поле В за 100 мкс увеличивается
с 1 Тл до 3 Тл, в результате чего плазма сжимается.
а) Покажите, что магнитный момент как у ионов, так и у электронов остается
инвариантным.
б) Вычислите температуры Т± и Тц после сжатия.
Рис. 32.18.
Рис. 32.19.
60
Гл. 2. Движение отдельных частиц
2.19. В тороидальной камере квадратного поперечного сечения содержится
однородная плазма (рис. 32.19). Магнитное поле создается током I, текущим
вдоль оси симметрии системы; размеры камеры а — 1 см, R = 10 см. Плазма
является максвелловской с температурой К.Т = 100 эВ, ее плотность п =
= Ю19 м-3. Электрическое поле отсутствует.
а) Нарисуйте типичные орбиты ионов и электронов с Цу = 0, дрейфующих
в неоднородном поле В.
б) Вычислите скорость накопления заряда на верхней крышке камеры в Кл/с
благодаря совместному действию дрейфов vvS и nr. Магнитное поле в центре
камеры равно 1 Тл; по необходимости можно пользоваться приближением
alR <К 1.
2.20. Предположим, что магнитное поле на оси симметрии пробкотрона имеет
вид Вг = Во (1 + a2z2).
а) Пусть при z=0 скорость электрона дается выражением а2 = Зо2у =
= 1,5 v2^. При каком z электрон отразится?
б) Запишите уравнение движения ведущего центра вдоль поля.
в) Покажите, что движение синусоидальное; вычислите его частоту.
г) Найдите величину продольного инварианта /, соответствующего этому
движению.
2.21. По бесконечному прямому проводу течет ток / в направлении положи-
тельных z. При t = 0 электрон, обладающий малым гирорадиусом, находится
в точке z = 0, г= г0, причем их0 = и ([ 0 (J_ и II п0 отношению к направле.
нию магнитного поля).
а) Вычислите величину и направление скорости дрейфа ведущего центра.
б) Предположим, что ток медленно возрастает таким образом, что в системе
индуцируется постоянное электрическое поле, направленное вдоль ± г.
Покажите на чертеже, как направлены I, В, Е и vg.
в) Уменьшаются, возрастают или сохраняются скорости ох и Су, когда ток
растет? Почему?
Глава 3
ПЛАЗМА КАК ЖИДКОСТЬ
3.1. Введение
В предыдущей главе мы рассмотрели движение заряженных частиц
в заданных электрических и магнитных полях. В плазме ситуация
гораздо сложнее; поля Е и В не заданы, а определяются положе-
ниями и движением самих заряженных частиц, поэтому для ана-
лиза поведения плазмы необходимо решать самосогласованную за-
дачу. Иными словами, мы должны найти такой набор траекторий
частиц и распределений полей, при котором частицы, двигаясь по
своим орбитам, будут генерировать эти поля, а возникшие поля
заставят частицы двигаться в точности по тем же самым орбитам.
И все это нужно сделать в нестационарном случае!
Мы видели, что типичная плотность плазмы составляет 1012
электрон-ионных пар в 1 см3. Если бы нужно было следить за каж-
дой из этих частиц, движущихся по сложным орбитам, то прогноз
поведения плазмы стал бы безнадежной задачей. К счастью, в этом,
как правило, нет необходимости, поскольку (что поразительно)
большинство плазменных явлений, наблюдаемых в реальных экс-
периментах (возможно, 80 %), можно объяснить с помощью
довольно простой модели, подобной той, что используется в гидро-
динамике; в ней пренебрегают отличиями отдельных частиц и рас-
сматривают только движения элементов объема жидкости. Разу-
меется, при анализе плазмы считается, что жидкость содержит
электрические заряды, В обычной жидкости частицы в элементе
объема движутся вместе потому, что они часто сталкиваются между
собой. Удивительно, что такая модель работает в плазме, где столк-
новения случаются редко. Однако мы увидим, что на это есть своя
причина.
В большей части настоящей книги мы будем рассматривать те
вопросы, которые можно изучить с помощью гидродинамической
теории плазмы. Более тонкий подход — кинетическая теория
плазмы — требует больше математических выкладок, чем это до-
пустимо во вводном курсе. Введение в кинетическую теорию изла-
гается в гл. 7.
В некоторых плазменных задачах для. описания поведения
плазмы недостаточно ни гидродинамической, ни кинетической тео-
62
Гл. 3. Плазма как жидкость
рии. Тогда нужно возвращаться к утомительному процессу отсле-
живания отдельных траекторий. Это по силам современным компью-
терам, однако их памяти хватает только на то, чтобы хранить по-
ложения и скорости около 104 частиц, и, за исключением отдельных
случаев, они могут решать только одно- или двумерные задачи. Тем
не менее численное моделирование стало в последнее время играть
важную роль, заполняя пробел между теорией и экспериментом
в тех случаях, когда даже кинетическая теория не позволяет при-
близиться к объяснению наблюдаемых в плазме явлений.
3.2. Связь между физикой плазмы
и обычной электродинамикой
3.2.1. Уравнения Максвелла
Уравнения Максвелла в вакууме имеют вид
80v-E=o, (3.1)
VXE=- В, (3.2)
у.В=0, (3.3)
VxB = p0(j + e0E). (3.4)
В среде они записываются следующим образом:
V-D = ct, (3.5)
VXE=—В, (3.6)
V-B=0, (3.7)
VxH=j + D, (3.8)
D=eE, (3.9)
B=pH. (3.10)
В уравнениях (3.5) и (3.8) о и j — это плотности «свободных» за-
рядов и токов соответственно. Плотности «связанных» зарядов и то-
ков, возникающих из-за поляризации и намагничивания среды,
включены в определения D и Н через е и р,. В плазме эквивален-
тами «связанных» зарядов и токов являются составляющие ее ионы
и электроны. Поскольку эти заряженные частицы движутся слож-
ным образом, то объединять обусловленные ими эффекты в две кон-
станты 8 и р непрактично. Поэтому в физике плазмы обычно рас-
сматривают уравнения Максвелла для вакуума (3.1) — (3.4), а
под ст и j понимают все заряды и токи,— как внутренние, так и внеш-
ние.
3.2. Связь между физикой плазмы и обычной электродинамикой
63
Заметим, что в уравнениях для вакуума мы использовали ве-
личины Е и В, а не их аналоги D и Н, связанные с Е и В через
s и р. Это объясняется тем, что силы <?Е и jxB зависят от Е и В, а
не от D и Н, и при работе с уравнениями для вакуума вводить по-
следние величины нет необходимости.
3.2.2. Классическая теория магнитных материалов
Любая вращающаяся заряженная частица плазмы обладает маг-
нитным моментом, поэтому казалось бы логично рассматривать
плазму как магнитный материал с проницаемостью рт. (Индекс
т у проницаемости мы поставили для того, чтобы отличить ее от
адиабатического инварианта ц.) Чтобы понять, почему на практике
так не делают, вспомним, как обычно исследуют магнитные мате-
риалы.
Ферромагнитные домены с магнитными моментами создают,
скажем, в куске железа намагниченность
(з.н)
V i
в единице объема. Эта намагниченность эквивалентна возникнове-
нию в веществе связанного тока с плотностью
b=VxM. (3.12)
В уравнение (3.4), определяющее магнитное поле в вакууме, мы
должны включить как этот ток, так и «свободный» ток от внешних
ИСТОЧНИКОВ jfl
p,o 'v X В = j/ + j(, + e0E. (3.13)
Запишем уравнение (3.13) в простом виде
VxH = jf + e0E, (3.14)
включив ji в определение Н. Это можно сделать, если положить
Н = р,Г'В—М. (3.15)
Чтобы получить простое соотношение, связывающее В и Н, пред-
положим, что М пропорционально В или Н:
М = ХтН. (3.16)
Постоянная %т называется магнитной восприимчивостью. Следо-
вательно,
B = Ho(l+Xm)H = HmH. (3.17)
Простая связь между В и Н оказалась возможной лишь потому,
что уравнение (3.16) линейное.
64
Гл. 3. Плазма как жидкость
В плазме, помещенной в магнитное поле, любая частица имеет
магнитный момент ра, а величина М есть сумма всех ра в единице
объема. Но теперь
О
mv \ п 1 1
В В В
Связь между М и Н (или В) уже не является линейной; мы не можем
записать, что В = ртН с постоянным и поэтому рассматривать
плазму как магнитную среду бессмысленно.
3.2.3. Классическая теория диэлектриков
Как известно, поляризация единицы объема вещества Р равна сумме
всех отдельных моментов электрических диполей р(-. Поляризация
диэлектрика приводит к возникновению в нем связанного заряда
с плотностью
<rfr=_V.P. (3.18)
В уравнение (3.1), описывающее электрическое поле в вакууме,
нужно включить как связанные, так и свободные заряды:
е0у-Е = о} + <Ть. (3.19)
Запишем это уравнение в простом виде:
yD = fff, (3.20)
включив Оь в определение D. Это можно сделать, положив
D = e0E + P = eE. (3.21)
Если поляризация Р пропорциональна Е, т. е.
Р = е0ХеЕ, (3.22)
то е является постоянной и определяется выражением
8 = (1 + Хе)е0- (3.23)
Заранее нельзя объяснить, почему соотношение типа (3.22) будет
в плазме несправедливо, поэтому можно попытаться получить
выражение для е в такой среде.
3.2.4. Диэлектрическая проницаемость плазмы
Как было показано в разд. 2.5, флуктуирующее поле Е создает
в плазме поляризационный ток jp. Это в свою очередь приводит к
возникновению поляризационного заряда, который определяется
из уравнения непрерывности
j£2-+V.jp = 0. (3.24)
dt
Уравнение (3.24) эквивалентно уравнению (3.18) с той лишь разни-
3.2. Связь между физикой плазмы и обычной электродинамикой 65
цей, что (как отмечалось ранее) поляризация в плазме возникает
только под действием нестационарного электрического поля. По-
скольку мы имеем точное выражение для jp, а не для сгр, удобнее
работать с четвертым уравнением Максвелла (3.4):
V X В = р-о (if + j₽ + е0Ё). (3.25)
Перепишем это уравнение в виде
V X В = р0 (jf + еЁ), (3.26)
где мы положили
8=е0 + (/р/Ё). (3.27)
Из уравнения (2.67), определяющего }р, имеем
8 = 80 + (р/В2), 8д^(8/ео)=1 + (Иорс2/В2). (3.28)
Это есть диэлектрическая проницаемость плазмы для поперечных
движений в низкочастотном пределе. Такое уточнение необходимо
потому, что использованное нами выражение для jp справедливо,
только если <о2 ®2> а электрическое поле Е перпендикулярно В.
Общее выражение для 8, естественно, очень сложное; оно вряд ли
поместится на одной странице.
Заметим, что при р-> 0 относительная диэлектрическая прони-
цаемость 8Л стремится к своему значению в вакууме, т. е. к единице,
как и должно быть. Если В —>- оо, то величина 8Л также стремится
к единице. Это связано с тем, что поляризационный дрейф vp здесь
отсутствует и частицы не откликаются на поперечное электрическое
поле. В случае обычной лабораторной плазмы второй член в пра-
вой части выражения (3.28) много больше единицы. Например,
если п = 10“ м-3, В = 0,1 Тл, то для водородной плазмы
ц0рс2 (4л-10~7)-(1016)-(1,67-10-27)-(9-101в) ,оп
---------— = 1оУ«
В2 (0,1)2
Это значит, что электрические поля, обусловленные наличием в
плазме заряженных частиц, намного превышают поля, приложен-
ные извне. Плазма с большим 8 экранирует переменные электриче-
ские поля аналогично тому, как плазма с малым дебаевским радиу-
сом XD экранирует постоянные поля.
Задачи
3.1. Вычислите диэлектрическую проницаемость плазмы в низкочастотном
приближении (3.28), рассмотрев совместно производную по времени от урав-
нения V-D = V- (еЕ) = 0 и уравнение Пуассона в вакууме (3.1). Исполь-
зуйте также уравнения (3.24) и (2.67).
3 Заказ 3170
66
Гл. 3. Плазма как жидкость
3.2. Пусть йс обозначает циклотронную частоту ионов, а ионная плазменная
частота определяется как Qp = (ne2/80Af)'^2> где М — масса иона. При ка-
ких Обстоятельствах диэлектрическая проницаемость приближенно равна
Пр/О2?
3.3. Гидродинамические уравнения
Уравнения Максвелла позволяют найти поля Е и В для данного
состояния плазмы. Чтобы решить самосогласованную задачу, нам
нужно иметь уравнение, описывающее отклик плазмы на данные
поля Е и В. В гидродинамическом приближении считается, что
плазма состоит из двух или более взаимопроникающих жидкостей,
каждая из которых соответствует определенному сорту частиц.
В простейшем случае, когда имеется только один вид ионов, нам
нужно получить два уравнения движения — одно для положи-
тельно заряженной ионной жидкости, а другое для отрицательно
заряженной электронной. В случае частично ионизованного газа
необходимо также уравнение движения жидкости, состоящей из
нейтральных атомов. Нейтральная жидкость будет взаимодейство-
вать с ионами и электронами только посредством столкновений.
Ионная и электронная компоненты взаимодействуют друг с другом
даже в отсутствие столкновений через генерируемые ими поля Е
и В.
3.3.1. Конвективная производная
Уравнение движения отдельной заряженной частицы имеет следую-
щий вид:
т (dv/dt) = g (Е 4- v х В). (3.29)
Предположим вначале, что столкновения и тепловое движение в
плазме отсутствуют. В этом случае все частицы элемента жидкости
движутся вместе и средняя скорость этих частиц и совпадает со
скоростью отдельной частицы v. Уравнение движения жидкости
при этом получается просто умножением уравнения (3.29) на плот-
ность частиц п:
тп (du/dt) — qn (Е u х В), (3.30)
однако в такой форме им пользоваться неудобно. Дело в том, что
в уравнении (3.29) производную по времени нужно брать в точке,
где находится частица. А мы хотим получить уравнение для эле-
ментов объема жидкости, зафиксированных в пространстве, потому
что делать иначе было бы неразумно. Действительно, рассмотрим
в качестве элемента объема жидкости каплю сливок в чашке кофе.
3.3. Гидродинамические уравнения
67
При перемешивании кофе капля скручивается в нить и в конце
концов распределяется по всей чашке, теряя присущие ей особен-
ности. Однако элемент объема жидкости в фиксированной точке
чашки сохраняет свою индивидуальность, несмотря на то что ча-
стицы непрерывно входят и выходят из него.
Для того чтобы перейти к переменным в фиксированной системе
координат, рассмотрим в одномерном случае любой параметр жид-
Рис. 3.1. Движение элементов жидкости в электронагревателе.
кости G (х, t). Изменение G со временем в системе отсчета, движу-
щейся с жидкостью, есть сумма двух членов:
dG (х, /) dG , dG dx dG . 3G
dt dt dx dt dt dx
(3.31)
Первый член в правой части этого равенства представляет собой
изменение величины G в фиксированной точке пространства, а вто-
рой отвечает изменению G при перемещении наблюдателя вместе
с жидкостью в область пространства с другим значением G. В трех-
мерном случае соотношение (3.31) обобщается следующим образом:
-^- = 4^+(U'V)G. (3.32)
at ut
Это выражение называется конвективной производной и иногда обо-
значается DtjlDt. Заметим, что (u-V) — скалярный дифференци-
альный оператор. Поскольку знак этого члена иногда вызывает
недоразумения, рассмотрим для иллюстрации три простых при-
мера.
На рис. 3.1 показан электронагреватель, в котором горячая
вода поднимается вверх, а холодная опускается на дно. Пусть
з»
68
Гл. 3. Плазма как жидкость
Рис. 3.2. Направление градиента солености в устье реки.
G (х, t) — это температура Т, тогда вектор vG направлен вверх.
Рассмотрим элемент жидкости у стенки бака. Если нагреватель
включен, то элемент жидкости при движении нагревается, и поэ-
тому dT/dt >0. Если же, кроме этого, с помощью вертушки соз-
дается дополнительный поток жидкости, то температура фиксиро-
ванного элемента будет понижаться из-за выноса холодной воды
со дна бака. В этом случае dT/dx>Q и их >0, поэтому u-v? >0.
Изменение температуры фиксированного элемента (dT/dt) опреде-
ляется разностью этих эффектов:
дТ dT п'т*
—— ----u-vT. (3.33)
ot dt
Ясно, что dT/dt можно сделать равной нулю, по крайней мере на
короткое время.
Рассмотрим второй пример. Пусть G — это соленость воды S
вблизи устья реки (рис. 3.2). Если ось х направлена вверх по те-
чению, то обычно градиент S такой, что dS/dx <0. Во время при-
лива граница между соленой и пресной водой сдвигается вверх по
течению и «х>0. Таким образом,
=_Ux-^- >0. (3.34)
dt дх
Это значит, что в любой данной точке соленость увеличивается.
Если же, скажем, в дождь, соленость всюду уменьшается, то для
описания этого процесса в центральную часть соотношения (3.34)
нужно добавить отрицательный член dS/dt.
Рассмотрим еще один последний пример. Пусть G — это плот-
ность автомобилей у въезда на скоростную магистраль в часы
пик. Приближаясь к переполненной автостраде, водитель видит,
что плотность машин вокруг него увеличивается. Этому явлению
соответствует конвективный член (u-v) G. В то же время местные
улицы могут заполнять автомобили, подъехавшие по другим до-
3.3. Гидродинамические уравнения
69
Рис. 3.3. К вычислению элементов тензора напряжений.
рогам, так что плотность будет увеличиваться даже в том случае,
если наблюдатель не движется. Этот процесс описывается членом
dG’dt. Общее увеличение численности машин, наблюдаемое води-
телем, есть сумма этих двух эффектов.
Возвращаясь к анализу плазмы, положим G равной скорости
жидкости и и запишем уравнение (3.30) в виде
тп[——(u -V)ul =<7п(Е + и х В), (3.35)
L dt J
где du/dt — производная по времени в фиксированной точке про-
странства.
3.3.2. Тензор напряжений
Для учета тепловых движений в правую часть уравнения (3.35)
нужно добавить силу давления. Эта сила отсутствует в уравнении
движения для отдельной частицы; она возникает из-за хаотиче-
ского движения частиц внутри и вне элемента жидкости. Пусть
центр элемента жидкости ДхДуДг расположен в точке (х0, Ау/2,
&z/2) (рис. 3.3). Для простоты будем рассматривать движение ча-
стиц только вдоль оси х через сечения А и В. Число частиц, про-
ходящих за секунду через торец А со скоростью vx, равно
ДпаижД//Дг, где Дп„ — число частиц в одном м®, имеющих ско-
рость vx:
Дпа = ДихЯ/(^> vy, vz)dvydvz.
Каждая из этих частиц имеет импульс mvx. (Считается, что плот-
ность п и температура КТ в каждом кубическом объеме опреде-
ляются их значениями в центре кубика.) При этом импульс Рл+,
который вносится через торец А в элемент жидкости с центром в
точке х0, равен
РА+= £Anvmu2xA.yAz== ЛуЛг[тохп/2]х_дх- (3.36)
70
Гл. 3. Плазма как жидкость
Суммирование по Дп0 приводит к усредненной по функции распре-
деления величине v2x. Множитель 1/2 возникает из-за того, что
только половина рассматриваемых частиц в кубе в точке х0—Дх
движется к поверхности А. Аналогично через торец В выносится
импульс Рв+ = АуЛг [mvx (1/2) п]%о, поэтому увеличение х-компо-
ненты импульса за счет движущихся вправо частиц равно
Ра+~ Рв+ = & (^/2) [(П0х)х0_дх—М\о] =
= —Аг/ Аг тл (—- Ах) д (пих) (3.37)
2 дх '
Этот результат нужно удвоить, чтобы учесть вклад частиц, дви-
жущихся влево, поскольку они несут отрицательный импульс, а
также движутся по отношению к градиенту nvx в противоположном
направлении. Таким образом, общее изменение импульса элемента
жидкости, расположенного в точке х0, равно
—— (птиА Дх Дz/ Дг = —т —— (nvx) \xkykz. (3.38)
dt дх
Пусть скорость частицы состоит из двух частей: vx = их+ vxr,
их — vx, где их — скорость жидкости, a vxr — скорость хаоти-
ческого теплового движения. Тогда для одномерного максвеллов-
ского распределения из уравнения (1.7) следует
Л-т&^Л-КТ, (3.39)
и уравнение (3.38) принимает вид
—(птих) = — т [и (их + 2ад? +1&)] =
dt дх
д Г / 2 , КТ \т
= — т — я I их Ч------)|.
дх L \ т 7J
Взяв частные производные:
дих , дп д (пих) дих д ,
dt dt дх х дх дх V ’
(3.40)
и воспользовавшись уравнением сохранения массы х)
-g- + -?-(nzzx)=O, (3.41)
dt дх
J) Если читатель раньше не сталкивался с этим уравнением, то можно
обратиться к разд. 3.3.5.
3.3. Гидродинамические уравнения
71
можно сократить два члена, которые стоят в соотношении (3.40)
по обе стороны знака равенства. Наконец, введя определение дав-
ления
р = пКТ,
(3.42)
приходим окончательно к уравнению
(dux , дих \
---—Ь «х —— I =
dt х дх )
др
’ дх '
(3.43)
В правой части этого уравнения стоит обычное выражение для силы,
связанной с градиентом давления. Добавляя к ней электромагнит-
ные силы и обобщая это соотношение на три измерения, получаем
гидродинамическое уравнение
тп —------h(u -V) u =<?n(E + u х В)—Vp.
L dt J
(3.44)
Полученное нами уравнение справедливо только в частном слу-
чае, поскольку мы исходили из того, что передача х-компоненты
импульса происходит из-за движения частиц в х-направлении, а
затем предположили, что жидкость изотропна, и поэтому аналогич-
ные результаты справедливы и для у- и для z-направлений. Однако
^-компоненту импульса можно передать и посредством движения
жидкости, например вдоль оси х. Предположим, что на рис. 3.3
uu = 0 при х = х0 и больше нуля с обеих сторон х0. Тогда при
движении частиц через А и В они внесут в элемент объема больше
положительной компоненты импульса, чем вынесут, и элемент
жидкости приобретает импульс в направлении у. Подобное сдвиго-
вое напряжение нельзя представить скаляром р, оно должно описы-
ваться тензором напряжений Р, компоненты которого =mnvtVj
определяют как направление движения, так и связанные с ним
компоненты передаваемого импульса. В общем случае член —Vp
заменяется на — V- Р.
Мы приведем здесь выражение для тензора напряжений только
в двух простейших случаях. Если функция распределения частиц
изотропная и максвелловская, то Р записывается в виде
/ Р 0 0 \
р _ 0 р о
ч о О р )
(3.45)
и v-Р в точности равно vp. В разд. 1.3 мы отмечали, что в при-
сутствии магнитного поля В плазма может иметь две температуры
72
Гл. 3. Плазма как жидкость
7\ и Тц. В этом случае и давлений тоже должно быть два: рх —
=пКТ± и р\\=пК1\. Тензор напряжений в такой ситуации за-
писывается в виде
/ Рх 0 0 \
Р = 0 О
к о о Р|| 7
(3.46)
где элементы третьей строки или третьего столбца связаны с движе-
нием частиц вдоль В. Тензор Р по-прежнему имеет’Диагональную
структуру; кроме того, он обеспечивает изотропию давления в пло-
скости, перпендикулярной вектору магнитного поля В.
В обычной гидродинамике недиагональные элементы тензора Р,
если они существуют, связаны, как правило, с вязкостью. Дело
в том, что в жидкости после столкновения частиц их средняя ско-
рость направлена вдоль вектора скорости жидкости и в месте их
последней встречи. При следующем столкновении их импульс пе-
редается другому элементу жидкости и т. д. Такой механизм стре-
мится выравнять и в различных точках пространства, а возникаю-
щее в результате этого сопротивление сдвиговому течению интуи-
тивно воспринимается нами как вязкость. Чем больше средняя
длина свободного пробега частиц, тем дальше передается импульс
и тем больше вязкость. В плазме аналогичный эффект имеет место
даже в отсутствие столкновений. Он связан с тем, что частицы,
в особенности ионы, в результате ларморовского вращения попа-
дают в различные точки пространства и поэтому скорости различ-
ных участков плазмы стремятся выравняться. Пространственный
масштаб подобной бесстолкновительной вязкости связан поэтому
не с длиной свободного пробега, а с ларморовским радиусом ча-
стиц. Таким образом, в плазме к столкновительной вязкости до-
бавляется эффект, который обусловлен конечной величиной лармо-
ровского радиуса и тесно связан с дрейфом v£ частиц в неоднород-
ном электрическом поле Е [см. уравнение (2.58)].
3.3.3. Столкновения
Если в плазме кроме ионов и электронов имеются и нейтральные
атомы, то заряженные частицы будут обмениваться с ними импуль-
сами посредством столкновений. Импульс, теряемый в столкнове-
нии, пропорционален относительной скорости и—и0, где и0 — ско-
рость нейтральной компоненты жидкости. Пусть среднее время
между столкновениями т приблизительно постоянно, тогда возни-
кающую при движении частиц силу трения можно приближенно
записать в виде —тп (и—и0)/т. Обобщим уравнение движения
3.3. Гидродинамические уравнения 73
(3.44), включив в него анизотропное давление и столкновения с
нейтральными частицами:
тп [du/d/+ (u-V) u] = <?n(E4-u х В)—V - Р —тп (и—и0)/т.
(3-47)
Столкновения между заряженными частицами сюда не включены;
они будут рассматриваться отдельно в гл. 5.
3.3.4. Сравнение с обычной гидродинамикой
Обычная жидкость удовлетворяет уравнению Навье—Стокса:
Р [-77- +(u-v)ul = — Vp + pvV2u. (3.48)
L dt J
Оно аналогично уравнению (3.47) для плазмы с той лишь разницей,
что здесь отсутствуют электромагнитные силы и столкновения ча-
стиц разного сорта (имеется лишь один сорт частиц). Описывающий
вязкость член pvV2u, где v — коэффициент кинематической вяз-
кости, соответствует столкновительной части выражения v-P—
в отсутствие магнитных полей. Уравнение (3.48) описывает жид-
кость с частыми столкновениями между частицами. Однако урав-
нение (3.47) было выведено без какого-либо предположения о ве-
личине частоты столкновений. Поскольку эти два уравнения тож-
дественны с точностью до членов, зависящих от Е и В, то возникает
вопрос: может ли уравнение (3.47) действительно описывать ком-
поненты плазмы? Ответ с некоторой осторожностью является ут-
вердительным. Выяснив, почему это так, мы установим пределы
применимости гидродинамической теории.
В действительности при выводе уравнения (3.47) мы неявно
предполагали, что и в плазме частицы одного вида сталкиваются
между собой. Это предположение было внесено в уравнение (3.39),
когда мы приняли, что распределение по скоростям является макс-
велловским. Обычно такое распределение возникает в результате
частых столкновений. Наше предположение, однако, использова-
лось только при вычислении среднего от v2xr. Любое другое распре-
деление с той же средней величиной дало бы аналогичный резуль-
тат. Следовательно, гидродинамическая теория в целом не очень
чувствительна к отклонениям от максвелловского распределения,
хотя в некоторых случаях эти отклонения существенны и тогда
для описания плазмы нужно применять кинетическую теорию.
Еще одно эмпирическое подтверждение действенности гидроди-
намической теории сделал Ирвинг Ленгмюр. Работая с электроста-
тическими зондами, которые сейчас носят его имя, Ленгмюр обна-
ружил, что функция распределения электронов оказалась гораздо
ближе к максвелловской, чем этого можно было ожидать, исходя
из значения частоты столкновений. Это явление, названное пара-
доксом Ленгмюра, иногда приписывают влиянию высокочастотных
74
Гл. 3. Плазма как жидкость
колебаний, однако удовлетворительного объяснения парадокса до
сих пор нет. Парадокс Ленгмюра — это, по-видимому, один из не-
многих случаев в физике плазмы, когда природа работает на нас.
Гидродинамическую модель можно применять к плазме еще и
потому, что при наличии магнитного поля оно в определенном
смысле может играть роль столкновений. Пусть, например, частица
ускоряется в электрическом поле Е. Если бы ей позволили двигаться
свободно, то ее скорость непрерывно бы росла. Однако при частых
столкновениях частица набирает только конечную скорость, про-
порциональную Е. В частности, электроны в медном проводе дви-
жутся вместе со скоростью v = цЕ, где р, — подвижность. Маг-
нитное поле также ограничивает свободу передвижения частиц,
заставляя их вращаться по ларморовским орбитам. Например,
электроны в плазме тоже дрейфуют как целое со скоростью, про-
порциональной Е: vE — Е х В/52. В этом смысле бесстолкнови-
тельная плазма ведет себя как жидкость со столкновениями. Разу-
меется, частицы могут свободно двигаться вдоль силовых линий
магнитного поля, и гидродинамическое рассмотрение не совсем
подходит для описания движения в этом направлении, однако для
движений, перпендикудярных В, гидродинамическая теория является
хорошим приближением.
3.3.5. Уравнение непрерывности
Из закона сохранения вещества следует, что общее число частиц N
в объеме V может меняться только в том случае, когда существует
поток частиц через поверхность 5, охватывающую этот объем. По-
скольку плотность потока частиц равна пи, из теоремы Остроград-
ского—Гаусса имеем
= — (f)nu-dS = — [y-(nu)dV. (3.49)
dt J dt j J
v v
Поскольку это справедливо для любого объема V, подынтегральные
выражения должны быть равны друг другу.
(dn/dt) + v-(nu) = 0. (3.50)
Такое уравнение непрерывности справедливо для любого сорта ча-
стиц. При наличии любого источника или стока частиц их нужно
добавлять в правую часть этого уравнения.
3.3.6. Уравнение состояния
Для того чтобы замкнуть систему гидродинамических уравнений,
необходимо еще одно соотношение. Для его вывода мы можем ис-
3.3. Гидродинамические уравнения
75
пользовать термодинамическое уравнение состояния, связывающее
Р и р:
p=Cpv, (3.51)
где С — постоянная, а у равна отношению удельных теплоемко-
стей Ср/С„. При этом величина vp определяется выражением
(Vp/p) = y(Vn/n). (3.52)
Если процесс сжатия изотермический, то vp = V (пКТ) =
= KTsjn, так что, очевидно, у = 1. При адиабатическом сжатии
температура КТ меняется, и потому величина у будет больше еди-
ницы. Постоянная у связана с числом степеней свободы N соотно-
шением
у = (2+ #)/#. (3.53)
Из применимости уравнения состояния следует, что тепловыми по-
токами в системе можно пренебречь, т. е. что теплопроводность
среды должна быть низкой. Опять-таки это положение справедливо
скорее для потоков, распространяющихся поперек магнитного
поля В, чем для параллельных ему. К счастью, большинство основ-
ных явлений в плазме можно описать в рамках простого приближе-
ния (3.51).
3.3.7. Полная система уравнений гидродинамики
Пусть для простоты плазма состоит только из двух компонент:
ионов и электронов. Обобщение на большее число компонент три-
виально. Плотности зарядов и токов в плазме даются соответст-
венно выражениями
= + j = MfV< + n4geve. (3.54)
Поскольку мы не будем больше рассматривать движение отдельных
частиц, скорость жидкости можно теперь обозначить через v, а не
через и. Пренебрежем столкновениями и вязкостыО, тогда уравне-
ния (3.1) — (3.4), (3.44), (3.50) и (3.51) образуют следующую си-
стему:
eov Е = щр<, 4- пде\ (3.55)
VXE=—В; (3.56)
V-B = 0; (3.57)
Цо"1 V X В = иды + пдече4-е0Ё; (3.58)
т^ [(dVjldt) 4- (v,• V) v;] = p^ (E 4- n,X B)—Vp,, j = i, e;
(3.59)
(dn.j/dt) + v-(n7v/) = 0, j — i,e- (3.60)
p^Cjriy, j = i, e. (3.61)
76
Гл. 3. Плазма как жидкость
скалярных неизвестных в системе 16: nt, пе, р(, ре, v{, ve, Е и В.
скалярных уравнений, очевидно, 18, поскольку каждое векторное
уравнение эквивалентно трем скалярным. Однако в этой системе
два уравнения Максвелла являются избыточными, поскольку со-
отношения (3.55) и (3.57) можно получить, взяв дивергенцию от
уравнений (3.58) и (3.56) [см. задачу (3.3)]. Совместное решение
системы из 16 уравнений с 16 неизвестными определяет самосогла-
сованный набор полей и движений в гидродинамическом прибли-
жении.
3.4. Дрейф жидкости перпендикулярно
магнитному полю В
Элемент объема жидкости состоит из множества отдельных частиц,
поэтому можно ожидать, что если ведущие центры отдельных ча-
стиц дрейфуют поперек магнитного поля, то и плазма как целое
будет совершать такой дрейф. Кроме того, поскольку в гидродина-
мических уравнениях появляется член Vp, существует и связан-
ное с ним дрейфовое движение, в котором участвуют элементы жид-
кости, а не отдельные частицы. Уравнение движения каждой ком-
поненты имеет следующий вид:
mn [(dv/d/)+ (v V) v] = срг (Е + v х В)—Vp. (3.62)
Рассмотрим отношение первого члена в левой части этого уравнения
ко второму слагаемому в правой части. Оно приближенно равно
тп icoy±
qnv^B
Здесь мы положили dldt — ico и учитывали только движение со
скоростью vx. Если дрейф медленный по сравнению с временным
масштабом ыу1, т. е. со < соС1 то первым членом в уравнении (3.62)
можно пренебречь. Мы пренебрежем также членом (v-V)v, а по-
том покажем, что это законно. Пусть поля Е и В однородны, а ве-
личины пи р имеют градиенты. Это типичная ситуация в том слу-
чае, когда столб плазмы удерживается магнитным полем (рис. 3.4).
Умножая уравнение (3.62) на В векторно и пренебрегая ле-
вой частью полученного равенства, имеем
О = <улг[Е X B + (v± х В) х В]—Vp X B = <7n[ExB-r(v± -В) —Vj-B2]—
—VP х В.
Следовательно,
v± = (ExB/B2) —(vpxB)/<7/iB2^v£ + vD, (3.63)
3.4. Дрейф жидкости перпендикулярно магнитному полю В
77
Рис. 3.4. Диамагнитные дрейфы в плазменном цилиндре.
где
v£ = ExB/B2.
(3.64)
vp = —(урх В)/дпВ2.
(3.65)
Скорость дрейфа v£ имеет такой же вид, как и в случае Е X В-
дрейфа ведущих центров. Кроме него появляется новый тип дрейфа
со скоростью Vp, который называется диамагнитным дрейфом.
Поскольку vp перпендикулярна направлению градиента, то
при Е = 0 член (v-v)v обращается в нуль, и мы правомерно им
пренебрегли. Если же Е = — #= 0, но и Vp направлены
в одну сторону, то (v-V) v по-прежнему равен нулю. В противном
случае должно существовать более сложное решение, связанное
с нелинейностью (v-V)v. Используя соотношение (3.52), скорость
диамагнитного дрейфа можно записать в виде
Vp± уКТ , (3.66)
еВ п - <
В частности, для изотермической плазмы в геометрии рис. 3.4, обо-
значив v« = n'r, мы получим следующие формулы, хорошо зна-
78
Гл. 3. Плазма как жидкость
Рис. 3.5. Происхождение диамагнитного дрейфа.
комые экспериментаторам, работавшим с Q-машинами1):
4Dl = {КТi/eB) {n'/n)Q, {п' == dn/dr<0), (3.67)
vDe= -{KTe/eB){n'/ri)Q.
Величину vD легко рассчитать по формуле
(3.68)
. — м/с,
В (Тл) Л
vD —
где Л — масштаб изменения плотности в метрах: Л = | п/п’ |.
Физическую причину этого дрейфа можно понять из рис. 3.5.
Здесь изображены орбиты ионов, вращающихся в магнитном поле.
Судя по густоте орбит, градиент плотности плазмы направлен влево.
Через любой данный элемент объема вниз движется больше частиц,
чем вверх, поскольку опускающиеся ионы выходят из области
с большим значением плотности плазмы. Таким образом, даже
в том случае, когда ведущие центры покоятся, существует
дрейф жидкости, скорость которого перпендикулярна V« и В.
Скорость диамагнитного дрейфа меняет знак вместе с q, поскольку
при перемене знака заряда направление вращения частиц меняется
на противоположное. Величина vD не зависит от массы частиц,
так как связь скорости с массой (~ /и-1/2) компенсируется зависи-
мостью от нее ларморовского радиуса (~ /и1/2); чем меньше масса
частицы, тем меньше перепад плотности на расстоянии порядка
ее гирорадиуса.
Поскольку ионы и электроны дрейфуют в противоположных на-
х) В Q-машине спокойная плазма создается посредством термической
ионизации атомов цезия или калия, ударяющихся о горячие вольфрамовые
пластины. Именно на Q-машинах были впервые измерены скорости диамаг-
нитного дрейфа.
3.4. Дрейф жидкости перпендикулярно магнитному полю В
79
Рис. 3.6. Дрейф частиц в огра-
ниченной плазме, иллюстриру-
ющий связь этого процесса
с гидродинамическим дрей-
фом.
Рис. 3.7. Измерение диамагнитного то-
ка в неоднородной плазме.
правлениях, в плазме возникает диамагнитный ток. При у = Z = 1
он равен
jD = ne(vD/-vDe) = (KTi + KTe)-^^ . (3.69)
Рассматривая движение отдельных заряженных частиц, каза-
лось бы, можно утверждать, что если их ведущие центры покоятся,
то тока в системе не будет. Однако при гидродинамическом описа-
нии плазмы в присутствии градиента давления диамагнитный ток
будет течь всегда, независимо от того, движутся ведущие центры
частиц или нет. Эти две точки зрения можно примирить, если учесть,
что все эксперименты ставятся в ограниченной плазме. Пусть плазма
находится в жестком ящике (рис. 3.6). Если вычислять полный
ток, исходя из теории движения отдельных частиц, то нужно учи-
тывать и частицы у стенок, траектории движения которых имеют
вид циклоид. Поскольку слева частиц больше, чем справа, то об-
щий ток будет направлен вниз, что согласуется с результатом, по-
лученным в рамках гидродинамического анализа.
Читателя^может не удовлетворить это объяснение, поскольку
в нем необходимо считать стенки отражающими. Если бы стенки
были поглощающими или их не было вовсе, то обнаружилось бы,
что в системе возникают электрические поля, потому что частиц
одного сорта (с большим ларморовским радиусом) в некоторых ме-
стах собралось бы больше, чем частиц другого сорта. В этом случае
возникает дрейф ведущих центров, и картина станет гораздо более
сложной. Приведем еще один пример, доказывающий существова-
80
Гл. 3. Плазма как жидкость
Рис. 3.8. В неоднородном магнитном поле В ведущие центры частиц совер-
шают дрейф, а элементы объема жидкости не дрейфуют.
ние диамагнитного тока. Пусть мы пытаемся измерить этот ток с по-
мощью зонда (рис. 3.7). Зонд представляет собой трансформатор
с сердечником из магнитного материала. Его первичная обмотка —
это плазменный ток, пронизывающий сердечник, а вторичная —
многовитковая обмотка вокруг сердечника. Пусть сердечник тон-
кий и поэтому не мешает движению частиц. Из рис. 3.7 ясно, что
прибор будет измерять результирующий ток, направленный вверх,
поскольку слева плотность частиц, вращающихся вокруг обмотки,
будет больше, чем справа. Следовательно, диамагнитный ток вполне
реален. Из этого примера видно, что с одиночными частицами ра-
ботать трудно, а гидродинамическая теория, если ее последова-
тельно применять, дает правильные результаты несмотря на то,
что она оперирует с «фиктивными» дрейфами наподобие димагнит-
ного.
А что можно сказать с гидродинамической точки зрения о гра-
диентном дрейфе и дрейфе из-за кривизны силовых линий, которые
имели место для одиночных частиц? При гидродинамическом опи-
сании дрейф из-за кривизны силовых линий по-прежнему сущест-
вует, поскольку при движении вдоль изгиба магнитного поля все
частицы в элементе жидкости подвергаются воздействию центро-
бежной силы. Для описания этого эффекта в правую часть уравне-
ния движения жидкости нужно добавить член Fct — nmv\lRc =
= пКТ и /Яс. Центробежная сила эквивалентна силе тяжести Mng,
где g = КТ ц/МЯс. Как и в случае одиночных частиц, она приво-
дит к дрейфу со скоростью ve = (ml q) (g X B)/B2 [выражение
(2.18) ].
Градиентный дрейф в жидкостях отсутствует. На основе термо-
динамических соотношений можно показать, что магнитное поле
не влияет на распределение Максвелла. Это связано с тем, что сила
Лоренца перпендикулярна скорости v и не может изменить энер-
гию частиц. Наиболее вероятное распределение в отсутствие маг-
нитного поля является также и наиболее вероятным распределением
3.4. Дрейф жидкости перпендикулярно магнитному полю В
81
при наличии В. Если f (v) в неоднородном поле В остается максвел-
ловской, а градиент плотности отсутствует, то импульс, передавае-
мый любому данному элементу жидкости, равен нулю. Дрейф в
жидкости отсутствует даже тогда, когда ведущие центры отдельных
частиц дрейфуют, поскольку скорости дрейфа частиц в элементе
жидкости взаимно компенсируются. Чтобы показать это наглядно,
рассмотрим орбиты.двух частиц, движущихся через элемент объема
жидкости в неоднородном магнитном поле (рис. 3.8). Поскольку
поле Е = О, ларморовский радиус меняется только из-за наличия
градиента магнитного поля В; ускорения частиц не происходит,
поскольку их энергия‘остается при движении постоянной. Если
две частицы имеют одинаковую энергию, то внутри элемента жид-
кости их скорости и ларморовские радиусы тоже будут одинако-
выми. Таким образом, когда при вычислении скорости элемента
жидкости складывают скорости пары частиц, они в точности ком-
пенсируют друг друга.
При наличии электрического поля Е картины движения жидко-
сти и отдельных частиц согласовать трудно. В этом случае эффект,
связанный с конечностью величины ларморовского радиуса, рас-
сматривавшийся в разд. 2.4, вызовет как дрейф ведущих центров,
так и дрейф жидкости. Но это не один и тот же дрейф. В действи-
тельности скорости этих дрейфов направлены в противоположные
стороны! Дрейф частиц мы рассматривали в гл. 2. Скорость гидро-
динамического дрейфа можно рассчитать, если известны недиаго-
нальные элементы тензора Р. Однако исключительно трудно объяс-
нить, почему так сильно разнятся эти два эффекта, ведь оба они
обусловлены конечностью ларморовского радиуса. Простая кар-
тина типа рис. 3.6 в этом случае бесполезна, поскольку при анализе
нужно учитывать очень тонкие эффекты, например такой: в при-
сутствии градиента п плотность ведущих центров не равна плот-
ности частиц!
Задачи
3.3. Покажите, что в системе уравнений Максвелла уравнения (3.55) и (3.57)
являются избыточными.
3.4. Покажите, что выражение для jo [правая часть формулы (3.69)] имеет
размерность плотности тока.
3.5. Покажите, что если при заданной ширине ящика ток, вычисленный по
движению остальных частиц, совпадает с током, величина которого рассчи-
тана по скорости диамагнитного дрейфа (рис. 3.6), то они останутся равными
при любой ширине ящика.
3.6. Изотермическая плазма удерживается между плоскостями х = ± а
в магнитном поле В = Вл. Распределение плотности имеет вид п =
= n0 (1—х2/а2).
а) Получите выражение для скорости диамагнитного дрейфа электронов voe
как функции х.
82
Гл. 3. Плазма как жидкость
б) Нарисуйте чертеж, показывающий, как распределена плотность и куда
направлена скорость по обе стороны от центральной плоскости, если
вектор магнитного поля В указывает на нас.
в) Оцените 0£>е при х = а/2, если В = 0,2 Тл, К.Т е — 2 эВ, а = 4 см.
3.7. В симметричном цилиндрическом столбе плазмы, помещенном в одно-
родное магнитное поле В, п (г) = поехр ( — г2/гц), nt = пе = поехр (еф/КТ^.
а) Покажите, что скорости V£ и у^е равны по величине, но противоположны
по направлению.
б) Покажите, что плазма вращается как твердое тело.
в) В системе отсчета, вращающейся со скоростью V£, некие плазменные
волны (так называемые дрейфовые волны) распространяются с фазовой ско-
ростью Уф = 0,5 Усе- Какова величина Уф в лабораторной системе? Нари-
суйте на плоскости г0 стрелки, показывающие относительные величины и на-
правления V£, У£>е и Уф в лабораторной системе.
3.8. а) Для плазмы, рассмотренной в задаче 3.7, найдите плотность диамаг-
нитного тока как функцию радиуса.
б) Вычислите jo в единицах А/м2, если В = 0,4 Тл, по=1О1вм_3, КТе~
— K.Tt = 0,25 эВ, г = r0 = 1 см.
в) Какие частицы переносят этот ток в лабораторной системе: ионы, элек-
троны, или и те и другие?
3.9. На какую величину поле В на оси цилиндра уменьшает диамагнитный
ток, рассмотренный в предыдущей задаче? Указание: можно воспользоваться
законом Ампера, выбрав соответствующим образом контур.
3.5. Движение жидкости параллельно
магнитному полю
Вернемся к уравнению движения плазмы в гидродинамическом
приближении; г-компонента этого уравнения имеет вид
mn [dvjdt + (v- V) vz] = —dp/dz + qnEz. (3.70)
Конвективным членом часто можно пренебречь, поскольку он много
меньше члена dvzldt. Мы не будем приводить здесь сложных до-
водов, а просто рассмотрим случай, когда vz пространственно одно-
родна. Пользуясь уравнением (3.52), получаем
dvz/dt = (q/rri) Ez—(yKTImn) (dn/dz). (3.71)
Отсюда видно, что вдоль направления В плазма ускоряется под
действием суммы электростатической силы и силы, связанной с гра-
диентом давления. Особенно важный результат получается, если
применить уравнение (3.71) к безмассовым электронам. Переходя
к пределу т 0 и полагая q = — е, имеем х)
qEz = е (дф/дг) = (уКТе/п) (дп/дг). ' (3.72)
х) Почему нельзя считать, что vz -> оо, а величина mvz сохраняется по-
стоянной? Посмотрите, как изменяется энергия частицы!
3.5. Движение жидкости параллельно магнитному полю
83
%.%•. s'г; °.°°»*
Vp ------------------
Fp ------ ------------
F£ ------*► ------
Е -*-----— ------►
Ф ~ +
Рис. 3.9. Физическое обоснование соотношения Больцмана, связывающего
плотность и потенциал.
Электроны настолько подвижны, что их теплопроводность почти
бесконечна, поэтому их можно считать изотермическими и поло-
жить у=1. Интегрирование уравнения (3.72) дает
еф — КТе1пп + С
или
п = п0 ехр (еф/КТе).
(3.73)
Это и есть распределение Больцмана для электронов.
Каков его физический смысл? Электроны легкие, поэтому они
очень подвижны. Если бы на них действовала сила, то электроны
быстро бы ускорились до высоких энергий. Однако электроны
в массе своей не могут покинуть какую-либо область, оставив по-
зади большой ионный заряд. Следовательно, полная сила, действую-
щая на электроны, должна быть близка к нулю, т. е. электростатичес-
ские силы и силы, связанные с градиентом давления, должны с хо-
рошей точностью уравновешивать друг друга. Это условие и при-
водит к соотношению Больцмана. Заметим, что выражение (3.73)
применимо к каждой силовой линии в отдельности. Если нет меха-
низма, заставляющего электроны двигаться поперек В, то раз-
личные силовые линии могут быть произвольным образом «заря-
жены» до разных потенциалов. Подобное действие могут оказывать
проводники, на которых оканчиваются силовые линии, поэтому
экспериментатору нужно очень тщательно учитывать эти краевые
эффекты.
На рис. 3.9 схематически показано, что происходит, когда в
плазме образуется локальный сгусток плотности. Пусть градиент
Глава 4
ВОЛНЫ В ПЛАЗМЕ
4.1. Представление волн
Любое периодическое движение с помощью фурье-разложения можно
представить в виде суперпозиции гармонических колебаний с раз-
личными частотами со и длинами волн X. Простейшая волна пред-
ставляет собой одну из этих компонент. Волна обычно имеет сину-
соидальную форму, когда амплитуда колебаний мала. Этот случай
мы и будем рассматривать.
Любую величину, меняющуюся по синусоидальному закону,
например плотность п, можно записать в виде
п = nexp [i (k-r—со/)], (4.1)
где в декартовых координатах
k-r = kxx + kyy + kzz. (4.2)
Здесь п — постоянная, определяющая амплитуду волны, а к —
волновой вектор. Если волна распространяется вдоль оси х, то к
имеет только ^-компоненту и соотношение (4.1) принимает вид
п = п ехр [i (kx—со/)].
Записывая величины в экспоненциальном виде, мы подразуме-
ваем, что физический смысл имеет только вещественная часть этого
выражения. Пусть п вещественна; вскоре мы увидим, что это соот-
ветствует определенному выбору источника колебаний. В этом слу-
чае вещественная часть величины п равна
Re (п) = и cos (fee—со/). (4.3)
Точка постоянной фазы движется в волне таким образом, что
{d!dt)(kx—со/) = 0 или
_^=_^иф. (4.4)
dt k
Величина иф называется фазовой скоростью. Если отношение со/£
положительно, то волна движется вправо, т. е. с увеличением /
4.1. Представление волн
87
значение х возрастает таким образом, что величина kx—сохра-
няется. Если величина a/k отрицательна, то волна движется влево.
Ясно, что функцию п можно также записать в виде
п = п ехр [i (kx + to/)],
и тогда положительным значением <о/Л будут отвечать волны, дви-
жущиеся влево. Иногда используют и такую запись, но мы этого
делать не будем. Заметим также, что одновременная смена знаков
как у to, так и у k приводит к тем же физическим значениям плот-
ности [см. (4.3)].
Рассмотрим теперь другую связанную с волной осциллирующую
величину, скажем электрическое поле Е. Поскольку мы уже пред-
положили, что фаза величины п равна нулю, необходимо приписать
Е некоторую отличную от нуля фазу б:
E = Ecos(fex—(0*4-6), E = Eei(Ax-<‘>/+6), (4.5)
где Е — постоянный вещественный вектор. _
Обычно информацию о фазе включают в Е, считая величину Е
комплексной:
Е = Ёе‘бе‘“О = Ёсе'
где Ее — комплексная амплитуда. Зная последнюю, можно найти
фазу 6, поскольку Re (Ес) = Е cos 6, a Im (Ес) = Е sin 6; следо-
вательно,
tg6 = Im(Ec)/Re(Ec)- (4.6)
С этого момента мы будем предполагать, что амплитуды всех вели-
чин являются комплексными и в дальнейшем будем опускать ниж-
ний индекс с. Любую осциллирующую величину можно записать
в виде
gi — gi ехр [i (к • г — to/)], (4.7)
поэтому в последующих формулах gx может обозначать либо комп-
лексную амплитуду, либо выражение (4.7) в целом. Путаницы это
не создаст, поскольку в линейной теории волн в обеих частях всех
уравнений возникает один и тот же экспоненциальный множитель
и его можно сократить.
Задача
4.1. В так называемой дрейфовой волне амплитуды колебаний плотности
пг и потенциала Фг связаны соотношением
еФх to* + i а
п0 КТе to 4- i а.
Остальные входящие в эту формулу величины (кроме i) положительны.
88
Гл. 4. Волны в плазме
а) Получите выражение для сдвига фаз бмеждуФгИ^ (считайте для про-
стоты, что величина п± вещественна).
б) Пусть ©«о*. Опережает ли потенциал Фх величину пг по фазе или за-
паздывает по отношению к ней?
4.2. Групповая скорость
Фазовая скорость волны в плазме нередко превышает скорость
света с. Это, однако, не нарушает теорию относительности, по-
скольку бесконечно длинный волновой пакет постоянной ампли-
туды не может переносить информацию. (Например, если несущая
радиоволна не модулирована, то с ее помощью нельзя передать
никакую информацию.) Информация же, содержащаяся в модуля-
ции, перемещается не с фазовой, а с групповой скоростью, которая
всегда меньше с. Для иллюстрации сказанного рассмотрим моду-
лированную волну, образованную сложением («биением») двух
волн с почти равными частотами. Пусть эти волны записываются
в виде
E1^£0cos[(/s + kk)x— (®4- Д<о)£], -4g
£2 = £0cos [(fe—Ak)x—(co — Aco) /].
Частоты волн £x и £2 отличаются на величину 2Асо. Поскольку
каждая из волн должна иметь в среде определенную фазовую ско-
рость a/k, в волновых числах возникнет разность 2А&. Используя
обозначения а = kx—at, b = (АЛ)х — (A©) t, получаем
£14- £2 = £0cos(a-|-b) + £0cos(a—ft) = £0 (cos a cos 6—sinasin& +
+ cos a cos b + sin a sin b) = 2£0 cos a cos b-,
Е^ + Е^ 2£0 cos [(Afe) x—(A©) t] cos (kx—at). (4.9)
Это синусоидально модулированная волна (рис. 4.1). Огибающая
волны дается выражением cos [(Д£) х— (A®) t] и является носи-
телем информации. Она распространяется со скоростью Дсо/А£.
Перейдя к пределу Асо —0, определим групповую скорость сле-
дующим образом:
vTp = da/dk. (4-Ю)
Эта величина не может превышать скорости света с.
Рис. 4.1. Пространственное распределение электрического поля суммы двух
волн с близкими частотами.
4.3. Плазменные колебания
89
4.3. Плазменные колебания
Если электроны плазмы сместить относительно однородного ионного
фона, то в системе возникнет электрическое поле. Оно будет на-
правлено так, чтобы восстановить нейтральность плазмы, т. е. сдви-
гать электроны в их первоначальное местоположение. Из-за инер-
ции электроны проскочат свое положение равновесия и бу-
дут колебаться вокруг него с характерной частотой, которая
называется плазменной частотой. Эти колебания являются на-
столько быстрыми, что ионы не успевают откликнуться на осцилли-
рующее поле и их можно считать покоящимися. На рис. 4.2 свет-
лыми прямоугольниками показаны типичные элементы ионной жид-
кости, а темными — смещенные относительно них участки элек-
тронной жидкости. Возникающие сгустки заряда создают перио-
дическое в пространстве поле Е, которое стремится вернуть элек-
троны в нейтральные положения.
Мы выведем выражение для плазменной частоты в простейшем
случае, сделав следующие предположения: 1) магнитное поле от-
сутствует; 2) в плазме нет теплового движения {КТ = 0); 3) ионы
равномерно распределены в пространстве и неподвижны; 4) плазма
является бесконечно протяженной; 5) электроны движутся только
вдоль оси х. Как следствие последнего предположения, мы имеем
У=хд/дх, Е = Ех, VXE = O, Е=—V</>. (4.11)
Таким образом, переменное магнитное поле также отсутствует и ко-
лебания являются чисто электростатическими.
Уравнение движения и уравнение непрерывности для электро-
нов имеют следующий вид:
тпе [{dve/dt) + (уе V) vj = — епеЕ, (4.12)
(3ne/a/) + V-(neve) = 0. (4.13)
Для анализа нам потребуется единственное уравнение Максвелла,
которое не содержит В, а именно уравнение Пуассона. Этот случай
является исключением из сформулированного в разд. 3.6 общего
правила, согласно которому нельзя искать Е, пользуясь уравне-
нием Пуассона. Плазменные колебания являются высокочастот-
ными, важную роль в них играет инерция электронов, поэтому
в данном конкретном случае главный эффект связан именно с от-
клонением от нейтральности. Согласно сделанным предположениям,
мы можем записать уравнение Пуассона в виде
£оУ-Е = еодЕ/дх = е{П{ — пе). (4.14)
Уравнения (4.12) — (4.14) нетрудно решить, применяя проце-
дуру линеаризации. Она состоит в том, что амплитуда колебаний
считается малой, и поэтому членами, содержащими высокие сте-
пени амплитуды, пренебрегают. Сначала мы разделим все перемен-
90
Гл. 4. Волны в плазме
ные на две части: «равновесную», обозначаемую индексом 0, и
«возмущение», которое пометим индексом 1:
ne = «o + ni; v^Vo + Vj; E = E0 + Ej. (4.15)
Равновесные величины описывает состояние плазмы в отсутствие
колебаний. Поскольку мы предположили, что, прежде чем элек-
троны сместили, плазма была однородной, нейтральной и находи-
лась в покое, то
Vn0 = v0 = Ео = О,
(dn0/di) = (dv0/dt) = (ЭЕ0/й) = 0. (4.16)
Уравнение (4.12) в наших предположениях принимает вид
tn [(dvjdt) + (Vi • V) vj = — eEi. (4.17)
О
Член (vx-v) vx квадратичен по амплитуде и, проводя линеариза-
цию, мы им пренебрежем. Линейная теория справедлива только
в том случае, если величина | их | достаточно мала и такими квадра-
тичными членами действительно можно пренебречь. Аналогично
уравнение (4.13) можно записать в виде
{dnjdt) + V (n0Vi + nivx) = 0,
~(Г
или
(3n1/aO + «oV-Vi + v1-Vno = O. (4.18)
О
Заметим, что в уравнении (4.14) в положении равновесия nia = пе0,
а пц = 0 потому, что ионы считаются неподвижными. Следова-
тельно,
eov-Ex= —епх.
(4.19)
4.3. Плазменные колебания
91
Будем считать, 'что осциллирующие величины изменяются по гар-
моническому закону:
vx= гухехр [i (kx—и 01 > «1 = nxexp [i (kx—©/)],
Ej = EjX exp [i (kx—®£)]. (4.20)
Таким образом, производную по времени можно заменить на — iсо,
а градиент V — на i kx. Уравнения (4.17) — (4.19) принимают
тогда следующий вид:
— im®Vi= —еЕг, (4-21)
— i ©«! = — noi kvu (4.22)
i /se0E'i= —en^ (4.23)
Исключая отсюда и Е1г из уравнения (4.21) получаем
, \ ( —е) (— "о i kvt) . п0е2 ,,
— 1 = (—е) ---— -3-----— = — 1 —2(4.24)
i Ле0 (— iw) е0<в
Если скорость Vr не равна нулю, то мы должны считать, что
со2 = пое2!тго. Таким образом, плазменная частота
<йр = (поёг/е.от)1 /2 р ад/с. (4.25)
Для численных расчетов можно пользоваться приближенной фор-
мулой
®р/2л = /р » 9д/«- (4.26)
Плазменная частота зависит только от плотности плазмы и яв-
ляется одним из основных ее параметров. Поскольку масса элек-
трона т мала, плазменная частота обычно очень велика. Например,
для плазмы плотностью п = 1018 м-3 имеем fp ж 9 (1018)12 =
= 9-109 с-1 = 9 ГГц. Излучение на fp чаще всего попадает в СВЧ-
диапазон. Можно сравнить ьзр с другой электронной частотой, а
именно с циклотронной частотой а>с- Численная формула для ее
расчета имеет вид
®с/2л = /Се«28 ГГц/В(Тл). (4.27)
Таким образом, если п яз Ю18 м-3, то при В = 0,32 Тл электрон-
ная циклотронная частота примерно равна электронной плазмен-
ной.
Из формулы (4.25) следует, что частота плазменных колебаний
должна зависеть только от п. В частности, и не зависит от k, поэ-
тому групповая скорость dmldk равна нулю, и возмущение плот-
ности в плазме не распространяется. Почему это происходит? При-
чину можно понять с помощью аналогии с механической системой
(рис. 4.3). Представим себе тяжелые шарики, подвешенные на пру-
92
Гл. 4. Волны в плазме
Рис. 4.3. Волна в системе независимых осцилляторов.
жилках на одинаковых расстояниях друг от друга. Если пружинки
одинаковы, то каждый из шариков будет совершать вертикальные
колебания с одной и той же частотой. Если шарики начинают дви-
жение при соответствующих фазах относительно друг друга, то
в системе может образоваться волна, бегущая в том или ином на-
правлении. Частота колебаний будет определяться пружинами,
однако длину волны можно выбрать произвольной. Заметим, что
такая волна не оказывает никакого воздействия на покоящиеся
концевые шарики; ясно, что начальное возмущение в этой системе
останется локализованным и никуда распространяться не будет.
Стоячие или бегущие волны, которые можно создать в такой це-
почке, напоминают волны на натянутой веревке, но в отличие от
первых волны на веревке могут распространяться вдоль нее и пере-
носить энергию, потому что каждый участок веревки связан с со-
седними участками.
Рассмотренная аналогия не является совершенно точной, по-
скольку в плазменных колебаниях частицы движутся вдоль вол-
нового вектора к, а не поперек него. Легко видеть, однако, что если
электроны не сталкиваются с ионами и друг с другом, то и в случае
продольных колебаний их все равно можно рассматривать как не-
зависимые осцилляторы, только двигаться они будут (рис. 4.3)
в горизонтальном направлении. А как поведет себя электрическое
поле? Сможет ли оно выйти из области начального возмущения
и вызвать колебания близлежащих слоев плазмы? В нашем при-
мере — нет, потому что электрическое поле, создаваемое равным
Рис. 4.4. В ограниченной среде плазменные колебания распространяются
благодаря полям, возникающим на границах системы.
4.4. Электронные плазменные волны
93
числом положительно и отрицательно заряженных бесконечных
плоских слоев, равно нулю; однако в любой конечной системе
плазменные колебания будут распространяться. На рис. 4.4 пока-
зана цилиндрическая труба, в которую заключены области с поло-
жительными и отрицательными зарядами, создаваемые плазменным
колебанием. Возникающее на торцах цилиндра электрическое поле
приводит к тому, что появляется связь между отдельными слоями,
и колебание больше не остается локализованным.
Задачи
4.2. Вычислите плазменную частоту с учетом движения ионов и подтвердите
таким образом наше предположение о том, что ионы остаются в покое. (Ука-
зание: включите в уравнение Пуассона член, пропорциональный п1(-, и вос-
пользуйтесь уравнениями движения и непрерывности для ионов.)
4.3. Для случая простого плазменного колебания, в котором ионы не-
подвижны, а зависимость от координат и времени имеет вид ехр [i (kx—со/)],
вычислите фазы величин Ф1Г Ег и vlt считая, что фаза плотности пг равна
нулю. Проиллюстрируйте фазовые сдвиги, нарисовав синусоидальные волны,
изображающие nlf Фх, Ег и v1 как функции координаты х и как функции
времени t при соМ>Ои при со/k < 0. Заметим, что временные зависимости
можно получить, перемещая изображения пространственных распределений
в соответствующем направлении, как если бы волны проходили мимо покоя-
щегося наблюдателя.
4.4. Запишите линеаризованное уравнение Пуассона, использованное при
анализе простейших плазменных колебаний, в виде V-(eE) = 0 и получите
выражение для диэлектрической проницаемости е, справедливое для про-
дольных высокочастотных движений.
4.4. Электронные плазменные волны
Кроме конечных размеров системы существует и другой эффект,
который может вызвать распространение плазменных колебаний.
Это тепловое движение. Тепловые электроны, проникающие в слои
плазмы, прилегающие к области, в которой имеют место колебания,
переносят информацию о том, что происходит в этой области. Плаз-
менные колебания в этом случае более точно можно назвать плазмен-
ной волной. Мы можем легко учесть этот эффект, добавив в урав-
нение движения (4.12) член —Vpe- Согласно формуле (3.53), в од-
номерном случае у = 3. Следовательно,
\7ре = ЗКТе\?пе = 3KTev («о + «1) = ЗКТех (дп^дх),
и линеаризованное уравнение движения принимает вид
тп0 (dvjjdt) = — еп0Е j—ЗК TJidnldx). (4.28)
Заметим, что при линеаризации мы пренебрегли членами (dv^dt),
п1Е1 и (vj-v) vx. С учетом соотношений (4.20) уравнение (4.28)
94
Гл. 4. Волны в плазме
можно записать в виде
— imci)n0o1 =—enoEj—3KTe\knr. (4.29)
Величины Ег и пг по-прежнему определяются из уравнений (4.23)
и (4.22), и мы имеем
i — [еп0 (—e/i fts0) + ЗКТе i ft] (n0 i ft/i to) Uj:
®2Vi = [(n0e2/e0m) + 3 (KTek2lm)] v^,
w2 = (o2p + ^-ft2vU. (4-30)
где Утепл = 2KTelm. Частота теперь зависит от ft, и групповая ско-
рость имеет конечное значение:
2(0 d w = -у- Vreim2ft dft,
Угр —d(i)/dft = - Отепл (ft/(i)) =: -— ^тепл/Уф- (4.31)
Групповая скорость оГр плазменных волн всегда меньше скорости
света с. Это легко увидеть из графика зависимости (4.30). Такая
дисперсионная кривая о (ft) изображена на рис. 4.5. Для данной
точки Р на этой кривой фазовая скорость равна тангенсу угла на-
клона прямой, соединяющей эту точку с началом координат. Наклон
касательной к кривой в точке Р определяет величину групповой ско-
рости. Ясно, что она всегда меньше, чем (3/2)12 итепл, что в свою оче-
редь для рассматриваемого нами нерелятивистского случая много
меньшее. Заметим, что при больших ft (малых X) информация перено-
сится с тепловой скоростью частиц. При малых ft (больших X) ско-
рость ее распространения остается меньше итепл, даже если Цф боль-
Рис. 4.5. Дисперсионная кривая
для электронных плазменных
волн (они же ленгмюровские ко-
лебания и волны Бома—Гросса).
Рис. 4.6. Схема эксперимента Луни —
Брауна по возбуждению плазменных
колебаний.
4.4. Электронные плазменные волны
95
Разрядный ток, мА
Рис. 4.7. Зависимость квадратов наблюдавшихся в эксперименте частот от
плотности плазмы, которая обычно пропорциональна разрядному току. На
вставке показаны наблюдавшиеся распределения интенсивности в колеба-
ниях. Они свидетельствуют о том, что каждой группе экспериментальных
точек соответствует своя стоячая волна. [Из работы: Looney D. Н.,
Brown, S. С., Phys. Rev., 93, 965(1954).]
ше Утепл- Это связано с тем, что при больших X градиент плотности
в волне мал и тепловое движение передает прилегающим слоям
очень небольшой импульс.
О существовании плазменных волн было известно еще
с 1920-х гг. со времен Ленгмюра. Однако только в 1949 г. Бом и
Гросс разработали детальную теорию, описывающую возбуждение
и распространение этих волн. Самый простой способ возбудить
плазменные волны — это приложить осциллирующий потенциал
к сетке или к набору сеток, помещенных в плазму. Однако в то
время генераторы гигагерцевого диапазона еще не были распро-
странены и вместо них в экспериментах по возбуждению плазмен-
ных волн использовались пучки электронов. Если электроны пучка
сгруппированы в сгустки, проходящие мимо данной точки с часто-
той fp, то они будут генерировать на этой частоте электрическое
поле и, следовательно, возбуждать плазменные колебания. Нет
необходимости заранее создавать такие сгустки электронов; после
того как в плазме возникнут колебания, они сами сгруппируют
электроны, а это в свою очередь приведет к росту плазменных ко-
лебаний благодаря положительной обратной связи. Первый экспе-
римент по проверке этой теории выполнили Луни и Браун в 1954 г.
Их прибор представлял собой стеклянную колбу диаметром около
10 см (рис. 4.6). Плазма, заполнявшая колбу, создавалась в парах
ртути при низком давлении (3-10~3 мм рт. ст.) с помощью электри-
ческого разряда между катодом К и анодным кольцом А. Электрон-
96
Гл. 4. Волны в плазме
ный пучок формировался в боковом отводе, где помещалась отри-
цательно заряженная нить накала. Эмиттированные электроны
ускорялись напряжением 200 В и выстреливались в плазму через
маленькое отверстие. Для регистрации колебаний использовался
тонкий подвижный проволочный зонд, подсоединенный к прием-
нику радиосигнала. На рис. 4.7 показана полученная в экспери-
менте зависимость квадрата частоты наблюдаемых колебаний f1
от тока разряда, который обычно пропорционален плотности
плазмы. Эта зависимость линейная, что в целом согласуется с вы-
ражением (4.26). Отклонения от прямой можно, казалось бы, при-
писать влиянию члена /г2г4епл из формулы (4.30), однако следует
заметить, что в эксперименте наблюдались не все частоты; вели-
чина k должна была быть такой, чтобы на длине плазменного столба
могло уложиться полуцелое число длин волн. Слева на рис. 4.7 по-
казаны распределения поля в таких стоячих волнах. Предсказан-
ные ранее распространяющиеся волны в этом эксперименте уви-
деть не удалось. Вероятнее всего, это объясняется тем, что пучок
был очень тонкий и вследствие теплового движения электроны по-
кидали его, унося с собой энергию колебаний. К тому же оказа-
лось, что электроны окончательно собирались в сгустки не в самой
плазме, а в колеблющихся слоях у концов плазменного столба.
Этот ранний эксперимент показал, что для создания в лаборатории
тех условий, которые предполагает теория однородной плазмы, не-
обходимо большое искусство.
Эксперименты, проведенные в последнее время, с большой точ-
ностью подтвердили, что дисперсионное соотношение Бома—Гросса
(4.30) справедливо. В качестве примера современного эксперимен-
тального метода рассмотрим работу Баррета, Джонса и Франк-
лина. Схема их установки показана на рис. 4.8. Цилиндрический
столб спокойной плазмы был получен на Q-машине посредством
термической ионизации атомов цезия на горячих вольфрамовых
пластинах (на рисунке не показаны). Сильное магнитное поле за-
ставляло электроны двигаться только вдоль столба плазмы. Волны
возбуждались с помощью проволочного зонда, подсоединенного
к источнику колебаний, а регистрировались вторым, подвижным
зондом. Плазма была окружена металлическим кожухом, представ-
лявшим собой волновод, частота отсечки которого была выбрана
так, чтобы не допустить взаимодействия между зондами из-за рас-
пространения в плазме обычных электромагнитных СВЧ-колебаний.
Бегущие плазменные волны регистрировались интерферометриче-
ским методом: переданный и полученный сигналы детектировались
кристаллическим смесителем, который давал на выходе большой
постоянный ток, если сигналы были в фазе, и не давал тока, если
сдвиг фаз между сигналами составлял 90°. На рис. 4.9 показаны
зависимости результирующего сигнала от положения зонда в плаз-
менном столбе при различных плотностях плазмы. Для понижения
уровня шумов в эксперименте использовался метод синхронного
4.4. Электронные плазменные волны
Рис. 4.8. Схема эксперимента по измерению параметров плазменных волн
[Из работы; Barrett Р. J., Jones Н. G., Franklin R. NPlasma Physicks,
10, 911 (1968).]
детектирования: сигнал возбуждения модулировался с частотой
500 кГц, поэтому и выходной сигнал должен оказаться промодули-
рованным с этой же частотой. Регистрируя только компоненту сиг-
нала с частотой 500 кГц, экспериментаторы избавились от шумов
на других частотах. Зависимости, представленные на рис. 4.9, по-
зволяют найти в каждом случае волновое число k. Изменяя частоту
<о, авторы получили зависимость величины (со/<ор)2 от ka, где а —
радиус плазменного столба (рис. 4.10). Разным кривым на этом
рисунке отвечают разные значения ира/уТепл- При игепл = 0
имеем кривую, отмеченную знаком оо. Она соответствует диспер-
сионному уравнению со = сор. В случае сы #= 0 кривые, изоб-
раженные на рисунке, соответствуют дисперсионной кривой, пред-
ставленной на рис. 4.5. Экспериментальные точки хорошо согла-
суются с теоретическими кривыми. Уменьшение со при малых ka
связано с влиянием ограниченности системы, которое иллюстри-
рует рис. 4.4. Впрочем, в данном эксперименте это отклонение мо-
жет быть связано и с другими причинами. Дело в том, что для вы-
полнения граничного условия, налагаемого из-за наличия прово-
дящего кожуха, т. е. условия Е = 0 на проводнике, плазменные
4 Заказ 3170
ШЛА
nQ - 2- 10ю см3
f = 950 МГц
X = 3,5 см
WVWWWvx
п0= 4'JO3 см'3
Г = 170 МГц
Л = 7,3 см
|М
п0 = !• 10 7 см ~3
F = 20 МГц
К ~ 5,1 см
Рис. 4.9. Пространственное распределение возмущения плотности в плазмен-
ной волне, измеряемое с помощью интерферометра, который перемножает
мгновенные значения сигналов от двух зондов и берет от произведения сред-
нее по времени. Интерферометр настроен на частоту волны, которая зависит
от плотности. Затухание, заметное при малых плотностях, вызвано шумами
в плазме. [Из работы: Barrett Р. J., Jones Н. G.t Franklin R. M.t Plasma
Physics, 10, 911 (1968).]
Рис. 4.10. Сравнение расчетной дисперсионной кривой с измерениями для
случая электронных плазменных волн, распространяющихся в цилиндре
радиусом а. [Из работы: Barrett Р. J., Jones Н. G., Franklin R, Л\, Plasma
Physics, 10, 911 (1968).]
4.4. Электронные плазменные волны
99
Рис. 4.11. Фронты волн, движущихся под углом к направлению магнитного
поля, вдоль поля разделены между собой расстоянием, которое больше длины
волны %.
волны должны распространяться под некоторым углом к магнит-
ному полю. Деструктивная интерференция между теми бегущими
волнами, у которых радиальная компонента волнового вектора к
направлена наружу, и теми волнами, у которых она направлена
внутрь, и позволяет удовлетворить граничному условию Е = 0.
Однако если волна распространяется под углом к магнитному
полю, то расстояние между ее максимумами и минимумами, изме-
ряемое вдоль поля, будет больше чем Х/2 (рис. 4.11). Поскольку
электроны в сильном магнитном поле В могут двигаться только
вдоль В, они будут взаимодействовать именно с этим, более длинно-
волновым колебанием. В результате электроны будут двигаться
медленнее, чем это предсказывается в теории волн в изотропной
плазме, и частота раскачиваемых ими колебаний окажется меньше
чем (ор.
Задачи
4.5. Электронная плазменная волна распространяется в однородной плазме
с параметрами КТе = 100 эВ, п = 101в м—3, В = 0. Пусть частота волны
равна f = 1,1 ГГц. Какова длина волны в сантиметрах?
4.6. а) Изучите влияние столкновительного затухания на распространение
плазменных волн (ленгмюровских колебаний). Для этого добавьте к правой
части уравнения движения электронов член —mnvv и заново выведите дис-
персионное уравнение при Те — 0.
б) Выпишите точное выражение для Im (св) и покажите, что его знак указы-
вает на затухание волны со временем.
4*
100
Гл. 4. Волны в плазме
4.5. Звуковые волны
В качестве введения в теорию ионно-звуковых волн кратко рас-
смотрим теорию звуковых волн в обычном воздухе. Пренебрегая
вязкостью, мы можем записать следующее уравнение Навье—Стокса:
р [(dv/dt) + (v • v) v] = — VP = — YPVp/p- (4.32)
Уравнение непрерывности имеет вид
(3p/dO + V-(pv) = 0.. (4.33)
Линеаризуя эти уравнения вблизи положения равновесия при по-
стоянных р0 и р0, имеем
— i wpoVx = — ур0 i kpx/po, (4.34)
— i (opi + poi k-Vi = 0. (4.35)
Здесь мы снова предположили, что зависимость всех величин в
волне от координат и времени имеет вид exp [i (к-г—at) ]. В случае
плоской волны, когда k = kx, v = vx, после исключения рх полу-
чаем
— i ®povx = — (уро/ро) i k (ро i kvji co),
co2^ = k2v3 (ypo/po)
или
(alk) (ypo/po)12 = (yKTIM)12 = cs. (4.36)
Это формула для скорости звуковых волн в нейтральном газе, ко-
торые представляют собой волны сжатия, распространяющиеся от
одного слоя к другому вследствие столкновений составляющих
его молекул. Аналогичное явление имеет место и в плазме, причем
даже если в ней нет нейтральных атомов, а столкновения проис-
ходят редко. Подобные колебания называются ионно-звуковыми
или ионными волнами.
4.6. Ионно-звуковые волны
В бесстолкновительной плазме обычные звуковые волны распро-
страняться не могут, однако из-за того, что ионы плазмы заряжены,
они могут передавать колебания друг другу через действие элек-
трического поля. Поскольку ионы, участвующие в таких движе-
ниях, обладают большой массой, эти колебания будут низкочастот-
ными и для их анализа можно применить плазменное приближение,
о котором шла речь в разд. 3.6. Таким образом, предположим, что
щ = пе — п, и не будем пользоваться уравнением Пуассона. Урав-
4.6. Ионно-звуковые волны
101
нение движения ионной жидкости в отсутствие магнитного поля
записывается в виде
Мп [(dv//dZ)+ (vr V) Vf] = enE — Vp= — епуф—ViKTffn. (4.37)
Здесь мы предположили, что Е = — и воспользовались урав-
нением состояния. Проводя линеаризацию и считая волны
плоскими, имеем
— i (лМпоиц = —enoi k<j>r—yiKT t i knr. (4.38)
Что касается электронов, то мы можем положить т = 0 и восполь-
зоваться аргументами, изложенными в разд. 3.5, где рассматрива-
лось движение вдоль магнитного поля В, применив их на этот раз
при В — 0. Для равенства сил, действующих на электроны, необ-
ходимо, чтобы
«р(-т^) - ".(1 + ~^+ )•
поэтому возмущение плотности электронов, а следовательно, и
ионов, будет равно
п1 = п0(^1/КТе). (4.39)
Величина п0 в распределении Больцмана равна плотности равновес-
ной плазмы, поскольку мы предположили, что в этом случае Ео=О,
и потому можем считать, что равновесный потенциал <j>0 = 0. За-
метим также, «что при выводе линейного уравнения (4.39) мы пре-
небрегли в разложении экспоненты членами более высоких поряд-
ков.
Теперь нам осталось рассмотреть лишь линеаризованное урав-
нение непрерывности для ионов. Из соотношения (4.22) имеем
i ©П1 = n0 i kv(1. (4.40)
Подставляя в уравнение (4.38) и гциз выражений (4.39) и (4.40),
получаем
i а>Мп0Уц — [еп0 i k (КТе!еп0) + yiKTtik] (noikvtl/ia),
co2 = /г2 [(KT'/M) + (yKTJM)],
to / KTe + yjKTj \П2
k k M )
(4.41)
Это дисперсионное уравнение для ионно-звуковых волн-, vs обозна-
чает здесь скорость звука в плазме. Поскольку мы предположили,
что рассматриваемые волны плоские, т. е. ионные облака сжимаются
только в одном направлении, то можно считать, что ft = 3. Элек-
троны по отношению к этим волнам движутся настолько быстро,
что их температура успевает повсюду выровняться, и поэтому для
них уе = 1. Если электроны не являются изотермическими, то в
формуле (4.41) перед КТе нужно поставить коэффициент уе.
102
Гл. 4. Волны в плазме
Дисперсионная кривая для ионно-звуковых волн (рис. 4.12}
ведет себя совсем не так, как кривая для электронных (ленгмюров-
ских) волн (см. рис. 4.5). Плазменные колебания представляют
собой волны с постоянной частотой, незначительные поправки к ко-
торой связаны с тепловыми движениями. Ионные колебания — это
волны, имеющие постоянную скорость-, они могут существовать
только в том случае, когда в плазме есть тепловое движение. Груп-
повая скорость ионно-звуковых волн равна фазовой. Причины раз-
Рис. 4.12. Дисперсионная кривая для ионно-звуковых волн в пределе ма-
лого дебаевского радиуса.
личия между плазменными и ионно-звуковыми волнами можно
понять из следующей физической картины. В случае электронных
колебаний частицы иного сорта (ионы) в них не участвуют. В ионно-
звуковых колебаниях, напротив, частицы другого сорта (электроны)
никак нельзя считать неподвижными; действительно, электроны
всюду следуют за ионами и стремятся скомпенсировать электриче-
ские поля, создаваемые ионными сгустками. Но это экранирование
не является полным; как показано в разд. 1.4, из-за теплового
движения электронов за пределы экранирующего облака может
просочиться потенциал порядка КТе1е. Поэтому в ионно-звуковой
волне происходит следующий процесс. Ионы перераспределяются
и создают области разрежения и сжатия, как в обычной звуковой
волне. Области сжатия стремятся расширяться и занять области
разрежения по двум причинам. Во-первых, ионы расплываются
из-за теплового движения; этому эффекту соответствует второй
член подкоренного выражения в формуле (4.41). Во-вторых, вследст-
вие того что ионы в сгустках положительно заряжены, они стре-
мятся рассеяться из-за возникающего в результате их взаимодейст-
вия электрического поля. Это поле, однако, почти полностью экра-
нируется электронами, и на ионные сгустки действует только era
малая часть, пропорциональная КТе. Упомянутый эффект приво-
дит к появлению первого члена в формуле (4.41). Ионы из-за своей
инерции проскакивают положение равновесия, и в плазме возни-
кает волна разрежений и сжатий.
Второй из рассмотренных эффектов приводит к интересному
следствию: ионно-звуковые волны существуют даже в том случае,.
4.7. Обоснованность плазменного приближения 103
когда величина очень мала. В нейтральном газе этого не про-
исходит [см. формулу (4.36) ]. Скорость звука в плазме при Ti = 0
дается выражением
ns = (KTe/M)I/2. (4.42)
Такие колебания часто наблюдаются в лабораторной плазме, для
которой обычно выполняется равенство Tt Те. В этом пределе
скорость звука зависит от температуры электронов (поскольку
электрическое поле в волне пропорционально 7г) и от массы ионов
(поскольку она является мерой инерции ионной жидкости).
4.7. Обоснованность плазменного приближения
При выводе выражения для скорости ионно-звуковых волн мы
пользовались условием нейтральности /г(- = пе, но считали Е от-
личным от нуля. Чтобы увидеть, какая при этом вносится погреш-
ность в решение, будем считать, что п, отличается от пе и запишем
линеаризованное уравнение Пуассона в виде
е0v • Ег = e0fe2^i = е (па—пе1). (4.43)
Возмущение плотности электронов определяется из линеаризован-
ного уравнения Больцмана:
nA = n0(e<hlKTe). (4.44)
Подставляя это соотношение в уравнение (4.43), имеем
eo^i [^ + (nZ/еоЯЛ)] = епп,
(1+ &2^d) = бЯлЛо- (4.45)
Возмущение плотности ионов можно определить из линеаризован-
ного уравнения непрерывности (4.40):
пц = (fe/to) п0Оц. (4.46)
Подставляя и п(1 из соотношений (4.45) и (4.46) в уравнение
движения ионов (4.38), находим
/ епп i k еХп \ / ь \
i = I--------------------------- {i k I (-----------) п0Оц.
V e0 l + fe2^ J
k1 ( n0e2eX~lXn \
®2 = — + У1КТ1 ’ (4’47>
M \ 1 + k%?D )
_____1___
k M 1 + /г2Х2о M J
Последнее соотношение аналогично выведенной ранее формуле
(4.41) и отличается от нее только множителем (1 + &2Xd)-1 перед
104
Гл. 4. Волны в плазме
КТе/М. Наше предположение о том, что гц = пе, внесло, таким
образом, в ответ погрешность порядка Ad = (2ctXd/X)2. Поскольку
в большинстве экспериментов очень мала, плазменное прибли-
жение справедливо почти для всех длин волн (за исключением са-
мых коротких).
4.8. Различие между ионно-звуковыми
и плазменными волнами
Если рассматривать коротковолновые ионно-звуковые колебания
полагая, что Ad > 1, то уравнение (4.47) примет вид
(332^k2{nQe2I^Mk2')^-- ще2/^М е=Й2, (4.49)
где Qp — ионная плазменная частота (для простоты мы также пе-
решли к пределу 7\ -> 0). Следовательно, при малых длинах волн
Электронные
волны
Ионно-звуковые
волны
Рис. 4.13. Сравнение дисперсионных кривых, отвечающих электронным плаз-
менным волнам (ленгмюровским колебаниям) и ионно-звуковым волнам.
Ленгмюровский зонд
Вакуумная камера
Генератор
синусоидально-
го сигнала
Соленоид
Горячая
вольфрамовая
пластина —
Напряжение
постоянного
смещения
.................|H!J
осциллографу
Пучок
нейтральных сетка
Возбуждающ Приема*. сетка
атомов
Рис. 4.14. Эксперимент по регистрации ионно-звуковых волн на Q-машине.
[Из работы: Wong А. У., Motley R, W., D'Angelo N.-> Phys. Rev., 133, A436
(1964).]
4.8. Различие между ионно-звуковыми и плазменными волнами
105
d-З (хм
Сигнал на возбужд.
сетке
Сигнал на прием,
сетке (xSu)
d-5,5 см
0 40 30 120 160 200
t, лткс
Сигнал на возбужд.
сетке
Сигнал на прием,
сетке (*60)
Рис. 4.15. Осциллограммы сигна-
лов от возбуждающей и прием-
ной сеток, разнесенных на рас-
стояние d. Видно запаздывание
сигналов во времени, которое
свидетельствует о том, что волна
движется. [Из работы: Wong
А. У., Motley R. W., D'Angelo N
Phys. Rev., 133, A436 (1964).]
Расстояние между зондами, cai
Рис. 4.16. Экспериментальные из-
мерения зависимости времени за-
держки от расстояния между зонда-
ми при различных частотах возбуж-
даемых волн. Фазовая скорость ко-
лебаний определяется по наклону
кривых. [Из работы: Wong А. У.,
Motley R. W., D'Angelo N., Phys.
Rev., 133, A436 (1964).]
частоты ионно-звуковых колебаний постоянны. Таким образом,
плазменные (ленгмюровские) и ионно-звуковые волны взаимно
дополняют друг друга: у первых при малых k примерно постоянные
частоты, а при больших k постоянные скорости, а у ионно-звуко-
вых волн — наоборот: при малых k скорости волн одинаковы и по-
стоянны, т. е. не зависят от k, а при больших k постоянны и не за-
висят от k частоты. Сравнение этих волн представлено графически
на рис. 4.13.
Первыми экспериментально доказали существование ионно-
звуковых волн Вонг, Мотли и Д’Анджело. На рис. 4.14 показана
схема их установки. Это снова Q-машина. (Мы не случайно так ча-
сто упоминаем Q-машины; только после того, как были разрабо-
таны способы создания спокойной плазмы, стали возможны тонкие
эксперименты по проверке плазменной теории.) Волны в экспери-
менте излучались и регистрировались с помощью погруженных
в плазму сеток. На рис. 4.15 показаны осциллограммы переданного
и полученного сигналов. Зная фазовый сдвиг, по этим осциллограм-
мам можно найти фазовую скорость волн, которая в этом случае
равна групповой. На рис. 4.16 эти фазовые сдвиги отложены как
функции расстояния между зондами, находящимися в плазме плот-
ностью 3-1017 м-3. По наклону этих кривых можно найти величину
фазовой скорости. На рис. 4.17 представлены фазовые скорости
ионно-звуковых волн для двух значений масс ионов М и разных
плотностей плазмы. Эксперимент показал, что скорость звука в
плазме vs постоянна и не зависит от ю и п0. Как видно из последнего
106
Гл. 4. Волны в плазме
f, кГц
Рис. 4.17. Измеренные в эксперименте фазовые скорости ионно-звуковых
волн в калиевой и цезиевой плазмах как функции частоты. Различные группы
точек отвечают разным плотностям плазмы. [Из работы: Wong A. Y., Mot-
ley R. W., D’Angelo N., Phys. Rev., 133, A436 (1964).]
рисунка, на котором представлены две группы экспериментальных
данных для случая калиевой и цезиевой плазмы, vs демонстрирует
установленную выше зависимость от М.
4.9. Электростатические электронные колебания,
распространяющиеся перпендикулярно
магнитному полю
До сих пор в этой главе мы считали, что В = 0. В плазме, находя-
щейся во внешнем магнитном поле, может существовать много
других типов волн. Мы рассмотрим только самые простые из них.
Начнем с высокочастотных электростатических электронных ко-
лебаний, распространяющихся под прямым углом к магнитному
полю. Прежде всего определим термины «перпендикулярный»,
«параллельный», «продольный», «поперечный», «электростатиче-
ский» и «электромагнитный». Слова параллельный и перпендику-
лярный будут использоваться для обозначения направления к по
отношению к невозмущенному магнитному полю Во. Продольный
и поперечный относятся к направлению к относительно электриче-
ского поля волны Ех. Далее, если осциллирующее магнитное поле
Вх равно нулю, то волна электростатическая, в противном случае
она является электромагнитной. Происхождение последних четы-
рех терминов связано с уравнением Максвелла
VX Ех = —Вх, (4.50)
которое можно записать в виде
кхЕх=®Вх. (4.51)
Если волна продольная, то к X Ех обращается в нуль; поэтому
продольная волна является также электростатической. В поперек-
4.9. Электростатические электронные колебания
107
ной волне, как следует из этого соотношения, Вх отлично от нуля,
и, следовательно, поперечная волна представляет собой электро-
магнитную волну. Разумеется, в общем случае волновой вектор к
может быть направлен под произвольным углом к Во или Ех; при
этом мы должны иметь смесь упомянутых выше типов колебаний.
Вернемся к электронным плазменным колебаниям, распростра-
няющимся перпендикулярно магнитному полю Во. Будем считать,
что ионы являются очень массивными и при рассматриваемых ча-
стотах колебаний не движутся, образуя неподвижный однородный
фон положительного заряда. Пренебрежем также тепловым движе-
нием электронов и положим КТе — 0. Как обычно, будем считать,
что в равновесии п0 и Во постоянны и однородны, а Ео и v0 равны
нулю. В этом случае движение электронов описывается следую-
щими линеаризованными уравнениями:
m (dvA/dt) = -е (Ex + vel X Во), (4.52)
dnjdt + nov • vel = 0, (4.53)
eo-VEi=— епл. (4.54)
Мы рассмотрим только продольные волны, у которых к || Ех- Без
ограничения общности можно выбрать систему координат так,
чтобы ось х была направлена вдоль к и Ех, а ось z — вдоль Во
(рис. 4.18). Таким образом, ky = kz = Еи = Ег = 0, к = kx,
Е = Ех. Запишем уравнение (4.52) покомпонентно и перейдем к
фурье-представлению, опустив индексы i и е:
— i —еЕ—evyBQ, (4.55)
— \.(йтоу= -\-еохВ?, (4.56)
— i comyz = 0.
Выражая vy из соотношения (4.56) и подставляя ее в (4.55), полу-
чаем
(4.57)
i cornu* = еЕ + eBovx (ieB0!ma),
eEHmas
vx =-----------------•
1 - (<*>2)
Заметим, что vx обращается в бесконечность на частоте циклотрон-
ного резонанса со = сос. Этого и следовало ожидать, поскольку
в таком случае электрическое поле, находясь в резонансе с цикло-
тронным вращением частиц вокруг оси z, всегда направлено в ту же
сторону, что и vx, и поэтому непрерывно ускоряет электроны.
[Если пренебречь членами (v-\z) v и Vp, то уравнения гидроди-
намики тождественны уравнениям движения отдельных частиц;
в этом приближении все частицы движутся вместе. ] Далее, линеа-
ризуя уравнение (4.53) и переходя к фурье-компонентам, получаем
«х = (/г/со) пйох. (4.58)
108
Гл. 4. Волны в плазме
Рис. 4.18. Плоская волна,
распространяющаяся под
прямым углом к магнитно-
му полю Во.
Рис. 4.19. Движение электронов в верхнегиб-
ридных колебаниях.
Переходя в уравнении (4.54) к фурье-компонентам и пользуясь
двумя последними соотношениями, имеем
/ 2 \ —1
. < г- k еЕ (, шс 1
1йе0Е = —е----п0-------I 1-----— I ,
<о im<o \ <о2 /
/ <в2 \ со2
1----£_ £=_Р_£. (4.59)
V <о2 J со2 V г
Следовательно, дисперсионное уравнение для этих волн имеет вид
(О2 =0)2(pgs (й%.
(4.60)
Частота соЛ называется верхнегибридной частотой. Такую частоту
имеют электростатические электронные волны, распространяю-
щиеся поперек магнитного поля В. Волны, движущиеся вдоль В,
представляют собой обычные плазменные колебания, их частота
® = <йр. Если не учитывать теплового движения, то групповая
скорость верхнегибридных колебаний, как и плазменных, будет
равна нулю.
Рис. 4.19 иллюстрирует физическую картину движения элек-
тронов в этих колебаниях. В плоской волне электроны образуют
области разрежения и сжатия подобно тому, как это происходит
в обычных плазменных колебаниях. Однако, поскольку в плазме
теперь имеется магнитное поле, перпендикулярное направлению
движения частиц, под действием силы Лоренца траектории движе-
ния электронов преобразуются в эллипсы. На электроны теперь
действуют две возвращающие силы: кулоновская сила, обусловлен-
ная электрическим полем, и сила Лоренца. Поскольку величина
возвращающей силы возросла, частота колебаний будет выше,
чем у плазменных волн. Если магнитное поле стремится к нулю,
4.9. Электростатические электронные колебания
109
Разрядный тон, мА
Рис. 4.20. Результаты эксперимента по измерению верхнегибридной ча-
стоты. Регистрировались параметры плазмы, при которых достигается мак-
симум поглощения (минимум коэффициента передачи) энергии СВЧ-колеба-
ний, распространяющихся поперек магнитного поля. На графике изображена
зависимость величины со2/®2, соответствующей напояженности магнитного
поля, при которой достигается максимум поглощения, от разрядного тока
(пропорционального плотности плазмы). [Из работы: Harp R. S., Proc. Se-
venth Intern. Confer, on Phenomena in Ionized Gases, Belgrade, 1965, II, 294
(1966).]
то в соотношении (4.60) частота сос также стремится к нулю и мы
имеем снова случай плазменных колебаний. Если же устремить
к нулю плотность плазмы, то сор тоже стремится к нулю, электро-
статические силы станут малыми и мы придем к случаю простого
ларморовского вращения частиц с частотой сос.
Существование колебаний на верхнегибридной частоте было
подтверждено в эксперименте по передаче СВЧ-волн поперек на-
правления магнитного поля. При изменении плотности плазмы эф-
фективность передачи волн с частотой со уменьшается при значе-
ниях плотности, соответствующих выполнению условия со = сод.
Это происходит потому, что энергия волн поглощается возбуждае-
мыми в плазме верхнегибридными колебаниями. Из соотношения
(4.60) ясно, что величина (ttyсо2 линейно зависит от плотности:
(со2/со2) = 1 — (<Ор/св2)= 1 — (/ze2/eowco2).
На рис. 4.20 показана полученная в эксперименте зависимость от-
110
Гл. 4. Волны в плазме
Рис. 4.21. Дисперсионные кривые
Трайвелписа—Гоулда для электро-
статических электронных волн, рас-
пространяющихся в проводящем
цилиндре, заполненном однородной
плазмой. Магнитное поле направ-
лено вдоль оси цилиндра. [Из ра-
боты: Trivelpiece A. IF., Gould R. IF.,
J. Appl. Phys., 30, 1784 (1959).]
Рис. 4.22. Проверка правильности
соотношений Трайвелписа—Гоулда
в эксперименте; при этом было так-
же показано, что в плазме суще-
ствуют обратные волны, у которых
групповая скорость, определяемая
по наклону дисперсионной кривой,
направлена противоположно фазовой
скорости. [Из работы: Trivelpiece
A. IF., Gould R. IF., J. Appl. Phys.,
30, 1784 (1959).]
ношения co2/co2 от тока разряда, который пропорционален плотно-
сти плазмы п. Видно, что эта зависимость линейная.
Рассмотрим распространение волн в плазме под углом 0 к маг-
нитному полю В. В этом случае в плазме могут существовать два
типа волн. Первые будут похожи на плазменные колебания, вто-
рые — на верхнегибридные, но свойства и тех и других будут за-
висеть от угла 0. Подробный анализ этих волн мы оставляем чита-
телю в качестве упражнения (задача 4.8). На рис. 4.21 схемати-
чески показаны зависимости со (&2) при фиксированных kx для этих
двух мод (здесь kx!kz = tg 0). Поскольку соотношение (4.60) сим-
метрично относительно сос и сор, случай сос >сор полностью аналоги-
чен случаю сор >сос, нужно лишь поменять у переменных индексы.
4.9. Электростатические электронные колебания 111
При больших kz волна распространяется параллельно Во и пред-
ставляет собой плазменное колебание с частотой со = Второе
решение, со = со^ при kz оо, является посторонним, поскольку
при 0 —> О величина Во в ответ входить не должна. При малых kz
мы возвращаемся к случаю поперечного распространения, kj_ Во»
уже рассмотренному в этом разделе. При kz -> 0 на нижней ветви
колебаний частота со стремится к нулю, а на верхней — прибли-
жается к верхнегибридной частоте coft. Кривые, приведенные на
рис. 4.21, впервые были получены Трайвелписом и Гоулдом, кото-
рые также подтвердили их в эксперименте (рис. 4.22). В экспери-
менте Трайвелписа—Гоулда использовался цилиндрический столб
плазмы; можно показать, что в этом случае изменение kz эквива-
лентно тому, что в плазме под различными углами к Во распростра-
няются плоские волны.
Задачи
4.7. Покажите, что в верхнегибридных колебаниях эллиптические орбиты
частиц всегда вытянуты вдоль волнового вектора к. (Указание: выразите из
уравнения движения отношение Vxlvy как функцию отношения со/сос.)
Рис. 34.8.
4.8. Получите дисперсионное уравнение для электростатических электрон-
ных волн, распространяющихся под произвольным углом 0 к магнитному
полю Во. Указание: выберите ось х так, чтобы векторы к и Е лежали в пло-
скости xz (рис. 34.8). В этом случае Ех = £jsin О, Ez — E^cos 0, Еу = 0.
Аналогичные соотношения имеют место и для компонент волнового вектора к.
После этого, как обычно, решите уравнение движения, уравнение непрерыв-
ности и уравнение Пуассона, полагая, что v0 = Е = 0, а плотность п0 П0‘
стоянна.
а) Покажите, что ответ имеет вид
со2 (со2 — со^) + со2со2 cos20 — 0.
б) Выпишите два решения этого квадратного относительно со2 уравнения
и покажите, что в пределах 0 0 и 0 л/2 из них следуют результаты,
приведенные нами выше. Покажите, что в этих пределах одно из двух реше-
ний постороннее и не имеет физического смысла.
в) Покажите, что дисперсионное уравнение, полученное в п. а, представляет
собой уравнение эллипса:
(У-1)2 *2
I2 а2
112
Гл. 4. Волны в плазме
в координатах z = cos 6, у в 2(02/<0ft, где а = со^/2сос<ор.
г) Нарисуйте этот эллипс при сор/сос = 1,2 и оо.
д) Покажите, что в случае a>c>wp при любом 0 >0 меньшее значение о
всегда меньше, чем сор, а большее всегда лежит между <£>с и со/,. Покажите
также, что при шр >сос меньшее значение <х> меньше, чем <ос, а верхний ко-
рень дисперсионного уравнения расположен между сор и сод.
4.10. Электростатические ионные волны,
распространяющиеся перпендикулярно В
Теперь посмотрим, что происходит с ионно-звуковой волной, если
к перпендикулярен Во. Казалось бы, можно считать, что произве-
дение к-В0 в точности равно нулю, но это приведет к результату,
который, хотя и является математически корректным, не описы-
вает процессы, происходящие в реальной плазме (см. разд. 4.11).
Вместо этого будем считать, что к почти перпендикулярен Во. Что
кроется за этим «почти», выяснится позднее. Как обычно, предпо-
ложим, что в состоянии равновесия плазма безгранична, параметры
п0<и Во постоянны и однородны, a v0 = Ео = 0. Для простоты по-
ложим Ti = 0; мы знаем, что при 7\ = 0 звуковые волны все равно
существуют, поэтому никаких важных эффектов при этом не поте-
ряем. Предположим также, что волны являются электростатиче-
скими, т. е. k х Е — 0, а Е = — V^>. Ориентация векторов к и Е
относительно магнитного поля показана на рис. 4.23. Будем счи-
тать, что угол (1/2) л—0 настолько мал, что при описании движе-
ния ионов можно положить Е = EjX, V = i kx и пренебречь в этих
соотношениях соответствующими z-компонентами. При описании
электронов, однако, далеко не все равно, считать ли (1/2) п—0
нулем или малой, но конечной величиной. Дело в том, что лармо-
Рис. 4.23. Электростатические ионно-циклотронные волны, распространяю-
щиеся почти под прямым углом к направлению магнитного поля Во.
4.10. Электростатические ионные волны
113
ровские радиусы электронов малы, и поэтому при 0 = л/2 они не
могут двигаться вдоль оси х и обеспечивать нейтральность плазмы;
поле Е заставляет электроны двигаться в прямом и обратном на-
правлениях лишь вдоль оси у. Если же угол 0 не в точности равен
л/2, то электроны могут двигаться вдоль показанной на рис. 4.23
штриховой линии (т. е. вдоль Во) и переносить отрицательный за-
ряд в области, заряженные положительно, осуществляя таким об-
разом дебаевское экранирование. Ионы же этого эффективно делать
не могут, поскольку из-за своей большой массы они не могут сме-
щаться за один период волны на такие большие расстояния. Именно
по этой причине при описании движения ионов мы пренебрегли
величиной kz. Критический угол, начиная с которого нужно учи-
тывать движение электронов, %0 = (1/2) л—0О, будет пропорцио-
нален отношению продольных скоростей ионов и электронов:
%0 « (mlM.)112 (в радианах). Если у = (1/2) л—0 больше этого угла,
то справедливо приближение, анализируемое ниже. Если же
X <%о> то применимо рассмотрение, представленное в разд. 4.11.
После этой длинной вводной части перейдем теперь к короткому
выводу результата. Уравнение движения ионов имеет вид
М (дУц/dt) = — eyfa + evu X Во. (4.61)
Предполагая, что рассматриваются плоские волны, распространяю-
щиеся вдоль оси х, запишем проекции последнего уравнения на
оси х и у.
— i<o/WulA.= — eviyB0,
— i co/H vly — — evixB0. (4.62)
Решая эту систему так, как и раньше, находим
vix = (ek/Ma>) [ 1 — (й2/со2)]“1 fa, (4.63)
где Qc = еВ01М — ионно-циклотронная частота. Из уравнения
непрерывности для ионов, как обычно, получаем
п(1 = (k/a) nov£x. (4.64)
Предполагая, что угол % =# 0 и электроны могут двигаться вдоль
Во, применим для их описания распределение Больцмана. В лине-
аризованной форме оно имеет вид
(nA/n0) = (efa/KTe). (4.65)
Замыкает систему уравнение плазменного приближения п£ = пе.
С помощью соотношений (4.64) и (4.65) уравнение (4.63) можно за-
писать в виде
[ 1 — (йс/co2)] vix = (ek/Ma) (КТе/еп0) (nofe/co) vix,
a2 — Q2 = k2(KTe/M). (4.66)
114
Гл. 4. Волны в плазме
Рис. 4.24. Схема эксперимента по возбуждению электростатических ионно-
циклотронных волн на Q-машине. [Из работы: Motley R. W., D’Angelo N.,
Phys. Fluids, 6, 296 (1963).]
Рис. 4.25. Измеренные зависимости частот электростатических ионно-цикло-
тронных волн от магнитного поля. [Из работы: Motley R. W.,D’ Angelo N.t
Phys. Fluids, 6, 296 (1963).]
Поскольку мы предположили, что КТ i = 0, уравнение (4.66) можно
переписать следующим образом:
co2 = Q^ + fe2vd (4.67)
Это — дисперсионное уравнение для электростатических ионно-
циклотронных волн.
Физическая картина процессов, происходящих в этих волнах,
во многом аналогична той, которая показана на рис. 4.19 для слу-
чая верхнегибридных колебаний. В ионно-циклотронных волнах
ионы совершают колебания, подобные ионно-звуковым, но теперь
на них действует дополнительная возвращающая сила — сила
Лоренца, что и приводит к появлению в соотношении (4.67) слагае-
мого й2. Роль электронов сводится к экранировке возникающих
при колебаниях электрических полей. Напомним, что именно де-
баевское экранирование электронами обеспечивает выполнение
дисперсионного уравнения для обычных ионно-звуковых волн со2 —
~ k2Vs. В случае ионно-циклотронных волн, для того чтобы прои-
4.11. Нижнегибридная частота
115
зошла экранировка, электроны должны пройти большое расстоя-
ние вдоль Во.
Электростатические ионно-циклотронные волны впервые экс-
периментально наблюдали Мотли и Д’Анджело и снова на Q-ма-
шине (рис. 4.24). Волны генерировались с помощью тока, который
протекал вдоль оси установки и попадал на маленький дополни-
тельный электрод. Возбужденные током волны распространялись
в радиальном направлении поперек магнитного поля. Механизм
возбуждения волн в такой системе довольно сложный, поэтому
здесь мы его рассматривать не будем. На рис. 4.25 представлены
полученные в эксперименте зависимости частоты ионно-циклот-
ронной волны от магнитного поля. В условиях эксперимента член
А2 а2 был мал по сравнению с Q2, поэтому измеренные частоты лишь
ненамного превышают йс.
4.11. Нижнегибридная частота
Рассмотрим теперь, что происходит, если угол 0 в точности равен
л/2: при этом электроны не могут свободно двигаться вдоль сило-
вых линий и обеспечивать нейтральность плазмы. В этом случае
плотность электронов нужно находить не из уравнения Больцмана,
а из полного уравнения движения (3.62). Если масса электрона
считается отличной от нуля, то это уравнение имеет нетривиальные
решения даже в том случае, если Те = 0 и членом Vpe можно пре-
небречь; мы это и предположим для простоты. Уравнение движе-
ния ионов совпадает с уравнением (4.63):
vix = (efe/Mco) [ 1 — (Q2/a>2)]~' fa. (4.68)
Решение уравнения (3.62) для электронов при Те = 0 можно вы-
писать сразу, заменив в соотношении (4.68) заряд е на — е, М на
m, a на —
vex = — (ek/mfa [ 1 — (сос/<о2) J""1 fa. (4.69)
Из уравнений непрерывности получаем
Пц = (£/®) novllt nel = (k/a)) novel. (4.70)
При этом из плазменного приближения tii = пе следует и1х = vel.
Приравнивая друг другу правые части соотношений (4.68) и (4.69),
имеем
Л4 [1 —(й2/<в2)] = —/и [1 —(со2/®2)],
w2(M+m) = m®2 + MQ2 = e2B2f -—h—Y
У tn М. )
со2 = - Йссос,
(4.71)
116
Гл. 4. Волны в плазме
Частота со/ называется нижнегибридной частотой. Если бы вместо
плазменного приближения мы воспользовались уравнением Пуас-
сона, то в результате получили бы соотношение
-у-----7-+^Г- (4'7|а>
В случае плазмы низкой плотности преобладающим является по-
следний член этого соотношения. Напомним, что нижнегибридные
колебания могут наблюдаться только тогда, когда угол 0 очень
близок к л/2.
4.12. Электромагнитные волны при Во=О
Следующими по степени сложности являются волны, у которых
собственное магнитное поле Вх 0. Примерами таких волн в плазме
могут служить свет или радиоволны, которые представляют собой
поперечные электромагнитные колебания. Вначале рассмотрим
кратко электромагнитные волны в вакууме. Поскольку в этом слу-
чае токи отсутствуют (/ = 0), а еоро = с-2, уравнения Максвелла
принимают вид
VXE1=-B1> (4.72)
c2vxBi = Ev (4-73)
Взяв ротор от уравнения (4.73) и выразив V X Et из соотношения
(4.72), получаем
c2v X (v X Bj) = v X Ё1= —Bp (4.74)
Предполагая, что волна плоская и все величины в ней пропорцио-
нальны ехр [i {kx—со/)], приходим к соотношению
со2Вх = — с2к х (к х Вх) = — с2 [к(к • Вх) — ^BJ. (4.75)
Поскольку из уравнения Максвелла (3.7) следует, что к-В! =
= — iv • Вх = 0, окончательно имеем
со2 = /г2с2. (4.76)
Таким образом, фазовая скорость электромагнитных волн в вакууме
равна скорости света с.
В плазме без магнитного поля уравнение (4.72) сохраняет свой
вид, а в правую часть (4.73) нужно добавить член чтобы учесть
токи, обусловленные движением заряженных частиц в первом по-
рядке по амплитуде поля:
c2VX B^fei-HW (4-77)
4.12. Электромагнитные волны при Во=О 117
Дифференцируя это соотношение по времени, получаем
c2V X Bi = Ex+её"' (djjdt). (4.78}
Кроме того, применим операцию ротора к обеим частям уравнения
(4.72):
v x(v X Ej) = v(v-Ej) —v2Ei= Hv X Br (4.79)
Исключая из двух последних равенств v X Bj и предполагая за-
висимость в виде ехр [i (к-г—со/)], получаем
—к (к Ех) + /г2Ех(ico/soc2) ji + (со2/с2) ЕР (4.80)
Считая, что волны являются поперечными, положим к-Ет = 0,
тогда уравнение примет вид
(со2—с2/г2)Ех =—icoji/eo. (4.81)
Частоты электромагнитных волн микроволнового и оптического
диапазонов столь высоки, что ионы плазмы можно считать покоя-
щимися. В этих случаях ток в плазме jx будет определяться исклю-
чительно движением электронов:
ji= — noeveV (4.82)
Из линеаризованного уравнения движения электронов мы имеем
(для К7\ = 0):
т (dvel/df) = —eEb
vei = eEi/imo). (4.83)
Уравнение (4.81) теперь можно записать в виде
(со2—c2k2) Ег — (ico/eo) Пов (eEx/i/nco) = (n0e2/s0m) Ev (4.84)
Легко заметить, что множитель перед Е2 в правой части этого со-
отношения равен со’; следовательно, мы имеем
со2 = cop-j-cV. (4.85)
Это дисперсионное уравнение для электромагнитных волн, рас-
пространяющихся в плазме без магнитного поля. Как видите, от
дисперсионного уравнения для волн в вакууме (4.76) оно отличается
членом со2, напоминающим о плазменных колебаниях. Фазовая ско-
рость электромагнитных волн в плазме выше скорости света:
Уф = со2//г2 = с2 + (со2/^2)>с2. (4.86)
Однако групповая скорость не может превышать скорости света.
Действительно, из соотношения (4.85) следует, что'
d&ldk = пгр = с2/Уф, (4.87)
так что при Уф>с величина игр<с. Дисперсионная кривая co
j । 118 Гл. 4. Волны в плазме
п
соответствующая уравнению (4.85), показана на рис. 4.26. График
напоминает кривую, изображенную на рис. 4.5 для случая плаз-
i менных волн, но на самом деле дисперсионные соотношения у этих
J волн совершенно различны, поскольку асимптотическое значение
фазовой скорости электромагнитных волн равно с (рис. 4.26), что
намного выше, чем асимптотическое значение фазовой скорости
Рис. 4.26. Дисперсионная кривая для электромагнитных волн, распростра-
няющихся в плазме в отсутствие постоянного магнитного поля.
плазменных волн (3/2)1/2 отепЛ (рис. 4.5). Еще более важно то, что
эти волны имеют различное затухание. Как будет показано на
основе кинетической теории в гл. 7, ленгмюровские (плазменные)
волны при больших А^тепл затухают очень сильно. Электромаг-
нитные же волны при больших k ведут себя как обычные световые
волны в вакууме и в этом пределе из-за присутствия плазмы не
затухают.
Из дисперсионного уравнения типа (4.85) следует существова-
ние явления, которое называется отсечкой. Если через плазму
распространяется микроволновый' пучок с частотой со, то длина
волны в плазме 2л/будет определяться соотношением (4.85). С уве-
2
личением плотности плазмы и, следовательно, величины сор зна-
чение k2 будет уменьшаться, а длина волны увеличиваться. При
дальнейшем увеличении плотность может достичь такого значе-
ния, что k2 обратится в нуль. Для плотностей, больших этого зна-
чения, уравнение (4.85) не удовлетворяется ни при каком вещест-
венном k и волна в плазме распространяться не может. Эта отсечка
волны происходит при такой критической плотности пс, для кото-
рой выполняется условие со = сор, а именно
пс = тейа2/е2. (4.88)
Если плотность п слишком велика или же частота со слишком мала,
то электромагнитная волна не может пройти сквозь плазму. В этом
случае из уравнения (4.85) следует, что k является мнимой величи-
ной:
cfe = (co2—cop)1/2=i|cop —со2|12. (4.89)
4.13. Экспериментальные приложения
119
Поскольку мы предположили, что зависимость всех величин в волне
от координаты имеет вид ехр (i kx), то при мнимых k волна будет
экспоненциально затухать. Длина затухания, или глубина скин-
слоя, определяется следующим образом:
eto = e~'*|x=e_*'e, 6 = 1^1-*=--------------. (4.90)
(со2-®2)1'2
Для лабораторной плазмы в большинстве случаев частоты отсечек
попадают в СВЧ-диапазон.
4.13. Экспериментальные приложения
Явление отсечки позволяет легко измерить плотность плазмы. Мик-
роволновый пучок, генерируемый клистроном, с помощью рупор-
ной антенны направляется в плазму (рис. 4.27). Прошедший через
плазму пучок принимается другим рупором и детектируется кри-
сталлическим детектором. Если менять частоту электромагнит-
ной волны или плотность плазмы, то сигнал на детекторе будет
пропадать всякий раз, когда где-нибудь в плазме выполняется со-
отношение (4.88). Этот метод позволяет измерить максимальную
плотность плазмы, но он не очень удобен и гибок, поскольку диа-
пазон частот, генерируемых СВЧ-генератором, ограничен.
Широко применяемый метод измерения плотности основан на
изменении показателя преломления, т. е. дисперсии, предсказы-
ваемой уравнением (4.85). Показатель преломления п определяется
как
(4.91)
Очевидно, что п зависит от со, поэтому плазма является дисперги-
рующей средой. Для измерения плотности используется СВЧ-
интерферометр, работающий по тому же принципу, что и интерфе-
рометр Майкельсона (рис. 4.28). Сигнал от клистрона разделяется
на два; одна его часть поступает через опорной канал прямо на де-
тектор, а другая с помощью рупорной антенны посылается в плазму.
п == С/Уф = Ck/to.
Плазма
Рис. 4.27. Измерение плотности плазмы по отсечке проходящего через нее-
СВЧ-сигнала.
320
Гл. 4. Волны в плазме
Волновод
Рис. 4.28. СВЧ-интерферометр для измерения плотности плазмы.
Детектор откликается на средний квадрат суммы амплитуд двух
принятых сигналов. С помощью аттенюатора и фазовращателя оба
сигнала регулируются таким образом, чтобы в отсутствие плазмы
их амплитуды были равны друг другу, а фазы сдвинуты на 180°,
так что на выходе детектора мы имеем нулевой сигнал. Когда в си-
стеме появляется плазма, фаза сигнала в плазменном канале из-
меняется, поскольку увеличивается длина волны (рис. 4.29) и на
выходе детектора возникает сигнал конечной величины. С увели-
чением плотности плазмы сигнал на выходе детектора проходит
через максимум и минимум всякий раз, когда разность фаз меняется
на 360°. Средняя плотность плазмы в каждый момент времени оп-
ределяется по величине фазового сдвига, т. е. по числу интерфе-
I 1ЛЛЛЛЛ
Ра определение
поля волны
в плазлю
Сигнал
на выходе
детектора
I Отсечка
Рис. 4.30. Показатель
преломления плазмы
меньше единицы, поэто-
му плазменные линзы
обладают необычными
оптическими свойствами.
1ЛЛАЛЛ
Плотность
Рис. 4.29. Сигнал на выходе интерферометра
при увеличении плотности плазмы (справа);
соответствующие распределения электрического
поля волны в плазме (слева).
4.13. Экспериментальные приложения
12В
Рис. 4.31. Плазма, удерживаемая в длинном линейном соленоиде, будет за-
хватывать используемое для ее нагрева излучение СО2-лазера только в том-
случае, если плотность плазмы минимальна на оси системы. Вакуумная ка-
мера на рисунке не показана.
ренционных полос. Обычно частота используемых волн настолько
высока, что сдвиг фаз оказывается малым. При этом он пропорцио-
нален плотности плазмы (задача 4.13). Чувствительность этого
метода при низких плотностях плазмы ограничена тем, насколько
устойчив к тепловому расширению материал, из которого выпол-
нен волновод опорного канала. Необходимо также вводить поправки
на затухание сигнала, обусловленное столкновениями, а также на
дифракцию и рефракцию волн за счет конечных размеров плазмы.
То, что у плазмы показатель преломления меньше единицы,
имеет интересные следствия. К примеру, выпуклые плазменные
линзы являются не собирающими, а рассеивающими (рис. 4.30).
Этот эффект используется в лазерно-соленоидальном «стартере»
для линейного реактора синтеза. В таком реакторе столб плазмы
длиной несколько сот метров удерживается сильным магнитным
полем. Нагрев плазмы осуществляется за счет поглощения излуче-
ния СО2-лазера (рис. 4.31). Если профиль плазмы имеет обычный
вид с максимумом на оси, то плазма ведет себя как рассеивающая
линза, что приводит к расфокусировке лазерного пучка, в резуль-
тате чего он попадает на стенки. Если же создать инверсный про-
филь плазмы с минимумом на оси, то плазменная линза становится
собирающей: при этом излучение фокусируется и захватывается
плазмой. Инверсный профиль плотности можно создать посредст-
вом сжатия плазмы с помощью импульсов тока в окружающей
ее обмотке или непосредственно с помощью самого лазерного пучка.
Когда пучок нагревает плазму, она расширяется, вследствие чего
ее плотность вблизи оси пучка уменьшается. СО2-лазер генерирует
излучение с % = 10,6 мкм, которая соответствует частоте / =
= с/К = 3-108/10,6-10-в = 2,8-1013 Гц. Как видно из соотношения
(4.88), этой частоте соответствует критическая плотность пс =
= Ш8О (2л/)2/е2 = 1025 м-3. Однако, поскольку лазерный пучок
проходит в плазме большое расстояние, рефракция становится су-
щественной уже при плотностях порядка 1022 м-3. Фокусировка
света в областях пониженной плотности плазмы была подтверждена
экспериментально.
Возможно, самое известное явление, связанное с отсечкой волн
в плазме, наблюдается при коротковолновой радиосвязи. Когда
122
Гл. 4. Волны в плазме
Ионосфера
Рис. 4.32. Иллюстрация влияния плазмы земной ионосферы на радиосвязь.
(На самом деле ионосфера расположена ближе к Земле, чем показано на
рисунке.)
распространяющийся в ионосфере радиосигнал достигает высоты,
на которой плотность плазмы достаточно велика, то он отражается
обратно (рис. 4.32), что позволяет радиосигналу огибать Землю.
Если считать, что максимальная плотность плазмы в ионосфере
равна 1012 м~3, то критическая частота будет порядка 10 МГц [см.
формулу (4.26)1. Именно поэтому для связи с космическими аппа-
ратами нужно пользоваться более высокими частотами, чтобы сиг-
нал мог пройти через ионосферу. При возвращении космического
корабля на Землю вокруг него из-за нагрева, вызванного силой
трения, образуется собственная плазма. Это приводит к отсечке
волн и обрыву связи с кораблем на участке спуска (см. рис. 4.32).
Задачи
4.9. Перед отсеком космического корабля, спускающимся в атмосфере Земли,
образуется ударная волна, в результате чего вокруг корабля возникает
плазма и связь с ним прерывается. Пусть радиопередатчик работает на ча-
стоте 300 МГц. Какова минимальная плотность плазмы в момент обрыва
связи?
4.10. Согласно предположению Ханнеса Альфвена, первого из специалистов
в области физики плазмы, удостоенного Нобелевской премии, на начальной
стадии развития Вселенной в ней было поровну материи и антиматерии.
Допустим, что Вселенная в то время представляла собой однородную смесь
протонов, антипротонов, электронов и позитронов, причем плотность частиц
каждого вида была равна п0.
а) Выведите дисперсионное уравнение для высокочастотных электромагнит-
ных волн, распространяющихся в такой плазме. Столкновениями, тепловыми
эффектами и аннигиляцией частиц можно пренебречь.
4.14, Электромаг. волны распространяющиеся перпендикулярно Во 12В
б) Пользуясь уравнением Пуассона, выведите дисперсионное уравнение для
ионно-звуковых волн. Можно считать, что лептоны удовлетворяют уравне-
нию Больцмана, и пренебречь температурой Ti (но не Те).
4.11. Покажите, что для электромагнитных волн показатель преломления
равен квадратному корню из относительной диэлектрической проницаемо-
сти плазмы (ср. с задачей 4.4).
8 см
Рис. 34.13.
4.12. В калиевой плазме Q-машины доля х электронов может быть замещена
на отрицательные ионы хлора С1_. При этом в 1 м3 плазмы будет содержаться
п0 ионов К+, хп0 ионов С1— и (1—х) п0 электронов. Пусть х = 0,6. Найдите
критическую плотность п0, при которой в плазме произойдет отсечка СВЧ-
сигнала с длиной волны 3 см.
4.13. Для определения плотности плазмы в бесконечном плоском слое тол-
щиной 8 см используется СВЧ-интерферометр, работающий на длине волны
8 мм (рис. 34.13).
а) Пусть плазма однородна, а фазовый сдвиг составляет 1/10 интерференци-
онной полосы. Какова плотность плазмы? (Указание: одна полоса соответст-
вует фазовому сдвигу 360°).
б) Покажите, что если фазовый сдвиг мал, то он пропорционален плотности-
плазмы.
4.14. Электромагнитные волны,
распространяющиеся перпендикулярно Во
Рассмотрим теперь распространение электромагнитных волн в
плазме при наличии магнитного поля. Сначала проанализируем
случай перпендикулярного распространения (kj_ Во). Если рас-
сматривать поперечные волны, в которых k_LEx, то возможны два
варианта: электрическое поле волны Ег может быть либо парал-
лельно Во, либо перпендикулярно Во (рис.4.33).
4.14,1. Обыкновенная волна (Ei || Во)
Пусть Ег параллельно Во, тогда можно положить Во == Boz, Ег =
= E^z, a k = kx. В эксперименте такую ситуацию можно реализо-
вать, если микроволновый пучок направить на столб плазмы ив
124
Гл. 4. Волны в плазме
Рис. 4.33. Электромагнитные волны, распространяющиеся под прямым уг-
лом к магнитному полю Во.
рупорной антенны, узкая сторона которой параллельна направле-
нию магнитного поля Во (рис. 4.34).
Волновое уравнение в этом случае по-прежнему записывается
в виде (4.81):
(со2—с2£2) Ег = — icoji/e0 = inoecouel/eo. (4.92)
Поскольку Ei = EjZ, из всех компонент скорости нужно рассмат-
ривать только vez. Она определяется из уравнения движения
т (dvez/dt) = —еЕг. (4.93)
Рис. 4.34. Обыкновенная'волна, падающая из волноводной антенны на столб
замагниченной плазмы.
4.14. Электромаг. волны, распространяющиеся перпендикулярно Во
125
Благодаря тому что уравнение имеет такой же вид, как и в случае
Во = 0, мы имеем то же дисперсионное уравнение
2 2 , 2t,2
(О = (Ор + С « •
(4.94)
Электромагнитная волна, в которой электрическое поле Ех || Во,
называется обыкновенной волной. Термины «обыкновенная» и «не-
обыкновенная» заимствованы из кристаллооптики, но в случае
плазмы их значения поменялись местами. В физике плазмы более
резонно называть обыкновенной ту волну, на которую магнитное
поле не влияет. По точной аналогии с кристаллооптикой волну
с Ех || Во следовало бы назвать «необыкновенной».
4.14.2. Необыкновенная волна (EjJ^Bq)
Если Е^Во, то магнитное поле Во будет влиять на движение элек-
тронов в волне и дисперсионное уравнение изменится. Казалось
бы, при анализе этого случая можно считать, что Ej — Егу,
Рис. 4.35. Необыкновенная волна эллиптически поляризована. Сдвиг фаз
между осциллирующими компонентами Ех и Еу равен 90°, так что конец
вектора электрического поля волны Ех за каждый период колебаний описы-
вает эллипс.
a k — kx (см.
рис. 4.33). Однако волны с E1J_B0 поляризованы не линейно,
а эллиптически. Это значит, что при распространении такой волны
в плазме у нее появляется компонента Ех, направленная вдоль к.
Таким образом, волна становится частично продольной и частично
поперечной. Чтобы правильно проанализировать поведение этой
волны, мы должны считать, что электрическое поле имеет как у-,
так и х-составляющие (рис. 4.35):
Е^Е^ + Еуу. (4,95)
126
Гл. 4. Волны в плазме
При КТе = 0 линеаризованное уравнение движения электро-
нов можно записать в виде
— im®vej = — е (Ej + vrt х Во). (4.96)
Не обращаются в нуль только х- и «/-компоненты скорости:
их = (—ie/ma) (Ех -ф иуВ0),
vg=(—\e/mai)(Ee—vxB0) (4.97)
(мы опустили индексы 1 и е). Разрешая, как обычно, эту сис-
тему относительно vx и vy, находим
В волновом уравнении (4.80) теперь нужно сохранить член
к-Е1 = /гЕ'х, отвечающий продольному распространению:
(со2—с2£2) Ех-|-с2/гЕхк — —iojjx/eo = in0coevel/e0. (4.99)
Разделяя это уравнение на х- и «/-компоненты и используя выра-
жения (4.98), имеем
Воспользовавшись определением <ар, можно записать эту систему
в виде
Эти уравнения совместны только в том случае, если составлен-
ный из их коэффициентов детерминат обращается в нуль:
А
С
В
(4.102)
__ л 2 2
Поскольку А = и —a>h, где — верхнегибридная частота, опре-
4.15. Отсечки и резонансы
127
делаемая выражением (4.60), условие равенства нулю детерминанта
AD = ВС можно записать в виде
(4.103)
Это уравнение можно упростить, сделав несколько алгебраических
преобразований. Заменяя в правой части на со2 + <»₽ и умножая
обе части уравнения на со2—со^, получаем
<^2 = t _ mp (tt2 - юй) + У»2) =
со2 (со2 — со2) (со2 — со);)
! СО2 (со2 - СО2) + СОрСО2 СОр
(со2 — со2) (со2 — со);) со2
= 1_____У . 0)2 (У ~ - юр (ю2~~
со2 (со2 — со2) (со2 - со2)
Это—дисперсионное уравнение для необыкновенной волны. Она
представляет собой продольно-поперечную электромагнитную
волну, которая распространяется под прямым углом к магнитному
полю Во. Собственное электрическое поле волны Ех также перпен-
дикулярно Во.
4.15. Отсечки и резонансы
Дисперсионное уравнение для необыкновенной волны гораздо слож-
нее любого из уравнений, с которыми мы имели дело до настоящего
времени. Чтобы его проанализировать, полезно определить поня-
тия отсечки и резонанса. Отсечка электромагнитной волны в плазме
имеет место тогда, когда показатель преломления обращается в
нуль или, поскольку п = ck!со, когда длина волны сигнала ста-
новится бесконечной. Резонанс возникает, когда показатель пре-
ломления становится бесконечным, т. е. длина волны обращается
в нуль. Если волна распространяется через область плазмы, в ко-
торой <Вр и сос меняются, то она может встретиться с точками отсечки
и резонанса. Как правило, в точке отсечки волна отражается, а
в резонансе — поглощается. 7
128
Гл. 4. Волны в плазме
Точки резонанса для необыкновенной волны можно найти, если
в уравнении (4.104) устремить k к бесконечности. При любой ко-
нечной со из условия k -> оо следует, что со -► сод; поэтому резо-
нанс возникает в той точке плазмы, где выполняется равенство
со* = ®р + со? = со1 2. (4.105)
Очевидно, это соотношение представляет собой дисперсионное
уравнение для электростатических волн, распространяющихся по-
перек Во [см. (4.60) ]. По мере приближения волны к точке резо-
нанса как фазовая, так и групповая ее скорости стремятся к нулю,
а энергия волны переходит в энергию верхнегибридных колеба-
ний. Как отмечалось выше, необыкновенная волна является ча-
стично электромагнитной, а частично электростатической; нетрудно
показать (задача 4.14), что в точке резонанса она теряет свой элек-
тромагнитный характер и становится чисто электростатической.
Частоты отсечки необыкновенной волны можно найти, положив
в уравнении (4.104) k = 0. Разделив получившееся равенство на
2 2
(о — сор, можно записать его в виде
Шп 1
1 = —р----------!---------. (4.106)
а2 !_
Выполнив несколько хитроумных алгебраических преобразований,
получаем простое выражение для со:
1 - (®2/®2) = (со2/со2)/[ 1 - (®2/со2)],
[1 —(<Вр/«>2)]2 = Ю2/(О2,
1 — (сОр/й)2) = -4- <ВС/<В,
со2=рсй(ос — (йр = 0. (4.107)
Знаки минус и плюс отвечают разным частотам отсечки; мы будем
обозначать их соЛ и coL. Корни квадратного уравнения равны
соЛ = -^-[сос-[-((о2 + 4а)р)12],
®£=~[—й)с+ (сос-р 4юр) ]. (4.108)
По принятому нами соглашению частота со всегда положительна,
поэтому в обоих случаях мы выбрали перед квадратным корнем
знак плюс. Заметим, что волнам, которые распространяются в на-
правлении отрицательных х, будут соответствовать отрицатель-
ные k. По причине, которая выяснится в следующем разделе, ча-
стоты соЛ и coL называются частотами отсечек соответственно
правополяризованной моды и левополяризованной моды.
4.15. Отсечки и резонансы
129
Рис. 4.36. Дисперсия необыкновенной волны, т. е. зависимость ее фазовой
скорости от частоты. В областях частот, заштрихованных на рисунке, не-
обыкновенная волна распространяться не может.
Частоты отсечки и резонанса разделяют график дисперсионной
кривой на участки, соответствующие распространяющимся и не-
распространяющимся волнам. Вместо обычного графика со (k) удоб-
нее пользоваться зависимостью фазовой скорости от частоты, или,
более точно, зависимостью величины со2/с2Л2 = 1/л2 от частоты со
(рис. 4.36). Чтобы объяснить эти зависимости, представим себе,
что частота сос задана и волна с фиксированной частотой со падает
на плазму извне. Когда волна проходит участки, где плотность
возрастает, частоты coL, сор, сол, соЛ увеличиваются, т. е. сдвигаются
на графике вправо. Это эквивалентно тому, что при фиксированной
плотности плазмы частота со уменьшается. Становясь на эту точку
зрения, мы видим, что при больших со (или низкой плотности) фа-
Рис. 4.37. Дисперсия обыкновенной волны.
5 Заказ 3170
1.30
Гл. 4. Волны в плазме
зовая скорость волны стремится к скорости света. По мере того как
волна движется дальше и плотность плазмы возрастает, фазовая
скорость волны увеличивается и наконец в точке отсечки правопо-
ляризованной моды она становится бесконечной. Между теми слоя-
ми плазмы, в которых <в=соЛ и со = сол, величина со2/Л2 отрицательна
и поэтому волна там распространяться не может. При со = a>h
наступает резонанс и фазовая скорость Цф обращается в нуль.
Между точками со = сой и со = сод волны опять могут распростра-
няться. Фазовая скорость волны в этой области будет больше или
меньше скорости света в зависимости от того, больше со, чем сор,
или же меньше ее. Из уравнения (4.104) ясно, что волна при со = сор
движется со скоростью с. При со <сод имеется еще одна область
нераспространения. Таким образом, у необыкновенной волны есть
две области распространения, разделенные полосой непропускания.
С целью сравнения на рис. 4.37 показана аналогичная диаграмма
для обыкновенной волны. В этом случае у дисперсионного уравне-
ния имеется только одна отсечка, а резонансы отсутствуют.
4.16. Электромагнитные волны,
распространяющиеся параллельно Во
Пусть теперь волновой вектор к направлен по оси z, а электриче-
ское поле волны Ех имеет обе поперечные составляющие Ех и Еу:
k — kz, Ех = Ехх + Еуу. (4.109)
Мы по-прежнему можем пользоваться волновым уравнением для
необыкновенной волны (4.99), поменяв в нем k = kx на к = kz.
Как следует из системы (4.100), проекции волнового уравнения
на оси координат имеют теперь следующий вид:
9 z . х
С0„ { 1С0- \
(®2-c2k2) Еу = -------( Еу + —°- Е J .
1—СО2/©2 V м /
Вводя обозначение
а = ©р/[1—и2/©2], (4-1П)
мы можем записать систему уравнений для Ех и Еу в виде
(со2—c2k2—а) Ех + i« (шс/а>) Еу = 0, (4.112а)
(ю2—c2k2—а)Еу—ia (©</©) Ех = 0. (4.1126)
Приравнивая нулю детерминант, составленный из коэффициентов
этой системы, получаем
(со2—c2k2—а)2 = (а©е/©)2, (4.113)
и2—c2k2—а = ±асос/<о. (4.114)
4.16. Электромаг. волны, распространяющиеся параллельно В,
131
Таким образом,
_______1 ± (<ос/и)
[1 +(<0с/«)][1-(«17/®)]
“р
(4.115)
Рис. 4.38. Право- и левополяризованные волны, распространяющиеся вдоль
направления магнитного поля Во.
Знаки й= показывают, что у системы уравнений (4.112) есть два
решения, которые соответствуют двум разным волнам, распростра-
няющимся вдоль магнитного поля Во. Дисперсионные уравнения
для этих волн записываются в виде
СД2 (о2/<о2
--------= 1-------------р!-------,
со2 1 — (ц>с/со)
С2^2 СО2/<02
а2 1 + (<ос/ш)
R -волна, (4.116)
L-волна. (4-117)
Оказывается, эти волны имеют круговую поляризацию. Символы
R и L означают соответственно правую тл левую круговые поляриза-
ции (задача 4.17). Ориентация векторных величин в этих волнах
показана на рис. 4.38. Вектор напряженности электрического
поля в правополяризованной волне с течением времени поворачи-
вается по часовой стрелке, если смотреть по направлению век-
тора Во. В левополяризованной волне он вращается в противопо-
ложную сторону. Поскольку дисперсионные уравнения (4.116) и
(4.117) зависят только от k\ направление вращения вектора Е не
132
Гл. 4. Волны в плазме
Рис. 4.39. Зависимость величины Оф/с2 от частоты со для право- и левополяри-
зованных волн. Области частот, в которых волны распространяться не могут
(г>ф/с2 < 0),не заштрихованы, поскольку для этих двух волн они различны.
зависит от знака величины k\ поэтому у волн, распространяющихся
в противоположных направлениях, поляризация будет одной и
той же. Таким образом, можно сделать следующее заключение:
основные типы электромагнитных волн, распространяющихся вдоль
магнитного поля Во,— это волны с правой (R) и левой (L) круговой
поляризацией; основные типы волн, распространяющиеся поперек
Во, — это линейно-поляризованная обыкновенная волна (О-волна)
и эллиптически поляризованная необыкновенная волна (Х-волна).
Рассмотрим теперь отсечки и резонансы право- и левополяри-
зованных волн. Для правополяризованной волны k становится
бесконечным при со — ас; в этом случае волна попадает в резонанс
с циклотронным вращением электронов. Направление вращения
плоскости поляризации этой волны совпадает с направлением вра-
щения электронов в магнитном поле; непрерывно ускоряя элек-
троны, волна теряет свою энергию и не может больше распростра-
няться. Напротив, левополяризованная волна не попадает в резо-
нанс с электронами, поскольку в ней вектор электрического поля
вращается в противоположную сторону. Как легко видеть из урав-
нения (4.117), при положительных со левополяризованная волна
не имеет резонансов. Если бы в нашем анализе мы учли движение
ионов, то обнаружили бы, что левополяризованная волна попадает
в резонанс при со = Qc, поскольку вектор электрического поля
в ней вращается в ту же сторону, что и ионы.
Чтобы найти частоты отсечек, в уравнениях (4.116) и (4.117)
нужно положить k = 0. В этом случае мы получим то же уравне-
ние, что и в случае отсечек необыкновенной волны [см. уравнение
4.17. Экспериментальные следствия
133
(4.107)]. Таким образом, при продольном распространении
частоты отсечек остаются теми же, что и в случае попереч-
ного распространения колебаний. Правополяризованная волна,
которой в уравнениях (4.116) и (4.107) соответствует знак минус,
имеет более высокую частоту отсечки aR, определяемую первым
из выражений (4.108). Частота отсечки левополяризованной волны
ниже. В уравнении (4.107) ей соответствует знак плюс, на оси со
она лежит левее a>R. Вот почему ранее мы обозначили эти частоты
<од и coL. Дисперсионные кривые для право- и левополяризованных
волн показаны на рис. 4.39. Полоса непропускания левополяризо-
ванной волны лежит в области низких частот; в целом она ведет
себя как обыкновенная волна, только отсечка ее происходит не
при со = ар, а при со = сод. Полоса непропускания правополяри-
зованной волны лежит между частотами со^ и сос, но ниже сос рас-
полагается еще одна область, где может распространяться волна
с фазовой скоростью Уф < с. В этой низкочастотной области волна
называется вистлерной (свистовой) модой. Вистлеры имеют очень
большое значение для изучения ионосферных явлений.
4.17. Экспериментальные следствия
4.17.1. Вистлерная мода
Первые исследователи ионосферного радиоизлучения были воз-
награждены за свои усилия разнообразными свистящими звуками,
прослушивавшимися в диапазоне частот, воспринимаемых на слух.
Рис. 4.40. Реальная спектрограмма вистлерных сигналов, изгибы на которой
связаны с дисперсией правополяризованной волны в области низких частот
(рис. 4.39). Приемник в каждый момент времени t быстро просматривает ча-
стотный диапазон от 0 до 20 кГц, что соответствует на спектрограмме верти-
кальной линии. Самописец рисует на этой линии точки, густота которых
пропорциональна интенсивности сигнала на данной частоте. Отклонение
точек от вертикали со временем свидетельствует о существовании в излуче-
нии нисходящего тона. [Из работы: Carpenter D. L., J. Geophys. Res., 71,
693 (1966).]
134
Гл. 4. Волны в плазме
Рис. 4.41. Схема, иллюстрирующая механизм распространения вистлеров.
Сигналы, распространяющиеся по каналам А, В и С, отмечены на рис. 4.40
этими же буквами.
На рис. 4.40 представлена частотно-временная спектрограмма
этого явления, т. е. зависимость частот принимаемых колебаний
от времени. На ней виден типичный ряд нисходящих тонов. Такие
свисты можно было также прослушивать через громкоговоритель.
Это явление легко объяснить, исходя из дисперсионных характе-
ристик правополяризованной волны. Когда в Южном полушарии
происходит вспышка молнии, генерируются радиошумы на всех
частотах. Среди возбуждаемых в ионосфере и магнитосфере волн
есть и волны с правой поляризацией, распространяющиеся вдоль
магнитного поля Земли. Эти волны перемещаются вдоль силовых
линий и регистрируются, скажем, наблюдателями в Канаде. Коле-
бания с разными частотами приходят туда в разное время. Как
видно из рис. 4.39, при со <сщ/2 фазовая скорость волн растет с ча-
стотой (задача 4.19). Можно показать, что и групповая скорость
также увеличивается с частотой (задача 4.20). Таким образом,
низкочастотные колебания приходят в точку наблюдения позже.
Это и приводит к тому, что тон становится нисходящим. Одна
вспышка молнии может вызвать несколько вистлеров, распростра-
няющихся вдоль различных трубок силовых линий А, В, С
(рис. 4.41). Частоты этих волн всегда меньше местной циклотрон-
ной, поэтому для того, чтобы вистлеры могли регистрироваться
в другом полушарии, их частоты должны быть ниже, чем мини-
мальная электронная гирочастота на всей длине силовой трубки.
Эта частота равна примерно 100 кГц. Частоты вистлеров либо не-
посредственно лежат в аудио диапазоне, либо их можно преобразо-
вать в этот диапазон посредством гетеродинирования.
4.17.2. Фарадеево вращение
Если в плазме вдоль магнитного поля распространяется линейно-
поляризованная волна, то ее плоскость поляризации поворачи-
вается (рис. 4.42). Это явление можно объяснить тем, что фазовые
скорости право- и левополяризованных волн различны. Действи-
тельно, из рис. 4.39 видно, что при больших а» правополяризован-
ная волна движется быстрее левополяризованной. Линейно-поля-
4.17. Экспериментальные следствия
135
Рис. 4.42. Фарадеево вращение плоскости поляризации волны, распростра-
няющейся вдоль магнитного поля Во.
ризованную волну можно считать суммой волн правой и левой
круговой поляризации (рис. 4.43). Частоты этих волн, естественно,
одинаковы. Совершив N оборотов, векторы электрического поля
право- и левополяризованной волн Ел и Ед возвращаются в их
исходные положения. Однако если линейно-поляризованная волна
прошла данное расстояние d, то составляющие ее Ел и Ед сделают
разное число оборотов, поскольку для того, чтобы пройти это рас-
стояние, право- и левополяризованной волнам требуется разное
время. Поскольку волна левой поляризации движется медленнее,
в точке, в которой вектор Е^ в правополяризованной волне сделает
N оборотов, вектор Et в левополяризованной волне успеет сделать
уже N + 8 оборотов, и векторы окажутся в положении, показан-
ном на рис. 4.44. Очевидно, что плоскость поляризации поверну-
лась. Измеряя угол поворота с помощью рупорной СВЧ-антенны,
можно вычислить величину сор и, следовательно, плотность плазмы
(задача 4.22). Явление фарадеева вращения было подтверждено
экспериментально, но как метод измерения плотности плазмы оно
оказалось не столь удобным, как СВЧ-интерферометрия, поскольку
к торцам плазменного столба обычно трудно подобраться. Другая
причина состоит в том, что при небольшой плотности среды этот
эффект очень слаб, а в противном случае нужно учитывать прелом-
ление волн в плазме.
При создании плотной плазмы с помощью мощных импульсных
лазеров, испаряющих твердую мишень, иногда спонтанно генери-
руются магнитные поля напряженностью до нескольких мегагаусс.
Они были зарегистрированы по фарадееву вращению лазерного
излучения с более высокой, чем у основного лазера, частотой. В меж-
звездном пространстве волны проходят настолько большие расстоя-
ния, что фарадеево вращение становится заметным, несмотря на
низкие плотности плазмы. Этот эффект использовался, в частности,
для объяснения поляризации микроволнового излучения, которое
на стадии образования новых звезд генерируется с помощью мазер-
ного механизма в облаках, состоящих из радикалов ОН- или мо-
лекул Н2О.
136
Гл. 4. Волны в плазме
Рис. 4.43. Плоскополяризованную волну можно представить как сумму
волн с левой и правой круговой поляризацией.
Рис. 4.44. После прохождения плазмы левополяризованная волна опережает
по фазе правополяризованную, и плоскость поляризации поворачивается.
Задачи
4.14. Докажите, что в точке резонанса необыкновенная волна является чисто
электрической. Указание: выразите отношение ЕУ!ЕХ через частоту со и по-
ложите <о = сод.
4.15. Докажите, что критические точки на рис. 4.36 расположены в правиль-
ном порядке, т. е. что сод <сор <со/г <со^.
4.16. Покажите, что групповая скорость необыкновенной волны в точках
отсечки и резонанса обращается в нуль. Движением ионов можете пренебречь.
4.17. Докажите, что право- и левополяризованные волны действительно так
поляризованы. Для этого:
а) покажите, что систему уравнений для ЕхпЕу можно записать в виде
F (<$)(ЕХ — \ЕУ) == О, G (со) (Ех + i Еу) = 0, где для правополяризованной
волны F (со) = 0, а для левополяризованной G(co) — 0;
б) заметьте, что для правополяризованной волны G (<о)=/=0 и, следовательно^
Ех ~ — i Еу. Восстановив экспоненциальные зависимости поля Е от вре-
мени [Е ~ ехр (— i со/)], покажите, что вектор Е% вращается в направле-
нии вращения электронов в магнитном поле; докажите, что в левополяризо-
ванной волне вектор Ед вращается в противоположном направлении;
в) нарисуйте спирали, которые описывает в пространстве в данный момент
времени конец вектора Е^ в правополяризованной волне; рассмотрите слу-
чаи 1) &2>0 и 2) й2<0; заметьте, что для неподвижного наблюдателя, рас-
сматривающего движущуюся мимо него спираль, вектор Е в обоих случаях
вращается в одну и ту же сторону.
4.18. Магнитогидродинамические волны 137
4.18. Левополяризованные волны распространяются в плазме вдоль одно"
родного магнитного поля В = Boz. Плотность плазмы растет с г. При какой
плотности плазмы произойдет отсечка волн, если f = 2,8 ГГц, а 80 = 0,3 Тл?
4.19. Покажите, что максимальная фазовая скорость вистлеров достигается
на частоте со = сос/2 и что она меньше скорости света.
4.20. Покажите, что в области частот со < сос (е >1) групповая скорость ви-
стлерных колебаний пропорциональна со1,2.
4.21. Покажите, что в позитрониевой плазме с равным числом позитронов
и электронов фарадеево вращение отсутствует.
4.22. В однородной плазме, помещенной в магнитное поле 0,1 Тл, изучается
фарадеево вращение СВЧ-колебаний с длиной волны 8 мм. Обнаружено,
что после прохождения 1 м плазмы плоскость поляризации повернулась на
90е. Какова плотность плазмы?
4.23. Покажите, что для линейно-поляризованной поперечной волны, рас-
пространяющейся вдоль магнитного поля Во, угол фарадеева вращения в гра-
дусах дается выражением
L
0= 1,5-lO-11^ f В (г) пе (г) dz,
б
где Ло — длина волны колебаний вне плазмы, a L — расстояние, пройденное
волной в плазме. Считайте, что со2 > со2 со2
р с
4.24. В некотором эксперименте по лазерному синтезу плазма создается с по-
мощью импульса излучения с длиной волны 1,06 мкм, падающего на твердую
мишень. Возникающие при этом термоэлектрические токи генерируют
очень сильные магнитные поля. Напряженность этих полей можно измерить
по фарадееву вращению излучения с удвоенной частотой (Хо = 0,53 мкм),
получаемого с помощью преобразования света от того же лазера. Пусть В =
— 100 Тл, п ~ 1027 м“3, а длина пути, который проходит свет в плазме, равна
30 мкм. Чему равен угол фарадеева вращения в градусах? (Считайте, что
МВ.)
4.25. Если плотность плазмы выше критической плотности пс, то для ее из-
мерения нельзя использовать СВЧ-интерферометр, работающий на обыкно-
венной волне. Для измерения больших плотностей можно использовать не-
обыкновенную волну.
а) Выпишите выражение для плотности ncx, при которой происходит .отсечка
необыкновенной волны.
6) На графике зависимости Цф/с2 от со покажите, на какой ветви дисперсион-
ного уравнения для необыкновенной волны будет работать такой интерфе-
рометр.
4.18. Магнитогидродинамические волны
В последней части нашего обзора основных типов волн в плазме
анализируются низкочастотные ионные колебания в присутствии
магнитного поля. Из многих возможных мод мы рассмотрим только
две: магнитогидродинамическую волну, распространяющуюся вдоль
магнитного поля Во, или альфвеновскую волну, и магнитозвуковую
138
Гл. 4. Волны в плазме
волну. У плоской альфвеновской волны волновой вектор к направ-
лен вдоль Во, Ei и jx перпендикулярны Во, а Вх и Vi перпендику-
лярны как Во, так и Ех (рис. 4.45). Из уравнения Максвелла, как
обычно, получаем
V X V X — k(k-E1)-yft2E1 = (<B2/c2)E1 + (iw/e0c2) ji (4.118)
[см. уравнение (4.80)}.
Согласно нашему предположению, k = kz и Ej — Е^х; поэтому
отлична от нуля будет только х-составляющая этого уравнения.
Рис. 4.45. Альфвеновская волна, распространяющаяся вдоль магнитного
поля Во.
Поскольку мы рассматриваем низкочастотные колебания, в ток
теперь вносят вклад как электроны, так и ионы. Проекцию урав-
нения (4.118) на ось х можно записать в виде
е0(®2—сЧг^Ег — —i<on0e (vix—vex). (4.119)
Тепловые движения для этой волны несущественны, поэтому ско-
рость движения ионов можно определять из формулы (4.63), полу-
ченной в предположении 7\- = 0. Для полноты анализа включим
в рассмотрение также компоненту viy, которая в явном виде нигде
ранее не выписывалась:
ie
Щх — ..
M(0
(4.120)
Решения уравнений движения для электронов получаются, если
сделать в этих формулах следующие замены: М -* т,
->---соС( а затем перейти к пределу <о2:
ie со2 „ Z4 е <о2 „
=--------— Е^О, иеу =--------------------~Ei =
та> щ ш2 ш2
£i
(4.121)
4.18. Магнитогидродинамические волны 139
В этом пределе ларморовским вращением электронов пренебре-
гают. Электроны совершают лишь Е X В-дрейф в направлении у.
Подставляя выражения для скоростей частиц в уравнение (4.119),
получаем
ie ( Г1
80 (со2—с2£2)Б1 =—iconoe------[1--------EL. (4.122)
Мы \ со2 /
Проекция скорости vx на направление у нужна нам лишь для того,
чтобы построить представленную ниже физическую картину рас-
пространения альфвеновских волн. Воспользовавшись определе-
нием ионной плазменной частоты Qp [см. формулу (4.49) ], имеем
/ Q2 \_|
ю2 _ Л2 = Q2 ( 1------- | . (4.123)
\ СО2 /
Теперь мы должны сделать еще одно предположение. Будем считать,
что со2 П2> т. е. что частоты магнитогидродинамических волн
значительно ниже частоты ионно-циклотронного резонанса. В этом
пределе уравнение (4.123) принимает вид
со2 — c2k2 = — ш2(йр/Й2)= — со2(п0е2/е0Л4) (Л42/е2^) = —со2(р/е0Во).
(4.124)
coW = с2/[ 1 + (p/e0Bg) ] = ?/[ 1 + (pp.0/Bg) с2],
где р — массовая плотность: р = п0Л4. Последнее выражение не
является неожиданным, поскольку знаменатель в нем равен от-
носительной диэлектрической проницаемости для низкочастотных
поперечных движений [формула (3.28)]. Уравнение (4.124) опреде-
ляет просто фазовую скорость электромагнитной волны в диэлек-
трике: a/k = с/(еЛрЛ)1/2 = с/е^2 при р^ = 1. Как было показано
ранее, в большинстве случаев для лабораторной плазмы е 1
и уравнение (4.124) можно приближенно записать в следующем
виде:
со//? = цф= В0/(р.0р)1/2. (4.125)
Такие магнитогидродинамические волны распространяются вдоль
магнитного поля Во с постоянной скоростью иА, которая называется
альфвеновской скоростью:
^а^Во/(НоР)1,2-'| (4-126)
Это — характерная скорость распространения возмущений сило-
вых линий. Диэлектрическую проницаемость (3.28) теперь можно
записать в виде
= е/е0 = 1(с/оА). (4.127)
Заметим, что для типичной плазмы плотность р достаточно велика,
и потому vk мала, а 1.
140
Гл. 4. Волны в плазме
Рис. 4.46. Соотношения между осциллирующими величинами в альфвенов-
ской волне и возмущение силовых линий магнитного поля (увеличено).
Чтобы понять физические процессы, происходящие в альфве-
новской волне, вспомним, что это электромагнитная волна, собст-
венное магнитное поле Вх которой определяется уравнениями
ухЕх= — Bi, Ех— (co//?) By. (4.128)
Когда к Во добавляется малая компонента Ву, на силовых линиях
появляется синусоидальная рябь; на рис. 4.46 она изображена
в увеличенном масштабе. В точке, отмеченной на рисунке, Вц на-
правлена в сторону положительных у, поэтому в соответствии с
уравнением (4.128) у волны, распространяющейся в направлении
положительных z, компонента Ех направлена в сторону положи-
тельных х. Электрическое поле Ех вызывает Ех X В0-дрейф в сто-
рону отрицательных у. Как следует из уравнений (4.120) и (4.121),
в выбранном нами предельном случае <о2 < Q2 ионы и электроны
дрейфуют с одинаковыми скоростями vy. Таким образом, на
рис. 4.45 плазма как единое целое будет двигаться взад-вперед по
оси у. Это же движение изображено на рис. 4.46. Амплитуда коле-
баний скорости в таких движениях равна | Ех/В0\. Рассмотрим
теперь движение силовых линий. Поскольку изгиб силовой линии
движется в направлении z со скоростью a/k, то силовая линия в
точке, отмеченной на рис. 4.46, движется вниз, туда же, куда и
плазма в этой точке. Скорость движения силовой линии равна
(<о/&) | Ву/В0\. Как следует из уравнения (4.128), эта величина
в точности равна скорости движения жидкости | ЕХ1ВО ]. Таким
образом, плазма и силовые линии колеблются вместе, как. будто
силовые линии вморожены в плазму. Иными словами, силовые ли-
нии ведут себя как нагруженные плазмой массивные струны, а
альфвеновскую волну можно считать возмущением, которое рас-
пространяется вдоль струн после щипка. Понятие о вмороженности
силовых линий в плазму и их совместном движении полезно для
понимания многих низкочастотных плазменных явлений. Можно
4.18. Магнитогидродинамические волны
141
Рис. 4.47. Направления
векторов скорости и эле-
ктрического поля в тор-
сионной (шировой) аль-
фвеновской волне, рас-
пространяющейся в ци-
линдрическом столбе
плазмы.
Рис. 4.48. Схема эксперимента по регистра-
ции альфвеновских волн. [Из работы: Wil-
cox. J. М., Boley F. I., DeSilva A. W., Phys,.
Fluids, 3, 15 (I960).]
показать, что если в плазме нет электрических полей, направлен-
ных вдоль Во, то это приближение является точным.
Нам осталось выяснить, какая сила поддерживает поле Ех,,
которое мы считали заданным. Дело в том, что в осциллирующем
поле Ех ионы из-за своей большой массы не успевают следовать-
за электронами и вследствие этого запаздывания в плазме возни-
кает поляризационный дрейф со скоростью vp, направленной вдоль
Ej. Компонента скорости этого дрейфа vix определяется уравнением
(4.120). Такое дрейфовое движение приводит к появлению тока jt
вдоль оси х. В результате на плазму действует направленная по-
оси у сила jx X Во, которая сдвинута по фазе относительно ско-
рости vx на 90°. Как всякая сила, действующая на осциллятор не
в фазе со скоростью, она поддерживает его колебания. Естественно^
источником колебаний является инерция ионов, проскакивающих
свое положение равновесия; в плазме их импульс с помощью элек-
тромагнитных сил сложным образом передается полю.
В системе с более реалистической для экспериментов геомет-
рией поле Ej будет направлено в радиальном, а скорость направ-
лена в азимутальном направлении (рис. 4.47). В этом случае плазму
можно считать несжимаемой и пренебречь в уравнении движения
членом VP- Возникающая при этом мода колебаний называется
торсионной альфвеновской волной. Впервые ее наблюдал в жидкой:
ртути Б. Ленерт.
Альфвеновские волны в плазме впервые возбуждались и реги-
стрировались в экспериментах Аллена, Бейкера, Пайла и Уил-
кокса в Беркли (шт. Калифорния, США) и Джефкотта (Англия)'
в 1959 г. Опыты ставились в водородной плазме медленного само-
стягивающегося разряда между электродами, вытянутыми вдоль-
142
Гл. 4. Волны в плдзме
Рис.14.49. Результаты измерений зависимости фа-
зовой скорости альфвеновских волн от магнитного
поля. [Из работы: Wilcox J. М., Boley F. I., De-
Silva'A. W., Phys. Fluids, 3, 15 (I960).]
Рис. 4.50. Магнито-
звуковая волна, рас-
пространяющаяся под
прямым углом к маг-
нитному полю Во-
направления магнитного поля (рис. 4.48), с помощью конденсатора
Ki большой емкости. Соединенный с металлической стенкой кон-
денсатор^Кг малой емкости использовался для того, чтобы создать
электрическое поле Еь перпендикулярное Во. После замыкания
этого конденсатора в плазме возникала волна, которая спустя не-
которое время регистрировалась зондами 3. На рис. 4.49 приведена
полученная в эксперименте зависимость фазовой скорости волны
от магнитного поля, которая, как и предсказывает формула (4.126),
является линейной.
Этот эксперимент был очень сложным, поскольку для того,
чтобы преодолеть затухание волн, нужно было создавать сильное
магнитное поле напряженностью 1 Тл. Однако если Во велико, то
vA и, следовательно, длина волны альфвеновского колебания ста-
новятся очень большими. Для уменьшения vA нужно было поэ-
тому создавать более плотную плазму. Чтобы достичь низкой альф-
веновской скорости 2,8-105 м/с, в эксперименте Уилкокса и др.
применялась плазма плотностью 6-1021 м-3. Заметим, что в экспе-
рименте нельзя увеличивать массовую плотность плазмы (р =
= п0/И), используя более тяжелые атомы. Дело в том, что частота
волны со = kvA пропорциональна /И~1/2, а циклотронная частота
Qc пропорциональна М~г. Таким образом, отношение co/Qc про-
порционально М1/2 и, применяя более тяжелые ионы, нельзя вы-
полнить условие со2 < Q2.
4.19. ^Магнитозвуковые волны
143
4.19. Магнитозвуковые волны
Рассмотрим, наконец, низкочастотные электромагнитные волны,
распространяющиеся поперек магнитного поля Во. Снова положим
Во = Boz и Ех = Epi, но теперь будем считать, что k = ky
(рис. 4.50). Очевидно, скорости Ег X В0-дрейфов направлены те-
перь вдоль волнового вектора к, так что в процессе распростране-
ния волн плазма будет сжиматься и расширяться. Следовательно,
в уравнении движения нужно сохранить член VP- Уравнение дви-
жения для ионов можно записать в виде
Mn0(5vil/5/) = en0(Ei +v/i х Во) —yiKT^ni. (4.129)
Направляя Ех и к так, как указывалось выше, уравнение (4.129)
можно записать в виде
vlx = (ie/Mco) (Ex+viyB^, (4.130)
viy = (.ielM<£>)( — vixB0) + (k/u>) (yiKTi/M) (гц/по). (4.131)
Уравнение непрерывности дает
«i/n0 = (k/a) vty; (4.132)
при этом уравнение (4.131) принимает вид
vly = — (ie/Al <о) vixB0 4- (/г2/®2) (yiKT {/М) vly. (4.133)
Введя сокращенное обозначение А == (Л2/®2) (т<КТ</Л4), уравне-
ние (4.133) можно переписать в виде
viy (1 — 4) = — (iQc/co) vix. (4.134)
Выражая отсюда компоненту v[y и подставляя ее в уравнение
(4.130), получаем
uix = (ieW®)Ex + (iQc/®)(—iQc/®)(l —4)-1щх,
/ о о\ (4»1о5)'
vix [ 1 — ($/ и )/( 1 — 4)] = (ie/M®) Ех.
Для дальнейшего анализа нам нужна только эта составляющая
вектора v^, поскольку единственная не равная нулю компонента
волнового уравнения (4.81) имеет вид
е0(®2—c2k2)Ex— —ia>noe(ViX—vex). (4.136)
Чтобы получить выражение для vex, необходимо лишь поменять
обозначения в уравнении (4.135) и перейти к пределу малых масс
электронов, т. е. считать, что ®2 < ®2 и со2 ^Цтепл.е:
ie <ог A fe2 УеКТе \
®2 \ Q? m /
-!*!_ -У'кт'- Ех. (4.137)
И
144
Гл. 4. Волны в п/азме
ео(со2—с2&2) Ех=- — i<on0e
—-------------W
1 — А — (й2/со2) )
1. (4.138)
Из последних трех уравнений получаем
ie /
~ Ех I
Мео I
ife2M уеКТе Е
еоВ2 еМ
Снова предположим, что со2 С й2, и поэтому разностью 1—А можно
пренебречь по сравнению с й2/со2. Используя определения величин
йр и vA, имеем
(ео2-с2А2) - -ео2(й2/й2)(1-4) + (^2/^)(уД7,е/м)>
/ х 9 z . (4.139)
/ уеКТе X Й2 ( yiKTi \ 4 7
со2 — с2&2 1 + —--- Н-----р- (О2 — А2 —--— = 0.
\ Mv\ / Й2 V М )
со2 —А2
Поскольку
^l2 = c2/v2Al
уравнение (4.139) принимает вид
(4.140)
где ^—скорость звука. Окончательно имеем
(4.141)
0)2 ^С2 Vl+VA
k2
(4.142)
Это — дисперсионное соотношение для магнитозвуковой волны,
распространяющейся перпендикулярно магнитному полю Во. В та-
кой звуковой волне области сжатия и разрежения образуются
не из-за движения частиц вдоль электрического поля Е, а из-за
их Е X В-дрейфа поперек Е. В пределе Во —0, vA -> 0 магнито-
звуковая волна переходит в обычную ионно-звуковую волну.
В пределе КТ ->-0, v5 -> 0 силы, связанные с градиентом давления,
становятся малыми и волна превращается в модифицированную
альфвеновскую волну. Фазовая скорость магнитозвуковой моды
почти всегда выше альфвеновской скорости vA, поэтому ее часто
называют просто «быстрой» магнитогидродинамической волной.
4.20. Основные типы волн в плазме
(сводка формул)
Электростатические электронные волны
3
-Bq = 0 ИЛИ к || Во : (0 = (О -| — k ^тепл (плазменные колебания или
И 2 ленгмюровские волны)
(4.143)
4.20. Основные типы волн в плазме (сводка формул)
145
k I Во : (О2 — (О2 Ci)2 = (0^ (верхнегибридные колебания). (4.144)
Электростатические ионные волны
Во=О или к || Во:
(ионно-звуковые
волны).
(4.145)
k X Во: СО2 = Q2 -|- ^2V2 (электростатические ионно-циклотронные
волны)
(4.146)
или
— 0)2 — (нижнегибридные колебания).
(4.147)
Электромагнитные электронные волны
9 9 »9 9
Bq = 0: (0 — Юр k С (световые волны).
(4.148)
& ± Во, Ej || BQ:
С2£2/(О2 — 1 _СО2/й)2 (обыкновенная волна).
(4.149)
-k _1_ Во, Ei J_ Во:
с2/г2
-------= 1
(О2
(О2
р
со2
со2 - *2Р
“2-“л
(необыкновенная
волна).
(4.150)
C-k2
*11 Во:
(О2
1 — ((0с/(0)
(правополяризованная волна);
(вистлерная мода).
(4.151)
C2k2
------ = 1
(О2
мр/'м2
1 + ((Ос/со)
(левополяризованная волна).
(4.152)
1
Электромагнитные ионные волны
Во = 0 : Нет
k J] Bq *. (О2 = Й2Уд (альфвеновская волна). (4.153)
z.2 ,,2 г _,2
СО Vs ~Р Од
k ± Bq! —~ = С2 — ------------— (магнитозвуковая волна). (4.154)
k2 с2 4- Од
Приведенный выше набор дисперсионных уравнений является очень
упрощенным; он охватывает только главные направления распро-
странения — вдоль и поперек магнитного поля. Тем не менее его
полезно запомнить как основу для анализа более сложных волно-
вых движений. Нередко сложную волну можно представить как
'.модификацию или суперпозицию этих основных типов Колебаний.
146
Гл. 4. Волны в плазме
4.21. Диаграмма Клеммова— Муллали— Эллиса
Если волна распространяется под углом к магнитному полю, то
ее фазовая скорость зависит от угла. Некоторые из типов колеба-
ний, перечисленных выше для случаев к || Во и kj_ Во, при измене-
нии угла плавно переходят друг в друга, другие же при некотором
критическом угле исчезают. Эту сложную картину помогает про-
яснить диаграмма Клеммова—Муллали—Эллиса (КМЭ), названная
так Т. X. Стиксом по фамилиям ее изобретателей. Такая диаграмма
1
Wp /<z)f или плотность
О
Рис. 4.51. Диаграмма Клеммова—Муллали—Эллиса, иллюстрирующая
классификацию волн в холодной плазме. Буквы R, L, О и X обозначают со-
ответственно правополяризованную, левополяризованную, обыкновенную»
и необыкновенную волны.
4.21. Диаграмма Клеммова—Муллали—Эллиса 147
изображена на рис. 4.51. КМЭ-диаграмма описывает только волны
в холодной плазме, когда Tt = Те = 0. Обобщение на случай ко-
нечных температур настолько усложняет диаграмму, что исполь-
зование ее теряет смысл.
На рис. 4.51 на осях координат отложены величины <ос/о> и
«р/®2 или пропорциональные им напряженность магнитного поля
и плотность плазмы. При данной частоте со любой эксперименталь-
ной ситуации, характеризуемой величинами сов и а>с, на диаграмме
отвечает определенная точка. Плоскость диаграммы разделяется
на участки кривыми, которые соответствуют уже знакомым нам
отсечкам и резонансам. Например, условие отсечки необыкновен-
ной волны со2 = со2 + <йр представляет собой квадратичную |зави-
симость величины сор/со2 от сос/со. Получающаяся в результате де-
ления дисперсионного уравнения на со2 парабола (сос/со)2 —
+ (cdp/®2)= 1 отмечена на рис. 4.51 надписью «верхнегибрид-
ный резонанс». Кривые, отвечающие отсечкам и резонансам, отде-
ляют области распространения различных типов волн от областей
непропускания. Таким образом, на различных участках диаграммы
могут существовать разные наборы волн.
Изображенные в каждой области маленькие диаграммы не
только показывают, какие волны существуют при данном наборе
параметров, но и демонстрируют, как фазовые скорости этих волн
зависят от угла. Условимся, что магнитное поле направлено на
диаграмме вертикально вверх. Тогда расстояние от центра малень-
кой диаграммы до любой точки на эллипсе или восьмерке вдоль
прямой, наклоненной под углом 0 к вертикали, будет пропорцио-
нально фазовой скорости волн, распространяющихся под углом 0
к магнитному полю. Например, в треугольной области, помечен-
ной на рис. 4.51 знаком * , при изменении угла 0 от нуля до л/2 ле-
вополяризованная волна переходит в необыкновенную волну. Фа-
зовая скорость у левополяризованной волны всегда больше, чем
у правополяризованной, а при 0 = л/2 скорость последней вообще
обращается в нуль. Правополяризованная волна не переходит в
обыкновенную, поскольку в этой области параметров со2<со2, и
обыкновенная мода вообще не существует.
Верхние участки КМЭ-диаграммы соответствуют случаю со < сос.
Здесь показаны характеристики низкочастотных ионных волн.
Электростатические ионные волны на диаграмме отсутствуют, по-
скольку они могут распространяться только в теплой плазме,
а тепловыми скоростями мы пренебрегли. КМЭ-диаграмму можно
рассматривать как «плазменный пруд». Если бросить в какой-ни-
будь участок такого пруда камень, то от него пойдут волны, форма
которых напоминает фигуры, изображенные на маленьких диаграм-
мах.
148
Гл. 4. Волны в плазме
Задачи
4.26. Водородная плазма газового разряда плотностью 101в м-3 помещена
в магнитное поле Во = 0,1 Тл.
а) Чему равна альфвеновская скорость va?
б) Предположим, что va оказалась больше с. Значит ли это, что альфве-
новские волны движутся быстрее света?
4.27. Вычислите альфвеновскую скорость в области магнитосферы, где
В = 10'8 Тл, п = 108 м-з, а М = Мн =- 1,67-10“27 кг.
4.28. Предположим, вы создали в лаборатории плазму, плотность которой
и — 1015 nt3. Плазма удерживается магнитным полем В ~ 10“2 Тл. Вы
подключаете к зонду, помещенному в плазму, генератор сигнала, работаю-
щий на частоте 160 МГц.
а) Нарисуйте КМЭ-диаграмму. Покажите на ней область, отвечающую па-
раметрам эксперимента.
б) Какие электромагнитные волны могут распространяться в такой плазме?
4.29. Предположим, что вы хотите поставить эксперимент по возбуждению
стоячих торсионных альфвеновских волн в цилиндрическом плазменном
столбе, причем амплитуда стоячей волны должна быть максимальна в цен-
тральной плоскости системы и обращаться в нуль на концах цилиндра. Чтобы
удовлетворить условию со < Йс, вы выбрали со = 0,1 Йс-
а) Какова должна быть длина плазменного столба, если вы можете создать
в магнитном поле 23~О,1 Тл плазму с концентрацией п=1019 м—3?
б) Какова должна быть длина плазменного столба для того, чтобы можно-
было поставить эксперимент в Q-машине, если напряженность магнитного
поля в ней Во ~ 0,3 Тл, а плазма имеет плотность п = 1018 м~3 и состоит
из однократно заряженных ионов цезия с атомным номером 133? Указание:
вынесите масштабные множители и примените результат, полученный в п. а
данной задачи.
4.30. Пульсар излучает широкий спектр электромагнитных волн. Они ре-
гистрируются приемником, настроенным на частоты, лежащие около f =
= 80 МГц. Из-за дисперсии групповой скорости, обусловленной межпланет-
ной плазмой, частота принимаемой волны дрейфует со скоростью dfldt =
= 5 МГц/с.
а) Пренебрегая межзвездным магнитным полем и считая в>2 > к>2, покажите,
что df/dt ж — (с/х) (f3/fp), где fp— плазменная частота, ах — расстояние
до пульсара.
б) Пусть средняя плотность электронов в космосе равна 2-105 м“3. Как да-
леко от нас находится этот пульсар? (1 парсек = 3-1016 м.)
4.31. В трехкомпонентной плазме плотность электронов п0, плотность ионов-
с массой М-! равна (1—е) п0, а плотность ионов с массой Л42 составляет 8п0.
Пусть Г11 = = 0, Те 0.
а) Выведите дисперсионное уравнение для электростатических ионно-цикло-
тронных волн в такой плазме.
б) Получите упрощенное выражение для to2 при малых е.
в) Оцените частоты волн в случае, когда е не мало, например для смеси из
равных количеств ионов дейтерия и трития, при условии что КТе = 10 кэВ,.
Во ~ 5 Тл, а волновое число k = 1 см-1.
4.32. Покажите, что в ленгмюровской плазменной волне усредненная по вре-
мени кинетическая энергия частиц, содержащихся в 1 м3 плазмы, равна плот-
ности энергии (1/2) е0 (£2), запасенной в электрическом поле.
4.21. Диаграмма Клеммова—Муллали—Эллиса
149
4.33. Покажите, что в альфвеновской волне усредненная по времени кинети-
ческая энергия ионов, содержащихся в 1 м3 плазмы, равна плотности энер-
гии магнитного поля волны ^В2у2р0-
4.34. На рис. 34.34 изображен лазер, работающий в дальней инфракрасной
области спектра на длине волны X = 337 мкм. В отсутствие магнитного поля
его излучение свободно проникает в плазму, если только сор меньше рабочей
частоты (о или п<згс = 1022 м“3. Однако вследствие того, что луч в плазме
проходит очень большое расстояние, в ней из-за дефокусировки образуется
оптическая полость с меньшей плотностью (ср. рис. 4.30) и излучение может
попасть в плазму только в том случае, когда ы? <£со2, где 8« 1. Для того
чтобы увеличить предельную плотность плазмы, а следовательно, и выход-
ную мощность лазера, на систему накладывается магнитное поле Во.
0 0 0 Во 0 0 0
Импульсный разряд
__ Загнутое
зеркало Плоское зеркало
и отверстие вывода
Пластиковое окно
Рис. 34.34. Схема импульсного HCN-лазера.
а) Покажите, что если в плазме распространяются левополяризованные
волны, то при неизменном е ее предельную плотность можно увеличить.
б) Пусть концентрация плазмы удвоилась. Насколько должна возрасти на-
пряженность магнитного поля, чтобы предельная плотность плазмы осталась
неизменной?
в) Покажите, что для вистлеров плазма является фокусирующей линзой.
г) Можно ли для увеличения предельной плотности использовать вистлер-
ную моду?
4.35. Используя уравнения Максвелла и уравнения движения электронов,
выведите дисперсионное соотношение для световых волн, распространяю-
щихся в однородной незамагниченной бесстолкновительной изотермической
плазме плотностью п, электронная температура которой Те отлична от нуля.
(Пренебрегите движением ионов.)
4.36. Докажите, что даже с учетом движения ионов член Vp не влияет на
поперечные волны с k X Во = 0.
4.37. Рассмотрим затухание обыкновенной волны, вызванное столкнове-
ниями между ионами и электронами с постоянной частотой v.
а) Покажите, что дисперсионное уравнение для необыкновенной волны в этом
случае имеет вид
с2£2/(о2 — 1 — wp/w (о) + iv).
150
Гл. 4. Волны в плазме
б) Покажите, что для волн, затухающих со временем (k вещественно), в пре-
деле v/co < 1 декремент затухания у s — Im со приближенно равен у
» (v/2) (сОр/ш2).
в) Покажите, что для волн, затухающих с расстоянием (со вещественна),
в пределе v/co^l характерная длина затухания 6=з(1т &)~1 приближенно
равна 6 as (2c/v) (со2/со2) [1—(<о2/(о2)]1/2,
4.38. Есть предложение построить в космосе электростанцию с большими па-
нелями солнечных батарей, которые собирали бы солнечный свет 24 часа
в сутки. Энергия должна передаваться на Землю с помощью микроволно-
вого пучка с длиной волны 30 см. Требуется оценить долю мощности излуче-
ния, которая теряется на нагрев ионосферы. Будем считать ионосферу слабо-
ионизованным газом, в котором частота столкновений между электронами
и нейтральными атомами постоянна. Какая доля энергии волн потеряется
после того, как они пройдут в такой плазме 100 км, если концентрации элек-
тронов и нейтральных молекул равны соответственно пе — 1011 м“3 и пп ~
= 101в м-3, а среднее от произведения сечения рассеяния частиц на скорость
частиц в плазме Cfv = 10"“14 м3/с?
4.39. Дисперсионное уравнение Эпплтона—Хартри для высокочастотных
электромагнитных волн, распространяющихся под углом 0 к магнитному
полю, имеет вид
Ai2/cd2 = 1 — 2о)2 (1 — со2/о2)/{2со2 (1 — (о2/со2) — co|sin20 ±сос X
X [со2 sin4 0 + 4со2 (1 — со2 /со2)2 cos20]1/2}.
Найдите из этого уравнения частоты отсечек и резонансов. Какие из них не
зависят от 0?
4.40. Микроволны, которые в свободном пространстве имеют длину волны
Л.о = 1 см, проходят через слой плазмы плотностью п0 = 2,8-1018 м“3 и тол-
щиной 10 см, помещенный в постоянное магнитное поле Во = 1,07 Тл. Вы-
числите число длин волн, укладывающихся внутри слоя, если (см. рис. 34.40):
а) волновод ориентирован так, что вектор электрического поля волны Et
параллелен оси z;
б) волновод ориентирован так, что вектор Ех параллелен оси у.
Рис. 34.40-
4.21. Диаграмма Клеммова—Муллали—Эллиса
151
4.41. Холодная плазма состоит из положительных ионов с зарядом Ze и мас-
сой и отрицательных ионов с зарядом — ей массой /И_. В состоянии
равновесия, когда в покоящейся плазме нет ни электрического, ни магнит-
ного полей, концентрации ионов равны соответственно л0+ и п0_ = Zn0-}-.
Выведите дисперсионное уравнение для плоских электромагнитных волн,
распространяющихся в такой плазме.
4.42. В плазме газового разряда, состоящей из смеси гелия и аргона, генери-
руются ионно-звуковые волны. Плазма состоит из следующих компонент:
а) электронов с концентрацией л0 и температурой КТе\
б) холодных ионов (Т ~ 0) аргона с массой Мд, зарядом + Ze и концентра-
цией Пд\
в) ионов гелия с концентрацией л/у, массой Мн, зарядом +е и темпера-
турой КТн= 0.
Пользуясь линеаризованной одномерной теорией в рамках плазменного
приближения и считая, что электроны удовлетворяют уравнению Больцмана,
получите выражение для фазовой скорости волн в такой плазме.
4.43. В отдаленной области Вселенной существует плазма, состоящая из
позитронов и полностью оголенных ядер атомов антифермия с зарядом —Ze,
где Z = 100. Выведите дисперсионное уравнение для плазменных колебаний
в такой плазме исходя из уравнений движения, непрерывности и уравнения
Пуассона с учетом движения ионов. Найдите плазменные частоты. Можете
считать, что ДТ = 0, Во = 0, а также ввести любые другие упрощающие
предположения.
4.44. Высокоразвитая цивилизация с планеты, находящейся в Крабовидной
туманности, пытается связаться с нами, «примитивными» земными сущест-
вами. Мы получаем от них радиосигналы в диапазоне 108—109 Гц, однако на
частоте 120 МГц спектр излучения резко обрывается. Из оптических измере-
ний можно заключить, что вблизи звезды верхний предел величины магнит-
ного поля составляет 36 Гс. (1 Гс == 10~4 Тл.) Оцените нижний предел плот-
ности вблизи звезды, считая, что она расположена в области НИ, которая
содержит ионизованный водород, а на распространение радиоволн в ней
влияет какая-то плазменная отсечка.
4.45. Космический корабль движется в ионосфере Юпитера со скоростью
100 км/с параллельно магнитному полю напряженностью 10”5 Тл. Если дви-
жение является сверхзвуковым (v >vs), то вокруг аппарата должны генери-
роваться ионно-звуковые ударные волны. Если же, кроме того, скорость
движения корабля превышает альфвеновскую (у >оа), то перед ним воз-
никнут также магнитозвуковые ударные волны. Приборы на борту корабля
показывают, однако, что наблюдаются ударные волны только первого типа.
Найдите пределы, в которых меняются плотность и температура плазмы.
Укажите, являются ли эти значения верхними или нижними пределами
параметров. Считайте, что атмосфера Юпитера состоит из смеси холодных,
однократно ионизованных молекул Н2, Не, СН4, СО2 и NH4, средняя моле-
кулярная масса которых равна 10.
4.46. На плазму извне падает необыкновенная волна с частотой со.
На рис. 34.46 показано, как изменяются с расстоянием г частота отсечки
правополяризованной волны сод и частота верхнегибридного резонанса (Од.
Из рисунка видно, что в плазме существует узкий слой, в котором не мо-
жет распространяться волна. Покажите, что расстояние d между точками,
в которых со — (0^ и со = сод, равно d « (<ос/<о) г0 (здесь г0 — характерный
масштаб изменения плотности в точке, где со « сод : | dnldr | « л/г0).
4.47. Если создать градиент магнитного поля Во, то для необыкновенной
волны, падающей извне на плазму, можно сделать достижимой точку верх-
негибридного резонанса.
152
Гл. 4. Волны в плазме
Рис. 34.46.
а) Нарисуйте на КМЭ-диаграмме в координатах у = (oc/w, х = со2/<о2 путь,
который прошла волна. Покажите, как можно обойти точку отсечки со =
(ср. с предыдущей задачей).
б) Покажите, что необходимое для этого изменение магнитного поля между
поверхностью плазмы и слоем, в котором со — со^, составляет АВ0 =
= S0°p/2“c-
4.48. Некая плазменная волна удовлетворяет дисперсионному уравнению
е2&2 i со2
= 1 ~ <ОА + -
top - и2 + COCQC
где со2 === со2 + Q2. Выпишите точные выражения для частот отсечек и ре-
зонансов (или для их квадратов) в пределе е г=т/Л4 <С 1.
4.49. Дисперсионное уравнение для необыкновенной волны с учетом движе-
ния ионов имеет следующий вид:
а) Покажите, что оно совпадает с дисперсионным уравнением, приведенным
в условии предыдущей задачи. (Автор предупреждает: эта задача может ока-
заться опасной для вашего здоровья.)
б) Пусть ш/ и — соответственно нижнегибридная частота и частота от-
сечки левополяризованной волны, удовлетворяющей приведенному выше
4.21. Диаграмма Клеммова—Муллали—Эллиса
153
дисперсионному уравнению. Покажите, что неравенства (0/ сод
справедливы всегда.
в) Используя полученные результаты и зная фазовую скорость колебаний
в пределе со-> О, постройте качественную зависимость величины с2 от
частоты со. Покажите области, в которых могут и не могут распространяться
волны.
4.50. С помощью нижнегибридных колебаний пытаются нагреть столб во-
дородной плазмы радиусом а, помещенный в однородное магнитное псле.
На оси плазменного цилиндра сор = сос/2, а при г = а плазменная частота
сор = 0. Антенна возбуждает в плазме необыкновенную волну с k ц = 0.
а) Постройте качественные зависимости величин сос, со^ и со/ от радиуса г.
Масштаб на графиках соблюдать не нужно, однако они должны давать пра-
вильное представление об относительных значениях этих величин на оси
и на образующей цилиндра.
б) Пусть на оси цилиндра частота со = сос. Вычислите толщину непропускаю-
щего слоя, лежащего между точками, в которых со = со/ и со = со^ (см. пре-
дыдущую задачу).
в) Повторите вычисления, проделанные в п. а и б для случая сор (шах) = 2сос.
Какой должна быть конструкция излучающей антенны?
4.51. Иногда для высокочастотного нагрева термоядерной плазмы исполь-
зуется электромагнитная ионно-циклотронная волна (волна Стикса). Выве-
дите ее дисперсионное уравнение. Для этого:
а) запишите волновое уравнение в виде (4.118) и пренебрегите током сме-
щения;
б) считая, что kykzEz « 0, k2 == k2 J- k2, kx ~ 0, запишите проекции этого
уравнения на оси х и у\
в) выведите аналоги уравнений (4.98) для ионов и получите из них выраже-
ние для vt-; считайте, что в низкочастотном приближении скорость электро-
нов ve равна скорости Е X В-дрейфа; зная V/ и ve, вычислите ток =
= nQe (yi—ve).
г) подставьте выражение для тока, полученное в п. в, в уравнения, выведен-
ные в п. б; пользуясь определением Q2 (4.49), получите систему из двух од-
нородных уравнений для Ех и Еу;
д) приравняйте детерминант этой системы нулю и решите полученное урав-
нение в наинизшем приближении по Q2, Вы должны получить следующее
дисперсионное уравнение:
Глава 5
ДИФФУЗИЯ И СОПРОТИВЛЕНИЕ
5.1. Диффузия и подвижность
в слабоионизованных газах
В предыдущей главе мы предполагали, что в состоянии равновесия
плазма является безграничной и однородной. Это, разумеется,
сильная идеализация. В любой реальной плазме всегда сущест-
вует градиент плотности, и плазма стремится диффундировать в об-
ласти с более низкой концентрацией частиц. Главная проблема
в реализации управляемых термоядерных реакций состоит в том,
чтобы с помощью магнитного поля уменьшить скорость этой диффу-
зии. Однако прежде чем браться за задачу с магнитным полем, рас-
смотрим диффузию в его отсутствие. Задача еще более упрощается,
если предположить, что плазма слабоионизована и поэтому заря-
женные частицы сталкиваются в основном не друг с другом, а с
нейтральными атомами. Анализ полностью ионизованной плазмы
мы отложим до следующих разделов, поскольку он сводится к рас-
смотрению нелинейного уравнения, для которого простых иллю-
стративных решений найдено мало. Впрочем, частично ионизован-
ная плазма встречается довольно часто: в эту категорию попадают
ионосферная плазма, плазма дуговых разрядов при высоком дав-
лении; большинство ранних работ по газовым разрядам было вы-
полнено при степенях ионизации 10~3—10-6, когда в плазме пре-
обладают именно столкновения заряженных частиц с нейтраль-
ными атомами.
Таким образом, мы будем анализировать неоднородное распре-
деление ионов и электронов на фоне плотного газа нейтральных
атомов (рис. 5.1), считая, что в процессе расширения плазмы под
действием градиента давления и электрических полей отдельные
ее частицы будут совершать случайные блуждания, часто сталки-
ваясь с нейтральными атомами. Начнем с краткого обзора понятий
атомарной теории.
5.1.1. Параметры столкновений
Пусть электрон сталкивается, скажем, с нейтральным атомом.
Тогда в зависимости от угла отскока легкая частица может поте-
рять любую долю своего начального импульса. При лобовом со-
5.1. Диффузия и подвижность в елабоионизоваиных газах
155
Рис. 5.1. Диффузия атомов газа,
обусловленная случайными стол-
кновениями.
Рис. 5.2. К определению [сечения вза-
имодействия.
ударении с тяжелым атомом изменение импульса электрона будет
в два раза больше его начального импульса, поскольку после (уп-
ругого) столкновения скорость легкой частицы меняет знак. Веро-
ятность изменения импульса можно выразить через эквивалент-
ное сечение о. Это площадь поперечного сечения, которое имел бы
атом, если бы он полностью поглощал импульс падающей на него
частицы.
На рис. 5.2 показаны электроны, падающие на плоский слой
площадью А и толщиной dx, в одном кубическом метре которого
содержится пп нейтральных атомов. Считается, что атомы пред-
ставляют собой неупругие шарики с поперечным сечением о; т. е.
попадая на участок слоя, занимаемый атомом, электрон теряет
весь свой импульс. Число атомов в слое равно ппА dx. Доля пере-
крываемой ими площади в сечении слоя составляет ппаА dx/A —
= nnadx. Пусть на слой падает поток электронов плотностью Г,
тогда с другой стороны слоя выходит поток плотностью Г' =
= Г (1—rinodx). Таким образом, изменение Г с расстоянием (dT7dx)
равно —ппаГ, откуда получаем
Г= Гоехр (—ппах) = Гоехр(— х/Хт). (5.1)
Пройдя расстояние %т, поток уменьшается в е раз по сравнению
со своим начальным значением. Величина '/.т называется средней
длиной свободного пробега между столкновениями:
\т = 1/п„о. (5.2)
Миновав расстояние %т, частица с большой вероятностью столк-
нется с атомом. Для частицы, движущейся со скоростью v, среднее
время между столкновениями равно т = Лт/г>, а средняя частота
столкновений дается выражением
т-1 = о/?.т = ппот. (5.3)
156
Гл. 5. Диффузия и сопротивление
Если теперь усреднить это соотношение по всем скоростям макс-
велловского распределения, то получим величину
(5.4)
которую обычно и называют частотой столкновений.
5.1.2. Параметры диффузии
Рассмотрим гидродинамическое уравнение, справедливое для лю-
бого сорта частиц с учетом столкновений:
mn(dv/dt) = mn [dv/dt + (v-V) v] = ± enE— ур—rnnvv, (5.5)
где + снова относится к знаку заряда. Здесь предполагается, что
для вычисления v использовался процесс усреднения. Нам нет
необходимости вникать в детали этих вычислений, достаточно счи-
тать, что они приводят к корректному уравнению (5.5). Это урав-
нение будет полезно только в том случае, если считать, что v =
= const. Рассмотрим стационарное состояние, в котором dv/dt = 0.
Пусть v достаточно мала (или v достаточно велика), тогда за время
между столкновениями элемент жидкости не успеет сместиться
в области, в которых Е и Vp сильно отличаются от исходных и кон-
вективная производная dv/dt тоже будет мала. Приравнивая нулю
правую часть уравнения (5.5), для случая изотермической плазмы
(Т = const) получаем
v = (± епЕ—KT\n)/mnv = ± (e/mv) Е—(K77mv)(vn/n)- (5.6)
Множители перед Е и \п/п в этом соотношении называются соот-
ветственно подвижностью и коэффициентом диффузии:
р = | g | !mv
(подвижность), (5-7)
D = KT/mv (коэффициент диффузии). (5.8)
Эти величины для разных сортов частиц различны. Заметим, что
D измеряется в единицах м2/с. Коэффициенты переноса р и D свя-
заны соотношением Эйнштейна:
y = \q\D/KT.
(5.9)
Используя эти выражения, формулу для потока частиц /-го сорта Г/
можно представить в виде
Г; = nV, — ± Р/пЕ — Dfyn.
(5.10)
5.2. Распад плазмы вследствие диффузии
157
Частным случаем этого соотношения является закон диффузии
Фика, который имеет место в том случае, если Е = О или же если
частицы не заряжены, и р, — 0:
Г= —D\n
(закон Фика).
(5.11),
Это уравнение отражает тот простой факт, что диффузия представ-
ляет собой процесс случайного блуждания. При этом поток частиц
из области большей их концентрации в область меньшей концен-
трации возникает благодаря лишь тому, что из объема с более вы-
сокой плотностью начинает свое движение большее число частиц.
Очевидно, поток частиц должен быть пропорционален градиенту
их плотности. В плазме закон Фика выполняется не всегда, по-
скольку в ней могут существовать согласованные движения (плаз-
менные волны), под действием которых плазма уже не будет расши-
ряться чисто хаотическим образом.
5.2. Распад плазмы вследствие диффузии
5.2.1. Амбиполярная диффузия
Рассмотрим, как распадается плазма, созданная в контейнере,
из-за диффузии на его стенки. Когда ионы или электроны дости-
гают стенки, они у нее рекомбинируют. Следовательно, плотность
плазмы у стенок почти равна нулю. Поведение плазмы описывается
гидродинамическими уравнениями и уравнениями непрерывности.
Пусть распад идет медленно, тогда в уравнении непрерывности
можно удержать только временную производную. В уравнении
движения (5.5), наоборот, при достаточно высокой частоте столк-
новений временной производной можно пренебречь. Поступая та-
ким образом, мы приходим к уравнению
(dn/^) + V-ry = 0, (5.12)
где Г,- определяется формулой (5.10). Ясно, что если бы выполня-
лось неравенство Г£=^ Ге, то очень скоро в плазме возникло бы
сильное разделение зарядов. Однако если размеры плазмы много
больше дебаевского радиуса, то плазма должна оставаться квази-
нейтральной, поэтому следует ожидать, что скорости диффузии
ионов и электронов будут как-то подстраиваться друг к другу, так
чтобы потоки этих частиц были одинаковы. Нетрудно понять, как
это происходит. У более легких электронов тепловая скорость
выше, поэтому они первыми стремятся покинуть плазму. В плазме
остается положительный заряд, вследствие чего в ней возникает
электрическое поле такой поляризации, что оно стремится замед-
лить вынос электронов и увеличить потери ионов. Напряженность
такого поля Е можно найти, положив Г£ — Ге = Г. Как следует
из уравнения (5.10),
158
Гл. 5. Диффузия и сопротивление-
Г=ргпЕ—Dtfn——иепЕ—De\n, (5.13)
Е = [(Of—Де)/(ц( + pj] (Vn/n). (5.14)
Таким образом, поток Г можно записать в виде
Г = R [(£>{—£>е)/(рг + Це)] уп—Dtyn = vn (jXfDf — рА — v-iDi —
— иЛ)/(Нг + Р-Л= — Vn(pA++ (5.15)
Это соотношение представляет собой закон Фика с новым коэф-
фициентом
Da s= ^tDe + H^>i)/(Hi + Р-Л (5 • 16)
который называется коэффициентом амбиполярной диффузии. Если
он является постоянной величиной, то уравнение (5.12) принимает
простой вид:
dnldt—D^n. (5.17)
Величину Da легко оценить, если считать, что > yit-. Из урав-
нения (5.7) видно, что это действительно так. Поскольку частота
столкновений v пропорциональна тепловой скорости, а та в свою
очередь пропорциональна т~12, то р. ~ т~1/2; следовательно,
в приближении ре Д р/ из уравнений (5.16) и (5.9) имеем
Da>^ Dt + (ц/иД=Dt 4*- (Te/Ti) Dh (5.18)
При Te = Ti
Da « 2Di. (5.19)
Таким образом, из-за наличия электрического поля, вызванного
разделением зарядов, коэффициент диффузии ионов увеличивается
в два раза, скорость же совместной диффузии определяется в ос-
новном менее подвижными ионами.
5.2.2. Диффузия в слое
Уравнение диффузии (5.17) легко решается методом разделения
переменных. Положим
и (г, 0 = T(/)S(r). (5.20)
При этом уравнение (5.17) принимает вид
S(dTldt) — DTy2S (5.21)
или
(l/T)(d7,/dO = (f/5)v2S (5.22)
(здесь индекс а мы опустили). Поскольку левая часть этого равен-
ства зависит только от времени, а правая — от пространственных
переменных, то обе они порознь должны быть равны некоторой
5.2. Распад плазмы вследствие диффузии
159
константе, которую мы обозначим через —1/т. Таким образом,
функция Т удовлетворяет уравнению
dT/dt— — Tlx, (5.23)
решение которого имеет вид
Т = Тоехр(—tlx). (5.24)
Функция пространственных переменных S удовлетворяет уравне-
нию
VaS=— (1/Z)t)S, (5.25)
которое в плоской геометрии принимает вид
d2S/dx*=—(VDx)S. (5.26)
Решение этого уравнения записывается следующим образом:
S - A cos[x/(Dt)12] + В sin [x/(Dt)12J. (5.27)
Мы вправе ожидать, что у стенок решение будет обращаться в нуль,
а внутри слоя иметь один или несколько максимумов (рис. 5.3).
Простейший вид имеет решение с одним максимумом. В этом слу-
чае из соображений симметрии в формуле (5.27) нечетное слагае-
мое (синус) можно опустить. Тогда из граничных условий S (— L) =
= S (L) — 0 следует, что L/(f)x)112 = л/2, или
т = (2Т/л)2/П. (5.28)
Рис. 5.3. Профили плотности при
различных временах в задаче о диф-
фузии плазмы на стенки.
Рис. 5.4. Начальное неоднородное
распределение плотности плазмы и
его эволюция со временем. Видно
быстрое исчезновение диффузионных
мод высоких порядков.
160
Гл. 5. Диффузия и сопротивление
Используя соотношения (5.20), (5.24), (5.27) и (5.28), имеем
п = поехр(— Их) cos(nx/2L). (5.29)
Это решение называется наинизшей диффузионной модой. В этой
моде плотность плазмы внутри слоя распределена по косинусу,
а максимум плотности экспоненциально уменьшается со временем.
Как и следовало ожидать, т увеличивается с ростом L и обратно
пропорционально коэффициенту диффузии D.
Существуют, разумеется, диффузионные моды и более высоких
порядков, имеющие несколько максимумов. Пусть начальное рас-
пределение плотности таково, как показано на рис. 5.4 (верхняя
кривая). Функцию, описывающую это распределение, можно раз-
ложить в ряд Фурье:
п = п0 а; cos [(z+-y-)nx/L] + уГ fyn sin [тлх/L]Ь (5.30)
’ l m >
При этой форме записи граничные условия при х = ± L удовлет-
воряются автоматически. Для анализа зависимости решения от
времени будем искать его в виде
п = п0 рЕ ai ехр (—t/xi) cos [(z + лх/L j +
+ У bm ехр (— t/xm) sin [mnxIL]
m
(5.31)
Подставив это выражение в уравнение диффузии (5.17), мы увидим,
что (5.31) является решением (5.17) только в том случае, если ко-
эффициенты при синусах и косинусах в правой и левой частях
получающегося уравнения равны между собой, т. е. если
— 1/т/ = — D л/Lj2 • (5.32)
Таким образом, характерное время затухания Z-й моды можно за-
писать в виде
1 \ 32
(5.33)
Отсюда видно, что тонкая структура распределения плотности, ко-
торой соответствуют гармоники с большими номерами Z, затухает
быстрее, с меньшими постоянными времени т2. Процесс распада
плазмы будет происходить так, как показано на рис. 5.4. Вначале
диффузия смажет тонкую структуру распределения плотности,
затем решение выйдет на наинизшую диффузионную моду, и плот-
ность распределится по косинусу, как показано на рис. 5.3. Потом
будет происходить уменьшение максимальной плотности плазмы,
в то время как форма распределения будет оставаться неизменной.
5.2. Распад плазмы вследствие диффузии
161
5.2. Распад плазмы вследствие диффузии
В цилиндрической системе координат пространственную часть урав-
нения диффузии (5.25) можно записать в виде
(PS/dr* + (1 /г) dS/dr + ( 1/£>т) S = 0.
(5.34)
Это выражение отличается от уравнения (5.26) только средним
членом, появление которого связано со сменой системы координат.
Из рис. 5.5 видно, почему нужно добавить к уравнению (5.26) это
слагаемое. В самом деле, рассмотрим вначале плоский слой плазмы
неизменной толщины, который движется в направлении больших
значений х; (на рис. 5.5 случай а). Ясно, что плотность вещества
в нем остается неизменной. Однако в цилиндрическом слое (случай б
на рисунке) при неизменном расстоянии между его стенками дви-
жение слоя в область больших г приводит к уменьшению плотности
вещества в нем пропорционально Mr. Это уменьшение и описывает
средний член уравнения (5.34). Отсюда, в частности, следует, что
решение (5.34) должно напоминать затухающий косинус (рис. 5.6).
Такая функция называется функцией Бесселя нулевого порядка.
а уравнение (5.34) — уравнением Бесселя нулевого порядка. В ци-
линдрической геометрии в решение уравнения диффузии вместо
cos всюду будет входить </0, и точно так же, как функция
cos [х/(£>т)й2] представляет собой решение уравнения (5.26), функ-
ция Jй (г/[От]1/2) является решением уравнения (5.34). Как cos kx,
так и J0 (kr) можно представить в виде бесконечных рядов. Значе-
ния этих функций можно также найти в таблицах. К сожалению,
микрокалькуляторы не содержат функций Бесселя.
Для того чтобы удовлетворить граничному условию п = 0 при
г — а, мы должны положить а/(Рт)1/2 равной первому нулю функ-
ции Бесселя, т. е. 2,4. Это условие определяет постоянную времени т.
Рис. 5.5. Движение плазменного слоя в плоской и цилиндрической геомет-
риях, иллюстрирующее разницу между косинусом и функцией Бесселя.
6 Заказ 3170
162
Гл. 5. Диффузия и сопротивление
Рис. 5.6. Функция Бесселя нулевого порядка.
Вследствие того что временная часть уравнения диффузии (5.23)
осталась неизменной, уменьшение концентрации плазмы со време-
нем по-прежнему будет происходить по экспоненциальному закону.
В этом разделе мы рассмотрели только наинизшую диффузион-
ную моду в цилиндре. По аналогии со случаем плоской геометрии
в цилиндрических системах существуют диффузионные моды и бо-
лее высоких порядков, имеющие внутри цилиндра несколько мак-
симумов. Эти моды можно выразить через функции Бесселя более
высоких порядков.
5.3. Стационарные решения
Во многих экспериментах плазма поддерживается в стационарном
состоянии путем непрерывной дополнительной ионизации или ин-
жекции плазмы, которые компенсируют ее потери. Чтобы рассчи-
тать плотность плазмы в этом случае, нужно добавить в уравнение
диффузии дополнительный член, описывающий источник:
dnldt—Dy2n = Q(r). (5.35)
Знак величины Q в этом уравнении выбран так, что при Q >0 до-
полнительный член описывает именно источник, т. е. приводит
к росту концентрации со временем. В стационарном состоянии
dnldt — 0, и для определения п (/?) остается решить уравнение типа
уравнения Пуассона.
5.3.1. Функция постоянной ионизации
Во многих случаях ионизация слабоионизованных газов происхо-
дит под действием высокоэнергетических электронов из хвоста мак-
свелловского распределения. В такой ситуации вклад от источника
Q пропорционален плотности электронов п. Полагая Q = Zn, где
Z — так называемая функция ионизации, получаем в стационарном
случае следующее уравнение:
V2n=—(Z/D)n. (5.36)
5.3. Стационарные решения
163
Это уравнение аналогично соотношению (5.25) для пространствен-
ной части распределения плотности S. Следовательно, как и при
распаде плазмы, профиль плотности описывается косинусоидальным
распределением или функцией Бесселя с той только разницей, что
в стационарном случае плотность плазмы не меняется со временем.
Несмотря на диффузионные потери, плазма находится в стационар-
ном состоянии благодаря тому, что источник тепла поддерживает
в ней постоянную температуру электронов, а малый поток ней-
тральных частиц заменяет те атомы, которые были ионизованы за
время эксперимента.
5.3.2. Плоский источник
Рассмотрим теперь вопрос о том, каким будет профиль плазмы
в случае плоской геометрии, если источник локализован в плоско-
сти х = 0. Таким источником может быть, например, коллимиро-
ванный с помощью щели пучок ультрафиолетового излучения,
если его интенсивность достаточно высока для того, чтобы ионизо-
вать нейтральный газ. В этом случае стационарное уравнение диф-
фузии принимает вид
d2n/dx2 = —(Q/D) 8 (0). (5.37)
Всюду, кроме точки х = 0, плотность плазмы должна удовлетво-
рять уравнению д2п!дх2 = 0, решение которого, очевидно, имеет
вид (рис. 5.7)
п = По(1 — |x|/L). (5.38)
Таким образом, по обе стороны от плоскости х = 0, в которой на-
ходится источник, профиль плотности плазмы линейный. Скачок
производной в точке, где находится источник, представляет собой
характерную особенность источников типа 6-функции.
-L О +L
Рис. 5.7. Треугольный профиль плот-
ности плазмы, возникающий при диф-
фузии от плоского источника.
6*
Рис. 5.8. Логарифмический профиль
плотности плазмы, возникающий при
диффузии от линейного источника.
164
Гл. 5. Диффузия и сопротивление
5.3.3. Линейный источник
В заключение этого раздела рассмотрим источник, расположенный
на оси плазменного цилиндра. Таким источником может быть, на-
пример, пучок энергичных электронов, который вызывает иониза-
цию при своем движении вдоль оси цилиндра. Плотность плазмы
всюду, кроме оси г = 0, должна удовлетворять уравнению
—---— (г—Vo. (5.39)
г dr \ dr ) v ’
Решение этого уравнения, обращающееся в нуль при г = а, имеет
вид
n = noln(a/r). (5.40)
При г = 0 плотность плазмы обращается в бесконечность (рис. 5.8).
Таким образом, если считать источник бесконечно тонким, то вблизи
оси симметрии плотность плазмы определить нельзя.
5.4. Рекомбинация
Если электрон сталкивается с ионом, то они с большой вероятностью
(особенно при малых относительных скоростях) могут рекомбиниро-
вать и образовать нейтральный атом. Для того чтобы обеспечить
выполнение закона сохранения импульса, в этом процессе должна
участвовать третья частица. Если этой частицей является излучае-
мый в результате взаимодействия фотон, то процесс называется
излучательной рекомбинацией. Если же это частица плазмы, то ре-
комбинацию называют трехчастичной. Уменьшение плотности пла-
змы из-за рекомбинации можно описать, введя отрицательный
источник в уравнение непрерывности. Ясно, что этот член будет
пропорционален пеп.( = л2, и тогда в отсутствие диффузионных чле-
нов уравнение непрерывности можно записать в виде
dnldt =—ап2. ’ (5-41)
Постоянная а называется коэффициентом рекомбинации, она имеет
размерность м3/с. Уравнение (5.41) нелинейно относительно п.
Поэтому его решение нельзя получить как суперпозицию частных
решений, удовлетворяющих граничным и начальным условиям.
К счастью, это уравнение имеет настолько простой вид, что его
решение можно сразу записать в явном виде:
л (г, t) По (Г)
где п0 (г) — начальное распределение плотности. Легко проверить,
что такое решение действительно удовлетворяет уравнению (5.41).
Как видно из формулы (5.42), после того как плотность станет
(5.42)
5.5. Диффузия поперек магнитного поля
165
Рис. 5.9. Уменьшение плотности заряженной компоненты слабоионизован-
ного газа в результате рекомбинации и диффузии. [Из работы: Brown S. С.,
Basic Data of Plasma Physics, John Wiley and Sons,- N. Y., 1959.]
существенно меньше своего начального значения, она будет убы-
вать обратно пропорционально времени:
п ~ Mat. (5.43)
Эта зависимость радикальным образом отличается от поведения
плазмы при диффузии, когда ее плотность уменьшается со временем
экспоненциально.
На рис. 5.9 показаны результаты измерений плотности плазмы
после окончания разряда в слабоионизированном водороде. Когда
плотность велика, ведущую роль в уменьшении концентрации иг-
рает рекомбинация, скорость которой пропорциональна п2, Плот-
ность при этом обратно пропорциональна времени. При низких
плотностях плазмы' главную роль начинает играть диффузия и
уменьшение плотности плазмы идет по экспоненциальному закону.
5.5. Диффузия поперек магнитного поля
Поместив плазму в магнитное поле, можно уменьшить скорость
диффузионных потерь. Именно в реализации этой задачи и состоит
проблема удержания плазмы при исследованиях по управляемому
термоядерному синтезу. Рассмотрим слабоионизированную плазму,
помещенную в магнитное поле (рис. 5.10). Оно не влияет на движе-
ние заряженных частиц вдоль В, поэтому в продольном направ-
166
Гл. 5. Диффузия и сопротивление
о ° ° о ° „о и
о°о ° -
О о____о ° о
° о О ° о °
о о 0 о о О ~
Рис. 5.10. Заряженная частица вращается вокруг одной и той же силовой
линии магнитного поля до тех пор, пока не столкнется с другой частицей.
лении частицы будут диффундировать в соответствии с уравнением
(5.10). Таким образом, для каждого сорта частиц
Гг=±рлЕ2—Dfinldz). (5.44)
Если бы в плазме не было столкновений, то в поперечном направ-
лении частицы вообще бы не диффундировали, поскольку они не-
прерывно вращались бы вокруг одних и тех же силовых линий маг-
нитного поля. Конечно, из-за того что в системе существуют элек-
трические поля или градиенты магнитного поля В, имели бы место
дрейфовые движения поперек В, но, изменив конфигурацию при-
бора, их можно было бы направить вдоль стенок. Например, в сим-
метричном цилиндре (рис. 5.11) градиенты всех параметров плазмы
направлены по радиусу цилиндра, поэтому скорости всех типов
дрейфа ведущих центров направлены по азимуту и с точки зрения
распада плазмы эти дрейфы опасности не представляют.
Если же в плазме имеют место столкновения, то из-за вызванного
ими процесса хаотического блуждания частицы будут перемещаться
поперек магнитного поля и могут попасть на стенки установки
(рис. 5.12). Механизм этого процесса следующий. Пусть ион стал-
кивается, скажем, с нейтральным атомом. После столкновения
1 направление движения иона изменится. Он снова начнет вращаться
вокруг силовой линии в ту же сторону, что и раньше, но фаза его
вращения испытает резкий скачок. (Может, конечно, измениться
и ларморовский радиус орбиты, но мы будем считать, что в среднем
Рис. 5.11. Дрейф частицы в симме- Рис. 5.12. Диффузия вращающейся
тричном плазменном цилиндре не заряженной частицы под действием
приводит к потерям плазмы. столкновений с нейтральными ато-
мами.
5.5. Диффузия поперек магнитного поля 167
энергия иона остается неизменной.) Следовательно, под действием
столкновений ведущий центр частицы случайным образом сдви-
гается. Частица в результате этого процесса будет диффундировать
против направления градиента Vra, причем шаг случайного блуж-
дания будет уже равен не длине свободного пробега Кт, как в слу-
чае диффузии в среде без магнитного поля, а величине порядка
ларморовского радиуса rL. Значит, уменьшая rL, т. е. увеличивая В,
можно ослабить диффузию поперек магнитного поля.
Чтобы количественно проанализировать этот процесс, запишем
перпендикулярную магнитному полю составляющую гидродина-
мического уравнения для каждого сорта частиц:
/7in(c!vj./dO = ±en(E + v± X В)—КТ\п—mnvv = 0. (5.45)
Здесь мы предположили, что плазма изотермическая, а частота
столкновений v настолько велика, что членом dv^/dt можно прене-
бречь. Проекции этого уравнения на оси х и у имеют вид
mnvvx = ± епЕх—КТ (дп/дх) ± envyB,
mnvvy = ± епЕу—КТ (дп!ду) + епихВ.
Используя определения коэффициента диффузии D и подвижности
р, мы можем записать эти уравнения в виде
vx=± p,Ex—(D/n)(дп/дх) ± (a>c/v) vu,
vy—± ^Ey—(D/n)(дп/ду) ± Mv)vx.
Подставляя во второе из предыдущих уравнений выражение для vx
из первого, находим vy-.
vy (1 ©2т2) = ± рЕу—(D/п) (дп/ду)— со2?2 (ЕХ1В) ±
± ©ст2 (КТ 1еВп) (дп/дх), (5.48)
где т = V-1. Компонента vx определяется аналогичным равенством:
vx (1 4- cd?t2) = ± uEx—(D/n) (дп/дх) + ©2т2 (Еу/В) Т
Т ®2т2 (КТ/еВп) (дп/ду). (5.49)
Последние два члена в каждом из этих уравнений пропорциональны
скоростям Е X В-дрейфа и диамагнитного дрейфа соответственно.
Действительно,
vEx~EylB, vEy— EJB, (5 50)
vDx = + (KT/еВп) (дп/ду), vDy — ± (KT/еВп) (дп/дх).
Первые же два члена в каждом из уравнений можно упростить,
если ввести определения подвижности в перпендикулярном направ-
лении и поперечного коэффициента диффузии,:
рг = р/(1 + (о2т2), £>± =£)/(! + ©2т2). (5.51)
168
Гл. 5. Диффузия и сопротивление
Пользуясь соотношениями (5.50) и (5.51), мы можем объединить
уравнения (5.48) и (5.49) и записать их в виде
Vi = ± |лЛЕ—(Vn/n) + (v£+vD)/[l+ (№/©!)]. (5.52)
Отсюда видно, что поперечная скорость частиц любого сорта
состоит из двух компонент. Во-первых, это обычные дрейфовые
движения: Е X В-дрейф и диамагнитный дрейф со скоростями v£
и vD, перпендикулярными направлениям градиентов плотности
и потенциала. Скорости этих движений меньше в 1 + (v2/<oc) раз:
из-за столкновений с нейтралами. (Заметим, что при v -> 0 этот
множитель стремится к единице.) Во-вторых, имеют место дрейфо-
вые движения, связанные с подвижностью и диффузией частиц.
Скорости этих движений направлены параллельно градиентам плот-
ности и потенциала, а соответствующие им коэффициенты ц и D
уменьшены из-за столкновений частиц в 1 + МП2 раз.
Величина сост является важной характеристикой магнитного-
удержания. Если «>2т2 1; то магнитное поле слабо влияет на
диффузию. Если же w-т2 1, то скорость диффузии поперек В
сильно уменьшается. Легко показать, что параметр <ост можно
также представить в виде
сод = ®c/v = рВ а* Xm/rt. (5.53)
В пределе )>> 1 мы имеем
= (KTImv) (1/^т2) = (5.54)
Сравнивая это равенство с соотношением (5.8), мы видим, что роль
частоты столкновений v стала иной: если для случая диффузии
вдоль В коэффициент диффузии D пропорционален V1, поскольку
столкновения мешают движению, то в случае диффузии поперек
магнитного поля величина D± пропорциональна v, поскольку
именно столкновения частиц обеспечивают их диффузию поперек В.
Зависимость от массы также иная. Вспоминая, что v ~ т~1/2, мы
видим, что D ~ m~i/2, a D± ~ т112. В случае диффузии вдоль маг-
нитного поля электроны движутся быстрее ионов, поскольку теп-
ловая скорость электронов выше; при диффузии же поперек поля
электроны движутся медленнее, поскольку их ларморовский ра-
диус меньше, чем у ионов.
Пренебрегая численными множителями порядка единицы, вы-
ражение (5.8) можно записать в виде
D — KT/mv ~ ОтеплТ ~ ^«/т. (5.55)
Из такой формы записи коэффициента диффузии (квадрат длины,
деленный на время) видно, что диффузия представляет собой про-
цесс случайного блуждания с характерной длиной шага Хт. Фор-
мулу (5.54) можно записать в виде
— KTvlm<s?c ~ ~ rt/т. (5.56)
5.5. Диффузия поперек магнитного поля
169
Отсюда ясно, что диффузия поперек магнитного поля — это про-
цесс случайного блуждания с характерным шагом rL, а не кт.
5.5.1. Амбиполярная диффузия поперек
магнитного поля
Анализ процесса амбиполярной диффузии при наличии магнитного
поля нельзя выполнить аналогично тому, как это было сделано
в случае В = 0, поскольку теперь подвижность и коэффициент
П±
Их
Пи
Ни-----
В
Рис. 5.13. Потоки частиц вдоль и поперек магнитного поля.
диффузии анизотропны. Рассмотрим компоненту потока частиц,
перпендикулярную В (рис. 5.13). Поскольку Ге± меньше, чем Г£±,
то в системе должно возникнуть поперечное электрическое поле,
которое будет направлено так, чтобы усилить диффузию электро-
нов и затормозить диффузию ионов. Это электрическое поле можно
экранировать, создав разность потоков вдоль магнитного поля.
В частности, отрицательный заряд, возникающий из-за того, что
Ге±<Гги_, можно скомпенсировать с помощью электронов, двигаю-
щихся вдоль силовых линий. И хотя в целом диффузия должна
быть амбиполярной, часть потерь, связанная с движением поперек
поля, не обязательно будет носить амбиполярный характер. Может
случиться и так, что электроны будут диффундировать главным
образом вдоль В, а ионы — в перпендикулярном к магнитному
полю направлении. Так ли происходит все на самом деле или нет,—
зависит от конфигурации плазмы в конкретном эксперименте.
Можно ожидать, что в коротких плазменных столбах, когда сило-
вые линии оканчиваются на проводящих пластинах, амбиполяр-
ное электрическое поле будет закорочено. В этом случае частицы
разных сортов будут диффундировать поперек поля с различными
скоростями. В длинных и тонких столбах плазмы, ограниченных
изоляторами, поперечная диффузия будет амбиполярной, потому
что в этом случае частицам трудно уходить вдоль магнитного
поля В.
С математической точки зрения исследование процесса диффу-
зии сводится к совместному решению уравнений непрерывности
(5.12) для ионов и электронов, причем в этом случае нужно при-
170
Гл. 5. Диффузия и сопротивление
равнивать не потоки Г7, а их дивергенции V-Гу. Выделяя в Г,- про-
дольные и поперечные составляющие, имеем
7-Г( = Vx— Dt^n) + (d/dz) [^nEz-Dt (dn/dz)], (5.57}
V ге = V X • (—He ± x — De X vn) + (dtdz) [ — penEz—De (dn/dz)].
Следует заметить, что уравнение, получающееся в результате при-
равнивания V-Г/ = ?-Ге, нельзя разделить на одномерные уравне-
ния. Кроме того, решение этого уравнения сильно зависит от гра-
ничных условий, т. е. от условий на концах силовых линий. Про-
стого ответа в задаче об амбиполярной диффузии поперек магнит-
ного поля не существует. Исключение составляет только тот слу-
чай, когда столб плазмы является настолько длинным, что диффу-
зией в продольном направлении вообще можно пренебречь.
5.5.2. Экспериментальная проверка
Действительно ли магнитное поле уменьшает поперечную диффу-
зию в соответствии с формулами (5.51)? Этот вопрос стал предметом
многочисленных исследований. Первый эксперимент подобного рода
был выполнен в Швеции Ленертом и Хохом в положительном столбе
гелиевой плазмы длиной 3,5 м и диаметром 1 см (рис. 5.14). Таким
образом, длина трубки, в которой создавалась плазма, была столь
велика, что диффузией через торцы трубки можно было пренебречь,
и уменьшение концентрации плазмы было связано только с диффу-
зией ее на стенки. Эти потери компенсировались посредством иони-
зации нейтральных атомов электронами из хвоста функции рас-
пределения по скоростям. В свою очередь быстрые электроны за-
мещались другими, ускоренными в продольном электрическом
поле Ег. Следовательно, можно было ожидать, что Ег будет, грубо
говоря, пропорционально скорости поперечной диффузии. Для
измерения Ег (В) на стенке трубки были установлены два зонда.
На рис. 5.15 показана зависимость отношения Ez (B)/Ez (0) от ве-
личины магнитного поля В. При малых В экспериментальные
точки в точности следуют зависимостй, рассчитанной на основе
уравнения (5.52). Однако, начиная с критического значения поля
Вс ~ 0,2 Тл, они отходят от теоретической кривой. Эксперимент
показал, что в действительности при В >ВС коэффициент диффу-
.f Зонды
^7 Катод
Анод. -----—
—[Г~ Z
--------------------- v j
В—*-
Рис. 5.14. Эксперимент Ленерта—Хоха по проверке влияния магнитного поля
на процесс диффузии в слабоионизованном газе.
/71
Рис. 5.15. Зависимость нормированного продольного электрического поля
от магнитного поля В при различных давлениях плазмы. Для сравнения при-
ведены теоретические кривые. [Из работы: HohF. С., Lehnert В., Phys. Fluids,
3, 600 (I960).]
зии растет с В. Было обнаружено также, что критическое поле Bs
увеличивается сдавлением, т. е. что критическая точка определяется
не просто магнитным полем, а некоторым значением параметра
год. При очень больших год с «классической» теорией диффузии
было что-то не так.
Причина расхождения вскоре была найдена советскими физи-
ками Кадомцевым и Недоспасовым. Они показали, что в сильных
магнитных полях должна развиваться неустойчивость, т. е. что
поле Ег должно возбуждать плазменную волну, которая и будет
усиливать радиальные потери. Теория правильно предсказала зна-
чение Вс. Позднее в эксперименте, выполненном в Беркли Алленом,
Пауликасом и Пайлом, эта волна непосредственно наблюдалась
в плазменном столбе в виде спиралевидного возмущения. Привле-
кая механизм спиральной неустойчивости положительного столба,
впервые удалось объяснить «аномальную диффузию» плазмы по-
перек магнитного поля. Это объяснение, однако, оказалось пригод-
ным только для случая слабоионизованных газов. Для полностью
ионизованной плазмы, каковой является плазма термоядерного
реактора, объяснение аномальной диффузии представляет собой
значительно более трудную задачу.
172
Гл. 5. Диффузия 41 сопротивление
Задачи
5.1. Для электронов с энергией 2 эВ, движущихся в гелии, сечение столкно-
вения с нейтральными атомами приближенно равно 6najj, где aQ —
= 0,53-10-8 см — радиус первой боровской орбиты атома водорода. Пусть
в положительном столбе гелиевой плазмы в отсутствие магнитного поля
и при комнатной температуре давление р равно 1 мм рт. ст. и %Те = 2 эВ.
а) Вычислите коэффициент диффузии электронов в м2/с, считая, что усред-
ненная по распределению скоростей величина ov равна <зу для электронов
с' энергией 2 эВ.
б) Пусть плотность тока, текущего вдоль столба, равна 2 кА/м2, а плотность
плазмы — 1016 м~3. Какова величина направленного вдоль столба электри-
ческого поля?
5.2. В плоском слое слабоионизованного газа плотность распределена по за
кону п (х) = n0cos (nx/2L) (—L^zx^L). Концентрация плазмы из-за
диффузии и рекомбинации начинает убывать. Пусть L = 0,03 м, коэффи-
циент диффузии D = 0,4 м2/с, а коэффициент рекомбинации а ~ 10~15 м3/с.
При какой плотности плазмы скорость ее убыли из-за диффузии будет равна,
скорости потерь из-за рекомбинации?
5.3. В кубическом алюминиевом ящике, длина которого равна Lt создана
плазма. Ее концентрация уменьшается из-за амбиполярной диффузии.
а) Выпишите выражение для распределения плотности в наинизшей диффу-
зионной моде.
б) Дайте для этого случая определение постоянной времени распада. Вычис-
лите ее при Da = 10~3 м2/с.
5.4. Длинный цилиндрический положительный столб имеет параметры:
КТс = 0,1 эВ, В = 0,2 Тл. Остальные характеристики плазмы такие жег
как в задаче 5.1. Распределение плотности по радиусу имеет вид и (г) =
= Jo (г/ [Dt]1/2) nQ, причем п= 0 при г ~ а = 1 см. (Заметим, что /0 (г) = О
при z = 2,4.)
а) Покажите, что рассматриваемый выше коэффициент амбиполярной диффу-
зии можно аппроксимировать величиной D Хе.
б) Пренебрегая рекомбинацией плазмы и ее потерями через торцы столба,
вычислите время удержания т.
5.5. Для профиля плотности плазмы, изображенного на рис. 5.7, выразите
максимальную плотность п0 через интенсивность источника Q и другие па-
раметры задачи. (Указание: приравняйте поток частиц от источника, про-
ходящий через 1 м2, к потоку частиц через 1 м2 поверхности стенок.)
5.6. Вы выполняете эксперимент по исследованию рекомбинации в слабо-
ионизованном газе, в котором главным механизмом потерь является именно
рекомбинация. С помощью внезапной вспышки ультрафиолетового излуче-
ния вы создали плазму плотностью 1020 м“3 и наблюдаете ее распад. Обна-
ружилось, что за 10 мс плотность плазмы уменьшилась вдвое. Чему равен
коэффициент рекомбинации а? Какова его размерность?
5.6. Столкновения в полностью
ионизованной плазме
Если плазма состоит только из ионов и электронов, то все происхо-
дящие в ней соударения представляют собой кулоновские столкно-
вения между заряженными частицами. Есть, однако, существенная
5.6. Столкновения в полностью ионизованной плазме
173
Рис. 5Л6. Сдвиг ведущих центров
двух тождественных частиц в резуль-
тате их столкновения под углом 90°.
Рис. 5.17. Сдвиг ведущих центров
двух противоположно заряженных
частиц после их столкновения под
углом 180°.
разница между а) столкновениями частиц одного сорта (столкнове-
ния иона с ионом и электрона с электроном) и б) столкновениями
между частицами разного сорта (столкновения иона с элек-
троном или электрона с ионом). Рассмотрим столкновение двух
идентичных частиц (рис. 5.16). Если столкновение лобовое, то ско-
рости частиц после него меняются на противоположные, т. е. ча-
стицы просто обмениваются своими орбитами, а два ведущих центра
остаются на прежних местах. Этот результат справедлив и при ка-
сательном соударении частиц, когда их траектории значительно
возмущаются. Сильнее всего смещаются ведущие центры в том
случае, когда частицы сталкиваются, двигаясь под прямым углом
друг к другу, и вектор скорости каждой из них после соударения
поворачивается на 90°. (Орбиты частиц после столкновения пока-
заны на рисунке штриховыми линиями.) Однако ясно, что и в этом
случае «центр масс» двух ведущих центров останется неподвижным.
Поэтому диффузия, вызванная столкновениями между частицами
одного сорта, является очень слабой. В частности, в любом ион-
ионном столкновении выполняется строгий баланс: на каждый
ион, движущийся в результате столкновения внутрь системы, при-
ходится другой, который движется наружу. Иное дело рассматри-
вавшиеся выше столкновения ионов с нейтральными атомами: ион
в результате ряда соударений с нейтралами будет совершать слу-
чайное блуждание, все более отдаляясь от своего первоначального
положения; скорости же нейтральных атомов после столкновений
нас обычно не интересуют.
Совершенно другая ситуация имеет место при столкновении
противоположно заряженных частиц (рис. 5.17). С точки зрения
174
Гл. 5. Диффузия и сопротивление
потерь из-за диффузии самый худший для нас случай теперь — это
столкновение под углом 180°, в результате которого направления
скоростей частиц меняются на противоположные. Поскольку после
столкновения частицы должны продолжать вращение вокруг сило-
вых линий в тех же направлениях, что и раньше, оба ведущих
центра частиц сдвинутся после их соударения в одну и ту же сто-
рону. Столкновения частиц разных сортов приводят к возникнове-
нию диффузии. Диффузия ионов и электронов происходит по-раз-
ному, что связано с разницей в их массах. Электроны отскакивают
от почти неподвижных ионов, и, как обычно, совершают случайные
блуждания. Ионы же при каждом соударении получают лишь лег-
кий толчок, они перемещаются с места на место в результате частой
бомбардировки их электронами. Однако, как мы покажем ниже,
скорости диффузии ионов и электронов одинаковы, поскольку при
столкновениях сохраняется общий импульс частиц.
5.6.1. Сопротивление плазмы
Гидродинамические уравения с учетом столкновений заряженных
частиц можно записать в следующем виде [ср. уравнение (3.47)]:
Afn(dv,/dO = en(E + vi х В)—vp£—у-л{+ Р{е,
(о.DO)
mn(dve/dt') ——en(E4-vex В)—Vpe—V-лг + Ре£. ' "
Члены Р£е и Ре£ описывают изменения импульсов из-за столкнове-
ний ионов с электронами соответственно ионной и электронной
жидкостей. Выписывая уравнения (5.58), мы расщепили тензор Ру-
на изотропную часть р, и анизотропный тензор вязких напряже-
ний Лу. В последний включены столкновения между частицами од-
ного сорта, приводящие к возникновению напряжений в каждой
из жидкостей в отдельности. Поскольку такие столкновения не при-
водят к возникновению сильной диффузии, мы в дальнейшем будем
опускать соответствующие им члены V-Л/. Что касается сил Рй£
и Р£е, которые описывают трение между двумя жидкостями, то из
закона сохранения импульса следует, что
Ple^-Pei. (5-59)
Мы можем выразить Ре£ через частоту столкновений с помощью
известного соотношения
Pei = mn(y{ — ve)vei. (5.60)
Аналогичное соотношение имеет место и для Р£е. Поскольку столк-
новения в плазме являются кулоновскими, можно ожидать, что Ре1
будет пропорциональна силе кулоновского взаимодействия, кото-
рая для однократно заряженных ионов пропорциональна е2. Кроме
того, сила трения Ре£ должна быть пропорциональна плотности
электронов пе и плотности рассеивающих центров п£, которая, ес-
тественно, равна пе. Наконец, Рг£ должна быть пропорциональна
5.6. Столкновения в полностью ионизованной плазме
175
относительной скорости ионной и электронной жидкостей. Таким
образом, из физических соображений мы можем записать Ре1 в виде
=Т]б2И2 (V; — Ve), (5.61)
где т) — коэффициент, пропорциональности. Сравнивая полученное
соотношение с формулой (5.60), мы видим, что
(5.62)
Постоянная ц называется удельным сопротивлением плазмы; вскоре
станет ясно, как оно связано с обычным удельным сопротивлением.
vei = (пе2!т) г].
5.6.2. Механика кулоновских столкновений
Рассмотрим процесс столкновения электрона с нейтральным ато-
мом. До тех пор пока электрон не приблизился к атому на расстоя-
ние порядка атомных размеров, никакие силы на него не действуют.
Такое столкновение похоже на соударение двух бильярдных шаров.
Столкновение электрона с ионом протекает по-иному: электрон
постепенно отклоняется приложенной к нему со стороны иона
дальнодействующей кулоновской силой. Тем не менее и для этого
вида столкновений можно вывести выражение для эффективного
сечения. Для наших целей достаточно оценить его по порядку
величины. На рис. 5.18 показан электрон, который со скоростью v
приближается к неподвижному иону с зарядом е. В отсутствие ку-
лоновских сил электрон пролетел бы мимо иона на минимальном
расстоянии г0, которое называется прицельным параметром. Из-за
кулоновского притяжения траектория электрона отклонится на
угол х, который зависит от г0. Сила кулоновского взаимодействия
дается выражением
F = — е2/4л е0г2. (5.63)
Электрон ощущает действие этой силы только в течение того проме-
жутка времени, когда он находится вблизи иона. Это время при-
ближенно равно
Т « r0/v. (5.64)
Рис. 5.18. Траектория электрона при кулоновском столкновении с ионом.
176
Гл. 5. Диффузия и сопротивление
Таким образом, изменение импульса электрона при соударении
описывается приближенным выражением
A (mv) = \FT]w e2/4n,e0r0v. (5.65)
Вычислим сечение взаимодействия для случая, когда электрон по-
сле столкновения отклоняется на большой угол % > 90°. Если ча-
стица рассеивается на угол 90°, то ее импульс mv изменяется на
величину порядка самого импульса mv. Таким образом,
A (mv) t&mvtt е2/4л80Г(А Го = еа/4л80тп2. (5.66)
Сечение рассеяния в этом случае
о = лгд = е4/16 л е^т2у4. (5.67)
Следовательно, частота столкновений равна
гге4/16ле2т2о3> (5.68)
а удельное сопротивление плазмы дается выражением
г] = vei (т/пе2) — е2/16леоти3. (5.69)
Если распределение электронов по скоростям является максвеллов-
ским, то в нашей оценке, справедливой только по порядку величины,
можно заменить v2 на K.TJm:
т) да ле2т‘ 2/(4л80)2 (КТ е)32. (5.70)
Формула (5.70) определяет удельное сопротивление с учетом
лишь тех столкновений, в результате которых электроны рассеи-
ваются на большие углы. Однако на практике из-за дальнодейст-
вующего характера кулоновских сил гораздо чаще происходит
рассеяние на малые углы. Оказывается, что последовательные от-
клонения на малые углы дают более значительный эффект, чем рас-
сеяние на большие углы. Как показал Спитцер, для учета этого
обстоятельства нужно умножить правую часть соотношения (5.70)
на коэффициент 1п А:
т] да ле2т1/2 In А/(4л80)2 (КТ/2,
где
A = %D/r0.
(5-71)
(5-72)
Величина А представляет собой максимальное прицельное рас-
стояние, выраженное в единицах г0 [см. (5.66)1 и усреднённое по
максвелловскому распределению. Считается, что максимальное
прицельное расстояние в размерных величинах равно XD, поскольку
при больших расстояниях кулоновское поле не действует на про-
летающую частицу из-за дебаевского экранирования. Хотя А за-
висит от плотности плазмы и ее температуры КТе, логарифм этой
5.6. Столкновения в полностью ионизованной плазме
177
величины нечувствителен к значениям плазменных параметров.
В табл. 5.1 приводятся типичные значения In Л. Из нее видно, что,
даже если параметры плазмы изменяются на много порядков ве-
личины, In Л меняется лишь в два раза. В большинстве случаев
независимо от вида плазмы с достаточной степенью точности можно
считать, что In Л = 10.
Таблица 5.1
КТе. эВ п, М—3 In Л
Q-машина 0,2 1015 9,1
Лабораторная плазма 2 -10” 10,2
Типичный плазменный тор 100 10” 13,7
Термоядерный реактор 10* ю21 16,0
Плазма лазерного синтеза 103 1027 6,8
5.6.3. Физический смысл величины т]
Предположим, что в плазме существует электрическое поле Е и что
возникающий вследствие этого ток целиком переносится электро-
нами как более легкими частицами. Пусть В = 0, 7<7\ = 0, так что
V-Pe = 0. Тогда в стационарном случае уравнение движения
электронов сводится к следующему [см. (5.58)]:
епЕ = Ре(. (5.73)
Поскольку j = еп (v£—ve), выражение (5.61) для Ре£ можно записать
следующим образом:
Р,г = rienj, (5.74)
в результате чего уравнение (5.73) примет вид
E = nj (5.75)
Это есть не что иное, как закон Ома, в котором константа т] является
удельным сопротивлением плазмы. Отметим некоторые особенности
величины г] в плазме, определяемой выражением (5.71) или (5.69),
А. Из формулы (5.71) видно, что т] не зависит от плотности
(если не считать слабой зависимости от нее In Л). Такой результат
является довольно неожиданным, поскольку из него следует, что
если к плазме приложить поле Е, то в ней, согласно формуле (5.75),
возникнет ток /, величина которого не будет зависеть от числа но-
сителей заряда. Это объясняется следующим образом. Ток j воз-
растает с ростом числа носителей заряда пе, а сила трения, дейст-
вующая на электроны со стороны ионов, растет с п£. Поскольку
пе = ni ~ п> эти Два эффекта взаимно компенсируются. Действи-
тельно, как видно из уравнений (5.68) и (5.69), частота столкнове-
ний пропорциональна п, а величина т] от п не зависит. В этом
178
Гл. 5. Диффузия и сопротивление
смысле полностью ионизованная плазма ведет себя совершенно
иначе, чем частично ионизованный газ: в слабоионизованной
плазме j = — nevf, ve = — реЕ, поэтому j = пеуеЕ. Вследствие
того что подвижность зависит только от концентрации нейтраль-
ных частиц, ток в слабоионизованной плазме пропорционален ее
плотности п.
Б. Из формулы (5.71) следует, что величина г] пропорциональна
е)-32. При нагреве плазмы сечение кулоновского рассеяния
уменьшается, и поэтому с ростом температуры удельное сопротив-
ление довольно быстро падает. При термоядерных температурах
(десятки килоэлектронвольт) столкновения в плазме происходят
очень редко. Именно поэтому большинство теоретических исследо-
ваний по управляемому термоядерному синтезу посвящено бес-
столкновительной плазме. Конечно, какие-то столкновения в плазме
обязательно должны быть, в противном случае в ней вообще не смо-
гут протекать реакции термоядерного синтеза. Самый простой спо-
соб нагреть плазму — это пропустить через нее ток. Связанные с
ним омические потери PR (или /2г)) приводят к росту электронной
температуры. Такой тип нагрева называется омическим нагревом.
Однако вследствие того, что ц ~ (К7’в)*3/2, до термоядерных темпе-
ратур плазму этим методом нагреть нельзя. При температурах выше
1 кэВ она становится настолько хорошим проводником, что омиче-
ский нагрев в этом диапазоне температур идет очень медленно.
В. Из формулы (5.68) видно, что частота столкновений vei про-
порциональна v~3. Поэтому быстрые электроны из хвоста функции
распределения сталкиваются с ионами очень редко. Иными словами,
ток в плазме переносят главным образом эти быстрые частицы, а не
электроны из основной части функции распределения. Сильная
зависимость vei от v имеет и другое интересное следствие. Если
к плазме внезапно приложить электрическое поле Е, то в ней может
возникнуть явление, известное как убегание электронов. Механизм
его следующий. В плазме имеется небольшое число электронов,
которые в момент приложения поля быстро двигались в направле-
нии —Е. До следующей встречи с ионами эти частицы успеют
настолько сильно ускориться, что совершат с ионами только
скользящие соударения. Это позволит электронам получить от поля
дополнительную энергию, и сечение столкновения этих частиц с
ионами еще более уменьшится. Если Е достаточно велико, то се-
чение столкновения уменьшается настолько быстро, что убегаю-
щие электроны вообще больше никогда не столкнутся с ионами.
Они образуют пучок ускоренных частиц, отделенный от основной
части функции распределения электронов.
5.6.4. Численные значения т)
Точное вычисление удельного сопротивления т], в котором учиты-
вается отдача ионов в каждом столкновении и выполняется усред-
нение по функции распределения электронов, было впервые выпол-
5.7. Уравнения одножидкостной магнитогидродинамики 179
нено Спитцером; поэтому величину т] часто, особенно для случая
водородной плазмы, называют удельным сопротивлением Спит-
цера. Полученная им формула имеет следующий вид:
г]ц =5,2-10-571пЛ/7’3/2(эВ) Ом-м. (5.76)
Здесь Z — заряд ионов, который всюду в этой книге мы считали
равным единице. Поскольку в приведенном соотношении все вели-
чины слабо зависят от массы ионов М, то эту формулу можно ис-
пользовать при анализе плазмы других газов. Индекс || у вели-
чины т] означает, что определяемое формулой (5.76) удельное со-
противление можно применять только для анализа движений, па-
раллельных магнитному полю В. Для описания движения поперек
В нужно пользоваться величиной j
^=2,07)11- (5-77)
Отсюда, разумеется, не следует, что продольная проводимость
только в два раза выше, чем поперечная; при вычислении послед-
ней нужно еще учитывать множители типа <о2т2. Коэффициент 2,0
в формуле (5.77) возник из-за того, что при вычислении удельного
сопротивления разные компоненты скорости электронов учиты-
ваются по-разному, В частности, медленные электроны, у которых
ларморовские радиусы малы, дают больший вклад в поперечное
удельное сопротивление, нежели в продольное.
При КТе = 100 эВ из формулы (5.76) получаем т] =
= 5-Ю-7 Ом-м. Сравним эту величину с удельными сопротивле-
ниями различных металлов:
медь Т|=2-10—8 Ом-м
нержавеющая сталь Г] = 7-10—7 Ом-м
ртуть Т) = 10-6 Ом-м.
Таким образом, мы видим, что проводимость плазмы, нагретой до
100 эВ, примерно такая же, как у нержавеющей стали.
5.7. Уравнения одножидкостной
магнитогидродинамики
Перейдем теперь к задаче о диффузии в полностью ионизованной
плазме. Поскольку диссипативное слагаемое Рес содержит разность
скоростей Vf—ve, проще считать, что неизвестными величинами
в задаче являются не сами скорости у{ и vc, а их разность Vi—ve,
и иметь дело с линейной комбинацией уравнений движения ионов
и электронов. До сих пор мы считали, что плазма состоит из двух
несмешивающихся жидкостей. Линейная комбинация гидродина-
мических уравнений, к которой мы собираемся перейти, будет опи-
сывать плазму как одну жидкость, аналогичную жидкой ртути.
Массовую плотность этой жидкости обозначим через р, а удельную
проводимость — через 1/т). Получающиеся в результате такого
180
Гл. 5. Диффузия и сопротивление
перехода уравнения называются уравнениями одножидкостной
магнитогидродинамики (МГД).
Для квазинейтральной плазмы с однозарядными ионами массовую
плотность р, массовую скорость v и плотность тока j можно опре-
делить следующим образом:
р== ntM + пет w п(М + т), (5.78)
v ss (riiMNi + n/nv^/p « (Mvt- + mvj/(M + rri), (5.79)
j~e(niv~neve) » пе(У{—ve). (5.80)
В уравнение движения мы добавим слагаемое Mng, отвечающее
силе тяжести. Этот член можно использовать для описания любой
силы неэлектромагнитного характера, действующей на плазму.
Уравнения движения ионов и электронов запишем в виде
Mn(5v(/5/) = en(E + v/ х В)—VPi + Mng + Ple, (5.81)
тп (dvjdt) = — еп (Е + ve х В)—vpe 4- rang + Pei. (5.82)
Для простоты, как и прежде, мы пренебрегли тензором вязких на-
пряжений л. Это можно сделать только в том случае, если лармо-
ровский радиус частиц много меньше характерных масштабов, на
которых меняются все параметры плазмы. Мы также пренебрегли
членами (v-V) v, поскольку в противном случае вывод уравнений
очень усложняется. Последнее упрощение обосновать труднее.
Не вдаваясь в длительное обсуждение, скажем просто, что v счи-
тается настолько малой, что квадратичным членом можно пре-
небречь.
Теперь сложим уравнения (5.81) и (5.82):
п (d/dt) (Mvt + mve)^= еп (У( — ve) х В—Vp + n(M + m)g. (5.83)
В полученном уравнении через р обозначено полное давление в
плазме:
P = Pt + P,- (5-84)
Электрические поля и столкновительные члены Pei и Р/е = — Pei
при сложении уравнений (5.81) и (5.82) взаимно уничтожаются.
Используя соотношения (5.78) — (5.80), уравнение (5.83) можно
записать в простом виде:
р (dvldt) = j х В — VP + pg- (5.85)
Это есть уравнение одножидкостной гидродинамики, описывающее
перенос массы. В его правую часть включены выражения для сил,
которые можно было ожидать из общих соображений. Электриче-
ское поле Е в силу общей нейтральности жидкости в явном виде
в уравнение не входит.
Менее очевидное уравнение получается в том случае, если из
уравнений для ионной и электронной жидкостей составить другую
линейную комбинацию. Умножим уравнение (5.81) на т, а урав-
5.7. Уравнения одножидкостной магнитогидродинамики 18Г
нение (5.82) на Л4 и вычтем их друг из друга. В результате получаем
следующее уравнение:
Mnm(d/dt)(v{—ve) = еп(М + m) Е 4-en(mVi + Mvs) х В—mVp(- +
+ Муре—(М +m)Pel. (5.86)
С помощью выражений (5.78), (5.80) и (5.61) это уравнение можно
переписать в виде
х (Мпт/е) (d/dt) (j/п) = ерЕ—(М + m)ner]j—mvpi + Mvpe +
+ еп (mvi + Мче) х В. (5.87)
Последний член можно упростить следующим образом:
mvi + М Ne = М vt + tnve + М (v£—vt) + т (vt- — ve) =
= (p/n)v—(M—т)Ц/пе). (5.88}
Разделив уравнение (5.87) на ер, с учетом (5.88) получаем
Е + v х В—т]j = (1 /ер) [(Мпт/е) (d/dt) (j/ri) + (/И — т) j х В +
+ mvpt—Mvpe]. (5.89)
При описании медленных движений, когда эффекты, связанные
с массами частиц (например, их циклотронное вращение), являются
несущественными, членом d/dt можно пренебречь. В. пределе
т/М -> 0 уравнение (5.89) записывается в виде
Е + v х В = г)j + (Men) (j х В—Vpe). (5.90)
Это — второе уравнение одножидкостной магнитогидродинамики,
которое, называется обобщенным законом Ома и описывает электри-
ческие свойства проводящей жидкости. Член j X В отвечает току
Холла. Последние два члена в правой части (5.90) часто являются
малыми, и ими можно пренебречь. В этом случае закон Ома запи-
сывается в виде простого соотношения
E + vxB = r]j. (5.91)
Уравнения непрерывности для массовой плотности р и заряда о
легко получить, складывая или вычитая уравнения непрерывности
для ионов и электронов. В результате мы приходим к следующей
системе МГД-уравнений:
рдv/dt = j х В—VP + pg, (5-85)
E + vxB = T)j, (5-91)
(5p/d/) + V-(pv) = 0, (5-92)
(3o./5/) + V-j = 0. (5.93)
Вместе с уравнениями Максвелла такая система уравнений нередко
используется для описания равновесного состояния плазмы. Ее
можно применять и для анализа волн в плазме, однако нужно по-
мнить, что точность этой системы уравнений значительно меньше,
182
Гл. 5. Диффузия и сопротивление
чем у использовавшихся нами ранее двухжидкостных уравнений.
Благодаря своей простоте МГД-уравнения весьма полезны при
исследовании вопросов, связанных с сопротивлением плазмы. Их
широко применяют астрофизики, работающие в области космиче-
ской электродинамики, специалисты по проблеме МГД-преобразо-
вания энергии, а также теоретики — специалисты в области управ-
ляемого термоядерного синтеза, рассматривающие магнитные си-
стемы сложной конфигурации.
5.8. Диффузия в полностью ионизованной плазме
В отсутствие силы тяжести для описания равновесного состояния
плазмы можно воспользоваться уравнениями (5.85) и (5.91), кото-
рые в стационарном случае принимают вид
j X В = Vp, (5.94)
E + vxB = T)j. (5.95)
Проекция последнего уравнения на направление магнитного поля
имеет простой вид Е ц ц/ ц и представляет собой запись обычного
закона Ома. Перпендикулярную компоненту скорости можно найти,
умножив уравнение (5.95) векторно на В:
Е х B + (Vj. X В) х В = тц] X B = r|j.Vp,
Е X В—-v±B2 = r|j.Vp,
Vj. = Е х В/В2—^±/В2)ур. (5.96)
Первый член в. правой части последнего равенства описывает сов-
местный Е X В-дрейф частиц обоих сортов. Второй член связан
с диффузией против направления градиента давления (— Vp). В ча-
стности, в осесимметричном плазменном цилиндре, где Ей Vp
направлены по радиусу,
Vq=—Er/B, vr=—(i\JB2)(dp/dr). (5.97)
Диффузионный поток частиц в полностью ионизованной плазме
равен
Г± =nv± = — [xun(KTi + KTe)/B2] \/п. (5.98)
Это соотношение имеет форму закона Фика [см. (5.11)] с коэффи-
циентом диффузии
КТ/В2,
(5.99)
который называется «классическим» коэффициентом диффузии в
полностью ионизованном газе.
Заметим, что, как и в случае слабоионизованного газа, D± про-
порционален 1/В2. Такая зависимость характерна для классиче-
5.9. Решения уравнения диффузии 183
ской диффузии, которую в конечном счете можно свести к процессу
случайного блуждания с шагом rL. Однако формула (5.99) имеет
три существенных отличия от выражения (5.54), описывающего
диффузию в слабоионизованном газе. Во-первых, в полностью
ионизованном газе коэффициент диффузии D_hc является констан-
той', он пропорционален плотности плазмы п. Это связано с тем,
что плотность рассеивающих центров определяется не плотностью
нейтральных атомов, а плотностью плазмы в целом. Во-вторых,
в полностью ионизованной плазме коэффициент диффузии D умень-
шается с ростом температуры, поскольку т] пропорциональна
^Т)-3/2. В слабоионизованном газе, наоборот, с ростом темпера-
туры диффузия усиливается. Это различие объясняется тем, что
сечение кулоновского взаимодействия зависит от скорости частиц
и, следовательно, от температуры плазмы. В-третьих, диффузия
в полностью ионизованной плазме автоматически является амби-
полярной (если не учитывать столкновений частиц одного сорта).
В такой плазме частицы обоих сортов дрейфуют с одинаковыми
скоростями, разделения зарядов не происходит, электрические поля
не возникают, поэтому плазма диффундирует как единое целое
с коэффициентом диффузии D_, определяемым формулой (5.99).
Такое поведение плазмы является следствием закона сохранения
импульса при электрон-ионных столкновениях. Это положение
станет более ясным, если проанализировать задачу о диффузии
в рамках двухжидкостных уравнений [см. задачу (5.15)].
Наконец, хотелось бы отметить, что в полностью ионизованном
газе отсутствует поперечная подвижность. В выражении (5.96),
определяющем vx, нет составляющей, зависящей от электриче-
ского поля Е и направленной вдоль него. Если приложить к одно-
родной плазме электрическое поле Е_|_В, то ионы обоих сортов
будут дрейфовать вместе со скоростью (Е X В)/В2. Поскольку от-
носительная скорость ионов разных сортов равна нулю, они не бу-
дут сталкиваться между собой и поэтому движения в направлении
Е не будет. Разумеется, в плазме происходят столкновения, вызван-
ные тепловым движением частиц, так что вывод об отсутствии по-
перечной подвижности является приближенным. Он обусловлен
тем, что при анализе задачи мы пренебрегли: а) столкновениями
между частицами одного сорта, б) массой электрона по сравнению
с массой иона и в) последними двумя членами в правой части вы-
ражения (5.90), представляющего собой обобщенный закон Ома.
5.9. Решения уравнения диффузии
Поскольку в полностью ионизованном газе коэффициент диффузии
D± не является постоянным, введем величину А, которая представ-
ляет собой константу:
А = г\КТ/В2.
(5.100>
184
Гл. 5. Диффузия и сопротивление
Здесь мы предположили, что КТ и В однородны, а слабой зависи-
мостью удельного сопротивления ц от плотности п через In Л можно
пренебречь. В таком случае при Tt = Те имеем
Рх=2пЛ. (5.101)
Уравнение непрерывности (5.92) можно теперь записать в виде
dn/dt = у.(Р±уп) = Л V • (2nvn)
или
dn/dt = Ау2п2. (5.102)
Уравнение для п является нелинейным, и простых решений у него
очень мало.
5.9.1. Зависимость решений от времени
Если разделить переменные, полагая, что п = Т (t) S (г), то урав-
нение (5.102) можно записать в виде
(\/T2)(dT/dt) = (AIS) V2S2= — 1/т, (5.103)
где —1/т — константа разделения. Зависящую от пространствен-
ных координат часть этого уравнения решить трудно. Что касается
его временной части, то она аналогична уравнению (5.41), с кото-
рым мы встречались при анализе процесса рекомбинации в плазме,
и решение T(t) можно выписать сразу:
При больших t, как и в случае рекомбинации, плотность убывает
как 1//. Выражение (5.104) описывает классическую диффузию в
полностью ионизованном газе. Напомним, что в слабоионизованном
газе диффузия протекает совершенно иначе: там плотность убывает
со временем экспоненциально.
5.9.2. Стационарные решения
Есть один случай, когда уравнение диффузии в полностью ионизо-
ванном газе можно решить довольно просто. Рассмотрим длинный
столб плазмы, на оси которого расположен источник (рис. 5.19).
Этот источник компенсирует потери плазмы из-за рекомбинации
и диффузии в радиальном направлении и поддерживает плазму
в стационарном состоянии. Вне области источника профиль плот-
ности плазмы будет определяться тем, какой из двух механиз-
мов—диффузия или рекомбинация — является преобладающим.
Если диффузия мала, а рекомбинация велика, то плотность плазмы
будет быстро уменьшаться с расстоянием от источника. В против-
5.9. Решения уравнения диффузии
185
ном случае ее уменьшение будет медленным. Из уравнения непре-
рывности следует, что в области вне источника
— Av2n2=— ап2. (5.105)
Это уравнение линейно относительно и2, и найти его решение не-
трудно. В цилиндрической геометрии его решением является функ-
Рис. 5.19. Диффузия поперек магнитного поля в цилиндрическом столбе пол
ностью ионизованной плазмы.
ция Бесселя. В плоской геометрии уравнение (5.105) принимает
вид
д2п2/дх2 — (а/А)п2, (5.106)
а его решение записывается следующим образом:
и2 = По ехр [—(а/Л)1/2х]. (5.107)
Характерный масштаб убывания плотности равен
/ = (Л/а)1/2. (5.108)
Поскольку Л зависит от напряженности магнитного поля, а кон-
станта рекомбинации а сохраняется постоянной, измерение зави-
симости I (В) позволяет проверить справедливость классической
теории диффузии. Такой эксперимент действительно пытались по-
ставить на Q-машине в полностью ионизованной плазме. К сожале-
нию, из-за наличия асимметричного Е X В-дрейфа в системе воз-
никли потери еще одного типа, а именно за счет конвекции, так
что однозначного вывода из эксперимента сделать не удалось.
В заключение следует заметить, что существует закон подобия,
справедливый для любой равновесной плазмы, поддерживаемой
постоянным источником Q в однородном магнитном поле В. В са-
мом деле, уравнение непрерывности для этого случая имеет вид
— Л v2n2 = —цКТу2 (п2/В2) = Q. (5.109)
Поскольку плотность п и магнитное поле В входят в это уравнение
только в виде комбинации п/В, профиль плотности при изменении
186 Гл. 5. Диффузия и сопротивление
В будет оставаться неизменным, а величина плотности будет ли-
нейно зависеть от В:
п~В. (5.110)
Казалось бы, в состоянии равновесия плотность п должна быть
пропорциональна В2, поскольку £>± ~ В-2, однако коэффициент
диффузии D± сам пропорционален п и потому п ~ В.
5.10. Диффузия Бома и неоклассическая диффузия
Хотя теория диффузии под действием кулоновских столкновений
была разработана довольно давно, до начала 1960-х гг. зависимость
Dx ~ В-2 не удавалось подтвердить в эксперименте. В большин-
стве выполненных до этого экспериментов коэффициент О. оказы-
вался пропорционален не В-2, а В-1 и концентрация плазмы умень-
шалась со временем не по закону \Jt, а экспоненциальным обра-
зом. Кроме того, абсолютная величина коэффициента диффузии D
была выше, чем предсказывала формула (5.99). Впервые на ано-
мально слабое магнитное удержание обратили внимание в 1946 г.
Бом, Бархоп и Месси, которые разрабатывали магнитную дугу для
разделения изотопов урана. Бом предложил для коэффициента
диффузии следующую полуэмпирическую формулу:
D±=KTe/16eB = DB. (5.111)
Эта формула неожиданно была подтверждена в большом числе раз-
личных экспериментов. Диффузия такого типа называется бомов-
ской диффузией. Поскольку DB не зависит от плотности, концентра-
ция плазмы со временем в режиме бомовской диффузии будет умень-
шаться по экспоненциальному закону. В цилиндрическом столбе
плазмы длиной L и радиусом R постоянную времени этого процесса
можно оценить следующим образом:
т « NI(dNldt) = rmRWr2nRL = nR/2Vr,
где N — полное число электрон-ионных пар в плазме, а Гг — ра-
диальная компонента потока частиц. Если Гг найти из закона Фика
с бомовским коэффициентом диффузии, то окажется, что
т л; nRI2DBdnidr « nRI[2DBnlR] = RZI2DB = тв. (5.112)
Величину тв часто называют бомовским временем.
Возможно, самая значительная серия экспериментов, подтверж-
дающих формулу Бома, была выполнена в Принстоне на шести уста-
новках, называемых стеллараторами. Стелларатор представляет
собой тороидальный контейнер, помещенный в магнитное поле,
5.10. Диффузия Бома и неоклассическая диффузия
187
Рис. 5.20. Результаты измерений времени удержания т в зависимости
от КТе/В для различных типов разрядов на стеллараторах модели С, под-
тверждающие справедливость бомовского закона диффузии. Данные норми-
рованы к величине магнитного поля 12,3 кГс и радиусу г = 5,0 см. (С лю-
безного разрешения Д. Грова из лаборатории физики плазмы Принстонского
университета. Работы выполнены при поддержке Комиссии по атомной
энергии США.)
силовые линии которого закручены таким образом, что в среднем
градиентный и центробежный дрейфы компенсируют друг друга.
(Эти типы дрейфовых движений были рассмотрены в разд. 2.3).
На рис. 5.20 приведена сводка данных, полученных за последнее
десятилетие при различных видах разрядов на стеллараторах мо-
дели С. Измеренные значения т почти в точности лежат на линии,
отвечающей бомовскому времени тв. Близкое соответствие наблю-
даемых процессов и бомовской диффузии имеет серьезные следствия
для проблемы управляемого термоядерного синтеза. Из формулы
(5.111) видно, что коэффициент бомовской диффузии с ростом тем-
пературы увеличивается. Что касается его зависимости от магнит-
ного поля, то хотя 2?в и уменьшается с В, но не так быстро, как
ожидалось. Кроме того, по абсолютной величине £>в намного
больше, чем D±. Например, для плазмы с температурой 100 эВ,
помещенной в магнитное поле 1 Тл,
£>в
1
16
(10») (1,6- ю-Ц)
(1,6- 10-м) (1)
= 6,25 м2/с.
188 Гл. 5. Диффузия и сопротивление
Если плотность плазмы равна 1019 м~3, то классический коэффи-
циент диффузии
JJ = (2) (1019) (109) (1,6 -10~19) (3,3) (5,2-10-5) (10) __
В9 ~ (I)9 (Ю0)3/2
= (1,06 • 10s) (5,2 • 10-7) = 5,49 • ю-4 м2/с.
Расхождение составляет четыре порядка величины!
Было предложено несколько объяснений бомовской диффузии.
Первое из них связано с возможным искажением магнитного поля.
Если установка, в частности термоядерный реактор, имеет сложную
форму, то не очевидно, что все силовые линии магнитного поля яв-
ляются замкнутыми. Они могут даже выходить из камеры, в кото-
рой находится плазма. Поскольку длина свободного пробега может
быть очень велика, то даже слабой асимметрии в магнитных обмот-
ках будет достаточно для того, чтобы электроны без каких-бы то
ни было соударений вылетели на стенки, а возникшее вследствие
этого электрическое поле вытолкнуло бы на стенки и ионы. Второе
объяснение связано с возможной асимметрией электрических по-
лей. Она может быть обусловлена наличием в плазме каких-либо
препятствий, асимметрией самой вакуумной камеры, наконец, тем,
что плазма создается или нагревается асимметричными источни-
ками. В этом случае скорость Е X В-дрейфа в постоянном поле Е
не обязательно будет направлена параллельно стенкам, в резуль-
тате чего на них будут одновременно выноситься и электроны и
ионы. Такие дрейфовые движения, называемые конвективными
ячейками, действительно наблюдались в плазме. Наконец, в плазме
могут существовать осциллирующие электрические поля, связан-
ные с неустойчивыми плазменными волнами. Если эти поля случай-
ным образом флуктуируют, то Е X В-дрейф даже в отсутствие
столкновений вызовет хаотическое блуждание частиц. Впрочем,
даже если волна является чисто синусоидальной, она все равно
может вызвать дополнительные потери, потому что фаза у скорости
Е X В-дрейфа может быть такова, что любая область с повышенной
концентрацией плазмы будет выталкиваться из нее наружу; такую
картину можно себе представить в виде движущихся конвективных
ячеек. Если в плазме есть аномальная диффузия, в ней действи-
тельно часто наблюдаются флуктуирующие электрические поля.
Можно, однако, показать, что во многих случаях влиянием только
этих полей все потери объяснить нельзя. В экспериментах, кото-
рые ставятся в полностью ионизованной плазме, могут одновре-
менно действовать все три рассмотренных выше механизма аномаль-
ных потерь.
Можно показать, что если потери вызваны Е X В-дрейфом ча-
стиц, то независимо от того, осциллирует электрическое поле или
нет, коэффициент диффузии DB будет пропорционален КТе1В
5.10. Диффузия Бома и неоклассическая диффузия
189
Рис. 5.21. Орбита частицы, удерживаемой в тороидальном контейнере с ио
мощью магнитного поля с закрученными силовыми линиями, по форме па"
поминает банан. «Орбита» представляет собой геометрическое место точек,
в которых частица при своем движении пересекает данное сечение тора.
Действительно, пусть поток покидающих плазму частиц пропор-
ционален скорости Е X В-дрейфа:
Г± = отх~пЕ/В. (5.113)
Вследствие дебаевского экранирования максимальный потенциал
в плазме определяется соотношением
ефмм^КТе. (5.114)
Если 7? — характерный масштаб длины, на которой меняется плЬт-
ность плазмы (например, величина порядка радиуса плазменного
цилиндра), то максимальное электрическое поле равно
Емакс«<£макс/Я « KTJeR. (5-115)
Отсюда следует, что поток Гх можно записать в виде
Г_ у (п/7?) (КТе/еВ) « — у (КТе/еВ) vn = — D^n, (5.116)
где у — некоторый множитель, меньший единицы. Таким образом,
не удивительно, что ~ KTJeB. Значение у = 1/16 не следует
из теории. Это эмпирический коэффициент, который с точностью
до множителя 2—3 обеспечивает согласие теории с большинством
экспериментов.
В последних экспериментах на тороидальных установках время
удержания плазмы было доведено до величин порядка 100 тв. Это
было достигнуто путем тщательного подавления колебаний и устра-
нения асимметрии в установках. Впрочем, в тороидальных прибо-
рах существуют и другие эффекты, усиливающие столкновитель-
ную диффузию. Рассмотрим кратко эти явления. На рис. 5.21 изо-
бражен тор, вокруг которого создано магнитное поле, силовые ли-
нии этого поля представляют собой спирали. Такая закрутка не-
обходима для того, чтобы устранить дрейфовые движения, связан-
ные с кривизной силовых линий и наличием градиента магнитного
поля. При движении вдоль силовых линий частицы попадают то
в область больших В у внутренней стенки тора, то в область мень-
190
Гл. 5. Диффузия и сопротивление
„ Банановая " диффузия
Рис. 5.22. Зависимость коэффициента неоклассической диффузии D ± от ча-
стоты столкновений v.
шей напряженности поля вблизи внешней стенки установки. Неко-
торые из частиц оказываются захваченными между магнитными
пробками и не делают вокруг оси тора ни одного оборота. Ведущие
центры таких частиц, последовательно проходя через данное сече-
ние тора, описывают орбиты, по форме напоминающие бананы
(рис. 5.21). Если частица участвует в столкновениях, то она после-
довательно может становиться то захваченной, то незахваченной
и таким образом, переходить с одной банановой орбиты на другую.
Вследствие этого пространственный шаг процесса случайного блуж-
дания будет равен не ларморовскому радиусу частицы гц, а ширине
банановой орбиты и коэффициент диффузии станет больше своего
«классического» значения. Такой режим называется неоклассиче-
ской диффузией. На рис. 5.22 показана зависимость коэффициента
диффузии поперек магнитного поля от частоты столкновений v.
В области малых v «банановая» диффузия больше классической.
При больших v диффузия снова становится классической, но ее
характер модифицируется из-за наличия токов, текущих вдоль
магнитного поля В. Теоретическая кривая для случая неокласси-
ческой диффузии была подтверждена в экспериментах, выполненных
Окавой в Ла-Холья (шт. Калифорния).
Задачи
5.7. Покажите, что средняя длина свободного пробега между электрод-
ионными столкновениями пропорциональна 7^.
5.8. Токамак представляет собой тороидальный контейнер, заполненный
полностью ионизованной плазмой, к которой прикладывается электриче-
ское поле, направленное''вдоль В. В результате в плазме возникает ток J
(рис. 35.8). Какова должна быть напряженность электрического поля в воль-
тах на метр, чтобы через поперечное сечение S = 75 см2 в плазме, нагретой
до КТе = 500 эВ, протекал полный ток 200 кА?
5.9. Пусть плазма в термоядерном реакторе имеет форму цилиндра диамет-
ром 1,2 м и длиной 100 м. Магнитное поле 5 Тл однородно всюду, кроме тор-
5.10. Диффузия Бома и неоклассическая диффузия
191
Рис. 35.8.
Рис. 35.9.
цов плазменного цилиндра, где оно образует магнитные пробки (этой неод-
нородностью можно пренебречь). Остальные параметры плазмы таковы:
KTt = 20 кэВ, КТС = 10 кэВ, п = 1021 м“3 (при г = 0). Экспериментально
обнаружено, что профиль плотности плазмы имеет примерно такой вид, как
показано на рис. 35.9.
а) Предполагая, что диффузия носит классический характер, вычислите
D ± при г ~ 0,5 м.
б) Вычислите величину dNldt, равную полному числу электрон-ионных пар,
выходящих за одну секунду из центральной области реактора в радиальном
направлении.
в) Оцените время удержания плазмы т, считая, что т та—Nl(dNldt). За-
мечание: в подобных задачах можно получить только грубые оценки. Оче-
видно, на профиль плотности плазмы кроме классической диффузии будут
влиять и другие процессы.
5.10. Оцените время классической диффузии для плазменного цилиндра ра-
диусом 10 см, считая, что плотность плазмы п — 1021 м-3, ее температуры
КТе = кп = 10 кэВ, а В = 5 Тл.
5.11. Распределение плотности в цилиндрическом столбе плазмы имеет вид
/г = n0 (1—г2/а2), где а = 10 см, а n0 — 1019 м”3. Пусть КТ е = 100 эВ,
KTi ~ 0, а магнитное поле на оси цилиндра равно BQ = 1 Тл. Чему равно
отношение коэффициента бомовской диффузии к коэффициенту классиче-
ской диффузии поперек Во?
5.12. Выражение для удельного сопротивления Спитцера справедливо и для
случая слабоионизованной плазмы, если только частота электрон-ионных
столкновений в ней выше частоты столкновений электронов с нейтральными
атомами: vet > ve0. Ниже приводятся данные о сечениях передачи импульса
при столкновениях электронов с нейтральными атомами в квадратных анг-
стремах (А2):
£ — 2 эВ £ - 10 эВ
Гелий 6,3
Аргон 2,5
4,1
13,8
Рассмотрим плазму, состоящую из однократно ионизованных атомов гелия
или аргона. Пусть электронная температура плазмы КТе составляет либо 2,
либо 10 эВ. (Возможно, таким образом, четыре случая: гелиевая плазма с
КТе = 2 эВ, гелиевая плазма с КТе ~ 10 эВ, аргоновая плазма с КТе =
= 2 эВ и, наконец, аргоновая плазма с КТе = 10 эВ.) Оцените для каждого
случая степень ионизации f = nf/(n0 + nz), при которой vel- = ve0, полагая,
что величину av (Те) можно грубо аппроксимировать выражением о (£) | v | (£
192
Гл. 5. Диффузия и сопротивление
Рис. 35.14.
где Е ~ КТе. [Указание: при вычислении veo пользуйтесь формулой (7.11);
величину vei рассчитайте по формулам (5.62) и (5.76).]
5.13. В тороидальном стеллараторе однородная плазма нагревается за счет
джоулева тепла током плотностью j = 105 А/м2, текущим вдоль магнитного
поля В. Плотность плазмы п == 1019 м~3 в эксперименте с течением времени
не меняется. Выделяющееся в результате джоулева нагрева тепло nJ2 пере-
дается электронам. Вычислите скорость нагрева плазмы в единицах эВ/мкс
в тот момент, когда ее температура равна КТе = 10 эВ,
5.14. При создании 0-пинча через одновитковую обмотку, окружающую хо-
рошо проводящую плазму, пропускается импульс тока большой силы. Маг-
нитное поле, возникающее внутри обмотки, индуцирует в плазме поверх-
ностный ток, который направлен против тока в обмотке и, следовательно,
стремится вытолкнуть магнитное поле из плазмы. Давление магнитного поля,
возникающего между обмоткой и плазмой, стремится сжать последнюю.
Этот механизм сжатия может работать только в том случае, если за время
импульса магнитное поле не успевает проникнуть внутрь плазмы. Исполь-
зуя формулу Спитцера для удельного сопротивления, оцените максималь-
ную длительность импульса для 0-пинча в водородной плазме с начальными
условиями КТе — Ю эВ, п ~ 1022 м-3, г ~ 2 см, если поле должно прони-
кать в плазму на расстояния, не превышающие 1/10 радиуса плазменного
цилиндра.
5.15. Пусть имеется осесимметричный плазменный цилиндр, в котором Е =
— Егг, В = Bz, a Vpt = Vpfi = г dpldr. Если пренебречь членом (v*V) v
или, что то же самое, центробежной силой, то в стационарном случае урав-
нения двухжидкостной гидродинамики можно записать в виде
еп (Е + V/ X В) — Vpi — e2n2rj (vt- — ve) = 0,
— еп (Е + ve X В) — Vpe + е2п2т) (vt- — ve) — 0.
а) Спроектировав эти уравнения на направление 0, покажите, что vir = ver.
б) Спроектировав их на направление г, покажите, что
VjQ = vE + vDj(J = i, е).
в) Получите выражение для vir и покажите, что эта величина не зависит от Ег.
5.16. В приближении одножидкостной магнитогидродинамики вычислите
фазовую скорость ионно-звуковой волны в неизотермической (Те Ti) од-
нородной незамагниченной плазме, воспользовавшись для этого уравнением
движения и уравнением сохранения массы.
5.17. Проанализируйте процесс затухания альфвеновских волн, обуслов-
ленного сопротивлением плазмы. Для этого выведите, дисперсионное урав-
5.10. Диффузия Бома и неоклассическая диффузия
193
некие для альфвеновских колебаний исходя из уравнений Максвелла (4.72)
и (4.77) и линеаризованных уравнений одножидкостной магнитогидродина-
мики (5.85) и (5.91), в которых пренебрегите силой тяжести, током смещения
и градиентом давления Vp.
а) Покажите, что
a?Ik2 = с2е0 [(Во/ро) — i ®п].
б) Выпишите явное выражение для Im (k) в случае вещественных © в пре-
деле малых т).
5.18. Плазменный цилиндр размывается под действием бомовской диффузии.
Рассчитайте радиальное распределение плотности п (г), пренебрегая тем
фактом, что оно может быть неустойчивым. Для этого предположите, что
при т = оо плотность п = 0, а при г = rQ она равна п0. '
5.19. В цилиндрическом столбе плазмы, помещенном в однородное магнит-
ное поле В = B2z, течет постоянный ток плотностью j = /2z, где z — единич-
ный вектор, параллельный оси цилиндра.
а) Рассчитайте распределение магнитного поля В (г), создаваемое этим током.
б) Выразите скорость градиентного дрейфа заряженной частицы с Оц = 0
через величины В2, /2, г, q и т, Можно предположить, что напряженность
поля, рассчитанная в п. а данной задачи, мала по сравнению с В2, но не равна
нулю.
в) Если сопротивление плазмы отлично от нуля, то в ней должно также су-
ществовать электрическое поле Е = Ezz. Вычислите скорость азимутального
дрейфа электронов, вызванного наличием этого поля, учитывая, что силовые
линии магнитного поля В представляют собой спирали.
г) Нарисуйте диаграмму направлений скоростей дрейфов ионов и электро-
нов, вычисленных в пп. б и в данной задачи, в плоскости г0.
7 Заказ 3170
Глава 6
РАВНОВЕСИЕ И УСТОЙЧИВОСТЬ
6.1. Введение
Если бы поведение плазмы определялось лишь движениями состав-
ляющих ее отдельных частиц, то создать магнитное поле для удер-
жания плазмы было бы довольно просто. Для этого нужно только
убедиться, что его силовые линии не упираются в стенки вакуум-
ной камеры, и обеспечить такую степень симметрии установки,
чтобы все скорости дрейфовых движений частиц (v£, vVB и т. п.)
были направлены параллельно стенкам. Однако с макроскопиче-
ской точки зрения не очевидно, что магнитное поле, созданное та-
ким образом, чтобы удерживать отдельные частицы, будет удержи-
вать плазму как целое. Дело в том, что независимо от конфигурации
внешних полей в плазме могут возникать внутренние поля, кото-
рые также будут влиять на ее движение. В частности, из-за группи-
рования частиц в сгустки в плазме может возникнуть электриче-
ское поле Е, которое вызовет Е X В-дрейф частиц к стенкам уста-
новки. Токи, текущие в плазме, могут генерировать магнитное
поле, которое приведет к выносу частиц из-за градиентного дрейфа.
Проблему удержания плазмы можно произвольным образом
разделить на две, а именно на задачу о равновесии и задачу об ус-
тойчивости. Разницу между равновесием и устойчивостью лучше
всего проиллюстрировать с помощью механической аналогии. На
рис. 6.1 показаны различные случаи равновесия шарика на твердой
поверхности. Равновесие представляет собой состояние, когда все
действующие на систему силы взаимно компенсируют друг друга
и возможно не зависящее от времени решение уравнений движе-
ния. Равновесие является устойчивым или неустойчивым в зависи-
мости от того, затухают или нарастают в системе малые возмуще-
ния. В частности, на рис. 6.1 в состоянии Е шарик находится в по-
ложении устойчивого равновесия (если только его не отклонять
из этого положения слишком сильно). Если же сдвинуть шарик
за показанный на рисунке порог, то система становится неустойчи-
вой. Такое поведение называется взрывной неустойчивостью. В слу-
чае Ж равновесие шарика неустойчиво, но он не может сильно от-
клоняться от положения равновесия. Такая неустойчивость не
6.1. Введение
195
А
В
Условное
равновесие
Б
Безразличное
равновесие
Равновесие
отсутствует
Д
Неустойчивое
равновесие
Г
Устойчивое
равновесие
Е
Равновесие, устойчивое
в линейном приближении,
но неустойчивое в нелинейном
режиме
Равновесие, неустойчивое
в линейном приближении,
но устойчивое в нелинейном
режиме
Рис. 6.1. Механическая аналогия
различных типов равновесия.
очень опасна, если нелинейная амплитуда колебаний достаточно
мала. В случае плазмы ситуация, естественно, гораздо сложнее по-
казанной на рис. 6.1, поскольку для достижения полного равновесия
плазмы нужно, чтобы уравновешивались силы, действующие на
каждый элемент ее объема. Из двух проблем — равновесия и устой-
чивости — легче решать последнюю. Для этого можно считать от-
клонения от состояния равновесия малыми и провести линеариза-
цию уравнений движения. При этом, как и в случае анализа волн
в плазме, мы придем к линейным уравнениям. Проблема равнове-
сия, напротив, сводится к нелинейной задаче, похожей на задачу
о диффузии. При наличии магнитных полей сложной конфигура-
ции исследование равновесия представляет собой весьма непростую
задачу.
7*
196
Гл. 6. Равновесие и устойчивость
6.2. Равновесие в МГД-приближении
Хотя в целом проблема исследования равновесия достаточно
сложна, некоторые полезные с физической точки зрения сведения
можно довольно просто получить из МГД-уравнений. Пусть уско-
рение свободного падения g = 0, тогда в стационарном случае,
d/dt — 0 плазма должна описываться уравнением [ср. с (5.85) ]
Vp = jxB (6.1)
и уравнением Максвелла
V X В = mj. (6.2)
Некоторые выводы о характере равновесия можно сделать уже на
основе простого уравнения (6.1).
1. Из этого уравнения видно, что имеется равновесие сил между
градиентом давления и силой Лоренца. Как это обеспечивается?
Рассмотрим плазменный цилиндр, в котором градиент давления Vp
направлен к оси цилиндра (рис. 6.2). Для того чтобы противодейст-
вовать силе давления, направленной к внешней границе плазмы,
в ней должен существовать ток, текущий в азимутальном направ-
лении, как показано на рисунке. Плотность тока, необходимого для
уравновешивания давления плазмы, можно найти, если умножить
векторно уравнение (6.1) на В:
h = (В х Vp)/B2 = (КЛ + K7\) (В X Vn)/B2. (6.3)
Эго выражение в точности совпадает с полученной ранее форму-
лой (3.69) для диамагнитного тока! Таким образом, с точки зрения
теории движения отдельных частиц диамагнитный ток возникает
из-за того, что при наличии градиента плотности средние скорости
частиц, совершающих ларморовское вращение, не обращаются
Рис. 6.2. В стационарном
состоянии сила Лоренца
j X В, связанная с диама-
гнитным током, равна гра-
диенту давления плазмы.
Рис. 6.3. Векторы j и В лежат на поверхно-
стях постоянного давления.
6.3. Понятие о величине 0
197
в нуль. С точки зрения магнитогидродинамики диамагнитный ток
генерируется потому, что поперек магнитного поля В действует
сила, связанная с градиентом давления Vp. Возникающий при
этом ток достаточен для того, чтобы уравновесить силы, действую-
щие на каждый элемент объема плазмы, и таким образом остановить
ее движение.
2. Из уравнения 6.1 очевидно, что в равновесии и вектор j, и
вектор В перпендикулярны vp- Это не тривиальное утверждение,
если учесть, что конфигурация системы может быть очень сложной.
Представим себе плазменный тор, в котором существует плавный
радиальный градиент плотности, так что поверхности постоянной
плотности (на самом деле — постоянного давления) представляют
собой вложенные друг в друга торы (рис. 6.3). Поскольку векторы
j и В перпендикулярны Vp, они должны лежать на поверхностях
постоянных р (изобарических поверхностях). Вообще говоря, си-
ловые линии магнитного поля и ток могут быть закручены как
угодно, но все равно в состоянии равновесия они не должны пере-
секать поверхности постоянных р.
3. Рассмотрим проекцию уравнения (6.1) на направление В.
Ее можно записать в виде
dp/ds — Q, (6.4)
где s — координата, отсчитываемая вдоль силовой линии. Отсюда
следует, что при КТ = const в состоянии равновесия плотность
плазмы вдоль каждой силовой линии должна быть постоянна. На
первый взгляд этот вывод может показаться ошибочным. В самом
деле, рассмотрим стационарный поток плазмы, который инжекти-
руется в область между двумя магнитными пробками (рис. 6.4).
При движении плазмы вдоль силовых линий она сначала расши-
ряется, а затем сжимается, поэтому ясно, что плотность на силовой
линии не является константой. Однако парадокса здесь нет. Все
дело в том, что в этой ситуации в системе нет статического равно-
весия. Производная dvldt действительно равна нулю, но член
(v-v) v, которым мы пренебрегли, в нуль не обращается. Мы же
должны рассматривать неподвижную плазму, в которой v = 0.
Если плазма покоится, то частицы оказываются запертыми в ло-
вушке, причем большинство из них группируется в центральной
плоскости системы, а не у ее краев, поскольку у торцов пробочное
отношение больше. Этот эффект компенсирует уширение ловушки
в ее центральной части, и в результате плотность вдоль силовой
линии магнитного поля оказывается постоянной.
6.3. Понятие о величине 0
Подставляя выражение для тока j из (6.2) в уравнение (6.1), по-
лучаем
Vp = Р?1 (V X В) х В = щГ1 £(В • V) В-VB2], (6.5)
198
Гл. 6. Равновесие и устойчивость
Рис. 6.5. В плазме с р =£ О диа-
магнитный ток уменьшает ма-
гнитное поле таким образом,
что сумма давления частиц и
давления магнитного поля со-
храняется постоянной. 1 —об-
ласть слабого магнитного поля
В и высокого давления р, 2—
область сильного поля В и
низкого давления р.
Рис. 6.4. Расширение потока плазмы при
его инжекции в пробкотрон.
ИЛИ
V [р + (В2/2|Ло)] = (В • V) В/Цо-
(6-6)
Во многих интересных для прак-
тики конфигурациях плазмы, на-
пример в виде прямого цилиндра, помещенного в магнитное поле,
параллельное оси цилиндра, правая часть этого уравнения обра-
щается в нуль, поскольку величина магнитного поля не меняется
вдоль В. В других случаях правая часть уравнения (6.6) отлична
от нуля, но мала. В этом приближении из (6.6) следует, что
р + (В2/2ц0) = const.
(6-7)
Поскольку величина В2/2р0 равна давлению магнитного поля,
отсюда видно, что в состоянии равновесия сумма кинетического
давления частиц и давления магнитного поля должна быть постоян-
ной. Иными словами, если в плазме есть градиент плотности
(рис. 6.5), то там, где концентрация частиц велика, магнитное поле
должно быть мало, и наоборот. Ослабление магнитного поля в
плазме, естественно, вызывается диамагнитным током. О величине
диамагнитного эффекта можно судить по отношению двух слагае-
мых, входящих в (6,7). Это отношение обычно обозначается грече-
ской буквой 0:
р 2 пКТ Давление частиц g^
В2/2р0 Давление магнитного поля
До сих пор, не оговаривая этого, мы рассматривали плазму только
с малыми Р, когда величина р заключена в диапазоне 10"3—10"6.
Следовательно, в рассматриваемых нами случаях диамагнитный
эффект был очень мал. Именно поэтому при анализе волн в плазме
мы могли считать поле BQ однородным. При малых Р все равно,
вычислять ли знаменатель в выражении (6.8) для случая магнит-
6.4. Диффузия магнитного поля в плазму
199
ного поля в вакууме или для поля в присутствии плазмы. Если’же
параметр р велик, то из-за наличия плазмы локальное магнитное
поле В может сильно уменьшиться. В этом случае в определение (J
обычно включают значение магнитного поля в вакууме. Плазма
с большими Р характерна для космического пространства и для
исследований по МГД-преобразованию энергии. Для того чтобы
термоядерный реактор был экономичным, значение Р в нем должно
существенно превышать 1 %, поскольку энергетический выход
реактора пропорционален квадрату плотности плазмы л2, а стои-
мость реактора растет с увеличением В по степенному закону.
В принципе может существовать и плазма с Р = 1, в которой
диамагнитный ток создает поле, в точности равное по величине и
противоположное по направлению внешнему магнитному полю.
В этом случае система должна разделиться на две части: область
плазмы без магнитного поля и область, в которой имеется лишь
магнитное поле, а плазма отсутствует. Если силовые линии магнит-
ного поля являются прямыми, то равновесие в этой системе будет
неустойчивым, поскольку такая конфигурация напоминает желе,
которое удерживают на натянутых резиновых лентах. Поэтому
надо еще доказать, можно ли вообще создать подобную плазму с
Р = 1. В некоторых магнитных конфигурациях поле В внутри
плазмы обращается в нуль, и локальное значение р в таком случае
должно равняться бесконечности. Это происходит, в частности,
в том случае, когда магнитное поле прикладывается вблизи поверх-
ности большого объема плазмы. Вследствие этого р обычно опреде-
ляют как отношение максимального давления частиц к максималь-
ному магнитному давлению, и в этом смысле у плазмы, удерживае-
мой магнитным полем, величина р не может быть больше единицы.
6.4. Диффузия магнитного поля в плазму
В астрофизике часто возникает задача о проникновении магнит-
ного поля в плазму. Пусть между областью, в которой есть плазма,
но нет поля, и областью, в которой есть магнитное поле, но нет
плазмы, существует резкая граница (рис. 6.6). Если электрическое
Только магнитное пале В
г • •• .•
Только плазма
Рис. 6.6. Между идеально проводящей плазмой и магнитным полем может
существовать резкая граница. Поверхностные токи выталкивают поле из
плазмы.
200
Гл. 6. Равновесие и устойчивость
сопротивление плазмы равно нулю, то эта граница будет оставаться
неизменной по той же причине, по которой магнитное поле не мо-
жет проникнуть в сверхпроводник: всякая ЭДС, создаваемая дви-
жущимися силовыми линиями, генерировала бы в плазме бесконеч-
ный ток, а это невозможно. Следовательно, и плазма при своем
движении будет выталкивать из себя силовые линии, а также из-
гибать и скручивать их. Возможно, этот эффект является причиной
образования нитевидных структур газа, которые наблюдаются
в Крабовидной туманности. Если же проводимость плазмы отлична
от нуля, то плазма может двигаться сквозь силовые линии магнит-
ного поля и, наоборот, магнитное поле может проникать в плазму.
Такая диффузия требует определенного времени, и если движение
происходит достаточно медленно, то силовые линии за время этого
процесса не успевают сильно исказиться. Время диффузии нетрудно
вычислить из уравнений
V X Е = —В, (6.9)
E + vxB = T)j. (6.10)
[ср. с уравнением (5.91)]. Для простоты будем считать, что сило-
вые линии проникают в покоящуюся плазму. Тогда v = 0 и
дЪ/dt <= —V х ту. (6.11)
Вспоминая, что j определяется выражением (6.2), уравнение (6.11)
можно переписать в виде
dB/dt = — (ц/^о) V X (V X В) — — (тр'Ио) [V (V В) — V2B]. (6.12)
Вследствие того что V-B = 0, мы приходим к уравнению диффу-
зии, с которым уже встречались в гл. 5:
дЪ/dt = (т]/Цо) V2B. . (6.13)
Его можно решить с помощью разделения переменных, однако мы
ограничимся здесь грубой оценкой времени диффузии. Пусть L —
характерный масштаб пространственного изменения магнитного
поля В; тогда
dB/ai = (T]/p0b2)B, (6.14)
В-Во ехр (± Z/т), (6.15)
где
т= p0L2/r]. (6.16)
Это и есть характерное время проникновения магнитного поля в
плазму.
Величину т можно также интерпретировать как время анниги-
ляции магнитного поля. Дело в том, что при движении силовых
линий сквозь плазму наводимые ими токи вызывают ее нагрев. На
этот нагрев тратится энергия магнитного поля. Потери энергии
6.4. Диффузия магнитного поля в плазму
201
в единице объема (м3) плазмы за время т равны т]/2т. Если прене-
бречь током смещения, то из уравнения Максвелла (3.4) следует,
что
|ioj = VX (6.17)
Отсюда можно найти диссипацию энергии:
П/Ч = т] (В/ИоЬ)2 (HoP/n) = Wo = 2 (В2/2Ио). (6.18)
Таким образом, величина т приближенно равна времени, которое
требуется для того, чтобы энергия магнитного поля рассеялась на
джоулев нагрев.
Задачи
6.1. Предположите,£что в дейтериево-дейтериевом реакторе из-за электро-
магнитной неустойчивости величина р не может превышать (т/М)1/2. Пусть
также из-за свойств материалов конструкции реактора магнитное поле огра-
ничено величиной В — 20 Тл. Найдите максимальную плотность плазмы,
которую можно удержать в этом реакторе, если KTif— КТе = 20 кэВ.
6.2. В экспериментах по лазерному синтезу у поверхности мишени вследст-
вие поглощения излучения лазера создается плазма плотностью п « 1027 м-3
с температурой КТе « « 104 эВ. Возникающие при этом термоэлек-
трические токи могут спонтанно генерировать магнитные поля до 103 Тл.
а) Покажите, что в такой плазме <осте£»1, и, следовательно, магнитное
поле сильно влияет на движение электронов.
б) Покажите, что р^>1, и поэтому такую плазму невозможно надежно удер-
жать с помощью магнитного поля.
в) Каким образом должны двигаться плазма и силовые линии магнитного
поля, чтобы одновременно удовлетворялись условия, сформулированные
в п. а и б, которые на первый взгляд противоречат друг Другу?
6.3. Цилиндрический столб плазмы радиусом а помещен в магнитное поле
В = Boz, параллельное его оси. Профиль давления плазмы имеет вид р —
= p0cos2 (nr/2а).
а) Вычислите максимальное давление ро.
б) Используя это значение ро, найдите распределение диамагнитного тока
j (г) и полного магнитного поля В (г).
в) Постройте зависимости / (г), Bq (г) и р (г).
г) Если этот цилиндр свернуть в тор таким образом, что силовые линии,
совершив один оборот, замкнутся сами на себя, то равновесие, при котором
макроскопические силы повсюду компенсируют друг друга, очевидно, бу-
дет нарушено. Можно ли так перераспределить давление р (г, 6), чтобы рав-
новесие в системе восстановилось?
6.4. Рассмотрите бесконечный прямой плазменный цилиндр, помещенный
в магнитное поле Во, считая что профиль плотности плазмы имеет форму
прямоугольника (рис. 36.4). Покажите, что при р — 1 магнитное поле на оси
цилиндра обращается в нуль. Для этого проделайте следующие операции:
а) Используя МГД-уравнения и считая, что КТ = const, найдите в стаци-
онарном состоянии ток j±.
202
Гл. 6. Равновесие и устойчивость
Рис. 36.4.
б) Проинтегрируйте уравнение Максвелла V X В = J по площади петли,
изображенной на рисунке. Используя теорему Стокса, покажите, что
СЮ
ВаХ - Во = Но X К Т J №п/дг)/В (г)] dr,
о
Вах = Вг=0.
в) Вычислите интеграл, считая, что производная дп!дг равна 6-функции и
потому В (г) при г = а есть среднее арифметическое величин Вах и Во.
6.5. Диамагнитная петля представляет собой устройство, которое приме-
няется для измерения давления плазмы путем регистрации диамагнитного
эффекта (рис. 36.5). Такая петля действует следующим образом: при воз-
никновении плазмы в ней нарастает диамагнитный ток и уменьшается В;
как следствие уменьшается магнитный поток Ф через поверхность петли.
В результате этого в контуре индуцируется ЭДС, которая затем усредняется
по времени с помощью йС-цепочки (рис. 36.5).
а) Покажите, что
J -МДФ= — MjBd-dS, Bd^B — Во.
По петле
Индуцированное
напряжение
I -»•
Рис. 36.5.
6.5. Классификация неустойчивостей
203
б) Пользуясь методом, применявшимся в предыдущей задаче, и полагая, что
п (г) = поехр [-—(г/г0)2], найдите Вд (г). При вычислении интеграла счи-
тайте, что р с 1, и поэтому в интеграле величину В можно заменить на Во.
в) Покажите, что J VdZ —Л’лГдРВ0, где Р определяется выражением (6.8).
6.5. Классификация неустойчивостей
При исследовании волн в плазме мы предполагали, что она нахо-
дится в невозмущенном состоянии полного термодинамического
равновесия, т. е. что частицы имеют максвелловское распределение
по скоростям, а плотность и магнитное поле являются однород-
ными. В этом состоянии энтропия системы максимальна, в ней нет
источника свободной энергии, который мог бы возбуждать волны,
и поэтому нам пришлось рассматривать колебания, генерируемые
в плазме внешними источниками. Исследуем теперь такое состоя-
ние плазмы, в котором она не является полностью термодинами-
чески равновесной, но находится в равновесии в том смысле, что
все действующие на нее силы компенсируют'друг друга, а урав-
нения движения могут иметь стационарное решение. Свободная
энергия, имеющаяся в системе, может привести к самовозбужде-
нию волн; при этом равновесие плазмы является неустойчивым.
Неустойчивость всегда представляет собой такое движение, кото-
рое уменьшает свободную энергию плазмы и переводит ее в состоя-
ние, более близкое к термодинамическому равновесию.
Неустойчивости можно классифицировать в соответствии с ви-
дом свободной энергии, приводящей к их раскачке. Существует
четыре основных типа неустойчивостей.
1. Потоковые неустойчивости. В этом случае через плазму
либо движется пучок частиц высокой энергии, либо протекает ток,
вследствие чего частицы разных сортов движутся относительно
друг друга. Энергия этого движения и используется для возбужде-
ния волн; колебания усиливаются за счет запаса кинетической
энергии, который имеется в начальном невозмущенном состоянии.
2. Неустойчивости Релея—Тейлора. В этом случае в плазме
существует резкая граница или градиент плотности; иными сло-
вами, плазму нельзя считать однородной. Кроме того, к плазме
должна быть приложена внешняя сила неэлектромагнитного ха-
рактера, которая и вызывает неустойчивость. Аналогию с неустой-
чивостями такого типа можно провести на примере перевернутого
стакана с водой (рис. 6.7). Хотя плоская поверхность раздела ме-
жду водой и воздухом находится в состоянии равновесия в том
смысле, что вес воды уравновешивается силой атмосферного дав-
ления, это равновесие является неустойчивым. Любой пузырек,
появившийся на поверхности, будет стремиться вырасти за счет
потенциальной энергии поля силы тяжести. Как хорошо известно
204
Гл. 6. Равновесие и устойчивость
Рис. 6.7. Гидродинамическая неустойчивость Релея—Тейлора ^возникает
в том случае, когда тяжелая жидкость покоится на легкой.
из гидродинамики, это явление всегда имеет место в том случае,
когда слой тяжелой жидкости лежит на более легкой.
3. Универсальные неустойчивости. Когда плазма тем или иным
способом удерживается в ловушке, то даже при отсутствии сил,
вызывающих ее движение, например электрических или гравита-
ционных, плазма все равно не находится в полном термодинамиче-
ском равновесии. Давление плазмы стремится ее расширить, а свя-
занная с этим процессом энергия может высвободиться в виде не-
устойчивости. Такого рода свободная энергия всегда присутствует
в любой ограниченной плазме, поэтому подобные неустойчивости
называются универсальными.
4. Кинетические неустойчивости. В гидродинамической теории
предполагается, что распределения частиц по скоростям являются
максвелловскими. Если же функции распределения отличны от
максвелловских, то в плазме существует отклонение от термодина-
мического равновесия и вследствие анизотропии распределений
по скоростям в ней могут раскачиваться неустойчивости. Напри-
мер, если Т|| #= Т±, то может возникнуть неустойчивость, которая
называется модифицированной неустойчивостью Харриса. В проб-
котронах из-за наличия конуса потерь существует дефицит частиц
с большим отношением vt/vj_; эта анизотропия приводит к так на-
зываемой «конусной» неустойчивости.
В последующих разделах будут приведены простые примеры
каждого из упомянутых выше типов неустойчивостей. Отметим,
что неустойчивости, раскачиваемые вследствие анизотропии, нельзя
описать с помощью гидродинамической теории и их детальный ана-
лиз выходит за рамки этой книги.
Не все неустойчивости одинаково опасны с точки зрения удер-
жания плазмы. Скажем, высокочастотные неустойчивости, в кото-
рых раскачиваются волны с частотами, близкими к <ор, не могут
влиять на движение тяжелых ионов. А вот низкочастотные неустой-
чивости с о « йс могут привести к аномальным амбиполярным
потерям из-за Е X В-дрейфа. Неустойчивости с о а йс не приво-
дят к эффективному переносу частиц поперек магнитного поля,
однако являются опасными в пробкотронах, где убыль частиц про-
исходит из-за их диффузии в конус потерь в пространстве скоростей.
6.6. Двухпотоковая неустойчивость 205
6.6. Двухпотоковая неустойчивость
В качестве простого примера потоковой неустойчивости рассмот-
рим однородную плазму, в которой ионы неподвижны, а электроны
движутся относительно них со скоростью v0. Иными словами, на-
блюдатель находится в системе отсчета, движущейся вместе с
ионами. Пусть плазма холодная (КТе = KTt = 0), а магнитное
поле отсутствует (Во = 0). Линеаризованные уравнения движения
частиц запишутся в этом случае в виде
Mn^dVii/dtj^en0Ei, (6.19)
mn0 [dvjdt + (v0 V) va] = —cn0Ei- (6.20)
В уравнении (6.20) мы пренебрегли членом (vel-y) v0, полагая,
что скорость v0 постоянна во всем объеме плазмы. Слагаемое
(v0-V) Vi в уравнении (6.19) отсутствует потому, что мы считаем
Vf0 — 0. Будем рассматривать электростатические волны в виде
Ех = Ex exp'[i (kx—со/)], (6.21)
где х— единичный вектор, направленный вдоль v0 и к. Уравнения
(6.19) и (6.20) можно переписать следующим образом:
— i’coMnoVn = еп0Е!, v£1 — (i е/Мсо) Ех, (6.22)
шпй (— i со + i kv9) vel = —ennEi, vel = —(i elm) Ех1(&—кий).
(6.23)
Поскольку все скорости частиц vyl направлены вдоль оси х, мы опу-
стили в уравнениях индекс х. Уравнение непрерывности для ионов
дает
dn^ldt + ИоУ • v£1 = 0,
= (kl&) nov{1 = (i enofe/M со2) E. (6.24)
Заметим, что другие члены вида у-(пу£) обращаются в нуль, по-
скольку Vn0 = v0< = 0. Уравнение непрерывности для электро-
нов можно записать в виде
dne-Jdt + n0V • vel + (v0 • V) пе1 = 0, (6.25)
(— ijco +1 kv0) пл + i kn^vel = 0; (6.26)
таким образом,
пе1 = knovel/(a—kvo) = — i ekn^Elm (co — kvof. (6.27)
Поскольку неустойчивые волны представляют собой высокоча-
стотные плазменные колебания, мы должны пользоваться не плаз-
менным приближением, а уравнением Пуассона:
1 e0V • Ei. = е (п{1—пе1), (6.28)
i йе0Е = е (i enBkE) Г—-— ----------1. (6.29)
° V ° ' L Me»2 m (<о - to0)2 J
206
Гл. 6. Равновесие и устойчивость
Разделив обе части последнего выражения на i£e0E, приходим к
следующему дисперсионному уравнению:
1 = 0)2 Г—+--------1----1. (6.30)
₽L Мы2 (ш -to0)2 J '
Выясним, устойчивы или неустойчивы колебания с веществен-
ными значениями Л. Умножая предыдущее уравнение на общий
знаменатель, можно получить уравнение четвертого порядка от-
носительно со. Если все его корни со, вещественны, то каждый из
них отвечает колебанию Ех = Ex exp [i (kx—©//)]. Если же не-
которые из корней комплексны, то они появляются в виде пар ком-
плексно-сопряженных величин. Запишем эти комплексные корни
как
= (6-31)
где а/ = Re (со,), у,- = Im (со,-). Таким образом, зависимость поля
от времени имеет вид
E1 = Exexp(y;/)-exp[i(fex—а/)]. (6.32)
Если Im (со,-) >> 0, то амплитуда волны экспоненциально нарастает
со временем. Отрицательное значение Im (со,) соответствует зату-
хающей волне. Поскольку соу появляются в виде пары комплексно-
сопряженных корней, один корень из этой пары обязательно отве-
чает неустойчивой волне (если только оба корня не являются ве-
щественными). Корни с отрицательными мнимыми частями не опи-
сывают самовозбуждающиеся волны и потому не представляют
интереса.
Анализ дисперсионного уравнения (6.30) можно провести, и не
решая уравнения четвертого порядка. Определим величины
х=со/сор, y = kvola>p. (6.33)
Подставляя эти величины в уравнение (6.30), его можно переписать
в виде
(6.34)
1 = ——+---------= F (х, у).
Мх2 1 (х — у)2
Для любого у можно построить график F (х, у) в виде функции от х.
Эта функция имеет сингулярности при х — 0 и при х = у (рис. 6.8).
Точки пересечения этой кривой с прямой F (х, у) — 1 дают значе-
ния х, которые удовлетворяют дисперсионному уравнению. На при-
мере рис. 6.8 видно, что таких точек четыре, и поэтому дисперсион-
ное уравнение имеет четыре вещественных корня со/. Если, однако,
взять меньшее значение у, то зависимость F (х, у) будет выглядеть
так, как показано на рис. 6.9. Теперь имеются лишь две точки
пересечения и, следовательно, два вещественных корня. Другие
два корня должны быть комплексными, и один из них будет обяза-
тельно соответствовать неустойчивой волне. Таким образом, при
6.6. Двухпотоковая неустойчивость
207
Рис. 6.8. Функция F (х, у) для двух-
потоковой неустойчивости. Плазма
устойчива.
Рис. 6.9. Функция F (х, у) для двух-
потоковой неустойчивости. Плазма
неустойчива.
достаточно малых &о0 плазма становится неустойчивой, а если
скорость и0 задана, плазма всегда неустойчива относительно длин-
новолновых колебаний. Если т!М < 1, то максимальный инкре-
мент неустойчивости, определяемый из (6.30), равен
1ш(ш/юр)«(т//И)1/3. (6.35)
Для реализации неустойчивости необходимо, чтобы величина
kv0 была достаточно мала. Иными словами, чтобы при данном вол-
новом числе k имела место неустойчивость, скорость у0 должна
быть достаточно мала. Это положение противоречит физическому
смыслу: ведь именно движение со скоростью v0 является источни-
ком энергии для неустойчивости. Парадокс возник потому, что для
описания плазмы мы использовали гидродинамические уравнения
в пределе К.Т = 0. В действительности всякая плазма имеет конеч-
ную температуру, и при ее анализе в рамках кинетической теории
нужно учитывать тепловые эффекты. При этом оказывается, что
для скоростей v0 отепЛ имеет место явление, которое называется
затуханием Ландау (см. гл. 7), и если v0 становится слишком ма-
лой, то из кинетического рассмотрения следует, что неустойчиво-
сти не будет.
Из физических соображений такую неустойчивость (ее назы-
вают бунемановской неустойчивостью) можно объяснить следующим
образом. Собственные частоты колебаний электронной и ионной
жидкостей равны соответственно сор и Qp = (m/М)1'2 ар. При не-
котором значении &v0 из-за доплеровского сдвига, вызванного дви-
жением электронной жидкости, в лабораторной системе отсчета эти
две частоты могут совпасть. При этом в плазме возникнет волна
потенциала, связанного с флуктуациями плотности ионов и элек-
тронов уравнением Пуассона. Можно показать, что электронные
колебания в этом случае обладают отрицательной энергией, т. е.
полная кинетическая энергия электронов при наличии волны
меньше, чем в том случае, когда волна отсутствует. Действительно,
в невозмущенном потоке электронов плотность кинетической энер-
гии равна (1/2) mnQV^. ЕслиТже в плазме имеются колебания, то
плотность кинетической энергии будет равна (1/2) т (п0 +
208
Гл. 6. Равновесие и устойчивость
+ «1) (ио + ^i)2- После усреднения этого выражения по прост-
ранственным координатам его значение оказывается меньше
(1/2) mnovo, поскольку из уравнения непрерывности следует, что
пх и v± определенным образом связаны между собой. Следовательно,
электронные колебания обладают запасом отрицательной энергии,
а ионные волны — положительной энергией, так что оба типа
волн могут раскачиваться одновременно, причем полная энергия
системы будет при этом сохраняться. Подобная неустойчивость
используется для генерации СВЧ-колебаний в клистронах. Моду-
ляция скорости в поле волны Ех заставляет электроны группиро-
ваться в сгустки. Проходя через резонатор, эти сгустки могут воз-
будить его собственные моды и, таким образом, вызвать генерацию
энергии в СВЧ-диапазоне.
Задачи
6.6. а) Выведите дисперсионное уравнение для двухпотоковой неустойчиво-
сти, возникающей в том случае, когда два холодных электронных потока
плотностью (1/2) л0 каждый движутся в противоположных направлениях
с равными скоростями v0 на фоне неподвижных ионов.
6) Вычислите максимальный инкремент неустойчивости.
6.7. Протонная компонента плазмы состоит из двух однородных потоков,
скорости которых равны + иох и — о0х7 а плотности — соответственно
(2/3) п0 и (1/3) п0. Нейтрализующая заряд протонов электронная жидкость
имеет плотность п0 и voe = 0. Обе компоненты холодные, магнитное поле в
плазме отсутствует. Выведите дисперсионное уравнение для потоковых не-
устойчивостей в такой системе.
6.8. В покоящуюся плазму плотностью падает пучок холодных электро-
нов плотностью п06 (6 — числовой параметр), движущийся со скоростью и.
а) Выведите дисперсионное уравнение для возникающей в такой системе вы-
сокочастотной плазменно-пучковой неустойчивости.
б) Максимальный инкремент неустойчивости ут в общем случае вычислить
трудно, однако если 6 С 1, то по аналогии с бунемановской электрон-ион-
ной неустойчивостью можно сделать приближенную оценку этой величины.
Воспользовавшись приведенной без доказательства формулой (6.35), выра-
зите Ут через 6.
6.9. Пусть в магнитном поле Boz на фоне нейтрализующей холодной элек-
тронной жидкости имеются два потока ионов плотностью (1/2) п0 каждый,
один из которых движется со скоростью + о0у, а другой — со скоростью
— гоу. Поле Во достаточно велико для того, чтобы удерживать электроны
(считается, что они совершают только одномерное движение), но не влияет
на траектории ионов.
а) Считая, что частоты электростатических волн, распространяющихся в на-
правлениях ± у, лежат в диапазоне й2 < со2 С (£%, выведите для этих волн
следующее дисперсионное уравнение:
2 (со — fa'o)2 2 (со + te0)2 со2
б) Получите закон дисперсии со (k), а также инкременту (й) и выясните, в ка-
ком диапазоне частот возбуждаются неустойчивые колебания.
6.7. Гравитационная неустойчивость 209
6.7. Гравитационная неустойчивость
Вследствие того что с точки зрения удержания плазмы магнитное
поле действует как легкая жидкость, удерживающая тяжелую
плазму, в ней может возникнуть неустойчивость Релея—Тейлора.
В случае искривленных силовых линий магнитного поля роль
эквивалентной силы тяжести играет центробежная сила, обуслов-
ленная движением частиц вдоль этих силовых линий. В качестве
простейшего примера такой неустойчивости рассмотрим поведение
границы плазмы, лежащей в плоскости yz (рис. 6.10). Пусть градиент
плотности v»o ориентирован в направлении —х, а поле силы тя-
жести g — по х. Для простоты будем считать, что КТ{ = КТг = 0
и рассмотрим случай малых 0, когда магнитное поле однородно.
В стационарном состоянии уравнение движения ионов принимает
вид
Mn0 (v0 • V) v0 = en0v0 х Во + Mnog. (6.36)
*V/z0 п”аз"а ®В
I и0
Вякуулг q 1
Рис. 6.10. Гравитационная неустойчивость поверхности плазмы.
Если g = const, то v0 тоже пбЬтоянна, и потому член (v0-v) v0
обращается в нуль. Умножив векторно уравнение (6.36) на Во,
получим (как и в разд. 2.2)
v0= (М/еВо) g X Во= —(g/£»y. (6.37)
Электроны движутся в противоположном направлении; скорость
этого движениям пределе mIM. -> 0 пренебрежимо мала. Поскольку
КТ = 0, диамагнитный дрейф в плазме отсутствует; нет и Ео X Во-
дрейфа, поскольку Ео = 0.
Если под действием случайной тепловой флуктуации на поверх-
ности раздела возникнет рябь, то из-за того, что слой движется
со скоростью v0, это возмущение будет нарастать (рис. 6.11). Фи-
зическая причина неустойчивости следующая. Дрейф ионов при-
водит к появлению зарядов на склонах изогнутой поверхности раз-
дела. Возникает электрическое поле, которое имеет неоднородный
характер; если двигаться вдоль поверхности раздела, то при каж-
дом переходе от горба к впадине электрическое поле меняет знак.
Как видно из рис. 6.11, на тех участках, на которых поверхность
сместилась вверх, скорость Ег X В0-дрейфа тоже направлена
вверх, а на участках, сместившихся вниз, она всегда направлена
210
Гл. 6. Равновесие и устойчивость
Рис. 6.11. Физический механизм гравитационной неустойчивости.
вниз, поэтому в результате Ех X В0-дрейфа начальное возмущение
будет расти.
Чтобы найти инкремент неустойчивости, нужно, как обычно,
рассмотреть уравнения движения в линейном приближении, счи-
тая, что волны распространяются вдоль оси у: k = ky. Уравнение
движения ионов с учетом поправок, связанных с волной, имеет
вид
М (п0 + nJ [(d/dt) (v0 + Vi) + (v0 + Vi) V (v0 + Vj)] = e (n0 + nJ x
X [Ex -j- (v0 + Vi) x Bo] + M (n0 -f- nJ g. (6.38)
Умножим уравнение (6.36) на 1 + (njnj. В результате мы полу-
чим следующее соотношение:
М («о + «i) (v0 • V) v0 = е (п0 + nJ v0 X Во + М (n0 + nJ g. (6.39)
Вычитая это равенство из уравнения (6.38) и пренебрегая членами
второго порядка, имеем
Мп0 [(dvjdt) + (v0 • V) Vx] = еп0 (Ex + Vx х Bo). (6.40)
Заметим, что g в конечный результат не входит. Информация об
этой величине, однако, содержится в выражении для v0. Рассмат-
ривая возмущения, пропорциональные ехр [i (ky—to/)], можно
записать следующее уравнение:
М (со—b0)Vi = ie(Ex4-ViX Во). (6.41)
Оно аналогично уравнению (4.96), за исключением того что вели-
чина со заменена в нем на со—kv0 и все величины относятся теперь
не к электронам, а к ионам. Следовательно, решение уравнения
(6.41) дается выражением (4.98), в котором сделаны соответствую-
щие изменения. Если Ех = 0, а
$»(<о—(6-42)
то решение имеет вид
vix = Ey!Ba, viy=—[(Ey/BJta—kvJIQc. (6.43)
6.7. Гравитационная неустойчивость 211
Последнее выражение представляет собой скорость поляризацион-
ного дрейфа в системе отсчета, движущейся вместе с ионами. Соот-
ветствующая величина для электронов в пределе т/М 0 прене-
брежимо мала. Следовательно, у электронов
vex = EuIB0, vey = Q. (6.44)
В^первом приближении теории возмущений уравнение непрерыв-
ности для ионов имеет вид
drh/dt + V (novo) + (v0 • V) «1 + niV v0 -b (vi • V) «о + «oV • Vi +
+ V-(«iVi) = 0. (6.45)
Член нулевого порядка V-(«ovo) обращается в нуль, поскольку
вектор v0 перпендикулярен Vn0; при постоянном v0 обращается
в нуль также слагаемое пх\!-\0. Следовательно, уравнение пер-
вого порядка теории возмущений можно записать в виде
— i conx + i + vtxno + i knnviy = 0. (6.46)
где «о = dnQldx. Уравнение непрерывности для электронов проще,
поскольку t>e9 = vey = 0:|
— i cont + vextio= 0. (6.47)
Заметим, что здесь мы воспользовались плазменным приближением
и положили Пи = пеХ. Это можно сделать только в том случае,
если неустойчивые волны имеют низкие частоты (что можно под-
твердить a posteriori). Из уравнений (6.43) и (6.46) получаем
(со—kv0) пх + i (Еи!В0) п'о + i kn0 (Ey/B0)(a—kv0)/Qc = 0, (6.48)
а из уравнений (6.44) и (6.47) —
conx + i (Еу/Во) п'о = 0, ЕУ!ВО — i ап^'по- (6.49)
Подставляя последнее выражение в уравнение (6.48), имеем
(со —kv0) пх—[«о + kn0 (со—fev0)/Qc] (corii/no) = 0,
со—kv0—[ 1 + (kn0/Qc) (со — kv0)/n0]a> = 0, (6.50)
со (со—kv0)= — voQcno/no. (6.51)
Заменяя в последнем равенстве величину о0 ее значением из фор-
мулы (6.37), получаем квадратное уравнение для частоты со:
со2—kvod) — g(n'o/no) = 0. (6.52)
Его решения имеют вид
со = kv0 ± (— fe2o2 + g (по/по)|1/2 • (6 • 53)
2 14 )
212
Гл. 6. Равновесие и устойчивость
Рис. 6.12. Желобковая неустойчи- Рис. 6.13. Дрейфовая неустойчивость
вость. в плазме цилиндрической конфигу-
рации. Область, заключенная в пря-
моугольнике, изображена в увели-
ченном виде на рис. 6.14.
Неустойчивость существует в том случае, если со комплексна, т. е.
если
—gno/nQ> — k2vl- (6.54)
4
Отсюда видно, что для реализации неустойчивости нужно, чтобы
g и пй!пй имели разные знаки. Это требование эквивалентно тому,
что тяжелая жидкость должна лежать на легкой; в противном слу-
чае частота со оказывается вещественной и плазма является устой-
чивой. Поскольку величина g моделирует эффекты, обусловленные
кривизной силовых линий магнитного поля, устойчивость системы
зависит от знака этой кривизны. Если силовые линии выгнуты
в сторону плазмы, то такая конфигурация устойчива. И наоборот,
когда силовые линии охватывают плазму, система оказывается не-
устойчивой. При достаточно малых k (больших длинах волн) ин-
кремент неустойчивости дается выражением
у = Im (со) « [ — g (по/ло)]1/2>
(6.55)
а вещественная часть частоты <о равна (1/2) kvn. Поскольку v0 —
это скорость ионов, колебания являются низкочастотными, как и
предполагалось первоначально.
Подобную неустойчивость колебаний границы плазмы с k | Во
иногда называют желобковой, потому что в плазменном цилиндре,
когда все силы направлены по радиусу, эти волны распространяются
в направлении 6, а поверхности постоянной плотности напоминают
рифленые греческие колонны (рис. 6.12).
6.8. Резистивные дрейфовые волны 213
6.8. Резистивные дрейфовые волны
Простой пример универсальной неустойчивости дает возбуждение
резистивной дрейфовой волны. В отличие от связанных с силой
тяжести желобковых мод в дрейфовых колебаниях волновой век-
тор к имеет малую, но конечную составляющую вдоль магнитного
поля Во. Поэтому поверхности постоянной плотности в этих ос-
цилляциях напоминают слегка закрученные желоба (рис. 6.13).
Если увеличить участок поверхности, обведенный на этом рисунке
прямоугольником, и выпрямить его, то он будет выглядеть так, как
показано на рис. 6.14. Единственная сила, которая может вызвать
неустойчивость,— это градиент давления КТ\/п0 (для простоты
предполагаем, что КТ = const). В этом случае скорости дрейфо-
вых движений в нулевом приближении по амплитуде волн записы-
ваются (при Ео = 0) в виде
V;o=vDi = (KT£/eBo)(no/no)y, (6-56)
ve0 = vDe = — (KTJeB^ (n'olno) у. (6.57)
По аналогии с желобковой неустойчивостью можно ожидать, что
фазовая скорость дрейфовых волн должна быть порядка vDl или
vDe. Мы покажем, что a>/ky действительно приближенно равна vDe.
В дрейфовых волнах величина kz =# 0, поэтому электроны мо-
гут двигаться вдоль Во, в результате чего они должны прийти в со-
стояние термодинамического равновесия (ср. обсуждение этого
вопроса при анализе нижнегибридных колебаний в разд. 4.10).
Рис. 6.14. Физический механизм дрейфовой неустойчивости.
214
Гл. 6. Равновесие и устойчивость
Следовательно, электроны должны удовлетворять уравнению Больц-
мана (см. разд. 3.5):
ni/no = ^i//<Te. (6.58)
Обратимся к рис. 6.14. В точке А плотность плазмы будет выше,
чем в состоянии равновесия, величина пх > О и, следовательно,
^х >0. По той же причине в точке Б пх и ^>х отрицательны. Раз
между точками А и Б имеется разность потенциалов, должно су-
ществовать и электрическое поле Ех. Как и в случае желобковой
неустойчивости, поле Ех вызывает дрейф частиц вдоль оси х со ско-
ростью vx = Ех х Во/Во- В процессе распространения волны вдоль
оси у наблюдатель, находящийся в точке А, будет видеть, что пх
и со временем осциллируют. Скорость дрейфа vx также будет
осциллировать со временем; фактически именно движение со знако-
переменной скоростью vx и вызывает колебания плотности. По-
скольку градиент плотности Vn0 направлен в сторону отрицатель-
ных х, из-за дрейфа со скоростью vx через точку А будет проходить
плазма разной плотности. Следовательно, плазма в дрейфовой
волне совершает колебания вдоль оси х, хотя сама волна распро-
страняется в направлении у.
Перейдем к количественным оценкам. Запишем величину vlx
в виде
vlx = Еу/В0 = — i ^1/Во- (6.59)
Будем предполагать, что vlx не зависит от х, a kz <£ ku, т. е. что
жидкость является несжимаемой и колеблется вдоль оси х. Вычис-
лим, какое число ведущих центров частиц пх вносится в единицу
времени в 1 м® плазмы, расположенный вблизи точки А. Очевидно,
dnjdt = —vlx дп01дх. (6.60)
Это условие представляет собой уравнение непрерывности для ве-
дущих центров, а они, естественно, не совершают дрейфа со ско-
ростью vD. Член n0V-vx обращается в нуль из-за сделанных нами
ранее предположений. Разница между плотностью ведущих центров
и плотностью частиц пх, вообще говоря, должна приводить к появ-
лению поправок в уравнении (6.60), однако эти поправки имеют
более высокий порядок и ими можно пренебречь. Используя соот-
ношения (6.58) и (6.59), запишем уравнение (6.60) в виде
—i wnx — i ky^n'o/Bo = — icon0(e^x^Te). (6.61)
Таким образом,
os/ky = — (KTe/eB0) (поЧ) == vDe. (6.62)
Следовательно, рассматриваемые нами волны движутся со ско-
ростью, равной скорости диамагнитного дрейфа электронов. Именно
поэтому они называются дрейфовыми волнами. Скорость этих волн
направлена вдоль оси у или (в цилиндрическом случае) по азимуту.
6.8. Резистивные дрейфовые волны
215
Кроме ky волновой вектор к имеет и составляющую kz. По причинам,
которые здесь не рассматриваются, величина kz должна удовлетво-
рять условиям
kZ<<. ky > ^тепл, i a/kz < Птепл, е- (6.63)
Чтобы понять, почему дрейфовые волны являются неустойчи-
выми, нужно учесть, что компонента скорости ионов vlx не равна
в точности Еу!В0. Существуют поправки к этой величине, связан-
ные с поляризационным дрейфом (2.66) и дрейфом из-за неоднород-
ности электрического поля (2.59). Под их влиянием распределение
потенциала в дрейфовых колебаниях отстает по фазе от распре-
деления плотности «j (задача 4.1). Из-за этого сдвига скорость Vj
будет направлена из плазмы на тех участках, где плазма уже сдви-
нута наружу (и наоборот); поэтому возмущения в дрейфовых ко-
лебаниях будут нарастать. Если бы дополнительного фазового
сдвига не было, то разность фаз между vx и </>! составляла бы 90°,
как показано на рис. 6.14, и дрейфовые волны были бы чисто ос-
циллирующими.
Роль электрического сопротивления в дрейфовых волнах состоит
в том, что оно не позволяет электронам, движущимся вдоль Во,
полностью экранировать электрическое поле волны Ех. Точнее,
если расстояние между гребнем волны и впадиной (1/2) Хг доста-
точно велико, а частота электрон-ионных столкновений значи-
тельна, то в системе из-за сопротивления среды может возникнуть
яма потенциала и, следовательно, отличное от нуля электрическое
поле Ev Дисперсионное уравнение для резистивной дрейфовой
волны с учетом этих эффектов можно приближенно записать в виде
со2 + 1стц(со —со*) = 0,
(6.64)
где
(6.65)
а
о И = Qc (/г|//г^) состе£. (6.66)
Если ст || со, то уравнению (6.64) можно удовлетворить только
при со « со*. В этом случае в первом члене уравнения частоту со
можно заменить на со*, и тогда
со « со* 4- i со2 ,/стц.
(6.67)
Отсюда видно, что величина Im (со) всегда больше нуля и пропор-
циональна удельному сопротивлению г|. Следовательно, дрейфо-
вые волны неустойчивы в любой плазме, имеющей градиент плот-
216
Гл. 6. Равновесие и устойчивость
ности. К счастью, инкремент этой неустойчивости мал, а сделав
поле Во неоднородным, ее развитие вообще можно остановить.
Заметим, что уравнение (6.52), описывающее желобковую не-
устойчивость, и уравнение (6.64) для дрейфовой неустойчивости
по своей структуре разные. В первом из них коэффициенты вещест-
венны, и со будет комплексной только в том случае, если дискрими-
нант квадратного уравнения отрицателен. Это типичная реактив-
ная неустойчивость. Коэффициенты второго уравнения комплексны,
поэтому со будет комплексна всегда — это характерная особенность
диссипативной неустойчивости.
Задача
6.10. Водородная плазма помещена в тор, большой радиус которого R =
= 50 см, а малый а = 2 см. Параметры плазмы следующие: Во = 1 Тл,
К.Те — 10 эВ, K,Tt = 1 эВ, п0 = 1019 м~3. Оцените инкременты для рези-
стивной дрейфовой волны и гравитационной желобковой моды, считая, что
n0/n0xal2, g^{KTe + KT^/MR, а обе волны характеризуются азиму-
тальным числом т = 1. (Обычно формулы, полученные для систем плоской
геометрии, можно применять к цилиндрическим системам, положив ky =
= т/г.)
6.9. Неустойчивость Вейбеля *)
В качестве примера неустойчивости, раскачиваемой из-за анизо-
тропии функции распределения, рассмотрим неустойчивость Вей-
беля, физическая интерпретация которой предложена Б. Фридом.
Эта неустойчивость сопровождается ростом возмущений магнит-
ного поля, поэтому она может также служить примером электро-
Рис. 6.15. Физический механизм неустойчивости Вейбеля.
!) Честь и слава старому другу Эрику Вейбелю (1925 —1983).
6.9. Неустойчивость Вейбеля 217
магнитной неустойчивости. Пусть ионы покоятся, а температура
электронов, движущихся вдоль оси у, выше, чем при движении
в х- и z-направлениях. В этом случае в плазме имеется избыток бы-
стрых электронов, движущихся вдоль оси у, однако вследствие
того, что вверх движется столько же частиц, сколько и вниз, полный
ток равен нулю (рис. 6.15). Пусть из шумового фона спонтанно
возникло распределение магнитного поля В = Вг z cos kx. Тогда
сила Лоренца —ev X В искривит траектории электронов так,
как это показано на рисунке штриховыми линиями, и в результате
частицы, движущиеся вниз, будут собираться в слое А, а
электроны, движущиеся вверх,— в слое Б. Возникающие при этом
токовые слои с j = — enove будут сфазированы в точности таким
образом, чтобы усилить возникшее вначале распределение магнит-
ного поля, и возмущение В будет расти. Хотя в общем случае ана-
лиз этой неустойчивости требует кинетического рассмотрения,
в пределе vy = г>тепл, vx = v? = 0 результат можно легко полу-
чить из этой физической картины. Инкремент при этом равен у =
— ^pVtennlc.
Глава 7
КИНЕТИЧЕСКАЯ ТЕОРИЯ
7.1. Функция распределения / (v)
Гидродинамическая теория, используемая нами до сих пор, пред-
ставляет собой простейшую теорию плазмы; нам действительно
повезло, что для описания большинства наблюдаемых явлений это
приближение является достаточно точным. Существуют, однако,
некоторые явления, которые гидродинамическая теория не может
описать адекватным образом. Для них мы должны рассматривать
функцию распределения / (v) частиц каждого сорта по скоростям;
такой подход называется кинетической теорией. В гидродинамике
все зависимые переменные являются функциями лишь четырех
независимых величин: х, у, z и t. Это возможно потому, что распре-
деление по скоростям для каждого сорта частиц всюду предпола-
гается максвелловским и может быть единственным образом задано
с помощью одного параметра, а именно температуры Т. Поскольку
столкновения частиц в высокотемпературной плазме происходят
редко, отклонение от теплового равновесия может в этом случае
поддерживаться в течение относительно длительного времени. В ка-
честве примера рассмотрим две функции распределения: fx (oj
и /2 (Цс) ДЛЯ одномерной системы (рис. 7.1). Эти две функции могут
вести себя совершенно по-разному, но если площади под кривыми
fi и /2 одинаковы, гидродинамическая теория не обнаружит разли-
чия между ними.
Плотность частиц есть функция четырех скалярных переменных:
п = п (г, /). Когда мы рассматриваем функцию распределения, то
Рис. 7.1. Примеры немаксвелловских функций распределения.
7.1. Функция распределения f (v)
219
имеем семь независимых переменных: f == f (г, v, t). Функция
f (г, v, t) означает, что число частиц в кубическом метре в точке
г в момент времени t с компонентами скорости между vx и vx +
+ dvx, vy и vy + dvy, vz и vz + dvz равно
f(x, y, z, vx, Vy, vz, t)dvxdVydvz.
Интеграл .от этого выражения записывается несколькими эквива-
лентными способами:
п(т, t) = J dvx J dvy J dvzf(r, v, t)= J /(r, v, =
—00 — OO —00 —00
= f f(r, V, t)dv. (7.1)
—00
Следует заметить, что здесь dv не вектор, а трехмерный элемент
объема в фазовом пространстве. Если / нормирована следующим
образом:
f f(r, v,) tdv = 1, (7.2)
—00
то / представляет собой распределение вероятности, которое мы
обозначаем через /. Таким образом,
f(r, V, O = n(r, Of(r, V, 0- (7-3)
Заметим, что / — по-прежнему функция семи переменных, по-
скольку форма функции распределения, как и плотность частиц,
может меняться во времени и пространстве. Из выражения (7.2)
ясно, что / имеет размерность с3/м3; следовательно, размерность /,
как видно из (7.3), равна с3-м-в.
Особенно важную роль играет функция распределения Макс-
велла
fm = (m/2nKT)3i2 ехр (— с/%тепл) > (7.4)
где v = ^vx + v2y + v2)'/2, a vTeiuI^ (2КТ/т)112. (7.5)
Используя определенный интеграл '
f ехр(—x2)dx = ^n, (7.6)
—оо
легко проверить, что интегрирование fm по dvxdvydvzjxaQT единицу.
Обычно используют несколько средних скоростей по максвел-
ловскому распределению. В разд. 1.3 мы видели, что среднеквадра-
тичная скорость дается выражением
(^)1/2=(ЗКТ/щ)1/2. (7.7)
220
Гл. 7. Кинетическая теория
Среднее значение скорости | v |, или просто среднюю скорость v>
определяют следующим образом:
V— J vf(v)d3v. (7.8)
—00
Поскольку fm изотропна, интеграл вычисляется наиболее просто
в сферической системе координат ^-пространства (рис. 7.2). Так как
элемент объема каждой сферической оболочки равен имеем
оо
u = (m/2nKT)3/2J и[ехр( — и2/г>тепЛ)]4ли2^о= (7.9)
О
оо
= (га»?епл)-3/2 4я0тепл J [ехр ( — г/2) ] у3 dy. (7.10)
о
Определенный интеграл равен 1/2, что можно найти интегрирова-
нием по частям. Таким образом,
v = 2л-1/2 отепл = 2 (2К77лт)1/2. (7.11)
Компонента скорости в одном выделенном направлении, скажем
vx, имеет другое среднее. В случае изотропного распределения vx,
разумеется, равно нулю, но | vx | не равно нулю:
Ы = f 1 Iк(V)d3v = (7.12)
/ т \з/2 ~ ( -v2 \ °° ( — о2 \
v^expо ) 1Лехр1"^ г
~ \ утепл / \ утепл /
00 / — V2 \
X f 2vx ехр I — х-) dvx. (7.13)
6 \ ^епл /
Из соотношения (7.6) видно, что каждый щз первых двух интегра-
Рис. 7.2. Трехмерное пространство скоростей.
7.1. Функция распределения f (v) 221
лов равен л1/2Птепл- Последний интеграл простой; его значение
равно Утепл- Таким образом, имеем
I Vx I — (ло^епл)-3/2 Л^епл = л-1/2итепл = (2КТ/лт)'/2 (7.14)
Случайный поток частиц через некоторую воображаемую плоскость
дается выражением
ГслУЧ = (1/2)п|йЛ=(1/4)пр. (7.15)
Здесь мы использовали соотношение (7.11) и тот факт, что лишь
половина частиц пересекает плоскость в каком-то одном направле-
нии. Таким образом, в случае распределения Максвелла мы имеем
следующие выражения:
иСр.кв = (3/Шт)’/2, (7.7)
[?| = 2 (2КЛлт)!-'2, (7.11)
К| = (2КТ/лт)1/2, (7.14)
vx = 0. (7.16)
Для изотропной функции распределения типа максвелловской
мы можем определить другую функцию g (о), которая представляет
собой функцию скалярной величины V, такую, что
j g(y)dv — f f(y)d3v. (7.17)
0 —oo
Для распределения Максвелла из уравнения (7.9) видно, что
g (о) = 4лп (m/2nKT)3/2v2 ехр (—о2/р2епл) • (7.18)
Рис. 7.3 показывает различие между g (и) и одномерным максвел-
ловским распределением f (их). В отличие от f (oj, которая при
vx — О максимальна, g (о) при v = 0 равна нулю. Это есть
следствие обращения в нуль элемента объема фазового простран-
Рис. 7.3. Одно- и трехмерные максвелловские функции распределения по
скоростям.
222
Гл. 7. Кинетическая теория
Рис. 7.4. Неоднородная одномерная
функция распределения f (х, vx).
Рис. 7.5. ЛинииЗпостоянных f для
двумерного анизотропного распреде-
ления.
Рис. 7.6. Линии|постоянных f в двух
измерениях для максвелловского рас-
пределения с дрейфом и «пучка».
Рис. 7.7. Линии постоянных f для
распределения с конусом потерь.
Здесь v ц и v L — компоненты v со-
ответственно вдоль и поперек маг-
нитного поля.
ства (рис. 7.2) при v = 0. Иногда функцию g (v) небрежно записы-
вают как / (о), чтобы отличить ее от / (v); но g(v) совсем по иному
зависит от своего аргумента, чем функция / (v) от своего аргумента.
Из соотношения (7.18) ясно, что g (у) имеет размерность с/м4.
До тех пор пока мы не уменьшим число измерений, невозможно
построить график функции / (г, v) в данный момент времени t. В од-
номерном случае f (х, vx) можно изобразить в виде поверхности
(рис. 7.4). Сечения этой поверхности плоскостями х = const пред-
ставляют собой распределения / (vj, а сечения ее плоскостями
vx = const дают профили плотности частиц, имеющих данную ско-
рость vx. Если форма всех распределений f (vx) одинакова, то кри-
вая, проходящая через максимумы этих распределений, представ-
ляет собой профиль плотности. Штриховые кривые на рис. 7.4 по-
казывают сечения плоскостями / = const, которые образуют ли-
7.2. Уравнения кинетической теории
223
нии уровня, или кривые постоянных /. Проецируя эти*линии на
плоскость хох, получаем топографическую карту значений f. Та-
кие карты оказываются очень полезными для получения предвари-
тельных представлений о поведении плазмы; в следующем разделе
мы приведем соответствующий пример.
Другой тип контурной карты для f можно построить, если рас-
смотреть /(v) в данной точке пространства. Например, если дви-
жение является двумерным, a f в переменных vx и vu изотропна,
то контуры f (vx, Vy) будут представлять собой окружности. Ани-
зотропное распределение должно описываться эллиптическими кон-
турами (рис. 7.5). Максвелловское распределение с дрейфом будет
иметь контуры в виде окружностей, смещенных относительно на-
чала координат, а пучок частиц, летящих вдоль оси х, проявится
как отдельный пик (рис. 7.6).
Функция распределения с конусом потерь для плазмы, удер-
живаемой в зеркальной ловушке, может быть представлена конту-
рами / в (и±, v^-пространстве. На рис. 7.7 показано, как выглядят
эти контуры.
7.2. Уравнения кинетической теории
Фундаментальным уравнением, которому должна удовлетворять
функция / (г, v, /), является уравнение Больцмана
+V-V/-+
dt
F df _( df "I
m dv \ dt Jc
(7.19)
Здесь F — сила, действующая на частицы, a (df/df)c — скорость
изменения / во времени вследствие столкновений. Символом V обо-
значен, как обычно, градиент в координатном пространстве х, у,
г. Символ dldv или Vu обозначает градиент в пространстве скоро-
стей:
(7.20)
Смысл уравнения Больцмана становится ясным, если вспом-
нить, что f есть функция семи независимых переменных. Следова-
тельно, полную производную от / по времени можно записать в виде
df df ! df dx df dy df dz
dt dt ' dx dt dy dt dz dt
df dvx df dvy df dvz
dvx dt dvy dt dvz dt (7-21)
Здесь df/dt представляет собой производную по времени при явной
224
Гл. 7. Кинетическая теория
временной зависимости. Следующие три слагаемых можно записать
в виде v-v/. С помощью второго закона Ньютона
dt
(7.22)
видим, что в (7.21) последние три члена записываются как
(F/zn)-(d//dv). В разд. 3.3 мы показали, что полную производную
dfldt можно интерпретировать как скорость изменения f в системе
отсчета, движущейся с частицами. Отличие состоит в том, что те-
перь мы должны рассматривать частицы, движущиеся в шестимер-
ном (г, у)-пространстве; dfldt в данном случае представляет
собой конвективную производную в фазовом пространстве. Согласно
уравнению Больцмана (7.19), до тех пор пока отсутствуют столкно-
вения, dfldt = 0. То, что это утверждение справедливо, можно ви-
деть из рис. 7.8 для одномерного случая.
Все частицы, попадающие в элемент dx dvx, обозначенный на
рис. 7.8 через Л, имеют скорость vx и координату х. Плотность ча-
стиц в фазовом пространстве х, vx равна f (х, vx). С течением вре-
мени эти частицы благодаря наличию у них скорости их переме-
стятся в другую точку х, и их скорость изменится под действием
приложенных к ним сил. Поскольку силы зависят лишь от х и vxt
все частицы в элементе А ускорятся на одну и ту же величину. Че-
рез время t все частицы окажутся в элементе В фазового простран-
ства. Поскольку все частицы движутся вместе, плотность в элементе
В будет такая же, как и в Л. Однако если в системе имеются столк-
новения, то частицы могут рассеиваться и f может измениться бла-
годаря наличию члена (dfldf)c.
В достаточно горячей плазме столкновениями можно пренебречь.
Если, кроме того, сила F полностью электромагнитная, то уравне-
ние (7.19) принимает частный вид:
J- +wf+^-(E + vxB)-4- =0.
dt т dv
(7.23)
Это уравнение называется уравнением Власова. Благодаря своей
относительной простоте это уравнение наиболее часто применяется
в кинетической теории. При наличии столкновений с нейтральными
атомами столкновительный член в уравнении (7.19) можно прибли-
женно записать в виде
@f/dt)c = (fn-f)/x, (7.24)
где fn — функция распределения нейтральных атомов, а т — ха-
рактерное время между столкновениями. Это выражение называют
столкновительным членом Крука. Оно является кинетическим обоб-
щением столкновительного члена в уравнении (5.5). Для случая
7.2. Уравнения кинетической теории
225
Рис. 7.8. Группа точек в фазовом
пространстве, описывающая поло-
жения и скорости группы частиц,
сохраняет плотность в фазовом про-
странстве по мере своего .перемеще-
ния со временем.
Рис. 7.9. Представление траектории
пучка электронов с одинаковыми
скоростями у0 в одномерном фазо-
вом пространстве. Функция рас-
пределения f (х, vx) бесконечна на
линии v = v0 и равна нулю вне ее.
Линия v = vQ является также тра-
екторией отдельных электронов. На-
правление их движения показано
стрелкой.
Рис. 7.10. Изменение траектории пуч-
ка, показанной на рис. 7.9, когда
в электронном пучке возникает плаз-
менная волна. Картина движется
вправо с фазовой скоростью волны.
Для наблюдателя, находящегося
в системе отсчета, связанной с вол-
ной, картина будет неподвижна,
а электроны будут двигаться вдоль
КрИВОЙ СО СКОрОСТЬЮ Vq—Пф.
Рис. 7.11. Распределение потенци-
ала плазменной волны, каким его
видит электрон. Распределение дви-
жется со скоростью Уф. Электрон,
имеющий малую скорость относи-
тельно волны, будет захвачен в по-
тенциальную яму и начнет двигаться
вместе с волной.
Рис. 7.12. Траектории электронов и линии постоянных f в системе отсчета,
связанной с волной. В этой системе картина неподвижна. Диаграммы такого
типа, типичные для конечных распределений f, представить себе легче, чем
распределения в виде 6-функции, показанные на рис. 7.10.
8 Заказ 3170
226
Гл. 7. Кинетическая теория
Рис. 7.13. Линии уровня в фазовом пространстве для электронов в случае
двухпотоковой неустойчивости. Заштрихованная область, которая первона-
чально представляла собой в лабораторной системе область малых скоростей,
не содержит электронов. По мере того как развивающаяся неустойчивость
выходит за линейную стадию, эта область фазового пространства закручи-
вается и принимает вид, напоминающий «водяной мешок». [Из работы:
Berk Н. L., Nielson С. Е., Roberts К. V., Phys. Fluids, 13, 986 (1970). ]
кулоновских столкновений уравнение (7.19) можно записать в виде
Л_=_^_.(КДу>)Л__£г:(/<д,ду>). (7.25)
Это уравнение называется уравнением Фоккера—Планка-, оно учи-
тывает только парные кулоновские столкновения (Av— изменение
скорости при столкновении) и представляет собой более короткую
форму записи достаточно сложного выражения.
Тот факт, что в отсутствие столкновений dfjdt — 0, означает,
что при своем движении в фазовом пространстве частицы следуют
вдоль линий постоянных f. В качестве примера того, как могут
быть использованы эти контуры, рассмотрим неустойчивость в си-
стеме плазма — пучок, рассмотренную в разд. 6.6. В невозмущен-
7.3. Вывод гидродинамических уравнений 227
ной плазме все электроны имеют скорость v0 и линия постоянных /
является прямой (рис. 7.9). На рисунке функция f (х, vx) представ-
ляет собой стенку, поднимающуюся от плоскости бумаги вдоль ли-
нии vx = v0. Электроны движутся вдоль этой прямой. При воз-
никновении волны ее электрическое поле Ех вынуждает электроны
изменять свою скорость vx при движении их вдоль траектории.
При этом на траектории развивается синусоидальная рябь
(рис. 7.10). Эта рябь перемещается с фазовой скоростью волны, а не
со скоростью частиц. При своем движении относительно волны ча-
стицы остаются на кривой. Если при увеличении амплитуды волны
напряженность Ех становится очень большой, а столкновения при
этом происходят редко, то некоторые электроны будут захвачены
в электростатический потенциал волны. В координатном простран-
стве потенциал волны имеет вид, показанный на рис. 7.11. Функция
/ (х, vx) будет максимальной в тех областях фазового пространства,
в которых имеется потенциальная яма (рис. 7.12). Поскольку кри-
вые постоянной f являются также траекториями электронов, видно,
что некоторые электроны в фазовом пространстве движутся по замк-
нутым орбитам; именно эти электроны оказываются захваченными.
Захват электронов — это нелинейное явление, которое не
удается исследовать с помощью непосредственного решения урав-
нения Власова. Однако расчеты с помощью ЭВМ позволяют рас-
считать траектории электронов, причем результаты их расчетов
нередко имеют вид кривых, аналогичных изображенным на
рис. 7.12. Пример получаемых при этом численных результатов по-
казан в виде графиков на рис. 7.13. Данный пример относится к
случаю двухпотоковой неустойчивости, когда линии постоянных f
первоначально имели щель вблизи vx = 0, которая разделяла элек-
троны, движущиеся в противоположных направлениях. Эволюция
этой незаполненной щели во времени показана на рис. 7.13 в виде
заштрихованных областей. Мы видим, что неустойчивость искажает
f (v) столь сложным образом, что едва ли все это можно описать
аналитически.
7.3. Вывод гидродинамических уравнений
Гидродинамические уравнения, которые мы использовали выше,
являются просто моментами уравнения Больцмана. Низший мо-
мент получается посредством интегрирования уравнения (7.19),
когда F представляет собой силу Лоренца:
[~~dv+ fv-vfdv+ —((E4-vxB)--^-dv= ( dv.
J at J mJ dv J \ dt )c
(7.26)
Первый член можно записать в виде
f-^-dv= = — • (7.27)
J dt dt J dt '
8*
228
Гл. 7. Кинетическая теория
Поскольку v — независимая переменная и, следовательно, на нее
не действует оператор V, второй член дается выражением
f v • vf dv = V • f fv dv = v • (nv) = V • (nu), (7.28)
где средняя скорость u по определению есть скорость жидкости.
Член, в который входит Е, обращается в нуль, в силу того что
f E--^-dv = (— -(/E)dv= f /E-dS = O. (7.29)
J dv J dv J
Sqo
Интегрирование полной дивергенции дает среднее значение вели-
чины /Е на поверхности при v = оо, которое равно нулю, если /->0
быстрее, чем v~2 при t оо, поскольку это необходимое условие
для любого распределения с конечной энергией. Член' с v X В
можно записать следующим образом:
f(vxB) • -^—dv = ( -(fvxB)dv— f/-^—x(vxB)dv = 0.
J dv j dv J dv
(7.30)
Первый интеграл снова может быть преобразован в поверхностный
интеграл. Максвелловская функция распределения f при v -> оо
спадает быстрее, чем любая степень величины v; следовательно,
этот интеграл равен нулю. Второй интеграл обращается в нуль,
поскольку вектор v X В перпендикулярен d/dv. Наконец, четвер-
тый член в уравнении (7.26) оказывается тоже равным нулю, по-
скольку столкновения не могут изменить полное число частиц (ре-
комбинация здесь не рассматривается). Таким образом, уравнения
(7.27) — (7.30) сводятся к уравнению непрерывности
+V(nu) = 0. (7.31)
dt
Следующий момент уравнения Больцмана получается умножением
уравнения (7.19) на mv и интегрированием уравнения по dv. Мы
имеем
т ( v dv + f mv(y-V)fdv + q ( v(E + v x В)- dv =
J dt J J dv
= m v ) dv. (7.32)
Правая часть этого уравнения представляет собой изменение им-
пульса вследствие столкновений и приводит к члену Pf/ в уравнении
(5.58). Первый член в левой части уравнения (7.32) записывается
в виде
т ( v -^—dv= т—— ( vfdv=—^— т(пи). (7.33)
J dt dt J dt
7.3. Вывод гидродинамических уравнений 229
Третий интеграл в (7.32) можно представить следующим образом:
( v (Е + v х В) • —— dv= { —• [fv (Е + v х В)] dv—
J dv J dv
— [fv —— (E4-v x B)dv— f f (E-f-v X B)- —— vdv. (7.34)
J dv J dv
Здесь в правой части первые два интеграла обращаются в нуль по
тем же причинам, что и выше, a dv/dv является единичным тензором
I. Следовательно,
f v (Е + v х В)« dv = —q f (Е + v х В) f dv = — qn (E + v x B).
J dv J
(7.35)
Окончательно, чтобы вычислить второй интеграл в уравнении (7.32),
используем сначала тот факт, что v — независимая переменная,
не связанная с |v, и запишем
f v(v-V)fdv=J V-(fvv)dv = V-J fvvdv. (7.36)
Поскольку среднее значение какой-либо величины равно взвешен-
ному интегралу этой величины по v, деленному на п, мы имеем
V-J/vvdv= V-nvv- (7.37)
Скорость v можно представить теперь в виде суммы средней (гид-
родинамической) скорости и и тепловой скорости w:
v = u + w. (7.38)
Поскольку и уже средняя величина, можно написать следующее
выражение:
V • (nvv) = V • (nuu) + V • (nww) + 2v • (nuw). (7.39)
Очевидно, среднее значение w равно нулю. Величина mnww есть
не что иное, как тензор напряжений Р:
Р = mnww. (7.40)
Оставшийся первый член в правой части уравнения ^(7.39) можно
записать в виде
V«(nuu) = uV-(nu) + n(u-V)u. (7-41)
Объединяя полученные нами результаты, а именно выражения
(7.33), (7.35), (7.40) и (7.41), уравнение (7.32) можно переписать
в виде
т —(nu)-(-muV*(nu)+ mn(u-V) u +V-Р —дтг(Е-|-и X В) = Р^.
(7.42)
Преобразовывая первые два члена с помощью уравнения непре-
230 Гл. 7. Кинетическая теория
рывности (7.31), окончательно получаем следующее гидродинами-
ческое уравнение:
тиГ-^- +(u-V)ul =^n(E + u х В)—V-P + P,-,-. (7.43)
L at J
Это уравнение описывает поток импульса. Чтобы вычислить
поток энергии, необходимо найти следующий момент уравнения
Больцмана, умножив его на (1/2) mvv и проинтегрировав по v.
При этом мы получим уравнение теплового потока, в которое вхо-
дит коэффициент теплопроводности х так же, как в гидродинами-
ческое уравнение тензор напряжений Р. Простейшей формой урав-
нения теплового потока при х= 0 является уравнение состояния
Р = Pv-
7.4. Плазменные колебания и затухание Ландау
В качестве элементарной иллюстрации использования уравнения
Власова выведем дисперсионное уравнение для плазменных коле-
баний, которые мы рассматривали с гидродинамической точки зре-
ния в разд. 4.3. Для этого нам потребуется контурное интегриро-
вание. Те, кто не знаком с ним, могут сразу перейти к разд. 7.5.
В разд. 7.6 мы дадим более простой, хотя и более длинный, вывод
без применения теории функций комплексного переменного.
Предположим, что в нулевом порядке плазма однородна и имеет
функцию распределения /0 (v), и положим Во = Ео = 0. Обозна-
чим возмущение функции f (г, v, t) в первом порядке как fx (г, v, t):
I (г, v, O = /o(v) + fj(r, v, t). (7.44)
Так как v теперь независимая переменная и ее не следует линеари-
зовывать, уравнение Власова для электронов в первом порядке
запишется в виде
_^l_+vv/1-^-E1. А=0. (7.45)
dt т dv
Как и прежде, предположим, что ионы тяжелые и неподвижные,
а волны являются плоскими и распространяются вдоль оси х:
fi ~ exp [i (kx—со/)]. (7.46)
При этом уравнение (7.45) принимает вид
-ico/i + ibj^ (7.47)
т dvx
_ i dfo/dpg a . (у
ГП (i) — kvx
7.4. Плазменные колебания и затухание Ландау
231
Уравнение Пуассона дает
eov Ej = i = — enL = — efff ^dtv. (7-49)
Подставляя сюда выражение (7.48) для Л и сокращая на i^So-E*,
получаем
1 =---------— ((f df^-dVx d3v.
km&0 J J J <в — kvx
VW
Множитель п0 можно факторизовать, если заменить /0 нормирован-
ной функцией /0:
9 00 ОО ОО / ч
1= С d„ f С у (7.51)
k J J J со — kvx
—со — оо —оо
Если /0 является распределением Максвелла или другой фактори-
зуемой функцией, то интегрирование по vz и vy легко выполняется
и остается одномерное распределение/0 (vx). Например, одномерное
распределение Максвелла имеет вид
L (vj = (т/2лКТ)1/2 ехр (—mt£/2KT). (7.52)
Следовательно, дисперсионное уравнение запишется в виде
1= 7 d„:
k2 J vx—(co/fe)
(7.53)
Поскольку мы имеем здесь дело с одномерной задачей, можно опу-
стить индекс х; при этом' следует быть внимательным и не путать v
(которое есть на самом деле vx) с полной скоростью v, используе-
мой выше:
«р г df0/dv
k2 Ju — (со//г)
dv.
(7-54)
Под /0 здесь понимается одномерная функция распределения, при-
чем мы считаем, что интегрирование по vy и vz выполнено. Соотно-
шение (7.54) справедливо для любой равновесной функции распре-
деления (о); в частности, если /о максвелловская, то следует ис-
пользовать выражение (7.52).
Интеграл в (7.54) нельзя вычислить непосредственно, поскольку
при v = alk имеется сингулярность. Эта сингулярность, однако,
не дает повода для беспокойства, поскольку на практике ® почти
никогда не бывает вещественной; обычно волны слабо затухают
вследствие столкновений или усиливаются благодаря некоторому
механизму неустойчивости. Поскольку скорость v является ве-
щественной, знаменатель в (7.54) никогда не обращается в нуль.
Гл. 7. Кинетическая теория
Рис. 7.14. Контуры интегрирования в задаче Ландау при Im (<о) >0 (а) и
Im (со) <0 (б).
Первым, кто правильно исследовал это уравнение, был Ландау.
Он обнаружил, что даже если сингулярность лежит вне пути ин-
тегрирования, ее наличие приводит к существенному изменению
дисперсионного уравнения плазменных волн — этот эффект не
предсказывается гидродинамической теорией.
Рассмотрим начальную задачу, когда задано синусоидальное
возмущение плазмы и, следовательно, величина k вещественна.
Если возмущение нарастает или затухает, то частота со будет ком-
плексной. Интеграл в (7.54) следует рассматривать как контур-
ный интеграл в комплексной v-плоскости. Возможные контуры
интегрирования показаны на рис. 7.14 для неустойчивой волны
с Im (со) > 0 и для затухающей волны с Im (со) < 0. Обычно интег-
рал вдоль вещественной оси v вычисляют с помощью теоремы вы-
четов:
J Gdu-j- j Gdv = 2n i 7?(со/й), (7.55)
с, с2
где G — подынтегральное выражение, Сг — путь вдоль веществен-
ной оси, С2 — полуокружность с радиусом, стремящимся к беско-
нечности, a R (со/А) — вычет при v = a>/k. Такое вычисление
справедливо, если интеграл по пути С2 обращается в нуль. К со-
жалению, это не имеет места в случае максвелловского распределе-
ния, которое содержит множитель
ехр(—о%тепл).
Этот множитель становится большим при и-> ± i оо, и вкладом
от С2 нельзя пренебречь. Ландау показал, что если задача рассмат-
ривается последовательно как начальная задача, то правильный
контур интегрирования следует выбрать так, чтобы кривая Ct
проходила ниже сингулярности. В общем случае этот интеграл
приходится вычислять численно. Фрид и Конте составили таблицы
численных значений этого интеграла для случая, когда функция f0
является максвелловской.
7.4. Плазменные колебания и затухание Ландау
233
Рис. 7.1$. Контур интегрирования
в комплексной плоскости v для слу-
чая малых Im (со).
Рис. 7.16. Нормированное максвел-
ловское распределение для случая,
когда Vф Птепл*
Несмотря на то что точное рассмотрение этой задачи сложно,
можно получить приближенное дисперсионное уравнение для слу-
чая больших фазовых скоростей и слабого затухания. В этом слу-
чае полюс при a/k находится вблизи вещественной оси v (рис. 7.15).
При этом контур интегрирования, предписанный Ландау, состоит
из прямой линии вдоль оси Re (о) и из небольшой полуокружности
вокруг полюса. Обход вокруг полюса дает величину, равную про-
изведению 2ni на половину вычета в этой точке. Таким образом,
уравнение (7.54) принимает вид J
(7.56)
где Р означает, что интеграл вычисляется в смысле главного зна-
чения Коши. Чтобы вычислить это выражение, начнем интегриро-
вание вдоль вещественной оси и остановимся перед самым полюсом.
Если фазовая скорость = a>/k достаточно велика, как мы и пред-
полагаем, то вклад от пренебрегаемой части контура будет мал,
поскольку как/0, так и dfjdu на нем очень малы (рис. 7.16). Ин-
теграл в выражении (7.56) можно вычислить интегрированием по
частям:
дК dv _ Г 7о
dv v — пфЧ [_ v — иф
(а — Оф)
‘00
С to dv
J f(f — Оф)2 ’
(7.57)
Поскольку последнее выражение равно среднему от (v—Оф)~2 по
функции распределения, вещественную часть дисперсионного урав-
нения можно записать в виде
1 = (®р//г2)(и —иф) 2.
(7.58)
234
Гл. 7. Кинетическая теория
Мы предположили, что Уф v, поэтому величину (и—Уф)-2 можно
разложить следующим образом:
2_.,—2/1 v Л-2 „2/1 I 2v , За2 , 4а3 , \
(v 1>ф) — Уф I 1 j — Уф j 1 4--------------1—— -j—-—(-...).
к аФ 7 к Оф Оф оф J
(7.59)
При усреднении нечетные члены обращаются в нуль, и мы имеем
(V-оф)~! « 1 + #-).
к оф 7
(7.60)
Вычислим у3 при условии, что функция/0 является максвелловской.
Вспоминая, что v на самом деле есть vx, мы можем записать
(7.61)
при условии что рассматривается только одна степень свободы.
При этом дисперсионное уравнение (7.58) принимает вид
, “р (} ,о k2
1 — — I 1 —г- <5 _ I,
А2 со2 к <в2 т 7
(7.62)
(7.63)
2 2 ,
СО = (£>р +
<2^.
со2 т
Если тепловая поправка мала, то во втором члене о»3 можно заме-
нить на со*, и мы имеем
(02=(!12 + 2£2k.fe2.
т
(7.64)
Это соотношение совпадает с дисперсионным уравнением (4.30),
полученным из гидродинамических уравнений при у = 3.
Теперь вернемся к мнимому члену в соотношении (7.56). При
вычислении этого члена можно с достаточной точностью пренебречь
тепловой поправкой к вещественной части со и положить со2« со*.
Из соотношений (7.57) и (7.60) мы видим, что главная часть интег-
рала в (7.56) приблизительно равна Л2/со2. Дисперсионное уравне-
ние (7.56) при этом принимает вид
9 9
1 “р , • “р df0
1 = —-—Ь 1 л —------~
со2 k* dv
»=°ф
(7.65)
фзЛ —^ = ©2. (7.66)
\ fe2 L dv Л°=«ф/
Считая мнимые члены малыми, их можно перенести в правую часть
и взять квадратный корень, используя разложение в ряд Тейлора.
7.5. Физический смысл затухания Ландау
235
В результате мы имеем следующее дисперсионное уравнение:
Если — одномерное максвелловское распределение, то можно
написать
2d____
v3
^тепл
-у—Y (7.68)
утепл Z
Здесь можно заменить приближенно на ар/k, но в экспоненте
необходимо учесть тепловую поправку, включенную в (7.64). При
этом затухание определяется выражениями
л <Ор 2<ор 1. / ®2
2 & ^епл к '
(7.69)
Im/—"1= —0,22 Yexpf -Y (7.70)
к “р J \ Непл ) I )
Поскольку Im (ю) отрицательна, существует бесстолкновительное
затухание плазменных волн; оно называется затуханием Ландау.
Из уравнения (7.70) очевидно, что при малых £ZD затухание чрез-
вычайно мало, но при = 0(1) оно становится существенным.
Этот эффект связан с flt т. е. с возмущением функции распределе-
ния, вызываемым волной.
7.5. Физический смысл затухания Ландау
Теоретическое открытие затухания волн в отсутствие столкнови-
тельной диссипации энергии явилось, возможно, наиболее выдаю-
щимся результатом исследований в области физики плазмы. То, что
этот эффект вполне реален, было продемонстрировано лаборатор-
ными исследованиями. Хотя в настоящее время имеется простое
физическое объяснение затухания Ландау, этот неожиданный эф-
фект был первоначально обнаружен чисто математически, а именно
в результате анализа контурного интеграла, что явилось подлин-
ным триумфом прикладной математики. Затухание Ландау харак-
236
Гл. 7. Кинетическая теория
Частица
получает
энергию
Волна
получает
энергию
Рис. 7.17. Физическая модель, иллюстрирующая затухание Ландау,
терно для бесстолкновительной плазмы, но оно имеет приложение
и в других областях. Например, при кинетическом рассмотрении
образования галактик звезды можно считать как бы атомами
плазмы, взаимодействующими через гравитационные силы, а не
посредством электромагнитных сил. Неустойчивости в газе звезд
могут вызвать образование спиральных рукавов галактик, но этот
процесс лимитируется затуханием Ландау.
Чтобы понять, чем обусловлено затухание Ландау, заметим
сначала, что Im (ю) определяется полюсом при и = v$. Следова-
тельно, эффект вызван теми частицами, которые имеют скорости,
почти равные фазовой скорости волны, т. е. «резонансными части-
цами». Эти частицы движутся вместе с волной и не видят быстро
флуктуирующего электрического поля; следовательно, они .могут
эффективно обмениваться энергией с волной. Простейший способ
понять этот обмен энергией — это представить спортсмена, зани-
мающегося серфингом, который пытается оседлать океанскую
волну (рис. 7.17). [Предупреждаем, что эта картина служит лишь
для того, чтобы направить наши мысли в нужную сторону; правиль-
ного объяснения уравнения (7.70) она не дает. ] Если доска стоит
на месте, то при прохождении волны она только болтается вверх-
вниз и в среднем не приобретает никакой энергии. Аналогично
доска, движущаяся много быстрее волны, не может получить
сколько-нибудь заметную энергию от волны. Однако если доска
имеет почти ту же скорость, что и волна, она может быть подхва-
чена и унесена волной; именно это и есть главная цель спортсмена.
В этом случае доска приобретает энергию и, следовательно, волна
должна терять энергию и затухать. С другой стороны, если бы доска
двигалась чуточку быстрее волны, она подталкивала бы волну,
взбираясь на нее; тогда волна приобретала бы энергию. В плазме
одни электроны движутся быстрее, другие медленнее, чем волна.
Однако если распределение максвелловское, то медленных электро-
7.5. Физический смысл затухания Ландау 237
нов больше, чем быстрых (рис. 7.18). Следовательно, большее число
частиц отбирает энергию от волны, чем отдает ей, и волна затухает.
Как только частицы с о « Рф захватятся волной, распределение
f (v) становится плоским вблизи фазовой скорости. Это искажение
есть не что иное, как возмущение Д (v), которое мы вычислили.
Как видно на рис. 7.18, возмущенная функция распределения со-
держит то же число частиц, но их общая энергия стала больше (за
счет энергии волны).
Исходя из проведенного обсуждения, можно прийти к заклю-
чению, что если /0 (и) содержит больше быстрых частиц, чем мед-
ленных, то возможна генерация волны. Действительно, из соот-
ношения (7.67) очевидно, что Im (со) положительна, если положи-
тельна производная df0/dv при v = Такая функция распреде-
ления показана на рис. 7.19. Волны с»ф в области положительного-
градиента функции f0 становятся неустойчивыми, поскольку они
получили энергию за счет частиц. Этот процесс аналогичен двухпо-
токовой неустойчивости, но только при наличии конечной темпе-
ратуры. Если рассматривать два холодных (/СТ = 0) электронных
потока в движении, то Д (к) будет состоять из двух 6-функций.
В этом случае мы имеем неустойчивость, поскольку величина
dfQldv является бесконечной; в самом деле, гидродинамическая
теория в этом случае предсказывает неустойчивость. Если потоки
имеют конечную температуру, то, согласно кинетической теории,
относительные плотности и температуры двух потоков должны быть
такими, чтобы между ними имелась область положительной ве-
личины df0/dv, точнее говоря, в случае неустойчивости полная:
функция распределения должна иметь минимум.
Физическая модель, в которой рассматривается спортсмен, пы-
тающийся оседлать волну, очень привлекательна, но она недоста-
точно точна, чтобы дать нам действительное понимание затухания:
Ландау. Фактически существуют два вида затухания Ландау: ли-
нейное и нелинейное. Оба этих затухания не зависят от механиз-
мов столкновительной диссоциации. Если частица оказывается
Рис. 7.18. Искажение максвеллов-
ского распределения в окрестности
v « Оф , вызванное затуханием Лан-
дау.
Рис. 7.19. Двугорбое распределение
и область, в которой будет разви-
ваться неустойчивость.
238 Гл. 7. Кинетическая теория
пойманной в потенциальной яме волны, то это явление называется
«захватом». Как и в примере с серфингом, захваченные частицы мо-
гут приобретать или терять энергию. Однако сам процесс захвата
нельзя описать с помощью линейной теории. То, что это так, можно
увидеть из уравнения движения
т (Px/dt? = qE (х). (7-71)
Если вычислять Е (х), подставляя точное значение х, то уравнение
будет нелинейным, поскольку Е (х) ведет себя примерно как
sin kx. В линейной теории х представляет собой невозмущенную
орбиту, т. е. х — х0 + vQt. При этом уравнение (7.71) является
линейным. Однако приближение становится несправедливым, когда
частица захватывается. Когда частица встречает потенциальный
горб, достаточно высокий, чтобы отразить ее, то на ее скорость и по-
ложение оказывает сильное влияние волна, так что эти величины
значительно отличаются от их невозмущенных значений. В гидро-
динамической теории уравнение движения имеет вид
_£5L+(v.v)vj =^Е(х). (7.72)
Здесь Е (х) должно быть вычислено в лабораторной системе коорди-
нат, что нетрудно выполнить; однако здесь имеется член (v-v) v.
Пренебрежение членом (vx-V) Vx в линейной теории означает то
же, что и использование невозмущенных орбит. В кинетической
теории нелинейный член, который не учитывается в уравнении
Х7.45), имеет вид
S-Ex-^-. (7.73)
т dv
Если частицы захватываются, то направление их движения относи-
тельно волны становится обратным, так что функция распределения
f (о) сильно искажается вблизи v = aylk. Это означает, что df\ldv
становится сравнимым с dfQldv и величиной (7.73) нельзя пренебре-
гать. Следовательно, в рамках линейной теории захват описать
нельзя.
Когда волна нарастает до большой амплитуды, происходит ее
бесстолкновительное затухание, связанное с захватом. При этом
волна не затухает монотонно; наоборот, ее амплитуда флуктуирует
в процессе затухания, в то время как захваченные частицы скачут
взад-вперед в потенциальных ямах. Это и есть нелинейное затуха-
ние Ландау. Поскольку результирующее соотношение (7.67) выве-
дено из линейной теории, оно должно быть связано с другим физи-
ческим механизмом. В связи с этим возникает вопрос: могут ли
незахваченные электроны, движущиеся со скоростью, близкой
к фазовой скорости волны, обмениваться с ней энергией? Прежде
чем ответить на этот вопрос, рассмотрим энергию.таких электронов.
7.5. Физический смысл затухания Ландау
239
7.5.1. Кинетическая энергия пучка электронов
Мы можем представить распределение электронов /0 (о) в виде боль-
шого числа моноэнергетических пучков (рис. 7.20). Рассмотрим
один из таких пучков: пусть он имеет невозмущенную скорость и
и плотность пи. Скорость и может быть близка к Оф, так что этот
пучок может состоять из резонансных электронов. Введем теперь
плазменные колебания Е (х, t) и рассмотрим кинетическую энергию
пучка по мере того, как он проходит через гребни и ямы потенциала
волны. Волна определяется самосогласованным движением сразу
всех пучков. Если плотность пи достаточно мала (число пучков,
достаточно велико), то рассматриваемый пучок оказывает прене-
брежимо малое воздействие на Волну и может быть рассмотрен как.
движущийся в данном поле Е (х, t). Предположим, что
Е = Ео sin (kx—at) = —d^/dx, (7.74)'
^>“(E0/fe)cos(Ax—ы/). (7.75)
Линеаризованное гидродинамическое уравнение для пучка запи-
шется следующим образом:
т + и = —eEosin(fex— at). (7.76)
\ dt дх J
Его возможное решение имеет
вид
еЕо cos (kx —
—------------------------------
т <в — ku
Рис. 7.20. Разбиение распределения
/о (у) на большое число моноэнерге-
тических пучков, имеющих скорость
и и плотность пи.
Рис. 7.21. Фазовые соотношения для
скорости и плотности электронов,
движущихся в электростатической:
волне.
240
Гл. 7. Кинетическая теория
Это выражение определяет модуляцию скорости электронов пучка
волной, когда пучок проходит вблизи волны. Сохранение потока
частиц требует существования соответствующих колебаний плот-
ности, которые описываются линеаризованным уравнением непре-
рывности:
dni । dni _ dvr
—г” И- fl,, " •
dt дх дх
Так как пропорционально cos (kx—cut), можно положить п1 =
= «xcos (kx—at). Подставляя это выражение в уравнение (7.78),
получаем
(7.78)
П1=_Пц_ЛМ-_со2(^-«>0 . (7.79)
т (<о — ku.)2
Смысл выражений (7.77) и (7.79) иллюстрируется рис. 7.21. Пер-
вые две кривые показывают на одной длине волны поле Е и потен-
циал —еф, как их «видят» электроны пучка. Третья кривая по-
строена в соответствии с выражением (7.77) для случая со—ku <0,
или и > Оф. Ее поведение нетрудно объяснить: когда электрон а
взбирается на потенциальный горб, его скорость мала, и наоборот.
Четвертая кривая описывает поведение ох для случая « < v$\ мы
видим, что знак величины ох обращен. Это обусловлено тем, что
электрон Ь, движущийся налево в системе отсчета волны, замед-
ляется по пути к вершине потенциального барьера; но поскольку
юн движется в противоположном направлении, его скорость ох
в положительном направлении оси х в этом месте максимальна.
Последняя кривая на рис. 7.21 демонстрирует поведение плотно-
сти п1( определяемой выражением (7.79). Она не меняет свой знак
вместе с и— Оф, поскольку в системе отсчета волны как электрон а,
так и электрон b на вершине потенциального барьера имеют наи-
меньшую скорость, и, следовательно, плотность в этом месте наи-
большая. Эго объясняется тем, что относительная фаза между «х
и о/ меняет свой знак вместе с и— цф.
Теперь можно вычислить кинетическую энергию IF* пучка:
Wk = т (пи + пг)(и + vtf =
т (пии2 + п uvl + 2un1v1-]-n1u2 + 2nuuvi + n1vT)- (7.80)
Последние три члена содержат нечетные степени осциллирующих
величин, и, следовательно, при усреднении по длине волны они
обратятся в нуль. Изменение величины Wk за счет энергии волны
можно получить, если вычесть первый член, который представляет
собой начальную энергию. При этом среднее изменение энергии
дается выражением
(AIF*) = -у- т (пио\ 4- 2ипгО1).
(7.81)
7.5. Физический смысл затухания Ландау
241
Из выражения (7.77) имеем
/ 2\ 1 е2Еп
Пи (о!) = — пи — - ; (7.82)
2 m2(co — ku)2
здесь множитель 1/2 представляет собой (cos2 (kx— Аналогично
из выражения (7.79) находим
e^E^ku
2и{п^ = пи 2 0 • (7.83)
т2 (со — ku)3
Следовательно,
1 е2Ел Г 2йи 1
W>==_Lm„u ° 2 Н+ --------— =
4 т2 (со — ku)2 L со — ли J
пи е2£ц со + ku
4 т (со — ku)3
(7-84)
Это выражение показывает, что (A W£) зависит от системы отсчета,
в которой находится наблюдатель, и не меняется со временем. Для
пояснения рассмотрим брусок, скользящий без трения по поверх-
ности тела, напоминающего стиральную доску (рис. 7.22). Из вы-
ражения (7.84) при св — 0 мы видим, что в системе отсчета, связан-
ной с доской, (АЙ7*) ~ — (ku)-2. Интуитивно ясно, что 1) величина
<А№\) отрицательна, поскольку брусок проводит больше времени
на вершинах, чем в долинах, и 2) после того как брусок начал дви-
гаться, его энергия в среднем сохраняется постоянной. Если те-
перь перейти в систему отсчета, в которой стиральная доска дви-
жется с постоянной скоростью ы/k (на скорость перемещения доски
движение бруска не влияет, поскольку мы предположили, что
плотность па пренебрежимо мала по сравнению с плотностью всей
плазмы), то по-прежнему ясно, что брусок в среднем не теряет и не
приобретает энергии. Однако из формулы (7.84) следует, что (AU7ft)
зависит от скорости aa'k и, следовательно, от системы отсчета, в ко-
торой находится наблюдатель. В частности, мы видим, что при на-
личии волны энергия пучка меньше, чем без нее, если со—ku <0,
т. е. и > Оф, или больше, чем без нее, если со—ku >0, т. е. и < оф.
Почему так происходит, можно понять из фазового соотношения
между п1 и vv Из рис. 7.23 ясно, что Wk является квадратичной
-функцией скорости V. Когда v колеблется между значениями
и— | | 'и и + | ох |, среднее значение энергии Wk будет больше
Рис. 7.22. Механическая аналогия для электрона, перемещающегося относи-
тельно движущегося распределения потенциала.
242
Гл. 7. Кинетическая теория
Рис. 7.23. Квадратичная зависимость кинетической энергии от скорости при-
водит к тому, что симметричное возмущение скорости вызывает увеличение
средней энергии.
равновесного значения W^o, при условии что частица затрачивает
одинаковое время на каждую половину колебания. Этим и объяс-
няется наличие первого члена в выражении (7.81), которое представ-
ляет собой положительно определенную величину. Второй член
в этом выражении является поправкой, учитывающей то обстоя-
тельство, что частицы неодинаково распределяют свое время. Из
рис. 7.21 можно видеть, что как электрон а, так и электрон b про-
водят больше времени на вершине потенциального горба, чем
в яме, но электрон а достигает этой точки после периода торможения,
так что величина ух здесь отрицательна, в то время как электрон b
оказывается в этой точке после периода ускорения (направо), и
здесь yt положительна. Благодаря этому изменяется знак величины
(AlFft) при и = Уф.
7.5.2. Влияние начальных условий
Результат, к которому мы только что пришли, по-прежнему не
имеет никакого отношения к линейному затуханию Ландау. Зату-
хание требует постоянного увеличения Wk за счет энергии волны,
а мы нашли, что для незахваченной частицы средняя энергия
(AlJ7fc) не меняется во времени. Если линейное затухание Ландау
не определяется ни захваченными, ни незахваченными частицами,
то чем же тогда? Ответ можно получить с помощью следующего-
наблюдения: если, скажем, величина (А1Га) положительна, то,
наверное, было время, в течение которого она увеличивалась. Дей-
ствительно, в первоначальном распределении имеются частицы,
скорости которых столь близки к Уф, что к моменту времени t они
еще не успевают пройти половину длины волны относительно
волны. Для них нельзя вычислять среднее значение (AW^). Эти
частицы могут поглощать энергию волны и обоснованно называются
«резонансными». С течением времени число резонансных электронов-
уменыпается, поскольку все большее их число будет смещаться
7.5. Физический смысл затухания Ландау 243
более чем на (1/2) X от своего первоначального положения. Однако
скорость затухания может оставаться постоянной, так как теперь
амплитуда волны меньше и требуется меньшее число электронов
для поддержания постоянной скорости затухания.
Влияние начальных условий наиболее просто понять с помощью
фазовой диаграммы (рис. 7.24). На этом рисунке изображены тра-
ектории электронов в фазовом пространстве, а также электроста-
тический потенциал —ефк, в котором они находятся. Мы предпо-
ложили, что этот электростатический потенциал существует, на-
чиная с t = 0, и что распределение /0 (^), которое на рисунке по-
мещено в плоскости, перпендикулярной листу бумаги, является
однородным в пространстве и монотонно уменьшается с |ц| в на-
чальный момент времени. Для ясности, размер волны на рисунке
сильно увеличен. Разумеется, наличие волны предполагает су-
ществование возмущения ft (v) при t = 0. Однако обусловленное
этим затухание есть эффект более высокого порядка и не учи-
тывается в линейной теории. Перейдем теперь в систему отсчета,
Рис. 7.24. Траектории электронов в фазовом пространстве (вверху) для слу-
чай частиц, движущихся в потенциале волны (распределение потенциала
показано внизу). Стрелки указывают направление движения электронов
относительно волны. Слева в плоскости, перпендикулярной листу бумаги,
отложена равновесная функция распределения.
244
Гл. 7. Кинетическая теория
связанную с волной, так что картина на рис. 7.24 оказывается не-
подвижной, и рассмотрим движение электронов. Электроны, рас-
положенные вначале в точке А, начинают двигаться от вершины
потенциала направо, поскольку их скорость v > Цф. Электроны,
находящиеся первоначально в точке В, движутся налево, так как
их скорость v < Цф. Те же электроны, что находились в точках С
и D, начинают двигаться от дна потенциальной ямы и перемещаются
соответственно направо и налево. Энергия электронов, находящихся
на замкнутых контурах Е, недостаточна, чтобы преодолеть потен-
циальный барьер, и они оказываются запертыми. В пределе малой
начальной амплитуды волны число захваченных электронов может
быть произвольно малым. После некоторого времени t, достаточно
короткого, чтобы ни один из электронов, находящихся в точках А,
В, С или D, не прошел более чем половину длины волны, электроны
переместятся в положения, обозначенные маленькими кружочками.
Видно, что электроны, находившиеся в точках А и D, приобрели
энергию, а в точках В и С потеряли. Если распределение /0 (у)
яыло вначале однородным в пространстве, то в 4 сначала было
больше электронов, чем в С, а в D больше, чем в В. Следовательно,
энергия у электронов возрастает, а у волны теряется. Это и есть
линейное затухание Ландау, которое критическим образом зависит
от начальных условий. Спустя некоторое время электроны
настолько размешаются по фазам, что начальное распределение-
забудется, и в полном согласии с результатом, полученным в пре-
дыдущем разделе, энергия частиц в среднем возрастать не будет.
В этом представлении энергия как электронов с v > иф, так и
электронов с v < vф при усреднении по длине волны будет увели-
чиваться за счет волны. Это кажущееся противоречие с моделью-
серфинга мы разрешим ниже.
7.6. Физический вывод затухания Ландау
Теперь мы в состоянии вывести формулу для декремента затуха-
ния Ландау без использования контурного интегрирования. Как
и прежде, разделим плазму на пучки со скоростями и и плотно-
стями пи и будем исследовать их движение в волне
E = Eisin(£x—at). [(7.85>
Из выражения (7.77) следует, что скорость каждого пучка равна
eEr cos (kx — at) (7 86)
m co — ku *
Это решение удовлетворяет уравнению движения (7.76), но не удов-
летворяет начальному условию = 0 при t — 0. Ясно, что это
условие должно быть наложено обязательно, иначе в окрестности
и = alk Oj будет очень велико и плазма будет находиться в специ-
7.6. Физический вывод затухания Ландау 245
ально приготовленном начальном состоянии. Добавляя произволь-
ную функцию величины kx—kut, выражение (7.86) можно под-
править так, чтобы оно удовлетворяло начальному условию. Ре-
зультирующее выражение по-прежнему будет удовлетворять урав-
нению (7.76), поскольку оператор в левой части выражения (7.76),
действуя на произвольную функцию f (kx—kut), дает нуль. Для
того чтобы получить vx = 0 при t = 0, функция f (kx—kut) должна
быть выбрана в виде —cos (kx—kut). Таким образом, вместо вы-
ражения (7.86) мы имеем
„ — еЕг cos (kx — «/) — cos (kx — kut) o-
---------------------------------- . (./ -Ot)
m co — ku
Затем нужно найти nlt решая уравнение непрерывности (7.78)
при начальном условии пг ~ 0 при t = 0. Поскольку мы стали
теперь умнее, попробуем искать решение в виде
пх = nx[cos(ta—at)—cos(kx—kut)]. (7.88)
Подставляя это выражение в (7.78) и используя формулу (7.87)
для vlt находим
7 „ eEjk sm(kx—at)—&\n(kx — kuf)
Ы11 ~ " —- --- ' •
т (а — ku)1
(7.89)
По-видимому, мы были недостаточно умны, так как множитель
sin (kx—at) не сократился. Для того чтобы получить член вида
sin (kx—kut), который возникает из-за добавленного к vx члена,
к п1 можно добавить член вида At sin (kx—kut). Этот член, оче-
видно, обращается в нуль при t = 0, а при действии на него опе-
ратора, стоящего в левой части уравнения (7.78), мы будем иметь
sin (kx—kut). Этот же оператор, действуя на sin (kx—kut), дает
нуль. Коэффициент А должен быть пропорционален величине
(со—ku)-1, чтобы производная dv-Jdx имела этот же коэффициент.
Таким образом, мы имеем
«1 = —пи —eElk-----!---[cos (kx— at)—cos (kx—kut)—
m (co — ku)1
— (co—ku)t sin (kx—kut)]. (7.90)
Мы видим, что при t = 0 это выражение обращается в нуль, и не-
трудно проверить, что оно удовлетворяет уравнению (7.78).
Записанные выше выражения для vx и пх позволяют вычислить
работу, производимую волной над каждым пучком. Сила, дейст-
вующая на единичный объем каждого пучка, дается выражением
• Fu——eE^infix—at) (пи + nx); (7.91)
246
Гл. 7. Кинетическая теория
следовательно, скорость изменения энергии этого объема можно
записать в виде
=Fu(u + Ui) = —eEi sin (kx—at) (nuu4-nuvr-\-n±u + n-jVj).
dt
(7.92)
Вычислим теперь среднее этой величины по длине волны. Первый
член исчезает, поскольку произведение пии = const. Четвертым
членом можно пренебречь, как числом второго порядка малости,
причем можно показать, что в любом случае среднее от него по вре-
мени равно нулю. Второй и третий члены можно вычислить с по-
мощью выражений (7.87) и (7.90), используя выражения
(sin(£x—(ot)cos(fex—kut)) —------— sin((ot — kut),
1 2 (7-93)
(sin(£x—at) sin (kx—kut)}—------cos(ot—kut).
Нетрудно показать, что среднее значение скорости изменения энер-
гии дается выражением
) dW \ е2Е2 Г sin (со/— kut)
\ dt /и “ L со — ku "1""
-|- ku
sin (at — kut) — (co — ku) t cos (co/ — kut)
(co — feu)2
(7.94)
Следует заметить, что в процессе усреднения уцелели лишь члены,
определяемые начальными условиями.
Полную работу, производимую над частицами, получаем сумми-
рованием по всем пучкам:
и
Подставляя сюда выражение (7.94) и используя определение ве-
личины ар, находим скорость изменения кинетической энергии:
/ dWь \ епЕ, 9 Г С sin (at— kut)
=-vL \ —------r^~du+
\ dt I 2 LJ co — feu
+(f. («) taJ=(7.96)
J (co — feu)2 J
= _L6oe^ f f0(U)du[....s.in^~to) =
2 J I co —feu du L co — ku JJ
—oo
(7.97)
7.6. Физический вывод затухания Ландау
247
----1- 80£^ f Го (и) du Ги 1. (7.98)
2 J du L <о — ku J
----00
Это выражение следует положить равным скорости потери плот-
ности энергии волны Ww. Энергия волны состоит из двух частей.
Первая — это энергия электростатического поля с плотностью
<Г£) = е0 (Е')/2 = e0£i/4. (7.99)
Вторая часть представляет собой энергию колебаний частиц в волне.
Если снова разделить плазму на пучки, то выражение (7.84) дает
энергию одного пучка:
2
4
<д^)и =
п„ е2£? Г
------------! +
т (со — ku)2 L
2ku
<0 — ku
(7.100)
При выводе этой формулы мы не использовали истинные начальные
условия, которые существенны только для резонансных частиц;
однако последние дают очень небольшой вклад в полную энергию
волны. Суммируя по пучкам, имеем
2 г?2 00
С -fo(“),-2 + (7.101)
4 т J (со — ku)2 L со — ku J
—оо
Здесь вторым слагаемым в квадратных скобках можно пренебречь
в пределе ®./£ итеПл, который мы используем, чтобы провести
сравнение с нашими предыдущими результатами. Дисперсионное
уравнение мы получим, используя уравнение Пуассона:
йеоЕ^ cos (fex—ш^) =—е^пг. (7.102)
и
Из формулы (7.79) для пг имеем
1 = — g2 V' • Пи —. & f (о (ц) cfu . (у ЮЗ)
eom (со.— k,u)2 епт J (со — ku)2
U —оо
Сравнивая это соотношение с (7.101), находим
с е2Е, гпт епЕ?
L_±_ = _o_l. =We> (7.104)
Таким образом,
Га,=.е0£?/2. (7.105)
Скорость изменения энергии.дается выражением (7.98), взятым
с отрицательным знаком:
d-Ww = — Wwa2p ( f0 (и)— \и -?*П..(Ю.-*Ц)Л du. (7.106)
dt J du L <o — ku J
248
Гл. 7. Кинетическая теория
Интегрирование по частям дает
dWtt> ____ ..у 2
— IF w<i>p
at
sin (<a — ku) t
и — ku
\u^ J.'n^-^Ldu
J du co — ku
—00
В случае регулярной функции /0 (и) проинтегрированная часть
равна нулю, и мы имеем
dWw
dt
оо
«в 2 Г •?'/ ,Г sin (ш — ku) t Т ,
= Ww — ЙР \ /о (И) ----1—I—— du,
k J L со — ku J
•• —oo
(7.107)
где и положено равным ы/k (постоянной), поскольку в интеграл
дают вклад только скорости, очень близкие к этой величине. Дейст-
вительно, при больших t квадратную скобку в (7.107) можно при-
ближенно заменить дельта-функцией
б (и-------—"j = — lim Г—^-1. (7.108)
\ k J Л L СО — ku J
Таким образом,
dW„, „л со ( со \ со
-Т- = —Г- h — ) = W>«0-£
at k k \ k / k2
(7.110)
(7.109)
Поскольку Im (о — это скорость нарастания (инкремент) величины
Ег, а энергия Ww пропорциональна £?, мы имеем
dWa/dt = 2[lm^)]Ww.
Следовательно,
Im (со) = (л/2) со (coPWo (со //г),
(7.1И)
что при co == cop согласуется с полученным ранее выражением (7.67).
7.6.1. Резонансные частицы
Теперь мы можем точно определить, какие частицы являются ре-
зонансными, т. е. какие частицы дают вклад в линейное затухание
Ландау. На рис. 7.25 показана функции/о (м), которая в (7.107)
стоит множителем в подынтегральном выражении. Мы видим, что
наибольший вклад дают частицы, у которых | со—ku | < л/t, или
| v—Рф | <л/А = М2; иными словами, это те частицы в начальном
распределении, которые не успели пройти половину длины волны
7.6. Физический вывод затухания Ландау 249
относительно волны. Как и ожидалось, ширина центрального мак-
симума с течением времени уменьшается. Дополнительные макси-
мумы в «дифракционной картине» на рис. 7.25 обусловливаются
теми частицами, которые прошли приблизительно одну половину
длины волны. Поскольку у этих частиц быстро нарастает разброс
по фазе, их вклад в среднем оказывается малым; начальное распре-
деление забывается. Заметим, что ширина центрального пика не
зависит от начальной амплитуды волны; следовательно, в группу
резонансных частиц могут входить как захваченные, так и незах-
ваченные частицы. Это явление не связано с захватом частиц.
7.6.2. Разрешение двух парадоксов
На рис. 7.25 видно, что подынтегральное выражение в уравнении
(7.107) является четной функцией переменной со—ku\ это означает,
что в затухание Ландау дают вклад как частицы, движущиеся бы-
стрее волны, так и частицы, движущиеся медленнее волны. Именно
так и происходит согласно физической картине, представленной на
рис. 7.24. Однако наклон кривой на рис. 7.25, который входит со-
множителем в подынтегральное выражение в (7.106), представляет
собой нечетную функцию переменной со—ku\ это означает, что ча-
стицы, движущиеся быстрее волны, отдают ей энергию, в то время
как частицы, движущиеся медленнее волны, отбирают от нее
энергию. Оба этих случая отличаются способом интегрирования
по частям. Рассмотрение в обоих случаях является правильным;
которое из них должно быть выбрано, зависит от того, что мы
хотим иметь под интегралом: /0 (и) или/0 («)•
Другой парадокс связан с галилеевской инвариантностью. Если
встать на точку зрения, что для затухания число частиц, движу-
щихся быстрее волны, должно быть меньше, чем более медленных
частиц, то до тех пор, пока мы находимся в системе отсчета, в ко-
торой плазма покоится, никаких проблем не возникает. Однако
Рис. 7.25. Функция, определяющая
относительный вклад частиц с раз-
личными скоростями в затухание
Ландау.
Рис. 7.26. Максвелловское распреде-
ление, в котором сточки зрения дви-
жущейся системы -отсчета может
быть область, приводящая к неу-
стойчивости.
250
Гл. 7. Кинетическая теория
если перейти в систему отсчета, движущуюся со скоростью V
(рис. 7.26), то частиц, движущихся быстрее волны, окажется
больше, чем тех, которые движутся медленнее ее, и волна на пер-
вый взгляд будет не затухать, а нарастать. Этот парадокс снимается,
если в выражении (7.100) восстановить второй член, которым мы
пренебрегли. Как показано в разд. 7.5.1, наличие этого члена мо-
жет привести к тому, что величина (AIFa) станет отрицательной.
Действительно, в системе отсчета на рис. 7.26 второй член в выра-
жении (7.100) не является пренебрежимо малым, величина
отрицательна и волна, по-видимому, имеет отрицательную энергию
(т. е. в невозмущенном распределении Максвелла с дрейфом заклю-
чено больше энергии, чем в том же распределении в присутствии
волны). И хотя волна «нарастает», добавление энергии к такой волне
с отрицательной энергией уменьшает ее амплитуду.
7.7. БГК-моды и моды ван Кампена
Мы видели, что затухание Ландау связано непосредственно с тре-
бованием, чтобы начальное распределение /0 (о) было однородным
в пространстве. Однако если с самого начала / (о, t — 0) сделать
постоянной вдоль траекторий частиц, то можно создать незатухаю-
щие электронные волны. Как нетрудно видеть из рис. 7.24, если
плазма приготовлена таким образом, что вдоль каждой траектории
плотность постоянна, частицы в среднем не приобретают и не те-
ряют энергии. Соответствующая волна называется БГК-модой
в честь Бернштейна, Грина и Крускала, которые первыми показали,
что возможно существование незатухающих волн с произвольными
<о, k, амплитудой и профилем. Образование БГК-моды опреде-
ляется относительным числом захваченных и незахваченных ча-
стиц, представляющим собой критический параметр при конструи-
ровании f (v, t — 0). В пределе малой амплитуды БГК-мода прев-
ращается в так называемую моду ван Кампена. В этом пределе за-
хватываются лишь частицы с ц = цф. Число захваченных частиц
можно изменить, если добавить к / (v, / = 0) член, пропорцио-
нальный 6 (о—Цф). Из рис. 7.24 следует, что добавление частиц
вдоль линии v — Оф не будет приводить к затуханию в последую-
щие моменты времени, поскольку при этом частиц, приобретающих
энергию, будет столько же, сколько и теряющих ее. Действительно,
выбирая распределения с 6-функциями при других значениях цф,
можно генерировать незатухающие волны ван Кампена с произ-
вольной Оф. Однако такие начальные условия не имеют физического
смысла. Для того чтобы получить гладко меняющуюся функцию
/ (о, t — 0), необходимо выполнить суммирование по модам ван
Кампена с распределением по скоростям оф. Теперь, хотя каждая
мода не является затухающей, полное возмущение проявит зату-
хание Ландау, поскольку фазы различных мод оказываются не-
синхронизованными друг с другом.
7.8. Экспериментальная проверка
251
7.8. Экспериментальная проверка
Хотя Ландау дал безупречный и четкий вывод бесстолкновительного
затухания, сначала было не ясно, что это имеет отношение к физи-
чески наблюдаемому явлению, до тех пор пока Даусон не выполнил
более длинного, основанного на интуиции вывода, воспроизведен-
ного в разд. 7.6. Даже после этого были сомнения относительно
того, удастся ли в лаборатории создать подходящие для наблюде-
10 Z0 30 40
Расстояние между зондами
Рис. 7.27. Интерферометрическая запись, показывающая распределение воз-
мущенной плотности в затухающей плазменной волне. (Из работы: Malm-
berg J. И., Wartbn С. В., Phys. Rev. Lett., 17, 175 (1966). ]
Рис. 7.28. Проверка затухания Ландау в эксперименте Малмберга и Вар-
тона. [Из работы: Malmberg J. Н., Warton С. В., Phys. Rev. Lett., 17, 175
1966).]
252
Гл. 7. Кинетическая теория
Рис. 7.29. Экспериментальное определение дисперсионной зависимости для
плазменных волн в плоской геометрии. [Из работы: Derfler И., Simonen Т.,
J.JAppl. Phys., 38, 5018 (1967).]
ния условия. Эти сомнения разрешил проведенный в 1965 г. экспе-
римент Малмберга и Вартона. Для возбуждения и детектирования
плазменных волн в столбе бесстолкновительной плазмы в этом
эксперименте использовались электростатические зонды. С по-
мощью интерферометрии были получены зависимости фаз и ампли-
туд волн от расстояния между зондами. На рис. 7.27 показана за-
пись волны, затухающей в пространстве. Поскольку в эксперименте
величина со вещественна, a k комплексна, полученный нами резуль-
тат в виде выражения (7.70) нельзя сравнить с экспериментальными
данными. Вместо этого мы должны вычислить отношение
Im (£)/Re (k) при вещественных со. Это отношение содержит также
множитель ехр (— 1>ф/утепл), который пропорционален числу ре-
зонансных частиц в максвелловском распределении. Следовательно,
логарифм отношения Im (£)/Re (k) должен быть пропорционален
(Цф/отепл)2- Из рис. 7.28 мы видим, что экспериментальные и тео-
ретические результаты согласуются друг с другом.
Аналогичный эксперимент в плоской геометрии выполнили Дер-
флер и Симонен; этот эксперимент позволил сравнить измеренные
7.8. Экспериментальная проверка 253
значения Re (со) с выражением (7.64). На рис. 7.29 представлены
результаты измерений для Re (k) и Im (k), полученные этими ав-
торами при различных частотах. Штриховая кривая построена
в соответствии с выражением (7.64) и является той же самой, что
и на рис. 4.5. Отклонение экспериментальных точек от штриховой
кривой обусловлено тем, что в разложении (7.59) мы не учитывали
члены более высокого порядка. Однако построенная в соответствии
с выражением (7.54) теоретическая кривая хорошо согласуется
с экспериментальными данными.
Задачи
7.1. В плазме с п= 101’м-3 и КТе= 10 эВ возбуждаются плазменные волны.
Вычислите приближенно декремент затухания Ландау | Im (со/сор) |, если
k = 10* м-4
7.2. В плазме с п = 1015 м—3 и КТе = 10 эВ возбуждается электронная плаз-
менная волна с длиной волны 1 см. Затем источник возбуждения отключается
и волна затухает бесстолкновительным образом (затухание Ландау). Через
какой промежуток времени амплитуда волны уменьшится в е раз?
7.3. Неограниченная однородная плазма с неподвижными ионами имеет функ-
цию распределения электронов, составленную из 1) максвелловского распре-
деления собственно «плазменных» электронов с плотностью пв и температу-
рой Тр, находящегося в покое в лабораторной системе, и 2) максвелловского
распределения электронов «пучка» с плотностью пь и температурой Ть, имею-
щего центр при v = Vx (рис. 37.3). Если плотность пь бесконечно мала, то
колебания вдоль оси х затухают. Ецли же плотность пь велика, то возникает
двухпотоковая неустойчивость. Критическое значение пь, при котором уста-
навливается неустойчивость, можно найти, полагая наклон общей функции
распределения равным нулю. Для того чтобы ограничиться простыми вы-
кладками, предлагается получить приближенный ответ следующим образом:
а) запишите выражения для fp(u) и fb(y), используя следующие сокра-
щенные обозначения: v = vx, а2 = 'i.K.Tplm, b2 = 2KTblm\
б) предположите, что фазовая скорость оф равна значению скорости v, при
котором fb (ц) имеет наибольший положительный наклон. Найдите оф и
4 (%)•-
в) вычислите f' (иф) и положите f'p (оф) + fь (°ф) = °!
Рис. 37.3. Невозмущенные функции распределения электронов плазмы fp (ох)
и пучка fb (ух) при рассмотрении взаимодействия плазмы с пучком.
254
Гл. 7. Кинетическая теория
г) покажите, что в случае критическая плотность пучка приближенно
записывается в виде
(nblnp) = (2e)V2 (TbITp) (Via) ехр (-V2/a2).
7.4. Предположите, что в некоторой модели теплой плазмы ионная и элек-
тронная функции распределения даются соответственно выражениями
7г0 (») = (Vя) (у2 + ае)~1 ’ • Ло (») = (Vя) О’2 + «?)"’ •
а) Используя уравнение Власова, получите точное дисперсионное уравнение
для электростатических возмущений.
б) Получите приближенное выражение для дисперсионного уравнения при
со йр. При каких условиях волны слабо затухают? Дайте физическое
объяснение, почему со.« в случае очень больших k.
7.5. Рассмотрите незамагниченную плазму с нейтрализующим неподвижным
фоном ионов. Одномерная функция распределения электронов имеет вид
[foe (f) = go (о) + йо (v),
где
go (°) = пр (ае/п) (о2 + а2)-1, h0 (о) = пь6 (о —1>0),
«о = пр + пь и пь < пр\
а) выведите дисперсионное уравнение для высокочастотных электростатиче-
ских возмущений;
б) в пределе со/А ае покажите, что существует решение, в котором
Im (со) > 0 (т. е. возмущения нарастают).
7.6. Имеется одномерная функция распределения
f(v)=A, |o|<om,
/(v) = 0, I о |>om.
а) Найдите выражение для постоянной А через плотность плазмы п0.
б) С помощью уравнений Власова и Пуассона попробуйте получить интег-
ральное выражение для электростатических электронных плазменных волн,
в) Вычислите интеграл и получите дисперсионную зависимость со (А) с точ-
ностью до членов третьего порядка относительно малой величины kvmla>.
7.9. Затухание Ландау на ионах
Резонансными частицами могут быть не только электроны. Если
фазовая скорость волны достаточно мала и оказывается сравнимой
с тепловой скоростью ионов, то становится возможным затухание
Ландау на ионах. В частности, сильно подвержены затуханию
Ландау ионно-звуковые волны. Напомним, что в соответствии с
(4.41) дисперсионное уравнение для ионных волн имеет вид
“ KT' + yiKTt у/2
T~Vs~{ м )
(7.112)
Если Те ==£ Т(, то фазовая скорость попадает в область, в которой
наклон функции распределения foi (о) отрицательный (рис. 7.30, а).
Следовательно, в этом случае ионные волны испытывают сильное
255
Рис. 7.30. К объяснению затухания Ландау ионно-звуковых волн, а —
Те « Тс, фазовая скорость волн лежит внутри ионной функции распределе-
ния; б — ТеСс Тс, очень немногие ионы имеют скорость, близкую к фазо-
вой; добавление легких ионов (штриховая кривая) приводит к увеличению
затухания Ландау.
затухание Ландау. Их можно наблюдать лишь в случае Те '^ Т}
(рис. 7.30, б), когда фазовая скорость лежит далеко в хвосте рас-
пределения ионов по скоростям. Алексеев, Джонс и Монтгомери
использовали хитроумный способ введения затухания Ландау кон-
тролируемым образом. В плазме с тяжелыми ионами (такими, как
ксенон) при Те Tt создавалась слабозатухающая ионно-звуко-
вая волна. Затем к плазме добавлялось небольшое количество лег-
ких атомов (гелия). Поскольку образовавшиеся ионы гелия имели
почти ту же самую температуру, что и ионы ксенона, но значительно
меньшую массу, функция распределения атомов гелия была более
широкой (на рис. 7.30, б это распределение показано штриховой
кривой). При этом волна испытывала затухание на резонансных
ионах гелия.
7.9.1. Дисперсионная функция плазмы
Рассмотрим теперь ионное затухание Ландау ионно-звуковых волн
в отсутствие магнитного поля; это позволит нам познакомить чи-
тателя с некоторыми общепринятыми понятиями кинетической
теории. Ионы и электроны подчиняются уравнению Власова (7.23),
а их возмущения описываются выражением (7.46), определяющим
распространение этих возмущений в виде плоской волны вдоль
оси х. Решение для Д дается выражением (7.48) с соответствующими
изменениями:
— dfoildvi , (7.113)
mj <о — kvj
Ex и vxj мы обозначили просто через Е и vjt причем /-й сорт
частиц имеет заряд qj, массу nij и скорость V/. Возмущение плот-
ности частиц /-го сорта можно записать в виде
nv = { fv(v,)dv, = —i-^-E ( dfoi,dvi dv,. (7.114)
J mj J co — kvj
256
Гл. 7. Кинетическая теория
Пусть равновесные функции распределения /0;- являются одномер-
ными максвелловскими распределениями:
f0 : = — _ °//®тепл» / (QKT Im V/2 1/2 6 > ^тепл, j—(21x1 jltTlj) итепл» (7.115)
Вводя немую переменную интегрирования s = vflцТепЛ, /, возму-
щение плотности можно записать в виде
i / 1_ C J4/4s)_e s_rf пб) km v2 л1/2 J s — Ъ Rrnj итепл» / 31
где s (в/^Отепл,/• (7.117)
Определим дисперсионную функцию плазмы Z (£):
? “~4^> Im(£)>0. (7.118) я1/2 j s-g — 00
В разд. 7.4 мы показали, что этот интеграл является контурным
и что, если Im (?) <0, следует использовать его аналитическое
продолжение на нижнюю полуплоскость. Величина Z (£) — это
комплексная функция комплексного аргумента (поскольку со или
k имеет, как правило, мнимую часть). В тех случаях, когда.Z(£)
не может быть аппроксимирована какой-либо аналитической фор-
мулой, можно воспользоваться таблицами Фрида и Конте или стан-
дартной подпрограммой для компьютера.
Чтобы выразить через Z (С), вычислим производную от Z
по С:
Z' (£) =
я1/2 J (S-02
—оо
Интегрирование по частям дает
Z' (С) =
1 Г — e~s! 1°° 1 С (d/ds) (e s3)
л1/2 L s-е
Как и для любой регулярной функции распределения, первый член
обращается в нуль. При этом выражение (7.116) можно переписать
в виде
=
i 4jEn0 j
кт^епЛ, j
(7.119)
7.9. Затухание Ландау на ионах 257
Запишем уравнение Пуассона
e0V • Е = i ke0E = X д{п1Г (7.120)
!
Объединяя последние два уравнения, выписывая явно электронный
член и определяя величину
QfJ = (n0lZ2e2/e,0M}y/2, (7.121)
получаем следующее дисперсионное уравнение
“n V ®2„,-
^Z'Z'&). (7.122)
итепл» е I утепл./
Отсюда, полагая Qp;- = 0 (для бесконечно тяжелых ионов), можно
получить электронные плазменные волны. Определим величину
&D = 2й>р/и?епл, е = ^D2- (7.123)
Тогда мы можем написать соотношение
WD=-i-Z'O (7.124)
которое есть не что иное, как соотношение (7.54), полученное для
случая максвелловского распределения /Ое.
7.9.2. Ионные волны и их затухание
Для того чтобы получить ионные волны, вернемся к соотношению
(7.122) и воспользуемся тем обстоятельством, что их фазовые Ско-
рости talk много меньше, чем Утепл.^; следовательно, мало и
можно разложить Z (£е) в степенной ряд:
Z(C)=iV^е"^-2?ер-^-Й+ . . (7.125)
Мнимый член возникает благодаря вычету в полюсе, расположен-
ному вблизи вещественной оси s [см. (7.56) ], и представляет элек-
тронное затухание Ландау. В случае t,e < 1 производная выраже-
ния (7.125) запишется в виде
-г2
Z'(Q=-2iVn tee s*-2+ . . ; «-2. (7.126)
Электронным затуханием Ландау обычно можно пренебречь, по-
скольку наклон функции fe (р) вблизи ее максимума мал. Заменяя
в дисперсионном уравнении (7.122) Z'(U на — 2, получаем диспер-
сионное уравнение для ионно-звуковых волн:
Y*! Q 2
X2d) -р' Z'(Cy)^ l+fe2X2D^ 1. (7.127)
/ ^тепл,/
Здесь член A2^d представляет отклонение от квазинейтральности.
9 Заказ 3170
258
Гл. 7. Кинетическая теория
Рассмотрим случай, когда имеется один сорт ионов. Так как
пОе ~ коэффициент при Z'(C/) в (7.127) запишется в виде
V п°^ М 1 ZT‘
^епл,. «о/ ео^ 2ЛТ, 2 г.
В случае £2Xd 1 дисперсионное уравнение принимает вид
(7.128)
Решение этого уравнения не простая задача. Предположим, что
для изучения затухания во времени мы выбрали величину k ве-
щественной, а и комплексной. При этом вещественную и мнимую
части величины со мы должны подобрать таким образом, чтобы вы-
полнялись условия Im (Z') = 0 и Re (Z') = 2TJZTe. В общем слу-
чае имеется множество корней со, удовлетворяющих этим условиям,
причем все они имеют Im со <0. Главным из этих корней является
тот, который дает наименьшее затухание, т. е. имеет наименьшую
величину-| Im (со) |. Затухание в пространстве обычно исследуют,
полагая частоту со вещественной, а волновое число k комплексным.
Снова мы получаем ряд корней k с. Im k > 0, которые определяют
затухание в координатном пространстве. Однако главный корень
здесь не соответствует тому же значению Сс, что и в случае комплекс-
ной величины со. Оказывается, при решении пространственной за-
дачи следует относиться с особым вниманием к механизму возбуж-
дения на границе и более аккуратно обращаться с членом Z'(Ce)
для электронной компоненты.
Чтобы получить аналитические выражения, рассмотрим пре-
дельный случай Zi 1, соответствующий большому отношению
температур Q = ZTJTt. Асимптотическое выражение для Z'(СО
записывается в виде
__ _£.2
Z'(C0 = -2iVn Ссе ‘ + СГ2+ -^-СГ4+ • • • • (7-129)
Если затухание мало, то в первом приближении можно пренебречь
членом, отвечающим затуханию Ландау. При этом выражение
(7.128) принимает вид
$ V 2 « ) 0
Поскольку мы предположили, что 0 велико, величина С; также ве-
лика; поэтому во втором члене Сс можно заменить на 0/2. Таким
образом, мы имеем
-—fn-— у=—’ <7Л30>
V е ) в 22
7.9. Затухание Ландау на ионах
259
или
о2 2KTt / 3 . ZTe \ ZKTe + 3KTi /7 iqi\
--------м~ + WJ = м (7’131}
Это есть не что иное, как дисперсионное уравнение (4.41) для ионно-
звуковых волн при yt = 3, обобщенное на случай'произвольных Z.
Подставим затем выражения (7.129) и (7.130) в'(7.128), сохранив
член, отвечающий затуханию Ландау:
14-----I— 21-ул £{е =—,
0 J 0
1 /
с? I
Раскладывая квадратный корень в ряд, мы имеем
~ RT О - 4~ ‘e“s?) <7-132)
Используя в мнимом члене выражение (7.130), мы находим прибли-
женное выражение для декремента затухания:
---1т^_ = 1тш_ = / _л_у/2 0 (3 0.1/2 е-(3+0)/2( (7.133)
Re Zi-------Re <0 \ 8 J 7 v
где 0 = ZTjTi, a Rea определяется формулой (7,131).
Выражение (7.133) является асимптотическим; оно справедливо
при больших 0 и показывает, что с ростом 0 затухание уменьшается
по экспоненте. В случае когда 0 <10, выражение (7.133) становится
неточным и затухание следует вычислять с помощью формулы
(7.128), в которой сохраняется Z-функция. Для экспериментально
интересной области 1 <0 <10 достаточную точность дает следую-
щая простая аналитическая формула:
Imco/Reco = 1,107/4ехр ( —02). (7.134)
На рис. 7.31 сравниваются результаты расчетов по приближенным
формулам (7.133) и (7.134) с точным расчетом по формуле (7.128).
Что произойдет, если к ионному затуханию Ландау добавить столк-
новения? Оказывается, удивительно немного. Столкновения ионов
с электронами малоэффективны, так как ионная и электронная
жидкости движутся почти совместно и трение между ними неболь-
шое. Ион-ионные столкновения (ионная вязкость) могут привести
к затуханию ионно-звуковых волн, но известно, что, несмотря на
столкновения, звуковые волны хорошо распространяются в воздухе.
9*
260
Гл. 7. Кинетическая теория
Рис. 7.31. Затухание Ландау ионно-звуковых волн на ионах. Кривая А —
точное решение с помощью формулы (7.128); кривая Б —асимптотическая
формула (7.133); кривая В —эмпирическая формула (7.134), справедливая
в области 1 <Й <10.
Действительно, столкновения нарушают резонансы частиц с вол-
ной, которые обусловливают затухание Ландау, и полное затухание
оказывается даже меньше затухания Ландау, если только частота
столкновений не слишком велика. Таким образом, ионное затуха-
ние Ландау почти всегда является доминирующим процессом для
ионных волн и экспоненциально зависит от отношения ZTJTi.
Задачи
7.7. В однократно ионизованной плазме из ксенона (Я= 131) с Те =1 эВ и
Tt — 0,1 эВ возбуждается ионно-звуковая волна с длиной 1 см. Сколько
времени понадобится на то, чтобы после отключения генератора амплитуда
волны благодаря затуханию Ландау уменьшилась в е раз по сравнению со
своим начальным значением?
7.8. В однократно ионизованной аргоновой плазме с пе— 1016 м—3, 7^—2 эВ,
Ti — 0,2 эВ возбуждается ионная волна с длиной Л. = 5 см и измеряется ее
декремент затухания «Ландау. Затем в плазму вводят примесь водорода с
плотностью пн — але. Вычислите значение а, при котором декремент зату-
хания увеличится в два раза.
7.9. В экспериментах по лазерному термоядерному синтезу кроме основного
распределения электронов с плотностью пе и температурой Те нередко встре-
чается группа горячих электронов с плотностью пь и температурой Т^. Гс-
7.10. Кинетические эффекты в магнитном поле
261
рячие электроны могут изменить затухание ионных волн и, следовательно,
повлиять на такие процессы, как вынужденное бриллюэновское рассеяние.
Предполагая, что Z = 1 для ионов с гц и определите = TjTit Од =
= ThlTiy а = nft/ni, 1—а = пе/щ, е = mlМ и &2d/ = nie2/s0KTi.
а) Запишите дисперсионное уравнение для ионно-звуковых волн в трехком-
понентной плазме, раскладывая в ряд электронные Z-функции.
б) Покажите, что с ростом nh электронное затухание Ландау не увеличивается
заметно, если 7\ » Те.
в) Покажите, что с ростом лд ионное затухание Ландау уменьшается и что
это явление можно представить как увеличение эффективного отношения тем-
ператур TelTi.
7.10. Дисперсионное уравнение для электронных плазменных волн, распро-
страняющихся вдоль Boz, можно получить из диэлектрического тензора е
(см. приложение Б) и уравнения Пуассона, v-(e-E) = 0, где Е = — уФ.
При этом для однородной плазмы
d /
л I22
дг \
= 8ггФ = 0
ИЛИ 8.22 = 0. Для холодной плазмы
задача 4.4 и уравнение (Б. 18) дают
8^ = 1 — (Ор/со2 или ш2=со2.
Для горячей плазмы из (7.124) имеем
ezz — 1
СО2
-----*—Z'
k2v2
к итепл
Используя разложение Z-функции в соответствующем пределе, покажите,
что это уравнение дает частоту волны Бома—Гросса [выражение (4.30)]
и декремент затухания Ландау [выражение (7.70)].
7.10. Кинетические эффекты в магнитном поле
Если имеется конечное постоянное магнитное поле Во или осцилли-
рующее магнитное поле Вп то в уравнение Власова для бесстолк-
новительной плазмы (7.23) следует включить член v X В. При этом
линеаризованное уравнение (7.45) заменяется уравнением
^ + у?Л + -^(ухВ0)--^-= --2-(E1 + vxB1).
dt m dv m dv
(7.135)
Движущиеся вдоль Bo резонансные частицы по-прежнему вызы-
вают затухание Ландау, если а>/Л итепЛ» но теперь появляются
два новых кинетических эффекта, которые связаны с компонентой
скорости Vj_, перпендикулярной Во. Один из них—это циклотрон-
ное затухание, которое мы рассмотрим ниже, другой — генерация
циклотронных гармоник, приводящая к возбуждению колебаний,
называемых обычно модами Бернштейна.
262
Гл. 7. Кинетическая теория
Гармоники циклотронной частоты возбуждаются, когда круго-
вое движение частицы по ларморовской орбите возмущается по-
лями Ех и Bj. В обычной гидродинамической теории пренебрегают
этими эффектами, связанными с конечным rL, но они могут быть
учтены до членов порядка Л2г2, если ввести тензор вязкости л.
Кинетический подход является аккуратным даже при Л2Гь = О (1).
Для того чтобы понять, как возникают гармоники, рассмотрим
движение частицы в электрическом поле:
E=£Jcei(^“°x. (7.136)
При этом уравнение движения [ср. с уравнением (2.10)1 запишется
в виде
+ w = (7.137)
т
Если krL не мало, то экспонента имеет различные значения на раз-
ных сторонах орбиты. В соответствии с (2.7) величину х в экспо-
ненте можно приближенно заменить невозмущенной траекторией
х = z-Lsin acf:
х+ысх = ^-Ех е‘ sin (7.138)
т
Для функции Бесселя Jn (z) производящая функция записывается
в виде
e2«-iW2= g tnjn^zy (7.139)
n=—oo
Полагая z = krv и t = exp (i ®c/), получаем
ei krL sin vct (fa) ei ; (7. 140)
—00
Нш2сх = -2-Е,ЕЛ(^)е',(в’ла')<. (7.141)
/71 —oo
Следующее решение можно проверить прямой подстановкой:
\ ------- (7.142)
т n“c)
—oo
Отсюда следует, что в движении присутствуют компоненты, ча-
стоты которых отличаются от ведущей на величину, кратную
и что амплитуды этих компонент пропорциональны
Л(^ь)/[<и2 — (м—п«с)2].
В случае когда знаменатель обращается в нуль, амплитуда стано-
7.10. Кинетические эффекты в магнитном поле 263
вится очень большой. Это имеет место при со—па>с = ± сос, или
со = (п ±1) сос, где /1—0, ±1, ± 2, . . ; иными словами, когда
поле Е (х, t) резонирует с какой-либо гармоникой основной час-
стоты сос, амплитуда резко возрастает. В гидродинамическом пре-
деле krL -> 0 функцию Jn (£/ь) можно аппроксимировать выра-
жением (krL/2)n/nl, которое стремится к нулю при всех п, кроме
п = 0. При п = 0 коэффициент в разложении (7.142) равен
(со?—со2)"1, что совпадает с результатом, полученным в рамках
гидродинамической теории [ср. с (4.57)] и содержащим только ос-
новную циклотронную частоту.
7.10.1. Диэлектрический тензор горячей плазмы
Проведя анализ Фурье для (г, v, f) в координатном пространстве
и во времени, уравнение (7.135) можно решить в случае максвел-
ловского распределения /0 (v) и затем использовать полученные ре-
шения для (k, v, со), чтобы вычислить плотность и ток, создавае-
мые каждым сортом частиц. Результат такого вычисления обычно
выражают в виде эквивалентного диэлектрического тензора 8, так
что при получении дисперсионных уравнений для различных волн
(см. приложение Б) в уравнениях Максвелла v-D = 0 и V X В =
= p,0D можно использовать вектор смещения D = е-Е. Алгебраи-
ческие выкладки имеют устрашающие размеры, и поэтому мы их не
приводим. Приведем здесь лишь частный результат, справедливый
для нерелятивистской плазмы с изотропным давлением (Tj_ = Тц)
в отсутствие дрейфа v0/ в нулевом порядке; этих ограничений легко
избежать, но для наших целей общие формулы слишком не-
обозримы. Таким образом, положим k = kxx + k2z, причем еди-
ничный вектор z направим вдоль вектора Во; поскольку в плоскости,
перпендикулярной Во, плазма изотропна, то, полагая ky равным
нулю, мы нисколько не теряем общности рассмотрения. Теперь вы-
пишем компоненты тензора 8Л = 8/е0:
2 ь +°°
1 + £ \ Со Е ”2 In {b)z (U
s —oo
4-oo
Еш2 e~6 V
+2fe2 z &),
S —oo
—oo
^xy ~ ^yx — i e Co n [Л (fc) — In (^)l 2 (Cn),
S —OO
(7.143)
264
Гл. 7. Кинетическая теория
—{-ОО
Z<o2n е~ь V
~2~ ,9, Л/2 -О / flln (&) Z' (£„),
(0 (ZD) ' / j
S —00
-1-00
ер2 = -e2i, = -i £ ±-^-(А)1'2^ £ [Z^)-4 (£)]/'(?„),
S —оо
-рое
егг = 1 - £ -J- е“Чп £ 1п (Ь) ^Z' (?„),
S —оо
где Z (?) — плазменная дисперсионная функция, определяемая вы-
ражением (7.118), 1п (b)— функция Бесселя n-го порядка мни-
мого аргумента, а другие величины определяются следующим об-
разом:
COps nOsZs € /8()/72s,
?«s — (® 4“ Я®р2)/^гПтепл, S’ toj — <й//г2Цтепл, s>
acs = | Z^eBolms |,
(7.144)
Утепл, s = 2KTslms,
bs = ±kVLs = £KTJms<£.
В выражениях (7.143) первая сумма берется по сортам частиц $,
причем предполагается, что <ор, Ь, ?0 и ?„ зависят от s и что знак +
определяется зарядом частиц. Второе суммирование производится
по номерам гармоник п. Штрих означает дифференцирование по
аргументу.
Как мы и предвидели, появились функции Бесселя от пара-
метра Ь, связанного с конечным ларморовским радиусом г^. [За-
мена Jn (b) на 1п (b) происходит при интегрировании по скоро-
стям. ] Компоненты тензора е, отвечающие составляющей движения
вдоль z, содержат функцию Z' (?„), которая приводит к затуханию
Ландау, когда п = 0 и a/kz « Щеп л- Наличие членов с п =# 0 при-
водит к другому возможному механизму бесстолкновительного за-
тухания, а именно к циклотронному затуханию, которое имеет
место При ((О ± п<лс)1кг « Щепл-
Задача
7.11. Покажите, что в пределе нулевой температуры компоненты тензора е
в выражениях (7.143) сводятся к компонентам диэлектрического тензора
для холодной плазмы, представленного в приложении Б.
7.10. Кинетические эффекты в магнитном поле 265
7.10.2. Циклотронное затухание
При определенной скорости частица, движущаяся вдоль внешнего
магнитного поля Во в волне с конечным kz, будет «видеть» волну
со сдвинутой вследствие эффекта Доплера частотой <о—kzvz =
± пас и поэтому под действием электрического поля волны Ех
она будет непрерывно ускоряться (замедляться). Энергия тех ча-
стиц, которые находятся в «правильной» фазе относительно Ех,
будет увеличиваться, а тех, что в «неправильной» фазе,— будет
уменьшаться. Поскольку изменение энергии есть произведение
силы на путь, более быстрые ускоряемые частицы приобретут за
единицу времени больше энергии, чем потеряют медленные частицы,
испытывающие торможение. Таким образом, в среднем происходит
увеличение энергии частиц за счет энергии волны, и волна затухает.
Этот механизм совсем не тот, что в случае затухания Ландау, по-
скольку усиление энергии происходит здесь в направлении, перпен-
дикулярном Во, и, следовательно, перпендикулярно компоненте
скорости частицы, дающей резонанс. Такое явление, как захват,
не может легко нарушить этот резонанс. Кроме того, для затухания
достаточно лишь наличие резонансных частиц; нет необходимости
иметь положительный наклон /о (vz), как в случае затухания
Ландау.
Для того чтобы прояснить физический механизм циклотронного
затухания, рассмотрим волну, у которой k = kxx + kzi, причем
составляющая kz положительна. Электрическое поле Ех можно
разложить на левую и правую циркулярно поляризованные ком-
поненты, как изображено на рис. 7.32. На рис. 7.32, а показано
расположение вектора Ех в точках А, В и С вдоль оси + z для ле-
вополяризованной компоненты. Так как волна распространяется
в положительном направлении оси z, неподвижный электрон уви-
Рис. 7.32. Механизм циклотронного затухания, а — для левополяризованной
компоненты; б — для правополяризованной компоненты.
266
Гл. 7. Кинетическая теория
дит эти векторы сначала в точке С, потом в В, а затем уже в А;
следовательно, он увидит поле Е, имеющее левое вращение. При
этом электрон не будет ускоряться, поскольку его ларморово вра-
щение является правосторонним (по часовой стрелке). Однако,
если бы скорость электрона в направлении z была больше, чем у
волны, то он увидел бы векторы в А, В и С, т. е. в прямой последо-
вательности и, следовательно, должен был бы ускоряться ре-
зонансно, когда его скорость удовлетворяет соотношению
<о—kzvz = — со^. Поведение правополяризованной компоненты Е
показано на рис. 7.32, б. Теперь электрон, если он движется мед-
леннее волны, будет видеть электрическое поле, вращающееся по
часовой стрелке, так что на него последовательно действуют век-
торы электрического поля в точках С, В и А. Этот электрон будет
ускоряться при выполнении условия w—kzvz = + <ос. Таким об-
разом, плоская или эллиптически поляризованная волна будет
затухать благодаря электронам, движущимся в любом направле-
нии в системе отсчета, связанной с волной.
7.10.3. Моды Бернштейна
Электростатические волны с частотами, кратными циклотронной,
распространяющиеся под прямым углом к Во, называются модами
Бернштейна. Их дисперсионное соотношение можно найти, под-
ставляя выражения (7.143) для компонент диэлектрического тен-
зора в уравнение Пуассона v-s-E = 0. Если предположить воз-
мущение электрическим, так что Ех = — v^i, и рассматривать
волны вида = ^Хехр [i (k-r—со/)], то уравнение Пуассона
можно записать следующим образом:
^хехх + 2Йх/ег8гх-|-/ггегг== 0. (7.145)
Заметим, что мы выбрали такую систему координат, что вектор к
лежит в плоскости xz, a ky = 0. Подставим в уравнение (7.145) вы-
ражения для sxx, exz, и ezz из (7.143) и выразим Z' (£„) через Z (£„)
с помощью тождества
Z'(U=-2U + U(S)]. (7.146)
Задача
7.12. Докажите тождество (7.146) непосредственно из интегральных выраже-
ний для Z (?) и Z' (£).
Уравнение (7.145) принимает вид
ОО
£Л(6)
S n=s—ОО
- 2 2 nkxkz (1 + ZnZj-Zk2^ (1 + £„Z)] = 0. (7.147)
7.10. Кинетические эффекты в магнитном поле
267
Пользуясь тем, что b = А2п2епл/2со2, а tn = (® + псое)/АгЦтепЛ, вы-
ражение в квадратных скобках с помощью небольших алгебраи-
ческих преобразований можно упростить и свести к виду:
2а2 [u« + &z (и].
Замечая затем, что для каждого сорта частиц 2A2co2to/tt)2 =
= 2(0р/и2епл = Ad, уравнение (7.147) можно переписать следую-
щим образом:
/£ + Аг + 2>2ое-6 £ ЛЖ[-Ло + и?0 = 0. (7.148)
S П——ОО
В этом уравнении член t-n/£o равен 1—гшс/<л. Поскольку 1п =
= 1_п (Ь), сумма слагаемых /„(Ь)п®с/ю по и от — оо до оо дает
нуль; следовательно, t-n/Co можно заменить на 1. Определяя А2 =
= А2 + А2, получаем общее дисперсионное уравнение для волн
Бернштейна:
1+ Е /W[l + :oZO = 0. (7.149)
S Х П=—ОО
1. Электронные моды Бернштейна. Рассмотрим сначала высо-
кочастотные волны, в которых ионы остаются неподвижными. Эти
волны не чувствительны к малым отклонениям от перпендикуляр-
ного распространения, и мы можем положить Аг = 0, так что tn ->-оо.
Следовательно, циклотронное затухание отсутствует; найденные
нами ниже щели в спектре волн обусловлены не этим затуханием.
В соответствии с разложением (7.129) мы можем заменить Z (tn)
при больших U на — 1/tn. Во второй сумме (7.149) слагаемое с
п = 0 сокращается, и эту сумму можно разбить на две следующим
образом:
Al + £ A2d е-6 £ In (b) (1 - to/U) + Е I-n (b) (1 - to/Un) = 0
$ Ln—1 П=1
(7.150)
или
оо
А2Х + У Ad е“6 У 1п (Ь) Г2----------------------------1 = 0. (7.151)
L + no>c <o — ntoc J
n=l
После приведения к общему знаменателю квадратные скобки сво-
дятся к единственному члену:
2 ;2
СО —
2л2ю2
(7.152)
268
Гл. 7. Кинетическая теория
Рис. 7.33. Функция а (со, Ь) для электронных волн Бернштейна. [Из работы:
Bernstein I. В., Phys. Rev., 109, 10 (1958).]
Используя определения величин kv и Ь, получаем известное дис-
персионное уравнение для случая kz = 0:
(со/лсос)2 — 1
(7.153)
Рассмотрим теперь конкретный случай электронных колебаний.
Опуская суммирование по сортам частиц, из уравнения (7.152)
получаем
ОО
А2 л о \ 1 е—ь1п (Ь)п2
= / 2 о (7Л54>
lrD / , or — пчгс
П=1
Функция а (со, 6) для Ь = 1 показана на рис. 7.33. Значения со
определяются точками пересечения графика функции а с горизон-
тальной прямой >0. Из рисунка видно, что возможные зна-
чения со лежат чуть выше каждой циклотронной гармоники и что
ниже каждой гармоники расположена запрещенная зона.
Чтобы перейти к гидродинамическому пределу, заменим в со-
отношении (7.153) функцию 1п (Ь) ее асимптотическим значением
(Ь/2)п/п\ при малых Ь. В пределе Ь -> 0 остается только член с
п — 1 и мы имеем:
9 х 2 \ — 1 О
<->р 2 6 / “ Л ЫР
со2 ь 2 ш2 J со2 —<в2
(7.155)
2 2 । 2 2
или со = сор + сос = сой, т. е. дисперсионное уравнение для верхне-
гибридных колебаний. Таким образом, при kx -> 0 частота сой
7.10. Кинетические эффекты в магнитном поле
269
Рис. 7.34. Дисперсионные кривые для электронной моды Бернштейна. [Из
работы: Crawford F. W., J. Appl. Phys., 36, 2930 (1965); рисунок приведен
с упрощениями. ]
должна быть одним из корней уравнения (7.154). Если а>Л попадает
между двумя высшими гармониками частоты wc, то вблизи со = <вЛ
форма кривой <в (k) изменяется таким образом, что при k± -+ 0
частота <в -> <вЛ. Для построения кривых со (Л) умножим уравне-
ние (7.154) на 2сор/®с и получим k^rl = 4co₽ а (со, Ъ). На рис. 7.34
представлены кривые зависимости величин со/сое от &±гь Для раз-
личных значений сор/со«. Заметим, что для каждого значения сор/сор
выше соответствующей этому случаю гибридной частоты характер
кривой заметно меняется. В крайней левой части данного графика,
где фазовая скорость приближается к скорости света в плазме,
в эти кривые следует включить электромагнитные поправки.
Электронные моды Бернштейна были зарегистрированы в ла-
бораторных исследованиях. В газовых разрядах при этом наблю-
дались также необъяснимо большие спонтанные колебания на выс-
ших гармониках сос. Однако это слишком долгая история, чтобы
ее здесь рассказывать.
2. Ионные моды Бернштейна. Среди волн с частотами, лежащими
вблизи гармоник ионно-циклотронной частоты, следует различать
чисто ионные моды Бернштейна, для которых kz — 0, и нейтрали-
зованные ионные моды Бернштейна, для которых kz имеет малое,
но конечное значение. Различие между ними состоит в том, что,
как и выше для нижнегибридных колебаний, это конечное значение
kz позволяет электронам перетекать вдоль Во, компенсируя разде-.
ление зарядов. Хотя предел kz = 0 уже был рассмотрен при ана-
270
Гл. 7. Кинетическая теория
лизе соотношения (7.153), различие между этими двумя случаями
станет яснее, если мы вернемся назад к соотношениям (7.148) и
(7.149). Отделяя член с п = 0 и пользуясь соотношением (7.146),
получаем
k 1 + 2 е bI0 (b) [ — — Z' (Co) j +
+ L fe2D e-6 Z In (6) [ 1 + CoZ (Cn)] = 0. (7.156)
s n^O
Линия раздела между чисто ионными и нейтрализованными ион-
ными -модами Бернштейна определяется электронным членом
с п = 0. Если для электронов Сое 1> то с помощью разложения
(7.129) можно записать Т (СОе) « 1/Soe- Поскольку в этом случае
ю/£г > Отепл, е. электроны не успевают достаточно быстро перете-
кать вдоль Во и нейтрализовать заряд. Если же Сое С 1, то нужно
использовать выражение (7.126), откуда имеем Z'(СОе) ~—2.
В этом случае a>lkz < итепл. е и У электронов достаточно времени
для установления распределения Больцмана (3.73).
Обратившись сначала к случаю Сое » 1> заметим, что при этом
обязательно и Cot 1 и, следовательно, член с п = 0 в уравнении
(7.156) принимает вид
^--^-е-Чо(й)
со2
—£
L <о2
Здесь мы перешли к пределу Ье -> 0 и положили b = bt. Члены
с п 0 в уравнении (7.156) рассматриваются, как и прежде; поэ-
тому электронные волны здесь определяются дисперсионным урав-
нением (7.155), а ионные — ионным членом дисперсионного урав-
нения (7.153). При этом дисперсионное уравнение для чисто ион-
ных мод Бернштейна принимает вид
Поскольку условие Сое 1 подразумевает, что k2 малы, то первое
слагаемое в (7.157) обычно пренебрежимо мало. Для анализа гид-
родинамического приближения мы можем положить вторые скобки
равными нулю, выделить слагаемое с п = 1 и использовать разло-
7.10. Кинетические эффекты в магнитном поле
271
Рис. 7.35. Чисто ионные моды Бернштейна; сравнение теории с эксперимен-
том, проводившимся на Q-машине. [Из работы: Schmidt J. Р. М., Phys. Rev.
Lett., 31, 982 (1973).]
жение In (b) при малых b. В результате мы придем к следующему
равенству:
!л=2
п2й2 (6/2)"—1
п\ (<в2 — п2Й2)
0. (7.158)
нуль, а оставшиеся члены
При b = 0 сумма здесь обращается в
равны величине S, определенной в приложении Б. Условие 5 = 0
дает верхнюю и нижнюю гибридные частоты [см.- выражения, сле-
дующие за соотношениями (4.70)]. Таким образом, при k± -* 0
низкочастотный корень дисперсионного уравнения стремится к сог.
При конечных b и ® « nQc один из членов суммы в (7.158) может
скомпенсировать электронный член, так что корни дисперсионного
уравнения будут находиться вблизи гармоник ионной циклотрон-
ной частоты. В этом случае дисперсионные зависимости co/Qc от
&±ги напоминают кривые для электронных мод, изображенные на
рис. 7.34. На рис. 7.35 показано поведение двух наинизших корней
для ионных мод, а также экспериментальные данные, подтверж-
дающие справедливость дисперсионных уравнений.
Нижняя ветвь дисперсионного уравнения для мод Бернштейна
проявляется в виде так называемой обратной волны', для нее кривая
<а (Л) имеет отрицательный наклон. Это указывает на то, что груп-
повая скорость волны противоположна по направлению фазовой.
Обратные волны действительно существуют. Это было подтверж-
дено в лабораторных экспериментах не только путем измерений за-
272
Гл. 7. Кинетическая теория
Рис. 7.36. Нейтрализованные ионные моды Бернштейна; сравнение теории
с экспериментом в высокочастотном разряде гелия. [Из работы: Ault Е.,
Ikezi Н., Phys. Fluids, 13, 2874 (1970).]
висимости со от k, но и данными интерферометрии, которые под-
твердили, что фазовые фронты в такой волне движутся в обратном
направлении — от приемника к передатчику.
В заключение рассмотрим нейтрализованные моды Бернштейна,
для которых СОе мало и Z' (СОе) « — 2. Электронный член в урав-
нении (7.156) при п — 0 оказывается равным Лг>е. Считая, что
неравенство £ос 1 по-прежнему выполняется, можно повторить
выкладки, с помощью которых было получено уравнение (7.157);
при этом уравнение (7.156) принимает вид
а при 1?г для нейтрализованных ионных волн Бернштейна
можно записать следующее приближенное соотношение:
1 р 1 —
СО2 — СО?
ЙР 2 e-6 V* zn W
о? b L-1 (ш/пОс—1)2
(7.160)
7.10. Кинетические эффекты в магнитном поле
273
Заметим, что теперь XD вычисляется по электронной температуре,
в то время как чисто ионные моды Бернштейна не зависят от КТ
[см. соотношение (7.157) ]. Если величина A2Xd мала, то выражение,
стоящее в формуле (7.160) в квадратных скобках, должно быть ве-
лико, а это возможно только вблизи резонанса со « nQc. Таким
образом, нейтрализованные моды оказываются нечувствительными
к нижнегибридному резонансу со « со/. Действительно, при
krLi 0 огибающая дисперсионных кривых приближенно опи-
сывается дисперсионным уравнением (4.67) для электростатических
ионно-циклотронных волн. Следовательно, в гидродинамическом
пределе нейтрализованные волны переходят в ионно-циклотронную
волну.
Нейтрализованные моды Бернштейна исследованы эксперимен-
тально не столь хорошо, как чистые моды Бернштейна. Один из
случаев наблюдения нейтрализованной моды в эксперименте пока-
зан на рис. 7.36.
Глава 8
НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
8.1. Введение
До сих пор наше внимание было привлечено почти исключительно
к линейным явлениям, т. е. к процессам, описываемым уравнениями,
в которые зависимые переменные входят в степени не выше первой.
В частности, весь анализ волн, выполненный в гл. 4, был основан
на процедуре линеаризации, при проведении которой считалось,
что члены высоких порядков малы и ими можно пренебречь. Это
позволяло нам рассматривать только отдельные фурье-компоненты
в полной уверенности, что всякую несинусоидальную волну можно
представить как соответствующую сумму фурье-компонент. Такое
приближение справедливо лишь до тех пор, пока амплитуда волны
достаточно мала и ее можно описать линейным уравнением.
К сожалению, во многих экспериментах ко времени начала на-
блюдений волны уже нельзя описывать с помощью линейной тео-
рии. Рассмотрим, например, дрейфовые волны. Такие волны яв-
ляются неустойчивыми, и поэтому в соответствии с линейной тео-
рией их амплитуды должны экспоненциально возрастать со време-
нем. В период роста эти волны чаще всего не наблюдаются, по-
скольку обычно не ясно, когда же именно начинать наблюдения;
колебания видят уже после того, как их амплитуды выросли до
больших стационарных значений. Прекращение роста колебаний
означает, что линейная теория уже несправедлива и рост ампли-
туды волны ограничивается каким-то нелинейным механизмом.
Теоретическое объяснение этого простого экспериментального факта
оказалось на удивление сложной задачей, поскольку амплитуды
волн в состоянии насыщения весьма малы.
Если амплитуда волны велика, то она может испытать целый
ряд модификаций. Может измениться форма волны; скажем, из
синусоидальной она может стать пилообразной. Иными словами,
в системе могут генерироваться фурье-компоненты с другими ча-
стотами (или волновыми числами). В конечном счете волна может
«опрокинуться» подобно набегающей на берег океанской волне.
Энергия волны при этом переходит в тепловую энергию частиц.
Волна большой амплитуды может захватить частицы в связанные
8.1. Введение
275
Рис. 8.1. Неустойчивая функция распределения электронов с двумя макси-
мумами.
с волной потенциальные ямы, изменяя таким образом свойства
среды, в которой она распространяется. С этим явлением мы уже
встречались при анализе нелинейного затухания Ландау. Если
плазма находится в сильно возбужденном состоянии, так что в ней
наблюдаются колебания с непрерывным спектром частот, то ее на-
зывают турбулентной. Для описания такого состояния плазмы
нужно привлекать статистические методы, подобные тем, которые
используются в обычной гидродинамике. Важным следствием плаз-
менной турбулентности является аномальное сопротивление, когда
движущиеся электроны замедляются не из-за столкновений с ионами,
а вследствие рассеяния на хаотических флуктуациях электриче-
ского поля. Это явление используется для омического нагрева
плазмы (разд. 5.6.3) до высоких температур, при которых обычное
сопротивление является недостаточным.
Нелинейные явления можно разбить на три большие группы.
1. Существенно нелинеаризуемые задачи. К ним, в частности,
относится нелинейная задача о диффузии в полностью ионизован-
ном газе (разд. 5.8), поскольку в этом случае коэффициент диффу-
зии зависит от плотности. Как показано в разд. 6.1, нелинейными
являются также задачи о равновесии плазмы в МГД-приближении.
Еще один пример подобной задачи будет дан в разд. 8.2, где речь
пойдет о таких важных объектах, как плазменные слои.
2. Взаимодействие волна — частица. Примером такого взаимо-
действия является захват частиц (разд. 7.5), который может при-
вести к нелинейному затуханию. Классическим примером служат
также квазилинейные эффекты, вызывающие изменение равновес-
ного состояния плазмы из-за присутствия в ней волн. Рассмотрим
плазму, в которой имеется электронный пучок (рис. 8.1). Поскольку
функция распределения частиц содержит область с положитель-
ными значениями df^/dv, знак декремента затухания Ландау в этом
интервале скоростей изменяется на противоположный. Как следст-
вие плазменные колебания, фазовые скорости которых иф лежат
в этой области, станут неустойчивыми [см. формулу (7.67)]. В пер-
вую очередь взаимодействие таких неустойчивых волн с частицами
276
Гл. 8. Нелинейные явления
скажется на резонансных электронах — под действием волновых
электрических полей их функция распределения изменится. Рост
волн остановится только после того, как в результате их взаимо-
действия с частицами функция распределения fe (о) станет совер-
шенно плоской, как показано штриховой линией на рис. 8.1, т. е.
установится новое состояние равновесия, при котором у функции
распределения уже не будет областей с положительной производ-
ной. Это и есть типичный квазилинейный процесс. Другим приме-
ром взаимодействия волна — частица является так называемое
плазменное эхо, которое мы рассмотрим в разд. 8.6.
3. Взаимодействие волна — волна. Взаимодействие волн друг
с другом можно описать уже в рамках гидродинамических урав-
нений, которые не учитывают эффекты, связанные с отдельными
плазменными частицами. Прежде всего плазменная волна может
генерировать другие волны на гармониках основной частоты. За-
тем гармоники могут взаимодействовать друг с другом и с первич-
ной волной, в результате чего на частотах биений будут возникать
новые волны. В свою очередь волны, частоты которых отвечают
этим биениям, могут вырасти до такого большого уровня, что на-
чнут взаимодействовать друг с другом, создавая все новые и новые
волны, и в конце концов спектр колебаний станет непрерывным.
Интересно выяснить, в каком направлении будет перекачиваться
энергия по спектру волн в турбулентной плазме. В гидродинамике,
как известно, длинноволновые моды распадаются на коротковолно-
вые, поскольку большие вихревые образования обладают большими
запасами энергии и могут распадаться только на вихри меньших
размеров, каждый из которых содержит меньшее количество энер-
гии. Кинетическая энергия движения жидкости в малых вихрях
в конце концов из-за затухания, вызванного вязкостью, переходит
в тепло. В плазме процесс перекачки энергии чаще всего идет в про-
тивоположном направлении: коротковолновые моды стремятся
слиться в длинноволновые, поскольку последние обладают мень-
шими запасами энергии. Это связано с тем, что плотность энергии
электрического поля в колебаниях равна Е2/8л = £2</>2/8л и при
фиксированных еф (обычно еф = КТе) моды с меньшими k (боль-
шими X) имеет меньшую энергию. Как следствие энергия плазмен-
ных волн, созданных неустойчивостями при больших k, будет пе-
реноситься в область меньших Л, где должен существовать некий
механизм диссипации энергии. При больших k искать такой меха-
низм не надо — это затухание Ландау. В случае малых k дело об-
стоит сложнее. Оказывается, что при движениях вдоль магнитного
поля таким механизмом является нелинейная «модуляционная»
неустойчивость, в результате развития которой энергия волн
с малыми Л передается ионам и идет на их нагрев. В случае попереч-
ных движений самые крупные вихри имеют размеры порядка раз-
меров самой плазмы и затухают из-за ее выноса на стенки установки
вследствие конвекции.
8.2. Слои в плазме
277
Хотя в линейной теории волн и неустойчивостей еще сущест-
вуют нерешенные проблемы, исследования по физике плазмы
сейчас ведутся главным образом в области гораздо менее понят-
ных нелинейных явлений. Примеры, которые будут приведены в по-
следующих разделах, дадут представление о некоторых нелиней-
ных эффектах, изучаемых теоретическими и экспериментальными
методами физики плазмы.
8.2. Слои в плазме
8.2.1. Почему в плазме возникают слои?
Во всех применяемых на практике плазменных установках плазма
удерживается в вакуумных камерах конечных размеров. Что про-
исходит с плазмой у стенки такой камеры? Рассмотрим для про-
стоты одномерную модель, описывающую плазму без магнитного
поля (рис. 8.2). Предположим, что электрическое поле в плазме
отсутствует; тогда потенциал ф внутри нее можно считать равным
нулю. Когда электроны или ионы ударяются о стенку, они на ней
рекомбинируют и в плазму не возвращаются. Поскольку тепловая
скорость у электронов намного выше, чем у ионов, потеря электро-
нов происходит гораздо быстрее и в плазме накапливается свобод-
ный положительный заряд. Вследствие этого потенциал плазмы
относительно стенки должен стать положительным, т. е. потенциал
стенки <l>w будет меньше нуля. Перепад потенциалов между стенкой
и плазмой не может распределиться по всему объему плазмы, по-
скольку из-за дебаевского экранирования (разд. 1.4) изменение
потенциала должно происходить у стенки в области толщиной в не-
сколько дебаевских радиусов. Эта область, которая должна сущест-
Рис. 8.2. Вблизи стенок потенциал еф
образует слои, которые отражают
электроны плазмы. Кулоновский ба-
рьер еФю подстраивается так, что о
стенку каждую секунду ударяется
равное число электронов и ионов.
Рис. 8.3. Распределение потенциала
Ф в плоском слое. Предполагается,
что холодные ионы проникают вслой,
имея постоянную скорость иа.
278
Гл. 8. Нелинейные явления
вовать у любой холодной стенки, граничащей с плазмой, и назы-
вается плазменным слоем. Такой слой создает потенциальный
барьер, благодаря которому в плазме за счет электростатических
сил удерживаются более подвижные частицы (обычно это элек-
троны). Высота потенциального барьера подстраивается таким об-
разом, чтобы поток электронов, энергия которых достаточно ве-
лика для преодоления этого барьера и выхода на стенку, был в точ-
ности равен потоку достигающих стенки ионов.
8.2.2. Плоский слой
В разд. 1.4 для анализа дебаевского экранирования и определения
дебаевского радиуса мы пользовались линеаризованным уравне-
нием Пуассона. Для того чтобы выяснить, как ведет себя потен-
циал ф (х) в слое, нужно решить линейную задачу. (Как будет по-
казано ниже, ее решение существует не всегда.) На рис. 8.3 изобра-
жено распределение потенциала вблизи стенки. Пусть ионы соз-
даются в основном объеме плазмы посредством ионизации и попа-
дают из него в слой, имея в плоскости х = 0 направленную ско-
рость и0. Такое движение ионов должно компенсировать их потери
из-за рекомбинации на стенке. Для простоты будем считать, что
Т{ = 0; иными словами, скорость ионов в плоскости х = 0 равна
v = и0. Мы будем анализировать задачу о стационарном слое без
учета столкновений, считая, что потенциал ф монотонно умень-
шается с увеличением х. В действительности потенциал ф может
иметь внутри слоя локальные максимумы, и тогда в стационарном
случае в слое могут существовать захваченные частицы. Однако
на практике этого не происходит, поскольку диссипативные про-
цессы стремятся разрушить эту столь «высокоорганизованную»
структуру.
Пусть и (х) — скорость ионов. Тогда из закона сохранения
энергии мы имеем
Ми2=~Ми20—еф(х), (8.1)
и = (ио—2еф/М)12. (8.2)
Из уравнения непрерывности для ионов плотность ионов тц можно
выразить через плотность фоновой плазмы п0:
no«o = rii (х) и (х), (8.3)
п{ (х) = п0 (1 —2e^/Af«o)-1'2- (8.4)
В стационарном состоянии электроны будут подчиняться распре-
делению Больцмана:
пе (х) = п0 ехр (е^/КТе).
(8-5)
8.2. Слои в плазме
279
С учетом этого уравнение Пуассона можно записать в виде
z0d2</>/dx2 == е (пе—ni) = еп0 Гехр f еф — fl-1/21 • (8.6)
L V КТ' J V м«02) J
Структура этого уравнения станет более понятной, если его упро-
стить, перейдя к безразмерным переменным
----«.-----
КТе J (КТ'/М)1'2
(8.7)
В этих переменных уравнение (8.6) принимает следующий вид:
Х" = (1+ -^гГ’2-е"Х’ (8-8)
\ JJl J
где штрих означает производную d/dc.. Это — нелинейное уравне-
ние, которое описывает распределение потенциала в плоском слое;
его решение имеет смысл, только если число Л достаточно велико.
(В разделе, посвященном ударным волнам, выяснится, почему мы
обозначили отношение скоростей через Л.)
8.2.3. Критерий Бома для образования слоев
Умножив обе части уравнения (8.8) на %', его можно один раз про-
интегрировать:
j М = j (1 + ^-) Ь2 X'^i - j (8-9)
0 0 0
где — переменная интегрирования. Интегрирование легко вы-
полнить, если учесть, что. при § = 0 функция х=0:
4-(х!-»г)=Х!Г(1+Л-)и-11+е->-1. (8.10)
Если электрическое поле в плазме отсутствует (Е = 0), то мы
должны считать, что при | = 0 величина %0 также обращается в
нуль. Второе интегрирование и определение % должно выполняться
численно. Следует, однако, отметить, что независимо от того, ка-
кой получится ответ, правая часть уравнения (8.10) должна быть
положительна при любом %. В частности, если считать, что % < 1,
и разложить правую часть уравнения (8.10) в ряд Тейлора
1’[1 + 7-тт+ • +
+ ^-х2+ • • . - 1>о,
280
Гл. 8. Нелинейные явления
—К стенке
0 Х=-еф/КТе
Рис. 8.4. Зависимости плотностей ионов и электронов в плазменном слое от
нормированного потенциала X (в логарифмическом масштабе). График плот-
ности ионов построен для двух случаев: «0 больше критической скорости
и «о меньше ее.
то получим
Л2>1 или u0>(KTJM)W. (8.11)
Это неравенство называется критерием Бома для образования слоев.
Из него следует, что скорость входящих в слой ионов должна пре-
вышать скорость звука vs. Чтобы разогнать ионы до скорости и0,
в плазме должно существовать электрическое поле конечной ве-
личины. Поэтому наше предположение о том, что при | = 0 вели-
чина %' = 0, является лишь приближенным. Оно справедливо
только потому, что размер слоя обычно много меньше размеров
основной плазменной области, в которой происходит ускорение
ионов. Величина и0 является до некоторой степени произвольной,
поскольку она зависит от того, где мы поместим границу к = 0
между слоем и плазмой. Ясно, однако, что, поскольку поток ионов
поио определяется скоростью их генерации внутри плазмы и по-
тому является константой, при изменении иЛ величина п0 при х = 0
будет обратно пропорциональна и0. Отметим также, что если тем-
пература Tt отлична от нуля, то критическая скорость и0 оказы-
вается несколько ниже vs.
Физический смысл критерия Бома легко понять, если построить
графики зависимостей концентраций ионов и электронов от вели-
чины % (рис. 8.4). В соответствии с уравнением Больцмана плот-
ность электронов экспоненциально убывает с ростом х- Плотность
ионов также уменьшается с ростом х, поскольку они ускоряются
потенциалом слоя. Если начальная скорость ионов достаточно ве-
лика, то связанное со слоем электрическое поле мало меняет их
скорости и уменьшение плотности ионов происходит медленно.
Если же начальная энергия ионов невелика, то ni (х) уменьшается
быстро и при некоторых х кривая nt (х) может пройти под кривой
8.2. Слои в плазме
281
пе (%). В этом случае вблизи точки % = 0 разность пе—п{ является
положительной и из уравнения (8.6) следует, что кривая ф (х)
должна быть вогнутой, а это противоречит требованию о том, что
слой должен отражать электроны. Чтобы такого противоречия не
возникало, наклон кривой п{ (%) в точке % = 0 по абсолютному
значению должен быть меньше, чем наклон кривой пе (%); это ус-
ловие тождественно требованию J(2 > 1.
8.2.4. Закон Чайлда—Ленгмюра
Поскольку пе (х) экспоненциально уменьшается с ростом %, в об-
ласти больших х, которая находится близко к стенке (или к любому
отрицательно заряженному электроду, помещенному в плазму),
плотностью электронов можно пренебречь и уравнение Пуассона
можно приближенно записать в виде
%" ~ (i + ^-)-1'2 « Ж)12.' (8.12)
Умножив его на х' и проинтегрировав от = £s до имеем
-j- (х'2-ъ!) = (х1'2—х','г) (8.13)
Здесь £5 отвечает той точке, начиная с которой мы пренебрегаем
вкладом пе в уравнение Пуассона. Можно переопределить функ-
цию х и считать, что при £ = ?s величина xs равна нулю. Мы можем
также пренебречь величиной х$ поскольку следует ожидать, что
наклон кривой, описывающей распределение потенциала в области
пе = 0, значительно меньше, чем наклон этой кривой в области,
где концентрация пе конечна. В этом приближении уравнение
(8.13) принимает следующий вид:
х'2 = 23/2^х1/2, %' = 23'4^Ь2х14 (8.14)
или
ВД/4 = 23/\<1/2<£. ' (8.15)
Интегрируя последнее равенство от £ = до £ = gs + dl'kD=
(нижний индекс w означает, что значение соответствующей вели2
чины берется у стенки), имеем
4^4=234^I'2d/XD’ (8Л6)
откуда находим __
jr = (4V2/9)(x^o/d2)- (8.17)
Возвращаясь к переменным и0 и <£ и замечаяТчто ток, переносимый
движущимися к стенке ионами, равен J — епаи0, приводим к вы-
ражению
J = (4/9)(2e/M)V2(eor|^|W). ‘ (8.18)
282
Гл. 8. Нелинейные явления
Это — хорошо известный закон Чайлда—Ленгмюра для тока в
плоском диоде, ограниченного пространственным зарядом.
Таким образом, распределение потенциала в системе плазма —
стенка можно разделить на три области. Ближе всего к стенке рас-
положена свободная от электронов область, толщину которой d
можно найти из условия (8.18), считая, что J определяется ско-
ростью генерации ионов внутри плазмы, а потенциал находится
из условия равенства ионного и электронного потоков. К этой об-
ласти примыкает другая, в которой пе 0. Как показано
в разд. 1.4, толщина последней области порядка дебаевского ра-
диуса экранирования. Наконец, в плазме существует так называе-
мый предслой, имеющий значительно большие размеры, в котором
ионы ускоряются до необходимой скорости разностью потенциалов
|</>| > (1/2) К,Те/е. В зависимости от условий эксперимента размер
предслоя может определяться размерами установки, средней дли-
ной свободного пробега или механизмом ионизации частиц. Разу-
меется, в реальной системе распределение потенциала является
плавным; разделение на упомянутые три области вызвано лишь
соображениями удобства и стало возможным лишь благодаря тому,
что размеры этих областей существенно различны. В ранних экс-
периментах по газовым разрядам плазменные слои наблюдались
в виде темных областей, в которых отсутствовали электроны, воз-
буждающие атомы и вынуждающие их излучать энергию. Профиль
потенциала в таких экспериментах измерялся по отражению в элек-
трическом поле тонкого пучка электронов, выстреливаемого па-
раллельно стенке газоразрядной трубки.
8.2.5. Электростатические зонды
Критерий образования слоя [(8.11) ] можно использовать для оценки
потока ионов, попадающих на помещенный в плазму зонд, который
находится под отрицательным потенциалом. Пусть площадь по-
верхности зонда равна А, а попадающие на зонд ионы имеют на-
правленную скорость п0 > (КТе/М)1!2; тогда собираемый зондом
ионный ток равен
I = п.еА (КТе/М)'2. (8.19)
Если зонд заряжен до значительного потенциала относительно
плазмы (в несколько раз больше, чем KTJe) и отталкивает все элек-
троны, кроме самых быстрых частиц из хвоста максвелловского
распределения, то электронным током, текущим через зонд, можно
пренебречь. В формуле (8.19) величина ns представляет собой плот-
ность плазмы у внешней границы слоя. Будем считать, что эта гра-
ница расположена в том месте, где скорость и0 в точности равна
(КТе/М)12. Для ускорения ионов до такой скорости необходимо,
чтобы в пределов существовал потенциал |^| > (1/2) КТе/е\ при
8.2. Слои в плазме
283
этом потенциал на границе слоя относительно плазмы будет равен
<l>s*-±-КТе/е. (8.20)
Считая, что электроны являются максвелловскими, определим
отсюда ns:
= = = (8.21)
С достаточной для наших целей точностью можно заменить 0,61 на
1/2; при этом ионный ток, текущий в состоянии насыщения через
отрицательно заряженный зонд, будет определяться приближен-
ным равенством
/в ~ поеА (КТе/МУ12. (8.22)
Ток /в иногда называют «бомовским» током. Зная эту величину
и температуру плазмы, легко найти ее плотность.
Если дебаевский радиус Xd и, следовательно, толщина слоя
много меньше размеров зонда, то площадь внешней поверхности
слоя будет близка к площади поверхности зонда А, независимо от
формы последнего. При низких плотностях плазмы величина ZD
становится большой, так что некоторые из попадающих в слой ионов
могут обогнуть зонд и не попасть на него. Расчеты траекторий дви-
жения частиц при различных формах зондов впервые были выпол-
нены Ленгмюром и Тонксом, поэтому прибор для измерения плот-
ности плазмы таким методом называется ленгмюровским зондом.
Несмотря на то что такие вычисления являются очень громозд-
кими, они позволяют достаточно точно определить плотность
плазмы, поскольку при таком анализе нет необходимости вводить
в рассмотрение понятие о границе слоя, которое, конечно же, яв-
ляется условным. Изменяя напряжение, подаваемое на зонд, ко-
торый помещен в плазму с максвелловским распределением частиц
по скоростям, можно построить вольт-амперную характеристику
прибора и определить по ней электронную температуру плазмы.
Электростатический (ленгмюровский) зонд был первым устройст-
вом, предназначенным для диагностики плазмы, и до сих пор ос-
тается самым простым и компактным измерительным прибором по-
добного рода. К сожалению, эти зонды можно использовать только
для измерения параметров холодной плазмы низкой плотности.
Задачи
8.1. Зонд,, собирающая поверхность которого представляет собой квадрат
из танталовой фольги размерами 2X2 мм, помещен в плазму, состоящую
из электронов и однократно ионизованных атомов аргона (атомная масса 40).
В состоянии насыщения через зонд течет ток 100 мкА. Пусть электронная
284
Гл. 8. Нелинейные явления
температура плазмы КТе — 2 эВ. Какова примерно плотность плазмы? (Ука-
зание-. ионы попадают на обе стороны зонда!)
8.2. На геостационарной орбите находится спутник, площадь солнечных бата-
рей которого равна 10 км2. Он окружен водородной плазмой плотностью
10“6 м~3 и температурой 1 эВ. Во время солнечной бури спутник бомбарди-
руется высокоэнергетическими электронами, в результате чего он заряжается
до потенциала — 2 кВ. Рассчитайте величину потока высокоэнергетических
ионов, проходящего через 1 м2 солнечных батарей.
8.3. Критерий образования слоя (8.11) выведен для случая плазмы с холод-
ными ионами. Пусть теперь функция распределения ионов по скоростям имеет
тепловой разброс, а средняя направленная скорость ионов по-прежнему
равна и0. Не производя математических выкладок, укажите, будет ли поро-
говая величина скорости выше или ниже бомовского значения. Почему?
8.4. Анализатор скорости ионов представляет собой цилиндр из нержавею-
щей стали диаметром 5 мм, один торец которого закрыт тонкой танталовой
сеткой (пусть это будет сетка 1). За этой сеткой (внутри цилиндра) находится
еще ряд параллельных сеток. Потенциал сетки 1 «плавает» — она не под-
соединена ни к какому источнику. На сетку 2 подано отрицательное смеще-
ние, в результате чего она отражает все электроны, прошедшие через сетку 1,
но пропускает ионы. Сетка 3 служит для анализа частиц; на нее подается
такое смещение, чтобы замедлить ионы, которые были ускорены сеткой 2.
Те ионы, которые смогли пройти через сетку 3, собираются коллектором.
Сетка 4 служит для подавления потока эмиттируемых с поверхности коллек-
тора вторичных электронов: она заворачивает их обратно к коллектору.
Если плотность плазмы достаточно велика, то вблизи сетки 3 может проис-
ходить накопление пространственного заряда, поскольку плотность ионов
там столь велика, что перед сеткой 3 образуется горб потенциала, который
отражает ионы и не позволяет им приблизиться к третьей сетке. Пользуясь
законом Чайлда—Ленгмюра, оцените максимальный ток, который может
течь через коллектор в случае гелиевой (Не+) плазмы, если диаметр коллек-
тора равен 4 мм, расстояние между сетками 2 и 3 равно 1 мм, а разность по-
тенциалов между ними составляет 100 В.
8.3. Ионно-звуковые ударные волны
Если реактивный самолет движется быстрее звука, то перед ним
возникает ударная волна. Она представляет собой существенно
нелинейное явление, так как наблюдается уже в виде оформивше-
гося образования; период роста из состояния с малой амплитудой
у такой волны отсутствует. Поскольку скорость самолета превы-
шает скорость распространения волн в воздухе, не существует сиг-
налов, которые могли бы «предупредить» невозмущенную среду
перед самолетом о том, что на нее надвигается ударная волна. Оп-
ределяющим процессом в гидродинамике ударных волн являются
столкновения. В плазме ударные волны существуют даже в отсутст-
вие столкновений. В частности, межпланетная плазма, обтекая
Землю по силовым линиям ее магнитного поля, образует магнит-
ную ударную волну, напоминающую по форме изогнутый лук.
Рассмотрим в качестве примера более простую бесстолкновитель-
ную одномерную ударную волну, которая образуется из ионно-
звуковой волны большой амплитуды.
8.3. Ионно-звуковые ударные волны
285
8.3.1. Потенциал Сагдеева
На рис. 8.5 изображен идеализированный профиль потенциала
в ионно-звуковой ударной волне. Пусть волна движется влево со
скоростью п0. Если перейти в систему отсчета, движущуюся вместе
с волной, то функция </> (х) не будет зависеть от времени, а поток
плазмы будет набегать на ударную волну слева со скоростью и0.
Положим для простоты Ti = 0, так что все ионы падают на волну
со скоростью uQ. Электроны будем считать максвелловскими. По-
скольку скорость ударной волны много меньше тепловой скорости
электронов, сдвигом максвелловского распределения на величину и0
можно пренебречь. Из закона сохранения энергии следует, что
скорость ионов внутри ударной волны определяется соотношением
Пусть плотность невозмущенной плазмы равна п0, тогда профиль
плотности ионов в ударной волне имеет вид
П{==_2о«о_=По/1---2еф_у12. (8 24)
и Ми% J
Плотность электронов удовлетворяет уравнению Больцмана. Рас-
пределение потенциала в ударной волне определяется уравнением
Пуассона
dx2
е(пе—= enol exp
(8.25)
которое аналогично уравнению (8.6), определяющему ход потен-
циала в плазменном слое. Другими словами, ударная волна пред-
ставляет собой не что иное, как слой, движущийся через плазму.
Введем безразмерные переменные:
х = + e$/KTet I = x/XD, Я=и./(КТе/МУ2. (8.26)
Рис. 8.5. Типичное распределение потенциала в ионно-звуковой ударной
волне. Волна движется в левую сторону, поэтому в системе отсчета, связан-
ной с волной, ионы налетают на нее слева со скоростью w0.
286
Гл. 8. Нелинейные явления
Заметим, что, определяя %, мы заменили знак этой величины на
противоположный [ср. (8.7)], с тем чтобы %, как и в задаче о слое,
была положительной. Величина .Ж называется числом Маха. В но-
вых переменных уравнение (8.25) записывается в виде
=-----~ (8*27>
Это уравнение отличается от уравнения (8.8) лишь знаком вели-
чины %.
Р. 3. Сагдеев объяснил поведение решения уравнения (8.27),
пользуясь аналогией с движением частицы, осциллирующей в по-
тенциальной яме. Для частицы, на которую действует сила
— т dV(x)/dx, смещение х определяется уравнением
d?x/dl?= — dV/dx. (8.28)
Если правую часть уравнения (8.27) обозначить через — dV/dyr
то оно станет тождественным уравнению движения осциллятора,
причем потенциал % будет играть роль х, а производная dldl, за-
менит d/dt. Квазипотенциал V (%) иногда называют потенциалом
Сагдеева. Функцию V (%) можно найти из уравнения (8.27), интег-
рируя его с учетом граничного условия V (%) = 0 при % = 0:
V(x)=l-ex + ^ri-fl-AV2!. (8.29)
L \ / J
При определенных значениях М график функции У(х) имеет такой
вид, как показано на рис. 8.6. Если бы это была обычная яма, то
частица, попав в нее слева при х = 0, дошла бы до правого края
ямы, отразилась и вернулась бы к точке х = 0, совершив таким
образом внутри ямы одно колебание. По аналогии и в нашем слу-
чае квазичастица совершит такое же движение: она дойдет до не-
которого положительного % и вернется к % = 0 (рис. 8.7). Подоб-
ное импульсное распределение потенциала или плотности назы-
вается солитоном; в нашем случае он движется влево со ско-
ростью и0.
Пусть теперь частица при движении в яме теряет энергию, тогда
она никогда не вернется в точку х = 0, а будет стечением времени
совершать колебания около некоторой точки х>0. Аналогично
небольшое затухание вызовет пространственные осцилляции по-
тенциала в ударной волне вокруг некоторого положительного зна-
чения ф, что и показано на рис. 8.5. В действительности для соз-
дания такого распределения в системе не обязательно должна су-
ществовать диссипация; тот же эффект дает отражение ионов от
фронта ударной волны. Чтобы понять это, допустим, что ионы
имеют малый тепловой разброс по энергиям, а высота потенциаль-
ного барьера в волне еф достаточно велика для того, чтобы часть
ионов от него отразилась и ушла влево, а часть перевалила через
8.3. Ионно-звуковые ударные волны
287
Рис. 8.6. Потенциал Сагдеева V (%). Верхняя стрелка соответствует траек-
тории движения квазичастицы, которая соответствует солитону. Эта квази-
частица отражается от барьера и возвращается к началу координат. Нижние
стрелки показывают траекторию движения квазичастицы, которая теряет
свою энергию и оказывается захваченной в потенциальную яму. Движение
такой квазичастицы взад-вперед в потенциальной яме описывает осцилляции
за фронтом ударной волны.
барьер и продолжала бы движение в правую сторону. Из-за нали-
чия отраженных ионов плотность плазмы вверх по течению от удар-
ной волны (на рис. 8.5 слева от нее) увеличится. Отсюда следует,
что величина
Г
Х' = — . (пе-и№ (8.30)
По о
уменьшится. Поскольку %' является аналогом dx/dt, это значит,
что наш воображаемый осциллятор теряет энергию и оказывается
захваченным в потенциальную яму (рис. 8.6).
8.3.2. Критические числа Маха
Решения типа солитонов или волновых пакетов существуют только
при определенных значениях Ж. Нижний предел этих чисел опре-
деляется из условия, что функция V (%) должна описывать именно
яму, а не горб потенциала. Разложение правой части (8.29) в ряд
при х С 1 дает условие
-уХ2-(Х2/2^2)>0, ЛГ2>1, (8.31)
которое и с физической, и с математической точки зрения совпада-
ет с бомовским критерием образования слоев [формула (8.11)].
~ л
л(или 5)
Рис. 8.7. Распределение потенциала в движущемся слева солитоне.
288
Гл. 8. Нелинейные явления
Верхний предел значений Л определяется тем обстоятельством,
что для существования потенциальной ямы функция V (%) должна
пересекать ось % при % >0; в противном случае квазичастица не
сможет отражаться, а потенциал будет неограниченно расти. Как
видно из формулы (8.29), для этого необходимо, чтобы при неко-
тором х >0 удовлетворялось неравенство
ех—1< ,<2[1— (1— (8-32)
Пусть число Маха больше нижнего, критического (Л/>1); тогда
при малых % левая часть неравенства (8.32), которая представляет
собой интеграл от электронной плотности по потенциалу в преде-
лах от нуля до %, будет больше, чем его правая часть, отвечающая
аналогичному интегралу от плотности ионов. Если число Л2
не очень велико, то с ростом х правая часть может стать больше
левой. Однако х не может расти до бесконечности; его максималь-
ное значение определяется из условия неотрицательности подко-
ренного выражения: Хмакс.= Х2/2. Физически это связано с тем,
что величина еф не может превышать (1/2) Мио; в противном случае
ионы не смогут проникнуть за ударную волну. Подставляя Хмгкс
в неравенство (8.32), приходим к условию
ехр(лГ/2)—1<лГ2, Л<1,6, (8.33)
которое определяет верхний предел чисел Маха. Таким образом,
ударные волны в плазме с холодными ионами существуют только
при 1 <Л <1,6.
Как и при анализе плазменных слоев, физическую причину
этого лучше всего понять с помощью графиков зависимостей и,
и пе от х (рис. 8.8). Поскольку мы сменили знак в определении х,
эти графики отличаются от тех, которые изображены на рис. 8.4.
Рис. 8.8. /Зависимость плотнос-
тей ионов и электронов от нор-
мированного потенциала % для
солитонного решения (логариф-
мическая шкала). Плотность ио-
нов изображена для двух случа-
ев: в первом число Маха Л<_
< 1,6, во втором — Л> 1,6.
Рис. 8.9. Ионно-звуковая волна боль-
шой амплитуды со временем укручается,
так что передние кромки горбов стано-
вятся круче задних.
8.3. Ионно-звуковые ударные волны
289
Ионы теперь не ускоряются, как в случае плазменного слоя, а за-
медляются, поэтому при %имеем tu -> оо. Поскольку
Л <1,6, при малых х кривая nt (х) лежит под кривой пе (х) и кри-
визна функции ф (х) имеет требуемый знак. При значениях х> со-
ответствующих условию fii — пе, потенциал ф в солитоне имеет
точку перегиба (рис. 8.7). Наконец, если х настолько велико, что
площади под кривыми пе (х) и (х) становятся одинаковыми, то
потенциал солитона достигает максимума, после чего $ начи-
нает уменьшаться и убывает до нуля, а плотности частиц тоже
стремятся к нулю, двигаясь по тем же кривым (х) и пе (х). Из
условия равенства площадей под кривыми следует, что полный
заряд солитона равен нулю; следовательно, вне солитона электри-
ческое поле отсутствует. Числу Маха Л >1,6 соответствует такая
кривая п;2, площадь под которой слишком мала и не может уравно-
весить вклад от электронов даже в том случае, когда х = Хмакс =
= лт.
8.3.3. Укручение волны
Пусть в плазме с холодными ионами распространяется ионно-зву-
ковая волна. Ее фазовая скорость определяется выражением (4.42)
и соответствует числу Маха Л = 1. Каким образом из нее можно
образовать ударную волну с Л >1? Для того чтобы ответить на
этот вопрос, вспомним, что формула (4.42) была получена в линей-
ном приближении и справедлива лишь для волн малой амплитуды.
Оказывается, с ростом амплитуды скорость ионно-звуковой волны
возрастает. Меняется и ее форма: из синусоидальной волна превра-
щается в пилообразную; передние кромки у бегущих вправо гор-
бов становятся круче (рис. 8.9). Это связано с тем, что электри-
ческое поле волны ускоряет ионы. Рассмотрим более подробно
механизм такого процесса. На рис. 8.9 ионы, находящиеся у пика
распределения потенциала, имеют более высокую скорость в на-
правлении Уф, чем частицы, находящиеся в яме, поскольку первые
были ускорены только что прошедшим мимо них максимальным
значением потенциала. Это различие в скоростях частиц учиты-
вается и в рамках линейной теории, однако вытекающими из него
различиями в положениях частиц линейная теория пренебрегает.
В нелинейной теории нетрудно показать, что ионы, находящиеся
у пиков потенциала, будут сдвинуты вправо, а частицы, распо-
ложенные у дна потенциальных ям,— влево, что и приведет к ук-
ручению профиля волны. Поскольку возмущение плотности на-
ходится в фазе с потенциалом, число ионов, ускоряемых волной
вправо, превышает число частиц, которые ускоряются влево. В ре-
зультате возникает поток частиц, движущихся в направлении рас-
пространения волны. При этом скорость волны превышает скорость
звука в невозмущенной плазме и число Маха Л становится больше
единицы.
Ю Заказ 3170
290
Гл. 8. Нелинейные явления
8.3.4. Результаты экспериментов
Ионно-звуковые ударные волны, похожие на ту, что изображена
на рис. 8.5, наблюдались в экспериментах Р. Тейлора, Д. Бейкера
и X. Икедзи. Для возбуждения волн был разработан специальный
G
Г
Рис. 8.10. Схема двухплазменной установки, на которой создавались и ре-
гистрировались ионно-звуковые ударные волны. [Из работы: Taylor R. J.,
Baker D. R., Ikezi H., Phys. Rev. Lett., 24, 206 (1970)1.
w
1 г
W
Рис. 8.11. Распределение плотности в ударной волне в различные моменты
времени по результатам наблюдений в эксперименте. [Из работы: Taylor R. J
Baker D. R., Ikezi H., Phys. Rev. Lett., 24, 206 (1970).] Заметно возникнове-
ние характерной структуры типа той, которая изображена на рис. 8.5.
8.3. Ионно-звуковые ударные волны
291
плазменный источник, так называемая двухплазменная установка,
схема которой показана на рис. 8.10. Принцип действия установки
следующий. В двух электрически изолированных камерах с по-
мощью разрядов между проволочными электродами F и стенками
W создается два плазменных сгустка с идентичными параметрами.
Они разделены сеткой G, на которую подается отрицательное сме-
щение, вследствие чего она отталкивает электроны и по обе стороны
сетки образуются ионные слои. Между двумя камерами пропу-
скается импульс напряжения (обычно треугольной формы). В ре-
зультате ионы из одной камеры попадают в другую и возбуждают
там плоскую волну большой амплитуды. Эта волна регистрируется
с помощью подвижного зонда или анализатора скорости частиц Р.
На рис. 8.11 представлены результаты измерений зависимости
плотности в ударной волне от времени и положения регистрирую-
щего зонда. Из них видно, что при распространении фронт ионно-
звуковой волны укручается и в конце концов в системе образуется
классическая ударная волна. Столкновения между частицами при-
водят к затуханию осцилляций плотности.
Задача
8.5. Вычислите максимальную скорость, которую может иметь ионно-зву-
ковая ударная волна, создаваемая в установке, изображенной на рис. 8.10,
если эксперимент ставится в аргоновой плазме с параметрами Те = 1,5 эВ,
Ti = 0,2 эВ. Какую максимальную амплитуду (в вольтах) может иметь та-
кая ударная волна?
(
8.3.5. Двойные слои
С плазменными слоями и ионно-звуковыми ударными волнами
тесно связано еще одно явление — так называемые двойные слои.
Двойной слой представляет собой неподвижный локализованный
внутри плазмы скачок потенциала, не связанный ни с какими гра-
ницами. Такое образование, как полагают, может естественным
путем возникнуть в ионосферной плазме. Название «двойной слой»
связано с тем, что для создания скачка потенциала ф (х) в плазме
должны существовать отделенные друг от друга области положи-
тельного и отрицательного зарядов. Такой скачок потенциала мо-
жет быть стационарным в пространстве, только если в системе
имеется поток плазмы и движущийся против него фронт ударной
волны имеет в лабораторной системе нулевую скорость или если
функции распределения прошедших и отраженных от разрыва
ионов и электронов по обе стороны от скачка потенциала специ-
ально подогнаны друг к другу. В лабораторных экспериментах
двойные слои создавались с помощью «трехплазменных» устано-
вок, которые похожи на двухплазменную машину, изображенную
на рис. 8.10, и отличаются от нее только третьей, безэлектродной
10*
292
Гл. 8. Нелинейные явления
камерой, располагаемой между двумя камерами, в которых соз-
дается плазма. Подбирая величины относительных потенциалов,
прикладываемых к трем камерам, разделенным между собой сет-
ками, можно создать потоки ионов и электронов, которые после
столкновения в центральной камере образуют двойной слой. В ес-
тественных условиях двойные слои, вероятнее всего, образуются
там, где существуют градиенты магнитного поля В, а не в однород-
ном поле или в незамагниченной плазме, как это происходит при
их моделировании в лабораторных условиях. В локализации двой-
ных слоев вдали от границ плазмы значительную роль может сыг-
рать сила F = — pvB 1см. формулу (2.38)]. Примером двойного
слоя, который образуется в результате магнитного захвата, яв-
ляется так называемый тепловой барьер, существующий в тандем-
ных зеркальных ловушках.
8.4. Сила высокочастотного давления1)
Обычно давление световых волн очень мало, и зарегистрировать
его трудно. Даже пример с загадочными кометными хвостами, об-
разуемыми под действием солнечного излучения, не является
в этом смысле идеальным: ведь кроме излучения на комету воздейст-
вуют и испускаемые Солнцем частицы. А вот радиационное давле-
ние, развиваемое мощными пучками лазерного или СВЧ-излуче-
ния, с помощью которых производится нагрев и удержание плазмы,
может достигать сотен тысяч атмосфер! Давление излучения воз-
действует на частицы плазмы довольно сложным образом. Связан-
ную с этим давлением силу называют силой высокочастотного (ВЧ)
давления. Пользуясь понятием этой силы, можно довольно просто
объяснить многие нелинейные явления.
Выражение для нелинейной силы ВЧ-давления проще всего
вывести, если рассмотреть движение электрона в осциллирующих
полях Е и В, связанных с волной. Пренебрегая постоянными по-
лями Ео и Во, запишем уравнение движения электрона в виде
m(dNldt)=—e[E(r) + vx В(г)]. (8.34)
Если поля Е и В вычисляются в точке, где находится электрон,
то уравнение (8.34) является абсолютно точным. Что касается
нелинейности, то одним из ее источников служит член v X В, ко-
торый представляет собой величину второго порядка малости, ибо
в равновесии как v, так и В обращаются в нуль. Вследствие этого
член v X В по абсолютной величине не может превышать произве-
дение vx X Вх, в котором векторы Vj и Вх определяются из линей-
ной теории. Другая нелинейность, как мы увидим, возникает вслед-
ствие того, что электрическое поле нужно вычислять в точке на-
') Ее называют также пондеромоторной силой.— Прим. пере».
8.4. Сила высокочастотного давления
293
хождения электрона в данный момент времени, а не в той точке,
где он находился вначале. Предположим, что электрическое поле
волны имеет вид
Е = Es (г) cos со/, (8.35)
где Es (г) — пространственное распределение поля. В первом при-
ближении по амплитуде волны в уравнении (8.34) можно пренебречь
слагаемым v X В и считать, что величина Е равна значению элек-
трического поля в точке г0, соответствующей начальному положе-
нию частиц:
т (dviJdt) = —еЕ (г0), (8.36)
vx = —(е/пмй) Es sin со/ = drjdt, (8.37)
6rx = (e/mco2) Es cos co/. . (8.38)
Следует заметить, что при вычислении нелинейных величин мы не
можем пользоваться зависимостями от времени в виде ехр (i со/),
а затем брать вещественные части получающихся функций; теперь
мы вынуждены писать временную часть в виде cos со/. Это связано
с тем, что в нелинейной теории мы будем иметь дело с произведе-
ниями величин, а операции умножения и нахождения веществен-
ной части комплексного числа не коммутируют между собой.
Переходя к анализу величин второго порядка по амплитуде
волны, разложим Е (г) в ряд вблизи точки г=г0:
Е(г) = Е(го) + (6г1-7)Е|г=Го+ . . . . (8.39)
В уравнении движения электрона нужно теперь учесть член
Vj х В1( где Вх определяется из уравнения Максвелла:
VxE = — dE/dt,
В= — (1/®) v X Es |г=Го sin со/. (8.40)
Часть уравнения (8.34), имеющую второй порядок малости, можно
записать в виде
mdv^dt= —e[(6rx-V) E + vx х Вх]. (8.41)
Подставляя выражения (8.37), (8.38) и (8.40) в уравнение (8.41)
и усредняя получающееся равенство по времени, получаем
т {dN^dt} = - у- (e2/mco2) [(Es • V) Es + Es х (V X Es)] — fнелин•
(8.42)
Здесь мы воспользовались тем, что (sin2®/) = (cos2®/) = 1/2.
Двойное векторное произведение можно записать в виде суммы
двух членов, один из которых сокращается со слагаемым (Es-V) Es.
Таким образом, мы приходим к выражению
Гнелии =—- (е2//и®2) V^s, (8.43)
4
294
Гл. 8. Нелинейные явления
определяющему эффективное значение нелинейной силы, дейст-
вующей на отдельный электрон. Сила, действующая на 1 м3 плазмы,
получается, если умножить 1нелин на плотность электронов п0,
которую можно выразить через а2р. Пользуясь тем, что Ef = 2 (Е2),
получаем следующую формулу для силы ВЧ-давления:
Fнелин =------ V ----- (8.44)
со2 2
Если волна является электромагнитной, то в центральной ча-
сти уравнения (8.42) преобладает второй член. В этом случае фи-
зический механизм действия Рнелин состоит в следующем. Элек-
троны осциллируют вдоль направления Е, но магнитное поле
волны искажает их траектории, поскольку сила Лоренца —ev х В
толкает электроны в направлении к (напомним, что скорость ча-
стиц v направлена вдоль Е, поэтому сила —ev х В действует
вдоль к). Фазы осциллирующих величин v и В таковы, что средняя
по периоду скорость частиц не равна нулю и они смещаются вдоль
направления к. Если бы амплитуда волны была однородной, то
для поддержания этого направленного движения не требовалось бы
никакой силы. Однако в неоднородной волне электроны будут на-
капливаться там, где напряженность электрического поля меньше,
и для преодоления возникающего при этом пространственного за-
ряда потребуется дополнительная сила. Именно поэтому эффек-
тивное значение силы Енелин пропорционально градиенту вели-
чины (Е2). Поскольку все электроны плазмы движутся одинако-
вым образом, сила Енелин пропорциональна плотности плазмы,
которой в формуле (8.44) соответствует множитель сор/со2.
Пусть теперь волна является электростатической, тогда в цен-
тральной части (8.42) доминирует первое слагаемое. Физический
механизм возникновения нелинейной силы в этом случае состоит
просто в том, что электрон, колеблющийся вдоль направления
к || Е, при движении из области более сильного поля в область
слабого поля сдвигается на большее расстояние, чем при движении
в обратном направлении.
Хотя Енелин действует главным образом на электроны, эта
сила при посредстве низкочастотных движений или постоянных
полей может влиять и на ионы. Если электроны под действием силы
Енелин будут сгруппированы в сгустки, то в плазме произойдет
разделение зарядов и возникнет электрическое поле Еразд. Полная
сила, действующая на электроны, будет равна
Fe = —бЕразд “И Енелин- (8.45)
Сила ВЧ-давления Енелин, действующая на ионы, в Wp/Qp = М/т
раз меньше силы, определяемой формулой (8.44), и ею можно пре-
8.4. Сила высокочастотного давления
295
Рис. 8.12. Самофокусировка лазерного луча под действием силы высокоча-
стотного давления.
небречь. Следовательно, на ионную жидкость будет действовать
только сила
Р.-=еЕра9д. (8.46)
Складывая два последних равенства, приходим к выводу, что пол-
ная сила, действующая на плазму, равна FHanHH.
С действием силы ВЧ-давления Fнелин непосредственно свя-
зана самофокусировка лазерного излучения в плазме. Из рис. 8.12
видно, что на плазму, через которую проходит лазерный пучок
конечного диаметра, действует сила ВЧ-давления, направленная
от оси пучка наружу. Эта сила выталкивает плазму из пучка,
вследствие чего плазменная частота <ор и диэлектрическая прони-
цаемость е внутри пучка становятся меньше, чем снаружи. Плазма
при этом действует как собирающая линза, фокусирующая лазер-
ное излучение в пучок меньшего диаметра.
Задачи
8.6. Лазерный пучок мощностью 10х2 Вт (1 ТВт) фокусируется на твердой
мишени в пятно диаметром 50 мкм. Созданная и нагретая таким пучком
плазма стремится расшириться. Сила ВЧ-давления, которая действует глав-
ным образом там, где плотность плазмы близка к критической (п — пс или
со = ®р), стремится вернуть плазму обратно, вследствие чего возникает так
называемая модификация профиля, а именно резкое изменение плотности
плазмы вблизи слоя с критической концентрацией.
а) Какое давление (в Н/м2) создает сила Енелин? (Указание: обратите внима-
ние на то, что эта сила измеряется в Н/м3 и что градиентный масштаб в ответ
не входит. При вычислении (Е2) считайте, что эта величина равна своему
значению в вакууме, а поток вектора Пойнтинга мощностью 1 ТВт равен
произведению плотности энергии в лазерном пучке на групповую скорость
волн в вакууме.)
б) Чему равна (в тоннах) общая сила давления лазерного пучка на плазму?
в) Какой скачок плотности может создать давление световых волн, если
KTt = КТе = 1 кэВ?
8.7. Исследуется процесс самофокусировки цилиндрического пучка лазер-
ного излучения с частотой со, распространяющегося в плазме докритической
плотности, у которой п <пс s евтпй)2/е2. В состоянии равновесия профиль
интенсивности излучения и профиль плотности плазмы определяются из
условия равенства кинетического и ВЧ-давлений (рис. 8.12). Пренебрегая
296
Гл. 8. Нелинейные явления
нагревом плазмы (т. е. считая, что КТ ss КТе + /ГЛ = const), докажите,
что плотность плазмы распределена по закону
п = n0 ехр (— е0 (Н2)/2п(;К7’) еэ па ехр [ — а (г)].
Величина а (0) является мерой отношения ВЧ-давления к давлению плазмы.
8.5. Параметрические неустойчивости
Из процессов нелинейного взаимодействия волн наиболее де-
тально исследованы параметрические неустойчивости, названные
так по аналогии с распространенными радиотехническими устрой-
ствами — параметрическими усилителями. Такого полного пони-
мания предмета удалось достичь потому, что теория этих процес-
сов в основном аналогична линейной и отличается от нее только
тем, что линеаризация уравнений задачи производится не около
стационарного, а около осциллирующего состояния равновесия.
8.5.1. Связанные осцилляторы
Рассмотрим изображённую на рис. 8.13 механическую модель,
которая состоит из двух осцилляторов Мх и М2, связанных с по-
мощью бруса, покоящегося на основании Р. Собственные частоты
осцилляторов равны и и2, а основание может двигаться взад-
вперед с частотой <оо. Ясно, что если Мх и М2 неподвижны, то в от-
сутствие силы трения основание может свободно колебаться, не
испытывая сопротивления. Если же основание Р неподвижно,
а осциллятор М2 пришел в движение, то и Мх начнет двигаться, од-
нако, вследствие того что собственные частоты осцилляторов раз-
личны, амплитуда колебаний Мх будет мала. Теперь предположим,
что двигаются как Р, так и М2. Тогда смещение осциллятора Мъ
пропорциональное произведению смещения осциллятора М2 на
длину плеча, будет меняться со временем по закону
cos <o2t cos (o0i — (1/2) cos [(®2 -j- ®0) + (l/2)'cos [(co2 — <oo) t]. (8.47)
Рис. 8.13. Механический аналог параметрической неустойчивости.
8.5. Параметрические неустойчивости
297
Если частота а1 равна ю2 + ®0 или ®2—со0, то Мх окажется в ре-
зонансе и амплитуда его колебаний начнет расти. Вследствие этого
М2 тоже будет получать дополнительную энергию, поскольку одна
из частот биений между сох и со0 в точности равна собственной ча-
стоте этого осциллятора <о2. Таким образом, после начала колеба-
ний одного из осцилляторов каждый из них будет возбуждаться
от другого, и система станет неустойчивой. Энергия колебаний,
разумеется, поступает от «накачки» Р, которая при своем движе-
нии должна преодолевать сопротивление наклонного бруса. Если
накачка достаточно сильная, то амплитуда колебаний основания
не будет зависеть от Мх и М2 и возникающую в системе неустойчи-
вость можно рассматривать в рамках линейной теории. В плазме
в качестве осцилляторов Р, Мх и М2 могут выступать различные
типы волн.
8.5.2. Резонансное взаимодействие волн
Уравнение движения простого гармонического осциллятора имеет
вид
d\ldt2 + <>hcr=Q, (8.48)
где «х — резонансная частота осциллятора. В случае когда на
осциллятор действует нестационарная сила, пропорциональная
произведению амплитуды накачки Ео на амплитуду смещения вто-
рого осциллятора х2, уравнение движения принимает вид
dfx-Jdt2 + (ofxx = CiX2Eq, (8.49)
где Cj — константа связи. Аналогичное уравнение имеет место
и для второго осциллятора:
d2x2!dt2 + (1)2^2 = с^Ео. (8.50)
Пусть х1 = %хСО8 со/, х2 = х2 cos со'/, а Ео = E0cos соо/, тогда из
уравнения (8.50) ^следует, что
(<В2 — со'2) *2 C°s СО' t = C2EoXr COS СОо t cos at =
= с2ЁоХ1 {cos [(соо ч- со) /] н-COS [(со0 — со) /]}. (8.51)
В правой части этого равенства стоит выражение для вынуждаю-
щей силы, которая заставляет второй осциллятор совершать ко-
лебания с частотами
со' = соо ± со- (8.52)
Если бы нелинейного взаимодействия не было, то второй осцилля-
тор мог бы совершать крлебания только с частотой со 2, т. е. должно
было бы выполняться равенство со' = со2. Однако наличие вынуж-
дающей силы вызывает сдвиг частоты, и со' будет равна со2 только
298
Гл. 8. Нелинейные явления
приближенно. Кроме того, если в системе существует затухание
(пока мы им для простоты пренебрегали) или неустойчивость, то
®' может быть комплексной величиной. Во всяком случае теперь
осциллятор х2 представляет собой систему с конечной добротностью
Q, т. е. может откликаться не только на чисто синусоидальное воз-
мущение с а = со2, но и на колебания, частоты которых находятся
вблизи ®2. Из условия (8.52) видно, что при малых <в оба значе-
ния со' могут лежать в полосе частот, на которые откликается вто-
рой осциллятор х2, и поэтому при анализе системы нужно учиты-
вать возможность существования двух осцилляторов: х2 (®0 + ®)
и х2 (со0—со).
Положим хг = х1 cos х2 = x2cos [(®0 ± ®) t] и подста-
вим эти выражения в уравнение (8.49):
(2 "2\ — " ±
(01 — (О ) Хх COS (О t =
= С1Ёо*2 ~ (cos {[®о + (®0 ± <о)1 О 4-C0S {[<о0 — (®о ± “)] Ф =
= ^£0X2 {cos [(2®0 ± ®) Л + cos со1}. (8.53)
Таким образом, вынуждающая сила, действующая на первый ос-
циллятор, возбуждает не только колебания с частотой со, но и ос-
цилляции с новыми частотами и" = 2соо ± со. Мы будем рассмат-
ривать случай |®0| )§> |©j|. При этом частоты 2соо ± ® распола-
гаются вне диапазона частот, на которые откликается первый
осциллятор, и амплитудой хх (2®0 ± со) можно пренебречь. Таким
образом, мы имеем систему из трех осцилляторов хг (®), х2 (соо—(л)
и х2 (со0 + <о), которые связаны между собой уравнениями (8.49)
и (8.50):
(со2—со2) Xj (со) — CjEo (со0) [х2 (со0— ®) + х2 («о + и)] = 0,
[®2—(®0“-®)2]х2(®() —®)—с2Ео(®о)х1(и)= О, (8.54)
[со2—(соо + ®)2] Х2 (со0 + и) — с2Е0 ((Оо) Xi (со) = 0.
Приравняв нулю детерминант, составленный из коэффициентов
этой системы уравнений, приходим к следующему дисперсионному
уравнен! сю: 2 2 (0 —С01 ciEq С1Е0
с%Е0 (С00 — со)2 — ©2 0 = 0. (8.55)
cJEo 0 ( ®0 + ®) — 0) 2
Если среди корней этого уравнения есть решение с Im (со) >0,
то это свидетельствует о неустойчивости системы связанных осцил-
ляторов.
8.5. Параметрические неустойчивости 299
В случае когда сдвиги частот или инкременты неустойчивостей
малы, частоты со и со' можно приближенно считать равными невоз-
мущенным частотам сох и со2. В этом случае из уравнения (8.52)
получаем следующее резонансное условие для частот:
со0 ?а <02 ± cox. (8.56)
Если осцилляторы представляют собой волны в плазме, то в преды-
дущих выкладках величину со/ нужно заменить на со/—к-г. Кроме
упомянутого условия, связывающего между собой частоты взаимо-
действующих волн, в последнем случае должно также выполняться
следующее условие для волновых векторов (условие пространст-
венного резонанса):
к0« к2 ± кг (8.57)
Физический смысл условий (8.56) и (8.57) легко понять из кванто-
вомеханической аналогии. Умножим равенство (8.56) [на постоян-
ную Планка h:
Й<оо« Йсо2 ± Й©!. (8.58)
Пусть Ео и х2 представляют собой, например, электромагнитные
волны, а осциллятору х1 отвечает ленгмюровская волна. Тогда ве-
личины Йсоо и /гсо2 соответствуют энергиям фотонов, a — это
энергия ленгмюровского плазмона. Таким образом, формула (8.56)
выражает просто закон сохранения энергии, а условие (8.57) яв-
ляется аналогом закона сохранения импульса Йк.
Одновременное выполнение условий (8.56) и (8.57) для волн
в плазме в одномерном случае возможно лишь при определен-
ных комбинациях волн. Необходимые соотношения лучше всего
уяснить с помощью диаграмм ю (й), представленных на рис. 8.14.
На рис. 8.14, а приведены дисперсионные кривые для электронной
плазменной волны (волны Бома—Гросса) и ионно-звуковой волны
(ср. с рис. 4.13). Плазменная волна (соо. ко) большой амплитуды
может испытать распад на движущуюся в обратном направлении
плазменную волну (со2, к2) и на ионно-звуковую волну ((d1; kJ.
Из построенного на рисунке параллелограмма следует, что <в0 =
= (о1 4- со2, a k0 = kj + к2. Для выполнения этих соотношений
положения точек (соо, к0) и (<ю2, к2) на дисперсионной кривой элек-
тронных волн нужно выбрать таким образом, чтобы вектор к1(
равный разности векторов к0 ик2, лежал на дисперсионной кривой
ионно-звуковых волн. Заметим, что ленгмюровская волна не мо-
жет распадаться на две ленгмюровские, поскольку конец разност-
ного вектора (к0—к2) не может лежать на дисперсионной кривой
электронных плазменных волн.
На рис. 8.14, б построен параллелограмм волновых векторов
для так называемой параметрической распадной неустойчивости.
В этом случае (соо, к0) представляет собой электромагнитную волну
большой амплитуды с высокой фазовой скоростью (со0/й0 « с). Она
300
Гл. 8. Нелинейные явления
Рис. 8.14. Распадные условия для частот <в и волновых чисел k при различ-
ных типах параметрических неустойчивостей: а — неустойчивость относи-
тельно распада электронной плазменной (ленгмюровской) волны; б — па-
раметрическая распадная неустойчивость; в — вынужденное бриллюэнов-
ское рассеяние, г — неустойчивость относительно распада на два плазмона.
В каждом из примеров со0 — частота первичной волны, Oj и со2 — частоты
волн, возникающих в результате распада. Прямые линии — дисперсионные
зависимости для ионно-звуковых волн; узкие параболы — для электромаг-
нитных волн; широкие параболы — для электронных плазменных (ленгмю-
ровских) колебаний.
возбуждает электронную и ионно-звуковую волны, распространяю-
щиеся в противоположных направлениях. Поскольку величина
| к01 мала, для этой неустойчивости мы имеем | kj | « — |к2| и
®о — ®1 + ®2-
На рис. 8.14, в представлена диаграмма со (&) для так называе-
мого обратного параметрического рассеяния, когда электромаг-
нитная волна возбуждает ионно-звуковую волну и другую элек-
тромагнитную волну, распространяющуюся противоположно пер-
вичной волне. Заметим, что в этом процессе вместо ионно-звуковой
волны может возбуждаться плазменная волна. По аналогии с по-
хожими явлениями в физике твердого тела эти процессы называются
соответственно «вынужденным бриллюэновским рассеянием» и «вы-
нужденным комбинационным рассеянием».
На рис. 8.14, г изображен распад электромагнитной волны на
два плазмона. Поскольку обе волны, получающиеся в результате
распада, представляют собой электронные плазменные колебания,
8.5. Параметрические неустойчивости
301
распадное условие для частот можно выполнить только в том слу-
чае, если со0 л; 2сор. Выразив частоты со0 и сор через плотность
плазмы, приходим к выводу, что последнее условие эквивалентно
условию п » пе/4, где пс — критическая плотность, отвечающая
частоте соо [см. (4.88)]. Таким образом, можно ожидать, что в не-
однородной плазме эта неустойчивость будет возникать только
в том слое плазмы, где ее плотность равна четверти критической
плотности.
8.5.3. Порог неустойчивости
Если затухание волн в плазме отсутствует, то параметрические
неустойчивости могут возникнуть при любой амплитуде колебаний.
На практике, однако, всегда существует небольшое столкнови-
тельное затухание или затухание Ландау, и потому неустойчивость
может развиваться только в том случае, когда амплитуда волны
накачки достаточно велика. Для того чтобы рассчитать порог не-
устойчивости, нужно ввести в рассмотрение декременты 1\ и Г2,
характеризующие затухание колебаний осцилляторов х1 и х2.
Уравнение (8.48) примет тогда вид
d^ldt2 + со?хх + 2ГХ (dx-Jdt) = 0. (8.59)
Если хх представляет собой, скажем, смещение груза под дейст
вием пружины, то в уравнении (8.59) последнее слагаемое описы
вает силу трения, которая пропорциональна скорости груза. Если
хх отвечает плотности электронов в плазменной волне, затухающей
из-за столкновений электронов с нейтральными атомами, то =
= vc/2 (ср. с задачей 4.5). Из соотношений (8.49) и (8.50) следует,
что зависимость амплитуд волн от времени можно искать в виде
экспоненциального множителя и, считая Ео вещественной величи-
ной, а хг и х2 — комплексными, заменить производную d/dt на
— i со. При этом уравнения (8.49) и (8.50) можно переписать в виде
(со?—со2—2i соГх) хх (со) = 'с^Ео»
[со?—(со—соо)2—2i(со — <о0)Г2]х2 (® —а0)=с2х1Е0. (8.60)
Сделаем еще одно упрощение: ограничимся случаем двухволнового
взаимодействия, т. е. будем считать, что со » сох, соо—со « со2, а
частота соо + со столь сильно отличается от со2, что соответствую-
щая ей волна является нерезонансной. В этом случае третью строку
и третий столбец в детерминанте (8.55) можно не рассматривать.
Если теперь выразить хх, х2 и Ео через их максимальные значения,
как это было сделано при выводе уравнения (8.53), то в правых
частях уравнений (8.60) появится множитель 1/2. Пренебрегая
302
Гл. 8. Нелинейные явления
нерезонансными членами и исключая и х2 из уравнений (8.60),
получаем
(со2—со2 4- 2i соГх) [(<о0—со)2—со2—2i (со0— со) Г2] = — с&Ед.
4
(8.61)
Можно считать, что на пороге неустойчивости Im (со) = 0. Наи-
низший порог соответствует точному выполнению резонансного
условия, он достигается при со — со1, со0—со = со2. При этом из
(8.61) следует, что
с1с2(£0)поР=16®1«)аГ1Г2. (8.62)
Если хотя бы одна из волн не затухает, то порог неустойчивости
равен нулю.
Задачи
8.8. Докажите, что при плотностях п>пс/4 не может быть вынужденного
комбинационного рассеяния.
8.9. В эксперименте по облучению мишени из твердого дейтерия (Z=]l, М—
= 2Л4н) лазером на неодимовом стекле (А, = 1,06 мкм) наблюдается вынуж-
денное бриллюэновское рассеяние. Длина волны рассеянного света оказы-
вается сдвинутой в красную сторону спектра на 21,9 А. Из измерения в рент-
геновской части спектра известно, что температура электронов К.Те =
— 1 кэВ. С помощью формулы (4.41) при ус = 3 оцените температуру ионов,
предполагая, что рассеяние идет в области частот «>2 < св2.
8.10. Анализируя процесс вынужденного бриллюэновского рассеяния, бу-
дем считать, что в системе уравнений (8.60) величина хг равна п1 — возму-
щению плотности в ионно-звуковой волне, а х2 — это электрическое поле
отраженной волны £2. Коэффициенты связи сг и с2 определяются при этом
выражениями q = e0fe2<o2/(o0<B2Af, с2 = со2(д2/пой>о, а пороговую амплитуду
накачки в однородной плазме можно вычислить по формуле (8.62). Обычно
квадрат амплитуды волны накачки выражают через (а2сц), средний квадрат
скорости осцилляций электронов в волне о2сц. Как известно [см. (8.37)],
цосц = еЕ^тЫц. Величину декремента Г2 в пределе v/a> 1 можно [найти
в условии задачи 4.376.
а) Покажите, что при Тс < Те порог вынужденного бриллюэновского рас-
сеяния определяется формулой
<4осцЖ = 4riv/(O1(O2,
где о2 = KTjm, <о1 = k^vs, a Tj —декремент затухания Ландау, опреде-
ляемый выражением (7.133).
б) Излучение СО2-лазера падает на однородную водородную плазму
(КТе = 100 эВ, КТ’с = 10 эВ, п0 = 1028 м~3). Вычислите пороговую интен-
сивность /0 лазерного излучения в Вт/см2, необходимую для возбуждения
вынужденного бриллюэновского рассеяния. (Указание: для расчета vec поль-
зуйтесь формулой Спитцера.)
8.5. Параметрические неустойчивости
303
8.11. Инкремент вынужденного бриллюэновского рассеяния в однородной
плазме вдали от порога неустойчивости можно найти из уравнения (8.61),
если пренебречь в нем членами, описывающими затухание. Предположим,
что O)=ais+i у, причем у2 < со2, а п пс. Покажите, что у = (1/2) уосц X
X Qp(wq/<bs)I/2, где оосц—максимальная скорость колеблющихся электронов.
8.5.4. Физический механизм неустойчивостей
Параметрическое возбуждение волн очень легко понять, рассмот-
рев силу ВЧ-давления (разд. 8.4). В качестве иллюстрации рас-
смотрим процесс распада электромагнитной волны (<о0, Ло) на элек-
тронную плазменную волну (tt>2> ^2) и низкочастотную ионно-
звуковую волну (®х, kr) (рис. 8.14, б). Поскольку частота сох мала,
<в0 должна быть близка к сор. Оказывается, однако, что при соо<;<вр
и ®0 система ведет себя совершенно по-разному. В первом
случае возникает так называемая осциллирующая двухпотоковая
неустойчивость (ее мы детально рассмотрим ниже), во втором —
распадная параметрическая неустойчивость.
Предположим, что в плазме существует возмущение плотности
вида rijcos Ахх; такое возмущение может, например, спонтанно воз-
никнуть как составляющая теплового шума. Пусть электрическое
поле волны накачки Ео cos о>0/ направлено по оси х (рис. 8.15).
В незамагниченной плазме дисперсионное соотношение, связываю-
щее между собой параметры соо и k0 в электромагнитной волне,
имеет вид соо = так что если ю0 т а>р, то ko « 0. Сле-
довательно, мы можем считать, что распределение поля волны на-
качки Ео почти однородно в пространстве. Пусть соо <юр (сор—
резонансная частота колебаний холодной электронной жидкости);
тогда электроны в волне будут смещаться против направления Ео,
а ионы за времена порядка со,Г1 вообще не успеют сместиться и ос-
танутся неподвижными. В системе, таким образом, возникнут раз-
деление зарядов (рис. 8.15) и электрическое поле Elt осциллирую-
щее с частотой ®0- Силу ВЧ-давления, обусловленную суммарным
полем Ео + Elt можно найти из формулы (8.44):
Рнелин =----— (сйр/соо) V ((Ео 4”£1) ) ео- (8.63)
Поскольку Ео однородно в пространстве и гораздо больше, чем Ех,
основной вклад в Рнелин дает лишь произведение Е0£х:
F™= (8.64)
2 ох
Среднее от E0Elt вообще говоря, не равно нулю, поскольку вели-
чина Ех сама зависит от Ео. Из рис. 8.15 видно, что Рнелин в точ-
ках минимума и максимума плотности пх обращается в нуль, но
там, где градиент v»i имеет значительную величину, сила Рнелин
304
Гл. 8. Нелинейные явления
Рис. 8.15. Физический механизм осциллирующей двухпотоковой неустой-
чивости.
также велика. Как следует из рис. 8.15, в системе возникает такое
пространственное распределение концентрации, что РнеЛин вы-
талкивает электроны из областей с низкой плотностью в области
высокой плотности. Возникающее при этом электрическое поле
втягивает в эти области и ионы, так что возмущения плотности
плазмы все время нарастают. Давление sjntl (KTi + /<Те) стре-
мится сгладить эту неоднородность концентрации. Ясно, что по-
роговое значение Рнелин будет достигнуто тогда, когда силе ВЧ-
давления удастся превзойти силу давления плазмы. Если Рнелин
становится выше этого порогового значения, то в системе разви-
вается неустойчивость, которую называют осциллирующей двух-
потоковой неустойчивостью, поскольку усредненная по времени
функция распределения электронов имеет два пика, совсем как в
случае двухпотоковой неустойчивости [разд. 6.6]. Заметим, что
у неустойчивых колебаний Re (<вх) = 0, поскольку возмущение
плотности представляет собой стоячую волну.
Если же частота а»0 больше, чем сор, то рассмотренный выше
механизм не работает. Дело в том, что в последнем случае направ-
ление силы, действующей на осциллятор, меняется с частотой, пре-
вышающей собственную частоту этого осциллятора, и поэтому
осциллятор движется против действующей на него силы, а это
приводит к стабилизации неустойчивости (подробнее мы расска-
жем об этом в следующем разделе). При ®0 ><ор направления ve,
8.5. Параметрические неустойчивести 305
Ех и Рнелин на рис. 8.15 меняются на противоположные. В этом
случае сила В Ч-давления выталкивает ионы из областей с повы-
шенной концентрацией частиц и нераспространяющееся возмущение
плотности будет со временем затухать. Однако если при соо>®р
имеется еще и бегущая ионно-звуковая волна, то ситуация корен-
ным образом меняется. Из-за инерции ионов между моментом при-
ложения силы Рнелин и моментом максимального смещения ионов
проходит какое-то время. За это время максимум плотности в
ионно-звуковой волне может сместиться именно туда, куда сила
Рнелин вытолкнула ионы, и концентрация частиц' в этой точке
начнет возрастать. Естественно, это может произойти только в том
случае, если фазовая скорость ионно-звуковой волны имеет необ-
ходимое для этого значение. Легко понять, что такое значение
равно vs. Последнее видно уже из того факта, что фаза силы Рнелин
в точности равна фазе электрической силы, действующей на ионы
в ионно-звуковой волне, где потенциал достигает максимума в точ-
ках максимума плотности, и наоборот (см. рис. 8.15, на котором
направления стрелок в этом случае нужно изменить на противо-
положные). Следовательно, сила ВЧ-давления Рнелин складывается
с электростатической силой, действующей на ионы в звуковой волне,
что приводит к увеличению амплитуды ионно-звуковых колебаний.
Что касается электронов, то амплитуда их колебаний также будет
достаточно велика, если частота волны накачки близка к собствен-
ной частоте осцилляций электронной жидкости: =
= <Ор + (3/2) ^2у?епл- Отметим, впрочем, что частота волны на-
качки соо не может быть в точности равна со2, поскольку разность
между соо и со2 должна быть равна частоте ионно-звуковой волны
coi = kх1»5. Это нужно для того, чтобы сила Риелин возбуждала
именно ионно-звуковые волны. Поэтому если частоты удовлетво-
ряют условию <ох = со0—со2, то в присутствии волны накачки в
среде будут возбуждаться как ионно-звуковая, так и электронная
плазменная волны. Таков механизм распадной параметрической
неустойчивости.
8.5.5. Осциллирующая двухпотоковая неустойчивость
Основываясь на физической картине, рассмотренной в предыдущем
разделе, выведем теперь уравнения для этого простейшего примера
параметрической неустойчивости. Пусть для простоты Tt = Те =
= ve = vj = 0. Тогда низкочастотные движения ионной жидкости
можно описать уравнениями
Мп0 (dv^ldt) = еп0Е — Рйеляа, (8.65)
(дпц/dt) + п0 (dvtl/dx) = 0. (8.66)
Предположим, что в состоянии равновесия плазма является
пространственно однородной, тогда мы можем произвести фурье-
306
Гл. 8. Нелинейные явления
разложение по х и заменить д/дх на \k. При этом из (8.65) и (8.66)
получаем следующее уравнение:
a2nn/3i2 + (i^/Af) Р нелин — 0, (8.67)
где /"нелин дается формулой (8.64). Чтобы найти Е1г нужно рас-
смотреть движение электронов. Оно описывается уравнением
т [dvjdt + ve (dvjdx)] = — е (Ео 4- Ег), (8.68)
в котором Ег связано с пе1 уравнением Пуассона
1/ге0Е1= — епл. (8.69)
Следует заметить, что любая из величин Elt ve и пе1 состоит из двух
частей: высокочастотной моды, в которой движение электронов
осуществляется независимо от движения ионов, и низкочастотной
моды, в которой электроны движутся вместе с ионами квазиней-
тральным образом. В наинизшем приближении по амплитуде волн
движение частиц представляет собой отклик на пространственно
однородное поле Ео:
dv^/dt = —(е/т) Ео — —(е/т) E0cos соо/. (8.70)
Линеаризуя уравнение движения ионов вблизи этого осциллирую-
щего положения равновесия, получаем следующее уравнение:
dvel/dt + i toeOuel = — (e/m)El = —(e/m)(Elfl + Eu), (8.71)
где индексами l и h помечены соответственно низкочастотная и вы-
сокочастотная части меняющихся величин. Вклад в первое слагае-
мое определяется в основном высокочастотной скоростью veh, опи-
сываемой уравнением
dvehJdt == — (e/m) Elh = nefte2/i keom, (8.72)
где мы воспользовались уравнением Пуассона (8.69). Низкочастот-
ная составляющая уравнения (8.71) имеет вид
i kveOveh = — (elm) Еа.
Правая часть этого выражения представляет собой силу ВЧ-давле-
ния, действующую на ионы плазмы [см. (8.65)]. Эта сила обуслов-
лена низкочастотными биениями между ve0 и veh. Левая часть этого
выражения определяется электростатической частью силы ВЧ-дав-
ления [см. (8.42)].
Уравнение непрерывности для электронов записывается в виде
dnel/dt + i kvebnel4- п0 i kvel = 0. (8.73)
Рассмотрим высокочастотную часть этого уравнения. Если пре-
небречь возбуждением волн с частотой 2со0 и более высоких гармо-
ник, то в среднем члене высокочастотная составляющая может
появиться только в результате наложения низкочастотной плот-
ности nei на уе0. Но, как следует из квазинейтральности плазмы
8.5. Параметрические неустойчивости 307
в низкочастотных движениях, nei = поэтому высокочастотная
часть уравнения непрерывности (8.73) принимает вид
dnehldt + i knovefl + i = 0. (8.74)
Продифференцируем последнее уравнение по времени и пренебре-
жем членом dnijdt. Используя для dveQldt и dveh!dt выражения
(8.70) и!(8.72), получаем
(?nehldt2 + <Ор«ел = (i ke/rri) п(1Е0. (8.75)
Пусть neh зависит от времени как ехр (— icoZ); тогда
(<о2- о2) пвЛ — (i]fee/m) п(1Е0. (8.76)
Уравнения (8.69) и (8.76) позволяют найти высокочастотную состав-
ляющую электрического поля:
тр __ &__________________&_____П-ilEp . /g 77)
9 9 о о V • /
еот а>р — <о ' eom со* — cog
(Предполагая, что скорость роста много меньше частоты волны
накачки Ео, мы заменили здесь со на соо.) Теперь из формулы (8.64)
можно найти силу ВЧ-давления:
^нелии « (e7/n) (cop/coo)i kn{1 (£о)/(®р—соо). (8.78)
Заметим, что знаки величин £lft и £нелин зависят от знака разно-
сти со2—®о- Именно по этой причине при coq >сОр механизм осцил-
лирующей двухпотоковой неустойчивости не работает. Максимум
силы ВЧ-давления достигается при соо « ®р (сор/соо « 1). Урав-
нение (8.67) в этом случае можно записать в виде
&пц!д1?« (Л2/2Л4т) Еолл/(®р—®о). (8.79)
Низкочастотное возмущение плотности в такой неустойчивости
является нераспространяющимся, поэтому можно считать, что
пи = лиехр (т^)> где У — инкремент неустойчивости. Таким об-
разом,
у2 « (e2fe2/2Mm)£o/(«>p —©о)- (8.80)
Величина у вещественна только в том случае, если со2 <w2. Факти-
ческое значение у зависит от того, насколько в действительности
мал знаменатель а»р—coq в центральной части выражения (8.77).
(Приближение ®р = соо является грубым.) При наличии затухания
мнимая часть разности —со2 будет порядка 2Г2сор, где Г2 — дек-
ремент затухания электронных плазменных волн. В этом случае
мы имеем
у~Ё0/ГУ2. (8.81)
Вдали от порога неустойчивости мнимая часть частоты со будет
308
Гл. 8. Нелинейные явления
определяться не значением Г2, а величиной у. В последнем случае
у2~£о/у или у~(£0)2/3. (8.82)
Такая зависимость у (Ео) характерна для всех параметрических
неустойчивостей. Для точного вычисления у и порогового значе-
ния Ео нужно более аккуратно, чем мы это сделали здесь, найти
сдвиг частоты ®р—со0. При этом П(1 нужно определить из (8.76)
и соответствующее выражение подставить в правую часть уравне-
ния (8.79):
= — (i kei2M) neflE0. (8.83)
Уравнения (8.75) и (8.83) при этом образуют систему уравнений,
напоминающую (8.49) и (8.50). Решение со (k, EQ) можно найти,
приравняв нулю определитель, составленный из коэффициентов
в уравнениях (8.75) и (8.83). Собственная частота первого осцил-
лятора ©! в этом случае в ответ не войдет, поскольку в пределе
Те = Tt = 0 ионно-звуковые волны в плазме отсутствуют и сох =0.
8.5.6. Распадная параметрическая неустойчивость
Анализ взаимодействия волн при соо ><ор можно провести по той
же схеме, которая была применена выше для случая ®0 <®р. Как
отмечалось ранее, при соо >сор электромагнитная волна распа-
дается на электронную плазменную (ленгмюровскую) и ионно-
Генератор
ВЧ-сигнала
(350 МГц)
Усилитель
ВЧ-мощности
(P^ZObrn}
Изолирующий
конденсатор
Металлическая
камера
{анод}
Гзрячие
проволочные
нита (катод)
= Зонд
с-----30 СМ
Рис. 8.16. Схема эксперимента, в котором было подтверждено существование
распадной параметрической неустойчивости. [Из работы: W'ong А. У. et
al. Plasma Physics and Controlled Nuclear Fusion Research.— liternational
Atomic Energy Agency, Vienna, 1971, v. I, p. 335.]
8.5. Параметрические неустойчивости
309
Ионно-звуковая
волна
Плазменная Волна
Низке
порога
Рис. 8.17. Частотные спектры колебаний, наблюдаемые с помощью устройства,
показанного схематически на рис. 8.16. В случае когда амплитуда возмуще-
ния чуть ниже пороговой, в низкочастотной части спектра наблюдается лишь
шумовой фон, а в высокочастотной — сама волна накачки. После неболь-
шого увеличения амплитуды накачки система выходит за порог неустойчи-
вости и в спектре появляются колебания, соответствующие частотам плаз-
менной и ионно-звуковой волн. [С любезного разрешения Р. Стенцеля, Ка-
лифорнийский университет, Лос-Анджелес. ]
звуковую волны. Мы не будем приводить здесь алгебраические
выкладки, описывающие этот процесс (они немного длиннее, чем
при анализе осциллирующей двухпотоковой неустойчивости). Вме-
сто этого рассмотрим некоторые эксперименты. Распадная пара-
метрическая неустойчивость хорошо изучена, она наблюдалась
как в лаборатории, так и в условиях ионосферы. Осциллирующая
двухпотоковая неустойчивость наблюдается гораздо реже. Ча-
стично это связано с апериодическим характером такой неустойчи-
вости [Re (со) = 0], частично — с тем, что данная неустойчивость
реализуется при соо <со„, когда волна, падающая на плазму, по-
глощается ею. На рис. 8.16 схематически показана установка, при-
менявшаяся в экспериментах Стенцеля и Вонга. Она состоит из
источника плазмы, аналогичного изображенному на рис. 8.10,
пары сеток, между которыми с помощью генератора создается поле
Ео, и зонда, подсоединенного к двум анализаторам спектра. Спектры
зарегистрированных в плазме сигналов показаны на рис. 8.17. Ниже
310
Гл. 8. Нелинейные явления
Рис. 8.18. Схема активного эксперимента для исследования ионосферной
плазмы, в котором наблюдалось поглощение СВЧ-колебаний, обусловленное
их параметрической неустойчивостью. [Из работы: Utlaui W. Е., Cohen R.,
Science, 174, 245 (1971).]
порога неустойчивости высокочастотный спектр состоит только
из волны накачки, частота которой /0 = 400 МГц. В низкочастот-
ном канале при этом наблюдается лишь слабый шум. После неболь-
шого увеличения амплитуды волны накачки в низкочастотной ча-
сти спектра образовалась ионно-звуковая волна с частотой /х =
= 300 кГц. Одновременно в высокочастотной части спектра воз-
никал сателлитный сигнал на частоте 399,7 МГц, представляющий
собой электронную плазменную волну с частотой, равной разно-
сти частот /0—волны накачки и ионно-звуковой волны. Наблю-
дались также биения волны накачки и ионно-звуковой волны, что
приводило к появлению слабого сигнала на частоте /0 + Л —
= 400,3 МГц.
Подобная неустойчивость наблюдалась также в ионосферных
экспериментах. На рис. 8.18 показана схема активного экспери-
мента по изменению состояния ионосферы, выполненного с помощью
большого радиотелескопа, расположенного в Платвилле (шт. Ко-
лорадо, США). Антенна телескопа посылала в ионосферу мощный
(2 МВт) поток СВЧ-излучения на частоте 7 МГц. В том слое ионо-
8.6. Плазменное эхо
311
сферы, где выполняется условие ®0 is <вр, наблюдалась генерация
плазменных и ионно-звуковых волн, а также нагрев ионосферных
электронов. В другом эксперименте, выполненном с помощью боль-
шой параболической антенны в Аресибо (Пуэрто-Рико), были из-
мерены параметры со и к возникших в результате неустойчивости
ленгмюровских волн. Авторы эксперимента зондировали ионо-
сферу лучом радара (частота 430 МГц) и наблюдали его рассеяние
от решетчатой структуры, образованной возмущениями плотности
электронов в плазменных колебаниях
Задачи
8.12. В установках лазерного синтеза луч лазера нагревает мишень в виде
таблетки, содержащей топливо для термоядерной реакции. Параметрическая
распадная неустойчивость может увеличить эффективность такого нагрева,
поскольку в процессе ее развития энергия лазерного излучения будет сна-
чала трансформироваться в энергию плазменных волн, а затем посредством
затухания Ландау передаваться электронам. При какой плотности плазмы
начнется параметрический распад, если используется лазер на иоде, кото-
рый излучает на длине волны А, = 1,3 мкм?
8.13. а) Получите следующее уравнение для возмущения плотности в ионно-
звуковой волне в присутствии силы ВЧ-давления ГнелиН:
(о2 + 2i Ги — k2v2s) Hi = i ^Гнелин/АГ.
Здесь Г —декремент затухания собственной моды (при ГНелин1 = 0)- (Ука-
зание: введите эффективную частоту столкновений v в уравнение движения
ионов, а после того, как будет получено дисперсионное уравнение, выразите
v через Г.)
б) Для случая вынужденного бриллюэновского рассеяния выразите -Рнелин
через амплитуды соответственно волны накачки Ео и рассеянной волны
Таким образом вы подтвердите, что константа связи с± в задаче 8.10 была
выбрана правильно. [Указание: см. формулу (8.64).]
8.14. На рис. 8.17 верхний сателлит с частотой <оо 4-cOi отсутствует. Это не
случайно. Оказывается, в большинстве параметрических процессов ампли-
туда верхнего сателлита меньше амплитуды нижнего. Объясните, почему
это так, пользуясь простыми энергетическими соображениями и квантово-
механическими аналогиями.
8.6. Плазменное эхо
Затухание Ландау не связано со столкновениями или диссипацией
энергии и потому является обратимым процессом. Наглядным под-
тверждением этого служит замечательное явление плазменного
эха. На рис. 8.19 приведена схема эксперимента по его регистрации.
Первая сетка возбуждает плазменную волну с частотой Oj и дли-
ной волны %!. Эта волна распространяется вправо. Вследствие за-
тухания Ландау ее амплитуда все время уменьшается и в конце
концов становится ниже порога детектирования. Вторая сетка,
расположенная на расстоянии I от первой, генерирует другую плаз-
312
Гл. 8. Нелинейные явления
менную волну, частота которой равна ш2, а длина волны —Х2*
Эта волна также затухает. Однако с помощью третьей, подвижной
сетки, которая подсоединена к приемнику, настроенному на частоту
и = со2—о»!, на расстоянии /' = Zco2/(co2—coj от первой сетки
в плазменном столбе можно обнаружить эхо. Каков механизм его
возникновения? Дело в том, что частицы, вызвавшие затухание
первой волны, сохраняют информацию о ней в своей функции рас-
пределения. Если с помощью второй сетки удастся восстановить
первоначальную функцию распределения резонансных частиц, то
в плазме снова может появиться затухшая было волна. Ясно, что
этот процесс может иметь место только в почти бесстолкновитель-
ной плазме. На практике именно по амплитуде эха часто опреде-
ляют, насколько велико столкновительное затухание в плазме.
Аналогичный механизм объясняет и появление эха при затухании
циклотронных волн. Физическая причина возникновения эха иллю-
стрируется рис. 8.20. На нем изображены зависимости положений
различных частиц от времени. Траектории частиц, движущихся
с постоянными скоростями, представляют собой прямые линии.
При х = 0 с помощью решетки в системе создаются сгустки частиц,
в каждом из которых имеется некоторый разброс по скоростям.
Из-за наличия этого разброса сгустки при движении перемеши-
ваются и после преодоления расстояния I плотность вещества,
как это показано на рисунке, снова становится постоянной во вре-
мени. Вторая, более частая решетка, которая расположена на рас-
стоянии I от первой, снова разбивает поток на сгустки. Такое раз-
деление частиц в пространстве и времени приводит к образованию
новых сгустков при х = I'.
Зависимость V (/) можно найти, исходя даже из упрощенной
физической картины, в которой не учитывается влияние электри-
ческого поля волны на траектории плазменных частиц. Пусть функ-
ция распределения электронов у первой сетки равна (i>). Если
с помощью первой сетки функцию распределения промодулиро-
вать по закону cos то при х >0 она запишется в виде
/(х, v, t) = f\ (о) cos [©j/ — ®хх/у]. (8.84)
Вторая сетка при х = I дополнительно модулирует эту функцию
распределения, причем вместо ©j и х в модулирующий косинус
входят соответственно <в2 и х—I:
f(x, v, 0 = /12 (у) cos (<0^— (0jx/u)cos[(»)2Z—со2(х—Z)/v] = (8.85)
=/i2(v)4“[cos [(«>2 + “О t - ^(x-0 + M1x j +
4-cos [(«2- сох) t - 0)2 (х -Z) - . (8.86)
Появление эха связано со вторым слагаемым последнего равенства,
х=0 х = I x = l'
Плазма-.
wz
Возбуждаю-
щие сетки
Приемник
a>z-wi
Рис. 8.19. Схема эксперимента по регистрации плазменного эха. [Из работы:
Wong A. Y., Baker Ь. R., Phys. Rev., 188, 326 (1969).]
9 т 2т 5т 4т 5т 6т
Время .
Рис. 8.20. Траектории частиц, прошедших через решетки. Видно образова-
ние сгустков частиц, ответственных за возникновение плазменного эха.
Справа показаны распределения плотности на различных расстояниях от
первой решетки. [Из работы: Baker D. R., Ahern N. R., Wong Д. Phys.
Rev. Lett., 20, 318 (1968).]
314
Гл. 8. Нелинейные явления
Расстояние между сетками, сл1
Рис. 8.21. Результаты измерений профилей амплитуды плазменного эха при
различных расстояниях I между возбуждающими сетками. Черные точки
соответствуют случаю <а2 <Wj, когда эхо наблюдаться не должно. [Из ра-
боты : Baker D. R., Ahern N. R., Wong A. Y., Phys. Rev. Lett., 20, 318 (1968). ]
осциллирующим с частотой co = co2—Qi и ПРИ выполнении усло-
вия (О g (х—I) = х или
х = со2//((о2— (Di) а V (8.87)
не зависящим от v. Таким образом, при х — Г разброс ио скоро-
стям в плазме не влияет на второй член в (8.86) и фазового разме-
шивания не происходит. Интегрируя второе слагаемое при х = Г
по скорости, мы придем к выводу, что оно описывает флуктуации
плотности с частотой со = со2—cov Вклад от первого члена в (8.86)
обнаружить нельзя, поскольку фазовое размешивание сглаживает
соответствующие этому члену осцилляции плотности. Ясно, что Г
является положительной величиной, только если co2 >(Oi- Физи-
ческая причина этого состоит в том, что вторая решетка, модули-
рующая распределение частиц, должна быть гуще первой, по-
8.7. Нелинейное затухание Ландау 315
скольку в противном случае она не сможет «распутать» флуктуа-
ции, созданные первой решеткой.
На рис. 8.21 представлены результаты измерений эха, созда-
ваемого ионно-звуковой волной; эти эксперименты выполнили Бей-
кер, Ахерн и Вонг. Измеренная зависимость V (/) соответствует
выражению (8.87). Черные точки, отвечающие случаю <о2 <«i,
как и ожидалось, указывают на отсутствие эха. Столкновения раз-
рушают когерентную картину модуляции скоростей, поэтому ам-
плитуда плазменного эха уменьшается с расстоянием.
8.7. Нелинейное затухание Ландау
Если проследить, как меняется с расстоянием амплитуда электрон-
ной или ионно-звуковой волны, возбуждаемой погруженной в
плазму сеткой, то окажется, что волна большой амплитуды не за-
тухает экспоненциальным образом, как это предсказывает линей-
ная теория. Вместо этого наблюдается уменьшение амплитуды,
затем снова ее рост, и в конце концов амплитуда, совершив несколько
колебаний, выходит на некоторый стационарный уровень. Подоб-
ное поведение электронной плазменной волны с частотой 38 МГц
иллюстрирует рис. 8.22. Такие колебания амплитуды хорошо ук-
ладываются в картину нелинейного захвата частиц, которая рас-
сматривалась в разд. 7.5, хотя, естественно, здесь могут иметь
место и другие эффекты. Частица, движущаяся со скоростью V,
будет захвачена волной только в том случае, если ее кинетическая
энергия в системе волны будет меньше, чем потенциальная, т. е.
если \еф | >т (v— Оф )2/2. Волны малой амплитуды могут захва-
тить лишь быстрые частицы, скорости которых близки к Пф . Для
того чтобы волна смогла захватить частицы с v « 0 из основной
части функции распределения, должно выполняться условие
\яФ\ mvl = -^-m(a/k)2. (8.88)
При таких больших амплитудах поведение волны уже нельзя опи-
сывать с помощью линейной теории. Поскольку \ф\ = \ E/k\, по-
следнее равенство эквивалентно условию
со « ®в, где ($=\qkElm\. (8.89)
Величина сов называется баунс-частотой. Она равна частоте ко-
лебаний частицы, запертой у дна потенциальной ямы, образован-
ной синусоидальной волной (рис. 8.23). Действительно, потенциал
вблизи дна ямы описывается формулой
ф = фо (1 —COS kx) ~ фо (-у + • • •
(8.90)
316
Гл. 8. Нелинейные явления
Рис. 8.22. Измеренный профиль амплиту-
ды нелинейной электронной плазменной
волны. Наблюдается немонотонное убыва-
ние амплитуды со временем. [Из работы:
Franklin R. N., Hamberger S. М., Ikezi И.,
LampisG., Smith G. J., Phys. Rev. Lett.,
28, 1114 (1972).]
Рис. 8.23. Запертые частицы
осциллируют в образованной
волной потенциальной яме.
Уравнение движения частицы у дна ямы имеет вид
т d2x/d/2 == —та>2х = qE= —qctyldx = —q$ok sin kx. (8.91)
Частота колебаний co является постоянной величиной только в том
случае, когда отклонение х мало (sin kx л; kx), а профиль потен-
циала ф (х) можно считать параболическим. В этом пределе час-
стота со равна величине сов, определяемой выражением (8.89).
Взаимодействие волны и запертых частиц происходит следующим
образом. В точке отражения резонансных частиц от профиля по-
тенциала они передают кинетическую энергию волне, и ее ампли-
туда увеличивается. Когда запертые частицы, совершив одно ко-
лебание, оказываются у противоположной границы ямы, то волна
возвращает им энергию и амплитуда ее уменьшается. Таким обра-
зом, можно ожидать, что в системе покоя волны ее амплитуда будет
осциллировать с частотой сов. В лабораторной системе частота
этих осцилляций будет равна со' = сов+ kv$ , а волновое число —
k' = со'/Уф= k [1 + (сов/со) ].
Оказывается, условие сов> со дает границу применимости
линейной теории и в том случае, когда поведение системы опреде-
ляется не захватом частиц, а какими-то другими процессами. Рас-
смотрим в качестве примера другой тип нелинейного затухания
Ландау, в котором главную роль играют биения двух волн. Пусть
в плазме имеются две высокочастотные ленгмюровские волны
(со 1( Aj) и (со2, &2). Биение этих волн приводит к образованию оги-
бающей амплитуды, распространяющейся со скоростью
(со2—со1)/(Л2—k-^ та угр. Если эта скорость достаточно мала и ле-
жит внутри основной функции распределения ионов, то может
8.8. Нелинейные уравнения физики плазмы
317
Рис. 8.24. Сила ВЧ-давления, обусловленная наличием огибающей волны,
может вызвать захват частиц, а при выполнении условия v « огр « (<о2~
—со1)/(й2—^i) привести к резонансному взаимодействию их с волнами.
наблюдаться обмен энергией между огибающей и резонансными
с ней ионами. Последние будут двигаться под действием силы вы-
сокочастотного давления (рис. 8.24). В результате в системе будет
наблюдаться нелинейное затухание Ландау или нарастание волн.
Поглощение огибающей двух плазменных волн резонансными с ней
ионами представляет собой эффективный способ нагрева ионов,
с которыми высокочастотные волны обычно не взаимодействуют.
Отметим также, что если функция распределения ионов по скоро-
стям имеет два максимума, то с помощью аналогичного механизма
в плазме можно возбуждать высокочастотные ленгмюровские ко-
лебания. Такая неустойчивость относится к классу модуляцион-
ных неустойчивостей.
Задачи
8.15. На основе анализа данных, приведенных на рис. 8.21, постройте зави-
симость /'(/) и выясните, насколько хорошо результаты эксперимента со-
ответствуют формуле (8.87).
8.16. Вычислите баунс-частоту колебаний электрона вблизи минимума по-
тенциала плазменной волны, среднеквадратичная амплитуда которой равна
10 В, а длина волны — 1 см.
8.8. Нелинейные уравнения физики плазмы
Среди уравнений, которые используются при анализе нелинейных
волн в плазме, наиболее подробно изучены два: это уравнение Кор-
тевега—де Вриза и нелинейное уравнение Шредингера. Каждое
из этих уравнений описывает определенный тип нелинейности.
В случае когда большой амплитуды достигает ионно-звуковая
волна, главный нелинейный эффект состоит в укручении фронта
волны, физический смысл которого мы объясняли в разд. 8.3.3.
Этот эффект возникает из-за наличия в уравнении движения ионов
члена (v-v) v и описывается уравнением Кортевега—де Вриза.
Это уравнение предсказывает также существование решений в виде
нелинейных волн и солитонов (см. рис. 8.5 и 8.7).
318
Гл. 8. Нелинейные явления
В случае когда нелинейной становится электронная плазменная
волна, преобладающим оказывается новый эффект, состоящий в
том, что сила ВЧ-давления волны приводит к выталкиванию фо-
новой плазмы из области больших напряженностей поля. В ре-
зультате в плазме возникают области пониженной плотности, на-
зываемые кавитонами. Запертые в такой области плазменные
волны образуют изолированную структуру, называемую солитоном
огибающей, или уединенной волной огибающей. Такие солитоны
описываются нелинейным уравнением Шредингера. Вызывает удив-
ление тот факт, что хотя физические модели и уравнения, описы-
вающие солитоны и солитоньГогибающих, различны, эти образова-
ния по форме похожи друг на друга.
8.8.1. Уравнение Кортевега—де Вриза
Это уравнение возникает при решении различных физических за-
дач, в частности при анализе эволюции слабо нелинейной ионно-
звуковой волны. Оно имеет следующий вид:
dU/дт + U (dU/д%) +^-dsU/dl3 = Q. (8.92)
Здесь U — амплитуда, а т и | — соответственно временная и про-
странственная переменные. Для приведения исходного уравнения
к подобному виду обычно требуется провести несколько процедур
замены переменных, однако физический смысл двух последних
членов в левой части (8.92) ясен и из такой простой формы записи.
Второе слагаемое в (8.92) соответствует конвективному члену
(v-y) v, который описывает укручение волнового фронта. Проис-
хождение третьего слагаемого связано с дисперсией волны, т. е.
с зависимостью ее фазовой скорости от волнового числа k. Напом-
ним, что при Т{ — 0 частота ионно-звуковой волны определяется
соотношением [(4.48) ]
+ (8.93)
Дисперсионный член k2^r> возникает из-за отклонений от нейтраль-
ности плазмы. Производя разложение в ряд Тейлора при малых
AA,d, находим, что
со = kvs' —k3v, (8.94)
т. е. дисперсионный член пропорционален k3. Именно поэтому по-
следнее слагаемое в левой части (8.92) содержит третью производ-
ную. Учет дисперсии позволяет предотвратить появление решений
с очень крутыми волновыми фронтами (им соответствуют очень
большие А).
8.8. Нелинейные уравнения физики плазмы
319
Уравнение Кортевега—де Вриза допускает решение в виде со-
литона, т. е. одиночного импульса, который движется с некоторой
скоростью с (не равной скорости света!) и при этом сохраняет свою
форму. Это значит, что решение U зависит от переменной t, = £—ст,
а не от величин | и т в отдельности. Вводя переменную ? = I—ст
и пользуясь тем, что д/дт = — cd/dt,, а д/д%, = d/dt,, мы можем
записать уравнение (8.92) в виде
—cdU№+ UdU/d£ + -~dsU/d^ = 0. (8.95)
Проинтегрируем (8.95) от ? до оо:
(8.96)
Если U (?) и ее производные на больших расстояниях от центра
солитона (| £ | -> оо) обращаются в нуль, то мы имеем следующее
уравнение:
cU-----------L_^L = o. (8.97)
2 2 dt2
Умножим обе части этого уравнения на dUldt, и еще раз выпол-
ним интегрирование:
—Lf_^£_y = o, (8.98)
2 6 4 V d£ J
или
(dUld®1 (3c— U). (8.99)
3
Этому уравнению удовлетворяет решение в виде солитона:
и(® = Зсзс№[(с/2)1/2&, (8-100)
что можно проверить непосредственной подстановкой, если вос-
пользоваться тождествами
(dldx) sch х = — sch’x th x (8.101)
и
schax + th2x= 1. (8.102)
Выражение (8.100) описывает структуру, похожую на ту, что
изображена на рис. 8.7: решение U (?) достигает максимума при
? = 0 и обращается в нуль при ?->-±оо. Скорость солитона
320
Гл. 8. Нелинейные явления
Рис. 8.25. Цепочка солитонов, движущихся вправо, с течением времени вы-
страивается по порядку, соответствующему их скорости, высоте и ширине.
равна с, амплитуда — 3 с и полуширина — (2/с)1/2. Все три вели-
чины связаны между собой, поэтому скорость с определяет также
и полную энергию солитона; чем больше энергия, тем выше ско-
рость и амплитуда солитона и тем меньше его ширина. Солитоны
могут возникать только из определенных начальных распределе-
ний поля. Для возникновения солитона энергия начального воз-
мущения должна быть достаточно велика, а фазы составляющих
его колебаний распределены заданным образом. Если хотя бы одно
из этих условий не выполнено, то в системе возникает не солитон,
а нелинейная волна большой амплитуды. Если же энергия началь-
ного возмущения столь велика, что ее хватит на несколько соли-
тонов, и фазы имеют необходимое распределение, то могут возник-
нуть N солитонов. Поскольку скорость солитонов пропорциональна
их амплитуде, спустя некоторое время после возникновения они
обязательно выстроятся по росту, как показано на рис. 8.25.
Докажем теперь, что уравнение Кортевега—де Вриза описы-
вает ионно-звуковые волны большой амплитуды. Рассмотрим про-
стой случай одномерных волн, распространяющихся в плазме с хо-
лодными ионами. Уравнение движения ионов и уравнение непре-
рывности запишутся соответственно в виде
dvi/dt + v( dvjdx = — (е/М) д&дх, (8.103)
dnildt 4- (д/дх) (п^) = 0. (8.104)
Предположим, что плотность электронов удовлетворяет уравнению
Больцмана [(3.73)1; при этом уравнение Пуассона принимает вид
е0 &ф/дх2 = е [n0 ехр (e<j>lkTe) — пг]. (8.105)
8.8. Нелинейные уравнения физики плазмы 321'
Чтобы все коэффициенты уравнений сделать равными единице,
перейдем к следующим безразмерным переменным:
х' == x/XD = х (п0е21ъйК.ту12,
t'= £ipt— t (пае2/е0М)1'2,
X = еф/К Те, п' = ntlПо, (8.106)
v'= v/vs = v(M/KTe)112.
При этом рассматриваемая нами система уравнений запишется
следующим образом:
dv' /dt' 4- v'dv’/dx' = — d’/Jdx', (8.107)
dn'/dt' 4- (d/dx') (n'v') = 0, (8.108)
02%/0x'« = e* —n'. (8.109)
Если теперь перейти в систему отсчета, которая движется со ско-
ростью v' = Ж, то мы придем к аналогу уравнения (8.27). Опи-
раясь на анализ уравнения (8.27), выполненный в разд. 8.3, можно
сделать вывод, что и система (8.107)—(8.109) при определенных
значениях числа Маха Ж допускает решения в виде солитонов.
Задача
8.17? Ъредполагая, что у, п' и v' зависят только от комбинации Vs *’—Mt’,
сведите систему (8.107)—(8.109) к аналогу уравнения (8.27). Дважды проин-
тегрируйте результат, как при выводе уравнений (8.96) — (8.98), и получите
уравнение
Y (W = ex- 14- Ж 1(Ж2 —2х)1/2~Ж].
Покажите, что решения в виде солитонов могут существовать только при
1 и0< Хмакс <1,3.
Для вывода уравнения Кортевега—де Вриза нужно произвести
разложение функций п’, у' и % по амплитуде волны и удержать
в этом разложении члены более высоких порядков (на единицу
выше, чем в линейной теории). Поскольку в солитонах амплитуда
и скорость связаны между собой, в качестве параметра разложения
можно взять величину 6, равную превышению числа Маха над
единицей:
Ъ = Ж — 1. (8.110)
Таким образом, можем написать
п' — 14- б/li 4- б2/г2 4- . . . ,
Х = бХ1 + 62Х2+ . . . , (8.111)
V' — 6oj 4- 62у2 4- ....
11 Заказ 3170
322
Гл. 8. Нелинейные явления
Произведем также масштабирование, т. е. перейдем к новым пере-
менным г)
I = fQ, Т = 6W. (8.112)
Таким образом, имеем
д _ ^з/2 д ^1,2 d
dt' dr 51
5 5 (8-113)
dx' d%
Подставляя разложение (8.111) в уравнение (8.109) и пользуясь
формулами (8.113), приходим к выводу, что члены наинизшего
порядка пропорциональны б, а
= (8.П4)
Производя аналогичные преобразования с уравнениями (8.107)
и (8.108)., находим, что в этом случае члены наинизшего порядка
пропорциональны б3/2, а
до1/д^=д%1/д^^дп1/д^ (8.115)
Поскольку все величины при £ -> оо обращаются в нуль, интегри-
рование равенств (8.115) дает
П1=Х1=У1>г/. (8.116)
Таким образом, наша нормировка оказалась настолько удачной,
что все линейные возмущения оказались равными и любое из них
можно выбрать в качестве U. Соберем в уравнении (8.109) члены
пропорциональные б2, а в уравнениях (8.107) и (8.108) — члены,
пропорциональные б5/2. В результате мы получим систему
^Нъ-^+4-Й. (8.П7)
-----^2_ J_ и = _ .д^. , (8,118)
dr 5? т 51 51
^-+4- fe+ад)-0- (8-Н9)
dr 51 51
Подставляя в уравнение (8.119) значение п2 из (8.117) и величину
dvjdt из соотношения (8.118), имеем
dni 53Х1 5%2 1 5Х2 5а/ 5», 5Хг
dr 513 51 2 51 т 5т 51 51
+ ~(ПЛ) = О. (8.120)
Ч Без объяснения причины. Цель оправдывает средства!
8.8. Нелинейные уравнения физики плазмы
323
.121)
К счастью, величина сокращается, и, заменяя все величины
первого порядка на U, мы приходим к уравнению
^L + (/2E_+J_^ = 0
dt 2 dla
которое тождественно уравнению (8.92). Таким образом, в следую-
щем после линейного порядке по амплитуде ионно-звуковая волна
описывается уравнением Кортевега—де Вриза.
Задача
8.18. В водородной плазме с плотностью п0 — 101вм~3 и температурой КТе =
= 10 эВ возбуждается солитон потенциала, амплитуда которого равна 12 В.
Вычислите скорость этого солитона (в м/с) и его полную ширину по половине
максимума амплитуды (в мм), предполагая, что солитон описывается урав-
нением Кортевега—де Вриза. (Указание: сначала покажите, что в нормиро-
ванных переменных скорость солитона равна единице.)
8.8.2. Нелинейное уравнение Шредингера
В безразмерных переменных это уравнение имеет вид
i dtyldt р д2ф/дх2 q | ф |2 ф = 0. (8.122)
Здесь ф — амплитуда волны, i = (—I)1'2. Физический смысл коэффи-
циентов р и q мы выясним ниже. От обычного уравнения Шредингера
i h dtyldt + (й2/2т) д^/дх2 — V (х, I) ф = 0
уравнение (8.122) отличается тем, что в последнем потенциал
V (х, /) сам зависит от ф, и потому третий член в левой части ста-
новится нелинейным. Следует заметить, что V зависит только от
квадрата амплитуды |ф |2 и не зависит от фазы функции ф. Для
случая электронных плазменных волн последнее обстоятельство
является естественным, поскольку нелинейность ленгмюровских
колебаний связана с действием силы ВЧ-давления, которая зави-
сит от градиента интенсивности волны.
Рассмотрим решения уравнения (8.122), имеющие вид плоских
волн. Оказывается, при выполнении условия pq >0 эти решения
становятся модуляционно-неустойчивыми; иными словами, моду-
ляция огибающей волны имеет тенденцию к росту. Картина про-
цесса во многом аналогична изображенной на рис. 8.24, несмотря
на то что мы рассматриваем, здесь движение жидкости, а не взаимо-
действие с волной отдельных частиц. Поясним, как сила ВЧ-давле-
ния может вызвать модуляционную неустойчивость плазменных
волн. Плазменное колебание с пульсирующей огибающей пока-
зано на рис. 8.26. Сила ВЧ-давления, обусловленная градиентом
интенсивности плазменной волны, будет сдвигать электроны и
ионы в те точки, где интенсивность волны минимальна. Эго при-
11*
324
Гл. 8. Нелинейные явления
Рис. 8.26. Сила ВЧ-давления, возникающая из-за неоднородности амплитуды
плазменной волны, заставляет ионы смещаться в точки минимумов интенсив-
ности колебаний. В результате в плазме образуются каверны плотности,
в которые захватываются ленгмюровские волны, и модуляция исходной плаз-
менной волны возрастает.
ведет к модуляции плотности плазмы. Из дисперсионного уравне-
ния для ленгмюровских волн
и2 = ®р + (3/2) А2у«пл (4-30)
следует, что волны с большими k могут существовать только там,
где мала локальная величина ®р и, следовательно, мала плотность п.
Вследствие этого плазменные волны окажутся запертыми в обла-
стях пониженной плотности плазмы. Захват части плазменных
волн еще более увеличит интенсивность плазменных колебаний
в тех областях, где они и без того были велики, и приведет таким
образом к дальнейшему росту амплитуды огибающей.
Какой смысл имеет в этом случае условие pq >0? Оказывается,
для плазменных волн р и q пропорциональны соответственно дис-
персии групповой скорости dvrp/dk и нелинейному сдвигу частоты
б®~д®/д|ф|2. Ниже мы покажем, что
p = (l/2)dvrp/dfe, q=—бю/d | ф |2 ~(8.123)
Модуляционная неустойчивость может возникнуть только в том
случае, когда pq >0, т. е. 6® и dvTV/dk имеют противоположные
знаки. Для того чтобы понять, почему это так, обратимся
к рис. 8.27. На рис. 8.27, а показана модуляция огибающей волны,
которая возникла вследствие случайных флуктуаций амплитуды.
Пусть б® <0. Тогда в области большей амплитуды ленгмюров-
ской волны частота ®, а значит, и пропорциональная ей фазовая
скорость (n/k станут несколько меньше исходной. Вследствие этой
неоднородности фазовой скорости распределение поля в левой ча-
сти образования станет гуще, а в правой — более разреженным
(рис. 8.27, б). Таким образом, локальное значение волнового числа
k в левой части пакета станет больше, чем в правой. Если
dv^ldk >0, то групповая скорость в левой части пакета при этом
окажется выше, чем в правой, и энергия волны локализуется в бо-
8.8. Нелинейные уравнения физики плазмы
325
Рис. 8.27. Модуляционная неустойчивость может возникнуть только в том
случае, когда нелинейный сдвиг частоты и дисперсия групповой скорости
имеют противоположные знаки.
Рис. 8.28. Солитон огибающей.
лее узкой области пространства. Иными словами, огибающая ста-
нет выше, а охватываемая ею область — уже (рис. 8.27, в). Если
же 6® и dvrp!dk имеют одинаковые знаки, то модуляционная не-
устойчивость возникнуть не может.
Несмотря на то что решения уравнения (8.122) в виде плоских
волн при pq >0 являются неустойчивыми, у этого уравнения мо-
гут существовать и устойчивые решения в виде так называемых
солитонов огибающей. Их можно получить из фундаментального
решения
w(x, i) = (2X/g)1/2sch[(4/p)1/2x]ei4i. (8.124)
326
Гл. 8. Нелинейные явления
Здесь А — произвольная константа, которая связывает между со-
бой амплитуду, ширину и частоту колебаний в волновом пакете.
В любой заданный момент времени решение (8.124) представляет
собой обычный солитон наподобие того, который описывается
формулой (8.100) (правда, теперь гиперболический секанс входит
в решение в первой степени, а не в квадрате). Из-за наличия экс-
поненциального множителя решение w (х, t) осциллирует между
максимальным и минимальным значениями. Существуют и другие
солитонные решения уравнения (8.122); среди них — солитон оги-
бающей, движущийся со скоростью V (рис. 8.28):
ф(х, t) =(——y/2sch —х°— ^)]ехр р х—
--—/+6о¥Ь (8-125)
4р Л
Здесь х0 и 0О — начальные положение и фаза колебаний в солитоне.
Из решения видно, что значение скорости V определяет число длин
волн, которые в каждый момент времени укладываются внутри
огибающей.
Задачи
8.19. Прямой подстановкой покажите, что выражение (8.124) является ре-
шением уравнения (8.122).
8.20. Докажите, что (8.125) является решением уравнения (8.122). Для этого
покажите, что если w (х, I) есть решение уравнения (8.122), то функция
ф = щ(х—х0 — Vt, t)exp[i(Vx/2p — V2Z/4p + 0o)]
также является его решением.
‘ Теперь мы хотим показать, что нелинейное уравнение Шредин-
гера описывает электронные плазменные волны большой амплитуды.
Для этого нужно решить самосогласованную задачу, которая оп-
ределяла бы образование каверны плотности под действием силы
высокочастотного давления и поведение волн в такой каверне. Вы-
сокочастотные движения электронов описываются уравнениями
(4.18), (4.19) и (4.28), которые мы перепишем в виде
duldt——(е!т)Е—(3KTeimn0) (дп/дх), (8.126)
dnldt 4- п0 (ди/дх) = 0, (8.127)
дЕ!дх~—(8.128)
где п0 — плотность однородной невозмущенной плазмы; Е, п и
и — соответственно возмущения электрического поля, плотности
электронов и скорости электронной жидкости. Эти уравнения ли-
неаризованы, поэтому нелинейности (u-v) и и V-(«u) в них отсутст-
вуют. Взяв производную по времени от уравнения (8.127) и произ-
8.8. Нелинейные уравнения физики плазмы
327
водную по х от уравнения (8.126), можно исключить из системы
величины и и Е и записать уравнение (8.128) в виде
дгп1д№—(ЗК.Те!т) дгп!дх2 + (п0е2//пе0) п — 0. (8.129)
Теперь заменим п0 на п0 + 8п, где 8п — возмущение плотности
в каверне; это единственный нелинейный эффект, который мы бу-
дем рассматривать. Естественно, линейному уравнению (8.29) удов-
летворяет любое линейное возмущение, однако для последующего
удобнее записать это уравнение для скорости и и воспользоваться
определением величины а>р. Таким образом, мы будем рассматри-
вать уравнение
(Paldt2—(ЗКТе1т) д2и/дх2-^^ (1 -|-бп/п0) и = 0. (8.130)
Скорость и состоит из высокочастотной составляющей, которая
осциллирует с частотой ®0, близкой к плазменной частоте сор, и
низкочастотной части щ, описывающей квазинейтральное движе-
ние электронов вслед за ионами, когда последние образуют каверну
плотности. (Заметим, что все пространственные вариации плотно-
сти, как крупномасштабные, так и мелкомасштабные, включены
В U{.)
Пусть
и (х, t)^=ut(x, /)e~io< (8.131)
Дважды дифференцируя это равенство по времени, получаем
d2uldt2 = (ui — 2ico0u/ — ®ow;) ,
где точки означают дифференцирование по «медленному» времени.
Поскольку вторая производная щ < ®о«/, ею можно пренебречь,
и мы имеем
д2и/д? = —(cooUi + 21®0й;) e-ioW . (8.132)
Подставляя это выражение в уравнение (8.130), получаем
Г Oirn it ! 2>KTg d2ui ,.2 \ "1 —ittoi p. zq 1 qq\
1 aIOqU/ i I (Oq (On ^p i 1 ® — 0» (о* 133)
L m dx2 \ nQ ) J
Переходя к безразмерным переменным
V— а>' = а/ар, x' = x/Xd,
(8.134)
и' = и (KTe/m)~l 2, 8п' = 8п/п0,
перепишем (8.133) в виде
[. ' du'i 3 <32u) 1 , „ „ ,1 — io'r
+ + е =0- (8ЛЗЗа>
at' 2 дх 2 2 J
Введем обозначение А для относительного сдвига частоты:
,\з (со0—(ор)/(ор = йо— 1 (8.135)
328
Гл. 8. Нелинейные явления
и будем считать, что Д < 1; тогда —1 » 2Д. Теперь можно
убрать штрихи (путаницы это не создаст), вернуться с помощью
соотношения (8.131) к функции и (х, t) и заменить в первом члене
(8.133а) величину ®0 на единицу. В результате мы придем к урав-
нению
j А_^_ + (д_Е1_б,Ли = о. (8.136)
dt 2 dx2 \ 2 7
Заметим, что в последнем соотношении производная d/dt берется
по «медленному» времени, хотя функция и содержит как быстро-
осциллирующий фактор ехр (— ia>0Z), так и медленно меняющийся
сомножитель ut. Таким образом, мы получили нелинейное урав-
нение Шредингера; осталось лишь выразить 8п через | ui |2.
Уравнение, описывающее движение электронов в низкочастот-
ном пределе, можно получить из уравнения (4.28), если пренебречь
в нем инерционным членом и добавить в правую часть этого урав-
нения выражение (8.44) для силы ВЧ-давления:
0= — епЕ—КТе—---------JL /.е.°£ \ . (8.137)
дх . т2 дх 2
шо
(Здесь мы положили уе = 1, поскольку низкочастотные движения
являются не адиабатическими, а изотермическими.) Если прене-
бречь тепловыми поправками, то из уравнения (8.126) следует:
(Е2) « (mVo/e2) (и2;. (8.138)
Положим Е = — и введем обозначение % = е$>/КТе-, тогда
уравнение (8.137) запишется в виде
(d/dx) (х—In n)—(m/KTe) (д/дх) (и2) = 0. (8.139)
Проинтегрировав это уравнение, положив п = п0 + 8п и перейдя
к безразмерным переменным, определяемым выражениями (8.134),
получим следующее соотношение:
(и2) =1 и |2 = х—In (1 + бп) яз х—6п. (8.140)
Теперь с помощью уравнений (8.103) и (8.104), описывающих
поведение холодных ионов, исключим величину х- Поскольку Qp =
= е®р, vs = 8 (K/Te/m)'12, где е == (m/M)1/2, то в безразмерных пе-
ременных (8.134) уравнения движения ионов запишутся в виде
— JTT+«i-Ti-+-F=0> (8.141)
е dt дх дх
— ^ + ^-[(1 + М^] = 0. (8.142)
е dt дх
8.8. Нелинейные уравнения физики плазмы 329
Здесь мы положили п£ = (п0 + 8п;)/п0 = 1 + 6лг£ и опустили
штрихи. Если в системе координат, движущейся со скоростью V,
решение является стационарным, то в лабораторной системе все
возмущения зависят от х и t только через комбинацию | =
= х—х0—Vt. Таким образом, д/дх = д/д%, d/dt — — Vd/dt, и по-
сле линеаризации безразмерные уравнения движения ионов за-
пишутся в виде
- —-^-+^- = 0, и£ = -^х,- (8.143)
8 д% di, V
V дбп; , ди; „ s 8 /о 1ЛЛ\
-------тг-н—— = 0, бп£ = — «,•. (8.144)
• е дс, V
Используя эти уравнения и условие квазинейтральности в медлен-
ных движениях, получаем
6ne = бп£ = e2x/V2. (8-145)
Выражая отсюда х и подставляя его в равенство (8.140), в котором
величина 8п в действительности равна 8пе, находим
8пе = (1/4) | и |2 (V2/e2— I)-1. (8.146)
Подставляя это выражение в уравнение (8.136), окончательно по-
лучаем
i —1V।«|21ы = о. (8.147)
dt 2 дх2 L 8 k е2 J J
Сравнивая последнее равенство с уравнением (8.122), мы видим,
что если пренебречь А, то (8.147) представляет собой нелинейное
уравнение Шредингера с параметрами
р = — , <?=----(----------Y (8.148)
Осталось показать, что р и q связаны с дисперсией групповой
скорости и нелинейным сдвигом частоты формулами (8.123). Это
действительно имеет место при V2 С tn/М. В самом деле, в безраз-
мерных переменных дисперсионное уравнение Бома—Гросса (4.30)
записывается в виде
<о'2 = 1 + 6п' + 3/г'2, (8.149)
где k' = k/k-D, а со выражена в единицах величины сор0, равной плаз-
менной частоте вне каверны плотности. Групповая скорость ленг-
мюровских волн дается выражением
Uгp = d(o7^^^, = 3fe7a),; (8.150)
поэтому dvrx>/dk' — 3/(о «3 и
p = ±-dv'TVldk’=(8.151)
330
Гл. 8. Нелинейные явления
При V2 <С е2 из формулы (8.146) следует 6м' = — \и' |2/4, так что
уравнение (8.144) можно записать в виде
(о/2= 1----- |u'|2 + 3fe'2. (8.152)
4
Следовательно,
2со'da' = —— d | и' |2,
4 (8.153)
6а' ~ da'Id | и' |2 да — 1/8.
При V2 е2 из второго выражения (8.148) имеем q да 1/8 =
= — d(o7dj и' |2.
Если условие V2 е2 не выполняется, то при анализе нели-
нейных процессов нужно более детально рассматривать динамику
движения ионов; в этом случае в плазме возникают нестационар-
ные взаимосвязанные солитоны ленгмюровских волн и плотности
ионов. Именно такая ситуация обычно реализуется в эксперименте
и изучается теоретиками.
Таким образом, функция (8.125) при р = 3/2 и q = 1/8 описы-
вает ленгмюровский солитон. При этом ф (х, t) равна низкочастот-
ной составляющей скорости и (х, t) (величины и, хи t безразмерны!).
Восстанавливая зависимость ехр (— i ©0/) и полагая х0 = 0О = О,
можно записать (8.125) в следующем виде:
и (х, t) = 4Л1'2 sch (х-И)] х
X ехр i ^cou------------A^t------(8.154)
Огибающая солитона перемещается со скоростью V, которая до
сих пор считалась произвольной. Для точного определения V од-
новременно с уравнением для ленгмюровских волн нужно решать
уравнение Кортевега—де Вриза, описывающее поведение каверны
плотности. Впрочем, физические соображения, лежащие в основе
этого решения, довольно просты. Если высокочастотные волны
заперты в каверне плотности и перемещаются вместе с ней, то
групповая скорость этих колебаний должна быть равна скорости
движения каверны V, т. е. (в безразмерных переменных)
V да Огр = 3k’/а да 3k' (8.155)
[см. (8.150)1. Следовательно, множитель i(V73)x в экспоненте вы-
ражения (8.154) равен именно величине i kx, показывающей, как
происходит движение ленгмюровской волны вместе с каверной
плотности. Член —i(72/6)/ в точности равен — i (3/2) k * t' и со-
ответствует сдвигу частоты в дисперсионном уравнении Бома—
8.8. Нелинейные уравнения физики плазмы
321
Z, см
Рис. 8.29. Каверна плотности, или кавитон, образованный вблизи критиче-
ского слоя под действием силы высокочастотного давления СВЧ-колебаний.
Высокочастотные волны (не показаны) генерировались с помощью пучка
электронов. [Из работы: Kim Н. С., Stenzel R. L., Wong А. У., Phys Rev.
Lett., 33, 886 (1974).]
Гросса (8.149) при 6п' = 0 (множитель 1/2 возник из разложения
квадратного корня). Поскольку соо « сор, то соо + (Г2/6) представ-
ляет собой частоту волны, удовлетворяющей уравнению Бома—
Гросса в однородной плазме. Следовательно, величина А равна
сдвигу частоты, вызванному присутствием каверны плотности 6п'.
Как видно из формулы (8.154), А определяет также ширину соли-
тона и его амплитуду. Интенсивность высокочастотного электри-
ческого поля можно найти из соотношения (8.138).
Кавитоны действительно наблюдались на установках, подоб-
ных той, которая изображена на рис. 8.16. На рис. 8.29 и 8.30 пред-
ставлены результаты экспериментов по созданию структур, на-
поминающих солитоны огибающих, путем подведения к спокойной
плазме высокой мощности СВЧ-колебаний. Благодаря этим экспе-
риментам была получена интерпретация данных по лазерному син-
332
Гл. 8. Нелинейные явления
Рис. 8.30. Взаимосвязанные ленгмюровский и ионно-звуковой солитоны.
а — низкочастотные ямы плотности, смещающиеся влево; б — интенсив-
ность высокочастотного электрического поля, измеренная проволочными
зондами; видно, что в минимумах локальной плотности интенсивность воз-
растает. [Из работы: Ikezi H.t Nishikawa К., Hojo Н., Mima К,- — Plasma
Physics and Controlled Nuclear Fusion Research, 1974, II, 609, International
Atomic Energy Agency, Vienna, 1975.]
тезу как «модификация профиля», т. е. изменение профиля плот-
ности плазмы под действием силы ВЧ-давления лазерного излу-
чения. Изменение профиля происходит вблизи критического слоя,
в котором (ор о)0 (со0 — рабочая частота лазера).
Задачи
8.21. Покажите, что нелинейный сдвиг частоты А связан с амплитудой со-
литона в соответствии с выражением (8.154), вычислив для этого среднее
уменьшение плотности плазмы в каверне и соответствующее ему изменение
величины top. (Указание: воспользуйтесь уравнением (8.146); считайте, что
среднее значение sch2 по ширине солитона равно примерно 1/2.)
8.22. В плазме с параметрами п0—1015м~3, К,Те = 2 эВ возбуждается ленг-
мюровский солитон огибающей, амплитуда которого равна 3,2 В. Пусть
у ленгмюровских волн Hd — 0,3. Найдите: а) полную ширину солитона
по половине максимума амплитуды (в мм); б) число длин волн, укладываю-
щихся на этой ширине; в) сдвиг частоты (в МГц) относительно значения,
предсказываемого линейной теорией Бома—Гросса.
8.23. В одномерной плазме, температура которой КТе = 3 эВ, создана пря-
моугольная каверна плотности. Плотность плазмы вне каверны п0 =
= 1016 м“3, а внутри нее nt — 0,4-1016 м~3. Пусть каверна достаточно про-
тяженная и резонансами, связанными с ее границами, можно пренебречь.
Какова длина самой короткой плазменной волны, которую можно запереть
в каверне?
Приложение А
СИСТЕМА ЕДИНИЦ,
КОНСТАНТЫ И ФОРМУЛЫ,
ВЕКТОРНЫЕ СООТНОШЕНИЯ
А.1. Системы единиц
Все формулы в этой книге записаны в системе СИ. Однако в большей част»
научных публикаций до сих пор используется гауссова система СГС. Ниже
представлены уравнения Максвелла в вакууме, гидродинамические уравне-
ния движения и закон Ома в идеальной плазме в этих двух системах:
СИ
V-D —е(п; — пе),
V X Е= — В,
V-B = o,
V xH = j +D,
D = е0Е, В = р0Н,
дч
т п----= qn (Е + v X В) — ур,
dt
Е + v X В =0,
СГС (гауссова)
V • Е = 4ле (п£ — ле),
eV X Е = — В,
V В = 0,
eV X В — 4лj + Ё,
е = р, — 1,
dv / , 1
тп -----= qn I Е + — v X В I — ур ₽
dt \ с J
1
ЕН------VXB = O.
с
Уравнение непрерывности в обеих системах выглядит одинаково.
В гауссовой системе единиц все величины, относящиеся к электрическим
явлениям, измеряются в электростатической системе единиц СГСЭ. Исклю-
чение составляет магнитная индукция В, которая измеряется в гауссах, т. е.
в единицах СГСМ. Чтобы учесть это исключение, приходится записывать
в явном виде множители, в которые входит скорость света с. В системе СИ
(МКСА) В измеряется в теслах (Тл), равных веберу на квадратный метр
(Вб/м2), причем 1 Тл = 10* Гс. Напряженность электрического поля Е в си-
стеме СГС имеет размерность 1 ед. заряда СГС/см, а в системе СИ — В/м..
Поскольку 1 ед. потенциала СГС равна 300 В, то 1 ед. СГС/см = 3-10* В/м.
Отношение Е/В в гауссовой системе единиц является безразмерным, так что
ve = сЕ/В. В системе СИ величина Е/В имеет размерность скорости, и по-
тому vg = Е/В. Это полезно помнить при проверке размерностей различных
членов уравнения в поисках алгебраических ошибок.
Плотность тока j = nev в обеих рассматриваемых системах записывается
одинаково. В СГС величины п и v имеют размерности соответственно см-*
и см/с, а е — 4,8-10~10 ед. заряда СГСЭ. Таким образом, j выражается в ед.
заряда СГСЭ/см2, причем 1 ед. тока СГСЭ = с-1 СГСМ или 10/с = 1/(3-109) А.
В системе СИ п и v измеряются соответственно в м~3 и м/с,! а е = 1,6-10“*® Кл;
следовательно, j выражается в А/м2.
334
Приложение А
Большинство формул, записанных в системе СГС, можно перевести в си-
стему СИ, если заменить В/с на В, а 4л — на еу1, где 1/4ле0= 9-Ю9. На-
пример, плотность энергии электрического поля в СГС равна В2/8л, а в СИ
это будет е0£2/2, плотность энергии магнитного поля в СГС равна В2/8л,
а в СИ—В2/2р.о. Здесь мы использовали соотношение (еор.о)—1|Z2=c=3-108 м/с.
Энергия КТ обычно выражается в электрон-вольтах. Для пересчета ее
в единицы энергии СГС, т. е. в эрги, мы должны умножить Тэв
на 1,6-10-12 эрг/эВ. Для пересчета в джоули (СИ) энергию в электрон-воль-
тах нужно умножить на 1,6-10—19 Дж/эВ. Это последнее число, как следует
из определения электрон-вольта, равно заряду электрона е в системе единиц
СИ.
А.2. Полезные константы и формулы
Константы си СГС
с скорость света е заряд электрона т масса электрона М масса протона Л1/т (М/т)‘1а К постоянная Больцмана эВ электрон-вольт температура, соответствующая 1 эВ лад поперечное сечение атома во- дорода плотность нейтральных ато- 3-108 м/с 1,6-10—« Кл 0,91-10—30 кг 1,67-10—27 кг 1837 43 1,38-10~23 Дж/К 1,6-10-19 Дж 11 600 К 0,88-10—23 м2 3,3-1019 м“3 3-1010 см/с 4,8-10-10 СГСЭ 0,91-10-2’ г 1,67-10-24 г 1837 43 1,38-10-18 эрг/К 1,6-10-12 эрг 11 600 к 0,88-10—16 см2 3,3-1013 см-3
мов при комнатной темпера-
туре и давлении 10~8 мм
рт. ст.
Формулы
Формулы для
СИ СГС (гауссова) расчетов
(п В СМ"8)
<0р плазменная частота электронная 40 с циклотронная частота дебаевский А'П радиус экранирования ларморовский rL радиус г пе* у/* / ълпе* у/* ,— (1 1 I fp — 9000 Vn с 1 еВ еВ fc = 2,8 ГГц/кГс т тс / 80КТ, \V2 / КТ, Y/2 / ТэВ ( ) ’“I » ) “ ,.R ’ ₽R R... ММ<Н>
Приложение А
335
альфеновская в
«А скорость (НоР)1'2
скорость / К Те у/2
t>s звука при П = 0 1 м J
скорость ЕхВ- дрейфа Е В
VD скорость диамагнитного дрейфа КТ п' еВ п
отношение пКТ
Р кинетического давления к магнитному В*/2ра
^тепл.е тепловая / скорость { электронов ' 2КТе у/2 < m }
Vei частота электрон-ионных столкновений
частота электрон- электронных столкновений
частота ион- 7i( - m
V» ионных столкновений м
средняя длина свободного пробега да ^ei‘
‘'’осц максимальная скорость коле- — баний электро- т(о0 нов в электро- магнитной волне
В (4лр)1/2 2,2-1011B/Vn см/с(Н>
( КТе А к м ) |1/2 106T*g см/с (Н)
сЕ 10в£ (В/см) см/с В (Гс)
сКТ п'
еВ п 111° _ „ СМ/С В R
пКТ
В2/8л
/ 2КТе > к m > )1/2 5,9- 107ТУв см/с
СОр Zne In Л
~ Nd да 1U ° с 1 у 3/2 п In Л 6 „3,2 С"1 1 эВ
\12/ Те \3/2
') ( Ti ) v“
у2 « 3,4- 104—гп— см (Н> п1пА
о2 -^=7>3/19К2>
/пю0 сг о2 = 3,7/13Х2/Т (эВ)
А.З. Полезные векторные соотношения
А(В хС) = В-(Сх А) = С-(Ах В) = (АВС),
А X (В X С) = В (А С)-С (А-В),
(А X В) (С X D) = (А-С) (В-D) — (A-D) (В-С),
(А X В) X (С X D) = (ABD) С — (ABC) D = (ACD) В — (BCD) А,
Г-(ФА) = A-V0 + Ф?-А,
V X (ФА) = V0 х А + 0V X А,
А X (V X В) = V (А- В) — (А-V) В — (В-V) А — В X (V X А)„
336
Приложение А
(А-V) А = V А2) —А X (V X А),
V (A X В) = B-(V X A)-A-(V X В),
V X (А X В) = A(v-B) —B(V-A) + (B-V) А-(А у) В,
V X [(A-V) A] = (A-V)(V X A) + (V-A) (V X A)-[(V X A)-V] А,
V X V X A = V(V-A)-(V V) A,
V X W = 0,
V-(VXA) = O.
Цилиндрические координаты (г, 0, z)
1 d f dф \ . 1 52Ф 52Ф
v r dr к dr J r2 562 ' 5г2
i a i a a
V A =-------— -----TX-Ae i-~A2
r dr r dQ dz
_ f 1 dA* _ dAe \ ~ / dAr __ dAz
\ r 50 dz J V dz dr
, Г 1 д 1 dAr
+ t- (rAe) — —
L r dr r 50
z,
V2A = (y • v) A = £v2A
1
r2
+ [v2Ae - (Ae - 2 0 + V2AZ£,
Л / dBr 1 dBr dBr 1
<л.у)в-г(л,^ + лвт^- + лг
+ 5(л,^- + ле 1
\ 5r
- / dB,
+ z (Ar—*-
\ дг
dz
дВв 1
' <36 ' "z dz r
, . 1 дВг , я дВг
VAq Г 50 +Az dz
Приложение Б
ТЕОРИЯ ВОЛН В ХОЛОДНОЙ
ОДНОРОДНОЙ ПЛАЗМЕ
При Те = Ti — 0 анализ волн, который был выполнен в гл. 4, легко обоб-
щить на случай произвольного числа сортов заряженных частиц и произ-
вольного угла распространения 0 по отношению к направлению магнит-
ного поля. В это рассмотрение мы не включаем волны, свойства которых за-
висят от температуры Т, например ионно-звуковые волны.
Прежде всего найдем тензор диэлектрической проницаемости плазмы.
Запишем четвертое уравнение Максвелла
V X В = |г0 (j + вое), (Б.1)
где j — ток в плазме, обусловленный движением s сортов частиц с плотностью
ns, зарядом qs и скоростью vs:
j=£ns?svs. (Б.2)
S
Считая плазму диэлектриком, плотность тока внутри которого равна j, урав-
нение (Б.1) можно переписать в виде
V X В = ЦоО, (Б.З)
где
D = 80Е + (i/co) j. (Б.4)
Здесь мы предположили, что все величины, описывающие движение плазмы,
зависят от времени как ехр (— icoZ). Пусть ток j пропорционален Е, но из-за
влияния магнитного поля B9z не обязательно направлен вдоль Е, тогда с по-
мощью соотношения
j = a-E (Б.5)
мы можем определить тензор проводимости о. Уравнение (Б.4) принимает
вид
D = e0(l Н-—5— а\е = в Е. (Б.6)
\ е0<а 7
Таким образом, диэлектрическая проницаемость плазмы представляет собой
тензор
в = е0 (I + ш/е0®), (Б.7)
где I — единичный тензор.
338
Приложение Б
Для вычисления о воспользуемся линеаризованным
ния частиц сорта s, пренебрегая членами, связанными
и давлением:
уравнением движе-
со столкновениями
ms (dvs/dt) = q$ (E + vs X Bo).
(Б.8>
Определяя циклотронную и плазменную частоты для каждого сорта частиц:
--14sB0/ms ьлр^п^1ейт3, (Б.9)
уравнение (Б.8) можно разбить на компоненты по осям х, у н г и найти со-
ставляющие вектора скорости vs:
iqs
vxs —
ms(a
[Ех ± i (cocs/co) Еу\
1 — (0>cS/(O)2
(Б.10а>
vys —
msd)
- + * (Ct»es/cp) Ex]
1 — (cocs/co)2
v2S — Ez>
(Б.106)
(Б.10в>
где знаки ± относятся к заряду qs. Ток в плазме
j = £ nos^vs;
$
(Б.Н>
поэтому
i
Jx
еосо
i/l0s
80СО 7И$СО
с ± i (<ocs/<o) ЕУ
1 — (G>cs/co)2
s
2
X ± 1 К» Еу
1 — (соС5/со)2
(Б.12>
S
Воспользовавшись тождествами
1
2 L СО 4= COcs
со
со
1 — (cocs/co)2
СО ± COes
(Б. 13>
cocs/co
со
со
уравнение (Б.12)
1_
1 — (COcs/co)2 2 L co + co cs co ± co cs
можно переписать в следующем виде:
1
ix =
eoco
со
со
СО -Ь C0cs СО ± C0cs
S
со
со
I __ ) iEy
\ CO 4- CO^s CO ± G)c$ /
Аналогично у- и z-компоненты плотности тока определяются равенствами
(Б. 14)
е0<о
iy =
со
со
S
, . . i&x +
co ± (O$s CO 4- C0cs J
Приложение Б
339
(Б.15)
(Б.16)
Определяя величину jx из (Б.14) и подставляя ее в (Б.4), получаем
2
со со
СО 4= dies О) ± COcs
Введем следующие обозначения:
(Б.17)
S
S
(Б.18)
S
С помощью этих определений уравнение (Б. 17) и аналогичные соотношения,
получающиеся, если спроектировать уравнение (Б. 11) на оси у и г и вос-
пользоваться формулами (Б.106) и (Б.10в), можно записать в виде
= SEX - iDEy, = \DEX + SEy,
= PEZ.
(Б.19)
Сравнивая последние равенства с
соотношением (Б.6), мы видим, что
(S — \D
\D S
О О
(Б.20)
e e08fl.
Теперь выведем волновое уравнение, взяв ротор от уравнения Максвелла
V X Е = — Ви заменив V X В на ц08*Е- Б результате получим уравне-
ние
VXVXE=-poeo(eJrE)= - —еЛ.Ё. (Б.21)
т) Заметим, что здесь D —это не вектор электрической индукции D,
-а величина, связанная с разностью величин Я и L.
340
Приложение Б
Предположим, что Е зависит от пространственных переменных как exp (ik-г)
и введем определение векторного показателя преломления:
р — ck/to. (Б.22}
Тогда уравнение (Б.21) запишется в виде
р X (р X Е) + £^-Е = 0.
(Б.23)
В плоскости ху однородная замагниченная плазма изотропна; поэтому без
потери общности можно выбрать ось у так, чтобы выполнялось равенство
ky ~ 0. Пусть угол между векторами к и Во равен 0, тогда
р* = р sin 0, pz = р cos 0, р^ = 0. (Б.24)
Теперь выпишем уравнение (Б.23) в компонентах, воспользовавшись соот-
ношением (Б.20) для составляющих тензора
R-Es
S — р2 cos2 0
iD
р2 sin 0 cos 0
— iD p2sin0cos0\ /^x\
S — p2 0 1^1=0. (Б.25)
0 P — p2sin20/ \EZJ
Отсюда видно, что компоненты Ех и Еу связаны с Ег только в том случае,,
когда угол 0 не равен 0 или 90°.
Матричное уравнение (Б.25) эквивалентно системе трех однородных
уравнений, решение которой существует, только если детерминант матрицы
R обращается в нуль: det || R || = 0. Раскладывая этот определитель по ми-
норам элементов второго столбца, получаем
(iD)2 (Р — р2 sin2 0) + (S — р2) [(S — р2 cos2 0) (Р — р2 sin2 0) —
— р4 sin2 0 cos2 0] = 0. (Б.26)
Заменив cos20 на 1—sin20, можно разрешить это уравнение относительно
sin20:
sin2 о = __+
и4 (S — Р) 4- р.2 (PS — RL)
Здесь мы воспользовались тождеством S2—D2 = RL. Аналогично
Sp4-(PS + PL)p2 + PRL
cos^ D = ----.
р4 (S-P) + p2(PS-PL)
Разделив последние два соотношения друг на друга, получим
Р(р4—2Spa+/?A)
Sp4 — (PS + PL)p2 + PRE
tg26=
(Б.27)
(Б.28)
Поскольку 2S = R + L, то числитель и знаменатель этого соотношения
можно разложить на множители, и в результате дисперсионное уравнение-
для волн в холодной -плазме принимает следующий вид:
Р(р2-Р) (р2 —- L)
(Sp2—PL)(p2—Р)
(Б.29)
Если положить 0 = 0 или 90°, то из (Б.29) можно получить основные
моды колебаний, рассматривавшиеся в гл. 4. Пусть 0 = 0, тогда уравнение-
имеет три корня: Р = 0 (ленгмюровская волна), р2 = R (правополяризо-
ванная волна), р2 = L (левополяризованная волна). В случае 0 = 90° мы
имеем два корня: р2 = RL/S (необыкновенная волна) и р2 = Р (обыкновен-
ная волна). Воспользовавшись определениями (Б. 18), можно показать, что
Приложение Б
341
получающиеся дисперсионные уравнения тождественны выведенным в гл. 4
с точностью до поправок, возникающих из-за учета движения ионов.
Полагая р оо, можно найти резонансы:
tg20pe3 = — Р/S. (Б.ЗО)
Из этого соотношения следует, что резонансные частоты зависят от угла 0.
При 0=0 возможными решениями являются Р = 0 или 5 = со. Первое
отвечает плазменному резонансу <о = сор. а второе реализуется либо при
R ~ оо (электронный циклотронный резонанс), либо при L = ос (ионный
циклотронный резонанс). В случае 0 = 90° возможны решения Р — оо или
5 = 0. Первому из этих равенств при конечных <ар и со удовлетворить нельзя;
второе позволяет получить выражения для верхне- и нижнегибридных резо-
нансных частот, а также для двухионных гибридных частот (в том случае,
когда в плазме имеются ионы двух или более сортов).
Частоты отсечек можно найти, если в уравнении (Б.26) положить р = 0.
Воспользовавшись тождеством 52—D2 = RL, получаем
PRL = 0. (Б-31)
Частоты отсечек не зависят от угла 0. Условия R = 0 и L = 0 приводят
к выражениям для частот отсечек со% и полученным в гл. 4 (с точностью
до поправок, учитывающих движение ионов). Условие Р = 0 (или со = (ор)
отвечает как отсечке (для поперечных волн), так и резонансу (для продоль-
ных колебаний). Это вырождение связано с тем, что при выводе дисперсион-
ных уравнений мы пренебрегли тепловыми движениями.
Диаграмма Клеммова—Муллали—Эллиса обобщает информацию, со-
держащуюся в дисперсионном уравнении (Б.29). Из него нетрудно получить
еще один, не показанный на диаграмме результат; из второго уравнения си-
стемы (Б.25) мы видим, что
iZ)^ + (S-lx2)££/ = O. (Б.32)
Таким образом, поляризация в плоскости, перпендикулярной вектору Во,
дается выражением
i (Ex/Ey) = (^-S)/D. (Б.33)
Отсюда нетрудно видеть, что в резонансе (р2 = оо) волны поляризованы
линейно, а в точке отсечки (р2 = 0) они имеют круговую поляризацию, по-
скольку в этом случае либо R = 0, либо L = 0, и, следовательно, S = ± D.
Приложение В
ЗАКЛЮЧИТЕЛЬНОЕ
КОНТРОЛЬНОЕ ЗАДАНИЕ
(ДЛЯ ТРЕХЧАСОВОГО ЭКЗАМЕНА)
Часть А (рассчитана на одночасовое выполнение
задания без права пользования литературой)
1. Число электронов в дебаевской сфере при п = 1017 м~3 и КТе = 10 эВ
приближенно равно
а) 135; б) 0,14; в) 7,4-103; г) 1,7-105; д) 3,5-1010 * *.
2. Для плазмы плотностью п = 1020 м-3 электронная плазменная частота
равна
а) 90 МГц; б) 900 МГц; в) 9 ГГц; г) 90 ГГц; д) с точностью до 10 %
не равна ни одной из приведенных выше величин.
3. Максимальный ларморовский радиус для ядра гелия с зарядом Z = 2
и энергией 3,5 МэВ, находящегося в магнитном поле В ~ 8 Тл, приближенно
равен
а) 2 мм; б) 2 см; в) 20 см; г) 2 м; д) 61 см.
4. В лабораторной плазме с п —• 1016 м~3, КТе ~ 2 эВ, = 0,1 эВ и В ==
= 0,3 Тл величина р (отношение газокинетического давления к давлению
магнитного поля) приближенно равна
а) 10"7 8 *; б) 10-6; в) 10~*; г) 10~2; д) 10”1.
5. Скорость градиентного дрейфа vv5
а) всегда направлена в ту же сторону, что и v^; б) всегда направлена
против V£j в) иногда параллельна В; г) всегда направлена против скорости
центробежного дрейфа v^; д) иногда параллельна вектору скорости диамаг-
нитного дрейфа Уд.
6. В плазменном торе, показанном на рисунке, диамагнитный ток течет в ос-
новном в направлении
а) + Ф;
б) —ф;
в) + 0;
г) - «9;
Д) + z.
7. В плазменном торе, изображенном на рисунке в п. 6, торсионные альфве-
новские волны могут распространяться в направлениях
а) ± г; б) ± 0; в) ± Ф; г) только в направлении + 0; д) только в направ-
лении — 0.
8. Плазма типа Л в 10 раз более плотная, чем плазма типа В, но имеет такую
же температуру и ионный состав. Сопротивление плазмы А по отношению
к плазме В
а) в 100 раз меньше; б) в 10 раз меньше; в) примерно такое же; г) в
10 раз больше; д) в 100 раз больше.
Приложение В
343
9. Средняя скорость электронов | v | в максвелловской плазме с температурой
10 кэВ равна
а) 7-Ю2 м/с; б) 7-Ю4 м/с; в) 7-Ю5 м/с; г) 7-Ю6 м/с; д) 7-Ю7 м/с.
10. Какие из следующих волн не могут распространяться в плазме без маг-
нитного поля (Во = 0)?
а) Электронная плазменная волна; б) обыкновенная волна; в) альфве-
новская волна; г) ионно-звуковая волна; д) волна Бома—Гросса.
11. Волна, «распространяющаяся назад»,— это такая волна, у которой
а) к направлен против Во; б) a>/k <0; в) da/dk <0; г) vt- = — ve; д) уф
направлена против угр.
12. Термины «отсечка» и «резонанс» относятся к условиям,'когда относитель-
ная диэлектрическая проницаемость £ равна соответственно
а) 0 и оо; б) оо и 0; в) 0 и I; г) 1 и 0; д) 8 нельзя вычислить, поль-
зуясь плазменным приближением.
13. Нижнегибридная и верхнегибридная частоты равны соответственно
а) (ЙРЙС)12 и (®р“с)1/2;
б) + и (to2-|-со2)1/2;
в) (“А)1'2 и (ир+“?)1/2;
г) (со2-со?)1/2 и (<о2+<о2)*'2;
д) (со^йд)12 и (<%О1/2.
14. В полностью ионизованной плазме диффузия поперек магнитного поля
В происходит главным образом вследствие
а) ион-ионных столкновений; б) электрон-электронных столкновений;
в) электрон-ионных столкновений; г) тройных соударений; д) диамагнетизма
плазмы.
15. Экспоненциальное уменьшение плотности со временем характерно
а) для классической диффузии в полностью ионизованной плазме; б) для
рекомбинации в полностью ионизованной плазме; в) для рекомбинации в сла-
боионизованной плазме; г) для классической диффузии в слабоионизованной
плазме; д) как для диффузии, так и для рекомбинации в полностью ионизо-
ванной плазме.
16. Вистлерная мода имеет круговую поляризацию, причем вектор электри-
ческого поля волны
а) вращается по часовой стрелке, если смотреть в направлении +
б) вращается по часовой стрелке, если смотреть в направлении — Во; в) вра-
щается против часовой стрелки, если смотреть в направлении + k\ г) вра-
щается против часовой стрелки, если смотреть в направлении — k\ д) вообще
не вращается, поскольку волна линейно поляризована.
17. Фазовая скорость электромагнитных волн в плазме
а) всегда больше с\ б) никогда не может быть больше с; в) иногда бывает
больше с; г) всегда меньше с; д) никогда не может быть меньше с.
18. Температуру плазмы нельзя повысить с помощью
а) нагрева на циклотронном резонансе; б) адиабатического сжатия;
в) омического нагрева; г) магнитной накачки за время пролета; д) процесса
неоклассического переноса.
19. Плазму нельзя удержать в
а) бейсбольной маске; б) диамагнитной петле; в) стеллараторе, свернутом
в виде цифры 8; г) системе из восьми одинаковых зарядов, расположенных
в вершинах куба; д) тета-пинче.
20. Затухание Ландау
а) вызывается резонансными частицами; б) всегда имеет место в бесстолк-
новительной плазме; в) никогда не возникает в бесстолкновительной плазме;
344
Приложение В
г) это математический результат, который не подтверждается в эксперименте;
д) связано с вычетом в точке сингулярности, лежащей на полуокружности
вне действительной оси.
Часть Б (двухч&совое выполнение задания;
пользуясь учебником, нужно решить четыре
задачи из пяти)
1. Рассматривается холодная плазма, которая состоит из ионов водорода
с концентрацией nQ, ионов Не++ с концентрацией (1/2) и0 и электронов с
плотностью 2 п0. Покажите, что в такой плазме существуют две нижнегиб-
ридные частоты. Получите для каждой из них приближенную формулу.
(Указание: можете пользоваться плазменным приближением, условием
ml М < 1 и формулами для vn приведенными в тексте. Заново решать урав-
нения движения не нужно, достаточно использовать известное решение.)
2. Разумные существа с далекой планеты пытаются связаться с Землей,
посылая мощные радиоволны, частота которых каждую минуту меняется
от 10 до 50 МГц. Линейно-поляризованные волны должны проходить через
плазму радиационных поясов таким образом, чтобы векторы Ей к были пер-
пендикулярны Во. Обнаружено, что во время солнечных вспышек (на их
солнце) волны с частотами от 24,25 до 28 МГц через радиационный пояс пла-
неты не проходят. Определите плотность плазмы и напряженность магнит-
ного поля в их радиационном поясе. (Указание: не округляйте полученные
числа раньше времени.)
3. Если величина р больше, чем т!М, то существует возможность связи ме-
жду дрейфовой и альфвеновской волнами, которая приводит к неустойчи-
вости. Для этого необходимо, чтобы продольные скорости волн вдоль Во
были одинаковы.
а) Покажите, что условие 0 > т!М эквивалентно неравенству Рл<иТепл-
б) Пусть в плазме КТе = 10 эВ, В = 0,2 Тл, ky = 1 см-1, а п =
= 1021 м~3. Найдите, какова должна быть величина kz для реализации
этой связи в водородной плазме. Можете считать, что n0/n0 = 1 см-1, где
n0 = dn^/dr.
4. Для аномальной диффузии, вызванной неустойчивыми колебаниями, за-
кон диффузии Фика выполняется .не всегда. Например, инкремент дрейфо-
вых волн зависит от Vn/n; поэтому и коэффициент дифузии D ± может сам
зависеть от Vn. Рассмотрев общее выражение для D± в цилиндрической си-
стеме координат, а именно
D . — Arsnp I---I »
\ dr J
покажите, что временная эволюция плазмы, распадающейся вследствие диф-
фузии, описывается уравнением
-^- = Г(г)пР+?+1.
ot
Покажите также, что в соответствующих пределах из этого соотношения
можно получить уравнения, описывающие диффузию в полностью и частично
ионизованной плазме.
Приложение В
345
5. В некоторых полупроводниках, например арсениде галлия, вольт-ампер-
ная характеристика выглядит так, как показано на рисунке:
На ней имеется участок, соответствующий отрицательному сопротивлению
или отрицательной подвижности. Допустим, что существует вещество, об-
ладающее отрицательной подвижностью при любых значениях тока. Исполь-
зуя уравнение движения холодной слабоионизованной плазмы без магнит-
ного поля, уравнение непрерывности для электронов и уравнение Пуассона,
проведите обычный анализ волн в линейном приближении и покажите, что
при <0 в плазме существует неустойчивость.
Приложение Г
ОТВЕТЫ К НЕКОТОРЫМ ЗАДАЧАМ
1.1.а. При нормальных условиях (давлении 760 мм рт. ст. и температуре
О °C) 1 моль идеального газа содержит 6,022-1023 молекул (число Авогадро)
и занимает объем 22,4 л. Следовательно, число частиц в 1 м3 равно
6,022-1023/2,24-10-2 = 2,69-1025 м~3.
б. Поскольку PV — NRT, то и = N/V = P/RT. Следовательно, n-Jn^ =
= PiTJPqT^. Зная плотность при нормальных условиях [она вычислена
в п. а)], имеем
IO"3 273
Л1 = (2,69-ю15)--------------------
' } 760 (273 + 20)
= 3,30-1019 М-3.
Заметим, что двухатомный газ, например Н2, при данном давлении содержит
в два раза больше ятомоа, чем, скажем, Не.
1.2. Рассмотрим интеграл
Z2 S3 [ е x'dx j е y'dy — f J е ^'^^dxdy
—оо —оо — оо
в двумерном пространстве. Переходя к полярным координатам, имеем
Z2 — [ f е~г7 dr d<t> ~ 2л ( e“rV dr — л j e~r*d (r2) = — ле—г21 “ = л.
6
Следовательно,
I = f e~*2dx =
и
1= J f\u)du= A (2KT/m)lz J e~m!‘?2J<Td[u(m/2](T)1‘2] = A/(2/(T/m)12;
------OO --00
поэтому A = (т/2лКТ)1^.
1.4. p n (KTe + KTi) = 1021 (4-104) (1,6-10-19) = 6,4* 106 Н/м2. 1 атм^
105 Н/м2, следовательно, p = 64 атм.
Приложение Г
347
1.5.
d20
dx2
е (rij — пе)
ео
---- n^e(^lKTi-^lKTe
паое / еФ , еф \
~ТГ\.кт{
Ф = Фое 1 х l/xD, где
4
9
”<х/ /___1
~ *0 I кте
Если Ti < Те, то XD^ (КТ^/п^е2)'^
Если Те Тс, то Xd ~ (КТе&о/п<х>е2)^2.
1.6.
a) d^/dx2= —nqizQ. Пусть 0 = Ах2 + Вх+С;
Ф' = 2Ах + В; Ф" = 2А. При х ~ 0 произ-
водная 0Z — 0 из симметрии. Следовательно,
В = 0. При х = ± d потенциал 0=0; поэтому
0 = Ad2 + С, С = — Ad2. Поскольку Ф" =
= 2А ~ — nq/z0, то А = — nq/2^0, а Ф ~Ах2—
— Ad2 = nq (d2—х2)/2е0.
б) Энергия, необходимая для того, чтобы
перенести заряд q из точки хх в точку х2,
равна изменению потенциальной энергии A(q$) = q (02— 01). При
х = d- d потенциал Ф = Фг = 0, а при х = 0 потенциал Ф = Ф2 =
= (1/2е0) nqd2; следовательно, S = п<?2с!2/2е0. Если d = Xd, то для одно-
мерного максвелловского распределения <S — (l/2e0)nQ2(ATe0/nq2) =
= (1/2) КТ = Вер. Следовательно, если d >Хп, то £ >£,ср. Если же функция
распределения по скоростям трехмерная, то £ср = (3/2) КТ и € > (1/3) £*ср.
Множитель 1/3 особой роли не играет; главное в другом: если заряд одной
компоненты плазмы не полностью нейтрализован зарядом другой компоненты,
то тепловой энергии частиц недостаточно для того, чтобы частицы могли
уйти в плазме на большие расстояния d > Xd.
1.7. a) XD= 7400 (2/1016)I 2= IO-4 m, Wd = 4,8-1010 m~«.
6) Z.D= 7400 (0.1/1012)1 2 = 2,3-10—3 m, ND = 5,4-1010 м~3.
в) XD= 74 00 (800/1023)1'2 = 6,6-10~? m, Nd = 1,2-1011 m~3.
2.1. E = (1/2) mv\-, следовательно, v± = (2£/m)I/2 и rL = mvJeB.
. Г (2) (104) (1,6.10-1») 11/2
a) "i = [—9;n.i0^—] = 5’93’10 M/c’
гъ =
(9,11-10~31) (5,93-107)
-----------------------=6,75 m<
(1,6-10~19) (0,5-10-4)
6)
= (300) (1000) = 3-105 м/с,
(1,67-1Q~27) (ЗЛ05)
(1,6-Ю"19) (5-10-9)
= 6,26-105 м = 626 км.
348
Приложение Г
v
_ Г И(№)||.б.!0?.;). w 10, И/С
L L (4) (1,67-10-27) J
(4) (1,67-10“ 27) (2,19-105)
• —----------------—--------------= (J,loo м.
L (1,6-10~19) (5,00-10-2)
Г)
rL =
<ШЕ
цВ
[(2) (4) (1,67-10~27) (3,5-106) (1,6-10~19)]1/2
= 3,38-10-2 м.
2
В®
(2) (1,6-1О“10) (8)
2.4. Пусть начальная энергия частицы равна <?0,
а ларморовские радиусы равны соответственно гг и г2»
как показано на рисунке. Энергия частицы в точке 1
равна = <£0 + еЕгг, энергия в точке 2 — £2 = —
—еЕг2. (Можно сказать, что 2 = <о0 ± еЕг^.) Очевид-
но, = 2<Г1(-2/Л/. В используемом нами приближе-
нии
Л^П.2 М (2Si.2\li2
Г1,2~ еВ еВ
_____if 2<go У 2 / еЕ \1 2
~ Qc I М J V+ £о Г1,27
При малых Е квадратный корень можно разложить
в ряд Тейлора:
1 / 2£0 \1/2
Г] о » -----I ---- I
Й. V М )
/ 2<£0 \ 1/2 Г X еЕ 1
к М ) L1 * 2 £0
/ 2£0 \ 1/2 г 1 еЕ
I I I 1 Ч; ----------—
k М J L 2 £0
Таким образом, независимо от величины <£0
Е- i
I
----*1
П I
И, 2 =
1
Й,
й.
1 еЕ
2 <£о
, \1/2т-1
М
еЕ 1 2<£0 2еЕ
г± — г2 =-------------— =------.
£0 Й* MQ2c
Иными словами, за время 2л/Йс ведущий центр частицы смещается на рас-
стояние 2 (гх—г2), поэтому
4еЕ 1 9 р Р
ve. = 2 (г, - г2) (йс/2 л) =
Мйс 2л п В В
т. е. скорость дрейфа ведущего центра не зависит от энергии иона 80. Если
бы мы работали в рамках более строгого приближения, то вместо 2/л полу-
чили бы множитель 1.
2.5. а)
П = П0^ КТе- = (7<Te/e) 1П (п/п0),
_ дф ~ КТе 1 дп ~ КТе ~
с = — “Г“- г = —----------------— г = —-— г.
дг е п дг еК
Приложение Г
349
б)
Для электронов УТепл “ (2^Te//n)1/Ч Следовательно, |с<е| = (КТе/т) X
Х(т/еВХ)== и2епл/(2(о<А). Теперь нужно найти rL, усреднив величину rL =
= mvJeB по функции распределения. Поскольку поперечной скорости
отвечают две степени свободы, то (1/2) mv2± = 2-КТе/2 = КТе. Удобнее всего
пользоваться среднеквадратичной величиной кв — (2КТе!т)х^2=
— ^тепл- Подставляя эту скорость в определение rL, находим | ге 1=(1/2)Х
Х(Утепл^) (ух/(ос) = (1/2) иТеплгЕ^> поэтому из условия ] иЕ | = утеПл сле-
дует, что rL = 2Х.
в) Если вместо электронов рассматривать ионы, то итеПл, i ~ (%KTi! М)^2 =
= rLi = и
утепл»^_и* 1 Ее
ТГ. ~ ~т~ Утепл’tTLl’’
Если | уе[ = ^тепл, г , то и в этом случае rjj, = 2Х, при условии, что Ti = Те
2.6. а) п == п0 ехр (е“г2/°2—1) = п0ее^к7\
е
~КТе
Ф (г) =е“г/а — 1,
р . дФ
Е = — V0 = — —-
дг
г,
дФ
Ег(г)= - —
дг
KTg
е
2г
Vе
dEr
dr
2КТе
еа2
2г2 \
~^)е'
= 0,
г2
а2
р КТе 2 .
макс^ еа л/2 е
-1/2 _
(0,2) (1,6-10~19)
(1,6-10-19) (1)
V2 е”1 2 = 17 В/м,
_1_
2
v£=—
р
Уе макс = М*КС = 17/0,2 - 85 м/с.
D
б) Сравним силу тяжести Mg с силой еЕ, действующей на ион (величина mg
для электрона будет в 1836 раз меньше). Ускорение свободного падения
g = 9,80 м/с2, Afg=(39) (1,67-10“27) (9,80) = 6,38-10~25 Н, еЕмакс =
= (1,6-10”19) (17) = 2,75-10“18 Н «4-106 Mg. Таким образом, гравита-
ционный дрейф слабее электрического в четыре миллиона раз.
в)
Mv.
fL = --- -- = 10-2 М,
еВ
350
Приложение Г
. i o Г (2) (0,2) (1,6-10”19) 112
,|67 ,o_g7)> ] _ 9,9.10. м/с,
(39) (1.67. !»-’) (S.9-101)
В =---------------------------------= 4,0* 10~2 Тл.
(10-2) (1,6-10-19)
2.8.
0,3-10-*
(г/7?)3
Тл,
В =
£
г
_ (1,6.10-»)(КТ)эВ _ (ЛТ)эВ .
(1,6-10-19)В в
„ , 0,3-10“*
в (г =57?) =-----------= 2,4-10—7 Тл,
5R = 3,2 -10’ м, vvB = 108 -2^Т^, = 0,39 (КТ)эВ м/с.
Таким образом, для ионов с температурой /СТ = 1 эВ скорость дрейфа
= 0,39 м/с, а для электронов с температурой 7<Т = 3-10* эВ скорость дрейфа
= 1,17-10* м/с.
б) Ионы дрейфуют на запад, электроны — на восток.
в) 2лг = (6,28) (3,2-107) = 2,0-108 м,
z _ 2jlr 2,0-IO8
“ vvB 1,17-ю4
= 1,7-10* с = 4,8 ч.
Приложение Г
351
г) Если пренебречь движением ионов, то / = nev^s— (107) (1,6-10“19)Х
Х(1,17-104) = 1,87-10-8 а/м2.
2.9, а) Поскольку энергия движения электрона вдоль направления 0 не
увеличивается, то 0. Вначале электрон покоится, поэтому после одного
оборота он снова окажется в состоянии покоя. Следовательно, траектория
его движения состоит не из петель, а из цепочки дуг, образующих между
собой острые углы (см. рисунок). Ясно, что
преобладающим будет электрический дрейф
ve, поскольку электрон вначале смещается
влево, а под действием силы Лоренца на-
чинает двигаться вверх.
б) В цилиндрической геометрии Ф —
=Л in г +В. Поскольку Ф (10~3) — 460 В,
а Ф (0,1 м) = 0, то
460 = A In (10-з) +В,
0 = Л In(0,1) + В, В= — Л1п(0,1),
460 = Л In (10-з) — Л In (0,1) = Л In (0,01),
Л = 460/ln (0,01).
460
ф (г) =----------- X
In (0,01)
X [In г — In (0,1)] = 460 В;
in (100)
£ — — 460 / г \ /
~ “ дг In (100) \ 0,1 А
----------= 104 В/м при г — 10“2 м;
4,6- 10—2
п /(Л)10-4 500 • 10“4
В = ——-------- =-------------= 0,01 Тл,
5г (5)(1)
104 В/м
| vE | = I Е/В I = п ------------= 106 м /с.
0,01 1л
Для того чтобы оценить скорость градиентного дрейфа, мы должны найти
в системе отсчета, движущейся вместе с ведущим центром. Напомним, что
при выводе выражения для считалось, что v± — это скорость движения
по невозмущенной круговой орбите. В нашем случае сама эта орбита дви-
жется со скоростью и движение в лабораторной системе никак нельзя
считать круговым, однако его можно представить в виде суммы кругового
движения со скоростью v± и Е X В-дрейфа ведущего центра. Рассмотрим
z-компоненту скорости частицы (скорость вдоль провода). В точке 1 скорость
vz = ve + v^cos act = 0, причем здесь cos соД — — 1, т. е. косинус дости-
гает максимальной отрицательной величины. Следовательно, = Ана-
логичное соотношение между ve и и±можно получить, если рассмотреть ско-
рость vz в точке 2: vz = v$ + y±(cos (ос/ — 1). Энергия частицы в этой точке
[(1/2) должна равняться энергии, которую получила частица от элек-
352
Приложение Г
трического поля, пройдя в нем расстояние 2/р Таким образом,
1 0 ти± £
— tn (vE + v . УЯггеЕ = 2eB —-— = 2mv . —- = 2mv . vp.
2 4 £ l eQ ± p x E>
ve + 2v±ve + v2j. = 4uxVE> (vE~ =
Теперь мы в состоянии вычислить
ув
В
7 ( — 1)-1Q—
1 А
V*B' 2 vc
dB
dr
со.
еВ (1,6-10~19) (1Q—2)
т
= 1,76-109 с"1
(9,1b Ю"81)
уВ
В
в
г
1 1012-102
=-------------— = 2,8-104 м/с.
2 1,8-109 -----------------
V.E-дрейф из-за того, что ларморовский
= 10а м-1,
га
1
^В~ 2 Ю2
На такую величину замедляется
радиус частиц меняется со временем, а траектория по форме напоминает е.
Невозмущенная орбита в этом случае напоминает траекторию ниппеля на
колесе движущегося велосипеда:
в
В заключение отметим, что поправка к v^, связанная с конечностью лармо-
ровского радиуса, пренебрежимо мала:
1 2v2_e_______LZL_L
4 L В ~ 4 г2 В
rL= =5)7.10_4м;
(1,6-10-19) (0,01)
а поскольку г = 10 2 м, то (1/4)(г^/г2) = 0,08 %.
2.12. Будем рассматривать скорости частиц в центральной плоскости;
пусть нижние индексы i и f относятся к начальному и конечному состояниям
(д® и после ускорения)
а) По условию Rm~ 5, v±i— Поскольку магнитный момент ц сохра-
няется, то v^f == v±i и только у й будет увеличиваться. Это увеличение будет
идти до тех пор, пока питч-уголл0 не превысит критический:
„2
1
1
1 + Rm
_1_
5
sin2 0m = —-----------
__। „2
Следовательно, 4, Уц^=2 и ±£. Энергия ^частицы
чальном состояниях равна соответственно
£/=4"л1(°м+р2хг):=4_Л1(4+|1)у2^=тМу2±£’
в конечном и на-
Приложение Г 353
Ei = V м (v II i + = V м (1 + °= МгЪ-
л £
Следовательно, Ef = 2,5Et = (2,5)(1) = 2,5 кэВ.
б) 1. Пусть частица, имеющая скорость v0 >0, ударяется о поршень, дви-
жущийся со скоростью vm <0. В системе отсчета, связанной с поршнем,
частица испытает упругое соударение и отскочит от поршня, имея скорость,,
равную начальной, но с противоположным знаком. Будем обозначать ско-
рости в системе отсчета, связанной с поршнем, буквами со штрихом. Тогда
начальная и конечная скорости частицы в этой системе будут равны соответ-
ственно
°i = v0~vm’ v'f = ~("o~V)'
(Напомним, что vm отрицательна.) Возвращаясь в лабораторную систему
отсчета, имеем
vf = vf +ym= ~vo + 2vm-
Поскольку vm <0, изменение скорости частицы равно 2| , что и требова-
лось доказать.
2. При каждой осцилляции между поршнями изменение импульса частицы
составляет Др ц = 2rnjvml . Если N —число таких осцилляций, то P||f =
= Pgf+ Л/ДРу. Таким образом,
N = = "Ilf-"II f = 2o±l-vxl = 1 v±i .
ДР|| 2vm 2vm 2 Vm
Et = = 1 кэВ - (103) (1,6-10-19) =1,6- IO-16 Дж.
/ 1,6*10-18 \l/2
Следовательно, u±i= ГуI = 3,1-105 м/с.
Поскольку vm— 104 м/с, то число осцилляций
2 104
3. Среднее значение и у равно
1 1 3
v = v("u< + "nf) = T<a±i’+2v^ =TI'±i = 4,6’10 ’
а поскольку L ~ 101Э m, to
• NL (15) (1013) o o 1ЛЙ 1Л 4
t = —=— = ——--------— = 3,2.108 c = 10 лет.
v 4,6-106
За это время расстояние между поршнями уменьшится на
Д£ = 2от/— (2) (104) (3,2-108) = 6,4-1012 м,
12 Заказ 3170
354
Приложение Г
так что в действительности время t « 2,5-108 с. Поскольку нас интересует
ответ с точностью до коэффициента порядка двойки, суммирования по всем
отражениям производить не нужно: точность приведенного выше ответа
(3,2-108 с) оказывается достаточной.
2.13, а) Поскольку J v у ds та v ц L = const, то v ц L + v ц L « 0.
б)
L Ъ .. vll (-i),
Uy • L T L
Ev у L 2v±f — vxi L 2 1013
i’ll (—i) + M 2Vm 3 2-104
= 3,3-108 с.
2.14. Как следует из уравнения Максвелла V X Е = — В, с увеличе-
нием В возникает электрическое поле Е. Это индуцированное поле Е имеет
компоненту вдоль скорости v и, следовательно может ускорять частицу. Если
В медленно возрастает адиабатическим образом, то поле Е будет мало, од-
нако интегральное действие этого поля за времена, превышающие лармо-
ровские, будет заметным. Инвариантность р, позволяет найти увеличение
энергии частицы, не рассматривая этот интегральный процесс.
3.1. Будем исходить из уравнения daldt + V-j = 0, где j = jp = (р/В2) Е.
Отсюда следует, что а = — V- [(р/В2) Е). Производная по времени от урав-
нения Пуассона имеет вид V-E = а/е0. Следовательно,
VE= V f 1 +—^-")Ё = 0.
\ е0 J \ В2 J \ е0В2 )
Предполагая, что относительная диэлектрическая проницаемость в не за-
висит от времени, имеем V-D = V-(eE) = 0. Сравнивая между собой два
последних равенства, заключаем, что е = 1 -f- р/е0В2.
3.2.
. , пМ Qp пе2 М2 пМ
е0В2 Q2 е0М е2В2 е0В2
Это справедливо, если е» 1.
3.3. Возьмем дивергенцию от уравнений (3.56) и (3.58):
V-(V X Е) = >-— \7-В= 0, —(V-B) = 0.
dt
Следовательно, если в начальный момент V-B =0, то это равенство будет
соблюдаться и в дальнейшем. Именно это и утверждает уравнение (3.57).
Далее,
V-E
V (V X В) = 0 = Цо [<7iV-(n£Vi) + ?eV-(n«ve)] 4--v •
Приложение Г
355
Из уравнения (3.60) следует, что V'(ni'vi) = — «1, 7-(«л) = — Пе, поэ-
тому
• • V- Ё
Но (— <Нп1 — qene) Н------— = 0,
с2
д г* 1 т
— v Е---------------(ntfi + neqe) = 0.
dt L e0 J
Если в начальный момент величина, стоящая в квадратных скобках, равна
нулю, то V-E = (1/е0) (mqi + neqe), что эквивалентно уравнению (3.55),
в X v« кт пе .
за + ------- —
Поскольку КТ ~ еФ, Е---------Ф/L, мы имеем KTleL ~ Е\ следовательно,
/о ~ пеЕ/В ~ nev, так как EiB — Ve-
3.5. Пусть /£> постоянен в ящике размером L. Из разности токов, текущих
по двум стенкам, получаем: Ди = n'L, |/£>| = |Дпецу| = \n'Levy\, По-
скольку этот ток распределен по ящику с длиной ребра L, то эквивалентная
плотность тока равна |/д| — |7д| IL = \n'evy\. Из уравнения (3.69) сле-
дует, что | j d | = \КТУп!В\= \К.Тп'1В\\ следовательно, если скорость vt
такова, что две формулы согласуются для одного значения L, то они будут
согласовываться и при любом L; ведь L в ответ не входит.
3.6. a) vDe = —-г-у--Уп
еВ п
Из условия изотермичности следует, что у = 1:
- КТе 2п0 х /. х2 \-1 ~ КТе 2х /. х2 \-1
Vn, = у--------2-----I 1-----I = V ------5----I 1-----I •
еВ a2 n0 к а2 / * еВ а2 к. а2 )
в) vDe = (2)/(0,2) Л:
Л-1 _ I n' I _ (2п0/а2) (д/2) Г 4/0,04
| п I по (1 — а2/4а2) j 3/4
Следовательно, = (10) (133,3) = 1333~м/с.
—г2/г2 еф/КТе
3.7. п = пое и = лое ,
12*
356
Приложение Г
а)
|п П КТе /
е пп е I
О \
дф - __ КТе 2г -
дг Г ~ е г20 Г’
Е X В
V£ = ----—
В2
__ В X ур
епВ2
__M=_§2£Zk
Вг еВ
КТе дп/дг 3
---------у =:
еВ п
2г
д
л КТе v . - л
— — О------------ 1п п = — 0
еВ дг
КТе 2г
--------— — уЕ
еВ г2
что и требовалось доказать.
б) Из результатов, полученных в п. а, следует, что частота вращения яв-
ляется константой, поскольку независимо от того, взять ли в качестве v
одну из величин v^, v^, vD/ или же их линейную комбинацию,
ие ~ г, а о = ив/г — const.
в) В лабораторной системе отсчета
v = Уф + У£ == 0,5vDe + ( — VDe) = — (1/2) VDe.
3.8.
а)
, / \ 3 na(KTe + KTi) 2r _г2/г2
iD = пе (vD£ - vD.) = - 0 —------е—-----• — е /го ,
о
б)
ь = 0018Ж5Н1^Г191 = о,147 А/м3
(0,4) (rg/2r) (2,718)
или
== ne(|l/Del+ I^Dil),
... . , (КТ)эв 2Г (0,25) 2г г
I VDe! — I vDi\ =-----------:-----------1— = 1,20 —- М/С.
В 0,4Г2О г2
0,4г2
В
D
Приложение Г
357
Пользуясь тем, что е== 1,6- 1О'И Кл, е = 2,718, получаем:
Г Q—
jD = (Ю?в) (1,6. 10'19) (2) (1,25) — -= 0,147 А/м2.
rl
в) Поскольку в лабораторной системе ve = V£ + v$e = vg — V£ —0, то ток
целиком переносится ионами.
3.9.
V X В = |1оЬ>
J (V X B)-dS = Но$ b'dS,
ф В-r/L = pt0 J ]d *dS.
Рассмотрим контур, одна сторона которого совпадает с осью цилиндра
(В — Во), а другая находится настолько далеко от него, что там В = Воо.
Поскольку ток направлен по — 0, мы можем выбрать направление ин-
тегрирования так, чтобы величина dS была положительна, как показано
на рисунке. Компонента Вг равна нулю; следовательно,
Lna(KTe+ KTt) Г.~'2/'о1Г ZLn.KT
J ” Boo
где Те = Ti. При вычислении этого интеграла мы считали, что В (г)= В оо,
поскольку такой малый ток j не может заметно изменить значение В. Таким
образом, D
AR R R 2л0КТ 2 (4л 10“7) (1016) (0,25) (1,6-10-19)
ЛВ = В, - В, = w -g— =----------------—---------•----=
= 2,5* 10-9 Тл.
358
Приложение Г
4.1. а) Найдем Ф^
, КТе Hi со + i а со* — i а
Ф1 ----------------------х-------------=
е п0 со* + i а со* — i а
__ КТе coco* + а2 + i а'(со*— со)
е со*2 + а2 по
Если величина Л1 вещественна, то
Im (Ф1) д(о)* —о) б.
Re (0j) coco* 4- <*2
следовательно,
л . Г а — °>) 1
о = arctg —ь--------L, .
L coco* + a2 J
б) Пусть пг = (kx а Фх — где А — положительная
постоянная. При со <со* величина 6 >0. Пусть в точке х0 в момент времени /0
фаза п1 равна нулю: kxQ—со/0 = 0. Если величины со и fe положительны, а
точка хй фиксирована, то фаза потенциала Фх обращается в нуль при
kxQ—со/ + 6 = 0, т. е. при t >/0. Следовательно, Фх запаздывает по времени
относительно При фиксированном /0 величина kx—со/о + 6 = 0 при
х <х0; поэтому в пространстве Фх тоже запаздывает относительно nt. (По-
скольку (n/k >0, а волна движется вправо, то ее начало находится при 66л ь-
ших х.) Если k <0, а со >0, то фаза потенциала Ф± обратится в нуль при
х >х0; однако, поскольку теперь волна движется влево, Фх по-прежнему
будет запаздывать относительно nv
— е (ni1 — пе1),
8о
— i corn^i = — eEt (для электронов),
— i (nMvii — eEi (для ионов),
— i conel = —i knovel (для электронов),
— i (on/! = — i kn^Vii (для ионов),
£ / — ie \ r- k / i e \ „
—---- n0 I ------- I El, nil —------По I ---- I El,
co \ m(a J co \ Meo 7
ikEi
4.3. Выразим Ф1, Ехи через пх; из уравнений (4.22) и (4.23) следует, что
со „ 4л i е
Vi^---------, =--------nv
k nQ k
Но, поскольку Ei~ —i то
4ле
01" ~~wnl-
Следовательно, разность фаз между Ег и пх составляет 90°, Фх и пх сдвинуты
по фазе на 180°, а либо синфазна с плотностью пх, либо сдвинута относи-
Приложение Г
359
гельно нее на 180° в зависимости от знака фазовой скорости a>/k. Далее, по-
скольку Е-l ~ — дФ^дх, то величина Е± определяется по наклону кривой
(случай а), В случае б мы имеем Е^Т/ц ~ i sign (й); следовательно, 6 ~
~ ±: п/2. Если m/k >0, то
Ег ~ ехр [i (kx ± | со ] t ± л/2)],
где ± соответствуют знакам величины k. Таким образом, Е^ на 90° опере-
жает П1 или отстает от нее, если со/й < О (см. рисунок).
Следовательно,
4.6.
СО2
а) «По ( — i со) t?i = — en0Ei — тпочиъ
А . iv \ ieEi
01 ( 1 Н-----) =-------
\ со / тсо
> 1
1 kEi =-----------eni,
ео
i kEi = -
nx =----not»i (из уравнения непрерывности),
(0
1 k i еЕг , i v Ч-1
— e------n0------— I 1 H----) ,
80 co mco \ co J
8 = 1
co2( 1 +
0 , . о
(0 + 1 VCO = CO*.
б) Пусть <0 == x + i у. Тогда дисперсионное уравнение принимает вид
х2 — у22ixy + ivx — vy — со2. Приравняем мнимую часть этого уравне-
360
Приложение Г
ния нулю: %ху + vx = 0, т. е. у = — v/2; следовательно, Im (со) = — v/2.
Поскольку х = Re (со), а г >0, то
Ех ~ е-1 ®*е^ = е—*
и колебание со временем затухает.
4.7. Рассмотрим уравнение /пл0 (— i со) Vj = епоЕг—еп^ (уг X Во). Пусть
вектор Во направлен вдоль z, а и к — вдоль х. Тогда ^-компонента этого
уравнения имеет вид
„ .. со
—1 tomvy — evxBQi —= — |i--------------
сос
Поскольку со = со/j ><ос, то | vx/vy \ >1 и орбита частицы вытянута в х-на-
правлении, которое одновременно является направлением вектора к.
4.8. а)
V-Bi =
1
— гяь
ео
Еу -— ky — 0,
к = k^x +
i (kxEx + kzEz) =------— erii.
«о
Запишем выражения для n-jt
дть
~~ + noV • Vi = 0, — i сопг + n0 i (kxvx + kzvz) = 0,
dt
и выражения для vx и vz.
MnQ ( — i co) vj = — en0Ei — en0 (Vi X Bo);
i e „ i toc
проекция на ось x: vx=----------Ex-------
проекция на ось у: mco co л ! i <°c Vy = 0 ч vx, to
ie р J- Vx - Ех+ Vx- mto co2 -ie ( = —Exi 1-4- mto \ co2 /
проекция на ось z: Vz Ez, mto
Из уравнения непрерывности следует, что
+kzEz
to \ mto J L \ to* /
^2^2
enQ / i e \ Г ( Y
kxEx + kzEz = i—-(---------ША I-----------------
eco \ mto / L \ co2 J
kx — k sin 0, kz = k cos 0,
“о Г ( “eV
feEi sin2 0 + kEr cos2 0 = —— I kE\ sin2 011---) 4- kEx cos2 0 1,
co2 L \ co2 / J
Приложение Г
361
2 г- ✓ 2 \ 1 т
sin2 е ( 1 — — I + cos2 0 t
©2 L \ ©2 / J
©2 Г ( 1
= —I 1 — cos2 04-11 -----------I cos2 0 ,
©3 L \ ©2 / J
2 А
—-----cos2 0,
©2
©2 (©2 — ©^) + ©р©2 cos20 = 0,
что и требовалось доказать.
б)
©2
(O2-a>2 _ш2
со2
СО4 — ©j*©2 4- ©2©2 COS2 0 = 0,
2©2 = ©? ± (©? — 4©2©2 cos2 0)1/2.
При 0->О величина cos20->l; поэтому
2<02 = со| ± [(®2 + СО2)2 - 4й)2 ш2] 1/2 = ^2 + щ2 ± ^2 _ ^2) ,
“2 = “р- “с-
Корень © = dtp отвечает обычному ленгмюровскому колебанию,
со = ©с является посторонним, поскольку при 0 -> 0 величина Во
входить не должна. При 0-> (л/2) величина cos20-> 0, а 2©2
т. е. © = 0, ©ft. Корень © ~ ©ft отвечает обычному верхнегибридному коле-
банию. Корень © = 0 не имеет физического смысла, поскольку вначале
предполагалось, что в системе существует осциллирующее возмущение.
в)
Корень
в ответ
9 9
= “Л ±4’
что и
г)
©4 — ©? ©2 + — ©1 = — ©1 — ©2©2 cos2 0,
** 4° 4 * “°
(1 \ / 1 \2
со2---со2 ) + (Wp<occos О)2 = ( —-<0А) ,
(^-1)3+ЛГ = Ь
а2
требовалось доказать.
(&р!($с я = (1/2) (©с/^р~|~
1
2
оо
1
5/4
oo
1 =
1
Уп
г
у = 2а?/а%
Д)
TU
(JUpfac Wc/(JUp
X= COS0
2
«2
- К + ®с] ± [(“₽ + - 4®Xc°s2 °]1/2-
2
362
Приложение Г
Для получения меньшего корня возьмем знак минус. Частота со достигает
своего максимального значения в том случае, когда величина cos20 макси-
мальна (и равна единице). Следовательно,
©L = <*>?, если (йр > ®с,
coL=wn, если <вг>соп.
Большему корню соответствует знак плюс. Частота достигает максимума
при cos2 0 — 0, в этом случае со2 = <йд. Следовательно, Этот ко-
рень принимает минимальное значение при cos20 = 1; таким образом,
2 2
= если соп>со.,
~ р р
9'2
<<L = <a7, если (o„>co„.
-f* С » 4- р
4.10. Обозначим через V+ и W+ соответственно скорость и плотность про-
тонов, а через V„ и 7V_ — соответственно скорость и плотность антипрото-
нов, через V— и — скорость и плотность электронов, а через уц- и п+ —
эти величины для позитронов.
а)
• Ё ( • Ё
VXE--B, + —, V X VX Е = — I poi + — L
с2 \ с2 /
[* • со2 т
(v+ — v_)------Е I ,
$2 J
— (k X k X Е) =Л2Е —к(к-Е),
' о
(ш2 — c2k2) Е = —— nQe (v+ — v__), тпоу± — ± en0E,
е0
v± = ± —— Е, со2—c2k2 == —— пое —— (1 + 1) = 2 со2,
т е0 т р
<0р == , о2 = + с2^2.
еот ---------;—£------—
(Множитель 2 можно включить в определение шр.)
б) V’Ei = (1/ео) (Л^+ ~N~ + «+ - n_)i, где п+ = п0е—е^'кг+>
= nQee^//<r_. Пусть = Т_ = Те, = т п^еф!КТе. (Заметим, что
^0± = П6±^П0.)
k k
-^ + »O±V-V±»o. и1±-Н,±Л.у±-^Ч±.
Приложение Г
363
<о2
М (— i(o) V± = ± е Ех —
у ±
± (о Я
.о е / k2 k2 \
пое3 2£2
-----------ф
8рЯ
(0«
k2k2D + 2
k2 2 + k2k2D
± i кеф (Я+ — Я_ = Я),
fe2 ПрвФ
со2 Я
jV
еФ
~КТе
k2_____1_\
<в2 X2, )’
w2 М
( KTe*0 V 2
А _ I с* U I
-----* D=== ------Г~
\ лое 7
-------1-----( — п0 — п0)
Я е0
2Ф = 2ф( Й2
гйКТе I р
2&2 О2л2
V2S
1 + (1/2) A2X2D
2of
4.11.
~ ck
п = -----
(0
си2 = w2 +c2k2,
C2k2
-----= 1
<o2
=
(О2
следовательно, п = уг •
4.12. Рассмотрим уравнение VX В= HoJi- Ток jj переносится только
электронами, поскольку ионы хлора очень тяжелые и не успевают отклик-
нуться на высокочастотный СВЧ-сигнал. Следовательно,
/1 = — nQeeve = —• (1 — х) noevel.
Если ввести <ор по правилу <о2 = n0e2/s0/n, то дисперсионное соотношение
принимает следующий вид:
c2k2 со2
-----= 1 _(1 _ X) —
Щ2 (02
Отсечка происходит при f = (1—х)1^2 fp = (0,4)^2 9 (л0)1/2, где
С =. 3‘1Q1° ^IQiQ
1 3
Таким образом,
1010 п2
----------- =3,Ы018 м-з.
(0,63)(9) J
4.13. а) Способ Г,
длине L = 0,08 м, а
Пусть N — это число длин волн, укладывающихся на
Л^о — это число длин волн, укладывающихся на той же
длине, но в отсутствие плазмы. “
Таким образом,
N =~, No= —
X Хо
л 2л
Л = — 1 "
k
д/v = _/v =—--------------
Лр 2л Хр
1-АГ
СО2 )
AJLh-jlV2
2л с
ck
(О
со2
364
Приложение Г
[✓ 2
\ (О2
_£=^08_ = 10.
Хо 0,008
Таким образом,
/ 0)2 Ч1/2 f2
1----- =1 — 10“2, 1---£-=1—2-10-2,
\ (О2 7 /2
п =
f2 = f-2-10"2
2,8-1019
92
= 3,5-1017 м-3,
Способ 2: Пусть Ло — волновое число в свободном пространстве. Тогда фазо-
вый сдвиг можно вычислить следующим образом:
L
&Ф = [ Д/г dx = (k0 — k) L = (0,1) 2л.
b
Этот способ приводит к тому же ответу.
б) Как видно из предыдущих рассуждений, если отношение со2/со 2 мало, то
величина AN также мала; поэтому квадратный корень можно разложить
в ряд:
AN
4
2 со2
1
1 — 1 1
Это и требовалось доказать.
4.14. Для необыкновенной волны из уравнения (4.101а) имеем
2
(<o2-£o2)^+i-^£i/=0.
(0
В резонансе со = сод; следовательно, Еу == 0, Е = £хх. Поскольку к = Лх,
то Е || к и волна является продольной и электростатической.
4.15. Поскольку со^ = со2 + со2, очевидно, что сор <toh. Кроме того,
<*>£ = ”Нс + (<0? + 4op)1'2]’
“L <у [-щстН + 4<осшр + 4ft)2)1'2],
<0£ = — [ — (йс + (<ос + 2(ор)] = (ор;
следовательно, сод < <ор. Аналогично
“« = V + (“? + 4шр)1/21 > “с
Приложение Г
365
— — = О 1см* (4.107)];
отсюда
<4 = “^+шр > +“р = ®h-
4.17 а) Умножим уравнение (4.1126) на i и сложим его с уравнением
(4.112а):
{аР-с№-а) (Ех 4- i Ев) + а (Ех + >£р) = 0.
(О
Теперь умножим снова (4.1126) на i и вычтем его из (4.112а):
(to2 — c2fe2 - а) (Ех — i £у) — а (Ех ~iEy) = 0.
О)
Следовательно,
F (&) — щ2 — Л2а — (1 + со^/со),
G(to) = со2 — c^kr— а(1 + <ос/со).
Поскольку
то
to2/со2 c2fe2
1 — со^/со со2
со2/со2 с2£2
G (to) = to2 1------------------------
\ 1 + ©с to со2
Из уравнений (4.116) и (4.117) слеаует, что для правополяризованной волны
F (со) = 0, а для левополяризованной G (со) — 0.
б) = “ i Еу, Еу = i Ех- Пусть Ex — f (2) тогда
Ey = f (г) ie“iG>< = f (г) е“*1 = f (г) e^ [<й^(л 2)L
Таким образом, Еу запаздывает относительно Ех на 90°; поэтому на рисунке
вектор Е вращается против часовой стрелки. В эту же сторону вращаются
электроны, которые создают ток, текущий по часовой стрелке. Последний
генерирует магнитное поле В, направленное против Во. Для левополяризо-
366
Приложение Г
ванной волны Еу = — i EXl так что Еу = f (z) е"*“1 [©*—(^/2)], и £ опережает.
Ех на 90°.
в) Для правополяризованной волны Еу = i Ех. Выделяя зависимости от
пространственных переменных, имеем Ех= f (0 elfe2, Ey — f (/) i elftz =
= f (t) el При k >0 Ey опережает \EX, поскольку при меньших z
имеет ту же самую фазу. При k <0 компонента Еу запаздывает относительно
Ех (имеет ту же самую фазу при больших значениях z).
4.19.
о>р/о>2
c2k2
1 — ос1о
do р
со2
— <о;
(-1)
(СО2 — (0(0С)2
^р/^2
1 — Ос/О
(2со — ос) = 0.
<Ч2
^(-^ф3
Следовательно»
2со — ос — 0,
1
О =-----Ос.
2
При со = toc/2 имеем
с2
----= 1
Л
ф
СО2
__________Р
1 2
1
2
“2
= 1
4<0р
“2
поэтому Уф с.
4.20.
со2
<Др/<й2
1 — ос1о
c22k dk — 2<dd(o
(6) — (0с) — (0
(ш — (Ос)2
с№ ='(о2 —
(0 — (Ос
“^р 1Я
----dco
о , I _
(йр do = 2(0 4
(со — (0г)2
cW
---= 1
2
®®р
Приложение Г
367
d(£> ____________,kc*________ ~ kc2____________
dk © + ©c©2/2 (© — ©c)2 ©-j-©2/2 ©с
Но
если © < ©с.
( СО2 \1/2 / СОСО2 Л1/2
ck = I ©2-------------I & I ©2 -j------— I , если © С а>С’
\ 1 — ©с/© / X ©С /
Следовательно,
da = с (а2 + аМр/Мс)1'2 = с (1 +<Ор/2асос)1/2
dk © + ©2/2©£ 1 + ©2/2 ©©^ '
Для того чтобы получить требуемый результат, нужно предположить, что
Оф < с2 (для вистлеров это действительно) так и считать, что ©2/©©с < L
Таким образом, получаем
— ^2сГ-Юс Y,2~co^2.
7
4.21. (©2 — c2^2)Ei =—— i ©ji [см. уравнение (4.81)],
ео
ji = nQe (Vp — ve) (vp — скорость позитронов).
Из уравнения движения имеем
следовательно,
£*=(
2со2
---------------Ех.
1 — со2/со2
Члены, содержащие Еу> взаимно сократились. Аналогично
2©2
(©^ - с^) Еу =--------р—~ Еу.
1 - ©2/©2
В этом случае сокращаются члены, содержащие Ех. Из обоих уравнений
следует, что
c2k2 2©2
-------- 1--------р---
<о2 (О2 — со2
Право- и левополяризованные волны вырождаются, их фазовые скорости
совпадают. Следовательно, фарадеево вращение в системе отсутствует.
368
Приложение Г
4.22. Поскольку разность фаз между право- и левополяризованной волнами
в два раза превышает угол фарадеева вращения, то
Р ( co2/w2 Y'2
J (*£-*Л)* = л, k^.L^’k, 1---------—р—— I
о \ 1 ± <йс1® /
Для того чтобы получить простое выражение для ki—йд, нужно разложить
квадратный корень. Предположим, что это можно сделать, а потом проверим
справедливость этого предположения:
kR, L » k01 1
1 “р/м2 \
2 1 ± coc/co J
o
1 t “p ( 1
«£ --- «Р =------«0 -----I -------------
2 co2 \ 1 — coc/co
1 , “p 2“p/“
— «0--------------------1
2 co2 1 — co2/co2
C0“<0. 1
я = L (kL — kR) = k0L ------------------; k0 = co/c;
<0 ю2_ш2
fc = 2,8-1010(0,1) Гц,
f = — = 3-108 =3,75-1010 Гц,
Ло 8-Ю-3
2 = (3 X IO3) _ (1,41-102i-7,8-1023) 5 1Q19 = 92n.
p (2)(1) (2.8-109)
n = 9,3-1017 М-».
Квадратный корень можно раскладывать в ряд, поскольку fc < f, так что
„ А_________= 0,05 «
1±сое/со /2 (3,75-1010)2
4.24. 12,7°.
4.25. а) Отсечка необыкновенной волны определяется из условия (4.107).
Таким образом,
2 I \ пе1 та>е0 . , .
со* = ш (со ± coJ =-------, псх =----------—(со + сос).
F ' е0/п е2
Мы выбрали знак -|-, соответствующий отсечке левополяризованной моды,
поскольку она отвечает большей плотности.
Приложение Г
б)
369
Левая ветвь соответствует волне, имеющей отсечку при со = сод. Каза-
лось бы, эта ветвь недостижима для волны, падающей на плазму извне, од-
нако если со <сос, то полосы непропускания между ©* и со^ можно избежать.
4.28. а)
fp = 9 д/п = (9) (1О15)1'2 = 2,85-108 Гц,
fp =28 ГГц/Тл = (2,8-10l0)-(10-2) = 2,8-108 Гц,
f = 1,6- 10s Гц; следовательно, сое/со > Г,
С0д=-^-[-ис±Н + 4й2)1/2] «-у-(-ос + л/Гис) =
= О,62сос при сос « а>р;
fL = (0,62) (2,8-108) = 1,73-108 > f.
Аналогично можно показать, что f больше всех ионных частот.
Участок кривой, помеченной на рисунке крестиком в кружочке, и соответст-
вует параметрам эксперимента. Он расположен на низкочастотной части
кривой, отвечающей отсечке левополяризованной моды. Частота волны ниже
электронной циклотронной частоты.
13 Заказ 3170
370
Приложение Г
б) Единственная волна, которая может распространяться в плазме при
этих условиях,— это правополяризованная (вистлерная) мода.
4.29. а)
в 1
пл —---------=------------------------------ - = 6,9*106 м/с;
(Р.ПЛ1) [(1,26-10~6)(1019) (1,67-10~27)]1/2
= <1^11=9;58.10. рад/с:
М (1,67,-10“ 27)
со = 0,1 Йс = 9,58* 10е рад/с;
G) = kVA = 2Л0лА»
Если X = 2L, то
L=-^- = "Х6’9-?06) =2,26 м.
со 9,58-10е
б)
L ~ va/<& ~ va/Qc ~ В (nM)~~xs2 В"1 М ~ (М/п)1/2;
следовательно,
(133 \1/2 / 1019 \1/2
V) (4£г) =82“-
Вот почему альфвеновские волны независимо от величины В нельзя изу-
чать на Q-машинах.
4.30. а)
<02=<02+Л2
2<в d<o — c22k dk\ vrp == dw/dfe = c2^/©;
z 2 \ 1/2
ck i <o„ V
=11— j
co \ co2 / ’
следовательно,
б)
/2 Г 1
V 2 со2
Игр — £ I 1 -----
\ (02
пГр/ = х; t = х/игр;
_ х Л_______1 mp V2
dco с \ 2 со2 )
df ~ _
dt
при со2» со2.
df
(______
I (О2
С Р
X /2
(Р
9
X
С (О3
(3-108) (8-Ю7)3
(9)2 (2 -105) (5 -10е)
cf3
X = ——
fp
X = (1,9-1018) (3- Ю16)-1 = 63 парсек.
1,9-1018 м,
Приложение Г
37Г
4.31 а) Пусть ~ (1—е) п0, = 8л0, пе = п$Ф/К.Те. В предположе-
нии 2 = 1 уравнение Пуассона принимает следующий вид:
i kEx = — —!— е (п<!> + лР — ле).
во
Из уравнения непрерывности следует, что
лР = (1 — е) Лл vp*, л!2) = en0 .
О) ш
Уравнение движения дает
, / q2 \-1
W = ~7Г — ф ( 1-----------7" ) tcM‘ (4 68)1-
Mj <0 \ со2 /
Следовательно,
(здесь использовано плазменное приближение). Следовательно,
*4
О)2 — fi2j
1 = (1 - 8)
4-е--------—
(О2 — Q%2
6) Существуют два корня: один из них расположен вблизи со=ЙС1, а дру-
гой — около (о = Оса- Если устремить а к нулю, то корень, лежащий вблизи
&С2, будет приближаться к QC2> поскольку второй член должен быть конеч-
ным. Обычный корень, лежащий вблизи ЙС1, будет сдвинут из-за присутст-
вия ионов с массой М2:
“2 - Й?1 = *4 - 8 *4 - *Чг
О)2 — fi2j "I
<В2 — Q%2 J
В последнем члене мы можем заменить со2 на Q2,-]-^2»^. Таким образом,
ш2 « Q2] 4- й2о2] -|- е
1 ^Ч21
В)
1 fe2psD 1 .
2 ^_^cD+ 2 0)2_Q2r :
о2д = KTe/MD = (104) (1,6- 10~1э)/(2) (1,67-10~27) = 4,79- 10n,
t>s2r =-|~tfD = 3,1910,‘;
13*
372
Приложение Г
--= eB/MD = (1,6-10~18) (5)/(2) (1,67-10~27) = 2,40• 10»;
Л 2 Л
— 1,60-108, k ~ 100 м”1;
3
(»г - »У (»’ - оу - -i- Ио (“! - ЙУ + й (»! - оу к
0)4 0)2 |^20 + н---------$ (vsD + °st) j + +
+ — $ (y^D^cT + = 0;
co4— (02 (8,32- 10ie + 3,99-1015) + 1,47-1033 + 1,53-1032 = 0;
tt>4 _ 8,72- 1016co2 + 1,63-1033 = 0;
fi)2 [8,72-10ie± (7,60-10^ — 6,52-1033)l/2] = 6,0-10ie и 2,72-1018;
4.32.
ш = 2,45, 1,65 10s c-1, f—39 и 26,3 МГц.
e
i mco
£;
e2
m2(o2
<£2>;
= nQ — tn
2
(£2> =
m2co2
ео<°р (E2}
co2 2
2 2 « 1
а поскольку co = <0p, to £=-—e0
4.33.
i>z«£i/b0;
— Mn0(E^jВй. Поскольку V X Ej =
-Bp to = (o>2M2) <B|),
S =
Mn0 co2
2B% k2
Для альфвеновской волны имеем
. в2 (в2)
й2 НопоМ 2р0
4.34. а) Отсечка левополяризованной волны происходит при (о == (Од,
так что необходимо выполнить условие (0д<8(о2. Поскольку при фиксиро-
ванной плотности п0 частота сод <(ор (задача 4.15), то, используя левополяри-
Приложение Г
373
зованную волну, можно при постоянном значении еш2 достичь большей плот-
ности и0.
б) При отсечке левополяризованной моды
со; . св ео/п(о / ок
со3 со е2 \ со
Таким образом, для того чтобы удвоить плотность, 80/п<о2/е2, при которой
происходит отсечка, нужно выполнить условие fc = Л
8 9-1011
fc = 28-10» Гц/Тл; следовательно, Bq =—-----------=31,8 Тл.
28-10»
Создание такого поля потребует непомерно больших затрат.
в) Плотность плазмы достигает своего максимума в центре, поэтому плазма
ведет себя как выпуклая линза. Такая линза при п >1 фокусирует лучи, а
при п <1 их рассеивает. Вистлерная волна распространяется с фазовой ско-
ростью иф <с (задача 4.19), так что n = c!v$ >1, и для этой волны плазма
является фокусирующей линзой.
г) Вопрос заключается в том, может ли эта волна достичь любой точки
плазмы. Если для всей плазмы выполняется условие со то в ней неза-
висимо от значения п0 будет распространяться вистлерная волна. Однако
если (о >й)с, то в областях пониженной плотности такая волна будет испыты-
вать отсечку. Из анализа, проведенного в п. б, следует, что для выполнения
неравенства ш <сос магнитное поле должно быть больше, чем 31,8 Тл. Это
значение слишком велико для того, чтобы предложенная схема нашла прак-
тическое применение.
4.35. Ответ такой же, как и для холодной плазмы.
4.36. Линеаризованное уравнение движения для каждого сорта частиц
имеет вид
— i co/nn0Vi = qnQ (Е + vx X Во) — уД’7’к«1.
Таким образом,
— i com/Zok-Vi = qriQ (k-E + k-Vi X Bo) — тКТА2Л1.
Для поперечной волны k-E — 0, a k-(vt X Во) =—vx-(k X Во) =0
по предположению. Линеаризованное'уравнение непрерывности имеет вид
— i сопх 4-п0 i k-Vi = 0.
Подставляя сюда значение k*vlf имеем
i <о2тП1 = i yKTk2nt.
Поскольку величина п1 произвольна, мы можем положить ее равной нулю,
откуда следует, что член Vp как для ионов, так и для электронов также об-
ращается в нуль.
4.44. При данной плотности плазмы максимальная частота отсечки равна
(Од, поэтому минимальное- значение п определяется из условия со =
- р _ 'р = 1________1_________kJ-----------------L—=0,16,
co2 f2 co (0,91-10-’°) (2л) (1,2-10»)
n = fp/q2 = (0,16) (1,2-IO8)2?-2 = 2,8-1013 m-3.
374
Приложение Г
4.46. Пусть при г = г± частота со = со^ (п — nlt сор — соР1), а при г = г2
частота со = (Од, п = п2, top = й)р2* Тогда
О)до = <02 — (D?, (4.105)
р*> **
(й^ = со2 — (о(ос. (4.107)
Таким образом,
“р2 - “pl = “с (“ ~ “с) = («2 - ”1) e2/e0m-
НО
п2 — П1 « d | dnldr | « nydlrQ = (e0/n/e2) (co) (co — coc) (dlrQ),
поэтому
d & (toclto)
4.47. a) Достижимый резонанс находится с дальней стороны, после мак-
симума плотности.
б) Пусть на левой границе слоя циклотронная частота равна coto, а в резо-
нансном слое, где со ~ top, циклотронная частота равна о)с. Потребуем, чтобы
. 2 2 2
сосО>со, где to* = toc-|- top.
Таким образом,
<°?0 > + wp> °>?0 —
(“с0 + “Л (“с0 ~ “с) » 2“Л“с > “р •
А“с Д50 “р
во 2ш2
4.48. Уравнение описывает верхне- и нижнегибридные частоты, а также
частоты отсечек лево- и правополяризованной мод с учетом движения ионов.
Заметим, что ш2/ш/,=
9 р* р с
Приложение Г
375
Резонанс:
ю4 “ (<°р + <*>* + + Qc) + wpQ? + “eQp + = О,
ш4- “й + ®р С1 — ®с/®ь) (верхнегибридный резонанс),
<oL & (о^/со^ или
J—=—1—+-—
©1. tt)cQc Qp
(нижнегибридный резонанс).
Отсечка:
i
(О2
отсечка правополяризованной
и левополяризованной волн.
Эти соотношения получаются более простым образом (без дополнительных
предположений) из дисперсионного уравнения, приведенного в условии
задачи 4.49.
5.1. a) De = KTelmv,
о = (6л) (0,53.10-10)2 = 5,29-10~20 м2;
_(2) (2) (1,6- lQ—1а) -|^8)39.108 м/с>
(9,11 • 10“31) J
Из ответов к задаче 1.1 следует, что
п0 = (3,3-1019) (103) = 3,3* 1022 м“3;
v = п0ои = п0ои = (3,3-1022) (5,29-10"20) (8,39-106) = 1,46- 10е с“\
(2)(1,6-10-19)
(9,11 • 10“31) (1,46* 109)
= 2,4-102 м2/с.
б) / = рпеЕ;
= eDeIKTe ^-lO^HM-lO2) = 1,2.щ2 м’/(В.с);
(2) (1,6-10-18)
Е = —--------------------------= 1,04 - Ю4 В/м.
цпе (1,2-102) (101в) (1,6-10-19)
5.2.
-----= £>V2n — ап2;
dt
р.-, ту / Л \2 ЛХ - г-ч / Л \2 _
D\2n = D-------= — Dn01-------1 cos------= — D |-------I n = — an2;
dx2 \2L J 2L \2L J
D f л \2
следовательно, n =----1-----]
a \ 2L J
0,4
lO-ie
(Л \2
——I =l,l-1013M“3.
0,06 7
5.4. а) Из ответа к задаче 5.1 (п. а) имеем ven = 1,46-109 с"1. Нужно
определить, является ли отношение большим или малым:
Н* M^in
Hl- т^еп
vjn= Ппт™л, j ~ т,- 112>
поскольку сечения а при столкновениях ионов с нейтральными атомами и
при столкновениях электронов с нейтралами приблизительно одинаковы.
376
Приложение Г
Таким образом,
« (— Y 2 = (4-1836)1 2 = [85,7;
Pi \ т J
_еВ_ = (1,6;10.-2!)(р.,2)_ =
т 9,1110~31
®ЛЯ
3,52-101° „.
-----------24,
1,46-10»
! + “?< = 58«;
Од, = оЛл — (—Y'2 = (24) (85,7)-1 = 0,28;
М \ т J
Hex
Не)!
Не
Hi
1±^L=(85,7)J^
1+а>?4 580
= 0,16 «
1;
следовательно,
D = ^^ex + Hex^ix xD |Нех р ' = р + 0J6p
fl± . Hix + Hex ‘ Hix
Кроме того,
Dix Н/х Ti .. 1 0.1 э.
дех Hex Те 0,16 2
Da± =DeL [1 + (0,16) (0,3)] = 1,05Г)г± «De±.
(2,4-10—2)2 DeX ’
2 4-102
D , ——:--------=0,4140 (см. задачу 5.1);
eX 580
т = 42 мкс.
5.5.
Г=— Ddnldx, n = n0(l ~ x/L)
V^DnJL (x>0);
Q = 2r = 2Dn0/L, n0=QL/2D.
5.7.
Xei ~ Итепл. eTei & °тепл. el^ei-
Поскольку отепл . ~ Tii2, a v , ~ Te 3/2,to
J Tenjii e ₽ ' ci c •
^i~Tlel2/T-3l2^T2e.
Приложение Г
377
5.8.
П„ = 5,2-10— 6------- Ом-м (предполагаем, что Z= 1);
11 тЗ/2
1 эВ
(5,2-10-s) (10) . ,а_я
п„ _ —------------—-=4,65-10 8 Ом-м;
111 - (500 )3 2
j = ЦА =.(2-105)/(7,5-10~3) = 2,67-10’ А/м2,
Е = Г) Ц / = (4,65- IO—») (2,67-10’) = 1,2 В/м.
5.9. а)
Пп (KTt + KTe)
В2
KTi= 20 кэВ;
КТ, = 10 кэВ, п = 1021 M-S;
г) = (3,3) (5,2-10-5) -1П- Ом-м = (1’-^10 4)/10) = l,7-10~9 Ом-м
Т3В2 (104)32
о _ О’7'10-9)0°21)(з-1Q4)(1t6-' 10~^-=3,3-Ю~4 м2/с.
х " 52
б)
dN _
dt —
дп п
дг 0,1 м
dN
д
2лгЬГг, rr=~Dl —
х дг
г = 0,50 м, L = 102 м;
(2л) (0,50) (102) (3,3- IO”1) (1021/0,10) = 1021 с"1
в)
т =
N _______ nnr2L
— dN/dt ~ —dN/dt
(1022)(л)(0,55)2(102)
(1021)
Гэфф — 0,55 м;
с.
5.13.
Пи = 5,2-IO-5-iSA. Ом-м = 5,2-10-5
11 Т3,2
1 эВ
Т)и/2 = (1,6-10—6)(106)2 = 1,6-10s Вт/м»= 1.6-105 Дж/(м3-с) =
= (1,6-105)/(1,610-19) = 1024 эВ/(м3-с) = аЕэ~-
dt
———=1,6-10—6 Ом-м;
Ю32
3 ЛЕэв 3 dT3B
2 dt 2 dt
L^- = —-------!—Ю24 = 0,67-105 эВ/с = 0,067 эВ/мкс.
dt 3 1019
378
Приложение Г
5.15. а)
о о
еп (Eq — virВ) — VePi — е2п2т) (viq — ад) = О,
о о
— еп (Eq — verB) — \/Qpe 4- е2п2т] (viQ — ад) = О.
Сложим два этих равенства:
— V[rB + VerB — О, Vir = Ver-
(Отсюда видно, что в системе существует амбиполярная диффузия.)
б)
о
еп (Er-\-vieB)
— еп (Er + v£qB)
dpi
—-----e2n2t) (vir — ver) = 0;
(»lr — Ver) = 0;
dr
Er . 1 dpt .
°» =------—4------—- ——=cb + oDj;
В enB dr
Er 1 dpe .
ад = —----------— + vDe.
В enB dr
в) Из первого уравнения, приведенного в п. а, имеем
е8/А1 . . ем\ 1 / dpi . dpe \ ri dp
vir=-------^(viQ - -ад) = —J-------- ( + -f- ) =-------= ver.
enB В enB \ dr dr / В2 dr
(Отсюда видно, что в системе отсутствует подвижность поперек магнитного
поля.)
5.17. а)
Po-^-==ji X Во;
dt
(1)
Ei + Vi X Во = i]h;
(2)
V X Ex — — Bi, V X Bi — pojb
VxVXEi=—VXBi= — Hoii»
o
— к (k - El) + &2E1 = i (O|ioh,
k-Ei = O (это поперечная волна).
(3)
Найдем Vx из соотношения (2):
Ei X Во + (vi X Во) X Во — ЯЙ X Во!
Ej X Во — V]±Bq = X Bo;
El X Bp TjJi X Bp .
p2 p2
#0 "0
v
Приложение Г
379
Подставим это выражение в соотношение (1), которое не зависит от компо-
ненты скорости, параллельной магнитному полю:
: f El х Во Tjji X Во V . D
— 1 СОРо I -------— ------------- I — J1 X О0.
к ^0 )
Поскольку, согласно соотношению (2), векторы Ej и jx параллельны друг
другу, будем считать, что они ориентированы вдоль х. Тогда //-компонента
последнего уравнения принимает вид
А / i Во y) \
__ = !---------]-—
Bo \ (OPo Bq j
Уравнение (3) записывается в виде
Е\ ( iBo nV ( В0 V‘
&2£'i = p,oico-----I-----—— I =PoW2l--------------------i сот] I Elt
Bq \ COpo Bq / \ po /
/42 / d2 \
° I ^0 . |
—— = Ho I------------1 (ОТ) I *
fc2 k Po /
6)
/ B2 \“12
k == (poco2)I/2 ( —-----i сот] ) =
k Po /
= ш / PoPo Y 2 A _ ’ а>ПРо Ч"1 2.
I Bo ) I B0 )
im (k) = w pppo- 2=—L.
2^ Uo2; 2 *3л
При малых n частота co л? kvA, где k = Re (k). Следовательно,
Im (k) .
2ул
6.4. a) j x B = Vp=KTVn (KT=KTe + KTi)-,
(j X В) X B = KTVn X B = B(j-B)—jB2.
Параллельная полю компонента последнего равенства дает нуль:
0 — j||B2—j||£2; следовательно, ток Jy произволен. Перпендикулярная ком-
понента имеет вид
б)
JV X B-4S = /л0Jj-dS,
j) B-dL = go $ j-dS = p0L J /и dr,
о
поскольку оба вектора (j и dS) направлены вдоль 0, а величина L равна
380
Приложение Г
длине петли в направлении z. Из симметрии ясно, что Вг = 0; следовательно,
в интеграл дают вклад только те два участка петли, которые параллельны
оси z. Подставляя в последнее равенство значение /©, имеем
00
(Вах — Во) В == Т f ----------&г• 1
J (г)
0 1
в) Функция dnldr равна нулю всюду, за исключением точки г — а, где она 1
равна минус бесконечности, а интеграл от этой функции равен — п0. Поэ- 1
тому можно считать, что dnldr = —п$(г—а). Таким образом, 1
оо
Вах -Во = ( (- n0) -б(Г~а) dr. ’
J В (г) I
0 i
Поскольку весь диамагнитный ток сконцентрирован вблизи поверхности !
г ~ а, магнитное поле В испытывает скачок от постоянного значения Вах j
внутри плазмы до другого постоянного значения Во вне ее. (Напомним, что 1
поле внутри бесконечного соленоида является однородным.) Проинтегриро-
вав поле вблизи этого скачка, получим среднее значение на двух сторонах
петли: В (а) = (1/2) (Вах + Во). Таким образом,
& ах “ Во = у^КТпъ — ;
(1/2) (Вах + ^о)
В2ах-в1= ~^п0КТ- ?
1-------------------s8= 1; следовательно, Вах == 0.
В2 В2 -
6.5. а) Согласно закону Фарадея, V = — йФ/dt\ поэтому
SC 4Ф i
Vdt = — N \ -5-=- dt= — #ДФ.
J dt
Поскольку изменение потока ДФ обусловлено диамагнитным эффектом I
(уменьшением В), то J
— JVA® = — jV J (В — B0)-dS. 1
Знак выражения зависит от того, какую сторону объема Усчитать положи- .
тельной. Практических следствий эта неопределенность не имеет, поскольку л
сигнал на экране осциллографа можно легко перевернуть, пользуясь пере- |
ключателем полярности. 1
б) Заметим, что в задаче 6.4 (п. б) петлю можно нарисовать так, чтобы ее
внутренняя сторона не лежала на оси цилиндра, а проходила бы на произ-
вольном расстоянии г от нее. В этом случае
ОО 00 I
п . . n zz^nC dnldr' dnldr' |
В (г)— Во= р-оХТх -—dr' « \^КТ I --------dr'. |
J В (г') J Во 1
г г 1
Приложение Г 381
(Здесь ТС Г = ЕКТ*/.) Поскольку
2 2
дп / 2г \ ~г /го
= «о (-I е ,
дг---------------I )
мы имеем
В (,) _ в. - -BstLL. 24- f .-/2'2,*' _ JMs" Г Г/2"Л” =
$0 г0 оо &0
= _ ' р,оло7СТ е-^2/<о
Во
Таково изменение В (г) из-за диамагнитного эффекта. Для того чтобы найти
сигнал, снимаемый с петли, нужно произвести интегрирование по попереч*
ному сечению плазмы:
J Vdt = - N J (В — B0)-dS = — W JJ [В (г) — Во] rdrdQ.
Здесь как В, так и dS ориентированы вдоль z. Подставляя сюда выражение-
для В (г) — Во и предполагая, что обмотка находится вне плазмы, имеем
f Vdt= » JH^a.L-'2"2 rdf=Nn <^KT ^[.^T -
Во о Во ц°°
= — Nnr2 ( 2^п«КТ Ъ
2 Ч В2 J
в) Величина в круглых скобках по определению равна р; следовательно^
= -L-Nn^BQ.
Обе части этого равенства имеют размерность потока.
6.6. а) Для каждого из потоков имеем
m ("Т1" + (*0’V) уЛ = — еЕ1 = (— i© + i Ло0) vlf
\ dt /
— i еЕг
V1 = ----------,
m (co — kv0)
-ТГ1- + no (V • Vi) + (v0-V) П1 = 0,
( — i © + i kvQ) nx + i = 0» ni = rto-----------------------;
© — kVo
следовательно,
Л1/
— i kE^e
m (© — &Vo/)a
382
Приложение Г
Из уравнения Пуассона следует, что i kEr = (e/ee) (nia + п^), где для по-
тока а скорость voa = VqX, а плотность поа = (1/2) л0; для^потока Ь: =
= — vox, поь = (1/2) п0. Таким образом,
i kEi = _ / g А / — Г (1/2) п0 (1/2) п0
1 \ е0 J \ т /!_(<» — Ьо)2 (о) + £у0)2
I = 1 г 1 I 1 ] •
еот 2 L (<о — £v0)2 (со + &v0)2 J ’
i = —ш2Г-------!--+------1---1.
2 "L (Ш— to0)2 (<0 + too)2 J
«)
1^(й2_..-2±^0_.
Р (ш2-^2)2 ’
И4 — (<о2 + 2£2vg) ш2 + А2^ (k2v$ — а2 ) == 0;
4-w+2As)±4-w+8“?A»)1'2-
Положим
2A2Vq 2<о2
У = U___ It = ____ •
тогда
уг = I + х ± (1 + 4х),/2.
Величина у будет комплексной, только если здесь выбрать знак минус.
В этом случае у будет чисто мнимой величиной и мы можем положить у — гу:
у2 = (1 + 4х),/2 - (1 + х),
—fL (?2) = 2(1 4-4х)~1/2 — 1=0, х= — .
dx 4
Таким образом,
т2 = (1 + 3),/2 — 7/4 = 1/4,
1 2<о«
2 “ ico2 ’
Im (<в) =
(йр
«.8. а)
6
1 = (В2Г_1
Р L о2 (<Й — ku)2
тде o)2=n0e2/s0m.
*б) Это уравнение отличается от уравнения (6.30) только тем, что отношение
jn/M з нем заменено на величину 6, которая также мала, а лабораторная
Приложение Г
зва
система заменена на систему отсчета, движущуюся со скоростью и. Макси-
мальный инкремент не зависит от системы отсчета. Это можно понять из
рис. 6.11, представив себе, что величина у отложена вдоль оси г как функция
х и у. Ясно, что сдвиг х не влияет на максимальное значение у. По аналогии
с уравнением (6.35) имеем
Умакс ~ 1 ®р*
Точное значение коэффициента, который должен стоять здесь в правой ча-
сти, равно 31/22—4/3 = 0,69. (Вывод выражения для умакс» который пред-
ставляет собой трудную задачу, поскольку дисперсионное уравнение — ку-
бическое, а также доказательство того, что в случае вещественных k вели-
чина уМакс не зависит от системы отсчета, оставляем в качестве упражнений
для подготовленного студента.)
6.9. а) Поскольку решение зависит только от ^-компонент векторов V/
и Е, приведенное в условии задачи соотношение легко получить, пользуясь
уравнениями (4.986) и (6.23), а также уравнением непрерывности и уравне-
нием Пуассона. Заметим, что при вычислении частоты берется не (1/2) и0,.
а п0.
б) Пусть а = -1- Q2 (1 + И2 /т2) 1 (
р = тогда дисперсионное уравне-
ние сводится к следующему:
со4 — 2 (а + Р) to2 + [J2 — 2сф = 0.
Закон дисперсии со (k) имеет вид
со2 = а + р ± (а2 + 4ар)12.
Неустойчивость возникает в том случае, если (а2 + 4ар)^2 > а + Р> или
р < 2а, т. е.
*2<(й>2)(1+<о>2)-*.
Если это условие удовлетворяется, то инкремент дается выражением
у = [(а2 + 4а₽)1/2 — (а + 0)]1/2-
7.3. а)
fb (о) =
пь -(v-VWV
6)
*'«6 — 2(о—V)
Г М = Г! _ 2(0- ЮЧ -Wlb’ = у
63л12 [ Ь3 J
о — V = ± Ь/^2 . Оф = V — &/V2 .
•/2 ПЬ
1 Ь*
е->/2
384
Приложение Г
В)
2прУ — 7а,а2
Ь \ — (V-6/V2 )2/аа
72 )
V^b.
г)
/ 2 \1/2 пь е—1/2 _ 2пру е— V2/a2
V л J b2 “ а№
Ць_ = (2е)! 2 Ve~V21a\ = Ть ,
пр а3 ’ а2 Тр ’
=(2e)1'2JYJLe-^.
Лр Тр и
a=
z < 2 “Й (1—1 40)
а==(40)1'2е А
МА 13
7.8. Из уравнения (7.127) получаем £a/Z' (£/) — 2Ti!Te, где а/ло//лое,
Е/ = ш/^тепл, /• Предположим вначале, что параметр a# мал, так что ад да 1,
а// = а. Малость а означает также, что Оф будет почти равна скорости звука vs
в аргоне. Для удвоения декремента затухания Ландау необходимо, чтобы
_ -£?
Im Z'(Eh) = Im Z'(£a), где Im Z'(Ef) = — 2i д/л E/e J. Таким образом,
__p2 _*
Еде A = agHe
Ед (MA У 2
Ен I MH J
____ ХТе -j- 31_________________.
A~ Ma * 2К1\ “ 2 ’
a = д/40е-6,5 (0’975> = 1,12-10-2 « 1%.
Таким образом, величина a настолько мала, что наши начальные предполо-
= Z' (Е») + -1^- z' (W + — Z’ (Ел).
ел
Z'(E)« — 2 — 2i V7 Ее"45-
б)
Поскольку < Ее < 1, то
|ImZ'&i)l«|ImZ'(k)|.
жения справедливы.
2k2
7.9. а)
k2
KDi
в) Поскольку Z' (Ел) да Z' (Ее) да — 2, то в уравнении, приведенном в п. а,
при выполнении условий 9ft 9« и <х < 1/2 членом, содержащим Ее, можно
пренебречь. В этом приближении дисперсионное уравнение принимает сле-
дующий вид:
6г Те
Tefe2
Т ki..
2 iKDi
Приложение Г
385
Последний член приближенно равен Л2Лр и, если в системе поддерживается
квазинейтральность, им можно пренебречь. Таким образом, дисперсионное
уравнение для ионно-звуковой волны имеет обычную форму, за исключе-
нием того, что отношение TtiTe в нем заменено на (1—a) TilT6. Поскольку
при малых TilTe затухание Ландау мало, горячие электроны уменьшают
затухание Ландау на ионах.
8.3. Обратимся к рис. 8.4. Рассмотрим ионы, имеющие скорости вблизи
v — и0, и разделим их на две группы — одну с v = и0 + Д, а другую
с v=u0—А. После ускорения в потенциале ф более быстрая часть ионов уве-
личит свою энергию на меньшую величину, поскольку она начинала движе-
ние с большей энергией. Следовательно, относительное уменьшение плот-
ности в этой группе частиц будет меньше. Для более медленной группы ча-
стиц ситуация будет противоположной, и в первом порядке общее умень-
шение плотности будет таким, как если бы все ионы имели v — и0. Однако
существует эффект второго порядка, когда преобладают более медленные
частицы. Это легко понять, если сделать Д настолько большим, что для мед-
ленных частиц будет выполняться условие и ж 0, из которого, очевидно,
следует, что плотность таких частиц должна заметно уменьшиться. Для того
чтобы компенсировать это уменьшение, скорость и0 должна увеличиться
и превзойти бомовское значение.
8.4. Максимальный ток через систему будет протекать в том случае, если
из-за наличия пространственного заряда замедленных ионов электрическое
поле вблизи третьей сетки уменьшится до нуля. Вследствие этого к области,
лежащей между сетками 2 и 3, можно применить закон Чайлда—Ленгмюра:
tJ = 4 Г (2) (ГбП0-19) T 2 (8,85-10-^) (100)3 2 = g
4 9 L (4) (1,67 -10—а7) J (10’3)2
А = (л/4) (4-10-3)2== 1,26-10-5 м2,
I = JA = 0,34 мА.
8.6. а) При со = <др имеем
нелик = - 8°^2> = ~ V/МФ =
следовательно, рэфф — —ео(£2)- Кроме того, /0 — се0{Е2) = P/А, где Р —
— 1012, и А = л/4 (50-Ю”6)2 = 1,96-10“9 м2, и мы
имеем
Р
Рэфф — “Г—Г
2с А
F = pA,
F = Mg,
1012
= 8,50-10й Н/м2;
(2) (3-108) (1,96-10“9)
«)
Р/2с = 1012/(2) (3-108) = 1667 Н;
М = Fig = 1667/9,8 = 170 кг = 0,17 т.
®)
2пКТ — Рэфф»
386
Приложение Г
откуда
8.7.
8,5-1011
(2) (10») (1,6-Ю-1»)
= 2,66 102Т м-з.
нелин — VP‘,
д
дг
(пКТ)=----------^—fe° -
пс дг
1 дп
п дг
Во
д <г2>.
2ncK Т дг
п = л0 ехр [ — е0 {Ег}!2псКТ}.
2псКТ
+ In По,
При г = О
2
Пмин = п0е-Е<>^!^акс/2«еКТ _ п^
следовательно,
__ Вр {£2)макс
~ 2псКТ
8.9,
k0 = 2л/Х0 = 2л/(1,06 - IO-6) = 5,93-Юз м~1;
ki»2k0= 1,19-10’ м-i;
К7\+ЗЛТ£^1/2 _ г (103) (1,6-10-!»)
(2) (1,67-10-2’)
1/2
м
/ з
со(- = Ди = kiVs = (1,19-10’) (2,19- 10Б) ( 1+ —
\ в
Дю ДХ
Хо
<оо
следовательно,
1/2
Дсо =-------^2- ДХ =--------ДХ = —
^0 ^0
3 3,67-1012 \2_о.
к 0 >1 2,61-1012 ) ~~
(2л) (3-108) 1()_10 = 101^
(1,06-10-e)«
т
= 3, откуда
0 =
Tt = — кэВ
3
8.10. а)
2^
2
8®!<В2Г 11 g
С1С2
80*1“р
CjC2 — ----------;
поИо^
4<o1r1<DQV
г —i.
“2*1 80“р
a2k2e2
V
2
Приложение Г
387
e2^/?^ tojTjVAt
m2a>0 a>2k2tn
а2М rfv2M (сф 4FjV
КТ, т ’ v2e ~ ®1(В2
б)
К) 41>»
2 ’
»е ®1“0
поскольку при п < пс частота со2 шо-
Таким образом,
= (2*)(М.О8) =1,78.1(И с
Хо (10,6-10-6)
= = .0(1,^). = j 76.10и м2/сг.
т (0,91-10-»°)
-А- = (-2LY 2 е (3 + 0)1/2 е- (3+е>2.
®i \ 8 7
Т г
0= — = 10, —-— =3,40-10-2;
Тс a>i
П = 5,2-10-6 - ?п А = (5,2' 10~5) (10) =5,2-10~7 Ом-м;
Т’эв (ЮО)32
v„- = пе^ __ (1О23)(1.6-1О-»)2(5,2-1О-7) = ! 46 ю, с_ь
т (0,91-10-3°)
= (4)(3’4-10~*)<1’46-10l>) (1 76. 1013) = ! 96.1Q7 М2/С2.
4 0/ (1,78-10м)
Из решения задачи 8.6 (п. а) следует, что
16 = сео (£2> = сео {vо) >
/о = (3-10») (8,854-10-2) (0-91-Ю-30)2 (1,78-10м)2 (1,96-102) =
(1,6-10-»)2
= 5,34-1010 Вт/м2 = 5,34-10е Вт/см2.
«.11.
(со2 + 2i T(0s — coj) [(<0s + i Y - coo)2 - co2] = -L C1c2£2.
Пусть <в2 = co2, (cos — (O0)2 = co|, a y/cos 1;
388
Приложение Г
тогда
(2i ?®s) [2i V (®s ~ и0)] = с^Ё1 2 = 4y2®sa2
Из решения задачи 8.10 следует, что
ео*1“р й1“ре2
<V2 = -----—— = —;
поа>цМ (ufjtnM
У2 = fei(0p^om ~ (2feo)2 Qp^0 _ MoQp^o .
16ы5<в2ШцтЛ1 16®sa2M 16®0as 4c2a0®s
O0 / ®0 \1/2
следовательно, у = —— [ —- 1 Яр.
2 \ ®s )
8.13. a)
Mn0 = en0E — YiKTiVn — Mnovv + Гнедин!
dt
Mn0 (— ia + v) v = en0 (— i k<t>) — ytKTi i knx + ГНелин-
Если еф!КТе = tiJriQ, то последнее уравнение принимает вид
(Ю + iv) v = Ь2 f нелин •
п0 Мп0
Из уравнения непрерывности следует, что
— i®n j + iknQv = — i con! -f- i kn0(<o + iv)—1 Г to2 ' ^нелин 1 = 0r
L n0 Mn0 J
(co2 + i vco - A2) nt = 1*Гнелин/Л4.
Если Гнедин = о, то
со2^1 + i—= Д»2, откуда
w w kvs (1-----— i —— = kvs-----------— v.
\ 2 а 7 2
б)
Следовательно, — Im <о = Г = v/2, поэтому (а2 21Га — k2u^ «j =
= 1^Гнелин/Л1.
нелин — —
“pVeo (Г0Г2)
аоа2
а2
----i йе0 (Е0Ег).
а0ш2
Следовательно,
i *Г„„ „„
нелин
1 f-®p . L А “р
-----------=-----1------ 1 Ае0 I = —-----
М (Г0Г2) М \ Шой>2 / а0ш2 М
Прилоложение Г
389
8.14. Частота верхнего сателлита определяется из условия =
= йш0 -|-йЮр Иными словами, энергия вторичного фотона больше, чем
энергия Й<о0; поэтому из энергетических соображений более предпочтительно
образование нижнего сателлита. Он образуется в результате экзотермиче-
ской реакции и имеет частоту <о2, такую, что й<о2 = Ясоо—ftwj.
8.18. U (? — ст) = 3 sch2 I(r/2)1/2 (g— ст)], где В = 61/2 (х'—Г), т = 63 2/',
х' = x/Xd, t' = Яр/, 6 = Л—1. Пусть
\ ad ad /
Поскольку ХоЯр = vs> то
д1'2
S = —------[х — (1 + 6с) vs/].
Ad
Солитон имеет максимум при £ = 0. Скорость этого максимума равна
dxldt = (1 + бс) vs. По определению
= Лщ = (1 + 6) vs.
dt
Следовательно, с= 1, а (7макс = 3с=3. Из уравнения (8.111) имеем
.. __ еФмаке ____S.. __Rri
Хмакс =----~ 0Х1 макс — ос/мако
КТе
откуда
6 = е ^макс = 1 = 0 4‘
КТе {/макс 10 3
Оф = (1 + 6) os = l,4os,
Vs== f 2ИЦ12 = Г <>Q) <!£•. = з,ю- ю«,
\ М J L 1,67-ю-2’ J
Оф = 4,33-104 м/с.
На половине максимума sch2a= 1/2, а -- 0,8814 = £/2,
В = 1,25 = 61/2xAd при / = 0.
SI/2 = Vo,4 = 0,632,
xD = (= io_t м = 0 235
к ное2 )
1,25Хр
0,632
= 0,46 мм.
Полная ширина по половине максимума 2х = 0,93 мм.
8.21.
| и | =4Л1/2 |sch х |; | и |2= 16Л | schx|aJ
390
Приложение Г
‘«=4-'Г
----| и | 2 = —4А | sch х |2;
4
6п = — 4 А | sch х |2 « — 2А;
^-JL_62_=---— (2Л)=—Д.
2 п 2
<0р
Следовательно, величина А представляет собой относительный сдвиг частоты
из-за наличия вариаций плотности 6п.
8.22. В реальных переменных
и =
( Г/ “О , 1 V* Л . V X ]
X ехр J — 1 |--— 4-------------Я I ------------1;
I 1Л “р 6 ve ) Ч Ч )
ve = (_AZkY/2 = 5>93.105 м/с, сор = (=1,78-10» рад/с;
\ т ) \ еот /
XD = _£е_ = 3,33.10-4 М, k = k'-D— = 0,3 = 9,02-102 м~1;
top Xd Xd
Up-p — 4Д1/2; — i amt) = — eE = — e (— i кФ), откуда Ф = — ;
ek
Фр_р « 4Л1/2ое; (O « (a2 + 3fe2v2)1/2 « 2,01 • 109;
1/2__ кефр—p к врфр—р KT e 1 kve ефр р
4mave 4<в KTe tn ve 4o> KTe
kve 3,2
4ш 2
= 0,106;
A = 1,13-Ю—2.
a)
sch X = — ,
2
X = 1,315 =
2A \V2 x
3 ) Xd ’
3_\V2 (1,315) (3,33-10-«) = 5 04.10_3
2 ) 0,106
Полная ширина по половине максимума 2х = 1,01 • 10~2 = 10,1 мм;
б)
Х =
1,01 -до—2
2nlk
= 1,45.
Приложение Г 391
в)
бсо = А(Ор = (1,13-10-2) (1,78-109) = 2-10’ рад/с;
6f = 6<о/2л = 3,2-10« = 3,2 МГц.
8.23.
,2 (3) (3) (1,6-10-19) , с0 ,П12 2/2
3vz = - v 7 v ~ 1,58-1012 м2/с2;
е 0,91 10“30
<о2(вне) = ______(10“)(1,6-Ю-»Г__ _3il8.10i9 рад2/с2;
р (8,824-10-12) (0,91 • 10-30)
<Вр (внутри) = О,4со2 (вне);
. со2 (вне)— а>2 (внутри) 3,18-1019
k2 = —----------------р = —-------------(1 — 0,4) =
макс п « .~19 v '
3v2 1,58 IO12
= 1,21-10’ м-2,
Отт
хмин = ——— = 1,81 • 10-3 м = 1,81 мм.
^макс
Предметный указатель
Авогадро число 346
Адиабатический инвариант 53
Адиабатическое сжатие 51, 52
Альфвеновская волна 137
---- затухание 192, 193, 379
----плотность энергии 149
---- торсионная 141
----шировая 141
— скорость 139, 151, 335
Анализатор скорости 284
Аннигиляция магнитного поля 200
Аномальное сопротивление 275
Антиматерия 122
«Банановая» диффузия 190
— орбита 189
Баунс-частота 315
Б ГК-мода 250
Бернштейна моды 266
---- ионные 269
---- нейтрализованные 272
---- электронные 267
Бесселя функции 161, 162
Больцмана постоянная 15, 334
— распределение 83
— уравнение 223
Бомовская диффузия 186
Бомовский ток 283
Бомовское время 186
Бунемановская неустойчивость 207
Ван Кампена моды 250
Ведущий центр 30
Вейбеля неустойчивость 216
Векторные соотношения 335
Верхнегибридная частота 108
Взаимодействие волна — волна 276
— волна — частица 275
Вистлерная мода 133, 134, 137
Вихри 276
Власова уравнение 224
Волна накачки 297
Волны Бома—Гросса 234
— в плазме, сводка формул 144, 145
------- холодной 337
— с отрицательной энергией 250
Восприимчивость магнитная 63, 64
— электрическая 64
Вынужденное рассеяние, бриллюэ-
новское 300, 302, 303, 311, 387
--- комбинационное 300, 302
Высокочастотный нагрев 153
Вязкость 72, 73
— бесстолкновительная 72
— магнитная 72
Газовый разряд 24
Гармоники 274
— циклотронной частоты 262
Гравитационная неустойчивость 209
--- инкремент 212
Групповая скорость 88, 136, 137
Давление 71
— магнитного поля 198
Двойной слой 291
Двухплазменная установка 291
Двухпотоковая неустойчивость 205
Дебаевское экранирование 18
---радиус 20, 334
Диаграмма Клеммова—Муллали —
Эллиса 146, 341
Диамагнетизм 30
Диамагнитная петля 202
Диамагнитный ток 78, 79, 96
Дисперсионная функция плазмы 255,
256
Дисперсионное уравнение для хо-
лодной плазмы 340
Дисперсия групповой скорости 324
Диффузионные моды 159, 160
Диффузия 182
— амбиполярная 157, 169, 183
— аномальная 170
— бомовская 186
— магнитного поля 199
Предметный указатель
393
— неоклассическая 190
— поперек магнитного поля 165
Длина свободного пробега, средняя
155
----------между электрон-ион-
ными столкновениями 190, 335
Дрейф гравитационный 34
— градиентный 36, 37, 80
— диамагнитный 77, 335
— поляризационный 49
— центробежный 38
Дрейфовая неустойчивость 212, 215
Дрейфовые волны 87, 214
— скорости 52
Диэлектрическая проницаемость 93,
139
---- в низкочастотном пределе 65
Желобковая неустойчивость 212
Захват 227
— электронов 225
Звуковые волны 100
Зеркало магнитное 39, 42, 197
Зонд электростатический 282
Изобары 197
Инвариант адиабатический* 53
____г. кд
----р. 41, 51, 53
----Ф 58
Ионно-звуковая ударная волна 284
Ионно-звуковые волны 100, 254,
311
----дисперсионное уравнение в ки-
нетике 258
— — нелинейные 317
---- скорость 101, 103
Ионно-циклотронные волны, элек-
тромагнитные 152
----электростатические 114, 148
Ионный двигатель 25
Ионосфера 25
Кавитон 318, 330
Касп 54
Квазилинейные эффекты 275
Квазинейтральность 21
Коллективное поведение 22
Конвективная производная 66
Конвективные ячейки 188
Конечный ларморовский радиус 47
Конусная неустойчивость 204
Конус потерь 43
Корона солнечная 25
Кортевега—де Вриза уравнение 318
Космическая физика 24
Коэффициент диффузии 157
---- амбиполярной 157
---- бомовской 186
---- в частично ионизованной
плазме 156
---- классический 182
Крабовидная туманность 25, 151, 200
Критерий Бома для образования
слоев 279, 280
Критическая плотность 121
Крука столкновительный член 224
Кулоновские столкновения 175
Кулоновский логарифм 176, 177
Лазер газовый 27
— на иоде 311
---- синильной кислоте 27, 149
---- углекислом газе 121
— работающий в далекой ИК-об-
ласти спектра 27, 149
Лазерный синтез 311
Ландау затухание на ионах 254,
259, 260
------- электронах 235
----нелинейное 238, 315
Ларморовский радиус 30, 334
Левополяризованная волна 131
Ленгмюра парадокс 73
Ленгмюровские колебания 99
---- плотность энергии 148
Ленгмюровский зонд 283
— солитон 323, 331
Ленерта—Хоха эксперимент 170
Линейный соленоид 121
Лошмидта число 18, 334
Луни—Брауна эксперимент 95
Магнитное поле, выталкивание из
плазмы 199
----диффузия в плазму 199
---- Земли 55
---- спонтанное генерирование 135
Магнитный момент 41, 64
Магнитогидродинамические волны
137
Магнитозвуковые волны 143
---- скорость 144
Магнитосфера 24
Максвелла уравнения 63
Максвелловское распределение 15,
219, 221
Малмберга—Вартона эксперимент
251, 252
Масса эффективная 26
Маха число 285, 286
МГД-преобразование энергии 25
МГД-уравнения 179
Модификация профиля 295, 331
Модуляционная неустойчивость 276,
317, 324, 325
394
Предметный указатель
Навье—Стокса уравнение 73, 100
Нагрев на нижнегибридной частоте
153
Накачка магнитная 54, 58
Нейтронные звезды 23
Нелинейное уравнение Шредингера
323
Нелинейный сдвиг частоты 324
Немаксвелловская функция распре-
деления 218
Необыкновенная волна 125—128, 152
Неоклассическая диффузия 190
Неустойчивость 203
— бунемановская 207
— в пространстве скоростей 204
— Вейбеля 216
— взрывная 194
— гравитационная 209
— двухпотоковая 205
— дрейфовая 215
— Кадомцева—Недоспасова 171
— кинетическая 204
— классификация 203
— конусная 204
— относительно распада на два плаз-
мона 300
— плазменно-пучковая 205
— потоковая 203
— Релея—Тейлора 203
—"универсальная 204
— Харриса 204
Нижнегибридная частота 115, 116
Обратное параметрическое рассея-
ние 300
Обыкновенная волна 123
--- затухание 149
Ома закон обобщенный 181
Омический нагрев 178, 192
Опрокидывание 274
Отрицательные ионы 123, 151
Отсечка 118, 127, 341, 375
— левополяризованной моды 128
— правополяризованной моды 128
Параллельное распространение волн
106
Параметрическая неустойчивость 296
--- порог 301, 302
--- распадная 299, 300, 305, 308
Перпендикулярное распространение
волн 106
Плазма, определение 13
— с большим Р 199
Плазменная линза 120, 121
— частота 89, 91, 334, 338
Плазменное Р 197, 335
— приближение 84, 103
— эхо 311
Плазменно-пучковая неустойчивость
253, 254, 383
Плазменные колебания 230
--- затухание 99
Плазменный параметр 21
Подвижность 156
— поперечная 183
Поляризационный ток 49
Поляризация 131, 132, 135
Пондеромоторная сила 292
Поперечные волны, определение 106
Правополяризованная волна 131, 136
Предслой 282
Прицельный параметр 175
Пробка магнитная 39, 42, 197
Пробочное отношение 43
Продольные волны, определение 106
Пространственный резонанс, усло-
вие 299
Пуассона уравнение 19
Пульсар 25, 148
Равновесие 195
Радиационные пояса 12, 25, 44
Радиосвязь 121, 122
Радиотелескоп 310
Распадная неустойчивость плазмен-
ных волн 299, 300
Распределение с конусом потерь 222
Реакция синтеза дейтерия и трития
24
Резистивная дрейфовая волна 213,
215
Резонанс 127, 341
Резонансное условие для частот 299
Резонансные частицы 248
Резонансный угол 341
Рекомбинация излучательная 164
— коэффициент 164
— трехчастичная 164
Релея—Тейлора неустойчивость 203,
209
Сагдеева потенциал 285, 286
Самофокусировка 295', 386
Caxd формула 12
Сверхзвуковое движение 151
СВЧ-интерферометр 119, 123, 137
СВЧ-колебания 119
Связанные осцилляторы 296
Сечение атома водорода 344
— определение 155
— передачи импульса 191
— столкновений электронов с ней-
тралами 191
Сила ВЧ-давления 292
Силовые линии 36
---вмороженность в плазму 140
Предметный указатель
395
Скин-слоя глубина 119
Скорость звука 335
— колебаний частиц в волне 335
Слабоионизованный газ 154
Слой в плазме 21, 277
Случайное блуждание 168
Солитоны 286, 287, 320, 323
— огибающей 318, 325
— связанные 330
Солнечный ветер 12, 24
Сопротивление плазмы 174, 176
— поперечное 179
— продольное 179
Спитцера сопротивление 176, 179
Спускаемый аппарат 122
Средние скорости для максвеллов-
ского распределения 221
Стелларатор 186, 187
Стикса волны 153
Столкновения кулоновские 175
— тождественных частиц 173
— частиц разных сортов 174
Температура 15
— плазмы 17
Тензор вязкости 174
— давлений 69, 71, 72
— диэлектрической проницаемости
337
--------в кинетике 263, 264
— напряжений 69, 229
Тепловая скорость 219
---- электронов 335
Термоядерный синтез 24
Тета-пинч 192
Точка поворота 55
Траектории частиц 225, 227
Трайвелписа—Гоулда дисперсион-
ные кривые 110—112
Транзистор полевой 27
Турбулентность 275, 276
Убегание электронов 178
Ударная волна 284
--- вблизи Земли 284
Укручение волны 289
Универсальная неустойчивость 204
Уравнения гидродинамики 75
— диффузии 183
---вывод 227
— непрерывности 74
— одножидкостной магнитогидроди-
намики 179
— состояния 74
— теплового потока 230
Ускорение космических лучей 44,45
Фазовая скорость 86 ’
— плоскость 226, 227
Фарадеево вращение 134, 137
Электронные плазменные волны 93,
230
------- дисперсионное уравнение в
кинетике 261
-------нелинейные 323
Электростатические ионно-циклот-
ронные волны 114
Электростатический зонд 282
Эпплтона—Хартри дисперсионное
уравнение 150
Эхо в плазме 311
Е X В-дрейф 32, 77, 335
Q-машина 78, 104, 114
/-функция 256
Оглавление
Предисловие редактора перевода 5
Предисловие ко второму изданию 7
Предисловие к первому изданию 10
Глава 1. Введение 12
1.1. Распространенность плазмы в природе 12
1.2. Определение плазмы 13
1.3. Понятие температуры 15
Задачи 18
1.4. Дебаевское экранирование 18
1.5. Плазменный параметр 21
1.6. Критерии существования плазмы 22
Задачи 22
1.7. Применения физики плазмы 23
Задачи 27
Глава 2. Движение отдельных частиц 29
2.1. Введение 29
2.2. Постоянные поля Е и В 29
Задачи 35
2.3. Неоднородное поле В 36
Задачи 44
2.4. Неоднородное поле Е 45
2.5. Нестационарное поле Е 48
2.6. Нестационарное поле В 50
2.7. Сводка формул для скоростей дрейфа ведущего центра 52
2.8. Адиабатические инварианты 53
Задачи 59
Глава 3. Плазма как жидкость 61
3.1. Введение 61
3.2. Связь между физикой плазмы и обычной электродинамикой 62
Задачи 65
3.3. Гидродинамические уравнения 66
3.4. Дрейф жидкости перпендикулярно магнитному полю В 76
Задачи 81
3.5. Движение жидкости параллельно магнитному полю 82
3.6. Плазменное приближение 84
Оглавление
397
Глава 4. Волны в плазме 86
4.1. Представление волн 86
Задача 87
4.2. Групповая скорость 88
4.3. Плазменные колебания 89
Задачи 93
4.4. Электронные плазменные волны 93
Задачи 99
4.5. Звуковые волны 100
4.6. Ионно-звуковые волны 100
4.7. Обоснованность плазменного приближения 103
4.8. Различие между ионно-звуковыми и плазменными волнами 104
4.9. Электростатические электронные колебания, распространяю-
щиеся перпендикулярно магнитному полю 106
Задачи 111
4.10. Электростатические ионные волны, распространяющиеся
перпендикулярно В 112
4.11. Нижнегибридная частота 115
4.12. Электромагнитные волны при Во = 0 116
4.13. Экспериментальные приложения 119
Задачи 122
4.14. Электромагнитные волны, распространяющиеся перпенди-
кулярно Во 123
4.15. Отсечки и резонансы 127
4.16. Электромагнитные волны, распространяющиеся параллель-
но Во 130
4.17. Экспериментальные следствия 133
Задачи 136
4.18. Магнитогидродинамические волны 137
4.19. Магнитозвуковые волны 143
4.20. Основные типы волн в плазме (сводка формул) 144
4.21. Диаграмма Клеммова—Муллали—Эллиса 146
Задачи 148
Глава 5. Диффузия и сопротивление 154
5.1. Диффузия и подвижность в слабоионизованных газах 154
5.2. Распад плазмы вследствие диффузии 157
5.3. Стационарные решения 162
5.4. Рекомбинация 164
5.5. Диффузия поперек магнитного поля 165
Задачи 172
5.6. Столкновения в полностью ионизованной плазме 172
5.7. Уравнения одножидкостной магнитогидродинамики 179
5.8. Диффузия в полностью ионизованной плазме 182
5.9. Решения уравнения диффузии 183
5.10. Диффузия Бома и неоклассическая диффузия 186
Задачи 190
Глвва 6. Равновесие и устойчивость 194
6.1. Введение 194
6.2. Равновесие в МГД-приближении 196
6.3. Понятие о величине р 197
6.4. Диффузия магнитного поля в плазму 199
Задачи 201
6.5. Классификация неустойчивостей 203
6.6. Двухпотоковая неустойчивость 205
398
Оглавление
Задачи 208
6.7, Гравитационная неустойчивость 209
6.8. Резистивные дрейфовые волны 213
Задачи 216
6.9. Неустойчивость Вейбеля 216
Глава 7. Кинетическая теория 218
7.1. Функция распределения f (v) 218
7.2. Уравнение кинетической теории 223
7.3. Вывод гидродинамических уравнений 227
7.4. Плазменные колебания и затухание Ландау 230
7.5. Физический смысл затухания Ландау 235
7.6. Физический вывод затухания Ландау 244
7.7. БГК-моды и моды ван Кампена 250
7.8. Экспериментальная проверка 251
Задачи 253
7.9. Затухание Ландау на ионах 254
Задачи 260
7.10. Кинетические эффекты в магнитном поле 261
Задача 264
Задача 266
Глава 8. Нелинейные явления 274
8.1. Введение 274
8.2. Слои в плазме 277
Задачи 283
8.3. Ионно-звуковые ударные волны 284
Задача 291
8.4. Сила высокочастотного давления 292
Задачи 295
8.5. Параметрические неустойчивости 296
Задачи 302
Задачи 311
8.6. Плазменное эхо 311
8.7. Нелинейное затухание Ландау 315
Задачи 317
8.8. Нелинейные уравнения физики плазмы 317
Задача 321
Задача 323
Задачи 326
Задачи 331
Приложение А. Система единиц, константы и формулы, векторные со-
отношения 332£*Г|
Приложение Б. Теория волн в холодной однородной плазме 337
Приложение В. Заключительное контрольное задание (для трехчасового
экзамена) 342
Приложение Г. Ответы к некоторым задачам 346
Предметный указатель 392
г
Уважаемый читатель!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие
просим присылать по адресу:
129820, Москва,
ГСП, 1-й Рижский пер., д. 2,
изд-во «Мир».