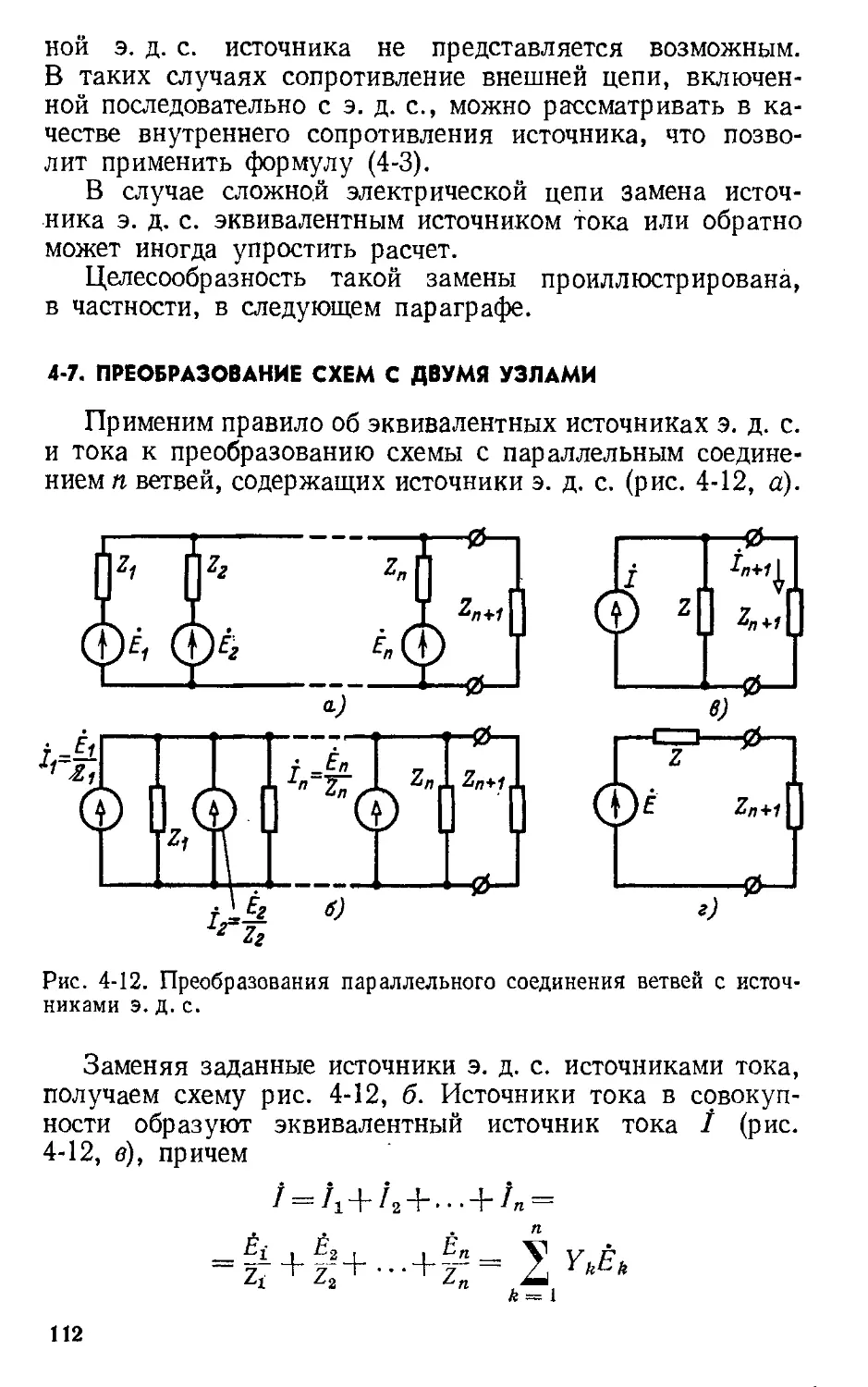
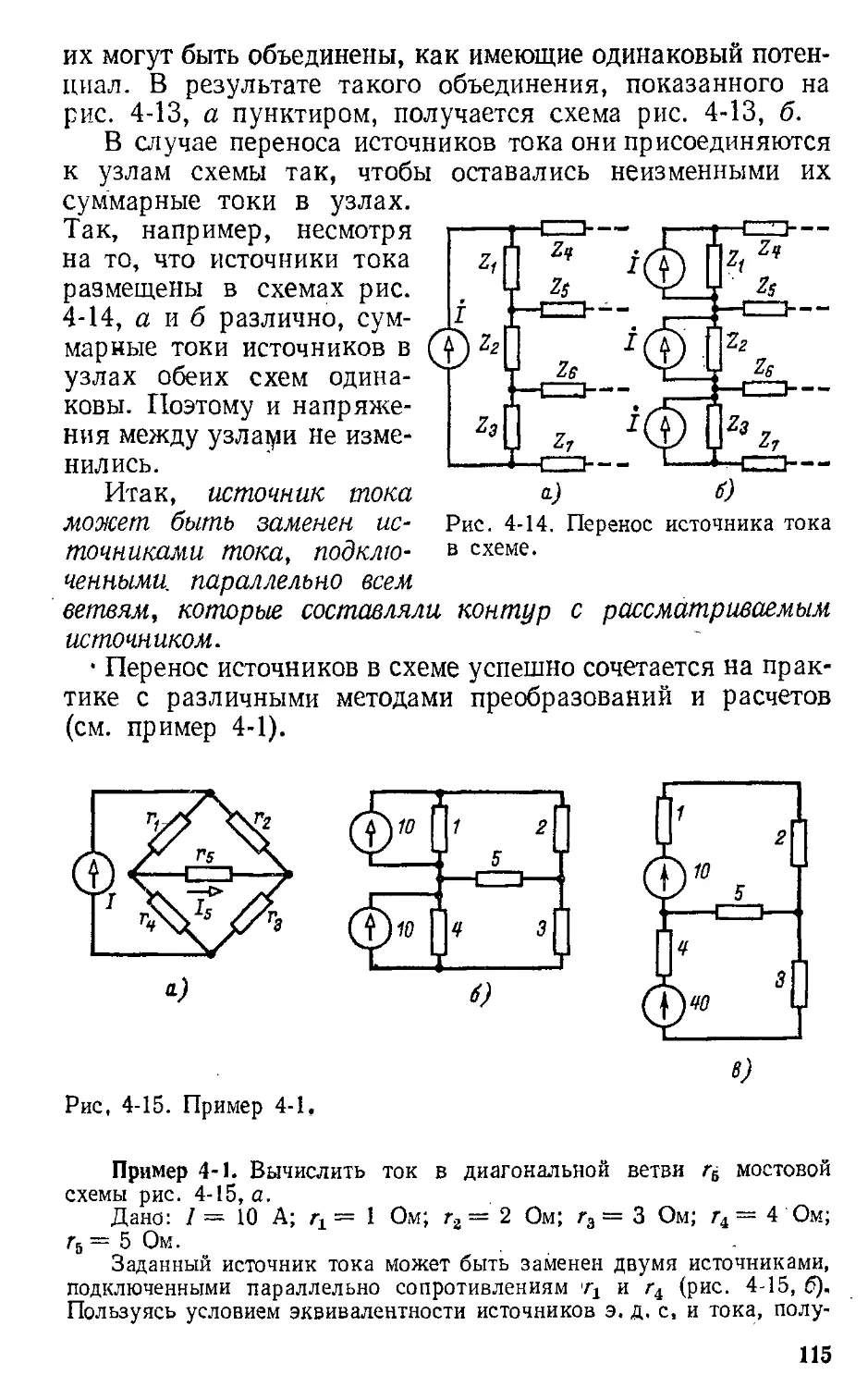
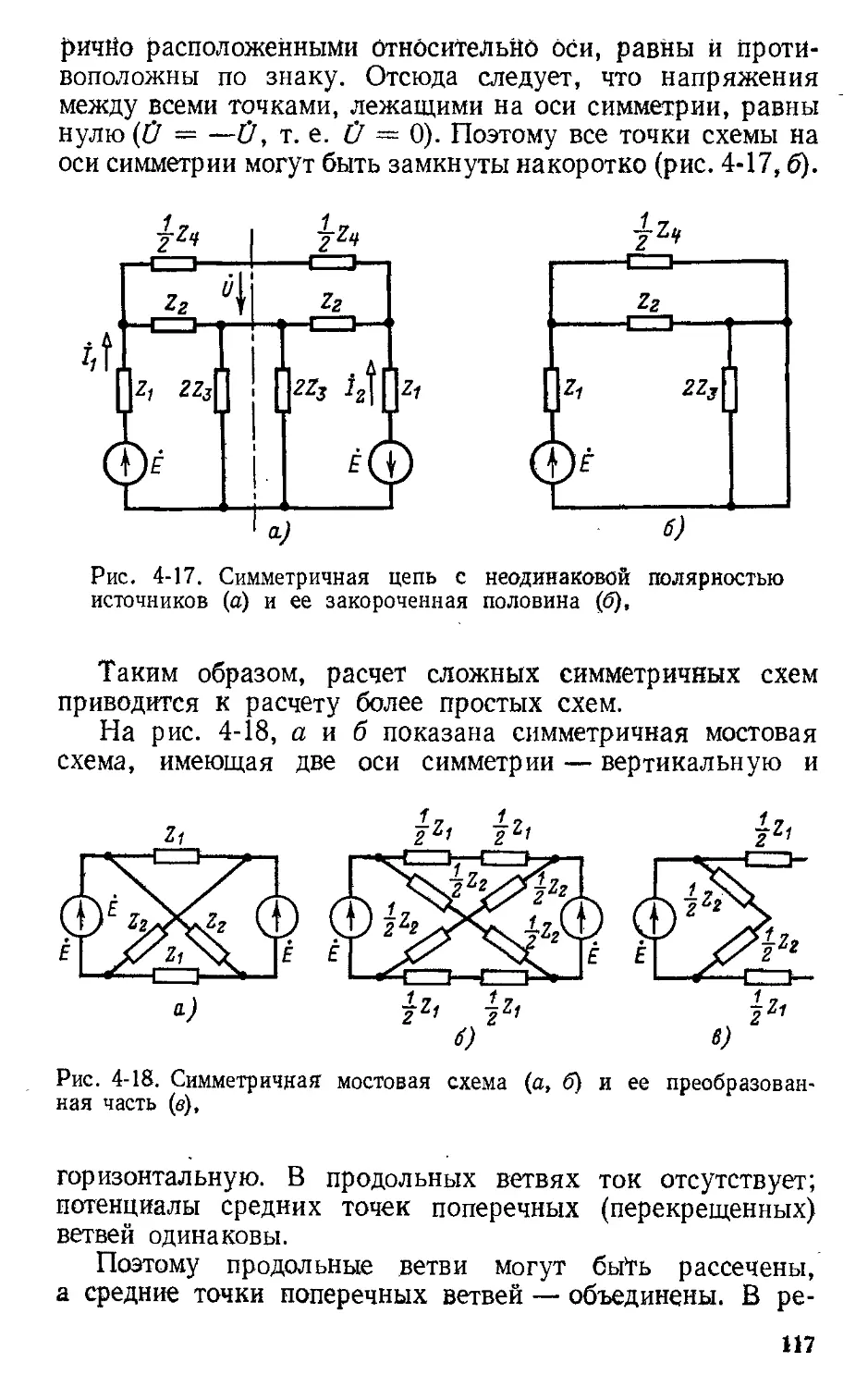
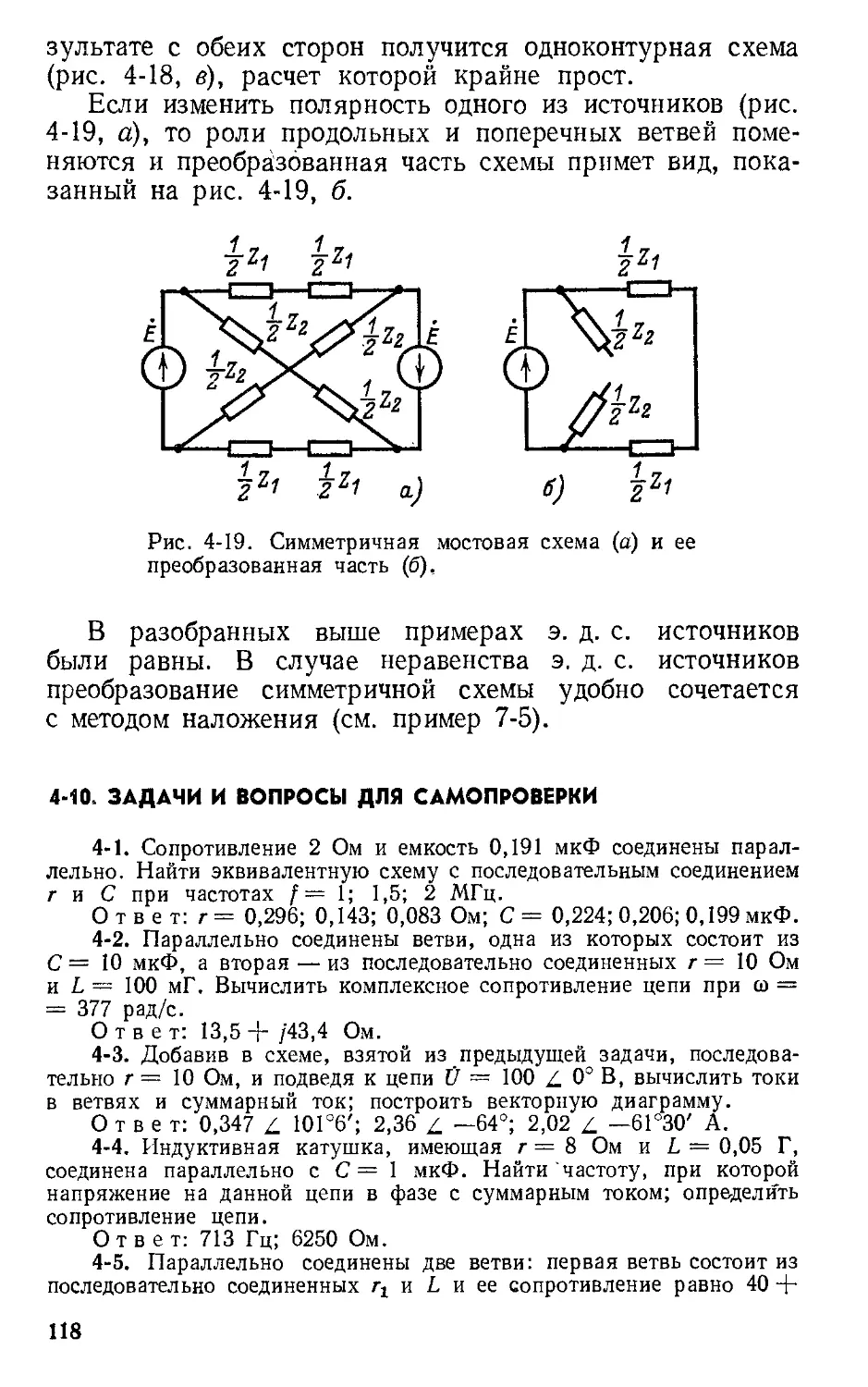
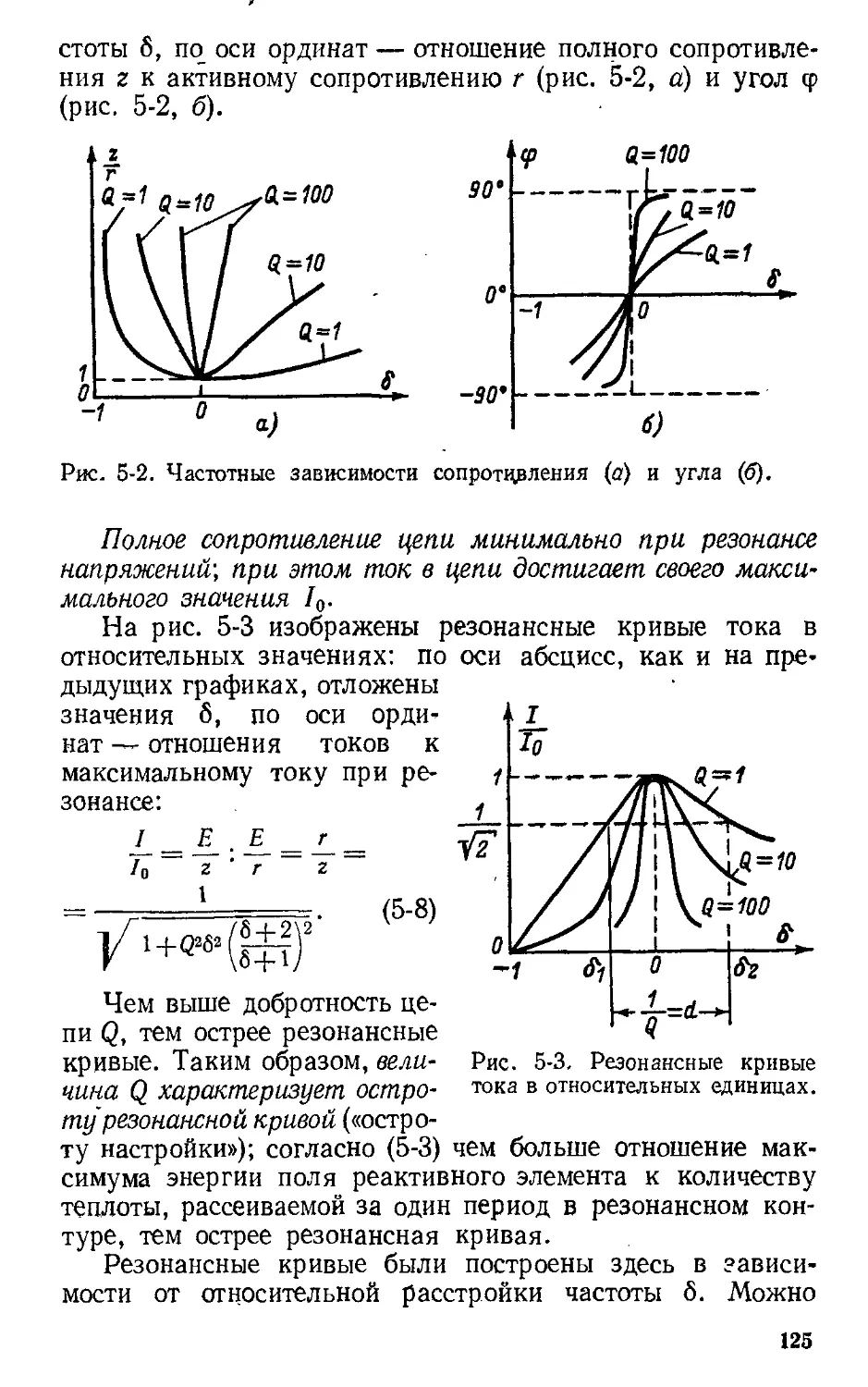
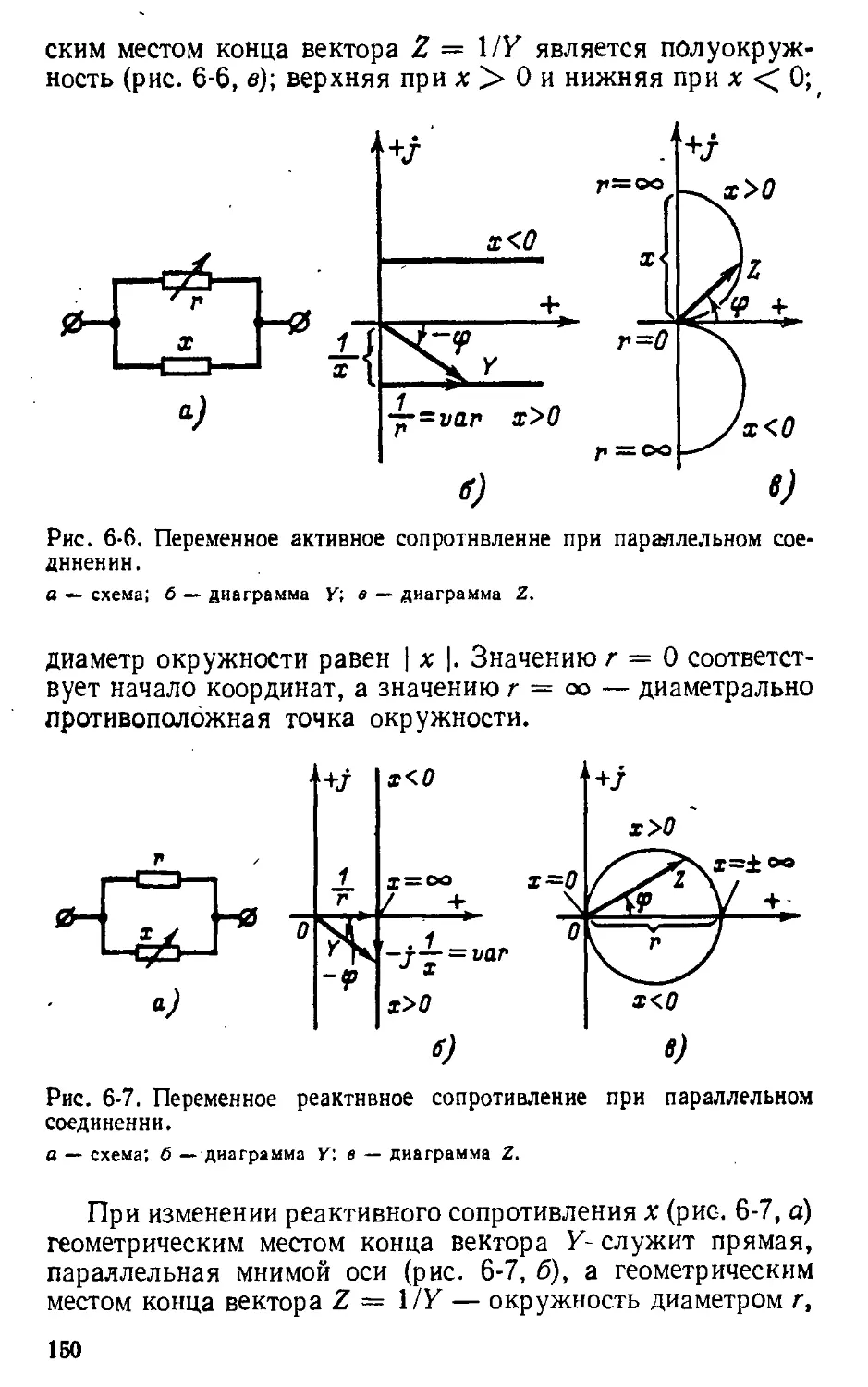
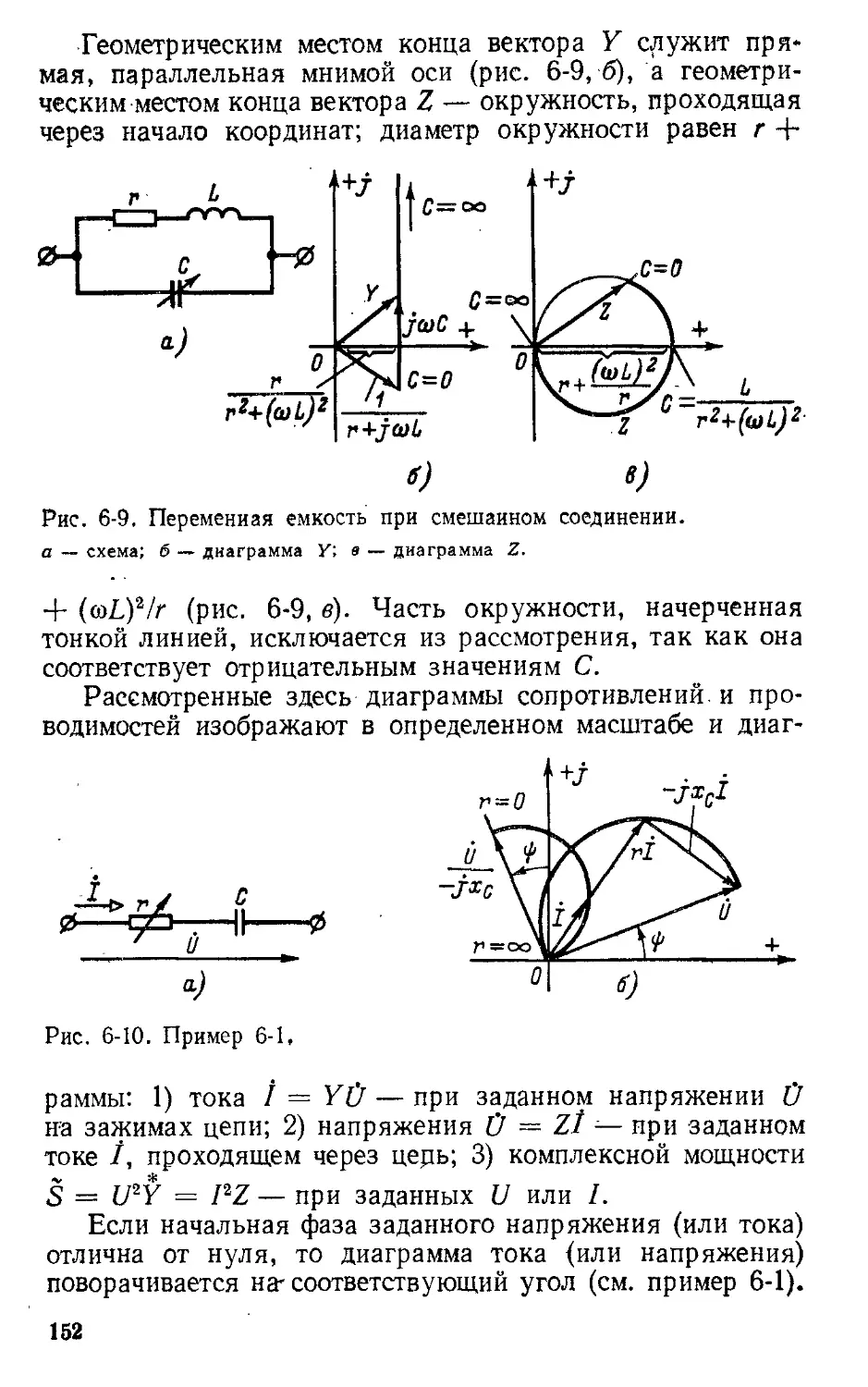
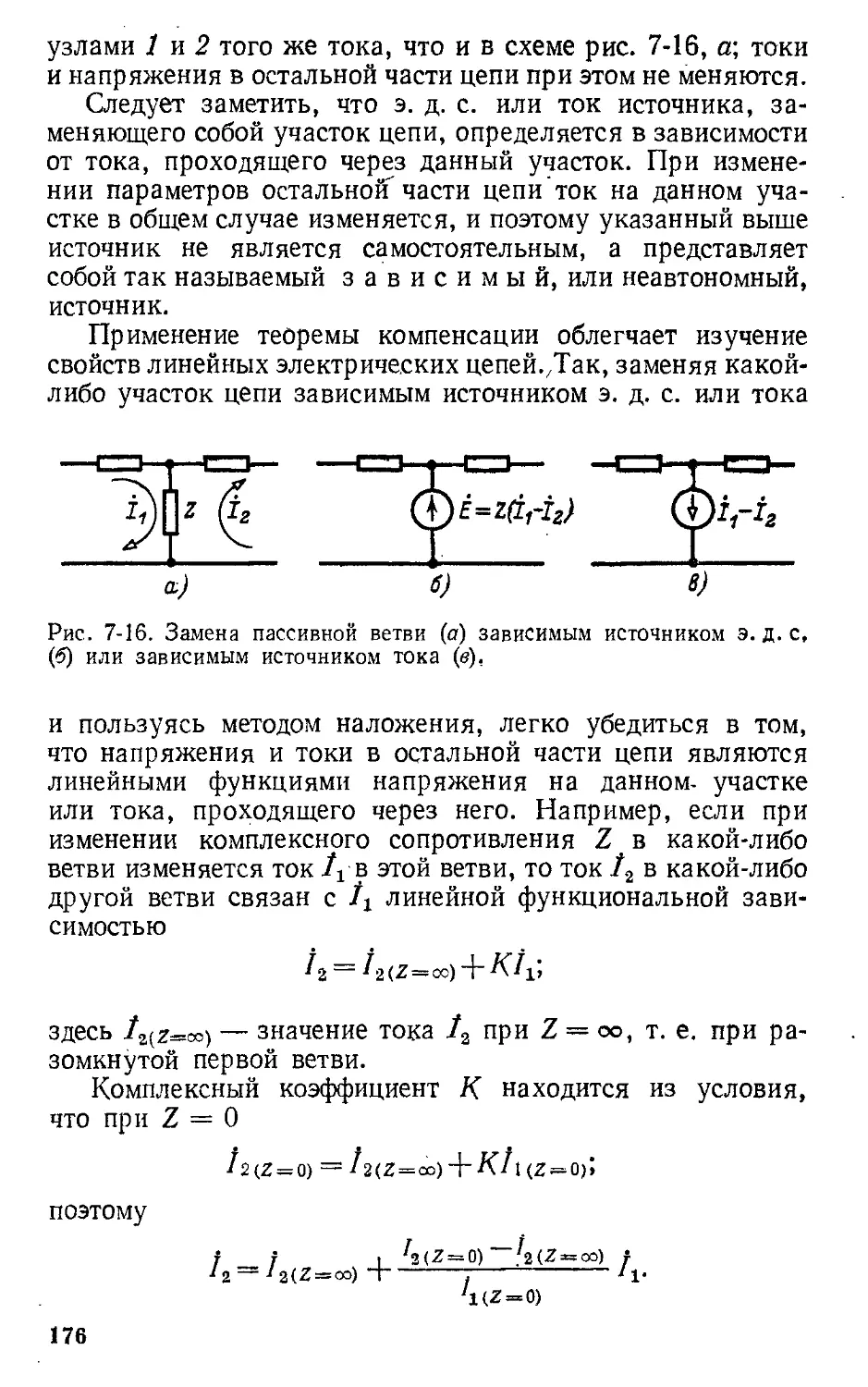
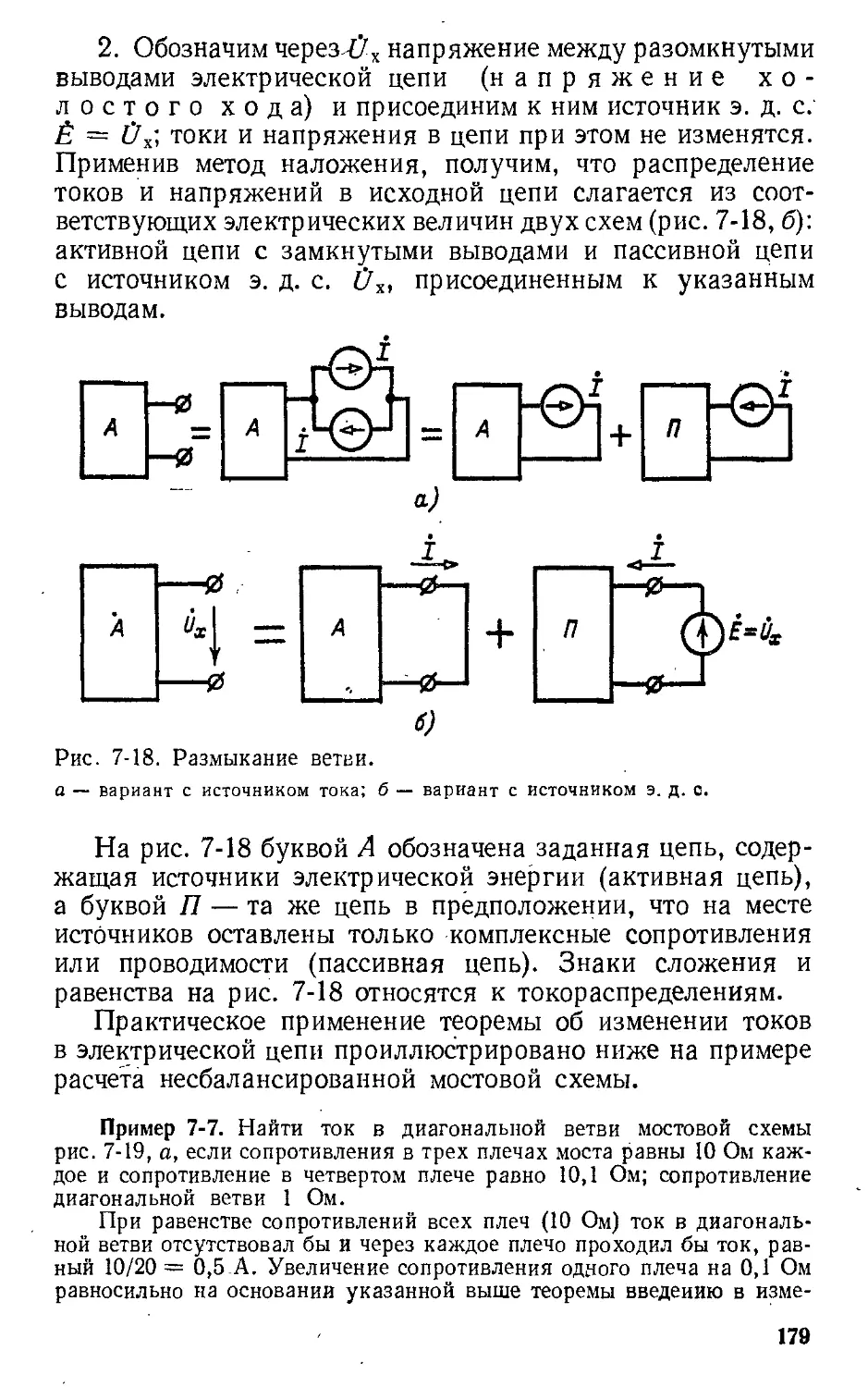
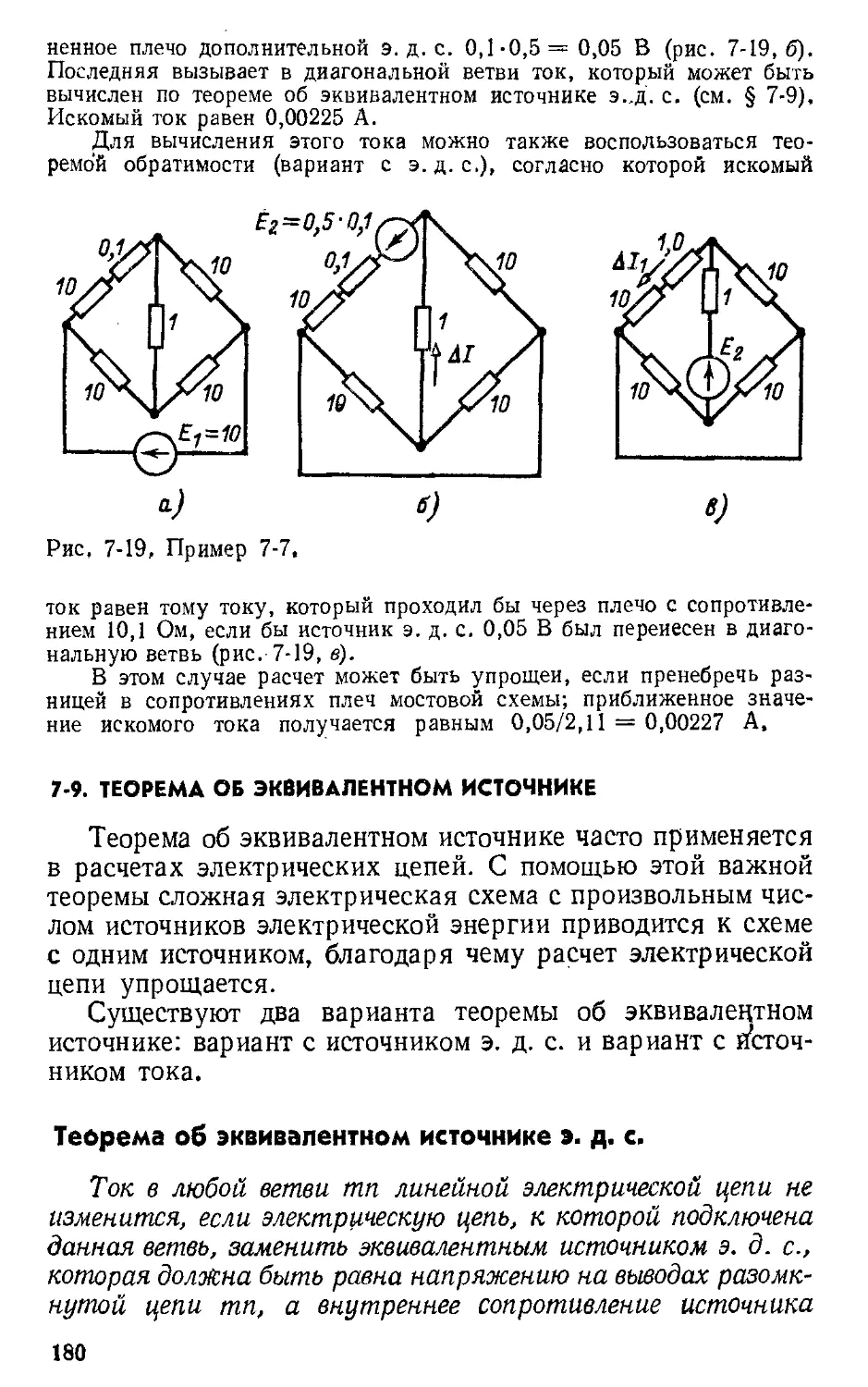
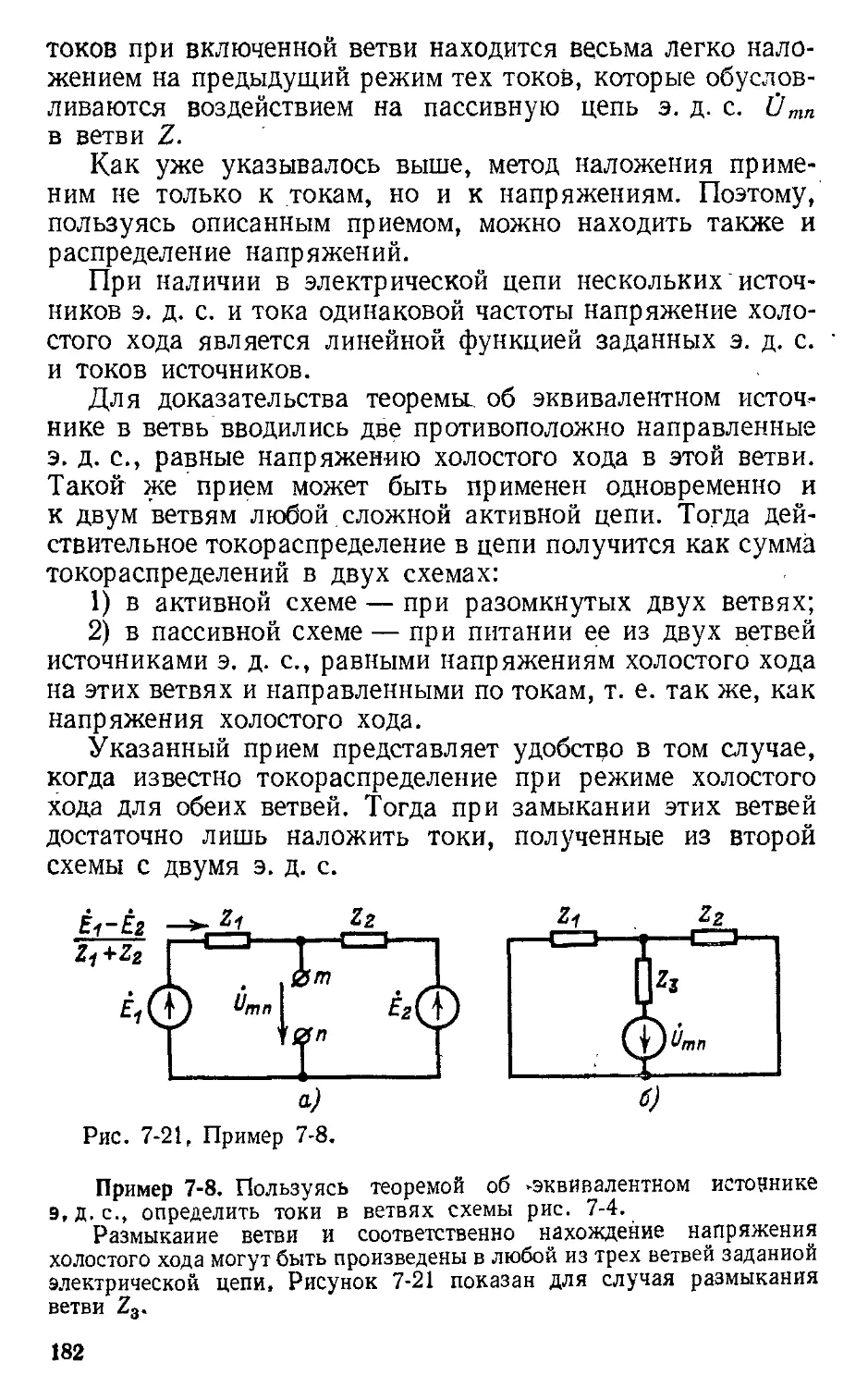
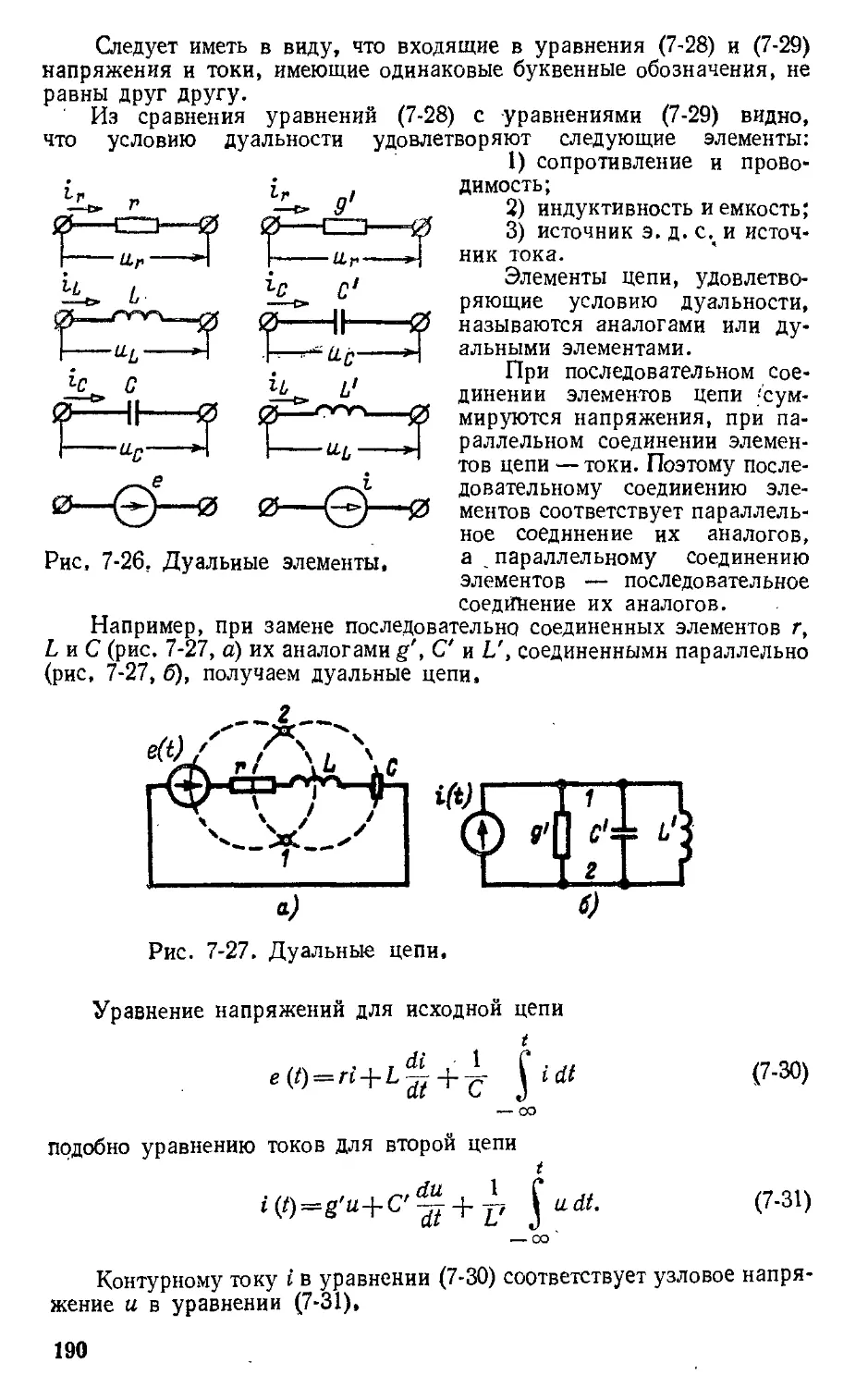
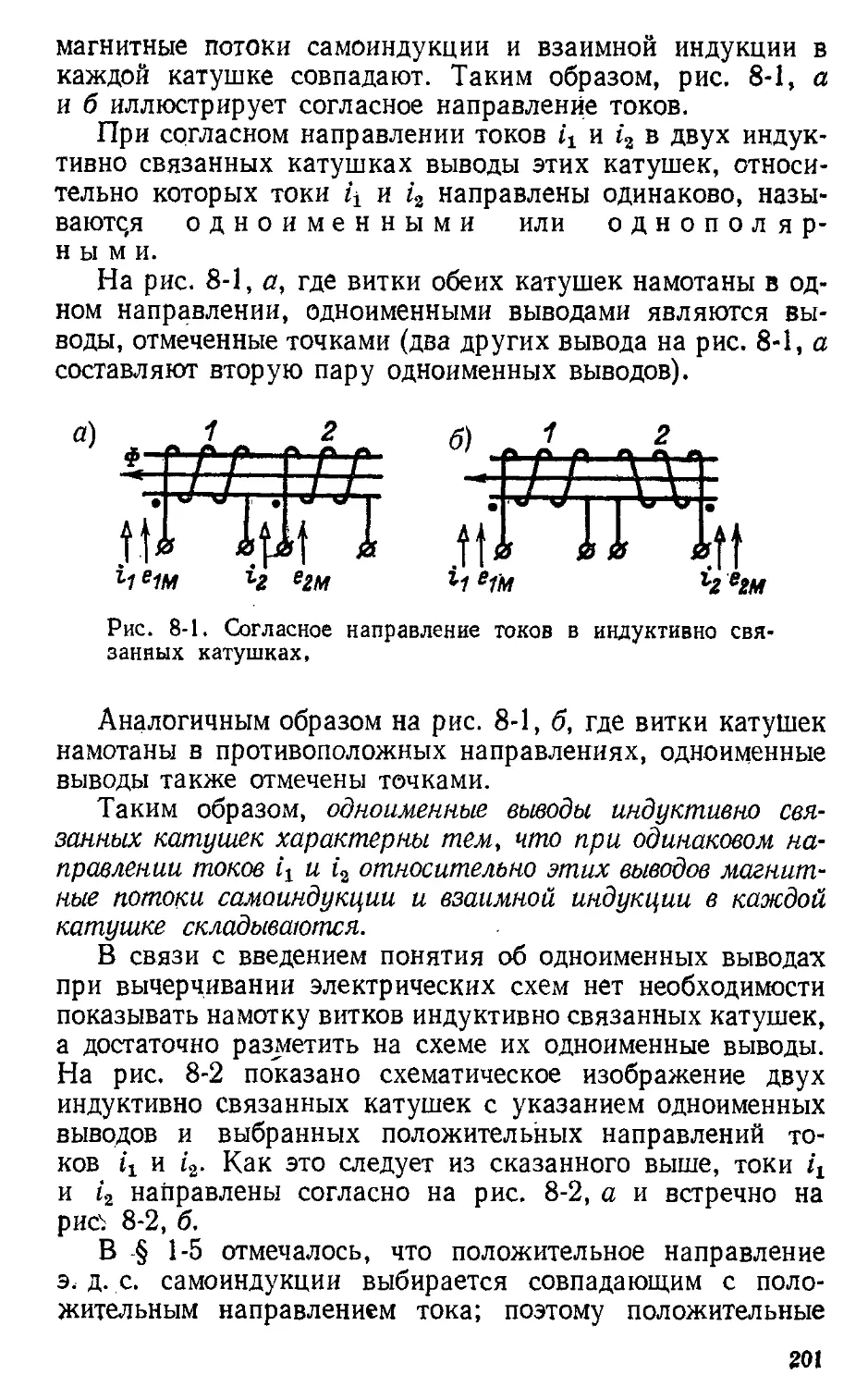
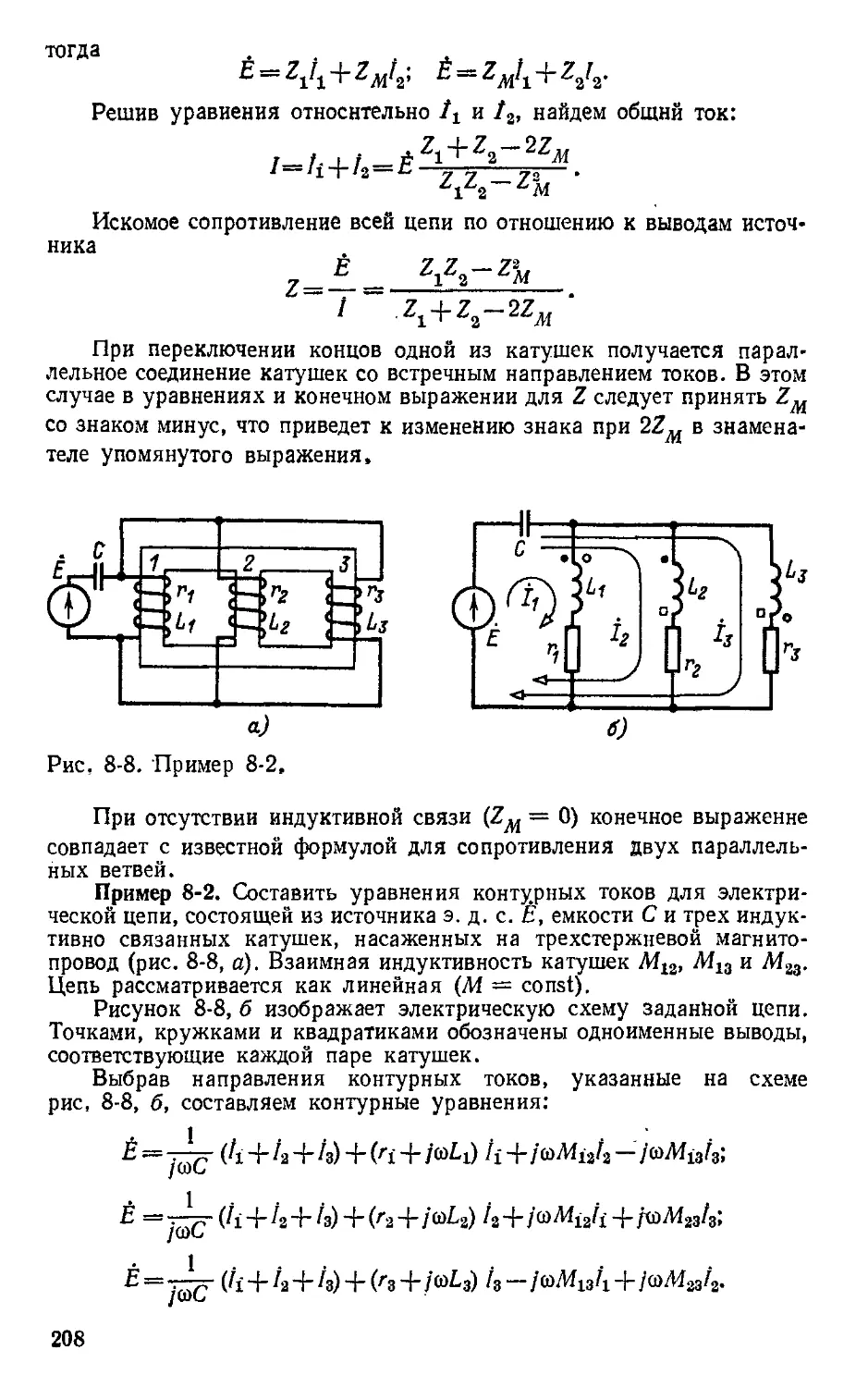
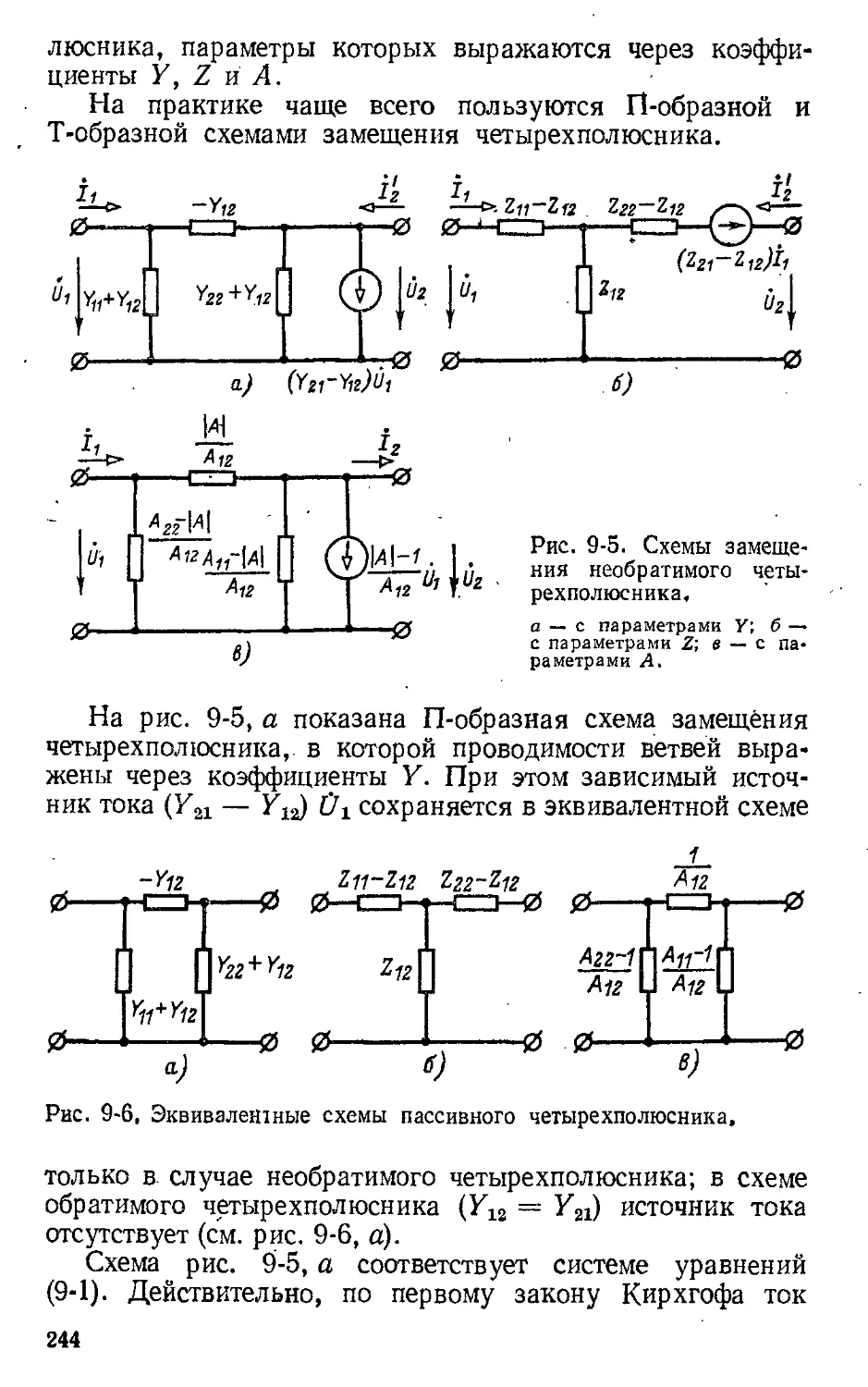
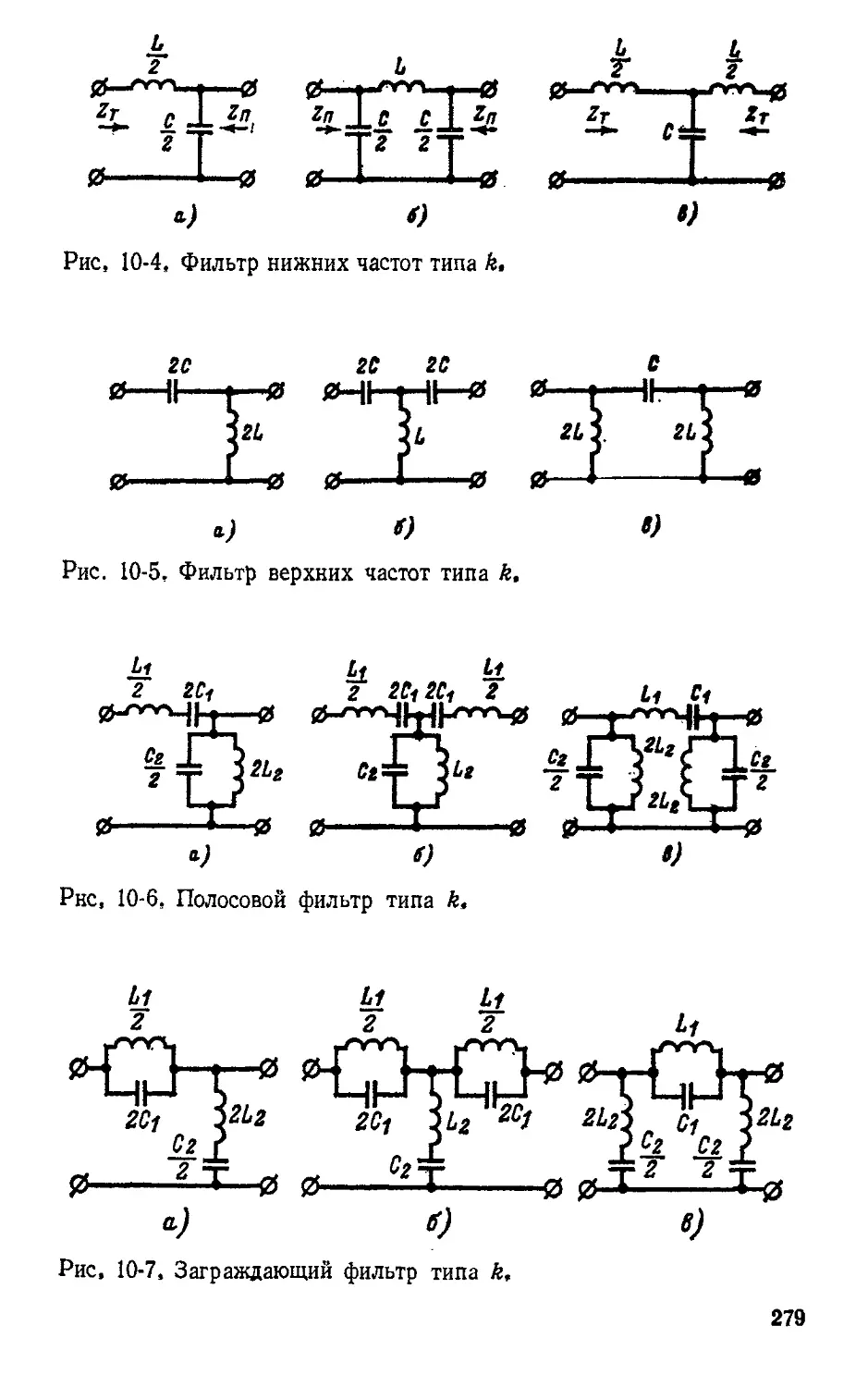
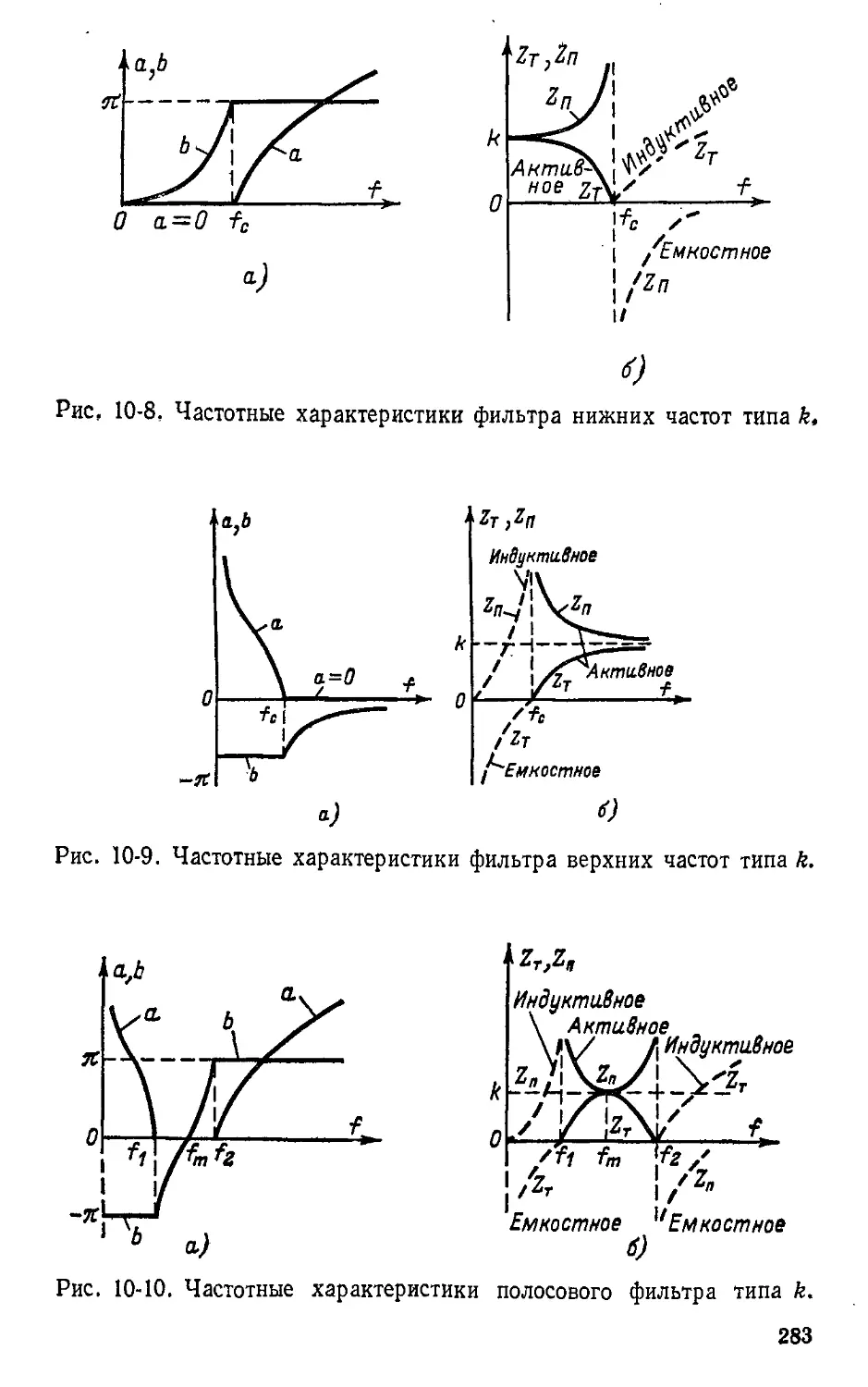
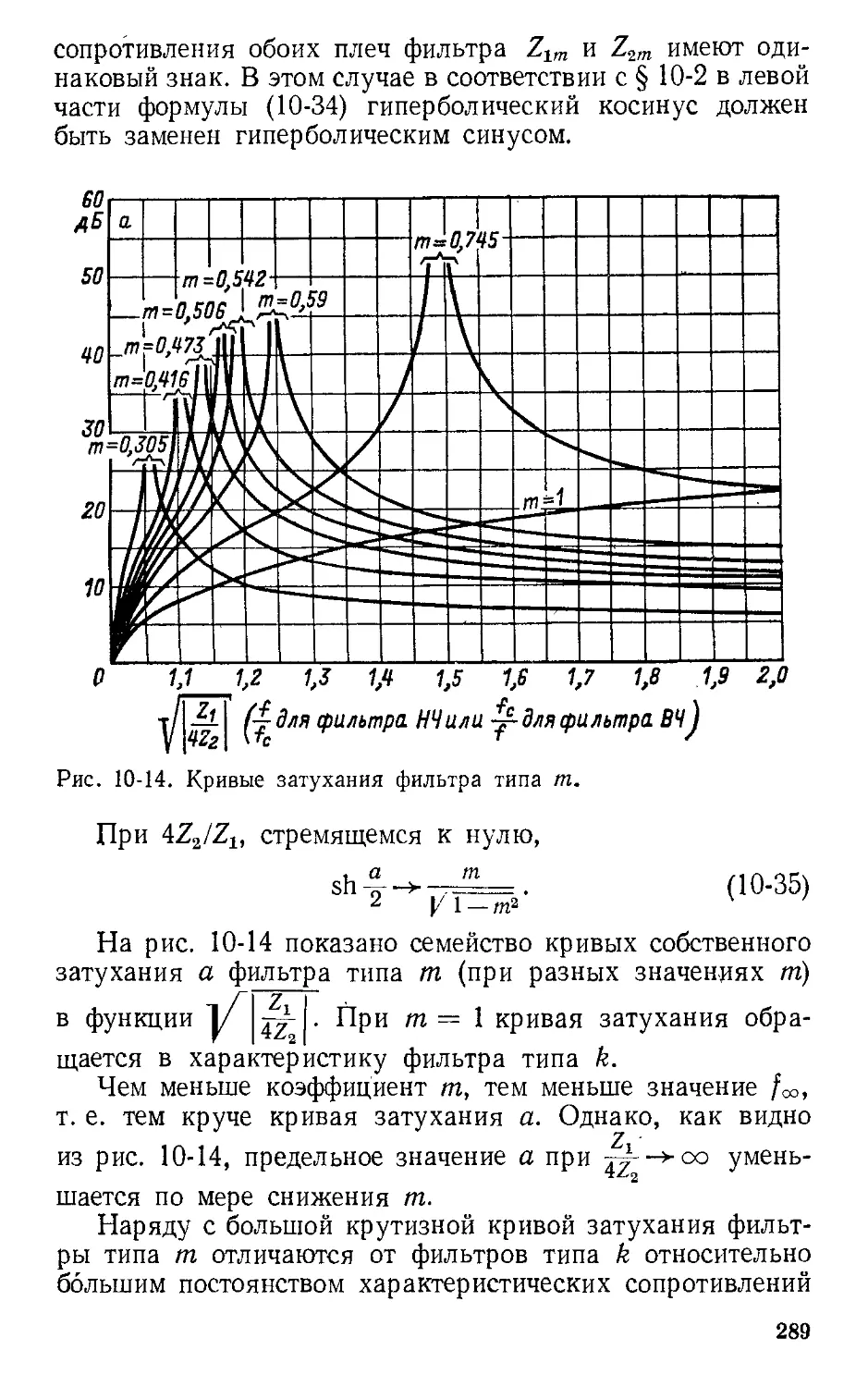
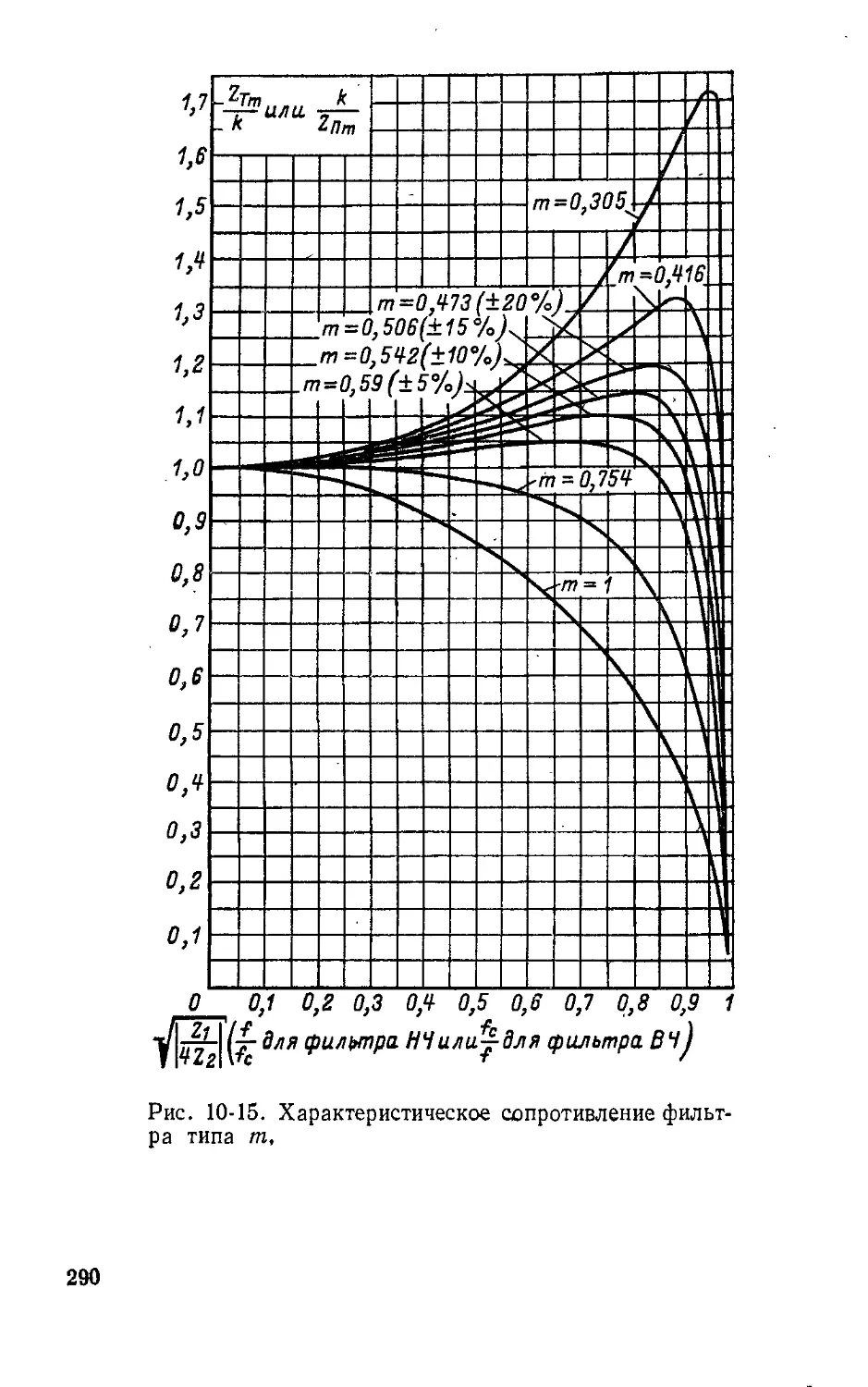
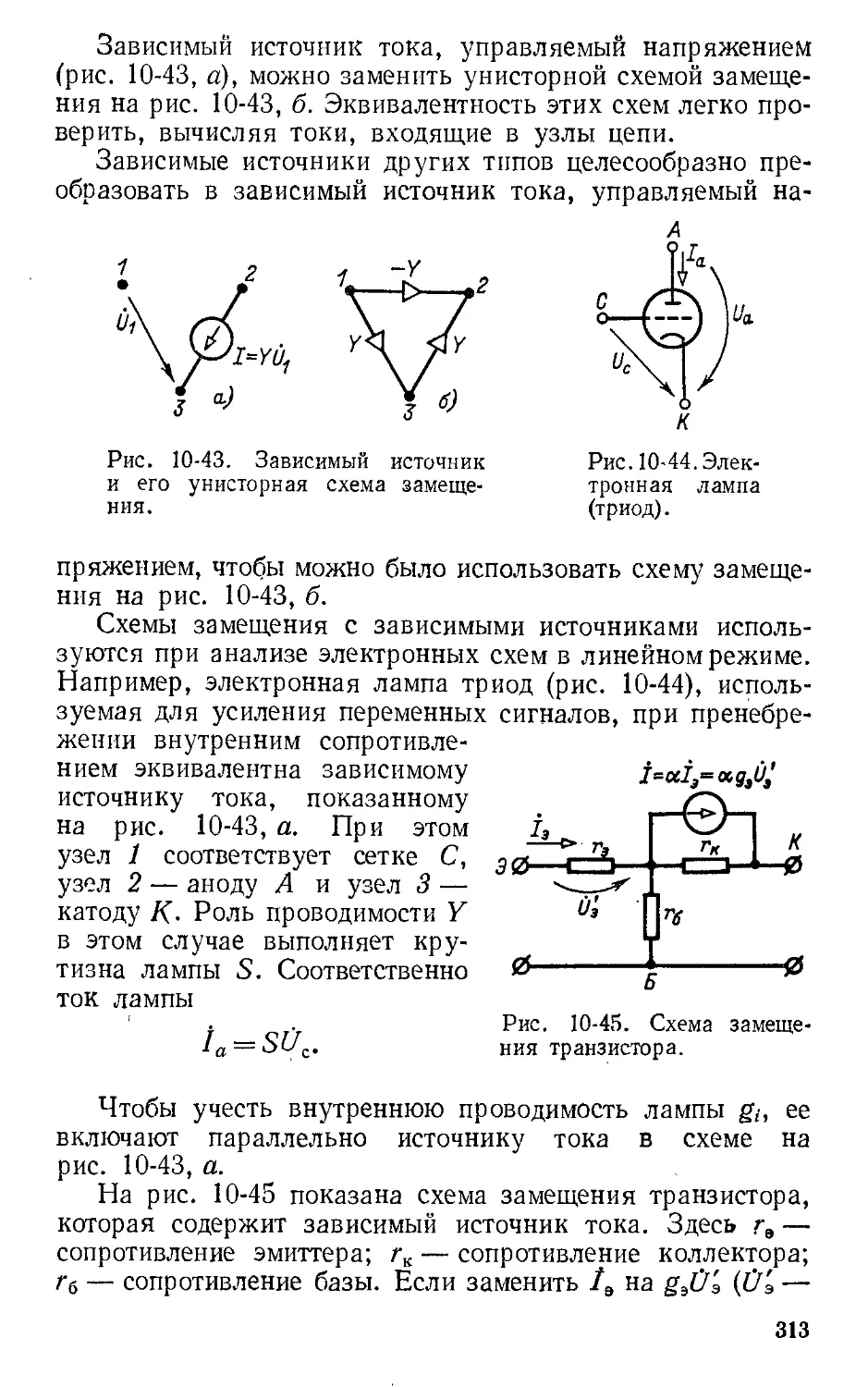
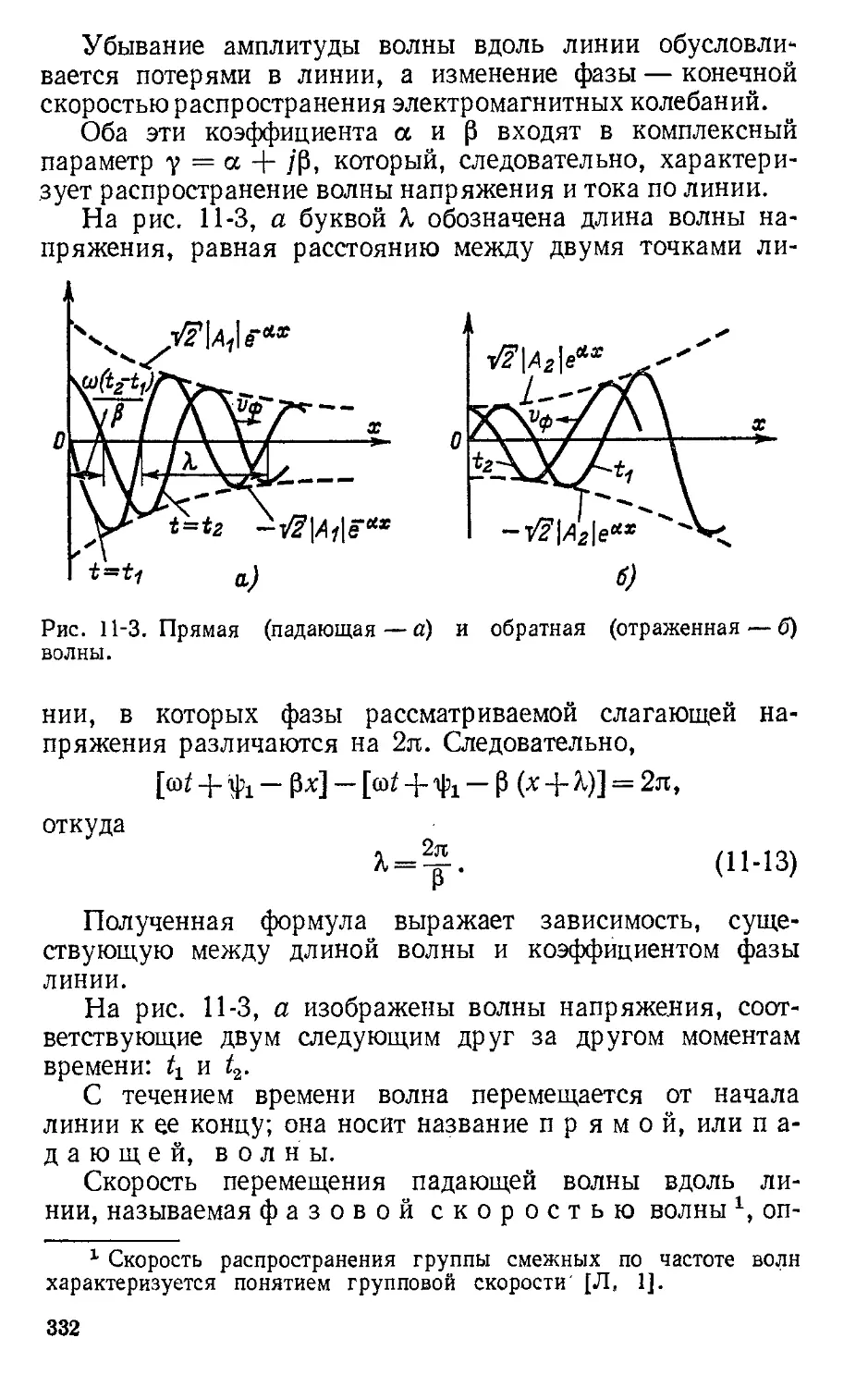
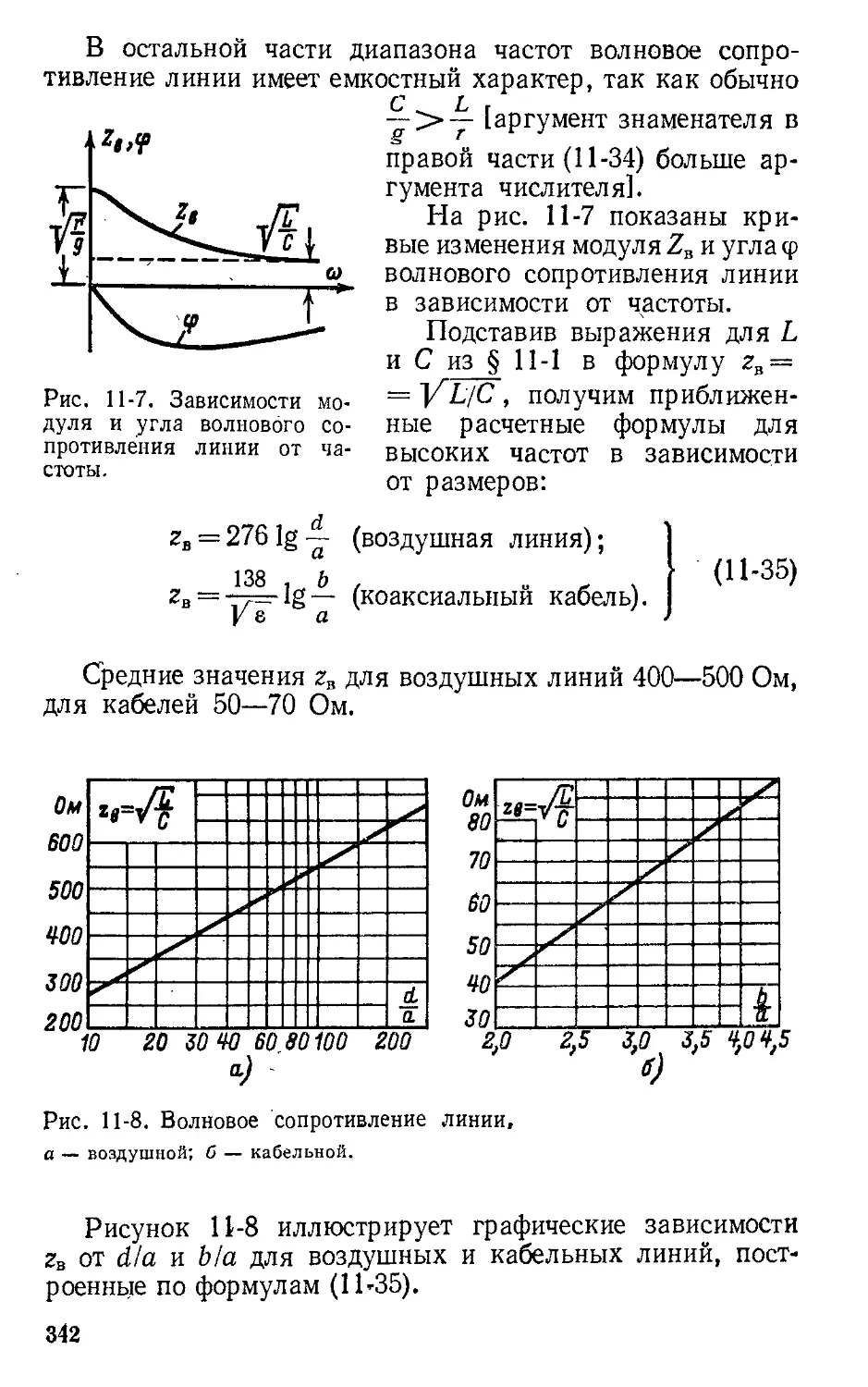
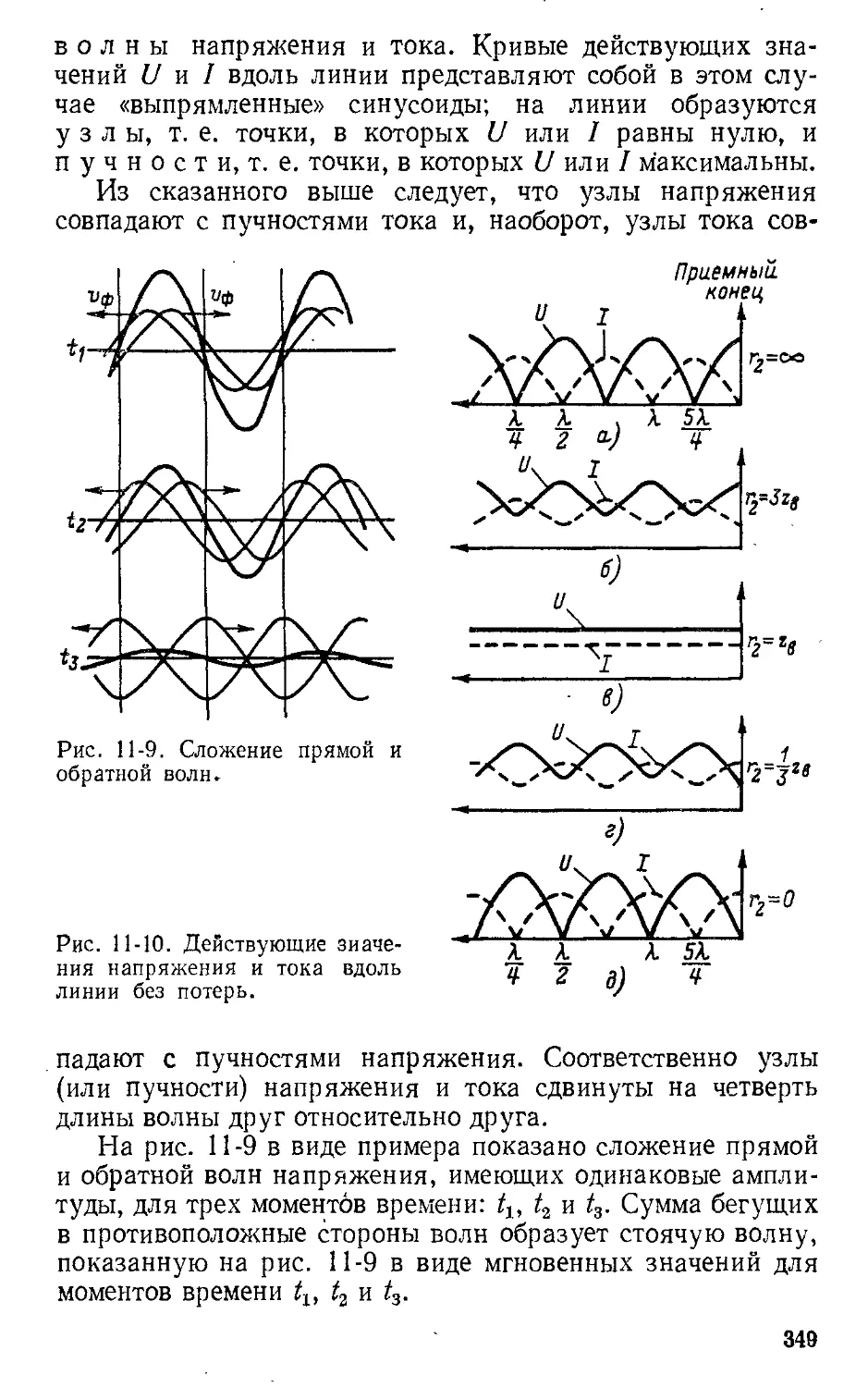
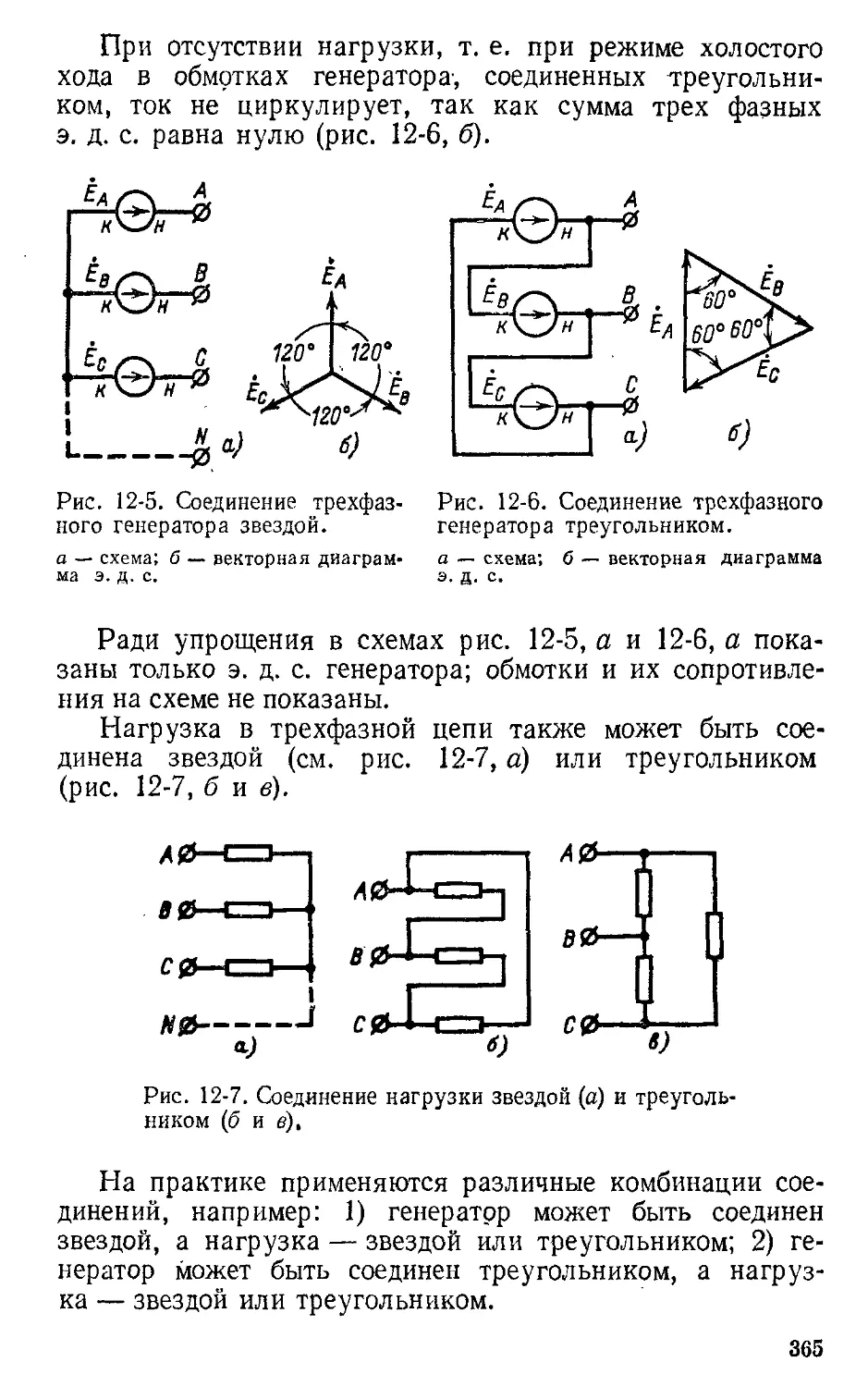
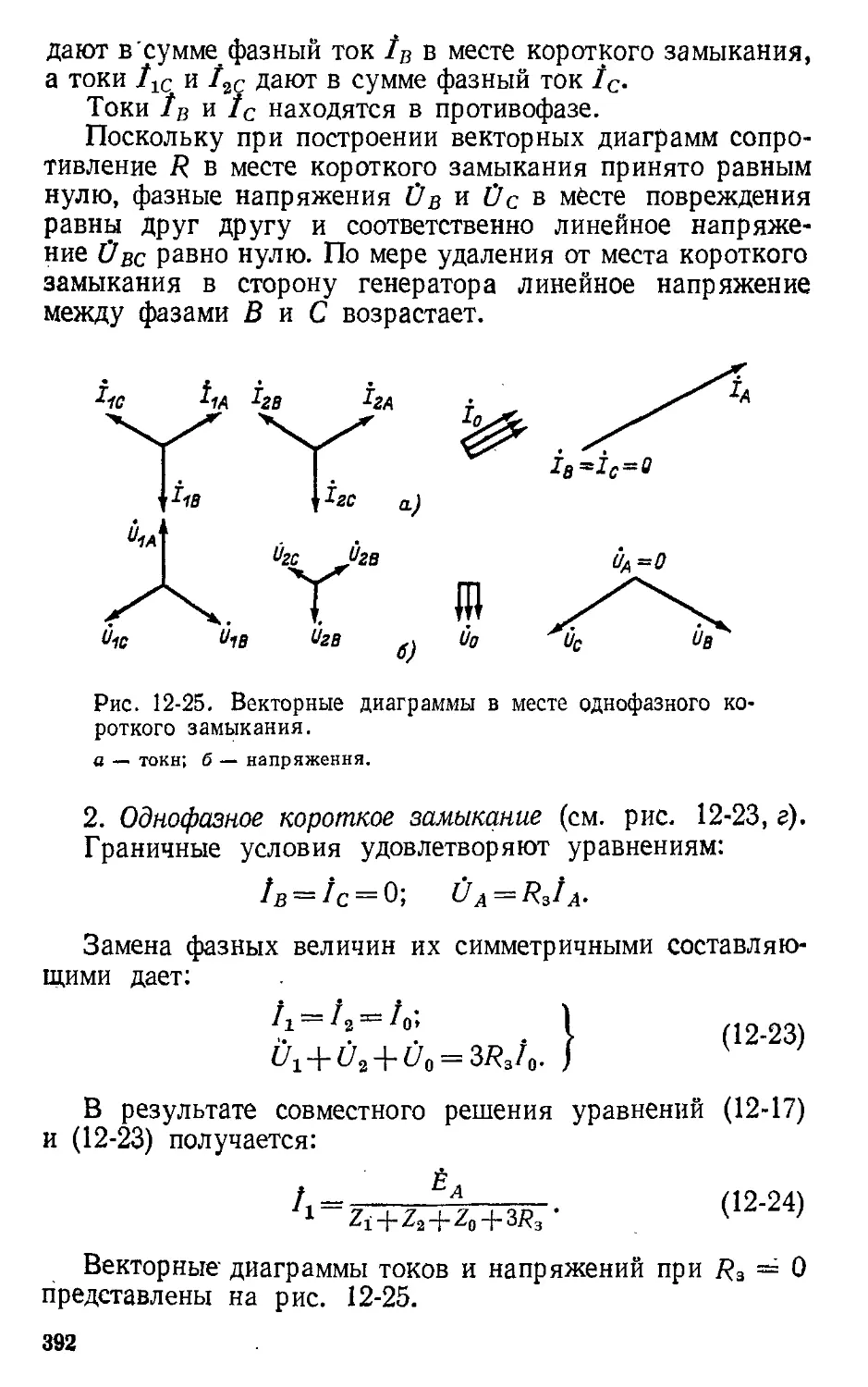
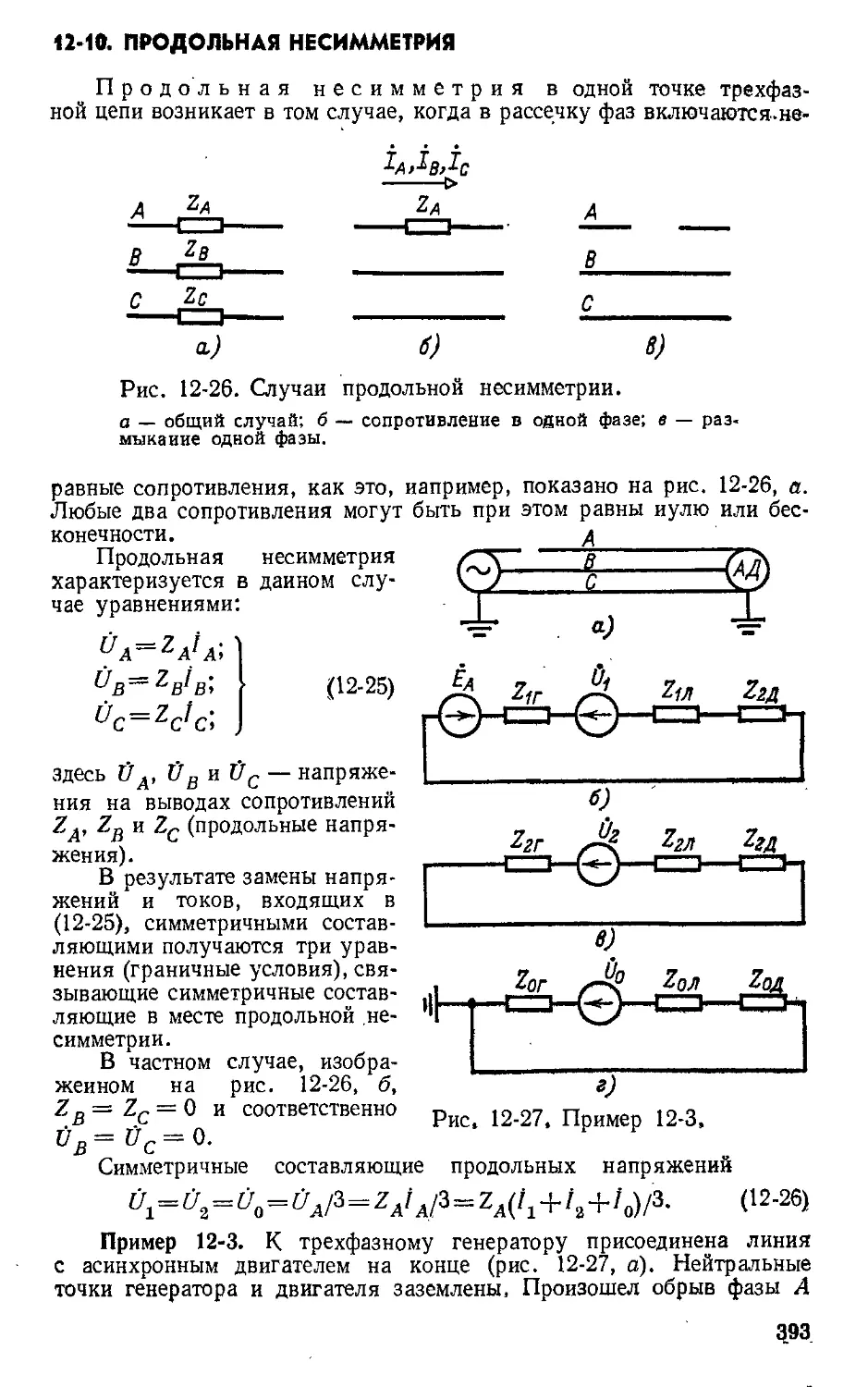
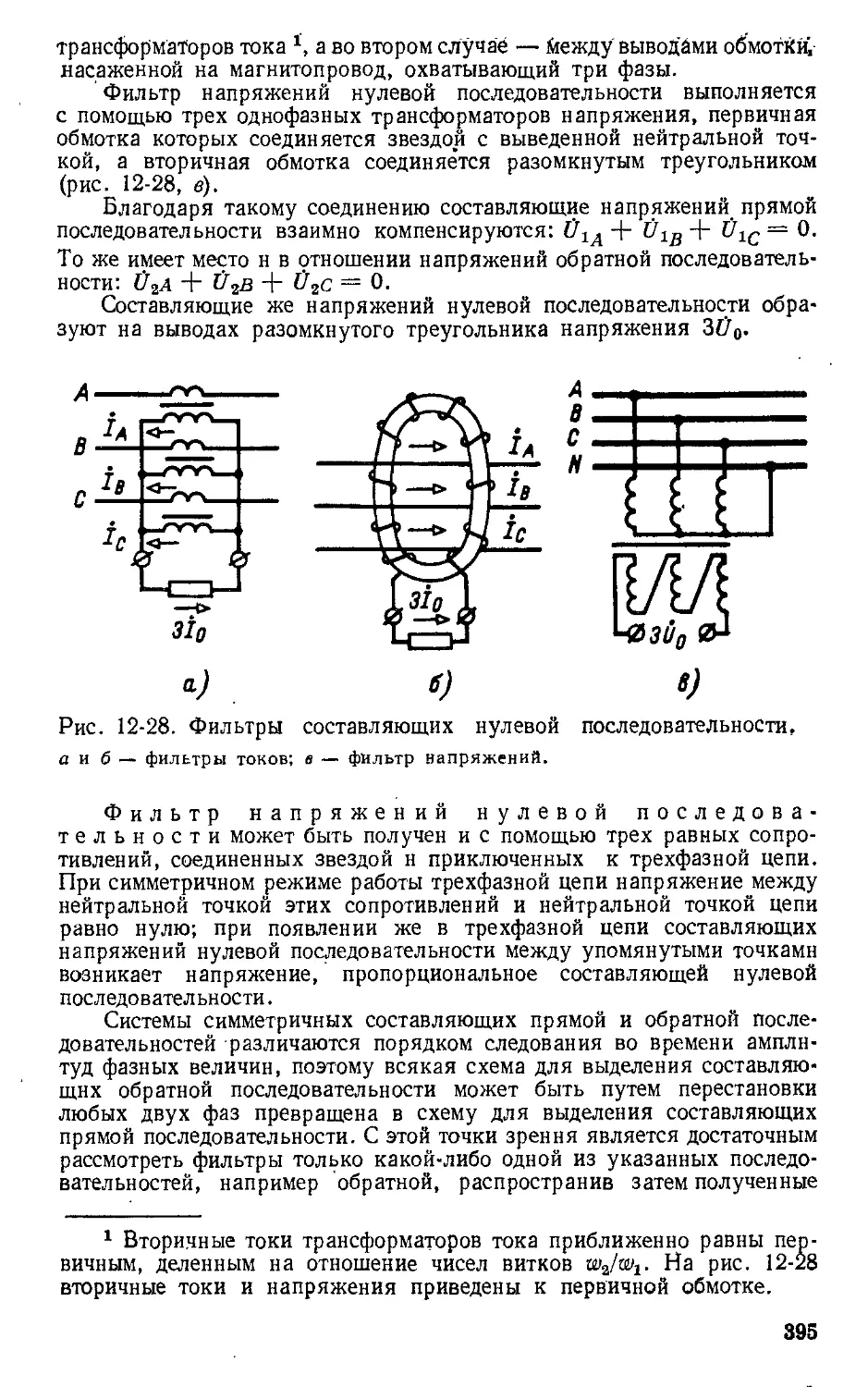
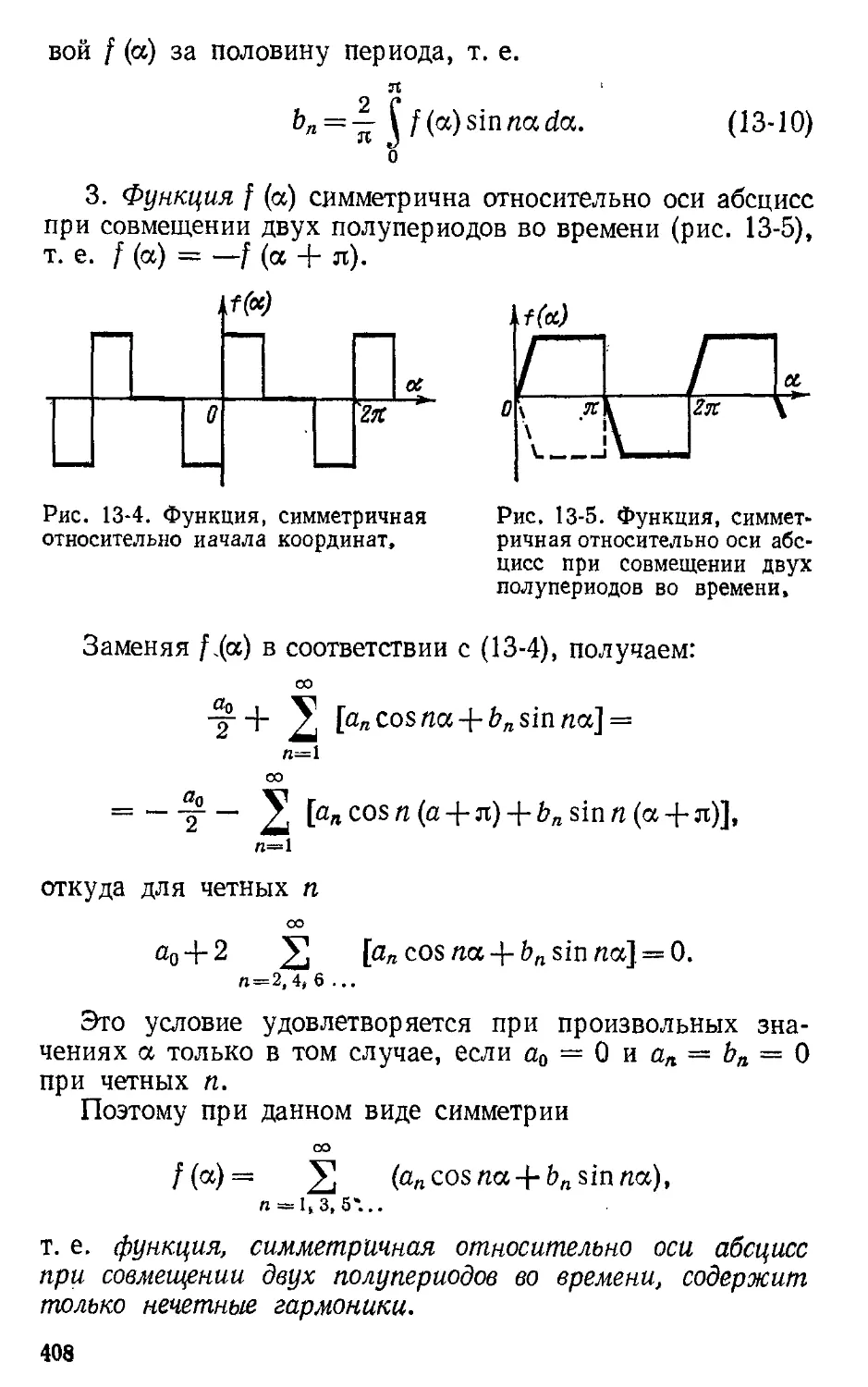
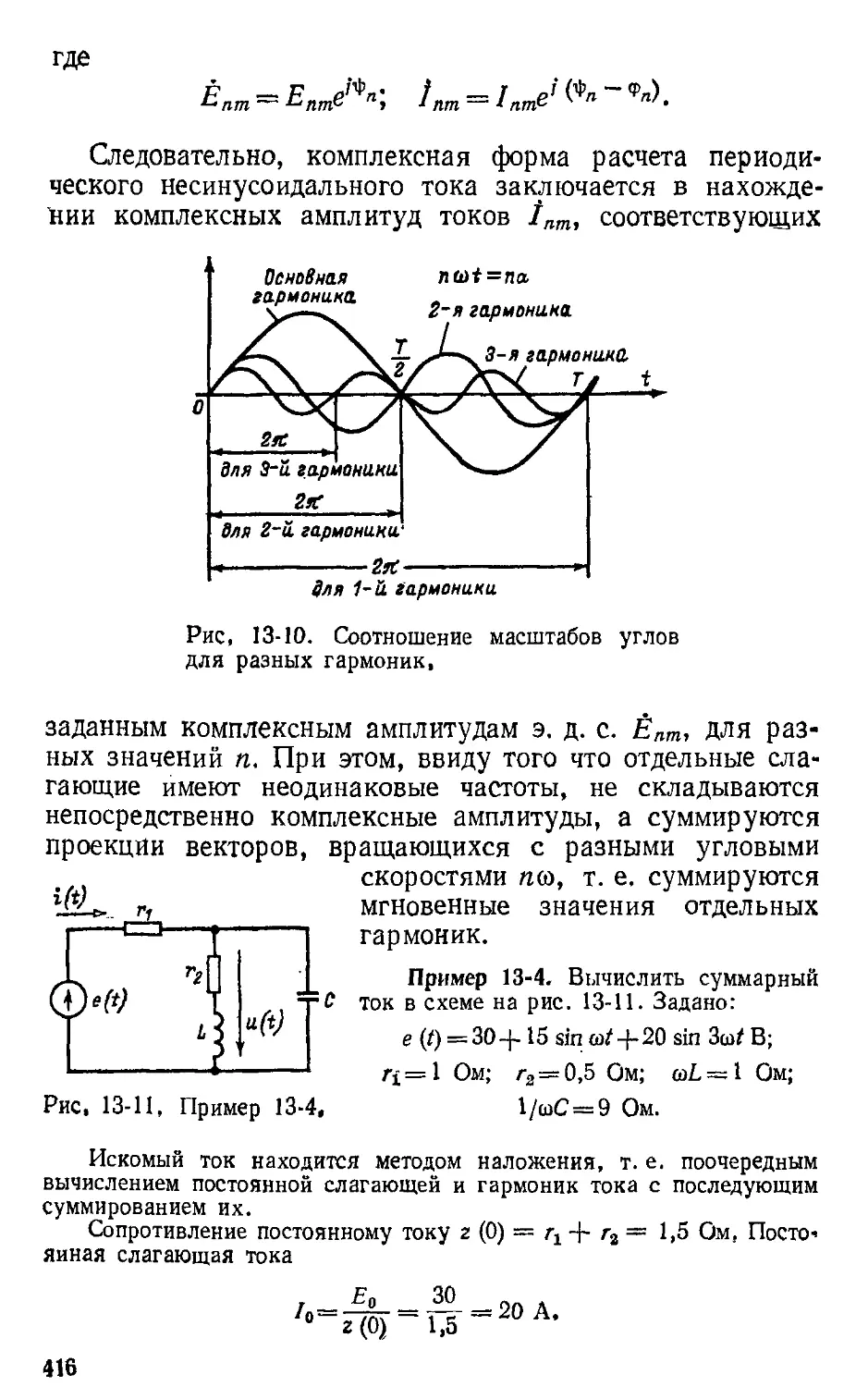
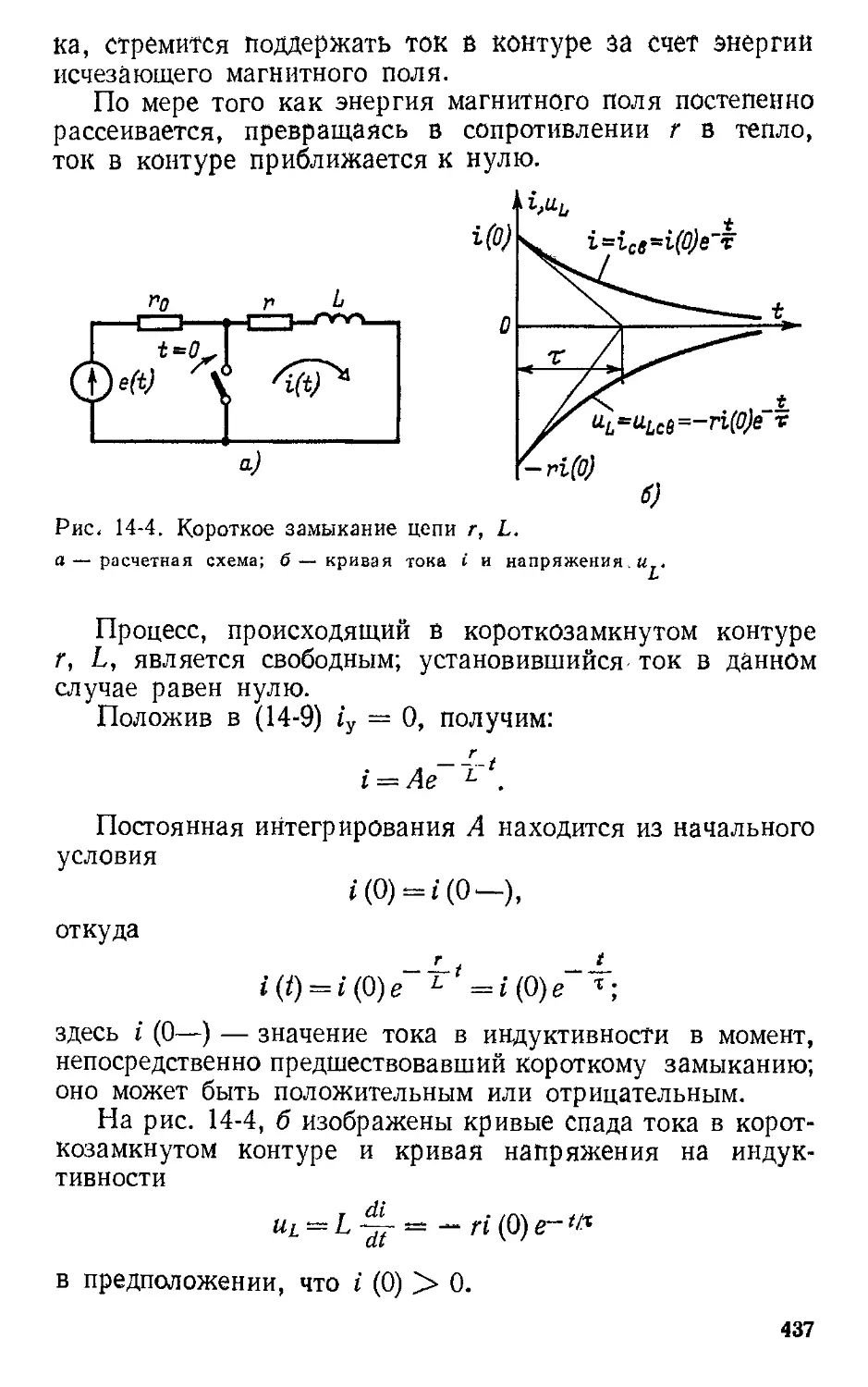
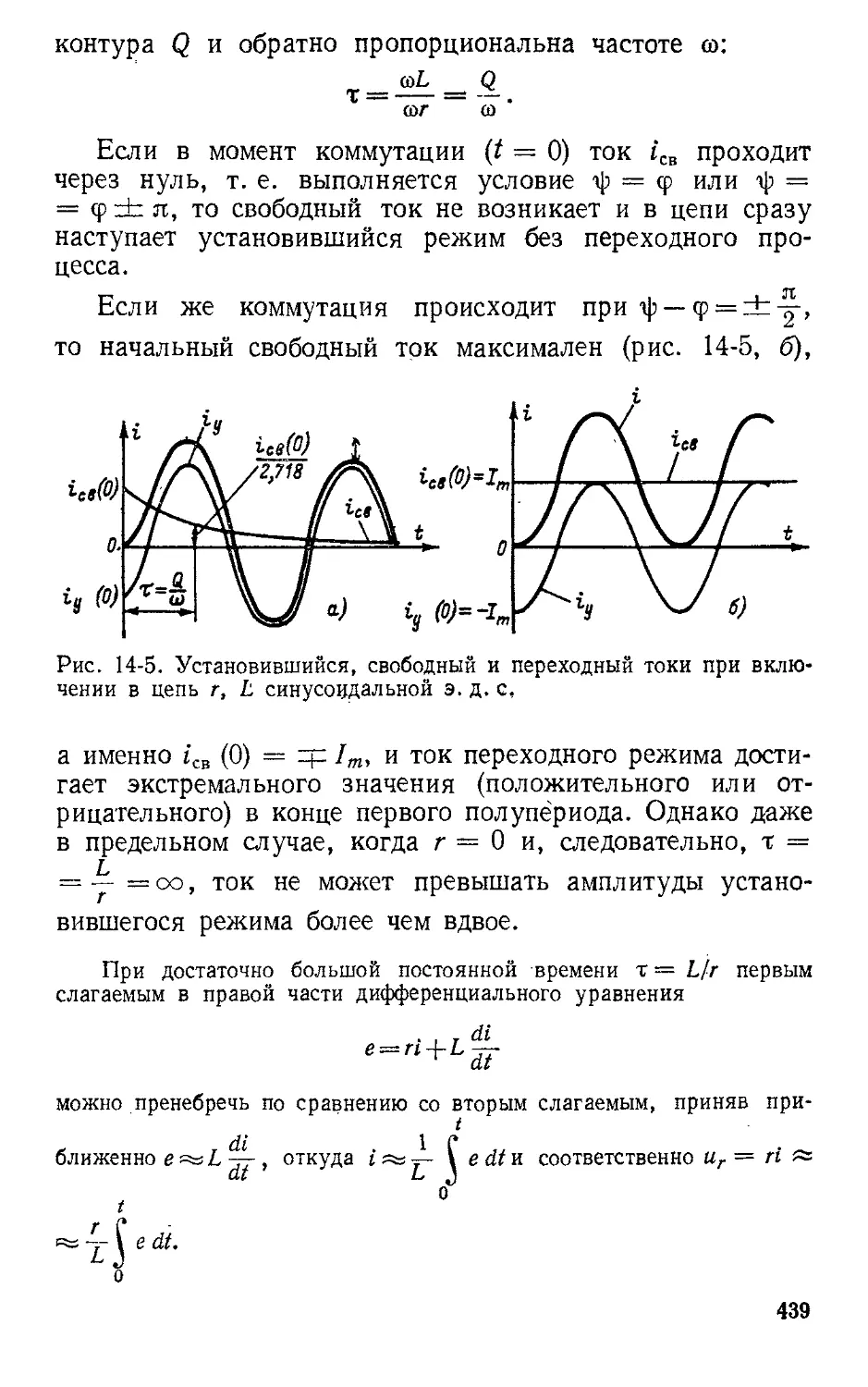
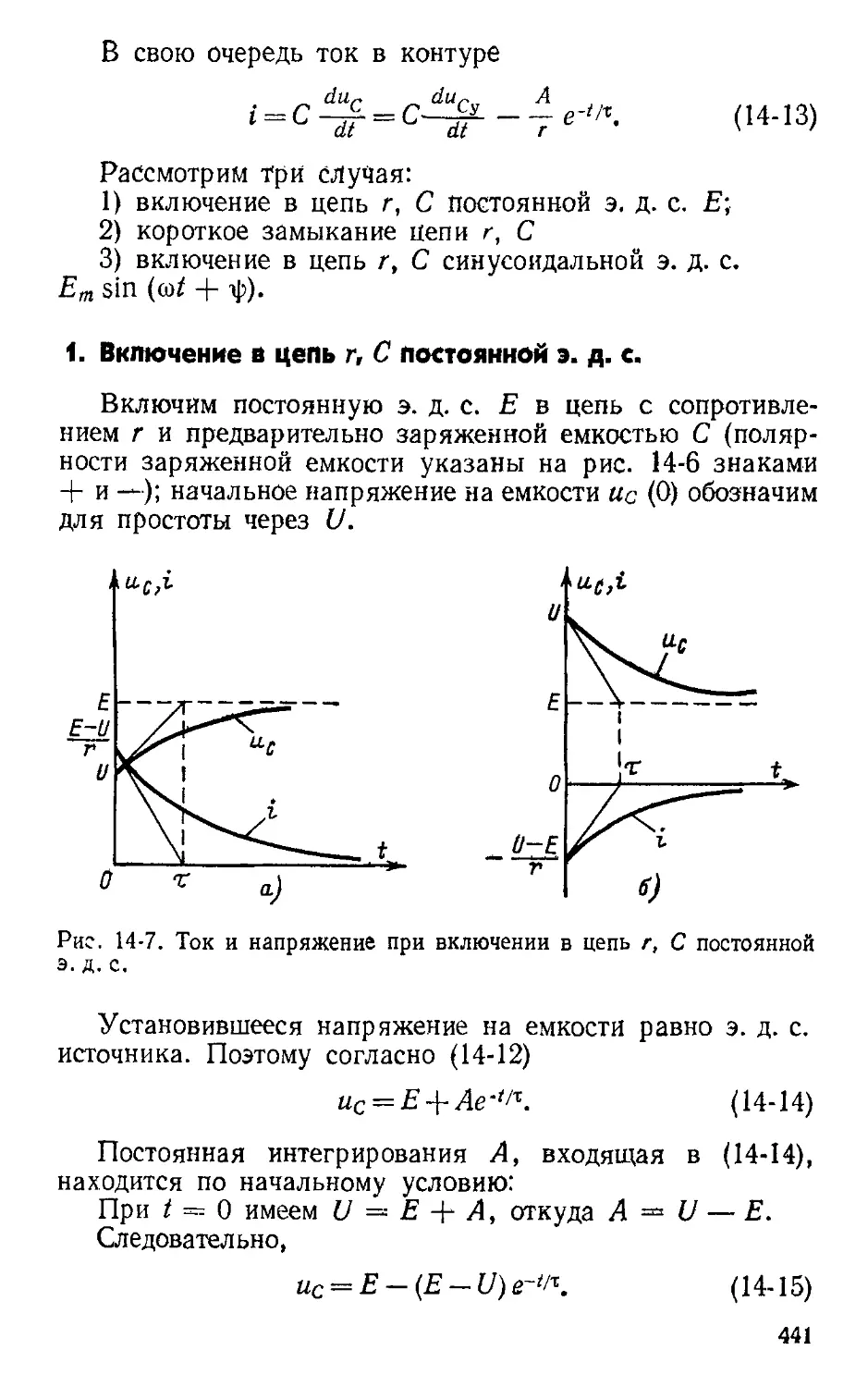
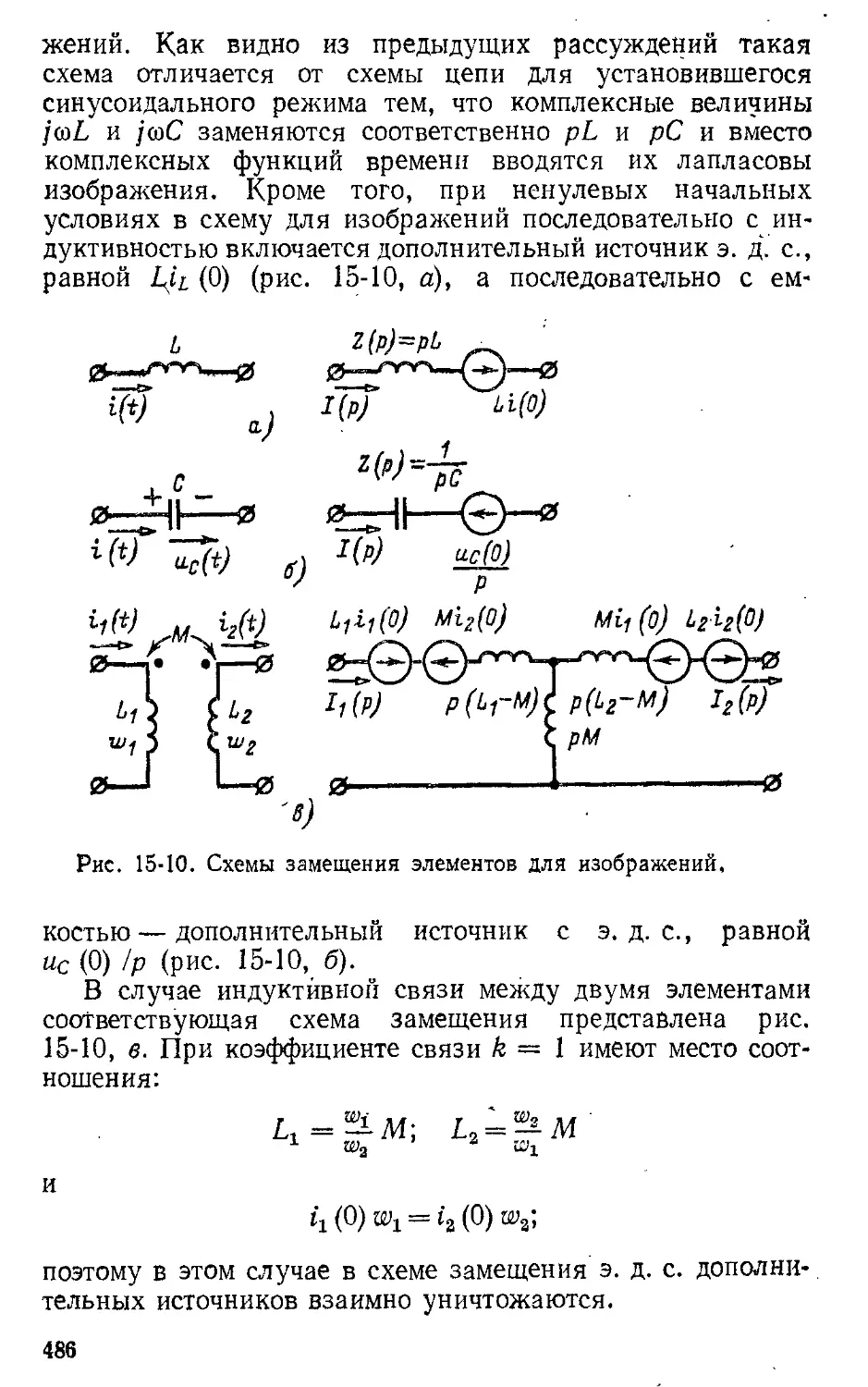
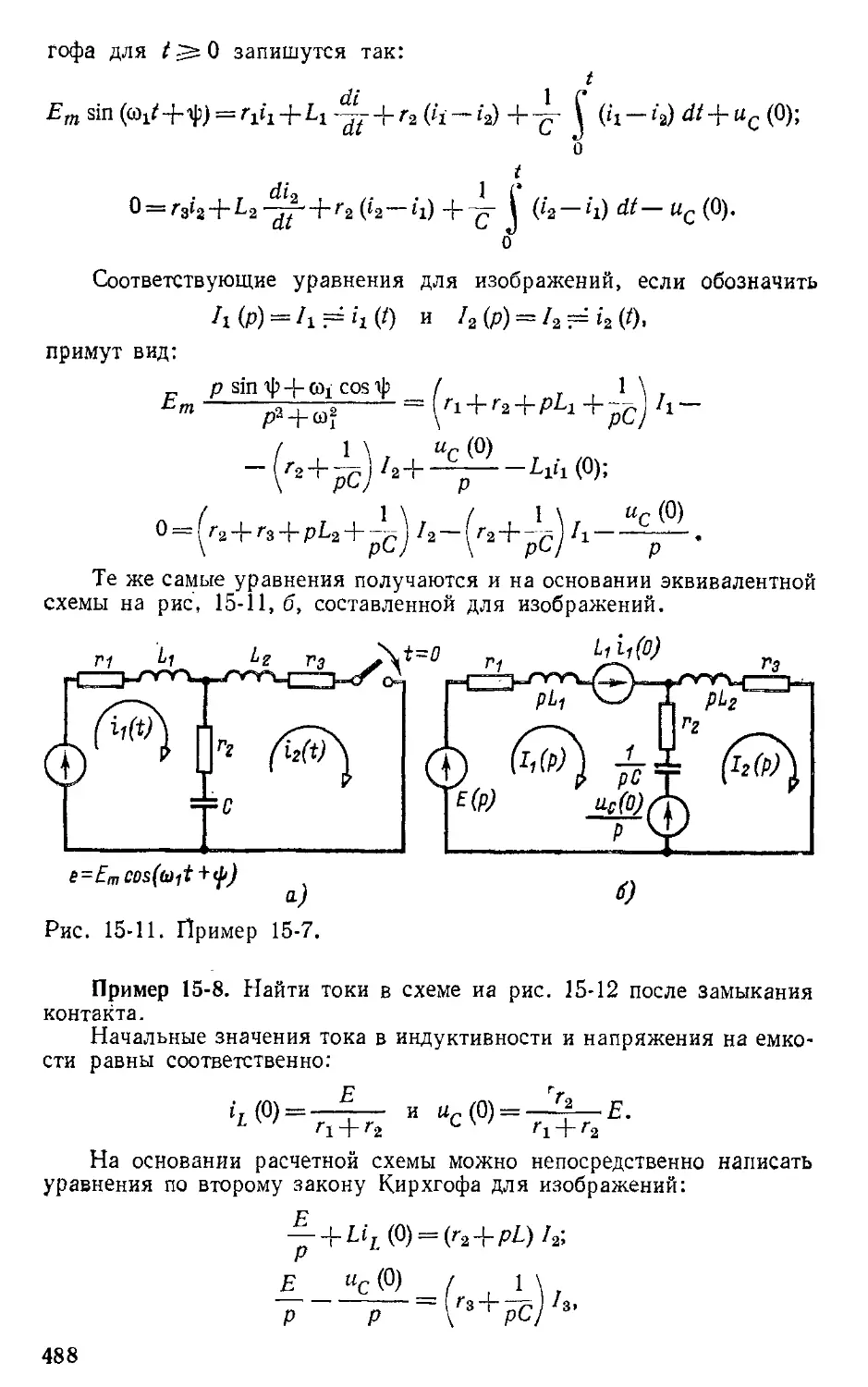
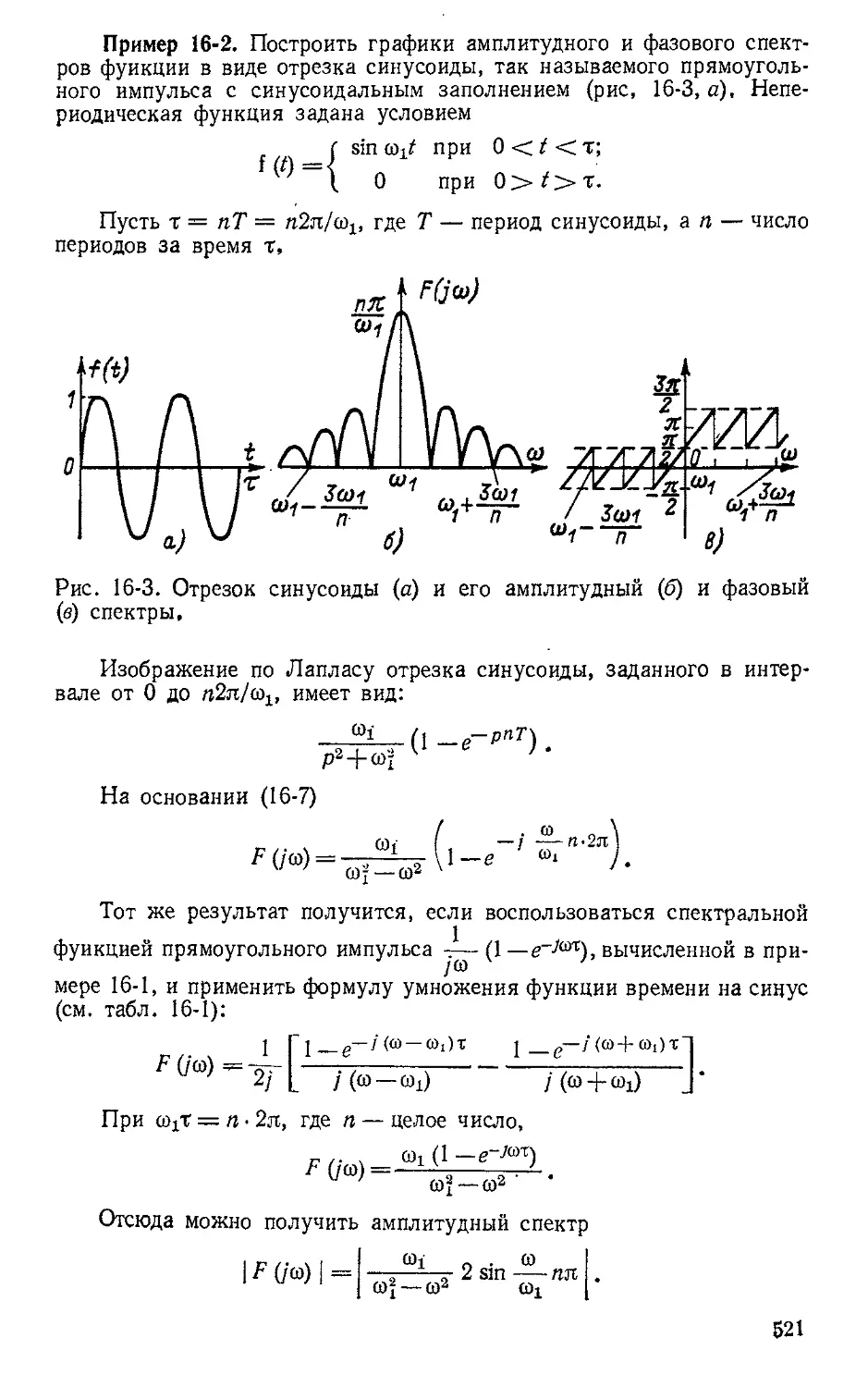
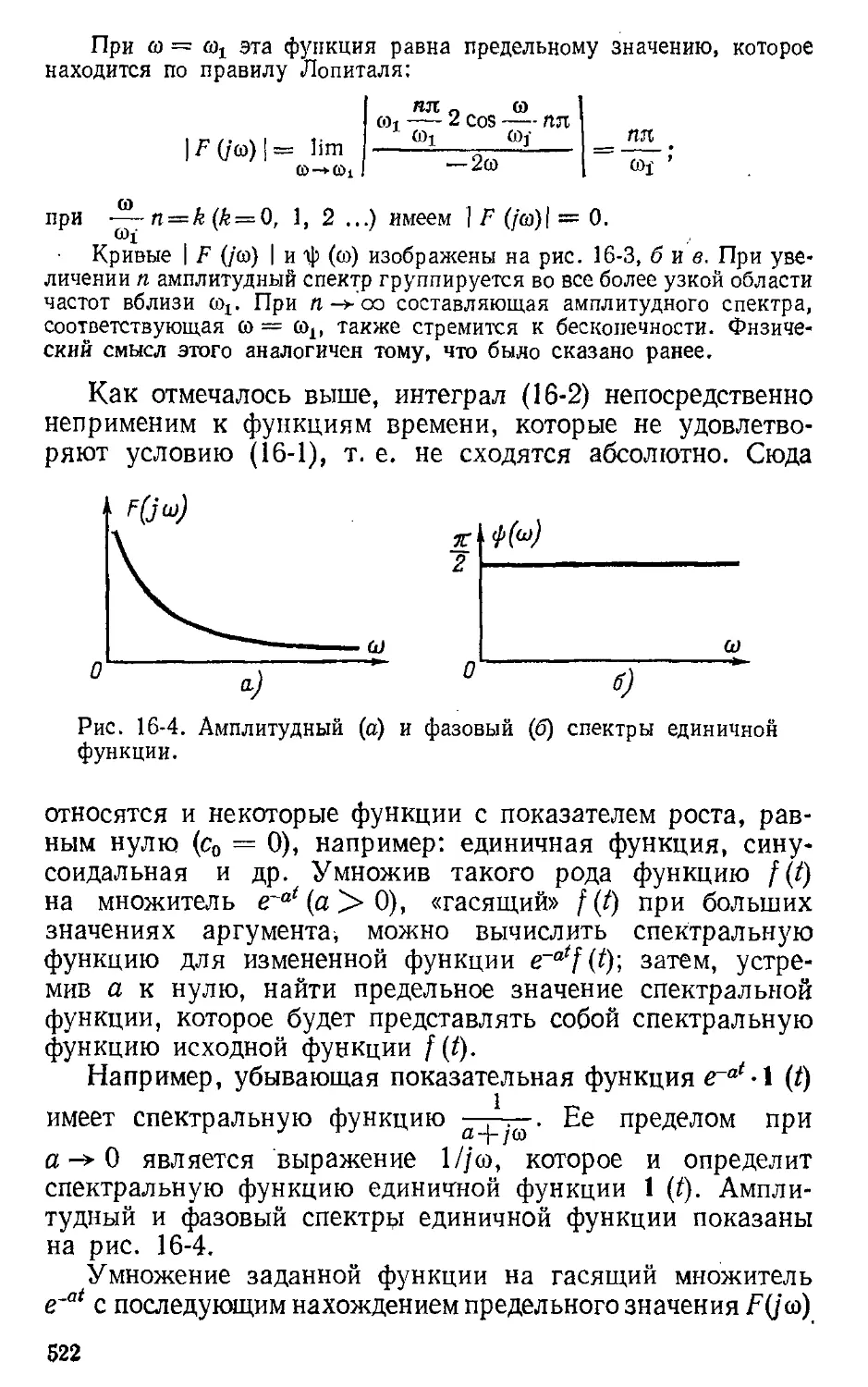
Автор: Атабеков Г.И.
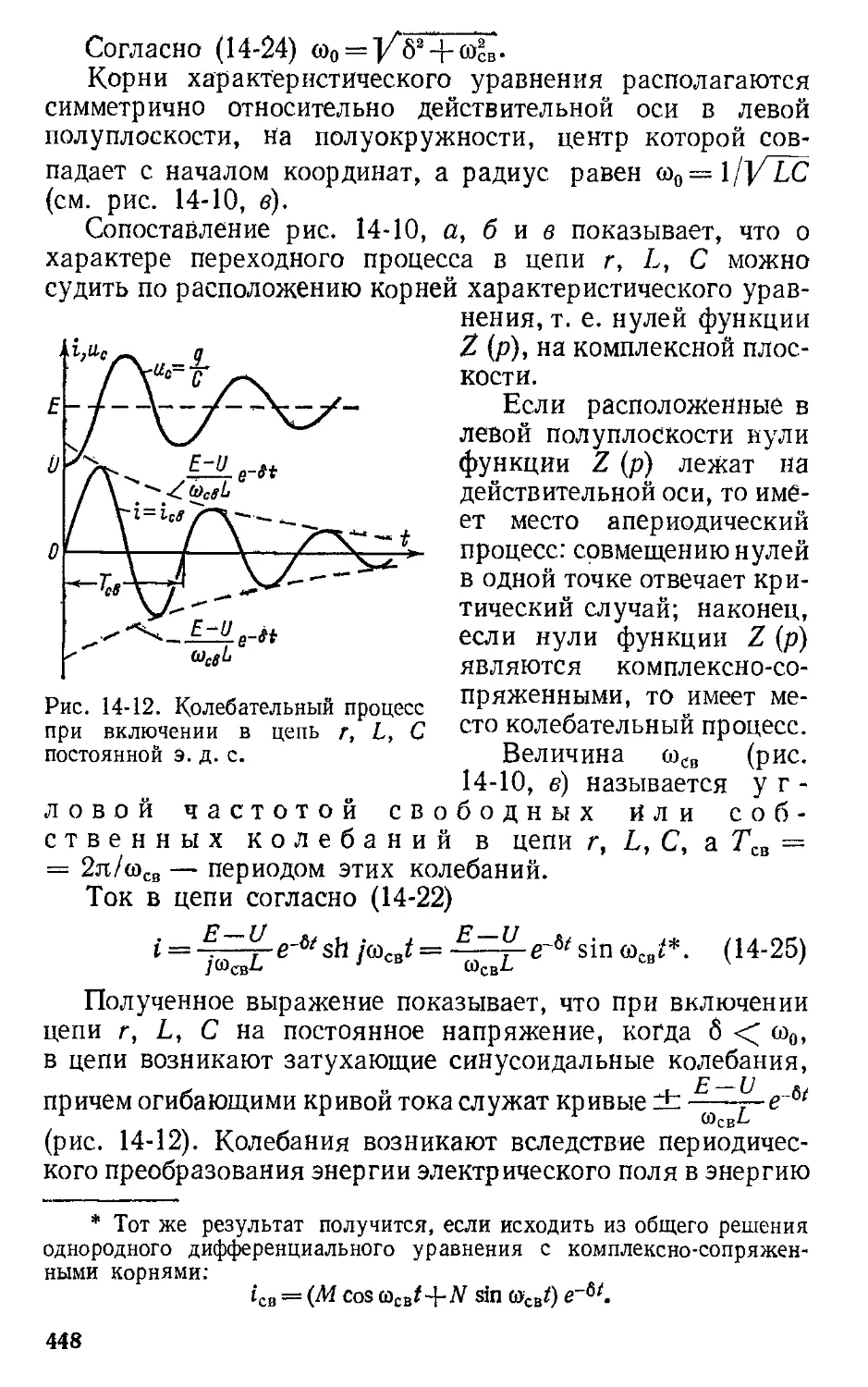
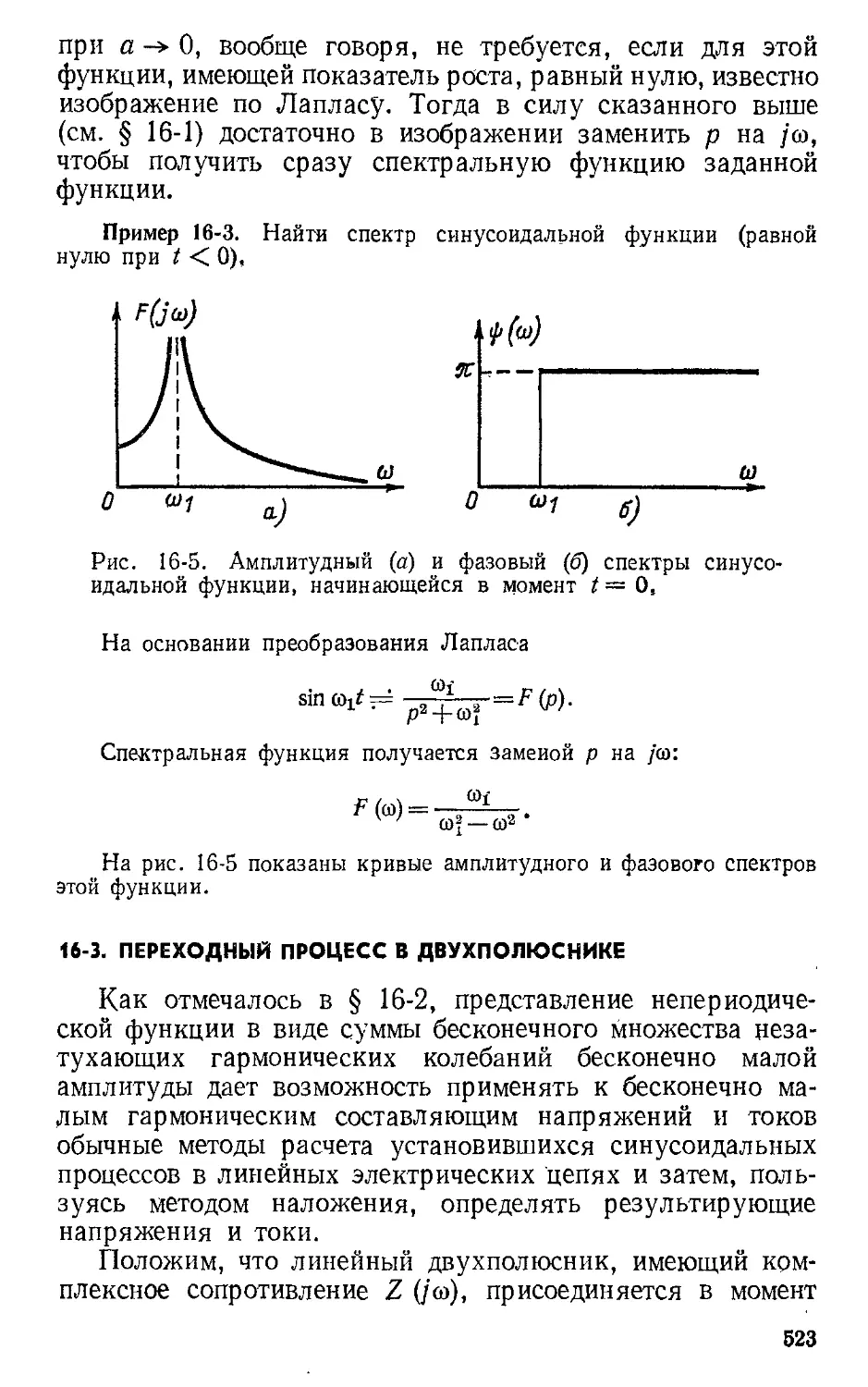
Теги: электроэнергетика электротехника электроника
ISBN: 978-5-8114-0800-9
Год: 2009
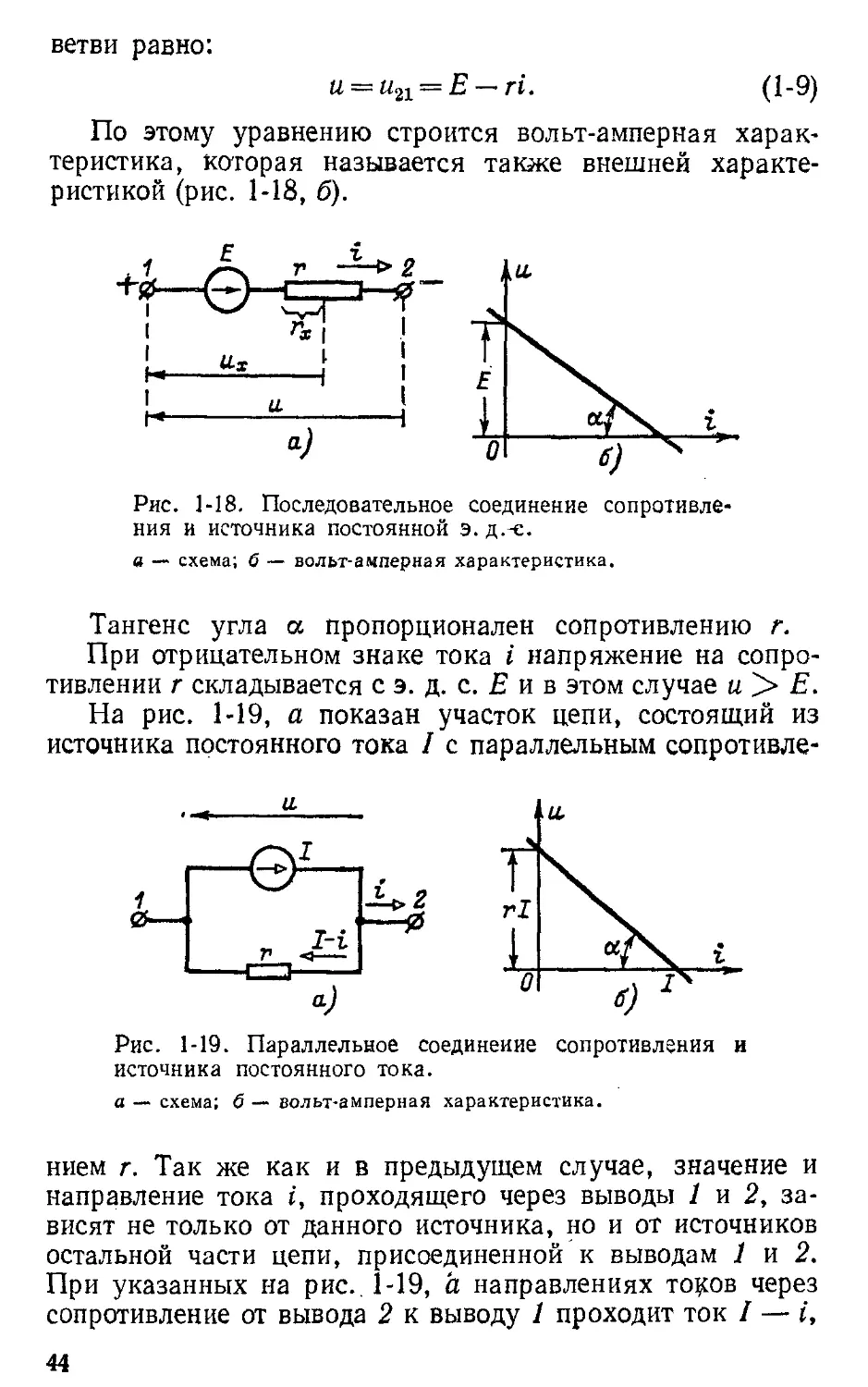
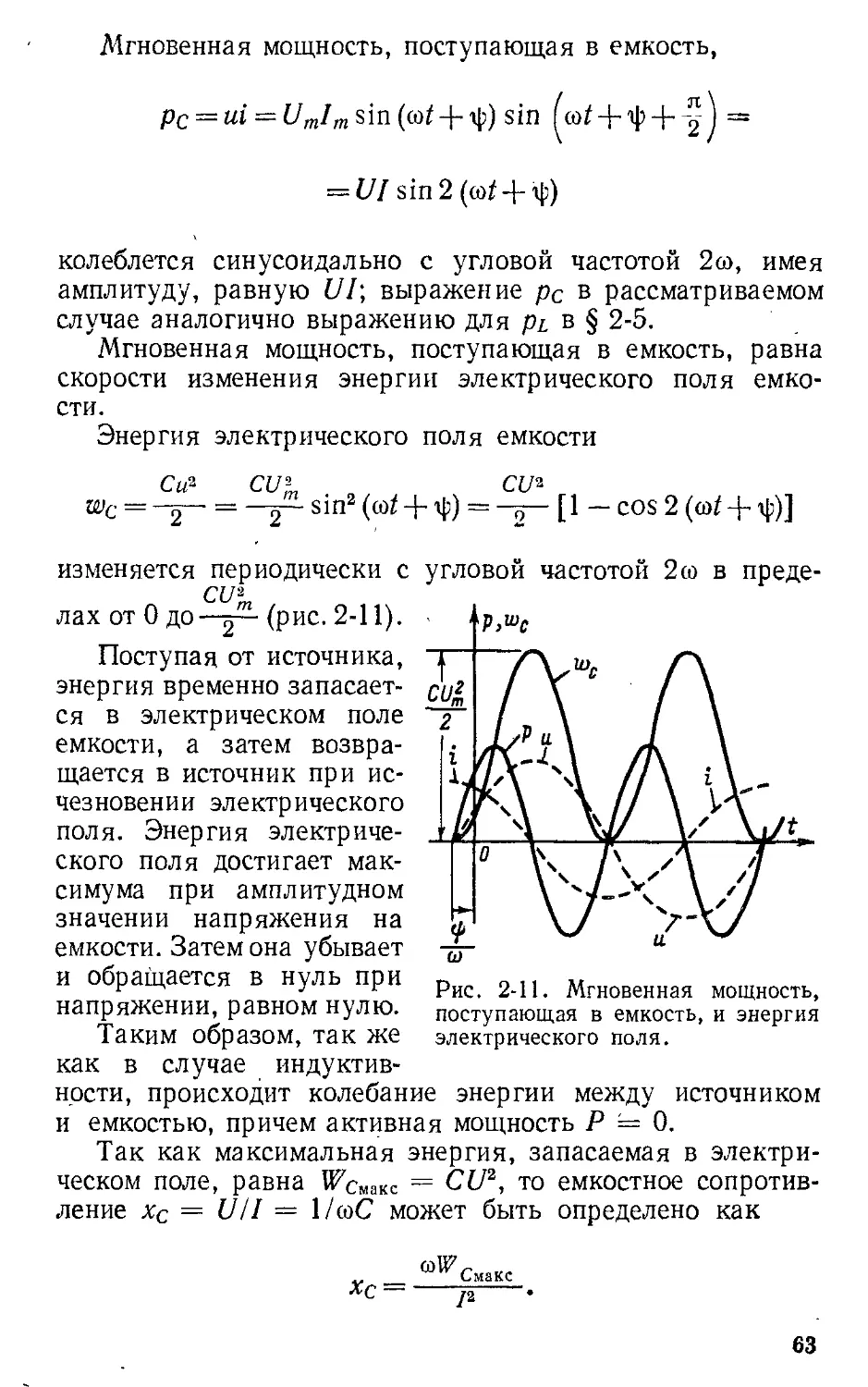
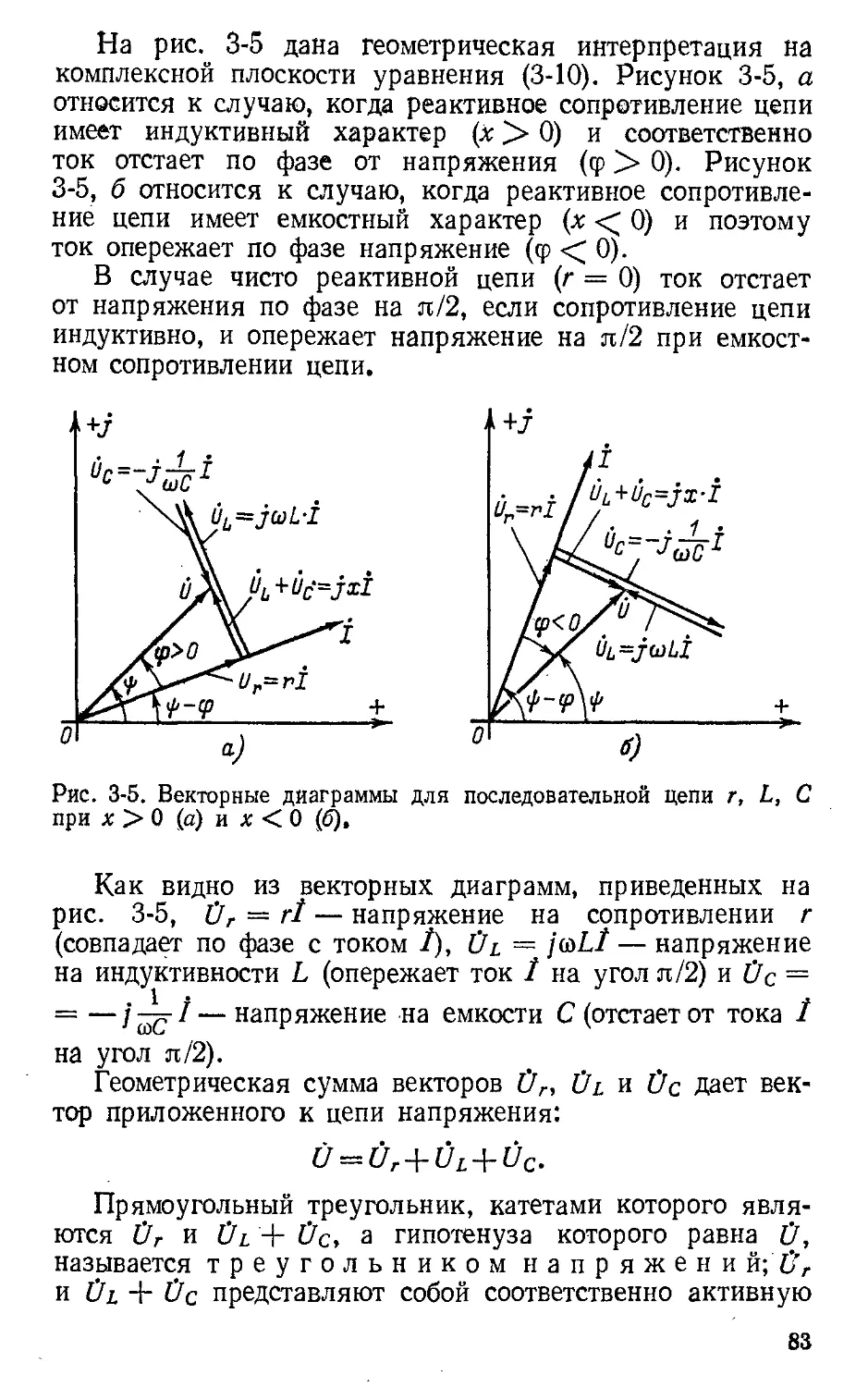
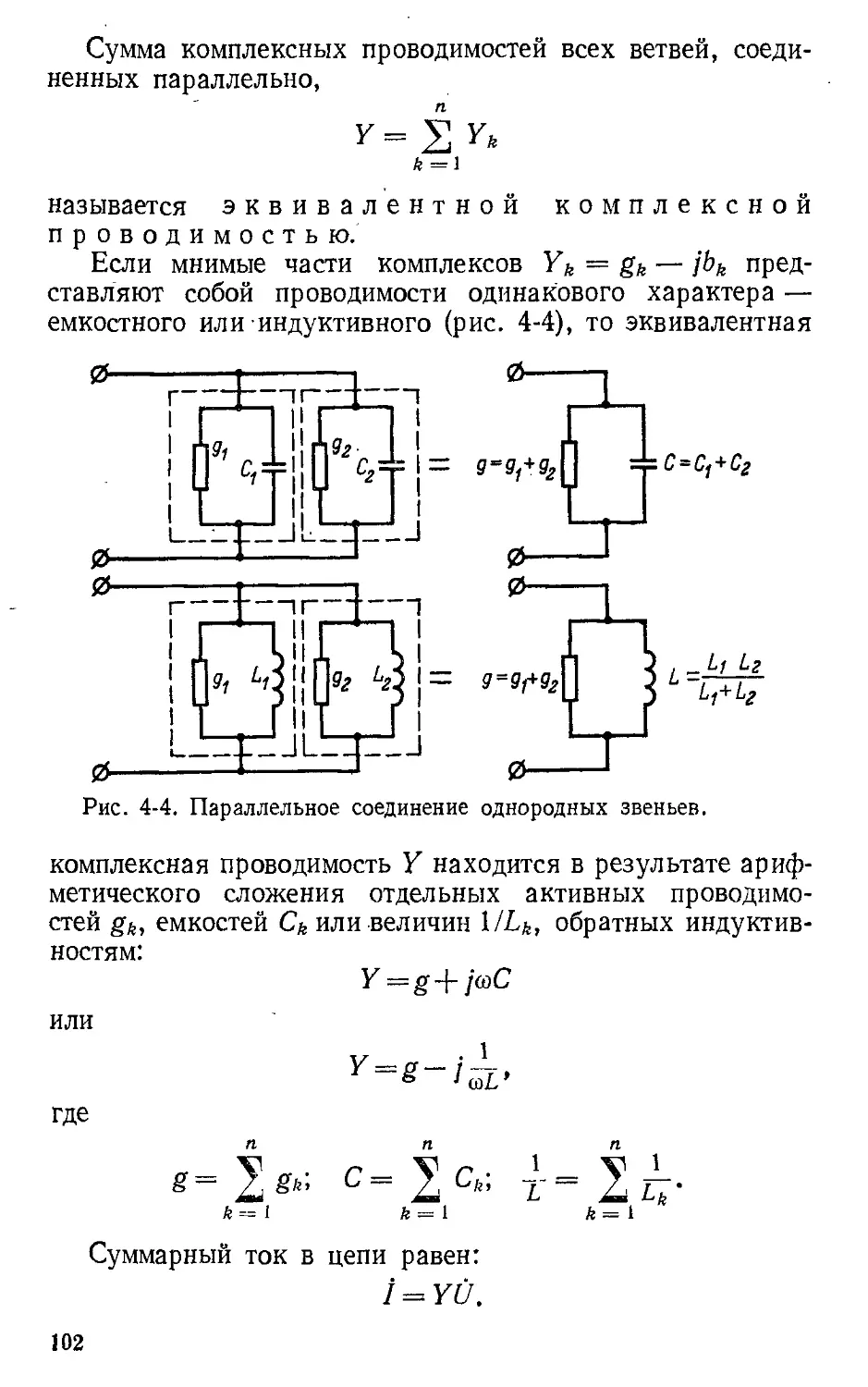
Текст
. ,. .
ТЕО - ЕТ ЧЕ КИЕ
.е 0:-1
- .
I
. -
.
. ..
.,
, ..
,..
..
,
@
"
х
.
l>
,
,..
,..
'-
ь
ЛАНЬ@
САНКТ.ПЕТЕРБУРr
МОСКВА
КРАСНОДАР
2009
r. и. АТАБЕКОВ
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ЭЛЕКТРОТЕХНИКИ
<:>
ЛИНЕИНЫЕ ЭЛЕКТРИЧЕСКИЕ UЕПИ
УЧЕБНОЕ ПОСОБИЕ
Издание седьмое,
стереотипное
ь
ЛАНЬ@
САНКТ.ПЕТЕРБУРr . МОСКВА. КРАСНОДАР
2009
ББК 31.21
А92
Атабеков r. и.
А 92 Теоретические основы электротехники. Линейные
электрические цепи: Учебное пособие. 7
e изд., стер.
СПб.: Издательство
Ланы, 2009.
592 с.: ил.
(Учеб
ники для вузов. Специальная литература).
ISBN 978
5
8114
0800
9
в учебном пособии рассмотрены основные свойства линейных
электрических цепей, электромаrнитные процессы в них и инженер
ные методы расчета. Рассмотрены цепи однофазноrо, трехфазноrо и
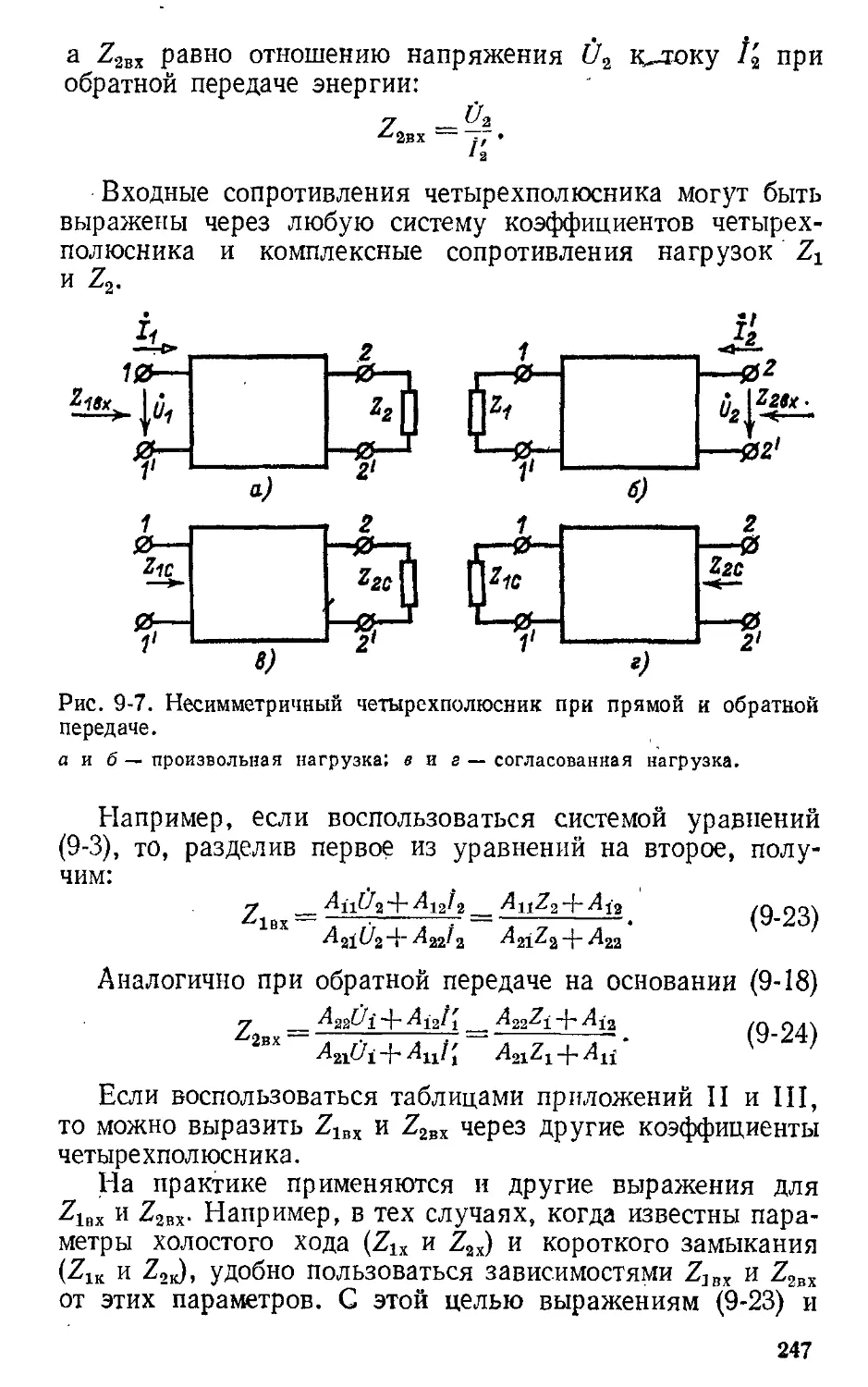
несинусоидальноrо тока, четырехполюсники и электрические фильт
ры, цепи с распределенными параметрами, переходные процессы и
синтез электрических цепей. Каждая rлава снабжена задачами и BO
просами для самопроверки. Рассмотрен машинный метод расчета элек
трических цепей.
Учебное пособие предназначено для студентов университетов и
технических вузов, обучающихся по электротехническим и радиотех
ническим специальностям.
ББК 31.21
ЛР NQ 065466 от 21.10.97
rиrиенический сертификат 78.01.07.953.П.004173.04.07
от 26.04.2007 r., выдан цrсэн в СПб
Изда тельство «ЛАНЬ,)
lan@lpbl.spb.ru; www.lanbook.com
192029, Санкт
Петербурr, Общественный пер., 5.
Тел./факс: (812)412
29
35, 412
05
97, 412
92
72.
Бесплатный звонок по России: 8
800
700
40
71
Подписано Б печать 28.04.09.
Бумаrа офсетная. rарнитура Литературная. Формат 84х108 1/32'
Печать офсетная. Усл. п. л. 31,08. Тираж 1500 экз.
3аказ N2 1331.
Отпечатано Б полном соответствии
с качеством предоставленных диапозитивов
Б ОАО <(Издательско
полиrрафическое предприятие «Правда Севера».
163002, r. Арханrельск, пр. НОБrородский, д. 32.
Тел./факс (8182) 64
14
54; www.ippps.ru
Обложка
А ю. ЛАПШИН
@ Издательство . Лань,} ,2009
@r. И. Атабеков, наследники, 2009
@Издательство .Лань,},
художественное оформление, 2009
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Настоящий учебник по курсу Йеоретические основы
электротехники» (ТОЭ) предназначен для студентов элек
тромеханических и радиотехнических специальностей, изу
чающих этот Rypc с отрывом или без отрыва от производ
ства. Он может также служить руководством для инженерно
технических работников, повышающих уровень теорети
ческих знаний.
Действующая в настоящее время проrрамма курса
ТОЭ.. утвержденная ,учебно
меТdдическим управлением по
вузам Минвуза СССР в 1964 r. для инженерно
техниче
ских ,специальностей высших учебных заведений, опре
деляет совокупность вопросов, составляющих содержание
курса. Курс ТОЭ должен читаться в соответствии с мето-
дикой, принятой кафедрой ТОЭ данноrо вуза, причем
в зависимости от имеющихся специальностей и учебных
планов института отдельные разделы проrраммы MorYT
излаrаться более расширенно или более сжато; очеред
ность ра
делов курса может варьироват,ься, Требуемая
степень детализации изложения тех или иных вопросов
устанавливается кафедрой ТОЭ по соrласованию со спе
циальными кафедрами данноrо вуза.
Теоретические основы электротехники представляют
собой непрерывно развиваюшуюся и обоrащающуюся HO
Выми сведениями дисциплину. По своему содержанию
курс ТОЭ разделяется на три явно выраженные части.
Первая часть охватывает теорию линейных электриче
ских цепей, вторая
теорию нешшейных цепей и TJ?e
тья
теорию электромаrнитноrо поля. В связи с этим и
учебник выпускается в трех частях, каждая из которых
содержит соответственную часть курса.
Деление теории цепей по принципу линейности и не-
линейности
естественный результат развития СОБре
менной электротехники и смежных с нею отраслей зна
ний; оно продиктовано спецификой нелинейных задач и
возросшим значением нелинейной электротехники в науке
6
и технике. В проrрамме курса 10Э специально Отмечено,
что теория нелинейных цепей выделена в самостоятель
ную часть в Связи с исключительно большим значением
нелинейных цепей во всех областях современной электро-
техники и в первую очередь в автоматике, вычислительной
технике, радиотехнике, элеКТРОНlIке и измерительной
технике.
Вместе с тем изучение нелинейных цепей после про
хождения теории линейных электрических цепей соrла-
суется и с принципом перехода от простоrо к сложному:
нелинейные задачи, как правило, сложнее линейных и
требуют предварительноrо знания теории линейных элек-
трических цепей.
При решении вопроса о содержании и методике изло-
жения отдельных разделов курса тоэ необходимо у'!И
тывать современный уровень Физико-математической под-
rотовки в средней и высшей школе.
Первоначальные сведения по электричеству, MarHe-
тизму и их практиче.скому применению учащиеся сред-
ней школы черпают из курсов физики и электротехники.
В последующем в высшей школе эти сведения уrлубляются
и расширяются Б курсе физики, действующая проrрамма
KOToporo для высших технических учебных заведений
предусматривает достаточно подробное изучение разделов
электростатики, постоянноrо тока и электромаrнетизма.
Поэтому при написании настоящеrо учебника учитывалось,
что комплекс знаний в области электричества и MarHe-
ТИзМа, приобретенныЙ учащимися до прохождения тоэ,
вполне достаточен для усвоения первой части тоэ
тео-
рии JшнеЙных электрических цепеЙ.
Устранение излишнеrо параллелизма и непроизводи
тельноЙ затрат,Ы времени на повторение некоторых вопро
сов, проЙденных в среднеЙ школе и по курсу физики в 1fН.
ституте, дает возможность освободить часть времени в курсе
тоэ для изучения новых важных вопросов современной
теоретической электротехники.
С друrой стороны, постановка математическоrо обра
зования в техниче.ских вузах с каЖДЫМ rодом все полнее
учитывает необходимость усиления математической ПОk
rотовки учащихся по соответствующим разделам мате-
матическоrо анализа (Специальные функции, матрицы,
преобразоваlIИЯ Фурье и Лапласа, функции комплексноrо
переменноrо и др.). Эrо обстоятельство позволяет изла-
raTh и изучать курс тоэ ца должном научно-техническом
7
уровне с привлечс:нием матема1'ическоrо аппарата, который
ранее в курсе тоэ либо вовсе не использовался, либо
давался в дополнительных rлавах курса тоэ, значительно
увеличивая ero объем (например, теория комплексных
чисел, теория вычетов, основы BeKTopHoro анализа и др.).
Настоящая, первая, часть курса тоэ, посвященная
линейным электрическим цепям, начинается с KpaTKoro
напоминания основных физических явлений и законов
электрических цепей и основных понятий, относящихся
К электрическим и маrнитным полям, В начале курса рас-
сматриваются такие основные вопросы, как положитель-
ные направления тока и напряжения; элементы и пара-
. метры электрической цепи; представление электротехни-
ческих устройств идеализированными схемами замещения
и т, п.
Читатель постепенно вводится в Kpyr вопросов, от НО-
сящихся К анализу линейных электрических цепей. Вна-
чале поясняются основные свойства простейших элект-
рических цепей синусоидальноrо тока, векторные диа-
траммы и комплексная форма расчета. Методика расчета
. простейших электрических цепей постоянноrо тока, уже
известная учащимся, в учебнике не повторяется,
ПоследОВательно накапливая сведения о преобразова-
ниях электрических схем, резонансных цепях и reoMeT-
рических местах на комплексной плоскости, учащиеся
ПОДrотавливаются к сознательному выполнению лабора-
торных работ и усвоению общих Teope
и методов расчета
сложных электрических цепей. Последние даются в общей
форме, применимой для цепеЙ постоянноrо и переменноrо
тока.
Вслед за теорией четырехполюсника приводится тео-
рия электрических фильтров, рассматриваемых, как част-
ные случаи четырехполюсника. Трехфазной цепью завер-
шается изучение синусоидальных режимов в линеЙных
цепях.
Периодические несинусоидальные процессы ИСС,7Iедуются
с помощью рядов Фурье, а после изучения переходных
процессов решения даются и в замкнутой форме.
В rлаве, посвященной применению преобразования
Лапласа, напоминаются основные теоремы и своЙства
преобразования Лапласа.. rлавное внимание уделяется
не доказательствам формул, которые должны быть из-
вестны учащимся из курса высшей математики, а прак-
тическому приложению этих формул к расчету переход-
8
ных процессов в линейных электрических цепях. PaCCMOT
рение преобразования Фурье как частноrо случая пре
образования Лапласа облеrчает исследование спектральных
характеристик и использование их для расчета переходных
процессов.
Первая часть курса завершается ознакомлением с син
тезом линейных электрических цепей.
В книrе приняты термины, рекомендованные КОМИ
тетом технической терминолоrии АН СССР. Для озна-
комления учащихся с определениями терминов, приве
денными в сборнике «Терминолоrиятеоретической электроте
хники» (ИЗkВО АН СССР, 1958,отв. редактор член-корр.
АН СССР Л. Р. Нейман), в сносках даны определения
основных понятий, заимствованные из этоrо сборника (сок-
ращенно и'менуемоrо ТТЭ) 1.
Буквенные обозначения в книrе приведены в COOTBeT
ствии с [ОСТ ,1494-61, а условные rрафические обозначе
ния для электрических cxeM,
в соответствии с
[ОСТ 7624-622.
В курсе применена Международная система единиц
(СИ) по [ОСТ 9867-61, включающая в себя электриче
ские и маrнитные единицы абсолютной практической
системы МКСА.
Уделено внимание сочетанию математичес'ких BЫBO
дОВ с физическими представлениями; изучение методов
расчета сопровождается рассмотрением физической CTO
роны явлений, причем содержание материала и порядок
ero изложения таковы, что учащийся лишь 'постепенно
переходит от более простых вопросов к более сложным.
Для облеrчения усвоения курса при заочном обуче-
нии основные положения теории иллюстрированы при
мерами, объем и содержание которых рассчитаны на то,
чтобы охватить принципиально важные разделы курса.
Кроме Toro, каждая rлава учебника снабжена вопросами
для самопроверки и задачами (с, ответами), которые уча
щимся предлаrается выполнить самостоятельно.
Студентам, в особенности занимающимся заочно, не
всеrда удается ОТЛИЧить все принципиальное и наиболее
существенное в предмете от менее важноrо. В связи с этим
1 В пятом издании терминолоrия была уточнена в COOTBeT
ствии с [ОСТ 19880-74. Электротехника. Основные понятия. Термины
и определения. (П рим. ред.)
2 В настоящее время [ОСТ 7624
62 заменен системой [ОСТ Еди-
ная система конструкторской документации. (П риА!. ред.)
9
при изложении материала в учебнике по мере необходи
мости оттенены курсивным шрифтом НЛII словесными ука-
заНI1ЯМИ принципиальные положения как данноrо курса,
T
K и последующих дисциплин.
Параrрафы и отдельные места, имеющие подчиненное
Или rtрикладное значение, набраны петитом.
В _ третьем издании в Ю-lиrу виесен ряд исправлений
и Д ' обавлений ( Е:.. 1 -5 1 -6 3-4 4.3 5-2 7-1 7-1 О 8-9
8-11
'::1 , , , , , , ,
и др.).
Автор rлубоко признателен коллективу кафедры тео-
ретической электротехники l\1ocKoBcKoro ордена Ленина
авиациош/оrо института имени Cepro Орджоникидзе И
рецензентам проф. В. Ю. Ломоносову и доц. Л. И. Столов)!
3<1 множество ценных замеЧаний и советов, СПQсобство"
вавших улучшению книrи.
Т. И. АТАБЕl(ОВ
успОВНЫЕ - ОSОЗНА ЧЕНИЯ
А
параметр четырехполюсника; обозначение фа:)ы трехфаз-
ной цепи;
а
собственное затухание четырехполюсника; фазовыЙ опе.
р атор e)120 Q ;
В
параметр четырехполюсника; обозначение фазы трехфазной
цепи; маrнитная индукция;
Ь
реактивная проводимость; коэффициент фазы четырехпо-
люсника;
Ь С
емкостная ПРОВОДИМОСТЬ;
Ь!.
индуктивная проrюдимость;
С
el\1KocTb; обозначение фазы Тi'ехфаююй цепи;
с
скорость света в пустоте (примерно 3 Х 108 м/с); деЦСТ6И-
телЬная часть комплексной частоты;
Е
постоянная э. Д. с.; действующее ЗН;Jчеиие переменвой
. э. Д. с.;
Е
комплексная э. Д. с.;
е
MrBoBeHHoe значение э. д, С.; основание натуральных ло-
rарифмов (примерно 2,718); -
F (jш)
спектральная функция;
F (р)
изображение фуикции по Лапласу; функция комплексной
частоты;
t
частота периодической функции;
O,
параметр четырехполюсника;
g
активная ПРОВОДИМОСТЬ; параметр чеТЬjрехполюсника (мера
или коэффициент передачи);
Н
параметр четырехполюсника;
1
постоянный ток; действующий переменный ток;
1
комплексный ТО/<;
i
мrИQвенный ток;
j==V
l;
К/
коэффициент передачи по току;
кu
коэффициент передачи по напряжению;
k
коэффициент связи; постоянная фильтра;
L
индуктивность;
Ls
индуктивность рассеяния;
М
взаимная индуктивность;
т
постоянная фильтра; индекс, обозначающиЙ амплитуду
переменной веЛИЧИfjЫ;
/l
коэффициент трансформации. коэффициеf!Т отражения;
р
активная МОЩНОСТЬ;
р
мrновенная МОЩНОСТЬ; комплексная частота;
11
Q
реак.тивная мощность; добротность катушки, конденсатора, _
контура;
q
электрический заряд (мrновенный);
,
активное сопротивление;
S
полная . мощность; площадь поперечноrо сечения;
т
период;
t
время; ,
и
Постоянное напряжение; действующее переменное напря-
жение;
(J
комплексное напряжение;
и
мrновеиное напряжение;
W
энерrия (постоянная);
W
число витков, мrновеННqЯ энерrия;
w и W c
энерrия, запасенная в индуктивности и емкости;
Х
реактивное сопротивление;
ХС
емкостное сопротивление;
X L
индуктивное сопротивление;
Хм
сопротивление взаимной индукции;
У
комплексная проводимость; параметр четырехполюсника;
Уа
входная проводимость i-ro контура (ветви) или узла;
У ki
передаточная проводимость контуров (ветвей) или узлов;
УН
собственная проводимость ветвей, сходящихся в узле;
Y rikJ
общая проводимость; между узлами i и k; ,
У (р)
операторная проводимость;
у
полная проводимость (модуль комплексной проводимости);
Z
комплексное сопротивление; параметр четырехполюсника;
ZB
комплексное волновое сопротивление линии;
Zc
характеристическое сопротивление;
Zii
входное сопротивление i-ro узла или контура (ветви);
Zki
передаточное сопротивление узлов или контуров (ветвей)
i и k;
ZriiJ
собственное сопротивление контура i;
ZrikJ
общее сопротивление контуров i и k;
Z (р)
обобщенное (операторное) сопротивление;
z
полное сопротивление (модуль комплексноrо сопротивле-
ния);
а;
коэффициент ослабления линии;
f3
коэффициеит фазы лииии; .
'v
коЭффициент распростраиения линии;
б
уrол, потерь; относитеЛЬ!fая расстройка частоты;
11
определитель системы уравнений;
l1 ik
алrебраическое дополнение элемента i-й строки k-ro столбца;
е а
абсолютная диэлектрическая проницаемость;
ft
температура;
А
маrнитная проводимость;
л
длина волны;
I-'-а
абсолютная маrнитная проннцаемость;
р
удельное электрическое сопротивление; воЛ!fовое сопротив'
ление контура;
1:
время, постоянная времени;
Ф
маrнитный поток;
<р
фазовый сдвиr; .
чr
потокосцепление;
:ф
начальная фаза;
J2
(i)
уrловая частота;
1,2 и О
индексы, обозначающие составляющие прямой, обратной
и нулевой последовательностей.
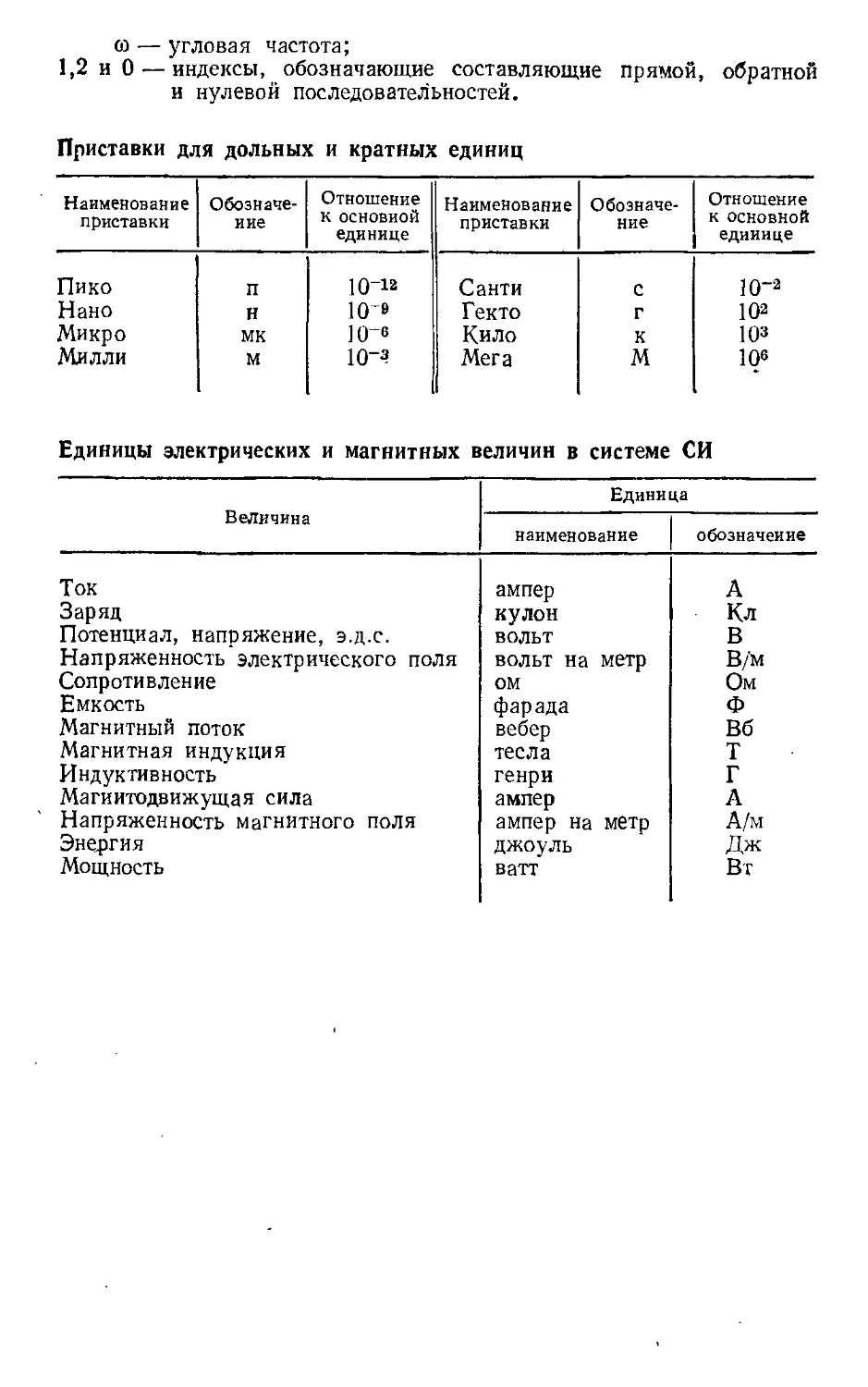
Приставки для ДОЛЬНЫХ и кратных единиц
Наименование I Обозначе- I Отношение
приставки иие к основиой
единице
Отношение
к основной
едииице
Наименование I Обозначе-
приставки ние
Пико
Нано
Микро
.милли
л
н
мк
М
10
12
10
P
]0
6
10
1!
Санти
[екто
к.ило
Mera
с
r
к
М
10
2
102
103
106
Единицы электрических и маrнитных величин в системе СИ
ВелИЧИна
обозначеиие
Единица
наименование
Ток
Заряд
Потенциал, напряжение, Э.Д,С.
Напряженность электрическоrо поля
Сопротивление
Емкость
Маrнитный лоток
Маrнитная индукция
Индуктивность
Маrиитодаижущая сила
Напряженность маrНИТНоrо поля
Эне-рrия
Мощность
ампер
кулон
вольт
вольт на метр
ом
фарада
вебер
тесла
rенри
ампер
ампер на метр
джоуль
аатт
А
к.л
В
В/м
ОМ
ф
Вб
Т
f
А
А/м
Дж
Вт
ВВЕДЕНИЕ
Роль и значение "Электрической энерrии в развитии
нарОДlюrо хозяйства общеизвестны. Электричество стало
основой развития всех отраслей техники, базой для раз
вития промышленности, транспорта, сельскоrо хозяйства,
электросвязи; оно стало основой комплексной механиза-
ции и автоматизации производственных процессов. Элек-
тричество и радио прочно вошли в быт. Исключительно
важное значение они имеют н в современной авиации;,
установленная мощность ИСТОЧН!1КОВ электрическоЙ энер
rии на самолетах, .исчислявшаяся долями киловатта в Ha
чальный период ра$ВИТИЯ авиации, в настоящее время
достиrает сотен киловатт на крупных самолетах. Продви
жение науки по пути освоения космическоrо пространства
и изучения планет солнечной системы было бы невозмож-
ным без применения электричества и радио.
Столь широкому распространению электриче<:кой энер-
rии во всех областях Народноrо хозяйства и всех отраслях
техники способствовали удобство пер
дачи электромаrнит-
ной энерrии на расстоянии и удобство преобразования
ее
в друrие формы энерrии: механическую, световую, тепло
вую, химическую и др.
Классики марксизма
ленинизма * с первых же шаrов
развития науки об электричестве предсказали ей великое
будущее. Известно, с каким пристальным вниманием сле-
ди-ли К. Маркс и Ф. Энrельс за опытами по передаче элек-
троэнерrии на расстояние, предсказав orpoMHoe револю
ционное значение применения электричества в промышлен
насти. В 1850 r. К. Маркс, обращаясь к В. Либкнехту,
rоворил: «Царствованйе ero величества пара, перевернув-
шеrо мир в прошлом столетии, окончилось; на ero место
станет неизмеримо более революционная сила
электри-
ческая иск ра». rоворя о передаче электрической энерrии
* Ссылки на док)'менты Съездов и Пленумов КПСС, а также на труды
В, И, Ленина, К. Маркса и ф, Энrельса в учебных изданиях были
обязательны для советскorо периода,
14
на расстояние, Ф. Энrельс в 1883 r. писал Э. Бернштейну,
что «это открытие окончательно освобождает промышлен
ность почти от всяких rраниц, пол'аrаемых местными усло-
виями; делает возможныМ использование также и самой
отдаленной водяной энерrии, и если в начале ОНо будет
ПОЛеЗНО только для еородО8, то в конце концов оно станет
самым мощным рычаrом для устранения противоположно-
сти между rородом и деревнеЙ. Совершенно ясно, однаКО,
что блаrодаря этому производительные силы настолько
вырастут, что управление ими будет все более и более lte
под силу буржуазии» 1.
Энерrетическая база дореволюционной России бьrла
крайне слаба. С первых дней существования Советской
власти Коммунистическая партия придавала решающее
ЗНачеНИе делу электрификации страны для победы HoBoro
общественноrо строя. Всем памятны Слова В. И. Ленина
«Коммунизм
это есть Советская власть плюс электри
фикация всей страны». Выступая в 1920 r. на VIII Bcepoc
сийском съезде Советов, В. И. Ленин rоворил: «...если
Россия покроется rустою сетью электрических станций и
мощных технических оборудований-, то наше коммунисти-
чеСКое Хозяйственное строительство станет образцом для
rрядуtцей социалистичеСJ\ОЙ Европы и Азии» 2. ,
Общеизвестно, что первый хозяйственный план, [осу-
дарственныЙ план элеКТРИфИJ\ации России (rоэлРо),
был назван В. и. Лениным второй проrраммой партии.
Блаrодаря преимуществам социалистической системы
планирования и раЗБИТИЯ нарОДНоrо хозяйства, обеспечив
ШИМ успешное выполнеНfIе и перевыполнение пятилетних
планов, в СССР создана мощная энерrетическая база,
которая дает возМожность быстрыми темпами повышать
электроснабжение и производительность труда во всех
отраслях промышлеНIЮСТИ и селЬскоr6 хозяйства. По про-
изводству электроэнерrии наша страна вылаa на первое
место в Европе и на второе в мире.
В СССР сооружена и rlущеllа в 1954 r. первая в мире
электрическая станция, используЮщая атомную энерrию.
Ведущая роль электрифиющии в развйтии всех ()'1'
раслей НарОДНоrо хозяйства, в осуществлении Bcero со-
BpeMeHHoro техническоrо проrресса раскрыта в Проrрамме
КПСС, принятой XXII съездом КПСС.
1 :К. м а р к с И Ф. Э н r, е ль С. Соч. 2-е ИЗД., т. 35, с. 374.
2 В. И, Л е н И н. Полн. собр. соЧ, 5-е ИЗД., т. 42, с. 161.
15
Советский Союз вступил в решающую стадию претво-
рения в жизнь идеи В. И. Ленина о сплошной электрифи-
кации страны. Планом развития народноrо хозяйства
СССР на 1976
1980 rr. предусмотрено довести производ-
ство электроэнерrии в 1980 r. до 1380 млрд. кВт .ч. Одно-
временно с дальнейшей электрификацией промышленности
и транспорта, автоматизацией производственных процес-
сов и т. п. будут также электрифицированы все колхозы,
совхозы и рабочие поселки. Создается и развивается Единая
энерrетическая система СССР, которая позвОляет перебра-
сывать энерrию из восточных районов страны в ее европей-
скую часть и связана с энерrосистемами друrих социали-
стических стран.
Большое внимание уделяется освоению новых источ-
ников энерrии и новых способов ее получения, в частности
решению проблемы прямоrо преобразования различных
видов энерrии в электрическую.
Электрификация народноrо хозяйства была бы немыс-
лима без развития учения об электричестве. В течение XIX
и ХХ вв. учение об электричестве непрерывно развивалось,
причем электротехника на ранних ступенях развития
являлась разделом физики.
Первый трактат по электричеству, вышедший на рус-
ском языке в 1753 r., принадлежит отцу русской науки
М. В. Ломоносову. Ero «Слово о явлениях воздушных,
от электрической силы происходящих» явилось одной из
крупных работ в области электричества, написанных уче-
ными XVIII в.
Исследования Ломоносова и ero друrа Рихмана, а также
Франклина, [альвани, Вольта и др., ПРИ:Е\едшие к изобре-
тению rромоотвода и источников электрической энерrии
(вольтова столба, rальванических элементов), положили
начало систематическому изучению электрических явлений.
В. В. Петров, производя опыты в электрической цепи,
обнаружил и исследовал в 1802 r. явление электрической
дуrи между уrольными электродами при атмосферном
давлении. Результаты этих исследований были опубли-
кованы им в книrе «Известие о rальвани-вольтовских
опытах» (1803 r.). '
В 1819 r. Эрстед обнаружил механическое воздейст-
вие электрическоrо тока на маrнитную стрелку, а в 1820 r.
Ампер открыл маrнитные свойства соленоида с током.
Таким образом, было установлено, что прохождение тока
сопровождается маrнитными явлениями.
16
в 1831 r. М. Фарадей открыл и описал явление элект
ромаrнитной индукции. В 1833 r. Э. Х. Ленц установил
правило определения индуктированноrо тока, выражаю
щее фундаментальный принцип электродинамики
прин
цип электромаrнитной инерции. В 1844 r. Ленцем и незави
симо от Hero Джоулем был открыт важный закон электро
техники, извёстный под названием закона Джоуля
Ленца.
На основании теоретическоrо обобщения эксперимен
тальных данных по электричеству и маrнетизму во BTO
рой половине XIX в. Д. Максвелл выдвинул rипотезу
существования электромаrнитноrо поля излучения. Раз
работанная им теория электромаrнитноrо поля изложена
в ero труде «Трактат об электричестве и маrнетизме»
(1873 r.).
В 1888 r. r. rерц опубликовал свои работы, в которых
экспериментально доказал существование поля излуче
ния. Однако r. rерц и современные ему физики, зани
мавшиеся исследованием электромаrнитноrо поля, не счи
тали ВОЗможным выйти за пределы своих лабораторий и
применить электромаrнитные волны для беСПРОВОЛО1jНОЙ
связи.
Такую задачу впервые поставил и блестяще разрешил
Выдающийся русский ученый Александр Степанович Попов,
практически осуществивший в 1895 r. первую в мире радио
связь. Изобретение радио открыло новую эру в истории
чеЛQвечества.
В России формирование самостоятельной дисциплины
«Теоретическое основы электротехники» относится к концу
XIX и началу ХХ вв. В 1904 r. проф В. Ф. Миткевич начал
читать курс «Теория электрических и маrнитных явлений»
в Петербурrском политехническом институте. Примерно
тоrда же началась подrотовка инженеров электротехниче
ской специальности в Московском высшем техническом
училище, rДе проф. К. А. Kpyr приступил в 1905 r. к чте
нию курса «Теория переменных токов».
Предметом курса «Теоретические осщ>вы электротех
ники» является изучение как с качественной, так и с KO
личественной сторон электромаrнитных процессов, про
исходящих в цепях и полях. Этот курс, базирующийся
на курсах физики и высшей математики, содержит инже
нерные методы расчета и анализа, применимые к широ
кому классу современных электротехнических устройств.
Он имеет исключительно важное значение для формиро
17
вания научноrо круrозора специатIСТОВ по электротех-
нике и радиотехнике и на нем основываются все спецl,-
альные электротехнические и радиотехнические дисци-
плины.
В курсе ТОЭ применяlOТСЯ два способа оI1исания элек-
трических и маrнитных явлений: при помощи понятий Тео-
рии цепеЙ и теории поля. Выбор Toro или друrоrо способа
диктуется условиями постановки задачи.
т е о р и я цеп е й исходит из приближенной замены
реальноrо электротехническоrо устройства идеализирован-
ной схемой замещения. Эта схема содержит участки цепи,
на которых опредмяlOТСЯ искомые напряжения и токи.
Теория цепей позволяет с достаточной для инженер-
ной практики точностью определять неПОСр,едственно на-
пряжение между концами рассматриваемоrо участка цепи,
не прибеrая к вычислению ero между промежуточными
точками. Токи также находят непосредственно, без вычисле-
ния их плотностей в различных точках сечения проводника.
т е о р и я п о л я изучает изменение электрических и
маrнитных величин от точки к точке в пространстве и вре-
мени. Она исследует напряженности электрическоrо и мзr-
нитноro полей и с ИХ помощью такие явления, как излуче"
ние электромаrнитной энерrии, распределение объемных
зарядов, плотностей токов и т. п.
Разrраничение областей применеlIия теории. Цепей и
теории поля является условным. Например, процессы рас-
пространения электрических сиrналов в линиях электрcr
проводной связи. исследуются как методами теQрИИ цепеЙ,
так и методами теории поля. Здесь сочетаюТся Такие по-
нятия, как напряжение и ток, характерные для Теории
цепей, и скорость распространения электромаrнитной эиер-
rии, характерная для теории поля.
Первая и вторая части настоящеro курса посвященыI
теории цепей; третья часть посвящена теории поля.
rЛАВА ПЕРВАЯ
ОСНОВНЫЕ ЗАКОНЫ,
ЭЛЕМЕНТЫ. И ПАРАМЕТРЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕй
1.1. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
Э л е к т р и ч е с к о й цеп ь ю называется совокуп-
ность устройств и объектов, образующих путь для элек
трическоrо тока, электромаrнитные процессыI в которых
MorYT быть описаны с riо
ощыо понятий об э. д. с., напря
жении и токе. В общем случае электрическая цепь состоит
из источuиков И приемников электрической энерrии и проме-
жуточных звеньев (ПРОБОДОВ, аппаратов), связывающих
источники с приемниками.
И с т о ч н и к а м и электрической эщ
рrии являются
химические источники тока, термоэлементы, rенераторы
и друrие устройства, в которых происходит процесс пре
образования химической, молекулярно-кинетической, теп
лавой, механической или друrоrо вида энерrии в электри-
ческую. К источникам можно отнести и приемные антенны,
в которых в отличие от перечисленных выше устройств
не происходит изменения вида энерrии.
При е м н и к а м и электрической. энерrии, или так
называемой наrрузкой,. служат электрические лампы, элек-
тронаrревательные приборы, электрические двиrатели и
друrие устройства, в которых электрическая энерrия прев-
ращается в световую, тепловую, механическую и др. К на-
rрузкам относяТся и передающие aHTef[HbI, излучающие
электромаrнитную энерrию в пространство.
Расчеты электрических цепей и исследования процес-
сов, происходящих в них, основываются на различных
допущениях и некоторой идеализации реальных объектов
электрических цепей. П о Д э л е м е н т а м и в теории
электрических цепей подразумеваются обычно не физи-
. чески существующие составные части электротехнических
19
устройств, а их идеализированные модели, которым тео-
ретически приписываются определенные электрические и
маrнитные свойства, так что они в совокупности прибли-
женно отображают явления, происходящие в реальных
устройствах. .
В теории электрических цепей различают активные и
пассивные элементы. А к т и в н ы м и э л е м е н т а м и
считаются источники электрической энерrии: источники
э. д. с. и источники тока. К п а с с и в н ы м э л е м е н -
т а м электрических цепей относятся сопротивления, ин-
дуктивности и емкости. Соответственно различают актив-
ные и пассивные цепи.
Эти важные понятия, лежащие в основе теоретической
электротехники, подробно рассмотрены ниже.
1-2. ПОЛОЖИТЕЛЬНЫЕ НАПРАВЛЕНИЯ ТОКА И НАПРЯЖЕНИЯ
Электрический ток в проводящей среде есть упорядо-
ченное движение электрическоrо заряда. Известно, что элек-
трический ток проводимости в металлах, так же как и в ва-
кууме, представляет собой перемещение отрицательно за-
ряженных частиц (электронов), а ток проводимости в элек-
тролитах и rазах
перемещение как положительно, так
и отрицательно заряженных частиц (ионов).
Электрическому току приписывается направление. Хотя
в общем случае ток представляет собой движение носителей
электрических зарядов Toro и друrоrо знаков в разные
стороны, однако за направление тока принимают направ-
ление перемещения положительных зарядов; это направ-
ление противоположно направлению движения отрица-
тельных зарядов.
Численно ток определяется как предел отношения ко-
личества электричества, переносимоrо заряженными ча-
стицами сквозь рассматриваемое поперечное сечение про-
водника за некоторый промежуток времени, к этому про-
межутку времени, коrда он стремится к нулю. Следова-
тельно, если обозначить через q количество электричества,
прошедшеrо через рассматриваемое сечение проводника
за время t, то MrHoBeHHoe значение тока, т. е. значение
ero в любой момент времени t, определится как производ-
ная q по t: i == dq/dt. Здесь q == q+ + q
, rде q+ И q
по-
ложительный и отрицательный заряды, переместившиеся
в противоположные стороны за время t.
20
в Международной системе единиц (СИ) i измеряется
в амперах 1 (А), q
в кулонах (Кл) или ампер-секундах
(А .с), t
в секундах (с).
Электрический ток может быть постоянным (неизме-
ияющимся) или переменным, т. е. изменяющимся в зави
симости от времени.
Направление тока характеризуется знаком тока. По-
Нятия положительный ток или отрицательный ток имеют
смысл, только если сравнивать направление тока в провод-
нике с некоторым заранее выбран-
ным ориентиром
так называемым
п о л о ж и т е л ь н ы м н а п р а в
1
2
л е н и е м. Ll.1Z
Положительное направление тока
выбирается проuзвольно; оно обычно
указывается стрелкой. Если в резуль
тате расчета тока, выполненноrо с
учетом выбранноrо положительноrо
направления, ток имеет знак плюс
(i> О), то это означает, что ero Ha
правление совпадает с выбранным положительным направ-
лением. В противном случае, коrда ток отрицателен (i < О),
он направлен противоположно.
Таким образом, выбранное для тока положительное
направление само по себе не означает направления, в ко-
тором перемещаются электрические заряды; оно только
придает определенный смысл знаку тока.
Изобразим некоторый участок электрической цепи,
через который проходит ток {, в виде прямоуrольника
и обозначим концы (выводы) этоrо участка цифрами 1
и 2 (рис. 1-1). Разность электрических потенциалов точек
1 и 2 представляет собой напряжение на данном участке
цепи 2. Напомним, что разность электрических потенциалов
...L.
)<
о( U.Z1
Рис. 1-1. Участок элек-
трической цепи с выб-
ранными положитель-
ными направлениями
тока и напряжения,
1 А м пер
величина неизменяющеrося тока, который, проходя
ПО двум параллельным прямолинейным проводникам бесконечной
длины и ничтожно малой площади сечения, расположенным на рас-
стоянии 1 м один от друrоrо в вакууме, вызвал бы между этими Про-
водииками силу, равную 2.1O
7 Н на каждый метр длины.
2 Э Л е к т р и ч е с к о е н а n р я ж е н и е
скалярная вели-
чина, равная линейному интеrралУ' напряженности электрическоrо
поля. Раз н о с т ь э Л е к т р и ч е с к и х п о т е н ц и а л о в
электрическое напряженне в безвихревом электрическом поле, харак-
теризующееся независимостью от выбора пути интеrрирования
(rOCT 19880-74). .
21
Or'Iределя
тся работой, затрачиваемой на перено
едиНИЧ-
Horo положительноrо заряда из ТОЧКИ 1 в точку 2.
Значение напряжения в любой текущий момент вре-
мени обозначается через и; оно может быть постоянным
или переменным. В системе СИ напряжение измеряется
в вольтах (В).
ДЛЯ придания определенноrо смысла знаку напряже-
ния на рассматриваемом участке цепи для напряжения,
так же как и для тока,. произвольно выбирается поло-
жительное направление. Чаще Bcero ero выбирают сов-
падающим с положительным направлением тока и ука-
зывают стрелкой.
В выбранном положительном направлении и отсчиты-
вается »апряжение. Пусть на рис. 1-1 отсчет напряже-
ния ведется от точки 1 к точке 2. Коrда потенциал точки 1
выше потенциала точки 2,
наI1ряжение положительно;
в противном случае оно отрицательно.
Для уяснения выбранноrо направления отсчета на-
пряжения можно вместО стрелки пользоваться обозначе-
нием с помощью индексов, при котором порядок располо-
жения индексов, соответствующих точкам цепи, отвечает
положительному направлению, выбранному для напряже-
ния. Так, применительно к рис. 1-1 напряжение, отсчиты-
ваемое в положительном направлении тока, равно и 12 .
Напряжение, отсчитываемое в обратном наI1равлении, имеет
ПРОТИВОПОЛОЖJIЫИ знак: и 2 1 ==
и12'
Двойное индексное обозначение возможно и для тока.
Например, i 12 обозначает 10К, который имеет I10ЛОЖl1тель-
ное направление на участке цеI1И от точки 1 к точке 2.
Однако на практике болршее распространение нашло Qбо-
значение с помощью стрелок.
Положительными направлениями токов и напряже-
ний пользуются при исследовании процессов, происхОдя-
щих в электротехнических устройствах, и расчете элект-
риче
ких цепей. Для краткости положительное направ-
ление будем называть просто наПравлением. ,
ОтчеТJIивое уяснение этих важных ПОЩIТий совершенно
обязательно для усвоения Bcero последующеrо материала.
и. MrHOBEHHASI МОЩНОСТЬ и ЭНЕрrиSl
Предположим, что через участок электрической цепи
(приемник энерrии) под воздействием приложенноrо на-
пряжения u проходит электрический заряд q. Совершае-
22
мая при этом элементарная работа, или, что то же, посту
пающая в nРIlеМIIИК элементарная энерrия, равна:
dw со= u dq == ui dt.
Производная энерrия по времени, т. е. скорость по
ступления в цепь электрической энерrии в данный момент
времени, представляет собой мrновенную мощность. Сле
довательно, мrновенная мощность, поступающая в при
еМI!ИК, равна произведению MrHoBeHHblX значений напря
жения и тока:
dw dq .
P==dt==U ([т==т.
Мrновенная мощность Р
величина алrебраическая;
значение ее положительно при одинаковых знаках и и
и отрицательно при разных знаках,
Если положительные направления для напряжения и
тока приняты совпадающими, то при Р > о энерrия посту
пает в приемник, а при Р < о она возвращается из pac
сматриваемоrо участка цепи к источнику.
Энерrиft, поступившая в приемник за промежуток Bpe
мени от t 1 до t 2 выражается интеrралом
"
w ==
Р dt.
t,
в отличие от мrновенной мощности р, которая может
иметь любой знак, энерrия, поступившая в приемник,
не может быть отрицательной.
В системе СИ работа и энерrия ИЗ)VIеряются в джоулях
(Дж), мощность
в ваттах (Вт).
1.4. СОП'ОТИВЛЕНИЕ
с о про т и в л е н и е м называется идеализированный
элемент цепи, приближенно заменяющий резистор \ в KO
тором происходит IIеобратимый процесс преобразования
электрической энерrии в теплоту. При этом терми1'I «сопро-
тивление» и соответствующее ему буквенное обозначение r
применя
ся как для обозначения caMoro элемента цепи,
так и для количественной оценки величины, равной OTHb
1 Стандартизованный в последние rоды термин «резистор» дает
возможность более ТОЧНd I1рllменять термин «СОПрd'tивление».
23
шению напряжения на данном элементе цепи к току, про-
ходящему через Hero:
Здесь предполаrается, что положительные направления
тока и напряжения совпадают; при этом знаки u и i одина-
ковы и r> О.
Величина g == 1/r, обратная сопротивлению, называется
про в о Д и м о с т ь ю. В системе СИ сопротивление r
измеряется в омах (Ом), а проводимость
в сименсах (См).
Формула (1-1) выражает закон Ома,
экспериментально установленный Омом в
1826 r.
Условное rрафическое изображение со-
противления (резистора) с указанием выб.
ранных положительных направлений тока
и напряжения приведено на рис. 1
2.
Мrновенная мощность, поступающая в сопротивление,
равна произведению MrHoBeHHbIx значений напряжения и
тока:
l'
Рис. 1
2. Услов
пое обозначение
сопротивления,
u
'==
.
t
(1
1)
Pr == ui == ri 2 == gu 2 .
Следовательно, параметр r может быть численно оп-
ределен как отношение мrновенной мощности к квадрату
MrHoBeHHoro тока, проходящеrо через сопротивление:
Pr
r==i2'
Электрическая энерrия, поступившая в сопротивление r
и превращенная в теплоту, наЧИН:ilЯ с HeKoToporo момента
времени, например, t == О, до рассматриваемоrо момента t,
равна:
t t t
W r ==
Pr dt ==
ri 2 dt ==
gu 2 dt.
О о о
В случае постоянноrо тока (i
/ == const) W r == r /Ч.
Превращение электрической энерrии W r В тепловую
впервые было доказано опытным путем Джоулем и Ленцем,
установившими тепловой ЭКВИвалент электрической энерrии,
равный 0,24 кал / Дж.
Выделение током тепловой энерrии впервые использо-
вано для целей освещения А. Н. Лодыrиным, создавшим
24
в 1873 r. лампу накаливания 1. Оно целесообразно ис-
пользуется в технике
электронarревательных приборах
и т. п. К вредным последствиям тепловоrо действия тока
относятся потери электрической энерrии В проводах, ма-
шинах, аппаратах, порча изоляции проводов от HarpeBa
и т. п.
Параметр r в общем случае зависит от тока i (напри-
мер, вследствие HarpeBa сопротивления током). Зависи-
мость напряжения на сопротивлении
от тока, проходящеrо через данное
сопротивление, называется в о л ь т -
амперной характеристи-
к о Й, которая в общем случае не-
линейна.
Если сопротивление r не зависит
от тока и ero направлеНия, то имеет
место прямая пропорциональность
между напряжением и током, Bыpa
жающая закон Ома. В этом случае
сопротивление называется л и н е Й - а
нелннейная; б
ли-
Н Ы м. На рис. 1-з показаны воЛЬТ- нейная.
амперные характеристики сопротив-
ления
неЛинейная (кривая а) и лиНейная (прямая 6).
В -этой книrе рассматриваются линейные сопротивления.
Очевидно, линейное сопротивление r пропорционально
TaHreHcy уrла наклона прямолинейной вольт-амперной
характеристики к оси тока:
r == !; == та АВ == !!!JL.. t а,
t т;ОВ т; g
u.
i
в
Рис. 1
3. Вольт
ампер-
ные характеристики
сопротивлен ий.
rде та и т;
масштабы нап'ряжения, В/мм, и тока, А/мм,
на чертеже.
1-5. ИНДУКТИВНОСТЬ
И н Д у к т и В н о с т ь ю называется идеализирован-
ный Элемент электрической цепи, приближающийся по
свойствам к индуктивной катушке, в которой накапливается
энерrия маrнитноrо поля 2. При этом термин «индуктив-
1 Эдисон изобрел лампу накаливания в 1879 r., после Лодыrина.
2 М а r н и т н о е n о л е
одна из двух сторон электромаrнит
Horo поля, характеризующаяся воздействием на электрически заряжен-
ную частицу с силой, пропорциональной заряду частицы и ее скорости
(rOCT 19880-74).
25
Носты И соответствующее ему условное обозначение L при-
меняются как для обозначения caMoro элемента цепи, так
и для количественноЙ оценки отношения потокосцепления
самоиндукции к току в Данном элементе 1:
чr
L=="""7"".
t
П о т о к о с цеп л е н и е м с а м о и н Д у к Ц и и це-
пи называется сумма произве,дений маrнитных потоков,
обусловленных только током В этой цепи, на числа вит-
ков, с которыми они сцеплены. Если все витки пронизы-
ваются одним и тем же маrнит-
ным потоком, то потокосцепление
равно произведению маrнитноrо
потока на число витков.
В Международной системе еди-
ниц ч.r измеряется в веберах (Вб),
L
в rенри (П. При этом всеrда
Потокосцеплени
и ток имеют бди-
наковый знак, так что L > О.
Рис. 1-4. Зависимости по- Зависимость потокосцепления
токосцепления от тока. от тока в общем случае нелиней-
а
неЛlIнеllная; б
линей- на, и пара метр L зависит от тока.
иая. .. в случае, коrда вебер-амперная
характеристика ч.r (i) прям:олинеЙ-
на, цндуктивность L постоянна (линеЙная индуктивность).
На рис. 1-4 показаны нелинеЙная и линейная зависимости
потокосцепления от тока. В этой части учебника рассмат-
риваются линейные индуктивности.
На основании закона электромаrнитноЙ индукции Фа-
радея
Максвелла изменение потокосцепления самоин-
дукции вызывает э л е к т р о Д в и ж у Щ у ю с и л у
(э. д. с.) с а м о и н Д у к ц и и, которая выражается фор-
мулой
'l!
i
о
dчr
eL==
([t.
(1-2)
По закону Ленца, выражающему принцип электро-
маrнитноЙ инерции, эта э. д. с. противодеЙствует измене-
нию потокосцепления, что и учитывается знаком минус
в (1-2), поскольку по.JIOжительное направление для eL
выбрано СОВПадающим с положительным направлением i.
1 Тер
ином «индуктивность» заменен ранее применявшиiiся в ли-
тературе и ныне не рекомендуемый термин «коэффициент самоиндукции»,
26
Ввиду совпадения положительных направлений eL и
i поло/Кительные направления маrнитноrо потока вдоль
оси витков и наводимой им э. д. с. самоиндукции, точно
так же как и положительные направления тока и созда-
BaeMoro им маrнитноrо потока, связаНы правилом право-
xoAoBoro винта.
Условное rрафическое изображение индуктивности с
указанием выбранных положительных направлений тоха
и э. д. с.саМоиндукции приведено на
рис. 1-5.
Если L не зависит от {, то предыду-
щая формула принимает вид:
di
eL ==
l, di '
L
(1-3)
IL/,
Величина
di
UL==
eL==L .
dt
(1-4)
Рис. 1
5. Условное
обозначение индук-
тивности и положи-
тельные направле-
ния тока, Э. Д. с.
самоиндукции и на-
пряжения.
Называется падением напряжения в ин-
дуктивности или, что то же, н а пр я -
ж е н и е м н а и н Д у к т И В Н О С Т и. Положительное
направление UL совпадает с положительным направле-
нием i (рис. 1-5).
На основании (1-4) ток в индуктивности
, 1 r
i == Т j Иr dt,
или
t
. 1 r
t ==т J
uLdt.
oo
Нижний предел ИlIтеrрэла принят равным
oo, так
как до рассматривземоrо момента времени t процесс Mor
Длиться сколр уrодно ДОJirо.
При t .......;. О ток в индуктивности равен:
о
i (О) == 11....
llLdt;
oo
следовательно,
t
i == i (О) +
UL dt,
О
27
т, е. в интервале времени от нуля до t ток в индуктив-
t
ности изменяется на величину
l S uLdt, определяемую
о
площадью, оrраниченной в этом интервале кривой на-
пряжения UL.
Мrновенная мощность, поступающая в индуктивность,
равна произведению MrHoBeHHbIX тока и напряжения:
. L . di
PL==t.l.Lt== t([i'
Она связана с процессом нС!растания или убывания
энерrии маrнитноrо поля. Энерrия маrнитноrо поля в
произвольный момент времени t определяется по формуле
t t
W L == S Р L dt == .\ и di == ;i 2 == :
.
oo О
Здесь учтено, что при t ==
00 ток в индуктивности
i (
oo) == О.
Если часть маrнитноrо потока, связанноrо с индук-
тивным элементом, связана одновременно и с друrим
индуктивным элементом, то эти два элемента, кроме па-
раметров L 1 и L2' обладают параметром М, называемым
в з а и м н о й и н Д у к т и в н о с т ь ю. Последний, как
это будет показано в
8-1, представляет собой отношение
потокосцепления взаимной индукции одноrо из элементов
к току в друrом элементе:
М == '1'12 == '1'2 !.. (1-5 )
i 2 i 1 '
здесь 'У 12
потокосцепление первоrо элемента, обуслов-
ленное током BToporo элемента; 'У 21
потокосцепление
BToporo элемента, обусловленное током первоrо элемента.
В этом случае в первом и втором элементах наводятся
э. д. с. взаимной индукции, равные соответственно:
d'1'12 М di2 )
е1ll1 ==
'([t'" ==
; (1-6)
d'1'2i М dti
е 2 М ==
'([t'" ==
&.
Выражения (1-6) получены в предположении, что М
не зависит от i 1 и i 2 , так как здесь рассматриваются линей-
ные цепи.
28
М измеряется, так же как и L, в rенри. Однако в от-
личие от параметра L взаимная индуктивность М обо-
значает не какой-либо самостоятельный элемент электри-
ческой цепи, а лишь маrнитную связь между индуктив-
ными элементами.
Вопрос взаимной индуктивности подробнее рассмот-
рен в rл. 8.
1-6. ЕМКОСТЬ
Е м к о с т ь ю называется идеализированный элемент
электрической цепи, приближенно заменяющий конден-
сатор, в котором накапливается энерrия электрическоrо
поля 1. При этом термин «емкость» и соответствующее
ему буквенное обозначение С приме-
няются как для обозначения caMoro Ч
элемента цепи, так и для количест-
венной оценки отношения заряда к
напряжению на этом элементе:
C==q/uc. (1-7) u.
о
Рис. 1
6. Зависимости
электрическоrо заряда
от напряжения.
а
нелинейная; б
ли..
нейная.
Если q и ис измеряются в куло-
нах (Кл) и вольтах (В), то С изме-
ряется в фарадах (Ф). При этом
всеrда заряд и напряжение имеют
одинаковый знак, так что С > О.
Зависимость заряда от напряже-
ния в общем случае нелинеЙна, и, следовательно, па-
раметр С зависит от напряжеНия.
В случае, коrда кулон-вольтная характеристика q (и)
прямолинейна, емкость С постоянна (линейная емкость).
На рис. 1-6 показаны нелинеЙная и линейная зависимости
заряда от напряжения. В этой части учебника рассматри-
ваются линейные емкости.
Предположим, что емкость образована двумя пласти-
нами, разделенными диэлектриком. Под влиянием прило-
женноrо напряжения на пластинах сосредоточатся рав-
ные КОличества электричества противоположных знаков;
пластина с более высоким потенциалом зарядится поло-
1 э'л е к т р и ч е с к о е п о л е
одна из двух сторон электро-
маrнитноrо поля, характеризующаяся воздействием на электрически
заряженную частицу с силой, пропорциональной заряду частицы и
не зависящей оТ ее скорости (rOCT 19880
74).
29
жительным электричеством, а пластина с более низким
потенциалом
отрицательным.
При изменении напряжения, приложенноrо к пласти-
нам, изменится в соответствии с (1-7) электрический заряд:
к пластине, потенциал котороЙ возрастет, поступит допол-
нительный положительный заряД, а к пластине, потенциал
которой снизится, поступит такой же отрицательный заряд.
Ток равен производной электрическоrо заряда по вре-
мени. Поэтому с изменением напряжения на емкости
в присоединенной К ней последовательно электрической
цепи создается ток, который определяется скоростью из-
менения заряда на' емкости:
. dq du c
t 0==
dt 0== С dt .
( 1-8)
Здесь знак заряда q соответствует знаку пластины, к
которой направлен ток i.
Этот ток рассматривается как т о к про в о Д и -
м о с т и в проводниках, присоединенных к емкостному эле-
менту (ток, обусловленный движением заряженных Ча-
стиц под действием электрическоrо поля в веществе, об-
ладающем электропроводностью), переходящий в т о к
с м е Щ е н и я 1 В диэлектрике eMKocTHoro элемента. По-
следнее понятие, применяемое в теории поля, означает ве-
личину, прямо пропорциональную скорости изменения
напряженности электрическоrо поля (в случае однород-
Horo поля и е 0== const.)
Напомним, что напряженность электрическоrо поля
определяется силой, действующей на электрический за-
ряд, равный единице 2.
Ток смещения имеет размерность тока. Блаrодаря
введению этоrо понятия ток в цепи с емкостью представ-
ляется замкнутым через диэлектрик.
Соrласно (1-8) ток положитеJlен, коrда заряд q и со-
ответственно напряжение ис 130зрастают.
На основании (1-8) напряжение на емкости
ис ,
i dt
1 т о к с м е Щ е н и я
скалярная величина, равная производ-
ной по времени от потока электрическоrо смещения сквозь рассматри-
ваемую поверхность (rOCT 19880-74).
2Напряженность электрическоrо поля
векторная величина, характеризующая электрическое поле и Оllреде-
ляющая силу, действующую на заряженную частицу со стороны элек
трическоrо поля (rOCT 19880-74).
30
lIЛИ
t
ие =-=
i dt.
co
Здесь, как и в предыдущем паРl:irрафе, предполаrается,
что до рассматриваемоrо момента времени t процесс Mor
длиться сколь уrодно долrо, и поэтому нижний предел
интеrрала принят равным
oo.
При t::.=: О напряжение на емкости
равно:
о
, 1. S
ие (О) ::.=:
C . . i dt.
co
...i..c,.
C
u.c' )
t
ие==ие(О)+
.\ i dt,
о
Рис. 1
7. Услов-
ное обозначение
емкости я llОЛО-
жительные на-
правления TOK
'
и напряжения.
Следовател ЬНо,
т. е.. в интервале времени от нуля до t напряжение на
t
емкости изменяется на величину
. i dt, определяемую
о
площадью, оrраниченной в этом интервале кривой тока i.
Условное rрафическое изображение емкости с указа-
нием положительных направлений тока и напряжения
приведено на рис. 1-7. Полярность емкости, указанная на
рис. 1-7 знаками + и
, соответствует положительному
напряжению ис, т. е. положительному заряду на пласти-
не +. '
Мrновенная мощность, поступающая в емкость, равна
du
Ре == Ие i == СИе" d
' Она связана с процессом накопле-
ния или убыли электрическоrо зарЯДа в емкости.
Коrда заряд положителен и возрастает, ток положи-
телен и в емкость поступает электрическая энерrия из
внешней цепи.
Коrда заряд положителен, но убывает, т. е. ток отри-
цателен, энерrия, ранее накопленная в элеlприческом
поле емкости, возвращается во внешнюю цепь.
Допустим, что к емкости С приложено некоторое на-
Пряжение ие. Энерrия электрическоrо поля в произволь-
31
ный момент времени i определяется по формуле
t ис С "
S r и-
We == Ре di == J Сие dUe ==т == 2С '
oo О
Здесь учтено, что при i ==
00 напряжение на емко-
сти ие (
oo) == О.
1-7. ЗАМЕЩЕНИЕ ФИЗИЧЕСКИХ УСТРойСТВ
ИДЕАЛИЗИРОВАННЫМИ ЭЛЕМЕНТАМИ ЦЕПИ
Представление о сопротивлении, индуктивности и ем-
кости как идеализированных элементах электрической
цепи основано на предположении, что потери энерrии,
маrнитное и электрическое поля сосредоточиваются в от-
дельных, не зависящих друr от друrа элементах цепи.
Раздельное рассмотрение сопротивления, индуктивности
и емкости представляет приближенный метод исследова-
НИя ц
пи. В действительности по
ери энерrии, маrнитные
и электрические поля сопутствуют друr друrу.
Электроп
оводность всякоrо изотропноrо вещества ха-
рактеризуется так называемой удельной электрической
проводимостью, равной отношению плотности тока прово-
димости к напряженности электрическоrо ПОЛя. Величина,
обратная удельной электрической проводимости, назы-
вается удельным электрическим сопротивлением.
Электрическое сопротивление проводника при посто-
янном токе, равное отношению постоянноrо напряжения
на рассматриваемом проводнике к постоянному току в
нем, зависит от длины проводника (м), площади попереч-
Horo сечения (м 2 ) и удельноrо сопротивления (Ом. м):
1
r==p Т'
В широких пределах изменения температуры зависи-
мость удельноro сопротивления проводника от темпера-.
туры практически прямолинейна, причем в случае метал-
лических проводников кр ивая р == f (9) с повышением тем-
пературы возрастает, а в случае неметаллических мате-
риалов (например, уrля) и электролитов
падает.
Если обозначить через Р1 и Р2 удельные сопротивле-
ния при температурах 91 и 92' а через 90
температуру,
соответствующую точке пересечения спрямленной ,xapCiK-
32
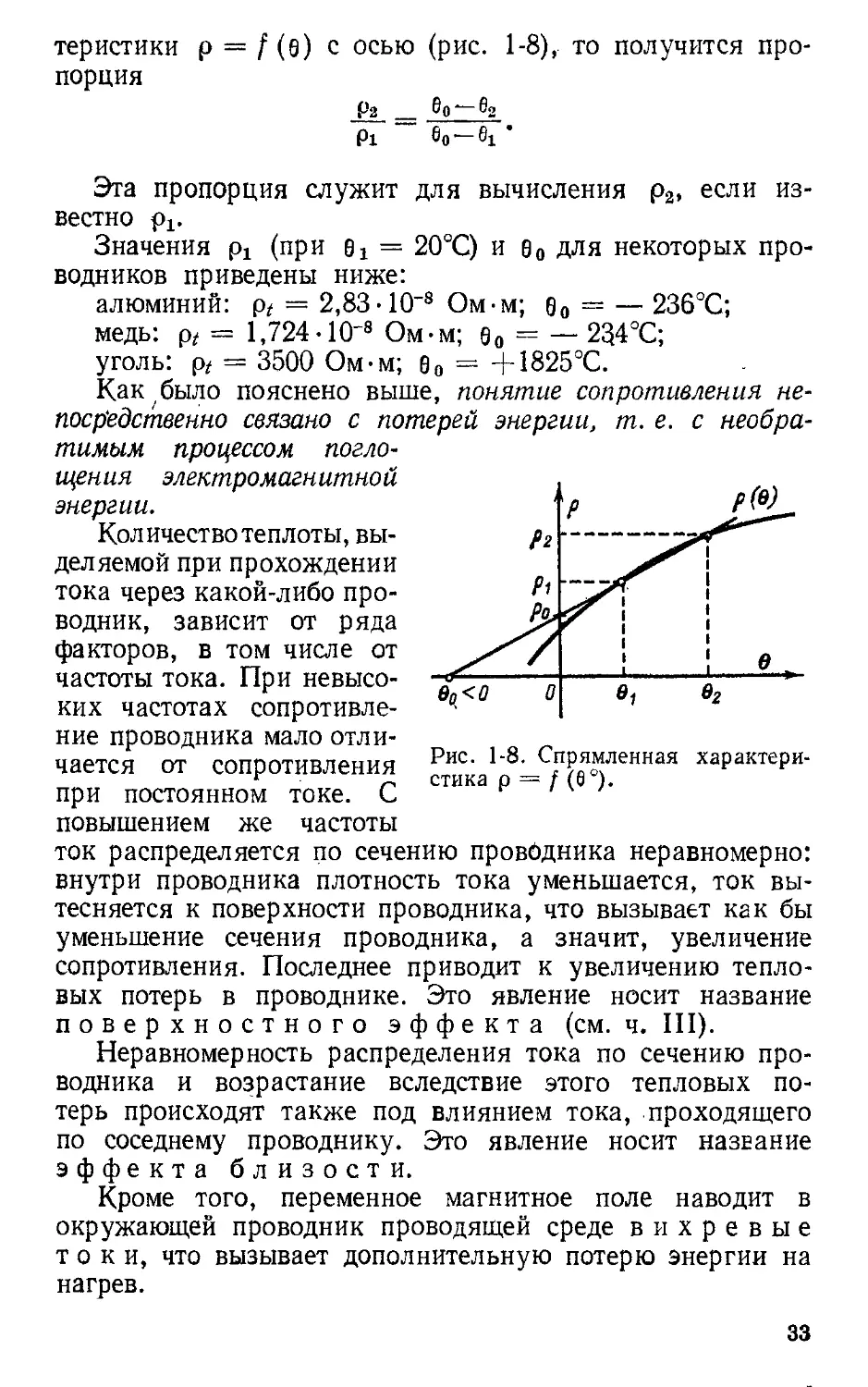
теристики р == f (6) с осью (рис. 1
8), то получится про-
порция
Р2
eo
e2
Pl
eO
el .
Эта пропорция служит для вычисления Р2' если из-
вестно 91'
Значения Рl (при 61 == 20 0 С) и 60 для некоторых про.
водников приведены ниже:
алюминий: Pt == 2,83 .10
8 Ом. м; 60 ==
236 0 С;
медь: Pt == 1,724.10
8 Ом. м; 60 ==
234 0 С;
уrоль: pt == 3500 Ом. м; 60 == +1825 0 с.
Как было пояснено выше, понятие сопротивления не-
I '
nocp'eдcmвeHHO связано с потерей энер
uи> т. е. с необра-
тимым nроцессом по
ло-
щения элек.троматитной
Эliер
иu.
Количество теплоты, вы-
деляемой при прохождении
тока через какой
либо про-
водник, зависит от ряда
факторов, в том числе от
частоты тока. При невысо-
80.<0
ких частотах сопротивле
ние проводника мало отли-
чается от сопротивления Рис. 1-8. Спрямленная характери-
стика Р == f (6 О).
при постоянном токе. С
повышением же частоты
ток распределяется по сечению проводника неравномерно:
внутри проводника плотность тока уменьшается, ток вы-
тесняется к поверхности проводника, что вызыван как бы
уменьшение сечения проводника, а значит, увеличение
сопротивления. Последнее приводит к увеличению тепло-
вых потерь в проводнике. Это явление носит название
n о в е р х н о с т н о r о э Ф Ф е к т а (см. ч. 111).
Неравномерность распределения тока по сечению про-
водника и возрастание вследствие этоrо тепловых по-
терь происходят также под влиянием тока,проходящеrо
по соседнему проводнику. Это явление носит наЗЕание
э Ф Ф е к т а б л и з о с т и.
Кроме Toro, переменное маrнитное поле наводит В
окружающей проводник проводящей среде в и х р е в ы е
т о к и, что вызывает дополнительную потерю энерrии на
HarpeB.
Р2
р
8
о
81
82
33
к этому можно еще добавить излучение 13 простран-
ство электромаrнитной энерrии, наблюдаемое при высо-
ких частотах и вызывающее дополнительное увеличение
сопротивления.
Вследствие наличия маrнитноrо и электрическоrо по-
лей проводник наряду с сопротивлением имеет некото-
pыe индуктивность и емкость.
Вычисление сопротивления, индуктивности и емкости
проводника с учетом указанных в'ыше факторов относится
к задачам теории поля. ,
Для уменьшения индуктивности и собственной ,емкости
проволочные резисторы выполняются в виде пластинча
тых или плетеных элементов. Применяются таКже непро-
волочные резисторы. Последние представляют сорой фар-
форовые цилиндрики, на которые наНесен слой уrлерода
(так называемые уrлеродистые резисторы), или стержни
из rлинистоrо материала, смешанноrо с rрафитом (объем-
ные карбокерамические резисторы).
Теперь представим себе простейшую и н Д у к т и вн У ю
к а т у ш к у в Виде нескольких кр yroBbIx витков ПрОВОk
ника, по которому проходит ток.
При постоянном токе напряжение на выводах катушки
определится падением напряжения на ее сопротивлении
в соответствии с (1-1) и ток БО всех TO
Kax будет одина-
ковым.
При переменном же токе изменяющееся маrнитное
поле будет наводить в витках э. д. с. самоиндукции. Между
витками, так же как и между отдельными точками смежных
витков, электрическое поле станет переменным. В свsри
с этим ток в различных витках будет неодинаковым, так
как появится ток смещения между витками. Чем выше
частота переменноrо тока, тем больше будут э. д. с. само-
индукции и ток смещения. При низких частотах током
смещения можно пренебречь; при высоких же частотах
ток смещения, обусловленный изменением напряженности
электрическоrо поля, может быть соизмерим по величине \
с током В витках или даже может превышать ero. Таким
образом, в зависимости от выбранноrо диапазона частот
индуктивная катушка может быть представлена либо как
сопротивление r (при постоянном токе
рис. 1-9, а),
либо как индуктивность L с последовательно включенным
сопротивлением r (при низких частотах
рис. 1-9, 6), либо
как индуктивность L и сопротивление r, соединенные парал-
лельно с емкостью С (при высоких частотах
рис. 1
9, в).
34
Если катушка имеет MHoro витков', то про ходящий
через нее ток создает маrнитный поток, пропорциональ
ный числу витков. -Считая, что этот маrнитный поток сцеп
лен со всеми витками катушки, приходим к выводу, что
потокосцепление самоиндукции и соответственно индук-
тивность катушки пропорциональны квадрату числа витков.
Положим, например, что катушка, состоящая из w
ВИТКelВ, насажена на тороидальный маrнитопровод или
достаточно длинный прямолинейный маrнитопровод, длина
KOToporo 1 (м) и площадь поперечноrо сечения S (м 2 ).
Обозначим через !1а абсолютную маrнитную проницае-
масть 1 маrНИТОПРОВОДа (равную про изведению относи-
L т'
" '"
с
а) () в)
Ри::. 1
9. Электрические схемы замещения индуктивнои катушки.
а
при постоянном токе; б
прн ниэких частотах; 8
прн высоких ча-
стотах.
тельной маrнитной проницаемости на маrнитную постоян-
НУЮ!1о == 4:rt.lO
7 r/M).
Маrнитный поток в веберах (В6) определяется отноше-
нием маrнитодвижущей силы (м. д. с.) всей катушки iw
к маrнитномусопротивлению маrнитопровода r M :::::: l/!1aS:
Ф
iwlta S
1 '
поэтому индуктивность катушки в rенри (r) соrласно оп-
ределению
L == wф
w 2 J.Lя S
i ,
l .
ОНа определяется rеометрическими размерами катушки,
маrнитной проницаемостью материала маrнитопровода и
квадратом числа витков.
Перейдем теперь к рассмотрению п л о с к о r о к о н -
Д е н с а т о р а, состоящеrо из двух параллельных пластин,
разделенных диэлектриком. При постоянном напряжении
lАбсолютная маrнитная проницаемость
для изотропноrо вещества
скалярная величина, характеризующая
маrиитные свойства вещества, равная отношению модуля маrнитнои
индукции к модулю напряженности маrнитноrополя (rOCT 19880-74).
35
и идеальном диэлектрике тока в цепи не будет. Если на-
пряжение переменно, то в процессе изменения электриче-
cKoro заряда возникает переменный ток, создающий пе-
ременное маrнитное поле. Эффект, вызываемый маrнитным
полем, может быть учтен в электрической схеме замещения
с помощью некоторой индуктивности, включенной после-
довательно с емкостью конденсатора. Обычно этой индук-
тивностью пренебреrают из-за ее относительной малости.
Наконец, в диэлектрике блаrодаря некоторой проводи-
мости возникают тепловые потери,
OTopыe возрастают
с частотой. Потери на HarpeB учитываются в схеме замеще-
ния конденсатора посредством сопро-
тивления r, включенноrо параллельно
емкосТИ С (рис. 1-10).
Емкость конденсатора определяет-
ся размерами обкладок, расстоянием
между ними и диэлектричесКИМИ
свойствами среды; заполняющей про-
странство между обкладками.
Если расстояние между обклад-
ками конденсатора (толщина диэлек-
трика) ,достаточно мало по сравнению с их размерами,
то емкость .конденсатора в фарадах (Ф) вычисляется по
формуле
Рис. 1-10. Электриче-
ская схема замеLЦения
конденсатора. .
с
8n S
d '
[де Ва
абсолютная диэлектрическая проницаемость изо-
ляции между пластинами 1 (равная произведению относи-
тельной диэлектрической проницаемости в на электриче
скую постоянную Во == 8,556 .10
12 Ф/м); S
площадь
поверхности каждой пластины, м 2 ; d
расстояние между
пластинами, м.
Чем выше частота и больше линейные размеры самих
устройств, тем в большей мере проявляются взаимосвязь
электрических и маrнитных параметров и неотделимость
друr от друrа электрическоrо и маrнитноrо полей, являю-
щихся лишь двумя сторонами единоrо электромаrнитноrо
поля.
1 А б с о л ю т н а я Д и э л е к т р и ч е с к а я про н и ц а е-
м о с т ь для изотропноrо вещества
скалярная величина, характери-
зующая электрические свойства ДИЭ.'lектрика, равная отношению элек-
трическоrо смещения к модулю напряженности ЭJ1ектрическоrо поля
(rOCT 19880-74).
36
CTporo разrраничить области частот, при катары х
справедлива та или иная схема замещения, не представ-
ляется возможным, так как это зависит от множества фак-
торов.
1.8. ИСТОЧНИК Э. Д. С. и ИСТОЦНИК ТОКА
В теории электрических цепей пользуются ид,еализи-
рованными источниками электрическоЙ энерrии: источни-
ком э. Д. с. и источником тока. Им приписываются следую-
щие свойства.
И Д е а л ь н ы й и с т о ч н и к э. д. с. представляет
собой активный элемент с двумя выводами, напряжени
1 а(')
0.)
+
s(t)=u(t)
e(t)
б)
Рис. 1-11. Источники э. Д. с.: идеальные (а, б) и
конечной мощности (6).
на которых не зависит от тока, проходящеrо через источ-
ник. Предполаrается, что внутри TaKoro идеальноrо источ-
ника пассивные элементы (r, L, С) отсутствуют и поэтому
прохождение через Hero тока не вызывает в нем падения
напряжения.
Упорядоченное перемещение положительных зарядов
в ИСТОЧНике от меньшеrо потенциала к большему возможно
за счет присущих источнику сторонних сил. Работа, затра-
чиваемая сторонними силами на перемещение единицы по-
ложительноrо заряда от вывода «
» к выводу «+», назы-
вается электродвижущей силой (э. д. с.) источника и обо-
значается е (t).
В соответствии со сказанным выше напряжение на вы-
водах рассматриваемоrо источника равно ero э. д. С., т. е.
u (t) == е (t).
Условные обозначения идеальноrо источника э. д. с.
приведены на рис. 1-11, а и б. Здесь стрелкой или знаками
+ и
указаны положительное направление э. д. с. QЛИ
полярность источника, т. е. направление возраСТания по-
З7
тенциала в источнике для моментов времени, соответствую-
щих положительной функции е (t}.
Ток в пассивной электрической цепи, подключенной
к источнику э. д. с., зависит от параметров этой цепи и
э. д. с. е (t). Если выводы идеальноrо источника э. Д. с.
замкнуть накоротко, то ток теоретически должен быть
бесконечно велик. Поэтому такой источник рассматривается
как источник бесконечной мощности (теоретическое ПОня-
тие). В действительности при замыкании зажимов реаль-
Horo источника электрической энерrии
химическоrо ис-
точника тока, reHepaTopa и т. п.
ток может иметь только
конечное значение, так как э. Д. с. источника уравновеши-
вается падением напряжения
от тока внутри источника
(например, в сопротивлении r,
индуктивности L).
Источник э. д. с. конеч-
ной мощности изображается
в виде идеальноrо источника
э. д. с. с подключенным к нему
последовательно пассивным
элементом, которыи характе-
ризует внутренние параметры
источника и оrраНичивает
мощность, отдаваемую во внешнюю электрическую цепь
(рис. 1-11, в). Обычно внутренние параметры источника
конечной мощности незначительны по сравнению с пара-
метрами внешней цепи; они MorYT быть отнесены к послед-
ней или в некоторых случаях MorYT вовсе не учитываться
(в зависимости от соотношения величин и требуемой точ-
ности расчета).
И Д е а л ь н ы й и с т о ч н и к т о к а представляет
собой активный элемент, ток KOToporo не зависит от напря-
жения на ero выводах. Предполаrается, что внутреннее
сопротивление TaKoro идеальноrо источника бесконечно
велико и поэтому параметры внешней электрической цепи,
от которых зависит напряжение на выводах источника,
не влияют на ток источника.
Условные обозначения идеальноrо источника тока при-
ведены на рис. 1-12, а и 6. Стрелка в источнике тока или
знаки + и
указывают положительное направление тока
i (t) или полярность источника, т. е. направление переме-
щения положительных зарядов, или, что то же, направле-
Ние" противоположное направлению движения отрицатель-
0.)
5)
Рис. 1-12. Источники тока:
идеальные (а, б) и конечной
мощности (6).
38
ных зарядов, для тех моментов времени, Rоrда ФУНКЦИ51
i (t) положительна.
По мере неоrраниченноrо увеличения сопротивления
внешней электрической цепи, присоединенной к идеаль-
ному источнику тока, напряжение на ero выводах и со-
ответственно мощность, развиваемая им, неоrраниченно
возрастают. Поэтому идеальный источник тока, так же
как и идеальный источник напряжения, рассматривается
как источник бесконечной мощности.
Источник тока конечной мощности изображается в виде
идеальноrо источника тока С подключенным к ero выводам
пассивным элементом, который характеризует внутренниа
и Источник и и
э.д.
;
/ ,
Источник / ,
тока I
I
i i I i
0.) 6) 8)
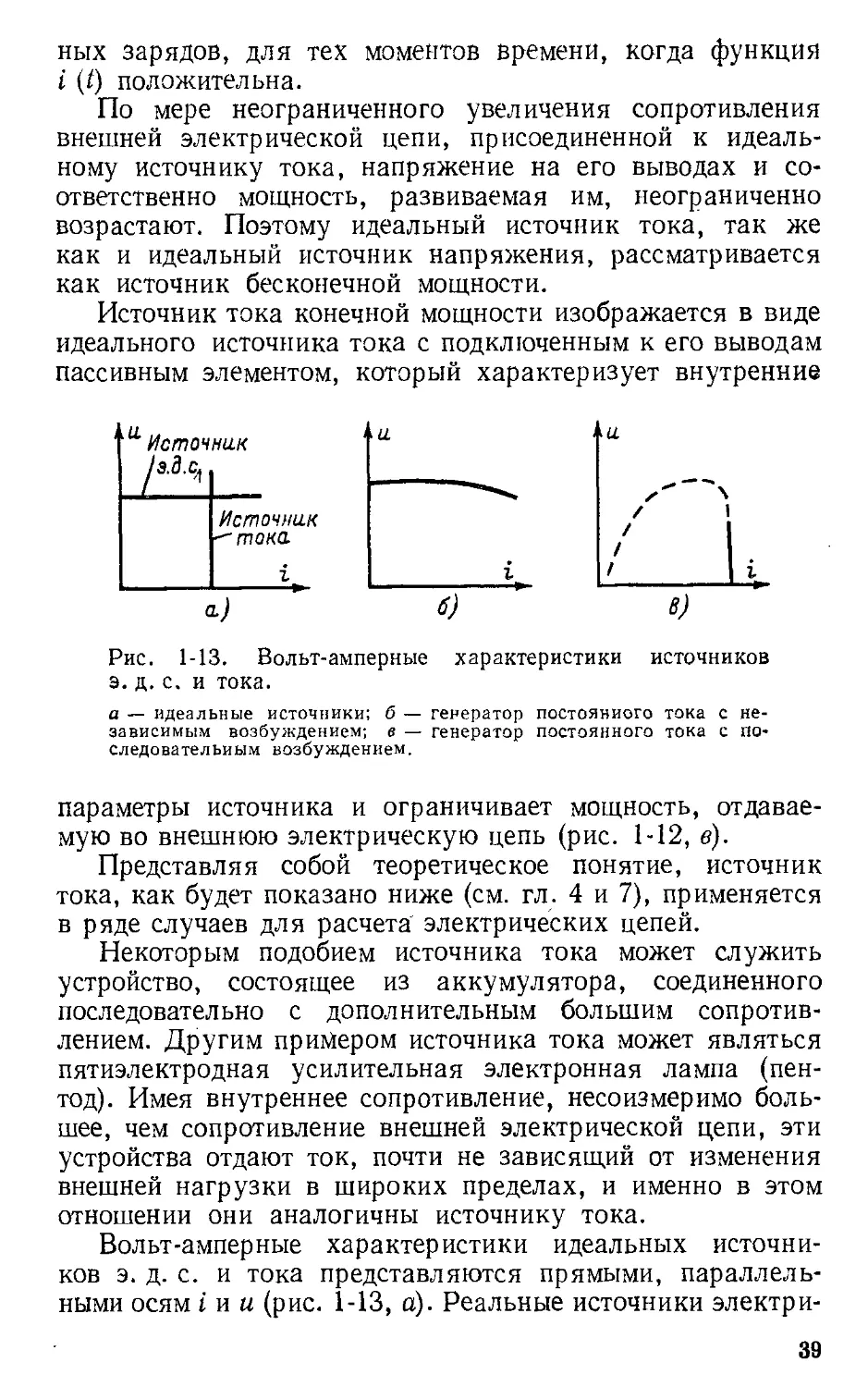
Рис. 1
13. Вольт-амперные характеристики источников
Э. Д. с. и тока.
а
идеальные источники; 6
[еРератор постояниоrо тока с не-
зависимым возбуждением; в
[енератор постоянноrо тока с ПО-
следовательиым возбуждением.
параметры источника и оrраничивает мощность, отдавае-
мую во внешнюю электрическую цепь (рис. 1-12, в).
Представляя собой теоретическое понятие, источник
тока, как будет показано ниже (см. rл. 4 и 7), применяется
в ряде случаев для расчета электрических цепей.
Некоторым подобием источника тока может служить
устройство, состоящее из аккумулятора, соединенноrо
последовательно с дополнительным большим сопротив-
лением. Друrим примером источника тока может являться
пятиэлектродная усилительная электронная лампа (пен-
тод). Имея внутреннее сопротивление, несоизмеримо боль-
шее, чем сопротивление внешней электрической цепи, эти
устройства отдают ток, почти не зависящий от изменения
внешней наrрузки в широких пределах, и именно в этом
отношении они аналоrичны источнику тока.
Вольт-амперные характеристики идеальных источни-
ков э, д. с. и тока представляются прямыми, параллеJIЬ-
ными осям i и u (рис. 1-13, а). Реальные источники электри-
39
ческой энерrии по своим вольт
амперным характеристикам
MorYT приближаться к идеальным источникам напряже-
ния или тока. Например, в значительной части характери-
стики u == f (i) напряжение на выводах reHepaTopa постоян-
Horo тока с независимым возбуждением 1, а также ток i
reHepaTopa постоянноrо тока с ,последовательным возбуж-
дением 2 изменяются незначительно. На рис. 1-13, в соот-
ветствующая часть характеристики Показана сплошной
линией.
1-9. ЛИНЕI1НЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Как уже указывалось выше, настоящая книrа посвя-
щена рассмотрению электрических цепей, в которых co
противления, индуктивности и емкости не зависят от токов
и напряжений и их направлений. Такие электрические цепи,
как и сами элементы, из которых они состоят, называются
л и н е й н ы м и, так как напряжение и ток в каждом эле-
менте связаны линейным уравнением
алrебраическим
или дифференциальным первоrо порядка.
Действительно, в случае если параметр r не зависит
от'и и i, то закон Ома (1-1) выражает линейную зависи-
мость между напряжением и током. Если L и С не зави-
сят от u и i, то напряжение и ток связаны линейным диф-
ференциальным уравнением (1-4) в случае индуктивно.
СПI и уравнением (1-8) в случае емкости.
Что каСается активных элементов линейных электри-
ческих цепей, то условием линейности идеальноrо источ-
ника э. д. с. является независимость напряжения от тока,
проходящеrо через источник, а условием линейности иде-
альноrо источника тока является независимость тока от
напряжения на ero выводах.
Реальные электротехнические и радиотехнические уст-
ройства, cTporo rоворя, не подчиняются линейному за-
кону. При прохождении тока через проводник выделяется
тепло, проводник наrревается и ero сопротивление из-
меняется. С изменением тока в индуктивной катушке
с маrнитопроводом соотношение между ПОТОКQсцеплением
и током, т. е. параметр L, не остается постоянным. В зави-
симости от диэлектрика в большей или меньшей степени
изменяет.ся и емкость конденсатора в функции заряда
1 Обмотка возбуждения питается от постоянноrо источника.'
2 Обмотка возбуждения соединена последовательно с цепью якоря.
40
(или приложенноro напряжения). К нелинейным устрой-
ствам относятся, кроме Toro, электронные, ионные и полу-
проводниковые приборы, параметры которых зависят 01'
тока и напряжения.
Если в рабочем диапазоне, на который рассчитывается
то или иное устройство, т. е. при заданных оrраничен-
ных пределах изменений напряжения, тока и т. П., закон
линейности с достаточной для практики степ€нью ТОЧНо-
сти сохраняется, то такое устройство рассматривается
как линейное.
Исследование и расчет линейных цепей сопряжены,
как правило, с меньшими трудностями, чем исследование
и расчет нелинеЙных цепей. Поэтому в тех случаях, Kor-
да линейный закон достаточно близко отражает действи-
тельность, цепь рассматривается как линейная.
1-10. ОСНОВНЫЕ ОПРЕДЕЛЕННЯ, ОТНОСЯЩНЕСЯ
К ЭЛЕКТРИЧЕСКОМ СХЕМЕ
Электрическая схема представляет собой ерафическое
изображение электрической цепи. Она показывает, как
осуществляется соединение элементов рассматриваемой элек-
трической цепи.
7..
.
е
Рис. 1-14. Изображения ветвей элекrрической схемы,
«Электрическими» элементами схемы служат актиs-
ные и пассивные элементы цепи. «rеометрическими» эле-
ментами схемы являются ветви и узлы.
В е т в ь 1 образуется одним или несколькими последо-
вательно соединенными элементами цепи (рис. 1-14). В об-
щем случае, если состав ветви неизвестен, последняя изо-
бражается прямоуrольником.
1 В е т в ь э л е к т р и ч е C
K ой цеп и
участок электриче-
ской цепи, ВДОЛЬ KOToporo протекает один и тот же ток (rOCT 19880-74).
41
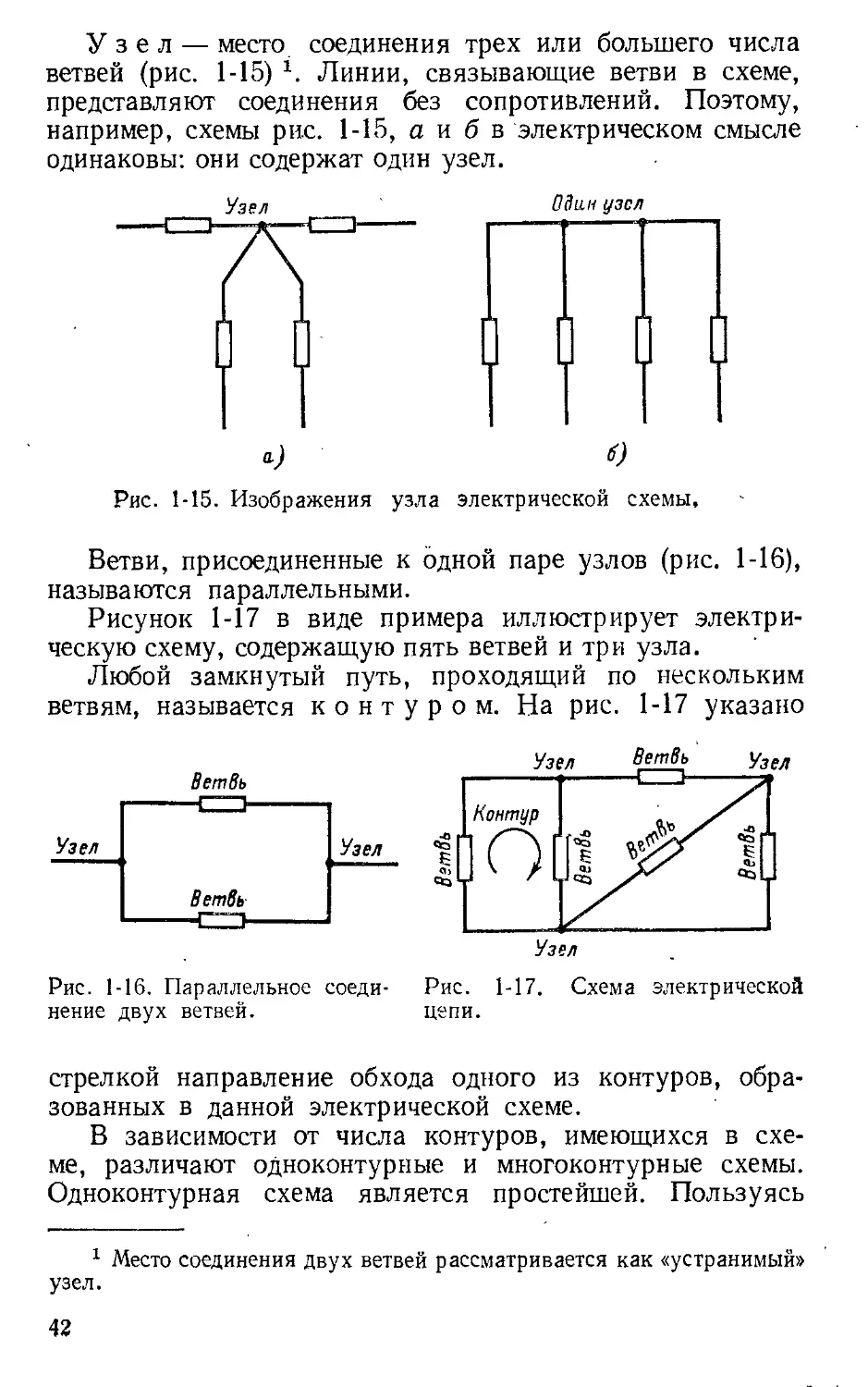
Узе л
место соединения трех или большеrо числа
ветвей (рис. 1-15) 1. Линии, связывающие ветви в схеме,
представляют соединения без сопротивлений. Поэтому,
например, схемы рис. 1
15, а и б в электрическом смысле
одинаковы: они содержат один узел.
Узел
ОдШI узел
а)
6')
Рис. 1-15. Изображения узла электрической схемы.
Ветви, присоединенные к одной паре узлов (рис. 1
16),
называются параллельными.
Рисунок 1
17 в виде примера иллюстрирует электри-
ческую схему, содержащую пять ветвей и три узла. .
Любой замкнутый путь, проходящий по н
скольким
ветвям, называется к о н т у ром. На рис. 1
17 указаНО
Вет8ь .
Узел
Узел
Контур
i п
а,
CQ
Вет8ь
в ет8ь'
Рис. 1
16. Параллельное соеди-
нение двух ветвей.
Узел
Рис. 1
17. Схема электрической
цепи.
стрелкой направление обхода одноrо из контуров, обра-
зованных в данной электрической схеме.
В зависимости от числа контуров, имеющихся в схе-
ме, различают одноконтурные и MHoroKoHTypHbIe схемы.
Одноконтурная схема является пр ост ей шей. Пользуясь
1 Место соединения двух ветвей рассматривается как «устранимыи»
узел.
42
rтравилами преобразования схем (см. rл. 4), в ряде слу-
чаев представляется удобным заменить мноrоконтурную
схему одноконтурной, что упрощает расчеты.
Если ток в электрической цепи постоянен, т. е. ero
значение не изменяется во времени, то отсутствует явле-
ние самоиндукции: производная потокосцепления по вре-
мени равна нулю и напряжение, например, на индуктив-
ной катушке определяется только падением напряжения
от тока в сопротивлении катушки. Схема замещения ин-
дуктивной катушки для эТоrо случая приводилась на
рис. 1-9, а.
В свою очередь, если не учитывать проводимости ди-
электрика конденсатора, т. е. ,рассматривать конденса-
тор как идеальную емкость, то ветвь с такой емкостью
представится в электрической схеме цепи постоянноrо
тока разомкнутой: постоянный ток через емкость не про-
ходит.
Таким образом, при рассмотрении электрической це-
пи ПОСтоянноrо тока в установившемся режиме, при кото-
ром напряжения и токи в цепи являются постоянными,
пассивНыми элементами схемы являются сопротивления,
а активными
источники постоянной Э. д. с. или поста-
янноrо тока.
Индуктивности и емкости УЧИТЫВaJОТСЯ в схемах це-
пей переменноrо тока и при переходных (неустано.вив-
шихся) процессах, возникающих в электрических цепях
при переходе от одноrо режима к друrому (см. rл. 14).
1-11. ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА УЧАСТКА ЦЕПИ
С ИСТОЧНИКОМ
Закон Ома может быть применен к участку цепи с источ-
никами, и для та Koro участка может быть построена волы-
амперная характеристика.
На рис. 1-18, а показана ветвь с последовательно сое-
диненными источником постоянной Э. д. с. Е и сопротив-
лением r. Через ветвь проходит ток i, значение KOToporo
в общем случае зависит не только от данноrо источника
э. д. с., но и от источников остальной Части электрической
цепи, присоединенной к выводам 1 и 2.
При указанных на рис. 1-18, а направлениях э. д. с.
и тока потенциал вывода 2 выше потенциала ВЫВОДа 1
на э. д. с. за вычетом падения напряжения от тока i в со-
противлении r. Следовательно, напр яжение на выводах
43
ветви равно:
u == и 21 == Е
ri.
(1
9)
По этому уравнению строится вольт
амперная харак-
теристика, }{оторая называется также внешней xapaKTe
ристикой (рис. 1
18, б).
Е i
+
I 7'
, I
,
I
t.. ": I I
I I
,. U I
а)
u.
i
Рис. 1-18. Последовательное соединение сопротивле-
ния и источника постоянной Э.д.
.
"
схема; б
вольт-амперная характернстика.
TaHreHc уrла сх. пропорционален сопротивлению '.
При отрицательном знаке ТОКа i напряжение на сопро-
тивлении r складывается с э. д. с. Е и в этом случае и> Е.
На рис. 1-19, а ПОКа3аН участок цепи, состоящий из
источНика постоянноrо тока 1 с параллельным сопротивле-
и u.
. ..
1
.,. I
i i
а)
Рис. 1-19. Параллелыюе соединение сопротивления и
источника постоянноrо тока.
а
схема; б
вольт-амперная характеРИС1'ика.
нием '. Так же как и в предыдущем случае, значение и
направление тока i, проходящеrо через выводы 1 и 2, за-
висят не только от данноrо источника, но и ОТ источников
остальной части цепи, присоединеннои - к выводам 1 и 2.
При указанных на рис. 1-19, а направлениях тщшв через
сопротивление от вывода 2 к выводу 1 проходит ток 1
i,
44
создающий напряжение
и == '!
ri.
По этому уравнению строится вольт-амперная харак-
теристика (рис. 1
19, б).
Таким образом, вольт-амперные характеристики уча-
стков цепи, состоящих из линейноrо сопротивления, сое-
диненноrо последовательно с источником э. д. с. или па-
раллельно с источником тока, прямолинейны.
Из сопоставления вольт-амперныIx характеристик
рис. 1-18 и 1
19 видно, что источник напряжения конеч
ной мощности эквивалентен источнику тока конечной
мощности при условии Е .:=: '! и потому они MorYT быть
взаимно заменяемы.
В общем случае этот вопрос разобран в 9 4.6.
t-t1. РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА ВДОЛЬ ЦЕПИ
С СОПРОТИВЛЕННЯМИ И ИСТОЧНИКАМИ Э. Д. С.
Допустим, что на участке цепи, изображенном на
рис. 1-18, а, ток i == ! задан.
Обозначив r х, ИХ Часть сопротивления r и соответствую-
щее напряжение относи-
тельно вывода 1, получим
по аналоrии с (1-9) ИХ ===
=== Е
rxl. Следовательно,
зависимость их (r x ) пред-
ставляется прямой линией
(рис. 1-20), причем TaHreHc
уrла наклона прямой к
оси абсцисс пропорциона-
лен 1:
tg Р == 8С ,
:
== 1 m r ,
АВ та m r та
и::
1
1
с
7'1
E,l
,
J "Z1
l
7'::
l'
Рис. 1-20. Зависимость напряже-
ния от сопротивления (при задан-
ном токе).
rде та и m r
масштабы, в которых отложены на рис.l-20
напряжения и сопротивления.
При переходе через источник
э. д. с. по направлению,
совпадающему с направлением действия э. д. с., потен-
циал возрастает скачкообразно на Е, затем пр и прохожде-
нии через сопротивление r x (по направлению тока) убывает
прямолинейно на падение напряжения rxl. Если не выде-
лять сопротнвление r, а рассматривать ero как сопротивле-
ние источника напряжения,' равномерно распределенное
45
внутри caMoro источника, то rрафик изменения потенциала
внутри источника представится в виде прямой ОА (рис. 1-20).
Теперь рассмотрим какую-нибудь неразветвленную элек-
трическую цепь постоянноrо тока, содержащую сопротив-
ления и источники э. д. с. (рис.
1-21, а), и построим для нее
rрафик изменения потенциала.
Приравняем нулю потенциал
одной точки этоrо контура. На-
чав обход контура с этой точки,
придем к исходному потенциалу.
Примерный rрафик распределе-
ния потенциала в этом случае
показан на рис. 1-21, б. Следует
обратить внимание на то, что
при переходе через источник
э. д. С. в направлении, противо-
положном э. д. с., потенциал
снижается на эту э. д. с.
На rрафике наклон прямых
линий одинаков, так как ток
во всех сопротивлениях один и
тот же (одноконтурная цепь). В случае разветвленной
цепи, rде токи в ветвях различны, наклон прямых линий
rрафика потенциала неодинаков.
Е,
"'2 .. ! t
6)
"]
Рис. 1-21. Распределение по-
тенциала вдоль цепи постоя!:!-
Horo тока.
а
схема;
циала.
б
rрафик потеи-
1.1]. ЗАКОНbI кирхrОФА
Основными законами теориИ цепей Наряду с законом
Ома являются законы баланса токов в разветвлениях
(первый закон Кирхrофа) и баланса напряжений на зам-
кнутых участках цепи (второй закон Кирхrофа).
Распределение токов и напряжений в электрических
цепях подчиняется законам Кир хrофа , которые должны
быть основательно усвоены для отчетливоrо понимания
материала всех последующих разделов курса.
Первый закон Кирхrофа
Алсебраuческая сумлю токов в узле равна нулю:
l:l==O. (1-10)
Суммирование распространяется на токи i в ветвях,
сходящихся в рассматриваемом узле. При этом знаки
токов берутся с учетом выбранных положительных На-
46
правлений токов: всем токам, направленным J{ узлу, Ь у'рав-
нении (1-10) приписывается ОДинаКОВJ,IЙ знак, напри-
мер положительный, и, соответственно все токи, направ-
ленные от узла, входят в уравнение (1-10) с противопо-
ложным знаком. Иначе rоворя, всякий ток, направлен-
ный от узла, может рассматриваться как ток, направлен-
ный к узлу, но имеющий противоположныЙ знак.
а) Из!)
Рис. 1-22. Иллюстрация к первому закону К:ирхrофа.
На рис. 1-22, а в качестве примера показан узел, в ко-
тором сходятся четыре ветви. Уравнение (1-10) имеет
в этом случае вид:
i 1 + i 2
i3
i 4 == О.
Первый закон Кирхrофа выражает тот факт, что в уз-
ле электрический заряд не накапливается и не расходуется.
Сумма электрических зарядов, приходящих к узлу, равна
сумме зарядов, уходящих от узла за один и тот же проме-
жуток времени.
Первый закон Кирхrофа применим не только к узлу,
но и к любому контуру или замкнутой поверхности, охва-
тывающей часть электрической цепи, так как ни в каком
элементе цепи. ни в каком режиме электричество одноrо
знака не может накапливаться.
Так, например, для схемы рис. 1-22, б имеем:
i 1
i 2
i3 == о.
Второй закон КирхrОфа
Алеебраическая сумма э. д. с. в любом контуре цепи
равна алzебраич(;ской сумме падений напряжения на эле-
ментах этоео контура:
е ==
и.
(1-11)
47
Обход контура совершается в произвольно выбран-
ном направлении, например по ходу часовой стрелки.
При этом соблюдается следующее правило знаков для
э. д. С. и падений напряжения входящих в (1
11): э. д. С.
и падения напряжения, сов-
Падающие по направлению
с направлением обхода, бе-
рутся с одинаковыми знаками.
Например, Для схемы
рис. 1-23 имеем:
е 1
е 2 == И 1 + и 2 + ИЗ
и 4 .
еl
и1
.........
и ч +
Напра8леНI.Lд
оохоаа
tI.L2
Рис. 1
23. Иллюстрация ко вто-
рому закону Кирхrофа.
Уравнение (1-11)
переписать так: ,
l:(и
е)==О.
можно
(1-12)
Здесь (И
е)
напряже-
ние на ветви. Следовательно,
алi!ебраuческая сумма напряженuй на ветвях в любом зам-
кнутом мнтуре равна нулю.
Формулы (1-10) и (1-11) написаны в общем виде для
мrновенпых значений токов, напряжений и э. д. С.; они
справедливы дЛя цепей как nepeMeHHoro, так и постоян-
Horo тока.
rрафик изменения потенциала, рассмотренный в щ5е-
дыдущем параrрафе, служит rрафической иллюстрацией
BToporo закона Кирхrофа.
'.14. ЗАДАЧИ И ВОПРОСbI для САМОПРОВЕРКИ
1.1. Определить сопротивление медноrо провода при 1O
С, если
при 600 С оно равно 5 Ом.
Ответ: 4,15 Ом.
1.2. Показать, что величины ,С, Ц, и V LC имеют размерность
времени.
1-3. Показать, что ,2С имеет Rазмсрность индуктивности, V L/C
размерность сопротивления
L/i
размерность емкости.
1-4, Ток i == e
a! проходит через ветвь, состоящую нз последова-
тельно соединенных сопротивления , и индуктивности L.
Определить напряжения на сопротивлении, индуктивности И на
всей ветви, приняв а == ,/ L; объяснить физически полученный резуль-
тат.
1.5. Начиная с момента t == О через сопротивление 1 Ом прохо-
дит ток i == 1
e
t А. Какая энерrия выделится в виде тепла к мо-
менту времени, коrда ток достиrнет значення 0,632 А?
О т в е т: 0,168 Дж.
48
1-6. Начиная с момента t == О через индуктивность L == 1 r про-
ходит ток i == 1
e
t А. Определить напряжение на индуктивности
и энерrию маrнитиоrо поля в момент времени, коrда ток достиrнет
Значения 0,632 А.
О т в е т: 0,37 В; 0,2 Дж.
1-7. Емкость С == 1 Ф, имеющая электрический заряд q == 1 Кл,
в момент t == О начинает разряжаться через сопротивление, == 1 Ом.
Ток изменяется по закону i == e
! [А]. Определить напряжение на ем-
кости и энерrию электрическоrо поля в момент, коrда ток достиrнет
значения 0,37 А.
О т в е т: 0,37 В; 0,068 Дж.
1-8. Сохранив условия предыдущеЙ задачи, определить, какое
количество энерrии выделится в виде тепла к моменту времени, коrда
ток достиrнет значения 0,37 А.
О т в е т: 0,432 Дж.
1-9. Сохранив условия задачи 1
7, убедиться в том, ЧТО энер-
rия, выделенная в виде тепла за бесконечно большое время. равна
энерrии электрическоrо поля до начала разряда. Определить эту
энерrию.
О т в е т: 0,5 Дж.
1-10. Плоский конденсатор состоит из двух листов фольrи, каж-
дый площадью 40 см 2 . разделенных парафинированноЙ бумаrой тол-
щиной 0,05 мм. Вычислить емкость конденсатора, приняв диэлектри-
ческую проницаемость в парафинированной бумаrи равной 1,8,
О т в е т: 1,275. ю
з мкФ.
1-11. ПЛоский конденсатор. диэлектриком Koтoporo служит слюда
толщиной 3 мм, имеет
eMKOCTЬ С == 0,0443. 10
3 мкФ. Площадь каждой
пластины конденсатора равна 25 см 2 > Чему равна диэлектрическая
проницаемость слюды?
О т в е т: 6.
1-12. Вычислить приближенно индvктивность катушки без Mar-
нитопровода, имеющей 300 витков, длину 10 см и сечение 1 см 2 .
О Т В е т: 0,113 Mr.
1-13. Тороидальная катушка Состоит из w витков. навитых на
маrнитопровод, поперечное сечение Koтoporo
прямоуrольник: а 1
и а 2
внутренний и внешний диаметры то\'юида; h
толщина тороида.
Доказать, что индуктивность катушки равна:
L == Pa w2h Jn
2
.
2л d 1
у к а з а н и е: Следует составить выражение для кольцевоrо Mar-
нитноrо потока бесконечно малоrо сечения и провести ИН1сrрирова-
ние по сечению тороида.
1-14. В цепи, изображенной на рис. 1-18, а. при токе i == 2 А
напряжение и == 10 В, а при i == 1 А и и == 12 В. Определить э. д. с.
Е и сопротивление ,.
О т в е т: 14 А; 2 Ом.
1-15. Определить 10К 1 источника тока и сопротивление, в схеме
рис. 1
19, а, если ток i и напряжение и изменяются так же, как и в
предыдущей задаче.
О т в е т: 7 А; 2 ОМ.
1-16. В цепи, изображенной на рис. 1
21, а, Е 1 == 10,5 В; Е з ==
== 19,5 В; '1 == 2 Ом; '2 == 3 Ом; 'з == 5 Ом. Найти э. д. с. Е 2 . при ко-
торой потеициал точки между сопротивлением '1 и источником э. д. с,
49
Е 2 равен и ПРО1Ивоположен по знаку потенциалу точки между сопро-
тивленнем '2 и источником Э. д. с. Е 2 .
Ответ: 15 В.
1-17. Сохранив условия предыдущей задачи, найти э. д. С. Е 2 .
при которой точка с нулевым потенцналом будет находиться посре-
динесопротивления '2'
О т в е т: О.
1-18. В цепи. изображенной на рис. 1
21, а, Е 1 == 17 В, Е 2 == 10 В,
Е з == 13 В, '1 == 6 Ом. 'з == 1 Ом. Определить сопротивление '2' ЩJИ
котором потенциал точки между сопротнвлением Т 1 И источником э. д. с.
Е 2 равен и противоположен по знаку потенциалу точки между сопро-
тивлением '2 и источником э. д. С. Е 2 .
О Т В е т: 3 Ом.
1-19. Сохранив условия предыдущей задачи, определить !;опро-
тивление '2' если известно, что точка с нулевым потенциалом нахо-
дится внутри со
ротивления '2' причем одна четвертая часть Т:1 нахо-
дится левее этон точки.
О т в е T:
35,5 Ом.
1-20. ЧТО такое положительное направление тока?
1-21. Зависит ли выбор положительiюrо направления напряже-
ния от положительноrо направления тока?
1-22. Что понимается под полярностью источника э. д. с. н истоЧ-
ника тока?
1-23. Почему результат расчета электрнческой цепи не зависит
01' выбора положительных направленнй токов?
1-24. Как выбрано положительное направление э. д. с. самоин-
дукцин в формулах (1-2) и (1
3)? Поясннть связь с законом Ленца.
1-25. Пояснить процесс прохождення nepeMeHHoro тока через
конденсатор.
1-26. Исходя из выражений энерrии, показать. что сопротивле-
ние, индуктивность и емкость всеrда положительны,
rЛАВА ВТОРАЯ
ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
ОДНОФАзноrо СИНУСОИДАльноrо ТОКА
1.f. СИНУСОИДАЛЬНblЕ ЭЛЕКТРИЧЕСКИЕ ВЕnИЧИНЫ
Электромаrнитный процесс в электрической цепи, при
котором MrHoBeHHbIe значения напряжений и токов пов-
торяются через равные промежутки времени, называется
пер и о Д и ч е с к и м. Наименьше
время, по истече-
нии Karoporo MrHoBeHHbIe значения
периодической вели-
чины повторяются, называется пер и о Д о м. Если ве-
личину, являющуюся периодической функцией времени t,
обозначить через F (t), то для любоrо положительноrо
50
или отрицательноrо значения aprYMeHTa t справедливо
равенство
F (t + т) ==р (t),
rде Т
период.
rеометрически это значит, что ординаты двух произ-
вольных точек rрафика F (t) с абсциссами, различающи-
мися на Т, одинаковы.
Величина, обратная периоду, т. е. число периодов
в единицу времени, называется ч а с т о т о й:
1
f
т'
Единицей измерения частоты служит rерц (rц); частота
равна 1 [ц, если период равен 1 с.
Преобладающим видом периодическоrо процесса в элек-
трических цепях является с И Н У с о и Д,а л ь н ы й ре-
жим, характеризующий-
ся тем, что все напря-
жения и токи явЛяются
синусоидальными функ-
циями одинаковой ча-
стоты. Это возможно
только при заданных
синусоидальных э. д. С.
и токах источников. Тем
самым обеспечивается Рис. 2-1. Синусоидальная функция.
наибол
е выrодный экс-
плуатационный режим работы электрических установок.
Как известно из курса математическоrо анализа, си-
нусоида является простейшей периодической функцией;
всякие друrие несмнусоидальные периодические функции
MorYT быть разложены в бесконечный ряд синусоид, име-
ющих кратные частоты (см. rл. 13). Поэтому ДЛя иссле-
дования процессов в цепях переменноrо тока в первую
очередь необходимо изучить особенности цепей синусои-
дальноrо тока.
На рис. 2-1 изображена синусоидальная функция
u==Uтsiп(wt+'ф); (2-1)
здесь И т
максимальное значение, или амплитуда; w
скорость изменения aprYMeHTa (уrла)
, называемая у r л о-
в о й ч а с т о т о й; она равна произведению частоты на 2л:
и измеряется в радианах в секунду (рад/с),
w == 2л:f;
lL
'фt
2К
(2-2)
51
'11'
н а ч а л ь н а я фаз а, определяемая смещением си-
нусоиды относительно начала координат; она измеряется
абсциссой точки перехода отрицательной полуволны в по-
ложительную.
Начальная фаза '11' представляет собой алrебраическую
величину. Уrол '11' положителен и отсчитывается вправо,
к точке t == О, коrда синусоидальная функция смещена
влево относительно начала координат (рис. 2-1).
Косинусоида может рассматриваться как синусоида
с начальной фазой '11' == л /2. Если функция задана
в коси-
нусоидальной форме u == и т cos (wt 1:- '11'1), то она может
быть приведена к виду (2-1) путем замены '11'1 == 'Ф.
л/2.
Поэтому к синусоидальным функциям (2-1) в общем случае
причисЛяются и косинусоидальные функции.
За aprYMeHT функции (2-1) может быть принято время t
или соответственно уrол wt. AprYMeHTY ,t соответствует
период Т, а aprYMeHTY wt
период шТ == 2л
Следует
иметь в виду, что aprYMeHT wt выражается в радианах,
причем в тех же единицах выражается и начальная фаза.
Если уrол '11' вычисляется в rрадусах, то aprYMeHT wt
также пере водится в rрадусы 1; в этом случае период со-
ставляет 3600.
Величина ш! + '11', определяющая стадию изменения
синусоидальной величины (2-1), называется фазовым yr-
лом или фаз о й. С течением времени фаза возрастает,
причем после увеличения фазы на 2л цикл изменения
синусоидальной величины повторяется.
РассмОтренные в данном параrрафе понятия, харак-
теризующие синусоидальные электрические величины, яв-,
ЛЯIOТся исходными при изучении электрических процессов
в цепях переменноrо тока.
2-2. rЕНЕРИРОВАНИЕ СИНУСОИДАЛЬНОЙ Э. Д. С,
Наиболее распространенным в промышленности спо-
собом получения синусоидальноrо тока является приме-
нение электромаrнитных машин, так называемых с и н-
х р О Н Н Ы Х r е н е р а т о р о в, приводимых во враще-
ние тепловыми, rазовыми, rидравлическими или друrими
двиrателями.
reHepaTop переменноrо тока состоит из двух частей
неподвижноrо с т а т о р а и вращающеrося р о т о р а.
1 Напомним, что 1 рад == 57,30.
52
На ОДНОМ из них (чаще на роторе) располаrаются полю-.
сы, т. е. электромаrниты, обмотка которых питается от
источника постоянноrо напряжения, или постоянные Mar-
ниты. На друrом (обычно на статоре) располаrается rлав-
ная обмотка, в которой наводится переменная э. д. с.
. [енератор может иметь одну или несколько пар полю-
сов. На рис. 2-2, а упрощенно показан явнополюсный re-
нератор с двумя парами полюсов, размещенных на рото-
ре. Указанному на рис. 2-2, а положению ротора относи-
тельно статора соответствует на рис. 2-2, 6 развернутая
на плоскость схема расположения обмотки и полюсов.
В каждом проводе обмотки, наХОДящемся в пазу ста-
тора, при вращении ротора наводится по закону Фарадея
Рис. 2-2, Принцип устройства синхронноrо [енератора,
э. д. с. е == Blv, rде В
маrнитная индукция поля ПОД
проводом; 1
длина провода; v
линейная скорость пе-
ремещения маrнитноrо поля. В Международной системе В
измеряется в теслах (Т), т.'е. Вб/м 2 .
При постоянных значениях 1 и v закон изменения э. д. с.
е (t) определяется законом распределения маrнитной индук-
ции В в воздушном зазоре машины. Блаrодаря специаль-
ной форме полюсных наконечников распределение маrнит-
ной индукции делается приблизительно синусоидальным
I вдQль всей окружности зазора между ротором и статором;
маrнитная индукция максимальна против середин и посте-
пенно убывает к краям полюсных наконечников. '
В момент времени, которому соответствует указанное на
рис. 2-2 положение ротора, маrнитная индукция под про-
ВОДОМ равна нулю и поэтому э. д. с. е также равна нулю.
После поворота ротора на одну восьмую часть полноrо
оборота (половина полюсноrо шаrа) э. д. с. достиrнет мак-
симума и будет направлена от вывода 1 к выводу 2 (по пра-
53
вилу правой руки) 1. Коrда ротор повернется еще на поло-
вину полюсноrо шаrа, э. д. с. вновь обратится в нуль. При
последующем вращении ротора еще на одну восьмую часть
оборота э. д. с. достиrнет максимума, но будет противо-
положно направлена
от вывода 2 к выводу 1 и т. д. Та-
ким образом, на выводах [енератора возникнет практиче-
ски синусоидальная э. д. с.
При числе пар полюсов р и числе оборотов ротора в ми-
нуту п частота наводимой переменной э. д. С. в reрцах
равна:
f === рп/60.
(2-3)
в энерrосистемах СССР и большинства друrих стран
частота промышленноrо тока равна 50 [ц. в США принята
частота 60 [ц.
в авиации с целью уменьшения массы оборудования
применяются машины с повышенной частотой вращения.
Частота f при этом получается повышенной (400 [ц). Напри-
мер, reHepaTop, имеющий р === 2 и п == 12000 об/мин,
reнерирует синусоидальную э. д. с. с частотой
f === 2.1:0000 400 [ц.
При большой окружной скорости (v > 50 м/с) крепление
полюсов затруднено и для обеспечения механической проч-
ности применяются неявнополюсные машины, у которых
обмотка возбуждения укладывается в пазы цилиндриче-
cKoro ротора неравномерно, так чтобы форма поля Былa по
возможности синусоидальной.
Проводная связь использует частоты порядка 104
105 [ц,
а радиотехника
еще более высокие частоты. rенерирова-
нне токов высокой частоты осуществляется с помощью
электронных или полупроводниковых устройств.
На рис. 2-3 в виде примера показаиа одна из схем
электронноrо [енератора высокой частоты. Анод трех-
электродной лампы (триода) присоединен через контур
LC к положительному полюсу источника постоянноrо на-
щiяжения, например аккумуляторной батареи. В конту-
1 это правило заключается в следующем: если вектор маrнитноЙ
индукцин входит в ладонь, а отоrнутый большой палец показывает
иаправление движения проводннка относительно поля, то остальные
четыре пальца указывают направление наводнмой э. д. с.
Аналоrично по правилу левой руки большой палец указывает
направление силы, действующей на проводник с то KO/,f.
54
ре LC, наЗываемом резонансным, возникаЮТ незатухаЮ-
щие синусоидальные колебания тока, частота которых
зависит от выбора параметров L и С. Электрическая энер-
rия, необходимая для поддержания этих колебаний, nocry-
пает от аккумуляторной
батареи.
Работа электронных re- С
нераторов здесь не рас- .
сматривается. Процессам,
происходящим в резонанс-
ных цепях, посвящена
rл. 5. Прющип действия
электронных rенераторmз
разобран во второй части Рис. 2-3. Упрощенная схема элек-
курса. Приведенная выше TpoHHoro reHepaTopa.
схема электронноrо reHe-
ратора предназначена для получения синусоидальных
колебаний высокой частоты.
Начало практическоrо внедрения nepeMeHHoro тока
относится ко ВТ9РОЙ половине XIX в., коrДа выдающийся
русский электротехник Павел НИколаевич Яблочков
(1847
1894) стал применять на практике изобретенные
им электрические свечи.
2-3. СРЕДНЕЕ И ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЯ ФУНКЦИИ
Среднее значение периодической функции f (t) за пе-
риод Т определяется по формуле
т
Fcp==
5 f(t)dt. (2-4)
о
Отсюда видно, что
peДHee значение за период равно
высоте прямоуrольника с основанием Т, площадь которо-
ro равна площади, оrраниченной функцией f (t) и осью
абсцисс за один период.
В случае синусоидальной функции среднее значение
за период равно нулю, так как площадь положительной
полуволны компенсируется площадью отрицательной по-
луволны синусоиды, Поэтому здесь пользуются понятием
среднеrо значения функции, взятой по абсолютному значе-
нию или, что то же, с р е Д н е r о n о л у пер и о Д н о r о
значения, соответствующеrо положительной полуволне си-
нусоиды (рис. 2-4).
55
В соответствии с эт'им среднее значениесинусоидаль-
Horo тока с амплитудой А == 1т будет:
" Т/2 Т/2
Icp== 2
т S siпсчtdt== 2:; l
cOS(J)tl ==
Iт
O,637Iт"
о о
(2-5)
Аналоrично среднее значение синусоидалъноrо напря-
жения
2
Uср==л- Uт
O,637Uт'
(2-6)
Измерительные приборы маrнитоэлеКТРl1ческой систе-
мы реаrируют на средние значения за период. Для изме-
рения среднеrо полуперио-
f(t) дноrо значения, соответ-
ствующеrо положительной
полуволне, синусоидаль:
t ный ток предварительно
пропускается через выпря-
мительное устройство.
Тепловое действие тока,
а та
же механическая сила
. Рис. 2-4. Среднее полупериодное взаимодействия двух про-
значение синусоидальной функции. водников, по которым про-
. ходит один и тот же ток,
пропорциональны квадрату тока. Поэтому о величине тока
судят обычно по так называемому Д е й с т В у Ю Щ е м у 1
(среднеквадратичному) значению за период.
Действующее значение периодической функции f (t)
вычисляется по формуле
F == V
J [f (t)]2 dt.
о
(2-7)
Из этой формулы следует, что величина F2 представ-
ляет собой, среднее знаllение функции [! и)]2 за период Т,
т. е. равна высоте прямоуrольника с основанием Т, пло-
Щадь Koтoporo равна площади/ оrраниченной функцией
[f (t)]2 и осью абсцисс за один период (рис. 2-5).
1 Этим термином заменен применявшийся ранее в литературе и
ныне не рекомендуемый термин «эффективное» значение,
56
В соответствии с (2-7) де йствующи й периодический ток
/ == V
s i 2 dt.
о
Возведя (2-8) в квадраТ
Horo выражения на ,Т,
найдем:
т
,РТ ==
ri 2 dt.
о
(2-8)
Это равенство показы-
вает, что действующий А'
периодический ток равен '2
такому постоянному току,
который, проходя через не-
изменное сопротивление "
за период времени Т выде- Рис. 2-5. Действующее значение
ляет то же. количество синусоидальной функции.
тепла, что и данный ток i.
Аналоrично действующее периодическое напряжение
{ Т
, 1 .
и == т
и 2 dt .
о
При синусоидальном токе
т т
i 2 dt ==
/
sin 2 rot dt ==
о о
/2 { /2
== 2т
(1
cos 2rot) dt ==т Т.
о
Следовательно, соrласно (2-8)
/ ==
O 707/
V2"""'" т'
АналоrичНО действующее синусоидальное
и т
U == V2
О,707и т .
(2-9)
(2-8а)
напряжение
(2-9а)
Номинальные токи и напряжения электротехнических
устройств определяются, Ka
правило, действующими зна-
57
чениями; поэтому действующие значения представляют
наиболее распространенный электрический параметр.
Для измерейия действующих значений применяются
системы приборов тепловая, электромаrнитная, электро
динамическая и др.
1.4. СИНУСОИДАЛЬНblЙ ТОК В СОПРОТИВЛЕНИИ
Если синусоидальное напряжение u === и т siп (wt + 'Ф)
подвести к сопротивлению, (рис. 2
6, а), то через сопротив-
ление пройдет синусоидальный ток
i=== и т sin(wt+1jJ)==/msin(ffit+\jJ).
,
Следовательно, напряжейие на выводах сопротивле-
ния и ток, проходящий через это сопротивление, имеют
одинаковую начальную фазу,
или, как rоворят, с о в п а
Д а ю т п о фаз е: они
одновременно достпrают своих
амплитудных значении U т И
/ т и соответственно одновре-
менно проходят через нуль
(рис. 2
6, б).
Разность начальных фаз
Рис. 2
6. Синусоидальный ток двух синусоид, имеющих оди-
в сопротивлении. наковую частоту, называется
фаз о в ы м с Д Б И r о м.
В данном случае фазовый СДБиr между напряжением u и
током i равен нулю:
i,U.
4
а)
(Ut
27r
ер == \jJu
\jJj == О.
При прохождении синусоидальноrо тока через сопро-
тивление, не только MrHoBeHHbIe напряжения на сопротив-
лении и тока В нем, но и амплитуды и соответственно дей-
ствующие напряжение и ток связаны законом Ома:
ит=='/т; U==,I.
Пользуясь величиной проводимости g == 1/" получаем:
/m===gU m ; /==gU.
Мrновенная мощность, поступающая в сопротивление:
Pr == ui == U т/ т sin 2 (wt + \jJ) == U / [1
cos 2 (wt + \jJ)]. (2-10)
58
изменяется с уrловой частотой, удвоенной по сравнению
с частотой напряжения и тока, и колеблется в пределах
от О до 2и 1 (рис. 2-7).
Как видно из (2-10), кривая Pr состоит из двух слаrаю-
щих: ПОСТОянной слаrающей U 1 и косинусоидальной функ-
ции, имеющей амплитуду U I и уrловую частоту 2ю.
Ввиду Toro что в рассматриваемом случае напряжение
и ток совпадают по фазе, т. е. всеrда имеют одинаковый
знак (плюс или минус), их
произведение всеrда поло-
жительно.
Среднее значение мощ-
ности за период Р ==
т
==
S Pr dt называется ак-
о
тивной мощностью И изме-
ряется в ваттах.
В рассматриваемом слу-
чае, как' это видно из
выражения (2-10) и рис. 2-7, активная мощность Р ==
== И/ == (Р. Это следует также из определений, данных
в предыдущем параrрафе.
Сопротивление r в свою очередь может быть опреде-
лено как отношение активной мощности к квадрату дей-
ствующеrо значения тока: r == Р/J2.
В
1-7 отмечалось, что сопротивление проводника
при переменном токе больше, чем при постоянном токе,
вследствие явлений поверхностноrо эффекта, возникно-
вения вихревых токов и излучения электромаrнитной
энерrии в пространство (при высоких частотах). В отли-
чие от сопротивления при постоянном токе сопротивление
проводника при переменном токе называется' а к т и в-
Н ы М сопротивлением.
-1/\7\1\[\."
о L
" T
2"
2
fJ)
fJ)
Рис. 2-7. Мrновенная мощность,
поступающая в сопротивление
N
О).
2-5. СИНУСОИДАЛЬНЫR JOK В ИНДУКТИВНОСТИ
Пусть через индуктивность L (рис. 2-8, а) проходит ток
i == 1 т sin (wt + "ф).
Электродвижущая сила самоиндукции определяется по
формуле (1-3):
eL ==
L
{
,==
юLl т cos (wt + 'ф) ==
и т sin( wt + 'ф +j).
59
Значит, напряжение на индуктивности
ИL ==....... eL == U т sin (rot+ 1Р+
).
Полученное выражение показывает, что напряженuе
на uндуктивности опережает ток на усол, л/2: максимум
напряжения смещен влево относительно максимума тока
на л/2 (рис. 2-8, 6), коrда ток проходит через нуль, напря-
жение достиrает положительноrо или отрицательноrо мак-
симума, так как оно пропорционально скорости изменения
тока (di!dt), которая в момент прохождения тока через нуль
максимальна (синусоида тока в этот момент имеет наиболь-
шую крутизну). Коrда ток до-
стиrает максимума, скорость
ero изменения, а следователь-
Но, и напряжение на индук-
тивности обращаются в нуль.
Под фазовым сдвucщ,t ер
тока относuтельпо напряже-
нuя понuмается разность на-
чальных фаз напряженuя u
тока (см.
2-4). Следователь-
Но, в данном случае
1(; .1, п
ер == 'Уа
'Yl == -2'
и).
Рис. 2-8. Синусоидальный ток
в иидуктивности.
UJt
Амплитуды, так же как и действующие значения на-
пряжения и тока, связаны соотношением, подобным за-
кону Ома:
Um==roL/m==xLl m ; U==xLI.
Величина xJ.. == roL, имеющая размерность сопротив-
ления, называется и н Д у к т и в н ы м с о про т и в л е-
н и е м; обратная ей величина b L == I!roL называется и Н-
Д У к т и в н о й про в о д и м о с т ь ю.
Итак,
/ т == bLU m ; 1 == bLU.
Индуктивное сопротивление представляет собой рас-'
четную величину, с помощью которой учитывается явле-
ние самоиндукции.
Мrновенная мощность, поступающая в индуктивность,
будет:
Р!. == ui , итI т siп (rot+'Ф +
) sin (rot+'ф) ==
== Ит;т 2соs(rot+'Ф)siп(rot+'Ф)==UIsiп2(rot+'Ф).
60
Она колеблется по синусоидальному закону с уrловЬй ,
частотой 20), имея амплитуду' UI, Мrновенная мощность
в данном случае равна скорости изменения энерrии Mar.
НИТlIоrо поля индуктивности (см.
1
3).
Энерrия маrнитноrо поля индуктивности
и2 и2 и2
WL ==2 == Т sin 2 (O)t+;p) == 2[1
cos 2 (O)t + '!')]
изменяется периодически с уrловой частотой 20) в nреде.
LJ2
лах от О до т (рис. 2-9).
Поступая от источника,
энерrия временно запасается
в маrнитном поле индуктив-
ности, затем возвращается
в источник при исчезновении
маrнитноrо поля. Энерrия
маrнитноrо поля достиrает
максимума n момент перехо-
. да тока в индуктивности че-
рез амплитудное значение,
затем она убывает и обра-
щается в нуль при токе, рав-
ном нулю.
Таким образом, происхо-
дит колебание энереии между
источником и индуктивностью, причем активная. мощ-
ность, поступающая в индуктивность, равна нулю.
Так как максимальная энерrия, запасаемая в маrнит-
ном поле, равна WLM"KC == L12, то индуктивное сопро-
тивление XL == O)L может быть определено к3!{
P,WL
Рис. 2-9. Мrновенная мощность,
поступающая в индуктивность,
и энерrия маrнитноrо поля.
Х
(i)W [макс
L
/2 .
2-6. СИНУСОИДАЛЬНЫй ТОК В ЕМКОСТИ
Пусть напряжение на емкости С (рис. 2-10, а) сину-
соидально:
и == и т sin (О)t+'Ф).
На основании (1-8)
i
С
; == О)СИ т cos (О)t+'Ф) == J т sin( O)t +'\1 +
). (2-11)
61
Изменение электрическоrо заряда происходит по си-
нусоидальному закону в соответствии с приложенным
напряжением и. При этом попеременное накапливание
. положительных и отрицательных электрических зарядов
на пластинах емкости обусловливает прохождение в це-
пи си;нусоидальноrо тока i. Он определяется скоростью
изменения заряда на емкости (dq/dt) ,
Выражение (2- 11) показывает, что ток. i опережает
приложенное напряжение и на УсОЛ л/2 (рис. 2-10, 6).
Нулевым значениям тока соответствуют максимальные
(положительные или отрицательные) значения напряже-
ния и. Физически это объясняется тем, что Korдa электри-
ческий заряд q и соответственно напряжение и == q/C до-
стиrают максимальноrо зна-
чения (положительноrо или
u)i отрицательноrо), ток i равен
нулю,
си! Под фазовым сдвиrом тока
относительно напряжения
здесь, как и раньше, подра-
б) зумевается разность началь-
ных фаз напряжения и тока,
Рис. 2
1O. Синусоидальный ток т. е. ер == 'Фtt
'Фi ==
л/2,
в емкости. Таким образом, в отличие
от цепи с индуктивностью,
rде ер == +л/2, фазовый сдвиr тока относительно напряже-
ния в случае емкости отрицателен (ер ==
л/2).
Амплитуды и соответственно действующие напряжение
и ток связаны соотношением, подобным закону Ома 1:
1 '
и т == юС /m==XC1m; U==Xc I .
Величина ХС == 1/О)С, Имеющая размерность сопротив-
ления, называется е м к о с т н ы м с о про т и в л е н и-
е м. Обратная ей величина Ь с == О)С называется е м к о-
с т н о й про в о Д и м о с т ь ю. Следовательно,
1т == ЬсИ т ; /==ьси.
1 Следует заметить, что 10ЛБКО в случае сопротивления r закон
Ома применим ,к MrHoBeHHbIM значениям напряжения И тока; в осталь-
ных случаях отношение MrHoBeHHbIx величин u и i, имеюшее размер-
ность сопротивления, представляет собой некоторую функцию вре-
мени, не имеющую физическоrо смысла и практическоrо применения.
62
Мrновенная мощность, поступающая в емкость,
Ре == ui == и т / т sin (ffit+ '\1) sin (ffit+1J1+
i) ==
== И/ sin 2 (ffit+ '\1)
колеблется синусоидально с уrловой частотой 2ш, имея
амплитуду, равную И/; выражение Рс в рассматриваемом
случае аналоrично выражению ДЛЯ PL в
2-5.
Мrновенная мощность, поступающая в емкость, равна
скорости изменения энерrин электрическоrо поля емко-
сти.
Энерrия электрическоrо поля емкости
Си 2 СИ' СИ2
Wc ==
== т sin 2 (
t+ '\1) ==
[1
cos 2 (ffit+ '\1)]
изменяется периодически с уrловой частотой 2ш в преде-
СИ2
лах от О дот (рис. 2-11).
Поступая. от источника,
энерrия временно запасает-
ся в электрическом поле
емкости, а затем возвра-
щается в источник при ис-
чезновении электрическоrо
поЛя. Энерrия электриче-
cKoro поля Достиrает мак-
симума при амплитудном
значении напряжения на
емкости. Затем она убывает
и обращается в нуль при
напряжении, равном нулю.
Таким образом, так же
как в случае индуктив-
н.ости, происходит колебание энерrии между источником
и емкостью, причем активная мощность Р , О.
Так как максимальная энерrия, запасаемая в электри-
ческом поле, равна WCMaKC == си2, то емкостное сопротив-
ление ХС == U / / == 1/ шС может быть определено как
Р,Шс
Рис. 2-11. Мrновенная МОЩНОСТЬ,
поступающая в емкость, и энерrия
электрическоrо поля.
шW Смакс
ХС == 12
63
1-7. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
При прохождении синусоидальноrо тока i == /т sin ш!
через электрическую цепь, состоящую из последовательно
соединенных элементов r,
L и С (р ис. 2-12), на выводах
этой цепи создается синусоидальное напряжение, равное
алrебраической сумме синусоидальных напряжений на
отдельных элементах (вто-
рой закон Кирхrофа):
U == U r + UL + "с.
Напряжение u r на со-
противлении r совпадает
...L,. L С
............
IL,. IL, ILС
.
IL
Рис. 2
12. Пос,'!еДовательное
соединение сопротивления,
индуктивности и емкости.
IL"J и, , ис
(A)t
Рис. 2-13. Напряжения на сопро-
тивлении, ИНДУКТИВi'!ости и емкости
(соединенных последовательно) при
синусоидалыJмм токе,
по фазе с током i, напряжение UL на индуктивности L
опережает, а напряжение ис на емкости С отстает по фазе
от i на л/2 (рис. 2
13). Следовательно, напряжение и на
вьпюдах всей цепи равно:
U т sil1 ((jJt+ rp) == r/ m sin (jJt+.(jJL/ m COS (j)t
ш
1т COS (jJt == '/ т sin (jJt +
+ ( (jJL
oo
) / m COS (jJt == / т [r sin ш! + х COS (j)t]. (2
12)
Уравнение (2-12) представляет собой триrонометри-
ческую форму записи ВТОlюrо закона Кирхrофа для MrHo-
венных напряжений. Входящая в Hero величина х ==
1
== XL
xc == (jJL
ыС называется р е а к т и в н ы м с о-
п р о т и в л е н и е м цепи, которое в зависимости от
знака может иметь индуктивный (х > О) или емкостный
(х < О) характер. .
В отличие от реактивноrо сопротивления х активное
сопротивление r всеrда положительно.
64
Для нахождения и т И ер воспользуемся триrонометри-
ческими соотношениями:
т sin a:t п cos а === V т 2 n + п2 sin (а + ер); ]
(2
13)
ер == arctg
.
т
Итак,
и т == v ,2+х 2 / т ;
х
tg ер ==
.
,
(2
14)
(2
15)
Выражение (2
14) показывает, что амплитуда и дейст-
вующее напряжение на цепи и ток, проходящий через дaH
ную цепь, связаны соотношением, аналоrичным закону
Ома:
Um==zI m ; U==zI,
rде
z === у ,2 +х2 (2
16)
называется n о л н ы м с о про т и в л е н и е м 1 рассмат-
риваемой цепи.
Активное, реактивное и полное сопротивления, OTHO
сятся К числу основных понятий, применяемых в теории
электрических цепей.
Выражения (2
12) и (2
15) показывают., что ток i отстает
х
от напряжения и на уrол ер == arctg
.
,
Если задано напряжение и == и т sin (O)t + 'Ф) на выво-
дах цепи с последовательно соединенными " L и С, то ток
определяется по формуле
. и m . ( t + ;,!; )
1. ==тSlП о)
ep.
Уrол ер, равный разности начальных фаз напряжения
и тока, отсчитывается по оси O)t в направлении от напряже-
ния к току и бывает острым или прямым
\ ер\
n/2.
УсОЛ ер положителен при индуктивном характере цe
пи, т. е. при Х > о; при этом ток отстает по фазе от напря
жения и ер отсчитывается по оси абсцисс вправо от напря-
жения к току (рис. 2
14).
1 ЭтИМ термином заменен применявшийся ранее в литературе н
ныне не рекомендуемый термин
<кажущееся>
сопротивлеиие.
65
Усол q> 011Jрицателеп при емкостном характере цепи,
т. е. при х < о; при этом ток опережает по фазе напряже-
ние и ер отсчитывается по оси абсцисс влево от напряже-
ния к току (рис. 2-15).
Итак, следует всеrда помнить, что УсОЛ ер положителен
при отстающем и отрицателен при опережающем токе.
Ток совпадает с напряжением по фазе при Х == XL
Хс == о, т. е. при равенстве индуктивноrо и eMKocTHoro
сопротивлений. Такой режим работы электрической цепи
называется рез о н а н с о м н а п р я ж е н и й' (см, rл. 5).
u,i.
blt
blt
tfu
Рис. 2-14, ТОК Отстает от на.
пряжения,
Рис, 2-15. Ток опережает на.
пряжение.
Из выражений (2-15) и (2-16) следует, что активное
и реактивное сопротивления цепи связаны с полным со-
противлением формулами:
r == z cos <р; Х == Z sin ер. (2-17)
Умножив правые и левые части выражений (2-17) на
действующий ток !, получим действующие напряжения
на активном и реактивном сопротивлениях, называемые
а к т и в н о й и р е а к т и в н о й с о с т а в л я ю lЦ и-
м и н а п р я ж е н и я:
и а == '! == z cos ер! == и cos ер; }
(2-18)
U р == Х! 7" z sin ер / == и sin ер.
MrHoBeHHble значения напряжений на активном и ре-
активном сопротивлениях, суммирующиеся алrебраиче-
ски в, соответствии с (2-12), имеют фазовый сдвиr л/2.
Поэтому непосредственное сложение действующих актив-
Horo и реактивноrо напряжений не дает действующ
ro на-
пряжения всей цепи: соrласно (2-18) активная и реак-
тивная составляющие напряжения связаны с действую-
66
щим суммарным напряжением формулой 1
и == у и: + U
.
ДЛЯ характеристики индуктивных катушек, представ-
ляемых цепью с последовательным соединением элемен-
тов r и L, пользуются понятием добротности катушки
QL == XL/r == шL/r, которое равнозначно TaHreHcy уrла
СДВИFа фаз ер для катушки. Чем меньше сопротивление (, тем
выше при прочих равных условиях добротность катушки.
Добротность индуктивных катушек, применяемых в ра-
диотехнике, автоматике и"' приборостроении, обычно не
превышает QL == 200 -7- 300. Для достижения более высо-
кой добротности применяются так называемые пьезоэлек-
трические резонаторы (см.
10-6). С понятием добротности
мы встретимся в rл. 5.
2.8. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Если к выводам электрической цепи, состоящей из
параллельно соединенных элементов " L и С (рис. 2-16),
приложено синусоидальное
напряжение u == И т sin шt,
то синусоидальный ток,
проходящий через эту цепь,
i
.......о-
lL
i,.
il. ! ic
,. L С
Рис. 2-16. Параллельное сое-
динение сопротивления, ин-
дуктивности и емкости.
i r , iL,ic
IL
wt
Рис. 2-17. Токи в сопротивлении,
индуктивности и емко
ти (соеди
неннЫХ параллельно) при синусои
дальном напряжении.
равен алrебраической сумме синусоидальных токов в парал-
лельных ветвях (первый закон Кирхrофа):
i==ir+iL+ic.
Ток i r в сопротивлении r совпадает по фазе с напря-
жением и, ток i L В индуктивНости L отстает, а ток ic в ем-
кости С опережает напряжение на л/2 (рис. 2
17).
1 И а И Ир MGrYT рассматриваться как катеты прямоуrольноrо Tpe
уrольника, rипотенуза KOToporo равна И; подобный прямоуrольный
треуrольник образуют также величины (, х и z (см. rл. 3).
67
Следовательно, суммарный ток i в цепи равен:
1т sin (rot
ер) ==
И m sin rot
L Иm cos rot +
, w
+ roСИ m cos rot == И m [+ sin rot
( (й
roС) cos rot] ==
==И m (g sin rot
Ь cos rot). (2-19)
Уравнение (2-19) представляет собой триrонометриче-
скую форму записи первоrо закона Кирхrофа для MrHo-
венных токов. Входящая в Hero величина Ь == b L
Ь С ==
1 С
== wL
ro называется р е а к т и в н о и про в о Д и-
м о с т ь ю цепи, которая в зависимости от знака может
иметь индуктивный (Ь > О) или емкостный (Ь < О) характер.
В отличие от реактивной проводимости Ь величина g == l/r,
которая в данном случае называется а к т и в н о й п р а-
в о д и м о с т ь ю, всеrда положительна.
Для нахождения 1т и ер воспользуемся соотношениями
(2-13):
Iт== V g2+b 2 Иm==уИ т ;
tg ер ==
.
g
Из (2-20) следует; что
1т == уИ m или I == уИ,
(2-20)
(2- 21)
rде
у == v g2 + Ь 2
(2-22)
п о л н а я про в о Д и м о с т ь 1 рассматриваемой цепи.
Активная, реактивная и полная проводимости отно-
сятся К числу основных понятий, применяемых в теории
электрических цепей.
Соrласно (2-21) ток i отстает от напряжения u на уrол
1
t ь WL
wc
ер == arc g
== arctg
g g
Если задано напряжение u == И m sin (rot + 'Ф) на выво-
дах цепи с параллельна соединенными r, L и С, то ток опре-
деляется по формуле
i == УИ m sin (rot+ 'ф
ер).
1 Этим термином заменен применявшийся ранее В, литературе и
ныне не рекомендуемый термин «кажущаяся* ПРОВОD,имость.
68
Уrол ер, как и в предыдущем случае, отсчитывается по
оси уrлов ffit в направлении от напряжения к току и яв-
ляется острым или прямым
I ер I
n/2.
УсОЛ ер положителен при индуктивном характере цепи,
т. е. при Ь > о; при этом ток отстает по фазе от напря-
жения.
УсОЛ ер отрицателен при емкостном характере цепи,
т. е. при Ь < о; при этом ток опережает по фазе напря-
жение.
Ток совпадает с напряжением по фазе при Ь == bL
Ь с == о, т. е. при равенстве индуктивной и емкостной
проводимостей. Такой режим работы электрической цепи
называется рез о н а н с о м т о к о в (см. rл. 5).
Из (2
21) и (2
22) следует, что активная и реактив-
ная проводимости цепи связаны с полной проводимостью
формулами:
g == у cos ер; Ь == у sin ер. (2-23)
Умножив правые и левые части выражений (2-23) на
действующее значение напряжения и, получим действу-
ющие токи в ветвях с активной и реактивной проводимо-
стями, называемые а к т и в н о й и р е а к т и в н о й
с о с т а в л я ю Щ и м и т о к а:
1 а == gU == у cos ер U == 1 COS ер; }
1 р == ьи == у sin ер U == 1 sin ер. (2-24)
,Активная и реактивная составляющие тока связаны
с действующим значением CYMMap Horo тока формулой 1
1 == V 1: + I
.
ДЛЯ характеристики конденсаторов, представляемых
цепью с параллельным соединением элементов r и С, при-
меняется понятие добротности конденсатора Qc == bc/g ==
== ffiCr, которое равнозначно TaHreHcy уrла I ер I конденса-
тора. Обратная величина называется т а н r е н с о м у r-
л а Д и э л е к т р и ч е с к и х п о т ерь конденсатора:
tg б == l/Qc (уrол диэлектрических потерь б дополняет
уrол I ер I до 90°).
1 lа и lр MorYT рассматриваться как катеты прямоуrольноrо тре-
уrольника, rипотенуза KOToporo равна 1; подобный прямоуrольный
треуrольник образует также величины g, Ь и у (см. rл. 3).
69
Чем больше сопротивление " тем больше (при прочих
равных условиях) добротность конденсатора и тем меньше
уrол потерь.
Добротность конденсаторов, применяемых в раДlIО-
технике, автоматике и приборостроении, определяется
сотнями и тысячами (tg б для разных частот и диэлектриков
колеблется в пределах от 10
1 до 10
4).
2.9. МОЩНОСТI, В ЦЕПИ СИНУСОИДАл&ноrо ТОКА
В
2-4
2-6 рассматривались энерrетические соотноше-
ния в отдельных элементах (, L и С при синусоидальном
токе.
Разберем теперь более общий случай участка элект-
рической цепи, напряжение на котором равно и ==
== и т sin (f)t, а ток
i == / т sin «(f)t
ер).
Мrновенная мощность, поступающая в цепь,
р == и т / т sin (f)t sin «(f)t
ер) ==
== u / [cos ер
cos (2(f)t
ер)] (2-25)
состоит из двух слаrающих: постоянной величины U / cos ер
и синусоидальной, имеющей удвоенную частоту по сравне-
нию с частотой напряжения и тока.
Среднее значение второй tлаrающей за время Т, в те-
чение KOToporo она совершает ,два цикла изменений, рав-
но нулю. Поэтому активная мощность, поступающая в рас-
сматриваемый участок цепи,
т
р == ;. S ui dt === U / cos ер. (2-26)
о
Множитель cos ер носит название к о э Ф Ф и ц и е н т а
м о Щ н о с т и. Как видно из (2-26), активная мощность
равна nроuзведению действующих значений напряжения
и тока, умноженному на коэффициент мощности.
Чем ближе уrол ер к нулю, тем ближе cos ер к еДИНице
и, следовательно, тем б6льшая при заданных значениях
U и / активная мощность передается источником прием-
нику.
Повышение коэффициента мощности nромышленных
электроустановок представляет важную техника-экономи-
ческую задачу.
70
Выражение активной мощности может быть преобра-
ЗQвано с учетом (2
17) и (2
23):
р == zI2 cos <р == r 12;
р == уи2 cos <р === gU 2 .
Активная мощность может быть также выражена че-
рез активную составляющую напряжения (и а == U cos <р)
или тока (Ia === 1 cos <р):
р === U aI; Р === U 1 а'
Приведенные общие выражения мrновенной и актив-
ной мощности применимы и к частным случаям, разоб-
ранным выше, Коrда <р === О
(см.
2-4), <р === n/2 (
2-5) и
<р ===
n/2 (
2
6); мы не бу-
дем здесь повторять получен-
ных ранее результатов.
Рассмотрим более общий
случай активно-реактивной
цепи, например цепи, содер-
жащей сопротивление и ин-
дуктивность; при этом
0< <р< nj2 и 0"< cos <Р< 1.
Соrласно (2-25) MrHOBeH-
ная мощность колеблется с
удвоенной уrловой частотой 2ю относительно линии, от-
стоящей от оси времени на Р === ИI cos <р (рис. 2-18).
В промежутки времени, коrда u и i имеют одинако-
вые знаки, мrновенная мощность положительна; энерrия
поступает от источника в приемник, поrлощается в со-
противлении и запасается в маrнитном поле индуктив-
ности.
В промежутки времени, Коrда u и i имеют разные зна-
ки, мrновенная мощность отрицательна и энерrия ча-
стично возвращается приемником источнику. Как видно
из рис. 2
18, в течение большей части периода MrHoBeH-
ная мощность положительна и соответственно ПЩIOжи-
тельная (расположенная над осью времени) ПЛощадь кри-
вой р преобладает над отрицательной площадью кривой р.
В результате средняя мощность за период, т. е. активная,
мощность, Р> О.
Аналоrичная картина получается и в случае активно
емкостной цепи (О> <р >
nj2).
i,u,p
Рис. 2-18. Мощность, поступаю-
щая в активно-индуктивную
цепь,
71
В электрических системах, в которых источниками
электрической энерrии являются reHepaTopbI переменноrо
тока, мощность получается от первичных двиrателей,
приводящих тенераторы во вращение. В радиотехнике и
электронике, тде синусоидальные колебания создаются
с помощью электронных или полупроводниковых прибо-
ров, мощность получается от источников постоянноrо тока,
питающих электронные тенераторы или друrоrо рода уст-
ройства.
Величина, равная произведению действующих тока и
напряжения на цепи:
S==И/,
(2-27)
называется п о л н о й м о Щ Н О С Т Ь Ю цепи и измеря-
ется в вольт-амперах (ва). Следует заметить, что амплитуда
синусоидальной составляющей мrновенной мощности (2-25)
численно равна полной мощности.
На основании (2-26) и (2
27) коэффициент мощности
равен отношению активной мощности к полной:
cosep==PjS.
При расчетах электрических цепей и на практике
в эксплуатации пользуются также понятием р е а к т и в-
Н а я м о Щ н о с т ь 1, которая вычисляется по формуле
Q == И/ sin ер
и является мерой потребления (или выработки) реактив-
Horo тока.
Эта мощность выражается в единицах, называемых вар.
Очевидно,
S2==P+Q2; sinep==
; tgep==
.
Выражение реактивной мощности может быть преоб-
разовано с учетом (2-17) и (2-23):
Q == zJ2 sin ер == хР; Q == уИ 2 sin ер == ьи 2 .
Реактивная мощность может быть также выражена
через реактивную составляющую тока (/р == / sin ер) или
напряжения (Ир === И siп ер):
Q == U / р; Q == U р/ .
1 Терминами «активная», «реактивная» И «полная» мощности за-
менены nрименявшиеся ранее в литературе и ныне не рекомендуемые
термины «sаттная», «безваттная» и «кажущаЯСЯ1> мощности.
72
В соответствии с принятым ранее правилом знаков
для уrла <р реактивная мощность положительна при от-
стающем токе (индуктивная НClZрузка) и отрицательна
при опережающем токе (емкостная НClZрузка).
Понятия активная (средняя), реактивная и полная
мощности являются удобными определениями мощностей,
которые прочно укоренились на практике.
Реактивные мощности, I'lQдводимые к ,индуктивности
и емкости, MoryT быть представлены в следующем виде:
:n; и2
Qz. == U / sin 2
== U / == wL/2 == (U т == ы W LMaKC;
Qc==U/sin(
)==
U/==
(UCU2;:
СИ'
==
(U 2 т ==
(U W Смакс'
rде WL 1 M8KC и W C 'M8KC
максимальные значения энерrии,
периодически запасаемой индуктивностью и емкостью.
Реактивная мощность цепи, содержащей индуктивность
и емкость, пропорциональна разности максимальных зна-
чений энерrии, запасаемой в маrнитном и электрическом
полях:
Q == (U (W LMaKc
W Смакс)'
(2-28)
Предлаrается читателям проверить и самостоятельно
убедиться в том, что эта формула справедлива при лю-
бом соединении индуктивности и емкости: последователь-
ном, параллельном или в какой-либо комбинации с со.
противлениями.
2.tO. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
2-1. Вычесть напряжение 5 sin ro! из напряження 10 sin (ro! +
+ :n;/2).
О т в е т: 11,2 sin (ro! + 116°30').
2-2. ТОК изменяется по закону i == 20 sin ш! А; частота равна f ==
== 50 rц. Определить наибольшую скорость изменения тока и соответ-
ствующее этому моменту зн'ачение тока,
О т в е т: 6280 А/с; О.
, 2-3. На выводах цепи, состоящей из послеДовательно соединен-
ных сопротивления , == 50 Ом и ннДуктивностн L == 0,1 r, задано
напряжение и == У2.100 sin ш! В. Частота f == 50 rц. Вычислить
полное сопротивление цепи и действующие напряжения на , и L; вы-
вести выражения для синусоидальноrо тока i (t); по 'Строить кривые
i (t), и (t) и напряжений на , и L.
О т в е т: 59 Ом; 85 В; 53,4 В; i == yi.l,7 sin (ш!
32°10') А,
73
2-4. В цепи, состоящей из последовательно соединенных r и L,
ток равен 1 А при частоте 400 [ц и 0,8 А при 800 {'ц. В обоих случаях
напряжение на цепи 20 В. Определить, и L.
О т в е т: 18 Ом; 3,45 Mr.
2-5. В цепи, состоящей из последовательно соединенных, и С,
ток равен 0,1 А при частоте 800 rц и 0,08 А при 400 [ц. В обоих слу-
чаях напряжение на выводах цепи 20 В. Определить, и С.
О т в е т: 180 Ом; 2;3 мкФ.
2-6. В цепи, состоящей из парэллельно соединенных r и С, ток
равен 0,08 А при чаСТGте 400 rц и 0,1 А при 800 rц. в обоих случаях
напряжение иа цепн 20 Б. Определнrь , и С.
О т в е т: 277 Ом; О, 688 мкФ.
2-7. В цепи, изображенной на рис. 2-12, при частоте 1000 rц и
сопротивлении, == 25 ом действуюшие Значения напряжений U r ==
== 25, UL == 100, ис == 120 В. Определить L и С.
О т в е т: 15,9 Mr; 1,33 мкФ.
2-8. На цепи, состоящей из последовательно включенных сопро-
тивления т == 30 ом и емкости С == 6 м!;Ф, задано напряжение u ==
== У2.120 sin oot В. Частота f == 400 [ц. Вычислить полное сопро-
тивление цепи и действующие значения напряжений на , и с; вывести
выражение для синусоидальноrо тока i (t); построить кривые и (t),
i (t) и напряжений на т и С. .
О т в е т: 72,8 Ом; 49,5 В; 109,5 В;
i== "У2. 1,65 sin (00/+65°40') А.
2-9. Напряжение на сопротивлении , == 3,63 Ом и индуктивно-
сти L == 0,02 r, соединенных параллельно, равно и == У2 х
х 120 sin (3,14 t + :n;/6) В. Вычислить полную проводимость цепи
и действующие токи в , и L; вывести выражение для cYMMapHoro сину-
соидзльноrо тока в цепи; построить кривые и (t), i (t) и токов в , и L.
О т в е т: 0,318 См; 33,1 А; 19,1 А;
i== "У2. 38,2 sin 3,14t А.
2-10. Напряжение на сопротивлении, == 1000 ОМ и емкости С ==
1 мкФ, соединенных параллельно, равно и == У2.120 sin 2512 t В.
Вычислить полную проводнмость И деЙствующие токи в , и с; вывести
выражение для cYMMapHoro синусоидальноrо тока i (t); постронть крн-
вые и и), i (t) и токов в , и С.
О т в е т: 0,00269 См; 0,12 А; 0,301 А;
i == У2. 0,323 sin (2512t+68°20') А.
2-11. Вычислить действующее напряжение на цепи, имеющей
активную проводимость 0,07 См и реактивную проводимость 0,044 См,
если действующий синусоидальный ток, проходящий через цепь, ра-
вен 10 А.
О т в е т: 121 В.
2-12. К цепи, состоящей из последС)вательно соединенных сопро-
тивления, == 1 Ом, индуктивности L == 0,1 r и емкости С == 101,4 мкФ,
приложено напряжение 33,8 sin 314 t В. Найти ток; пострсщть кривые
тока и напряжений на сопротивлеиии, индуктивности и емкости.
О т в е'т: 33,8 sin 314 t А.
74
2-13. Определить напряжеlIие на 1.{епи, состоящей из т, L и С,
соединенных последовательно, если напряжение на С равно и т sin wt,
О т в е т:
U т V (l
w
LC)
+ (,шС)
(sil1 wt + а);
t тшС '
CG="arc g l
w2LC'
2-14. Напряжение на т, L и С, соединенных паралле.льно, РЩJНО
и т sil1 wt. Определить суммарный ток.
О т в е т;
'т==и т vиJ+( w
WCYSil1(wt
rp);
q>== arctg, ( ;L
ШС).
2-15. Через цепь, состоящую из ЩlралЛl:ЛЬНО соединенных со-
противления , == 8,33 Ом и индуктивности L == 6,36 Mf, проходит
ток 0,141 cos wt А, частота равна 500 [ц. Опред.елить напряжение на
параллельных ветвях.
О т в е т: Ц cos (wt + 22036') В.
2.16. На цепи, СОСJоящей из последовательно соединенных ,
и L, напряженне равно 120 В, ток 0,5 А, активная мощность 30 Вт,
частота 400 rц. Определить т и L.
О т в е т: 120 O
; 83 Mr.
2-17. Цеl1Ь состоит из источника э. д. с. 100 sil1 400 t В, сопро-
тивления, == 50 Ом и индуктивности L == 0,1 r, соединеиных последо-
ватеЛЬН0. Считая ток синусоидальным, найти для момента t == :rt/200 с
MrHoBeHHbIe токи, напряжения на элементах и мощности, подводи-
мые к ним; определить действующие токи и напряжения на элементах.
О т ве т:
0,975 А;
48,8 В; 48,8 В; 47,5 Вт;
47,5 Вт; 1,1 А;
55 В; 44 В.
2-18. Сохранив условия задачи 2-17, заменить индуктивность ем-
костью 100 мкФ.
О Т В е т: 0,8 А; 40 В;
40 В; 32 Вт;
32 Вт; 1,26 А; 63 В; 31,5 В.
2
19. Цепь состоит из источника э. д. с. 10Q sin 300 t В, сопро-
тивления , == 40 Ом и индуктивности L == 0,1 r, соединенных последо-
вательно. Считая ток синусоидальным, найти MrHoBeHHble ток и напря-
жения на элементах при t == 0,01 с; вычнслить энерrию, поступающую
от источника с момента t == О до t == 0,01 с.
Ответ:
1,42 А; 56,8 В;
42.4 В; 0,833 Дж.
2-20. Цепь состоит из источника э.д; с. 100 sin 400 t В, сопро.
тивления , и индуктивности L == 0,025 r. Найти " если при t == :rt/800 с
MrHoBeHHoe напряжение на L равно 35,35 В; получить выражение для
синусоидальноrо тока; вычислить для t == п/800 с энерrию, запасен-
ную в маrиитном поле, и мrновенную мощность, поступающую от источ-
ника.
О т в е т: 13,55 Ом; 5,95 sin (400 t
36030') А; 0,284 Дж; 478 Вт.
2-21. Цепь состоит из источника э. д. с. 100 cos 1000 t В, сопро-
тивления r и емкости С, соединенных последовательно. Ток в цепи
равен 10 cos (1000 t + п/3) А. f-Iайти , и С; вычислить для t == п/1000 с
MrHoBeHHbIe значения напряжения на , и С и мощности, поступающие
в иих.
О т в е т: 5 Ом; 115 мкФ;
25 В;
75 В; 125 Вт; 375 Вт,
75
2-22. Цепь, состоящая из " L и С, соединенных ПQследовательно,
питается от источника э. д. с. 110 В переменной частоты. Определить
коэффициент мощности цепи при 60 rц, если известно, что при частоте
45 rц напряжение на емкости, так же как и на индуктивности, состав-
. ляет 200,8 В.
У к а З а н и е. При 45 rц имеет место резонанс напряжений,
т. е. шL == ljшС.
Ответ: 0,69.
2-23. Что такое положительное направление синусоидальноrо
тока?
2-24. Что понимается под полярностью источника синусоидальной
9. д. С. или источника синусоидальноrо тока?
2-25. ЧТО такое фазовый сдвиr тока относительно напряжения?
Чем вызван фазовый сдвиr?
2-26. Какова разница между активной, реактивной и полной мощ-
ностями? В каких единицах они измеряются? .
2-27. Почему в общем случае активная проводимость ветви не
равна величиие, обратной активному сопротивлению этой ветви? В ка-
ком частном случае выполияется такое равенство?
2-28. Для чеrо стремятся повысить коэффициент МОЩRОСТИ элек-
трической установки?
rЛАВА ТРЕТЬЯ
ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
И ВЕКТОРНЫХ ДИАrр АММ
К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕй
3.1. ПРЕДСТАВЛЕНИЕ СИНУСОИДАЛЬНblХ ФУНКЦИЯ В ВИДЕ
ПРОЕКЦИЯ ВРАЩАЮЩИХСЯ ВЕКТОРОВ
Триrонометрическая форма расчета электрических це-
пей синусоидальноrо тока, рассмотренная в преДЫДУLЦей
rлаве, практически применима только для простейших
электрических цепей, не содержаLЦИХ большоro числа кон-
туров и источников, взаимных индуктивностей и т. п.
С усложнением электрических цепей триrонометриче-
ская форма расчета становится крайне затруднительной
и требуется метод, ПОЗВОЛЯЮLЦий рассчитывать электри-
ческие цепи nepeMeHHoro тока алrебраически аналоrично
цепям постоянноrо тока. Таким удобным расчетным ме-
тодом служит м е т о Д к о м п Л е к с н ы х а м n л и т у Д
(комплексный метод), основанный на замене рассмотре-
ЩIЯ синусоидальных функций рассмотрением враLЦаю-
щихся векторов. Все послеДУЮlI!ее изложение курса таэ
76
и друrих электротехнических и радиотехнических дисцип-
лин базируется на этом методе 1.
Известно, что каждая точка на комплексной плоско-
сти определяется радиус-вектором этой точки, т. е. векто-
ром, начало Koтoporo совпадает с началом координат,
а конец находится в точке, соответ-
ствующей заданному комплексному чи- +j
слу (рис. 3-1). А,
Пользуясь показательной или по-
лярной формой записи комплексноrо
числа, имеем 2:
А:::::: Ae Jct =::: А L а;
здесь А
м о Д у л ь; а
а р r у - о
м е н т или Ф а 3 а; j == v 1 (в элек-
тротехнике не пользуются обозначе-
нием i == V
1 , так как буква i обоз-
начает ток).
Применив формулу Эйлера, можно получить т р и r о-
н о м е т р и ч е с к у ю форму записи комплексноrо числа:
А == А cos а+ jA sin а
ИЛИ соответственно а л r е б р а и ч е с к у ю форму:
А=::: А 1 + jA 2 .
+
Рис. 3-1. Вектор,
изображающий
комплексное число.
rде
А 1 == А cos а; А 2 =::: А sin а,
Очевидно.
A2==Ai+A
;
t А2
а == arc g A
.
1
Вектор, вращающийся в положительном направле-
нии, т. е. против хода часовой стрелки, с уrловой скоро-
стью (U может быть выражен сле.дующим образом:
AeJ,(oot-tU) == Ae ioot , (3-1)
rде А =::: Ae ict == А L а
к о м п л е к с н а я а м п л и-
т у Д а, представляющая данный вектор в момент t == О
1 l(омплексный метод расчета электрических цепей введен в инже-
неРН1Ю практику А. Е. l(еннели и Ч. П. Штейнметцем в 1893
1894 rr.
В зарубежной литературе по электротехнике и радиотеХНИК(О1
для комплексных величин часта применяется жирный шрифт а отличие
от модулей, обозначаемых светлыми буквами.
77
(рис. 3-2). Иначе roвop5t, это 1Wмплексная величина, не
зависящая от времени, модуль и арсумент которой равны
соответственно амплитуде и начальной фазе заданной
синусоидальной функции.
Множитель ej(J)t является о пер а т о р о м в р а Щ е-
н и я; умножение КОМП-!lексной амплитуды А на e/(J)t озна-
чает поворот вектора А на уrол юt в положительном на-
правлении.
Записывая комплексную функцию (3-1) в триrонометри-
ческой форме .
Aej((J)t+C/.) == А cos (юt+ а) + jA sin (юt + а),
заключаем, что синусоидальная функция А sin (юt + а)
может рассматриваться как мнимая часть комплексной
- +j ФУН1щии (3:1), взятая без
множителя], или, чпw то
же, как nроекция враЩaIOще-
2ОСЯ вектора на мнимую ось.
Условно это записывается
так:
.....
...
'"
/
/
I
I
I
I
,
I
\
\
\
\
\
,
.....
....
....
I
I
I
/
/
/
"
".
".
+
А sin (юt+а) == 1т (Aej(J)t).
С,имвол 1т обозначает,
что берется мнимая часть ком-
плексной функции.
Аналоrично косинусоидаль-
Рис. 3-2, Вращающийся вектор, ная функция может быть
в случае необходu.мости nре-
дставлена как действительная часть комплексной функ-
ции (3-1)
А cos (юt + а) == R е( Aei(J)t) ,
rДе символ Re обозначает, что берется действительная
часть комплексной функции.
Если синусоидальные функции имеют одну и ту же
частоту, то. соответствующие этим функциям векторы
(<врашрются с одинаковой условой скоростью и поэтому
УZЛbl между ними сохраняются неизменными.
На рис. 3-3, а показаны две синусоидальные функции:
и1 == и 1т sin (юt + "'1) и и 2 == и 2т sin (юt
"'2)' имею-
щие одинаковую уrловую частоту ю. Функция и 1 опере-
жает по фазе функцию и 2 , причем фазовый сдвиr равен
разности начальных фаз:
Ip==Wl
(
wz) == Wl +11'2'
78
Этот уrол и образуют между собой векторы, показан-
ные на рис. 3
3, б.
При равенстве начальных фаз) т. е. при фазовом сдви2е)
равном нулю) векторы напра8леныв одну и ту же сторону
(совпадают по фазе).
При фазовом сдви2е 1800 векторы направлены в диа-
метрально nротueОnОЛОЖНble стороны (находятся в nро-
тueофазе) .
. Диаrрамма, изображающая совокупность векторов, по-
строенных с соблюдением их взаимной ориентации по фазе,
называется в е к т о р Н О Й д и а r р а м м о й 1.
I.L
+j
111т
+
0.)
б)
Рис. 3
3. Фазовый сдвиr,
а
между синусоидами; б
между векторами.
Векторное представление синусоидальных функций, Ча-
стота которых одинакова, облеrчает операции сложения
и вычитания этих функций. Ввиду TOro что сумма проекций
двух векторов равна проекции reометрической суммы
этих векторов, амплитуда и начальная фаза результирую-
щей кривой MorYT быть найдены из векторной диаrраммы.
Например, если двум синусоидальным функциям со-
ответствуют комплексные амплитуды А и В, то сумме
этих синусо.идальных. функций соответствует комплексная
амплитуда С == А + в (рис. 3
4, а).
Из rрафическоrо построения следует:
с== у A2+B2+2ABcos(ct
);
t .
А sin а+В sin
g 'у
А cos а + В cos
.
(3
2)
(3
3)
1 В отличие от векторных диаrрамм кривые MrHoBeHHbIX значе-
ний называются в р е м е и и ы м и диаrраммами.
79
Здесь уrол "'( находится с учетом знаков числителя и
знаменателя, определяюlЦИХ знаки синуса и косинуса.
+]
+j
6=А+8
+
+
,
а.)
6)
Рис. 3-4, Сложение (а) и вычитание (6) векторов,
в случае, Коrда вектор В вычитается из вектора А
(рис. 3-4, 6), уrол р в (3-2) и (3-3) заменяется р + пили,
что то же, р
n.
3.2. ЗАКОНЫ ОМА Н кнрхrОФА в КОМПЛЕКСНОЯ ФОРМЕ
Рассмотрим применение метода комплексных ампли-
туд в случае последовательноrо и парадлельноrо соедине-
ний элементов " L и С.
Поспедоватепьное соединение r, L и С
Положим, что в уравнении Кирхrофа
u == ri + L
+
S i dt
(3-4)
заданными являются параметры " L, С и синусоидаль-
ное напряжение u == и т sin (ro' + 1jJ) на цепи, а искомой
величиной является ток i. Ввиду Toro что здесь рассма-
тривается установившийся режим цепи синусоидальноrо
тока, решение этоrо дифференциальноrо уравнения должно
дать синусоидальную функцию вида:
i == 1 т sin (rot + 'ф
<р),
rде 1 т и (ф
<р)
пока неизвестные амплитуда и началь-
ная фаза тока.
Пусть в соответствии с предыдущим параrрафом задан-
ное синусоидальное напряжение символизируется комплекс-
ной функцией (J mej(jJt, а искомый синусоидальный ток
комплексной функцией 1 mej(jJt; комплексные амплитуды
80
напряжения и тока равны соответственно:
й m == U mef1lJ; i m == I mej(1!J
!P).
Сложение, дифференцирование и интеrрирование сину-
соидальных функций в уравнении (3-4) заменяются теми
же математическими операциями над мнимыми частями
комплексных функций: '
1т (й mej(j)() == r 1т (i mej(j)() +
+ Lft 1т (i mej(j)() + .
S 1т (i mej(j)() dt. (3-5)
Операции над мнимыми частями комплексных функ-
ций MoryT быть заменены операциями над самими ком-
плексными функциями с последующим выделением мни-
мой части полученноrо результата. Объясняется это ком-
мутативностью операций сложения, дифференцирования и
интеrрирования относительно символической операции 1т.
Итак, (3-5) преобразуется следующим образо
Im(rjmei(j)()==lm(rimejrot+L
imej(j)t+
S imej(j)(dt).
Полученное уравнение удовлетворяется для любоrо
момента времени. Поэтому заключенные в скобки комп-
лексные выражения, от которых берется мнимая часть,
должны быть равны друr друrу. Производя дифферен-
цирование и интеrрирование, получаем:
rj mej(j)t == r i mej(j)t + j(f)Li mej(j)t + ' l С i mej(j)t. (3-6)
/Ш ,
Здесь следует обратить внимание на то, что при инте-
rрировании функции ej(j)( постоянная интеrрирования опу-
щена, так как в рассматриваемом установившемся режиме
цепи синусоидальноrо тока электрические заряды или
напряжения на емкостях представляют собой синусои-
дальные функции, не содержащие постоянных слаrающих.
В результате сокращения всех частей уравнения (3-6)
на множитель ei(j)t получается алеебраическое комплексное
уравнение
- . .' 1.
и т == rl m + J(f)LJm+
c 1т.
/Ш
(3- 7)
Ток J m может быть вынесен за скобки. При этом вво-
дится условное обозначение для к о м п .ТI е к с н о r о
81
с оп р о т и в л е н и Я рассматриваемой электрической
цепи:
Z ==,+ j( wL
ro
) ==,+ jx. (3-8)
Таким образом, получается уравнение
и т == zj т' (3-9)
выражающее закон Ома для комплексных амплитуд.
Разделив обе части уравнения (3-9) на у2. получим
закон Ома для к о м п л е к с н ы х Д е й с т в у ю I.Ц и х
з н а ч е н и й 1:
.
u == zj.
(3-1 О)
'. Следовательно, комплексное сопротивление электриче-
ской цепи равно отношению комплексносо напряжения
на данной цепи к комплексному току в этой цепи.
Комплексное сопротивление Z представлено в выра-
жении (3-8) в алreбраической форме. Та же величина
в триrонометрической' и показательной (полярной) фор-
мах имеет вид:
z == z cos <р+ jz sin <р; }
Z == ze jCP == z L <р. (3-11)
Здесь z == IZI
модуль комплексноrо числа Z
пред-
ставляет собой полное сопротивление цепи, а qJ
apry-
мент комплексноrо ч исла Z:
z == V ,2 + х 2 ; , <р == arctg
.
На основании (3-9) комплексная амплитуда тока
j == О т == l/ m ej(
cp) == и m L ( .1,
т )
т z Z z 't: '1"
rде 'ф
rp
начальная фаза тока. Следовательно, иско-
мый ток в триrонометрической форме
i == 1т (i mej(iJt) ==
т sin (wt+ Щ
<р),
что совпадает с результатом, полученным ранее (см.
2-7).
1 Комплексный действующий синусоидальный ток (комплексный
ток)
комплексная величина, модуль и aprYMeHT которой равны
соответственно действующему сннусоидальному току и ето начальной
фазе (по rOCT 19880-74).
82
На рис. 3-5 даНа rеометрическая интерпреТация на
комплексной плоскости уравнения (3-10). Рисунок 3-5, а
ОТНQCится к случаю, коrда реактивное сопротивление цепи
имеет индуктивный характер (х > О) и соответственно
ток отстает по фазе от напряжения (rp> О). Рисунок
3-5, б относится к случаю, коrда реактивное сопротивле-
ние цепи имеет емкостный характер (х < О) и поэтому
ток опережает по фазе напряжение (rp < О).
В случае чисто реактивной цепи (, == О) ток отстает
от напряжения по фазе на л/2, если сопротивление цепи
индуктивно, и опережает напряжение на л/2 при емкост-
ном сопротивлении цепи.
+j
. . 1 .
иC=
J
I
шС
U/,==jcиL.j
+j
+
+
6)
Рис. 3-5. Векторные диаrраммы для последовательной цепи " [, С
при х > О (а) и х < О (6).
Как видно из векторных диаrрамм, приведенных на
рис. 3-5, (Jr == ,1
напряжение на сопротивлении ,
(совпадает по фазе с током 1), (J L == jffiL1
напряжение
на индуктивности L (опережает ток 1 на уrол л/2) и (J с ==
1 . 1
==
j шС 1
напряжение на емкости С (отстает от тока
на уroл л /2).
rеометрическая сумма векторов (J r, (J L И (J С дает век-
тор приложенноro к цепи напряжения:
(; == (;r+ (; L + (;с.
Прямоуroльный треуroльник, катетами KOToporo явля-
ются (J r И (J L + (J с, а rипотенуза KOToporo равна (J ,
называется т р е у r о л ь н и к о м н а п р я ж е н и й; (; r
И (J L + (J с представляют собой соответственно активную
В3
и реактивную составляющие напряжения (О а == О r; О р ==
== OL+ ос).
Если все CTopOHЫ
BeKTOpы 9Toro треуrольника разде-
лить на вектор 1, то получится т р е у r о л ь н и к с о -
про т и в л е н и й, подобный треуrольнику напряжений
и повернутый относительно последнеrо на уrол Ф
ер
по ходу часовой стрелки,
+j +j
х<о
+ +
о .,. о
а.) j:r=
jlжl
о)
Рис. 3.6, Треуrольник сопротивлений при х > О (а) их < О (6).
. .
Треуrольник сопротивлений представляет собой reo-
метрическую интерпретацию уравнения (3
11). Ero поло-
жение не зависит от начальных фаз О и i; сопротивление,
откладывается на комплексной плоскости в положитель-
ном направлении действительной оси, а реактивное со-
противление Х в зависимости от ero знака откладывается
в положительном (х> О) или отрицательном (х < О)
направлении мнимой оси (рис. 3
6, а и 6).
В треуrольнике сопротивлений уrол ер отсчитывается
от катета, к rипотенузе Z по аналоrии с тем, как отсчиты
вается УI:ОЛ ер в треуrольнике напряжений от Or == ,1
к U == Zl.
Параnnеnьное соединение r, L и С
Пользуясь рассуждениями, аналоrичными приведен-
ным выше, можно прийти к комплексной форме законов
Ома и Кирхrофа для электрической цепи, состоящей из
элементов " L и С, соединенных параллельно.
Оrраничиваясь записью для комплексных действующих
значений, пропорциональных комплексным амплитудам,
имеем в соответствии с первым законом Кирхrофа:
j ==g(; +
L (; + jroСЙ == J r + i L +ic; (3-12)
}ОО
здесь lr == g(;
ток в сопротивлении r (совпадает по фазе
.' 1 .
с напряжением И); IL==
j шL и
TOK в индуктивности
(отстает от напряжения на л/2);
lс =-, jwC(;
ток в емкости (опережает напряжение
на л/2).
Выражение
У ==g
j ЦL
шС) ==g
jb
(3-13)
представляет собой к о м п л е к с н у ю про в о Д и -
м о с т ь рассматриваемой цепи; g и Ь
активная и реак-
тивная проводимости цепи.
. Уравнение
J == У(;
(3
14)
выражает закон Ома в комплексной форме. Следовательно,
комплексная проводимость электрической цепи равна отно-
шению комплексною тока в данной цепи к комплексному
напряжению на ее выводах.
Триrонометрическая и показательная (полярная) формы
комплексной проводимости имеют следующий вид:
У == У cos rp
jy siп <р; У == ye
N == у 1.
<р;
здесь у == 'УI
модуль комплексноrо числа У
пред-
ставляет собой полную проводимость цепи, а (
cp)
aprYMeHT комплексноrо числа У:
у == v g2 + Ь 2 ; rp == arctg
.
g
На основании (3
14) комплексный ток равен:
J == уUеj('Ф
fjJ) == уи 1. ('1'
<р),
что соответствует синусоидальному току
i == 1т (1 mejriJt) == уи т siп (wt + ф
<р).
На рис, 3-7 дана rеометрическая интерпретация на
комплексной плоскости уравнения (3-12). Рисунок 3-7, а
относится к случаю, коrда реактивная проводимость цепи
имеет индуктивный характер (Ь > О) и соответственно
ток отстает по фазе от напряжения (rp> О). Рисунок 3-7, б
относится к случаю, Коrда реактивная проводимость цепи
имеет емкостный характер (Ь < О) и соответственно ток
Qпережает по фазе напряжение (rp < О).
l$5
Лрямоуrольный треуrольник с катетами J r и (J L + lс)
и rипотенузой 1 называется т р е у r о л ь н и к о м т о -
к о в; lr и (l L + lс) представляют собой соответственно
активную 1I реактивную слаrающие тока lа и l р .
+]
+]
. 1 . '
1" =
] OIL и
.
i" +ic=
jbи и
. 1.
I,,=
j fIJL и
ic=jfIJси
i" +ic=
jbIj
i,.=giJ
"'
tp +
+
4)
б)
Рис. 3.7. Векторные диаrраммы для параллсльной цепи " L, С при
Ь > О (а) и Ь < О (6).
Если все стороны-векторы этоrо треуrольника разде-
лить на вектор О, то получится т р е у r о л ь н и к
про в о Д и м о с т е й, подобный треуrольнику токов и
повернутый относительно последнеrо на уrол 'ф по ходу
+j
+j
о
+
jb=jlbl
+
о
Ь<О
Ь>О
а) б)
Рис. 3-8. Треуrольник ПрОБодимостей при Ь > О (а) и
Ь < О (б).
часовой стрелки. Треуrольник проводимостей служит
reометрической интерпретацией выражения (3-13): актив-
ная проводимостъ g откладывается на комплексной пло-
скости в положительном направлении действительной
оси, а реактивная проводимость Ь в зависимости от ее знака
86
откладывается в отрицательном (Ь> О) или положитель-
ном (Ь < О) направлении мнимой оси (рис. 3-8, а и 6).
В треуrольнике ПРОВОДимостей уrол ер отсчитывается
от rипотенузы У к катету g по аналоrии с треуrО?IЬНИКОМ
токов, rде уroл ер отсчитывается от 1 == УИ к Ir == g(j.
в табл. 3-1 дана сводка уравнений основных элемен-
тов цепи в общей форме (дифференциальной, интеrраль-
ной) И при синусоидальном режиме в триrонометрической
комплексной формах.
Уравнения элементов цепн
Элемент
Общая форма
Сопро-
тивление
u ==,i
i==gu
ИНДУК-
тивность
di
и==L
dt
t
. 1
(
L
oo
Емкость
t
U == Ь
i dt
00
. , с du
(==
dt
Синусоидальный режим
Триrонометрнческая
форма
и==,l m sin (ооt+ф)
i==gU m sin (ооt+ф)
(
и==оои т sin «(М+,\,)
иdt i==
L и т cos «(М+,\,)
и==
C 1т sin (oot+,\,)
i==(f)cU m cos (ш' +'\')
Таблица 3-1
l<омплексиая
форма
{; ===,/
j == gИ
(; == j(f)Li
. 1.
1==
i
U
ooL
. 1 1
U==
j
ооС
/ == j(f)СИ
Следует обратить внимание на то, что комплексное
сопротивление индуктивноrо элемента равно j(j)L, а ем-
1 . 1
KOCTHoro элемента jooC ==
J ооС ; комплексные проводимости
. 1. 1 . С
составляют соответственно jooL ==
J ooL и J(j) .
При последовательном соединении " L и С складыва-
ся в комплексной форме сопротивления, а при парал-
лельном соединении
проводимости.
В табл. 3
2 приведены выражеЮfЯ комплексных сопро-
тивлений и проводимостей цепи для различных сочетаниЙ
элементов " L и с.
87
Таблица 8-2
Выражения комплексных сопротивлений и проводимостей
Цепь I z при ПОСЛедо"ательном У при параллельном
соединении соединении
'. L r+jooL 1 1
j
r ooL
(, С 1
+jooc
r
j
ооС ,
(, L, С r+j (OOL
C )
j (
ooc)
r ooL
].]. ЗАВИСИМОСТЬ МЕЖДУ СОПРОТИВЛЕНИЯМИ
И ПРОВОДИМОСТЯМИ УЧАСТКА ЦЕПИ
Пользуясь комплексной формой записи, при заДанном
комплексном сопротивлении Z == , + jx HeKoтoporo участка
цепи находим для Toro же участка цепи комплексную
проводимость 1:
у 1 1 r . Х 'Ь ( 3 15 )
==2' == ,+ix' == ,2+х2
J ,2+X2 ==g
J . .
в своЮ очередь если задана комплексная проводи
мость HeKoтoporo участка цепи У == g
jb, то комплекс-
ное сопротивление Toro же участка цепи
Z 1 1 1 + . ь + . (3 16)
== у == g
jb == g2+b 2 J g2+b2 ==, JX. .
Выражения (3-15) и (3-16) показывают, что реактив-
ное сопротивление х и реактивная проводимость Ь одНОеО
и таеО же участка цепи имеют одинаковый знак.
Кроме Toro, каждая слazающая nроводимости (g и Ь)
зависит как от активНОеО, так и от реактиВНОеО сопротив-
лений (т. е. от , и х). Соответственно каждая слаrающая
сопротивления (, и х) является функцией активной и реак-
тивной проводимостей (g и Ь).
Соотношения g == 11, и Ь == lIх справедливы только
в частном случае, КоrДа элемент " L или С рассматрива-
1 В зарубежной литературе под реак1ИВИОЙ проводимостью обычно
Х
Понимается величина b==
+ 2 и соответственно комплексная "ро-
, х
водимость записывается в виде У == g + jb,
88
ется в отдельности, например:
1 1 1
b L ==
==
L ' ЬС ==
== юС.
x L ш' Хс
Предлаrается учащимся в виде упражнения написать
выражения для активноrо и реактивноrо сопротивлений,
активной и реактивной проводимостей для всех случаев,
указанных в табл. 3-2.
3-4. КОМПЛЕКСНАЯ ФОРМА ЗАПИСИ МОЩНОСТИ
Допустим, что через электрическую цепь проходит си-
нусоидальный ток, причем положительные направления
тока и напряжения на выводах цепи приняты совпадаю-
Ц!ими (рис. 3-9).
1..z
18
+
() 0.)
Рис. 3-9. Положительиые направлении (а) и комплекс-
ные напряжения и ток (6).
Комплексные ток и напряжение равны соответственно:
j == 1 L '11'1 И (; == U L '11'2'
Фазовый сдвиr тока относительно напряжения равен
разности начальных фаз:
ер == '\1'2
1151'
*
Умножим И на комплексное значение 1 == 1 L
'Ф1'
сопр яженное с 1:
(; j == U 1 L ('1'2
'\1'1) == U 1 L ер.
отсюда следует, что
S == (; j == U 1 cos ер + jU 1 siп ер == Р + jQ.
Так как напряжение И может рассматриваться как
сумма активной и реактивной слаrающих: И == И а + Ир
(см. 9 3-2), то почленное умно?Кение этих слаrающих на
89
'"
1 дает активную и реактивную мощности:
u,i +и р l === U cos rp/ L 00+ U sin rp/ L. л/2 == Р+ jQ.
Аналоrично мощность может быть выражена через
активный и реактивный токи.
Таким образом, комплексная величина S определяет
действительной частью активную мощность, а мнимой
частью реактивную мощность,
поступающую в цепь.
Модуль S равен полной мощ-
ности. S носит название мощ-
ности в комплексной форме,
+ или к о м п л е к с н О й м о Щ -
н о с т и.
На комплексной плоскости
S изображает rипотенузу пря-
моуrольноrо треуrольника, ка-
тетами KOToporo служат Р и Q
(Р,ис. 3-10).
Треуroльник мощностей, изображенный на рис. 3-10,
подобен треуrольнику сопротивлений:
Q х
Р == r == tg <р.
+j
jq,
р
о
Рис. 3-10. Треуrольник мощ-
ностей на комплексной плос-
кости.
Если комплексно сопряженное напряжение й умно-
жить на комплексный ток 1, то получится:
* .
U/ == ИI cos <p
jU / sin <p==P
jQ.
Поэтому мощности Р и Q на выводах цепи MorYT быть
записан'ы в следующем виде:
1 . * * .
Р ==2"(ИI +и/);
1 . * *.
Q== 2j (ИI
и/).
Комплексное сопротивление цепи леrко вычислить,
если известны комплексная мощность S и действующее
значение тока 1:
откуда
. s == uj == zJi == ZJ2,
Z s P + .Q
== j2 ==72 172'
00
Воспользовавшись выражением (2-28), получим:
Z ==
+ j * (W LMaKc
W Смш)'
Эта формула справедлива при любой схеме соединений
сопротивлений, индуктивностей и емкостей.
Энерrетический метод определения комплексноrо co
противления применим и к комплексной проводимости:
.11< .*11< * 11<
*
S == ИI ==ииу == и 2 У, откуда У == S/U 2 , rде У
ком-
плексная ПРОБОДИМОСТЬ, сопряженная с У. Следовательно,
у == :;
j 32 ==
2 + j ;';2 (W с макс
W L макс)'
Итак, активные сопротивление и проводимость цепи за-
висят от поrлощаемой цепью активной мощности, а реак-
тивные сопротивление и проводимость
от разности мак-
симальных значений энерrии, запасаемых в маrнитных и
электрических полях' (см.
2-5, 2-6 и 2-9).
3-5. УСЛОВИЕ ПЕРЕДАЧИ МАКСИМУМА АКТИВНОй МОЩНОСТИ
ОТ ИСТОЧНИКА К ПРИЕМНИКУ
Пусть требуется подобрать комплексное сопротивле-
ние наrрузки таким образом, чтобы при заданном ком-
плексном сопротивлении источника
обеспечивалась пере,цача максиму-
ма активной мощности от источ-
ника к приемнику. Обозначим
комплексные сопротивления источ-
ника напряжения и наrрузки со-
ответственно через
Zo == ro+ jx o
и Z == r+ jx
(см. рис. 3-11).
Активная мощность, потребляемая наrрузкой, равна:
,Е 2 ' ,Е 2
P==r/ 2 ==
I Zo+Z 12 ('0+r2)
(xo+X)2 .
Будем сначала изменять реактивное сопротивление х.
Очевидно, при любом значении r ток и соответственно
активная мощность достиrают наибольшеrо значения х ==
,Е2
;;:::;
хо
При этом Р == (,0+,}2 .
.>
Е
Zo
.......
!1
Z
Рис. 3
11. Передача энер-
rии от источника к при-
емнику.
91
Найдем теперь условие максимума полученной функ-
ции в предположении, что ,
переменная величина, т. е.
из условия, что dP Id, == о; это даст:
(ro + r)2
2, (ro +,) == о,
откуда
, == '0'
На основании найденных равенств заключаем, что
условием передачи максимума активной мощности источ-
ником приемнику является равенство
*
Z == Zo,
(3-17)
'"
rде Zo
комплексное сопротивление, сопряженное с Zo.
При соблюдении этоrо условия приемник потребляет
мощность
Е2
Р макс ==
4
То
и К. п. д., определяемый как отношение активной МОщно-
сти, потребляемой приемником, к суммарной Мощности,
поrлощаемой активными сопротивлениями цепи, равен 0,5.
В том случае, коrда комплексное сопротивление источ-
ниКа имеет индуктивный характер, комплексное сопро-
тивление приеМIIика на основании (3-17) должно быть
eMKocTHOro характера. Такая компенсация реактивноrо
сопротивления цепи осуществляется на практике С помощью
конденсаторов, включаемых последовательно или парал-
лельно наrрузке.
Если условие (3-17) не выполняется, то относительное отклонение
передаваемой активной мощности от максимальной составляет;
PMaKC
P (,o
,)2+(xo+x)2
Р макс == (,0+,)2+(хо+х)2'
В тех случаях, коrда реактивное СОПРОТИВJlение источника отно-
сительно невелико по сравнению с ero активным сопротивлением, yc
ловия, близкие к оптимальным, получаются при активной. наrрузке,
если Сопротивление приемника принято равным активному или пол-
ному сопротивлению источника.
Например, при Zo == 618 L
140 и Z"'" 618 LO° поступающая
в приемник активная мощность отличается от максимально ВОЗможной
только на 1,5%; в этом случае компенсации реактивноrо сопротивле-
ния источника практически не требуется.
Формулы, приведенные выше, справедливы и для цепей
Постоянноrо тока; при этом комплексные величины заме.
няются действительными.
92
3.6. УСЛОВИЕ ПЕРЕДАЧИ ИСТОЧНИКОМ МАКСИМУМА
МОЩНОСТИ ПРИ ЗАДАННОМ КОЭФФИЦИЕНТЕ
МОЩНОСТИ ПРИЕМНИКА
На практике часто возникает необходимость подбора
комплексноrо сопротивления наrрузки таким образом,
чтобы при заданных комплексном сопротивлении источ
ника и коэффициенте мощности приемника обеспечивалась
передача максимума полной и соответственно активной
мощности от ИСТОЧНика приемнику.
Пользуясь условными обозначениями, принятыми в пре-
дыдущем параrрафе, находим полную мощность на выводах
наrрузки:
S 2 zE2
. z/ == \20+Z\2
ZE2
I Z 1 2 '
z5 1 + Zo L (<p
<Po)
rде ер и еро
уrлы комплексных сопротивлений Z и Zo.
После преобразования получим:
s
( Е ) 2 Z ( 3 18 )
Z ( Z ) 2' -
1+2
cos(<p
<po)+
Zo Zo
Приняв величину z за переменную, записываем условие
максимума функции S:
==o
dz '
откуда
Z ( Z ) 2 [ 1 Z ]
1+2
cos,(ep
epo)+
z 2
cos(ep
epo)+22 ==0,
Zo Zo Zo Zo
или
1+(
Y
2(
Y==0.
Следовательно,
z == zo.
(3-19)
Подстановка (3-19) в (3-18) дает:
Е2
SMaKc == 2z0 [l + cos (ер
<ро)] .
Таким образом, передача максимума мощности в на-
ерузку при заданном cos ер достиеаеmcя при равенстве
полных сопротивлений НCl2рузки и истОЧНИКа. При этом
передаваемая мощность тем больше, чем больше по абсо-
93
лютному значению разность уrлов сопротивлений наrрузки
и источника Icp
CPol.
Если условие (3
19) не соблюдается, то отиосительное отклонение
передаваемой полной мощности от максимальной составляет:
(I
Z
/
z ( z ) 2
1 +2
cos (<I'
<1'0) +
Zo Zo
Практически допустимы отклонения от условия (3-19), при кото'
рых значение (3-20) не превышает заданноrо предела.
SMaKC
S
SMaKC
(3-20)
Условия передачи максимума мощности широко исполь-
зуются в радиотехнике, электропроводной связи, авто-
матике и пр иборостр оении. В энерrетических же систе-
мах, reнерирующих и потребляющих большие мощности,
стремятся обеспечить Высокий к. п. д. reH
paTopoB; поэтому
сопротивления наrрузок значительно превышают сопро-
тивления reHepaTopoB.
3-7. БАЛАНС МОЩНОСТЕА
Из закона сохранения энерrии следует, что для любой
электрической цепи соблюдается закон баланса активных
мощностей: активная мощность, Zl:нерируемая источни-
камИ, равна активной мощности, потребляемой всемИ
пр шмниками.
В свою очередь можно по казать, что и сумма отдавае-
мых реактивных мощностей равна сумме потребляемых
реактtЮных .мощностей.
Если воспользоваться комплексной формой записи то-
ков, напряжений и мощностей, то высказанные положения
будут вытекать из следующих рассуждений.
Для электрической цепи, содержащей q узлов, можно
написать по первому закону Кирхrофа q
1 уравнение
вида: .. * .. ..
1 kl+ I k2 +...+ Ik. q
l + I kq == О,
rде положительные Itаправления всех' токов приняты
от узла k к узлам 1, 2, ..., q.
Умножим каждое из этих уравнений на комплексное
напряжеиие, отсчитываемое от соответствующеrо узла
к узлу q, и просуммируем эти произведения:
u 1q (j12+ j lЗ+" .+jlQ) +U 2q (j21 +12:+" .+1 2q ) + ...
+.. .+U q
l. q (!q
l. 1 + jq
l. 2 +.. .+jq
l. q) == О,
94
откуда с учетом Toro, что
(; kq
(; тg === (; km
и
., *
/mk ==:,.."..,.., 1 km,
,получим:
. * . * . *
U 12 1 12 + U 1з l 1з +...+ и q
l, qlq
l. q === О.
Итак сумма 'комплексных мощностей, потребляемых
всеми ветвями электрической цепи, равна нулю; следова-
тельно, также равны нулю в отдельности алreбраические
суммы действительных и мнимых частей мощностей.
Иначе rоворя, равны нулю как алreбраическая сумма
потребляемых всеми ветвями цепи активных мощностей,
ТаК И алreбраическая сумма потребляемых реактивных
мощностей.
Поскольку отрицательные потребляемые мощности пред-
ставляют собой мощности отдаваемые, то отсюда следует
закон баланса как активных, Так И реактивных моЩ-
ностей.
В случае цепи nосmoЯННО20 moка сумма мощностей ucmoч-
ников равна сумме мощностей, расходуемых в сопротивле-
ниях, причем знаки мощностей источников определяются
по указанному выше пр ав илу: мощность положительна при
совпадении направлений э. д. с. Е и ТОКа 1, проходящеrо
через источник, и отрицательна при встречных направле-
ниях э. д. с. и ТОКа. В последнем случае, если источником
энерrии служит аккумулятор, мощность Е/ расходуется
на ero зарядку; если же источником служит тенер, атор
то мощность Е! расходуется на м:еханическую работу
(тенератор работает в режиме двиrаТеля).
3-8. ПОТЕНЦИАЛЬНАЯ IтопоrРА.ФИЧЕСКАЯJ ДИАrРА.ММА.
В 9 1-12 рассматривался rрафик распределения потен-
циала для простейшей цепи постоянноrо тока. В случае
цепи синусоидальноrо тока аналоrично строится друrой
rрафик, который называется п о т е н Ц и а л ь н о й или
топоrрафической диаrраммой напряжений. Эта диаrрамма
представляет собой векторную диаrрамму, на которой
отложены комплексные ПO'feнциалы отдельных точек за-
данной цепи по отношению к одной точке, потенциал
которой принят за нуль. Таким образом, порядок рас-
ЩJЛожения векторов падения напряжения на диаrрамме
95
cTporo соответствует порядку расположения элементов
цепи на схеме. Конец вектора напряжения на каждом
последующем элементе примыкает к началу вектора Ha
пряжения предыдущеrо элемента. При таком построении
векторной диаrраммы напряжений каж,дой точке электри-
ческой цепи соответствует определенная точка на потен-
циальной диаrрамме.
Потенциальная диаrрамма позволяет весьма просто
находить напряжения между любыми точками цепи: дей-
ствующее значение и фаза искомоrо напряжения опре-
деляются прямой, соеДИНяющей соответствующие точки
потенциальной диаrраммы.
1
"1
2 L J
rz
'1-0
! й15 01;
....,..........
ии
Uзц
иЧ5
t i
i
2
U2Ч / й 1 2 = "1 !
. l'
.
UЧ5=
j щС I / Uи=j(JJl,I
'1- J
uJч="zi 5)
Рис. 3.12. СхеМа (а) и потенциаЛЬная диаrрамма (6).
1
5
а.)
На рис. 3
12 изображена схема неразветвленной элек-
трической цепи и для нее построена потенциальная диа-
трамма напряжений. Направления векторов напряжений
на потенциальной диаrрамме увязаны. с произвольно вы-
бранным направлением вектора Тока 1.
Обход схемы
едется навстречу положительному на-
правлению тОКа 1. В соответствии с порядком располо-
жения в схеме элементов С, '2' L, '1 на диаrрамме изобра-
жены векторы напряжений:
. . 1. '. .. 1 . .
U45==
j (j)c l; U з4 ==r 2 1; U 2з ==j(i)L; U 12 ==r 1 1.
Начала и концы векторов (рис. 3
12, б) пронумерованы
в соответствии с нумерацией точек, принятой на схеме
(рис. 3-12, а).
Напряжение между какими-либо двумя точками схемы,
например, на участке 2
4 схемы, взятое в положитель-
ном направлении тока 1, определяется по потенциальной
диаrрамме вектором О 2Q, соединяющим точки 2 и 4 диа-
траммы и направленным на диаrрамме от точки 4 к точке 2.
96
Это соответствует известному правилу вычитания BeKTO
ров, соrласно которому какой-либо вектор [) тп, представ-
ляющий собой разность напряжений (или потенциалов)
[) m
(; п, направлен от конца вектора Оп К концу век-
тора О т' Итак, вектор напряжения на диасрамме направ-
лен к точке высшее.о (уменьшаемое.о) потенциала, а то же
напряжение на схеме указывается стрелкой, направлен-
ной от высшеrо потенциала к низшему.
Если при построении потенциальной диаrраммы обход
схемы сооершался бы в положительном направлении тока 1,
то изменилась бы нумерация начала и конца каждоrо
вектора напряжения на потенциальной диаrрамме, что
противоречило бы принятому правилу расстановки индек-
сов при вычитании векторов.
3-9. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
3-1. Произвести вычисления: а) 10 L 30° + 5 L 60°,
Ответ: 14,53 L 400.
б) 10 L 30°
5 L 600.
Ответ: 6,2 L 6012'.
в) (8,66 + j5) (3,53 + j3,53).
О т в е т: 50 L 750.
r) (8,66 + j5) : (2,5 + j4,33),
о т в е т: 2 L
300.
д) (5 + j5)З.
О т в е т:
25 0 + j250.
е) -v 5 + j8,66.
о т в е т: 1,78 L 15°, 1050,
750 или
165°.
ж) In (50 е!70 0 ).
О т в е т: 3,91 + jl,22.
3-2. Решить в комплексной форме следующие задачи:
а) Сложи
ь напряжения Ul == 10 sin (oot + n/3) и и2 ==
== 5sin (oot+ л:/12).
б) Сложить .токи i 1 == 10 sjn oot и i 2 == 10 cos (oot + Л:/4).
О т в е т: U == 14 siп (oot + 45030'); i == 7,65 sin (оо! + 67030').
3-3. К цепи, состоящей из , == 7 Ом и L == 63,7 Mf, соединенных
последовательно, приложено напряжение 250 sin 377 t В. Найти три-
rонометрическое и комплексное выражения тока, комплексные напря-
жение и сопротивление; построить векторную диаrрамму,
О т в е т: 10 sin (oot
73°40') А;,
;2 L
73040' А;
LO° В; 25L 73 G 40' ОМ.
3-4. к: цепи, состоящей из , == 20 Ом, L == 100 Mr и С == 50 мкФ,
соединенных последовательно, приложено напряжение U == 14,14 Х
Х sin 377 t В. Вычислить комплексные ток и напряжения На " L и С;
построить векторную диаrрамму.
О т в е т: 0,396 L 37025 А; 7,92 L 37025' А; 14,95 L 127025' В;
21,15 L
52035' В. '
97
3-5. Сохранив условия предыдущей задачи, вычислить мrновеи-
ные значения тока и напряжений на " L и -е при t == 0,01 с.
О т в е т:
0,538 А;
10,76 А;
6,22 В; 8,52 В.
3-6. На выводах цепи, состоящей из ПОС.'1едователь-но соединенных
, и С, напряжение равно 127 В, ток 27,6 мА, частота 400 [ц; напряже-
ние на сопротивлении 63,5 ,В. Определить, и С.
О т в е т: 2300 Ом; 0,1 мкФ.
3-7. Индуктивная катушка L == 5 Mf, , == 5 Vз == 8,66 Ом и
соединенная с нею параллельно емкость С == 100 мкФ находятся под
напряжением u == 100 V2 siп 1000 t В. Найти комплексные токи и
показания приборов. Построить векторную диаrрамму.
О т в е т: 1 == 10 L 300; 1 с == 10 L 900; 1 к == 10 1.
зоо А.
3-8. Комплексное сопротивление равно 3 + j5 Ом. Вычислить
активную и реактивную проводимости.
О т В е т: 0,0882 См; 0,147 См.
3-9. Комплексная ПРОВОДИМQCть равна 0,2
jo,2 См. Вычислить
активное и реактивное сопротивления.
О т в е т: 2,5 Ом; 2,5 Ом.
3-10. Заданы в комплексном JЗиде напряжение на ветви (j ==
== 30 В и ток 1 == 6 + jO,9 А, ПРОХОДЯЩИЙ через эту ветвь. Определить
комплексное сопротивление и комплексную проводимость цепи; по
строить векторную диаrрамму.
О т в е т: 4,95 L
8030' Ом; 0,202 1. 8030' См.
3-11. Через ветвь, комплексное сопротивление которой равно
5 L 300 Ом, проходит ток 1 == 10 L 300 А. Определить напряжение
на ветви в комплексной и триrонометрической форме; построить век-
торную диаrрамму.
О т в е т: 50 L л/3 В; У"2. 50 sin (О)t+л/3) В.
3-12. К , и L, соединенным последовательно, 1/0дведено напряже-
ние и == 100 L 3{)0 В; , == 30 Ом; O)L == 40 Ом. Написать выражение
для мощности в 'комплексной форме.
Ответ: 120+ j160 В.А.
3-13. Напряжение на индуктивной катушке " L равно 100 В при
прохождении через катушку как постоянноrо тока 25 А, так и сину-
соидальноrо тока 10 А с частотой 400 [ц. Определить емкость, которую
следует включить последовательно с катушкой, чтобы синусоидальный
ток возрос до 20 А, а напряжение на цепи было равно 100 'В.
Рассмотреть два случая, удовлетворяющие этому требованию,
найти напряжение на катушке и построить векторные диаrраммы.
Ответ: 64,6; 32,7 мкФ; 200 В.
3-14. В цепи, изображенной на рис. 3
12, а, '1 == 25 Ом, L == 8 Mr,
'2 == 15 Ом, С == 8 мкФ.
Построить потенциальную диаrрамму и определить (j 13' (j 24 И (j 15,
если ток в цепи 1 == 2 L 00 А и уrловая частота о) == 2500 рад/с.
О т в е т: 64 L 38040'; 50 L 53010'; 100 L
36050' В.
3-15. Доказать, что
1 .* *
P==
2 (U! +ul);
1 .* * 1
Q== 2j (U!
U).
3-16. Как переходят от MrHoBeHHbIx значений токов к комплекс-
ным?
3-17. На какую ось проектируют вращающийся вектор при пере-
Ходе от комплексных выражений к триrGнометрическим?
98
3
18. В чем заключается удобство комплексной формы расчета
электрической цепи?
3
19. Построить синусонды Н векторы напряжений и токов по
табл. 3-1.
3-20. Определить модули и apryмeHTbI (уrлы) комплексных со-
противлений и ПрОВОДимостей, приведенных в табл. 3
2, и построить
треуrольники 'сопротивлений и проводимостей,
rЛАВА ЧЕТВЕРТАЯ
ПРЕОБР АЗОВАНИЕ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕй
4.1. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ
При расчете электрических цепей часто возникает целе-
сообразность преобразования схем этих цепей в более
простые и удобные для расчета. Так, при одноМ или не-
скольких исТdчниках электрической энерrии в ряде слу
чаев удается преобразовать электрическую схему в одно-
контурную или 'в схему с двумя узлами, что весьма упро
щает последующий расчет.
Описываемые ниже приемы nреобразования схем элек.
трических цепей nримеНИМbl для цепей nостоянное.о и nере-
менное.о тока; ради общности изложения они приводятся
В комплексной записи.
Одним из основных видов преобразования электриче-
ских схем, часто применяемых на практике, является пре-
образование схемы со Сj\iешанным соединением элемен-
тов. Смешанное соеДИНение элементов представляет собой
сочетание более простых соединений
последовательноrо
и параллельноrо, рассмотрению которых и посвящен дан-
ный параrраф. Смешанное соединение разбирается в Э 4
2.
Поспедоватепьное соединение
На рис. 4-1 изображена ветвь электрической цепи,
в которой последовательно включены комплексные сопро-
тивления 21' 22' ..., 2n. Через все участки цепи, соединен-
ные п.оследовilТельно, проходит один и тот же ток 1.
Напряжения на отдельных участках цепи обозначены
через 01' 02, ..., Оп.
99
По второму закону Кирхrофа
и:=;; й 1 + й 2 +. ..+и n ,
или, ЧТО то же,
и:=;; Z11 +Z21 +...+ Zn1.
Сумма комплексных сопротивлений всех последовательно
соединенных участков цепи
п
Z == 2; Zk
k
l
называется Э к в и в а л е н т н ы м
с о про т и в л е н и е м.
комплексным
i
z, ........ [, [.,
--c::::J---o0
.
и, и,' Utt
If
i Z = Е Zk
......е> k : 1
u'
Рис, 4-1, Последовательное соединение.
Если мнимые Части комплексов
Zk:::=; rk+ jXk
представЛЯЮТ СQбой сопротивления одинаковоrо XapaKтepa
индуктивноrо или eMKQCTHorO (рис. 4-2), ТО эквивалент-
ное комплексное сопротивление Z нахоДИТСЯ в результате
r
II
;
1 '" ", 11 '" /" I "=,,,+'" /'=/'1+/"
=
. 1 '
L
L
c
CIC'
r
" r
, с +-с
1 ,"1 СI 11'" С, 1 ,,=,.,+r,"
0, '
=
L
..JI,..
...I
Рис. 4-2. Последовательное соединение однородных
звеньев.
арифметическоrо сложения в отдельности сопротивлений rk,
иНдуктивностей Lk или величин l/C k , обратных емкостям:
Z == r+ jwL
или
Z . 1
':'" r
1 ыС '
100
rде
n
(== .! fk;
k
1
n
L == .! L k ;
k
l
n
== .! d k .
k
l
Ток в цепи равен:
. (;
I==y.
Напряжения на участках цепи, соединенных последо-
вателыiO, относяtr/.Cя как комплексные сопротивления этих
участков: напряжение на k-M участке равно произведению
cYMMapHoro напряжения [) на отношение комплексНоrо
сопротивления k-ro участка к эквивалентному комплекс-
ному сопротивлению цепи:
. . Zk
Uk==U у'
Приведенные выше формулы справедливы при любых
значениях Zk'
Параnnеnьное соединение
На рис. 4-3 изображена схема электрической цепи
с двумя узлами. Между этими узлами параллельно соеди-
нены ветви с комплексными проводимостями Уl' У2, ...
..., Уn. Напряжение на всех ветв'ях одиl:1аковое, равное [).
j,
..........с>
"t ч У, Ч ,,
y.
и
y=д;,
Рис. 4-3. Параллельное соединение.
Токи в ветвях обозначены через 11' 12' ..., 1n.
По первому закону Кирхrофа
j == i 1 + i2+" .+in,
или, что то же,
i == У/; + Y,iJ +...+ Уnи,
101
Сумма комплексных проводимостей всех ветвей, соеди
ненных параллельно,
n
У == S Y k
k
J
называется э к в и в а л е н т н о й к о м п л е к с н о й
про в о Д и м о с т ь ю.
Если мнимые части комплексов Y k == gk
jb k пред
ставляют собой проводимости одинаковоrо характера
eMKocTHoro или 'ИНДУКтивноrо (рис. 4-4), то эквивалентная
g=g,+ g 2
c=c , +cz
g=gr+ g 2
L = L, Lz
L , + Lz
Рис. 4-4. Параллельное соединение однородных звеньев.
комплексная проводимость У находится в результате ариф-
метическоrо сложения отдельных активных ПРОВОДимо-
стей gk, емкостей C k или величин l/L k , обратных индуктив-
ностям:
У == g+ j(iJC
или
У . 1
==g
J ши
rде
n
g== ! gk;
k
1
n
С==
C k ;
k
1
n
L 1 k .
k
l
Суммарный ток в цепи равен:
j == У(;.
102
Токи в ветвях относятся, как' их комплексные прово-
дщюстu: то!{ в k
й ветви равен произведению CYMMapHoro
тока всех ветвей на отношение комплексной проводимости
k
й ветви к эквивалентной комплексной проводимости:
. . Y k .2
1 k == 1 У == 1 2k .
Данным выражением особенно удобно пользоваться
при п> 2. При этом значения Y k MorYT быть любыми.
В случае параллельноrо соединения двух ветвей (п ==
== 2) обычно пользуются выраженияМи, в которые входят
сопротивления Z1 == 1/ У 1, И Z2 == 1/У 2 ветвей; эквива
лентное комплексное сопротивление равно:
Z
1
2122
Yl+Y2
+
21+22'
21 22
Токи В параллельных ветвях:
. . 22 " 1 2i
11==1 21+22 ; 12== 21+22 '
т. е,ток одной из двух параллельных ветвей равен сум-
марному току, умножеННОАtу на сопротивление друеой
ветви и деленному на сумму сопротивлений обеих ветвей.
4-2. СМЕШАННОЕ СОЕДИНЕНИЕ
Электрические схемы, имеющие смешанное соединение,
MorYT быть преобразованы в более простую электрическую
схему путем замены парал-
лельных ветвей одной ветвью Zf h
и соответственно последова
тельно соединенных участков й I i 2 ' Z2 ia I Z3 jчl Z,
цепи
одним участком. t V V V
На рис. 4
5 показан при-
мер элеКтрической цепи со
смешанным соединением. Эта Рис. 4-5. Смешанное соедине-
схема леrко прив.одится к ние.
одноконтурной. Первоначаль
но вычисляется эквивалентная комплексная проводимость
параллельных ветвей; затем находится величина, обрат-
ная проводимости, т. е.' общее комплексное сопротивление
параллельных ветвей; найденное комплексное сопротивле-
ние суммируется с комплексным сопротивлением последо
вательно включенноro участка. Полученное суммарное
103
комплексное сопротивление эквивалентно сопротивлению
исходной цепи со смешанным соединением.
Расчетные выражения для рассматриваемоrо случая
будут следующие:
У э == У 2 + уз+ У 4 == Z l
+
Z I
+
Z
'
2 З '1
СуммарНое комплексное сопротивление всей цепи равно:
Z Z + 1 Z + Z2ZЗZ4
== 1 Уа == 1 Z2ZЗ+Z2Z4+ZЗZ4 t
а суммарный ток
. й
11 == Z .
Токи в ветвях относятся, как комплексные проводи-
мости ветвей:
. . У 2 . . Уз '. . У4
12==IIY
; Iз==IIУ
; 14==Ily
'
Таким
бразом, мноrоконтурная электрическая схема
со смешанным соединением приводится к одноконтурной.'
'Z1 ' Zl Z5 Z7
1
I 1 Zz
{
'.!; ,-Т;
{z' Z'l /'1 Z,
11;
J/' Z,
Рис, 4-6, Цепная схема.
имеющей суммарное комплексное сопротивление Z или
соответственно суммарную комплексную проводимость У.
Распределение токов и напряжений в смешанной цепи
подчиняется правилам, указанным в предыдущем пара
rрафе.
Описанный выше порядок преобразования схемы и
нахождения распределения токов принципиально приме-
ним и для так называемой цеп н о й с х е м ы, показан-
ной на рис. 4-6. Просуммировав комплексные сопротивле-
ния Z7 и Z8 В последней ветви, найдем комплексную про-
водимость ветви, которую алrебраически сложим с. 1/Z6
И получим суммарную комплексную проводимость двух
последних ветвей; вычислив обратную величину, т. е. KOM
плексное сопротивление, прибавим к ней Z5' Продолжая
Jt}4
таким образом дальше, получим в итоre результирующее
комплексное . сопротивление цепи и соответственно сум-
марный ток 11' который может быть путем последователь-
ных вычислений распределен между всеми ветвями сложной
цепи.
Однако такой способ расчета цепной схемы является
достаточно трудоемким и утомительным. Более целесо-
образно в этом случае воспользоваться друrим методом,
который известен под названием м е т о Д а n о Д о б и я
или еДИНИЧНоrо тока.
Задавшись током в последней ветви, равным единице
(1; ==:: 1), находим напряжение На комплексном сопротив-
j " 2 +2
лении Z6, равное (Z7 -+- Z8) :1. При этом ток 6==
'
Следовательно,
j "
j ", + j "
27 + 28 + 1
5
6 7
.
Прибавив к напряжению на Z6 падение напряжения
от тока 1
в комплексном сопротивлении Z5, получим на-
пряжение на Z,.. Продолжая таким образом дальше, найдем
в конечном итоre ток 1; и напряжение [)'. Ввиду Toro
что ток 1; был произвольно выбран равным единице, полу-
ченн
напряжение не будет равно заданному напряже-
нию и на выводах цепи. Для нахождения действитеЛЬНоrо
распределеяия токов в схеме необходимо все вычислен-
ные значеяия токов умножить на отношение [) /[)'.
4-3. ЭКВИВАЛЕНТНЫЕ УЧАСТКИ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ
И ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЯМИ
Обозначим комплексное сопротивление участка цепи,
состоящеrо из двух последовательно соединеняых эле-
ментов, через Z == r + jx. Комплексная проводимость дан-
Horo участка цепи равна У == I/Z == g
jb, . причем актив-
ная и реактивная проводимости:
g
. b
(2+х2'
,2,+xZ'
Если два элемен-rа с проводимостями g И Ь, вычислен-
ными по этим формулам, соединить параллельно, то сум-
марная комплексная проводимость будет равна У и соот-
ветственно комплексное сопротивление будет равно Z.
103
Такие две цепи с последовательным и параллельным
соединениями, имеющие одинаковые сопротивления на вы-
ВОДах, называются э к в и в а л е н т н ы м и.
Ввиду Toro что реактивное сопротивление х, входящее
в расчетные формулы, в общем случае зависит от чаСТОТЫ,
условие эквивалентности этих цепей выполняется только
при той частоте, для которой вычислено х.
Пусть, например, задана схема с последовательным
соединением сопротивления '1 и индуктивности L 1 (рис.
4-7, а). Преобразуем ее в схему с параллельным соедине-
нием элементов (рис. 4-7, 6).
Активная и реактивная проводимости исходной цепи:
'! . Ь
фLi
g
'i + (ФL 1 )2'
,i + «(j)L 1 )2'
ИЗ условия эквивалентности цепей следует, что пара-
метры новой цепи будут:
r 2 ==
== 'i + «(j)L 1 )2 . (f)L 2 == Ь 1 == 'r +
Ll)2 .
g '1' ,(j) 1
Вычислив по этим формулам '2 и L 2 . получим схему
цепи, эквивалентной исходной при данной частоте (1). При
друrих значениях частоты (f) параметры '2 и L 2 будут
иметь друrие значеНffЯ, сле
довательно эквивалентность
цепей нарушится.
При (
< ((f)L 1 ) 2, наПри-
мер, при достаточно высокой
частоте:
а) б)
Рис. 4-7. Активно-индуктивные
цепи, эквивалентные при опре-
деленной частоте,
«(j)L 1 )2 L
'2
и 2
l'1'
'1
Если исходной является схема рис. 4-7, б и заДан-
ными параметрами являются '2' L 2 И Ш, то параметры экви"
валентной цепи (рис. 4-7, а) определятся из выражений:
1
g '2
'1 == g2+b2 == (
) 2 + (
) 2;
'2 (j)L 2
1
L ь . wr;
(f) 1 == g2 + Ь2 == (
) 2 (
) 2'
'2 + (j)L 2
106
Из полученных выражений видно, что числовые зна-
чения '1 и L 1 эквивалентной цепи зависят от частоты.
у СJLOВИЯ эквивалентности для цепей с последователь-
ным и параллельным соединением сопротивления и емко-
ти имеют вид:
'2 =='1 [1 + ((J)C:r 1 )2 ]: С 2 == C 1 1 + (
C1r1)2 ;
'1 == '2 1 + (
C2r2)2 ; С 1 == С 2 [1 + ((J)c:r z )2 J.
При достаточно высокой частоте (ШС 2 '2) 2> 1, и тоrда
1
'1
( С ) 2 ;
'2 (J) 2
С 1
С 2 .
4-4. ПРЕО6РАЗОВАНИЕ ТРЕУrОЛЬНИКА в ЭКВИВАЛЕНТНУЮ
ЗВЕЗДУ
Преобразованием :rреуrольника в эквивалентную звезду
называется такая замена части цепи, соединенной по схеме
треуrольником, цепью, соединенной по схеме звезды,
при которой токи и напряжения в остальной части цепи
а
b
,[]
Рис. 4-8. Упрощение схемы hреобразованием
треуrольника в звезду.
сохраняются неизменными. Иначе rоворя, эквивалентность
треуroльника и звезды понимаетсяв том смысле, что при
одинаковых напряжени.ях между одноименными выводами
токи, входящие в одноименные выводы, одинаковы. Это
равносильно тому, что мощности в этих цепях одинаковы.
На' рис. 4.8 показан случай, коrда преобразование тре-
уrольника в эквивалентную звезду дает возможность пр е-
образовать мноrоконтурную схему в ОДНО контур ную.
Для вывода расчетных выражений, слу
{ащих для
преобразования треуrольника в эк
ивалентную звезду,
ниже приняты следующие обозначения (рис. 4-9):
Z12' Z23' Z31
сопротивления сторон треуrольника;
107
11, !-'''' Z3
сопрОтивления лучеЙ звезды:
11, / } ' 13
токи, подходящие к выводам 1, 2, 3;
112' 23, /з1
токи В ветвях треуrольника.
Выразим токи в ветвях треуrольника через приходя-
щие токи.
Рис, 4-9, Соединения треуrольииком (а) и звездой (6).
б)
По второму закону Кирхrофа сумма напряжений в кон-
туре треуrольника равна нулю:
ZI2 i 12+ Z2з i 23 + Z31i31 == о.
По первому закону Кирхrофа для узлов 2 и 1
i 23 == i 12 + i 2; i 31 == i 12
i l'
Решение этих уравнений относительно 112 дает:
i
23111
22з12
12
212+223+231 .
Напряжение между выводами 1 и 2 схемы рис. 4
9, а
будет:
й
Z i
231212ii
Z12Z2зI2
12
lZ 1:2
412 + Z23 + Z31 '
а в схеме рис. 4
9, 6 оно равно:
(;12 ==> Zl i 1
Z2'2'
ДЛЯ эквивалентности необходимо равенство напряже-
ний 012 при всяких токах 11 и 12' Т. е.
231212 j 212223 j Z j z!
Z12 + 223 '+ 2: п 1
Z12+ 2 2з+ 2 31 2. == 1 1
2. 2'
108
Это ВОЗМоЖНо при условии:
Z
Z31 Z 12
1
Z12+ Z 2З+ Z 31
Z
Z12 Z 2:J
2
Z12+ Z 2з+ Z зi
Z
Z2З Z 81
3
Z12+ Z 23+ Z 3i
: I
I
. J
(4
1)
Третье выражение получается В результате круrовой
замены индексов.
Итак, Комплексное сопротuвление луча звезды равно
проuзведению комплексных сопротивлений прилеzающих сто-
рон треуzольника, делеН/юму на сумму комплексных сопро-
тuвлений трех сторон треУсОАьника.
Выше было получено выражение для тока в стороне
1
2 треуrольника в заВисимости от токов 11 И 12' Kpyro-
вой заменой индексов можно получить токи в двух друrих
сторонах треуrольника:
i
Z12i2
Z31/з' i
Z2зiз
212i1
23
Z12+ Z 2З+ Z 31 И 31
212 + 223 +Z31 .
4-5. ПРЕОБРАЗОВАНИЕ ЗВЕЗД'" В ЭКВИВАЛЕНТНЫ,",
ТРЕуrольник
В расчетах также возникает необходимЬСтЬ замены
звезды эквивалентным треуrольником. На рис. 4
10 пока-
зан, например, случай, коrда такая замена позволяет
,
{]
Рис. 4-10. Упрощенне схемы преобразованием звезды в треуrольник,
преобразовать сложную электрическую схему в однокон-
турную.
При переходе от звезды к треуrольнику заданными
являются сопротивления звезды Zl. Z2. Z3. Выражения для
искомых сопротивлений треуrольника находятся в резуль-
тате COBMeCТHoro решения трех уравнений (4
1).
109
Деление TpeTbero уравнения на первое, а затем на вто.
рое дает:
.
2.! И Z:
231
21
212 22
212 .
Выражая отсюда Z23 и ZЗ1 через Z12 и подставляя их
в первое уравнение (4-1), получим:
Z1[ Z12 + Z12
; + Z12
: ] == Z
2
: '
откуда
Z12 == Z1 + Z2 + Z
2 .
Аналоrично круrовой' заменой индексов
Z
Z + Z +22ZЗ
23
2 3 zi
(4-2)
получим:
(4-2а)
и
Z Z Z 2з2f
31== 3+ 1+Z-;'
( 4-2б)
Следовательно, комплексное сопротивление стороны тре-
уеольника равно сумме комплексных сопротивлений прилееаю-
ЩUX лучей звезды u проuзведения их, деленноео на сопротивле-
ние третьеео луча.
Токи в лучах звезды леrко выражаются через токи
в сторонах треуrольника. С учетом положительных направ-
лений на рис. 4-9 имеем:
j1==j12
j31; J2==j2з
j12; jз==j31
j23'
4-6. ЭКВИВАЛЕНТНЫЕ ИСТОЧНИКИ Э. Д. С. И ТОКА
Два разнородных источника электрической энерrии
источник э. д. с. и источник тока
считаются эквивалент-
ными" если при замене одноrо источника друrим токи и
напряжения во внешней электрической цепи, с которой
эти источники соединяются, остаются неизменными. На
рис. 4-11 изображены эквивалентн,ые источники тока,
посылающие во внешнюю цепь ток 11 и поддерживающие
на своих выводах одинаковое напряжение а.
Условием эквивалентности источников, именуемым
в дальнейшем п р а в и л о м о б э к в и в а л е н т н ы х
и с т о ч н и к а х э. д. с. и т о к а, служит следующее
соотношение между э. д. с. Ё источника э. д. с. и током 1
110
источника тока:
E
z!,
(4-3)
rде Z
внутреннее комплексное сопротивление как источ
ника э. д. с., так и источника тока.
ДеЙствительно, напряжение (J на источнике э. д. с.
получается в результате вычитания из э. Д. с. Ё падения
напряжения от тока 11 в комплексном сопротивлении Z
источника (р ис. 4-11, а).
CoOTвeTCTB
HHO напряжение (J на источнике тока при
том же токе 11, посылаем<?м во. внешнюю цепь, равно паде
нию напряжения от тока 1
11 В комплексном сопротивле
нии Z источника (рис. 4
11, 6).
В обоих случаях напря
жения на выводах обоих ис
точников одинаковы:
(; == Ё
Zll == Z (1
/1) ==
==ZI
Zll'
т. е. получается условие .(4-3),
не зависящее от тока /1 Ha
rрузки. Рис. 4
11. Эквивалентные источ-
При отсоединении экви
ники Э. Д. с. (а) и тока (6).
валентных источников э. д. с.
и тока от внешнеЙ цепи (11 == О) напряжение на выводах
обоих источников равно Ё. Именно это обстоятельство и
равенство внутренних комплексных сопротивлений обоих
источников и обеспечивают их эквивалентность при .любом
режиме работы (см. Э 7-9).
Следует заметить, что мощности, расходуемые во вну-
тренних сопротивлениях эквивалентных источников э. д. с.
и тока, неодинаковы. В первом слу
ае полная мощность,
расходуемая в источнике, равна zI
, во втором случае
. . 2
Z I 1
/1 I .
'Например, при отсоединении источников от внешнеЙ
цепи в первом случае мощность в источнике не расходу-
ется, а во втором случае она составляет zJ2.
Поэтому эквИ8алентность источниКQ8 следует nони.мать
пwлько в СМblсле неизменности тОК08, наnРЖ)fсений и мощ-
ностей 80 8нешней электрической цепи, присоединенной
к источникам.
Если внутреннее сопротивление источника э. д. с. равно
нулю, то непосредственное применение формулы. (4-3)
для нахождения эквивалентноrо источника тока по, задан-
EI Z
' m
.
i
i,
+ Ё и! i
z й!
0.) 5)
111
ной э. д. с. источника не представляется возможным.
В таких случаях сопротивление внешней цепи, включен-
ной последовательно с э. д. С., можно рассматривать в ка-
честве BHYTpeHHero сопротивления источника, что позво-
лит применить формулу (4-3).
В случае сложноЙ электрической цепи замена источ-
ника э. д. с. эквивалентным источником тока или обратно
может иноrда упростить расчет.
Целесообразность такой замены проиллюстрирована,
в частности, в следующем параrрафе.
4.7. ПРЕО6РАЗОВАНИЕ СХЕМ С ДВУМЯ УЗЛАМИ
Применим правило об эквивалентных ИСТОЧНИКах э. д. С.
и тока к преобразованию схемы с параллельным соеДине-
нием п ветвей, содержащих источники э. Д. с. (рис. 4-12, а).
Zn
Zn+1
Ё п +
а.)
б)
jn+1 *
z Zn+1
8)
Z
Е Zn+1
z)
Рис. 4-12. Преобразования параллельноrо соединения ветвей с источ-
никами э. д. С.
Заменяя заданные источники э. д. с. источниками тока,
получаем схему рис. 4-12, б. Источники тока в С9ВОКУП-
ности образуют эквивалентный источник тока 1 (рис.
4-12, в), причем
i==il+i2+...+in==
Ё' . n
== 21 +
+ . ..+
'! == ! УkЁk
1 2 n k
1
112
и
z==
п
Y k
k
l
Пользуясь этим соотношением, можно в конечном
итоrе перейти от схемы рис. 4
12, в к схеме рис. 4
12, 2,
являющейся эквивалентом исходной схемы рис. 4
21, а.
Здесь .
n
У kEk
Ё == zi == k
1
п
Yk
k
l
Таким образом, п параллельных ветвей с источниками
э. д. с. между двумя узлами MorYT быть заменены
одним источником тока (рис. 4
12, в) или источником
э. д. с. (рис. 4
12, е).
Ток во внешней цепи (в ветви с сопротивлением Zп+l)
равен:
1 . z Е
п+1 == 1 z + Z ,== Z + Z ' .
п+l п+1
Напряжение между двумя узлами находится по фор-
муле
(; == i [ ZZMf ] == i 1
Z+Zп+i п+ 1
Y k
k
l
п
У k E k
k
l
п+l
Y k
k
l
(4-4)
Выведенные здесь выражения широко используются
для расчета электрических цепей с двумя узлами, а также
более сложных цепей, приводящихся к двум узлам.
4.8. ПЕРЕНОС ИСТОЧНИКОВ В СХЕМЕ
Расчет электрической цепи облеrчается в ряде случаев
в результате переноса в схеме источников э. д. с. или
тока. Как это видно из уравнений Кирхrофа, токи в схеме
определяются заданными величинами суммарных э. д. с.
в контурах независимо от Toro, из каки/х отд€'льных сла
rающих они состоят. Поэтому измеllение расположения
113
в схеме источников э. д. с., при котором суммарные э. д. с.
во всех контурах сохраняются неизменными, не влияет
на токи в ветвях. Аналоrично напряжения на ветвях опре
деляются задан-ными суммарными токами источников тока
в узлах, и поэтому изменение расположения в схеме И{;точ
ников тока, при котором их суммарные токи во всех узлах
сохраняются неизменными, не влияет на напряжения
в схеме.
Если, например, требуется исключить источник э. Д. с.
из какой-либо ветви, то в данную ветвь вводится компен-
сирующая э. д. с., причем точно такая же э. д. с. вво-
дится одновременно во все остальные ветви, сходящиеся
а)
б)
Рис. 4-13. ПереНQС источников Э. Д. с. в схеме.
в одном из узлов данной ветви. Компенсирующая и допол-
нительные э. Д. с. имеют одинаковое направление по отно-
шению к рассматриваемому узлу. В результате Э10rо
источник э. д. с. из ветви исключается и появляются
источники э. д. с. в друrих ветвях схемы. Суммарные
э. Д. с. во всех контурах и соответственно токи в ветвях
остаются прежними.
Итак, источник э. д. с. может быть nepeHereH из какой-
либо ветви схемы во все друеие ветви, nрисоединенные к узлу
данной ветви, без uэмененuя таков в cXeAte.
Справедливо и обратное положение: если БО всех вет-
вях, кроме одной, СХОДящихся в узле, имеются одинаКОI1ые
источники э. д. с. (рис. 4-13, а), направленные все к одному
узлу или все от узла, то они MorYT быть заменены одним
источником э. Д. с. в ветви, в которой источник OTCYТCTBO
вал (рис. 4.13, 6). '
Это положение подтверждается тем,ЧТО суммарные
э. д. с. в контурах схем на рис. 4
13, а и б'одинаковы.
Имеет<;я и друrое доказательство данноrо положения:
ввиду равенства э. д. с. всех источников вторые выводы
114
их MOrYT быть объединены, как имеющие одинаковый потен-
циал. В результате TaKoro объединения, показанноrо на
рис. 4-13, а пунктиром, получается схема рис. 4-13, б.
В случае пере носа источников тока они присоеднняIOТСЯ
к узлам схемы так, чтобы оставались неизменными их
cYl\iMapHbIe токи в узлах.
Так, например, несмотря
на то, что источники тока
раэмещены в схемах рис.
4-14, а и 6 различно, сум-
маряые токи источников в
узлах обеих схем одина-
ковы. Поэтому и напряже-
ния между узла
1И не изме-
нились.
Итак, источник тока
может быть заменен ис-
точниками тока, подклю-
ченными, параллельно всем
ветвям, KOпwpbte составляли контур с рассматриваемым
источником.
. Перенос источников в схеме успешно сочетается на прак-
тике с различными меТОДаМИ преобразований И расчетов
(см. пример 4-1).
а)
Рис, 4
15. Пример 4-1,
ZI
i
Z2
Z3
j
z Z,
, t
Zs
i
Z2
Z6
i
Z3 Z1
0.) о)
Рис. 4-14. Перенос источника тока
в схеме.
8)
Пример 4-1. Вычислить ток в диаrональной ветви '5 мостовой
схемы рис. 4-15, а.
Дано: 1
10 А; '1 == 1 Ом; '2 == 2 Ом; 'з == 3 Ом; '4 == 4 Ом;
'5 == 5 Ом. , .
Заданный источник тока может быть заменен двумя источниками,
подключенными параллельно сопротивлениям 'Т1 и '4 (рис. 4-15,6).
Пользуясь условием эквивалентности источников э. Д. с. и тока, полу-
б)
115
чаем схему рис. 4-15, в с двумя узлами. По формуле (4-4) напряже-
40 10
иие иа ветви '6 равно 1 "'7
3" 1 3,52 В. ИСКОМЫЙ ток
7 +
3
+ 5'
1,,== з,
2 ==0,704 А.
4-9. ПРЕО&РАЗОВАНИЕ СИММЕТРИЧНЫХ СХЕМ
Схема электрической цепи, в которой имеется ось
симметрии, называется симметричной. Например, схема
рис. 4-16, а симметрична относительно вертикальной оси.
В симметричных схемах леrко выявляются точки или
узлы с одинаковым потенциалом. В ветвях, присоединен-
ных к таким узлам, токи равны нулю. Поэтому эти ветви
1
2 Z ,
Z'I
4)
6)
6)
Рис. 4-16. Симметричная цепь (а и 6) и ее отсеченная по-
ловина (8), .
можно разрезать, не нарушая распределения токов и на-
пряжений в схеме. Точки, имеющие одинаковый потен-
циал, MorYT быть объединены. Рассечение ветвей, по кото-
рым не проходит ток, и объединение точек paBHoro потен-
циала упрощают схему и облеrчают расчет.
Так, в симметричной схеме рис. 4-16, б токи в соедине-
ниях, пересекающих ось симметрии, отсутствуют. Раз-
резав схему по оси симметрии, получим с обеих CtOpOH
одноконтурную схему рис. 4-16, в, которая леrко рассчи-
тывается.
Допустим теперь, что полярность источников в симмет-
ричной схеме неодинакова (рис. 4-17, а). В этом случае
(равенство э. д. с. источников и различие их полярности)
токи в симметричных ветвях (например, 11 и 12) и напря-
жения между соответствующими парами выводов, симмет-
116
рично расположенными Относительно оси, равны iI проти-
воположны по знаку. Отсюда следует, что напряжения
между всеми точками, лежащими на оси симметрии, равны
нулю (О ==
O, т. е. О :::::: О). Поэтому все точки схемы на
оси симметрии MorYT быть замкнуты накоротко (рис. 4-17,6).
1 1 fZ1f
2 Z 'l 2 Z 'l
Z2 Z2 Z2
11 t jzl
Z, 2ZJ 2ZJ Z1 2Z з
б)
Рис. 4-17. Симметричная цепь с неОДИН8КОВОЙ полярностью
ИСТОЧНИКОВ (а) и ее эакороченная половина (6),
Таким образом, расчет сложных симметричных схем
приводится к расчету более простых схем.
На рис. 4
18, а и б показана симметричная мостовая
схема, имеющая две оси симметрии
вертикальную и
Z,
1
2 Z,
!..Z,
2
а)
-JZI i Z I
о)
8)
1Z 1
2
Рис. 4
18. СимметрнчнаЯ' мостовая схема (а, 6) и ее преобразован-
ная часть (в),
rоризонтальную. В продольных ветвях ток отсутствует;
потенциалы средних точек поперечных (перекрещенных)
ветвей одинаковы.
Поэтому продольные .ветви MorYT быть рассечены,
а средние точки поперечных ветвей
объединены. В ре-
117
зультате с обеих сторон получится одноконтурная схема
(рис. 4-18, 8), расчет которой крайне прост.
Если изменить полярность ОДНоrо из источников (рис.
4-19, а), то роли продольных и поперечных ветвей поме-
няются и преобра:зованная часть схемы примет вид, пока-
занный на рис. 4-19, б.
1
2 Z1
1
gZ1
1 1
Z Z1 z Z 1
а)
1
ZZ1
1
gZz
б)
1
Z Z 1
Рис. 4-19. Симметричная мостовая схема (а) и ее
преобразованная часть (6).
в разобранных выше примерах э. д. с. источников
были равны. В случае неравенства э. д. с. источников
преобразование симметричной схемы удобно сочетается
с методом наложения (см. пример 7-5).
4.10. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
4-1. Сопротивление 2 Ом и емкость 0,191 мкФ соединены парал-
лельно. Найти эквивалентную схему с последовательным соединением
, и С при частотах f == 1; 1,5; 2 мrц.
о т в е т: , == 0,296; 0,143; 0,083 Ом; С == 0,224; 0,206; 0,199 мкФ.
4-2. Параллельно соединены ветви, одна из которых состоит из
С == 10 мкФ, а вторая
из последовательно соединенных, == 10 Ом
и L == 100 Mr. Вычислить комплексное сопротивление цепи при Q) ==
== 377 рад/с.
о т в е т: 13,5 + j43,4 Ом.
4-3. Добавив в схеме, взятой из предыдущей задачи, последова-
телыю , == 10 Ом, и подведя к цепи (j == 100 L 0° В, вычислить токи
в ветвях и суммарный ток; построить векторную диаrрамму.
О т в е т: 0,347 L 101°6'; 2,36 L
640; 2,02 L
61030' А.
4-4. Индуктивная катушка, имеющая , == 8 Ом и L == 0,05 r,
соединена параллельно с С == 1 мкФ. Найти 'частоту, при которой
напряжение на данной цепи в фазе с суммарным током; опре-делйть
сопротивление цепи.
О т в е т: 713 [ц; 6250 Ом.
4-5. Параллельно соединены две ветви: первая ветвь состоит из
последовательно соединенных '1 и L и ее (;опротивление равно 40 +
118
+ j30 Ом; вторая состоит из последовательно соединенных '2 и С и
ее сопротивление равно 80
j150 Ом. Определить сопротивление и
проводимость всей цепи, если частота возрастет в 1,5 раза; начертить
на комплексной плоскости сопротивления и проводимости ветвей и
всей цепи.
О т в е т: 58,4 L 21°35' Ом; 1,71'1(}2 L
21035' См.
4-6, Параллельна соединены три ветви: первая состоит из '1 ==
== 25 Ом, вторая
из С == 50 мкФ, третья
из индуктивной ка-
тушки, имеющей '2 == 10 Ом и L == 50
Mr. Напряжение на ветвях
равно 100 sin 400 t В. Вычислить действующее значение суммар-
Horo тока и активную мощность цепи,
О т в е т: 4,47 А; 300 Вт,
4-7. Индуктивная катушка, имеющая, и L, соединена параллельна
с емкостью С. Найти L и С, при которых сопротивление всей цепи равно
500 L 0° Ом, если, == 100 Ом и уrловая частота (i) == 105 рад/с.
О т в е т: 'L == 2 Mr, С == 0,04 мкФ,
4-8. Последовательно с С подключена цепь, состоящая из , ==
== 500 Ом и L, соединенных параллельно. Приняв w == 105 рад/с,
найти L и С, при которых общее сопротивление равно 100 L 0° Ом.
О т в е т: 2,5 Mr; 0,05 мкФ.
4-9. Доказать, что полное сопротивление цепи, состоящей из
параллельно соединенных индуктивной катушки (', L) и емкости (С),
при уrловой частоте w == I/V 2LC не зависит от ,.
4-10. Сопротивления 50
j20, 100 + jO и 40 + j60 Ом соедннены
треуrольником. Преобразовать данный треуrольник в эквивалентную
звезду.
О тв е т: 18,5 + j7,7; 23,1
Л5,4; 26,5 + j26 Ом.
4-11. Индуктивная катушка, имеющая сопротивление 15 + j20 Ом,
последовательно ПОДКЛl9-чена к участку цепи, состоящему из параллель-
, 1
но соединенных, == 10 Ом и С== ЗОw Ф. Определить действующие ток
в индуктивной катушке и напряжения на , и С, если ко всей цепи при-
ложено напряжение 100 L 0° В.
О т в е т: 2,76
jl,96 А; 19
j26 В.
4-12. Два reHepaTopa, имеющие одинаковую частоту, работают
паралл
льно.на общую наrрузку. Заданы: комплексные э. д. С. reHepa-
торов Е 1 и Е2' комплексные сопротивления reHepaTopoB 21 и 22' ком-
плексное сопротивление наrрузки 23.
Определить ток в иаrрузке.
О т в е т:
2 2 Ё i +2 1 Ё 2
2122 +2223 + 7.з2i'
4-13. В чем заключается удобство. расчета схемы с двумя узлами?
4-14. В каких случаях целесообразно применять метод единичноrо
тока?
4-15. Привести пример, в котором требуется. преобразовать звезду
в треуrольник (или треуrольник в звезду).
4-16. Вывести условия эквивалентности (при определенной ча-
стоте) активно
емкостных цепей с последовательным и параллельным
соединением сопротивления и емкости.
4-17, Пользуясь условиями (4
1), выразить токи в сторонах тре-
уrольника через токи эквивалентной звезды,
119
rЛАВАПЯТАЯ
РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
5-1. РЕЗОНАНСНЫЕ (КОЛЕEiА ТЕЛЬНЫЕ) Ц.ЕПИ
Резонансными или колебательными
цеп я м и называются электрические цепи, в которых
MorYT возникать явления резонанса напряжений или токов.
Резонанс представляет собой такой режим пассивной
электрической цепи, содержащей индуктивности и емко-
сти, при котором реактивное сопротивление и реактивная
проводимость цепи равны нулю; соответственно равна
нулю реактивная мощность на выводах цепи.
Рез о н а н с н а П р я ж е н и я наблюдается в элек-
трической цепи с последовательным соединением участков,
содержащих индуктивности и емкосТи. Неразветвленная
цепь, состоящая из последовательно соединенных элемен-
тов " L и С, рассмотренная В
2-7, представляет собой
один из простейших случаев такОЙ цепи. В радиот
хнике
ее называют п о с л е д о в а т е л ь н ы м к о л е б а -
т е л ь н ы м к о н т у ром.
При резонансе напряжений индуктивное сопротивле-
ние одной части цепи компенсируется емкостным сопро-
тивлением друrой ее части, последовательно соединенной
с первой. В результате реактивное сопротивление и реак-
тивндя. .мощность на выводах цепи равны НУЛЮ.
В свою очередь рез о н а н с т о к о в наблюдается
в электрической цепи с параллельным соединением участ-
ков, содержащих индуктивности и емкости. Один из про-
стейших примеров такой цепи, состоящей из параллельно
соединенНЫХ элементов " L и С, был рассмотрен в
2-8.
В радиотехнике такую цепь называют пар а л л е л ь -
н ы м к о л е б а т е л ь н ы м к о н т у ром.
При резонансе токов индуктивная проводимость одной
части цепи компенсируется емкостной проводимостью дру-
rой ее части, параллельно соединенной с первой. В резуль-
тате реактивная пP080дuмocтb и реактштая мощность
на 8ыiздахx цепи равны НУЛЮ.
Частоты, при :которых наблюдается явление резонанса,
называются рез о н а н с н ы м и ч а с т о т а м и.
Исследование резонансных режимов в электрических
цепях заключается В нахождении резонансных частот,
120
зависимостей различных величин от частоты 1 или пара-
метров L и С, а также В рассмотрении энерrетических
соотношений при резонансе.
Резонансные цепи очень широко применяются в элек-
тротехнике и представляют собой неотъемлемую часть
всякоrо радиотехническоrо устройства. Изучению явления
резонанса, свойств и Частотных характеристик простей-
ших резонансных цепей посвящена данная rлава. Элек-
трические фильтры, которые также являются резонансными
цепями, расмотрены в rл. 10.
$-2. ПОСЛЕДОВАТЕЛЬНЫА КОЛЕ&АТЕЛЬНЫЯ КОНТУР. РЕЗОНАНС
НАПРЯЖЕННА
РезонаНсная цепь с последовательным соединением
(, L и С (рис. 5-1) является простейшей цепью для изу-
чения явления резонанса напряжений и подробно рас-
сматривается ниже. Комплексное сопротивление такой цепи
зависит от часТотЫ:
Z == r + j ( (OL
Ю
) . (5-1) l' L
Резонанс напряжений наступает
t Ё ' ]
при частоте (00' Коrда
(О L==
'
о юоС'
1
UJo == -V LC .
MrHoBeRHbIe энерrии выражаются формулами:
(5-2)
Рис. 5
1. Последова-
тельиый колебатель-
ный контур.
отсюда
и 2 Си?:
WL ==
2
; Wc ==2'
Если принять i == 1т sin (Oot, то ис ==
UCт cos (00/'
Поэтому
и7п .
'WL ::::: 2 sш 2 UJot
и
CUtm
Wc :::::
cos 2 UJot.
1 Такие зависимости называются частотными характериСтиками.
121
Максимальные значения этих энерrий равны друr
друrу, так Как
СUЁт с ( 1т ) 2
Ll
==T (fJoC
2'
Это следует и из TOrO, что реактивное сопротивление
цепи, содержащей индуктивность и емкость, при любой
схеме соединений пропорционально разности максималь
ных значений энерrии, запасаемой в маrнитном и электри-
ческом полях (см. 9 3-4):
(fJ
х == 72 (W LMaKc
W С макс)'
Поэтому условию резонанса (х == О) соответствует
равенство
W L макс == W Смакс'
MrHoBeHHbIe значения WL И Wc колеблются с удвоен-
ной частотой около среднеrо зНачения Ll':,,/4, причем
происходит непрерывное перераспределение энерzии .мazнит-
НОсО и электрическоzо полей, СУМАюрное значение которой
постоянно:
L
Lt
WL + Wc == т [sin 2 (i)ot + cos 2 (i)ot] == ---i!.
в рассматриваемом случае (резонанс напряжений, рис.
5-1) в цепи не происходит обмена энерrии между и('точ
НИКОМ и реактивными элементами цепи, а вся электриче-
ская энерzия, поступающая от источника, расходуется
в сопротивлении r.
Мы уже встречались с понятием добротности индук-
тивной КатушКи QL == (i)L/r (см. 9 2-7) и конденсатора
Qc == (i)Cr (9 2
8). Умножив и разделив выражение дЛЯ
QL на {- 1
, получим:
1 2
L1 m W
Q 2 2 L макс
L==(i)
== Л;рt
.
'Im
2
Здесь WLMaKc
максимум энерrии, периодически за-
пасаемой индуктивностью L; Р
активная мощность,
расходуемая в сопротивлении при амплитуде тоКа 1т'
122
Аналоrично рассуждая, т, е. умножив и разделив выра-
жение Qc на } И'!N, получим:
1 2
-? СИт,
Q
ш
С
1 Иiп
2
r
W C а .-
2л
РТ'
rде W с макс
максимум энерrии, периодически запасае-
мой емкостью С, а Р
активная мощность потерь в парал-
лельном сопротивлении r при амплитуде напряжения
на емкости И т . Следовательно, в обоих случаях доброт-
ность определяется в, зависимости от отношения макси-
мума энерrии реактивноrо элемента к энерrии РТ, выде-
ляемой в виде тепла за период.
В случае резонансной цепи также пользуются поня-
тием Д о б Р о т н о с т и цеп и, подразумевая под этим
в общем случае величину
Q
W макс
== ШО Р ;
(5-3)
здесь шо
резонансная частота;
W MaKc
сумма макси-
мальных значений энерrии, периодически запасаемой при
резонансе в индуктивных (или емкостных) элементах;
Р
активная мощность на выводах цепи при резонансе.
Знак
в (5-3) относится к случаю, коrда число индук-
тивных (или емкостных) элементов превышает единицу.
В рассматриваемом нами случае резонанса напряжений
в цепи рис. 5-1 знак
опускается.
Для схемы рис. 5-1 на основании (5-3) получаем:
Q
bloL
V
P
r
ЫоС'
---т------
r'
(5-4)
rде
P==Y
называется х а р а к т е р и с т и ч е с к и м (а также вол-
новым) сопротивлением резонансноrо контура.
Условимся называть о т н о с и т е л ь н о й р а с -
С Т рой к о й ч а с т о т ы по отношению к резонансной
123
частоте контура величину 1
б== ОО
ООо ==
1.
000 000
(5
5)
Сопротивление контура соrласно (5-1) и с учетом (5-2)
и (5-4)
Z == ' [ 1 + J ' rooL (
)] == , [ 1 + J 'Q (
JJ )] ,
, 000 oooooLC. 000 ro
00 000 1
откуда, используя (5-5), 000 === б + 1 или ro == 0+ 1 ' ло
лучаем:
Z==r[1 + jQ(б+ 1
O
I )J=='(l +jQб
t
). (5-6)
Следовательно, полное сопротивление цепи
z==rV 1 +Q262(
t
Y
и уrол
ер == arctg QOo(
2) .
Ток в цепи
1 Ё Ё
== z ==. ( 1 + 'Q6 0 +2 ) '
, 1 б+ 1
При частоте, близкой к резонансной, I б I значительно
меньше единицы, и поэтому при ближенно
Z
, (1 + j2Qб) ==, Уl + (2Qб)2 <'ер; )
ер
arctg 2Q6;
. Ё
1
, (1 + j2Qб) .
(5-7)
Выражения (5-7) практически достаточно точны при
I б 1< 0,1. При I б I == 0,2 поrрешность в сопротивлении z
меньше 10%.
На рис. 5-2 кривые даны в относительных значениях:
по оси абсцисс отложена относительная расстройка ча-
1 СJlедует обратить виимание на ТО, что чаСТОТам ВЫше резонансной
(ro > (00) соответствуют положительные значения расстройки б, а ча-
стотам НИЖе резоиансной (00 < (00)
отрицательные значения б;
нулевой частоте (00 == О) соответствует о ==
l; при резонансной ча-
СТОте 6 == о.
124
стоты б, п
оси ординат
отношение полноrо сопротивле-
ния z к активному сопротивлению r (рис. 5-2, а) и уrол ер
(рис. 5-2, б).
О
а)
РИС. 5-2. Частотные зависимости сопротцвления (а) и уrла (6).
Полное сопротшзленШ! цепи минимально при резонансе
напряжений; при этом ток в цепи достиzает своесо макси-
.мальноzо значения 10'
На рис. 5-3 изображены резонансные кривые тока в
относительных значениях: по оси абсцисс, как и на пре-
дыдущих rрафиках, отложены
значения б, по оси орди-
нат
отношения токов к
максимальному току при p
зоиансе:
8
90'
ер Q=100
r
I
О'
1
I
I
9r
L
б)
1
10
1
..J.....
y'i'
i..
E .
!....
10
z . ,
z
1
V I+Q 2 б 2 (
t
Y'
Чем выше добротность це-
пи Q, тем острее резонансные
кривые. Таким образом, вели- Рис. 5.3, Резонансные кривые
чина Q характеризует остро- тока в относительных единицах.
ту'резонансной кривой (<<остро-
ту настройки»); соrласно (5-3) чем больше отношение мак-
симума энерrии поля реактивноrо элемента к количеству
теплоты, рассеиваемой за один период в резонансном кон-
туре, тем острее резонансная кривая.
Резонансные кривые были построены здесь в ::>ависи-
мости от ощосительной расстройки частоты б. Можно
(5-8)
125
вывести расчетные выражения и построить резонансные
кривые в зависИМости от ш или относительной частоты
ш/ шо. Следует заметить, что максимумы резонансных кри-
вых на рис: 5-3 равны, таК как по оси ординат отложено
отношение 1 !I o . Если откладывать ток 1, то при разных
r максимумы резонансных крив-ых, естественно, не совпа-
дут в одной точке.
Полосу частот вблизи резонанса, на rраницах которой ток снижа-
ется ДО I/V2 == 0,707 максимальноrо (резонансноrо) значения 10'
принято называть п о л о с о й про п у с к а н и я резонансноrо
контура. При токе / == /o/V2 мощность, расходуемая в сопротивле-
нии " равна: '
, (
y == .
,Ig,
т. е. составляет половину мощности, расходуемой при резонансе. Поэ-
тому полосу пропускания характеризуют как полосу, rраницы кото-
рой соответствуют ПОЛОfiине МaJ,симальной мощности. На rраницах
полосы пропускания резонансноrо контура активное и реактивное со-
противления равны '2 == J х 1. Это следует из условия ,
, Е2 lЕ2
, ,2+х2
2
' fii'
что дает ,2 + х 2 == 2r2.
Соответственно и фазовый СДвиr между напряжением на выво-
дах цепи и током составляет 450; на нижней rранице комплексное
сопротивление цепи имеет емкостный характер (ток опережает напряже-
ние) и q> ==
450; на верхней rранице комплексное сопротивление цепи
имеет индуктивный характер (ток отстает от напряжения) и q> == 450.
На основании (5-8) условие для rраницы полосы про пускания
записывается в следующем виде: .
-v I+Q2&2 (
ti Y == V2,
или
&+2
Q& & + 1 =ч 1,
откуда
1 ,; 1
151.2==
1 :+ 2Q + V 1 + 4Q2
(5-9)
(знак минус перед корнем, получающийся в результате решения ква-
дратноrо уравнения, опускается, как не имеющий смысла). Индексы
1 и 2 и соответственно знаки минус и плюс в выраженин (5
9) относятся
к rраницам ниже и выше резонанса.
По определению полоса про пускания резонансноrо контура нахо-
дится из условия
1
152
151 ==
(i'
126
или
Cl)2
(()i == 1 d
(()о Q == .
(5-10)
Величина d, обратная добротности контура, называется 3 а т у-
х а н и е м контура.
При достаточно высокой добротности резонансноrо контура (Q
1)
подкоренное выражение (5-9) может быть приравнено единице, OT
1
куда ()1, 2::::::: +: 2Q ; т. е. полоса пропускания практически симметрична
относительно резонансной частоты.
В радиотехнических устройствах к одному из peaK
тивных элементов колебательноrо контура, например e
кости, подключается наrрузка в виде сопротивления r H .
Вследствие этоrо возрастают потери в цепи и COOTBeT
ственно уменьшается добротность. Для определения доброт
ности наrруженноrо контура параллельное соединение r и
и С может быть заменено эквивалентным при резонансной
частоте последовательным соединением емкости и «вноси
Moro сопротивления» r ви , С этой целью используются
условия эквивалентности цепей с последовательным и
параллельным соединениями (см. Э 4
3).
1
Так как обычно (i)оСr и :> 1, то r BH
( С)2 ' С учетом
'и (()о
1
Toro, что
c ==p, получаем: r ви ::::::: p2/ rH . При этом, как
(()о
отмечал ось в конце Э 4
3, емкости эквивалентных схем
MorYT быть практически приравнены друr друrу.
Таким образом, добротность наrруженноrо контура
равна:
Q
р
р
Il
'+'ви """ ,+р2j,и'
а затухание увеличивается на вносимое затухание d BH :
d ==
+ 2
==d + d .
н Qи р 'н ви
Если вносимое сопротивление r BH значительно превы-
тает сопротивление r, то
Q
'2I. d
k==d .
н р , и 'н рн
Внутреннее сопротивление источника э. д. с. Rj,
добавляемое к сопротивлению r, влияет на добротность
и полосу пропускания колебательноrо контура: чем боль
ше RI' тем ниже добротность и шире полоса пропускания
127
контура. Поэтому с точки зрения сокращения полосы
пропускания последовательноrо колебательноrо контура
8Ы20ден источник напряжения с малым внутренним сопро-
тивлением.
В условиях, близких к резонансу, напряжения на индук-
тивности и емкости мосут быть весьма велики, что необ-
ходимо учитывать во избежание повреждения изоляции.
На рис. 5-4 показана векторная диаrрамма тока и
напряжений при резонансе. Напряжения на реактивных
элементах при резонансе определяются из выражения
. . Ё . .
U Lo ==
U СО ==
f(OoL == fEQ.
,
(5-11 )
При Q> 1 эти напряжения превышают напряжение
U == Е, приложенное к резонансному контуру. Однако
значения, получаемые на ос-
новании (5-11), не являются
максимальными: максимум На-
пряжения U L располаrается
i =,. io
Io
. 1 . .
uLo-j(z)оl..i о иco=
j (z)oc 1o
Рис. 5.4. Векторная диаrрам-
ма при резонансе напряже-
ний.
! JL @
Е Е
в
Рис. 5-5, Частотные зависи-
мости напряжений на индук-
тивности и емкости в отно-
сительных е.ZJ.иницах.
несколько выше (правее), а максимум и с
ниже (левее)
резонансной частоты (рис. 5-5).
Напряжение на индуктивности U L == (OLI, равное нулю
при (о == О, с увеличением (о может возрастать только
до тех пор, рока ток не начнет снижаться быстрее, чем
возрастает (о. После этоrо U L спадает, стремясь, в пределе
к Е. Напряжение На емкости ис == I/(OC, равное при
(о == о приложенному напряжению' U == Е, увеличивается,
I!OKa ТОК растет быстрее, чем (О; затем и с спадает, стре-
мясь в пределе к нулю. Кривые U L и ис пересекаются
при резонансе, причем ордината точки пересечения в соот-
ветствии с (5-11) равна QE.
128
Это также вытекает из аиализа следующих ниже выражений. полу-
ченных с учетом (5-5) и (5
б):
т.j
F .i(j)L
E jQ (6+ 1)
L
Z
1 + 'Qб & + 2
! 6+1
и
. Q
.
! &+ 1
Е & <') .
1+ 'Qб +..
! 0+ 1
Напряжение U L достиrает максимума при
, 1
!
, . wC
ис==Е z
б
1
1,
У 1
2
а напряжение U с
при 1
б== Y1
2
2
l.
Пренебреrая б по сравнению с единицей. получаем приближен.
ную формулу
. . -А. jQ
UL
UC
C 1+j2Q& .
(5-12)
Возвращаясь к определению понятия добротности рщ>
сматриваемой резонансной цепи, мы видим, что наряду
с формулами (5-3) и (5-4) добротность цепи характеризуется
выражениями (5-10) и (5-11), а именно:
Q == ЩО . Q == '!J...o == U Со
002
(J)l ' Е Е'
Последняя формула показывает, что добротность рас-
сматриваемой цепи определяется как кратность перена-
пряжения на L и С при резонансной час10те.
Выше была рассмотрена неразветвленная электриче-
ская цепь с последовательно соединенными r, L и С. ДЛЯ
ИсследоваНИЯ явления реЗОItаItса в более сложных раз-
!етвленных цепях, rДе резонанс напряжений может воз-
1 Следует отметить,' что при Q
I/V2 максимум функции U L
наступает при & == 0:>. т. е. в этом случае U L с ростом
aCTOTЫ не'пре-
рывно стремится к значению приложенноrо напряжения U == Е; MaK
симум же Фуикции и с в рассматриваемом случае имеет место при & z=
==
1. т. е. при нулевой частоте (00 == О). коrда и с == Е.
129
НИ кать на ОДНОЙ или нес1<ОЛЬКИХ частотах, наряду с ана-
литическим методом расчета, иллюстрированным выше,
целесообразно также пользоваться методом rеометрических
мест (см. rл. 6).
'-3. ПАРАЛЛЕЛЬНЫА КОЛЕIАТЕльнЫА КОНТУР. РЕЗОНАНС ТОКОВ
Явление резонанса токов удобно изучать примени-
тельно к электрической цепи с параллельно соединенными
" L и С (рис. 5-6), так каК при этом можно непосредст-
венно воспользоваться результатами, полученными в пре-
дыдущем параrрафе. .
Действительно, выражение для. комплексной проводи-
мости такой цепи
т
и
у == g
j (
L
roС)
структуре аналоrично выражению (5-1),
резонансная частота определяется
но (5-2).
Добротность резонансной цепи
НОВаНИИ (5
3)
сu 2 ,
Q == 6)0 u
== 6) о С' == р'
2
-
,
(5
'13)
по своей
причем
соrлас-
На ос-
По аналоrии с предыдущим ВЫРi3же-
Рис, 5-6. Парал- ние (5-13) приводится к виду:
лельный колеба-
тельный контур. У (1 + . Q
+ )
==g J v
+; .
Сравнивая полученный результат с (5-6), убеждаемся
в том, что выражение У /g для схемы рис. 5-6 имеет тот
же вид, что и выражение Z/r для схемы рис. 5.1.
Поэтому кривые рис. 5-2 применимы и в данном слу-
чае: кривые рис. 5
2, а выражают зависимость от 6 dтHO-
шения y/g, а кривые рис. 5-2, б
зависимость уrла
<p от 6.
Кривые рис. 5
2, а показываюr, что при резонансе то-
ков\полная проводимость цепи минимальна, т. е. входное
сопротивление достисает максимума.
При заданном напряжении () на выводах цепи ток,
идущий от источника в цепь, равен:
. . . ( 15+2 )
1 == У U == gU 1 + jQб б + 1 .
130
Этот ток достиrает минимума при резонансной частоте,
так как при этом
Jo==gU. .
Следовательно, отношение, токов 10 и 1 определяется
из выражения
!Q,
1
1
11 1 +Q21\2(
t
Y ,
правая часть KOToporo полностью совпадает с (5-8).
В связи с этим резонансные кривые рис. 5.3 выражают
применительно к схеме рис. 5-6 зависимость 10/1 от 6.
В случае резонанса токов токи в индуктивном и емкост-
ном элементах схемы рис. 5-6 равны и противоположны
по знаку:
i Со ==
j Lo == jUJoC(; == j/oQ.
Полученное выражение показывает, что добротность
рассматриваемой цепи определяется как кратность токов
в L и С по отношению к суммарному току 10'
При Q> 1 эти токи превышают 10'
Если параллельный колебательный контур питается
от источника тока с внутренним сопротивлением Ri' то чем
меньше сопротивлен'ие Ri' присоединяемое параллельно
сопротивлению r, тем ниже добротность и шире полоса
пропускания контура. Поэтому в отличие от последова-
тельноrо колебательноrо контура с точки зрения сокра-
щения, полосы пропускания параллельноrо колебательноrо
контура вЫ20ден источник тока С большим внутренним
сопротивлением.
Для схемы рис. 5-6 при резонансе токов остается в силе
вывод, сделанный в предыдущем параrрафе о непрерыв-
ном обмене энерrией между индуктивным и емкостным
эле,ментами при резонансе напряжений.
Схема рис. 5-6 является идеализированной, так как
она не учитывает активных.nотерь в ветвях L и С, Поэтому
рассмотрим друrие схемы, приняв во внимание аКтивные
сопротивления в ветвях L и С (рис. 5-7; а и 6).
Условие резонанса токов для схемы рис. 5-7, а запи-
сывается в виде равенства реактивных проводимостей:
1
(j)oL
ro;;c
'f+«(j)oL)2
( 1 ) 2
,
+ ЫоС '
(5-14 )
131
откуда
(
'1/1 C
'l
000== У LC 1
,
.
Явление резонанса возможно при этом ТОЛЬко в случае,
если подкоренное выражение (5-15) имеет положительный
L . L .
знак или, что то же, величины с
fi и с
'2 имеют
одинаковый знак. Если '1 =='2 == vi
, то цепь резони-
рует на люб
й частоте.
(J
O
C
Рис. 5-7. Колебательные контуры
с .1I.ВУМЯ параллельными ветвями.
(5-15)
1сl.
Рис. 5-8. Векторная диаrрам-
ма при реЗОНБнсе токов.
На рис. 5-8 показана веКТорвая диаrрамма при резо-
нансе токов в цепи рис. 5-7, а. Токи в индуктивной и eMK
CT-
ной ве.твях слаrаются из активных (1 La. 1 Са) И реактивных
(1 Lp, 1 Ср) составляющих, причем
1 Lp ==
lcp; i La + /Са == 10'
1
Чем меньше r 1 и r 2 по сравнению с (J)oL и
C ' тем ближе
ыо
к 180" уrол фазовоrо сдвиrа между J Lo И j СО; при этом токи
в ветвях образуют как бы один контурный ток I K ;:;:::: I Lo ;:::;:
;:;:::: 1 со, замыкающийся в колебательном контуре.. !
При резонансе вся цепь имеет ТОЛЬКо активную ПРОБО-
ди:мость
у '1" '2
0== go == 'r+(WoL)2 + ,
+(:o
У '
откуда с учетом (5-14)
у
ri+Цu
LС
О
,f + ((UoL)2
Для колебательноrо контура с малыми потерями можно
пренебречь слаrаемqrм r} по сравнению с «(J)OL)2
и считать,
132
что w
LC
1. При этом проводимость колебательноrо
контура приближенно выразится формулой, широко' рас-
пространенной в практике радиотехническ
х расчетов:
У '1+'2 ('i+'2)с
О
(ШоL)2
.
При '1 == '2 == , соrласно (5-15)
1 2,
WO== V T и Уо==Яо==
'
С ,2 +
с
Кроме Toro, если r == V
' то У == V
при любой
частоте (резонанс в такой цепи называют «безраз.iшчным»
резонансом).
Леrко убедиться в том, что и в, случае резонансной
цепи с двумя параллельными ветвями (см. рис. 5-7) соблю-
дается условие W LMaKe == W Смаке' Для этоrо достаточно
умножить обе части уравнения (5-14) на
2
Uin,
Ша
Выше отмечалось, что в схеме с пзраллельно соединен-
ными " L и С (см. рис. 5-6) полная ПРОВОДимоеть всей цепи
имеет минимум при резонансной частоте.
Для схемы рис. 5-7, б нетрудно показать, что при изме-
нении частоты (i) или индуктивности L минимум полной
проводимости цепи, а также минимум общеrо тока насту-
пают не при резонаНСIiОЙ частоте, В том же случае, коrда
переменным параметром является емкость С, проводимость
и общий ток достиrают минимума при резонансе токов
IЛ.2).
Добротность параллельноrо колебательноrо контура рис. 5-7, а
на основании (5-3) равна:
W L макс Шi U ;' Ш(jL
Q== Ша
-
== 2zigД '2' %: zigo '
но
'i '2 '1 + '2 Ш б l . С
ga== z
-i+ z
i== Z2 ,
1 2 1
откуда
Q
(,)о!'
'1+'2ш
LС '
тде резонансная частота Ш О определяется ПО формуле (5-15).
Часто в ветви с емкостью сопротивлением '2 можно пренебречь.
Тоrда формулы значитеЛI?J.!О упрощаются.
133
Рассмотрим ЭТОТ случай (см. рис. 5-7, 6).
Резонанасиая час тота TaKoro контура cor ласно (5- 15)
000== 11 L
(i)2 == /LC 11 1
(
J. (5-16)
а добротиость цепи в соответствии с полученным выше, выражением
Q == oooL . (5-17)
,
Из сопоставления (5-16) и (5-2) видно, что при одних и тех же па.
раметрах " L и С резонансные частоты для схем рис. 5-1 и 5-7, ботли,
чаются МНожителем
J! 1
(, /р)2.
При ,/ р < 0,1 разность резонансных частот не превышает 1 % .
Кроме Toro, выражение (5-16) показывает, что резонанс токов возмо'
жеи в охеме рис. 5-7, б только при ,/ р < 1.
Общее сопротивление колебательноrо контура (см. рис. 5.7,6)
(,+ jooL) (
j ы
) L 1
j :L
z
r+j ( {j)L
) '
,C l+j {j)L ( I
) '
ооС , oo 2 LC
На основании соотношений (5-16) и (5-17) моЖНо получить:
(
у == ;,2 == 1 + Q2.
Учитывая также соотиошения
, Ыо' 1
ooL ==(; OOoL
Q(6+1)
1 Ю
1
I +Q2
oo 2 LC == {j)2{j)
LC
(1
i
) (6+ 1)2
Q2 (6+ 1)2 ,
ПОJ1учаем выражеиие для сопротивления КОJ1ебательноrо контура:
'(I+Q2)[I
jQ(6
1)]
[ 1 +Q2 ] .
l+iQ(6+1) 1 Q2(6+1)2
При резонансиой частоте (6 == О) Zo == , (1 + Q2).
в тех случаях, коrда Q2 весьма велико по сравнению с единицей
выражение (5-18) упрощается:
Z
(5-18)
. 1
1
I
Z
rQ2 Q(6+1j .
1 + . Q 6 6+
J 6+ 1
134
В режиме, близком к резонансу, коrда I б I иесоизмеримо меньше
единнцы, данное выражение заменяется приближенным:
1
j
1
Q
Z
,Q2 1 + j2Qб
При высокой добротности колебательноrо контура
,с:р.
Z
1 + j2Qб .
Прн iТOM токн В ве твях
i L:= ,
ooL i
i 1 J;2Qб ; j
. "Q
lc:= jooCZ!
' 1 ,!j2Qб .
Здесь J
ток, входящий в цепь.
Напряжение на аыводах цепи (J связано с током / следующим
образом:
(5-19)
. . . ,Q2
и == Zl
1 1 + j2Q6 (5-20)
Приближеииые выражеиия (5.19) и (5-20) аналоrичны при задан-
иом Q выражениям "(5-12) и (5-7), выведениым для цепи рис. 5-1, при
условии замеиы напряжений токами и обратно. Поэтому кривые со-
противлений. токов и иапряжений, соответствующие схеме рис. 5-1.
в известиом Масштабе приближеино выражают проводимости. напря-
жения и токи в схеме рис. 5-7, б.
Следует обратить внимание на то, что в схеме рис. 5-6 мrновеи-
иая мощность в цепи при резонансе токов равна мrновенной мощности,
расходуемой в сопротивлении ,; в схемах с двумя параллельными вет-
вями (рис. 5
7) мrновенная мощность на выводах цепи отлична от MrHo-
венной мощности, расходуемой в сопротивлениях ветвей. Например,
в тот момент, коrда ток, входящий в цепь, проходит через иулевое
значеиие, мrновеннаи мощность на выводах цепи равиа нулю; в этот
момеит токи в ветвях, сдвинутые по фазе относительно cYMMapHoro
тока цепи, отличиы от нуля И поэтому мrновенная мощность, расходуе-
мая в сопротивлениях ветвей, также не равна нулю. Объясняется это
тем, что в схемах рис. 5
7, а'и б энерrия, накапливаемая реактивными
элементами, периодически преобразуется частично в теплоту (в сопро-
тивлениях ветвей), а затем вновь пополняетси за счет энерrии источ-
ника.
Для повышения крутизны резонансных характеристик.
необходимой для более четкоrо разделеиия колебаций раз-
ных частот, в радиотехнике широко применяются двухкон-
турные резонансные цепи: два резонансных контура, На-
строенных каждый -Б отдельности на одну и ту же частоту,
Связываются индуктивно или электрически. В отличие от
«одноrорбой» резонансной кр ивой одиночноrо контура в свя-
135
заllНЫХ цепях получаются «двуrорбые» кривые; например,
ток в каждом контуре может иметь максимумы при двух
частотах, расположенных ниже и выше резонансной ча-
стоты одиночноrо контура (см.
8-9
8
11).
Индуктивно связанные резонансные контуры как фильт-
рующая система рассмотрены в
lO
5.
5-4. ЧАСТОТНblЕ ХАРАКТЕРИСТИКИ СОПРОТИВЛЕНИЯ
И ПРОВОДИМОСТЕА РЕАКТИВНЫХ ДВУХПОЛЮСНИКОВ
д в у х п о л ю с н и к о м называется любая электри-
ческая цепь или часть электрической цепи, имеющая два
вывода. Ниже рассматриваются только линейные двух-
полюсники, т. е. такие, которые состоят из линейных эле-
ментов.
Различают двухполюсники активные и пассивные.
А к т и в н ы м называется двухполюсник, содержащий
источники электрической энерrии, которые не компенси-
руются взаимно внутри двухполюсника.
6
Рис. 5,9. Двухполюсник, внутреllние источники
KOToporo взаимно компенсированы.
П а с с и в н ы м называется двухполюсник, не содер-
жащий источников электрической энерrии; в случае линей-
Horo ДВУХПОJIюсника он может содержать цсточники элект-
рической энерrии, взаимно компенсирующиеся таким обра-
зом, что напряжение на ero разомкнутых выводах равно
нуЛю. Такои линейный двухполюсник относится к KaTe
rории пассивных; ero сопротивление, измеренйое на выво-
дах, не изменится, если источники электрической энерrии
внутри Hero заменить пассивными элементами
внутрен-
ними сопротивлениями источников э. д. с. или COOTBeTCT
веllНО внутренними проводимостями источников тока. При-
мер двухполюсника, содержащеrо компенсированные источ-
ники, показан на рис. 5
9.
По числу элементов, входящих в двухполюсник, раз-
личают о Д н о э л е м е н т н ы й, д в у Х Э л е м е н т н ы й
и м н о r о э л е м е н т н ы й двухполюсники.
136
По характеру этих элементов двухполюсники делятся
на р е а к т и в н ы е, т. е. состоящие из индуктивностей и
емкостей, и Д в у х п о л ю с н и к и с п о т е р я м и,
содержащие активные сопротивления. Реактивные двухпо
люсники представляют собой идеализированные электриче-
ские системы, приближающиеся по своим свойствам к физи
чески существующим цепям с маЛЫМ!l потерями.
Частотные характеристики сопротивлений или прово
димостей двухполюсников, образующих электрическую
цепь, предопределяют частотные и резонансные свойства
цепи, т. е. зависимости амплитуд и фаз токов и Напряже
нии от частоты.
Настоящий параrраф посвящен изучению частотных xa
рактеристик пассивных реактивных двухполюсников.
Одноэпементные реактивные двухпопюсники
Индуктивность и емкость представляют собой IJростей
IlIl1е одноэлементные реактивные двухполюсники. Знак
комплексноrо сопротивления и комплексной проводимости
каждоro из этих двухполюсников не зависит от частоты;
этим они существенно отличаются от друrих, более слож-
ных реактивных двухполюсников, содержащих HeOДHOpoд
Вые реактивные элементы, т. е. индуктивность и емкость
в разных сочетаниях.
Комплексное сопротивление индуктивноrо элемента Во
всем спектре частот имеет положительный знак, а комплекс
ная проводимость
отрицательный:
Z . . L У . ь . 1
L==jX,.==jro; L==
j L==
jwr'
Комплексное сопротивление eMKocTHoro элемента во
всем спеКТре частот имеет отрицательныЙ знак, а комплекс-
ная проводимость
положительный:
Zc ==
jxc ==
j
6 у с == jb c == jroC.
В рассматриваемом случае реактивных двухполюсников
КОМПJIексные сопротивления и проводимости являются.
мнимыми. Поэтому для сохранения знаков частотные Xa
рактеристики сопротивлений и ПРОВОДимостей удобно рисо
вать в прямоуrольной системе координат, в которой вверх
откладываются мнимые величины со знаком плюс, а вниз
со знаком минус.
137
Частотные характеристики ZL и У с, построенные в пря-
моуrольной системе координат, представляют собой пр,я-
мые линии, а частотные хаjJактерНСТИКИ Zc и У L
равно-
бочные rиперболы (рис, 5-10). Таким образом, кривые ZL
и Zc аналоrичны кривым УС и У [.
Следует заметить, что как сопротивления, так и прово-
димости рассматриваемых здесь одноэлементных реактив-
L
(u
UJ
Рис. 5-10. Частотные характеристики индуктнвноrо (а)
и eMKoCTHoro (6) элементов.
ных Дl3ухполюсников возрастают (с учетом знака) по мере
повышения частоты, т. е.
dZ dY
d >0;
d >0.
1 ro 1 ro
Это является общим свойством всех реактивных ДBYX
полюсников, а не только одноэлементных.
Двухполюсник, состоящий из последовательно или
параллельно соеДИl1енных однородных элементов (индук-
тивностей или емкостей), относится к числу одноэлементных
двухполюсников, так как последовательно или параллельно
соединенные однородные элементы MorYT быть заменены
одним эквивалентным реактивным элементом Toro же Ха-
рактера.
ДвухзлемеНТНIt,е реактивные ДВУХПОЛJOсники
Двухэлементные двухполюсники, составленные из ин-
дуктивности и емкости, представляют собой лростейшие ре-
зонансные цепи,_
При последовательном соединении индуктивности и
емкости алrебраически складываются комплексные сопро-
тивления. На рис. 5-11, а жирной линией показана частот-
ная характеристика ДВУХПОЛЮСl:lIlка, полученная в резул
138
Тате rрафическоrо сложения кривых ZL и Zc. Она пересекает
ось абсцисс при резонансной частоте UJ o == 1/V LC (резонанс
напряжений). Эта частота, при которой функция Z ==
== ZL + Zc обращается в нуль, называется н у л е м дан-
ной функции; точка на оси абсцисс, которая соответствует
нулю функции, обозначается кружком.
+j
+j
'"
I
I
I
I '"
I"' f:!
I r
I
i б)
о
Рис. 5-11. ЧаС1Отные характеристики двухэлемеит-
Horo двухполюсника последовательиосоединен
нЫми нндуктивностью и емкостью,
Частотная характеристика проводимости Toro же двух-
полюсника представляет собой функцию, обратную сопро-
тивлению: У === 1/Z.
Кривая у показана на рис. 5-11, б.
При резонансной частоте проводимость рассматриваемоrо
двухполюсника обращается в бесконечность; эта тачка
носит название п о л ю с а функции У и обозначается На
чертеже крестиком
Частотные характеристики Z и У, построенные таКим
образом l , соответствуют уравнениям:
Z == jx === j (XL
хс) == jL ( UJ
oolc)
и
у ==
jb ==
j ( 1 1 ) '
L ы
ooLc
или с учетом (5-2):
х == L Ы 2 :Ы 5 ; )
Ь== ы .
L (ы 2
ыВ)
1 На осях ординат частотных характеристик чисто реактивных
цепей откладываются мнимые значения сопротивлений и проводимо-
стей.
(5- 21 )
139
В области частот ниже резонансной (ш < ооо) сопротивле
ние eMKocTHoro элемента превышает по абсолютному значе
нию сопротивление индуктивноrо элемента; при этом со-
противление двухполюсника имеет емкостный характер.
В области частот выше резонансной (оо > ооо) абсолют
ное значение eMKocTHoro сопротивления меньше, чем индук
тивноrо; сопротивление двухполюсника имеет индуктивный
характер.
При параллельном соединении индуктивности и емкости
алrебраически складываются их комплексные проводи-
мости. На рис. 5
12, а жирной линией показана частотная
+j
+j I
I
I
О fAJ О I
f::: Х
yt. а.) ! z 6)
Рис. 5
12. Частотные характернстики двухэлементноrо
двухполюсника с параллельно соединенными индуктнв-
ностью и
мкостью.
характеристика двухполюсника, получеННая в результате
rрафическоrо сложения Y L и Ус.
Частотная характеристика сопротивления Toro же двух-
полюсника представляет собой функцию, обратную прово
димости: Z == 1/У. Кривая Z показана на рис. 5-12, б.
Частота, при которой характеристика У пересекает ось
абсцисс (нуль функции У), а характеристика Z уходит
в бесконечность (полюс функции Z), является резонансной
частотой (резонанс токов).
Частотные характеристики, построенные на рис. 5-12,
соответствуют уравнениям:
у '"'"
jb ==
j (Ь 1
Ь с ) ===
j ( .
ооС ) ==
J 'C (
Ш )
. wL wLC
и
Z== jx == j (1 1 )
С
ш
wLC
140
или с учетом (5-2):
Ь == С ro
Ц)2 . )
ro '
(5-22)
х == C(Ц)
Ц)2) '
В области частот ниже резонансной проводимость индук-
тивноrо элемента перекомпенсирует проводимость емкост-
Horo элемента и сопротивление двухполюсника получается.
индуктивным. В области частот выше резонансной наблю-
дается обратное явление и сопротивление двухполюсника
имеет емкостный характер.
Таким образом, в зависимости от частоты двухэлемент-
ный реактивный двухполюсник может иметь либо индук
Тивное, либо емкостное сопротивление. При этом, так же
как и в случае одноэлементноrо реактивноrо двухполюс-
ника, кривые Z и У возрастают, т. е. производные от Z/j
и у /j по частоте положительны.
В отличие от сопротивлений одноэлементных двухполюс-
ников, которые выражаются только через текущую частоту,
сопротивления двухэлементных реактивных двухполюсни-
ков зависят также и от разности квадратов резонансной и
текущей частот [формулы (5-21) и (5-22)].
Как видно из выражений (5-21), для построения частот-
ных характеристик двухполюсника, состоящеrо из последо-
вательно соединенных элементов L и С, достаточно знать
нуль функции Z или, что то же, полюс функции У. Пара-
метр L, входящий в (5-21), влияет только на выбор мас-
штаба Z и У по оси ординат.
Аналоrично в соответствии с (5-22) для построения ча-
стотных, характеристик двухполюсника, состоящеrо из
параллельно соединенных элементов L и С, достаточно
знать полюс Z или, что то же, нуль У, причем параметр С
влияет только на масштаб Z и У.
Двухполюсники, имеющие одинаковые частотные ха-
рактеристики Z или У, эквивалентны.
Мноrоэпементный реактивный ДВУХПОПlOсник
Мноrоэлементный реактивный двухполюсник может быть
получен в результате различных сочетаний одноэлементных
и двухэлементных двухполюсников. i10ЛЬЗУЯСЬ частотными
характеристиками, приведенными выше, можно построить
частотные характеристики для трех-, четырех- и MHoro-
элеl',1ентных реактивных двухполюсников. При этом одно-
141
родные элементы (или rруппы элементов с одинаковыми
резонансными частотами), соединенные параллельно или
последовательно, должны быть сначала заменены одним
элементом (или эквивалентной rруппой элементов, как 'это,
например, показаНО На рис. 5
13).
L nL (n+1)L
С ic
o
n n+1
Рис. 5-13. Прим('р приведен!"я схемы к двухэлемент-
ному дв
хполюснику,
Такие двухполюсники будем наЗЫВать «приведенными».
Из свойства положительности производной dZ/jdw (или
dY /jdw) следует, что Ну,ли и полюсы функций Z (или У)
должны чередоваться, так как при наличии двух послеДова-
тельных нулей, не разделенных полюсом, имелся бы уча-
сток характеристики С отрицательной производной.
L.,2 L.,2п
2
CLf':"L '!
м, чi--J
--
С2 а.) C2п
2
Рис. 5-14. Схема (а) и частотная характеристи-
ка (6) мноrоэлементноrо двуХПОJlюсника.
в общем случае, если при w == О сопротивление реактив-
Horo двухполюсника равно нулю, т. е. имеется путь для
постоянноrо тока, то первым наступает резонанс токов, за
ним следует резонанс напряжений и т. д.
В противном слуЧае порядок расположения резонансов
обратный: первым наступает резонанс напряжений, BTO
рым
резонанс токов и т. д.
142
На рис. 5-14, а дана схема мноrоэлементноrо двухполюс-
ника, а на рис. 5-14, 6
соответствующая ему частотная
характеристика сопротивления.
,У реактивных двухполюсников сумма чисел полюсов и
нулей (не считая точек w === О и w == (0) на единицу меньше
числа элементов даННоrо «приведенноrо» двухполюсника.
Расположение нулей и ,полюсов, как указывалось выше,
поочередное, а все ветви частотной характеристики с уве-
личением w возрастают.
5.5. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
5-1. В цепи с последовательно соединенными " L и С иаступает
резонанс напряжений при уrловой частоте 500 рад/с; ,:=: 34 Ом; L =:;
== 400 Mr; напряжение на цепи (j :=: 120 L 00 В. Определить С и MrHO-
венные значения тока и напряжений на элементах цепи; построить век-
торную диаrрамму. .
О т в е т: 10 мкФj 5 sin 5О0'! А; 170 sin 500 t В; 1000 sin (500 t :!:
:!: 11:/2) В.
5-2. Цепь состоит из индуктивной катушки (" L) и емкости, сое-
диненных последовательно. Напряженне на ц€пи равно 120 В. Опреде-
лить напряжение на катушке при резонансе, если при этом иапряже-
ние на емкости равно 208 В.
О т в е т: 240 В.
5-3. Вычислить резонансную частоту и частоты, при 'которых
напряжения на L и С максимальны в цепи с последовательно соеди-
ненными ':=: 50 Ом, L:=: 10 Mr и С == 1 мкФ.
О Т В е т: 10000, 10 700; 9350 рад/с.
5-4. Вычислить резонансную частоту и добротность контура,
состоящеrо из последовательно соединенных, == 5,1 Ом; L == 65. lO
б [;
С:=: 1,56.1O
gф. Определить сопротивление цепи при частоте, превы-
шающей резонансн
ю на 1 % .
О т 8 е т: 5.10 rц; 40; 6,53 L 38°35' Ом.
5-5. Резонанс напряжений в контуре " L и С наступает при ча-
стоте 1 мrц. Полоса пропускания резонансноrо КОН1:ура равна 5000 rц,
сопротивление цепи при резонансе 50 Ом. Найти " L и С.
О т в е т: 50 Ом; 1,59 Mr; 15,9 пФ.
5-6. Резонанс напряжений в контуре " L и С наступает при
1,5 мrц, добротность контура равна 250. Вычислить частоты, соот-
ветствующие половинной мощности.
Ответ: 1,497 и 1,503 мrц.
5
7. Последовательно с L включен участок цепи, состоящий И3
параллельно соединенных, и С. При 1000 rц индуктивное и емкостиое
сопротивления элементов L и С равны каждое 100 Ом; , == 200 Ом.
Вычислить резонансную частоту и проводимость цепи при реЗ0нансе;
пояснить явление резонанса в заданной цепи.
О т в е т: 866 [ц; 0,02 См.
5-8. Если в цепи на рис. 5-7, б сопротивление r превЬ!сит опреде-
ленное значение, то резонанс токов будет невозможен. Пояснить это
физически и привести условие, при котором резонанс невозможен.
О т в е т: ,?: V ЦС .
143
5-9. Индуктивная катушка и последовательно сбединеиная с нею
емкость питаются от источника синусоидальиой э. д. с.; частота равна
1 кrц. Максимальное sначение тока в цепи 1,1 А достиrается при
С == 10,4 мкФ, при этом напряжение на емкости в 11,1 раза превы-
шает приложенное к цепи напряжение. Вычислить СОПiYотивление и
индуктивность катушки и напряжение на емкости при токе 1,1 А.
О т в е т: 1,38 Ом; 2,44 Mr; 16,3 В.
5-10. Коитур, состоящий из, == 100 Ом, L == 10 Mf и С == 1 мкФ
питается от источника переменной частоты. Найти наибольшее отно-
шение напряжения на L (или G) к приложенному к 'контуру напря-
жению.
Ответ: 1,155.
5-11. Цепь состоит из , == 100 Ом, L == 10 Mf и С, соединенных
последовательно; уrловая частота равна 104 рад/с. При каком значе-
иии С напряжение на С максимально? Во сколько раз оио превышает
приближенное к цепи напряжение?
... О т в е т: 0,5 мкФ; 1,41.
5-12. Найти минимальное значеиие С, при котором наступит ре-
зонанс в цепи на рис. 5-7, а, если '1 == 10 Ом; L == 50 Mf; '2 =: 5 Ом;
f == 50 [ц, определить сопротивление цепи при резонансе.
О т в е т: 152 мкФ; 25,2 Ом. .
5-13. Резонанс напряжений в контуре " L, С наступает при
500 кrц. При этом сопротивление контура равно 75 Ом; полоса пропу.
скания равна 3 кrц. Найти L и С.
О т в е т: 3,98 Mr; 25,4 пФ.
5-14. Что такое ПрИведенный реактивный двухполюсник?
5-15. Чем определяется число нулей и полюсов приведенноrо ре-
активноrо двухполюсника, а также их последовательность на харак-
теристике?
, 5-16. Разобрать резонансные явления в трехэлементном реактив-
ном двухполюснике.
5-17. Доказать эквивалентность схем, изображенных на рис. 5-13.
rЛД8ДШЕСТДJII
rЕОМЕТРИЧЕСКИЕ МЕСТА НА КОМПЛЕКСНОй
ПЛОСКОСТИ
6-1. rРАФИЧЕСКОЕ ИЗО&РАЖЕНИЕ ЗАВИСИМОСТЕR
КОМПЛЕКСНblХ ВЕЛИЧИН ОТ ПАРА МЕТРА
Исследование зависимости какой-либо комплексной ве-
личины (или отношения комплексных величин) от перемен-
HOrO параметра сводится к нахождению зависимостей мо-
дуля и уrла от.параметра.
При пользовании прямоуrольной системой координат
строятся кривые модуля и уrла, которые в совокупности и
характеризуют изменение исследуемой величины. Вместо
144
зависимостей модуля и уrла в пря
оуrольной С,истеме коор-
динат MorYT быть построены зависимости от параметра дей-
ствительнЬЙ . и мнимоЙ частей исследуемой комплексной
величины,
Таким образом, rрафическое изображение исследуемой
зависимости в прямоуrольной системе координат осуществ-
ля
тся с помощью двух кривых: модуля и уrла или соответ-
ственно действительной lf мнимой частей.
При комплексной форме записи полнре представление
о зависимости исследуемой величины от параметра может
быть достиrнуто с помощью одной кривой, изображаемой
на комплексной плоскости. Сущность TaKoro rрафическоrо
изображения заключается в TQM, Что исследуемое комплекс-
ное выражение предстcmляется на комплексной плоскости
вектором) 2еометрическое место конца котОРО20 при изме-
нении входящею в это выражение параметра изображается
кривой. Эта кривая, называемая также rодоrрафом, на-
rлядно показывает изменение модуля и фазы рассмат-
риваемой комплексной величины в зависиМОсти от пара-
метра.
Такой rрафический метод применим к комплексным
амплитудам
напряжениям, токам, Мощностям
и ком-
плексным сопротивлениям, ПрОВОДИмостям, передаточным
функциям и 1'. п.
Переменным параметром электрической цепи может
служить какая-либо из величин, характеризующих источ-
ник электрической энерrии или пассивный элемент: модуль
или фаЗ8 э. д. с, (или тока) источника, частота cu, .сопро-
тивление r, индуктивность L, взаимная индуктивность М,
емкость С или соответственно реактивная составляющая
сопротивления или проводимости и т. д:
в качестве переменноrо параметра может рассматри-
ваться полное сопротивление z при неизменном зн
чении
aprYMeHTa (j), или, наоборот, переменным параметром может
служить уrол (j) при постоянном z.
Изменение каждоrо из этих параметров может быть
rрафически представлено на комплексной плоскости. На-
пример, изменение активноrо или реактивноrо сопротивле-
ния изображается прямой, .параллельной соответственно
действительной или мнимой оси. Изменение полноrо сопро-
тивления при постоянном уrле (j) изображается прямой
линией, образующей с действительной осью уrол (j). В свою
очередь изменение уrла (j) при неизменном z изображается
окружностью радиусом z.
145
6.2. ПРЕО&РАЗОВАНИЕ ВИДА Y;:1/Z
Положим, что вектор Z при изменении соответствующеrо
параметра описывает на комплексной плоскости окружность
или прямую. Требуется построить rеометрическое место
конца вектора У == l/Z.
Пусть точка Zo на комплексной плоскости Z служит
центром окружности, радиус которой равен R. Комплекс
ная форма ураI\нения такой окружности может быть пред
"
ставлена так:
(Z
Zo) (i
Zo) ==R 2 ,
или
* * * *
ZZ'
ZZo
ZZo + ZoZo == R2.
Подстановка Z == llУ дает:
(6
1)
уу
У * Zo
ZOZo
R2
что то же,
>1: ..
, YZ o
.;о
ZOZO
R2
+ ..
ZoZo
R2
о
или,
*
уу
У /0 У /0 +
ZOZO
R2 " Z.ZO
R2
'"
+ ZoZo == R2 (6
2)
(Zoio
R2Y (ZOZo
R2)2 .
Из сопоставления (6
2) с (6-1) следует, что вектор У
R
описывает окружность радиусом р == * с центром
ZoZo
R2
*
Z
В точке * о комплексной плоскости У.
ZOZO
R2
Наиболее удаленной от начала координат точке Ь окруж-
ности Z соответствует наиболее близко расположенная
к началу координат точка Ь' окружности У, f" и наоборот.
Диаметры соответствующих окружностей, проходящие через
начало координат, образуют с' действительной осью одина-
ковые уrлы, отсчитываемые в противоположных направле-
ниях (рис. 6-1). Следует заметить, что координаты центров
окружностей векторов Z и У не подчиняются ус
овию
У == lIZ; иначе rоворя, У О =1= l/Zo.
В случае, коrда окружность проходит через начало
*
координат, ZoZo == R 2 И на основании (6-1)
* * *
ZZ
ZZo
ZZ!) == О. (6.3)
146
Вектор У описывает при этом прямую, находящуюся на
расстоянии 1/2R от начала координат (рис. 6
2). Диаметр
+j
+j
+
у
Рис. 6-1. Преобразова-
ние окружности Z в
окружность У.
Рис. 6-2. Преобразование
окружности Z в прямую У.
окружности Z, проходящий через начало координат, и пер-
пендикуляр, опущенный из начала координат на прямую У,
образуют с действительной осью одинаковые уrлы (отсчиты-
ваемые в противоположныIe стороны).
Уравнение прямой У получается, +j
е'сли обе части уравнения (6-2) умно- Z
*
жить на ZZo
R2 и затем перейти к
*
пределу ZZo
R2
O. Тот же резуль-
тат можно получить непосредственно
из {6-З), заменяя Z == l/Y: +
>1< '"
YZo+YZo
l==O. (6-4)
в свою очередь уравнение прямой
линии в плоскости Z, не проходящей
через начало координат, записывается
по аналоrии с (6-4):
"''''
ZYo+ZYo
1 ==0.
Рис. 6.3. Преобрвзова-
ние прямой Z в пря-
мую У.
При этом уравнение окружности, описываемой Beктo
ром у t имеет вид:
:1< '" '"
УУ
YYo
УУо==О,
Если rеометрическим местом вектора Z служит прямая,
проходящая через начало координат под уrлом <р к дейст-
147
В,ительнод оси. то rеометрическое место вектора У пред-
С,тавляer. собой прямую, также проходящую через начало
координат и образующую с действительной осью уrол
ер
(рис. 6
3).
Преобразования прямой в окружность н окружности
в окружность иллюстрированы ниже На примерах простей-
ших электрических цепей.
6.3. ДИАrРАММЫ СОПРОТИВЛЕНИЙ И ПРОВОДИМОСТЕй
ПРОСТЕйШИХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Рассмотрим диаrраммы сопротивления и проводимости
цепи с последовательным, параллельным или смешанным
соединением при изменении одНоrо параметра.
Поспедоватепьное соединение
При изменении сопротивления r (рис. 6
4, а) reoMeT-
рическим местом комплексноrо сопротивления Z:=: r +
+ jx ,служит прямая, параллельная действительной оси
0.)
+j
+
+
+j
:&>0
о
1
:&<0
r=O
б)
8)
Рис. 6
4. Переменное активное сопротивление при послеДова-
тельном соединении.
а
схема; б
диаl'раММа z; в
диаrрамма У.
(рис. 6-4, 6). rеометрическим местом комплексной ПРОВО-
1
димости У ==
+ . является полуокружность, проходя-,
, JX
щая через начало координат комплексной ПЛ,оскости У,
диаметр котороЙ равен 1/ I х I (рис. 6-4, в).
148
Вторая половина окружности, соответствующая оТрИ-
цательным значениям r, из раССМОТреНИЯ исключается.
Значению r == О соответствует наиболее удаленная точка
окружности У, а значению r == 00
точка О в плоскости У.
При х > О rеометрическое Место конца вектора Z рас-
полаrается в первой четверти, а при х < О
в четвертой
четверти комплексной плоскости.
Соответственно полуокружность У при х> О распола-
rаеrся в четвертой четверти, а при х < О
в 'первой чет-
верти.
а.)
+j
х<О
х>О
j:r = va.r
х=О +
.:& =:!:оо
+
+j
х<О
6)
8)
Рис. 6
5. Переменное реактивиое сопротивление при последо-
вательном соединении.
а
схема; б
диаrрамма Z; 8
диаrрамма У.
При изменении реактивноrо сопротивления х (рис. б-5, а)
reрметрическим местом вектора Z служит прямая, парал-
лельная мнимой оси (рис. б-5, 6). rеометрическим местом
К0нца вектора У == l/Z является окружность, проходящая
через начало координат комплексной плоскости; диаметр
окружности равен l/r (рис. б-5, 8).
Значениям х> О соответствует нижняя, а х < О
верхняя полуокружность.
При х == О цепь имеет только активное сопротивление
и соответствен.но активную проводимость. При х == + 00
проводимость цепи равна нулю.
Параппепьное соединение
При изменении сопротивления r (рис. б-б, а) rеометри-
У 1 . 1
чески м местом конца вектора ==
-
J
служит прямая,
, х
параллельная дейcrf!ительной оси (рис. б-б, 6). rеометриче-
149
ским местом конца вектора Z == l/У является полуокруж-
ность (рис. 6-6,8); верхняя при х > О и нижняя при х < о;
,
+j
7' == Q()
ж<О
ж
l' +
it
а) 1 ж>О
;;-=val'
!) 6)
Рис. 6.6, Переменное активное сопротнвленне при пармлельном сое-
днненин.
Q
схема; 6
j!иаrрамма У; 11
диаrраМма Z.
диаметр окружности равен I х 1. Значению r == О соответст-
вует начало координат, а значению r == 00
диаметрально
противоположная точка окружности.
+j
<O
+j
ж>О
" /
:=00
+ +
j
=va1'
4) :>0 :&<0
6) 8)
Рис. 6.7, Переменное реактнвное СОПРОТИВJ\ение при параллельном
соединенни.
Q
схема; 6
.диаrрамма У: 11
диаrраммв Z.
При изменении реактивноrо сопротивления х (рис. 6
7, а)
reометрическим местом конца вектора y
служит прямая,
параллельная мнимой оси (рис. 6-7, 6), а rеометрическим
местом конца вектора Z == 1 /У
окружность диаметром т,
150
проходящая через начало координат (рис. 6-7, в). Значе-
ниям х> О соответствует верхняя, а х < О
нижняя
полуокружность. При х == О полное сопротивление цепи
равно нулю, а полная проводимость беСl.{онечно веЛИКа.
При х == + 00 сопротивление и проводимость цепи яв-
ляются активныМИ.
Смешанное соединение
Рассмотрим в качестве примеров две схемы цепи со
смешанным соединением элементов.
На рис. 6-8, а показана схема цепи, в которой перемен-
НЫМ параметром является реактивное сопротивление х.
+j
::&>0
7"1
+
а.)
6')
Рис. 6-8. Переменное реактивное сопротивление при сме.
шанном соединении.
а
схема; б
диаrраМ'dа.
Диаrрамма Z такой цепи (рис. 6-8, б) отличается от диа-
rpaMMbI Z (рис. 6-7,8), тем, что окружность смещена отно-
сительно начала координат на величину сопротивления r 1 .
Изменение х может быть обусловлено изменением частоты
или параметра L и С.
На рис. 6-9, а показана схема цепи, в которой перемен-
ным параметром является емкость С. Проводимость ветви r,
L равна:
'
j(j)L .
, + j(j)L
,2+ «(j)L)2 ,
проводимость ветви с емкостью равна jwC. Следует отме-
(j)L
тить, что резонанс токов наступает при wC == ,2+ «(j)L)2 .
При этом комплексная проводимость всей цепи равна
,
у == ,2+ «(j)L)2 ' а комплексное сопротивление Z == r +
+ (wL)2/ r .
151
Теометрическим местом конца вектора У С{lУЖИТ пря-
мая, параллельная мнимой оси (рис. 6
9,б),а rеометри-
ческим,местом конца вектора Z
окружность, l'Iроходящая
через начало координат; диаметр окружности равен r +
+j
t с== 00
+j
а)
[,
r Z +(lIJL)Z'
6')
8)
Рис. 6
9. Перемениая емкость при смешаином соединении.
а
схема; 6
.(\иаrрамма У; g
J1.иаrрамма Z.
+ «(f)L)2Ir (рис. 6-9, в). Часть окружности, начерченная
тонкой линией, исключается из рассмотрения, так как она
соответствует отрицательным значениям С.
Рассмотренные здесь диаrраммы сопротивлений и про-
Бодимостей изображают в определенном масштабе и диаr-
+j
k
<
/ .
.......... и
а.)
с
I
+
о
Рис. 6
1O. Пример 6
1,
раммы: 1) тока i == У[)
при заданном напряжении [)
н:а заJ!<имах цепи; 2) напряжения [) == zj
при заданном
токе 1, проходящем через церь; 3) комплексной мощности
*
s == U 2 У == [2Z
при заданных и или 1.
Если начальная фаза заданноrо напряжения (или тока)
отлична от нуля, то диаrрамма тока (или напряжения)
поворачивается на- соответствующий уrол (см. пример 6-1).
152
Пример 6-1. Напряжение на вЫводах участка цепи, состоящеrо
из последовательно соединенных сопротивлеиия , и емкости С, задано
(J
и L 1jJ (рис. 6-10, а). Построить KpyroBbIe диаrраммы тока и
иапряжения на сопротивлении при изменении , от нуля до бесконеч-
ностн.
Круrовая диаrрамма тока j == у(J повернута отиосительно диа-
rpaMMbI проводимости, изображенной на рис. 6
4, в (для случая х < О),
на уrол 1jJ, равиый начальиой фазе приложенноrо НaIJряжения.
Д u и
иаметр круrовои диаrраммы тока равеи току
соответству-
/Xc'
ющему зиачению , == О и опережающему (j на л/2 (рис. 6-10, б).
Напряжение на. СОПР9тивлении совпадает по фазе с током. В силу
равенства ,1
jX c l == U конец вектора ,1 описывает окружность,
диаметром котороЙ служит и.
6.4. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
6-1. Найти с помощью круrовой диаrраммы емкость С в цепи,
изображенной на рис, 5-7, а, при которой сопротивление всеЙ цепи
максимально. Дано: '1 == 10 Ом; '2 == 5 Ом; L"== 50 Mr; (j)
377 рад/с.
О т в е т: 85 мкФ.
6-2. Найти иаименьшее из двух значеиий емкостн С, которые соот-
ветствуют резонансу токов в цепи предыдущей задачи,
Ответ: 115 мкФ.
6-3. Показать с помощью круrовоЙ диаrраммы, как изменяются
иапряжения на элементах, и L, включенных послеДОlj.ательно, если,
изменяется от нуля до бесконечности, при неизменном напряжении
200 В иа цепи. Построить линию, переменноrо параметра , и найти
rрафически напряжение на L и фазовыЙ сдвиr тока относительно при
ложенноrо напряжения при f == 400 rц; L"== 31,8 Mr и , == 6{) Ом,
От вет: 160 В; 530.
6-4. Найти 'с помощь!}> круrовой диаrраммы комплексноrо сопро.
тивления емкость С, соединенную последовательно с ,
34 Ом и L ==
== 400 Mr, при которой наступает резонанс напряжений; (j)
500 рад/с.
О т в е т: !о мкФ.
6-5. Найти с помощью круrовой диаrраммы значения индуктиа-
ности L катушки, имеющей сопротивление ,
10 Ом и включенной
параллельно емкости 10,5 мкФ, при которых наступает резонанс токов.
Частота f == 400 [ц.
Ответ:14иlмr.
6-6. Построить в зависимости от частоты rеометрическое место
для комплексноrо сопротивления (или комплексной проводимости)
цеШI, изображенной на рис. 5-7, а, n найти резоиансную частоту, при-
няв '1
8 Ом; '2 == 6 Ом; L == 5 Mr; с
50 мкФ, Найти значения С,
при которых резонанс неаозможен.
О Т-В е т: 1500 рад/с; 80 .;;; С .;;; 140 мкФ.
6-7. Решить задачи 5-3, 5-8 и 5-10 rрафически.
6-8. Пояснить ход построения круrовой диаrраммы по заданному
комплексному выражению.
6-9. Пояснить ход построения лииии перемеиноrо параметра.
6-10. Как определяется рабочая часть круrовой диаrраммы?
6-11. В чем заключается преимущество метода rеометрических
мест перед аналитическими методами?
153
rЛАSАСЕДЬМАЯ
МЕТОДЫ РАСЧЕТ А СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕй
1.1. ПРИМЕНЕНИЕ ЗАКОНОВ кирхrОФА для РАСЧЕТА
СЛОЖНЫХ ЦЕПЕ'"
В предыдущих rлавах рассматривались простейшие
схемы электрических цепей
одноконтурные схемы, цеп-
ная схема с одним источником электрической энерrии и
схемы с двумя узлами, Были описаны методы преобразова-
ния схем, с помощью которых в ряде случаев удается
упростить. расчет разветвленной электрической цепи. При
этом под расчетом цепи подразумевается вычисление значе-
ний электрических величин или их отношений при заданных
схеме и параметрах цепи.
В случае, коrда схема электрической цепи достаточно
сложна и не приводится к схеме одноконтурной цепи или
цепи с двумя узлами, пользуются более общими методами
расчета.
OnUCbleaeAtble ниже методы и теоремы применимы для
цепей постоянною и перемеННО20 тока; ради общности
изложения они приводятся в комплексной форме.
В общем случае искомые значения электрических вели-
чин и их соотношения MorYT быть найдены в результате сов-
MecTHoro решения системы уравнений, выражающих пер-
вый и второй законы l5.ирхrофа для заданной электрической
цепи. .
Положим, что в схеме, содержащей р ветвей и q,узлов,
заданными являются источники э. д. с., а искомыми
. токи в ветвях. Следовательно, число неизвестных равно
числу ветвей.
Поп е р в о м у з а к о н у К и р х r о Ф а, выражаю-
щему равенство нулю алreбраической суммы токов в узле,
может быть записано q -
1 независимых уравнений; урав-
нение для посJiеднеrо, q-ro, узла является следствием пре-
дыдущих q""'""': 1 уравнений. Действительно, ввиду Toro, что
каждая ветвь Связывает два узла, ток каждой ветви входцт
дважды с различными знаками в уравнения, записанные
для q узлов. Поэтому если просуммировать q уравнений, то
получится тождество вида О ' О. Следовательно, одно из
этих уравнений является зависимым, т. е. вытекающим из
всех остальных уравнений.
154
Узлы, для которых записываются независимые ypaBHe
иия по первому закону Кирхrофа, можно назвать незави
симыми узлами. Из сказанноrо следует, что из общеrо
числа q узлов любые q
1 узлов являются независимыми, а
оставшийся последний узел является зависимым.
П о в т о р о м у з а к о н у К и р х r о Ф а, выражаю-
щему равенство алrабраической суммы э. д. с. в контуре
алreбраической сумме падений напряжения в нем, может
быть записано р
q + 1 независимых уравнений. В самом
деле, если ко всем ветвям применить заКон Ома, то полу-
чатся р уравнений вида:
(;ik:=;(;i
(;k:=;
En+Znl(t; (7
1)
здесь Uik
комплексное напряжение между узлами i и k;
Еn, 1 n
комплексные э. д. с. источника и 'I'oK в n
й ветви,
направленные от узла i к узлу k; Zn
комплексное сопро-
тивление той же ветви.
В систему уравнений вида (7
1) входят р неизвестных
токов 1 n и q
1 неизвестных потенциалов иЕ, U k И Т. д.
(потенциал одиоrо из узлов принимается равным нулю).
Если из имеющейся системы уравнений исключить эти
неизвестные потенциалы, останется р
q + 1 уравнений,
связывающих комплексные э. д. С. источников с напряже
ииями на комплексных сопротивлениях; полученные таким
путем уравнения выражают второй закон Кирхrофа.
Итак, расчет электрической цепи с помощью перВоrо
и BToporo законов Кирхrофа сводится к решению (q
1) +
+ ( р
q + 1) :=; р уравнений
по числу ветвей.
Контуры, для которых уравнения, ,записанные по вто-
рому закону Кирхrофа, являются независимыми, назы.
ваются н е з а в и с и м ы м и К о н т у р а м И.
На рис. 7
1 в виде примера показана электрическая
схема с числом ветвей р == 9 и числом узлов q :=; 6. Соот-
ветственно число уравнений по первому закону Кирхrофа
равно 9
6 == 3 и ПО второму закону Кирхrофа 9
6 +
+ 1 == 4. В схеме рис. 7.1 независимыми являются четыре
контура. На рис. 7-1 показан один из мноrих возможных
вариантов выбора независимых контуров. '
Для Toro чтобы уравнения по второму закону Кирх-
rофа, а следовательно, и сами контуры были независимыми,
достаточно, чтобы каждый последующий контур отличаЛС5;l
от предыдущих хотя бы одной новой ветвью. Например,
если в схеме рис. 7-1 обходить контур 4 не в последнюю
155
очередь, то каждый последующий контур будет содержать
новую ветвь.
Независимый контур в отдельных случаях может не
содержать навои ветви схемы, например контур 4 в схеме
рис. 7
1, если обходить контуры в порядке их нумерации.
При выборе независимых контуров заданную схему' цепи
удобно изображать в виде r раф а, в котором ветви пред-
ставляются отрезками линии; идеаЛЬНЫЙ источник Э. д. с.
учитывается как короткозамкнутая ветвь, а идеаЛЬНЫЙ
источник тока
как разомкну-
тая ветвь. На рис. 7-2, а пока-
зан rраф схемы рис. 7-1.
Рис. 7-1. Электрическая схе.
ма с четырьмя не"аIJИСИМЫМИ
контурами.
()
0.)
Рис. 7-2. fраф схемы на рис, 7-1 (а)
и ОДНО из ero возможных деревь-
!еВ (6).
[раф содержит всю информацию, относящуюся к reo-
метрической структуре соединения ветвей.
Часть rрафа, содержащая все узлы, но не содержащая
ни одноrо замкнутоrо контура, называется Д е р е в о м
r раф а.
Леrко ПОК8зать, что число ветвей дерева на единицу
меньше числа узлов схемы, т. е. равно q
1.
Ветви rрафа, не входящие в состав дерева, называются
r л а в н ы м и в е т в я м и дерева или хордами. Под-
ключение к дереву каждой Из rлавных ветвей создает по
одному независимому контуру. Совокупность rлавных вет-
вей дерева называется дополнением дерева. Так как rраф
содержит р ветвей, 'а дерево q
1, то число rлавных ветвей
дерева равно р
(q
1) == Р
q + 1, т. е. числу неза-
висимых контуров,
На рвс. 7
2, б сплошными линиями показано одно из
возможных деревьев rрафа, а пунктирам
rлавные J3етви
дерева.
Из сказанноrо следует способ выбора независимых коН-
туров: чертится дерево схемы и затем поочередно добав
156
ЛЯlO'fся rлавные ветви. Любой контур, образуемый добав
лением новои ветви, является независимым, та:ККаК о'Н
отличается от предыдущих контуров новой ветвью. В итЬrе
Коrда к дереву добавятся все rлавные ветви, получится rраф
схемы и число независимых контуров станет достаточным
для ра:счета цепи. См. также
10-8
10-13.
Предлаrаем читателям выбрать таким способом незави-
симые контуры в схеме рис. 7-1.
. Для' получения независимых контуров, достаточны
для расчета цепи, можно начать и не с построения дерева,
а с caMoro rрафа схемы, а затем поочередным размыканием
rлавнЫх ветвей донти До дерева. В этом случае руководст-
вуются следующим правилом: в заданной схеме выбирается
какой-либо контур, раЗМЬJкается одна из ветвей Этоrо КОН-
тура и в оставшейся части схемы выбирается новый контур,
затем размыкается одна
ветвь этоrо HOBoro контура
и т. д. до тех пор, пока в
схеме не останется ни од-
Horo контура.
Предлаrаем читателям
применить для выбора не-
зависимых контуров и это
правило. '
Пример 7
1. [Л. 9]. В мо-
стовой схеме, представленной на Рис. 7-3. Пример 7-1.
рис. 7-3, заданы все комплекс;
иые сопротивления и э. д. с. Е. Требуется определить ток 15 в вет-
ви Z5 (ток В диаrонали мостовой схемы).
Схема содержит четыре узла и шесть ветвей. Следовательно, мо,
rYT быть составлены три уравнения по первому закону Кирхrофа и
три уравнения по второму закону Кирхrофа:
для узла А
16
........-i>
Z6
.D
в
.
+ Е
ii
i2+i6==0;
для узла В
i2
iз+15"""0;
для узла С
iз+i4
16==О;
для KCJHTypa ABDA
Zl11 + z2i2
2515 ==0;
для контура BCDB
2313
2414 + 2515 ==0;
ДJlЯ контура АВСА
2212+ 2313+ 26;б==Е.
157
В полученной системе из шести уравнений неизвестными являются
токи в ветвях. Решая систему уравнений относительно искомоrо тока,
находим:
. Ё
15
M (l2Z4
212з),
rде
М
Z5 [(Z1 +Z4) (Z2+2З)+Z6 (21 +Z2+ ZЗ+ Z 4») +Z1 Z 4 (Z2+ 2з)+
+ Z223 (Z1 +
4) + 26 (21 + Z2) (ZЗ + Z4)'
Полученное выражение показывает, что ток в диаrонали равен
иулю, если выполнено условие Z1ZЗ == Z224 (условие равновесия мосто.
вой схемы),
7-2. МЕТОД КОНТУРНЫХ ТОКОВ
Метод контурных токов является одним из основных
методов расчета сложных электрических цепей, которым
широко пользуются на практике. Этот метод заключается
в том, что вместо токов в ветвях определяются на основа-
нии BToporo закона Кирхrофа
так называемыIe к о н т у р "
н ы е т о к и, замыкающиеся
в контурах.
Е2 На рис. 7-4 в виде при-
мера ПОказана двухконтурная
электрическая цепь, в кото-
"Рис. 7-4. Иллюстрация. к ме- рой 11 И 12
контурные токи.
тоду контурных токов. Токи в сопротивлениях Z1 и
Z2 равны соответствующим
контурным токам; ток в сопротивлении Zз, являющемся
общим для обоих контуров, равен разности контурных
токов 11 И 12, так как эти 'токи направлены в ветви Z3
встречно 1. При этом если положительное направление
искомоrо тока в ветви Z3 принять совпадающим с направле-
нием KOHTypHoro тока 11' то ток В ветви. будет равен 11
12'
В противном случае он будет равен /2
11'
Число уравнений, записываемых для контурных токов
ПО второму закону Кирхrофа, равно числу независимых
. контуров, т. е. дЛя электрической схемы с числом узлов q
и числом ветвей р задача нахождения контурных токов
сведется к решению системы р
q + 1 уравнений. Так,
в схеме рис. 7-4 q == 2, Р == 3; следовательно, число урав-
нений равно 3
2 + 1 == 2 (число независимых контуров).
Z1
Z2
fE)"
fF;\
ZЗ
)
1 Следует отметить, что если положительное направление одноrо
из контурных токов (11 или 12) Изменить на обратное, то ток в ветви ZЗ
будет равен сумме этих токов,
158
Условимся сумму комплексных сопротивлений, входя-
щих в контур. называть с о б с т в е н н ы м с о про -
т и в л е н и е м контура, а комплексное сопротивление,
принадлежащее одновременно двум или нескольким KOHTY
рам.
о б щ и м с о про т и в л е н и е м этих контуров.
Положительные направления контурных токов задаются
произвольно. 'Направление обхода каждоrо контура при
нимается обычно совпадающим с выбранным положитель
ным направлением KOHTypHoro тока; поэтому при составле
нии уравнения по второму закону Кирхrофа падение на-
пряжения от данноrо KOHTypHoro тока в собственном со-
противлении контура берется со знаком плюс. Падение
напряжения от тока смежноrо контура в общем сопротивле-
нии берется со знаком минус. если контурные токи в этом
сопротивлении направлены встречно. как это, например.
имеет место в схеме рис. 7
4. rде направление обоих кон-
турных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независи-
мыми контурами (рис. 7
4) MorYT быть записаны два урав-
нения по второму закону Кирхr6фа. а именно:
E 1 == (Zl +Zз) i 1
z з i 2 ;
Ё 2 ==
ZЗ;l + (Z2+Z8) i 2 ,
rде Zl + Z8 и Z2 + Z8
собственные сопротивления кон-
туров 1, и 2; Z3
общее СОПРО'УИвление контуров 1 и 2
(знак минус в уравнениях обусловлен выбором положитель-
ных направлений контурных токов).
Если заданная электричесная схема содержит п незавИ-
симых контуров, то на основании BToporo закона Кирхrофа
получается система из п уравнений:
E 1 === Z(щi 1 + Z(12)i 2 +... + z(ln)i n; I
.2
.Z
2
/:1
.Z
2
)
2
: .:-: .i
21:)
n;.
Еn == Z(nl)! 1 + Z(n2)i 2 +...+ Z(nn)i n'
Здесь Е ;
контурная э. д. с. в контуре i (i == 1,2. .... п),
т. е. алrебраическая сумма э. д. с.. действующих в данном
контуре; э. д. с., совпадающие по направлению с напра-
влением обхода, берутся со знаком плюс, а направленные
BCTpe!IHO
со знаком минус;
Z(it)
собственное сопротивление контура i;
Z(ik)
общ ее сопротивление контуров 1 i и k.
, 1 Индексы собственных и общих сопротивлений контуроа заклю-
чены в скобки для отличия их от входных и передаточных сопротивле-
ний, приводимых в последующих разделах книrи.
(7-2)
159
В соответствии со сказанным ранее собсТвенные сопро-
тивления Z(ii) войдут со знаком плюс, поскольку обход
контура принимается совпадающим с положительным на-
правлением KOHTYPHoro тока 1 i . Общие сопротивления Z(ik)
войдут со знаком МИНус, коrда токи 1; и 1 k направлены
в них встречно.
Решение уравнений (7
2) относительно искомых контур-
}lbIX токов может быть найдено с помощью определителей:
E 1 Z(12) ... Z(1n)
1 1 E 2 Z(22)' ., Z(2 n )
1 == Д;: .........
E n Z(п2) ... Z(nn)
Z(l1)E1 '" Z(1n)
1
1 Z(21)E 2 . .. Z(2 n )
2
Д;: .........
Z(n1)E n ... Z(nn)
И т. д., rДе определитель системы 1
Z(11)Z(12) ... Z(1n)
/'1;: == Z(21)Z(22) ... Z(2n)
Z(пI)Z
n2) .,. Z(nп)
Соrласно правилу разложения определителя по элемен-
там столбца определитель равен сумме iIроизведений эле-
ментов столбца на их алrебраические дополнения. Поэтому
решение уравнений запишется в виде 2:
/ . 'Дl! . Д2! . Дп!
1 == Еl Т + Е 2 т +. . . + Еn т;
z z, z
. . L'.12 . Д22 . Дп2
/
== Е 2 у+ Е 2Т +...+ Еn '"'""л"';
z z L1z
(7-3)
/ . Е . L'.ln +E ' А2п + +Е дпn
n== lТ 2Т'" nТ'
z z z
1 Определитель снабжен индексом Z, Т81{ как ero элемеНтамн на-
ляются комплексные сопротивления. '
2 На nрактике во мноrих случаях решение системы уравиений (7-2)
может быть выполнено более просто последовательным исключением
неизвестных,
160
Здесь 8ik
алrебраическое ,1{ополнение элемента Z(ik)
определителя системы, т. е. умноженныЙ на (
l)i+k минор
элемента Zik (минор образуется
из определителя системы
исключением из Hero i
Й строки и k
ro столбца).
Сокращенно система уравнениЙ (7
3) записывается в
Биде:
n
. 1 "\1
Ik == 6
1:. 1 8 Ik .
z i
l
(7
4)
Первый индекс алrебраическоrо дополнения i, обозна
чающиЙ номер строки, вычеркиваемоЙ в определителе си-
стемы, соответствует номеру контура, контурная э. д. с.
KOToporo умножается на данное алrебраическое дополне-
ние. ВтороЙ индекс k, обозначающиЙ номер столбца, вы-
черкиваемоrо в определителе системы, соответствует номеру
контура, для KOToporo вычисляется контурный ток.
Уравнения (7-2), выражающие второй закон к.ирхrофа,
записаны в предположении, что источниками электрическоЙ
энерrии служат источники э. д. с. При наличии в электри
ческой схеме источников тока они MorYT быть заменены
эквивалентными источниками э. д. с.
Если проводимости источников тока равны Нулю, то
целесообразно выбрать заданные токи в качестве KOHTYP
ных; тоrда число неизвестных контурных токов и COOTBeT
ственно число уравнениЙ сокра1;ЯТСЯ на число заданных
токов.
Если в заданной электрической схеме имеются парал
лельные ветви, то замена их эквивалентным комплексным
сопротивлением сокращает число контуров (за счет тех,
которые образованы параллельными ветвями).
Электрические цепи MorYT быть планарными или непла-
Нарными.
П л а Н а р н а я, или плоская, электрическая цепь мо-
жет быть вычерчена на плоскости в виде схемы с непере
крещивающимися ветвями. В некоторых случаях пересече-
ние ветвей в электрической схеме, являющееся результатом
IJринятоrо способа начертания схемы, устраняется при
ДРуrом способе изображения данной планарной элек-
трической цепи, как это, например, пр.едставлено на
рис. 7-5.
Электрическая цепь, приведенная на рис. 7
5, а, пла-
нарна, так как имеющееся пересечение ветвей устранимо
в соответствии с рис. 7.5, б.
161
Не п л а н а р н а я электрическая цепь не может быть
вычерчена на плоскости в виде схемы с неперекрещиваю
щимися ветвями. Примером такой электрической цепи слу-
жит приведенная на рис. 7
5, в непланарная цепь, пересе
чение ветвей в которой не может быть устранено.
Если направление контурных токов во всех контурах
планарной электрической цепи одинаково, например COB
падает с ходом часовой стрелки, то общие сопротивления
смежных контуров входят в систему уравнений (7
2) со
знаком минус, так как контурные токи смежных контуров
.2
()
з
а)
б)
8) '1
Рис. 7-5. Планарные (а и б) и непланарная (8) элеК1рические цепи.
направлены в общих ветвях встреЧНQ. Направление KOH
турных токов по ходу часовой стрелки принимается во
всех контурах, кроме BHelUHero. охватывающеrо всю схему.
В последнем контурный ток направляется против часовой
стрелки'(см. пример 7-2). Это правило, однако, не является
обязательным.
В случае непланарной электрической цепи не преk
ставляется возможным иметь в общих ветвях только раз
ности контурных токов, как это, например, видно из схемы
рис. 7-5, в.
Пример 7-2. [Л. 9]. Пользуясь методом контурных токов, опре-
делить ток в диаrонали мостовой схемы рис. 7-6. .
Выбранные положительные направления контурных токов 11'
12 И 13 указаны на схеме стрелками. Число уравнений, заПНСЫl;jаемых
по второму закону К:ирхrофа, равно трем (по числу независимых кон-
туров):
O
(Z1 +22+25) i 1
Z5i2
22iз;
O
Z5i1 +(Z3+Z4+Z5) i2
zз/з;
E==
Z2i.i
zзi2+(Z2+ZЗ+Z6) i3.
162
Решение полученной системы уравненнй относительно контур.
ных токов 11 И 12 дает:
, Ё
11-:=:
.М [lз l б+ Z 2 (ZЗ+ Z 4+ Z 5Н;
, Е
12-:=:
М [Z2 Z б+ Z З (Zi+Z2+ZoH,
rде М имеет то же значение, что и в прнмере 7.1.
ИСКОМЫЙ ток в диаrонали мостовой схемы равен разности кон-
турных токов:
. .'. Е
lo==12
li == М (Z2Z4
Z1ZЗ)'
что совпадает с получениым в
примере 7.1 ответом.
Следует заметить, что если
в заданной схеме контуры выб-
рать так, чтобы через ветвь Z5
проходил только однн контур-
ный ток, ТО искомый ток в
ветви Z:i будет равен именно Рис. 7-6. Пример 7
2.
этому контурному ТОКУ, т. е.
задача сведется к нахождению ТОЛЬКО OD,Horo KOHTypHoro тока (вместо
двух).
7.3. МЕТОД узловых НАПРЯЖЕННА
.
Iа
,
Е
Метод узловых напряжений заключается в том, что на
основании первоrо закона Кирхrофа определяются потен
циалы в узлах электрической цепи относительно HeKoToporo
б а з и с н о r о узла. Эти' разности потенциалов назы-
ваются у з л о в ы м и н а п р я Ж е н и я м И:, причем
положительное направление их указывается стрелкой от
рассматриваемоrо узла к базисному.
Напряжение на какой-либо ветви равно, очевидно,
разности узловых напряжений концов данной ветви; про
изведение же этоrо напряжения на комплексную проводи-
мость данной ветви равно току в этой ветви. Таким обра
зом, зная узловые напряжения в электрической цепи,
можно наЙти токи в ветвях.
Если принять потенциал базисноrо узла равным НУЛю,
то напряжения между остальными узлами и базисным узлом
будут равны также потенциалам этих узлов. Поэтому дан-
ный метод называется также методом узловых потенциалов.
На рис. 7
7 в виде примера изображена электрическая
схема с двумя источниками тока, имеющая три узла: 1,
2 и 3. Выберем в данной схеме в качестве базиса узел 3 и
163
обозначим узловые напряжения точек 1 и 2 через и 1 и и 2 .
Соrласно принятым на рис. 7-7 обозначениям комплексные
проводимости ветвей равны соответственно:
1 1 1
У 1 == Zi ; У 2 == z;; У з == z;'
Для заданной электрической цепи с тремя узлами MorYT
быть записаны два уравнения по первому закону Кирхrофа,
а именно:
для узла 1
i 1 == У 1 й 1 + УЗ (и 1
й 2 ) == (У 1 + УЗ) (;1
У З V 2 ;
!!.ля узла 2
/2 == У 2 й 2 + У З (U 2
й 1 ) ==
У Э U 1 + (У 2 + Уз) V'l'
Величина У 1 + УЗ, представляющая собой сумму ком-
плексных проводимостей ветвей, сходяЩихея в узле 1,
называется с о б с т в е н н о й про в о Д и м о с т ь ю
узла 1; величина УЗ, равная комплексной проводимости
ветви между узлами 1 и 2,
1 Z3 2 ВХОДящая в уравнения со зна-
ком минус, называется о б -,
щей проводимостью
между узлами 1 и 2.
Если заданы токи источн!!-
ков тока и комплексные про-
водимости ветвей, то узловые
напряжения нахоДЯТСЯ сов-
Рис. 7
7. Иллюстрация к методу местным решением уравнениЙ.
узловых напряжений. В общем случае если элек-
трическая схема содержит q
узлов, то на основании первоrо закона Кирхrофа полу-
чается система из q
1 уравнений (узел q принят За ба-
зисный):
i 1 == У(ЩU 1 + У(щL\+...+ Y(l.q
lPq
l; )
;2 == У Щ )U 1 + У(22)й 2 +...+ Y(2,q
l)Uq
l; (7-5)
,i:
;q'l.:)Й:
(:
.
)Й2'
': .
. ;(;
i'.q
l;Й q
l'
Здесь ток источника тока, подходящий к узлу, берется
со знаком плюс, а отходящий от узла
со знаком минус;
У(и)
собственная проводимость всех ветвей, сходящихся
в данном узле i; Y(ik)
общая проводимость между уз-
164
.!Iами i 11 k, входящая со знаком минус при выбранном на-
правлении всех узловых напряжений к базису, независимо
от Toro, является ли данная электрическая цепь планарной
или непланарной.
Решив систему уравнений (7
5) при помощи определите-
лей \ получим формулу для k-ro узловоrо напряжения отно-
сительно базиса:
q
l
. 1
.
и k == F:"
J i !!!fk'
у i
1
(7-6)
rAe !:.у
определитель
Vщ)
У(21)
!:. у ==
системы. 2 :
У(12) V(l. q
l)
У (22) У(2. q
l)
Y(q
1.1) Y(q
1.2) .., Y(q
.l.q
l)
!:.ik
алrебраическое дополнение элемента V(lk) данноrо
определителя.
Первый индекс i алrебраическоrо дополнения, обозна-
чающий номер строки, вычеркиваемой в определителе си-
стемы, соответствует номеру узла, заданный ток источника
тока KOToporo умножается на данноеалrебраическое ДОПОk
нение. Второй индекс k, обозначающий номер столбца,
вычеркиваемоrо в определителе системы, соответствует
номеру узла, для KOToporo вычисляется узловое напря-
жение.
Уравнения (7-5), выражающие первый закон Кирхrофа,
записаны в предположении, что в I<ачестве источников эле-
ктрической энерrии служат источники тока. При наличии
в электрической схеме источников э. Д. с. последние должны
быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д. с.
(проводимости таких ветвеЙ бесконечно велики), то эти
ветви следует рассматривать как источники неизвестных
токов, которые затем исключаются при сложении соответст-
вующих уравнениЙ. Дополнительными связями между не-
известными узловыми напряжениями будут являться извест-
ные напряжения между узлами, равные заданным э. д. с.
1 См. сноску 2 на с. 160.
2 Определитель сиабжен индексом у, так как ero элементами ЯВ
JlЯЮТСЯ комплексные ПРОБОДИМОСТИ.
11'11'>
При наличии только одной ветви с э. д. с. и бесконеч-
ной проводимостью целесообразно принять за базисный
узел один из узлов, к которому примыкает данная ветвь;
тоrда цапряжение друrоro узла становится известным и
число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед
методом контурных токов в том случае, ко!'да число урав-
нений, записанных по первому закону Кирхrофа, меньше
числа уравнений, записанных по второму ЗaJЮНУ Кирх-
rофа. Если заданная электрическая схема имеет q узлов
и р ветвей, то в соОтветствии со сказанным выше, метод
узловых напряжений представляет преимущеС1ВО при
q
1 < Р
q + 1, или, что то же, при 2 (q
1) < р.
Здесь имеется в виду общиЙ случай, коrда число урав-
нений не сокращается за счет известных контурных токов
или узловых напряжений.
Пример' 7-3. [Л. 9]. Поль-
зуясь методом узловых напря-
жений опр.еделить ток в диаrо-
2 нали мостовой схемы (см.
рис. 7-6).
В результате замены за-
данноrо источника э. д. с. .эк-
вивалентным источником тока
получается схема (рис. 7-8), со-
держащая четыре узла. Для этой
Рис. 7-8. Пример 7-3. схемы по первому закону Кирх-
rофа заПИСЫlJаlOТ 4
1 == 3 урав-
. нения (по числу независимых
узлов). Если выбрать в данной схеме в качестве базиса узел 4. и на-
править узловые напряжения к базису, то уравнения примут вид:
для узла 1
УвЕ== (У 1 + У 2 + У в ) и 1
Y2и2
Vви З ;
для узла 2
o==
V2и1+(V2+VЗ+V5) U2
VЗUЗ;
для узла 3
Y6E==
у в и 1
v з и 2 +(v з + У 4 + У в ) из.
Решение получеиной системы уравнений относительно ТJ 2 даст
. Е
и 2 ==7{ У в (V2V4
V1VЗ)'
I'де
,
N == У 5 [(У 1 +У 2 ) (V з + У 4 )+ У в (У 1 + У 2 + V з + У 4 )] +
+ УУ4 (У 2 + V з )+ V 2 V з (У 1 + V.v + У в (Vi+ У 4 ),(У 2 + Vз)'
166
Умножив иайденное узловое напряжение (J 2 на прgВОДИМОСТЬ y
диаrональной ветви мостовой схемы и изменив знак в С00тветствии
с выбраниым ранее направлением тока 15 (см. рис. 7;3), иайдем иско-
мый ток:
. Е
/5== 7'/ У5 У в (УIУЗ
У2 У 4)
1-4. МЕТОД НАЛОЖЕНИЯ
в линеЙноЙ электрическоЙ цепи, содержащей источники
э. д. с., контурные токи (и соответственно токи в вет-
вях) представляют собоЙ линеЙные функции контурных
э. д. с. Математически они выражаются формулой (7-4):
n
. 1".
/ k ==
-'- E l l1 lk .
z i
l
ФизическиЙ смысл этой формулы заключается в том,
что ток 8 любо!.! коюпуре линейной электрической цепи
может бblть получен как алzебраическая сумма токов, вы-
ЗblваеА!ЬLX в этом контуре каждоЙ из э. д. с. в отдельности.
Метод расчета токов, основанныЙ на определении токов
в одном и том же контуре (или в
тви) при поочередном воз-
действии э. д. с. и последующем алrебраическом сложении
этих токов, называется м е т о Д о м н а/л о ж е н и я.
При определении частичных слаrающих токов по методу
наложения необходимо считать включенными внутренние
сопротивления тех источников э. д. с., Iюторые принимаются
отсутствующими при вычислении слаrающих токов. Если
в цепи заданы идеальные источнйки э. д. С., т. е. внутрен-
ние сопротивления источников равны нулю; то при опреде-
лении ТOIЮВ, вызываемых какой-либо э. д. С., все осталь-
ные источники э. д. с. закорачиваются.
В свою очередь в линейной электрической цепи, содер-
жащей источники тока, узловые напряжения (и соответст-
венно напряжения на ветвях) представляют собой линейные
функции задающих токов источников. Математически они
выражаются' формулой (7-0):
q
l
(; k ==
j I l1/ k .
У J;:, 1
Физический смысл этоЙ фор мул ь! заключается в том,
что узловое напряжение для любос.о узла линейной электри-
ческой цепи мвжеm быть получеыо как алс.ебраическая сумма
напряжений, вblЗblваемьLX в этом узле каждым из задающих
167
таков в отдельности. Таким образом, формула (7
6), так
же как и (7-4), представляет собой математическую запись
метода наложения, справедливоrо для линейных электри
ческих цепей.
При определении частичных слаrающих узловых напря-
жений по методу наложения необходимо считать включен
ными внутренние проводимости тех источников тока, Кото-
рые принимаlOТСЯ отсутствующими при вычислении слаrаю-
щих напряжений. Если источники тока заданы без внутрен-
них проводимостей, т. е. проводимости их равны нулю, то
при пользовании методом наложения ветви с неучтенными
источниками тока разрываются.
Если в линейной электрической цепи заданными яв-
ляются одновременно ист
чники э. д. с. и источники тока,
то метод наложения применим и в этом случае. Например,
ток в каком
либо контуре данной цепи может быть получен
в результате алrебраическоrо сложения токов, вызываемых
в этом контуре поочередным действием источников э. д. с.
и тока. При этом отсутствующие источники Э.д.с. заменяются
внутренними сопротивлениями, а отсутствующие источники
тока
внутренними проводимостями.
Пример 7-4. Пользуясь методом наложения, определить ток а веТ-
ви ZЗ схемы рис, 7-4,
Z1 ZZ Е1 Е2
ZЭ
, iЭ!
.
ZЭ E
0.)
Рис, 7
9. Пример 7-4.
6)
Искомый ток l з ' опp€деляется как сумма токов 1
и 1;, ПР9-
ходящих через. ветвь Z3 под воздействием источников э. д. с. Е 1
(рис. 7
9, а)' и Е 2 (рис. 7
9, б), взятых порознь. '
Токи 1
и J; суммируются, а не вычитаются, так как положитель-
ные направления их выбраны совпадающими:
j'
E f Z2[:,f .
8
Z2+Z3 2 Z2 2 3 Z122+'Z2Zз+Zз21 ,
1+ 2 2 +2 з
j",",,
Е 2
21[:,2 .
8 Z1+ZЗ Z2+
Z1Z2+i2lз+23Z1'
21 + Z3
168
/
/'+I"
Z
Ei+Z1EI!
з
8 3
Z1Z2+Z2Zз+ZзZi .
Пример 7.5. Задана симметричная схема с нерзвными э. Д. с.:
Еl == 12 В и Е 2 == 8 В (рис. 7-10, а). Значения сопротивлений
(в омах) указаны по схеме. Вычислить токи 11 И /2' Заме-
тив, что Е == Ч 2 (Е 1 + Е 2 ) +
+ lb (Е 1
Е 2 ) и Е 2 == 1/2 (Е 1 +
+ 1;2)
1/2 (Е1
Е 2 ), можно
вместо заданной схемы рас-
смотреть две симметричные схе-
мы, в каждой из которых
Э. д. с. источников равны. В
первой схеме источники имеют
э. д. с. 1/2 (Е 1 + Е 2 ) == 10 В и
полярность их одинакова; во )
второй схеме исroЧlIИКИ имеют а.
э. д. с. 1/2 (Е 1
Е 2 ) == 2 В и Z 2
полярность различна.
Пользуясь методикой, опи-
санной в
4-9, пронзведем соот-
ветствующие рассечения и за-
мыкания накоротко по оси сим-
метрии (рис. 7.10, б и в).
Искомые токи найдутся ме-
тодом наложення:
10 2
11 == 4
+
6 == 2,83 А;
10 2
12== 4
6 ==2,17 А.
следова1eJlЬНО,
7-5. ВХОДНЫЕ И
ПЕРЕДА ТОЧНЫЕ
ПРОВОДИМОСТИ
И СОПРОТИВЛЕНИЯ
2
d)
2
8)
в электротехнике, pa
диотехнике и теории aBTO
Рис. 7
10. Прнмер 7-5,
матическоrо реrулирова-
ния широко используются поняТия о входных и переда-
точных ФУНКШIЯХ,
Условимся называть источник э. д. с. н е 3 а в и с и -
м ы м или автономным (самостоятельным), если э. д. с.
источника не зависит от напряжений и токов в цепи (с По
нятием «зависимый» источник мы встретимся в
7-7).
Пусть в какую-либо ветвь контура электрической цепи
включен независимыЙ источник э. д. с. Её (рис. 7-11, а),
причем данная ветвь не является общей, а ПрИНадлежит
16:)
только контуру i. Если вся остальная часть электрической
цепи не содержит независимых источников электрической
энерrии, то в соответствии с формулой (7
4) заданная э. Д. С.
ЕI вызовет в данном контуре i и в каком-либо друrом кон-
туре k токи
. tJ.i"
Ii==
El
Дz
(7-7)
11
. l1 ik . (7 8)
Ik==
Ei' -
На рис. 7-11, а показаны контуры i и k заданной элект,
рической цепи.
rn
i
k
Q71
0.)
Uk
Рис. 7-11. Определеиие ПОНЯ1ИЙ ВХОДных и передаточных
ПрО!Jодимостей и сопротивлений.
Отношение KOHTypHoro тока к э. Д. С., действующЕ'Й
в том же контуре, при отсутствии независимых источников
во всех остальных контурах называется iз х о д н о й про-
в о д и м о с т ь Ю электрической цепи:
1/ 'tJ.ii
...
==........... == Уи. (7-9)
ЕI LJ.z
В свою очередь отношение KOHTypHoro тока к э. Д. С.,
действующей в npyroM контуре, при отсутствии независимых
источнйков во всех ОСТi1ЛЬНЫХ контурах называется пер е -
Д а т о ч н о й (или взаимной) про в о д и м о с т ь Ю кон-
о туров:
/k == tJ.ik
Y k .
El tJ.z
,.
(7 -1 О)
Элементами определителя системы и алrебраических
дополнений в ,выражениях (7-9) и (7-10) служат собственные
и общие сопротивления контуров заданной электрической
цепи. Определитель Ll. z имеет размерность сопротивления
в степени n, rne n
порядок опредеJIИтеля (равный числу
независимых контуров данной цепи); алrебраические до-
НО
полнения !1и и !1'k имеют размерlIОСТЬ сопротивления
в степени п
1. В результате деления алrебраическоrо
дополнения на определитель системы получается веЛИЧИRа,
меющая размерность проводимости.
На основании (7
9). и (7-10) заключаем, что ВХОДНая и
передаточная проводимости численно равны токам в кон-
турах i и k, Korдa в контуре i действует э, д. с., равная 1 В.
С учетом обозначений (7-9) и (7-10) выражения для
токов (7-4) принимают вид:
n
j k '='=
YkiE j .
,== 1
(7 -11)
Аналоrичные рассуждения MorYT бытьпроведены и
в отношении узлов i и k электрической цепи в предполо-
жении, что к узлу i подключен независимый источник
тока 1 J" а вся остальная часть цепи не содержит незави-
симых источников (рис. 7
11,6). В соответствии с (7-6)
заданный ток 1" обусловит появление узловых напряжений
для узлов i и k:
.
iI'
иС==Т/1
у
(7 -12)
и
ik .
Uk==T1j'
у
(7 -13)
Отношение напряжения в узле к току, заданному в том
же узле, при отсутствии в схеме друrих независимых источ-
ников называется в х о Д н ы м с о про Т И В Л е н и е м
электрической цепи:
(;; ==
== Zjj;
/;
y
соответственно отношение напряжения в узле к току, за-
данному в друrом узле, при отсутствии в схеме друrих
источников называется пер е Д а т о ч н ы м (или взаим-
ным) с о про т и в л е н и е м узлов:
(;k == /l. jk == Zkl' (7-15)
/; /l.у
, Элементами определителя сисrемы и, алrебраических
дополнений в (7
14) и (7-15) служат собственные и общие
проводимости узлов заданной электрической цепи. Опреде-
(7 -14)
1 ИСТОЧНИК тока называется независимым, или автономным, если
ток источника не зависит от иапряжений и токов в цепи.
171
литель l1у имеет размерность проводимости в степени т,
rде т
порядOI{ определителя (на единицу меньший числа
узлов в заданной схеме); алreбраические дополнения du
и l1 i k имеют размерность проводимости в степени т
1.
В результате деления алrебраическоrо дополнения на опре-
делитель системы получается веЛИЧИНа, имеющая размер-
ность сопротивления.
На ОСНовании (7-14) и (7-15) заключаем, что входное и
передаточное сопротивления узлов численно равны напря-
жениям в узлах i и k (относительно базисноrо узла), коrда
в узле i задан ток, равный 1 А.
j.
ф
[]15i +1
i
'#(+1
k
О н
tikf1
4)
-= ()
Рис. 7-12. Отношение токов (а) и напряжений (6).
с учетом обозначений (7-14) и (7-15) выражения для
напряжений (7-6) принимают вид:
q
l
(; k ==
Zkl1l' (7-16)
i
l
Следует иметь ввиду, что входным сопротивлением
может также называться величина, обратная выражению
(7-9), а входной проводимостью
величина, обратная
выражению (7-14).
Очевидно, что для одной и той же пары выводов элект-
рической цепи, не содержаЩеЙ источников, величины Уа
и Z/i, определяемые. из (7-9) и (7-14), взаимНО обратны, т. е.
Zu == 1jY/i.
ОТНОllIение двух контурных токов i k И ikj--l' вызываемых
в контурах k и k + 1 источником э. д. с. Е (, включенным
в контур i (рис. 7-12, а), определяется на основании (7-10),
отношением соответствующих передаточных проводимо-
стей, а именно:
i k
==
ik+i
УkiЁi
У k+i. {Ё!
==
у k+i. 1 .
172
Аналоrично отношение двух уЗловых напряжений (j k И (j k+l'
обусловливаемых в узлах k и k + 1 источником тока /j, заданным
в узле i (рис. 7-12, б), определяется на основании (7
15) отношением
соотаетствующих передаточных сопротивлениЙ:
Uk ZkJi Zki
иlHi == Zk+i, i/i == Zk+!, i .
Входные и передаточные сопротивления и проводимости, а также
отношения одноименных электрических величин (токов, напряжениЙ)
подробнее рассмотрены в f.'1. 9.
7.6. ТЕОРЕМА О&РАТИМОСТИ (ИЛИ ВЗАИМНОСТИ)
Пассивные линейные электрические цепи обладают важ-
ным свойством, известным под названием о б Р а т и м о -
с т и. Основанная на этом свойстве теорема обратимости
(или взаимности) может быть сформулирована в двух ва-
риантах: примеНИтельно к источникам э. д. с. и ТОКа.
Оrраничимся рассмотрением первоrо варианта.
t21 .
s
CS
а.)
б)
Рис. 7-13. Теорема обратимости (вариант с источни-
ком Э. Д, с.),
в а р и а н т с и с т О ч н и к о м э. д. с. На рис. 7-13
условно показана электрическая цепь с выд,.еленными кон-
турам!! i и k. Электродвижущая сила E i в контуре i
(рис. 7-13, а) вызывает ТОК в контуре k, который соrласно
(7 -1 О) равен:
lk=== YkjE i .
Соответственно э. д. С. Ея В контуре k (рис. 7-13, б)
вызывает ток в контуре '.
ii == YikE k .
Отсюда следует, что
!.li. == У ki E i
/1 Y ik Ek'
Алrебраические дополнения !J.. jk и Дki, входящие в вы-
ражения У ki И Y ik , различаются только тем, что в них
173
строки заменены столбцами с учетом Toro, что их элементы
общие сопротивления контуров заданной цепи
не изме-
няются от перестановки индексов.
Поэтому l1ik == I1kl И, следовательно,
Y ki == Y ik .
(7 -11)
Электрические цепи,. для которых выполняется усло-
вие (7-17), называются обратимыми цепями.
Для таких цепей имеем:
==
EI
/1 Ek'
Если принять E i == E k , то 11 ==. lk'
Таким образом, для обратимых цепей справедливо
следующее положение: если некоторая э. д. О,) находящаяся
j5 L
z i!
Е
Рис. 7
14. Пример 7-6.
8 каком-либо контуре эле1\трической цепи, вызывает ток
в друеом контуре данной цепи, то та же э. д. С., будучи
перенесенной во второй контур, вызовет в первом KOHmypJ
ный ток с таки.ми же модулем и фазой.
При соответствующем выборе контурных токов ток
в ветви равен контурному току. Поэтому данная теорема
справедлива также для токов в ветвях.
Использование свойства обратимости пассивных линей.
ных электрических цепей в ряде случаев упрощает расчеты.
С этим важным своЙством пассивных линейных цепей нам
придется неоднократно встречаться далее, особенно в rл. 9.
Практическое применение теоремы обратимости иллю-
стрировано в примерах 7-6 и 7-7.
Пример 7-6. Воспользовавшись теоремой обратимости, вычислить
ток 1 в схеме р'ис. 7-14, а при любом конечном значении сопротивле-
ния Z. Дано: Ё == 10 L 0° В.
Применение теоремы обратимости облеrчает в данном случае рас-
чет тем, что после переноса э. д, с. в ветвь Z (рис. 7-14, б) получается
174.
схема резонанса токов, в которой ток источника равен нулю; поэтому
искомый ток, равный току в емкости схемы рис. 7
14,,6, иаходится
как отношение э. д. С. к сопротивлению емкостей ветви:
I
10 L,0 5 °
j2 А .
]
7-7. ТЕОРЕМА КОМПЕНСАЦИИ
Токи в электрической. цепи не изменятся, если любой
учm;ток цепи заменить э. д. С., равной напряжению на
данном учm;тке и направленной навстречу току, проходя-
щему по данному учm;тку. '
Справедливость этоrо положения, носящеrо название
т е о р е мы' к о м п е н с ац и и, вытекает из Toro, что
любое из слаrающих падения напряжений,. входящих
в уравнение по второму закону Кирхrофа, может быть
r4
"
4)
Е i
z
"
l
zi
6)
Рис. 7-15. Теорема компенсащш.
перенесено в друrую сторону уравнения с противополож-
ным знаком, т. е. может рассматриваться как дополни-
тельная э. д. с., направленная навстречу току.
'Иллюстрацией сказанноrо выше служит .рис. 7
15;
уравнение по второму закону Кирхrофа, записанное для
схемы рис. 7-15, а как Е == z11 + zl, может быть пред-
ставлено в виде Е
z1 == Z/.
Последней записи уравнения соответствует схема
рис. 7-15, б, в которой вместо сопротивления Z включена
"3. д. с. Zl, направленная противоположно току 1.
Данная теорема справедлива и для разветвленных элек-
трических цепей. Рисунки 7-16, а и б иллюстрируют воз-
можность замены комплексноrо сопротивления Z источни-
OM э.. д. с. Ё
Z (11
12), действующим навстречу току
/1
12' про ходящему через сопротивление Z.
Вместо источника э. д. с, может быть включен источник
тока (рис. 7-16, в), обусловливающий прохожд..ение между
П5
узлами 1 и 2 Toro же тока, что и в схеме рис. 7-16, а; токи
и напряжения в остальной части цепи при этом не меняются.
Следует заметить, что э. д. с. или ток источника, за-
меняющеrо собой участок цепи, определяется в зависимости
от тока, проходящеrо через данный участок. При измене-
нии параметров остальной части цепи' ток на данном уча-
стке в общем случае изменяется, и поэтому указанный выше
источник не является самостоятельным, а представляет
собой так называемый з а в и с и м ы Й, или неавтономный,
источник.
Применение теоремы компенсации облеrчает изучение
свойств линейных электриче.СКИХ цепей./Так, заменяя какой-
либо участок цепи зависимым источником э. д. с. или тока
=
T(
i,):E
CL) б) 8)
Рис. 7
16. Замена пассивной ветви (а) зависимым источником э. Д. С,
(6) или зависимым источником тока (в),
и пользуясь методом наложения, леrко убедиться в том,
что напряжения и токи в остальной части цепи являются
линейными функциями напряжения на данном- участке
или тока, проходящеrо через Hero. Например, если при
изменении комплексноrо сопротивления Z в какой-либо
ветви изменяется ток l 1 в этой ветви, то ток 12 В какой-либо
друrой ветви связан с 11 линейной функциональной зави-
симостью
i 2 == i 2 (z==co) + Ki 1 ;
здесь l z (z"",-oo)
значение TOJc{a 12 при Z == 00, т. е. при ра-
зомкнутой первой ветви.
Комплексный коэффициент К находится из условия,
что при Z == о
i 2 (z==o) == i 2(Z==
) + Kit (z==O);
поэтому
i
J . + 12(z==O)
!2(Z==OO) 1
2
2(Z==OO) '1'
11(z==o)
176
7-8. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ТОКОВ В ЭЛЕКТРИЧЕсКОR
ЦЕПИ ПРИ ИЗМЕНЕНИИ СОПРОТИВЛЕНИЯ В ОДНОН ВЕТВИ
На основании методов наложения и теоремы КОмпенса-
ции вытекает {:,'!едующая теорема об изменении токов
в электрической цепи, вызываемом изменением параметра
в одной ветви данной цепи.
Если комплексное сопротивлеiше какой
либо ветви элек-
трической цепи изменится на + Z', то изменение токов
в цепи будет таким же, какое ВЫЗblсается действием в ветви
.
1 Z
...........с>-
...........
0
1+j' а) . ,. iz=z'j
z z' E 1 =ZI
...............
6') l.
z1
i z z' 1
............j>
i' 8) Ez=z'i
z z,
...........с>-
1'"' ............
а)
Рис. 7-17. Изменение сопротивления ветви,
z + Z' э. д. С., . направленной противоположно первона-
чалЬflOМУ току 1 в данной ветви и равной по модулю и
знаку + Z'j.
Сказанное поясняется на рис. 7
17.
Положим, что в ветви, комплексное сопротивление
которой равно Z, проходит ток j (рис. 7
17, а). Спраши
вается, как изменится ток, если сопротивление ветви изме-
нится на +Z', т. е. станет равным Z + Z'.
На рис. 7
17, б показана ветвь с измененным сопро-
тивлением; щ)едполаrается, что в результате изменения
сощ
отивления Z на Z' первоначальный ток 1 изменился
., . .,
на 1 , т. е. стал равным 1 + 1 .
Включим в данную ветвь две противоположно направ-
ленные э. д. с. Ё 1 И Ё 2 , равные z'j каждая (ток в цепи при
этом не изменится), и, пользуясь методом наложения, pac
смarрим действие этих э. д. с. поочередно. При OTCYTCT
вии Ё 2 получаются условия, тождественные первоначаль-
ным, так как схемы рис. 7-17, а и в эквивалентны: падение
177
напряжения от тока J в Z' компенсируется на основании
теоремы компенсации дополнительной э. д. С. Е 1 == Z' i.
Следовательно, изменение тока в цепи обусловливается
действием э. д. с. с Е 2 == Z'1, направленной навстречу i
(рис. 7-17, ё), что и требовалось доказать.
Применение данной теоремы бывает целесообразным в тех
случаях, коrда известны токи в цепи до изменения пара-
метров ветви.
Кроме Toro, измерив ток в электрической цепи с по-
мощью амперметра, сопротивление KOToporo известно, мож-
но, основываясь на этой теореме, уточнить значение тока
в цепи, т. е. исключить поrрешность, вызванную сопро-
тиВлением прибора. Дополнительный ток, обусловленный
сопротивлением прибора, соrласно те.ореме равен:
/ "
Ё 2
iz'
Ze
Ze '
rде 1
истинный ток (без амперметра); Z'
сопротивление
амперметра; Zэ
эквивалентное сопротивление пассивной
цепи (с амперметром).
Через амперметр проходит ток
ia==j+j'
i(1
:J .
Следовательно, имея показание амперметра /а, можно
вычислить искомый ток по формуле
I==lal Ze
z, l.
Следует заметить, что размыкание какой-либо ветви
заданной электрической цепи cooTBetcTByeT предельному
случаю Z' == 00, Коrда решение по приведенной выше тео-
'реме становится неопределенным. В этом случае применим
любой из следующих приемов:
1. Включим между разомкнутыми точками два источ-
ника тока 1, соединенных параллельно. При принятом на
рис. 7-18, а направлении этих источников ток в данной
ветви в соответ<;твии с первым законом Кирхrофа равен
нулю. Применяя метод наложения и считая, что ток 1
выбран равным току в ветви до ее размыкания, приходим
к выводу, что размыкание ветви равносильно добавлению
к токам предшествующеrо режима новой системы токов,
обусловленных действием в данной ветви пассивной элект-
рической цепи источника тока, paBHoro току, ,протекавшему
в той же ветви перед ее размыканием.
178
2. Обозначим через-V х напряжение между разомкнутыми
выводами электрической цепи (н а п р я ж е н и е х о
л о с т о r о х о Д а) и присоединим к ним источник э. д. с;
Е === ох; токи и напряжения в цепи при этом не изменятся.
Применив метод наложения, получим, что распределение
токов и напряжений в исходной цепи слаrается из COOT
ветствующих электрических величин двух схем (рис. 7
18, б):
активной цепи с замкнутыми выводаМИ и пассивной цепи
с источником э. д. с. ОХ, присоединенным к указанным
выводам.
[J::= I А
=
+
_.. а)
ш=m+ffii=
б)
Рис, 7
18. Размыкание ветви.
а
вариант с источником тока; 6
вариант с источником Э, Д. С.
На рис. 7
18 буквой А обозначена задаННая цепь, COДep
жащая источники элеI(трическо
энерrии (активная цепь),
а буквой П
та же цепь в предположении, что на месте
источников оставлены только комплексные сопротивления
или проводимости (пассивная цепь). Знаки сложения и
равенства на рис. 7
18 относятся к токораспределениям.
Практическое применение теоремы об изменении токов
в электрической цепи проиллюстрировано ниже на примере
расчета несбалансированной мостовой схемы.
Пример 7
7. Найти ток в диаrоналыюй ветви мостовой схемы
рис. 7-19, а, если сопротивления в трех плечах моста равны 10 Ом каж-
дое и сопротивление в четвертом плече равно 10,1 Ом; сопротивление
диаrональной ветви 1 Ом.
При равенстве сопротивлений всех плеч (10 ом) ток в диаrональ-
ной ветви отсутствовал бы и через каждое плечо проходил бы ток, рав-
ный 10/20'== 0,5А. Увеличение сопротивления ОЩlOrо плеча на 0,1 Ом
равносильно на основании указанной выше теоремы введеиию в изме
179
ненное плечо дополнительной э. Д. с. 0,1.0,5 '=' 0,05 В (рис. 7
[9, 6).
Последняя вызывает в диаrональной ветви ток, который может быть
вычислен по теореме об эквивалентном ИсточНИКе э.,,1.. с. (см.
7-9).
Искомый ток равен 0,00225 А.
ДЛЯ вычисления этоrо тока можно также воспользоааться Тео-
ремой обратимости (вариант с э. Д. с.), соrласно которой искомый
а.)
Рис, 7-19, Пример 7-7,
6)
в)
ток равен тому току, который проходил бы через плечо с сопротивле-
нием 10,1 Ом, если бы источник э. д. с. 0,05 В был переиесен а диаrо-
нальную ветвь (рис. 7-[9, в).
В этом случае расчет может быть упрощеи, если пренебречь раз-
ницей в сопротивлениях плеч мостовой схемы; приближенное значе-
ние искомоrо тока получается равным 0,05/2,11 '=' 0,00227 А.
7-9. ТЕОРЕМА 06 ЭКВИВАЛЕНТНОМ ИСТОЧНИКЕ
Теорема об эквивалентном источнике часто применяется
в расчетах электрических цепей. С помощью этой важной
теоремы сложная электрическая схема с произвольным чис-
лом источников электрической энерrии приводится к схеме
с одним источником, блаrодаря чему расчет электрической
цепи упрощается.
Существуют ДВа варианта теоремы об эквивалецтном
источнике: вариант с источником Э. д. с. и вариант С петоч-
ником тока.
Теорема об эквивалентном источнике 1. д, с,
Ток в любой ветви тп линейной электрической цепи не
изменится, если электРl-lческую цепь, к которой подключена
дающя ветвь, заменить эквивалентным источником э. д. С.,
копwрая должна быть равна напряжению на выводах разом К-
нупwй цепи тп, а внутреннее сопротивление источника
180
должно равняться входному сопротивлению пассивной
электрической цепи состорОliЫ выводов т и n при разомкну-
той ветви тn.
Данная теорема доказывается следующим образом:
в ветвь тn вводятся две равные и противоположно направ-
ленные э. д. с" О тn при условии, что О тn равно напряже-
нию между выводами т и n при разомкнутой ветвн тn,
т. е. напряжению холостоrо хода (рис. 7-20).
.
I
I А t!]
1 А
.
= 1 А
+ I п
= 1 А I ""'! + I п
п
j й т " О тп
=
j и тп
=
. .
1 и т "
Рис. 7.20, Теорема об эквивалентном источнике напря-
жения,
Применение метода наложения в соответствии е р ие. 7-20
приводит к выводу, что ток в ветви Z равен:
! . (; тn
=== 20+Z '
rде Zo
комплексное сопротивление всей пассивной це-
пи П. Таким образом, ток в ветви Z получается впредпо-
ложении, что
анная ветвь подключена к источнику э. д. с.,
которая равна О тn, а внутреннее сопротивление равно Zo.
Следует заметить, что в соответствии с рис. 7-20 ток в какой-
либо друrой ветви заданной электрической цепи может
быть получен в результате алrебраическоrо сложения тока,
проходящеrо через эту ветвь при разомкнутых выводах т
и n, с током, возникающим в ней под воздействием э. д. С.
О rnn В ветви Z (коrда остальная цепь пассивна). Поэтому,
если известно распределение токов в электрической цепи
при разомкнутой ветви Z, то последующее распределение
(7 -18)
181
токов при включенной ветви находится весьма леrко нало-
жением на предыдущий режим тех токов, которые обуслов-
ливаются воздействием на пассивную цепь э. д. с. О тn
В ветви Z.
Как уже указывалось выше, метод наложения приме-
ним не только к токам, но и к напряжениям. Поэтому,
пользуясь описанным приемом, можно находить также и
распределение напряжений.
При наличии в электрической цепи нескольких
источ-
ников э. д. с. и тока одинаковой частоты напряжение холо-
cToro хода является линейной функцией заданных э. д. с.
и токов источников.
Для доказательства теоремы... об эквивалентном источ-
нике в ветвь вводились две противоположно направленные
э. д. с., равные напряжению холостоrо хода в этой ветви.
Такой
e. прием может быть применен одновременно и
к двум ветвям любой сложной активной цепи. То.rда дей-
ствительное токораспределение в цепи получится как сумма
токораспределений в двух схемах:
1) в активной схеме
при разомкнутых двух ветвях;
2) в пассивной схеме
при питании ее из двух ветвей
источниками э. д. с., равными напряжениям холостоrо хода
на этих ветвях и направленными по токам, т. е. так же, как
напр яжения холостоrо Хода.
Указанный прием представляет удобст
о в том случае,
коrда известно токораспределение при режиме холостоrо
хода для обеих ветвей. Тоrда при замыкании этих ветвей
достаточно лишь наложить токи, полученные из второй
схемы с двумя э, д. с.
.
Е 1
Z2
Z1
Z2
i1
Ez
11 +Zz
а)
Рис. 7-21, Пример 7-8.
6)
Пример 7-8. Пользуясь теоремой об .ЭКВl1валентном ИСТОllнике
9, Д. с., определить токи в ветвях схемы рис. 7
4.,
Размыкаиие ветви и соответственно нахождение напряжения
холостоrо хода MorYT быть произведены в любой из трех ветвей заданиой
электрической цепи, Рисунок 7-21 показан для случая размыкания
ветви ZЗ'
182
Напряжение холостоrо хода ТJ mп находится в Этом случае как
.
'
разность э. д. с. Е 1 И падения напряжения оттока Z + z в комплекс-
1 2
иом сопротивлеини Z1 (р ИС. 7-21, а):
(;,
E
Z Ei
E2
Z2 E i+ Z 1 E 2
mп
1 1 Z1+ Z 2
Z1+ Z 2
Под воздействиеы э. д. с. и mп В схеме рис. 7-21, б через ком-
плексное, сопротивление Z3 идет ток
/
и mп Z2t1 +Z1 E 2
3
Z3 + Z1 Z 2 Z1Z2+Z2ZЗ+ZЗZ1'
Z1 + Z2
который разветвляется в Z1 и Z2: через Z1 проходит ток
Z2 .
Z1 +Z2 'з,
а через Z2
ток
.
i I
Z1 +Z2 з.
Искомые токи в ветвях Zt' и Z2 определяются в результате сложе-
ния токов, проходящих в схемах рис. 7-21, а и б, т. е.
J1= J1
E2 +
Z2 t i+ Z 1 E 2
Z1 +Z2 Z1 +Z2 Z1Z2+Z2Zз+ZзZi
( Z2 + Z3) Е 1
ZзЁ2 .
== Z1Z2+Z2Zз+ZзZi '
i2==
i
t2
Z2t1 + Z1 t 2
Z1+ Z 2 Z1+Z2Z1Z2+Z2Zз+ZзZi
{Zl + Z3) Е 2 + ZзЁi
ZlZ2+Z2Zз+ZзZi .
Даиный пример иллюстрирует применение теоремы об эквива-
лентном источнике э. д. С. дЛЯ вычисления токов в разных ветвях,
причем не Сfавится цель получить решение кратчайшиы путем.
Рис. 7-22. Пример 7-9.
Пример 7-9. Пользуясь теоремой об ЭквиваJlентном ИСТОЧНике
Э. д. с., определить ТОК Бдиаrоцальной веТl3И мостовой схемы рис. 7-22, а.
183
Разомкнув ветвь 25' находнм напряжение холостоrо хода (J тп
как разность напряжений на участках 24 н 23 (рис. 7
22, б):
. Ё Ё 2224
212з Ё
и тп ==2 4 21 +24
Zз 22+23 == (21 +24) (22+23) .
Сопротивление между т н п при Е == О н разомкнутой ветви 2i
равно (рнс. 7-22, в):
2124 2223
20== Zl+Z4 + 22+23 '
На основании (7-18)
i (; тп
5== 20+25 '
Теорема об эквивапентном источнике тока
ТОК в любой ветви тп лиНЕйНОй ЭЛЕктрической цепи не из.llенится,
если ЭЛЕктрическую цепь, К которой подключена данная ветвь, заменить
эквивалентным источником тока; ток этоео источника должеп быть
равен току, проходящему между
выводами т и п, замкнутыми
накоротко, а внутренняя прово-
дUЛtoсть источника должна рав-
няться входной проводимости
пассивной электричеасой цепи
со стороны выводов т и п при
разомкнутой ветви тп.
Данное положение выте-
кает нз условия Эквивалентно-
Рис. 7
23. Теорема об эквнвалент- сти источников напряжения н
тока, а именнЬ: неточник
ном неточнике TOK1j..
э. д. с., которая равна
а[JрЯ-
жению холостоrо хода и тп' а
(рис. 7
23, а), может быть заме-
6
.4
Zo
z
а)
б)
внутреннее сопротивление равно 20
нен источником тока (рис. 7-23, б)
J limn .
тп==
== уои тп .
Последнее выражение есть не что иное, как ток, проходящий
меЖдУ выводами т и п, замкнутыми накоротко (т О к К о р о т к о r о
з а м ы к а н и я). Искомый ток в цепи равен:
. 20' у..,
1== 20+2 Imn== yo+y I mn , (n9)
rде
1
y==Z'
Если известно распределение токов в электрической цепн при за-
короченных выводах т и п, то распределение токов в цепи при включен-
ной ветви 2 может быть найдено посредством наложения на предыду,
щин режим тех токов, которые получаются в результате ПрНсоедине-
184
ния ИСТОЧника тока 1 тп к ветви Z (коrда остальная часть цепи
пассивна).
При наличии в электрической цепи нескольких ИСточников э. Д. с.
и тока одинаковой частоты ток KopoTKoro замыкаиия является лиией-
ной функцией заданных э. д. с. и токов источников.
Пример 7
10. Пользуясь теоремой об эквивалентном источнике
тока, определить ток l з в ветви ZЗ схемы рис. 7-4,
Е1 Zz
. i«! ,
E' ф i. ',
Е 1 Ez
а) 6')
Рис, 7
24. Пример 7-10,
ТОК эквивалентноrо источника равен току KopoTKoro :замЫ:кания
(Zз == О, рис. 7
24, а):
. . Е! Е 2 . .
/тп ==IK == zi + 22 == Y1E 1 + У 2 Е 2 .
К:омплексная проводимость эквивалентноrо источиика равна Уg:Ж
с: У 1 + У 2 . Следовательно, на основании (7-19) искомый ток равен:
jз===
iк=== Уз i K == Z2Ёl+Zl
.
Уо+Уз Уl+У2+ У З Z1Z2+Z2ZЗ+ZЗZf.
7.10. ПРИМЕНЕНИЕ МАТРИЦ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЯ
Математическая СИМволика и правила матричной алrебры позво-
ляют упростить запись систем уравнений, получающихея при расчете
сложных электрических цепей. В Этом отношении матричную алrебру
можно сравнить со стеноrрафией, которая облеr'чает и ускоряет запись.
Напомним, что м а т р и ц а представляет собой совокупность
величин, называемых ее элементами и расположенных в виде прямо-
уrольной таблицы 1. Если чиСло строк равно числу столбцов, то мат-
рица ,называется квадратной. Матрица, содержащая один столбец,
называется столбцовой или матрицей-столбцом.
ПрИ13еденная в
7-2 система уравнений, записанных по второму
закону К:ирхrофа для контурных э. д. с. и контурных токов, может
быть представлена в виде произведений квадратной матрицы собствен-
ных и общих сопротивлений контуров на столбцовую матрицу контур-
1 Матрицу не следует смешивать с определителем. Определитель
может быть вычислен, матрица же не может быть приравнена числу,
а может равняться только матрице. Две матрицы считаются равными,
если онИ содержат одинаковое чиСло строк и столбцов и если равны
все их соответственные элементы.
185
ных токов. При этом следует помнить, что про изведением двух матриц
иазывается матрица, элементы которой равны сумме произведений
всех элементов соответствующей строки первой матрицы на COOTBeT
ствующие элементы столбца второй матрицы. Итак, уравнеиия (7
2)
в матричной форме имеют вид:
Ё 1
Ё 2
Z{ll)
Z(21)
Z(12) ... Z(1n)
Z (22) ... Z (2n)
ii
i 2
Ё
n
Z(nf) Z(n2) ... Zl1m>
/-п
или сокращенно
11 Ё 11==11 Z 11'1] ill.
Данное матричное уравнение может быть решено относительно
матрицы 11111. Для этоrо обе стороны уравнения должны быть умно-
жены на матрицу, обратную матрице 11 Z /1:
11 Z 11
1'11 Ё II==I!Z 11
1,1I Z1j'll ill.
l(aK известно, для получения обратной матрицЫ неоёiходимо заме-
нить в исходной матрице. каждый элемент ero алrебраическим дополне.
нием, затем заменить строки соответствующими столбцами 1 и получен-
ную таким образом матрицу разделить на определитель исходной мат-
рицы. Напомним, что алrебраическим дополнением элемента квадратной
матрицы называется умноженный на (
I)i+k определитель, получаю-
щийся из элементов матрицы после исключения i-й строки и k
ro столбца.
В ,свою очередь определителем матрицы называется определитель, со-
ставленный из элементов квадратной матрицы, расположенных в том
же порядке, что и в матрице. Итак, обратная матрица имеет ВИД:
[\11 Д2! ... Дп1
1'112 А 22 .... Д,.2 .
,
1
11 Z 11
1 ==
Дz
Д1n Д2п ... Дnnl
здесЬ Дz
тот же определитель системы, что и в
7-2.
Произведение обратной матрицы на исходную матрицу равно еди-
ничной матрице, т. е. квадратной матрице, у которой все элементы rлав-
ной диаrонали (идущей от левоrо BepxHero уrла к прааому нижнему)
равны еДинице, а остальные элементы равны нулю.
Следовательно,
11 Z 11
1'11 ZII==11 1 11
и
11 Z Р .11 Ё 11 == 11111 . 11 i 11.
rде 111 11
единичная маiрица.
1 Матрица, получающаяся в результате замены строк соответст-
вующими столбцами, называется сопряженной или транспонирован-
ной относительно исходной
атрицы,
186
Произведение единичной матрицы на матрицу 11111 раВНО матрице
11111. поэтому
11 i 11 ==" z 11
1 . 11 Е 11.
или в развернутой форме
li Ан A 2 f .. . Anf. Ei
/2 1 Ai2 А 22 .. . А п2 Ей
А...
ln Ain А 2п .. . А пп Е п
в результате умножения матриц получаются выражения для кон.
турных токов вида (7-4).
Аналоrично решается маТрИЧиое уравнение для узловых напря.
жений
11/11==11 у 11'" (;11.
r
e 11111 и 11 (J 11
столбцовые матрицы токов, заданиых В узлах, н
НСКомых узловых напряжений; 11 У 11
квадратная матрица собствен-
ных и общих проводимостей 'узлов;
11 у II
I . 111 [1 ==" у I[
:t . 11 у 11 ' 11 (; 11.
откуДа
11 (;[1==11 у 11
A '11/11.
В результате умножения матрнцы 11 У 1I
1 на матрицу 11111 noлу-
чаются выраження для узловых напряжений вида (7-6).
Матричная алrебра широко прнменяется для расчета сложных
четырехполюсников (см. rл. 9). .
В случае относительно простой электрической схемы без взiшм-
ной индукцин матрица контурных сопротивлений леrко записывается
непосредственно по заданной схеме. В более сложных случаях матрица
контурнык сопротивлений может быть получена с помощью матрицы
сопротивлений ветвей. Ниже показана связь, существующая между
матрицамн контурных сопротивлений и сопротивлений ветвей 1. Вывод,
сделанный в общей форме, проиллюстрнрован на примере простой
схемы рис. 7-25. леrко решаемом обычным способом.
.Обозначим токи, напряження, э. д. С. и сопротивлення ветвей ИН-
дексом «в», а соответствующие контурные велнчины
нндексом «к».
Связь между токами в ветвях и контурными токами выражается зави.
Симостью .
11 / в 11 == [[ с 11 . [1 i к 11.
(7 -20)
ЗдесЬ 11 с Ilf
М а т р и ц а к о н т у р о в .(ннциденций). Чнсло
ее строк равно чнслу ветвей, а число столбцов числу контурных токов.
Элементами матрнцы контуров служат чнсла + 1,
1, н О, + 1 означает,
что выбранные на схеме положнтельные направления тока и ветви и
KOHTypHoro тока совпадают;
1 берется, КоrДа их направления раз-
личны
наконец, О означает, что данная ветвь Не вход.ит в рассматривае-
мый контур. .
1 Существует также и зависимость между матрицами проводимостей
[Л. 9. 15 и 16]
187
Наqример, для CX
MЫ рис. 7-25 HM
eM:
ia 1 О О
b 1
1 О
1
1 с О 1 О. 12 .
id О 1
1 i3
'с О О 1
Урзвн
ния вида (1-12) по второму закону Кирхrофа в матричной
форме записываются так:
IICIIT' 11 ив 11==11011, (7-21)
rде 11 С II Т
матрица, транспонированная относительно матрицы кон-
туров 11 С 11 и отличающаяся от последнеЙ тем, что строки заменены
столбцами.
Строкз 11 С II T , так же как и столбец 11 С 11, содержит кроме нулей
единицы на местах, соответствующих ветвям ЦЮIНо!'о контура; поэтому
«про изведение» ее на 11 О в 11 дает алrебраическую сумму напряжений
ветвей этоrо коитура. Соrласно второму закону Кирхrофа алrебраиче-
екая сумма напряжений на ветвях в любом контуре равна нулю, т. е.
«произведение» любой строки
11 С II T на столбец 11 О в 11 должно
равняться нулю, что и выра-
11, жаеr (7-21).
v' Например, для схемы рис.
7-25 имеем:
rz
И а
1 1 О О ИЬ
.
О
1 1 О И с ==
О O'
1 1 j И d
IИ с
Рис. 7
25. Схема к примеру расче-
та матричным методом,
Считая, что направления э. д. с. и токов в ветвях совпадают, полу-
чаем матрицу напряжений на ветвях в виде
11 ив 11==11 ZB 11'11 i B II
[I Ев 11.
[Jодстановка (7
20) и (7-22) дает:
11 ZB 11.11 С 11'11 ' к II
II Ев 11==11 ив 11,
а подстановкой (7
23) в (7-21) получаем:
1I C[IT .11 ZB 11.11 С 11.11 i K II
II С I
.11 Ев 11==0,
I1 CIIT .11 ZB II'IICII'II i K 11== 1I СlIт 'IIEBII.
Сопоставив это уравнение с уравненнем для контурных токов
11 ZK II.II/ K 11==11 Е к 11,
(7-22)
(7
23)
откуда
приходим К выводу, что э. Д. с. в ветвях и контурные э. д. с. связаны
матричным уравнением
11 С IIT .11 Ев 11== I1 Е к 11, (7
24)
а матрица контурных сопротивлений получается по формуле
11 ZK 11 == 11 G-IIT .11 ZB [1.11 С 11.
(7 -25)
188
Для схемы рис. 7-25 матрица сопротивлений ветвей записывается
в виде
l'
i О О О О
j(f)Li О О О
1
IIZB 11== О о j(f)C 2 О О (7-26)
О О О j(f)L 2 О
О О О О '2
Матрица контурных сопротивлеиий соrласно (7-25) равна:
I
i О О О О 1 О О
1 1 О О О j(f)l"i О О О 1
1 О
1
О
1 1 1 О 'О О j(f)C О О О О
О О О
1 1 О О О j(f)L 2 О О 1
1
О О О О '2 О О 1
'i + j(f)Li
j(f)Li О
j(f)Li j(f) (L 1 +L 2 )+7
jш1"
. (7
27)
. 1Ю
О
j(f)L 2 '2 + j(f)L 2
7.11. ДУАПЬНЫЕ ЦЕПИ
ПОД условием Д у а л ь н о с т и понимается такое соответствие
электрических цепей, при котором закон изменения контурных токов
в одной цепи подобен закону изменения узловых напряжеиий в друrой
цепи.
Для элементов электрической цепи, изображенных на рис. 7-26
(слева и справа), 3ависимосТи между напряжениями и токами имеют
ВИД:
и т == ,lr;
di r .
U L
Ldt ;
t
Uc==
5 (с dt;
oo
(7-28)
ir
g'ur;
. , dll C 1
lс==С сп-; 1
iL==
' SULdt.
(7.29)
co
189
Следует иметь в виду, что входящие в уравнения (7
28) и (7-29)
напряжения и токи, имеющие одинаковые буквенные обозначения, не
равны друr друrу.
, Из сравнения уравнений (7-28) с уравнениями (7-29) ВИДно,
что условию lJ.уальности удовлетворяют следующие элементы:
. 1) сопротивление и проВо.
димость ;
2) индуктивность и емкость;
3) источник э. д. С. и Источ-
ник тока. .
Элементы цепи, удовлетво-
ряющие условию дуальности,
называются аналоrами или ду-
альными элементами.
При последовательном сое-
динении элементов цепи '-СУМ-
мируются напряжения, при па.
раллельном соединении элемен-
тов цепи
токи. Поэтому После-
довательному соедииению эле-
ментов соответствует параллель-
ное соедннение их аналоrов,
а _ параллельному соединению
Элементов
последовательное
соед
ение их аналоrов.
Например, при замене послеДоватеЛЬНQ соединенных элементов "
L и С (рис. 7-27, а) их аналоrами g', с' и L', соединеннымн параллельно
(рис. 7-27,6), получаем дуальные цепи,
1"
9'
L
с'
t=1
ic С i" [/
e
Рис. 7-26, Дуальиые элеМентЫ,
а)
Рис. 7-27. Дуальные цепи,
1
g' с'
2
б)
L'
Уравнение напряжений для исходной цепи
t
di . 1 S
е (t) ==,i + L
+
i dt
dt С
о:>
(7-30)
подобно уравнению токов для второй цепи
. (t) , С , du 1
t ==g и+ dt + L'
t
S tL dt.
(7 -31)
o:>
Контурному току i в уравнении (7.30) соответствует узловое напря-
жение и в уравнении (7-31),
190
Если э. д. с. и ток источников подчинены одному и тому же закону,
например синусоидальны, и имеют одинаковую начальную фазу, то
законы изменения KOHTypHoro тока в схеме рис. 7
27, а и узловоrо на-
пряжения в схеме рис, 7-27,6 совпадают при соблюдении пропорции
, L L'
g' == С' == С'
в случае сложной электрической цепи каждой ее области, оrрани
ченной независимым контуром, с учетом также области, внешней по
отиошению ко всей цепи, соответствует узел дуальной цепи, Следова-.
тельно, число областей заданной цепи равно ЧИСJIУ узлов дуальной
цепи.
При построении дуальной цепи по отношению к заданной планар-
ной цепи удобно пользоваться следующим rрафическим приемом
(рис. 7-27).
В каждой области, оrраниченной независимым контуром заданной
цепи, наносится точка, рассматриваемая в качестве будущеrо узла
дуальной цепи.
а)
(7-32)
Рис. 7-28. fрафический прием построения дуальных цепей,
Узлы, соответствующие каждой паре смежных областей, соеди-
няются параллельными ветвями, число которых равно числу элементов,
последовательно включенных в цепь, rраничащую с указанными обла
стями. Элементами параллельных ветвей являются аналоrи элементов
заданной цепи.
fрафический способ построения дуальной цепи иллюстрирован
ииже на примере рис. 7-28.
Исходная цепь (рис. 7-28, а) содержит три независимых контура.
Виутри этих контуров фиксируем три точки (J, 2 и 3), соответствующие
узлам исходной дуальной цепи. Четвертую точку, соответствующую
узлу 4, фиксируем в области, внешней по отношению к заданной цепи,
Проводим между этими точками пунктирные линии, пересекающие
элементы цепи и представляющие собой ветви дуальной цепи; пересекае-
мые элементы заменяются их аналоrами, включенными между соответст-
вующими узлами дуальной цепи.
, При соrласовании направлений э. д. с. и токов дуальных источ-
ников руководствуются следующим правилом; если э. Д. с. источника
ействует в положительном направлении контура (по ходу часовой
191
стрелки), то ток источника тока в дуальной цепи направлен к узлу,
соответствующему данному контуру исходной схемы.
Следует заметнть, что еслн rрафический способ построения дуаль-
ной цепи повторно применить к схеме рис. 7-28, б, то получится исход-
ная схема рис. 7-28, а.
Существуют дуальные электрические цепи, имеющие одинаковую
схему, например MOcToBoro типа (аВТОДУ'альные схемы).
При соблюдении пропорцнн (7-32) комплексное сопротивление
цепи, общей для двух смежных контуров схемы, пропорционально ком-
плексной проводимости цепн, соединяющей два соответствующих узла
дуальной цепи. Например, в схеме рис, 7-27, а комплексное сопротив-
ление цепи равно:
z
' + j ( rol,
ы
) .
а в сХеме рис. 7-28,6 комплеКСН2Я проводимость цепи
У , , . ( 1 С ' )
== g
1 VJL'
ro .
Полаrая
fI'==F; L'==k 2 C; С' == k
'
rде k
коэффициент пропорциональности, имеющий размериость со.
противления, получаем:
Z==k 2 Y'.
Аналоrичная пропорциональность получается и между входным
сопротивлением н проводимостью более сложных дуальных цепей. Это
свойство используется, в частности, в теории электрических фильтров
(см, rл, 10).
'7-t1. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАлоrии
Явления, исследуемые на основе законов физики, описываются
математически при помощи систем уравнений. Исходя из единстаа
уравиений, соответствующнх некоторым двум явлениям, происходящнм
в различных областях, например в электрической цепи и механической
системе, можно установнть аналоrню между этими явлениями. «Един-
ство природы обнаруживается в «поразительной аналоrичности» диф-
ференциальных уравнений, относящихея к различным областям явле-
ний» 1.
Блаrодаря единству уравнений электрических и механических
систем исследование явлений в механической системе может быть за-
менено исследованием процессов в электрической цепи. Выполнение
электрических цепей обычно сопряжено с меньшими трудностями,
чем выполнение механических систем; они более компактны и, что
особенно важно, измерения в них более точны и удобны. Процессы
в электромеханических снетемах, представляющих совокупность Э,1ект-
1 В. И. Л е н }f н. Материализм и эмпириокритицизм, Полн. собр.
соч, б-е изд., т, 18, с, 306.
192
ричеСkИХ и механичеСКИХ устройств, таКЖе MorYT с успехом исследо-
ваться с помощью электромеханических аналоrий.
Механические системы с сосредоточенными параметрами, которые
по аналоrии с электрическими цепями будем называть механическими
цепями, состоят из активных элементов (источников энерrии) и паСС}lа-
ных элемеитов. '
Рассмотрим идеализированные элементы простейших линейиых
механических цепей, совершаЮЩ!lХ поступательиое или вращательное
движение (комбииированное поступательно,вращательное движение
ОI:IУСТИМ)'
. В случае поступательноrо движения задаиная внешияя сила, при- _
ложениая к цепи, рассматривается как источник силы, а заданяая ско-
рость какой-либо точки цепи
Kaj< источник скорости.
В случае вращательноrо движения задаиный вращающий момеит,
приложенный К цепи, рассматривается как источник момента, а задан-
ная уrловая скорость какой-либо точки
как источник уrловой ско-
рости.
Роль пассивных Элементов в механических цепях выполняют
массы, моменты инерции, пружины и механические (демпфирующие)
сопротивления. ' .
М а с с о й называется идеализированный элемент механической
цепи, обладающий инерцией. В нем накапливаетсЯ кинетическая энер-
rия. При этом термин «масса» И соответствующее ему условное обозна-
чение m примеияются для обозначения как caMoro инерционноrо эле-
мента, так и ero количественной характеристики. Сила F (ньютон
Н),
приложенная к U.eHTPY тяжести свободиоrо твердоrо тела, сообщзет
ему лииейную скорость v (м/с) и линейное ускорение dv/dt (м/с 2 ), сов-
па}J,ающие по направлению с силой. Еслн масса неизменна, то
do
Е==т dt ' (7-33)
т. е. масса m (Kr) представляет собой коэффициент пропорциональ-
ности между силой и ускорением.
На вращение тела влииет не только масса, но и распределение ее
оТносительно оси вращения. Поэтому вращающийси инерционный эле-
мент характеризуется моментом инерции J == т,2, rде ,
радиус
инерции тела относительно оси вращения. это пассивный элемент,
а котором накапливается кинетическая эиерrия враLЦения.
Момент М (Н. м), приложенный к свободному твердому телу, сооб-
щает ему уrловую скорость 00 (рад/с) и уrловое ускорение dw/dt (рад/с 2 ).
Если момент инерции постоя неи, то
doo
M==J dt '
(7 -34)
т. е. момент ииерции J (Kr'M 2 ) представлиет собой коэффициент про-
порциоиальности между момеитом и уrловым ускорением.
Кинетическая энерrия поступательноrо движения равна ти 2 /2,
а кинетическая энерrия вращательноrо движения Joo2/2 (Дж).
Пру ж и н а Иrрает роль пассивноrо элем
нта, в котором накап-
ливается потеициальная энерrии, Сила натяжения или давления, раз-
виваемая соответственно растянутой или сжатой пружиной при данном
отиосительном перемещении х (м) ее конца, пропорциональна ее жест-
кости К, измеряемой в Н/м == Kr/c 2 .
193
Сила Р, необходимая для относительноro перемещения х конца
пружины, действует вдоль оси х и равна по закону [ука:
Р==Кх==К S v dt.
Продифференцировав обе части уравнения, получим:
M
V==KI d,t '
(7-35)
Величина, обратная К, называется податливостью пружины.
Момент, необходимыи для создания уrловоrо перемещения ер
конца пружины, подверrающейся скручиванню, пропорционален жест.
кости К (Н'м/рад):
м ==Кер==К S (i) dt,
откуда
dM
(i) == K
I
ёJ.[ .
(7
36)
В этом
лучае коэффициент пропорциональиости К: 1 называется
податливостью при кручении.
Потенциальная энерrия при растяжении или сжатии пружины
1 1
равна "2 Кх 2 , а потенциальная энерrия при скручивании "2 Kq.>2 (Дж).
Демпфирующее механическое сопротивле-
н и е создается вязким трением. Вследствие механическоrо сопротивле-
ния происходит необратимый процесс преобразования кинетической
энерrии в тепло.
В линейной механической цепи с поступательным движением сила
трения пропорциональна первой степени относительнон скорости точек,
прннадлежащих трущимся поверхностям:
F == {rJ, (7 -37)
rде f
коэффициент трения (Н,с/м == Kr/c).
При вращателыlOМ движении МOM
T силы трения проnoрционален
первой степени относительиой уrловой скорости:
м == f lJ!f. == f(j).
dt
(7-38)
В этом случае коэффициент трения f измеряется в Н'м,с/рад ==
== кr.м 2 /(с.Р&Д).
Мощность, расходуемая на трение, равна при поступательном
движении fv 2 , а при вращательном f(i)2 (Вт).
Сопоставление уравнений (7
33)
(7-38) с уравиениями элементов
электрических цепей
L di . С dи .
и== dl;
== dt ; и==п
показывает, что механическая сила и вращающий момент соответствуют
иапряжению, линейная и уrловая скорости
току, масса и момент
инерции
индуктивности, податливость пружины
емкости, меха-
ническое сопротивление
сопротивлению,
194
На рис. 7-29 приведены изображения пассивных элементов механи-
ческой цепи с поступательным движением 1 и повазаны их электриче-
ские аналоrи.
Рассмотreнная Система электромеханических аналоrий, сведенная
в табл. 7
1, не является единственной. Взяв дуальную электрическую
цепь, можно заключить, что механическая сила и вращающий момент
соответствуют току, линейная и уrловая скорости
напряжению, масса
и момент инерции
емкости, податливость пружииы
индуктив-
ности, мехаиическое сопротивление
проводимости.
Дифференциальные уравнения движения механической цепи MorYT
быть выведены на основе в т о р о r о з а к о н а Н ь ю т о н а, кото-
рый для поступательноrо движения rласит: если на тело действует
несколько сил, то ero ускорение совпадает по направлению с равно-
действующей этих сил и пропорционально отношению последней
к массе тела.
11
..........
0
F=m k
dt
2.с:. L
...............
LL
, di
и=и
dt
11
'{
F :/.
х
i с
F=Kx
I
dx I<
1 dF
11 =Е= ёlt LL
u. = ...!L.
с
. dq dи
1..= dt = С dt
.j
F=f11
1'
и
u. = 1'1..
Рис. 7-29. Пассивные элементы механической цепи с поступа-
тельным движением и их электрические аналоrи.
ДЛя вращательноro Движения применяеп:я следующая формули-
ровка Bтoporo закона Ньютона: если относительио оси вращения тела
действует несколько моментов, то ero уrловое ускорение относительно
той же оси пропорционально отношеllИЮ реаультирующеrо момента
к моменту инерции тела.
Дифференциальные уравнения движения механической цепи MorYT
быть также получены на основаниИ при н ц и п а Д а л а м б е р а:
при движении тела действующие на Hero силы и сила инерции удовлет-
воряют уравнению равновесия сил.
УравНения TaI{oto же типа, получаемые для электрlltJеских Цепей
на основании зllконов I<ирхrофll, MorYT быть либо уравнениями напря-
жений, либо уравнениями токов.
В качестве примера рассмотрим простейшую механическую систему:
масса т находится под воздействием снлы F и опирается на пружину
(рис. 7-30, а). Тело движется между неподвижными направляющими,
и Между ним 11 lIаl1равляющими- возникает вязкое трение, Массой пру-
жllilы преllеб реr.!leМ.
1 Механическое соПротивление изображаеТСJI в виде демпфера.
195
Электромеханические анапоrии
Таблиц" 7-1
еханическая цепь
Электрическая цепь'
Сила F (н) или вращающий момент
M(H.
'
Перемещение линейное х (м) нли уrло-
Бое ер (р ад)
Скорость линейнаЯ v (м/с) или уrло-
вая m (рад/с) .
Масса т (Kr) или момент инерции J
(Kr . м 2 )
Податливость K
l при поступательном
движениИ (м/н) или кручении
[рад/(Н . м))
Коэффициент трения f при поступа-
тельном движении (Kr/c) или вра-
щении [Kr. м2/(с. рад)]
1
Кинетическая энерrия 2" ти 2 или
1
2" Jm 2 (дж)
Потеициальная эиерrия
1
Кх2 или
2 .
1
2" К ер2 (Дж)
Мощность от ,трения 'и 2 или 'ы 2 (Вт)
МОЩНОС1Ь Ри или МФ (Вт)
Напряжение и (8)
Заряд q (кл)
Ток i (А)
Индуктивность L (r)
Емкость С (Ф)
Сопротивление , (ом)
Маrнитная энерrия
и2 (дж)
2
Электрическая эиерrия
1
2" Си 2 (дж)
Мощность В СОПРОТивлеиии
,i 2 (Вт)
Мrновенная мощиость иi (Вт)
На рис. 7-30, б изображена схема даниой механической цепи. По
IlТОРОМУ закоиу Нью
на
dv S
т iп==F
fv
К v dt
или
dv S
F.:=fv+т dt +К v dt.
Польsуясь первой системой электромеханических аналоrий (сила
иапряжение, табл. 7-1), получаем уравиение электрической цепи, по-
казаиной иа рис. 7-30, 8: '
e=='i+L
+
S i.dt.
В свою очередь, применив вторую систему аналоrий (сила
ток),
получим уравиение электрической цепи, показанной из рис. 7-30, е:
i.:=g'и+c'
+l
S иdt.
196
Таким образом, можно пользоваться двумя системами. электромеха-
нических аналоrий: в одной из них напряжение, а в друrой
ток
являются аналоrом силы или вращающеrо момента. Две электрическне
цепи, аналоrичные одной и той же механической цепи, являются дуаль-
ж Шj
1
а.) б)
1 iИЕG'
"
В) а)
Рис. 7-30. Механическая цепь .(а и б) и ее электрц-
ческие аналоrи (8 и е).
ными, так как контурные токи одной цепи соответствуют узловым
иапряжениям друrой.
Электромеханические аналоrии находят практическое применение
в электрических моделях. Вопросы, затронутые в этом параrрафе,
подробно рассмотрены в [Л, 5].
7-t3. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
7-1., Методом контурных токов определить ток в ветви Zз рис. 7-4.
О т в е т см. в тексте (пример 7-4).
7-2. Методом узловых напряжений ОПРеАелить напряжеиие иа
ветви Zз рис. 7-7. '
О т в е т:
V2/i
Vii 2
VIV2+V2Vз+VзVi'
7-3, Решить задачу 7.2,-методом наложения.
7-4. Решить задачу 7-1 по теореме об Иiменении токов в электри-
ческой цепи, зная ток в ветви при
з == о. .
7-5. В схеме рис. 7-4 принять Е 1 == 230 L 300; Е 2 == 230 L 00 В;
Zl == Z2 == jl; Zз ==
jl0 Ом. Используя решение задачи 7-1, в общем
виде вычислить активные мощности и построить векторные диаrраммы,
О т в е т: Р 1 ==
P2 == 13,
кВт.
7-6. В схеме рис. 7-4 Е 1 == 100 L 00 В; Zl == Z2 == jlO; Zз ==
== 20 L 00 Ом.
Найти Ё 2 . если мощность nepBoro источника активная, а BToporo
реактивная.
О т в е т: 212 L
450 В.
7-7. В схеме рис. 7-4 Е 1 == 120 L 00; Ez == 110 L 00 В; Zl == 0,4 +
+ jO,6; Z2 == 0,3 + jl,2; Zз == 10 Ом.
197
ПО теореме об эквивалентном источнике вычислить напряжение
на сопротивлении Z3'
О Т В е т: 113,9 '-
20 В.
7-8. ВычиCJIИТЬ ток В диаroн.а.льной ветви Мостовом схемы рис. 7-22,
если Е == 10 В; Z1 == 20 + j10; Z2 ==
j10; Z3 == 20; Z4 ==
j20;
Z& == 10 Ом.
О т в е т: 0,351 А.
7- 9. Доказать, что при наличии комплексноrо с'опротивления Z
в одной ветвИ электрической цепи ток в какой-либо друrой
Тви равен:
i
t + i(Z
IJ)
i(z
ф) Z
(Z
oo) Z+Zo о,
rде l(Z
YJ)' l(Z
o)
токи во второй ветви при соответственно разомкну-
той и замкнутой первой ветви; Zo
комплексное сопротивление цепи,
к которой подключено сопротивление Z, при отсутствии источннков.
. 7-10. Вычислить ток в индуктивности L 2 схемы рис. 7
29, а, если
е1 == 10 sin rot; е 2 == 20 cos rot В; '1 == '2 == 'з t:=: 1 Ом; L 1 == L 2 ==
== 0,1 Mr; С 1 === С 2 == 1 мкФ; f === 400 [ц. .
Применить: а) метод контурных токов; б) метод узловых Ifапряже-
ний; в) теорему об эквивалентном истоqнике.
7-11. На примере рис: 7-28 показать, что если отношение Комплекс-
ных э. д. с, и тока источников дуальных цепей равно k, то их актив-
ные мощности равны, а реактивные различаются только по знаку (смысл
коэффициента k пояснен в
7-12).
7-12. Пояснить целесообразность применения различных методов
расчета электрических цепей к схемам разной конфиrурации.
7-13. Проиллюстрировать на примере пракrическую целесообраз-
ность применения теоремы об изменении токов в электрической цепи.
7-14. В чем заключается различие между общим и передаточным
взаимным) сопротивлениями?
rЛАВА ВОСЬМАЯ
ИНДУКТИВНО СВЯЗАННЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
8.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ Н ОПРЕДЕЛЕНИЯ
При изменении маrнитноrо поля, связанноrо с каким-
либо витком, в последнем наводится э. д. С. j которай
в соответствии с законом элеRтромаrнитной индукции оп-
ределяется скоростью изменения маrнитноrо потока не-
зависимо от Toro, чем вызвано изменение потока. В ка-
тушке, состоящей из большоrо числа витко!З, наводится
Э. д. с" пропорциональная скорости изменени.я потоко-
сцепления, т. е. скорости изменения суммы маrнитных
потоков, сцепленных с отдельными витками данной Ка-
I
тушки. Если все витки катушки пронизываются ОДНИМ и
тем же маrнитным потоком, то, как указьща.лось в
1-5,
потокосцепление равно произведению маrнитноro потока
на число витков.
При рассмотрении цепей синусоидальноrо тока до
сих пор учитывалось явление самоиндукции, т. е. наве-
дение э. д. с. в электрической цепи при изменении пото-
косцепления самоиндукции, обусловленноrо ТОКОМ в этон
цепи. Отношение потокосцепления самоиндукции к току
характеризовалось скалярной величиной
индуктив-
ностью L.
Теперь нам предстоит заняться рассмотрением явле-
ния в з а и м н о й и н Д у к Ц и И, т. е. наведения э. д. с.
в электрической цепи при изменении потокосцепления
взаимной индукции, обусловленноrо током в друrой элек-
трической цепи. Цепи, в которых наводятся э. д. с. взаим-
ной индукции, называются и н Д у к т и в н о с в я з а н-
н ы М и цеп я м и.
Связь потокосцепления взаимной индукции одной элек-
трической цепи с током в друrой цепи, равная отноше-
нию потокосцепления взаимной индукции 13 одной цепи
к току в друrой цепи, характеризуется в з а и м н о й
и н Д у к т и в н о с т Ь ю 1 М, которая, так же как и индук-
ТИВНОСТЬ, представляет собой скалярную величину.
Если потокосцепление WI Ф М2 первой цепи обуслов-
лено током i 2 второй цепи, то взаимная ИНДУКТИВНОСТЬ
цепей определяется как
М WIФ М2
12==
i 2
(8-1 )
Соответственно если потокосцепление
цепи обусловлено током i 1 первой цепи, то
М
W 2 Ф Мl
21
'
11
w 2 Ф Мl второй
(8-2)
Для линейНых электрических цепей всеrда выполняется
равенство
М 12 :!::: М 2Н
И поэтому индексы у параметра взаимной индуктивности
MorYT быть опущены.
1 ЭтИМ термином заменен применявшийся ранее в литературе и
ныне не рекомендуемый термин «коэффицнент взанмной индукцни».
199
Справедливость последнеrо равенства можно доказать,
если выразить потоки взаимной индукции ФМl и ФМ2
через соответствующие м. д. с. i1Wl И i 2 w 2 И маrнитную
проводимость путей, по которым замыкаются эти по-
токи 1:
Ам == 1, I1i. S ;
Wl (i 2 W\lЛ М ) , }
М 12 == .
W 1 w 2 A M ;
2
w 2 (il W l Л М)
М 21 == i l W 1 w 2 A M ,
Отсюда также ВИДНо, что величиНа М пропорциональна
произведению чисел витков катушек и маrнитной про-
водимости пути общеrо потока, которая заВисит от Mar-
нитной проницаемости среды и взаимноrо расположения
катушек.
На основании сказанноrо формулируется свойство вза-
имности для индуктивно связанных цепей: если ток, про-
ходящий в первой цепи, обусловливает во второй цепи по-
токосцепление взаимной индукции W 2 ФМl' то такой же
ток, проходящий во второй цепи, обусловит в первой цепи
потокосцепление взаимной индУК1{ии U'l Ф М2 той же вели-
чины.
(8-З)
8-2. ПОЛЯРНОСТИ индуктивно СВЯЗАННЫХ КАТУШЕК;
ЗДС ВЗАИМНОЯ ИНДУКЦИИ
Напомним, что положительные Нанравления тока п
создаваемоrо им маrнитноrо потока соrласуются всякий
раз по правилу ПРЗВОХОДовоrо винта, Условимся положи-
теЛЬные направления токов i 1 и i 2 В двух индуктивно свя-
занных катушках считать с о r л а с н ы м и, если поло-
жительные направления создаваемых ими маrнитных пото-
ков самоиндукции и взаимной индукции совпадают.
На рис. 8-1, а и б по казаны индуктивно связанные ка-
тушки, насаженные на общий маrнитопровод; здесь в За-
висимости от направления намотки витков выбраны такие
положительные направления для токов i 1 И i 2 , при которых
1 Картина распредеJIення MrHoBeHHblX силовых трубок потоКов
Ф Мl И Ф М2 не зависит от токов i 1 И i 2 . т. е. при любых токах она одина-
кова; поэтому проводимость Л М для каждоrо из этих noтot<oB одна и
та же,
200
маrнитные потоки самоиндукции и взаимной индукции в
каждой катушке совпадают. Таким образом, рис. 8-1, а
и б иллюстрирует соrласное направление токов.
При соrласном направлении токов i 1 и i 2 В двух индук-
тивно связанных катушках выводы этих катушек, относи-
тельно которых токи ii И i 2 направлены одинаково, назы-
вают
я о Д н о и м е н н ы м и или о Д н о n о л я р-
н ы ми.
На рис. 8-1, а, rде витки обеих катушек намотаны 8 од-
ном направлении, одноименными выводами явля
ся вы-
воды, отмеченные точками (два друrих вывода на рис. 8-1, а
составля
вторую пару одноименных выводов).
а) 1 2
flf1
'Ч е1М 1., е2М
б
.Н .Н
1 цм t,ezM
Рис. 8-1. Соrласное направление токов в индуктивно свя-
занных катушках,
Аналоrичным образом на рис. 8-1, б, rде витки катушек
намотаны в противоположных направлениях, одноименные
выводы также отмечены тс>чками.
Таким образом, одноименные выводы индуктивно свя-
занных катушек характерны тем, что при одинаковом на-
правлении токов i 1 и i 2 относительно этих выводов мazнит-
ные потоки самоиндукции и взаимной индукции в каждой
катушке складываются.
В связи с введением понятия об одноименных выводах
при вычерчивании электрических схем нет необходимости
показывать намотку витков индуктивно связанных катушек,
а достаточно раЗ}1етить на схеме их одноименные выводы.
На рис. 8-2 показано схематическое изображение двух
индуктивно связанных катушек с указанием одноименных
выводов и выбранных положительных направлений то-
ков i 1 И i 2 . Как это следует из сказанноrо выше, токи i 1
и i 2 направлены соrласно на рис. 8-2, а и встречно на
рис; 8-2, б.
В
1-5 отмечалось, что положительное направление
э, д. с. самоиндукции выбирается совпадающим с поло-
жительным направлением тока; поэтому положиТельные
201
направления маrнитноro потока и наводимой им э. д. с.
самоиндукции связаны правилом правоходовоrо винта.
Точно так же и положительное направление э. д. с. вза-
имной индукции е1М, наводимой в катушке 1 током i 2 ,
прииимается совпадающим с положительным направле
нием Тока i 1 . Соответственно положительное направление
э. д. с. Езаимной индук
ции е2М, наводимой в Ka
тушке 2 током i 1 , совпа-
дает с положительным на.
правлением i 2 . При таких
условиях и соrласном на-
правлении токов i 1 и i 2 В
формуле э. д. с. взаимной
индукции имеется знак
«минус», так же как в фор-
муле э. д. с. самоиндукции
(1
2), причем положитель
ное направление маrнитноrо потока и наводимой э. д. с.
взаимной индукции связано правилом правоходовоrо винта:
W 1 dФМ2 di }
е1М ==
а! ==
M t#;
w 2 dФ М1 dif
е2М ==
dt ==
м dt.
Рассмотрим случай, коrда через катушку 1 проходит
ток i 1 , причем di 1 /dt > О. На основании (8-4) в катушке 2
di.
наводится э. д. с. взаимной индукции е2М ==
м CIf < О.
в этом случае потенциал вывода катушки 2, одноимен-
ный с тем, в который входит ток i 1 , оказывается выше потен-
циала BToporo вывода катушки 2.
Oтi;юда можно заключить, что одноименные выводы двух
индуктивно связанных катушек обладают той особенностью,
чnw подведение к одной из них возрасmающеео тока 8bfЗbl(J(JRт
пО8ышение потенциала на одноименном выводе вnwрой ка-
тушки.
На указанном свойстве основано экспериментальное
нахождение одиоименных выводов индуктивно связанных
катушек. Одна из них включается в цепь источника по-
стоянноrо напряжения, а к друrой присоединяется вольт-
метр постоянноro тока (рис. 8-3).
Если в момент замыкания цепи источника стрелка изме-
рительноro прибора отклоняется в сторону положительных
202
i 1 i2 if i2
:J е5 е
а)
6)
Рис, 8-2. Схематическое изображе-
ние ИИДУКТИDНО свйзанных кату-
шек с обозначением одноименных
выводов и выбраиных Положений,
(8-4)
показаний, то выводы индуктивно с
язан'ных катушек,
подключенные к положительному пOJlЮСУ источника элек-
трической энерrии и положительному ВЫВОДУ измеритель-
Horo прибора, являются одно-
именными.
Теперь рассмотрим случай
в с т р е ч н о r о направления
токов i 1 и i 2 , схематически изо-
браженный на рис. 8-2, б, rде
токи i 1 и i 2 направлены раз-
лично относительно одноимен-
ных выводов.
Ввиду Toro что положитель-
ные направления маrнитных по-
токов самоиндукции и взаимной индукции в этом случае
противоположны, э. д. с. взаимной индукции при встреч-
ном направлении токов вычисляются по формулам, содер-
жаIЦИМ знак плюс:
Lfv
G
Рис. 8-3. Экспериментальное
определение одноименных BЫ
ВОДОВ,
W 1 dФ М2 М di 2 . )
еlМ
dt dt '
w 2 dФ Мl di 1
е2М == dt
М ' dt .
(8-5)
Рассмотрим последовательное соединеиие двух индук-
тивно связанных катушек (рис. 8-4, а и 6).
При соrласном направлении токов (рис. 8-4, а) э. д. с.
. М di2 М dii
взаимнои индукции е 1 М ==
dt и е2М ==
d{' СОВ-
падаЮLЦие по направлению с токами, MorYT быть при об-
ходе контура в том же направлении заменены падениями
напряжения от взаимной индукции и1М ==
e1M и и2М ==
==
e2M' Поэтому суммарное напряжение на обеих катуш-
ках с учетом Toro, что i 1 == i 2 == i, равно:
. + L dii М di2 . L di2 + М dil
u cor =='1 l 1 17+ d{+'2 l 2+ 2Т ([t ==
==('1+ r 2)i+(L 1 +L 2 +2M)
t ' (8-6)
Полученное выражение покаэъrвает, что две индук-
тивно связанные катушки, соединенные последовательно,
при соrласном направлении токов эквивалентны катушке,
имеЮLЦей активное сопротивление '1 + '2 и индуктивность
L 1 + L 2 + 2М.
203
Таким образом, как и следовало ожидать, наличие
взаимной индукции при соеласном напрi18лении тo
oв в Ка-
тушках, соединею!ых последовательно, увеличивает индук-
тивность цепи.
При встречном направлении токов (рис. 8-4, б) паде-
ние Iiапряжения от взаимной индукции при обходе контура
в направлении тока получается со знаком минус:
. . + L dii М di2 + . L di2 М dif
и аСТ =='1 / 1 1dt
dt '2/2+ 2dt
dt==
==('1+t
)i+(L1+L2
2M) :
. (8-7)
Данное выражение показывает, что две индуктивно
связанные катушки, соединенные последовательно, при
встречном направлен ии' токов
эквиваJ1ентны катушке, имею-
щей активное сопротивление
'1 +'2 и индуктивность L 1 +
+ L 2
2М.
Следовательно, наличие
взаu;мLOй индукции при встреч-
ном направлении токов в ка-
тушках, соединенных последо-
вательно, уменьшает индук-
тивность цепи.
На основании сказанноrо
можно сделать следующий вы-
вод: при СО2Ласном направле-
нии токов падение напряжения от взаимной индукции
имеет ЗНак плюс, а при BCmpeqHOM
Знак минус (обход
цепи в обоих случаях соверщается в положительном На-
правлении тока).
L1 ,.....M
1 Lz 1'Z
. .
.,...-1>,/
'1.1 а) 'I.Z
.L1
Mr;:;----..Lz. 1'Z
...,...-i>
7.1
б)
-r-1>
'1.Z
Рис. 8-4. Сеrласное (а) и встреч-
ное (6) направления токов в
индуктивно связанных катуш-
ках, соединенных последова-
тельно.
8-З. КОМПЛЕКСНАЯ ФОРМА РАСЧЕТА ЦЕПИ С ВЗАИМНО,",
ИНДУКЦИЕIit
Представив ток в комплексной форме, получим вы-
ражение ;), д. с. взаимной индукции для случая соrласноro
направления токов в комплексной форме:
М :t / meffiJt ==
j(J)M i пl!jfiJt ,
ОТКуда комплексная действующая э. д. с. взаимной индук-
ции
204
Ем ==
j(J)Mi
и соответственно падение напряжения от взаимной индук-
ции
{; м == j(j)M/,
.
rде j(j)M --:-- комплексное сопротивление взаимной индук-
ции; в радиотехнике ero называют с о про т и в л е н и е м
с в язи.
Комплексные напряжения, соответствующие (8-6) и
(8-7), запишутся так:
(;cor == ['1 +'2 + j(j) (L 1 + L 2 + 2М)] /;
. (;вст == ['1 +'2 + j(j) (L 1 + L 2
2М)] /.
Отсюда, между прочим, вытекает -следующий способ
нахождения взаимной индуктивности М: если через X cor
обозначить Индуктивное сопротивл
ние цепи при соrлас-
ном направлении токов последовательно соединенных эле-
ментов, а через Х ВСТ
то же при встречном направлении,
т. е. положить
X cor == (j) (L 1 + L 2 + 2М); . }
Х ВСТ ==, (j) (L 1 + L 2
2М),
(8-8)
то в результате вычитания BToporo равенства из первоrо
получим:
м
X cor
Х вст
4ы .
На рис. 8-5 изображены векторные диаrраммы для
случаев соrласноrо и встречноrо направлений токов двух
индуктивно связанНыХ катушек, соединенных последова-
тельно. При построении векторных диаrрамм принято,
что L 1 > М И L 2 > М. При этом как при соrласном, так и
при встречном направлениях токов ток 1 отстает по фаз
от результирующеrо напряжения {). Если принять L 1 < М,
TO
И В этом случае ток получится отстающим, так как
всеrда L 1 + L 2
2М > О (см.
8-4). Условия L 1 < М И
L 2 < М одновременно существовать не MoryT.
Порядок расчета разветвленных электрических цепей
при наличии взаимной индуктивности иллюстрирован
ниже на примере схемы рис. 8-6. Предполаrается, что эле-
менты L1' L 2 и L з , входящие в схему, связаны индук-
тивно.
Заданными являются э. Д. с. Ёi и Ё } и все параметры
цепи. Искомыми являются токи 11,12 И 8'
205
Если бы в каждом контуре был только один индуктивно
связанный элемент, то запись уравнений для контурных
токов не вызывала бы затруднений. В данном же случае
о
j шL , 1
1"111
j шL 2 i
7'21
jшм1
jшм1
jfIJL 2 1
j шL 1 1
Рис. 8
5. Векторные диаrраммы при соrласном (а) и
встречном (6) направлениях токов,
удобнее писать уравнения непосредственно для токов в вет-
вях, по первому и второму законам Кирхrофа. Совершая
обход контуров по направлению токов 11 и 12. будем со-
ставлять уравнения напряжений по второму закону Кирх-
.
1
Z1
Ь1
'11f".." Ь: z.
.
.
M1J
. ;)Ми,
i.r
· j u s Е,
Z.r
Рис. 8-6. Разве1вленная электрическая цепь со взаим-
ной индукцией, .
rофа с учетом падений напряжения в сопротивлениях
взаимной индукции. При соrласном направлении токов
падение напряжения в со?ротивлен
и взаимной индукции
входит со знаком плюс (и м == j(j)M/), а при встречном
206
со знаком минус (О м ==
jwMj):
Е 1 == (Zl + jwL 1 ) i 1 + jWM 12 i 2
jwм 1з i э + (;з;
Е 2 == (Z2 + jfJ.)L 2 ) i 2 + jWM 12 i 1
jwм 2з i з + (;з;
(;з == (Zэ + jwL s ) i э
jwM 1 sil
jwм 2з i 2 ; i 1 + i 2 == i з ;
здесь ИЗ
напряжение между узлами схемы. Решение
уравнений дает токи.
Отметим, что слаrаемые с одинаковыми взаимными
индуктивностями входят в уравнения с одинаковыми зна
ками, что может служить проверкой правильности записи
уравнений.
Таким образом, расчет разветвленной электрической
цепи при наличии взаимНОЙ индуктивности может быть
приведен одним из описанных ранее методов с учетом па-
дений ,напряжений в сопротивлениях взаимной индукции.
Метод узловых напряжений в данном случае непо-
средственно неприменим 1, так как токи в ветвях зависят
не только от напряжений между узлами, к которым при
соединены эти ветви, но и от токов друrих ветвей, с кото-
рыми они связаны через взаимную индукцию.
В разобранном выше примере одноименные. ВЫВОДы
всех трех индуктивно связанных элементов были обозна-
чены одинаково (звездочкой), так как предполаrалось,
что эти элементы имеют общий
неразветвленный маrнитопровод.
В том случае, коrда три или
большее число элементов распола
"2
rаются на сложном, разветвленном
маrнитопроводе, необходимо одно-
именные выводы каждой пары ин- rz
дуктивно связанных элементов обо-
значать разными условными зна-
ками (см. пример 8
2). Рис, 8-7. Пример 8-1.
Пример 8
1. Определить комплексное
сопротивление на входе электрической
цепи, состоящей из двух параллельно соединенных катушек, связанных
индуктивно при соrласном направлении токов (рис. 8-7).
Для положительных направлений контурных токов, показанных
на рис. 8-7, составляем контурные уравнения:
Ё == (ri + jwL 1 ) ii + jwMi 2 ; Ё == (r2 + jwL 2 ) i 2 + jwMii.
Обозначим:
Zl"""l+ jwL l; Z2==r 2 +jwL 2 ; ZM==jwM;
1 См. сноску на с. 214.
207
тоrда
Е == Z1/1 + Z М/2; Е == Z М/1 + Z/2'
Решив уравиения относнтельно /1 и 12' найдем общнй ток:
. ...Zl+Z2
2ZM
I==/i+I 2 ==r. Z Z
Z2
12М
Искомое сопротивление всей цепи по отношению к выводам источ.
ника
Ё Z1Z2
Z7u
z
J
Z1 +Z2
2ZM
При переключении концов одной из катушек получается парал-
лельное соединение катушек со встречным направлением токов. В этом
случае в уравнениях и конечном выражении для Z следует принять Z м
со знаком минус, что приведет к изменеНИЮ знака при 2Z м в знамена-
теле упомянутоrо выражения.
а)
Рис. 8
8. Пример 8-2.
L;s
б)
При отсутствии индуктивной связи (z м == О) конечное выраженне
совпадает с известной формулой для сопротивления 1J.BYX параллель-
ных ветвей.
Пример 8-2. Составить уравнения контУ.рных токов для электри-
ческой цепи, состоящей из источника э. д. с. Е, емкости С и трех индук-
тивно связанных катушек, насаженных на трехстержневой маrнито-
провод (рис. 8-8, а). Взаимная индуктивность катушек М 12 , М 1З и М 2З .
Цепь рассматривается как линейная (М == сопst).
Рисунок 8-8, б изображает электрическую схему заданной цепи.
Точками, кружками и квадратиками обозначены одноименные выводы,
соответствующие каждой паре катушек.
Выбрав направления контурных токов, указанные на схеме
рис, 8
8, б, составляем контурные уравнения:
Е== . l С (li+J2+JЗ)+('i+jroL1)Ji+jroМi212
jroМiз/з;
Jro
Е == . l С (/i+ J 2+ I з ) + ('2+jroL 2 ) J2+jroМi2/i+jWМ2зlз;
Jro
. 1 . . . '"
Е == jroc (fi+ 12+ lз) + ('з+ jroL з ) [з
jroМ 1З [1 + jroМ 2З [2'
208
Совместное решение уравнений дает токи.
Предлаrается читателям приведенную выше систему контурных
уравнений получить матричным методом, рассмотренным в
7-10..
У к а з а н и е. Матрица соединений JJ:ЛЯ схемы рис, 8
8 имеет
ви
:
I! CII==
1 1 1
1 О О
О 1 О
О О 1
Матрица сопротивлений ветвей равна:
I j
C о о
11 ZjJ 11 == о '1 + jwLf jwM 12
О jwM 12 '2 + jwL 2
О
jwМ 1з jwМ 2з
о
jwМ 1з
jwМ 2з
'3+ jwL31
8-4, КОЭФФИЦИЕНТ ИНДУКТИВНОМ СВЯЗИ.
ИНДУКТИВНОСТЬ РАССЕЯНИЯ
Рассмотрим картину маiнитноrо поля индуктивно свя-
занных катушек, схематически представленную на рис. 8.9
(для соrласноrо направления токов). .
ПоЛожим, что первая катушка состоит из Wl витков,
а вторая из W 2 витков, расположенных в каждой катушке
настолько близко друr к
друrу, что маrннтный по-
. ток охватывает целиком
витки данной катушки.
В общем случае, коrда
по обеим катушкам прохо-
дят токи i 1 И i 2 , маrнит-
ные потоки MorYT быть
представлены как резуль-
тат наложения потоков, Рис. 8-9. Маrнитные потоки двух
создаваемых каждым током индуктивно связанных катушек.
В отдельности.
На рис. 8.9 приняты следующие обозначения маrнитных
потоков: \
Фl
весь поток, созданный током i 1 первой катушки;
ФМl
поток взаимной индукции первой катушки,
пронизывэ,ющий витки второй катушки;
, ФSl
поток рассеяния первой катушки, пронизываю-
Щliй только витки этой катушки;
209
Ф2' ФА12 , ФS2
аналоrичные потоки, созданные током 12
второй катушки;
Ф м
общий поток взаимной индукции, пронизываю-
щий витки обеих катушек.
Из сказанноrо следует, что
Ф1==ФS1+ Ф М1; Ф2 == ФS2 + ФМ2; ФМ==ФМ1+ Ф М2'
Чем меньше потоки рассеяния ФS1 И ФS2' тем больше
приближается ФМ1 к Ф1 И соответственно ФМ2 к Ф2'
При изменении токов i 1 и i 2 во времени изменяются
также и потоки, создаваемые этими токами. Индуктив-
ность каждой катушки, как изВ€стно, определяется отно-
шением потокосц
пления самоиндукции к току данной
катушки:
L == W 1 Ф 1 == W 1 Ф S1 W 1 Ф М1 ' }
1 if if + if '
W 2 Ф 2 W 2 Ф S2 W 2 Ф М2
L2==
==
+
i э i э ia'
(8-9)
Первые слаrаемые этих выражений:
L
WI Ф sf . L
W2 Ф sа
S1
if ' S2
i э
(8-10)
называются и н д у к т и в н о с т я м и р а с с е я н и я
к а т у ш е к.
Маrнитные потоки MorYT быть выражены через пр()изве-
дения м. д. с. на маrнитные проводим()сти путей, по ко-
торым замыкаются эти потоки:
ФS1 == i 1 w 1 A s1 ; ФS2 == i 2 w 2 A s2 ;
Ф1И1 ==-i 1 w 1 А м ; ФМ2 == i 2 w 2 A M .
Следовательно,
L 1 == wi (A S1 + А м );
L 2 == wHA s2 + А м ). (8-11)
Таким образом, индуктивность катушки пропорцио-
нальна квадрату числа витков и сумме маrнитных про-
водимостей путей потоков рассеяния и взаимной индук-
ции (см. Э 1-7).
Маrнитная проводимость в свою очередь зависит от
формы и размеров катушек, их взаимноfо расположения
и маrнитной проницаемости среДЫ (см. Э 8-1). На осно-
вании (8-1), (8-2), (8-9) и (8-10) индуктивности рассея-
210
ния L S1 И L S2 можщ) выразить через Ll
L 2 и М следующими
формулами:
wi W
L S1 == L1"'....,.
М; L S2 ==L2
М. (8-12)
W2 Wi
Эти выражения нам понадобятся в следующем пара
rрафе при рассмотрении схемы замещения трансформа
тора.
Степень индуктивной связи двух катушек характери-
зуется к о э Ф Ф и ц и е н т о м с в я з и k, определяемым
как среднее reометрическое из отношении потока взаимной
индукции ко всему потоку ка тушки, т. е.
k== ,j Ф Мl ФМ2 (8-13)
r Фi Ф2'
Если выразить потоки через параметры L 1 , L 2 и М по
формулам (8-1), (8
2) и (8-9) , то получим :
k == ' j Mil
i Mi 2 w. 2
r W2 L l l 1 WI L 2 1 2
или
k == м . (8-14)
V L 1 1" 2
ИЗ формулы (8-13) видно, что коэффициент связи всесда
меньше единицы (так как ФМl/ Ф l < 1 и ФМ2/ Ф 2 < 1).
КоэФI>ициент связи возрастает с уменьшением ПQТQКQJ;J
рассеяния ФSl И ФS2'
С учетом (8-3) и (8
11) коэффициент связи может быть
выражен через маrнитные проводимости:
k==:. Ам .
V(ASl +Л м ) (Л S2 +Л М )
Повышение коэффициента связи достиrается бифиляр-
ным способом намотки катущек (рис. 8-10, а) и применением
маrнитrщровода, так как с увеличением маrнитной прони
цаемости и соответственно маrнитной проводимости маrни-
топровода доля потоков рассеяния снижается.
При перпендикулярном расположении осей катушки
(рис. 8-10, б) коэффициент связи обращается в нуль. Поэ-
тому, перемещая одну катушку относительно друrой, можно
плавно изменять коэффициент связи в широких пределах,
а при последовательном соединении этих катущек плавно
изменять 'их результирующую ИНДУКТИВНость. Такое уст-
ройство называется в а р и о м е т ром.
211
При наличии маrнитопровода цепь теряет СВОЙСТВО ли-
нейно,СТИ. Однако в тех случаях, коrда по условиям работы
маrнитная индукция в маrнитопроводе не выходит за пре-
делы прямолинейноrо участка кривой. намаrничивания и
ero маrнитная проницаемость может быть пр.инята постоян-
ной, данная цепь рассматривается как линейная и изложен-
ная выше теория сохраняет силу.
Как уже указывалось, схематическая картина Mar-
нитноrо поля на рис. 8-9 соответствует соrласному на-
правлению токов. Если изменить на рис. 8-9 положитель-
ное направление тока i 2 ,
то изменится направление
ма.нитных потоков ФS2 II
ФМ2' что будет соответ-
ствовать встречному на-
правлению токов.
В этом случае в урав-
нениях, приведенных вы.
ше, должен быть изменен
знак перед i 2 , ФS2' ФМ2 И
Ф2' При этом, как видно
из предыдущих формул, величины Ll' L 2 , М, k, L S1 И L S2
сохраняются неизменными.
В предыдущем параrрафе было показано, что при
встречном направлении токов в двух катушках, соеди-
ненных последовательно, результирующая индуктивность
равна L 1 + L 2
2М.
Докажем теперь, что величина L 1 + L 2
2M всеrда
положительна. Дляэтоrо воспользуемся двумя неравен-
ствами:
:t: J Кп
4) ()
Рис. 8-10. Катушки с коэффициен-
том связн. близким к единице (а)
и нулю (6).
и
(1I L1 ,
1I L2 )2 == L 1 + L 2
2 V L 1 L 2
О
1I LIL2 >M.
Заменив в первом неравенстве 11 L 1 L 2 меньшей вели-
чиной М, подучим:
L 1 +L2
2M >0.
Пример 8-3. Индуктивная катушка имеет w витков, соединенных
последовательно.соrласно. Индуктивность каждоrо витка равна [.
Приняв коэффициент связи ВИТкоВ равным единице, определить резуль-'
тирующую индуктивность катушки.
При отсутствии рассеяния ВЗаимная индуктивность каждой пары
виткоа равна L. По аналоrии с (8-6) результирующая индуктианостъ
212
катушки определится суммой индуктивностей всех витков и взаимRой
индуктианости, умноженной на. число размещений из w витков по два:
Lрез==wL+А
L.
Так как
A
w!
(w
2)! == (w
1) w,
то
Lрез==wL+(w
1) wL==w 2 L.
Как и следовало ожидать, па основаиии выражений (8-11) резуль-
тирующая индуктивность катушки пропорциоиальиа квадрату числа
витков,
а.5. УРАВНЕНИЯ И СХЕМЫ ЗАМЕЩЕНИЯ
ТРАНСФОРМАТОРА &Е3 МАrНИТОПРОВОДА
Т р а н с фор м а т о р представляет собой аппарат, пе-
редающий энерrию из одной цепи в друrую посредст-
вом электромаrнитной индукции. Он применяется для
различных целей, но чаще Bcero предназначается для пре-
образования переменных напряжений и токов 1. Трансфор-
матор состоит из двух или
нескольких индуктивно
. связанных обмоток, наса-
женных На общий маrнито-
прОВQД.
В настоящем параrрафе
рассматривается двухобмо-
точный трансформатор без Рис. 8.11. Трансформатор без Mar.
маrНитопровода. Такой нитопровода;
трансформатор может слу-
жить СОставной частью линейной электрической цепи
в устройствах электроавтоматики, и
мерительной техники
или связи.
Если пренебречь распределенными емкостями, суще-
ствующими как между витками каждой из обмоток транс-
форматора, так и между самими обмотками и обмотками и
землей, то трансформатор может быть представлен .схемой
рис. 8-11, в которой активные сопротивления обмоток
условно вынесены и изображены отдельно.
Обмотка трансформатора, ПРИGоединяемая к источнику
питания, называется пер в и Ч н о Й, а обмотка, к которой
i .
....1.0. 7'1
, 7'2!!.
00
1 Отсюда происходит само назаание «трансформатор», т. е. преоб-
раЗоаатель,
213
подключается наrрузка,
в т о р и ч н о й. Соответственно
напряжения и токи на выводах этих обмоток называются
перв!;;!чными и вторичными. Следует заметить, что такие
наименования в некоторых случаях являются условныIи,,
если в зависимостц от режима энерrия может передаваться,
,как в одну, так и в друrую стороны.
При заданной полярности выводов обмоток транс-
. форматора на схеме рис. 8-11 токи направлены встречно
(что в данном случае не имеет принципиальноrо значе-
ния).
Уравнения трансформатора в дифференциальной форме
при встречном направлении токов имеют вид:
. L dii М di2 . L di2 М dii
и 1 == '1 t 1 + 1&
dТ;
и 2 == '2 t 2+ 2 dТ
&.
Если напряжения и токи синусоидальны, то уравне-
ния трансформатора в комплексной форме запишутся
следуюЦJИМ образом:
(;1 == . ('1 + jюL . 1 ) i1
jЮМ . i2; }
(8-15)
и 2 == ('2 + ]юL 2 ) i 2
]юМi 1 ,
Эти ура:внения равносильны следующим:
(;1 == ['1 + jю (L 1
М) + jюМ] i 1
jюмi 2 ;
(;2 == ['2 + jю (L 2
М) + jюМ] i 2
jюмi 1 .
Последние уравнения являются контурнь
ми ypasHe-
ниями, которые соответствуют схеме рис. 8-12.
Следовательно, эта схема может рассматриваться в ка-
честве схемы замещения трансформатора без Маrнитопро-
вода. В отличие от рис. 8-11 в схеме замещения первичная
и вторичная цепи трансформатора связаны не индуКтивно,
а rальванически 1.
Если L 1 == L 2 , то L 1
М > О и L 2
М > О, так как
коэффициент связи k:t=% M/V L 1 L 2 < 1. При неравных ЗНа- .
чениях L 1 и L'lJ одна из разноетей (L 1
М или L 2
М) мо-
жет оказаться отрицательной, Например, если W 1 :> W2,
то на основании (8-12) L1> М И L 2 < M
В этом случае
схема замещения рис. 8-12 может быть практически осу-
ществлена толъко при фиксированной частоте, Коrда от-
рицательная индуктивность может быть замещена емко-
1 Такая схема замещения дает возможность, например, приме.
нить метол узловых напряжений в цепи со взаимной индукцией,
214
стным элементом; в общем же случае схема с линейным
элементом, имеющим
рицательную индуктивность, прак-
тически нереализуема.
Входящие в схему рис. 8-12 разности L 1
М И L 2
М
имеют физический смысл только при одинаковом числе
витков первичной и вторичной обмоток (Шl == Ш 2 ); в этом
случае, как видно из (8-12), они представляют собой ин-
дуктивности рассеяния L S1 и L S2 первичной и вторичной
обмоток трансформатора.
При неодинаковых числах витков первичной и вторич-
ной обмоток (Wl:f= Ш 2 ) на практике часто пользуются так
называемой при в е Д е н -
н ой. схемой замещения
трансформатора, показан-
ной на рис. 8-13. Приве- 1Ut
дение заключается в том, t
что напряжение (;2 и ток 12
заменяются величинами,
приведенными к первичнqй Рис. 8-12. Схема замещения транс-
обмотке: напряжение U 2 форматора без маrнитопровода.
умножается на п, а ток 12
делится на 'п. Здесь п == ШI1Ш2
отношение чисеЛ вит-
ков, которое называется к о э Ф Ф и ци е н т о м т р а н с-
фор м а ц и и.
Придав уравнениям (8-15) следующий вид:
й 1 == (r 1 + j(f)L 1 ) 11
jronM /2 ;
n
nU2==n2(r2+ j(f)L 2 )
j(f)nM/ 1t
"'1
и1
M
,.,
L2
M
M
й2 t
!)
можно преобразовать их таким образом:
(;1 == [rl + j(f) (L 1
nМ)] j 1 + j(f)nM/ 1
j(f)nM ь-.;
n
и . 2 [ + . (L М )] ;2 + . М 12 . _ М/ '
п 2 == п r 2 J(f) 2
n n J(f)n n
J(f)n l'
Полученные уравнения являются контурными уравне-
ниями для приведенной схемы замещения трансформатора
(рис. 8-13).
Схема замещения трансформатора, приведенная к пер-
вичной обмотке, содержит: сопротивление '1 и индуктив-
ность рассеяния L S1 первичной обмотки трансформатора;
индуктивность Wi М В поперечной ветви (эта ветвь назы-
Wa
215
вается в е т вью н а м а r н и ч и в а н и я); сопротивле-
ние '2 и индуктивность рассеяния L S2 вторичной обмотки,
приведенные к первичной обмотке трансформатора, т. е.
умноженные на n 2 == (шl/ш2)2 (квадрат отношения чисел
витков).
Индуктивные сопротивления roL S1 и roL S2 представляют
собой сопротивления рассеяния первичной и вторичной
обмоток трансформатора, а индуктивное сопротивление
nroМ
сопротивление ветви намаrничивания. Маrнито-
движущая сила, определяющая общий маrнитный. поток,
который пронизывает первичную и вторичную обмотки,
(W 1 Y (Ш1 )2
1'1 LS1 Ша L S2 w "а
. а
и1
j) !!!.1 м
i
Ш1 .
иa
Ша Ш1 z Ша
Рис. 8
13. Схема замещения, приведенная к пер-
вичной обмотке.
при встречном направлении токов равна i 1 W 1
i 2 w 2 ==
( . W2' )
( . i 2 ) Т . i 2
== t 1
tn Ш 1 == t 1
шl' ок t 1
И соответствую-
Wl . n n
щий ему комплексный ток i 1
i 2 , который В схеме заме-
n
щения трансформатора, приведенной к первичной обмотке,
проходит через ветвь намаrничивания, принято называть
на м а r н и ч и в а ю Щ и м т О к (j м трансформатора.
Схеме рис. 8
13 соответствует векторная диаrрамма,
показанная на рис. 8
14. При построении векторной диа-
rpaMMbI в качестве исходных MorYT быть приняты приве-
денные вторичные напряжение и ток.
Падения напряжения от приведенноrо вторичноrо тока
1 2 /n в приведенных активном сопротивлении '2n2 и индук-
тивном сопротивлении рассеяния roL S2 n 2 вторичной обмотки
rеометрически складываются с приведенным вторичным
напряжением па 2' Полученное напряжение равно паде-
нию напряжения от намаrничивающеrо тока В индуктивном
сопротивлении ветви намаrничивания jronM (il
!}), при-
чем намаrничивающий ток отстает от полученноrо напря-
жения на 90". Первичный ток находится как rеометриче-
216
ская сумма намаrничивающеrо тока и привеДенноrо Вто.
ричноrо тока:
(/1
) +
! == 11'
Падение напряжения от тока 11 в аКifИВНОМ сопротив-
лении и индуктивном сопротивлении рассеяния первич-
ной обмотки rеометрически складывается с напряжением
на ветви намаrничивания, образуя первичное напряжение.
Ввиду Toro что вторичные электрические величины
напряжение й2 и ток 12
В схеме рис. 8-13 приведены
к первичной обмотке, т. е.
изменены пропорционально
отношению числа витков,
данная схема приведенноrо
трансформатора не экви-
валентна исходной схеме
трансформатора. Для Toro
чтобы схема замещения
стала эквивалентной задан-
ной схеме'трансформатора,
можно воспользоваться так
называемым и Д е а л ь -
ным трансформа-
т о р о м, которому будем
приписывать следующие
свойства: при любых усло,:-
внях отношение первич- Рис. 8-14. Векторная днаrрамма
Horo напряжения к вторич-=-- К схеме на рис. 8-13.
ному на выводах идеаль-
Horo трансформатора равно отношению ВТОрllчноrо тока к
первичному и определяется коэффициентом трансформа-
ции п; идеальНЫЙ трансформатор не имеет потерь энерrии и
при разомкнутой вторичной обмотке через ero первичную об-
мотку ток не проходит. В действительности TaKoro транс-
форматора не существует, однако по своим свойствам к нему
приближается трансформатор с коэффициентом связи, близ-
ким к единице, и столь большим числом витков, что сопро-
тивление ero ветви намаrничивания jюпМ == jюwjА м прак
тически равно бесконечности.
Дополнив схему рис. 8-13 идеальным трансфор.мато-
ром с коэффициентом трансформации п, получим экви-
валентную схему трансформатора (рис. 8-15).
Рисунки 8-12
8-15 соответствуют в6речному направ-
лению токов, принятому в исходной схеме рис, 8-11.
о
!!с
2' .
. 12
I
1 п
217
Схема замещения с измененным положительным на-
правлением вторичноrо тока соответствовала бы соrлас-
НОМУ направлению токов в исходной схеме.
"'1 L1
nM n Z (L2'. Л:) nZl"z
и1 ] (f . @.
пй е
Ш 1
Рис. 8
15. Схема замещения с идеальным трансформатором
(п == W1!1JI.'2)'
Пример 8-4. Решить пример 8-1 с помощью схемы замеЩения
трансформатора (см. рис. 8
12).
Рассматривая иидуктивно связаниые элементы схемы рис. 8-16, а
в качестве траисформатора с попарно соединенными первичными и
вторичными выводами и пользуясь схемой замещения рис. 8-12 (с из
менением направления тока 12)' получаем эквивалентную схему
рис. 8-16, б без индуктивных связей. .
i
..........j>
i
..........j>
iz
а)
Рис. 8-16. Пример 8
4,
а
НСХОj!ная схема; 6
схема аамещения.
')
Комплексиое сопротивление всей цепи равно:
Z Е . М+ ['f+jw (Lf
M)] [r2+jw(L2
M)]
'='
'-'Jw .
j 'i+'2+jW (Li+L2
2M)
Применяя сокраЩеННую запись
Zl =='1 +jwL 1 ; Z2=='2+ jwL 2; ZM==jwM,
находим:
(Zl
ZM) (Z2
ZM)
Z==ZM+ Z +Z
2Z
l' _ 2 М
ZlZ2
ZM
Zl+Z2
2ZM
218
8-6. ЭНЕрrия ИНДУКТИВНО СВЯЗАННЫХ 06МОТОК
--
Рассмотрим вопрос об энерrии индуктивно связанных обмоток.
Дифференциадьные уравнения двух индуктивно связанных обмоток
при встречном направлении токов (см. рис. 8-11) имеют вид:
. di 2 dif
0== U2+,./2+L2
M
. dt dt .
. dii М di2
щ==r1 / i+ L i
.
dt dt'
Умножив первое уравнение на i 1 , а второе на ё 2 , сложив И сrруппи-
ровав слаrаемые, получим:
. . + '2 + " +L ' dii +
L ---.di2 М ( . di2 + ' di 1 )
Pi==и1 / i==U2 / 2 '1/1 '2/2 1/i([[ 2/2dY
li dt 12&
или
dw
'2 + '0 + м + .
Pi=='1 / 1 '2/2 dt
и2 / 2'
rДе Ш м
энерrия Маrнитноrо поля:
L '2 L '2
1/1 + 2/2 М .,
шм==т T
11/2'
Как и следовало ОЖидать, мrновенная Щ)ЩНОСТЬ,подводимая к траис-
форматору через первичные выводы, равна сумме MrHOBeHHbIx значе-
ний мощностей, расходуемых иа HarpeB обмоток, скорости изменеиия
энерrИII Ш м , наliоплеинои в маrиитном поле, и мощности, передаваемой
наrрузке.
Первое слаrаемое энерrии маrнитноrо поля равно энерrии поля
первой обмотки при 12 == о; второе слаrаемое равно энерrии поля вто-
рой обмотки при i 1 == о; третье слаrаеМQе представляет собой энерrию,
связанНую с взаимнЫМ расположением обеих обмоток.
При соrласном направлении ТОКов третье cJtaraeMoe в выражении
энерrии будет иметь знак плюс.
Первое и второе слаrаемые положитеJlЬны, третье же в зависимо-
сти от знаков MrHoBeHHbIx токов i 1 и ё 2 МОжет иметь положительиый или
отрицательный знак. Поэтому энерrия системы, состоящей из двух
индуктивно связанных обмоток, может быть больше или меиыl1e суммы
анерrий обеих обмоток, взятых отдельио.
Пример 8-5. Две ИНДУКТИвно связанные катушки имеют индуктив-
но<:ти L 1 == 4 r и L 2 == 25 r; коэффициент СВsiЗИ k == 0,5.
Определить энерrию ПОЛ$!, создаваемую ЭТими катушками при то-
ках ;1 == 10 А It ё 2 == 20 А.
Взаимиая индуктивность катушеК'
M==kJ! L 1 L 2 ==0,5J! 4.25 ==5 r.
3нерrия каждой катушки, взятой отдельно, составляет:
L 1 iI
4. 102
200 Д . L2i
25. 202
5 /V\(\ Д
ж, """'2
vvv Ж.
Энерrия вввимн:оrо раСПОJlожения
Мё 1 ;2==5. 10.20== 1000 Дж,
219
Энерrия поля всей системы при соrласном направлении ТОКОВ
W M == 200 + 5000+ 1000==6200 Дж,
а при встречном направлении токов
wM=='200+5000
1000==4200 Дж.
1-7. ВХОДНОЕ СОПРОТИВЛЕНИЕ ТРАНСФОРМАТОРА
Если наrрузка 2 и присоединена к источнику эле.ктро-
энерrни не непосредственно, а через трансформатор
(рис. 8-17), то соrласно (8-15):
(;1 == (r 1 + jюL 1 ) 11 + jюмl 2 ;
0== + jЮМ/ 1 + (r2 + jюL 2 + 2 и ) /2'
ел / =+ jooMii
едовательно, 2 == + . L + z ' откуда солротив-
'2 100 2 и
ление на входных выводах трансформатора
Uf . (ы.М)2
2!вх == '"7'" == r1 + fюL 1 + +. L +Z ' (8-16)
lf '2 100 2 и
Третье слаrаемое в правой части выражения (8-16)
представляет собой комплексное сопротивление, в н о с и-
.li.o.
и1
i,
M
.
.
11 ",
11
.......
Рис. 8-17. Присоединение'
наrрузки К ИСТОЧНИКУ че-
рез трансформатор,
1"1 .,
(r.иM)'
rz+jru '-Z+ZH
Рис. 8.18. Схема для оп-
ределения входноrо со-
противления наrруженно-
ro трансформатора,
м о е и з в т о р и ч н ОЙ, Ц е tI и в пер в и ч н у ю;
схема рис. 8-18 эквивалентна схеме рис. 8-17. В зависимости
от' характера 2 и мнимая часть вносимоrо сопротивления
может быть положительной или отрицательной.
Допустим теперь, что наrрузка 2 и присоединена к иде-
альному трансформатору. Учитывая у
ловия [)1/02 ==
== 12/11 == п, которыми характеризуется идеальный Tp
HC-
220
форматор, получим входное сопротивление
1 Ui nи 2 2 1
lBX:::O
:::о
:::O n И'
li
i 2
n
(8-17)
Следовательно, идеальный трансформатор, включен-
ный между наrрузкой и источником электроэнерrии, из-
меняет сопротивление нazР!Jзки nроnорционально квад-
рату коэффициента mрансформации без изменения ееО
уела. '
Это свойство практически используется в различных
областях электротехники, проводно
связи, радио, при-
боростроения, автоматики для уравнивания сопротивле-
z
.
L 1
Р1
а.)
Рис. 8.19. Пример 8.6.
а
ИСХОj!,иая схема; б
схема эамещеНН!I.
!)
ний источника и наrрузки (с целью повышения отдавае-
мой источником мощности). Поэтому в том случае, KorAa
требуется изменить сопротивление какой-либо наrрузки
без изме
ения самой наrрузки, включается промежуточ-
ный трансформатор, по свойствам приближающийся к иде-
альному трансформатору с коэффициентом трансформации,
определяемым на основании (8-17):
n:::о ... / Zlsx ,
r Zи
rде Z1sx
требуемое сопротивление.
Формула (8-17) непосредств
нно вытекает также нз
приведениой схемы замещения трансформатора (см.
рис. 8-13), поскольку идеальный трансформатор не имеет
активных сопротивлений и индуктивностей рассеяния (r 1 :::о
:::о '2 :::о о; L S1 :::O L S2 == о) И ero взаимная индуктивность
равна бесконечности.
221
Входное сопротивление идеальноrо трансформатора при
замкнутых выходных выводах равно нулю, а при разомкну
тых
бесконечности.
Пример 8
6. Определить входное сопротивление цепи, показанной
на рис. 8
19, а.
Пользуясь СХЕ:МОЙ замещения, представленной на рис. 8.19, б,
находим:
Z== _ + . ( L
M )+ f'2+j(t) (L2
M)] fj(OM +Zol
'1 }(О 1 + . L +Z .
'2 }(О 2 О
Пример 8.7. Определить входное сопротивление цепи, состоящей
из двух трансформаторов, включенных каскадно с наrрузкой 'н на вы-
ходе (рис. 8-20, а). Активные сопротивления обмоток трансформаторов
не УЧитываются.
5)EjMtJ
а)
Рис. 8-20. Пример 8
7.
а
IIсходная схема; б
cxe
la заАiещениЯ.
L1
M1 L1
M1 L2
MZ L2
MZ
6)
в соответствии с (8
16) входное сопротивление Bтoporo трансфор-
матора будет:
. ((ОМ 2 )2
22==J(OL2+ ' L + .
J(O 2 'н
Рассматривая Z
в качестве наrрузки nepBoro трансФОРtdатора,
определяем входное СОПрОТИI.'Леиие цепи по той -же формуле (8-16):
. ((ОМ 1 )2
Z==J(OLi+ . L +2 .
J(O 1 2
После преобразоваиия находим:
Z== (о'н (Li+LIL2
Mi)+/(02 (
,iL2
I---L1L
L]М
L2Мj) .
(O(I
IL2+L2
M2)
J'H (Li+L2)
К тому же результату можно прийти на основе схемы замещения,
показаНIIОЙ на рис. 8.20, б.
8.8. АВТОТРАНСФОРМАТОР
А в т о т р а н с фор м а т о р отличается от трансфор-
матора тем, что ero оБМОТl{а низшеrо напряжения является
частью обмотки высшеrо напряжения (рис. 8-21, а). Так
же как и трансформатор, он может быть понижаюI.ЦИМ
или повышающим,
222
Уравнения автотрансформатора в комплексной форме
для указанных на рис. 8
21, а положительных направле-
ний токов и напряжений записываются так:
й 1 == [Т1 + jw (L 1 + М)] i 1 + [Т2 + jw (L2 + M)](i 1
i 2 );
й 2 == [Т2 + jw (L 2 + М)] i 1
(Т 2 + jroL 2 J i 2 .
Эти уравнения соответСТl3уют схеме замещения, пока-
занной на рис. 8-21, б. Правая ветвь схемы состоит из
практически неосуществимоrо линейноrо элемента
от-
рицательной индуктивности (
M). Поэтому полученная
схема замещения рис. 8
21, б может быть использована
только для расчета. Практически осуществить ее можно
только для фиксированной ,частоты, Korдa элемент
M
r>1L1+M
M
1 : ( 7i':. 1",
1JpL2
и2 t
1"1 W(Ш
Ш2)L
W2(Ш
W2)l.,
1"2
WW2!.
0.)
6)
Рис. 8-21. Автотрансформатор без маrнитопровода (а) и ero схемы за-
мещения (6 и в).
замещается емкостью. Однако если индуктивность на-
rрузки, подключенной к выходным выводам, комriенси-
,PY
T отрицательную индуктивность, то схема замещения
автотрансформатора в сочетании с наrрузкой практиче-
ски осуществима.
Итак, схема замещения автотрансформатора представ-
ляет собой трехлучевую звезду. Сопротивления лучей
этой звезды MorYT быть найдены и друrим способом, если
поочередно приравнять суммы сопротивлений двух лучей
сопротивлениям между соответствующими выводами авто-
трансформатора (при разомкнутом третьем выводе).
Обозначим: индуктивность каждоrо витка L, общее
число витков W, число витков обмотки низшеrо напря-
жения W2; приняв коэффициент связи равным единице,
т. е. пренебреrая рассеянием, подучим в этом случае схему
замещения автотрансформатора, показанную на рис. 8-21, 8.
В режиме холостоrо хода автотрансформатора (Т. е.
при разомкнутых выходных выводах), если не учитывать
223
рассеяния, отношение первичноrо напряжения й 1 к вто-
ричному И 2 равно отношению ,cYMMapHoro числа витков
обмотки к числу витков обмотки низшеrо напряжения:
и 1 /и 2 == W/W 2 == п;
п
коэффициент трансформации автотрансформатора.
При наrрузке подводимая к автотрансформатору мощ-
ность передается на вторичную сторону как посредством
электромаrнитной индукции (через маrнитное поле), так
и непосредственно через электрическую связь.
Применение автотрансформатора вместо обычноrо транс-
форматора той же мощности и с таким же коэффициен-
том трансформации дает экономию в меди, затрачиваемой
на обмотку. Экономия достиrается за счет СОI<ращения
общеrо числа витков и уменьшения толщины провода об-
мотки, через которую проходит ток, равный разности пер-
вичноrо и вторичноrо токов.
Экономия в меди тем больше, чем ближе к единице
коэффициент трансформации, так как npll этом умень-
шается разность токов 111
12 1.
8-9. ИНДУКТИВНО СВЯЗАННЫЕ КОЛЕ&А ТЕЛЬНЫЕ КОНТУРЫ
В радиотехнике широко распространены двухконтур-
ные колебательные системы, в которых связь между кон-
турами осуществляется при помощи взаимной индукции.
11 1z 11 i 2
ф:
>
f,;:J fZ
Z"'l cp::
Z "' l
а) б) В)
Рис. 8.22. Индуктивно связанные колебательные контуры (а) и их
схемы замещения (6 и 6).
На рис. 8-22, а показаны колебательные контуры с ин-
дуктивной (трансформаторной) связью. Обозначим 'соб-
ственные сопротивления контуров через Z1::;::'1 + jX 1 и
Z
== '2 + jx 2 . На основании
8-7 сопротивление, вносимое
из вторичной цепи в первичную, равно:
. (ооМ)2 ( ООМ ) 2 . ( ООМ ) 2
ZlBH == '1ВН + /Х lВн ==
== z;- '2
/ z;- Х 2 .
224
На рис. 8-22, б изображена схема замещения для пер-
вичноrо контура. Первичный ток .равен:
. Е
/1== (ffiM)2 ' (8-18)
21+
22
а вторичный ток
/ .
jffiM!i
2
22 .
(8-19)
Следует заметить, что напряжение Z1вп11 на сопротив-
лении, ВНОСИ!>:lОМ из вторичноrо контура в первичный,
равно
j(f)M1 2 .
Подставив (8-18) в (8-19) и умножив числитель и знаме-
натель на Z.iZl' получим;
Ё !5Е М
/ 21
2 == (ooi'v1)2 '
22+
Выражение (8-20) моrло быть выведено и по теореме
об эквивалентном источнике.
Числитель полученной дроби равен э. д. с., наводимой
во вторичном контуре, коrда он разомкнут, а знаменатель
представляет собой эквивалентное сопротивление вторич-
Horo контура, в котором влияние первичноrо контура уч-
тено сопротивлением Z2BH == (roM)2/Z 1 , вносимым из пер-
вичноrо контура во вторичный.
Схема замещения для вторичноrо контура показана
на рис. 8-22, в; здесь
Z2ВИ == '2ВН + jX 2BH == (
y '1
j ( 00: у Хl'
(8-20)
Активные составляющие вносимых сопротивлений всеrда
положительны, а знаки реактивных составляющих Х 1ВН
и Х2ви противоположны знакам реактивных сопротивле-
ний Х 2 и Xl соответственно.
Как 'lвн и '2ВН' так и ХIвн и Х2вн зависят от частоты. По
мере приближения частоты источника
к резонансной ча-
стоте вторичноrо контура 'lВН возрастает, стремясь к макси-
мальному значению 'lBH. мак\: == «(оМ)2/'2' а Х 1ВН стремится
к нулю. В свою очередь если частота приближается к резо-
нансной ч.астот.е первичноrо контура, то '2ВН растет, стремясь
к '2ВН. макс == (roM)2/'l' а Х 2ВН стремится к нулю.
225
8-10. НАСТРОЙКА СВЯЗАННЫХ КОНТУРОВ
На практике часто добиваются получения максималь-
Horo тока /2 (или максимальной мощности Р2) во вторич-
ном контуре. ЭТО достиrается соответствующей настройкой
связанных контуров. Существуют различные способы на-
стройки, а именно:
1) изменением параметров первичноrо контура, на-
пример емкости С 1 ; резонанс, который при этом возни-
кает, называется пер в ы м ч а с т н ы м рез о н а н-
с о м;
2) изменением параметров вторичноrо контура, напри-
мер емкости С 2 ; в этом случае возникает в т о рой ч а с Т-
н ы й рез о н а н с;
3) изменением параметров ОДНоrо из контуров и со-
,противления связи; резонанс в этом случае назыmtется
с л о ж н ы м;
4) изменением параметров обоих контуров и сопро-
тивления связи; в этом случае резонанс называется п о л-
н ы м.
Первый частный резонанс. Соrласно (8-19) вторичный
ток прямо пропорционален первичному, Поэтому максимуму
тока /1 соответствует и максимум 12'
Первый частный резонанс наступает при
Х 1
( ro:: у Х 2 == О. (8-21)
в этом случае:
Е EroM
/lмакс == ( roM ) 2 ; /2макс == (ыМ)2'
'1+
'2 '1Z2+
'2
Z2 Z2
Второй частный резонанс наступает при
( roM ) 2
X2
х 1 ==о.
(8-22)
При этом
/2ыакс ==
ЕооМ
(ооМ)2
'2Z1+
'f
Z1
Сложный резонанс. При настройке первичноrо кон-
тура оптимальное сопротивление связи найдем, прирав-
226
няв нулю первую производную /2М3КС по шМ:
[ (<оМ)2 <оМ ]
д / Е '1z2+
'2
2<oM
'2
2"акс Z2 Z2 О
д (<оМ) == [ + (<оМ)2 ] 2
.
'1 Z 2
'2
Z2
Отсюда
r 1 == ( <Oz
1 У r 2 .
Следовательно, оптимальное сопротивление связи
f 'i
(UМ опт == Z2
.
'2
(8-23)
в этом случае получается максимум максиморум вто-
ричноrо тока:
Е
/2М8кс.М8КС ==
.
2
'1'2
Условия (8
21) и (8
23), которые при этом выполня
Ю'fся, означают, что собственное сопротивление первич
Horo контура равно сопротивлению, комплексно сопря-
женному с сопротивлением, вносимым из вторичноrо кон-
тура в первичный, т. е.
*
Zl == ZlBH'
Из S 3-5 [формула (3-17)] известн
, что это и есть усло-
вие передачи максимума активной мощности от источника
l{ приемнику .
Аналоrично при настройке вторичноrо контура опти-
мальное сопротивление связи равно:
(UМ опт == Zl -.! '2 , (8-24)
V '1
причем условия (8-22) и (8-24) в совокупности означают,
что
*
Z2 == Z2BR>
т. е. и в этом случае выполняется условие передачи мак-
симума активной мощности от источника к приемнику.
При этом
Е
/2макс. макс == . V
.
2 '1r 2
Следовате.ТIЬНО, при сложном резонансе максимум мак-
симорум вторичноrо тока не зависит от Toro, какой из
KOHTypOIj настраивается на резонанс.
227
Полный резонанс. При настройке на полный резонанс
сначала настраивают первичный контур при разомкну
том вторичном, т. е. добиваются условия Х 1 == О. Затем Ha
страивают вторичный контур, добиваясь условия Х 2 == о.
Наконец, подбирают оптимальное СQпротивление связи.
При Х 1 == Х 2 == О
ЕыМ
J2MaKc == '1 r 2+(wM)2 .
Оптимальное сопротивление связи находится из ус-
ЛОВия
д/2макс Е [r1'2+(wM)2,.....2 (ыМ)2]
д (ыМ) == [r 1 r2 + (ыМ)2]2
О,
откуда
roМ опт == v '1'2 '
При этом вторичный ток равен:
Е
J2MaKc.MaKc == 2 ,/
.
r r1'2
(8
25)
Хотя максимум максиморум вторичноrо тока при На-
стройке на ПQ.7JНый резонанс и получается таким же, как
при настройке на сложный' резонанс, насmройка на пол-
ный резонанс имеет то преимущество) что сопротивление
связи меньше, чем при сложном .резонансе; оно как и
актИ1!ные сопротивления '1 и '2' исчисляется еДИНИцамИ ом.
Эффективность передачи энерrии из первичноrо кон-
тура во вторичный оценивается к о э Ф Ф и ц и е н т о м
п о л е з н о r о Д е й с т в и я двухконтурной системы,
равным отношению мощности, поrлощаемой сопротивле-
нием '2' к сумме мощностей, поrлощаемых сопротивлениями
'1 и '2:
Р2
'Il == p
p .
1. 2
Очевидно, Р1 == '1п : Р2 == '2П == '1внп Поэтому
'iBH
'I'J==
.
.'1 + r1BH
I(оrда вторичный контур настроен на частоту источ-
Ника,
(шМ)2 (ыМ)2
'lВН ==
И 'I'J == 'l r 2+ (ыМ)2 .
228
При настройке на полный резонанс <ом == 1/ '1'2 и
11')==0,5.
Если колебательные контуры идентичны и частота
близка к резонансной, то оптимаЛbflЫЙ коэффициент
связи при настройке На полный резоНанс с учепwм (8-25)
примерно равен затуханию контура:
оооМ " 1
k опт ==
L
L ==
Q == d.
000 000
Например, для радиотехнических контуров с доброт-
ностью Q ==:;; 100 оптимальный коэффициент связи соста-
вит k опт
0,01.
8.Н. РЕЗОНАНСНЫЕ КРИВЫЕ И ПОЛОСА ПРОПУСКАНИЯ
СВstЗАННЫХ КОНТУРОВ
Оrраничимся рассмотрением случая, Коrда связанные
колебательные контуры имеют одинаковые резонансную
частоту <00 и добротность Q.
Для построеIffiЯ резонансных кривых вторичноrо тока
воспользуемся выражением (8-20), приняв Z1 == Z2 == Z.
При рассмотрении последовательноrо колебательноrо кон-
тура В
5.2 встречалось выражение
Z == , [ 1 + jQ (
:0 )] == , (1 + j
).
Величина S == Q ( .
(00 ) называется о б о б щ ен н о й
000 00
р а с с т рой к о й контура.
При частотах, близких к резонансной, <оМ
<OoLM/ L==
== Qrk. Поэтому
. ЁjQrk
/2 == ,2 (1 + j
)2+(Qrk)2 '
откуда
1
EQk
2
, v (1 +Q2k2
2)2+4
2'
Отнеся вторичный ток к току J2MaKC. макс == Е/2" полу-
Чим:
/2
/2l\18KC.bl8KC
2Qk
У (1 +Q2k2
2)2+4G2'
(8-26)
229
Если контуры настроены на частоту источника, то
==Ои
120
12макс. маКс
1 + Q 2 k 2 .
Выясним, каким значениям S соответствуют максимумы
резонансной кривой 12112макс. макс' Приравняв нулю ,про
изводную по
от подкорен-
Horo выражения (8-26), полу-
чим три корня:
o == о;
1,2 == + lIQ 2 k 2
1.
При Qk < 1 второй и тре-
тий корни лишены физиче-
cKoro смысла и резонансная
кривая имеет только один
максимум
при 60 == о «О ==
== (00)' Вторичный ток при
этом меньше 12макс. макс'
ПриQk == 1 и
== о полу-
чаем 12112макс. макс == 1, т. е.
, вторичный ток достиrает зна-
чения максимума максиморум.
При Qk > 1 резонансная
кривая получается двуrорбой,
причем впадина двуrорбой
кривой соответствует значению
== о, а 12112макс.макс ==
1 соответствует
==
1 И
==
2'
Сказанное иллюстрируется рис. 8-23.
Леrко показать, что при Qk:> 1, коrда 61,2
+ Qk,
максимумы вторичноrо тока соответс твуют частотам
(01, 2
(00 [ V 1 + (
у +
J.
Коэффициент связи k == 1/Q == d, при котором полу-
чается предельная одноrорбая резонансная кривая, на-
зывается к р и т и ч е с к и м. Он совпадает с оптимальным
коэффициентом связи двух идентичных контуров, настро-
енных на полный резонанс (см.
8-10).
П о л о с о й про п у с к а н и я связанных колеба-
тельных контуров, как и в случае одиночноrо колебатель-
Horo контура, условно считается область частот, на rрани-
цах которой резонансная кривая снижается не более чем
в 112 раз по сравнению С максимумом.
12
IZ/lf4llc. /lfIJNС
Qи=1
Рис. 8
23. Резонансные кривые
связанных колебательных кон-
туров.
230
(8-27)
Так как
l
(00
(O2
(O
(O
(Oo (;)+U)Q
Q
(oo w
(оо(\)
.
"", (О + (00
то приняв вблизи резонанснрй частоты
2, можно
считать, что I G I/Q == 2 I () 1" определяет полосу пропуска-
Ния связанных контуров при Qk;;::: 1 (здесь ()
относи-
тельна5;I расстройка частаrы
см.
5-2), Решением урав-
нения
..!....
2Qk
V2
V(l +Q2k2
2)2+4
a
служит
== + YQ2k2+2Qk
1.
, (8-28)
Это выражение справедлщю до тех пор. пока впади-
на резонансной кривой находится выше или совпадает
1 2Qk
с 1 /V2. В предельном случае V2 == 1 + Q2k2 ' откуда
Qk == 2,41.
ПодстаВИБ э
о значение Qk 2 (8-28), найдем:
Ш
З,1
31d
Q
Q
. .
т, е. при Qk == 2,41 полоса пропусканuя в 3}1 раза больше}
чем у одuночноео колебательною контура.
Если Qk == 1, то I G 1 == У2 и I G I/Q == V r 2d, т. е. поло-
са пропусканuя в lАl раз БОЛbUlе, чем у одuночноео кон-
тура,
При Qk == 0,68 полоса пропускания связанных конту-
ров равна полосе пропускания одиночноrо коитура, а при
Qk < 0,68 она меньше полосы пропускания одиночноrо
контура,
Величина Qk в радиотехнической литературе носит
название пар а м е т р а с в язи.
8-f2. ЗАДАЧН Н ВОПРОСЫ дЛЯ САМОПРОВЕРКН
8-1. Перекрестив в схеме 'рис. 8
7 КОНЦЫ ОДНОЙ Н3 индуктивно свя-
занных катушек, определить сопротивление параллельно соединенных
катушек без учета активных сопротивлений,
j(O (l'lL2
M2)
О Т В е т: [1 + L 2 + 2М .
231
8-2. В, ветвь первой катуl,IIКИ схемы РЦС. 8-7 последовательно вклю-
чена емкость 50 мкФ; '1 == 20 Ом; '2 == 10 Ом; L 1 == 0,2 [; L 2 == 0,1 [;
коэффициент связи равен 0,4. Вычислить напряжение на емкости, если
напряжение на параллельных ветвях равно 100 L 00 В; (j) == 40Q рад/с.
О т в е т: 83,6 L .
1430 В.
8-3. Заданы параметры трансформатора: сопротивление 40 Ом и
индуктивность 0,05 f
для первичНОЙ обмотки, сопротивление 50 Ом
и индуктивность 0,05 r
для вторичной обмотки, коэффициент
связ
0,6. Первичная обмотка присоединена к источнику Э. д. с.
100 L ООВ, вторичная обмотка
к источнику Э. д. с. 150 L 30 0 В;
уrловая частота равна 400 рад/с. Электродвижущие силы источников
направлены к одноименным выводам трансформатора. Вычислить актив-
ные мощности, поступающие от обоих иСточников и идущие на потери
внутри трансформатора. .
Ответ: 128,360 Вт.
8-4. Две индуктивно связанные одинаковые катушки с сопроти-
влением 10 + jl0 Ом каждая, соединены последовательно и соrласно;
сопротивление взаимной индукции равно j4 Ом. К общему выводу кату-
шек подключена емкость
i20 Ом. К свободным выводам катушек под-
ключеиы источники э. д. с. 10 L 00 и 10 L 300 В, вторые выводы
KOТOpЫ
присоединены к свободному выводу емкости.
Наити напряжение на емкости.
. О т в е т: 10,95 L
1018' В.
. 8-5. Трансформатор, имеющий две обмотки на общем маrнитопро-
воде, характеризуется следующими данными: '1 == 100 Ом; L 2 == 1 [;
общее сопротивлен-ие вторичной, обмотки и наrрузки 10 000 Ом; отно-
шение чис.ел витков W2 : W 1 == 10; коэффициент связи k == 0,5. Вычи-
слить параметры схемы рис. 8-12.
, О т в е т: L 1
М ==
0,04 [; L 2
М == 0,95 [; М == 0,05 [.
8-б. Вывести формулу (8-17) на основании выражения (8
16),
положив, что L 1 и L 2 стремятси к бесконечности, М2 == L 1 L 2 ;'1 == '2 == О.
8-7. Какие выводы называются одно полярными?
8-8. Что называется током намаrничивания?
8-9. Пояснить понятие «идеальный тра'нсформатор».
8-10. В чем заключается приведение схемы трансформатора К пер-
вичной цепи?
8-11. Построить векторную диаrрамму токов и иапряжений для
цепи, показанной на рис. 8
7.
8-12. Как применить трансформатор в качестве соrласующеrо
устройства?
8-13. Почему в случае двух индуктивно связанных катушеК не
MorYT одновременно выполняться условия L 1 < М И L 2 < М?
8-14. Пользуясь схемой замещения рис. 8-22, б, построить веюор-
ную диаrрамму токов и напряжений для индуктивно связанных коле.
бательных контуров, настроенных на частоту источника. Уредиться,
что в этом случае пеgвичный ток1 1 совпадает по фазе с э. д. с. Е, аток 12
опережает 11 на 90 .
8-15. Что называется обобщенной расстройкой контура?
8-1б. Как определяется полоса пропускания индуктивно связанных
колебательных контуров?
8-17. Показать, что максимумы двуrорбой кривой рис. 8-23 соот-
ветствуют
1.2 == :!:2,19.
8-18. Как зависит rлубина впадины двуrорбой резонансной кривой
от параметра связи Qk?
232
rЛАВА ДЕВЯТАЯ
ЧЕТЫРЕХПОЛЮСНИКИ
9.1
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КЛАССИФИКАЦИЯ
ЧЕТЫРЕХПОЛЮСНИКОВ
Часть электрической цепи, рассматриваемая по отно-
шению к J1юбым двум парам ее выводов, называется ч е-
ты ре х п о л ю с н и к о м (рис. 9-1). Понятием «четырех-
полюснию> пользуются тоrда, коrда интересуются токами
и напряжениями только в двух ветвях или двух парах
узлов электрической цепи. Так, в качестве четырехполюс-
ника MorYT быть представ-
лены длинная линия, элек-
t=: '
трический фильтр, транс-
форматор, усилитель, кор-
ректирующее и всякое дру-
roe устройство с двумя
парами выводов, включен-
ное между источником и рис, 9-1, Четырехполюсник,
приемником электрической
энерrии, Korдa предметом исследования являются токи
и напряжения на этих выводах, а не токи и напряжения
внутри caMoro четырехполюсника.
Выводы четырехполюсника, к которым присоединяется
источник электрической энерrии, называются в х о Д н ы-
J::
б)
8)
е)
В)
Рис, 9-2, РазновидностИ четырехполюсников.
233
м и, а ВЫВОДЫ, к которым присоединяется наrрузка,
в ы х о Д н ы м и. Ради краткости применяются также тер-
мины «вход» и «выход» четырехполюсника.
На практике возможны случаи, коrда обе пары выво-
дов четырехполюсника являются входными (случай дву-
CTopOHHel"O питания четырехполюсника) или выходными
(случай четырехполюсника, содержащеrо независимые ис-
точники электрической энерrии и наrруженноrо с обеих
сторон).
Четырехполюсники MorYT быть классифицированы по
различным признакам.
. По признаку линейности элементов, входящих в них,
четырехполюсники разделяются на линейные инелинейные.
Ниже рассматриваютсЯ л и н е й н ы {е четырехполюсники.
По схеме внутренних соединений четырехполюсников
различают r-образный (рис. 9-2, а), Т-образный (рис. 9-2, 6),
П-образный (рис. 9-2, в), мостовой (рис. 9-2, е), Т-образно-
мостовой (рис. 9-2, д) и друrие.
Четырехполюсники делятся на активные и пассивные.
Четырехполюсник называется а к т и в н ы м, если он
содержит внутри источники электрической энерrии. При
этом, если эти источники являются независимыми, то
в случае линейноrо четыреХПОЛlOCника обязательным до-
полнительным условием активности четырехполюсника яв-
ляется наличие на одной или обеих парах ero разомкну-
тых выводов напряжения, обусловленноrо источниками
электрической энерrии, находящимися внутри Hero, т. е.
необходимо, чтобы действия этих источников не компенси-
ровались взаимно внутри четырехполюсника. Такой актив-
ный четырехполюсник называется а в т о н о м н ы м.
В случае, коrда источники внутри четыреХПОЛlOCника
являются зависимыми, как это, например, имеет место
в схемах замещения электронных ламп и транзисторов,
то после отсоединения четырехполюсника от остальной
части цепи напряжение на разомкнутых выводах ero не
обнаруживается. Такой активный четырехполюсник назы-
вается н е а в т о н о м н ы м.
Четырехполюсник называется п а с с и в н Ы м, если он
не содержит источников электрической энерrии; линей-
ный четырехполюсник может содержать источники элект-
рической энерrии, взаимно компенсирующиеся таким об-
разом, что напряжения на обеих парах разомкнутых выво-
дов четырехполюсника равны нулю. Так, четырехполюсник
на рис. 9
3, а пассивен, так как любые две э. д. с. четырех-
234
полюсника взаимно компенсируются в контуре (в ypaBHe
ниях Кирхrофа эти э. д. с. взаимно уничтожаются); четы
рехполюсник, изображенный на рис. 9
3, б, пассивен вслед-
ствие Toro что напряжение на выводах ветви с ИСТОЧJ-Iика/v1И
всеrда равно нулю.
Если все э. д. с. в схемах рис. 9-3 приравнять нулю,
то получатся четырехполюсники, эквивалентные в элект-
рическом смысле исходным. Под э к в и в а л е н т н o
.с т ь ю двух четырехполюсников понимается возможность
взаимной замены их в электрической цепи без изменения
токов и напряжений в остальной ее части.
0.)
5)
Рис. 9
3. Четырехполюсники, внутри кото-
рых' действия источников електрическон
энерrии компенсированы.
Различают четырехполюсники симметричные и несим-
меrричнъrе. Четырехполюсник является с и м м е т р и ч-
н ы м в том случае, коrда перемена местами ero входных
и выходных ВЫВОДов не изменяет токов и напряжений
в цепи, с которой он соединен. В противном случае четы-
рехполюсник является н е с и м м е т р и ч н ы М.
Четырехполюсник называется о б р а т и м ы м, если
выполняется теорема обратимости, T
е. отношение Ha
пряжения на входе к току на выходе, или, что то же, пе-
редаточное сопротивление входноrо и выходноrо контуров
не зависит от Toro, какая из двух пар выводов является
входной и какая выходной. В противном случае четырех
полюсник называется н е о б р а т и м ы м.
ПасСU8ные линейные четырехполюсники являются обра
тимыми, несимметричные же активные (автономные и
неавтономные) четырехполюсники необратимы. Симметрич-
ные четырехполюсники всеrда обратимы.
Основной смысл теории четыреХПОЛIOсника заключается
в том, что, пользуясь некоторыми обобщенными пара-
235
метрами четырехполюсника, можно находить токи и напря-
жения на входе и выходе четырехполюсника.
Сложная электрическая цепь (например, канал связи),
имеющая входные и выходные выводы, может рассматри-
вать как совокупность составных четырехполюсников,
соединенных по определенной схеме.
Теория четырехполюсника лозволяетвычислить Пара-
метры TaKoro сложноrо четырехполюсника по парамет-
рам составных четырехполюсников и, таким образом,
получить аналитическую зависимость между токами и на-
пряжениями на входе и, выходе резулыирующеrо слож-
Horo четырехполюсника, не производя расчетов токов Н
напряжений внутри заданной схемы.
Получаемые таким путем значения величин на входе
и выходе позволяют оценить
режим работы передачи
в целом. При этом пользование обобщенными парамет-
рами четырехполюсника дает возможность сопоставлять
и правильно оценивать передающие свойства электрических
цепей, различных по своему типу и структуре.
Теория четырехполюсника позволяет также решать
задачи- синтеза, т. е. находить структуру и элементы
четырехполюсиика по заданным характеристикам (см.
rл. 17).
Основы теории пассивноrо четыреХПОЛIOСllика разра-
батывались мноrими отечественными и зарубежными уче-
ными. Понятие четырехполюсник может быть применено
и к механизму, служащему для передачи силы и скорости
от источника механической энерrии к приемнику. Такой
«механический четырехполюсник», имеющий два полюса
(вход и выход), может быть описан линейными уравне-
ниями, связывающими силы и скорости на полюсах
[Л. 5].
Механическому четырехполюснику соответствует элек-
трический четырехполюсник, построенный по одному из
двух принципов электромеханических аналоrий, указан-
ных в
7-12: силы заменяются напряжениями, скорости
токами, либо силы заменяются токами, а скорости
напряжениями.
В настоящей rлаве рассматриваются активные (не авто-
номные) и пассивные четырехполюсники, имеющие одну
пару входных и одну пару выходных выводов. Рассмотре-
ние общей теории мноrополюсника не входит в рамки дан-
Horo курса.
236
9-2. СИСТЕМЫ УРАВtlЕНИМ ЧЕТЫРЕхпопЮСНИКА
Положим, что имеется четырехполюсник, не содержа-
щий неЗRВИСИМЫХ источников электрической 'энерrии. Обоз-
начим левую пару выводов четырехполюсника цифрами
1
1', а правую пару выводов
цифрами 2
2'. Этоrо
условноrо обозначения будем придерживаться во всем
последующем изложении, приписывая индексы 1 и 2 токам
и напряжениям, относящимся соответственно к левой и
правой парам выводов четырехполюсника. Теми же ин-
дексами 1 и 2 будут обозна-
чаться входной и выходной кон-
туры четырехполюсника.
На рис. 9-4 обозначены при-
НЯТЬJе положительные направле-
ния для токов и напряжений на
выводах четырехполюсника. Ва-
риант с токами 11 и j 2 принято
называть п р я м о й пер е -
д а чей (см. уравнения по фор-
ме 11 А 11), вариант с' токами
1
и 1
о б Р а т н о й пер е -
Д а чей (см. уравнения .по фррме 11 В 11). Используется
такж
вариант с токами 11 И 1;, который будем называть
третьим вариантом (см. уравнения по формам Н У 11, 11 Z 11,
11 Н 11, 11 G 11). Во всех случаях каждое из напряжений 01
и 02 понимается .как разность потенциалов BepxHero
(1 или 2) и нижнеrо (1' или 2') выводов четырехполюс-
ника.
Напряжения и токи на выводах четырехполюсника обус-
ловливаклся присоединением акти
ных цепей к обеим па-
рам выводов либо присоединением активной цепи к одной
паре, а пассивной цепи к друrой паре выводов
четырехпо-
люсника.
Электрические цепи, присоединенные к выводам 1
1'
и 2
2', MorYT быть на основании теоремы компенсации
в любом режиме замещены источниками э, д, с. Ё 1 == 01
И Ё 2 == 02' которые MorYT рассматриваться как контурные
э. д. с., включенны
в два неза.ВИСИМЫJF контура четырех-
полюсника, .а токи 11 ==
1
и 12 ==
I
как контурные
токи.
Соотношения между напряжениями и токами на BXOД
и выходе четырехполюсника MorYT быть записаны в виде
следующих ниже шести форм уравнений:
. "
11
.,
12
..".......
1
Рис. 9-4, Положительные на-
правлендя тОков и напряже-
иий четырехполюсника,
237
1. Форма 11 у 11 : 11 и 1
выражаются 13 заВИСИМОСТИ 01'
(;1 и 02:
11 == Yll U 1 + У12 й 2; }
1
== У21й1 + У 22 й 2 .
2. .Форма 11 Z 11 : (;1 и 02 выражаются в зависимости от
11 и 1
:
1 == ZlJ1 + Z12i
; }
u 2 == Z21 1 1 + Z22 i 2'
3. 9>орма 11 AII : (;1 и 11 выражаются Б зависимости от
(;2 и 12:
(9-1 )
(9-2)
(;1 == A ll U 2 + A 12 i 2 ; }
. (9-3)
11 == А 21 и 2 +А 22 / 2 .
4. Форма 11 В 11 : (;2 и 1
выражаются в зависимости от
(;1 и 1
:
2==Bll
I+BI2!
; } (9-4)
12 == В 21 U 1 + В 22 1 l'
. 5. Форма 11 Н 11 : (;1 и 1
выражаются в зависимости от
11 и (;2:
1==Hll!I+H12?2; } (9-5)
12== Н 21 1 1 + н 22 и 2 .
6. Форма 11 О 11 : 11 И (;2 выражаются в зависимости от
(;1. и 1
:
i. 1 == 01l Li .l + 012/
: } (9-6)
U 2 == оц..и 1 + 022[2'
Из перечисленных выше шести форм уравнений pac
смотрим более подробно формы IL у 11 и 11 А 11.
Коэффициенты и опредеJIИ
ЛИ каждой системы ypaB
нений четырехполюсника MorYT быть выражены через коэф-
фициенты и определители любой друrой системы (см.
приложения II и 111). Таблицы облеrчают переход от одной
формы записи уравнений четырехполюсника к друrой.
Контурные токи 11 И 1
связаны с контурными э. д. С.
Е 1 == (;1 И Е 2 == (;2 (рис. 9-4) линейными уравнениями
(9-1), которые непосредственно___ следуют из (7-11) (см.
7-5), поскольку рассматриваемый четырехполюсник не
содержит независимых ИСточников электрической энер
rии.
238
Коэффициенты У представляют собой входные и пере-
даточные проводимости контуров 1 и 2. В общем слу-
чае
это комплексные величины, зависящие от частоты;
они опредеJI
ЮТСЯ следующим образом:
Ун :::::: (
)
входная проводимость со стороны
Иf и2
O
выводов 1 при закороченных выводах 2;
У 22 == (
)
входная проводимость со стороны
И 2 и,==О .
выводов 2
ри закороченных выводах 1;
( /
)
У 21 ::::::
передаточная проводимость при за-
И 1 и.
o
короченных .выводах 2;
У 12 == (
f )
передаточная проводимость при за-
И 2 и,
o
короченных выводах 1.
В случае обратимоrо четырехполюсника
У 12 == У 21 , (9.7)
т. е. только три коэффициента в уравнениях (9-1) являются
независимыми.
Если четырехполюсник симметричен, то наряду с (9-7)
выполняется условие
УН == У 22 8 (9.8)
В этом Случае число независимых коэффициентов равно
двум (например, УН и У 12 ).
Коэффициенты Z11> Z22' Z21' Z12 В общем случае комплексные и
зависят от частоты. Они имеют размерность сопротивления и MorYT
быть опреде{lены следующим образом:
Zif == ( и-! )
входное сопротивление со стороны выодовB 1
, /! I;
O
при раЗОМКI!УТЫХ выводах 2;
Z22 == ( и:: )
входное сопротивление со стороны выводов 2
/2 I,
o
при разомкнутых выводах 1;
Z21== ( '-:2 )
передаточное сопротивление при разомкнутых
/1 I
O
B1?lВoдax 2;. -
Z12== (
)
передаточное сопротивление при разомкнутых
/2 I,
o
выводах 1.
В случае обратимоrо четырехnолюсиика
. Zi2 == Z2f, (9.9)
239
т. е. ТO.1IbKO три коэффициента в уравнениях (9-2) являются независи-
мыми.
Если четырехполюсник симметричен,' ТО наряду с (9-9) выпол-
няется условие
Zli ==Z22'
(9. iO)
в этом случае остаются только лва независимых коэффициента
(например, Zl1 и Z12) *.
9-Э. УРАВНЕНИЯ ЧЕТЫРЕхпопlOСНИКА В ФОРМЕ 11 AII
Как уже отмечал ось в Э 9-2, при записи уравнений
в форме 11 А 11 положительное направление токэв 11 и 12
выбирается соrласн6 рис. 9-4. Удобство . выбора именно
TaKoro положительноrо направления тока 12 связано Б дан-
ном случае с тем, что форма 11 А 11 применяется обычно при
передаче электрической энерrии от входных выводов к вы.
/ходным, причем четырехполюсник, включенный между
источником и приемником, может состоять из нескольких
четырехполюсников, соединенных каскадно;
xoд каждоrо
последующеrо четырехполюсника совпадает с выходом
предыдущеro четырехполюсника.
Выведем форму 11 A.l1 из ФОрмы.1I у 11. Для этоrо 8 урав-
нениях (9-1), заменив 12 через
12, получим;
J
==Y1ll\+Y1202; }
/2 == У21 и l + У22 и 2 .
Из BToporo уравнения (9-11) следует:
r', У22 . 1.
Иl:;;:;;
У и2
Y /2'
21 2i
(9-11)
(9-12)
Подстановка этоrо выражения в первое уравнение (9-11)
дает;
J [ У22 . 1. ] У ,
1 == Y1l -
y
и 2
'У2/ 2 + 12. и 2 ==
I у 1(; Ун i
Y2! 2
Y21 2'
(9-13)
rде I у I == Y 1l Y 22':"'" У12 У 21'
11< к.оэффициенты четырехполюсников по форме 11 Z 11 не являются
обратными величинами по опюшению к коэффициентам по форме
li у 11, так что, например, У21 i= I/Z 21 или У11 i= I/Z 11 .
240
Положив в (9-12) и (9-13):
A ll
Y
' А l
!.... }
У21' 2
Y2i'
(9-14)
А 21 ==: ......,.... l y Y 1 ; А 22 ==:
y Yii ,
21 2!
получим систему уравнений четырехполюсника 1 (9-3).
Коэффициенты Ан, А 12 , А21' А 22 В общем случае комплекс-
ные и зависят от частоты: Ан и А 22
безразмерные, А 12
имеет размерность сопротивлений, А 21 имеет размерность
проводимости. Эти коэффициенты мщут быть определены
аналоrично .предыдущему следующим образом:
Ан ==: ( и- i )
отношение напряжений при разомК-
И 2 1.
O
нутых Bbj.XO
HbIX выводах;
А 22 . (/ /i )
отношение токов при закороченных
2 и.
o
выходных выводах;
А 12 ==: ( И / ' i )
величина, обратная передаточной
2 и.
O
проводимост
при закороченных выходных выводах;
А 21 ==: (
i )
величина,. обратная передаточному со-
И 2 1.
O
противлению при разомкнутых выходных выводах.
Определитель, составленный из коэффициентов А, ра-
вен:
I А 1== Al1A22
А 12 А 21 == Y Yi2 . (9-15)
21
В случае обратимоrо четыреХПОЛlOCника У12 == У21' И
поэтому
I А 1== А н А 22
А12 А 21 == 1, (9-16)
т. е. только три любых коэффициента в уравнениях (9-3)
являются независимыми; четвертый коэффициент связан
с остальными условием (9-16).
Если четырехполlOCНИК симметричен, то на основании
(9-14) с учетом (9-8)
Al1 == А22' (9-17)
т. е. число независимых коэффициентов равно двум (на-
пример, Ан и А 12 ).
1 Коэффициенты Ан, А12' A 2 i и А 22 часто также обозначаются через
А, В, С и D. .
241
В случае перемены направления передачи электриче-
ской энерrии, а именно при передаче энерrии от выводов 2
к выводам 1, в уравнениях четырехполюсника связывают
напряжения и токи (; 2, j
И (; 1, j
[см. уравнения (9
4)
по форме 11 в 111. Если заменить в (9-3) токи 11 на
j
и j2
на
1
и решить уравнения относительно (;2 и j
, то полу-
чим уравнения четырехполюсника в форме 11 в 11, выра-
женные через коэффициенты формы 11 А 11. Для обратимоrо
четырехполюсника :
2 == А22?l + A12
; } (9-18)
12== А 21 и 1 + Ан! l'
Сопоставляя уравнение (9
18) с уравнениями (9
3),
соответствующими направлению передачи энерrии от выво-
дов 1 к выводам 2, заключаем, что с переменой направления
передачи энерrии коэффициенты A1l и А22' входящие в си-
стемы уравнений, меняются местами.
'-4. ПАРАМЕТРЫ XoпoCToro ХОДА И KOPoTKoro ЗАМЫКАНИЯ
В
9-3 было показано, что коэффициенты Y1l и У 22
представляют собой входные проводимости чеrырехполюс-
ника рис. 9-4, измеренные слева и справа при закорочен-
ных противоположных ВЫводах; соответственно Zl1 и Z22
представляют собой входные сопротивления четырех по-
люсника при разомкнутых выводах.
Введя индексы «к» И «х» для обозначения режимов КОрОТ-
Koro замыкания (выводы замкнуты) и холостоro хода (вы-
воды разомкнуты), получим пар а м е т р ы х о л о с 1'0-
r о х о Д а и к о р о т к О r о з а м ы к а н и я:
1 1 }
ZlK==
Y .; Z2K==' Y
;
11 22
Zlx == Zl1; Z2X == Z22'
(9
1 9)
Этих параметров достаточно для составления уравне-
ниЙ обратимоrо четырехполюсника. Для записи уравне-
ниЙ необратимоrо четырехполюсника недостаточно пара-
метров холостоrо хода и KopoTKoro замыкания, так как
из них только три являются независимыми.
Действительно, на основании (9-19) и таблицы прило-
жения 11
ZiK 1 I У I
Zfx == YfiZif == Yil Y 22
242
и
Z21<
,1 I У I
Z2X
Y22 Z 22 == Yl1 Y 22 '
откуда
Zil<
Z21<
ZlX
Z'2X '
(9
20)
Таким образом, параметры холостоrо хода и KopoTKoro
замыкания, выражаемые формулами (9-19), принудительно
связаны уравнением (9-20).
В случае симметричноrо четырехполюсника
Z1K == Z2K' Z1x == Z2x,
Т. е. симметричный четырехполюсник характеризуется толь-
ко двумя параметрами.
Параметры холостоrо хода и KopoTKoro замыкания мо-
rYT быть выражены через любую систему коэффициентов,
например через коэффициенты А:
Z Ai2 Z Ан }
1К-==Т; 1х==Т;
22 21 (9-21)
t Ai2 Z А 22
2К == A ll ; 2х == А 21 '
в свою очередь любая система коэффициентов обра-
тимоrо четырехполюсника может быть выражена через'-
параметры холостоrо хода и KopOТKoro замыкания. На-
пример, для коэффициентов А получае м 1:
А
, r Zix (9-22)
11
JI Z2X
Z2K
и, используя (9-21), выражаем все остальные
енты через А 11:
А
А Z . А
Ай. А
А Z2X
12
11 2к' 21
ZlX ' 22
11 Z'fy .
коэффици-
(9-22а)
9-5. СХЕМЫ ЗАМЕЩЕНИЯ ЧЕТЫРЕХПОhЮСНИКА
На основании уравнений четырехполюсника MorYT быть
построены различные схемы' замещения, которые облеr-
чают исследование общих свойств рассматриваемой цепи.
Ниже показаны некоторые схемы замещения четырехпо-
1 Эта формула дает двузначное решение, так как входящие в нее
параметры не меняются от перекрещивания любой пары выводов.
243
люсника, параметры которых выражаются через коэффи-
циенты У, Z и А.
На практике чаще Bcero пользуются n
образной и
Т-образной схемами замещения четырехполюсника.
i4 ./ 11
Y12 12
<!------
Z11
Zf2 ,
U I !'I11+ Y I2
Й2 t й 1 (Z21
Z 12)11
У 22 + У 12 Z12 Й2
а) 6)
i l 1.4-1 12
......:..р. А12
t UI AzzlAI Рис. 9-5, Схемы эамеще.
А 12 A11
IAI ния необратимоrо четы-
А;;- рехполюсника.
а
С пара метрами У; б
8) с пара метрами Z; в
с па.
раметрами А.
На рис. 9
5, а показана П
образная схема замещения
четыреХПОЛlOсника, в которой ПРОВОДИМОСТИ ветвей выра-
жены через коэффициенты У. При этом зависимый источ-
ник тока (У21
Уа) а 1 сохраняется в эквивалентной схеме
1
Y12 Z11
Z12 Z22
Z12 A1Z
Yzz + У12 Z12 Aи
1 A11
1
А12 А12
1+ У12
а) 6) 8)
Рис. 9-6, ЭквивалеIlIные схемы пассивноrо четырехполюсника,
только в случае необратимоrо четырехполюсника; в схеме
обратимоrо ч
тырехполюсника (У 12 === У21) источник тока
отсутствует (см. рис. 9-6, а).
Схема рис. 9
5, а соответствует системе уравнений
(9-1). Действительно, по первому закону Кирхrофа ток
244
11 равен сумме токов, входящих в ветви с проводимостями
Ун + У 12 и
YI2' Ток, входящий В первую ветвь, равен
(УН + У12) (;1, а ток, входящий ВО вторую ветвь, равен
Y12 ((;1
(;2)'
Итак,
11
(У u + У 12 ) (;1
У 12 Фl
(;2) == У 1l й 1 + У 12 Й 2 .
в свою очередь ток 12 paBeH
сумме токов, входящиХ
в ветви с проводимостями У22 + У12 и
Y12' И тока источ
ника (У 21
У 12) (;1' Следовательно, '
J;
(У 22 + У 12 ) (;2
У12 (О 2
й 1 ) +
+ (У 21
Уа) (;1
У 21 (;1 + У 22 (;2'
На рис. 9
5, б показана Т
образная схема замещения,
в которой сопротивления ветвей выражены через коэффи
циенты Z четырехполюсника. Применив второй закон
Кирхrофа, леrко убедиться в тсм, что данная схема
соответствует уравнениям (9-2).
Схема замещения четырехполюсника содержит зави-
симый ИСТОЧ5IИК э. д. с. или тока в случае, коrда четырех-
полюсник необратим. В схеме обратимоrо четырехполюс
ника (Z12
Z21) зависимый источник отсутствует (рис. 9-6, 6).
Параметры схемы замещения четырехполюсника MorYT
быть выражены также через коэффициенты А. Так, напри-
мер, пользуясь таблицей приложения II, MOlJ{HO в П-об
разной схеме (см. рис. 9-5, а) проводимости ветвей выра-
зить через коэффициенты А; при этом получится схема
рис. 9-5, в; в случае обратимоrо четырехполюсника будем
иметь с:хему рис. 9-6, в, которая часто применяется для
расчетаэнерrетических систем.
Пассивный П -образный четырехполюсник может быть пре-
образован в Т -образный (или наоборот) по правилу преоб-
разования треуrольника в эквивалентную звезду (см.
4-5).
Следует заметить, что П-образная и Т-образная схемы
,замещения четырехполюсника не всеrда физически реали-
зуемы 1.
Под физически реализуемой пассивной схемой пони-
мается такая схема, в которой паря.метры r, L и С положи-
тельны (см. rл. 17). Если в какой-либо ветви схемы данное
условие не выполнено, то схема физически нереализуема.
1 Это не относится к четырехполюсникам, не СО.Q.ержащим реак-
тивных элементов,
245
Например, схема рис. 9-6, б нереаJ1изуема при отрицат'ель-
ном знаке деЙствительной части Z12' т. е. если
ReZ12 < О.
Схемой замещения четыреХПОЛIOCника может служить
и мостовая схема (см.
9-15). Мостовая схема является
физически реализуемым эквивалентом для любоrо реаль-
но осуществимоr
симметричноrо пассивноrо четырехпо-
люсника.
Схемы замещения необратимых четырехполюсников, опи-
санные выше, применяются для анализа и расчета электри-
ческих цепей, содержащих электронные лампы и тран-
зисторы. К этому вопросу предстоит вернуться во второЙ
части курса.
Пример 9-1. Рассматривая автотрансформатор (см. рис. 8-21, а)
как четырехполюсник, построить для Hero Т-образную схему замеще-
ния.
Выбрав положительные направления токов по третьему варианту
и воспользовавшись параметрами Z, найдем:
Zl1 =='i +'2+ jш (Li+I'2+2M); Z22=:' '2+ jшL 2 ;
Z12==Z2i== (
: ) =='2+jш (L2+M).
I
I,
o
На основании рис. 9-6, б получаются следующие сопротивления
ветвей Т-образной схемы:
Zii
Zi2=='1 +jш (Li+ М); Z22
Zi2==
jшМ;
Z12=='2+jш (L2+M).
Полученный результат совпадает с данными
8-8 (см, рис. 8-21, 6).
9.6. ВХОДНОЕ сопротивпЕНИЕ ЧЕТЫРЕхпопЮСНИКА ПРИ
произвопьноя НАrРУЗКЕ
Обозначим через Z1BX входное сопротивление четырех-
полюсника со стороны выводов 1, Коrда к выводам 2 присо-
единено произвольное комплексное сопротивление Z2
(рис. 9-7, а); соответственно через Z2BX обозначим ,входное
сопротивление четырехполюсника со стороны выводов 2,
Коrда к выводам 1 присоединено произвольное комплексное
сопротивление Z1 (рис. 9-7, 6).
Следовательно, вхо.дное сопрот.ивление Z1BX равно отно-
шению напряжения и 1 к току /1 при прямой передаче
энерrии:
Z1BX ==
! .
[!
246
а Z2BX равно отношению напряжения (;2 К,.д'
KY l
при
обратной передаче энерrии:
Z2BX ===
;- .
/2
. Входные сопротивления четырехполюсника MorYT быть
выражены через любую систему коэффициентов четырех-
полюсника и комплексные сопротивления наrрузок. Z1
и Z2'
i 1
.......;,.(>
E1",1
а)
t;D
1/
8)
1
.,
12
......-.
"
б)
2
1)
Рис. 9
7. Несимметричный четырсхполюсник при прямой и обратной
передаче.
а и б
произволыIяя lIаrрузка: в и е
соrласоваllllая IIнрузка.
Например, если ВОСПользоваться системой ура:внений
(9
3), то, разделив перво
из уравнениЙ на второе, полу-
чим:
Z1BX == Al1Ug+A19
9
A l1 Z g +Ai9 (9
23)
AgiUg+A9219 A21Z2+A29
Аналоrично при обратной передаче на осНовании (9-18)
Z
A99Ui+Aigi
AggZi+Ai9 (9 - 24)
2вх
. А . .
A 21 U i+ 111; A 91 Z 1 +A 1 i
Если восполЬЗоваться таблицами ПрIIJIожений II и III,
то можно выразить Z1BX и Z2BX через друrие коэффициенты
четырехполюсника .
На практике применяются и друrие выражения для
ZlBx и Z2BX' Например, в тех случаях, коrда известны пара-
метры холостоrо хода (Z1X и Zgx) и KopoTKoro замыкания
(Z1K и Z2.J, удобно пользоваться зависимостями ZlBX и Z2BX
от этих параметров. С этой целью выражениям (9-23) и
247
(9-24) с учетом (9-21) придается следующий вид:
А
Aii
+Z2
Z
A 1 i
Z ? 2K+Ё
.
lВХ
А
lХ Z Z'
А - 22+Z 2Х+ :1
21 А 21 2
А Ai2 Z
22 A
+ 1. Z - +z -
Z 22 Z 1К 1
2вх == А. == 2Х Z + z .
А .......!! + z - 1х 1
21 А 21 - 1
Рассмотренные выше функциональные зависимости
Z1BX == Р 1 (Zz), ZZBX == Fz (Z1) преДС1:авляют собой дробно-
линейные преобразования, связывающие СОПРОТИВJ.Iения на
выводах четырехполюсника; они иллюстрируют одно из
свойств четыреХПОJIюсника
способность преобразовывать
сопротивления.
9.7. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ЧЕТЫРЕхпопЮСНИКА
Положим, что сопротивления Z1 и ZZ В схемах
рис. 9-7, а и б подобраны таким образом, что Z1BX == Z1 И
ZZBX == Zz. Иначе rоВОрЯ, будем считать, что существуют
два сопротивления: Z1 == Z1C И Zz == Zzc, которые удовлет-
воряют следующему условию: входное сопротивление Z1BX
четыреХПОЛIOCника, наrруженноrо сопротивлением Zzc, рав-
но Z1C (рис. 9-7, в); входное сопротивление ZZBX четырех-
полюсника, наrруженноrо сопротивлением Z1C, равно Z2C
(рис. 9-7,8).
Такие два сопротивления называются х а р а к т е р и-
с т и ч е с к и м и с о про т и в л е н и я м и несиммет-
ричноrо четыреХПОЛIOCника.
Условие, коrда четырехполюсник наrружен _ соответст-
вующим характеристическим сопротивлением, наЗЫВается
условием с о r л а с о в а н н о й н а r р у 3 К И или соrла-
cOBaHHoro включения.
ПОЛОЖИВ в (9-23) и (9-24)
ZlBX == Zi == ZlC
и
ZZBX == Zz == Zzc,
получим:
Z
A l1 Z 2C + Ai2 . Z
A 22 Z ic + Ai2
lс
A21Z2c+A22' 2С
A21Z1C+A1i .
248
Совместное решение этих уравнений относительно Z!C
и Z2C дает:
Z .:::.. 'J j Al1 A i2 .
lс
JI А 21 А 22 '
Z2C == ... / A 22 Ai2 .
JI A 21 Aii
, (9-25)
Введем для раСQматриваемоrо обратимоro четырех по-
люсника новый параметр g, У
Qвлетворяюl.ЦИЙ условиям:
th g i 11 Ai
A2Z ; }
(9-26)
shg== У А 12 А 21 .
Эти условия всеrда осуществимы, так как параметр g
может быть комплексным., Кроме Toro, эти
условия взаим-
но дополняют друr друrа, так как имеющая место связь
между коэффициентами (9-16) соответствует триrономет
рич(;;ской формуле
ch2g
sh2g== 1.,
. Параметр g в общем случае комплексный; g == а + jb
называется мерой передачи 1 четырехполюсника. Это
третий характеристический параметр обратимЬrо четырех-
полюсника. Ero действительная часть а называется с о б-
с т в е КН ы м 3 а т у х а н и е м четырехполюсника, а
мнимая часть Ь
к о э Ф Ф и ц и е н т О м фаз ы.
Физический смысл этих коэффициентов будет пояснен
ниже. Выразим коэффициенты четырехполюсника формы
lIA11 через характеристические параметры.
На основании (9-25):
.. / '!ic ==... / Ан
JI Z2C JI Ааа
(9-27)
и
v ZlC Z 2C == .. /
12 .
JI 21
(9-28)
Умножение (9-26) на (9-27) и (9-28) дает:
А V ZiC h
11 == Z
c g;
2С
А 12 == V ZlC Z 2C sh g.
(9-29)
(9-30)
1 Иноrда ЭТОТ параметр называется КОЭффИIl.иентом передачи, ero
не следует смешивать с терминами «коэффициеит передачи по напря-
жению» и «коэффициент передачи по TOKY
. В литературе ранее при-
МСнялось обозначение g:;;;:: ь + ja.
249
Деление (9
26) на (9
27) и (9
28) дает:
А 22 0== y
:: chg;
1
A 21 O== V
shg.
ZlC Z 2C
(9- 31 )
(9-32)
в результате подстаноI3КИ (9-29)
(9-32) в (9
3) полу-
чаются уравнения несимметричноrо обратимоrо четырех-
ПОJIюсника в rиперболической форме., соответствующие
положительным направления
токов 11 и 12. указанным
на рйс. 9-4:
(;10== y
(U 2 chg+Z 2 )2 sh g); !
11=="'/
2C ( 12chg+
(;2Shg ) . J
v lc 2с .
(9-33)
При соrласованно подобранной наrрузке (Z2 == Z2C)
имеет место равенство
.' 1..
Z2cl2 == и 2 или Z
и 2 0== 12'
. 2с
Если воспользоваться известным математическим соот-
ношением
ch g + sh g == e g ,
то уравнения (9-33) упростятся:
и 1 == y
: U 2 e g ; 110== y
:: j2
' (9
34)
Отсюда следует, что при соrласованно подобранной
наrрузке модули напряжений и соответственно токов на
входе и выходе четырехполюсника связаны уравнениями:
и
",/ ZiC' Uea. 1
"'/ Z2c lea
1
V Z2C 2 , 1
V ZlC 2 .
Множитель V Zlc/Z2C е а равен отношению амплитуд
или действующих ЗНачений напрнжений на входе и выходе
четырехполюсника при соrласованной наrрузке. В свою
очередь множитель V Z2c/Zlc е а равен отношению ампли-
туд или действующих значений токов при той же наrрузке.
Если aprYMeHTbI (уrлы) комплексных характеристичес-
ких сопротивлений Zlc и Z2C обозначить через СР1С И СР2С,
то фазовый сдвиr напряжения на входе относительно напря-
250
жения на выходе определится величиной Ь +
(СРIС
ЧJ2С)'
а фазовый сдвиr тока на выходе относительно тока на
выходе
величиной Ь +
. (СР2С
ЧJIС)'
В общем случае коэффициент фазы Ь может быть опре-
делен как полусумма фазовых сдвиroв между напряже-
ниями и соответственно между токами на входе и выходе
четырехполюсника, наrруженноrо соrласованно. При ра-
венстве уrлов ЧJIС и tp2C И соrласованно подобранной наrрузке
фазовые сдвиrи между напряжениями и соответственно
между токами четырехполюсника одинаковы и равны Ь.
Характеристические параметры ZlC, Z2C и g MorYT быть
выражены через параметры холостоrо хода и KopoTKoro
замыкания, а именн о: на основании (9-21), (9-25) и (9-26)
ZlC == V ZlX Z IK; Z2C == V Z2X Z 2K; }
th g == ... / ZH == ...!
2K . (9-35)
JI Zlx JI l2X
Подстановка (9-26) в формулу ch g + sh g == e g приводит
к выражению, связывающему характеристический параметр
g с коэффициентами четыр ехполю сника формы !!AII,
e g == eae jb == V А ll А 22 + V А 12 А 21 . (9-36)
По этой формуле g вычисляется однозначно, если под-
ставлять под радикалы коэффициенты А в показательной
форме с последующим сложением уrлов и делением их
суммы на 2. По формуле (9-35) Для TaHreHca принципиально
невозможно получить однозначное решение, так как в.ход-
ные сопротивления под радикалом не изменяются от пере-
крещивания выводов четырехполюсника. Поэтому формула
(9-36) предпочтительнее формулы (9-35) для th g.
Вычисление g по формуле для th g ведется в следую-
щем порядке:
e g
e
g
thg== eg+e
g '
откуда
2g
1 +thg
М L .
е
1
thg
ЧJ,
в результате лоrарифмирования
+ . ь 111 м + . <р
g==a J ==
J
2
'
251
Следует отметить, что параметр g может быть также
получен как половина натуральноrо лоrарифма отноше-
ния произведений комплексных напряжения и тока на
входе и выходе четырехполюсника при соrласованной
наrрузке.
Действительно, на основании (9-34)
( (;111 ) ==e2g
(;212 Z2
Z2C '
откуда
1 / (;111 ) (9 - 3 7 )
g
2 п! . , .
\И 2 1 2 Z2"",Z2C
В случае симметричноrо четырехполюсника (Ан == А 22 )
характеристические сопротивления ZlC и Z2C равны друr
друrу:
ZlC == Z2C == Zc == 11
.
Следовательно, входное сопротивление симметричноrо
четырехполюсника, наrруженноrо характеристическим со-
противлением Zc, равно Zc. Это означает, что ВСЯКОМУ
симметричному четырехполюснику соответствует некото-
рое характеристическое сопротивление Zc, обладающее
следующим свойством: если на.ерузить даннтй четырех-
полюснU1C сопрО1iluвлениеАt Zc, то отношения напряжения
к току на входе и выходе четырехполюсника будут
одина-
ковыми, т. е.
И / ' 1 == L:2 == Zc.
f 12
На основании (9-33) уравнения симметричноrо четы-
рехполюсника при произвольной наrрузке записываются
в rиперболической форме (для положительных направлений
рис. 9-4) так:
.. . .. 1 .
и 1 == и 2 chg+ZC l 2 shg; /1 == /2 chg+z
U 2 shg.
С
?сли наrрузка подобрана соrласованно, т. е. ZJ2 ==
== и 2 , то
& :....... eae jb == ( (;! 1 == ( lf ) .
(;2/Z2
ZC 12 Z2""'ZC
В этом случае амплитудные изменения напряжения и
тока опреде.ляются множителем е а , а фазовый сдвиr между
(9-38)
252
напряжениями или токами
уrлом Ь. Собственное зату-
хание а будет:
( И 1 ) ( /1 )
а == In И
z
z == In
I z
z .
2 2 С 2 2
С
Величины g, а и Ь
безразмерные. Уrол Ь вычисляется
в радианах (рад); собственное затухание а, входящее
в (9
39), принято вычислять в б е л а х (Б) или д е ц и.
б е л а х (дБ), которые определяются следующим образом.
Если полная мощность на выходе четырехполюсника
в 10 раз меньше мощности на еео входе, то затухание со-
ставляет 1. Б; €сли мощность уменьшается в 100 раз, то
затухание оценивается в 2 Б и т. д. Поэтому
8! И 1 /f
аб == Ig 82 == Ig И 2 / 2 .
(9-39)
В случае соrласованно наrружеНIJоrо симметричноrо
четырехполюсника
8! == ( И f ) 2 == ( /i ) 2
82 И 2 12
и, следовательно,
И. lf
аб == 2 19 и: == 21g 12 .
Децибел
еДИНИЦа затухания, в 10 раз меньшая бела
Затухание 1 дЕ соответствует уменьшению полной АЮЩ-
ности 8 1,26 раза или уменьшению напряжения и тока
в 1,12 раза.
Затуханию 1 Нп соответствует уменьшение амплитуды
и действующеzо значения напряжения или тока в е ==
и, и )
== 2,718 раза (так как при ln и: == 1 имеем и: == 2,718 .
Табл. 9-1 иллюстрирует зависимость затухания в деци-
белах от отношений полных мощностей 81/82 на входе и
выходе четыреХПОЛIOCника;
Таблица 9-1
Затухание при различных отношениях 81782' дБ
а, дБ I 5, а,дБ I 5, а, дБ I 5,
s; s; s;
0,1 1,02 4 2.51 8 6,31
1 1,26 5 3,16 9 7,94
2 1,58 6 3,98 10 10
3 1,99 7 5,01 10п 10 п
253
соответствующие им отношения веЛИЧliН напряжений или
токов симметричноrо четырехполюсника, наrруженноrо со.
rласованно, состаВJJЯЮТ 11 51/52 '
Для перехода оТ децибелов к неперам или обратно
можно воспо.дЬЗ0ваться приведенным выше условием:
Ui а
адБ == 20 19 и
== 20 19 е Нп == 20анп 19 е ==
" \\
== 20. 0,4343анп == 8,686анп,
т. е.
1 дЕ == 0,115 Нп.
или
1 Нп == 8,686 дЕ.
'.8. ВНОСИМОЕ ЗАТУХАНИЕ ЧЕТЫРЕхпопЮСНИКА
в н о с и м о е 3 а т у х а н и е (или усиление) является мерой
оценки изменения условий передачи при включении четырехполюсника
между источником и приемником.
Лоложим, что между источником напряжения, имеющим внутрен-
нее сопротивление Z1' и приемником Z\\ включен четырехполюсник,
i 1
Z1 Z1
Ю €l
, 0.)
i 2
Zt
б)
Рис. 9-8. Питание приемник а непосредственно от источ-
ника (а) и через четыреХПОЛЮСНI1К (6).
Под вносимым затуханием четыреxnолюс,ника подразумевается
десятикратное значение десятичноrо лоrарифма (в децибелах) или поло-
вина натуральноrо лоrарифма (в неперах) отношения полной мощно-
сти 81' которую непосредственно отдавал бы ИСтоЧник сопротивлению Z2
(рис, 9-8, а), к полной мощности 82 на выходе четырехполюсника, на-
rруженноrо сопротивлением Z\\ (рис, 9-8,6):
8i
а вн . дВ == 1 О 19
8 "
, \\
1 8i
а вн . Нп ==
2
ln -S;.
Мощности 81 И 82 выражаютси следующим образом:
81 " U 2 z 2 . 8
Z " / 2
: Zl +Z212' \\
2 2'
(9.40)
или
(9-41 )
254
Соrласно (9-41)
а
}
ln и 2 'п U ( 942 )
ПН
2 IZ1+Z212f
[ZI+Z2112'
Отношенне U/1 2 . входящее в (9-42), может быть выражено через
характеристические параметры четырехполюсника и сопротивления
ZI и Z2' ,
Пользуясь обозначениями рис. 9-8, б и уравнениями четырехпо-
люсника, записанными в форме 11 А 11, находим:
(; ;:;(;1 + ZI/i == AIlU2+AI2i2+Z1 (А 21 (;2+ A 22 i 2 ) ==
::= (AllZ2+AI2+A21Z1Z.+A22Z1) 12'
откуда
(;
7;==AilZ2+Af2+ A2iZlZ2+A22Zf.
На основании (9-29)
(9-32)
A'
"'(' Zic eg+e
g .
11
JI Z2C 2 '
lr
eg
e
g
А 12 == r l1C Z 2C 2 ;
(9-43)
А
1 eg
e
g
21
V ZiCZ2C 2
А'
.. (' Z2C eg+e
g
22
JI ZlC 2 .
Подстановка (9-44) в (9-43) дает:
!L == ( -.; Z!C Z2+ V Z1C Z 2C +
+ ... (' Z2C ZI )
' +
12 JI Z2C V Z1CZ2C r Zic ,2
+ ( -.; ZlC Z2
V Z1CZ2C y
+ ... (' Z2C Z1 ) e
g .
JI Z2C ZlCZ2C JI ZIC - 2
После рида алrебраическнх преобразований получается:
(;
egVZ'h (Zi+Zic) (Z2 + Z2C) (1
пlп2e
2t)
/2
2 V ZI Z ic y
Z2 Z 2C
(9-44)
rде
21
ZIC Z2
Z2C
nl== ZI+ Z 1C и п 2 ==l2 2 +Z 2C
так иазываемые к о э Ф Ф и и: и е н т ы о т р а ж е н и я на входе
и выходе четырехполюсника.
, В связи с этим выражение (9-42) принимает следующий вид:
ави==а+lП ! Zl+
\ +ln ) Z2
1 +
2У 2 1 2 1с 2 V Z2Z2C
I 21 + 22 I
+In 11
п
п2e
2gj
ln 2Y Z I Z 2 .
255
Следовательно, вносимое затуха'ние состоит из пяти слаrаемых.
Первое слаrаемое
собственное затухание четырехполюсиика, вто-
рое
затухание вследствие несоrласованности сопротивлений на
входе четырехполюсника, третье
затухание вследствие Hecor ласо-
ваН\lОСТИ сопротивлений на выходе, четвертое
затухание вследствие
взаимодействия несоrласоваииостей на входе и выходе и пятое со зна-
ком минус
затухание вследствие несоrласованности сопротивлений
источника И приемника.
Если вносимое затухание равно Иулю, то это означает, что мощ-
ности на входе и выходе четырехполюсника равны между собой.
I(оrда четырехполюсник является усилителем мощности (например,
в случае ламповоrо триода или транзистора), выражения (9-40) и (9-41)
дают отрицательные значения а вн ;, это указывает на то," что вместо за-
тухания в данном случае имеет место уснление (измеряемое в децнбе-
лах нли неперах).
9-9. ПЕРЕДАТОЧНАЯ функция
Передаточной функцией называется зависимость от
частоты отношения комплексных амплитуд или комплекс.
ных действующих значений электрических величин 1 на
выходе и входе четырехполюсника при заданном режиме
передачи. Необходимо помнить, что именно выходная
электрическая величина делится на входную, а не обратно.
Передаточные функции, соответствующие отношению
одноименных электрических величин,
коэффициент пе-
редачи по напряжению
K U ==U 2 I U r.
и коэффициент передачи по току
KI == i 2/ i 1
представляют собой безразмерные, в общем случае комплекс-
ные, зависящие от частоты величины. Применительно
к усилительным устройствам они носят название коэффи-
циентов усиления по напряжению и току.
Отношения разноименных элеК1'ри:ц:еских величин
передаточное сопро,!-,ив.ление Z == U 2/ J 1 и передаточная
проводимость У == 1 2 /U 1
имеют соответственно размер-
ности сопротивления и проводимости и также являются
в общем случае комплексными величинами, зависящими
от частоты.
Зависимости модулей комплексных отношений представ-
ляют собой а м п л и т у Д н о-ч а с т о т н ы е, зависи-
1 Под передаточной фуикцией понимается часто отиошение опера-
ториых изображений (см. rл, 15) электрических величин на выходе
и входе чеrырехполюсника, .
256
мости их aprYMeHToB
Ф а 3 о - Ч а с т о т н ы е Характе-
ристики четырехполюсника. Эти характерис,!:ики имеют
важное значение для работы устройств автоматики и радио-
техники.
В общем случае четырехполюспика, натруженноrо про-
извольным сопротивлением Z2' передаточные функции MorYT
быть выражены через любую систему коэффициентов четы-
реХIюлюсника. и сопротивление Z2'
Через коэффициенты формы '!АН они выразятся следую-
щим образом (положительные направления для токов
соответствуют прямой передаче):
К и ==
2 == . (;2
Z2
Ut AiiV2+ А 12 1 2 _ AiiZ2+A12'
К] == {
== . 12' 1 .
, li А 21 U 2 + А 22 1 2 A21Z2+A22
При холостом ходе и коротком замыкании эти коэффи-
циенты примут вид:
1 1
KиX==' A
; K]K==
A .
11 22
В случае обратной передачи, очевидно, можно напи-
сать (при IA I == 1):
К , 1 К , 1
их ==
A и ] к.==
A '
22 11
Отсюда видно, что для обратимоrо четырехполюсника
коэффициент передачи по напряжению при холостоМ ходе
и прямом направлении передачи энерrии равен коэффи-
циенту передачи по току при коротком замыкании и обрат-
ном направлении передачи энерrии. В свою очередь коэффи-
циент передачи по току при коротком замыкании и пря-
мом направлении передачи равен коэффициенту передачи
По напряжению при холостом ходе и обратном направлении
передачи.
9.10. КАСКАДНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ,
ОСНОВАННОЕ НА соrЛАСОВАНИИ ХАРАКТЕРИСТИЧЕСКИХ
СОПРОТИвлеНИR
На практике широко распространено к а с к а Д н о е
или цепочечное соединение четырехполюсников, при кото-
роМ входные выводы каЖдоrо последующеrо четырехполюс-
ника присоеДИНЯIOтся к ВЫХОДНЫМ выводам предыдущеrо
четырехполюсника; цепи, служащие для передачи электри-
257
ческои энерrии' (каналы связи и т. д.) обычно состоят из
звеньев, следующих друrза друrом.
Каскадное соединение четырехполюсников, выполнен-
ное по принципу соrласования характеристических сопро-
тивлении, заключается в том, что ВХОДНое сопротивление
на выводах любоrо четырехполюсника равно характери-
стическому.
Рисунок 9-9 иллюстрирует каскадное соединение двух
четырехполюсников. Ввиду Toro что комплексное сопро-
тивление наrрузки соrласовано с выходным характеристи-
ческим сопротивлением ZЗС BToporo четырехполюсника,
входное сопротивление этоrо четырехполюсника равно
характеристическому (Z2C); при этом оно служит соrласо-
ваннои наrрузкои для первоrо четырехполюсника. Поэтому
входное сопротивлениепервоrо четырехполюсника также
равно характеристическому (ZlC).
i,
- . I
Ia I,
"
z,,=
Zac
12
иа,
Рис. 9-9. Соrласованное каскадное соединение четырехполюсников,
Отсюда следует, что каскадно соединенные четырех-
полюсники с соrласованными характеристическими сопро-
тивлениями MorYT быть замещены одним четырехполюсни-
ком, имеющим характеристические сопротивления, равные
входному характеристическому сопротивлению первоrо и
выходному характеристическому сопротивлению послед-
Hero четырехполюсников (рис. 9-9). Мера передачи g резул(,-
тирующеrо четырехполюсника определяется алreбраичес-
кой суммои мер передачи составныХ четырехполюсников.
В самом деле, применительно к схеме рис. 9-9 в соот-
ветствии с (9-34)
. y z' g
u
и е б.
2
ZЗС 3 ,
1
"'/
'iJ!:.. j е gб '
2
V Z2C 3 ,
'. y 2 1c ,. .
..
и 1 == Z
и 2 е-- а ,
2С
. y Z 2C / . g
/1== '[
2 еа ,
1с
откуда
(; 1 == "'/
Z .1C U
pga +gб; j
"'I Zз
j ega +gб .
V 3С ;r- 1
V ' ZlC 3 '
258
Полученные выражения подтверждают сказанное выше:
результирующий четырехполюсник имеет характеристи-
ческие сопротивления Zlc и Zзс И меру передачи g == g. +
+ gб' Соответственно собственное затухание р
зультирую-
щеrо четырехполюсника а
а. + аб, а фазовый коэффи-
циент Ь == Ь а + Ь б .
в rл. 3 (см.
3-5) было показано что передача макси-
мума активной мощности обеспечивается, коrДа комплек-
сные сопротивления ИСТОЧНИКа И наrрузки являются сопря-
женными. Это условие не выполняется в случае соrласо-
ваНи я характеристических сопротивлении каскада в прямом
и обратном направлениях, если характеристические сопро-
тивления комплексные. Однако если они активные (ВКЛЮ-
чая сопротивление источника), как это нередко имеет место
на практике, то обеспечивается оптимальное условие пере-
дачи мощности.
Соrласование Характеристических сопротивлений ,ши-
роко применяется в аВтОМатике, приборостроении и элек-
тронике.
9-Н. УРАВНЕНИЯ СПОЖНЫХ ЧЕТЫРЕХПОПЮСНИКОВ
в МАТРИЧНОЙ ФОРМЕ
Для получения параметров результирующеrо четырехполюсника,
СОСтавленноrо из более простых четырехполюсников, параметры кото-
рых известны, удобно пользоваться матричной записью (см.
7-10).
Аа.
i Z a.=i 1 /
ц
i 1 =i 1 a.
ti,=Jit .[j
i26= i z
А! 'tJ ".ti2
Рис, 9-10. Каскадное соединение четырехпoJIЮСНИКОВ.
в зависимости от схемы соединения Сложноrо четырехполюсника
применяется та или иная форма уравнений, а именно:
1) при каскадном соединении (рис. 9-10)
форма 11 А 11 или 11 в 11;
2) при последовательном соединении (см. рис. 9-11)
форма 11 z 1/;
3) при параллельном соединении (см. рис. 9-12)
форма 11 у 11.
Каскадное соединение четыIехполюсннковB (рис. 9-10), 'Уравнения
составных четырехполюсников в матричной форме 11 А 1/ имеют ВИд:
11
;lIa
II
:
:: Ila '/I
: IJa
11 Аа II'II
: Ila;
!I
: 116 ==11
::
:: 116 .(\
: 116
11 Абll. \\
: Ilб'
259
Здесь индексом а отмечены веJlИЧИНЫ, относящиеся к первому четы-
рехполюснику, а индексом б
величины, относящиеся ко второму
четырех полюс нику .
При каскАЦНОМ соединении
(;1== (;la; k==/ia; (;2==(;26; i 2 == 126; (;2a==<(;i6; i 2а ==iiб'
Следовательно,
11
: 11 == 11 Аа 11 . 11 А6 I1 .11
11 == 11 А 11 .11
:[I.
Таким образом, матрица" А " результирующеrо четырехполюсника
равна произведению матриц составных четырехполюсников:
11 А 11 ==11 Аа 11.11 А6 11.
это правило распространяется на случай каскадноrо соединения
любоrо числа четырехполюсника: При этом матрицы, подлежащие
i, ==i la .,
,
12а==I", 114 iJIL
<1-----
O'a
+ Z4
Й2а
]й,
1, ;:;i flf
'
Uf6
Zt
и2t
Рис. 9-(1. Последовательное
соединение четырехполюсников.
Рис. 9-12. Параллельное соедине-
ние четырехполюсников,
перемножению, записываются в порядке С;1едования соответствующих
четырехполюсников, так как умножение матриц не подчиняется пере-
местительному закону.
Последовательное соединение" четырехполюсников (рис. 9-11)
Уравнения составных четырехполюсников в матричной форме
" Z 11 имеют вид:
I11 g; \\а == 11 Za 11 .11
I[a; 11
[16==11 Z6 ",!!
116'
ЗдесЬ
Если при этом
(;i == (;ia + (;i6; (;2 == (;2а + (;26'
i 1 ==i 1а ==i t б И i
==i
а==i
б;
то
== { I
all +11 Z611 } \\
\1==11 z 11. \\
a
260
Матричные уравнения сложных четырехполюсннков
Таблица 9-2
Соединение
Схема
МаТричное уравне-
ние
Каскадное
I10слеiо
ательное
Параллельное
Последовательно-nа-
раллельное
Параллельно-последо-
вательное
ПА 11==IIA a 11'!IАбll
11 z 11==11 Za 11+11 Zбll
IIY!I== Уаll+IIУб\1
11 н 11 ""'11 На 11 +11 Нбll
/1 о /1==11 Оа 11+11 Обll
Таким образом, матрица" Z " результирующеrо четырехполюсннка
равна сумме матриц составных четырехполюсников:
IIZ 11==IIZall+11 Zбll.
Параллельн.ое соединение четырехполюсника (рис. 9-12)
Уравнения составных четырехполюсннков в матричной форме
11 У 11 имеют вид:
i\
\Ia ==/1 у а /1'"
:"a; 11
\!б /1 у бll.11
:llб'
При параллельном соединении четырехполюсников:
и 1 == Uia== U 1б ; и 2 == (;2а == (;2б; 11 ==l ia + l 1б ; 1
==I
a +j
б.
261
Следовательно,
11
11== {II у all +11 у 611}"
: 11==11 у 11.11
:II.
Таким образом, матрица 11 у 11 результирующеrо четыреХПоЛЮСlIика
равна сумме матриц составных четырехполюсннков
11 у 11==11 у а; 11+11 у 611.
Правила иахождения матриц сложных четырехполюсников све-
деиы в табл. 9-2. Они справедливы при любом числе COCTaBHЫ
четырех-
полюсников. Одиако правила сложения матриц применимы только при
равенстве токов входящеrо и выходящеrо в каждой паре выводов со-
ставных четырехполюсников, которое должно быть обеспечено тем
или иным способом.
Соединение четырехполюсников, удовлетворяющее этому условию,
называется реrулярным [Л. 2 и 6].
9-12. ОДНОЭЛЕМЕНТНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
Простейшими четырехполюсниками являются одноэле-
ментные четырехполюсники, состоящие из последователь-
Horo (рис. 9-13, а) или параллельноrо (рис. 9.13, б) двух-
полюсника.
Уравнения первоrо из них в форме IIAII записываются
следующим образом:
U 1 ===u 2 +z/ 2 ; 11==0+/2'
или, что то же,
\\
1
==
I] '11
2\\.
Уравнения одноэлементноrо четырехполюсника с парал-
лельной ветвью (рис. 9-13, б) в форме IIAII записываются
следующим образом:
.. . 1. .
и 1 == и 2 +0; [1 ==z и 2 + [2
или, что то же,
(\ 1 О (;2
/1 1 /2
Z
Если в первом четырехполюснике (рис. 9-13, а) положить
Z == о или, что то же, во втором четырехполюснике
(рис. 9-13, б) принять Z == 00, ТО получится уравнение
262
в форме НАН: . ..
Ilrlll==ll
[I'II
2\!==lj
2Ij,
соответствующее непосредственному прямому соединени,Ю,
показанному на рис. 9-14, а.
f21
0.) б)
1
o
1/
f21
2
2'
f21
0.)
1 2
DG,
6)
Рис, 9-13. Однсэлементные че. Рис. 9-14. Соединения: прямое Са)
тырехполюсники с последова. и перекрещенное (6),
тельной (а) и параллельной (6)
ветвями,
Леrко убедиться, что перекрещенному соединению
(рис. 9-14, б) соответствует уравнение в форме IIAII:
ll
l\\==\!
II' 11
21!==
=
211.
Поэт
)Му при перекрещивании входных или выходных
выводов любоrо четырехполюсника ero матрица IIAII умно-
жается на 11
11, что равносильно перемене знаков
коэффициентов А.
9.13. r.О&РАЭНЫЯ ЧЕТЫРЕХПОЛЮСНИК
Коэффnциенты r.образноrо четырехполюсника. (см.
рис. 9-15) MorYT быть получены непосредственно по форму-
лам, приведенным в
9-2 и 9-3. Например, для схемы
рис. 9-15, а коэффициенты формы HAII соrласно формулам
9.3 будут:
( (;'
Al1 ==
) == 1;
и 2 1.
0
A2
== (
i ) == /! ==1+
C ;
12 u.
o ..............E
11 а
Z а + Zc
А ( (;1 ) (;1 Z А ( 11 ) 1
12 ==
. ==
== с; 21 == 7""' ==
.
12 u.
o
(;:j. и 2 1.==0 Za
Zc
263
Аналоrично MorYT быть вычислены и друrие коэффи-
циенты.
Характеристические параметры r-образноrо четырех-
полюсника MorYT быть вычислены по формулам (9-25)
и (9-26).
f
1: ::r "':[:
0.) О 8)
Рис, 9.15. f-образный четырехполюсник,
Для схемы рис, 9-15, а:
ZlC==; Z a 1I
; 1
Z2C == V Zc (Za + Zc);
chg==; 11 1 +
. J
Для схемы рис. 9-15, б:
ZlC ==; V Zb (Za + Z' b); I
Z2c==;Za 11 Za
Zb ;
ch g == 11 1 +
. J
i.z 1
Z
2Zt z,
е)
(9-45)
(9-46)
При расчете электрических фильтров (см, rл. 10) и
в ряде друrих случаев за исходные схемы r-образных
четырехполюсников принимаются схемы рис. 9-15, в и е,
причем мера передачи r-образноrо четырехполюсника обо-
значается через g/2, для Toro чтобы при соrласованном
каскадном соединении двух таких четырехполюсников
получалея Т-или П-образный четырехполюсник с мерой
передачи g (см.
9-14), При этом характеристическое сопро-
тивление со стороны параллельной ветви обозначается
через Zп, а со стороны последовательной ветви
че-
рез ZT.
264
На основании (9-45) или (9-46):
ZT == 11 Zl Z 2 (1 +ii;); I
Z == V Z1 Z2 .
П Z '
1+
1..
4Z 2
g --. / Zf J
сЬ
2
::::: JI
= 4Z 2 ; ,
sh
::::: 11 {i 2 .
(9-47)
(9-48)
Эти выражения используются в теории электрических
фильтров.
9.14. T-ОEiРАЗНЫА И П.ОEiРАЗНЫА ЧЕТЫРЕХПОЛЮСНИКИ
в
9-5 рассматривались схемы замещения чет.ырехполIOС-
ника и приводились схемы Т-образноrо и П-образноrо
четырехполюсников. Коэффициенты таких ,четырехполюс-
ников вычисляются по общеЙ мето-
дике, описанньЙ в
9-2
9-4.
Так, для Т-образноЙ схемы рис.
9-16 получим:
1 +
I!.. Zb+Zc+ Zblc
11 А 11 == za za
1 + z
c..
za za
.
Рис. 9
16. Т-образный
четырехполю
ник .
Характеристические параметры находятся по формулам
(9-25) и (9-26).
СиммеТричные Т- и П-образные четырехполюсники можно
получить соrласованным каскадным соединением двух оди-
наковых [-образных четырехполIOcников (рис. 9-17, а и 6).
Результирующие четыр
хполlOCНИКИ имеют характеристи-
ческие сопротивления ZT и Zп, определяемые соrласно
(9-47), и меру передачи g, вдвое превышающую меру пере-
дачи r-образноrо четырехполюсника.
С учетом (9-48) имеем:
h 2 Ь 2 2g Zi
С g== 1 + s
2== 1 +2Z
'
(9-49)
265
Тот же результат получается на основании (9-26).
1 1
"2 Z , Z Z , r
'. r
,
I Zw I j-ZI !!Т
1-4
r....-
I I 2Zz I
11
=
2Z1
I 2Zz
I
L
...
Z7
Zz, Zr
.......
_
...!
4)
Z,
Zn 2ZZ 2ZZ =
6)
Рис. 9.17. Разложение симметричных Т-образноrо (а) и
П.образноrо (6) четырехполюсников на f-образные.
9-f5. СИММЕТРИЧНЫА МОСТОВОА ЧЕТЫРЕХПОЛЮСНИК
ДЛЯ симметричноrо MOCTOBoro четырехполюсника (см.
Z, рис. 9-18) в соответствии с
9-3
можно получить коэффициенты фор-
мы IIAJI:
Zi + Z2 2Z 1 Z 2
IIA 11 == Z2
Zi Z2
Z1 .
2 Zi+Z2
Zi
Z2 Z2
Z1
Рис. 9.18. Мостовой
четырехполюсник.
Характеристические параметры симметр ичноrо
Boro четырехполюсника находятся по формулам:
ZM == V
: == 1/ Z 1 Z 2;
h А Z1 + Z2
с g== 11== Z2
Z1 ;
h '/ A
A 2 V Z 1 Z 2
sg==Y12"1== Z Z ;
2
1
sh .!L == --. / chg
1 == --. / Z
2 JI 2 JI Z2
Z1 '
ch Л. == --. /1+ shz[. == --. / Z2 ;
2 JI 2 JI Z2
Z1
th д-- == l/Zf J
2 JI z;'
мосто-
(9-50)
266
Как уже отмечалось в
9
5, мостовой четырехполюс-
ник является физически реализуемым эквивалентом для
любо,ю реально осущесmвuмоzо сuмметричноzо пaccU8Hozo
четырехполюсника [Л. 2 и 16].
Последовательно
параллельное соединение двух четы-
рехполюсников представляет собой один из основных видов
цеп и с о б Р а т н о й с в я 3 Ь ю, В которой напряже
ние на выходе воздействует на входные напряжения си-
стемы. Пусть некоторое уст-
ройство, которое назовем ос-
новным, представляет собой
четырехполюсник с переда-
точной ;Рункцией К' (jw) ==
== (;21(;1 (рис. 9-19). Если
выходное напряжение и 2
подвести К выводам друrоrо
четырехполюсника, называе-
Moro 'устройством обратной
связи, и включить ero про- РИС. 9-19, Цепь с обратной
тивоположные выводы после- СВЯЗI;>Ю.
довательно с входными вы-
BoдaM
основпоrо устройства, то ПОЛУЧIjТСЯ система с об-
ратньй связью по напряжению.
Обозначим передаточную функцию устройства обратной
связи через К" иш) == (;1/(;2' Очевидно, (;1 == u1
Ь;.
Следовательно, передаточная функция всей системы
К ( 'ш ) == (;2 == (;2
J И ', И ', И 'н,
1 l
1
9.16. О&РАТНАЯ СВЯЗЬ
Осно8ное
устрой.ст80
ЙZ
или, если разделить числитель и знаменатель на (;;,
К'
К == 1
К' К'"
(9-51)
Если поменять полярность одной из пар выводов уст-
ройства обратной связи, то в знаменателе (9-51) вместо
знака минус получится знак плюс.
Обратная связь, при которой напряжение, пропорцио-
нальное выходному напряжению, добавляется к входному
напряжению системы так, что IK I > 'К' \, называется поло-
жительной; если же IKI < IK' 1, то обратная связь назы-
вается отрицательной.
267
Выражение (9-51) может быть переписано так:
1 [('К"
К == [(" 1
[(' K tt .
Если IK' К"I >- 1, то
1
K
K'"
Это выражение показывает, что передаточная функция
системы зависит от передаточной функции устройства обрат-
ной связи. Реrулируя последнюю, можно воздействоваТI7
на передаточную функцию всей системы.
9.17. ЗАДАЧИ И ВОПРОСЫ для САМОПРОВЕРКИ
9-]. Доказать, что в случае симметрИЧ1Iоrо четыреХПОЛIOСlIика.
наrруженноrо cor щrеованно, коэффициент передачи по напряжению
равен:
1
r
'
Аl1+ V Ail
1
9-2. Доказать, что
Z21 ==:!: V Z2X (ZlX
ZlK)'
rде ZlX' Z2X' ZlK
параметры холостоrо хода и KopoTKoro замыкания,
9-3. Доказать, что
e
2g
Zic
ZjK
Zlc + ZlK
Z2C
Z2K
2 2C +Z 2K .
9-4. Доказать, что коэффициент передачи по напряжению четы-
рехполюсника, наrруженноrо произвольным сопротивлением Z2' равен
коэффициенту передачи по напряжению при холостом ходе, деленному
Z
на 1 + .......!!'...
Z2 .
9-5. Доказать, что коэффицнент передачи по току четырехполlOС-
ника, наrруженноrо произвольным сопротивлением Z2' равен коэффи-
циенту передачи по току при коротком замыкании, деленному на
1+ 22
2 2х .
9-6. Определить коэффициент передачи по напряжению при холо-
стом ходе и коэффициент передачи по току при коротком замыкании
для П-образноrо четырехполюсника, продольная ветвь Koтoporo со-
стоит из L. а поперечные ветви
из С (каждая). .
1
О т в е т: 1
(jJ2LC .
9-7. В схеме рис. 9-16 заданы: Za == 30
j40; Zo == Zc == 12 +
+ j16 Ом. Определить а и Ь.
О т в е т: 4,88 дБ; 0,703 рал,
268
9-8. Определить коэффициенты А трансформатора (см. рис. 8-11).
Дано: '1 == 15 Ом; L 1 == 20 Mf; '2 == 45 Ом; I
2 == 60 Mr; м ;:: 25 Mr;
u) "'" 1Ооо Р ад/с.
О т в е т: 1 L
36C50'; 72,3 L 3020' Ом; 0.,04 L 90° См;
3 L
36050'.
9-9. Определить характеристическое сопротивление и меру пере-
дачи симметричноrо MOCТOBoro четырехполюсника.
9-10. Доказать для симметричноrо
MOCTOBoro четырехполюсника,
что
1
Zl1 ==
2 (Zl +Zv;
1 ( 1 1 )
Yi1;::2 z1 + z; ;
1
Z12=="2 (Z2
Zl);
Y12==J.
(
) .
2 Z2 Zl
9-11. Вывести условия эквивалентности симметричныХ Т-образ-
Horo и MOC"ТOBoro четырехполюсников.
9-12, Несимметричный четырехполюсник наrружен сопротивле-
нием Z2' Пользуясь формулой 11 Z 11, доказать, что коэффициент пере-
Z.
дачи по току равен Kj==
Z
lZ ,а коэффициент передачи по на-
22 2
пряжению
к == Z21 Z 2
и Zl1Z22
Z12Z21 + Zl1 Z 2 .
9-13. Опыт холостоrо хода со стороны входиых выводов И опыты
холостоrо хода и KopoTKoro замыкания со стороны выходных выводов
четырехполюсника дали следующие результаты: Iа == 0,24 А; Р 1Х ==
== 13 Вт; I
x ==1,11 А; Р 2х == 92,3 Вт; I
K == 1,04 А; Р 2К == 89,2 Вт.
Напряжение источника питания при всех опытах было равно 100 В,
и все три тока отставали по фазе от напряжения.
Определить коэффициенты А.
О т в е т; 7,44 L 120°30'; 715 L 151°30' Ом; 17,9'lO
2 L 63°25' См;
1,59 L 97°.
rЛАВАДЕСЯТАЯ
ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ И тополоrИЧЕСКИЕ
МЕТОДЫ АНАЛИЗА ЛИНЕйНЫХ ЭЛЕКТРИЧЕСКИХ
ЦЕПЕЙ
10-1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КЛАССИФИКАЦИЯ
ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ
Изучая свойства резонансных цепей (см, rл. 5), мы
встретились с понятием полосы пропускания колебатель-
Horo контура. Было установлено, что чем выше доброт-
нОСть контура, тем уже ero полоса пропускания и соот-
269
ветственно острее резонансная кривая. Острота резонанс-
ной кривой характеризует частотную избирательность
колебательноrо контура, т. е. ero способность пропускать
или задерживать электрические колебания только опреде-
ленной частоты
резонансной или близкой к ней.
Однако на практике встречается необходимость Bыдe
ления не только одной какой-либо частоты, но целой полосы
частот. Например, для передачи по радио разrовора тре-
буется отделить определенную полосу частот, в пределах
которой ведется - данная передача, от всех друrих частот.
Такое разделение частот ОСУЦl,ествляется с помощью элект-
рических фильтров.
Э л е к т р и ч е с к и й фи л ь т р представляет собой
пассивный четырехпоЛiОСНИК, пропускающий некоторую
определенную полосу частот с' малым затуханием; вне
этой полосы частот затухание велико. Полоса частот, при
которых затухание мало, называется - п о л о с о й п р о-
п у с к а н и я фильтра. Остальную область частот со.
ставляет п о л о с а з а Д е р ж и в а н и я (или затухания)
фильтра.
Практическое применение электрических фильтров весь-
ма широко и разнообразно. Они применяются не только
в ,аппаратуре связи, но и в автоматике, приборостроении
и друrих областях техники, rде используется принцип
разделения частот.
Система одновремеННоrо телеrрафирования и телефо-
нирования по одному и тому же проводу с использованием
индуктивностей и емкостей для устранения влияния ОДНоrо
вида связи на друrой была применена в России впервые
в 1880 [. военным инженер-капитаном [. [. Иrнатье-
вым, осуществившим разделение двух каналов связи (теле-
фона и телеrрафа) с помощью индуктивных - катушек и
конденсаторов.
Эти элементы, примененные в целях отделения полосы
нижних частот от полосы верхних частот, ЯВЛЯЛИСЬ про-
стейшим видом фильтрующих устройств.
Совершенствование электрических фильтров неразрывно
связано с последующим развитием высокочастотной тех-
ники и электроники. Создание мноrоканальной ПРОВОДНОЙ
связи и радиосвязи сопровождалось разработкой теории
электрических фильтров и методов их расчета и непрер
IВ-
ным совершенствованием самих фильтров. Теория электри-
ческих фильтров базируется на общей теории четырехпо-
люсников.
270
Электрические фильтры MOrYT быть классифицированы
различным образом.
Классификация по про пускаемым частотам. В зависи-
мости от пропускаемоrо спектра частот фильтры разде-
ляются на фильтры: а) нижних частот (низкочастотные);
б) верхних частот (высокочастотные); в) полосовые; r) за-
rраждающие (режекторные).
Классификация по схемам звеньев. Фильтры MorYT со-
стоять из звеньев [-, Т-, П-образных, мостовых и др. В зави-
симости от числа звеньев фильтр может быть однозвенным
или мноrозвенным.
Классификация фильтров по характеристикам. В отли-
чие от простейших фильтров типа k различают фильтры
более BbICOKOtO класса
производные фильтры типа т
и др. Смысл коэффициентов k и т будет пояснен ниже.
Классификация фильтров по типам эл(}ментов. Разли-
чают фильтры: а) реактивные (состоящие из элементов L
и С); б) пьезоэлектрические (состоящие преимущественно
из кварцевых пластин); в) безындуктивные (состоящие
из элементов r и С) и др.
10.2. УСЛОВИЕ ПРО ПУСКАНИЯ РЕАктивноrо ФИЛЬТРА
Наименьшее число элементов, из которых может состоять
фильтр, равно двум ([-образное звено). Фильтры, содер-
жащие Т-и П-образные звенья, MorYT рассматриваться
в качестве комбинаций, составленных из [-образных звеньев.
h Z1
:
Z1
CJ
2Zz
Q ZZ' :
Рис. 10-1. Симметричные Т- и П-образные фильтры.
в случае симметричноrо Т- или П-образноrо фильтра
(рис. 10-1) параметры А 11 и g вычисляются по формуле
(9-49)
А Zf
11 == ch g == 1 + п
.
(10-1 )
Мера передачи g симметричноrо Т - или П-образноrо филь-
тра может быть определена как удвоенная мера передачи
271
g/2 [-образноrо фильтра. Соrласно (9-48)
sh { == у
.
(10-2)
Полосой пропускания peaKmuel-lOсо фильтра является
область частощ при KOпwpыX робственное затухание peaK
тивносо фильтра равно нулю (а == О).
Покащем, что четырехполюсник, состоящий из одних
индуктивностей или одних емкостей (
шаки Zl и Z2 одина-
ковы), не может иметь полосы пропускания. Иначе rоворя,
такой четырехполюсни:к не является фильтром; Действи-
тельно, пусть [-образный или симметричный Т:: или П-об-
разный четырехполюсник состоит из чисто реактивных
элементов, т. е.
Zl ==::t jX.l' Z2 == + jx 2 ;
(10-3)
здеСЬ.Х 1 и Х 2
модули реактивных сопротивлений; положи-
тельные знаки относятся к индуктивным, drрицательные
к емкостным элементам.
Соrласно (10-2)
h g h ( а + . Ь ) h а ь + . h а . Ь + ... / Xi
S 2
== s "2 ]"2 == s 2 cos 2
] с
2
810
2 ==
JI 4х 2 '
откуда, разделяя действительные и мнимые части, полу-
чаем
а Ь У Х:-
sh
Cos
== + .
.
2 2
4Х 2 '
h а . Ь О
с 281Оу== .
(10-4)
Ввиду Toro что rиперболический косинус деиствитель-
HOrO aprYMeHTa не может быть равен нулю (ch
;:::: 1),
на основании (10-4)
. ь О ь +1
SШ 2 == и cos
2==
.
Таким образом, при одинаковом характере СОПРОТИВле
нии Zl и Z2 затухание фильтра определяется по формуле
sh .
.. == у 4:
'
т. е. а> О (четыреХПQЛЮСНИК не имеет полосы пропуска-
ния).
272
Четырехполюсник обладает свойствами фильтра только
в том случае, коrда сопротивления Zl и Z2 имеют разные
знаки, т. е.
Zl == + jx 1 ; Z2 == + jx 2 .
(1 0
5)
При этом
sh fL == + J . ... /
X!
2 r 4Х2
Н, следовательно,
а Ь
sh
cos
О'
2 2
,
h а . Ь ... /
Х!
С 2 810
2 == + JI 4Х2 '
Уравнение (10-6) удовлетворяется при
sh
О
2
(10-6)
(1 o
7)
(10-8)
или
ь
cos2" == О.
(10-9)
Условие (10
8) соответствует полосе пропус;кания (а ==
а
== О). В этом случае ch 2" == 1 и соrласно (10-7)
. ь + ... /
Xl
8Ш
2==
JI 4Х2 '
(10-10)
По такому закону изменяется коэффициент фазы фильтра
в полосе пропускания (Х1 и Х 2 зависят от частоты).
В свою очередь условие (10-9) соответствует полосе
задерживания. В этом случае Ь == + л; Sin
== + 1 и на
основании (10-7)
ch i === У 4:; '
( 1 0-11 )
По такому закону изменяется затухание фильтра в
поJIосе задерживания. Формулы (10
10) и (10-11) спра
ве.дливы для r -образных и симметричных Т-и П-образных
фильтров. При этом под а/2 и Ы2 подразумеваются собст-
венное затухание и коэффициент фазы каждоr6 r -образноrо
звена. Т- или П-образный фильтр состоит из двух r-об
разных звеньев, и поэтому ero собственное затухание и
коэффициент фазы равны соответственно а и Ь.
273
Для любоrо симметричноrо реактивноrо фильтра в по-
лосе пропускания, т. е. при а :=;: О, выполняется условие
А ll (ro) == chg == ch (а + jb) == ch jb == cos Ь.
Поскольку косинус изменяется от
1 до + 1,
1
Ан (ro)
,1.
Это условие в случае Т- или П-образноrо фильтра при-
Нимает вид:
Zi 1
1
1 + 2Z 2
или
Zf
2
2Z 2
O.
Разделив все части неравенства на 2, получим
1 Zi О 10
422
. ( -12)
Таким образом, предельные частоты, лежащие на rpa-
нице полосы пропускания (так называемые ч а с т о т ы
с рез а), удовлетворяют условиям:
Zl==
4Z2; Zl==O. (10-13)
Неравенство (10-12) носит название у с л о в и я пр й.
п У с к а н и я реактивноrо фильтра (r-, Т- или П-образ-
Horo).
Z1 Ь
2 Z
1
Zz о
0.)
z
z ЛОIIОСа.
IfPO"!lcKaHUJI
Z1
ш
5)
о)
Рис. 10-2. fрафическое определение полосы пропускания на основа-
нии условий (10-13).
Частоты среза наХОJ]:ЯТСЯ из уравнений (10-13) анали-
тически (если заданы функциональные выражения Zl и
Z2 В зависимости от частоты) или rрафически (если заданы
частотные характеристики Zl и Z2)'
На рис. 10-2, б в виде примера показаны частотные
характеристики Zl и Z2 фильтра, изображенноrо на рис.
274
10-2, а; полоса пропускания rрафически найдена на
рис. 10-2,8.
Частоты среза MorYT быть также получены из рас-
смотрения частотной характеристики входноrо сопротив-
ления фильтра, наrруженноrо соrласованно, т. е. при по-
мЬщи характеристическоro сопротивления фильтра.
В случае Т -образноrо фильтра характеристическое со-
противление
ZT == -V Z l Z2 (1 + 41J ;
в случае П-образноrо фильтра
Z ' V Z1Z2
п==
1+42;'
Как было доказано выше, условие а == О может быть
получено только при разных знаках Zl и Z2' В этом случае
(10-14)
(10-15)
Z1 О
4Z 2
,
(10-16)
а произведение Z l Z2
действительное число.
Выражения '(10-14) и (10-15) получаются действитель-
ными при
Z'
1 +4Z;?=0,
т. е. при
Z1
1
4Z 2 .
(10-17)
Сопоставление (}0-16) и (10-17) с (10-12) показывает, что
условие, при котором характеристическое сопротивление
рассматриваемоro фильтра имеет действительное значение,
совпадает с условием пропускания фильтра. Поэтому пре-
дельные частоты полосы, соответствующей действительным
значениям характеристическоrо сопротивления, являются
частотами среза.
Физически это объясняется следующим образом. В по-
лосе Частот, при которых характеристическое сопротивле-
ние фильтра действительно, фильтр наrружен активным
сопротивлением " равным характеристическому по усло-
виям соrласованноrо включения.
Рассматриваемая здесь теория фильтров предполаrа-
ет наrрузку фильтра соrласованной, хотя в действитель-
275
насти соrласовать наrрузку На, Бсех частотах невоз-
можно.
Мощность, потребляемая этоЙ наrрузкой, является ак-
тивной мощностью. Она равна
Р 1 2 Щ
2==r2::::;
,
,
(10-18)
rде /2 и U 2
действующие ток и напряжение на ВЫХОДе
фильтра.
Входное сопротивление симметричноrо фильтра, Harpy-
женноrо соrласованно, в зоне пропускания таюке равно r,
и поэтому мощность На входе фильтра равна:
U 2
Р1 == (]1 ==
;
,
(10-19)
здесь /1 и U 1
действующие ток и напряжение на входе
фильтра.
Поскольку рассматривается идеальный фильтр, т. е.
фильтр, состоящий из чисто реактивных элементов, 'актив-
ная мощность внутри фильтра не расходуется и поэтому
Р1 == Р2'
На основании (10-18) и (10-19) сле-дует, что
11 == 12; U 1 == U 2 .
т. е. затухание ра.вно нулю.
Итак, 8 полосе пропускания фильтр имееrn активное
характеристическое сопротивление. В полосе задержива-
Ния хара'ктеристическое сопротивление фильтра является
реактивным.
Отсюда вытекает простой способ rрафическоrо нахож-
дения частот среза по частотным характеристикам входных
сопротивлениЙ холоcrоrо хода (Zx) и KopoTKoro замыка-
ния (ZK)'
Характеристическое сопротивление Zc фильтра связа-
но с Zx и ZK формулой
Zc == V ZXZK ' (10-20)
Очевидно, что Zc будет действительным числом при
разных знаках Zx и Z".
На рис. 10
3, б показаны кривые Zx и ZK дЛЯ фильтра
рис. 10-3, а. После перемножения Zx на ZK и извлечения
корня получается кривая рис. 10-3,8; полоса частот, в
пределах которой Zc имеет действительное значение, т. е.
276
представляет активное сопротивление, соответствует полосе
пропускания фильтра 1.
Очевидно, что эта полоса оrраничена частотами <Ul и
<U 2 (рис. 10-3, 6); в пределах этой полосы Zx и ZK имеют
разные знаки. Вне этой полосы Zx и ZK имеют одинаковый
z
Zc = vz ж Z,;
Ин8укти8ное
А кти8ное
...
,
Ы2' ы
=0
0.)
ПОЛQСо.
nропуснания
о)
о Ы1
;'
l'
Емкостное
Полосо.
пропускания
8)
Рис. 10-3. fрафическое определение полосы пропускания на основа-
нии условия (10-20),
знак и, следовательно, характеристическое сопротивление
в соответствии (с 10-20) имеет мнимые значения (реактив-
ное сопротивление), показанные на рис. 10-3, в пункти-
ром.
Данное положение является общим для фильтров без
потер ь всех типов.
10.3. ФИЛЬТРЫ ТИПА k
П усть составные элементы r -образноrо звена явл яются
взаимно обратными двухполюсниками. Это означает, что
произведение их комплексных сопротивлений во всем
диапазоне частот ПОСТОяНно, т. е. не зависит от частоты:
1
2' Z1 . 2Z 2 === Z l Z2 === k 2 ,
( 1 0- 21 )
rде k
действительное число.
Можно покаЗ8ТЬ, что и произведение характеристических
сопротивлений ZT и Zп Toro же r-образноrо звена также
1 ПО оси ординат откладывается или действительное, или миимое
значение характеристическоrо сопротивления в зависимости от обла-
сти частот,
277
равно k 2 . Действительно, умножая (10-14) на (10-15), полу-
чем: .
ZтZп == Z l Z2 == k 2 .
Фильтры, удовлетворяющие условию (10-21), получили
название Ф и л ь т р о в т и п а k. ,
С учетом (10-5) и (10-21) выражения (10-10J
(10-12),
(10-14) и (10-15) принимают вид
. Ь " . k Х}
51°2== + 2хз == + Zk;
ch !:. ==
== Х} .
2 2Х2 2k'
1 k О . 1 Х} О .
2хз
,
2k
'
V ( k ) 2 V ( X'l \ 2
Z Т == k 1
== k 1
'"
) ;
2хз", 2k
."." '"
k k
Zп
V l
(2;J2
Yl
(
?
(10-10а)
(10-11а)
(10-12а)
(10-14а)
(10-15а)
Таким образом, при заданном значении k достаточно
воспользоваться только одной из частотных функций Хl
или Х 2 (представленной аналитически или rрафически)
для определения всех прочих характеристик фильтра типа
k*.
Приведенные выше формулы справедливы для r
, Т-
и П-образных звеньев. Иначе rоворя, при одних и тех же
значениях k и Х 1 (или Х 2 ) ширина полосы пропускания и
характеристические сопротивления r-образноrо фильтра
получаются такими же, как и в случае Т- и П-образных
фильтров. Разница заключается лишь в собственном зату-
хании и коэффициенте фазы, которые при переходе от r.
образноrо звена к Т. или П-образному звену удваиваются.
На рис. 10-4
10-7 показаны схемы фильтров нижних
частот, верхних частот, полосовых и заrраждающих (для
[-, Т- и П-образных звеньев).
Физическое действие таких фильтров леrко объяснить
тем, что на низких частотах индуктивные сопротивления
малы, а емкостные велики; на высоких же частотах имеет
* в расчетах коэффициент k выбирается из условия соrласования
сопротивления наrрузки с характеристическим сопротивлением фильтра
при определециой частоте.
278
L
Т
...... z T.... 1
11.)
L
JffJ:
1)
Рис, 10-4, Фильтр нижних частот типа k,
t t
--ф- с 1 ....
(IJ
tlS
')
2С 2С 2С
::r I :1
с
11. "L
')
4)
Рис. 10-5. Фильтр верхних частот типа k.
()
1,1
Т 2С1
:+:}:'
4)
f! !!
2C12
Lf .Cf
!! " 2Lz Cz
С, Lz Z 2
2L,
Рнс, 10-6. Полосовой фильтр типа k,
1)
L1
2
2С1 2!.1 2LZ
2Т
0.)
L1
2'
.;
l1
2'
L1
Рис, 10-7. 3arраЖJ(aIOЩИЙ фильтр типа k.
279
место обратное явление
индуктивные сопротивления ве...
лики, а емкостные малы. Поэтому например, в фильтре,
нижних частот (см. рис., 10-4) токи нижних частОТ проходят
через индуктивность в наrрузку, лишь в малой степени
ответвляясь в емкость.
В области же верхни.х частот индуктивнрсть представ-
ляет большое сопротивление и, кроме Toro, ток высокой
частоты, прошедший через индуктивность, замыкается в
основном через емкость, 'представляющую ;ДЛя Hero малое
сопротивлен ие.
Аналоrичные рассуждения применимы и к фильтрам
верхних частот (см. рис. 10-5), которые блаrодаря eMKOCT
ному характеру сопротивления продольной ветви и индук-
'тивному характеру сопротивления поперечной ветви обус-
ловливают' большое затухание на нижних частотах и малое
затухание на верхних.
В свою очередь в полосовых и заrраждающих фильтрах
(рис. 10-6 и 10-7) проявляются частотные зависимости
сопротивлений двухполюсников, состоящих из последо-
вательно и параллельно соединенных индуктивностей и
емкостей.
Частотные характеристики а, Ь, ZT и ZП рассматри-
ваемых фильтров типа k изображены на рис. 1 0.8
1 0-11,
а расчетные выражения основных характеристик и пара-
метров фильтров сведены в табл. 10-1 * и 10-2. '
Как видно из расчетных выражений и характеристик
(рис. 10-8 и 10-9), в пределах полосы пропускания напря-
жение на входе симметричноrо фрльтра, наrруженноrо
соrласованно, опережает напряжение на выходе (Ь > О
фильтр нижних частот) или отстает от Hero (Ь < О
фильтр верхних частот);. в случае полосовоrо фильтра
(рис. 10-10) знак Ь изменяется в пределах полосы пропуска-
ния с минуса на плюс. В полосе задерживаНИst симметрич-
oro фильтра коэффициент фазы Ь равен п (фильтр ниж-
них частот) или
л (фильтр верхних частот); в с"lучае
симметричноrо полосовоrо фильтра коэффициент фазы ниже
полосы пропускания равен
л, а выше полосыl пропуска-
ния
равен л.
· При м е ч а н и е к т а б л. 10-1.
t 'т
F == 'Т;;;
т , rде t m ==
'2 lт
" 1т
Т;
=== У М2 .
280
6
t:!
;':' S
::! .е.
'" ""
'g :::
h ::r
52
'"
'"
:!!
'"
о.
<-.
'"
C'J
111
Q
1-
,.Q
"=
::
-&
::
::о:
::
1-
'"
..
1-
::о:
са
..
:а
=:
111
Q
=:
u
Q
IG:- l...ilc$
Iit'
::;, ::;,
i"- !
+
+ 11
.. "- +1 ;....,
I,JI
I
,
1...i]c3'
'
"
t::
If 11
"- "- i+ I,JI
';;;...
<1 I
/
u!
.
I
1-..J1c.J
.....[
............... ...............
f-<
l
, t:: +
+
g
I"'" I
u I
со
о'
..
.....1 u
::: '
Iч......
1
1-..J1c.J
'" ............... ...............
'" ......I
.t:: +
+ l
g
I
......
,Q'"
>;
'"
ео
[ с t:!1
'" ':::'
N
II
'" .= .:::,
'и; С:: t:! u
с) f-< t::
'" t-.J
о. "'* t-.J
cl!
... t\1,t;;
'" 15
g;
'" u >.::s:
о. о t:: :r:
Q) :r:
'"
о t\1 00=(0;:
><: 00.::<:
t::t::U t::
a:a
,Q
>;
:::
-9<
.:::
о
'"
о
и
О
"
О
t::
х
'"
о.
cl!
'"
С.
>;
:::
ео
х
281
с'о
с::) 1+
.....
g. фlcJ
...
-..1
": r:- ::? +
'g I
'" ::?
I
I
t.... о: I
!
I
I
.,.
,.
I 1=: :::,
I=:
:r
t:: 1=: 11
1+
52
., '<j< '<j<
10{ 11 11 CJ \..............
i!i ... '" 11
1J3
., ч -..1 '...
""
.. с,,)
., 11
(у) ...
'"
о:
==
-&
.:s:
о
'"
о
и
о
о:
о
t::
......
... ...
ц.....ц.....
I 1 ц.:;
C'I
:t t:;
""'"
1=:
11
..
..$ ч
.... I
ц..;... 1
I I
...... ..
t:;
'<j< -«
I
111=:
с,,) .1
с,,)
1+
I CJ
...
.,..:1
+J""""""'"
l
II
,
I+
lcG
11
...
'...
ц..;
><
Ii I
==
,. '
>< 1=:
""....
:i\
'<j<-
са 11 11
со
11
joo с,,)
.а '" -..1
"= о:
:: '"
-& Э
:11
со
joo II
i >< l.tt
==
I'i
'"
i!i....
с
t':
01.1 ",,16 11 11 11
:11
'" ч с,,)
:с
joo о: I
01.1 :s:
:r I э
aI
g,.
282
а,Ь
о
f
fc
а.)
I
I (iy.<::'
I
"
I 'f.
",
I t-y.
,. Zr
1,,/ f
IfC "....
: ,/Емностное
I 'Zп
11
11
Рис. 10-8. Частотные характеристики фильтра нижних частот типа k,
б)
4,Ь
"
а)
т
Zr ,Z"
Ин8fjктIJ.8ное
,,
Zn
: Zn
1 1
k
T"'
l' I
I I Zr
,"ТС
I Zr
/"'Емносmное
о
Рис. 10-9. Частотные характеристики фильтра верхних частот типа k.
5)
а.,Ь
f
0-)
ZT,ZIl
ИндуктиВное
\ Акти8ное
I I ИндуктиВное
I 1. I '\.- ,
k Z.!!.
п
+
,,}:
T
I I I Z I /
О / т т
.1'(1 f m
I'
T
I
Емкостное I/EMKocmHoe
б)
Рис. 10-10. Частотные характеристики ПОЛОСОБоrо фильтра типа k.
283
Выше отмечалось что коэффициент фазы r -образноrо
фильтра равен Ь!2, и поэтому в полосе задерживания он
равен л/2 или
л/2, в зависимости от типа фильтра.
Если r -образный фильтр наrружен соrласованно, то
уrол фазовоrо сдвиrа между, напряжениями на входе и
1
выходе составляет 2" (Ь + <Рlс
<Р2С)' rде <РIС И <Р2С
уrлы
характеристических сопротивлений рассматриваемоrо r-об-
разноrо фильтра (см.
9-7).
В полосе задерживания характеристические сопротив-
ления мнимые, разноrо знака и соответственно разность
Zr , ZП
о
k
й}Ь
Рис. ld
ll. Частотные характеристики заrР<J>кдающеrо фильтра типа k.
уrлов (jJlc
(jJ2C составляет л или
л. В этом случае уrол
между входным и выходным напряжениями r-образноrо
фильтра, наrруженноrо соrласованно, с учетом Toro, что
в полосе затухания Ь!2 == + л/2, получается piJBHbIl.\'j + л.
Это соответствует физическим представлениям о фазовых
сдвиrах в реактивных цепях, поскольку в полосе задержи-
вания наrрузка,фильтра предполаrается также реактивной.
Следует заметить, что если, напр имер, r -образный
фильтр нижних частот cOrJIaCOBaHHo наrружен со стороны
выхода, имеющеrо характеристическое сопротивление ZП,
то в полосе пропускания наrрузка фильтра, равная Zп,
активна.
Можно показать, что в результате параллельноrо соеди-
нения активноrо оопротивления наrрузки (Zп) с емкост-
ным сопротивлением поперечной ветви r -образноrо звена
(2Z 2 ) получится активно-емкостное сопротивление, емкост-
284
ная составляющая KOToporo компенсирует индуктивное
сопротивление продольной ветви (Zl/2). В результате
остаиется только активная составляющая, равная xapaK
теристическому сопротивлению ZT при данной частоте t.
lXля определения знака характеристическоrо сопротив
ления фильтра В полосе задерживания (+ j или
j) удобно,
пользоваться формулами табл. 1 O
l, в которых под корнем
сохранен множитель j. В полосе задерживания слаrаемое,
содержащее множитель j, больше единицы; поэтому при
отбрасывании слаrаемоrо 1 под корнем остается выраже-
ние с множителем j в числителе или- знаменатеJiе в зависи
мости от типа фильтра и от Toro, рассматривается лИ ZT
или Zп.
Преимуществом фильтров типа k является их простота,
'а также то, что в полосе задерживания затухания по мере
удаления частоты от частоты среза неуклонно возрастает.
Что касается недостатков фильтров типа k, то они в
основном заключаются в следующем:
, 1. Характеристические сопротивления ZT и ZП В полосе
пропускания фильтра очень резко изменяются в зависи
мости от частоты, всЛедствие чеrо соrласовать' наrрузку
с фильтром удается только в оrраниченной части полосы
пропускания.
2. Кривая затухания вблизи частоты . среза имеет недо-
статочную крутизну, вследствие чеrо не обеспечивается
четкое разделение частот.
Для увеличения крутизны кривой затухания прихо
Дится применять мноrозвенный фильтр.
, tO-4. ФИЛЬТРЫ ТИПА т
В целях наилучшеrо соrласования наrрузки с фильт-
ром необходимо, чтобы характеристическое сопротивление
, фильтра было по возможности постоянным в полосе про-
пускаемых частот. В связи с этим попытаемся изменить
продольную или поперечную ветвь r-образноrо звена типа
k таким образом, чтобы полуЧИJ):ОСЬ новое r -образное звено
с хараК"fеристическим сопротивлением, мало меняющим<,:я
в зависимости от частоты в полосе пропусн:ания. Второе
характеристическое сопротивление этоrо звена должно
быть равно характеристическому сопротивлению исход-
Horo звена типа k (именуемоrо «прототипом»).
Равенство характеристических сопротивлений HOBoro
фильтра (так назыВаемоrо фильтра типа т) и прототипа
285
позволяет включать их соrласованно и образовывать, таким,
образом, комбинированные фильтры, сочетаЮlJ1,ие в себе
преимущества фильтров обоих типов. Ввиду Toro что r
рб
разный прототип имеет два характеристических сопротив
ления, в данном случае возможны два вариаf!та:
1. Одинаковыми остаются характеристические сопро-
тивления ZT (рис. 10
12). Полученное при этом звено т
носит название п о с л е Д о в а т е л ь н о . про и з в о Д .
н о r о.
2. Одинаковыми остаются характеристические СQПрО
тивления Zп (рис. 10-13). В этом случае звено m носит
НаЗВание пар а л л е л ь н о - про и з в о Д н о r о.
тZ1
2'"""
Z1 Z1m
2 :;Е ' 2 Zп",
...... 2Z2
ZT
2Z 2m
а) 6)
Zr
2Z2
т ZПm
1
т2
2т Z1
8)
Рис. 10-12. Образование последовательно-производноrо звена ТИПi\ т.
Рассмотрим первый вариант. Из условия равенства
характеристических сопротивлений ZT звеньев, изображен-
ных на рис. 10
12, а и б, следует:
ZT == V Zl Z 2 (1 +
1J == V Zlт Z 2т (1 + 4
)' (10-22)
Пусть
Zlт == mZ 1 ,
причем
1
m
О.
(10-23)
(10
24)
Подстановка (10
23) в (10
22) и решение полученноrо
уравнения относительно 2Z 2т дают:
2Z
2Z 2 + Zi 1
т2 ( 10-25 )
2т
m 2 m .
Из Этоrо выражения ВИДно, что поперечное плечо пос
ледовательно-производноrо r -образноrо звена типа m co
стоит ИЗ двух последовательно включенных сопротивлений
/ (1
т2) Zi
2Z 2 m и 2т (см. рис. 10
12, в).
286
Рассмотрим теперь второй вариант. Исходя из условия
равенства характеристических сопротивлений примени-
тельно к рис. 10-13, а и б, и меем:
ZП == "1 f 2122 == I 2iт22m . (10-26)
V 1+
L 1 1+ 21т
. 422 42 2т
Пусть
Z Z2
2т ==
,
т
(10-27)
причем сохраняется условие (10-24).
После подстановки (10-27) в (10-26) решение уравнения
относительно 21Z l1 11, дает:
+
1
m2 (10-28)
21т
т2 1 222т'
Значит, продольное плечо параллельно-производ!!оrо
r-образноrо звена типа т состоит из сопротивлений тZ l /2
2т2 2
и
1 2' соединенных па р аллельно (рис. 10-13, в).
m
Z1 21т
т ZП
:::LZп
Рис. 10-13. Образование параллельно-производноrо звена типа m.
в соответствии с (10-25) и (10-28) MorYT быть найдены
выражения харак:rеристических сопротивлений ZTm
(рис. 10-13) и ZПm (с.м. рис. 10-12):
1
2 '
1+(1
т2)
422
ZПm == ZП [1 + (1
т 2 ) 4
J .
ZTm == ZT
(10-29)
(10-30)
Очевидным является соотношение
ZТmZПm == ZтZп == k 2 . (10-31)
Полосы пропускания фильтров типа k и полученньiх из
них фильтров типа т совпадают. Действительно, на основа-
287
нии (10-23) и (10
25) можно получить:
m т
42 2т == 4 (
+
,
1
т 2 )
Z2 + 1
т2
т 4 т 21
то же самое выражение получается на основании (10-27)
и (10-28) для друrоrо варианта фильтра типа т. Подстав-
ляя в (10-32) условия (10-13), отвечающие предельным
частотам фильтра типа k, получаем при Zl == О и Zl ==
==
4Z 2 :
(10-32)
2im О .
4Z 2m == . ,
21т 1
422111 ==
.
(10-33)
Эти условия соответствуют предельным частотам фильтра
типа т (имеroщеrо последовательно- или параллельно-
производное звено).
Следовательно, частоты среза для обоих типов фильт-
ров совпадают.
О 'совпадении полос пропускания ПрОТQТипд и произ-
водных от Hero звеньев можно также судить на основании
равенства характеристических сопротивлений (в полосе
пропускания характеристические сопротивления имеют
действительные значения).
В полосе задерживания в соответствии с общей форму-
лой (10-11)
сЬ ;
V I,Zi::.1
vl,z,т , .
.
+ 1
т 2
Zi
(10-34)
3атухаН!1е обращается в бесконечность при частоте
foo, при которой 4;: + 1
т 2 == О, или, что то же
21 1
4Z
==
1
т2 '
При этом условии Z2111' выражаемое формулой (10-25),
обращается в нуль. Это означает, что
при foo наступает
резонанс напряжений в поперечной ветви (в случае после-
дователыю-производноrо звена). При этом' же условии
Zlm, выражаемое формулой (10-28), обращается в беско-
нечность, что означает резонанс токов в продольной ветви
(в случае параллельно
производноro звена.) Частота foo
называется частотой бесконечно большоrо затухания.
При переходе частоты через значение foo, т. е. в области
частот f> foo (коrда foo> fc) или f < foo (коrда foo> fc),
2ВВ
сопротивления обоих ПJIеч фильтра Zlm И Z2m имеют оди
наковый знак. В этом случае в соответствии с
10
2 в левой
части формулы (10-34) rиперболический косинус должен
быть заменен rиперболическим синусом.
60 I I mJl!.7
5
АБ а
I I
50
f-------- т=0542 \
r=0,5
O,59
\
40 miO/'
16 i\ J
30
У. \ / "'-
m =O,J05 \ i\.,/ ["0..........
rf':,.
20 '1 /' ,'\
< ""....... т",1
" X'I'-::::-
;>< >с ....
10
.......
-т
о 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0
VI4;
l' (fc аля фильтра НЧ или ;с для фильтра 8Ч)
Рис. 1O
14. Кривые затухания фильтра типа т.
При 4Z 2 , IZ 1 стремящемся к нулю,
а т 5
sh
2 -+
. (10-3 )
V 1
т 2
На рис. 10-14 показано семейство кривых собственноrо
затухания а фильтра типа т (при разных значеНJIЯХ т)
в функции У \4;'2/' При m == 1 кривая затухания обра-
щается в характеристику фильтра типа k.
Чем меньше коэффициент т, тем меньше значение f со,
т. е. тем круче кривая затухания а. Однако, как видно
z.
из рис. 10-14, предельное значение а при 41 2 -+ СХ) умень-
шается по мере снижения т.
Наряду с большой крутизной кривой затухания фильт-
ры типа m отличаются от фильтров типа k относительно
б6льшим постоянством характеристических сопротивлений
289
117
z .
...!!Е ил u. ..2....
k ZПт
I
т=0, 3О5
I J
т =-0/116
т =О,Ч73 (f20%) / ",....
m=0, 506 (::t15%) ..( \
m=0)5't2(i:.10%)
t><
т=О 59 (f 5%)" у .x
.....
1 I '1 I
I
.....
...... '\
r-- '" --- --- in = О,7Н \Ш
...... .......
....... ""
..... т=1 '\
"
" \
\ \
r\
,
\
1)6
1)5
1/'1
1)3
1/2
1,1
1)0
019
018
017
0)8
015
О,Ч
013
0)2
0/1
О 0/1 012 013 О,Ч 015 018 017 q,8 0,9 1
1'IЦ
21Ц для фил/tmра ff'fи.ЛIJ.
fJля фильтра 8'1)
Рис. 10-15. Характеристическое CDпротивление фильт-
ра типа m.
290
L
'2
Z r; 2 т :
т!.
"7
т!.
тС
Z Тт zT
; 1
т с у : Zn
2т
1
mZL Znm
2т тС'"
T2es
ZT
..........
o
Рис, 10-16. Фильтр нижних частот типа т,
2С
т
ZT 2[, Z"",
.......... т 2 .......
C
т 1
т2 .
o 0
20
TZп
:J:
Zn
Рис. 1O
17. Фильтр I!ерхних часто'r типа т,
.!:f 2 С ,
'
С2
Z r ...... -т
2[,2 Z
-+-"
.yL1 ZC1
т
1
mZ
L,
2т 2т Z 1
т! С
I
Zb
Zпт
zт z
тС2 2Ц тС!
....", 2
J?J
Zt
X!J
Рис. 10-18. ПолосовоЙ фильтр типа т,
291
" Zrт . Znm .,
11 I
;
,1 I
k k 1 /
r-i ,
ь=о f / If"" f I I f
О fc Q fC, ,fco
I I ,
11 11
11
Рис. 10-19. Частотные характеристики фильтра нижних частот типа m.
znm,\
'1
k
--/r
;00' I f
О
I 'с
I
,
ZTm i.
,1
k
--i+
,';",,'
О
I ,fc
11
\1
f
I
b=
x
Рис, 10-20, Частотные характеристики фильтра верхних частот типа m.
ZПт ,1 1
k
\
'1 \
, I /
, '1 I .I.........!.....
о '" 1 ' 2 1 /foo2
/ 00 11
1 l'
",
/
/
ь ,1
,1
, I
I
, \f"",2 f
I ",
I I
1с I 1
l'
Рис, 10-21, Частотные характеристики полосовоrо фильтра типа m.
292
ZTm или ZПm (по сравнению с частотными характеристи-
ками ZT и Zп).
На рис. 10-15 изображены кривые ZTm1k И соответствен-
но k/Z Пm в зависимости от величины V I4;; " равной f /f с
ДЛЯ фильтров нижних частот и fclf для фильтров верхних
частот.
В спектре частот, соответствующем V 14i
1 == 0+0,9,
характеристические сопротивления ZTm И ZПm отклоняются
от k на + 5% при т == 0,59 и на + 10% при т == 0,54.
Типовые схемы [-образных звеньев фильтров нижних
частот, верхних частот и полосовых фильтров типов k и т
а)
о
-f
Рис. 10-22. Комбинированный фильтр.
а
схема; б
характеристика затухания.
приведены на рис. 10-16
10-18; частотные характеристики
фильтров типа т показаны на рис. 10-19
10-21.
Как видно из частотных характеристик, фильтры типа т
имеют более постоянное характеристическое сопротивление
в полосе пропускания, чем фильтры типа k. Кроме Toro,
они обладают большей крутизной кривой затухания.
Недостатком фильтров типа т является СНижение зату-
хания при f < foc> (фильтры верхних частот и полосовые)
и f> fco (фильтры нижних Частот и полосовые).
Соединяя последовательно звенья типов k и т, можно
достиrнуть HeKoToporo постоянства характеристических
сопротивлений и крутизны кривой затухания при одно-
временном сохранении необходимоrо затухания ниже или
выше частоты бесконечно большоrо затухания. На рис.
10-22, а в виде примера показан полосовой фильтр, состоя-
щий из Т-образноrо фильтра типа k (в середине) и двух
[-образных звеньев типа т (по концам). На рис. 10-22, б
изображена характеристика затухания TaKcro фильтра.
293
iO-5. ИНДУКТИВНО СВЯЗАННЫЕ КОНТУРЫ КАК ФипЫРУЮЩАЯ
СИСТЕМА
Индуктивно связанные КОНТуры при соответствующем
подборе параметров представляют собой полосовой фильтр,
пропускающий заданную полосу частот.
Положим, что в первичную и вторичную цепи трансфор-
матора включены емкости С (рис. 10-23, а).
Индуктивности обмоток трансформатора примем рав-
ными L; коэф;рициент индуктивной связи обозначим через ko.
Llt
T
м
а) 5)
Рис. 10-23. Фильтрующая система.
а
ИIщуктивно связанные реЗОН<iНСИЫЕ! К6нтуры; 6
tХёМЗ замеЩення.
Трансформатор с емкостями С предстаВЛяет собой сим-
метричный четырехполюсник, эквивалентная схема кото-
poro показана на рис. 10-23, б. Выше мы уже встречались
с аналоrичной схемой полосовоrо фильтра (см. рис. 10-2).
Исследуем теперь более подробно фИЛЬТРУЮLЦие свойства
рассматриваемоrо четырехполюсника в предположении, что
ОН наrружен соrласованно. Ero характеристическое сопро-
тивление может быть вычислено по формуле (10-14), куда
следует подставить:
21 == j2 [О) (L
М)
ш
]; 22 == jO)M.
После прео бразования получим:
Zc == (O
у
(0)2С (L +М)
I][О)!!С (L
М)
1].
Приняв 0)5 == 1Л,С и введя КОзффициент индуктивной
связи ko == М IL, ПОЛУЧИ1\! ОКОНЧательно:
2с ==
c V
[( с: ) 2 (1 + ko) ,
1] [( с: У (1
ko)
1].
Характеристическое сопротивление 2с действительно
при условии, что выражения в квадратных скобках имеют
294
разные знаКИ J В именно:
с: У (1 +ko)
1 > о; с: У (1
)
1 < О,
откуда
<(й< шо ;
Vl+ko Vl
ko
ffil И
(й:.! представляют
а.,Ь
z,
i i I
II :
II I .
/!o-(f{
:... I I".,.,..;J
о ""'0 ш,
j,'
Рис. 10-24. Частотные характе-
ристики индуктивно свяsанных
резонаисных контуров,
(()
.
1
V l+ko '
ШО
(й2 == Vl
ko ;
CL)
собой частоты среза данноrо
полосовоrо фильтра.
В области частот ниже
(й 1 характеристическое со-
противление фильтра ем-
костное и с. уменьшением
частоты приближается к
j/2cuC.
В области частот выше
Ю 2 характеристическое со-
Z1
Рис. 10
25. Мостооой
фильтр.
противление фильтра индуктивное и с увеличением частоты
приближается к jcu ц/ 1
k
.
При частоте
(й == (йо == I/V LC ,
Zl ==
j2cu()M
и
м koL "1/У:
Zc == (йоМ == VLc == VLC ==ko JI С'
На рис. 10-24 показаны частотные характеристики дан-
Horo фильтра.
295
10-6. МОСТОВЫЕ ФИЛЬТРЫ. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ
РЕЗОНАТОРЫ
Соrласно
9
15 [формулы (9-50)] характеристическое
, сопротивление и мера передачи симметричноrо MocToBoro
фильтра (рис, 10
25) находятся по формулам:
ZM == Y Z 1 Z 2; )
th ,
== 1
. (10-36)
Полоса пропускания фильтра (а == О) имеет место при
мнимых значениях корня V Z1/Z2 и деиствительных зна-
чениях корня V Z 1 Z2' При этом Z1 И Z2 имеют разные знаки.
Коэффициент фазы определяется в этом случае по фор-
муле
tg
== + 1 1
1.
(10
37)
в полосе задерживания Z1 и Z2 имеют одинаковые знаки.
В этой полосе. возможны два случая:
Ь == О или Ь == + N.
В первом случае
th
== th
== 1 \
1.
Это решение соответствует условию IZ11 < IZ21, так как
rиперболический TaHreHc не может превышать единицу.
Во втором случае
th
f == cth
== 1 1
[.
Данное решение соответствует условию IZ11> IZ21,
так как rиперболический KOTaHreHc не может быть меньше
единицы.
а
При Z1 == Z2 затухание а == 00, так как при этом th"2 ==
1 и напряжение на выходе мостовой схемы равно нулю.
Физически это объясняется тем, что мост уравновешен.
На рис. 10-26 показаны простейшие схемы мостовых
фильтров: нижних частот, верхних частот, полосовоrо и
заrраждающеrо.
Основываясь на том, что в полосе пропускания Z1 и
Z2 имеют разные знаки, а в точке пересечения кривых
296
Zl I! 2?" т. е. при 21 == 2?, а :=-
00, можно леrко найти частоты
СрЕ'за tf бесконечно большоrо затухания. В Биде примера
ХХХ
[1
L
л.С2
:
8)'
Рис. ]O
26. Мостовой фильтр нижних частот (а), верхних частот (6),
полосовой (6) И заrраждающий (е).
это показано применительно к фильтру нижних частот
на рис. 10
27. При отсутствии пересечения кривых 21
и 22 частота бесконечно большоrо затухания отсутствует
или удалена Б бесконечность (при асим-
птотическом приближении 21 к 22)' +]
На практике применяются также мостовые
схемы с дифференциальным трансформатором
(дифференциально
мостовые схемы), эквивалент
ные по своим электрическим качествам мосто-
вым схемам, но имеющие меньшее число эле-
ментов (рис. ]0
28).
Следует заметить, что в соответствии' с
(l0
З6) ZM зависит от произведения, а g
от
отношения сопротивлений плеч MocToBoro
фильтра, Поэтому характеристические парамет-
ры ZM и g MocToBoro фильтра не связаны друr
с друrом в той мере, как это, например, имеет
место в Т-и П
образных фильтрах (см. задачу О fc foo
]0-]6) и, следовательно, ZM и g MorYT выби-
раться независимо друr от друrа. Это свойство
является одним из преимуществ мостовых
фильтров по сравнению с друrими.
Мостовые фильтры часто выполняются с по
мощью пьеЗОЭ,1ектрических резонаторов. Послед-
ние представляют собой электромеханическую
систему, состоящую из пьезоэлектрической пластинки 1, электродов
и держателя. Пьезоэлектрическая пластинка под воздействием пере-
MeHHoro электрическоrополя совершает механические колебания
с частотой приложенноrо напряжения. При этом на ее поверхностях
возиикают электрические заряды. При совпадснии частоты поля с ча-
стотой собствеиных колебаний пластинки наступает резонанс: ампли-
туда колебаний и соответственно заряд на пластинке достиrают мак-
симума,
l'
f
Рис. ]0
27. Нахож-
дение частот среза
и бесконечно боль-
шоrо затухания мо-
cToBoro фильтра.
1 В технике связи применяюТСЯ преимущественно кварцевые пла-
стинки,
297
Эквивалентная электрическая схема пьезоэлектрическоrо резо-
натора представляет собой двухполюсник (рис. 10-29, а). Частотная.
характеристика реактивноrо сопротивления резонатора изображена
на рис. 10-29, б,
Z nZ
1У
2Z1 U
C :E
Рис. 10-28. Диффереициально-мостовые схемы.
2Z1
Zz
т
в отличие от иидуктивных катушек, добротность кморых в луч-
шем случае измеряется сотнями единиц, добротность пьезоэлектриче-
ских резонаТОРОА достиrает десятков тысяч.
С помощью таких резонаторов удается получить полосовые фильтры
с весьма узкой полосой пропускания и ВЫСокой крутизной кривой за-
:r:
.o
а.)
I
I
I
lcut
i
,.,
Рис. 10-29. Пьезоэлектрический резонатор.
а
ЭКllИвалентная схема: 6
частотная характернстнка
реактивноrо элемента.
тухания вблизи частот среза (кварцевые мостовые фильтры допускают
полосу пропускания порядка 20
50 [ц при частоте 500 Krri).
Емкость с 2 , входящая в систему замещения пьезоэлектрическоrо
резонатора (рис. 10
29, а), значительно превышает емкость' с; поэтому
частоты Ш 1 и Ша (рис, rO
29, б) располаrаются весьма близко I1pyr
к друrу.
10-7. &Е3ЫНДУКТИВНЫЕ ФИЛЬТРЫ
Изrотовление индуктивных катушек для фильтров, работающих
в области низких частот, сопряжено с трудностями, особенно коrда
катушки должны иметь большую индуктивность при высоком коэф-
фициенте добротности. Увеличение сечения обмотки повышает массу,
размеры и стоимость катушки, прнменение же маrнитопровода СОЗl1ает
зависимоСТЬ индуктщmости от тока, проходящеrо по обмотке,
2ВВ
Применение пьеЗокварrJ.евых реЗонатороВ для фильтров низких
частот также не всеrда возможно, так как самая низкая .частота, на ко-
торую изrотовляется кварц, составляет несколько сотен rерц.
ВО избежание получения rромоздких фильтров с низкой доброт-
ностью катушек применяют б е 3 ы н Д у к т и в н ы е Ф и л ь т р'ы
(,С-фильтры), состоящие из активных сопротивлений и емкостей.
На рис. 10-30 показан ,С-фильтр нижних частот. При низких
частотах, коrда емкостное сопротивление велико, напряжение на вы-
ходе фильтра немноrим меньше напряжения на ero входе И, следова-
тельно, затухание мало. С повышением частоты емкостное сопротивле-
ние убывает, напряжение на выходе уменьшается И, следоuательно,
затухание возрастает.
l' ,..,..
z z z
" С Т flJ
4) 6)
Рис. 10.30. rC-фильтр нижних частот.
fc
)
На рис. 10-30, в показана частотная характеристика собственноrо
затухания TaKoro фильтра. Ввиду малой крутизны кривой затухания
однозвениоrо 'С
фильтра применяют двух- или трехзвенный фильтр,
однако при этом увеличивается затухание и в полосе пропусквния.
На основании (10-1)
ch g==ch (a+ib)==ch а cos b+i sl1 а sin Ь== 1 +j оо;с ,
откуда
h . Ь оо,С
s asm ==
.
ch а cos Ь == 1;
(1 0
38)
При постоиином токе (ш == О)
ch а cos Ь == 1; sh а sin Ь == о. (10-39)
Эти равенства удовлетворяются при а == О и Ь == О одновременно.
/ П О WrC, h О
ри ы> "2> о и sщ Ь > О, так как s а > "
Итак, в отличие от реактивных фильтров, рассмотрениых в пре-
дыдущих параrрафах, ,С-фильтр не имеет области частот, а пределах
которой собственное затухание а равно нулю.
Частотные характеристики ,С-фильтра нижних частот MorYT быть
построены по выражениям для а и Ь, которые получаются в результате
cOBMecTHoro решения уравнении (10-38), первое из к:оторых можно
представить в следующем виде:
(l + вЬ 2 а) (1
sin 2 Ь) == 1.
Подставляя сюда выражение для sin Ь, получаемое из Bтoporo
уравнения (10-38), приходим к биквадратному уравнению
sh" а
( ы;с / Sh2 а
(ы;с у -= о,
299
bTKYJiI'l
sli а== V «(O
C)2 + ы;С V 1 +( ы;С у.
wrC
При значениях ы, при которых
<: 1,
(10-40)
-.! ытС
sha
a",=, JI
.
За частоту среза тС
фильтра нижних частот условно принимается
частота, при которой равны активное и емкостное сопротиалеwия вет-
вей r-образноrо звена, т. е. '
, 2 ыстС 1
') С или
4 ==.
==
выражение (10-40) дает sh а == 2,2, откуда а ==
в этом случае
13,3 дБ.
На рис. 10
31 представлен тС
фильтр верхних частот с примерной
частотной характеристикой затухания.
а}
)
о ; fr:
2С 2С 2С
::Е ::r:
6)
Рис. 10
31. тС
фильтр верхних частот.
При низких частотах, коrда емкостное сопрdтивление велико,
напряжение на выходе фильтра мало, т. е. получается большое зату-
хание (при постоянном токе
бесконечно большое). С увеличением
чаСТi)ТЫ емкостное сопротивление" уменьшается и напряжение на выходе
возрастает, т. е. затухание убывает. Частотная характеристика соб-
cTBeHHoro затухания TaKoro фильтра показана на рис. 10-31, в.
Для повышения крутизны кривой затухания применяются не-
сколько звеньев, однако при этом неизбежно увеличивается затухание
и в полосе пропускания.
Пользуясь формулой (10
1), получаем в рассматриваемом случае:
chacosb==l; shаSiПЬ==
2Т
С ' (10
41)
При бесконечно большой частоте (ы == 00) получаются условия
(1O
39), которые, как было установлено выше, выполняются, если одно-
временно а и Ь равны нулю.
При значениях О < w < 00 Sll а sin Ь < о; поскольку а > о, ь < О.
Совместное решение уравнений (10
41) приводит к биквадратному.
уравнению
h 4 1 h 2 1 О
s а
(2ытС)2 s а
(2ытС)2 .
300
откуда
sh а== у 8 «(!)lrC)2 + 2(!)
C У 1..+ (4w
C)2 .
1
При значениях 00, при которых 2(!)rC
1,
sha.""a:::::::"1i 1
r 2(!),С'
Если за частоту среза условно принять частоту, при которой
сопротивления ветвей f-образноrо звена равны друr друrу,
1 1
2,==
или
4 С ==1,
2(!)с С (!)c r
то на основании (10-42) будем иметь:
(10-42)
sha==2,2; a
1,53 Нп.
Простейшие схемы полоСовоrо и заrраждающеrо ,С
фильтров
и примерные частотные характеристики затухания приведены на
рис. 10-32 н 1O
33.
С1
0----1
I"z
/J.
1"1
С,
'v:
ri.)
fo б)
Рис. 10-32. Полосовой ,С-фильтр.
I10ЛОСОВОЙ ,С
фильтр основан иа том, что емкость первоrо звена
обусловливает затухание более низких чаСТОТ, а емкость BToporo звена
затухание более высоких частот. Средняя частота полосы пропускания,
при которой собственное затухание фильтра минимально (рис. 10-32, 6),
ориентировочно равна:
1
/0 :=::::.
2лV r1'2C1C2
При r1 == '2 == r и С 1 == С 2 == С
1
10::::::: 2лrС .
Как видно из рис. 10-33, а, заrраждающий ,С
фиJiьтр состоит
из двух параллельно соединенных Т
образных rC-фильтров верхних
и нижних частот. Соответствующим подбором параметров элементов
можно добиться Toro, что при определенной частоте токи на выходе
обеих T-образн!olХ схем будут равны и противоположны по знаку,
301
вследствие чеrо ток в наrрузке будет равен нулю. Следовательно, зату-
хание на 9'I'ой частоте будет бесконечно большим (рис. 10-33, б).
7'2 7'2
а.
I
\
f
'о б)
С1
С,
а.)
Рис. 1O
33. Заrраждающий ,С
фильтр.
о
,С
фильтры часто применяются в сочетании с усилителем. В этом
случае в полосе пропускания не только отсутствует затухание, но,
наоборот, имеет место усиление.
10-8. тополоrИЧЕСКИЕ ФОРМУЛЫ НАХОЖДЕНИЯ
ОПРЕДЕЛИТЕЛЕ Я И АлrЕ&РАИЧЕСКИХ ДОПОЛНЕНИЯ
При анализе линейных электрических цепей используют
два основных тополоrических метода
метод деревьев (или
тополоrических формул) и метод сиrнальных rрафов.
Расчет электрических цепей по методу узловых напря-
жений требует соrласно формуле (7-6) вычисления опреде-
лителя системы и ero алrебраических дополнений. Эта
задача может быть облеrчена, если: применить метод де-
ревьев.
Определитель системы по методу узловых напряжений
для цепи на рис. 7-8:
(У 1 + У 2 + У в )
Ду ==
У 2
Yв
У 2
(У 2 + V з + У 5 )
УЗ
У в
V З
(V З + У 4 + Ув)
Раскрыв определитель, получаем выражение, содержа-
щее алreбраическую сумму 38 произведений проводимо-
стей ветвей. После приведения подобных Ч!lеНОБ в выра-
жении останется только 16 членов. 22 члена взаимно унич-
тожаются и получаем:
==
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ V 2 V Б V в + V з V 4 V в + VзVБV в + V 4 V Б V в . (10-43)
302
Выражение (10
43) можно получить без ЗIШИСИ лишних
взаимно уничтожающихся членов, основываясь на том, что
каждый член уравнения содержит произведение проводи-
мостей ветвеЙ,принадлежащих некоторому дереву rрафа
цепи,
Произведение проводимостей ветвей дерева называется
величиной (весом) дерева.
Для любоrо дерева, которое можно выбрать в rрафе
цепи, в выражении (10-43) имеется соответствующий член.
Отсюда следует правило: определитель системы уравнений
по Meпwдy узловых напряжений равен сумме величин всех
деревьев ерафа цепи.
Поскольку в соответствии с приведенным правилом опре.:
делитель системы уравнений вычиtляется по rрафу цепи,
To.ero называют также определителем rрафа цепи.
Обозначим величину k
ro дерева через f k , тоrда выраже-
ние для определителя можно записать так:
Д у == 2: t k == Т,
k
(10-44)
rДе k
все деревья.
Суммирование в формуле (10-44) распространяется на
все деревья rрафа цепи.
Чтобы не пропустить ни одно дерево, располаrаемветви,
принадлежащие дереву, в порядке возрастания их номеров,
а сами деревья записываем в порядке возрастания номеров
как первых, так и последующих ветвей. Именно по та-
кому прИIIципу записаны величины деревьев' в выражении
(10-43).
Для нахождения алrебраическ.их дополнений исполь-
зуются понятия 2
дepeвa и величины (веса) 2-дерева.
2-деревом ерафа цепи называется такая часть ерафа
(подсраф) , которая содержит все узлы срафа, не содержит
ни oaHoeQ контура и состоит из двух изолированных частей.
2-дерево содержит q
2 ветви, так как при добавлении
к нему одной ветви, соединяющей изолированные части,
оно превращается в дерево.
Лримером 2-дерева rрафа цепи на рис. 7
8 может слу-
жить подrраф из ветвей У 1 и Vз. Ветви У 1 и У 2 тоже обра-
зуют 2-дерево. Одна часть Этоrо 2
дepeBa содержит ветви У 1
и У2' а также узлы 1, 2 и 4. Вторая часть состоит только
из узла 3.
Проuзведение проводимосmeй ветвей 2-дерева называется
величиflOй (весом) 2-дерева.
заз
Рассмотрим алrебраическое дополнение Д12 определи-
теля l1у цепи на рис. 7-8:
I
У 2
V З I
1112==
У 6 (Уз+ У 4 + У6) == V 2 V З + у 2 у 4 + у 2 у 6 +
+ V З V 6 .
Последнее выр.ажение содержит сумму величин 2-де-
ревьев. В этой сумме учтены не все 2-деревья, а только
такие, которые содержат узлы 1 и 2 в одной части 2-дерева,
а базисную вершину 4
в друrой.
В результате получаем правило: алеебраическое дополне-
ние l1 ik определителя Ду равно сумме величин таких 2
дe-
ревьев, у которых узлы i и k находяrr.ся в одной части 2-дерева,
а базисная вершина q
в друеой.
Обозначим величину упомянутоrо выше 2-дерева через
Пk,q, тоrда можно записать:
l1 ik ==
Пk, q == nk, q'
(10-45)
rде суммирование распространяется на все 2-деревья, у ко-
торых вершины, разделенные запятой в обозначении 2-де-
рева, находятся в разных ero частях.
tO-9. тополоrИЧЕСКИЕ ФОРМУЛЫ РАЗЛОЖЕНИЯ
Приведенные выше тополоrические формулы имеют тот
недостаток, что приходится в сложных rрафах находить
1
3 Ц е h
б)
2
Рис. 10
34. Исходный rраф G и rраф Gk' соответствующий пути ad.
большое число деревьев. Так, в rрафе на рис. 7-8 число
деревьев равно 16, а в rрафе на рис. 10-34
128.
304
С ростом числа ветвей число деревьев быстро увеличи-
вается. Для облеrчения задачи нахождения суммы величин
деревьев и для более компактной записи этой суммы исполь-
зуются формулы разложения.
Формула разложения по путям
Путем в ерафе называется такая последовательность
ветвей, в которой начало последующей ветви совпадает
с концом предыдущей. Величиной (весом) пути называется
проuзведение проводимостей ветвей пути. Путь, а также
еео величину обозначим буквой Р.
, Определитель ерафа цепи, получающейся после закорачи-
,вания всех ветвей пути P/i, называется алеебраически,}f. до-
полнением пути P/i и обозначается через !1k.
Формула разложения определителя по путям записы-
вается следующим образом:
!1 у ==
P/i!1/i.
k
(10-46)
rде суммирование распространяется на все пути в rрафе
цепи между двумя выбранными узлами.
Таким образом, определитель системы уравнений по ме-
тоду узловых напряжениЙ равен сумме произведений вели-
чин путей между двумя
выбранными узлами на соответст-
вующие им алrебраические дополнения.
Докажем последнее утверждение, для чеrо рассмотрим rраф неко-
торой цепи, который обозначим буквой а. Для любых выбранных узлов
существует путь по ветвям дерева rрафа а, соединяющий эти вершины.
Закоротим в rрафе G ветви пути Р k между выбранными узлами, тоrда
получим новый rраф G/i' в котором оставшиеся незаКОРО'IеНIIЫМИ ветви
дерева rрафа G образуюr дерево rрафа G k .
Например, если в дереве, которое показано толстыми лиииями
на рис. 10,34, а, закоротить ветви а и d пути между узлами 3 и 4, то
получим rраф G k , IlQказаниый на рис. 10
34, б. В этом I'рафе ветви Ь,
k и h образуют дерево.
С друrой стороны, если в rрафе G k выбрать любое друrое дерево,
то оно вместе с веrвями пути P k образует дерево rрафа а.
Таким образом, для каждоrо дерева rрафа а, содержащеrо путь Pk.
существует единственное дерево rрафа Gk. и наоборот.
Величина i-ro дерева, содержащеrо путь P k , равна pif), rде
t
k)
величииа i
ro дерева rрафа G k . Сумма величин всех деревьев,
содержащих путь Pk, равна:
pA k ) ==P k
t
k) == PktJ. k .
i i
305
так как сумма lIеличин всех деревьев. типа ,t
k) равна определителю
цепн, соответствующей rрафу G k , т. е. !!/z.
Определитель .. /j,y равен сумме всех деревьев для всех возможных
путей rрафа а, т. е. члены вида Pk!ik нужно просуммировать для всех
путей, что приводит к формуле (10-46).
Вычисляя алrебраическое дополнение Дk, можно также
использовать формулу разложения по путям.
Пример 10-1. Найти определитель цепи на рис. 7-8 разложением
по путям между узлами 2 и 4.
Между узлами 2 и 4 можно ПрОС,'1едить следующие пять путей:
;
;
;
После закорачивания ветвей nepBoro пути Рl получаем rраф,
состоящий из трех параллельных ветвей с проводимостями Уз, У 4 и Ув'
Определитель TaKoro rрафа !!1
== У з + У 4 + У в . так как любая
из трех ветвей является деревом.
Если закоротить ветви пути Ра
(т. е. ветвь с проводимостью У 5 ),
получим rраф, показанный на
рис. 10.35, а. После замены парал-
лельных ветвей ЭIшивалентными
преобразуем ero к rрафу на рис.
10-35, б, определитель KOToporo
!i2
У в (Yi+ У 2 +У з + У 4 )+
+(У 1 + Уа) (У з +У 4 ).
:.>6
а)
Рис. 10-35. rраф, соответствую-
щий /j,a. .
Для пути Р 4 , алrебраическое дополнение /j,4
1, так как при
закорачивании ветвей пути Р4 все ветви оказываются закороченными.
Аналоrичным образом находим алrебраические дополнення
!iз==У 1 +У 2 +У в и !i 5 ==1.
П6дставляя найденные величины путей и алrе6раических дополне-
иий в формулу (10-46), получаем:
!i y == У 1 У а (У з + У 4 + У в )+ Y
[Ув (Yi+ У 2 +У З +У4) +
+(У 1 + У 2 ) (У з + У 4 )] +У З У 4 (У 1 + Уз+У в ) + УЗУ4Ув+У1УЗУU'
Разложение определителя по уэлу
Пусть к некоторому узлу s подходят ветви с проводимо-
стями У 1, У 2, ..., У п' Поскольку все деревья касаются
узла 5, то любое дерево содержит хотя бы одну ветвь,
касающуюся узла s. Среди .этих деревьев имеются содержа-
щие одну, две, три и т. д, ветвей, подходящих к узлу 5.
Сумма величин деревьев, содержащих ветвь с проводи-
мостью Y i , равна ViДi, rде Д;
определитель rрафа, полу-
306
чающеroся при заКораЧИВаНШI: :ветви с проводимостью У !
и удалении остальных ветвей, подходящих к узлу s.
Аналоrично сумма величин деревьев, содержащих ветви
с ПРОВОДИМОСТЯМИ У ! и Y k , равна. YiYk
ik, rде
ik
опре-
делитель rрафа, получающеrося при закорачивании ветвей
с ПРОВОДИМОСТЯМИ Y i И У k И удалении остальных ветвей,
подходящих к узл у S.
Суммируя величины деревьев всех типов, получаем
n n
I:I== 1: Yi
i+ 1: YiYk
ik+
i == 1 1: == 1, k == 1
+
YiYkYI
ikl+"'+YIY2".Yn
12...n'
i
1, k
1, 1
I
(10-47)
Под знаком суммы в форМУ.'Iе (10-47) стоят произведения
разных проводимостей (i =1= k, k =1= 1, 1 =1= i). Леrко убе-
диться, что
i ===
1'
:'v 2
J
Пример 10-2. Найти определитель цепи на
рис. 7-8, используя формулу разложею,я по
узлу 1. ,
Для Данноrо примера формулу (10-47) запи-
шем в виде
ЛУ==(V 1 + У 2 + Уа) Лi+ V 1 V 2 Лi2+
+V 1 V 6 Л 16 + У 2 У 6 Л20+VIV2V6 Л 126 .
Определитель Л 1 соответствует rрафу на рис.
10-36 и равен У 5 (Уз + У 4 ) + VзУ,. После закора-
чиваниЯ ветвей 1 и 2 и удаления ветви 6 останутся
параллельно соединенные ветви 3 и 4, т. е.
A 12 == V З + У 4 . Аналоrично Л 16 == V З + У 5 , а Л 26 == У 4 + У 5 . После
закорачивания ветвей 1, 2 и 6 все ветви будут закорочены, т. е.
Л 126 == 1.
С учетом приведенных выше значений находим:
Лу==(Vi+ У 2 + У О ) [У 5 (Vз+V,) + V з V 4 J+
+ V 1 V 2 (V З + У,) +V 1 V 6 (V З + У 5)+ У2 У 6 (У 4 + У5)+ У l У 2 У 6'
Рис. 10
36. rраф,
соответствую-
щий Л 1 .
Рвзпоженне апrебранческнх допопиеинм по путям
В соответствии с формулой (10-45) алrебраическое до-
полнение
ik равно сумме величин всех 2-деревьев типа t'k,q,
у которых узлы i и k находятся в одной части 2-дерева,
а базисный узел q
в друrой. На рис. 10-37 условно изоб-
ражено ОДНо из таких 2-деревьев. '
Добавим к 2-дереву ветвь с проводимостью, равной еди-
нице, и соединяющую узлы k и q (показано пунктиром на
рис. 10-37). В результате получаем ,дерево, величина кото-
307
poro равна величине исходноrо 2-дерева и которое coдep
жит путь от узла i к узлу q через узелk и единичную ветвь.
Можно осуществить обратную операцию: добавить еди-
ничную ветвь к исходному rрафу цепи и выбрать в нем
произвольное дерево, содержащее
путь от узла i к узлу q через еди-
ничную ветвь. Если удалить из этоrо
дерева единичную ветвь, то оно пре-
вращается в 2-дерево типа tl k . q ,
т. е. между деревьями и 2-деревья-
ми указанноrо выше типа сущест-
вует взаимно однозначное соответ-
ствие.
Из сказанноrо выше следует, что
алrебраическое дополнение Дik равно
сумме величин всех деревьев, содержа'щих путь от узла i
к узлу k через единичную ветвь, т. е.
Дik ==
P1M,
rде Рl
величина l-ro пути от узла i к узлу q
через единичную ветвь; 1
М
алrебраическое ' дополнение
этоrо пути.
i . ""\. \. T k
./
\1
I
q
.""\... "
./
Рис. 10-37. Преобра-
зование 2
дepeBa в де-
рево.
Пример 10-З. Найти алrебраическое допол-
нение ':\12 rрафа цепи на рис. 7-8.
После добавления единичной ветви, соеди-
няющей узлы 2 и 4 (базисный) ПОf1!УЧИМ цепь,
rраф которой изображен на рис. 10
38. Ветвь 5
удалена из rр
фа, так как она шунтируется лю- 3
бым путем, проходящим через единичную ветвь, Рис. 10-38. При-
и не может поэтому принадлежать алrебраиче- мер 10-3.
скому дополнению пути.
Записываем пути меЖдУ узлами 1 и 4, а также их алrебраические
дополнения:
Следсвательно,
Р i == V 2 . 1; ':\1 == V з + V 4 + V в;
Р 2 ==V в V з .l; ':\2==1.
':\12== У 2 (V з + У 4 + У в ) + VвV з .
10-10. тополоrИЧЕСКИЕ ФОРМУЛЫ ДЛЯ ПЕРЕДАТОЧНЫХ
ФУНКЦИЙ
В
9-9 было отмечено, что передаточная функция опре-
деляеТСя как отношение выходной величины четырехпо-
люсника к входной, причем это отношение зависит от на-
З08
rрузки. Ниже при рассмотрении передаточных функций
в качестве выходной величины примем напряжение холо.
cToro хода или ток KopoTKoro замыкания. Это не нарушает
общности, так как, если сопротивление наrрузки отлично
от нуля или бесконечности, то ero можно внести внутрь
четырехполюсника.
К входу четырехполюсника подключим идеальный источ-
Ник Э. д. с., если ВХОДНая величина
напряжение, или
идеальный источник тока, если вХодная величина
ток.
На выходе подключим вольт
метр в случае холостоrо хода
или амперметр при коротком
замыкании. На рис. 10-39 yc
ЛоВНо показано подключение
источника И и измеритель-
Horo прибора П. Полярности
иеточника и прибора соответ-
ствуют выбранным положи-
тельным направлениям напря-
жений.
Передаточные функции любоrо типа для схемы на
рис. 10-39 определяются с помощью тополоrическоrо закона
передачи, который выражается формулой
К === 2:. P k l1f)l1,
2
t U1
п
Uz
l'
2'
Рис. 1O
39. Четырехполюсник
для определения тополоrиче-
CKoro закона передачи.
(10-48)
rде К
передаточная функция;
Pk
величина пути от плюса источника к ero минусу,
проходящеrо через измерительный прибор;
I1 k
алrебраическое дополнение пути P k ;
11
определитель rрафа цепи, получающейся после
закорачивания источника э. д. с. и амперметра,
а также удаления источника тока и вольтметра.
При определении величины пути P k проводимость при-
бора считаем равной единице (единичная ветвь). Путь P k
берем с плюсом, если измерительный прибор проходим
в положительном направлении, иначе P k берем с минусом.
Определитель 11 можно находить разложением по путям
между любыми вершинами.
Доказательство справедливости формулы (10-48) сделаем
на примере передаточноrо сопротивления
(;2 (;21'
(;2'1'
Z21 ==
== ,
/f 11
rде 11
ток источника тока на входе цепи.
309
Подставив в последнее уравнение выражения узловых
напряжений О 21 . и О 2 , 1 , соrласно формуле (7
6), получим;
d12
d12'
Z21::=::: .d y (10
49)
Алrебраическое дополнение Ll 12 соrласно формуле (10-45)
равно сумме величин 2-деревьев типа ti2,1', у которых
узлы 1 и 2 находятся в одной части 2-дерева, а базисный
узел 1',
B друrой. Что касается узла 2'. то он может
быть или в той части, rде находятся узлы 1 и 2, или в той,
rде узел 1', т. е. .
Ll 12 == Tk1' == п22',1' + п2,2'1'.
в этом уравнении, как и ранее, запятая разделяет HO
мера узлов, принадлежащих разным частям 2-дерева.
По аналоrии можно записать, что
Ll 12 , == Ti2',1'::=::: T;
'2,1' + Ti2',i1"
ПодставлS!я полученные ВЫРj1жения для .6.12 и .6.12'
В уравнение (10
49), находим:
ri2,2'1'
Т;2' ,21'
Z21 == d
у
2-деревья типов ti2,2'1' и ti2',21' преобразуются в деревья
добавдением единичной ветви, соединяющей узлы 2 и 2'.
Эrи деревья содержат путь
от плюса источника к ero
минусу через единичную
ветвь (рис. 10-40). Причем
для 2-дерева ti2,2'1' единич-
ная ветвь проходится в
пути от узла 2 к узлу 2',
Рис. 10-40, Преобразование 2-де- а для 2-дерева ti2',21'
в
ревьев в деревья. обратном направлении.
Соответственно в выраже
2-дерево входит с плюсом, а второе
(10-50)
t '2 ,2'"
+ . ,..., '-
:1
I
./ l '
. - """
l'
t,1' 21
:)(11
l' 2'
ние (10-50) первое
с минусом.
Разлаrая суммы 2
дepeBьeB п2,2'l' и Ti2..21' по путям
описанноrо выше типа, получаем формулу (10-48), в KOTO
рой f{ == Ll y .
Аналоrичным образом можно доказать справедливость
формулы (10
48) для друrих типов передаточных функций.
Тополоrический закон передачи можно использовать
также для определения входноrо сопротивления и проводи-
310
мости, если считать, ,что вход и выход совпадают. В этом
случае имеется единственный путь Р;' от узла 1 к узлу l'
непосредственно через измерительный прибор. Величина
этоrо пути равна еДИНице, а алrебраическое дополнение
равно определителю цепи при закорс>ченном входе.
Следовательно, входное сопротивление
ZBX == /).11//).У,
rде /).11
определитель цепи при закороченном входе;
/).у
определитель цепи при разомкнутом входе.
Пример 10-4. Найти передаточную ПРОВDДИМОСТЬ для цепи на
рис. 1O
41, а в режиме KopOTKoro замыкания и коэффициент передачи
по напряжению в режиме XO.'JQCTOrO хода,
Рис. 10-41. Пример 10-4,
2
., f6-.,
'+ 1+
У1 Уз'
112
,.J flJ--.J
1 УЧ
2 d)
При определении передаточной проводимости на входе включаем
источник Э. Д. с., а на выходе
амперметр. Используем формулу (10.48).
В числителе этой формулы сумма произведений величин путей 'от узла 1
к l' через амперметр на их алrебраические дополиения. В цепи суще-
ствуют только два таких пути: p
== У 1 У 6 У 4 И P
==
VЗV6V2' Алrе-
браические дополиения путей равны единице.
Следовательно,
' ,
Pk
k== У 1 У 6 У 4
V з V 6 V 2 .
В зиаменателе формулы (lO
48) стоит определитель rрафа цепи,
которая получается из исходной после закорачиваиия э. д. с. и ампер-
метра. Этот rраф совпадает с rрафом на рис. 10.35, определитель кото-
poro
== У 6 (У 1 + V 2 +V з + V4)+(Vi+V2) (V З + У 4 ).
Подставляя найденные величины В (10-48), находим:
V
(VIV4
VЗV2) У в
21
У6(Уl+ У 2+ У З+ У 4)+(Уl+ V 2) (УЗ+ V 4) .
При определении коэффициента передачи по напряжению на входе
цепи вместо амперметра следует включить вольтметр. Поскольку сама
схема цепи и характер включения, измеР!lтельноrо прибора не изменя-
ются, то пути от узла 1 к узлу 1 останутся теми же, Соответственно
числитель формулы (10-48) не измеиится.
811
Для вычисления определителя .1 нужно закоротить вход и уда-
лить вольтметр. [раф результирующий цепи показан на рис. 10-41, б.
Определитель этоrо rрафа
.1== (Yi+ У 2 ) (У з + У 4 ) У 6 .
Окончательно получаем:
К
YIY2
V З У 2
и
(У 1 + У 2 ) (V з +V 4 ) ,
Проводимость У 6 В числителе и знаменателе сокращается. Это
можно было учесть с caMoro начала, подключив вольтметр к точке 2",
так как напряжение на ПРОВОДИМОСТII У в равно нулю,
tO-11. ТОПОЛоrНЧЕСКИй АНАЛИЗ АКТИВНЫХ ЦЕПЕй
Рассмотренный выше тополоrический анализ линейных
цепей применим К пассивным обратимым цепям без взаим
ноЙ индуктивности. Если имеется взаимная индуктивность,
то от нее можно избавиться, используя развязКу индуктив
1ky 2 1.k.y 2
)2 "\/
а)
6
у
б)
Рис. 10-42. Унисторная (а) и обычная (6) ветви.
ных связей (см. rл. 8). Необратимые цепи MorYT быть заме
нены эквивалентными схемами замещения с зависимыми
источниками энерrии (см.
9-5).
Для Toro чтобы можно было применить тополоrические
методы для анализа электрических цепей с зависимыми
источниками, вводится в рассмотрение элемент, называе
мый унистором (рис. 10
42, а).
Унистор
несимметричный элеме!lТ, пропускающий ток
только в одном направле.нии,
казанном стрелкой. Ток
определяется равенством 1 == YU 1 .
ДЛЯ обычной ветви ток
j == У ((;1
92) == уи 1
УU 2 .
Следовательно, обычная ветвь эквивалентна параллель-
НОМУ соединению противоположно направленных унисторов
с проводимостью, равноЙ проводимости ветви (рис. 10-42,6).
312
Зависимыи источниК тока, управляемый напряжением
(рис. 10-43, а), можно заменить унисторной схемой замеще
ния на рис. 10-43, 6. Эквивалентность этих схем леrко про
верить, вычисляя токи, входящие в узлы цепи.
Зависимые источники друrих ТIIПОВ целесообразно пре-
образовать в зависимый источник тока, управляемый на-
А
Ia
c
)и,
пряжением, чтобы можно было использовать схему замеще-
ния на рис. 10-43, 6.
Схемы замещения с зависимыми источниками исполь
зуются при анализе электронных схем в линейном режиме.
Например, электронная лампа триод (рис. 10
44), исполь
зуемая для усиления переменных сиrналов, при пренебре-
жении внутренним сопротивле
нием эквивалентна зависимому
источнику тока, показанному
на рис. 10-43, а. При этом
узел 1 соответствует сетке С, 3
узt:л 2
аноду А и узел 3
катоду К. Роль цроводимости У
в этом случае выполняет кру-
тизна лампы S. Соответственно
тоК лампы
j а === SИ С '
1 2
;\;4" УО I
J а.)
'
2
J 6)
Рис. 10-43. Зависимый источник
и ero унисторная схема замеще-
ния.
к
Рис. 10-44. Элек-
тронная лампа
(триод) .
.. ",
I=IXIз
()(,g6и6
к
Б
Рис. 10-45. Схема замеще-
ния транзистора.
Чтобы учесть внутреннюю цроводимость лампы g/, ее
включают параллельно источнику тока в схеме на
рис. 10-43, а.
На рис. 10
45 показана схема замещения транзистора,
которая содержит зависимый источник тока. Здесь '&
сопротивление эмиттера; r к
сопротивление коллектора;
rб
сопротивление базы. Если заменить 1& на g90
(O
313
НаПр5lжеlше На сопротивлеНИИ эмиттера), то получим
источник тока, управляемыЙ напряжением (;
, который
заменяется унисторной схемой на рис. 10-43, б с У =:;;
=== ag g .
Основные тополоrические:правила, применимые к обыч-
ным цепям, справедливы и для цепей, содержащих уни-
сторы. Все отличия сводятся к следующему:
1) в рассмотренных выще тополоrических формулах
учитываются только такие деревья, 2-деревья или пути,
в которых вс;е унисторы направлены в сторону базисноrо
(заземленноrо) узла;
2) в случае 2-дерева базисный узел выбирают в каждой
части 2-дерева;
3) при использовании тополоrическоrо закона передачи
заземленным узлом должен быть один из выводов измери-
теЛЬНоrо прибора.
Пример 10-5. На рис. lO
46, а показана схема катодноrо повтори-
теля. Определить для нее передаточную проводимость, представляющую
собой отношенне тока катода к входному напряжению,
с
s
Ё
т -:-
Рис. 10-46. Схема Катодно-rо повторнтеля (а) и ее
унисторыый rраф (6).
На анод схемы подано постоянное по отношению к земле напряже-
ние. Поскольку, анализнруя усиление сиrналов, постоянную составляю-
щую отбрасывают, можно счнтать, что анод присоединен к земле. С уче-
том .этоrо после замены лампы унисторной схемой замещения получаем
rраф на рис. 1O
46, б. В .этой схеме существует лишь один путь P 1 ==
== SgK
от плюса иСточника к минусу через амперметр. Эт()т путь сле-
дует учесть, так как унистор направлен к заземленному узлу. Алrе-
браическое дополнение .1; == 1.
Для нахождения определителя .1 в знаменателе формулы (1O
48)
закорачиваем источник и амперметр. Получаем rраф из проводимостей
gi, gK И даух унисторов, соединенных параллельно. Любая из этих
314
вет,вей образует дерево. Однако
один из уиисторов следует отбросить,
так как он направлен от заземленноrо узла. Сле.довательно,
L\==gt+gK+S
и передаточная провоДИМоС1Ь
j SgK
У 21 == -----т- ==
Е gi+gK+S
10-12. сиrНАПЬНЫЕ rРАФЫ и МЕТОДЫ их ПРЕО6РА308АНИЯ
Выше был рассмотрен тополоrllЧ
СКИЙ метод, исполь-
зующий понятие деревьев. Особенность этоrо метода в Том,
что он оперирует с rрафом электрической схемы, отобра-
жающим ее тополоrию.
Сиrнальные rрафы, применяемые для анализа электри-
ческих цепеЙ, не отображают тополоrию, электрических
схем. Они используются для решения систем линейных урав-
нений и их конфиrурация определяется этой системой.
Возьмем, например, систему уравнений, полученных для
схемы рис. 7-6 в примере 7-2. Дл.я построения сиrнальноrо
rрафа необходимо сначала разрешить каждое уравнение
относительно одной переменной (разной для разных урав-
нений). Разрешим, например, первое уравнение относи-
тельно 11' второе
относительно 12 и третье относи"
тельно 13:
jl==tI212+tlзjз
)
j 2 == t 21 i 1 + t 2З 1з;
j 3== t 31 i 1 + t з ) 2+ t з /::.
Здесь коэффициенты
Z5 t Z2
tI2== Z1+Z
+Z5 ; lЗ== Z1+Z2+Z
;
z t Z3
t 21 == i 8 +z:+Z 5 ; 2З==' ZЗ+ Z 1+ 2 5 ;
Z z
t 31 == Z
+Z:+Z6 ; [ 32 == i2+ Z:+ZG ;
1
t 34 == 22+Z3+ 2 6 '
Полученной СИс1'еме уравнений соответствует сиrналь-
ный rраф, изображенный на рис. 10-47, а.
Сиrнальный rраф обладвет следующими свойствами:
1. С и r н а л ь н ы й r раф состоит из у 3 Л О В И
В е т в е Й. Ветвь изображается направленным отрезком,
(10-51)
315
соединяющим два узла сиrнальноrо rрафа: Направление
ветви указывается стрелкой.
2. Каждая ветвь rрафа характеризуется пер е Д а -
чей ветви t ik . Первый индекс ветви (i) соответствует
номеру узла, в который входит ветвь, а второй (k)
номеру
узла, из KOToporo она выходит.
3. В Каждом узле rрафа имеется с и r н а л, который
передается от узла по всем ветвям, выходящим из Hero.
При решении уравнений электрических цепей ПОД сиrналами
понимаются токи, напряжения и т. д.
4. При прохождении по ветви сиrнал умножается на
передачу ветви.
ц.
Ё
f l' Ц. t;JЧ
.
..
11 11 Ё
tZ;J t
z
t;J1 + tZ1 t JZ t1Z tZ1
1
11
t1
+t1ztZJ
б)
Рис, 10-47, Сиrнальные rрафы для системы (10
Ы).
5. Результирующий сиrНал в узле равен сумме всех
сиrналов, приходящих в данный узел по ветвям, входящим
в этот узел. .
В соответствии с вышесказанным ток 11 представляет
собой сиrнал в вершине 1 rрафа на рис. 10-47, а, ТОК 12
сиrнал в вершине 2, ток 13
сиrнал в вершине 3 и э. д. с.
Ё
сиrнал в вершине 4. Соrласно первому уравнению си-
стемы (10-51) в вершину 1 должны входить ветвь с переда-
чей t 12 , выходящая из вершины 2, и ветвь с передачей '13'
выходящая из вершины 3 (рис. 10-47). Аналоrичные рас-
суждения относятся и к остальным ветвям rрафа, изобра-
женноrо на рис. 10-47, а.
Выше отмечалось, что для построения сиrнальноrо rрафа
следует каждое уравнение разрешить относительно одной
переменной. Очевидно, это можно сделать по-разному.
Например, первое уравнение рассмотренной выше системы
уравнений можно разрешить о
носительно 12' а не 11' BT
-
рое уравнение
относительпоl з , третье
относительно 11'
В результате получится система уравнений, отличная по
форме от системы (10-51), и соответственно сиrналы-!ий rраф
для таКой СИСтеМы будет отличен от rрафа на РИС. 10-47, а.
316
Таким образом, для данной системы уравнений можно
построить различные rрафы, но данному rрафу соответст-
вует совершенно определенная система уравнений.
После построения сиrнальноrо rрафа для данной системы
уравнений ее решение сводится к вычислению передачи сиr-
нальноrо rрафа.
Передачей сиенальноео ерафа от ucmOKa J откуда только
6ыходят ветви ерафа, к стоку, куда только входят ветви
ерафа, называется отношение сиенала в стоке к сиеналу
в исnwке. Узел 4 rрафа на рис. 10-47, а является источни-
ком. Узел 1 не является стоком, но можно добавить узел l'
с сиrналом 1; и соединить ero с узлом 1 ветвью с единичной
передачей, Что соответствует уравнению 1; == 11' Узел l'
является стоком, тоrда передача от узла 4 к узлу l'
i; 11
Tl'i==
==
,
Е Е
откуда 11 == Т 1 '4Ё, т. е., зНая передачу rрафа от узла 4
к узлу 1', можно определить ток 11'
Ниже рассмотрены ДВа метода нахождения передачи
сиrнальноrо rрафа: 1) последовательным упрощением rрафа
и 2) вычислением передачи по формуле Мейсона.
Метод упрощения сиrнальноrо rрафа основан на следую-
щих правилах:
1. Параллельно соединенные ветви, направленные в одну
сторону, заменяются одной ветв.ью, передача которой
равна сумме передач параллельно соединенных ветвей
(рис. 10-48, а).
2. Последовательно соединенные ветви, направленные
в одну сторону, заменяются одной ветвью, передача которой
равна произведению передач ветвей (рис. 10-48, 6).
3. Если в точке соединения двух ветвей с передачами t 12
и t 2З имеется петля с передачей t 22 (петля
это ветвь,
ВЫХодящая из Toro же узла, куда она входит), то все эти
три ветви заменяются одной ветвью с передачей (рис. 10-48, в)
t
t 12 t 2з
13
1
t22'
Указанные выше правила являются частными случаями
общеrо правила устранения вершин. При устранении вер-
шины rрафа устраняется и сиrнал, соответствующий этой
вершине, т. е. устранение вершины равносильно исключе-
Нию переменной из системы уравнений. Вообще всякому
317
преобразованию rрафа соответствует определенное преоб-
разование системы уравнений.
При устранении некоторой вершины (рис. 10-48, 2) уда-
ляются все ветви, входящие или выходящие из этой вер-
шины. Передачи оставшихся ветвей (вблизи удаленноrо
t1Z
= > I "
t'Z=t'Z+ t 1Z
.
t" а.)
12
) t'2 t2J J< ='
t1J'"' t1Z t и f(
I . . .
2
5)
tzz
) Q з< =
t
t'Z t 2J $<
t1! tи 1J
1
t22
. ... .
2
8)
2 I
т tz", Z
I tZk
tim
I
i. tik k
)
Рис. 10-48. Преобразование сиrнальных rрафов.
узла) соответствующим образом меняются. Емн n исход-
ном rрафе имеется ветвь, идущая из узла k в узел s с пере-
дачей t sk , и ветвь, идущая из узла s в узел i с передачей tl-r
(рис. 10-48,2), то новая передача ветви между узлами k и i
вычисляется по формуле
t
t- + t1stsk
Ik
Ik 1 t .
S5
(1 О-52)
rAe t S5
передаЧа петли в вершине s.
818
Если в исходном rрафе отсутствует ветвь между узлами k
и i, то:в формуле (10-52) следует положить t ik == О. Анало-
rично t ss == О при отсутствии петли в вершине s. В частном
случае вершины i и k MorYT совпадать, что приведет к по-
явлению петли в новом rрафе. Передачи tiт, ttт и tl k нахо-
дятся по формуле, аНалоrичной формуле (10-52).
В качестве примера применения формулы (10
52) устра-
ним вершину 2 из rрафа на рис. 10-47, а. В результате полу-
чится rраф, изображенный на рис. 10-47, б. Выражения
ДЛЯ передач ветвей указаны на рисунке.
Далее можно удалить узел 3 из rрафа на рис. 10-47, б;
получится rраф, содержащий узлы 1 и 4, причем в узле 1
будет петля. Для удаления этой петли можно добавить
ветвь с един11.ЧНОЙ переДачей, как указано было ранее
(пунктирная лиНия на рис. 10
47, а) и устранить узел 1.
Окончательно получится rраф, содержащий единственную
ветвь с передачей Т 1 '4 == i 1 /Й. Указанные преобразования
преДлаrается выполнить в качестве упражнения- и резуль-
тат сравнить с (10-57).
В rрафе на рис. 10-47, а узел 4 5!вляется истоком. Соот-
ветствующий ему сиrнал(э. д. с. Е) считается известным
и находится только в правой части уравнений (10-51).
Может возникнуть обратная задача определения э. д. с. Е,
которую в этом случае необходимо перенести в левую
часть уравнения, после чеrо узел 4 перестает быть истоком.
Ветвь с передачей t 34 после TaKoro преобразования будет
входить в узел 4.
Операция изменения направления ветвей называется
и н в е р с и е й.
Рассмотрим сначала инверсию одной ветви, выходящей
из ИСТОКа i и входящей в узел k. Поскольку узел i является
истоком, то соответствующий ему сиrнал Xl находится
только в правой части системы уравнений, т. е. нет уравне-
ния, выражающеrо сиrнал Xi через друrие сиrналы. Для
k-ro узла такое уравнение имеет вид:
Xk == t k1 X 1 + t k2 x 2 +...+ tkiXi+"'+ tkkXk' (10-53)
Определим из этоrо уравнения сиrнал Xj:
(н tk2 1
tkk 5
Xi==
t
Xl
t
X2
"'+
t Xk' (10- 4)
kj ki kl
Уравнению (10-53) соответствует часть rрафа, показанная
на рис. 10-49, а. После преобразования уравнения (10
53)
сиrнал узла k переходит в правую часть уравнения, т. е.
319
узел k становится истоком. rраф, соответствующий ураВ-
нению (10
54), показан на рис. 10
49, б. Сравнивая эти rрафы,
получаем правило для инверсии ветви t ki :
1) устраняем петлю в узле k (если она имеется);
2) инвертируемую ветвь t ki заменяем ветвью с переда-
чей t!k == (1
tkk)/t lli , имеющей противоположное напра-
вление;
3) концы ветвей, входивших в узел k, переносим в узел i,
умножая передачи этих ветвей. на
lItki'
После инверсии ветви с передачей t ki узел k становитсЯ
истоком. В связи с этим можно инвертировать любую ветвь,
выходящую из узла k, скажем, ветвь t 1k . в результате ока-
Рис. 10.49. Инверсия ветви.
жется инвертированным путь tkit 1k . Таким образом, исполь-
зуя приведенное выше правИЛО, можно инвертировать путь,
начинающийся в истоке.
Описанный выше метод является rромоздким. Ero целе-
сообразно использовать лишь для предварительных упро-
щений и преобразований сиrнальных rрафов. Более удобно
вычислять передачу rрафа по формуле Мейсона.
Передача сиrнальноrо rрафа от истока к стоку
РkДk
Т== k Д (10-55)
rде 11
определитель rрафа;
P k
передача k
ro пути в rрафе от истока к стоку;
I1 k
'алrебраическое, дополнение пути.
Суммирование выполняется по всем возможным путям.
Путь в rрафе берется с учетом направления ветвей,
т. е., идя от истока до стока, необходимо все время идти
320
в направлении стреЛОk. Передача пути ршзна проuзведению
передач всех ветвей пути.
Определитель rрафа
Ll == 1
L i +
* LiLk
* LiLkLm +..., (10-56)
,i i, k [, k, т
rде L i
передача i-ro контура, равная произведению
передач всех ветвей контура. Контуры выбираются так,
чтобы все ветви в контуре были направлены в одну сто-
рону. Звездочки у знака сумм означают, что следует брать
произведения величин двух, трех и т. д. некасающихся
контуров.
Алrебраическое дополнение Ll k вычисляется по той же
формуле (10-56), но при этом следует учитывать во всех
суммах лишь контуры, не касающиеся пути P k .
Пример 10-6. Вычислить передачу rрафа на рис. 10-47, а от узла 4
к узлу 1.
Поскольку все контуры rрафа касаются друr друrа, то в COOTBeT
ствии с формулой (1O
56) в выражении определителя необходимо учесть
единицу и взятую со знаком минус сумму передач контуров, Следова-
тельно, определитель rрафа
t:. == 1
(t 2з t 32 + ti2t2i + tзitiз + ti:l21t32 + t2зti2(31)'
В rрафе на рис. 10-47, а имеютс
два пути от истока к стоку: Р 1 ==
== t з4 t 2 А2 И Р 2 == t з4 t 1з , Алrебраические дополнения этих путей равны
единице, так как все контуры касаются их.
Теперь остается подставить выражения 'определителя, передач
путей и их алrебраических
ополнений в выражение JIO-55) или в ра-
венство
Тй
P 1 t:.i + P 2 t:. 2
t:.
что дает
т i4 == i
== t З 4 t 2з t i2 + t 3 4 t iз . (1 О-57)
Е 1
(t 2з t 32 + ti2t2i + tiзtзi + ti:l21t32 + t2з(i2tзд
10-13. ПОСТРОЕНИЕ сиrНАЛЬНЫХ rРАФОВ ЭЛЕКТРИЧЕСКИХ
ЦЕПЕR
Как указывалось ранее, для любой системы линейных
уравнений можно построить сиrнальный rраф. При ана-
лизе электрических цепей в качестве такой системы урав-
нений можно взять уравнения или по законам Кирхrофа,
или по методу контурных токов, или по методу узловых
напряжений. Чтобы исключить промежуточную операцию
составления уравнений, нужно найти метод построения
rрафа по схеме электрической цепи. Ниже рассмотрены
321
, nрА1ШJiа n6c'tpoeНtH! rрафа для расчетов методами контур-
ных токов и узловых напряжений.
Независимо от схемы электрической цепи уравнения по
методу контурных токов имеют. например, для трех конту-
ров, такой вид (см.
7-2):
Z11 i 1 +Z12 / 2 +Z1з 1 з== Б 1 ;
Z21 / 1 +Z22 1 2 + Z2З/З == Ё 2 ;
ZЗ1 1 1 +ZЗ/2+ zзз1з== Б s .
Перенесем все члены этих уравнений в правую часть.
Прибцвим к обецм частям первоrо уравнения 11. BTO
poro 12, Tpeтbero 1 з' В результате получаем систему урав-
нений:
11== (1
Zl1) 1 1
Z12 1 2
Z1з l з + Е 1; . )
i 2 ==
Z21 11+ (1
Z22) i 2
Z2з 1 3+ 1:.2;
i з ==
Z31/1
Z32/2 + (1
zзз) 13 +Е з .
Эrой системе уравнений соответствует сиrнальный rраф.
показанный на рис. 10-50, Ero можно построить. не запи
сывая системы уравнений, при
любом числе контуров, имея в
виду следующие свойства rрафа:
1. В k-M узле rрафа, соответ-
твующем k-MY контурному току
1 k. имеется петля. с передачей
(1
Zkk)'
2. Между k-M И i
M узлами
IIмеются две ветви. Одн'8 с пере-
з' дачей
Zik направлена от узла
k в узел i, друrая с передачей
Еl
ZIIi .....:. из узла i в узел k.
3. К k-MY узлу ПО.f{ходит ветвь
.из узла с сиrналом Ek. имеющая
единичную передачу.
По этим правилам леrко по-
строить сиrнальный rраф, не со-
ставляя системы уравнений. В
этом нет необходимости, так как сам сиrнальный rраф
представляет собой rеометрическую запись системы урав-
нений. Передачи ветвей rрафа вычисляются по тем же пра-
вилам, по которым вычисляются собствеЮlые и общие со-
противления контуров.
1
Zll
Рис, 10-50. Сиrнальный rраф
уравнений по методу контур-
ных ТОКОВ,
322
(10-58)
Аналоrично можно составить сиrнальный rраф для урав-
нений по методу узловых напряжений. Для случая трех
узлов имеем такие уравнения:
УН И 1
У1Z И 2
V 1З И З == 11;
V 21 U 1 + у 22 и 2
У2З U з== 12;
VЗ1И 1
V ЗZ И 2 + V ззUз == i з .
Преобразуя эти уравнен
я аналоrично тому, как это
делаJ']QСЬ с уравнениями по методу контурных токов, полу-
чим:
и,1 == (1
. ун) И 1 + У12и.2+ У1З
З +
1:. }
U 2 == У2Р1 + (1
У 22 ) и 2 + У2:РЗ +12' (10-59)
и з == V З1 U 1 + УЗ2 U 2+(l
Vзз) из+i з .
Полученные уравнения отличаются по структуре от
уравнений (10-58) только знаками при общих проводимо-
стях. Соответственно этому и правило составления rрафа
будет отличаться тем, что знаки передач ветвей, соединяю-
щих разные узлы, будут положительны. К:онфиrурация же
rрафа не изменится.
10-14. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
10-1. Рассчитать фильтр нижних частот с частотой среза 1000 [ц
и характеристическим сопротивлением 100 Ом при нулевой чаСТОте.
О Т в е т: L == 31,8 Mf; С == 3,18 мкФ.
10-2. Задан Т
образный фильтр нижних частот, состоящий из двух
индуктивностей, каждая из которых равна О, I Mf, и емкости 2 мкФ.
Определить частоту ср.еза и построить rрафик характеристическоrо
сопротивления.
О Т в е Т: (йс =:: 10. рад/с; ZT
10 V 1
(й2. 10
lO Ом.
10-3. Задан П-образный фильтр. нижних частот, состоящий из
индуктивности 0;2 Mf и двух емкостей по 1 мкФ каждая. Определить
частоту среза и построить rрафик характеристическоrо сопротивления,
О т в е т: (йс =:: 10. рад/с;
zп 10 Ом
Vl
w2.10
lO .
10-4. Пользуясь результаТом решения задачи 9-1, доказать, что
в случае Т- или П-образноrо фильтра нижних частот (см. рис. 10-4),
i1arруженноrо соrласованно, передаточная функция по напряжению
имеет вид:
(J. [у ( ' ) 2 ]
2
"= 1
+i
.
Ui (йс (йс
10-5. Основываясь на предыдущей задаче, показать, что в полосе
пропускания коэффициент передачи по напряжению равен единице.
10-6. Два f-образны". фильтра верхних частот, каждый из которых
состоит из емкости 1 мкФ И индуктивности 10 Mf, образуют Т-образ-
323
ный фильтр. Вычислить для Т-образноrо фильтра частоту среза fc,
характеристическое сопротивление и собственное затухание при 2fc;
характеристи:еск
е сопр?тивление. и к
эффици
нт .фазы при 0,5 fc.
О т в е т. 10 рад/с, 86,6 Ом,
J 730 Ом, О,
п.
10-7. Два r-образных фильтра верхних частот, указанные в пре-
дыдущей задаче, образуют n-образный фильтр. Вычислить для П
образ-
Horo фильтра то же, что в задаче 10-6.
О т в е т: 104 рад/с; 116 Ом; j 57,7 Ом; о;
п.
10-8. Пояснить, исследуя формулы для симметричноrо фильтра
без потерь, почему в полосе пропускания фильтра ero характеристи-
ческое сопротивление активное, а в полосе задержания реактивное.
10-9. Как определить характеристические сопротивления несим-
метричноrо фильтра по данным опытов ХОЛОСто,Q хода и KopOTKoro
замыкания?
10-10. Как найти полосу пропускания фильтра по заданной частот.
ной зависимости ero характеристическоrо сопротивления?
10-11. Пояснить физическую сущность коэффициента фазы фильтра.
10-12. Как определяется в полосе пропускания и в полосе задер-
живания уrол фазовоrо сдвиrа между напряжениями на входе и выходе
r-образноrо фильтра, наrруженноrо соrласованно?
10-13. Начертить схемы последовательно-производноrо и парал-
лельно
производноrо звеньев заrраждающеrо фильтра типа m.
10-14. На примерах схем реактивных мостовых фильтров, пока.
занных на рис. 10-26. убедиться в том, что при разных знаках 21 и l:J
появляются полосы прспускания.
10-15. Доказать, что в полосе пропускания реакrивноrо МОСТО-
Z
Boro фильтра выпЬлняется условие
1
Z 1 Z '
О, что равно.
2
1
Z,
сильно условию
<X>
z:
О. Пояснить физический смысл послеД.
Hero условия.
10-16, Вывести для фнльтра типа k зависимости
2 T ==kch
и zп==.......!......
ch g
2
10-17. Пояснить с помощью табл. 10-1 построение частотных
характеристик фильтров типа k (см, рис, 1O
8
1O-1l).
rЛАВАОДИННАДЦАТ АЯ
ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
tt.t. ПЕРВИЧНЫЕ ПАРАМЕТРЫ ОДНОРОДНОЯ ЛИНИИ
ДО сих пор рассматривались электрические uепи с со.
средоточенными параметрами, т. е. предполаrалось, что
электрическая uепь представляет собой совокупность не-
324
которых самостоятельно существующих элементов " L
и С, сосредоточенных в различныIx точках ее. Напряже
иие и ток этих элементов связываются соотношениями
di . dиc
u r == ri; UL == L dt ; t == С dt'
основанными на предположении, что ток, входящий в каж-
дый из этих элементов цепи, равен току, выходящему
из Hero. Решение этих уравнений дает закон изменения
исследуемой электрической величины в зависимости от
времени, но не от координаты длины, которая в эти урав-
нения не входит.
Однако представление электротехнических устройств
в виде цепей с сосредоточенными параметрами не всеrда
возможно. Например, рассматривая электромаrнитные про-
цессы, происходящие в элеI(трических линиях, при по-
мощи которых электрическая энерrия или сиrналы пере-
даются на расстояние, необходимо иметь в виду, что Mar-
нитное и электрическое поля распределены по всей длине
линии и превращение электромаrнитной энерrии в терло
также происходит по всей длине линии. Таким образом,
линия является цеп ь ю с р а с п р е Д е л е н н ы м и
пар а м е т р а м и.
Если мысленно выдеЛИТЬ какой
либо конечный уча-
сток этой линии, то токи на концах этоrо участка ока-
жутся неодинаковыми вследствие наличия токов смеще-
ния, обусловленных емкостью между токоведущими про-
водниками, и токов утечки через изоляцию. Только при
бесконечном уменьшении участков линии токи на концах
их можно считать равными друr друrу.
Следовательно, приведенные выше уравнения непо-
средственно не применимы ко всей линии в целом или
конечным участкам ее; cTporo rоворя, они MorYT быть
применимы только к участкам бесконечно малой длины.
Маrнитный поток, который сцепляется с контуром тока,
образуемым токоведущими ПрОБодниками, определяет ин-
дуктивность цепи.
Емкость между проводами, а также емкости этих про-
водов по отношению к земле (или соответственно к кор-
пусу машины, самолета, ксраБJiЯ и т. д.) И друrим сосед-
ним проводам определяют емкость цепи.
Тепловые потери в проводах с учетом поверхностноrо
эффекта и эффекта близости обусловливают продольное
активное сопротивление цепи.
325
Наконец, несовершенство изоляции (проводимостьизо-
ляции И диэлектрические потери, возникающие в ней)
определяет поперечную активную проводимость цеr.rи.
В качестве цепи с распределенными параметрами ни-
же рассматривается о Д н о р о Д н а я Д в у х про в о д-
н а я JI И Н И я, т. е. такая линия, индуктивность, емкость,
активное сопротивление и проводимость которой равно-
мерно распределены вдоль всей длины линии. Эти элект-
рические параметры, отнесенные к единице длины линии,
называ
ся первичными
параметрами линии; они
обозначаются через L, С,
r и g*.
Однородная двухпро-
водная линия является
распространенным типом
линии; она используется
в электропроводной связи
и радиотехнике и выпол-
няется в виде параллель-
(рис. 11-1, а) или коаксиальноrо кабеля
: ::::::::::::::::C
_а а
а) б)
Рис. 11-1. Двухпрdводные линии.
а
ВОЭ,IJ;ушная; 6
коаксиальный
кабель.
ных ПрОБОДНИКОВ
(рис. 11-1, б).
Уравнения для напряжений и токов такой линии в прин-
ципе применимы и к друrим типам линий
трехфазным
и мноrопроводным.
Первичные параметры линии зависят от ее конструк-
ции и частоты. Вычисление первичных параметров отно-
сится к задачам теории электромаrнитноrо поля, состав-
ляющей содержание третьей части курса «Теоретические
основы электротехники».
в области радиочастот первичные параметры однородной двух-
проводной линии с медными проводами вычисляются по следующим
формулам (размеры в метрах).
Воздушная линия (параллельные провода) (рис, 11-1, а):
,::::::; 8,3
Vf
Hr8, Ом/м (линии);
L::::::;O.921Ig
10--6 [/м;. С::::::; 12,
lO
12, [/м.
Ig
а
* Следует обратить внимание на то, что здесь , i= l/g, так как
Щlраметры линии r и g не связаны друr с друrом: параметр ,
про-
дольный (активное сопротивление проводов), параметр g
попереч-
ный (активная проводимость изоляции).
326
к.ОQксltаltЬныllкабель (рис. 11-1, 6):
r"""4.16(
+
)Vl.10
8, Ом/м; g==roCtg8. См/М
(8
уrол диэлектрических потерь);
L
O,461g!!... 10--6, r jM; с
0.24;8 10
lO, Фjм
а Ig
а
(8
относительная диэлектрическая проницаемость изоляции).
С повышением частоты уrол потерь 8 уменьшается, Изоляция,
применяемая для коаксиальНЫХ кабелей, обычно имеет tg 8 порядка
10
1O
4,
Активная проводимость g между параллельными про-
ВОДамИ, заВИСЯЩая от метеоролоrических условий, состо-
яния изоляторов, к которым подвешены провода, и друrих
факторов. определяется экспериментально.
Практически во мноrих случаях можно считать, что
g
O.
На высоких чаСТОТах ввиду значительноrЬ преобла-
дания индуктивноrо сопротивления токоведущеrо провод-
ника над ero активным сопротивлением последним можно
во мноrих случаях'пренебречь.
Следует заметить, что на низких частотах и при Ма-
лой длине линии, коrда емкостная и активная проводи-
мости незначительны, токи В начале и конце линии прак-
тически одинаковы; В' этом случае линия _ с достаточной
точностью может рассматриваться как цепь с сосредото-
ченными параметрами. Разrраничение понятий «корот-
кая» и «длинная» линии связано с частотой, на которой
работает рассматриваемая линия; этот вопрос освещен
В & 11-3.
,И. ДИФФЕРЕНЦИАЛЬНblЕ УРАВНЕНИЯ ОДНОРОДНОЙ ЛИНИИ
Напряжение и ток В линии являются функциями двух
независимых переменных: пространственной координаты х.
определяющей место наблюдения, и времени t. определяю-
щеrо момент наблюдения. Здесь предполаrается, ЧТО На-
правление координатной оси х совпадает с направлением
оси линии.
Нашей ближаЙшей задачей является нахождение про-
ctpaHctbehho-временноrо распределеНИ5j\ тока в линииi (х, t)
и напряжения между проводами u (х, t). При ЭТОМ в общем
327
случае мо)Кет рассматриваться передача электромаrнитной
энерrии по линии, коrда источник и приемник имеются
на обоих концах линии.
Выберем поло)Кительное направление тока в линии
слева направо (рис. 11-2) и условимся наЗЫВаТЬ «нача-
лом» линии левый конец, а «концом» линии
праВЫЙ
конец. Расстояние до произвольной точки линии от нача-
ла обозначим через х, а от конца
через х'. Таким обра-
зом, вся длина линии 1 ==
== х + х'.
Выделим элементарный
участок линии длиной дх,
находящийся на расстоя-
нии х от начала. Поль-
зуясь первичными пара-
метрами r, g, L и С, отне-
сенными к единице длины
линии, прибли)Кенно пред-
ставим рассматриваемый
элементарный участок ли-
нии в виде последовательно
rLlx и индуктивности LLlx
активной проводимости gLlx
i+..H"
Рис. 11-2. Элементарный участок
цепи с равномерно распределен-
ными параметрами.
включенных сопротивления
и параллельна включенных
и емкости Сдх.
Обозначим:
u
напря)Кение ме)Кду верхним и ни)Кним проводами
в точке х;
ди
приращение напря)Кения на участке Llx;
i
ток в точке х;,
Лi
приращение тока на участке дх.
Уравнения для приращений напря)Кений и тока на
элементе длины дх запишутся следующим образом:
ди == (ri + L
) дх; )
Lli == [g (и + ди) + с д (и-;tди) 1 дх.
(11-1)
Ввиду наличия двух независимых переменных (х и t)
уравнения записываются в частных производных.
По мере стремления дх к нулю степень точности этих
уравнений повышается, причем величина BToporo порядка
малости [gLlu + с д (
) ] дх в правой части ни)Кнеrо урав-
нения (11-1) мо)Кет быть опущена.
328
Итак, линия рассматривается как цепная схема с бес-
конечно большим числом звеньев, электрические параметры
которых бесконечно малы.
Разделив обе части уравнений (11-1) на дх и перейдя
к пределу ДХ == О, получаем дифференциальные уравнения
линии:
ди . ai )
дх, == rt + L дt;
ai С ди
дх == gu + at '
(11- 2)
Эти уравнения известны в литературе под названием
т е л е r раф н ы х у р а в н е н и й.
Ес,ли за Начало отсчета принять конец линии, т. е.
ввести координату х', то уравнения примут вид:
:' == ri + L
; }
ai С ди (11-3)
дх' == gu + дi'
Уравнения (11-2) или (11-3) MorYT быть решены од-
нозначно при использоваНИИ начальных и rраничных
условий. Н а ч а л ь н ы м и у с л о в и я м и будут ЗНаче-
ния напряжения и тока в начале или конце линии в момент
времени, принятый за нуль. r р а н и ч н ы е условия опре-
деляются связями между напряжением и током в начале
или конце линии, зависящими от заданноrо режима ра-
боты линии.
Решение указанных выще уравнений дает функцио-
нальные ЗавИСИМОСТИ напряжения и тока в линии от пе.
ременных х (или х') и t.
11-3. СИНУСОИДАЛЬНЫЙ РЕЖИМ В ОДНОРОДНОЙ ЛИНИИ
При периодическом режиме под воздействием при-
ложенноrо к линии СИНУСОИДальноrо напряжения в лю-
бой точке линии напряжение и ток изменяются СИНУСQ-
идально с часТОТОЙ Ист01Jника 1. Обозначим комплексные
действующие значения напряжения и тока на расстоянии
х ОТ начала линии через О == О (х) и j == j (х).
1 Обоснованием высказанноrо положения является линейность
уравнений (11-2) и (11
3), так как только в таких уравнениях сохра-
няется синусоидальность всех функций,
329
Применяя комплексную форму записи, перепишем урав-
нения в комплексном виде:
dd
== (r+ jшL) i; )
== (g+ jшС) U.
Ввиду Toro что комплексные значения (; и 1 не за-
висят от t и являются только функциями Х, при переходе
от уравнении (11-2) к (11-4) частные производные по х
заменены обыкновенными.
Исключая из системы (11-4) ток 1, получаем уравне-
ние относительно (;:
(11-4)
d2() . .'
dx 2 ::=: (r+ ]шL) (g+ ]шС) u.
(11
5)
Аналоrично, исключая из .(11-4) нацр яжен ие {), полу-
чаем уравнение относительно 1:
d 2 j > 1
dx 2 == (r+ jшL)(g+ jшС) .
(11-6)
Обозначим квадратнь!и корень из комплексноrо мно-
жителя при (; или j через
'1' == V(r + jшL) (g + jшС) == CG + j
( 11-7)
и назовем эту величину к о э Ф Ф и ц и е н т о м р а с п р о-
с т р а н е н и я 1. Смысл TaKOro названия ВЫЯСНИТСя позже.
Итак, уравнения (11-5) и (11-6) записываются в виде
dЦ) 2 . . d 2 j
2 /
dx 2 == '1' И, dx 2
'1' . ( 11
8)
Получились одинаковые однородные линеИНЫе диф-
ференциальные уравнения BToporo порядка. Решение пер-
Boro из Них имеет вид:
Li == Ale
'YX + А 2 е'У Х . (11-9)
Ток 1 после этоrо получаетёя подстаНQВКОИ (11
9) в пер-
вое уравнение (11
4):
i == 1. (А
'e
'YX
А
'e'YX) == ... [' g+
ooC ( А e
'YX
А е'У Х )
,+/wL 11 21 V'+JwL 1 2'
1 В литературе ранее применялось обозначение у ==
+ ja..
830
или
. 1 А
1 == Z
(A.le
'I'x
2 еУХ ) ,
(11-10)
rде
z
-.; ,+jffiL
в
JI g+jffic
(11-11)
называется в о л н о в ы м с о про т и в л е н и е м ли-
нии.
Смысл TaKoro названия объяснен дальше.
Подставив (11-7) в (11-9), получим:
(; == A.le--cx.xe
;13x + A2ecx.Xei13x.
Мrновеиное значение напряжения в точке х равно мни-
мой части выражения У2 uei(j)t:
u (х, е) == 1т [У2 A.leaxe
iJ3xej(j)t + У2 A2eaxei13xej(j)t] ==
== У21 A.lI e
ax sin (ffit+Wl
x) +
+ У2! А 2 1 е ах sin (ffit + 1)5; +
x); (11-12)
здесь 'Ч'1 и 'Ф2
арrументы комплексньtх величин А 1 и А 2 .
Таким образом, MrHoBeHHoe значение напряжения в лю-
бой ТОЧI{е линии слаrается из двух функций.
Рассмотрим вначале первую из этих слаrающИх функ-
ций.
Если считать точку х фиксированной и рассматривать
изменение напряжения в данной точке в зависимости от
времени, то первая слаrающая выражения (11-12) npek
ставит собой синусоидальную функцию с постоянной ам-
плитудой.
Если же считать момент времени t. фиксированным и
рассматривать изменение MfHoBeHHoro напряжения вдоль
линии (т. е. в зависимости ОТ х), то получим затухающую
синусоидальную волну напряжения, амплитуда которой
V21 А 1 1 e
ax убывает с ростом Х, т. е. по мере удаления-
от начала линии к концу.
Величина а, характеризующая изменение амплитуды
волны на единицу длиныI линии, называется к о э Ф Ф и-
ц и е н т о м о с л а б л е н и я \ а величина
, равная из-
менению фазы на единицу длины линии, называется к о.
э Ф Ф и ц и е н т о м фаз ы.
! Ранее применялся термнн к О э Ф Ф и ц и е н т з а т у х а н и я.
331
Убывание амплитуды волны вдоль линии обусловли-
вается потерями в линии, а изменение фазы
конечной
скоростью распространения электромаrнитных колебаний.
Оба эти коэффициента а и
входят в комплексный
параметр у == а + j
, который, следовательно, характери-
зует распространение волны напряжения и тока по линии.
На рис. 11-3, а буквой "л обозначена длина волны на-
пряжения, равная расстоянию между двумя точками ли-
t=t1
3:
3:
...
Рис. 11
3. Прямая (падающая
а) и обратная (отраженная
б)
волны.
нии, в которых фазы рассматриваемой слаrающей На-
пряжения различаются на 2л. Следовательно,
[ffit + 1171
x]
[ffit + '1/'1
(х + "л)] == 2л,
откуда
2:rt
"л == 13' (11-13)
Полученная формула выражает зависимость, суще-
ствующую между длиной волны и коэффициентом фазы
линии.
На рис. 11-3, а изображены волны напряже.ния, соот-
ветствующие двум следующим друr за друrом моментам
времени: t 1 и t 2 .
С течением времени волна перемещается от начала
линии к
e концу; она носит IIазвание п р я м о Й, или п а-
Д а ю щей, в о л н ы.
Скорость перемещения падающей волны вдоль ли-
нии, называемая фаз о в о й с к о р о с т ь ю волны 1, оп-
1 Скорость распространения rруппы смежных по частоте волн
характеризуется понятием rРУППОI!ОЙ скорости' {Л. 1].
ЗЗ2
ределяется как скорость перемещенля точки, фаза коле-
бания в которой остается постоянной. Это условие запи-
сь
вается для прямой волны в виде
ro' + '1/'1
X == const,
откуда
a
(ffit + '1'1
x) == О
и, следовательно,
dx (j)
dt == VJP == Т'
(11-14)
Аналоrичное исследование BToporo слаrаемоrо выра-
жения (11-12) показывает, что для произвольноtо момента
времени оно представляет синусоидальную волну, ампли-
туда которой V21 А 2 1 еах возрастает с увеличением х,
т. е. по мере удаления от начала линии к ее кониу. С те-
Чением времени волна перемещается от конца линии к ее
началу (рис. 11-3, б); она называется о б р а т н о й, или
о т р а ж е н н о Й, в о л н о й.
Фазовая скорость обратной волны получается равной
(j)
Vф ==
lf; знак минус указывает, что обратная волна
движется в направлении, противоположном направлению
прямой волны.
Итак, MrHoBeHHoe напряжение можно рассматривать
как сумму двух волн, движущихся В противоположных
направлениях, причем каждая из этих волн затухает Б на-
правлении движения.
На основании (11-13) и (11-14)
==
== 2лf ; }
VФ VФ
VФ
л== т == VфТ,
т. е. за время, равное одному периоду, как падающая,
так и отраженная волны перемещаются на расстояние,
равное длине волны.
Линии, физическая длина которых соизмерима с дли-
ной волны, считаются Д л и н н ы м и линиями. При до-
статочно высоких частотах практически любая протяжен-
ная электрическая uепь становится «длинной» по отно-
шению к длине волНы.
Как будет п<жазано ниже, фазовая скорость в воз-
душной линии близка к скорости света (около 3.108 м!с),
(11-15)
ззз
и поэтому частоте 50 [ц будет соответствовать Д./lина в6лны
6000 км, а частоте 3. 109 rц
ДЛИН;:1 волны 1 О см. Сле-
довательно, в первом случае длинной Линией будет линия,
измеряемая мноrими сотнями или тысячами километров,
а во втором случае
цепь протяженностью в несколько
сантиметров.
Возвращаясь к уравнениям (11-9) и (11-10) и запи-
сывая прямую и обратную волны в комплексной форме,
Имеем:
(; == (; n + (;0;
. и п и о . .
1 == z;;
ZB == 1 n
10'
rде
и '
А e
yx. и
A е ух
п
1 , 'o
2 .
Напряжение И ток прямой И соответственно обратной
волн связаны законом Ома:
и п
и о
Z
.
.
В'
1 п 10
Это соотношение объясняет смысл названия ZB
вол-
новое сопротивление.
Постоянные интеrрирования А 1 и А2' входящие в (11-9)
и (11-10), находятся в зависимости от напряжения и тока
в начале линии (rраничные условия), если они заданы.
При х == О
(; (О) == (;1 == А 1 + А 2 ; ZB i (О) == ZBi1 == А 1
А2'
откуда
А 1
и 1 +ZB i 1. А
Ui
ZBji
2 . 2
2
Введем поня:rие к о э Ф фи ц и е н т а о т р а ж е н и я
ВОЛНЫ в начале линии:
и о (О)
А 2
Ui
ZB/f
Z1
ZB (11 - 16)
n1
,
(;п (О) А! (;1 +ZBii' 21 -t-ZB
rде Zl == (j 1/11
входное сопротивление линии
Подстановка вырджений дЛЯ А 1 И А 2 В (11-9) и (11-10)
с учетом (11-16) дает:
. u. + z/. )
и == 1 2 в 1 (e
YX + n 1 е"Х);
. (11-17)
i === и 1 tz ZB/f (e
YX
n 1 е УХ ).
в
334
Если задан
ы rраничные условия на конце линии, то
удобнее отсчитывать расстояние от конца, приняв коор-
динату х'.
Заменяя в уравнениях (II
9) и (11
10) х На (1
х')
и используя заданные rраничные условия О (l) == 02;
1 (!) == 12' получаем дЛЯ А 1 и А 2 следующие выражения:
А
li 2 +Z B i 2 у! А
li2
ZB/2
y!
1
2 е, 2
2 е.
Подставив их J3 (11-9) и (11
10), получим окончатель-
ныевыражения для О и 1:
r
U2+ZBi2 ( v x' +
vx' ) , }
u
2 е п 2 е ,
. . (11-18)
J
U2+ZB12 ( ух'
Vx' )
2Z B е п 2 е ,
rде аналоrично предыдущему п 2
коэффициент отраже-
ния в конце линии:
п 2 ==
o (1) ::;:: А 2 е У! ==
2
Zn
2 == Z2
ZB ; (11
16a)
и п (1) Ale
yl U:i+ZB/a Z2+ZB
Z2 == 02/12
выходное сопротивление На конце линии или
в случае приемника входное сопротивление ero.
Если сопротивление приемника равно волновому со-
противлению линии (Z2 == ZB), то коэффициент отраже-
ния равен нулю (п 2 == О). При этом в линии имеется только
одна прямая волна; обратная волна отсутСтвует. '
Это важное свойство реализуется в линиях связи, от-
ражения в которых нежелательны по ряду причин.
Во-первых, если затухание в линии невелико, то от-
раженная волна создает эффект эха в начале линии.
Во-вторых, отражения связаны с потерей энерrии.
Часть энерrии, ДQстиrшая приемноrо конца, не поступает
в приемник, а возвращается по линии в виде, энерrии от-
раженНой волны. При этом возникают дополиительные
потери энерrии в сопротивлении r и проводимости g ли-
нии. Если сопротивление источника, питающеrо линию, не
равно волновому сопротивлению линии, то .отраженная
волна, достиrнув начала линии, претерпевает повторное
отражение и т. д, Происходящая вследствие этоrо потеря
энерrии в линии понижает общий к. п. д. передачи.
В-третьих, в случае отражений может иметь место
нежелательное увеличение напряжения или тока в линии
(см. Э 11
6).
ЗS!)
Вследствие указанных причин на практике стремятся
соrласовать сопротивление приемника с волновым сопро-
тивл
нием линии. При соrласовании наrрузки с линией
выражения (11-18) упрощаются: с учетом Toro, что ZB12 ==
== (;2, находим:
(; == (; 2е'УХ'; i == /2е'УХ'. (11-19)
Эти выражения показывают, что при перемещении точки
наблюдения вдоль линии, наrруженной соrласованно, на
конце, в направлении от конца к началу линии, модуль
напряжения возрастает в е ах ' раз, а фаза
на
x' рад.
Уравнения (11
19) аналоrичны уравнениям симметрич-
Hor6 четырехполюсника при соrласованной наrрузке. По-
этому показатель распростране-
НИя на всю длину линии "(l
эквивалентен мере передачи
четырехполюсника g, а волно-
вое сопротивление линии ZB ана-
лоrично характеристическому
сопротивлению четырехполюс-
ника Zc'
Выражения (11-19) показы-
вают, что при соrласованной
наrрузке (Z2 == ZB) rеометриче-
ским местом конца вектора на-
пряжения (; является лоrариф-
мическая спираль. На рис. 11-4,
иллюстрирующем сказанное,
(вектор (;2 направлен по дей-
+J
Рис. 11-4. rеометрическое
место конца вектора напря-
жения при соrласованной на-
rрузке.
+
принято (;2 == U 2 L 00
ствительной оси).
Большой интерес представляет также рассмотрение
двух частных случаев наrрузки линии, а именно случаев,
коrда лиНИя на конце разомкнута (режим холостоrо хода)
или замкнута (режим KopOТKoro замыкания). В первом
случае Z2 == 00 И соответственно коэффициент отражения
п 2 == 1; во втором случае Z2 == О И п 2 ==
1.
К. рассмотрению этих двух случаев мы вернемся не-
сколько позже.
Система уравнений (11-18) может быть переписана в сле-
дующем виде:
. . е'У Х ' +e
'УХ' + . е'У Х '
e
'УХ' }
и==и 2 2 ZB l 2 2 ;
. и 2 e'Yx'
e
'YX' . e'Yx'+e
'YX' (11-20)
I== ZB 2 +/2 2
336
Уравнения (11
18) и ('11-20) представляют собой ypaB
нения линии в п о к а з а т е л ь н о й (или волновой)
форме при отсчете расстояния от конца линии. Они пре
образуются с помощью rиперболических функций:
(J == [;2 сЬ ух' + ZBi2 sh ух'; }
.. 1 .
1 == 12 сЬ ух' + ZB ' и 2 sh ух'.
(11-21)
Положив в этих уравнениях х' == 1, получим уравнения
линии в r и пер б о л и ч е с к о й форме, выражающие
напряжение и ток в начале через шщряжение и ток в конце
линии:
(;1== (;2 сЬ уl + ZB i 2 sh yl; }
" 1 .
11 == 12 сЬ у! + ZB и 2 sh yl.
(11
22)
Обращает на себя внимание сходство полученных
уравнений с уравнениями симметричноrо четырехполюс
ника (см.
9-7). Эти ура
внения показывают, что OДHO
родная линия представляет собой симметричный четырех-
полюсник с характеристическими параметрами g == уl и
Zc == ZB'
Применяя параметры 11 А 11 четырехполюсника, получим
связь между коэффициентами ero и параметрами ' линии:
Ан == А 22 == сЬ yl; 1
А 12 ==
B sh yl; (
А 21 == ZB sh yl. J
Показательная и rиперболическая. формы записи
уравнений линии (11-18) и (11-21) дополняют друr друrа
и применяются в зависимости от условий задачи.
Преимущество показательной формы записи уравне-
ний заключается в большей наrлядности рассмотрения
физических процессов в линии с помощью прямых и об-
ратных ВО.1Н и удобстве построения rеометрических мест на
комплексной плоскости. Поэтому уравнения (11
18) широко
использованы в последующих параrрафах данной rлавы.
rиперболическая форма записи уравнений также пред-
ставляет в ряде случаев известныIe удобства с точки зрения
исследования и расчета электрических величин в ЛИНИ,и и
их фазовых соотношений.
Рассмотрение линии как четырехполюсника базируется
обычно на rиперболическойформе записи уравнений.
(11
23)
337
Н... ВТОРИЧНЫЕ ПАРАМЕТРЫ ОДНОРОДНОЙ ЛИНИИ
В т о р и ч н ы м Н, или Х а р а к т е р и с т и ч е с к и-
м и, параметрами линии ЯВЛяются коэффициент ослабления,
коэффициент фа
ы
и волновое сопротивление ZB' кото-
рые в свою очередь выражаются через первичные пара-
метры линии и частоту.
Из выражения
'1' == 1/(' + j(l)L) (g + j(l)C)
== v 'g
(l)2LC + j(l) (Lg+ С,) ==а+ j
следует, что
а 2 + j2CG
2== 'g
(l)2LC + j(l) (Lg+ С,),
откуда
а 2
2 == rg
(l)2LC; 2a
== (l)Lg + (l)С,.
Совмес тное решение этих уравнений дает:
CG == -v --} [,g
(l)2LC + у(,2 + (l)2L2) (g2 + (l)2С2) ] ; (11-24)
== -v
[(I)2LC
'g + у(,2+ (1)2[2) (g2 + (l)2С2) ]. (11-25)
Из полученных выражений следует, что CG и
в об-
щем случае зависят от частоты. Однако, как показьiвает
исследование, в отличие от коэффициента ослабления, ко-
торый изменяется в сравнительно оrраниченных пределах,
коэффициент фазы неоrраниченно растет с частотой.
Формула (11-25) позволяет 'выразить фазовую ско-
рость распространения электромаrнитной волны через пер-
вичные Параметры линии и частоту по формуле (11-14).
Выражения (11-24) и (11-25) неудобны для практиче-
CKoro использовайия ввиду их rромоздкости. Существует
ряд приближенных расчетных формул для ,вычисления
вторичных параметров линии, учитывающих, что в обла-
сти высоких частот (порядка 1 мrц и выше) сопротивление,
весьма мало по сравнению с (l)L, а проводимость g ничтожно
мала по сравнению с (l)С. Первое допущение «(I)L > ,)
обусловлено тем, что индуктивное сопротивление прямо
прощ)рционально частоте, между тем как сопротивление
проводов , пропорционально квадратному корню из ча-
стоты вследствие поверхностноrо эффекта (см. 9 11-1).
Второе допущение справедЛИВО для высокочастотных фиде-
ров, которые, будучи «длинными» по сравнению с длиной
338
волны, имеют весьма малую физическую длину и поэтому
MorYT иметь надежную изоляцию между ПрОВодам,И. Осо-
бенно ничтожно мала проводимость g кабельных линий.
Используя для выражения
-..r
( , ) 1/2 ( . g ) 1/2
l' == jffi r LC 1
j шL 1
J шс .
(11-26)
бином Ньютона, оrраничиваясь первыми двумя членами
разложения
l'
j(;) V'LC (I
j 2
L )(I
j 2
C ) (11-27)
. ,g
и пренебреrая ввиду малости слаrаемым
J 4оо V i.c '
получим окончательно:
a
; V Z +{V
;
i3
fJ) V LC .
(11-28)
(11-29)
Эти формулы представляют собой пределы, к кото-
рым стремятся коэффициент ослабления и коэффициент
фазы с ростом частоты.
Выражение (1I-28) не следует понИмать в том смысле,
что а не зависит от частоты; входящие в Hero параметры r и g
сами являются функциями частоты (см. 9 11-1).
Первое слаrаемое в правой части выражения (11-28)
определяет ту долю ослабления, которая обусловливается
продольным активным сопротивлением линии. Второе сла-
raeMoe определяет долю ослабления, которая вносится
в передачу вследствие наличия поперечной активной про-
водимости линии.
Для уменьшения потерь при передаче электромаrнит-
ной энерrии по линии стремятся к тому, чтобы сопротив-
ление линии r И проводимость изоляции g были по воз-
можности малы.
Фазовая скорость соrласно (11-14) И (11-29) равна:
ш 1
VФ ==
VLc
. (11-30)
Это предельная фазовая скорость распространения вол-
ны вдоль линии при бесконечно большой частоте. При
постоянном токе (ffi == О) понятия коэффициент фазы и
фазовая скорость теря.ют физический смысл; на основа-
339
нии выведенной ранее формулы для l' (11-7) при <u == О
а == V rg ; {3 == О.
На рис. 11-5 показан характер изменений а и
в зави-
симости от частоты; коэффициент
с ростом частоты асим-
птотически приближается к
rl..' прямой, образующей с осью <u
уrол
rде т
масштабный коэффи-
циент.
Для кабельных линий ха-
рактерна резко выраженная
емкостная проводимость roС,
по сравнению с которой про-
Рис. 11
5. Частотные характе- водимость изоляции g ничтож-
ристики а; и
. но мала. Кроме Toro, если
частота не очень велика, то
индуктивное сопротивление roL мало по сравнению с актив-
ным сопротивлением r Из-за малоrо расстояния между
жилами. Поэтому в случае кабельной линии, пренебреrая
параметрами g и L по сравнению с r и С, получаем
упрощенные расчетные формулы
l:
+
J.1t\1.
М;I
arctg (У LC т),
O/
V jr<uC == V rwC L 45 q
или
, y
c ( У2 + . У 2 )
1'
(ш
J
.
Следовательно,
.. j тшG
a
V
.
(11-31)
Соответственно фазовая скорость распространения волны
в кабельной линии равна
ш .. j2W
VФ == 13
V ,С '
(11-32)
т. е. прямо пропорциональна корню квадратному из ча-
стоты.
В теории электромаrнитноrо поля доказывается, что
про изведение удельных значений индуктивности и емко-
340
сти В линии
LC === efl/C 2 , (11
33)
rде с
скорость света в пустоте (около 3.108 м/с);
е и fl
диэлектрическая и 'маrнитная проницаемости
среды, окружающей токоведущие проводники.
Предел,' к которому с ростом частоты стремится фа-
зовая скорость волны, равен на основании (11-30) и (11-33):
с
VФ === VEfJ. .
В случае воздушной линии е
1 и
L
1, и потому
фазовая скорость в пределе стремится н: скорости света
в пустоте.
'Ка(елu.
телефонные u. Mop
снu.е
телеарафные т
20 '10 80 160 820 6'10 1280 2560 5120 102'10rч,
Рис. 11-6. Зависимость фазовой скорости распространения
волны от частоты и типа линии,
в случае кабельной линии е === 475 и поэтому предель-
ная фазовая скорость примерно вдвое меньше скорости
света в пустоте.
Рисунок 1l
6 иллюстрирует заВИСI:{МОСТЬ фазовой ско-
рости волны от частоты и типа линии.
Волновое сопротивление линии
-.(' ,+j(j)L ( ' l+j(j)
ZB=== V g+j(j)C === g 1+ ' С
l(j)
i
при постоянном токе (ю === О) и бесконечной частоте (ю == 00)
имеет действительные значения
ZB == 11 ;
(11-34)
(ю==О)
и
Zs == 11
(ю == (0).
341
В остальной части диапазона частот волновое сопро
тивление линии имеет емкостный характер, так как обычно
с L
>
[aprYMeHT знаменателя D
g , ,
правой части (11-34) больше ар-
rYMeHTa числителя].
На рис. 11-7 показаны кри-
вые изменения модуля ZB и уrла ер
волновоrо сопротивления линии
в зависимости от частоты.
Подставив выражения для L
и С из
11-1 в формулу ZB ===
=== V LjC , получим приближен-
ные расчетные формулы для
высоких частот в зависимости
от размеров:
Z, ,'!
Рис, 11-7. Зависимости мо-
дуля и уrла волновоrо со-
противления линии от ча-
стоты.
ZB === 276 Ig : (воздушная линия); )
138 Ь
ZB === Y
Ig
(коаксиальный кабель).
8 а
, (11-35)
Средние значения ZB дЛЯ воздушных линий 40Q........500 Ом,
для кабелей 50
70 Ом.
Ом
600
500
1100
300
200
10
z,=/f
"
./
./
./
Loo"
d.
а
20 30 'ю 60 80100 200
а.}
.
т;f
1....
1....-
/
l/
/
1/
./
/
!
Ом
80
70
50
50
110
30
ZJO
215
O 315 'ljО I.f J 5
5)
Рис. 1l
8, Волновоесопротиаление линии,
а
воздушной; ci
кабельной.
Рисунок 11-8 иллюстрирует rрафические зависимости
ZB от d/a и Ь/а для воздушных и кабельных линий, ПОСТ4
роеннь.rе по формулам (11-35).
342
ft.J. ЛИНИЯ 6ЕЗ ИСКАЖЕНИЯ
Сиrналы, передаваемые по линии связи, представляют
собой совокупность множества различных частот: дис
кретных
в случае периодических несинусоидальных сиr-
налов (см. rл. 13) и образующих непрерывный спектр
в случае непериодических сиrналов (см. rл. 16).
Н е и с к а ж е н н о й передачей сиrнала называется
такая передача, при которой qюрма сиrнала в начале и
конце линии одинакова, т. е. все ординаты кривой напря-
жения или тока в конце линии прямо пропорциональны
соответствующим ординатам кривой в начале линии.
Такое явление имеет место в том случае, коrда коэффи
циент ослаблеI;IИЯ
ЛИНI:'и, а также фазовая скорость на
всех частотах одинаковы.
Неодинаковое затухание на разных частотах создает
так называемые амплитудные искажения, а неодинаковая
скорость .волн Ha
разных частотах
фазовые искажения.
Соrласно (11-31) и (11-32) коэффициент ослабления
и фазовая скорость в случае кабельных линий пропор-
циональны квадратному корню из частоты. В случае воз-
душных линий также существует зависимость (Х и Vф от
частоты. В результате этоrо получаются амплитудные и
фазовые искажения.
Итак, для неискаженной передачи требуется, чтобы
коэффициент ослабления (Х не зависел от частоты, а коэф-
фициент фазы
был прямо' пропорционален частоте; в пос
леднем случае фазовая скорость Vф == ю/
получается не
зависящей от частоты.
Такое положение имеет место при условии, что
L С
:::::
(11-36)
r g
В этом случае коэфф ициент распространения раве н:
,\,== Y (r+jffiL) (g+jffiC) ==Vrg(l+ju>
)(I+jffi
);
с учетом (11-36)
'\' ==-V rg +jffivrg
r
или
'\' == V rg + jffi V LC .
Если считать, что пеРВl1чные параметры линии не за-
висят от Частоты, то коэффициент ослабления в данном
:И3
случае будет постоянен:
сх == v rg , (11
37)
а коэффициент фазы
прямо пропорционален частоте:
== u) vrc. (11-38)
Линия, параметры которой удовлетворяют условию
(11
36), называется л и н и е й б е з и с к а ж е н и й, по-
скольку любые сиrналы распространяются по ней с со-
хранением их qюрмы. Линия без искажений является
одновременно и линией с минимальным затуханием, ко-
торое только и возможно при заданных параметрах r и g.
Волновое сопротивление линии без искажений
дей-
ствительное число, что равносильно активному сопротив-
лению, не зависящему от частоты; в соответствии с (11-34)
оно выражается простой qюрмулой
ZB=='V ; == V
.
(11-39)
Фазовая скорость в линии без искажений постоянна
и совпадает с полученным ранее выражением (11-30) для
предельной скорости распространения волны вдоль линии
при бесконечно большой Частоте:
1
vф== VLc .
Для устранения искажений, вызываемых несоrласо-
ванностью сопротивления приемника с сопротивлением
линии, т. е. во избежание возникновения отражений на
приемном конце, сопротивление приемника должно быть
равно ZB' Коэффициент полезноrо действия линии имеет
в этом случае наибольшее возможное значение, равное
e
2(J.l, как в линии при соrласованной наrрузке.
Ввиду TOrO что волновое сопротивление линии без ис-
кажений является активным, при соrласованной наrрузке
напряжение и ток в любой точке линии совпадают по
фазе. Отношение мrновенных значений напряжения и тока
в любой точке такой линии равно:
==Y
,
откуда
Li'J. Cи'J.
""'2 == '""2'
(11-40)
344
Следовательно, на любом отрезке линия без искаже-
ний, наrруженной cOrJIaCOBaHHo, энерrия маrнитноrо поля
в каждый момент времени равна энерrии электрическоrо
поля.
Следует заметить, что на практике условие (1l
36),
как правило, не выполняется; отношение L/r обычно зна-
чительно меньше отношения C/g. Вследствие этоrо зату-
хание линии всеrда превышает минимальное. Наименее
соответствуют условию (11-36) кабельные линии.
Чтобы линия наиболее соответствовала условию (11-36),
следовало бы изменить какой-либо первичный параметр,
например уменьшить r или С либо увеличить g или L.
Уменьшение активноrо сопротивления r возможно за
счет применения проводов большеrо диаметра, что, од-
нако, значительно удорожало бы линию. Увеличение про-
водимости изоляции g невыrодно, так как при этом воз-
росло бы затухание линии.
Наилучшим средством для приближения первичных
электрических параметров к оптимальному соотношению
(11-36) является искусственное увеличение индуктивно-
сти включением в линию через определенное расстояние
индуктивных катушек или применением кабеля, прово-
Дящие жилы KOToporo обмотаны тонкой лентой из мате-
риала с высокой маrнитной проницаемостью [Л. 1).
11-6. ЛИНИЯ БЕЗ ПОТЕРЬ
Независимо от Toro, соблюдается ли оптимальное со-
отношение первичных Параметров (11-36) или не соблю-
дается, во всех' случаях желательно, чтобы активное со-
противление r и проводимость изоляции g были по воз-
можности малы (для уменьшения потерь энерrии).
В воздушных линиях обычно индуктивное сопротив-
ление линии юL превышает активное сопротивление r,
а емкостная проводимостъ юС превышает активную прово-
димость g. С ростом частоты разница между указанными
величинами становится еще более значительной.
& ряде случаев оказывается полезным в первом при-
ближении рассматривать линию, не имеющую поreрь,
т. е, пренебреrать активными СОПРОТИВo/Iением и проводи-
мостью по сравнению с соответствующими реактивными
составляющими. Такая идеализация допускается для при-
ближенной качественной и количественной оценки иссле-
дуемых явлений. При этом весьма 'упрощаются расчетные
345
выражения и rиперболические уравнения линии переходят
в триrонометрические.
Итак, основным исходным предложением, которое де-
лают при рассмотрении линии без потерь, ,является при-
ближенное условие, что "
о и g
о. в этом случае вто-
ричные пара метры линии принимают весьма простой вид,
а именно:
'V == jffi V LC; ct == о;
== ffiV LC ; Zs == Zз == V
.
Следовательно, в линии без потерь ослабление отсут-
ствует. Ввиду постоянства фазовой скорости
1
vф== V LC
отсутствуют также фазовые искажения.
Выражения для коэффициента фазы, фазовой скоро-
сти и ВОЛНОвоrо сопротивления линии без потерь совпа-
дают с выражениями, полученными ДЛя линии без иска-
жений. Следовательно, все сказанное о линии без иска-
жений полностью относится и к линии без потерь.
Ввиду Toro, что rиперболические функции с мнимым
aprYMeHToM преобразуются в триrонометрические функ-
ции, rиперболические уравнения линии (11-21) принимают
триrонометрическую форму:
й == {\ cos рх' + j
Bj2 sin
x'; }
. . и
1 == 12 cos рх' + j
sin рх'.
ZB
(11-41)
Эти уравнения ИСПОЛЬЗУIОТСЯ ниже при рассмотрении
стоячих волн в лиН1IИ без потерь (см.
11-7).
Энерrия, передаваемая по линии, складывается из
энерrии электрическоrо и маrНитноrо полеЙ.
В том случае, коrда к концу JIиlIии без потерь при-
соединено сопротивление, равное волновому, на любом
отрезке линии соблюдается условие (11-40), полученное
для линии без искажениЙ. При этом вся энерrия, достав-
ляемая падающей волной, поrлощается в сопротивлении
наrрузки.
Если сопротивление наrрузки отлично от ВОЛlIовоrо,
то в Месте присоединения наrрузки энерrия перераспре-
деляется между полями, Б результате чеrо возникают от-
ражения.
346
В предельном случае, коrда линия на конце разомкну-
та, падающая волна встречает бесконечно' большое со-
противление; ток в конце линии обращается в нуль, и
соответственно энерrия маrнитноrо поля переходит в энер-
rию эa:rектрическоrо поля. Напряжение на разомкнутом
конце линии УДВаивается, и возникает отраженная волна
Toro же знака, что и падающая [П 2 === 1; см. (11-16а)J.
В друrом предельном случае, Коrда линия на конце
замкнута накоротко" падающая волна встречает сопро-
тивление, равное нулю, напряжение в конце линии 15б-
ращается в нуль и соответственно энерrия электрическоrо
поля переходит в энерrиюмаrнитноrо поля. Ток на ко-
роткозамкнутом конце линии удваивается, и возникает
отраженная волна, знак котороЙ противоположен знаку
падающец волны (П 2 ===
1).
При активной наrрузке и r 2 > 28 коэффициент отраже-
ния п 2 > о; п 2 < О при r 2 > 28' Поэтому В первом случае
возрастает напряжение и убывает ток, а во втором слу-
чае, наоборот, убывает напряжение и возрастает ток по
сравнению с режимом соrласованной нзrрузки (па ==-
-= о).
tf.7, РЕЖИМЫ РА&ОТЫ ЛИНИИ &Е3 ПОТЕРЬ. СТОЯЧИЕ ВОЛНЫ
ИСCJlедуем закон распредел
ния действующих напря-
жения и тока вдоль линии без потерь. С этой целью вос-
пользуемся уравнениями линии (11-18) и (11-41) в ком-
плексной и rиперболической формах.
Приняв в (11-18) мнимый коэффициент распростра-
нения у == 'j
== j2л/л, получим для любой точки линии на
расстоянии х' от конца:
{; == {- v 2 ( 1 +
) (/
х' + па e
j
х' ) ; )
( . 21С ,121C . ) (11-42)
j == 2:0 и 2 ( 1 +
z;) е l т х'
П 2 е
/ Т х .
Входящий в эти уравнения коэффициент отражения
Z2
Z8
П 2 == Z2+ZS
представляет собоЙ в общем случае комплексную величину.
Выражения (11-42) наrлядно свидетельствуют о том,
что комплекс!:юе напряжение в любой' точке х' слаrается
847
из падающей и отраженной волн напряжения, амплитуды
которых находятся в соотношении 1 : 1 п 2 .1; 'в свою очередь
комплексный ток равен разности падающей и отраженной
волн тока с тем же соотношением амплитуд.
Точкам х' == k
(k
целое число), 'удовлетворяющим
условию
I . 2л , . 2п ' !
/Т Х +п2e
J1::'x ==1+lп 2 I, (11-43)
соответствует максимальное действующее значение и, так
как при этом фазы падающей и отраженной волн напря-
жения совпщщют. На расстоянии л/4 от этих точек падаю-
щая и отраженная волны оказываются в противофазе и
действующее напряжение имеет минимум. При этом удовлет-
воряется условие
I J 2л , . 2л ' 1
е Т Х
п2e
JTX ==1
lп21. (11-44)
Координаты максимумов и минимумов и, являющиеся
мноrозпачными функциями п 2 и Л, не зависят от вре-
мени, т. е. с течением времени они остаются на одном и
том же месте; минимум и располаrается посредине между
двумя соседними' максимумами и, причем расстояние
между ближайшими максимумами (или минимумами) со-
ставляет Л/2.
Таким образом, кривая действующих значений на-
пряжения вдоль линии без потерь представляет собой
волнообразную кривую, максимумы и минимумы которой
чередуются (см. дальше рис. 11-10, б и е).
Аналоrичные рассуждения приводят к выводу, что и
кривая деЙСТБУЮЩИХ значений тока вдоль линии без по-
терь представляет собой волнообразную кривую, смещен-
ную относительно кривой действующих значений напря-
жения на четверть длины волны. Места максимумов на-
пряжения совпадают с местами минимумов тока и, наобо-
рот, минимумы и совпадают с максимумами 1.
При отсутствии отраженной волны (п 2 == О) действую-
щие значения и и 1 вдоль линии без потерь не изменя-
ются.
Чем больше приближается коэффициент отражения
I п 2 I к единице, тем больше разнятся максимумы и мини-
мумы и (или 1).
При I п 2 I === 1, т. е. при равенстве амплитуд прямой и
обратной волн, в линии устанавливаются с т о я ч и е
348
в о л н ы напряжения и тока. Кривые действующих зна-
чений и и 1 вдоль линии представляют собой в этом слу
чае «выпрямленные» синусоиды; на ,ТlИнии образуются
у злы, т. е. точки, в которых и или 1 равны нулю, и
п у ч н о с т И, т. е. точки, в которых и или 1 максимальны.
Из сказанноrо выше следует, что узлы напряжения
совпадают с пучностями тока И, наоборот, узлы тока сов-
Прu.еМН&lй.
конец
Рис. 11
9. Сложение прямой и
обратной волн.
Рис. 11-10. Действующие зиаче-
ния напряжения и тока вдоль
линии без потерь.
и
rz =с.о
ь ь ) л. 5л.
)..
rz= JZ 8
" ............; .............; ....
.
6)
,
:
У
Щ
'zО"
8)
1
.. ,
... ,
/ .....
... rz=J Z 8
а)
.. \. r.
o
'1 ,1 \ / 2
· л. л. л. 5л
7[ '2 д) q:
падают с пучностями напряжения. Соответственно узлы
(или пучности) напряжения и тока сдвинуты на четверть
длины волны друr относительно друrа.
На рис. 11-9 в виде примера показано сложение прямой
и обратной волн напряжения, имеющих одинаковые ампли
туды, для трех моментов времени: t 1 , t 2 и t з . Сумма беrущих
в противоположные стороны волн образует стоячую волну,
показанную на рис. 11-9 в виде MrHoBeHHbIx значений для
моментов времени t 1 , t 2 и t з .
349
Из этоrо рисунка ВИДНО, что на протяжении Bcero участка
между двумя соседними узлами стоячеЙ волны синусоидаль-
ное изменение напряжения во времени происходит с одина-
ковой начальной фазой: при прохождении узла начальная
фаза синусоидальных колебаниЙ изменяется скачкообразно
на величину л. Сказанное в равной мере относится и к стоя-
чей волне тока.
На основании приведенноrо выше выражения для ко-
эффициента отражения п
можно заключить, что условие
I п 2 ! =:: 1 выполнимо в трех случаях: при Z2 == 00 (холостой
ход), Z2 =:: О (короткое замыкание) и Z2 == jx (реактивная
наерузка). Этим усло&иям соответствуют стоячие волны,
возникающие G линии без потерь.
Распределение действующих значений напряжения и
тока вдоль линии для холостоrохода и KopoTKoro замы-
кания иллюстрируется на рис. 11-10, а и д.
Для сравнения на рис. 11-10 показано распределение
напряжения и тока для друrих режимов работы линии.
При активной наrрузке Z2 =:: r 2 =:: 3z B , п 2 == 0,5 (слу-
чаЙ 6) максимумы и минимумы и и 1 совпадают по своему
местоположению с аналоrичными значениями для режима
холостоrо хода; при активной наrрузке Zo}. =-
r 2 =-= l/ зzв ;
п 2 =::
0,5 (случай е) максимумы и минимумы расположены
так же, как при коротком замыкании; при соrласованной
наrрузке Zz == r 2 == ZB' п 2 == О (случаЙ в) кривые и и 1
изображаются прямыми, параллельными оси абсцисс.
Стоячие волны леrко исследуются с помощью уравне-
ниЙ (11-41) ЛИНии без потерь.
При холостом ходе (/2 =:: О)
. . 2Л;, }
и == и 2 COS
'i: х ;
(11-45)
! . '(;2' 2л; ,
==l
Sln
X .
ZB '),.
Узлы напряжения находятся в ТОЧКах, для которых
2л; , О
cosT X ==
или
2л;, Л + k
т Х =::
2
зt,
отку да
, 2k+ 1
Хуз==
""
350
Пучности напряжения находятся в точках, для Ko
торых
2л , + 1
cosT x ==
или
2л; , k
Т Х == п.
откуда
, k
Х пуч == "2 "'.
Разомкнутый конец линии совпадает с узлом тока и
пучностью напряжения (рис. 11-10, а).
Как видна из (11-45), ток опережает по фазе напря-
90 0 . 2л; , 2л ,
жение на ,коrда sш
'i: Х и cos
'i: Х имеют одинако-
u (О ' '), '), ,. 3
)
выи знак
X
4.; '2
X
4 '" и т. д. , И отстает
90 0 . . 2л; , 2л;,
на от напряжения, коrда знаки sш
i;" Х и cos т Х
( '), , л 3'А ,
)
различны 4
X
2; 4'"
X
'" и т. д. .
При коротком замыкании, положив в (11-41) и 2 == О,
получим
. . J . . 2л; , }
U==JZB 2 S1П т Х ;
.. 2л;,
1 == J 2 COS т. Х .
(11-46)
На замкнутом конце линии х' == О и в точках, удален-
ных от Hero на целое число полуволн х' =:= k'A/2, находятся
узлы напряжения и пучности тока, а в точках, удален-
ных от конца на нечетное число четвертей волн
[Х' == (2k+ 1)
], находя:rся пучности напряжения и узлы
тока (рис. 11.10, д).
Как видно из (11-46), ток отстает по фазе от напря-
90 0 . 2л , 2л ,
жения на ,коrда sш т Х и cos
Х имеют одинако-
(о " '), '), , 3
)
вые знаки
X
4; "2
X
4'" и т.. д. , и опере-
жает на 900 напряжение, коrда знаки siп
Л; х' и cos 2; х'
( "'А. , '), 3
,
)
различны 4
X
2; 4'"",
x
'" и т. д. .
351
Следует заметить, что наличие хотя бы самых малых
потерь в реальных линиях приводит к' тому, что действу-
ющие значения и и 1 не снижаются до нуля, а достиrают
некоторых минимальных значений в точках, соответству-
ющих узлам. .
В случае стоячих волн моЩность в узлах напряжения
и тока равна нулю. В остальНых точках линии имеет место
только реактивная мощность, так как напряжение и ток
сдвинуты по фазе на 900. В этом случае энерrияне пере-
дается вдоль линии, а происходит лишь обмен энерrией
между электрическим и маrнитныM полями на участках
линии, оrраниченных узлами напряжения и тока.
Если в линии имеются потери или приемник потреб-
ляет активную мощность, то узлы исчезают; амплитуда
падающей волны превышает амплитуду отраженной вол-
ны, и за счет разности амплитуд происходит процесс пере-
дачи энерrии вдоль линии, .
Для количественной оценки степени соrласования ли-
нии с наrрузкой в радиотехнике используется к о э ф-
Ф и ц и е ы т б е r у щей в о л Н Ы, под которым пони-
мается отношение минимума кривой распределения и или 1
к максимуму той же величины:
Кб === UM
H === JM
H . (11
47)
и маКс 1 маКс
с учетом (11-43) и (11-44) иМеем:
К 1
ln21
б== 1+l n 21'
(11-48)
откуда
'п 2 !== 1 1
К к б == UмаJ(С
UМИН . (11
49)
+ б имакс+имнн
В случае активной наrрузки выражение (11-48) упро-
щается. П р и , 2 > Z B l п I 'Z
ZB И соrласно ( 11-48 )
I 2 == 'Z+ZB
'Z
Кб==
'
'2 '
(-11-50)
при '2 < ZB I п 2 1
ZB
'2
ZB +'2
И, следовательно,
К б ==!!..
ZB
(11-51)
в реальных условиях коэффициент беrущей волны
обычно не ниже 0,5
0,6.
352
КРИВУЮ расnред.еленйя д.ействующих ЗНачений ltаf1рЯ
жения ВДОЛЬ линии ис.пользуют на практике для изме-
рения длины волны или частоты. Длина В9ЛНЫ "опреде-
ляется удвоенным расстоянием между соседними макси-
мумами или минимумами КрИВОЙ распределения, а частота
вычисляется по длине БОЛНЫ на основании (11-15).
tt-a. ВХОДНОЕСОПРОТНВЛЕНИЕ линии
Входное сопротивление' линии, измеренное в произ-
вольной точке на расстоянии Х' от конца, определяется
отношением Z ==: [) /1 и может быть представлено в ком-
плексной ,или rиперболической форме. Ради, общности
рассмотрения вопроса будем считать, что линия Harpy-
жена на конце некоторым сопротивлением 22' которое
в зависимости от условий может быть любым.
Комплексная форма выражения для входноrо сопро-
тивления линии получается на основании (11-18):
(J е УХ ' +п2e
YX'
z ==
==: 2 в УХ'
YX'
1 е
п#
или
1 + п2e
2ax' e
j2f>x'
2 == 2 в 1
2a.x'
j2f>x' .
п2e е
(1l-52)
Данное выражение показывает, что с изменением коор-
динаты Х' модуль входноrо сопротивления линии ко-
леблется между некоторыми максимумами и миниму-
мами (которые в общем случае отличаются друr от
друrа) .
Допустим, что МОДУЛЬ Z достиrает HeKoToporo макси-
мума В точке X
xto Тоrда максимумы будут также в точ-
ках, соответствующих изменению aprYMeHTa 2
x' на ве-
личину 2kл, что даст:
2
xt + 2kл ==: 2
.(x
xt + k
), ==: 2
(x
xt +ok
}).
Следовательно, максимумы чередуютс!} через каждые
полволны. ПосреДИfJе между максимумами будут мини-
мумы, которые также чередуются через каждые полволны.
Если вместо координаты х' варьировать коэффициентом фазы
== 2n/'л, меняя частоту источника, то получится аналоrичная ВОЛН0-
образная кривая, причем максимумы и соответственно минимумы будут
отстоять друr от друrа на n/х' (здесь х' == coпst). ИсслеJlУЯ изменение
353
входноrо сопротивления Линии прн плавном иЗменении частоты источ
ника, можно зафиксировать два следующих друr за друrом макси.
мума (нли минимума) z, соотаетстаующих частотам 11 и 'а.
в ЭТОМ случае
(i)i
2лli.
2==
(i)2 == 2лl2
1
'vi" ' "'2"'2
и, следовательно,
R 2
R 1 == 2л ( А.
А ) ==
1-' 1-' "'2"'1 х' ·
откуда
, "'1"'2
== 2 (vJ2
dJl) .
Uри малом расхождении частот 11 и 12 фазовые скорости "'l и "' 2
почти одинаковы: "' 1 ::::; V 2 ::::; "'ф.
При этом
"'ф
2 (f2
fr)
Данная формула позволяет определить расстояние от точки наблю-
дения До ближайшей точки линии, в которой имеет место отражение
(например, при коротком замыкании на ЛИНИИ), производя измерение
только в одной точке.
x'
Волнообразный характер кривой z подчиняется в об-
щем случае закону изменения модуля rиперболическоrо
TaHreHCa с комплексным aprYMeHToM, что видно из сле-
дующеrо вывода.
Непосредственно из (11-21) следует:
Z == и 2 ch УХ' + Z.Bi 2 sh УХ'
22 + ZB th УХ' (11-53)
и 2
12 сЬ УХ' +у sh УХ' 1 +
Z 2 th ух'
В. в
Обозначив Z2/ZB == th М, имеем:
th М + th УХ' , 5
Z===ZB l+thMthyx' === ZBth(yX +М). (11- 4)
При холостом ходе (Z2 === 00) входное сопротивление
линии соrласно (11-53) равно:
Zx === ZB cth ух', , (11-55)
а при коротком замыкании (Z2 === О)
ZK === ZB th ух' . (11-56)
С учетом (11-55) и (11-56) входное сопротивление Z
леrко Выразить через Zx и ZK:
Z
Z 22+2к
xl2+ZX'
354
Этой формулой пользуются в том случае, коrДа из
опытов холостоrо хода и KopoTKoro замыкания известны
Zx и ZK'
Данные опытов холостоrо хода и KopoTKoro замыка-
ния используются также для вычисления характеристи-
ческих параметров линии.
На основании (11-55) и (11-56)
,ZB == V ZXZK ; th ух' == V {: . (11-57)
Эти формулы совпадают с (9-35). Ввиду Toro что коэф-
фициент фазы
определяется по (11-57) неоднозначно, при
вычислении производится провер.ка на основании (11-14),
причем первоначально фа-
зовая скорость VФ выби-
рается ориентировочно.
Вычисление характеристи-
ческих пара метров по фор-
MY.'l3M (11-57) иллюстриро-
вано ниже примероl\t 11-1.
На рис. 11-11 показаныI
кривые изменения модулей
Zx и ZK В зависимости от
координаты х'. В пределе,
т. е. при х'
00, макси-
мумы и минимумы кривой
стремятся к значению Zп.
Входные сопротивления
линии без потерь при холо-
стом ходе и коротком замыкании MorYT быть получены
из (11-55) и (11-56) заменой у == j
== j2л/л.:
Z . t 2л;, Z . t 2л; ,
X==
JZBC g-1
X; K==JZB gT X '
,
,
Эти реактивные входные сопротивления с учетом их
знака изображаются котанrенсоидами и танrенсоидами
(рис. 11-12). AprYMeHToM может служить также величи-
на
, если изменять частоту при постоянной длине х'.-
Сопоставляя эти rрафики с частотными характери-
стиками сопротивлений реактивных двухполюсников (см.
rл. 5), леrко убедиться в их сходстве: резонансы напря-
жений и токов чередуются; однако в отличие от двухпо-
люсников, имеющих оrраниченное число резонансов, ли-
ния без потерь имеет бесконечное число резонансных то-,
355
чек, что соответствует представлению линии как цепочки
из бесконечноrо числа индуктивностей и емкостей.
А
Входное сопротивление линии без потерь при х'
4
индуктивно в случае KopOТKoro замыкания и емкостно
в случае холостоrо хода. При х' == Л/4 в первом случае
наступает резонанс токов (z == (0), во втором случае
резонанс напряжений (z == О).
ж'
Рис. 1l-12. Входные сопротивления линии без пот€рь,
а
холостой ход; б
короткое замыКание.
Следует отметить, что в реальных условиях вследст
вие наличия потерь входное сопротивление линии никоrда
не снижается до нуля и никоrда не достиrает бесконеч-
Horo значения.
При этом короткозамкнутая линия при х' == Л/4 имеет
большее входное сопротивление, чем разомкнутая линия
при х' == ')../2, а разомкнутая линия при х' == ')../4 имеет
меньшее 'входное сопротивление, чем короткозамкнутая
при х' == ')../2.
Пример 1 t -1. Даны результаты измерения входных сопротивле-
ний линни длиной 160 км на частоте 1000 [ц при холостом ходе и ко-
ротком замыкании: Zx == 887 L
350; ZK == 540 L 21° Ом. Требу-
ется вычислить первичные Ц вторичные параметры линии.
Расчет начинается с вычисления волновоrо сопротивления и коэф-
фициента распространения:
ZB==V ZXZK ==V(88 7 L
350) (54 0 L 210)==692 L
7° Ом;
th "l== .... / ZK == .... / 540 L 21° 0,78 L 280==0,688 +1 '0,366' ,
I V Zx V 887 L
35°
2yl
1+tgyl
1,688+jO,366
1,7'26 L 12°15'
е
l
thyl
0,312
jO.366
0,480 L
49°35'
:=3,6 L 61°50' ==3,6 L 61,83°==3,6 L (1 ,08 + 2nk).,
356
Целое число k находится на основании ориентировоЧноrо расчета
величины 2
l; если исходить из приближенноrо значения фазовой
скорости VФ z 300 000 км/с (если линия воздушнаи), то
') . (О 6280 о
l==2l
vф ::;:,;:320 300000 ::;:,;:6,7 рад==384.
Следовательно, надо принять
k==! и Z
l==1,08+6,2B==7,36 рад.
Итак,
е2У! ==el,28ei7,36,
откуда
2a;l == 1,28 Нп== 11,12 дБ.
Коэффициент ослабления
11,12
а; == 2. 160 == 0,0348 дБ/км == 0,004 Нп/км;
коэффициент фазы
7,36 .
== 2. 160 ==.0,023 рад/км;
коэффициент распространении
y==a;+j
==0,004+jO,023==0,0233 L 8008' KM
l;
фазовая скорость
(О &280
Vф==13== 0,023 ==273040 КМ/С;
длина волны
2:п; 6,28
л == т == 0,023 == 273,04 км.
Первичные параметры линии иаходятся на осиовании выражеиий:
уzз==,+j(ОL и }. ==g+j(OC;
8
r + j(OL== (О,02ЗЗ'L 8008') (692 L
70) ==
== 16,12 L 7308' == 4,
7 + j15,426 Ом/км;
g+ .(ОС 0,0233 L 8008' 10
6. 33 , 6 L 8708' ==
J 692 L 7"
==(1,68+j33,6) .10
6 См/км.
Таким образом,
у==4,887 Ом/км;
15,426
L== 6280 ==0,00245 r/KM; g==l,б8.10
6 См/км;
33,6. 1<r 6
С== 6280 0,00535 мкФ/км.
357
11-9. ЛИНИЯ КАК ЭЛЕМЕНТ РЕЗОНАНСНОЙ ЦЕПИ
Четвертьволновая линия с малыми потерями. разомкнутая иа конце,
обладает свойствами резонансной цепи, состоящей из последовательно
соединенных У. L и С. При частоте, при которой на линии укладыва-
ется четверть волны (такую частоту условимся называть резонансной).
входное сопротивление линии будет активным и притом минимальным.
При малом отклонении частоты от резонансной модуль входноrо
сопротивления линии резко возрастает: входное сопротивление при-
обретает емкостный характер при понижении частоты и индуктивныЙ
характер
при повышении.
Входное сопротивление линии с малыми потерями. разомкнутой
на конце, можно получить из (11
21), разлаrая sh ух' и ch ух' по фор-
мулам триrонометрии и приняв ввиду малости CG ch CGx'
,1, а sh CGx'
CGx'.
Выражение примет вид:
Z
cos
x' + jCGx' siп
x'
х
ZB CGX' COS
x' + j siп
x' .
Вблизи резонансной частоты
x'
п/2 и sin
x'
1, а cos
x'
1. Поэтому
ZX""'=ZB (CGx'
j cos
x') == ZB CGX ' ( 1
j co
!x' ).
Если через
o обозначить коэффициент фазы при резонансной
частоте, т. е. принять
oX' == п/2, и учесть соотношение VФ == (O/
z (Oo/
o, то cos
x' можно преобразовать следующим образом:
(о
cos
x'
cos Ro
х' == cos (
oX' +
oX' б) ==
t' (00 '
==cos C
+
ох'б )==
sin
ох'б
х'б.
" (o
(oo
Здесь. так же как и в rл. 5, и'==
расстройка частоты
(00
по отношению к резонансной. Следовательно,
Zx
zBCGx' (1 + j
б ).
(11-58)
В rл. 5 было показано, что при частоте, близкой
Korдa б значительно. меньше единицы, комплексное
резонансной цепи равно:
к резонансной,
со противление
i
r (1 +j2Qб).
(11-59)
Рассматривая четвертьволновую линию как резонансную цепь.
можно в силу одинаковой структуры выражений (11-58) и (11-59) счи-
тать. что добротность линии равна:
Q ==
/2CG.
При этом резонансные характеристики, приведенные в rл. 5, при-
менимы и к рассматриваемой линии.
358
Соответственно полоса про пускания, представляющая собой ве-
личину, обратную добротности (см.
5
2), равна:
1 2и
б2
бi==Q ==13'
Здесь под полосой пропускания, так же как и в
5
2, подразуме-
вается отнесенная к резонансной частоте ширина резонансной кривой
между точками, соответствующими половине максимальной мощности
(коrда r == I х 1).
При малых значениях коэффициента GG добротность получается
высокой, достиrая примерно 1000
4000, что HaMHoro превышает доб
ротность контуров Т, L и С. в связи с этим возрастает и острота иаст-
ройки,
11.10. ИСКУССТВЕННЫЕ ЛИНИИ
И С К У с с т Б е н н о й л и н и е й называется цепь
с сосредоточенными параметрами, приближающаяся по сво-
им частотным характеристикам (в заданном диапазоне
частот) к цепи с распределенными параметрами.
Искусственные линии находят широкое применение
в лабораторных условиях и в особенности в COBpeMeH
ной импульсной радиотехнике для получения требуемоrо
запаздывания сиrналов.
В
11-3 отмечалось, что всякая однородная линия
представляет собой симметричный чеТрlрехполюсник с. ме-
рой передачи, равной
l==lV(r+j(i)L) (g+j(i)C) ,
и характеристическим сопротивлением, равным волно-
вому:
z =="1/ ' + jroL .
в V g+jroc
Заменяя линию эквивалентным Т
образным четырех-
полюсником, соrласно рис. 9
17, а получаем на основании
формул (11-23) расчетные выражения: .
Zi ==z th 1
. Z
( 11-60 )
2 в 2' 2
sh V l .
Для какой
либо фиксированной частоты ТаКОЙ Т -об
разный четырехполюсник может быть осуществлен. Од-
нако при передаче сиrналов в некоторой заданной поло-
се частот величины Zl и Z2 представляют сложные функ
ции от частоты, Не реализуемые в виде простейших эле
ментов. В этом случае искусственная линия создается
359
вnиДе цепной схемы, кажДое звено которой с достаточ-
ной степенью точности заменяет весьма малый участок
однородной линии.
Н-Н. ЗАДАЧИ И ВОПРОСЫДПЯ САМОПРОВЕРКИ
11-1. Вычислить при частоте 1000 [ц волновое сопротивление одно-
родной линии, коэффициент распространения н фазовую скорость
по заданным первичным параметрам:
, == 6,5 Ом/км; L == 2.29.1O
[/км; с== 5,22-.10
3 мкф/км; g == О,5х
Х 1O
6 См/км. .
О Т В е т: lB == 692 '-
120 Ом; У == (49,2 + j 222) 1O
4 км
1; VФ ==
==,283000км/с.
11-2. l( линии, указанной в предыдущей задаче, присоединена
активная наrрузка 200 Ом. Вычислить коэффициент отражения,
О т в е т: 0,558 '- 173°.
11-3. Входное сопротивление ЛИНИИ длиной 200 км ПрИ частоте
800 [ц равно: при холостом ходе 747 L
26,50. Ом, при КороТкоМ за-
мыканин 516 '- 0,50 Ом. Вычислить вторичные и первичные параметры.
О т в е т: 19 == 620 '- 13° Ом; У == (47,5 + j180) .1O
4 KM
l; , ==
== 5,4 Ом/км; L == 2,04 .1O
3f/KM; с== 6.1(}9 Ф/км; g == 8,7 .1O
? См/км.
11-4. Входное сопротивление ЛИНИИ длнной 50 км при частоте 800 [ц
равно: при холостом ходе 328 '-
290 12' Ом, при коротком, замыка-
нии 1548 '- 6°48' Ом. Вычислить вторичные и первичные параметры;
Ответ: lB== 712 '-
11°12' Ом; у== (91,6+ j280) .1O
4KM
1;
, == 10,25 Ом/к м; L == 3,66.10
[/км; с == 8,22.IO
B Ф/км; g ==
== 5. 1O
6 См/км.
11-5. Однородная линия имеет параметры: , == 5 Ом/км;С ==
== 5.1O
мкФ/км; g == 1(}6 См/км.
При какой индуктивности в линии отсутствовали бы искажения?
О т в е т: 25 Mf/KM.
11-6. Вычислить входное сопротивление ЛИНИИ без потерь при
коротком замыкании. Длина линни 35 м; длина волны 50 м; волновое
сопротивление линии 505 Ом.
О т в е т: 1554 '- 900 Ом.
11-7. Условия и требование предьщущей задачн, но принять длину
линии равной 23 м.
О т В е т: 129 L.
900 Ом.
11-8. Волновое сопротивление ЛИНИИ без потерь ZB == 500 Ом.
Определить амплитуду тока на расстоянии 1 м от разомкнутоrо конца
линии при частоте f== 108 [ц, если действующее значение напряжения
на разомкнутом конце равно 10 В.
О т в е т: 0,0245 А.
11-9. Однородная ЛИНИЯ с первичными параметрами , == 1О,40м/км,
L == 3,67 Mf/KM, С == 0,00835 мкФ/км и g == 0,8.10
6 См/км длиной
100 км подключена к источнику Э. д. с. 100 В; частота равна 1000 [ц;
лнн.ия наrружена активным сопротивлением 200. Ом. Вычислить: токи
в начале и КОНце линии; напряжение в конце линии; активную мощность
в начале и КОНце линии. ,
О т в е т: 0,167 L 0°30' А;0,113 L
200030' А; 22,6L
200°30' В;
16,7 Вт; 2,55 Вт.
11-10. Чем отличаются цепи с распределенными параметрами
от цепей с сосредоточенными lIараметрами?
360
1l
1l. В каких линиях и при каких условиях возникают стоячие
волны?
11-12. Будет ли передаваться эн
рrия по линии без потерь, замкну-
той на реактивное сопротивление?
11-13. Каковы первичные и вторичные параметры линии без по-
терь?
11-14. Как определяются параметры А11о А12' А 21 И А 22 однород-
ной линии?
11-15. Как определяются напряжение и ток в начале (или конце)
линии в зависимости от напряжения и тока в конце (или начале) ли-
нии?
1l
6. При каких условиях отношение и 1 /и 2 равно e IX1 ?
rЛАВА ДВЕНАДЦАТАЯ
ЦЕПИ ТРЕХФАзноrо ТОКА
'12.... ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
т р е х Ф а 3 н а я электрическая цепь может быть
представлена как совокупность трех однофазных цещ
й,
в которых действуют э. д. с. одной и той же частоты, сдви-
нутые друr от.носительно друrа на одну треть периода,
или, что то же, на уrол 2л/З.
Эти три составные части Tpex
фазной цепи называются Ф а -
з а м и 1 И им ниже будут при
писываться буквенные обозна
чения А, В и С.
На рис. 12-1 схематично
показана трехфазная цепь,
фазы которой электрически
не связаны друr с друrом.
Таки
трехфазные цепи на-
зываютrя н е с в я з а н н ы
м и (В настоящее время не
применяются).
На рис. 12-1 для упрощения обмотки трехфазноrо reHe-
ратора не показаны. Сопротивлениями обмоток и шести
соединительных проводов ввиду их малости по сравнению
с сопротивлениями наrрузки можно для начала пренебречь.
iA
ф Ё А
zO
[ А
<r---
i8
ic.......f>
Рис. 12-1. Несвязаниая
фазная цепь,
трех-
1 Таким образом, термином «фаза}> В электротехнике обознача-
ются два поиятия: уrол, определяющий стадию периодическоrо про-
цесса, и составиая част!? мноrофазной цепи.
361
Фазы А, В и С изображены на рис. 12-1 под уrлом
120°, для TOrO чтобы подчеркнуть, что э. д. С. ЕА, Ев и Ее
сдвинуты друr относительно друrа на одну треть пери
ода. При равенстве амплитуд э. д. с. и одинаковых соп
ротивлениях в фазах токи 1 А, 1 в и 1 с также равны по
величине и сдвинуты друr относительно друrа на одну
треть периода, образуя так н'азываемый трехфазный ток.
Сумма этих токов в любой момент времени равна нулю;
поэтому если три провода, по которым токи возвращаются
к источникам, объединить в один провод, ТО ток в этом
проводе будет равен нулю. При отсутствии в ПРОБоде тока
излишним в данном случае является и сам провод; от Hero
i можно отказаться, r;ерейдя,
...А.с:. таким образом, к, схеме
рис. 12-2. В результате
этоrо достиrается экономия
материала ПРОБОДОВ; кроме
Toro, по сравнению с не свя
занной трехфазной цепью
исключаются потери мощ
ности ОТ токов 1 А , 1 в И lе
Рис. 12-2. Связанная трехфазная в обратных проводах.
цепь. Трехфазная цепь на
рис. 12-2, фазы которой
соединены электрически, . представляет собой одну из разно-
видностей с Б Я З а н н ы х трехфазных цепей.
Блаrодаря теХНИКО
ЭКОНомическим преимуществам свя-
занных трехфазных цепей они получили широкое распро-
странение.
Для получения связанной трехфазной цепи не требу-
ются отдельные однофазные reHepaTopbI, <';l используется
трехфазный reHepaTop, схематически ноказанный на
рис. 12-3. Обмотки, в которых наводятся э. д. с., помеща
ются в пазах статора 1. Обмотки фаз сдвинуты друr OTHO
сительно друrа на уrол 120 0 /р, rде р
число пар полю-
сов. В случае двухпстюсноrо [енератора (рис. 12-3) р ==
== 1 и уrол равен 1200 (подробнее см.
12-6).
При вращении ротора в силу идентичности трех об-
моток [енератора в лих наводятся э. д. С., имеющие оди
наковые амплитуду и частоту, причем эти э. д. с. сдвинуты
по фазе по отношению друr к друrу на одну треть пери-
1 Следует отметить, ЧТО на практике применяются также трехфаз-
ные rенерзторы, в которых полюсы неlIoдвижны' а обмотки вращаются.
362
ода. Векторы, изображающие эти э. д. с., равны по модулю
и расположены под уrлом 1200 (рис. 12
4, 6).
MrHoBeHHbIe э. Д. с. трехфазноrо reHepaTopa, показан-
ные на рис. 12-4, а, выражаются аналитически следующим
образом:
еА == Е т sin rot;
eB==Emsin (rot
2; );
ее == Ет sin ( ro! + 2; ).
MrHoBeHHbIe значения э. д. с.
равны соответствующим проек
циям трех векторов: Ё тА , ЁтВ
И Ё те (рис. 12
4, 6), образую
щих симметричную звезду и
вращающихся в положительном
направлении с уrловой CKO
ростью ro (на рис. 12-3 положе
ние ротора соответствует момен-
ту t == О).
Положительные направления э. д. с. в обмотках ука-
заны на рис. 12-3 точками и крестиками; точка означает
острие, а крестик
конец стрелки, совпадающей с поло-
жительным направлени
ем э. д. с. (положительное нап-
е
еА
ее
ОсьА
Рис. 12
3. Принцип выпол-
нения трехфазноrо синхрон-
иоrо rеиератора.
"" lIJ
cиt
t ЕтА
а.) 6)
Рис. 12
4. Мrиовеииые э. Д. с. (а) и векторная диа-
rpaMMa Э. д. с. (6) трехфазноrо reHepaTopa.
равление э. д. с. не следует смешивать с действительным
направлением э. д. с. в произвольный момент времени).
Создание в 1889 r. связанной трехфазной цепи пере-
MeHHoro тока явилось важным событием в истории элект
роrехники.
363
Впервые такую цепь осуществил ВЫДающийся рус-
скиЙ инженер и ученый Михаил, Осипович Доливо-Доб-
ровольскиЙ (18б2
1919). Им были. разработаны основ-
ные звенья rенерирования, передачи, распределения и
преобразования электроэнерrиц трехфазноrо тока, именно:
трехфазные reHepaTop, трансформатор и асинхронный дви-
rатель. Изобретение М. О. Доливо
Добровольским асин-
((pOHHOro двиrателя, являющеrося простеЙшим и самым
деш
вым двиrателем переменноrо тока, существенно спо-
собствовало широкому промышленному внедрению трех-
фазноrо тока.
Технические и экономические преимущества трехфаз-
Horo тока обеспечили ему ведущую роль в современной
электротехнике.
Неуклонно возрастает также роль трехфазноrо пере-
MeHHoro тока в авиации.
12.2. СОЕДИНЕНИЕ ЗВЕЗДОЯ И ТРЕуrоnьником
Каждая фазная обмотка имеет две крайние точки или
два вывода, которые условно называются н а ч а л о м
и к о н Ц о м обмотки. За начало обмотки reHepaTopa
обычно принцмается тот вывод, к которому направлена
положительная э. д. с. На рис, 12-2 одноименные выводы
фазных обмоток reHepaTopa обозначены буквами н (на-
чало) и к (конец).
Показанное на схеме рис. 12
2 соединение обмоток
трехфазноrо reHepaTopa называется з в е з д о Й: все концы
фазных обмоток reHepaTopa соединены в одной общей
точке. В дальнеЙшем для упрощения мы не будем распо-
лаrать фазы reHepaTopa под уrлом 1200, а будем изображать
их параллельно (рис. 12-5, а).
Общая точка фазных обмоток reHepaTopa называется
н е й т р а л ь н о й точкоЙ. В зависимости от требова-
ниЙ нейтральная точка может быть выведена к отдельному
выводу, обозначенному на рис. 12
5, а буквой N.
При соединении обмоток трехфазноrо reHepaTopa тре-
уrольником (рис. 12
6, а) начало одноЙ фазноЙ обмотки
соединяется с концом следующеЙ по порядку фазноЙ об-
мотки так, что все три обмотки образуют замкнутый тре-
уrольник, причем направления э. д. с. в контуре треуrоль-
ника совпадают и сумма э. д. с. равна нулю. Общие точки
соединенных обмоток reHepaTopa выводятся к выводам,
к которым присоединяются линейные провода или наrруз
а.
364
При отсутствии наrрузки, т. е. при режиме холостоrо
хода в оБМ9тках reHepaTopa, соединенных -rреуrольни-
ком, ток не циркулирует, так как сумма трех фаэных
э. д. с. равна нулю (рис. 12-6, 6).
ЕА
120.
I Ее
I Н )
L
, (J,
Рис. 12-5. Соединение трехфаз-
Horo reHepaTopa звездой.
а
схема; б
I!екторная диаrрам.
ма э. д, С.
Е А
6)
Рис. 12-6. Соединение трехфазноrо
reHepaTopa треуrольником.
а
схема; б
I!екторная диаrрамма
э. 11. с.
Ради упрощения в схемах рис. 12-5, а и 12-6, а пока-
заны только э. д. с. reHepaTopa; обмотки и их сопротивле-
ния на схеме не показаны.
Наrрузка в трехфазной цепи также может быть сое-
динена звездой (см. рис. 12-7, а) или треуrольником
(рис. 12-7,6 и в).
:3 А
А
8 8
I
N.........J с с 1)
4) б)
Рис. 12-7. Соединение наrрузки звездой (а) и треуrоль-
ником (6 и е),
На практике применяются различные комбинации сое-
динений, например: 1) reHepaT9P может быть соединен
звездой, а наrрузка
звездой или треуrольником; 2) re-
нератор может быть соединен треуrольником, а наrруз-
ка
звездой или треуrольником. .
365
Соединение наrрузки звездой по схеме рис. 12
2 при
меНяется только при одинаковоЙ наrрузке всех трех фаз.
Между тем условие равномерной заrрузки фаз на прак-
тике не всеrда выполняется (например, в случае освети
тельноЙ наrрузки). При неравномерной наrрузке напря-
жения на фазах, т. е. на сопротивлениях лучей звезды
наrрузки, получаются неодинаковыми (см.
12-4). Кроме
Toro, в схеме рис. 12-2 недопустимым является включе-
ние или отключение одной фазы наrрузки.
В этом отношении соединение наrрузки треуrольни-
кем имеет преимущество: сопротивления фаз, т. е. сторон
треуrольника, MorYT быть неодинаковы и даже в край-
ЕА
ЕА
Ев
а)
б)
Рис. 12-8. Соединение звезда
звезда с нейтральным
проводом (а) и заземленными нейтральными точками (6).
нем случае MorYT включаться и отключаться независимо
друr от друrа.
Такая же возможность имеется при соединении reHe-
ратора и наrрузки звездой, если их нейтральные точки
соединены н е й т р а л ь н ы м про в о Д о м или через
землю (рис. 12-8, а и 6). На Gамолетах и кораблях ней-
тральным проводом может служить металлическая об-.
шивка (корпус), к которой присоединяlOТСЯ нейтральные
точки reHepaTopoB и наrрузок.
Электродвижущие силы, наводимые в фазных обмот-
ках [енератора, напряжения на их выводах, напряжениЯl
на фазах наrрузки и токи в них называются COOTBeTCT
венно фазными э. д. с., напряжениями и токами и обозна-
чаются Е ф , и ф и 1 ф.
Напряжения между линейными проводами и токи
в них называются л и н е й н ы м и напряжениями и то-
ками и обозначаются и Л и 1 Л'
При соединении фаз звездой фазные токи равны ли-
нейным токам: 1 ф == 1 Л' При соединении фаз треуrольни-
366
ком фазное напряжение равно соответствующ
му линей
ному напряжению: И Ф == И JI *.
, Различают симметричный и несимметричный режимы
работы трехфазной цепи. При симметричном режиме co
противления всех трех фаз одинаковы и э. д. с. образуют
симметричную систему; в противном случае имеет место
несимметричный режим.
12-3. СИММЕТРИЧНЫй РЕЖИМ РМОТЫ ТРЕХФАЗНОй ЦЕПИ
Расчет трехфазной цепи, так же как и расчет всякой
сложной цепи, ведется обычно в комплексной форме.
Ввиду Toro что фазные э. д. с. reHepaTopa сдвинуты друr
относительно друrа на 1200, для краткости математиче
ской записи применяется фазовый оператор
комплекс-
ная величина
а == еjl20 0 == cos 1200 + j sin 1200 ==
+ j
З ,
Умножение вектора на оператор а означает поворот
вектора на 1200 в положительном направлении (против
хода часовой стрелки).
Соответственно умножение вектора на множитель а 2
-означает поворот вектора на, 2400 в положительном нап
равлении или, что то же, поворот ero на 1200 в отрица-
тельном направлении.
Очевидно,
а 2
e j240°
e
jI20'
J
J . Vз
2 2'
Если э. д. с. фазы А равна Ё А , то э. д. с. фаз В и С
равны соответственно:
Е в == а 2 Е А ; Е е == аЕ А .
в простейшем случае симметричноrо режима работы
трехфазной цепи, коrда reHepaTop и наrрузка соединены
звездой (рис. 12
9, а), векторная диаrрамма э. Д.с. и то-
ков имеет вид, показанный на рис. 12-9, б.
Ток в каждой фазе отстает от э. д. с., той же фазы на
х .
уrол ер == arctg т' rде r и х
активное и реактивное со-
противлени я фаз.
* Кроме тoro, применяется понятие «фазное напряжение в дaH
ном сечении» трехфазной цепи по отношению к какой
либо точке, при-
нимаемой за нуль, напрнмер земле, нулевой точке reHepaтopa или ис-
кусственной нулевой точке. '
367
Ток в фазе А находят так же, как в однофазной цепи,
потому что нейтральные точки reHepaTopa и наrрузки
в симметричном режиме MorYT быть соединены как име-
ющие одинаковые потенциалы:
. БА
IA===z.
Соответственно токи в фазах В и С через ток J А:
i B ===a 2 i A , ic===ai A .
Наличие нейтральноrо провода
He вносит при сим-
метричном режиме никаких изменений, так как сумма
токов трех фаз равна нулю и ток в H
M отсутствует:
iN==iA+iB+ic===(l +а 2 +а) iA==o.
Т
ким образом, при симметричном режиме работы
трехфазной цепи задача сводится к расчету одной из фаз
f A .
z ЕА
i 8 , Z
..........р.
Ее ic z
CL)
Рис. 12-9. Симметричны.й режим работы трехфазной
цепи.
а
трехфазная цепь; б
векторная диаrраМма.
аналоrично расчету однофазной цепи. При этом сопро-
тивление обратноrо (нейтральноrо) провода не учиты-
вается, так как ток в нем и соответственно падение на-
пряжения на нем отсутствуют.
По мере удаления от reHepaTopa фазные напряжения,
определяемые падениями напряжения до нейтральной точки
наrрузки, изменяются по модулю (обычно убывают) и по
фазе. Линейные напряжения определяются как разности
соответствующих фазных напряжений, например: О АВ ===
=== (J А
(J В' В любом месте трехфазной линии при сим-
метричном режиме
соблюдается следующее соотношение
между модулями линейных и фазных напряжений:
и л === уз и ф'
368
ДеЙствительно,
(; АВ === (; А (1
а 2 ) == vз (; А 1. 300,
т. е. О АВ опережает по фазе О А на 300, причем модуль
И АВ В vз раз превышает И А'
В случае соединения треуrольником линейные токи
определяются в соответствии с первым законом Кирхrофа
как разности фазных токов и при симметричном режиме
соблюдается соотношение 1 л == уз 1 ф'
Соединение фаз rеиератора или наrрузки треуrольни-
ком должно быть для расчета заменено эквивалентным
соединением фаз звездой; вследствие этоrо расчет трех-
фазной цепи с соединением фаз треуrольником приво-
Дится в конечном итоtе к расчету эквивалентной трех-
фазной цепи с соединением фаз звездой.
Между сопротивлениями сторон треуrольника (lA) и
лучей звезды (l)..,) имеет место соотношение l).., ==
l6,.
вытекающее из формул преобразования треуrольника со-
противлений в эквивалентную звезду (см.
4-4). Этосоот-
ношение справедливо как для сопротивлений симметрич-
ной трехфазной наrрузки, так и для сопротивлений сим-
метричноrо ,трехфазноrо . reHepaTopa. При этом фазные
э. д. с. эквивалентноrо reHepaTopa, соединеННоrо звездой,
берутся в vз раз меньшими фазных э. д. с. заданнorо reHe-
ратора, соединенноrо треуrольником (кроме Toro, они
должны
ЫTЬ сдвинуты на уrол 300). Это леrко усмотреть
tiз векторной потенциальной диаrраммы напряжений reHe-
ратора.
Активная мощность симметричной трехфазной наrрузки
равна:
р == 3И ф I ф cos <р.
Ввиду Toro что при соединении Наrрузки звездой
VЗ И ф == и л И 1 ф === 1 ЛI а при соединении наrрузки тре-
уrольником И Ф == ИЛ и VЗ/ ф ==1л, активная мощность
трех-фазной цепи независимо от вида соединения выра-
жается через линеЙные напряжения и ток следующи.м
образом:
р === уз И л/ л cos <р;
здесь <р
уrол сдвиrа фазноrо тока относительно одно-
имеННоrо фазноrо напряжения.
369
Аналоrичным образом для реактивной и полной мощ-
ностей симметричной трехфазной наrрузки имеем:
Q==VЗUлlлsiпq>; S==VЗUлl л .
Приведенные выражения не означают, что при пере
соединении наrрузки со звезды на треуrольник (или Ha
оборот) активная и реактивная мощности не изменяются.
При пересоединении наrруЗКИ со звезды на треуrольник
при заданном линейном напряжении фазные токи, возра-
стут в Vз раз, в линейный ток
в 3 раза и поэтому мощ.
ность возрастет в 3 раза.
А А
Си.мметричная Си.мметричная
трехфазная треХфазная
С наzрузка. С наzрузка.
N
а) N б)
Рис. 12-10. Измерение активной мощности при симметричном режиме.
Если нейтральная точка симметричной трехфазной Ha
rрузки выведена, то измерение активной мощности может
быть осуществлено одним ваттметром, включенным по
схеме рис. 12
10, а (одноименные или так называемые reHe
раторные выводы последовательной и параллельнойцепей
ваттметра отмечены на рис. 12
10, а звездочками). Утроен-
ное показание ваттметра равно суммарной активной мощ-
ности трех фаз.
Если неЙтральная точка не выведена или наrрузка
соединеНа треуrольником, то можно воспользоваться схе-
мой рис. 12-10, б, rде параллельная цепь ваттметра и два
добавочных активных сопротивления r доб, равные по вели
чине сопротивлени
параллельной цепи ваттметра, обра-
зуют искусственную нейтральную точку О *.
* Следует заметить, что здесь применим только электродинамиче-
ский или ферродинамический ваттметр, сопротивление параллельной
цепи KOToporo является чисто активным. Индукционный ваттметр
неприменим по той причине, что сопротивление параллельной цепи
T3Koro ваттметра имеет реактивное сопротивление; для создания ис-
кусственной нейтральной точки в этом' случае потребовались бы ре-
активные добавочные сопротивления.
370
Для получения суммарной мощности, как и в предыду-
щем случае, показание ваттметра утраивается.
На рис. 12
11 показан способ измерения реактивной
мощности в симметричной трехфазной цепи при помощи
одноrо ваттметра: последовательная цепь
ваттметра включена в фазу А, а парал-
лельная
между фазами В и С, при
чем reHepaTopHbJe выводы ваттметра при-
соединены к фазам А и В.
Показание ваттметра в этом случае
равно:
и Ее! A'COS (ер
900) == и Ее! А sin ер.
с
Рис. 12-11. Изме-
рение реактивной
мощности при сим-
метричном режиме.
Для получения суммарной реактив-
ной мощности показание умножается
на Vз.
Разделив активную мощность На полную мощность,
получим:
р
COS ер == S.
Пример 12-1. Определить ток в reHepaTope при симметричном
режиме работы трехфазной цепи, представленной на рис, 12-12, а.
Z1
ZJ
Z3
Ё А
.....
Ев Z1
.......
ZJ
Z2
а.)
Рис. 12-12. Пример 12-1,
Z1
ZJ
1
"3 Zч
Z2
6)
Сопротивления Z4' соединенные треуrольником, заменяютСЯ экви-
валентной звездой из сопротивлений Z4/3'
При симметричном режиме нейтральные точки reHepaTopa и наrруз-
ки. как было указано выше. моrутбыть объединены. Тоrда режим работы
каждой фазы, например фазы А, может быть рассмотрен в ОАнофаз-
ной расчетной схеме (рис, 12.12, 6).
371
Результирующее СОПРОТивленне цепи ОДНОИ фазы равно:
Z==Zl+ ?2(ZЗ+ Z 4/ З ) ,
Z2+Z3+ 2 4/ 3
ИСКОМЫЙ ТОК в фазе А
I А ==Е A/Z,
12-4. НЕСИММЕТРИЧНЫЯ РЕЖИМРА60ТЫ ТРЕХФАЗНОЯ ЦЕПИ
Несимметрия в трехфазной цепи может быть вызвана
различными причинами: 1) неодинаковым сопротивлением
фаз (несимметричная наrрузка); 2) несимметричным ко-
ротким замыканием (например, между двумя фазами или
фазой и нейтралью); 3) размыканием фазы; 4) неравенством
э. д. с, и т. п.
Расчет токов
несимметричном
-+:---
U N
Рис. 12
13. Несимметричная
трехфазная цепь, соединенная
звездой (с нейтральным прово-
дом).
и напряжений в трехфазной цепи при
режиме может производиться теми же
методами, которые применяют-
ся для расчета однофазных
цепей.
Рассмотрим несколько про-
стейших вариантов (без вза-
N' имной ИНДУIЩИИ между фа-
зами).
1. Несимметрuчная трех-
фазная цепь, соединенная звез-
дой, с нейтральным проводо,м
(рис. 12-13).
Несимметричная трехфаз-
ная цепь, показанная на
рис. 12-13, может рассматри-
ваться как трехконтурная
цепь с тремя э. д. с. Такая
цепь может быть рассчитана
методами контурных токов,
узловых напряжений и друrими. Поскольку в схеме имеют-
ся только два узла, наиболее целесообразно в данном слу-
чае опред
лить узловое напряжение (напряжение смеще-
ния) между неЙтральными точками N' и N по формуле,
аналоrичн6й (4-4): ...
. . УАЕА+УвЕв+УсЕс
UN'N==UN
У +У +У +У ..,
А 11 .с N
rде у А, У в, У с и У N
ПРОВОДИМQСТИ соответствующих
ветвей.
i A
.......с-
ZA
Z8
N
Zc
ь ZN
(12-1 )
372
После этоrо найдем ТоЮ1:
/А==УА(ЁА
ИN);
jB==YB(EB
(;N);
/C==YC(EC
(;N)'
в симмеТРj1ЧНОЙ. трехфазной цепи У А == У в == Ус.. и
поэтому при Е А + Ев + ЕС == О узловое напряжение U N
равно нулю.
Случаю размыкания какой-либо фазы или шtйтраль-
Horo провода соответствует равенство нулю проводимости
данной фазы или нейтраль-
Horo провода.
При отсутствии нейтраль-
Horo провода, полаrая в (12-1)
У N == О. имеем:
. УлЕл+УвЁв+УсЁс
U N === У +У +У .
А В С
2. Несимметричная трех-
фазная наерузка) соединенная
звездой (без нейтралЬНО20 nро-
вода) с заданными линейными
напряжениями на выаодах
(рис. 12-14).
Если заданы линейные на-
пряжения [) АВ. [) ВС И [) СА
На выводах наrрузки, соединенной звездой, ТО токи в фа-
зах звезды определяются следующим образом.
Обозначив фазные напряжения на выводах наrрузки
через [) А. [) В И [) С (рис. 12.14). получим
j А == У АИ А; i B == УвИв; lc == УсИ с ,
А
.
IA
ZA
""1
. I
1 иАВ. I
+8 Д
йА
ZB
. 1..........
+ и вс . I .
Ic и в
с..... Zc
--:+-
ис
Рис. 12-14. Несимметричная
трехфазная наrрузка, соединен-
ная звездой (без неЙтральноrо
проnода),
rде УА, У В И Ус
проводимости фаз наrрузки.
Равенство нулlO суммы токов трех фаз заЩiсывается
в виде:
У А (; А + УвИв +УсU с == О.
(12- 2)
Фазные напряжения [) В И [) С MorYT быть выражены
через [) А И заданные линейные напряжения:
(; В == И А
(; АВ; (; с == И СА + и А'
( 12-3)
373
Подстановка (12-3) в (12-2) дает:
. YB(;AB
YC(;CA
и А == У +У +У .
А В С
Круrовой заменой индексов (с порядком следования
АВСА и т. д.) находятся:
. .
YC(;BC
YA(;AB . )
иB
У +У +У ,
А В С
. У A(;CA
У В(;ВС
и С == У +У +У .
А В С
По фазным напряжениям наrрузки находятся фазные
токи. ,.
в случае симметричной наrрузки У А == У в == у с век-
тор фазноrо напряжения Р"1вен одной трети диаrонали
параллелоrрамма, построенноrо на со-
ответствующих линейНых напряжениях.
Фазные напряжения в этом случае оп-
ределяются векторами, соединяющими
центр тяжести треусольника напряже-
ний (тDчка пересечения медиан) с верши-
нами треуе.ольника.
На рис. 12-15 построение сделано для
фазы А по формуле (12-4):
. 1.. 1..
U А==з(U AB
иCA) ==
з(U ВА +и сА ).
,
\ I /
\ , /
\ ,/
\//
Рис. 12.15. Нахож-
дение фазных на-
пряжений.
(12-4 )
в качестве примера раСсМОТРИМ схему фазоуказателя,
используемую для определения чередования фаз по вре-
мени, состоящую из конденсатора и двух одинаковых элект-
рических ламп, соединенных звездой 1.
Положим, что конденсатор присоединен к фазе А,
лампы
к фазам В и С; емкостное сопротивление конден-
сатора берется равным по модулю сопротивлению лампы,
т. е. ZA ==
jxc, ZB == Zc == r, причем хс == r.
Неравенство напряжений на лампах проявится в том,
что накал ламп будет разным. Отношение напряжений
соrласно выведенным выше выражениям (12-4) равно при
1 Для определения чередования фаз на практике обычно поль-
зуются специальным прибором, в котором создается вращающееся
маrнитное поле (см. 9 12-6), увлекающее за собой диск в ту или друrую
сторону.
374
симметрии линеЙных напряжений:
Ив I a2
a
/(I
a2) I / З,23+/0,8661.
---и--; == j (a
1)
(a2
a) == O,23+jO,866 l..
3,73.
Следовательно, лампа, присоединенная к фазе В (т. е.
к фазе, опережающеЙ ту, к которой присоединена Вторая
лампа), будет светить ЯрКо, а лампа, присоединенная к от-
стающеЙ фазе,
тускло.
Вместо конденсатора можно применить индуктивную
катушку, подобрав ее индуктивное сопротивление при-
близительно равным по МС;>-
дулю сопротивлению лампы.
В этом случае ярче будет све-
тить лампа, присоединенная
к отстающеЙ фазе. Эти соот-
ношения также MorYT быть
получены непосредственно из и СА
векторной диаrраммы.
3. Несимметричная трех-
фазная на
рузка, соединенная
треу
ольником, с заданными
напряжениями на выводах
(рис. 12-16).
Если на выводах несиммет-
ричной трехфазноЙ наrрузки,
соединенной треуrольником, заданы линейные напряже-
ния О АВ, О ВС И О СА (рис. 12-16), то токи в сопротивлениях
наrрузки равны:
i A
.............,.
! UA8 .
18
ZA8
ZCA
! д вс .
Ic
.............,.
ZSC
Рис. 12-16. Несимметричная
трехфазная наrрузка, соединен-
ная треуrольннком.
И АВ И ВС И СА
lAB ' lBC И ZCA'
Токи В линии определяются как ра3f:IОСТИ с<;>ответству-
. И АВ И СА
ющих токов наrрузки, например: 1 А ==
т----- и т. д.
АВ СА
Если на выводах несимметричной трехфазной наrрузки,
соединенной треуrольНИКОМ, заданы фазные напряжения
О А, (; В И (; С источника, соединенноrо в звезду, то линей-
ные напряжения на выводах наrрузки находятся как раз-
ноети соответствующих фазных напряжениЙ, в результате
чеrо задача сводится к только что рассмотренному случаю
(рис. 12-16).
Пример 12-2. Сопротивления фаз наrрузки, соеднне.нной звез-
дой: l А == 40 + j 30 == 50 L. 36°54'; lB== 30 + j 40 == 50 1. 53°6'; lC ==
== 20 1. 00 Ом.
375
Сопротивление нейтральноrо провода
ZN==3+j4==5 L 5306' Ом.
Напряжения на цепи представляют собой симметричную
(J А == 100 L 00; (J в == 100 L
1200 ==
50
j86,6;
== 100 L 1200 ==
50 + j86,6 В.
Требуется определить фазные напряжения наrрузки.
Проводимости фаз наrрузки и нейтральноrо провода
у А ==f-==0,02 L
36054' ==O,016
jO,012 См;
А
У в == Z 1 - == 0,02 L
5306' == 0,012
jO,016 См;
-п
звезду:
Ое==
1
У е==у==о,05 L 00 См;
с
1
У N==Z==0,2 L
5306' E::0,12
jO,16 См.
N
На основании формулы (12
1)
(; == 100 0,02 L
36054' +0,02 L
173°6' +0,05 L 120"
N 0,016
jO,012+0,OI2
jO,OI6+0,05 +0,12
jO, 16
==
14,9+jO,39 В.
Искомые фазные напряжения наrрузки:
(; А
(; N== 100+ 14,9
jO,39== 114,9
jO,39== 114,9 L
ool2' В;
(;B
(; N==
50
j86,6+ 14,9
jO,39==
==
35,1
j87,0==93,5 L.
1120 В;
(;e
(; N==
50+ j86,6+ 14,9
jO,39==
==
35,1 + j86,2 == 93,0 L 112050' В.
12-5. МОЩНОСТЬ НЕСИММЕТРИЧНОЯ ТРЕХФАЗНОЯ ЦЕПИ
Пользуясь комплексной формой записи мощности, можно
написать общее выражение для мощности трехфазной цепи:
. * . * . *
S ==UAIA+UBIB+Uele.
(12
5)
Действительная часть этоrо выражения представляеr
собой активную мощность
р == U АI А COS СРА +UBI B COS CPB+Uel e cos <Ре.
Суммарная активная мощность, потребляемая несим-
метричной трехфазноЙ цепью, может быть в соответствии
с этим измерена при помощи трех ваттметров, включенных
на подведенные к данной цепи фазные напряжения относи.
376
тельно нейтраJlIt й ОДноимеНI:Iые с НиМи токи. Активная
мощность равна сумме показаний трех ваттметров. Такой
метод измерения применяется при наличии нейтральноrо
ПрОБОДа (рис. 12
17) или искусственно созданной нейтраль-
ной точки.
В случае отсутствия нейтральноrо ПрОБода измерение
может быть произведено с помщцью двух ваттметров
i A *'
..........с-
-- -- -- .. .. w
*
18 *'
w
j Те *'
,
и А .
и 8 lЧ
А
.......
--
Трех
фазнан
наарузка
Рис. 12
17. Измерение МОЩности при наличин нентраль-
Hcro провода,
i A
""""'"!>
ТреХфазная
ffailP!i3Ka.
. 1 je
и АС .....=..{>
t U8C
а.)
Рис. 12-18. Измерение мощности двумя ваттметрами (при от-
сутствии нейтральноrо провода),
(рис. 12-18). В этом случае выражение (12-5) преобразуется
*
следующим образом: исключая ток 1 С с помощью условия
* * *
1 С ==
! А
! в,
получаем:
. . * . . 41-
s== (и А
UС)!А +(UB
U С ) !в,
или
. * . *
s ==u АС! А +UВС!В.
( 12
6)
377
В соответствий с (12
6) прй измереl:lИй активной мощ-
ности двумя ваттметрами к одному из них подводятся на-
пряжеf!ие (; АС И ток 1 А, а ко второму
напряжение (; ВС
и ток 1 в (рис. 12
18, а). Показания ваттметров складыва-
ются алrебраически.
Круrовой заменой А, Д и С в выражении (12-6) можно
получить выражения для друrих равноценных вариантов
включения двух ваттметров.
Следует иметь в виду; что если стрелка одноrо ваттметра
отКлоняется по шкале в обратную сторону, то, изменив
направление напряжения или тока, ПОДВОДИМоrо к данному
ваттметру, записывают полученное показание со знаком
минус. При симметричном режиме работы трехфазной цепи
такое положение имеет место при
I ер I > 600,
что видно непосредственно из векторной диаrраммы
(рис. 12-18, 6).
При симметричном режиме показания двух ваттметров
в схеме рис. 12-18, б будут следующие:
Р 1 == U АС! А cos (ер
300) == U! cos (ер
300);
Р2 ==u вс ! В cos (ер+ 300) ==UI cos (ер+ 300).
Сумма и разность показаний ваттметров соответственно
равны:
P 1 + Р 2 == UI 2 cos ер cos 300 == уз UI cosep;
Р 1
P2 == UI 2 sin epsin 300== UI sin ер.
Следовательно, при симметричном режиме работы трех-
фазной цепи TaHreHC уrла сдвиrа фаз может быть вычислен
по формуле
t Y
3 Pl
P2
gep== Pl+PS.
11-6. ВРАЩАЮЩЕЕСЯ МАrНИТНОЕ ПОЛ
Пусть через катушку проходит ток i == !msin (rot + '1)1).
На рис. 12-19, а катушка условно изображена в виде вит-
ка, причем точка и крестик указывают положительное на-
правление тока. Принятому положительному направле-
нию тока соответствует по правилу буравчика положи-
378
тельное направление вектора маrнитной индукции 1 В ==
== Втsiп (rot + 'Ф), указанное стрелкой вдоль оси катушки
(Вт
максимальное значение маrнитной индукции в центре
катушки); коrда ток отрицателен, вектор маrнитной индук-
ции имеет противоположное направление, показанное на
рис. 12-19, а пунктиром.
Таким образом, маrнитное поле изменяется (пульси-
рует) вдоль оси катушки; такое маrнитное поле называется
п у л ь с и р у ю щ и м.
Условимся К Р У r о в ы м в р а Щ а ю Щ и м с я Mar-
нитным полем называть маrнитное поле, ось KOToporo равно-
мерно вращается, причем значение маrнитной индукции на
....
8
(AJ
jTe
jUJt
+j p';-e ifllt
..J+
.
j
т e jfllt J
(AJ
а.) 5)
8) Pre
jfllt
Рис. 12-19. Разложенне пульсирующеrо маrнитноrо поля катушки (а)
на два вращающнхся: при сннусоидальном (6) и. КОСННУСОН./Iальном (в)
токах (в момент t == О),
В+
+
этой оси неизменно. Леrко убедиться в том, что маrнитное
поле, пульсирующее по закону синуса или косинуса, может
рассматриваться как результат наложения двух KpyroBblx
полей, вращающихся в противоположные стороны с уrло-
вой скоростью, равной уrловой частоте переменноrо тока,
и имеющих максимальную индукцию на вращающейся оси,
вдвое меньшую амплитуды индукции пульсирующеrо поля
(рис. 12-19, б и в). Это следует из формул
sin rot == f (ej((Jt
e
joot)
1
и cos rot ==
(ei((Jt + e
j((J
.
Положения векторов на рис. 12-19, б и в соответствуют
моменту t == о.
Допустим теперь, что через две катушки, расположен-
ные взаимно перпендикулярно, проходят токи одной и
1 Предполаrается линейная зависимость нндукцни от тока.
379
тоЙ же амплитуды и частоты, сдвинутые по фазе друr
относительно друrа на четверть лериода. На рис. 12
20. а
катушки обозначены цифрами 1 и 2. Принятым положи-
тельным направлениям токов i 1 == 1 msin(i)t и i 2 == J msin «(i)t +
+ л:/2) == 1 mCOS(i)t соответствуют взаимно перпендикуляр-
ные пульсирующие маrнитные потоки с индукциями в точке
пересечения осей катушек В 1 == Bmsin(i)t и В 2 == BmcoS(i)t,
направленными по действительной и мнимой осям.
Заменив каждое из пульсирующих полей двумя вра-
щающимися (рис. 12
20, б и в), убеждаемся в том, что
+j
81 +
+j
j 8т e
jlJJt j 1L e j X
2 + 2 (J)
j B; ejllJt
/
(J)
б)
+j
8z
ы
""j Вт e
jllJ't
2 +
i z
1
z
а)
8)
Рис. 12-20. Образование KpyroBoro вращающеrося MarHHTHoro поля
из двух пульсирующих.
векторы маrнитНоИ индукции
j В; ej(fJt (рис. 12.20, 6) и
j
т ej(fJt (рис. 12
20, в), вращающиеся в положительном
направлении, взаимно компенсируются (их сумма равна
нулю). Два друrих вектора образуют в сумме вектор Mar-
нитнои индукции jBт,tr/(J)t, вращающийся в отрицательном
направлении (по часовой стрелке).
К тому же выводу приходим и на основании выраже-
ния, получаемоrо для результирующеrо вектора маrнитнои
индукции,
13== В 1 + jB 2 == Вт (sin (i)t + j cos (i)t) == jBme
/(fJt.
Это выражение показывает, что ось результирующеrо
маrнитноrо поля равномерно вращается с уrловой ско-
ростью ш, причем значение индукции на оси неизменно
равно Вт, т. е. получается KpyroBoe вращающееся Mar-
нитное поле.
Направление вращения маrнитноrо поля зависит от
положительных направлений маrнитных индукций и от
380
Toro, какая из индукциЙ является отстающеЙ. В рассмат-
риваемом здесь случае индукция В 1 отстает по фазе на
п/2 от индукции В 2 И маrнитное поле вращается в отри-
цательном направлении. Если изменить направление тока
в одной из катушек, например в катушке {, что равно-
сильно изменению фазы тока i 1 на п, маrнитное поле будет
вращаться в положительном направлении. В этом можно
убедиться, повернув векторную диаrрамму рис. 12-20, б
На 1800 или воспользовавшись выражением ,
В == Вт (
sin wt + j cos wt) == jBmejrfJt.
Таким образом, от сложения двух взашщо перпенди-
КУЛЯрНblХ пульсирующих MaeUU/JlHblX полей, сдвинутых по
фазе на четверть периода,
получается круеовое Маенит-
ное поле, вращающееся с уело-
вой скоростыо в сторону от-
стающеео по фазе вектора ин-
дукции.
Описанный способ получе-
Ния KpyroBoro вращающеrося
маrнитноrо поля с помощью
двухфазной системы токов ши-
роко используется в приборо-
и электромашиностроении.
БоЛьшое удобство с точки
зрения возможности получе-
ния KpyroBoro вращающеrося
поля представляет трехфаз-
ный ток.
Расположим три одинаковые катушки таким образом,
чтобы их' оси были сдвинуты друr относительно друrа
в пространстве на уrол 1200 (рис. ,12-21), и подключим эти
ЩlТушки К симметричной трехфазной цепи. Тоrда через
катyIUКИ будут протекать токи:
i A == 1 т sin wt;
i B == 1 т sin (wt
2;) ; ic == 1т sin (wt + 2; )..
Положительным направлениям токов, обозначенным на
рис. 12-21 с помощью точек и крестиков, соответствуют
по правилубуравчика указанные стрелками положитель-
ные направления маrнитных потоков (векторов индукций),
создаваемых токами i A , i B и ic.
+j
...
...
с:::.
НА
+
Рис. 12-21. Получение вращаю-
щеrося маrнитноrо поля при
помощи трехфазной системы то-
ков.
З8J
При пропорциональной зависимости индукций от токов
MrHoBeHHbIe значения индукций фаз выразятся следующим
образом:
Б А == Вт sin rot; )
Бв==БтSiп( rot
2; );
Б е == Вт sin ( ro' + 2; ),
rде Вт
амплитуда индукции на оси каждой из катушек.
При выбранном на рис. 12
21 направлении осей + и +j
результирующI:!.Й ве!5ТОР индукции находится сложением
векторов БА, Б в и Б е :
В == j (В А + а 2 В в + аВе). (12-8)
Подстановка (12-7) в (12-8) дает:
В == jB m (sin ro! + а 2 sin rot cos 120°
а 2 cos rot sin 120° +
+а sin rot cos 1200+a
cos ro! sin 120°) ==
== j 1 ,5В т (s in rot + j cos rot),
( 12-7)
или
в ==
1,5Bme
j(jJf.
Полученное выражение показывает, что результирую-
щий \вектор масн.итнО20 поля имеет постоянный модуль,
равный 1,5 Вт, и равномерно вращается С условой скоростью
ro от оси фазы А по направлению к оси фазы В и Т. д.
(на рис. 12
21
по ходу часовой стрелки), т. е. получается
KpyroBoe вращающееся поле.
Для изменения направления вращения поля достаточно
поменять местами токи в каких
нибудь двух катушках,
например i B и ic.
При несимметрии токов в катушках, например если
концы одной катушки поменять местами, или при несим
метрии питающих напряжений вместо KpyroBoro враща-
ющеrося поля получится э л л и П т и ч е с к о е вращаю-
щееся поле, результирующий вектор индукции KOToporo
описывает эллипс и имеет переменную уrловую скорость.
В электрических машинах вращающееся маrнитное поле
осуществляется с помощью обмоток, размещаемых в пазах
неподвижноЙ части машины
статора (см. rл. 2).
Линии маrнитной индукции замыкаются по телу ста-
тора, воздушному зазору и телу. рОТ9ра. Место выхода
382
линий индукции IIЗ статора можно рассматривать Как се-
верный полюс, а место входа их в статор
как южный
полюс маrнитноrо поля обмотки статора.
Крива
я распределения индукции В вдоль воздущноrо
зазора имеет ступенчатую форму, которая при большом
числе пазов статора близка к трапеции с уrлом наклона
боковой стороны 600, и может быть приближенно заменена
Синусоидой.
Синусоидальный ток частоты !, проходя через фазную
обмотку статора, создает поле, пульсирующее с той же
частотой. Таким образом, маrнитное поле одной фазы
изменяется сиНусоидально как во времени, так и В про-
странстве (по окружности зазора).
Обмотки ТреХ фаз расположены на статоре так, что
иХ оси, а' следовательно, и оси трех пульсирующих Mar-
НИТНЫХ полей сдвинуты в пространстве на 1200. Поэтому
при прохождении через обмотку трехфазноrо тока пуль-
сирующие поля. образуют в сумме двухполюсное враща-
ющееся в зазоре синусоидальное поле, амплиТуда индук-
ции KOToporo постоянна и равна 3/2 амплитуды слаrающих
фазных полей.
За один период переменноrо тока такое маrнитное поле
совершит один оборот, а за 1 мин 60! оборотов.
Если обмотку статора выполнить мноrополюсной, т. е.
с полюсным шаrом 180 0 /р, то три пульсирующих поля
будут <;:двинуты В пространстве на 120 0 /р и в результате
получится 2р-полюсное вращающееся поле, имеющее ча-
стоту вращения, равную 60!/р об/мин.
12-7. ПРИНЦИП ДЕйСТВИЯ АсинхРонноrо И синхРонноrо
двиrАТЕЛЕй
Простейшим по устройству и наиболее распространен-
ным в промышленности типом двиrателя переменноrо тока
является трехфазный асинхронный двиrатель, изобретен-
НЫй в 1888 r. М. О. Доливо-Добровольским. Ero ротор
выполняется в виде Стальноrо цилиндра, собранноrо из
стальных листов, с обмоткой, размещенной в пазаХ по ero
поверхности. Вращающееся маrнитное поле, созданное
обмотками статора, наводит в замкнутой обмотке ротора
токи. Механическое взаимодействие этиХ токов с вращаю-
щимся полем приводит ротор во вращение в том же направ-
лении, в котором вращается поле.
383
Ротор вращается асинхронно, т. е. частота вращения
ero (п, об/мин) меньше частоты вращения маrнитноrо поля
(пl' об/мин).
Разность частот вращения поля и ротора, отнесенная
к скорости поля, НазыВается с к О л ь ж е н и е м:
пi
п
s
пl .
Скольжение не может быть, равно нулю, ТаК' как при
одинаковых частотах вращения поля и ротора прекрати
лось бы наведение токов в роторе и, следовательно, отсут-
ствовал бы вращающий момент.
В рабочем режиме асинхронный двиrатель находится
в динамическом равновесии, коrда создаваемый блаrодаря
скольжению вращающий момент уравновешивает тормо-
зящий момент наrрузки на ero валу.' С увеличением меха-
нической наrрузки тормозящий момент становится больше
вращающеrося и скольжение увеличивается. Вследствие
этоrо возрастают индуктированные в обмотке ротора э. д. с.
и токи, что вызывает увеличение вращающеrо момента
до HOBoro СОСТОяния динамическоrо равновесия (при боль-
шем скольжении).
Однако вращающий момент может расти С увеличением
скольжения только до определенноrо предела, так назы-
BaeMoro критическоrо значения при критическом сколь-
жении, после чеrо он падает, а двиrатель затормаживается.
При нормальной наrрузке скольжение асинхронных
двиrателей в среднем составляет 2
4 % .
Трехфазный reHepaTop (см. рис. 12-3), как и' мноrие
друrие типы электрических машин, обладает свойством
обратимости: он может работать как с и н х -р о н н ы й
д в и r а т е л ь. Поэтому конструктивно синхронный ДЕИ-
rатель мало отличается от reHepaTopa.
Если присоединить J>бмотку статора к источнику (се.ти)
трехфазноrо тока, а обмотку ротора (обмотку возбужде-
ния)
к источнику постоянноrо тока, то вращающееся
маrнитное поле статора бу.дет периодически создавать на
валу моменты разных знаков. Поэтому ротор не сможет
прийти во вращение
он будет вибрировать.
Для пуска двиrателя необходимо сначала (при ра-
зомкнутой обмотке возбуждения) привести ротор во Bpa
щение до частоты вращения, близкой к синхронной. Если
после этоrо включить обмотку возбуждения, то двиrатель
384
«втянется В синхронизм». Ротор будет вращаться синхронно
с полем статора.
Для пуска синхронноrо двиrателя можеТ быть исполь
зована специальная пусковая обмотка ротора, действую
щая так же, как в асинхронном двиrателе.
При cTporo синхронном вращении ротора имеется уrло-
вой сдвиr между осями полей статора и ротора, зависящий
от наrрузки (от момента сопротивления на валу). С увели-
чением наrрузки этот уrол увеличивается, БЛаrодаря чему
момент вращения также увеличивается. Максимальный
вращающий момент получается при уrле между э. д. с.
двиrателя и напряжением сети около 900, после чеrо даль
нейшее увеличение наrрузки приводит к остановке двиrа-
теля и (\выпадению» erO из синхронизма.
Если изменять постоянный ток в цепи возбуждения
ротора, то можно в широких пределах реrулировать cos ер
двиrателя. Так, при «недовозбуждении» двиrателя уrол ер
положителен, т. е. ток отстает от напряжения, а при «пере
возбуждении» уrол ер отрицателен
ток опережает напря
жение. Это свойство синхронных двиrателей весьма ценно
и широко используется в промышленности для повышения
cos ер электроустановок.
Синхронные двиrатели выполняются обычно для номи
нальных режимов работы при cos ер == 1 и cos ер == 0,8 (опе-
режающем).
Более подробное изучение конструкций, электрических
процессов и режимов работы асинхронных и синхронных
двиrателей отНосится к курсу электрических машин.
12-8. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ.
Метод расчета несимметричных режимов трехфазных
цепей, описанный в Э 12-4, ОТНОсился к частным случаям
таких режимов, коrда не было взаимной индукции между
фазами или она моrла быть учтена в эквивалентном сопро
тивлении на фазу (при отсутствии нейтральноrо провода
(см., например, [Л. 14]), не было вращающихся машин
с несимметричным ротором, отсутствовали токи в земле
с неизбежным индуктивным влиянием на фазыые обмотки
или провода.
Для расчета несимметричных режимов трехфазных
электрических цепей в общем случае применяется м е т о Д
с и м м е т р и ч н ы х с о с т а в л я ю Щ и х, основан-
ный на представлении любой трехфазной несимметричной
385
системы электрических или маrнитных величин (токов,
напряжений, маrнитных потоков) в виде суммы трех сим
метричных систем. Эти симметричные системы величин,
образующих в совокупности несимметричную систему, но-
сят название симметричных составляющих п р я м о й,
о б Р а т н ой и н уле во й последовател ь н О -
С Т е й. При этом под последовательностыо подразумева-
ется порядок следования во времени максимумов фазных
величин.
На рис. 12-22 в виде примера показаны симметричные
составляющие токов всех трех 'последовательностей. Как
видно из рисунка, симметричные составляющие обозна-
чаются цифрами
l, 2, О.
y .*
. . а) 1 1 б)
1 1с . 118 28 2С
iOA=ioB=Ioc
lli \
В)
Рис. 12-22. Симметричные составляющие токов прямой (а), обратной
(6) и нулевой (в) последовательностей.
Система прямой последовательности образует симмет-
ричную трехлучевую звезду 1 1А , 118, 1 1с С порядком сле-
дования фаз А, В, С.
Система обратной последовательности образует трех-
лучевую звезду 1 2А , 128, 1 2с С порядком следования фаз
А, С, В.
Система нулевой последовательности состоит из трех
равных векторов: 1 0А == 108 == 10С'
Векторами, показанными на рис. 12
22, MorYT изобра-
жаться как комплексные амплитуды, так и комплексные
действующие значения ТОков трех последовательностей.
MrHoBeHHble (синусоидальные) значения симметричных
составляющих мыслятся в виде проекций на мнимую ось
комплексных ампЛИТУД, вращающихся с уrловой CKOpO
стью (U В положительную сторону. Следует обратить внима-
ние на то, что направление вращения у всех трех систем
векторов одно и то же.
386
Взаимное расположение и модули векторов прямой,
обратной и нулевой последовательностей зависят от харак-
тера несимметрии и электрических параметров трехфазной
цепи.
На
основании рис. 12-22:
11B==a2ilA; !lc==ai 1A ; }
. . . 2.
12B == aI 2A ; J 2С == а J 2А'
Токи В фазах А, В и С определяются как суммы соот-
ветствующих симметричных составляющих:
A==
1A+i2A+
OA; )
J в == I 1В + i 2В + 1 оВ;
Iс == i 1C + i 2C + lос.
( 12-9)
(12-10)
В дальнейшем ради упрощения записи индекс А при
симметричных составляющих фазы А опущен, т. е.
1 1 ==i 1A ; i 2 ==1 2A ; 10 == i oA ' (12-11)
С учетом (12-9) и (12-11) выражения (12-10) принимают
вид: .. . .
IA==/l+/2+/o; )
1 В ==a2jl +ai2+io;
1 . 2' 1
с==а[l+ а 12+ о.
Эти формулы служат для нахождения фазных токов
по их симметричным составляющим.
Если известны фазные токи, то симметричные состав-
ляю:цие служат решением системы уравнений (12-12).
Умножив вторую стр.ОКУ на а и третью строку на а 2 и
сложив уравнения (12-12), получим (с учетом Toro, что
1 + а + а 2 == О):
i 1 ==(lA+ajB+a 2 !C)/3' (12-13)
Аналоrичным образом, умножив втор ую строку на a
и третью строку на а и сложив уравнения (12-12), найдем:
i 2 == (j А + a 2 j В+ а! С)/3. (12-14)
Наконец, сложив уравнения (12-12), получим:
10 == (i А + j в+ jc)/3. (12-15)
выаженияя (12-12)
(12-15) являются общими; они
применимы также для напряжений, маrнитных потоков
и друrих величин.
(12-12)
387
i1.9. ПОПЕРЕЧНАЯ НЕСИММЕТРИЯ
Поп е р е ч н а я н е с и м м е Т р и я в одной точке
трехфазной цепи возникает в том случае, коrДа к фазам
присоединяются неравные сопротивления, как это, на-
пример, показано на рис. 12
23, а. Такое включение может
иметь место при несимметричном коротком замыкании или
несимметричной наrрузке.
Любые два сопротивления из числа включенных в звезду,
а также сопротивление Z3 MorYT быть равны нулю или
бесконечности. Таким образом, различные виды несимметрии
или KopoTKoro замыкания, изображенные, например,
на рис. 12-23, б, в и е, получаются как частные случаи из
общеrо случая, представленноrо на рис. 12-23, а.
А
В
С
ZA
0.) ZJ
'='
Zc
А
В О
С R R
"2 "2
j8
jG
б)
'1!IA
2)
А
8
С R R
Z. '2
18* *1с
RJ *1.!' О)
'='
Рис. 12
23. Случаи поперечной несиммстрии.
а
общий случай;' б
двухфазиое замыкаиие; в
ДВУХФазное заМЫI<ание
на землю (или на корпус); 8
однофазиое замыкание.
в случае KopoTKoro замыкания сопротивления в месте
замыкания складываются из сопротивлений электрических
дуr и заземлений. Эти сопротивления, как показали экспе-
риментальные исследования, явЛяются активными. Поэтому
сопротивления ДЛя упомянутых выше частных случаев
приняты активными, а именно:
1) при двухфазном замыкании. между фазами В и С
(рис. 12
23, б)
ZB == Zc == Р/2; Z А:;= Z3 == 00;
2) при двухфазном замыкании на землю (или корпус
самолета) (рис. 12-23, в)
ZB == Zc == R/2; Z3 == R з ;
3) при однофазном замыкании На
(рис. 12
23. е)
ZA == о; Zз == R з ; ZB == Zc == 00.
888
ZA==oo;
землю (корпус)
Поперечная несимметрия в общем случае (рис. 12-23, а)
характеризуется уравнениями:
А==ZА:А+3ZЗ!0; ]
ив == ZBI в + 3Z 3 / 0;
U C == Zc i с+ зzJ о ;
здесь (; А, (; В И (; С
фазные напряжения в месте несим-
метрии относительно земли.
Входящие в (12-16) фазные напряжения и токи MorYT
быть с учетом формул (12-12) заменены симметричными
составляющими. При этом получаются три уравнения, свя-
зывающие симметричные составляющие в месте попереч-
ной несимметрии (так называемые rраничные условия).
Дополнительные три уравнения, необходимые для вы-
числения шести неизвестных (симметричных составляющих
напряжений и токов в месте несимметрии), даются соотно-
шениями между напряжениями и токами одноименных по-
следовательностей для фазы А:
Z1
1+
1==EA; )
Z2/2 + и 2 == о;
zoi 0+ li о === о;
(12-16)
(12-17)
здесь Z1' Z2 и Zo
результирующие фазные сопротивления
всей цепи (без сопротивлений в месте несимметрии) для
токов прямой, обратной и нулевой последовательностей;
Ё А
Э. д. с. фазы А эквивалентноrо reHepaTopa.
Формулы (12-17) выражают второй закон Кирхrофа для
каждой последовательности в отдельности. Поскольку
э. д. с. reHepaTopa трехфазноrо тока образует симметрич-
ную звезду с прямым чередованием фаз, в уравнениях
(12-17) э. д. с. reHepaTopa входит только в уравнение для
составляющих прямой последовательности; в остальных
двух уравнениях, связывающих составляющие напряже-
ний и токов обратной и нулевой последовательностей,
э. д. с. reHepaTopa отсутствует.
Сопротивления прямой, обратной и нулевой последо-
вателы;Ioстейй для электрических машин (reHepaTopoB, элект-
рических двиrателей, трансформаторов) берутся по завод-
ским данным.
Равенство Z1 == Z2 имеет место только для статических
не вращающихся устройств
трансформаторов, линий
и т. п.
389
Для вращающихся электрических машин обычно
Z2 < Z1' Разница в сопротивлениях прямой и обратной по-
следовательностей электрических машин обусловлена раз
личными направлениями вращения маrнитных полей, обра-
зуемых токами прямой и обратной последовательностей:
направление вращения маrнитноrо поля, созданноrо токами
прямой последовательности, совпадает с направлением
вращения ротора, маrнитное же поле, образованное токами
обратной последовательности, вращается в противополож-
ную сторону. Более подробно этот вопрос рассматривается
в литературе по электрнческим машинам и токам KopOТKoro
замыкания в трехфазных системах.
Сопротивления прямой и нулевой последовательностей
трехфазной линии (кабельной или воздушной) находятся
расчетным или опытным путем, причем сопротивления
прямой и обратной последовательностей для линий оди-
наковыI, а, сопротивление пулевой последовательности мо-
жет в 2
3 раза превышать сопротивление прямой после-
довательности. Объясняется это различием э. д, с. взаим-
ной индукции, Наводимых в фазе токами прямой и нулевой
последовательностей, протекающими по двум друrим фазам,
а также сопротивлением земли или обшивки транспортноrо
средства, по которому проложена сеть.
Методика определения симметричных составляющих
токов и напряжений и построения' соответствующих век-
торных диаrрамм иллюстрирована ниже на примере част-
ных случаев поперечной несимметрии.
1. Двухфазное короткое замыкание (рис. 12-23, 6). [ра-
яичные условия удовлетворяют уравнениям:
lA==o; jB==
ic;
iJ в
U с == R (i в
j с)/2.
Подстановка (12-18) в (12-13) и (12-14) дает:
11 == (а
a2) i в/3; /2 == (а 2
a) i 8/3'
(12-18)
(12-19)
ОТкуда
Jl==
i2'
Подстановка (12-18) в (1
15) дает:
i 0== О.
Кроме Toro, на основании (12-19)
(a2fj1 + а( 2 )
(аЙ 1 + а 2 и 2) == (а 2
а) (01
й 2) ==::
== (a2
a) R (/1
i 2 )/2,
(12-20)
390
или
(;1
(;2 == R (i 1
i 2 )/2.
(12-21)
Уравнения (12-20) и (12-21) вместе с дополнительными
первыми двумя уравнениями (12-17) достаточны для На-
хождения четырех неизвестных: 11, 12' {) 1 И {) 2' В резуль-
тате cOBMecTHoro решения этих уравнений получается:
J Ёл
1 == Z1 +Z2+R . (l2
22)
На рис. 12-24 предсrавлены векторные диаrраммы то-
ков и напряжениЙ в месте двухфазноrо KopoTKoro замыка-
1 1с 1м
J(
\
. \
118 {'
\..i8
28 "
.
и1А
li1
. I "
и8
<
и28
12C
.
.
12A 128
а)
.
и2А
и2
)
18
иА
и с
.
ив
Рис. 12-24. Векторные диаrраммы в месте двухфаз-
Horo KopoTKoro замыкания.
а
токи; б
напряжения.
Ния при R == О (металлическое короткое замыкание).
В этом случае в соответствии с (12-21) {)1 == {)2'
Векторные диаrраммы построены в предположении, что
вектор э. д. С. Ё А направлен вертикально вверх, причем
уtлы комплексных сопротивлений прямой и обратной по-
следовательностей одинаковы (например, 600). Поэтому
01А совпадает по фазе с Ё А и ток 11A отстает от {)lА на
заданный уrол.
Сумма токов l 1А и 1 2А В месте двухфазноrо KopoTKoro
замыкания равна нулю, поэтому 1 А == О. Токи 1 1B И 1 2в
891
Дают В'сумме фазный ток l в в месте KopOТKoro замыкания,
а токи l 1С и 1 2с дают в сумме фазный ток 1 с.
Токи 1 в и 1 с находятся в противофазе.
Поскольку при построении векторных диаrрамм сопро-
тивление R в месте KopOТKoro замыкания принято равным
нулю, фазные напряжения О в и О с в месте повреждения
равны друr друrу и соответственно линейное напряже-
ние ОБе равно нулю. По мере удаления от места KopoTKoro
замыкания в сторону reHepaTopa линейное напряжение
между фазами В и С возрастает.
i 1C 1 1А 1 2в i 2A
./
'(
18 =Ic={l
0.)
Л. "уй" иА=О
m
и1С и,в UZB б) ио ис ив
Рис. 12-25. Векторные диаrраммы в месте однофазноrо ко-
pOTKoro замыкания.
(j
токн; б
напряження.
2. Однофазное короткое замыкание (см. рис. 12-23, е).
rраничные условия удовлетворяют уравнениям:
1 в == 1 е == о; (; А === R31 А'
Замена фазных величин их симметричными составляю.
щими дает:
11==12==10; }
&1 + (;2 + (;0 === 3RJo.
В результате cOBMecTHoro решения уравнений (12-17)
и (12-23) получается:
. Е
11 == Zi+Z2+
о+3Rз . (12-24)
(12-23)
Векторные' диаrраммы токов и напряжений при Ra ::::;; О
представлены на рис. 12-25.
392
Про Д о. л ь н а я н е с и м м е т р и я в ОДНОЙ точке трехфаз-
ной цепи возникает в том с
учае, коrда в расс
чку фаз включаются,.не-
iA/ i 8,ic
ZA
равные сопротивления, как это, иапример, показано на рис. 12-26, а.
Любые два сопротивления MorYT быть при этом равны иулю или бес-
конечности. А
Продольная несимметрия
/J..
характеризуется в даином слу- . '"V
С
чае уравнениями:
а)
A==ZA,iA; )
Z/ Ё й.
и в == В в; (12-25)
Ztr
ZtЛ
Uc==Zcic;
здесь (J А' (J В И (J С
напряже-
ния на выводах сопротивлений 6) .
Z А' ZB и Zc (продольные напря- (j
a
Z2r
'Z Z2Л
жения).
.
в результате замены напря-
жений и токов, входящих в
(12-25), симметричными состав-
ляющими получаются три урав-
нения (rраничные условия), свя-
зывающие симметричные состав-
ляющие в месте ПрОДОЛЬНОЙ .не-
симметрии.
В частном случае, изобра-
жеином на рис. 12-26, б,
Z в == Zc == о и соответственно
(; в == (J с == О.
Симметричные составляющие продольных напряжений
й 1 ==й 2 ==й О ==й A/ 3 ==Z A i Ai 3 == 2 A (i 1 +i 2 +i 0)/3' (12-26)
Пример 12-3. I( трехфазному reHepaтopy присоединена линия
с асинхронным двиrаrелем на конце (рис. 12-27, а). Нейтральные
точки rеиератора и двиrателя заземлены, Произошел обрыв фазы А
12-10. продопЬНАЯ НЕСИММЕТРИЯ
А
ZA
Z8
в
с
А
в
с Zc
а)
б)
8)
Рис. 12-26. Случаи ПРОДОЛЬНОЙ несимметрии.
а
общи!! случа!!; б
сопротивление в ОАНО!! фазе; 8
раз-
Каиие одно!! фазы.
8)
а)
Рис. 12-27. Пример 12-3.
l
]
1
93
вблизи выводов reHepaтopa. Требуется определить токи в фазах В и С
и напряжения в месте обрыва.
Обозначим: Zlr' Z;ro Zor
комплексные сопротивления прямой,
обратной и нулевоЙ последовательностей reHepaTopa; ZI.о' Z2.о' Zо.о
то же для линии; Z111.' Z211.' ZOI1.
то же для асинхронноrо .двиrателя;
Е А
э. д. с. фазы А reHepaтopa.
Для сокращения записи обозначим:
Zi == Zir + 2i.о + Zil1.;
22 == Z2r + 22.0 + Z211.;
Zo == Zor + ZОЛ + ZOI1.'
На основании схем замещения для отдельных последовательностей
(рис, 12-27, б
е) можно написать основные уравнения (12-17):
Ё А
(;1 == Z/ 1;
(;2 == Z/2; --:--(;0 == Z/ о'
Для данноrо случая добавочные уравнения соrласно (12-26) при
Z А == со будут:
(;i==(;2==(;0 и ii+i2+io;==o.
Совместное решение этих уравнений дает:
(;1 ==(;2== (;0== Ё A 2 2 Z i N ;
io==
E A Z 2 /N; i2==
Е AZiN;
i 1 ==Ё А (Z2+Zo)/N,
rде
N == Z1Z2 + Z1Z0 + Z220'
Полные токи и напряжения MorYT быть леrко найдены суммирова-
нием отдельных состав
яющих.
12-11. ФИЛЬТРЫ СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
ф и л ь т р а м и с и м м е т р и ч н ы х с о с т а в л я ю Щ и хна-
зываются устройства, служащие для выделения соотвеТС1ВУЮШИХ
составляющих напряжений или токов трехфазной цепи. Фильтры
имеют входные и выходные выводы. К входным выводам фильтра под-
водятся напряжения или токи трехфазной электрической цепи; на вы-
ходнЫх выводах фильтра получается напряжение или ток, пропорцио-
нальные соответствующим симметричным составляющим электриче-
ских величин, подводимых к входным выводам.
Напряжения и токи, выделяемые фильtрами симметричных состав-
ляющих, используются на практике для цепей автоматики, защиты
от несимметричных режимов или сиrнализации. С этой целью к выход-
ным выводам фильтров симметричных составляющих riрисоединяются
соответствующие аппараты, приборы, реле и т. п.
Наиболее простой тип фильтра симметричных составляющих пред-
ставляет собой Ф и л ь т р т о к о в н у л е в о й п о с л е Д о в а -
т е л ь н о с т и, в котором суммируются токи трех фаз (рис. 12-28, а)
или создаваемые ими маrнитные потоки (рис. 12-28, 6). В первом слу-
чае реаrирующий прибор включается в нейтралыlйй провод трех
394
трансформаторов тока 1, а во втором случае
между выводами обмотКК
насаженной на маrнитопровод, охватывающий три фазы.
Фильтр напряжений нулевой последовательности выполняется
с помощью трех однофазных трансформаторов напряжения, первичная
обмотка которых соединяется звездой с выведенной нейтральной точ-
кой, а вторичная обмотка соединяётся разомкнутым треуrольником
(рис. 12
28, в).
Блаrодаря такому соединению составляющ
е наПР!lжений. прямой
последовательности взаимно компенсируются: и 1А + и 1В + и 1С == о.
То же и
еет M
TO н в 9тношении напряжений обратной последователь-
ности: и 2 А + и 2 В + и 2 С == о.
Составляющие же напряжений нулевой последовательнос.ти обра-
зуют на выводах разомкнутоrо треуrольника напряжения за о .
A
В i A
С 18 <r:
1 с <1---
з10
0.)
6)
А
В
С
N
[И!j
6)
Рис. 12-28. Фильтры составляющих нулевой последовательности.
а и б
филстры токов; в
Фильтр вапряжеиий.
Фильтр напряжений нулевой последов а-
т е л ь н о с т и может быть получен и с помощью трех равных сопро-
тивлений, соединенных звездой н приключенных к трехфазной цепи.
При симметричном режиме работы трехфазной цепи напряжение между
нейтральной точкой этих сопротивлений и нейтральной точкой цепи
равно нулю; при появлении же в трехфазной цепи составляющих
напряжений нулевой последовательности между упомянутыми точкамн
возникает напряжение, пропорциональное составляющей нулевой
последовательности.
Системы симметричных составляющих прямой и обратной После-
довательностей 'различаются порядком следования во времени амплн-
туд фазных величин, поэтому всякая схема для выделения составляю-
щнх обратной последовательности может быть путем перестановки
любых двух фаз превращена в схему для выделения составляющих
прямой последовательности. С этой точки зрення является достаточным
рассмотреть фильтры только какой.либо одной из указанных последо-
вательностей, например 'обратной, распространив затем полученные
1 Втори
ные токи трансформаторов тока приближенно равны пер-
вичным, деленным на отношение чисел витков W 2 /W 1 . На рис. 12-28
вторичные токи и напряжения приведены к первичной обмотке.
395
результаты на фильтры' симметричных составляющих друrой (прямой)
последовательности.
Принцип выполнения фильтров токов и напряжений обратной
последовательности иллюстрирован ниже на примере двух схем: схемы
фильтра токов трансформаторноrо типа (РИС. 12-29) и схемы четырех-
$лементноrо активно-емкостиоrо фильтра напряжений (рис. 12
30).
В фнльтрах обоих типов суммируются напряжения, находящиеся
в определенных соотношениях С токами или напряжеииими, подводи-
мыии к входным выводам фильтров.
Фильтр токов обратной послеДовательно-
с т и, изображенный на РИС. 12
29, состоит из активных сопротивле.
ний, между которыми проложен нейтральный провод трансформаторов
тока, и промежуточноrо трансформатора, токовые обмотки Koтoporo
в фазах В и С связаны ИИДУКТИвно с третьей обмоткой в выходной
цепи; параметры фильтра УДовлетвориют условию R == уз шМ, rде
3/0
А
i A
l.R
Э
1R
3
А
В
С
J
1
и
.........
'>.
Рис. 12
29. Фильтр токов об.
ратной последовательности,
Рис. 12-30. Фильтр иапряжений
обратной последовательности.
w
уrловая частота тока, на которую рассчитан фильтр; М
взаим-
ная индуктивность первичной и вторичной обмоток промежуточноrо
трансформатора.
Блаrодаря тому, что маrнитопровод промежуточноrо трансформа-
тора имеет воздушный зазор, обеспечиаается линейная зависимоСтЬ
э. д. с. взаимной индукции от токов.
Напишем уравнение Bтoporo закона I(ирхrофа по выходному
контуру:
2' 1,. , .
U==з R ' А
ЗR (l в+/ с)
jwM ( B+1C).
с учетом первоrо закона I(ирхrофа
(' в+'с)==' А
з'о
и соотношений между симметричными составляющими
'A=='1+'Z+'o;
'B
/ c==
i VЗ ('1
' 2)
получим окончательно:
U ==R ('i.+'2)
VЗ ооМ ('i.
'2) == 2Ri 2 ,
( 12-27)
396
Т.е. выходное напряжение пропорционально току обратной nоследо-
-вательности.
Влияние токов нулевой последовательности отсутствует в рас-
сматриваемом фильтре блаrодаря взаимной компенсации падений
напряжения от токов 1 о и 210 в сопротивлениях
}R и
}R. Друrой воз-
можнЫй способ устранения влияния токов нулевоЙ последовательности
заключается в том, что к фильтру токов обратноЙ последовательности
вместо фазных токов 1 А' 1 в и 1 С подводятся разности фазных ТОКОВ
1 А
1 в, 1 в
1 С и 1 С
1 А' В которых составляющие нулевой после-
довательности отсутствуют.
Аналоrичным образом для устранения влияния напряжений нуле-
вой последовательности фильтры напряжениЙ обратной п
след<?ва-
тельности включаются обычно на линеЙные напряжения и АВ' и ВС
и (J СА'
На рис. 12
30 показан четырехэлементный фильтр напряжений обрат-
ной последовательности, прпменяемый в релейной защите. Пара-
метры элементов фильтра подбираются из условия
Ri: Xi
X2: R2
уз. (12-28)
При холостом режиме работы фильтра, т. е. при разомкнутых вто-
ричных выводах, напряжение на этих выводах равно сумме
уз . ух .
2"'""' u АВ L 30 Q И 2'""""" U вс L
30' .
Если (J АВ и (J ВС выразить через симметричные составляющие ли-
нейных напряжений, то напряжение на выходных выводах фильтра
будет равно:
и
I,бli2АС'
(12-29)
т. е. пропорционально составляющей обратной последовательности.
Если на выходе фильтра присоединена наrрузка (реаrирующий при-
бор), ТО ток или напряжение в выходной цепи MorYT быть получены
на осиовании теоремы об эквивалентном источнике.
Пример 12-4. I( выходным выводам фильтра токов обратной после-
п.овательиости, показiшноrо на рис. 12-29, подключена наrрузка
ZH
rIl+j(i)LH'
Определить ток в наrрузке при подведении к входным ВЫВОДам
фильтра системы несимметричных токов.
Будем исходить из предположения, что к выходным выводам филь-
Тра подключены источиики токов 1 А' 1 в и 1 С, так как эти токи не завн-
сят от сопротивлений наrрузки.
Соrласно (1
-27) напряжение иа разомкиутых выходных выводах
фильтра равно и
2R1 2 .
ПО теореме об эквивалентном источиике ток в наrрузке равен:
li
'H
Zф+Zк '
rде Zф
сопротивление фильтра, измеренное со стороны ero выход-
ных выводов при разомкнутых, входных выводах, так как внутрен-
ние сопротивления источников тока равны бесконеЧности.
397
Обозначив через Z == , + jroL сопротивление вторичной обмотки
промежуточноrо трансформатора, включенной в выходную цепь, полу
чим:
/ == 2R/ 2 ,
и , +, и + R + jro (L + L и )
Таким образом, при заданном значении Zи пропорциональность
тока / и току /2 сохраняется.
Пример 12
5. I( выходным выводам фильтра напряжений обратной
последовательности, показанноrо на рис. 12
30, подключена наrрузка ZИ'
Параметры элементов фильтра, удовлетворяющие соотношению (12
28),
выбраны следующим образом:
Ri
Xi == V 3 ; Х 2 == Rl;
Ri
R 2 == Vз .
Определить напряжение на наrрузке при подведении к входным
выводам фильтра несимметричных напряжений.
Будем исходить из предположения, чro к входным выводам фильтра
подключены источники э. д. с. (J АВ и (J ВС' Corласно -(12-29) напряжение
на разомкнутых выходных выводах фнльтра равно:
U == 1 ,5и 2Ас == 1:5 УЗU 2А L. 300.
ПО теореме об эквивалентном источнике напряжение на наrрузке
равно:
. ZИ ,
ии== zф+zи и,
rде ZФ
сопротивление фильтра, измеренное со стороны ero выходных
выводов при закороченных входных выводах, так как внутренние
сопротивления источников э. д. с. равны Нулю.
Следовательно, в соответствии с заданием
Z
j ( RIXi + R 2 X 2 )
ф
Rl
jXi R2
jX2
Ri R 1
( Rl уз уз Ri )
==
J . Ri + Ri . ==0,965Ri L
450;
\ Rl
J уз уз
JRi
отсюда
u
и.
1,5 уз и 2А L 30 0 Z и
0,965Rl L
450+ Zи'
При любом заданном значении Z8 сохраняется пропорциональ-
ность между (J и и (J 2А .
11-11. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
12-1. В симметричной трехфазной цепи наrрузка Z == 10 + j5 Ом
(на фазу) соединена звездой; линейные напряжения на наrрузке равны
230 13. Вычислить ток.
Отает: 11,9 А.
398
12-2. В симметричной трехфазной цепи наrруэка Z АВ == lBC ==
== ZCA == 10 L. 300 Ом соединена треуrольником; линейные напряже-
ния на наrрузке равны 100 В. Определить активную и реактивную мощ-
ности наrрузки.
О т в е т; 2600 Вт; 1500 вар.
12-3. В симметричной трехфазной цепи наrрузки Z == 10
jl4 Ом
(на фазу) соединена звездой; комплексное сопротивление линии от reHe-
ратора до наrрузки равно 1 + j2 Ом (иа фазу). Линейные напряжения
на выводах reHepaTopa равны 100 В, Вычислить фазное напряжение
на наrрузке.
Ответ; 61,2 В.
12-4. Несимметричная трехфаэиая наrрузка соединена треуrоль-
ником; Z АВ == 100 L. 00; Z ВС == 100 L.
900; ZCA == 141 L. 450 Ом,
Линейные напряжения на наrрузке симметричны и равны
OO
. Вы-
числить линейные токи и активную мощность наrрузки, приняв и АВ ==
== 200 L. 0° В.
О т в е т; 2,13 L.
40°; 1,04 L.
105°; 2,73 L. 120° А; 600 Вт.
12-5. Решить ту же задачу при тех же напряжениях, но при обрат-
ном чередовании фаз.
О т в е т: 3,39 L. 60; 3,86 L.
165°; 0,735 L. 600 А; 600 Вт.
12-6. Нссимметричная трехф"азная наrрузка соединена звездой:
Z А == 100 L.
90°; ZB == 100 L. 0°; Zc == 141 L. 45° Ом. Линейные
напряжения на наrрузке симметричны и равны 200 В. Вычислить ли-
нейные токи и активную мощность наrрузки.
О т в е т; 1,34 L 32°; '1,72 L.
138°; 0,463 L. 72° А; 317,4 Вт.
12-7. Несимметричная трехфазная наrрузка соединена треуrоль-
ником: Z АВ == 8,66 + j5; ZBC == 3 + j4; ZCA == 5
j5 Ом; линейные
напряжения на наrрузке симметричны и равны 100 В каЖДое. Опре-
Делить активную, реактивную и полную мощности наrрузки при пря-
мом и обратном чередовании подведенных напряжении.
. Ответ; 3066 Вт; 1100 вар; 3260 В.А.
12-8. Несимметричная трехфазная наrрузка соединена треуrоль-
ником: Z АВ == jЗ; ZBC == з; ZCA ==
j3 Ом; активная мощность из-
меряется двумя ваттметрами, включенными по схеме рис. 12-18. Напря-
жения на наrруэке симметричны и равны 100 В каЖДое, Определить
показания ваттметров.
О т в е т; 2885; 448 Вт.
12-9. Вычислить линейные токи, реактивную и полную мощности
в симметричной трехфазной цепи по показаниям двух ваттметров,
включенных по схеме рис. 12-18, а, 1986 и 2517 Вт. Линейиое напря-
жение равно 208 В.
Ответ: 12,8 А;
919 вар; 4600 В.А.
12-10. К трехфазному reHepaтopy, соединенному звездой и имею-
щему фазную э. д. с. 100 В, подключена с помощью четырехпроводной
линии несимметричная наrрузка; между фазой А и нейтральным про-
водом 50 Ом; между фазой В и нейтральным проводом
j50 Ом; между
фазами В и С 40 + j20 Ом. Комплексные сопротивления линейных про-
БОдов и нейтральноrо провода одинаковы и равны 1 + j2 Ом. Вычис-
лить линейные токи и активную мощность на выводах reHepaтopa,
приняв сопротивление ero равным нулю.
О т в е т; 1 А == 1,92 А; 388 Вт. "
12-11. Трехфазный reHepaтop, соединенный звездой, имеет фазные
Э.д.с. 135,
67,5'
jI17 и
67,5 + jl17 В и внутреннее сопротив-
399
Jteние 0,1 + Л,5 ОМ (на фазу). От reHepaTopa отходит линия, имеющая
сопротивление 0,9 + jO,5 Ом; в конце линии несимметричная наrрузка
соединена в треуrольник; Z АВ == 40 + j60, ZBC == 100; ZCA == 50
j20 Ом.
Вычислнть линейные токи.
О т в е т: 7,06 L
20° 24'; 2,85 L
161° 42'; 5,15 L 139024' А.
12
12. Пользуясь решением предыдущей задачи, вычислить фаз-
иые токи, напряжения и активную мощность наrрузки.
О т в е т: 2,97 1.
28,7°; . 2,33 1.
92,4°; 4,15 < 165,4° А;
214,5 1. 27,6°; 232,8 1.
92,4°; 224 L 143,6° В; 1760 Вт.
12-13. В чем заключается преимущество трехфазноrо тока перед.
однОфазным?
12-14. Как определяется чередование фаз опытным путем?
12-15. В какую сторону вращается маrнитное поле, созданное двумя
пульсирующими полями, оси которых сдвинуты на уrол 90°, а токи
в обмотке сдвинуты по фазе на четверть периода?
12-16. Пользуясь правилами правой и левой руки, показать, что
короткозамкнутый ротор, выполненный' в виде беличьей клетки, при-
ходит во вращение в том же направлении, в котором вращается маrнит-
ное поле.
12-17. Как изменить направление вра[Цения поля?
12-18. Определить симметричные составЛяющие для заданной
системы токов: 1 А == 6,6 L 120°; 1 в == 6 L 0°; 1 С == 5,4 1. 240° А.
О т в е т: ii ==
3 + j5,2; 12 ==
0,3 + jO,17; 10 == jO,35 А.
12-19. Для чеrо несимметричная система векторов раскладывается
на симметричные составляющие?
, 12-20. Почему сопротивление нулевой последовательности линии
превышает сопротивление прямой послеДоватеЛЬЩJСТИ линии (пояс-
иить физическую сторону явления)?
12-21. Показать, что уrол фазовоrо сдвиrа напряжения и тока
нулевой (или обратной) последовательности не зависнт от сопротив-
ления в месте повреждения.
.12-22. Доказать, что мощность трехфазной цепи выражается через
мощности прямой, обратной и нулевой последовательностей по формуле
S ==3 (Uili+U2i2+uоiо)==з (8i+82+80).
12.23. В каких случаях и какое возникает напряжение нулевой
последовательности в трехфазной цепи с изолированной нейтралью?
r Л, А В А Т Р И Н А Д Ц А Т А Я
ЦЕПИ ПЕРИОДИЧЕскоrо НЕСИНУСОИДАльноrо
ТОКА
f3-1. триrОНОМЕТРИЧЕСКАЯ ФОРМА РЯДА ФУРЬЕ
ДО сих пор изучались линейные электрические цепи
однофазноrо и трехфазноrо токов, в которых все э. Д. С.,
токи и напряжения изменялись синусоидально с одинако-
вой частотой.
400
---
При разборе принципа rенерирования синусоидальной
э. д. С, (см,
2-2) отмечалось, что для получения СИНУС9И-
дальной э. д. с. в обмотке как явнополюсноrо, так и неявно-
полюсноrо reHepaTopa стремятся получить синусоидальную
форму распределения маrнитной индукции в воздушном
зазоре между статором и ротором, В действительности,
однако, распределение маrнитной индукции может отсту-
пать от синусоиды, вследствие чеrо э. д. с., наводимая
reHepaTopoM,
ожет быть не точно синусоидальной. Элект-
ронные reнераторы, применяемые в технике высоких ча-
стот, rенер.ируют токи, которые в зависимости от режима
работы электровакуумных и полупроводниковых пр ибо-
ров также MorYT в большей или меньшей степени отличаться
от синусоидальных. По этим причинам, а также если источ-
ники синусоидальных э. д. с., присоединенные к цепи,
имеют разные частоты, напряжения и токи В цепи оказы-
ваются н е с и н у с о и Д а л ь н ы м и.
Во мноrих электротехничеСIШХ и радиотехнических
устройствах несинусоидальный режим работы цепи явля-
ется нормальным режимом. Особенно характерен такой
режим для нелинейных цепей, Даже при синусоидальной
э. д. с. форма кривой тока может резко отличаться от
синусоиды при наличии в цепи нелинейноrо элемента 1
(электрической дуrи, индуктивной катушки с насыщенным
маrНИТОЛРОВОДОМ,полупроводниковоrо прибора и т. п,).
Настоящая rлава посвящена исследованию периодиче-
ских процессов в линейных электрических цепях, На-
ходящихся под воздействием несинусоидальных э. д. с.
Электрические и маrнитные величины в таких цепях пред-
ставляют собой периодические несинусоидальные функции.
Явления, происходящие в линей
ой электрической цепи
с периодической несинусоидальной э. д. с., проще Bcero
поддаются исследованию, если эту э. д, с. разложить на
сумму постоянной и синусоидальных слаrающих (назы-
.ваемых r а р м о н и к а м и), затем на основе уже изу-
ченных методов расчета линейных электрических цепей
определить токи и напряжения, вызванные каждой сла-
rающей э. д. с. в отдельности, и, наконец, просуммировать
соответствующие величины. Полученные таким образом
токи и напряжения будут представлять собой периодиче-
ские несинусоидальные функции времени, причем их пе-
1 Несинусоидальные процессы в неЛинейных цепях рассматрива-
ются во второй части курса,
401
риод будет равен периоду заданной несинусоидальной
э. д. с.
Кроме вычисления токов и напряжений в электриче-
ской цепи по заданной несинусоидаЛЬНQЙ э. д. с. источника
(или заданному току источника тока), на практике может
возникнуть необходимость выявления rармоническоrо со-
става или степени отклонения от синусоиды той или иной
периодической' функции времени, полученной, например,
экспериментально в результате осциллоrрафирования.
На рис. 13-1 в виде примера показана периодическая
несинусоидальная функция времени с периодом Т:
f (t) == f (t + Т).
Вид разложения такой функции зависит от выбора
начала отсчета (см.
13-3).
В пределах интервала времеНИ Т функция f (t) может
быть либо непрерывной, либо иметь точки разрыва непре-
рывности. Будем считать,
f(t) что все эти точки разрыва
непрерывности обладают
следующим свойством: если
функция f (t) претерпевает
разрыв непрерывности в
точке t == t 1 (рис. 13-1), то
существуют конечные пре-
Рис. 13-1. Периодическая несинусо- делы функции f (t) при при-
идальная функция времени. ближении к точке разрыва
как справа (т. е. от зна-
чений t> t 1 ), так и слева (т. е. от значений t < t 1 ).
Эти пределы условно обозначаются f и1 + '0) и f и1
О)
или, что то Же, f (t 1 +) и f и1
). Как известно, такие
точки разрыва непрерывности называются т о ч к а м и
разрыва первоrо рода.
Будем также считать, что в пределах интервала вре-
мени Т число разрывов первоrо рода, а также число макси-
мумов и минимумов функции f (1) конечны.
Таким образом, будем рассматривать функции, удовле-
творяющие у с л о в и я м Д и р и х л е; следует заме-
тить, что э. д. с., токи и напряжения в реальных электри-
ческих цепях удовлетворяют этим условиям.
Известно, что периодическая несинусоидальная функ-
ция, удовлетворяющая условиям Дирихле, может быть
представлена в виде бесконечно rармоническоrо ряда
ряда Фурье. Сумма этоrо ряда совпадает со значениями
402
f (!) для всех точек непрерывности этой функции, а в точках
разрыва дает среднее арифметическое левоrо и правоrо
предельных значений f (t), т. е.
1
2
и и
) +f (t+)].
Обозначим ro :::= 2л/Т и будем называть ro основной уrло-
вой частотой. Синусоидальная и косинусоидальная сла-
rающие с уrловои частотоЙ ro образуют основную rapMo-
нику. Слаrающие с более высокими уrловыми частотами
представляют собой высшие rармоники.
r армонuческuй ряд в mрuеономеmрuческойформе имеет
вид:
00
f (t) ==
O + -! (а п cos пrot + Ь п sin пwt),
п
l
(13-1 )
rде
t.+T
2
а п :::= т
f (t) cos пrot dt; _
t.
t.+T
2 ('
Ь п :::= т J f (t) sin пrot dt;
t.
(13-2)
(13
3 )
здесь а о /2
постоянная слаrающая; а п и Ь п
амплитуды
КОСИНусоидальных и синусоидальных членов ряда.
f(t)
Рис. 1
3"2. Несинусоидальная'
функция, среднее значение ко-
торой за период равно нулю,
t
т
Постоянная слаrающая 0.0/2, определяемая на основа-
нии (13-2) при п :::= О, представляет собой среднее значение
ФУНКции f (t) за период. Она равна Нулю, коrда площади
положительных и отрицательных значений f (t) одинаковы
(рис. 13
2).
Коэффициенты ряда Фурье а п и Ь л не зависят от t o ;
поэтому значение t o может быть выбрано произвольно.
В этом леrко убедиться, если учесть, что подынтеrраль-
403
ные функции в (13-2) и (13-3) имеют период Т. Обозначив
подынтеrральную функцию через g (t), получим:
4+Т о Т
+T
g(t)dt==
g(t)dt+
g(t)dt+
g(t)dt.
4
О Т
Так как g (t) == g (t
Т), то
t o + т ( о + т
g(t)dt ,
g(t
T)dt.
т т
Заменой переменной х == t
Т находим:
(.+Т (. (.
g (t) dt ==
g (х) dx ==
g (t) dt.
т о о
Следовательно,
( о + т /.
g (t) dt ==
g (t) dt.
т о
Полученный результат можно еще объяснить так: пло-
(. + т т
щади, выражаемые интеrралами
и
, равны, так как
t o О
В силу периодичности подынтеrральной функции любое
изменение t o не меняет площади, оrраниченной данной функ-
цией и осью абсдисс за период.
Положив t o == О и введя новую переменную а == wt,
найдем (с учетом Toro, что, шТ == 2л и da == wdt):
00
f(a)==
Q+ ! (ancosпa+bnsinпa), (13-4)
n
l
rде
2п
а п ==
S 1 (а) cosпada;
о
2п
Ь п ==
s f (а) sin па da.
о
(13-5)
(13-6)
т
Если принять t o ==
2' то пределы интеrрирования
будут равны соответственно
л и +л.
404
Сумма косинусоид и синусоид, выражаемая формулой
(13-1) или (13-4), может быть представлена в виде суммы
только одних СИЕУСОИД С соответствующими рачальными
фазами.
Так, если принять
а n cos па + Ь/l sil1 па == Fn sin (па + 6/1)' (13-7)
rде
F /1 :::::: V а; + b
; 6 n == arctg
/I ,
/1
то ряд получит вид 1:
ro
f (а) ===
O + ! F/I sil1 (па + 6 п ).
n
1
( 13-8)
Напомним, что уrол е п находится с учетом знаков а п
и Ь п , определяющих знаки синуса и косинуса.
Форма (13-8) удобна в том случае, коrда требуется
знать процентное содержание каждой rармоники;, она
обычно применяется для расчета несинусоидальных токов
и напряжений в электрических цепях (см.
13-5).
Хотя теоретически ряд Фурье содержит бесконечное
число слаrаемых, однако он обычно быстро сходится.
Сходящийся ряд может выражать заданную функцию с лю.
бой требуемой степенью точности; если он сходится быстро,
то практически достаточно взять небольшое число rapMo-
ник для получения требуемой степени точности.
ВстречаlOщиеся на практике периодические несинусои-
дальные функции MorYT быть Разбиты на две rp уппы.
Первая rруппа включает в себя кривые rеометрически пра-
вильной формы. Вторая rруппа включает в себя кривые
более сложной формы; разложение их в ряд Фурье произ-
водится rрафоаналитически.
rрафоаналиmический меmод разложения в ряд Фурье
представляет приближенный метод численноrо интеrриро-
1 Иноrда периодическую функцию представляют В ВИДе слеДУЮ-
щеro ряда:
со
а о '\1 F 1(.
,(а)==2+
псоs(nа
'Фп)' rAe 'Фп==2
вп'
/1==1
что следует из равенства
соэ (nа
'Фп)==siп (nc:t
'Фп +
).
вания, при котором вычисление опрецеленноrо интеrрала
заменяется нахождением суммы конечноrо числа слаrае-
мых. С этой целью период функции f (а) , ращIЫЙ 2л, раз-
бивается на т равных интервалов Да, так что тДа ==: 2л.
Расстояние от начала координат до середины k-ro интер-
( 1 ) 2л
вала составляет уrол а==: k
2 т'
Пусть fk (а) есть значение периодической несинусои-
дальной функции в середине k-ro интервала.
Интеrралы, входящие в (13-5) и (13-6), заменяются
суммами:
2.1t
a'l
.! f (а) cos па Да
о
т
2
( 1 ) 2Л
т
fk (а) cos п k
2 т;
k
1 \
2i't
bп
.!f(а)siппаДа
о
2
. ( 1 ) 2Л
т
fk(a) sшп k
2 т'
k
l
Если в пределах периода имеются точки разрыва, то
при указанном rрафическом методе разложения целесооб-
разНо делать разбивку на интервалы так, чтобы '10ЧКИ
разрыва не были в' серединах интервалов.
В описанной выше технике выполнения rрафоаналити-
ческоrо разложения в ряд Фурье брались значения функ-
ции в середине интервалов; если вместо этоrо брать зна-
чения в конце или начале интервалов, то в случае четной
функции Наряду с косинусоидами в разложении появятся
и синусоиды, которых четная функция не содержит.
13-1. СЛУЧАИ СИММЕТРИИ
Периодические несинусоидальные функции, изобра-
жающие электрические и маrнитные величины, обладают
обычно каким-либо видом симметрии и это облеrчает раз-
ложение их в ряд Фурье.
Рассмотрим следующие случаи симметрии:
1. Функция f (а) си.л.tметрична относительно оси орди-
нат (рис. 13-3), т. е. f (а) =:: f (.........а). Такие функции назы-
406
ваются ч е т н ы м и. Поскольку синусоиды любых частот
яв;rIЯЮТСЯ нечетными функциями, они не входят в состав
ряда.
Поэтому при данном виде симметрии
00
f (а) ==
O + ! а п COS па,
п
l
т. е. четная функция может содержать только косинусоиды
и постоянную составляющую.
Рис. 13-3. Функция, симмет.
ричная относительно оси ор.
динат,
(\
ф
)
27С
Важным свойством четных функций является также
то, что для определения коэффициентов а п достаточно
пользоваться кривой f (а) за половину периода, т. е.
:n:
а п :=:
f (а) cos па da.
о
( 13- 9)
Это следует из равенства
:n: о :n:
f (а) cos па da ==
f (а) cos па da+
f (а) cos па da.
:n:
л: О
Замена в первом интеrрале а на
a приводит к (13-9).
2. Функция f (а) симметрична относительно начала
координат (рис. 13-4), т. е. f (а) ==
f (
a). Т<!кие функ-
ции называются н е ч е т н ы м и. Поскольку постоянная
слаrающая и косинусоиды этому условию не удовлетво-
ряют, при данном виде симметрии ряд примет вид:
со
f(a)::;:: 2: bnsinпa,
п
l
т. е. нечеmная функция
toжеm содержать только сину-
соиды.
В этом случае, так же как и в предыдущем, для опре-
деления коэффициентов Ь п достаточно пользоваться кри-
407
вой f (а) за половину периода, т. е.
n
bп
S f(a)sinпada.
о
3. Функция f (а) СJlмметрична относитеJIЬНО оси абсцисс
при совмещении двух полупериодов во времени (рис. 13-5),
т. е. f (а) ==
! (а + л).
f(oe) f(rt.)
Рис. 13-4. Функция, симметричная
относительно иачала координат.
(13-1 О)
Рис. 13-5. Функция, Симмет-
ричная относительно оси абс-
цисс при совмещении двух
полуnериодов во времени,
Заменяя f ,(а) в соответствии с (13-4), ПОJIучаем:
со
i + ! [aпcosпa+bпsinпa]==
п
l
со
==
O
1: [апсоsп(а+л)+Ьпsiпп(а+л)],
п
l
откуда для четных п
со
а о +2
[aпcosпa+bпsinпa}==O.
п
2,4.6...
Это уc.rrовие удовлетворяется при ПРОИ3ВОJIЬНЫХ зна-
чениях а только в том случае, еСJIИ ао == О и а п == Ь п == О
при четных п.
Поэтому при данном виде симметрии
со
f(a)==
(aпcosпa+bпsinпa),
п==I.3,S.....
т. е. функция, симметричная относительно оси абсцисс
при совмещении двух полупериодов во времени, содержит
тоЛЬКО нечетнЬ/.е i!apMOHUKU.
408
Коэффициенты а п и Ь п MorYT вычисляться в этом слу-
чае по формулам (13-9) и (13-10).
Раскладывая периодическую несинусоидальную функ-
цию в ряд Фурье, следует предварительно выяснить, не
обладает ли заданная функция каким-либо видом симмет-
рии. Наличие симметрии позволяет заранее предсказать,
каких rармоник следует ожидать в разложении.
Если одновременно выполняются условия симметрии
по пп. 1 и 3, то в разложении содержатся только нечетные
косинусоиды, если по пп. 2 и 3, то содержатся только
нечетные синусоиды.
Допустим, что функция, содержащая только нечетные
косинусоиды, удовлетворяет, кроме Toro, условию f (а) ==
==
f (л
а). Так как при нечетных n cosna ==
==
cos п (л
а), то в этом случае для определения ко-
эффициентов а п достаточно пользоваться кривой f (а) за
четверть пер иода:
111
2'
а п ==
f(a)cOSпada.
в свою очередь если функция, содержащая только не-
четные синусоиды, удовлетворяет условиюf (а) == f (л
а),
то ввиду Toro что при нечетных п sin па == siп п (л
а) и
в этом случае для определения коэффициентов Ь п доста-
точно пользоваться кривой f (а) за четверть периода:
( 13-9а)
те
2
Ь п ==
Sf (а) sin па da.
о
Виды симметрии зависяТ от выбора начала отсчета.
Если начало отсчета может быть выбрано произвольно, то
целесообразно выбрать ero так, чтобы получить наиболь-
шую симметрию.
Данные о коэффициентах ряда Фурье, относящиеся к
разобранным выше случаям симметрии, сведены в табл. 13-1.
Пример 13-1. Требуется разложить в ряд Фурье nилообрllЗНУЮ
ФУНКЦИЮ, nоказаииую на рис. 13.6. Эта функция удовлетворяет УСЛОВИЮ
(l3-10a)
а
f(a)==I
при 0<а<2л:.
л:
Задаиная функция является нечетной, поэтому в разложении в ряд
отсутствуют постоянная состаВЛЯЮЩая н косинусои.llЫ; на основа-
409
....
.....
::<-
:::!
":
\с>
Q;)
ОА
0&
с;
Q.,
:11
!-о
=
4j
=
:::f
i
-&
'"
Q
:о:
=
=
=
Q.,
!-о
4j
=
...
=
IC
Q
410
:о
..
'"
"
'"
::;
'"
.е-
.е-
"
б
::<;'
"
'"
'>
u
:>.
"
б
:<:
u
"
..
'"
..
'"
::!
"
..
g
,Q
'>
"
..
=:
u
б
=:
S
'"
=:
'"
..
=:
U
i;"
1:
с:
""
с:
'"
Q
'"
=
"<;:
:>,
::r::
,.Q
!-о
U
tIJ
,.Q
!-о
U
tIJ
=
<;:
:>,
::r::
...
.а
!-о
u
tIJ
.а
;>,
::r::
.......
tI
1
........
11
:[
........
-g-
1
........
t
I
11
........
а
:о:
:r:
1:':
'"
:r:
t
.z.
1:':
'"
:r:
!-о
о)
:>'
о)
.3
f-<
'"
:r:
=
о..
О
=
О
!-о
'"
:r:
=
о..
о
O
:':1:':
=
",:::f
@
::r::
<:-:1
с:>
:':0)
.а ::а
3 :r:
i:--
.Q :>'
!-о о)
'-':>::
tIJ
о
:.:
.a
-"::>::
!-o
Q)
[;
'-':>::
tIJ
.а
о:;
:>,
::r::
?
+
з..
........
I
11
........
=
=
:r:
о)
:;;
о
u<n
О
=
0..=
o..
Q)
ti
=0:;
:::fO
'" :><
:>,
5
о
=
:>,
::r::
о
:0:0)
:a
;:
о)
Z
'-':>::
tIJ
.а
::r::
?
+
з..
........
I
\\
-g-
1
ч--.
1\
:[
ч--.
с:>
:r:
==
о)
:2
о)
о..
о
:r:
о
=
=:
'"
:>'
:>,
о:;
u
о
:':Q)
.а :а,
3 :r:
!-o
"':>::
tIJ
=
:>,
::r::
,.Q
о::
:>,
::r::
?
+
з..
........
I
11
-g-
1
........
I
11
ч--.
о
:r:
:r:
о)
:2
о)
о..
<:Q
О
:r:
о
=
<:-:1
=
'"
:>'
:>,
о:;
u
'=1'
LC)
Q
8
'>
:>.
'"
о
'"
gj
""
'"
о
=:
""
"
r::
'"
'"
=:
е
:<:
.е-
"
=:
'"
"
..
'"
11;
"
'"
1!i
"
'"
u
'"
о
:<:
,;
'"
..
:>.
'>
u
р
u
'"
..
r:Q
нии (13-10)
:rc
Ь п ==! \ ( 1
.::.. ) sin па da == 2...
л j л nл
о
Следовательно,
f
)
.! ( sin rt + sin 2rt + sin 3rt + )
,rt
Л 1 2 3 ... .
в точках rt == О, 2:n:, 4:n: ... сумма ряда равна нулю, т. е. среднему
арифметическому левоrо и правоrо предельных значений функции f (л).
f(
)
Рис. 13-6. Пример 13-1.
Рис, 13-7, Пример 13-2,
Пример 13-2. Требуется разложи'FЬ в ряд Фурье знакопеременную
прямоуrольную функцию, показанную на рис. 13-7. Эта функция удов,
летворяет условиям
f(rt)== { 1 при О<а<:n:;
1 при л <а < 2:n:.
Заданная функция нечетна и, кроме Toro, симметрична относительно
оси абсцисс при совмещении полупериодов. Поэтому в разложении в ряд
отсутствуют постоянная составляющая, все косинусоиды и четные си-
Hycoиды. Кроме тoro, выполняется условие f (а) == f (л
а). Поэтому
для определения коэффициентов Ьп. воспользуемся формулой (13
lOa):
:rt
2
Ь п ==
\ siп nrt drt == ..!.. ,
л j n:n:
о
rде п
нечетно, отсюда
f ( ) == i. ( Sin rt siп 3а + sin 5rt + )
а :n: 1 + 3 5 '" .
0.3. ПЕРЕНОС НАЧАЛА ОТСЧЕТА
Положим, что для некоторой периодической несину-
саидальной функции f (а) коэффициенты а п и Ь п являются
заданными, т. е. известно разложение данной функции
в ряд Фурье:
00
f (а) ==
!!. + 1: (а п cos па + Ь п siп па).
п
1
411
Если сместить начало отсчета на некоторый отрезок
вправо или влево относительно исходноrо начала коорди
нат, то разложение в ряд Фурье относительно новой коор-
динатной системы будет получено заменой а на аl +
,
rде аl
абсцисса в новой системе координат; положи-
тельное значение
соответствует смещению HOBoro начала
отсчета вправо, а отрицательное
влево. Итак,
00
f(al+
)==fl(al)==
O + ! [anCOsп(al+
)+
n "'" 1
+Ь n siпп(а 1 +Ю]. (13-11)
Эта формула позволяет быстро находить разложение
в ряд Фурье функции, если известны коэффициенц,I ряда.
ypьe для друrой функции,
1 f!(щ) получаемой в результате сме-
щения первой по оси абсцисс
на постоянное значение.
Рис. 13
8. Пример 13-3.
Пример 13
3. Требуется найти
разложение в ряд Фурье функции,
изображенной на рис. 13-8, исполь-
зовав результаты примера 13-2.
Функция на рис. 13-8 получает-
ся при переносе начала координат
на отрезок
== 1[/2. Следовательно,
на рис. 13-7 (точка О) вправо
в соответствии с (13
1l)
4 [ sin ( rч +
) sin 3 ( Щ +
)
12 ((Z1) ==;т: 1 + 3 +
+ sin 5 ( (Z1 +
) + ] == i ( cos (Zi
cos 3(Zi cos 5(Z1
)
5 ... 1[ \ 1 3 + 5 ... .
0-4. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ
Триrонометрическая форма ряда Фурье может быть
преобразована в комплексную следующим образом. Исходя
из Toro, что
e Jncx + e
Jncx
cos па =::: 2 ;
sin па
412
e Jncx
e
Jncx
2!
выражение, заключенное в скобки в формуле (13-4), при-
водится к виду
Ь . a n
J 'b n . N a n+J 'b n '
а n cos па + n sш па == 2 eJn
+ 2 e
Jncx
и ряд (13-4) записывается следующим образом:
со
f(a) ==
O + ! ( an
jbn ejncx+ antjbn e
jna).
п
l
На основании (13-5) и (13-6) а п четная, а Ь п нечетная
функция относительно п, т. е. а п сохраняет свой знак при
отрицательных значениях п, а Ь п меняет ero:
а п ==a
п, Ь п ==
b
п'
Поэтому с учетом Toro, что
ао
( ап
jb n ;па )
2'
e n
O'
00
f (а) ==
O + ! an--;jb n e jna +
Ii
1
oo 00
+ ! an
jbn ejncx== ! an
jbn e ina .
п
l
co
Таким образом, ряд Фурье в ком,nлеКС1-tОй форме имеет
вид:
00
1
.
f (а) == 2' """ Fne jnCX ,
(13-12)
co
rде комплексный коэффициент (комплексная амплитуда)!
соrласно (13-5) и (13-6)
2
Р п == а п
jb n =r=
f (а) e....jncx da
о
(п == О, + 1, + 2 . ..).
(13-13)
1 Применявшаяся ранее для преДСТ8:влення синусоидальной функ-
ции комплексная амплитуда, например и т. связана с введенным з,!{есь
одноименным понятнем соотношением
1т [UmeJ(йI] ==
} [F 1 е JФ ! +АеiФ!],
откуда следует:
Re [
jUmeJUJ!]==Re [l\е М !] и Um==jFf.
413
Как указывалось выше, а == ffit; следовательно, ряд
(13-12) содержит два бесконечных ряда сопряженных отно-
+ . 2я сительно действительной
/
ш=пт оси векторов, вращаю-
2Рп" щихся в противополож-
" + ные стороны с уrловыми
скоростями пш. reoMeT-
рическая сумма каждой
пары сопряженных веК-
торов дает только дей-
О ствительное значение
(рис. 13-9). В результате
Р п
т
2Я
n
nш
Рис. 13
9. Синусоидальная
функция как сумма двух
сопряженных векторов, вра-
щающихся -в противополож-
ных направлениях.
t
суммирования двух бесконечных рядов сопряженных век-
торов получается действительная функция f (ffit).
13-$. ПРИМЕНЕНИЕ РЯДА ФУРЬЕ R РАСЧЕТУ ПЕРИОДИЧЕскоrо
НЕСИНУСОИДАпьноrо ПРОЦЕССА
Пусть требуется найти ток в электрической цепи под
воздействием периодической несинусоидальНОЙ э. д. с.
со
е (t)==Ео+
Епт(siппffit+'Фп).
п
1
Здесь индексом т обозначеныI амплитуды rармоник.
Если цепь линейна, т. е. параметры r, L, М и С неиз-
менны, то ток в цепи находится методом наложения, путем
суммирования токов, создаваемых каждой из слаrающих
э. д. с. в отдельности:
00
i(t)==Io+
Iпmsin(пffit+'I'п
qJп),
п
l
(13-14)
rде
1
ь-.. 1
Е пт
o
z(O)' I пm
z(п(j))'
Под Z (О) подразумевается сопротивление n:епи при
частоте, равной нулю, т. е. сопротивление постоянному
току; z (пш)
полное сопротивление при частоте пФ.
414
Уrол ЧJп определяется как apKTaHreHc отношения реак-
тивноrо сопротивления цепи к ее активному сопротивлению
при частоте пф.
В случае, Korдa цепь состоит из последовательно соеди-
ненных элементов. r, L и С,
,(' ( 1 '2
Z (пф) == V r 2 + nФL
пшС ) .
1
nwL
пшС
ЧJп == arctg
r
При этом z (О) == 00, так как цепь для Постоянноrо тока
разомкнута.
По мере повышения номера rармоники, т. е. с увели-
чением частоты пФ, индуктивное сопротивление nФL растет
по закону прямой линии, а емкостное сопротивление 1/nФС
убывает по закону rиперболы. Поэтому в цепи, состоящей
из последовательно соединенных r и L, rармоники тока
выражены слабее, чем В э. д. с. источника. В отличие от
этоrо высшие rармоники тока в цепи, состоящей из r и С
MoryT достиrать больших значений.
В смешанной индуктивно-емкостной цепи при nФL
1 О u
пшС == наступает явление резонанса для n-И rapMo-
ники.
В общем случае цепи, состоящей из элементов r, L и С,
как реактивное, так и активное сопротивления являются
функциями частоты пф (см., например,
3-3).
Периоды различных rармоник обратно пропорциональны
номеру rармоники. Поэтому если по оси абсцисс отклады-
вается не время t, а уrол СХ п == nФt == тх, то уrлу tX основ-
ной rармоники соответствует на той же абсциссе уrол ntX
для n-й rармоники (рис. 13-10).
Расчет периодических несинусоидальных токов и на-
пряжений в разветвленных электрических цепях ведется,
как правило, В комплексной форме.
Если периодическая несинусоидальная э. д. с. задана
в триrонометрической форме ряда Фурье Вида (13-8), то
э. д. С. и ток MorYT быть представлены так:
00
e(t)==Eo+
1т (Ёпmеiп(J)!);
п
l
00
i (t) == 1 о +
1т (i nтejn(J)!).
п
1
415
rдe
. j1jJ .
Е пт =: Епте п,
1 1 j ( 1jJ
!p )
пт == пте п п.
Следовательно, комплексная форма расчета периоди-
ческоrо несинусоидальноrо тока заК?Iючается в нахожде-
нии комплексных амплитуд токов 1 пт, соответствуюI.ЦИХ
ОСНDВНа.я
,а.рмонцка.
t
n:
для
Ц ,-а.рмонини
2к
длл
й. еармонцни:
2к
qЛR 1
11 'армонцкц
Рис. 13-10. Соотношение масштабов уrлов
для разных rармоник.
заданным комплексным амплитудам э. д. С. Е пт , для раз-
ных значений п. При этом, ввиду Toro что отдельные ела-
rающие имеют неодинаковые частоты, не складываются
непосредственно комплексные амплитуды, а суммируются
проеКЩ1И векторов, вращающихся с разными уrловыми
скоростями пю, т. е. суммируются
MrHOBeHHble значения отдельных
rармоник.
Прнмер 13-4. Вычислить суммарный
С ТОК в схеме на рис. 13
11. Задано:
е (t) == 30 + 15 siп ш! + 20 siп 3ш! В;
ri.== 1 Ом; r)!==O,5 Ом; (j)L==:: 1 Ом;
lJ(j)C==9 Ом.
i{t) ,.
,
1
7'2
I.(t)
Рис. 13-11, Пример 13-4,
Искомый ток находится методом наложения, т. е, поочередным
вычислением постоянной слаrающей и rармоник тока с последующим
суммированием их.
Сопротивление постоянному току z (О) == '1 + '2 == 1,5 Ом, Посто-
яиная слаrающая тока
Ео 30
10== z (О) == l,5 == 20 А,
416
Комплексное Сопроtивление цепи для ОСНОВной частотЫ
Z иш)
1,63 + j1 ,09 Ом.
Комплексная амплитуда тока основной частоты
, 15
Jlm
1 63+'1 69
7,65 L
33,60 А.
, J,
Комплексное сопротивление цепи для утроеНной частоты
(r 2 +j3юL) (
j 3 1с )
Z(j3{i)==rl+ ( 1Ш) ==19
j3 Ом.
r 2 + j 3u:JL
3шС
Комплексная амплитуда тока третьей rармоники
20
l зm == 19
j3 == 1,04 L 8,90 А.
MrHoBeHHoe значение cYMMapHoro тока
i (t) == 20+ 7,65 sin ({i)t
33,60) + 1,04 sin (3ы! + 8,90) А.
в заключение следует отметить, что в простых СЛУ'lаях установив-
шийся периодический ток может быть получен не только в виде суммы
rармоник, но и в более удобной форме аналитическоrо выражения,
справедливоrо для определенноrо интервала времени (например, полу-
периода). Для Э1'оrо интервала заПисывается дифференциальное ypaB
нение для тока, которое решается так называемым классическим мето-
дом (см. rл, 14) или с помощью преобразования Лапласа (rл. 15). ПО-
лученное решение включает в себя неизвестное начальное значение
тока, которое затем находят из условия периодичности.
Рассмотрим простой прнмер. Пусть в цепи последовательно соеди
ненных , и L действует периодическая знакопеременная э. д. с. TaKoro
вида, как изображено на рис. 13-7. Тоrда для первоrо полупериода
справедливо уравнение ri + L di/dt == Е, решение KOToporo имеет вид
Е
.!.....t
i == ....... + Ае L. При t == О, i == i (О), следовательио, А == i (О)
,
Е Т1'
. l\ривая тока, так же как и кривая э. д. с., будет симметрична
,
относительно оси времени и не будет иметь скачков блаrодаря индук-
тивному характеру цепи. Поэтому i (
) ==
i (О). Это дает:
,Т
i (
) == ; + [i (О)
] е
2L ==
i (О).
Отсюда находится i (О)
i ( О )
Е (e
a
1)
, (era+ 1) t
rде а == ,T/2L.
417
Подставив это в выражение для тока, получим окончательно для
nepBoro полупериода (о < t <
) :
Е ( 2
t )
i==
1
e L .
, 1 + e
a
Во втором полу периоде кривая тока будет иметь тот же вид, но
противоположный знак.
Итак, периодическая несинусоидальная функция представляется
не только в виде ряда Фурье, но и в замкнутой форме, т. е. в виде ана-
литическоrо выражения с конечным числом слаrаемых, справедливоrо
для выбранноrо интервала времени. Друrой метод решения в замкнутой
форме описан в
15
12.
13-6. ДЕЙСТВУЮЩЕЕ И СРЕДНЕЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОЙ
НЕСJ04НУСОИДАПЬНОЙ ФУНКЦИИ
Д е й с т в у ю щ е е з н а ч е н и е пер иодической Не-
синусоидальной функции f (t) определяется по формуле
(см. Э 2-3)
F == V
f2 и) dt.
о
Если функция задаНа в виде (13-8), то после возведения
ее в квадрат интеrрал под знаком. корня разложится на
ряд интеrралов, дающих в результате сумму квадрата
постоянной слаrающей (a o /2)2, и средних значений квадра-
тов отдельных rармоник (которые соrласно Э 2-3 равны
F2 n I2), средние же значения удвоенных произведений rap-
моник разных порядков или произведений постоянной
слаrающей на отдельные rармоники будут равны нулю.
Следовательно, действующее значение периодической
несинусоидальной функции выражается формулой
р== {(
Y + i
h .
n
l
Поскольку F n
амплитуда пой rармоники, F пlV2
действующее значение rармоники. Таким образом, полу-
ченное выражение показывает, что действующее значение
периодической несинусоидальной функции равно корню
квадратному из суммы квадраnwв действующих значений
zapMOHUК и квадрата постоянной слazаюШf!Й.
418
Отсюда следует, что действующее значение функции,
представляющее собой сумму rармоник разных частот,
не зависит от начальных фаз этих rармоник, а всецело
определяется их действующими значениями.
Например, если несинусоидальный ток выражается
формулой (13-14), то де йствующее зна чение тока равно:
1 == Vl
+li+I
+...
Действующее значение периодической несинусоидаль-
ной функции может быть измерено, так же как и при си-
нусоидальных токах, с помощью электроизмерительноrо
прибора электромаrнитной, электродинамической, тепло-
вой или друrих систем.
Наряду с понятием действующеrо значения периоди-
ческой несинусоидальной функции в электротехнике и ра-
диотехнике пользуются понятием с р е Д н е r о з н а ч е -
н и я Ф у н к ц и и, взятоrо по абсолютному значению;
последнее в соответствии с
2-3 выражается интеrралом
вида
т
i
1 f (t) I dt.
о
Этот интеrрал равен среднему значению функции f (t)
за положитедьный ПО.'1упериод, если f (t) имеет одинаковые
положительную и отрицательную полуволны:
т
т
2
Рср ==i
I f (t) I dt ==} 5 f (t) dt.
о о
Среднее значение функции за полупериод измеряется
с помощью маrнитоэлектрическоrо прибора с выпрямите-
лем (маrнитоэлектрический прибор без выпрямителя изме-
ряет постоянную слаrаЮЩУI9).
13-7. МОЩНОСТЬ В ЦЕПИ ПЕРИОДИЧЕскоrо
НЕСИНУСОИДАльноrо ТОКА
В соответствии с (2-26) активная мощность равна сред-
нему значению мощности:
т
1
' .
Р == т J ш dt.
о
419
Если вместо и и i подставить их выражения через три-
rонометрический ряд вида (13
8), то интеrрал разложится
на ряд интеrралов, дающих в результате сумму произве-
дения постоянных слаrающих напряжения и тока и сред-
них значений произведений rармоник напряжения и тока
одноrо и Toro ,же порядка. Остальные интеrралы будут
равны нулю, так как они представляют собой средние зна-
чения произведений rармоник разных порядков или про-
изведений постоянной слаrающей на отдеЛьНые rармоники.
Итак,
со
Р ==: и 01 о +
U пl п COS qJп,
п
l
(13-15)
т. е, активная мощность периодuческоС?о несинусоuдальноzо
тока рщзна сумме активных мощностей отдельных еармо-
ник плюс мощность пОСf1WЯННblХ СЛG2ающих.
ИIiаче rоворя, активная мощность от взаимодействия
разноименных rармоник напряжений и токов или взаимо-
действия rармоник с постоянными слаrающими равна Нулю.
По аналоrии с понятием реактивной мощности для
синусоидальных функций может быть введено понятие
р е а к т и в н о й м о Щ н о с т и в цепи с периодическими
несинусоидальными величинами. Она определяется как
сумма реактивных мощностей отдельных rармоник.
Содержание в одной из кривых (напряжения или тока)
rармоник, отсутствующих В друrой кривой, не отражается
на величинах активной и реактивной мощностей, но повы-
шает действующее значение той функции, которая содер-
жит эти rармоники. Поэтому, если п о л н у ю м о Щ н о с ть
В рассматриваемой цепи определять как произведение дей-
ствующих напряжения и тока S === и 1, то на основании
сказанноrо можно заключить, что в отличие от синусоидаль-
Horo режима сумма квадратов активной и реактивной мощ-
ностей в цепи с периодическими несинусоидальными вели-
чинами не равна квадрату полной мощности:
р2 + Q2 == S2
Т2.
Величина Т носит название м о Щ н о с т и и с к а ж е -
н и я; ОНа характеризует степень различия в формах кри-
вых напряжения и и тока i. Если сопротивление цепи
активное, то кривые напряжения и тока подобны; при
этом Q == о и Т == О.
420
Пример 13
5. Вычислить активную мощность, поступающую в цепь
в примере 13.4.
е (t) == 30 + 15 siп wt + 20 siп 3wt;
i (t) == 20 + 7 ,65 sin (wt
33,60) + 1,04 sin (3wt+ 8, 90).
На основании (13-15)
р == 30.20 +
5 .; ,65 cos 33036' + 20.; ,04 cos 8054' == 600 + 47,9 +
+ 10,2==658,1 Вт.
13.8. КОЭФФИЦИЕНТЫ, ХАРАКТЕРИЗУЮЩИЕ ПЕРИОДИЧЕСКИЕ
НЕСИНУСОИДАЛЬНЫЕ ФУНКЦИИ
По аналоrии с синусоидальными функциями отношение
активной мощности qри несинусоидальных токах к полной
мощности называется к о э Ф Ф и ц и е н т о м м о Щ н о -
с т и и обозначается х:
т
f ui dt
р б
х ==сТТ == l /{ и2 dt .f iZ dt
о о
(13
16)
Отношение в правой части (13
16) обращается в единицу
только при наличии прямой пропорциональности между
u и i.
Положим, что напряжение синусоидально, а ток неси
нусоидален. В этом случае активная мощность в соответ-
ствии с (13-15) определяется мощностью первой rармоники:
р == UJ./1 COS!jJ1 == и/ 1 COS !jJ1'
При этом действу ющее значение т ока
1 == VI8+Il+/2+'" > 11'
Следовательно, коэффициент мощности
U /1 cos !J1i /1 k
х== И/ ==
TCOS!jJ1== иСОS!jJ1'
/
М н о ж и т е л ь k и == + < 1 называется к о э Ф Ф и -
ц и е н т о м и с к а ж е н и я.
В радиотехнике и электротехнике пользуются также
коэффициентами формы кривой (k ф ) и амплитуды (k a ).
К о э Ф Ф и ц и е н т фор м ы кривой определяется
как отношение деЙствующеrо значения функции к среднему,
421
взятому по абсолютному знач ению,
V
f2 (/) dt
о
т
S [! (t) [ dt
о
k ф ==
Для синусоиды
:rt
k Ф == 2V2
1,11.
К о э Ф Ф и n и е н т а м п л и т у Д ы определяется как
отношение максимальноrо значения функции к действую-
щему значению ее:
ka ==
'т
V
s f2 (t) dt
о
Для синусоиды
ka == 112
1 ,41.
Несинусоидальные кривые напряжения и тока заменя-
ются в ряде случаев э к в и в а л е н т н ы м и с и н у .
с о и Д а м и. Замена производится таким образом, что
действующие значения синусоидальных функций прини-
маются равными действующим значениям несинусоидаль-
ных функций, а уrол сдвиrа фаз между эквивалентными
синусоидами принимается равным уrлу arccosx, rде Х опре-
д.еляется из (13-16).
13-9. ВЫСШИЕ r АРМОНИКИ в ТРЕХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ
ЦЕПЯХ
При установившемся режиме в симметричных трехфаз-
ных электрических цепях кривые напряжения и тока во
второй и третьей фазах аналоrичны кривой напряжения
и тока первой фазы со сдвиrом на треть периода. Так, на.
пример, если напряжение иА (t) в фазе А выражается
функцией
00
иА ==
и nт sin (пffit + 'Ч'n),
n
1
422
то
00
ив== 2: UптSiп[пф(t
- ; )+'i'n];
п
l
00
ис==
UптSiп[пф(t+ ; )+'i'n]o
п
l _
rармоники ПОРЯДка, KpaTHoro 3 (п == 3, 6, 9, ...), во
всех фазах тождественны, так как
sin [пФ (t
; )+'i'n] == sin [пФ (t + ; ) + "'п] ==
== S i 11 [пфt + "'n].
Поэтому они образуют систему напряжений нулевой
последовательности.
rармоники Порядка п == 3k + 1, rде k
любое целое
число, т. е. при п === 1,4,7, 10, 13 и т. д., образуют симмет-
ричную систему напряжений прямой последовательности,
,так как при этом:
sin [ пФ (t
)+'Рn] == sin [ пфt
2; + "'п];
Siп[пф(t+ ; ) + "'n] === Siп[пфt+ 2 з л +'i'n]
и, следовательно, поя rармоника в фазе В отстает от пой
rармоники в фазе А на 1200, а в фазе С опережает ее на 120".
Наконец, rармоники при п === 3k
l, rде k
любое це-
лое число, т. е. при п === 2,5,8, 11, 14 и т. д., образуют
симметричную систему Напряжений обратной последова-
тельности, так как при этом:
sin [пФ (t
; ) + "'n] == sin[ пфt +
Л + "'п];
sin [пФ (t + ; ) + 'Рn] == sin [пфt
2 з л + "'n]
и, следовательно, поя rармоника в фазе В опережает пою
rармонику в фазе А на 1200, а в фазе С отстает от нее На
1200. Все эти случаи весьма наrлядно представляются на
векторных диаrраММах, построенных для каждой чаСТОТЫ
в отдельности.
В практически встречающихся случаях постоянная со-
ставляющая и четные rармоники обычно отсутствуют, и
423
поэтому в дальнейшем можно оrраничиться рассмотрением
только нечетных rармоник.
При соединении источника электроэнерrИ1СИ наrрузки
звездой с нейтральным проводом в последнем в соответ-
ствиис изложенным выше протекает ток, равный сумме
всех rаРМОIIИК с порядковым номером, кратным 3:
i N == i A + i n + ic == 31зm sil1 (3rot
<rз)+
+ 3/ 9т SiIl (9rot
'CP9) + . . .
Действующее значение этоrо тока определится соrлаСНQ
13-6:
1 N == 3 У 15 + 1
+ ...
. При отсутствии нейтральноrо провода токи в фазах не
содержат rармоник ПОрЯДКа, KpaTHoro 3.
В линейных напряжениях, равных разностям фазных
напряжениЙ, будут ОТСУТСТВОЕаТЬ rа'рмоНики c
порядковым
номером, кратным 3. .
Ввиду отсутствия в линейных напряжениях rармоник
порядка, l{paTHoro 3, отношение действующеrо линейноrо
напряжения к действующему фазному напряжению при
несинусоидальных напряже ниях получа ется меньше УЗ:
U J1 ==УЗ УUf+Щ+ ...;
Uф'==УUi+U
+U
+ ...
Если фазы reHepaTopa соединены треуrольником, 1'0
во внешней цепи rармоники ПОрЯДКа, KpaTHoro 3, отсут-
ствуют; Б обмотках же [енераторов, соединенных треуrоль-
ником, действует э. д. с., равная утроенной сумме высших
rрамоник, кратным 3. Однако она полностью уравновеши-
вается падением напряжения В контуре треуrОЛЬНИка от
токов этиХ rармоник. Поэтому rармоники, порядок которых
кратен 3, отсутствуют не толькО в линейныХ токах и напря-
жениях, но и в фазных напряжениях.
Разность потенциалов на выводах вторичной обмотки
трансформатора напряжения, соединенной разомкнутым
треуrольником (см. рис. 12-28,8), в случа:е несинусоидаль-
ных фазных напряжений равна:
иА + ив + ис == 3U зт sin (3rot + \jJз) + 3U 9т sil1 (9rot + 'Р9) + ...
Действующее значение этоrо напря жения
U ==3УЩ+U:+...
424
Поэтому даже при симметричной трехфазной электри-
ческой цепи возможно появление составляющих токов и
напряжений нулевой последовательности, обусловливае-
мых несинусоидальностью фазных э. д. с. reHepaTopoB.
13-10. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
'3
1. Разложить в триrонометрический ряд Фурье периодическую
функцию, получаемую при однополупериодном выпрямлеиии косину-
соиды:
t (t)
cos оо! при
п л:
.c2
<oot<2'
о т в е т:
1 ( Л 2 2 )
л ,1 +2
cos ооt+з
cos 2v)t
iK cos 4oot+.." .
13
2. Разложить в триrОllомеТРИ<lескиЙ ряд Фурье периодическую
функцию, получаемую при ДВУХllолупериодном выпрямлении косину-
соиДЫ.
О Т 8 е т:
2 ( 2 2 2 )
n 1 + 3
cos 2оо!
15 cos 4оо! + 35 cos 6оо!
... .
13
3. Разложить в триrонометрический ряд Фурье выпрямленное
трехфазное напряжение, изменяющееся по закону u == cos ш! в пределах
л: ' п
3 <oot<
3'
О т в е т:
3 V3 ( 1 2 cos 3оо!
2 cos 6ш! + 2 cos gwt
) '
2л + 8 35 80 '" .
13
4. В цепи, состоящей из индvктивности L == 5 r и емкости
С
10 мкФ, соединенных последовательно, действует э. д. с., полу-
ченная в результате двухполупериодноrо выпрямления косинусоидаль-
ной э. д. с. Параллельно емкости присоединено сопротивление ,
== 2000 Ом. Найти напряжение на сопротивлении, приняв w
377 рад/с.
о т в е т:
2
Е т [1 +0,0242 соэ (2oot
176°)
0,0012 cos (4ш!
178°) +.. .].
л:
13-5. Индуктивность lJ присоединена к источнику. Э. Д. С. кото-
poro задана кривой прямоуrольной формы вuда, показанноrо иа рис. 13
8.
Найти ток.
О т в е т:
оо1п ( sin (д!
&in Зw! + ;5 sin 5ш!
.. . ) .
425
13-6. Разложить в триrонометрическиЙ ряд Фурье функцию тре-
уrольной формы
f( ) '2
n
t ==
"it oot при
2 < ы' < 2;
2
3
f (t) ==л (
oot) при 2
< ф! < 2
'
О т в е т:
n
(sin ф'
sin 3оо! + 215 sin 5rot
...).
13-7. Сопоставив результаты двух предыдущих задач, поясниТь,
какова форма кривой тока в Задаче 13
5.
1 n л
Отв'ет: rt при
2<wt<2'
13-8. Вычислить действующее значеиие функции в задаче 13-2.
Ответ: 0,707.
13-9. Вычислить амплитуду n-й rармоники периодической функции,
симметричной относительно начала,координат. Наклоиная часть тра-
пеции на участке от а == О До а == аl выражается уравнением f (а) ==
а
== А
, rде А
высота трапеции. Сопоставить результаты вычисле-
al
ний по формулам (13-6) и (13
lOa).
О т в е т;
Ь n == 29
siпnщ(l
соsпл);
Лn--v.l
при четных n Ь п == о; при нечетных n
Ь 4А.
n==
sш naf.
nn аl
13
1 О. Вычислить мощности: активную, реактивную, полную и
мощность искажения, если
u == 141 sin oot + 11 sin (3оо' + 30") В;
i == 10,19 sin «(j)t
11,3°) +2 cos 3(j)t + siп 5ш' А.
О т в е т: Р == 709,5 Вт; Q == 123,8 вар (инд.); S == 738 В. А;
Т== 160,5 В.А.
13-11. НаЙти эквивалентные СЦНУСОIIДЫ напрнжения и тока, если
и== 156 siп (ш' + n/6) + 50 siп (3oot
/3) +2 sin (5Ф! +.тtj4);
i==31,1 sin (oot+25°)+5 sin 5oot.
О т в е т: 164 sin (ы' + 300); 31,55 sin (001 + 9,20).
13
12. Вычислить действующий несинусоидальный ток, если
мrновенный i == 5 + 10 sin oot
10 cos oot А.
О т в е т: 11,2 А.
13-13. Вычислить действующее несинусоидальное напряжение для
и == 10 sin 400t + 5 sin 800t + cos 12001.
О т в е т: 7,95 В,
426
t3
14. Вычислить действующий ток, соответствующий разности
двух несинусоидальных токов: i 1 == 5 + 4 cos (ш'
'Л/3) + 2 cos (2mt+
+ 'Л/6) и i z == 3
5 cos ш'
3 cos (2mt + 'Л/4) А.
О т в е т: 6,85 А. .
13-15. Сопротивление 50 Ом и емкость 50 мкФ, соединенные парал-
лельно, подключены к источнику Э. д. с. 50 + 100 sin (400t + 'Л/б) +
+ 50 sin (1200t
'Л/4) В ,с внутренним сопротивлением 30 1. 00 Ом.
Определить действующее напряженn:е на параллельных ветвях и сум-
марный ток.
О т в е т: 54 В; 1,62 А.
13-16. Сохранив условия предыдущей задачи, вычислить активную
мощность, расходуемую' в обоих сопротивлениях, и энерrию, запасен-
ную в емкости при t;;: О. .
О т в е т: 95,5 Вт, 0,01 Дж.
13
17. Вычислить напряжение u (t) в схеме рис. 13-11
(см. пример 13-4).
О т в е т: 10 + 9,64 sin (mt + 260 12') + 18,97 sin (3ш!
40 48')В.
13
18. Входное напряжение трансформатора (см. рис. 8
1l) и1 ==
== 20 + 100 sin 1000t + 40 sin 3000t В, выходные выводы замкнуты:
'1 == 20 Ом; L 1 == 15 Mr; '2 == 40 Ом; L 2 == 30 Mr; м == 20 Mr. Опре-
делить токи i 1 и i 2 . .
О Т В е т: i 1 == 1 + 3,54 sin (1000t
21010') + 1,09 sin (3ОООt
180 5'); i z == 1,42 sin (1000t + 320) + 0,665 sin (3000t + 60) А.
13
19. Зависит ли действующее значение несинусоидальной функ-
ции .от начальных фаз и частот отдельных rармоник?
13
20. Покаэать, что линейные напряжения трехфззиоrо reHepa
тора не содержат rармоник, кратных трем,
rЛАВАЧЕТЫРНАДЦАТАЯ
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ.
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА
14-1. ВОЗНИКНОВЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В предыдущих rлавах рассматривалисъ установившиеся
процессы в линейных электрических цепях, т. е. такие
процессы, при которых напряжения и токи либо неизменны
во времени (цепи постоянноrо тока), либо представляют
собой пеРиоАические функции времени (цепи переменноrо
тока).
Наступлению установившеrося процесса, отличноrо от
первоначальноrо режима работы цепи, предшествует, КаК
правило, пер е х о Д н ы й про Ц е с с, при котором
напряжения и токи изменяются непериодически.
Переход от ОДIIоrо режима работы цепи к друrому MO
жет быть вызван изменением парамеТРОБ или схемы цепи,
йазываемым в общем случае в электротехнике к о м м у т а -
ц и еЙ.
Можно теоретически считать, что коммутаЩlЯ цепи
ПРОИ3ВОДllТСЯ MrHoBeHHo, т. е, на включение, выключение
или переключение цепи время не расходуется. Тем не ме-
нее переход от исходноrо режима работы цепи к после-
дующему установившемуся процессу происходит не MrHo
венно, а в течение HCKoToporo времени. Объясняется это
тем, что каждому состоянию цепи соответствует опреде
ленный запас энерrии электрических и маrнитиых полей.
Переход к новому режиму связан с нарастанием или убы-
ванием энерrии этих полей. Энерrия WL == ии2, запа-
саемая в маrнитном поле индуктивности L, и энерrия
Wc == СиЫ2, запасаемая в электрическом поле емкости С,
не MorYT изменяться мrновеино: ЭlIерrиЯ может изменяТься
непрерывно, без скачков, так как в противном случае
мощность, равная производной энерrии по времени, ДОСТИ-
rала бы бесконечных значении, что фИЗИчески невозможно.
Именно поэтому, например, в случае размыкания ветви
с индуктивной катушкой в месте размыкания неизбежно
возникает искра, в сопротивлении которой расходуется
энерrия, накопленная в маrнитном поле индуктивной ка-
тушки. Аналоrично если замкнуть накоротко выводы кон-
денсатора, который был предварите.льно заряжен, то за-
пасенная в нем электрическая энерrия рассеется в COI1pO
тивлении соединяющеrо провода и между контактами.
Если исключить случаи размыкания индуктивности 11
замыкания накоротко емкости и рассматривать цепи, в ко-
торых энерrия, накапливаемая в маrнитном или электри-
ческом поле, может рассеиваться в виде теплоты в сопротив-
лениях, то, считая, что коммутация происходит мrновеино,
можно искрообразование не учитывать.
Для завершения переходноrо и наступления YCTaHO
вившеrося процессов теоретически требуется бесконечно
БОJIЬШое время. Практически, однако, время переходноrо
процесса определяется малым интервалом, по истечении
Koтoporo токи и напряжения настолько приближаются к
установившимся значениям, что разница оказывается прак-
тически неощутимой. Чем интенсивнее происходит рассея-
ние энерrии в сопротивлениях, тем быстрее протекает
переходныЙ процесс.
Если бы электрическая цепь состояла только из сопро-
тивлений и не содержала индуктивностей и емкостей, то
переход от одноrо установившеrося состояния к друrому
428
tовершался бы MrHoBeHHo, без затраты Времени. В реальных
элеIПРОlехнических устройствах тепловые потери, обуслов-
ленные током, маrнитные и электрические поля сопутствуют
друr друrу. Применяя специальные схемы и подбирая
соответствующие параметры цепи, можно в завнсимости
от необходимости ускорить или замедлить переходный
процесс.
В одних случаях переходные процессы в электр!
ческиХ
цепях нежелательны и опасны (например; при коротких
замыканиях в энерrетических системах). В друrих случаях
переходный процесс представляет собой естественный, Нор-
мальный режим работы цепи, как это, например, имеет место
в радиопередающих и радиоприемных устройствах, систе-
мах автоматическоrо реrулирования и друrих цепях.
Существуют раЗJlичные методы расчета переходных про-
цессов в линеИI;IЫХ электрических цепях. Настоящая rлава
посвящена к л а с с и ч е с к о м у м е т о д у решени я
дифференциальных уравнений, описывающих переХQдные
процессы,
14-2. ЗАКОНЫ КОММУТАЦИИ И НАЧАЛЫ'/ЫЕ УСЛОВИЯ
Высказанные выше положения о том, что запас энерrии
маrнитноrо или электрическоro поля может изменяться
только плавНО, без скачков, выражают npUl-щип непре-
рывности во времени потокосцепления индуктивности и
электрическосо заряда емкости и называются законами
коммутации.
Нейозможность скачкообразноro измеНения потоко-
сцепления следует из TOI'O, что в противном случае на
индуктивности появилось бы бесконечно большое напря-
жение UL == d'l' /dt == 00, что лишено физическоrо смысла.
Ввиду раnенства 'l' == Li ПРИНЦИП непрерывности потоко-
сцепления означает, что при неизменном L ток i не может
изМеняться скачком. Итак, в начальныii момент после КОМ-
мутации ток в индуктивности остается t1zаким же) каким
ОН был непосредственно перед коммутацией) а затем плG.8Нй
изменяется.
Аналоrично невозможность скачкообразноrо изменения
элекtрическоrо заряда q следует из Toro, что в противном
случае через емкость проходил бы. бесконечно большой
ток ic == dq/dt ....c
00, что также лишено физическоrо смысла.
Ввиду равенства q == СИе ПРИНЦИП непрерывности электри
ч
скоrо заряда означает, что при неизменном С Напрпже
429
ние ис не может изменяться СКачКОМ. Итак, в начальный
момент после КОМ.l1-утации напряжение на еШФСtШl оста-
ется таким же, каким оно было непосредственно перед KOM
мутацией, а затем плавна изменяется.
При этом следует отметить, что в цепях с идеализиро-
ванными сосредоточенными параметрами скачкообразно MO
rYT изменяться: 1) токи в сопротивлениях и емкостях и
2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емко-
сти в момент коммутации называются н е з а в и С, и мы -
м и н а ч а л ь н ы м и у с л о в и я м и.
Обычно принимают, что коммутация происходит в мо-
мент времени t == о; тоrда ток в индуктивности и напря-
жение на емкости в момент времени непосредственно перед
коммутацией обозначаются через iL (()........) и ис (()........), а в на-
чальный момент переходНоrо процесса после коммутации
через iL (О) и ис (О).
На основании законов коммутации:
iL(O
)==iL(O); } (14-1)
ис (o
) == ис (О).
Эти равенства выражают начальные условия цепи, в KO
торых происходит коммутация.
При нулевых начальных условиях, т. е. коrда i L (o
) == О
и ис (o
) == О, индуктивность в начальный момент после
коммутации равносильна разрыву цепи, а емкость равно-
сильна короткому замыканию.
В случае ненулевых начальных условий, т. е. коrда
i L (О) =1= О и ис (О) =1= О, индуктивность в первый момент
равносильна источнику тока iL (О), а емкость равносильна
источнику э. д. с. ис (о).
Независимые начальные условия характеризуют энер-
rию маrнитноrо н электрическоrо полей, запасенную к MO
менту коммутации, и для расчета переХОДНоrо процесса
обязательно требуется знание этих начальных условий
причем совершенно безразлично, каким образом эти усло-
вия в цепи были созданы.
При расчете переходных процессов в разветвленных
электрических цепях наряду с независимыми начальными
условиями используются так называемые з а в и с и м ы е
н а ч а л ь н ы е у с л о в и я, а именно: значения токов,
напряжений и их ПРОИЗБОДНЫХ В начальный момент вре-
мени (t == О), Методика вычисления зависимых начальных
условий и их использование в расчете описаны в
14
7.
430
До сих пор нами исключались. из рассмотрения случаи
коммутации, при которых неизбежно между контактами
возникает искра или дуrа. Один из таких случаев показан
на рис. 14
1, а. До коммутации ток проходит через индук
ТИВНОСТЬ L 1 и контакт, шунтир ующий индуктивность L 2 ;
ток в L 2 равен нулю. В Момент t == О контакт размыкается
и индуктивности L 1 И Lz оказываются включенными после
довательно; ток в них принудительно становится одинако
вым. Поскольку в момент коммутации ток в L 1 не изменя
ется, а ток в L 2 равен нулю, в силу первоrо закона Кирх-
rофа ток, должен замкнуться через дуrу, образовавшуюся
между контактами. Кроме Toro, если под L 2 подразумевать
реальную индуктивную катушку, то ток может частично
Электрц
'fecKC1.R
цепь
i,(o--)
"'1
; i;;J\ /"z
iJ:};
3лектDu.
Л)I
'1eCKaR "'119
цепь
;:,-t=О
qt(tr)l QI07
С, С: .
0.)
6)
Рис. 14
1. Случаи размыкания (а) или замыкания (6) при частичной
потере энерrии.
замкнуться и через межвитковую емкость. После быстроrо
поrасания дуrи токи в L 1 И L 2 уравниваются. Эта началь
ная стадия переходноrо процесса протекает столь быстро,
что ею практически можно пренебречь, считая, что токи
в L 1 И L 2 уравниваются MrHOBeHHO. Именно в этом смысле
можно условно rоворить о скачкообразном изменении токов
в индуктивностях, кот.орое предшествует исследуемому пере
ходному процессу в цепи. При этом для расчета переХОk
Horo процесса используется nринциn неnрерЫ8ности сум-
марною nоmoкосцеnления при коммутации, т. е. L 1 i (o
) ==
==, (L 1 + L 2 )i (О). Скачкообразное изменение токов и COOT
ветствующих ИМ потоков в L 1 И L 2 В момент коммутации
не сопряжено в данном случае с наведением бесконечно
большой суммарной э. д. с. самоиндукции, поскольку CYM
мар ное лотокосцепление не претерпевает скачкообразноrо
изменения. При НОВЫХ значениях токов в L 1 И L 2 маrнит
ная энерrия, запасенная в катушках, будет меньше энер
rии, запасенной в первой катушке до коммутации. Часть
энерrии превратится в тепло в искре, а также излу
чится.
431
Найденный таким образом ток i (О) в L 1 И 1-2 может
рассматриваться как независимое начальное условие для
расчета переходноrо процесса во всей цепи на рис. 14-1, а
после разрыва дуrи.
При коммутациях в цепях с емкостями при отсутствии
сопротивлений также возможны весьма быстрые перерас-
пределения зарядов, условно рассматриваемые как MrHo-
венные. В этом случае применим принцип непрерывности
суммарною заряда. Полученные при этом значения зарядов
и напряжений на отдельных емкостях используются в рас-
чете последующеrо переходноrо процесса как независимые
начальные условия.
Например, в случае схемы на рис. 14-1, б принцип не-
прерывности cYMMapHoro заряда до и после коммутации
выражается равенством
q1 (O
) + q2 (O
) == q1 (О) + q2 (О) == ис (О) (С 1 + C
).
При сделанном допущении в остальной электрической
цепи, соединенной с емкостями, Не возникает бесконечно
большоrо ТОЕ:а, так как суммарный заряд не изменяется
скачкообразно при t == О.
в процессе рассматриваемой коммутации энерrия эле кт-
рическоrо поля уменьшится, так как часть ее превратится
в тепло в очень малом сопротивлении проводника при
очень большом токе, а также сможет выделиться в искре
и излучиться.
14-3. УСТАНОВИВШИЯСЯ И СВО&ОДНЫЯ РЕЖИМЫ
В общем случае анализ переходноrо процесса в ли-
нейной цепи с сосредоточенными параметрами r, L, С и
М сводится к решению обыкновенных линейных неодно-
родных дифференциальных уравнениЙ, выражаюших за-
коны Кирхrофа. Эти уравнения представляют собой ли-
н
йную комбинацию напряжений, токов, их первых пре-
из водных и интеrралOl
по времеии.
Например, если какая-нибудь э. д. с. е (t) включается
в цепь, состоящую из последовательно соединенных r, L и С,
то интеrродифференциальное уравнение имеет вид:
ri+L
+
5 idt==e(t). (14-2)
Это уравнение после дифференцирования приводится
к неоднородному дифференциальному уравнению BТOpOro
432
пор ядка
d2i di i de
L dt2 + 'ат +
C ==
dt.
( 14-3)
Как известно, общий Иllтеrрал TaKoro
уравнения равен
сумме частноrо решения неоднородноrо уравнения и
общеrо решения однородноrо уравнения.
Частное решение выражает у С т а н о в и в ш и й с я
р е ж и м, задаваемый источником.
Расчеты установившихся токов рассмотрены в пре-
дыдущих rлавах. Нахождение частноrо решения в друrих,
более сложных случаях будет изложено в
14-7, а также
в 15-12.
Общее решение физически определяет поведение uепИ
при отсутствии внешних источников электрической энер-
rии и заданных начальных условиях. Функции, опреде-
ляемые общим решением, называются с в о б о д н Ы м и
составляющими (токов, Нdпряжений и пр.).
В случае, рассмотренном выше, однородное уравнение
имеет вид:
dZi di i
L(Тta+r dt + С==О
( 14-4)
и соответствующее ему характеристическое уравнение
1
L p 2+ rp + c ==0. (14-5)
Если корни характеристическоrо уравнения обозна-
чить через Рl и Pz, то общее решение запишется в виде:
i CB (t) =0= A 1 e ptt + A 2 e p2t , (14-6)
rде А 1 и А 2
постоянные интеrрирования, которые опре-
деляются из начальных условий (см.
14-7).
ПолныЙ переходный ток в цепи равен сумме уста но-
вившеrося и СБободноrо токов:
i (t)
iy (t) + i CB (t).
( 14- 7)
Аналоrично напряжение, заряд, маrнитный поток и
друrие функции на любом участке цепи в переходном ре-
жиме состоят из установившейся и свободной состав-
ляющих.
На основании законов коммутации (см.
14-2) можно
найти начальные независимые условия i L (О) И иС (О).
После этоrо можно написать соrласно (14-7):
i L (О)
iLy (О) + i LcB (О); ис (О) == ису (О) + иС СВ (О),
433
откуда
i LcB (О) == i L (О)
iLy(O); }
иС СВ (О) == иС (О)
ису (О).
Итак, начальные значения свободных функций i L
O) И
СВ
иС (О) определяются изменениями в момент коммутации
св
соответствующих установившихся функций.
В частном случае при нулевых начальных условиях:
i LcB (О) ==
i Ly (О); иС СВ (О) ==
ису (О).
В зависимости от порядка дифференциальных ypaB
нений, описывающих иссЛедуемые переходные процессы,
различают цепи перВоrо, BToporo и более BbIcoKoro порядков.
В цепях первоrо порядка накопление энерrии проис
ходит только в одном элементе, L или С в форме маrнитной
энерrии (в цепИ с индуктивностью, см.
14-4), или электри-
ческой энерrии (в цепи с емкостью, см.
14-5). Однокон-
турная цепь, содержащая элементы, в которых накапли-
вается энерrия обоих видов
маrнитная и электрическая,
представляет собой цепь BToporo порядка (цепь r, L, С
14-6). Разветвленные цепи MorYT быть более BbIcoKoro
порядка (см.
14-7).
( 14-8)
14.4. ПЕРЕХОДНЫй ПРОЦЕСС В ЦЕПИ " L
Положим, что в момент t == О цепь, состоящая из co
противления r и индуктивности L, включенных последова-
тельно, присоединяется К Ис-
точнику э. д. с. е (t) (рис. 14-2).
ДиффереНЦИiJ.Льное урав-
нение для времени t?'=: О за-
писывается в виде
. +L di
е==п -(j{'
еЮ ;-{ =0 l' L
Рис. 14-2. Включение цепи '. L.
Характеристическое уравнение имеет вид r + pL == О
,
и соответственно корень уравнения Рl ==
Т'
Отсюда свободный ток
.!.....I
i CB == Аер,l == Ае L
Переходный ток в цепи определится суммой установив-
шеrося и свободноrо токов:
.!.....I
i ==iy+Ae L .
( 14-9)
434
у становившийся ток может быть найден, если задана
э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь r, L постоянной э. д. с. Е;
2) короткое замыкание цепи r, L;
3) включение в цепь r, L синусоидальной э. д. с.
Eтsin «(iJt + 'Ф).
1. Включение в цепь r, L постоянной
э. д. с.
При включении в цепь r, L постоянной э. д. с. Е YCTa
новI1вшийся ток равен E'/r. Поэтому соrласно (14-9)
Е
.!..
t
i == r + Ае L . (I 4-1 О)
Постоянная интеrрирования А находится по Началь
ному условию
i (О) == i (O
) == О.
Е
ОТкуда А ==
.
,
Следовательно,
Е (
.!.
t )
i==r.I
e [. ==
== J (I
e
t/1:);
здесь 1 == Е /r
пре-
дельное значение, к ко-
торому стремится ток
i и) по мере неоrраниченноrо возрастания " называемое
у с т а н о в и в ш и м с я т о к о М.
В начальный момент t == О э. д. с. самоиндукции eL ==
di
==
L {[[ (О) ==
Е и полностью компенсируется э. д. с.
источника, так как ток' i (О) равен нулю.
С течением времени э. д. с. самоиндукции убывает,
а ток в цепи возрастает, асимптотически приближаясь
к установившемуся значению.
На рис. 14-3 показаны кривые установившеrося, сво-
бодноro и переходноrо токов; на том же рисунке изображена
Соrласно уравнению
(14-10) при t == О
Е
O==
+A,
,
i
1
t
I
Рис. 14
3. Установившийся, свободный
и переходный токи пр,И включении в
цепь '. L постоянной э. Д. с.
435
kривая напряжения наИНДУКТИВllОСТИ
di
'...
Щ == L dt == Ее 1;
Из курса математическоrо анализа известнО, что если
у == f и), то подкасательная равна 11
1. В данном случае
при любом значении t
I и
1 == I
1 ==1:.
I UL 'св
( 1 4- 1 1)
Величина
в р е м е 'н и.
-r == L/r носит название п о с т о я н н о Й
Постоянная времени измеряется в секундах:
, [
] ==
Ом. с == С.
, ОМ Ом
Выражение (14-11) показывает, что постоянная вре-
мени ерафически определяется длиной пьдкасательной к кри-
вой i CB или UL при любом значении t.
Нарастание тока происходит тем быстрее, чем меньше
постоянная времени и соответственно чем быстрее убывает
э. д. t. самоиндукции. Для различных моментов времени
ток в цеПи, выраженный в процентах конечноrо (установив-
шеrося) значения составляет:
(0=:.1: 21: 3.
+ 100%0=:.63,2 86,5 95,0
4т
5.
со
98,2
99,3
100
Следовательно, n.oстоянная времени цепи " L равна
промежутку времени, в течение котороео свободная состав-
ляющая тока убывает в е == 2,718 раза и сооrrюетсrrюенно
ток в этой цепи, включенной на n.oстоянное напряжение,
достиеает 63,2%' своею установившееося значения.
Как видно из рис. 14-3 и приведенной выше таблицы';
переходный процесс теоретически длится бесконечно долrо.
Практически же можно считать, что он заканчивается
спустя t == (4 -+- 5) -r.
2. К о Р о т к о е з а м ы к а ни е цеп и " L.
Положим, что цепь " L, присоединенная К ИСТОЧНИКу
постоянноrо или переменноrо напряжения, замыкается
при t ==.0 накоротко (рис. 14-4, а). В образовавшемся при
этом контуре " L блаrодаря наличИ:Ю маrнитноrо ПОЛя
и:ндуктивной катушки ток исчезает не MrHoBeHHo: Э. д. с.
самоиндукции, обусловленная уБЫМНliем маrНИТlIоrо пота-
436
ка, стремиТСЯ ПОДДер>кать ТОК в контуре за счет энерrии
исчезающеrо маrнитноrо поля.
По мере Toro как энерrия маrНИ'1'ноrо поля постепенно
рассеивается, превраща5lСЬ в сопротивлении r в тепло,
TOI{ в ко.нтуре приближается к нулю.
i)u./,
l' /., t
О
0.)
l'i(O)
б)
Рис. 14-4. Короткое замыкание цепи " L.
а
расчетная схема; б
кривая тока i и иапряжения, U L .
Процесс, происходящий 13 короткозамкнутом контуре
" L, является свободным; установившийся, ток в данном
случае равен нулю.
Положив в (14-9) iy == О, получим:
!".
!
i == Ае L .
Постоянная интеrрирования А нахоДИТСя из начальноrо
условия
i(O)==i(O
),
откуда
.!....!
!....
i(t)==i(O)e L ==i(O)e 1:;
здесь i (O
)
значение тока в индуктивности в момент,
непосредственно. предшествоваВШlIЙ короткому замыканию;
оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в корот-
козамкнутом контуре и кривая напряжения на индук-
тивности
UL == L
::=
ri (О) e
t/1:
в предположении, что i (О) > О.
437
Постоянная времени контура 't' == L/r может быть
найдена rрафически как подкасательная к кривой i (t)
(например-, в момент t == О).
Переходный процесс в короткозамкнутом контуре за-
канчивается теоретически при t == 00. За это время в соп-
ротивлении r выделяется в виде тепла энерrия
00 00
s ri 2 dt== r(i (0)]2 S e
2f.
t dt==
iiO)]2 ,
о о
т. е. вся энерrия, запасенная в маrнитном поле катушки
до коммутации.
Так же как и в предыдущем случае, переходный про-
цесс в короткозамкнутом контуре можно практически счи-
тать законченным спустя t == (4 ...;-. 5) т.
3. В к л ю ч е н и е в цеп ь r, L с и н у с о и Д а л ь -
н о й э. Д. с.
При включении в цепь r, L синусоидальной э. д. с.
е ::= Е т sin «(()t + 'Ф) установившиЙся ток будет:
i пр == I т sin «(()t + 'Ф
rp),
rде
Е roL
1
т т== arct g
.
т
.v,2+(roL)2 r 't' ,
На основании (14-9)
i == 1 т sin «(()t + 'ф
rp) + Ae
t/'t,
rде
1: == L;r.
Постоянная интеrрирования определяется по началь-
ному условию i (О) == i (O
) == О.
Следовательно, О == 1т sin (1.jJ
rp) + А, отКуда А ==
::::
/т sin (ф
({'). Поэтому искомый ток будет:
i == /m[sin «(()t+'Ф
rp)
sin ('Ф
({') e
t/'t].
На рис. 14-5, а изображены кривые i y , i CB и i. Начальные
ординаты iy (О), { СВ (О) одинаковы и противоположны по
знаку; поэтому ток в начальный момент равен Нулю. Сво-
бодный ток убывает по показательному закону. По исте-
чении времени t == 't' свободный ток умеНЬшается в е ==
== 2,718 раза по сравнению с начальным значением i CB (О).
Постоянная времени прямо пропорциональна добротности
438
контура Q и обратно пропорциональна частоте 0):
1: == ooL ==
t{ .
00, 00
Если в момент коммутации (t == О) ток i CB проходит
через нуль, т. е. выполняется условие 'Ф == ер или 'Ф ==
== ер + n, то свободный ток не возникает и в цепи сразу
наступает установившийся режим без переходноrо про-
цесса.
:rt
Если же коммутация происходит при 'ф
ер == + 2'
то начальный свободный ток максимален (рис. 14-5, 6),
i
i
ic, (О) =Im
t
i
ig
ig (0)=
Im
Рис. 14
5. Установившийся, свободный и переходный токи при вклю-
чении в цепь " [; синусщщальной э. д. С.
а именно i CB (О) == + 1 т, и ток переходноrо режима дости-
raeT экстремальноrо значения (положительноrо или от-
рицательноrо) в конце первоrо полуш€риода. Однако даже
в предельном случае, коrда r == О и, следовательно, 't' ==
L
== r == ею, ток не может преВЫШаТЬ амплитуды устано-
вившеrося режима более чем вдвое.
При достаточно большой постоянной времени .. === [/, первым
слаrаемым в правой части дифференциальноrо уравнения
. +L di
е === rt dF
можно пренебречь по сравнению со вторым слаrаемым, приняв при-
t
di 1 r
ближенно е""" L dt ' откуда i """ L J е dt и соответственно и r === ,i
о
t
, S -
<=:::::т edt.
о
439
Следовательно, цепь с последовательно соединенными сопротивле,
нием и индуктивностью при большой постоянной времени можно рас-
сматривать как и н т е r р н р у ю щ е е 3 в е н о.
В свою очередь при достаточно малой постоянноЙ времени, пре-
небреrая вторым слаrаемым уравнения, приближенно получаем:
е
ri
отдуда
di L de
U L """L{j[
, dt '
т. е. цель с последовательно соединенными сопротивлением и индуктив-
ностью при малой постоянной времени представляет собой д и Ф -
Ф е р е н ц и р у ю Щ е е 3 в е и о.
В обоих случаях функция е (t) может быть произвольноЙ.
Интеrрирующие и дифференцирующие звенья входят в Ka'IecTBe
Элементов в системы автоматическоro управления и реrулирования.
f4-S. ПЕРЕХОДНЫЯ ПРОЦЕСС В ЦЕПИ " С
Положим, что В момент t == О цепь, состоящая из соп-
ротивления r и емкости С, включенных последовательно,
присоединяется к источнику Э. д. с. е (t) (рис. 14-6).
На основании BToporo закона Кирхrофа уравнение Для
времени t?'=: О имеет вид:
e==rl+uc,
[де ис
напряжение на емкости.
du c
С учетом 1'oro, что 1::= С &' получим:
du c
е == ,С ------ёft + ис:
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение 1 + rCp == О и соот-
ветственно корень уравнения Pl ==
lJr-С. Следовательно,
(t) свободная слаrающая напря-
e :\ t::;O т'. С жения на емкости
...... о
]
ц;:r +"'
"С"
Ae
II'C
Ae
I
,
[де т == rC
постоянная вре-
мени контура r, С (измеряется
Рис. 14-6. Включение цепи " С. В секундах: [rC] == Ом. Ф ==
== Ом' А. с/В == с).
Переходное напряжение на емкости равно сумме при-
НужденНоrо и свободноrо напряжений:
Uc==ucy+Ae
t/'t. (14-12)
440
В свою очередь ток в контуре
. dи C du c А
t==C
==C
e
//'!;
dt dt , .
(14
13)
Рассмотрим fри случая:
1) включение в цепь r, С постоянной Э. д. с. Е.
2) короткое замыкание I1епи r, С
3) включение в цепь {, С синусоидальной э. д. с.
Е т sin (ш! + -ф).
1. Вкmoчение .. цепь r, С постоянноJi э. д. С.
Включим постоянную Э. д. с. Е в цепь с сопротивле-
нием r и предварительно заряженной емкостью С (поляр-
ности заряженной емкости указаны на рис. 14-6 знаками
+ и
); начальное напряжение на емкости ис (О) обозначим
для простоты через U.
ис ,i
ис, !
I
1
1'[' t
О
t
IJ
E
'т: l' 6)
а)
Ри('. 14-7. Ток и напряжение при включении в цепь " С постоянной
Э. Д. С.
Установившееся напряжение на емкости
источника. Поэтому соrласно (14-12)
ис == Е + Ae-//'t.
равно э. д. с.
Постоянная интеrрирования А, входящая в
находится по начальному условию:
При t == О имеем и == Е + А, откуда А == и
Е.
Следовательно,
(14-14)
(14-14),
ис == Е
(Е
И) e
//'t.
(14-15)
441
Соrласно (14-13) ток в контуре
. Е
u (/
==
e.. 'с.
,
(14-16)
Если Е> и, то с течением времени напряжение на
емкости возрастает, стремясь к установившемуся значе-
нию Е, а ток убывает, стремясь в пределе к нулю; на
рис. 14-7, а изображены кривые нарастания ис и спада i.
Чем больше постоянная времени, тем медленнее происхо
дят нарастание ис и спад i.
Если Е < и, то кривые и с и i имеют вид, показанный
на рис. 14-7, б.
Постоянная времени 't == ,С может быть найдена так
же, как раньше, rрафически как подкасательная к кри-
вой i в любой точке (например, при t == О).
Закон изменения напряжения на емкости li тока в дан-
ной цепи аналоrичен закону изменения тока и напряже-
ния UL в контуре " L, рассмотренном ранее. Поэтому все
сказанно
о постоянной времени в предыдущем случае
сохраняет силу для данноrо случая.
}, Короткое замыкание цепи r, С
Замыкание накоротко цепи, состоящей из последова-
тельно соединенных r и С, равносильно принятию в пре-
дыдущем случае 9. д. с., равной нулю. Предполаrается,
что емкость С заряжена, т. е. в момент включения H
вы.
водах имеется напряжение U.
Положив в (14-15) и (14-16) 9. д. с. Е равной нулю,
получим:
ис == Uc
t/'t;
i ==
/et/-r,
rде
и
1 ==
.
,
При коротком замыкании цепи " С электрический ток
идет от вывода + к выводу
Следовательно, при выбран-
ной на рис. 14-6 полярности емкости ток проходит через
сопротивление r в направлении, противоположном тому,
которое принято на рис. 14-6 за положительное. Поэтому
в выражении для тока стоит знак минус. На рис. 14-8
изображены кривые спада ис и i.
442
В отличие от напряжения на емкости, которое изме.
няется непрерывно, ток в контуре " С, пропорциональный
скорости изменения ис, совер-
шает при t == О скачок.
Энерrия, рассеиваемая в со- и
противлении r в течение Bcero
переходНоrо процесса, равна
энерrии, запасенной в электри-
ческом поле до коммутации:
5 "" И2 "" ,
СИ 2
ri 2 dt ==
е ТС dt ==
.
, . 2
о о
ис,1:
t
I
Так же как и в случае це-
пи " L, переходный процесс
может считаться законченным
спустя t == (4 + 5) 't', так как
к этому времени емкость разрядится на 98,2
99,3%
и напряжение на емкости снизится до 1 ,8
0, 7% первона-
чальноrо (см.
14-4, случай 1).
Рис. 14-8. ТОК и напряже-
ние при коротком замыкании
цепи " С.
Э. ВКПlOченне в цепь r, С CHHYCOHAanbHoji э. Д. С,
При включении в цепь " С синусоидальной э. д. С.
Е т sin (wt + 'Ф) установившееся напряжение на емкости
1 т . ( t . N )
ису== шС sш w +ф
ep
2' ,
rде
lm
V Е( 1 )"
arctg(
):
,2+ шС
на основании (14-12)
ис ==
cos (wt + 'Ф
ер) + Ae
t/'t.
Если предполаrать, что конденсатор не был заряжен,
то постоянная интеrрирования определится по начальному
условию ис (О) === о:
o==
'ё СОS('Ф
ер)+А,
отку да
1
А == ооС cos ('Ф
ер).
443
Тоrда искомое напряжение на емкости будет:
ис ==
::с [cos ((Ot+ 'IjJ
rp)
COS ('ф,
rp] e
tf't],
а ток в цепи
i == С d;
== 1т [sin ((Ot + 'ф
rp)
Ш
С cos (ЧJ
rp) e
t/'J
Из написанных выражений ВИДно, что если включение
цепи " С происходит в момент, коrда установившийся'
ток должен достиrать максимума
положительноrо или
отрицательноrо (т. е. 1\J
rp '=' + i) , а установившееся
напряжение на емкости должно быть равно нулю, то сво-
бодной слаrающей напряжения на емкости не возникает
. и в цепи сразу же без переходноrо процесса наступает
установившийся режим.
Так как цепь r, С по протеканию переходноrо процесса
подобна цепи r, L, то при соответствующем подборе пара-
метров r и С она также может
служить дифференцирующим
и интеrрирующим звеном.
i(ij ц' с
Рис. 14
9. Включение цепи "
L, С.
14.6. ПЕРЕХОДНЫЙ ПРОЦЕСС
В ЦЕПИ " L, С
При включении в цепь r,
L, С э. д. с. е (t) (рис. 14-9)
переходный процесс иссле-
дуется с помощью дифференциальноrо уравнения (14-3):
d'Ч di i de
L dt2 + rdi
+ с ==
Л'
Соответствующее ему характеристическое уравнение
( 14-5)
1
Lp2+ rp+
c== О
имеет корни
Pl'2==
{T + Y(
;{Y
l.
==
<'3
V <'32
(O
,
rде
, 1
<'3 == 2L ; (00 == VIё
резонансная частота.
444
(14-17)
Свободный ток соrласно (14
6) равен:
i CB == А 1 е Р ,! + А 2 е Р2! .
Ток в цепи определяется суммой установившеrося и
свободноrо токов:
i == iy+ А 1 е Р '! + A 2 e p2f . (14
18)
'Установившийся ток находится в соответствии с задан
ной э. д. с. е (t). Что касается свободноrо тока, то ero
характер зависит от знака подкоренноrо выражения (14-17).
1. ВКПlOченне в цепь r, L, С постоянной а, Д. С,
Рассмотрим сначала случай, коrда э. д. с. источника
постоянна: е == Е, и емкость имеет начальное напряжение
ис (О) === U.
Ввиду наличия индуктивности начальное значение тока
i (О) == О.
Исходное уравнение
Е . L di +
:=:; rt + (j[ ис
для начальноrо момента записывается Б виде
di
Е:=:; L (j[ (О) + ис (О),
u di ( О)
откуда находится начальное значение производнои d{ ,
которое является зависимым начальным условием, необ
ходимым для вычисления А 1 и А 2 :
(О) == Е
И . (14-19)
При установившемся режиме ток будет равен нулю,
что следует как из физическоrо смысла, так и из вида
праВОЙ части дифференциальноrо уравнения (14
3). Про-
дифференцировав (14-18) с учетом Toro, что i пр == О, по-
.rrучим:
di
А Р е р,! +А Р е р,!
dt
ll 22'
(14-20)
Подставляя в (14
18) и (14-20) t == О и используя (14
19),
получаем:
0== Al + А 2 ;
Е
И А А
== lРl + 2Р2'
445
Из этих уравнений следует:
А E
U
1 ==
А 2 ==
L (Р1
P2)
E
U
r
,
2L V 62
ю
поэтому
E
U
i == .' (ер,1
ep,t).
2L V 62
ю
(l4
21)
Рассмотрим возможные три случая.
. С л у н ай 1. б> шо, т. е. r> 2 y
(аперuoдuчесюuй
процесс) .
Р2
+ P1=P2=
6'
+
8)
+j
+'
J
о
о
а.}
5)
j (J)o
Рис. 14-10. Расположение корней характеристическоrо уравнения на
комплексной плоскости.
Соrласно (14-17) корни характеристическоrо уrавнения
Р1 и Р2
отрицательные действительные числа (рис. 14-1 О, а).
Если индекс .1 соответствует верхнему знаку перед корнем,
то I Рl I < I Р2 I и поэтому кривая еР'! спадает медленнее,
чем eP.t. На рис. 14-11 показана кривая i, построенная по
выражению (14
21).
При больших значениях С влияние eMKOcTl1 мало и кри-
вая тока приближается к кривой тока в цепи r, L (см.
рис. 14-3); при малых значениях L влияние индуктивности
незначительно и кривая тока близка к кривой тока в цепи r,
С (рис. 14
7).
Выражение (14-21) может быть преобразовано вrипер-
болическую форму
i == Е
U е бt sh V б2
Ш
t.
L V62
(j)
(14-22)
446
Следует заметить, что при коротком замыкании цепи
" L, С, т. е. при Е == О, ТОК В цепи обусловливается раз
рядом емкости.
С л у чай 2. {) == (00, т. е. '== 2 V
(критический
случай) .
Соrласно (14
17) корни характеристическоrо уравнения
одинаковы:
,
Р1 == Р2 ==
2L ==
б
(см. рис. 14
10, 6).
Выражение (14-21) приводит в этом случае к неопре
деленности ВИда 010.
Раскрьщая неопределенность по правилу Лопиталя
дифференцированием числителя и знаменателя по Р1, полу
чаем:
i== Нт
E
и (ep,t
ep2t)== E
и tе
бt.
р,
Р2 L (Рl
Р2) L
То же выражение получится, еCJfи воспользоваться об
щим решением однородноro дифференциальноrо уравнения.
с кратными корнями:
i CB == (В 1 + B 2 t) е
бt.
В рассматриваемом слу-
чае i CB (О) == В 1 == О И
d'
== в е-' бi
В tбе
бt
dt 2 2 .
i.,uc
Е
А 1
\
q
IJ.c=-ё-
i.tc8=At eP ,t
Следовательно,
di Е
U
dТ (О) ==B2==
'
t
Кривая тока аналоrич
на кр ивой i на рис. 14-11. Az=
At
С л У чай 3. {) < (00,
т. е. r < 2 "1 / [ С (колеба- Рис. 14-11 . Апериодический про-
JI цесс в цепи r, L,- С.
тельный процесс).
Корни характеристическоrо уравнения комплексные и
сопряженные:
Р1,2 ==
{) + jю св ,
(14-23)
rде
(ОСВ == v Ю
{)2.
(14-24)
447
Соrласно (14-24) <00 == Vб 2 + Ю
В'
Корни характеристическоrо уравнения располаrаются
симметрично относительно действительной оси в левой
полуплоскости, на полуокружности, центр которой сов-
падает с началом координат, а радиус равен <00 == 1/ У LC
(см. рис. 14-10, в).
Сопоставление рис. 14-10, а, б и в показывает, что о
характере переходноrо процесса в цепи r, 1., С можно
судить по расположению корней характеристическоrо урав-
нения,Т. е. нулей функции
Z (р), на комплексной ПJ10С-
кости.
Если расположеIНIЫе в
левой полуплоскости нули
функции Z (р) лежат 11а
действительной оси, то име-
ет место апериодический
процесс: совмещению нулей
в одной точке отвечает кри-
тический случаи; наконец,
если нули функции Z (р)
являются комплексно-со-
пряженными, то имеет ме-
сто колебательный процесс.
Величина <OtB (рис.
14-10, в) называется у r -
лавой частотой свободных мли со б-
с т в е н н ы х к о л е б а н и й в цепи r, L, С, а Т СВ ==
== 2л/<осв
периодом ЭТИХ колебаний.
Ток в цепи соrласно (14-22)
Е
U А ! h Е
и A t . * ( 1 25
i==
e
V s 1 '<0 t==
e
u SШ<О [. 4- )
}wcBL св wcBL св
Полученное выражение показывает, что при включении
цепи r, L, С на постоянное напряжение, коtда <'J < <00,
В цепи возникают заТУХающие синусоидальные колебания,
. E
и fu
причем оrибающими кривои тока служат кривые -+-
L e
Ю СВ
(рис. 14-12). Колебания возникают вследствие периодичес-
Koro преобразования энерrии электрическоrо поля в энерrию
....
.....,..
E
U e
8t
WeB/'"
Рис. 14-12. Колебательный процесс
при включении в цепь " L, С
постоянной Э. Д. с.
* Тот же результат получится, если исходить из общеrо решения
однородноrо дифференциальноrо уравнения с комплексно-сопряжен-
ными корнями;
i CB == (М Cos oocBt+N sin OO'CBt) е
бt.
448
маrнитноrо поля и обратно, причем эти колебания сопро-
во)Кдаются потерей энерrии в сопротивлении.
При t == 1/6 ордината оrибающей в е == 2,718 раза мень-
ше начальнorо значения оrибающей. Поэтому величину
1/6 == 2L1, называют постоянной времени колебательноrо
контура.
На рис. 14-12 показана так)Ке кривая напря)Кения ис
на емкости, которая в друrом масштабе выра)Кает так)Ке
зависимость электрическрrо заряда q от времени. Функции
ис и i имеют одинаковый мно)Китель затухания. При
нулевыIx начальных условиях (U ;:= О) кривая ис начинается
с нуля.
. О')ЫО
О t
а.)
. 6'=шо
О t
6)
i
i
t
Рис. 14
13. Изменение харак-
тера переходноrо процесса
с уменьшеннем 6.
Как видно из (14-23) и рцс. 14-10, в, уrловая частота
этих колебаний (ОСВ определяется абсолютным значением
ординаты корня характеристическоrо уравнения, которая
при б:f=. о всеrда меньше резонансной частоты (00'
Чем меньше б по сравнению с (00' тем медленнее зату-
хает колебательный процесс и тем больше частота собствен--
ных колебаний цепи " L, С прибли)Кается к резонансной
частоте.
В пределе, при б == О (ОСВ == (00' колебания не затухают
и корни характеристическоrо уравнения располаrаются
на мнимой оси (см., рис. 14-10, в).
О быстроте затухания колебательноrо процесса судят
. 6Т св u . б
по величине е ,называемои декрементом коле ания,
или величине 6 == lп е 6Тсв == 6Тсв, называемой лоrарифми-
ческим декрементом колебания.
449
На рис. 14-13, a
2 показано изменение характера пере-
ходноrо процесса при уменьшении б.
Приведенные выше величины <ОСВ и е связаны с парамет-
рами последовательноrо резонансноrо контура
доброт-
ностью Q == OOoL/r и затуханием d == 1/Q, введенными
в rл. 5:
ООСВ == 000 -v 1
( 2
oL )2 == <00 -v 1
(
2
/ .
При достаточно высокой добротности <ОСВ
000' в этом
б2л л
случае е ==
Q .
' откуда d
е /л. Для контура сред-
(й СВ
Hero качества d;::::::; 0,01 и лоrарифмический декремент
6
0,03.
2. ВКПlOчение в цепь r, L, С синусоидапьной ). д. С.
Если цепь r, L, С присоединяется к источнику сину-
соидальной э-. д. с. Е т sin (оо! +- 'Ф), то установившийся
ток равен:
iy == 1 т s in (<ot + 'Ф
'Р)
и переходный ток соrласно
(14-18) равен:
i == 1 т sin (oot + 'Ф
'Р) +
+ A1ep,t + A 2 e p2t .
Кривые установившеrо-
ся, свободноrо и'переход-
Horo токов при апериоди-
ческом и колебательном
процессах поКазаны в виде
примера на рис. 14-14.
Частота установившеrо-
ся тока равна частоте ис-
точника синусоидалъноrо
напряжения, свободный же ток при б < 000 изменяется
с собственной частотой цепи <ОСВ' Частота <ОСВ может быть
в зависимости от параметров r, L и С меньше, больше или
равна частоте 00.
Свободные колебания тока накладываются на устано-
вивщийся ток и затухают пропорционально множителю
e
{i. По мере затухания свободноrо тока кривая переходноrо
тока приближается к кривой установившеrося тока.
Lc8
О
а)
о
Рис. 14
14. Апериодический (а) и
колебательный (б) процессы при
включении в цепь " L, С сину-
соидальной Э.Д.с.
450
Та из двух слаrающих тока i, частота которой меньше,
служит как бы криволинейной осью для друrой слаrающей,
колеблющейся относительно нее (рис. 14-14, б). При близ
ком совпадении частот (J) и (J)CB В цепи возникают биения.
Этот вопрос подробнее рассмотрен в [Л, 12 и 14).
14-7. РА.СЧЕТ ПЕРЕходноrо ПРОЦЕССА. в РА.ЗВЕТВЛЕННОЯ ЦЕПИ
Переходный процесс в разветвленной линейной элект-
рической цепи описывается системой линейных дифферен-
циальных уравнений с постоянными коэффици
нтами, об-
щее решение которых находится как сумма установившейся
и свободной составляющих.
Рассмотрим сначала методику расчета установившеrося
рещима.
e(t)
e(t)
о
t
с=о
8)
Рис. 14-15. «Синусоиды» с возрастающей (а), убывающей (6) и неиз-
менной (в) амплитудами.
Во мноrих случаях воздействующая функция, например
э. д. с. источника, может быть представлена в обобщенной
форме Eme N e Pt , rде р === с + j(J)
комплексное число.
В зависимости от значений буквенных величин, входящих
в приведенное выражение, получается тот или иной закон
изменения э. д. с., причем MrHoBeHHbIe значения э. д. с.
определяются мнимой или действительной частью выраже-
ния.
Условие (J) =1= О соответствует rармонической э. д. с.
с возрастающей (с > О), убывающей (с < О) или неизменной
(с === О) амплитудой (рис. 14
15).
Условие (J) === О соответствует возрастающей (с > О) или
убывающей (с < О) показательной функции; при с === О
э. д. с. постоянна (рис. 14-16).
Задавшись э. д. с. EmeNePt, ищем устаIЮВИВШИЙСЯ ток.
в виде 1 пl!jae Pt . Данная ФУНКlLИЯ пр и дифференцировании
(по переменной t) умножается на р, а при интеrрировании
451
делится на р. Поэтому подстановка выражения [mе/аеР!
в исходное дифференциальное (или интеrродифференциаль-
ное) уравнение приводит к алreбраическому, уравнению,
которое отличается от уравнения для установившеrося
режима, записанноrо в комплексной форме, только тем,
что j(f) заменяется на р. Таким образом, установившийся
ток получается равным
Е еf'Фе рt Е еС/е;' ((о)i+ф)
[y(t)== Z(p) == Z(c+iro)
в зависимости от схемы и постановки задачи Z (р)
означает обобщеlшое входное сопротивление или вели-
чину, обратную обобщенной передаточной проводимости;
Z (р) получается из соответствую-
щеrо комплексноrо сопротивле-
ния заменой j(f)L на
pL и lIj(f)C
на l/pC.
MrHOBeHHbIe. значения тока
определяются мнимой или дей-
ствительной частью [ПР (t).
В случае синусоидальной
э. д. с. (с == о; р == j(f)) устано-
вившийся ток также синусои-
дальный
[у (t) == Ете/(rot+Ф) /Z (j(f)).
e(t)
о
Рис. 14-16. Возрастающая
(с > О) и убывающая (с < О)
показательные функции и по-
стоянная (с"= О).
t
Если э. д. с. есть пЪказательная функция ('1' == о;
р == с; Е т :=: Е), то установившийся ток изменяется также
по показательному закону
iy (t) == EeciJZ (с).
rде
Z (с) == [Z (p)JI'
c'
При постоянной э. д. с. ('Ф == о; р == о; Е т == Е) уста-
новившийся ток равен постоянному току
[== E/z (О),
rде z (О)
сопротивление при постоянном токе.
Перейдем теперь к рассмотрению свободноrо режима.
Свободные составляющие представляют собой общее
решение системы однородных линеЙных дифференциальных
уравнений. Для. заданной цепи степень характеристичес-
Koro уравнения не зависит от выбора контуров, для кото-
452
рых составляются уравнения
по второму закону Кирхrофа.
Однако если выбрать контуры так, чтобы порядок диффе
ренциальных уравнений был наименьшим, то степень
характеристическоrо уравнения не будет превышать суммы
порядков исходных дифференциальных уравнений системы.
При этом, как будет показано ниже, для получения харак-
теристическоrо уравнения отнюдь не обязательно приводить
систему дифференциальных уравнений к одномууравне-
нию относительно одной неизвестной функции.
Корни характеристическоrо уравнения MorYT быть дей-
ствительными или комплексными. Если корни комплекс-
Ные, то они Bcerдa образуют комплексно сопряженные пары.
В связи с этим характеристическое уравнение нечетной
степени BcerAa имеет хотя бы один деЙСТВJ.JТельный корень,
остальные же корни MorYT быть действительными или комп-
лексно
сопряженными; характеристическое уравнение чет-
ной степени имеет четное число действительных или комп-
лексно-сопряженных корней. Действительные части всех
lю.рней характеристическоrо уравнения BcerAa отрицатель-
НЫ, что физически обусловлено затуханием свободных сос-
тавляющих в пассивных цепях с течением времени. При
этом все коэффициенты характеристическоrо уравнения
должны быть действительными и положительными.
Корни единоrо характеристическоro уравнения исполь
зуются для нахождения в данной цепи свободных состав-
ляющих как ТОIЮВ, так и напряжений.
Допустим, что характеристическое уравнение имеет п
корней. Тоrда свободный ток в любой ветви
n
i CB (t) ==
Ake"k t ;
ko:l
здесь Pk
корни характеристическоrо уравнения, Ak
постоянные интеrрирования.
Аналоrичная структура решения получается и для
свободных составляющих напряжений.
. В случае, Коrда Pk ==
6k является дейсmвитеЛЫ-lЬtМ.
корнем той кратности} решение для этоrо корня записы'
вается в виде
(14-26)
т
e
fJkt
Btti
l,
i == 1
Если имеются сопряженные комплексные корни} напри-
мер Pk,ktl =:
6k + j())k, то выражение Ake Pkt + A k + 1 e Pk +1
453
преобразуется в е
бkt (Ake!(J)k t + Ak+l e
J(J)kt) == е
бkt Х
Х (М cos (f)kt + N sin (f)kt).
Для т-кратных сопряженных комплексных корней реше
иие принимает вид:
т
e
kt Е ti
l(MICOS(f)kt+NISin(f)kt).
i,,= 1
Методика получения характеристическоrс уравнения
иллюстрирована ниже на примере двухконтурной схемы,
изображенной На рис. 14-17. .
Первый контур содержит сопротивления '1 и 'з И индук-
тивность L, второй контур содержит сопротивления '2 и '3
И емкость с; поэтому по-
рядок дифференциалъноrо
уравнения для каждоrо из
fZ этих контуров равен еди-
нице:
( . + . ) + . + L di[
С r з t 1 l2 '1'1 dt == е;
'3 и1 + i 2 ) + '2 i 2 +
1 ('
+C
J i 2 dt ==е.
L
е
Рис. 14-17. Пример двухконтурной
схемы.
Соответственно степень характеристическоrо уравне-
ния равна 2.
Для получения характеристическоrо уравнения при-
меняется следующий прием. Система дифференциальных
уравнений для свободных слаrающих токов
( . + . ) + . + L dii
B О
'з lHB l2
B 'l t HB
' ;
'з иl
B + i2
B) + r2i2
B + + s i2
B dt == О
записывается в символической алrебраической форме, при
которой символ р замеНяет операцию дифференцирования,
а символ l!р
операцию интеrрирования:
('1 +'3 + pL) il
B + ,зi2
В === о;
'зi]
В+{'2+r8+ p
)iZCB==:O.
Данная система уравнений имеет решение, отличное
от нулевоrо, если определитель системы равен нулю,
т. е.
'1+,з+рL
д (р) ==
'3
'3
1
'2+'3+ рС
или
('1 +'3 + pL) ('2 +'3 + р l с )
,i ==
== p
{('2 + (3) LC p 2 + [('1'Z + '1'3 + '2'З) с +
+L]Р+'1+'з}:;;;:О.
Таким образом, получается характеристическое ypaB
нение второй степени
('2 + (3) LC p 2 + [('1[2 + '1'3 + '2'З) с + L] р +'1 +'3 == О.
Ввиду прямой пропорциональности, существующей меж-
ду входным сопротивлением цепи Z (р) и определителем
системы д (р) [см., например, (7-9) в
7-5], то же характе-
ристическое уравнение получается и по формуле Z (р) == о.
Операторное сопротивление Z (р) получается из комп-
лексноrо сопротивления Z (j(f)) заменой j(f) на р. При этом,
разомкнув любую ветвь в пассивной цепи, находим в месте
размыкания BxoДНDe сопротивление Z (р) "'.
Если характеристическое уравнение имеет степень п,
то искомыми являются п постоянных интеrри
вания
(А 1 , А2' ..., Аn), входящих в выражение (14-26) . По-
стоянные интеrрирования находятся в результате решения
системы п уравнений, соответствующих моменту BpeMe
Ни t == О. Эта система уравнений получается путем
* Предыдущие рассуждения основывались на уравнениях контур-
ных токов. Аналоrично, исходя из метода узловых напряжений, можно
показать, что У (р) == о также является характеристическим уравне-
нием, если под У (р) подразумевать операторную проводимость между
любыми двумя узлами заданной схемы пассивной цепи.
* * Методика вычисления постоянных интеrрирования остается
такой же и в случае кратных или комплексных корней характеристи-
ческоrо уравнеиия.
455
(п
l)
KpaTHoro дифференцирования уравнения (14
26):
п )
i CB (О) == i (О)
i np (О) == В A k ;
k
J
п
i
B (О) == i' (О)
i
p (О) ==
PkAk;
k
l
(14-27)
n
i
J) (О) == i(п
J) (О)
i
J) (О) ==
k
J
. . . . . J
n
J A
Pk k'
Значения свободноrо тока и ero производных при t == О,
входящие в (14-27), нахОДятся предварительно на основании
законов коммутации (см.
14-2) и уравнений Кирхrофа.
Для определения начальных значений токов и напря-
жений в цепи можно для наrлядности воспользоваться
схемой замещения, которая составляется из исходной
схемы после коммутации, если заменить индуктивности
идеальными источниками тока с токами, равными iL (О),
а емкости
идеальными источниками э. д. с. ис (О). Эта
схема замещения справедлива только для t == О.
При нулевых начальных условиях индуктивность рав-
носильна разрыву ветви, а емкость
короткому замыка-
нию.
По этой схеме замещения можно найти друrие токи
и напряже-ния в момент t == О, если воспользоваться УРаВ-
нениями Кирхrофа или правилами преобразования схем.
Итак, в соответствии со сказанным выше расчет пере-
ходноrо процесса классическим методом провОдится В сле-
дующем пор ядке:
1. Производится расчет режима до коммутации, из
Koтoporo определяются конечные значения (т. е. при t == O
)
функций, не меняющихся скачком (токов в индуктивностях,
напряжений на емкостях). Далее с использованием зако-
нов коммутации находятся независимые начальные усло-
вия, т. е. i L (О), и<:. (О).
2
Составляется система дифференциальных уравнений
Кирхrофа, описывающая процесс в цепи после коммута-
ции.
3. Находится общее решение системы однородных диф-
ференциальных уравнений.
4. Находится тем или иным методом частное решение
системы неоднородных дифференциальных уравнений, ука-
456
занных в п. 2, соответствующее принужденному режиму
цепи.
5. Определяются зависимые начальные условия для
искомых функций на основании найденных в п. 1 незави-
симых начальных условий и уравнений Кирхrофа из п. 2,
примененных для t == о.
6. По начальным условиям определяются постоянные
интеrрирования, содержащиеся в общем решении.
7. Найденные установившиеся и свободные токи и на-
ПряжеНИЯ складываются 1.
Приведенный ниже пример 14-1 иллюстрирует нахож-
дение начальных условий; в примере 14-2 дан численный
расчет переходноrо процесса в цепи на рис. 14-17.
Пример 14-1. В цепи, изображенной на рис. 14-18, моменту {== О
предшествовал установившийся режим постоянноrо тока. При t == О
замкнулся контакт К. Найтн на-
=
з:а:
:. :;д
:
7'2
костях И их первых производ-
ных.
,Независимыми начаЛIJНЫМИ
условиями будут ток в ин-
дуктивности . i4 (О) == ё4 (О
) == + Е
Е '
ilf
i,
9 ,
IL,
К
t=O
iz
С ,
IJ.,
i з !
7',
и наПряжения на
'1 +'2
емкостях U 1 (О) == и 1 (O
) И
и 2 (О) == и 2 (O
).
Напряжения на емкостях
до коммутации находятся из р 14 18 П 14 1
условий равенства их зарЯДОВ ис. -. . ример -.
(так как емкости соединены
последовательно) и раВ2нства CYMMapHoro иапряжения на емкостях
напряжению на сопротивлении '1:
С1и1 {0
)==C2и2 (o
);
иl (o
) + и2 (O
) == 'liз (O
) == '1ё4 (О
),
L
откуда
щ{0
)=='li4(0
) C1
C2
и 2 (0
)==rli4 (o
) C1
C2 '
Требуемые Зависимые начальные условия определятся из ypaBHe
ний
C 1 d
r (О) == ё 1 (О) И С 2
! (О) == ё 2 (О),
1 В случае, коrда э. д. с. изменяется в виде импульса, имеющеrо
кусочно-аиалитическую Ф02МУ, представляется часто целесообраз-
ным применять интеrрал Дюамеля (см. Э 15-11).
токи же i 1 (О) И i 2 (О)
из уравнений Кирхrофа ПОС.'lе коммутации:
Ei2 == '2i5 + иl + и2' иl == 'l i з; i 1 + i з == i2+ i4 == i5'
Подстановка в эти уравнения найденных значений i4 (О), и 1 (О) И
и 2 (О) дает:
i (О)
Е
Щ (О)
и 2 (О) . i (О) == иl (О) .
5 '2' 3 rl '
i 1 (О) == i5 (О)
i3 (О); i 2 (О) == i5 (О)
i4 (О)
и далее
dщ ( О ) == i 1 (О) . dи2 ( О ) == i 2 (О)
dt Ci' dt С 2 .
Начальное значение производной тока в индуктивности опреде
ляется также из уравнения Кирхrофа:
Е . + . +L di$
== '2/5 '1/з ат'
откуда при t == О
l:i ( 0 ) == E
'2i5 (О)
'liз (О)
dt L'
Пример 14-2. Определить ток i в цепи на рис. 14.17, если известно,
что е == Е == 100 В, '1 == 5 Ом, '2 == 3 Ом, 'з == 100 Ом, L == 0,1 r,
С == 100 r.iкФ, Ц С (О) == О.
Подстановка заданных значений в приведенное выше характери-
стическое уравнение дает:
1,03 .10
3p2+0,1815p+ 105==0,
или
р2+ 176р + 1,02. 105 ==0;
корни характеристическоrо уравнения комплексные:
Рl. 2 ==
88 :!: j307.
Искомый ток
i 1 <=Z iiy + i 1C . B .
Установившийся ток
100
i 1y == 105 == 0,952 А.
Свободный ток
iicB ==e
BB! (АlеfЗО7t + А
jЗО7t) ==e
BBt (М cos 307! + N siI1 307t).
В начальный момент i 1 (О) == О, следовательио, О == 0,952 + М,
откуда М ==
0,952.
Производная тока по времени
d d i i == e
88! (
307 М sin 307 t + 307 N cos 307 ()
88e
в8! (М cos 307 t +
t .
+ N sin зо7t).
4,58
В начальный момент и с (О) == О, i} (О) == О и i 2 (О) =: {
== 0,971 А.
Следовательно, в начальный момент напряжение на ветви '2С ( и парал-
лельной ей ветви 'IL) равно 3.0,971;:: 2,913 А. Начальное значение
производной di 1 /dt (О) определяется из уравнений 2,913:=0,1 d:: (О),
d'
откуда
: (О) == 29, 13 А/с.
d'
Следовательно, подставляя значение
(О) в выражение для про-
изводной при t -= О, получаем:
29,13==307N
88M =-=307 N +8з,8,
откуда
N ==
0,178.
Итак,
i 1 == 0,952
e
BB! (0,952 cos ЗО7t + О, 178 sin 307t) А.
i4-8. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
Переходные процессы в цепях с распределенными
параметрами (в линиях, обмотках электриqеских машин
и т. п.) возникают при коммутациях, передаче неперио-
дических сиrналов или под влиянием внешнеrо электро-
маrнитноrо поля (например, при rрозовыIx разрядах).
Для исследования переходных процессов В однородных
цепях с распределенными пара метрами пользуются диф-
ференциальными уравнениями (11-2) в частных ПрОИЗБОД-
ных, выведенными в rл. 11:
ди . ai ai ди
дх == rt + L дt
;
ах == gu + с дТ '
rде т, L, g и С
параметры цепи на единицу длины; х
Координата рассматриваемой точки, отсчитываемая от на-
чала цепя.
В общем виде решение этих дифференциальных уравне-
ний достаточно сложно. Решение упрощается, если пре-
небречь потерями, т. е. считать, что r и g равны нулю.
В этом случае
ди Ji
==L
'
дх at '
C
дх
at'
( 14-28)
(14-29)
Дифференцируя (14-28) па К:
д 2 и i} ( ifi ) д ( дi ' )
дх2 ==
L дх ' ar ==
L дi дХ
и используя (14-29), получаем:
д 2 и д2и
дх 2 == LC (jj2 .
(14-30)
Дифференциальное уравнение (14-30) известно в мате-
матической физике под названием у р а в н е н и я к о ,.
л е б а н и й с т р у н ы. Ero решение дано Даламбером
и имеет вид:
u == f1 (x
vt) + f2 (х+ vt),
(14-31)
rде
1
v == V LC .
Первая слаrаюrцая представляет собой одиночную
п Р я м у ю в о л н у напряжения, которая без изменения
перемеrцается в сторону возрастаюrциХ х, т. е. от начала
к концу цепи. Для всех значении х, при которых х
vt ==
== const, эта слаrаюrцая имеет одно и
то же значение, т. е.
волна ДВlIжется со скоростью v == dx/dt.
Вторая слаrаюrцая представляет собой одиночную о б -
р а т н у ю , в О Л Н У напряжения, которая без изменения
перемеrцается в противоположном направлении.
Для нахождения тока про изведем замену переменных,
обозначив
== х
vt и '1') == х + vt. На осНОвании (14-29)
и (14-31)
;o:
c
и +f ) ==
с (
д
+
Тj ) ===
дх дt 1 2 \ дs дt дТj дt
== Cv (
дf2. . ) .
дs дч
Но
дfl дfl дs дfi
дх == д[ 7ii == д;
и
дf2
дf2 дТj
дf2
ах
дТ] дх
-дч'
Следовательно,
дi
== CV (
J
& )
дt дх дх'
460
Интеrрирование последнеrо уравнения Дает 1:
i==-V
[f1(X
Vt)
f2(X+Vt)]. (14-32)
Выражения (14-31) и (14-32) записываются сокращенно:
U == и п + и о ; , (14-33)
i ==
(и п
и о ) == i n
io. (14-34)
ZB
здесЬ i n и io
прямая и обратная волны тока; ZB == -v
волновое сопротивление.
Следовательно, напряжение и ток прямой и соответ-
ственно обратной волн связаны законом Ома:
!!!l
.
.
ZB'
'п 'о
Аналоrичный результат был получен в
11-3 для уста-
новившихся прямой и обратной волн при рассмотрении
синусоидальноrо режима в однородной линии. Физически
установившиеся волны представляют собой бесконечные
суммы прямых и обратных одиночных волн, отраженных
от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с рас-
пределенными параметрами напряжение и ток MorYT быть
представлены как сумма и разность двух волн, движущихся
С одинаковой скоростью v == l/V LC в противоположных
напряжениях, без изменения их формы. При этом в любой
точке однородной цепи отношение, шrtrряжения и тока для
прямой и обратной волн равно волновому сопротивлению ZB'
Если на пути распространения волны встречается не-
однородность, например воздушная линия переходит в
кабельную или волна достиrает конца линии (разомкнутоrо
или замкнутоrо через сопротивление или на короткое),
происходит о т р а ж е н и е волны. В зависимости от ха-
рактера неоднородности отражение может быть частичным
или полным. В первом случае наряду с отраженной волной
возникает п р е л о м л е н н а я волна, распространяю-
щаяся за место нарушения однородности; во втором случае
преломленная волна отсутствует.
Обозначим и 1 и i 1
напряжение и ток в месте отражения;
иlп И i 1n
напряжение и ток падающей (прямой) волны;
1 Постоянная интеrрирования может быть отнесена к функцням
11 И I'J.'
461
И 1О И Ё 1о
напряжение и ток отраженной (обратной)
волны;
И 2 и Ё 2
напряжение и ток преломленной (прямой)
волны;
21 И 22
волновые сопротивления для прямой и об-
ратной волн (Z1) и преломленной волны (Z2)'
В месте неодНОрОДНОСТИ выполняется условие равенства
натrряжений и токов:
И 1 == И 2 , Ё 1 == Ё 2 .
Следовательно,
И 1П + И 1О == И 2 ;
i 1п
i 10 == i 2 .
( 14-35)
( 14-36)
Подстановка в (14-36) значений i 1п == И 1п /Z 1 , Ё 1о ==
== И 1О /Z 1 И Ё 2 == И 2 /2 2 дает:
Щп
Що
Z1
Z2 .
( 14-37)
в результате cOBMecTHoro решения уравнений (14-35)
(14-37) находятся отраженная (И 10 ) и преломленная (и 2 )
волны:
И 10 == пи 1п ; }
И 2 == (1 + п) И 1Ш
rде п == Z2 +
Zf
коэффициент отражения.
Z2 Zl
Соответственно ток отраженной волны
. иI O иI П
E1o==
==п
,
Zf Z1
а ток преломленной волны
. и 2 (1 +п) Щп
2щп
'2 == z; == Z2
Z1 + Z2 .
Последнее выражение показывает, что ток в конце
линии после отражения можно найти как тnK в ЭК8ивалент-
ной цепи, в которую включается напряжение, равное двой-
ному напряжению падающей волны, и которая состоит из
волновосо сопротивления первой линии 21 и последовательно
соединенносо с ним сопротивления нazрузки (в которое
входит вторая линия своим волновым сопротивлением 22)'
Опишем процесс включения однородной линии без
потерь. После присоединения линии к источнику Э. д. с.
по линии начнет распространяться зарядная волна, соз-
дающая напряжение и ток. Если в конце линии присое-
динена наrрузка, равная волновому сопротивлению линии,
(14-38)
462
то падающая волна, достиrнув ее, не отразится и в линии
сразу наступит установившийся режим. Если же наrрузка
с линией не соrласована, то падающая зарядная волна,
достиrнув конца линии, претерпит отражение. Распростра-
няясь в обратную сторону, отраженная волна сложится
с падающей, причем напряжения волн суммируются, а токи
вычитаются (алrебраически). Достиrнув начала линии,
обратная волна снова отразится от источюiи,а э. д. с., как
от короткозамкнутоrо конца; появится новая прямая волна
напряжения и тока, которая также отразится от конца,
и т. д. Процесс будет продолжаться до наступления уста-
новившеrося режима. Теоретически в идеальной линии без
потерь при чисто реактивной наrрузке процесс колебаний
будет продолжаться бесконечно долrо. В реальной линии при
наличии потерь волны напряжения и тока будут постепенно
затухать в направлении распространения.
Напряжение и ток в ЛИНИИ в произвольный момент
времени определятся как алrебраические суммы и соот-
ветственно разности напряжений и токов прямых и об-
ратных волн.
Пользуясь формулами и схемой замещения, описанной
выше, можно найти напряжение и ток, возникающие
в месте присоединения сосредоточенной наrрузки или
перехода одной линии в друrую (см. пример 14-3).
Следует отметить что индуктивность, включенная по-
следовательно в линию, или емкость, включенная парал-
лельно проводам линии, сrлаживает фронт преломленных
волн; активное сопротивление, включенное в линию па-
раллельно, уменьшает преломленную волну.
Различные случаи отражения и преломления волн рас-
смотрены в IЛ. 5, 12 и 141.
Пример 14-3. К !Юнцу линни, имеющей волновое сопротивление ?Ь'
присоединена индуктивная катушка " L. Определить ток в катушке и
напряжение на ней под воздействием прямоуrольной волны и.
l' Z
1" L
L ZUt :
а) о)
Рис, 14-19. Пример 14-3.
На рис. 14-19 показаны расчетная схема и эквивалентная схема
замещения, Днфференцнальное уравнение Кнрхrофа для такой цепн
463
запишется так:
2и ='= ёа (zs +,) +L .d
; ,
откуда
.
2и (1
t/T )
la
e
Zs+'
и
2и .'. 2и (
t/T )
и2==
ZsI2==
+ ,+zse ;
<'в ,
L
здесь 't' ==
+ ; t == О соответствует моменту падения ВоЛНЫ
%в ,
на ка-
тушку.
14-9. ЗАДАЧИ,И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
14-1. Сопротивление, == 1000 Ом и незаряженная емкость С ==
== 1 мкФ, соединенные последовательно, подключаются при t == О
к источнику постоянной Э. д. с. Е == 100 В. Вычислить ток и первую
производную тока по времени для t == О, не находя функциоиальной
зависимости i (t). '
Ответ: ё(О)== 0,1 А.
di
dt (О) ==
100 А/с.
{4-2. Сопротивление, == 10 Ом и индуктивность 1. == 1 r, соеди-
ненные последовательно, подключаются при t == О к источнику Э. Д. с.
Е == 100 В. Вычнслить ток И первую производную тока по времени
для t == О, не находя функциональной зависимости i (t).
di
О 'l' в е т: i (О) == о; dt ' (О) == 100 А/с.
(4-3. Сопротивление, == 10 Ом и незаряженная емкость с== 10 мкФ,
соединенные ПОС,1едовательно, подключаются при t == О к источнику
Э. д. с. 10e
t siп t В. Определить i и).
О т в е т: i == 10
'e
t (cos t
siп t)
1O
4е
lO<t А.
{4-4. Цепь, состоящая из послеДоватеJIЬНО соединенных сопротив-
лений, == 75 Ом, индуктивност!!': L == 3. 10
4 r и незаряженной емкости
С == 12.1<r 10 Ф, подключается при t == О к источнику постоянной Э. д. с.
Е == 100 В, Определить i (t).
О т в е т: i == 0,2e
12.5 'lo't siп (l,66.10 6 t) А.
{4-5. Сопротивление, == 20 Ом и емкость С == 5 мкФ, соединенные
последовательно, подключаются при t == О к источнику постояиной
Э. д. с. Е == 25 В. Определить i (t), если начальное напряжение из ем-
кости равно 50 В. ,
О т в е т: i == з,75е
lО'i, нли i ==
1,25
lo.t А.
(4-6. Сопротивленне , == 50 Ом и незаряженная емкость С ==
== 3,75 мкФ, соединенные последовательно, подключаются при t == О
к источнику Э. д. с. Е == 20 В. Определить i (t).
О т в е т: i == 0,4е
БЗЗЗ: А.
14-7. В цепи на рис. 14-17 '2 == О и е == Е. Определить: 1) иапря-
жения на '1 и на L, дЛЯ t == О и t == со; .
464
2) первые производные напряжений на '1 и L по времени для t == о.
О т в е т: и r1 (О) == U L (О) == о,
,- dи
U r l (оо)==Е
+ 1 ; U L (00) "",о;
d r t !_:(O)==O;
'1 'з
dU L F
(O)
dt
'зС'
14-8. Заряженная емкость С 1 == 10 мкФ С начальным напряжением
1000 В присоединяется при t == О к двум параллельным ветвям. Первая
ветвь состоит нз одноrо сопротивления '1 == 106 Ом, вторая ветвь состоит
из сопротивления '2 == 2'106 Ом И незаряжеНRОЙ емкости С 2 == 20 мкФ,
соединенных последовательно, Вычислить вторую производную тока
во - второй ветви hля t == О, не находя функциональной зависимости
MB
eo. -
Ответ: 1,41.1O
б А/с 2 ,
14-9. Сопротивление, == 100 Ом и заряженная емкость с== 100 мкФ,
соединенные последовательно, подключаются к источнику э. д. с.
е == 141 sin (377t + л/6) В при t == о. Определить i (t), если начальное
напряжение на емкости равно 50 В.
О т в е т: i == 1,37 sin (377t + 44048') + O,241e
1001 А или i ==
== 1,37 sin (377t + 44° 48')
0.75ge
100' А.
14-10. ,Возможно ли включение на переменное синусоидальное
напряжение контуров " L, " С и " L, С, не сопровождаемое переход-
ным процессом (пояснить физическую сторону SlВления)?
14-11. Может ли частота колебательноrо разряда в контуре (, L.. С
быть равной или больше резонансной частоты этоrо контура?
14-12. Пояснить физнческий смысл постоянных вр
мени цепей" L и
(, С. Почему с увеличением, постоянная времени для nepBoro контура
уменьшается, а для BToporo контура увеличивается?
14-13. Пепь " L подключается при t == О к источнику синусоидаль-
ной э. д. с. Выбрать начало отсчета -Времени так, чтобы свободный ток
отсутствовал.
14-14. Изменив в схеме на рис. 14-6 полярность заряженной емко-
сти, начертить кривые тока и напряжения при включении в цепь " С
постоянной э. д. с.
- 14-15. Зависит ли характеристическое уравнение (и соответственно
порядок цепи) от воз,!(ействующей функции?
rЛАВА ПЯТНАДЦАТАЯ
ПРИМЕНЕНИЕ ПРЕОБР АЗОВАНИЯ ЛАПЛАСА
К РАСЧЕТУ ПЕРЕХОДНЫХ ПРОЦЕССОВ
.
15-1. 06ЩИЕ СВЕДЕНИЯ
Необходимость определения постоянных интеrрирова-
ния из начальных условий в ряде случаев сильно ослож-
няет расчет переходных процессов классическим методом
465
решения линейных дифференциальных уравнений, обыкно
венных или с частными производными, описывающих
исследуемые процессы. По мере усложнения электрических
схем и возрастания порядка дифференциальных уравнений
трудности, связанные с нахождением постоянных интеrри-
рования, увеличиваются.
Для инженерной практики, более удобным является
метод решения линейных дифференциальных уравнений,
при котором заданные начальные условия включаются
в исходные уравнения и для нахождения искомых функций
не требуется дополнительно определять постоянные ин-
теrрирования.
В прошлом столетии в математике развивалось так
называемое симsолическое исчисление, построенное на
системе формальных операций над символом р: произ-
водная df (t)/dt представлялась как результат действия
на функцию f (t) символа р; операция интеrрирования
рассматривалась как применение символа 1/р и т. д. В числе
работ, посвященных этому вопросу, большоrо внимания
заслуживает моноrрафия М. Е. Ващенко-Захарченко «Сим-
волическое исчисление и приложение ero к интеrрированию
линейных дифференциальных уравнений» (Киев, 1862).
В конце XIX в. анrлийский инженер-электрик О. Хеви-
сайД успешно применил и развил символический метод
решения линейных дифференциальных уравнений для
расчета переходных процессов в электрических цепях
с сосредоточенными и распределенными параметрами. Orpo-
roe обоснование символическоrо, или, как ero стали назы-
вать, о пер а Ц и о н н о r о и с ч и с л е н и я, было да-
но лишь в 20-х rодах нашеrо столетия на баdе общей теории
функциональных (интеrральных) преобразований.
В настоящее время формально-операционное исчисле-
ние Хевисайда полностью вытеснено более общим и строrим
методом
преобразованием Лапласа, нашедшим широкое
применение в технике.
Идея этоrо метода заключается в том, что из области
функций действительноrо переменноrо решение переносится
в область функций комплексноrо nepeMeHHoro 1 р == с + jro,
rде операции n
ринимают' более простой вид, а именно:
вместо исходных дифференциальных или интеrродифферен-
циальных уравнений получаются алrебраические ypaBHe
1 В современной литературе наряду с обозначением комплекс-
Horo nepeMeHHoro р широко распространено также обозначение s,
466
ния; затем полученный решением алrебраических уравнений
результат «интерпретируется», т. е. производится обратный
переход в область функций действительноrо переменноrо.
Этот переход осуществляется с помощью формул или
таблиц.
В этом отношении преобразование Лапласа можно
сравнить с лоrарифмированием, коrда от чисел переходят
К лоrарифмам, над лоrарифмами производят действия, соот-
ветствующие действиям Над числами, причем умножен:ию
чисел соответствует более простая операция сложения
лоrарифмов, И' т. д.; наконец, по найденному лоrарифму
определяют искомое число (пользуясь таблицами).
15.2. ПРЯМОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. оРиrИНАП
. и ИЗОБРАЖЕНИЕ
Пусть f (t)
функция действительноrо переменноrо t,
заданная в области t> О и равная нулю при t < о, воз-
растает не быстрее показательной функции, т. е. I f(t) I <
<Me ci при t> о; здесь М и СО
постоянные (положитель-
ные и действительные); t
переменное (время). Постоян-
ная СО называется показателем роста
функции f (t). rоворят, что функция
имеет оrраниченный рост, если показа-
тель роста конечен.
Из курса математическоrо анализа О
известно, что если f (t) имеет оrрани-
ченный рост, то интеrрал
+j(,zJ
+с
СО
00
F (р) ==
f (t) e
P! dt
о
(15-1 )
Рис. 15-1. Комп-
лексная ПЛОскость.
сходится абсолютно и является аналитической функцией
комплексноrо переменноrо р == С + jro в полуплоскости
Re р == С> СО (рис. 15-1).
Интеrральное уравнение вида (15-1) представляет собой
прямое преобразованuе Лапласа. Функция f (!) называется
о р и r и н а л о м, а функция F (р)
и з о б р а ж е н и-
е м по Лапласу. Следовательно, ориrинал и изображение
представляют собой пару функций действительноrо пере-
MeHHoro t и комплексноrо переменноrо р, связанных пр е-
образованием Лапласа.
Из определения изображения следует, что каждый
ориrинал имеет единственное изображение. В свою оче-
467
редь ориrинал вполне определяется своим изображением
с. точностью до значений в точках разрыва ориrинала.
Фразу «ориrинал f (t) имеет своим изображением F (р)>>
будем записывать символически (с прмощью знака соответ-
ствия : ): .
,f(t) .' F(p) или F(p) .' {(t).
Такая сокращенная запись раВНОСflльна интеrральному
уравнению (15-1). В литературе применяется также друrая
условная форма записи прямоrо преобразов.ания Лапласа,
а иМенно:
L [f (t)] === F (р).
Для обоснования операционноrо исчисления Хевисайда
в свое время испоJiьзовалось изображение по Карсону 1
00
F (р) === р
f (t) e
P! dt,
. о
отличающееся от изображения по Лапласу множителем р.
В
настоящее время в теории автоматическоrо pery-
лирования и радиотеХНИКе применяется преобразование
Лапласа, имеющее прямую связь со спектральным пре-
образованием Фурье (см. rл. 16). Поэтому все последую-
щие рассуждения будут относиться к изображениям по
Лапласу, а не по Карсону.
15-3. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ ПРОСТЕАШИХ ФУНКЦИА
При исследовании переходных процессов в электри-
ческих цепях часто предполаrается, IIТО в некоторый мо-
мент времени, принимаемый за начальный (t === О), в элек-
трическую цепь включается источник постоянной сину-
соидальной или какой-либо друrой э. д. с., выражаемой
функцией f (t). Для всех значений t < О функция f (t)
принимается равной нулю; это означает, что данная э. д. с.
не воздействует на рассматриваемую электрическую цепь
до момента ее включения.
Если функция f (t) имеет оrраниченный рост, то на
основании
15-2 она рассматривается как ориrинал.
Простейшими ориrиналами являются единичная и по-
казательная функции.
1 Изображение по Карсону имеет ту же размерность, что и ориrи-
нал, однако эта особенность ие имеет для практики существенноrо
значения. '
468
Е д и н и Ч н а я Ф у н к ц и я (рис. 15-2), заданная
условием
f (t) == { О при t < о;
1 при t> о,
соответствует случаю включения постоянной э. д. С., рав-
ной 1 в.
Единичная функция имеет условное обозначение 1 (t).
Однако для простоты записи в дальнейшем будем условно
писать f (t) == 1, помня, что всякий ориrинал (в том числе
и единичная функция) по определению равен нулю при t < О.
Изобра}кение единичной функции
соrласно (15-1) имеет вид:!(t)
F (р) == f e
P! dt == e
: 1
.
1
Следовательно,
1 .'
при Re р>Оl.
t
(15- 2)
о
Рис. 15-2. Единичная
функция.
Умножение единичной функции на любую функцию
времени оставляет последнюю без изменения при t > О
и дает нуль при t < О. Поэтому, умножив, например, еди-
ничную функцию на показательную функцию e qt , получим
функцию-ор иrинал
{ Опри t < о;
f (t) == eqt при t> о,
ДЛЯ которой, применяя в дальнейшем сокращенную за-
пись f (t) == e Qt , условно сохраним название п о к а за-
т е л ь н о й Ф у н к Ц и и 2.
Найдем изображение этоrо ориrинала, полаrая, что
q
произвольное комплексное число:
00 00
S e
{P
q)t 1 1
F (р) == e
pfeQf dt ==
==
p
q p
q
о
1 При Re р
O интеrрал расходится.
2 Данная условность распространяется и на друrие функции вре-
мени: синусоидальные, косинусоидальные и Т, П.
469
при Re (р
q) > О, т. е. при Re f5 > Re q. Итак,
e qt .'
p
q при Re р > Re q. (15-3)
Полученное выражение справедливо также для дей-
ствительных или мнимых ЗНачений q.
15-4. ОСНОВНЫЕ СВОЙСТВА ПРЕО&РАЭОВАННЯ ЛАПЛАСА
Математическим операциям над ориrиналами соответ-
ствуют определенные операции НаД изображениями и на-
оборот .
Знание этих оrrераций, или, как их называют, свойств
преобразованuя Лапласа) облеrчает нахождение изобра-
жений:. оно позволяет переходить от дифференциальных
(или ийiеrродифференциальных) уравнений, записанных
для функций-ориrиналов, к «операторным» уравнениям,
записываемым для изображений, и облеrчает последующее
нахождение искомоrо ориrинала по вычисленному изобра-
жению.
Основные свойства преобразования Лапласа, извест-
ные из курса математическоrо анализа, приведены в табл.
15.1. Во всех соотношениях предполаrается, что f (t) .. F (р).
Пользуясь соответствием (15-3) и свойством линейности
преобразования Лапласа (изображение линейной комбина-
ции есть линейная комбинация изображений), леrко найти
изображения следующих функций-ориrиналов, часто встре-
чающихся в задачах по электротехнике:
e i (UJ,t+w) ....!. eN . ( 15-4 )
7" p
jWl '
sin(oo l i+1.\J)== 2
(ei(UJ,t+1jJ)
e
i(UJ,t+1j;)] .'
рsiп'Ф+WIСОS'Ф . ( 15-5 )
7" p2+wr '
os ( t + .1' )
Р cos 'Ф
Wi sin 'Ф ( 15 - 6)
с 001 't'
p2+wr .
Такие изображения соответствуют, например, Э. д. с.,
ВКЛючаемым в электрическую цепь, если эти э. д. с. за-
даются в комплексной (показательной), синусоидальной.
или КОСИНУСОИДальной форме (амплитуда равна единице).
Ниже приводятся дополнительные разъяснения к
табл. 15-1 и применение некоторых свойств преобразо:ва-
ния Лапласа иллюстрируется на примерах.
470
Таблица 15-1
'Основные свойства одностороннеrо преобразования Лапласа
Наименоваиие
Формула
Свойство линейности
n n
Gili (t) . .
aiFi (р)
i
l i
l
Свойство коммутативности
преобразований Лап-
ласа и операций Re и
1т
Re 1 (t) . . Re F (р)
1т 1 (t) :
1т F (р)
Дифференцирование ори-
rинала (теорема диффе-
ренцирования)
l' (t) . . рР (р)
1 (О)
Интеrрирование ориrина-
ла (теорема интеrриро-
вания)
Дифференцирование изо- ,
бражения
t
1 (t) dt . . F
)
о
(
()n 1 (t)
d
)
Интеrрирование изобра-
жения
ro
1
t) . .
F (р) dp
о
по I
ix
1 (t, х)
..: :х F (р, х)
Дифференцирование
параметру
Интеrрирование по пара-
метру
:к: х
1 (t, х) dx . .
F (р, х) dx
хо хо
Изменение масшта6а не-
зависимоrо перемеllноrо
(теорема подобия)
I(
t)
F (
)
Смещение в области дей-
ствительноrо перемен-
Horo (теорема запазды-
вания)
f(t
to) . ' e
ptoF(p)
471
Продолжение таб.л. 15-1
Наименование
Формула
Смещение в области КОМ-
плексноrо nepeMeHHoro
(теорема смещения)
e"i:.M 1 (t) . . F (р :+ л)
Предельные соотношения:
начальное значение
ориrинала
конечное значение
ориrинала
liт t (t) == liт рР (р)
t
O р
cD
liт 1 (t) == liт рР (р)
t
cD p
O
Умножение изображений
(теорема свертывания)
t
S 11 (т) 12 (t
t) dT . . Р 1 (р) Р 2 (р)
О
Следствие теоремы свер-
тывания
t
:t
f1(r)f2(t
T)d;;C'
'pF1(P)F2(P)
о
ИитеrраJ1 Дюамеля
t
f1 (О) 12 (t)+ J f
(т) f2 (t
T) d.=-
t
==f1 (t) 12 (0)+ S 11 (t) I
(t
T) dT . .
о
. . pFi (р) Р 2 (р)
Умиожение ориrинала на
косииус или синус
t (t) cos OJ1t ,;--=,
} [Р (р
jOJ1) + F (р + j OJ 1) 1
f (!) sin OJ1t
'
j [Р (р
jOJд
F (р + jOJ11
Особоrо внимания заслуживают преобра:;ювания, свя-
занные с дифференцированием и интеrрированием ориrина-
лов (теоремы дифференцирования
и интеrрирования).
По теореме дифференцирования
" (t) .' рР (р)
f (().
( 15- 7)
Здесь, как и ранее в rл. 14, под f (О) подразумевается
предел f (О +), к которому стремится f (t), коrда t иеоrра-
ниченно убывает, оставаясь положительным. В случае,
коrда ориrинал в начальной точке непрерывен, т. е. f (О) ::::=
472
== f (O
) == О, ero дифференцированию соответствует опе-
рация умножения изображения на р:
" (t) .' рР(р). (15-8)
Повторным применением операции, выражаемой фор-
мулоЙ (15-7), можно распространить теорему о дифферен-
цировании на производные высших порядков:
f" (/) .' Р [рР (р)
f (О)]
f' (О) == р2Р (р)
р! (О)
f' (О)
и т. д., откуда
п
f(n)(/) .' рnр (р)
f(k
l) (О) pn
k,
k
1
rде f(k
l) (О)
правое предельное значение, т. е.
lim f(k
l) (/).
t
o+
Если, в частности, f (О) == [' (О) == ... == f(n
1) (О) == О,
f(n) (t) .' рnр (р)
то
и, следовательно, п-кратному
rинала соответствует п-крат-
ное умножение на р (если
все производные при t == О
равны нулю).
По теореме иптеерироеа-
пия
дифференцированию ори-
f(t):=F(p)
f(t
ta):le
PfoF(p
t
t
f(t)dt .
F:) . (15-9)
о ta
Рис. 15-3. Смещение в области
действительноrо nepeMeHHoro.
Повторное применение операции, выраженной этой
формулой, дает:
t t
S ... S f (t) (dt)n .' Pp
) .
о о
Теоремы дифференцирования и интеrрирования пока-
зывают, что комплексное переменное р можно рассматри-
вать как оператор (оТсюда и наименоваНl1е «операторный
метод») .
По meopeJ;te запаздЬ/8ания
f(t
to) .' e
pt.P(p). (15-11)
(15-1 О)
473
Форму:ла (15-11) показывает, что умножение изображе-
ния на e
pto сдвиrает rрафик ориrинала вправо На 'о
(рис. 15-3).
Пример 15-1. Найти изображение функции (РИС. 15-4, а)
f (t) == { e
a! при О < t < ' о ;
О при ',> ' о
(а
положительное
ейстаительное число),
}e
ctfo t
to а)
t
О.
5)
Рис. 15-4. Пример 15-1,
Соrласно (15-1)
' о
F (р) == \ e
ate
Pt dt==
[l
e
(Pta)tO].
J р+а
о
Тот же результат получится, если рассматривать f (f) как сумму
двух функций, показанных на рис. 15-4,6; f (!) == 11 (t) + 12 (t), Функ,
.р, (tJ
t
а.)
Рис. 15-5. Пример 15-2.
1
ция 11 (!) имеет изображение
+ . Поэтому f3 соответствии с (15-11)
р а
функция {2 (t) имеет изображение
e
at.e
pt.
р+а
Искомое изображение функции f (!) в силу лииейности преобразо-
ааиия Лапласа равно:
[l
e
(р +а) ( о ).
р+а
474
Пример 15
2. Найти изображение ПОJIупериодз СИНУСОИДЫ
(рис. 15-5, а) с амплитудой, равной единице, и ОСНОl!анием, равным Т/2.
Такой импульс можно получит!;> сложением двух синусоид, сдви,-
нутых на полпериода (рис, 15-5, 6),
По теореме запаздывания
F (р) ==
+
e
рТ/2 ==
р2 + roi р2 + Фl
f(t)
==
(1 +е
p Л/UJ, ) . t
р2 + roi
При мер 15-3. Найти изображение
«выпрямленной» синусоиды, т. е. функ-
ции f (t) == Isin ro 1 t\ (рис. 15-6). Рис. 15-6, Пример 15-3.
Заданная кривая получается пе-
риоднческим повтореннем полуволн
синусоиды, для которой в предыдущем примере найдено изобра
жение Е 1 (р). По теореме запаздывания изображение «выпрямленной»
синусоиды будет:
F (р) ==Е1 (р) (1 +e
рТ/2 +e
рТ +...) == E
(P)T/2 .
l
e р
Следоnaтельно,
F ( )
roi (1 +e
рп/ф,) ==
cth
.
р
(р2 + ro
) (1
e
рл/ro,) р2 + ro; 2ro1
При мер 15-4. Найти изображение пилообразной функции по
рис. 15.7,а.
f(t)
а.)
Рис. 15-7. При:мер 15-4.
Заданная пилообразная кривая получается периодическим повто-
ением кривой рис. 15.7, б. Последняя слаrается из трех функций:
прямолинейных 1 и 2 и единичной 3. TaHreHcbl уrлов наклона прямых
равны соответственно 1/т. и
l/T.
ПО таблице приложения II 1 и теореме запазДыванця рассматри-
. ваемая кусочная функция f1 и) имеет изображение
1 e
рТ e
рТ
Е 1 (р) == Тр2
'fiJ2"'
475
То же получится, если применить непосредственно формулу (15-1)
и вычислить интеrрал
т
Р 1 (р) == S
e
pt dt.
О
Изображение задаиной функции f ('> иаходится сложением изобра-
жений одинаковых треуrольников с учетом сдвиrа:
F(p)==Fi(P)(I+e
pT +e
2pT +...)== Ft(p) т
l
e
P
1 e
рТ
== Тр2
Р (1
e
рТ) .
Теорема смещения
ei:Mf (t) .' F (р + л)
(15-12)
показывает, как изменяется изображение при умножении
ориrинала на показательную функцию. При этом следует
иметь ввиду, что число 'л может быть как действительным,
так и комплексным. Если F (р) определено при Re р> СО,
то изображение (15-12) определено при Re р > со + Rе'Л.
п редеЛ6ные соотношения
Первое предельное соотношение соrласно
Нт! (t1::;;; Вт рР (р)
t.....o р.....оо
табл. 15-1
(15-13)
дает возможност
найти начальное значение функции
f (t) при t --== О непосредственно по изображению. Эта фор-
мула устанавливает существование равенства между двумя.
частными значениями: значением функции f (t) в tIачале
координат (при подходе справа) и значением функции
F (р) в бесконечно удаленной точке (в предположении,
что р стремится к бесконечности внутри уrла I arg р I < п/2,
т. е. в правой полуплоскости).
Второе предельное соотношение
liтf и)::;;; Нт рР (р) (15-14)
t.....oo р.....О
дает возможность найти предел функции f (!) при t
00
по значению функции F (р) в начале координат.
Эта формула имеет смысл только в том случае, коrда
предел фун'кции f (t) при t
00 существует.
Предельные соотношения (15-13) . и (15-14) полезны-
для проверки вычислениЙ с помощью преобразования.
Лапласа. .
476
Теорема умножен.ия изображений (теорема свертывания)
t
. Р 1 (р) Р 2 (р) ..
'1 (-r:)f2 (t
т:) dT (15-15)
о
устанавливает, что умножению в области комплексноrо
переменноrо соответствует свертывание в области дейст-
вительноrо переменноrо.
Если произведение представляет собой произведение
более чем . двух сомножителей, то теорема свертывания
может быть применена к попарно сrруппированным со-
множителям (в любом порядке).
Применение интеzрала Дюамеля.
t
РР 1 (р) Р 2 (р) .' fl (О) f2 (t) +
,
(т) 12 (!
т) d1: ==
о
t .
:=='1 (t) f2 (О) +
'1 (т) f
(!
т:) dT (15-16)
о .
облеrчает вычислеНия по сравнению с формулой
t
рР 1 (р)Р 2 (р) .'
Sfl(Т)'2(t
т)d-с (15-17)
о
в тех случаях, коrда после дифференцирования функ-
ции '1 (т:) или '2 (t
-с) подынтеrральное выражение упро-
щается и вычисление интеrрала в результате этоrо облеr-
чается. Следует иметь в виду, что функция f2 и
-c) в (15-16)
дифференцируется по переменной' t.
В
15-11 будет специально рассмотрен метод расчета
переходных процессов в электрических цепях с помощью
интеrрала Дюамеля.
f5.5. НАХОЖДЕНИЕ оРиrИНАЛА ПО ИЗОБРАЖЕНИЮ
С ПОМОЩЬЮ O&PATHOro ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
ИЗ теории функции комплексноrо переменноrо извест-
Но, что если' функция F (р) аналитична в полуплоскости
Re р> Со. стремится к нулю при '.р 1---)000 в любой полу-
плоскости Re р :== С> СО равномерно относительно apry-
c+irx>
мента р и интеrрал
F (р) dp абсолютно сходится,
c
Joo .
477
то F (р) является изображением ФУНКЦИИ
c+joo
f (t) == 2
j S F (р) е Р! dp.
c
joo
Эта формула, носящая название обратНОёО преобразо
ванuя Лапласа, представляет собой решение интеrральноrо
уравнения (15
1) относительно функции f (t).
В литературе применяется также условная форма за-
писи обратноrо преобразования JIапласа:
L
1 [Р (р)] == f (t).
За путь интеrрирования в (15-18) может быть принята
любая бесконечная прямая, параллельная мнимой оси,
расположенная на расстоянии С > СО от последней (см.
рис. 15-1), так чтобы все особые точки функции F (р) оста-
вались левее пути интеrрирования. Интеrрал в (15-18)
принимаетсяв смысле rлавноrо значения 1.
При практичеСRОМ применении обратноrо преобразо-
ванин Лапласа путь интеrрирования вдоль прямой, парал-
лельной оси мнимых величин, заменяется замкнутым кон-
туром 2, что дает возможность применить теорему о вычетах,
соrласно которой ориrиналом F (р) служит функция
f(t)=::;SResF(p)e Pt и>о), (l5
19)
Pk
[де сумма вычетов берется по всем особым точкам p
функ-
ции F (р).
При t < О функция f (t) равна нулю.
Формула 05
19) позволяет вывести теорему разложеНИ$!
(см.
15
6) применительно к мероморфной функции F (р),
т. е. коrда особенности интеrральной функции в конечной
области
только полюсы.
( 15-18)
Н.6. ТЕОРЕМА РАЗЛОЖЕНИЯ
Пусть изображение задано в виде прав ильной дроби
F (р) =::; Р 1 (p)/f 2 (р), причем числитель и знаменатель не
имеют общих корней. Положение полюсов функции F (р)
определяется корнями уравнения
Р2 (р) == о. (15-20)
1 То есть как предел интеrрала вдоль отрезка (с
jro, с + jro)
при ro --+- СО.
2 Возможность такой замены основывается на лемме Жордана.
478
Обозначим n корней уравнения (15
20) через Рl, Р2' ...
..., Рn. При этом возможны два случая: а) все корни простые;
б) некоторые или все корни кратные.
Рассмотрим эти случаи в отдельносТИ.
а) Спучай простых корней
Из теории функций комплексноrо переменноrо известно,
что вычет функции ер (р)/1Р (р) по полюсу первоrо порядка
Р ::; Р" равен:
Res Ip (р) ::; [ (Р
Pk) Ip (р) ] ==
(Pk) . (15-21)
Р" Ф (р) Ф (р) P
P" Ф (Pk)
Если, как в формуле (l5
18), функция комплексноrо
переменноrо Р имеет вид ;
e pt , причем все корни урав-
нения (15-20) простые (полюсы первоrо порядка), то на
основании (15-19) и (15-21)
n р t
Fl (р)
Fl (Pk) е k
Р 2 (Р) 7""' "'::1 [ Р2 (р) ]
P
P" P
P"
n Р t
'\'1 Fl (Pk) е k
""" p
(Pk) .
"
l
( 15-22)
Это общая фор.ма теоремы разложения для случая простых
корней. Выражение в квадратных скобках в знаменателе
сначала надо сократить на множитель (P
Pk), после чеrо
произвести подстановку Р == Pk.
В случае комплексных корней получаются два сопря-
женных слаrаемых, сумма которых равна удвоенному
значению действительной части (см. пример 15-11).
Пример 15-5. Пользуясь reoремой разложения (15-22), найти ори-
rинал по изображению
1
Р (р+а) (Р+Ь) .
В данном случае Fl (р) == 1; Р 2 (р) == Р (р + а) (р + Ь).
Корни уравнения Р 2 (р) == о равны соответственно:
Pl==O, P2==
a, рз==
Ь.
Следовательно, на основании (15-22)
1 . 1 e
ac
р (р+о) (р+Ь)
оЬ + (
a)(
а+Ь) +
е Ь! 1 ae
Ы
be
at
+ (
Ь)(
Б+а) ==аъ+ ab(b
a) .
479
6) Сnучаji кратных корней
Допустим, что корень Pk повторяется т раз. Из теории
функций комплексноrо переменноrо известно, что если
функция ;
е Р! имеет в точке Pk полюс порядка т, то
вычет функции в этой точке равен:
R Fl (р) р!
1 [ dm"'l Fl (р) (
) т pt ]
P
s Р 2 (р) е
(m
1)1 dpm
l Р 2 (р) Р Pk е P
Pk'
Как и в предыдущем случае, все операции ПРОИ3ВО-
дятся после сокраще,ния
на множитель ( Р
Pk)т. Обозна-
F '
чив А (р) == p
j (р
Pk)m, продифференцируем А (Р) e pt
по рm
1 раз:.
d
dp А (p)ept==ePt[tA (р)+А' (р)];
d d22 А (р) e pt == еpl [t 2 А (Р) + 2tA' (р) + А" (p)J,
р.
. . . . . . . . . . , . . . . . '! . . . . . . . . . .
:;
l А (Р) e Pt == е Р! [tm
lA (р) + (т
1) tm
2A' (р) +
+ (m
1
m
2) tm
ЗА" (р) +.. .+A(т
1) (р)]*.
Следовательно,
Res Fl (р) еР! ==
Pk Р 2 (р)
Pkt [ tm
lA (р) tm
2A' (р) tm
3A" (р) Arm
l) (р» )
e (m
I)1 + (m
2)1 + (т
3)!21 +"'+ (т
I)! P
Pk
т
'р t " tm
iA'HI (Pk)
== е k
(m
i)1 (i
1)1 .
i
1
Формула (15-23) универсальна; ОНа справедлива для
любоrо корня. Здесь предполаrается, что О! == 1. Поэтому
если 8 (15-23) принять т == 1, то получится выражение
Р t Р t
е k tOAO (Pk) Fl (Pk) е k
о! 01
[ Р2 (р) ] ,
P
Pk P
Pk
( 15-23)
* То же получается иепосредственно прн формуле Лейбница
п (п
1)
(uv)rnl == uv Ш1 +nu'vrn
l) + 21 и(2)vШ
2) +... +u'n1v.
480
соответствующее случаю простоrо корня Pk' Это В равной
мере относится и к приведенной выше исходной формуле
вычета функции Б полюсе порядка т, I<оторая при т == 1
переходит в формулу (15-21).
Если уравнение (15-20) содержит несколько кратных
корней, то формула (15-23) применяется поочередно для
каждоrо корня, после чеrо полученные результаты сумми-
руются.
Если имеются одновременно простые и кратные корни,
то формулы (15-22) и (15-23) применяются раздельно соот-
ветственно для простых и кратных корней; затем произво-
дится суммирование.
15-6, Найти ориrинал по изображению
Рl (р)
р+2
Р2 (р)
(р
1)2 р3 .
Заданная функция имеет полюс BToporo порядка Pl == 1 и полюс
TpeTbero порядка Р2 == О. Применив формулу (J5
23) ПOQчередно для
случаев т == 2 и т == 3, получим:
е! [ t р+2 +
Р+2 ] ==(3t
8) ef;
р 3 dp р3 Р
1
O [ !
p+
р+2
!
p+
]
2 5
е 2 (р
1)2 + t dp (р
1)2 + 2 dp2 (р
1)2 р
о
t + t + 8.
Следовательно,
(р
t); р3 . . (3t
8) е ! + t 2 +5t+8.
Друrой способ нахождения ориrинала при наличии
кратных KopHei;I, не требующий дифференцирования, за-
ключается в том, что заданное дробное рациональное
выражение раскладывается на простые дроби; для перехода
от простых дробей к ориrиналу используется соответствие
1 .
ti
lePkt
(P
Pk) t . (t
1)!
Разложение на простые дробlI может быть произве-
дено известным в математике методом неопределенных
коэффициентов, который, однако, связан с решением си-
стемы уравнений, что практически не всеrда удобно,
Если заданная рациональная дробь имеет т-кратный
полюс pk, то разложение на простые дроби может быть
осуществлено непосредственным делением полиномов, рас-
положенных по восходящим степеням р. Например, в рас-
481
смотренном выше примере в результате деления полиномов
получаем
Р 1 (р)
+p
+
.l2 +
11p3
8e
Р 2 (р)
p3
2pl+p
р3 р2 I Р p3
2p4+p
.
Остаточный член в данном случае разлаrается весьма
просто:
8 (p3
p4)+3p3 8 3
" "
"
,.
==
+
(p
1)2 p
p
1 (p
1)2 .
Если имеется т-кратный полюс Pk, отличный от нуля,
1'0 после замены Р
Pk == Z производится деление поли-
номов, расположенных по восходящим степеням Z.
Пусть, Например,
Р! (р) р3
Р 2 (р) == (р+2)4 (р+ 1);
здесь Pk ==
2
полюс кратности 4. ,
ОбознаЧ!IВ Р + 2 == Z И--соответственно Р == Z
2; Р +
+ 1 == z
1, получим:
(Z
2)3
8+ 12z
6z2+z3
!3"
i.' E
+ J:
z4(z
l)
Z4+Z5
Z4 Z3 + Z2 Z z
l'
Следовательно,
F 1 (р) 8 4 2 1
1
Р 2 (р) == (р+2)4
(р+2)3 + (р+2)2 + р+2
р+ 1 .
В заключение отметим, что Для разложения F 1 (p)/F 2 (p)
на простые дроби при наличии m-кратноrо полюса Pk можно
пользоваться формулой
т
Рl (р)
К;
Р 2 (р) ==
(p
Pk)P
i
l
rде
К
1 А (m
i) ( )
l
(m
i)! Pk'
Данное разложение приводит к формуле (15-23).
15-7. ТАБЛИЦЫ оРи.rИНАЛА И ИЗОБРАЖЕНИЙ
Теорема разложения для случаев простых и кратных
корней (см.
15-6) в сочетании с друrими свойствами преоб-
разования Лапласа (см.
15-4) дает возможность составить
таблицы орисиналов и изображений, весьма облеrчающие
и ускоряющие расчеты переходных процессов. Такие таб-
лицы широко применяются на практике.
482
Наиболее полные таблицы приводятся в справочниках
по операционному исчислению и специальных трудах,
посв
щенных преобразованию Лапласа. При практическом
пользовании той или иной таблицей во избежание возмож-
ных недоразумений надлежит в первую очередь проверить
форму записи изображения: дается ли изображение по Лап-
ласу или по Карсону. Если изображение дается по Карсону,
то в соответствии с
15.-2 ero надлежит разделить на р для
получения изображения по Лапласу. '
В ряде типовых примеров, разобранных в предыдущих
параrрафах, были приведены ориrиналы и изображения
по Лапласу. Эти пары функций, а также некоторые друrие,
встречающиеся на практике, помещены в сводной таблице
в приложении IV (в конце книrи).
Возможность пользования таблицами ориrиналов и
изображений наряду с теоремами и различными свойст-
вами преобразования Лапласа представляет большое удоб-
ство, Поэтому преобразование Лапласа широко приме-
няется на практике для расчета переходных процессов
в линейных электрических цепях. К этому следует добавить,
что изображения по Лапласу, приводимые в таблицах,
непосредственно связаны с rармоническим анаЛИЗОl\! непе-
риодических функций (см. rл, 16), что делает этот метод
€ще более универсальным.
15-8. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНЮI ЛАПЛАСА !( РЕШЕНИЮ
диффЕрЕнциАльныx УРАВНЕНИЙ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Рассмотрим цепь с нулевыми начальными условиями,
показанную на рис. 15-8. Допустим, что в момент вре-
мени t == О участок " L С подключается к источнику
э. д. с. е (t). Требуется
найти изображение тока
на этом участке.
По второму закону
Кирхrофа для t;::: О имеем:
. +L di +
е== rt
dt
t
+
.\ idt+uc(O); (15-24)
о.
т'
L
с
Рис. 15-8. Включение источника
э. д. с. в цепь с ненулевыми усло-
ВИЯМИ.
здесь ис (О)
начальное напряжение на емкости, обусловлен-
ное э,'!ектрическим зарядом емкости в момент коммутации.
48З
Будем рассматривать е (t), ис (О) и i (t) как функции
ориrиналы, имеющие изображения Е (р), ис (О)/р и 1 (р).
На основании свойства линейности преобразования
Лапласа и теорем дифференцирования и интеrрирования
исходному уравнению (15
24) соответствует следующее
уравнение для изображений:
E(p)==rI(p)+pLl(p)
Li(O)+ I C (P) + ис(О) ; (15-25)
р р
здесь i (О)
начальный ток в индуктивности.
Блаrодаря тому, что операция дифференцирования и
интеrрирования ориrинала соответствует операции умно-
жения и деления изображения на р, уравнение для изо
бражений получается алrебраическим, т. е. более простым,
чем исходное интеrродифференциальное уравнение, Ero
решение относительно 1 (р) дает:
Е (р)
и с (О) + Li (О)
l(р)== р 1
r+pL+ pC
Далее после. преобразований получим:
1 рЕ (р) + ри (О)
и с (О)
1 (р) == т r 1 .
р2 + .L
P+ LC
Искомая функция i (t) (ориrинал) Находится по изобра
жению (15-26а) однпм из указанных выше способов, а
именно: с помощью теоремы разло-
жения (или друrих правил) или по
rOToBbIM таблицам.
Для схемы, показанной на рис.
15-9, ypaBHeHII
заПИСывается по пер
вому закону I<.ирхrофа (при t> О,
т. е. после подключения сопротивле
ния r):
t
i ==
U + с
+.!
(' u dt + i L (О)
r си L J I '
О
l'
i (t)
.,::r-
Рис. 15
9. Включение
ветви в цепь с источ-
ником тока.
(15-26)
(15-26а)
rде i
ток источника тока; u (t)
напряжение между
узлами; i L (О)
ток в индуктивности при t == О.
Полаrая i (t)
1 (р) и u (t) .. U (р), нахоДИМ:
I(p)== и(р) +рСИ(р)
Си(О)+ и(р) + iI.(O) . (15-27)
, pL р'
484
здесь u (О)
начальное напряжение между узлами, рав-
ное напряжению на емкости.
После преобразований получается изображение иско-
Moro напр яжения
1 р! (р) + рСи (О)
i E (О)
и (р) ==с 1 I '
рЧ
р ,С + [С
для KOToporo указанными выше способами находится ори-
rинал u (t).
При нулевых начальных условиях, т. е. при включе-
нии источников в пассивные цепи, выражения (15,26) и
(15-27) упрощаются, а именно:
1 (р) ==
Е (р)
Е (р)
1
Z (р)
'+pL+ рС
и
1 (р) == ( ; +
p
+ ре) и(р) == у (р) и (р).
Здесь Z (р) и У (р) представляют собой сопротивление
и проводимость соответствующих цепей при комплексной
частоте р == с + j(J). Это те же сопротивление и проводи-
мость, которые уже встречались в rл. 14. Они называются
о пер а т о р н ы м и сопротивлением и ПрОВОДИмостью.
В общем случае порядок решения задачи следующий:
1) записываются интеrродиффереНЦ1Iальные уравнения
Кирхrофа для цепи, в которой исследуется переходный
процесс;
2) записываются те же уравнения для изображений
с учетом нез.ависимых начальных условий:
3) уравнения для изображений решаются алreбраически
относительно изображения искомой функции;
4) на основе полученноrо изображения находится ори-
rинал искомой функции.
При достаточном навыке или если схемы относительно
просты, уравнения для изображений записываются непо-
средственно, без предварительноrо составления интеrро-
дифф.еренциальных уравнений (см. примеры 15-8, 15-11
и др.).
В случае сложной схемы также можно обойтись без
записи интеrродифференциальных уравнений, если пред-
варительно нарисовать эквивалентную схему для изобра.
485
жений. Как видно из предыдущих рассуждений такая
схема отличается от схемы цепи для установившеrося
синусоидальноrо режима тем, что комплексные вели
ины
jroL и jroe заменяются соответственно pL и ре и вместо
комплексных функций времени вводятся их лапласовы
изображения. Кроме Toro, при ненулевых начальных
условиях в схему для изображений последовательно с,ин-
дуктивностью включается дополнительный источник э. д. С.,
равной L,/L (О) (рис. 15
10, а), а послеДовательно с ем'
t
'
........
i(t) а) 1 (р) L, i(O)
С Z(p) = :с
.0
i
i (t) u.c(t) 6) I(p) (1 0 )
i 1 (t) М iz(t) L1 i 1 (о) Miz(O)
y
- -Т; I;(p)
(L1
M)
:J
, 8)
Mi 1 (о) Lziz(O}
p(L2
M)
рМ
Рис. 15.10. Схемы замещения элементов для изображений.
костью
дополнительный источник с э. д. с., равной
ис (О) /р (рис. 15-10, 6).
В случае индуктивноЙ связи между двумя элементами
соответствующая схема замещения представлена рис.
15
10, 6. При коэффициенте связи k :::::: 1 имеют место соот-
ношения:
L
Wi М .
1
Ша '
.... w.., .
L 2 ==: .....::с М
Wl
и
i 1 (О) W 1 ==: i 2 (О) W 2 ;
поэтому В этом случае в схеме замещения э. д. с. дополни-
тельных источников взаимно уничтожаются.
486
После введения дополнительных 1iСТОЧЮIК6в 3аt1исЬi-
ваются уравнения I(ирхrофа непосредственно для изо-
бражений; структура этих уравнений аналоrична струк-
туре уравнений для установившеrося синусоидальноrо
режима. Сказанное проиллюстрировано в примере 15-7.
Если воздействующая функция, например э. д. с. источ-
ника, синусоидальна, то переходный процесс можно рас-
считывать в действительной или комплексной форме. При
комплексной ф?рме расчета начальные значения токов
в индуктивНостях и напряжений на емкостях учитываются
Б виде КОI
лексных амплитуд и уравнения записыва
ся
для изображений комплексных функций токов' и напря-
жений. Искомые функций времени определяются мнимой
частью наЙденных комплексных ориrиналов (подробнее
см. пример 15-10). Любая из указанных здесь форм решения
уравнений для изображений приводит в конечном итоrе
к необходимости нахождения ориrинала по теореме раз-
ложения или таблице; ориrинал получим в виде суммы
установившейся и свободной составляющих.
. Вычисления во мноrих случаях мОРут быть 06леrчены,
если предварительно рассчитать установившийся режим
и определить по формулам (14-8) начальные значения
свободных токов в индуктивностях i L (О) И свободны
св
напряжений на емкостях ис (О). Используя эти значения
СВ
как начаЛьные условия в уравнениях для свободноrо ре-
жима или соответствующих эквивалентных схемах заме-
щения с дополнительными источниками, но без основных
источников, можно получить изображение свободноrо
тока. ОНо будет иметь более простой вид, чем изобра-
жение полноrо тока. Соответственно облеrчится и на-
хождение ориrинала по изображению. Полный ток
определится как сумма установившеrося тока, найден-
Horo отдельно, и ориrинала свободноrо тока (см. при-
мер 15-11).
Такой метод' расчета целесообразен в том случае, коrДа
установившийся ток, входящий в состав полноrо тока,
значительно усложняет лапласово изображение для пол-
Horo тока и тем затрудняет нахождение ориrинала.
Пример 15-7. Составить уравнения для изображений контурных
токов схемы на рис. 15
11, а после замыкания контакта. Начальные
значения тока в индуктивности L и напряжения на емкости С обозначим
через i 1 (О) и ic (О), приняв положительное направление напряжения
на емкости в напраВ.'lении тока i 1 . Уравнения по второму закону .кирх-
481
rофа для t
О запишутся так:
t
Е т sin (W1 t +'Ф) == 'l i 1 +L1
+'2 (ii
i 2 ) +
S (i 1
iJ dt+ и с (О);
о
t
о==,з i 2+ L 2
2 +'2 (i2
i1) +
S (i2
i1) dt
и с (О).
о
Соответствующие уравнения для изображений, если обозначить
11 (р) == 11:= i 1 (t) И 12 (р) == 12:= i 2 (t),
примут вид:
Е рsiп'Ф+WiСОS'IjJ == ( , + , + L +
) I
т р2 + WI 1 2 Р 1 рС 1
( 1 ) ис (О) .
'2+ рС 12+
L111 (О);
( 1 ) ( 1 ) ис (О)
0== '2+,з+рL 2 + рС 12
'2+ р С 11
'
Те же самые уравнения получаются и на основании эквивалентной
схемы на рис. 15-11, б, составленной для изображений.
1,1 i l (о)
7'3
pL I
t
/с
Е(р) щ(а)
р
pLz
"z
(rМ)
а.)
Рис. 15.11. I1ример 15-7.
е=Е т COS(6Jl t +,/,)
6)
Пример 15-8. Найти токи в схеме иа рис. 15-12 после Замыкания
контакта.
Начальные значения тока в индуктивности и напряжения на емко-
сти равны соответственно;
i L (O)==
и и с (0)== ' + '2 Е.
'1+'2 '1 '2
На основании расчетной схемы можно непосредственно написать
уравнения по второму закону к.ирхrофа для изображений:
+LiL (О) == ('2+pL) 12;
р
иср(о) == ('3+ p
) 1з,
488
откуда
, Е + Li [, (О) Р
/2==
Р ('2+pL)
{+ i L (О) Р
p(p+ 'i )
и
Е
И С (О)
1з== 'з ( Р +
) .
. '3 С
Переходя к ориrиналам, по формуле (15-22) находим:
Е (
1 )
!3. t
i 2 (t) == '2 ,1
е L + i L (О) е L ;
Е
и ( О)
!
. ( t )
е rзе
13
'з е
i 1 (t) == i 2 (t) + i3 (t).
Пример 15-9. Определить ток в контуре цепи на рис. 15-13 после
размыкания контакта, если до размыкания в цепи был установившийся
постоянный ток.
t=:O
"2 "з
7'
/'z
L i3! с
Рис. 15-12. Пример 15-8. Рис. 15
13. Пример 15-9.
в задаче пренсбреrают временем rорения дуrи на контакте;
считается, что токи в индуктивностях L 1 И ['2 уравниваются MrHOBeHHO.
В
14-2 укаЗhlвалось, что решение TaKoro рода задач основано на прин
ципе непрерывности cYMMapHoro потокосцепления до и после KOMMY
тации.
Дифференциальное уравнение для заданной цепи запишется так:
. di di
Е == rt + Li di + L 2 dt .
При t == О токи в индуктивностях были i 1(0
) == О И i 2 (o
) ==
== Ej,.
. Начальиым условием для процесса после разрыва дуrи будет:
L 2 i 2 (o
) == (L1 + L 2 ) i (о),
489
откуда
. ( О )
i 2 (O
) L 2
l
L 1 + L 2 .
Переходя к изображеНИЯ
f, напишем:
Е ;:: r! (р) + (Lf + Li'J р! (р)
([-1 -+ L 2 ) i (О);
Р
откуда
Е + Н2, р
,
( , \ .
(Li + L 2 ) р + Li + [ 2 ! р
ПО формуле (15-22) найдем ориrинал:
. (t) Е (1 Lf
L,
L. [ )
l ==
е .
, L 1 + L 2
При мер 15
10. В момент t;:: О цепь, состоящая из послеД9вательно
соединенных, и [, присоединяеrся к источнику синусоидальной э. д. с.
е (t) == Е т sin (I0 1 t + 'Ф).
Определить ток i (t), пользуясь комплексной формой расчета
переходноrо процесса.
При t
О
Emei(w,t+1j,)==.,[ (jIOt) + L d[ (jmt)
dt
Е + L 2 i 2 (o
)
р
1 (р)== r+2(L1+L2)
Переходя к изображениям, приняв ! иIO!) =j;; ! (р), получаем:
',1, 1
E m eJ't'
==,[ (р ) +рLl ( о).
,p
/IOi '
откуда
Е теl'Ф
1 (р) (р
j (0 1) (r+ pL) .
Ориrинал НаХОДим по формуле (15
22):
Е ei(CiJ,t+1)J) Е eJI\1
f t
1 (jIOt) == т,
": е
,+/I011, r+/ I0 1 L
Искомый ток определяется мнимой частью этоrо выражения, т. е.
i и) == Е т sin (I01t+'Ф
«р)
у,2+( I0 1Ц2
r
Е т siп ('Ф
«р)
у; t
У е.
r 2 +(I01L)2
rде
I01L
ер == arctg
.
r
Пример 15
11. Найти методом оТДелениg свободноrо тока от YCTa
новившеrося ток в цепи на рис, ]5
!4 после замыкания контакта.
490
Дано: Е т "'" 10 1?; (й1 == 400 раД/С;'l == 10 Ом;'2 == 5 Ом; L :о:: 0,1 (;
С == 100 мкФ.
Обычным методом расчета устаНОDнвшеrося синусоидальноrо ре-
жима леrко найти до коммута-
Цни ток и наприжение и с :
i==0,472 sin (400t
л/4)А;
uc==
11,8cos (400t
л/4) В.
1'2
"
с
Отсюда находятся началь-
ные условия:
i(O)==i (0
)==
0,332 А;
и с (О) == и с (O
) ==
8,З4 В, Рис. 15-14. Пример 15-11,
Аналоrичным расчетом после коммутации находятся те же устано-
вившиеся значения:
и
iy (t) == 0,633 sin (400!
71030') А
и с (t)==
15.8сos(400t
71ОЗ0') В,
у
ЧТО дЛЯ t == О дает:
iy (0)=;;
0,6 А и и с (0)==
5 В.
у
Соrласно (14-8) начальные независимые значения свободных состав-
ЛЯЮЩнх будут:
i CB (О) ==
O,332 + 0,6== 0,268 А;
ic (0)==
8,34+5==
3,34 В.
св
Изображение свободноrо тока для такой цепи имеет вид:
и с (О)
Li CB (О)
СВ
/СВ (р)==
'2+pL+
c ,
. р
О,268р+33,4
О,268р+33,4 .
р2+50р+l0 0
(P
P1).(P
P2J'
здесь Р1.2 ==
25 :!: /315.
По формуле (15-22) находим ориrинал:
. (t)
O,268(
25+/315)+33,4 01t +
B 2./315 е
+ 0,268 (
25
j315)+33,4 ep,t==:
2 ' j315
== 2Re [о, 141e
j\7° 30' e
25/ e i 315t] == 0,282e
25/ сos (31Бt
17030') А.
0,1 . O,268
3,34
р
106
5+рО,1 + р. 100
Как видно, ориrинал СDободноrо тока найти достаточно просто.
Пример 15-12. Найти ток в контуре ,С в случае включення в Hero
источника э. д. с. треуrольной формы (рис. 15:15).
Начальные условия нулевые,
491
Функцию е (i) можно представить в виде СУмм!,! ТреХ прямолиней-
ных функций, изображенных на рис. 15-15, а. TaHreHcbI упlOВ наклона
первой и третьей прямой равны I/T, а второй прямой (
2/T). Исполь-
зуя теорему запаздывания для функции е (t), получаем изображение
1 2
т 1
2 Т
E(p)==
e р +
e Р.
Тр2 Т р 2 Тр2
Тот же результат получится, если применить непосредственно фор-
мулу (15-1) и произвести интеrрирование,
t
Рис. 15-15. Пример 15-12.
5)
Изображение искомоrо тока будет:
1 (р) ==
(pi
;
,+
рС
пераое слаrаемое э. д. с. даст:
1
/1(Р)== ( l'
Тр 2 ,+ рс )
. ,с 0 + 1
?=?l'e ( l ) е
,т
ТС
t ( t )
С
,С С
,С .
y е == т l
e ==li (t).
1
,Тр (Р+ ,
)
t
,С С
==
T
Второе и третье слаrаемые имеют тот же вид, но запаздывают от-
носительно nepBoro соответственно на Т и 2Т (второе слаrаемое учи-
тывается при t> Т, третье
при t > 2Т). Поэтому при t > 2Т
i (t) == i 1 (t)
2il ((
Т) +il ((
2Т).
15-9. УЧЕТ НЕНУЛЕВЫХ НАЧАЛЬНЫХ УСЛОВИIit МЕТОДОМ
ЭКВИВАЛЕнтноrо ИСТОЧНИКА
Если в электрической цепи при ненулевых начальных
условиях (т. е. при наличии токов в индуктивностях или
напряжений на емкостях) происходит замыкание или
492
размыкание какой
либо ветви, то переходный процесс,
вызываемый изменением схемы, может быть рассчитан
методом эквивалентНО20 источника. В случае замыкания
ветви удобно применять теорему об эквивалентном источ
нике э. д. с., а в случае ра.змыкания
- теорему об экви-
валентном источнике тока (см. rл. 7).
На рис. 15
16, а показан случай замыкания ветви элек
трической цепи в момент 1 == О. Так же как в
7-9, буква А
означает активную, а буква Ц
пассивную цепь; их (/)
напряжение, существовавшее до момента замыкания ветви,
условно продолженное на время 1 > О.
'A
\A
lп
6') 2)
А
>..t=O
/&1
а)
Рис. 15
16. Замыканне ветви электрической цепи.
Режим электрической цепи при 1> О MOr быть как
установившимся, так и переходНЫМ. Ход рассуждений
в обоих случаях остается одним и тем же. Включив в зам-
кнувшуюся ветвь две э. д. с., равные их (/) и противо
положно направленные (рис. 15
16, б), и пользуясь мето-
дом наложения, приходим к двум схемам на рис. 15
16, в
и с, в первой из которых токи те же, что и в первоначаль-
ной схеме.
Таким образом, nереходный процесс при замыкан.ии
ветви находится в результате наложения токов nредшесm-
вующе20 режима (при разомкнуmоu. ветви), условно про'.
должеННО20 на вре.МЯ 1 > О, на токи, получаемые в резуль-
тате включения в пассивную цепь источника э. д. с. их (/).
При этом если при 1 < О режим бьiл установившимся,
то напряжение их (/) может быть как постоянным, так и
переменным (синусоидальным).
При их (/) == и == сопst в расчет вводится изображе
ние ИХ (р) == И/р, а при синусоидальном напряжении
493
их (t), записанном в комплексной форме u т ei(UJ,f+1P), в рас-
чет вводится изображение Uтej\j)
.
P
J[j)1
ТОК В замыкаемой ветви находится по изображению
1 ( ) их (р) 5 28
р == z (р) , (1
)
rде Z (р)
оператор ное сопротивление всей пассивной
цепи, рассматриваемой со стороны места замыкания. При
менительно к схеме на рис. 15
16 ОНо равно входному опе-
раторному сопротивлению пас
сивноrо двухполюсника.
Рассмотрим для иллюстра
ции изложенноrо метода один
простейruий пример.
Пример 15
13. Найти ток i (!) в
ветви с сопротивлением '2, замыкае-
мой при '== О (рис. 15-17).
Напряжение на разомкнутых кон-
тактах равно Е. СледоватеЛЬНQ, изо-
бражение ИХ (р) p;JBHO Е/р. Входное операторное сопротивление
пассивной цепи, рассматриваемой со стороны замыкающеrо контакта,
/.,
r 1
i (t)
Рис. 15-17. Пример 15-13.
Z 'lpL
(p)=='2+
+ L '
'1 Р
Следовательно, на основании (15-28)
I (P)
Е E
+
( ,pL ) P['1'2+('I+'2)pLJ'
р '2+ '1 +pL
Переходим к ориrиналу:
'," t
. Е 'IЕ (Т, +Т 2 ) L
(!)
r;
'2 ('1 +'2) е
На рис. 15
18 показан случай размыкания ветви элек-
трической цепи в момент t == о. Здесь i K (t)
ток, суще-
ствовавший до момента размыкания ветви, условно npo
долженный на время t >0.
Включив параллельно в месте размыкания два источ-
ника тока i K (t), действующие в противоположных направ
лен иях (рис. 15
18, 6), и пользуясь принципом наложе
ния, приходим к двум схемам (8 и с). В первой схеме токи
те же, что и в первоначальноЙ схеме а.
Таким образом, переходный процесс при размыкании
ветви находится в результате наложения токов предшест-
вующесо режима (при замкнутой ветви), условно продолжен-
494
ноео на время t> О, на распределение токов, получаемое
в результате включения в пассивную цепь ucточника тока i K (t).
Напряжения в исследуемом переходном режиме также
находятся методом наложения, т. е. алrебраическим сло-
жением напряжений на одинаковых участках цепи на
рис. 15-18, а и с.
.l!=O
а)
iK(t)
---1>
А
!)
iH(t)
е)
Рис. 15-18. Размыкание ветви электрическоЙ цепи.
Ток i K (t) заменяется изображением I K (р), И напряже-
ние в месте размыкания опp€деляется по изображению
и (р)=== z (р) I K (р); (15-29)
здесь Z (р)
входное операторное сопротивление пассив-
Horo двухполюсника (схема с).
Если исследуемый переходный процесс вызывается
изменением схемы электрической цепи не при t == О, а при'
t === t 1 , то заменоЙ переменной
t' === t
t 1 начало отсчета вре-
мени переносится в t 1 (см. при-
меры 15-14 и 15-15).
Пример 15-14. [Л. 5]. В схеме на
рис. 15
19 при t == О замыкается кон-
такт К 1 . а при t == ( 1
контакт К 2 .
Требуется определить ток в цепи кон-
такта К 2 методом Эквивалентноrо ис- Рис. 15-19. Пример 15-14.
точника.
При t < ( 1 , т. е. до замыкания контакта К2' напряжение на нем
определяется напряжением на- сопротивлении '2:
Е'2 t
их (t)==
(I
e
a).
'1 +'2
[де
'1 +'2
a==
.
rf
f;f
К2
i(t)
495
Произведем замену переменной: t::= ( 1 + (', Следовательно,
их (t'):= ЕУ 2 (1
e
atle
at.).
(У1 + (2)
Пусть ИХ ({') =;lc ИХ (р), т. е.
И ::=
(
e
at. ) ::= ЕУ 2 [а+ р (1
e
Qt,)]
х(р) '1+ У 2 р р+а (У1+'2)р(р+а)'
Изображение искомоrо тока находится по формуле (15-28):
/ (р)
их (p)/Z (р),
rде
z (р)
'2 ('1 + pL) .
'1 +r2+pL
Пщставляя выражения ИХ (р) и Z (р) в выражение для / (р), по-
лучаем:
Е [а+р (1
e
atl)]
/(p)
(У1+'2) (р+Ь)р
здесЬ
b
'1/L.
Переходя к ориrиналу, находим:
. (t ' ) Е Е( '1 l
e
atl )
Ы'
t
"
е (t' > О).
(1 ( 1 '1+'2
Пример 15-15 [Л. 51. в схеме на рис. 15:20 при (
О замыкается
контакт К1' а при t
( 1 размыкается кнопка. Требуется определить
методом эквивалентноrо источника
напряжения на выводах кнопки
...L.. после ее размыкания.
При t
( 1 , т. е. до размыка-
r1 ния кнопки, проходящий через нее
ток равен:
r2
i K (t)
l!..
c at ,
(1
rде
Рис. 15
20. Пример 15
15.
а::= 1/'1С'
Производим замену переменной: t
(' + ( 1 .
Следовательно,
. ( t' )
Е
at,
at'
lк
ri е е .
Полаrая i K (t') ;" /к (р), имеем:
Е
at, 1
/к (p)
т
e
.
'1 р+а
4116
Обозначим через Z (р) входное операторное сопротивление пассив-
ной цепи, рассматриваемой со стороны выводов кнопки:
'2 ( 'i+ p
l c
)
p+a
Z(p)== 1
'l+'2P+b'
'1 +'2+ рС
rде
1
Ь== ('1 +(2) С .
Изображение искомоrо напряжения на выlодахx кнопки находится
по формуле (15-2
):
Е"2 (р+ а) e
al, E'2e
al,
и (р) == Z (р) 1 к (р) == ('1 + (2) (р + Ь) (р +а) == ('1 + '2) (р + Ь) .
Ориrинал искомой функции
u(t')== Er
e
(all+bI') (t'>O).
'1 +'2
15-10. ФОРМУЛbI ВКЛЮЧЕНИЯ
Как было показано выше, включение источника э. д. с. в пассивную
(без энерrии) электрическую ц
пь вызывает ток
1 (р)==Е (P)/Z (р).
Операторное сопротивление Z (р) может пред::тавлять собой либо
входное сопротивление [в этом случае 1 (р) является входным током],
либо величнну, обратную передаточной проводш!Ости.
Если включаемая э. Д. с. задана в виде экспоненциальной функции
Ee?I, то
Е
Е (p)==
p
q
и соответственно
Е
1 (р) == (р
q) Z (р) .
Применяя теорему разложения (15-22), получаем ФОРМУЛУ 6КАЮ-
<;ения для экспоненциальноЙ э. д. с. 1
n р I
. . Ee ql '\1 Ее k
1 (p);='t (t)== Z (q) +
(Pk
q) Z' (Pk)'
k
l
(15-30)
Первое С'лаrаемое представляет собой установившийся ток; сумма
остальных слаrаемых образует свободный ток.
Нанболее распространенными на практике случаями являются
случаи включения источников постоянной или синусоидальноЙ э. д. с.
1 Здесь по аналоrии с Э 14-7 предполаrается, что уравнение Z (р) ==
== о имеет n корней,
497
При включении испючнu"а nостояннойа. д. с. (q == О) формула (15-30)
принимает вид:
. Е
Ee Pkt
l (t) == Z (О) + "'- PkZ' (р k) .
k
l
В случае включения источника синусоидальной э. д. с. (В комплекс-
ной форме) q == jO)l' причем вместо Е должна быть введена комплексная
амплитуда Eme jro ;
I
Emei(ro,t+li')
EmeNePkt
(!)
Z иО)1) + ""'" (Pk
j Ш l) Z' (Pk) .
k
l
(15
31)
(15-32)
Нетрудно убедиться в том, что формулы включения (15.30)
(15-32) остаются справедливыии и в том случае, коrда Z (Р) представ-
ляет собой дробную функцию вида Z (Р) == А (р)/В (Р), однако при этом
удобнее пользоваться теоремами разложения (l5
22) и (15-23).
Н-Н. РАСЧЕТ ПЕРЕходноrо ПРОЦЕССА С ПОМОЩЬЮ ФОРМУJ'l
НАЛОЖЕНИЯ
Если пассивную электрическую цепь (без запаса энер-
rии), имеющую операторное сопротивление Z (р), при-
соединить к источнику э. д. с, е (t) .' Е (р), то возникнет
ток i (t) .' 1 (р) == Е (р) /Z (р). Изображение искомоrо тока
равно произведению двух функций: 1/Z (р) иЕ(р).
Рассматривая функцию 1/Z (р) как изображение, соот-
ветствующее некоторому ориrиналу У6 (t), можно ВОСПОль-
зоваться формулой (15-15) умнqжения изображений (теоре-
мой свертывания). В результате получим:
t ' t
i (t) ==
е (1") У6 (t
-r) d-r ==
е (t
-r) Уа (-r) d-r. (15-33)
о о
Выражение 1/Z (р) может трактоваться как изображе-
ние тока, возникающеrо в данной цепи под воздеЙствием
э. д. с., изображение которой равно еДИнице. Функция,
изображение которой равно единице, представляет собоЙ
предел прямоуrольноrо импульса длительностью'( и высо-
той 1/'( при '( --+ О. Действительно прямоуrольный импульс
на рис. 15-21, а, заштрихованная площадь KOToporo равна
еДИНице, может быть представлен как разность двух функ-
ций (рис. 15-21, б и в), имеющих изображения l/-rp и е
Рt/-rр.
Следовательно, изображение прямоуrольноrо импульса рав-
1 ,
но т:р (1
e
pt). При '( --+ О данное выражение принимает
498
неопределенный вид 0/0. Раскрывая неопределенность по
правилу Лопиталя, находим:
Нт
(1
e
P'C) == Нт 1?..e
P'C == 1.
'C"'-+оТР Р
Хотя физически этот предел нереализуем, ОДНаКО на
основани!! сказанноrо выше условно считается, что функ-
ция, изображение которой равно единице, означает бес-
конечно большой импульс бесконечно малой продолжи-
тельноети; площадь, оrраниченная импульсом, равна едини-
це. Такая функция называется
импульсной функ-
Ц И е й и обозначается б (t).
Итак, ориrинал Уб (t) пред-
ставляет собой не что иное,
как реаКцию цепи на импульс-
ную функцию. Если функ-
ция Уб (t) известна, то пере-
ходный процесс в той же цепи
под воздействием произволь-
ной э. д. с. е (t) рассчитывает-
ся по формуле (15-33), пред-
ставляющей собой одну из
разновидностей формул нало-
жения.
Друrие разиовидности
формул наложения основаны
натом, что первоначально
исследуется переходный процесс под воздействием еди-
ничной функции, т. е. в предположении, что заданная
цепь присоединяется к источнику постоянной э. д. с.,
равной 1 В.
Ток, возникающий под воздействием единичной функ-
иии, имеет изображение l/pZ (р). Функция Yl (!) .' l/pZ (р)
Носит в литературе название пер е х о Д н о й про в о -
Д и м о с т и.
Ток i (t), возникающиЙ под воздействием э. д. с. е (t),
имеет изображение
Е (р) 1
1 (р) == z (р)' == рЕ (р) pz (р) .
;;
11
lb
о
t
"
а)
t
.
о)
.t
.
'с'
8)
Рис. 15-21. Прямоуrольный им-
пульс как разность двух еди-
ничных функций.
(15-34)
Следовательно, задача сводится к нахождению ориrи-
нала по .изображению, сомножителями KOToporo являются
р, Е (р) .' е (t) и.l/рZ (р) .' Yl (t).
499
В данном случае можно воспользоваться следствием
теоремы свертывания, т. е. одной из формул интеrрала
Дюамеля (15
16):
t
i (t) == е (О) Уl (t) +
е' (т) Уl (t
т) dT ==
о
t
== е (t) Уl (О) +
е (т) Y
(t
т) dT. (15-35)
О
Таким образом, зная реакцию электрической цепи на
илтульсную или единичную функцию, можно найти peaK
цию той же цепи на произвольную функцию с помощью
одной из интесральнЬ/х фОРАtул (J5
33) или (l5
35). Эти
формулы MorYT быть также выведены на основе метода
наложения.
e(t)
I
I
I
t I t
О A't' 2л't' 8
'C' О
't"" 2A't"" 3
'C'
0.) 5)
Рис. 15-22. Иллюстрация к ВЫВОДУ формул наложения.
Заданную кривую э. Д. с. е (t) можНо приближенно
заменить ступенчаТ0Й кривой в виде серии прямоуrоль-
ных импульсов длительностью ДТ (рис. 15-22, а). При
достаточно малом ДТ реакция цепи на первый прямоуrоль-
ный импульс приближенно равна реакции цепи на импульс-
ную функцию, умноженную на площадь первоrо пр ямо-
уrольноrо импульса е (О) ДТУб (t). Реакция цепи на вто-
рой прямоуrольный импульс приближенно равна е (ДТ) Х
Х ДТУб (t
ДТ), rде е (ДТ) ДТ
площадь BToporo прямо-
уrольноrо импульса, Уб (t
ДТ)
реакция цепи на им-
пульсную функцию, соответствующую моменту времени Дт.
Следовательно, для рассматриваемоrо момента вре-
мени, t == пДт реакция цепи приближенно выражается так:
п
i (t)
е (k ДТ) ДТУб (t
k ДТ).
k
O
500
Коrда ,11'.....,. О, п .....,. 00. в этом случае
11.
i (t) == Нт
е (k L\T) ,1чJ6 (t
k L\T).
.:I.'.....Ok
O
11......""
По мере приближения L\T к нулю изменение k,11' вме-
сто скачкообразноrо (дискретноrо) становится непреры
HblMj операция суммирования превращается в операцию
интеrрирования по переменной т == kL\1':
t
i (t) ::::=
е (т) уб (t
т) d1'.
о
На рис. 15-22, б кривая е (t) приближенно заменена
серией ступенчатых функций, запаздывающих друr OTHO
сительно друrа на L\'t. Реакция цепи на первую ступень
равна реакции цепи на единичную функцию, tIомножен
ную на высоту первой ступени: е (О) Уl (t), Реакция цепи
на вторую ступень равна L\e 1 Yl (t
,1т), rде L\el
высота
второй ступени, Уl (t
L\1')
реаКция цепи на единичную
функцию, смещенную в сторону, запаздывания L\1'.
Следовательно, для рассматриваемоrо момента времени
t == nL\'t реакция цепtI равна:
п.
i (t)
е (О) Уl (t) + L: L\ekYl ('
k L\'t').
k
l
При L\1'-+ О И п -+ 00
11.
i (t) == е (О) Уl (t) + liт
ek Уl (t
k L\T) L\T ==
.:1.'.....0 k
l 't'
n.......оо -
t
== е (О) Уl (t) + \ е' (т) Уl ('
т) d't.
О
Метод инте2рала Дюамеля целесообразно пРИАlенять
в тех случаях, КО2да известна или леека находится реак-
ция на единичную функцию, а воздействующая функция
имеет кусачна-аналитическую форму.
Если Боздействующая функция является разрывной
при t> О, то удобнее пользоваться той формой интеrрала
Дюамеля, которая не содержит производной .этой функ-
ции. В противном случае должна быть учтена реакция
цепи на соответствующий скачок функции.
501
Пример 15-17. Сопротивление f и емкость С, соединенные nосл!!-
довательно, подключаются при t
О к источнику Э. д. с. в виде тре-
уrольноrо импульса (см. рис:' 15-15, а). Определить ток при t> 2Т,.
1
Реакция цепи на единичиую фуикцию равна У 1 (р) 1 ) .
Р (,+ рС
t
1
тС
Следовательио, У1 (t)
, е .
Воспользуемся первой формулой (15-35):
t
i (t) =-= е (О) Yi и) + S е' (т) Yi (t
') dT;
О
Т t
, 2Т t
,
. r 1
-ТC r 1
те
t (t)
J т; е dT
J т, е d..
о т
Проинтеrрировав, получим ток после окончания действия нмпульса,
т. е. для t > 2Т:
i (t)
ce
T
(1
/C у.
Нетрудно убедиться, что полученный результат совпадает с резуль-
татом примера 15
12, найденным с помощью преобразования Лапласа.
В данном случае ннтеrрал Дюамеля дал очень леrкое решение.
Пример 15-18. Сопротивление, и индуктивность L, соединенные
последовательно, подключают при t =; О к источнику ступенчатой э. д. с.,
показанной на рис. 15-23. Определить ток при t 2 > t > t 1 И t > t 2 .
e(t)
e(t)
жО ,. L
1
о
t1
t
t2
Рис. 15-23. Пример 15-18.
Решение находится проще Bcero методом наложения. Суммируются
реакции цепи на две единичные ступени иапряжения, одна из которых
запаздывает на t 1 ; при t > t 2 вычитается реакция цепи на удвоеииую
ступень напряжения, смещенную в сторону запаздывания на t 2 .
Итак, при
t 2 > t> ti
1 [
!
('
t') l 1 [
t (
t. )]
i(t)==, l
e
+1
e
, 2
e
l+e
.
502
При !>!z
1 [
!.. t ( !. (, )
!. «(
(') ]
i(t)==, 2
e L 1+6'L
2+2e L ==
r ( r r )
1
Т. ( L (, L (,
==
е 2е
е
1 .
r
Для сравнения приведем решения по формулам (15-33) и (15-35).
t
По первой формуле (15-33) i (t) == S е (т) Уб (!
T)'dt.
о
Изображение реакции цепи Н1! импульсную функцию равно:
1
Уб (р) == r+pL .
Следовательно,
r
1
т. t
Уа (t) ==
е
L
При '2> t> ti
r t r
(' 1
(t
't) S 1
«(
't)
i (t) == J I: е L dT + 2 I: е L dT ==
О
[ r ( r ' ]
1
t
" .
== r 2
е L 1 + e L ) .
r
1
Т. (t
't)
Уа ('
T)==E е
При ! > '2
" r (, r
{' I
,
«(
't) \' 1
(t
't)
i(t) ==.1 те L d1'+2 J уе L dT==
й (,
1
( (
"
(, )
== 7 е L 2е L .......е L
1 .
По второй формуле (15-35)
t
i (t) ==е (t) Уl (О) +
е (т) Y
(!
't') d-r.
Реакция цепи на единичную функцию равна:
1 (
( )
Yi(t)==, l
e L .
Следовательно,
r
1
(t
't)
У! (О) == О, y
(t
т) == т- е L
Т. е. получаются те же интеrралы, которые были вычислены выше.
503
15-12. НАХОЖДЕНИЕ В ЗАМКНУТОй ФОРМЕ УСТАНОВИВШЕйСЯ
РЕАКЦИИ .ЦЕПИ НА ПЕРИОДИЧЕСКУЮ
НЕСИНУСОИДАЛЬНУЮ ВОЗДЕйСТВУЮЩУЮ ФУНКЦИЮ
В
13-5 было показано, что в случае периодической
несинусоидальной воздействующей функции установив-
шаяся реакция цепи может быть получе
а не только как
сумма rармоник, но и в замкнутой форме с конечным,
относительно малым числом слаrаемых. Решение ОСНО-
вывал ось на И!Iтеrрировании дифференциальноrо уравне-
ния в определенном интервале времени и нахождении
постоянной интеrрирования из условия периодичности
процесса.
Друrой метод решения этой задачи основан на приме-
нении преобразования Лапласа. Допустим, что первыЙ
период воздействующеЙ периодической функции (равной
нулю при t < О) имеет изображение Р 1 (р). Тоrда изобра-
жением периодической фунrщии-ориrинала будет:
F (р) == Р 1 (р) (1 +e
P! +e
2pT +...) == Fl (
) Т '
1
e р
rде Т
период.
Обозначив передаточную функцию цепи 1 через К (р),
получим реакцию цепи на периодическую функцию-ори-
rиНаЛ как сумму вычетов функции:
Fi (р) К (р) e Pt .
1
e
pT
у становившаяся реакция цепи ра13на сумме вычетов
относительно полюсов воздействующей функции Fl
) Т '
. l
e р
а свободная реакция
сумме вычетов относительно полю-
сов передаточной функции К (р).
Число полюсов воздействующей функции бесконечно
. т
велико, так как уравнению 1
еР == О соответствует
. ')
бесчисленное множество корней: Pk == jk
; (k
целые
числа). Поэтому находить установившуюся реакцию цепи
непосредственно по и
ображению 1
e
;T К (р) нецеле-
сообразно (получится ряд Фурье).
1 Ход рассуждений останется тем же, если вместо передаточной
функции воспользоваться сопротивлением или проводимостью цепи,
504
Свободная же реакция цепи определяется суммой ко-
нечноrо числа слаrаемых, так как ЧИСJIО полюсов переда-
точной функции К (р) щраН'ичено (здесь рассматривается
цепь с сосредоточенными параметрами).
Если из полной реакции цепи вычесть свободную реак-
цию, то получится установившаяся реакция цепи. При
этом для первоrо периода полная реакция цепи на функ-
цию F (р) не отличается от реакции на функцию Р 1 (р) И
поэтому находится по изображению Р 1 (р) К (р).
Поясним сказанное на примере, приведенном в
13-5.
Периодическая знакопеременная э. д. с. прямоуrольной
формы, равная нулю при t < о, имеет изображение
( Т )
p!....
Е
P
Е 1
e 2
1
2е 2 + 2e
pT
. ., ==,
т .
р р
P
l+е 2
Сопротивление цепи Z (р) == r + pL.
Изображение тока в цепи
т
Е 1
e
P
ij
I(P)==
. ( Т ) .
р 1 +e
P2 (r+pL)
Свободный ток
. Е ( 1
е
Р
) е Р! Е 1
e
a
t
t CB == R es
( 1 ' ) ==
е L
r р
P
, l+e
a ,
P
L
1 +е 2 (,+pL)
rде а == rT/2L.
Переходный ток в течение первоrо полупериода
i 1 ==
(1
е
f t).
, .
Следовательно, искомый установившийся ток
iy==il
icB==
(1
l:e
a e
ft)
(o
t
{
),
что совпадает с результатом, полученным в примере 13-4.
Ниже приводятся два типовых примера для цепей
первоrо и BToporo порядков.
505
Пример 15-19 [Л. 16]. Сопротивленне, == 2 Ом и емкость С == 1 Ф.
соединенные последовательно, подключены к источнику пилообразной
э. д. с. вида, изображенноrо на рис. 15
7, а; период Т == 1 с. Найти
установившееся напряжение на сопротивлении.
Из примера 15
4 известно изображение nepBoro периода (см.
рис, 15-17, б):
1 e
P e
P
Ei (p)==
p
7
и всей пилообразной функции (рис. 15-7, а): .
Еl (р)
Е (р) l
e
P .
Передаточная функция равна:
,
2 Р
==
.
2+ р р +2'
1
'+ре
Изображение реакции цепи на пилообразную функцию
1
e
P
pe
P
U (р)
р (p+
}) (1
e
P)
1 e
P
== р (p+'
)
(Р+
) (1
e
P) .
Свободное напряжение на сопротивлении
[ ерl ] [ eP(I
l) ]
и ев == Res 1 р (Р+ 1/2)
Res 1 (Р+ 1/2) (1
e
P) ==
P
2 P==
2
e
1/2 е 1/2
==
2e
I/2
1
ei/2
1/2
2
1/2 е
е + 1
J/2 '
e
Переходное напряжение на сопротивлении в течение nepBoro пе-
риода (т, е. реакция цепи на первый «зубец»)
[ e Pt ]
1/2 _
щ== Res 1 р(р+l/2)
2
2e (O
t< 1).
P
2
Здесь принято во внимание только первое. слаrаемое изображения
«зубца», так как два вторых слаrаемых не относятся ко времени t < 1.
Установившееся напряжение на сопротивлении в течение nepBoro
периода
uу==щ
иев==2
2е
1/2
(
1/2 \
1/2
2
1/2 е 1 2 е
е + 1 +e
I/2 ) ==
1
e
I/2
(O
t<I).
506
Правильнасть ответа может быть проверена по условию непрерыв-
ности усrановившеrося напряжения на емкости:
1 +2e
1/2
и су (О) == и су (1) == 1
lj2 .
e
При мер 15.20 [л. 161. Сопротивлеиие ''''''' 3 Ом, индуктивность
L == 1 r и емкость С == 1/2 Ф, соединенные последовательно, подклю-
чены к источнику периодической 3. д. с. треуrолъной формы;
{ t O
t
l,
е (!) ==
2
! 1
t
2 и т, д.
Найти установившееся напряжение на емкости.
Из примера 15-12 известно изображение треуrольника(см,
РИС. 15
15, а);
1 1
Е 1 (р) ==
(1
2e
P +e
2P) """
(1
e
P)2.
р2 р2
Периодическая э. д. с, треуrольной формы, равная нулю при t < О,
имеет изображение
Е (р)
Е 1 (р)
1
e
2P
1
e
P
р2 (l +e
p ) .
Передаточная фуикция равна:
1
ре
1
r+pL+ рС
1
1 3
"2р2+ 2 р+l
2
(Р+ 1) (р+2)
Изображение реакции цепи на периодическую э. д. с.
2 (1
e
P)
и(р)== p2(I+e
P)(p+l)(p+2) .
Свободное напряжение на емкости
2 (l
e
P) еР!
и св == P
I р2 (1 +e
P) (р+ 1) (р+2) +
2 (1
e
P) еР!
+p
e"='2 p2(l+e
P)(p+l)(p+2) .
Изображение напряжения на емкости в первом периоде
, 2 ' 2 (1
2e
p +e
2P)
и 1 (р) ==Ei (Р) (р+ 1) (р +2) == р2 (р+ 1) (р+ 2)
имеет простые ПОЛЮСЫ Рl ::=
1 и Р2 ==
-2 и полюс BToporo порядка
рз == О.
в интервале О :( t < 1 принимается во вниманне только первое
слаrаемое числителя, так как второе и треТЬе слаrаемые относятся
к последующим интервалам времени.
На основании (15-22) и (15-23) переходное напряже!fие на емкости
1 1.
Щ (t)
2 (2t
3+4e
'
e
21) (О
t < 1);
и2 (t)
иl (t)
2щ (t
1) (1
t < 2).
Искомое установившееся напряжение на емкости
3 4e
(t
l) e
2 (t
l)
Uy
t
2 + '+е
l+е 2 (O
t<I);
3 4e
(t
2J e
2 (t
2)
иу
и
2)+ 2
l+е + '+е 2 (l
t<2).
Проверка:
3+5e
5e2+3e3
И у (О)
и у (2)
2 (1 +е) (1 +е2) .
15-13. ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПЯХ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ С ПОМОЩЬЮ
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В rл. II (см.
11-2) были выведены дифференциаль-
ные уравнения однородной двухпроводной линии; ввиду
наличия двух независимых переменных (t и х) дифферен-
циальные уравнения получились в час'I'ных производных:
== ri + L
i. ]
дх дt'
дi ди (15-36)
дх == gu + с дЕ'
Минусы в левой части уравнений (15-36) соответствуют
случаю, коrда расстояние хотсчитывается от начала линии,
или, точнее, в положительном направлении тока.
Формула дифференцирования по параметру (табл. 15-1)
позволяет применить преобразование Лапласа к уравне-
ниям (15-36), в которых х является пара метром.
Если изображения искомых функций обозначить через
и . (х, t)
-'... . U (х, р) == И; }
(15-37)
,(х, t)
I(x, p)==I,
то системе дифференциальных уравнениЙ в частных произ-
водных (15-36) будет соответствовать система уравнений:
== (r+pL) 1
Li (х, О); ]
dl' (15-38)
d == (g+ рС) U
Си (х, О);
.У;
508
здесь i (х, О) и u (х, О)
начальные (по времени) значе
ния тока и напряжения в точке х.
Ввиду Toro что р не зависит от х и в уравнениях (15
38)
производные по р отсутствуют, при переходе от ypaBHe
ний (15-36) к (15-38) частные производные по х заменены
обыкновенными.
Исключая из системы (15-38) 1, получаем уравнение
относительно и:
d 2 U С U di (х О)
dx 2 ==(r+pL)(g+p) +L d
C(r+pL)u(x, О).
( 15-39)
Аналоrично, исключая из (I5
38) и, получаем уравне-
ние относительно 1:
== (r+ pL) (g+ рС) 1 +С d/l
; О)
L (g+pC) i (х, О).
( 15-40)
Эти уравнения решаются как обычные дифференциаль-
ные уравнения BToporo порядка.
Обозначим:
'\' (р) == 11 (r + pL) (g + рС)
и назовем это выражение о пер а т о р н ы м к о э Ф -
фи Ц и е н т о м " р а СП Р о с т р а н е н и я.
При нулевых начальных значениях уравнения (15-39)
и (15-40) упростятся:
2и ==
,2и' )
dx2 r ,
d 2 f
dx 2 == у2/.
Обращает на себя внимание сходство полученных опе
раторных уравнений (l5
41) при нулевых начальных усло
виях с дифференциальными уравнениями однородной ли
нии при установившемся режиме.
Соответственно остаются в силе для (15-41) решения,
полученные в rл. 11 (см.
11-3), если под U и 1 подразуме-
вать изображения напряжения и тока, а под
Z ()
1 ,+рL
в Р == JI g+pC
операторное волновое СОПРОТИВЛение
линии 1 .
(l5
4 1)
1 Если в выражениях для 'V (р) и ZB (р) заменить р на jro, то полу-
чатся извеСтные выражения для параметров линии при синусоидаль-
ном режиме,
509
В общем случае переход от изображений и (х, р) и
1 (х, р), являющихся трансцендентными функциями р,
к ИСКомым ориrиналам u (х, t) и i (х, f) представляет зна-
чительные трудности. При решении задач обычно дела-
ются какие-либо упрощающие предположения [Л. 2 и 8].
15.14. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
15-1. Сопротивление, === 2 Ом и индуктивность L === 1 r, соеди-
нениые последовательно, ПоДКЛЮчаются при t:::;; О к источнику Э. Д. с,
е (t) === t В. Определить' i (t). .
1 1 1 I
О Т В е т: '2 t
'4
+ 4' e
2. А.
15-2. Применить обратное преобразование Лапласа к изображе-
ниям:
.' 3р . р+l
(р2+ 1) (р2+4) , p
+2p ;
1 1 . р2
(p+l) (р+2)2 , р(р2+2р+5)' (р2+1)2'
о т в е т:
cos t
cos 2t;
} (1
e
2/); e
t
e
2t (1 +t);
[1 +-
e
t (
2 Cos 2t
sin 2t)]; -+ t cos t+
sin t.
15-3. Примеиив преобразование Лапласа, решить задачи преды-
дущеii rлавы: 14
3
14
6 и 14
9. .
15-4. Цепь, состоящая из последовательно соединенных сопроти-
вления , === 2 Ом, индуктивности L == 1 r и незаряженной емкости
С == 0,5 Ф, поАключена при t == О к источнику Э. д. с. е (!) == sin t В.
Определить i (t).
О т в е т: 0,2 (cos t + 2 sin t
e
1 Cos t
3e
t sin t) А.
15-5. Два одинаковых iшдуктивных контура " L, С связаны взаим-
ной индуктивностью М. В ОДин из них при t == О включена постоянная
э. д. с. Е. .
Найти ТОК в друrом контуре.
О т в е т:
[
e
{\t sinwlt e
62t s inw 2 t ] .
2 .ооl(к+м) W2(L
M)'
, 2 1
<"ы 2(L::!::M) ; ())ы C(L::!::M) б
'2'
15-6. Сопротив.'Iение , === 10 Ом и индуктивность L === 0,1 r, со-
единенные последовательно, подключаются прн t == О к источнику
Э. Д. с. lOe
4t В. Определить i (t).
О т в е т: 1 ,04 (e
4t
e
loot) А.
15-7. Сопротивление, == 1000 Ом и незаряженная емкость С ===
.=== 10 мкФ, соещпiенные .J10сл:едовательно, подключаются при t == О
к источнику Э. д. с. 2,5.104 (1
e
41) В. Найти i (t).
О т в е т: 1 ,04 (e
M
e
10ot) А.
510
15-8. Найти ориrннал по изображению
p2
p+ 10
(Р+ 1)2 (рЧ--IОО) .
О т в е т:
0,119te
t
0,027e
! +0,027 СоЭ 10/+0,086 sin 10/.
15-9. В контуре, состоящем из сопротивления 40 Ом и индук-
тивности 0,1 [, при установившемся режиме действует' Э. д. с. е
== 100 соэ 400 t В.
Найти i (1) при 1 > О,если, начиная с момента t == О, амплитуда
а. д. с. становится равной 40 В.
О т в е т:
0,707 соэ (40ot
лj4)+0,75е
400t В.
15.10. При нулевых начальных условиях в контур ,L включается
источник Э. д. с. Ee
at, Определить токи при а =F ,jL и а == ,jL,
О т в е т:
( e
at
e
t).
te
{ t
,
aL . , L .
15-11. Решить предыдущую задачу, если э. д. с. равна Ete
at.
О т в е т:
Е EL (
! ) Е
!
fe
at+ е L
e
a! .
t2e L .
,
aL (r
aL)2 1 2L
15-12. Источннк тока, посылающий ток i'=:; 1 А в виде прямо-
уrольноrо импульса длительностью 0,001 с, подключен при t == О к со-
противлению, == 100 Ом и емкости С == 10 мкФ, соединенным парал-
лельно. Начальные условия нулевые, Определить напряжение на 'вы-
водах цепи.
О т в е т:
100(1
e
10.t)
100[1
e
10'(t
O,OOI)] 1 и
O,OOI) В.
15-13. Пользуясь решением примера 15-12 (см. рис. 15-15), найти
установившийся ток в , и С, соединенных последовательно и подклю-
ченных к источнику периодической э, д. с, треуrольной формы.
О т в е т:
( т
t, )
С е ТС
т 1
2
(O
t<T);
1 +е ,С
( 2T
t )
С rc
т
1+2 e
(T
/<2T).
\ 1 + е ,С
15-14. Доказать прнменимость теоремы об ЭКl3ивалентном источ-
нике э. д. с. к иgображеНИЯ
I.
511
15-15. Как учитывается энерrия маrнитноrо и электрическоrо по-
лей, имеющаяся к началу исследуемоrо переходноrо процесса?
15-16. На каком основании при обратном преобразовании Лапласа
применяется теория вычетов?
15-17. Что такое импульсная функция? Показать, что
t
S б (t) dt== 1.
о
15-18. Найти изображение импульса произвольной формы, если
известно изображение функции, получаемой периодическим повторе-
нием данноrо импульса,
rЛАВА ШЕСТНАДЦАТАЯ
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ К РАСЧЕТУ
ПЕРЕХОДНЫХ ПРОЦЕССОВ
16-1. ПРЕО6РАЗОВАНИЕ ФУРЬЕ КАК ЧАСТНblй СЛУЧАА
ПРЕО6РАЗОВАНИЯ ЛАПЛАСА
Допустим, что заданная непериодическая функция f (t)
преобразуема по Лапласу, причем показатель роста СО
отрицателен, т. е. для всех t> о.
I f (t) I < Me
lco It.
(16-1 )
Это означает, что функция не превосходИт некоторой
со
затухающей экспоненты; следовательно, интеrрал
I f (t) I dt
о
равен конечному числу (условие абсолютной интеrрируе-
мости функции). В таком случае изображение F (р) .'
. . f (t) является аналитическоЙ функцией в полуплоскости
Re р > Со, а следовательно, и на мнимой оси; поэтему
В формулах прямоrо и обратноrо преобразований Лапласа:
со
F (р) === S f (t) e
P! dt;
о
c+joo
1
.
f (t) , 2Л1 J F (р) е Р! dp
c
joo
можно положить С == О и р === j(j), т. е. за путь интеrриро-
вания в формуле обратноrо преобразования Лапласа вы-
брать мнимую ось. '
512
Тотда будем иметь:
(f)
F (j(j) ==
f (t) e
iUJt dt;
о
(f)
f и) == 2
S F (j ш) e iUJt d(j).
ф
( 16
2)
( 16-3)
Эти формулы, известные под названием одностороннеео
преобразованuя Фурье, имеют более узкую область при
менения, чем преобразование Лапласа. Это связано с тем,
что для схОдимости несобственноrо интеrрала (16
2) на
функцию f (t) наложено оrраничение (16
1), которое ЯБЛЯ
ется более жестким, чем условие I f (t) I < Me Co1t , предъ-
являемое к функциям-ориrиналам (см.
15
2).
Например, такие функции 1, как единичная, возрастаю
щая показательная, периодические и некоторые друrие
функции
ориrиналы, имеющие лапласовы изображения,
не Moryт быть непосредственно представлены в виде ИНте-
rрала Фурье (16-3).
Если заданная функция, преобразуемая по Лапласу,
удовлетворяет условию (16.1), то свойства преобразова-
ния Лапласа сохраняют силу при р == j(j). Соответственно
свойства преобразования Фурье получаются на' основании
свойств преобразования Лапласа заменой р на jш. В этом
смысле можно rоворить, что преобразование Фурье явля-
ется частным случаем преобразования Лапласа.
Из изложенноrо выше следует, что всякая функция,
для которой применимо одностороннее преобразование
Фурье, всеrда 'может быть преобразована по Лапласу.
Значит, для нашей функции по изображению Лапласа
можно находить F иш) (заменой р на j(j).
f6.2. СПЕКТРАЛЬНАЯ ФУНКЦИЯ
Формулы преобразования Фурье представляют собой
взаимно связанные интеrральные уравнения, каждое из
которых служит решением друrоrо. Эти формулы позво-
ляют преобразовать непериодическую функцию времени
f (t) в функцию частоты F аш) и обратно.
Для выражения связи между F (j(j) и f (t), накладывае-
мой преобразованием Фурье на эти функции, может быть
применен тот же знак соответствия .' , которым мы поль-
1 Здесь имеются в виду функции, равные нулю при t < О,
513
зовались в предыдущей rлаве. Итак, сокращенная услов
ная запись F (jro) .' f и) обозначает, что F (jro) и f (t)
связаны уравнениями (16-2) и (16-3).
Функция F (jro) носит название с п е к т р а л ь н о й
Ф у н к Ц и и, которая является функцией текущей ча
стоты ro.
Соrласно (16-3) непериодическая функция f (t) пред
ставляется совокупностью бесконечно большоrо числа rap-
моник с бесконечно малыми .амплитудами 2
F (jro) dro
во всем диапазоне частот от
oo до +00. Иначе rоворя,
представление непериодической функции в виде интеrрала
Фурье подразумевает суммирование незатухающих rap-
монических колебаний бесконечноrо сплошноrо спектра
частот. .
Такой метод представления непериодических функций
несколько сходен с методом разложения периодических
несинусоидальных функций в рЯд Фурье (при комплекс-
ной форме ряда, так'же как и в (16-3), присутствуют поло
жительные и отрицательные частоты). Однако в отличие
от представления периодических функций в виде дискрет
Horo ряда rармоник в данном случае суммируются еармо-
нические колебания сплошноео спектра частот. При этом
,интеrрал Фурье (16-3) обладает тем ценным свойством,
что, правильно описывая функцию f (t) при t> о, он
тождественно обращается в нуль при t < о.
Например, если на электрическую цепь с момента t ==
== О воздействует функция f (t), то представление ее инте
rралом (16-3) подразумевает существование бесконечноrо
числа колебаний всевозможньiХ частот с бесконечно Ma
лыми амплитудами во всем интервале времени от t ==
oo
до рассматриваемоrо момента [, причем при t < О' все эти
колебания дают в сумме нуль.
Если заданная непериодическая функция f (t) не равна
нулю для отрицательных значений [, то в формуле (16
2)
нижним пределом интеrралаберется
oo, а не о:
со
F иro) ==
f (t) e
j(fJt dt.
co
(16-4)
в этом случае преобразование Фурье называется дву-
спwронним 1. Для сходимости несобственноrо интеrрала
1 В теории преобразования Лапласа иноrДа также пользуются
двусторонним преобразованием Лапласа.
514
(16-4) должно ВЫПОЛНЯТЬСЯ условие абсолютной интеrри-
руемости функции в бесконечных пределах, т, е. должен
существовать и иметЬ' конечное значение интеrрал,
00
/f и)1 dt.
co
Спектральную функцию можно представить как оrи-
бающую коэффициентов ряда Фурье, т. е. как предел ли-
нейчатоrо спектра частот периодической функции, коrда
ш;риод стремится к бесконечности. Если непериодическая
функция f (t) задана в конечных пределах, то всеrДа можно
подобрать такое Т, чтобы выполнялось равенство
т
со 2'
риro):-:=
f(t)e
j(jJtdt==
t(t)e
j(jJtdt.
co т
2
Соответствующая этому случаю периодическая функция,
т т
совпадающая с t (t) в пределах от
2 ДSJ 2 и имеющая
период Т, характеризуется коэффициентами разложения
в ряд Фурье соrласно формуле (13-13):
т
2'
. 2 r t .
Р1l ==
T J (t) e
/поо,! dt,
т
2
( 16-5)
rде ro 1 == 2л/Т
основная уrловая частота; она имеет
индекс 1 для отличия ее от текущей частоты ro в (16-14).
Из сопоставления (16-4) с (16-5) ВИДНо, что спектральная
функция F иro) заданной в конечных пределах неперио-
дической функции f (t) в масштабе 2/Т изображает оrибаю-
щую дискретноrо рЯДа коэффициентов F п разложения,
соответствующеrо периодическому повторению заданной
функции:
т . .
2 Р п == [Р иro)]оо==поо"
( 16-6)
По мере возрастания периода Т интервал по шкале
частот между составляющими ряда Фурье уменьшается
и линемчатый спектр все более сrущается, стремясь перейти
в пределе в сплошной спектр.
Рисунок 16-1 иллюстрирует ПQстепенный переход от
коэффициентов разложения к спектральной функции.
515
Периодические функции на рис. 16
1, а и б в интервале
(
'
-) заданы условиями:
при
t 1 < t < t 1 ,
при
t 1 > t > tl'
Для непериодической функции (рис, 16-1, в)
условия сохраняют силу на всей оси времени t.
Соrласно (16
4) и (16-5):
f (t) == {
те же
11
F иш) == r e
jwl dt == 2t 1 Si::t i ;
J 1
11
11
Р п ==
S e
jпw,1 dt == 4t 1 sin nUJlti .
т т nUJltl
11
Представление непериодической функции в виде сово-
купности rармонических колебаний позволяет На основа-
+
t;1 t1 . t
0.)
n
f (t)
Jf (t)
n t
т
"[Р п
(J)
,
T
ZF"
.... ,,". ... J
.1'1'1. ,_ (J)
'..1.>'
IJ.'
J.I; "j,j' ,.
б)
т:
,
$ F(j (J)).
..... ,....
,....,.
......., "-" '-'''''''''
В)
Рис. 16-1. Переход от коэффициентов разложения к спек-
тральной функции.
нии спектральной функции судить о распределении энерrии
в спектре и оценивать значимость отдельных частотных
полос этоrо спектра. Например, полученное выражение
F ( 'ш ) == 2! sin UJti
J 1 UJtt
516
показывает (рис. 16
1, в), что функция F (jw) обращается
в нуль при ш
k (k
1, 2 ...). По мере уменьшения t 1
интервал между нулями функции F (jw) возрастает.
Рассматриваемая здесь непериодическая функция f (t)
(рис. 16
1, в) выражается формулой (16
3) как совокуп-
ность rармонических колебаний бесконечноrо спектра ча-
стот. Если же используется часть спектра, то для доста-
точно правильноrо воспроизведения функции f (!) требу-
ется тем БОльшая полоса частот, чем меньше t 1 .
Спектральная функция F (jw) может быть действитель-
ной или комплексной.
Приняв в общем случае F (jw) == I F (jw) I e
/1IJ«())) полу-
чим две частотные характеристики, а именно: амплитуд-
ный спектр I F (j ш) I и фазовый спектр 'Ф (ш).
Амплитудный спектр
всееда четная, а фазовый
спектр
всееда нечетная функция ш.
Из формул одностороннеrо преобразования Фурье и
Лапласа видно, что если выполняется неравенство (16
1),
то при замене комплексноro переменноrо р, входящеrо
в изображение по Лапласу, мнимой величиной jw получа-
ется выражение для спектрально,Й функции
F (jw)
[Р (p)Jp
Jw'
(16
7)
Такой способ нахождения спектральных функций явля-
ется наиболее просты.м и удобным, так как он позволяет
использовать таблицы ориrиналов и изображений (см. при-
меры 16-1 и 16
2).
Родственная связь, существующая между преобразова-
ниями Лапласа и Фурье, вносит, таким образом, физиче-
ское содержание в понятие «изображение» как обобщенную'
форму спектральной функции. Она распространяется \ и
на основные свойства преобразований Фурье и Лапласа.
В табл. 16-1 приведены основные свойства односторон-
Hero преобразования Фурье, которые в ряде случаев облеr-
чают нахождение функций времени или их спектральных
функций. Если НаД некоторой функцией времени, спек-
тральная функция которой извеСТНа, производится ОДна
из операций, указанных в табл. 16
1, то спектральная функ-
ция, соответствующая полученной НОвой функции времени,
Находится по соответствующему правилу из первоначаль-
ной спектральной функции (см. пример 16-2).
В свою очередь если спектральная претерпевает какую-
либо операцию, то, функция времени, соответствующая
517
Таблица 16-1
Основные свойства одностороннеrо преобраЗ0вания Фурье
Наименование
Формула
СВОЙСТВО линейности
n n
G/I/ (/)
щF/ (jw)
/
1 /
1
Дифференцирование функ- I
ции времени
l' (/) ;
jwF ию)
1 (О)
Интеrрирование функции
времени
t
f (/) dl . . F j
w)
о
Дифференцированне
спектральной xapaKTe
ристикн
(
j/) f (t) "
:ы F ию)
Изменение масштаба не-
зависимоrо nepeMeHHoro
f (at)
F (j : )
f (t ::!: 10)
е:!:. jwt o F (jw)
Смещение функции вре-
мени
Смещение спектральной
характеристики
e-i:.jw,t f (t)
. F [j (ю =+ (1)]
Умножение спектральных
.характеристик
t
11 (с) {2 и
c) d't';
Р 1 ию) Р 2 ию)
О
Умножение функции вре-
мени на косинус или
синус
518
f (/) cos Ю1/
:
{F [j (Ы
Ю1)]+
+ F и(Ш+Ю 1 )]};
1(/) sin Ю1 / . .
.. .
i {F[j(W
W1)]
F[j(w+Wl))}
новой спектральной, также находится по известным Пра
вилам.
Указанные в табл. 16
1 основные свойства односторон-
Hero преобразования Фурье имеют важный физический
смысл. Например, соrласно теореме 06 изменении мас-
штабов независИмоrо переменноrо при изменении мас-
штаба времени в а раз масштаб частот меняется в l/а раз.
Это означает, что ширина спектра увеличивается при
сжатии сиrнала во времени и сокращается при растяжении
сиrнала (без изменения caMoro характера спектра). Поэтому
бесконечно короткий импульс должен иметь бесконечно
широкий спектр. Здесь под шириной спектра сиrнала
понимается область частот, в пределах которой заключена
основная доля ero энерrии.
Представление непериодической функции в виде сово-
купности незатухающих rармонических колебаний дает
возможность исследовать переходный процесс в линейной
электрической цепи, применяя к спектральной функции
общие - методы расчета установивIIfИХСя синусоидальных
процессов (см.
16-3) и (16
4).
Пример 16-1. Построить rрафики амплитудноrо и фазовоrо спект-
ров прямоуrольноrо импульса (рис. 16-2, а).
f(t)
F(jш)
ф (ш)
а)
t
7:
?(
1
о
(JJ
lI-7С
б) 7f"
Рис. 16-2. Прямоуrольный импульс (а) и ero амплитудиый (6) и фазо-
вый (в) спектры. '
Непериодическая функция -задана условием
f (1) == { 0 1 при О < t < <;
при 0>1>'t'.
На основании (16
2)
т
' 1 [ 2 Сйт ]
f
F(j(j)== e
J(i)Tdt==
(I
e
j(i)T)==
siп
е 2.
!Ы (j) 2
о
519
Тот же результат может быть получен на основанин (16-7), если
в изображении по Лапласу
1
F (Р)==р (1
e
Pt)
заменить р через joo.
Амплитудный спектр равен:
I F иоо) I == I ; sin
' 1.
00'1:
Нули функции F(joo) соответствуют Значениям т==kл (k==
=: 1, 2...).
00, л
При "'"2 ==
2 (2k+ 1)
I F (joo) I ==
I 2 I == '1:
00
(2k+1)
2
с учетом ЗНака sin
'I: фазовый спектр 'Ф (00) определяется следую-
щим образом:
'Ф (00) == 0),/2
при 0<оо<2л/'I:;
'Ф(ОО)==ОО'I:/2
л при,2л7,<оо<
и т, Д.
,
Кривые I F (joo) I и 'Ф (00) изображены На рис. 16
2, б и в,
Следует обратить вНиМание на то, что в соответствии
с формулой смещения функции времени (см. табл. 16-1)
перемещение импульса неизменной длительности
вдоль
оси времени на t o не влияет на амплитудный спектр, а изме-
няет только фазовый спектр на уrол (j)t o ; это видно и из
сравнения амплитудных спектров на рис. 16-1, в и 16-2, б.
С увеличением длительности импульса
амплитудный
спектр rруппируется во все более узкой области частот
вблизи нулевой частоты, причем значение амплитудноrо
спектра при нулевой Частоте, равное
, возрастает, стре-
мясь в пределе к бесконечности. Это физически означает,
что энерrия сиrнала, выражаемоrо рассматриваемой функ-
цией, при 't'
00 стремится к бесконечности и в основном
сосредоточивается около частоты (j) == О. Функции, опре-
деляющие сиrнал с бесконечной энерrией, не удовлетворяют
условию абсолютной интеrрируемости, и интеrрал (16-2)
к TaKoro рода функциям непосредственно неприменим.
Чтобы обойти оrраничения, накладываемые условием абсо-
лютной интеrрируемости, применяют искусственный прием
(см. ниже),
520
Пример 16-2. Построить rрафики амплитудноrо и фазовоrо спект-
ров фуикции в виде отрезка синусоиды, так называемоrо прямоуrоль-
Horo импульса с синусоидальным заполнением (рис, 16-3, а), Непе-
риодическая функция задана условием
{ sin (j)lt при 0< t < т;
f(t)== О при O>t>T.
Пусть Т == пТ == п2Л/(j)1' rде Т
период синусоиды, а п
число
периодов за время т.
о
f(jw)
Рис. 16-3. Отрезок синусоиды (а) и ero амплитудный (6) и фазовый
(в) спектры,
Изображение по Лапласу отрезка синусоиды, заданноrо в интер-
вале от О до п2Л/(j)1' имеет вид:
(j) l ' Т
(1
e
pп ).
p2+(j)i
На основании (16-7)
(j)" (
}
п'2Л )
F(j(j)== (j)"
(j)2 l
e w, .
1
Тот же результат получится, если воспользоваться спектральной
фуикцией прямоуrольноrо импульса
(1
e
JW'!), вычисленной в при-
J(j)
мере 16-1, и применить формулу умножения функции времени на СИl!УС
(см. табл. 16-1):
. 1 l l
e
j(W
W')'C 1
e
i(W+W')'C J
F(j(j)==2[ j«(j)
(j)l) j«(j)+(j)l) '
При (j)lT == п. 2:n, rде п
целое ЧИсло,
.
(j)1 (1
e
MT)
F (j(j)
2 2' .
(j)l
(j)
Отсюда можно получить амплитудный спектр
I F(j(j)I== 1 2(j)i 2 2Sin
n:n ! .
(j)l
(j) (j)l
521
При ro == ro 1 эта функция равна предельному значению, которое
находится по правилу Лопиталя:
I (01
2 Cos
- пл \
I F (jU) I == lim :7 =З' ==
;
ro
ro,
2ш U)f
при
n==k (k==O, ], 2 ...) имеем/ F Uro)I::::: О.
,
Кривые I F (jU) I и'\Р (ш) изображены на рис. ]6-3, б и в. При уве-
личении n амплитудный спектр rруппируется во все более узкой области
частот вблизи Ш1' При n --+ CXJ составляющая амплитудноrо спектра,
СООТfJетствующая U) == Ш1' также стремится к бесконечности. Фнзиче-
ским смысл этоrо аналоrичен тому, ЧТО было сказано ранее.
Как отмечалось выше, интеrрал (16-2) непосредственно
неприменим к функциям времени, которые не удовлетво-
ряют условию (16
1), т, е. не сходятся абсолютно. Сюда
F(j ш) ф(UJ)
7с"
2
ц) ц)
о (1) о б)
Рис. 16-4. Амплитудный (а) и фазовый (6) спектры единичной
функции.
относятся и некоторые функции с показателем роста, рав-
ным нулю (со == О), например: единичная функция, сину-
соидальная и др. Умножив TaKoro рода функцию f (t)
на множитель e
a! (а > О), «rасящий» t (t) при больших
значениях aprYMeHTa, можно вычислить спектральную
функцию для измененной функции e
att (t); затем, устре-
мив а к нулю, найти предельное значение спектральной
функции, которое будет представлять собой спектральную
функцию исходной фУlIКЦИИ t (t).
Например, убывающая показательная функция (;a t .l (t)
1
имеет спектральную функцию
+ . . Ее пределом при
а JU)
а
О является выражение l/j(f), которое и определит
спектральную функцию единичной функции 1 (t). Ампли-
тудный и фазовый спектр
единичной функции показаны
на рис. 16
4.
Умножение заданной функции на rасящий множитель
e
at с последующим нахождением предельноrо значения F(j(f).
522
при а
О, вообще rоворя, не требуется, если для этой
функции, имеющей показатель роста, равный нулю, известно
изображение по Лапласу. Тоrда в силу сказанноrо выше
(см.
16
1) достаточно в изображении заменить р на jw,
чтобы получить сразу спектральную функцию заданной
функции.
Пример 16-3, Найти спектр синусоидал!>ной функции (равной
нулю при t < О),
tp (щ)
.
lZJ
а)
о
tJJ
Ы1
б)
Рис. 16-5. Амплитудный (а) и фазовый (6) спектры синусо-
идальной функции, начинающейся в момент t == О,
На основании преобраэования Лаплас'а
. t ' Wi F (р)
SШ Wl . p2+W
.
Спектральная функция получается замеиой р на jw:
Wi
F (w) == 2 2 .
Wl
W
На рис. 16
5 показаны кривые амплитудноrо и фазовоrо спектров
этой функции.
16-3. ПЕРЕХОДНЫй ПРОЦЕСС В ДВУХПОЛЮСНИКЕ
Как отмечал ось в
16-2, представление непериодиче-
ской функции в виде суммы бесконечноrо множества неза-
тухающих rармонических колебаний бесконечно малой
амплитуды дает возможность применять к бесконечно ма-
лым rармоническим составляющим напряжений и токов
обычные методы расчета установившихся синусоидальных
процессов В линейных электрических цепях и затем, поль-
зуясь методом наложения, определять результирующие
напряжения и токи.
Положим, что линейный двухполюсник, имеющий ком-
плексное сопротивление Z иш), присоединяется в момент
523
t == о при нулевых начальных УСЛО!!lИЯХ к источнику
Э. д. с. е (t).
Если через Е (jffi) обозначить спектральную функцию
воздействующей э. д, С., то спектральная функция тока
найдется по формуле
1 (jffi) == у (jffi) Е (jffi); (16-8)
здесь у (jffi)
комплексная проводимость цепи; она опре-
. деляется в установившемся режиме для Bcero спектра
частот.
Переходный ток в двухполюснике следует найти по фор-
муле (16-3): .
00 00
i (t) == 2
S 1 -иш) e jffi ( dffi == 2k S у иш) Е (jffi) e jffi ( dffi. (16-9)
oo
oo
Вычисление i и) непосредственно по формуле (16-9)
не имеет преимуществ по сравнению с вычислением' при
помощи обратноrо преобразоващiЯ Лапласа.
Для вычисления i (t) можно ВОСПОЛьзоваться одним
из правил нахождения функции времени по спектральной
функции, которые аналоrичны правилам нахождения ори-
rинала по изображению Лапласа (с заменой р на jffi).
Рассматривая функцию У (jffi) как спектральную функ-
цию некоторой функции времени Уб (t) и имея B
виду,
Что Е (jffi) соответствует е (t), можно также применить
фQрмулу умножения спектральных функций (см. табл. 16-1):
t t
i и) ==
е ('t) Уб (1
.) d. ==
е (t
т) Уб (т) dT. (16-10)
о о
Данная формула совпадает с формулой (15-33), при-
веденной в
15-11, причем Уб (t) означает реакцию цепи
на импульсную функцию.
В случае, коrда воздействующая э. д. с. е (t) задана
в виде единичной, синусоидальной или косинусоидальной
функции, причем известна частотная характеристика актив-
ной или реактивной проводимости двухполюсника" можно
воспользоваться интеrральной формой выражения этой
функции, вытекающей из преобразования Фурье.
Р
ссмотрим, Н,апример, включение в момент t == О
источника постоянной э. д. с. Е в цепь двухполюсника,
имеющеrо комплексную проводимость
у Ош) == g (ш)
jb (ш).
524
Пользуясь известной интеrральноЙ формой выражения
единичной функции [л. 2]
,
+
r sin (j)t dro == { 1
2 11: J (j) о
о
при t>O;
при t< О,
находим ток в контуре:
со
. Е Е r sin «(j)t
<p)
t (t) == 2Z (О) + 11 J (j) I Z (j(j) I dro ==
о
со со
==
+.!i. r cos <р sin (j)t dro
Е S sin <р cos (j)t dro
22 (О) 11: J (j) I Z иы) j 11: (j) I 2 иы) : .
о о
Вводя в подынтеrральное выражение активную и реак-
тивную проводимости
COS <р Ь ) sin <р
g(ro)== IZ(j(j)j и (ш == 12(j(j)j '
получаем:
со со
i (t) == Eg (О) +.!i. r g (ro) sin (j)t d(i)
Е S Ь (ro) соэ (j)t dro.
2 11: J . (j) 11: (j)
О О
( 16
11 )
Эrо выражение, справедливое для любоrо момента
времени, должно {)бращаться в нуль при t < О. Следова-
тельно, при t> О i (
t) == О, или, что то же,
со со
Eg(O)
Е r g(ro) sin(j)t dro
Е S b(ro) cos(j)t dro==O. (16-12)
2 . 11: J (j) 11: (j)
О О
Вычитая (16-12) из (16-11), находим:
со
i(t)==i(t)
i(
t)== 2E r g(ro) sin(j)t dro (при t>O). (16-13)
11: J (j)
о
По этой формуле вычисляется переходный ток в двух-
полюснике, если известна частотная характеристика только
ero активной проводимости g (ro). Знания частотной харак-
тер истики реактивной проводимости Ь (ш) пр и этом не тре-
буется, потому что последняя функционально связана
с первой.
Аналоrичная формула может быть получена и для
включения синусоидальной э. д. с. [Л. 2].
525
Таким образом, если задана характеристика g «((),
то указанный метод расчета переходНоrо тока является
наиболее целесообразным.
16-4. ПЕРЕХОДНЫЙ ПРОЦЕСС В ЧЕТblРЕХПОЛЮСНИКЕ
,Для линейной электрической цепи общие методы и
теоремы, относящиеся к установившемуся синусоидаль-
ному процессу (см. rл. 7 и 9), применимы К спектральным
функциям непериодических функций переходноrо режи'ма.
Например, если к входным выводам четырехполюсни-
ков подведено напряжение, спектральная функция кото-
poro равна U 1 (j((), то спектральные функци'и напряжения
и тока на выходе четырехполюсника выражаются соот-
ветственно через передаточную функцию по напряжению
Ки (j(() и передаточную проводимость У21 (j(() установив-
шеrося режима:
U 2 и(() == Ки и(() U 1 и((); /2 Оro) == У21 (jro) U 1 иro).
Напряжение и ток на выходе четыреХПОЛlOCника вычис-
ляются по формулам (16-3), (16-10). В частном случае,
коrда передаточная функция '
Ки (jro) == I Ки (jro) I e
j8 (ю)
имеет постоянный модуль, а фазу, пропорциональную
частоте, т. е.
IKu(j(()I==K==const, 6(ro)==(()t 3 , (16-14)
то напряжение на выходе четырехполюсника на основа-
нии теоремы смещения функции времени (см, табл. 16-1,
строка 6) равlЮ:
U 2 (jro) == U 1 иro) Ke
jwt'З .. Ки 1 (t
t з ).
Таким образом, если модуль коэффициента передачи
по напряжению не 'зависит от частоты, а фазо-частотная
характеристика линейна, то кривая напряжения на выходе
четырехполюсника подобна кривой напряжения на входе:
, она изменяется в К раз и сдвиrается по оси времени на t з
в Р е м я з а паз д ы в а н и я; последнее определяется
крутизной фазо-частотной характеристики
t == dб ((О) == 6 ((О)
3 d(o) (о) .
Иначе rоворя, условия (16-14) характеризуют отсут-
стВие амплитудных u фазовых искажений при передаче
любых электрических сиеналов ,через чеmырехпОЛЮСNUК.
526
Частотные свойства линейной электрической цепи при
установившемся синусоидальном режиме однозначно опре
делЯIОТ перехоДНЫЙ процесс в этой цепи при нулевых началь-
ных условиях.
Применение преобразования Фурье к исследованию
переходных процессов в линейных электрических цепях
позволяет распространить на переходный режим мноrие
понятия и свойства цепей, рассмотренные ранее для уста-
новившеrося режима.
Например, ввиду равенства
У12 (jUJ) И У21 (jUJ), которое свой-
ственно обратимым цепям, теорема
обратимости или взаимности (см.
7
6) сохраняет силу и в пере-
ХОДном режиме.
Рис, 16-6, Пример 16
4,
Пример 16-4. Найти спектр и времен-
ную зависимость напряжения на выходе
четырехполюсника, изображенноrо на рис. 16-6, если на входе при-
ложено напряжение и 1 (t) == Ие
а! 1 (t).
Коэффициент передачи по напряжению
1
v ( ' ) 7WC
'\ U J(j) == 1"
'+
C
J(j)
",(t)
9J U
1
Ч-.j(j)С'
Приложенное напряжение имеет спектральную функцию
и 1 (j(j)) == + и, .
а J(j)
Следовательно, спектральная функция выходноrо напряжения:
и 2 (j(j)) == (а+ j(j))
+ j(j)'C) .
Заменяя j(j) на р и пользуясь таблицей изображений по Лапласу,
получаем:
и2(t)== 1 U С (e
at
e
,
').
a'
ТоТ же результат получается и по формуле (16-10), если рассмат-
ривать функцию Ки (j(j) как спектральную функцию времени:
1
!
Уб (t) == ,с е ,С
t 1 ( 1 )
. U
(t
't) U
.!
и2 (t) ==
'
, e
aТ;e ,с d.. == e
a!
е тС .
J ,с 1
а,С
о
527
16.5. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
16-1. Найти амплитудный и фазовый спектры непериодической
убывающей показательной функции e
at. 1 (t) и построить частотные
характеристики.
16-2. Найти амплитудный и фазовый спектры непериодической за-
тухающей синусоиды e
at siп (j)lt. 1 (t) и построить частотные характе-
ристики.
16-3. Найти амплитудный и фазовый спектры прямоуrольноrо
импульса с косинусоидальным заполнением (число периодов целое) и
построить частотные характеристики.
16-4. Решить задачу 16
3, применив формулу дифференцирования
функции времени, если известна спектральная функция прямоуrоль-
Horo импульса с синусоидальным заполнением.
16-5. Симметричный Т
образный четырехполюсник, состоящий из
двух сопротивлений, в продольных ветвях и емкости С 'в поперечной
ветви, закорочен на выходе и затем подключен к источнику постоЯнной
э. Д. с. Е. Определить ток в закороченных выводах четырехполюсника
спектральным методом.
Е (
' )
О Т В е т: 2, 1
e ,С .
16.6. Найти спектральную функцию треуrольноrо импульса.
16.7. Сопротивление " индуктивность L и емкость С, соединен-
ные параллельно, подключены при t
О к источнику постоянноrо тока 1.
Найти напряжение на выводах цепи при нулевых начальных условиях
спектральным методом.
16-8. Доказать, что пилообразная функция с высотой зубцов, рав-
ной 1, и шириной каждоrо зубца, равной а, имеет спектральную функ-
цию
1 e
Jaro
а (j(j)2
j(j)(l
e
Ja(J).
16-9. Сравнить спектральные функции затухающих синусоид
вида e
at sin 314 t при а
50 и а
500.
. 16-10. Какая связь существует между' спектральной функцией и
коэффициентом ряда Фурье?
16-11. В чем заключается родственность преобразований Фурье
и Лапласа?
16.12. О чем можно судить на основании спектральной функции
электрическоrо сиrнала?
16-13. Доказать применимость теоремы обратимости (взаимности)
в переходном режиме линейной цепи при нулевых начальных условиях.
16-14. Доказать применимость теоремы об эквивалентном источ..
нике к расчету переходных процессов с помощью преобразования Фурье.
16-15. Сформулировать условия, ПрИ которых переходный процесс
на выходе четырехполюсников, имеющих разную структуру, одинаков.
16-16. Пользуясь теоремой об эквивалентном источнике, ВЫВеСТИ
общее условие эквивалентности источников э. д. С. и ,тока Е (j(j)
== Z (j(j) 1 иш), rAe Е (j(j) и 1 (j(j)
спектральные функции э. Д. с. и
соответственно тока эквивалентных источников; Z (j(j)
их внутрен-
нее комплексное сопротивление (т. е. сопротивление последовательной
BeTBIj источника напряжения, равное сопротивлению параллельной
ветви источника тока),
528
r Л'А В А С Е М Н А Д Ц А Т А Я
СИНТЕЗ ЛИНЕйНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
11.1. ХАРАКТЕРИСТИКА ЗАДАЧ СИНТЕЗА
При проектировании различноrо рода устройств авто-
матическоrо управления, каналов электропроводной и ра-
диосвязи и т. п. возникаеТ необходимость подбора схем и
параметров электрических цепей, отвечающих определен-
ным требованиям. Нахождение схемы и элементов электри-
ческой цепи, удовлетворяющей заданным условиям, со-
ставляет задачу с и н т е з а электрической цепи.
Ввиду Toro что установившийся и переходный процессы
во всякой линейной электрической цепи зависят от частот-
ных свойств цепи, задача синтеза обычно сводится к нахо-
ждению цепи по заданной частотной характеристике.
Искомым может быть двухполюсник с заданной зависимо-
стью сопротивления (или проводимости) от частоты либо
четырехполюсник с заданной передаточноЙ функцией или
частотной зависимостью ero параметров. Построение схемы
пассивной цепи по заданноЙ частотной функции принято
называть р е а л и з а Ц и е й или о с у Щ е с т в л е -
н и е м функции.
В отличие от задачи анализа, в которой искомая вели-
чина
реакция цепи на приложенное воздействие
полу-
чается однозначно, задача синтеза может иметь несколько
решений или вовсе не иметь решения в заданном классе
электрических цепей. Данная rлава посвящена синтезу
пассивных обратимых цепей, поэтому заданную частотную
функцию будем считать реализуемой ИЛи осуществимой,
если соответствующая ей электрическая цепь может быть
составлена из сопротивлений, индуктивностей и емкостей
(возможно также применение трансформаторов).
Поскольку задача синтеза может иметь несколько реше-
ний, возникает необходимость сопоставления полученных
вариантов и выбора оптимальноrо решения.
В этом вопросе не имеется вполне определенноrо крите-
рия, так как приходится сравнивать схемы с разнородными
элементами. При этом обычно руководствуются следующими
соображениями. Желательны схемы с наименьшим коли-
чеством элементов, имеющие практически приемлемые па-
529
раметры, прич
м предпочтение следует отдавать схемам,
содержащим простейшие элементы
сопротивления и ем-
кости.
Индуктивность
менее желательный элемент цепи. Если
в схеме последовательно включены индуктивность и сопро-
тивление, то они MorYT быть практически выполнены в виде
индуктивной катушки. Однако -при этом приходится счи-
таться с витковой емкостью, которая может внести в работу
цепи искажения при высоких частотах.
Еще менее желательным элементом схемы является
трансформатор, практическое осуществление Koтoporo со-
пряжено с появлением тепловых потерь и межвитковых
емкостей. Кроме Toro, коэффициент связи может не сов-
падать с расчетным.
В задачах синтеза частотные характеристики сопротив
лений, проводимостей или передаточных функций MorYT
быть заданы rрафически или аналитически. Если характе-
ристика задана rрафически или не является рациональной
функцией, ,то она приближенно аппроксимируется рацио-
нальной функцией, т. е. отношением двух полиномов, кото-
рое по определенным правилам синтеза реализуется в виде
двух- или четыреХПОЛЮСlIика.
Таким образом, первым этапом в задаче синтеза является
аппроксимация заданной частотной характеристики рацио-
нальной функцией; этот этап, относящийся 1{ области ма-
тематики, здесь не рассматривается. Второй этап заклю-
чается в реализации рациональной функции, что и состав-
ляет основное содержание данной rлавы.
11-2. ИССЛЕДОВАНИЕ ДВУХПОЛЮСНИКА ПРИ КОМПЛЕКСНОЙ
ЧАСТОТЕ
При исследовании переходных процессов в линейных
электрических цепях мы пользовались понятиями комплекс-
ной частоты р == с + jw и операторноrо сопротивления
Z (р). Если Z (jw) представляет собоЙ комплексное сопро-
тив
ение цепи, то операторное сопротивление получается
заменой iw через р.
В общем случае, пользуясь комплексной частотой р,
можно представить операторное сопротивление Z (р) как
отношение двух полиномов, которые. не имеют общих корней
Z ( ) == aпpп+aп
lpп
l+.., +a1P+ao
р bmpm+bm
lpm
l+...+blP+bo'
(17-1)
530
'1. е. Z (р) является рациональной функцией р. Обозначив
через Рl, рз, ... , P2п
1 корни числителя (число их равно сте-
пени пслинома п) и через Р2, р", ... , Р2т корни знаМf'нателя
(число их равно степени полинома т), разложим числи-
тель и знаменатель' на множители:
Z (р) == н (p
Pl)(P
Рз)... (p
Р2IН) .
(P
P2) (P
P4) '" (P
P2т) ,
(17
2)
здесь Н === а 1l /Ь т
постоянный множитеJIЬ (действитель-
ное число); P2k
1
нули функции Z (р); P2k
полюсы Z (р).
Расположение полюсов и нулей функции Z (Р) на ком-
плексной плоскости характеризует частотные свойства ли-
нейной электрической цепи, от которых в свою очередь
зависят установившийся и переходный процессы в данной
цепи.
Нули функции Z (Р) двухполюсника являются корнями
характеристическоrо уравнеНЩI (см. rл. 14). Они MorYT
быть любыми числами, но обязательно с отрицательной
деиствительной частью, так как эта часть определяет фи-
зически затухание свободных токов в данной цепи. В пре-
дельном случае незатухаю[Цих колебаний в цепи действи-
тельная .часть корней равна нулю. Это условие распростра-
няется также на нули функции Z (р) дуальноrо двухполюс-
ника, которая равна функции У (Р) исходноrо ДВУХПО. 1 IЮС-
ника, rдe у (р) == I/Z (р). Но нули функции У (р) есть
в то же время полюсы функции Z (р). Поэтому полюсы Z (р),
так же как и нули, располazаются в левой части комплекс-
ной пЛОСКDсти и на оси мнимьа чисел.
Из выражения (17
2) СJlедует, что свойства функции
Z (р) полностью определяются расположением нулей и по-
люсов. Если У двухполюсников, имею[Цих разные струк-
туры, НУJ1И И полюсы функции Z (р) совпадают, а множп-
тели Н одинаковы, то такие двухполюсники эквивалентны.
Рассмотрим основные свойства функций сопротивления
и проводимости.
Функция сопротивления Z (р) и функция проводимости
У (р) являются положительными действительными функ-
циями.
Функция Z (р) комплексноrо переменноrо р называется
положительной действительной функ-
Ц И е Й, если она удовлетворяет двум требованиям:
1) комплексным числам р в правой полуплоскости соот-
ветствуют значения Z (р), расположенные также в правой
полуплоскости, т. е. действительная часть функции Z (р)
531
при положительных действительных частях р положительна
(отсюда название «положительная» функция);
2) функция Z (р) действительна при действительных ::ша-
чениях р (отсюда название «действительная» функция).
Убедимся теперь в том, что обобщенное сопротивление
двухполюсника Z (р), представляющее собой рациональ-
ную функцию вида (17-1), удовлетворяет указанным выше
двум условиям.
В самом деле, поскольку полюсы Z (р) MorYT находиться
лишь в левой полуплоскости и На мнимой оси, Z (р) анали-
тична в правой полуплоскости. Кроме Toro, при любоЙ ча-
стоте ffi средняя мощность, поступающая в пассивную цепь,
не отрицательна:
Р === Re [Z ию)]12:;=: О.
Так как 12 > О, то и действительная часть комплексноrо
сопротивления не отрицательна:
Re [Z ию)]:;=: О.
(17 -3)
На основаНии принципа максимума и минимума модуля
следует, что наибольшие и наименьшие значения действи-
тельной части функции Z (р), аналитичной в правой полу-
плоскости, достиrаются только в rраничных точках обла-
сти. В данном случае rраницей области является мнимая
ось, rде Z (р) принимает значения Z аш).
Следовательно, с учетом (17-3)
Re[Z(p)]:;=:O при Rep:;=:O.
(17 -4)
Если на мнимой оси расположены полюсы, то они MorYT
быть обойдены дуrами окружностей сколь уrодно малоrо
радиуса и предыдущие рассуждения MorYT быть отнесены
к оставшейся части.
Итак, соrласно (17-4) для Z (р) выполняется первое
условие: Z (р)
положительная функция.
Коэффициенты полиномов в числителе и знаменателе
(17-1) должны быть положительными и действительными,
так как только в этом случае корни этих ПОЛИНОМ0В, соот-
ветствующие нулям и полюсам функции Z (р), как уже было
отмечено выше, располаrаются в левой полуплоскости.
В этом случае при действительных значениях aprYMeHTa
функция Z (р) принимает действительные значения. Сле-
довательно, выполняется второе УCJIOвие: Z (р)
дейст-
вителыщя функция.
532
Таким образом, оператор ное сопротивление любоrо
пассивноrо двухполюсника представляет собой положитель-
ную деЙствительную функцию.
Операторная проводимость паССИВlIоrо двухполюсника
также является положительной действительной функцией.
В этом леrКо убедиться" приняв Z (р) ::::: , (с, ш) + jx (с, ш),
rде р === с + jw.
Очевидно,
у 1 1 ,
jx
(р)::::: Z (р) == ,+ jx ::::: ( 2 +х 2 .
В правой полуплоскости r> О и ,/(,2 + х 2 ) > о; при
этом действительным значениям р соответствуют действи-
тельные значения У (р).
Таким образом, У (р) удовлетворяет требованиям,
предъявляемым к положительным действительным функ-
циям.
Остальные свойства функций сопротивления и проводи-
мости вытеКают из свойств положительных действительных
функций.
1. Если на мнимой оси иJ.tеются нули или полюсы, то
все они простые, причем вычеты в полюсах и проuзводные
в нулях действительны и положитеЛЬflЫ.
Допустим, что функция Z (р) имеет т-кратный полюс в точке Р "'"
== jro o . Разложение Лорвна в окрестности полюса записывается в виде
Z (р)
C
т
(p
jroo)т
c
(m
i) +
( ' ) m
...
P
Jroo
ro
...+ C
+
CI,(P
jroo)k.
р
}roo
k
O
В достаточно малой окрестности точки Р == jro o поведение функ-
ции Z (Р) определяется первым членом разложения
Z ( ) C
11l
< Р
(p
jroo)т,
Пусть С т === Ae i9 и Р
jro o === ре iФ , rде р > о сколь уrодно малая
величина (рис. 17
1).
Для действительной части функции Z (р) получается выражение
А А
ReZ (р)",=:: Rc
eJle
т1/)) ==
cos (тф
е).
рl1l рl1l
При обходе BOKpyr точки jro o по окружности радиусом р уrол 'i>
измеияется от О ДО 2л, значение же е сохраняется неизменным. Знак
действительной части определяется в этом случае знаком cos (тЧ>
6),
который при обходе m-кратноrо полюса изменяется 2т раз.
533
Если Z (р)
положительная функция, то действительная часть
ее в правой полуплоскости положителr.на и не меняет
HaKII. Следова-
телЬно, полюс, расположенный на мнимой оси, должен быть простым
(т == 1), причем уrол е должен быть равным
+ . й) нулю, а ве
ичина А == Ct должна быть по-
J ложительнои, только пуи этих условиях
С .
Re Z-(p)
cos1j' сохраняет положитель-
jo>o вый знак в р правой полуплоскости р, rде
л/2 <
, < л/2; здесь C
l
вычет функ-
ции Z (р) в точ!,е р == jffio.
ПОСКОЛЬКУ У (р) == I/Z (р)
положи-
тельная действительная функция, то указан-
ное выше свойство распространяется и на
+ у (р), а именно: если на мнимой оси имеются
О полюсы функции У (р), ТО они простые и
вычеты в этих полю.:ах действительны и
Рис. 17
1. Полюс на положительны. Но простой полюс функции
ни й оси у (р) есть простой нуль функции Z (р), а
м мо. вычет функции У (р) в простом полюсе об-
ратен производной dZ (p)7dp в нуле Функ-
ции Z (р). Следовательно, на мнимой оси нули MorYT быть только про-
стыми, причем производные в них действительны и положительны;
2. Нули и соответственно полюсы рациональной поло-
жительной действительной функции MOf!.ym быть действи-
тельными или комплексно-сопряженньо'!и.
Данное положение следует из Toro, что рациональная
функция является положительноЙ деЙствительной функцией
только в }ом случае, если все коэффициенты полиномов
в числителе и знаменателе действительны и одинаковоrо
знака. Замена комплексноrо aprYMeHTa Р сопряженной
*
величиной р дает при таком условии сопряженную функцию
* *
z (р) == z (р).' Поэтому если ро
комплексный нуль функ-
ции Z (р), то наряду с равенством Z (Ро) == О обязательно
* ,. *
должно выполняться равенство Z (ро) == Z, (ро) == О; ИНаче
*
rоворя, ро является также нулем функции Z (р).
То же положение распространяется На нули функции
у (р) == llZ (р), т. е. на полюсы функции Z (р).
На основании сказанноrо комплексные нули и полюсы
Z (р) располаrаются симметрично относительно действи-
тельной оси, т, е, образуют сопряженные пары. То же можно
сказать о функции У (р).
3. Наибольшие и
coomвeтcтвeHHO наименьшие показа-
тели степеней р в числителе и Знаменателе положительной
действительной функции не ,мощт различаться более чем
на единицу.
534
Сростом [р \ ФУНI\ция (17-1) или, Что то же, (17-2)
стремится к Hpп
т. Ввиду Toro что бесконечно удаленную
точку. можно считать лежащей на мнимой оси, на основа-
нии свойства 1 соответствующий нуль или полюс функции
должен быть простым.
Если р == со есть простЬй нуль или полюс, то степень
числителя на единицу ниже или выше степени знаменателя.
Возможны три случая при р
00:
1) Z (р)
Нр, коrда п
m == 1;
2) Z (р)
н /р, коrда п
m ===
1;
3) Z (р)
н > о, коrда п
m == О.
Поскольку точка р == О (начало координат) ПрИнадле-
жит мнимой оси, на основании свойства 1 нуль или полюс
в точке р == О должен быть простым. Следовательно, наи-
меньшие показатели степеней в числителе и знаменателе
положительноЙ деЙствительной функции не MorYT разли-
чаться более чем на единицу. Возможны три случая при
p
o:
1) Z (р) === ао/Ь о , коrда а о =1= о, Ь о =1= о;
2) Z (р) == GO/b1P, коrДа G =1= о, Ь О === о;
3) Z (р) == а]р/Ь о , коrда Go == о, Ь о =1= О.
При исследовании частотных свойств двухполюсника
текущая переменная р берется на мнимой оси' (р == jw).
Частотные свойства двухполюсников 'определяются при
этом расположением нулей и полюсов на мнимоЙ оси.
Выражение (17-2) может быть переписано в показатель-
ной форме. Обозначив через M2k
] и a2k
] модуль и apry-
мент бинома (р
P2k
]), а через M2k и a2k модуль и apry-
мент бинома (р
- P2k), получим:
Z (р) == н MIM3... M
'!::!. L а; (17-5)
М2 М 4 ." М 2т
а== (а] +аз+.. .+a 2n - 1 )
(аз+а4 +.. .+а 2т ).
Следовательно, для выбранноrо значения р модуль функ-
ции Z (р) определяется отношением произведения модулей
(р
p2k
]) К произведению модулей (р
p2k); aprYMeHT
функции Z (р) определяется разностью суммы aprYMeHTOB.
(р
P2k
1) И суммы aprYMeHToB (р
P2k)'
Из выражен ия (17-5) в виду симметр ии расположения
нулей и полюсов относительно деЙствительной оси следует,
что модули функций Z иш) и У иш) четны относите,fJЬНО (1),
так как все модули для +jw и
jw одинаковы, а aprYMeHTbl
их нечетны относительно ш.
535
Итак, по расположению на комплексной плоскости
нулей и полюсов (операторноtо) сопротивления Z (р) можно
судить как о характере самой цепи, так и о ее частотных
свойствах.
17.3. УСЛОВИЯ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ ФУНКЦИИ
В задачах синтеза функция Z (р) может быть задана
непосредственно или получена из частотной характери
стики Z (jw) с помощью подстановки jw === р.
Функция С1штается физически реализуемой, если соот-
ветсm.eующая ей электрическая цепь может быть состав-
лена из элементов (сопротивлений, индуктивностей, ем-
костей) с положительными действительнылщ парамет-
рами.
Для всякой действительной положительной функции
может быть построен двухполюсник, для KOToporo она яв-
ляется обобщенным сопротивлением (или проводимостью).
Поэтому условие положительности и действительности
функции является достаточным для ее реализуемости.
В связи с этим, если требуется построить двухполюсник
по заданноЙ рациональной функции, предварительно выяс-
няют, является Ли она положительной и действительной.
В соответствии с тем, что было сказано в предыдущем
параrрафе, рациональная функция является положителъ
ной и действительной, если одновременно выполняются сле
дующие условия:
1) все коэффициенты полиномов действительны (условие
действительности функции);
2) в правой полуплоскости полюсы отсутствуют (усло-
вие аналитичности функции);
3) в бесконечно удаленной точке функция ведет себя,
как Нр, Н или Н /р (свойство 3);
4) полюсы на мнимой оси MorYT быть только простыми
С действительными и положительными вычетами (свойство 1);
5) действительная часть функции на мнимой оси не
отрицательна lусловие (17-3)].
Перечисленные условия являются необходимыми и до-
статочными, чтобы заданная рациональная функция была
положительной и действительной. Если хотя бы одно из
этих условий не выполнено, то заданная функция не есть
положительная действительная функция.
Условия 1 и 3 проверить леrКо непосредственно по виду
функции. Для проверки условий 2 и 4 существует метод,
536
не требующий определения расположения всех полюсов
ФУНКЦИИ и использующий свойства полиномов rурвица.
Полиномом rурвица называется полином, КОрНИ KOТO
poro расположены в левой ПОЛУПЛОСКОСТИ и на оси мнимых
чисел, причем полюсы на мнимой ОСИ простые. Из этоrо
опредедения следует, что числитель и знаменатель положи
тельной действительной фУНКЦИИ должны быть полиномами
rурвица.
Чтобы проверить, является' ли данный полином А (р) полиномом
fурвица, ero представляют в виде суммы полиномов с четными и не-
четиыми степенями.
Полином А (р) является полиномом fурвица, если функция
А ч (р)/ А и (р) или обратная ей функция MorYT быть разложены в не-
прерывную дробь вида
СОР +
С1Р + 1
С 2 Р+
. 1
+ СпР
с положительными коэффициентами со, С 1 , С 2 , ..., Сп' Последователь-
ность разложения в непрерывную дробь описана в
17-4.
Действительная часть функции на мнимой оси [Re Z (j(j)] сравни-
тельно просто находится, если полиномы А (р) и В (р) в числителе и
знаменателе (17-1) представить как суммы полиномов с четными и
нечетныМИ степенями р:
А (р)==А ч (р)+А и (р); В (Р)==В ч (Р)+В и (р).
При этом
Z (р) А (р) В (
p)
[А ч (р) + Ан (р)] [В ч (
р) + В и (
p)]
в (р) в (
p)
в (р) в (
p)
откуда с учетом равенств В ч (
p) == В ч (р) и В и (
p) "'"
Ви (р)
Z (р) А ч (р) В ч (р)
Ан (р) В н (р) + Ан (р) 'В ч (р)
А ч (р) В и (р)
B
B
. B
B
При р == j(j) первое слаrаемое, четное относительно частоты (j),
выражает активное СОПрОТИВJ1(
ние двухполюсника, а второе слаrаемое,
нечетное относительно частоты, выражает реактивное сопротивление.
Итак,
RеZ(j(j)== [ Ач(Р)Вч(Р)
АИ(Р)Ви(Р) J . (17-6)
B(p)B(
p) p
j(f)
Знаменатель выражения (17
6) на мнимой оси В (j(j) В (
j(j) ==
1 в (j(j) 12 положителен. Следовательно, условие неотрицательностн
действительной части функции можно 3iшисать в виде
[А ч (р) В Ч (Р)
Аи (р) В И (p)]p
j(f)
O'
537
в случае реактивноrо двухполюсника выражение (17-6) обращается
в иуль, т. е. выполняется условие (при р == jO)
А ч (р) В ч (р) == Ан (р) В Н (р).
При этом
Z(P)
А ч (р)+А н (,о)
В Ч (,о) + в н (,о)
А ч (,о) + А ч (,о) В Ч (,о)
В и (,о)
А ч (,о)
Ан (,о)
В Ч (Р)+Вн (р)
В и (,о)
Б ч (,о) .
Следовательно, в случае реактивН020 двухполюсника полином в
числителе (17-1) содержи т 1110.1 ЬКО четные, а в знаменателе
только
нечетные степени, или наоборот.
Пример 17-1. Проверить положительность и действительность
фуикции
Р(р)== р2+р+2 :
р+l
1) коэффициенты полиномов действительны;
2) в правой полуплоскости полюсы отсутствуют;
3) в бесконечиости фуикция ведет себя, как р;
4) на мнимой оси полюсов нет;
, 2
5) Re Z (/0) == 1 + 0)2
О.
Проверка показывает, что заданная функция Является положи-
тельной действительной.
i7-4. СВОйСТВА ДВУХЭЛЕМЕНТНЫХ ДВУХПОЛЮСНИКОВ
И ИХ РЕАЛИЗАЦИЯ
Под двухэлементными двухполюсниками понимают двух-
полюсники с элементами двух типов (L и с; t и С или r и L).
В случае, коrда Двухполюсник состоит 1rолько из реак-
тивных элементов, т. е. если потери электрической энерrии
в нем отсутствуют, aprYMeHT сопротивления составляет
--+
900. В соответствиН с (17-5) пр ямой уrол возможен только
при условии, что все нули и полюсы лежат на мнимой оси.
Как показано выше, функция Z (р) реактивноrо двух-
полюсника представляет собой отношение полиномов, один
из которых содержит четные, а друrой
нечетные степени
р. При этом общее число нулей и полюсов нечетно, следова-
тельно, в начале координат (т. е. в точке р == О) должен
находиться нуль или полюс.
Нули или полюсы должны обязательно чередоваться.
Если бы за нулем следовал нуль или за полюсом
полюс,
то в соответствии с (17-5) при некоторых частотах уrол был
бы равен + 1800, что противоречило бы условию, что на
выводах реактивноrо двухполюсника фазовый уrол между
напряжением и током не превышает 900. Таким образом,
538
для реактивных ДВУХПОЛЮС1-IИКОВ характерным является
расположение нулей и полюсов, показанное на рис. 17
2,
a
e.
В случае, коrда двухполюсник состоит из элементов
r, L или 1', С, нули И полюсы Z (р) располаrаются по дейст-
вительной оси (в левой полуплоскости). AprYMeHT комплекс-
Horo сопротивления TaKoro двухполюсника не достиrает
+ 900, поэтому нули и по
люсы должны быть не толь-
ко простыми, НО И чередо-
ваться. Числа нулей и по-
люсов MorYT разниться не
более чем на единицу.
При частоте, равной
нулю, сопротивление двух-
полюсника типа r, L, в за-
висимости от ero структуры
равно пулю или имеет дей-
ствительное значение. По-
этому нуль Z (р) TaKoro
двухполюсника либо сов-
падает с началом коорди
нат (рис. 17-3, а), либо
смещен влево 'по действи-
тельноЙ оси (рис. 17
3, б);
при этом ближаЙшим к на-
чалу координат является
нуль, а не полюс. При бес-
конечноЙ частоте сопротив-
ление двухполюсника ти-
па 1', L деЙствительно или
бес!(онечно велико.
Что касается сопротивления двухполюсника типа r, С,
то при частоте, равной нулю, оно имеет деiicтвительное зна-
чение (рис. 17-3, в) или бесконечно велико (рис. 17-3, с).
Ближайшим к началу координат является полюс, а не нуль.
При бесконечной частоте сопротивление обращается в нуль
или действительное число.
Поменяв местами нулн и полюсы Z (р), получим кар-
тину расположения нулей и полюсов У (р).
Следует заметить, что при наличии потерь, коrда нули
и полюсы функции являются действительными или комплекс-
ными величинами, сопротивление и проводимость не MorYT
принимать нулевые или бесконечно большие значения
f +j+
а.)
+
i:
Рис. 17
2. Расположение нулей и
полюсов Z (р) в случае реактианоrо
двухполюсника,
539
в точках, лежаЩI1Х на мнимой оси. Однако при частоте,
соответствующей проекции полюса на мнимую ось, абсо
лютное значение исследуемой функции проходит через
максимум, а при частоте, соответствующей проекции нуля
на мнимую ось, оно проходит через минимум. Чем меньше
4
4
а)
6)
8)
е)
Рис. 17-3. Расположение нулей н полюсов в случае даух-
полюсников " L (а н б) н " С (6 Н с).
действительные части полюсов и нулей, тем резче выража-
ются максимумы и минимумы функции.
Рассмотрим реализацию двухэлементных двухполlOC
ников по методу канонических схем Фостера и методом раз-
ложения в непрерывную дробь (реализация по Кауэру).
Метод канонических схем Фостера
Рассмотрение решения задачи синтеза начнем с более
простоrо метода реализации функции сопротивления Z (р)
реактивноrо двухполюсника.
540
Е
ли
тепень числителя превосходит степень знамена-
теля, то
Z (р) === (/.,;др + Zo (р);
(17-7)
здесь (/.,00 === Н
действительная положительная величина.
Если степень числителя меньше степени знаменателя, то
в выражении (17-7) схс:о == О.
Действительная часть (/.,а:;Р на мнимой оси равна Нулю,
поэтому
Re Zo (jш) == Re Z (jш);;:;:: О.
ВВИДУ Toro что функция Zo (р), получившаяся из Z (р)
после выделения (/.,с:ор, не отрицательна на мнимой оси,
Zo(p)
положительная действительная функция.
201:1Р 201: ч Р
p2+w2 p2+w 2
o
Рис. 17
4, Первая каноническая схема Фостера цепи
L, С,
Полюсы Zo (р) совпадают с полюсами Z (р) за исключе-
нием полюса в бесконечности. Следовательно, Zo (р) имеет
полюсы + jШk и О на мнимой оси с вычетами (/.,k и схо, причем
на основании свойства 1 (см.
17-2) эти полюсы простые,
а (/.,k и СХО
действительные положительные числа. В СВЯЗИ
С этим разложение Zo (р) на простейшие дроби дает 1:
q q q
Z ( ) == "о + '\'1 .......!!:.!... +
== "о + '\'1 2щр
орр "'" р + jOOk "'" Р
jOOk Р "'" р2 + OOk .
k
l k
l k
l
(17 -8)
Подставляя (17-8) в (17-7), находим:
q
Z "о '\'1 2щр
(р) == (/.,с:ор + р + "'" р2 + 00" .
k
l k
Полученному выражению соответствует схема, изобра-
женная на рис. 17-4, которая называется первой канониче-
ской схемой Фостера.
(17 -9)
1 Вычеты "k в сопряженных миимых полюсах равны в силу Toro,
ЧТО они действительиы,
541
Полюс р == 00 обусловлен наличием в схеме индуктив-
ности Loo == а оо , а полюс р == о
наличием емкости СО ==
== 1/а о . Паре комплексно сопряженных мнимых корней
+ j(j)k соответствует параллельное включеНие емкости C k ==
== 1/2ak и индуктивности Lk == 2CGk/(j)2k'
Аналоrично можно показать, что функция проводимости
реактивноrо двухполюсника может быть записана в виде
q
у ( ) ==
== а + C:
+ '\'1 2щ,.р
Р z (р) оор р "'" р2+шх. '
k
l '
rде ak и ао
вычеты У (р) в полюсах + j(j)k и О.
Выражению (17-10) соответствует схема на рис. 17-5,
которая носит название второй каноничесКОЙ схемы Фо-
стера.
Реализацию фУНКЦИЙ двухполЮсников типа " L и " С
получим,' используя реализацию двухполюсников типа L, С.
rtoop Сопротивление произвольной ветви
. цепи L, С можно записать в виде
(Ха 1 1 ( 1 '
p
ZLC (р) == pL +
C
==
... p2L + с-).
Еа1Р р р ,
р2+ы; (17-11)
I
: 2rtqp I
Рис. 17
5. Вторая ка-
ноническая схема Фос-
тера цепи L, с.
(17-10)
Если в ветви отсутствует индуктив-
ность или емкость, то отсутствует соот-
ветствующиЙ член выражения (17-11).
Сравнивая уравнение (17-11) с вы-
ражением для сопротивления ветви "
L, в котором оператор р заменен
на р2,
ZrL (р2) == p2L + "
приходим К выводу, что выражение для сопротивления
ветви r, L в функции от р2 можно получить из выражения
для сопротивления ветви L, С, умножив ero на р (замена
1/С на r не меНяет характера функции). Чтобы получить
ZrL (р), остается заменить р2 на р. Это справедливо и для
получения выражения сопротивления любоrо сложноrо
двухполюсника, т. е. для любых двухполюсников типа
,., L и L, С, имеющих одинаковую схему соединения эле-
ментов,
ZrL (р2) == pZLC (р). (17-12)
Справедливость равенства (17-12) следует из формулы
(7 -9) для входноrо сопротивления или проводимости двух-
542
полюсника. Соrласно этой формуле входное сопротивление
определяется как отношение определителя матрицы кон-
турных сопротивлений к ero алrебраическому дополнению.'
Определитель матрицы контурных сопротивлений пред-
ставляет собой алrебраическую сумму произведений, каж-
дое из которых содержит п сопротивлений ветвей (п
число независимых контуров). Сопротивление каждой ветви
цепи " L в функции от р2 отличается от сопротивления соот-
ветствующей ветви цепи L, С множителем р, тоrда выраже-
ния определителей цепей " L и " С отличаются множите-
лем рn.
Поскольку алrебраическое дополнение представляет
собой алreбраическую сумму произведениЙ, каждое из ко-
торых содержит п
1 сопротивлений ве
вей, то алrебраи-
ческие дополнения цепей " L и L, С отличаются множителем
pn
l. После сокращения множителей pn
l В числителе и зна-
менателе входноrо сопротивления получим равенство (17 -12).
Если указанное выше правило получения выражения для
сопротивления двухполюсника типа " L прпменить непо-
средственно к разложению (17-9), то, обозначая 2CGk через
CGk и CUk через
k, получаем разложение для функции сопро-
тивления произвольноrо двухполюсника типа " L в виде
q ,
"\1 (7.,kP
Z(p)==CGooP+CG o +
P+Pk '
k
l
(17 -13)
Величина
k определяет действительный полюс функ-
ции, а CGk
вычет в этом полюсе. Функции в выражении
(17-13) соответствует реализация на рис. 17-6.
Аналоrичным методом, сравнивая выражения для сопро-
тивлений ветвей цепей типа L, С и " с, получаем разло-
жение для функции сопротивления двухполюсника типа
" с:
q ,
(7.,0 ! (7.,k
Z(P)==CGoo+'
+
+ A"
. р Р t'k
k
l
(17-14)
котор.ому соответствует реализация на рис. 17-7.
Из выражений (17-13) и (17-14) вытекают свойства двух-
полюсников типа " L и " с, описанные выше.
Полученные реализации двухполюсников типа " L
и " С представляют собой первую каноническую схему
Фостера. Для второй схемы Фостера выражения для прово-
димостей двухполюсников типа " L аНалоrичны выражению
543
(17-14), а для двухполюсников типа r, С
выражению
(17-13). Схемы реализации отличаются от второй канониче
ской схемы Фостера, реализующей двухполюсник типа L, С,
зяменой емкости или индуктивности на сопротивление.
Значения сопротивлений, индуктивностей и емкостей
реальных электрических цепей обычно имеют резко отлич
ные порядки. Для удобства вычислений применяется норма-
лизация значений параметров цепи таким образом, чтобы
коэффициенты полиномов функции цепи были пQ возмож-
ности близки к единице.
.
IX1P
IXчР
Р+!1 . Р+Рч
Рис. 17
6. Первая каноническая
схема Фостера цепи r, L,
"'
ф-e::::.--j'ЧrJ
.ч
tXr "' q
р +11 . р +Iч
Рис. 17
7. Первая канони-
ческая схема Фостера цепи
" С,
Нормализация осуществляется по отношению к базис-
ному сопротивлению rб и базисной частоте CUб' При этом HOp
.
мализ&ванные значения параметров определяются из фор
мул
{ Н == r/rб; ш Н == CU/CUб'
Из соотношения (CUL)H == ffiL/rб находим L!! == LCUб/rб
аналоrично С I1 == СCUб/'б'
В приведенных ниже примерах заданные функции ДBYX
полюсников предполаrаются нормализованными.
Пример 17-2. Требуется реализовать положительную действитель-
ную функцию
Z ( ) == pl+4p2+3
Р р3+2р'
Заданиа
функция сос>тветствует реактивному двухполюснику и
имеет полюсы в точках р == О, р ==:!: j v"2 и в бесконечности. Вычеты
в полюсах функции
асс == Res p
roZ (р) == liт Z (р) == 1;
p
ro р
( р4+4р2+3 ) 3
ао == R"sp
oZ (р) == р2 + 2 р
o == 2";
( р4 +4р2 +3 ) 1
al==Res .
Z (р)==
==
.
. P
1Y2 Р (p+j V2) p
jV2 4
544
В результате получаем разложение функции в виде
3 р
2 (р)
p + 2р + 2 (р2+2) '
которому соответствует схема на рис. 17
8.
Пример 17-3. Требуется реализовать положительную действитель-
ную функцию
2р3+ Ilp2+ 8р
2 (р) == (р+2) (2р+ 1) '
Эта функция может быть преобразована в реактивную функцию
заменой р на рЗ и делением на р, что соответствует равенству (17-12).
1/ч
12
I
ч
2
Рис. 17.8. Пример 17-2.
2 1
Рис. 17-9. Пример 17-3.
Следовательно, заданная функция определяет двухполюсник типа r, L
и имеет разложение вида
( rf-\p.. rf-2P 2р 2р
2 р) ==rf-со Р + р +2 + Р + '/2 ==Р+ р+2 + 2р+ 1 .
В результате получаем цепь на рис. 17-9.
Метод разложения в непрерывную дробь
Наряду с рассмотренными выше схемами двухэлемент-
ных двухrюлюсников существуют цепные схемы типа изобра-
женной на рис. 17-10, сопротивления которых MorYT быть
выражены непрерывной дробью (в схеме на рис. 17-10 по-
следовательные ветви обозначены сопротивлениями, а па-
раллельные
проводимостями):
1
z ==о ZI +
У 2 + 1
23 + 1
v 4 +
+ 1
, 1
Z'H+y
'
n
Разложение задаННQЙ дробно-рациональной функции
Z (р) == А (р)/В (р)
545
Б. непрерывную дробь осуществляется в такой последова
тельности. Сначала определяем частное Z1 от деления поли
нома числителя А (р) на полином знаменателя В (р) и OCTa
ток R 1 (р) этоrо деления, т. е.
Z ( ) Z R1 (р) Z 1
Р == 1 + в (р) === 1 + в (p)/R 1 (р) .
(17-15)
Далее делим полином В (р) на R 1 (р), определяя новое
частное У2 и остаток R 2 (р). Затем делим остаток R 1 (р)
на R 2 (р) и так далее, пока не получим нулевоrо или леrко
реализуемоrо остатка.
В приведенной выше процедуре разложения Б непреРЫБ
ную дробь частное от деления полиномов имеет вид ар, а
или а/р и реализуется соответственно индуктивностью, aK
тивным сопротивлением и
емкостью. Выполняя деле
иие, нужно следить, чтобы
коэффициенты полиномов
были положительны.
Следует заметить, что
непрерывные дроби и co
ответствующие им цепные
схемы различны в зависи
мости от Toro, распола
rаются ли полиномы Б числителе и знаменателе за
данноЙ дробно-рациональной функции по возрастающим
или нисходящим степеням р. Кроме Toro, вместо функции
Z (р) в непрерывную,дробь может быть разложена функция
у (р) === I/Z (р). Рдзложение функции У (р) отличается от
разложения Z (р) тем, что первое частное представляет
собой проводимость У1' Соответственно схема, реализующая
разложение функции У (р) в непрерывную дробь, начина
ется не с последовательноrо сопротивления, а с параллель-
ной проводимости.
Наконец, возможно разложение в непрерывную дробь,
при котором в процессе деления сначала соблюдается один,
а затем друrой порядок расположения степеней р. В отдель
ных случаях некоторые варианты расположения степеней
приводят к появлению отрицательных коэффициентов потI
номов, т. е. не дают физическую реализацию.
Методом разложения в непрерывную дробь можно реали
зовать любые двухэлементные двухполюсники, а также не-
которые ДВУХПОЛЮСНIIКИ типа " L, С. Построение двухпо
Z,
Z.1
[5
Z7I
'
У,
B
1..у,
I
'14
Рис. 17-10. Цепная схема:
546
люсника методом разложения Z (р) в непрерывную дробь
проиллюстрировано ниже примерами.
Пример 17-4. Требуется реализовать положительную действитель-
ную функцию
р2 + р + 1
Z (р) == р3+р2 +2р + 1 .
Заданная функция разлаrается в непрерывную дробь:
1
z (р) ==
р+ 1
р+ р+l '
Этому выражению соответствует цепная схема, изображенная на
рис. 17
11.
С=1 С=1
r=f
iз
L=1
Рис. 17
11. Пример 17-4.
Рнс. 17-12. Прнмер 17
5.
При мер 17-5. Требуется реализовать положительную действитель-
ную функцию
2р3+3р2+ 2р+ 1
z (р) == 2р2+2р+l .
Степень числителя выше степени знаменателя, следовательно, функ-
ция нмеет полюс в бесконечности, что указывает на наличие послеДова-
тельной индуктивности.
Начав с расположения полиномов по возрастающим степеням и
измеиив в процессе деления порядок расположения степеней, можно
заданную функцню представить в следующем виде:
1
Z(P)==p+ 1+2р+2р2
1 +р+р2
1
р+ 1
1 + 1 + р + р2
р+р2
::= Р+ 1
1+ 1 1
+
.
р
+1
р
Полученной непрерывной дробн соответствует схема n
Ника, показанная на рис. 17-12. "вухполюс,
547
17.5. О&ЩИй СЛУЧАй РЕАЛИЗАЦИИ ФУНКЦИй ДВУХПОЛЮСНИКА
Процесс реализации положитеJIЬНОЙ действительной
функции двухполюсников начинается с выделения реактив-
ной части цепи, соответствующей полюсам на мlIИмОЙ оси,
включая начало координат и бесконечность. После чеrо
функция сопротивления примет вид:
р
а о
2CGkP Z ( )
Z (р) == (хоор + р + "" р2 + (i):k + 1 р .
k
l
(17-16)
На мнимой оси выделенные члены, не входящие в Z1 (р),
принимают мнимые значения, поэтому
Re Z1(jffi) == Re Z Ош);:?:: О
и, следовательно, Z1 (р)
положительная действитель-
ная функция.
Целесообразность первоначальноrо выделения членов,
соответствующих полюсам на мнимой оси, определяется
не только тем, что это всеrда допустимо, но и тем, что мнимые
корни знаменателя В (р) функции Z (р) можно найти, не
Qпределяя всех корней.
Полином знаменателя можно записать в ВИДе
в (р) == N (р) + м (р) == N (р) + pN 1 (р),
(17-17)
rде четный полином N (р) объединяет члены В (р) с чет-
Ными степенями, а полином М (р)
с нечетными степе-
нями.
При р == jffi четные степени jffi дают действительные
числа, поэтому N аш) И N 1 иш) В уравнении (17-17) дают
действительные значения. Тоrда N(jffi) представляет собой
действительную часть В иш), а ffiN 1 аш)
мнимую часть.
Поскольку комплексное число равно Нулю, коrда дей-
ствительная и мнимая части равны нулю, то, если jffik
корень полинома В (р) или В иш), он должен обращать
в нуль и N (jffik), и N 1 (jffik)' Таким образом, мнимый ко-
рень ПОЛИНома В (р) является одновременно .корнем поли-
номов N (р) и N 1 (р).
Так как полиномы N (р) и N 1 (р) содержат лишь четные
степени р, то, заменяя р2 на s, получим полиномы N' (s)
и N; (s). Степень этих полиНомов по меньшей мере в 2 раза
меньше степени полинома В (р), что облеrчает нахождение
мнимых корней (см. пример в конце параrрафа).
548
Функция Zl (р) В уравнении (17-16) носит название
функции мииимальноrо реактивноrо
с о про т и в л е н и я. Если функция Zl (р) имеет нули
на мнимой оси, тоrда функция Y 1 (р) ИМеет полюсы на мни-
мой оси. В этом случае можно выделить из Y 1 (р) члены,
соответствующие полюсам на мнимой оси. В остатке полу-
чаем функцию Yz (р), не имеющую полюсов на мнимой оси.
Такая функция носит название Ф у н к Ц и и м и н и-
м а л ь н о й р е а к Т и в н о й про в о Д и м о с т и.
Функция У 2 (р) может иметь нули на мНимой оси, Torдa
процесс выделения реактивных элементов нужно продол-
жИ'!;ь для функции Zz (р) и т. д. В конечном итоrе получим
функцию Z k(P), не имеющую ни нулей, ни полюсов на
мнимой оси. Такая функция называется Ф у н к Ц и ей
минимальноrо реактивноrо сопро-
т и в л е н и я и про в о Д и м о с т и.
Для реализации функции Z" (р) выделяют из нее актив-
ное сопротивление, равное минимальной действительной
части Zk (р). В этом случае минимальная действительная
часть оставшейся функции
Zo (р) == Zk (р)
'мик (17-18)
равна нулю, причем этот минимум достиrается на мнимой
оси при (i) == ШО. Функция Zo (р) называется Ф у н к Ц и ей
минимальноrо активНоrо сопротив-
л е н и я.
Для нахождения 'мик и ШО нужно определить минимум
выражения (17-6) и часТоту ШО, при которой оН достиrа-
стся.
В простейшем случае, коrда ШО равно нулю или беско-
нечности, функция Zo (р) позволяет продолжить процесс
выделения реактивных элементов и может быть получена
окончательная реализация. В противном случае функция
Zo (р) представляет собой отношение полиномов одинаковой
степени, не имеющих корней на мнимой оси. Такая функция
может быть реализована методом Брунэ.
Пусть функция Zo (р) представляет собой отношение
полиномов А (р) и В (р) пой степени. Эта функция принимает
чисто мнимое значение Zo ишо) == jx o при р == jw o , которое
реализуется индуктивностью Ll == Хо/Шо' .
Так как хо может быть отрицательным, то соответствую-
щая индуктивность Ll будет тоже отрицательной. Отрица-
тельная индуктивность не может быть реализована На
практике, но, как показано ниже, от нее можно избавиться.
54\J
После выделения индуктивности L 1 остаВI1Iаяся функция
ZOI (р) == Zo (р)
pL 1 == А 1 (p)IB (р) (17-19)
имеет нули при р == + jffio, следовательно, обратная функ-
ция имеет в этих точках полюсы.
После выделения члена, соответствующеrо полюсам
+ jffio, получаем функцию
у ( ) У ( ) 2аор А 2 (р) (17 20)
02 Р == 01 Р
р2 +- (i)
== 82 (р) , -
rде степень полинома А 2 (р) р?виа п
2, а В 2 (р)
равна
п
1; таК КаК они На 2 меньше степеней полиномов числи-
теля. и знаменателя УОl (р).
1.,1 1.,1 Выделенный член реали
зуется ветвью из последова-
тельно соединенных индук-
ZОЗ(Р) тивности L 2
1/2а о (а о
вы-
чет функции У01 (р) В полюсе
jffio) и емкостью С == 1!ffi
L2
(рис. 17-13).
Рис. 17
13. Цепь с выделенным Функция Z02 (р) == 11У02 (р)
циклом Брунэ, имеет полюс в бесконечности,
так как степень полинома чи-
слителя больше степени полинома знаменателя. Этот полюс
реализуется индуктивностью L з , которая равна вычету
в этом полюсе:
1-3== lim ZО2 Ш.
р.....оо Р
Выражая Z02 (р) через Zo (р) с помощью уравнений
(17-20) и (17-19), находим, что
L3 ==
L 1 L 2 . (17-21)
L 1 + L 2
После выделения индуктивности L3 получаем функцию
Z ( ) Z ( ) L 82 (р) L 8 з (р)
03 Р == 02 Р
Р 3 == А 2 (р)
Р 3 == А 2 (р) .
На рис. 17-13 ПоКазан результат рассмотренных эта-
пов. Выделенная часть цепи, состоящая из индуктивностей
L 1 , L2' L3 И емкости С, называется циклом Брунэ.
Проанализируем физическую реализуемость на каждом
этапе. Если индуктивность L 1 отрицательна, то Z(J1 (р)
является положительной действительной функцией и по-
слеДУЮЦI.ие этапы дают физическую реализацию.
550
Если индуктивность L 1
положительна, то ZOl (р)
не является положительной действительной функцией.
Это означает, что она не может быть реализована с помощью
положительных элементов типа r, L, С. Действительно,
соrласно формуле (17-21) при положительной индуктив
насти L 1 индуктивность L3
отрицательна.
Таким образом, в схеме на рис. 17-13 одна из индуктив-
ностей L 1 и L3 обязательно отрицательна и не может быть
реализована. В связи с ЭТИм индуктивности L 1 , L 2 И L3
заменяют трансформатором с индуктивностями обмоток
Ц == L 1 + L2' L2 == L3 + L 2 и взаимной; индуктивностью
, М == L 2 .
в результате получаем схему на рис. 17-14, эквивалент-
ную схеме на рис. 17-13. В этой схеме индуктивности Ц и L
положительны. Коэффициент связи трансформатора
k == м == L 2
1.
VL
L; V(Li+L2)(L2
L
tJ
Трансформатор с коэффициентом связи, равным еди
нице, .называется совершенным. Для реальноrо трансфор
матара k < 1, но можно с дo
статочной для практики сте-
пенью точности приблизиться
к значению k == 1 и реал и-
З0вать таким образом совер-
шенный трансформатор.
Оставшаяся функция Zоз(р)
представляет собой отношение
полиномов степени п
2.
Для реализации этой функ- Рис. 17-14. Схема цепи, эквива-
ции может быть применена лентная цепи на рис. 17-13.
описанная выше процедура,
которая может потребовать выделения HOBoro цикла Брунэ.
Однако, поскольку после выделения цикла Брунэ степени
полиномов снижаются на 2, в конечном итоrе функция
будет реализована.
.
Lz
Zo;s(p)
Выше был рассмотрен простейший метод реализации функции
минимальноrо активноrо сопротивления, который требует использо
вания совершенноrо трансформатора. Имеются бестрансформаторные
методы реализации, такие как методы Ботт-Даффина, Мията и др.
Пример 17-6. Реализовать положительную действительную функ-
цию
Z ( ) === 4рЧ-6р3+ 12р2+ 16р+ 10
р р4+ р 3+бр2+2р+8
(17-22)
55.
Сначала определяем мнимые корни знаменателя, решая уравнения
для четной и нечетной частей:
р4+6р2+8=:О или s2+65+8==O, (17-23)
рЗ+2р=:0 или s+2==0.
Из последнеrо уравнения находим sl ==
2 или Pi,2 == :!: j У2.
ЭТИ корни удовлетворяют уравнению (17-23) и, следовательно, являются
полюсами функцни (17
22).
Вычет фуикции в полюсе Pi==j У2 равен 3/2, поэтому можно запи-
сать, Что
3 '
2 (р) == p2
2 +2i (р).
ПервыЙ член реализуется параллельно соединенными индуктив-
ностью и емкостыо (рис. 17-15), а второй члеи
2 ( ) == 2р2 + 2р + 5
1 Р р2 + р + 4
реализуется по методу Брунэ.
Используя формулу (17-6), находим, что д'еЙСТl\ительная часть
функции Z1 (р) имеет минимальное значение 'мин == 1 при частоте ШО ==
== У2. Выделяя сопротивление 'мин, получаем:
21 (р) == 1 +
:
t
.
21 (р) при частоте шо обращается в j/y2 == jш о L 1 ,
Второй член
ОТКуда LL == 1/2.
После выделения индуктивности L4
L
= уч
Т=У,/
получаем в остатке функцию
(р2 + 2) (
Р + 1)
Zз(р)== 2 (Р2+.о+4), ,
ДЛЯ, которой
1
Уа (р) == 23 (р) ==
2р 4
р3 +2 +
р + 1 .
L = 312
Первый член последнеrо
выражения реализуется после-
довательным соединением ин-
дуктивности L 2 == 1/2 и емкости С == 1. Второй член
последова-
тельным соединением индуктивности L3 ==
1/4 и сопротивления
r == 1/4. После замены индуктивностей Ll' L 2 и L з совершенным
трансформатором получаем схему на рис. 17-15.
Рис. 17.15. Пример 17-6.
11.6. ИССЛЕДОВАНИЕ ЧЕТЫРЕхпопЮСНИКА НА КОМПЛЕКСНОR
ЧАСТОТЕ
Так же как и в случае двухполюсников, введение комп
лексной частоты р == с + j(j) расширяет возможности ис-
следования общих свойств четырехполюсников.
552
Передаточная функция четырехполюсника может быть
выражена отношением полиномов ВИДа (17-1). При этом
в отличие от сопротивления или проводимости двухполюс-
ника степени полиномов в числителе и знаменателе переда-
точной функции четырехполюсника MorYT разниться более
чем На единицу.
Передаточная функция четырехполюсника, представ-
ляющая собой отношение электрических величин в двух
разных контурах или узлах, свободна от некоторых оrрани-
чений, свойственных сопротивлению и проводимости двух-
полюсника. Так, передаточное сопротивление и проводи-
мость четырехполюсника MorYT иметь отрицательную дей-
ствительную часть.
+ jw
+ jw
+
+
0.)
РЗ"
Р1
б)
Рис:. 17
16. Размещение нулей и полюсов передаточных функций ми-
нимальной (а) инеминимальной (6) фаз.
Что касается полюсов передаточной функции, то, так же
как и в случае двухполюсника, полюсы не MorYT иметь
положительной действительной части: они располаrаются
в левой полуплоскости, так как совпадают с полюсами
входноrо сопротивления или проводимости четырехпол
-
Ника. ,
Однако подобное оrраничение не распространяется на
нули передаточной функции четырехполюсника: нули м'йеут
находиться как в левой, так и в правой полуплоскостu.
Передаточная функция, не имеющая нулей в правой
полуплоскости, называется Ф у н к Ц и е й м и н и м а л ь -
н о й фаз ы, а передаточная функция, нули которой рас-
ПQлаrаются и в правой полуплоскости, называется Ф у Н К -
Ц и е й н е м и н и м а л ь н о i1 фаз ы. Соответственно
различают и цепи минимальной и неминимальной фазы.
На рис. 17-16 в виде примера показано размещение нулей
и полюсов передаточных функций минимальной (рис. 17-16,а)
и неминимальной (рис. 17-16, б) фаз.
553
Амплитудная и фазовая характеристики MorYT быть
поtтроены на основе (17
5). В рассматриваемом случае
отношения M/NI 2 равны друr друrу, и поэтому при paBeH
стве множителей Н амплитудные характеристики совпадают.
Фазовые же характеристики неодннаковы: передаточная
функция минимальной фазы характеризуется всеrда
меньшим в алreбраическом смысле фазовым сдвиrом,
чем фу'нкция неминимальнойфазы при той же аМПЛИТУk
ной характеристике. Эт(l) видно из рис. 17
16, rДе уrол аl
меньше уrла, дополняющеrо ero до 180°.
Существенной особенностью функций минимальной
фазы является то, что амплитудная и фазовая характери-
стики однозначно определяют друr друrа: имея одну, из
этих характеристик, можно наЙти друrую характери-
стику.
В цепных схемах ток в наrрузке может быть равен
нулю в том случае, коtда какое-либо из сопротивлений
продольных ветвей бесконечно велико или какое-либо из
сопротивлениЙ поперечных ветвеЙ равно нулю. Поэтому
передаточная функция цепной схемы всеrда являетсяфунк-
цией минимальной фазы: ее нули обусловливаются полю-
сами сопротивлений продольных и нулями сопротивлений
поперечных ветвей цепной схеМЫ,которые всеrда распола-
rаются в левой полуплоскости.
Интересной разновидностью передаточных функций не-
минималыrой фазы служит функция, нули которой распо-
лаrаются в правой полуплоскости в виде зеркальных изо-
бражений полюсов. Четырехполюсник, обладающий такой
передаточной функцией, пропускает Бсе частоты с одина-
ковым затуханием. Действительно, для всех точек мнимой
оси модуль выражения (17
3) сохраняется постоянным.
AprYMeHT этоrо в
!ражения, т. е. фазовый сдвиr между
электрическими величинами на выходе и входе четырех-
полюсника, при этом зависит от частоты. rодоrраф переда
точной функции на комплексной плоскости представляет
. собой акр ужность.
Такое изменение фазы при ПОСТОЯННОй амплитуде своЙ-
ственно, например, симметричному мостовому четырехпо-
люснику , Harp уженному соrласованно. Четырехполюсники
подобноrо типа применяются в технике связи в качестве
устройств, корректирующих фазу.
Построение четырехполюсника по заданным частотным
характеристикам представляет собой в общем случае задачу
более сложную, чем построение двухполюсников [Л.2 и 8].
554
в зависимости от условий задачи в основу построения че
тырехполюсников в ряде случаев MorYT быть положены
общие методы синтеза двухполюсников.
17.7. СИНТЕЗ рЕАктивныx ЧЕТЫРЕХПОЛЮСНИКОВ
В качестiзе примера рассмотрим построение четырех-
полюсника в виде симметричной мостовой схемы (см. рис.
9
18) по заданной функции передаточноrо СОПРОТИJ:\-
ления
Z (р):;;;о. и 2 (р)/ [1 (р)
при холостом ходе.
Полаrая в уравнениях четырехполюсника в форме Z
[см. уравнение (9-2)], 1; == О, находим, что Z (р) - Z21 (р).
Соrласно формулам (9
19) и соотношениям между пара
метрами четырехполюсника
Z1K==-
== Zl1Z22
Z
! == Z1x
zg! ,
Ун Z22 Z2X
откуда для симметричноrо ч етырехполюс ника
Z21 == + v Z1x (ZlX
ZlK)'
Из полученноrо равенства следует, что полюсы функ-
ции ZlX (р) являются одновременно и полюсами функции
Z21 (р). Поскольку ZlX (р) представляет собой функцию со-
противления двухполюсника, полюсы этой функции рас-
положены в левой полуплоскости и вычеты в них положи
тельны. Что касается вычетов функции Z21 (р) В этих полю
сах, то они MoryT быть как поЛОжительНыми, так и отрица-
тельными.
Для упрощения задачи синтеза примем, что вычеты
функции Z21 (р) равны по модулю вычетам функции Zlx (р),
тоrда разложение Z21 (р) на элементарные дроби будет отли-
чаться от разложения ZlX (р) только тем, что часть элемен
тарных дробей будет иметь отрицательные знаки.
В этом случае можНо записать, что
Z21 (р) == z
t) (р)
Z
l) (р);
-Z1x (р) == Z
1) (р) + Z
l) (р).
(17 - 24)
(17
25)
(+)
rде Z21 (р) объединяет элементарные дроби Z21 (р) с поло-
(
)
жительными коэффициентами, а Z21 (р)
элементарные
дроби с отрицательными коэффициентами. .
555
Для мостовой схемы (см. рис. 9-18)
Z21 (р) == (Z2
Z1)/2; Z1x (р) == (Z1 + Zz)/2.
Сравнивая эти выражения с равенствами (17-24) и
(17-25), находим:
Z1 == 2Z
l' (р);
Z2 == 2Z
1' (р).
(17-26)
( 17 - 27)
Если полученные выражения дЛЯ Z1 и Z2 удовлетворяют
условиям положительных действительных функций, то
114 они MorYT быть реализованы
схемами двухполюсников. За-
менив в цепи на рис. 9-18 со-
противления Z1 и Z2 найденны-
24 2
ми схемами двухполюсников,
получим искомую реализацию
четырехполюсника.
При мер 17-7. Реализовать Функ-
цию передаточноrо СОПРОТИБ.'Iения
2
Рис. 17-17. Пример 17-7.
Z2i (р)
р3
(р2+3) (р2+2)'
Путем разложения на элемеитариые дроби представим заданную
функцию в виде
2
Z21 (р) == р2
3
р2
2 == Zkt' (р)
Zki' (р).
Используя формулы (17-26) и (17-27), находим:
4р 2р
Zi
р2+2 ; Z2
р2 +3 '
Этим выражеииям соответствует схема, показанная на рис. 17-17.
17.8. ЗАДАЧИ И вопросы ДЛЯ САМОПРОВЕРКИ
17-1. Показать, ЧТО
р2+р+4 . р3+3р2+ 2р+2.
р2+р+1' р3+3р2+3р+1 '
Р (р2+2)
(р2+ 1) (р2 +4)
положительные действительиые функции,
556
17-2. Показать, что
р (р2+5) . р2+2р+ 1 .
(р2 + 1)2 ' р2 '
р3+ 7р2+ 15р +9
р4+6р2+9
не являются положительными действительными функциями.
17-3. Осуществить,
Z (р) (р+ 1) (р+3) . У (р)== р4+4р2 +3
Р (р+2) , р3+2р
разложением на простейшие дроби.
17-4. Решить задачу 17-3 разложением в неПР2РЫВНУЮ дробь.
17-5. Осуществить
z (р) == (р2 + 1) (р2 + 9)
Р (р2+4)
последовательным выделением полюсов и нулей.
17-6. Осуществить по методу Брунэ функцию
Z ( ) == р3+5р2+2р+ 1
р р2 + р + 1
17-7. Решить задачу 17
5 разложением в непрерывиую дробь.
17-8. Основываясь на формуле (l7
3), riоказать, что для реактив-
'Horo двухполюсника нули и полюсы чередуются.
17-9. В каких случаях полином, все корни Koтoporo расположены
иа мнимой оси, содержит только нечетные степени р?
17-10. Почему полюсы передаточной функции не MorYT находиться
в правой полуплоскости, между тем как на нули передаточной функ-
ции это оrраничение не распространяется? '
17-11. Почему обобщенные сопротивления и проводимости двух-
полюсников представляют собой положительные действительные функ
1J.ии?
17-12. Осуществить реактивные функции
р3+4р
p
Z (р) р4+5р2+6 и Z (р) 2 р 4+3р2 + 1
в виде схем симметричных мостовых четырехполюсников.
ПРИЛОЖЕНИЕ 1
МАШИННЫЙ РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕI(ТРИЧЕСКИХ ЦЕПЕЙ
1. Последовательность решения задач на ЭВМ
ДЛЯ расчета с помощью ЭВМ должна быть сформулирована задача
н определена конечная цель. Это является первым этапом решения
задачи. Затем должна быть создана математическая модель. Состояние
электрической цепи в каждый момент времени определяется значениями
токов в ее ветвях или напряжениЙ между узлами цепи. При paCCMOTpe
нии электрической цепи с распределенными параметрами, помимо вре-
мени, в качестве второй независимой переменной должно учитываться
раССТОЯl!ие. Обычно существует несколько способов построения MaTe
матической модели одноЙ и той же задачи, имеются также существен
ные отличия от подrотовки и решения задач ручным способом. ЭТО под-
робно рассмотрено в ряде соответствующих пособий 1.
Второй этап решения связан с численным анализом.
Математическая запись задачи может оказаться непереводимой
непосредственно на язык ЭВМ, поскольку машина выполняет только
арифметические действия. Все уравнения должны быть выражены через
арифметические операции. При этом следует иметь в виду различие
свойств точных арифметических операций и свойств операций, выпол-
няемых на ЭВМ. Машинная арифметика имеет свои характерные осо-
бенности. Ошибки окруrления неизбежны на ЭВМ. Но какими бы
малыми они ни были, их появление существенно меняет математические
свойства арифметических операций. Точные операции являются ком-
мутативными, ассоциативными и связаны между собой законом дистри-
бутивности. Операции на ЭВМ уже не являются таковыми; Поэтому,
чтобы указать алrоритм вычисления любоrо арифметическоrо выраже-
ния, -необходимо определить порядок выполнения входящих в Hero
операций.
Таким образом, всякая задача при постановке на ЭВМ определяет
совокупность вычислительных алrоритмов, отличающихся друr от
друrа порядком выполнения арифметических операций. Несмотря на
математическую эквивалентность этих модификаций в точном смысле,
различие в вычислительном аспекте может быть чрезвычайно большим,
Б особенности с точки зрения численной устойчивости. Среди всех мо-
дификаций существует такая, которая обеспечивает наиболее точное
решение задачи.
1 r о л е м б о З. Б. Алrоритмизация и проrраммирование электро-
технических задач на электронных вычислительных машинах, М.,
«Высшая ШКОJlа
. 1974.
558
Рассмотрим, например, два основных способа решения уравнеНЮ1
узловых напряжений (7
5) или контурных токов (7
2)
методами
исключения и итерационным методом rау
са
Зейделя 1.
Метод исключения конечен и теоретически с ero помощью можно
решить любую невырожденную систему уравнений. Итерационный
метод rаусса
Зейделя сходится только в том случае, если выполняется
неравенство
I Znn I >
I Zmn при т =F п,
при соблюдении KOToporo неизвестное R уравнениях (7-2) и (7
5) иуме-
руют так, чтобы максимальные коэффициеиты заполняли rлавиую диа-
rональ матрицы. l(оrда итерационные методы сходятся, они обычио
предпочтительнее при расчетах на ЭВМ. Для некоторых систем, напри-
мер при расчете разветвленной сети питания с различными отноше-
ниями х/, в ветвях, метод исключения является единственно возмож-
ным.
Следует также заметить, что с точки зрения классической мате-
матики все прямыe методы решения систем линейныx алrебраических
уравнений эквивалентны, поскольку сводятся в конечном счете к вы-
числению одних и тех же арифметических выражений, определяющих
зависимость caMoro решения от входных данных. С позиций численноrо
ана,1Иза различие здесь весьма значительно. Используя один метод,
можно получить точное решение, а используя друrой метод, не полу-
чить ни одноrо BepHoro знака в решении. Например, различные вари-
анты метода raycca также приводят к существенно различным резуль-
татам.
Составив численный алrоритм решения задачи, ero необходимо
выразить в виде точно определенной последовательности операций иа
ЭВМ. Таким образом, третьим этапом является проrраммирование
иа ЭВМ.
В процессе проrраммирования вначале оБыноo составляется схема
вычислительной процедуры. Используя схему метода решения, показы-
вающую предстоящие операции, пцшут проrрамму на одном из алrо-
ритмических языков. Для электротехнических задач весьма удобным
языком является ФОРТРАН (FORTPAN
FORmula TRANslator).
Отличительными чертами ero являются: простота и леrкость изучения,
близость записи арифметических выражений и лоrических условий
к принятым В обычной математической записи, состоящей из последо-
вательности операторов. Одни из них определяют арифметические
операции, являющиеся основным содержанием алrоритма, друrие
определяют порядок ввода и вывода информации, например ввода
чисел с перфокарты или вывода чисел на печать. Друrоii: тип операто-
ров изменя('т порядок выполнения операций. Имеется тип операторов,
содержащих информацию об алrоритме, но никаких действий не опре-
деляющих. Вместе взятые все операторы составляют исходную про-
rpaMMy. Нанесенная на перфокарты исходная проrрамма преобразуется
с помощью транслятора ФОРТРАН в рабочую проrрамму, Рабочая
проrрамма
последовательность элементарных команд дЛЯ ЭВМ.
Такое преобразование необходимо, так как язык ФОРТРАН является
rораздо более сложным, чем язык команд ЭВМ. Расчеты на ЭВМ про-
изводятся именно по рабочей прorрамме.
1 М а к - l( р а к е н Д., Д о р и У. Численные методы и про-
rраммирование на ФОРТРАНе. М., «Мир», 1969.
559
Проrраммирование заканчивается отладкой nporpaMMbI, поскольку
в процессе проrраммирования обычно совершаются ошибки.
По отлаженной проrрамме можно про изводить расчет сразу для
иескольких вариантов набора исходных даниых.
2. Особенности реализации алrоритмов расчета
переходных процессов в Лииейных цепях
Переходные процессы в электрических цепях описываются диффе-
ренциальными уравнениями. Решение их связано с известными труд-
ностями, которые изложены в rл. 15. Использование преобразования
Лапласа для расчета Переходных процессов также не всеrда обеспечн'
вает тривиальный обратный переход в область функций действитель.
Horo переменноrо с помощью формул или таблиц.
Машина не может оперировать с непрерывно изменЯЮЩИМИСЯ ве-
личинами и, следовательно, не может находить их предельные значения,
так как она использует вычислительный процесс с конечным числом
операций. Поэтому вместо исходной непрерывной задачи решается
друI'ая
дискретная, аппроксимирующая непрерывную задачу в том
смысле, что ее дискретное решение аппроксимирует непрерывное ре-
шеиие исходной задачи. Единственной непрерывиой задаче соответст-
вует бесконечное множество дискретных задач. Переход от дискретной
задачи к непрерывной не является взаимно ОДнозиачным и может при-
водить киеопределенности.
Таким образом, при численнЫХ методах моделирования иекотороrо
процесса, протекающеrо в электрнческой цепи и заданноrо в виде ана-
литической снетемы
dz/ '
dt ==Z/ ==1 (t, zi, '2' '" , 'т)' (== 1, 2, ..., n
(П.l)
с начальными условиями
Z/ (t") == Z/O,
исследование свойств процесса заменяется изучением Свойств решений
некоторой системы конечно
разностных уравненнй.
Пусть при' алrоритмизацин примеияется метод решения с помощью
рЯДов Тейлора. ,
Напишем разложение функции Zi (t) в ряд. Тейлора в окрестиости
точки t:= t m
q ",
, Zm 2т 2
Zi (t)==zm+zm (t
tm)+2 (t
tm)2+T (t
tт)З+.." (п-)
rде Z<,f.>
j-я производиая фуикции Z (t) в точке t =>:: t m ,
РеШение в точке 10 даетсЯ начальным условием. Предположим, что
найдено nрнближенное решение уравнения для т + 1 точек иа оси,
т, е. для t o , t 1 , t 2 , ... , t m , Последовательные значения t[ раСПОЛQжены
иа расстоянии h друr от друrа, т. е.
tc='= t o + ih,
rде h
шаr ннтеrрирования.
Приближенное решение для точки t m + 1 можно найти, подставив
{ т + 1 == t m + h в выражение (П-2)
, h 2 . h З '"
'т+1 ==zm+ hZm +
2 zrn+6 Zm +... (П-З)
560
Чем больше членов ряда, теМ точнее будет приближение. Если
пользоваться решением с помощью рядов, Тейлора, необходимо вычис-
лять различные производные функции Z (t). Все значения функции и
ее производных вычисляются при t == t m , т. е. i == zт, Для вычисле-
ния Zт+l требуется информация только об одной предыдущей точке t m ,
Zm' поэтому нахождение решения с Помощью ряда Тейлора является
одноступеичатым методом.
Для получеиия лучшеrо приближения, т. е. меньшей ошибки orpa-
ничения, необходимо вычислить более высокую производную, а это
сделать весьма сложно, а иноrда даже просто невозможно. С точки
зрения практических вычислений этот метод обычно неудобен, хотя
теоретически приrоден для решения любых дифференциальных урав-
нений. Метод ценен тем, что он дает некоторый эталон дJ)я сравнения
различных практических удобных методов; показывает, насколько
тот или ииой метод соrласуется с разложением в ряд Тейлора. Ряд
численных методов cor ласуется вплоть до членов порядка h, друrие
до членов порядка h 4 и т. д. Этот критерий применяется несмотря на
то, что практические методы не предусматривают вычисления произ-
водных от функции.
Таким образом, изучение свойств (п-!) заменяется изучеиием
свойств численноrо решения дифференциальноrо уравнеиия.
Поэтому основная задача при создании алrоритмов цифровых мо-
делей состоит в достижении оптимальноrо соответствия между свойст-
вами воспроизводиМоrо в машине и заданноrо процессов.
3. Особенности численных методов расчета переходных процессов
rлавным недостатком численноrо решения является то, что оцеика
ошибки, вносимой методом решения, оказывается сложиой задачей и
часто невозможно сказать, какова достоверность решения.
ДЛЯ ЭВМ нельзя точно указать предела точности, которой можно
достиrнуть. ,
Ошибки, возникающие при решении, вызываются несколькими
причинами.
ошибки окруrления обусловливаются имеющейся разрядиой сет-
кой и правилами окруrления при выполнении арифметических опера-
ций на ЭВМ. Чтобы обнаружить ошибку окруrления, необходимо, оче-
видно, увеличить разрядную сетку, т. е. нужно произвести расчет
этой же задачи с удвоенной точностью.
Поскольку обычио дифференцирование увеличивает малые ошибки,
важно иметь заметный запас точности при вычислении функции, подле-
жащей дифференцированию,
запас, который сам по себе должен
соответствовать точности, которую дают ЭВМ.
Ошибки вызываются также случайными сбоями или неисправио-
стью ЭВМ. Часто на практике считается, что если машина дважды под-
ряд выдает один и тот же ответ, то ero можно считать правильным.
Однако каждая машина и каждая nporpaMMa MorYT иметь свои специ-
фические ошибки, в силу чеrо тот же самый неверный ответ может быть
получен какое уrодно число раз.
)::динственной удовлетворительной проверкой для обнаружения
ошибки, вызываемой случайными сбоями, является введение избыточ-
ности в виде осуществления повторноrо расчета на друrой ЭВМ и соста-
вления новой np6rpaMMbI. Часто случается, что такая ошибка улавли-
вается имеющимися тестами для проверки машин,
561
Наилучшим контролем !JравильнОСТи полученноtо решениЯ остается
проверка заранее известноrо контрольноrо соотношения, Например,
для задачи
dx
dt == у;
dy.
dt ==
x
\
критерием правильности является проверка известноrо соотношения
х 2 + у2 == ( 2 , которое- должно выполняться в любой момент времени.
Этот способ контроля является наиболее эффективным, так как он сразу
фиксирует сбой в работе ЭВМ. ошибку в nporpaMMe, а также совокуп-
ную ошибку метода и вычислений.
Наиболее эффективным для решения дифференциальных уравне-
ний с помощью ЭВМ является метод PYHre
Кутта, который дает воз-
можность получить значение у == (х + h), если ИЗВ,естны только у (х)
и шаr интеrрирования h, не используя у (х
h), У (х
2h) и т. д.
Следовательно, при вычислении точки х т + 1 . Ут+l используется
информация 'ТОлько о точке х т , Ут' что не вызывает затруднений при
изменении шаrа h. Метод не требует вычисления производных от t (х, у),
вычисляется только сама функция. Но для вычисления каждой после-
дующей точки решения приходится вычислять функцию t (х, у) несколько
раз при различных значениях х и у.
4, Формирование алrоритмов для аиализа электрических цепей
Основой для описания процессов в электрической .цепи Являются
уравнения Кирхrофа совместно с уравнениями, связывающими ток и
напряжение каждоrо элемента цепи через ero параметры. Для обычноrо
. линейноrо сопротивления уравнение протекающеrо процесса соста-
вляется на основании закона Ома, для линейной индуктивности на
основании' закона Фарадея и т. д. Уравнеиие, связывающее ток и на-
пряжение в линейном элементе, весьма просто, так как имеет лишь
один коэффициент пропорциональности, являющийся электрическим
параметром.
, Пример П-l. Составить проrрамму иа алrоритмическОМ языке
ФОРТР АН и рассчитать цепь nepeMeHHoro тока, состоящую из после-
довательно соединенных " L, С (рис. 5-1) и найти зависимость тока,
протекающеrо в цепи, от набора значений частоты. Приложенную
э. д. с. и- параметры цепи считаем заданными, Ток в цепи из ура13не-
ния (2-14)
[== Е
у,2 + (2лt L
1 f2лfС)2 .
Проrрамму составляем так, чтобы возможно было произвести вы-
числения для любоrо дискретноrо набора значений частоты при любых
заданных значениях Е, " L и С.
В исходной информации предусматриваем считывание с перфокарт
последовательных значений частоты. Проrрамма предусматривает пе-
чать этой частоты и вычисленноrо для нее значения тока. Проrрамму
составляем таким образом, чтобы можно было про извести ВЫЧИсления
ДЛЯ лю60ro конечноrо числа перфокарт, на которые нанесены дискрет-
иые значения частот. Эталоном окончания счета условимся считать
перфокарту , которая содержит отрицательную частоту. Все вычисле-
ния проводятся для положительных частот, Поэтому карту с отрица-
562
тельной частотой нет оснований спутать со всеми друrими входными'
картами. При использовании алrоритмическоrо языка ФОРТРАН после
чтения очередноrо значения частоты остается только применить опе-
ратор IF, чтобы определить, не дошла ли очередь до эталонной карты.
110сле печати очередноrо результата прочитывается очередная входная
перфокарта и так до тех пор, пока наконец не будет введена эталонная
карта с Qтрицательной частотой и оператор IF не передаст управление
оператору STOP для остановки вы-
числений. Последовательность опера-
ций приведена на схеме рис. П-l. Как
следует из этой схемы, сначала прочи-
тываются значения четырех парамет-
ров Е, (, L, С, которые остаются
неизменными. На схеме эти величины
обозначены такими же символами
как
и в проrрамме, поэтому можно сравнить
схему и проrрамму на ФОРТРАНе.
Чтение с перфокарты величин, кото-
рые не будут меняться в ходе вычис-
лений, производится один раз; все ос-
тальные стадии повторяются всякий
раз после ввода HOBoro значения ча-
стоты. Для поочередноrо ввода, значе-
иий частоты (CYCLE) независимо от
ввода остальных параметров, исполь-
зуется отдельный блок. После ввода
'очередноrо значения частоты с по-
мощью оператора IF задается вопрос:
не является ли частота отрицательной?
Цикл вычислений может повторяться
неизвестное заранее число раз, так
как может оказаться различное число
перфокарт со значением частоты. Поэтому проверку по эталону
необходимо производить каждый раз, кроме первоrо. Если перфо-
карта со значением частоты не является эталонной, то переходят
к блоку вычисления тока в цепи (AMPERE). В проrрамме этому вы-
числению соответствует длинный арнфметический оператор; на схеме
фермула не приведена. После вычисления тока печатают частоту и
соответствующий ей ток и возвращаются, чтоБЫ прочесть сперфокарты
новое значение частоты. Проrрамма будет продолжать считывание с пер-
фока рты очередноrо значения частоты, вычисление и печать значений
тока и возвращение для ссчитыванияновой карты пока не закончится
цикл с помощью перфокарты с эталоном окончания.
Определив процесс вычислений с помощью схемы, переходим к на-
писанию проrраммы на ФОРТРАНе. Проrрамма имеет следующий вид:
Рис. П
I. Схема проrраммы
для расчета цепи перемен-
Horo тока,
5
6
7 FORТRAN STATEMENT
200
READ 2ОО VOLT, ОНМ, HENRY, FARAD
FORMA Т (4Р 10.. .0),
READ 200, CYCLE
23
563
Продолжение
601
о
I IF (CYCLE) 600, 601, 601
I STOP
I AMPERE==VOL TjSQRT (OHM**2+(6.2832*CYCLE)
I *HENRY
1/(6.2832*CYCLE*FAR.AD)**2)
I PRINT 201, CYCLE, AMPERE
I FORMAT (IР2ЕI6,6)
I GO ТО 23
I END
600
201
Номера присвоены операторам FORMA Т и трем операторам, к ко-
торым возможен переход от операторов IF и GO ТО. Если частота,
введенная с перфокарты, отрицательна, то управление передается на
оператор STOP, который стоит сразу же после IF. Оператор STOP
можно поместить и в друrое место nporpaMMbl. В операторе IF необхо-
димо предусмотреть случай, коrда выраженне в скобках равно Нулю,
так как правила ФОРТРАНа требуют указать оператор, которому будет
передано управление при каждом из трех возможных значений в скоб-
ках оператора IF: отрицательном, нулевом и положительном. Естест-
венно, что вычисление тока по этой проrрамме бессмысленно проводить
для частоты, равной нулю.
Оператор GO ТО определяет, что после печати значения частоты и
соответствующеrо ей тока управление будет передано второму опера-
тору READ, которому присвоен номер 23.
Для вычисления по этой проrрамме была составлена входная пер-
фокарта со следующими значениями параметров: Е == 10 В, r
== 1000 Ом, L == 0,1 r, с == 0,5 мкФ. Частота менялась от 1000 до
3500 rц с шаrом 50 rц.
Ответная информация печатается на выходном бланке. Результаты
расчета приводятся ниже
1,000000 03
1,500000 03
2,000000 03
2,500000 03
3,000000 03
3,500000 03
3,644963
03
6,466553
03
9,482350
03
9,584666
03
7, 717787
оз
6, 127667
оз
Во втором операторе FORMA Т использован коэффициент шкалы lР,
чтобы десятичная точка была напечатана между первой и второй зиа-
чащими цифрами мантиссы. Порядок автоматически уменьшается при
этом на единицу. Коrда 21tfL == lj21tfC, то имеет MeCT
резонанс на;
пряжений. В решении хорошо прослеживается широкии резонансныи
пик с вершиной оКоЛо 2200 rц.
564
Пример П-2. ДЛЯ цепи постоянноrо тока (рис. П-2) рассчитать
токи
11' 12' I з , 14' 15' протекающие через извеСтные сопротивления '1'
'2' '8' '4, '5' если заданы напряжения Е 1 , Е 2 .
По законам Кирхrофа для неизвестных токов 11' ..., 15 имеет
место следующая система уравнений:
'1/1+'2/2
'2/2+'818
'818 + r 414
13
==Е 2 :
+'5 / 5==Е 2 ;
==Е 2 ;
+ 15 == о;
/5 ==0.
/1+/2
/4
Неизвестные в ИсхоДной системе обозначим х (I), rде 1 == 1 (1) N,
N
ЧИСЛо неизвестных, равное числу уравнений.
Коэффициенты исходной системы заданы в виде А (/, К), rде
1, К == 1 (1) N, Элемеиты правой части системы обозначены через
Аи, N+l), rде 1==/(I)N.
Число неизвестных определяется
размерностью массива А в опера-
торе DIMENSION. В Проrрамме
примем N
100. применителы!o
к рассматриваемому случаю введем
оrраничение N == 5 с помощью опе-
раторов FORMA Т с метками 50 и
52. Если нужио будет решить си-
стему уравнений при N i= 5 и в
удобной форме отпечатать резуль- Рис. П-2, Пример 2,
таты, то необходимо соответст-
венно изменить эти операторы.
Алrоритм расчета построен на методе исключения (метод raycca).
Схема проrраммы последовательности операций ПрИ8едена на рис. ПОЗ.
Процесс исключения неизвестных не изменяет абсолютноrо значения
определителя системы, хотя знак определителя и измеияется при
каждой перестановке уравнений. После окончания процесса значение
определителя равно произведению диаrональных элементов, причем
знак Этоrо произведения надо изменить на обратный, если ЧИСЛо пере.
становок было нечетным.
Проrрамма так составляет столбцы заданной системы уравнений,
что элемент с максимальным абсолютным значением становится диаrо-
нальным. это приводит к тому, что диаrональные элементы не близки
к нулю.
Исходной информацией является N (первая перфокарта), значения
коэффициентов и правые части уравнений исходной системы (на по-
следующих перфокартах). N
записывается на формате 15, а осталь-
ные значения
в столбцы по 10 Значений на каждой перфокарте в
формате F8.З.
Проrрамма имеет вид:
7"s
PROGRAM GAUSS
Решение линейной системы уравнений
DIMENSION А(1О0, 101), Х(1О0)
READ 100, N '
Nl == N + 1
565
4
5
6
N2 ... N
1
REAO 101, «А (1, J), 1 == 1, N), J == 1, Nl)
PRINT 50, Н.«А (1, J), J == 1, Nl). 1 == 1. N)
001К == 1, N2
р==о
002 1 == К, N ,
Н == ABSF (А (1, К»
IF (Н. GT. Р) 3,2
р == н
L==I
CONТINUE
004 J == К, Nl
Р == А (К, J)
А == (К. J) == А (L. J)
А (L, J) == Р
IF (ABSF (А (К, К)/А (1, 1» LT.l.E
06) 5,6
PRINT 51
GO ТО 10
Ю==К+l
001 1 == Ю, N
Р == А (1, К)/А (К, К)
А (1, К) == о
001 J == Ю, Nl
А (1, J) == А (1, J)
Р'" А (К, J)
Х (N) == А (N, Nl)/A (N, N)
007 L == 1, N2
Р == А (N
L, Nl)
008 М == 1,' L .
р == Р
А (N
L, NI
. М) '" Х (Nl
М)
X(N
L)==P/A(N
L, N
L)
PRINT 52, (Х (1). 1 == 1, N)
CONТINUE
FORMAТ (3Х, 15)
FORMAT ( ) F8, 3)
FORMA Т (11 5Х)
FORMAT (115X) ЭlН
ENO
3
2
8
7
10
100
101
51
52
Для вычисления по приведенной nporpaMMe была составлена вход-
ная перфокарта со следующими значениями параметров. E
== 3 Б;
Е 2 == 2 В; '1 == 40 Ом; '2 == 35 Ом; 'з == 25 Ом; '4 == 20 Ом; '5 == 30 Ом.
Ответная информация печатается на выходном бланке и имеет сле-
дующий вид в соответствии с оператором FORMAT с меткой 51,
Решение линейной системы уравнений.
Число неизвестных N == 5
Матрица коэффициентов
40.000 35.000
О
35.000
О О
1.000 1.000
О О
о
25.000
25.000
О
1.000
о
о
20.000
О
1.000
о
30.000
О
1000
1.000
Правые части
3.000
2.000
2.000
О
О
иеизвестные значения х (1) равны
0,0579 0,0196 0,0615 0,0232 0,383 А.
566
Mact:u.8: А(100)О1), Х(1О0)
ДА
А BS F (А(К,К){А,11)) < 1E
0.8
Рис. П-з, Схема проrрзммы GAUSS.
567
5. Алrоритмизация задач с использованием методов
контурных токов и узловых наприжений
Проrр
ммы расчета разветвленных цепей, составленные на основе
законов 1\нрхrофа, как правило, получаются чересчур ,rромоздкими.
Для сложных разветвленных цепей более компактными получаются
проrраммы, составленные на основе метода контурных токов или узло-
вых напряжений. Следует иметь в виду, что некоторые виды преобра-
З0ваний, эффективные при ручном счете, не дают аналоrичноrо эффекта
при машиином расчете цепей.
Orраничеиием применения метода контурных ТОКов с целью созда-
ния алrоритмов являетсЯ трудность выбора наиболее удобной системы
независимых контуров.
В СВЯЗи с тем, что реализация алrоритма является процессом авто-
матическим, не представляется возможным (<подправлять» что-либо
в процессе вычислений с целью лучшеrо выбора независимых контуров,
как это имеет место, например, при ручном счете. В принципе можно
разработать тактический алrоритм, который бы проrраммным путем
составлял оптимальный выбор независимых контуров. Однако при пол-
иом исследован.ии поставленной задачи это весьма сложно. Следует также
заметнть еще одно существенное обстоятельство, состоящее в том,
что при использовании итерационных методов решения неудачно выб-
ранная Система независимых контуров не дает должной сходимости
процесса.
Алrоритм, построенный на основе метода контурных токов в сочета-
нии с итерационными методами применительно к системе контуров,
образованных элементами с несоизмеримыми по значениям сопротивле-
ниями, может также не дать сходимости процесса. Поrрешность вы-
числений падений напряжений по замкнутому КОНТУРУ на некотором
этапе может оказаться настолько большой, что контроль правильности
решения реально не может быть осуществлен. В этом случае процесс
вычислений обрывается. 1\ числу таких цепей относятся, в частности,
электрические системы, схемы замещения объектов с распределенными
параметрами. Друrим весьма важным обстоятельством, оrраничиваю-
Щим построение алrоритма при использовании метода контурных токов,
является то, что иЗменение rеометрической структуры цепи связано
с необходимостью выбора новой системы независимых контуров. При
изменившихся условиях невозможно использовать предыдущие ре-
зультаты расчета на ЭВМ. Приходится заново со[тав.лять исходную
информацию как в части rеометрической структуры цепи, так и для
rраничных условий. Таким образом, в случае повторяющихся расчетов
при любом, даже незначительном изменении конфиrурации цепи расчет
проводится заново с соблюдением всех расчетных этапов.
Алrоритмы, основанные на уравнеииях контурных токов, эффектив-
но используются при расчете цепей, содержащих взаимную индуктив-
ность между участками.
Алrоритмы, созданные на основе метода узловых напряжеиий, MorYT
быть' эффективно использованы для решения широкоrо Kpyra задач.
Так, в ОСНОВУ расчетов электрических сетей положен такой алrоритм,
поскольку напряжения узлов определяют режим в э1'их системах. При
принятой системе узлов и ветвей матрица коэффициентов составляется
один раз. это цениое качество метода позволяет довольно просто видо-
изменять сопутствующую информацию в случае частичноrо измене
иия rеометрической структуры цепи при рассмотреиии различных
вариантов.
568
Мюематические преимущества применения метода узловых напря-
жений, помимо удобства для вычислений и значительноrо сокращения
числа арифметических операций, заключаются в наличии более быстрых
средств для vлучшения приближенноrо решения задачи. Для опреде-
ления распределения наrрузок в системе методом узловых напряжений
используется в качестве критерия первый закон Кирхrофа.
Уравнение узловых напряжений для k-ro узла имеет вид:
.. *.
(Ul
Uk) У kl===Sk/Ul,
i
rде У kl
проводимость ветви kij (j i' (j k
узловые напряжения;
"'
Sk
комплексная мощность, подведенная к узлу k.
Следует также заметить, что метод узловых напряжений поЗволяет
использовать линейные преобразоваиия для повышения точности рас-
чета в случаях, коrда значения
напряжений смежных узлов мо-
rYT оказаться близкими.
Пример П
3. Составнть алrо-
ритм расчета напряжениЙ в уз-
лах цепной схемы (рис. П-4) со
сколь уrодно большим числом
узлов n.
К такому виду приводится
схема замещения однородной Р П 4 Ц
ис. -. епная схема с пуз-
линии с распределенными пара- лами.
метрами. При расчетах' линию
представляют состояшей из ко-
нечноrо ЧИСЛi\ соединенных между собой четырехполюсников. Пара-
метры четыре"полюсника MorYT быть определены по п- или Т-образ-
ной схеме замещения.
Для построения> математической МОl(ели воспользуемся методом
узловых напряжениЙ. Система уравнеиий применительио к пузлам
схемы (рис. п-
) имеет вид:
(;o
(;i у (/ (;i
(;2
O'
zi
1 1
,
[, 1 [, f [, .!!. 4 [.".
и
D
(;i
(ji+i
ZI+l
у (; , (;i+i
rJi+2
i+1 1+1
ZI+2
о.
,
(П-4)
(; n
i
(; п
Z.п
(;nУп ==0,
тде Z1' Z2' ..., Zn; У 1 , У 2 , ''', У n
соотвеТственно сопротивления и про-
ВРДИМОСТJ;I схемы зам
щения элементарных четырехполюсников; t) l'
и 2 , ..., u п
неизвестные узловые напряжения.
Полученная математическая модель представляет собой систему
линейных алrебраических уравнений с комплексными коэффициентами.
Существует MHoro способов решения такой системы. При непосредствен-
ном вычислении разностей (j i+1
(j 1 MorYT теряться размеры чнсла,
поэтому для алrоритмизации предлаrается следующиЙ способ.
569
Обозначим
(Jo
(Jf
l' (J/
(J/+i ==<l/;
о, . 2/+f
(Jn
i
(Jn J .
2 == n
i'
n
Тоrда исходная система. (П-4) представляется в ВИДе
lп
i==YnUn+O; (Jn
i==ln
izп+(Jп; )
1 п
2== У n
iUn
i +1 n
i; U п
2==1 n
2Zn
1+(Jn
1;
f
J
1/== YI+1 U i+1 +//+1;
й/== l/l i +1 + UI+ 1 ;
, {П-5}
li== У 2 И 2 +1 2 ; Ui==1 1 Z +(J2;
10== Y1Ui + i 1 ; Uo
loz1+Ui'
Очевидно,
211.1 п
i==1 п
i
U 11.; 211.1 n
i==U n
2
(;n
1;
..., 2 2 i 1 ==U 1
и2; 21io==(;o
Uf'
поэтому, чтобы получить нужные разности, можно ВЫЧИСлять произ-
ведения Znln
l; Zп
11n
2 ит. д.
Поскольку рассматриваемая электрическая схема состоит из ли-
нейных элементов, то все веЛIj'JИНЫ 1 i И (;1 пропорциональны (;11.. Это
также леrко усмотреть из системы (П
5).
Обозначив коэффициенты пропорциональности соответственно че-
рез
I и ai' имеем:
lп
i==
n
iUп;
(;п
i ==an
lUn;
lп
2==
n
2(;п;
[1 ==
1ип;
(;1 == а1(; 11.;
10==
ои 11.;
ио==аои n .
Если положить (;11.== 1 + jO, '[о из (П
5) вместо 1/ и (;1 найдем
/
и al' ВЫЧИСЮIВ ао, определяют и 11. из последнеrо равенства (П-6).
Затем по формулам (П
5) определяют все неизвестные напряжения.
Такой процесс решения самоконтролируем, так как в случае правиль-
Horo решения правая часть последнеrо уравнения системы (П-5) должна
оказаться равной напряжению на входе. Коэффициенты системы (П
4)
вычисляются в машине по известным формулам Т- или П
образных схем
замещения линий. Для этоrо в машину вводятся следующие параметры:
аКтивная проводимость g; длина каждоrо замещаемоrо участка линии 1,
Индуктивное сопротивление участка лиНии L, проводимость на участке
линии у, относительная частота k. Также указывается число участков,
которыми представлена линия. Кроме Toro, для решения системы (П.4)
(П-6)
570
задается напряжение в начале линии. Таким образом, проrрамма пре-
дусматривает расчет параметров линии.
Заметим, что при решении систеМ
I (П-5) потребовалось Bcero
одно действие деления (для нахождения и п)' Коэффициент аа в зависи-
мости от параметров электрической цепи может оказаться малым, так
что деление на аа в ЭВМ окажется невозможным; машина остановится
из
за переполнения. В этом случае в проrрамме предусмотрено увели-
чение коэффициентов пропорциональности в ЮР раз, rде р
подби-
рается так, чтобы правая часть последнеrо уравнения системы (П-6)
была возможно близкой к 1 ОР. Последнее и является контролем правиль-
ности решения. Проrрамма выводит на печать как исходные данные, так
и все вычисленные значения.
При мер П
4. Составить схему проrраммы применительно к алrорит,
мическому языку ФОРТРАН дЛЯ решения системы из n уравнений
(7
5). составленных на основе метода узловых напряжений
расчет-
ной схемы rаусса
Зейделя.
Система (7
5) tостоит из n уравнений с n неизвестными. Чтобы
проиллюстрировать метод, рассмотрим систему из трех уравнений,
аl1 Х l + a 12 x 2 + аlЗХЗ == Ь 1 ;
a21 x i +а 2 2 Х 2 +а 2 з х з== Ь 2 ;
а:Н Х l + аЗ2 Х 2 + аззхз === Ь з .
Представим систему в следующем виде:
хl == (bi
а12Х2
аlзХз)/Щi;
Х2 == (Ь 2
a21xl
а2з х з)/а22;
хз== (Ьз
аЗIХl
аЗ2Х2)/азз.
(а)
(б)
(в)
Возьмем некоторое первое приближение к решению этой системы,
обозначив ero xiO', x
O), x'
), Подставим ero в (а) и вычислим новое
значение хl:
xi 1 ) == (Ь!
a12x
O)
ЩзХ
О)/ай.
Используя вычисленное xi1> и начальное значение x
o), аычислим
из (б) новое значение Х2
x
1> == (Ь 2
a21X'p
а2зх
О')/а22'
Используя значения хр) и x
l', найдем из (в) новое значение х з
x
1> == (Ь З
аЗlхi1)
аЗ2Х2)/азfJ,
Этим заканчивается первая итерация. Теперь можио заменить
исходные значения xi°J, XkO) и X
O) на xi 1 ', x
l), x'i' и вычислить следую-
щее приближение, Текущие неизвестные сразу же испо.1JЬЗуются для
последующих вычислений. Нельзя вычислять, иапример, x
k), пока
не получено x\k). Аналоrично этому для вычисления x
k) надо сначала
определить x!k) и x
k).
В случае n уравнений k
e приближение к решению будет задаваться
формулой
x
k)==(bi
ailxik)
...
ai,i
lx
I
ainXhk
l), i"""l, 2, .... n.
571
Рис. П-5,
572
Итерационный процесс продолжается до тех пор, пока все xi k ) не
станут достаточно близкнми к x
k
I). '
Критернй близостн можно, например, задать в следующем виде:
мШ ==шах I x
k)
x
k
1) 1 < 8.
Схема проrраммы для вычислений по методу rаусса
Зейделя
приведена на рис. П-5.
ДЛЯ решения системы (7-5) начальное приближение принимается
равным нулю, а счетчик числа итераций получает значение 1. Для под-
счета числа итераций используется переменная целоrо типа ITER.
При дальнейших вычислениях эти начальные действия не повторяются.
В конце Этой части схемы стоит кружок с цифрой 1, что означает, .что
следующая схема начинается с этой позиции.
Переменная BIG используется для Toro, чтобы определять
шах 1 x
k)
x}k
l) 1. Сначала этой переменной присваивается значение
нуль, а затем с ней сравниваются абсолютные значения I x}k)
x
k
l) 1.
После вычисления всех x}k) наибольшая разность будет равна значению
переменной ВIО. '
Затем в схеме следует rруппа действий для вычисления суммы всех
членов уравнения кроме диаrональноrо. В начале проrраммы с перфо-
карты прочитано число МАХ, которое определяет максимально допусти
мое число итераций.
Исходная информация вводится в ЭВМ извне и результаты печа-
таются.
Ориентировочно дЛЯ МАХ можио принять значение 50, если система
(7-5) состонт нз 50 уравнений.
6. Уменьшение нзбыточностн исходной информацни
в линейных цепях
Система уравнений, составленных по методу коитурных токов
нли узловых напряжений, сводится к решению типа
Ax
b==O,
rде А
квадратная матрица порядка п; х и Ь
векторы 1 n-ro порядка.
Решение системы может быть произведено либо непосредственным
нахождением х, либо сначала может быть решена более общая задача
определения матрицы, обратной А, после чеrо искомое решенне системы
уравнений получается в виде
х == A
1b.
Сравнивая различные подходы к решению уравнений, сле"цует
отметить, что первый подход требует меньшеrо времени. В большинстве
применяемых методов время умножений сокращается примерно на 1/3.
Число умножении составляет примерно n 3 /3.
1 Подразумеваются столбцовые матрицы.
573
Определение обратной матрицы и преобразоР.ание посредством
отыскания каждоrо из векторов Ь вносит дополнительно п 2 умножений
и n записей для каждоrо вектора п
о сравнению с первым случаем.'
Не всеrда удается хранить в оперативной памяти машины всю
исходную информацию. Обращение к внеШней памяти и создает ряд
затруднений в части проrраммной реализации и, кроме Toro, снижает
темп работы машины, Оrраничения, налаrаемые объемом памяти машины
и временем выборки чисел из нее, выдвиrают важную проблему сокра-
щения количества первоначальной информации, а также уменьшения
числа операции в применяемом числениом методе и структуре формиро-
вания электротехнических алrоритмов. '
,Используя свойство взаимности в линейных электрических цепях,
применяем при построении .алrоритма численные методы, предназна.
ченные для решения уравнении с симметричными
матрицами А. Эти
методы требуют значнтельно меньше ;записей, что обеспечивает эконо-
мию времени при реализации алrоритмов на ЭВМ. Методы, предназна-
ченныедля р.ешения уравнений с симметричными матрицами, в принципе
должны обладать большей точностью, так как-при каждои записи про-
изводится одно окруrление и появляется связанная с этим ошибка.
Одним из недостатков, прliСущих алrоритму, составленному с использо-
ванием метода исключения, даже в наиболее блаrоприятном случае,
коrда матрица симметрична, является то, что значительная часть вре-
мени расходуется на запись цифр, применяемых на различных стадиях
вычислении.
Симметричный вид коэффициентных матриц, возникающих при
исследовании электротехнических задач, позволяет создат!, экономную
вычислительную схему.
Число записей при работе над симметричной матрицей сокращается
с 2п 2 + 4п до 3п 2 /2 + 9п/2. Число ОСновных операций для решения
системы уравнений, составленных по методу контурных токов для
узловых напряжений, уменьшается с п 3 + 1,5 п 2 + 1,5 п до п 3 /3 +
+ п 2
п/3. ,,'
Наличие симметричной матрицы обусловливает возможность при-
менения наиболее эффективных -методов последовательиых приближе-
нии для определения собственных чисел, предлаrаемых специально
применительно к симметричным матрицам. При этом представляется
возможным рассматривать только верхнюю или нижнюю треуrольную
матрицу. При рассмотрении симметричной матрицы вместо п 2 элементов
матрицы в оператиВНОЙ памяти машин
будет храниться (п 2 + п)/2
элементов,
.....
.....
IЦ
::.::
::t:: CQ
::.::
Q.,
t:::
<
::.::'
=
::с
.(,)
s=
t:::
о
с
;.(
'"'
со
:t:
!о-
'"'
:r
=
::!:
<
!о-
::
'"'
=
::r
=
>е-
е
(!)
о
;:.::'
:.-.
'"'
::;;:
=
::
'"'
:3
о
::
!о-
о
О
(,)
I.
IIJ
I
I
.
\
I
...
rE
., rEcQ Q:)CI:j
rE
Q:)
CI:j !
I
I
Q:) !J '
I
I ... Q:)
CI:j!Q:) riirE
Q:) r:Er:E '
rE
I
I
I
.'/
"<'
....[
[
....!
'" '"
I
.
I
'
I
I
1[
! ., II
.,;: .
l.' ' ... '"
..r:
"'<:"'<:
I
'=' 1= "'!
!J Jj '=' JI '='
'='
... '"
,'='
'=' '=''=' I
....]
....1
l;!
'
I .,1
cl' ,=,
!
'='
cl'1 '='
.... cl'l tS I
'='
'=' j'='
.'! '"
lJ 1!
S;
!= '" '"
'"
::t:: ::t:: ::t::
:з.! J '
r
!
.
....
'" ....] .
1:rE'
'
:Е
I >- ....I
l >- [ =
'"
=
l>-
I
>- >-. 1>-
>-
....1
1 >-
>- .
... "
....[
I
>:
..;:
;;:I
....[
"'\ '"
IJ
.1 '" ,,"(," ....N
'"
N '
""
"'1
'
.
....1 N!
'J
'" "'I
N' N
N N N' N
N
I
N >- ::t::
575
....
....
о
"=>
::
р..
=
4)
::
::
:х:
t;
о
с:(
о
р..
t::
576
\:>
II
I
I
::I
""
cQ'
.1
'
]
IJ J!
.cxfl
.
..
I
I
"fl
"'1;
I
I "'I;
'
"'1;"'1; "'I;
..
"'1;
I
.
J!
. '
I
.1 .
'''t:
"'1; "'1; "'1; '
"'1;"'1;
I
I
I
I
(,)
cs r. <$ <$ 1(,) ir.$
1.::>
[J
I 11 cS
.
(,)0;;,
I
(,)
r.$
..
1
cS
(,)(,)
I
=!
11
I[
I
.
'
I
..
I
I
JI
I ;;1
I
I
.'1
о;;,
'
I
I I
..\
I
II
!
IT
fl
:::::=
::-
] >.i:J
I
I
r
'
I
I
.,
>.
'
>. ..
I ::
1>- i>-
fl J
I ::
I
I
I
I
l
I
I
1
!
.'1"
I
I
..
..
t'OO.J
t'OO.J
(,) "'1;
:t:
;:...
.....
.....
.....
::t::
tц
а
"'"
14,
1::::
о(
::
:с
(,J
2
о
=
;<
gJ
с..
:а
!-
gJ
:r
:а
!-
:с
gJ
::
::r
::
е
е
tI') ::r:
о
м
gJ
с..
gJ
:r
gJ
:а
:с
:с :>..
gJ
о(
с..
:а
-=
::
gJ
!-
::
gJ
с..
=
Q
"1
'"' ""1 .. "'1 '"' ....1 ..
I 'Q
I
r:S
'Ir:S
'"'
..
"'t:
..
...
Т'"' '"'[ .. ...., .. "1 '"' "'t:
...:
' .. "" -i:";: I
"'t:"'t: "'t:"I
..
..
...
"'t:
''"'
r$
..
... ..) ...
"1 '"' -"",1 e.:t
I G I tSr$
r$1б' tSl
' .. I
r$
'"'
б'
'"'
..
"1 ...
"'! '" "'1'"'
I ::t::
,
,
I I
..
'
""
...
::t::
'"'
..
I
I "1 '"' '"'/ '" "'1 '"'
.. .;:-;: -;::.;: -;:-;:
-;::
'"'
""
....
..,
..
""
N
I
1
I
I "-, "1 ...
"" ..
.. NN NjN
,
..
N
'"'
...
N
N
::t::
"'t:
'"'
..
'Q
..
...
'Q
I
..
..
Q:;I
'"'
...
,Q:;I
I "'t:
"" 1 ..
.. ...
I
'"" ..
1:t7
I
'"' 1 ..
.;:
'"' fJ
.. ...
N
'Q
577
при.лОЖЕНИЕ IУ
оРиrИНАЛЫ и ИЗОБРАЖЕНИЯ ПО ЛАПЛАСУ
Р(р) fft)
! Нт
при О < 1 < 1:;
б(/)== '1:...01:
О при О> 1> 1:
1
р
1
р3
рп
1
р+а
1
р (р+а)
]
р2 (р+а)
1
(р + а)2
р
(р+ а)2
1
(р+а)3
р
(p+a)
578
,п
(n
1)1 ; n
целое
число
положительное
e
a!
1
а (1
e
at)
1
(e
al +a/
1 )
а 2
'e
a!
(1
at) e
at
1
12e
at
2
I(I
t)e
at
Пр одолжение при л о ж. IV
.
F (р) f (1)
1 1 I
(р + а)n
tn
le
at
(п
1)!
1 ( "
I]
J.. 1
e
a(.! (at)k I нмоо
р (р+а)n а n
kl положи-
k
O тельное
n ЧИСЛО
рn e
al 1: п! (
a)k k
(p+a)n+
(п
k)! (k)12 t
k
O
1 1
(р+а) (р+Ь)
(e
al ...;... e
bl)
b
a '
1 I ..!. +
( e
b!
e-- al )
р (р+а), (р+Ь) аЬ . Ь
a Ь а
р I 1
(р+а) (р+Ь)
(be
Ы
ae
al)
b
a
1 I 1 .
р2 + а2
sщаt
а
1 I 1
р (р2 + а2)
(1
cos at)
а 2
р I
р2 + а2 соэ а!
1 I 1
р2
а 2
sh а!
а
р I chat
p2
а2
pcosb
asinb I соэ (at+b)
р2 + а2
р sin Ь + а cos Ь I sin (at+ Ь)
р2 + а2
1 I sin at t cos а!
(р2 + а2}2 2а:!
"2a2
579
Продолжение при л о ж. IV
F(p) f (t)
Р 1 t .
(р2+а 2 )2 2а sm at
р2 1 .
(р2+а 2 )2 2а (sm at + at сos at)
p2
a2
(р2 + а2)2 t сos at
1 t ch at sh at
(р2
а2)2 "2а2
2a
р 1
(р2
а2)2 2а t sh at
1 e
a! sin bt
(р+а)2+Ь 2 ь
р+а
(р+ вfI+b 2 e
at cos bt
(р + а) сos 'Ф
ь sin 'Ф I e
at сos (Ы + 'Ф)
(р+а)2 +Ь 2
(Р+а) siп 'Ф+Ь сos'Ф I e
a! sin (Ы + 'Ф)
(р+а)2+Ь 2
1 I e
a! sh bt
(р+ a)2
b2 Ь
р+а I
(р+а)2
b2 e
a! ch bt
t I 1
T
р Vлt
3 I 2J/
2
р
580
список ЛИТЕРАТУРЫ
1. Акульшин П. К., Евланов С. Н. Основы теории электрической
связи. М., Связьиздат, 1960.
2. Атабеков r. И. Теория линейных электрических цепей. М.,
«Советское радио», 1960.
3. Атабеков r. И. ОСНОВЫ теории цепей. М., «Энерrия», 1969.
4. Бессонов Л. А. Теоретические основы электротехники. М.,
«Высшая школа», 1973.
5. rарднер М. Ф., Бэрнс ДЖ. Л. Переходные процессы в линейных
системах. М., Физматrиз, 1961.
6. rоноровский И. С. Радиотехнические цепи и сиrналы. Ч. 1.
М., «Советское радио», 1971.
7. Жуховицкий Б. Я., Неrиевицкий И. Б. Теоретнческие осиовы
электротехники. Т. 2. М., «Энерrия», 1972.
8. Основы теории цепей. М., «Энерrия», 1975. Авт.: [. В. Зевеке,
П. А. Ионкин, А. В. Нетушил, С. В. Страхов.
9. 3елях Э. В. Основы общей теории линейных электрических
цепей. М., Изд-во АН СССР, 1951. .
10. Теоретические основы электротехники. М., «Высшая школа»,
1965. Авт.: П. А. Ионкин, Н. А. Мельников, А. И. Даревский, Е. С. Ку-
харкин.
11. Караев Р. И. Переходные процессы в линиях большой протя-
жеиности. М., «Энерrия», 1978.
12. Kpyr К. А. Основы электротехники. Ч. 1 и 2. М.
Л., [ос-
энерrоиздат, 1946.
13. Поливанов К. М. Теоретические основы электротехники. Т. 1.
М., «Энерrия» , 1972.
14. Неймаи Л. Р., Демирчян К. С. Теоретические ОСНОВЫ электро-
техиики. Т. 1. Л., «Энерrия», 1975.
15. Реза Ф., Сили С. Современный анализ электрических цепей.
М.
Л., «Энерrия», 1964.
16. Сешу С." Балабаияи Н. Анализ линейных электрических цепей.
М.
Л., fосэиерrоиздат, 1963.
ПРЕДМЕТНЫй УКА.ЗА ТЕЛЬ
Автотрансформатор 222
Активные элементы цепи 20
Алrоритмы расчета 560, 562
Амплитуца 51
комплексная 76
Амплитудные искажения 343
Аналоrии электромеханическне 192
Апериоднческнй процесс 446
Базисный узел 163
Баланс мощностей 94
Близости эффект 33
Варнометр 211
Вебер
амперная характеристика 26
Вектор вращающийся 77
Векторная днаrрамма 79
Величина (вес) дерева 303
пут!! 305
Ветвь схемы 42
намаrннчивання 216
Взаимная нндукция 199
Вихревые токн 33
Виешняя характеристика 44
Вноснмое затух анне 127
четырехполюсника 254
Волна обратная 333, 460
отраженная 333, 460
падающая 332
преломленная 461
прямая 332, 460
стоячая 348
Волновое сопротивление линии 331,
334, 338 ,
операторное 509
. (характеристическое) сопротив-
ление 'контура 123
Вольт-амперная характеристика 25,
43, 44
Вольт
амперные характ
ристнки ис-
точников энерrин 39
Время запаздывания 526
Вторичные параметры линин 338
Вход четырехполюсника 233
Высшне rармоннки 401
в трехфазной цепи 422
Выход четырехполюсника 233
Вычеты функцни 504
rармоннческий ряд 403
rеометрическое место комплексноrо
вектор а 146 '
rрафоаналнтическое разложеиие в
ряд Фурье 405
rрафы 156
снrнальные 302, 315
Двухполюсннкн 136, 523, 530
активные 136
двухэлементные 138
мноrоэлементные 141
одноэлементные 137
пассивные 136.
приведенные 142
реактнвные 137
с потерями 137
582
Двухфазное короткое замыкание
388. 390
Действующее зи ачение комплекс-
ное 82
несинусоидальной . функции
418
сннусоидальной функции 56
Декремент колебаний 449
Дерево 156, 39З
Децибел 253
Диаrраммы проводнмостей и сопро.
тивленнй 149
Дирнхле условия 402
Дифференцнрующее звено 440
Диэлектрнческая проницаемость 36
Длина волны 322
Длинная линня 331
Добротность 450
катушкн 67
коиденсатора 69
контура (цепи) 123. 130
Дуальные цепи 189
Емкость 29
кабел я 327
конденсатора 36
линии 326
Закон Джоуля
Ленца 24
Ле;ща 26
Ома 24
82' при переменном токе 60, 65,
Фарадея
'Максвелла (электро-
маrнитной индукции) 26
Законы Кирхrофа 46, 154
коммутацни 429
Затухание вноснмое 254
контура 127
собственное четырехполюсника
249
Идеализация элементов цепи 20, 32
Изображение по Карсону 461
Лапласу 467. 578
Инверсня ветви 319
Иидуктивная катушка 122
связь 234
Индуктнвно-связанные контуры
198, 294
Индуктивность 25
взаимная 28, 199
кабеля 327
катушки 35
лИнии 326
ра,ссеяння 210
Интеrрал Дюамеля 472, 477" 501
.
Фурье 513
Интеrрирующее звено 440
ИНциденций матрица 187
Исток 317
Источннк бесконечной мощности 38
зависимый (неавтономный) 176
независнмый (автономный) 169
тока 38, 184
электрической энерrии 19
Источник S. д. с. 37. 180
Источннки энерrии эквнвалентные
110, 180 .
Канонические схемы Фостера 540
Каскадное соединение четырех по-
люсников 257, 259
Класснческнй метод расчета пере-
ходных процессов 427
Колебания затухающие 449
энерrии 61, 63
Колебательные контуры 120, 121
процессы 447
Коммутацня 429
Комплексная форма расчета 76
ряда Фурье 412
Кондеисатор 29, 35, 69, 122
Коитур 42
незавИсимый 155
параллельный колебательный
120, 130
последовательный колебатель-
ный 120
с малыми потерямн 132
Короткое замыканне 184, 436, 442
однородно!\. линни 350, 351
Коэффицнент амплитуды 421
беrущей волны 352
искаження 421
мощности 70. 421
ослабления 331, 338
отражения 255, 334
передачн (передаточная функ-
ци я) 256
полезноrо деllствия 92, 94, 228
распростр анени я 330
операторный 509
связи 211
критический 230
траисформацин 215
УСИJ)ени я 256
фазы линнн 331. 338
чстырехполюсннка' '2.49
формы кривой 421
Коэффицненты ряда Фурье 403, 515
четырехполюсника 238, 575
Кулон-вольтная характеристика 29
Линейныll элемеит цепи 40
.'1ини я длинная 333
без искажеиий 343
потерь 345
искусственная 359
как элемент резонансной цепи
358
однородная 326
Маrнитная нидукция 53
проводимость 210
проницаемость 35
аrнитиое поле 25
вращающееся 378
-:-
пульсирующее 379
аrнитодвижущая сила 35, 216
атрица контуров (инциденций) 187
атрицы 185
атричные уравнения 186, 251
ашинный расчет цепей 558
epa передачи 249
eTOД двух узлов 112
деревьев 302
единичноrо тока (метод подобня)
105 ,
комплексиых амплитуд 76
Метод контур-ных ТОКОВ 158
иаложеиия 167
подобня \метод единичноrо тока)
105
сиrнальных rрафов 302
симметричных составляющих 385
узловых напряжений 163
одуль 77
ощность актнвная (среДНЯЯ) 59,
71, 419
искажени я 420
комплексная 90
мrновенная 22, 28, 31, 58
полная 72
реактивная 72. 420
трехфазной цепи 369, 376
Напряженне 21
активное 66
комплексное 82
линейное 366
реактивное 66
смещения нейтрали 372
узловое 163
холостоrо хода 179
Неискаженная передача 343, 526
Нсйтральна я точка 364
Ненулевые начальные условня 430,
492 '
Непер 253
Несимметрия поперечиая 388
продольнаf! 393
Несннусоидальные токи 414
Несинусоидальный периодический
процесс 401
Нулевая последовательност. 386
Нуль функции 139, 531
Обратимые цепи 174
Обратная передача 237
последовательность 386
связь 269
Обратиое преобразоваиие Лапласа
477
Обрыв фазы 393
Однофазное короткое замыкание
388, 392
Однофазный синусоидальный ток 50
Оператор вращения (поворота) 78
Опережеиие по фазе 66
Орнrиналы 467. 578
Отражеиие волн 461
Отставанне по фазе 66
Параллельное соединение 67, 84,
101, 149
четырехполюсннков 260
Параллельно-последовательное со-
единеиие четырехнолюсннков 260
параметр с&язи 231
Параметры однородиой лииии Вто-
ричные 338
первнчные 326
холостоrо хода и KopoTKoro за-
MыKaHия четырехполюсиика 242
четырех полюс ника 237
характеристические 248
Пассивиые элементЫ цепи 20
Передача максимума мощиости 91
ветви 316
сиrнальиоrо rрафа 317
Передачи прямая и обратиая 237
583
Переходные процессы 427, 561
в цепи распределенными Па
раметрами 459, 508
сосредоточеииыми
параметрами 427
Переходный ток 433
Поверхиостный эффект 33
Положительная действительная
функция 531
Положительные иаправлеиия тока
и напряжения 21 .
Полоса задержнвания(затухания)290
пропускания 126, 230, 270
Полюс функцни 139
Последовательное соедннение 64,
80. 99. 148
четырехполюсников 259
Последовательно
параллельное со-
едннение четырехполюсников 261
Последовательность (чередованне)
фаз 374, 386
Постояиная времени 436, 440, 449
Маrинтная 35
электрическая 36
Постоянная составляющая 403
Потенциала распределенне 45
Потенциальная AHarpnMMa 95
Поток маrннтный 35
рассеяния 210
Потокосцепление 26
Правила левой и правой руки 53, 54
Правило правоходовоrо винта 27
Предельиые соотиошення 472. 476
Преобразование звезды в треуrоль.
ник 109
.'Iапласа 465
снмметричных схем 116
сХеМ с двумя узламн 112
источниками 110, 113
со смешанным соединением
103
треуrольника в звезду 107
Фурье 512
Приемник электрической энерrин 19
Принцип непрерывн.ости заряда 432
потокосцепления 431
Проводимость 24
активная 68
Взаимная (передаточная) 170
входная 170
емкостная 62
индуктнвная 60
комплексная 85
общая узлов 164
операториая 185
передаточная 452
(взаимная) 170
переходиая 499
Полиая 68
реактивная 68
Процесс переходный 427
пернодический 50
Прямая Передача 237
последовательность 386
Путь .в rрафе 305
Разложенне алrебраическоrо допол-
иени я 307
определНтеля 306
Разность потенциалов 21
фаз 58, 65
Расположеиие нулей ФУНКЦИИ 448.
531
584
Реакция цепи 500. 504
Реализация четырехполюсннка 246
фуикции 529, 536
Режим периодический 32'9
свободиыЙ 433
синусоидальный 51
установившиЙся 433
Резонанс «безразличиыЙ» 133
на rармонике 415
напряжениЙ 66, 120
полныЙ 228
сложный 226, 228
токов 69. 120. 130
частный 226, 228
Резонаисная кривая 125, 229
цепь 120. 358
частота 120
Резонаторы пьезоэлектрическне 297
Ряд rармоиический (Фурье) 403
Связанные колебательные контуры
234
Сдвиr фаз 58
Сиrнал 316
Сиrнальные rрафы 302, 315
Симметричная трехфазная цепь 367
Симметричные составляющие 335
Синтез электрических цепей 529
Скольжение 384
Скорость волны rрупповая 332
фазовая 332
Смешанное соедннение 103, 151
Смещение иейтрали 372
Соботвенная проводнмость узла 164
Собственное сопротнвление контура
159
Соrласование сопротнвлений 221,
248. 257, 336
Сопротнвление 23
актНвное 59
ВетвИ иамаrничивання 216
взаимное (передаточное) 171
взаимной индукции 205
волновое 334. 338
входное 171. 220, 246, 353,
452
линии 353
трансформатора 239
четырехполюсиика 276
ДВУХПОЛЮСННI(а 137.
емкостное 62
ИНДуктивное 60
кабеля 327
комплексное 81
линии 326
общее коитуров 159
операториое 485, 530
передаточное (взаимное) 171
полное 65
прнведенное к первичной обмот-
ке 216
проводника 32
рассеяния 216
собственное контура 159
характернстическое 123. 248. 275
Сопротивлення прямой. обратноJ\ и
нулевой последовательиостей 389
tпектральиая функция 513
Среднее значенне косн'нусоидальноlI
функцни 419
периодической фУНКЦНИ 55
СреднеквадРатичное значение функ.
цНИ 56
СХема замещеНИ я
втотрансформа-
тора 223
индуктнвной катушки 35
конденсатора 36
трансформа10ра 215
четырехполюсника 243
Мостовая 117, 157, 163, 166, 234
симметрнчная 116
цепная 104
электрическая 41
Теорема взаимности (обратимости)
173
дифференцирования 471, 472
запазды1анияя 471
интеrрирования 471, 473
компенсацни 175
об ИЗМеиении токов при Измене-
нии сопротивленнй 177
Эквивалентном источнике тока
184
Э. д. с. 180
подобия 471
разложения 478
свертываН>lЯ 472
смещения 472, 476
Тепловые потери в диэлеКТРllке 36
Ток 20
активный 69
комплексный 82
контурный 158
KopoTKorO замыкания 184, 388
лннеЙный 366
иамаrиичнвающий 216
однофазный 50
переменный 21
переноеа 20
переходный 433
ПостОЯННЫй 21, 44
проводнмости 20, 30
реаКТИВНЬП"1 69
свободный 433'
синусоидальный 57
СМещения 30
трехфазныЙ 361
устаиовившийся 433
фазный 366
Токи несинусоидальные 400
Топоrрафическая диаrрамма 95
Тополоrические методы 302
формулы разложения 304
Точка нейтральиая 364
Трансформатор 213
идеальный 217
Треуrольник мощностей 90
напряжений 83
проводимостеЙ 89
соПротивлений 84
токов 86
Треуrольннком соединение 366
Трехфазная цепь 361
несвязанная 361
иесимметричная 372
связанная 362
снмметричная 367
Трехфазный ток 361
Триrонометрическая форма ряда
Фурье 403
Уrловая чаСтота 51
собственная 448
Уroл диэлектрических потерь 69
сдвнrа фаз 58
Узел 42
Узлы стоячих волн 349
Унистор 312
Уравнения контурных ТоКов 159
линии телеrрафные 329
матричные 186, 259
мех анических цепей 196,
трансформатора 214
узловых напряжений 164
характеристические 433, 452
четырех ПОЛЮС ника 237, 250, 259
стаиовнвшийся процесс 427
Фаза 52, 361
начальная 52
Фазоуказатель 374
Фильтров классифнкация 271
Фильтрующие системы 294
Фильтры 270
безындуктивные 298
верхних частот 278, 282, 283,
291, 297, 300
заrраждающие' (режекторные)
278, 282, 283, 297. 300
мостовые 296
инжних частот 278, 282, 283,
291. 297, 299
полосовые 278, 282, 283, 291,297.
300
реактивные (идеальные) 271
снмметричных составляющнХ 394
типа k 277
типа т 285
Формулы разложения тополоrичес;:-
кне 304
ФОРТР АН 559
Фостера схемы 540
Функции единичная и показатель-
ные 469
минимальноrо реактивноrо со-
противления и ПРОВОДимостн 549
мииимальной и иеминимальноl!
фазЫ 553
Функция воздействующая 451, 504
импульсная 499
передаточная 256
периодическая 50, 401
несинусоидальная 401
спектральная 514
Цепи дуальиые 189
Цепная схема 104
Цепь активная 20
линейиая 40
мехаиическая 193
непланарная 162
однофазная 50
пассивиая 20
плаиарная (плоская) 161
резонансная 120
с обратной связью 167
распределеиными параметра-
МII 324
трехфазная 361
эквивалентная 105
электрнческая 19
Частота 51
комплексная 485, 530
основная 403
резонансиая 120, 225
собствениых (свободных) коле-
баиий 448
585
Частота среза 274
уrловая 51
Частотные характеристнки 125, 136
Чередованне нулей н полюсов 142
(последовательность) фаз 374
Четырехполюсники 309, 520, 552
актнвные 234
r
образные '233. 263
механические 236
мостовые 234, 266
необратнмые 234, 246
неснмметричные 234
обратнмые 234
одноэлементные 262
пасснвные 234
П
образные 234. 245. 265
симметричиые 234, 265, 266
ЧетыреХПОЛЮСНIIКИ Т-образные 233,
245, 265
Численные методы расчета переход-
ных процессов 561
Эквнвалентные звезд
и треуrоль-
ннк 107
нсточннки э. д. с. и тока 110
цепи 105
Электродвижущая сила 53
взанмной нндукцин 202
самоиндукЦии 26, 59
Элементы механической цепи 193
электрической цепн 19
Энерrня маrнитиоrо поля 28, 61
электрнческая 23
лектрическоrо поля 31, 63
оrЛАВЛЕНИЕ
От издательств а о . . о о о . . . . 5
Предисловие к третьему изданию 6
Условные обозначения о . . о . . 11
Введение о о о . о . . о о о . о . . 14
r л а в а пер в а я. Основные законы, элементы и параметры
электрических цепей . . . . . . . . о . 19
1
1. Электрическая цепь о . . : . . . . . . . . . . . . . 19
1
2. Положительные направления тока и напряжения. 20
1
3. Мrновенная мощность и энерrия . 22
1-4. Сопротивление . . . . . . . . . . . 23
1-5. Индуктивность . . . . . .. . . . . 25
1-6. Емкость.... о . . о . . . . . . . . . . . . . . . . . .. 29
1-7. Замещение физических устройств идеализированными
элементами цепи . . . . . . . . . . . 32
1
8. Источник э. д. с. и источник тока . . '.' . . . . . . о 37
1-9. Линейные электрические цепи . . . . . . . . . . . " 40
1-10. Основные определения, относящиеся к электрической
схеме . о . . о . . . . . . . . . . . . . . . . о . . . .. . 41
1-11. Вольт-амперная характеристика участка цепи с источ-
ником о . . . о . . . . . . . . . . . . . . . . . . . . .. 43
1
12. Распределение потенциала вдодь цепи с сопротивле-
ниями и источниками э. д. с. . . . . . . . . . . . . .. 45
1-13. Законы Кирхrофа . . . . . . . . . . . . . . . . . о .. 46
1-14. Задачи и вопросы для самопроверки. . . . . . . . .. 49
f л а в а в т о рая. Электрическая цепь однофазноrо сннусои-:
дальноrо тока. . . . . . . . . о ' 50
'2
1. Синусоидальные электрические 'величины . 50
2-2. fенерирование синусондальной э. д. с. .' . 52
2
3. Среднее и действующее значения функции 55
.2
4. Синусоидальный ток в сопротивлении . . 58
2-5. Синусоидальный ток в индуктивности 59
2-6. Синусоидальный ток в емкости. . . . 61
2-7. Последовательное соединение . . . . . 64
2-8. Параллельное соединение . ... . . . . 61
2
9. Мощность в цепи синусоидальноrо тока 70
2
1O. Задачи и вопросы для самопроверки. . 73
r л а в а т р е т ь я. Применение комплексных чисел н векторных
диаrрамм к расчету элек
рических цепей 76
3
1. Представление синусоидальных функций в виде проек-
ций вращающихся векторов . . . . . . о . . . . . . .. 76
3-2. Законы Ома и Кирхrофа в комплексной форме . . .. 80
587
3-3. Зависимость между сопротивлениями и проводимостями
участка цепи. . . . . . . . . . . . . . . . . . . . . . .. 88
3-4. Комплексная форма записи мощности. . . . . . . . .. 89
3-5. Условие передачи максимума активнЬй мощности от ис-
точника к приемнику . . . . . . . . . . . . . . . . . .. 91
3-6. Условие передачи источником максимума мощности при
заданном коэффициенте мощности приемника . 93
3-7. Валанс мощностей. . . . . . . . . . . . . . . . . . . .. 94
3-8. Потенциальная (топоrрафическая) диаrрамма. . . . .. 95
3-9. Задачи и вопросы для самопроверки. . . . . . . . .. 97
r л а в а ч е т в е р т а я. Преобразоваиие схем электрических
цепей. . . . . . . . . . . . . 99
4-1. Последовательное и параллельное соединения. . . .. 99
4-2. Смешаиное соединение . . . . . . . . . . . . . . . ... 103
4-3. Эквивалентные участки цепи с последовательным и па
раллельным соединениями. . . . . . . . . . . . . . ... 105
4-4. Преобразование треуrольника в эквивалентную звезду 107
4-5. Преобразование звезды в эквивалентный треуrольник 109
4-6. Эквивалентные источники э. д. с. и тока 110
4-7. Преобразование схем с двумя узлами 112
4-8; Перенос источников в схеме . . . . . . . 113
4-9. Преобразование симметричных схем . . . 116
4-10. Задачи и вопросы для самопроверки. . . 118
r л а в а n я т а я. Резонанс в электрических цепях 120
5-1. Резонансные (колебательные) цепи. . . . . " .... 120
5-2. Последовательный колебательный контур. Резонанс Ha
пряжений. . . . . . . . . . . . . . . . . . . . . . . . .. 121
5-3. Параллельиый колебательный контур. Резонанс токов 130
5-4. Частотные характеристики сопротивлений и проводи-
мостей реактивных двухполюсников. . . . . . . ., 136
5-5. Задачи и вопросы для самопроверки . . . . . . " 143
r л а в а ш е с т а я. rеометрические места на комплексиой
плоскости . . . . . . . . . . . . . . .. 144
б-l. rрафическое изображение зависимостей комплексных
величин от параметра . . . . . . . . . . . . . . . . . .. 144
б
2. Преобразование ВИда У == 1/2 . . . . . . . . . . . . .. 146
6
3. Диаrраммы сопротивлений и проводимостей простей-
ших электрических цепей. . . . . . . . . . . . . . . .. 148
6-4. Задачи и вопросы для самопроверки . . . . . . . . .. 153
r л а в а с е Д ь м а я. Методы расчета сложных электрических
цепей . . . . . . . . . . . . . . . . . .. 154
7-1. Применение законов Кирхrофа для расчета сложных
цепей . . . . . . . . . . . . . 154
7-2. Метод контурных токов . . . . 158
7-3. Метод узловых напряжений. . 163
7-4. Метод наложения. . . . . . . . 167
7 -5. Входные и передаточные проводимости и сопротивле-
ния. . . . . . . . . . . . . . . . . . . . . . . . . . . ., 169
7 -б. Теорема обратимости (или взаимности) ........ 173
7-7. Теорема компенсации . . . . . . . . . . . . . . . . ., 175
7-8. Теорема об изменении токов в электрической цепи при
изменении сопротивления в одной ветви. . . . . . .. 177
588
7
9.
7-10.
7-11.
7-12.
7-13.
rлава
8-1.
8-2.
8
3.
8-4.
8-5.
8-6.
8-7.
8-8.
8
9.
8-10.
8.11.
8-12.
rлава
9-1.
9
2.
9-3.
9.4.
9-5.
9-6.
9-7.
9-8.
9-9.
9-10.
9.11.
9-12.
9-13.
9-14.
9-15.
9-16.
9-17.
rлава
Теорема об эквивалентном источнике . . . . .
Применение матриц к расчету электрических цепей
Дуальные цепи . . . . . . . . . . . . .
Электромеханические аналоrии . . .
Задачи и вопросы для самопроверки. . . . . .
в о с ь м а я. Индуктивно связаниые электрические
цепи. " . " " " " " " " " " . " " " " , " 11
Основные положения и определения . . . . . . . . . .
Полярности индуктивно связанных катушек; э. д. с.
взаимной индукции ..................
Комплексная форма расчета цепи с взанмной нндук-
цией. . . . . . . . . . . . . . . . . . . . . . . . . . . .
Коэффициент индуктивиой связи. Индуктивность рас-
сеяния. . . . . . . . . . . . . . . . . . . . . . . . . . .
Уравнения и схемы замещения трансформатора без
маrнитопровода. . . '. . . . . . . . . . . . .
Эиерrия индуктивно связанных обмоток. . . . .
Входное сопротивлеиие трансформатора . . . . .
Автотрансформатор. . . . . . . . . . . . . . . . . .
Индуктивно связаиные колебательн'ые коитуры .
Настройка связанных контуров. . . . . . . . . . . . .
Резонансные кривые и полоса пропускания связанных
коитуров . . . . . . . . . . . . . . . . . .
Задачи и вопросы для самопроверки. . .
д е в я т а я. Ч'етырехполюсники . . . . .
Основные определения и класснфш<ация четырехпо-
люсииков . . . . . . . . . . . . . . . . . . . . . . .
Системы уравнений четырехполюсникз.
. . . . . . .
Уравнения четырехполюсника в форме 11 А 11 . . . . .
Параметры холостоrо хода и KopoTKoro замыкания. . .
Схемы замещения четырехполюсника . . . .
Входное сопротивление цетырехполюсника при про-
извольной наrрузке . . . . . . . . . . . . . . . . .
Характеристические параметры четырехполюсника . .
Виосимое затуханне четырехполюсника ',' . . . . . .
Передаточная функция. . . . . . . . . . .'. . . . . . .
Каскадное соединение четырехполюсников, осиованное
на соrласовании характеристических сопротивлений
Уравнения сложиых четырехполюсииков в матрнчной
форме . . . . . . . . . . . . . . . . . . . . . . . . . . .
Одноэлементные четырехполюсиики. . . . . . .
r -образный четырехполюсник . . . . . . . . . .
Т.образный и П-образный четырехполюсники .
Симметричный мостовой четырехполюсник .' . .
Обратная связь. . . . . . . . . . . . . . . . . .
Задачи и вопросы для самопроверки. . . . . .
д е с я т а я. Электрические фнльтры и тополоrическне
метады анализа линейиыХ электрических
цепей. " " " " " " " " " " " . " . " " " " ..
180
185
189
192
197
198
198
200
204
209
213
219
220
222
224
226
229
231
233
. 233
237
240
242
243
246
248
254
256
257
259
262
263
265
266
267
268
269
10-1. Осиовиые определения и классификация электри.
ческих фильтров .............'....... 269
10-2. Условие пропускания реактивноrо фильтра . . . .. 271
589
10-3. Фильтры типа k. . . . . . . . . . . . . . . .
. . . .. 277
10-4. Фильтры типа т . . . . . . . . . . . . . . . . . . .. 285
l(
5. Индуктивно связанные контуры как фильтрующая
система. . . . . . . . . . . . . . . . . . . . . . . . .. 294
1O
6. Мостовые фильтры. Пьезоэлектрические резонаторы 296
10-7. Безындуктивные фильтры . . . . . . . . . . . . . " 298
10
8. Тополоrические формулы иахождения определителей
и алrебраических дополнений . . . . . . . . . . . " 302
10-9. Тополоrические ФОРМУЛЫ разложения. . . . . . . .. 304
10
10. Тополоrические формулы для 'передаточных функций 308
10-11. Тополоrический анализ активных цепей . . . . . .. 312
10
12. Сиrнальные rрафы и методы их преобрэзования. .. 315
10,
iз. Построение Сиrнальных rрафов электрических цепей 321
10-14. Задачи и вопросы для самопроверки . . . . . . . .. 323
r л а в а о д и н н а Д Ц а т а я. Цепи с распределенными пара-
метрами . . . . . . . . . 324
11-1. Первичные параметры однородной лииии. 324
11-2. Дифференциальные уравнення однородной линии 327
11-3. Синусоидальный режим в. однородной линии. 329
11-4. Вторичные параметры однородной линии. . . 338
11-5. Линия без искажений ............. 343
11
6. Линия без потерь. . . . . . . . . . . . . . . . 345
11-7. Режимы работы линии без потерь. Стоячие волны 347
11
8. Входное сопротивление линии . . . . . 353
11-9. Линия как элемент резонансf!oй цепи 358
11-10. Искусственные линии. . . . . . . . . . 359
11-11. Задачи и вопросы для самопроверки. 360
r л а в а
Д в е н а Д Ц а т а я. Цепи трехфазиоrо тока. 361
12-1. Трехфазные электрические цепи. . . . . . . 361
12-2. Соединение звездой и треуrол!'ником . . . . _ 364
12-3. Симметричный режим работы трехфазной цепи . . . .' 367
12-4. Несимметричный режим работы трехфазной цепи 372
12-5. Мощность несимметричной трехфазной цеци . . . .. 376
12-6. Вращающееся маrнитиое поле . . .
. . . . . . . .. 378
12-7. Принцип деЙствия асинхрониоrо и синхронноrо дви-
rателей . . . . . . . . . . .
. . . . . . . 383
12-8. Метод симметричных составляющих. 385
12-9. Поперечная несимметрия . . . . . . . . 388
12-10. Продольная несимметрия. . . . . . . . 393
12-11. Фильтры симметричных составляющих 394
12-12. Задачи и вопросы для самопроверки . 398
r л а в а Т р И н а Д ц а т а я. Цепи периоднческоrо несииу-
соидальиоrо тока . . . . 400
13-1. Триrонометрическая форма р'яда Фур'ье " 400
13-2. ,Случаи симметрии. . . . . . . . . . . . . .. .... 406
13-3. Пере нос иачала отсчета ................ 411
13.4. Комплексная форма ряда Фурье . . . . . . . . . . _ 412
13
5. Применею!е ряда Фурье к расчету периодическоrо
несинусоидалr,ноrо процесса . . . . . . . . . . . . ., 414
13-6. Действующее и среднее значения периодической
несинусоидальной функции. . . . . . _ . . . . . . .. 418
13-7. Мощность в цепи периодическоrо несинусоидальноrо
тока ........ . . . . . . . . . . . . . . . . . .. 419
590
13
8. Коэффициенты, характеризующие периодические не- .
синусоидальные функции. . . . . . . . . . . . . . .. 421
13-9. Высшие rармоники в трехфазных электрических цепях 422
13-10. Задачи и вопросы для самопроверкн . , . . . . . .. 425
r л а в а ч е т ы р н а Д Ц а т а я. Переходные процессы в элек-
трических цепях. к.,iассиче-
ский метод расчета . 427
14-1. Возникновеиие переходных процессов . . . 427
14
2. Законы коммутации и начальные ,условия 429
14
3. Установившиися И свободный режимы .
. 432
14
4. Переходный процесс в цепи '. L . . . . . . . 434
14
5. Переходный процесс в цепи '. С . . . . . . . 440
14-6. Переходный процесс в цепw" L, С . . . . . . . . .. 444
14-7. Расчет Переходноrо процесса в разветвленной цепи 451
14-8. 'Переходные процессы в цепях с распределенными
параметрами . . . . . . . . . . . . . " . . . . . . " 459
14
9. Задачи и вопросы для саМОПрОВерки. . . .'. . . . .. 464
r л а в а n я т н а Д Ц а т а я. Применение преобразованtfЯ Лап-
ласа к расчету переходиых про-
цессоа . . . . . . . . . . . . . .. 465
15-1. Общие сведения. . . . . . . " . . . . . . . . . . . . '. 465
15-2. Прямое преобразование Лапласа. Ориrинал и изоб-
ражение . . . . . . . . . . . . . . . . . . . . . . . .. 467
15-3. Изображения некоторых простейших функций. . .. 468
15-4. Основные свойства преобразования Лапласа. . . .. 470
15-5. Нахождение ориrинала' по изображению с помощью
обратноrо преобразования Лапласа. . . . . . . . " 477
15-6. Теорема разложения . . . . . . . . . . . . . . . . .. 478
15-7. Таблицы ориrиналов и изображений. . . . . . . . .. 482
15-8. Примеиение преобразования Лапласа к решению диф-
ференциальных уравиеиий электрических цепей. .. 483
15-9. Учет ненулевых начальных услоаий методом эквива-
лентноrо источника. . . . . . . . . . . . . . . . . .. 492
15-10. Формулы включения . . . . . . . . . . . . . . . . .. 497
15-11. Расчет Переходноrо процесса с помощью формул раз-
ложения . . . . . . . . . . . . . . . . . . . . . . . ., 498
15
12. Нахождение в замкнутой форме установившейся
реакции цепи на периодическую несинусоидальную
воздействующую функцию . . . . . . . . . . . . . " 504
15-13. Исследование переходыых ПР9цессов е цепях с рас-
.пределенными параметрами с помощью преобразова-
ния Лапласа . . . . . . . . . . . . . . . . . . . . .. 508
15-14. Задачи и вопросы для самопроверки . . . . . . . .. 510
r л а в а ш е с т н а Д ц а т а я. Применение преобразоваю.я
Фурье к расчету переходных
процессов . . . . . . . . . . . '. 512
16-1. Преобразование Фурье как частный случай преобра,
зования Лапласа. . . . . . . . . . . . . 512
16
2. Спектральная функция. . . . . . . . . . . . 513
16
3. Переходный процесс в двухполюснике. . . 523
16
4. Переходный процесс в четырехполюснике 526
16.5. Задачи и вопросы для самопроверки. . .. 528
591
r л а в а с е м н а д ц а t 11 я. Сиитез ЛинеilныJt Электрических
цепей . . . . .
. . . . . . . . .
17
1. Характеристика задач синтеза . . . . . . . . . . . . .
17
2. Исследование двухполюсника при комплексной частоте
17
3. Условия физической реализуемости функции . . . . .
17.4. Свойства двухэлементных" двухполюсников и их реа-
лизация . . . . . . . . . . . . . . . . . . . . . . . . . .
17
5. Общий случай реализации функций двухполюсника
17 -6. Исследование четырехполюсника на комплекснОй
частоте. . . . . . . . . . . . . . . . . . .
17 -7. Синтез реактивных четырехполюсников
17-8. Задачи и вопросы для самопроверки. .
Приложения:
1. Машинный расчет линейных электрических цепей
11. Соотношения между коэффициентами четырехполюсника
111. Определители, выраженные через коэффициенты четы-
рехполюсника . . . . . . . . . . . . . .
lУ. Ориrиналы и изображения по Лапласу
Список литературы . .
ПредмеТНqJЙ указатель
529
529
530
536
538
548
552
555
556
558
575
577
578
581
582
r ДЕ КУПИТЬ
ДЛЯ орrАНИ3АЦИЙ:
Для то,о, чтобы зан:азать uеобходuмые Вам н:ии,и, достаточuо обратuться
в любую uз тор,овых н:омnаиии И здательсн:о,о Д ома ,<ЛАНЬ,}:
по России и зарубежью
<.ЛАНЬ
ТРЕЙД.. 192029, Санкт
Петербурr, ул. Крупской, 13
тел.: (812) 412
85
78, 412
14
45, 412
85
82; тел./факс: (812) 412
54
93
e
mail: trade@lanpbl.spb.ru; ICQ: 446
869
967
www.lanpbl.spb.ru/price.htm
в Москве и в Московской области
<.ЛАНЬ
ПРЕСС.. 109263, Москва, 7
ая ул. Текстильщиков, д. 6/19
тел.: (499) 1 78
65
85; e
mail: lanpress@ultimanet.ru
в Красиодаре и в Красиодарском крае
<.ЛАНь
юr.. 350072, Краснодар, ул. Жлобы, д. 1/1
тел.: (8612) 74
10
35; e
mail:lankrd98@mail.ru
ДЛЯ РО3НИЧНЫХ ПОКУПАТЕЛЕЙ:
U1iтеР1iет
ма2аЗU1iЫ:
<.Сова.: http://www.symplex.ru; <.Ozon.ru.: http://www.ozon.ru
<.Библион,: http://www.biblion.ru
также Вы можете отправить заявку на покупку книrи
по адресу: 192029, Санкт
Петербурr, ул. Крупской, 13