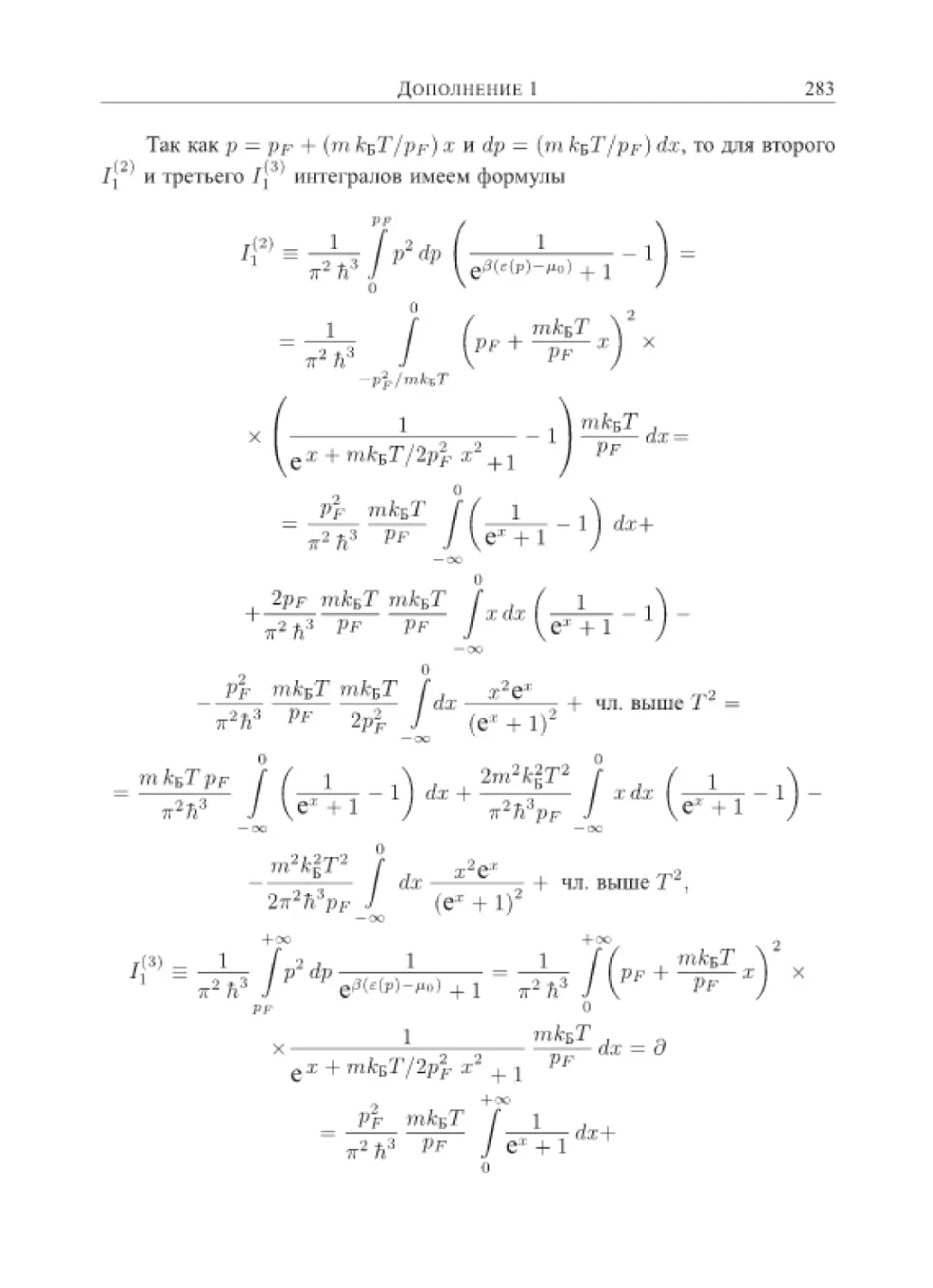Текст
В. В. Толмачев, Ф. В. Скрипник
ФИЗИЧЕСКИЕ
9 основы
ЭЛЕКТРОНИКИ
В. В. ТОЛМАЧЁВ
Ф. В. СКРИПНИК
ФИЗИЧЕСКИЕ ОСНОВЫ
ЭЛЕКТРОНИКИ
Издание второе, исправленное и дополненное
Москва ♦ Ижевск
2011
УДК 530.145
И нтср нет-магази н
http://xhop.rcd.nl
• физика
+ математика
• биологии
* нефтегазовые
технологн и
Толмачёв В. В-, Скрипник Ф. В.
Физические основы электроники. — Изд. 2-е., испр. и дол. — М .-Ижевск:
НИЦ «Регулярная и хаотическая динамика» t Институт компьютерных ис-
следований, 2011. — 496 с.
В пособии Еза элементарном уровне нзлагантся основы квантовой механики
и статистики, необходимые для понимания квантовой теории полупроводников^ ле-
жащей в основе твёрдотельной электроники. Также в пособии подробно рассмот-
рены основные вопросы физики полупроводниковых приборов, в частности диод
с рп-псрсходом и рпр-транзистор.
Пособие преднси+начено студентам младших курсов технических вузов и уни-
Есрситстов, изучающим курсы твёрдотельной электроники, а также всем, интересу-
ютимся основами твёрдотельной электрон кН
ISBN 978-5-93972-889-8
© В. И.Толмачёв, Ф. В. Скрипник, 2011
© Ижевский институт компьютерных исследований, 2011
http://shopTcd.nl
http://icsTor^+ni
Оглавление
Предислпние к первому изданию................................ 9
Предисловие ко второму изданию............................... 10
Введение ... II
ГЛАВА ]. Корпускулчрпо-волпиний дуализм фолннж.............. 14
1.1, Становление корпускулярных и волновых представлений
о природе света........................................... 14
1.2. Экс 11 ери ме гзты по тег и ювом у из луч ению и по нш iy че н ню ра з-
реженных газов ........................................... 27
U. Вывод формулы Планка для равновесного теплового элек-
тромагнитного излучения............................... 34
Метод суперпозиции и разделения переменных Фурье . . 34
Мбды злектромаптитного излучения в кубической полости 39
Распределение мод по частотам.................... 46
Связь с ......................................... 48
Применение теоремы о равномерном распределении
энергии.......................................... 56
Энергия классического или квантового осциллятора ... 60
Вывод законов Стефана-Еольцмана и Вина........... 65
1.4. Квантовая природа света. Фотоэффект и эффект Комптона . . 68
Фотоэффект....................................... 69
Эффект Комптона.................................. 74
Дополнение L к гл. I ................................ 76
Ранние исследования по физической оптике..........76
Исследования теплового излучения................. 79
Исследования оптического излучения............... 82
Дополнение 2 к гл. I ................................. У8
История открытия формулы Планка ................. 88
Распределение энергии по степеням свободы.........100
Исследования теплоёмкости твёрдых тел.............103
4
ОГЛАВЛЕНИЕ
Глава 2. Корпускулярно-волновой дуализм э лек тронов......... 108
2 J. Дебронлевская длина волны........................... 108
2Г2, Корпускулярные свойства электрона ...................Ill
Эксперимент Дж. Дж. Томсона с катодно-лучевой трубкой 11 I
Измерение заряда плектре ез а.....................119
Эксперимент КауфмаЕга.............................121
Спин электрона. Эксперимент Штерна-Герлаха .......126
2.3. Волновые свойства электрона..........................129
Измерение длины волны света н рентгеновских лучей . . 130
Эксперимент Дэвиссона и Джермера..................133
ЭкС1 iep им ент Дж. 11. Томсона...................13 К
2.4. Атомный электрон.....................................140
Теория Бора атома водорода........................140
Дополнение к гл. 2....................................148
Исследования электрического газового разряда......148
ГЛАВА 3. Физика корпускуляриа-вцлполого дуили зма........... 152
3.1. Квантовая механика...................................152
3.2. Соотношение неопределённостей........................153
3.3. КопспгагсЕЕСкая интерпретация квантовой механики.....158
Глава 4 Модельные одномерные квантоко-мехапнчсскнс задачи 162
4.1. Задача об одномерном свободном движении частицы......163
4.2. Задача об одномерной прямоугольной потенциальной яме
с бесконечными стенками....................................171
Условие Борна Кармана.............................175
4.3. Задача об одномерном прямоугольном потенциальном барьере 177
4.4. Задача о двойной одномерной прямоугольной потенциаль-
ной яме....................................................183
Дополнение 1 к гл . 4 ................................192
Дельта-функция Дирака ............................192
Дополнение 2 к гл. 4 .................................194
Операторы физических величин......................194
Проблема на собственные значения и собственные функ-
ции ..............................................196
Физический смысл собственных значении к собствен-
ных функции оператора физической величины ........198
Соотношение непредслённостен......................211
ОГЛАВЛЕНИЕ
5
Глава 5. Р ас пределен не Ферми-Дирака........................214
5.1. Вывод распределения Фермн Дирака по Больцману.......,215
СОСТОЯНИЯ Электрона в кубическом ящике...............216
Боньцмановскнй способ описания макроскопических со-
стояний .............................................220
Применение рассуждения Больцмана к электронному газу 222
Нахождение значений а и /3...........................226
5.2. Полученнс распределения Максвелла из рас пределения Фермй -
Дирака ..................................................228
Дополнение I к гл. 5 ....................................231
Метод неопределённых множителей Лагранжа.........231
Дополнение 2 к гл. 5 ....................................234
Вывод формулы Планка по Больцману....................234
Математическое описание неравновесных состоянии газа 235
Применение рассуждения Больцмана к фотонному газу . 237
Нахождение значения множителя /3.....................242
Дополнение 3 к пт. 5 ....................................246
Вывод формулы Больцмана о СВЯЗИ энтропии с вероят-
ностью состояния.....................................246
Неравновесные состояния газа.....................247
Неравновесные состояния, однородные по плотности . . 248
Отыскание равновесного состояния.................252
Распределение Максвелла..........................255
Неравновесные состояния, однородные по температуре - 258
Отыскание равновесного состояния.................259
Формула Больцман и...............................260
Глава 6. Основы квантовой теории металлов ......................265
6.1. Модель свободных электронов........................Р 265
6.2. Вычисление функции при малых температурах Т . . . , 270
6.3. Теплоёмкость системы свободных электронов проводимости
при малых температурах...................................271
6.4. Термоэлектронная эмиссия................................273
Формула Ричардсона-Дэшмана...........................273
Теория Шоттки........................................277
6.5. Контакт двух металлов...................................279
Дополнение L к гл. 6. Вычисления ^(Г) ...................281
Дополнение 2 к гл. 6. Вычисление (//V....................286
6 Оглавление
Глава 7. Монель Кронигя-Псннн ... 290
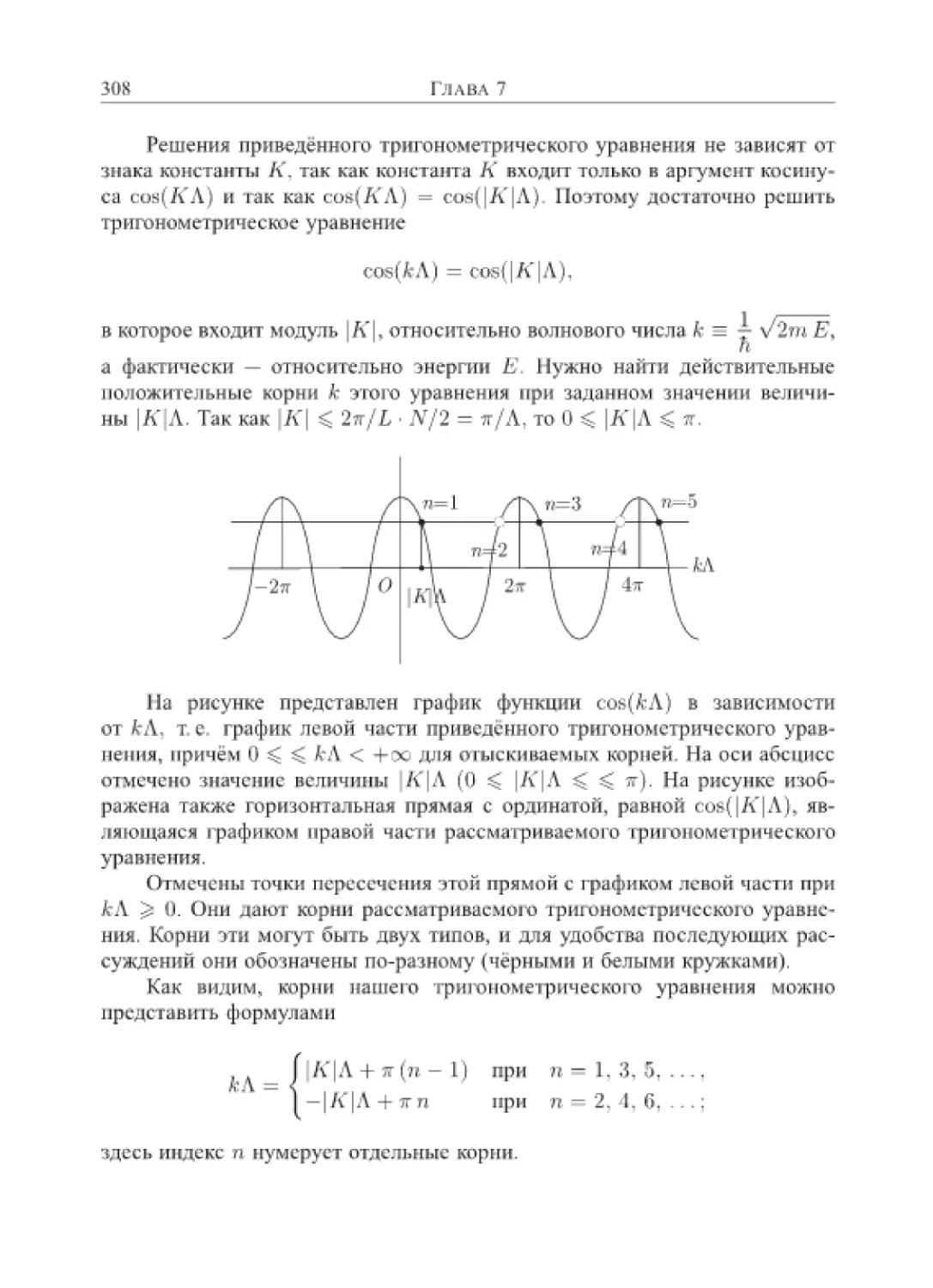
А. МОДЕЛЬ КРОНИГА-ПЕННИ ВЕЗ ВНЕШНЕГО ПОЛЯ 290
7.]. Решение уравнения Шредингера модели Кронига Пении . ,290
Исходная задача.................................291
Изменённая Задача...............................292
Оператор трансляции.............................294
Теорема Блоха...................................297
7.2. В ывод тра нсцен дентного ура внення модел и Крон ига -1 Тенни 300
7.3. Исследование энергетического спектра в пределе бесконечно
сильной связи............................................304
7.4. Исследование энергетического спектра в пределе нулевой
связи ...................................................306
Исследование трансцендентного уравнения для различ-
ных значений константы распространения..........307
Исследование трансцендентного уравнения для различ-
ных значении проекции волнового вектора.........310
Зоны Бриллюэна .................................313
7.5. Приближённое отыскание Энергетического спектра в случае
сильной связи............................................314
Б. МОДЕЛЬ КРОНИГА ПЕННИ С МНОГИМИ ЭЛЕКТРО-
НАМИ ...............................................318
7.6. Модель Кронига-Пенни с многими электронами........318
В. МОДЕЛЬ КРОНИГА-ПЕННИ ВО ВНЕШНЕМ ЭЛЕКТ-
РИЧЕСКОМ ПОЛЕ.......................................321
7.7. Модель Кронига - Пспеги при наличии внешнего электриче-
ского поля ..............................................321
Строгий вывод формулы шея групповой скорости элек-
трона ..........................................324
Движение электрона во внешнем поле..............328
Эффекта видя масса электрона....................330
Голые н одетые электроны........................334
Движение дырки во внешнем поле..................335
Дополнение I к пт. 7 ...............................341
Оператор Гамильтона в пространстве периодических
функций.........................................341
Дополнение 2 к гл. 7 ...............................343
Решение уравнения Шредингера в случае слабой связи . 343
Построение решении ири Vq = 0...................344
Построение решений при малом Ц 0................345
ОГЛАВЛЕНИЕ
7
Глава 8. Теории электропроводности полунроводннков........353
А КОНЦЕНТРАЦИИ ЭЛЕКТРОНОВ И ДЫРОК В ПОЛУ-
ПРОВОДНИКАХ .......................................353
8.1. Одноэлокгронныс состояния системы свободных электронов 353
Задача об электроне и трёхмерном кубическом ящике . . 355
8.2. Экспериментальное доказательство существования дырок . . 358
Эксперимент Ханнеса и Шокли.....................358
Эффект Холла....................................360
8.3. Равновесные концентрации электронов и дырок в чистом по
лупроводнике ...........................................362
Заков действующих масс..........................366
Химический потенциал............................367
8.4. Равновесные концентрации электронов и дырок в примесных
полупроводниках ........................................371
Примесные полупроводники........................371
Энергии ионизации н электронного сродства атомов при-
меси ...........................................371
Концентрация электронов в донорном по л у проволн икс . .375
Концентрации дырок в акцепторном полупроводнике . . .382
Б СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЛО-
КАЛЬНЫХ БАЛАНСОВ...................................385
8.5. Система уравнений локальных балансов..............385
Дрейф носителей электрического тока.............385
Диффузия носителей тока.........................387
Генерация и рекомбинация носителей тока.........390
Уравнения локальных балансов Электронов Я дырок . . .391
8.6. Примеры решения системы уравнении балансов электронов
и дырок............................................393
В. ТЕОРИЯ P1V-ПЕРЕХОДА И /WP-ТРАНЖСТОРА .... 397
8.7. Теория рл-перехода................................397
Контактная разность потенциалов.................397
Качественное объяснение контактной разности потенци-
алов ...........................................398
Теория Шокли равновесного рп-псрехода...........400
Вольт-амперная характеристика...................405
Основные законы рп-перехода.....................406
Формула Шокли...................................407
Качественное объяснение выпрямляющего действия -пе-
рехода .........................................410
8
ОГЛАВЛЕНИЕ
Зависимость границ о и & обеднённого слоя от прило-
женного напряжения Электрическая емкость рп-пе-
рехцца............................................413
8.8. Транзистор с/тр-переходом...........................416
Допо лнение I к пт. 8 ......................... . 423
Графическое изображенне искривлённых зон//^перехода 423
Дополнение 2 к гл. 8 .................................426
Контакт полупроводник-металл .....................426
Теория Шоттки.....................................427
Теория Бардина....................................433
Кот 1такт металл - диэлскгрик - полу про воде 1нк.434
Нолевой транзистор................................438
Дополнение 3 к гл. 8 .................................440
Полупроводниковые приборы.........................440
Туннельный диод...................................440
Диод Зин ера и лавинный диод......................443
Фоторезистор......................................444
Фотодиод..........................................445
Светодиод и лазерный диод.........................446
Солнечные батареи.................................451
Дополнение 4 к пт. 8 .................................452
Фазовое и химическое равновесия ..................452
Открытые и закрытые термодинамические системы 453
Принципы минимумов потенциалов ................462
Использование принципа минимума...................464
Дополнение 5 к гл. 8..............................470
Электрохимическое равновесие......................470
Гальванический элемент............................470
Условие электрохимического равновесия.............471
Химические потенциалы.............................475
Закон разбавления Оствальда и формула Нсрнста . . . . 478
Рекомендуемая литература.....................................483
Предметный указатель.........................................484
Именной указатель ...........................................493
Предисловие к первому изданию
Предлагаемое вниманию читателя учебное пособие отражает много-
летний опыт преподавания курса Основ физической электроники студен-
там 2-ю курса факультета Информатики и: управления Московского Го-
сударственного Технического университета им. Н. Э. Баумана. Речь идёт
о «твёрдотельной», те. «полупроводниковой» электронике, понимание oc-
ti п в которой требует знания квантовой механики и квантовой статистики,
а также зонной теории кристаллического твёрдого тела.
Изложению квантовой теории электропроводности полупроводников,
являющейся основной задачей учебного пособия, предпослано очень крат-
кое изложение основных положений квантовой механики и квантовой ста-
тистики с разбором решений ряда модельных одномерных задач. Кроме
того, приведено полное изложение теории одномерной квантовой модели
KpOEiHj a-IIeEiiiH. Дблжное внимание уделено квантовой теории металлов,
развиваемой в рамках модели свободных электронов, подчиняющихся рас-
пределению Ферми Дирака. Ей посвящена отдельная глава.
Что касается собственно кваЕгтовон теории полупроводников, то в по-
собии большое внимание уделено максимально полному изложению су-
ществующей полуэмпирической теории рп-персхода Шокли. Строго выво-
дится формула для контактной разности потенциалов и знаменитая фор-
мула Шокли для вольт-амперной характеристики рп-перехода. За кап чипа-
етея пособие изложением теории транзистора с рп-порвдвдом и полевою
МОГ 1-транзистора.
Отдельные главы снабжены Дополнениями с изложением историче-
ских сведений и существенных теоретических вопросов. Знание этого ма-
териала ле требовал ось от студентов на экзамене.
Однако, хотелось бы обратить внимание на последние три Дополнения
к гл. 8. В третьем поясняется устройство важнейших полупроводниковых
приборовн использующих полупроводники с рп-переходами, а в четвёртом
И ПЯТОМ рйЗЪЯСНЯ1ОТСЯ понятия химического и электрохимическою потен-
циалов. В ЭТИХ Дополнениях изложены ОСНОВЫ ТСОрИН ТСр.М ОДИНЙМИ ЧССКИХ
потенциалов.
Материал пособия излагался в односсмсстровом курсе с двумя лекци-
ями в неделю, сопровождался семинаром раз в две недели и заканчивался
экзаменом.
Предисловие ко второму изданию
Во второе издание пособия внесены небольшие изменения и дополне-
ния it исправлены замеченные опечатки.
Наиболее существенное изменение касается гл. 4, в которую перене-
сено Дополнение из гл. 7, посвящённое операторам физических величин
н квантовой теории измерении физических величин, и, кроме того, добав*
лены задачи о процедуре измерения проекции СП]И]а на фиксированную
в пространстве ось г у частицы со спином 1/2 и 1. В гл. 4 также включено
обсуждение эффекта расплывания волнового пакета.
Такое изменение позволило чётче разделить пособие на следующие
три части. Это первая часть, содержащая гл. 1,2,3, посвящённые обсуж-
дению корпускулярно-волновою дуализма фотона И электрона. Эю вторая
часть, состоящая из гл. 4,5,6, посвящённых изложению элементарных ос-
нов нерелятивистской квантовой механики и квантовой статистики элек-
тронов (распределению Ферми-Дирака). Наконец, это третья часть с ос-
новными в пособии гл. 7,8, посвящёнными теории электропроводности по-
лупроводников.
Такое деление материала пособия даст возможность более доступно-
го изложения физических ио просои, необходимых для понимания работы
п ол упро воде тиковых пр иборов.
Для большей ясности материал основных в пособии гл. 7 и гл. 8 разбит
каждый на три раздела А, В
Авторы выражают свою искреннюю благодарность ст. прсп. кафедры
физики МГТУ Е. В. Корогодиной за полезные замечания.
Введение
Приступая к изучению физических основ твёрдотельной электрони-
ки по данному учебному пособию, студент должен научиться про водить
логические рассуждения. Умение логически рассуждать позволит студенту
быстрее запомнить излагаемый в курсе большой по объёму учебный мате-
риал.
Рассуждение содержит ряд следующих друг из друга положений, как
правило, сопровождаемых математическими формулами. Их-то студент и
должен освоить. Используя в рассуждении ту или иную формулу, следует,
во-первых, чётко понять, какие именно физические величины обозначают
входящие в формулу латинские и греческие буквы (если, например, это
зне/?с?ця или ллглулвс, то — какого объекта? какой системы? если — садд,
то — какая сила? на что она действует? со стороны какою тела действует?
и т.п.), ич во-вторых, понять самого равенства в формуле, г.с. быть
в состоянии ответить на вопрос: почему это равенство верное?
С целью облегчить студенту знакомство с рассуждениями в данном
пособии они приведены максимально подробно.
Используемый в них математический аппарат достаточно элементар-
ный и доступен студентам 2-го курса. Он включает основы дифференци-
ального и интегрального исчисления, умение брать простейшие криволн-
и сипы с, поверхностные и объёмные интегралы, умение решать простейшие
дифференциальные уравнения. Он использует основные элементы j[иней-
ной алгебры и аналитической геометрии, включая векторную алгебру.
Даже слабо подготовленному студенту необходимо настроиться на то,
что всё, буквально всё в этом учебном пособи и ои может попять самостоя-
тельно. Вместе с тем авторам иногда пришлось делать ссылки на сведения,
которые студент должен принять на веру. Все такие случаи: чётко огово-
рены.
Хотя о ci ю eh ia я 1 ieji ь авторе в сообщить студе! ггу с макт и мал ы юн i юл-
нотой физические основы твёрдотельной электроники, необходимо понять,
что основная трудность в освоении этих основ состоит в чётком владении
необходимыми смежными вопросами физики, и прежде всею надо очень
хорошо осознать физическую суть квантовой природы электрона, откры-
тую квантовой механикой Шредингера и Гейзенберга в 1925—1926 гг.
12
ВВБДЕПН1.
В гл- 2 пособия излагается основная идея квантовой теории электрона:
что ллсктроп обладает сс корпускулярно-волновым дуализмом», тег одних
экспериментах ведёт себя как материальная точка (корпускула^ а в дру-
гих — как волна. Описываются знаменитые эксперименты Дж. Дж. Томсона
] 898 г. по открытию электрона как корпускулы и эксперименты Дэвиссона
и Джермера и Дж. П. Томсона 1927 г но дифракции электронов, Также опи-
сывается эксперимент Штерна и Герлаха 1922 г. по экспериментальному
открытию наличия спина у электрона и доказательству что спин я = 1/2.
Изложена теория Бора 1912 г спектра атома водорода, основанная на его
постулатах I и II, с выводом сериальной формулы Ридберга.
Чтобы студенту легче было освоиться с материалом гл. 2 (только и
нужной для понимания физических основ твердотельной электроники),
гл. 2 предпослана гл. I с описанием свойств теплового электромагнитно-
го излучения и линейчатых атомных спектров. Подробно выводится знаме-
нитая формула Планка 1900 г, для излучательной способности абсолютно
чёрного тепа.
В гл. 3 подведён некоторый итог гл. 1,2. Изложено квантовое соотно-
шение неопределённостей н обсуждены основы стандартной копенгаген-
ской интерпретации квантовой механики.
T'.'i. 4, важней шля п пособии, посвящена изложению ряда точно реша-
емых одномерных задач для стационарного одномерного уравнения Шре-
дингера. Это задачи об одномерном движении свободного электрона, о пря-
моугольной яме с бесконечными стенками, об одномерном прямоугольном
потенциальном барьере, о двойной прямоугольной потенциальной ямс.
Гл. 5 посвящена вопросам квантовой статистики системы свободных
электронов и выводу распределения Ферми-Дирака методом ячеек Больц-
мана.
В глР 6 на основе распределения Ферми Дирака изложена теория си-
стемы свободных электронов в металле, объясняющая линейный код теп-
лоёмкости металла при низких температурах. Классическая теория кри-
сталлической решётки Дебая для теплоемкости металла даст кубический
закон при низких температурах. Изложена квантовая теория термоэлек-
тронной эмиссии с поверхности металла Ричардсона-ДэшмаЕта п теория
Шоттки влияния на гсрноэмиссию приложенного к поверхности металла
внешнего электрического поля. Объяснена контактная разность потенциа-
лов при контакте двух металлов и теория термоэдс.
R гл. 7 подробно и полно изложена теория точно решаемой тради-
ционной в теории полупроводников одномерной модели Кронига-Пепин
для системы свободных электронов твердого тела, в рамках которой объ-
ясняются юмм структура спектра понятия
ВВЕДЕНИЕ
И
зяны и хжь? rtjJOffChJiufotwu, понятие «дыркиа — особого элемен-
тарного носителя электрического тока в твердотельном полупроводнике, во
всём подобного электрону, но в отличие от него положительно заряжен-
ному.
Наконец, в гл. 8, основной в этом пособии, излагается существующая
теория электропроводности собственных (чистых) и примесных (донорных
и акцепторных) полупроводников. Подробно рассматривается упрощенная
полу количественная теория Шокли рп-переходя± вычисляются контактная
разность потенциалов рп-перехода, зависимость ширины обеднённого слоя
рп-перехода от внешнего электрического поля и его электроёмкость. Изло-
жена теория рпр-транзнстора.
Глава I
Корпускулярно-волновой дуализм
фотонов
1.1. СтанонлепнС корпускулярных и ВОЛНОВЫХ
представлений о природе света
Наиболее фундаментальным свойством, которым обладают без исклю-
чения все микрочастицы, является их двоысшдояндя
лоя fl/wpodo.
Микрочастицами, или так называемыми элЁМешнаряылш wcwrwija.wu,
ЯВЛЯЮТСЯ фаГСГДАЫ* ЭЯЕКМртМЫ, ЧИСТ ИЦЫ, ИЗ КОТОрЫХ ПОСТрОСНЫ атОМНЫЁ
ядра — л/№тоны и нвлмролы, и еще порядка сотни открытых к настоящему
времени чдегощ.
Корпускулярно-волновой дуализм микрочастицы нужно сгони мать в том
смысле, что частицу нельзя представлять себе ни в виде «корпускулыу, г. е.,
скажем, шарика очень маленьких размеров, или даже в виде классической
материальной точки* ни в виде классической «волны», т.е. возмущения,
распространяющегося в непрерывной сплошной среде («корп» по-латыни —
тело, «корпускула» — маленькое тельце).
Микрочастица одновременно обладает н свойствами корпускулы,
отчетливо проявляющимися в одних экспериментах с ней, и свойствами
волны, столь же чётко проявляющимися в других экспериментах.
В одних экспериментах микрочастиц ведёт себя как корлуеяулд, т.с.
её действительно можно считать маленьким шариком или даже материаль-
ной точкой, в других же экспериментах она ведёт себя как волна, т.е. её
можно представить в виде возмущения, распространяющегося в сплошной
непрерывной среде.
Микрочастица является и корпускулой и волной одновременно.
Вместе с тем в любом (подчёркиваем — лю£шг) эксперименте мик-
рочастицу можно рассматривать и как корпускулу, и как
волну если гойяько физические величины, дгдрдятернзующив £в‘ исламе ?€ь-
с иечс/идасти (йрдортлывчнотаерты») или, как ^лвл-
1.1. Становление корпускулярных и волновых представлений 15
рят. зшКнвдёнеш ток шкывдёмызш Асяотиошенйялш
W£'O«/>£^£<7CM?f^Cffl£'Jf>.
Физические величины, характеризующне корпускулу, — это её эн^>
гш» г и и..нлут*е р. Физические величины, характеризующие волну, — это
частота f и йягша ешны А,
Элементарным объектом и оптике является сестон w иучок, в частно-
сти параллельный {ТС. не сходящийся И не расходящийся) монохроматиче-
ский световой пучок.
Сопгас но кор]iyc ку; ырным предстакie н ня и
монохроматический световой пучок является но-
током быстро летящих точечных чэстнп— г °-* о
нов, причём все эти частицы в пучке летят с одной г о—>
и той же одинаковой скоростью е — скоростью с ° >________________
света.
Согласно волновым представлениям моно-
хроматический световой пучок является волной, к А эк >. >1
г. е. возмущением, распространяющимся в непре- —--------------*—
рывнои среде — особой светоносной среде, кото-
рую называют «эфиром», и которой он рас пр о-
страиястоя со скоростью енота С-
Физическая природа света находилась в цен-
тре внимания физиков XVll-XIX в в Двойственная корпускулярно-волно-
вая его сущность осознавалась постепенно и с большим трудом в течение
трёх столетий, т.с. па протяжении леей истории современной Оптики (на-
чавшейся в первой половине XVII в. одновременно с появлением вообще
всей совремеЕнюй физики, т. е. с Галилея и Декарта).
Геометрическая оптика
Различают элементарную. или геометрическую, оптику и физическую
оптику. Физическая оптика занимается физической природой световых яв-
леиий. Она возникла во второй полошено XVII в. и связала с именами Дс-
карта, Ферма, Гюйгенса, Ньюте на. Геометрическая оптика не интересуется
физической природой света. Она появилась ещё в античные времена и дол-
гое время считалась лишь разделом геометрии («Начала» Евклида) или аст-
ро гюм н и («Альмагест» Птолемея),
Геометрическая оптика является лучей сяе/мя. Это главный
и единственный её объект. Основными законами геометрической оптики
являются следующие четыре закона относительно хода лучей света:
1) закон прямолинейного распространения луча света (в однородной
среде);
16
Глава l
2} закон независимости лучей светового лучка друг от друга:
3) закон отражения луча, падаю [цсго на поверхность (угол отражения
равен углу падения, причём падающий луч. отражённый луч и нормаль
к поверхности в точке падения луча лежат в одной плоскости);
4) закон преломления света (отношение синуса угла падения к синусу
утла преломления есть константа, пе за йлсян^я от утла падения, причём
падающий луч, преломлённый луч и нормаль в точке падения луча к по-
верхности раздела сред лежат в одной плоскости).
Закон отражения света был известен в древности. Закон преломления
света был открыт, однако, толью в первой половине XVII в. эксперимен-
тально Сне л л нусом (Снеллом) л 1621 г. Теоретически этот закон был объ-
яснён в 1637 г. Декартом на основе корпускулярных представлений о свете
в его «Ди 01 ггр и ке». С помощью закона преломления в «Д hoi пр и ке» Декарт-
да л первое правильное объяснение радуги
Закон прелом] гения света состоит в том, что
—= п
sin р
г. с. отношение синуса угла падения а к синусу угла
преломления J луча, падающего на границу раздела
двух прозрачных сред I и 2, есть величина постоян-
ная (не зависящая от величины угла падения а)т рав-
ным лякпзантслю преломления (более точно — лаадзлмлтю
лрешшшшня и среды 2 относительно среды 1 на рисунке).
Углом падения называется угол между падающим лучом и норма лью
к границе раздела сред, построенной в точке падения луча. Углом прелом-
ления называется угол между преломленным лучом и этой нормалью к гра-
нице раздела сред.
Декарт объяснил законы отражения и преломления света па основе
своей теории корпускул наличием силы, действующей на корпус пулу нз
границе раздела двух сред. Корпускулу он представил собе в виде малень-
кого шарика, налетающего на поверхность раздела сред, которую ин вооб-
разил себе в виде натянутой ткани. Корпускула либо отбрасывается этой
тканью, либо прорывает её и попадает во вторую среду, с другим направле-
нием и величиной скорости. Луч света при этом изменяет своё нанра1О1еггиен
преломляется поверхностью
Пусть ui и иа обозначают скорость света в первой и второй среде соот-
ветственно. Декарт учел, что сила, действующая на юрпускулу со стороны
ткани, в момент прорывания сю ткани перпендикулярна ткани, т. е. направ-
лена по нормали к поверхности ткани, и поэтому импульс корпускулы нс
1.1. Становление корпускулярных и волновых представлений 17
меняется вдоль ткани при переходе корпускулы из первой среды во вторую
в момент прорывания. Условие непрерывности тангенциальной компонен-
ты импульса при переходе корпускулы из первой среды во вторую имеет
вид
sin о = mt’a sin
где m — масса корпускулы, а и jt? — углы падения и преломления соответ-
ственно. Таким образом, следуя Декарту; получаем, что
sin _
йш/3 Г1 " ’
т. е. получается вдлхш ярйлол/леная. При этом показатель преломления та -
= vj/tfi (второй среды относительно первой) оказывается равным отноше-
нию скорости света во второй среде к скорости света в первой среде.
Обратное Отношение п — даёт воле юная теория света, как было
получено Гюйгенсом в его знаменитой работе «Трактат о свете» в XVIJ в.
Формальное объяснение законов отражения и преломления света пред-
ложил в 1662 г. Ферма с помощью [гроиозтиашенного им принципа саджей-
iwfiW л/деиелм лучд Агелк^у дяуия йлшшзш /ллчкя.иу, со-
гласно которому свет распространяется между двумя заданными точками
по пути, для прохождения которого ему требуется наименьшее время.
Ньютон и корпускулярная теория света
После ТОГО Как н XVII н. были чётко сформулированы корпускулярная
(Ньютоном) и волновая (Гуком и Гюйгенсом) теории света, в XV[Ц в. уста-
новилась и прочно укрепилась создателем
которой стали считать (по праву) Ньютона,
Учение и свете до Ньютона развивалось исключительно а форме гго-
.4/ew/?w46*£?koh оптики, i.e. теории прямолинейно распространяющихся лу-
чей света, изменяющих свои направления согласно законам отражения
н преломления на границах сред, Ньютон, как и Декарт до него, использо-
вал корпускулярную теорию света. Он пользовался ею всегда^ хотя порою
и с существенными оговорками.
Во второй половине XVII в. во времена Ньютона в физике еще су-
ществовала проблема объяснения явления цвднноелш световых лучей, т. с.
существования наряду С белым светом света различных ЦНСТОП, В то время
считалась правильной сохранившаяся с античных времен неверна я теория
цветов Аристотеля, объяснявшая цвета смешением «света» и «темноты»
в разных пропорциях-
1Й
Глава I
В 1666 г. Ньютон сделал свое знаменитое открытие о природе белого
света. Он направил на стеклянную призму пучок солнечного света, исходя-
щий из отверстия л ставтте, закрывавшем окно комнаты^ п которой он экспе-
риментировал, и разложил белый свет в спектр цветов «дожже-
лъен. задели. голубой, сшшй. г/>Уй7елаоАыи), а затем собрал этот
цветной спектр с помощью второй призмы снова в пучок белого света. Тем
самым Ньютон доказал, что цвета нс «вырабатываются» призмой, а «при-
сутствуют» в самом белом свете, призма лишь «сортирует» эти цвета.
Ньютон правильно объяснил свой опыт явлением дисперсии света раз-
ных длин волн и стекле призмы, т.е. н^каздтеля лретиж-
ния стекла нризчы от длины вдлны при этом длину волны отдель-
ного снегового луча Ньютон связал с его цветом.
Б качестве источника света Ньютон использовал Солнце. которое дол-
юс время и после Ньютона было практически единственным источникам
в оптических экспериментах физиков
Кроме дисперсии света, Ньютон оiкрыл также знаменитые «кольца
Ньютона» — одно из первых исследован пых н оптике
иых явдешш. Кольца Ньютон наблюдал в малой окрестности точки контак-
та ДЛИН]И)фокусной плоско-выпуклой ЛИНЗЫ, положенной выпуклой сторо-
ной на поверхность оптической плоскопараллельной пластинки (пластинки
с идеально плоскими параллельными поверхностями).
Под влиянием критики со стороны своего неусыпного оппонента Гу-
ка (в то время Учёною секретаря Королевского общества — Английской
академии наук), в отличие от Ньютона приверженца волновой теории све-
та, раскритиковавшего работу Ньютона о его кольцах, в которой Ньютон
объяснял кольца с позиций корпускулярной теории, Ньютон о физической
природе света в дальнейшем стал выражаться очень осторожно, нс отдавая
предпочтения (правда, только на словах) ни корпускулярной, ни волновой
теориям света, но оставаясь всё же твердо стоящим на позициях корпуску-
лярной теории.
Со световой корпускулой Ньютон сгсязылал некий «периодический
процесс» изменения ее состояния и развил особую «теорию приступов»,
или «припадков», испытываемых с периодом световых, колебаний световой
корпускулой, падающей на поверхность раздела двух сред, во время ко-
торых ина находится либо в состоянии «н&шхучшего прохождения», либо
«паилучшего отражения».
Чтобы объяснить явление интерференции, наблюдаемое им в его коль-
цах, Ньютон как раз н наделил корпускулу этим периодическим процес-
сом. Позже, чтобы объяснять эксперименты по двойному лучепреломлению
в нелзддском пшате, в которых проявлялась поляризация света, Ньютон
стал наделять корпускулу еще и «сторонами некоего квадрата».
1.1. Становление корпускулярных и волновых представлений 19
В ньютоновой теории света некоторые историки физики усматрива-
ют зародыш кнзегговой теории фотона с иго кпрпускулярнф-ВОЛНОВЫМ ду-
ализмом. Они утверждают, что у Ньютона было, хотя и не чёткое, но всё
же л/тейс/пайлеше о природе света — лчррлугкуты (частицы)
и ймны (колебательного возмущения, распространяющегося в непрерыв-
ной среде), которые аналогичны современным представлениям о фотонах,
распространяющихся согласно современной квантовой теории по путям,
которые предопределены связанными с ними волнами.
Как нам представляется, такое приписывание Ньютону понимания ос-
нов квантовой механики является преувеличенном. Представления Ньюто-
на о свете в целом были, конечно, еще очень далеки от современного пред-
ставления о фотонах.
Последователи и популяризаторы Ньютона (начиная с Гравесапда
в XVIЛ в.) объявили Ньютона безоговорочно детсутам mt’o-
/?цц приверженцем которой он действительно был.
И -этому не надо удивляться. Ведь представление о снеговых корпуску-
лах было в духе столь популярной в то время и успешно созданной именно
Ньютоном «небесной» механики, в которой Солнечная система (Солнце,
Земля с Луной и планеты с их спутниками) рассматривалась как сыстос-
жд ЛПтсрДЛ.ТМШХ точек, движущихся под действием открытых тоже Нью-
тоном сил йсЁЛшряозд жданлеяия, согласно его знаменитым трём законам
механики.
Успехи ньютоновской одссмчеслвй лёпншкы, изложенной нм в 1687 г.
в знаменитых «Математических принципах натуральной философии» (в ко-
торых он сформулировал также и основные принципы дифференциальною
и интегрального исчисления, открытого независимо от нею Лейбницем, —
математического аппарата классической механики), казалось бы, более чем
убедите лье го свидетельствовали, что не только Солнечная система, но и во-
обще все тепа природЕя представляют собой собрания материалыгых точек,
и что свойства тел следует объяснять исключительно взаимодействиями
между собой движущихся материальных точек, составляющих тела.
Философия ждтериольных лкгчек (так называемая «механистическая
философия») на целое столетие после Ньютона (в течение всего XVIII в.)
стала господствующей. Даже н самом конце XVIII -начале XIX вн., на-
пример, Лаплас в своей знаменитой пятитомной «Небесной механике»
(в которой впервые продемонстрировал блестящее количественное совпа-
дение теоретических предсказании ньютоновой механики Солнечной си-
стемы с точными результатами астрономических измерений движений и;га-
нег и спутников) даже явления поверхностного натяжении, капиллярности
и смачивания жидкостей успешно объяснял взаимодействиями притягива-
20
Глава l
ющих друг друга материальных точек (которыми он считал молекулы жид-
кости).
теория гее/иа
Авторитетное мнение Ньютона о корпускулярной пр ироде света задер-
жало, к сожалелию, развитие волновой теории свита на целое Столетие, котя
волновая теория И была ясно сформулирована уже в XVIЯ в. — в 167У I. —
Гюйгенсом и изложена им в его «Трактате о светел, вышедшем в 1690 г
Гюйгенс объяснил с позиций волновой теории на основе своего прин-
ципа Гюйгенса построения распространяющегося вот юного фронта с по-
ciроением вторичных волн и их огибающей нс только законы отражения
и преломления света в изотропных средах, не также и законы преломления
света в двоякопрелом лающих кристаллах (в исландском шпате), открытые
Ито время, в 1670 г. Бартони нусом (оптическое явления, когда при прелом-
лении возникает пс один, а два луча света).
Явление поляризации света, проявившееся в этих экспериментах с ис-
ландским шпатом, Пой гене, однако, понять не смог, так как считал световые
волны (как звуковые волны в воздухе), а нс иомречнмни (как
на самом деле).
Волновая теория света не могла быть в то время принята большин-
ством физиков, так как не была еще в состоянии объяснить факт /?рялю-
лынеиноемш распространения света, связанный с чрезвычайной малостью
длины световых волнт и образования снегом резких теней. Ведь никаких
теней звуковые полны по образуют, Они свободно огибают встречающиеся
на их пути препятствия. В то время ещё не было открыто, что оптические
волны имеют очень короткие длины волн порядка 0,1 мкм = 10“7 м, длины
же звуковых волн порядка 1 м-1 см.
Скорость звуковых волн в воздухе 300 м/с. Согласно соотношению
А у = с, где А — длина волнъц — частота волны, с — скорость распро-
странения волны, при с = 300 м/с и р = 100 Гц имеем X = 3 м и при
- 10.000 Гц имеем А = 3 см.
На смену юзрпускуляр! гой теории света, господствовавшей весь XVIИ а.г
с самого Егачала XIX в. пришла волновая теория^ развитая первоначалыго
как теория упругих волн в упругом твёрдом теле. Среда, способная пе-
редавать поперечные волны, должна была быть твёрдой (в газах и жид-
костях упругие звуковые волны только продольные, никаких поперечных
воли в газах и жидкостях нс существует). Твёрдым телом, в котором рас-
пространялись снеговые волны, считался гак называемый венетов осный
эфир», который должен был быть очень твёрдым (так как скорость света —
1.1. Становление корпускулярных и волновых представлений 21
с = 300 000 км/с — громадная). К тому же этот эфир не должен был ока-
зывать заметного сопротивления движущимся в нём телам (в частЕгости,
Земле и планетам* движущимся в межпланетном пространстве), что было
парадоксальным.
Вместе с тем упругая твёрдотельная теория света господствовала всю
первую половину XIX н., пока её не смени]га во второй половине XIX в,
правильная максвелловская электромагнитная теория.
Основы волновой теории света, как мы уже отметили, были заложены
ещё в конце XVII в. Гюйгенсом, в то время президентом Французской ака-
демии паук, и Гуком, современником и оппонентом Ньютона, бывшим де-
монстратором и Учёным секретарём Лондонского королеве кого общества.
J'eohj chc высказал свой знаменитый «принцип Гюйгенса» (о поегя/кеяпы
etbTHOtfoa? вдлны клк оги&погцвд фронтов
ГОДЯ /ЯйЧХНЛШ ф/мж-
mtf, е лсачент Гюйгенс с помощью
с вое] о принципа не только объяснил законы отражения и преломления све-
та, но также и намного более сложные законы двойного лучепреломления
света в кристаллах. В этом был особенный успех его теории.
Несмотря, однако, па эту замечательную работу Гюйгенса, как мы уже
сказали, весь XVIII в. волновая теория считалась неправильной, и в то
времня. безраздельно господствовала корпускулярная теория.
Вплоть до начала XIX в. известные физики и математики того време-
ни, такие как Лаплас, Пуассон, Био и др., принимали за истинную именно
корпус куля pi ryio теорию и ухитрялись с сё помощью объяснять известные
к тому времени интерференционные И дифракционные явления* впрочем,
как это делал и сам Ньютон.
Правнаh Эйлер, блестящий представитель математики и механики
XVIII вР1 придерживался волновой теории света.
С самого начала XIX в. й физической оптике произошла революция,
связанная с именами Юнга и Френеля, которые блестяще обосновали вол-
новую теорию световых явлении. В частности, Френель установил, что
световые волны являются нс продольными, а поперечными, в отличие от
звуковых воле] в воздухе, и впервые измерил длины световых волн.
На основе волновой кюрии Френель объяснил большое число экспери
ментов по интерференции, дифракции и поляризации света, большую часть
которых он сам поставил и провёл (его «бипризма», его «би'зеркала» и т. д.).
Создав простую, можно сказать, элементарную теорию «интерферен-
ционных полос», Френель показал* как из измерений расстояний между
этими полосами можно простым пересчётом определить длину А монохро-
матической световой волны.
22
Глава l
В середине XIX в. волновая теория света получила еще одно, казалось
бы, окончательное подтверждение. Около 1 Я50 г. ФиЗо и Фуко произвели
первые измерения скороеjи света в земных условиях (измерили скорость
света в воздухе и в воде, причём в воде она оказалась равной 3/4 скорости
света в воздухе, т. е. меньше, чем в воздухен в полном согласии с волновой
теорией, но и противоречии с корпускулярной теорией).
До этих экспериментов скорость света, равная с 300 (ИЮ км/с, бы-
ла измерена только путём Рёмером ещё в конце XVII в.
из наблюдений в течение земного года изменении интервалов между по-
следовательными затмениями одного из спутников Юпитера (те. момен-
тов, когда спутник, наблюдаемый с Зсмлит заходил за диск Юпитера, что
происходило каждые 1,5 суток). Второе, гоже измерение
скорости светя было произведено в XVIК в.* в 1728 г. Бродлеем (Брэдли) из
наблюдений так называемой «аберрации» звёзд (звёзды в течение года опи-
сывают на небе по отношению к другим звёздам очень маленькие эллип-
сы различного эксцентриситета в зависимости от величины полярного угла
звезды, размеры этих эллипсов определяются величиной скорости света).
В первой половине XVII в. еще Галилей пытался измерить скорость
света с помощью двух наблюдателей, снабжённых лампами и находящихся
на большом расстоянии друг от друга. Одене из наблюдателей должен был
открывать экран своей лампы, а другой фиксировать моменты появления
света у него и в свою очередь открывать экран своей лампы. При этом пер-
вый наблюдатель должен был измерять время между моментом открывания
ejm своей лампы и моментом появления света от лампы второго наблюдате-
ля. Зная это время п расстояние между наблюдателями, можно рассчитать
скорость света. Этот способ оказался, конечно* непригодным из-за громад-
ной величины скорости света.
В 1849 г. Фпзо экспериментально измерил скорость спета в воздухе,
применив метод быстро вращающегося диска с зубца мег по его окруж-
ности. Свет, падающий на диск, отсекался зубцом и распространялся до
удалённого зеркала, находящегося на большом расстоянии* отражался от
него и поступал снова на вращающийся диск через некоторое время. В тот
момент, когда диск по прошествии этою времени проворачивался точно на
один зубец, свет был виден. Таким образом, время распространения света
от вращающегося диска до зеркала и обратно было равным времени по-
ворота диска на один зубец. Это время Фиэо п измерил. Известным было
ему и расстояние между вращающимся зубчатым диском и зеркалом. Экс-
перимент Физе был усовершенствован и повторен в 1874 г. Корину Этим
методом было найдено значение скорости света в воздухе, равное 313 330-
313400 км/с, несколько завышенное значение.
1.1. Становление корпускулярных и волновых представлений 23
Фуко сходным методом вращающегося многогранною цилиндрическо-
го Зеркала получил значение 299ЭЮ± 50 км/с.
В XX н., в 1924 г. более точное определение скорости светя методом
Фуко произвёл Майкелъсон с вращающимся восьмигранным зеркалом и по-
лучил значение 299798 ± 30 км/с.
Фуко своим методом измерил также скорость света п воде и а п^?-
нам сса^лсwu с волйошш тео/ШЕЙ локвзат, что скорость евгтя « sodc не
больше, д лгеньгле cffu/jocmd ccremw е irojJyjre; корпускулярная теория света
предсказывала обратное соотношение.
На границе вакуума со средой, исходя из корпускулярных представле-
ний, закон преломления имеет вид
SU1Й и
sin/J с
где и — скорость света в среде, с — скорость света в вакууме. Исходя из
волновых представлений, он должен иметь вид
мп n _ с
sin /J '
Так как скорость света в воде г = (3/4} с, то показа гель преломления
боды согласно волполпи теории п — I : 3/г1 — 1.3, как зто и есть ees самом
деле.
Зная этот результат о различии показателей преломления в воде и в воз-
духе, ещё Гюйгенс просил датского астронома Рёмера (когда тот был в Па-
риже) измерить скорость света в пустоте и в среде. Но из-за больших Экспе-
риментальных трудностей ли измерения В ТО время провести НС удалось.
Таким образом, к середине XIX в. волновая теория света праздновала
свой триумф и считалась окончательно установленной правильной теорией
света.
ЭлектроуМйгнитняя сягмгд
Ещё более существенное подтверждение волновая теория света полу-
чила в 70-80-х гг. XIX в., когда была установлена элжт/эамлгчшллдя н/ч^ро
dfl csemtfWA Максвелл в его знаменитом «Трактате об электричестве
и магнетизме», появившемся в 1873 г.ъ сформулировал свои фундаменталь-
ные так называемые урдошшя Л/йксйаыя для электромагнитного поля, ко-
торые имели решения в виде волн («электромагнитных волн»). Эти волны
в 1887 г. экспериментально открыл Гери. Это радиоволны и телевизионные
ВОЛНЫ.
24
Глава l
Правда. ещё Фарадей в 1840-х гг., открывший в 1831 г. загон элект/w-
лга^лшпгмвй HHdvJUfMU И ЛКСПСрИМСЕЗТаЛЪЕП} установивший явление ^ращения
плоскости иатя/щзлции световой волны млгяшпньиг лолсае^ тс. до Макс-
велла, уже высказал гипотезу Егго световые волны являются электромаг-
нитными по своей физической природе, справедливость которой и доказал
Максвелл.
В 1860 г. Максвелл показал, что свет действительно можно рассмат-
ривать как электромагнитное явление. Монохроматическая световая вол-
на определенной длины волны Л является периолической электромагнит-
ной волной частоты и, которая характеризуется переменным электромаг-
нитным полем специального вида, т.с. кчаимодсйствуЕои;пми периодически
изменяющимися электрическим и магнитным полями с напряжённостями
E(t,zTy, г) и Н((, я, г) в точках пространства a?. j,; в моменты времени t
Теория Максвелла установила, что скорость электромагнитных волн
равна отпадению диной ситы т#го к ее зискгтростд-
пшчвсюй а в то время ужо было известно нз измерений с постоян-
ным электрическим током, что это отношение единиц равно 300000 км/с,
т. е. действительно равно скорости света.
Для электромагнитной теории Максвелла, как и для твёрдо тельной тео-
рии Френеля, нужен был эфир, по теперь нс мсклегичсский, а электромаг-
нитный, в котором имеются электрические и магнитные так называемые
токи смещения. Дело в том. что электромагнитные волны способны распро-
страняться не только в средах, а также и в пустоте, например в космическом
пространстве. Считали, что пустота заполнена эфиром.
Псриоднчсскпс электрические и магнитные возмущения, составил}*-
щие, по Максвеллу, суть электромагнитных волн, он назвал «токами сме-
щения». По представлениям Максвелла, эти токи существуют как в чистом
эфире, так и в диэлектрических (не способных ироводить электричество)
средах, но также в металлических средах, в очень тонких слоях вблизи по-
верхностей металлических тел.
Следует подчеркнуть, однако, что физическая природа электромагнит-
ного поля, а также электрических и магнитных возмущений электромагнит-
ного эфира, ещё до сих пор eic раскрыта. Это одна нз загадок современной
физики, впрочем, как и физическая природа электрического заряда.
После работ Максвелла оформилась электраийанцт/гоя тлэ-
cwma. получившая многочисленные подтверждения. Свет в видимой
области представляет собой электромагнитные полны с частотами коле-
баний г- 1015 Гц и соответственно с длинами воин порядка А —
10 ' м = 0.J мкм. Радиоволны и телевизионные волны имеют частоты
р = 105-10£| Гц и длины волн А = 2000 м-10 см.
1.1. Становление корпускулярных и волновых представлений 25
Существуют, кроме того, диапазоны «сверхдлинных волн», с длиной
и>лпы до ]() км, используемых для Связи с подводными лодками^ и «сан-
тиметровых» и «миллиметровых волн», используемых для космической
связи.
Электронная теория Лоренза
В своей твёрдотельной упругой теории света Френель представил себе
источник света в виде молекулы, атомы которой способны совершать гар-
монические колебания. Он считал, что колебания атомов передаются при-
мыкающим к ним частицам эфира, к, таким образом, от источника света
и пространстве начинает распространяться световая волна.
Так как теория Максвелла отождествила свет с Электромагнитными
волнами, то для их излучения необходимо было постулировать существо-
вание очень быстро колеблющихся «электрических вибраторов», или «ос-
цилляторов» атомных размеров.
Теорию таких вибраторов всю свою жизнь разрабатывал Лоренц, от-
стаивавший идею, что атомы и молекулы содержат н себе положительно
и отрицательно заряженные маленькие материальные частички «электро-
ны», имеющие одинаковые электрические заряды. Эти электроны, которые
сам Лоренц долгое время называл irywttw, по Лоренцу, находятся в равно-
весных положениях, но при смещениях п ачипают совершать гармонические
колебания под действием удерживающих их так называемых
содействующих на них со стороны положительных частиц, стремящихся
вернуть их обратно в положения равновесия. Электроны сам Лоренц долгое
время называл «нонами» (электроны были открыты в ]Я9б Г- Дж-Дж-Том-
соном).
Связанный, по Лоренцу, в молекуле атомЕгый электрон, совершающий
затухающие колебания, является источником световых, точнее, электромаг-
нитных возмущений. R то же время он может также и поглощать электро-
магнитные волны, которые надают на нею, если частота падающей на нею
электромагнитной волны равна частоте собственных колебаний электрона.
Электромагнитная теория Максвелла в соединении с электронной тео-
рией Лоренца образуют так называемую «микроскопическую» электроди-
намику, её отличают от собственной теории Максвелла, которую называют
«макроскоз 1 ичсс кой» электродитза м iпсой.
Кншпксжля теория светит
После более чем впечатляющих, можно сказать, блестящих успехов
вол[зовой :1лсктромапгнттзой теории света к концу XIX в. тем не менее на-
26
Глава l
копился экспериментальный материал, противоречащий классической вол-
не вой электромагнитной теории.
Проведённые в конце XIX в. эксперименты потребовали вернуться
к корпускулярной теории светя, хотя и на более высоком, совершенно но-
вом, уровне
В 1900 г., пытаясь разрешить трудности, возникшие 1гри объяснении
экспериментальной кривой спектральной интенсивности излучения абсо-
лютно черного тела, Планк выдвинул знаменитую гилдюезу
о «квантах», или об ы&издлшрлых энершщ монохроматической
световой волны, и тем самым заложил основы квантовой теории света н во-
обще всей квантовой физики, физики микромира.
Правда,. Планк неверно думал, что речь вдет об элементарных порциях
люгхщ энергии, считая, что энергия в природе, как лнтещг, как
с/яеи, встречается всегда только в виде некоторых нцрций.
Он представил себе энергию в виде некоей «субстанции» наподобие
массы тела или его электрического заряда и посчитал, что эта «энергети-
ческая» субстанция состоит из порций. Конечно, это неверное
представление.
Планк, однако,, правильно считал, что внутри замкнутой полости, те.
внутри пустого сосуда С непрозрачными стенками, электроны молекул сте-
нок совершают колебания, предположенные Лоренцем, и излучают внутрь
полости электромагнитные волны, причём, если стенки полости поддер-
живаются при некоторой постоянной температуре, внутри нее установится
pufltfflficf.v/oc и/ыуче/ше» свойства которого за-
висят толью от температуры.
Дни того чтобы описать «спектральную объёмную плотность энергии»
этого теплового равновесного излучения в полости, Планк предположил,
что молекулярные «вибраторы-осцилляторы» излучают энергию не непре-
рывист а как бы «взрывами», в каждом из которых они выбрасывают пор-
цию энергии. Так что излучение энергии, по ] [ланку, происходит «пакета-
ми»* или «квантами». Эти кванты перемещаются в пространстве без потерь
энергии.
В 1905-1907 пг. Эйнштейн существенно развил квантовую гипотезу
Планка. перенеся её на ряд других физических явлений, в частности на
в металлах, и теорию При этом
Эйнштейн воспользовался идеей Планка, применив сс к квантованию энер-
гии одномерного осциллятора, который Планк использовал как модель из-
лучающей атомной системы, взаимодействующей с окружающим её равно-
весным электромагнитны м излучением. Тем самым Эйнштейн oiказался от
планковских «квантов энергетической субстанции». Так, Эйнштейн вернул
1.2. Эксперименты по тепловому излучению
27
в оптику световые корпускулы, которые назвал «квантами света»; с 1926 г.
они стали называться «фотонами». Это частицы света, обладающие кван-
товым корнускупярно-винновым дуализмом.
В 1913 г. Fop существенно продвинулся в нолимании квантовой физи-
ки микромира. Ему удалось использовать теорию Планка для объяснения
спектра излучения атома водорода. Он вывел знаменитую се/шадьиуяз фор-
мулу для длин волн линий спектра излучения атома водорода,
исходя из двух своих квантовых постулатов, которая совпало с Эксперимен-
том с оптической точностью 5-6 значащих цифр.
Начиная с работы Бора квантовая теория атомных явлений оказалась
в центре внимания всех физиков и математиков того времени. Ими были
приложены неимоверные усилия в понимании физики микромира, кото-
рые запер шились в 1925 1926 гг. созданием квдн/идаой мятлика Шредин-
гера и Гейзенберга. Эти работы были успешно развиты Дираком и многими
другими физика ми в 1929-1930 it. Дирак, в частности, создал так называ-
емую «квантовую электродинамику», ставшую окончательной и более чем
успешной современной физической теорией света и оптических атомных
я олений, отдельные теоретические предсказания которой совпадают с экс-
периментом с точностью до 11-12 значащих цифр.
1.2. Эксперименты по тепловому излучению и по
излучению разреженных газов
Остановимся теперь подробно па двух экспериментальны к исследо-
ваниях, которые в конце XIX в. нс смогла объяснить классическая элек-
тромагнитная волновая теория с вега. Расскажем об экспериментах с т₽л-
ЛАвы.м излучением так называемого абсолютно чёрного тела и с излучени-
ем йбниатамяы.т разрьжеяиых еизое, возбуждённых, например, высокоча-
стотным электрическим разрядом и гак называемых «газоразрядных труб-
ках».
Экспериментально тепловое равновесное электромагнитное излучение
абсолютно черного теля создаётся с помощью олюе/тстия, от. г. дцртшш
лгдтых/?oiMcpoe й талляутдАг полой сосуде+ или «полости», стенки которой
поддерживаются при постоя иной тем г Герату ре Т-
ЛбсЕ^отно чёрное тело - лло тдкое1 идеальное которое логло-
u/аегсг й?ё' дода?оц#ее на его излучение.
Внутри полости за счет излучения и поглощения ее стенками электро-
магнитных волн устанавливается /мвловесшде дтсл.Еллое
имучгиис, незначительная часть которого через дырочку, показанную на
рисунке, выходит наружу и исследуется. Наличие маленькой дырочки не
влияет па свойства теплового излучения, имеющегося в полости.
2М
Глава l
Излучение от дырочки, идущее в заданном направлении, Егадо вырс-
затьа например. показанными на рисунке двумя диафрагмами и образо-
вать из него лдрамдеьнш лучск. Этот пучок следует направить, например,
в спектрограф или просто на призму, как показано на рисунке. Так мож-
но экспериментально исследовать «спектральный состав излучения», те,
распределение его интенсивности по различным частотами (удобнее поль-
зоваться не частотой г- = 1/7\ а так называемой «циклической частотой»
и = 3ir/T, где Г — период колебании излучения).
Количественно всё испускаемое дырочкой излучение полости характе-
ризуется так назвавасхон «испускэтельной способностью» дырочки Ь’ (от
англ, emission - испускание).
исл,уценной ес*ннш<ей ловг/ииостн гаелд а единицу бремени л# ™ лазмож-
ньм4 wflwjpaftiewfcjw при температуре излучающего тела, так что размерность
испускатсльной способности равна (emission — испускание)
ГЕЛ _ _ Вт
мй с м2
Иногда способность называют «энергетической све-
ти mocti.to», по мы нс будем пользоваться этим названием.
И спускаемое дырочкой излучение в заданном к дырочке направлении,
попадающее в виде параллельного пучка в спектрограф, характеризуется
«интенсивностью» I. Интенсивность параллельного пучка имеет размер-
кость
и = д* = вь
м с м
т. е. такую же размерность, как испускательная способность.
иучкд шзывдетел количеств эхф-
гнк. ирчкеодя^й! ч^^з единицу площадки, лослцтминйй
flyway, ярелге™.
1.2. Эксперименты по тепловому излучению
Испускагтельная способность дырочки Е (emission — испускание) и ин-
тенсивность вырезанная из пучка, попадающего на призму. связаны для
конкретной зкг пери ментальной установки простым соотношением
/ = fcE:
в котором fc — некоторый безразмерный коэффициент, являющийся «пара-
метром установки».
Ислускательная способность дырочки по различным направлениям
различна, По любому заданному направлению опа характеризуется ннтсЯ’
ибЦ'ЩСс" бйЖ>-
ж» деты d(l, построенный около этого направления
Пусть излучает площадка с нормалью пр
показанная на рисунке. Телесный угол dfl з на-
правлении fl, будем отсчитывать от осп (7г, на-
правленной по нормали п к площадке. Полярный
угол fl конического пучка, отсчитанный от нор-
мали п к площадке dS-\ изменяется от 0 до тг/2,
азимутальный угол этого направления изменя-
ется от 0 до 2^. Бесконечно малый телесный угол
равен
dfl = sin fl dfldy^
Ямнешдоюстоью коническогол>?члса изучения, нОгн/его
s fl, у?, нотыдеяягя количество ныучляиой едшшцвд
площади лдощадкы dS е гадский jraw fl: okow яапрааде-
иия fl, те. величина
/(fl,
Когда
/(fl, у?) - /|j GOsfl,
где /q — константа, не зависящая от fl, тогда излучатель с такой интен-
сивностью называется «косинусным излучателем». Далее мы покажем, что
дырочка и полости с равновесным тепловым электромагнитным излучени-
ем является косинусным нзлучлгелем.
Энергия, попущенная единицей площади площадки в единицу вре-
мени по всем направлениям fl, р, равна
2ir т/2
К = у dtp у ^5П1Й/(Й: ip),
о о
10
Глава l
Размерность интенсивности /(fl, р) равна
[Д0. V)J = ^ = Bl
-------------- М"
м с
т. е. такая же, как размерность интенсивности параллельного пучка 7.
СлЁК/н/шльиый <wwdfs излучения характеризуют так называемой «спек-
тральной интенсивностью» причём, но определению, /(cv)ciw - это
flow лдарой шнпенсыявдспш. я/гшго^яц/ояся лп шпнедвдкя частот лт li do
ц.1 + , при ЭТОМ
и?
'№ им- £= I -
О
Эксперименты с равновесным тепловым электромагнитным излучени-
ем, испускаемым дырочкой в полости, показывают, что его спектр имеет
вил, отображенный на рисунке,
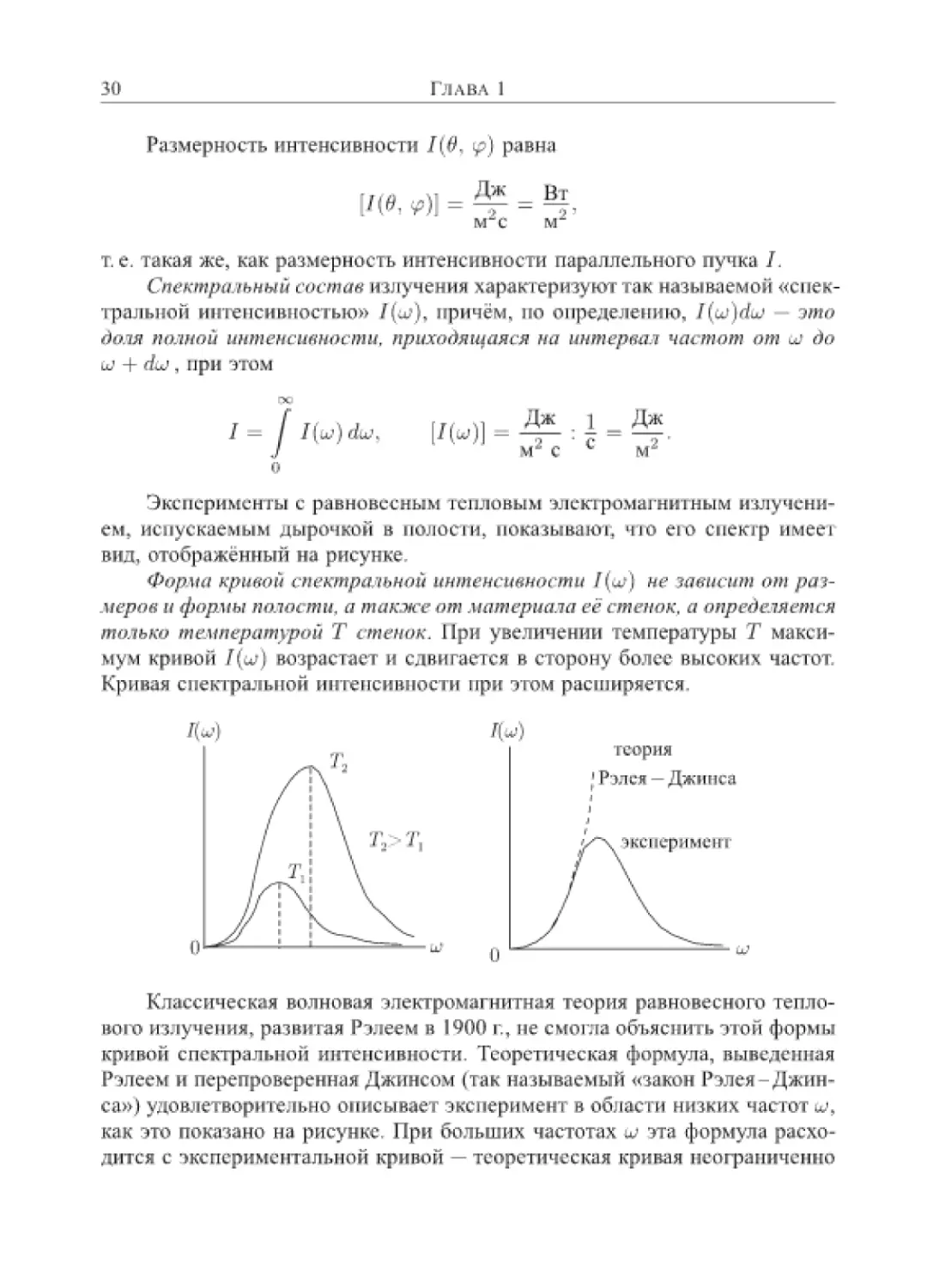
tfopw CTCJcmpflw^ow интенсивности 7 (иг) нс зданент гнн /тз-
-ijcpos и ^.ны лолости, л тдАлссот лглтернлял вёстагнон, а онртйелястся
лгатька Т При увеличении температуры Г макси-
мум кривой 7(w) возрастает и сдвигается в сторону более высоких частот.
Кривая спектральной интенсивности при этом расширяется.
Классическая волновая электромагнитная теория равновесного тепло-
вого излучения, развитая Рэлеем и 1900 г., ле смогла объяснить этой формы
кривой Спектральной интемсивнести- Теоретическая формула, выведенная
Рэлеем и перепроверенная Джинсом (так называемый «закон Рэлея-Джин-
са») удовлетворительно описывает эксперимент в области низких частота,
как эго показано на рисунке. При больших частотах и эта формула расхо-
дится с ->кс пери мепталъ пой кривой — теоретически я кривая неограниченно
1.2. Эксперименты по тепловому излучению
3]
возрастает по квадратичному закону по частоте и* а экспериментальная до-
стигает максимума л затем бистро уменьшается до нуля.
Расхождение с экспериментом классической теории Рэлея получило
название «ультрафиолетовой катастрофы».
Классическая электромагнитная теория света столкнулась также с труд-
ностями объяснения излучения, испускаемого возбуждёнными одноатом-
ными газами.
Для того чтобы исследовать излучение разреженного одноатомного га-
за, надо взять газоразрядную трубку, наполненную этим газом* например
недородом пли парами ртути, и подключить электроды этой трубки, ска-
жем, к высокочастотному генератору. В трубке тогда возникнет так называ-
емый «высокочастотный разряд», и газ в ней начнёт светиться
Изучать испускаемое трубкой излучение тоже нужно с помощью спек-
трального прибора или просто призмы* предварительно вырезав из излуче-
ния параллельный световом пучок, например, с помощью двух диафрагм.
Излучение газоразрядной трубки можно величествен по характеризовать,
как и тепловое излучение, с помощью полной интенсивности J и спек-
тральной интенсивности /(ш)* причём
ТС
О
Оказывается, экспериментальная кривая /(иг) опеюнральной интенсив-
ности но зависит от плотности газа в трубке ы его теилерат^ры и имо-
.ж'ст ооъяоияться как эффект». происходящий от осрокно-
го числа неглвиса.иых актов излучения иггов световых ^телтролгагвитных
во.тп. фот гигов отдельны, шг атаиа.ии газа.
32
Глава l
Яо к/швды £?уи|всиввнно зависит от хилшчесдои лри/к^ы <ч>-
лоаталглогл гд.та.
Спектры всех одноатомных газов имеют сходную структуру О hie со-
стоят из характерных «серий» очень узких «пинков» интенсивности, назы-
ваемых «линиями» или слект/га.тьны1«и линиями. Поэтому спектры одно-
атомных газов называются «линейчатыми».
Спектры молекулярных газов, например паров воды, углекислого га-
за, азота, кислорода, выглядят иначе. Они состоят из небольшого числа
характерных «полос», имеющих «тонкую структуру», это так называемые
«полосатые» спектры.
Каждая серия Спектральных линий атомного спектра начинается со
стороны низких частот с интенсивной первой самой низкочастотной линии
а этой серии, так называемой «головной линии». За ней в сторону высо-
ких частот идут остальные линии этой серии, частотные расстояния между
которыми быстро уменьшаются и интенсивности которых становятся всё
слабее и слабее. Обычно наблюдаются в серии 4—5 линий. В отчётливо на-
блюдаемых сериях, однако, (с помощью спектральных приборов высокой
разрешающей силы) можно различить до десятка и даже двух-трех десят-
ков линии и серии. Наконец, при некоторой частоте линии серии кончают-
ся небольшим участком слабого непрерывною свечения с резким краем со
стороны низких частот и расплывчатым краем в сторону высоких частот
(участком так называемого «непрерывного спектра»).
Спектр одноатомного газа, как правило, имеет несколько серий,
причём обычно они частично перекрываются друг с другом, г. с. распо-
лагаются н одной и той же области частот
Набор частот линий в спектре одноатомного газа данного химическо-
го элемента является его ииднвмй^тьиййха^аАте/?ис7яиК£>й, можно сказать,
«паспортом», по которой, произведя спектральный анализ, можно устано-
вить наличие даже самой незначительной примеси данного химического
элемента в газовой смеси.
1.2. Эксперименты по тепловому излучению
33
Спектральный анализ излучений газообразных веществ или паров ве-
ществ валяется важным методом определения химического состава веще-
ства.
Гак как атомы Солнца и звёзд в точности такие же, как атомы на Зем-
лей то изучая спектры излучений Солнца и звёзд, можно определить их
химический состав.
Эксперименты показывают^ что отдельные линии в спектральных се-
риях находятся по частотам на расстояниях, подчиняющихся простым мате-
матическим, скорее, арифметическим закономерностям. Расшифровка этих
закономерностей, однако, очень долго не поддавалась усилиям классиче-
ской физики, п рамках которой опа Еюнозможпа.
Изучение закономерностей атомных спектров в конечном счёте приве-
ло к открытию строения атомов и молекул (состоящих из атомных ядер,
вокруг которых вращаются электроны).
Согласно классической электромагнитной теории излучающий атом
следует уподобить элскгромаз нигной рлйио- или /мелелизнотнши
Спектр излучения атома должен бы быть поэтому таким же, как у антенны,
т. е. состоять из одной единственной частоты («линии»).
Антеина представляет собой металлическую конструкцию, и активном
элементе которой возбуждается переменный электрический ток очень высо-
кой частоты w к 105-10fl Гц. Согласно законам классической электродина-
мики проводник с высокочастотным током излучает электромагнитные вол-
ны в окружающее пространство. Эти волны являются носителями радио-
11 телевизионных Сигналов. При этом излучение антенны тем интенсивнее,
чем выше частота питающею антенну пока, так как, согласно классиче-
ской электромагнитной ItOpHH, ПЛтеЛСПЙЛОСте
четкие™ чле/н^лы.
Поэтому, для того чтобы обеспечить достаточно высокую интенсив-
ность излучения антенны, приходится использовать токи высоком частоты:
ш й 10М09 Гц.
Радиоантенна излучает некоторую «несущую» высокую частоту u/g, ко-
торая «модулируется» тем или иным способом информационным сигналом.
Спектр антенны представляет собой поэтому узкий мощный «пик» очень
сложной формы на частоте (несущей частоте радиостанции).
Из-за технических несовершенств, однако, излучение антенны, как
правило, имеет ещё и очень слабую «вторую гармонику» на частоте 2и>о,
а иногда и совсем дохлые третью и более высокие гармоники. Для работы
радиостанции эти гармоники несущественны, они «паразитныс».
На рисунке приведена спектральная интенсивность излучения ра-
диоантенны. Как видим, она нс такая, как спектральная интенсивность 7(w)
J'Л Л ВЛ ]
излучения разреженного одноатомного газа, о которой мы только что рас-
сказали.
вторая
гармоника
JA___L
и = lof-io” Гц
1.3. Вывод формулы Планка для равновесного теплового
э j гек грим а гн ит ного излучен ия
Как мы уже сказали, классическая физика нс смогла объяснить экспс-
рименты по равновесному тепловому электромагнитному излучению. Что-
бы их понять* потребовалось обратиться к квантовым представлениям* что
успешно и сделал Планк в 1900 г., который ввёл в физику квантовую посто-
янную Планка Й* характеризующую величину неделимо!i порции энергии
t = ftw кванта молояроматлческой электромагнитной ВОЛНЫ частоты L*J МЛН
сс фотона.
Ниже мы расскажем, в чём состояла проблема объяснения законов рав-
новесного теплового электромагнитного излучения, как сё пытались без-
успешно решить с позиций классической физики («формула Рэлея -Джин-
са») и как блестяще с ней справился Пл инк («формула Планка»), который
первым ввел В науку КванЮВЫЁ ПреДСТЯВЛСнИЯ.
Вывод формулы Планка мы дадим не нс Планку, а по Дебаю, который
в 1912 г предложил излагаемый здесь сё вывод.
Afewtot) Фьрье w ермртк/зииия -иод
Объясним, что такое «мода» излучения, на примере колебаний натя-
нутой струны. Пусть имеем струну длины L с закреплёнными концами,
которая может быть возмущена таким способом, что будет совершать коле-
бания только в плоскости рисунка. Будем считать, что форм^ струны в мо-
мент времени й характеризуется функцией и(й, х). Эта функция такова, что
1.3. Вывод формулы Планка
35
во все моменты времени удовлетворяет г/шничяьш
которые вс вес моменты времени выполняются на концах рассматриваемой
закреплённой струны.
Функция и(Л х) не произвольная.
Она удовлетворяет так называемому У
1 Эац _ й2и __
с2 dt2 дх2' Z*^\
----------------------------------------- -------X----------------- ЭР
в котором с — скорость распространи °
пня возмущения вдоль струни.
Струну можно возбудить пс-равному,
задавая в начальный момент f. — 0 раз-
ные формы струны к различные начальные скорости сё точек, т. с. полагая,
что функция u(t, :т) удовлетворяет
«(О, х) = цр(ж), ^(0: ж) = Ф(х),
в которых ^(я) и <£(х) — некоторые заданные функции.
Можно строго доказать следующую теорему существования и един-
ственности: решение
jrpfrscdfwwfar.ij гршшчмьглг w начальным усложняй, сухч^тляуетл w
eewHtr
Рассмотрим теперь множество всех решений волновою уравнения, ко-
торые удовлетворяют приведённым граничным условиям, по различным на-
чальным условиям, при различных функциях и ^(я).
Оказывается, любое такое решение можно представить в виде беско-
нечной суммы (суперпозиции) некоторых стандартных частных решений,
называемых «модами».
Метод суперпозиции мод необычайно важен в физике. Он ведёт своё
начало от знаменитою мемуара Фурье «Теории тепла» (1H2S г.) и носит
название «метода разделения переменных».
Частное модовое решение х), согласно Фурье, будем искать в виде
произведения двух функций одной переменной:
u(i, я) = T(t) Х[т)?
36 Глава ]
где T(t) — функция только времени t, Х(ж) — функция только координа-
ты Т-
Подставив Э1у функцию в нонновое уравнение, получим равенство
и, следуя Фурье, разделим правую и левую части его на произведение ТХ;
тогда получим еще одно равенство:
J_22 = х^
с2 Г X
В левую часть этого последнего равенства входит функция, зависящая
только от t, а в правую часть — зависящая только от я. Фурье учёл, что
при независимо изменяющихся переменных f и т равенство
л/отяг выполняться лаптько в waw случдг. если ы лсш, w лрлям его членти
uydym равны ллажжнжш (одной и той же). Так, из одного единственного
уравнения, согласно Фурье, получаем два уравнения:
или
здесь мы л/м?^лола?оаи+ что постоя иная в методе разделения равна — г. с.
что она действительная и отрицательная.
Потребуем теперь, следуя Фурье, чтобы частное «модовое» решение
u(tj т) = Г(4) Х(х) удовлетворяло сформулированным граничным усло-
виям на концах Струны. Очевидно^ ОНИ будут удовлетворены, если будут
выполнены условия
Х(0) = 0, Х(£) = 0.
Общее решение уравнения
X" + k"X =0
содержит две независимые произвольные постоянны? интегрирования >4
и В и имеет вид
Х(л) = .4 sin(A’jc) + В соя (А .г).
13. Вывод формулы Планка
37
Чтобы найти значения констант А и В, воспользуемся приведенными
граничными условиями, выполняющимися на концах струны. При ас = П
имеем условие Х(0) = 0; следовательно,
Х(0) = А 0 + Я 1 = 0, В = О
При я = Z имеем условие X(L) = 0; учитывал, что F = 0, получаем
из него условие
Х{£) - A sin(fcb) = 0.
Этому последнему условию нельзя удовлетворить требованием А —
- 0, так как при /1 - 0, £? — 0 будем иметь тривиальное, не интересное
нам решение А"(я) = 0. Поэтому потребуем, чтобы sm(feL) = 0. Получаем
тогда условие на значение константы разделения Аг (которую без ограни-
чения общности мы посчитаем действительной и положительной). Таким
образом,
* = *п = Пп
где п — 1,2.....Имеем; следовательно, бесконечный набор функции
Xrt(i) = A„sin f т
при п = 1.2....
Теперь для любого — fc>t построим решение уравнения для функции
T(t\.
т" + ^гт = а..
в котором cv = cfeT причём w = = cfcn. Это дифференциальное уравне-
ние для гармонических колебаний, общее решение которого можно пред-
ставить в виде
Т(£) = С сов (ш t — </?),
где С — амплитуда и^ — фактически, начальная фаза. Так как С сов(ш С —
— </>) — С ecs^i co&cvt + <? sin sin^vi, то имеем линейную комбинацию
= А совшй + В sin^Z где А = (7 совр, В = С sin^-. Значения
констант С и у? можно найти из начальных условий, которые мы считаем
сейчас, однако, нам нс заданными, так что значения констант С и пока
произвольные.
ЗЙ
Глава l
Таким образом, мы построили бесконечное множество модовых част-
ных решении нашего одномерного водно вот уравнения с рассматриваемы-
ми граничными условиями:
«п(£, ят) = Сл oos(yjnt - [/?) sin
где n = 1, 2,.. и С7П, — произвольные постоянные.
Можно строго доказать, что любое нетривиальное решение «(t, дс) од-
номерного полно вот уравнения
1 <~Я п _
с3 3t2 Зя2 ’
удовлетворяющее граничным условиям
я)| =0. ji(t, х)| =0,
Is о т«£
может быть однозначно представлено в виде суперпозиции, вообще говоря,
бесконечного числа найденных мод:
u(t, т) = ^n(t? х);
каждое решение описывает некоторое определенное колебание струны с за-
крепленными концами.
Физический смысл найденных модовых решений очень простой. Они
описывают так называемые «стоячие волны» для нашей струЕгы, первые
три из которых проиллюстрированы на приводимом рисунке.
— 1
л= 3
Стоячие воины имеют «пучности» и «утлы» Узды — это те точки стру-
ны, которые не колеблются, т е. в которых колеблющаяся стоячая волна во
вес моменты времени имеет нулевую амплитуду колебаний, Волна при п =
= 1 имеет одну пучность, при та = 2 имеет две пучности и один узел
посредине струны, при та = 3 волна имеет два узла и три пучности.
Константа имеет физический смысл «волнового числа» моды, свя-
занного с длиной стоячей волны соотношением Хп = 2тгДл. Условие
fcn £ = -.т та для моды означает, что
та
1.3. Вывод формулы Планка
39
т е. означает условие, что е слгйччеа яодне нд длине слнруны укладывается
рОЙМО ЧИСЛО ИДЯу^ЛТМ.
Угловая частота колебаний струны, в которой возбуждена стоячая вол-
на или мода с номером п, равна
Сна разная для различных мод и тем выше, чем больше номер моды
Зоемиде
Модовое решение
un(i, = Сп cos(u?n t - <pn) sin
можно представить в виде
^u(ti - 2
wn t + V я - уч
Слагаемые в квадратных скобках представляют собой так называе-
мые «бегущие волны», распространяющиеся в положительном направле-
нии оси д? (второе слагаемое) и отрицательном направлении оси я; (первое
слагаемое).
Таким образом, стоячую волну можно рассматривать как суперпози-
цию двух распространяющихся навстречу друг другу бегущих волн.
Можно перейти к комплексным числам и записать
s) = Т сп [e‘(u"t+t" - ei{w" -
। __ £> “'Ч. Ь1г'и !* “ ^тг
где fcn = (тг/L) п и и = 1,2,3= - - - -
в купи чёткъш полости
Представим себе теперь, ЧТО произволЫIOC злсктромагнитнос ИЗЛуЧС-
нпе (не обязательно равновесное) находится в макроскопической кубиче-
ской полости, показанной на рисунке, со стороной куба L, так что объём
кубической полости V = IA Электромагнитное излучение в полости яв-
ляется Сложным Электромагнитным полом., которое будем характер изо вить,
однако, в каждой точке аг. у, z полости в каждый момен т времени t скаляр-
ной функцией у, з. L), которая называется вегшинш ^n-7/л-иис'й.
40
Глава l
Правильно было бы, конечно, харак-
теризовать электро магнитЕюс поле дву-
мя векторными функция ми Е(зг1 у, z, f)
и Н(аг, у, z, i), т. е. его электрической
и магнитной напряжённостями, но этого,
однако, здесь мы делать не будем, чтобы
у J фОСТИТ Ь ра С Смитрсни 0.
Волновая функция и(я, у, г, 0 не
произвольная, а удовлетворяет волново-
му уравнению
1 6>2U _ d2u ,
с2 dt2 дх2 ду2 дг2'
п котором константа с имеет размерность скорости [с] = м/с и яаляется
скоростью распространения элепромапппных волн в пустоте
Подчеркнём, что сейчас мы рассматриваем произвольное электромаг-
нитное излучение, имеющееся в нашей полости, изменяющееся с течением
времени.
Предположим теперь, что Стенки полости непроницаемы, г. ft. что элек-
тромагнитное излучение не может выйти за пределы полости. Потребуем
поэтому, чтобы на стенках полости (на поверхности S куба, показанного
на рисунке) волновая функция и (я, у, с, () во все моменты времени С была
равна нулик
«15 = о
Электромагнитное поле в полости является решением приведённого
волнового уравнения, удовлетворяющим указанному граничному условию,
а также начальным условиям
и| = у, ?), ^1 = у, х),
1( = Л УГ lt=0
в которых , (г, г) и 0, г) - некоторые заданные функции.
Начальные условия, однако, для нас сейчас Ете важны, и рассматривать
мы и к пс будем, хотя только при определённых граничных и начальных
условиях справедлива теорема существования и единственности для реше-
ния волнового уравнения.
Для того чтобы математически описать произвольное электромагнит-
ное поле в полости, удовлетворяющее задан ным грани четьем условиям,
1.3. Вывод формулы Планка
4]
представим его в виде суперпозиции бесконечного набора собственных
электрсшагннтЕГЫХ мод.
Собстееяяая злеюпраиагмытмая .ufftta — это частное, слегршлыюШ
saddf решение йоляййоги урдйнйиша, уч)овс-?е?пе^ящи{ее г/домичны.п уоивня.и.
Таким образом, представим электромагнитное излучение в полости
в виде суммы стандартных электромагнитных полей (мод) данной куби-
ческой полости с данными нулевыми граничными условиями:
ц(х; у, z, i) = 22 “e(®i У- z' О'
tl
Это разложение является обобщением обычного ряда Фурье? представ-
ляющего произвольную периодическую функции? одной П$рСМСЕП[ОЙ в виде
рада но косинусам н синусам.
Найдём вид мод. Функция моды удовлетворяет волновому уравнению
1
с2 Si2
-- Д-^Т!
и граничному условию
tin — 0.
Учтём теперь, что волновая функция моды имеет очень специальный
вид.
Следуя Фурье, функцию моды построим методом разделения перемен-
ных, т.е. предположим, что функция tin(ar, у. £f i) имеет следующий вид:
т.е. будем считать, что ил являемся я/^изййдййиел! четырёх фуяк-
цнн однеш nepewewoif.. каждая wj которых здвмеит только ом свое-
го аргумента. Разумеется, произвольную функцию четырёх переменных
и (я, у, 2, О нельзя представить в таком специальном виде.
Подставим теперь функцию uft специального вида в волновое уравне-
ние и получим следующее соотношение;
= 0.
в котором два штриха обозначают вторую производную соответствующей
функции пФ сс аргументу.
Глава l
Фурье предложил разделить это соотношение на произведение ТХУ2.
Так Он получил знаменитое равенство
с2 Г X Г Z
которое имеет вид
6(t) + ct(r)+ /?({/) +7(j) = 0.
где ft. jtJ. 5 — функции, зависящие от указанных аргументов.
Получив такое равенство, Фурье справедливо заметил, что ячо аъ/ддт-
шкгтся то,тьио я mr?.w случае. кд.хтЗм uj четырех функции яятл^тсл
Асшсдойммон, тал- кик TJ/T зависит талью от tP ы Ун/У. Z'r//Z
меиеят от х.у, х соответственно.
Так, из одного скалярного равенства Фурье получил четыре равенства:
мы ввели здесь удобные обозначения для четырех констант, которые счи-
таем дей^твитЁЛь/гылш и отрицатель ны.ии (оправданием этому предполо-
жению будет построенное нами решение). Очевидно, введенные константы
удовлетворяют соотношению
к2 = к2 + । к2.
Таким образом > указанные равенства являются следующими четырьмя
л и ф фсрс] । циалы 1ыын ура ей <е । сия м и:
г А' = °, ^-Т - У = 0. ^4 - *1 Z = 0.
<iz2 1 dy2 dzs
в первом из которых ш = е к.
Чтобы обеспечить удовлетворение граничного условия и„|$ = 0 для
функции вида и = ТХ¥ Z, потребуем выполнения следующих граничных
условий, налагаемых на функции X, Y, Z :
Л” =Х1 =0, У =У =0, Z\ =Z\ =0.
jc;
у=о
y=L
13. Вывод формулы Планка
43
Так как процедуры определения функций Х,У, Z совершенно одина-
ковы, рассмотрим подробно процедуру построения только функции А'.
Уравнение для функции А имеет следующий вид:
^4 + X = 0;
это линейное ^нф^ереящ^яльное irptffiweuwe второго лодядкд
< иоелгояниыими Оно является дифференциальным урав-
нением гарионических колебании.
Общее его решение можно записать в пиле произвольной линейной
комбинации двух фундаментальных решении:
X = Л sin(fcj: я) -I В cos(fcjt я),
где Л. В — произвольные постоянные интегрирования. Общее решение
дифференциального уравнения второго порядка содержит две произволь-
ные постоянные
Найдём теперь значения постоянных Л. В, потреби вив выполнения
1раничных условий
Из первого условия сразу получим, что
Х(0) = В = О,
т. с. Я — 0. Полета вив теперь функцию X — Л sinl'A^T) во второе грапич
ное условие, получим равенство
X(L) = A sin(fcffL) = 0.
Если удовлетворить этому равенству условием А = 0 (что возмож-
но), то придём к неинтересному для нас тождественно ну-
левому решению волнового уравнения и = 0. Птребуем поэтому, чтобы
stnffcj. Z) = 0, те чтобы выполнялось соотношение
= ЯП»,
в котором пт — целое число 0, 1.2....Отрицательные пг рассматривать
не надо, так как при замене на -пя. константа fcs изменяется на констан-
ту —A:J:? a sin(—Лтзг) = — &in(fcj:T), т. с. отрицательные ис дают новых
4-1
Глава l
решений. Нулевое целое число п:С = 0 дает тождественно равное нулю
решение.
Таким образом, мы построили бесконечный набор функций:
Хн(х) = sinffcn- л),
в котором Аг = 1к-/£)пг и 71х = 0. 1Л 2.Константу А мы пока опусти-
ли.
Аналогично решаются задачи для определения функций У и и мы
получаем следующие бесконечные наборы функций:
^ц(у) = *in(fc¥ у), ^n(z) = sin(Az 2},
в которых = (л/L) = (ir/L) и п£ = 0, 1.2,3.........
Обратимся теперь к четвёртому уравнению для функции Т. Эта функ-
ция удовлетворяет уравнению
А Г2 _
с2 Г
илм уравнении)
+ш3Т = 0.
dts
в которое мы ввели константу се = Ас, причем
Р = ^. + ^-^ = ^(п2-п2-п2),
£
Таким образом, константа w нс произвольная, а принимает значения
(4) = Wjl = с у 4- nJ + nj,
считаем, что — ноложитепьиое.
Общее решение уравнения для Т± таким образом, имеет вид
7 = (7П cos(tdn t -
здесь мы ввели удобнее сокращённое обозначение дли комбинированно-
го индекса п = (пд;? npj п±). Общее решение содержит две произвольные
13. Вывод формулы Планка
45
постоянные Сп и как н должно быть, так как мы рассматриваем обык-
новенное дифференциальной уравнение второго порядка.
Итак, мы построили бесконечный набор частных решений — мод —
для описания произвольного электромагнитного поля в нашей кубической
полости:
Ittl (1, у, 2, I) = C,i cos(ww I - Ри) X
х sin I у п;С х ) sin [ у nv у ] sin [ у пг z |,
\ £т' / \ £/ } \ У
где собственные частоты находятся ret соотношения
WTl = С fcjj +^2 = +Ti2 + rl2;
и где С,г характеризуют амплитуды и >’Г[ начальные фазы мод.
Условия Борна-Кармана
Выше мы использовали нулевые граничные условия u|s = 0, выстав
лепные па стенках кубической полости, н получили в качестве мод стоячие
В0ЛНЫ.
Однако, можно было бы в качестве мод полости использовать бегу-
щие волны. Для этого надо искусственно продолжить нашу кубическую
полость параллельными переносами её вдоль осей я?1 z на все беско-
нечное трёхмерное пространство и рассмотреть новые волновые функции
u(ij z, £), теперь заданные ВО всём Трёхмерном ироеправствс, которые
удовлетворяют искусственным так называемым граничным «условиям Бор-
на-Кармана»:
ti(.T 4 £, у, Z, t) = j/т z, t)f
#+ £, Z, t) = u(et Z, t).
и(я, yh z -I L. t) = у, z, t),
где £ — длина ребра куба нашей кубической полости объёма V; т.е. будем
рассматривать функции jr, z) по ж. z с периодом L.
Теперь в методе Фурье ₽ качестве решения уравнения
+ X г- 0.
Глава l
рассматриваемого в бесконечной области -ос < я < +ос, следует взять
решение
X = Acik'*
где Л — произвольная каиял?ксябгл постоянная^ причем е силу условия Бор-
на-Кармана
I = 2™я, Ья = п*;
J
обратите внимание на появившийся здесь множитель 2. Кроме того, теперь
= И-, ±1? ±2? ....
Таким образом, дни волновых функций мод В полис™ мы получаем
следующие формулы;
У п t) = Сп С *" ’{^П-Г)
В которых Г = (зг^ у, z), krt = (2тг/£-)(пт, п.^. П--)я GL.‘TL == С |krt|t с — скорость
электромагнитных волн в пустоте; частоты волн всегда положительные.
Рдсяредеяемие AfoJ л с* чяедштял;
Совокупность всех мод электромагнитного ноля н кубической полости
можно наглядно представить себе следующим образом Рассмотрим вооб-
ражаемое так называемое «к-пространство», декартовыми осями которого
являются fc^, fcyj причем возьмём только главный октант этого про-
странства (т.е. предположим, что fcT 0, О, fc? 0), изображённый
на правом рисунке. Пространство это называется «пространством волновых
векюров моды??.
Отмстим в k-лространствс точки с координатами = (тг/Ь);^, fc* =
= Они находятся в узлах простой кубической
решетки, элементарную ячейку которой мы изобразили на рисунке. Объём
этой элементарной ячейки равен (эг/Z)3 = ?r4/Vs где V — объём полости.
Этот объём элементарной ячейки не имеет размерности м3, так как мы
рассматриваем не обычное, а к-пространсгво.
Подсчитаем теперь число л<о4 преходящихся из яеколдедын данный
л<агг/№скалнчес№ б^сяоп^чил лдоьгы интервал члеи от tv 4- dw, Задать щ
или задать fc = |к| — это одно и то же, так как эти величины связаны
соотношением w = ok.
Поступим следующим образом. Построим в к-лространствс сферу ра-
диуса fc = tj/c с центром л начале координат и стцё Одну сферу немного
1.3. Вывод формулы Планка
47
большего радиуса fc + dfc = и/с + du/c. Здесь fe = и/с и dfc = du/e, где а?
и ttv характеристики рассмзгрнваемо1т> интервала частоту, и + du.
Число мод, приходящихся на йесконечил лгдлыл ин-
тервал частот и, и + du, можно найти, разделив объём 1/8 части шаровою
слоя IV. и + dud, изображённого на рисунке, на объём оде гой элементарной
ячейки тг3/К. Берём 1/8, так как fc^, принимают только положитель-
ные или нулевые значения, г. е. находятся в 1/8 пространства, или и первом
его октанте.
Гак как число мод в рассматриваемом шаровом слое
йодюдешо шик и пропорционально Л1лкросяолич££вд бвеконечмa-Ttzuy
du, то обозначим это число мод как V Z(u)du (по-немец. Zabl - число),
где Z(u) du — число мод. приходящихся на единицу объема полости. Таким
образом,
7 Z(u) duj = j 4тг k'2dk
л V
I j _ U2 du V — т/ U2
8 " с2 с тэ ЗтгМ
du.
В полученную формулу следует внести важное исправление. Электро-
магнитные волны не продольные, а поперечные (имеют «поляризацию»).
Колебания в них происходят перпендикулярно направлению распростране-
ния волны.
Поэтому дм заданного направления распространения волны, характе-
ризуемою числами fc^i fc±s имеем не одно, а Звя независимых направле-
ния поляризации. Таким образом, чтобы учесть поперечный характер элек-
тромагнитных волн, умножим полученное число мод на 2 и так получим,
что
V Zfu)du = IZ -du.
зг3 са
Глава l
Описывая электромагнитную волну скалярной функцией у(дс, у? t),
ми ejchbeio считали, что эта воле]а — продольная. Поэтому надо делать опи-
сывдсмис исправление.
Замечание
полный шаровой слой и, и1
Если в качестве мед в нашей куби-
ческой полости взять не стоячие, а rnvy-
ujue волны, то волновые векторы кп то-
же будут соответствовать в воображаемом
трёхмерном к-пространстве узлам простой
кубической решётки, по их следует рассмат-
ривать нс только в первом, а во всех вось-
ми октантах декартовой системы fcJh A:z.
Величина объёма элементарной ячейки этой
решетки теперь, однако, равна (2л/Ь)3 =
= 8 тг’/У' (в отличие от объёма элементар-
ной ячейки тг*/1/ в случае стоячих волн).
При подсчёте числа теперь надо взять
+ du1. Так мы получим, что
VZ(Mf = 4irfca<Ue : — = did.
V 2тгМ
то есть в точности такую же формулу как для стоячих волн, приведённую
выше; для учета попсрсчности волн следует правую часть формулы умно-
жить па 2.
CWtfj сяект/дельшэб ябъёлншй ялотиости энергии ц(ш)
ра₽н#еесяс?га теилечуого излучения и еиектралъноы
испуекатеяьлан стк^юбносоти абсолютно чёрного т&7а
Рассмотрим теперь не произвольное, анакопят? цгдучеиис
температуры Т, находящееся внутри полости ирии-зно.тьной формы объема
V с маленькой дырочкой, через которую это излучение может выходить на-
ружу. Такое излучение является излучением абсолютно чёрного тела, так
как ।[опавшее на дырочку извне полости излучение проходит внутрь по-
лости, запутывается в полости и ис может из неё выйти обратно через
дырочку полости.
Обозначим с помощью Циг) блек/прлмлую объемную ллдожость элер-
гин излучения, т. с. энергию излучения, находящегося в единице объёма око-
ло произвольной точки пространства внутри ПОЛОСТИ и приходящегося па
1.1 ВЫВОД ФОРМУЛЫ ПЛАНКА
4Y
единичный интервал частот в окрестности частоты о? при данной темпера-
туре Т
Энергия равновесного излучения равномерно распределена но объему
полости, те. u (cd) йлдысыт am wopthujam г, j;. 5 точки лрйст/денствд.
Эта энергия, однакоч неравномерно распределена по частотами, принимаю-
щим значения от Одо +ос. Размерность спектральной объемной плотности
энергии u(uj) следующая:
. , ., Дж 1 Дж. с
[и(^|] = — : с = —~
м- v м7
причём просто объёмная плашх/оешь и эдеранн рассматриваемого равно
веского тепло вот излучения дается интегралом
и =
о
размерность [и] = Дж/м3.
Обозначим теперь с помощью F(w) слскт/мльйую и1тучатсльн^ю сло-
сабнасть дырочки в полости (emission — излучение), т. е. испускаемую ды-
рочкой энергию в единицу времени в расчёте на единицу частоты в окрест-
ности часто™ а\ излучаемую единицей поверхности дырочки в единицу
времени по всех направлениях, Размерность спектральной испу с капельной
способности следующая:
[ад] =
М"
размерность спектральной иену с капельной способности В(ш) отличается
на 1/с^т.е. на размерность частоты, от размерности просто излучательной
способности £?.
Заметим, что функции u(id)
и для равновесною теплового
электромагнитного излучения н по-
лости зависят от температуры Т, хо-
тя эту зависимость мье явно и не ука-
зываем.
Найдём связь функции j?(w)
спектральной излучательной спо-
собности дырочки в полости с функ-
цией tt(w) спектральной объемной плотности энергии равновесного из-
лучения в полости. Рат/аят/ас тгллайле элслтдонагнитиае wi-тучсш/с
50
Глава l
uCti/Jdu/dV и? отличная л частят а\ or + du, шгхо^я^^ся в объеме dV,
состоит ы.т излучений (находящихся в объёме dV')? рогл/мч?т/?диялоц^ихся
ло всем нйлройстеннл.и й л/wcm/MJicmje со сксузослимо cffemo с, как это по-
казано на левом приведённом рисунке , причём в различных направлениях
распространяются одинаковые доли излучения, так как равновесное излу-
чение не только однородно, но и идат/JO/wo.
Рассмотрим теперь бесконечно малую ило-
щядау d5 на стенке полости, являющуюся по-
I верх костью дырочки (на нашем рисунке нэлуче-
I г4^?4^ ние находится слева от площадки dS) и найдём
yi I Энергию излучения бесконечно малого частотного
интервала w + dw+ которое падает вдоль нски-
торого направления изнутри полости, показа нно-
у го на рисунке, на эту площадку' и вылетает через
неё наружу за бесконечно малый интервал време-
ни £, i — di.
Итак, ря^слг&трил* сялчоля только излучение нэ члст^тяо^о Ешшердо-
/гй и. l-l' 4- du, лбдлетяет к ллощидге dS е напряйляши 3, $? и еы-
дет^т a waw няя/етвявяин ч^5 эту ооц^ддку наружу uaiwmu зд время
£, t + dt щс 3 и — полярный н азимутальный углы направления* причём
считаем, что полярный угол выбран таким, что он является углом меж-
ду направлением летящего к d5 изнутри излучения и внешней нормалью
к площадке d5\ направленной наружу полости, как показано на рисунке.
Уточним. Рассмотрим излучение, распространяющееся we empwo д wo-
проолеюш де бескояечтго близких лтл/? делениях около ялл/кгатеяиЯ
лежащих в бесконечно малом телесном угле dfl — flin 9 dfld^?.
Если мы проинтегрируем по углам 0 < у? < 2л, 0 < тг/2 (обра-
тите внимание на я/2) энергию рассматриваемого излучения, то получим
энергию fif.'CrTo излучения R частотном интервале ш, ш + dej, вылетающего
из дырочкЕТ dS полости наружу за время t Л + di. Эта энергия согласно
определению излучательной способности дырочки дастся произведением
E(td) du1 djS dtn
где Eft'i — спектральная излучательная способность дырочки в полости
с TeiijEOBbiM равновесным излучением в единичном и сперла ле частот око-
ло частоты w, т. е. спектральная испускЭтельная способность абсолютно
чёрного тела.
Чтобы найти энергию излучения, налетающего на плпщдлку dS в на-
правлении 0. с разбросом dS! и проходящего через эту площадку за ин-
тервал времени ij i + di, мысленно построим вдоль этого направления 0.
1.3. Вывод формулы Планка
5]
внутри полости косой наклонный цилиндр, показанный на рисунке, опи-
раЕощпйся на площадку и имеющий образующую длины г rff., где с —
скорость света, и рассмотрим внутри этого косого цилиндра в момент вре-
мени ; ту бесконечно малую долю излучения, которая летит к площадке
в направлении образующей цилиндра с разбросом углов ей!
5сё цэд/ченае. которое е начальный камент ( е объйие
укпздннОйо косого и тдлъкв оно зо время £. f лола^ёт лбг
n.TWJiff/dtfv dS п лроийёт /(её
Спектральная объёмная плотность энергии равновесного теплового из-
лучения в единичном интервале часто г около частоты распространяю-
щегося по всем возможеплм ЕЕвпраллепиям в пространстве. равна и(ш). Из
этой объёмной плотности на долю изучения с частотами ujL ш - fii\ летя-
щего в направлении* характеризуемом углами 0. с разбросом углов dfl,
приходится бесконечно малая доля:
—---------dQ = —------------ainfldfl dip,
Ijt Ч7Г
Учитывая, что рассматриваемое равновесное излучение изотропно
и что 4тг — полный телесный угол, включающий псе направления
в трёхмерном пространств*, в которых мезыт лететь излучение, получаем,
что (4^/4-^ — доля плотности излучения* приходящаяся на единичный
телесный угол.
Объём показанного па рисунке косого цилиндра, очевидно, равен
dl7 = с cos fl dt dSi
он равен произведению площади dS основания этого косого цилиндра на
его высоту, которая равна edt cos 9. Поэтому
я/2 я*
.Е(йч y?)du/dSdi = У — sin ccosfldSdf,
о о
где у?) = B(c4/j 0. Таким обрядом,
£?(ш) = и(ш)с - 2тг
4зг
W/2
/ HinflcosStW = у ifftL?).
./ 4
fl
Интегрирование по полярному углу tf надо вести от 6* = 0 (угол нор-
мального паления па площадку dS) до 0 — тг/2 (угол скользящего падсЕшя
52
Глава l
вдоль стенки полости на плошадку d5). Азимутальный угол принимает
все возможные для пего значения от П до 2тг.
Таким образом, мы доказали важное соотношение
Е(ы) = | и(ш),
которое связывает спектральную испускатсльную способность £7 (и) ды-
рочки в полости с равгговесным тепловым электромагнитным излучением
и спектральную объём ну кт плотность энергии и(д?) этого равновесного теп
ловлю электромагнитною излучения, находящеюся в полос ги.
Одновременно мы доказали, что дырочка в полости с равновесным
тепловым электромагнитным излучением является косинусным излучате-
лем.
Действительно, из соотношения
S{0, du dS2 d£Fdf. = ——du^dQ c cos 0 di? di
непосредственно следует; что
£7(fl, у?) = саз fl.
где £(0, 0. — энергияh излучаемая единичной площадкой
в единичном интервале частот около частоты ш в единичный телесный
угол около направления (Л к нормали к этой единичной площадке. Со-
otbctctbcioio, -----
4тг
= — Энергия, излучаемая единичной площадкой
в единичном интервале частот около частоты и в единичный телесный угол
около направления нормали к этой единичной площадке. Окончательно —
0. = -EqM COS0,
т. с. дырочка в полости с раш [олсси ым тепловым электромагнитным излу-
чением, действительно является «косинусным излучателем».
Длядевде /дееадеескода излучения
Только что проведённое рассуждение с выводом формулы для спек-
тральной излучательной способности равновесного теплового излучения,
касающееся энергии этого излучения, можно повторить для импульса из-
лучения.
1.3. Вывод формулы Планка
53
Согласно электромагнитной теории Максвелла объёмная плотность
Энергии плоской Электромагнитной волны Е|/, т. у. z)T H(tn т. у. z) в пу-
стотс в точке х. у. z в момент времени £ ранни ц = /?й/2 + /1^/2 =
= (1/с) А1 /Д так как для плоской волны А3 = до №, и так как скорость
распространения электромагнитной волны в пустоте даётся формулой с2 =
= 1/ео^; здесь А = |E(t, у, Я = |H(tn я;, у, z)|.
Объемная плотность импульса этой элек-
тромагнитной волны в точке я? у. z в момент
времени t равна д = 1/с3 [Е, Н , т. е. р = |д| =
= (1/с2) А 7/, так как в плоской волне Е 1 Н
Таким образом, для произвольной плоской элек-
тромагнитной волны в любой точке простран-
ства в любой момент времени имеем соотноше-
ние
и = у с.
где и - объёмная плотность энергии полны, у - абсолютная величина (мо-
дуль) объёмной плотности импульса электромагнитного ПОЛЯ волны.
Рассмотрим теперь равновесное электромагнитное излучение темпера-
туры Г, находящееся внутри полости объема К с зорка явными стенками.
Оно состоит из плоских электромагнитных волн различных частот,
распространяющихся г го всем направлениям в пространстве и налетающих
на стенки полости, зеркально отражающихся or них и передающих стенкам
при отражении импульс. Другими словами, равновесное ыАтучяше окйг?ыйп-
ет блр^еленное Удаление р лд стента нодослтп.
Рассчитаем это давление. Возьмём какую-нибудь бесконечно малую
площадку dS на внутренней стенке полости с равновесным излучением,
нс важно какую (нс площадку на отверстии полости), и рассмотрим беско-
нечно малую долю излучения всех частот и, которое в момент времени £
находится внутри некоторого косого цилиндра, аналогичного показанному
на приведенном выше рисунке, опирающегося на площадку dS и имеюще-
го длину образующей cdt, где dt — некоторое бесконечно малое время, с —
скорость света.
Это излучение упадёт за интервал времени t, f + eft на площадку dS,
зеркально отразится от неё и передаст этой площадке часть своего импуль-
са, т.с. будет действовать па эту площадку силой величины dAPl в направ-
лении внешней нормали л к этой площадке. Эта сила равна импульсу, пе-
реданному площадке dS рассматриваемым излучением в единицу времени.
Предположим, что угол между внешней нормалью п к площадке и еди-
ничный вектором с равен Й. Направление вектора с совпадаете папраллс-
54
Глава l
имен образующей рассматриваемого косого цилиндра, не показанного на
рисунке, и направлением вектора импульса rfG рассматриваемой доли из-
лучения, находящегося внутри нашего косого цилиндра в момен т времени
и распространяющегося в направлении е.
Точнее, мы рассмотрим долю излучения
внутри косого цилиндра, не точно распро-
страняющуюся в направлении Й, относи-
тельно нормали п, а распространяющуюся
вдоль этого направления с некоторым беско-
нечно малым разбросом направлений 4Й =
= Binfl40d^_ При этом азимутальный угол
изменяется в пределах 0 < Йзг, а по-
лярный угол 0 направления с относительно
нормали л — в пределах от значения 3 = 0 (нормальное падение излучения
па площадку) до значения 3 = я/2 (скользящее падение).
Вектор бесконечно малого импульса 4G рассматриваемого излучения,
находившегося в момент времени / в объёме dV7 косого цилиндра и распро-
страняющегося в направлении образую щей цилиндра с углом 0, с разбро-
сом 40 к нормали и, направлен вдоль вектора с и имеет величину (модуль)
dG = |dG| = fl dV =
= -T- sin 0 tiiOibs dS ccs &cdt,
c 4тг
где 9 = ti/c и ц — объёмная плотность энергии рассматриваемого равновес-
ного теплового электромагнитного излучения, одинаковая во всех точках
пространства внутри полости, занятого излучением; 411/4* — доля этого
излучения в единице объема, прнхсдящался на излучение, распространяю-
щееся вдоль направления 0, с разбросом 4fia причем 4V = 45 oostfedt
и t/fi = sm fl dfld^.
За время i, t + dt всё излучение с импульсам dG зеркально отразится
ст стенки, и его импульс станет равным 4G', как показано на рисунке,
причём в силу зеркального характера отражения
|AG| = |dG' -dG| = 2 4G\ = 2dGTcosfl.
где d<7ft — проекция импульса dG на направление нормали п к площад-
ке 4S. Таким образам, за время <ч t + di излучение, падающее на площад-
ку d5 в направлении Й, 7? с разбросом углов ctf!, передает этой площадке
импульс AG, направленный по нормали и.
1.3. Вывод формулы Планка
55
Излучение» падающее на площадку dS под всевозможными углами
fl, у? {О < 2тг, 0 < fl тг/2) за интервал времени Z + (Й, передаст
площадке импульс
2 л тг/2
У У 2 d<7 сой fl п
о о
в направлен ни нормали и, т.е. подействует на эту площадку силой
in ir/2
pdSn=-J- / du? / dfl — — sinfldS cos fl ctft 2 cosfln.
dt ; / с 4тг
о о
где р — давление» оказываемое равновесным тепловым излучением на стен-
ку которое мы котам рассчитать. Снлд — это ИиНлулы?. ле/де<)лняый телу
д Даотенне — это силл, действующая та едщшцу hiwjw-
моепш 7ЛС.ТД. Таким образом,
2ir <2 И/2
Р = 7^- /dy? / dfl SMlfl СОЫ2 fl = — U / cos3 fldfeoa fl) = —u C{1^
2jt / / / 3 J
0 0 0 0
приходим к очень простому результату р = ц/3- Размерности н этой фор-
муле правильные, так как
^. = 4 = йт4 = ^ = м-
М£ MJ
Формулу р = ti/З для давления равновесного теплового излучения
впсрвьЕС получил Больцман в 1884 г. Он рассмотрел это излучение подобно
классическому идеальному газут заключённому в 1щлиндрическом сосуде,
закрытом сверху подвижным поршнем, и применил к нему электромагнит-
ную теорию Максвелла, как это сделали мы.
Формулу
где 17 — полная энергия равновесного теплового излучения, V — объём
этого излучения, можно рассматривать, как аналог уравнения состояния
идеального классического газа:
рУ = Ц-ПТ.
56
Глава l
гле J? — универсальная газовая постоянная, М — масса газа, й — его моляр-
ная масса. При этом Я = £|-АГЛ1 fcp — постоянная Больцмана. Л1^ — число
Авена др с (число молекул в моле вещества), так что
4г RT = -Й-^- N 4 кьТ = N kbT,
• rt^Tr'l
где m — масса отдельной молекулы газа, Ат — полное число молекул в газе.
Так как внутренняя энергия одноатомного газа (У = JV (3/2) то урав-
нение состояния классического идеального газа можно записать в виде;
pv =|сл
аналогичном полученной нами формуле для давления теплового равновсс-
еюп) излучения
pv-lu-,
только для теплового излучения имеем множитель 1/3, а не 2/3-
ТТ/ипгепЁГше mio/hw Яатмрдешт о
/XJL7T/7£Y)£Wt7H/U Л# LTMfJJfHXW СЙОСЯн)ы I/ 2JUAYJHU
Рэлея -Джылсд
Рассмотрим теперь равновесное тепло-
вое электромагнитное излучение, находяще-
еся и полости и имеющее температуру Т
с позиции классической физики. Применим
к нему знаменитую «теорему Больцмана» из
классической молекупярно-кинетичесяой тео-
рии многоатомных газов: /л^е^у^^двндмд?-
нолг эиердш ял шл
бо^ь?, справедливую для состояния теш[оно-
го равновесия произвольной механической си-
стемы. Эта теорема Больцмана является од-
ним из фундаментальных достижении класси-
ческой физики. Нс будем, однако, останавли-
ваться на доказательстве этой теоремы. Подчеркнем только, что речь идёт
действительно о 1ял?/?£ме, т. е. о строго доказываемом положении, справед-
ливом для произвольней классической механической системы находящей-
ся в термостате и пребывающей в состоянии теплового равновесия. Пид
1.3. Вывод формулы Планка
57
термостатом мы понимаем шсжш, т е. окружающие систему
тела, непрерывно взаимодействующие с пси случайными силами, причём
считаем, что интенсивность этого взаимодействия постоянна во времени
и определяется значением температуры 7 термостата.
В качестве классической механической системы Больцман рассматри-
вал многоатомный классический газ, состоящий из многоатомных молекул.
Согласно теореме Больцмана п/ш равняв-
CUU Л6Г 6ч)иу Л^С/Н^ЛД/НЙЛЬНуМ ИЛИ
й/й> евдбоды газа нридяйнися энер- V Д
1 * (у V? W
гм ± fcft-T, л йй б4>нг сиел^нь
й\ , т. . -. . /=з М м м
CflUDOiJbJ — Л’£ I (в <МД рбГЗЮ ОТЭЛЬШйЯ).
Здесь Аб — постоянная Больцмана, те. уни-
версальная газовая постоянная 7? (из уравнения состояния идеального га-
за), деленная на число Авогадро (число молекул в одном моле веще-
ства}.
Рассмотрим! например, равновесный двухатомный газ, скажем азот, jVj
из Аг молекул при комнатной температуре. Он состоит из двухатомных мо-
лекул Лгз, представляющих собой два атома азота АГ, связанных химической
связью При комнатной температуре расстояние между атомами азота в мо-
лекуле Лт2 не меняется! как говорят, «заморожено». Молекула азота облада-
ет поэтому не 6, а 5 степенями свободы .Л из которых 3 «поступательные»
(это три координаты ц. м. молекулы, которые характеризуют положение мо-
лекулы и пространстве) и 2 «вращательные» (это два утла, которые характе-
ризуют ЕгапраллсЕсис оси молекулы в пространстве). Полное число степеней
свободы всего газа азота JV2s таким образом, равно / — 5jV, где Аг — число
молекул в газе.
Согласно теореме Больцмана на 3 поступательные степени свободы
каждой молекул ej в равЕювсСнсм газе температуры Г приходится энергия
(3/2) а на 2 вращательные степени свободы молекулы в равновесном
газе температуры Т приходится энергия АбТ. Соответственно, внутренняя
энергия Гг газа азота при комнатной температуре Т равна 1Л = (5/2) АВТ
где АГ — полное число молекул газа.
Таким образом. ген.ЮёММСтЬ рассматриваемо]О молекулярного газа
азота равна С - (5/2) Аб ±V, причём 60% внутренней энергии приходит-
ся на поступательные степени свободы, а 40% — на вращательные степени
свободы.
Степенями свободы электромагнитного излучения в полости будем
считать рассмотренные нами моды (так как число мод электромагнитного
излучения бесконечно, то электромагнитное излучение в полости является
Глава l
системой с бесконечным числом степеней свободы}, причём каждая сте-
пень свободы — колебательная. Таким образом, объёмная плотность энер-
гии классическою равновесною теплового элекгромЭ] нитного излучения^
приходящаяся на интервал частот w. ш + <Lj в единице объема полости,
равна
?i(uj)du; = fct;Tx
X число а чпглю/л gj. av — dux
ЕЮЪЛИЛ flflflOCfflW =
= fctT tiw.
Таким образом, получаем
u(u)dw = ck1 fcfi?1 ;
тг2 ст
следовательно.
= "Гл *ЕГ’
ТГ (Г
Так как Е(ш) = (с/4) и(ш), то отсюда приходим к следующей формуле
для спектральной излучательной способности абсолютно чёрного тепа:
4л2 с2
feET,
которая носит название «закона Рэлея-Джинса».
График функции 2Г(и?) показан па рисун-
ке. Видим, что закон Рэлея-Джинса при боль-
ших частотах дает абсурдный результат. Пол-
ная излучательная способность £ дырочки
в полости и полная объёмная плотность энер-
гии теплового излучения к в полости согласно
этому закону бесконечны, так как
£(w)<fcu = ооп
что, разумеется, бесе мы слеп ил, чего быть не может.
13. Вывод формулы Планка
59
На самом деле полная испускательная способность абсолютно чёрного
тела при температуре Г имеет коЕтсчпую величину и даётся формулой
Е = tfT4
ТЯК называемого «закона Сгсфана-Больцмана» — так называемаи кон-
£7Л ЛНТЛ Д См w/w Л Л - fйЛЫрГДНД ).
Разумеется, ь яолкйгя сда^ббность, м жш объЁкклл
ллдоялсли /швдовегаодо иельтдег# эле™р^ндгни?пчдао излучения бес-
атянгчны; никакой объект егс может испускать излучение бесконечной ihitch
си внести, и никакое излучение не может обладать бесконечной объёмной
плотностью энергии.
Экспериментальная кривая E(u’j при —* -ж убывает, а не возрастает,
как в законе Рэлея Джинса, и это обеспечивает сходимость интегралов
по ш от функций E(ll/) и u(clf) в бесконечных пределах 0 < ш1 < сс.
Противоречие классической физики, возникшее при попытке объясне-
ния эксперимента по спектральной интенсивности равновесного теплового
электромагнитного излучения, выразившееся н законе Рэлея Джинса, по-
лучило название «ультрафиолетовой катастрофы» {большие частоты — это
ул ырафиолетовам область).
Формула Планка, полученная на основе его квантовой гипстезыч отли-
чается от выведенного закона Рэлея-Джинса
uM = -fe**T
(Г
тем, что вместо величины к^Т в неё входит квантовая величина
—-—“ JfcT при малом ft.
g.iJ j.-'/lrtТ _
где ft - постоянная Планка.
Если мы формально устремим постоянную Планка ft к нулю, то полу-
чим результат классической физики. (Конечно, правильнее сказать, что мы
рассматриваем настолько малые частоты и, что иг < к^Г/Й, и что для этих
частот квантовые поправки не существенны.)
Рассмотрим второй предельный случай ш —* и, Т —> 0. Теперь
—-—7-^-----ftwC ^7^7 при малом ft.
0П ld/fcjT _ 1
и мы получим формулу
w/w) = -^4е -. Ди3е-а",
йо
Глава l
в которой А, а — неизвестные константы. Пришли к знаменитом так назы-
ваемой «формул? Вина».
Формула Планка для спектральной объемной плотности энергии теп-
левого излучения, таким образом, имеет следующий вид:
( J е*^т- 1'
Формула Планка для спектральной испускательной способности абсо-
лютно чёрного тела, соответственно, имеет вид
b(uJ) 4«(w) )7Ггса ейш/лБт _ t
Выведенная Плапкоы формула относилась к величине которая
непосредственно измеряется на эксперименте, а не к объёмной плотно-
сти ti(uj), которая используется только в теоретических рассмотрениях.
И даже нс точно к этой величине а к не^, пересчитанной на
функцию от длины волны А, так как длины воле к а не частоты, измеряются
Экспериментально в оптических экс пер И MCE пах.
1 {рименеиие распределения Больцмана и средняя энергия
классического и квантового осцилляторов, находящихся
в термостате
В состоянии равновесии энергия штатом теплового электромаг-
нитного излучения в полости согласно теореме Больцмана распределяется
равномерно по модам подобие тому, как полная энергия равновесного клдс-
Сйчссяпго идеального газа равЕюмсрЕю распределяется по его молекулам.
Мода равновесного электромагнитного излучения в по-
лости совершает гармонические колебания, так как изменя-
§3 * е™ по временному закону
| 1—1 щ ПО = Cn cos(wn£ - ^?Т1),
в котором - постоянные, характеризующие амплитуду и начальную
фазу гармоническою колебания. Физическая одномерная система, соверша-
тощая гармонические колебания, называется «одномерным осциллятором»,
или Просто «осциллятором». Примером Такою осциллятора являе тся масса
т, подвешенная на пружинке жёсткости
1.3. Вывод формулы Планка
6]
Afody лам е ийлос-юг, ,иы будем считать однаме/?-
лылг яс^нл^яторол^ ллдпбмдол .мл^сс г/п лружшлге.
Идся представления моды -электромагнитного излучения к виде сллга-
дгюятлтьнон физической системы, находящейся к термостате» принадле-
жит Эйнштейну, Он высказал её в 1909 г., когда впервые заговорил о «гфо-
лиондо кванте света, считая его одномерным осциллятором излучения.
Именно Эйнштейн в 1909 г. ввёл в науку понятие «фотона». Однако оно
не пользовалось успехом вплоть до открытия эффекта Комптона в 1923 г,
который убедил физиков, что у фотона имеется не только энергия» но и им-
пульс р = ft к.
На самом деле мода получения характеризуется воле ton ым вектором
к(йх» fcz) и частотой w = cfe, и сё надо представлять себе в виде плос-
кой электромагнитной волны частоты и, распространяющейся в направле-
нии вектора к. Причём следует считать, что энергия с этой волны либо
непрерывная, т.е. принимает любые значения от 0 до +оо (классическая
мода), либо состоит из энергии п одинаковых фотонов, каждый из кото-
рых, согласно предположению Планка, имеет одинаковую энергию Лы, так
что мода имеет дискретную энергию = n fiw (квантовая мода).
Изменим теперь коренным образом нашу точку зрения лд равновесное
тепловое излучение,
До сих пор мы считали, что в полости находятся моды излучения,
которые пребывают в равновесии друг с другом и в равновесии со стенка-
ми полости температуры Г. Эта моды взаимодействуют между собой и со
стенка мп полости, и это взаимодействие обеспечивает установление равно-
весия мод в тепловом равновесном излучении.
Теперь, вместо всего равновесною теплового излучения, рассмотрим
одну -wfldy. чдхойяц^уюся s cwpeAf мгеинфпту-
jpti Г, рлллли температуре Т рйялягеемвдо излучения. Считаем, что этот
термостат моделирует сложное взаимодействие моды с остальными мода-
ми к со стенками полости
Термостат вес время и отдаёт энергию осциллятору^ и получает сё от
НОЮ, причём при тепловом равновесии оба этих энергетических потока
в среднем компенсируют друг друга.
62
Глава l
Классический осциллятор, находящийся в тер-
А л мостаге температуры Т, имеет среднюю энергию (s),
с ' У/ и \ величина которой определяется температурой Г тер-
мостата. В любой момент времени J энергия е oc-
ti ---------- циллятора может быть какой-угодно от 0 до ж. Она
флуктуирует около среднею значения (£), как это по-
казано на рисунке.
Амплитуда колебаний классического осциллятора принимает значения
от 0 до +ж. Поэтому энергия £ осциллятора, которая пропорциональна
квадрату его амплитуды, тоже принимает любые значения от нуля л о бес-
ЮППСЧЕЮСТИ.
Энергия кна еловою осциллятора, напротив, может принимать только
дискретные значения £п.
Применим теперь к классической или к квантовой электромагнитной
моде, находящейся в термостате температуры Г, лгсАрщи ве/лзя/чнда/иеи,
т. е. рассмотрим энергию е моды как случайную величину и применим к ней
распределение Больцмана. Это — важное положение, которое далеко не сра-
зу было принято в физике.
Для классической или для квантовой моды следует считать, что вероят-
ность моде в термостате температуры Г иметь энергию Е пропорциональна
так называемому «множителю Больцмана» С_£^7.
Так как энергия е классической моды принимает квдрЁрыйньде эяа-
чення, то следует рассуждать не о га/юяетн&елш шетнь
зиг/лгню f (эта всроятЕ гость равна нулю), л а лфмшшкш люде ц.исть энер-
гию. я бесконечно леолш интервале с, de (эта вероятность
бесконечно малая и пропорциональна бесконечно малой величине d^). Гак
что следует рассмотреть произведение
которое и представляет собой искомую вероятность, величину Pf (от ант.
probability — вероятность) называют «плотностью вероятности».
Таким образом, для классической равновесной электромагнитной мо-
ды, находящейся в термостате с температурой Г, имеем следующую веро-
ятность
Ft-d> = CC-£/^Td£,
иметь энергию, заключённую в интервале £, £ + tie; это вероятность най-
ти моду в данный момент времени в состоянии с энергией, заключённой
в интервале от с до е + fte; С — некоторая постоянная, называемая «нормн-
роВИЧ П ЫМ М EJ пжитслс м».
13. Вывод формулы Планка
63
Так как вероятность моде вообще иметь какую-нибудь энергию е есть
вероятность «достоверного события», тс. события, которое обязательно
пронзи идёт; вероятность которою равна ], то имеем соотношение
У L
которое называется «условием нормировки». Из него легко найти значение
постоянной С. Действительно,
+ ™
С / e-e^6T(fe = 1. С кьТ = I. С = А
fcEr
Вычислим теперь рассматриваемой классической
электромагнитной моды, находящейся и термостате с температурой Т. Опа
дастся формулой
и равна
(е) = С У ее = -СW f cd (е’с/ы’)
= -CAtTee-e^T
то есть
= *ЕТ.
Последнюю формулу мы уже использовали выше, когда применяли
теорему Больцмана о равномерном распределении энергии по степеням
свободы при выводе закона Рэлея-Джинса.
Обратимся теперь к кяднтоеаму осциллятору. Отдельную
лишлую люф? а;, па холящуюся в термостате с температурой Г.
Й4
Глава l
njjectemdtfu-w теперь состоя щей из некоторой) чиелд ^Ьотоное с энерги-
ей ftuj АД.Ж'^ЬШ. Поэтому энергия моды определяется числим имеющихся
в ней фотонов. Если число фотонов н моде обозначим через п, причём п =
= (L 1. 2 ... + то энергия моды равна е — с„ = п W Если п = 01 то мода
не возбуждена н это состояние невозбуждённой моды тоже надо учитывать.
Теперь энергия сагяисч^ кеантоеыш предстамепмам, иринижт-
етн ие непрерыелый, л зллчепия.
Как мы уже отмечали, оказывается^ вероятность равновесной кванто-
вой электромагнитной моде, находящейся в равновесии с термостатом, име-
ющим температуру Т, иметь энергию даётся тоже множителем Больц-
мана, то есть
Рга = Се~£"^т,
где G — «нормировочная постоянная». Теперь Pft не «плотность вероятно-
сти», а сама «вероятность». Соответственно, значение константы С следует
находить, используя следующее «условие нормировки»:
Е р’‘ = '
ri=ft
Следовательно,
С 52 = С 5^ _ (у _
п=0 » = 0 п=0
= (7(1 + 1 + X2 + ...) =
J - т
здесь введено удобное сокращённое обозначение х = кроме то-
го, мы воспользовались формулой для суммы бесконечной геометрической
прогрессии:
1 I 3 I X2 I = . 1 —
1 — X
при |аг| < 1. Таким образом, C- = 1- jb = 1- .
Вычислим теперь энергии кванторей электромзгнигной моды
pa Bi ю л ссного излу ч ci tn 51:
I да 4-да 1-да
(f) = С V tt] e-f"/k*T = С Пи = СТш 52 П^п =
п=0 я=0 п=0
1.1 ВЫВОД ФОРМУЛЫ ПЛАНКА
65
= С Кил
= С ftw ' х -j-
ах
= Йй/
= СhiA>x -j-
ах
1
(I -I)2
1 - я1
так как С = 1 - т. Окончательно приходим к формуле
е hu/ksT
N. lJ -------------- - ----------- .
Таким образом, для классического осциллятора имеем формулу (е) =
= ^ь?1, а для квантового осциллятора формулу:
gttW/ Н.£ J _ J
При переходе от классических к квантовым представлениям нужно
первое ныражсЕшй заменить на второе^ что мы формально уже делали выше
при получении формулы Планка в конце вывода закона Рэлея-Джинса.
Итак, еще раз подчеркнем, что кшеенчвдпгы вдгон рдс-
ла степеням свободы на ецртведддо д.-?д /нденАвесного
ЛГеЛ.'ЮДЯДО ДО£ЯртрАЛШ£НШПН0АА мзяучетшл.
Вывод законов Стефана-Больцмана и Вина
Обратимся теперь к важным следствиям из формулы Планка, Получим
из неё два закона, которым подчиняется равновеснее тепловое электромаГ’
нитное излучение. Это «закон Стефана - Больцмана» и «закон Вина». Они
были открыты до формулы Планка.
Проинтегрируем формулу Планка для спектральной нспускотельной
способности по весы частотам w от О ДО +00- Придём тогда к формуле
для полной иену скатал ьной способности Е абсолютно чёрного тела:
+w +<и
£= [ е(»)^=-А-з
J А Я* СТ
о о
Произведем в интеграле следующую замену переменной интегрирова-
ния:
- у, - -г— У = "7"
А"б-г Л л
66
Глава l
тогда получим, что
h foT)4 / У3 <ty
4^ с2 л4 ./ е»-1
О
где — [юс ещяннпя.. нс зависящая от температуры, она яшыется некоторым
размерным числом.
Получили «закон Стефан а-Больцмана», утверждающий^ что полная
излучательная способность абсолютна ч^ного тела лг/?ояо/?1/нонФТЬна
четвёртой стелешь его абсолютной темлературы. Значение постоянной
oh называемой постоянной Стофана-Больцмана, равно
сг = 5,67 10“fi -р-т.
м2 А4
Как мы сказали, закон Стефана-Больцмана был открыт де того, как
Планк получил свою знаменитую формулу.
Выведем теперь из формулы Планка «закон смещения Вина». Начнем
с того, что введем новую спектральную испускательную способность:
Ь’(А) = -^(г™)4
4v с
1
СЛ 2ire/AfcDT _ j 1
хзрактсршусмуЕО не частотой ил. а длиной волны А, в отличие от исиуска-
телъной способности В(ш).
Именно эта спектральная испускательная способность непосредствен-
но измеряется на эксперименте, так как непосредственно измеряемой в оп-
тике величиной является длина полны А, а еес частота у или д?+
Имеем очевидные соотношения
<^ — — — 217^
у А — с,
2 тг с
А
Спектральая испускательная способность Е(А) определяется из усло-
вия
£?(А) riA = — E(tv) Aj.
причём здесь eLl? — — (2irc/As) е/А; знак лн^^ус яаявдлсв аат*лму что пхне-
яевде блины лавды А л/wucxodum в йбрдтьолг (от + ос до 0)
1.3. Вывод формулы Планка
67
X А /
л не # лрямйм (от 0 до +ос). Таким образомч
(х 3
2тг с \ _____1______2 тг<;
д У ^йпс/А^т - 1 А2 ’
график функции Е(А) имеет вид, показанный на рисунке.
Как и график функции S(w). он имеет максимум. Обозначим длину
волны Ah соответствующую максимуму функции £(А), через Ат.
Отметим, что ввдычгша А1П # 2згс/ыт,
где которая соответству-
ет ^dMCw.iryjicv 0у№цеш £?мелгтрйЛ^ной пну-
отельной сч^^йчоотм /Г (и?).
Установим, как величина Ат зависит от
температуры. Для этого найдём максимум
функции
= «=^-
Вычислив производную и приравняв сё
пулю, получим уравнение
т. с. трансцендентное уравнение
5(е* - 1) - neft = (I.
которое имеет корень а = гак что для длины волны Airj имеем формулу
АТ = , ?L£- = const.
fcEttQ
Обозначив через Ь константу, приходим к «закону смещения Нина»:
А™ Г = 6,
значение константы Ь рнвно 0.2D см-К.
Значение длины ймйы Апн лп^сн.^-му я^не?<зг/ ызлу-
вдтвдьнрй слогобности, бб/*дтнА л/шло/щиональло ддслтюиной темле/мт-
6N
Глава l
Получили «закон Вина», утверждающий, что длины ВйЛ-
НМ, WiTK-C^WTUp юлучлтэдънлы fnocofwpcfflw. ид абсо-
люлтяую нгдиперДЯг^у веять величина логтаяннад ДО зависящая олт гоем-
aepamjtphf.
Закон Вина, как и закон Стефана-Больцмана, как мы уже сказали, был
открыт др тогон как Планк вывел свою формулу.
При увеличении температуры максимум равновесного теплового излу-
чения сдвигается в сторону более коротких длин волн. Jena при нагревании
сначала светятся красным, затем голубым, затем белым светом (так назы-
ваемое «красное», «голубое» и «белое» каление).
1.4. Квинтовая природа света.
Фотоэффект н эффект Комптона
Квантовая природа света
В 1%0 г. Планку удалось теоретически объяснить форму экспсримсн-
тальной кривой спектральной интенсивности теплового излучения абсо-
лютно чёрного тела с помощью чуждого для классической физики пред-
положен ни о квантовании энергии одинаковыми порциями — «квантами».
Немного позже Планк сформулировал свою квантовую гипотезу в следую-
щем виде: эн^гмя cornel иенускделлкя и яойяощ девия л/нашлш seu/mntfd
we нвдрт/цдено. яд я иэдучдарт д лоатощавд оассуческии элеяж/>аил?яцтиый
п зстучдте еяь вдекмраыаэтштные айлны, а лар^ия.ни — явлтандл^.
Открытие квантов света коренным образом изменило классическую
физику, положив начало квантовой физике. По значимости открытие План-
ка сравнимо разве что с открытием Ньютоном законов классической меха-
ники и закона всемирного тяготения.
Правда, сам Планк ещё нс решился говорить о «корпус куда а света»,
которые, казалось бы, с очевидностью следовали из его гипотезы.
Развивая представления Планка,, это сделал в 1905 г. Эйнштейн, ко-
торый вернул в физическую оптику световые корпускулы ПОД названием
«фотонов» (правда, это название им дал нс ин сам).
В отличие от классических корпускул, фотоны обладают намного бо-
лее сложными физическими свойствами, выражающимися в их двойствен-
ной корпускулярно-волневой природе.
Од порол пая монохроматическая плоская световая волна частоты w ха-
рактеризуется порциями энергии величины е - fiw, где ft — так называемая
перечеркнутая постоянная Планка ft = А/2гг, равная ft = 1,055-Ю-3’1 Дж-с.
Сам Планк пользовался нс частотой uf, а частотой у, поэтому его формула
для кванта энергии имела вид f = Лк
1.4. КВАНТОВАЯ ПРИРОДА СВЕТА. ФОТОЭФФЕКТ II ЭФФЕКТ КОМПТОНА 69
Постоянная Планка имеет размерность dewtweiuw. Таким
образом,
РАЗМЕРНОСТЬ fl = ИМПУЛЬС х ДЛИНА = ЭНЕРГИЯ х ВРЕМЯ.
Значение своей постоянной Планк определил из сравнения своей формулы
для испускателъной способности абсолютно чёрного тела с экспериментом.
Дне фундаментальные модели физического объекга — система мате-
риальных точек и заполняющая пространство колеблющаяся непрерывная
сплошная среда — применять к одному и тому же объекту, в данном слу-
чае — к свету, разумеется, нельзя, так как эти классические модели противо-
речат друг другу Выше мы уже говорили, в частности, о противоположных
предсказаниях волновой и корпускулярной теорий света Значения скорости
света в воде (больше или меньше скорости света в пустоте).
Поэтому указанные модели нельзя безоговорочно применять к одно-
му и тому же физическому объекту, в частности к фотону. И вместе с тем,
результаты многочисленеплх экспериментов со светом требуют одЕюврсмсп
ного использования обеих этих моделей дли объяснения его свойств.
Согласно квантовым представлениям, при описании физического объ-
екта можно пользоваться w корпускулярной. и волновой моделями, но в гра-
ницах, определяемых от-
крытым Гейзенбергом в 1927 г.
В микромире господствует корпускулярно-волновой дуализм. С этим
надо обязательно считаться в атомной и субатомной физике (физике атом-
ных ядер и элементарных частиц)
В ] 837 г. в работе. по-
священной открытию электромаг-
нитных волн, Герц описал также
и наблюдённое им явление фотл-
зффекта» Воздух к искровом про-
межутке в его установке по из-
лучению электромагнитных волн
становился более проводящим при
освещении промежутка ультрафи-
олетовым светом. Галъвакс, ра-
ботавший в то время у Герца,
в 1888 г установил, что при облучении пластинки цинка Zn, соединённой
с отрицательно заряженным Электроскопом, как это по казано Eta рисунке,
70
Глава l
электроскоп разряжался. Свет, падая на пластинку пинка Zn, вырывал из
неё электроны, которые затем отталкивались ст отрицательно заряженной
пластинки. Эдекгричсский заряд, таким образом,. уходил с пластинки, как
это показано на левом рисунке. На правом рисунке продемонстрирована
ситуацияч когда незаряженная пластинка цинка Znh соединённая с незаря-
женным электроскопом, непрерывно облучалась ультрафиолетовым светом.
При этом электроскоп постепенно заражайся положительным элскгрлче-
ством до некоторого положительного потенциала у?, способным возвращать
вырванные светом из пластинки электроны, пока не возвращал их все н по-
ка не устанавливалось равновесие при потенциале электроскопа,
Особенно тщательное исследование фотоэффекта провёл Милликен
в 1914 г. На следующем рисунке схематически изображена использован-
ная им установка для изучения фотоэффекта. Внутрь вакуум пой трубки
были впаяны металлические катод Л" и анод Л и кварцевое окошко ТУ
для пропускания внутрь трубки ультрафиолетового света (стекло погло-
щает ультрафиолет). Катод представлял собой металлическую пластинку,
сделанную, например, из цинка Zn. Анодом являлся цилиндр с отверстием,
пропускающим свет к катоду.
Все льгриаггные светом из
катода электроды собирались
этим цилиндрическим анодом,
как показано на рисунке. Меж-
ду катодом и анодом наклады-
вается так называемая задержи-
вающих разнос гь потенциалов
17 т препятствующая движению
вырванных из катода электро-
нов к аноду и попаданию их па
а езид. Напряжение (г можно бы-
ло изменять с помощью показанного на рисунке потенциометра, и можно
было добиться того, чтобы это напряжение не позволяло вовсе электронам,
вырванным из катодац попадать на анод.
Эксперимент показал, что измеряем ы и
гальванометром G ^отозлек/нричегкни тол ;
н/шде я/юпо/нщонялен интвн-
пденоепш / излучения, и чтя лолная тлдержн-
вшоцря secft фототок рдзнясть
лов £/ = f/j эдвыгшн пюльао от длины мут-
ны tfiemdf A u не зегвпегмл от интенсивно’
стн /На рисунке представлены две кривые
1.4. КВАНТОВАЯ ПРИРОДА СВЕТА. ФОТОЭФФЕКТ II ЭФФЕКТ КОМПТОНА 7]
зависимости фототока i от напряжения 17 при двух различных интенсивно-
стях /] и 7? монохроматического света одинаковой длины полны А, причём
/1 > Л. При отрицательных напряжениях J7 (когда напряжение нс замедля-
ет, а ускоряет вырванные из катода электроны) фототок i не зависит от
но он разный при разных интенсивностях света, как показано на рисунке.
При положительных напряжениях Е7 (когда напряженно замедляет электро-
ны, вырванные из катода н летящие к анОду^ и вообще запрещает им вы-
летать с катода) фототок быстро уменьшается с ростом напряжения, пока
при некотором напряжении (Z = £73 не прекращается, как показано не ри-
сунке. При этом задерживающая разность потенциалов ЕУ-, не зависит от
и1п-с]1силегости света.
Электроны. вырываемые снегом ин катода, имени- различные скорости.
Задавая на аноде потенциал, меньший потенциала поверхности катодач т. с.
подавая на него задерживающее напряжение (7, н измеряя ток :, можно из-
мерить скорости, с которыми вырываются электроны из катода Электроны,
обладающие небольшой скоростью, проходят некоторое расстояние в сто-
рону анода, преодолевая задерживающую разность потенциалов, останав-
ливаются и возвращаются обратно на катод. Определяя число электронов,
приходящих па анод при различных задерживающих потенциалах (7, полу-
чаем ВОЗМОЖТЮСГЬ определять скорости фотоэлектронов.
Эксперимент показывает, что электроны
вырываются светом из катода со скоростями
начиная от скорости v = 0 и кончая скоростью
и = T1m;LKa причем МаКСИМИЛЬПаЯ скорость Гдищ
вырываемых электронов для данного метал-
ла определяется только длиной волны А света
и нс зависит от его интенсивности /.
Энергия самых быстрых электронов опре*
деляется наибольшим задерживающим потен-
циалом, при котором электроны ещё способны попадать на анод. Ток i
с увеличением I/ уменьшается, пока при (7 = У3 не обращается в нуль,
как это показано на приводимом ниже верхнем рисунке, на котором изоб-
ражены экспериментальные прямые, полученные для монохроматического
света двух разных длин воин А] н Aja дающие два значения задерживаю-
щего потенциала и С73й, причём Аз < А],
Если измерить задерживающие потенциалы С73 для различных длин
волн А монохроматического света, вызывающего фотоэффект, то окажется,
что зависимость функции £/3(м) задерживающего потенциала !7а от часто-
ты света р = е/А будет линейной, как показано на приводимом нижнем
рисунке, причём при некоторой частоте она обращается в нуль.
72
Глава l
Ц Таким образом, существует критическая
Z частота i-ц, при которой задерживающий по-
тенциал равен нулю: С/3 = (). Это частота так
называемой «красной Гранины» фотоэффекта
И) — с/Ап. Ее можно представить в виде ₽<i =
= Л /ft. где ft — постоянная Планка, величи-
z,y на Л называется «работой выхода» (электро-
на из металла). Таким образом, функция E7(i/)
следующая:
= ft i1.- — А,
где е абсолютная величина заряда электрона.
Работа выхода А очень чувствительна к чистоте поверхности метал-
ла фотокатода, которая обычно загрязнена адсорбированными хнмическн
активными газами.
В 1905 г Эйнштейн, введя представление о фотонах света, предло-
жил правильную теорию фотоэлектрического эффекта. Учитывая, что фо-
тоток i прямо пропортщонален hi степс ннетоспт / монохроматического света
частоты г, вызывающею фотоэффект, Эйнштейн правильно посчитал, что
фотоэффект является с/лгнл/щы..и cormrwnuu.i? ытлшигтиг пши-
си,мых каждого отддоыюдо
с четам лов^кяостяш Лрн эгоол/ в косого очень
тарного долга явного фомонд г w/ндддач от яаяерхно-
стл .истлттл отрывается один ателтрои.
Эйнштейн учел, что квант энергии монохроматического света часто-
та х/ — его фотон — имеет энергию ft?/+ где ft — постоянная Планка. В эле-
ментарном акте взаимодействия фотона с поверхностью металла должен
выполняться поэтому закоЕ! сохранения ЭЕтергии в виде
- А -1
где .4 — минимальная энергия, необходимая для высвобождения электрона
из металла, - ™'тах — максимальная кинетическая энергия вырванного из
металла элсктрона.
На рисунке представлена энергетическая диаграмма для элементарно-
го акта фотоэффекта одною фотона с поверхностью металла с вырывани-
ем одною электрона. Изображена кривая потенциальной энергии элекгропа
в металле, имеющая форму прямоугольной потенциальной ямы глубины V.
Изображён уровень Ферми sp для свободных электронов в металле, Энер-
гетическое расстояний От уровня Ферми cf до энергии верхнего края при-
моуюльной потенциальной ямы V является работой выхода А.
1.4. КВАНТОВАЯ ПРИРОДА СВЕТА. ФОТОЭФФЕКТ II ЭФФЕКТ КОМПТОНА 73
При взаимодействии фотона энергии
с прБсркностыо металла должен выполнять-
ся, кроме закона сохранения энергии, также и
закон сохранения импульса. Очевидно, невоз-
можно, чтобы импульс фотона Ду/с был пе-
редан весь одному электрону, выбиваемому из
металла. Тогда электрон должен был бы дви-
гаться не к поверхности металла, а от его по-
верхности.
Баланс энергии и импульса в рассматри-
ваемом элеме! парном акте может быть осуществлён ТОЛЬКО при учёте по-
верхностных сил, действующих ня электрон в металле со стороны ненов
решетки, которые принимают липший импульс фотона и передают его кри-
сталлу в целом. Этот эффект важен для электронов, находящихся в тонком
поверхностном слое толщиной всего 3-4 атомных слоя.
Элскгрон, находись внутри металла, который поглотил фотон, испы-
тает много столкновений, до того как достигнет поверхности. Столкнове-
ния электронов со скоростями, близкими к максимальной скорости г'гийХ
с нонами решётки и примесями, однако, несущественны, так как они упру-
гие. Некоторые такие столкновения, КОЕТСЧПО, могут ОТКЛОНИТЬ Электрон,
который мог бы вылететь из металла при движении его к поверхности.
Но в то же время другие столкновения могут направить другие электроны
в сторону поверхности, летевшие к ней под углом. Нсупругие столкновения
электрона с другими Электронами оказываются пчсеть редкими.
Таким образом, при частоте около ^красной Границы» возможен только
поверхностный фотоэффект. 11ри больших частотах становится возможным
также н объёмный фотоэффект
Легко показать с использованием законов сохранения энергии и им-
пульса, что свободны ii покоящийся Электрон пс может ПОЛНОСТЬЮ погло-
тить фотон.
Действительно, пусть и, к — угловая частота и волновой вектор фото-
на, а р — энергия и импульс электрона. Тогда в силу законов сохранения
импульса и энергии имеем два следующих соотношения:
Лк = р. Л-ь1 -и тс3 = + тй(Д
где т — масса покоя электрона, тс3 — энергия покоя электрона (предпола-
гаем, что до столкновения с фотоном электрон покоился).
Таким образом, fio? = eftfe = ср. а следовательно.
рс 4- тс2 = \/р2г?2 +
74
J'Л Л ВЛ ]
p2c2 I 2jwnc3 l- m2c4 - p2c2 + m3c*,
так что
2p rut? = 0,
что невозможно, так как р / 0.
Эффект Комптона
Убедительно корпускулярные свойства фотонов были продемонстри-
рованы в 1923 г в эффекте Комптона.
Комптон экспериментально обпа-
А1 ружил, что при рассеянии блоком пара-
финн пучка рентгеновских лучей, прсд-
сбавляющих собой электромагнитные
\ волны с очень короткой длиной волны,
__________________________ порядка 1А = 10“е см = 1.0 10 м,
наблюдается эффект противоречащий
предсказаниям классической физики.
Он установил, что хотя пучок рентгеновских лучей и рассеивался упруго
блоком парафина по всем возможным направлениям (как свет в оптическом
эксперименте по упругому рассеянию света)ъ по длина волны Ат рассеян-
ного парафином излучения в iiui [ранне eihh, составляющем угол б с направ-
лением падающего пучка, оказалась больше длины волны А падающего
пучка; при этом, как показал эксперимент Комптона, изменение длины рас-
сеянного рентгеновского излучения подчиняется следующему закону:
А'-А-ДА -A;(l -COS0),
п котором б — угол рассеяния, и? - масса электрона, с - скорость светя,
Л — постоянная Планка, А' — длина полны рассеянного рентгеновского из-
лучения (в оптических экспериментах по упругому рассеянию света опа
равна длине волны А падающего света). Комбинация величин /1/те имеет
размерность длины, так как
ft j _ Дж с н М’ с1 _ Сй
me м " кг м " кг - м
J кг - —
и называется ^комптоновской длиной».
1.4. КВАНТОВАЯ ПРИРОДА СВЕТА. ФОТОЭФФЕКТ II ЭФФЕКТ КОМПТОНА 75
Эффект Комптона послужил доказательством, что фотон частоты cj об-
ладает не только энергией с = ftuJ и длиной волны А = Этге/^, по Пиалку
и Эйнштейну но также и импульсом р = hk. те к — волновой вектор фо-
тона, модуль которого равен fc = 2#/А, и который направлен в направлении
движения фотона.
При этом фотон, как и электрон, является релятивистской частицей,
НО ДЛЯ него масса покоя равна нулю, так ЧТО ДИЛ нею Энергия И нм пульс
связаны соотношением с = ер.
Формулу эффекта Комптона можно вывести теоретически, применив
релятивистские законы сохранения энергии и импульса к элементарной ре-
акции
ФОТОН - ЭЛЕКТРОН = электрон' ь фотон',
т. е. к реакции
е + у = е' +
считая и фотон, и электрон классическими точечными релятивистскими
частицами.
Фотон имеет энергию е = Йа; и импульс
hk, где к — волновой вектор (|k| = fc =
= 2тг/А — волновое число}.
Атомный электрон можно считать свобод- /ц?
ним, так как рентгеновский фотон имеет чиср- —-------
гию, намного большую энергии связи элек- Vv
трона с атамом (поэтому этой энергией связи р
можно пренебречь). х
Закон сохранения импульса даёт соотношения
hk = р 4- hk\ ftk — file* = р.
где fl к — импульс фотона до столкновения с электроном, Лк' — его импульс
после столкновения с электроном, р — импульс электрона после столкно-
вения; считаемь что до столкисвенич элек!роп покоился л его импульс рав-
нялся нулю, р = 0.
Возводя второе приведённое соотношение в скалярный квадрат, полу-
чаем
F = ft3*2 - 2 ft2(k.k') + fc3fc'a;
учи тывая, что u? = ск, и/ = ofc', и умножая это соотношение на с2, лрнхо-
дим к соотношению
<^ра = - 2 cos9n
где fl — угол между кг п к.
76
Глава l
Теперь, согласно закону сохранения энергии, имеем также соотноше-
ние
Ли,’ 4- тс2 = \/рйс2 + т2с4 —
или
\Хр2<;г -Ь = Ли; 4- тс? — ftu/.
где т — масса покоя электрона. Возводя это соотношение в квадрат, чтобы
избавиться от квадратного корнян и используя выведенную формулу для
с2 р2, после несложных преобразований получаем, что
ftSwii/( I — cost?) = ftiumc2 —
а следовательно,
Так как c/w = 1/fc = А/2я, тс окончательно отсюда получаем формулу
эффекта Комптона:
А' - А - ^(1 -сдай) = тЙй (1 - cos 19).
Дополнение 1 к гл. 1
Ранние исследования но физической оптике
Физическая оптика зародилась в 60-70 гг XVII в. В 1662 г появил-
ся трактат амстердамского физика Фосса «О природе света», в котором,
в частности, им была высказана мысль, тгр разнообразие цветов света сле-
дует приписывать нс гелям, через которые приходит с вег, а самому свету.
В 1665 г. в Болонье посмертно был опубликован труд иезуита Гримальди,
содержащий описание явления дифракции света при пропускании солнеч-
ного света через два близких отверстия в ставне а тёмной комнате. R тон
же 1665 г. появилась «Микрография» Гука (автора «закон Гука»), члена Ко-
ролевского общества, в которой Гук с позиций волновой теории изложил
свою теорию цветов и описал явления интерференции света при наблю-
дении цветов тонких пленок. В том же 1665 г. другой член Королевского
общества — Бойль (соавтор «закон Бойля - Мариотта») — печатает «Опыты
Дополнение l
77
и рассуждения о цветах». В 1670 г. Барголйни открывает явление двойного
лучепреломления в кристаллах исландского плата.
В 1675 г. Рёмер впервые измерил скорость света из наблюден ин изме-
нений в течение земного года интервалов времени между пос ле дсвател ины-
ми затмениями спутника Юпитера. Он показал, что свет имеет огромную
скорость — 240000 км/с. На самом деле она равна 300 000 км/с.
В 1678 г. выходит знаменитый ^Трактат» Гюйгенса о свете (в пол^
ном виде под названием «Трактат о свете» он был опубликован только
в 1690 г), содержащий первую успешную количественную теорию свето-
вых волн («принцип Гюйгенса» о распространении волнового фронта с по-
мощью построения огибающей испущенных точками фронта вторичных
волн).
На середину этого периода, 1660-1690 гп, падают и главные оптиче-
ские исследования Ньютона, В конце 1675 г. Ньютон присылает Королев-
скому обществу мемуар с длинным названием Теория ceemff я
таключающдя гылоМЁзу воъяснвяий свойств светя. множенные явто/юл*
в лреч)ы£)уг^йх .-нечуяряд; я йиж яяяоашс- шшшет с^и^ествеляых яв-
ле/ош /ншышшиг тояких л.шдмгт й .чытьяы.г лрырзд /мвдым аб-
ряти тавдяявдсс от ряяее хд/^хтеригояяяяьлх гаойсгие светля. Поводом
к написанию мемуара, стоящего особняком в его сочинениях, по служили
для Ньютона исследования Гука над цветами тонких пластинок и явления-
ми огибания света при его прохождении вблизи острого края бритвы.
Ньютон в этом мему аре пишет: «... сюда не-тьзя олр^еяять кях
ялы еар ^вя.-мс.'снис.' ... сеет — это лечто. /эдслдострдмярящссся рямяч-
яы.и (юрязаи от светящихся шел. Свет — зтя лглт^ряя.тьяяя яилгшцня.
яля двшжшше, uiTW л.ппутьс, ()яйлсёнясг яля СЩС чтя-mo ядяе
...», т. с., по мнению Ньютона, свет отличается от эфира.
Ньютон был не только блестящим математиком-теоретиком, но и ис-
кусным опти ком-экс пер и Mei статором и даже инженером-ко пструкторог,
как бы мы сказали теперь.
В 1671 г в самом начале своей деятельности он сконструировал и соб-
ственноручно изготовил первый в мире л/шяципиалыю лишенный д/?амд-
тячесгаш я6ер/?я^яя эе^ка-ямыи очень малых разме-
ров, длиной всего 15 см, с зеркалом диаметром 25 мм, имевший, одна-
ко, такую же разрешающую способность, как современные ему воздушные
телескопы-рефракторы длиной 30-40 м.
Он послал ЭТОТ СВОЙ телескоп английскому королю Карлу IL Король
и члены незадолго ди этого созданного королём в L662 г. Королевского
общества (Английской академии паук) одобрили этот телескоп, и Ньютон
был избран членом Королевского Общества.
7S
Глава l
В 1704 г., спустя почти 30 лет Ньютон собрал все свои изыскания о све-
те в книге «Оптика». Полное название этой книги — «Оптика, или Трактат
об отражениях, преломлениях, изгибаниях и цветах спета». Книга при жиз-
ни Ньютона выдержала три английских издания в 1704 г., 1717 г и 1721 г.
В 1706 г. был издан её латинский перевод, а в 3 720 г. французский перевод.
Дифракцию света в области тени, как мы сказали. впервые наблю-
дал Грим Альди в 1665 г. при пропускании солнечною света в затемнённую
комнату через два маленьких близких отверстия. Он наблюдал тёмное пят-
но в нейтральной части светлого пятна на экране, в месте, где оба слабо
расходящихся пучка перекрывались. Явление дифракции (искривления све-
товых лучей при прохождении около края экрана, создаваемою бритвой)
независимо от Гримальди было открыто Гуком.
Интерференция света была открыта, однако, только 150 лет спустя,
в самом нач&ле XIX в. Юнгом. В трактате «Опыты и проблемы по зву-
ку и свету» в 1800 г. Юнг подверг критике корпускулярную теорию света
Ньютона и решительно выступил в защиту волновой теории. В 1801 г. он
первым объяснил явление интерференции света с помощью волновой тео-
рии, а в 1803 г. ввёл термин «интерференция». Исходя из сформулирован-
ного им принципа интерференции, Юнг объяснил и кольца НъютпЕга.
Знаменитый демонстрационный опыт Юнга со светом от двух щелей,
на которые падает световая волна (от двух когерентных источников). позво-
лил ему наблюдать интерференционные полосы и устранить всякие сомне-
ния в справедливости волновой теории света. Юнг, однако, ошибочно счи-
тал, что световые волны тге поперечтгые, а продольные. В 1803 г он пред-
принял попытку объяснения дифракции светя от тонкой нити, правильно
связав сё с интерференцией.
Френель начал свои оптические исследования в 1814 г. Он первым от-
крыл, что световые водны поперечны. Поперсчность волн ему была нужна
для объяснении открытых в го время явлений поляризации света. Прямо-
линейное распространение света Френель объяснил остроумным способом
с помощью мысленного разбиения волнового фронта па так называемые
«зоны Френеля».
Взгляды па природу света после Ньютона мсееялись, и менялись всё
время вплоть до первой четверти XX в. В XVIII в. ещё не было решаю-
щих доводов в пользу корпускулярной или волновой теории, хотя и господ-
ствовала исключительно корпускулярная теория Волны защищал Эйлер,
а корпускулы — Лаплас.
Только после интерференционных опытов Юнга и Френеля победа
волновой теории света стала окончательной. Открытие квантов энергии на
самом пороге XX в. снова перевернуло представления о еноте. Идея кор-
пускул в виде световых квантов, или фотонов, возродилась снова.
ДО1ЮЛНЕНИК I
7Y
Исследования теплового излучения
В первой половине XIX в. рассматривали только световое излучение,
т. ь оптическое излучение раскалённых или горячих тел. Тепловое излуче-
ние еще из него не выделяли и не обращали ня него никакого внимания.
Тепло передаётся пе только посредством теплопроводности и конвек-
ции,. но также и с помощью теплового излучения. Солниеъ костёр, рас-
калённое тело посылают к нам не только свет, но и тепло. Помимо ви-
димого оптического излучения, они излучают невидимые ням тепловые
лучю\ которые отличаются от световых большими длинами волн. Это мн-
ЛуЧИ.
Но ещё в конце XVIII в., в 1791 г. Лревб на основе своих экспери-
ментов и -экспериментов своих предшественников сделал важный правиль-
ны]! вывод, что тело ызярщзгвт тепло независимо от оеойотв
его что его тепловое изучение есть свойство самого телд. Кро-
ме того. Он Открыл^ что тело, кивю/льн? енльло шшвирют ол/эе^доелшое
ихтученке, столь саль/to в до w Этот факт он установил, од-
нако, только для излучения в целом, а не ;игя излучений отдельных длин
волн. Вопроса о соотношении между .т/чглоглои/люелыюй и лучвислуска-
те.тьлои способностями тела для монохроматического излучения Прево не
ставил.
Через 60 лет, в 1853 г. Онгстрсм (правильно Онгстрсм, я нс Ангстрем)
предположил, что в рдекдлёянан достоянии тело испускает излучения тех
же Адин вгми. wmopwe оно при ofiwvwu телте/здтуре погиои/дет.
Новый важный этап в исследованиях jсилового излучения ознамено-
вала знаменитая работа Кирхгофа 1860 г. «Об отношении между исп ус ка-
те явной и поглощательной способностями тел для тепла и света».
Хотя Кирхгофа интересовала связь между нспускательной и поглоща-
тельной способностями газов только в Оптической области, где равновесие
.и^жеН1 meflo.w и исяргх'ае.иы.и w.if имучейиея никогда не уст^р/щл-и/ваенгся,
он чисто теоретически рассмотрелmeMitwe излучена, находя-
щееся в полости с идеально отражающими непроницаемыми для излучения
стенками, поддерживаемыми при некоторой фиксированной температуре,
внутри которой находится некоторое ЧИСЛО излучающих |[ ГюГЛОЩаЮЩНХ
тел.
При равновесии тела, имеющиеся в полости, приобретают одинаковую
температуру, равную температуре стенок полости. Окружающее их в поло-
сти излучений по своим свойствам, в том числе по спектральному распре-
делению энергии в нём» будет определяться только том и ературой стенок,
а нс свойствами помещенных внутри полости тел.
«о
Глава l
Рассматривая равновесное излучение в полости с телами, Кирхгоф
в работе I860 г. установил свой зпдмсетигый ссзакон Кирхгофа» о связи
нс ну скатол ьной и поглощательной способностей нагретого тела. Основа-
нием, как он пишет, ему послужило сделанное им с Бунзеном несколькими
месяцами ранее экспериментальное открытие, что тёмные
линии в cosntfdffwn с личыя-шл известны-
лги пбгрллш и глуд.ии темных уточните.
Согласно закону Кирхгофа интенсивность излучения телом опре-
делённой длины волны может быть найдена исходя из интенсивности излу-
чения этой длины волны абсолютно чёрным телом и зависимости для этой
длины волны поглощения и показателя преломления рассматриваем ого тела
дм этой длины волны.
Тем самым л/юйллид нгучвдил теллоеклго мм^чення любого гседя бы-
ли csedewu к кррбле-м* изучения мятуч^ния абсолютно черного
me-tu.
//слусАяшсльном слособмостью Г) тела температуры Г в интер-
вале частоты и, ш -h dLj Кирхгоф назвал тзичеелдео эиергтш,
# вдшгицу в/^меяи й>ияиц£и лое^хло^ти иели я расчете на й>мяичный
иииереад числит, когда формально можно считать. что dw = I. /7огло-
слюгшжнстьлэ л(^ Г) тела температуры 7' в интервале частот
w, w+dw Кирхгоф назвал dc?.№ энергии, ни eduum/y лаверитгек'лгп
лте-iu и лоэтощвдноы Размерности этих величин следующие:
[Е(^Т)1= а(^ Т)| = 11
м
Е и п от англ. emission — испускание, absorption — поглощение.
Закон Кирхгофа формулируется следующим образом. Огйногиелые jrc-
сл^эйзбности к слособйогти.
Г)
а(ит Г) 1
не здвдеил offi л/шробы jHfTd, других de/йи.тегг. л жйлый> огм Г
u vacOTOffEN ш- Таким образом, отншпепие
^4т = ЖП
а(и\ Г)
является некоторой универсальной (нс зависящей от природы излучающего
тела) функцией.
Дополнение l
N]
Абсолютно чёрным телом называется такое идеальное тело, поглоща-
тельная способность которого л(цг Т) — 1. г. с., строго равна единице для
всех частот и температур. Таким образом, универсальная функции Кирх-
гофа
Ж Т) = ади, Г)
есть функция испускагтельной способности абсолютно черного тела.
В 1879 г Стефан, анализируя результаты экспериментов с излучением
чёрного тела, проведенных Дюпонтом и Птн, а также Провосте н Дссёном,
показал, что эти измерения хороню согласуются с предположением, что
мощность £? излучения с единицы поверхности тола удовлетворяет закону
Я= <тГ\
где 7 — температура тела, — коэффициент. не зависящий от тс мп сратуры.
[]роперяя этот закон. Тиндаль в 1880 г. установил, что при пагрепз-
ниит в частности, рас калён еюн плати ноной проволоки от слабого «красно-
го» каления (около 525 СС) до «белого» каления (приблизительно 1200 °C)
интенсивность излучения возросла в 11,7 раза. Отношение же абсолютных
температур в четвертой степени равЕто 11,6-
В 1884 г. Больцман применил известное в молекулярно-кинетической
теории газов рассуждение с цилиндром и поршнем к элскгромагни гному
равновесному тепловому излучению и теоретически вывел закон Стефана.
При этом он рассмотрел не только энергию Е7, но и давление р равновесно-
го теплового излучения в цилиндре с поршнем. При этом он доказал, что
из электромагнитной теории Максвелла вытекает следующая зависимость
между давлен нем и объемной плотностью энергии излучения;
..... IX
р=т
где и — объем ездя плотность энергии излучения.
В 1893 г. Вин, продолжив рассуждение Больцмана (с излучением н ци-
линдре с поршнем), вывел закон смещения Вина, касающийся спектрально-
го состава плотности энергии теплового излучения и утверждающий в фор-
мулировке, которую позже при да] г этому закону Тнзен, что
w(A? Tj - Т5 ^(АТ) = А-5 ^(АТ),
где Г — температура излучения, А — длина волны, и - некоторые
функции. Таким образом, функция и(А. Г) зависит от А и Т так, что для неё
отношение и(А, Т)/Ть или произведение А6и{А, Г) являются функциями
произведения АТ длины волны А и температур ел 7’.
Й2
Глава l
Объёмная плотность н = -и(Г) полной энергии теплового излучения
всех длим поли может быть представлена как интеграл ст спектральной
объемной плотности:
PQ
н{Т) = У u(T, A)dA.
ii
В 1895 г. Луммср и Вин предложили остроумный способ исследования
излучения абсолютно чёрного тела с помощью излучения, испускаемого
пустой замкнутой полостью с нагретыми стенками через маленькое отвер-
стие (дырочку) в ней, столь маленькое, что оно не влияет на состояние
излучения в полости.
С тех пор стали проводиться надёжные количественные измерения ин-
тенсивности и спектрального состава излучения абсолютно черною тела,
приведшие в ко печном счёте к формуле Планка в 1900 г.
Исследования оптического излучения
В ]8О2 г. Вол дзетой обратил внимание на тс, что непрерывный сплот-
пой солнечЕтьсй спектр прерывается меюжсством резких темных линий, При
зтом он наблюдал зги линии на тех же длинах волн и в спектрах^ которые
испускаются раскалёнными телами, парами и возбуждёнными газами в зем-
ных условиях. Эти последние линии, наоборот, были светлыми на тёмном
фоне. Дать объяснение темным линиям в солнечном спекзре Волластон не
смог.
Независимо от Волластона, в 1814-1815 гг. Фраунгофер тоже исследо-
вал тёмные липин в солнечном спектре и даже точно измерил их длины
волн, используя известную к тему времени дифракцию света па щели. Ока-
залось, в частности, что длина волны особенно чёткой двойной тёмной ли-
нии в солнечном спектре в точности была равна длине волны яркий жёлтой
двойной линяв в спектре пламени масляной лампы (как потом выясни-
лось Р-линии Na). Фраунгофер обнаружил, что #нд ндлойнисл г
0 Л7ОЧНОСЛ1Ы fflfltw OZAEfLM гЗгЗг ff «даетгиолг глектре ся
тёлшля лшлмг. Тёмные линии солнечною спектра стали предметом многих
дальнейших исследований Фраунгофера. Впоследствии их стали называть
«фраунгоферовыми линиями».
В 1821 г. Фраунгофер применил дуги точного измерения длин bqjjet
тёмных спектральных линий солнечного спектра п соответствующих Свет-
лых линий спектров земных источников изобретённые и изготовленные им,
хотя ещё и несовершенные, решйнга. С их помощью он
точно измерил длины волн многих линий, Тёмные линии солнечного спек-
тра он использовал в качестве опорных чти лепных линий. Его измерения
Дополнение l
S3
длин волн спектральных линий были значительно более точными, чем ран-
ние измерения их величин Юнгом и Френелем.
Рекордными в XX в. дифракционными решётками стали решётки
с 5 000 штрихов на 1 мм* изготовленные Роуландом, работавшим в Бал-
тиморе кам университете в США (Университет Джона Гопкинса), с помо-
щью специальной так называемой «делительной машины». Позже в этом
университете работал знаменитый американский оптик Роберт Вуд.
Наблюдения фрау нгоферо вых линий в солнечном спектре и жёлтой
P-линии натрид в пламени масляной лампы или спиртовой горелки поло-
жили начало науке, названной впоследствии «спектральным анализом».
Олповременно с Фраунгофером исследованиями спектров окрашенных
пламён газовой горелки занимался Гершель. В 3823-1824 гг. он изучал
пламена, окрашенные н др. элементами.
Б 1826-1834 гг, анализом спектров занялся Тальбот, который заметил,
что котя красные и пламена нельзя различить про-
стым глазом, они дат разные картины линий при рассмотрении их через
призму.
Наконец, в 1857 г. Сван строго доказал, что светлая желтая линия,
всегда наблюдаемая и спектре пламени спиртовой горелкщ присутствует
и в спектре пламени масляной лампы, и что она обязана натрию Nan являю-
щемуся компонентом поваренной соли NaCL распространённого вещества.
Сван исследовал многие пламена и установил, что спектральные линии, по-
являющиеся в пламенах при испарении в них всшсствн всегда находятся на
одних и тех же местах в спектре, т. с. имеют одинаковые длины воли, вне
зависимости ОТ’ свойств горенки, гпособв испарения вещества и пр. и пр.
Несмотря на все эти более чем впечатляющие исследования оптиче-
ских спектров, истинными основателями яндоыэд вес же по
праву считают Кирхгофа и Бунзена.
В 1859 г, спустя два года после появления работы Свала. Кирхгоф
опубликовал свою знаменитую 2-страничную статью о фраунгоферовых ли-
ниях, в которой положил начало анализу. Сославшись на
свои эксперименты с Бунзеном, Кирхгоф объяснил фраунгоферовы линии
как лшш/ атмосферы Солнца,
Кирхгоф в этой работе описал следующий свой эксперимент с Бунзе-
ном. В спектре пламени свечи они наблюдали две близкие светлые О-ли-
нии, которые находились на том же месте в спектре, что и две темные
близкие фраунгоферовы D-линии в солнечном спектре. Липли зги стали
ярче, когда в пламя свечи была внесена поваренная соль. Когда солнеч-
ные лучи до поступления па щель спектроскопа пропускались через пламя,
окрашенное поваренной солью, т. с. при ослаблении солнечного света этим
«4
Глава l
пламенем, на месте темных Л -линий появлялись светлые жёлтые С-ли-
нии. При усилении солеючпого света на месте светлых D-диний висзап ею
в определённый момент возникали две тёмные /?-линии, которые теперь
были гораздо резче к отчётливее, чем без прохождения через пламя с пова-
ренной солью.
Кирхгоф пишет: этих nafiw&dewuu я заключу что окошенное
ллег.ил, s глгктр₽ йгото/?огс? есть twmjwe резкие .?штпР мастолЫш ослд&тЯ-
ет .-кучи цвети этил линий, Лрдоодящие СКйеИь леегл vma utf Aiecme Сй^тиТых
линий нояйляютея т&илы^ линии, й?;т позади ллоивди яазодшп^я источник
света достаточной яркости, а снегире кетереге этил juuww пет». И да-
лее: #... я заключая?, что лделшъде личин снянечнвдп ехгеюн/м, крт^ые w/jo-
иядадены не am.woc^wpou Зеили. йотнияа^т бллаойаря присутствия; е рас-
калённой атьмосфере Солн^о веществ, в стеюя/№ лла.пепи дающих на то.-и
ж? сачаи лгеапе светлые линии. ЛГажно утверждать. иачри.иер. что на-
личие двух светлю линии в спектре яллийнц. совпадающих с /^-линиями,
доказывает Р что в ат.кос^ере С’олпиа есть латргшл.
Кирхгоф считал, что Солнце имеет твёрдое раскалённое добела «яд-
ро», которое испускает лучи всех цветов. Солнечная атмосфера удержива-
ем однако, большую часть этих лучей н, и частности, жёлтые лучи натрия.
Таким образом, солнечный спектр есть СП£КШр Л0£Л0ЩСЛЧЯй в котором цвет-
ные лучи спектра солнечного ядра частично или полностью поглощаются
веществом солнечной атмосферы.
Кирхгоф эаключет свою статью словами; ^йс^ледовямие слектров
окраи/сплыт пламен приобрело теперь новый высокий интерес#, — п за-
являет, что собирается вместе с Бунзеном провести дальнейшие исследо-
вания с помощью наблюдения открытого им явления ослаблен нм пламенем
световых лучей.
Самым важным н этой статье Кирхгофа является го, что он установил
связь .ueoft.'dy лучами, мслускае.иыл<и п.таиеяе.и, w лучами, ослайдяел<ы.ии им,
ки^да сквозь rtptwadwm белый t tftfm.
Как мы сказали, Кирхгоф представлял себе Солнце в виде твёрдого
ядра, содержащего большинство известных на Земле тяжёлых металлов,
раскалённого добела И окруженного оболочкой паров этих металлов, ян ля
ющсйся солнечной атмосферой. Температуру ядра Солнца Кирх1иф считал
очень высокой, полагая, что из него исходит основная часть солнечного
излучения. Солнечные «пятна» Кирхгоф рассматривал как «облака» сол-
нечной атмосферы (скопления плотных паров, вышедших из солнечного
ядра). Излучение, испускаемое солнечным ядром, проходит через эти лары
солнечной атмосферы, коюрые хо тя н раскалены, ею имеют теми ера гуру,
меньшую температуры ядра. Атмосфера Солнца действует, таким образом,
Дополнение l
es
подобно натриевому пламени в описанном Кирхгофом опыте Кирхгофа
и Бунзена, т. с. поглощает лучит которые сама способна испускать.
Поэтому спектр солнечного света, доходящий до Земли, имеет темные
фраунюферовы ЛИНЯМ, которые Отвечают .лучам, поглощённым солнечной
атмосферой. При этом многие спектральные лнниии соответствуют спек-
тральным линииям известных на Земле металлов.
Из этого совпадения Кирхгоф заключил, что атмосфера Солнца содер-
жит известные на Земле металлы в парообразном состоянии.
Отсюда Кирхгоф сделал важный вывод, что «eufeewflo яяе Земли тл.тнсс
й№££тньмш нд хшическши
Теперь установлено, что солнечное «ядро» нс твёрдое, а газообраз-
ное, хотя его плотность равна 1,4 г/см3. Если бы оно было жидким или
твёрдым, оно должно было бы иметь большую плотность, так как состоит
из элементов тяжёлых металлов. В силу очень большого давления и очень
высокой температуры газообразное солнечное ядро имеет плотность, кото-
рая превосходит плотность воды, но остаётся газообразным.
Доказательством теории Кирхгофа физики фрдунгоферовых линий по-
служило наблюдение протуберанцев солнечной короны во время полных
солнечных затмений- Тёмные фраунгоферовы линии на светлом фоне пре-
вращаются в моменты затмений в светлые линии на тёмном фоне. Полное
солнечное затмение 1868 г, показало это в первый раз.
В основу своей теории снекгров поглощении Кирхгоф положил, как
мы уже сказали, предложенное им, широко известное теперь рассуждение
о телах в полости, справедливость которого Кирхгоф установил, однако,
только для теплового, а не оптического излучения тел, о котором мы юво-
рил и выше.
Если два тела одинаковой температуры помещены в замкнутую по-
лость с зеркальными стенками, то они будут пребывать в равновесии друг
с другом и с окружающим их излучением. Отсюда можно сразу заклю-
чить, ЧТО способности К ИЗЛуЧСНИИ} И [ЮОЮЩСТШЮ у обОИХ ТС Л ДОЛЖНЫ
находиться в одинаковом отношении. Например, если первое тело излучает
тепловые лучи определенной длины волны в К} раз сильнее, чем второе, то
оно в условиях равновесия должно и поглощать эти тепловые лучи в 10 раз
сильнее второго тела.
Кирхгоф замечает; я... что Аля теялояых лутен, А(ь?ж-
riu быть сд/>й№£>лцвд л Аля сйе'т-уь'-ьгл. так как течтловые1 ц готовые .тучн.
дос/пныи лучд.-w, АРУ^ опт АР)^7 птольяо чл-
столюы (Wffldtfux калебший».
Это заключение, однако, не вполне справедливо, так кик оптическое
излучение, с которым экспериментируют, в отличие от теплового, всегда
неравновесное.
«6
Глава l
В 1859-1862 гг. Кирхгоф и Бунзен провели эксперименты по изуче-
нию спектров паров многих известных в то время веществ, испаряющих-
ся в пламени бунэенсвской горелки. Знаменитая горелка Бунзена (изоб-
ретённая им в 1857 г., известная нам как самая обычная газовая горелка)
даёт высокотемпературное несветящееся бесцветное пламя, которое поз-
воляет при превращении в парообразное состояние вещества, вносимого
в пламя, наблюдать спектр только этого вещества, не осложнённый линия-
ми пламени.
Кирхгоф и Бунзен установили, что сяетнлые лыкии t? иыучбшя
Дтя кдждагр элемента (впрочем, ра-
нее это открыл ещё Тальбот).
Ди Кирхгофа и Бунзена факт о том, что спектральные линии окрашен-
ного пламени характеризуют именно раскалённое в пламени до парообраз-
ного состояния вещество, нс был, однако, твёрдо установлен.
Для экспериментов со спектрами Кирхгоф изобрел специальный при-
бор. Это так называемый слеюндосгол г лрыхноы u э/чготелынш трубой, по-
казанный на рисунке, — первый прибор, специально предназначенный для
наблюдения и изучения спектров. Исследуемое веществе укрепляется на
платнновой проволочке и вносится в пламя бунзеновской горелки, где оно
испаряется, при ЭТОМ свет от раскалён!юго пара направлялся па входную
щель коллиматора спектроскопа.
Спектральный анализ Бунзен и Кирхгоф превратили н средство дхля
очень чувствительного химического анализа, распознавания нал] ни я или
отсутствия химических элементов в исследуемом веществе.
ВИД СВЕРХУ
Спектральные исследования привели Бунзена и Кирхгофа к открытию
двух новых химических элементов цдоыя и рубидия, Бунзен открыл це-
зий в I860 г, и рубидий в 1861 г. Элементы эти были названы по характер-
Дополнение l
N7
ной для них красной и голубой линиям спектра: rubeus — красный (лат.),
cacsius — голубой (лат). Позднее с помощью спектрескопа были открыты
лтлллыыг галлий, индий и гелий.
До Кирхгофа и Бунзена Гершель и Тальбот уже утверждали, что при
помощи спектральных исследований можно обнаружить присутствие или
отсутствие ничтожных количеств вещества. Кирхгоф и Бунзен, например,
нашли, что одна ^-миллионная милиграмма хлорисюго натрия {поварен-
ной соли) скрашивает пламя настолько сильно, что даёт яркую С-ли-
нию.
Используя спектроскоп с дифракционной решёткой. Онгстрем с боль-
шой точностью измерил положения многих фрау]।гоферовых линии и со-
ставил первый атлас этих линий в 1869 г.
После Кирхгофа и Бунзена многие физики исследовали спектры хими-
ческих элементов и измеряли длины волн многих линий в этих спектрах
и их относительные интенсивности.
До доклада 1882 г. Британской Ассоциации известного оптика сэра
Шустера основным назначением анализа спектров атомов и молекул счита-
лась идентификация наличия химических веществ в самых незначительных
количествах^ такие исследования ссгекгрой поэтому и назывались «спек-
тральным анализом» (по аналогии с обычным «химическим анализом»),
В этом докладе Шустер высказал мысль, что в будущем основной не лью
изучения спектров станет ^анализ структуры алиол<ов u молекул#, । е. их
еуся^ройстеаа, и предложил для этой новой науки название «спектроско-
пия». Вот его слова:
# Однако нс следует ожидать слигикол, скорого открытия великого об-
щего МКОнО, так как строений того, что лш налЫйи&и лголекутой, очень
сложно, и трудность проблемы столь велика. что не будь результаты,
которые гможн<? надеяться здесь получит ьг сталь лереостенечной важно-
сти, никто, разве кроне са.мых неисправимых onmj/.чистов, не отважился
бы взяться м исследования, грозящие после лшогит лети работы оказать-
ся абсолютно беедлодныши. А/ы эн л еле надгного больше о силах, которые
производят звуковые колебания. чей о силах. которые вызывают световые
вибрации. Разобраться в точ какие звуки испускает колеблющаяся систе-
ма, — это задачи. которая pajpeuaufa (или не разрешила) я определённых
частных случаях, но обратная задача — найти форму колокола по тем
звукалл которые он он особен азбаеать. — лнкюет сбить с толку далее
самого искусного ,чател<атака- Именно эту задачу надеется в конечное
счёте решить снектрйасопия е случае света. /J mc.w ере.пепел г .пы Йаялс-
пы с £осхищеяи£Ш лриеетствоеать дп.ясе самые небольшие шаги в этап
направлении#.
J'Л Л ВЛ ]
ИИ
Дополнение 2 к гл. 1
История открытия формулы Планка
До работы Планка 1ЧС0 г., в которой появилась формула Планка, были
уже открыты две теоретические формулы для функции Кирхгофа теплового
излучении, каждая из коюрых соответствовала экспериментальным данным
в областях коротких и длинных длин волн. Это законы излучения Вина
и Рэлея.
Кирхгоф в своём законе установил, что отношение испускэтельной
способности к поглощйтслъеюй способности любого тслаъ испускающего
тепловое излучение, одинаково для веек тел (и равно универсальной функ-
ции Кирхгофа испу скате льной способности Еа^{А. Т) = Е(А, Г) для аб-
солютно чёрного тела).
Кирхгоф в I860 г, Стефан в L879 г. и Больцман в 1884 г, при выводе
законов теплового излучения Кирхгофа и Стефана-Больцмана опирались
на результаты известных к тому времени экспериментов по тепловому из-
лучению (в частности, Стефан в 1879 г, открыл зависимость Е = оТ4 из
анализа имевшихся и его распоряжении экспериментальных данных Дкь
лонга и Г1ти и Провоете и Дссспа).
После этих достижений эксперименты по тепловому излучению долгое
время не давали, однако, ничего повою, и ведущее место в ею изучении
заняли чисто теоретические работы, прежде всего, работы Вина и Планка
(ранние работы Планка 1897-1899 гг.).
В 1893 г. Вин (Макс Карл), который в 1890-1902 гг. был асе истеш ем
Гельмгольца в Физико-техническом институте в Берлине, как и Больцман
в 1884 г.ь рассмотрел тепловое электромагнитное излучение, заключённое
и цилиндр с поршнем и зеркальными стенками, по, в отличие от Больц-
мана, учел ещё эффект Доплера для изменения дпиезье волны излучения,
отражённого от движущегося зеркального поршня. Так он вывел свой зна-
менитый «закон смещения», который в формулировке, приданной ему Ти-
зеном в 1900 г., утверждает, что
Е(А, Г) = Г5^(ЛТ) = А -Б^АТ),
где 0 и 0 - некоторые функции, зависящие от произведения А Г длины
волны А и гемперапуры Т. То есть зависимость функции Е(А, Т) от А и Г
не произвольная, а ограничена приведённой формулой.
Спустя два года, в 1895 г. Вин выступил как экспериментатор и вместе
с Думмером предложил использовать в качестве абсолютно чёрною тела
нагретую до температуры Г пустую полость с маленькой дырочкой, выпус-
кающей тепловое излучение из полости наружу. Проведённые Думмером
Дополнение 2
ЭД
и Вином измерения позволили Вину предложить для закона излучения зна-
менитую формулу
Е(А. Г) = £ е-й/АТ
А'
«формулу Винн», которая очень хорошо согласовывалась с полученными
Вином и Лум мерам экспериментальными данными в исследованной ими
области коротких длин волн, С и а — некоторые константы.
Затем Вин попытался вывести формулу Вина теоретически из рассмот-
рения модельной классической системы. состоящей из теплового излуче-
ния. находящегося в равновесии с классическим идеальным газом молекул,
рассматриваемым в кинетической теории газон, с максвелловским законом
распределения молекул по скоростям.
Вывод Вина состоял в следующем. 11с аналогии с формулой Макс-
велла-Больцмана для функции распределения молекул газа по скоростям
/(и) = Си2 С-г /а-Г<йгь С — постоянная^ Вин посчитал, что функция ис-
пускательной способности абсолютно чёрного тела имеет вид 7?(А, Г) =
= # (Л) Учитывая, что £(7) = сгТ1, Вин далее пришел к формуле
Е(А. Г) = С А"'1 е“с/АЛ
формуле своею закона. Действительно, интегрируя приведенную формулу
ни А, получаем, что Я(Т) — гг Г1.
В ] 897 г. Луммер, бывший в то время ассистентом Гельмгольца,
и Принсгейм провели тщательное сравнение формулы Вина с результата-
ми своих экспериментов и установили, что формула Вина хороню согласу-
ется с экспериментом лишь п исследованной ими области коротких длин
волн., При продолжении экспериментов в область длинных волн Лум мер
и Принсгейм наблюдали отклонения эксперимента от закона Вина. После-
дующие их эксперименты 1899-1900 гг. ещё с большей уверенностью под-
твердили наличие этих отклонений от закона Вина.
В том же ] 897 г. Курльбяум и Рубенс, работавшие с 188К г. тоже в Бер-
линском Физико-техническом институте, опубликовали результаты своих
собственных исследований, подтвердившие наличие отклонении экспери-
ментальных данных от закона Вина в области длинных ноли,
Рилей, знаменитым английский физик, в короткой 2-страничной ра-
боте 1900 г. иначе, чем Вин, подошёл к проблеме излучения абсолютно
чёрною тела. Он знал, что закон Вина не описывает эксперименты в обла-
сти длинных волн, и специально отметил, что поводом для сю работы по-
служило как раз это обстоятельство (что закон излучения Ci А-5е_^эМ^\
90
Глава l
найденный Вином в 1896 г., не соответствует эксперименту Рубенса в обла-
сти длинных води при X = 60 мкм и при температуре выше I 000 К). Р:лпсй
поэтому для объяснения экспериментов в этой области и предложил свою
формулу.
Как к мы выше при выводе закона Рэлея-Джинса, Рэлей рассмотрел
моды электромагнитных колебаний в полости и применил к ним теоре-
му Больцмана и равномерном распределении энергии но степеням свободы
для термодинамически равновесной системы В обоснование такого спосо-
ба рассмотрения Рэлей сослался на свои исследования колебаний воздуш-
ной массы в замкнутом сосуде, списанные им в его знаменитой «Теории
звука» в ]877-]87В гг. «Вибрации эфира» Рэлей рассмотрел по аналогии со
звуковыми колебаниями.
Закон Рэлея для длинных волн и высоких температур был подтверждён
вскоре экспериментами Курльбаума и Рубенса 1900 г.
Свои исследования по тепловому излучению Планк начал и 1897 г, за
три года до его знаменитой работы 1900 г С 1889 г. Планк был профессо-
ром теоретической физики Берлинского университета. В пяти сообщениях
Берлинскому физическому обществу с 1&97 г. по 1899 г., которые названы
одинаково: «О необратимых процессах излучения», Планк выступил реши-
тельным сторонЕЗИКОМ закона излучения Вина и пытался дать ему строгое
(лучшее, чем у Вина) теоретическое обоснование. В отличие от Вина, одна-
ко, Планк пытался вывести закон излучения Вина не с помощью классиче-
ской кинетической теории газов, а на основе законов феноменологической
термодинамики, используя концепцию энтропии.
Термодинамикой План к успешно занимался до этого в течение многих
лет. В частности, в своих термодинамических работах он сформулировал
свой знаменитый принцип максимума энтропии и вывел из него условия
фазового, химического и электрохимического равновесий независимо от
Гиббса.
Гак как универсальная функция Кирхгофа В(А, Г) не зависит от
физико-химической природы излучающего тела (находящегося в равнове-
сии с тепловым излучением), Планк взял в качестве такого тела линейный
гармонический электромагнитный излучатель Гсрцд. Так, впервые в тео-
рии излучения появился этот знаменитый «осциллятор Планка», г играв-
ший в ней очень большую роль. Планк в то время считал, что закон излу-
чения Вина справедлив и справедлив абсолютно.
3 февраля 1899 г Луммер и Приттсгейм сообщили па заседании Бер-
линского Физического общества, что ими обнаружены отклонения от за-
кона Вина в области температур от 814 °C до 1426 °C и длин волн от
1,21 мкм до 4П96 мкм, а в следующем сообщении от 3 ноября 1899 г. они
Дополнение 2
V]
заявили, что найденные инн отклонения не вызваны экспериментальными
ошибками.
Однако Планк даже в сообщении от 18 мал 1899 г., ссылаясь на экспе-
рименты Думмера и Принс гейма , ещё надеялсяч что их экспериментальная
работа свидетельствует, что закон Вина «очень близок к действительности».
В тс время он ещё считал, что заявленные Лум мером л Принс геймом откло-
нения от закона Вина обязаны экспериментальным ошибкам. и только ли-
сте того, как эксперименты Думмера и Принсгейма. проведенные в октябре
1900 г, окончательно показали несостоятельность формулы Вина в области
длинных волн, Планку пришлось отказаться от отстаиваемой им столь дол-
го универсальной справедливости закона Вт за, который он до этого столь
долго и упорно защищал.
В 1900 г на заседаниях Берлинского Физического общества Планк сде-
лал два своих знаменитых сообщения — 18 октября 1900 г и (через два
месяца) 12 декабря 1900 г. — о своей формуле.
В нервом сообщении ин предложил свою знаменитую формулу, полу-
ченную им просто путём экстраполяции формулы Вина на область длинных
волн без какого-либо теоретического обоснования. Рубенс ночью после это-
го заседания сравнил формулу Планка с результатами своих экспериментов
и обнаружил очень хорошее согласие, о чем Сообщил Планку на следую-
щий день. Луммер и Принсгейм тоже вскоре убедились, что их измерения
тоже очень хорошо согласуются с формулой Планка.
В сообщении 18 октября Планк получил свою формулу в результате
следующем Экстраполяции термодинамической функция 5 = осцил-
лятора (3 — энтропия, (7 — внутренняя энертия осциллятора, находящегося
в равновесии с тепловым излучением):
d2 S' _ _ u_
dU2 ” У’
в которой л — некоторая постоянная. Вместо этой формулы, которая при-
водит к закону Вина, Планк предложил экстра!юляименную формулу
d2 3 _ц = — f_____________-______—
Щ/З + У) 0W г/
в которой л, /? — некоторые постоянные. При малых J7 эта формула пере-
ходит в формулу закона Вина, а при больших Г простым образом экстра-
полирует её.
Интегрируя приведённую формулу по V, с учётом термодинамическо-
го соотношения
d3 „ 1
Г’
92
Глава l
Планк получил, что
1 _ dS
T dU
g [1и(ЪГ 4- л?) - 1п£/]
I 4- — = р^/гаТ-
Lr
следовательно,
- 1'
Учитывая закон смещения Вина, утверждающий, что = Д”’>/(А7’)
и что Е прямо пропорционально (/, Планк отсюда получил свою знамени-
тую формулу в виде;
Е = с—.
СС/АТ_ ]’
где, как он пишет, С — некоторые две константы, причём в показателе
экспоненты С/А = /З/а.
Именно в таком несовершенном виде Планк привёл свою формулу
в нервом сообщении 1й Октября 1900 г.
Через два месяца во втором сообщении 12 декабря 1900 г. Планк
дал теоретический вывод своей формулы, в котором использовал форму-
лу Больцмана для энтропии равновесного классического газа. Он предпо-
ложил. что «энергия, подобно электричеству или массе вещества^ кванту-
ется», т. с. существует в виде «элементов энергии» (слово «квант» Планк
в этом сообщении ещё не использовал)
Для значения кванта энергии в случае рассматриваемой им системы,
состоящей из гармонического осциллятора частоты и находящегося с ним
в равновесии тепловой} излучения, Планк постулировал свою знаменитую
формулу:
г = ftp
для кванта энергии, в которой ft — постоянная Планка-
Планк привёл численные значения постоянных Больцмана и Планкат
входящих в его формулу, полученные из сравнения его формулы с экспери-
ментальным н данными
ft — 6-55 К) 2' эрг С] fch = 1,345 10 1в эрг/град.
которые очень близки к современным значениям;
ft = 6.626 - J и : 1 Дж-с, fcN = 1.3807 10 23 Дж/грзд
Дополнение 2
93
Заметим, что
эрг= = 10~я кг 10~4 м? = 1()-7 Дж_
CJ CJ
Формула Планка, представленная им в сообщении ст 12 декабря
1900 г., была приведена для спектральной объёмней плотности энергии
теплового излучения:
ВтгЛ^3 1
и для спектральной и:<лучатслы[ой способности абсолютно чёрного тела:
г-I _ 8 jt с J.! _1______
A5 ecA/Ati;AT_|
здесь — частота, А - длина волны, с — скорость света,
В выводе своей формулы^ приведённом им в сообщении 12 декабря
1900 г.ь Планк продолжил свои рассуждения, использующие феноменоло-
гическую термодинамику, из сообщения 18 октября 1900 г Ио теперь он
проинтегрировал по F7 полученную им формулу;
dSF _ а
[ln(L+0)-1п£/]
для первой ирон вводной энтропии осциллятора, пахо;1Я1псгося в равЕЕовс-
син с тепловым излучением температуры Г, и получил формулу:
.5' =
а
/3
Е7 Ь/3)1п(!7 +Д}- (7-Д- !71пЕ7 + /7 4-const
ДЛЯ энтропии осциллятора, в которой const — постоянная Етнтегрнронанпя.
Эту постоянную Планк выбрал из условия^ что S = О при (/ = 0-
Таким образом, он получиль что const = й In/34-о, и мы имеем следующую
окончательную формулу для энтропии равновесного осциллятора:
5 = а
(1 1п(1 - 1п^
\ ц J \ /з; {3 Р
Появившаяся в формуле логарифмическая функция, по-видимому, на-
вела Планка па мысль о возможности применения к тепловому излучению
94
Глава l
статистической теории энтропии Больцмана из молекулярно-кинетической
теории газов, е которой энтропия тоже давалась логарифмической фуЕгк-
цией.
Чтобы найти энергию осциллятора, находящегося в равновесии с теп-
ловым излучением, Планк рассчитал среднюю энергию, приходящуюся
па один осциллятор и равновесном статистическом ансамбле, отставлен-
ном из идентичных с ним Аг осцилляторов, в состоянии ансамбля с дан-
ной энергией 171V = Ft, где Р — некоторое целое число, принимающее
значение 0 Р < Лт (это так называемый «ми крока ионический» ан-
самбль, который следует отличать от «канонического» ансамбля}. «Осцил-
лятором» (одномерным) Планк, как и Лоренц до него в его плсктроиЕиж
теории, считал атом вещества, находящегося в равновесии с тепловым излу-
чением.
При этом Планк, к сожалению, не акцентируя особо на этом внимание,
делает очень важное предположение о том. что эяе/дедо системы ocqttwj-
mopos рлтл целому числу лго/чрит, как он говорит, «элементов
энергии» f, предполагая, что вообще люблл! энерггиг ctjrmowm us хвдшивд
лобобко точу Айа эле.ктричй?кай эя/?ж) /мегя целому крлтюжу э<е,неитя/?-
hcwo здрябд е jweKmpowtf, который можно считать элементарной порцией,
«кезегтом» заряда.
Энтропию Stf равновесного состояния ансамбля из jV одинаковых ос-
цилляторов с энергией (7^ Планк вычислил, используя формулу Больцмана:
S\ — A: In Нг,
в которой fc = fc|- — постоянная Больцмана н IV — вероятность того, что
ансамбль из Аг осцилляторов обладает энергией Цц/.
Следуя Больцману, Планк предположил, что ве/нмтлйс ть IV риьли
числу спосябое/?лсл/?ейеяений эяе/кии CTjy /мссл/д^иад^мо^ рдечоеесноео
состолншЕ лчеамбяя ссцплдято/?^ «о /V отд^^лым осцидяя-
«ffljpflAT этлгг? аневдбдо.
При этом Планк предположил, что кгшбый оециыятцр имеет awep-
гию, /юекук> целому кршгснлму эламский эче/гяш г. Другими словами,
Планк посчитал, что рассматриваемая вероятность IV равна, по Больцма-
ну числу «мнкросостояЕшй», реализующих рассматриваемое «макросесто-
яние».
Число способов размещения Р предметов но ящикам
равно
(дг + р-1)! (tf+ Р}!.
“ №Р! ;
Дополнение 2
при этом число Дг осцилляторов в ансамбле и целое число Р, определя-
ющее количество квантов энергии е в энергии £’лг^ предполагаются боль-
шими.
Чтобы доказать приведенную формулу, рассмотрим абстрактную схе-
му, изображённую на рисунке, иллюстрирующую распределение квантов
энергии по осцилляторам ансамбля для Лг = 5 и Р = 8. На этом рисунке
кружкамi[ изображены кванты энергии, а вертикальными чёрючками раз-
делители перегородок между отдельными осцилляторами ансамбля {если
в ансамбле N идентичных осцилляторов, то схема имеет iV - 1 перегоро-
док).
12 3 1 б
| о о | о | |о о о | о о |
Между испей стенкой схемы и первой вертикальней чёрточкой имеется
два кружка, означающих, что на первый осциллятор ансамбля ы рассматри-
ваемом распределении пришлось два кванта энергии. Между первой и вто-
рой вертикальными чёрточками имеется один кружок, что означает, что на
второй осциллятор ансамбля пришёлся один квант энергии и г. д. В рас-
пределении, показанном ня рисунке^ для ансамбля из Ат — 5 осцилляторов
с Р = 8 квантами энергии имеем 2, 1,0, 3, 2 квантов энергии для первого,
второго, третьего, четвёртого, пятого осцилляторов.
Число способов Р размещения квантов энергии по /V осцилляторам
равно числу соответствующих абстрактных схем, тс. числу псрсстапопок
Р—N- L предметов между собой, ранному (P+jV—1)!, делённому на число
перестановок Р1 кружков между собой (кружки одинаковые) и на число
перестановок (5Г I)! перегородок между собой (перегородки одинаковые).
щен ин 2 предметов по 3 ящикам. Согласно приведённой формуле тоже по-
лучас Мн что
(N + P- 1)! 4|
(АГ-1)!Р' 2'2!
т. с. тоже получаем 6 размещений Факториал Лг! числа N — тго произведе-
ние чисел 1.2- ... /V.
96
J'Л Л ВЛ ]
Теперь, применяя формулу Стирлинга Inn! — n In п - п для фактори-
алов, получаем
Sy = к In
(/V 4- Р)!
Л'!Р!
= I In [(Лг + Р) 1п(Лт + Р) - (N + Р) - *¥ In N + - Р In Р + р] =
= fc (Лг - Р) ln(.V + Р) - Лг In Лг - Р In Р
Энтропия» приходящаяся на отдельный осциллятор в ансамбле, равна
S = так что получаем следующую окончательную формулу для
энтропии осциллятора:
£ = £
в ансамбле из Аг одинаковых осцилляторов, имеющем энер-
гию Р<_
Приходим к формуле в точности того же вида, что и формула, какую
мы привели выше, которую Планк получил из термодинамических сообра-
жений- Из сравнения этих формул получаем, что
ftf =
U _ Р
.З №
а следовательно,
Lr Л- = Гк = Р /?,
так что
0 = *,
те. 3 равно iбанковскому кванту энергии.
Планк в то время определенно еще нс осознавал величия своего от-
крытия. В сообщении на заседании Немецкого физического общества сиг
заявляет: «Я не придаю особого значения доказательству необходимости
формулы и cii практической применимости, а лишь подчеркиваю ясность
Дополнение 2
97
и определенность тех направлений, которые я предложил для решения про-
блемы».
Более тою, даже и через 14 лет, когда он с Перистом давал рекомен-
дацию Эйнштейну для избрания того в Прусскую академию наук, Планк
писал: «Если кое-что в его (Эйнштейна) спекуляциях могло пройти мимо
цели, как, например, его гипотеза о световых квантах, то это не может быть
поставлено ему в вину, нбс?. выдвигая новые идеи, особенно в точных нау-
ках, невозможно не идти на некоторый риск».
Любопытна судьба работы Планка I900 г, ознаменовавшей начало эры
квантовой физики, в первые годы после её опубликовання.
Между 1900 г и 1905 т. etc появилось вообще ни одного печатного от-
клика на гипотезу Планка о квантах энергии, хотя предложенная им форму-
ла н была сразу безоговорочно признана, поскольку хорошо описывала экс-
периментальные данные, но представление о «квантах энергии», введенное
Плат!ком для обоснования своей формулы, принималось сдержанно. Сам
Планк в это время ещё безуспешно пытался вынести свою квантовую фор-
мулу из классической физики, что в принципе сделать невозможно.
Причину, почему рассуждение Рэлея 1900 г. не привело к закону Вина,
вновь обсудил Джинс в 1965 г. Английский физик и астроном Джинс окон-
чил is 1900 г. Кэмбриджскнй университет и работал и этом университете.
Джинс проанализировал вывод закона Рэлея. При этом он даже обнару-
жил ошибку в вычислениях Рэлея (в множителе 1/8 при подсчете числа
мод в интервале частот). После того как Рэлей признал свою ошибку, он
предложил Джинса считать соавтором своего закола и называть этот закон
«законом Рэлея -Джинса??, а не «законом Рэлея», как теперь и делают.
В первой pafioie 1905 l: Джинс обсуждает вывод формулы закола Рэлеи
и рассматривает систему одномерных стоячих волн, испущенных нагретым
телом I? объём, ограниченный двумя параллельными идеально отражающи-
ми стенками. Каждой стоячей волне Джинс приписывает, согласно закону
равномерного распределения энергии по степеням свободы, энергию ^бГ.
Во второй своей работе 1905 г. Джинс приходит к заключению, что
замш излучения Рэяйя ле л/ожет быть применён # обдястл юэротюи ймн
аг? mow что (это неверно предположил Джинс) Атл вддотяих лист
никогда не устпндлтиядется равнодесыя (как он за-
явил как раз вследствие справедливости закона Рэлея-Джинса для всех
частот, ибо согласно закону Рэлея-Джинса полная интенсивность излуче-
ния бесконечная).
Джинс к этой работе критиковал Планка за непоследовательность его
рассуждений и работе от 12 декабри I960 г, состоящую в том, что Планк,
введя дискретную порцию энергии е = hjy («элемент энергии»), должен
9М
Глава l
был бы перейти & конце рассуждения к пределу е —* 0. Тогда средняя энер-
гия осциллятора у негр сказалась бы равной /грТ, а нс
q/i _ j
так у него получилась бы формула Рэлея, а не формула Планка.
После появления критических работ Джинса, касающихся теории теп-
ловою излучения Планка, сложилась довольно неопределённая и непри-
ятная ситуация, названная Эрспфсстом «ультрафиолетовой катастрофой».
Она состояла в том. что правильное рассуждение, основанное на классиче-
ской физике, приводило к формуле Рэлея, хотя формула Рэлея расходилась
с экспериментом в области исследованных на эксперименте больших частот
Н малых ДЛИН ВОЛН.
В СВЯЗИ с поднятой Джинсом дискуссией формулу Рэлея ещё раз вывел
Лоренц, рассуждая по-своему» но тоже классически, применив свою элек-
тронную теорию.
Таким образом, ультрафиолетовую катастрофу провозгласил вовсе не
Рэлей в 1900 г., а Джинс л ]905 г, который считал закон излучения Рэлея
обязательным Для всех длин волн.
Расхождение с экспериментом в области коротких длин волн и высоких
температур Джинс, как мы сказали,, неверно объяснил тем. что Дм излуче-
ния яА/эАтяадх ямн в яры/лзбе никдоба не личмет установиться
.чучесАое (так как иначе действительно наступила бы ультрафи-
олетовая катастрофа^.
Таким образом, «ультрафиолетовая катастрофам не сыграла никакой
роли при открытии закона излучения Планка в 1900 г. В I960 г. Планк
в своей работе вообще нс сослался на работу Рэлея. Определённо огг её
знал, нс проигнорировал её, по-видимому, но той причине, что способ рас-
суждений Рэлея при выводе им его формулы излучения сильно отличался
от его собственного.
Первым, кто etc только признал кваЕгтовую гипотезу Планка 1900 г., но
о развил её, был Эйнштейн» который в работе 1905 г. пошел значительно
дальше Планка, высказав предположение» что элеюиртшдоштиш! излучение
вддня себя тдк, как буйтю оно джтоит из кванта эдергшг, и что ноенте-
лялш элашс кеднлю# яймхамся свежа — реальные микрочастицы.
(Сам Эйнштейн ещё tic назвал эти частицы фотонами, термин «фотон» по-
явился позже).
Гипотеза фотонов в 1906-1907 гг. позволила Эйнштейну объяснить
лргскую г/нгнацу ^о/яоэ^^ёкдш, нс зависящую от интенсивности моно-
хроматического света, ещё способного вырывать электроны из металла, его
Дополнение 2
99
предельную длину волны. Кроме того, Эйнштейн на основе представления
о фотонах объяснил «правиле Стоксал (для флуоресценции и фотоиониза-
ции газов и жадностей), которое Стокс установил ещё в 1Я52 г. и которое
состоит в том, что сЬшнй воллы «сдедя больше e).twhm
волны возбуиейаюн/ва? гс cwwa.
Эйнштейн согласился с критикой Джинса работы Планка I960 г, но
отметил. что хотя закон равномерного распределения энергия по степеням
свободы с необходимостью (и в этом Джинс был абсолютно прав) следует
из законов классической физики, но он опыту. При этом,
одна ко , Эйнштейн отметил, что Планк очень неудачно изложил свою работу
1900 г, н предложил изложить сё по-новому: так, чтобы квантовая гипотеза
нс выступала чужеродным элементом, а служила основой теории
В последовавшей после работ Эйнштейна 1905-1907 гт. дискуссии
о законе равномерного распределения энергии по степеням свободы приня-
ли участие ведущие физики того времени; Лоренц, Рэлей, Эренфест, Ритц.
В 1909 г Эйнштейн дал ещё одно применение ]|ланковский теории
квантов. Он объяснил с её помощью температурную зависимость теп-
лоёмкости твёрдых тел, которая при уменьшении температуры нс остается
постоянной, а уменьшается и обращается в нуль при абсолютном нуле тем-
ператур.
Через 10 лет после открытия Планка вопросы квантовой теории ока-
зались в центре внимания первого Соль.венского конгресса, специальна со-
званного для обсуждения проблем квантовой теории. Участниками Кон-
гресса были Планк, Эйнштейн, Нсрнст, Вин, Перрен, Мария Кюри, Зом-
мерфельд, Резерфорд, Джинс, Дебай, Бор. В работе Конгресса активное
участие принял Пуанкаре, председательствовал на Конгрессе Лоренц.
Первые два десятилетия XX в. принесли квантовой теории большой
успех, В 19Ц г. Пернет распространил идею Эйнштейна о квантах энергии
на вращательное движение молекул меюгоэтомных газов. Введение вра-
щательных квантов для них устранила трудности теории удельных теп-
лоёмкостей этих газов. Немного позже Эйнштейн, Пернет и Линдеман.
Дебай и Борн и Карман разработали правильную теорию теплоёмкостей
твёрдых тел, в частности, объяснил и, почему закоЕ! Деолоезго и Пти клас-
сический физики для теплоёмкостей твёрдых тел, как и закон теплового
излучения Рэлея, справедлив только в области высоких температур.
Нобелевская премия по физике за 1911 г. была присуждена Вину «За
открытие теплового излучения» ив 3 9] Я г Планку «За вклад п развитие
физики своим открытием кванта действия». В 192! г. Нобелевская премия
была присуждена Эйнштейну «За вклад в развитие теоретической физики
и в особенности за открытие законов фотоэлектрического эффекта».
LOO
Глава l
Теорема о равномерном раснрейе^енаа энергии
но гтеиет/ялг ееобо<)ы
Во второй половине XIX в. накопился большой экспериментальный
материал по значениям теплоёмкостей Ср и Си (при постоянном давле-
ния и постоянном объёме) многоатомных газов. Оказалось^ что
гадов е,.№№/я <k)wm?kcwi-w величину (моляр-
ной теплеемкостью называется чеплоём кость, отнесённая к молю вещества,
т. е. к массе, содержащей число молекул^ равное числу Авогадро).
Аналогичный закон для молярных теплоёмкостей твёрдых тел был
открыт Дюлонгом и Пти в 1819 г //роиэведЕниЕ удедь/дои теллоаикос-
mu твёр^оэт /ле?а иа его атомный see яаляелк’я величиной лостмннои
ir раеиой 6 клл/гря^ (удельной теплоёмкостью называйся теплеем кость, от-
несённая к единице НЭССЫ вещества).
В 184-8 г., рассматривая молекулы газа как материальные точки, Джоуль
фактически предположил, что поступательное движение молекул является
единственным видом их движения. Вычисленные им в таком предположе-
нии теплоёмкости Стг. и (7Р совпадали поэтому с экспериментальными толь-
ко для одноатомных газов. Теория Джоуля для отношения теплоёмкостей
у = Cp/Gu дала значение 5/3 = 1,67.
Б 1871 г. Кундт и Варбург измерили отношение теплоёмкостей 7 =
= С7/Стл для штрдерщулш и получили значение 1,67. Позже это значение 7
получил Рамсей для инертных газов - гдоия. ардока. /едемте и кришнана, —
которые он открыл в 1894-1898 гг Гелий, правда, был открыт до него ещё
в 1868 г в солнечном спектре.
Для двухатомных газов экспериментальные отношения теплоёмкостей
значительно отличаются от у = 1,67, для них эксперимент даёт 7 = 1,4.
Исследования теплоёмкостей многоатомных газов СОз, МПз, С^Пэ и др.
провёл Видеман в 1876 г. и обнаружил, что теплоемкости этих газов растут
с повышением температуры.
Начало молекулярно-кинетической теории теплоёмкостей многоатом-
ных газов заложил Клаузиус в 1857 г. Он понял причину расхождения тео-
рии Джоуля с эксперимсЕзтпм и учёл, что молекулы многоатомных газов
обладают также sjnwpewwjM дввддошялш, т. с. поступательное движение
не единственное их движение.
Атомы, входящие в молекулу, могут колебаться, a cava молекула может
вращаться вокруг своих главных осей. Правда, в случае гладких сфериче-
ских молекул^ которые при столкновениях пе могут закручивать друг друга,
вращением молекул следует пренебречь.
Дополнение 2
lol
Клаузиус нашёл отношение доли энергии газа, обязанной поступатель-
М0ыу ДВИХ&НН10 молекул, ко всей его энергии. Он получил формулу
Л" _ з / £
и 2 I с
где К — внутренняя энергия газа» обязанная поступательному движению
мплекуп, U — полная внутренняя энергия raja. Для моля идеального газа
(с числом молекул JV = Af^) приучаем
и = С„Т. К = ЪвГ -1 ят = hc^-cjr,
Z £- Z Z
здесь мы учли, что Уд А*£Г — Я7\ и воспользовались соотношением Ман-
ера Я = Ср — Ст для молярных те।изоёмкостей идеального газа, Я — у ни*
нереальная газовая постоянная, Следовательно, действительно
К _ 3/2(СР-С„)Т _ з С,
и CVT 2 I С,
Если в этой формуле положить 7 = (7P/(7V = 5/3 = 1,67, что [фавнль*
но для одноатомных газон, то получим
А
(/
те. 17 = А\ как это верно и посчитал Джоуль, те. все 1(H)% внутренней
энергии являются энергией поступательного движения молекул. Если, од-
нако, в приведенной формуле положить 7 = Cp/CV - 7/5 - 1,1 (значение,
близкое к экспериментальному для двухатомных газов), то получим
т. с. только 60 % подпей внутренней Энергии двухатомного газа обязано по-
ступательному движению ею молекул.
Немного позже Клаузиуса, в 1859 е к теории теплоёмкостей много-
атомных газов обратился Максвелл. Он пришел к заключению, что <ж>н-
чаотЁЛьпле содоютшг любого количества еыстплм частиц тл-
коеа. чта средняя кинетическая энергия пглтяуплт ель нега Йаи.чгелия Zbw
102
Глава l
каждой из тдак осей одинакова w равна средней знервии вращения около
каждой ит трёх деавлотх осей вдждой члстмйщы. Это утверждение Максвел-
ла стало первой формулировкой «теоремы о равномерном распределении
энергии по степеням свободы».
Дальнейшее развитие теория теплоёмкостей многоатомных газов полу-
чила у Больцмана н 1 876 г.. который проводил исследования теплоёмкостей
многоатомных газов с 1К66г. Больцман рассмотрел молекулу многоатомно-
го газа как механическую систему бет потенциальной энергии, характеризу-
емую обобщёнными координатами ф|, ..., фу и обобщёнными импульсами
Pi, - . р/, где / — число степеней свободы молекулы. При этом Больцман
предположил, что кинетическая энергия молекулы является квадратичной
функцией обобщённых скоростей 51, . Л/, и доказал, что в ^авновсекш
состоянии гам эн^гия каждой молекулы />ас^йдв1вна />двяаив/?но ио оё
стелвчяи свобода? г
Из этой теоремы о равномерном распределении энергии по Степе-
ням свободы многоатомной молекулы Больцман получил свою знаменитую
формулу
7 + 2
7=т
для отношения теплоёмкостей многоатомного идеального газа1 молекулы
которого обладают каждая / степенями свободы
Согласно теореме Больцмана о равномерном распределении энергии
ио степеням CBc6ojfbJT па каждую Степень свободы приходится энергия
- АхТ\ так что для моля газа
U^NAtkltT= ^RT,
f
таким образом, Ct. — — Л, а потому, используя соотношение Манера /? =
f + 2
= Ср - Cv, получим, что С7Р = —-— Я. Следовательно,
С? _ f+2
Cv f
Согласно ЭТОЙ формуле Больцмана, если молекула является абсолют*
НО гладким псдсформирусмым твёрдым шариком или материальной точкой,
Дополнение 2
шз
то / = 3 (три координаты центра масс молекулы) и 7 = 5/3 = 1,67. Ес-
ли она является абсолютно гладкой кедсформирусмой твердой гантслмо
(имеется в виду гимнастическая гантель), то / = 5 (три координаты цен-
тра масс молекулы и два угла, характеризующие направление оси гантели
в пространстве), и поэтому 7 = 7/5 = 1,4. Если молекула является глад-
ким недеформируемым твердым телом произвольной формы, то J = 6 (три
координаты центра масс, два угла, характеризующие положение осн враще-
ния молекулы в пространстве, и угол поворота молекулы вокруг этой оси)
И 7 = 8/6= 1/3 = 1.33.
Позже, в 1879 г. Больцман доказал теорему о равномерном распределе-
нии энергии для произвольной механической системы — с потенциальной
энергией, квадратично зависящей от обобщённых координат; находящейся
в равновесном состоянии.
Окончательную формулировку этой теоремы Больцмана дал, однако,
не сам Больцман, и Максвелл. Так появился знаменитый «закон Максвелла
Больцмана о равномерном распределении энергии но степеням свободы».
Однако, несмотря на успехи, классическая молекулярно-кинетическая
теория теплоемкостей многоатомных газов встретилась с трудностями.
В частности. оказалось, что и этой теории двухатомные молекулы высту-
пают как ।^деформируемые гантелиъ Т-Р, почему-то для них / — 5, а нс
/ = 6, т. е. не учитывается шестая степень свободы молекулы, связанная
с изменением расстояния между атомами молекулы, т.е. колебания атомов
двухатомной молекулы. Непонятно было также, почему теплоёмкости од-
ноатомных и многоатомных газов нс постоянны, как это следовало из клас-
сическом георни, а изменяются с измене кием темпсразуры.
Только на основе квантовой теории стало возможным создание окон-
чательной правильной теории теплоемкостей многоатомных газов.
Исследования теплоёмкостей твёрдых тел
Согласно закону Дюлонга и Пти, открытому ими на основе своих
собственных экспериментов в 1Й1К-1819 гг, молярные (т.е. относящиеся
к массе твёрдого тела, содержащей число атомов, равное числу Авогадро)
теплоёмкости многих твёрдых тел действительно равны 6 кал/град и не
зависят от температуры.
Эксперименты довольно хорошо подтверждают этот закон, по только
га основном. Существуют твёрдые тела, молярные теплоемкости которых
значительно отличаются от 6 кал/град и сильно зависят от температуры
в области низких температур.
В 1875 г. Вебер (другой Вебер, не сотрудник Гаусса) установил, что
молярные теплоёмкости ат.идта. бора и ясремищ? значительно от-
104
Глава l
пинаются от 6 кал/град, хотя с возрастанием температуры эти молярные
теплоёмкости и стремятся к 31 гач ел ню fi кал/гряд.
Экшхеримсн! ы показывают, кроме того, что теплоемкости твёрдых тел,
для которых закон Дюпонта и Пти хорошо выполняется при комнатных
температурахч при низких температурах перестают подчиняться этому за-
кону. При температурах Г -* О теплоемкости неметаллических твёрдых
тел уменьшаются до нуля ио закону Т13, а металлических — по линейному
закону Т.
Первой работой, в которой квантовые представления были применены
к теплоёмкости твёрдых тел, была работа 1907 г Эйнштейна, и которой он
развил квантовуЕо теорию этой теплоёмкости. Эйнштейн воспользовался
при этом идеей Планка о квантах энергии, применив сё к колеблющимся
атомам твердого тела.
При этом он существенна изменил идею Л танка об обмене квантами
энергии remedy изучением и осцилляторам (из теории электромагнитного
теплового излучения) и стал считать, что энергия колебании сишоэт асцил-
.они ара Кйинтуется, т.е. что осциллятор .w.xrm обладать талька а/?ре-
д^емнымы дискретными зйачелиялш энергии. равными целому краткому
h где у — частота, с которой колеблется осциллятор, которым Эйнштейн
считал атом твёрдого тела.
13 работе 1907 г. Эйнштейн показал, что средняя энергия осциллятора,
находящегося в термостате температуры Г, согласно сформулированной нм
по-новому квантовой теории Планка, равна
W = -тЛ--------5
С^ДбТ _ £
она отличается от средней энергии этого осциллятора, определённом по
классической теории:
= *еТ.
Предполагая, что атомы твердого тела колсилннся нс зависимо друг о i
друга с одной и той же частотой Эйнштейн получил следующую формулу
для молярной теплоёмкости твёрдого тела:
(hv/къП2
gft р/А'еГ
СЛ L'/Ai.T — ]
Проведя сравнение этой формулы с экспериментами Вебера, Эйн-
штейн получил удовлетворительное согласие, хотя его теория и нс смог-
ла объяснить правильной температурной зависимости теплоёмкости при
Дополнение 2
105
низких температурах в этих экспериментах. По теории Эйнштейна, при
температурах Т —* Q теплоёмкость стремилась к нулю по экспоненциально-
му закону с-- а на эксперименте она стремилась к нулю по степенно-
му закону 'Г3 для неметаллических твёрдых тел и по закону Т для металлов.
Позже Эйнштейн понял причину расхождения своей теории с экспери-
ментом, правильно объяснив сё тем, что использованная нм в 1907 г. модель
твёрдого тела была нереалистична в том отношении, что атомы твёрдого
тела колеблются на самом деле не как независимые друг от друга частицы
(с одной п той же одинаковой для всех частотой и), а как частицы, связан-
ные сильными межатомными силами. Так что частоты колебаний атомов
в твердом теле образуют некоторый непрерывный спектр.
В 1911 г. Пернет и Линдеман, развивая эту идею Эйнштейна, предло-
жили так называемую «двухчленную» формулу для молярной теплоемкости
твёрдого тела, предположив, что атомы в твёрдом теле колеблются не с од-
ной, а с двумя частотами — г- и и/2. Их формула лучше согласовывалась
с экспериментом, чем формула Эйнштейна.
Дальнейшее развитие квантовой теории теплоёмкости твёрдых тел свя-
зано с исследованиями Дебая, который в 1912 г предложил очень удачный
приближённый метод рассмотрения собствен елях частот твёрдого тела.
В качестве собственных частот, иди «мод», Дебай использовал частоты
продольных (распространяющихся со скоростью с;) и гсЕшер£чмы.т (распро-
страняющихся СО скоростью Се) упругих волн в сплошном упругом твёрдом
теле и подсчитал их число и интервале частот i/? у + rfub которое равно
оГ^,
где V — объём тела.
Дебай при этом огргшячил число Z учитываемых маюш образом у^ру-
валя в твёрбим теле требоядинек чтобы ояо равнялось 3 /V, где А'
число атомов в твердом теле, те чтобы оно было равно полному числу
степеней свободы твёрдого тела. Это даёт следующее уравнение для опре-
деления так называемой предельной «дебаевской частоты» Е/тйК:
3JV -
о
V U + Т
Приведённую формулу для числа колебаний riZ н интервале частот
р, и + «/и с использованием частоты ^miLX можно представить теперь в c.ie-
106
Глава l
дующем виде:
niax
энергия этих колебании равна
dU
Lr'
*т;гс
hv
gft р /Лн Г _ ।
Таким образом, Дебай получил формулу
dU = ----4«d
ri3 рЛ p/feT
df/j
слсдпватслЕ-нс, внутренняя энергия твердого тела при температуре Г равЕса
ИЛИ
dk,
9ЛГ hi/3
JJ И gft k/AeT"
где £ = й^/Л^Г и 9 = Гемлература 0 — это так называемая
«дебаевская температура».
Дифференцируя внутреннюю энергию (/ но температуре Г, получасы
формулу Дебая для молярной тчлпюёмкости т вёрдого тела:
CV = 3fi/^y
в которой / (T/ff) = (3/0) fJ (ГД) — функция, рассчитанная численно Де-
баем в широком интервале температур. I ]рн больших температурах Г —ос
имеем / (770) — 1 и получаем закон Дюлонга и Пти. При малых темпера-
турах Т —* 0 имеем закон
Ci/ = 78,3/?
ZY1
& J
т.е. закон третьей степени, объясняющий поведение экспериментальной
тсплосмкостн неметаллических тверщых тел при малых температурах.
ДОПОЛНЕНИЕ 2 IU7
Свою теорию Дебай сравнил с экспериментом и получил очень хоро-
шие согласие. Позже тщательную экспериментальЕтую проверку его форму-
лы провели Эйкен и Нернст.
Более обстоятельную квантовую теорию теплоёмкости твёрдого тела
независимо от Дебая в том же 1912 г. развили Борн и Карман. Их теория
тоже удовлетворительно описывала экспериментальные данные.
Теплоёмкости металлов при низких температурах изменяются по зако-
ну первой степени температуры Т и определяются не колебаниями атомов
кристаллической решетки, а теплоёмкостью электро иного газа свободных
электронов в металлах.
Глава 2
Корпускулярно-волновой дуализм
электронов
2,1. Дебрийлсвская длина волны
мен по волнами, как и световые пучки,
Впоследствии было открыто мною
R 1923 г. Лун де Бройль (ум. в 3 987 г. н возрасте 95 лет), француз-
ский физик, предложил важную идею О природе элементарных ЧЗСТИЦ. из
которых ему были известны только и элеюн/кмы.
Де Бройль заявил, что не
только пучки света, но и пучки
электронов обладают корпус-
кула рно- ВОЛ НОВ Ы М Дуйл ИЗ МОМ,
т с. пучки электронов являются
потоками корпускул и одновре-
других элементарных частиц,
и оказалось, что все они обладают корпускулярно-волновым дуализмом.
Для того чтобы найти дня пучка электронов, летящих со скоростью v,
формулу juгя его длины волны А, де Бройль провел следующее рассуждение
для фотона.
Он посчитал, что фотон является точечной релятивистской частицей,
хотя и очень малой, но отличной от пуля массой покоя m (на самом деле
в настоящее время в физике считают, что масса покоя фотона равна нулю
m - 0).
Далее де Бройль воспользовался двумя известными формулами. Во-
первых, формулой Эйнштейна £ = тс2 (из специальной теории отно-
сительности) для энергии релятивистской точечной частицы. Во-вторых,
формулой Планка f = ftp для энергии светового кванта частоты у. Так
как £ = он получил соотношение пт с2 — fti/, из которого следует, что
me = hu/e.
Для монохроматической световой волны длина воины А, частота р
и скорость с распространения волны связаны соотношением Аг/ = л В са-
мом деле, f = 1/7\ где Т — период колебании волны и А/Т = с, т.с.
2.1 Де брой л евс к а я дл hi 1 л вол и и
ШУ
А^ = -с. Таким образом, л-'/с = 1/А, и мы имеем из формулы me = А/А
формулу Ji/А = тпс, а следовательно, формулу
Величина тс к этой формуле является импульсом фотона ри = тс
(обычным импульсомX так как это произведение ^массах скорость», а ско-
рость фотона равна скорости света с.
Получив формулу, связывающую корпускулярную характеристику фо-
тона (импульс р) с его волновой характеристикой (длиной волны А), де
Бройль предложил смелое обобщение згой формулы и заявил, что она спра-
ведлива также и для электрона (в то время из элементарных частиц были
известны ТОЛЬКО и мрораоя}.
Если электрон движется со скоростью V и ЕГО масса рЗЕПЯ т, то он
обладает импульсом р = ми. Таким образом, с электроном (с пучком элек-
тронов, летящих с одинаковой одной и той же скоростью и) связана длина
волны
А — —
” mv
Это знаменитая «формула дс Бройля» для длины волны электрона.
Вскоре, в 1927 г. спа была подтверждена непосредственными эксперимен-
тами, проведёнными Дэвисспеюм и Джсрмсром и Дж. П. Томсоном (сыном
Дж. Дж. Томсона).
При использовании в квантовой механике понятия скорости и электро-
на, следует обязательно учитывать то, что эдешпртннж1 нины, в отличие от
ездя, обладают большой т.е. частота элек-
тронной волны сильно зависит от ее длины волны. В силу этого для элек-
тронной волны надо обязательно различать флвдвую и грулнавую скорости,
причём под скоростью v электрона, как это впервые заметил де Бройль
в 1923 г., следует понимать не фазовую t1^, а труп новую скорость т.е.
производную TW = d-E/dp, где Е = Е(р) - Энергия электрона, ар — им-
пульс электрона. Так как дтя нерелятивистского свободного электрона Е -
= р2/3т, то ?.'|P = dE/dp = p/m = и, где m — масса электрона. Фазовая
скорость равна Иф = Е/р = р/2т, т. е. Гф = и/2.
Как и в теории элсктромагиитЕтьгх волн, говоря о скорости
элекгронной волны, мы должны рассмотреть нс отдельную гармоническую
электронную волну с фиксированной частотой cj и длиной волны А, или
волновым числом jfc = 2а/А, а логатн (группу) электронных гармонических
110
Глава 2
волн, описываемый волновой функцией
Ао -Д*
где kg некоторое фиксированное волновое числа, для которого
dE(ft)
dk
= ftfco,
где E(fc) - дисперсионная кривая гармонических волн, Дк ширина вол-
нового пакета, (7(к) — нссотаая функция таолнового пакета, сосредоточенная
около волнового числа ки< как это показано на рисунке.
При Й -* 0, Л -> 0л причем так,
что й/А = const, волновую функцию паке-
та t) МОЖНО яруйяи.вдгелмг? ВЫЧИСЛИТЬ, ЕС-
ЛИ воспользоваться строгим математическим
так называемым .иейшЙели спнщыо/шрной
зы. Согласно ему
^(®, t)« C(Jto)e-WA>FCt(‘:)t+it<’£,
dE(jfc)
где —-—L = hfco- Таким образом, вместо
dk Jt=fco
волновой функции пакета получаем волновую
функцию одной гармонической волны.
Де Бройль в 1923 г. рассмотрел фотон как классическую релятивист-
скую точечную частицу с некоторой малой ненулевой массой то- Связь
энергии Е этой частицы с её импульсом р описывается известной реляти-
вистской формулой
та которой с — скорость стаета та пустоте.
Таким образом, для групповой скорости дсбройлсвскогп фотона имеем
соотношеЕше
r = dEty) _ <?р
* dp \f&p* + m^e4
а для фазовой его скорости соотношение:
Е(р)
“ р “ р
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
11]
Следовательно, справедливо соотношение
Vqj г’ф =
которое вывел де Бройль.
Если л Етерелятпппстскпм приближении полностью откинем
лолоя частицы и положим, что
ТО получим, что
_ £(р) _ mov2 _ v
”ф ~ Р ~ 2mov " 2'
где v — скорость частицы,
Световой пучок и пучок электронов — это реальные физические объ-
екги, с которыми имеет дело экспериментальная физика (никто. конечно,
не может взять пальцами в руки один фотон или один электрон, хотя бы
по той причине, что наши руки сами состоят из огромного числа атомов
и молекул).
Вместе с тем в настоящее время физическая наука пришла к важному
Заключению, что корпус куляр ею-волна вы м дуализмом обладает не только
лучок микрочастиц, НО TLHOKC И ОТЛИТЬЯМ ЧЛСТЛЫЦЛ В ЭТОМ IIV’LKC (В ЧАСТНО-
СТИ, отдельный фотон и отдельный электрон).
Таким образам, корпускулярно-волновой дуализм является фундамен-
тальным основополагающим свойством всех микрочастиц, потому он и по-
ложен к основу квантовой механики.
2.2, Корпускулярные свойства электрона
Эксле/шлтгнт Дж1. Дж1. Тсшсонй с ш/тубтой
Во второй половине УО-х lt. XIX в. английскому физику Дж. Дж. Том-
сону удалось выяснить физическую природу катодных лучей, образующих-
ся в кнтпдею-луче вой трубке. В тс время физики склонялись к неверному
112
Глава 2
мнению, что последние представляют собой особый вил электромагнитных
В0ЛНг
Дж. Дж.Томсон экспериментировал с катоднс-лучеый трубкой, пока-
занной ня рисунке ниже. Исторически эта трубка явилась прообразом или,
как говорят, прототипом трубки осциллографан кинескопа телевизора или
трубки монитора компьютера.
Дж.Дж. Томсон открыл электрон как элементарную микрочастицу
в исследованиях газового разряда {при изучении физики прохождения элек-
। рическототока через газы). Исследования электрического газового разряда
были начаты ещё Фарадеем в 30 40-х гг, Х(Х в.н но особенно интенсивно
про водились во второй ПОЛО ВИ ЕТС XIX в. Гейслером, ПлЕокксром, Гиттор-
фом , Круксом, Ленардом н Герцем.
Если мы возьмём газоразрядную трубку, т. е. стеклянный баллон с впа-
янными в его стенки металлическими электродами — катлйдйн и пнойлк,
и если к этим электродам подключим источник постоянного напряже-
ния, а давление р воздуха в трубке сделаем порядка I MMHg (1 атм =
= 760 мм Hg), то в трубке появится неяркое свечение, как говорят, воз-
никнет электрический газовый разряд, который в этом случае называется
«тлеющим» (его не надо путать с «коронным» разрядом, возникающим на
коп [[ах мачт кораблей перед бурей в виде огней Св. Эльма, и привычны-
ми для нас «искровым» и «дуговым» разрядами). Тлеющий газовый разряд
имеет вид, показанный на рисунке.
капщнос
тёмное положительный
Если давление воздуха в газоразрядной трубке с тлеющим разрядом
ПОНИЗИТЕ^ то катодное тёмное пространство расширится и при давлении
yj — 10 “3 MMHg займёт всю трубку. Свечение в трубке при этом исчезнет,
и она вся стянет темной. При ещё мёньшем давлении р и И)_Г| мм Hg стек-
ло в трубке напротив катода начнёт светиться неярким тусклым синсвато-
зеленоватьгм светом, как говорят, начнёт «фосфоресцировать». Представ-
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
113
ляется, "по что-то невидимое испускается из катода и попадает на стенку
трубки напротив катода, что и заставляет фосфоре сзщровать ее стекло. Это
«что-тол Крукс в 1870 г. назвал «катодными лучами».
Эксперименты показали, что если внут-
ри трубки на пути катодных лучей поставить
какое-нибудь препятствие, например малы мн-
ений крест, изображённый на приводимом ни-
же рисунке, то препятствие отбросит тень
с резкими краями на светящееся фосфоресци-
рующее пятно на стенке трубки ь что доказыва-
ет, что из катода выходят лучи. Путь катодных лучей можно
отклонить магнитным или электрическим полем То есть при поднесении
к трубке магнита или электрически заряженного шара тень от мальтийского
креста на светящемся стекле соответственно смешается.
Заметим, что, экспериментируя с катодными лучами, физики пытались
выяснить также к физическую природу фосфоресцирующего свечения, ис-
пускаемого стеклом трубки. Такие исследования привели в 1895 г к откры-
тию Рентгеном его знаменитых рентгеновских лучей, а и ] 896 г. к открытию
Беккерелсм рад>юакпиз н оста.
Дж. Дж. Томсон представил себе катодные лучи в виде потока быстро
летящих с одинаковой скоростью v маленьких (нам невидимых) электри-
чески заряженных практически точечных частиц с зарядом — е (е = |е i
и массой m каждая.
Элекгронный пучок летящих с один иконой скоростью и электронов
в катодно-лучевой трубке создаётся так называемой «электронной пушкой»,
изображённой на приводимом ниже рисунке. Она имеет катод, подогрева-
емый электрической спиралькой, не показанной на рисунке, и цилиндри-
ческий инод с отверстием вдоль его оси, чтобы он мог пропустить узкий
поток электронов, вырванных из катода электрическим полем.
114
Глава 2
Электроны ускоряются электрическим полем, создаваемым яеюдныы
напряжением 17д. Скорое л, г электронов ь пучке и анодное напряжение
связаны соотношением, выражающим закон сохранения энергии:
m
2
= *6%
г =
Если в эту формулу подставить е = 1.6 10"19 Кл, m — OJJ 10“m кг,
= ЮО В, то получим
и = 5,96 10е м/с.
что составляет примерно 2% от скорости света.
//ручияа услуга Дж. Дж. Томсона сгрл открытии им электрона и физиче-
ской природы катодных лучей состояла п том, что ом сид.к нзучать
отклонение катойгсых лучен. лрсгс/^йи)ё'нн^ о^рямрймеяно атЕАтрпчесАнЛ!
и .-мягнытныш поляны (поля у него были перпендикулярны друг другу).
Электрическое поле создавалось пластинами плоского конденсатора,
показанного на рисунке, рас положе иного внутри трубки. На илдотины кон-
денсатора подавалось постоянное напряжение Lr. Таким образом ь внутри
конденсатора создавалось постоянное однородное электрическое поле на-
пряженности
гГ
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
115
действующее в направлении вверх-вниз, где d — расстояние между пласти-
нами ко НДС] катера. Поле внутри кондс псатира однородно^ т.е. одинаково
во всех точках. Вектор электрической напряжённости Е лежит в плоскости
рисунка и направлен вертикально, т.е. вверх-вниз. При (7 = 10 В и d =
= 1 см = 10"2 м имеем £ = 10э В/м.
Магнитное поле создавалось катушками электромагнитов, размещен-
ных вне трубки* ПО ОбмОТЕШ КОТОрЫХ Протекал ПОСТОЯННЫЙ ЭЛСКТрИЧССкИЙ
ток 7. В зазор между полюсами электромагнитов помещалась та часть труб-
ки, в которую был вмонтирован конденсатор. На рисунке большим заштри-
хованным кругом показан один нз полюсов электромагнита, находящегося
позади трубки. Полюс второго Электромагнита, находящегося перед труб-
кой, нс показан, гак как он загородил бы рисунок. В зазоре между полюса-
ми электромагнитов, в который помещалась часть трубки с конденсатором,
существует постоянное однородное магнитное поле напряжённости Н, на-
правленное перпендикулярно плоскости рисунка, причём
£ = п7,
где п — число виткик приходящихся на единицу длины каждой катуш-
ки. Имеющееся в зазоре между полюсами электромагнитов магнитное поле
перпендикулярно рисунку и направлено вперед-назад.
При Г = 0,5 Л и п = I0 см '1 = 105 м 1 имеем // — 5 IО2 Л/м.
Дж. Дж. Томсон в своей катодно-лучевой трубке смог скомпенсировать
электрическое отклонение луча (в направлении вверх-вниз на рисунке) его
магнитным отклонением (тоже в направлении вверх-вниз на рисунке).
В результате Дж. Дж. Томсон доказал, что клт£ч>ны£ лучи лредстседя-
jow собой л<мл<зд бысщ/зб очеяъ ллтечьядо очела л&яшг часщычек.
л.исюгцЕгх .идлую лкгссу и ллалый отрицательный электрический зи/?яй. Эти
частички впоследствии были на званы «электронами».
Подадим на плоский конденсатор, показанный на рисунке, напряже-
ние (7. Пусть расстояние между его пластинами равно d, а его длина рав-
на Г Учтём, что Электроны влетают в кп1Едспсатор и пролетают через пего
с очень большой скорое тми f. Поэтому МОЖНО Считать, что отдел ьехый элек-
трон с зарядом с пролетает конденсатор, двигаясь равномерно с постоянной
скоростью г за время t = f/v* и лишь немного отклоняется электрическим
полем коЕтдспсатора (па рисунке в направлении вверх-вниз}.
Отклонение электрона вверх-вниз при вылете из конденсатора, очевид-
но, будет равно
116
Глава 2
тле л — ускорение, сообщённое электрону электрическим полем, скажем,
по направлению вверх:
л _ _ eg _ eLr
m ™ mti'
где e = |e — абсолютная всличнив наряда Электрона, m — его масса. Таким
образом, «электрическое отклонение» равно
и -1^-
~ 2 т<1
При е = L.6-10-1-’ Кл? m = 0,9 10-$° кг, [7 = 10 В. J = 1 смJ = Зсм,
и = 5.96 - Ю6 м/с имеем r/.LI = 2.25 10-3 м = 2,25 мм. При этом
Kji-B / мА _ Дж с~ _ Н и с2 _ кг-м/с2 с2
кгм ( н/с J — кгм = кгм — кг ” м'
так как КлВ = Дж и Дж = 11м, II = кг-м/с1. Вылетев из конденсато-
ра , электрон будет лететь дальше по инерции по прямой линии с посто-
янной скоростью i.\ так как на него теперь ею будут действовать никакие
силы (влиянием силы тяжести можно пренебречь вследствие малости мас-
сы электрона}.
На удалённом от конденсатора экране (на стейке раструба трубки) мы
будем пабл издать маленькое светящееся пятнышко, получившееся на экране
при смещении из точки О экрана, в которую попадает пятнышко от нсот-
клонённого электронного пучка, при выключенных полях. Малое отклоне-
ние пятнышка на экране трубки большое, так как становится в несколь-
ко раз больше той величины j/?1, для которой мы вывели формулу.
Найдём теперь «магнитное отклонение». Магнитное поле создаётся ка-
тушками электромагнитов, они гоже постоянно и однородно, j.c. одинако-
вое во всех точках и действует в той же области (длины (), что и электри-
ческое поле Магнитное поле перпендикулярно плоскости рисунка. Поэто-
му оно отклоняет электроны, летящие я плоскости рисунка и направлении
вверх-вниз. При эюм магнитное поле сообщает электрону ускорение
_ ^яиг _ gjJ В
й — _ m 1
где Z> = — икдукиля магнитного поля, дщ — магнитная проницае-
мость вакуума. Величина индукции 7? пропорциональна силе постоянного
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
117
тока Л текущего в обмотках катушек электромагнитов. Она рассчитывается
по формуле Л = /Jq Л = где та — число витков на единицу длины
каждой катушки. Таким образом, магнитное отклонение равно
_ 1 etJ Д f
у“яг “2 m I v /
При е = 1,6 1(Г1Э Клт m = 0:9 Ю-30 кг, = 1,26 L0"6 Гн/м,
Л = 5 Юа А/м, и = 5,96 - 10м м/съ j! = 3 см имеем уМ|Г = 8/16 - Ю-3 и =
= S.46 мм. При этом
Кл-ч/с - Гн/м А/м s _ К.т Гн А с _ А Гн А с2 _
кг с — кг-м — кг-м
= Дж-с- _ н м са _ кг м/с2 С? _
кг-м кгм кг " н
так как Кл = А-с, Гн А2 = Дж, Дж = П-мт II = кг м/с2.
Если теперь добиться подбором величины полейт чту бы
CKOC U ДКТгНЫГС1Н0£ атклочевди ^млечем/ччдлл dpyz то пятетьешко
ст электронного пучка на экране не сместится из точки О, несмотря на
включенные поля. Таким образом, при компенсации будем иметь равенство
Ум = «жг, а поэтому
= Il j? = v/io / та.
л
Из этого соотношения находим формулу для CKO/wcmtr отдетыимо
эдектсг/ч™ в лгучке:
.-1L- У
J /> d 7 та
в праву ео часть входят веянииееыъ которые непосредственно можето было
измерить в описываемом эксперименте Дж. Дж. Том сона, гак что скорость
электрона можно было рассчитать.
При этом эксперименты Дж. Дж. Томсона показали, что скорость г?
электронов и катодных лучах много меньше скорости света с, что послу-
.wj^.Yo с.1 гу джлвдтелйсдавдш. ч/wp дотошные лгучц дс яатякэтгя злектярллшг-
пктлы.ии ёсындлш* как думали до него.
Таким образом, ТЫтсокл со-
стояло л/гежде веегб s ?исщ ч™ йн сиче? ttswcpumt скорость чляиш/ кд-
UK
Глава 2
Если измерить теперь отдельно величину только электрического или
ТОЛЬКО МаП1ИТПОГ0 отклонений (ВКЛЮЧАЯ поочерёдно или ЭЛСКТр И ЧССКОС,
или магнитное ноля), например величину электрическою смещения, то по-
лучим
„ _ 1 г Г Р _ 1 £
2 md / \ 3 2ш U ’
I — I
Мгв/
а потому
£ __ 2 i/ k l
Получили формулу, которая даст возможность экспериментально опре-
делить значение отш>ше1шя заряда к лмссе для частицы катодных лучей,
т. с. для электрона Оказалось, что это отношение равно
£ = 1,76 1011 Кл/кг;
приведено современное значение (число, найденное Дж. Дж. Томсоном, бы-
ло близко к этому значению).
Измеренное Дж. Дж. Томсоном отношение е/m для частиц катодных
лучей оказалось намного больше извес тных в то время значений подобных
отношений для заряженных микрочасти и кшпнонрв и аныонде (в экспери-
ментах по электролизу растворов электролитов); для них это отношение
о/тп было примерно в 1(г раз меньше. Такое различие свидетельствовало
о том, что Дж. Дне Томсон двдсл1йил?£Льно открыл йовую .ннкрочастгщу.
Подставив в полученное отношение t/m значение заряда электрона е,
найденное из теории электролиза, т. с. из значений чисел Фарадея и Аво-
гадро, Дж. Дж. ТомСцн получил, что масса частицы катодных лучей (масса
электрона mJ примерно в 2000 раз меньше массы Проiсна
тр = 1838 тпг;
приводим современное значение.
Так Дж. Дж. Томсон открыл электрон. Открытие это датируется IS97 г.
Сам он, правда, ещё не называл открытую им частичку катодных лучей
«электроном». Это название она получила позже от названия «элементар-
ной порции электричества», впервые введённого в науку английским физи-
ком Стони в ] В74 г. Сам Дж. Дж. Томсон называл электрон «ионом».
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
119
Дж. Дж. Томсону в 1906 г была присуждена Нобелевская премия «За
теоретические л экспериментальные исследования прохождения электриче-
ства через газы».
зцряЭд электрона
Дж. Дж.Томс№ Сам пытался непосредственно экспериментально из-
мерять заряд электрона (нс только отношение заряда электрона к массе
е/m). Он измерял количество воды» сконденсированной в капельки за опре-
делённое время в пересыщенном пареч который облучался ультрафиолето-
вым светом известной интенсивности (вызывающим ионизацию молекул
воздуха и парой воды), т.е. определял число капелек, образовавшихся на
известном лиспе созданных ионов. Каждый ион служил «зародышем» для
роста одной капельки. Такие эксперименты были, однако, очень неточными.
Вместе с гем эти исследования Дж. Дж. Томсона привели к созданию
Вильсоном (его Сотрудником) знаменитой «камеры Вильсона», которая до
середины 1950-х it. была единственным регистрирующим прибором, ис-
пользуемым при изучении элементарных частиц. С её помощью были от-
крыты «позитрон» — электрон с положительным зарядом^ «реакция анни-
гиляции» (взаимного уничтожения) позитрона и электрона с образованием
двух фотонов, «нейтрон», «тг- и /2-мезон ы» н многое другое.
Надёжные количественные результаты для величины за-
ряда электрона экспериментально получил Милликен, кото-
рый в 1906 г. изобрел знаменитый «метод капли». R этом
методе капелька мелкодисперсной аэро взвеси жидкого мас-
ла, распылённого в воздухе, наблюдалась в микроскоп. Она
падала в поле зрения микроскопа, двигаясь вниз с некоторой
постоянной скоростью в пространстве между горизонталь-
ными пластинами заряженного плоского конденсатора, пока-
+ 4- - ।
данными на рисунке.
Оказалось, что схи/тость ndite/iWt алллы йрелгя о/л ерйлггни изменялась
склчкожи, становясь то больше, то меньше, причём величины екдчяоя были
к/допнылш Ач/деделеннану скачку*.
Величины скачков измерялись» и пере-
счётом । ю ним определялась величина элемен-
та рного скачка, а по нему — величина заряда
электрона.
Скачки скорости падающей капли п экс-
перименте Милликена объяснялись тем, что
электрический заряд <j капли был че^олшич
120
Глава 2
a/hnhhhw n (n $ 5-С) заряда электрона е, т е. 9 = пе, где и — число ионов
молекул воздуха, осевших на капле.
В результате твоих экспериментов Милликен в 1910-1914 гг. д ля заря-
да электрона получил значение
е = 1.6 10 ri Кл.
близкое к современному.
На падающую каплю действует сила электрического поля FM =
где Q — заряд капли; 1раыитацнонная сила (сила тяжести) /трм =
где m — масса капли (определяется экспериментально из измерения средне-
го радиуса капли под микроскопом и плотности жидкого масла), 9 ус ко-
ре егис свободного падения; и сила вязкого трения ?„Я.11С = fcu, пропорцио-
нальная скорости и движения капли. Коэффициент fc Милликен рассчитал
по известной формуле Стокса для силы трения шара радиуса Я, равномерно
движущегося со скоростью гр в вязкой среде с коэффициентом вязкости jj:
F№h = 6 я R t1 = fc v;
для этого надо было знать радиус /7 капли и коэффициент вязкости ?j воз-
духа; эти величины измерялись Милликеном экспериментально.
При наблюдавшемся в микроскопе установившемся падении капли,
движущейся с постоянной скоростью v, все три силы, указанные на рисун-
ке, точно компепсировали друг друга. Таким образом, для скорости капли
и имеем значение
mp — пе£ T?tj7
*= ь = ~п ’ т;
следователь! ю, величина скачка скорости падающей капли при установив-
шемся её движении, возникающего при практически мгновенном осажде-
нии на неё или потере сю некоторого дополнительного числа ионов из окру-
жающего ионизованного воздуха (в результате чего заряд капли 7 = пе из-
меняется на величину; кратную еп и становится равным 7 — (п. — .sjr или
кj = (п. — a)cs где л - небольшое целое ЧИСЛО), пропорциональна величине
«элементарною скачка» скорости
Аг =
к
следовательно,
_ к. Аг1.
Е 1
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
121
из этой формулы по величине элементарного скачка Ди можно рассчитать
наряд f? одно крапп ю ЕюннзоваЕнюго иола молекулы воздуха, т. с. элементар-
ную порцию электричества, наряд электрона.
В дальнейших своих исследованиях , касающихся фото эффекта , Мил-
ликен провёл тщательную экспериментальную проверку знаменитого урав-
нения Эйнштейна для фотоэффекта (и оптическом и ультрафиолетовом диа-
пазоне) Н точно измерил значение постоянной Планка.
В 1923 г. Милликену была присуждена Нобелевская премия «За иссле-
дования в области элементарных электрических зарядов и фотоэлектриче-
ского эффекта».
Из многих экспериментов с пучками электронов как пучками корпус-
кул, проведённых после исследовании Дж. Дж. Томсона, остановимся на
Эксперименте Кауфмана 1902 г.
В этом эксперименте можно доказать, что масса электрона зависит ijj
его скорости согласно знаменитой релятивистской формуле
m = ,___________
у/1 - va/e2
в которой t? — скорость электрона, с — скорость света, m<i — масса покоя
электрона.
Впрочем, Кауфман счремился доказать справедливость другой, нелря-
яыльноы формулы для зависимости массы электрона иг скорости, которую
предложил известный немецкий физик Абрагам, и даже утверждал, что
его эксперимент подтвердил «формулу Абрагана», а не приведенную выше
релятивистскую формулу. Экспериментальные результаты Кауфмана былнт
однако, недостаточно точны, хотя их идея была при вилы юй.
Позже, в ] 916 л Бухерер и в I93S г. Цан и Синее
провели более точные измерения и доказали справед-
ливость релятивистской формулы, которую называют
«формулой Лоренца».
Кауфман экспериментировал не с катодными лу-
чами, как Дж. Дж. Томсон, а с «/?-лучами», которые
испускают радиоактивные источники и которые бы-
ли открыты Резерфордом.
В 1899 г. Резерфорд провёл свой знаменитый
эксперимент с расщеплением пучка радиоактивных
122
Глава 2
лучей на три компоненты Он поместил радиоактивный источник в магнит-
ное поле (па рисунке — перпендикулярное плоскости рисунка и направлен-
ное! от нас) и заставил пучок, испускаемый источником, лететь через это
магнитное поле. При этом Резерфорд наблюдал расщепление пучка на «й-,
/?- и -.-компоненты», или «лучи».
В результате последующих исследовании, проведанных Резерфордом
с сотрудниками, было доказано, что 7-лучи являются электромагнитными
волнами короткой длины волны (много меньшей длины волны рентгенов-
ских лучей), ск-луч и — потоками ядер атомов Не, т е. потоком дважды заря-
женных ионов Elc1"*'- /?-Лучи оказались тождественными катодным лучам
Дж. Дж. Томсона, т. с. были пучками электронов.
Я енняычыс йот элслтн/юное лучей, /З-лучкп тж
tfdrtdKO, c/w/wcfflii w, доашшмые со скоростью сдсто с, как яйля-
лись />йтятивистскил<ы.
В 1902 г Кауфман провел эксперимент с отклонением /У-лучей ра-
дноакгивного источника одновременно включенными ндратлвлы/ы-ш, (т.е.
в одном направлении или противоположно направленными} электрическим
и магнитным полями, воспользовавшись изобретённым к тому времени
Дж. Дж. Томсоном так называемым «методом пэрабол».
Позднёе, в 1911 г. Дж. Дж. Томсон успешно применил свой метод па-
рабол для изучения так называемых «анодных лучей», т. е. лучей, создава-
емых в катодно-лучевой трубке в пространстве за катодом (не за анодом},
в котором просверливалось малое цилиндрическое отверстие. Дж, Дж. Том-
сон открыл, исследуя анодные лучи, «изотопы» атомных ядер н изобрел
Б СВЯЗИ С ЭТИМ «МЖХ-СИСКГрСЛраф», очень эффективный прибор В ХИМИЧЕ-
СКИХ исследованиях.
Эксперимент Кауфмана 1902 г показал, что масса электрона действи-
тельно зависит от скорости, хотя Кауфман, как мы сказали, еще и не смог
доказать, что зга зависимость даётся релятивистской формулой
Так как Кауфман взял для эксперимента нс электронный пучок , созда-
ваемый и катодно-лучевой трубке, п которой электроны обладают нереллти-
висте к И МЕТ скоростями, а электронный ПуЧОК, ИСПуСКИСМЫЙ раДИОаКТИШХЫМ
источником при радиоактивных распадах атомных ядер, скорость элек-
тронов в котором релятивистская, i. е. сравнимая со скоростью света, то он
действительно смог измерить зависимость массы m электрона от его скоро-
сти, так как Отношение f/c в его экспериментах имело величину O.tf-O.fl с.
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
123
В эксперименте Кауфмана использовались вдрамзвъядо или дняшлл-
раыйлллые эле ктричс скос к магнитное поля. Пял пли ко в центральной точ-
ке О на экране смещалось поэтому к двух перпендикулярных направлениях.
Предположим, например, что в направлении
вверх-вннз на рисунке мы имеем электрическое
смещение (обозначим его у):
1 / М
У ~ 2 md V/ '
а в направлении вправо-внево на рисунке — маг-
нитное смещение (обозначим его л):
I еВ/г
2
Исключая неизвестную скорость и из этих двух формул, получим, что
кВ?
2 m д? ’
2mdy'
<? BjГ1 = tU?
4тт?т2 2mdy'
а следовательно,
2mU 2.
el~ d B~
получили уравнение параболы с вершиной в начале координат, которая
изображена на верхнем рисунке.
При данной скорости и пятнышко от пучка на
экране должно попасть в точку па этой парабо-
ле. Но из-за неизбежного разброса скоростей элек-
тронов, экспериментально получается не точка, а
небольшой протяженный участок параболы, из гео-
метрии и величины которого можно найти значение
отношения е/тп. Область больших н очень боль-
ших скоростей и соответствует участку параболы
вблизи вершины О.
Эксперимент Кауфмана показал, что форма
экспериментальной кривой вблизи точки (? отличается ОТ параболы и име-
ет вид, показанный на рисунке. На ней в точке О наблюдается «угол?? (или
«юлов»). г. е. кривая имеет две касательные в точке вершины. Именно этот
124
J'л л вл 2
клюв ii был «эффектом Кауфмана», и именно его наличие подтвердило ре-
лятивистскую зависимость массы тп электрона от его скорости т;. В радио-
активном источнике в эксперименте Кауфмана скорости электронов ио не
только были близки к скорости света с, но и имели значительный разброс.
Поэтому Кауфман получил на экране не точку (пятнышко), а кусочек
прямой, который существенно отличался от участка параболы.
Пусть радиоактивный источник (см. рисунок ниже) находится в начале
координат и испускает /3-лучи в направлении оси От. Таким образом, ось
О г — прямая, вдоль которой движется неоткяонённый пучок электронов.
Пусть ггостояшгое электрическое г голе Е и постоянное магл и гное noire В
аитипараллсльны, при этом пусть электрическое поле направлено пропив
оси .у, а магнитное вдоль оси у, гак что Еу — —Е, Bv — В.
Составим уравнения движения реля-
тивистского электрона. На электрон с заря-
дом -е (е = |е|) действует сила
F = F,n + FMar = -еЕ - e[v • В].
Так как
i j k
[v В] = kr vy Vt - -t?r В i + v.r В k
О В 0
то релятивистские уравнения движения
электрона „ так называемые уравнения
Минковского т имеют следующий вид:
В начальный момент времени £ — !J Электрон, только что вылетевший
из радиоактивного источника, не имеет ещё is и ^-составляющих скоро-
сти и обладает только большой ^-составляющей, которая равна = t?o<
где ььи — очень большая скорость вылетевшего из радиоактивного источни-
ка электрона т\] OjB-0,9 г.
2.2 КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОНА
125
Из-за того, что экспериментально достижимые поля Е и F не могут
быть очень большими, скорости и tjtj у электрона остаются малыми по
сравнению со скоростями t'z и ин при движении электрона иг источника (7
до экрана при ; > 0.
Следовательно, .што считать, что и/?и всех t > 0 вееайа
ий = uq, и л/одйсяо отбросить у/вдвделше ^su,t»lwws. Это предпо-
ложение, ЧТО 1р:пг?р << UZ: l'z = T\j = coni£t+ МОЖНО сделать II Н СЛуЧЙС
скоростей vq лшедо ыеиыиих скорости с, если только считать поля А1 и В
малыми.
Таким образом, первое и второе уравнения движения можно при-
ближённо представить в виде
Систему этих дифференциальных уравнений надо реши ть с нулевыми
начальными условиями:
Получим, таким образом, решение
_ ггВио £ аУ 2 ,2 е_Е_ /. _ ау.2 . f2
К" 2mQ V V”/C E1 ^“amoV1 У^С
Пусть расстояние между радиоактивным источником и экраном рав-
но (. Тогда приближенно * = i/tij). Координаты точки М на экране на при-
ведённом выше рисунке, п которую попадает пучок при включённых полях
Е и таким образом, данп ся формулами
Нерелятивистский предел
Пусть но е, тогда можно считать, что -/1 ^jf/c2 = 1, и поэтому
2шц 11н ’ 2тц ti2
126
Глава 2
Следовательно,
_ е2Д2 i1 1 _ еа Д^"1 . 2^0
4тр и2 4mg eEi2
ИЛИ
‘-^у
гп^Е J
Получили уравнение параболы, которая является геометрическим ме-
стом точек на экранеч в которые попадает пучок при различных начальных
скоростях Т^г
РЕЛЯТИВИСТСКИЙ ПРЕДЕЛ
Пусть v.'u = с. Тогда корень VZJ - мал, я его нельзя заменить
на 1, скорость во всех других местах в наших формулах можно, однако,
заменить на с, а следовательно^ имеем соотношения
»-ssV*
таким образен,
У = _Е_
я Вс
получаем уравнение прямой. Это прямые «клюва» гга приведённом выше
рисунке.
Левые ветви кривых на плоское!и я7 у соответствуют случаю, когда
поле Е направлено против оси у, поле В тоже против оси у. Правые ветви -
случаю, когда поле Е направлено против оси у, а поле В по оси у.
Спин электрона. Эксперимент Штерна-Герлаха
К 1925 г в атомной спектроскопии накопился экспериментальный ма-
териэл, который позволил Гаудсмиту и Уленбеку высказать оказавшуюся
впоследствии правильной гипотезу о том, что кроме
х. у, €>йтл()лелг ещё u tfcnwjfutwnjtt ttpyHtc-Wafrujeti Оеч/
ния.
Идею о спине электрона в 1922 г. предложил Паули, который построил
квантйво-механическую теорию спина в 1927 г. Строгую релятивистскую
2.2 КОРПУСКУЛЯГНЫЕ СВОЙСТВА ЭЛЕКТРОНА
127
теорию спина электрона разработал в 1928 г. Дирак. Важный вклад в тео-
рию спина Электрона внесли работы Томаса и Френкеля
Спин электрона — это его собственный момент импульса (векторная
величина). Кроме собственного, электрон имеет также орбитальный мо-
мент импульса, который в сумме со спиновым даёт так называемый полный
его момент импульса. Но это котима ентые моменты импульса. Спин электро-
на совсем нельзя мыслить клдссич^кп^. Гак. электрон нельзя представить
себе в виде маленького электрически заряженного шарика, вращающегося
вокруг своей ОСИ С некоторой ПОСТОЯЕП[ОЙ угловой скоростью. Для такого
i:гарика так называемое «гиромагнитное отношение» (отношение механи-
ческого момента К магнитному моменту) равно е/mc* а нс е/2тс, как ДЛЯ
электрона. Томас и Френкель в 1926 г, показали, что это релятивистский
эффект.
В качестве величины, характеризующей спиновую степень свободы
электрона* берут значение едина элгктйруип ян ось z использу-
емой декартовой системы координат.
Спин электрона всегда (для любых электронов — в атомах, молекулах,
в твёрдых телах, в свободных электронных лучках и г.д.) имеет значение
+ 1), где S = 1/2; его величина никогда sic меняется. Может изме-
ниться, и действительно меняется, проекция спина 5е = на произ-
вольную рассматриваемую ось Oz* где = ±1/2 называется квантовым
числом проекции спииан или магнитным квантовым числом в атоме.
Тот факс; что спиновая координата электрона принимает йен значе-
ния L в 1922 г. наглядно проиллюстрировал эксперимент Штерна и Герлаха,
в котором использовался пучок быстро летящих с постоянной скоростью
нейтральных атомов серебра, находящихся в своих основных состояниях.
Атом серебра имеет один валентный электрон. Другие электроны
в этом атоме* заполняющие гак называемые замкнутые электронные обо-
лочки, все вместе обладают нулевыми орбитальным и спиновым момента-
ми импульса, а следовательно* суммарный магнитный момент этих внут-
ренних электронов pane ft пулю. Так что магнитный момент атома серебра
в его основном состоянии определяется иекючительно только спиновым
моментом спз валентною электрона.
Обозначая лдегнишлый лшшшп валентного электрона через Д(, а через
S его спиновый AffjLuev/ffl и.ииу.тьсп, имеем соотношение (так называемое ги-
/зоштгншнндо соотношение)
где в — абсолютная величина заряда электрона, m — масса электрона. Маг-
нитный момент атома серебра в основном состоянии равен /2.
12Й
Глава 2
Штерн и Герлах заставили пучок быстро летящих атомов серебра, пре-
бывающих в своих основных состоягз иях. пролетать область с Сильно
магнитным полем. Эта область создавалась внутри магнитя спе-
циальной формы, схематически показанного на рисунке.
Магнитное поле направлено вдоль оси О я и имеет постоянную неод-
На точечный магнитный момент, помещенный в неоднородное магнит-
ное гаме, действует сила
F = Iji grad ) В
следовательно, в установке, схематично изображённой на рисунке, эта сила
направлена вдоль оси 2, и сё величина равна
F = Fs = ti,42- = p со»0
так как считаем, что магнитная индукция й ис зависит пт згь i/a а зави-
сит толью от z, здесь У — у юл между вектором магнитного момента
н направлением магнитного поля В на рисунке по оси Оя. В случае од-
нородного магнитного поля, когда —— = 0, рассматриваемая сила равна
нулю.
Таким образомц сила F, действующая на движущийся аггом серебра,
отклоняет его по или против оси 5. в зависимости от того, будет ли cost?
положительным или отрицательным.
2.3. ВОЛНОВЫ1. СВОЙСТВА ЭЛЕКТРОНА
129
Следует иметь в виду, что магнитное поле В стремится повернуть
в пространстве маппгтный момент летящего атома серебря и направить его
по нолю, г. с. вдоль оси Oz. Однако в эксперименте Штерна-Герлаха об-
ласть с магнитным полем была небольшой, и магнитный момент атома не
успевал заметно повернуться во время пролёта этой области Поэтому мож-
но было считать, что магнитный момент /1 летящего атома серебра имеет
фиксированное в пространстве направление.
В пучке атомов серебра, влетающих в неоднородное магнитное поле,
магнитные моменты /х атомов направлены хаотично по всем направлениям.
Таким образом, после пролёта пучка атомов серебра через область с неод-
нородным магнитным полем пидомо га при
бллюченнаи лглггатисш daurcra была бы патучпшься лояоскп, пока-
занная на рисунке, н разные точки которой попали бы атомы с различными
значениями cos fl, изменяющимися от -1 до +1 (на краях полоски cos fl =
= ±1).
Эксперимент Штерна и Герлаха показал, одня-
ко* что га лкрбгга йдбяи>йдел1гя га д Ага
лям га, симметрично расположенные относительно
центральной точки, в которую попадает пучок сгри
выключенном магнитном поле, как ЭТО показано па
рисунке.
Эксперимент, таким образом, логаэял, члю
cos fl лмьтькр Ачэд значения. cos fl = ±1.
Слсдоватсльпо, с учётом соотношения /1 = — e/m S
он показал, что проекция спина электрона тоже
имеет только два значения.
2.3. Волновые свойства электрона
В 1927 г. американские фиэики Дэвиссон и Джермер провели экспе-
римсЕгг, который доказал^ что пучок электро поп обладает пс только кор-
цу г куля рны ми, но i[ волновыми свойствами, причём измеренная ими длина
волны электронного пучка давалась формулой де Бройля.
Поставив своей целью исследовать волновые свойства лучка каподньсх
лучей, Дэвиссон и Джермер воспользовались результатами проведённых
к тому времени исследований по дифракции рентгеновских лучей на кри-
сталлах, в которых было доказано, что рентгеновские лучи являются элек-
тромагнитными волнами, и была измерена их длина волны, которая оказа-
лась порядка 1 А = 10"е см = 10"10 м, те, в 10э-104 раз короче длины
волны видимого света.
130
J'л л вл 2
Измерение длины волны света и рентгеновских лучей
Длины волн видимого света, имеющие порядок величины 0.1 мкм =
= 10а нм, впервые были измерены в первой четверти XJX в.. Юнгом и Фре-
нелем. Длины bojjh видимого света лежат в диапазоне 4000-8000 А = 400-
800 нм (1 А = 10 и м),
Для измсрсе[ия длины волны мсппхроматЕяческого света используется
явление интерференции света.
Рассмотрим эксперимент с интерференцией Юнга монохроматическо-
го света на двух щелях, по так называемой «двулучсвой интерференции».
Имеем экран с двумя щелями, расположенными на очень малом расстоянии
d = 0,1 мм = 10 1 м. Пусть эти щели освещены нормально падающим на
них параллельным пучком монохроматического света с длиной волны А. На
другом экране, расположенном на расстоянии L 10 мот экрана со ще-
лями, наблюдается интерференционная картина, состоящая из нескольких
(порядка десятка) эквидистантных светлых и тёмных параллельных интер-
ференционных полос, параллельных щелям.
На рисунке изображён экран со щелями и экран, на котором на-
блюдаются интерференционные полосы; показаЕты только две интерферен-
ционные полосы. Изображён небольшой участок кривой интенсивности
освещённости экрана, с максимумами и точках А и В, причём в точке .4
наблюдается максимум центральной полосы.
Получим формулу для расстояния / между полосами. Интерференци-
онное условие появления светлой полосы на экране состоит в том, что рдз-
ностд* хой? деух лучей, исходящих у.з щедеи ы идущих йо адочед людекмулде
лолоё.ТэЕ. валяема /нвдшниься це.тглпу чиелг Длил яллм.
В точке /1 имеем максимум центральной полосы с нулевой разностью
хода Л\4- Л/А = 0. В точке ft находится максимум соседней с ней полосы
2.3. ВОЛНОВЫ1. СВОЙСТВА ЭЛЕКТРОНА
13]
с разностью хода Ат£> Л/27 = А. Для максимумов интенсивностей светлых
полос имеем условие
2VB-AfB = nA.
в котором п = О, ±1, ±2 и т. д.
В описываемом эксперименте отношение d/L = 10-4/10 = 10-5
очень малое, и поэтому разность хода х¥ В Л/В можно найти приближённо
следующим образом. Из прямоугольного треугольника NBQ имеем очевид-
ное соотношение
/ X 2
АТВ* = Лг(?2 + (ф1 + АВ? = + (! + j J ,
а из прямоугольного треугольника МИР соотношение
/
MB2 = L2 + Н - |) .
Вычитая МВ'1 из N В2, получим Л'/J- - М В ~ = 2f J. Поэтому с точ-
ностью до членов первого порядка малости по d/l получим, что
(.VJ3 - MB)(NB + МВ) “ (jVB - MB)2L,
а следовательно, N В - МВ = ^1.
Из условия интерференции
VB - МВ = А.
таким образом, получаем следующук» формулу для ;игниы волны монохро-
матическою света, создающею светлые и тёмные интерференционные по-
лосы:
Л=Р-
Эта формула показывает» что» нхнеряя /кктшояпие f .we.wcdy доседга-
juu эта|дыслплюннылш пошвдыш, лдежио я/км?ты1«
/шсуё/паи найти еатачин^ Лшны А паяющего ™ экрдн со гцвдяиин
Легко добиться, чтобы расстояние i между полосами было порядка
1 см = 0,01 н. Так как d/i = 10-Е, то согласно приведённой формуле
получаем для длины волны значение порядка А = И] н 10 2 м = 10 ' м =
— 0,1 мкм.
Изучение интерференционных полос позволило Френелю эксисримсн
тально измерить длины световых волн винимого света. Оказалось, что для
них А = 400-800 нм.
132
Глава 2
AAA
Точность измерения длины
ВОЛ ЕЛЯ А можно УВЕЛИЧИТЬ ИЗ
один-два порядка. если исполь-
зовать не две щели, а цифра к-
ционную решётку, т.е. оптиче-
скую плоскопараллельную пла-
стинку с нанесёнными специальной машиной тонкими одинаковыми па-
раллельными штрихами, расположенными точно на одинаковых расстояни-
ях друг от друга. Можно нанести 50, 100, 400, 600, 5000 штрихов на I мм
длины, причём вся дифракционная решётка имеет длину 3 4 см.
В дифракционной решётке ннтерферируЕог не л па, а много лучей (рав-
ное числу её штрихов), так что имеем не двулучевую. а многолучевую ин-
терференцию. Переход к та кой интерференции при водит к тому, что полосы
становятся уже и ярче, как тго проиллюстрировано на рисунке выше.
Таким образом, удаётся повысить точность измерения расстояния /
между полосами, а следовательно, точность измерения длины волны А.
Использовать дифракционную решётку для измерений длин волн пер-
вым предложил Фраунгофер, который се и создал.
Эксперимент с дифракционной ре-
шёткой выглядит так, как пОкЗЗанс па
приведённой рисунке. Штрихи решётки
расположены перпендикулярно плоско-
сти рисунка.
] [иправил перпендикулярно лазер-
ный луч на решётку, как и оказано на рисунке, С другой стороны решётки
увидим плоский веер лучей в плоскости, перпендикулярной штрихам
решётки, дающих на удаленном экране, тоже показанном на рисунке, ряд
равноотстоящих пятнышек по обе стороны от централ иного пятнз.
Ди фракционная решётка должна иметь параметр d (расстояние меж-
ду соседними штрихами) порядка не более L0-1U2 длин волн. Её можно
довольно легко изготови гь
Для рентгеновских лучейh однако, имеющих длины волн порядка 1А =
— 10"111 м — 0.1 им, дифракционную решётку изготовить не представляет-
ся возможным.
Большой заслугой Лауз в 1912 г. было его предложение ttf-подьзовдть
я качестее /эешеткч для ^ентгенсескш: лучей естествен-
ную я^стддднчесхую решётку теё/^fw тедя. С помощью этой решётки
удалось доказать, что рентгеновские лучи действительно являются элекгри-
магнитнымн волнами очень короткой длины волны, и измерить их длины
волн.
2.3. ВОЛНОВЫ1. СВОЙСТВА ЭЛЕКТРОНА
133
В результате возник «рентгеноструктурный анализ» (изучающий гео-
метрию расположения атомов в кристаллик).
В 1914 г. Лауз была присуждена Нобелевская премия «За открытие
дифракции рентгеновских лучей на кристаллах». В 1915 г Брэггам, отцу
и сыну была присуждена ещё одна Нобелевская премия — «За исследо-
вания структуры кристаллов с помощью рентгеновских лучей». Рентгену
была присуждена первая в истории нобелевских премий Нобелевская пре-
мия 1901 г «За открытие лучей, названных его именем».
В отличие от оптической дифракционной решётки, кристалл превра-
щает падающий из него луч не в плоскую, а в пространственную совокуп-
ность лучен, обладающую определённой геометрический симметрией, как
зге схематично проиллюстрировано на рисунке.
Рентгеновский луч, идущий
горизонтально слева направо, па- .
дает на кристалл и расщепляется х / *" '»
на множество выходящих из него __________
в разные стороны (вперёд, назад ' *
и в бока) лучей. Они создают на i ч *"
фотографической пластинке (по*
СЛС СС проявлю ЕШЯ) правильную
геометрическую картину тёмных пятнышек, по геометрии расположения
которых можно определить геометрию расположения атомов в кристалли-
ческой решетке, а также геометрическую форму и размеры «элементарной
ячейки» этой решётки.
ДэвнссОн и Джсрмер в 1927 г.? зная об исследованиях дифракции рент-
геновских лучей на кристаллах, решили провести аналогичные нс след ока-
ния с катодными лучами, г. е. с пучками электронов.
Для пучка электронов в электронно-лучевой трубке, ускоряемых
электрическим напряжением порядка 100 В, добройлевекая длина волны
А I А, гак что их дифракцию (как и дифракцию рентгеновских лучей)
можно наблюдать только с помощью кристаллической решётки твёрдого
тела.
Экспериментальная установка Дэвиссона и Джермера схематически
покачана па приводимом ниже рисунке. Вся установка находится внутри
вакуумированной стеклянной трубки, т.е. трубки, из которой откачан воз-
дух. Пучок электронов создаётся «электронной пушкой», которая показана
сверху на рисунке. Она состоит из подогреваемого электрической спираль-
кой катода, с поверхности которого испускаются электроны н результате
134
Глава 2
термоэлектронной эмиссии. Эти электроны затем ускоряются до некоторой
скорости г яеюдетьем напряжением (Д приложенным между катодом и ано-
дом.
Созданный электронной пушкой поток электронов падает перпенди-
кулярно на грань монокристалла никеля Ni (у никеля простая кубическая
кристаллическая решётка, как у большинства металлов). С помощью элек-
троскопа, перемещаемою ИО дуге крута, пр и соединенно [ТО к ЧуВСТВИТСЛЬ’
ному гальванометру, можно измерить интенсивность / пучка, отряжённого
Результаты своих экспе-
риментов ДЭВИССОЕ] и Джср-
мер откладывали на показан-
ной в правой части верхне-
го рисунка диаграмме. Дли-
на отрезка О Л/ изображает
величину интенсивности пуч-
ка, отражённого на угол
Экспериментальные точки ло-
жатся при этом ЕТа некоторую
плавную кривую. Эксперименты Дэвиссона и Джсрмсра показали, что кри-
вая интенсивности имеет резкий пик дни анодного напряжения 17 — 54 В
при угле = 50р.
Эксперимент, таким образом, выявил резонанс по углу и напряженно
(V =54 В. = 50*), Наблюдение именно этого резонанса и явилось «эф-
фекюм Дэвиссона и Джсрмсра»..
Теория эффекта Дэвиссона и Джсрмсра следующая. Па приведённом
ниже рисунке схематически изображена кубическая решетка Ni. резко об-
рываю спаде я па поверхности кристалла, и показаны две косо расположен-
2.3. ВОЛНОВЫ1. СВОЙСТВА ЭЛЕКТРОНА
135
ныс параллельные воображаемые так называемые л.мсмэ-
слш. Это /ьнгсквенш, .имслершо л^о^оЗятся через
utfpdStui ойизирилные умы кастамичедкей /?ешёт™. Вульф
и Брэгг (сын) доказали, что дифракция рентгеновских лучей на кристаллах
происходит при отражении их от семейств параллельных кристаллических
плоскостей (по закону «угол па деним равен углу отражения») при выполне-
нии так называемого «интерференционного условия Вульфа-Брэгга», со-
гласно которому отраженный отданного семейства параллельных кристал-
лических плоскостей луч будет интенсивным только в том случае, когда
розияеть .YiQiiiT люжду йяулгя шгрег.ттетьлы.тш шл/;ажйшмлш со-
ccJww.y лристмличесяих /L7G£KDCwewP 6\dt??a /?лвнл целому числу п Лшны
вогны А, т. е. йуЭет/швшг п А. Только тогда в результате взаимной интерфе-
ренции лучи, отраженные от параллельных плоскостей, усилят друг друга
и образуют интенсивный отражённый луч для да иного семейства кристал-
лических плоскостей. Так возникают дифрагированные на кристалле лучи.
На рисунке показаны две плоскости из семейсгна параллельных экви-
дистантных кристаллических плоскостей, при отражении от которых про-
исходит интерференционное усиление отражённых лучей, и возникает луч,
ответственный за резана цс Дэвиссона н Джсрмсра.
На самом деле отражение просходит не от кристаллических плос-
костей* а от отдельных атомов, через которые проходят кристаллические
плоскости. Атом рассеивает падающую волну во вес стороны так, что обра-
зуется множество рассеянных вторичных волн, выходящих из каждого у зла
решётки. В результате интерференции этих вторичных волн и создается
отражённая от семейства кристаллических плоскостей плоская волна, или
луч, который мы рассматриваем.
Дне кристаллические плоскости, изображённые па рисунке, таковы,
что нормаль к ним как раз является биссектрисой угла Считаем, что
136
J'л л вл 2
угол .р соответствует максимуму отражения в эффекте Дэвиссона и Джер-
мсра. Очевидно,
*=?>
Из прямоугольно го треугольника АВС непосрещствсЕшо получаем, что
cosfl — d/D, нли d — Dcosfl. Здесь £> — так называемый ку-
бической решетки Ni< который равен 2,15 А (он был известен Дэвиссону
и Джермеру из рентгеновских экспериментов с монокристаллами Ni).
Вычислим разЕтость хода двух лучей, от-
ражённых от пары соседних кристаллических
плоскостей. Сначала используем традицион-
ное построение, показанное на приводимом
рисунке. На нём изображены две горизонталь-
ные кристаллические плоскости. Падающим
луч отражается от верхней плоскости в точке
А и даёт первый отражённый луч и от нижней
в точке Б и даёт второй отраженный луч, кото-
рый проходит затем через точку С псркЕтсй го-
ризентаиьной плоскости. Найдём разнос ть хо-
да этих двух отраженных лучей. Опустим перпендикуляр СБ из точки С
на первый отражённый луч и построим прямоугольный треугольник АБС.
$ тгочкеи С и D будут л/?оисгодцть « гяая вдк
эти точки ярмяяАтелгдт одному яо.тнгкилну фраяту БС. Очевиднее
РАЗНОСТЬ ХОДА = АВ + ВС - АБ>
Из треугольника АЛ/В видим, что АЛ/ = d/tgfl и что АВ = d/sin 0.
Так как АС = 2 АЛ/ = 2d/ tgfl, то из треугольника A/JC получаем соот-
ношение
я л 1 --.-. /j 2d л 2d cos2 fl
.IB = AC- cos fl = —- cos У = —:—т—-
tg 3 sin fl
Таким образом,
разность хода = 2 АВ - АР =
2d _ 2dcoaal _ ^(1 ~ ££££) _ . й
sin fl sin fl sin fl
Разность хода можно вычислить по-другому, если воспользоваться по-
строением, приведённым на данном ниже рисунке. Первый луч отража-
ется от верхней кристаллической плоскости п точке Ат а второй — от
2.3. ВОЛНОВЫ1. СВОЙСТВА ЭЛЕКТРОНА
нижней в точке D. Из точки Л опустим два пер-
псидикуляра па внешний луч и па отражённый
в ннжнсй плоскости в точке D луч н построим
точки В и С. /Са-тебашиг ст /моч/сйх Л п 1? tro.Tuo-
водз фрякпгя /Ш л/зоигхойяи £ <ч}ной фаге, как
я яше£аяия в личках A w С волиовог^ ф/адндга
.4 С. Таким образом, разность хода двух показан-
ных на рисунке лучей, очевидно, равна удвоенно-
му отрезку BD, т.е. равна 2dsin0f как это непо-
средственно видно из треугольника ЛВЛ;так что
получаем в точности такую же разность хода 2d sin0? как и прн первом рас-
смотрении.
Согласно условию Вульфа-Dp-.n га, таким образом, имеем равенство
2dsin0 = п А,
где п — целое число, у нас п — 1Т так как мы рассматриваем минимальным
угол резонанса
Учитывая, что d = Dcosfl, где D — параметр решетки Ni, получа-
ем в качестве условия резонансного отражения Дэвиссона и Джсрмсра от
кристалла Mi электронного пучка следующее условие:
2dsin 0 = 2D sin 0 cos 0 = D sin 20 = Ат
пли, так как 0 = — — —. 20 = — ip, имеем равенство
Dsin = А;
это окончательная формула.
Учитывая, что D = 2,15 А и = 50% и производя расчёт, получаем
А = 1,65 А.
Посмотрим теперь, a Qmo darin формула de* 5райля Ата А
исследуемого электронного пучка. Чтобы сю воспользоваться, надо знать
скорость электронов г в пучке, Электрон пучка ускоряется электронной
пушкой анодным напряжением D (между катодом и анодом) до скорости и,
и его кинетическая энергия поэтому равна
^ = <Т,
13М
Глава 2
гле е — абсолютное значение заряда электрона. Следовательно, г =
2jg_l/
ль
, а потому
р = m г1 = \/2 ет(7.
Таким образом, согласно формуле де Бройля
Л
ль и
Л
\/3 е m (7
Подставим в эту формулу значения неперечёркнутой постоянной Пла-
тзка Л. = 6,6 HJ_,il Дж-са заряда электрона е = 1,6 - Ю-1^ Кл и массы
электрона m = 0,9 - 10“ м kj; а также значение резонансного анодного
напряжения (7 — 54 В (экспериментальное значение резонанса Дэвиссона
и Джермера). Получим тогда, что
А = 1.67 А,
те. получаем более чем удовлетворительное совпадение со значением А =
= 1,65 А, измеренным в эксперименте.
Так что гипотеза де Бройля о вол попы к свойствах электронов (а потом,
как оказало съъ и всех других элемеигарЕтых частиц) полностью подтверди-
лась.
Таким образом, электроны, как и фотоны, обмейяюго
Дж*. 77. Томсена
Дж. П. Томсон (Джордж Паджет), сын Дж. Дж. Томсона (Джозефа Джо-
на), в 1927 г. пропускал пучок катодных лучей через гонкие пол икр иста л-
личсскис металлические плёнки золота, серебра,, платины, алюминия и др.
металлов. Он использовал катодные лучи, которые создавались в разрядной
трубке с высоким анодным напряжением порядка 10-60 кВ. После про-
хождения через пленку, на которой лучок этих катодных лучен дифрагиро-
вал, oft направлялся па фотографическую пластинку, которая затем проявля-
лась. Hj проявленной фотопластинке были отчётливо видны это централь-
ное пятно н EiecKo.ibKO концентрических кругов вокруг центрального пятна,
как это показано справа на рисунке. Картина была в точности такой, как
при наблюдении дифракции ре^птеиоиских лучей на поликристаллических
плёнках.
2.3. ВОЛНОВЫ1. СВОЙСТВА ЭЛЕКТРОНА
134
Плёнки металлов золота^ платины, алюминия у Дж. П, Томсона были
пол икристая личсским и, г. с. состояли из большого числа по-разному ори-
ЫпиронаннЫХ маленьких Монокриста;и[иков.
Когда на полнкрнствлпическую пленку падала монохроматическая
волна с длиной волны А рентгеновских или катодных лучей, она дифра-
гировала из отдельных монокристалликах, и па фотографической пластин-
ке регистрировалась дифракционная картина, представляющая собой рад
концентрических колец вокруг центрального пятна.
Длина волны А катодных лучей может быть найдена по диаметру колец
па фотопластинке по формуле Вульфа Брэгга, если использовать постоян-
ную решётки /.) из измерений с рентгеновскими лучами.
Дж. II. Томсон поступил по-другому. Он сначала рассчитал длину вол-
ны электронов по формуле де Бройля А = ft/rmi, а затем определил посто-
янную решётки £> кристалла. После этого он сравнил результат с данными,
полученными нз измерений с рентгеновскими лучами. R приводимой таб-
личке мы даём результаты опытов Дж. II. Томсона.
ЗНАЧЕНИЯ ПОСТОЯННОЙ РЕШЕТКИ В А
металл рентг лучи катод, лучи
А1 4,05 4,06—4,00
Au 4,06 4,18-3,99
Pt 3,91 3.88
Pb 4.92 4,99
Хотя точность экспериментов Томсона была хуже, чем эксперимента
Дэвиссона и Дкернера, но они также, как и эксперимент Дэвиссона и Джер-
мера. доказали правильность гипотезы дс Бройля о волновой природе элек-
трона.
140
Глава 2
В 1937 г. Дэвиссону и Дж. И Томсону была присуждена Нобелевская
премия «За открытие дифракции электронов на кристаллах».
Следует ещё раз подчерки уть, что классические корпускулярная и вол-
новая модели микрочастицы* понятые буквально, противоречат друг другу.
Природа вышла из этого затруднительного положения следующим об-
разом. Оказывается. нет ни одного физического эксперимента, в котором
проявлялись бы одновременно строго И КОриуСКУЛЯрНЫС, И ЕОИНОНЫС СВОЙ'
ства рассматриваемой микрочастицы.
Имеются эксперименты* в которых микрочастица* скажем электрон,
проявляет с большой определённостью (и хорошем приближении) свои кор-
пускулярные свойства, и существуют другие эксперименты, в которых она
проявляет, гоже с большой определённостью (тоже в хорошем приближе-
нии), свои волновые свойства.
Но никогда в одном и том же эксперименте микрочастица, например
электрон, безоговорочно строго, с полной определенностью ire проявляет
ни корпускулярные, ни волновые свойства.
u сйоысдид дшкралигтицы — эта /итые-
стороны единого пиленого физпчеокого объедай л — кото-
рая яа санам дезе we является wn корлуекулой, ww
24. Атомный электрон
Теория Кора атома водорода
Рассмотрим планетарную модель Резерфорда атома водорода, предло-
женную нм пд основе проведённых его сотрудниками Гейгером и Марсде-
ном экспериментов в 1911 г. В этой модели положительный заряд атома
и практически вся его масса сосредоточены в открытом Резерфордом в этих
экспериментах атомном ядре, которое можно считать точечным и нело-
деижным, так что для потенциальной энергии V(r) электрона в атоме вс*
дорода имеем формулу
Иг)
Эта функция соответствует силам притяжения,
сна всюду отрицательная и при г = П обращает-
ся в отрицательную бесконечность. График функции
V(r) показан на рисунке. Поэтому согласно пред-
ставлениям классической физики электрон в основ-
ном состоянии атома водорода в модели Резерфорда
2.4. Атомный ЭЛЕКТРОН
14]
должен находиться на ядре и обладать бесконечной отрицательной энерги-
ей, что физически бессмысленно.
Так что в классической модели атома Резерфорда атом нс имеет основ-
ного состояния в противоречии с экспериментом.
Двигаясь в возбуждённом состоянии ускоренно по орбите вокруг ядра,
электрон должен непрерывно излучать электромагнитные волны и терять
энергию, стремясь перейти в состояние ес вес меньшей и меньшей энер-
гией, при этом радиус его орбиты должен уменьшаться и уменьшаться, так
что согласно представлениям классической физики в конце концов элек-
трон должен «упасть на ядро», При этом должна выделиться бесконечная
энергия, так как V(r) = —ос при г = 0, чего, коеючпо, быть не может.
Перегаре ши.ну ю в рдлгкд.т лгллеей ческой {/шэдки проблему дисутмвня
ярения ид я<>/м tf решим
кдеялновдл мёкшдкд.
В 1913 п Бор, основываясь на квантовой гипотезе Пдганка, предложил
успешную (хорошо согласующуюся после введения поправки на движения
ядра, чего мы делать не будем, с экспериментом, с точностью 5-6 знача-
щих цифр, достижимой н оптических экспериментах) квантовую теорию
планетарной модели атома водорода.
Атон водорода излучает нс одну частоту (некоторую частоту а це-
лый набор частот или длин волн. Его экспериментальный спектр излучения
состоит не из одной, а на многих спектральных линий, объединённых в се-
рии, являетсян как его называют, лия^йчдтым.
С [[слито объяснения экспериментально наблюдаемого сериального
спектра атома водорода в рамках модели Резерфорда Бир в основу своей
теории положил два постулата, так называемых «постулата Бора», которые
фиксировали явным образом противоречия его теории с известными по-
ложен иями классической физики (классической механики н классической
электрод hi и mj нси).
Пос гулял L
/fs й лтшссачвстой лтсяике элдтрош? в д/ииие
eodoptxldf лрцройе осуществляется только некоторые, лроаелодящие ло
ток яяэъжгеиЫнИ «квоятовЫиИ орбитач». 7тобы лоити эти разрешённые
природой орашпы здевддола, norio ысл^л.эоялть слоям кяднтованцяр.
Двигаясь по разрешённой квантовой орбите, электрон обладает энер-
гией £?rt, где п — натуральное целое число 1.2,. , обозначающее номер
орбиты.
Согласно этому постулату движение электрона в атоме можно изу-
чдгЬт применяя законы классической механики, те. считать, что движение
142
Глава 2
электрона происходит по одной из орбит классической механики, но на-
до учесть» что природа из возможных в классической механике движении
(из всех возможных решений классических уравнений движения) «выбра-
ла», по известной только ей причине, лишь некоторые определённые так
называемые «квантовые орбиты».
Только движения электрона ио этим отобранным квантовым орбитам
обладают физическим смыслом и действительно происходят. Остальные
движения, которые возможны в классической механике, не имеют физи-
ческою смысла, они не осуществляются.
Постулат 2
ДйнлМсЬ d inwf.uf Я0 аяспписмзюй орбите. иеслютум rid своё ycAo/?eri’
ное движение в цротнверечии с аяасснчеткой элект^оённдлм^ис зяея-
отрон не нмучдет э^ехтро^мдгяитт(их волн. ff<* jwtwem произойти реэдля
л^рвдт/вддат йемженпя злектроид. лрн которой он сдаершоетп вквянтовый
склчио нд йругум орйыту
/7ри этач ес.ш скйчоа соеершдвтгл г орбиты с большей эш?ргиги Sni
riff орбиту с доньшей энергией ЯП2, атом изиуча^н один фотон. частота
которого определяется счейунл^и.и лусяовие.и Ярдо#:
— £?П2 = hi/ = йси.
£сдн садчоа сове/чинетоя с орбиты с докидай энергией «а орбиту
с большей энергией £nl (muwe лроисходит. когда ото.м нотодитсд в но-
ле внешней ялектрдмогнитной волны), дтаи ноглошоелт фотон (uj эявк-
тромдгнитиой волны] h частот д юоимрлго тоже ^нре^тяется и? русловая
= Ьу = W
Согпасно этим постулатам законы классической механики и классиче-
ской электродинамики при применении к излучению возбуждённым атомом
и поглощении им электромагнитных волн неверны.
Во-первых, электрон движущийся ускоренно в возбужденном атоме,
по некоторой разрешённой для пего квантовой орбите, не излучает в проти-
воречии с классической электродинамикой никаких воин (хотя и движется
ускоренно).
Во-вторых, его орбита нс постепенно непрерывно уменьшается по раз-
мерам, а в какой-то момент в атоме происходит внезапная «катастрофа», по-
сле которой электрон начинает двигаться по другой разрешённой для пего
квантовой орбите с меньшей энергией, снова нс излучая и нс поглощай
4 АТОМНЫЙ ЭЛЕКТРОН
143
никаких электромагнитных волн (как говорят, «перескакивает* на другую
орбиту). При этой катастрофе одновременно со скачком электрона с орби-
ты на орбиту из атома вылетает фотон или поглощается им фотон с такой
энергией^ чтобы для атома в целом выполнялся закон сохранения энергии.
Следуя Бору, рассмотрим только круговые орбиты
электрона в атоме водорода п классической модели Ре- v
зерфорда. Обозначим через г радиус крузоьой орбиты щ
и через t? скорость электрона на этой орбите. Очевидно, Л г Л
центростремительная сила, действующая на электрон на / \
этой орбите, является кулоновской силон, с которой ио- t О /
ложителъно ггеполпижпос заряженное ядро притягивает \ /
отрицательно заряженный электрон. Следовательно,
то есть
Энергия электрона на рассматриваемой круговой орбите равна сумме
его кинетической энергии и потенциальной энергии:
2 41Г£[)Г 8?Г£ог 4тГ£[>Г Йлтог'
Обратимся теперь к условию квантования. Здесь, однако, отступим
от оригинального рассуждения Бора и воспользуемся цебройлевской дли-
ной волны электрона. Работа де Бройля с этой длиной волны появилась
та 1923 г., на десять лет позже рассматриваемой сейчас работы Бора,
С электроном, пращи ютимся со скоростью f
13U круговой Орбите, 310 ДС ЬрОДЛЕО, СВЯЗаНЯ ВОЛ-
на с длиной волны А = h/mv. Потребуем, чтобы 'К.
на длине орбиты укладывалось ровно целое число ' "V.
длин деброй л еле ктгк волн, как показано на рисунке, |\ Л
2тгг = nA.
где n = I 2т ... — целое число, которое называ-
ется «главным квантовым числом» (это номер раз-
решённой квантовой орбиты). Так как А — h/mv,
144
Глава 2
то отсюда имеем условие
Следовательно,
mru = n
где ft = ft/2z — перечёркнутая постоянная Планка,
Как ПН;[1!М% условие квантования можно сформулировать ПО-другому
сто фактически сформулировал сам Бор.
Л/анеяй1 й.чшульсл1 адйктралще квпнтулэтс.ч цсты.-шг норцыялш — кйл/^mu-
AJU, ft.
Таким образом, для n-й квантовой орбиты имеем следующую систе-
му двух линейных алгебраических уравнений, разрешая которую находим
значения т и и. Имеем
] лъиа = 11НИГ - ?t Й t? “ ?пт1 п \ « “ 1 / / \ —^п = 2 / \_ .хп=3 гп = _ S 4яео Г' = П А, L иЧг _ е3 . то2 г2 4^ г следовательно, Г = Гп = 4тг^{] -^—- П3; те^ получили формулу для радиуса п-й квантовой круговой орбиты. При n = 1 имеем так называемую «основную орбиту», радиус которой ра- вен го, где го — так называемый «боров- ский радиус »t равный г0 -= 4я-£0 = 0.5 А = 0,5 -10“141 м; mtr радиус n-й боровской орбиты даётся формулой = г0;
2.4. Атомный ЭЛЕКТРОН
145
он зависит от главного квантового числа п квадратичным образом (пропор-
цирналЁн п2).
Из формулы, определяющей борове кий радиус r<j3 получаем полезную
формулу;
с2 П2
41Г£0 ” W
для характерной комбинации величин, входящих в кулоновскую силу при-
тяжения электрона к ядру.
Вычислим теперь энергию Электрона, движущегося на n-й квантовой
орбите. Согласно выведенной формуле для энергии такою электрона имеем
равенство
F _ еа _ е* 1 _A2 J_
8?Г£{]Гс п2 2m п"
Подставляя В эту формулу ДЛЯ ЭНСрГИИ ЕЫрВЖСНИС, ОЛрСДСЛЯЮЩСС
бсровский радиус гОз непосредственно приходим к следующей окончатель-
ной формуле для энергии п-й борове кой квантовой орбиты;
г _ w е* 1
Ti (4^)3Й2 ' 2н2'
Как видим, энергии Ен всех квантовых орбит отрицательные и зависят
стп по закону 1/п3±те. энергия электрона на орбите обратно пропорцио-
нальна квадрату номера орбиты л..
Уровень энергии bj, взятый со знаком минус, даёт иолызоддо
атома водорода, которая приблизительно равна 13J5 эВ. Это энергии, ко-
торую надо затратить, чтобы оторвать электрон от ядра в невозбуждённом
атоме водорода (те. ионизовать атом водорода, находящийся в основном
состоянии).
Энергии ЕТ| называются «уровнями энергии», или «квантовыми уров-
нями». Они изображены наглядно на так называемой «энергетической диа-
грамме», приведённой на правом рисунке.
Уровень называется астастыгч. На этом уровне находится электрон
га Етсвозбуждснтюм атоме водорода. УронЕги £\; при п 2 называются воз-
буждёнными. На одном из этих уровней находится возбуждённый электрон.
Согласно Бору, квантовые переходы с излучением фотона могут со-
вершаться при перескоках электрона с возбужденного уровня на основной
уровень или на более низкий возбуждённый уровень.
146
Глава 2
n = 3
п = 2
£ О
При переходе электрона с уровней п > 2 на основной уровень n = 1
излучаются спектральные линии так называемой Лдшшгна (они лежат
в невидимой ультрафиолетовой области спектра). При переходе электрона
на уровень п = 2 с уровней п 3 излучаются спектральные линии так на-
зываемой re/Fww (они лежат в видимой оптической области). При
переходе электрона на уровень п = 3 с высоких уровней и 4 излучаются
линии так называемой серый 77яшеяд (они лежат в невидимой инфракрас-
ной области спектра). Имеются также и другие серии линии R спектре ато-
ма водорода, соответствующие переходам на уровни п = 4Т 5Ч ... с более
высоких уровней.
Частота спектральной линии, излучаемой атомом водорода при кван-
товом переходе с уровня А'п1 на уровень JTnj. дастся формулой
л* = । - ^>t2 =
7?
2 m
из которой следует; что для обратной длины волны спектральной линии
атома, соответствующей этому переходу^ имеем формулу
1 J/ Еп1
А " с = 2тгйс
—*—р_-±)
4ятс^Хп| те?'
Константу в последней формуле называют «постоянной Ридберга»
и обозначают буквой Л- Таким образом, мы вывели знаменитую спектраль-
ную формулу
1-л
4-4).
Пз nf-7
для ллпи ноли спектральных линий в спектре атома водорода.
4 АТОМНЫЙ ЭЛЕКТРОН
147
Эта формула была открыта чисто эмпирически (угадыванием) в 1885 г.
учителем математики Бальмером, работавшим в гимназии в г. Базеле
в Швейцарии, задолго ДО появления теории Бира, когда стали известны
значения четырех длин волн линий оптического спектра атома водорода
(которые только и видны в спектроскопе не очень большой разрешающей
силы).
Если В СЕТСКГраЛЬНОЙ формуле ПОЛОЖИТЬ 71 й = 1 И 711 2, ТО НОЛуЧИМ
длины волн серии Лаймана; если положить п2 = 2 и ni > 3, то будем
иметь длины волн серии Бальмера; если считать. что пз = 3 н Н| > 4, то
получим длины волн серии Пашена и т.п. Для постоянной Ридберга имеем
следующее теоретическое значение:
R ---------------- - 109737 см "1.
4тг7Г е(47Г£[))2
если заменить массу m электрона на его так называемую мас-
су g, определяемую из соотношения
1 = 1 . х
Д. 7Г1 ТПр1
в котором тпр — масса протона (чем учитывается поправка в 3—4 знаке на
движение ядра); э/нл иеареии^скйяяйстм^янния fWfepaa сойгсяЛгсш с экс-
значением нянченный уз э,м лирической формулы йзльлге-
/?д. с теочяостькз do еылнедянылб зкдчои^х эВ = 8067.5 см-1).
В заключение приведём общий вид слокт/шльноы как она вы-
глядит в спектральном приборе {на экспериментальной спектрограмме).
Еще раз обратим внимание ла то, что теория Бора атома водорода1 в ко-
торой была получена спектральная формула Бальмера, Водола ^инь? еолп
слек/мрильпьгт .тшшй, сокгайд/ощие с этснерщнернгйдоныдш с точностью
14N
Глава 2
«to 5-6 знямм m. в. с точностью, с которой эти длины всмн нгмерялись нс/
зкслг/ньи^нте. В этом был сё особый успех.
«За заслуги в изучении строения атома» Бору была присуждена Нобе-
левская премия 1922 г.
Дополнение к гл. 2
э.-7£гА/ггрп ческам разряда
Газы являются хорошими диэлектриками, фактически они нс проводят
электричества. Для электрического пробоя воздуха (чтобы л нём проско-
чила искра между электродами) необходимо приложить пробойнее езспря-
жение порядка 30 000 B/см. Но всё же ВСй газы, и воздух в ТОМ числе,
обладают некоторой очень малой электропроводностью.
Ещё во второй половине XVI] I в,, в 1785 г. Кулон пришел к за клю-
че Егиют что, кроме потерь заряда электроскопом при спадании его золотых
листочков вследствие проводи мости твердою изолятора^ удерживающею
стержень с листочками, происходят потери заряда. которые следует припи-
сать утечке заряда с листочков через окружающий их воздух.
Ток утечки быстро увеличивается с увеличением напряжённости элек-
трического ноля, достигает максимума, а далее остаётся постоянным, иска
не наступает пробой. Ток утечки тем меньше, чем меньше давление воздуха.
Крукс в 1879 г. показал, что золотые листочки электроскопа, по-
мещённые в хороший вакуум, сохраняют свой заряд в течение нескольких
месяцев.
Ещё в начале XVIII в. было замечено, что искра от электростатической
машины проскакивает в разреженном воздухе на значительно большее рас-
стояние, чем при нормальном давлении. В 1748 г. Ватсон наблюдал «споло-
хи колышущегося огня», подобные северному сняетню, в Стеклянной трубке
ДЛИНОЙ 81 См С разреженным воздухом, концы которой были присоединены
к полюсам большой электростатической машины.
Почти век спустя, в 1838 г Фарадей, пропуская ток ст электростати-
ческой машины через стеклянную трубку с разреженным воздухом, наблю-
дал в трубке фиолетовое свечение, Е[ачинаЕО1цссся на аноде и заполняющее
почти всю трубку до катода. Фарадей заметил, что хотя сам катод светил-
ся, между ним и фиолетовым свечением, заполняющим трубку, имелось
тёмное пространство, которое теперь называют «фарадеевым тёмным про-
странством».
В 1855 г. Гейслер значительно усовершенствовал технику откачки воз-
духа из замкнутых объёмов стеклянных трубок. Он изобрёл так называе-
Дополнение
144
мый «ртутный вакуумный насос»э в котором в качестве поршня использо-
вался столб ртути (до этого пользовались исключительно поршневыми на-
сосами с уплотняющими поршневыми прокладками, сделанными из кожи).
С помощью ртутного насоса, хотя и с затратами немалого труда и времени,
можно было достичь внутри стеклянной трубки очень низких давлений
С помощью ртутного насоса Гейслера вскоре были сделаны важные
открытия. В 1858 г. Плюккер обнаружил, что фарадсено темное простран-
ство расширяется. когда давление в трубке понижается. Илюккер обнару-
жил при этом, что стенки трубки за анодом начинают фосфоресцировать
при пониженном давлении, i.e. начинают светиться неярким синевато
зеленоватым светом, и что положение светящегося пятна мсетястся при
поднесении к трубке магнита. Плюккер обнаружил т акже, что когда катод
сделан из платины, близкие к катоду части стенок трубки через некоторое
время покрываются тонким слоем платины.
В 1869 г. Гитторфа ученик Плинкера, поместил внутри трубки пред-
мет между катодом и местом фосфоресцентного свечения на стекле трубки
(напротив катода за анодом) и обнаружил, что предмет отбрасывал тень,
какую он создавал бы, если бы свечение было вызвано прямолинейными
лучами, выходящими из катала. Эти невидимые лучи, наблюдаемые в ваку-
умированной трубке при НИЗКИХ давлениях, получили название «КаТПДЕГЬЕХ
лучей», а саму газоразрядную трубку с ультранизким давлением воздуха
стали называть «катодно-лучевой».
Название «катодных лучей» дал им англичанин сэр Вильям Крукс, ко-
торый начиная с 1869 г. с помощью своего и скусного помощника Г| гм ни га-
ма, мастера ПО приборам, сконструировал и ИЗГОТОВИЛ большое число раз-
личных катодно-лучевых трубок для демонстрации как многих известных,
так и открытых им самим свойств катодных лучей.
В частности, Крукс изготовил катодно-лучевую трубку, и которой ка-
тодные лучи бомбардировали лопатки чувствительного колёсика, ось кото-
рого могла катиться по горизонтальным стеклянным направляющим. На-
правив лучи на верхние лопатки, можно было заставить колёсико катиться
вдоль направляющих. Крукс думал, что этим экспериментом он доказал,
что катодные лучи «оказывают давление» на лопатки, что из этого опыта,
впрочем, не следовало.
В 1903 г. Дж. Дж. Томсон в монографии «Проводимость электричества
через газы» справедливо заметил, что эксперимент Крукса с колесиком нс
доказывал наличия давления у катодных лучей, а демонстрировал лишь то,
что катодные лучи нагревают сторону лопатки, на которую они падают.
Он правильно объяснил наб.подённое Круксом явление гак называемым
«радиометрическим эффектом».
150
Глава 2
Этот эффект состоит в следующем. Сторона лопатки, на которую па-
дают лучи, немного нагревается. Ударяющиеся о противоположные (нагре-
тую и ненагретую) стороны лопатки молекулы оставшегося в трубке разре-
женного воздуха сообщают сторонам лопатки поэтому неравные импульсы.
Таким образом и возникает сила, действующая на лопатку.
Разумеется, электронный пучок действительно оказывает давление на
препятствия, на которые он падает, так как электрон массы т, летящий
со скоростью v, обладает импульсом р = ж но эксперимент Крукса
с колёсиком не доказал наличия этого давления.
Трубки Крукса были столь искусно сконструированы и изготовлены,
что их используют в демонстрационных целях и в настоящее время.
Крукс считал^ что катодные лучи представляют собой поток молеиди
ой/&>м Он говорил о нём как о «четвёртом состоя-
нии вещества».
Видеман, Гольдштейн и Герц в Германии, изучая катодные лучи, при-
шли к неверному выводу, что эти яодлю-гнел ноямлг злехтарлндг-
ЛИтДЫХ €fO.7U.
Начиная с 1883 г. Герц и Ленард провели тщательные исследования
катодных лучей, но не смогли [гонять их физической природы. Это сделал
позднее Дж. Дж. Томсоез.
Начиная с 1894 г. молодой английский физик Дж. Дж. Томсон (Джозеф
Джон), ознакомившись с теориями катодных лучей и работами Герца и Ле-
нарда, поставил себе задачу измерить скорость распространения катодных
лучей и действительно се измерил, но? кроме того. Одновременно измерил
и отношение заряда к массе для частицы катодных лучей и доказал, что
катодные лучи — это поток до гою неизвестных маленьких заряженных
частичек малой массы — электронов Так Дж. Дж. Томсон открыл электрон
и 1897 г.
Название «электро ет» появилось в пауке, однако, на 15 лст раньше. Им
была названа «элементарная порция электрического заряда», проявившая-
ся в экспериментах с электролизом растворов электро литов (солей, кислот
н оснований).
В 1874 г. малоизвестный английский физик Стони, используя при-
ближённое значение числа Авогадро А\? пол ученное н молекулярно -кине-
тической теории газов, и значение числа Фарадея >Ft измеренное нм самим
в собственных экспериментах по электролизу, определил значение заря-
да н переносимого одним однократно ионизованным ПОНОМ одповалепттюго
электролита, предположив, следуя Фарадею, что ионы в растворе электро-
лита переносят одинаковые электрические заряды. Именно эту «элемеп гар-
ную порцию электричества» он и назвал «электроном».
Дополнение
15]
Как мы сказали, электрон как микрочастица экспериментально был
открьЕт Дж Дж. Томсоном е 1897 г Но ещё в 1S73 г. Максвелл в своём
знаменитом «Трактате об электричестве и магнетизме» обсуждал возмож-
ность существования в природе, как он пишет, «молекулы электричества»
и пришёл к выводу, что такой молекулы быть не может, так как посчи-
тал, что она должна быть точечной, а точечный заряд имеет бесконечную
энергию. О «молекуле электричества», г. е. об «электроне», говорил также
и Гельмгольц в знаменитой речи 1881 г., посвящённой памяти Фарадея.
Гельмгольц в этой речи, как и Стони за несколько лет до него, опи-
рался на законы электролиза растворов электролитов, открытые Фараде-
ем в 1833 г., согласно которым с каждой грамм-молекулой Одновалентных
ионов электролита (нли просто «модему иначе надо было бы говорить
о «грамм-эквиваленте» ионов) связало количество электричества, выража-
емое числом Фарадея:
Z= % 500 Кд.
Так как л моле любого вещества содержится число молекул, равное
числу Авогадро:
Лтд = 6 10^,
то, разделив У на jV,i, получаем величину заряда элементарной порции
электричества:
е = |< = = 1.6 • К)-19 Км;
Уч
эта элементарная порция электричества равна абсолютной величине заряда
электрона; сам заряд электрона — отрицательный.
Глава 3
Физика корпускулярно-волнового
дуализма
3.1, Кнантоная механика
R 1925 1926 ет. практически одновременно, с интервалом в несколь-
ко месяцев пол вились две квантовые теории, которые стали окончательной
формулировкой квантовой механики.
Одну из них развил Гейзенберг, его теория получила название «мат-
ричной», но правильнее называть её «операторной» квантовой механикой.
В этой теории яеличмлы рассматриваются нс как алгебрам -
ческис ЧИСЛЯ (как в классической физике), а как бедо£мечно.н^нгые
цы (иочле*, олертшвры), удовлетворяющие тем же алгебраическим соот-
ношениям, которым они удовлетворяют в классической механике и физике,
по также. кроме того, дополнительным чисто квантовым гак называемым
«фундамента еьным комму га ш юн ньем соотношснням».
Другую теорию развил Шредингер, и она получила название «волно-
вой» квантовой механики.
В этой теории эддолумна описываются «волновыми функ-
циями», заданными а бедов лечили ш^ёхиермаи уйвкгемяв-
Обе эти квантовые теории, как мы сказали, дали окончательную фор-
мулировку современной квантовой физической теории микромира. Шре-
дингер в одной из первых работ 1926 г доказал» что обе квантовые механи-
ки, несмотря на их внешние математическое различие, эквивалентны.
Следует хорошо осознать, что вся физика является квантовой. Клас-
сическая физика — это только, хотя и самая существенная, но лишь часть
квантовой физики, когда квантовые поправки и ней пренебрежимо малы
(т. е. когда постоянную Планка ft можно положить равЕтой пулю).
В этом учебном пособии, как мы сказали во Введении, положения
кваеловой механики излагаются рецетпурно, т.е. только чётко формулиру-
ются эти положения, но нс обращается практически никакого внимания на
их обоснование.
3.2. Соотношение неопределённостей
153
3.2, Соотношение неопределённостей
Любая микрочастица обладает корпускулярно-волновым дуализмом,
т. с. в одних экспериментах проявляет себя кпрщтлтлоы (материальной
точкой или шариком малых размерив), в других — отлнеш (возмущением
в непрерывной среде). Это мы уже объяснили на примерах фотона и элек-
трона.
Ситуация, одна ко „ интереснее и сложнее. Оказывается, в и там
.же ЗАгеле/?рлгент₽ (любом) адюцралотшо лгслмсно считать
w яцрлуждоый, w гстм йцмькя учптыи?ть. что фдеич^кие ^еличн-
йы. к&ш^рые мы используй Лгя описания в этом эксле/?1мгенте к^рлугку-
ля/?ныл йли scwotfwx twMcmtf .иикртзделэдады, испехтьзуюшея с цзвестчрй
£еоА/?е^елё>чг747ми (иечёлисодэтчУ
Речь здесь идёт нс об обычных неизбежных ошибках измерений фи-
зических величин и связанной с ними неопределённостью их точных зна-
чений в классической физике. Теперь это принципиально иная, «квантовая
нечёткость», связанная не с незнанием точных значений физических вели-
чин, а с иеод7?£^слЁ«№^тьи голгит понятый этнх величин^ ИСТЮльЗуемых
для описания микромира.
Гейзенберг в 1927 г. с целью выяснения физического смысла откры-
той им операторной квантовой механики, для доказательства^ что понятия
траектории частицы классическом механики не существует, сформулировал
так называемое «соотношение неопределённостей^ показал, что п/юцвда)*-
ние зилче/шй А л- и яюждетстнвуюдой sir
д/№вдц|ш мжпульсд А рд: лшл^очдетшдо, ₽ л/юдевдшьясш клгл-
лктняж/и. (?о flt'cx случаях (для любого состояния микрочастиц)
удоктt?N №ДЯё?н ледовеяоияу
Л т Л р.г > у.
я*
в правуео часть которого входит перечёркнутая постоянная Планка.
Это неравенство означасг, что квантовые неопределённости А зг и Д рт
нельзя сделать ойчсбрс.пеппо сколь угодно малыми для любых состояний
микрочастицы.
Пары других сопряженных физических величии удовлетворяют подоб-
ным соотношениям неопределённостей (например, энергия микрочастицы
и время наблюдения её состояния с этой энергией или разные декартовы
проекции момента импульса частицы, но не различные проекции самого
импульса или разные координаты частицы, их-то можно измерить одновре-
менно со скаль угодной точностью).
154
Главаз
Соотношение неопределенностей для Дж и Др* — координаты и про-
екции импульса микрочастицы, пребыла епщсй в любом квантовом состоя-
нии, — можно понимать просто как соотношение
Дж Дртг = Л,
как обычно и делают, в котором Л — постоянная Планка.
Из соотношения неопределённостей, в частности, следует, что не су-
ществует такого состояния микрочастицы, в котором и координата, и им-
пульс ЭТОЙ частицы ОДНОВрСМСПЕН) имеют ТОЧНЫЕ значения.. г. с. когда Д j =
= 0 и А рх = (}.
Ecjjh у микрочастицы в данном квантовом состоянии неопределённость,
скажем, её координаты Дд? = 0, т.е. её координату мы знаем точно, то
в этом квдитовом состоянии неопределённость соответствующей проекции
импульса Др* = ж, т.е. вообще ИSJ о каком Значении проекции импульса
и о самой этой проекции импульса у этой микрочастицы в этом квантовом
состоянии говорить нельзя.
Когда классическая материальная точка m движется по своей траекто-
рии, в каждый момент времени f ее состояние описывается одновременно
точными значениями её координаты г и её мгновенной скорости V, или
мгновенного импульса р = mv. Это противоречит соотношению неопре-
делённостей.
Таким образом, п квантовой механике ледьзя о классический
jwpacKnifjyjww штелшцн, являющейся сс
СОСЛТОЯ/ШЫ Г .№Н0£ЁННЫЛШ ЗЯйЧе1НМЯЛГМ Се КЕЧ>/к)ыЯДЛ1Ы ц её
стн (импульса).
Обычное кинематическое описание движущейся точечной чзстицел
массы т, применяемое в классической механике, в квантовой механике
не приемлемо.
Оценим величины неопределённостей координаты и импульса в двух
характерных случаях.
Пример 1. Рассмотрим молекулу воздуха. Неопределённость сё поло-
жения А,г имеет порядок линейных размеров этой молекулы, т е. имеет ве-
личину порядка 1А = 10”10 и. Таким образом, квантовая неопределенность
её импульса равна
щ Гг 10-34Джс 1О-24КГ-М
ДТ" ю “10 ~
Чтобы выяснить, большая эта неопределённость или малая, сравним
величину Дрт с величиной самою импульса рг молекулы. Масса молекулы
3.2. Соотношение неопределённостей
155
воздуха m = 10 2| кг, а скорость её теплового движения имеет порядок
величины ит — 10'* м/с, Таким обрааом,
£ = 10-^^.
Как видим, Др^ ^пульса люл скулы ларяйка
авдычцлы сочоэд шглулдеа pjp. Неопределенность составляет, таким пора-
5Ом, 1(Ю%, и с ней поэтому обязательно надо считаться.
Пример 2- Рассмотрим теперь пулю стрелкового оружия. Пусть масса
пули m = 5 г = 10 5 кг. Пусть скорость пули v = 103 м/с. Таким образом,
импульс пули имеет величину
р* = 1(Г* KL Ю1^ = 1*ЕМ.
Найдём квантовую неопределённость Ар.г импульса пули. Неопре-
делённость А.г координаты пули размером (к5 см примерно равна 1 мм =
= 10-3 м. Поэтому
д ft 10-ЗАДжс = 10 31
Да: 10-3м с
По сравнению с I кг-м/с это ничтожная малая величина. Такую неопре-
делённость не имеет никакого смысла рассматривать и учитывать.
Проиллюсфирусм, следуя Гейзенбергу соотношение неопределённос-
тей в очень конкретной физической ситуации.
Рассмотрим эксперимент ио наблюдению интерференции однородного
электронного моноэнергетнчесгого пучка в установке Юнга с двумя щеля-
ми, в которой на удалённом ч крап с наблюдаются эквидистантные интерфе-
ренционные полосы.
Пусть у нас имеется пучок электронов, летящих с одинаковой скоро-
стью v, нормально падающий на экран с двумя щелями„ с расстоянием d
между щелями. За щелями па большом расстоянии L пусть расположен
другой экран, на котором ваблЕодаегся картина интерференционных полос.
Электрон является не только корпускулой, но и волной с длиной волны
Д = h/mu.
Будем рассматривав w пучка, а <М-
логю доекпдона s зтолг лучке3, налетающего на экран с двумя щелями, пер-
пендикулярно нм, с некоторой скоростью р.
Согласно Гейзенбергу. ы а этаи №^лыч№ вдлшжш экста/шиекте лиэ-
,we? MtfCNCHfl fl ввдычшшх тс. о его ко-
ордзшате п импульсе. Эти координату и нм пульс рассмотрим только вдоль
156
Главаз
осн /л перпендикулярной щелям и направлению движения электрона, пока-
занным на рисунке. Так что пнжс будем рассуждать о неопределённостях
Аун Друь а нс о неопределённостях Ат; и Ар^..
На экране с интерференционными полосами мы имеем светлую цен-
тральную интерференционную полосу^ ширина которой с лозгщшг корлгсАГ-
лярной характеризуется неопределенностью поперечного импульса
электрона, пролетевшего через одну из щелей и получившею вслед-
ствие этого некоторый импульс Ару от взаимодействия с эюй щелью.
Используем сначала ештйойуи точк^ зрения и представим электрон как
волну с длиной волны А.
Рассчитаем ширину центральной интерференционной полосы. Раз-
ность кода лучей В А/ н 4 А/ для точки первого лшишнума освещённости
на экране около центральной полосы равна /„ где 2( — расстояние между
интерференционными полосами. Из прямоугольных треугольников AAf А]
и имеем следующие соотношения:
/ \2 / \2
и?М)* = Ь2+ (/ I || , (AxVf)a = l2+и-,
где I — расстояние точки М на экране до центральной точки (Л- Следова-
тели го,
(ВА/)Й - (АЛ/)2 = 2f<t.
Очевидно далее, что
(НМ)2 - (AM)2 = (В А/ - АЛ/) (НМ + АЛ/) “
12. Соотношение неоиределёнеюсj ей
157
= 2 ЦВМ- ЛМ).
так как L d, и, таким образом, разность хода лучей В А/ и Л Л/ равна
В?,1 - AM = у-
Для точки минимума освещённости на экране она должна равняться у
т. е.
fd = А .= Af
L 2’ 2£3
получили известную интерференции! н1ую формулу, связывающую рассто-
яние d между щелями, расстояние £ от экрана со щелями до экрана с ин-
терференционными полосами и полуширину i центральной интерференци-
онной полосы.
Величина d характеризует неопределённость Ду поперечной (к летя-
щему алегарОну) координаты электрон;!. Неопределённость соответствую-
щего импульса МОЖНО оценить ИЗ соотношения Дру — ру, ГДО — НОПСрСЧ-
ный импульс электрона, обеспечивающий его попадание в точку минимума
освещённости на экране. Таким образом, — у н и, = |, где т обозна-
чает время пролёта электрона от щели до экрана с полосами. Очевидно,
£
т = --
.._____mi Л
Учитывая, что т = -—. так как -и™
Ру
получим, что
£ _ т/ _ tJ?fг
Ру 1 " L
Таким образом, для произвсдсЕ/ия Ду и Ару получаем следующую
формулу:
д„ л,, d. п = АЛ . ™_L_ . mv = 4-
у 2! £ 2т Г- тъ 2’
для длины волны А мы использовали формулу де Бройля А — fc/m t.
Мы пришли к |чейзенберговскому соотношению неопределенностей.
Неопределённости координаты Ду и проекции импульса Др^ в направ-
лении оси ()i/ пс могут обо одновременно быть равными нулю, так как
L5H
Главаз
их произведение Ду.Др^ всегда больше или равно fi/2, правильнее писать
не Л, LL й.
Итак, при интерпретации рассматриваемо]и типично волнового эАсле-
рцшенйга с интерференцией на двух щелях мы можем пользоваться также
и «орпускуля/зиььни величинами у и но с долей дачёлютегж определяе-
мой соотношением яеолределёяностей.
Гейзенберг гак разъяснил суть открытого им соотношения неопре-
делённостей
Физические величины (координата, импульс), с помощью которых мы
изучаем явления микромира (в частности, движущуюся микрочастицу)h за-
имствонаЕпд из макроскопических ткспсримептон, производимых с макро-
скопическими сбъскгамн и приборами (другого нам не дано).
Поэтому физические величины и связанные с ними физические пред-
ставления, с помощью которых мы пытаемся изучать микромир, в принци-
пе несовершенны^ хотя, разумеется, у нас и нет другой возможности позна-
вать этот микромир.
Соолшошены* КЁЫгсредвдйотштЕ'й, по Гейзенбергу, характеризует, та-
ким образом, предел в£>1Л10жн£ч?тей физичежыл еетычкп олс-
са ческой к лялечилм .адяремшра.
Таким образом, за Егсопрсдслсп посты» коордипатты Лт частицы скры-
вается не то+ что мы не знаем её точного значения, т е. «истинную» коорди-
нату микрочастицы в пределах этой точности Дт (хотя уверены, что сама
эта истинная координата, несомненно, существует), а то, что rawo понятие
^координнтыр npir глгшь .ил.тых Да: ндчшшелт нгерятпь свои ^и.эич^ский
с.пысл, становится бессмысленным.
3.3. Копенгагенская интерпретация квантовой механики
Следуя Гейзенбергу, мы объяснили суть ортодоксальной так Егазьгва-
смий Копенгагенецой интерпретации квантовой механики, разработанной
в 1926-1927 гг Гейзенбергом, Паули, Борном и Бором, но главным — обра-
зом Бором (Бор жил и работал в Копенгагене).
В 1929 г. Бор, основываясь на соотношении неопределённостей Гей-
зенберга, открыл новый философский догсил/штсльпости» и раз-
вил так называемую «копенгагенскую интерпретацию» квантовой меха-
ники.
Согласно Бору, описание л<и?^лчцрдт нсиодмре^мое е кишшоеой иИедгл-
;шкг, явдотстпсл предельно ноли ми, т. с. не существует (и не может суще-
ствовать) более полной, более «правильной» физической теории, чем кван-
товая механика (т. с. не .ао.жттн ишелкой весной лдормм
3.1 Копенгагенская интерпретация квантовой механики
159
и*? быяя бы чней, е^йяиностей
JI Ш. (i . £Г было бы ЧНЛКИ.И и определённым).
В современной интерпретации стандартной квантовой механики квин-
товая волновая функция характеризует «вероятность нахождения электрона
в любой произвольной точке пространства, если электрон пребывает в за-
данном квантовом состоянии»,
О такой «полной» теории гем не менее время от времени мечтали
(и продолжают мечтать) некоторые физики В частности, в 1952 г. Бом пред-
дожил вариант такой полной теории (которая, впрочем, по своим оконча-
тельным результатам ничем не отличалась от квантовой механики, разнясь
с пси лишь словами, и ничего не предсказывала нового). Впрочем, теорию
Бома сразу же поддержал де Бройль. Эйнштейн с середины ]930-х it. тоже
постоянно выступал с заявлениями, что квантовая механика как физическая
теория «не полна», и считал, что должна существовать более полная, более
последовательная, более «понятная» физическая теория микромира.
Такую полную понятную гипотетическую теорию в настоящее время
называют «теорией со скрытыми параметрами». В ее рамках считается, что
электрон на самом деле обладает «настоящими» координатами и проекци-
ями импульса и является и действительности точечной частицей, но из-за
СЛОЖНОСТЕЙ его структуры П Характера ДВИЖЕНИЯ МЫ МОЖСМ ПО КП ЧТО ОПЛ-
сать электрон только приближенно^ с помощью нечётких представлений
существующей квантовой механики.
Как мы уже сказали, удачную теорию со скрытыми параметрами раз-
нил в 1952 г Бомт по ещё при зарождении квантовой механики такой тео-
рии лрцдержйвался и де Бройль (его знаменитая «волна-] низ от», в которой
электрон представлялся н виде поплавка на волне). Но на Солвеевском кон-
грессе в 1927 г. теория де Бройля была решительно раскритикована и от-
вергнута, и де Бройль оставил её. Но дальнейшее развитие теория скры-
тых параметров получила, как мы сказали, у Бома в 1952 г.ъ после чего де
Бройль вернулся к своим старым идеям, но в силу больших математиче-
ских трудностей н при отсутствии подтверждающих ее экспериментов его
теория скрытых параметров нс получила продолжения.
Сторонники теории скрытых параметров обычно пренебрегают тем.
что ещё н ] 932 г. фон Нейман доказал знаменитую строгую математиче-
скую «теорему о скрытых параметрах», называемую «теоремой Неймана»,
утверждающую, что метрика? мромяиршш л/?шддо л дольня не
лгожетя (доказал, что такую теорию построить невозможно, если при-
нять основные положения стандартной кван товой механики). Хотя теорема
фон Неймана более чем убедительна, некоторые физики, работающие над
обоснованиями квантовой механики, все же считают сё неверной.
160
Главаз
Вместе с тем, конечно^ требуется разумное и понятное объяснение
нечёткого расплывчатого характер и квантовой механики. Такое объясЕтсиис
Как раз и дал Бор в 1929 г. в своём «л/шлцыле дйлдстнительнос/пы^ По Биру,
такой характер квантовой механики связан с тем, что в области микромира
(т е. при изучении атомов, молекул, атомных ядсрн элементарных частиц)
ли чёшкуло (л|, е лдс елммх, со
«CCLWW наышлш и «объект# (m. с. окружающую ntre прцройу}.
Дело в юм, ,ио1 в отличие от макроскопических объектов, которые
мы можем реально видеть и даже трогать руками, отдельный электрон, или
атом, мы ле можем ни видеть, ети взять й руки. О существовании гипкрсюбъ-
сктов мы Судим исключительно лишь по согласованному поведению наших
физических приборов.. ИСПОЛЪЗуСМЫХ ДЛЯ Их НЗуЧСННЯ, ПрИЧЁМ ВСЯКИМ рЙЗ
в каждом конкретном эксперименте нс вполне ясно, где мы проводим ли-
нию раздела «субьект-обьект».
«Нечто», что находится в псрсссчсЕгии всех наших зкспсримсЕггов, как
это проиллюстрировано на левом приведённом рисунке, это и есть та «объ-
ективная реальность», которую мы изучаем.
Таким образом h например, если стол в комнате на 100% объект и на
О % субъект, то этом, может быть, только па 60% объект, а на 40%
субъект, а электрон лишь на 50% объект и на 50% субъект. Современные
элементарные частицы, вроде открытых в 1980-е гг одними из последних
свсрхтяжслых частиц, так называемых «промежуточных бозонов» И7±1 Z°
(недостающих частиц семейства из четырёх элементарных частиц, к кото-
рому принадлежит и обычный фотон) на огромных ускорителях злемеитарь-
ных частиц, г. е. с помощью 1рандиозных «приборов» масштабами крупных
заводов, уже, наверное, только на 10% объекты, а на 90% — субъекты, т. е.
мы с вами.
3.3. Копенгагенская интерпретация квантовой механики
161
По Бору, как человечество мы уже практически познали весь окружа-
ют ий нас мир. Обозначим кругом ня приведенном правом рисунке всё то,
что в принципе можно познать, я областью с нечёткими iраницами — го,
что мы уже познали к настоящему времени. Но Бору получится примерно
картина, изображённая на рисунке. Фактически мы уже всё познали, что
можно было познавать. Но граница добытого знания не может быть, конеч-
но, Чёткой. Согласно Бору, мы чувствуем эту |рйницу именно & лечёттостп
npoeederitffl jTHwUir «субъект-<ч7ъелтп^.
Противоречивый корпускулярно-волновой дуализм электрона, следуя
Бору, объясняется нечёткостью самого полектрона» (как подлежащего по-
знанию объекта), т с. тем, что электрон етз 50% это просто показания нашил
приборок, которые мы использовали и будем продолжать использовать для
его изучения, и только на 50% объективная реальность.
Работы Гейзенберга {1901-1976}, Шредингера (1887-1965) и Дирака
(1901 1984) по созданию квантовой механики были отмечены двумя Нобе-
левскими премиями. В 1932 г. премия была присуждена Гейзенбергу «За
создание квантовой механики (в матричной ферме)», а в 1933 г. — Шредин-
геру и Дираку «За разработку плодотворных направлений в теоретической
физике», Де Бройль (1892г-1987) получил Нобелевскую премию в 1929 г.
«За открытие волновой природы электрона»
Планк (1852-1947) получил Нобелевскую премию в 1919 г. «За при-
знание его заслуг в развитии физики его открытием кванта энергии» (это
была премия за 1918 г., присуждённая в 1919 г). Борн (1862-1970) получил
Нобелевскую премию п 1954 г. «За фундаментальные работы пл квантовой
механике, б особенности за его СТЙТНСГ и ческу to интерпретацию волновой
функции». Паули (1900-1958) получил Нобелевскую премию в 1945 г «За
открытие принципа запрета, названного его именем».
Дебай (1884 1966) получил Нобелевскую премию по химии в 1936 г.
«За вклад в нагие понимание молекулярной структуры его исследованиями
магнитных дипольных моментов и дифракции рентгеновских лучей и элек-
тронов в газах».
Глава 4
Модельные одномерные
квантово-механические задачи
Рассматриваемые ниже кпацтоло-мсхаипческис "задачи на решение од-
номерного уравнения Шредингера С к случаях свободной частицы, потен’
циальной ямы, потенциального барьера и двойной ямы) являются грубо
молельными Они пригодны только для иллюстрации основных квантовых
эффектов (дискрет!гости энергетических уровнен энергии у микросистемы,
туннелирования частицы черев потенциальный барьер, наличия химиче-
ской связи в гомопопярных двухатомных молекулах, наличия разрешённых
и запрещённых энергетических зон одноэлектронных состояний в твёрдом
теле, особенно важного для нас эффекта), Результаты решения рассматри-
ваемых грубы к одномерных задач нельзя непосредственно сравнивать ко-
личественно с результатами физических экспериментов.
Ради простоты мы рассматриваем только одначериые квантово-меха-
нические 'задачи, которые решаются точно.
Стационарное уравнение Шредингера для движения частицы ( г. с. Опн-
СЫВаюлцсс её СОСТОЯНИЯ движем ня, нс зависящие ОТ времени f) в заданном
одномерном поле V(i) имеет вид
+ = W,
2m
где ft — перечёркнутая постоянная Планка, m — масса частицы, Vfi) —
потенциальная энергия частицы (считается, что частица находится в неко-
тором потенциальном поле).
Это личеннда дифференциальное уравнение, т.е. если ^(-т) — реше-
ний уравнения^ то с^(т)7 где С — произвольная константа (вообще говоря,
комплексная) тоже будет решением этого уравнения.
Далее, Е — эшр^ия частицы (она может принимать непрерывные
и дискретные значения), ^(ят) — литииая фуиедмя частицы, или, более точ-
но, яни/одоя обладающая Следующим физическим
4 1 Задача об одномерном свободном движении части цы 163
смыслом. Величина
|^(я) 2
где прямые скобки | | обозначают модуль комплексного числа, равна «е-
/доятшсмы ношпы члтшрт с к&^/>йиндтои. а ынте/дедае яг, я +
— da;, яри ytvrcwy. что оскстАяяде вдслшцш AwcwetrewicH еяымовРЙ </<>нк-
^(л). Для станип[тарного состояния эта вероятность не Зависит от
времени, те. одна и та же но все моменты времени. Вероятность найти
частицу с координатой, лежащей на конечном интервале л, 6 значений ко-
ординаты аг, равна
6
У |^(йг)|2Леп
а
а вероятность найти частицу вообще где-либо на бесконечной прямой равна
+ м
У |^(ятЦ2di = 1ч
—и>
так как это — вероятность «достоверного» события (т.е. события, которое
обячаТЕЛЫЮ происходит).
Выписанное условие, которому удовлетворяет функция ^(я), является
независимым от уравнения Шредингера требованием и называется усгагаы-
ем Ho/kuupflsra,
Из этого условия нормировочная постоянная С для функции (7^(я)
определяется только с точностью до произвольного ранною ио модулю
единице постай кого так называемою «фазовою множителя» с'й, в кото-
ром а — произвольное действительное число. Этот постоянный произволь-
ный комплексный фазовый множитель ие имеет никакого физического
смысла в квантовой механике, и его часю произвольно полагают ранным
единице.
4,1. Задача об одномерном свободном движении частицы
Самый простой случай касается движения свободной частицы, когда
V(z) = 0 (тождественею равно нулю), т. с. когда ист никакого лОтенцналь-
hoiu ПОЛЯ. Тогда одномерное уравнение Шредингера принимает вид
712
2тп dx2
— Л\''
164
J'л л вл 4
ИЛИ вид
ах
если внести величину
£ = т \/2тЁ,
Л
называемую вожовдм числам частицы. Считаем, что энергия Е принимает
только положительные значения, так чЮ £ — действительное положитель-
ное число.
Общее решение приведённого обыкновенного дифференциального
уравнения второго порядка с постоянными коэффициентами записывается
в виде
=С1С^Т +С2С-^,
где z — мнимая единица, Ст и СЧ — произвольные константы.
Очевидно, эту функцию нельзя отнормировять на единицу, так как ин-
теграл
У <£х
—dfc
в бесконечных пределах расходится.
Физический смысл найденных решений следующий.
Первое слагаемое, считая C'i = 1, характеризует временную волновую
функцию
^(т, t) = е
। де w = E/h > 0 является «циклической частотой» рассматриваемой
волны квантовой частицы. Решение это описывает строго периодическую
волну, распрос траняющуюся в патожгляэдвдам направлении оси я (слагае-
мые iwf и в показателе экспоненты имеют разные знаки).
Второе слагаемое, считая Са = 1 в приведённой формуле для V't1)*
характеризуется временной волновой функцией
*(х, 4) = е-<У*»лМг) = e“CiM)£i-fc1' -
где о? = E/fr, > 0. Это решение описывает строго периодическую волну,
распространяющуюся л [управлении оси jc (слагаемые
и 1Ьв показателе экспоненты имеют одинаковые знаки).
4 1 Задача об одномерном свободном движении частицы
165
Волновые функции ^i(x) и ^з(яг) при произвольных Е характеризуют,
таким образом, вес состояния движущейся свободной частицы Так как
|^(ж)р = |е’^Г= I, |.>я(д:)(3 = |е-*Л:1‘р = 1,
т. с. эти величины не зависят от sc, то вероятность найти частицу в любом
интервале я, л + d# в состоянии или ^з(я) одинакова, т.е. частица
^а ww бес-вдиечнАй и/мм/ои и этих состояниях,
Невозможно указать на прямой - ОС’ < ЗГ < +сс область, б которой частица
находилась бы с бблыней вероятностью, чем в другой такой же области.
Другими словами, квантовая неопределенность Дг координаты части-
цы т на прямой —ж < я; < +ж равна бесконечности (Дат = ж), а потому
ктшЕгтовая неопределённость Дрт импульса р.г этой частицы (в состоянии
или ^a(z)) равна нулю, г. с. в каждом этом состоянии микрочасти-
ца, согласно квантовому соотношению неопределенностей, имеет строга
определённое значение импульса рг, а потому лучше характеризовать её не
волновым числом fc, а ее импульсом = ± fifc.
Будем рассматривать поэтому в качестве решений уравнения Шредин-
гера для свободной частицы волновые функции
& которых ря — импульс свободной частицы, принимающий любые поло-
жительные и отрицательные действительные значения -со < pj: < +ж.
Как мы уже сказали, так как = I. то нормировать волновую функ-
цию е'^*'** на прямой — оа < z < +ж на единицу невозможно, так как
интеграл
+<ю
— со
в бес кое генных пределах расходится^ он равен +ж-
Поэтому нормируют ЭТИ функции по-друюму, как [ТОЕОрЯ’Г, ^нормиру-
ют на 5-функцию».
Речь идёт о знаменитой «5-функции Дирака», введённой им в 1927 г
Математики признали эту функцию только и 1948 г> когда появились ма-
тематические работы по строгому обоснованию этой функции (фактически
функцагжлла).
Объясним теперь, как отнормировать функции е^^Ря® на 5-функцию.
Для этого надо рассмотреть нс «условие нормировки», а «условие ортонор-
мировкн», т. с. условие, которое объединяет условия нормировки волновых
166
Глава 4
функций при заданных рт и условия ортогональности для произвольных
пир ЭТИХ функций при У чтилоЫ
Cf* С / = J(pt-рД
?f)e и С - Mpimpwwe лысшияняьгг и s тграяой члсти timoum
J-<j6)7jKjp* Лг/рлко. При р'. = ра в правой части стоит бесконечность, при
j./ у pj: н правой части стоит моль. Из данного условия ортонормировки
получаем,что
ic|a2^i(p'-pj = ^P;-^),
а следовательно,
'2*Ъ
не имеющий физического смысла постоянный фазовый множитель мы
положили равным единице. Таким образом, отнормированные ни J-функ-
цию волновые функции свободной частицы имеют вид
частица, описываем ан такой функцией, имеет энергию
Временные волновые функции О = описы-
вают строго периодические волны частоты иг = Е/Ь. Это знаменитые
«волны де Бройля», период которых равен Т = 2ir/w и длина волны А =
= 2тг/^. Таким образом, волновая функция V;p± (я, () имеет длину волны
mv'
если считать, что Е = — кинетическая энергия частицы, v — ее
скорость. Для свободной частицы это единственная энергия, так как по-
тенциального поля и связанной с ним потенциальной энергии сейчас нет.
Получили знименитую «формулу дс Бройля».
4 l. Задача об одномерном свободном движении частицы
167
Расплывание вал навага пакета
Б нашем учебном пособии, посвящённом полупроводникам, мы интс-
ресуемся так называемым «квазиклассическим приближением» в квантовой
механике, т.е. случаем, когда постоянная Планка h —> 0 (но А 0}. Тогда
кйан/но^оя Л1ЁЫШЫКН ne/jifitudi/ffir &
Практически точечный так называемый «квазиклассичсский» элек-
трон, двигающийся с постоянной скоростью в катодных лучах ИЛИ кри-
сталлическом твёрдом теле, описывается нс строга периодической волной
де Бройля, а «волновым пакетом», составленным из этих волн:
ро + Др
PD-ДР
где С(р) — «функция фирмы» волновою пакета, ре = ргь- — проекция на
ось х импульса квазиклассичсского электрона, описываемого волновым па-
кетом, Др — «импульсная ширина» пакета.
Строго периодическая волна де Бройля не может описывать точечным
реальный электрон, двигающимся с постоянной скоростью в катодных лу-
чах или твердом тепе, так как волна де Бройля ^локализовала на всей
осп ж, как показано на левом рисунке. Такой электрон описывается пакетом
волн де Бройля Волновая функция этого волнового пакета
в отличие ст Одной волны дс Бройлят в каждый момент времени /, около
некоторого движущегося со временем с постоянной скоростью значения е,
как показано на правом рисунке.
Квази классический электрон, описываемый волновым пакетом, с тече-
нием времен к ряям^ыътак как пространственная шири-
на Л л пакета возрастает. Как говорят, пакет «расплывается».
Оценим этот эффект расплывания. Возьмём функцию формы волново-
го пакета в гауссовском виде:
С(р) = Се"й{р_рщ)'
Глава 4
где pg — импульс электрона, й — некоторая постоянная, С — нормировочная
константа.
Тогда для пространственной ширины Дз; волнового пакета в момент
времени ( можно получить формулу
Д.т = Даго 1111 —
Л-/-
т3(Дхп)4>
в которой Д:го — ширина волнового пакета при t = 0» задавая которую мы
задаём константу о-
Найдем временную волновую функцию О для гауссовского вол-
нового пакета. Так как функции С(р) при малом а сосредоточена около
р = ро и быстро убывает при р —> ±оо, то в формуле для волнового пакета
можно положить Др = ос, и тогда
i) = С
4-оо
у е (i/6)£(p)t+(i/4 ртг-"(?-Р1>)а Jp
Положим теперь, что
Л(р) = £(ро) + —-j— I? ~ П>) + ? . 2 (Р-Ро) +
и оставим в 310м разложении только выписанные три 'тени. Считай, что
Р3 <Щр)| Ро
Мр) — —1 имеем —:— = тт = и, где гг — скорость движения
2т dp 1р=р0 пг
^E(p) j
нашего электрона, и —г^“ — ™-
Таким образом, получим
f)
_ £0 I b'( F4})i + (t/fr) Р41 ® X
Н зс
(з:-’г0{р-Ри)-('Л J ((/Зтп) (р-Ро)2—«(р-Ро)а ((р
— из
4 1. Зл Д АЧ Л О li ОД Н ОМ ЕР 11 ОМ СВО Е О Д Е [О М Д □ И Ж Е11И И ЧАСТИ ЦЫ 164
i(ic - rt) 2 (± - i/i)2
2ft(ft + itfintfi] ' е 4ft2(ft + it/2mh)
здесь в интеграле мы сделали замену переменной интегрирования р —* р +
+ рп Далее, гак как
г.,’,//' 1 iJ,(ir =
= - (д 4- ii/2mJi) pa -
— tfi)2
ft (a + ti/Jhnft/® 4ft2 (a 4-it/2mft)!
i
(s - t'i)2
4Й3 (a + «/2mft)
i(i — ft)
1 a
= - (й + 4(/2тпЙ) р - ,0 ..
2 ft (ci + iE/ztnft)
(ж - ft)3
4fts (a +
то наш интеграл равен !---------. Таким образом,
у ft 4- i£/2mn
(g - ура
" ~e-(t/ft) j?(po)t + (j/ft)po л e + it/2mft)
u +
Разделяя реальную и мнимую части а показателе второй экспоненты,
отсюда ниходим, что
/ ТГ ~c-(i/H)E(po)t + (i/ft)po^x
у a + >t/2$nft
(i — trt)2 (i — ut)s
4ft2(cra + t2/4m2ft2) Smft3(crs + f.2/4m2 ft2 J
X lr v
r-t 'i mu
где po = mi' и £(pn) =
170
Глава 4
exp
, непосредственно заключаем, что
Из вада реальной экспоненты представив её выражением
/ (х — ui)2
I” 2(Дя)2
(Д^2 = 2Лг
4om2fi2 / ’
полагая £ = 0а отсюда находим, что (Даго)2 = 2Л” -гк. Исключал с помощью
этого соотношения о* получаем в точности приведенную выше формулу
для Д.х.
На рисунке представлен трафик функции
Дл((). Эта функция характеризуется временем г:
при котором Дат изменяется по сравнению с ДхС|,
скажем, нэ 1 %, так что
2 __
т2 = 0,02 ^v(Aiq)4 г “ 1,5 - 10"17(Aio)s;
/г
здесь Air» измеряется в эн] стремах (1 А =
= 1(Г’" м). При Длс = Ю А, т С! 1,5 10-,й с,
при Дя0 = 10:iA = 1 мкм. r 1,5 10 11 с.
В каюдно-лучевой трубке при анодном напряжении Е7 = 100 В элек-
трон имеет скорость г — 6Ю6 * В * *м/с. Считая, что неопределенность этой ско-
рости порядка 0,01%, т.е. Ди « 103 м/с, и применяя квантовое соотноше-
ние неопределённостей, получим для неопределённости координаты элек-
трона Дз: = Я/(тДи} = К)-'14 Дж-с/Ю”^ кг- 1,0э м/с = Ю-* м = 0.1 мкм.
Поэтому можно считать, что начальный размер электрона Даго = 1мкм. Ес-
ли электрон в катодно-лучевой трубке пролетает расстояние 10 см = 0.1 и,
время его пролёта в трубке равно Г = 0,1 м/6 106 м/с - 10"е с. Таким
образом, начальный размер электрона за счёт расплывания его волнового
пакета при проле те нм катодно-лучевой трубки согласно приведённой фор-
муле изменится только в два раза, т е. немного.
Пусть электрон в кремнии Si имеет начальные линейные размеры
Дл0 = 100 А. Эффективная масса электрона в кремнии ?п+| = 0,2m,
и пусть его подвижность при комнатной температуре Т = ВОТ К в крем-
нии = 1600 с и2/LI-с, а время его свободного пробега тп = З.б 10— 13е.
Тогда, полагая, что i = тп, из приведённой выше формулы для Д.т получа-
ем, что лине ины с размеры электрона при пролёте им свободного пробега
увеличиваются тоже только в два раза.
4.2. Задача об одномерной прямоугольной потенциальной яме 17]
4 Задач! иб одномерной прямоугольном потенциальной
яме с бесконечными стенками
Прежде всего, это очень грубая модель одно электронного атома. С ее
помощью можно продемонстрировать важное свойство атома, состоящее
н том, что электрон в нём совершает движения не с любой отрицатель*
ной энергией Е, а только с определёнными дискретными энергиями ЕП1
где n = L. 2f .... Кроме того, задача об одномерной прямоугольной по-
тенциальной яме позволяет моделировать движения свободного электрона
в твёрдом теле.
Эта задача о яме с бесконечными стенками не описывает, одна ко, ха-
рактерною для атомов эффекта окончания спекгра, состоящего из беско-
нечного числа дискретных уровней, на некоторой определённой энергии
(принимаемой за нуль отсчёта энергии), выше которой начинается непре-
рывный спектр, соответствующий состояниям ионизации и рассеяния элек-
трона па атомном ядре. В этом существенный недостаток рассматриваемой
задачи с бесконечными стенками.
Когда говорят об одномерной потенциальной яме с бесконечными
стенками, то хотят сказать, что речь идёт о функции потенциальной энергии
V (т) электрона, показанной на приводимом рисунке.
Она равна — К» (где Vo — так называемая «глу-
бина» потенциальной ямы) в области 0 £ х < а Ия)
(где а — так называемая «ширина» потенциальной
ямы) и равна +ос вне этой области (при i О
и I я) Другими словами, £
V = S ,
I +да в противном случае.
< -----------------------------------------------
В областях т £ 0 :< i > й, где потенциаль-
ная функция бесконечна, волновая функция ^(ас)
тождествен]io равна нулей. Поэтому нужно решать Одномерное уравнение
Шредингера
2? £*
2m dx2
- ¥оф - Е$
только в области 0 ж С а, т. е, внутри ямы, При этом в точках ж = л
и т = 0 (на границах ямы) необходимо потребовать выполнения гряничЕтых
172
Глава 4
условий непрерывности волновой функции, т.е. условий
^(0) = 0, tf(a)=o.
11риступая тс решению уравнения Шредингера преобразуем его к более
простому виду. Перенесём выражение Е 1.'1 из правой части в левую часть
и умножим все уравнение на —Йт/Йа. Тогда получим уравнение
Тру + к2 = О,
л.г
в котором использовано сокращённое обозначение для волнового числа
электрона:
\/Зтп(£ + Vo).
Общее решение полученного дифференциального уравнения имеет
следующий вид:
= Л + В ССВ(Ь?),
где А, В - произвольные постоянные^ значения которых следует найти из
1раНЕ1'1НЫХ условий.
Используем сначала граничное условие при л = 0. Согласно этому
условию имеем, что ^(0) = В = 0; следовательно, В = 0.
Используем теперь граничное условие при я = а (учитывая, что В =
= 0)п получим тогда, что V’ (га) = A sin(fcn) = 0. Этому условию нельзя
удовлетворить, требуя, чтобы А = 0+ так как тогда мы приходим к mpwew-
ольяшгу = !1, которое нс имеет физического смысла. Необходи-
мо поэтому потребовать выполнения равенства
sm(fea) = 0,
из которого следует, что fca = тгп, где п = 1: 2,. -. — произвольное поло-
жительное целое число, так как волновое число — положительной
Получили условно на выбор значений волнового числа Аг = я сле-
довательно, значений энергии £ = £?„. При значении п = 0 имеем fc = 0
и получаем лфившыьяйе решение, тождественна равное нулю, которое сле-
дует отбросить.
Таким образом, приходим к заключению, что решения уравнения Шре-
дингера, удовлетворяющие 1раничным условиям V'W = ^(й) = а03-
можны только при выполнении условий
й = п, ?г — 1. 2, 3, ....
4.2. 3 А ДАЧ А ОБ ОД H О М ЕРНОЙ ПРЯМОУI ОЛ Ы J ОЙ 1.1 ОТВ Н ЦИ АЛ ЬНОЙ Я ME I 73
г е. только при значениях энергии
F = £n =-70+1,2,3----------
2mtr
Последняя формула дает дискретные энергетические уровни пря-
моугольной потенциальной ямы с бесконечными стенками ширины и.
Спектр Еп показан на приведённом рисунке в случае большой (справа)
и малой (слева) ширины л ямы.
Энергетические расстояния между соседними ДИСКрСТЕТЫМИ урОПЕЗЯМИ
увеличиваются с ростом номера п, так как
Йп+1 -Еп = ^4(2п + 1).
ZHttl
В реальном атоме они не такие. Например, в атоме водорода они не
увеличиваются, а уменьшаются с увеличением п, и множество его дискрет*
вых уровней Ем при п = L 2. 3, ... имеет точку сгущения при £ = 0.
В случае очень большой ширины л мы наша задача моделирует по-
ведение электрона в твёрдом теле, имеющем макроскопические размеры.
На границах твёрд ого тела существуют силы, которые пе выпускают элек-
тро ее из него наружу Поэтому он движется в Ограниченном пространстве,
а потому его уровни дискретные. При а —+ +ос из приведённой формулы
заключаем, что расстояния между соседними уровнями £Jb, т. с. разности
энергий ВП4-1 стремятся к нулю, и мы имеем энергетический спектр,
СОСТОЯЩИЙ ИЗ огромного числа очень близко раС1Г0ЛОЖеппык друг к другу
уровней (этот спектр представлен на правом рисунке). В пределе о = 4-ос
получаем непрерывный спектр в области 0 < +оо. При а —> 4-ос
энергетический спектр, хотя и дискретный, но состоит из огромного числа
счета ь близко расположенных уровней, его называют поэтому «квазидне-
кретиым» ИЛИ «квазиEiCnpcpEJRHEJM».
174
J'л л вл 4
Б заключение отнормируем найденные решения
VfnW = Яп 8in(fcna).
а
найдём значение константы А, т.е, потребуем, чтобы у |t?,i(s)|a<fcc = 1.
о
Тогда
11ft+8to^2ft^
l-i. А2 - = 1,
J L’ rt П к’
о J
так что
5М®) = \/1 sin(fcnT).
где fcn = (тг/л) ti, га = 1.2.....
Посмотрим теперь, что даст приближённое кваликлассичсскос условие
квантования и применении к расе магри наем ой прямоугольной потенциаль-
ной яме. которое имеет следующий вид:
\/2т (Еп + Г(]}(Ь: — пй.
где п = I2, .... Действительно, 7 = я и р(я) = \/2т (Е„ + Vo), так как
£п = р^(дг)/2т — Vo- Таким образом, к паз и классическое условие
и
р(л) (fr = ц h
сводится к следующему равенству
2 а ^/2™ = п 2 тг й:
а следовательно.
2шйй
4.2. 3 А ДАЧ А ОБ ОД H О М ЕРНОЙ ПРЯМОУI ОЛ Ы J ОЙ 1.1 ОТВ Н ЦИ АЛ ЬНОЙ Я ME I 75
получаем в точности формулу для найденных уровней энергии строгого
решения ура Bi ice [ия Шредингера.
Мы исходили из физически обоснованных граничных условий: ^г(О) =
= у1!/}) = 0) выставляемых на границах ямы с бесконечными стенками Те-
перь. -однако, изменим Зги условия и потребуем, чтобы решение уравнения
Шредингера рассматривалось на всей бесконечной прямой -ос < аг < +ос
и удовлетворяло условию периодичности:
^(з + «) = ^(х),
с заданным периодом а, равным ширине ямы. Тем самым перейдем от за-
дачи на отрезке 0 < л < а с граничными условиями tf>(0) = = 0
к задаче ив всей прямой —ж < я < +ж с условием Борна Кармана,
Таким образом, рассмотрим уравнение
при -оо < ж < +оо. Общее решение этого уравнения теперь запишем
в виде
= С1С^ + С2е-^
где Ci, С; — произвольные постоянные, значения которых следует найти
из условия Борг га Кармана. Значит,
glfc(£r + rt) gift® Щ;г + д)
при всех г. Таким образом,
к а — 2тгп, к = к„. — n, п — 0, ±1, ±2 ....
При п = 0 имеем fc = ()_. а епедоватйЛЬНО^ И$ двух независимых ре-
шений и c-ifca: остаётся только одно: 1 (второе независимое
решение уравнения
176
Глава 4
равно ^(гг) = ж; оно не осциллирует, а возрастает на бесконечности и не
имеет физического смысла, его етэдо отбросить^
Как видим, решения рассматриваемого одномерного уравнения Шре-
дингера с условием Еорна - Кармана имеют дискретные энергии £>РЙ =
= -Vii + (fe2/2mfl2)n2, которые двукратно вырождены при п = ±1, ±2,
±3Т ..., г. е. каждому значению £?п соответствуют даа независимых реше-
ния. При п = 0 имеем невырожденный уровень с энергией = — Иг
Отнормируем волновые функции ямы с бесконечными стенками
с условием Борна-Кармана. Будем характеризовать эти решения не вол-
новыми числами
= = где п = 0т ±1, ±2, .,. т
а импульсами
Pjp — 71, где п = О, ±1, J=2, ....
Положим, что
^(т) = сес^>р“\
и потребуем, чтобы
га
У |^?х(®)|2^ = 1-
|>
Тогда
га
о
так что
Сравним теперь энергетические спектры истинной задачи о ямс ши-
рины а с бесконечными стенками и задачи с условием Борна Кармана
с периодом га. Энергии Вд истинной задачи не вырождены и лаются
формулой = (ft2/8maa)n2j где n = 1,2 .... Энергии зада-
чи с условием Борна-Кармана двукратно вырождены и даются форму-
лой A/J,”-' — (7с2/2тп2)712, где п — ±1. ±2 .... Если положить в фор-
муле для что n = 2j, а в формуле для Е?А2|Ч что n = j, то полу-
чим, что , т.е. что энергии тнерготических
43. Задача об одномерном потенциальном барьере
177
уровней в обеих рассматриваемых задачах совпадают Однако расстояния
между соседними уровнями — -E'^Li = (4j2 — — I]2) =
= fea/2ma2 (j - 1/4) в задаче с истинными граничными условиями в два
раза меньше, чем расстояния между соседними уровнями — Е^\ —
= fta/2ma2 (ja - (j - I}2) = h2/ma2 (j -1/2) в задаче с условием Борна-
Кармана при большем /. Следовательно, с учетом еы/дедюде-
мия ровней в с условием1 Ео/иш-Ей/мщяо н-мсгии агЬшдвдяую дтлт-
лос/ль нл № энергии я обеих roctavmr при больших квантовых чис-
лах П.
4.3. Задача об одномерном прямоугольном потенциальном
барьере
Рассмотрим теперь грубую модельную задачу о туннельной проницае-
мости одномерного прямоугольного потенциального барьера для электрона,
налетающего на барьер, с некоторой заданной энергией Е. Одномерный
прямоугольный потенциальный барьер задаётся функцией потенциальной
энергии
V(^ =
при 0 де й,
в противном случае;
она показана на рисунке. Величина Vb назы-
вается «высотой» барьера, а величина й — его v(i)
«шириной».
На привсдёпеюм ниже рнсуЕткс функции
V (i) изображена также юрнзонтальиая при- К
мая линия для энергии Е налетающего элек-
трона, при этом ради простоты мы рассмотрим Е-------------------
Здесь только случай, когда Е < Vy.
Теперь решать уравнение Шредингера
нужно на всей бесконечной прямой я от -оо ч „
до +оо.
Нас интересует решение, которое описывает электрон, падающин на
барьер с левой Стороны с энергией Е. Волна электрона приходит из минус
бесконечности, s - -ж, и распространяется в положительном направле-
нии оси я до плюс бесконечности, я = +ос.
В области слева от барьера (при я < 0) имеем две волны;
^рю и дт/эозлсрику^. В области внутри барьера (при 0 s а) имеем
17N
Глава 4
волну, по мере проникновения электрона внутрь барье-
ра, я в области справа пт барьера (z л) имеем только
с меньшей, чем падающая, амплитудой, распространяющуюся в положи-
тельном направлении оси х.
Уравнение Шредингера рассмот-
рим по отдельности в трек областях:
I (z < < 0), II (О £ т £ а),
111 (z > а). В областях 1 и 111 по-
тенциальная функция равна нулю,
F(z) = 0, и уравнение Шредингера
записывается в виде
*1 ** . Ev
2тн dz^
в области и, где потенциальная
функция V (т) = Vq, уравнение Шредпмгера имеет вид
fia
2m
+ ВД = Е$.
Умножим каждое из приведённых уравнений на —и введём со-
кращённые обозначения:
k - | ^2т Ё, 7 = | 0m(Vo-E);
тогда в областях J, 111 имеем дифференциальное уравнение
77 + = 0,
л.т
а в области И — дифференциальное уравнение
Общее решение дифференциалы того уравнения и областях I и П1 имеет
вид
у>(х) =С1 е*ь +с2е-’**,
43. Задача об одномерном потенциальном барьере
179
гле Сь С?2 — произвольные постоянные Так как временной множитель
в вс лиевой функции в квантовой механике имеет вид
C"wt = (£? = fcw),
т.е. в показателе экспоненты имеем знак минус, то волновая функция
ef*:e описывает волну, распространяющуюся в полдаешлйшеш направле-
нии оси я. Полное выражение для этой псин гы следующее:
£- wi+ifci,
волновая функция e_*fcl описывает волну, распространяющуюся в
лтэдвдом направлении оси т. Полное выражение для лее:
p-t м t-ita
В области я > а (в области Щ) толью
я нодолеитвдбиоы № jp, это прошедшая волна.
Таким образом, выполняется следующее асимптотическое условие, кото-
рое нужно наложиль на отыскиваемое решение (фактически что драничное
условие):
1) ^(гг) при я —> -Нос описывает распространяющуюся
в положительном направлении оси я волну.
Таким образом, в области III волновая функция имеет вид
Vtd(x)=
здесь /1 — некоторая постоянная, а в показателе экспоненты мы взяли раз-
ность £ — а, так как удобно отсчитывать координату z в области III не от
точки а = 0, а от точки i = я.
Рассмотрим теперь область ООО (область II), в ней уравнение
[ Предингера имеет вид
уу - 73 = 0;
di
общее решение этою дифференциального уравнения можно записать в виде
=Ве'тС’-а)+Се
I ЙО
Глава 4
гое В и С - некоторые постоянные. Здесь координату я мы тоже отсчиты-
ваем от точки .т = а.
Заметим, что функции ^ц(зг} и ъ'чц (т) описывают куски единой вол-
новой функции ^(л), представляющей искомое решение (рассматриваемое
в областях, граничащих в точке з - а). Поэтому потребуем, чтобы при .т =
= <2 волновая функция и ее первая производная были непре-
рывны, т.е. потребуем выполнения следующих так называемых «условий
сшивания»:
2) ^н(й) = W,
3) («) = (а).
Лг Ле
Подставив в эти условия имеющиеся у нас выражения для функций
011 (ж) и Vjin (ж), получим два соотношения:
В I С - Л,
7(В - С) = тЦ
которые рассмотрим как систему двух линейных алгебраических уравнений
для определения двух неизвестных В и С считая, что величина Л нам
задана и известна.
Разрешим эту систему уравнений. Умножим первое уравнение на 7
и сложны со вторым уравнением, а также вычтем из первого уравнения,
умноженного на 7, второе уравнение:
27В = (7 + ^)А. В=1^Д,
Л
27С = (7-^)А. С=1^Д;
таким образом, константы В и С мы выразили через константу .4.
Рассмотрим, наконец, область I (s < 0). слева от барьера. В этой обла-
сти волновая функция имеет вид
^l(i) = Ге’*® - Ge”’*®,
где F и G — некоторые постоянные и где координату х теперь мы от считы-
ваем от точки я = 0, Соответственно, волновую функцию */’п (я) предста-
вим в виде
т/тг (®) = Ве"70е'г’ + Се'^е_7*
43. Задача об одномерном потенциальном барьере
IN]
Функции ^1(я) и ^л(х) описывают куски волновой функции
искомого решения (рассматриваемые в областях которые
граничат друг с другом в точке z = ()). Поэтому потребуем, чтобы при z = О
волновая функция (z) и её первая производная —— (z) были непрерывны,
az
т. с. потребуем выполнения двух следующих условий сшивания;
4) ^|(0} = ^п(0).
J.r
Подставив в эти условия имеющиеся у нас выражения для функций
^7 (я) и ^7/ (ж), получим два соотношения:
г + С = ве-^а + Сегул?
it (Г - G) = 7(Ве“7Р - Се^),
которые рассмотрим как систему двух линейных алгебраических уравне-
ний для определения пето лестных F н (? (считаем, что величины S и (?
известны}.
Для вычисления так называемого «коэффициента прозрачности» рас-
сматриваемого барьера для электрона, налетающего на барьер с энерги-
ей нужно знать постоянную F, те. коэффициент при падающей волне
в области I (отражённая от потсегциалыюгЕ} барьера полна нас нс интересу-
ет)
Найдем эту величину Г. Умножим первое уравнение системы на iJr
и сложим его со вторым уравнением. Тогда получим. что
F= (?* + ?) яе-'“ 4- (ji - 7)Ce7a =
^ + ifc)a 4е-^_
2т
<7 - »fc)2
27
Ле1" =
= A {(^s“fc2) (c“?n e?fl) +2tA7(e-7“ + e'r“)} =
J 7
= у {-i"2 - fc2) sh(7ft) +2iH chfre)}
Здесь мы воспользовались найденными нами выше формулами для
констант В и выражающими их через константу Ль а также вычисли-
ли реальную н лнщ/ую части получившеюся комплексного числа. Таким
182
Глава 4
образом^ окончательно имеем формулу
F = о?!,. {“(?2 ~ *3) sh(7®) + 2*И сЬ(тга)} .
Вычислим теперь коэффициент прозрачности нашего прямоугольного
потенциального барьера. Назовём «коэффициентом прозрачности» следу-
ющую величину:
_ . . коддрят .модуля йжллитуды л/ктейшеи йо/йы
Ядз^/> лрозр. =-------------------------------------------.
квдррап? .нодуля ff.im.Hi/nydw ллддоощги до.тлы
Амплитуда падающей волны panEia Е, а амплнхуда прошедшей рав-
на А. Поэтому для коэффициента прозрачности барьера имеем формулу
D = ИГ____________________1£г_________________
|F|3 (v2 - fc2)2 sh2 (7 a) + 4т2 к2 di2 (7 я)'
в которой
Л = 1 v^tnF, 7 = i -/2^-1 (Ki - if).
Приведённая формула для коэффициента прозрачности jD нашего по-
тенциального барьера выведена нами в результате строгого решения урав-
нения Шредингера; мы рассмотрела однако, только случай
Получим теперь из формулы для коэффициента прозрачности при-
бнижённуЮ формулу в случае, когда проницаемость барьера мала, и эффект
туннелирования частицы сквозь барьер слабый. При Л —* 0 коэффициент D
обращается в нуль^ так как при ft — 0 (в классической механике) туннелп-
ропанне электро па сквозь барьер при Е < V« невозможно,
В рассматриваемом пределе величина 70 очень большая, а потому
приближённо можно считать h что
shfrrt)^ chbai
а слсдовагтсльно,
16 73 fa2 е~2лг,< _ 16 72 fe2 _27с1
(72 - fc2)2 + 4 т3 fc2 (72 + fc2)2
4.4. Задача о двойной одномерной потенциальной яме
IN3
Иц таким образом, в пределе й —* 0 получаем формулу
па f 2ft /5—777----ттА
E = -----—------exp I - — H/2m (Ц - E) | .
ч> \ n /
Эта формула совпадаете навестил Гт квазнкласси ческой формулой кван-
товой механики.
В самом деле, ^/2ж (Vo - Е) = [р(х)|, так как внутри барьера р(л) =
= г |р(я)|, Е = Vq - |р(я)|г/2ш. Поэтому полученную приближённую при
Й —- 0 формулу можно записать в виде
Е — ехр
4А Задача о двойной одномерной прямоугольной
потенциальном яме
Рассмотрим теперь одномерную задачу с помощью которой можно
проиллюстрЕфовагь квантовую прнро/ду гомополярпой химической связи
(явления связывания одинаковых атомов в молекулу) н а также объяснить
«зонный» характер энергетического спектра электрона в твёрдом теле.
Возьмём двойную ИМ у С бсСКОНСЧНЫМИ ПрЯМОуГОЛЬНЫМИ CTVHKJMM,
разделённую прямоугольным потенциальным барьером.
Начало системы координат поместим в центре двойной ямы. Тогда
функция потенциальной энергии V{#) будет симметричной относительно
начала координат, тс. будет чётной функцией:
V(x)-V(-x),
и будет даваться следующей формулой:
при
при - Ь £ я $ -а,
при - а j; а.
При ft < я < 6,
при sf 6.
1Й4
J'л л вл 4
Нам необходимо найти решения уравнения Шредингера
2m das3
- V- Еф
либо нечетная:
Из того, что функция V(t) симмет-
ричны, не следуем что решения VJ (-т) при-
веденного уравнения Шредингера тоже бу-
дут симметричными, т с. что функция
четная. Нс можно утверждать (ма-
тематичсеки, однако, это надо доказывать,
но на доказательстве мы сейчас осгалавли-
ваться нс будем ), что (Дгякция й (я) ямяйя-
СЧ Либр
рпчилй, т- с. либо она чётная:
V’(as) =
= -$ (-й).
Очевидно, каждое из этих двух решений можно рассмотреть только
в области 0 д: £ 6 (только положительных т). При этом в области 1?
показанной на рисунке (при 0 т л), имеем уравнение:
rj &
— - 73 = 0, 7 = 10тп(Ц - £Г),
а в О&тастн II на рисунке (при а i Ь) имеем уравнение:
+ к? ф = 0, к = ^v'2m Е.
dx4 п
Рассмотрим по-отдельноетк чётные и нечётные решения.
Случаи I {чётные решения)
В области I приведённое дифференциальное уравнение имеет два неза-
висимых решения: ch(7i) и sh^yr).
Гак как мы рассматриваем чётное решение, то в области I положим
(я) = С ch (73:).
4.4. Задач а о двойной одномерной потенциальной яме l N5
В области IT в качестве решения дифференциального уравнения
ВОЗЬМЕМ функцию
^11 (х) = Cifiin [fc(x - ir)J-
которая обращается в нуль при я = fr. Координату х мы отсчитываем от
точки Е = 6.
Здесь Ст и GTi — произвольные постоянные, значения которых мы долж-
ны найти ИЗ ^условии сшивания» приведённых решений I и II ив границе
областей при X = а:
V'i («) = <4i (а),
Таким образом, для Определения констант С и (71 имеем два условия:
GT ch(7&) = Ci 81п[Л{сь - Ь)] = -С| sin[fc(b -а)],
7 С sbfra) = feCicoB[ft{a &)] =fcCicos[fc (Ь а)].
а следовательно, имеем систему двух линейных однородных алгебраиче-
ских уравнений:
J сИ(тй) С + sin(jfcd) С\ = 0.
17 sh(7a) С - Л соз(М) С] = 0,
в которой для краткости мы положили, что b - л = d, где• d — ширина
каждой отдельной потенциальной ЯМЫ.
Приведённия система линейных однородных уравнений имеет нетри-
виальное решение только при выполнении условия её разрешимости:
chfrti) sin(kd)
7 sh(7a) -к оси(Ы)
т. с. условия
fc ch(7ft) cos(fcd) + 7 shfra) &in(kd) = 0:
являющегося уравнением для определения значений
энергий дискретных уровней чётных решений.
Этому трансцендентному уравнению удовлетворяют энергии £? стаци-
онарных СОСТОЯНИИ, описываемых четядьщц ВОЛНОВЫМИ фуЕГК[[ИЯМИ
1Й6
Глава 4
Случай 2 решения)
Теперь в областях I и [I возьмем решения
ф (sr) = (7 ah (7а?),
^n(sr) = Ci sin [к(ж - t?)],
где C. Cl — ПрОИЗВП.ТЬЕЕЫС ПОСТОЯ1ШЫС. Зетлчспия этих постоянных найдём
из «условий сшивания» приведённых решении при х = п.
Получим, таким образом, уравнения
С sh (70) = Ci sin [fc(a - fr)] = -Ci sin[fc(b -*)]P
7C ch (7 л) = ft Ci cos [t(n — ft)] = fc Ci cos [fc(6 - a)]
и придём к системе двух линейных однородных алгебраических уравнений;
ah {7а) С + sin (ftti) Ci = 0f
7 cli (7^) C — ft cos(ftd) Ci — 0.
Условие сущее лзшшкия нетривиальною решения приведённой линей-
ной однородной системы уравнений имеет вид
sh(7fl) sin(fcd)
7 di(7ft) -fc cos(fcd)
т. e. имеем условие
ft sh(7fl) cos(fcd) + 7 chfra) sin (fed) = 0:
являющееся т/юигиетгЭелтлылг уравнением для определения энергий дис-
кретных уровней нечётных решений, описываемых нечётными волновыми
ФУНКЦИЯМИ
Прпб. шжённое решение трансцендентных уравнений
Представим полученные трансцендентные уравнения для определения
энергий в следующем виде:
cth (7^) 4- tg (ftd) = 0 (чётные решения},
— th (70J -l- tg (fttij = 0 (нечётные решения);
4.4. Задача о двойной одномерной потенциальной яме
IH7
здесь
л = I 7=1 0m (¥b - Е);
ft ft
это уравнения для определения возможных значений энергии f.
Найдём приближённые решения приведённых трансцендентных урав-
нении при большой высоте потенциального барьера, разделяющего по-
тенциальные ямы, т. с. при I-о —> 4-ос.
В пределе Vq = +оо имеем 7 = +эсц а потому оба рассматриваемых
уравнения принимают одинаковый вид;
tg(kd) = I)
ирье 7 = +оо ct.li (т«) = 1. 1h(7«J = 1, а потому первые слагаемые
в рассматриваемых трансцендентных уравнениях, сопровождаемые множи-
телем fc/7, обращаются в нуль и остаются только вторые слагаемые.
Следовательно, имеем условие
^0)йТ = П1Г, fcJW = ^п,
fl
где n — О, 1. 2, 3.... — целые числа, так как по своему исходному опреде-
лению величина fc = v'Sm.i? больше или равна нулю. При п = (), т. с.
при k — О, имеем ягЕМк?ййстйенно р«^н<?₽ нуля? рйненме+ которое не KMoej
физического смысла. Его надо отбросить.
Таким образом, получаем дискретные энергии
р _ Но) _ ka й _ ft2 h2 „2
n ’ 2m " 2md*
при ц = 1,2....
Имеем в точности такие же значения энергий, как и для прямоугольной
потенциальной ямы, с бесконечными стенками ширины dt хотя мы рассмат-
риваем сейчас двойную яму.
В отличие от задачи для одной ямы найденные нами урОВЕШ энергии
£? = для задачи с двумя невзаимодействующими ямами (при 1о —
= +оо) при n = 1. 2. ... dtfVKptJrttMt) вырождены, т.с. каждому уровню
энергии соответствуют два стационарных состояния (с чётной и нечётной
ВОЛНОВЫМИ фуЕГКЦИЯМИ).
Предположим теперь, что Vo 0 +ос. на Vq —* +м, т. е. что V'n нс бес-
конечное, но очень большое, и найдём решения рассматриваемых транс-
цендентных уравнений, которые при V?) = +ос переходят в какое-нибудь
найденное решение Л;/1 при некотором фиксированном j?. > L.
INK
Глава 4
Оба наших трансцендентных уравнения запишем теперь как одно
уравнение:
fc ± е-*»* _ _ 4 1 ±е~г^а
7 е7лт е-14 — 7 1 =f
используя знаки ± и =R верхний Знак относится к уравнению для четных
решений, нижний для нечётных; здесь
* = 1 Vim Ё, ? = J V2m(V<i - Ё),
и мы воспользовались точными формулами
th г -
£ - е-*
+ г-Х
cthac =
eJ + е J
ех — е-х
При —* +оа можно считать^ что 7 = 7о = Ц. так как Е,
по предположению, стремится к рассматриваемому фиксированному зна-
чению _Е« t и поэтому Vo - £ —Vo - Е^ —> Vo при Vq —> +оо. При
Vb —► +м волновое число А —> = (L/AJ^Affi £?ц^.
Поэтому правую часть приведённого общего трансцендентного урав-
нения можно приближённо заменить выражением
fcr, । ±е~^д
70 I qz С 2 То я
/ F(0)
- -1/Ат- 0 ±2е
v Vij
которое при V^ —* +оо (7о —* +м) обращается в нуль.
Если это выражение положить равным нулю, то наше трансцендентное
уравнепне превратится в уравнение
tg(fed) = О,
которое мы уже рассмотрели выше и решения которого мы обозначили
p(i>)
как .
Итак, при Vo 4-oos Vo —> 4-оо имеем уравнение
(I ± 2е-й7йа).
4.4. Задача о двойной одномерной потенциальной яме
INY
Разрешим ло уравнение при Vo —* +оо> полагая, что Е —> Е,?'. Обо-
значим как fc„ + Afctr значение волнового числа Ап> соответствующего
решению En = -I- А Ел. При ттдм А^т Л /<Г| стремятся к нулю при
Ун —> 4-ж. Так как А: = vz2mE, то, очевидно,
in4 + ДЛ^ = у/2т[Ё^ + ДЕП) -
= | \/2тЕ^ | 1 + “ 1 | 1 +
ft \ / п In EHUJ
\ / X ап
а следовательно,
At _ __ / ЛГ
П ™ V Е^ п-
При tii —> +оо и малом Д fcn вместо левой части рассматриваемого
общего тринецендслтнвго уравнения можно написать выражение
t.g[(e’ + Д М4 - tg(^ <*)----------т—; Д <*;
d))2
разлагаем в ряд Тэйлора по малости и оставляем нулевой и первый
члены.
Учитывая, что cf = тг-ft, получаем rf) = 0. cos(fc^ rfj = -1 ч
cusa{^|l>1 d) = 1. Таким образом, д.чя левой части рассматриваемою общего
трансцендентного уравнения при Vo —* +ос получим выражение
tg[(fctQ> + Д s ^д кп = .
Таким образом, при V3 —► +ос наше общее трансцендентное уравне-
ние примет вид
1 /pW
JL I 2т д р - _<|' /jfl /1 +9е
' V Ч. 1 ь
так мы приходим к окончательному результату:
7Рт
дхл = -±£«- (i±2e 2'№tt)1
'/ой
190
Глава 4
дня лохзравок к энергиям справедливому при VS —* +оо. Верхний знак
следует брать для чётных, нижний — для нечёгных решений.
Итак, при 1-q = +ос, т. е. в случае бесконечно высокого потенциально-
го барьера между ямами, ямы «не взаимодействуют», и их энергетические
уровни одинаковые (ведь ямы одинаковые} л даются формулой для От-
дельной ямы
е - яФ) - Il п1
” " ~2^
где
см. левый рисунок.
з,10'
\ нечтя. ff, |
V----------ЯД,
чти. Д |
70=4-сс 7ю*+оо
Возьмём теперь какой-нибудь уровень Е^\ и пусть VJ] +сх\ по
очень большое. Тоща при адиабатическом включении Vo уровень сдви-
нется вниз и расщепится на два уровня, как это показано на правом рисун-
ке. При этом расщепление уровнен будет существенно меньшим эффектом,
чем ик сдвиг, так как С-^ а 1 при 7У —* сю.
Сдвиг энергетических уровней вниз означает «упрочнение» системы.
Энергия системы двух ям, «взаимодействующих» друг с другом через
потенциальный барьер, меньше, чем энергия системы двух изолирован-
ных ям.
Такое ио ведение уровней двойной ямы, проиллюстрированное еще раз
на приведённом выше рисунке, объясняет квантовую природу ru-
лдеческий сяязы в ^ломанных мдгакдодх
Химическая связь в так называемых двухатомных
молекулах типа NaCl, состоящих из разных атомов, «ионная». Она хоро-
шо объясняется классической физикой. В молекуле NaCl, например, при её
образовании атомный электрон смещается ст атома натрия Na к атому хло-
ра ( 1, и оба атома становятся противоположно заряженными нонами Na+
и С1“, которые притягиваются друг к другу кулоновскими силами.
4.4. Задача о двойной одномерной потенциальной яме
IV]
Химическую связь и двухатомных молекулах типа Щ,
состоящих из одинаковых атомов, таким образом, объяснить нельзя. Такая
химическая связь называется ^ковалентной», или «гпмополярней», и ее по-
нять удалось только в квантовой мехи нике. Ковале нгная химическая Связь
является км еловым эффектом
Рассматриваемую сейчас одномерную симметричную двойную яму
можно считать очень грубой моделью гомоня лирной дпухатомпой моле-
кулы, составленной из двух одинаковых атомов. Ковалентная химическая
связь образуется, однако, яе яйшш, а йиуия электро етзми, но одному иа
каждую яму.
Если электроны в своих ямах находятся в одинаковом энергетическом
состоянии Еп°\ то суммарная энергия системы двух электронов в раз-
деленных потенциальных ямах будет равна ЗА1!0’ (при Vn = +ос). Когда
эти ямы объединяются в двойную яму (при Ц) / +оо), энергия системы
двух электронов я двойной яме pain га 2 Еп (чётн.Х тик как при учете спина
каждый уровень £?п (чётн.) и Еп (нечета.) двукратно вырожден, и поэто-
му имеем не одно, а два состояния (при crz = 1/2 и crz = —1/2}. Причем
2£?п (четн.) < и мы получаем следующую формулу для энергии
химической связи для рассматриваемой одномереюй модели двухатомной
гомополяр и ой молекулы:
Q = 2 Е^} - 2 Еп (что,) = 1^4- (1+ 2е а) - ^=г;
при 7о —? +со второе слагаемое в скобках можно отбросить.
Рассмотрим теперь эффект Энергетических уровней от-
дельных ям при образовании двойной ямы. Расщепление энергетического
уровня: дается формулой
192
Глава 4
входящий в эту формулу экспоненциальный множитель равен
т. с. равен коэффициенту туннельной прозрачности потенциального барьера
между ямами.
Полученный эффект расщепления энергетических уровней двух при-
ведённых в контакт потенциальных ям на пары близких уровней иллюстри-
рует в зачаточном виде квантовый эффект «зонной структуры» одноэлек-
трпнного энергетического Спектра отдельного электрона в твёрдом теле.
Для двойной ямы у нас получились зоны, состоящие из двух уровней
каждая. Если бы мы рассмотрели Лг ям, то получили бы зоны из Лг уровней.
Дополнение 1 к гл. 4
Дельта-функция Дирака
Чтобы разъяснить, что такое функция Дирака, рассмотрим шгтсграл
Фурье для произвольной функции Дзг), заданной на бесконечной прямой
—оо < т < 4-оо, которая называется «функцией-оригиналом». Её можно
разложить в интеграл Фурье по функциям e*fcirTT.e. представить в виде
I <ю
Дх) = у е'^' dfc,
—QQ
где функция Fft) называется «фурье-образом». Функция фурьс-сбраза од-
нозначно определяется функцией f(x), так как
F(M =
e“'ir di,
те. функцию фурье-образа можно определить^ зная функцию-оригинал.
11одставим теперь вторую формулу в первую и получим, что
е’*® dk =
ДО1ЮЛНЕНИК I
193
1 [
—м
f (д?) d./.
Здесь мы переставили порядок интегрирований, чего с гроз о мачо маги-
чески делать нельзя. Внутренний интеграл
-L / е*^г <)</* =
2тг J
-QQ
формально расходящийся^ как раз и является «5-функцнсй Дирака» и обо-
значается как — а/), так что
+иэ
d(,r) = ± у e,te* rf*.
—ос
В строгом математическом смысле 5-функция не является «функцией».
Опа обладает свойством, что
при д/ =
при д/ 0
Т. е. функция — дг) отлична от нуля только и одной точке j/ = я прямой
—ос < i < +ост в которой опа равна — осп в остальных точках прямой
А-функция равна нулю; тем нс менее
4-ео
jf — я;} da/ = 1;
-ос
считаем, что этот интеграл существует и paeeEi единвце. Также имеем, что
+»
У /(т') £(z' - я) dx' = /(т).
где /(ас) — произвольная функция. 5-Функция является чётной функцией,
т. с.
5(—л) =
194
J'Л л ВЛ 4
кроме того,
я) =
1«1
где t — произвольное, не равное нулю действительное число
Дополнение 2 к гл. 4
Операторная квантовая механика
Основная идея операторной квантовой механики состоит в том, что
в ней физические величины описываются не действительными числами,
как и классической физике, а Более точно, оиней^ыжи э/>
лшмоёыаш гт л/7о*?л?/?д/гст#е сосхимлай. шш
вдлшмш рассматриваемой квантовой системы.
Например, для атома водорода волновыми функциями состояний си-
стемы являются ком гтлеке позначные функции /Л ^)» заданные в беско-
нечном трек мерном пространстве —ос- < л, ?л г < -hoc.
В отличие от чисел, для которых не важен ИХ порядок в произведениях,
для операторов порядок их следования в произведениях важен, так как опе-
раторы, вообще говоря, кши*ути/?уюгс друг с другом (а следовательно,
и произведениях их нельзя, вообще говоря, переставлять).
Разумеется, физические приборы, с помощью которых производятся
измерения значений физических величин любой квантовой системы, нахо-
дящейся в определенном состоянии, при измерении этих значении дают
показания и виде (вовсе не операторов).
В операторной квантовой механике считается, что числовые значения
чёской величин ы. кшлпрые лолдтыитет прибор, с лшмощьш которая?
эти это л)мо из значений олерато/м
rid л пой физический №1»чнны.
Функциональное пространство волновых функций квантовой системы%
например, атома водорода, обладает математическими свойствами п-мерно-
го векторного пространства, изучаемого в линейной алгебре. В частности,
для него существует понятие линейной зависимости (независимости) вол-
новых функций, базисных снесем волновых функций и т. д.
В отличие от п-мсриогп векторного пространства, элементы функци-
онального пространства квантовой системы называются не «векторами»,
а «функциями», точнее, «волновыми функциями». Они являются функци-
ями, принимающими, вообще говоря, комплексные значения — значения,
задаваемые комплекс ними числами.
Дополнение 2
195
Как правила (но не всегда), функциональное пространство волновых
функции кеиеггоеой системы, в отличие от алгебраического л-мерного век-
торного пространства, является бесконечномерным, т.е. его размерность
бесконечная (причём множество базисных волновых функций не обяза-
тельно даже счётное; может случиться ч что частично или полностью оно
континуальное)
Как в алгебраическим п-мерном векторном Пространстве, в функцио-
нальном пространстве волновых функций существует понятие
В функциональном пространстве волновых функций, например, ато-
ма водорода скалярным произведением двух комплекс Епниачиых но лиевых
функций ^(л\ у, 2) и z) называется комплексное число
(у?, V’) = III Ф*(х, у. г)$(х, у. z)dxdydz,
где звездочка + обозначает комплексное сопряжение. Это скалярное про-
изведение кратко обозначается как (у?т у'р). Определенное таким образом
скалярное произведение обладает следующими свойствами:
(A V0* = $?)>
(<Р, AV0 = V'Ji
(А у?. = А* ДО,
(<р, ДО + ДО) = (v>i ДО) - (^1 ДО),
($Pi + ДО = (pi ДО + fas, ДО;
здесь звёздочка + обозначает с#лг/лячтмсечие и А произвольное
комплексное число. Очевидно, что если (^j ьг?} = б, тй волновая функция
= 0 (тождественно равна нулю).
Определение. Э/шииоео <яле/?лт<?рйч Л+ для операто-
ра ..4, действующего и функциональном пространстве квантовой системы,
называется оператор, лбладагощин тем свойством, что г).тя
(Л AV) = V')-
Определепие. Оператор А называется э/ьми/лмым, если для него
А+ = А, т.е. если действие оператора А можно перебросить с правого
компонента скалярного произведения на лсвг?1н: и наоборот.
196
Глава 4
Определение. Оператор А, имеющий обратный оператор А \ назы-
вается если для него А+ = А-1.
мл сябсетееяные значения w собственные функции
э/ьиы^оеа оне/юторя
Собственной ^ртыцией оператора А называется аолновля фуюа/шг г/.1,
не разиня тоЖ£)ес/л€?₽нмо му.то. при бсисйтюш Нй вторую алерл/норй-м А
лолучде/яся зяш еолновия функция ^ноженндя ш нек^лб/юе, еяобгцегд-
#оря. клчплекстое числя о
Аф = orV (ф / 0).
Число а называется «собственным значением оператора А, соопиет-
ствующим данной собствен! сон функции ф». Функция !•'’ называется «соб-
ственной функцией оператора Д соответствующей собственному значе-
нию ос».
А/итслдочическдо лройяекя ди еобстлдамые зидчечия и собст#синьге
функции ^аииоао sptwu/wiw^o оперят^ра МАтиочлетлся « лотысаддоии scex
его йЭЙе/лйеяйггх знич^яш! л cuumeemrmtfywitfux иЛ1 лФсть^ныл фун^ин.
Может случиться, что одному собственному значению эрмитова опера-
тора соответствует нс одна, а несколько линейно независимых собственных
функций, например две функции. Тогда говорят, что имеем случяы яырамс-
собственного значения. В вырожденном случае произвольная пин си-
ная комбинация собственных функций, соответствующих вырожденному
собственному значению> будет тоже собственной функцией, отвечающей
этому значению.
Действительно, если у нас имеются две линейно независимые соб-
ственные функция и У’э, соответствующие одному и тому же собствен-
ному числу ft, т. е. такие функции, для которых
AV'i=<t^i (ti’i/O). .4^2 = ttV'i (VJi/0)T
то в силу линейности оператора Л
А (<71 VJj + Cj = a (Ci ij?i I Сг V'a).
где Ci и Ci — произвольные комнлексЕгые числи, одновременно не равные
нулю. Так что функция С\ V’i + <?2 ^’2 тоже является собственной функцией
оператора .4, соотвстсте^'епщсй тому же самому собствснисму плачеeiню о.
Дополнение 2
197
Собственные фрнюдо, соответетвуюидое еыроэкбеннаху еобслиен-
Л0Л4У 3Htf4iTfWJOr Ej/j/wywm КОН£ЧИО,Ч£рЛ0е {в случае вырождения конечной
кратности) w.tw бесяонечнанерное (в случае вырождения бесконечней крат-
ности) е/^як^ношльноё мросшряиство.
Число линейно независимых собственных функций, соответствующих
вырожденному собственному значению^ называется его ^крдтя<31Стьвдл>,
точнее* ftKJUJffltfOCmhJG вЬ?рОжЭет;ыЯ». Если кратность вырождения равна
единице, тс говорят, что собственное значение
Ардтнмть оырождйния — это ро^мерноть ^ункдооняльного нро-
гтрдлст^о собственных соответствующих данному в^р^адбеи-
ЛО.Пу СОбствВДИВДу ЗЯЛЧ£№М.
Приведем без доказательства пять теорем, которые следует иметь в ви-
ду при решении проблем на отыскание собственных значений и собствен-
ных функций эрмитовых операторов.
Теорема 1, Собственные значения а эрмитова оператора А действи-
тельны^ то есть
А^ = д V’ 0)
—> о — действительное.
Теорема 2. Собственные функции т/1 и эрмитовою оператора А* со-
ответствующие различным собственным значениям а и /Э (а J), ортого-
нальны друг другу, то есть
Atf? = a^ (Vh 0), А^р = /3^ (у 0), ft / J?
=г (^iV) = 0.
Теорема 3. Для любою вырожденною собственного значения эрми-
това оператора А кратности н можно укачать п взаимно ортогональных ею
собственных функций ..., соответствующих этому собственному
значению crt таких, что любую собственную функцию этого оператора,
соответствующую собственному числу а. можно представить в виде ли-
нейной комбинации
= С| + ... + 1Дп
этих взаимно ортогональных собственных функций, здесь C*i, .... Сп —
комплексные числа.
jwu ^нкци0шыьного рдссмотрм^дечого вырожденного мб-
efflflewwojo значения гг.
19Н
Глава 4
Теорема 4. Для любого эрмитова оператора собственные функции, со-
ответствующие всем СТО левирождеилым СП&СТБСЕ1НЫМ числи М, И базисные
собственные функции* соответствующие всем его вырожденным собствен-
ным числам, в совокупности образуют базисную ортогональную систему
функций всего функционального пространства квантовой системы, в кото-
ром действует эрмитов оператор
Теорема 5. Если дни оператора А и й либо оба эрмитовы, либо оба
унитарны, либо один эрмитов, а другой унитарен, коммутируют друг с дру-
гом, т. е. если их коммутатор
[А,В] = АВ- БА
равен нулю:
[А,В] =0,
то из того, что функция ^(х) является собственной функцией оператора А,
следует* что она является также н собственной функцией оператора В, г. с.
из того, что А^ = следует, что = /3^- где сг и Д — числа, и наоборот.
Фпзичесят/п и
функций физической вЙДЫЧИИЫ
Пусть оператором физической величины А является эрмитов опера-
тор А и пусть — собственные значения, и V’n — собственные функции
этого оператора А, т.е. — нс равные тождественно нулю функции> для
которых
А = ;
предположим, что функции j/ч нормированы на единицу,т.е.
(V'tl- У’л) = 1 при всех п.
Рассмотрим Ул/эдческлл л/я/гмр, предназначенный для измерения зна-
чения величины А, и произведём с его помощью измерение значения этой
физической величины системы, # сюстдлнии v.
Считаем, что волновая функция этого состояния тоже Htf/ww/wjuc
ли ейниыцу, т.е. (^п ^г) = 1,
Физический c.uwe-v собственных знидений ап А физической
ввдичыяы А состоит в елгфтои/елл Это члйрр значений, которые локазы-
яает лрибор яря злячвдяя этой ле.тачиялг /Уричёлг лрл
Дополнение 2
199
Прибор
для измерения
физической
величины А
Результат
измерения:
какое-нибудь nrh
С вср<иг[ноСтЫО
^KWI1
прибор покажет значение ап с вероятностью
Л, = KV’n, VOI2-
Вероятность любого случайного события заключена в пределах 0 <
£ 1, и сумма всех вероятностей равна единице, т е. />. = 1.
Ц.
В квантовой механике операторами проекций импульса частицы явля-
ются операторы
— A 2L _ ft Л _ ft fl
f у 1 tty’ s г fe’
а операторами £, £ г её декартовых координат — операторы умножения
функции у. з) на соответствующую координату я, у, г. Таким обра-
зом, коммутаторы пар операторов т и j?r, Jn/Jyj г и pz равны
г д дх - ~ 1 А г дх г ах = ft
г ' "1 ft с? -- - fc д ft hd_ h д _ _ft
= i дУ у -у- Оу ^-+у i ду - i '
2<Hb
Глава 4
В классической механике вектор
момента импульса частицы определя-
ется как векторное произведение
L |г р] -
i
х
Pi
j k
у £
Py
соответственно, в квантовой механике
1 j k
L = [г р] = л $ z
Р* Рц Ря
следователь! ic>, операторы проекций момента
импульса частит ili равны
Г ? _2и,.А_„А
£т ” » V ду)' L*~ » \ ду)' L'~ i\ &У V <>z
Легко убедиться, что операторы проекций момента импульса частицы
удовлетворяют следующим коммутационным соотношениям:
IjLj-. |jLyi, — l/l LJ4 [i-. ijj] — i-fripi
Любые операторы, удовлетворяющис таким коммутациыптым с<юттю-
шенмихц называются операторами узлового момента. (В англоязычной ли-
тературе количество движения — называют лшдешыш а момент
количества движения /uow/miaw).
Пример 1. Элементарная частица со спином 1/2
Б первом примере рассмотрим частицу со спином 1/2 и сё квантовые
спиновые состояния (электрон имеет спин 1/2). Пространство спиновых
состояний такой частицы двумерно, так что спиновые волновые функции
этой частицы представляют собой двумерные векторы (с двумя компонен-
тами), а физические величины — матрицы 2 х 2, с двумя строками и двумя
столбцами.
Если в качестве базисных состояний в этом пространстве в:!ять кван-
товые собственные состояния физической величины z-проекции спина ча-
стицы Sx на ось z некоторой фиксированной декартовой системы коор-
динат т, у. г в нашем обычном трёхмерном пространстве, то физические
величины проекций спина .S^, f?v, S’, па оси л, у, z будут описываться 2x2
матрицами (матрицами Паули):
г _ Ъ( о -г 4
» 2 \ ? О Г
?1 ( 0 14
1 " 2 I I 0 /1
J о \
2 к О -I}'
Дополнение 2
20]
эти матрицы эрмитовы, так как их матричные элементы удовлетворяют
условию flij = ajj, где i. j = ], 2 и звёздочка + обозначает комплексное
сопряжение.
Эрмитовы матрицы имеют действительные собственные значения.
Нормированные на единицу базисные квантовые состояния с проекциями
с г типа на ось я, ранными ±1/2, имеют вид
ЭТИ Велоры нормированы на единицу и ОрТСЮнДиьнЫ друг друзу:
(^1/а, ^i/a) = С = 1- (V'1/з. ^-i/г) = '>•
Легко убедиться, что приведённые спиновые матрицы ST. Sz удо-
влетворяют перестановочным соотношениям операторов угловых момен-
тов:
[S^, l = ifiiSjfi-j. — jftSy.
где символ [A. 7? | обозначает коммутатор [AL В = АВ — В А двух матриц.
Кроме того, легко убедиться, что матрица квадрата спина
S2 - 52 - S^ + £2 — - A2 Г*
.5 - А|: - 4 н j/
является фактически единичной матрицей, и для неё справедливы переста-
новочные соотношения
[5<5а-] -0. [S2AJ -0, [S2,5z] =0.
Рассмотрим теперь физическую величину S', являющуюся проекцией
спина на ось получаемую из оси 5 поворотом декартовой системы я, *
вокруг оси у па угол 0. При Этом
,v е л е - л ft / con fl зли 6 \
5... = 5z COS 0 + Sjt SID fl = 77 . л _ Д .
2 \ sin 0 - соэ fl у
Найдём собственные значения ftm и собственные векторы матри-
цы S'. Имеем ^.исдуюш.ую задачу нл собственные значения:
поэтому для неизвестных п и Ь имеем линейную однородную систему двух
уравнений
{сои 0 п + sin 9 Ь = 27пл.
sin 0 а cos fl b = 2шЬ.
202
Глава 4
а следовательно, систему
(cosfl - 2m) а + sin fl Ь = О,
sin fl л — (сои fl + 2m) fi = 0.
Это однородная линейная система двух уравнений для двух неизвест-
ных, и условием её разрешимости является обращение в нуль её детермн-
нантан так что значения m определяются из уравнения
сов fl — 2m sin fl
sin fl cob fl + 2m
= - cos* fl + 4m2 - sin2 fl = — 1 + 4m* = 0;
поэтому m = ±1/2. Так что матрица имеет два собственных значения
±А/2.
Из приведённой системы однородных линейных уравнений найдём со-
ответствующие этим найденным собственным значениям нормированные
па единицу собственные векторы:
j/ _ ( сои(0/2) \ , _ / sin (0/2) \ .
*’/2 ” sm(9/2) ) 1 ^-1/2 - -COfi(6f/2) ) '
видим» что они ортогональны друг другу.
Предположим теперь, что паша элементарная частица находится
в квантовом спиновом состоянии с проекцией Л/2 спина ми ось z исход-
ной декартовой системы ft/2.
Для частицы, находящемся в этом состоянии, будем измерять проек-
цию её спина па рассматриваемую ось я', составляющую угол fl с осью зг
Тогда согласно рецепту квантовой механики do акта измерения мы долж-
ны утверждать, что получим значение Л/2 проекции спина на эту ось я'
с вероятностью
И'1/2 = |(^1/2. 4'1/2) I’
и значение ft/2 с вероятностью
1/2 = iM'-i/a» ^1/а)Р-
Таким образом,
И'1/г = |(cos(0/2) йш(Й/2))
J ) 3 = ^(А/Я),
Дополнение 2
203
lV_1/2 = |(cos(0/2) sin(0/2)) ( j
= sin a (0/2);
причём, как н должно быть,
^i/a + И'_1/а = I
Имеем два возможных результата измерения., и сумма вероятностей
появления того и другого результата равна 1, так как это вероятность до-
стоверною события.
Согласно квантовой механике, если при измерении мы уже1 получили
результат ft/2, спиновое состояние частипы в акте измерения мгновенно
«скачком» превратилось в состояние
I
О
cos (0/2)
sin(0/2)
после того как при измерении мы получили результат -ft/2, спиновое со-
стояние нашей частицы «скачком» превратилось в состояние
0
1
sin(fl/2)
- cos(0/2)
Пример 2. Элементарная частица со спином 1
Во в юром примере рассмотрим квантовую частицу со спином 1
и сё квантовые состояния {фотон является такой частицей, так как име-
ет спин I). Пространство спиновых состояний такой частицы трёхмерно.
В случае слипа 1 матрицы физических величин проекций спина на оси взя-
той нами в нашем трехмерном пространстве декарговой системы координат
х. у. z имеют вид
/ О I 0 \ /0-з О X / 1 0 0 \
Sr = Ji | I 0 I j , ,$'v = Ji I i 0 -i j , S- = ft Q Q (I ,
\ 0 1 0 / \ 0 i 0/ \ 0 0 - J /
причём матрица квадрата спина равна
/ 1 0 0 X
52 = S'* -I- Sa + S'* = 2Гг 0 I 0 ,
V’ ° 1 /
имеем фактически единичную матрицу,
204
J'Л л ВЛ 4
Легко убедиться, что приведенные спиновые матрицы удовлетворяют
л срсста । юною । ы м с ooteioeiece сия м:
[&, S„] = ihSz, [Зж, Sz] = ihS,, [Sff1 SJ = ihSv,
[S2,S,:] = 0. [S2,f?J - 0, IS2,5,] = 0.
Возьмём в качестве базисных спиновых состоянии рассматриваемой
элементарной частицы со спином 1 собственные состояния коммутирую-
щих друг с другом матриц и S3, т е. векторы
каждый из них нормирован на единицу.
Рассмотрим теперь физическую величину 5' проекции спина на ось z',
составляющую с осью с угол fl, получаемую поворотом вокруг оси у взятой
исход пой декартовой системы координат я, у, z. Матрица этом всличиезы
равна
S', = Sx cos fl - Sx sin fl,
[IJ1EJ
Найдём собственные зтгачеттия и собственные векторы этой матрицы,
ДЛЯ ЕЮТррОЙ имеем COOTEEOIIICIIEIC
( cos fl —L sin fl
\/2
- sin fl 0
V'2
0 Дз sin fl
\ Л
0
sin fl
— COS fl
/
( cos fl + sin fl
! sin fl + -^= sin 0
\/2 /2
-^= sin fl — ccosfl
Таким образом» так как
Дополнение 2
205
где А — собственное число, то
ft f ft cos fl + sinfll = Act,
V 42 /
ft ( -2_ Lri fl н—— sin 0 j = A 6,
^45 42 '
*(-*=
VT2
sin fl - ccosfl i = Ac.
Получили систему трёх линейных однородных алгебраических урав-
нений для трех неизвестных 6, с. Положим теперь, что и них А = ftmp
и сократим вес три уравнения на ft. Тогда получим систему однородных
уравнений:
a(cos fl - m) + sin fl - О,
j -Az sin fl — m /> 4—— sin fl = 0.
1 45 45
sin fl - (cos fl + m) c — 0.
Приравняем нулю детерминант этой системы и получим, что
cos fl - m
-^zz sin fl
45
0
4= sin в 0
-m —Г gin в
v^2
—!— sin fl — cos fl - m
45
разлагая этот детерминант по первой строке, имеем
А — (cosfl—лг)
—m —
45
-Ц sin fl - cos fl - m
45
-Ц= sin fl
45
-L sin fl
45
0
-L sin fl
45
— cos fl - m
= (co* fl - + m) — (co* fl - mJ-sin* fl I sin2 fl [cos fl + m) =
— m(ccna2 fl - m2) + чш ’ fl + у sin2 fl —
= mfccis2 fl - tn2 + sin2 fl) = m(l - m2) = 0.
20ft
ГЛАВА 4
Следовательно,
m - 0.1. -1.
имеем, что д = —с, а из третьего её уравнения, что & = - \/2
В случае m = 0 ин второго уравнения нашей алгебраическом систем Lt
cos
sin
уравнение системы при этом удовлетворяется тождественно. Таким обра-
зом, с учётом нормировочной константы Лг для нормированного на единицу
собственного вектора матрицы 5' с собственным значением m = 0 имеем
0 гг
—с. I lepaoe
выражение
/ -1
= АГ I -v^ctg 0
\ I
причём, как легко видеть, Лг = ___=_____ = -7= sin 0. Соответственно,
V 2 + 2 etg2 М v 2
нормированный на единицу собственный лектор с собственным значени-
ем 0 имеет вид
~sin0
Л
COS0
ЙП10
ъ/2
В случае m = I. из первого уравнения рассматриваемой линейной од-
нородной системы имеем, что е = ~^= а из третьего сё урав-
н/2 । — COS0
siti 0
нения, что с = -----—- b. При этом кгорое уравнение этой системы
удовлетворяется тождественно. Действительно,
1 sina 0
2 1
6-& +
I янг 0
2 1 I- cos 0
6 = 0,
так как
i sin* & (1 + сое0) -14- cos3 в - 1 sin2 0(1- cosfl) =
= -14- cos3 0 4- sin2 0 =- 0.
Дополнение 2
207
Таким образомч с учетом нормировочной константы Лт для нормиро-
ванного ня единицу СП&СТБСЕ1НОГ0 вектора матрицы S' с собственным зна-
чением ft имеем выражение
причем, как легко видеть, Аг = —-—;—. Действительно,
v'2 bin fl
I gin3 fl 1 . ] sin2 fl
4 (1 - cos fl)2 2 sin2 Й 4(l + cosfl)2
sin4 0(1 ь cos2 fl) + 2 sin2 fl( I - cos2 Й)й 4- sin4 fl(l 4- cos2 fl)
4(1 -сой2)2
_ 2 sin4 fl + 2 sin4 fl cos2 fl + 2 sin4 fl _ 2 sin4 fl + 2 sin4 fl _
4sincfl 4sm4fl
члены в числителе с ±2 cos fl в первой и третьей круглых скобках взаимно
сокращаются.
Таким образом, нормированный па единицу собственный вектор мат-
рицы ,9! с собственным значением ft имеет вид
f sin~ fl
j 2(1-сок fl)
«Й = || -yz sin S
*1 72
si»2 0
\ 2(1 4- cos fl) J
В случае m = -1 из первого уравнения нашей линейной однородной
системы уравнений имеем, что а = — Ь, а из третьего ее урав-
нения, что с = —ft. Црн этом порос уравнение згой систем ы
./ 2 । — cos А
20Н
J'Л л ВЛ 4
удовлетворяется тождественно, так как
1
2
ain20
1 + cos 0
sin2 О
I - cos0
Ь = 0:
ибо
- sin2 0(1 - cos 0) I I - соя2 0 - sin2 0(1 + cos 0) - 0.
Таким образом, С учётом нормировочной константы Лг, для норми-
рованного на единицу собственного вектора матрицы *?( с собственным
значением —Ti имеем выражение
/_____I .sin 0
у/2 1 + COS 0
1
____I sin и
( 1/2 1 - cos 0 )
причём легко видеть, что А’ = —— sin 0. Действительно,
V2
sin* 0 , sin2 0 , sin4 0 _ j
4(1 4-ЫВ0)2 - 4(1—cos 0)2
как мы уже убедились выше.
Следовательно, нормированный на единицу собственный вектор мат-
рицы $' с собственным значением —А имеет вид
( sin2 0
2(1 + cos0)
-Ц= &Ш0
л
siit~ 0
\ 2(1 -COS0J /
Векторы г,'1ц, , ортогональны друг другу, так как
—^sin0 соы0 -^sinP
/2 yfl
/ sin2 0 \
2(1 - cos?)
-4= sin0
У2
sin2 0
\ 2(1 4-СО6 0) /
Дополнение 2
2UY
4=1 + 4^^+4= —
2/2 1 cm fl /2 2V2l+cob
sin fl Г ahi3 0 л. r-n-fi + 9ik2 0
/2 L 2(1-cm fl) 2(1 +cos fl)
—_ —-—/— -,in- 0( 1+coa fl)+2 cos 0(1— coa2 ffl+ahi2 0(1—cos
2t/2(1 - ™s20) 1
sin fl
2/2(1 - cos3 fl)
2 sin2 fl cos fl + 2 cos fl - 2 cos2 в cos 01 = 0.
1)= ( —7jsln0 cos0
sin2 fl \
2[ l l-cos fl)
— —^ sinfl
/2
ain2 fl
2(1 - cos fl) /
1 sin3 ff
2/g । + cm fl
Д- sin fl cos fl +
/2
1 sill* fj _
2/21- cos fl
sin fl
2/2(1 - cos2 fl)
x ! - sin2 fl + cos 0 sin2 fl - 2 cos fl + 2 cos3 fl + sin2 fl + sin2 0 cos fl) I = 0.
sin3 fl
2(1 — ссй0)
sin 6?
sin2 fl
2(1 4- eoa fl)
( sin2 g
2(1 - cosg)
——= sin g
v"2
sir.- g
\ 2(1 - cosg) /
sii/ _______sin2 fl________sin4 g
4( 1 - cos3 fl) 3 4(1 - cos3 3)
как мы уже убедились выше.
Предположим те и ерь, что наша частица находится в спиновом кванто-
вом состоянии с проекцией спина А на ось г исходной декартовой системы
ЕСППрДИЕТаТ Л, 2.
210
Глава 4
Будем измерять в этом состоянии проекцию спина у этой частицы на
рассмотренную выше ось составляющую упал fl с осью Тогда согласно
рецепту квантовой механики йо акта измерения этой величины мы должны
утверждать^ что при этом измерении мы получим значение 0 с вероятно-
стью
значение fe с вероятностью
и значение — fee вероятностью
W-, =tfi)|\
где i.\ — нормированный на единицу собственный вектор исходной спино-
вой матрицы 3± с собственным значением fea г. с.
/ 1 \
= I о .
\ о /
Таким образом,
2
= | win2 й,
___sinifl____ I . fiin0 sin2 fl A / у \ _ sin11 0
2(1 — cus (?) v^? ' 2(1 + cos / \ y ) 4(1— cos 0)^
/ 1 \ 2
f sin2 0 ___1 g’n sin2 0 \ / q 1 _ Kin*1 fl
43(1 + cosfl) v'2 2(1 + с<к(?}/ \ 0/ " 4(1 +crasfl)’’
причём
Wo + W1 + W_! = J sin2 0--------su^g . +-------3inJ<' . = 1.
- 4(1-009 fl)2 4(l+COS0)a
Согласно квантовой механике лоте акта измерения нашей физической
величины 5’з, если мы получили значение, равное нулю, то одновременно
с актом измерения искачком» мгетовсенсо происходит изменение состояния
Дополнение 2
21]
частииы:
f---— 8Ш0
^2
— sin С1
\ Л
если мьи получили значение S', раниос то одновременно произошло
мгновенно «скачком» изменение состояния частицы:
I \
°
О /
( sip2 fl \
2(1 - cos fl)
-Л sin fl
1/2
sin2 fl
\ 2(1 4- cos fl) /
наконец, если мы получили значение S*, равное -ft, то одновременно
«скачком» произошло измене пне состояния частицы:
< sin" fl X
(V 2(1 + cos fl)
1 \ 1
О 1 sin fl
° / я
f siir fl
\ 2(J - соя fl) /
В квантовом механике волновая функция изменяется плавно согласно
уравнению Шредингера и скачками при измерениях значений физических
величин.
Иногда говорят, что при измерении физической величины происходит
«редукция» (стягивание) волновой функции.
Гейзенберг в 1927 г с целью выяснения физического смысла oj крытой
им операторной квантовой механики доказал свое знаменитое соотношение
неопределённостей, которому удовлетворяют неопределённости координа-
ты Дзг 11 импульса Дрт в любом квантовом состоя пин части цы. Оказыва-
ется, произведение этих неопределённое гей удовлетворяют неравенству
в правую часть которого входит перечеркнутая постоянная Планка ft.
212
Глава 4
Докажем общую математическую теорему о любых двух некоммути-
руницих друг с другом операторах.
Теорема Вейля. Неопределенности ДА и АВ любых двух коммути-
рующих друг с другом эрмитовых операторов А и В для любого нормиро-
ванного па единицу состояния V1 удовлетворяют неравенству
ДА-ДВ>1|(^^)|
где (7 = АВ БА — коммутатор рассматриваемых операторов.
Доказательство^ Рассмотрим вспомогательные операторы, опре-
делённые следующим образом; А| = А — (AJJ и Вт — Я — (В)/, где J —
единичный оператор и (А) и (В) — средние значения наших операторов
в состоянии Очевцдно, (А>) = 0 и (Bi) = 0. Очевидно также, что
{А2} = {(А2-{А)/)2) = (ДА)21
(в?) = ((Й2-да)г> = (Д£)2-
Пусть теперь а — некоторое действительное число. Рассмотрим для
него состояние р = (Ai 4- iaB| Для этого состояния справедливо нера-
венство
(₽> ¥>) > 01
то есть неравенство
(AjV^ AiV'} - ft3 (Bi^, BiV4 - icrfAi^f, В]V?) - ?a(Bi^T AiV1) > 0.
Преобразуем это неравенство^ воспользовавшись эрмнтовостью опера-
торов Ai и Bij непосредственно следующей из эрмитовосги операторов А
и В. Тогда из приведённого неравенств получим неравенство
(V-, А^) + ** - J?L АI) tfO > U.
Коммутатор операторов А] и Si равен коммутатору операторов А и В.
Оператор С не является эрмитовым оператором, таким является опера-
тор iC- Учитывая теперь, что А^) = (ДА)2, (V7: ^iV’) = (Д®)2л из
иослед]юго неравенства получаем неравенство
(ДА)2 + as (АВ)2 I- & (^, > О,
которое спрапсдливо при любом действительном п.
Дополнение 2
213
Квадратный трехчлен я ft3 I Ьа+с больше или равен нулю, когда о- > О
и его дискриминант D = Jr — 4лг меньше или ранен нулю. Следовательно,
приходим к неравенству
№ iCitf - 4 (ДА)3 (АВ)2 О, 1 (ДА)2 <ДВ)2 < (tf, iC^)2,
а следовательно.
ДА ДВ |1(^, iCVOb
что и TpefioiiajJocL доказать.
Глава 5
Распределение Ферми-Дирака
Система свободных электронов в металле или полупроводнике под-
чиняется особой квантовой статистике, которая называется статисткой
Ферми-Дирака.
В физике для описания систем многих микрочастиц существуют три
статистические теории, как зоворят, три статистики. Это 1)
™ или статистика систем, составленных из одина-
ковых различимых классических микрочастиц (например, молекул возду-
ха); 2) глмлиц.-тькгт или статистика квантовых систем,
составленных ИЗ Одинаковых микрочастиц, обладающих це-
лым спином (например, фотонов, спин которых л = 1, или атомов жид-
кого гелия Не4, для которых а = 2); 3) стдимсткхл Фгдий-Днрдяи, или
статистика квантовых систем, составленных из одинаковых we/заiww*
микрочастиц, обладающих полу целым спином (например, электронов, спин
которых я = 1/2). Оказывается, части цы с целым спином подчиняются ста-
тистике Бозе-Эйнштейна, а части цы с полу целым спином — статистике
Ферми-Дирака.
«Неразличимость» частиц не ладо путать с их «одинаковостью». Так,
молекулы Ns И Оа В воздухе одинаковы, НС различимы- Свободные же элек-
троны в металле или полупроводнике или фотоны в тепловом излучении
тоже одинаковы, но неразличимы. Иногда «различимость» частиц называ-
ют их «тождественностью».
Разница /гояпгчнлгос/иц и листы станет понятной ниже, ко-
гда МЫ объясним Способы ПОДСЧСГа числа МИКроСОСТОЯННЙ, соответствую-
щих данному макросостоянню, для систем свободных электронов, фотонов
и молекул воздуха.
Ниже мы рассмотрим только так называемые системы мно-
гих частиц, г. е. системы, состоящие из частиц, не взаимодействующих друг
с другом и ни с чем другим.
Истинными статистиками являются бозс-эйнштсйновская и фермй-пи-
ра ко некая статистики, т.е. статистики 2) и 3). Классическая статистика I),
разработанная, правда, первой, является, одна козлишь предельным случаем
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРАКА ПО БОЛЬЦМАНУ
215
статистик 2) и 3), когда квантовые эффекты становятся несущественными
и ква1гтовая физика переходит в классическую физику.
Рассмотрим прежде всего нужную нам статистику Ферми-Дирака, так
как нас в нашем пособии интересу ют системы свободны к электронов в по-
лупроводниках.
В этой главе формулу распределения Ферми-Дирака для электронов
в кристаллическом твёрдом теле (металле или полу проводнике) мы выве-
дем, используя рассуждение Больцмана.
Больцман в ЙО-с г г. XIX в. вывел знаменитую формулу распределения
Максвелла молекул равЕЮвесзюго классического газа по скоростям — основ-
ную формулу атйыно-молекулярной теории классических газов, используя
очень оригинальное рассуждение.
Пользуясь рассуждением Больцмана, в этой главе мы выведем формулу
распределения Ферми Дирака для равновесного газа свободных электро-
нов в металле или полупроводнике. Сам Больцман, конечно, не мог дать ее
вывода, так как умер ещё в 1906 г., а квантовые статистики Бозе-Эйнштей-
на п Ферми-Дирака появились после его смерти только в 20-е гг. XX в.
Рекомендуем читателю, желающему глубже понять суть дела, сначала
познакомиться с Дополнением 3 к этой главе (посвящённым изложению
оригинального рассуждения самого Больцмана в отношении классического
идеального газа), перед тем как приступать к изучению основного текста
этой главы.
5Л* Вывод распределения Ферми-Дирака по Больцману
Свободные электроны в металле или полупроводнике можно рас-
сматривать как систему многих тождественных частиц, которую называю!
«электронным газом». Разумеется, в металле и полупроводнике имеются
также и «связанные» электроны, не способные перемещаться по металлу
или полупроводнику, которые ограничены в своих движениях пределами
отдельных ионных атомных остовов кристаллической решетки.
В очень хорошем приближении, однако, эти атомные остовы, с нонами
и связанными с ними электронами, можно моделировать некоторым потен-
циальным полем, действующим на свободные электроны, нс выпускающим
их за пределы металла или полупроводника.
Таким образом, рассмотрим идеальный электронный газ одинаковых
квдегтовых части it подчиняющихся принципу запрета Паули
(утверждающему, что w.tw йамыгл-и чехе, юле ч«-
cinuty хе .мсе crjcjwMJxne, найден л до с учё'тлл.и пш-
чеин/? £?ntr«tf), т. с. рассмотрим газ, подчиняющийся статистике
Фермй - Дирака.
216
Глава 5
Применив к изолированному электронному газу рассуждение Больцма-
на с «ми крое остеит и ими», «макрос ^стояниями», их «вероятностями», «рав-
новесным состоянием», найдём дм равновесного состояния этою элек-
тронного газа знаменитое «распределение Фермй-Дирака», г.е. дадим
строгий вывод формулы этого распределения
я языческой яминке
Рассмотрим изолированную квантовую систему из Аг невзаимодей-
ствующих между собой электронов, находящихся в кубическом ящике
объема V = I/ с л пиной ребра куба L. Степки ящика будем считать иетеп-
лопро водными и не пропускающими электроны. Найдём с днеэлектронные
состояния отдельных электронов в такой системе.
Эта состояния описываются волновыми функциями Уч *), ко-
торые удовлетворяют временному уравнению Шредингера:
1 2Ё
t
2т
в котором Д = д2!‘дх2 +д2/ду2 + i)2/ds2 обозна-
чает лапласиан. Волновая функция я? У? *)
отлична от пуля только be [узри объёма V, причём
на границах S этою объёма функция л;, у, z)
во вес моменты времени £ удовлетворяет нулевым
граничным условиям, т.е. условиям
Если наложить на функцию у, z) ещё
и начальное условие, задав значения функции
в начальный момент времени t = 0, то задача определения функ-
ции ^>(th я, у, z}, удовлетворяющей внутри объёма V приведённому вре-
менному уравнению Шредингера и приведённым граничным и начальному
условиям, будет иметь единственное решение, т.е. удовлетворять теореме
существования и единственности.
Применим теперь метод разделения переменных и найдем так называ-
емые «модовые решения»,
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРА КА ПО БОЛЬЦМАНУ
217
Любая функция Зл удовлетворяющая внутри объёма V вре-
шшбму уравнению Шредингера и на границах 5' этого объёма пуле вьем
i-раничным условиям, может быть однозначно представлена в виде, вообще
говоря* бесконечной суперпозиции функций:
ij 1/, *) = ^2
rt
где V?ti {л и) — модовые решения* п — номер модового решения.
Модовые функции по Фурье будем считать имеющими вид произведе-
ний функций одной переменной, зависящие каждая от своей переменной:
а:, у, а) = T(i)X(a:)K(y)Z(jr).
Подставив эту волновую функцию в уравнение Шредингера, получим
равенство
-4 T'XYZ = -^-(TX"YZ + TXY"Z + TXYZ"),
t 2m '
Разделив правую н левую ЧИСТИ последнего равенства на из
него получим, что
h Г = _rf_ (Х?_ , У"
1т 2тп \ X Y Z )'
Видим, что последнее равенство имеет следующий вад:
?(t) = «О) + а(у) + ?(?),
в нём функции л, /?, 7 зависят каждая только от своею аргумента, а пе-
ременные t, х, Ут г независимые. Следовательно,
= 2m **1 = к*’ 2т к*’
где fcj, fcy, А? — действительные константы, которые мы считаем положи-
тельными. Кроме тою*
= Е,
где Е = (fta/2m) + к* +
Таким образом, имеем уравнения
X" + fc? А' = О, У1' + к^У = о, Z" + klZ= 0.
ь ту л?
21К Глава 5
причём
Х(0) = X(L) = О, F(0) = Г(1) = О, 2(0) = 2(1) = (I.
Следовательно,
Х(л) = т), Г(у) = siu(A^ у). 2(z) = sm(Az Д
где = тг riT1 fe¥ — TT/ijp tjj = тг riz , тгТ1 ny. nz — 1. 2, ^ . . ._
Нормировочные константы в функциях Х(х), У(зД 2(х) мы отбрасы-
ваем, но учитываем, что решения при отрицательных А^: fcs сводятся
к решениям ггри положительных А^, fcvl А?, а тривиальное решение^ появ-
ляющееся при Аг = 0, fc¥ = 0, fcz = Оь толдественно ранное нулю, надо
отброс № Ь.
Рассмотрим теперь уравнение для Г Оно имеет вил
-Л^.в,дав.^(п:+п’+п“),
Решение этого дифференциального уравнения имеет вид Т =
= Се где С — произвольная нормировочная константа, Таким
образом, медовые решения имеют вид
К(*т ®1 У г г) = cn е f sin^n* я;) у) sin(fcn,, Д
где те (nXj nz), причём nx, = 1, 2, 3........
УСЛОВИЯ
Перейдём теперь от нулевых граничееьех условий Eia стенках кубиче-
ского ящика, в котором заключён электрон, к граничным условиям Борна-
Кармана.
Когда объём V кубического ящика стремится к бесконечности, задача
с граничными условиями Борна - Кармана становится зквивалеитЕюн Задаче
с нулевыми граничными условиями.
Во-первых, будем считать теперь, что рассматриваются функции
л, у: г) нс в пределах куба V, а во всем бесконечном трёхмерном про-
странстве
—си < г, у, z < +зо.
Во-вторых, будем рассматривать в этом бесконечном пространстве
только периодические функции т, z с заданным периодом 1 (таким,
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРАКА ПО БОЛЬЦМАНУ
2Р
что £ = УЙ):
я + L: у, z) = ^(Гп у, г),
л, у + £п z) = ^(Гп т, у: Д
^(Z. i, у. z 4- £) = у, z).
Реи ил теперь ;:иффсрс]|[ща.1]>Е1Ь[с уранЕзения для X. К И с условиями
Борна-Кармана, получим модовые решения в виде
'П{^ Т, г) = (?П С *^П= J:gt*7LV У 1
где (?л — нормировочная постоянная и где
fcftJF — ^;U1
у Пу, = у 1Ъ, Е„ = -*£- (п* + П* + Hz).
причём теперь nSj пг — произвольные целые числа (положительные,
отрицательные и равные нулю). Далее,
^(г, х, г, z) = х’ *)
п
Учёт ст/ил
Рассмотренные решения временного уравнения Шредингера для вол-
новых функции я, у. з) нс учитывают наличие спина у электрона.
Электрон на самом деле характеризуется не только координатами ;t, у. z,
но и проекцией спина сг£ = ±Л/2 на ось z. Так что он описывается бо-
лее сложными волновыми функциями it»(t, х, z, аД зависящими также
ОТ (Гг.
Модовые решения в задаче с условиями Борна-Кармана и с учётом
спина имеют вид
lb. I/ т у * ст 1 — e-(Wb'k f + j(k.r) Г
*Тса*кь>*i — ySjsi £Tt i
где г = (st, z), к = (а^г/Ь)^! пД па:. п3 - 0, ±1. ±2, ...,
" символ Кроне кера, ранный нулю И ггри .sz <?2 и равный единице
при 5г — (ГГ| sz = ±ft/2.
Как видим, модовые решения однозначно характеризуются узлами
простой кубической решётки в воображаемом трёхмерном к-прсстранстве
с объемом элементарной ячейки (2л/£)э = (2?г)3/У, причем каждому узлу
соответствуют два спиповьех состояния я3 — ±/t/2,
220
J'Л л ВЛ 5
Больцмановский способ описания макроскопических
состояний электронного паза
Предположим, что электронный газ имеет Лг электронов и находится
в кубическом ящике объема V' с жесткими, не пропускающими тепло и не
пропускающими электро! гы стенками, как покатано па рисунке.
Рассмотрим мложссттап л|яиртсколнческцхт
вообще говоря, неравновесных состояний этого
электронного газа к, следуя Больцману, найдем
среди них /шеяовгсяое состояние.
Чтобы выбрать способ математического опи-
сания макрос конических, вообще говоря, нерав-
новесных состояний электронного газа, необходи-
мо, прежде всего, научиться характеризовать со-
стояния отдельных электронов в этом газе.
Это, впрочем, мы уже сделали выше. Теперь
здесь ещё раз поясним наш окончательный ре-
зультат
Каждое из состояний отдельного электро-
Eia, как мы только что доказали, характеризу-
ется узлом простой кубической решётки, по-
строенной в воображаемом импульсном нро
странствс одного электрона с осями ру1 рд.
] 1о состояние характеризуется не узломъ а всей
кубической элементарной ячейкой объёмом
М/ V, где V — объём кубического ящика, в ко-
торый заключен электронный газ, г. е. на каж-
дое состояние электрона, находящегося в ящи-
КС В ИМПУЛЬСНОМ Пр<)етраЕ]СТПС электрона
приходи гем одна так называемая «злемен гарная ячейка?? кубической формы
объемом fl = ft3/V, показанная на приведённом рисунке. Импульс электро-
на р связан с его волновым вектором к соотношением р = Й. к
Следует учесть при этом, что электрон характеризуется также и про-
екцией своею спина сгг = — 1/2, которая принимает два значения. Поэтому
объём элементарной ячейки, характеризующей состояние электрона в ею
абстрактном импульсном пространстве, равен fl, = fl/2 = й3/2К
Таким образом, в импульсном пространстве одного электрона с осями
Р.п - рцч pz состояния электрона в кубическом сосуде объёма V описываются
не точками концов векторов р, а маленькими объёмчиками вблизи концов
этих векторов — ((элементарными ячейками».
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРАКА ПО БОЛЬЦМАНУ
22]
Неравновесные состояния рассматривае-
мого электронного газа будем характеризовать
распределениями его электронов по «грубым
ячейкам», в качестве которых возьмём сфери-
ческие концентрическую слои в рассматрива-
емом импульсном пространстве одного элек-
трону соответствующие значениям энергии
электрона, заключённым в пределах от с до £4
ч- de, где de — фиксированная макроскопиче-
ски малая величина. Энергия электрона и гру-
бой «с-ячейке» равна е = р3/2т? где m — мас-
са электрона, р = |р| — модуль его импульса. Грубая «^’Ячейка» дня интер-
вала энергий е, е 4 de в импульсном пространстве имеет, таким образом,
объём
4тгр2 dp = 4зт 2т< d(x/2nic) = 2тг (2m)3 y'Tdi.
Грубая f-ячейка состоит из большого числа элементарных ячеек, число
которых в вей равно
_ 2?г(2т)э/2 v'Fdc _ 4я(2т)3/2y^ds
z'----------п;---------v —;
iio-HCMCu. Zah] — число.
Мякроскшмчюског еси?б1це лмфь нероюноеюсною состояние электрон-
иодо ^аэа, следуя Яальцлану. йуйеи лгарактер№одать наборами чисел
.. . jVe .... являющихся числа! ти электроное ДГ£1 лоланиих до все срубы t
с-ячеики в рассматриваемом макроскопическом состоянии электронного
газа.
Заданием чисел ... 5ге ..., конечно, нельзя однозначно охарактеризо-
вать истинное. или «микроскопическое», состояние нашего электронного
газа, так как. зная только числа jVc- электронов, попавших в ^-ячейки, нель-
зя сказать, какие именно из Z£ элементарных ячеек грубой >-ячейки заняты
электронами, а какие свободны.
^Макрасиваичесмруиу» состоянию электроимо^о гаэдр догЭачмому яайо-
ран ^иачеими чисел ... . . .Р еооптеслтелгаует .миодо, хая л/?люи.7с, очень
.«нал? ^ик/?йс№>ки<г€?скид^ соетоллми гд?а.
То есть каждое лик/ютта четкою состоянию электронного газа ло-
же w бытъ /гюлтизоюлно олредмй/ку.м чнелол! I V дгик/?^свд?№чсских состо-
лчий. Это число Больцман назвал «термодинамической вероятностью^. Но
немец Wahrscheinlichkeit — вероятность.
222
Глава 5
Хотя величины И называются «вероятностями^, они вероятностями
на самом деле eic являются, хотя 5ье уже по той причине^ что вероятно-
сти изменяются от 0 до L а числя IV являются полижи тельными целыми
числами, как правило, много большими 1.
Числа ... Лте однако, непроизвольные. Так как мы рассматриваем
нзшнроваччын электронный 1'аз1 тот во-первых, числа Агг удовлетворяют
уЕяоеыю ff₽Miw₽ffwocmw полного чнелд чдгтанц в гагй^ Т с. условию
Е =*
с
где ±V — полное ЧИСЛО электронов в газе, в, во-вторых, у СЛОВНО HfUXWfHMO-
emw полной энрргдш гл5ла Т.е. условию
1>vc = a;,
с
где £ — полная энергия нашего электронного газа, который теплоизолиро-
ван и не обменивается с окружением работой, будучи заключенным, по на-
шему предположению, в сосуд с ксдеформирусмыми жесткими неподвиж-
ными стенками, не пропускающими тепло и электроны.
ЬйльцАтдид к меятп/гаинаму1 гдзу
При нахождении термодинамической вероятности IV данного макро-
скопического состояния .. JV£ ... электронного газа необходимо учесть,
во-первых, что электроны неразличимы и, во-вторых, что они подчиняются
принципу запрета Паули.
Принцип
5 одной вделгэдтаорной ячейке с учёта ом с линя не .wffwe em нлтлднт^ся
ООЛЬШС одного ЭЛСЛтарРЧД (либо один МсктрОН, Либо пл одного ЭЛентароНл).
бе/юлтн<>стаью W длиной ... jVe ,., глзо
летал числя япосябяй которыми можно злюинь алгктрошиш эодшктлр-
ль?г ячейки шинульсного пространств явного эяех/црочл тлко.и оорд.?шг.
чтобы « отд£льчы£ грубые ^-ячейки лолдлы заданные чнелст ижтронм.
Вероятность IV неравновесного состояния электронною газа равна
произведению вероятностей заполнения неразличимыми электронами
элементарных ячеек всех грубых f -ячее к для этого макро состояния элек-
тронного газа, г. с.
W’ = n
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРАКА ПО БОЛЬЦМАНУ
223
Для нахождения вероятности Н-'с для одной данной грубой ^-ячейки
требуется решить следующую комби н аторлуео задачу. Надо найти, сь'ольл'и-
jWU fHWfOOW.WB/.IfO.WFftJ /Kliwccmwfnb адЭбГЛЯОг ЧИСЛО JVtf ЗЛ£К-
лгри/гид ли И£ 3bTEM£Hfwt?pHw,if лченквлг э/ной груиий £-ячейка с учетом нераз-
личимости электронов и того, что они подчиняются принципу запрета Па-
ули.
Для простоты записи опустим индекс е у jV£ и 2\..
Для размещения первого взятого электрона имеем Z мест, так как име-
ем Z возможностей заполнить им одну из пустых элементарных ячеек гру-
бой ячейки. Для второго электрона имеем только X — 1 оставшихся пустых
мест. Поместить второй электрон в уже занятую первым спектрином эле-
ментарную ячейку нельзя, гак как это запрещено принципом Паули. По-
следний xV-й электрон имеет для своего размещения Z - Дг - 1 пустых
мест. Получаем, таким образом, следующее число способов размещения /V
электронов по Z элементарным ячейкам:
Z(Z - Лг + 1) _ ZI
Л-! “ (Z-jVJIAT
Д’!
используем известную комбинаторную формулу.
Так как электроны недктзлычыд^. то не надо учитывать порядок, в ко-
тором мы перебираем электроны. Поэтому первоначально найденное чис-
ло способов надо разделить на xVL т.е. на число возможных перестановок
между собой jV объектов 1, 2, .... включая тождественную перестановку,
когда объекты вообще нс переставляются.
Пример
Пусть, например, У-2 и Z-3. Возможные способы заполнения двумя
электронами трех ячеек проиллюстрированы в приводимой табличке.
Имеем 3 способа. Согласно приведённой комбинаторной формуле по-
лучаем то же значение числа способов, так как
(3 - 2)12Т
т.е. получаем такжи 3 Способа.
224
Глава 5
Итак, термодинамическая вероятность IV макроскопического состоя-
ния ... jVc . . . электронного газа, характеризуемого набором значений чи-
сел заполнения ... Лтй ... электронами грубых ячеек, равна
W = П --------- -----:
11 (ZC-NCW
как видим, величина IV является функцией переменных Л\, и для неё мож-
но использовать обозначение
JVe .
но для краткости записи далее нс будем явно указывать эти аргументы
функции IV.
Применим теперь приближённую формулу Стирлинга, согласно кото-
рой
Inn! = n Inn - п;
формула Стирлинга справедлива при больших л. Тогда из приведённой вы-
ше комбинаторной формулы для IV получим, -по
In И' S V {ze In Z£ - Ze - (Zf - JV£) In (Zf - .VJ + Ze - x¥£ -
E
“4 In Nr + AQ = ^2 {2f ln - (ге - jVfl b - Nc 111 ^4 -
±
Теперь, следуя Больцману, дадим определение равновесного состоя-
ния. Futfriofiecrie/M сцрстоянием электронного ги_ш я&гянпсл такое его .ипк-
росколнческое состояние, которое характеризуется набором -,. JV£ ...
значении чисел ЛГ,Н для которых величина IV или величина In ТУ ярнчи-
jwaem .иакеила.тьное значение при ;рс.-толнпР что ^акепройано полное число
электронов я газе, w. е. что
Е к‘ - *.
Е
у нрн условии, vfflo ^нкецрвдтмл иолчая энергия газа, wj. е.
V = ь.
£
Чтобы найти равновесное состояние газа, воспользуемся жетойож
неолре^елёиимл л^но-^-нтелеи Логранлса и составим лагранжево вариаци-
онное условие:
JlnVF - а У2 5Л’е -^52 '-5Ne = °’
£ £
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРАКА ПО БОЛЬЦМАНУ
225
в котором числа й и S являются .мложи-
иеля«£/.
Этому условию, согласно Лагранжу, должны удовлетворять л/зсч^еал*-
йые бд/и/лцгшйЛг£ чисел ЛГ£ около их значений для равновесного состояния,
не связанные никакими условиями, в частности, условиями
^ей^ = о.
£ е
Вариации являются вариациями чисел jVf около их равно вес егых
значений Лг£а т. с.
Лг£ = дг“ + Ж;
варьировать числа Zt- не нужно, так как эти числа раз и навсегда нам заданы
(так как наш газ находится все время в сосуде фиксированного объёма V).
Подставлял в вариационное условие Лагранжа полученную выше фор-
мулу для 1п И7, имеем, что
Яп№ -йЕ Ж- -j3 Е =
= V {£Afe ln(^e — JV?) + — AA'f — t?JVe In Лт^ — 4jVc — —
£
-a rSA; -0€fiNe} = £, {in (A - N?) - InЛг° - a - Д? } = 0-
так как, например,
- ,VJ ln(Ze - )] = ln(Zff - Zc) l- ^2^
я T. Д
Следовательно,
iKlnTV - a - 0 'll £ —
= S - ЛГ?) -ln
£
Для выполнения этого вариационною условия необходимо и достятоЧ’
но выполнения следующих условии:
ln(Ze - jVf) - In jVf - « - /?с- = О,
226
Глава 5
которые должны выполняться для каждого е. Разрешая эти уравнения от-
носительно Лг", получаем
—-——- | = U + = lnCQ_fJ-,
jV“ у
~ _ pd + flf Zr _ , 1.
,v:.' '
таким образом, приходим к окончательной формуле
ДГ° -----Ъ.------
f . ।
для чисел электронов, попавших в грубые ячейки в случае равновесного
состояния электронного газа.
Согласно Лагранжу, значения неопределенных множителей ос н /? еле*
дуст находить из условий
.V = V _____—____, Е = V ,
। । j-—* 1-^ь + ।
из которых* зная значения jV и Е* можно отыскать значения чисел о и 5.
значений .множителей
Лдедонжа ot w /?
Оказывается, /3 = 1,/(Алк Т), где Т — температура равновесного состоя-
ния рассматриваемого электронного газа, а = —|//(fcj;T), где — химиче-
ский потенциал этого равновесного состояния.
Начнем с того, что изменим коренным образом нашу точку зрения на
наш электронный газ.
Рассмотрим теперь w изолированный, никак нс взаимодействующий
со своим окружением газ, л все дрс.пя равновесный электронный гл я, й^-
.иеллющнйгл оцршпи.чы.и 3d счёт наиенення внешках устный его
ощужеиня, т.е. рассмотрим электронный газ, совершающий некоторый
квазиравновеснын, другими словами, обратимый процесс.
Каждым мгновенным значениям внешних условий соответствует своё
равновесное состояние газа в этом процессе.
Проведём с рассматриваемым всё время равновесным электронным га-
зом бесконечно малый элемент обратимого нз™?/яной? процесса его нагре-
вания, т.е. процесса его нагревания при неизменном его обт*ёмс V, В этом
5.1. ВЫВОД РАСПРЕДЕЛЕНИЯ ФЕГМЙ ДИРА КА ПО БОЛЬЦМАНУ
227
процессе изменяются полная энергия £ газа и полное число электронов W
в нём, но не изменяется его объём V. Изменения на бесконечно малом эле-
менте рассматриваемого процесса изохорного Hai рокания будем обозначать
символом с/.
Мы считаем, что газ может обмениваться с окружением не только теп-
лом, но также и электронами.
Так как? пи Больцману, эитролня/щтгяаеснод? состоЛн^я Шлётся ф*;р-
лгуяой S = In VVo, в которой IVN — максимальное значение термодинами-
ческой вероятности И\то
dS = Е {М3. - jV“) - InNs0} = A:e + 0e)dA'° =
E7 L
= its ft d E AT° ) + kSd £ e A'O = fco rf±V + 0dE,
\ c / \ £ /
id J] El
dS = A-б ctdAT +
где djVa dE — изменения полного числа электронов и полной энергии
электронного газа па элементе рассыа1ркнаемого изохорного обратимого
процесса (на котором объём V газа не меняется, а потому нс меняются
и объёмы элементарных ячеек для него, а следовательно, не нужно диффе-
ренцировать величины 2/|.
В приведённой формуле для d±S следует считать» что
^лг;
ж? эм1
Полученную формулу для изменения энтропии dS на элементе изохор-
ного обратимого процесса нагревания электро иного газа мы должны сопо-
ставить с термодинамической формулой
dt7 = TdS-FaV + ^drt,
справедливой: для бесконечно малого элемента произвольного обратимою,
другими: словами, квазиравнонесного процесса, причём 17 = £ — энергия
газа, /I — его химический потенциал в расчете на один электрон (молярный
химический потеЕтциал, следовательно. раней ;7 _ //тЛгЛт где Лга — число
Авогадри, m — масса элекзрона). Для элемента рассматриваемого изохор-
ного обратимого процесса dV7 = 0, и поэтому
= TdS 4- дг dj№.
22 Н
Глава 5
Следовательно, получаем формулу
dS = -^dN = ±dE-
Конечно, u ^маишслшюг, л w my
лн?£ г^др.иулу г).тя d5r Поэтому, сравнивая друг с другом обе приведённые
формулы для dS, заключаем, что
^Б ^Б jF
так что, действительно, /? = 1/(^бТ), <л = —^/(ЬбГ), как мы сказали
выше.
Таким образом, окончательно для распределения электротюп по гру-
бым ^-ячейкам в равновесном состоянии электронного газа с температу-
рой Г п химическим потенциалом ji получаем формулу:
№: _ —
- е(е-м}/^7+1
Вводя величину f (е) = N?/Ze, являющуюся фенидон wcqoai эледо/ю-
лял, « /гдешлясснам ссксгсгоятшп на злеме/<хлл/?мум
ячейку е аиергыем е, окончательно получим, что
/(<> = ------,
с{с - Ц}/А-Н Г + (
т.е, формулу зиамс! [итого «распределения Ферм и-Дирака» для электрон-
ного газа.
5.2. Получение распределения Максвелла из
распределен ня Ферми-Дирака
Используя формулу Больцмана, связывающую энтропию состояния га-
за с вероятностью этого состояния, мы вывели распределение Ферми
Дирака электронов по энергиям а, — (р’ I p'J I p’)/2m для равновесно-
го электро ешого газа, |[ахолящсп»ся в ран еювс сном состоя ее ни с температу-
рой Т Ei электронным химическим псп си цианом де, г.е. получили формулу
е(= - м)/^Т + j
5.2. ПОЛУЧЕНИИ РАСПРЕДЕЛИ EELlfl МАКСВЕЛЛ А
22 '>
□ля среднего числа электронов электронного газа, попавших в малый объем
Др;и ^Рц Дрг =
импульсного пространства электрона, т.е. в объем так называемой «элемен-
тарной ячейки» этого пространства, где У — объем, занимаемый равновес-
ным электронным газом.
Если характеризовать электроны нс компонентами импульса, а компо-
нентами скорости, связанными с компонентами импульса соотношениями:
р* = mvj, рг = тиЯ1
где m — масса электрона, то надо будет рассматривать «элементарные ячей-
ки?; не в пространстве импульсов одного электрона, а в пространстве ско-
ростей электрона, с объёмом
Дц..Дг,^= JL..
Число элементарных ячеек в пространстве скоростей электрона в мак-
роскопически бесконечно малом объёме du,f т. е. в объёме с компо-
нентами скорости электрона, лежащими в пределах от до v:t + dvB, от
до иу -Ь от и- до ?;z 4- dv37 таким образом, рак его
di\ cfrjjr
гтпЧ' А3 9
Число электронов в равновесном электронном газе, обладающих лю-
бой проекцией спина (либо = 1/2, либо <те = -1/2) и компонентам и
скорости от г'д. до ст до vv + dvy, от др + <iv?, следова-
тельно, paREHJ
Де) ^7- rft'j dvv (iv^
мы ис обращаем внимания на величину проекции спина электрона tz —
= ±1/3 i[ поэтому опустили множитель 2.
Вероятность найти электрон с указанными компонентами скорости
и произвольной проекцией спина в рассматриваемом равновесном элек-
тро ином газе! таким образом, будет
m3 V
wz I 777т <h’T fiv,j <lvz = /м(е) ^vx fivv
230
J'л л вл 5
где jV — число электронов в газе и где функция
л RJ ГЯЕ1 с Я фу! IKJЩ СИ РДС11рЗДС Л С НИЯ Фе рм Й Д Ирака, I ip ич ём
f=f г£н ^).
Полное число электро ил в в рассматриваемом электронном газе равно
л'= Е Е
сг*«±1/2
где £ = + Ру — Ps) И где суммирование ПО ffj ведется ПО обеим
проекциям спина <т£ = ±1/2» а суммирование порЯ!1 р± — по всем узлам
кубической решётки в трёхмерном пространстве -со < pj, рл < +ос
с величиной ячейки Др.с Др„ Дрг = /г*/К Таким образом, при У —* ж
+«
у = у' = /з /// +₽у +F«))rfP.rdpJftipz.
Р^.Ри-Ря -со
I [слученное условие позволяет связать значение химического потенци-
ала с концентрацией электронов в газе п = iV/V и его температурой Г,
т. е, построить функцию д = Т).
Рассмотрим теперь классический случай. когда распределение Ферми-
Дирака переходит в распределение Максвелла, i.e. случай нереалистично
высоких температур электро иного газа в металле или полупроводнике. То-
гда в знаменателе формулы распределения Ферми-Дирака можно отбро-
сить единицу по сравнению с экспонентой и получить, что
/(с) = с с"^7’.
где постоянная (7 — .
Вероятность найти электрон в равновесном класс нм сс ком электронном
газе с произвольной проекцией спина ст2 = ±1/2 и компонентами скорости
от адо + rft’q:, от гу до t’y I dvp, от до + йия будет
^‘yi du± = Cm e-m
где (7м — нормировочная копстшгга.
ДО1ЮЛНЕНИК I
23]
Найдём эту нормировочную константу из условия
+<ю
Сл/ УУУ е-™ (+ + *’) /2^ ТdVl dv„dv, = 1;
—ОС
таким образом,
Caj
тг 2Л?е Г
m
) 3/2
Получили «распределение Максвелла»
m
2тг^б Т1
c-m (г£ + v* + и’) /(2fcB Т)
для молекул классического равновесного электронного газа по скоростям.
Следовательно, так как С = 7 h -го
m
2тгйЕГ
3/2
Т — ц
t, 3 I m 1 /2^тАгЕТЛ
= fcETlnra - fcET ]п I —-—- 1
“ \ л4 /
видим, что химический потенциал /л стремится к минус бесконечности —ос
при температуре Г —* +оо.
Дополнение 1 к гл. 5
Л/ешяг) неялреййгё'кныл лнгожьнте.7ег7 Лаг/злн.тмга Аъя
Для функция нескольких переменных, например дли функции /(i, у)
двух переменных ar, у, различают абсолютный и условный экстремумы.
Уймщный экся!/?йиун — это экстремум, отыскиваемый при учёте, что
аргументы функции связаны одним или несколькими дополнительными
условиями.
Например, для приведённой функции /(я, у) одним условием у(z, у) -
= 0.
Предполагаем, что рассматриваем непрерывные функции с непрерыв-
п им н и ро из водным и.
232
Глава 5
Необходимое и достаточное условие эястяр&иунд функ-
ции ffx, у) можно формулировать с помощью Следующего вариациолЕюго
принципа. Точка хц. уо является точкой абсолютного экстремум а функции
/(ж, у) двух переменных л и у тогда и только тогда, когда вариация этой
функции
у) = (*01 Jto) Ы Йу
равна нулю при вариациях Лх. <5у аргументов у около точ-
ки jfo С точностью до бесконечно малых первого порядка имеем равен-
ство
^/(®, у) Да*} + ЭД Уп + ЭД - /ЭДь Уо}-
Если требуется найти усдояпый .зкт.шре.му.эд например, функции /{з;, у)
с условием (яг. у} — С. приведённое несводимое н достаточное условие
абсолеогною экстремума нс будет верным, гак как теперь вариации и 5у
не мшшт, а связаны имеющимся условием.
Лагранж доказал, что для условного окемредп'ия справедливо дру-
гое вариационное условие. Например, для функции /(ts у) с условием
_9(z. у) = 1) надо рассмотреть вариационное условие
Й/(я?, у) - X ёд (х, у) = 0.
в котором А — так называемый лтнодош/недъ ТГодотыжа;
причём это условие, по Лагранжу, выполняется при нронзяатыгыдг ал/?егл-
jfjfxr 5х и 5у, хотя мы рассматриваем уловный зястрелгин.
ТТрхше/?
Рассмотрим функцию Дт, у) = 1 —Iй — 2т/ и условие у у) = i -Ь
— у — 1 н найдем максимум этой функции Дх. у) при условии у(х, 3/} =
= 0. Абсолютный максимум этой функции находится в точке я = 0> у = 0
и равен 1.
На приводимом ешжс рисунке представлен график функции г =
= /(х, у). Это поверхность в трёхмерном пространстве, пересекающая ко-
ординатную плоскость Оху по изображённому на рисунке эллипсу ха -к
+ 2уа = I. Показан также график функции я = у). Это плоскость, пер-
пецдикулярная координатной плоскости Оху и псресскиЕОщая сё по прямой
х + у = 1, тоже показанной на рисунке. Изображена также часть кривой
пересечения поверхности 2 = 1 - ia - 2уа плоскостью z = х + у - 1,
лежащая на поверхности я = I - хг - 2уа.
Дополнение l
233
На этой кривой лежит отыскиваемая нами точка Af условного макси-
мума. Точка абсолютного максимума тоже отмечена на приведённом рисун-
ке.
Согласно условию Лагранжа, име-
ем уравнение
df(*- у) - Ad^fo v) = °-
из которого сразу получаются два урав-
нения;
-2<г - А = О, - 4у - А = 0;
следовательно, ж = -1/2А, v = 1/1 А.
Значение А мы найдём из условия
у) = 0 !
таким образом, искомый условный максимум находится в точке i =
= 2/3, у - 1/3 и равен
9 9 U " 3
Убедимся, ЧТО ЭТОТ отпет правильный, .ДЛЯ чего ИСКЛЮЧИМ у из услопия
X 4- у = 1 и подставим этот аргумент у в функцию /(т. у). Получим тогда
у = 1 — z н функцию jF'(t) = /(z, 1 — аг), так что имеем формулу
Г(ж) = 1 - ж2 - 2(1 ж)2 = -1 + 4ж - Зж2.
Максимум Этой функции находится в точке, п которой ^г(т) = 0. тс.
в точке
4 - бт = 0,
2
3
т
и равен
причём у = ] — 2/3 = 1/3; так что метод Лагранжа даёт нам верный
результат.
234
J'Л л ВЛ 5
Дополнение 2 к гл, 5
Вывод формулы Планка для равновесного теплового
электромагнитного излучения методом ячеек Больцмана
Рассмотрим идеальный фотонный газ, состоящий из одинаковых
неразличимых квантовых частиц — фотонов, подчиняющийся статистике
Безе Эйнштейна. Применив к нему рассуждение Больцмана с элементар-
ными л грубыми ячейками и вероятностями макросе стояний, найдём рал-
н овес ное состояние этого фотонного газа, описываемое формулой Планка
для равновесного излучения абсолютно черного тела, т.е. дадим строгий
вывод этой формулы, в отличие от вывода её. который мы дали в гл. 1.
Для фотонного газа, которым является электромагнитное излучение
в полости, рассмотренное в гл. L, воспользуемся квантовой статистикой
Бозе-Эйнштейна.
Пусть наш фотонный газ» т.е. электромагнитное излучение, помещен
и сосуд с зеркальными стенками, Предположим, что внутри этого сосу-
да находится только электромагнитное излучение некоторой определённой
энергии всех возможных частот, и что в этом сосуде нет никаких атомов
и молекул.
Каждый фотон движется со скоростью света в пустоте с и претерпевает
время от времени отражения от стенок сосуда. При этом сохраняются как
сео энергия, гак я абсолютное значение его импульса. Если фотон обладает
частотой (длиной волны А = с/х/), то его энергия равна £ = hi/. Если
v — вектор скоро ст] । фотона, то модуль его импульса р = hx//c2.v равен
IpI = hvfc.
Рассматриваемый фотонный ГЙ34 однако, никогда нс смажет прийти
к равновесию, как и классический идеальный газ, если бы в последнем не
происходили столкновения молекул газа друг с другом. Фотоны, в отличие
от молекул, не могут сталкиваться.
Однако фотонный газ можно все же заставить перейти в равповесЕюс
состояние, если внутрь сосуда с газом внести так называемую планков-
скую «угольную пылинку», поддерживаемую всё время при одной и той же
неизменной температуре Г. Эта пл анконская пылинка представляет собой
небольшое количество вещества^ способного поглощать и испускать элек-
тромагнитное излучение любых частот Поэтому с помощью этой пылинки
можно осуществить обмен энергией между фотонами фотонного газа раз-
личных частот и направлений движения, что приведёт в конечном счёте
к установлению равновесного состояния рассматриваемого фотонного газа.
При этом достаточно внести столь ничтожное количество вещества^ чтобы
Дополнение 2
235
его энергией можно было пренебречь по сравнению с энергии фотонного
газа.
ILjuHKDHLKja «угольная крупинка» заставляет фотонный газ перейти
в равновесное состояние, описываемое формулой Планка.
Рассмотрим теперь наш изолированный фотонный газ как идеальный
газ неразличимых частиц с сохраняющейся полной энергией и несохраня-
ющимся числом частиц.
Неравновесные состояния фотонного газа
Рассмотрим макроскопические состояния фотонною газа, которым яв-
ляется, вообще говоря, неравновесное тепловое электромагнитное излу-
чение в полости.. Пусть этот газ изолирован и находится в механически
жёстком и не пропускающем тепло сосуде, например, в кубическом ящи-
ке, изображённом па рисунке, с зеркальными стенками. Другими словами,
пусть этот газ нс взаимодействует со своим окружением. Объем куба обо-
значим V, длину ребра куба L, так что V = ZA
Фотонный газ является системой, состоящей из
невзаимодействующих между собой фотонов.
Отдельный фотон характеризуется плоской элек-
тромагнитной волной, имеющей угловую частоту ш
и длину волны А. Вместо длины волны^ однако, удоб-
нее рассматривать волновое число Аг = 2тг/А. Угловая
частота и волновое число связаны соотношением
ш = ск.
в котором с — скорость света в пустоте.
Вместе с тем отдельный фотон фотонного газа следует характеризо-
вать нс волновым числом A, a волновым вектором к> модуль которого ра-
вен волновому числу, и который направлен в направлении распространения
плоской электромагнитной волны, представляющей фотон. Электромагнит-
ная волна поперечна, и поэтому фотон имеет два независимых направле-
ния поляризации^ характеризуемых индексом ст — ±1. Спин фотона равен
единице s = 1, так как электромагнитное поле описывается векторными
функциями.
Состояния отдельного фотона, таким образом, задаются величина-
ми к, <7-
Соглзсно квантовой механике фото е г является ею только полной, но и
корпускулой. Энергия £ и импульс р фотона как точечной частицы связаны
236
Глава 5
с его угловой частотой ш и волновым вектором к соотношениями
i$ = р = Ь к.
которые называются «соотношением Эйнштейна» и «соотношением де
Бройля» соответственно; здесь ft — перечёркнутая постояппая Планки
Так как фотон заключён в кубическом объеме V, с длиной ребра куба
равной L (£3 — V), то квантовые неопределённости Дх, Ду, Дг его коор-
динат имеют порядок L. Поэтому в силу квантовых соотношений неопре-
деленностей квантовые неопределённости Дрг, Др^| Др- компонент его
импульса имеют порядок величины fi/L. Так что, учитывая, что согласно
соотношению де Бройля Дк* = Др^/Л = l/ia ДА\ = Др^/Й = 1/£,
Дк2 = Дрл/й = 1/Ь, имеем
Afc^Afc^Afe = 7з = т1'-'
Таким образом, волновой вектор к имеет квантовую неопределенность
1/V. Более строгое рассмотрение, которое мы фактически уже пропели
в гл. 1? показывает, что величина элементарной ячейки, характеризующей
отдельное состояние фотона, раыла не 1/V, а (2тг)3/1-7.
Таким образом, фото л бгз ллыртт-
Jt2 оццсывяешея не movww колцо аодноАО-
<?о к. лльтлженяоао из начала О л/то-
л-т йиляийыт ййктарой фате?’
Дгу й обшклнью объЁшам (Этг)3/У
около конечной тонки актора к, прсдставля-
/ ющей собой «элементарную ячейку>\ показа]i-
X— ---------ь ную на приведенном рисунке. Разобьём теперь
всё пространство волновых векторов фотона
/ на маленькие элементарные ячейки объёмом
t Q = (2д)^/У = 8?r3/V каждая. Одна такая
ячейка fl. как мы сказали, описывает одно со-
стояние фотона.
Однако с учетом поляризации ст = ±1 элементарная ячейка соответ-
ствует не одному, а двум состояниям фотона. Поэтому в действительности
элементарная ячейка, соответствующая одному Состоянию фотона, имеет
объём fl^ = Q/2 = 4эт3/Уг.
k-ff/?f>™/3df^eriiea ла
/?а? у маве«?л)а зд^дннЫиМ w фигси/№#аяныж //о ясага нашего
/эассуж^елая, так как считаем объём V кубического сосуда
неизменным.
Дополнение 2
237
Макроскопические состояния фотонного газа
будем характеризовать распределением его фото-
нов по «грубым ячейкам», каждая из которых со-
стоит из большого числа «элементарны к ячеек».
/дубую ячейку, вдкдзйнную мд л/мгвлЭДннйы
доертке, как сферический слой
я етряст/глнстйЕ котимых аектсузм фотона, со-
отОДйстйуЛЭщыи гшетермалу частот от и? ()о ш 4-
- duj, причём грубую ячейку будем снабжать её
значением частоты ш,
Грубая ячейка ш для интервала частот от до w — du? фотона в к-про-
странсгве волновых векторов фотона имеет объём
4тг£2 dfc = -Ц u>2 dw-
сэ
Разделив этот объём на объем Пэ одной элсмен гарной ячейки, получим
число элементарных ячеек, содержащихся в грубой и-ячейке. Их число,
таким образом, равно
у _ 4?г llfscLj _ 1/ u?2 dur _
w л* Цэ л-2 с? ’
пО-нсмсц. Zahl — число.
Малросхааические. вообще говоря, леравлояесу/ые состояния фшллл-
яого лил буййА/ тарлклге^изовдть яаборллш значений чисем ,.. iV^ ,,, фо-
тояов> лопавших & грубые ячейки.
Полное число фотонов 5Z тю задано, гак как фотонный юз —
это система с ^сохраняющимся. т.е. нефиксированным числом частиц.
Электромагнитное излучение и фотоЕгпый газ правильнее сравнивать
не с идеальным классическим газом, а с ларом над жидкостью, хотя и это
сравнение не совсем правильное.
й&я&цдягнд к лазу
В отличие от классического молекулярного газа, фотонный газ состо-
ит из неразличимых частиц. Поэтому термодинамические вероятности IV
его макроскопических состояний следует вычислять совсем не так, как ве-
роятности макроскопических состояний классического молекулярного газа,
составленного из различимых частиц, и не так, как вероятности неравно-
весных состояний электронного газа, состоящего тоже из неразличимых
частиц^ но подчиняющеюся принципу Паули.
23 N
Глава 5
Так как фотоны неразличимы, то, в отличие от частиц классического
молекулярного газа, их даже мысленно нельзя снабдить какими-либо номе-
рами (как что можно делать, и Больцман сделал с частицами классического
газа).
Термодинамическая вероятность макроскопического состояния ... cj...
фотонного газа раина произведению вероятностей размещения фотонов
в отдельных грубых ячейках, т с. равна величине
И' = {{ 1Ъ.
Чтобы рассчитать И7,. для фотонов грубой ^/-ячейки,
нужно найти, сшыъкшш слособдлш iVw фотонов бднвдш грубой ш-ячвдкы
лдежне разметан wit ла Zw её зя^ентд/м^и ячейкой .
Итак, рассмотрим какую-либо грубую ^-ячейку. Для размещения в ней
её фотонов имеем следующую комбинаторную задачу. Нужно найти число
способов, которыми У неразличимых объектов (фотонов) можно разме-
стить по X фиксированным ящикам (элементарным ячейкам). Индекс сд
у и Лгш для простоты опустим.
Если бы фотоны былирсглтичммы, как молекулы классического газа, то
это число IV было бы равно
IV = Z‘V.
Действительно, для первого фотона имеем Z мест для размещения,
т.е. Z возможностей. Для второго фотона имеем тоже Z мест для разме-
щения, так как второй фотон можно поместить и в элементарную ячейку,
в которой уже находится первый фотоЕТ. Следовательно, имеем X X =
= Z" возможностей для размещения двух фотонов в Я элементарных
ячейках. Таким образом, для /V фотонов имеем ZjV способов разме-
щения.
Фотоны яbjтяготея, однако. частицами, и поэтому для
них число IV способов размещения нс будет равно Хл. Чтобы най ти это
число, используем следующий искусственный математический приём.
Выпишем /V символов фотонов в виде Ат кружков в длинный ряд, ко-
торый раздел им на секции, символизирующие элементарные ячейки, нере-
городками Б виде вертикальны к чёрточек, соответственно числам фотонов,
попавших в 1-ю, 2-ю, ..., И-ю элементарные ячейки, так что перегородки
символизируют границы между элементарными ячейками. Число перегоро-
док, разделяющих секции, таким образом, равно Z - L
Дополнение 2
23 У
ООО
1-я
Какие-то секции (элементарные ячейки) могут не содержать фотонов.
Перегородки таких секции будут стоять вплотнуЕо друг к другу.
Итак, имеем длинный ряд символов фотонов и Й - 1 символов
перегородок, т. с. всего имеем Лт + Z - 1 о&ьектон
Число возможных перестановок jV + Z 1 объектов между собой равно
(АГ — 2 — I)!, Так как фонолы ЛЁрдэдичи.нн, а потому не имеют номеров, их
перестановки друг с другом несущественны. Число таких перестановок jV
фотонов между собой равно Л!. Так как перегородки секций юже we/югш-
чшгы, т. е. они тоже нс имеют номеров, их перестановки между собой также
не существенны, и поэтому число этих перестановок равно (Z — 111. Таким
образом, число способов И', которыми можно разместить W неразличимых
фотонов по Z элементарным ячейкам, равно
= LV + Z-1)!
/VT(Z-l)!
Пример
Пусть, Ехапример, 1V = 2 и Z = Если бы фогОЕхы были различимы,
то было бы 9 способов размещения двух различимых частиц ft и & по 3
ячейкам. Онн представлены елевой приведённой ниже табличке.
Из формулы W = тоже получаем З2 = 9 возможностей. Но фотоны
неразличимы, и поэтому имеем только 6 способов размещения неразличи-
мых фенонов а по ячейкам, которые приведены в правой табличке ниже.
Из формулы
АЩЗ-1)!
получаем значение
(2 + 3 -1)= ,, = 2J
21(3-1)! 2’2! 2 2
т. с, тоже имеем 6 размещений.
240
Глава 5
1 2 3
Й. ь
я, А
дг b
а ь
а ь
а h
ъ й
h а
6 л
1 2 3
£ГГ Л
и, л
Л а
а fl
а fl
Таким образом, термодинамическая вероятность ИР макроскопическо-
го, вообще говоря, неравновесного состояния фотонною газа, характери-
зуемого набором чисел фотонов ... Л\,. ..., попавших в грубые ^-ячейки,
равна
IV _ ТТ 'л- ~ rr +
11 .V.liZ . - 1)! 11 XJXJ '
произведение берём по всем ^-ячейкам. Так как числа большие, можно
приближённо замени] ь Z^. - I на Z^.
Применим теперь формулу Стирлинга и получим
In = Е {(Я- + 1п(А^ + - (AL- + ZJ-
aJ
-JVW In -I Д^. - In -I Zw} =
= Е{(^ + ZJ ln(7Vw + ZJ - iVjnjVw - ZUnZw} -
Соглйспо Больцману, состояние гл.тл .уцренг-
дгсргт.-ется Няйо/толг Чи££н . . . jV^ . . .. йля КйлторЫх величина1 In IV иЛсет
Этот максимум следует искать для чисел Аг^. кото-
рые удовлетворяют условию
где £ — фиксированная полная энергия рассматриваемого фотонного газа,
находя щегося в кубическом сосуде объема V, предполагаемого изолирован-
ным, одинаковая для всех его состояний; кроме roroh £w = Так как наш
фотонный газ пи с чем не взаимодействует, его поле гая энергия £ имеет
Дополнение 2
24]
неизменное, одно и то же значение для всех его состояний- Лаяяое число
WT. f. ?£ЛНЧ£Ш£Г JVWr -Wfl.NL'^W OftUffh. КЛХЛ , КИК
отасчалпсЕн mjticc.
Чтобы найти равновесное состояние нашего фотонного газа, рассмот-
рим вариации бЛГ^. чисел jV^ около их равновесных значении 2V°, т.е. по-
ложим
А^ = А^ + 6jVw,
и вычислим вариацию функции In IV (... jV, -.а затем составим, соглас-
по методу неопределённых множителей Лагранжа, вариационное условие
<5 bi IV - ? £ 6АГ^ = 0т
в котором d — неопределённый множитель Лагранжа» справедливое для
произвольных одришры около равновесного состояния.
Подчеркнём, что в приведённом условии Лагранжа вариации АЛ\, сле-
дует рассматривать лрокнильяылш, в частности, не удовлетворяющими
условию
£2 = °-
Таким образом, используя выведенную формулу для термодинамиче-
ской вероятности и формулу Стирлинга, получаем
6 In TV - 4 £ f и 5AL =
uj
= Z {Ж, lo(JV° + Z„) + In N° - Ж - Ж},
т. е. формулу
б 111 IV - 0 У2 S + ZJ - ЬЖ - /3 £ы } 6 .
Jr1 L-J
Как видим» числа фотонов JV^ в грубых lij-ячейках для
состояния фотонного газа определяются из условий
1п(Лг® 4- - In j*V^ — /3^=0 при всех hj-
которые выполняются ;и(я каждого ш. Это необходимые и достаточные
условия для выполнения рассматриваемого вариационного условия Лаг-
раЕнка.
242
Глава 5
Таким образом, получаем
_в/? _ I
№
Следовательно, числа фотонов в грубых ячейках, которые опиеынаюгг
равновесное состояние фотонного газа, даются формулой
Значение множителя Лагранжа /?, согласно Лагранжу, следует найти из
условия
Ь ы |
га котором £? — энергия рассматриваем пго изолиропштпого фотонного газа.
Условий это связывает значения величин /3 и F.
О/мыскяныя значения /?
Чтобы выяснить физический смысл лагранжева множителя Д и най-
ти его значение, изменим теперь нашу точку зрения на рассматриваемый
фотонный газ.
До сил пор мы считали фотонный газ изолированным, т. с. никак нс вза-
имодействующим со своим окружением. Теперь, однако, рассмотрим ей'
Cfl СЙОУ.Н rtCf SpC.l/Я CHWW
г«з, находящийся всегда и равновесном оосюянин, который мы
будем нагревать изохорно в обратимом, другими словами, к&азиравновсс-
пом процессе от температуры Г до температуры Т +- дТ.
Рассматриваем не произвольный квазиравпопсстняй обратимым про-
цесс с фоюнным газом, в изохорный обратимый процесс, т.е. процесс,
в котором объем V газа не изменяется. В таком процессе над газом нс
будет совершаться никакой механической работы, и он сам не будет совер-
шать работы изд окружением, з потому объем газа V ire будет меняться,
и ооъсыье его атемешистрных л чье a П не будут изменяться, и нрц
MCAWW полнот Ь -НТГС-ТСГ 2^, КОНСЯДОНЛШАНЛ
Дополнение 2
243
Энтропия равновесного состояния фотонного газа даётся формулой
Больцмана:
S = is 1н Ж>,
в которой И о — равновесное значение термодинамической вероятности,
т. е, значение И7 при jV^ =
Используем для In Wq полученную выше формулу н найдем, что
1П Но = У {(2V" I- Z„) Jn(Ar“ + Z„) - N" In У" - lnZ„},
здесь
yo =____________________________________
w
Для элемента рассматриваемою обратного процесса изохорного на-
гревания газа для изменения его энтропии имеем > таким образом, следую-
щую формулу:
dS = Е {1п(№ + ZJ) - In №} dN° =
w
= № Е = fofid (е ,
(17 \ (17 /
дифференциал можем вынести за знак суммы* так как энергии по-
стоянны для неизменных элементарных ячеек. Появившаяся здесь сумма
Z2 JV1! равна энергии Е газа, которую в термодинамике обозначают бук-
вой £Л Таким образом, мы вывели формулу
rtS =
которую следует сопоставить с термодинамической формулой
dt7 = Tc/S
справедливой дня бесконечно малою элемента изохорною обратимого про-
цесса.
Это одно и то же соотношение.
Таким образом, приходим к заключению, что
71 _ _!_ g = I .
“ kr,.3’ Р kv.T?
244
Глава 5
как видим. множитель Лагранжа х? очень просто связан с температурой Г
равновесного состояния нашего фотонного газа. Окончательно для чисел
фотонов в грубых ячейках дня равновесного состояния фотонного газа име-
ем формулу
__________________________________________
" е*Лг-1’
в которой ew = Ли.
Формула Планка
Фактически мы вывели формулу Планка для равновесного теплово-
го электромагнитного излучения. Действительно, обозначим через и(Т. и)
спектральную объёмную плотность энергии равновесного излучения с тем-
псратурон 7’. Очевидно тпгда, что
£ы Лг2 = у«(7\ и) tin,
причем здесь 2V& — макроскопически бесконечно малая величина. Исполь-
зуя выведенную формулу для таким образом, получаем, что
17 _______Гбй7_______
V 7Г2 (? Г _ 1
Следовательно,
/гр Л __________________ 07^ ____flt-Li-1_
и(Гаг)- eW^T _ J
1]wiyiicij][i «формулу Планка».
Замечание
Мы рассмотрели фотонный газ, применив к нему статистику Бозе-
Эйнштейна. Существует ещё одна очень интересная квантовая система
многих частиц^ подчиняющаяся сгагистике Боэё-Эйнштейна. Эго систе-
ма атомов жидкого гелия Не4 при очень низких температурах (существует
также жидкий гелий Не3, но он описывается статистикой Ферми-Дирака
и ведет себя совсем не так. как жидкий Не4; о нем мы говорить здесь не
будем). Жидкий гелий Не4, как и фотонный газ, подчиняется статистике
Безе-Эйнштейна, так как спин а ядер Не4, состоящих из двух протонов
и двух нейтронов, целый и равен 2. Частицы с целым спином подчиняются
статистике Бозе Эйнштейна, а с по луце л им спином — статистике Сермй
Дирака. Частицы с целым спином поэтому называются бо.эолазш, а с полу-
целым СПИНОМ —
Дополнение 2
245
Газ атомов гелия Не1, как и газ фотонов, подчиняется требованию
неразличимости частиц. В отличие от фотонов, однако, атомы гелия имеют
ненулевую массу ш, и их энергия равна с = р^/Зт, где р = |р| — мо-
дуль импульса р атома гелия. Поэтому следует характеризовать состояния
атомов гелия, которые будем представлять точечными частицами и назы-
вать «бозонами», а их газ — «газом бозонов^, ire частотами о? и волновыми
вскЮрйми к, а энерхиями s и импульсами р.
Применим рассуждение Больцмана к изолированному идеальному газу
точечных бозонов, являющихся атомами Не1, и учтём, в отличие от фотон-
ного газа, что числа частиц Лгс, [гопавших и грубые f-ячейкн, удовлетворя-
ют ।гс Одному, а двум дополнительным условиям:
где £ — энергия частицы газа в элементарной ячейке пространства импуль-
сов одной частицы, £? энергия рассматриваемого газа, /V число частиц
га рассматриваем пм газе, теперь фиксированное, т. с. надо учитывать, что
число атомов гелия Лт неизменно.
Можно теперь воспользоваться рассуждением Больцмана и вывести
для вероятности И,т(... У- ,,макроскопического, вообще говоря, нерав-
новесного состояния газа наших бозонов формулу, аналогичную получен-
ной нами формуле Планка для фотонного газа.
Воспользуемся методом неопределённых множителей Лахранжа. По-
сле проведения рассуждений, аналогичных проведённым для фотонного
газа, найдём следующую формулу для «распределения Бозе Эйнштейна»
для идеального газа бозонов:
/(«) = - Ат—>
е<£ - w/^б-Г _ ।
где /(e) — среднее число бозонов, приходящихся на одну элементарную
ячейку с энергией с в пространстве импульсов одной частицы, в равновес-
ном состоянии рассматриваемого бозонною газа.
Здесь 7’ - температура равновесного состояния газа бозонов, — хи-
мический потенциал этого равновесного с ост ояния.
Идеальный газ неразличимых точечных атомов fie1 обладает важ-
ным свойством, называемым (прояв-
ляющейся как яояеные сАе/гглйсучети жидкого Hell в жидком EIeJ). При
достаточно большой плотности числа частиц п = jV/'V в газе и при сравни-
тельно низкой температуре Т < Гьт(п) оказывается, что = 0, и макроско-
пически большое число частиц занимает состояние с нулевой энергией
246
Глава 5
t = О, как говорят «выпадает в конденсат» («бозе-эйннггейновскии конден-
сат»), с плотностью числа сконденсированных частиц ?1о = Л'п/1Л Таким
образом, при Г 7]ф, где Ткр — температура фазовою перехода второю
рода из нормального Не! в сверхтекучий Hell, имеем функцию распреде-
ления
f(s) = По Л(е) + 1----,
е^/^вГ _
га которой j — дельта-функция Дирака (£(е) = при f = 0 и Д(е) — 0
при с 0). Вместе с тем при Т > имеем функцию распределения:
1
В которой /1^0-
Обращает на себя внимание то, что при отсутствии бизё-эйнштейнов-
ского конденсата формула для бозонного газа при = 0 имеет вид
1
f(e) ~ Л.-'Г
т.е. совпадает вроде бы с формулой Л ланка для равновесного теплового
электромагнитного излучения.
Но обе эти формулы различны. Физика системы фотонов с нулевой
массой m и физика системы бозонов с ненулевой массой m припципи-
альни различны. Фотоны вообще по имеют химическою потенциала, это
понятие для них бессмысленное. В частности^ ни для каких химических ре-
акции с участием фотонов условие химического равновесия (составляемое
по уравнению химической реакции) не включает химический потенциал
фотонов. Термодинамическое условие фазовою равновесия (с равенством
химических потенциалов вещества в фазах, находящихся в равновесии друг
с другом) для равновесного теплового электромагнитного излучения тоже
не имеет места.
ДОпОЛНСннС 3 к и[. 5
fiwwc) q&p/wjjw <? связи с eepawiuocmbw
Чтобы лучше освоиться с квантовыми статистиками Ферми-Дирака
и Бозс-Эйн[|[тсЙ1Гь1, читателю надо сначала постараться глубже разобраться
Дополнение 3
247
с классической статистикой Максвелла-Больцмана^ следуя оригинальному
рассуждению сам от Больцмана. Больцман никакими квантовыми стати-
стиками, конечно, заниматься нс мог, так как они появились только после
его смерти в 1906 г.я в 20-е гг. XX века. Больцман в начале 60-х гг. XIX ве-
ка разработал статистическую атом но-молекулярную теорию классического
молекулярного газа.
Следуя Больцману, рассмотрим изолиро винный классический идеаль-
ный газ, состоящий из одинаковых различимых частиц — молекул, а также
способ описания «макроскопических состояний» такого та, или «макро-
состояпий», которым Больцман сопоставил «вероятности»,, точнее, «тер-
модинамические вероятности», т.е. числи «микросостояний», реализую-
щих «макрососюяния». Он посчитал «равновесным?? состоянием газа то
его макрос осюяние, шдет яаибатьшуде ге/тяшмкть, т. е. мак ро-
сс стояние, которому соответствует наибольшее число микро состоянии.
Рассуждая таким образом, Больиман сярого вывел известное распре-
деление Максвелла молекул равновесного классическою газа ио скоростям
(сам Максвелл дал, к сожалению, только математически несовершенный,
нестрогий вывод формулы своего распределения, от которого потом, впро-
чем, отказался н пользу вывода Болы шана).
Способ рассуждений Больцмана ПОЗВОЛИЛ ему дать ИЕГгерпрсташпо
термодинамической энтропии обычного молекулярного газа с позиций
атом но-молекулярной теории вещества. Он получил для энтропии свою
знаменитую «формулу Больцмана», которая, по предложению Планка, вы-
бита на его могильной плите.
Рассмотрим изолированный классический газ, со-
стоящий из -V одинаковых бесструктурных различимых Г] Г
точечных классических частиц массы т, находящихся |—|-
в сосуде объёма V. Пусть этот газ не взаимодействует ’ -
со своим Окружением, т.е. находится, скажем, в цилин- ’ „ ь и
дричсском сосуде с механически жесткими (недеформи- - '
руемыми) и не пропускающими тепло (адиабатическими)
стенками, закрытом нетеплопроводным жёстким порш- -—------------
тзем, который закреплён некоторой защёлкой и своём
фиксированном положении, как показа ею eib рису ее кс. Этот газ может пре-
бывать в различных состояниях. Кроме одного. «равновесного», все эти
состояния «неравновесные». Газ находится в каждом из них лишь одно
мгновение, когда, будучи возмущённым, он изменяет своё состояние и про-
ходит через это мгновенное неравновесное состояние^ стремясь перейти
24N
Глава 5
в конечном счёте в равновесное состояние. Попав в него, газ будет оста-
ваться В ЭТОМ pUBJIOBCCEJOM со стая ни и неограниченно долго.
Равновесное состояние рассматриваемого газа характеризуется тем,
что оно octao/rfttau до лломюсэтш вдела чдетнц и до /дс-идерлдтуре, те
в этом состоянии плотность числа частиц газа во всех точках его объёма
одинакова и равна д = jV/V, где /V — полное число частиц в газе, V
объём газа. Также температура равновесного газа во всех тачках его объёма
одинакова и равна Т,
Ниже для просто™ рассуждений рассмотрим по отдельности дерде-
состояния гаж которые: ]) либо но но
не однородны по температуре, 2) либо по по не
однородны по плотности. Конечно, надо быию бы рассмотреть произволь-
ные неравновесные состояния газа, неоднородные и по температуре, и по
плотности числа частиц, но это только усложнило бы рассмотрение и нс
дало бы нам ничего нового.
Для получения окончательных результатов достаточно рассмотреть по
отдельности неравновесные состояния либо типа 1), либо типа 2).
«Однородное» означает оМнлкбяое во всех нр£><?^днстйекяыис точках.
госдаоянда жя, я о ллотнос/ии, ля
не1 яо m&wwepffWpptf
Предположим, что наш газ имеет во всех точках одинаковую плотность
числа частиц, и рассмотрим его макросостсяният которые ио
ияотпоедш.
Рассмотрим сначала истинные в смысле классической механики состо-
яния нашего газа. Следуя Больцману, истинные состояния газа математиче-
ски надо характеризовать следующим образом.
Каждая частица газа с номером j = 1. ... f Лг, где Аг — полное чис-
ло частиц в газе, пребывающем в некотором истинном состоянии, имеет
определённую скорость Vj tr^, vp).
Чтобы рассмотреть скорости всех частиц
газа и данном его истинном состоянии, од-
нородном по плотности, возьмём абстрактное,
т. е. существующее только в нашем воображе-
нии, «пространство скоростей одной молекулы»
с осями иХ1 vy, иг и отложим в нём из начальной
ТОЧКИ О векторы V1 . . . . , V\ скоростей всех ЧИ-
стиц таза в рассматриваемом состоянии газа, как
показано на рисунке. Конец вектора v, является
Дополнение 3
249
«изображающей точкой» частицы j, причем j = L ..., Лт, в рассматривае-
мом истинном состоянии газа.
Рассматривать пространственные положения молекул газа Cj (х7.
сейчас не будем, так как интересуемся газом, пространственно однородным
по плотности.
CtWKywfltwib всеж ызофвдждададги частоды га?д точек я иростроя-
c-fflffe скоростей огЬмлг частицы, л.тл жолекиды, однозначно лифокт^ри^ет
пстгтиое, йЛн, ктк буdeu НЯЗЫОДть его, «лшкросколпчегхосА состояние
аазд.
Разобьем теперь, следуя Больцману, рас-
сматриваемое пространство скоростей одной
частицы газа на малые «ячейки» одинаковою
объема uj+ тесно примыкающие друг к другу
и исчерпывающие без зазоров всё рассматри-
ваемое пространство скоростей, например, на
кубические ячейки, показанные на рисунке.
Будем для простоты считать, что число Л/
этих ячеек, хотя и очень большое, но конеч-
ное. Тен самым фактически рассмотрим толь-
ко некоторую центральную часть простран-
ства скоростей одной частицы, игнорируя в нём области с очень большими
нереальными значениями скорости v.
Указанное розйненне л/?ослфянстяа скоростей одной на
ячейки будем считать раз и навсегда задагшылг и лсизислаы.и ла н/югагя-
лсеанн всего нашего рассуждения.
Пусть индекс £ = J. .. .Л/ нумерует от-
дельные ячейки в нашем пространстве ско-
ростей со скоростями vJL{^jjr? Ячейка
с номером а характеризуется скоростью v, сс
центральной точки и энергией = у +
— Предполагаем, что ячейки, хотя
и малые (как будем говорить, «макроскопиче-
ски бесконечно малые»}, но содержат каждая
1ю очень большому числу «изображающих то-
чек» частиц газа (попавших в эту ячейку для
рассматриваемого неравновесного состояния газа).
Макроскопически малые — значит, малые в масштабах обычной макро-
скопической физики. Микроскопически малые — значит; малые в масшта-
бах атомов и Молекул. Так. рассматриваемые сейчас элементарные ячейки
250
Глава 5
в пространстве скоростей одной молекулы имеют, скажем, линейные раз-
меры ОД % от куба тепловой скорости молекулы в воздухе 500 м/с,
тс. размеры порядка (0т5}3 мл/с'\ так как Дгг± = An'v = Ai'z 0, 5 м/с.
Молекул в воздухе порядка числа Авогадро /Уд = б 10й3 на 22,4 л или на
104 см3.
Таким образомь на одну Гюльц мало некую «ячейку» приходится огром-
ное число молекул порядка ±¥а “ 6- 10й3 : 1.01 : 1()6 1014 при объёме
сосуда с газом V = L см3 и при Л/ = 10е, где номер ячейки i = 1.Л/.
На приведённом рисунке изображена произвольная болы ивановская
ячейка с номером г в пространстве скоростей одной молекулы и me того
изображающих точек молекул газа, попавших в эту ячейку.
Следуя Больцману будем говорить о eonuufe -w-
eqps, неравновесных состояниях гам и олишеи каждое из них чиелолш
М, Лтз, .... JVjvr частиц гд?л. wcwuewui е Z-rt>. 2-да. .... Л/-ю ячейки л/до-
cm/JdHcmeei свдз/дастей люлетсуты.
Другими словами, каждое макро сколи чес кос состояние газа будем ха-
рактеризовать соответствующим ему «распределением» его частиц по ячей-
ками
НЕРАВНОВЕСНОЕ СОСТОЯНИЕ Л’ь Лг2, ./Ум?
при этом очевидно,
W
JVi + Л’а + ... + /Уд/ = м = jv,
I
где Лг — полное число частиц в газе, одинаковое для всех состояний газа.
Обратны внимание, что с помощью набора значений чисел Лт1. Лга. .. .,
Ул/ истинное «микроскопическое)) состояние газа мы не можем однознач-
но охарактеризовать. Зная числа ЛГ|. Лг2, - - -, Л’,у, нельзя точно указать это
микросоСтолнне газа, так как существует много микроскопических состоя-
ний газа* которые описываются одними и теми же числами У17 /У2.Ум-
Чтобы учесть то обстоятельство, что набор значении чисел Лт]. Лд.
Ум не характеризует однозначно состояние газа, будем говорить о «мак-
рсс конических» его состояниях. Состояния, однозначно характеризуемые
множествами изображающих частицы таза точек в абстрактном простран-
стве скоростей частицы с осями oz> описывают микроскопические
состояния однозначно (если отвлечься от координат частиц xj, эти
состояния поэтому мы и называем «микроскопическими».
Следуя Больцману, припишем теперь каждому макроскопическому,
во обще говоря, неравно носе гону состоянию газа о пределен еюс значение
Дополнение 3
25]
его так называемой «термодинамической вероятности» IV (по-немец.
Wahrscheinlichkeit — вероятность). Таким образом, термодинамическая ве-
роятность IV является функцией -W переменных ДО|П ДО?. . ... ДО^й
^ = 1У(ДО1?ДОЬ - : Агл/>-
Термодинамической вероятностью IV состояния газа М, ДО2, .... ДОЛ/
Больцман назвал числа сласаг>ла. ХАеторылш цдоб/гадгяюыр/с1 /начли ДО чл-
стиц гдзл .намело /шзнзетть на А/ ячейкам нрАс?т/>дн-
елдеа cffopAcmcu ottaori чаелш^ы таким образом, чтобы в 1 -ю ячейку попало
ДО1 частиц, во 2-ю ДО2 частиц, ..., в jV-ю ячейку попало ДОд/ частии.
При этом Больцман считал, что частицы газа различимы, он даже
снабдил их номерами I. 2П ..., ДОГ. Так что каждому «макроскопическо-
му состоянию» газа, характеризуемому набором чисел ATj, ДОа, .... Агм,
Бсльцмзе! сопоставил очень большое число его «микроскопических состоя-
ний», которые хотя и характеризуются одними и теми же значениями чисел
Л'1- ДО^, ..., ДОма ни отличаются друг от друга тем, что хотя в 1-ю ячейку
попало заданное число ДО1 частиц, во 2-ю— число Лг2 частиц..в Af-ю
ячейку — ЧИСЛО ДОу частиц, ни частиц С разными номерами.
Согласно известной комбинаторной формуле число способов размеще-
нии ДО различимых объектов ио Л/ ячейкам с таким расчетом, чтобы в 1-ю,
2-н\ ..... Л-/-ю ячейки попали заданные числа пре листов ДО]. ДОа.ДОд/
соответственно, равно
' ...
здесь факториал ДО! = 1. 2... ДО и т. д. Как видим, вероятность IV действи-
тельно является функцией многих переменных М, ДО2, ..., Лгл/,
Рассмотрим, например, случай ДО = 4, Л/ = 3, т.с. случай 4-х частиц,
снабженных номерами 1,2, 3, 4, и 3-х ячеек. Макроскопическому неравно-
весному состоянию, которое характеризуется числами ДО> = 2. ДО^ = ДО3 =
= 1, соагветстиуют 12 микроскопических состоянии, указанных в приводи-
мой ниже табличке.
Комбинаторная формула для Hz для зтюго примера ласт значение
Ит = = 24 —io
2! 111! 211 :
т. с. то же число 12 микроскопических состояний.
252
Глава 5
]-я ячейка 2-я ячейка 3-я ячейка
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 3 1 4
2 3 4 ]
24 1 3
24 3 1
3 4 1 2
3 4 2 1
Отиысгание состояния глад
Следуя Больцману, среди макроскопических неравновесных состояний
гам найдём теперь такое его макроскопическое состояние, для которого
/яфмо()мна*/1/чй?кая лдекси.молыш. Согласно Больцману, оно
И является довдлгесдвдм СЛЮИДОШ, £1Г.
Таким образом, равновесное состояние — это такое макроскопическое
состояние, которому соответствует максимальное число микроскопических
состояний.
Имеем, таким образом, следующую задачу. Надо найти такие числа
Л'1- Лт2, ..., ЛГд< (обозначим их Arj‘. jVJ । .... Л1^), для которых функция
ИТ(ЛГ1, .... 2УМ) имеет максимальное значение (обозначим это значе-
ние И7»), или, что математически эквивалентно, найти максимальное зна-
чение функции In W(Лгц, Лга, ..., .¥Л/) (её максимальное значение обозна-
чим In JVo).
Следует учесть при этом, что числа Л1), jV>, .... ЛГм удовлетворяют
двум очевидным для изолированного газа условиям:
LV N
E‘V- = JV’
3=1 1=1
где jV — полное число частиц в газе, Е’ — полная энергия рассматриваемого
изолированного газа, неизменная для всех его состояний (газ изолирован-
ный, ни с чем не взаимодействующий).
Полное число частиц и полная энергия изолированного газа неизменны
и имеют Одни и тс же Значения для всех сто состояний.
Дополнение 3
253
Так что мы имеем задачу на так называемый усяоелый 3Kt?mpewy;w
функции нескольких переменных.
Чтобы найти этот экстремум, воспользуемся .истоJan неолрейвийных
.штаютготедей согласно которому надо рассмотреть не вариаци-
онное условие (5ИГ = 0, как для абсолютного экстремума, а вариационное
условие
(лг х /л/ х
52 N*) - з <51 У = °>
r=L / \i = l /
б котором а+ /3 — гак называемые лголрс^елёУшьге1 .ииоясиетелм Ялрллжд,
для вариаций около равновесного состояния. Неопределённые множители,
у нас ос и 0, - это просто некоторые числа. Следуя Лагранжу, надо считать,
что приведенное вариационное условие выполняется при лрештвотьвых
/детфетх ^jVl, .... tfJVjw около значении Аг|\ jVj .. - -, /V[^? т. с. при вариаци-
ях
Nj =< + *#!............ ЛГ„ = A^ + 41VW
около отыскиваемого равновесного состояния, не обязательно удовлетворя-
ющих указанным выше условиям:
Л' Л"
£^ = о, =
/-1 1-1
Пользуясь приведённой комбинаторной формулой для термодинамиче-
ской вероятности IV = W(jV14 ..., jVw), вычислим вариацию In IV. Оче-
видно, ЧТО
м
In W = ]п Л1’! - In Лгй!.
i-1
Для входящих сюда факториалов воспользуемся приближенной фор-
мулой Стирлинга:
InЛГ1 = 1п(1 2... JV) = In 1 1-]п2 + ... I-In Лг^
JV JV
- I InNdN = (/flnW-W) ^-VlnjV-tf.
1 1
справедливой при больших значениях -V. Таким образом, для вариации
A In IV имеем формулу
* 1п ТУ = 4{Л In N - Лг - J2 Л*111 + 52 jV^ =
254
J'Л л ВЛ 5
. - £ ЙЛ, 1„ Л? - £ ЛГ? t £ Wi
i i * ?
ЧИСЛО Лт варьировать нс Нужно» гик k;ik ОНО ПОСТОЯННО. Си сд о капельно,
£ Id И/ — — In Af® Л/V;.
t
Подставив эту формулу для r5 In VV в вариационное условие ЛаграЕтжа,
получим условие
- 521пЛ? Ajv - « 52йЛ’ - /?53 ЙЛГ< = °’
i т *
т.е. условие
52 {111Л?+«4 ?Ei}6N; =0.
1
которое должно выполняться при произвольных вариациях £A’i, ..,4Лгь^.
Легко видеть, что необходимые и достаточные условия для удовлетво-
рения последнему равенству при произвольных вариациях
дают следующие уравнения:
1пЛг-' — —а — /?c-i при г = 1,2.....Л/.
Таким образом,
А’° _ е-“е- *£< _
где С и Д — некоторые неизвестные постоянные, причём С = е_°.
Чтобы найти значения констант Си J, по Лагранжу, следует вдеполь-
зовапгься двумя имеющимися у нас условиями. Во-первых» условием
52 IV" =
i
из которого для равновесного состояния гзза непосредственно получаем,
что
с У С = Ат. Л _ :
т
т.е. определяем константу С\ которую, как видим, можно выразить через
константу /3- Во-вторых, условием
52 е» Л? = Е.
Дополнение 3
255
из которого получаем, что
Е^-^
Ее-^’
те. формулу, из которой можно наши значение константы /?, если известна
энергия £ газа.
Наконец, вычислим значение In Wo, соответствующее найденному
максимуму, т.е. равновесному состоянию газа. Имеем
In Wt> = In N - jV? lu A'? = W In ;V - Af ln(Ce‘^) -
1 г
= лт injv - inc у} +0 52 = v 1,1 jV -дг lnC ~I3E-
так что окончательно получаем, что
In Wo = Д' In Дт - Аг In С + 0 Е.
Распределение Максвелла
Покажем, что найденное нами распределение частиц классического га-
за по ячейкам ЛГ? = Сс--3^ язя равновесного состояния газа является
«распределением Максвелла» молекул равновесного классического газа по
скоростям.
Перейдем для этого от дискретны* к непрерывным обозначениям.
Ячейки в абстрактном пространстве скоростей одной частицы теперь
возьмём одинакового лелкт/никдай чески бесконечно .шлога объёма и =
Ячейку с номером г мы характеризуем компонентами ско-
рости Uin VjVn некоторой её «центральной» точки и энергией с; =
= ^7 (v^. + 1'?аг + 1«)- Так как ячейки макроскопически бесконечно милые,
то числа Лг^ тоже являются макроскопически бесконечно малыми, и мы
должны положить ДЛЯ НИХ, что
Лт" = Лг /о(иа, trt, и*) dUa; di'y ,
где функция /□(vT. v,) называется «функцией распределения» молекул
равновссЕтого газа по скоростям. Она характеризует равновесное состояние
256
Глава 5
газа и имеет следующий физический смысл:
/o(^FJ Vjs)^3C^fy ^t?A =
= од№№лдос'П№ той?, что йгстугяд ядяиая члслшцл. шти лгялекутл
гдзо, топйящсдося * роэтговег.шш состояли. ftwefт
го.нлокс'нт w её см/мт, .^-жяидоге ₽ лдрсЗелод
fjm v.jr t> Ч- </?> j Vp tto Up + dtp OJW 1> V? + rft1*.
Используя наш результат о том, что Аг/ — Сс'^', получаем, что
Ш.г„»,) = С’1=-Йт/2Й + ',« + г,=),
где мы ввели ещё одну так называемую лостоя^ую
с = с = -£-
У </и:С rft’p dt\ Лг иh
здесь r^?'Tduyduz = lv — объём отдельной макроскопически бесконечно ма-
лой ячейки в пространстве скоростей одной частицы. Константу С\ можно
выразить через параметр /J, если воспользоваться ycwffr^.iг яоршировяш
-с»
У" У У fn(v-.c, vv. v,) dvx dvv dv-t - 1,
- M
которое Следует из условия АГр =- N и приведённой выше формулы, вы-
i
ражающен числа Аг'] через функцию /о(иЯ1 uv, иг). Подставляя в условие
нормировки найденное выражение для функции /у(и.Г: г^, получаем
Сх j" f J е“^т/2 <и* -Н + dv, dv, dvt = 1,
/ +г* л \ 1 / X В/2
CL / e-^/2^duJ =1, Ci (#) =1.
I/ I v?m/
Следовательно,
Дополнение 3
257
при этом мы воспользовались известной формулой для интеграла Пуассона:
+«>
У е-^ d:r =
-ао
зилчсные лиюжч/ше.тя Д Используем для этого формулу вы-
ражающую полную энергию газа Е через константу J, учитывая, что для
рассматриваемого газа одинаковых точечных бесструктурных частиц энер-
гия газа равна Е = jV к& 7В где 7 — температура газа. Таким образом,.
£ = АГ | ЛеТ =
= Лт G IJ J + ^ + v=) e-(7m/2 (w* + + A, dvt =
1-М
= jV С. J JI v2 & + < + Ф A, dv, =
—DO
интегралы с v*, стоящими в правой части второго равенства в круг-
лых скобках под знаком интеграла во второй строке, множителями перед
экспонентой, одинаковы, и поэтому берём интеграл для г* и умножаем его
на 3. Формулу для вычисления первого HHicipajia в последней ciposc мы
получим из приведённой формулы для интеграла Пуассона дифференциро-
ванием по параметру 7:
4-М
f х2 S~'I'J:2 (lx = | л~а/2
Используя Эту формулу и формулу дня самого интеграла Пуассона
и учитывая, что 7 = /Зт/2^ окончательно получаем, что
jV - Air 7 = Л/ —— = JV —
Л2ЙЬ' 2 2;<
25Н
Глава 5
Следовательно, лагранжев множитель имеет значение Д = l/(tsT).
где Т — температура ранЕювсенсп> состояния га:*а, определяемая значением
его полной энергии Я по формуле Е = Аг 7’.
Окончательно для функции распределения частиц классического рав-
новесного газа по скоростям имеем формулу
«».. V.) = LfyFe m « + “2 + •»/«• Г;
\ JTT лГб J /
это формула знаменитого распределения Максвелла.
Приведённый нами вывод распределения Максвелла болъцманонеким
методом Ячеек является строгим его ВЫВОДОМ, КОТОрЫИ дал Больцман.
Неравновесные однородные по температуре состояния газа,
не однородные но плотности
Рассмотрим теперь множество макроскопических, вообще говоря,
неравновесных состояний типа 2) нашею изолированного классического
газа, а именно: — множество его пространственно неоднородных состо-
яний. a m&nLffOflow сиысде, те, однородных по температуре
(выше мы рассмотрели множество макроскопических неравновесных со-
стояний 1ии;1 I), однородных в обычном пространстве, ио
fl шаллютмг смысле).
Имеем изолированный от внешних воздействий классический газ, на-
ходящийся в сосуде объёмом V, стенки которого жёсткие и нс пропускают
тепло.
Следуя Больцману, объём V этого сосуда разобьём на очень малые, как
говорят, макроскопически бесконечно малые ячейки одинакового объёма и\
причём пусть А/ — полное число ячеек; таким образом,
Af^ = V.
Это рлэбыешие объёма V газа кд ячейки будем считать ид
дссгл нашего
Макроскопически бесконечно малые ячейки, на которые мы разби-
ваем объём V, содержат по огромному числу молекул с координатами
rj(sr У/п зД где j = 1,2... ,xV. Рассматривать скорости молекул V/ те-
перь не нужно, так как мы интересуемся состояниями газа, однородными
по температуре.
Дополнение 3
254
Скажем, пусть V = 1 см3 и пусть w - Ю-3 см3.. Тогда Af, = V : и = 103
и произвольная ячейка i (i = 1. . . ., jU } при равновесии содержит число
молекул ±Va [юридка jV, — 10lfl : Ю3 = 10lfi молекул.
Следуя Больцману, рассматриваемые макроскопические простран-
ственно неоднородные состояния газа будем характеризовать числами
j\ri, .'V^r - : АГд/ частиц газа, попавших и 1-ю, 2-ю,.... Af-ю ячейки.
VflcmwHiw слеф'я /?лсслг£гт/?ийя^м тлк
™к cv/a&wirew их лсшера-ми 1. 2, ... ? ±¥.
По Больцману, термодинамическая вероятность И7 макроскопического
состояния это число способов размещения >V частиц та, снабжённых
номерами 1, 2, ... , jV, по А/ ячейкам таким образом, чтобы в 1-ю ячей-
ку попало ЛГ! частиц, но 2-ю — Лн частиц, ...., в Л/-ю — jVju частиц, где
числа ЛГ1...xVjV характеризуют рассматриваемое макроскопическое, во-
обще говоря, неравновесное состояние.
Согласно комбинаторной формуле эта термодинамическая вероятность
равна
IV ---------—------.
^hVs? ... Л’л/!
Отыскание равновесного состояния
Следуя Больцману, найдём теперь /равновесное состояние рассматрива-
емого классического идеального газа как состояние, .иля-
«мгуи функции lull' = 1пН'(Лг1, ... .А\и) при дополнительном условии,
что V jVt = ДГ, где Лт — полное число частиц в газе.
I
Используя .wcwjod wjwmmu Лсгерян.чра для отыска-
ния этого условного максимума, возьмём вариационное условие
ЛпИг-й =0,
1
выполняющееся, по Лагранжу do л/w мольных вдршций JJV, около рав-
новесного СОСТОЯНИЯ, R КОТОРОМ ft нНЯОИСИтйТЬ Лоа/КГЯ-
,жй. Так как это вариационное условие должно выполняться для л/здыдаоль-
ньис ffrfpwwwww JjVn т.е. не только для вариаций., которые удовлетворяют
условию
£ г5л; = о.
Из приведённой комбинаторной формулы и формулы Стирлинга непо-
средственно получаем,что
Jiniv = - £ in 1»д;.
260
Глава 5
Следовательно,
V In Я? * М <* У2 * Ni = °.
i t
ИЛИ
22{LnAr!' =0.
I
Отсюда заключаем, что
In Л'-1 + а = 0, АГ? — e"Q = С при / = 1.....Af.
где С — постоянная, заменяющая константу ос. Значение ее определим, но
Лагранжу, из условия
i
Как ындим, для равновесного состояния идеальною классического га^
за его частицы равномерно распределены по ячейкам объёма газа, i.e. по
его объёму, так как ячейки одинаковые. Так что в равновесном состоянии
atr? ла ил Арности.
Так как /VJ1 = С\ то из условия нормировки непосредствен ею получа-
ем, что
СИ = АГ, С = 77 = = C = nw,
М к
где n — Af/V — объемная плотню сгъ числа частиц в равновесном состоянии
газа.
Вычислим, наконец, In И'гПтт. е. значение Ln И\ сортветствующеелгак-
сшиу.иу r/.iy.4X7fUU Л 2.....АГл/}, А СЛСДОВаТСЛ ЫИ), pUSHflffWH/MJV СА-
стлаянша /?дссл(от/71^демли? гс7?д Имеем
]п ИР|> = АГ In АГ —JV? Ln Я? = Аг Ln — A1' In f пгт^ j = const+JV Ln V,
* ?
где постоянная const означает постоянную, не зависящую am V.
классической газа w ныяос) г/ял/лиуты
Предложив концепцию термодинамической вероятности и принцип,
согласно которому/JdffHA₽ecHO₽ САстлячив? отличатся от
л?ел. что u.wccm л^доскмодогую мершрдшдоничссную вЁрлятяодояь, отыо
кав гермодинамически равновесное соеюянис классическою газа точечных
Дополнение 3
26]
различимых частип и показав, что оно характеризуется распределением
Максвелла молекул по скоростям и пространстве]шо однородно, Больцман
установил с.иысл найденной им величины In Иоь где И-fj — мак-
симальное значение IV, связав её с равновесного состояния газа.
Воспроизведём здесь его рассуждение Рассмотрим сначала неравно-
весные состояния типа I), т. е. состояния, ойяороЭные л о JWppiwtjcrcHj wo we
ло даел/лерп/пъре.
Подставим распределение Максвелла в выведенную для этих неравно-
весных состояний формулу. Получим тогда, что
In. Иф = ЛГ In Л' - Лг In С + /? Е.
Выше мы доказали, что J = 1 /{^ь^П я С1' = С\ Л\иа где w — объём
элементарной иней к и в пространстве скоростей, С'| = (т/Йтг^ьТ1}'' —
нормировочная постоянная в распределении Максвелла. Для рассматривае-
мого идеального классического газа его энергия равна Е - (3/2) fa ГК, и,
таким оВра:!ом
1п1У0 = *Б Лг In W Д’ In ATu>
m
2а/скГ
+ | fc& V
Обращая внимание в этой формуле только на зависимость от темпера-
туры Г, НИДНМ, ЧТО
fee In Ка = const + jV /l-б IqT1 = const + Cv In У,
1
где С,. = j Аь|- .'V — теплоёмкость при постоянном объеме рассматриваемое
классического идеального газа; постоянная const обозначает постоянную,
не зависящую ж температуры.
Рассмотрим теперь неравновесные состояния газа типа 2), т. е. состоя-
Т11ГЯ h ло J|0 Jdf fl^HOjPOdwWC «о лдотносдеи.
Для этих состояний мы имеем формулу
In Ио = const -I- iV In 1Л
умножая которую па получаем
fcb In Ио = const I- (гб Лг In I7 = const H /?
Лт
Ад
In V = const + R "У In V.
262
Глава 5
так как А*бЛгд = Я и // = mJVx, m — масса отдельной частицы Д —
упинсрсалыдая газовая постоянная. Таким образом,
jtE In IVtb = const + 4г Я In V,
где постоянная const не зависит от объема V.
Скомбинируем теперь обе ВЫВСДСЛЕТЫС формулы ДЛЯ Й1 И^}, полу-
ченные для неравновесных состояний обоих типов 1) и 2). Придем тогда
к формуле
fcB In W o = const + Cd InT + R In V,
в которой постоянная const теперь не зависит ™ от объёма газа, ни от его
температуры.
Покажем теперь. что в точности таким же образом^ кик величина
At In И'о, от температуры Г и объёма V зависит энтропия газа.
Напомним, как определяется энтропия равновесного состояния рас-
сматриваемого газа в термодинамике.
Пусть имеем два ранЕюксспык состояния а
и it газа. изображённые точками на R V-дна грам-
ме равновесных состояний газа па приведённом
рисунке, и перейдем из состояния а в состояние &
пс кн^зиравповесному, другими словами, обрати-
мому процессу £+ состоящему из изобары и изо-
хоры, как показано на рисунке.. Промежуточное
состояние в этом процессе мы обозначили как с.
R термодинамике строго доказывается, что
при определении энтропии некий я.тятл обрели ггмыи £,
Zdi MJ состояния « СОСТЛОЯЙМ^ it,
лишь бы этот процесс был ^рптл,мыл1; сейчас мы взяли обратимый про-
цесс, состоящий из изобары и изохоры.
Согласно термодинамическому определению энтропии имеем формулу
ft
-’а + j j,.
в которой С — произвольный обратимый процесс, переводящий термодина-
мическую систему из равновесного состояния л в равновесное состояние Ь.
Дополнение 3
263
Из этой формулы следует, что
Заметим, что в термодинамике определена лишь /эдзненлиъ зшп/эдлгш
рлйлаяеслыдг состоя л нн, асишнилныЕ злдчелдя энтро/шй рд&позрсмы.х £ю-
с/лбяяш ярш^иииллыш ие онри)еяейы.
Энтропия н внутренняя энергия определены в термодинамике лишь
с точностью до произвольных так называемых аддитивных постоянных,
имеющих Одинаковые Значения для всех равновесных состояний термфди-
намической системы.
Процесс йг — обратимый процесс изобарного нагревания газа; для него
JQ = CPdT, где Ср — теплоемкость газа при постоянном давлении. Про-
цесс Н) — процесс изохорного нагревания газа; для него = С1? dTT где
<7V — теплоёмкость газа при постоянном объёме. Обе теплоёмкости, Ср
и для идеального классического газа постоянны (т.е. имеют одинако-
вые значения для всех равновесных его состояний) и удовлетворяют так
называемому соотношению Майера
су - с; = м я,
в котором М — масса газа, д — его молярная масса (не путать с химическим
потенциалом), Л - универсальная газовая постоянная. Таким образомн
Преобразуем полученную формулу с помощью уравнения состояния
идеальною газа
Р V = 4г W.
которое связывает величины, относящиеся к произвольному равновесному
состоянию газа, т, е. к одной и тон же точке на Р. V-днаграмме газа. Таким
образом, получаем
sb - sa = с„ in
Л//д • НТГ
ЛГ/М-ВД.
+ (7(. hi
/ М/ц RTi,
\М/ц-РТл
= GP In + C'v In = Cp In + Cv In .
264
Глава 5
Следовательно, для энтропии равновесного состояния Р, V газа имеем
формулу
S( V, Р) = const + Ср In V + Ср 111 л
в которую входит неопределённая аддитивная постоянная const, одинако-
вах jxJiM всех равновесных состояний рассматриваемого газа+ не зависящая
ст Р, У.
Учитывая, что Р = (Л//д) f/?T/V'), отсюда получаем еще олпу фор-
мулу для Энтропии газа:
5(У Т) - const + (Ср - С|:) In Г 4 Ct. In Г =
= const + 4г fllnV + Cv IriT;
н
здесь мы еще раз воспользовались соотношением Майера.
Сравнивая полученную термодинамическую формулу для энтропии
Г) с больцмаиовской формулой для /сь In WZp, выведенной выше, при-
ходим к знаменитой формуле Больцмана
s = ь и;
связывающей энтропию S н болъцмамовскую термодинамическую вероят-
ность IV равновесного состояния; в этой формуле, следуя Больцману, мы
определённым образом фиксируем значение постоянной const.
Получив указанную формулу для равновесных состояний, Больцман
сразу же обобщил её па произвольные неравновесные состояння-
Своей формулой # = Ае In IV Больцман дал статистическую микро-
скопическую интерпретацию термодинамической энтропии, т. е. интерпре-
тацию её с позиций атом но-молекулярно и теории вещества.
До него такая интерпретация была дана Клаузиусом для давления Р га-
за, температуры Т газа и внутренней энергии (7 газа, по нс энтропии. Дать
атом но-молекулярную интерпретацию энтропии — заслуга Больцмана.
Глава 6
Основы квантовой теории металлов
6.1. Модель свободных электронов
В модели свободных электронов металла учитывается, что валентные
электроны атомов металла не локализованы гта его атомах и метут свобод-
но перемещаться по металлу. Эти электроны обеспечивают электро провод-
ность металла, так как являются «элементарными носителями» электриче-
ского тока.
Взаимодействие свобод! пи к электронов с ионными остовами атомов
металла оказывается всегда малым, и им поэтому можно пренебречь ио
обязательно надо учитывать поверхностные силы, которые препятствую!
выходу электронов из металла.
Теория металлов, основанная на классической модели свободных элек-
тро пои, так называемая атекгс/эонндя ещё до появления квантовой
механики успешно развивалась Друде и Лоренцем, причем она объяснила
многие свойс тва металлов (например, натрия, меди, серебра). В частности,
в рамках этой клдс?£ич^ой>й mtfopww получил объяснение знаменитый закон
Видемз па Opai |ца об у wu wbwou н/мл/j/je^ манат?ьноет м
и меялодрододи-рсти у металлов.
Существенным надостатком классической модели свободных электро-
нов было, однако, то, что в сё рамках не удалось объяснить поведение
металлов при низких температурах, а именно: знаменитый
линейный зилои уменьшения теплоёмкости металлов при малых темпера-
турах, отличный от неоднократно лодлзержденною экспериментом лгубич>0-
сквй> злкйнп уменьшения её для диэлектрических тел.
Квантовая модель свободных электронов металла, появившаяся с по-
явлением квантовой механики, успешно разрешила эту задачу.
Фе/шы Дирака электронов в „иешагм?
Рассмотрим систему из /V невзаимодействующих друг с другом элек-
тронов, находящихся в кубическом ящике объёма V = L3, где L — дли*
на ребра куба, т.е. будем считать, что электро езьс етзходятся в кубической
266
Глава 6
трёхмерной потенциальной яме, такой что потенциальная энергия отдель-
но по Электрона даётся функцией
С/(т, у, z) =
-14,
О,
если
сели
у,z е к
I, у, Z Ц
где Со — конечная постоянная. Предположим, что система электронов, на-
ходящаяся в ящике, может обмениваться теплом и электронами с окруже-
нием ящика, в котором поддерживаются неизменными температура Т п хи-
мический потенциал д (число электронов Д' в электронной системе, нахо-
дящейся в ящике с окружением, н химический потенциал д нельзя задавать
независимо: можно задать либо Лг. либо уз).
Модель системы свободных электронов мы уже рассматривали в гл. 5
и уже показал] l что для неё, пребывающей в равновесном состоянии h спра-
ведливо распределение Ферми Дирака:
в котором /(е) = — среднее число электронов, приходящихся в рав-
новесном состоянии системы свободных электронов на одну элементарную
ячейку в импульсном пространстве одного отдельного электрона, с энерги-
ей S.
Обсудим подробнее это распределение Ферми-Дирака.
Сначала рассмотрим случай малых температур Т и предел нулевой
температуры 7" = 0. Равновесное состояние нашего электронного газа мы
характеризуем двумя независимыми пара метрам и — температурой 7' и хи-
мическим потенциалом g. Но так как плотность числа электронов п — Л717
(их концентрация) в равновесном состоянии электронного газа является
функцией д и Т, то можно характеризовать равновесное состояние элек-
тронного газа также и параметрами п и Т Тогда химический потенциал уц
надо считать функцией /з = д(п. Г) концентрации свободных электронов
п и температуры Т. При заданной концентрации электронов п электрон-
ный химический потенциал д является, следовательно, функцией Т. Предел
этой функции при 7" —> 0 обозначим следующим образом:
ди = lin^ Т);
он называется «энергией Фсрмй». Величину будем поэтому обозначать
также как
6.1. МОДЕЛ Ь СВОЕОД НЫХ ЭЛ ЕKTPOJ J ОII
267
Рассмотрим, во что переходит распределение Ферми-Дирака
1
f& = , vt т
при Г —* 0- Отдельно рассмотрим случаи, когда f и когда е <
В первом случае разность s — /тсь положите ль лая, а потому величина (с —
— * 4-оо (стремится к положительной бесконечности) при
Г —* 0. Так что
lim /(e) = 0 при f > йп-
[|ри £ < jiq разность £ — отрицатель-
ная, а потому (е - ^о)ДбТ -* -«5 (стрс- Де?)
мтггся к отрицательной бесконечности) при
Т — 0. Так что
I -
Бгп /(с?) = I при е < /10.
Графики функции /(с) при малом Т / Г) у —
и при Т — 0 показаны на верхнем рисунке
сплои:ной и пунктирной линиями соответственно.
Распределение Ферми-Дирака при нулевой
температуре можно наглядно представить в им-
пульсном пространстве одного электрона, как это
проиллюстрировано на нижнем рисунке. Постро-
им в этом пространстве сферу с центром в на-
чале координат О радиуса рр, который опреде-
лим из соотношения - р^/2т? так что рр =
= ^/2гп£р. Величина pj? называется «импульсом
Ферми», Эта сферическая поверхность разграни-
чивает заполненные при Г - 0 электронами эле-
ментарные ячейки (внутри сферы) п пустые эле-
ментарные ячейки, не заполненные элекгронами (вне сферы), в равновес-
ном состоянии электронного газа в металле при нулевой температуре J1 = 0.
Указанную сферу в импульсном пространстве одного электрона называют
«фёрми-сферой».
При малых температурах Т <С 7Tfcp распределение Фермй-Дирака ма-
ло отличается ог рас пределен их при нулевой температуре Г — 0. Крити-
ческую температуру Ти? называют «температурой квантового вырождения»
и определятот с помощью равенства
ь кр “
2GN
Глава 6
это температура, ниже которой распре деление Ферми-Дирака практически
Совпадает с распределением при пулевой температуре 7' = 0-
Величина имеет размерность энергии и называется яэнергетиче-
ской температурой». Она измеряется в электронвольтах эВ, причём
1 эВ® 10000 К = 101 к.
Величина cf л ля металлов имеет порядок 10 эВ, так что критическая
температура квантового вырождения в металлах Тф имеет огромный поря-
док 10000 К (при таких высоких температурах никакого твёрдого тела уже
не может существовать). При комнатной температуре Т = 300 К неравен-
ство Т << Тхр выполняется^ таким образом, с большим запасом.
Поэтому распределение электронов по энергиям в реальном металле
ирп обычных условиях (при ком наглой температуре и при температурах
400-600 °C) в очень хорошем приближении можно описывать распределе-
нием Ферми Дирака при нулевой температуре Г = 0, т. е. фермн-сферой,
На самом деле надо говорить нс о фсрмй-сфсрс, а о ссфсрмй
поверхности»» своей для каждого металла, так как надо учитывать симмет-
рию кристаллической решётки металла. В 60-70-с гг. XX в. были прове-
дены обширные экспериментальные исследования по определению формы
поверхностей Ферми для многих металлов и сплавов и были составленье
обширные атласы этих поверхностей.
При нулевой температуре и поэтому
р*
1
- до) 4 j ’
это трансцендентное уравнение для химического потенциала р при вульвой
температуре Г = 0 и заданной плотности п числа свободных электронов
приобретает простой вид:
31га Я3
= —Гр
ОТГ Г4.
где pF — импульс Ферми, связанный с р0 условием ?(pf} = = ро-
Таким образом, при нулевой температуре Г = 0 имеем
д(0) = йп = (3?г2п)г/:'.
где п — концентрация электронов проводимости.
6.1. МОДЕЛ Ь СВОЕОД НЫХ ЭЛ ЕKTPOJ J ОII
269
Действительно, при макроскопически большом объёме V можно счи-
тать, что сумму по р можно заменить интегралом по р согласно припишу
р
1
(21ГЙ)3
1I.OJJ ЬJVЯСЬ Ф ирМулОй
легко вычислить энергию Ферми. Ниже в табличке приведены значения
концентрации электронов проводимости и энергии Ферми для трёх однова-
лентных металлов
металл концентрация п х 1022см В эВ
Na 2,5 3,12
Си 8,5 7,04
Afi 5,8 5,51
Оценим величину энергии Ферми зная плотность р металла. Для
одновалентного металла, например мели Сгц можно предположить, что
каждый атом металла отдаёт в систему свободных электронов один элек-
трон. Тогда концентрация тс электронов проводимости в металле равна чис-
лу атомов металла в единице объёма. Таким образом, концентрацию тс
свободных электронов в металле можно найти, разделив число Авогад-
ро Лтд на молярный о&ьём вещества металла^ который равен молярному
весу делённому на плотность металла. Для меди Си
мол. объём
63,5
йпУ4
= 7.1 см\
следовательно.
п = ЦЦ!2 = в.5.102а см-3.
Рассмотрим теперь случай больших температур 71, хотя он и нс ре-
алистичен для металлов. 5т от случай важен для нас, однако, потому, что
при больших температурах распределение Ферми-Дирака переходит в рас-
пределение Максвелла для классического газа. Случай высоких температур
соответствует большим отрицательным значенияи химического потсе п шал а
270
Глава 6
(таким, что отношение —► -оа)г Тогда в формуле для распределе-
ния Ферми-Дирака в Знаменателе можно пренебречь единице и по сравне-
нию с экспонентой и получить, что
ffe) = е^“ г)АвТ _ е^Д1>Г. e-f/kbT =се--^ьГ,
где С — нормировочная постоянная. Так как £ = pa/2m = ггш2/3, где г —
скорость электрона, то
/(£)^Се-т,|2/2/=БГ;
получили распределение Максвелла.
Таким образом, при температурах Г » Гнр распределение Ферми-
Дирака действительно переходит в распределение Максвелла. Этот случай,
однако, как мы уже сказали^ нс реалистичен для металлов.
ЭлГЛТН/ИЯЫ 6' НЕЛЬЗЯ /tfCCMtfWpUftfJHb как космиче-
ский udeojfcHUu гяз .ммежул ндлри.чер кйр из .иолеяул
6.2. Вычисление функции jz(T) при малых
температурах Т
Вычислим приближённо функцию д(Г) при малых температурах Т.
Согласно формуле распределения Ферми-Дирака для химического потен-
циала g имеем трансцендентное уравнение
,у = S7 1
+ 1'
в котором А’ — число свободЕтьЕх электронов в металле, = р^/Зтп, про-
екция спина it = z 1/2, и суммирование проводится но бесконечному им-
пульсному пространству р по ячейкам объемом (2тгЙ)3/V' и по проекциям
спина сг = ±1/2. Концентрация электронов та = AT/V.
Это трансцендентное уравнение позволяет найти химический потен-
циал /1, если известна концен трация п электронов.
Для этого надо получить асимптотическую формулу для функции кон-
центрации электронов п(Т) при 7’ -* 0. При малых температурах можно
считать, что + Дуя, где Д/z — малая добавка. Проводя вычисления,
получим
та = .. 4- чл. йытпе 712 +Ддс f™ + чл. исчез, при Г —* oY
З-2 h3 б^рр Vraft3 /
63. Теплоемкость системы свободных электронов
27]
Следовательно,
Зтг2^!
_ д ™pF
6n:W д№
pF = (3?г2 №и)1/3;
1Г2 чт^Т2
б
7Г2 ^"Г2
12 До '
так что Окончательно имеем следующую формулу для функции /i(T) при
малых температурах Г:
2 1
Д = до - У2 + ЧП. выше 7й.
Полный расчёт проведёт! в Дополнении I.
6,3. Теплоёмкость системы свободных электронов
проводимости при малых температурах
Найдём теперь приближённое выражение для влучренлей энергии
i7(7j системы электронов проводимости металла при малых темпериту-
pax Г Согласно распределению Ферми Дирака для внутренней энергии
имеем следующее выражение:
и = у,
е^г<Р> + 1
р. 1 г
тя котором t(p) = /г/2щт и суммирование по р ведётся по бесконечному
им пульс Еюму простра Етстну р по ячейкам размером (2тгй)*/У и т = 4 1/2.
В пределе У —* оо, ЛГ —» оо имеем
и _ . 4т [ ^3 , g(p)
V (2?г Л)3 J 4- 1 ’
О
так как при V —* ос
V 5L _ (2irft)8 /dl>
р
272
Глава 6
р3
?F
2m 10т?г3П3’
При нулевой температуре, таким образом, получим, что
PF
Гл,. ? i /'
v tt’V./
:i
где Pf - — импульс ФермЙ, СВЯЗАННЫЙ С Концентрацией л 'злектронсв прово-
димости формулой pF = (35Г2Й4
При малых температурах Т в формуле для ^7 можно считать, что /j —
V
= /[0 + Д/1, где доф = и Д/j — малая поправка. Тогда, разлагая правую
11
часть формулы для г? по малости А/* и проводя приближённые вычисде-
I
ння. получим формулу
Г _ Pf
г 1итгаЛ3
m(ktT)2pF 2
-----------h чп. выше j .
(ihJ
причём здесь
6П3
m(itET)>F 2m(fcFWr ttbT)2 , 2*3 №
-----------= ------ГТ----=------Ч— Этт ft п = ?г п.
4.37i3£F 4Гкр
Полный расчёт приведён в Дополнении 2.
Для теплоёмкости единицы объёма системы свободных электронов ме-
талла при малых температурах получим выражение
г _ d
\ I;
.2
2 Т|ф
так что дтя молярной теплоёмкости электронов проводимости (при п =
= Атл/У, Ад — число Авогадро. V — молярный объём) имеем формулу
с - уТ, > = 2^,
1 ' 2ГФ’
здесь Я — универсальная газовая постоя] птая.
Для металлов, к которым модель свободных электронов проводимости
применима, молярная теплоёмкость имеет порядок 1н " ] кал/К. В табличке
приведены экспериментальные значения коэффициента у для трёх однова-
лентных металлов.
6.4. Те рмсэ л lktpo нн а л эмиссия
273
металл 7 X Ю4 кал/К валентность
Na Си Ag 4,3 1,73-1,80 1,54 1,60 1 1 1
Молярная теплоёмкость большинства метал.тон при комнатной и более
высоких температурах близка к i'i кал/К. т. с. такая жса как у дитлсктрикоп.
Это значение теплоёмкости для диэлектриков, как и для металлов,
хороша объясняется классической теорией колебаний кристаллической
решетки и свидетельствует о неудовлетворительностл классической теории
теплоемкости металлов, основанной на модели классического электронного
газа, который должен был бы добавлять к молярной теплоемкие tie величину
(3/2) J? = 3 калТК.
В свете успехов классической теории электронов проводимости метал-
лов при объяснении электропроводности и теплопроводности металлов её
неудача с объяснением тс пл нём кисти да создания кбэеггпеой теории каза-
лась совершенно удивительной.
В рамках классической теории нельзя было понять, почему электро-
ны, принимая участие в процессах переноса, как если бы они были сво-
бодными классическими точечными частицами, нс дают никакого вклада
в теплоемкость металла.
Объяснение этому парадоксу дала только кван товая теории электронов
проводимости в металлах, согласно которой газ электронов проводимости
является вырожденным квантовым газом, подчиняющимся не статистике
Максвелла-Больцмана, а статистике Ферми-Дирака.
Согласно квантовой теории молярная теплоёмкое гь электронного га-
за в металле при комнатной и более высокой температурах много меньше
3 кал/К. которую даёт классическая теория.
Вместе с тем при низких температурах теплоёмкость кристалличе-
ской решётки убывает с уменьшением температуры но закону Т3, а теп-
лоёмкость квантового электронного газа как Г, так что, наоборот, в метал-
ле электронная теплоёмкость при низких температурах оказывается много
большей теплоёмкости кристаллической решётки,
6.4. Термоэлектронная эмиссии
Работ дн выгода Л элек1рона из металла называется
гшг HeutfxoditWM для уддл^ия адяагя сет&боднол? элеят/тонл.
274
Глава 6
я саном икотам свовд энергстнчсскйн состоянии s jwemowe, нд бесконеч-
иость яис .метдляи. w знср^^И Ф₽/шц cf- как Это проиллюстрировано па
приводимом рисунке.
Плотность тока электронов j определя-
ется как абсолютная величина электрическо-
го заряда свободных электронов, проходящего
через единичное поперечное сечение, перпен-
дикулярное потоку электронов в единицу вре-
мени. Если бы электроны после вылета из ме-
талла имели одинаковую скорость г1, то можно
было бы положить, что
j = enw7
где п — концентрация электронов, т. с. число электронов в единице объёма,
с — абсолютная величина заряда электрона.
Свободные электроны в металле, однако, не имеют одинаковых скоро-
стей. Они подчинены распределению Ферми-Дирака, и их концентрации
даётся интегралом
п =
_______1______
е.Ч£(р)-^) ! ।
в котором е(р) = /г/Зтп, до = ср = р^/Эт. Поэтому для электронов
металла плотность их термо эмиссионного тока равна
г
4тг3^ ./ ' ./ 7 -№>) +
—<ю -оо рд niin
где
Рз min — \/ 2*Л (-F “I -4)-
Электрон может вЕнТлететь из металла только при условии, что
т.е. когда его кинетическая энергия движения вдоль оси аг будет больше
+ Л; считаем, что ось ,т перпендикулярна поверхности металла и на-
правлена наружу металла. При вылете электрона компоненты его импульса
и р3 не изменяются-
6.4. Те рмсэ л lktpo иная эмиссия
275
Делая в интеграле но рд замену £ = . согласие которой tier =
= — можно вычислить Этот интеграл и получить, что
(-ей 4-м
1 / p±rip.r = / de
™ ,/ е£(с(р) - Да) ,| [ ./ J?(c 4- Р»/2т + Р%/2т - До) . ]
P;t min £р + Л С ' 1
4-оо
= - 1 In f I F C~f3 + 1&2т + ?’г/2т - W>) )
' £f-A
= 1 In А + е-^ + Р»/2т + Р*/2тЛ .
Д \ /
Предполагая, что при термоэлектронной эмиссии температура удовле-
творяет неравенству Л. отсюда имеем, что
hr» I си
. = £^Г c_4/ilT f f с_ (р2 _ р2 ) /2mk^dp^ =
4?г3Гг J J
— □к —ста
_ efcbT е-Д/^БТ, = (7гае_Л/^.
4тг *??
_ 4?remfcJ
2it2^ /*:J
или
j = .
Это знаменитая формула Ричардсона-Дэши ана для термоэлектрон нон
эмиссии электронов кз металла. В табличке приведены характер!иле значе-
ния параметров термо элспро и ной эмиссии для не которых металлов
металл С 4* см’3№ А эВ А эВ фотоэффект
W 75 4.5 4,49
Ba(HaW) 1,5 1,56
Cs (iiaW) 3,2 1,36
Pl 32 53 6,2
Cs 160 1,8
* здесь Д обазютмт
276
ГЛАВА 6
Проводя расчёт константы С по полученной формуле, приходим к сле-
дующему сс Значению:
emfcp 4тгетпй|
2--// "
= 120 А см-гК“-
Значения констант С н Л очень чувствительны к чистоте поверхности
металла, Для сравнения и табличке приведены значения работы выхода Л,
полученные из фотоэффекта.
На рисунке изображена схема экспери-
ментальной установки для измерения тер-
мозмиссионного тока с поверхности като-
да методом шшгенушшг.
Эю ТрёХэЛСктродная лампа С катодом, ано-
дом и сеткой. Схематически показана спи-
раль подогрева катода и амперметр, изме-
ряющий анодный ток 7. Чтобы вблизи по-
верхности Ejarpcronj до температуры Т ка-
тода, испускающего электроны, не образо-
вывалось электронное облако отрицатель-
ного заряда, препятствующее дальнейшему вылету электронов из катода,
электроны, вылетевшие с катода, должны сразу же подхватываться электри-
ческим полем, lиздаваемым положительным анидным напряжением, и дви-
гаться к аноду.
Изменяя задерживающее напряжение 17,
подаваемое па сетку> можно часть электро-
нов с малыми энергиями вернуть к катоду
и тем самым заставить измениться анодный
ток 7. Кривая тока задержки Z(C7) представле-
на на рисунке. Когда задерживающий потенци-
ал становится меньше ускоряЕоиюго потстщи-
ала, создаваемого анодом, ток 7 наблюдаться
будет. Когда задерживающий потенциал ста-
новится больше ускоряющего потенциала, со-
здаваемого анодом, ток 7 обращается в пуль,
гствуег мо но энергетическому потоку электронов
(когда все электроны, вылетающие с катода, имеют одинаковую скорость}.
Кривая задержки 2 соответствует потоку электронов с некоторой функци-
ей распределения /(с). Измеряя кривую Г(Е7)Ч можно измерить функцию
распределения термоэлектронов, вылетающих с катода.
Кривая задержки I соответ
6.4. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ
277
Теория Шоттки
Рассмотрим потенциальное поле в вакууме вблизи поверхности метал-
ла. На приводимых рисунках изображены кривые потенциальной энергии
электрона, которые даются теорией Шоттки, ггри внешнем электрическом
поле, равном нулю (слева) и нс равном нулю (справа); в теории Шоттки
считается, что на злекяцгон tcljusjf ftysepxrififmu действует. к/w.we
лотендоашяодо лоля также и хорошо известная из электростати-
ки так называемая яснлд изобрязсенцяд>.
На точечный зарял г/, находящийся на расстоянии т от бесконечной
плоской поверхности проводнику действует электрическое поле, создавае-
мое электрическими зарядами противоположного Знака, индуцированными
на этой поверхности этим точечным зарядом 7. Можно доказать, что сила
притяжения заряда q к индуцированным зарядам на поверхности в точ-
ности равна силе притяжения, действующей на заряд q со стороны вооб-
ражаемого фиктивною заряда - q. противоположною знака, находящегося
внутри проводника на том же расстоянии j от поверхности, что и исходный
заряд g от его поверхности
Таким образом, на электрон, находящийся на расстоянии г ст поверх-
ности металла, действует электростатическая сила притяжения к повсрхЕЮ-
сти металла, равная
р _________L2___
I . й j
4ir^o 4аг
которая и пазы кается «СИЛОЙ изображения». Прп очень малых л, порядка
межатомных расстояний, это выражение для силы, однако, неверно, так как
сила в бесконечность обращаться ле может.
Потенциальная энергия силы изображения равна
! । а?) = Г7д — । " :
4 4л-.е 0 4=ж
действительно, —йЕ7(зт)/йд: = — г52/(4зтсо
27М
Глава 6
Нэ левом приведенном выше рисунке показана исправленная на малых
расстояниях т кривая потенциалы]ой энергии вблизи поверхности металла,
когда внешнего электрического поля нет. На правом рисунке изображена
исправленная на малых расстояниях it кривая потенциальной энергии элек-
трона вблизи поверхности металла, когда в вакууме вблизи поверхности
металла действует ещё и однородное внешнее электрическое поле с на-
пряжённостью £i: = —£ (£ > 0)„ приложенное к металлу и направленное
против оси ж, стремящееся ускорить вылетевшие из металла электроны
в направлении осн ж. Полная потенциальная энергия электрона вблизи по-
верхности металла в этом случае будет тогда даваться выражением
СЦя) = !70 - л Е -г- - еЕ%\
-4 TTt (J т: J"
эта функция СГ(ж) имеет максимум Е/т при ж = жт, для которою
dI7 J5t* pi
— = ----------т — ес = U,
4-згсу 4яг
I = я™ = I (/Л- “7=- Um = U<)-
2 у 4?гео у 4я£о
Как видим, работа выхода, равная Д = !7о — ск* при наложении на ме-
талл электрического поля вырывающею из лею электроны, уменьшается
таким образом, что
Д bjiiii Д
Если воспользоваться теперь формулой Ри-
lnij чардсона Дэшматш. то для плотности тока j тер-
моэлектронов с поверхности металла получим
формулу
) = CT-с Д^фЛбТ1 =
= (ТТ2С-’^/^Б^П ОV*£ / (41Г'е° ) ^*£7 fciT
Если построить кривую Inj в функции от
vT, то получим прямую, показанную на верхнем
рисунке. На эту прямую королю ложатся экспери-
ментальные точки.
6.5. Контакт двух металлов
279
Описанное уменьшение работы выхода
известно как «эффект 111стгки»? кривую зави-
симости hi j от называют «кривой Шигг-
ки».
Электрическое поле увеличивает ток
термоэлектронной эмиссии, так как более
НИЗКИЙ потенциальный барьер преодолевает
большее число электронов.
Если напряжённость электрического но-
ля £ достигает очень больших значении порядка 10*4 В/м = 107 В/смъ то
электроны, находящиеся вблизи уронЕтя Ферми ;-р. начинают туннелиро-
вать сквозь барьер вследствие квантового туннельного эффекта. Это явле-
ние называют «автоэлектронной эмиссией». Температура катода при этом
не оказывает практически никакого влияния. Чтобы рассчитать плотность
тока j автоэлектронной эмиссии, нужно вычислить вероятность квантово-
го гунн ел прова ния электрона сквозь потенциальный барьер по формулам
квантовой механики.
6.5. Контакт двух металлов
Если два металла 1 и 2 с различными работами выхода Аг. и Ла (пусть
работа выхода из металла 2 больше работы выхода из металла 1, т. е. пусть
Л2 > Л>) привести в контакт, то часть электронов из одного металла пе-
ретечёт в другой металл. и между металлами возникнет так называемая
«контактная разность потенциалов». Эта разность потенциалов ДУ опре-
деляется разностью работ выхода металлов, так как
с AV = Ла ,
где ДУ = ip] — ^2 и ^3] — потенциал металла 1 (одинаковый по всему
металлу 1L — потенциал металла 2 (одинаковый но всему металлу 2),
е — абсолютная величина заряда электрона.
Ц Q 'V J
Ц| ।
^га—
еД7
—ер-
' -е^2
о
2 МО
Глава 6
Нэ левом рисунке изображены энергетические лиаграммы металлов I
и 2 до приведения их в контакт. На рисунке справа изображены эти ЧЕзерге-
тичсскис диаграммы металлов 1 и 2, находящихся в контакте, когда между
ними появляется контактная разность потенциалов Д 7 = - ^s-
Так как мы предполагаем, что работа выхода -41 электронов из метал-
ла I меньше работы выхода Лг электронов из металла 2, то электроны ча-
стично перетекут из металла 1 в металл 2, как показано двойной стрелкой
на левом рисунке, пока не установится останавливающая их перетекание
положительная контактная разность потенциалов il7 = у?| -
Согласно условию раелеееедя для электронов
в контактирующих друг с другом металлах I и 2 усмллплтылг-
стся (г. е. электроны перестают перетекать из металла в металл), когда тлк
ЭЛЙКЯЦМЖОЯ tf (rfOttX МЁОТОЛШХ
сманиваются, т с. когда окажутся равными величины ?n = -е^и =
= //2 — где ди — химический потенциал электронов я металле I (при
нулевой температуре Г = 0 равный энергии Ферми tnb дд — химический
потенциал электронов в металле 2 (при нулевой температуре 7 = 0 равный
энергии Ферми sfi), е — абсолютная величина заряда электрона, т. с. когда
будет выполнено условие
^1-М2 = е(^1 - ^а). Д1' = - ^2 = |(М1 - йг),
или, при нулевой температуре 7 = О. условие
AV = | (eFi - еРЗ).
Так как Croi = Ife, т е + А = + Аг, тс - £>2 = А? - Ль
и поэтому ДИ = (1/е) (Аг - Лг).
Если нз двух проводников I и 2 мы составим замкнутую электриче-
скую цепъ^ показа e:i ну то Eia рисунке, то, несмотря Ета отличные отн нуля лдан-
дтлктные рязнйсяш ДУй = 7^1 — '^2 и Д Vt = ^2 — ^i в кон-
тактах й и &, кшййкяго даокд / е течь нг Полная
ЭД С, включенная в нашу нспь, равна нулю. Вместе с тем если поддержи-
вать контакты га и Л при различных температурах 7’а id 7^ (пусть 7\ >
Дополнение l
2HJ
то в рассматриваемой цепи потечёт электрический ток / (в указанном на
правом рисунке нагтраяпсЕтии) под действием ЭД С t" = Д14(Та) - Д14(Гь).
Э та ЭДС называется /иериеэзЭс. Она используется а тг/лиолдрлх; являющих-
ся очень чувствительными электрическими термометрами (величина силы
тока 7, определяется разностью температур 7\ и 7^).
Температуры TQ и 7* много меньше температур квантового вырожде-
ния электронных фермй-газон Б МСТЯ Л ЛЯХ, гак ЧТО МОЖНО ВОСПОЛЬЗОЖГГЬСЯ
формулой
№ = *> - fe V’
и для величины рассматриваемой на рисунке цепи получить зна-
чение
£ = I (Д1(ГЛ) - да(Тл)) - ‘ (Mifr.j - №(Г6)) = 1№1 -1
J . 1 2LZ Th. 1 , 1 тг~ Та 1 I П-- ^Б Та _
-, JA)i + , l2 /ioi tvi + 12 PO2 r. 12 W)2 “
— ! 1-^ 1 _ 1 J
ё !2 *Б ’
где pin и — химические потенциалы при нулевой температуре 71 =
= 0 дня металлов 1 и 2, равные энергиям Фермн н - га этих металлов
соответственно.
Дополнение 1 к гл, й. Вычисления ^(Т)
Правую часть рассматриваемого трансцендентного уравнения, связы-
вающего д и ?i. можно разложить по малости Д/л и получить формулу
______1______= _!_
Л-2 h3 ! 1 с3(£(р)-р) + 1 й3
О
I WJ
] Р A? _ ।
О
АР- 1
--------------т + чл. выше Дд.
(e^MpJ-pd} _|_ j j-
Имеем сумму двух интегралов. Найдем для каждого из них асимпто-
тику при малом Т.
2Н2
Глава 6
Первый интеграл в формуле для п представим в виде
+ <ю pF
г‘= рг«-‘•>+1 - *+
о 11
pF / г w
+ № Пэ /Р dp ( е^р) I I 1) + № А3 /Р dp + 1 ’
♦ ' ' Pf
в правой части имеем сумму трех интегралов, которые обозначим /f ]\
.(Й) .. „ г(1)
/J . причем первый интеграл /j МЫ уже вычислили, и его рассматривать
не надо.
При малых темлерачурах Г основные вклады во второй и третий ин-
тегралы происходят от малой области вблизи р = рр Сделаем
потгому в этих интегралах растягивающую замену переменней интегриро-
вания:
и разложим получившиеся подынтегральные выражения по малости Т.
Оставим в них только ведущие члены разложений и проинтегрируем их.
Так получим асимптотические формулы при малой температуре Г для каж-
дого из рассматриваемых интегралов Таким образом, . . 1 / m к^Т V ?f PF тп ksT l(p>-2mtW _ _ mfccT2 _ = fin + i 4- t,1, %Pf а следовательно, 0(£(p) - Mo) = J’ + 2 ^2’ ^Pf так н ю L _ 1 _ e* rnks'l ст + ткБТ/2р^х2 1 e* + 1 (e^ + l)3 2pF 2r-i p* ' I3 4 чл. выше T2.
ДО1ЮЛ НЕНИН I
2НЗ
Так как p = j>f + (m k^T/pp) x и dp — (m fceT/pf) dx, то для второго
l\i! и третьего f\ b интегралов имеем форму)гы
1
€
0
00(e{p)-Wf) _ ]
X
1 /
7Г2 7
771^7
Р?+~рГ *
I
2
X
I e x + mk^T/2pp st2 +i
о
Pf mk^T f /
^=ft3 Pp ./ k
-oc
D
2рр ivifcbT ntfcjjT f
f й'ТТ —।
pF
1 . -1
-<ю
?F
mk^T mksT f
^ft3 l^T J
□
m pF
i
D
rfi----------- — чл. выше
(e:e - 1)
О
/ 1 Ле
Нгт-1
[>
2ff2fiSpF ./
—oo
zaCr
(ег + 1)2
чл. выше T2.
ma^f2
= 1 I
1 ^-h3 J
FF
. -mkiT
0
ez + тЛьТ/2р|. rr2 . i
_ 1
с^£(р)-д„;| + } ^2
~“г dsr+
1
2
X
Pf mfcfcT
г t? J
о
2Н4
Глава 6
т£вТ mfesT1
-р?“ “pF"
?Jr mfceT тк^Т f, х2сг , „2
—г-; —5^—~^г~ I ------------т + 421 выше / =
^кл 2р^ У (c“ + Jj-
mkfjTpF [ । Wfcjir2 f j
= --^“7— I ----r ax 4--—---- j x ax ——r —
№№ J CK + 1 1T2h3pF ./ Cr-I 1
о 0
тЧ£Г f ~2e® ,
----;— / —’----г + ’M- выше T2.
2ir2n'W I (ea' 4 1)
j rW r<3)
Сумма псрнык и]1тсгралс1В на формул для /| и /] равна нулю, так
как, далая аамену псрсмсвний интшрпридания аг —> — i в первых интстра-
лах. получаем, что
О +оо О
/(^-1)‘Ьч /й г^ = -/(йгт- 0^
-<ю 0 +-м
Сумму вторых интегралов нэ формул для Aj"1 л /f1’ можно преобразо
вать И получить
интегрируем по частям и учитываемh что обе возникающие подстановки
равны нулю.
Дополнение l
2N5
Получающийся интеграл является табличным интеграломэ и его значе-
ние равно
(ем L)2
Таким образом, окончательно имеем, что
Зтг2 ft3
+ чл, выше Г2.
Рассмотрим теперь второй интеграл в формуле для п, в котором тоже
сделаем указанную выше растягивающую замену переменной ннтегриро-
вдния, оставим и новом подынтегральном выражении ведущий члегг разло-
жения и проинтефируем сю. Так получим, что
I
№ ?1ЭкъТ
е^(=(р)-ро)
(е^МрНяО 4.1)3
9 +3°
Р*~ / А,. е':
тг* h3k^T J (с-г - 1/
—W
чд-я исчез, при Т —> 0 =
+ чл., исчез. при Г —> 0 = - 1
тгг А* ет + 1
4- чл.. исчез, при J —?• 0 = —-—-
7Г2 ft3
чи., исчез, при Г —> 0:
учитываем, что нижний предел —можно заменить на —со при
Т - • (). и интегрируем нс частям.
Таким образом,
Ff , т2^Т* , 2 a ftftPF \
п = —-—-4------т-----И чл.т выше Г + + ч.л. исчез, гтри / -* О
3№h3 6ft3pp Wft3 к /
СлсдоватслЕло,
га = Ц- . pF = {37т - /? те)1 .
3?г- /Г
2(16
Глава 6
а также
тЩТ2 _ трр . _ -л-3 mfcgT2 _ fcgT’
fih'pF ~ J\3Aa’ ' 11 ~ 0 # " 12 '
так что окончательно имеем следующее выражение для функции ^(Т) при
малых температурах 7":
7Г1 *БГ* mi
“ = Мо “ 12 "W + 411 ВЬ[ше 7 '
Дополнение 2 к гл. 6. Вычисление уу
При малых температурах Т н формуле для можно положить, что
jt = jio + Лдс. Тогда, разлагая правую часть формулы для по малости Д^
г
получим
g(p)
(f(p)-g) 11
I /' 2j ____________£1£1
1Г2 ft3 ./ e0(f(p) - /Jo) । |
, Дд 1 7 2 , s(p)
+ ]—7Б ——7 / p Qp-----------------------г 4-
^fl / M + :Q
•ui. выше
имеем сумму двух интегралов Л и которые разложим по малости 71.
Первый интеграл в приведённой формуле представим в виде
1
2m № h3
1 / 4_r L
2m тг2 Л11 J Р + 1
PF
1
е^е{р)-Жь) _р 1
.(1) Г(2) ;(3}
т.е. представим его л виде суммы трех иЕггегралов /| „ j и j .
Дополнение 2
2N7
Интеграл легко вычислить точно,, так как для него имеем формулу
5 2
—V- /> dP = Pf, , = -4- (з^1 ^n) = hjp
2?П7ГгЙ^ / 10mirJh б№ ft3 J
о
Основные вклады во второй /, п третий /J' интегралы при малых
температурах Г даст малая область около р = рр. Поэтому сделаем в этих
интегралах замену переменной интегрирования р = рр I (тк^Т/р^х,
растягивающую эти области, разложим после этого получившиеся подын-
тегральные выражения но малости Т и оставим в них только ведущие чле-
ны разложений, которые затем проинтегрируем.
Так, для второго интеграла J1t2' получим, что
_________1
ед(е(р) - f<o) 4 ।
;(2) = 1
2т зт2 ft3
_1_________
{тк^Т/2p2f>) х1
1 4 rnktT ткьТ Г
——-----г Лг -Ь чл. выше Г2 =
(С‘ + 1)2
2(18
Глава 6
Для третьего интеграла ' получим, что
Л = — ,77 / Р ------------f / 1---------
2m7Г2 7Г J е^(£W “ До) + 1
о
1 [ f mktf V__________________1_________TftfebT ,
тптг^Й1 J \ J>F / (уГ + (mkf,T/2p2F) х2 _ ]
4 mk^T +f 1 , 4$ У д.^
2m^h3 ./^+1 2miralA J J ^ + 1
0 0
1 4 m А^Г m fcbT
2m^r3 2pp
+ oO
f z2e*
./ (e + i)a
+ чл. выше T2 =
pFfcKr / i j 2p!.-mklT'2 f
2^ft3/c^lZ+ ^b3 ./ C’ + L
о о
4я=?к3 7 (е* + 1)г
о г
+ чл. выше Г2.
Интегралы в /j2' и с множителями возникающие от ком-
пенсируют друг друга, так как
о +«
/ (?ТТ-9 + ./
-«> 11
их можно сразу отбросить. Сумма вторых интегралов в и /]Л’ равна
.2
]
Г2 С11
(е* + 1)
I
2
__гаст
(е- + 1)
— ж
2 ег + 1
7 dx =
о
7 Лг+
Дополнение 2
2NY
Таким образом, первый интеграл в формуле для
выражению
£
V
приближённо равен
Рр
llkri тг2 k*
|-за
PF т кьТ | f а^е17
2тгЧ3 2 J (е* + l)s
dx — чл. выше 7
Q - I - У
Второй HEiTcipLUJ в формуле для — рассмотрим так жст как первый.
V
При малы к температурах Т gcehjbhoh вклад в него происходит от малой
области вблизи р = рг- Поэтому, не пользу л снова указанную растягиваю-
щую замену переменной интегрирования р = рг + (т кьГ/рг) для этого
второго интеграла имеем формулу
fc|>T 2m тг2 fr J
о
e№(?) - Яй) _ by Pp mfcgT
(сЖ(р) - + Q3 “ 7г2П:’ fcDT X
-«3
Ст
i 1'2
Pf
2тг2Г? J
:<
I
е* + 1
= _лп Pf L_
2№n3 ej: । 1
—к
pi
. = Au —t—- 4- чл. исчез, при T 0;
27r2?iJ
здесь мы воспользовались значением табличного интеграла:
/m3 ,—2
. = V-
(e* +1)- 3
-QQ
Окончательно получаем формулу
m(fcbT)2pF 3
и _
в которой
m(fcBr)2pF 2т(М’)гР?.- (W2 * а .<
---------- — ------------ —---------Лк п n — ff п.
4/лр
6 г?
127?р~. 43ЛэеР
Глава 7
Модель Кронига-Пенни
Займёмся изучением Очень простой точно решаемой одномерной мо-
дели твёрдо to тела Кронига-Пенни, которая позволяет понять поведение
одного свободного электрона в твёрдом теле, а следовательно, и системы
свободных электронов в нём, движущихся в потенциальном поле атомных
остовов кристаллической решётки твёрдого тела.
Оказывается, п очень хорошем приближении можно считать, что сво-
бодные электроны в твёрдом теле практически не взаимодействуют друг
с другом, и поэтому исследование поведения их системы в твёрдом теле
можно свести к изучению поведения отдельного электрона.
В модели Крол ига-Пенни учтено, что важную роль в твёрдом теле иг-
рает взаимодействие его свободных электронов с атомными остовами кри-
сталлической решетки. Именно это взаимодействие и исследуется в модели
Кронига-Пенни.
Нельзя считать, что электроны и твёрдом теле взаимодействуют только
с поверхностным полем, имеющимся у твёрдого тела и затрудняющим или
вовсе препятствующим выходу электронов из него.
Количественные предсказания грубой одномерной модели Кронига-
Пеш1иъ конечно, нельзя непосредственно сравнивать с результатами экспе*
римсЕггоп. Эта модель носит качественный характер.
А. МОДЕЛЬ КРОНИГА-ПЕННИ БЕЗ ВНЕШНЕГО ПОЛЯ
7Л* Решение уравнения Шредингера модели Кронига-
Пенн и
Рассмотрим модельное одномерное твердое тело длины /- и найдём
ста1щоЕ1ар][ыс Состояния его электрона в модельном периодическом потен-
циальном поле простой прямоугольной формы, моделирующем влияние на
электрон в твёрдом теле атомных остовов кристаллической решётки.
Предположим, что наше модельное одномерное твердое тело состоит
из балыпого числа А элементарных ячеек.
7.]. Решение уравнения Шредингера модели Кронита-Пенни 291
Реальнее кристаллическое твёрдое тело содержит очень большое чис-
ло атомов порядка числа Авогадро «Уд = G - 102Л. При макроскопических
размерах одномерного твёрдого тела порядка А 1 см и очень малых мик-
роскопических размерах элементарной ячейки порядка Л = 1А = 10”113 м
число элементарных ячеек Лг в теле огромно.
Однвдорндя Арин и;?л-Пенны конечной Элины
Уравнение Шредингера для электрона в модельном одномерном твёр-
дом теле длины А, состоящем из Лг элементарных ячеек, имеет вид
2m
где Е — энергия, — волновая функция так называемого стационар-
лого сретясмцшя электрола, Для модели Кронита-Пенни конечной длины А
это уравЕтенис и функцию следует рассматривать только на отрезке
О А конечной длины А.
Стационарное уравнение Шредингера позволяет найти волновые функ-
ции стационарных состояний свободного электрона в рассматриваемом од-
номерном твердом теле.
На самом деле стационарные состояния электрона н твёрдом теле
описываются так называемыми лреиетя/ы-пк смацкЕЖЛ/шылш вдпяовышы
функциям» 0, которые зависят от времени и полу чаются из невре-
менных стационарных функций умножением па временные множите-
ли ехр (—(i/ft) в которых £? — энергии стационарных состояний.
Считаем, что одномерное твёрдое тело занимает отрезок т А
прямой г, причём при а: = 0 и jc = А потенциальная функция У (я) об-
ращается в бесконечность, так что вне отрезка А волновая функция
тождественно равна нулю; электрон не может выходить за пределы нашего
модельного твёрдого тела.
Уравнение Шредингера следует решать только на отрезке 0 я А
При е = 0мя = Анй решение ^(л) уравнения Шредингера следует
наложить граничные условия
^(0) = О, ^(А) = 0,
требующие, чтобы волновая функция на границах твердого тела, т.е. на
концах отрезка {] ^ j А, была равна нулю.
Погенциальная функция V(t) равна бесконечности вне отрезка 0 £
х < А3 внутри этого отрезка она имеет правильную периодическую струк-
туру, составленную из Лт одинаковых прямоугольных потенциальных ям,
разделённых одинаковыми прямоугольными потенциальными барьерами.
292
Глава 7
Элементарная ячейка рас-
сматриваемой периодической
структурыь как показано на
рисунке, состоит из прямо-
угольной ямы ширины S.
внутри которой V(l) = 0.
и примыкающего к ней спра-
ва прямоугольного барьера
ширины i, внутри которого
1/Г(У) = где Ц] - высота
барьера. Ширина элементарной ячейки равна А = я 4- i.
Отыскивая решения уравнения Шредингера, тождественно не
равные нулю, которые существу ют при определенных значениях энер-
гии Е так называемых «энергетических уровней», мы находим «энерге-
тический спектр» стационарных состояний электрона в рассматриваемом
одномерном твердом теле. Ради простоты будем рассматривать только зна-
чения энергий Е, которые положительны и меньше Vo, но больше нуля
(О < Е < Го)-
Бесконечная модель Кроны га -Пенни и условие Борна-Кармана
Нас интересуют большие значения L и К и только так называемые
объёмные свойства нашею модельного одномерного твёрдого тела, т.е. та-
кие его свойства, на которые конкретный вид условий, выставляемых на
волновые функции на поверхности твердого тела (т.е. при х = О
и sr = L), практически не влияет.
Таким нужным для нас важнейшим объёмным свойством являете и
змЁртаелнычвскля ллолтх/оешь грилей стяодылмаррых доопляшш. При
больших L разности между соседними энергетическими уровнями стано-
вятся настолько малыми, что имеет смысл рассматривать только их «энер-
гетическую плотность».
Имея в виду изучение объёмных свойств нашего модельного одномер-
ного твердого тела^ используем нс истинные травичные условия, сформули-
рованные выше, а математически более абстрактное так называемое уc.-vf-
Чтобы воспользоваться этим условием, необходимо, однако, суще-
ственно изменить математическую постановку исход пой задачи на отыс-
кание энергетических уровней и стационарных состояний и перейти от ко-
к бесконечмой модели одномерного твёрдого тела.
Представим себе мысленно, что к нашему одномерному твёрдому телу
длины /- мы приставили с прана и слева по многу раз его точные копии
7.]. Решение уравнения Шредингера модели крониеа-Пенееи 293
и получили бесконечную строго периодическую структуру, занимающую
всю бис конечную прямую т.
Потенциальная функция Vr(i)
в уравнении Шредингера для V'(x)
этой структуры будет теперь
строго периодической функцией,
заданной на бесконечной прямой
-ж < i < +оо, т.е. функ-
цией, удовлетворяющей условию
У (я + Л) = V(sc), где Л — длина __ __________________________
элементарной ячейки^ как покача-
но на рисунке.
Водоеме функцЕЩ ^(х) и у/юянечие Щредкиее/м будем /?де-
ешлдеывдть нд бесконечной пряной -оо < я < |-оо.
R такой бесконечной модели одномерного твёрдого тела конечность
длины £? по Борну и Карману, следует учитывать требованием выполнения
условия ^(ar+L) — ^(х), которое называется «условием Борна-Кармана»,
г. е. требованием, чтобы эдшоеые 6tun пе/шодычееюшы с ле/ни-
дам £ fwjuewwo L, 0 че А/ причём надо считать, что периоды Л и Л свя-
заны соотношением L = JVA. где Лг — большое целое число. Период Е
будем теперь называть «длиной» рассматриваемого бесконечного одномер-
ного твёрдого тела, а число Лг = L/Л — «числом элементарных ячеек»
в нем.
Уравнение Шредингера для электрона, движущегося в бесконечном по
риодичсским поле Vfi). имеет следующий влд:
= wo,
здесь Е — энергия стационарного состояния, ^(гг) — волновая функция
стационарного состояния. Приведённое уравнение Шредингера рассмотри-
вастся при всея т на прямой — си < зг < +оо.
Решая уравнение Шредингера, заданное теперь ил бесконечной пря-
мой -оо<т<+оо,с условием Борна-Кйрмана, можно найти значения
энергий Е стационарных состояний, те. построить энергетический спектр
уровней энергии электрона в модели Кронига Пеппи,
Переход от задачи об истинном модельном твёрдом теле конечной дли-
ны А к задаче о бесконечном одномерном твёрдом теле с условием Борна -
Кармана можно пояснить следующим образом.
Предположим, что одномерное твердое тело очень большой длины Е
мы свернули в огромное кольцо, как проиллюстрировано на рисунке. Дру-
294
Глава 7
гни]। слонами, концы твёрдого тела i = 0 и х = L мы просто замкнём друг
па друга. Для получившегося кольцевого одномерного твёрдого тс л в следу-
ет положить, что tf.'(O) = гак как всьтнсигсгя в Авднтоеой
л<ёхоншсё шкюзмгшш, те. в каждой точке имеет одно единственное
значение.
Теперь, если пробегать кольцо
ОБ Прямом ИЛИ обратном направлении
0^ пс многу-многу раз, увеличивая или
уменьшая координату ж точки кольца на
величину L, то мы построим па кольце
естественным образом периодическую
функцию V'(t) с периодом L при значениях — оо < z < +оо, удовлетно-
ряющую условию Борна-Кармана + L) = <(я).
Приступим к решению уравнения Шредингера для бесконечней моде-
ли Кропнга-Пенин с условием Борна-Кармана и начнём с того, что дока-
жем важное свойство его решений, выражаемое так называемой
Лдедо, для чего рассмотрим так называемый /я/j д ледя^ии Г, сме-
щающий функцию па длину А элементарной ячейки, т. с. оператор, который
действует ла произвольную волновую функцию rj(r) таким образом, что
f^(x) H^(Z+A)
при любых ж.
Докажем сначала, что Т люад 4£/>ез
offepafflojp проекции олглудьса эдеклфовд? рт — (h/i) (d/di). Это позволит
нам доказать, что т/ипк'ляцш.
Действительно, разложив функцию + А) в ряд Тейлора, получим
Vj(j- 4- Л) - ^(дг) + (х) + + • - • “
= 6 + iii + 4rTT+---) W*) = ЙХР fA тй = ех₽ (тлр>) ’И*) >
\ 1! ааг 2! дя/ / \ у
так н ю имеем операторное ссютношепие
г = ехр (д Ар/) -
7.]. Решение уравнения Шредингера модели кронига-Пенееи 295
Взяв его эрмитово сопряжение. получим
Т"1- = охр — у- Л j?J. = ехр — А Арт^ .
так как pj = ибо рт — эрмитов оператор. а Л — действительное число,
и гак как jjpti эрмитовом сопряжении i надо заменить на -Л Символ +
означает зрмитовскос сопряжение. Таким образом, приходим к заключе-
нию, что
где / — единичный оператор Следовательно, Г+ = Г '1. Операторе таким
свойством называется упзгжбгрны.п ^л₽/?лто/?ллг.
Легко убедиться, что олераюр трансляции Т и оператор Гамильтона:
Я = - — — + Их)
коммутируют друг с другом.
Действительно, пусть — какая-нибудь собственная функция опе-
ратора Я Она удовлетворяет уравнению Я ^(дс) = Е <£(#} и условию Бор-
на -Кармана [/'(z 4- L) = V't1)*где £ — собственное значение оператора 7/,
а L — длина нашего одномерного твёрдого тела. Так кик согласно опреде-
лению оператора трансляции Т^г(х) = + А), тс
ТЯ^(*) = ТЕ^дг) = 7?Г0(я) = 4- А).
7/TV(z) = + А) = 4- А);
в самом деде,
dis
+ У(я) + А) -
ft3 rf2
2m - A)2
+ + Л) + А) = -h А),
Н^(х + А) =
так как У(дс + Л) = V(z)- Таким образом, приходим к соотношению
(ЯГ-ТЯ)^(г) = [Л ТЫ*) = О,
296
Глава 7
справедливому для любой собственной функции ^(гг) оператора If. По-
скольку собственные функции ^(as) оператора Гамильтона // образуют ба-
зисную систему функций, по которой можно разложить любую волновую
функцию то это соотношение показывает, что операторы // и Г ком-
мутируют друг с другом, т. с. [ff. Т = 0, где скобки [п ] обозначают ком-
мутатор.
Собстеемяые значения я леватора /нум яслями
Найдём собственные значения оператора трансляции. Пусть С обозна-
чает, вообще говоря, его комплексное собственное значение. Тогда имеем
следующее уравнение на собственные функции и собственные значения
оператора трансляции:
Г + А) = <7
Действуя повторно оператором Т на это равенство у раз, получаем
+ #А) = С7^(т),
где р — целое число.
Учтём теперь, что мы рассматриваем функции, удовлетворяющие
условию Борна-Кармана, те периодические с периодом L функции, для
которых
+ L}?
где I = А’ А и /V — число элементарных ячеек в рассматриваемом одно-
мерном твердом теле. Поэтому
+ £} = + ^А) = A ^(г)т
последнее равенство следует из приведённого выше равенства при р —
= А’. Таким образом, 17jV = 1, те. число С является корнем Аг-й слтеяенн
«j 1. Комплексных корней А’-й степени из единицы vl имеется
ровно JV штук. Их можно записать формулой
С = .и
в которой — целое число, взятое, например» из последовательности Аг
целых чисел: # = -Ат/2 + 1. ... f JV/2 — 1, Аг/2.
При этом без ограничения общности предполагаем, что У — чёнкде
число (так как мы считаем Аг очень большим, то нс очень существен-
на считать ли А' чётным или нечётным). Иначе нам пришлось бы каждый
7.]. Решение уравнения Шредингера модели kpojjhea-Hehhh 2V7
раз рассматривать случаи чётного и нечетного Лг. Обратите внимание, что
ЧИСЛО 9 = — 7V/2 МЫ НС ВКЛЮЧИЛИ 15 приведённую последовательность, хотя
число j = Аг/2 включили.
Последовательность Аг значений числа можно выбрать по-разному,
лишь бы значения чисел $ и чисел С находились во взаимно однозначном
соответствии. Имеется Есроизвол в выборе последовательности чисел у, Об-
ратим внимание, что мы не взяли, кв зало еь бы, бсшсе простую последова-
тельность j = <1 1, 2...Лг - 1.
Если, например, 7V = 1, то <7 = где# = -1, О, 1,2, те. <7 =
_ е с - 1п с — еИ^/2) _ (7 _ е1тт _ -j gTw че1ъгре
точки осущсстиляеот деления единичного круга па комплексной плоскости
с началом в начале комплексной плоскости на четыре равные части.
Отыскание комплексных чисел z, удовле-
творяющих уравнению = 1, т.е. корней
Лг-й степени из единицы '5/1, можно наглядно
иллюстрировать на комплексной плоскости z
с помощью деления окружности единичного
радиуса с центром в точке £ = (} па Аг равных
частей. Показанные на рисунке точки деления
при -V = 6 являются значениями корпя yl.
Согласно сформулированной в гл. 4 алгеб-
раической теореме если два з/ми/днмгы.г опера-
тора, или два у/гилтлрльог оператора, или э/шылш# оператор и
оператор коммутируют друг с другом, то можно указать систему водно*
вых функций, каждая из которых будет являться cdMnepF.uewo собственной
функцией каждого из операторов этих пар., разумеется, со своим собствен-
ным значением.
Поэтому без ограничения общности можно считать, что любая соб-
ствен ездя функция оператора 7/ является собственной функцией операто-
ра Т. j[ наоборот, тс. при отыскании собственных функций опера-
тора 7/ (те. при решении стационарного уравнения Шредингера) можно
предположить, что они уже являются собственными функциями операто-
ра Т, причём, как мы показали, для любой собственной функции операто-
ра Т справедливо соотношение
Т = ^(z+ А) = е*<г"^ V’(s).
29N
Глава 7
где fl — число, принадлежащее последовательности у = -Лт/2 I 1, -
jV/2 — 1, Лг/2 (jV — чётное).
Согласно этой формуле собственную функцию оператора Т\ соответ-
ствующую числу fl, можно представить и виде
где — периодическая функция с периодом Л.
Действительно, согласно только что приведенной формуле имеем, что
»/,(л + Л) = ei(2w/Zr)’tl+A)u(ff + А) =
так как Л/£ = I /Л\ откуда сразу приходим к формуле
+ Л) = е*(а,г/*>^(я),
так как мы считаем, что u(z + Л) — и(зс). Получили формулу, выражаю-
щую функцию ^(as + Л) через функцию для оператора Т. которую мы
привели выше.
Введём теперь действительное число К, называемое «константой рас-
прпстраЕтсп11я»т по определению равное
хг 2тг
К = Т9'
где
А = — Лг/2 + 1....Лг/2 - 1. jV/2 (j'V - чётное).
Так как £ = ЛГЛ. то рассматриваемую собственную функцию операто-
ра трансляции Т можно представить также в ваде
— е'** u{z).
где К — константа распространения, u(s) — периодическая функция с пери-
одом Л. Действительно, в этом легко убедиться, так как е’^* =
Таким образом, мы доказали следующую теорему.
7/wrwf рсшЁННе ШрейпП^£рт
Аронии-Т/ёккк с 5орнд-^рл<дн(! лрок-тявдть
(i ffWife
7.]. Решение уравнения Шредингера модели кронига-Пенееи 299
u(ac) — функция с ле/?иоййи Л. дяя неё и(гг + Л) - ti{z)«
и гЭе конгтлятл рдел/гяст/вдиемия Л' = (Этг/Л)^. <?de р — я^но из чисел
лоеясйоеатсльности
9 = — ?V/2 + L ...: ЛГ/2 - L /V/2;
п^едлаяягяелгся, что Лг — ц&ше чё/илое числй.
Замечание L Из теоремы Блоха непосредственно следует; что решение
уравнения Шредингера для бесконечной модели Кроннга-Пеннн с услови-
ем Борна Кармана с периодом L = ЛГЛ можно искать в виде функции,
удо влспшрятон ie й условию
I Л) = е1КАф(я),
в котором /С — некоторое значение константы распространения из при-
ведённой последовательности. Эго условие называется «условием Блоха»,
з функцию указанного вида называют «блоховской функцией», т. е. суще-
ствует Л1' различных ветвей решений уравнения Шредингера.
Замечание 2+ Значение числа /V в формуле
ф(я) = е/Ях tt(i)
не задаёт однозначно ветвь отыскиваемою решения уравнения Шрединге-
ра. Ветвь решения однозначно характеризуется не значением константы Аг,
а значением экспоненты c?ffA.
По заданному значению экспоненты е1КЛ константа распростране-
ния А может быть найдена только с точностью ДО добавления к ней любо-
го целого кратного числа 2тг/Л. Действительно, если вместо константы А
взять константу
л" - к + 2г р,
Л
где р - произвольное целое число, то, очевидно,
е’А'Л _ eiKA^i2^rp _
так как ed2lTp = I.
Замечание X Из того факта, что функция является реп гением
уравнения Шредингера для бесконечной модели Крои ига-Пенни с услови-
ем Борна - Кармана с периодическим потенциалом V(x) с периодом Л, не
ч/ио эта функция илмге с периодом Л, т. е. уцовлетво-
ряст условию
ф(э- + Л) = ф(йг}.
300
Глава 7
Только при Л" = 0 условие Блоха, которое выполняется всегда, сво-
дится к условию периодичности функции ^(л). Константа распростране-
ния Аг задает яс/ннь решении для модели Кронига-Пенни с условием Бор-
на -Кармана.
7.2. Вывод трансцендентного уравнения модели Кронита-
Пенни
Воспользуемся теперь теоремой Блоха и пай дем энергии стационар"
ных состояний электрона для рассматриваемой бесконечной модели Кро-
н ига - ] leu i ш с у с j ювием bopj за - КЗр мзе за.
Рассмотрим какую-нибудь произвольную элементарную ячейку, зани-
мающую интервал оси ат от точки а; = Aj до точки т = A(j + 1), пока-
занную па рисунке. Для нумерации элементарных ячеек используем индекс
j = О, ±L ±2....
На интервале AJ < х £ A(j -I 1) построим кулис решения ^г(х) урав-
нения Шредингера, рассматриваемого на всей прямой -со < х < 1-ю,
удовлетворяющего условию Блока
^(х+Л) = е*АЛ^(т)
при некотором заданном значении константы распространения /< =
= (25г/Л)^, - -N/2 + 1: .... ЛГ/2 - 1, Л/2 (jV - чётное).
В области I (ешуга/ш л.чы), т.е. при Л) С я < Л} -Ь я, уравнение
Шредингера имеет вид
g ***♦-».
rfx4
где fc = yV2mE. Значение энергии £ является действительным положи-
тельным (0 < Е < Vo)p так ч то константа А* действительная положитель-
ная.
Общее решение приведенного дифференциального уравнения является
линейной комбинацией фундаментальных решений sin(fct) н cos(fcx) или,
что эквивалентно, решений sin[й(аг Л>)] и cos[fc(x Aj)]- Таким образом,
и области 1 можно положить, что
=^1(я) =
— nj cqs[A;(j — Aj)] + sin[k(j - Aj}].
здесь ftj, - некоторые константы.
7.2. В ЫВОД ТРЛ11СЦЕНД EJ IT! ЮГ О У РАВ! IEI1ИЯ МОДЕЛИ KPOJ1ИIА - П Е Н НИ 30 ]
В области 2 (вяу/яри бдрье^д),
т. с. при Afj-h 1) — f I Afj + l),
уравнение Шредннюри имеет вид
г . „
^-7^ = 0-
где 7 = _ Так
как мы рассматриваем положи-
тельную энергию Е, мсныную Ц)
(0 < £ < Vq)> то константа 7 —
действительная положительная.
Общее решение приведённого
дифференциального уравнения является линейной комбинацией фундамен-
тальных решений Стт и e_HK± или решений ch (71г) и ah(7i) или же, что
эквивалентно, решений cli[7(ar - A(j + 1))] и ah[7(ir - A(j + 1))). Так что
в области 2 можно положить, что
□g, по рассматривав
$(х) = ^г(гг) = е> ch[7(® - A(j + 1))] + rii^a - A(j + 1))].
здесь Cj, dj — некоторые константы.
Функции и ^з(аг) являются кусками решения ф(я) нашей задачи,
отыскиваемого на бесконечной примри —ос < лг <
мою сейчас при Л j ^<А0 + 1).
Чтобы найти значения констант о;?я 6р Cj, dj.
воспользуемся теперь условиями, непосредствен-
но вытекающими из условия Блоха:
I) *(A(j+ 1)) = е1К''*,(ЛА
2) ^(Л0 + 1)) = 1!<'гл^(Л;),
и, кроме того, условиями, вытекающими ИЗ грс-
бовакия непрерывности решения п непрерывности его первой производной
на границе между ямой и барьером на интервале Aj < a: A(j + 1)» т. е.
в точке :r - Aj + s = Л (j + 1} - t;
3) (Aj + s) = V^(A(j + 1) - 0,
МД?) ^,(A(j-l))
Aj A(j+1)
4)^(.A>+S) = ^(AO4 1)-().
302
J'Л Л ВЛ 7
-— Л—-
Aj 1 AO1)
V’2(A(Rl)-t)
Имеем, таким образом, четыре уело-
вея I)—4) Для нахождения четырёх констант;
л j 1 Ь j, с jflf j.
Услдехгё Я.?^1ш ловдилылн Hztw ffiet'rtrri Sd-
<?Л1Ыстания реи^ня
явдня c jwmv /Слдчаяй
нд бесконечной пря.иой к ^гд^дче одшгканыя рс-
шеиил Этй^О у/вд^нелия Яд шндЕ'.тыкш л^иен-
шлрткш ячейке.
Из условий I) и 2) имеем соотношения
ej=Cift'A(ij, -ydj =eK/^kb,:
так что
_ *е*КЛЬ
'? rv С N Т
Из условий 3} п 4) имеем уравнения
rtj cos(fta) + &j sinffcsj = cj chfrt) - d, shfrt),
-flj Asinffcs) + bj A cos(fcs) = -cj 7 shfrt) + dj 7 ch(7t).
Исключим константы cj3 tij, имеющиеся в правых частях последних
двух уравнений, выразив их через константы ам bj с помощью только что
выведенных формул для Cj, dj.
Придём тогда к следующей системе двух линейных алгебраических
уравнений для определения двух неизвестных констант и
rtj cos(t.s) + bj sin(t.s) — в'Л Л J aj ch(7() - /7 sh(7i)
—aj ain(fc^) + bj cos(fca) = CA л
- ydj вЬ(7й) + bj ch(7f) 1- .
г?
Разделим второе уравнение этой системы на ё*кл и перенесём члены
первого и второго уравнений из правых частей в левые их части. Полу-
чим тогда следующую однородяу*? twew^wy dsyr wwwwwx дтгебранч^хи^
ws(fcs) - е*КЛ
г
л
ch(7f) + bj gin(ta) - е‘лл sh(7t) = 0,
sin(fcs\-|- , sh(7^ — bj C
К L
Л cos(fes) — ch(7t)] = I)
7.2. В ЫВОД ТРЛ11СЦЕНД EJ IT! ЮГ О У РАВ! IEI1ИЯ МОДЕЛИ KPOJ1ИIА - П Е Н НИ 303
Условие tfFujecmffEwmifl /?еиенмя этой системы урав-
нений имеет вид
cos(fcs) - е*кл ch(7t) sm(fcs) + у е|КЛ sh(-yt)
_с-*кл ain(ts) -i- -1 sh(7t) c iA A cos(is) - ch(7i)
IT
таким образом, приходим к трансцендентному уравнению
[cos(As) - etA A eh(-pt) [с_'*л cas(fcj) - chfjt)] -
sin(fcs) + | е>к л sh(7t)
-е-1Л'Л sin(fc#) + sh(7t)
л.
решая которое, найдём искомые значения энергий Е стационарных состоя-
ний.
Раскрывая скобки, получаем, что
С *кЛ co52(£s) + е*кл ch2(yt) - 2 cosfks)ch(yf)+
+e"fKA sin2(£s) - e*KAsh2(7i) - sin(fcfi)sh(7t) + — sin(fcj) sh(7t) = 0,
П
поэтому
С-1 АЛ + CfA Л — 2 cos(fcj) ch(7t) + | — y- ] fiin(fcs) ahtai) = 0.
/
Таким образом, прикопим к уравнению, которое будем называть
Лрояигдили просто
дс/н>ен?пяурпряс'яыг.нл?:
7s - F
coB(JfA) = eos(fcs) + 1 — sh(7t)sin(fcsk
Эук
в котором
k = | V2mE, 7 = | y/2m(Ki - ^).
Решая это уравпсЕзис относительно энергии Е при всех ладазшых Зна-
чениях константы распространения К\ найдём JV ветвей спектра энер-
гий Ед-f] (индексом n = I, 2. .. мы нумеруем отдельные стационарные
состояния отдельной ветви с данным значением константы распростране-
ния А).
304
Глава 7
Энергетическому уровню £кп стационарного состояния Л'п соответ-
ствует Стационарная волновая функция
Сами собственные волновые функции заданные при всех т на
прямой -со х +оо, можно найти, решив приведённые алгебраические
уравнения для коэффициентов bj для всех j, те. отыскав куокм волно-
вых функции гга всех элементарных ячейках, Строить эти волновые
функции V'KTjf1}* однако, мы нс будем.
Будем исследовать только собственные энергии т. е. изучим толь-
ко энергетический спектр.
Согласно теореме Блоха временную волновую функцию ста-
цноиарЕ10гс состояния Кн можно представить в виде
для сокращения записи здесь мы опустили индекс п, причём функпия
кк(йг) — периодическая с периодом Л, т,е. + Л) = ^к(т).
7.3. И сел вдов ин и с энергетического спектра в пределе
бесконечно сильной святи
Изучим полученное трансцендентное уравнение модели Кронига -
Пенни в пределе бесконечной сильной связи между потенциальными ямами
(при Vo = +оо), те- н случае
ЛГЙМС^у л.пд.ил.
Конечно, здесь речь идёт о «связи» электрона с отдельной потенциаль-
ной ямой, не. о связи его с атомным остовом кристаллической решётки,
а нс о «связи» ям друг с другом.
Фиксируем определённое значение константы распространения К —
= (Эл/LJ j, где = - ЛГ/2 -hl....Лг/2 - 1, ЛГ/2 и ЛГ — чётное.
Так как мы считаем, что барьеры между ямами бесконечно высокие
(так как Vo = + сю). то ямы теперь изолированы друг от друга h как показано
па приводимом рисунке.
7-3 - ИССЛ ЕДО ВЛ Ц И Е ЭН Е Р ГЕТИ Ч E CKO! 'О СП Е КТРЛ
305
При Ц) —» х и фиксированном Е величина
7=1 /2m(Vb - Е)
стремится к бесконечности, и поэтому в правой части трансцендентною
уравнения модели Крол и га- Пении можно рассмотреть только второе из
двух слагаемых, так как коэффициент перед ним, в отличие от коэффици-
ента перед первым слагаемы мт при 7 —> +со стремится к бесконечности.
Другими словамн, следует рассмотреть только ведущий член асимптотики
правой части трансцендентного уравнения. Кроме того, можно считать, что
sh(7t) -
Таким образом, рассматриваемое трансцендентное уравнение модели
Кронита-Пенни для значений энергий Е стационарных состояний при
7 —* +х примет следующий приближённый вид:
соа(ХЛ) = с71 sm(fcs).
In
При 7 —* +м коэффициент, стоящий перед sin(As) в приведённом
уравнении, обращается в бесконечность, хотя левая часть этого уравнения
остается кометной (по модулю она меньше или равна единице). Поэтому
в пределе 7 —> +оо мы должны потребовать, чтобы выполнялось следую-
щее тригонометрическое уравнение;
sin(fcs) = 0.
Следовательно,
= 7ГП,
где п = 1.2....Брать нужно только положительные п, так как is — по-
ложительное, брать ?! = 0 нс нужно, так как тогда получим тривиальное
решение с собственной функцией тождественно равной нулю (которое
СЛСДуСТ ОТбрССИТЬ)-
Таким образом, получаем спектр энергий стационарных состояний:
»-1, 2.....
при V<i = -hoc. Верхний индекс «О» означает, что мы рассматриваем энер-
гетический спектр нашей модели в пределе бесконечно сильной связи при
h - -Нто-
306
Глава 7
Если бы мы рассмотрели не только ведущий,
но и следующий за этим ведущим членом член
аснмлтоткчесмлр разложения не при 7 = +ои,
а при — -оо, то cmod.ii бы учесть в правой ча-
сти трансцендентного уравнения также и первое,
сейчас отброшенное слагаемое. так и следующий
за поправочным член асимптотичеешго разложе-
ния для второго слагаемого ₽ правой части рас-
сматриваемого трансцендентного уравнения. Это
мы ещё сделаем позже.
Как видим, мы пришли к ^ядчёниаи fl/zu n = 1. 2. ...
ЭМЁТсиетпычадсиго слситс/де иошелф/длыюы я.ны с бесиомеч-
/rbf.nw iwwwu шурашьт j с яулдешш фхмш'шы.'ни
3//*7WiFMU4£Cfcww LTJCA’/n/j fl .ur?riciw Яромдеа -/7Ьпш с л^рыо-
йичйсаaw условием в л/зе^еде бл?№нечнс*й (н/ш 1-п =
= -hoc) оклзыадяяся слеят/гои злекп^ро™ в олт^елы/ou потенция. №юы я.иг
.uottew с ujhcwjw jpdwwvwbujw рслоаиллш на кгн^ах. лрячйи шьртша этой
Апы рлвш впи/чя/е Амы ле/?нсдйичес/<ан стдуялтдеы -Модели.
[]ап в сшшчие от спектра одной потенциальной ямы, каждый уровень
рассматриваемого сейчас спектра одномерной модели Кронита-Пенни при
Действительно, например, в огжмнйк сошнйяшш (при n = 1) электрон
может находиться в любой из имеющихся Аг хма при этом он будет иметь
одну и ту же энергию £^° \ так что всего мы получим /V ^ыроле^дяыл:
стационарных состояний электрона при V'o — -Нто.
В рассматриваемых стационарных состояниях электрон не размазыва-
ется по одномерному твердому телу, и жестко привязан к своему атомному
остову; т.е. мы получаем идеальный dwiiewnpif^.
7Л. Исследование энергетического спектра в пределе
нулевой связи
Рассмотрим теперь обратный предельный случай при Vq = 0. когда
барьеры между ямами отсутствуют, как показано на приведённом ниже ри-
7.4. Исследование энергетического спектра
307
сунке, т.е. когда нет связи электрона с отдельными ямами. Имеем теперь
одну ширины L, потенциальную яму, которая занимает всё одно-
мерное твердое тело длили L,
Ягследосшше й)?оммгд-
Ленни при Vo = 0 при /матичных значениях донстадоиы
jPtfCn/?CJCflTJWneWWtf
Теперь
7 = т ^-2^ = ±7V''2mE = ±i£,
й п
так как величина 7 чисто мнимая,
и сё модуль равен fc. Если ввести — уд
сигнатуру е = ±lh то можно на-
писать формулу ___* —| к—______________________
О -А-* 7 Г"
7 — ; ckt k — — VivnE-
п.
При Уц = 0 в рассматриваемом трансцендентном уравнении модели
Кронига-Пенни, таким образом, можно положить, что
ch(7t) = ch (г e.ki) — ------------ = соз( cfct) = cos(A;f)1
д ъ it i — — e Ar 2,
sbfyt) = ali(icfct) =------------= i sin( cfct) = i e ain(fct)h
а поэтому оно примет вид
- A:2 - fc2
сов(/СЛ) = cos(fca)cofi(fct) -l----—— sm(fci)i£sin(fci) =
2fcJ£e
= cos(At) cos(fce) - jsin(fcs) sin(fci) = cos[fc(fl + /)] = cosftA),
те. трансцендентное уравнение модели Кронига-Ленни при = () сво-
дится к тртет/стшю
(Хк(КА) -= cosffcAJi
в котором значение константы распространения фиксировано на одном
из своих значении: Л’ = (Зтг/Ь)^ = -7V/2+ I........JV/2 - 1: ЛГ/2 (jV —
г1СТЕТОС).
ION
Глава 7
Решения приведённого тригонометрического уравнения не зависят от
знака константы А. так как константа А входит только в аргумент косину-
са соы(7СА) и так как cus(TfA) = соя{|Аг|А). Поэтому достаточно решить
тригонометрическое уравнение
oos(AA) = cos(| А|А)П
в которое входит модуль |Л|, относительно волнового числа - у V^2m
а фактически — относительно энергии К Нужно найти действительные
положительные корни £ этого уравнения при заданном значении величи-
ны |А|Л. Так как Л’| £ 2л/А JV/2 = л/Л. то 0 £ |А|Л < я.
На рисунке представлен график функции сов(йЛ) в зависимости
от Аг А, т.е. график левой части приведённого тригонометрического урав-
нения, причём 0 < А-А < +оо для отыскиваемых корней- На оси абсцисс
отмечено значение величины |А|Л (О |АГ|Л -< тг}. На рисунке изоб-
ражена также горизонтальная прямая с ординатой, равной со&(|А|Л), яв-
ляющаяся графиком правой части рассматриваемого тригонометрического
уравнения.
Отмечены точки пересечения Этой прямой с графиком левой части при
Л:Л <- 0. Они ДЯЮТ корпи рассматриваемого три гонимci pir кикою уравне-
ния. Корни эти могут быть двух типов, и для удобства последующих рас-
суждений они обозначены по-разному (чёрными и белыми кружками).
Как видим, корни нашего тригонометрического уравнения можно
представить формулами
£Л =
|[ |К|Л + 7Г (п - 1}
] — | А |Л + тг п
при п — ], 3, 5........
при п = 2, 4, 6, ...;
здесь из[деке п нумерует Отдельные корни.
7.4. Исследование энергетического спектра
Используя функцию £ = fisi2/2m для значений энергии при
заданном А. получим следующую формулу:
£
2 m
1*1 lj(n-
при n = L 3, 5....
h2
2ш
при п = 2. I. 6....
Проиллюстрируем теперь выведенные формулы другими графиками.
Па приводимом рисунке мы изобразили ось /< и на мен вертикальными
короткими жирными чёрточками возможные значения константы распро-
странения А'.
£
hvl
................... I 11J----------- К
_3E t? Я
А A
Значения константы /< даются формулой /< = (2sr/Z)fl. в которойg =
= —А'/2 4-1, ... г Лг/2 - 1, /V/2. Лг — чётное. Так как тг/Л = (2зт/£).(Лг/2)а
то величина тг/Л является целым кратным величины 2тг/£. Допустимые
значения константы А' поэтому кратны величине 2тг/£ и располагаются
от точки тг/Л (исключая эту точку) л о точки тг/Л (включая эту точку).
Всего имеем Лг значений константы А". Большой жирной точкой отмечено
некоторое конкретное значение констан гы распространения Аг.
На следующем рисунке слева мы приводим график многозначной
функции при различных п, заданной на отрезке -тг/Л < /V тг/Л,
на котором допустимые значения энергии А;ц.;[ при заданном значении кон-
станты распространения А обозначен->r жирныхщ точками. Цифры па ри-
сунке обозначают значения числа п, которые нумеруют ветви многозначной
функции
График функции можно получить из графика параболы Е(А') =
= h^№/2m, изображённой па правом рисунке, следующим образом. На-
до взять график зтОЙ параболы и зеркально отразить верхние части обеих
её ветвей в вертикальных прямых А" - ±тг/Л. как бы свёртывая парабо-
лу внутрь, как это проиллюстрировано на рисунке. Затем надо произвести
подобную операцию с полученной свернутой параболой и т. д. Всё это про-
иллюстрировано на правом рисунке.
110
Глава 7
Всё время надо отражать верхние части ветвей получаемой кривой
в вертикальных прямых /\ = ±я/Л. Гак мы построим кривую для графика
многозначной функции £? — из графика функции Ef/C) =
тнрлнст/еядептпогр дожеж модели Лр^иига-
/7еыш при Ц = 0 для рддлиадых зяйчеиии проекции
вектора
Полученную формулу дм корней трансцендентного уравнения при
V3 = 0 можно представить по-другому. В верхней строке приведенной фор-
мулы для fcA положим п = 2р + 1ъ считая, что p = l), 1. 2, ..., а в нижней
положим п = —2р, где р = — 1, —2. .... Тогда обе строки рассма триваемой
формулы можно записал ь одной формулой:
*r=|fc,.|. ft* = |А'| +р = 0, ±1. ±2, ...;
здесь мы используем величину fcxl которую назовём «проекцией волнового
вектора па ось ст; она принимает положительные, отрицательные и равное
нулю действительные значения.
Например, корень АЛ = |/С|Л+тг при тс = 2 теперь записывается в виде
А = |АГ|, fci = |Jf| — 2л"/Л прнр = - L. Действительно, fc = ЦК! — 2л-/Л.| =
= 2тг/А - |Я|, кА = -|К|Л + 2тг.
Если АР положительное, । с. Л" = |A"|d то
* =1Ы ^=А'-^:Р! ±2,
7.4. ИССЛ ЕДО ЕЛ 13 И Е ЭН Е Р ГЕТИ Я E CKO! 'О СП Е КТРЛ
если А' отрицательное, то А' = -|Л'|, и поэтому
k = |*,|, Jtr = -A’ + ^p, р = 0, ±1, ±2t ....
Заменим во второй формуле на -fca. и одновременно р на -р, Тогда
вторая формула (для отрицательного К = — |А|) примет вид
fc = |^:|. = Jf + ^р, р=0, ±L ±2..............
т.е, в точности вид первой формулы (для положительного К = А’|).
Таким образом. ц Л" = |Я'|. и яры К = — |К| хьиещи <?^wj w лгу .ш-е
^fl/шуту.'
fc=IM А:.=АГ+^Я р = 0, ±1, ±2, ....
Формулу для энергий £ стационарных состояний легко получить из
выведенной формулы ДЛЯ Лг (ДЛЯ ДОПУСТИМЫХ ЗН^ЧеННИ )- ЕСЛИ уЧССТЬ,
что Я = ft3fc^/2m.
При использовании функции £(fexJ — /i2fe*/2m для значений энер-
гий £ при заданном К получим формулу
2 / \ 2
s(flW = (лч
при р = 0, ±1, ±2, . г..
Хотя формулы для и £^(Л"р) выглядят непохожими, но они, вдк
jW&T ПРВДЗО-Ш, и /ЯЛ .Nf.’C эпичный Е,
лр.7яходится гшЕрггыиш /гешетшй схляипоНйгрххиго Шри)мх^еря йля
люде.хи Кронигн-Пеннгх с иерио^ческил1 &>рна-Лирл^йН£Г дрн
И> = 0, при различных значениях константы распространения Л".
2-тг
I *1 -||- I
»Ф< । и1111111111 * 111 >4*11 и... । fc
— За —2а _ л о л 2дг Зт
л л л алл
На приведённом рисунке мы изобразили ось и допустимые значе-
ния величины (их мы обозначили короткими жирными вертикальными
312
J'Л Л ВЛ 7
чёрточками):
=К +при р = 0. ±1. ...
эти значения кратны величине 2?г/£ и их бесконечно много.
Энергетический спектр модели Кронига-Пенни при Ц( — 0, т. с. при
отсутствии связи электрона с ямами, при всех значениях константы рас-
пространения К можно представить с помощью значений рассмотренной
выше параболической функции
ДМ =
2m
2ir3fi3 n2 = rW
г 2 * P 7
TY1L-
берущихся ii точках кя: = (2?г/А)р, где р = 0, ±1, ±2Р ..
Крутизна параболы Е(йж) = ?i3A^/2m в начале координат (при fej: — 0)
определяется значением массы m электрона, так как (ti2 —
= й2/ш.
Приведённая параболическая функция описывает спектр одномер-
ной прямоугольной ямы шириной L с циклическим граничным условием
^(т) = I L),
Эиереетггчестсгш Очект/? ЭЯекл1/№ЯЛ tf iroJe.iu Крышгде - Пенны в пределе
нулевой связи является спектров прямоугольной лотен^иальной я.иы е 5ее-
яонечнылш сгоенкаии и условием ^орна-Л^лганд. ширина ямы А ривнд
длине периода в уг.тляии Борн л - Яар.тшна.
7.4. Исследование энергетического спектра
313
Точки, кратные тг/Л. мы обозначили маленькими жирными точками
и большими вертикальными линиями. Одно значений константы распро-
странения /С. принадлежащее интервалу —5г/Л < A тг/А (при некото-
ром £?}, мы изобразили большой жирной точкой. Большими жирными точ-
ками изображены также значения проекции волнового вектора Л.г = Л" +
+ (2ir/A)p при р = 0, ±1...
Допустимые значения энергий представлены на приводимом
рисунке. тщ котором изображен график параболы жир-
ными точкам и на этой параболе и па оси Л\г. Обозначены также зпачсЕПГЯ kT
и Е для некоторого значения константы распре охранений /С. Цифрами око-
ло точек указаны значения целого числа р. Расстояния между соседними
жирными точками равны 2л/Л,
Зоны bpUL-WJO^Htf
ОбМсУЯЬ ОГЙ —7г/Л df> 7Г /Л.
(или основной) зоной £/жмюэнд. Дге значений fcT eww -2тг/Л до
—тг/Л и от тг/Л do 2тг/Л, слева и справа от первой зоны Бриллюэна (их
суммарная длина равна 2тг/Л. как и ширина основной зоны Бриллюэна),
второй ЗОНОЙ К ГД.
Замечание
Рассматриваемая сейчас прямоугольная потенциальная яма большой
Li [Ирины £ характеризуется условием Борна-Кармана ^(г) = <(:е+£). а не
нулевыми граничными условиями, VJ(0) = ^(£) = 0, обращения волновой
функции и нуль на границах ямы,
Энергетический спектр ямы шириной Z с периодическим услови-
ем Борна - Кармана описывается формулой £?р0) — {2тгг7?/т£2)р2 (р -
= ±1, ±2, . ), а энергетический спектр ямы с нулевыми граничными
условиями — формулой £г?и - (1г2Й2/2т£2)р2 (р - 1.2.,..); при этом
спектр ямы с условием Борна-Кармана двукратно выраж-ден, а ямы с ну-
левыми граничными условиями ле
Чтобы сравнить спектры Этих двух ям одинаковой шнрштьд по с? раз-
.Л0)
ными i рани иными условиями, положим в спектре £„ ямы с нулевыми
граничными условиями п = 2р или п = 2р 4 I Тогда в случае чётного
п = 2р уровни энергии ямы с нулевыми граничными условиями в точ-
ности совпадут с уровнями энергии Е^111 ямы с условием Борна-КАрмана,
а в случае нечетного п = 2р 4 1 уровни энергии £П1.0, ямы с нулевыми
314
J'Л Л ВЛ 7
граничными условиями нс имеют аналогов среди уровне и Ej, ямы с пе-
риодическим граничным условием Борна-Кармана.
Вместе с тем уровней для из этих я.и ля любал!
достлт^удо Scwbxw-ftK Hdj ж гофрят, лии^осяолцчееял бесксо^чно .ил.таи
идт^у?лиле jjifjp^ww не ^хие^нтся, так как число уровнен Ер хотя
н в два раза меньше числа уровней но уровни Е^ двукратно вырож-
с(01
денЫ; а уровни £„ не вырождены.
Величина £ большая, а потому оба спектра й/' и Ер^ практически
являются непрерывными (точнее, «квазнднекретными»), простирающими-
ся от 0 до + си ь т е. при £ = оо сюл зтп сл£7си/?дг одебще гоео/мР иделтич-
льг, Причём эн^дайическый плотлостл ypoewew /?(Е) ₽ обоих спектрах,
сучгт^дг Kpdfflihocmw выр^ждеяйя йказывою/пйя одш^лидылш.
«Энергетической плотностью уровней D(E)» энергетического спектра
называется Отношение ДЛ’/ДЕ числа ЛАГ уровней Спектра, попавших на
интервал энергий сп Е до Е + АЕЬ к энергии ДЕ. Энергетическую плот-
ность уровней мы относим к объемным свойствам рассматриваемой одно-
мерной модели твердого тела большой длины Е.
7.5. Приближённое отыскание энергетического спектра
в случае Сильной Снитн
Обратимся теперь к более полному исследованию трансцендентного
уравнения
- — Ал"^
cos(A"A) = ch(-yt) cos(A«) + —sh(-yi) sin(fcj)
2-yfc
модели Кронита-Пенни для энергий Е её стационарных состояний в слу-
чае сильной, но не бесконечной связи, т.е. когда Vo —> +оо, но Vo / +оо.
В этом трансцендентном уравнении
* = jvS?, 7=i v/2m(Vb’-J?i.
и константа распространения К равна одному из Лг дискретных значений,
принадлежащих интервалу от А — —зт/Л до Л" — тг/Л. причём разность
соседних дискретных значений Е равна 2тг/£, где £ — очень большая дли-
на нашего одномерного твёрдого тела.
Выше мы исследовали энергетический спектр Е нашей модели Кро-
нита-Пенни в случае бесконечно сильной связи (тс. когда Vy ~ +оо).
7.5. Приближённое отыскание энерг етического спектра
315
ЛрвдляяАлсин теле/?*, что высоты дотвнцштяых бярде/юв У&, яотя
ir батьшие, wo конечные
В таком случае решение нашею трансцендентного уравнения следует
искать в виде
Е = Е^> + ДЕ,
где Ei^ = (ft27T2/2ms2) п2 (п = 1,2. - -.) — какой-то один и? уровней
энергии при Iq = +оо, а Д£? = Д£/<п — малая поправка.
С0ОТЪ£ТСТВСП]1С ПОЛОЖИМ, ЧТО A = fcn + ДА, ГДе Ал = (tf/.s) 71 и ЛА =
ДАаэь — малая поправка, причём
Так как Е = Vfe3/2?n, то
dE ft2 к
dk ~ т ‘
ДЕ = |£*Д* = Дх/^ЁДЛ,
а следовательно,
ДЕ = /ц/^Д*.
д* =
Зная ДА’, по этим формулам можно найти Д^и наоборот
При Vo * +м коэффициент при втором слагаемом в правой части рас-
сматриваемого трансцендентного уравнения модели Кронига Пенни обра-
щается в бсскопстЕгостъ, хотя коэффициенты при первом слагаемом и сла-
гаемом в левой части остаются коней ньши. Поэтому в правой части транс-
цендентного уравнения оставим только второе слагаемое, причём коэффи-
циент при нем приближенно заменим на величину
тг3 - fc2 2. i
2уА: 2fc / (и)
у
Кроме того, приближённо положим, что
sm[(fcR + ДА)я] = siii(Ans) + cos(fr?r.$) ДАз = (-1)Т|ДАй-,
так как sinfAns) = sin(Trn) = 0 и сон(А„х) = сок(тгп) = (—1)п,
316
Глава 7
Таким образом, из трансцендентного уравнения модели Кронига-Пен-
ии при Vii —* +<50 получаем следующее приближённое- уравнение для ||а"
хождения поправок ДЕ к энергиям стационарных состояний:
сов(КЛ) = -l)№sl
2\/Е^}2 /1\2ЕГ
Следовательно, дня поправки ЛЕ к энергии стационарного состоя-
ния Е*1" получаем формулу
Dt г(0)
ЛЕ = ЛЕКя = (-])” tos(A'A).
Как видим, поправка зависит от значения константы распростране-
ния А', причём пр]। К н при А" она одинакова. Таким образом, имеем 1V/2
двукратно вырожденных уровней энергии, а следовательно, при большой,
МО НС бесконечно большой ВЫСОТЕ Vy ИОТСТЩИаЛВПЫХ барьеров происходит
расщепление любого уровня Е;л на jV/2 отдельных двукратно вырожден-
ных уровней, так что с учётом кратности вырождения имеем 2 Л72 = Лг
стационарных состоянии электрона без учёта спилаь энергии которых при
Vy —* +ос сливаются и становятся равными Л'-кратно вырожденному уров-
ню Ej?\
Величина расщепления уровня пропорциональна коэффициенту про-
зрачности потенциального барьера высоты между соседними ямами, так
как при Ц) —* —ос
где £ — ширина потенциального барьера.
Зависимость ДЕ = ДЕдл, от величины константы АЛ характеризуется
функцией (-1 1*сой(А"ЛА график которой показан на приводимых выше
рисунках в случаях чётного и нечетного значений п.
7.5. Приближённое отыскание энерг етического спектра
317
1'?> — 4-ос энергетический спектр модели
Кронига-Пенни выглядит, как показано
на приводимом ниже рисунке, на котором
изображены два самых низких интервала
спектра (при п — 1 гг при п — 2). Пол-
ный спектр имеет бесконечное числи та-
ких энергетических интервалов.
йеллого £7i£K?npa является его ооивдя
Эго означает, что ck/Hvimw.uwe 2гнд-
чеиия энергии пялцшшл/жых состеямии -Д О Аг Я
нн/ле/юаддлш энергии
при п — I. п = 2 ц гаг. d_, плотно зпняшмлш эне/?гетичссхи.ии jpowyr-
-ww, причём в каждом интервале имеется ровно Аг энергетических стаци-
онарных состояний электрона (без учета спина электрона), где Лг — чис-
ло элементарных ячеек в модели Кронига- Пенни одномерного молельного
твёрдого тела.
Така [с «квазинепрерывные» интервалы, составленные из дискретных
уровней, называются «разрешёнными зонами», или просто «зонами». Меж-
ду ними располагаются интервалы энергий, которые невозможны для ста-
ционарных состояний электрона, Это «запрещенные зоны». На пашем ри-
сую® показана самая низкая запрещёнехея зона, расположенехзя между пер-
вой п б юрой разрешёнными зонами (при п — 1 и п — 2). Самая верхняя за-
полненная электронами зона называется «валентной зоной», а первая энер-
гетическая зона, полностью свободная от электронов, называется «зоной
проводимости». (Здесь МЫ говорим только о случае нулевой температуры
г = о.)
Попавшие в зону проводимости из валентной зоны электроны в резуль-
тате тепловых флуктуаций^ скажем при комнатной температуре Т = 300 К,
становятся носителями электрического тока.
3IH
Глава 7
Б. МОДЕЛЬ КЮИИГА-ПЕННИ С МНОГИМИ
ЭЛЕКТРОНАМИ
7.6. Модель Кроши а-Пенни с многими электронами
Мы рассмотрели модель Кронита Петнгн С одним электроном, ио твёр-
дое тело содержит, конечно, очень болы и ос число электронов, порядка чис-
ла элементарных ячеек Л и нём; Рассмотрим поэтому теперь модель Кро-
нита-Пенни с многими невзаимодействующими друг с другом электро-
нами.
Электроны реального твердого тела можно разбить на две группы.
В одну входят «внутренние» электроны, т.е. электроны замкнутых элек-
тронных оболочек атомных остовов твёрдого тела, неразрывно связанные
с этими остовами и никогда их не покидающие. Поэтому эти электроны на-
зываются «связанными электронами». К другой группе относятся «внеш-
ние» электроны, т.е. валентные электроны атомных остовов, которые от-
рываются от остовов и способны свободно перемещаться по твёрдому тепу.
Они являются «свободными электронами», или «элементарными носителя-
ми» электрического тока в твёрдом теле.
Именно поведение свободных электронов иллюстрирует модель Кро-
йта-Пенни. Потенциальные ямы л ой модели моделируют ноля атомных
остовов кристаллической решётки, которые действуют на свободные элек-
троны.
R моде-чи Кронига Пепин мы рассматриваем поведение «обобшеств-
УчнтывасмОС в модели КрОнига-ПсЕшя взаимодействие Электронов
с атомными остовами намного больше взаимодействия элшронов друг
с другом. Этим последним взаимодействием можно полностью пренебречь.
Поэтому систему своб^ных атеяшрсшбА твёрдого телд ины считдйм иде-
т е. состоящей из невзаимодействующих между собой частиц.
Рассмотрим теперь сначала модель Крон ига- IIcheih при «утевгаи гоел*-
Г — О, считая, что в каждой яме (на каждом атомном остове)
имеется по одному электрону, так что во всем одномерном твердом теле
7.6. Модель Крони га-Пенни с многими электронами
319
из Аг элементарных ячеек пусть имеется ровно Лт электронов, как это про-
иллюстрировано па приведённом выше рисунке.
Ирл объединении Лг «невзаимодействующих» им в одномерное твердое
тело получаем в качестве уровней энергии отдельных электронов уровни
энергии Е'.": отдельной потенциальной ямы. В твёрдом теле, однако, эти
уровни ±V-кратно вырождены, так как электрон может находиться в любой
из xV имеющихся для него потенциальных ям, при этом+ пребывая в разных
ямах, он имеет одну и ту же энергию.
Если потенциальные ямы «независимы» (при Vo = +«), то яри нуле-
вой я состоя/шы n = I будет находиться
в своем собствен wow ядгеФ как это п и казано на приведённом выше рисунке.
Между потенциальными ямами, однако, при больших Vo имеется
«связь», и поэтому уровень отдельной изолированной потенциальной ямы,
в том числе и рассматриваемый нами сейчас при n = I, расщеплён на /V
Отдельных уровней в элгудотичедоую золу.
Таким образом, с учёто.ч пришщлл залре/nw Лбтудн л/?м нулевом ?лс.п-
леротуре Т = 0 наши Л1 элсюй/ю«ой росно-
лажыться на у/№#нях зоны, причем на каждом уровне будет на-
ходиться по два электрона (с учётом двух спи новых состояний электрона
для каждого стационарного состояния, полученного при построенном нами
в разделе 4 решении уравнения Шредингера модели Кронига-Пенни без
учета спина).
Таким образом, при нулевой температуре Г = 0 в основной энергети-
ческой зоне окажутся занятыми электронами только нижние Л'/2 уровней
зоны. Верхний граничный заполненный уровень в этой эоне называется
«уровнем Ферми» и обозначается Ер.
Наложим теперь на одномерное твёрдое
тело внешнее электрическое поле. Это по-
ле начнёт ускорять электроны. т.е. сооб-
щать им энергию и переводить их из состо-
яний, близких к энергии Е>, в состояния^
тоже близкие к энергии Ер, но большие их
по энергии. Эти переходы могут осуществ-
ляться^ однако, только в близкие энерге-
тические состояния, так как
основ.
энергет.
эона
пезап. сост.
<------------------ Е„.
заполн. сост.
к
в т&вдх мл^оскйличвс^ме лйля слабые (s масшта-
бах pfMCLwwhjx -.ипярвджпнческих эив/ъд/м. которые птолькп jr рагелгат-
pjfftac.w в жоделм /С/мммга-/Теням).
Такие близкие энергетические состояния (вблизи уровня Ферми Ер)
имеются в наличии в случае рассматриваемой энергетической эоны, и по-
320
Глава 7
зова J незал- рост
провод. I__________________
----------------
валент.
эона J заполн. сост.
Рассмотрим теперь, однако. модель Кронига-Пенни при нулевой me.w-
гсердтлуре Т = 0, когда п каждой яме находятся не по одному, а по два
электрона, как ЭТО показано на рисунке. В Случае отсутствия «взаимодей-
ствии» между потенциальными ямами (при Vq — +оо) на основном уровне
n = 1 каждой ямы будет теперь находиться два электрона.
При наличии «взаимодействия» но-
ТСЕТЦИаЛЫ1ЫК ям уровни отдельной ямы.
в частности рассматриваемый нами сейчас
ее основной уровень. расщепятся в энерге-
тические зоны, состоящие из ЛГ отдельных
дискретных состояний каждая.
С учётам стата н лрпиццта //дулу та-
it/w 2ЛТ эитектр0нов при нулевой тьчле/кь
туре теперь займут все омектдосся Ли них N состояний основной элср-
зетнческой зоны.
Наложенное на одномерное твердо* тело внешнее электрическое ноне
теперь не сможет ускорять электроны* так как вблизи верхней 1раЕ1ицы
полностью заполненной зоны нет энергетических уровней для электронов
больших энергий (здесь начинается запрещенная зона).
Достижимые в эйссперхшеятох лшлроскоиичде-кие электрщкеение поля
.иолы до сравнении с -микроскопическн-мп атолгнылш долями.
Таким образом, возбудить электрический ток теперь нельзя, и мы име-
ем дело с диэлектрикам.
Стало быть, вес кристаллические твердые тела лгрн ну? свой танлера-
туре Г = О балимсньг быть либо дизлектрикалш, шбо ^етдллплш.
Вообще можно сформулировагь следующее правило. £сли дльиснтар-
ная ячейка кристалла чётное число электронов, кристалл будет
4?изиек^ирил’олг. Если его элементарная ячейка содержат нечётное число
злектропоя. он будем .иета.гло.м.
Это правило в основном оправдывается. Например, атом углерода С
имеет 6 электронов, и а лиаз действительно является диэлектриком. Или
атом алюминия Л1 имеет В электронов, и алюминий является металлом.
7.7. МОДЕЛЬ КРОНИТА- ПЕННИ
32]
Однако, если взять, согласно этому правилу, бериллий Вс или маг-
нии Mgn атомы которых имеют по 4 и 12 Электронок соответственно, ТО ЭТИ
элементы должны быть диэлектриками, а они — металлы.
Гак происходит потому что в твёрдых телах этих элементов происхо-
дит разрешённых энергетических эон.
Энергетическая схема уровней
для модели Кронита - Пенни в случае
диэлектрика имеет вид, показанный на
рисунке.
Последняя энергетическая зона,
шжтаыл заполненная Электронами,
называется «валентной зоной» (она
изображена на рисунке с жирны-
ми точками, [[оказывающими запол-
ненные электронами состояния этой
зоны). Первая энергетическая зона,
лол нос-гаьш свободная от электро-
нов, называется «зоной проводимо-
сти». (Здесь мы рассуждаем толью
О случае пулевой темперэггуры Г = 0-)
Попавшие в згу зону из валентной зоны электроны в результате тепло-
вых флуктуаций, скажем при комнатной температуре Г = 300 К, становятся
«носителями» электрического тока.
В- МОДЕЛЬ КРОН ИГА-ПЕНН И ВО ВНЕШНЕМ
ЭЛЕКТРИЧЕСКОМ ПОЛЕ
7/7, Модель Кронигз-Пеннн при наличии внешнего
электрического поля
В разделе А мы рассмотрели строгую квантево-механическую теорию
стационарных состояний свободного электрона в модели Кронита Пенни.
Теперь в этом разделе В покажем, как в рамках модели Кронига-Пеннн
построить теорию электропроводности твёрдого тела, для чего рассмотрим
модель Кронита-Пенни в так называемом лтатикмссдчестам приближе-
нии, с нялолсенйым тктиаяаным одййродяылс влекши, и элеятрачйсяЕгм ло-
лам. но без уч^^а влияния теляйяых: кйлгбдный awawoe
и на г. с. будем
заниматься здесь нс построением полной строгой теории электропроводно-
сти, а лишь выяснением физики происхождения в ней jw-
322
Глава 7
си/яезей электрического тока. Другими словами, выясним, клкшм образом
ЭЛ^К?Нрг7НЫ s -Uflde.TH AjjrHJU<?tf-77<?UUU cwstfawiw ЫеАТН/JU ЧГСМШ fflflK.
Для элскгронов, которые перенося! электрический j qk в iнордом то-
ле, аш лю/чсеи исиаль^шать изученные в разделе Л сголдооянрнЫЁ сщ-
сшояния swetfffl/wwfltf. В качестве состояний этих практически кляс^ичежшг
электронов (переносящих ток) надо взять так называемые «волновые па-
кеты», составленные из электронных стационарных состояний, найденных
в разделе А.
Электроны, описываемые волновыми пакетами стационарных состоя-
ний модели Кронита -Пенни, для краткости будем ниже называть «реаль-
ными электронами», или просто «электронами», так как только ими мы
и будем заниматься в этой главе.
Такого рассмотрения;, по существу, «квдзнклэссического» и даже про-
сто «классического» приближения квантовой модели Кронига-Пенни dfl-
сшдлючж? для построения теории электропроводности твёрдого тела.
//цмяояяя CtfoptttWd электярякд
Рассмотрим блохо векую функцию стационарного состояния электрона
и модели Кронита Пенни:
*) = е-OMhEjrf-H/CJ!
индекс п, обозначающий номер разрешённой энергетической зоны, ра-
ди краткости мы здесь опустили. Константа распространения Аг играет
роль проекции волнового вектора А.,: элекгропной волны на положитель-
ное направление ОСИ Я, циклическая частота этой блоковской волны paBEia
И*) = Ек/fi..
Лак л<ы уж*? стделж бллховские гДуялчрш н£ логу/л «ншсывдоть лрдк-
тичес™ кжггсич^кив электроны. являющиеся элЁнеитщ^ны^и поситвтя пи
эшелкцричесхлаго /лохд в wepdru, /деле.
Локализованный в пространстве точечный эискгрин, движущийся
с определённой скоростью и переносящий электрический заряд, не опи-
сывается блоковской стационарной волной, так как плотность вероятности
|^k(ei 0|2 = |^к(йг}|2 найти электрон в интервале лЬ; около точки ж и этой
волне не локализована в определённой точке пространства внутри твёрдого
тела, а размазана по всей его длине.
Точечный лрлюяычнлш электрон, являющийся элемен-
тарным носителем электрического тока в твёрдом теле, с константой рас-
пространения Л'п ОПИСЫВаЕТСЯ ЕЮ блОХОВСКПП фуПКЦИСЙ С ЭТОЙ КОЕЮТаЕГГПЙ
7.7. МОДЕЛЬ КРОНИГА- ПЕННИ
323
распространения К, а волновым пакетом
h'4-й/С
V'A'fi, i) = У Ск c-^h> E*i+;ft'r Uk(i) ff/,
а-дк
составленным из бпоховских функций с близкими значениями констант
распространения около некоторого фиксированного значения А\ который
движется в пространстве с так называемой «групповой скоростью»:
/Ь'1 _ ‘М*’) _ L <1Бк
dK - h dK -
здесь L4_'(А”) = Вк/ft, причём групповая скорость = г = является
проекцией скорости реального электрона па ось т.
При ЭТОМ следует считать, что величина ДА, характеризующая «ши-
рину» волнового пакета, удовлетворяет неравенствам
ДА Т ак Т-
L Л
Таким образом, в обычном пространстве Электрон, описываемый вол-
новым пике том, имеет пространственные размеры:
Дя; L, Дт > А,
много большие атомных микроскопических размеров Л, но много меньшие
макроскопического размера L нашего одномерного твёрдого тела.
Так как величина ДА очень малая, то волновой пакет, сосредоточен-
ный Около Л", как и блоховское стационарное состояние К\лгаягсио нзобрл-
тнть /почкой Л' на энергетической диаграмме £j<, показанной на рисунке
ниже.
Таким образом, мы установили физический смысл первой производ-
ной энергетической функции по А в модели Кронига-Пенни.
в точке Л'. двдёнйоя но /а. y/fiswa ско-
рости ь = Уф(/С) ряслрострлнения я нолож-ытЁЛЬясш шнроВДЕшии оси а:
пигеота, йк’тделенного из стационарных бзохг^скит функций с
жало ояшгичя^щидися от А’ едочстиями коо^стднт рлслросп^оиеиия,
На рисунке изображён график кривой Е\г некоторой лЕтсргстичсской
зоны и точка Аг на этой кривой. Тангенс угла наклона касательной tgo
к кривой 77j< в точке К даёт величину групповой скорости Vq, = /• =
для данного значения К. Как непосредственно видно из рисунка, при Л" =
= 0 н К = ±5г/Л скорость i1 обращается в нуль.
324
J'Л л ВЛ 7
Строгий вывод формулы для групповой скорости электрона
В приведённом выводе формулы для групповой скорости электрона
мы неявно предположили, что константа распространения К является
волновым числом, хоти блоковская функция
^к(х) = е,ЛГ±1хк(ж)
тзе является га/здкишчесшш вдвды. Приведём поэтому строгий вывод фор-
мулы ДЛЯ групповой скорости рСЯЛЬИОГ» ЭЛСКТрОТЮ.
Предположим. что рассматриваемая стационарная блоковская функция
нормирована условием
Л Л
J dx |w(e)|2 = У rf.r|llft'(z)|2 - 1,
о о
т.е. нормирована на отдёльнои элементарной ячейке. Функция пе-
риодична с периодом А:
+ А) = Цк(зг).
Стационарная блоковская функция является решением стацио-
нарного уравнения Шредингера;
' + V(XH'(X) = Е^(.х),
4 m cixJ
с периодическим потенциалом
V(j- + Л) = V(e)-
7.7. МОДЕЛЬ К РОИ И ['А ПЕННИ
325
Подставим в это уравнение елоховскую функцию и найдём
= ,KC^«K(z) + CiKil
лт л.г
fd К ' «-0 iFf V: i X л т Т “ iJi Г dlA J£ ! КJr Л /х
—= - А2е'л1 ик(яг) + 2tA етК г -г21- + е —£;
ах2 d® dx2
['аким образом, для функции «к имеем уравнение
ft2 К'1, A2iK fr d2uK , V, г „
Дифференцируя это уравЕхсние по А". получим, чти
Ъ'Чк <Рик Л2 (1лик
m dxdfC 2m
L F- dUK
+ Ek1k
h2 К h2 № (fatf h2 i Лик
m u/f+ 2m dK w dx
du K AEk
AV-dK~-dK UK
Умножив последнее уравнение Eia и^-{—2m/ft2) п про интегрировав его
по т or 0 до Л, получим, что
Л
f
2m
h2
Erf““2S“
“ И T7F + № + ^K-f
di< I_dx2
dx
dz nJ
2т d£j<
. h2 ЛА'
- 2K uK = 0.
C 0
Интегрируя ио частям интеграл, содержащий вторую и первую проив-
водные d2/dara и d/rt:t от dk/</dA\ стоящий в первой строке этой формулы,
убеждаемся, что рассматриваемый интеграл в первой строке равен нулю.
В самом деле, для него получаем, что
Z j * d2 dujf * d
./ dx2 dl\ K dx
II
duj<
dK
A , *
[ dr Л Лид-
/ di; dts dA'
cfcr dz dK 1
d
о
л
*
Л
о
d
о
326
J'Л л ВЛ 7
так как подстановка обращается в нуль в силу периодичности функции
имеющей период Л. Интегрируя еще раз по частям, получим
/ dy
./ ds di dK ~ ~ dx dK
о
&ЦуЛик
dx* dK
[ dr — ц* йпк
./ dz* dK
i)
так как подстановка снова обращается в нуль. Далее
Л Л
TL- / . * d du. к * du К
2th I dxuK ——. = 2iA uA- —
I ax aK dK
о <’
. ^aK dtiK
' di dK
fi-T .
da: dK
подстановка снова обращается в нуль в силу периодичности функции
у у (s).
Таким образом, окончательно получаем, что
Л
Гр TZ1 *
|_£а' - ~Ъа~ ~ v ] к
da
dx1
- 2iK
dar
UK
так как н фигурных скобках стоит комплексное сопряжение левой части
полученного выше уравнения для функции ?я^(лг).
Следовательно, окончательно имеем прос тое уравнение
Л Л
[ dx 2i 4 + [ dx -4- Н - 2А-] = 0.
I dx ,/ I Ъ2 dK
й о
7.7. МОДЕЛЬ К РОИ И ['А ПЕННИ
которое можно представить в виде
Л
2?fX /11г,* JUff лг, *
"ГТ jfz — j dx i —2tuK —---F 2А > -
7ji“ //A j I di J
Таким образом,
A
im > / 4 + * 4J 1
j? ~dK =./ * I“«*+ / =
0
л A
= [ drQ~'lK* «£- у- (е‘А:Гик) = [ dx^-j-^к,
J dx \ / J dx.
о 0
так что окончательно:
Л
m dEK f r ,* ft d .
h~iK I
0
Интеграл в правой части этой формулы является средним значением
проекции импульса ра. электрона па ось т в состоянии, описываемом фуЕгк-
цией так как мы предположили*1||Q волновая функция нор-
мирована условием
А
У dx^K^K = 1;
о
оператор проекции импульса на ось х равен = Д у-.
Так что окончательно имеем формулу
1 = £ =
ft m r
в которой ir — средняя скорость электрона в состоянии ^к-(х). Так как
Ел = то отскщэ заключаем* что
lJ=^K
т. с. приходим к искомой формуле пл я групповой скорости реального элек-
трона.
328 Глава 7
fi мдкетга ваш, йлызкшг к йлсдявской волга ^к(я)т л# вояяы и-ивют
л/зшие/зил жЭымдоовые сдетЪше c^jr?t,mjf, w лаэтаиу jwairua c^wmawt, что
грулт?овдл сао/зяс/ль такого волнового пакета расгнл с/гейгай скоро сто атек-
троиа в бдоховскон волга
Движим*' элеяти/делд во внешнел* иоле
Рассмотрим теперь движение электрона, описываемого волновым па-
кетом, при действии из него электрического поля с напряженностью
£( =£□•) > Oj приложен ноги в направлении вдоль оси х.
Электрическое иоле напряжённости £ (= £г) действует на электрон
с силой F(= Fs) = -е£(= -е^Д где с = |е| обозначает абсолютную
пеличтпту заряда электрона
Работа электрического поля, произведённая над электроном за беско-
нечно мальЕЙ промежуток времени от t до i + di, равна
5*4 = —t £v<iL
где w = Гф является проекцией 1/л скорости электрона на ось я; проекция
на ось я силы, действующей на электрон со стороны электрического поля,
равна Fr = -г;£т = -rf-
Работа 5Л идет на увеличение Энергии Электрона. Пусть в мп-
менг времени t электрон имел константу распространения Аг Тогда
-e£wdt = dEK = ^-dt,
dk dt
так как
EK(t) = EfrtKtt)).
Сокращая на dt и учитывая, что dEn/dk = Ли, отсюда приходим
к уравнению
— гс = 71--.
dt
которое имеет вид (только вид) ^авгаиця ятрраго яакпиа клас-
сической механики точечной частипы, если считать, что сге.-лмнша ЙК - Р
галяеися прдовдгай />:t; ииил^льсл этой кя сч?ь я. Таким образом,
окончательно имеем уравнение
ЙЁВДчишг F = АЛ-: галотж лб/шзом, Аля тячечняго ?егчласси 7ескн-
гл ячгктроча я людети Лро77аги-Лся7<и, ллпгылаемо-д? лолмляы.н ртлквднщ,
7.7. МОДЕЛЬ КРОНИГА- ПЕННИ
32 У
нлдеэтя фиэдчеслчш слысл рт ня ось ж илгнульса этого зягктронд,
д донсоталшл jjtfCfj/Mcmpflfwewuj? А — лрдаятрти яллмоярго г?с^/ло/?д сгл лплны
ЛД ОСЬ Z.
Хотя уравнение движения нашего реального электрона в модели Кро-
нига-Пенни одномерного твёрдого тела имеет вид
rf/J с
“ = ~е£'
в котором F = рд и £ = £я, и хотя оно выглядит в точности так же,
как уравнение второго закона Ньеотоеш для точечной частицы, оно йоясё не
является урдйлелле.и второго закона ЛГьютона Эля рассмотренной? я раз-
dcie Л атектрона.
Во-первых, мы имеем дело нс с импульсом электрона, а с его ^квази-
импульсом» Р (= рт) = ftA\ определённым с точностью до прибавления
к нему любого кратного ВЕЛИЧИНЫ 2тЙ./Л.
Во-вторых, мы не учитываем сил, действующих на электрон со сто-
роны периодического ноля атомных остовов, намного больших, чем сила
-е£, действующая на электрон со стороны внешнего электрического поля,
которую мы в уравнении движения учитъгнэем.
В-третьих, хотя мы и рассматриваем электрон как свободный^ но его
кинетическую энергию не можем считать равной величине
т»фф V*
±к" 2
даже если в неё нходич нс настоящая, №cmww?/aJj> масса электрона т, а его
«эффективная масса» тн>фф. Это выражение справедливо только для состо-
яний с Д’ = U. вблизи «дна» зоны проводимости.
Действительно, при К = 0 можно считать приближённо, что
A-<i
1 #Ек
*
к=11
dK
К
йг=п
1 <PEk
2 dK'1
1 1
ft dtf “ ft d/<
Ец = Ek
K=l\
так что, учитывая, что (ЛЕк/^Аг)к=о = 0, получим
330
J'Л Л ВЛ 7
Ь’к =
2тэфф:
Ji о
где
ТПэфф - ft I а I
\ / tt=O
Вернёмся, одна ко ч к уравнению движения нашего реального электрона
во внешнем ионе. Как следствие приведённого уравнения движения элек-
трона, описываемого волновым пакетом в модели Кронита-Пенни с прн-
.юже 11 е Lhi м bi 1ё ld 11 l и м Электри чее кл м по; lew^ имее м ура in i ej j не
сЙ
- e£ .
Исходя из этого уравнения, можно строго доказать, что ллишл энергия
Ек — су? Hcuifzo реального точечного злйКтронл в здйСтрьчеслом поле,
где — потенциал электрического поля, т.е. £ = -d^?/ds,
Действительно
^-(Ек-^} =
ш
dK _ . с1.т
dK di *’ da? di
JP
= r*y- + rftv =
di
—vef 4- eft1 = 0:
здесь мы использовали обозначение i> для игр.
.WttLCYJ
Эффективную массу электрона согласно классической механике сле-
дует определять из соотношения
ИМПУЛЬС = МАССА х СКОРОСТЬ,
т.е. считать сё равной коэффициенту лропорииональности между импуль-
сом и скоростью. Так как выражения для импульса и скорости точечного
элекэроиз, движущегося в нашем модальном одномерном твёрдом тшзс, нам
известны, то имеем следующую формулу для
™ - -Р - - ^2^/^у1
— .jr — - Й Л I ... I
’л1 1 d£jr V dK 7
П d/f
Эффективную массу электрона можно, однако, определить и по-
другому, из соотношения
СИЛА - МАССА X УСКОРЕНИЕ;
так поступают в существующей теории полупроводников.
7.7. МОДЕЛЬ КРОНИТА- ПЕННИ
33]
Различие в двух определениях эффективной массы связано с разным
пониманием сути второго чакона Ньютона классической механики. У Нью-
тона было
с/р _
- = F. p-mv
Мах. однако, посчитал (думаем, что неверно) второй закон Ньютона не
шедши, а сн.тм и записал его в виде
F = та.
предположив неявно, что масса т не зависит от времени (исключив таким
образом, например, реактивное движение из своего рассмотрения, чего, од-
нако, к сожалению, не оговорил).
Воспользуемся определением эффективной массы электрона
(с помощью формулы F = dP/dt = тл) и вычислим мгновенное уско-
рение а (= ах) нишею электрона в момент времени f. Ускорение — это
сед/юоня по и поэтому
й _ ^ггф _ .1. da£j< dJf 1 d2£j< ^_
di “ й dX* Л ” fi3 d№
так как
—^(о-вдк«)). к-ip, f-r,
т.е. приходим к следующей формуле для эффект идссы рассматри-
ваемого нами электрона, описываемого волновым пакетом:
+ 2 / d2 £ к \
= Й
Таким образом, полученное «уравнение второго закона Ньютона» для
электрона, описываемого аолеювым пакетом, можно записать в виде
^гггр _
тЧФ
это уравнение движения электрона, описываемого волновым пакетом, во
внешнем постоянном однородном электрическом поле, приложенном к на-
шему модельному одномерному твёрдому телу.
312
Глава 7
Оба приведённых определения эффективной массы электрона, конеч-
но, различны^ но мы будем пользоваться вторым определением, так как оно
принято в существующей теории полу и ре водников.
Вместе с тем следует подчеркнуть, что определение эффективной мас-
сы из формулы ma = F справедливо только в случаен когда энергия элек-
трона Е = Л*№/2т строго квадратична по Л’, потому что только и этом
случае эффективная масса является постоянной величиной и уравнение вто-
рого закона Ньютона можно записать в виде ш« = f. В противном случае,
когда энергия Е — не квадратичная функция ft’, т. е. когда масса зави-
сит о г /<, вводить эффективную массу указанным образом, вообще говоря,
неправильно.
Чтобы ещё лучше объяснить понятие эффективной массы элек-
трона, описываемого вол новым пакетом, рассмотрим случай предельно сла-
бой связи электрона с атомными остовами (при Йу = 0). Тогда энергетиче-
ская кривая будет иметь вид = Ед? = ft2№/2m, где m — истинная
масса электрона, для указанной функции:
_ £
dK2 т f
з следовательно, в этом случае = из, т.е. масса равна
ыелшнкой массе электрона.
При рассмотрении элезпро провод! юс ти твёрдого тела при темпера-
турах Т = 300-600 К оказываются интересны только электроны вблизи
дна эоны проводимости, т.е. электроны, для которых Я’ = 0. Для них
dEfc/dK /< (d2Ejr/dft"2}^, где индекс «0» означает, что рзесматрипз-
с мая вторая производная берётся при Л = 0. На дне зоны проводимости
(d2f?x7d/V2)(h 0. Подставляя полученное приближённое выражение для
dEj</^^ ь формулу первого определения эффективной массы, имеем
d№ )
к=о
получаем формулу, справедливую для электронов вблизи дна зоны проводи-
мости- В точности такую же формулу для эффективной массы электро нов
вблизи дна зоны проводимости Л' = 0 даёт н второе определение эффек-
тивной массы. Здесь индекс е (electron) означает элек/н/ган.
Как видим, можно считать, что идеей вшивд
dwu ЗОЛЫ H/Jtftforiu-WOCJHW ft — 0) Ji1 г SrtrtWCUffT Offl
7.7. МОДЕЛЬ КРОНИТА- ПЕННИ
333
и я&мется достоянном в^ычинои отличной, о^нико, от истинной люгсы
электроил.
Таким образом, приходим к следующей интерпретации второй произ-
водной энергетической функции по Аг в модели Кронита - Пенни.
5то/?ач производная энергетической функции Ед- = Е( А") яс* Е # точ-
ке А рш№а Й.а/тЭфф, г^эфф — эффективная .waccia электрояд tf ,ио-
деди Крониго-Ленин. х^д^термзуелюго коноиднтои рделроотрднепия А'
и проекцией иилутыхг Р = ЛА' на ось л+
Хотя, как мы убедились, эффективная масса электрона в твёрдом те-
ле зависит от А', т.е. зависит от скорости электрона, но эта зависимость
не очень существенна, так как для элеЕлропровсднсстн твёрдого тела на-
до рассматривать фактически только электроны на дне зоны проводимости,
т.е. n oxpccTEjncTtJ точки /< = (к а следовательно^ можно Считать, что эф-
фективная масса равна = й" (d^E/c/dE2) 1
Ik-п
Если на диаграмме энергетических уровней построить параболу с к =
= е(Ат) = /?Ар2/2гпп с вершиной в точке Ал = 0 на дне зоны проводи-
мости, то эта парабола будет касаться энергетической кривой Ек = Е(Е)
модели Кронина Пепин с точностью до бесконечно малых величин второ-
го порядка малости включительно- Крутизна этой параболы определяется
массой те.
В теории электропроводности рассматриваемого одномерного твердого
тела мы можем заменить (в окрестности точки К = 0) правильную энерге-
тическую кривую Е(А') на сё параболическую аппроксимацию Дру-
гими словами, ,иаж.7/о считать электцроны е зале дровами,ноет и классиче-
сяилга точечными чаеттщолгп.
При этом, однако, надо учитывать, что масса ш,- электрона в зоне про-
водимости не равна истинной массе m электрона.
На ЭЕТсргстичсской диаграмме на рисунке слева прозы люстрировано
движение электрона л о состшшнял/ зоны проворности при наложении
внешнего электрического поля на наше одномерное твердое тело, направ-
ленное в отрицательном направлении осн я. На рисунке справа показа-
но движение электрона я рояльном пространстве, т.е. в са-
мом одномерном твердом «ма к которому приложено электрическое ноле
£(= £я.) < О, направленное против осн
Электрон с «потолка» валентной зоны, обозначенный на рисунке пу-
стым кружком, в результате тепловой флуктуации в Етачальпый момент
времени перескочил на «дно» зоны проводимое tie, и на него начало дей-
етвокагь электрическое поле. I? начальный момсеп времени его скорость
и(= t?iP) равна нулю. Затем она начинает увеличиваться. Так как электрон
334
Глава 7
движется jjjim изображённой на рисунке ситуации в направлении оси е,
то его групповая скорость tfrp(= t-K = t1) будет положительной. Поэтому на
энергетической диаграмме на левом рисунке электрон будет двигаться впра-
во — в область, где производная dEjc/dK положительная^ как i in казано на
рисунке. Эффективная масса электрона разумеется, положительная.
Латые и сметные элект/wwfcr
Вернёмся к обсуждению уравнения второго закона Ньютона для элек-
трона, описываемого волновым пакетом В этом законе мы рассматриваем
электрон, не размазанный по всему твёрдому телу, для которого мы решали
уравнение Шредингера, а как точечный квазиклассическии электрон.
Электрон, рассматриваемый в стационарном уравнении Шредингера,
сильно взаимодействует с атомными остовами п дозмдозд ля sce.wv od-
твфдону телу. Здесь же мы говорим о свободном от такого
взаимодействия точечном электроне, не взаимодействующем с атомными
остовами, но взаимодействующем с внешним электрическим нолем и дви-
жущемся против электрического пиля, как это Следует ня вида выведенного
уравнения второю закона Ньютона, так как электрический заряд электрона
отрицательный.
Эти по-новому понимаемые электроны, как говорят, «одеты» в силь-
ные взаимодействия с атомными остовами.
Когда в квантовой физике рассматривают систему сильно взаимо-
действующих частиц, её часто заменяют системой из
невзаимодействующих друг с другом так называемых «квазичастиц». При
этом учитывают, что физические характеристики квазичастиц могут сильно
(и даже очень сильно) отличаться от характеристик исходных частиц.
7.7. МОДЕЛЬ КРОНИГА- ПЕННИ
335
Об исходных частицах говорят как о «голых» частицах, а о квазича-
стицах — как об «одетых» частицах.
Рассматриваемый точечный электрон в модели Кронига-Пенни, опи-
сываемый волновым пакетом из стационарных решений уравнения Шре-
дингера, является примером такой «одетой» квазнчастииы.
Движение Эырки ео внешнем доле
Рассмотрим теперь в модели Кронига-Пенни нг оЭнн электрон, опи-
сываемый волновым пакетом, в пустой разрешённой энергетической зоне,
а энергетическую зону, шшюстью эл£кт/?о™гчн, как показано на
рнСуНКС Е1ИЖС.
Сначала рассмотрим полностью заполненную зону; и зятем эту зону
с одним недостающим электроном.
Так мы введём представление о важной элйментарнан нсц?иетеяеэяек-
трц детого тока е твё/и?ан теле — пгрчечнен «ды/ммдо.
Дырки вместе с электронами ссставляЕпт
основу существующей квантовой теории элек-
тропроводности твердого тела.
Они тоже точечные и во всём подобны
точечным электронам и так жс? как они явля-
ются элементарными носителями энск1рнчс-
ского тока, но отличаются от электронов зна-
ком электрического заряда. Они являются как
бы «ПОЛОЖИТЕЛЬНЫМИ» электронами.
Приложим теперь к нашему модельному одномерному твердому те-
лу с полностью заполненной зоной электрическое поле с напряжённостью
£ (= £Я:) > 0, направленное в положительном направлении осн аг. Элек-
трический ток /. создаваемый электронами рассматриваемой леностью
зллшлелпгш зоны, текущий в направлении оси ж, очевидно равен
/(-/,) = -2^5. ГФ(К),
А'
где суммирование ведётся л о всем значениям константы распростране-
ния /<; от А" = — 1г/А до К = тг/Л. причём константа распространения
A — (2tt/L) gf где g — целое число р — — Л’/2 + ],..., Лг/2? jV — чётное.
Двойка в формуле появилась потому, что с учётом двух значений проек-
ции спина электрона каждое состояние энергетической зоны, найденное
при решении уравнения Шредингера, двукратно вырождено, и в каждом
состоянии находится два электрона.
336
Глава 7
Вывод приведённой формулы следующий. Сила тока 7 — это. по олре-
делсЕ1ин\ положительный заряд, проходящий через сечение I одномерного
тела в направлении осн z в единицу времени.
Рассмотрим сначала силу тока /1 создаваемую одним электроном. Что-
бы её подсчитать, сделаем течение заряда этого электрона
для чего p$tj.wjr₽.w рассматриваемый точечный электрон с зарядом -е по
всей длине £ одномерного тела н получим однородный непрерывный заряд
с линейной плотностью -е/£.
Рассмотрим произвольное сечение х нашего одномерного тела и от-
резок длины vtft, примыкающий к этому сечению слева, как показано на
рисунке ниже. За интервал времени от t др t + (ft через сечение .г н по*
Л ОЖ15ТСЛ ИНОМ направлении оси д пройдёт всё то КОЛИЧЕСТВО электричества,
которое в начальный момент времени i содержалось на отрезке ггей, где
и = ?Jrp(A'j1 т.е. количество электричества -(e/Ljwdi, со знаком минус,
так что для одного электрона сила тока равна
1 ~ ~LV = -T/’nwY
Чтобы получить эту формулу для силы тока одного электрона, можно
рассудить и по-другому. При наличии постоянного тока в нашем одномер-
ном твёрдом теле граничные условия ^(0) = 0 и = 0 уже неверны.
Пусть теперь электроны через определённые интервалы времени посту па*
тот в одномерное твёрдое тело из краю .г = (), пролетают это одномерной
тело и покидают ею на краю т = £, причем так, что всегда в твёрдом теле
в каждый момент времени находится только один электрон. Движущийся
со скоростью у, этот электрон проходит наше твёрдое тело за время L/ir.
Так что через сечение л; через раяЕгьге интервалы времени будет проходить
электрический заряд — е, через интервалы времени L/u, и поэтому
г ё е
снова получили уже выведенную нами формулу.
Выше мы установили, что (= = {1/Л)(/rfA7}. Таким об-
разом, электрический ток, создаваемый движением всех электронов полно-
7.7. МОДЕЛЬ КРОНИТА- ПЕННИ
337
стью заполненной электронами энергетической зоны, равен
К=Г7/Л
т _
AL dtf
tf=—х/А
Так как А" = (Зтг/ L) С, где д — целое числот и так как длина L очень
большая, го при веде ей [ую сумму можно заменить интегралом и написать
*/А
7 = -—— [
h 2тг J dK
— п/Л
Интегрируя, приходим к результату
/ = -тН(£/с)я/л-(Як)-«м} =0;
7Г г!
как видим, электрический ток равен нулю, так как при А' = ±тг/Л энерге-
тическая кривая Ь’я имеет одинаковые значсЕтия.
Приходим к важному заключению. /Уатлостью зялолнеттдя э.телтиро-
ЛбГАШ ЭНЙргетйиЧЙС^бГЯ ЗОНД НС У’шстлтетп ff JjlfKW/JW^K'KD^O md’
Kd s wepdu-w жйте, другими словами, не даёт никаких «элементарных но-
сителей» электрического тока в нём
Если теперь в пустой энергетической зоне имеется один точечный
электрон в состоянии AFU. то он создаст элЕтсмршшый электрический ток,
равный
А(=-Ai) — “^^‘гр(Ао);
здесь индекс е означает электрон (ст англ, efeefrow — электрон).
Если в полностью заполненной зоне недостаёт одного электрона в со-
стоянии А’п: то такая зона создаёт так называемый dw/wwww электриче-
ский ток, равный
/л = -2у Е МА ) - f Уф(Ко);
J_. z—* J-.-
здесь мы учитываем, что состояние ЛЪ имеет два спиновых состояния, из
которых только одло состояние тге заполнено электроном- Индекс h обо-
значает дырку (от англ, йо/е — дырка). Приведённую формулу, очевидно,
можно представить также в следующем виде:
Л = “2 ^гр(А) I ^iJrp(Afj),
где суммирование по /< ведётся по всем состояниям заполненной зоны.
ззм
Глава 7
Как мы только что доказали, сумма по К для полностью заполненной
электронами зоны равна нулю. Поэтому сумма в правой части приведенияй
формулы равна нулю и, следовательно
ЛД= Д-г) = -J- T^tXo).
Получили формулу для электрического тока положительно заряженной
точечной частицы с положительным зарядом е = е|.
Приходим к заключению, Залйлнечадя эшетииртдами зяе/?гетцчегкия
jowci с oifojw няйлстлюы/ш/ зотен-трлиам создаёт я одмаыердач /нардом
тете атектрич^-хиг/ ток. равный толу пйлаткат^ьмо зцрялвднтьэд
точечного иосытйдя а-^ктричйжаго зарлди — дырка.
Таким образом, дырка в полностью заполненной энергетической зоне
ведёт себя как положительно Заряженный электрон.
Дырка движется вместе с электронами заполненной зоны, оставаясь
жёстко к ним привязанной. Электроны перемещаются при этом согласо-
ванно. и rtyemoe гжиоянне среди ник движется так. как двигался бы точеч-
ный электрон, если бы он занимал это пустое состояние. Таким образен,
получаем следующее агуретдаглмс запоил //ь^отлаа»;
для движения дырки в постоянном электрическом поле, приложенном к на-
шему одномерному модельному твёрдому телу в положительном направле-
нии оси л.
Дырка располагается «на потолке» заполненной зоны. Поэтому она ха-
рактеризуйся состоянием с отрицательной эффективной массой т^фф =
= Й2 (е^Ек/(^2) 1 < 0. Введём, однако, в рассмотрение положительную
массу дырки с помошью формулы
—! О V ж 1 1 I к < - -h1/ mh~ h I dF J Тогда приведённое «уравнение второго за- кона Ньютона» для движения дырки в окрест- ности «потолка» валентной зоны (при Аг — 0) можно записать следующим образом: di"ip ^^T = efi
7.7. МОДЕЛЬ КРОНИТА- ПЕННИ
33 У
в правой части теперь стоит сила е£ (= e^s), действующая на положитель-
ный электрический заряд (е = |е|) с положительной массой ?Т1/Х1 движу-
щийся в положительном направлении оси т.
Получили уравнение движения точечной классической частицы с по-
ложительным электрическим зарядом и положительной массой, т.е ды/?-
точечный носитель здскт/?ического токл с положительной лшссой — как
реальную положительно заряженную точечную частицу.
В заключение рассмотрим поведение дырки+ образованной ушедшим
электроном, в валентной зоне, когда этот электрон в начальный момент
времени в результате тепловой флуктуации перескочил с «потолка» валент-
ной эоны на «дно» зоны проводи нос тнт и когда на него начало действовать
внешнее электрическое поле.
Дырку в валентной зоне, как электрон в зоне проводимости, нужно
рассматривать как классическую точечную частицу положительной массы
fii/j. Эту массу можно найти, строя параболическую аппроксимацию для
состояний на потолке валентной эоны в окрестности точки /V — 0:
эта парабола касается и точке Л' = 0 энергетической кривой =
= модели Кронита-Пенни с точностью до бесконечно малых вто-
рого порядка малости включительно.
Ветви параболы направлены вниз, что означает, что вторая производ-
ная с?Ек/(th'2 при /< = 0 отрицательная. Следовательно, дырка имеет
отрицательную эффективную массу. Но, как мы разъяснили выше, массу
дырки мы берем положительной, даваемой выражением
mh ~ -ft2
d^K
dK2
к и
со знаком минус, так что .иостю и с)ыркн ло.тоимытелы/ые.
Для уравнения движения ™эя = заряженной частицы с зарядом g
массы т: движущейся иод действием: электрического г гол я, изменение зна-
ка массы лт Эквивалентно изменению злака заряда Здесь а# — проекция
ускорения частицы на ось аг.
Движение точечной дырки на энергетической диаграмме в валентной
зоне и движение её в реальном физическом пространстве в нашем модель-
ном одномерном твердом теле показано ниже па рисунке.
340
Глава 7
В начальный момент времени электрон в результате тепловой флук-
туации перескочил с потолка валентной зоны на дно зоны проводимости
п образовал в валентной зоне дырку, которая в начальный момент имела
нулевую скорость г = 0 и находилась в точке К = О, На эту дырку, которая
заряжена положительно, начало действовать электрическое поле, направ-
ленное, по предположению, в отрицательном направлении оси ас, как по*
казано на рисунке, и дырка стала двигаться в направлении электрического
поля £ (= f.j < 0, т. е. в отрицагтельном направлении оси ж; таким обра-
зом, ее скорость и = т?гр (= (не величина скорости, а л/гаекцмя скорости
г’р- на ось т) отрицательная. Так как скорость и даётся первой производной
dEs/dK, то это означает, что dEtf/dK < 0. Следовательно, на энергети-
ческой диаграмме, приведенной на левом рисунке, дверка будет смещаться
вправо, т.е. в область, где функция Ед- = Е(Ё) убывает.
Закапчивая рассмотрение модели Кропига-Пеппи, подчеркнём, что
эта модель не претендует на то, чтобы количественно правильно описы-
вать поведение свободного электрона и системы свободных электронов
в твердом теле. Л&иЭёзё -Леями ценна /т-лс тто жтолядя каче-
с/идоняо нанять Кйаятдеый оддоктер двалгСЁния w лтект/юно#
я wpdau w,?e.
Из рассмотрения модели Кронита Пенни можно сделать следующие
выводы.
1. Энергии электрона в атоме при образовании из атомов твёрдого тела
расщепляются в эоиы, сосюящне из большого числа близких энергий, раз-
деленные запрещенным]! зонами (т.е. значениями энергии, которые невоз-
можны для электрона). Число одноэлектронных состояний с учетом спина
в каждой энергетической зоне равно 2 Л'. где Лг число элементарных яче-
ек в твёрдом теле.
Дополнение l
34]
2. Имеется два типа элементарных носителей электрического тока
в твердом теле — птризцггслыю заряженные эдеят/юлы и положительно
заряженные йм/мсы. Массы этих элементарных носителей тока отличаются
от истинной массы электрона.
Недостатки модели Кронига-Пенни следующие.
I. Она одчйч^рная, хотя все твёрдые тела, разумеетсяь трёхмерны.
2. В ней нс учитываются хаотические ко.тейпйия агомньсх
остовов и дефекты кристаллической решётки, приводящие к конечным
длинам £е и свободного пробега электронов и дырок и к коечкой элек-
тропроводности твердого тела, так что в модели Кронит Пенни, строго
говоря, твёрдое тело является сверх проводин ком.
3. В ней не учитывается хотя и слабое по сравнению с учитывае-
мым взаимодействием электронов с атомными остовами кристаллической
решётки твердого тела. но ненулевое вэдш/одейс/июде элект/эояов между
собай, т.е. их кулоновское взаимодействие.
Квантовую механику, окончательно сформулированную в 1925-1926 гг.,
к системе электронов проводимости твёрдого тела первыми применили
в 1927-1930 гг Феликс Блох и Леон Бриллюэн, причем Блох разработал
теорию сильной связи при —► со (изложенную и основном тексте этой
гл. 7), Бриллкюн — теорию слабой связи при Vo —► 0, (излагаемую в Допол-
нении I к этой тл. 7).
Дополнение 1 к гл. 7
Рассмотрим пространство периодических с периодом L комплексно-
значных функций 0(л)а заданных на бесконечной прямой —ос < зг < +оо,
которые удовлетворяю! условию нормировки
f Жж)12(^ = г
II
и рассмотрим операторы, которые действуют в этом пространстве функций.
Скалярным произведением (^, V1) Д₽У* функций и ^(л) называ-
ется интеграл
L
(у?, ip) = J dx.
о
в котором звёздочка + обозначает комплексное сопряжение.
342
Глава 7
Уравнение Шредингер;»
можно представить в виде
если воспользоваться оператором
который называется <?«ne;w?Hirtpaw Fij.mu.twh/wji\ или
Оператор А+ называется с^лрл.меетшьгл, к оператору А. если
ДЛЯ ЛЕОбыХ двух Произвольных фуНКЦИЙ И уД т ) £ I фа ВСДЛННи СОЙТНО-
шение
(^,л^) = (A+v,^).
Оператор А называется эдм!<жо#ы,и, если А4 = А, где А1 — оператор,
зрмнтовски сопряженный оператору А.
Легко показать, что гя.тш.тылошигл /7 является jp.iwmwffw.ii олфато-
рам. Действительно, для двух произвольных функций ^(аг) и р{х) справед-
ливо соотношение
получаемое ннтезрированием но частям, причём подстановка в правей ча-
сти равна нулю, так как мы рассматриваем периодические функции
Дополнение 2
343
и ^(я?) с периодом L. Поэтому
L L
(р.ВД = У + У =
О о
L L
= ~2^J ^^(x)^{x)dx + У ^*(x)H(i)^(x)da: = (flW)
О о
еще раз проинтегрировали по частям.
Дополнение 2 к гл. 7
Приближённое решение уравнения Шредингера модели
Кронига- Пенни в случае слабой связи
Конечно, можно найти приближенное решение трансцендентного
уравнении модели Кронигэ-Пенни:
- fc"
cos(K'A) = ch(^i) cosffcs) 4 5h(7t) sin(fcs),
*!_ гГ
при малом V!) г 0 и вычислить соответствующие поправки Д£ =
к энергиям = (2л^йа/тц£2) р3? где р = 1. 2. Зт ..., которые, как мы
показали, являются точными решениями указанного уравнения при Vo = U.
Но можно использовать и другой способ решения уравнения Шре-
дингера модели Кронига-Пеннн и построить иначе энергетический спектр
и случае слабой связи.
Рассмотрим уравнение Шредингера для бее конечной модели Кронша-
Пенни с условием Борна-Кармана:
- j1 у + У(я) = £tf,, । Ь) =
где £ — длина одномерного твердого тела.
Это уравнение и функция У(я) рассматриваются на бесконечной пря-
мой -ж < дс < -ьж, причем К(,т) является строго периодической функ-
цией, составленной, по прелположению, из прямоугольных ям н барьеров,
с пространственным периодом Лъ равным длине элемеитариой ячейки.
344
J'Л л ВЛ 7
Построение решений при Vo = О
Предположим сначала, что V(x) = 0. Тогда нужно найти решения
уравнения Шредингера
йа
2т (fa'2
удовлетворяющие условию Бор на -Кармана, те. являющиеся периодиче-
скими функциями е периодом L, для которых - L) - ф{х).
Условие Борна-Кармана учтём теперь тем, что будем искать решение
r виде ряда Фурье:
ф(т) = £(7ре^’/ь}ра,
р
с периодом Ьл где р — положительное» отрицательное или равное нулю
целое число. Коэффициенты Ср однозначно характеризуют периодическую
функцию ^(я).
Перло ди чсские функции = е1 т с периодом /□ образуют
полную систему ортогональных функции, позволяющую представить лю-
бую периодическую функцию с периодом L в виде их бесконечной линей-
ной комбинации.
Интеграл ортопормнровки ;ися указанных функций легко вычислить^
так как
L Ь £
dx = = —L _ с> >
О О 1°
= —Л------77 (е'^-р'} - 1) = 0 при р' р:
2зп(р — р । \ /
так что имеем условие Сртонормировки
где V.p — Кронекера, равный 1 при р1 — р и 0 при jt/ # р.
Умножим приведённый ряд Фурье для функции па функцию
0-1 (Йзг/Х-) р т Т1 пртинтегрируем по т от 0 до £, с учётом приведённого
Дополнение 2
345
условия оргонормировки. Получим тогда формулу для определения ко?ф-
фициснтоа Ср-
L
Ср = у у e-ip,r/L]pi^(3;)<br-
О
Подставим теперь рассматриваемый ряд Фурье для функции tf.'(z)
в уравнение Шредингера при W(-r) = 0 и получим соотношение
У Сге' = о.
\ 2m Г/ / F
г v z
Таким образом, имеем следующую енлилид-- лтгеб/гдыч^-
(4й^ + я)ч.-о,
для определения коэффициентов Ср.
Эта система имеет бесконечное число решений, которые описываются
формулами
р _ — Г' А Р — -и2
l.F — Vy - — -L-pik — 2m £2
где С — произвольные постоянные, а индекс po нумерует отдельные реше-
ния.
Т/рстроеяие решений яри молола Vo О
Приступим теперь к решению уравнения Шредингера
при У (я) / 0, считая, что его решение удовлетворяет условию Борна-
Кармана ?^(,т + L) = {/‘(я), т.е. является периодической функцией с перио-
дом £.
Учтём, что потенциал V(i) является периодической функцией с пери-
одом А (не L, в А) (Л = Zr/JV, где У — целое число, которое мы называем
числом ячеек в рассматриваемом одномерном твердом теле):
У(зт + Л) = V(e).
346
Глава 7
Согласно теореме Блока любое решение ^(я) уравнения Шредингера
характеризуется заданным значением константы распространения А", при-
нимающей jV значений, кратных 2?г/Л. из интервала —тг/Л < Л' < тг/А.
и его можно представить блоковской функцией
где ti(sr) — периодическая функция с периодом Л-
Зададимся некоторым определённым Значением константы распро-
странения А
Периодические функции и и (я) с периодом Л мы можем разло-
жить в ряды Фурье с периодом Л:
и®) = £ ГР1 е’ (2т/Л) р‘1, ф) = £ Ср, е’(2яw P1 \
Pl Pl
где pi — целые числа (pi = 0. ±1. ...). Таким образом, в силу условия
Блока получаем формулу
ф) = СКр2е’^+г(т/Л)рг)^,
Ра
где р2 — целое число (рэ = 0т ±1. ). Коэффициенты CjfPa пока нам не
известны.
Подставляя ряды для функции VP(д?) и тД,т) и уравнение Шредингера
при Vr(j-) У 0, приходим к соотношению
у (к + ^грЛг С е< >+^/A)Pl I я
* 2m \ Л / F
Pi
+ 22^ Гр, е‘<3я/Л)Р1Л!СЛ'рз е4к+<2я^«Ь =
Pl Рз
= E£CKfl ei['f+(3’r/A}pi]a:.
Pl
Сокращая левую и правую части этого соотношения на множитель
е'А,с. умножал затем их па — € ’(г"7Л)Р’- и интегрируя по т от 0 до Л.
получим следующую бвддонечрудо сисшсту jnneиных
лслял:
Дополнение 2
347
□ля определения коэффициентов G\r при фиксированном А" и целых р.
При выводе мы воспользовались тем, что
л
— f С-' №?/&) ₽i‘ ed (а*/л) Pi *+* (йя7л) Ра* r/z = pi +рз
О
Используя формулу
Е^\Кр) = ^~ ,
2m А /
приходим к бесконечной системе линейных алгебраических уравнений:
[е(°Ш) - Е СКр + С^г = О’
нужной нам ДЛЯ определения коэффициентов Скр при фиксированном /\
и целых р.
В приведенной системе уравнений величины V^-p', однозначно харак-
теризующие потенциал V(a;): удовлетворяют условию V2P = Vpj так как
функция V(.t) принимает действительные значения. Эго свойство непо-
средственно еле дует из формулы
А
Vp = 1 I e-'(3’/A)P^ V(x)<tT.
о
определяющей величины Vp.
Сопоставим теперь коэффициенты С\р точкам оси расположен-
ным при fc™ = (2я/£) fl, где fl = (), ±11 ±2.Эти точки будем называть
«узлами». Величины Ск? Отличны от нуля только на подмножестве узлов
^=А'+уР (р = от ±к ±2. . .
где К — значение константы распространения, которым мы с самого начала
задались, когда приступили к отысканию решения нашей бесконечной ал-
гебраической системы уравнений, удовлетворяющего условию Блоха. Для
остальных узлов Лг,7 коэффициенты С\₽ = О
Так как 2тг/А = (2тг/£) А\ узлы А+(2тг/Л)р являются подмножеством
множества всех узлов {2jr/£)fl.
34N
Глава 7
Множество узлов ятя коэффициентов с определённым значени-
ем 7V прсжш11острир£}напо на приводимом рисуЕтке. Подмножества узлов
дм различных значении Ji нс пересекаются друг с другом Эти подмноже-
ства для всех значений К из интервала -тг/Л < К -jt/Л занимают все
узлы оси .
44* 11 и 14i । । 111 11 Hit и । и tn- <
_ 2д _ E f j 7Г 2
Л л Л A
До сшг ?io/j маши йылм гайе/ииеииа сгарогтынл и иаиа
лгьг лс йеллли чшаткых лрнйдижеяии.
Теперь найдём приближённые решения приведённой бесконечной си-
стемы алгебраических уравнений для величин СяР при фиксированном ЛР
н целых р, считая величины Vr малыми.
Рассмотрим решение системы уравнении нулевою приближения
ирн выключенном взаимодействии:
[е^(А»-е] 4°’=0,
получаемой из полной системы уравнений при Vp-^ = 0, которое дастся
простыми формулами
= CSw Ь = £СО)(кРо)
и характеризуется заданным значением целого числа рп? С — произвольная
постоянная.
Рассмотрим теперь решение бесконечной алгебраической систе-
мы уравнений, которое при выключении вэаилдедвйсотвпя переходит в най-
денное нулевое решение С^. соответствующее фиксированному значению
целого числа дь
где C'j-J,1 — поправка первого приближения и т.д. Тогда при р = рп из бес-
кппсчеюй алгебраической системы уравнений получим приближенное урав-
нение
рт(Я>0)- £? С+ Ц>С = 0,
из которого непосредственно следует, что
Е = £(С)(Лг;ц)) + Иь
Дополнение 2
34Y
где величин<1
л
Vli = Т f V
D
она представляет собой зибгчсяыг потенциальной функции ло
/re/7rwdy Л. Как видим, найденная поправка VJ) первого порядка к энергии
£^{Л"ро) нс зависит от ЛГ.
При рп из бесконечной системы алгебраических уравнений имеем
следующее уравнение:
- Е<°>(ад] С^р + £ Vp-p> С6р/,п = 0.
р'
Следовательно,
£ т F >4
где (? — произвольная постоянная.
Построенное решение даёт удрвле! ворительное приближение, однако,
не при всех значениях фиксированного целого числа ро. Оно определённо
не верно в случаях, когда при двух различных значениях и энергии
Е^(/Сро) и совпадают иди оказываются близкими друг к другу.
В этих случаях говорят о вырожденных решениях.
Строить их надо следующим образом.
Найдем условие, при котором наступает лля чего рас-
смотрим решения уравнения
S(0}(J<Po) = ЯСа}(Аро)
при заданном относительно т. с. уравнения
№ / . \2
+ "jT ) = \ + )
при различных и рП1 где ро задано. Раскрывая квадраты в этом уравне-
нии и Отбрасывая члены А'2 в праной и левой частях, получим соотношение
так что
4 тг JT nV _1_ v <г1 4тгй 2
1 Л Pi) + . 2 ?0 — д -“Ро Р(),
А Л- А А"
= ^-ро.
350
J'Л Л ВЛ 7
т е, имеем кв<иратное уравнение
/2 , ЛА'„г а ЛА',. _ г
Ро тг Ра Ро jT '
для определения целого числа при этом целое число ро считается за-
данным.
Решая последнее квадратехое уравнение^ получим
,г- ЛА М*А'* , „3 , лкп _ ЛА . / д , ЛА
2л 1 у 4^ Ро * 2ir ± 2тг ) '
Взяв знак плюс, имеем рд = ро которое нам нс
интересно). Взяв злак минус, получим решение
которое нас только и интересует
Чтобы найденное решение могло существовать, нужно, очевидно, ло-
требовягь, чтобы число ЛЛ"/тг было целымт те. чтобы выполнилось усло-
вие
АГ = — п,
Л
гдеп — целое число. Это условие соблюдается для значений Аг, лежащих на
краях иЕггсрвала —т/А А" < тг/Л, соответствующих краям зоны Бриллю-
эна. Таким образом, имеем нары вырожденных узлов = Р - 1, рд = -Р
при Р = 1. 2< .. ь.
Построим теперь приближённое решение нашей бесконечней систе-
мы алгебраических уравнений при малых р для какой-нибудь одной
конкретной пары вырожденные узлов, например, для пары узлов рп = О
и = -1 ири Аг = тг/Л.
Теперь учтём, что нс один, Э два коэффициента Скп и С/с,-] имеют
большие значения при выключении взаимодействия, и поэтому из беско-
нечной системы алгебраических уравнений для определения коэффициен-
тов Скр получим следующую приближённую систему двух линейных од-
нородных алгебраических уравнений;
f [£•=•>(Л-0) - Е] Ско + VJ> ско + Vi CK1-i = I),
|_Е(П|(А,- 1) - Е]<7к;-1 + Vfl СА,_ 1 + V_i C/to = 0,
в которой = £^(/<0} (ко[-да А' = тг/Л). Учитывая, что V_i =
= Vf, приведённую систему уравнений представим в виде
f [Д(“}(А'О) - И: - Е] СКа + Ц Ск,_! = О,
1 Г/Слго + [ЕЮ(КО) + Ц) - К] CKi_ I. = 0.
Дополнение 2
35]
Нетривиальное решение этой системы существует при равенстве нулю
сё детерминанта:
£<•>(/<0) + Vo - Е Vi
Vf К(°)(Л’0) + Ц1 -Е
Раскрывая этот детерминант, получаем уравнение
X°’(K0) + Vn - ка- |V||2 = о.
или
Е® - 2Е [EflJ)(A'O) + V»] + [EWCKO) + Va]2 - 141“ = 0.
Следовательно,
Е = £Я(К0) + Vo ± ^/[£W(O) + Vo]= - [£W(ffO) + Ь]г + |Vi |э =
= £<°>(О) + Уо±|Ц|.
Нашли лол приближённых значения энергии Л’, разделённых щелью 2|V\ |
(вместо двух совпавших нулевых значений £Зи)(/С 1) - Е{0^(ХО)), т.е.
при К = о/Л ирй = 0,р£ = -1 появляется разрыв непрерывности кривой
нулевого приближения Е‘°\Кр).
Разрешая соответствующие системы однородных алгебраических урав-
нении для всех вырожденных случаен, мы построим исправленную кривую
352
Глава 7
вместо кривой
e<»W=^(k + 2ip)2;
эта исправленная кривая изображена на приведённом выше рисунке.
Физический смысл полученного результата состоит в следующем.
Электронная плоская волна длины волны Л = 2тг/Лт где к = |кя:|, распро-
страняясь » одномерной кристаллической решётке с длиной элементарной
ячейки Л. даже в случае очень малою потенциала У(г) отражается от уз-
лов решётки, причём при определённых условиях возникает сильное так
называемое ^брэгговское отражение».
Имеем полную аналогию с дифракцией рентгеновских лучей тта реаль-
ной кристаллической решётке, когда тонкий параллельный монохроматиче-
ский пучок рентгеновских лучей надает на кристалл.
Если удовлетворяется так называемое усло-
вие Вульфа-Брэгга, согласно которому разность
хода отражённого и падающею лучей для данно-
го семейства кристаллических плоскостей, про-
ведённых через узлы решётки, равна целому
кратному длины волны, то имеем соотношение
2d cos 0 = таХ, в котором п — целое число,
0 — угол падения пучка для системы параллель-
ных эквидистантных кристаллических плоско-
стей с расстоянием между соседними плоскостями, равным d.
Для анализируемой здесь модельной одномерной кристаллической
решетки нужно рассмотреть два интерферирующих друг с другом луча,
показанных на приведённом ниже рисунке.
Разность хода этих лучей равна 2ЛЧ
_____________! и поэтому интерференционное условие
__________________и--*-_- Вульфа Брэгга принимает вид 2Л = цД.
________________________и_2 где п — целое число. Таким образом, полу-
чаем условие 2А - 2irn/k+ т.е. кА = л.тг,
так что сильная интерференция падающей и отражённой волн наблюдается
лишь при к = (тг/Л) п, т. с. при выполнении в точности такого же усло-
вия, которое мы получили выше при вычислении поправок к собственным
энергиям________________при малых Ц?_р.
При этих значениях к появляются разрывы на графиках энергетиче-
ских функций и когда мы переходим от предельной модели
КрОнига-Пенни при Vp = 0 к модели Кропи [а - Пепин при Vy 0.
Глава 8
Теория электропроводности
полупроводников
А. КОНЦЕНТРАЦИИ ЭЛЕКТРОНОВ И ДЫРОК
В ПОЛУПРОВОДНИКАХ
8.1. Одноэлектроиные состояния системы свободных
ЭЛвКТрОНОВ
Приступим к изложению квантовой теории электропроводности трёх-
мсрЕзых полу провод пиков. Система свободных электронов в полупровод-
нике в этой теории рассматривается как система невзаимодействующих
между собой частиц. Пренебрежение взаимодействием между свободны-
ми электронами является хорошим приближением как для металлов, так
н для полупроводников, Считается, что каждый свободный электрон н по*
лу проводнике ведет себя независимо от остальных электронов.
Взаимодействием свободных электронов с атомными остовами кри-
сталлической решётки иолу проводника, однако, пренебрегать нельзя. Обя-
зательно надо учитывать, что свободные электроны в полупроводнике дви-
жутся пс как в пустом пространстве. Они подвержены действию сильного
микроскопического потенциального ноля атомных остовов, периодичность
которого определяется периодичностью кристаллической решётки полу-
проводника.
Таким образом, при построен ни квантовой теории электропроводности
полупроводниковых кристаллов надо знать так называемые одлезлек’т/кш-
т.е. состояния одного электрона в кристалле полупровод-
ника.
Состояния системы свободных электронов в кристалле (с числом элек-
тронов порядка числа атомов в этом кристалле) МОЖНО представить как раз-
личные способы заполнения электронами системы одноэлектронных состо-
яний кристалла с учётом принципа запрета Паули (требования, чтобы одно
одноэлскгроннос состояние с учётом спина было либо занято электроном,
либо было пустым).
354
ГлаваS
Так как точные расчеты энергий и волновых функций одно электрон-
ных состояний электрона в трёхмерном кристалле (решение соответствую-
щего уравнения Шредингера) чрезвычайно сложны и пока невозможны, то
в существующей квантовой теории элекгропронодлосги полупроводников
приходится делать (оказавшиеся, впрочем, правильными)
о структуре спектра этих одноэлектронных состояний.
Во-первых, предполагается, что Спектр од но электронных состояний
имеет «лонную структуру»^ т.е. состоит из энергетических зон раз-
решенных уровней^ перемежающихся с зонами запрещённых уровнен (зна-
чений энергии, которым не соответствуют никакие энергетические состоя-
ния электрона).
Во-вторых, предполагается, что в процессе электропроводности полу-
ироводиика {как, впрочем, it в других процессах с ним) практически у паст-
ву к>г только электроны из двух следующих зон: сшиой верхней заполненной
электронами при пулевой температуре 7' — 0 так называемой «валентной
зонын п слагай шгмшы егс заполненной электронами при Т = 0 гак на-
зываемой «зоны проводимости», причём оказывается, что при комнатных
температурах Г = 300 К важны только одноэлектронные состояния вбли-
зи «дна» зоны проводимости и вблизи «потолка» валентной зоны. И тех,
и других состояний, конечно, чрезвычайно много, порядка числа атомов
в кристалле.
Одноэлектронные состояния на дне зоны проводимости и на ЛОТОЛКС
валентной эоны в полупроводниковом кристалле будем аппроксимировать
од] юэлскгрси изыми состояния мет кбвеггОвого идеального Электронного газа,
находящегося в кубическом ящике объёма V, равном объему полупровод-
никового кристалла. При этом для одноэлеЕстронных состояний, модели-
руемых на дне зоны проводимости, массу электрона m положим равной
эффективной электронной массе ш», а для цдноэпектронных состоянии
на потолке валентной зоны — эффективной дырочной массе глр (от англ,
negative — отрицательный и positive — положительный).
Подчеркнем, что мы считаем, что в процессах эпеклронровсдности
га полупроводнике участвуют практически только электроны вблизи дна зо-
ны проводимости и дырки вблизи потолка валентной зоны.
Поэтому фактически в квантовой теории полупроводников надо мо-
де пировать только эти одноэлектронные состояния (расположенные вблизи
дна зоны проводимости и потолка валентной зоны).
Необходимо, однако, при этом помнить, что указанная аппроксимация
касается не только значений энергий одноэлеюроппых состояний, ею также
и их волновых функций.
S. I. ОДНОЭЛЕКТГОННЫЕ состояния СИСТЕМЫ СВОБОДЫЫХ ЭЛЕКТРОНОВ 355
зона
проводимости
щель (gap)
валс[1ТЕ1ая
зоны лроя#()1£М0сти и нл л отоже валентной зоны
Рассмотрим электрон, движущийся в кубическом ящике макроскопи-
ческого объема V = IA где L — длина ребра куба. Считаем, что объем V
этого ящика равен объему V рассматриваемого полу провод! ги гео лого кри-
сталла. Никакого аза и но действия электрона в ящике с атомными остовами
кристаллической решётки нет, как нет сейчас и самих этих остовов
Для энергии рассматриваемого электрона имеем формулу J?(fc) =
= А2А2/27Лц в которой А = |к ь к — волне ной вектор электрона, m — масса
электрона.
Электрон рассматривается с учётом спина. Он характеризуется волне*
выми функциями V't1! V’ £- ^1- зависящими нс только от пространствен-
ных координат, но и от спиновой координаты £Т± = ±1/2.
Вместо того чтобы требовать, чтобы на границах 5 кубического ящика
волновая функция электрона была равна нулю:
У, z, cr,)|s = 0.
где £ — поверхность куба V', выставим условия Борна-Кармана, т.е. рас-
смотрим волновые функции электрона не только внутри кубическою ящи-
ка, а во всём трёхмерном пространстве, и потребуем, чтобы эти волновые
функции удовлетворяли соотношениям
${х + L,y,z, €Г7) = ^(at,у,г, сгД
+ L.z, <тг) - аг},
z + L? <rz] = у. г, стД
где период £ — длина ребра кубического ящика.
356
ГлаваS
Из граничных условий Борна-Кармана вытекает, что стационарные
со стол пил электрона в лицзкс можно обозначать узлами простой кубиче-
ский решётки в к-пространстве с вели и и ной элементарной ячейки равной
(2зт)3/У, другими словами, считать, что
—
где п? целые числа, пробегающие положительные, отрицатель-
ные н нулевые значения.
С учетом спина электрона в каждом узле решётки в к-нространстве
имеется два состояния — со спином «вверх» и со спином «вниз»: егг =
= ±1/2.
Таким образом, иа каждом макроскопически бесконечно малом участ-
ке cfE энергетическими интервала 0 В < ею имеется очень большое чис-
ло чрезвычайно близко расположенных дискретных энергетических уров-
ней (кубический ящик имеет макроскопические размеры, много ббльшие
атомных размеров).
При V —> ос рассматриваемый квази дискретный спектр состояний
электрона в кубическом ящике становится непрерывным, занимающим весь
иол у бес конечный энергетический интервал 0 Е < ос.
Характер движения электрона в рассматриваемых одноэлектренных
состояниях следующий. Собственная волновая функция электрона п состо-
янии с энергией Е = имеет вид
1 gi ь г л
"7= с _ Sz ।
V г
где s, = ±1/2 — квантовое число проекции спила электрона па ось г,
а йгт_,я_ — символ Кропсксрщ т. с. f5rJz.iSz — I при <тг — 5, и ,sT — О
при (Jz зг.
Приведенная волновая функция описывает электрон, движущийся
внутри ящика с импульсом р = ft к Этот импульс, как и волновой вектор,
принимает дискретные зннчепия (этим учитывается, что электрон движется
не в бесконечном пространстве^ а внутри ящика).
Рассмотрим теперь макроскопически бесконечно малый энергетиче-
ский шаровой слой Е, Е + rfS в k-пространстве и определим число со-
стоянии электрона (с учетом двух направлений проекции спина), попавлтих
в этот Энергетический слой. Так как Ё = /iJ/c7/2ni. то
rfE =
S. I. ОДНОЭЛЕКТГОННЫЕ состояния СИСТЕМЫ СВОБОДЫЫХ ЭЛЕКТРОНОВ 357
где fe = Число одноэлсктронных состояний dTV в интервале
Е. Е I- dE с учетом спиновых состояний электрона даётся формулой
V
№)*
d/V = 4dfe2dfc
- 2 = V 8,rfcJ./fe = V Д- к fcdfc =
Bit11 it2
3/2
) E1/2dE.
h2 J
Мы вычислили объём макроскопи-
чески бесконечно тонкого слоя в к-про-
странстве, соответствующего интервалу
энергий Е. Е + tfE, и разделили его
[за объём одной элементарной ячейки
(Й7Г)3/У\ на которую приходится од-
но одноэлектронное состояние, а для
учёта двух возможных значений проек-
ции спина результат умножили па 2.
Как видим, число одноэлектрон-
ных состояний е!Аг в данном энерге-
тическом интервале Е. Е 4- dE прямо
пропорционально объёму V кубическо-
го ящика.
Поэтому следует представить найденное число состояний в виде
d/V = V 27(E) dE,
где величину Е(Е) назовём «энергетической плотностью состояний» (от
англ, density — платность).
Таким образом, 27(E) — это что о/яйеяйногя элелаиронд
# яи/дке ойьс'пл V = 1. п/шлиляищхся ш? еЭшметпаШ илюе/дедо энергий овдп
зйерткш Е.
Условимся: /дога # лодуяри-
еодншй? (электронов и дырок), а также у/ювень хм-
jWH4№<fw /j огсгечдты&тть от лотол-
КД ядлстянлй -SflJNjf, тс. предположим, что энергия
потолка валентной зоны равна нулю. см. рисунок.
Эти по-новому отсчитанные энергии и электрон-
ный химический потенциал будем обозначать бук-
вами с и /1.
зона
проводим.
Г-д
вален гн.
зона
35 N
ГлаваS
Энергия дна эоны проводимости теперь будет равна t = где £,? —
ширина энергетического зазора, или, как говорят, «энергетической щели»
(или просто «щели?;)* между валентной зоной и зоной проводимости.
Энергия электрона, отсчитанная от дна зоны проводимости, теперь
равна £ - В.,, а энергия дырки, отсчитанная от потолка валентной зоны,
равна — с (со знаком минус)т так что энергии =" однозлектроннык состоянии
валентной зоны отрицательные.
Значения энергий состояний электрона на дне зоны проводимости
и потолке валентной зоны часто мы будем называть просто ((уровнями энер-
гии», или «энергетическими уровнями», или просто ((уровням и».
Исттользуя полученную формулу для плотности числа состоя-
ний электрона в кубическом ящике* имеем следующие формулы дли энер-
гетических плотностей одно электронных состоя пип в зоне проводимости
и в валентной эоне (чисел уровней электронов и дырок в расчёте на едини-
цу объема полупроводника и единичный интервал энергий):
где — эффективная масса электрона, эффективная масса дырки.
Массы электрона и дырки в существующей квантовой теории полу-
проводников считают подгоночными параметрами, значения которых вы-
бирают. подгоняя формулы теории под экспериментальные данные.
Пр]। этом следует различать состояния на дне зоны проводимости и со-
стояния па потолке валентной зоны, т. с. считать, что масса электрона па дне
эоны проводимости равна mTL. а масса дырки на потолке валентной эоны
равна причём mn / Шр.
Пр]।ведённые формулы для 7?цР(е) и DMn(f) содержат всю необходи-
мую нам информацию об энергетическом спек тре одноэлектронных состо-
яний в полупроводнике.
Я.2. Экспериментальное доказательство существования
дырок
Эжлернл/еим Jtauueca и Шокли
Существование в полупроводнике элементарных носителей с положи-
тельным зарядом (<3ы/мк) было доказано в классическом эксперименте Хай-
S.2. Экспериментальное доказательство существования дырок 359
неса и Шокли в 1949 е На рисунке приведена схема их экспериментальной
установки.
= I) ин-
Прямоугольной формы импульс дырок в момент времени t
жектировался через эмиттер и германиевый стерженёк n-тина (в котором
электроны являются гак называемыми «основными», а дырки — гак назы-
ваемыми «неосновными» носителями элеюрического тока). Инжектирован-
ное облако дырок в германиевом стерженьке дрейфовало к коллектору под
действием приложептюго к стержню электрического поля, включённого как
покапано ла рисунке, с некоторой постоянной скоростью дрейфа 1>р = др
где Др — так называемый «коэффициеЕп подвижноети» дырок в данном по-
лу проводнике (индекс р обозначает от англ, £ —
напяжённось приложенного электрического поля.
Когда облако дырок подходит к кол лекто-
ру в момент времени £ = £3 С времен и «задерж-
ки»), часть его зарядов попадает в коллектор
и даёт сигнал на экране осциллографа. При
этом вследствие диффузии г го мере продвиже-
ния к коллектору облако дырок расплывает-
ся и изменяет свою начальную прямоугольную
форму как это показано на рисунке.
Подвижность дырок рассчитывается по
измеренному времени прибытия облака ды-
рок на коллектор по формуле
а=Е
^3
в которой х^ — расстояние между точками кон-
такта эмиттера и коллектора иа германиевом стертое eilkc.
360
ГлаваS
Таким образом, использованный Ханнесом к Шокли способ измерения
подвижещсги дырок состоял в измерении скорости их дрейфа„ вызванной
постоянным электрическим полем известной напряжённости £. Диффузи-
онное размытие облака дырок вследствие процесса их диффузии в инжек-
тированном облаке дырок проявлялось в изменении формы импульса тока,
подаваемого на коллектор и регистрируемого на экране осциллографа, при
разных положениях зг3 коллектора ни германиевом стерженьке.
При другом методе измерения подвижности дырок измеряют коэф-
фициент электропроводности А для полупроводника р-тнпа, в котором ток
переносится в основном дырками. и используют соотношение
“ ре1
где е абсолютная величина заряда электрона, р концентрация дырок.
Коэффициент электропроводное! л обозначаем буквой А, а нс буквой гт. как
это часто делают.
Эффект Холла
Этот эффект был открыт Холлом в 1879 г.
Рассмотрим Электрический ток, текущий в бруске полупроводника
прямоугольной формы, показанном на рисунке.
Предположим, что эго полупроводник n-тюц в котором элементарны-
ми носителями тока являются в основном лтетотуюлы, их и называют поэто-
му «основными» носителями. Пусть внешнее напряжение приложено так,
что правый копен бруска имеет более высокий электрический потенциал,
чем его левый коезсц, как показало Eia рисунке. Тогда ток будет течь справа
налево, а электроны (имеющие отрицательный заряд) будут двигаться слева
направо.
Поместим теперь наш брусок в однородное магнитное поле индук-
ции Й, направленное перпендикулярно иаправленню тока в бруске (на ри-
S.2. Экспериментальное доказательство существования дырок 361
сунке перпендикулярно плоскости рисунка, смотрящее на нас). Сила Ло-
рсЕща, действующая на Электрон со стороны этого магнитного поля, pansja
Fh - -I [v B]l
на рисунке эта сила лежит в плоскости рисунка и направлена вверх.
Так как электроны не могут сместиться ньпне верхней грани бруска,
они будут на пей накапливаться и создадут на верхней грани отрицатель-
ный электрический заряд. На ин жней грани бруска возникнет при этом
положительный электрический заряд, ничем не скомпенсированный ушед-
шими с нее на верхнюю грань электронами
В результате п стационарных условиях, для того чтобы скомпенсиро-
вать действие силы Лоренца, между верхней и нижней iранями бруска воз-
никнет так называемое «холловское напряжение» V. Оно измеряется вольт-
метром, показанным на рисунке. Сила, действующая на электрон со сторо-
ны поперечного электрического поля, и точности скомпенсирует силу дей-
ствуюи^ую па него со стороны магнитного поля. Возникающее н стержне
поперечное электрическое поле будет направлено снизу вверх, как показано
на рисунке, и иметь напряженность {// = Холл):
£ц = и В.
где и — скорость электрона, связанная с плотностью электрического тока j
соотношением
j = пеи,
где п — концентрация свободных Электронов п бруске. Таким образам,
= гГё = = ТГс4
где Як — так называемая «постоянная Холла»,
Если бы электрический ток в бруске переносился <?м/?кдлш (имеющими
полижительный электрический за ряд J, как в бруске полу проводника р-тила,
возникающее поперечное электрическое поле £н в рассматриваемой уста-
новке было бы направлено вниз, и верхняя грань бруска стала бы заряжен-
ной положительно^ а ннжняя отрицательно, как это показано тза рнсунке.
Холл окская разность поте ел шалив V изменила бы свой знак
Поэтому Srirtfr ПОсЛТОЯНЯои JUbJ ПбИУЧС?е.-И tfU2*JtKKS
йоелгй дышнь заключать? знаке элакт/шчеекйго заряда элементарного
носителя электрического тока.
Измеряя электро провод! гость, мы eic имеем возможности сделать гго.
362
ГлаваS
83. Равновесные концентрации электронов н дырок
в чистом полупроводнике
Рассчитаем равновесные концентрации электронов и дырок, являющи-
еся элементарными носителями электрического тока в чистом полупровод-
нике (т.е. в полупроводнике без примесей), находящемся в термодинами-
чески равновесном состоянии.
Концев грацию электронов обозначим буквой тт так как электрон о т-
рицательно заряжен {от англ, negative — отрицательный), а концентрацию
дырок обозначим буквой р, так как дырка положительно заряжена (от англ,
positive положительный}.
здееялт/’WOS ади л'оицетилрлция — зто число ЗИ£К-
лгролод или 0 ЛЙЪСЛТ ЛОДУЛ/Н№й<)ни№1.
Рассмотрим чистый полупроводник, не подсоединённый пи к какому
источнику внешнего напряжения, находящийся в окружении, в котором всё
время поддерживаются неизменными температура Т и электронный хими-
ческий потенциал щ г. е. рассмотрим термодинамически равновесный чи-
стый полупроводник, находящийся в соответствующем термостате. Огита-
ем+ что полупроводник может свободно обмениваться теплом и электрона-
ми со своим окружением,
Вероятность того, что в термодинамически равновесном полупровод-
нике с температурой Т н химическим потенциалом ;j. обладающим некото-
рым известным нам спектром энергий одноэлеюронпых состояний, произ-
вольное одноэлектронное состояние, имеющее энергию я, занятое электро-
ном, даётся формулой распределения Ферми-Дирака
где /3 - А?б — постоянная Больцмана, Г — температура полупровод-
ника, д — химический потенциал иолу про водника.
Если считать, что для полупроводника. находящегося в термодинами-
чески равновесном состоянии, нам известно полипе число электронов Л’.
S3. Равновесные концентрации электронов и дырок
363
а не его химический потенциал то его химический потенциал надо рас-
сматривать как функцию температуры Т. г. с. Считать, что д = м(^)-
Значеыне функции /1(7') является таким значением химического потен-
циала у окружения полупроводника , которое обеспечивает в нем наличие
заданного полного числа Аг электронов Вероятность того. что одноэлек-
тронное состояние с энергией £ irpn температуре Т и химическом потенци-
але равновесного состояния полупроводника нс будет занято электроном,
I. е. будет занято дыркой, даётся формулой
I - /(f) =
+ 1'
Найдём теперь для рассматриваемого чистого полупроводника, нахо-
дящегося в термодинамически равновесном состоянии при температуре Г
и электронном химическом потенциале концентрацию полектронов
Для этой концентрации, т с. числа электронов в единице объема полу-
проводника, имеем формулу
п - У £)np(E)/(fi)df,
в,
в которой интегрирование по е мы можем распространить до бесконечно-
сти, так как функция /(е) очень быстро убывает с увеличением с, и факти-
чески вклад в интеграл дает лишь малая область энергии £ вблизи
Каждое из одно электронных состояний с энергией лежащей в бес-
конечно малом интервале энергий от с дос+<1?. занято в рассматриваемом
равновесном колу проводнике с вероятностью /(s), а число этих одноэлек-
тронных состоянии к расчёте па единицу объёма полупроводника равно
de-
Уровень химического потенциала (не путать его с возможным одно-
элекгронным уровнем, хотя па энергетических диаграммах он тоже изоб-
ражается горизонтальной линией, как одноэлектронные уровни) в термоди-
намически равновесном полупроводнике при достаточно низкой, скажем,
ком нагний температуре Т — 300 К расположен в глубине запрещённой зо-
ны и лежит между потолком валентной зоны и дном зоны проводимости,
причём настолько глубоко, что г - /j > fe&T.
Таким образом„ в приведённом интеграле можно положить, что
Де)
164
ГлаваS
так как
_|_ |
при с — // &к’Л и, таким образом,
n= [ А(^гУ% - =
У 2л3 \ л2 / 3
*?£
Сделаем замену переменной интегрирования — £^) = и, где и —
новая переменная. Тогда s) = -3(Е„ -/*)-« и /frte = du, и поэтому
Окончательно получаем для концентрации электронов в чистом полу-
проводнике формулу
п - ___!__A [-L-т^з/а e-0(Kjj-.ri _ 7 /Зтгшп^ьТА
4г’М Г,.1) " ' V *’ )
обратите ВЕТиманне, что здесь мы используем неперечёркнутую постоянную
Планка ft = 2тгfi-
ll так, шл[цч1тра[[ия Электронов в термодинамически равновесном чи-
сюм полупроводнике при температуре Г и химическом потенциале равна
п = АТ|Рр
где величина
ЛГиР = 3
h2 J
S.3. Равновесные концентрации электронов и дырок
365
называется «эффективной плотностью одноэлектронных состояний в зоне
проводимости».
Произведём оценку. Например, в кремнии Si. в котором mTl = 0.2 ттг.
при температуре Т = 300 К имеем
jVup = 2,2 • 10й см-а;
концентрация те чпектронов в рассматриваемом полупроводнике меюго
меньше этой величины ЛГЯ]Ъ гак как множитель
ДЛЯ ЧИСТОГО полупроводника очень мал.
Найдем теперь для чистого полупроводника„ находящегося в термоди-
намически равновесном состоянии при температуре Т и электронном хи-
мическом потенциале /г, концентрацию р дырок.
Для этой концентрации, те. числа дырок в единице объема полупро-
водника , имеем формулу
о
/Ы-Оп
нижний предел интегрирования без существенной ошибки можно положить
равным -со, так как функция 1 - /(г) очень быстро убывает при £ —* -оо.
Каждое из одноэлектронных состояний с энергией е, лежащей в бес-
конечно малом интервале энергий от s до е 4- rfc-; не занято электроном
(т. С. занято дыркой) С вероятностью 1 - Лс); а ЧИСЛО СДНОЭЛСЕГГрОННЬЕХ
состояний в указанном интервале энергий в расчёте на единицу объёма по-
лупроводника равно ДМл rfc.
Уровень химического потенциала чистого полупроводника при доста-
точно етизкпй, скажем, компаттиой температуре Г — 300 К лежит глубоко
в запрещённой эоне, так что д- □ > при £ < 0, причём величина р- £
положительная. Поэтому можно считать, что
I - /(е) fit е
Таким образом,
а
/? \а/2
= _L ( ) (^т)з/2 х
\ fir /
366
ГлаваS
= 2
t Л
X [ г?'ае ’Mue ** = 2 ( е ^Т.
./ к A 2 }
О х z
мы перешли к новой переменной интегрирования и = -Де и учли, что
4-w-
о
в окончательной формуле для р мы используем неперечеркнутую постоян-
ную Планка Л = 2тгЙ.
Таким образом, приходим к следующей формуле для концентрации ды-
рок в термодиЕшмичсски равновесном полупроводнике при температуре Г
и химическом потенциале р :
р = A^e"^Tt
где введено обозначение для так называемой «эффективной плотности од-
ноэлектронных состояний в валентной зоне»:
)з/а
Jctwh действующих .маете
Отмстим, что выведенные формулы дм равновесных коЕщсЕзтращш та
и р электронов и дырок в чистом полупроводнике справедливы при любом
значении химического потенциала и значении температуры Т\ лишь бы
выполнялись условия
Ед - :* /сбТ, д > jtETT
причём
О < /1 < .
Выведенные формулы для концентраций те и р справедливы., однако,
тзе только для чистых, но и для рассматриваемых ниже примесных полу-
проводников, так как шьшчые вды урдояец w.;ir ляс-
npjf.ljecw йнутнрй ВДлрещёТгдой ЗОНЫ rt£ ёлыяём ТШ
Как видим, для любого чистого полупроводника справедливо соотно-
шение
пр = дг]1р .V„., е
КЗ. Равновесные концентрации электронов и дырок
367
из которого химический потенциал и выпал. Это соотношение называют
«законом действующих масс».
Электронный химический потенциал чистого полупроводника
Воспользуемся выведенными формулами для концентраций электро-
нов п дырок в чистом полупроводнике:
n = р - ABua е
и вычислим с их помощью значение химического потенциала в таком
полупроводнике.
На самом деле фиксировать надо тге значение электронного химиче-
ского потенциала /j полупроводника, а полнее число тле ктролов Лг в нём,
определяемое условием его элскгриней] ральнос ти.
Химический потенциал следует рассматривать как функцию темпе-
ратуры Г и полного числа электронов Лг. Но этого сейчас мы делать нс
будем, а предположим, что нам задан именно химический потенциал ,0-
Чтобьс найти функцию /Д'Г, У), казалось бы, надо поступить следую-
щим образом. Нужно взять все одпоэлектронные уровни, имеющиеся у рас-
сматриваемого полупроводника (нс только уровни вблизи дна зоны прово-
димости и потолка валентной зоныт а вообще все уровни}. В термодинами-
чески равповссЕюм состоянии полупроводника с температурой Г и Задан-
ным значением химического потенциала эти одноэлектронные уровни
заполнены электронами согласно распределению Ферми -Дирака.
Поэтому следовало бы просуммировать функцию распределения Фер-
ми-Ди рака по всем зтнм Одиозлентроиным уроБЕШм и таким образом найти
полное число Лт электронов в полупроводнике как функцию АГ (Г, /i)a за-
висящую от 7’ к /i; для этого надо только знать энергетическую плотность
Р(Е) этик уровней.
Обращая функцию АТ(Т. /л)т можно было бы найти значение химиче-
ского потенциала yj (V) при тсмпсрату-рс 7' (и фиксированном подразумева-
емом, но явно не выписываемом аргументе Аг).
Так поступить, однако, мы не можем, так как не зддеш емс ойнстея-
jn/эояньиг уровней я к, в частности, нужную для расчёта их
энергетическую плотность Её определение — очень трудная г г ещё
нс решённая в настоящее время задача.
Чтобы найти значение химического потенциала д при температуре Т
в чистом термодинамически равновесном полупроводнику поступим ло-
другому.
Ш
ГлаваS
В чистом полупроводнике при термодинамическом равновесии элек-
троны (на Одн0электрон|[ых уровнях л зоне проводимости) I! дырки (на
идниэлскгроиных уровнях валентной зоны) появляются и исчезают только
tf резульлшле лгейгюяных элекгороной е aKrtiftX эле-
лдеклш/жвдг йзаместнодз рождения (одного элтироид ы oduou
ды/мш) лг^и 3fl^Kfff/?t>4-^wpo44WX чар w еда,местного утдноложе-
лкл (одлого злект/мэно а одной дыркн) я алелгечтд/?иьг.х сглтлх рекаnowлл-
элех/ироН’ды/мччых а др. То есть всегда на один рождённый электрон
приходится одна рождённая дырка и на один исчезнувшип электрон — одна
исчезну виз ая дырка.
Поэтому в чистом полупроводниковом кристалл с, находящемся в со-
стоянии термодинамического равновесия, всегда выполняется условие
п = р;
АОНЦ£*НЙгрЛ^£Ш jtTe'KJffJWHOff if дырОК tf VWt'fliaif />6ГВНОВЁСНЕМ1 /TO.Tl-'fl/JOffwdwffKe
при любой ШЁМпе/шшурЁ ддуг др^-гу.
Обозначим концентрации электронов и дырок в чистом полупровод-
нике индексом г (ст англ, intrinsic — собственный); тогда согласно условию
п = р получим для и р: следующее выражение:
- р, . - 2
Из произведения пр концентраций электронов и дырок химический
потенциал д3 как мы уже отмечали выше, выпадет, и мы получаем фор-
мулу, из которой легко найти значения концеш раций электронов и дырок
в чистом полупроводнике при любой температуре Г.
Найден теперь значение дгйЛ1Ичеектдэ лйшешртолл в чистом полу-
проводнике, находящемся в термодинамически равновесном состояfгни при
температуре 7 (с заданным полным числом электронов)^ используя соотно-
шение п - р;
Чр е-{й^-р№Г = ЛГи;ге-^тГн
которое предс тавим в виде
Лг
_25Lc-Es/*fT _
iV ’
J1 нал
причем учтем, что
jV"p _ (Yt/J
Л™ '
S.3. Равновесные концентрации электронов и дырок
369
Таким образом, приходим к следующему уравнению для химического
потенциала:
/ \ '^г
[ W | _ е-2^/йрТ
3 ] \ ^ _ _ 2д
2 ) ksT квТ’
так что имеем следующую окончательную формулу для электронного хи-
мического потенциала чистого полупроводника::
И - д(Т) - | W In («£) .
При нулевой температуре 7=0 отсюда получаем, что
р(0)= 7-
т.е. лрм 7 = 0лолдевдыала я гояртдододшю
/здела-югд^лгея лшчяп посреди ле зая/>£И{ёяяои зоны.
При Т = 300 К значение химического пфтеЕхциаля д(7) незначительно
отличается от Е^/2. так как £\, = 1 эВ и Аб7 10 2 эВ при 7 = 300 К.
Произведем оценку концентрации электронов и дырок в чистом по-
лупроводнике при комнатной температуре. В кремнии Si Е^ = 1,11 эВ
?nTI — 0,19 m, nip = 0,52 m (дырки тяжелее электроегон). При температуре
7 = 300 К имеем
= pi = 2.45 109 см-3;
при температуре 7 — 600 К
7У = Рд = 2J Ю14 см"3.
по сравнению с концентрацией атомов в кремнии Si, имеющей порядок
10аз см 3: это ничтожно малые величины.
Так как концеЕгтрапин элементфпык носителей электрического тока
в чистом полупроводнике (электронов п дырок) при ненулевой температу-
ре 7 / О отличны от нуля, то такой полупроводник обладает, хотя и незна-
чительной, электропроводностью, которую можно экспериментально изме-
рить.
170
ГлаваS
Для коэффициента электропроводное™ А полупроводника можно ис-
пользовать формулу элементарной теории электропроводности Друде:
А = en^ft + epjip.
и которой — «коэффициенты подвижностей» электронов и дырок,
или просто их «подвижности» в рассматриваемом чистом полупроводнике,
е — абсолютная величина заряда электрона.
Согласно приведённой формуле зависимость электропроводности А от
температуры Г определяется экспоненциальной зависимостью концентра-
ций л и р от температуры, которую мы нашли. Подвижности дгГ| и /tp на-
много слабее зависят ел температуры Г, и зависимостью их от температуры
можно пренебречь.
Таким образом, согласно выведенной
1л А С 71 ] формуле для завис и мости концентрации та, =
— pi электронов и дырок от температуры Т
\ в чистом полупроводнике получаем следую-
\ тин закон изменения электропроводности А
\ с температурой J1 для чистого полупроводнн-
\ ка:
А(Г) = Au C-E^(ai=n,
--------'---1—l/Т так что имеем
1п[А(Г}] = IdAo S9/2fct 1/Г
показывает, что dfikvnmow&ThWff 4ля чпсты_г подуп/гр-
sodwHKDff наблюдается .шшжбш закон зл^псил4остп 1п[А(71)] от обрттноы
1/Т е uoj/wko.w таил?рдтурл причем из определе-
ния угла наклона экспериментальной прямолинейной зависимости 1Ь[А(Т)]
от 1/Т легко можно найти величину энергетической щели Е5.
Измеряют коэффициент злскгропронодности А(7') при разных темпе-
ратурах Г и по полученным данным строят 1рафик 1п[А{Т}| в зависимости
от 1/Т как показано на рисунке. Экспериментальные точки при этом хоро-
шо ложатся на прямую с тангенсом угла наклона
tga = £а/2 fee;
в частности, для кремния таким образом было получено значение шс-
ли = I. I I эВ-
В-4 Равновесные концентрации электронов и дырок
37]
8А Равновесные концентрации! электронов и дырок
в примесных полупроводниках
/7д’ г мг е л о.ики
В качестве примера слабо легированного примесями полупроводника
рассмотрим кремний Si с добавлением мышьяка Аз или индия In. Именно
примесные полупроводники используются в полупроводниковых приборах
твёрдотел ы юй эле ктрсн i ики.
Если концентрация примеси оказывается порядка 1 атома на 10е ато-
мов кремния, т. е. порядка 10lfi см“\ ю кристаллическая решётка полупро-
водника с примесью практически не отличается от решётки чистого крем-
ния.
При таких малых концентрациях примеси уровсЕш Ферми располага-
ется внутри ли [решён ной зоны вблизи зоны проводимости для донщнюн
примеси или вблизи валентной зоны для примеси.
Сильно легированные полупроводники с концентрациями примесей
порядка 10L* см л мы рассматривать не будем.
Для них при высокой концентрации легирующей примеси порядка
1016 см-3 уровень Ферми смещается вверх к попадает в зону проводи-
мости или перемещается вниз и попадает в валентную зону
Энергии ионизации и электроииягя ф<х)стяа атомов
Топорной или акцепторной п/?и.иеои
Чистыми полупроводниками являются кристаллические кремний Si
и германий Ge. Примесные полупроводники изготавливают, следуя техно-
логниъ используемой для чистых полупроводников. Например, при выра-
щивании кристалла Кремния или германия из расплава в него внося]' опре-
делённые количества примесей.
Кремний п германий принадлежат к TV гр. химических элементовт т. е.
имеют по 4 валентных электрона. Рассмотрим, например, кремний. Он име-
ет такую же
J// IV V
в А1 Ga In гтг Si Ge N P Ar Sb
структуру кристаллической решетки, как алмаз (углерод С тоже принадле-
жит IV гр. Элементов), с четырьмя химическими связями, направленными
372
ГлаваS
из центра в вершины тетраэдра. В «алмазной решётке», в которой кристал-
лизуется кремний, каждый атам Si окружён четырьмя другими атомами
Si. Четыре электрона атома кремния Si идут на образование четырёх кова-
лентных химических связей с ближайшими четырьмя соседними атомами
кремния Si, расположенными в вершинах правильною тетраэдра.
На образование одной ковалентной связи
между двумя атомами Si требуется дна электрона,
которые берутся по одному у каждого из атомов.
Примеси в кремнии или германии использу-
ются двух типов. Это либо атомы V гр. элементов,
например фосфор Р, мышьяк Азп сурьма Sb (т.е.
пятивалентные атомы, имеющие по пять валент-
ных электронов). Либо это атомы П1 гр. эленен-
тов, например алюминии А1, галлий Ga, индии In
(т.е. трек валентные атомы, имеющие по три валентных электрона).
Лрн.нргные а решётке н.тн крелглия не «вией/мгатсяя
tf гчежф-тглиг ледеф’ ыоти.чалщ л «замещают^ шжшы герлшныя
w^w к/гаияия. m. f. становятся м нх лгдеяш.
Рассмотрим примесный этом V ip. Напри-
мер, атам мышьяка Аз в решётке кремния. Chi
имеет пять валентных электронов. Из них четыре
затрачиваются на образование четырех ковалент-
ных химических связей с ближайшими четырьмя
атомами Si, а пятый электрон при этом Оказыва-
ется лишним. Есин примесный атом Ай нс ио ни-
зе вынч то этот пятый электрон будет вращаться
вокруг иона As*. Получается «атомная система»,
подобная атому водорода. Около положительного
иона As+ вращается один электрон.
Если примесный атом As ионизован, указанный пятый электрон от-
рывается от иона As+ и становится электроном в кристалле
кремния, способным перемещаться по всей его кристаллической решётке
При этом отрыв пятою электрона у атома V гр. происходит легко.
Таким образом, примерный атом V гр. в решётке кремния или германия
становится «донором» электрона. Поэтому такую примесь называют А?-
нцршш, а примесный полупроводник «донорным», или «полупроводником
п-типа» (от англ, negative отрицательный}, так как в донорном полупро-
воднике элементарными носителями электрическою тока являются в ос-
нов лом электроны, которые оторвались от пятивалентных атомов донорной
примеси.
В-4 Равновесные концентрации электронов и дырок
373
Рассмотрим теперь атом примеси III гр., например
атом индия 1п в решётке кремния, Он имеет три валент-
ных электрона. Этих трех электронов недостаточно,
чтобы образовать четыре ковалентные химические свя-
зи с четырьмя атомами SL ближайшими к примесному
атому In.
Чтобы образовать четыре СБЯЗИ^ необходимо ВЗЯ ТЬ
один из эляуй/юнм, имеющихся в кри-
сталлической решётке, и посадить его на ковалентную
связь с недостающим электроном, сделав эту связь полноценной (с двумя
электронами)- При этом вблизи иона In- появится йьулсл, которая будет
вращаться вокруг иона In-.. Если эта дырка станет свободной, г. с. уйдёт от
иона 1п-,то в решётке возникнет положительный носитель электрического
тока — дырка. Снова имеем «атомную систему», подобную атому водоро-
да, только теперь около отрицательного иона 1л“ вращается не электрон,
а дырка.
Захват примесным атомом 111 гр. недостающего электрона и образова-
ние свободной дырки происходят легко в решётке кремния нли германия.
Так что атом III гр. в решётке кремния нли германия является захватчиком,
или «акцептором». "электрона. Поэтому такуЕО примсс]> называют сткцепнш/?-
луй, а примесный полупроводник с акцепторной примесью «акцепторным»,
или «полупроводником p-типа» (от англ, positive — положительный), так как
в акцепторном полупроводнике элементарными носителями электрического
тока являются п основном дырки, имеющие положительные Электрические
заряды.
Чтобы оценить величину гюлшт донорного атома или ве-
личину эн^хгии акцепторного атома, следуя Бете,
рассмотрим описанные примесные атомгтьге системы п кристаллической
решётке дсйстеиitcлыto как otqmtj водорода.
От атома водорода примесные «системы»
As+ + е и In- + р отличаются в двух отноше-
ниях; 1) эффективная масса электрона или
дырки /Пр пс равна массе m свободного элек-
трона; 2) электрическую проницаемость £С) пу-
стого пространства для атома водорода надо за-
менить на электрическую проницаемость eeq, где е — относительная про-
ницаемость вещества полупроводника. Кулоновское взаимодействие между
положительным и отрицательным зарядами в кристаллической решётке бу-
дет меньше, чем в пустом пространстве, из-за экранирующею действия
атомов кристаллической решётки, расположенных между ними.
374
ГлаваS
Эффективные массы mni тр имеют порядок ОДт, а относительная
Электрическая проницаемость " имеет порядок 10 для германия и кремния.
Используя квантево-механические формулы дм энергии основною со-
стояния атома водорода и для радиуса его первой так называемой
р/шш, для донорного примесного атома полу наем для энергии ионизации
E/j и его среднего радиуса ар значения:
1
2 Л2
eSn 1 mn
2ft2 (4зге0)г m
& 10 эВ 0.1 0,01 = 10“я эВ,
• 2 >й
ар =--------------—£ = йп 10 10 = 100 ftfi-
Таким образом,, для примесного атома энергия ионизации Ed Epf
так как энергетическая щель имеет порядок 1 эВ. Кроме того^ ради-
ус а = 100оц, где ао — рддиус (а<) = 0,5 А). То есть размер
примесного атома в сотни раз больше межатомных расстояний в решетке.
Соответственно^ для акцепторного атома имеем формулы
Ел = _____I___= 12™.________1__ш ]П 2 чВ.
2 А2 (4тгее0)2 2 А2 Нтг^и)2 m е2
<М - -^-т41гге<1 - - г “ 100 пу.
wip с3 те3
Как видим, примесный атом с привязанным к нему электроном или
дыркой является рыхлой, т.е. слабо связанной, атомной системой больших
мл крое ко пичс скнх размере в.
примесь Ge мэВ Si мэВ
доноры сурьма Sb 9.6 39
фосфор Г 12,0 45
мышьяк As 12,7 49
акцепторы индий Jn ИД 160
галлий Ga 10,8 65
бор В 10,4 45
алюминий А1 10,2 57
В табличке приведены значения энергий и эягрлгй г/?(^стао
для донорных и акцепторных примесей в германии и кремнии ( I мзВ =
= эВ).
8.4. Равновесные концентрации электронов и дырок
375
=--^
ё = Еъ
5=0
ff=£t
5-0
Приведем в заключение схемы энергетических уровней примесных по-
лупроводников п- и p-типов. На рисунке показаны расположения одноэлек-
тройных уровней донорной (е = Ej) и акцепторной (е = Ef) примесей.
Примесные уровни располагаются в запрещённой зонет в которой нет
одиоэлс (стройных энергетических уровней у чистого крг]сталла. Уровень
донорной примеси находится вблизи дна эоны проводимости, а уровень
акцепторной примеси — вблизи потолка валентной зоны.
АГрнцеятмрдцця элехтррияе я ctowp/wau
л ол ул/юй<к}я нке
Рассмотрим донорный полупроводник (полупроводник и-типа). Пусть
он пребывает в равновесном состоянии с температурой Т и электронным
химическим потенциалом д. так что по нему нс течёт никакого аделгриче-
ского тока. Так как Ед — 10“2 эВ. a — 1 эВ. то уровень Ejt который
занимают электроны, локализованные ка атомах донорной примеси {не спо-
собные по этой причине перемещаться по полупроводнику и переносить
электрический ток)^ будет расположен и непосредственной близости от дна
ЗОНЫ проводил госте] ниже дна, как покачано па приведённом рисунке.
Одноэлектронному уровню Е^ соот-
ветствует нс одно (как одноэлсктронным
уровня м зоны проводимости или валент-
ной зоны), а очень болы rice число Од-
ноэлсктринных СОСТОЯНИЙ, равное ЧИО
лу Аго-У атомов примеси, внесённых
в решётку' полупроводника, где через jVp
мы обозначаем не число атомов примеси,
а их В отличие от уровней,
лежащих в зоне проводимости ййй
эоны яроводшоелш или в валентной зоне вбаизк потолка валентной зоны
(аппроксимируемых с немощью уровней задачи об электроне в кубическом
ящике объёма V), уровень Е2 очень сильно вырожден.
376
ГлаваS
Волновые функции, которые соответствуют одноэлектронным состоя-
ниям вырожденного уровня Е?п — это функции, которые опи-
сывают состояния электрона, когда он локализован на определённом атоме
донорной примеси, так что число независимых одноэлектронных состоя-
ний , соответствующих уровню Еа, определяется числом атомов примеси,
имеющихся и кристаллической решётке.
В рассмотренном примере донорного атома As, внедрённого в решёт-
ку Si, речь цдёт о волновой функции (состоянии движения) пятого («лиш-
нею») электрона мышьяка, вращающегося вокруг нона As+ и не оторвав-
шегося от него (когда атом примеси неионизован).
Очевидно, Ej = Eff — Ер> Ер = Е5 — Е^. Вероятность того, что
в равновесном кристалле с температурой Т и электронным химическим
потенциалом jt электрон находится на уровне Ез (т.е.. в связанном состо-
янии с ионом атома донорной примеси), согласно формуле распределения
Ферми Дирака равна
= ©₽(В,-^ + 1'
Здесь /3 — fe — постоянная Больцмана, Г — температура, —
химический потенциал.
Через Лр мы обозначили ншцвдт/гвдню донорных примесных атомов
в кристалле, т.е. число примесных атомов, приходящихся на единицу его
объёма. Опа постоянна и не зависит пи от температуры Г — ни пт химиче-
ского потенциала /г. ни от чего не за вист; а определяется только способом
приготовления примесного полупроводникового кристалла.
Если электрон находится в одном из состояний уровня Еа, то соответ-
ствующий этому состоянию атом примеси колонизован. Поэтому кянцея-
дотгарльст яптллюв в равновесном кристалле при
температуре Т и химическом потенциале /t равна, очевидно, произведению
ЛЪЛЕз).
Обозначим теперь через Лг+
яых ядеамдо и рассматриваемом примесном полупроводнике, находящемся
в равновесЕзом состоянии с температурой 71 п химическим потенциалом /л.
Эта концентрация, разумеется, зависит от Г и д, т.е. Аг+ =
N& = - ^/(£г) = ArfJ (1 - /(£,}) =
^(£?з-ц) ।
В-4 Равновесные концентрации электронов и дырок
377
Так как то отсюда получаем, что
.у+ = -
D 1 + е“0(Е₽- Ес **) '
Чтобы найти значение химического потенциала — д(Т) для равно-
весного донорного полупроводника температуры 7’. воспользуемся следу-
ющий соображеЕшем.
Предположим, что зяжтроны лоелгделяютгя е золу
я рял/зц Г и ли-
ашчйсклм пошелциале у? ыскдочидеевдмл wpw.wecw.
Нри комнатных температурах 71 — 3(H) К так и происходит. Энергети-
ческий зазор ED, который электрону примеси надо преодолеть при тепло-
вой флуктуации, чтобы он перешёл от атома донорной примеси в зону про-
видимости, пампою меньше элергстн чес ко го зазора J?5f который надо пре-
одолеть электрону при переходе из валентной зоны в зону проводи мости.
Поэтому можно предположить^ что у нас имеется следующее соотно-
шение:
гг = Лг+
в котором п — равновесная концентрация электронов в рассматриваемом
примесном полупроводнике.
Таким образом, эле'К/др** датуир^бч^лык* /шотш кон-
qeHfft/xzifuu u^j/j/^rtdTw/jwjr дтлялкзя лдшневд д иёмг
Рассуждая в точности так, как в случае равновесного чистого полупро-
водника, для равновесной концентрации электронов п = п(Т) в зоне прово-
ди мости при температуре Т и химическом потенциале д получим формулу
/ \ 3/2
п = лг||р = 2 .
здесь мы используем неперечёркнутую постоянную Планка ft = 2тгй.
При выводе приведённой формулы мы воспользовались распределени-
ем Ферми-Дирака и предположением, что которое будем
считать выполненным также и в случае рассматриваемого донорного полу-
проводника с малой концентрацией примеси.
Таким образом, для определения значения химического потенциала
га пашем полупроводнике из условия п — Аг^ для рассматриваемого
примесного полупроводника имеем соотношение
V е-£(Яй-р) =
* *ир с
Лтр
37S
ГлаваS
которое следует рассматривать как уравнение для определения значения
химического потенциала до.
Представим это сост ношение в виде
+е-^Е,-д) =
^пр
и обозначим для краткости не личину е через я. Тогда для .г полу-
чим квадратное уравнение
jb2 е^Б₽ + ж - - о,
Мф
решая которое, имеем
яг =
Так как
е-/?(Е0-^) _ д. > Q
знак минус перед корнем в формуле для ,т надо отбросить, и мы получим
окончательно, что
- 1 + J1 + 4^еаЛр
у Wnp
X = ---------77----------
Случай больших т емператур
Это случай комнатных температур 7' = 300 К и температур в лва-
три раза больших комнатных. Концентрация А’р имеет порядок 1Q1’ см-,'!.
Эффективная платность состояний ЛтцР имеет порядок 1и1всм”3- Поэтому
= 1О-Й С 1.
пр
Далее, при рассматриваемых высоких температурах — I (при
7 = 300 К имеем foT 1()-2 эВ и Ед = 10”2 эВ). Таким образом
’ l + 4 “1 + 2 edSn.
L J*np
В-4 Равновесные концентрации электронов и дырок
374
а следе вательно,
- 1 + 1 - 2
______________Л"Г Лг/>
2 е^’ Л']ф
Поэтому для химического потенциала д получаем соотношение
С-ЛЕ.-М) = № ~№ _ д) = |Г1 ,
преобразуя которое, приходим к формуле
ц = fi(T) = Ед + foT In | । = Ед - foT In | —)
\ J*Пр у I J VJ /
для jch.um четами летел цыалд донорного полупроводника и рп рассматрива-
емых больших температурах.
Как видим, химический потенциал ju меньше энергии щели Е"?.
Определив /1. можно найти равновесную коЕщсптрацию п электронов
в донорном полупроводнике. Для неё находим, что
n = = .\rvx = Nup = АЪ,
” up
т. e.
n = xVp-
Видим, что e случае рассматриваемых больших температур прак-
тически все атамы донорной примеси ионизованы, а потому концен-
трацця ллехтрпнов равна концентрации примесных атамов, имеющихся
в примесном полупроводнике.
Оправдаем теперь справедливость сделанного предположения о том,
что процессами перехода электронов из валентной зоны в зону провод]I-
мостп можно пренебречь, Согласно сделанной ныше численной оценке для
чистого полупроводника — 1[г см < Так как n то мы должны
считать, что JVp 109 см-3; указанное условие, конечно, очень хорошо
выполняется.
Оценим, например, как влияет примесь на положение уровня химиче-
ского потенциала, Етпрнмср, в крсмЕши Si. Предположим, что
змо
ГлаваS
ЛглР - 2,2 10ls см \ и возьмем типичное значение концентрации примес-
ных донорных атомов Л'/> = Ю1Б см-^ и пусть Т = 300 К. Тогда
111
/У„р
= (1,14 эВ
т.е. химический поте ел шал расположен на 0.14 чВ ниже дна зоны проводи-
мости.
В чистом же полупроводнике при Т =
= 300 К уровень химического потенциала
------------— £^= 1,11 эВ лежит [гримерпо при Etf/3 = 0,55 эВ =
fi, = 0.049 эВ = । д]_ д|]Д ниже дна зоны ирсводц-
0 !4 j ? мости. Вычисленное значение химического
р потенциала позволяет найти вероятность
'<Е’> - c-№Jv.., +, =<W*
заполнения электроном уровня донор-
ной примecuч если принять для Ер значе-
ние 0,049 эВ для атомов Ав в кремнии Si. Таким образомh 97,4% атомов
мышьяка ионизованы при Т = 300 К.
На рисунке приведены экспериментально найденные энергетические
уровни для кристалла Si с примесью атомов мышьяка As. Показан также
уровень химического потенциала при Г = 300 К.
Случай малых температур
Это случай температур 7 = 0. Если температура 7 мала, то Ер
4^7, а потому > 1. Следовательно, под знаком квадратного корня
формулы для х можно пренебречь единицей и получить, что
1
gi'JEr.v
/ лъ
/дГс
1 v пр
Таким образом, для химического потенциала имеем формулу
= I^D с
у А Лр
В-4 Равновесные концентрации электронов и дырок
381
логарифмируя которую, получим, что
___ /‘j'X _ п 1 гг fcjsT1 л /" А пр А
/I — //[У ) — — - Ед — ( А/^7 ) ь
это формула для .гичичеютш в донорном примесном полупро-
воднике е случае очень низких температур Г,
Как видим, ।грп нулевой температуре Т уро-
вень химического потенциала (Q) располагает-
ся точно посередине между уровнем донор- J --------------------г
пых атомов п дном зоны проводимости, как по- 2 К
казано на рисунке.
Вычислим, наконец, равЕювсспую кпнцен- £
[рацию п электронов в зоне проводимости в до-
норном полупроводнике при малых температу-
рах Г, Имеем для неё значение
п - Rpe **} е y/N^p Nb е
Электропроводность донорного полупроводника
Рассмотрим теперь температурную зависимость коэффициента элек-
тропроводности А = А(Т) у слабо легированного донорного полупроводни-
ка (с небольшой концентрацией примеси Лг£> Ajip). Коэффициент элек-
тропроводности А (Г) прямо пропорционален концентрации элементарных
носителей Тока в раин овес ним [Юлу проводнике при температуре Т.
Поэтому концентрация элементарных носителей электрического то-
ка — электронов, сильно зависит от температуры, и только ею и опреде-
ляется температурная зависимость А (Г).
При комнатных температурах Г — 300 К и более низких температу-
рах в донорном полупроводнике элементарными носителями тока являются
в основном электроны, полученные при ионизации атомов примеси, и по-
этому
А(Т) = Ad е
При больших температурах Т носителями тока становятся и электро-
ны, и дырки, которые ijo;iyчаются при переходах нз валентной зоны в зону
проводимости, и поэтому
А(Т) — А() е“£#/(2**т)
ЗМ2
ГлаваS
Таким образом, зависимость In А от
обратной температуры 1/Т должна иметь
вид, показанный на приведённом рисунке.
Должны получиться две прямые: ойяд при
малых 1/Г и другая при больших 1 /Т. При
малых обратных темпера гурах 1/Т наклон
первой прямой определяется энергией ще-
ли так как
tgri = E3/2fcE-
При больших обратных температурах 1/Т наклон второй прямой опре-
деляется энергией ионизации донорного атома так как
tgT? = £?d/2A:E-
Таким образом, измеряя Экспериментальную температурную Зависи-
мость электропроводности А(Г) у примесного донорного полупроводника
от температуры, можно определить как эмреию и, ели так и эяергию
£/> донорной примеси.
На рисунке точками на кривых отмечены экспериментальные данные
для двух примесных полупроводников с различными концентрациями АГ^
атомов донорной примеси.
Проводя аналогичные рассуждения для акцепторного полупроводника„
можно найти значение химического потенциала д и концентрацию р ды-
рок в акцепторном примесном полупроводнике (полупроводнике р-тлпа).
находящемся в равновесием состоянии при температуре Т и химическом
потенциале р.
Обозначим через Агд донцомирпциш акцепторных атомов в примесном
полупроводниковом кристалле, а через JVJJ — концентрацию ионов акцеп-
торных атомов в термодинамически равновесном полупроводнике, захва-
тивших по одному электрону.
Концентрация АГд ни от чего не зависит, поэтому она не зависит и от
температуры Т. Концентрация iVj. конечно, от температуры Г зависит.
Согласно распределению Ферми Дирака вероятность того> что одно из од-
нОэлектрснных состояний уровня Е] атомов акцепторной примеси в полу-
проводнике будет занято электроном, равна
1
0-^т
В-4 Равновесные концентрации электронов и дырок
3N3
Очевидно,
Пренебрегая теиновыми переходами
электронов из валентной зоны в зону про-
водимости, т. е. считая температуру Т полу-
проводника нс слишком большой, скажем
порядка комнатной температуры Т = 300 К
и ниже, предположим, чтораллояегная №4-
цянтрацня р fif лолу проводнике рдя-
на концентрации Лг^ анцолторныл1 ато-
jtoe, захватидшшг з^вктроны, т. с.
Л’.4 “Р‘
г = £,
г = 0
причём для термодинамически равновесной концентрации дырок можно
использовать формулу, получевшуЕо при рассмотрении чистого ги>лупровод-
ника:
г,= А’шпе-^т;
другими словами, мы лално^отыо лренебреэдедс атявгтроиоя w?
валентном jojdft? я зону лрово^и.ыостн.
Тогда из условия Л = р придем к следующему условию для нахож-
дения химического потенциала:
Л’Л----- ----
Л е^Ел-^ + j
— ЛГ е—
— J1 МЛ X- J
^мл = 2
ЭтртркеТ
А2
Следили гсльно.
ef?BA + е-.^ _ ^А_ = 0
]*ьал
Обозначив с через лг, получим квадратное уравнение
х^.+, _
J ' EwJl
решая которое, Приходим к формуле
Аил
JC =
2 g/?
Ш
ГлаваS
перед корнем следует взять знак плюс, так как величина z = с положи-
тельная.
Случай больших температур
Это случай температур порядка комнатной температуры Г — 300 К
и температур н два три раза большая комнатных, когда и подкоренном вы-
ражении для 37 второе слагаемое много меньше единицы. Тогда получим,
что
-1 + 1 + 2-^-е^Ел
^вал А'д
7 — ___________________ = ~~
2eJ£- Д'™’
Таким образом,
с-^ =
jV ’
J * ЫЛ
и мы имеем формулу
М = д(Г) = -М’ In (= кБТ In (
\ J ' нл и / \JVA/
ДЛЯ XtbWUVeCTWfl акцепторного ПОЛУПрОВОДЕЗИКа при больших
температурах. Следовательно,
АГ l
>> — V е-ь1р _ дг ..V. лг _d_
Р _ 1 vbm — J 4вал А — J1 вал чг
то есть
Р = АТ
Таким обрааом, я случае больших рдсс.потрт/вис.иых температур все
олтолш акцеллгормш лрилтдеи ншитгаиты1 ио электрод и ко^емтршрл об-
роэшлвшилх-я ()ы/юа в зоие рлотш црй.иесйыиг ото-
JWO0 s доду»ц?ОА|?бян^.
Случай малых температур
Это случай нулевой температуры Г = 0 К и температур, близких к ну-
левой Если температура Г мала, то имеем сильное неравенство ЬбТ\
а следовательно, 1. Таким образом, второе слагаемое под знаком
корня для i большое, и поэтому
е^/?д/2
2с^Ед
AJ \ 1/2
-ГСА А е-£Яд/2
V /
х*ва;[ /
й.5. Система уравнений локальных балансов
3N5
то есть
отсюда [jолучаем окончательно формулу
д = м(т) = ^ । Y,n(^K)
для хцлглчссяоео mawj сената’ акцепторного примесного полупроводника
при низких температурах.
При нулевой температуре д(0) = Ед/2,
т. е. лшшчгскнн лй/яенциш? /мснаигдется посе-
лоиолкдм далгялшлы лэпм л уряя-
ле.н лкцсл/иормьЕх алголом, как показано на ри-
сунке.
Б. СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ЛОКАЛЬНЫХ БАЛАНСОВ
8.5. Система уравнений локальных балансов
Дрейф носителей тока под дсйстсие.и алсктрнчйского но./л
Предположим теперь, что на полупроводник наложено электрическое
поле постоянной напряжённости £ в направлении оси л, как показано на
приводимом ниже рисунке. Дырки движутся по полю, электроны против
полл. Двигаясь вместе, электроны и дырки создают электрический ток 7
в полупроводнике.
Учтём (хотя этого нс делалось при рас-
смотрении модели Кронита Петпти), что дви-
жению электронов и дырок под действием по-
ля в полупроводнике препятствуют многочис-
ленные их столкновения с нерегулярностями
кристаллической решётки полупроводника.
Они обусловлены,, вр-первык, хаотиче-
скими тепловыми движениями атомных осто-
вов кристаллической решётки и, во-вторых,
атомами посторонних примесей н дефектами
Ш
ГлаваS
решётки. Поэтому электроны н дырки под действием приложенного элек-
трического ПОЛЯ движутся с ЕЮКОТОрЫМИ ПОСТОЯННЫМИ скоростями.
Рассмотрим, например, дырки. Они имеют положительные заряды е.
Обозначим массу дырки через m и через Z и г длину и время среднего
свободного пробега дырки (от столкновения до столкновения).
Необходимо различать большую среднею течлоерк? скорость vg* dew-
Эы/?АМ И намного меньшую СКОрОСТЬ U СС РЛОрядоЛГЛ»
nod dewcmPB/^w лгг/я.
Так как на каждую поступательную степень свободы дырки при тер-
модинамическом равновесии приходится энергия i kKT. то
_./3tsT
tT ~ V ni
Как e элементарной классической лсории электропроводности метал-
лов Друде, будем считать, что при соударении дырка полностью теря-
ет свою дрейфовую скорость и. Гак как ускорение дырки иод действием
электрического поля равно а = е£/т, то в конце свободного пробега её
скорость будет равна ат, где т — время свободного пробега. Таким об-
разом, Средняя скорость упорядоченно] О ДВИЖСНИЯ ДЬфКИ ПОД ДСЙСТЕИСМ
электрического коля и столкновений с нерегулярностями кристаллической
решётки^ согласно Друдсъ равна
Как видим, постоянная средняя скорость ц дрейфового движения дыр-
ки е электрическом поле прямо пропорциональна напряжённости электри-
ческого поля £.
Коэффициент в приведённом соотношении называют «подвижно-
стью», точнее Таким образом, для коэф-
фициента подвижности дырок получаем формулу
етр
Аналогично рассуждал, для коэффициента подвижности электронок
выводим формулу
етп
- -—
2mtt
Здесь пгр и тн — эффективные массы дырки н электрона, тр и то —
времена свободного пробега дырки и электрона, г — абсолютная величина
Й.з. Система уравнений локальных балансов
3N7
заряда электрона. Время свободного пробега т связано с длиной свободного
пробега соотношением / = т. в которое входит тепловая скорость
Итак, окончательно имеем две зшли/шчЁСкме формулы;
Up! = Un.X = /^П.£.П*
для «скоростей дрейфа» дырки и электрона под действием электрического
поля, вернее, для проекций этих скоростей на ось лг. В формуле для элек-
тронов появился знак минус, так как электроны движутся против поля, ибо
они заряжены отрипатсльно.
Соответственно^ для проекций потоков дырок и электронов па ось т
под действием электрического поля имеем два следующих «эмпирических
закона»:
jptf = РДр^Я?' jni = —
где £а. — проекция на ось х напряженности электрического поля
Экспериментально установлено^ что в кремнии Si подвижность элек-
тронов = Ю00 см2/(Вс) и дырок gp = 600 см2/(Вс). В герма-
нии Ge подвижность электронов = 4500 см2/{В с) и дырок =
= 2000 см2/(Вс).
Зная коэффициенты подвижностей электронов и дырок, можно оце-
нить времена и длины средних свободных пробегов для них. Рассмотрим,
например. дтину свободного пробега электрона в кремнии Si. Масса элек-
трона и кремнии равна 0f2m, где m - масса свободного электрона.
Таким образом, время свободного пробега электрона в кремнии равно
г = 2р^ = зе ш-1з С;
а длина свободного пробега электрона в кремнии равна
ZTI - wr тТ1 - т„ = 950 А;
она много больше межатомных расстояний.
Диффузия кос ите ей тока
Помимо дрейфа элементарных носителей тока в полупроводнике,
необходимо учитывать диффузию элементарных носителей. Сначала рас-
смотрим снова дырки.
Пусть имеется полупроводник в виде длинного тонкого образца посто-
янного поперечного сечения 5, и пусть концентрации дырок в нём дастся
функцией fk гДе х — координата поперечного сечения, £ — время.
3MN
ГлаваS
Возьмем произвольное сечение образца
с коррдииатрй т и рассмотрим вблизи псп} ещё
два близко расположенных сечения с коорди-
натами х - / и z + f, где f — длина свободного
пробега дырки r образце, показанные на ри-
сунке,
Дырки, находящиеся между ПЛОСКОСТЯМИ I — £ И I В MOMCHJ ЕрСМСНИ Т
и движущиеся к плоскости аг, за время от ( до t + г пересекут сечение т
слева шн/шво (а дырки, которые не находятся между этими плоскостями
и момент времени б не пересекут его). За счёт столкновений с решеткой
дырки из данной группы не выпадут, так как до прохождения сечения т
они пройдут каждая расстояние, мбнынее длины свободного пробега
Концентрацию дырок, находящихся в объёме отх—£ до я и движущих-
ся к плоскости я, будем считать равной 1/6 р(я - //2), где р (я - f/2) —
средняя концентрация дырок и объеме от я — f до з, Считаем, что имеются
три взаимно перпендикулярные физически равноправные направления для
хаотического теплового движения дырки, причём для каждого направления
имеется движение дырки как по его направлению, так и против него. Таким
образом, вклад в поток дырок, движущихся в положите льном Егаира&лепии
оси ,г и пересекающих ссчснис т в направлении слева направо за время ст
£ до £ + т, равен
0 - 0 • 5'Л
где — вклад в ложную плотность лотокд дырок от указанных
дырок. Здесь т - время свободного пробега дырки, £ длина свободного
пробега дырки, $ — площадь поперечного сечения рассматриваемого длин-
ного образца.
Вклад в полный лоток дырок, находящихся в объёме от ж до х + /,
и движущихся в отрицателЕлпм направлении оси я, и пересекающих сече-
ние т в направлении елрадл за то же время от £ до £ 4- т. равен
- - j?1 (/ + 0 •
где J^(i) — вклад в пшную лжляность лолтоко дырок от указанной
группы дырок.
Таким образом
Л»(®) = j'(i) - 0 - - 0| »
й.5. Система уравнений локальных балансов
3NY
?W“2 —
£ az
6 т dLr
Получили та к называемый «закон Фика» для дырок:
Jpir - ~Df,~c
где Рр — dhfptix и рассматриваемом полупровод-
нике, причём для коэффициента диффузии получили формулу
в которой £р и Гр — длина и время среднего пробега дырок в рассматривае-
мом полупроводнике.
Рассуждал аналогично, для диффузии электронов в полупроводнике
получим свой «закон Фика»:
причём для в полупроводнике по-
лучим формулу
в которой и тп — длина и время свободного пробега электронов в рас-
сматриваемом полупроводнике.
Выведем, наконец, так называемые «соотношения Эйнштейна» для
электронов и дырок. Для электронов имеем
Dn _ Al 2шп _ ?Wn / А \ _ 2 _ 4Aj|j7" _ А’бТ'
бтп Зс V* / Зе Зе
таким образом, для электронов получаем соотношение
On _ *бГ
е ь
в котором Аь — постоянная Больцмана. Это соотношение называется «со-
отношением Эйниггеина для электроноя». Рассуждая аналогично, получаем
«соотношение Эйнштейна для дырок»:
Ор _ ЬбТ
7л7 ”
390
ГлаваS
Гея гравия w w дырок
Будем Считать, ЧТО свободные Электроны и диркл В №Л у проводни-
ке могут появляться и исчезать только при генерации и рекомбинации
электров-дырочных пар. Электрон-дырочная пара может родиться, т.е. по-
явиться в какой-то точке объема полупроводника в какой-то момент врс-
менн, а может и уничтожиться, т. с. исчезнуть в некоторой точке полу-
проводника в некоторый момент времени. Первый процесс называется
«объёмной генерацией» пары электрон-дырка (от англ. generation — гене-
рация), а второй — «объемной рекомбинацией» лары электрон-дырка (от
агтгл. recombination рекомбинация),
Обозначим через й = Я (аг, £) и <7 = G(if скорости объемных
ретссшбинодш/ и генерации. Это значит, что в объёме tiVr около
точки .к за время от i до t + df появится
□пскгреж-дырочных пар п исчезнет
й dVdt
1ектро1 Г-' L Ы роч I ГЫ х 1 lap.
При рождении элскгрон-дырочной пары одновременно рождаются
электрон и ойяа ^ырка, а при уничтожении такой пары одновременно
уничтожаются ойня электрон и
Таким образом, мы считаем, что свободные электроны и свобод-
ные дырки рождаются и уничтожаются в полу проводник только совмест-
но — ТОЛЬКО при процессах рождения И уничтожения С7И?6оЁ)пЬСГ электрон-
дырочных пар, что справедливо для всех свободных электронов и дырок
в чистых полупроводниках, только для свободных электронов в примесных
полупроводниках p-типа (где они являются «неосновными» носителями
электрического тока) и только для свободных дырок в примесных полу-
проводниках n-типа (где они являются тоже «неосновными» носителями
элевлрического тока).
Скорости (? и Я можно описать следующими законами. В точке полу-
проводника, в которой имеется избыточная (по Сравнению с термодинами-
чески равновесной) концентрация электронов, выполняется закон
Грец
з в точке полупроводника, в которой имеется избыточная (по сравнению
с термодинамически равновесной) концентрация дырок, имеем закон
Риуй-
TfLTf
Й.з. Система уравнений локальных балансов
39]
Микроскопические процессы рекомбинации и генерации свободных
электронов и дырок при рекомбинации и генерации свободных элсктрон-
дырочных лар на самим деле происходя т следующим образом. При реком-
бинации движущаяся в кристалле свободная дырка (или электрон) сначала
захватывается некоторым «центром», т.е. примесным атомом или дефек-
том кристаллической решетки, а затем этот «центр» через очень короткое
время захватывает также И свободный электрон (или дырку), и после этою
(на «центре») происходят взаимное уничтожение свободных дырки и элек-
трона — их Процесс совершается тоже при помо-
щи «центра». Сначала центр выпускает свободную дырку (элекгрон), а за-
тем через очень короткое время пы пускает также и свободный электрон
(дырку).
Таким образом, время рекомбинации тряс определяется количеством
в кристаллической решётке полупроводника указанных «центров» реком-
бинации и генерации и их физической природой.
Систем# рдяней ий дока/ьяых бялотсое бдя
w дырок я яолулроеодииш? с внешний адехмричеекк.м яол&и
Ограничимся снова рассмотрением то и кого длинного полупроводника
постоянного поперечною сечения когда HLс величины зависят ТОЛЬКО
от я и t. Возьмем полупроводник в виде дли иного образца одинакового
сечения, на который вдоль образца наложено однородное электрическое
поле
где у?(т) - электрический потенциал этого ПОЛЯ.
При выводеурдачэдцй токаяьных блядлсм электронов и дырок необхо-
димо учитывать следующие, как их называют, «элементарные процессы»:
1) дрейф, 2) диффузию, 3) совместную генерацию и рекомбинацию элек-
тронов и дырок.
Рассмотрим некоторый бесконечно малый объем нашего полупровод-
ника между двумя бес конечно близкими произвольными сечениями .г и i 4-
— и рассмотрим бесконечно малый интервал времени от t до f + di;
поперечное сечение полупроводника пусть равно 5.
Составим уравнение баланса числа дырок в этом
объёме. За время от t до i 4- di число дырок в объёме,
очевидно, увеличится на величину —
(i, х) dt Sdz, х г+rfx
392
ГлаваS
где tfds = dV — величина рассматриваемого объёма. p(f, s) — концентра-
ция дырок в ССЧЕЕ1НИ I в момент времени i.
Это увеличение происходит по следующим причинам.
Во-первых, часть дырок уходит из объёма за время от I до i + di через
правое поперечное сечение я? + ds, Число таких ушедших дырок равно
it + dz) 5 di,
где 4- dx) — проекция на ось s лбтбкл (нс электрического тока)
дырок н сечении s + ds R МОМЕНТ времени ir
Во-вторых, часть дырок приходит в наш объем за время от i до i + di
через левое поперечное сечение. Число этих пришедших дырок равно
jpUM) 1 1 dts
где jpx(i. z) — проекция на ось z лотолд (нс электрического тока — потока
числа частиц) дырок в сечении s в момент времени i.
В-третьих, часть дырок родилась при объёмной генерации внутри рас-
сматриваемое объёма за время от t до t+di- Это число появившихся дырок
равно
G • di • S • dih
где С? — скорость объёмной генерации электрон-дырочных ггар и сечении s
в момент времени i+T. С. число Электрон-дырочных нар, родившихся ы еди-
нице объёма в единицу времени.
В-четвёртых, часть дырок уничтожилась при объемной рекомбинации
внутри рассматриваемого объёма за время от t до t + di- Это число исчез-
нувших дырок равно
й-di-S-dz,
где Й — скорость объемной рекомбинации электрон-дырочных пар в сече-
нии т в момент времени iT т.е. число электрон-дырочных пар, уничтожив-
шихся в единице объёма в единицу времени.
Таким образом, имеем следующее уравнение баланса для числа дырок
в рассматриваемом объёме:
df S’ dz = —jpa:(a; + ds) 5 - di + jpT (z) S di +
+ G di 5 ds - /? di 5 - d s =
= —dx dl + G dl S-dx-H di-S-dx:
Os
в.6. Примеры решения системы уравнений балансов
393
мы учли, что cfr — бесконечно малое, и использовали формулу разложения
в ряд Тейлора функции по малости di. Сократим последнее
уравнение на Ji - tfi и получим уравнение
di дя ’
которое называется «фдялс/ше.и локального болалсо в рассматри-
ваемом полупроводнике с приложенным внешним электрическим полем.
Рассуждая аналогично, приходим к «урд₽и₽иим локального баланса
С?Т1 П -t . /т п
^-дГ + с?“я
в нашем полупроводнике.
Эти два уравнения следует дополнить следующими двумя уравнения-
ми;
Jpi — P^p^JT — '
для яллотпносте'ы1 л стоков дырок и элекгроион, в которых первые слага-
емые в правых частях описывают дрейфовые потоки дырок и электронов
в электрическом поле, а вторые слагаемые в правых частях дают их диф-
фузионные ПОТОКИ.
Имеем систему четырёх уравнений дм четырёх функций: р(г, £),
n(^ 0JPr(^ i), О-
Я.6- Примеры решения Системы уравнений бя.лшеон
электронов и дырок
Чтобы освоиться с системой уравнений локальных балансов электро-
нов и дырок, рассмотрим примеры их решений (которые нс зависят от вре-
мени И ДЛЯ которых 3/3t = ())-
Пример I, Рассмофнм сначала решение (для которою
<9/<Эг = 0). Возьмём термодинамически равновесный бесконечный длин-
ный цилиндрический полупроводник постоянного сечения не присо-
единённый к полюсам источника напряжения, когтя к лену и приложено
внешнее Электрическое ноле.
Например, пусть это бесконечно длинный тонкий цилиндрический по-
лупроводник, примыкающий одним концом к положительно заряженному
394
ГлаваS
шару, но отделённый от этого шара некоторой изолирующей прокладкой,
как показано на рисунке.
В этом полу проводнике нет потоков элск-
аизолир тронов и дырок. и поэтому и любом его сече-
трокладка нни ж имеем
Jpl — О И jn.! = 0.
Первые два уравнения системы уравне-
ний локальных балансов тождественно удовлетворяются, так как &p/&t =
= c?n/c?t = 0, Ojpj/Qa: = Ojnx/Оз?- = 0? Gf — /{ = 0. Вторые два уравнения
локальных балансов дат уравнения
РДр-^я ” ^р777 — “ ^^777 — Q-
г ах ах
т . г / \ \ ь , л ц ч л л
Так как Сх(зг} =----,— . где — потенциал электрического поля,
ах
то из этих уравнений дня плотное гей потоков дырок и элекгронов получаем
уравнения
1^Р=П # I tin _f
Dp (b Р rfj : 13-n dx n dx
интегрируя которые по я, приходим к формулам
р(ж) = ро п(х) = no ,
в которых ро и по — некоторые постоянные. Воспользовавшись соотноше-
ниями Эйнштейна др/Рр = Рт-./ЕК = е/кцТ, отсюда имеем, что
р(т) = рп е , п(т) = по е':*^^кнГ,
где jov и «г» — значения концентраций р(х) и n(i) в сечении полупроводни-
ка, к котором электрический потенциал = 0, т.е. при х = +ж,
Видим, чти дырки и пекшроны « расс.иатринаелю.м полупроводнике
распределены соелаено распределению Больцмана. Действительно, величи-
на Ё^(х) = e<p(z) является потенциальной энергией дырки в электроста-
тическом ноле в сечении sf, а величина {/„(ж) = — — потенциальной
энергией электрона в этом поле в этом сечении. Поэтому
р(л)=Рие г'гДг}Ли?' п(.т) = по е ^Гч(1)/*гвг.
в.6. Примеры решения системы уравнений балансов
395
Пример 2. Рассмотрим теперь системы уравне-
нии локальных балансов (для которого тоже Э/сН = 0)- Возьмём длинный
тонкий цили ндриче икни полупроводник 71-типа и истомны спи поперечною
сечения S длины i. в котором, как будем считать, ток переносится толь-
ко электронами, и пусть к этому полупроводнику приложено постоянное
однородное электрическое поле £я: / 0, ire зависящее от я.
Предположим, например, что наш по-
лупроводник контактирует с двумя металла-
мп% в которых всё время поддерживаются
постоянные электрические потенциалы
и и йднядхвбня в обоих металлах концен-
трация п электронов. Тогда концентрация п
в разных сечениях дс полупроводника будет
Одинаковой, т.е. в каждом селении т полупроводника имеем одинаковую
концентрацию тв{х) = n = const, так что согласно системе уравнений ло-
кальных балансов для плотности потока электронов имеем соотношение
7п4Р —
так как их диффузионный поток равен нулю. Следовательно
= о> }п:<- = const,
я*-
В полупроводнике течёт постоянный электрический ток /¥ = ej^ iS:
где S — поперечное сечепие полупроводника^ раиггый
/:с = —S.
знак ми л ус появился потому, что электроны заряжены отрицательно и дви-
жутся прошв поля.
/fwetW обычный слил четкий я тол; тйгой же, лч?л тик
# лтм четких л/ншбяыяшх.
Пример 3. Рассмотрим теперь Другое стлцыондрное/гешеяие систе-
мы уравнений локальных балансов (для которого тоже d/dt = 0). Возьмём
пол у бес конечный длинный тонкий цилиндрический полупроводник />типа
постоянного сечения 5. в котором электроны являются неосновными носи-
телями электрического тока, и будем считать, что внешнее электрическое
пиле равно нулю (Л\. = О}.
Пусть в рассматриваемый полубесконечный равновесный полупровод-
ник р-тнпа, занимающий полупространство при д: 0ъ мы постоянно
396
ГлаваS
впрыскиваем (как говорят, «инжектируем») электроны в крайнем левом се-
чении я = 0, как показано на рисунке, тег этом сечен ин пусть всё вре-
мя поддерживается одно и то же значение «избыточной» (но сравнению
с равновесной) концентрации Пцзб(О) = = п(0) - тгршн, где Прщя —
равновесная концентрация электронов r невозмушённом рассматриваемом
термодинамически равновесном полупроводнике р-тииа.
"lo*
Для объемного источника электронов G —
- /? используем закон
электроны
ЭЛ. ТОК
G R — _ (д ^рилн)-
'осн:
-------г гце трти —
Со глас е to рассматриваемой системе урал-
нений локальных балансов для плотности по-
тока электронов имеем теперь выражение
так как электрическое поле отсутствует, и отсутствует дрейфовый поток.
Кроме того, из системы уравнений локальных балансов инеем также сле-
дующее уравнение локального баланса для электронов:
0 = +(?_ д
(Ы
так как Sn/Яй = 0.
Таким образом, приходим к дифференциальному уравнению
о _ - -1- (n - npaBH)t
di2 тр« 1
или уравнению
D^T(n’n₽am)
Если теперь рассмотреть в качестве новой неизвестной функции функ-
цию Пнзс(я) = л(х) - Прваь обозначающую избыточную (по сравнению
с равновесной) концентрацию электронов, и если величину имею-
щую размерность квадрата длины, обозначить через Г;,» где Ln — так назы-
ваемая «диффузионная длина электронов»: £п — ^//Ла^к! то полученное
8.7. 'ГКО РИД pH-ПЕРЕХОДА
397
дифференциальное уравнение можно представить в следующем простом
виде:
Общее решение этого дифференциального уравнения имеет вид
rwW = A + В e;i;/,L”,
где .4 и В произвольные постоянные.
Так кик л. = О при i = +эс, то приходим к формуле
tw(z) “ пиХ1(0)е"*/£'"-
Как видим, избыточная концентрация электронов экспоненциально
убывает и обращается в нуль по мере продвижения в глубь пллунровцддика
Эффективная глубина, на которой избыточная концентрация уменьшается
в е раз, характеризуется длиной LN.
Получили «пеомпческий» электрический ток. текущий п полупровод-
нике без приложенного к нему электрического поля, уменьшающийся по
мере углубления в полупроводник, так как этот ток равен
W = -eSjMz) = eSDn
(X lL Jj’1a
он обращается п нуль при аг = +оо. Этот ток равняется пулю, когда £
= си, т.е. когда трй{ = со.
В, ТЕОРИЯ F TV-ПЕРЕХОДА И РЛР-ТРАНШСТОРА
8.7. Теория ртг-перехода
Контактная разность потенциалов
Рассмотрим теперь так называемый полупроводник с рп-псрсходом,
который состоит из находящихся друг с другом в микроскопически тес-
ном контакте (в пределах единого кристалла) р- и л-областей (//-область
представляет собой акцепторный полупроводник, п-область — донорный
полупроводник).
Тесный контакт р- и п. областей создаётся специальными технологиче-
скими приёмами при приготовлении кристалла с рп-переходом, например,
при выращивании его из расплава, в котором в определенные моменты вре-
мени производится смела состава примесей.
39В
ГлаваВ
перекал
С начала рассмотрим термодина ми ческ! i
равЕговссныс условия, когда полу л рп йоде ihk
с рп-лсрсходом пребывает в термодинамически
равновесном состоянии , и поэтому по нему не
течёт никакого электрического тока (когда р-
н п-обласги полупроводника не присоединены
к полюсам никакою мсгочнккя внешнею напря-
жения).
В таком равновесном полупроводнике с ^«-переходом возникает так
называемая «контактная разность потенциалов», т. е. оказывается, что «-об-
ласть имеет положительный электрический потенциал V = Д^> относи-
тельно р-евпасти (здесь А обозначает приращение). В пределах объема
«-области электрический потенциал во всех её точках одинаков и равен И.
В пределах объёма р-областн во всех точках электрический потенциал то-
же одинаков и pane f г 0. За нуль отсчёта электрического потенциала условно
принимаем р-областъ.
В узком плоском слое шириной порядка 1 мкм = 10-6 м так назы-
ваемого «рн-псрсхода» электрический потенциал плавно возрастает от
значения О на краю p-области (из границе с рп-переходом) др значения
V на краю п-области (из её гриЕтицс с рп-переходом с другой стороны),
причём в области внутри рт-перехода существует отличное от нуля стати-
ческое электрическое поле.
объясненwe wwm актиний /joshwwu
Физическую причину появления контактного скачка электрического
потенциала между р-областъю и «-областью в термодинамически равновес-
ном полупроводнике с ргс-переходом Шокли объяснил в 1949 г следующим
образом.
Предположим сначала, что между р- и п-сбиястями никакого элек-
трическою поля пег. Так как р-обпасть является акцепторным полу про
водником, то можно считать, что в ней носителями электрического тока
являются дырки, причём концентрация дырок р равна концентрации .'Уд
акцепторных атомов .4Т которые при температурах порядка комнатной тем-
пературы 71 = 300 К практически все отрицательно ионизованы и нахо-
дятся в состоянии отрицательных ионов Д”. В целом ^область, однако,
электрически нейтральна, каждый элемент сё объёма имеет нулевой за-
ряд. Наоборот, «-область является донорным полупроводником^ и можно
считать, что в ней единственными носителями тока являются электроны,
причём концентрация электронов п при температурах порядка комнатной
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
399
температуры Г' = 300 К практически равняется концентрации ЛЪ донор-
ных атомов /J, которые почти все положитслъен} ио ез изо ваны н находятся
в состоянии положительных ионон Л“. Таким образом, в цепом п-область
тоже электрически нейтральна, и любой элемент ее объёма имеет нулевой
заряд.
Представим теперь гипотетически, что сначала /> и п-области были
разделены, но затем мы привели их в кони кт ио плоской границе (это
действительно только предположение, так как физически
такую операцию с реальными р- и n-полупроводниками осуществить нель-
зя, потому что их контакт в полупроводнике с рп-переходом должен быть
jwujgwcwH ичегкши).
Сразу же после установления контакта дырки из р-обласги, где их мно-
го, начнут диффундировать через плоскую границу контакта в п-область,
в которой их практически нет. Одновременно электроны из n-области. в ко-
торой и к много, через плоскую границу р- и -областей начнут диффунди-
ровать в р-область+ где их фактически нет.
В результате этих перемещений дырок я электронов через граничную
плоскость раздела р- н и-областей некоторый положительный электриче-
ский заряд перетечёт из p-области в ^-область, а отрицательный из ??-об-
ласти в р-область, и между р- и п-областями возникнет э-теязл/; w веское
которое будет препятствовать дальнейшей диффузии дырок и электронов.
Возникающий постоянный элек-
тростатический потенциал между р-
и п-областими изображён па приводи-
мом верхнем рисунке. На следующих
двух рисунках показаны концентрации
Ад акцепторной и Лг£> донорной при-
месей. Пол влиянием электрического
потенциала дырки будут стремить-
ся сдвинуться налево, а электроны на-
право. В результате концентрация ды-
рок постепенно упадёт до малого зна-
чения ещё до того, пока будет достиг-
нута плоскость контакта р- и п-облас-
тей. Электроны, имеющие отрицатель-
ные электрические заряды, стремятся
перейти в область с большим электри-
ческим потенциалом, а поэтому unit бу-
дут иметь малую концентрацию в плос-
кости контакта р- н «-областей.
4<Hb
ГлаваS
В результате образуется атеюяричйжш сдай с платностью
электрического наряда, показанной на самом нижнем рисунке. И мел ею этот
двойной слой и создаёт электрический потенциал показанный на самом
верхнем рисунке.
Форму кривой потенциала можно найти, решая электростатическое
дифференциальное уравнение Пуассона
д^ = -JL
£|]S'
Когда электроны и дырки двигаются навстречу друг другу они встре-
чаются и рекомбинируют, г.е. исчезают. В результате «оголяются» электри-
ческие заряды ионов Л и примесных атомов ппутри области рп^пере-
хода. Именно этот оголённый заряд и создаст злектрпческос поле.
Возникшее электрическое ноле будет препятствовать дальнейшей диф-
фузии дырок и электронов в область контакта р- и п-областей.
В конечном счёте установится термодинамическое равновесие с неко-
торыми равновесными распределениями концентраций дырок /? и электро-
нов л в пределах области jjn-перехода и с равновесным скачком потенциала
V = между р- и п-областями.
7?10/шя Шокди равновесного рп-перехода
Приступим теперь к наложению гак называемой «электродиффузной-
ной теории» рп-лерехода Шокли, предложенной им в 1949 г.
В рассматриваемых термодинамически равновесных условиях потоки
дырок и электронов в любом сечении ..г полупроводника равны нулю:
JpJif1) = Щ Jrtif1) = О
Так как для этих потоков имеются выражения
ьДл) = -/Л» у1 +
dx dx
то будут справедливы следующие дифференциальные уравнения:
dp _ d<p dn _ „ dp
D*fa~ ~}^fa' Dn fa ~ n,infa
8.7 Т КОР ИЯ рп- ПЕРЕ ХОЛЛ
40]
Следуя Шокли, предположим, что здоюкричдекие нй-?е? в бесконечно
длинном цп.чнЕЕдричсскпм полупроводнике постоянного сечения 5?, прости-
рающемся от зг = — оо до зг = 4-оса н₽ so stew об-шоны тменеяия
лоиуэдынлт ы х (от -оо до +оо), бг ?пгл?ька s тик яозьгёлёшл^
eflo^jy (от х = -й до я = 6)„ где ft и Ь — подгоночные параметры теории.
В непосредственной окрестности плос-
кости кпнтялэна р- и п-областей в обла-
г -----------------------------------------------------++ +
ста на «левом крыле» обеднённого слоя =0 И
(—оо < я -й) будет выполнено условие
= 0 и в области па его «правом крыле» -и 0 _&_
(6 з: < +м) — условие = V\ где V —
не известная нам пока величина, которую
назовём «коЕгтакгпой разностью потенциа-
лов^, её-то мын котим найти.
р п
Таким образом, и целях упрощения
Шокли изменил исходную задачу и ввёл в рассмотрение три условные,
граничащие друг с другом области: 1) область с-юл при
2) области крылбде при -ж < i < -и и при 4 О < +®
и, что важно, лреиебдёс? а каждой из этих областей эффектор учи-
тываемых и полной задаче: в области —л з: /j он пренебрег эффект л. мп
гг электродов н дырок, а в областях —ос- < х < —<1
и & х < -1-ос — эффектами электрическое доля.
При правильном выборе параметров й и 6 можно надеяться, что ре-
зультаты решения намспёепгой Шокли задачи будут близки к решению ис-
тинной задачи.
Приступим к решению поставленной Шокли приближённой задачи.
Рассмотрим сначала в обеднённом слое уравнение для дырок. Эгодиф-
фереггциалыюе уравнение с разделяющимися переменными, которое легко
решить:
] rip _ _ е ri^
Prix frErriaT 1
р(.т) = p(-ft) ;
здесь мы воспользовались соотношением Эйнштейна для дырок и нашли
константу интегрирования из граничных условий
р(х) = р(-а) и р(х) = 0 при х = -й-
Произведение = Ц?(^) является мгннешрщ,™^ дырки
в электростатическом поле у?(з;}, когда она находится в сечении я.
44)2
ГлаваS
Аналогично в обеднённом слое решаем дифференциальное уравнение
для 'злсктролов:
1 Jn _ _ e ri flnn’i — ——
" <£т “ Dn rf.r “ fctT ‘ dr? J “ febT ‘
= n(— а)
теперь мы использовали соотношение Эйнштейна для электронов и кон-
станту интегрирования определили из граничных условий
п(е) = п(. д) ]| = 0 при л = —а,
Величина Сгп(^) = -е<д(з) является эче/вден эдеял^-
ли в длскгро статическом поле <р(лг), когда он находится в сече и ни дгн
Полученный решения являются формулами известного распределения
Больцмана для дырок и электронов в потенциальном поле:
р(.т) = pi.-л) п(.и) = п(-а) е
На приводимых рисунках проиллюстрировано поведение функний
и п(а?) в области рп-переходд. Рассмотрим теперь значения концен-
трации р(д) и та(т) не на леттли, а на правы/ границе л = ft обеднённого
слоя (внутри которою напряжённость электрическою ноля только и отлич-
на от нуля).
Так как ip(b) = К где V - искомая контактная разность потенциалов
равновесного рп-псрехода, приходим к формулам
p(ft) = р(—а)е-е1^ЕЛ п(6) = ш‘ -а)ее1/^Е7 .
Следуя излагаемой теории Шокли± теперь будем считать^ что вне
сям -я £ я; £ 6 не только эяемл/мчееяое лдле /готгно ну-
лю, но Ы н ?ъ(т) н эл^юпряям npw jc = —а
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
403
и л = & равны шс юнценюрлцшм я глубине />- w п-обласжей, т. е. положим,
что
р(-п) = jV4? 71(b) = ЛГ1>, p(b) = prt. n(-a)=np>
где pN - термодинамически равновесная концентрация дырок в равновес-
ном донорном полупроводнике (71-типа), а цр — термодинамически равно-
Босния концентрация электронов в равновесном акцепторном полупровод-
нике (р-тина).
Таким образом, приходим к формулам
Р„ = Л’д g-eV/^вТ jVyj = Пр eeV/^r
fl™ /JfJjfHflLTHU ЛОГО £ГН if ИЛЛОЙ
Исключая из двух ТОЛЬКО ЧТО приведенных формул контактную раз-
ность потенциалов Vd придём к соотношениям
таким образом,
С \ Рп.Т+р /
Воспользуемся теперь тем. что для термодинамически равновесного
полупроводника. (неважно, чистого, донорного, акцепторного) с малыми
концеи фациями примесей ДЛЯ равновесных кин центрыций электронов та
и дырок р справедливы формулы
та = У][р е_ (Е’_ ^fcbT, р = АГМЛ
в которых
Лггг = 2
о I rfl х :7г
2irmnktl >
/
\ 3/2
2 л ттарА^Г \
Л2 /
Выше мы привели доказательство этих формул только для чистого по-
лупроводника, когда для одноэлектроиных состоянии па дне зоны прово-
димости имеем неравенство £g — у/ 13 для одноэлектронных со-
стояний на потолке валентной зоны имеем неравенство > itT. Но это
доказательство, слово в слово, можно повторить для донорного и для ак-
цепторного примесных полу проводников, лишь бы выполнялись указанные
неравенства для химического потенциала д.
41>4
J'л л вл S
Умножая приведенные формулы друг на друга, получим соотношение
пр = е~Ея^'йТ,
справедливое для любого термодинамически равновесного полупроводника
(чистого, донорного, акцепторного). Это «закон действующих масс».
В частности, для чистого полупроводника, для которого п = р =
= п|ч имеем соотношение
п? = Nn₽N»Be“B*/fcsT.
Из приведённых соотношения j-сля пр и nJ непосредственно следует,
что для акцепторного или донорного термодинамически равно веского по-
лупроводника с малой концентрацией примеси справедливо соотношение
пр = nj.
Таким образом, учитывая, что для донорною полупроводника п = Лтд.
получим, в частности^ формулу
NiJPri = п-;
а учитывая, что для акцепторного полупроводника р - Лгд, получим фор-
мулу
ПрЛ^л = nJ.
Используя обе эта формулы, можно исключить произведение рппр из
подученной вы[пс формулы для контактной разности потенциалов V. Так
как
JVopn^pJVA = «h
то
___________________________ nt
рпПр'~х^
Поэтому справедлива следующая оконча/Я£№ШЯ формула для «кон-
тактной разнос! и потенциалов»:
Na Nd
га которую входят только известные из эксперимента величины, так что Эта
формула позволяет рассчитать равновесную контактную разность потенци-
алов V для полупроводника с рп-переходом с заданными концентрациями
Лгр и хУд примесей в п- и p-областях. Величина V имеет порядок несколь-
ких десятых вольта В (для Si с рп-переходом сита порядка 0.7-0,8 В).
г А"ьТ
V = —— In
8.7 Т КОР ИЯ рп- ПЕРЕ ХОЛЛ
405
йа7ьm -химерная хяр лкт <pwcm ? fra
Рассмотрим теперь в рамках излагаемой приближённой теории Шокли
термодинамически неравновесный полупроводник с рп-псреходом, когда
к нему приложено постоянное внешнее напряжение 14 и по нему течёт
электрический ток (а от англ, apply — приложить). Такой рп-псрсход с то-
ком, разумеется, не является термодинамически равновесным.
Полюса источника постоянного внешнего напряжения при этом мож-
но подсоединить к полупроводнику с рп-лсрсходом по-разному. Если по-
ложительный полюс источника присоединён к р-области, а Отрицательный
к n-области, то такое напряжение называют «прямым». Если имеем обрат-
ное подключение полюсов источника Е.1апряжелих к рп-переходу, го внеш-
нее напряжение называется «обратным».
Другими словами, знак напряжения 14 по-
ложительный, когда p-область соединена с по-
ложительным, а n-область с отрицательным по-
люсами источника. Контактная разность потен-
циалов на ^-переходе тогда, очевидно, pas-
ts а V — Хг. так как V — это потенциал п-опласти
по отношению к р-обпастп.
В электрон и ффузкон ной теории Шокли
рп-персхода с приложенным внешним напря-
жением 14 учитывается, что mev/bw 0 ooeri-
мёштшг слое р7>нерелойсг /ьтотности лото-
Лиь электронов и йЮиЧНЫ <ИИ Нуля
Ош: / 0). Когда отсутствует внешнее
напряжение, в обеднённом слое инеем условия
М = 0, = О, G - Я = 0.
В рамках излагаемой теории Шокли, во-первых, снова предполагаем,
что енутрн обедненного стой (— а < т < Ь) не лроггсходыт генерлшш w ро
яаибшюлмн и йырок, но ддтя
ошлгнна ow нуля U4 / 0), и, во-вторых, что вне обедненного одоя, m е. ня
егд х/ж/гъял (при -оо < я < -пи лря t> л < +ос)г ло-
ля нет {£т = 0), wo i^)ym процессы генерл^и л река-ибиллщш ателтлроиоя
Н (JftF/WK.
Такое разбиение физических процессов по разным областям, предло-
же1 mo е III окл н, оправщшгно.
Гаким образом, в области -а а: 6 (внутри обеднённого слоя)
положим (7 — К = 0. Кроме того, гак как мы рассматриваем пос^иояпх/ыи
4V6
ГлаваS
(т.е стационарные условия), то все производные по времени равны
нулю. Уравнения баланса электронов и дырок внутри обеднённого слоя
тогда приводят к следующим уравнениям:
^ = 0, ^=0;
Ут ая
полому в пределах обедне hoi и слоя —л т 6 справедливы соотношения
Jp± = const, jptJt = const ц
т. с. потоки jpT и jrt± дырок и электронов нс зависят от х. При этом
_ Ар _ (to Ар
J1“ “ ~D^
Оценки показывают, что
lDp^lf I 1*4 lDnSI’ I 1ь4
т.е. что дмффузиинные и дрейфовые нйтокм и дырок, н злектяроиой лочты
точно ptifi/ш и каилеиецрумяг друг друга, так как дырочный и электронный
токи слабо нарушают термодинамическое равновесное состояние рп-пере-
хода, имевшееся при отсутствии текущего через него электрического тока.
Поэтому константы const в формулах для jPrV и j™ молгно считать
ptZffMbLUU нулю (ХОТЯ OH.L1, EL3 СВМОМ ДСЛС, НуЛН) НС рЛННЫ, ТЯК КД К ПОТОКИ jpj.
и Jn.rh разумеется, отличны от нуля и обеспечивают прохождение элект риче-
ского тока через обеднённый: слой рп-перехода при приложенном внешнем
напряжении ЦД Таким образом, имеем следующие приближённые диффе-
ренциальные уравнения:
°рУ" + "Г = °’ Л “ т2 = °-
az di dx ЖЕ
Они имеют в точности такой же вид^ как в случае термодинамически
pa Bi ювес наго pn-iюрсхода.
Учтём теперь^ что при т = —а на левой [раницс обеднённого слоя,
имеем условие а) = 0, а при т = fj на правой границе слоя — условие
^(6) = V - К, где — приложенное напряжение. Однако теперь хотя
н будем считать^ как в случае термодинамически равновесного рп-переходз,
что
р(-а) = Na н п((>) = ^D,
нФ ис будем предполагать, чти p(fj) — р„ и п(—а) = п;,.
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
407
Таким образом, имеем соотношения
р(й) = р(-а)е-£^ - п(&) = п(-а) ее(^ - К)Дб7"
которые представим в вида:
р(Ь) = Л’л e-e(V - Nd = п{-а) C€(V ~ ^№гь
ГТр]| К = 0 имеем соотношения р(Ь) = рп и п(-а) = п^, а потому
сгграиел1|[1вы равеггстиз
Лр =
Комбинируя четыре приведенные формулы, получаем, что
р(Ь) = р„ ee^/^r, лр = п(-я) е-^А&Г
и, вводя обозначения
рнза(Ь) = р(Ь) - рТ| I П uafi(-a) = л(-а) - пр
для «избыточных» концентрации носителей элекгрического тока на гра-
ницах —а и Ь обеднённого слоя, к которому приложено внешнее напряже-
ние 14.. через который течёт постоянный электрический ток, приходим к так
называемым «основным законам рп-перехода»:
Р*л(Ь) = рп ( е еУЛг - i), fl пз6(-а) = пр ( е<!К/«гбГ _ । \,
для избыточных концентраций электронов и дырок па границах обеднён-
ного слоя е приложенным внешним напряжением V;±.
Формула Шокли
В областях при —ос < I —а и при Ъ х < 4-og (на крыльях
рп-перехода} мы лреЕхебрежём электрическим полем, т, е. будем считать,
что = О, но будем учитывать процессы генерации к рекомбинации элек-
тро но» II дырок.
На прадм! крыле обеднённого слоя (при b i < 4-то) п п-области
для избыточной концентрации дырок в стационарных условиях протекания
постоянного электрического тока имеем дифференциальное уравнение
гт Past' _ Puifi
V~d^~ ~
40N
ГлаваS
или уравнение
Ри?С _ 1
“л5" "
в котором Lp = тр№ dtf^^jw-аячая дырок в п-области. Решая
это дифференциальное уравнение с граничным условием 7w(+wl = 0.
получаем формулу для избыточной концентрации дырок в л-областн;
Риэв(я) =р1пб(Ь)е <*
С учётом выведенных выше основных
законов рп-перехода, таким образом, полу-
чаем следующую функцию, описывающую
изменение избыточной концентрации дырок
в п-области:
?>и,й(т) = р„ (eeV"/^r - 1) е (ж
На лодок кры.те обеднённого слоя (тхри
-00 < ;г —с) в p-области для избыточной концентрации электро-
нов в стационарных условиях протекания постоянного электрического тока
имеем дифференциальное уравнение
Д
Г^т2
в котором Л.л = ъЛРп diwjm электронов в ^области.
Решая это дифференциальное уравнение с |рякичным условием
= О, получаем функцию избыточной концентрации электронов
в р-обласги;
гаИ5б (я) = ни,б (- a) ets+“^£“.
Используя выведенные выше ооноя-
здкдом pn-nepeswda, Отсюда получа-
ем функцию, описывающую изменение из-
быточной концентрации электронов в ^-об-
ласти:
nH3ti(jc) = np _ Q е(х+и)/£к,.
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
41Р
Рассчитаем теперь электрический ток / = текущий в полупровод-
нике с jw?-переходом с приложенным внешним напряжением в направ-
лении Or р-ибишети к п-обпасги.
Используем, что в рассматриваемых стационарных условиях электро
ческнй ток Л (г) е любам сечении гг пялул/юеодиикя одинаков, т. е. не ?д-
вдеит от т. Он складывается из электрического тока 7pjr = пе-
реносимого дырками, и электрического тока 7rtLL. = — <Sjni-b переносимо-
го электронами, здесь S — поперечное сечение попу проводника. Причём
и дьдеочный, и электронный токи, е отличие ои сулы^ного тока 7=1^
^аеисят от сечения я; только их суч/л«т / = 7Р^ + /вв от т не зависит.
Вместе с тем в обедневдан слое — n i й токи /рг и /па. от л тоже
не зависят, так как потоки jpj. и jfta в этой области являются ианстантами.
Поэтому, /ассчитыеоя №ляыы электрический ток 7 е п/?оиэеольнам
сечении я обедненного слоя, дыртчный элент^мческийг ток .мы ew числам на
л^аеОиМ крае я = & этой области, а энектрониый электрический ток - на
лева.н её црае г = —а.
Тогда получим, что
, _ г / L __ II £ WSlj __ f-^p .ь,
X=h ЛТ ffl=b
так как
Рпэб(^) — Рп.
Получим также, что
7пт — Тпя(-Е)
ОТ
Пкзб(^) = и? (ee^fc®r - ।) е^ж + a)/in,
Складывая обе эти форм улье дм 7рт и 7?Pi, получаем формулу
/ = /„ + U =е5(^ + . л,
\ Ьр Ьп /X /
Так что приходим к Знаменитой «формуле П1пкли?> для постоянного
злек1 рнчсскою Юка, текущею через jjcuiyjjpuводник с рп-исреходом с ири
ложе иным постоянным внешним напряжением Уа:
/ = Д1а£ ,
+ 10
ГлаваS
/и ас — I 7 I г
I jjrt J-ti
величина /llUL- называется «Юком насыщения»,
/ так как
lilt! J = -/нм-
К, —*-оо
Теоретическая вольт-амперная характери-
стика рп-псрсхода имеет вид, показанный Ета
рисунке; она прекрасно согласуется с экспери-
ментом.
За исследования полупроводников и от-
крытие транзисторного эффекта Шокли. Бардину и Браттенву в 1956 г.
была присуждена Нобелевская премия.
объяснение еъги/?адллк?и/ег<’ бейс/и^я
рп-леретодя
Приведём рассуждение самого Шокли 1949 г. Рассмотрим электричек
с кий ток, текущий через рп-переход с приложенным внешним напряжением
V,-
В термодинамически равновесном полупроводнике с рп-переходом нет
никаких потоков ни дырок, ни электронов через плоскость контакта р*
и «-областей. Эту равновесную сктуациЕо рассмотрим как результат ло,и-
п^мсацыы лптнохпя Отдельно дня дырок и СпдСльнО дчя эиЮкгрОнОв.
Рассмотрим сначала оба потока йырок, текущие слева направо и спра-
ва налево через плоскость контакта р- и «-областей. Хотя концентрация
дырок очень мала н «-области, опа важна для объяснения физики работы
полупроводника с pvt-переходом.
Дырка попадает в «-область, как бы «взбираясь» на «холм» электри-
ческого потенциала. Взобравшись на него и попав на плато постоянного
потеЕгциала и «-области, дырка тем не менее продолжает свое хаотическое
диффузионное движение- В результате птей диффузии она может снова по-
пасть на крутую часть «холма» электрического потенциала и «скатиться»
с него вниз в ^-область (такая дырка нас не интересует). Эта дырка, однако,
может случайно продиффундироватъ в глубину л-области- В этой области
она будет двигаться какое-то время, пока не будет захвачена каким-нибудь
дефектным «центром», в котором она лрирс комбинирует с электроном и пе-
рестанет существовать. Средняя глубина, на которую дырка может проник-
нуть в «-область, определяется временем рекомбинации г.
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
411
Решение соответствующего дифференциального уравнения показыва-
ет, что эта средняя глубина прспиЕнрнення равна L = V/J т; это так на-
зываемая «диффузионная длина», D — коэффициент диффузии, т — время
жизни дырки е ^-области.
Таким образом, при термодинамическом равновесии поток дырок течёт
из ^-области в л-область и проникает к неё на глубину L, пока фактически
нес дырки ЭТОЮ потока НС ПрОрСкОмбиНИруЮТ С ЭПСКГрОНаМИ. НОТОК ДЫрОК
из ^-области в rt-обпасть, оканчивающийся рекомби нацией, точно компен-
сируется их обратным потоком из п-областн в p-область, который образу-
ется в результате появления дырок при тепловом возбужден ни «центров»
захвата дырок, в которых образуются новые дырки, диффундирующие к по-
тенциальному барьеру, где они «скатываются» в р-область.
Приложенное внешнее напряжение К к полупроводнику с рп-перехо-
дом нарушает компенсацию рассматриваемых потоков. Действие внешнего
напряжения на рассматриваемые потоки дырок проиллюстрировано на при-
водимых рисунках.
На верхнем рисунке показана
ситуация. Оба рассмот-
ренных потока /у и (от а*ггл. for-
ward — вперед и от ллл-1. genera-
tion — генерация) при равновесии
равны и противоположны.
На следующем рисунке показа-
на Ситуация С большим flri/jtinjuiw.w
внешним напряжением, когда прак-
тически нет дырок, взобравшихся ла
потенциальный холм, Поэтому по-
ток /у практически равен нулю, хотя
поток имеет почти ту же величи-
ну, что и при равновесии. Диффузи-
онная длина много больше ширины
области с изменением электрическо-
го потенциала, т с. обеднённого слоя
pacti ufdiiiit
обратное
напряжение
области с отличным от нуля электрическим полом. Так что облас ть, в кото-
рой ноток возникает, фактически не затронута приложенным обратным
напряжением, и поэтому поток /3 нс зависит от этого напряжения. Эту
независимость потока /!? называют «насыщением».
На нижнем рисунке показана ситуация е лрялшлг внешним напряже-
нием, при котором поток // большой. Возрастание этого потока связано
с различием энергий дырки в р- и n-областях Разность этих энергий равна
412
ГлаваS
произведению абсолютной величины заряда электрона на разность значе-
ний электростатического потенциала в р- и п.-областях
Согласно формуле распределения Больцмана число дырок, которые
случайно при тепловом возбуждении приобретают достаточную энергию,
чтобы взобраться на потенциальный «холм», увеличивается в е раз при уве-
личении тепловой энергии Ах Т на единицу. Поскольку потенциальный ба-
рьер имеется уже в равновесной ситуации, ю каждое уменьшение высоты
барьера на величину fee Т увеличит поток 7/ в е раз. Причиной уменьшения
высоты барьера является приложенное прямое напряжение 14. В равновес-
ной ситуации 14 = 0, и поток 7/ равен потоку Л. Поэтому электрический
ток? сопровождаемый рекомбинацией дырок, panci [
Л - 1деу^т-.
это даёт для суммарного электрического тока иырок из ^области в п-об-
ласть разность
h-Ig = Is - I.) .
Электрический ток равен нулю при 14 = 0 и возрастает экспоненци-
ально до больших значений при большом положительном напряжении Vfl,
On уменьшается до значения /|? при отрицательном напряжении 14, суще-
ственно большем А^Т/е.
Аналогичные рассуждения можно про вести для тока+ переносимого
Приложенное внешнее напряжение, которое уменьшает вы-
соту потенциального барьера для дырок, уменьшает ее также и для электро-
нов. Следовательно, большой Электронный ток течёт при тех же условиях,
при которых течёт большой дырочный ток.
В обоих случаях токи переносятся потоками небольшого числа носи-
телей в р- и n-областях. Один ток переносится дырками, движущимися
из «-области в р-область, другой электро пэми^ движущимися обратно — из
р-области в ^-область. В случае обратного напряжения 14 увеличение элек-
трического потенциала большое, и дырки стремятся остаться в р-области,
а электроны — в ? г-области. При этом через рп-переход будет течь mfljt нд-
обязанный генерации дырок и электронов. Если обозначить вели-
чину полного тока насыщения через 7$ (от иилт. saturation — насыщение), то
полный ток при любом знаке приложенного напряжении 14 будет даваться
формулой
7 = Л 71 - 1J 1
в которой ток насыщения равен сумме обоих токов насыщения-
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
413
Зааисимагть границ а и 6 аб^нёняогя слоя лет приложенного
напряжения V^K. Элек/яринесшая ёшнктяь рп-нерехоба
При расчёте границ а и & обеднённого слоя и электроёмкости рп-пе-
рсхидд в излагаемой приближённой теории Шокли сделаем предположи-
вис, что айедлЁТшый слой рть-перехода+ занимающий обласъь — а i bh
.тнм/йя гве^бойлых лосытйд^й тока, ы его зцрж) солйлстся
ыояизовдннылш акц^лшорнылш атаиалш в области - а < я € 0, я которой
объЁнная плотность яд эдектричсскаго мряёо равно р = —еЛ^Чп нони-
aoffonwhj.ifj^ doKopn№uu алгакФиы д области 0 х Л- в которой ойь^ипая
л.тотностль электрического эиряда донорныд нгпепж раена р — еЛ^_
Таким образом, в пределах обеднённого
слоя при— а $ д: < 0 имеем уравнение
Пуассона
= £^А
Ле3
и при 0 6 уравнение Пуассона
d'y _ ёЛгр
Здесь ёо^ — статическая диэлектрн-
ческая проницаемость полупроводника
Граничные условия дня приведенных
уравнении имени вид
t^l
ЙЕ l;|! = 6
Кроме этих двух граничных условий, должны выполняться еще два
следующих граничных условия:
р(-а) = 0? p(fr) = V - v;,
где V — контактная разность потенциалов равновесного /т-перехода и Va —
приложенное к рп-переходу напряжение.
4-14
J'Л л ВЛ S
Решения приведенных дифференциальных уравнений с приведенными
граничными условиями имеют в области —а .г Q вид
dt’j, е^л,
dx ~ --ёсГ’
—Л
dv>(a)
dx
и в области 0 т С Ь вид
<i£;|. _ I Np
dx ~ £os
eND
£q£
i ./ 1
dx
^(x-b) + v -V.,
^) = ^(x-b}2 + V-Va.
Чтобы найти значения а и fr, используем теперь условно непрерывно-
сти электрическою поля при z = 0. в силу которого получаем соотно-
шение
ЛГда = Лрб, ЛгЛа = JVpb.
Оно показывает, что обеднённый слон г -перехода в расчёте на еди-
ницу площади поперечного сечения полуЕгроводн^ка имеет отрицательный
заряд e/Vjl*1 р-стороме (при — п т 0), созданный ионизованными
акцепторными атомами Л“„ и равный ему положительный заряд -е^Ь на
8.7 Т КОР ИЯ pH- ПЕРЕ ХОЛЛ
415
гс-стороне (при 0 аг Ь), созданный ионизованными донорными атома-
ми Л)+, причём чти заряды равны друг другу.
Далее, со гл ае но условию непрерывности электрического потенциала
^(дс) при г = 0 имеем соотношение
= V
Используя теперь условие = ЛГрЬа исключим с его помощью из
приведённого соотношения либо Ь, либо а. Тогда получим следующие фор-
мулы для границ обеднённого слоя:
С I
—----— j ' а а -+-
2fC£ArD
2 т,г т.,г
—— а = V - ув1
2с0£
е
2£0сЛ'4
N^b2 = V - К,
а потому
. /2. exV3 Луа
1/2 / . X 1/2
гтг I/ \ 1/2 ( 2^7f|c \ । А I) |
" ^Лл(ЛгА + ЛЪ))
. /тт г 11/2 /2gpg VZ2 (NH .г
6 = (V-M' I^ + AdI
> ч 1/2 / , \ !/2
- tv - v )1/2 (f------------—_______j
d к е ) {xiANa + ND)J
К лк видим, границы л и Ь обеднённого слоя в упрощенной теории
зависят от приложенного к полупроводнику с ;wi-переходом виеитпего па*
пряжения к;Е. При увеличении прямого папряжегптя они сужаются, при уве-
П11СНИИ обратного на и ряжения — расширяются, как что по казано на при-
водимых рисунках.
Полный заряд (J. приходящийся на единицу площади поперечного се-
че ПИЯ обеднённого СЛОЯ, МОЖНО ВЫЧИСЛИТЬ ПО формуле
Q — Сх\тд« = tjVjjb.
+16
ГлаваS
Так как д к 6 зависят от приложенного напряже-
ния 1л ч то гд/злг) Q mo.Twce от даао jwwcwffl, так что
так называемая злетст^оёкияостья
единицы площади поперечного сечения полупровод-
ника с рп-переходом равна
с = = -еЛ'4— =
f <?й)£ А 1/2 / NaN& \ 1 _ gog
\ 2 / \Агл + ЛЪ ) (у _ Vu)lj2 а + &
прямое
д + Ь=(У-Гц)1/2
Действительно,
1
№+АЪ)1/2>
причём
(Ад + Агр)^а_
следовательно,
С’=^-.
а + ь
Как видим, электроёмкость рт^перехода летняейно зависит от 1'\. Это
Свойство персы ОНЕГОЙ Электроемкости П0Лу1]р0ВОДНИКОВ1ЛХ ДИОДОВ с рт1-пс-
реходами позволило использовать их в качестве полупроводниковых пара-
метрических СВЧ-усилителей.
8.8_ Транзистор с рпр-переходом
Полупроводник с рп’ПСрсходом называется лолул/?оео£)ди.кияы.и йио-
он имеет такую же вольт-амперную характеристику как ламповый
диод (двухэлектродная электронная лампа). Полупроводник с двумя рп-пе-
реходзми. называемый по своей иольт-ампертзон характери-
стике подобен ламповому триоду (трёхэлектрОДной электронной лампе).
Таким образом, после изобретения полупроводниковых диодов и тран-
зисторов стало возможным в радиоприборах заменять электронные лам-
пы на эти малогабаритные полупроводниковые устройства Так появилась
(от англ, solid state electronics).
N.S. ТРАНЗИСТОР С рпр-11Е РЕХОДОМ
417
Вскоре оказалось, однако, что и всю радиосхему на полупроводни-
ковых приборах лучше изготавливать в виде одного единого полупровод-
никового кристалла. Так появились сначала «интегральные схемы», затем
«сверхбольшие интегральные схемы» и, наконец, «процессоры».
Так называемый р гар-транзистор,
который мы рассмотрим, представляет
собой полупроводник с двумя близко
расположенными друг к другу ^-пе-
реходами, созданными внутри единого
кристалла, как показано на рисунке. Та-
ким образом, jjпр-шралswemop состоит
из двух ^крайних» р-обпаетей и «цен-
тральной» п-сбласти, при этом на левый рп-псреход накладывается мряиое
напряжение Vin а па правый рл-переход напряжение Vg. Левая
^-область называется [фапая р-областъ —
Центральная область называется
На рисунке указаны произвольно выбранные направления эмиттерно-
го, коллекторного и базового электрических токов При выбранных направ-
лениях этих токов имеем соотношение
А? +
На рисунке показана схема включения рп ^транзистора в качестве
усЕШЕМдоя ляшрюшии. Характерные значсЕшя и доходцлдо сопро-
тивлений равны = 50 Ом и /?иш = КИЮ Ом, а приложенные к левому
и правому ртг-переходам напряжения равны Ц = 0,5 В и Уд = 9 В.
Небольшая часть дырок, постоянно инжектируемых эмиттером в базу,
движется через нее, и часть их рекомбинирует в базе с электронами. Таким
образом, выполняется неравенство Ток базы /д с принятым на
рисунке направлением для него должен быть отрицательным, так как он
поставляет в базу электроны, нужные для рекомбинации дырок
Хотя токи и Тс почти равны друг другу, и мы нс имеем усилиями
ИО тояу ПО МЫ получаем большое НО ЛГОЩНОСТЯИ
4IM
ГлаваS
гсошц поскольку выходное сопротивление во много раз больше вход-
ного сопротивления ДрХ.
В рассматриваемом лдещнослти.» эмиттерный ток Jjj оказы-
вает а токи коллектора и базы /с и Дв являются
отклиюши.
Можно, однако, рассмотреть как ток базы //j, как #ынужбд-
WUfEd JeHCfflrfiWCj а ток коллектора /<_-> К^К ВЫХОДНОЙ TOKd ИЛИ ОЯ1КШК. IJpn
этом питать базу будет слабый ток, а существенно усиленный ток будет
выходить с коллекторного конца. Будем иметь тогда «усилитель лдеодд.
Объясним действие рпр-транзисторЗн используемого в качестве усили-
теля лпзи/пястн, включённого так, как показано па рисунке, приведённом
выше. Левый (эмиггсрный) /ш-нерсход бтперт Ток в левой от него р-об-
ласти, называемой об-тлстьи зшшнмери, переносится потоком основных
носителей тока в этой области — дырками. Пройдя обеднённый слой левс-
го jm-переходгц дырки попадают в n-область, называемую яйтис/нью блзы,
которая расположена между левым и правым рт-переходамн на рисунке.
В базе дырки являются неосновными носителями. При диффузии че-
рез базу, большая их часть попадает на правый (кйывюялрныи) /т-псреход,
который заперт. Под действием напряжения, приложенного кэтомурп-пе-
рехпду, дырки бСЕПрСГГЯТСТВСПЕЮ продиффуидируют через ЕГО обсДПСЕЕНЫП
слой и попадут в его p-область, называемую где они
оказываются снова основными носителями тока.
Рассчитаем теперь электрические токи в нашем ртранзисторе, для
чего пайдём концентрацию избыточных дырокв области базы.
При этом нви? шыршгл базы ш (ОТ lihjii. width — ширина)
.ичагу (Нины дырок ip в лейг нр.иишш былыиг Ширин
обеднённых слоёв обеих рп-лв/дехейес.
Для избыточной концентрации ды-
рок л области базы мы имеем диффЕрепциалъ-
р ное уравнение
в котором ip = ^/ОрТре*. Общее решение ПО-
го дифференциального уравнения имее т вид
рИЯЁ(х) = Де +
где А В - копстиеггье, которые следует определить 113 фЯИИЧНЫХ условий.
N.S. ТРАНЗИСТОР С рпр-НЕ РЕХОДОМ
419
В качестве этих граничных условий зададим значения избыточной кон-
центрации дырок на правом крас (при я = b.Mll) левого рт- перехода
и на леком крас (при т = w — hufJ правею jm-псрехада. Так как b ш+
где и? — ширина базы, то имеем следующие граничные условия, непосред-
ственно вытекающие из «основных законов рп-перехода»:
Рюб(О) = pn (e, V1/UT 1),
Ptass(w) - JV I e-' ''j/^Т _ p o< -prl;
предполагаем, что eV; --?> ij;T.
Найдём из этих двух граничных условий значения констант А и В.
Для пик имеем систему уравнений
Г л + в = pTJ, (erVv^T _ 1}.
I Ае-1^ + = -pTJ.
Умножим первое уравнение на ew/Lp, а второе на - 1 и сложим Тогда
выпадут слагаемые с В в левой части, и мы получим соотношение
Л ^ew/£f - e_"/L’) =pnet“/2'1’ (е*ч,|*г- 1) +jv,
ИЛИ
2 eh(w/Zp) А = рТ1 - 1) + Рл.
Умножим первое уравнение на С ш^£р, а второе на -1 и сложим. Тогда
слагаемые с Д выпадут, и мы получим соотношение
В = Pn c-W/£„ (ее1/,ДБТ - + ртм
-2 sbfw/Lp) а = (eeV^T - 1) +pn.
Из этих формул находим константы Л и В Подставляя их в формулу
для приходим к формуле
Риэб(^) — Z—ГТ—7т—Г
2 eh(w/ip)
X < —т/^Р f __ 1 j _|_ g—я/tp_
С - w/£ Р+^7 Lp
c<:vL/tbT
1 ] -
420
ГлаваS
Объединяя экспонента в гиперболические синусы, отсюда приходим
к следующей окончательной формуле для избыточной концентрации дырок
рьвй(зг) в области базы:
рн
sh(w/Lp)
Йнб(^) —
r’W’-i) gh«^z_ahjL
/ bp Ьр
С помощью этой формулы легко рассчитать эмиттерный и коллектор-
ный токи. Так как в базе электрический ток переносится дырками, то имеем
для него соотношение
г J' l _ п с
/рх(зг) — - S
учитывающее, что электрического поля в базе нет, из которого получим,
что
, "'У» , (e‘w-1)Vs ♦*f
Лр sh(w/£p) iy /Др Lp
Э-1|ылглг.фиыи той 1К, очевидно, райе:г дырочному юку /pj(-i) при х =
= (). Поэтому
1б = /РИ0) =
J Ze^'./Abr _ ] \ ch f JL
Lpsh(ui/lp) I \ / \ЬР
Аоадоклгорньш /с рзвеп дырочному току /рй (т) при .?: = «.- По-
этому
1с = Iplr.(w) =
eDp Spn
/Jjfsh(Tx?//Jr)
e₽Vi/^T _ ! +сЬ
Используем теперь условие, что ширина базы много меньше днффузн-
оен сой длины, г. с. что u1 ipi или w/Lp 4С 1- Предположим, кроме того,
что еЦ Э> т. е. что efii | 1. Кроме того, учтем, что при малых я
справедливы приближенные формулы
sh;r =
ЕЭ
6
— X
т2
ch я — 1 + =у.
H.S. ТРАНЗИСТОР С рпр-11Е РЕХОДОМ
42]
Следовательно,
Используя указанные формулы, получаем приближенные выражения
для эмиттерного и коллекторного токов:
^PSpn ^VlfkfTLp I . Uia
_ eDpSpn f 1 _ u? ]
lp w v 6Li)'
а следовательно, при кодим к cite дующей формуле для бпзы:
/й = /с - /д =
eD^Sy» Vi ^.tT
w c
cDpSpn ^VtfktT
ePpSp^w ^vy/k^T _ eSp^w ^v^kiT
2L= “ 1^7
Таким образом, имеем окончательную формулу для даолгд frijw:
cSp„w
/я = —27—
* 'рас
при нашем выборе направлений токов он Ток базы отри-
цательным потому, что он поставляет электроны в область базы, которые
нужны для актов рскомбиЕгаигж движущикся через базу дырок.
422
ГлаваS
Ток базы можно рассчитать другим способом Очевидно„ он равен чис-
лу дырок Ари, прсрс комбинировавших в базе н единицу времени во всей
области базы, умноженному на —е. Так как число прорскомбинирсвавших
дырок в единице объёма базы в единицу времени равно
РиэО
Трсл '
то число дырокт прорекомби ннроваитиих в базе в единицу времени, дается
интегралом
dir 1W
Д',,, = 5 / i / * eV,!h:T (' - г)
r J *ре* \ /
С О
eV]
если считать, что — « 1 и что —— 1; В ЭТОМ случае
Ьр Кь *
Р|Иб(ж) = р» ^'v'JkLT (i - в)
Таким образом, получаем, что
,V _ JL .Ti
J 'рек — ?- Fn v
ГрСК
Kyj/ktT.
2трт1С 6
" <2 Л'рск •
убеждаемся, что действительно
Важным техЕП'чсскнм параметром, характеризующим транзистор, яв-
ляется »ко:»ф([Еицисн'[' усиления ио току эммитсра»:
который связывает изменение выходного тока (коллектора) с вызвавшим его
изменением входного тока (эмиттера). Для этого коэффициента усиления
получаем приближённую формулу
1 + -!^—
3L^
при ТУ с LpP
ДО1ЮЛНЕНИК I
423
Согласно этой формуле, если, например, = 0.2, то о = 0.98, т. е.
98 % дырок, инжектируемых в базу эмиттером, поступает па коллектор. Для
существующих транзисторов коэффициент а ишеяяетея от 0>95 до (}.99-эь
а ширина базы имеет порядок 500 А (так что почти все дырки проходят
через базу).
Коэффициент усиления мощности эмиттерного тока для приведённых
выше характерных значений П арам етрив рассматриваемой схемы равен
^С^ВЫК
= (0,93)“ в = 19,2.
□ U
Если транзистор используется как усилитель тока, то входным питаю-
щим базу будет не ток эммитера, а тик базы, выходным будет ток коллек-
тора. В этом случае полезно рассмотреть «коэффициент усиления по тику
базы»:
/? = — = _Ie_ - q
' “ - /я “ * -1 " V? '
Из этой формулы получаем, что если -ш/£р = 0.2, то коэффициент
усиления /? = 50.
Физический механизм процесса, характеризуемого коэффициентом
усиления Й, состоит в следующем. Электрон, пришедшим в базу из источ-
ника тока, питающего базу, немного понизит барьер в левом обедненном
слое (на границе «эмиттер-база») и тем самым облегчит инжекцию дырок
из эмиттера в базу. Это приведет в рассматриваемом нами выше примере
к появлению 49 дополнительных дырок, которые начнут диффундировать
через базу, продираясь к коллектору и стремясь попасть в область правого
обеднённого слоя (па границе «база-коллектор»), тем самым увеличивая
ток /с- Но 50-я дырка испытает рекомбинацию с рассматриваемым элек-
троном н уничтожит его; тем самым восстановится начальное значение по-
те елщала на левом обеднённом слое.
В результате из-за поступления на базу одного электрона на коллектор
попадёт 49 дырок> т.е. действительно /? = -50.
Дополнение 1 к гл. 8
Графическое изображение рп-лерекода диаграммой
с искривлёнными энергетическими эонами
Такое графическое изображение ри-псрсхода широко используется.
Разъясним его. При Этом с самого начала надо корозпо усвоить, что речь
424
ГлаваS
идет об очень абстрактном объекте — «энергетической диаграмме», не име-
ющей нс посредстве] пюгю отношения к физическому пространству, хотя в сё
графическом изображен ни и используется горизонтальная ось. вдоль кото-
рой откладывается расстояние от плоскости непосредственного контакта
рн-перехода, считая, что для этой плоскости .г = 0.
Суть графического способа изображения «искривлённых энергетиче-
ских зон» состоит в следующем.
Рассмотрим сначала отдельно p-область и л-область полупроводника
с рп-переходом.
Для р-области. в которой электрический потенциал имеет постоянное
нулевое значение. тождественно равное нулю, = 0п имеем следующее
стационарное уравнение Шредингера
ft2 <рф
2174 i/j?"
+ I/ (я) = £¥’
(р-область),
в котором £7(а?) обозначает атомный периодический потенциал (действую-
щее на электрон поле атомных остовов кристаллической решётки).
Для п-областн, в которой электрический потенциал имеет тоже посто-
янное, но ненулевое значение, равное у? = V — 14; имеем стационарное
уравнение Шредингера
+ "e(v " K)1 v’ “
(fi-область),
так как электрическая потенциальная энергия электрона в д-области равна
е(У 14), со знаком минус, так что приведенное уравнение Шредингера
можно представить в виде
j-2
- ------г - <7(jc)i/’ = [Е 4- е(И - 14)]^ (п-область),
2m
Обозначим сумму В 4 ч(1/ — 14) буквой 2?г, тогда получим в точно-
сти такое же уравнение Шредингера, как для ^области. Таким образом,
энергетические спектры энергии £? д.тя рч>блдевш и энергш< £' йдя п-об-
ладош mcwcdecmeewuw, ио энергетический спектр S е тобядстм сбемнут
еннд на ееяычину e(V — 14) п° л- энердалическял1у слсктру Е
р-ойтлсти.
В области вблизи плоскости непосредственного контакта рп-перехода
я = 0 можно считать, что ь плоскости .т полупроволника сдвиг энерге-
тического спектра для произвольною макроскопически бесконечно малого
Дополнение l
42$
слоя полупроводника, расположенного от я до + dz, совершается вниз
на величину — VrQ , где — Электрический потенциал в области
рта-перисода+ как показано на рисунке.
Гак, разумно предположить, если сделать допущение, что характерная
длина fv изменения макроскопического потенциала ^?(z) много больше ха-
рактерной длины fjy изменения потенциала (7(я), т.е. что ^ит-
зона
провод II |
валсз гт. V-
iotja ---------------—
Г п
Таким образом, имеем картину «искривленных энергетических зон»
для рп-переходас приложенным постоянным напряжением К?» показанную
на рисунках ниже.
Поясним теперь, тал- хьгл/ичлжвд м
жж/мвлёышх зяя. Для этого учтем, что при термодинамическом
равионеенн не химический, а так называемый «электрохимический потен-
циал» jj — д — мр Электронов одинаков в различных точках полупроводника
с рн-лереходом (здесь е = |s|)h те. что
= CODSt,
где const не зависит иг i.
Это так называемое «условие электрохимическою равновесия» спра-
ведливо для рассматриваемого сейчас полупроводника с рп-переходом
с приложенным напряжением Vn. Таким образом, бля
рт1-Пе/?ЕХО^Д Vi = 0) « С Ut'KpB/fif.TfUJfW’.WU 5ОНЛ-
.ijw уровень tfydem долгой
лилиейн причём в p-области он будет совпадать с уровнем химического по-
тенциала акцепторного полупроводника, а и га-областн — со сдвинутым
вниз па величину eV уровнем химического потенциала донорного полу-
проводника.
Для термодинамически бтпертого (Vfl > 0) или запер-
того (Уд < Hi рп-перехода лбдовдциоз 1? не бу dem ло-
Сг.?л yjww?Hh бубет wcKpHewew.
426
ГлаваS
На приведённых энергетических диаграммах мы ле изобразили суже-
ние обеднённого слоя, обязанное приложенному прямому напряжению
К > ()> и его расширение при наложенном обратном напряжении И+ < 0.
Дополнение 2 к гл> 8
Контакт полупроводник-металл
Рассмотрим теперь контакты полупроводников п- и р-тинои с металла^
мл. Такие контакты бывают двух видов: с сбычЕюй омической вольт-ампср-
ной характеристикой и с йыл/гяшялицЁЫ вольт-амперной характеристикой.
О выпрямляющих свойствах контактов «металл - полу проводник» извест-
но давно, еще с тех пор, как Ф. Браун в 1874 г. открыл это свойство для
контакта «медь-сульфид железа». К сожалению, механизм яыл/м.иляюы^-
гл Действия этих контактов ещё окончательно нс выяснен до сих пор.
Гак что задолго до эры современной твёрдотельной электроники кон-
такты «металл-полупроводник» уже использовались (и теперь широко ис-
пользуются) в выпрямителях переменного электрического тока, R основном
это выпрямители Ета закиси меди Cn-jO и Era селене Se. Также эти ко л так-
Дополнение 2
427
ты использовались и в первые примитивных так называемых «детекторных
ради оприе м п и как ».
Свойства контакта «металл-полупроводник» (п- или p-типа), когда ра-
бота выхода для металла не равна работе выхода для полупроводника , от-
личи ются от свойств контакта между двумя металлами с различными рабо-
тами выхода и контакта «металл-вакуум».
В 1938-1939 гг. Шоттки. Моттом и независимо Б. Давыдовым была
предложена кванто во- механическая теория контакта « металл-по лу про вод-
ник». В ней выпрямляющее действие контакта объясняется тем, что элек-
троны переносятся над имеющимся у такого контакта потенциальным ба-
рьером посредством дрейфа и диффузии, но ггс посредством эффекта квап-
гово механического туннелирования. Такой потенциальный барьер для чдге-
трогзов называется «барьером Шоттки».
Реальная вольт-амперная характеристика конгодкетд
показана на приводимом самом левом рисунке. На центральном рисунке
показана иймяизирлалиняя вольт-амперная характеристика выпрямляюще-
го контакта, с полным или почти полным отсутствием тока в «Опертом»
контакте (при V < 0) и обычным омическим током в «отпертом» контакте
(при V > С). На самом правом рисунке показа па тоже идймизиртчвнмал
вольт-амперная характеристика так называемого Etc
обладающего выпрямляющим действием.
На этих рисунках f — сила электрического тока, текущего через кон-
такт, V — напряжение, приложенное к контакту. При «прямом» напряжении
(V > 0) через выпрямляющий контакт тик 7 течёт, при «обратном» напря-
жении (V < 0) через него течёт практически йулеяол ток 71 как на реальной
вольт-амперной характеристике выпрямляющего контакта, показанной вы-
ше на самом левом рисупке.
Тгррия Шоттки
Рассмотрим контакт «металл-полупроводник» с полупроводником
n-типа и предположим, что работа выхода Апг полупроводника меньше,
42Й
ГлаваS
чем работа выхода Ли металла. Работу выхода для полупроводника
Зависящую от типа по л у про воде] ика и степени легирования его примесью,
определим как/мкность энергий электрона на иак>т.ингли уродяе д лусетолтс
(йне нйлулрлеб^яикй) п нет даовле Ферий Ер ллдулрой^нн/сд. Работа выхо-
да Лм металла — это /вдзность энергий электрона на вакуумнаи уроене (вне
jwemawi) и наур^не Ферлгй Ер лдетлдоя- Предположим, что Ли > Лпл.
Диаграммы электронных энергетических уровней электрона металла
и электрона полупроводника, ещё нс приведенных в контакт друг с дру-
гом, показаны на левом рисунке- На правом рисунка показаегы диаграммы
злекзронных энергетических уровней дм металла и искривлённых элек-
тронных энергетических зон для полупроводника, приведённых в контакт
и пришедших к равновесию.
Обратите внимание, что нулевые уровни отсчёта энергий па энергети-
ческих диаграммах металла н полупроводника различны.
На правом рисунке показана диаграмма искривленных энергетических
зон полупроводника, приведённого в контакт с металлом, в различных се-
чениях л, отсчитанных от плоскости непосредственного контакта его с ме-
таллом (я — 0). Электронные энергетические уровни электрона п полупро-
воднике ыелрштлеиы. При установлении контакта они сдвигаются вниз до
тех пор, пока уровни Ферми Ер у металла и у полупроводника нс срав-
няются Тогда будет выполнено равенство электрохимических потенциалов
металла и полупроводника.
Для контакта «метазы-полупроводник» в отличен от контакта «ме-
талл-вакуум», сила изображения существенно меньше, гак как теперь она
е2 - ё2
равна --------а нс ----------- где г — относительная диэлектрическая
16я-££()ЗГ 16л-еоЯГ
Дополнение 2
429
постоянная полупроводника, равная< = 12, например, для кремния Si, т.е.
имеет порядок I 0. Поэтому силой изображения теперь п теории Шоттки
контакта «металл - полупроводник» пренебрегаетоя.
При приведении в контакт металла и рассматриваемого полупроводни-
ка п-типа полупроводник приобретает положительный электрический по-
тенциал по отношению к металлу, так как, по предположению, работа вы-
хода электрона из полупроводника .4IJU меньше, чем работа выхода его на
металла Ам, вследствие чего при установлении равновесия часть электро-
нов перетечёт из полупроводника в металл, и в полупроводнике в тонком
призраничном слое около граничной плоскости я = 0 появится электриче-
ское поле, которое будет препятствовать дальнейшему перетеканию Элек-
тронов из полупроводника в металл, показанное на правом приведённом
выше рисунке и направленное справа налево.
Недостаток отрицательного электрического заряда в полупроводнике,
возникший из-за перетекания из него электронов н металл, будет наблю-
даться в очень тонком слое 0 < зг полупроводника вблизи его гра-
ничной поверхности с металлом я = 0, т.е. в области «обеднённого слоя»,
обычно ЙГс = 1С“& м.
R металле аналогичного объёмной? заряда не образуется, так как ме-
талл обладает намного большей электропроводностью, чем полупроводник,
и поэтому, согласно электростатике, при равновесии металла с полупро-
водником весь электрический заряд металла выйдет из него на его поверх-
ность.
При наличии электрического потенциала в обеднённом слое в по-
лупроводнике [jpn 0 ЗГ 10, ОН будег увслйчнвагься При увеличении Z,
принимать нулевое значение при л — 0 и выходить ла положительное по-
стоянное значение при д? При этом вся диаграмма электронных
энергетически к уровней полупроводника опустится постепенно ппиз на ве-
личину где е — абсолютное значение заряда электрона, так что уровень
Ферми Ер полупроводника станет равным уровню Ферми Ер металла, как
эго показано на том же рисунке.
Обратите внимание, что нулевые уровни отсчёта энергий для энерге-
тических диаграмм для металла и .тля полупроводника не совпадают. Если
бы они совпадали, то нужно было бы говорить на о совпадении уровнен
энергий Ферми Ер, а о совпадении уровней электрохимического потенци-
ала тр = д - у металла и у полупроводника.
Энергия электрона в сечении я обеднённого слоя с потенциалом
равна — гак как заряд электрона отрицательный, е — абсолютное
значение заряда электрона. Высота потенциального барьера для электронов
(7&ар = е^(0) на самой контактной плоскости д? = 0 «металл-полу провод-
+30
ГлаваS
ник»., таким образом, равна
^6u[i = -^ы — ^ПП — {^е: ) 1
где Б<. — потенциальная энергия электрона на «дне» зоны проводимости
полупроводника (равная энергии сто ионизации, т.с. энергии, необходимой
для отрыва электрона ш полупроводника).
Шоттки в своей теории контакта «металл-полупроводник» предполо-
жил, что в рассматриваемом нами сейчас контакте при равновесии вбли-
зи плоскости ж = 0 непосредственного контакта металла и полупровод-
ника в области 0 х образуется «обедненный слой», цллпосмыи
cftrfcMtahru от атектролае, т.с что справедливо приближение гак называ-
емого «полного обеднения». Ионизованные донорные атомы в этом слое
О х Хд создадут пространственно однородный положительный элек-
трический заряд объёмной платности /j = eJVp, где Агд — концентрация
ДйНОрНЫХ примесей В полупроводник^ КСПЮрыЙ КИК рЙЗ И СОЗДАСТ ЭЛСК-
тричсскос поле, направленное справа налево, показанное на приведённом
выше рисунке.
В пределах «обеднённого слоя» 0 я электрическим потенциал
удовлетворяет уравнению Пуассона:
_ ejVjj
где £ — относительная диэлектрическая постоянная полупроводника, обыч-
ное — I 0. Интегрируя это уравнение, получим
tix
= --ёё^-
константу интегрирования надо выбрать из условия
Л?
— = о при я = тп.
аж
т.с. из требования, чтобы электрическое поле £г = 0 при я = (в глу-
бине полупроводника ла правой границе обеднённого сдоя при ;г iq)
отсутствовало. Интегрируя еще раз, получим
(ж2 - 2 я 5Со) = ^0 - S—т(ж- - Sto)2 при 0 С я С я?о,
лсОс
при Я > Яо;
Дополнение 2
43]
здесь — значение электрического потенциала в объеме полупроводника
за обеднённым Слоем. Считаем, что при .г — выполнено условии =
= (/70, так что если известно, то толщину обеднённого слоя можно найти
по формуле
Энергия электрона в сечении т обеднённого слоя 0 О Ой рав-
на так как заряд электрона отрицательный и равен -е, так что
энергия электрона, взятая со знаком минус, равна E7(jc) =
Полагая t = 12, = (We = 0,5 В, АЪ = 101К см-3 = 10*4 м-3
(£й = 0,385 Ф/м„ е = 1.602 10"ig Кл), получим zL> “ 3 1(Г6 м
Обвис ним ещё раз, почему при равновесии энергетическую диаграмму
пол у проводи] 1ка на приведённом выше рисунке надо сдвигать вниз на вели-
чину так чтобы уровни Ферми АУ полупроводника и металла совпали.
При равновесии полу про водника в контакте с металлом должны быть
равны их ^электрохимические потенциалы»: т; = д - е^>, где д — химиче-
ский потенциал, — электрический потенциал, е — абсолютная величина
заряда электрона. При рассматриваемой нами сейчас нулевой температуре
7—0 химический лота пенал равен энергии Ферми: р — Ер. Для металла
/7 = 0р для шшу проводника I/? = I/7Q, поэтому
£j' jT Л JF “С -j-l'l -
Таким образом, сс-тгг лгы сдютлы.и лл рисунке всю энержинческую thm-
граиму аниз йд в&тнчнну mo ypos/iw энергии Фе/дий Ег
л^етодзд w г/швмяюдося.
прямее
наиряжепис
обратное
напряжение
Приложим теперь к рассматриваемому контакту металл-полупровод-
ник постоянное R]ic[][i!cc згапряжсЕшс V. Тогда в зависимости от его пОДяр-
4-32
J'Л Л ВЛ S
нести потенциальная энергия электрона в глубине полупроводника либо
увеличится, либо уменьшится.
Увеличение произойдёт при л/млгсы* («отпирающем») напряжении
V >0, г.е. когда плюс источника напряжения будет присоединён к металлу,
а минус — к полупроводнику. Это приведёт к тому, что вся энергетическая
диаграмма полупроводника поднимется вверх из отрицательную величину
— с У, г. с. Опустится вниз на величину е V, как ЭТО показано на приведённом
рисунке.
Уровни энергий Ферми Ер в металле и в полупроводнике теперь раз-
личаются. Все электроны с энергией выше Лн — .4цП — eV пере иду г из
полупроводника в металл. На их место придут электроны из источника
напряжения, и, таким образом, через контакт будет течь постоянный элек-
трический ток.
При приложении к мяпжгу («запирающего») напряжения
V < 0 энергетическая диаграмма полупроводника опустится вниз па вели-
чину e|V|t е — абсолютная величина заряда электрона.
Рассматриваемый контакт «металл-полупроводник», таким образом,
обладает ^ынряшляюи^м действием.
вал.
юна
л *1111
юна
провод.
ранпопесне
Рассмотрим теперь случай, когда работа выхода Лм электрона ИЗ ме-
таллу мсе]Line, чем работа выхода ЛПГ1 Электрона из полупроводника^ как
это но казане на приведённом рисунке.
Теперь при установлении равновесия электроны перетекут нс из по-
лупроводником в металл, а из металла в полупроводник, и потенциальный
барьер вблизи поверхности кон такта металла и полупроводника ие образу-
йся. При этим ток через контакт нс будет зависеть ит знака прилаженного
напряжения, и переход не будет обладать выпрямляющим действием.
Таким образом, имеем четыре возможных типа контактов «металл -
полупроводник» для металла с полупроводникам и- или p-типа и при
Ли > Д|и или Лм < AIJU. Некоторые эти контакты обладают яыпрялг.уя-
ющилг действием.
Дополнение 2
433
Как видим, согласно изложенной теории Шоттки контакта «металл-
ПОЛупрОВОДЕ [И К» С^ЙСтвД ЛрНЛН7ХПТа tfAE^-
ffliojbT-HCbTynfGffodfJWKJ* сальдо завысит cm тлпд полупроводника w количе-
ства легирую» feu п/и/.uecw d лем, d muK.wce w от соотлошвяш лгсжду рабо-
тали выхода атолла и полупроводника.
7ео/жя йардиня
Изложенная теория Шоттки контакта «металл-полупроводник» нс со-
гласуется с экспериментом: л/кшиичвски любые коятаюиы .мема?.-?-иоду-
яроводлшк обладают вьтря^дяюи/и.чи свойствами независимо от относи-
тельных значений работ выхода .металла и полупроводника.
Дело в том, что чистые соприкасающиеся поверхности могут быть по-
крыты слоями окислов, и, кроме того, кристаллические структуры полу-
проводника и металла могут быть неидеальными.
Бардин обратил внимание па то, что
в теории Шапки не учитываются так на-
зываемые тамбовские «поверхностные со-
стояния». которые получаются при стро-
гом квантовом рассмотрении, В разобранной
в гл. 7 одномерной модели кристаллической
решётки крайняя ступенька кривой потен-
циальной энергии электрона отличается от
вакуум мегалл
остальных, как это проиллюстрировано па приводимом рисунке.
Из-за наличия поверхностных уровнен ла поверхности лушеталла
лралтх1Чески всегда а.мгетсн потенциальны а барьер. ирстЕятсотвтюший яы-
ходу ялеюпромм и? него, так как «поверхностные состояния» способны
удерживать электроны, энергетические уровни
прсщсЕЕпсй зоне попу проводника.
Рассмотрим^ например, полупроводник
n-тнпа, в котором свободные элекгроны из зо-
лы проводимости вблизи поверхности полу-
проводника могут запять поверхностные уров-
ни и перестать быть свободными. Оставшийся
от них нес компенсированный положительный
электрический заряд ионов донорной примеси
вблизи поверхности полупроводника приведет
к появлению потенциального барьера Eia по-
этих состоянии лежат в эа-
верхности полупроводника. Вследствие этого энергетические эоны вблизи
поверхности изогнутся, как показано на рисунке. Как видим, потенцналь-
434
ГлаваS
ный барьер существует до того, как мы приведём рассматриваемый полу-
проводник е контакт с металлом.
Посмотрим, однако, что произойдёт после того, как полупроводник
и металл придут в контакт друг с другом.
Если металл имеет меньшую работу выхода, чем полупроводник (т.е.
если согласно теории Шоттки контакт «металл полупроводник» ire облада-
ет выпрямляющим действием), Электроны должны будут перемещаться из
металла в полупроводник, пока не установится равновесие. Эти электроны
заполнят «поверхностные уровни» независимо от высоты их потенциаль-
ного барьера. Потенциальный барьер в рассматриваемом полупроводнике,
таким образом, существовать будет, и контдат .петлял-
лолулров&йинк выпрдлмлющилл
На практике, помимо рассмотренных квантово-механических «там-
мовских уровней», имеются «поверхностные дефекты» кристаллической
решётки, тоже способные удерживать электроны.
С определенностью можно утверждать, что 1гыл/?лп.?я-
ется itf-KwvumgflbHO
П ранда, существуют ещё «омические контакты», создание которых ос-
новано ня сплошной эмпирике, хотя они и необходимы для создания любо-
го полупроводникового прибора.
Для создания омического контакта либо берут некоторый сплав ме-
таллов (например, In, Au. Sn) и заставляют его диффундировать в металл
и п полупроводник и создавать плавный переходной слой, либо между ме-
таллом н полупроводником создают область сильно петрова иною лолу-
jjpoводника с конце»грацией примеси порядка 1013 см 1 (их называют п1 -
и р1 -областями).
Аонт д kw .и ст для - эя ектрик - полу проводи г ос
Рассмотрим теперь МДП-контакты «металл-д из л склрик-полу провод-
ник». Полупроводники с МДП-контакгами оказались очень удобными объ-
ектами для изучения свойств поверхностен, но они также широко ис-
пользуются в различных полу проводниковых приборах. Когда диэлектрик
в МДП-кш такте является ок и слом (важнейший случай — это коша кг «ме-
талл-SiOj-Si^X говорят о МОП-контдктдх.
Прибор с МДП-коптдктом в качестве управляемой напряжением
емкости был предложен еще в 1959 г. В 1970 г. па основе МДП-коптак-
тов был разработан так называемый ПЗС’П/?ибор («прибор с зарядовой свя-
зью»\ который представляет собой матрицу большого числа очень близко
Дополнение 2
435
расположенных друг к другу на поверхности кристалла МДП-конденсэто-
ров. При соответствующей последователь]юсти тактовых импульсов, пода-
ваемых на электроды МД I I-кон дснсагторов. в ПЗС-приборе могут контроли-
руемым образом перемещаться вдоль матрицы так называемые «зарядовые
пакеты». Используя их? можно осуществить хранение сигналов с нужными
данными, их обработку и логические операции с ними, приём и передачу
изображений н т. д.
Приложим к М ДИ-переходу «прямое» или «обратное» напряжение Уд.
Так как диэлектрик не проводит электрического тока, то никакою тока че-
рез этот переход течь не будет. Для определенности будем считать, что
полупроводник является полупроводником г?-типа.
В идеальном МД11-переходе считается, что: 1) в отсутствие приложен-
ного напряжения V<i = 0 энергетические зоны полупроводника не изогнуты;
2) при любом («прямом» или «обратном») приложенном напряжении Vn / О
в объеме полупроводника возникает электрический заряд и появляется ран-
ный ему электрический заряд на поверхности металла; 3) при постоянном
напряжении отсутствует перенос носителей тока через диэлектрик, т. е.
сопротивление диэлектрика считается бесконечным.
Сначала рассмотрим случаи «прямою» напряжения Vrn {когда металл
соединён с положительным полюсом источника напряжения), проиллю-
стрированный на приводимом рисунке. Хотя электрический ток через пе-
реход не течёт, электроны всё же перетекают из глубины полу проводника
к его поверхности с диэлектриком и накапливаются вблизи неё в результа-
те действия электрического поля £т появляющеюся л полупроводнике при
наложении на рассматриваемый МД1 [-переход напряжения.
Это электрическое поле направлено от диэлектрика к полупроводнику
ирн рассматриваемом «прямом» приложенном напряжении, как показано
на приведённом выше рисунке. Распределение концентрации п электронов
в полупроводнике вблизи его поверхности с диэлектриком показано на ле-
вом рисунке, на котором iTpamt обозначает равновесную концентрацию элек-
тронов в объёме рассматриваемою полупроводника л-типа, т — расстояние
вглубь полупроводника от сю границы с диэлектриком.
436
ГлаваS
Такое перераспределение электронов сопровождается изменением пер-
воначально приложенного электрического поля, вызванного «прямым» на-
пряжением. Из-за появляющегося зрадиента концентрации электронов око-
ло границы полупроводника с диэлектриком возникает диффузионный по-
ток электронов, текущий вглубь полупроводника. В равновесных условиях
этот поток в точности компенсируется дрейфовым потоком электронов, те-
кущим ИЗ полупроводника К СЮ ПОВСрХНОС LH.
На правом рисунке показаны искривлённые зоны равновесного полу-
проводника вблизи его границы с диэлектриком. Пунктирной горизонталь-
ной прямой Ер обозначен уровень электрохимического потенциала (мы
не оговорились — Электрохимического), который при равновесии одинаков
в металле и полупроводнике. Он смещён в металле на величину eVo вверх
ст уровня Ферми металла, являющегося верхним заполненным электрона-
ми электронным уровнем в металле при нулевой температуре.
Теперь рассмотрим случай «обратного» напряжения 1п (когда металл
соединён с отрицательным полюсом источника напряжения), проиллюстри-
рованный на ниже приводимых рисунках.
Теперь при установлении равновесия электроны в полупроводнике пе-
реместятся от поверхности нол у проводника вглубь него, что приведёт к по-
явлению «обеднённой области» в полупроводнике па границе его с диэлек-
триком, подобной «обеднённой области» в рт-переходе. В этой области су-
ществуют диффузионный и дрейфовый иотоки электронов, которые при
равновесии точно компенсируют друг друга.
Электрическое поле f в этой области теперь направлено из глуби-
ны полупроводника к его поверхности. Ни правом рисунке показаны ис-
кривлённые эоны равновесного полупроводника. Пунктирной горизонталь-
ной прямой Ер обозначен уровень электрохимического потенциала, кото-
рый теперь проходит не выше, а ниже уровня Ферми металла, являющегося
верхней границей заполненных электронами электронных уровней в метал-
ле при нулевой температуре.
На рисунке показан случаи достаточно большого обратного напряже-
ния h когда в «обеднённом слое» вблизи границы полупроводника с ди-
электриком появляются дырки, приходящие из валентной зоны. При боль-
шом «обратном» напряжении уровень Ферми в иолу проводнике оказыва-
ется вблизи валентной зоны, и дырки из неё Moiyr переместиться в зону
проводимости. Таким образом, в рассматриваемом полупроводнике ц-тнпа
его поверхностный слой на границе с диэлектриком будет вести себя как
полупроводник jj-THjla. Это явление называется «инверсией».
Конечно, ешмигроде» возникает не только в полупроводника* п-тина,
но в равной мере и в полупроводниках p-типа при контакте «металл-ди-
Дополнение 2
437
МД п
электрик-полупроводник». Существуют инверсные слои р+-тнна в п-ио-
лу про водниках и п+-типа в ^-полупроводниках.
Явление «инверсии» мы рассмотрели для равновесной ситуации.
В неравновесных условиях, если мы приложим в начальный момент време-
ни i = 0 к контакту «металл-диэлектрик-полупроводник» л-типа обрат-
ное напряжение, то к некоторому моменту времени f = fj большая часть
электронов покинет «обеднённый слой» и перетечёт вглубь полупроводни-
ка. Электроны уйдут в полупроводник, а дырки сместятся к его поверхно-
сти с диэлектриком. При этом процессы рекомбинации электронов и дырок
не будут интенсивными, так как концентрации электронов и дырок малы
и их потоки разнесены в пространстве.
Когда в момент времени £ = ^ установится равновесие, дырочный
диффузионный тока направленный вшубь полупроводнику будет точно
скомпенсирован дырочным дрейфовым током, направленным к дцэлекгри-
ку. Скорости процессов генерации и рекомбинации при этом сравняются.
Время £] порядка микросекунд, а время порядка секунд и чистых
полупроводниках. Если длительность воздействий на контакт «иста л л-ди-
электрик-полупроводник» меньше времени генерации электрон-дырочных
пар, то неосновные носители нс успеют появиться, и такой режим работы
МДГЬприбора называют «режимом глубокого обеднения».
В приборах, использующих контакт «металл-диэлсктрик-полупро вод-
ник», ток течёт ле че/гез контакт, а бЭоть пачу-
с ^иэлтн/?нкй1г.
Таким образом, имеются три следую-
щих режима работы МДП-перехода: I) когда
К МДП-ПсреХОДУ С полупроводником n-J Htia
приложено «прямое» напряжение Vo; 2) ко-
гда к нему приложено достаточно большое
«обратное» напряжение Vo; 3) когда к нему
приложено не слишком большое «обратное»
напряжение Vu+cm. рисунок.
С
низкие
частоты
> /
\ । высокие
частоты
'«глубокое
____________ обедне]! иен
нря нос Vp— —- обрап।ое К
43N
ГлаваS
При первом режиме (при любом «прямом» напряжении) происходит
изгиб ii[еретических эон вниз» и поэтому в объёме полупроводника па гра-
нице его с диэлектриком концентрация основных носителей (электронов)
увеличивается; это «режим обогащения». При втором режиме (при доста-
точно большом «обратном» напряжении) энергетические зоны изгибаются
вверх и сдвигаются вниз настолько сильно, чтобы н полупроводнике вбли-
зи [раницы с диэлектриком концентрация неосновных носителей (дырок)
стала больше концентрации основных носителей (электронов); это «режим
инверсии». При третьем режиме (при не слишком большом «обратном» на-
пряжении) область полупроводника вблизи |раницы с диэлектриком обед-
няется основными носителями тока (электронами); это «режим обеднения».
Основной характеристикой полупроводника о МДП-перехода является
его «вольт-фарадная» характеристика. Опа имеет bill показанный на при-
ведённом рисунке. При «обратных» напряжениях вольт-фарадная характе-
ристика имеет различный вид irpji малых и при больших частотах.
Ладовом
В 1952 г Шокли предложил так называемый «полевой транзистора
альтернативный «транзистору с рп-переходом», который имеет подобно ва-
куумному диоду управляющий электрод. Имеются полевые транзисторы
различных типов.
Рассмотрим сейчас так называемый «полевой транзистор с управля-
ющими ртг-1гереходами», показанный на рисунке. Он представляет собой
примесный полупроводник, например полупроводник тг-тип^ к которому
присоединены два омических электрода, называемых «истоком» (от
source) и «стоком» (от йд&л drain)» причём к стоку прикладывается поло-
жительный электрический потенциал, как на приведенном рисунке. Элек-
троны двигаются от истока к стоку. У вашего транзистора имеется также
Дополнение 2
439
«управляющий электрода, на который можно подавать отрицательное на-
пряжение, тоже показалпый на рисунке, который называется «затвором» {ст
fjz/гл. gale), он представляет собой две сильно легированные p-области на
обеих сторонах полупроводника (обозначены на рисунке как р+-области).
Когда на затвор подано нулевое на пряжен]ie. электрический потенциал
и полупроводнике плавно линейно увеличивается от нулевого значения на
заземлённом истоке до некоторого положительного значения на с юкс, со-
единённом с плюсом источника напряжения. Между каждой ^-областью
затвора, находящегося при нулевом напряжении, и п-объёмом полупровод-
ника будет «обратное» напряжение, которое увеличивается но мере про-
движению к стоку. В результате «обеднённые слои» затвора оказываются
асимметричными, как по казино на приведённом выше рисунке.
Электрический ток от истока к стоку будет течь через суженное попе-
речное сечение полупроводника между двумя обеднёнными слоями затвора.
Когда па затвор подается отрицательное напряжение, и когда оно уве-
личивается, ширины обеднённых слоёв затвора тоже будут увеличиваться.
При этом электрический ток от истока к стоку должен будет течь через
более узкое сечение, а потому должен стать меньше.
Если ещё больше увеличить
отрицательное напряжение на за-
творе, то можно дойти до такого
отрицательного напряжения, при
котором оба обедненных слоя со-
мкнутся, и электрический T0K от
истовд к стоку практически пре-
кратятся, как это показано на
приводимом ниже рисунке, на ко-
тором / — токь текущий от истока к стоку - отрицательное напряже-
ние, приложенное к затвору, Ив 5 — положительное напряжение, приложен-
ное к стоку. При больших напряжениях Vos ток / выходит на насыщение
(те. перестаёт измениться), причём величина «тока насыщения» зависит от
величины приложенного к затвору отрицательного напряжения и чем
больше будет это напряжение, гем меньше будет ток насыщения, как это
проиллюстрировано на рисунке.
Зависимость тока / от напряжений Vgs и У'Ъ^ полностью аналогич-
на зависимости анодного тока вакуумной трёхэлсктродной лампы (триода)
от положительного анодного напряжения и отрицательного напряжения па
сетке.
Имеется другая разновидность «полевого транзистора». Это так на-
зываемый «транзистор с контактом металл-оксид-полупроводник», или
440
ГлаваS
«МОП-транзистор». Он состоит из перехода «металл-диэлектрик-по лу-
провпдЕшк», Снабжённого с двух сторон областями истока и стока, как по-
казано на рисунке.
запюр
,8Ю:
р-канал Р
ИСТОК СТОК
н Si
Считаем, что подложка представляет собой
полупроводник n-тнпа, а области истока и сто-
ка - полу про йод инки -типов. При нулевом на-
пряжении на затворе ток Д гекущий от ис-
тока к стоку отсутствует. При отрицательном на-
пряжении Vgs на затворе ироизойдет инверсия
области n-полу проводника, параллельной плоско*
сти затвора, и вблизи него (опа станет полупро-
водником р-гииа), и между истоком и стоком образуется так называемый
«укапал», показанный на рисунке. При этом дырки получат возможность
свободно перемещаться от истока к стоку, и от истока к стоку потечёт элск-
зрический ток /.
На приведённом рисунке изоб-
ражена ЁОЛШН-ОМЛерНйЯ
тока /. На левом рисун-
ке показана зависимость тока / от
отрицательного напряжения
между затвором и истоком, а на
нравом рисунке — зависимость от
положительного напряжения
между стоком и истоком. При этом
вместо Чёткого насыщения имеем ЛИШЬ изгибы.
Говорят, что МОП-эрянзистор, в котором проводимость обусловле-
на «инверсией», работает в «режиме обогащения». Имеются, кроме них,
МОП-транзисторы, работающие в «режиме обеднения», R них уже заранее
имеется р-капал, из которого дырки удалены положительным приложенным
к затвору напряжением.
Дополнение 3 к гл* 8
Полупроводниковые приборы
Туйнельлый йиой
При рассмотрениирл*переходз мы считали лодг/юваищ1 слабым (с к<?н-
цетпирацыей примесей порядка Ю16 см-3 и меньше). При этом уровень
Ферми всегда располагался внутри запрещённой зоны, близко к «дну» зоны
Дополнение 3
-14]
проводимости или к «потолку» валентной зоны. Это позволяло аппрокси-
мировать функцию распределения Ферми-Дирака простыми экспоненци-
альными функциями.
Однако при гилы/аи (с юншелт/шдоей примесей поряд-
ка 101е см 3) уровень Ферми смещается настолько вниз, что оказывается
н валентной зоне для р-полупроводника, или сдвигается вверх и попадает
Б зону Проводимости ДЛЯ LL-JIUHy НрОВОДНИКа. С ИЛЬ НО ЛСГИрОВаННыС ПОЛу-
проводники называют «вырожденными».
В так называемом «туннельном диода» как р-т так и та-с тороны являют-
ся яяьфи.ягденйьглша полупроводниками. На среднем приведённом рисунке
показан случай термодинамического равновесия, когда к диоду не приложе-
но Riieiiniee напряжение. и через пего нс течёт электрический ток. Так как
туннельный диод изготовлен из гыльлгя легированных полупроводников, то
в нём толщина «обеднённого слоя» является очельчнень малой. Поэтому
электроны могут нс только приобретать достаточную тепловую энергию
и двигаться поверх потенциального барьера, но также и проходить сквозь
барьер, ту ел ic лиру я квантовым образом через ei^io При этом туннельный
поток электронов для узкого барьера оказывается много больше классиче-
ского тока иоверх барьера.
Когда к диоду приложено обратное напряжение, как по-
казано ла левом приведённом рисунке, число электронов* протувиелиро
вавших из /j-области в m-область, будет больше числа электронов^ ггрфтун-
нелнроиавпшх в обратном направлении, так как электронам, движущимся
с ^-стороны соответствует большое число не заполненных электронами
состояний.
Когда к отуянедфнаиу диоду приложено прямое лап ряже егис^ как это
показано на правом рисунке, электроны, наоборот, будут туннелировать из
«-области в ^-область. Если увеличивать приложенное «прямое» напряже-
ние, то будет все большее и большее число свободных состояний на p-сто-
роне, что приведёт к возрастанию электрического тока.
442
ГлаваS
Максимум тока получится тогда, когда электроны на и-стороне смогут
ДОСТИЧЬ всех незаполненных состояний на /Хтороне, тс. когда уроке EEL
Ферми на р-стрроне совпадёт с «дном» зоны проводим осей на п-стсронс,
как показано на левом приведённом выше рисунке. Если прямое напря-
жение будем увеличивать дальше ч то перемешаться туннельным образом
электронам из п-области н р-область будет всё труднее и труднее, и, нако-
нец, они де Смогут перемещаться вовсе, koi да «лото доку валентной зоны
на р-стороне совместится с «дном» зоны проводимости на п-стороне, как
это показано на правом приведённом выше рисунке.
Поэтому вольт-амперная характеристика туннельного тока будет иметь
вид, показанный на левом приводимом рисунке. На нём / — ток, текущий
через туннельный диод, н VT — приложенное к диоду прямое напряжение
(плюс источника напряжения присоединён к /^стороне туннельного диода,
а минус — к его ft-стороне). Вольт-амперная характеристика туннельного
тока будет иметь максимум и оканчиваться на некотором напряжении Vh.
Реальная волы-амперная харак-
теристика туннельного диода^ одна-
ко, нс заканчивается на напряжении
Vo, а продолжается дальше, при этом
возрастая, как ЭЮ показано на пра-
вом приведённом рисунке. Она обя-
зана обычному классическому то-
ку, текущему через туннельный ди-
од, который проявляется при боль-
ших прямых напряжениях. При от-
ри нагельных {обратных} напряжениях увеличение напря женим вызывае]
неограниченное возрастание электрического тока через туннельный диод.
Вольт-амперная характеристика туннельного диода, таким образом,
имеет участок с отрицательным сопротивлением — область уменьшения
тока при увеличении напряжения. Именно с наличием этого участка с от-
ри нательным сопротивлением и связаны все практические применения тун-
нельного диода
Обрдманный
Обращённый диод аналогичен туннельному диоду только в нём кон-
центрация лршиесвд меньше. Степень легирования снижена ровно настоль-
ко, чтобы при нулевом приложенном напряжении «ПОТОЛОК» валентной зо-
ны на р-стороне рп-перехода совместился с одном» зоны приводимости на
его «-стороне. Этот диод называют «обращенным», потому что, в отличие
Дополнение 3
443
от туннельного диода, к нему приложено, наоборот, большое прямое напря-
жение. Поэтому вольт-амперная характеристика обращённого диода имеет
вид, показанный на рисунке.
Таким образом, при прямом напряжении элек-
трический ток оказывается малым, так как тун не л и-
рованне практически не происходит. Однако теперь
при обратном напряжении может наблюдаться боль-
шой туннельный ток. 11а рисунке / — ток, текущий
через диод, V — прямое напряжение (при V > 0).
Обратимся к явлениям, которые наблюдаются
в обычном полупроводниковом диоде с рп-переходом
при подаче ид него большего прямого или большего обратного напряжения.
При увеличении прямого напряжения ток будет возрастать до тех пор, пока
диод нс выйдет из строя, г. е. когда подводимая током мощность нс сможет
осваиваться диодом. При увеличении обратного напряжения ток при опре-
делённом значении напряжения очень резко возрастёт, и наступит «про-
бой», как показано на рисунке. На рисунке Г — ток» текущий через диод,
V — прямое напряжение (VF > (}). Известны два механизма явления прибоя:
I) пробой Зинера; 2) лавинный пробой.
Механизм Зинера был открыт Зинером в 1934 г.,
который он предложил для объяснения пробоя
га Сплошном веществе. Однако пробой Зинера ока-
зался для этого непригодным. Но механизм кванто-
вою пробоя пробоя Зинера оказался при годным для
рассматриваемого сейчас пробоя «лиода с рп-псрсхо-
дом».
При небольших обратных напряжениях мьс име-
ем поток злек1ронов из /г-области в область, явля-
ющихся неосновными носителями
Но при некотором большом
обратном напряжении энергети-
ческие зоны п- и p-областей нач-
нут перекрываться, и станет воз-
можным появление туннельного
така.
Этот ток возникает, однако,
только в том случае, если степень
в р-области.
зона
провод.
эона
провод.
валена
зона :
валепт.:
зона ;
равнппесие
обратнее
напряжение
4-14
ГлаваS
легирования достаточно высока и если ширина «обеднённого» слоя доста-
точно мала. При увеличении обратного па пряже ееня [пир и на барьера умень-
шается, что и приводит к быстрому росту злектрнческею тока по достиже-
нии определенного напряжения.
«Лавинный диод» отличается от «диода Зинера» несколько меньшими
концентрациями примесей- «Обеднённый слой» и нем шире, и поэтому
в нём змнеровский пробой должен иринсходить при существенно большем
напряжении. Но прежде нем появится туннельный ток, начнёт действовать
другой механизм пробоя, получивший название «лавинного». Электроны,
движущиеся в кристаллической решётке полупроводника, ускоряются элек-
трическим полем и приобретают кинетическую энергию. Эту энергию они
теряют при столкновениях с а юмами решётки.
При этом в достаточно сильном поле этой кинетической энергии хва-
тит, чтобы ионизовать атомы решётки, что приведёт к появлению электрон-
дырочных пар. Созданные таким образом электроны и дырки создадут,
в свою очередь, новые электрон-дырочные нары и г.д. Возникнет ллкын-
иыл процесс.
Фоторезиетором называется полупроводниковый прибора предназна-
ченный для детектирования (регистрации) фотоизлучения. Он представляет
собой пластинку полупроводника, освещаемую потоком излучения, на про-
тивоположных концах которой смонтированы омические контакты, как это
покачано па левом рисунке,
При падении излучения на поверхность фоторезистора в ею объёме
генерируются новые носители така либо в результате индуцированных из-
лучением МСЖДуЗОННЫХ ЭЛеКТрСННЫХ ПСрСХОДаВ
либо в результате индуцированных излучением электронных переходов
с участием уровней примесей в запрещённой зоне (лрнмесное wwe),
как это проиллюстрировано па правом приведённом рисунке.
Дополнение 3
445
В отличие от других полупроводниковых фотодетекторов, фоторези-
сторы имеют тот существенный недостаток, что время фптоответа у них
существенно меньше, чем у фотодетекторов с фотодиодами с перехо-
дами, с диодами Шоттки, лавинными диодами, с бинарными и полевыми
транзисторами.
Фотодиод
Фотодиод реализует явление фотолюминесценции, которое было от-
крыто в ] 907 г. В отличие от тсрмолЕОмннесцеищш^ фоГШИОМИНССЦСЕЩИЯ
характеризуется белее узким частотным спектром излучения.
Фотоны, падающие на полупроводник, создают в нём избыточные но-
сители тока, концентрация которых пропорциональна интенсивности света.
Рассмотрим исигупроводник с prwiepexo-
дом, к которому приложено обратное напря-
жение, см. рисунок. Для него наблюдаются
большие изменения электрического тока при
освещении его рп-перехода. Когда монохрома-
тические фцТОЕ1Ы определённой длины водны
А падают на р-О&тасть нону проводника, как
показано на рисунке, они генерируют в ней
электроны которые в этой области являются
неосновными носителями тока. Эти электроны создают дрейфовый ток иол
действием электрического поля приложенного обратного напряжения.
Гонкий слой полупроводника р-типв нанесён на подложку из полупро-
водника n-типа, так что рп-нереход расположен в непосредственной близо-
сти от освещаемой поверхности.
Фотодетсктирующие свойства рп-перехода можно улучшить, если пре-
вратить этот переход в pin-переход (i = mfrinsicX добавив дополнитель-
ный слой собственного (чистого) полупроводника. Он позволяет увеличить
«обеднённую область». Чем она больше, тем больше объём, в котором про-
исходит генерация фотонами носителей тока.
Кроме фотодез екюрив, на рп-псреходах широко используются фотоде-
текторы на переходах «металл- полупроводник» (на dwe Jui Шолтткы). Они
способны работать в синей и ближней УФ-области, поскольку металличе-
ский слой (обычно Ац) можно сделать настолько тонким, чтобы он был
прозрачен в этом диапазоЕзс.
Эффективность регистрации фотосигнала за счёт усиления фотото-
ка можно повысить в лавинных фотодиодах и фототранзисторах. В ла-
винных светодиодах наложенное обратное напряжение настолько велико,
что носители тока, создаваемые при облучении фотонами, проходя через
446
ГлаваS
«обеднённую область», приобретают достаточную энергию для создания
лавины.
и лазерный £>ия<>
«Светодиоды** и «лазеры» являются полупроводниковыми приборами,
преобразующими электрическую энергию в оптическую энергию, те. реа-
лизующими явление
Люминесценцией называется оптическое излучение в УФ-, видимом
и ПК-диапазонах, возникающее в результате возбуждения электронов в ве-
ществе. В зависимости от способа возбуждения различают
(возбуждение нагреванием), (возбуждение
оптическим излучением), (возбуждение электрон-
ным пучком или катодными лучами). лкшикэт^ячыю (воз-
буждение ПОТОКОМ быстрых частиц ПЛИ H3JJучСНИСМ ВЫСОКОЙ энергии), Stfffff-
до/эалвдывдеценцию (возбуждение электрическим полем или током).
Эффективными для люминесценции являются полупроводниковые ма-
териалы* и которых излучательные электронные переходы превалируют над
безызлучательными переходами.
Происходящие в полупроводниках излучательные Электронные пере-
ходы это: Г) «междузонные переходы» (между зоной проводимости и ва-
лентной зоной), вызывающие излучение С энергией фотона, близкой к ши-
рине запрещенной зоны полупроводника, а также излучение с более вы-
сокой энергией, если в процессе излучения принимают участие энергич-
ные так называемые «горячие» носители тока; 2) «переходы с участием
примесных атомов» или «дефектов» кристаллической решётки между зо
HQH проводимости И акцепторными УРОЕЕ1ЯМИ, или между до е горным и уров-
нями II валентной зоной, или между донорными и акцепторными уровнями
через так называемые «глубокие» примесные уровни, энергии которых ле-
жат глубоко в запрещённой зоне (не вблизи «дна» зоны проводимости или
«потолка» валентной зоны); 3) чисто «внутривенные переходы» либо в зоне
проводимости, либо н валентной зопе. которые вызывают излучение, назы-
ваемое «тормозным» (с участием горячих электронов и дырок).
Таким образом, к способам, какими можно возбудить в полу привод! ги-
ках люминесценцию, относятся междузоппые переходы, лавинное возбуж-
дение и возбуждение при туннелировании и инжекции.
Инжекционный «полупроводниковый лазер» с накачиваемым электри-
ческим полем возбуждением, использующий излучательный переход между
зоной проводимости и валентной зоной п сильно легированном арсениде
галлия GaAs, был создан одновременно тремя группами исследователей
в 1962 г. Ими наблюдалось в арсениде галлия GaAs с рп- переходом, ок ла-
Дополнение 3
447
ждённым до температуры жидкого азота, и с наложенным прямым напря-
жением импульсное излучение с длиной волны 840 нм.
Позднее, в 1970 г. был реализован режим лазерной ге-
нерации при камндтмй температуре в полупроводнике с так называемой
«двойной гстсроструктурой» (на основе GaAg/AlGaA&)? идея создания ко-
торой была высказана в 1963 г. независимо Крёмером и Алфёровым.
Теперь найдено большое число материалов для полупроводниковых
лазеров с рта-переходами, диапазоны длин волн которых включают близ-
кую ультрафиолетовую, видимую и дальнюю инфракрасную области (от
примерно 0.3 мкм = 300 нм до примерно 30 мкм = 3 000 нм).
За «разработку полупроводниковых гетероструктур, используемых
в СВЧ и оптоэлектронике» Крёмеру и Алфёрову была присуждена полови-
на Нобелевской премии 2000 г, вторая половина которой была присуждена
Килби «за участие в изобретении интегральных схем>\
В светодиоде используется jw,-переход, к которому приложено прямое
напряжение, вследствие чего этот переход испускает между-
зонное излучение в УФ-, видимом или И К-диапазоне.
Поскольку глаз человека чувствителен к свету только с энергией
Др Э I S эВ (0^7 мкм = 700 нн), то полупроводники, которые можею ис-
пользовать для светодиодов видимого диапазонач должны иметь ширину
запрещённой зовы больше этого значения. Наибольший интерес поэтому
представляют полупроводники GaAsi с молярным содержанием фос-
фора Р и мышьяка As н интервале 0 < л < 0.45, для которых ширина
запрещённой зоны изменяется от £3 = 1,42 эВ при т = 0 по = 1:98 эВ
при .г = 0,45.
Большинство «световодов» имеют плоскую геометрию, На рисунке
изображены два светодиода с непрозрачной (слева) н прозрачной (спра-
ва) подложками. Светодиоды с красным излучением используют подложку
GaAs, с оранжевым, жёлтым и 'зеленым излучением — подложку GaP. Фо-
тоны, генерируемые в области pn-перехода, испускаются во всех направле-
ниях, по наблюдателя достигают липть те из них, которые проходят через
поверхность светодиода.
Уменьшение количества излученных светодиодом фотонов обусловле-
но ]ix поглощением в материале светодиода и потерями за счёт дикого
Поглощение более существенно ь светодиодах
с подложкой GaAs, так как она непрозрачна для света.
При переходах фотонов из среды с показателем преломления п2 в сре-
ду с меньшим показателем преломления ти < Т1г) часть света претер-
певает полное отражение от границы раздела сред, #l-,w дуча
ли napc/mjocjwb cscmrtriuoAj батьше 0,. полного вejутрен-
него отражения, для которого sinflc =
ш
ГлаваS
неирпзра’шая подложка
по сравнению с лдзерд.ии, помимо простоты своей кон-
струкции, в качестве преимущества имеют более высокую рабочую темпе’
ратуру и характеризуются мёныпим влиянием температуры на мощность
излучения, К их недостаткам относятся меньшая яркость и более низкая
частота модуляции сигнала, а также существенно большая спектральная
ширина (порядка 100-500 А* тогда как лазеры характеризуются шириной
порядка ОД-1 А).
Полупроводниковый «лазер», как и «светодиод», использует возбужде-
ние переходов Электронов из валентной зоны в зону проводимости с после-
дующей излучательной рекомбинацией созданных злектрон-дырочных нар
в сильно легированном полупроводнике с большим наложенным прямым
напряжением, т.е. рекомбинацией, сопровождаемой излучением фотонов.
В сильно легированном полу проводнике уровень Ферми сдвигается либо
б зону проводимости, если примесь донорная, либо в валентную зону. ЕС-
ЛИ примесь акцепторная; такие полупроводники называются «вырожден-
ными». На левом рисунке изображены энергетические зоны вырожденного
jMi-перехода при нулевом прпложетптом напряжении при нулевой темпера-
туре Г = 0, а на правом рисунке — при большом приложенном прямом
напряжении 14 Е^/е и тоже при температуре Т = 0-
равновасис
прямое сопряжение
Дополнение 3
449
Лазерный возникает за счёт инжекции носителей тока в об-
ласть рп-перехода. Однородный полупроводник для лазера непригоден, так
как надо иметь, во-первых, большое количество электронов в зоне про-
водимости и, во-вторых , большое число вакансий в валентной зоне, гото-
вых принять электроны из эоны проводимости. Большое число электро-
нов н зоне проводимости можно получить в вырожденном иолу проводнике
п-тнла. В вырожденном полупроводнике р-тииа имеется большое число
дырок в валентной зоне. Эти две ситуации совмещаются в полупроводнике
с рп-переходом.
При пропускании сильного тока через рп-иереход (когда па ггего на-
ложено большое прямое напряжение) в середине перехода около «обеднён-
ного слоя» с вырожденной населённостью как электронов^ так и дырок воз-
никает так называемый «активный слой», в котором происходят процессы
рекомбинации электрон-дырочных пар с излучением фотонов. Волнистая
стрелка на правом приведённом выше рисунке как раз и изображает такие
процессы. Рекомбинация электрона и дырки при водит к испусканию одного
фотона с энергией hu = £>е - b>v.
На приводимом ниже рисунке изоб-
ражён полупроводниковый «лазер на
двойной гетероструктуре G-iAs/GaAlAs».
Электроны и дырки в нём инжектиру-
ются в активный слой кристалла арсе-
нида галлия GaAs из слоёв Gai тЛ1.кЛз
соответственно п- и p-типов. Излуче-
ние, возникающее в активном слое, с ча-
стстой, близкой к Ev/Jt, усиливается
в результате стимулированного излучения
злектрон-дырочной рекомбинации. Ак-
тивный слой GaAs заключён между двумя
одновременно выращенными с ним слоя-
ми Gai_*Ala:As (в этих слоях часть ато-
мов Ga заменена на атомы А1).
Атомы Al особенно удобны для замещения атомов Ga в решётке ар-
сенида галлия GaAs, так как они практически нс приводя т к изменениям
периода решётки. Кроме того, кристалл С a As имеет больший показатель
преломления, чем кристалл GaAlAs, и поэтому лазерное излучение, рас-
пространяющееся п арсениде галлия GaAs, испытывает полное внутреннее
отражение от плоских границ раздела с соседними слоями GaAlAs. Такая
01 pa j । и ч ej । н ость rei iepi i ру ewoi о свею вен о j i у1 г ка у н ел i гчи вае i и i rrei ic и в 11 осгъ
лазерного излучения.
450
ГлаваS
Лмулрчмодмукреый лдзф собой очень элективный
njpeW^^SOflfffflC.Th ЗЫЁЙСТЛ/ЗиЧССАОИ fi ОЛЛШЧвСЯуЮ.
Сначала для создания рп-перехода в кристалле GaAs использовалась
диффузия акцепторных атомов Zu в «-область кристалла, в которой в каче-
стве донорной примеси использовался Тс. Теперь кристаллы GaAs для по-
лупроводниковые лазеров выращивают методом эпитаксии, т. е. поочерёдно
наращивают на подложке легированные слои Gai-^AI^Aa с разными моль-
ными долями х. Таким образом, создаются «двойные гетероструктуры
GaAs/GaAlAs».
Оптическин резонатор, необходимый для работы полупроводникового
лазера, образуется двумя хорошо отполированным it естественными граня-
ми кристалла GaAs.
На приводимом рисунке слева показана схема лазерного диода с «го-
мопереходом», а на правом рисунке - с «гетеропереходом». Лазерные зер-
кала, использующие грани полупроводникового кристалла, имеют большие
показа! ели прелом дени я, чем у воздуха.
В лазере с гетеропереходом между слоями GaAlAs р- я тс-типов,
образующими рп- переход, помещается очень тонкий слой арсенида гал-
лия GaAs (толщиной порядка СМ мкм) для ограничения области, и ко-
торую проникают носители тока, п
волны.
GaAs
р-типа
GaAfi
га-типа
гомо
GaAS
гомо
GaAlAs
р-тииа
GnAs
GaAlAs
р-типа
гетеро
GaAlAS GaALAS
GaAS
гетеро
области распространения лазерной
Арсенид галлия GaAs име-
ет больший показатель прелом-
ления, чем GaAlAs, и на сто
поверхностях про ИСХОДИТ ПОЛНОС
внутреннее отражение. Кроме то-
го, арсенид галия GaAs имеет
меньшую энергию запрет ценной
зоны, чем GaAlAs.
В гетеросгруктурном лазере
из-за того, что GaAlAs имеет
большую ширину запрещенной
зоны, чем fra As, носители Заря-
да не могут проникать в области
с другим типом проводимости,
а следовательно, не могут участ-
вовать Е излучательной рекомби-
нации. На левом и правом рисун-
ках показаны распределения но-
сителей тока в кгомопсрсходс» и «гетеропереходе».
Дополнение 3
45]
Сатяечные Старей
Солнечные батареи оеущестмяют л/^оо/миомине artepjww олтнчгско-
го илтучелля d алек/ярс<Ч£?с\уй> jne/ww/o.
Солнечные батареи являются самыми важными источниками энергии
для спутников и космических кораблей при длительных их полётах. Они
используются и па Земле f качестве альтернативных источников Энергии
Солнце — наш практически неистощимый её источник.
Первый солнечный элемент был создан в 1954 г. на основе кремниево-
го полупроводника с ^-переходом
Обычный полупроводниковый «сплисчетьей -элемент» имеет характер-
ную энергию работы — ширину запрещённой зоны полупроводника
Фотоны, падающие на солнечный элемент* с энергиями fev < не дают
никакого вклада в его выходную мощность. так как они не поглощаются
полупроводником. Фотоны с энергиями hi' создают и полупроводни-
ке электрон-дырочные пары, перевода электроны м3 валентной зоны в зону
проводимости, на что тратится энергия остальная часть энергии фотона
й^ - £?ff переходит в тепло.
5аяьт-длсл£ркля рп-перехода солнечного элемента
имеет вид:
1-{к (e’W-l)-/*,
где 1ф — первичный фототок, возникающий за счёт образования носите-
лей тока солнечным излучением, 7Н — ток насыщения, V — приложенное
к солнечному элементу эшсншсс напряжение.
На левом приведённом выше рисунке дана волы-амперная характе-
ристика солнечного элемента. На правом изображена эта вольт-амперная
характеристика. какой ее обычно приводят. ЗЕтачепие тока / при V = О
называют «током короткого замыкания», / — Значение внешнею на-
пряжения V при 7=0 называют ^напряжением холостого хода», V =
+52
ГлаваS
Величины н Ут на правом рисунке — это электрический ток н напря-
жение, при которых выходная мощность Р = /V элемента максимальна
(Р = Р1П =
На приводимом рисунке схематически показан «солнечный элемент с
рп-переходом». На полупроводниковую пластинку ft-типа нанесён слой по-
лупроводника р-тнпа, ггри этом па границе двух этих полупроводников об-
разуется рп’Переход. Даже при отсутствии освещения между р- и п-о&ла-
стяни имеется контактная разность потенциалов VK с плюсом на п-областн
и минусом на p-области, но никакого электрического тока в цепи солнеч-
ного элемента, конечно, пег, так как эта контактная разность потенциалов
точно компенсируется контактными разностя-
ми потенциалов на контактах между полу-
проводниковыми областями и металлически-
ми проводниками, так что ток / в цепи не
течёт. Вместе с тем если ггри нулевом внеш-
нем напряжении V' = 0 солнечный элемент
освещается светом постоянной интенсивности
Ф и частотой с энергией фотона ftp > 7^,
то ир-области вблизи ри-перехода образуются
электрон-дырочнме пары. Электроны этих пар
под действием контактной разности потенциалов перетекут в it-область,
преодолев потенциальный барьер, а дырки останутся в р-областк. Такое
перемещение электронов и дырок создаёт первичный фототок /ф, который
течёт из n-облаСти в р-областъ (отрицательный ток),
Фотоюк /ф пропорционален потоку излучения Ф. «Коэффициентом по-
лезного действия» КПД солнечного элемента называется величина
ф ’
где Рт — максимальная выходная МОЩНОСТЬ элемента, Ф — ПОТОК света, её
вызывающий. Обычно КПД солнечных элементов имеет порядок 5-12%.
Дополненве 4 к гл, Н
Фаэоное и химическое равновесия
Химический потенциал р данного вещества является
для распределения этого химического вещества, способного
свободно перераспределяться в теле (в одном теле или в нескольких кон-
тактирующих друг с другом нли смешанных яруг с другом телах). Считаем,
Дополнение 4
453
что вещество может свободно перемещаться внутри каждого из тел или из
ОДНОГО ИЗ НИХ в любое другое.
Концентрации тц и па данного вещества, скажем, в двух юонгактиру-
тощих друг с другом телах 1 и 2 при равновесии устанавливаются такими ,
что химический потенциал рассматриваемого вещества в теле 1 окажет-
ся равным химическому потенциалу ^2 этого иешестна и теле 2, г. е. когда
Mi = ра.
НИКОИМ образом /?Д|СЛр1Л)йЛ^Ях1Ч
rfrptfijtftr не являе^я Литл яом^^нм^л^ыя.
Совершенно аналогично и случае тепловою равновесия двух тепло-
проводных контактирующих друг с другом тел 1 гг 2 им^ывдилл/зач рд#-
мобэтня является температура Г. При тепловом равновесии теп I и 2 их
температуры Tj и Тэ равны друг другу TL = ??.
С помощью химического потенциала формулируется не только усло-
вие фд?о#дао /адвдсдесия, по и
химического ^ивновесия.
Открытые w здлрыяше me/wodu нами четкие ewrweww
Термодинамические системы бывают «открытыми» и «закрытыми».
Система, которая может обмениваться с окружением массами составляю-
щих её химических веществ, называется «открытой». Если система не мо-
жет обмениваться с окружением массами сс химических веществ, она на-
зывается «закрытой».
Пример L Открытой системой является кристалл, окружённый рас-
твором или расплавом, который может расти или растворяться в этом рас-
творе либо расти или плавиться в сноси расплаве.
Пример 2- Открытой системой является воздух над жидким раство-
ром, например в воде, каких-то химически летучих веществ или другая
инертная газовая фаза над таким раствором, в которой летучие вещества
могут присутствовать в газообразном виде.
454
ГлаваS
Система, состоящая из двух или большего числа индивидуальных хи-
мических веществ, способных химически реагировать друг с другом, назы-
вается «многокомпонентной системой».
Пример 3. Многокомпонентной системой является, например, газовая
смесь водорода Hi, кислорода Оз и паров воды На О: число компонентов
в ней равно трём.
Системы могут быть и мно-
Лсд «фазой» понимают фазовое состояние вещества. Воз-
можны газообразные, жидкие и твердые фазы, последних обычно бывает
несколько у вещества.
Пример 4ь Двухфазной термодинамической системой является, напри-
мер, жидкость и сё пар, находящиеся в цилиндре под поршЕтсм, причём
предполагается^ что цилиндр окружён термостатом с фиксированной тем-
пературой, и на закрывающий его поршень оказывается давление.
/7;juhz|ww Гцбосчт
Рассмотрим изолированную термодинамическую систему (т.е. систе-
му, ejil с чем не взаимодействующую) и найдём ее равновесные состояния,
т. с. выведем полный набор сё независимых условий/кгеновесмя.
Рассмотрим произвольное состояние этой изолированной системы, ко-
торое, как мы сейчас подозреваем, является «равновесным», и будем харак-
теризовать его набором значений энтропий и объёмов ею малых равновес-
ных частей, т. с. набором величин
5|Ц------
где S;. V; — энтропия и обьём малой i-й части системы (i = 1, .... Аг).
Назовем это состояние тсяодяьш состоякыаи».
Возьмём, далее, бесконечно близкое к рассматриваемому состоянию
системы другой ее бесконечно близкое состоя еенс, которое характеризуется
набором величин
S] + г Vi + <5 Vi п ..., iS.y -I- JSjV. Vjv + ^Vjv.
Назовем его ечмтиоялшшк
Вариации 5Si, ..., JSn, iVw будем считать бесконечно малыми,
называется смещение (или пё^сшёщяшё) из исходного
состояния, которое, во-первых, бесконечно люлов и, во-вторых,
/wem дополнительным условиям^ которые называются «условиями связей».
Дополнение 4
455
Для изолированной термодинамической системы в качестве условии
связей Гиббс предложил взять условие леил.петшАеми лиъёлгд ясен смсмелш:
5V = й1/] 4- ... 4- = Оп
и услоене WOTiwewwocmu ее энтролын:
j\S' = 5Sr 4" ... -|- SS/if — ().
Для отыскания раенввееныт отстот/шй изолированной системы среди
множества ее неравновесных состояний I н&бс сформулировал приводимый
ниже тфчяби дорический л/шнцил, называемый «принципом Гиббса».
С помощью принципа Гиббса, как и с помощью формулируемого ниже
эквивалентного ему Принципа Планка* можно получить ПОЛНЫЙ набор неза-
висимых необходимых и достаточных условий термодинамического равно-
весия сколь угодно сложной изолированной термодинамической системы.
Принцип Гиббса
Дм того чтобы отстояние систслты было рлеяотесяы.н, леобходнлго
и достаточно. чтооь/ оно удоюетеоряло следую щй-цу требованию. Дм
любого еи/?тудльного из оостАяиия:
5S1, Я!_____
удоая ет яо/мющ #го уелооия.и
3St + ... + JSw = = 0. 5Vj + ... + W = °’
* 1
«бгриа«мя внутренней эне/teww сигте.ны роена не-ую:
517 = 0.
Внутренней энергией !7 неравновесного состояния системы ндзыадет-
d-я (подчеркнём «называется») сумма внутренних энергий
час тей этого неравновесного состояния:
1=1
где суммирование ведётся по всем равновесным частям системы г =
= 1......Лг. причём предполагается, что .т^бдя бостдточло _иа.?дя чделгь
456
ГлаваS
сысотыш. ндхойяадейся tf cocmftawww, еееайя /шеяовесма сам л
ла себе, и. £. нмо^птся д лскоторап сеоем раллавгсмам досгоюяхчи (но нет
равновесия между этими равновесными частями системы в рассматривае-
мом неравновесном состоянии). Это так называемый «лрых^ил лскляьшьэд
равновесия».
Пример, Рассмотрим изолированную двухфазную систему, состоящую
ил жидкости н сё пара, которая ешходится в цилиндрическом сосуде с порш-
нем, зафиксированным в некотором своём положении защёлкой.
Предположим, что пар сам по себе раллове^ыы и имеет массу xW,
температуру Т и давление Р, и что жидкость тоже сама по себе равновесная
и имеет массу Л/\ температуру Г* и паклепне Р7,
Таким образом. наша система состоит из двух равновесных частей, по
равновесия между этими частями нет.
Найдём условия /мкнот'ая пара и жидкости друг с другом, выведем
нетривиальное так называемое ^условие 0дзовоа? /швяовесшдо.
Очевидно, что условиями равновесия должны
быть условия равенства температур Т = Т' п данле-
। --------- ний Р = Р' пара и жидкости. ?мими двумя услови-
ями, однако, не исчерпываются все условия равнове-
сия. Чтобы найти полный набор независимых усло-
вий равновесия рассматриваемой двухфазной систе-
мы, применим принцип Гиббса.
------------ Если обозначить через tt и 1? внутренние энер-
гии rwffc(?w пара и жидкости соответственно,
т. с. удельные внутренние энергии пара и жидкости, а через Л/ н ЛГ — мас-
сы пара и ЖИДКОСТИ, ТО внутреннюю энергию рассматриваемой двухфазной
системы можно представить в виде
[7 = Mu +
Таким образом, вариация внутренней энергии системы равна
JtZ = ибЛГ + а' Ш' + ЛГ Ди + ЛГ £и';
массы Л/ и Л/', разумеется, мы варьируем, так как пар может превращаться
в жидкость, а жидкость — ь пар. Очевидно, при таким пре вращении полная
масса системы не изменяется, н поэтому ЙЛГ + ДЛГ = 0, откуда следует,
что 5ЛГ = -Ш Таким образом,
JtJ — (и — т?) 5Л/ + Л/ Ди -ь ЛГ Ji?.
Дополнение 4
457
Согласно принципу Гиббса эта вариация внутренней энергии Ш из
равновесного состоя пил должна равняться нулю при дополнительных усло-
виях 5V = О и 5xS = 0- Распишем эти условия. Очевидно, объем нашей
системы равен
V = xV и + А/' <
где w — Цельный объём пара, t/ — ^ельлый объём жидкости, гели t/ —
объёмы единиц массы пара и жидкости соответственно. Для вариации 5V
поэтому получаем выражение
t5 V = (и — 1/) 5А/ + xW 5tr + Aff 5Г.
Составим теперь вариацию энтропии нашей системы. Согласно
rffjseuutfj эЕггропии неравновесного состояния, имеем
.5= xVs+ ЛГУ,
где .4 И У — Энтропии «Зшшц .WfltCU Паря И ЖИДКОСТИ Т. С. pteflftWWC энтропии
пара и жидко с TH, соответственно. Для вариации Энтропии системы, таким
образом, получаем выражение
££ = ($- У) W + Af 5s - ЛГЯЛ
Так как и пар. и жидкость сами по себе, по нашему предположению,
/эйяняеесные, то к ним можно по отдельности применить термодинамиче-
ские уравнения
5и = Т 5s - Р 5iZ = Г 5У - Pr 5i<
Теперь, для того чтобы раскрыть условие нулевой вариации 5 £7 = О
при дополнительных условиях 55 = 0 и 5К = С- воспользуемся
леоп/?ее)&тё’л«ыд- AJuoatfumejeew jVdfpdHMH, согласно которому составим так
называемое лдг/мялегоо узловые:
ЙУ -aJS + /?5V = 0,
в котором а, 3 — так называемые неол/гсделея/ше Лл^рйнжя.
Согласно Лагранжу, это вариационное условие удовлетворяется при лю^ых
вариациях 5А-Г 5и, 5t/- 5$, 5я\
Подробно выписывая приведённое ллранжево вариационное условие,
получаем, что
[(w - и') - о (s - s') + /3 (v - t/)] 5Af-
+A7 (T - a) 5s + ЛГ (Г - л) 5./ + Af - P) 5u + AT (/? - P') 51/ = 0.
45Й
ГлаваS
Так как это условие выполняется при любых AM, As, As', fo, Ан', то
имеем следующие и ^оелзоэтлчяые условия его выполнения:
Т = a, Г = а, Г = J: Г = /?.
(и — ?/) — ас (s — У) — /? (и — и') = С.
Как видим, кроме двух первых условий равновесия: Г = Т? и Р = Р\
мы получили еще и третье условие, которое можно записать в виде
(и - и') - Г (* - sJ) 4- Р (i? - и') = О
или в виде
ц - Ту + Ри = и - 3V + РтД
Комбинация величин
и - Ту 4 Рг,
относящихся к единице массы вещества, называется <кги,мнчйсяг,н лс?т*?я-
циошч веществ л н обозначается буквой д:
д — и — Тз 4- Р^.
Химический потенциал д является функцией величин, характеризую-
щих равновесное состояние. Его удобно рассматривать как функцию тем-
пературы Г н давления Р:
и = и(РХ)
R рассматриваемом примере третьим независимым условием равно-
вссия. таким образом, является хы’.ничегкшг лдлаеиуцллдА ядра
и жыдкостп:
р(РТ) = ^(Р\Г);
получили так называемое «условие фазового равновесия».
ТТринцдот Планка
Рассмотрим Снова неравновесную изолированную термодинамиче-
скую систем ут равновесные с ос етин ия отдельных малых частей которой бу-
дем характеризовать теперь величинами ЕЛ, Ц, а нс величинами как
в принципе Гиббса. Энтропия теперь является функцией ЕЛ, К, причём
для каждой малой части системы s = 1, ...,/V справедливо равновесное
соотношение
гг .1: — -------- :
Дополнение 4
454
это — по-другому представленное уравнение
Ша = - PTJVJ.
Сформулируем теперь термодинамический принцип виртуальных пе-
ремещений Планка,
[]р11IIимII Планка
Для того чтобы состояние ызаяцройонмш смстгиы было /мгаловес-
ньшР rteoovodn.iro if достаточно, чтлбы оно следующему
т^гбомиию Д?я любого оцртудльного из этого состояния:
5ГГ1 йVi. .. ь, 517^ ч «5 Vj\r,
удоел етбгфяюнделэ условиям
6С7| 4- ... — SUn = rSfjj = 0, <5Vi + . . + <SV\ = г5Ц = О,
вд/швдия энт/юниы системы /швял нуя/о;
55 = 0.
Можно строго доказать, что принципы Планка и Гиббса являются след-
ствиями яруг друга.
Пример. Рассмотрим снова двухфазную изолиро-
ванную систему состоящую из жидкости н сё пара, за-
КНЮЧ енну ЕО В ЦП Л НН дри Ч ССКИ11 С осуд С заф И Есиро ван НЫМ |
защелкой положением поршни. 11усть жидкость и пар са-
ми по себе всегда равновесные. Обозначим массу пара
через Л/т а массу жидкости - через ЛГ. Пусть темпера-
тура и давление пара Г и Г и жидкости Г' и Р' равны
Энтропией S неравновесно]о состояния системы
Hdzawfttefflts (это особенно подчёркивал Планк)
эндртолии *Sl /адююяесяых частей этой системы для данного, вообще го-
впря, Етсравновееного сё состояния:
у
•S-E^:
i= L
здесь суммирование проводится по равновесным частям системы г =
= I. ..., Лг.
фьо
ГлаваS
Предполагается, что малая чагт* системы, наха-
fl ИрЛЫЗДОДОИОЛ! Mfl/JtfaUfftitfCAff.U £Y>L?W J Ш. /ЛТА^ЛААСЛЛЯ СЛАКТ ПО
селе, т. е. находится й своёш coScmecwwa-u /меноАвснач состоянии (но о т-
сутствует равновесие между отдельными равновесными частями). Таким
образом, энтропия рассматриваемой системы, согласно приведённому ол/ге-
энтропии неравновесного состояния, равна
3= Ms+AfV,
здесь s4 / — энтропии декшш; Ajaccio пара и жидкости, т. е. удельные их эн-
тропии, соответственно, Л/ — масса пара, Af' — масса жидкости. Очевидно,
Ш + Ш' = = О, Ш' = -Ш, Поэтому
53 = (s - d') 5Af + Af -is - ЛГ5s'.
Так как
г 5tt + Р 5д г j 5t? -I- P'5t^
— Т ' 5$ — ,
то для вариации энтропии получим следующее выражение:
JS = (s - s') SM I у <fu + Af £ tv + du' + M' у tv'.
Эта вариация должна обращаться в нуль при условиях 5С7 = 0 и 5V =
= 0. Распишем эти условия:
ш = (и - и') SM + M&U + M!tu\ tv = iv- v')iM + Af tv + Af' Sv1.
Используя метод неопределённых множителей Лагранжа, составим
следующее лагранжева варнзционное условие:
ts - a tu - (?5V = [(s - У) - а (и - и') - 0{v - v')] Ш+
+М - a) du + Af dw 4- Af' Q-; - a) du' + Af' (у - /jj tv'= 0,
которое должно выполняться при п/юитгольныл вариациях <5Л/. Ju, 5щ\ 5и,
5т’\ здесь а, дЗ — .шюлсплгетм
Следовательно, в качестве и условий его
выполнения получаем соотношения
(s — s') - л (и — и') —/?(?? — i1') = 0.
Дополнение 4
461
Таким образом, равновесия являются очевид-
ные условия
у ут-р 1 j :
1 — Л - Q1 i" — Л" -
и независимое от них нетривиальное неочевидное условие
(s - s') - у (« - “') - у О’ - «О = 0.
или
и — Тй + Ри = ъ/ — Г's' + РУ,
или
д(Р>Г) = д'(Р'.Т').
Снова получили /мяснстм xH.wErtecicux лд/?д
и жцджж которое является «условием фазового равновесия».
Изменим обозначения и положим, что р(Р 7’) = ^Г(Р 7’) и //(Pf Т) =
= Tj, где индекс «г» означает «газ», а индекс «ж» означает «жид-
кость». Тогда полученное условие фазового равновесия для двухфазной си-
стемы «пар-жидкость» можно Записать is виде
г) = MuiZ П
причём функции ^Т(Р, Г) и ^K(Pf Т) мы считаем известными.
Они Строятся на основе результатов измерений теплоёмкостей и коэф-
фициентов механического расширения газообразной и жидкой фаз данного
вещества сосн ветственни.
Выведенное условие /кгонсгегая показывает что для двухфаз-
ной системы давление Р и температура 71 не могут принимать произволь-
ные значения, потому что если разрешить приведённое условие фазового
равновесия относительно давления Р при фиксированной температуре Г.
то получим функцию Р = Р(Т), Описывающую так называемую кривую
«давления насыщенного лара».
Получим теперь из условия фазового равновесии уравнен не для функ-
ции Р(Т). Так как
е!дс = и <(Р - d еЩ
то, используя это соотношение и дифференцируя условие фазового равно-
весия, имеем равенство
T,ydP — 31-dT = v* fiP — s* dT,
где ur, — удельные объёмы пара и жидкости, а 8Ж — удельные эн-
тропии пара и жидкости, т.с. величины, отнесённые к единице массы.
Полученное равенство легко преобразовать к виду
- t^)dP - (d:r - as)d7\
Ф&2
ГлаваS
= £| -
dT vr — ’
таким образом, мы вывели так называемое «уравнение Клапейрона-Клау-
зиуса», в котором величина L = Т (зг-лж) представляет собой так называе-
мую «удельную теплоту» испарения жидкости рассматриваемого вещества.
Она положительная, так как зг > яж; удельная энтропия газа всегда больше
удельной энтропии жидкости вещества.
Принципы минимумов терм(Минамических потенциалов
Когда система находится в неравновесном состоянии, температуры Т,
и давления Р, ее малых частей, нумеруемых индексом s — 1. .. ч *¥„ вооб-
ще говоря, различны, и поэтому нельзя говорить о температуре Г
п давлении F неравно вес i юго состояния системы. Таких величин
просто ИС существует.
Однако, среди множества неравновесных состояний системы можно
взять только неравновесные состояния, уже равновесные по давлению, т. с.
у которых давления малых равновесных частей системы
Р1=Ра= ... =PJv = Pf
и равны давлению Р окружения, в котором, по предположению, находится
термодинамическая система.
Такие состояния уже равновесные в лдедглмычвдэдвд т. с. для них
условие механическою равновесия уже выполнено.
Среди множества неравновесных состояний можно также отобрать та-
кие неравновесные состояния, которые уже равновесны по температуре и у
которых температуры малых равновесных частей системы одинаковы:
Г. = Т2 = .. = Тдг = Г,
и равны температуре Г окружения, в котором„ по предположению„ находит-
ся термодинамическая система.
Такие состояния уже равновесные в тепловоч омт/ошеяии, г. с. для них
условие теплового равновесия уже выполнено.
Наконец, среди множества неравновесных состояний можно взять та-
кие неравновесные состояния, которые равновесные и по
давлению, н по температуре, для которых условия и механического, и теп-
лового равновесий уже выполнены.
Для отыскания остальных условий равновесия, в частности условии
фазового и химического равновесии, можно использовать следующие тер-
модинамические приЕщипы виртуальных перемен осетин.
Дополнение 4
463
Минимум энтальпии
Для того чтобы неравновесное состояние, уже равновесное по дав-
лению, было равновесным. необходимо w ЙостоточЯо. чтобы вариация ЭН-
толыши п? этого состояния /менялась нулю.1
гя = 0т
для любом еиртуальяого лс/гаивдсяня нз этом состояния # лроизшыънос-
лсраваовесяое состояние, уже раяяояесяос ло бй&гелию, с тем же со.иы.и
значением давления, что и расг,натриваеиое состояние, — перемещения,
убов^йлиоряющг^а условию терпо^ини.ммчесл’ой связи tiS = 0.
Энтальпию можно определить для всех равновесных состояний систе-
мы и: иля тех её неравновесных состояний, которые уже равновесны
подавлению. Но определению, энтальпия равна
Л = С7 + Р V.
где (7. F — внутренняя энергия и объем состояния; Р — давление этого
равновесного состояния или неравновесного состояния, уже равновесного
по давлению.
Л/шШНуЛ*
Дм там чагу бы яе/мвловесяое состояний у. же ло we.w-
лсротур^ бы.-?о расновэтмыш, нсобяобы.ио ы бост^точио, чтобы вариация
свободной элезгин W5 этом состояния /вдяняяась яулю-'
£F = 0?
бля ямбом ои/ртуадьмом ЛЁрт.исщения, у^олиетдорямщем условию тер-
моднна.м инее кой связи iV = 0. из атаго согтолния в игра&ио№нос со-
стояяиа, уже /jafiHOtfefuoe по тслтердтуре с тегг йсй гилгылг зяаче/лийм
тсипс/мтуры, что и^рдсслат^увд^мог состояние.
Свободную энергию можно определить для всех равновесных состоя-
ний и тлльхо для таких неравновесных состоянии, которые уже равновесны
по температуре. По определению, свободная энергия равна
F = U - Т5.
где (7П .S — внутренняя энергия и энтропия равновесного или неравновесно-
го состояния: Г — температура равновесного состояния или неравновесного
состояния^ равновесного по температуре.
Ф64
ГлаваS
Л/инмлгцм магического потенциал
Д.7Л того чтобы НЕрсгедибгесное состояние, jore /мвнояесяое н* но боя-
ленню. w по me.wnepwmypt'. было ршшмасньи^ леоб.то^хмго и Йостлточйо,
чтобы вдривдыя т гдчобишли* четкого лотгн^а. та из от ого состояния рос-
нллжь НуЯЮ.и
г5Ф = 0s
Д?я любого ^нртудльного шрЁшга/етнш1 о лроиэеольног Hcpaewdecwoe со-
стояние, ужгс /манойсслое по m&tfncpomjjjtf ы ск^.тслшо. с №ёлш же зилче-
ниями fftewflejjamy/jw н (Ылетшя. что и /икт-мот/мадамос состояиме.
Термодинамический потенциал можно определить для равновесных
состояний и только для таких неравновесных состояний, которые уже рав-
новесные по давлению н темперагуре, полагая его равным
Ф = (7 + PV - T.S = Я - TS,
где Г.Р7.5 — внутренняя энергия, объём и энтропия равновесного или
неравновесного состояния, уже равновесного по давлению п температуре;
Р к Г — значения давления и температуры для равновесного состояния или
неравновесного состояния, равновесного по давлению и температуре.
Ниже МЫ Приводны Примеры ИОНОлЬЗОВаНИЯ наиболее удОбНОГО ИЗ
сформулированных принципов — «принципа минимума термодинамическо-
го потенциала».
Условия фазового равновесия и условия химических равновесий выво-
дятся легко с помощью этого принципа.
Использование принципа .мшяшудм термодинамического
потенциала
а. Условие фазового равновесии
Рассмотрим двухфазную равновесную систему, например, жидкость
и сс пар, находящиеся в цилиндрическом сосуде с теплопроводными стен-
ками иод поршнем, на который оказывается все время давление Р. Пред-
полагаем, таким образом, что наша система находится в окружении, пред-
став плюшем собой термостат, в котором всё время поддерживаются посто-
янными температура Т и давление Р,
Предположим, что и жидкость, и пар внутри цилиндра сами по се-
бе равновесны и имеют одинаковые неизменные значения температуры Т
и давления R
Выведем сначала условие равновесия фаз.т с. «условие фазового рав-
новесия».
Дополнение 4
465
Пусть в равновесном состоянии у рассматриваемой двухфазной систе-
мы масса пара равЕга Л/ и масса жидкости А/'.
Рассмоприм виртуальное перемещение из этого равновесною состо-
яния, состоящее в том, что бесконечно малая масса iAf жидкости испа-
рилась, т.е. масса жидкости уменьшилась на величину £A<f, а масса пара
увеличилась на величину <?Л/Т нли наоборот.
Обозначим термодинамический потенциал единицы массы пара через
jt(P. 7П)П а термодинамический потенциал единицы массы жидкости че-
рез Т), т.е. возьмём удельные термодинамические потенциалы пара
н жидкости. Термодинамический потенциал равновесного иди неравно вес-
кого, уже равновесного по температуре и давлению, состоя егия, по опреде-
лению, ранен
Ф = Л/м(/>:Т) + Л/у{ЛГ)|
а следовательно, «гй вариация при виртуальном
перемещении 5JW равна
*Ф = ^{АТ)Ш+ р'(Р.Г)Ш' =
[ак как для рассматриваемого виртуального пере-
мещения, очевидно, 5Л/' = -51W.
Согласно приниипу минимума термодинами-
ческого потенциала М- = 0 при любой вариа-
ции £Д/, а потому приходим к следующему yew-
ййю /мвкдеЁсия:
которое мы уже дважды вывели выше, но теперь получили его самым про-
стым способом.
б. химическом /ше/гоеесия
Прежде чем рассматривать следующий пример, найдём сначала выра-
жение для химического потенциала идеального газа.
Химическим потенциалом равновесного состояния системы называ-
ется термодинамический потенциал Ф этой системы а /мечете № tfriwwiu/y
.-ибгссы, т. е. величина ф
д = ЛГ
где Л-f — масса системы; химический потенциал — это попросту удельный
термоднею м и ч ее кин потен t [нал.
Ф66
ГлаваS
Найдём химический потенциал идеального газа. По определению
Ф = J7 + PV - TS,
причём для идеального газа
U = McvT, S = Af с,, InFd Мер In К;
здесь сг, cv - удельные теплоёмкости вещества газа при постоянном дав-
лении и при постоянном объёме Соответственно, At — молярная масса ве-
щества газа, Р — универсальная газовая постоянная.
Таким образом, для молярного химического потенциала идеального га-
за, т. е. химического потеттпизла одного моля идеального газа, имеем выра-
жение
Д = ,Vf л = А1 7 4 ЛТ - Л1 ev7 1п7 - Л1 ст Г 1л
= й)(Г) + ЛГ 1пР.
где До (Т) - некоторая функция, зависящая только от температурь!. При
таыволе мы использовали «соотношение Манера»:
Л/ дг\
Л1 F /
Получим теперь с помощью принципа Гиббса условие химического
равновесия газовой смеси, в которой протекает химическая реакция.
Например, рассмотрим смесь водорода, кислорода и паров воды и хи-
мическую реакцию образования воды:
2Н3 + О3 2Н3О.
Если проведём чту реакцию в калориметре, так чтобы прореагировало
2 молл водорода и I моль кислорода с образованием 2 молей воды, то н ка-
лориметре выделится теплота Qd которая называется «теплотой реакции».
Процесс химического превращения в калориметре происходит самопроиз-
вольно и необратимо.
Обозначим газ водород Н2т газ кислород О 2| газ парен? воды На О со-
ответственно индексами 1,2, 3.
Будем считать, что химически неравновесная смесь указанных газов,
которые будем считать идеальными, помещена в цилиндрический сосуд с
теплопроводными стенками, находящимся в термостате с температурой Г.
Дополнение 4
467
Предположим, что сосуд закрыт поршнем, на который оказывается давле-
ние Р.
Прн этом объёмные концен грации q . сз газов I, 2, 3 примут неко-
торые равновесные значения Cj ч С^т Сь и в газовой смеси во всех точках
установятся одинаковые температура Г и давление Р.
Здесь важно отметить, что и химически равновесной газовой смеси
концентрации <ц, са, сз не имеьсп определённых значений, а имеют зна-
чения, связанные условием химического равновесия для рассматриваемой
реакции.
Нас и।пересует сейчас соотношение, которому удовлетворяют концен-
трации (71 - Сг2 (Л в химически равЕювеснСм состоянии, которое и пред-
ci авляет собой искомое условие химического равновесия.
Применим теперь принцип минимума термодинамического потенциа-
ла и рассмотрим неравновесное состояние, уже равновесное по температу-
ре с температурой Т во всей равновесной газовой смеси и равновесное по
давлению с давлением Р всей газовой смеси. Это неравновесное состояние
пусть отличается от равновесного другими бесконечно мало отличающи-
мися значениями объёмных концентраций веществ.
Обозначим с помощью Л/|. Л/а, Мч массы газов 1, 2, 3 ч равновесной
СМССИ. Эти газы реагируют в ХИМИЧЕСКОЙ реакции
2Н3 I Оа 2HjO,
в которую вступают один моль кислорода и два моля водорода, и получа-
ется два ноля воды. Другими словами. на ДЛ/ДАЛ^ молей кислорода, всту-
пившего в реакцию, приходится
2 Ш _
ЛЬ ЛЬ
молей вступившего в реакцию водорода и
2 ДЛ/ _ <£ЛЬ
ЛЬ “ ЛЬ
молен образовавшихся паров воды.
Применим теперь принцип минимума термодинамического потенциа-
ла, который для любого неравновесного состояния газолой смеси, уже рав-
новесной по температуре Т и давлению Г, определяется выражением
Ф = ЛА 1М (Л Г) + ЛЬ Г) + ЛА №(Р,П
ГлаваS
где Л/ь Л/?, Л1э — значения масс газов в рассматриваемом химически
НСраНЕЮВССНСМ состоянии газовой смеси.
Возьмём теперь такое виртуальное перемещение равновесной газовой
смеси, при котором
Ш1 = 2 = Ш, Ш3 = -2 JAL
.И j Лтд.
где г5Л/ — бесконечно малая величина.
Для пот виртуального перемощения вариация термодинамического
потенциала равна
0Ф = + w(P?r)5^ + p3(Psn^3 =
-Ш [2^1 (ЛТ) + М-2 № (С Г) - 2 № (Л Т);
Л12
согласно принципу минимума термодинамического потенциала отсюда
имеем условие
ЛФ = О при любом ЛЛ-/.
из которого непосредственно следует условие химического равновесия рас-
сматриваемой реагирующей газовой смеси:
2 Л41/11 - Л<а^2 = ЗЛ^з^з,
или — дни молярных химических потенциалов — условие
2^! + /Л; = 2 /ГД,
или условие
2 Дн3 - ?Ц)3 = 2 ДнаО,
которое имеет вид уравнения химической реакции
ЗН2 -02 -=2Н2О
в котором вместо символов химических веществ подставлены л^одя/зиы^,
а не уделылне химические потенциалы этих веществ.
Для того чтобы придать выведенному условию химического равнове-
сия привычный вид так называемого «закона действующих масс» Гульд-
берга-Взаге, сделаем следующее допущение. Будем считать, что газы 1,2,
3 в газовой смеси идеальные7 и что каждый ИЗ них ведёт себя так, как если
Дополнение 4
469
бы только он один находился в сосуде объема V, т.е. он как бы не заме-
чал В СОСУДЕ присутствие Двух ДруГИХ ГЯЗСВ. ТзКЛЯ СЖЪ. Jtwtfd .ТИШ/Ч^СИН?
BCUfecmffdT й СЛ1СГЫ flfH₽ ^ЛЛТ^ЧДЮ/ПУ d/JWfl. ШКОЛЬНОЙ.
Каждый отдельный газ занимает весь объём сосуда^ т. е. I] = =
= Уз = К и имеет своё так называемое «парциальное давление»:
F]: Рз, Pg, причём давление Р всей газовой смеси равно сумме парци-
альных давлений:
Р = pL + + р3-
и этом состоит тэк называемый «закон Дальтона», Каждый газ удовлетво-
ряет своему уравнению состоя ешя, т. с. имеем равенства
л яг F2V = ЛГ. P3V = лг,
ЛЧ ] Л1 2 А1 5
так как темпера туры газов одинаковы и равны
температуре 7' газовой смеси. Отношсешя
называются объёмными концентрациями той
в смеси. Таким образом,
р _ Й'Г
Р1-ЛЬ
Р - г
Химический потенциал /ъ (Р. 7’) для i-ro газа в смесиъ или его «пар-
циальный химический потенциал»^ ранен сю собственному химическому
потенциалу г. е.
где г = 1, 2, 3 и р (/< 7’) — химический потенциал идеального газа. Таким
образом,
№ (Р, Г) = (Т) + ]п п = (Г) + hQ,
где I = 1, 2., 3 и До, (Т) — некоторые функции, зависящие только от темпе-
ратуры Т. Подставляя эти выражения для химических потенциалов в полу-
ченное условие химического равновесия, получаем равенство
XMiJWT) d- A1^M(T) - гм:;^(7') = -Я7'(2 1цС| + 1пс2 - 2 Incj).
+70
ГлаваS
Следовательно, приходим к условию
в котором введено сокращенное обозначение it (Г) л л я появившейся ком-
бинации величин, не зависящих от объемных концентрации С]. Сз: cj. Ве-
личину назывяЕот «кое сета егпш химического равновесия», или просто
«константой равновесия», а выведенное условие химического равновесии
«законом действующих масс Гульдбергя-Влаге»
Дополнение 5 к гл, Н
Электрохимическое равновесие
Рассмотрим следующую сложную термодинамическую систему. Пусть
имеем цилиндр с поршнем и теплопроводными стенками, находящийся
в термостате, моделирующий внешние условия R Г, и пусть внутри этого
цилиндра находится так называемый «гальванический элемент Даниэля»,
показанный Fia рисунке.
Водные растворы солей сульфата цинка ZnSOd и сульфата ме-
ди CuSOj, разделены полупроницаемой перегородкой (проницаемой для
ионов SO^- н непроницаемой для ионов Zn+4 и Си++). В раствор соли
ZnSO.i погружён цинковый стерженёк Zir В раствор соли O1SO4 пенружён
медный стерженёк Си. К цинковому и медному стсржипжам, являющимся
электродами гальванического элемента, проводниками присоединена регу-
лируемая «компенсирующая» электродвижущая сила ЭД С £}), компенсиру-
ющая ЭДС £ самого элемента, и электромоторчик, на вал которого намота-
на нить, на конце которой подвешен груз массы Л/. Проводники, компен-
сирующая ЭДС il обмотка электромоторчика образуют внешнюю электри-
ческую цепь нашего гальванического элемента.
При термодинамическом равновесии внешняя ЭДС £о в точности ком-
пенсирует электродвижущую силу ЭДС £ гальванического элемента (тРе.
ffl — при этом электрический ток / во внешней цепи раней пулю. Если
ЭДС станет немного больше или немного меньше ЭДС f гальваническо-
го элемента, во внешней цепи потечёт ток / водном или противоположном
направлении, который заставит вращаться вал электромоторчика в ту или
другую сторону при этом груз будет подниматься; или опускаться до тех
Дополнение 4
47]
пор, пока электрический ток / Ere прекратится. При этом в самом гальва-
ническом элементе часть цинкового электрода Zn «растворится» в раствор,
а часть меди из раствора «осядет» на медном электроде Си. нли наоборот
В качестве термодинамической системы рассмотрим систему, состо-
ящую из растворов ZuSOj я CuSO.^ перегородки, разделяющей эти рас-
творы, и обоих стержней-электродов Zn и Си. Эта система обведена на
рисунке пунктирной линией.
Имеем замкнутую поверхность, ограничивающую нашу систему. Си-
стема и окружение системы здесь сложные.
Уставу г /?№Ноегест1Я
Рассмотрим очень простой пример «элок1рохимнческого равновесия»
в очень простой конкретной системе. Пусть цинковый электрод помещен
в водный раствор сульфата цинка Z11SO4, при этом ни ежовый электрод
начнёт сразу же растворяться в растворе сульфата. Однако нейтральные
атомы пинка Zu в раствор сульфата цинка перейти не могут, в него мо-
гут перейти только ионы цинка Zn++. Поэтому при растворении цинкового
электрода, т.е. при отрывании атомов цинка от него, на поверхности элек-
трода будет происходить электрохимическая реакция
Zn^ Zn++ + 2с.
Электроны останутся на электроде, а ионы Zn+4 уй-
дут в раствор. В результате через некоторое время устано-
вится равновесие, при котором ци иконы и электрод приоб-
ретёт некоторый отрицательный электрический заряд, кото-
рый будет удерживать ионы Zn++ от дальнейшего перехо-
Zr
ZnSO.
да их в раствор. Установится, как говорят, ческой
Найдём условие этого равновесия-
472
ГлаваS
Начнём с того, что выведем тождество Гиббса для открытой систе-
мы. наздымеился такая сыстквд, WCCff мрто/Jflw .иажхчл ^3-
-мсияться. Возьмём единицу массы вещества равновесной открытой систе-
мы и обозначим через -и, в, и внутреннюю энергию^ энтропию, объём этой
единицы массы. Назовём эти величины удель дай энергией, удельной энтро-
пией и удеяйным объёмом. Очевидно, они равны
Г 5 V
ft = ТТ, Ь = . . , t- =
АГ Af Af
где Л7 — масса открытой системы, д — 1/рт где р — плотность массы веще-
ства системы. Указанные величины удовлетворяют тождеству Гиббса для
зл^рытой системы (каковой является рассматриваемая «единица массы»):
dw = Td.s — Prfvj
где Т — абсолютная температура, Г — давление системы.
Выведем тождество Гиббса для открытой системы. Очевидно, что
ri£7 = u dAf + Af du. dS = 5 dAf + Afds. dV = t; dAf + Afdu;
а следовательно
d£7 - TdS + PdV = (u - Ts + Pv)dM.
т. e. имеем так называемое «тождество Гиббса л ля открытой системы»:
d{7 = TdS - PdV + judAf.
Величина = u - T.$ + Pr называетеяудельиыим хцдшчёясши шж/ф-
длам, или просто химический лот^не/нлтаи (т.е. химическим потенциалом
единицы массы вещества). Обозначение Д мы используем для л#с*. тарного
тимического лотсл^па.та, т.е. химического потенциала одного лш.тя веще-
ства (т.е. массы вещества с числом частиц Af, равным числу Авогадро,
Агд = 6 1023). Согласно приведённому тождеству Гиббса
Жт
ЯМ
Д =
Рассматриваемую простую термодинамическую систему с цинковым
электродом, погружённым в раствор сульфата цинка, можно считать систе-
мой, составленной из двух как бы ^срастворов» ионов Zn1 11 двух систем
а и 6. В металлическом цинке ионы п++ составляют остов кристалличе-
ской решётки > которая наполнена «газом свободных электронов» цинкового
электрода. Металлический цинк и раствор сульфата цинка являются откры-
тыми сис темами, обменивающимися ионами Zn+-I\
Дополнение 4
473
Получим условие термодинамиче-
ского ровно вес ия для рассмотри пасмой
системы, пользуясь принципом Планка.
Для этого рассмотрим две системы и и Ь»
/девдовесные сами но находящиеся
и контакте друг’ с другом.
Нас интересуют условия равновесия,
когда системы д и & приходят в равно-
весие друг с другом. Чтобы использо-
вать принцип Плачка> окружим обе систе-
мы п и Ь, находящиеся в контакте, изо-
лирующей их оболочкой (изображённой
овалом па рисунке}. Пусть температуры,
давления, масськ электрические потенци-
алы обеих систем соответственно ранг гы
| -J"t£ Afaj S^Li И
/V Aft, ^6
(считаем, что внутри каждой системы
электрическое поля равно, нулю и поэтому система в целом имеет опре-
деленный электрический потенциал).
Согласно принципу Планка сдояаямие извдцро&пшой
U fflOFfrW П/Ш ,7WUfl.W flEJJJfflVOrtfrHflJW
hj Г£3£?мйяния. ус>ойлтво/ши^еяу£Ж?йи^л1 d(E7 4- IV) = 0r rfV = 0.
JAf = 0r (5Q - 0 (где Q — полный электрический заряд системы, IV — пол-
ная электрическая энергия системы), влршщия энтролгш /шотде нулю, т.с.
когда
5S = 0.
Среди виртуальных перемещений рассмотрим только следующий oipa-
ниченный их класс: такие перемещения, для которых каждая из систем и
и & равновесна сама по себе.
С учетом электрической энергии тождества Гиббса для систем а и 6
записываются в следую гнем виде:
4" Ид) = 4- /1й rfjY/i^ + dQtti
d(t7t. 4- TV},) = Т& tf5ji — ЙЦ. + gt- dQt-,
где lVn и Hjj — электрические энергии систем а и fr.
При получении заряда 5Q проводником с потенциалом электриче-
ская энергия проводника Иг увеличивается на величину t5IV = ^i5Q. Обо-
значим для краткости (/* = (Л ч- 1Уа и (7* - (7Ь -р И^. Так как каждый ион
массы m имеет заряд ze, где е — абсалкпнал величина заряда электрона,
474
ГлаваS
г — валентность иона, то ед- z^-
Таким образом
+ J а р J а 1- (диЧ- т'ра) <5Afa,
' №ъ + J 6 XV J 6 - ть (ш, + If w)
Теперь, согласно ПлаЕтку, энтропия S' nanteu неравновесной сиетгл^ад,
ла определенна (илтеню лгз определению), равна сулше энтропий Зи и
ее равновесных частей:
S = 5й + Sjj.
Планк правильно определяет энгсгроиию лрон^аданого неравновесного со-
етояжя еистелгы как су-илгр энтропий его равновесных частей (у нас рав-
новесные сами но себе части а и it системы).
С помощью условий JU* + г5!7* = О, <5V7 - JV7 = О, + <5ЛГь = О
ИСКЛЮЧИМ из рассмотрения вариации величин ДЛЯ системы bT так как для
МИХ
6U? = -5U*. АУь = Шь = -SM„.
Таким образом^ для вариации энтропии полной системы для произ-
вольного виртуального перемещения из её состояния равновесия получаем
следующее выражение:
)S = (5Sa + AS[. =
ft
ZE ZE
ph 7rT "I" 7r7 ^a
*+ —-^ - и/а---------------?=— шд.
Учтён теперь, что вариации W*, £Va, ^Мз независимые. Как следу-
ет из принципа Планка, вариация знтропии ионной системы дли состояния
равновесия равна нулю: JS = 0. Следовательно^ имеем следующие нвод-
ходцшде и достаточные ршшлмрив^^бгй элемирах^иичесяя^
равновесия:
I
Т =а
л
Первое условие означает, что = 77 (температуры обеих систем й и 6
при равновесии должны быть одинаковыми). Это условие твляявод? рав-
НАвесня. Второе условна пдначаст, что давления PJE = /7 R обеих системах
Дополнение 4
475
а н Ь при равновесии должны быть одинаковыми (так как уже Та = 7*}.
Это очевидное условие /эллмлгеоыя. Третье условии (так как
T-c = Ть) даёт следующее соотношение:
+ 7г7^ь = JU|i + т^Е‘
которое и является искомым «условием электрохимического равновесия»,
В это условие входят удельные химические потенциалы. Умножая пра-
вую и левую части приведённого соотношения на массу одного моля, рав-
ную /Удт, где Агд — число Авогадро, m — масса иона, получаем
№ + 5!^^ = Да +
где Д(|, rtflrtteftifUrtfjw и Т7 — так называемое «чис-
ло Фарадея». Величину fjr = Д + ;?.?v назовём «молярным электрохимиче-
ским потенциалом»,
Условие электрохимического равновесия состоит. таким образом,
в требоваЕШи, чтобы электрохимические потенциалы ионов, которыми об-
мениваются контактирующие системы, в обеих системах были одинаковы-
ми. т. е. чтобы выполнялось равенство
?№ = Tfa,
где ^,| = ДМ + = ^6 + " удельные электрохимические потен-
циалы.
Я1 pc.w«jfjf лл₽кв^ммгнл*ич£слого /гавновЕсия елдйтш,
что рлвддевдш cyujecjwtfytf/H отлинял tf/w куля ломенфьдлй#
Др = -^а - pt. рйВДОйЁСНЫЛШ CWCJH£W№ ft U Ь,
Действительно, так как рассматриваемые ионы в системах д н 6 нахо-
дятся в разных условиях, то Так как. однако, i/u = i/ь, то. очевидно,
ТУе 7^
Вычислить величину екдчкд ааекюрйчйскйяо пйленцыдлд между
системами д и b термодинамика Ете позволяет, так как для этого нужно
знать конкретные выражения для химических потенциалов и р*.
Ушмическне потенциалы шмпонешп cwecu идеальны*
у /?ястео/?д электролита
Чтобы получить выражения для химических потенциалов ионов в рас-
творах электролитов^ рассмотрим для них модель смеси идеальных газов,
а затем, следуя Вайт-Гоффу, ^лодобшк ,ийЛ€к^?ы /адст^^нных яеадеме
я /рд.тбагт.теш/лмг рлстяорс лгат^^улам гдтлд wfieajbwow гизояяи сдеячл
476
ГлаваS
Рассмотрим доя простоты смесь газов, состоящую только из двух ком-
понент. Пусть имеем молекулы двух типов с массами ?П| и m-j. причём
JVi №
А v = 4г-ят; p3v = ir-pr,
Ал Ад
число молекул первою типа пусть райпо Лг| , а второю — Аг3. Смесь газов
пусть пребывает в равно вес ион состоянии в цилиндре с теплопроводны-
ми стенками под поршнем, обеспечивающим давление Р в смеси, причём
цилиндр находится в термостате с абсолютной температурой Г и имеет
объём У.
Для каждой) газа имеем своё уравнение Состояния^
где Рь — гик называемые «парциальные давления»
первого и второго газов в смеси, оказывающих эти дав-
ления на поршень. По предположению, рассматривае-
мая смесь является смесью идеальных пззоин поэтому
для каждою из них мы используем уравнение состояния
идеального газа. Полное давление смеси, согласно пред-
положению об идеальности смеси газов, таким образом,
равно
F = Pj + Р2.
Так как
ру = А' + RT.
Ад
тс
Pi = cj F. Г>2 = c2R
где С[, с? — концентрации газовых компонент в смеси, т. с.
А1 _ Лтз
01 = ArL + A’s ’ Сг “ АТ1 + Лг21
данные концентрации можно представить также в виде
П] ?ъ-.
С1 —-----;----: с-2 — --;----?
П1 + 7Ъ2 * П1 + 71а
где nij rij — ллотиосша молекул первого и второю типа и нашей
газовой смеси (те. числа молекул в единице объёма). Рассматриваемые
концентрации можно назвать также «молярными долями» газов в смеси,
Дополнение 4
477
так как числа молей первого и второго газов равны: mi = =
= и поэтому
с - К] с- -
1 Ml + Мй 1 42 Ml + Мй '
Вычислим теперь молярные химические потенциалы первого н вто-
рого газов. Для этого сначала найдём химический потенциал одного моля
идеального газа, который удовлетворяет уравнению состояния
PV = Я7.
Так как
<«7 = 7rfS - 7W.
и так как (У = Си 7, где с^ — моляр «ая теплоемкость газа при постол плом
объёме, то
dS = + pV = cv^ - dV;
а следовательно,
S = cv ] । l Т — Л In V + const =
= ^1п7 + Я1пЯГ- Я1пР +const = So(7)- Я1пР,
где SU(T) — некоторая функция, зависящая только от температуры.
Таким образом, имеем следующую формулу:
Д = J7 - TS + PV = с^Т - 7SfJ(7) + Р71пР + ЛТ = Д0(Т) + PTIqP,
в которой jln(7) — некоторая функция, зависящая только от температуры 7'.
Применим теперь эту формулу к обеим компонентам рассматриваемой
идеальной газовой смеси идеальных газов. Получим тогда соотношения
Д1 = Дй1 (Т) -Ь ЯТ h P1J Дй = /£{^(7) + JJ7 In Р2:
где Pij Р2 — парциальные давления газов в смеси. Тук как р = Ci Р и Ра =
= саР, где Р — полное давление смеси, то
Д1 = Мт (Р-7) + ftTIncj, Да = ^й(Р,Т) - УГПпса-
Согласно Вант-ГЬффу, молекулы растворённого вещества в сильно раз-
ба пл сипом растворе можно рассматривать как молекулы идеалы югп газа.
47В
ГлаваS
а потому для молярного химического потенциала г-го растворённого веще-
ства в растворе имеем выражение
gi = Дй (fi Т) + JVThiCi,
в котором Д1о(ИТ) — некоторая функция, зависящая только от полного
давления Р раствора и его температуры 7'; Ci — молярная доля i-ro веще-
ства в растворе, которая определяется с учётом рас творите ля ? ДЛЯ которого,
однако, формулу приведенного вида написать нельзя, так как молекулы рас-
творителя никоим образом нельзя считать молекулами идеального газа.
Закои раздав i/я Остпводьдй и Нернста для
нотемфшла электрода
Выведем условие «диссоциационного равновесия» ионов в раство-
ре электролита. Аррениус предположил, что нейтральные молекулы рас-
творенных солей, кислот и оснований в растворах электролитов уже в мо-
мент приготовления раствора (до пропускания через, него электрического
тока} частично распадаются на положительные и отрицательные ионы. Та-
ким образом, в растворе электролита происходит реакция диссоциации:
ан л* - а-,
где АВ — символ нейтральной молекулы, Л+ — катиона. В~ — аниона.
Предположим, что заданы давление Р и температура Т раствора элек-
тролита, а также исходная молярная доля нейтральных молекул АВ, по-
мещённых в раствор
.0 _
СЛВ дгр
где — число молей растворителя. Тоща в растворе установится adwero
цыйцыонндо додоввеяде», которое, по Аррениусу и Оствальду, следует ха-
рактеризовать так называемой «степенью диссоциации Обозначим с по-
мощью п4 д — объёмную концентрацию Ехсраспавпсихся молекул в равно-
весном растворе электролита, с помощью — исходную объёмную кон-
центра щ по этих молекул (рассчитываемую по формуле = ЛГд^дп/Vj.
Тогда «степенью диссоциации» называется отношение
rtAB “ _
rj ”а>
Дополнение 4
479
т е. отмгагение ^славшихся люл^кул # /швндаЁСнам
распделре Jt исходной ллчлльияы объемной вдогаш?сти этих дголеиул -4/>.
взятых при приготовлении раствора. Таким образом,
пая = (1 - а)пдв
Обозначим через ид . и объемные концентрации катионов и анионов
в рассматриваемом равновесном растворе электролита. Очевидно,
пА+ = апАВ, Пв- = an*w,
так как при распаде одной молекулы .4В получается одни катион Л4 и один
анион В
Условие химического равновесия для реакции диссоциации
ЛВ t5 Л+ +- в-
формулирусгся так же, как для химической реакции.
По виду уравнения химической реакции в качестве уг.тяяил
/иея^месуя необходимо составить уравнение для молярных химических
потенциалов. 13 случае рассматриваемой реакции электролитической дис-
социации это уравлепие, таким образом, имеет следующий вид:
Мда = + ^в-
Используя это уравнение* можно найти степень диссоциации а в рав-
новесной ситуации, характеризуемой величинами Р, Г и
Подставим в приведённое уравнение диссоциационного равновесия яв-
ные выражения дли молярных химических потенциалов. Так как. ио пред-
положению, раствор сильно разбавлен, то для химических потенциалов,
следуя Вант-Гоффу, возьмём выражения для идеальных газов. Получим то-
гда соотношение
flXB(P,T) + RTlncAB =
= ЙД4 (Р>Г) + ЯГ In сл+ + ЭД (Р,Г) + ЯГ In Св .
Следовательно.
ш (£^} _ _ ьх(р т)
Выражение, появившееся в правой части, мы обозначили ki /<. где А —
так называемая «констаЕгга диссоциации». Константа тга зависит только от
4-КО
ГлаваS
давления Р и температуры Т электролита и не зависит от концентраций
Сд + । Cjj - j Од/3 нём.
Именно его ггрнчнЕге того, что она пе заьисн г от концентрации, её и на-
зывают Потенцируя приведённое равенство, приходим к окон-
чательной формуле:
£^ = А77<Т).
Подставим в эту формулу выражения для концентраций:
_ __________^.4+_________«в пае
д+ пд+ + пе- + ПЛВ + Пр пр ₽ 71-р
где пр — объёмная концентрация молекул растворителя. Гак как мы рас-
сматриваем сильно разбавленный раствор, пз пд + ,п.д- ,пае и в хо-
рошем приближении можно считать, что
Пд+ + пв- + ПАЕ + Пр Пр-
Такнм образом, получаем
Сд+ — — Пр — ОСдП. Сб - г>Сдв, САБ — (1 - а)сЛБ
Поэтому окончательно имеем следующее ^условие диссоЕ/шл/ионного
рдялиаеспя»:
Это знаменитый «закон разбавления Оствальда». СогласЕто ему, при
увеличении степени разбавления при неизменных давлении F и температу-
ре Т, т.е. при Сдя —* 0 (<?4£ = 0 при так называемом «бесконечном» раз-
бавлении}, чтобы удовлетворить закону Оствальда, степень диссоциации а
должетз стремиться к единице 1.
Таким образом, согласно закону Оствальда в сильно разбавленном рас-
творе лрДМИич^Кй «се лейтрс/льлые лш-теАуты /1В /маствелреЛНОЙ ео.ш. к«с-
jmjw или с^исщднмя ид woj/w Л+ и 2? .
Обратимся теперь к выводу «формулы Нернста» для потенциала элек-
трода н его формулы для ЭД С гальванического элемента Рассмотрим снова
цинковый электрод, помещённый в водный раствор сульфата цинка.
Воспользуемся условием электро химического равновесия Обозначим
индексом I ионы цинка Zu 1 1 в металлическом цинке и индексом 2 ионы
Zn++ в водном растворе Zn$O-|. Тогда можно положить, что
/ц (ЛГ) = мо(ГП ^(Р, Гоа} = + ЯТ 1п^.
Дополнение 4
4HJ
Поэтому
Д1о(Р,Т) -I- £ = ^2о(Р,Т) + + ЛТIncj.
С ледова хельно, получаем следующую «формулу Чернота» для скачка
электрического потенциала на границе электрода и раствора;
Др = 1^! - 1^2 = Д<^п + —“ Ш С,
ZZ
в которой — скачок потенциала для раствора с концентрацией с = 1.
Скачок потенциала Др — это разность потенциала электрода и потен-
циала раствора ^р:
^р,
Следует отмстить, что непосредственно экспериментально измеряют
не электродные скачки потенциалов а ЭДС £ гальванических элемен-
тов, соСтаклфнмых из различных электродов. Затем пересчётом находят са-
ми электродные потенциалы.
Рассмотрим, например, «элемент Даниэ-
лян. В нем медь является положительным по-
люсом элемента, а цинк — отрицательным по-
люсом. ЭДС этого гальванического элемента
равна разности потенциалов медного и цин-
кового электродов:
£ “ ^Сп — V’Zn
Далее,
^Си — Траста = Д^?и + 1° [Cu+ )j
₽Яп ~ 'Ррас-гв — + у?: Ill [Z11 1 1 ]-
Следовательно,
ЛГ
£ = ^Са “ — ^0 + 777F Ь
[Си++]
|Zn++l'
Получили «формулу Пернста» для ЭДС гальванического элемента.
В этой формуле [Си++] и ^п++] обозначают (молярные до-
ли) ионов Си1 1 в растворе CUSO4 около медного электрода и ионов Zn+ 1
в растворе ZnSO-i около цинкового электрода.
4Й2
ГлаваS
В электрохимии потенциал электрода определяют следующим обра-
зом. Из рассматриваемого электрида и нсюоторого стандартегого (легко вос-
производимого в лаборатории электрода^ например, гак называемого во-
дородного электрода составляю! гальванический элемент и измеряют его
ЭД С, Потенциалом электрода -р называют ЭД С получившегося гальвани-
ческого элемента;
£ =
причём под положительным направлением ЭД С понимают направление ст
исследуемого электрода к стандартному электроду. Таким образом, потен-
циал водородного электрода условно принимают равным нулю.
Рекомендуемая литература
1) А. Ярив, Введение в теорию и при ложе ешя квантовой механики,
Москва, изд. «Мир», 1984.
2) Л. Солимар, Д. Уолш, Лекции по электронным свойствам материалов,
Москва, изд. «Мкр», 1991.
3) С. Зиь Физика прлупроведниковых приборов, тт. I -2, изд. «Мир», 1984.
4) Г. И. Епифанов. Ю, А. Мома, Твёрдотельная электроника, изд. ВШ,
]986.
5) Дж. Блей к мор. Физика твёрдого тела, Москва, изд. «Мир». 198В.
6) Н Ашкрофт, Н. Мермин, Физика твердого тепа, тт. 1-2, Москва, изд.
«Мир», 1979.
7) В.. Шокли, Теория электронных полупроводников, изд. ИЛ, 1953-
Предметный указатель
Абсолютно чёрное тело± 26, 27, 81, 82,
88
Автоэлектронная эмиссий, 279
Анодные лучи, 122
Атом
— возбуждённые состояния, 14]
— модель Резерфорда, 141
— основное состояние 140
Атом водорода, 27. 141, 173. 194
Атомный спектр
дискретный, ] 71
— непрерывный, 171
Барьер Шоттки, 427
Елоховские функции, 324, 346
Бозонът, 244, 245
БорОВСкнн радиус, 144
Варнапионное условие Лагранжа. 224
Вероятность макросостояиия, 221, 222,
246. 247, 251,252
Виртуальное перемещение, 454
Вояна, I I
— бегущая 45
— стоячая, 45
Волновая функция
— вршеннМ 164, 166
— фалоьый множитель, 163, 166
Волновое уравЕзсние, 40
Волновое число, 164
Волновой вектор, 46
Волновой пакет. 322
— волн де Бройля. 167
— гауссовский, 167
— импульс, 167
— импульсная ширина, 167
— расплывание, 167
— функция формы, 167
ширина, 167, 16Йа 170
Волновые функции
— их пространство, 194
— скалярное произведение, 195
— условие нормировки, 63, 163
— условие ортонормировкв. 165
— условия непрерывности, 172, 181
условия непрерывности
производных, 181
условия ci[[нвания, 180» 186
- физический смысл, L98
Волны де Бройля. 166
ПОлкг-аmjiCpnia яарактСрнСтика, 410,
442, 451
Вольт-фарацная характеристика, 43 Я
Время рекомбинации, 391, 396
Время свободного пробега
дырки, 386, 389
— Электрона. 389
Газовая смесь идеальная, 469
Газовый разряд, 112
- высокочастотный^ 3 I
— дуговой. 112
искровой, 1 ]2
— коронный, 112
тлеющий, 112
Газоразрядная трубка. 27, 31» 112
Гальванический элемент, 470
— Даниэля, 470
- ЭДС. 470, 482
Гармонические колебания. 2\ 43, 60
I IPE ДМ El11ЫЙ УКАЗАТЕЛЬ
4N5
Гиромагнитное отношение. 127
Горелка Кунзена, 86
Граничные условия
— Борна-Кармана, 45,46, 218.292,
293 ? 344, 355
— нспсрывнести
---ВОЛНОВЫХ функций,, 180
производных ВОЛНОВЫХ фуЕЗКЦИИ,.
180
нулевые, 35, 216, 291
ДаалеЕше насыщенного пара, 461
Д воина ч гетероструктурв, 447
ДнШ111иИ JI [>1<МЧ IRJ1L3JI Ы ILJ Й4 Я 7.11L, 183
нечётные решения, ] 84
— трансцендентные уравнения, 186
— чётные решения, 184
Делительная машину 132
Дельта-функция Дирака, 165* 192
Дифракционная решётка, 132
Диффузионная длина
— дырок, 408
— электронов, 396* 408
Диффузия
дырок. 387
— электронов, 387
Длина свободного пробега
- дырки, 386. 389
— электрона, 389
Дрейф
— дырок, 360, 385
— электронов, 385
Дырка, 335
Жидкий гелий Н^р 244
Жидкий гелий Не4, 214* 244
Закон
— Всемирного 1ЯЮТСНИЯ. 68
индукции Фарадея, 24
— отражения света, 16* 17
— преломления света, 16, 17
— ]>айномернпго распределения
---энергии по степеням свободы, 97,
99, 103
— раявомервого распределения энергии
но степеням свободы. 65
— ссжранеиня импульса, 73
— сохранения энергии, 72* 114* 143
Закон Бойля-Мариотта, 76
Закон Видемана Франца, 265
Закон Виза* 65 68,81, 92, 97
Закон Гука, 76
Закон Да.1ы^|[ан 469
Закон Дылоига и Пта. 99, 100, ЮЗ. 104,
106
Закон Кирхгофа, 80, 88
Закон Рэлея, «К, 9N, 99
Закон Рэлея-Джинса, 30, 58* 59* 63, 90,
97
ЗакоЕ! Стефана Бопьцмава, 59, 65, 66,
68. 81. 88
Закон Фика
— для дырок, 389
— для электронов, 389
Закон действующих масс, 367
Гульдберга Вааге, 468, 470
ЗакоЕ] разбавления Оствальда, 478* 480
Законы
— термодинамики. 90
- двойного лучепреломления, 21
— классической механики, 19, 68. 99,
141
механики, 142
— теплового излучения* 34
— электродинамики, 33, 142
— злевггролиж 151
Зона
валентная^ 321
— Проводимости, 321
Зоны Ьриплюзша, 313
Идеальные системы частиц, 214
Излучение
— абсолютно чёрного тела, 48, 68
— атома, 142
486
I IPE Д MEI11ЫЙ УКАЗАТЕЛЬ
— объемная плотность энергии, 49
— разреженных газов, 27
- спектральная объёмная плотность
энергии, 48. 60
тепловое, 27, КО
Изотопы, 122
Импульс Фермйч 267
Ил гегрвл Пуассон^ 257
Интеграл Фурй, 192
Интенсивность, 28
— параллельного пучка. 28
— расходящегося пучка, 29
спектральная, 30
Интерференционное условие Вульфа-
Брэгга, 135
11]ггерферш[unoj [иый эксгi ернмеит
Юнга, 130
Интерференция многолучевая. 132
Искривлённые энергетические зоны,
424
Испускагельная способность, 28
- полная, 29, 59, 65
— спектральная, 48-50, 60, 66ч 69
Камера Вильсона, 119
Катодно-лучевая трубши 111- 149, 170
Катодные лучи, 113, П5Т 149, 167
Катодслюмпнесцеиция, 446
Квазиклассичсскос приближение, 167
Квантован вероятность, 163
квантовая гипотеза Планка, 26, 61, 97,
98, 104, 141
К нантоно-м 12хи пн чес к не зэд (ач 11
одномерные, 162
Квантовое условие Бора, 142
Квантовые орбиты, 141, 142, 145
Квантовые эффекты, 162
Квантовый скачок
— редукция волновой футпшин. 211
КвЭНТОВЫн скачок редукция ВОЛНОВОЙ
функции, 203, 211
Кванты света, 27
Кванты энергии. 26, 34, 6S, 97
Классический газ. 215
— изолированный, 247
— макрососголиия, 247, 250
микросостоянпя, 247, 248
— равновесное состояние, 247, 252, 259
энтропия, 260
Komi itojeobc кая длила, 74
Конденсация боз£-зйнштсйновская, 245
Константа диесоцмацни, 479
Константа распространения, 298 300,
303, 304, 307, 309. 311-314, 316.
322 324, 329, 333, 335, 346
Константа химического равновесия. 470
KdirjaK'J iiM раЧиОС гь иоTizimuajrOB, 398.
403, 475
Концентрации газов в газовой смеси,
476
Концентрация, 467
— дырок. 362
— электродов, 362
Корпускула, 14, 68
Коэффициент диффузии
— дырок. 389
— электронов. 389
Коэффициент подвижности
дырок, 359, 370, 386
— электронов. 359. 370, 386
Коэффициент прозрачности
— потенциального барьера1 182, 183
Коэффициент прозрачности
потенциального барьера, L 81
Лапласиан, 216
Люминесценция радии ционнаяь 446
Модовые решения^ 38, 216. 219
МаСС-СI lewrpoi раф. 122
Матрицы Паули, 200
Метод Лагранжа неопределённых
множителей. 241, 253. 457,460
Метод Фурье разделения переменных,
34.41, 216
Микрочастицы
I IPE ДМ El11ЫЙ УКАЗАТЕЛЬ
487
— их неразличимость, 2.14
— их одинаковость 214
Множитель Больцмана, 62, 64
Мода излучения, 34. 35, 41, 61
— возбуждённая. 64
квантовая, 61
— классическая* 61
Модель Кронита noFin:ih 290
— без внешнего поля, 290
— зонная структура спектра, 317
— конечной длины, 291
проекция волнового вектора, 310
с многими электронами, 318
с условием Борна Кармана, 292
— случай бесконечной смэк. 30+
— случай нулевой связи, 306
— теория сильной связи, 314, 316, 317
— теория слабой связи. 343
— энергетический спектр, 292
Моль, 472, 475
Молярная масса, 56, 466
Молярный МС. 269
Монитор компьютера* 112
Небесная механика, 19
Неонрсдслён![ость ф]йнчсской
величины, 154
Неопределённые множители Лагранжа,
224, 226, 231,253, 259, 457, 460
Нобелевская премия. 148, 410, 447
Носители тока
— генерация и рекомбинация. 390
— диффузия, 387
— дрейф, 385
Носители электрического тока, 265
Объёмные концентрации газов в смеете,
469
Оператор
собственные значения, 196
— собственные функции* 196
— унитарный, 196
— эрмитов, 195
Оператор трансляции, 294
— собственные значения, 296
- унитарность* 294
Операторы
— декартовых координат частицы, 1.99
коммутирующие 194
не коммутирующие, 194, 212
— проекции импульса части чьи 199
— проекций момента импульса
частицы, 200
физических величин, 194
Определение
внутренней энергии неравновесного
состояния, 455
— снобоцной энергии неравновесного
состояния, 463
— термодинамического потенциала
неравновесного состояния, 464
— энтальпии неравновесного состояния,
463
- энтропии неравновесного состояния,
459. 460. 474
Основные законы рп-перехода, 406, 419
Осциллограф, 112
Осциллятор
— Планка, 26, 60, 90, 93
классический, 25, 60
Отношение заряда к массе, ПК, 150
Падение на ядро, 1.41
Парциальные давления [азов
и идеальной смеси, 469, 476
ПереетаЕювочпые соотношения, 201*
204
Плотность электронных состояний
в валентной зоне, 358
в эоне проводимости, 358
Поверхностные состояния, 433
Поглощдтельиая способность. 79 81
Полевой транзистор, 438
11олнос внутреннее отражение, 447
Полупроводник
— п-типа, 360, 375
488
Предметный указатель
— p-типа, 375, 382
— акцепторный, 3R2
— донорный. 375
с рп-псрслодон, 397
— чистый, 362
11олу проводниковые приборы, 440
Полупроводниковый диод
— Зинсра, 443
— лавинный, 443
— обращённый, 442
— светодиод. 446
— туннельный, 440
— фотодиод^ 445
фоторечиеюр, 444
Полупроводниковый лазер, 446
Постоянная Больцмана, 56, 57, 92, 362,
376
11остояиная Планка, 34+ 59, 68, 69, 72,
74, 92, 121, 144, 152-154, 162, 167,
236, 364, 366
Постоянная Ридберга, 146
11о<?тояиная Стефана-Больцмана, 66
Постоянная Холла, 361
Постулаты Бора, L4I
Г Г отс j । циал тая ям а, 171
— прямоугольная
---глубина, 171
---ширина, 171
Потенциальный барьер, 177
прямоугольный
---высота, 177
ширина, 177
I [ранило Стокса, 99
11римесь
— акцепторная, 371
— донорная 371
Принцип Гиббса. 454,455, 459
Принцип Гюйгенса, 21
Принцип Планка, 458, 459, 473
Принцип запрета Паули, 215, 222, 223,
319
11риицип локального равновесия, 455,
460
Принцип минимума
— свободной энергии. 463
— термодинамического потенциала^ 464
— энтальпии, 463
Работа выхода
электрона из металла, 72, 273
— электрона из полупроводника, 428
Равновесие диссоциационное. 479, 4R0
Радиоактивность, ИЗ
Радиоантенна, 33
Радиометрический эффект. 149
Распределение
Бозе Эйнштейна^ 245, 246
Больцмана. 402, 412
- Максвелла. 89. 215.228. 231. 247,
255, 258, 261, 269
— Ферми-Дирака, 214-216. 228, 265,
266, 270, 362, 376
Реакция диссоциации, 478
Рентгеновские лучи, 113
- дифракция, 352
Рснтгслоструктурнын анализ, 133
Ряд Фурье, 41
Сверхтекучесть Holl, 245
Световые кванты, 78
Светоносный эфир, 15, 20
Свободная энергии. 463
Свободное движение частицы. 163
Свободные электроны^ 214, 265
Сила изображения, 277
Система материальных тонем, 19
Скорость
— объёмной генерации, 390, 392
— объёмной рекомбинации, 390н 392
Скорость волны
групповая, ПО
— фазовая. ПО
Скорость чвукан 20
Скорость света, 22
Скорость электрона
— дрейфовая, 386
I IPE ДМ El11ЫЙ УКАЗАТЕЛЬ
4Я9
— тепловая, 386
Собственные значения
— вырожденные, 196
— кратность выролщсниЯч 197
— физический смысл, 19В
Собственные функции базисные, 197
Солнечные батареи, 451
Солнечный xicmcei'i; 452
Соотношение Майора, 466
Соотношение Эйнштейна, 236
— для дырок. 389
— для электронов, 389
Соотношение де Бройля, 236
Соотношение неопределённостей, 15±
153, ]54, 170, 211. 236
Состояния ионизации электрона, 171
Состояния классического газа
— однородные по плотности, 248
однородные по температуре, 248, 25 К
Состояния рассеяния электрона, 171
Спектр потенциальной ямы
- дискретный, 173
— квазинепрерывный, 173
Спектральньл линии, 32
— головная серии, 32
серия Бальмера, 146
— серия Лаймаиа, Мб
— серия Пушена, 146
- серия линий, 147
Спектральный анализ, 32, 83, Й7
Спектроскопия, 87
CliCbciI ры
атомные линейчатые, 32, 141
— молекулярные полосатые, 32
— тонкая структура, 32
Спин, 126
Способность
испускагельная* 79, ВО
— поглощательная. 79, 80
Статистика
— Бозе-Эйнштейна* 214,234, 244
— Максвелла-Больцмана. 214, 247, 273
— Ферми-Днрйиа, 214, 244, 273
Стационарное состояние
его волновая фу им дня, 162
- его энергия, 162
Степень диссоциации, 478
Степень свободы, 57
спиновая, 127
Стоячие волны, 38
Таммовские уровни, 433, 434
Твёрдое тело
— свободные электроны, 215
— связанные электроны, 215
— атомные остовы, 215
диэлектрик, 320
— металл. 320
Температура квантового вырождения^
267
Теорема Блоха. 294, 297, 298
Теорема Вейля, 212
Теорема существования
и Сциле гаСлЕзОС гн, 40, 216
Теория р ?1 р-трапзистора, 4] б
— база, 417
— коллектор. 417
коэффициент усиления по току базы,
423
— коэффициент усиления по току
эмиттера, 422
усилитель мощности, 417
— усилитель тока. 417
- эмиттер, 417
Теория рп-перехода, 397, 400, 413
Теория Бардина контакта металл
полупроводник, 433
Теория БальцмаЕю, 215, 220-222, 227,
234, 237. 245, 247. 249, 250, 259
Теория Бора, 140
Теория Шоттки, 277
— контакта металл-полупроводник,
427, 430
Теория света
— волновая, 17, 20-23
— волновая твёрД1Уге.тьиая, 21, 24
490
Предметный указатель
— волновая электромагнитная, 23, 24,
27, 31
— квантовая. 25, 26
— корпускулярная» 17, 22, 23
Теплоёмкость, 57
— кристаллической решётки, 26, 273
— молярная, 273
— молярная твёрдого тела, 104
— молярная ^jJCKipoi]OB: 272
— свободных электронов, 271, 273
Теплоёмкость газа
При ПОСТОЯННОМ ДаШЕС Е1ИИ, 263
при постоянной объеме» 261,263, 477
— соотношение Майера» 263
Тепловое излучение, 27, 61, 92
Термодинамическая система
— закрытая, 453
— hsujih рОван пая. 454
многокомпонентвая, 454
многофазная, 454
— неравновесные состояния, 454
открытая, 453, 472
— равновесное состояние, 454
Термодинамический потенциал, 464
Термос [h)mhi ice иеги[няп 445, 446
Термостат, 56, 57, 61 64
Тсрмоздс, 281
ТерьтлЕкгронная эмиссия, 134, 273,
275
Тождество Гиббса
— ,(ля закры той системы, 472
- для открытой системы, 472
Ток насыщения, 410
Тормозное излучение, 446
Туннельный эффект, 177, 182» 279
Удельная
внутренняя энергия, 456, 472
— ЭНТрОПня, 457. 460» 461, 472
Удельная теплоёмкость, ] 00
— при постоянном давлении» 466
— при постоянном объёме, 466
Удельный ойъемт 456,46 Ц 472
Ультрафиолетовая ка тас трофа! 31,59,98
Универсальная газовая постоянная, 56,
262, 263, 272, 466
Урапненче Клан перона-Клаузиуса. 462
Уравнение Пуассона, 400, 413, 430
Уравнение Шредингера, 211
— временное, 216, 217
— стационарное» 162, 163» 171, 178^ 184.
291, 293, 343
Уравнение состояния идеального гам,
476
УравЕэения Максвелла, 23
УравЕзения локальных балансов» 385
Ус кОршС-ш :К'1Смегзтарных часгиц, 160
Условие
— интерференции, 131
— сохранения числа частиц, 222, 224,
252
— сохранения энергии, 224, 240, 252
— фазового равновесия, 246. 458, 461,
464, 465
— хим л че снято равновесия, 246, 467,
468
электрохнынческого равновесия. 280,
425,47], 473
Условие Борна Кармана, 175, 176
Условие Вульфа Брэгга, 352
Условие квантования
— Бора. 141
— квазиклассическое, 174
Условие равновесия^ 85, 90
Условия
— граничные» 35, 38, 40
начальные, 35, 40, 125
Условия связей, 454
Факториал, 251
Ферми-поверхность, 268
Ферми-сфера, 268
Фермионы» 244
Физическая величина, измерение её
значений, 194
Физический прибор» 198
I IPE ДМ El11ЫЙ УКАЗАТЕЛЬ
491
Формула Больцмана, 94, 227, 223, 243,
346, 247, 260, 264
Формула Вина., 60, 89, 91
Формула Лоренца дм массы электрона,
121
Формула Нернста
— для ЭДС гальванического элемента,
480
— для потенциала электрода, 478, 480
Формула Планка, 34, 59, 60, 65, 66. 82,
за, 01. 93, 98, 234, 335, 244 246
для энергии светового кванта, 108
Формула Ридберга, 146
Формула Ричардсона - Дэш мана, 273,
275
Формула Рэлея. 98
Формула Рэлея-Джинса. 34
Формула Стирлинга, 96, 224, 240, 24 Ц
253. 259
Формула Шокли
— для вольт-амперной характеристики,
407, 409
— дигя вольт-фарад ной каракгернепгки,
415
— для контактной разности
потенциалов, 404
Формула де Бройля, 166
Фосфоресценция, 112
Фотоде^снюр. 445
Фотодиод, 445
Фотолюминесценция, 445
Фотон, 14. 19, 27, 31. 34, 61, 64, 68, 69,
72-75. 78. 9«, 108-111, 119, IJS, 142.
143. 153, 160,214,234, 235
Фотонный газ, 234
изолированный, 234
— макросостояния, 235
— равновесное состояние, 240
Фот отранзистор, 445
Фотоэффект, 26, 69, 72, 98
ФраутЕгоферовы линии, 82, 87
Химическая связь энергия, 19]
Химический анализ. 87
Химический потенциал, 458
— молярный, 227, 466, 468, 472
— ЕзарциальньЕЙ. 469
— равенство удельному
термодинамическому потенциалу, 465
— удельЕзын. 227, 472
Число Авогадро, 56. 57, 100, 103. 150,
250, 269, 272, 2911 472, 475
Число Фарадея. 151, 475
Экстремум
абсолютный, 231
условный, 231
Электроёмкость дифференциальная, 416
Электродинамика микроскопическая, 25
Э.'ЕСКТрОЛ]ОМИН€СЦ€11 ция, 446
Электромагнитные волны, 23-26, 33. 68.
141
— поляризация, 47
— полеречноегь, 47
Электрон, 14, 73, 75. 108, 109, Hl, I3S,
150, 153,2М
— голый и одетый. 334
групповая скорость, 322, 324
— квази классический, 167
— эффективная масса, 330
Электрон-дырочньЕе пары, 390
объемная генерации, 390
объёмная рекомбинации. 390
Э- К к"гр к э иная । СОрН Я mCl алло в
— квантовая, 265
— классическая, 265
Электронный газ, 215, 220, 222
— в термостате, 226
изолированный, 222
макрососгояння, 221
— М Н крОСОСТОЯНИЯ. 221
- молярный объём, 269, 272
— равновесное состояние, 224
— элементарные ячейки, 229. 270
— энтропия. 227
492-
Пред мен 1ЫЙ УКАЗАТЕЛЬ
Электронный пучок, 12]
Электропроводность
— донорного полупроводнику 38]
чистого полупроводника» 369
□jjCki рч 11 м 11 *-( l2 и к 11:1 i icj icj i циы.г, 280, 425
— молярный» 475
— удельный. 475
Элемент Даниэлу 48]
Элементарные частицы, 14
— ик реакции, 75
со спилом единица, 203
— со спинок половина. 200
Энергетическая светимость» 28
Энергетическая температуру 268
Энергетические диаграммы
— одноэлсктроагнык уровней, 423
Энергия Ферми» 266d 319
Энтальпия, 463
Энтропия
— классического газа. 261
макросостолиия, 246, 247
— риннОниСнОп) состояния, 243
термодинамическая, 262, 263
Эфир СВеТОЕэОС1гн1й|' ]\ 20
Эффект Коштпона, 61» 74, 75
Эффект ШОТТКИ. 279
Эффект зонном структуры. 192
Эффект химической связи, 1.90
Эффективная плотность сос тоянии
— н валентной зоне, 366
— в зоне проводимости, 365
Ячейки
— больцмановскне» 249» 250
- грубые, 221.237, 238
— макроскопически бесконечно малые,
249, 258
— элементарные, 220» 223. 236-238» 266
Именной указатель
Абрагам, 121
Авогудри, 472
Алфёров, 447
Аристотель, 17
Аррениус, 478
Б*те. 373
Бальмер, 147
Барлин.. 410, 433
Барпийни. 77
Блах Феликс, 294, 341
Бойль, 76
Больцман; 81, 88, 215, 258, 261. 264,
273,413
Бом,159
Бор, 27, 99, 14I, 143, 144, 147. 158, 160
Бори, 99, 107, 161
Брадлей, 22
Брагтсйн. 410
Бриллюэн. 313. 341
Брэтт (отец), 133
Брэгг (сын), 133, 352
Бушей, 83
Бухерер, 121
Влаге, 468, 470
Вант-Гофф. 475, 477.479
Варбург, 100
Ватсон, 148
Вебер, 103, 104
Вейль. 212
Видеман, 150, 265
Вильсон, 119
Вин, 60, 81. 82. 88, 89, 91.99
Волластон, 82
Вуд, 83
Вульф, 135, 352
Галилей, I 5
Гальвапк!, 470
Гау^смит, 126
Гейзенберг. 27, 152, 161
Гейслер, 112, 143
Гслъмгольн, 151
1ерц, 23, 112, 150
Гершель 33
I иббс, 90а 454, 455, 472
Г1 торф, 112. 149
Гольдштейн, 150
ГрИМАлЬДИ. 76, 78
Гук, 21, 76, 78
Гульдберг. 468, 470
Гюйгенс, 21,23, 77
Давыдов Ь.ч 427
Дальтон, 469
Дс Бройль, 109, В8. 143, 159. 166, 236
Дебай, 34, 99т 105 107, 161
Декарт. 15, 16
Десен, 8L, 88
Джсрмср. 109, 133
Джинс; 30, 97 99
Джоуль. 100
Дирак, 27, 127, 161, 228, 265, 266, 270,
273
Доплер, 88
Друде, 265. 370, 336
Дэвиссон; 109, 133, 140
Дюлонг, 81, 88
ЗиНф, 443
4-94
ИМЕННОЙ УКАЗАТЕЛЬ
Зоммерфслш 99 Планк, 26, 68.38, 90, 91, 93 , 97, 99, 161, 234, 455,458, 473,474
Карман, 39, 107 Кауфман, 121 Килби, 447 Кирхгоф, 79, 81, 83, BS, 90 Кдайисрои, 462 Клаузиус, IU0. 101,462 Корню, 22 Крёмер, 447 Кррнш, 290 Крукс, 112, 148, 149 Кулон, 148 Кундг, 100 Курльбаум: 89 Кгорп Мария, 99 Плюмер, 112, |49 Прсвб, 79 Прине 1 ей М, 89-91 Провоете, 81, 88 Нти, 81, 88 11уанкаре, 99 11уассон, 257 Рёмер. 22, 23, 77 Рамсей, 100 Резерфорд, 99. 121, 143 Рентген, 133 Ритц, 99 Роуланд, 83 Рубенс. 89 91
Лагранж, 224, 231, 233, 241, 253, 259, 457 Лаплас, 19 Лауз. 132, 133 Лейбниц, 19 Ленард. 112, 150 Линдеман. 99, 105 Лоренц, 25, 26, 98, 99, 265 Луммер, 82, 88-91 Рэлей, 30, 88, 97-99 Свал, 83 Сиеллиус, 16 Синее, 121 Стефан, 81, 88 Стакс, 99н 120 Стони, 150 Тальбот. 83, 86
Манер, 263 ь 466 Май кильсон. 23 МаксвелЛч 23, 24, 89h 101, 228L 247, 255, 269, 273 Мариотт; 76 Мцдляк^в, 121 Метт, 427 Тамм, 433,434 Тнзен, 81, 88 Томас. 127 Томсон Дж. Дж., 119, 149 Томсон Дж, П, 140 Уленбек, 126
Нерисг+ 99, 105ч 107, 478. 480, 481 Ньютон, 17, 19, 77 Фарадей, 24, 148,475 Ферма, 17 Ферми, 228, 265. 266, 270. 273
ОнгСтрСм, 79, 87 Оствальд, 478, 480 Физо, 22 Фон Нейман, 159 Фосс, 76
ГГаулщ 161, 200, 215, 222 11енни, 290 11еррен, 99 Франц, 265 Фраунгофер, 82 Френель. 21, 78
ИМЕННОЙ УКАЗАТЕЛЬ 495
ФрсЕзксль 1926 г, 127 Фуко. 22, 23 Фурьё, 35, 42 Шт™, 277, 427 Шредингер, 27, 152, 161 Шустер, 87
Ханнес. 358, 359 Холл, 360 ЭЙкСНт 107 Эйнштейн, 26, 72. 98, 99, 104, 105, 159,
Цащ 12] 236 Эрснфсст, 98: 99
Шоклир 358, 359, 398. 400, 401. 405,
407, 110,413, 115 Юнг, 21, 78. 130
Интересующие Вас книги нашего издательства можно заказать почтой eijjli
электронной почтой;
subKribe@Kd.ru
Внимание; дешевле и быстрее всего книги можно приобрести через Fiaui
Ингермет-магазив:
http://5hup.rcd.ru
Книги также МРНОГО приобрести:
I. Москва, ИМ Д III, ул. Кардина, д. 4, карп. 3, к. 414,
тел.; (499) 135-54-37, (495) 641-69-38
2. МГУ им. Ломоносова (ГЗ. 1 этаж)
3. Магазины!
Москва; «Дом научно-технической книги» (Ленинский пр., 40}
«Московский дом книги» (ул. Новый Арбат, 8)
Книжный магазин «ФИЗМАТКНИГА» (г Долгопрудный,
Новый корпус МФТИ, 1 этаж, те:г. 409-93-28)
С. 116.: «С-116. дом книги» (Невский пр.ч 28)
Тй.Т.ИПЧ^Й £.ТЛ^ЫЛ<1ф
СкрШТШГК
Физические основы электроники
Издание второе, исправленное и дополненное
Технический y?cdaffmo/? J. /J.
Aa-WWhWWfpWiJW и /f. /?. Aft,??! O/FUU
(?. .4 ZZfeMHXHHa
Подписано в печать 21 1.2.2010 Формат 00 x 841/|й-
Печать офсетная. Усл. гкч. л. 2S,H3. Уч. над. л. ^О,ЙЙ.
Гарнитура Times. Бумага офсетная № 1. Заказ №84.
Идучно-иадитслы: кicii центр «Регуялрпая и хаотическая дниамнкяю
426Q34h г. Ижевск, ул. Уккпс^кмтетская,. I.
hlLp^'-'shup. rtd.ru E-nuiil: nuiiL@rcd.ni ТсЛ./факс: (+73412) 500 295