Автор: Говоров В.М. Дыбов П.Т. Мирошин Н.В. Смирнова С.Ф.
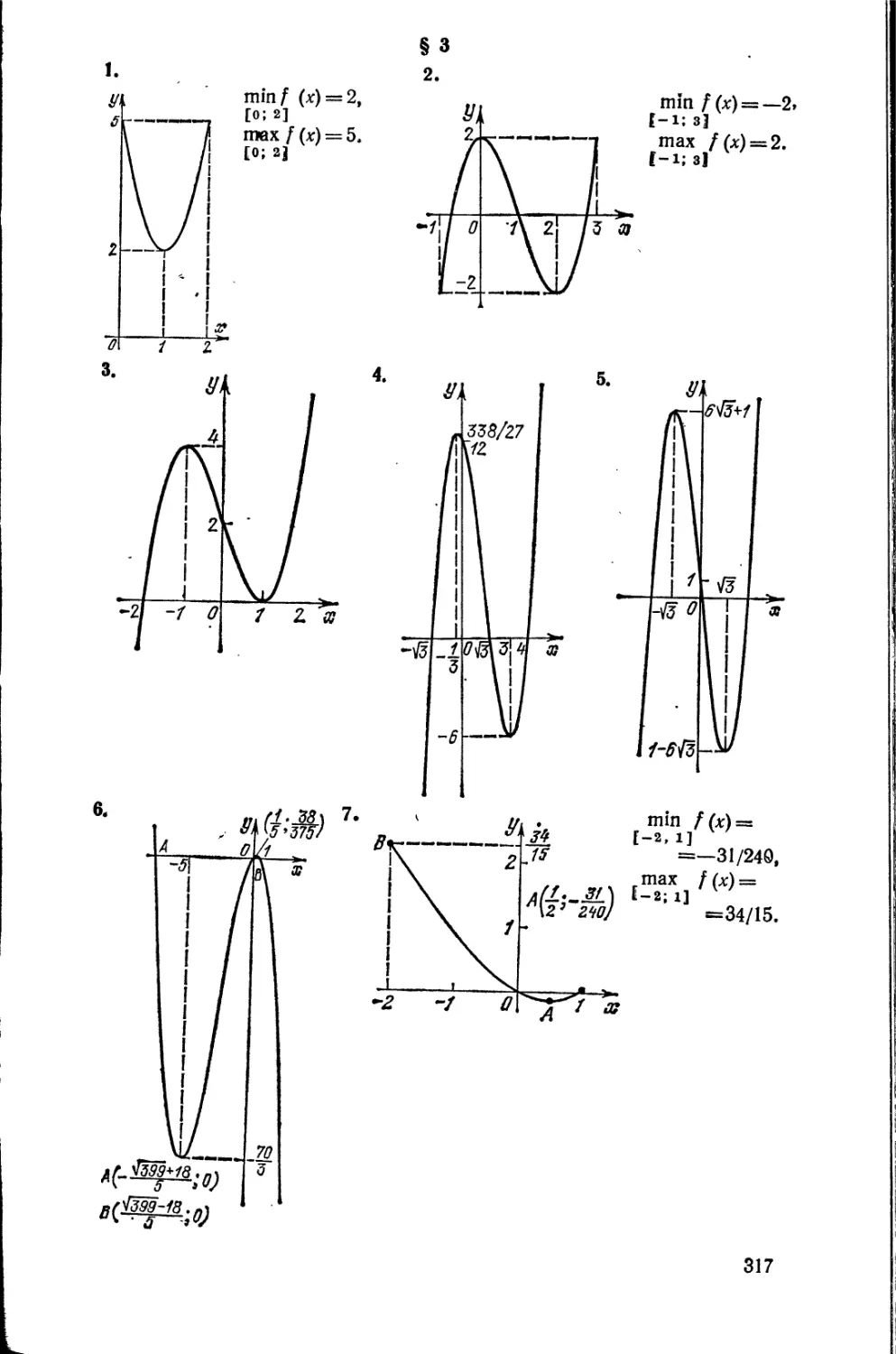
Теги: математика задачи по математике
Год: 1983
Текст
В. М. ГОВОРОВ
П.Т ДЫБОВ
Н. В. МИРОШИН
С. Ф. СМИРНОВА
СБОРНИК
КОНКУРСНЫХ
ЗАДАЧ
ПО МАТЕМАТИКЕ
В.М. ГОВОРОВ, П.Т. ДЫБОВ
Н. В. МИРОШИН, С.Ф. СМИРНОВА
СБОРНИК
КОНКУРСНЫХ
ЗАДАЧ
ПО МАТЕМАТИКЕ
с методическими
указаниями
и решениями
Под редакцией А. И. ПРИЛЕПКО
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособия для слушателей
подготовительных отделений вузов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 3
22.1
Г 57
УДК 51
Говоров В. М., Дыбов П.Т., Мирошин Н. В., С м и р н о в а С. Ф.
Сборник конкурсных задач по математике (с методическими указаниями и ре-
шениями).—М.: Наука, Главная редакция физико-математической литературы,
1983. — 384 с.
Основу сборника составляют задачи, предлагавшиеся на письменных и
устных вступительных экзаменах по математике более чем в ста вузах разных
профилей. Все задачи снабжены ответами, а ряд задач — указаниями и реше-
ниями.
Сборник может быть использован для самостоятельной подготовки к кон-
курсным экзаменам в вузы различной ориентации, на подготовительных отде-
лениях и курсах. Учителя средних школ найдут в книге материал, который
смогут использовать в своей работе.
1702030000— 1 32 Q_ оо
Г ОЬЗ (02)-83 88-83
© Издательство «Наука»
Главная редакция
физико-математической
литературы, 1983
Г
СОДЕРЖАНИЕ
Предисловие............. • . ...............• 5
Раздел I. Алгебра, тригонометрия и элементарные функции .... 7
§ 1. Задачи с целыми числами. Признаки делимости ....... 7
§ 2. Действительные числа. Преобразования алгебраических выра-
жений ........................................................ 10
§ 3. Метод математической индукции. Элементы комбинаторики.
Бином Ньютона............................................... 21
§ 4. Уравнения и неравенства первой и второй степени ..... 30
§ 5. Уравнения высших степеней. Рациональные неравенства . . 35
§ 6. Иррациональные уравнения и неравенства.................. 41
§ 7. Системы уравнений и неравенств .......................... 49
§ 8. Область определения и множество значений функции .... 62
§ 9. Показательные и логарифмические уравнения и неравенства 67
§ 10. Преобразования тригонометрических выражений. Обратные
тригонометрические функции.................................... 89
§ 11. Решение тригонометрических уравнений, неравенств и систем
уравнений ..................................................... 97
§ 12. Прогрессии............................................ 119
§ 13. Решение задач на составление уравнений.................. 126
§ 14. Комплексные числа ...................................... 140
Раздел II. Начала анализа .................................... 142
§ 1. Последовательности и их пределы. Бесконечно убывающая
геометрическая прогрессия. Пределы функций . ................. 142
§ 2. Производная. Исследование функций с помощью производной 145
§ 3. Графики функций ........................................ 154
§ 4. Первообразная. Интеграл. Площади криволинейных трапеций 156
Раздел III. Геометрия и векторная алгебра......................... 162
§ 1. Векторная алгебра........................................ 162
§ 2. Планиметрия. Задачи на доказательство.................... 168
§ 3. Планиметрия. Задачи на построение........................ 174
§ 4. Планиметрия. Задачи на вычисление........................ 182
§ 5. Стереометрия. Задачи на доказательство................... 193
§ 6. Стереометрия. Задачи на вычисление....................... 197
3
Раздел IV. Задачи и вопросы устного экзамена...................... 218
§ 1. Экзаменационные билеты................................... 218
§ 2. Задачи устного экзамена.................................. 221
§ 3. Программа по математике вступительных экзаменов в вузы . 241
Ответы и методические указания.................................... 247
Приложение ....................................................... 368
Список высших учебных заведений страны, материалы которых исполь-
зованы в сборнике задач....................................... 379
ПРЕДИСЛОВИЕ
Настоящий сборник содержит более трех тысяч самых разно-
образных задач по всем разделам школьного курса математики.
Он составлен в соответствии с ныне действующей программой,
все используемые обозначения и терминология соответствуют обо-
значениям и терминологии, принятым в средней школе.
Основной фонд задач сборника составили задачи, поступившие
на отделение математики телевизионных подготовительных курсов
Центрального телевидения (отделения математики и физики
работали на базе Московского инженерно-физического инсти-
тута). Почти все задачи, включенные в сборник, предлагались на
вступительных экзаменах по математике в различных вузах.
В сборнике приведены задачи 120 вузов различных городов и
республик нашей страны. Авторы стремились представить вузы
самых различных профилей наиболее характерными для них за-
дачами, предлагавшимися на вступительных экзаменах. Материал
сборника разбит на четыре раздела: алгебра и тригонометрия,
начала анализа, геометрия и векторная алгебра, задачи и воп-
росы устного экзамена.
Материал сборника охватывает оба варианта ныне действую-
щей программы. Кроме того, авторы сочли необходимым вклю-
чить в сборник материал, относящийся к комплексным числам,
элементам комбинаторики, формуле бинома Ньютона, простейшим
тригонометрическим неравенствам. При подготовке к вступитель-
ным экзаменам в вузы изучение этого материала не обязательно,
так как он не входит в программу вступительных экзаменов.
Однако этот материал, не входящий в школьную программу и
в программу для поступающих в вузы, начинает использоваться
при изучении вузовского курса буквально с первых дней и часто
без необходимых объяснений. Включение этого материала в сбор-
ник поможет читателям расширить свои знания, будет полезно
для физико-математических школ, дневных подготовительных
отделений, для работы школьных математических кружков.
5
Все задачи снабжены ответами, а многие и методическими
указаниями к решению. Типичные задачи и многие задачи повы-
шенной трудности снабжены краткими решениями. Задачи повы-
шенной трудности и задачи олимпиадного характера помечены
звездочками. В некоторые параграфы включен справочный мате-
риал. В разделе «Вопросы и задачи устного экзамена» печатается
программа по математике для поступающих в вузы.
Авторы надеются, что собранный воедино большой материал
вступительных экзаменов в вузы самой различной ориентации
будет полезен как учащимся, готовящимся к поступлению в выс-
шие учебные заведения, так и учителям средних учебных заведений,
а также всем лицам, желающим углубить свои знания по мате-
матике.
Авторы
Раздел I
АЛГЕБРА, ТРИГОНОМЕТРИЯ
И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
§ 1. ЗАДАЧИ € ЦЕЛЫМИ ЧИСЛАМИ. ПРИЗНАКИ ДЕЛИМОСТИ
1. (МПИ, 1979 г.). Сумма цифр двузначного числа равна 6.
Если к этому числу прибавить 18, то получится число, записан-
ное теми же цифрами, но в обратном порядке. Найдите это число.
2. (МИНХ, 1977 г.). Если некоторое двузначное число умно-
жить на сумму его цифр, то получится 405. Если число, напи-
санное теми же цифрами в обратном порядке, умножить на сумму
его цифр, то получится 486. Найдите это число.
3. (МТИЛП, 1977 г.). Найдите три числа, из которых второе
больше первого на столько, на сколько третье больше второго,
если известно, что произведение двух меньших чисел равно 85,
а произведение двух больших чисел равно 115.
4. (МХТИ, 1977 г.). Сумма двух чисел равна 15, а их сред-
нее арифметическое на 25% больше среднего геометрического.
Найдите эти числа.
5. (МИНХ, 1979 г.). Разность двух чисел равна 48, разность
между средним арифметическим и средним геометрическим этих
чисел 18. Найдите эти числа.
6. (МИНГП, 1977 г.). Среднее геометрическое двух чисел на
12 больше меньшего из этих чисел, а среднее арифметическое
тех же чисел на 24 меньше большего из чисел. Найдите эти числа.
7. (ВЗИИЖТ, 1979 г.; МТИЛП, 1980 г.). Найдите двузначное
число, зная, что число его единиц на два больше числа его де-
сятков и что произведение искомого числа на сумму его цифр
равно 144.
8. (МЭСИ, 1980 г.). Произведение цифр двузначного числа
в два раза больше суммы его цифр. Если из искомого числа вы-
честь 27, то получится число, записанное теми же цифрами, но
в обратном порядке. Найдите это число.
9. (МИХМ, 1979 г.). Произведение цифр двузначного числа
в 3 раза меньше самого числа. Если к искомому числу прибавить
18, то получится число, записанное теми же цифрами, но в об-
ратном порядке. Найдите это число.
19. (МИНХ, 1979 г.). Сумма квадратов цифр двузначного
числа равна 13. Если из этого числа вычесть 9, то получится
число, записанное теми же цифрами в обратном порядке. Найдите
это число.
2
11. (МИНХ, 1979 г.). Двузначное число втрое больше суммы
своих цифр, а квадрат этой суммы цифр равен утроенному иско-
мому числу. Найдите это число.
12. (МИХМ, 1977 г.). Найдите двузначное число, которое на
12 больше суммы квадратов его цифр и на 16 больше удвоенного
произведения его цифр.
13. (МИХМ, 1977 г.). Сумма квадратов цифр двузначного
числа равна 10, а произведение искомого числа на число, запи-
санное теми же цифрами, но в обратном порядке, равно 403.
Найдите это число.
14. (МГПИ, 1978 г.; МИНХ, 1979 г.). Если двузначное число
разделить на сумму его цифр, то получится в частном 4 и
в остатке 3. Если же это двузначное число разделить на произ-
ведение его цифр, то получится в частном 3 и в остатке 5. Най-
дите это двузначное число.
15. (МИНХ, МЭСИ, 1977 г.). Если двузначное число разде-
лить на число, написанное теми же цифрами в обратном порядке,
то в частном получится 4, а в остатке 15; если же из данного
числа вычесть 9, то получится сумма квадратов цифр этого числа.
Найдите это число.
16. (МЭСИ, 1977 г.). Найдите двузначное число, частное от
деления которого на произведение его цифр равно 8/3, а разность
между искомым числом и числом, написанным теми же цифрами,
но в обратном порядке, равна 18.
17. (МИНХ, 1977 г.). Найдите двузначное число по следую-
щим условиям: частное от деления искомого числа на сумму его
цифр равно 8; частное от деления на эту же сумму произведе-
ния цифр равно 14/9.
18. (МИНХ, 1979 г.). Если неизвестное двузначное число
разделить на число, записанное теми же цифрами, но в обрат-
ном порядке, то в частном получится 4 и в остатке 3. Если
же искомое число разделить на сумму его цифр, то в частном
будет 8, а в остатке 7. Найдите это число.
19. (МИНХ, 1979 г.). Если двузначное число разделить на
сумму его цифр, то получится в частном бив остатке 2. Если
же это число разделить на произведение его цифр, то получится
в частном 5 и в остатке 2. Найдите это число.
20. (МИНХ, 1979 г.). Какое двузначное число меньше суммы
квадратов его цифр на 11 и больше их удвоенного произведения
на 5?
21. (ЯГУ, 1980 г.). Найдите два последовательных натураль-
ных числа, если квадрат суммы этих чисел на 112 больше суммы
их квадратов.
22. (МАИ, 1979 г.). В первый раз знаменатель положительной
дроби увеличим на 3, а во второй раз—-уменьшим на 5. Сумма
полученных таким образом дробей оказалась равной 2/3. Найдите
знаменатель дроби, если ее числитель равен 2.
23. (хМАИ, 1977 г.). Знаменатель несократимой дроби на 2
больше чем числитель. Если у дроби, обратной данной, умень-
8
шить числитель на 3 и вычесть из полученной дроби данную
дробь, то получится 1/15. Найдите дробь.
24. (МИФИ, 1976 г.). Рассматривается дробь, знаменатель
которой меньше квадрата числителя на единицу. Если к числи-
телю и знаменателю прибавить по 2, то значение дроби будет
больше, чем 1/3, если же из числителя и знаменателя вычесть
по 3, то дробь останется положительной, но будет меньше 1/10.
Найдите дробь.
25. (ЛатвГУ, 1980 г.). Существует лишь три положительных
двузначных числа, обладающих следующим свойством: каждое
число равно неполному квадрату суммы своих цифр. Требуется
найти два из них, зная, что второе число на 50 единиц больше
первого.
26. (ГГУ, 1978 г.). Найдите сумму всех двузначных чисел,
которые при делении на 4 дают в остатке 1.
27. (МИФИ, 1979 г.). Найдите сумму всех трехзначных чисел,
которые при делении на 5 дают остаток, равный 4.
28. (ТартГУ, 1980 г.). Найдите сумму всех двузначных чисел,
которые при делении на 7 дают в остатке 3.
29. (ТбГУ, физфак, спец, радиофизика и электроника, 1978 г.).
Найдите сумму всех нечетных трехзначных чисел, которые делятся
на 5.
30. (МИФИ, 1976 г.). Произведение двузначного числа и чис-
ла, записанного теми же цифрами в обратном порядке, равно 2430.
Найдите это число.
31. (МИФИ, 1976 г.). Найдите пары натуральных чисел, раз-
ность квадратов которых равна 45.
32. (МИФИ, 1975 г.). Существует такое натуральное число,
которое равно квадрату натурального числа, если к нему приба-
вить 100, и равно квадрату другого натурального числа, если
к нему прибавить 168. Найдите это число.
33. (МИФИ, 1976 г.). Найдите два натуральных числа, зная,
что их сумма равна 85, а их наименьшее общее кратное равно 102.
34. (МИФИ, 1975 г.). Найдите все пары натуральных чисел,
наибольший общий делитель которых равен 5, а наименьшее
общее кратное равно 105.
35. (МИФИ, 1976 г.). Найдите два трехзначных числа, сумма
которых кратна 504, а частное кратно 6.
36. (ГГУ, мехмат, физфак, 1979 г.). Представьте число 19
в виде разности кубов натуральных чисел.
37. (МИФИ, 1975 г.). Найдите три числа, если куб первого
числа на 2 больше их произведения, куб второго числа на
3 меньше их произведения, а куб третьего числа на 3 больше их
произведения.
38. (МИФИ, 1976 г.). Найдите все двузначные числа, удов-
летворяющие следующим условиям: сумма цифр числа не менее 7;
сумма квадратов цифр не более 30; число, записанное теми же
цифрами, но в обратном порядке, по крайней мере вдвое меньше
данного.
9
39. (МИФИ, 1980 г.). В четырехзначном числе сумма цифр
тысяч, сотен и десятков равна 14, а сумма цифр единиц, десят-
ков и сотен равна 15, причем цифра десятков на 4 больше цифры
единиц. Из всех чисел, удовлетворяющих указанным условиям,
найдите такое, у которого сумма квадратов цифр принимает наи-
меньшее значение.
40. (МИФИ, 1980 г.). В четырехзначном числе сумма цифр
тысяч и десятков равна 4, сумма цифр сотен и единиц равна 15,
а цифра единиц больше цифры тысяч на 7. Из всех чисел, удов-
летворяющих указанным условиям, найдите такое, у которого
сумма произведения цифры тысяч на цифру единиц и произведе-
ния цифры сотен на цифру десятков принимает наименьшее зна-
чение.
41. (МИФИ, 1981 г.). Докажите, что если число а равно сумме
квадратов двух неравных натуральных чисел, то 2а также равно
сумме квадратов двух неравных натуральных чисел.
42. (ТбГУ, мехмат, спец, прикладная матем., 1978 г.). Най-
дите сумму всех несократимых дробей между 10 и 20 со знаме-
нателем 3.
43. (ТбГУ, мехмат, спец, прикладная матем., 1977 г.), т и п —
натуральные числа. Найдите все дроби m/n, знаменатель которых
на 16 меньше числителя, сама дробь меньше чем сумма утроен-
ного обратного и 2, а числитель не больше 30.
44. (ТбГУ, мехмат, спец, прикладная матем., 1980 г.). Дана
последовательность
(1+(-!)”) + !
Un~ 5п+6
Определите количество членов последовательности (zzn), которые
удовлетворяют условию ип С] 1/100; 39/100[.
§ 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. ПРЕОБРАЗОВАНИЯ
АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Смешанная бесконечная действительная периодическая дробь
в простую дробь обращается по формуле
0,^^
п /о о о \_____ txioc2.. .awPiP2« • • Р/л—аха2...ап
• • <МР1Р2• • • PzzJ - 99...900...0
т
Представьте в виде простых дробей следующие смешанные бес-
конечные десятичные периодические дроби (1—4).
1. (МИСИ, 1977 г.). 7,5(3).
2. (МТИЛП, 1980 г.). 2,1(32).
0,23(7)+^
3. (МТИЛП, 1979 г.). -------
0,5(60-^
10
4. (МЭСИ, 1979 г.). Найдите х, если х = 10.
0,(3) +1,1(6)
Вычислите (5—31).
5. (ТартГУ, 1980 г.). (l)-10.27-3 + 0,2-4-25-2 + (64-i/’)~!i.
6. (МЭСИ, 1980 г.). (]/2 + КЗ +}/2 —/3 )\
7. (МЭСИ, 1980 г.). з/—J----h-rJ-------L-1
’ \/104-5 V10-2 /10/
8. (МЭСИ, 1980 г.). ,
’ /75—5/2
9. (МТИМБО, 1979 г.). 1+sec20°-/3ctg40°.
10. (МГМИ, 1979 г.). •
11. (МЭСИ, 1980 г.). (6 —4 (5/16)°)-2 +(2/3)-1 —3/4.
12. (МЭСИ, 1980 г.).
13. (МЭСИ, 1980 г.).
14. (РПИ, 1980 г.).
2-2 + 2°
(1/2)-2-5-(-2)-2+(2/3)~2 •
(0,6)° —(0,1)-1
(3/23)~i-(3/2)3+(—1/3)~1 •
31/3/%o-si/±/4/6+5/1/5+/20-Ю/0,2
3V2/32—/^/а+г/^в+б/2/#—140/0,02 ¥
15. (РПИ, 1980 г.).
2,4/8i/s-9/i/3+/2i/ia_+V2/i/3-+3/g7
IVa^/a-/0,5+1,5/2+20/1/50-/32 /s’
16. (МГМИ, 1980 г.).
()/ (/2-4)2-У (1-/2)3У+ 2-3/2cos^.
17. (МГМИ, 1980 г.).
( /(^-4)’-j/(|-К5)3)1/2 -/-2зш^.
18. (МГМИ, 1980 г.).
(//3 + /2-(И"3-Г2)1/2) ((/3 + /2)1/2 +
+ /ГЗ- /2)’1- cos^ .
19. (МГМИ, 1980 г.).
(/ 2 + /3 +(2-2 cos(lln/6)),/2} X
X (/2+2cos(л/6)-2-/з).
20. (МТИЛП, 1980 г.). /251/1ое»5 + 491/1о«»7.
21. (МВМИ, 1977 г.). cos Qj (log, | + log1/eз)).
11
22. (МВМИ, 1977 г.). log1/2 (log3cos (л/6) — log3sin (л/6)).
23. (МГМИ, 1979г.). (-З”'08’6 + 1V sin^.
24. (МГМИ, 1979 г.), ^/з.з-ю^7.tg + 31/2 + 2р/г-cos^.
25. (МГМИ, 1979 г.).
((128з/7 • 27V». Ю-’в«)-1/2 4. ctg~1 -у-)2 + 2• 61'2.
26. (МГМИ, 1979 г.). (s^-S^’-sin^ + ^^y^cos-
27. (МАТИ, 1977 г.).
(%1/з + Z/1/3) (%2/з— %1/з^1/з -]~у2/*) при Х=45/7,
28. (ВЗИТиЛП, 1980 г.).
1/2 I vl/4
х
6 ’
X— 1
хЗ/4+х1/2’
29. (ПГУ, 1980 г.).
я3— а—2Ь — —
а
\ г а а2 /
при а = 23, Ь — 22.
30. (МАТИ, 1977 г.). х’ + Зх—14 при
3Л , с i/-»' 1
• X1/4 + 1 при x= 16.
x
a2—b2
31. (МГУ, мехмат, 1978 г.). Разность jZ]40K2 —57| —
— 40 j/2 + 57 является целым числом. Найдите это целое число.
Избавьтесь от иррациональности в знаменателе (32—33)/
32. (МГИ, 1979 г.). --
' 1+К2+ГЗ
33. (ЯГУ, 1980 г.). —.......7,- .-
У 2/3—К 2 j/ v 2+j/3
9
34. (РПИ, 1977 г.). Сравните два числа а = -^==—и 6 =
— 6
“ з— У~з
35. (ГГУ, 1978 г.). Дано: 1 < а < Ь + с < а+ 1, &<с. Дока-
жите, что а < Ь.
36. (МВМИ, 1977 г.). Что больше: log3108, или log3 375?
Расположите в порядке возрастания следующие числа (37—39).
37. (МИЭМ, 1979 г.). 0; kW; 1,2; 11/30; 0,91846.
12
38. (МИЭМ, 1979 г.). 1; 0,37; 65/63; 6J/59; tg 33°; tg(—314°).
39. (МИЭМ, 1979 г.). 0,02; 1; 0,85; Кз/2; ^0,762; —cos571°.
40. (ГГУ, радиофиз. фак., 1979 г.). Докажите, что 535 s —ЗЗ35
делится на 10.
Разложите на множители (41—43).
41. (МИНХ, 1979 г.), и4+ 4.
42. (МИНХ, 1979 г.). 1 + п4 + п8.
43. (МИНХ, 1979 г.). 1+х3.
Упростите следующие выражения (44—166).
44. (ОГУ, 1980 г.).
' ’ ' а—Ь а2—Ь2
45. (ВТУЗЗИЛ, 1977 г.).
___!_____+_____!_____+______1___
(а—Ь) (а —с) ‘ (Ь—с)(Ь—а) ‘ (с—а) (с — Ь)
46. (ВТУЗЗИЛ, 1977 г.). (« + „4»)
47. (ВТУЗЗИЛ, 1977 г.). (41-+&)2—1б") f(a+b)2-ab\^-^
48. (ВЗФЭИ, 1977 г.). +
v ’ 7 \ (a—b)2 1 a2—b2) (a—b)2
49. (ВЗФЭИ, 1980 г.; ВЗИТиЛП, 1980 г.).
/ , 4mn \ f m n 2mn \
\ 1 \m-\-n n—m m2— n2 J
50. (ВЗФЭИ, 1980 г.; ВЗИТиЛП, 1980 г.).
((/n-h п)2 ( т2 п2 ) п
51. (МТИПП, 1980; ВЗПИ, 1980 г.),
52. (МИИЗ, 1978 г.), -у—а") (а + Ь + с)’2.
а b с
53. (РПИ, 1980 г.). -|^(1+Ц^1!.,);114=£.
54. (МИИЗ. 1978 г.). ^;(x3-s=)+ -&-_А.
55. (МЭСИ, 1979 г.).
56. (МИИЗ, 1979 г.).
67. (МГМИ, 1980 г.). +
13
58. (ТартГУ, 1980 г.).
„ ((\6—а)а , 3+2а
а I а2—4 ”* 2—а
За—2\ а—1
а-|-2 / а(а24-4а-{-4) *
59. (ВТУЗ ЗИЛ, 1979 г.).
(6»> + 5<I-1+^±‘):(3O-2 + jAi).
60. (МарПИ, 1977 г.). (-рДгт + ^^Т^)'
61. (РПИ, 1980 г.).
/1,1 2с \ , . . . о . / 1 . 1 , 2 4с2 \
\а +b ab) (а + Ь + %с)'-[аг+ bz+ ab а2Ь2)'
62. (МИИЗ, 1979 г.).
63. (ВЗИИЖТ, 1979 г.). ( —
64. (ВЗИТиЛП, 1979 г.),
(УТ75)372 (1/
65-(M™™.1979r.).l-^^.^7XT5A.
66. (ВЗИИЖТ, 1979 г.). ( -1^ + -£±1) (1+1).
67. (ВЗИТиЛП, 1980 г.; ВЗФЭИ, 1980 г.).
f (^°+ р У.
\ /\ а~ь /
x1/24-x’-1^ l—r-Va
68. (ВЗПИ, 1977 г.; ПГУ, 1980 г.). х ,+*-+ х 7=-.
1 —х 1 + У х
69. (ВЗПИ, 1977г.).
70. (ВЗПИ, 1978г.).
71. (МТИЛП, 1980 г.). (^ + /Т - и ,: ( + 1)
(1 —х) (1 —Х~’1/2)
72. (ВЗПИ, 1980 г.). x^ + x-^-i
73. (МарПИ, 1977 г.)
74. (МИИЗ, 1977 г.; ВЗПИ, 1977 г.; РПИ, 1980 г.).
(а^+Ьр--У^}: (а_Ь)+^-О
14
a—b
75. (ВЗПИ, 1980 г.). --а~°
а+Ь+г^аЬ а~1/2+Ь~1/2
76. (МПИ, 1977 г.). (- а1/--+2---.alf2~2\. gV2 + L.
' \а+2а1/2 + 1 а~1 J а1/2
77. (МПИ, 1977 г.). (х4-Кх2^1)2 + (х4-Их2^Л)"24-2(1 —
78. (ВЗПИ, 1977 г.). - “У b----------ь . —УаЬ
(К а+К b)(a—b) У а+КЬ а—Ъ
79. ВТУЗ ЗИЛ, 1977 г.; ЯГУ, 1980 г.). xV'+1 !----.
- ’ 7 х- + л-1/2 + 1 X3/2 —1
80. (ВТУЗЗИЛ, 1977 г.). (23/2 4-27z/3/5): -1/2 H-Sz/Vs)
X — у X— у
81. (ВЗИИЖТ, 1979 г.). |С^'~ТС£—
/ х-/у У х+К у У~*
х—у х — у
82. (ВЗИИЖТ, 1979 г.).
2 (а + 6)- W (1 +1 ( - /А /)'’.
h — Y h3/2 — Y3/2
83. (МПИ, 1977 г.). — ° —.
v ’ у Ъ-У х ь—х
84. (МТИПП, 1978 г.; МГМИ, 1980 г.).
85. (МТИПП, 1980 г.; ВЗПИ, 1980 г.).
/ /п4~ Ут2—п2 т—Ут2—п2\ п2
\т—Ут2—п2 т+Ут2—п2 / 4тУ т2—п2
86. (ВЗИИЖТ, 1979г.).
87. (МАДИ, 1977 г.).
Уа^Т . _________________Уа+1___________
1 1 ' (о—1) Уа+1— (а4-1) Уа^-1 ’
Уа+1 У а— 1
88. (МТИПП, 1977 г.).
V <!+1 -- +________-\(у~а 4 л*'
2 \ 14-К 54- У а'1 — У 54-К a J\
89. (МТИПП, ВЗПИ, 1980 г.).
/х1/2+{/1/2 х1/2_у1/2\
\+/2_у1/2 х1/2+у1/2)(У
1_
2У~а
а— 1
90. (МИИЗ, 1977 г.
15
81. (МТИММП, 1977 г.; МАДИ, 1977 г.).
(а + о1/2) (й + b)-1 (Ка (V~а-/Ь)"1—().
92. (МТИММП, 1980 г.).
—2 УТ . /а3/2+&3/2--1--\ , _ „ _J
(ab)"1/2/^ ’ •
93. (ВЗПИ, 1980 г.).
94. (ВЗПИ, 1980 г.).
95. (РПИ, 1980 г.).
/ V д+1 | 1^6+ Vе а | \/ V д+1 Ка&+ К а . j \
Х^+1 "Г УаЬ — 1 /X УаЬ+1 УаЬ—1 *" /
96. (РПИ, 1980 Г.). + Y (а_&)+ 2]£ft
X у а-\- у Ь / у а+ у b
97. (МПИ, 1977 г.).
— а
b-----------
(ab)~ °-5
ai/2 + i \ 1—а
98. (МАДИ, 1977 г.).
1 , ,Г--г
V ab J +
-1/3
1 1 ' (а— 1) Уа+1 — (а+1)Уа— 1
У'а+1 У а— 1
99. (ВЗИИЖТ, 1979 г.).
(aVb)~1/2 (-------.
X а+УаЬ/ а—Ь
100. (ВЗИИЖТ, 1979 г.).
/ а3—8 (а+1)24-3 а2+а\. Уab
а2—5а+> Д—3 4/^ J' 4/^ip ’
а^-ЗаУЧ .(. ,
101. (ВЗИИЖТ, 1979 г.).
102. (МТИММП, 1977 г.).
/а+ЬХ1/2 2аУа2—Ь2
\a^b) ~ b2(ab~l+Г)2
1
1— ba-'
1+&а-1
103. (МТИПП, 1978 г.). . >2—. я/_=г.
(а2/—а2/л) (^/;д'л+1+ у/оет+1)
104. (МТИПП, 1977 г.; МИИЗ, 1979 г.).
16
105. (МТИМБО, 1981 г.).
2 р+1
а \а3— 1
106. (МПИ, 1977 г.).
1
а2 +^+1
_2_ А
1— а)
а34-«2 + 2а
a-j-b a—b
а2/3_а1/361/3+&2/3 а2/3+а1/3Ь1/3+г,57Г
107. (МПИ, 1977 г.).
/ ХЧ3-у3/3 х1/2+у1/2 \х3^3у1^3
Уху1/2 +Х1/2!/ Х1/1/2 -хг/3у / Х+У
108. (МТИПП, 1977 г.; МИНХ, 1979 г.).
а2/3_&2/3
’aV3_bi/3-
2у
х—У '
t + (/ + 4)1/2 + 4 (/ + 4)- V2.
109. (КишПИ, 1980 г.). • а2/3 (уГа3 .
v ’ 7 ^/а2(а-&)2 (а-Ь)1'3
ПО. (МИНХ, 1979 г.).
2 Х~1/ х(у2_а2)-1/2+1 /х_(х2_а2)1/2у1
*а-Я2/' к а(х-в)-1/3+(х_а)1/2 А а2(х+о)1/3 J
111. (РПИ, 1980 Г.).
((/1 - /4 /т + /4 -2)Х‘+/I) •
112. (ВЗИТиЛП, 1980 г.).
(2а-\-Ьх'3ах13 V1 / a3'3 -Ь3'3 a~b X
\ За J \ a-aV26i/2 уГа+VbJ'
113. (ВТУЗ ЗИЛ, 1977 г.).
(/7-1)(/~7+1)
.2/3 х2—4x4-3’
2 (а—Ь)-1
(ab)-V3 '
114. (ВТУЗ ЗИЛ, 1977 г.).
2х~ ________х2^3
х2/3 —Зх~ !/2 х»/3—.
115. (МПИ, 1977 г.).
у ((У a3 b~3 — V Ь3а~3):^-
116. (МТИМБО, 1982 г.).
Л2 /1 _ й2\- 1/2 . /___J______________________
U ' • Vn-(«(1—а2)-1/2)2 1~а"
117. (ВТУЗ ЗИЛ, 1977 г.; ЛГПИ, 1978 г.).
(/7- 1<у)34-2х2: /Т4-у/у . З/^-Зу
х!< х+иУ и х—У
118. (ВТУЗЗИЛ, 1977 г.).
/ I—х”2 2 . х~2—х \ /1 . 2
1/2 Х2. у- + ^1/2 _х - 1/2 Д -Г X2 )
17
119. (ВТУЗ ЗИЛ, 1977 г.).
(х1/з — у)2 (х~ 1/3у + х1/3у~1 + 1) . , /3
Х~ 2/3^2—х- 1/Зу_^х2/3 у-2-x1/3t/“l
120. (ВЗПИ, 1977 г.). [+//а+а+у/ °2 _|_ 1_
1 — у/ а i/ а~3
121. (ВЗИИЖТ, 1979 г.).
/ (1-Х)1/4 , (1+х)1/4(1-Х)-3/Ч . /1 „т/4
\2(14-х)3М 2 х> •
122. (ВЗИИЖТ, 1979 г.). (х>м+^/4)
123. (ЛПИ, 1980 г.). У
Х3/2+у3/2_х1/2у1/2 (т<-+Г-) 2у~
(*-«/) (*1/2+z/1/2) П+У~У '
124. (ЛПИ, 1980 г.).
(a—b)3(Vl-\-V~b)~3 + 2aVl + bV"b 3(УаЬ—Ь)
аУ~а+ьУ~Ь а—Ь
125. (ВЗФЭИ, 1980 г.).
/1 + ГаУi ,_2_,ГГ1/г
< 1-Уа + у~а Д+ЛД
126. (МТИМБО, 1982 г.).
(8V^+8l/~b)4(]A'-t/~by (у-а+уГЬ+у-ьЦу-а-У^Ь+у-Ь)
а—УаЬ * т/а3Ь—b
127. (МТИММП, 1980 г.).
(\ _21/± Y—Д4/3-8^8<> V1 |/~~г~
\ V а A a3'3 4-2j/Hb + 4b2/3/ V «~2 ’
128. (МТИПП, 1977 г.).(х /^+у===.)’ :(х--1)«-.
129. (ВЗПИ, 1980 г.)/-—
130. (МТИПП, 1977 г.).
, 8~х , ’ f24- .[ (I/
131. (МТИММП, 1977 г.).
i/а3—b 12 ,-\~
зх-ь-З1^3/
i/ а— у & J
132. (МТИПП, 1980 г.)
133. (МИНХ, 1979 г.).
т1^ —п1^ X
miM+ni/4 / J
: 2 +
2p/Z х р/ х2 —4
/7—2/ УГ2 + 2,3/
а—
\У~а+1/~Ь V )'
- --Д~ь -Ь^3.
18
134. (МТИММП, 1980 г.).
а2+10а + 25+2 5 (/~д3+5/а)
(а2—25) ((/а3 — К125) (а+/5^4-5)-,)~1 ’
136. (МАИ, 1977 г.).
137. (МТИПП, 1977 г.).
д—26 |/2fl* 2& + j/4a&2 \
р/а2 — р/462 р/д2 + ^/4&2+ f/lGab J*
а^/а+бу2д+Ь^/7+ву2&
_ ’ а-\-Ь
138. (МЭИ, 1979г.). (3 * * * * * *~уГа Н-1—— 6^16У
v ' \ 9—д 1 3—]/^a T2S—&) 1 54
139. (МЭИ, 1977 г.).
_/7Га+-оуг________________уу____________У1 ^Iog4(
\\р/а— р/6/ йз/4_а1/Ч1/2+а1/г61/4_вз/4 J -ТУ
140. (МЭИ, 1977 г.).
(______3________3 , У а-1 \ -Х С а-1/3-!-Л2 -1 log, А.
^р/а2"—у~а-\-\ а4~1 р/а2 —1 / \ д1/3 J й
141. (МЭИ, 1977 г.).
]<Нб(/д-/3) т/16а&(К a+y^b+Vab)
(у-ь-уъуу-b У^-У^
142. (МЭИ, 1978 г.).
2 л/ а 2 Л
(а1/4—aV84-l)-x-|_(ai/4_|_ai/e_|_i)-;i-Z_V а~У—\ _2i°&4fl-8.
Vа— Уa+l J
143. (МЭИ, 1978 г.).
д+10 / а+У20(Уа^+5У а)+25
(а-25) (рЛГ3- /125)"1 (Ка+ р/25^ +б) '
144. (МЭИ, 1977 г.).
145. (МЭИ, 1978 г.).
/ (У а+У ьУ—У КаЬ ._____1 __/ а—Ь X-1 \-Х
а—Ь + у д+ у-Ц yj) ) ’
146. (МЭИ, 1979 г.). ( 2У а+.3У °-К7~3 У
\/16а+12 У а+9 2р/а+3/
Х(2-310&»а + 3).
19
147. (МИРЭА, 1977 г.).
2^ + /^TT)(f<^ + l) 1 +± + ]/(*2-1)К 1-рг) *
148. (МЭИ, 1980 г.).
2а i/ab*—a Vab*-ab _ 21 + 2logs a+loge 6>
У a2b— У ab
149 (ЯГУ 1980 г 1 (a ^~д2 1,2_a+ Уа--^\. 4 Уа*—а2Ь2
’ * ’ ’ '\a+Va2—b2 a— Va2—b2)’ (56)2
150. (МТИМБО, 1982 г.).
1 1/ ( в । 3°4 i а*ь* i 1 \2/3 , Г (&2/3 —a2/3)3 — 2a2 — &21 -?
a2 У +/)-2 -Г 3-1 + b-S j + [ a2_|_(62/3_a2/3)3_|_2&2 J ’
151. (МТИМБО, 1980 г.). ( ^3>2~ a+ Y 4-
v ’ \ a+ /2^4-2 /
4-/(a2 4-2)2 —8a2.
152. (МТИМБО, 1980 г.).
Z +2x+a \ _|_j/'(a3—За2х + Зах2 — х3)2/3 :a при x>a.
XV x— V a) -(x-\-2a)J ________
153. (МИФИ, 1978 г.). ^а2~2а&+г,2_|—Q<a<b.
v 7 Уа2 + 2аЬ + Ь2 «+*
154. (МТИ, 1977 г.).
(_1+_LIE£_4. I— >/~Нгу V %2—1 ,
\ 1— x+VT^x + 14-X— УТ+х / 2 +
155. (МТИПП, 1977 r.).
x= '(/« /А),
*4- V 14-х2 2\Y b Ya)'
156. (МГМИ, 1980 г.).
(m4-x)1'24_ (m—x)1/2 ___ 2mn
(m-^-x)1'2—(m—x)1'2’ X n24-l ’
1, 0<x<l.
a > 0, b > 0.
tn > 0, 0 < n
157. (МЭИ, 1977 г.).
((3&24-2a2)2—24fl2&2)!/2
3b—a2-21~l°S2b
i-У a—b2 — jY a + 2b У a — b2,
a/b > У 3/2, &>0, a>62.
158. (МТИПП, 1977 r.).
l)a4~b>0, a — & > 0; 2) a + b<.®, a — b<.§.
159. (МГМИ, 1980 г.). a+ .
v 1—a2
<^4-Р<^+ уУ+Ьс+3
160. (МТИ, 1981 г.). А у.а+'Г4 --L------.
' К*с4-3
20
161. (МВИМУ, 1981 г.). .(a .1-+fe-1-)-(a_^-2.
v aPyf а-2
162. (МТИПП, 1981 г.). 1 ----а-1------ и вычислите
при а = 5.
163. (МТИПП, 1981 г.). ?Т+^13 : a~L и вычислите
v ’ (fl2-ab)2i* aV a—bV b
при а — 1, 2; Ь = 3/5.
164. (МТИПП, 1981 г.), —* § ** . Л2-У (-4т—Ай")
' ’ ' \a-\-b a2-[-2ab-\-b2 ] \ a-j-b а2—b2 j
и вычислите при а = —2,5; & = 0,5.
165. (РГУ, физфак, 1981 г.).
и вычислите при х = 9, t/ = 0,04.
166. (ЛатвГУ, 1980 г.). Докажите тождество
b^—Zb—ib—X} ]Л^4-}-2 ,/~У+2~_ 1 —&
62 + 36 — (&+1) lrb2^4+2 У Ь—2 1+6'
167. (МИНХ, 1977 г.). Укажите область определения функции
и упростите заданное выражение
У=+ (х+4)0’- + 4 (*+4)"°’5'
168. (МЭИ, 1976 г.). Докажите, что если
]/ х2+ v/Vyi + yr y2+}/^yi = a,
то л+3 + «/2/3 — а213.
169. (ЛГПИ, матфак, 1979 г.). Найдите значение выражения
7 (х2+а2)У2+(х2-а2р/2 \-2 ( т2+п2 У/* 0 0
V (х2+а2)х/2—(х2—а2)1/2 ) ПРИХ~ 2тп } ’ а > и» /И > О,
п > 0, т > п.
170. (ЛГПИ, 1981 г.). Найдите область определения и упро-
. ’ а-Ь-b f a + b b , а \
стите выражение А — - >.+—=: ( —4------------т= + -7=— ) _
/«+К* \a~b b—Yab Yab^a)
V{Y-a-Y-b)2
2
§ 3. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ. ЭЛЕМЕНТЫ
КОМБИНАТОРИКИ. БИНОМ НЬЮТОНА
Метод математической индукции
Метод доказательства, называемый методом математической
индукции, основан на принципе, который является одной из ак-
сиом арифметики натуральных чисел.
21
Принцип математической индукции*. Предложение А (п) счи-
тается истинным для всех натуральных значений переменной, если
выполнены следующие два условия:
1. Предположение А (п) истинно для п = 1.
2. Из предположения, что А (п) истинно для n — k (где k —лю-
бое натуральное число), следует, что оно истинно и для следую-
щего значения n = k+l-
Доказательство методом математической индукции состоит из
двух частей: в первой части проверяют истинность Л (1); во вто-
рой части предполагают истинность А (п) для п = k и доказывают
справедливость А (п) для n = k+l, т. е. А (£)=>Л (k+ 1).
Если доказано, что А (1) истинно, и из истинности А (п) для
n — k следует истинность А (п) для n — k-\-\ (при любом нату-
ральном А), то А (п) истинно для всех натуральных п.
Пример 1. Докажите, что при х>—1 неравенство (Я. Бер-
нулли)
(1+х)"> \+пх (1)
верно для любого натурального п.
1) При п = \ имеем (1 4-х)1 = 1 4-я. Одно из соотношений >
или = имеет место, поэтому Л(1) истинно.
2) Докажем, что из истинности A (k) следует истинность
Л(й + 1) для любого натурального k. Пусть неравенство
(!+*)*> 1+kx (2)
истинно. Умножим обе части неравенства (2) на 14-х. Так как
14-я > 0, то
(1 4-я)Л+х > (1 +kx) (1ч+х),
или
(14- я)*+1 > 1 4- (k + 1) Х + kx2\
учитывая, что £х2^0, заключаем:
(1 4-x)*+1 > 1 + (Л +1) я,
т. е. Л(й)=фЛ (fe+1).
Так как неравенство (1) верно при п—\ и из истинности это-
го неравенства при n — k для любого натурального k следует его
истинность при п = ^4-1, то согласно принципу математической
индукции неравенство (1) истинно при всех натуральных п.
Методом математической индукции доказываются предложения,
определенные при целых отрицательных п (проведя замену п — —т),
а также предложения, определенные на множестве целых чисел,
начиная с п = т. В последнем случае доказательство основывает-
ся на следующем обобщении принципа математической индукции.
Если предложение Л(п), в котором п — целое число, истинно
при n = m и из истинности этого предложения-для n — k, где& —
любое целое число, большее или равное т, следует, что оно верно
для и = &4-1, то предложение А (п) истинно для любого целого
п^т.
22
Пример 2. Докажите, что неравенство
2” > 2я + 1
(3)
верно при всех натуральных я^З.
1) Если п — 3, то 23> 2 -3 + 1, т. е. Л(3) истинно.
2) Докажем, что из истинности неравенства при п — k для лю-
бого натурального Z>+=3 следует его истинность для я = &+1.
Итак, пусть
2*>2^+1; (4)
тогда 2ft + 2ft> 46+ 2, т. е.
2*+х > 2(&+1)+1+ (2&—1). (5)
Так как при всех натуральных k > 1 2k— 1 > 0, то из справед-
ливости (5) следует справедливость неравенства
2*+1 > 2 (Л + 1) + 1,
т. е. Л(6)=М(£+1).
Таким образом, обе части доказательства проведены, следова-
тельно, неравенство (3) справедливо для любого я^З.
Докажите утверждения следующих задач (1 —10).
1. (КПИ, 1981 г.). Докажите, что я3 + Зя2+ 5я + 3 при любом
натуральном п делится на 3.
2. (ЛьвГУ, 1980 г.). Докажите, что при любом натуральном
п число 4л+15я—1 кратно 9.
3. (МИФИ, 1977 г.). Докажите, что 2" > я2 при любом нату-
ральном я ^5.
4. (МИФИ, 1977 г.). Докажите, что при любом нечетном я
выражение я3 —я делится на 24.
5. (КГУ, мехмат, физфак, 1977 г.). Докажите, что для произ-
вольного натурального я^2: -р=+^|+-^=+...+^= > |/"я?
6*. (КГУ, мехмат, физфак, 1979 г.). Докажите, что для лю-
бого натурального я выполняется равенство
\ 9Д 25/ у1 (2п — I)2 J 1—2+
7*. (МИРЭА, 1977 г.). Докажите, что при любом натуральном
я > 1 выполняется неравенство ^рт + '^+2 + ' ‘> 24 ‘
8. (МИНХ, 1977 г.; КуйбГУ, 1977 г.; ЛГУ, матмех, 1977 г.).
Докажите, что | sin яга | яг | sin а | при любом натуральном т и
любом a^R.
9*. (МИФИ, 1977 г.). Докажите, что при любом целом неот-
рицательном я: Цп+2+122л+1 делится на 133.
10. (МИФИ, 1977 г.). Докажите, что при любом натуральном
. (2/г)! 4”
(п!)2 ^п+1 ’
23
Комбинаторика
Перестановки. Число перестановок. Установленный в конеч-
ном множестве порядок называют перестановкой его элементов.
Число перестановок конечного множества элементов зависит толь-
ко от числа элементов, для множества из п элементов число пе-
рестановок обозначают через Рп. Множество из одного элемента
можно упорядочить единственным образом: единственный элемент
множества считается первым, поэтому Рх=1. Методом математи-
ческой индукции доказывается, что Рп равно произведению п
первых натуральных чисел:
Р„=1-2-3 ... п. (1)
Произведение 1-2-3... п обозначается п! . Поэтому Р„ = п1. По
определению считают Ро = О! — 1.
Размещения. Число размещений. Множество вместе с задан-
ным порядком расположения его элементов называют упорядочен-
ным множеством. Упорядоченные множества записывают, распо-
лагая в круглых скобках его элементы в заданном порядке. На-
пример, (А; Б\ В) —упорядоченное множество с первым элемен-
том А, вторым элементом Б и третьим элементом В.
Конечные упорядоченные множества называются размещениями.
Число размещений по т элементов в каждом, составленных из
данных п элементов, обозначают через А™. Методом математиче-
ской индукции доказывается, что
= . (2)
Эта формула записывается также в виде
A^ = n(n— 1) ... (п — т+ 1). (3)
Сочетания. Число сочетаний. Свойства числа сочетаний. В
комбинаторике конечные множества называют сочетаниями. Число
сочетаний из п по т (т. е. число подмножеств по т элементов в
каждом, содержащихся в множестве из п элементов) обозначается
через С™.
Подсчитывая число размещений из п по /п, можно получить,
что
^ = С,Т-Рга, (4)
откуда
С'« =____-_______________________ (51
п ml (п—т)\ ’ ' '
Эта формула записывается также в виде
rm— л (я—1) (п—2)... (n—m+1) /fix
“ 1-2... т • v '
Для любых п и т (0 т п) верно равенство
Q = (7)
24
Действительно,
n!
run __ __________ni___________ Г>п-т
п т\(п—т)\ (п—т)\ (я —(n—т))! п
Методом математической индукции можно доказать, что
C,? + Q + ^+...+Q = 2\ (8)
Доказать это равенство можно также, положив в формуле Нью-
тона а = Ь=1. Справедливость формулы следует также из того,
что сумма
C«+Q + C^+...+Q
есть полное число подмножеств множества из п элементов, а оно
равно 2я.
Для любых п и т таких, что 0^/п<п, справедливо равен-
ство
С^ + СГг = С^. (9)
Доказательство можно провести, представив С™ и С™4-1 по фор-
муле (5) и сложив полученные дроби.
Решите следующие уравнения (11—26).
И. (МТИММП, 1977 г.). = x£N.
Czx + I d
12. (МТИПП, 1977 г.). Л2_х-С* = 79, x£N.
13. (МИХМ, 1977 г.). ЗС*+1-2Л*=х, х^АГ.
14. (МТИММП, 1977 г.). |, x$N.
15. (МТИПП, 1977 г.). 12Cl + Q+4 = 162, x£N.
16. (МАТИ, 1977 г.). Л’+1 + С*;1= 14 (х+ 1), x$N.
17. (ЯПИ, 1977 г.). Л’ + С*-2= 14х, x£N.
18. (МТИММП, 1977 г.). СЩ=^А3х+1, x^N.
19. (МИХМ, 1977 г.). Cx+l: С‘ = 6:5, x£N.
20. (МИХМ, 1980 г.). Cx+1-Ax — 4x3 = (Alx)2, x$N.
21. (МИХМ, 1980 г.). ЗСх+1 +Р2-х = 4А3х, x£N.
22. (МЭСИ, 1977 г.; РГУ, мехмат, спец, прикладная матем.,
1977 г.). =5:5:3.
23. (МАТИ, 1977 г.). ~х+3 - = 720, x£N.
Ах'Рх-ь
24. (МГУ, фак. вычислит, матем. и киберн., 1978 г.).
Л.?+3 = С£+2 + 20, x$N.
25. (МТИМБО, 1978 г.). С3 +Q = 11 Q+1, x£N.
26. (РГУ, мехмат, вечери, отд., 1977 г.). llC2 = 24CJ+i.
27. (МИФИ, 1977 г.). Упростите выражение
C“ + 2Q + 3Q+...+(n+l)C", п£ЛГ,
освободившись от С„ (k = 0, 1, ..., п).
25
Решите следующие неравенства (28 — 37).
28. (РГУ, мехмат, 1977 г.). < GW2, m£N.
29. (РГУ, физфак, 1977 г.). С^>С^, tn^N.
30. (РГУ, мехмат, 1977 г.). С®<С„, n£N.
31. (РГУ, мехмат, 1977 г.). 5С2 <C*n+i, n$N.
32. (РГУ, мехмат, 1977 г.). С'^-С^—A*_s <0, x£tf.
33. (МТИЛП, 1977 г.). С*+\ > 3/2, x^N.
34. (МТИММП, 1977 г.). С*;} <21, х£Н.
35. (ЯГУ,. физфак, 1978 г.). 2Съп > 11С®_2, п$Ы.
36. (ЯГУ, физфак, 1978 г.). С";?-С";К 100, ti^N.
Л 4
37. (МАИ, 1977 г.). 14Р3, п^Ы.
Сп-1
38. (МГУ, физфак, 1977 г.). Сколько отрицательных членов
в последовательности (хп), где x„ = Q+5 —, ti^N.
*п + 3
39. (МГУ, физфак, 1977 г.). Сколько положительных членов
/ \ 195 Ап+з — «у
в последовательности (х„), если хп = -гъ-n£N.
*п + 1
40. (МГУ, физфак, 1977 г.). Найдите отрицательные члены
/4/2+4 143 _
последовательности хп = —-гр-, n£N.
*п + 2
41. (КГУ, мехмат, 1977 г.). На одной стороне треугольника
взято п точек, на другой— т точек и на третьей —& точек, при-
чем ни одна точка не является вершиной этого треугольника.
Сколько существует треугольников с вершинами в этих точках?
42. (КГУ, геофак, 1977 г.). За одним столом надо рассадить
5 мальчиков и 5 девочек так, чтобы не было двух рядом сидя-
щих мальчиков и двух рядом сидящих девочек. Сколькими спо-
собами это можно сделать?
43. (КГУ, геофак, 1977 г.). Двенадцати ученикам выданы два
варианта контрольной работы. Сколькими способами их можно
посадить в два ряда, чтобы рядом не было одинаковых вариан-
тов, а у сидящих друг за другом был один и тот же вариант?
44. (МИУ, 1978 г.). В 12-ти этажном доме на первом этаже
в лифт садится 9 человек. Известно, что они выйдут группами
в 2, 3 и 4 человека на разных этажах. Сколькими способами
они могут это сделать, если на 2-м этаже лифт не останавливается?
45. (МИЭМ, 1977 г.). В хирургическом отделении работает
40 врачей. Сколькими способами из них можно образовать бригаду
в составе: а) хирурга и ассистента; б) хирурга и четырех его
ассистентов?
46. (ЛГУ, матмех, 1977 г.). Сколькими способами можно 10
одинаковых подарков распределить между 6 детьми так, чтобы
каждый ребенок получил хотя бы один подарок?
47. (ЛГУ, физфак, 1977 г.). Сколькими способами можно раз-
местить п одинаковых шаров по k ящикам?
48. (ЛГУ, фак. прикладной матем. и процессов управления,
1977 г.). В 10 урнах "распределены 6 белых и 6 черных одина-
26
ковых по размеру шаров, причем в каждой урне имеется хотя бы
один шар. Сколько существует различных вариантов распределе-
ния шаров?
49. (УрГУ, матмех, 1977 г.). На один ряд, в котором 8 стульев,
рассаживаются 5 юношей и 3 девушки. Сколькими способами они
могут сесть, чтобы не все девушки оказались сидящими рядом?
50* . (МИУ, 1978 г.). Семь различных предметов нужно рас-
пределить между тремя людьми. Сколькими способами это можно
сделать, если одному или двум из них может не достаться ни
одного предмета?
51* . (ЛГУ, биол.-почв. и географ, фак., 1977 г.). Сколько
существует натуральных чисел меньших 104 и делящихся на 4,
в десятичной записи которых встречаются только цифры 0, 1, 2,
3, 5, которые ни в одном из этих чисел не повторяются?
52. (ЯГУ, матфак, 1978 г.). Сколько различных шестизначных
чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, чтобы цифры
не повторялись и крайние цифры были четными?
53. (ВЗЭИС, 1978 г.). Сколько различных четырехзначных
чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5?
54. (ЛГУ, фак. экономической кибернетики, химический, психо-
логии, 1977 г.). Сколько существует натуральных чисел меньших
104, в записи которых в десятичной системе все числа различны?
55. (ЛФЭИ, 1977 г.). Сколько различных пятизначных чисел,
не содержащих одинаковых цифр, можно написать при помощи
цифр 1, 2, 3, 4, 5, 6, 7, 8, 9?
56*. (УрГУ, 1977 г.). Сколько есть четырехзначных чисел,
запись которых в десятичной системе счисления содержит не более
двух разных цифр?
57*. (КГУ, мехмат, 1978 г.). Сколько существует различных
семизначных чисел, сумма цифр которых четная?
58*. (КГУ, ВМК, 1978 г.). Сколько различных 4-х значных
чисел можно написать, пользуясь цифрами 1, 2, 3, 4, 5, 6, 7, 8
так, чтобы в каждом из них была только одна единица, если
любая другая цифра может встречаться в записи этих чисел не-
сколько раз?
59*. (КГУ, 1978 г.). Сколько различных семизначных чисел
можно написать, пользуясь только тремя цифрами 1, 2, 3, при
условии, чтобы цифра 2 в каждом числе встречалась 2 раза?
60*. (ЛГУ, матмех и фак. прикладной матем. и процессов
управления, 1977 г.). Сколько шестизначных чисел содержит
точно четыре различных цифры?
61*. (КГУ, мехмат, 1978 г.). Сколько различных чисел, мень-
ших чем 2-108, которые делятся на 3, можно написать при помощи
цифр 0, 1 и 2 (начинаться с 0 числа не могут)?
62*. (КГУ, мехмат, 1977 г.). Сколько есть четырехзначных
чисел, запись которых в десятичной системе счисления содержит
не более двух разных цифр?
63*. (МИНХ, 1978 г.). Из 18 разных цветков нужно составить
букет так, чтобы в него входило не менее 3-х цветков. Сколь-
27
ко различных способов существует для составления такого
букета?
64*. (КГУ, мехмат, 1978 г.). Сколько различных чисел, мень-
ших 2 • 10е, можно написать при помощи цифр 1 и 2?
65*. (КГУ, мехмат, 1978 г.). Сколько существует различных
шестизначных чисел, у которых три цифры четные, а три нечет-
ные?
66*. (КГУ, ВМК, 1978 г.).’Сколько различных четырехзначных
чисел можно написать, пользуясь только по разу цифрами 1, 2,
3, 4, 5, 6, 7, 8 так, чтобы в каждом из них была единица?
67*. (КГУ, мехмат, 1978 г.). Сколько существует различных
шестизначных чисел, сумма цифр которых нечетная?
68. (МИФИ, 1978 г.). В шахматном турнире среди участников
были две женщины. Каждый участник турнира играл с осталь-
ными участниками по 2 партии. Число партий, сыгранных муж-
чинами между собой, оказалось на 66 больше числа партий,
сыгранных мужчинами с женщинами. Сколько всего было участ-
ников в турнире и сколько всего партий было сыграно?
Бином Ньютона
Формула
(а + Ь)п = С°ап + + ... + + ... +СппЬп, (1)
справедливая при любом натуральном п, называется формулой.
Ньютона или биномом Ньютона. Коэффициенты С„ формулы (1)
называются биномиальными коэффициентами'. (&+1)-е слагаемое
суммы (1) считается k-м членом разложения и обозначается
через Tk:
Tk = Cknan~W (6 = 0, 1, ..., и). (2)
69. (МИУ, 1978 г.). Найдите наибольший коэффициент раз-
ложения (« + &)", если сумма всех коэффициентов равна 4096.
70. (МТИЛП, 1977 г.). Найдите средний член разложения
Г-тУ-
71. (ВЗЭИС, 1978 г.). В разложении (аКо-|-^л коэффи-
циент второго члена разложения на 44 больше коэффициента пер-
вого члена. Найдите п.
72. (МХТИ, 1977 г.). Найдите член разложения (Х+“У»
не содержащий х.
73. (ЛФЭИ, 1977г.). Найдите член разложения (-^=+ аЛ 1,
\у а2 /
не содержащий а. ___
74. (МТИПП, 1977 г.). Найдите член разложения (f/х~а+х)\
содержащий х во второй степени.
75. (МТИММП, 1977 г.). Найдите второе слагаемое разложе-
ния бинома а+ '^===^ , если Ст:С^ = 4:1.
28
76. (МТИММП, 1977 г.). Найдите третий член разложения
если сумма всех биномиальных коэффициентов
этого разложения равна 2048.
77. (МИЭТ, 1977 г.). Определите х в выражении ( f/2 +-^Y
15
если отношение седьмого слагаемого от начала в разложении
бинома к седьмому слагаемому от конца равно 1/6.
78. (МИУ, 1978 г.). Определите номер члена разложения би-
нома + который содержит а7.
79. (МЭСИ, 1977 г.). В разложении + биномиаль-
ный коэффициент второго члена на 44 больше биномиального
коэффициента первого члена. Найдите номер члена, не содержа-
щего х.
80. (МХТИ, 1978 г.). Найдите член разложения
не содержащий х.
81. (МТИПП, 1978 г.). Коэффициент при х во втором члене
разложения — равен 31. Найдите степень п.
82. (ЛГУ, фак. экономический, химический, психологии,
1978 г.). Сумма коэффициентов трех первых слагаемых разложения
(2 \ т
X2 — —) равна 97. Найдите член разложения, содержащий х4.
83. (МАТИ, 1977 г.). Определите А„, если пятый член разло-
жения (j/x +“£)" не зависит от х.
84. (МИЭТ, 1977 г.). Найдите, при каких значениях х в раз-
(1 1 \т
у 2х -^-’^====j сумма третьего и пятого сла-
гаемых равна 135, а сумма биномиальных коэффициентов трех
последних слагаемых равна 22.
85. (МИЭТ, 1977 г.). При каком х четвертое слагаемое разло-
жения бинома (Гх1/(1^+1) + ^хГ равно 200?
86. (МИНГП, 1978 г.). В разложении ^2^+^у сумма бино-
миальных коэффициентов первого и второго членов разложения
равна 36, а второй член разложения в 7 раз больше первого.
Найдите х.
87. (МИЭТ, 1977 г.). Найдите, при каких значениях х раз-
ность между четвертым и шестым слагаемыми разложения бинома
f й
) равна об, если известно, что показатель бинома т
\у 8 V^x)
на 20 меньше, чем биномиальный коэффициент третьего слагае-
мого разложения.
88. (МИФИ, 1977 г.). Найдите х,' если известно, что второй
член разложения бинома (х-фх1®*)5 равен 1000000.
29
89. (МАИ, 1977 г.). При каком значении х шестое слагаемое
(1 XI \ 7
2iogtV»-«->+7_|_2 s og2~ paBe
но 84?
90*. (МИНХ, 1977 г.). Докажите неравенство nn+1 > («+1)”,
п^З, n£N.
91. (МИФИ, 1977 г.). Найдите показатель п бинома
если 9-й член разложения имеет наибольший коэффициент.
92. (МИСиС, 1978 г.). Найдите наибольший по модулю член
разложения бинома (a-f-&)?°, если |а| = Кз|&|.
93. (МФТИ, 1979 г.). В разложении бинома (1-(-х)п по воз-
растающим показателям степеней х третье слагаемое в четыре
раза больше пятого, а отношение четвертого слагаемого к шестому
равно 40/3. Найдите п и х.
94. (РГУ, мехмат, 1977 г.). Упростите выражение
\ X2/3—хг^3+1 X—х1^ )
и найдите член разложения, который не содержит х.
95. (РГУ, мехмат, 1977 г.). Сумма коэффициентов первого,
/ 1 \/я
второго и третьего слагаемых разложения (х2 + у) равна 46.
Найдите член разложения, не содержащий х.
§ 4. УРАВНЕНИЯ И НЕРАВЕНСТВА ПЕРВОЙ И ВТОРОЙ СТЕПЕНИ
Решите следующие уравнения (1—3).
1. (КишПИ, 1980 г.). |x-f-2 = 2(3—х).
2. (МАТИ, 1979 г.). |Зх-2 + х=11.
3. (МИИГАиК, 1980 г.). |х|-|х-2| = 2.
4. (МЭСИ, 1980 г.). Найдите наименьшее целое значение х,
удовлетворяющее уравнение [х — 3|4-2|х4-1| = 4.
5. (МАИ, 1981 г.X Найдите все a^R, при которых уравнение
а3 + а21 а + х | +1 а2х -f-11 = 1 имеет не менее четырех различных
решений, являющихся целыми числами.
Решите следующие неравенства (6—11).
6. (МСИ, 1977 г.). |5 —2х|< 1.
7. (МСИ, 1977 г.). |3х—2,5 >2.
8. (КишПИ, 1980 г.). |х —2 <|х + 4|.
9. (МТИЛП, 1977 г.). |2х-4|<х-1.
10. (МГУ, географ, фак., 1967 г.). 2]хЧ-1|>х-}-4.
11. (МАТИ, 1977 г.). |х + 2|-|х-1 |<х-3/2.
12. (МЭСИ, 1980 г.). Решите неравенство |х+1 | + |х —4| > 7,
указав наименьшее целое положительное х, удовлетворяющее этому
неравенству.
13. (МТИЛП, 1981 г.). Найдите наибольшее целое х, удовлет-
2лг+ 1 Зх— 1 !
воряющее неравенству $ '-------2— >
30
Квадратные уравнения и квадратный трехчлен
14. (СимфПИ, 1981 г.). Найдите Ь, если корни уравнения
24Х2 + Ъх + 25 = 0 действительны и Xj=l,5Xf.
15. (МГМИ, 1979 г.). Найдите все решения уравнения (|х|4-1)2—
s=4|x|4-9, принадлежащие области определения функции у =
=/5=^2х.
16. (МГМИ, 1979 г.). Найдите все решения уравнения
(3|х) —3)2 = |х)4-7, принадлежащие области определения у =
х (х—3).
17. (МГМИ, 1979 г.). Найдите все решения уравнения
(2|х| —1)2= |х|, принадлежащие области определения функции
y = lg(4x —1).
18. (МГМИ, 1979 г.). Найдите все решения уравнения 9х2 —
— 18|х|4-5 = 0, принадлежащие области определения функции
У = In ((х-f-l) (х —2)).
Решите аналитически и графически следующие уравнения
(19—22).
19. (МИСиС, 1979 г.). |х2 + 4х + 2| = (5х4-16)/3.
20. (МИСиС, 1979 г.). | х2 — 2х — 1 [ = (5х + 1 )/3.
21. (МИСиС, 1979 г.). |х2-4х + 2| = (5х-4)/3.
22. (МИСиС, 1979 г.). |х2-6х+7| = (5х-9)/3.
Решите уравнения (23—25).
23. (ЯГУ, 1980 г.). х2 + |х-1| = 1.
24. (ПГУ, 1980 г.).
(х2 4- х + 1)+(х2 + 2х + 3)+(х2+Зх 4-5) +... + (х24-20х-|-39)=4500.
25. (МАТИ, 1979 г.). х|х-4|4-а = 0.
26. (ЯГУ, 1980 г.). При каких значениях а уравнение 9х2—
— 2х4-а = 6—ах имеет равные корни?
27. (РПИ, 1980 г.). Найдите значение k, при котором урав-
нение (k — 1)х24- (64-4) х 4-6 4-7 = 0 имеет равные корни.
28. (ОГУ, 1980 г.). Найдите значения а, при которых корни
уравнения (2а — 5)х2 — 2(а— 1)х4-3 = 0 равны между собой.
29. (МАМИ, 1976 г.). При каких значениях т уравнение
х2—х4-/и = 0 не имеет действительных корней?
30. (МАМИ, 1977 г.). При каких значениях т уравнение
х2—х-|-/п2 = 0 не имеет действительных корней?
31. (МСИ, 1980 г.). При каких значениях т уравнение тх2—
— (т 4- 1) х 4- 2/п—1=0 не имеет действительных корней?
32. (МСИ, 1980 г.). При каких значениях с уравнение
(с—2)х24-2(с—2)х4-2 = 0 не имеет действительных корней?
33. (МЭСИ, 1980 г.). Найдите целые значения k, при кото-
рых уравнение (k—12)х24-2(6—12)х4-2 = 0 не имеет действи-
тельных корней.
34. (ВГУ, геолог, и географ, фак., 1980 г.). При каких зна-
чениях а уравнение x24-2aj/a2 — Зх4-4 = 0 имеет равные корни?
35. (МХТИ, 1977 г.). Найдите значение коэффициента а, при
котором кривая z/ = x24-ax4~25 касается оси Ох.
31
36. (МВМИ, 1977 г.). Найдите значение k, при котором кри-
вая г/ = х2 + #х + 4 касается оси Ох.
37. (МТИЛП, 1980 г.). Составьте квадратное уравнение, кор-
1 1
нями которого являются числа ----------------=.
г 10—1^72 10 + 6 К2
38. (МарПИ, 1977 г.). При каких значениях k неравенство
х2 — (k — 3)х — & + 6>0 справедливо при всех действительных х?
39. (УрГУ, матмех, 1979 г.). При каких значениях а нера
венство ах2 + 2ах + 0,5 > 0 выполняется на всей числовой оси?
40. (МЭСИ, 1980 г.). При каком целом k неравенство
х2-2(46- 1)х+ 15Л2 — 2k-1 > 0
верно при любом действительном х?
41. (МЭСИ, 1980 г.). Найдите наименьшее целое значение k,
при котором уравнение х2 — 2(^ + 2) х+ 12 + &2 = 0 имеет два раз
личных действительных корня?
42. (МИСиС, 1977 г.). При каких значениях а сумма корне
уравнения х2 + (2—а —а2)х—а2 = 0 равна нулю?
43. (МИТХТ, 1977 г.). При каких значениях а уравнение
х2 —(2а—1)х —3(4а-1 —2а-2) = 0 имеет действительные корни?
44. (ПГУ, 1980 г.). При каких значениях а графики функций
у = 2ах +1 и у = (а — 6) х2 — 2 не пересекаются?
45. (МИНГП, 1979 г.). При каких значениях р вершина пара-
болы г/ = х2 + 2рх+13 лежит на расстоянии 5 от начала коор-
динат?
46. (РПИ, 1980 г.). Найдите значение а, при котором один
корень уравнения х2 + (2а —1)х + а2 + 2 = 0 вдвое больше другого.
47. (РПИ, 1977 г.). При каких значениях а отношение кор-
ней уравнения х2 + ах + а + 2 = 0 равно 2?
48. (РПИ, 1977 г.). При каких значениях а отношение кор-
ней уравнения ах2 — (а + 3)х + 3 = 0 равно 1,5?
49. (МАИ, 1977 г.; МГИ, 1979 г.). При каких значениях а
корниXj и х2 уравнения х2 —(За + 2)х + «2 = 0 удовлетворяют
соотношению хх = 9х2? Найдите эти корни.
50. (РПИ, 1978 г.). Определите а так, чтобы один из корней
15
уравнения x2 — -^x-}-a = Q был квадратом другого.
51. (ВГУ, 1980 г.). Корни xt и х2 уравнения х2 + рх + 12 = 0
обладают свойством х2 — хх=1. Найдите р.
52. (ВГУ, геолог, и географ, фак., 1980 г.). В уравнении
5х2 — kx-\-1 = 0 определите k так, чтобы разность корней уравне-
ния равнялась единице.
53. (РПИ, 1977 г.). При каком значении а разность между
корнями уравнения (а — 2) х2— (а — 4) х— 2 = 0 равна 3?
54. (МЭСИ, 1979 г.). В уравнении 5х2 + &х — 28 = 0 найдите
если корни уравнения хх и х2 находятся в зависимости 5хх +
+ 2х2 = 1 и b — целое число.
55. (МХТИ, 1979 г.). В уравнении х2 — 4% + р = 0 найдите р,
если известно, что сумма квадратов его корней равна 16.
32
56. (МТИПП, 1978 г.). При каких значениях а разность кор-
ней уравнения 2х2 — (а + 1) х + (а — 1) = 0 равна их произведению?
57. (БГУ, 1980 г.). Найдите все значения а, при которых
сумма корней уравнения х2 —2а (х—1) —1 = 0 равна сумме квад-
ратов его корней.
58. (ВГУ, геолог, и географ, фак., 1980 г.). Определите коэф-
фициенты уравнения х2 + рх + ^ = 0 так, чтобы его корни были
равны р и q.
59. (ЛатвГУ, 1980 г.). При каких значениях а уравнения
х2+ах + 1=0 и х24-х + а = 0 имеют общий корень?
60*. (ТбГУ, физфак, спец, радиофизика и электроника, 1978 г.).
Даны два квадратных уравнения х2—х + т = 0, х2 — x + 3m = 0,
ш#=0. Найдите значение т, при котором один из корней вто-
рого уравнения равен удвоенному корню первого уравнения.
61. (МГМИ, 1979 г.). Трехчлен ах2-}-&х + с не имеет дейст-
вительных корней, а + & + с<0. Найдите знак числа с.
62. (ЯГУ, 1980 г.). Выразите Xi + xf через коэффициенты урав-
нения х2 + рх+# = 0, где х£, х2 —его корни.
63. (КГУ, 1978 г.). Пусть xf и Xj —корни уравнения Зх2 — ах-Ь
-f- 2а — 1 = 0. Вычислите х?+х%.
64. (БГУ, 1980 г.). Не решая уравнения Зх2 — 5х—2 = 0, най-
дите сумму кубов его корней.
65. (КГУ, 1977 г.). Вычислите -^ + -4-, где хо х2 —корни
Х%
уравнения 2х2 —Зах—2 = 0.
66. (РПИ, 1978 г.). При каких а уравнение (2 —х)(х+1) = а
имеет действительные и положительные корни?
67. (МТИММП, 1977 г.). Найдите все значения р, при которых
корни уравнения (/? —3)х2 —2рх-)-5/7 = 0 действительны и поло-
жительны.
68. (РПИ, 1978 г.). Найдите все значения а, для которых не-
равенство (а + 4) х2 — 2ах + 2а—6 < 0 выполняется при всех х £ R.
69. (РПИ, 1978 г.). Найдите все значения а, для которых не-
равенство (а — 3) х2 — 2ах + 3а — 6 > 0 выполняется при всех зна-
чениях а.
70. (ВГУ, матфак, 1979 г.). Найдите все значения а, для ко-
торых неравенство (а— 1) х2 — (а-\-1) х+а+ 1 > 0 выполняется при
всех действительных х.
71. (МЭСИ, 1980 г.). При каком наименьшем целом k трехчлен
(k — 2)х2 + 8х+& + 4 положителен при всех значениях х?
72. (КПИ, 1978 г.). Решите неравенство х2 + ах+а> 0.
73. (КиевГПИ, 1978 г.). Найдите все действительные значе-
ния т, при которых неравенство /их2—4х + 3/п+1>0 удовлет-
воряется при всех положительных х.
74. (МИТХТ, 1979 г.). Найдите все значения а, при которых
оба корня уравнения х2 — бах+ 2 — 2а + 9а2 = 0 больше 3.
75. (МАИ, 1979 г.). Составьте квадратное уравнение, произве-
дение корней х± и х2 которого равно четырем, и - . 4-Ц = .
Xi ~~ 1 & *
2 В. М. Говоров и др. 33
76. (МАИ, 1979 г.). Составьте квадратное уравнение, сумма
„ 1— Xi , 1— х2 оЧа24-15
корней Xi и Xi которого равна двум и = 2 4aic_i'»
77. (МИИГАиК, 1978 г.). При каких значениях а корни урав-
нения х2 — 4ах-4-1 = 0 действительные и удовлетворяют условиям
х^ ^а, х2 0?
78. (МАИ, 1979 г.). При каких значениях a£R уравнение
ох2 + х-j-а — 1 = 0 имеет два различных действительных корня хх
I 1 I к н
и xi, удовлетворяющих неравенству----------> 1?
I Х1 *2 I
79. (МАИ, 1979 г.). При каких значениях a^R уравнение
х24-1=х/а имеет два действительных различных корня х£ и х2,
удовлетворяющих неравенству |х’ — х||> 1/а?
80. (МИТХТ, 1979 г.). Найдите все значения а, при которых
неравенство (х — За)(х—а—3) < 0 выполняется при всехх таких,
что 1 х sC 3.
81* . (МГУ, геофизика, 1977 г.). Найдите все значения k, при
которых любое действительное х является решением хотя бы одного
из неравенств
х24-562-|-8£ > 2(ЗЛх-4-2)
и
x2 + W>Jfe (4х+1).
82*. (КиевГПИ, 1981 г.). При каких действительных а корни
уравнения х2 — 2х — а2 4- 1 =0 лежат между корнями уравнения
х2—2 (а 4- 1)х-}-а (а — 1) = 0?
83. (КиевГПИ, 1981 г.). При каких значениях а всякое реше-
ние неравенства х2—х—2 <0 больше любого решения неравенства
ах2 — 4х— 1 ^0?
Решите следующие неравенства (84—109).
84. (МИИЗ, 1978 г.). Зх2—7х4-4<0.
85. (ВЗИИЖТ, 1979 г.). Зх2-7х+6<0.
86. (ВЗИИЖТ, 1979 г.). Зх2-7х-6<0.
87. (ВЗИИЖТ, 1979 г.). х2-Зх4-5>0.
88. (ВЗИИЖТ, 1979 г.). х2-14х-15>0.
89. (ВЗИИЖТ, 1979 г.). 2-х-х2>0.
90. (МИНХ, 1979 г.), х2-51 х 14-6 < 0.
91. (БГУ, 1980 г.), х2-|х|-2>0.
92. (МИИГАиК, 1977 г.). |х2-4х|<5.
93. (МАТИ, 1980 г.). [х24-х|—5<0.
94. (МИИГАиК, 1977 г.; БашГУ, 1980 г.) | х2 - 5х | < 6.
95. (МИФИ, 1980 г.). |х2 —2х|<х.
96. (МИНХ, 1980 г.). |х2—2х —3|<3х —3.
97. (МИЭТ, 1977 г.). |х2-Зх|4-х-2 <0.
98. (МИИГАиК, 1978 г.). х2-7х4- 12 < | х-41.
99. (МГУ, геофизика, 1977 г.), х2—|5х — 3|—х < 2.
100. (МИИГАиК, 1978 г.). | х—61 > х2—5x4-9.
101. (МИИГАиК, 1978 г.). |х—6| <х2-5х4-9.
34
102. (МГУ, геофизика, 1977 г.). |х—2|^2х2—9x4-9.
103. (МГУ, геофизика, 1977 г.). Зх2—|х—3|>9х—2.
104. (МГУ, геофизика, 1977 г.). x24-4^|3x4-2j—7х.
105. (МАТИ, 1980 г.), х2—15x4-81 > 0.
106. (МИНХ, 1979 г.). 31jc —114-х2—7 > 0.
107. (МИУ, 1978 г.). |х—6|>|х2—5х4-9|.
108. (МАТИ, 1977 г.). (| х— 11—3) (| х + 2|—5) < 0.
109. (ЯГУ, 1980 г.), (х2—2х—8|>2х.
НО. (МТИПП, 1981 г.). При каких значениях k уравнение
&х24-12х —3 = 0 имеет корень, равный 1/5?
111. (МГУ, химфак, 1981 г.). При каких значениях параметра а
неравенство (а34-(1—К2)а2—(34-К2)а4-3|/г2)х24-2 (а2—2)х4-а>
> — J/^2 выполняется для любого х > 0?
112. (МГУ, психфак, 1981 г.). Найдите все числа а, при каж-
дом из которых наименьшее значение квадратного трехчлена 4х2 —
— 4 ах 4-а2— 2а 4-2 на отрезке 0^х^2 равно 3.
113. (ТбГУ, физфак, спец, радиофизика и электроника, 1980 г.).
При каком значении а корни уравнения 2x34-6x-f-a=O удовлет-
воряют условию 47 + “ < 2-
§ 5. УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Уравнения высших степеней
1. (МАТИ, 1980г.). Решите уравнение(х — j/з)4 — 5 (х — j/*3)2 4-
4” 4 = 0.
2. (МГМИ, 1979 г.). Найдите все решения уравнения
(2| х |—З)2—|х|—6
4х-|-1
принадлежащие области определения функции у = (2х4-1)/(х2 — 36).
3. (ПГУ, 1980 г.). Покажите, что если
г = а4-Кд2 4* Ь3 — J^a24-b3 — а,
то z34-3&z — 2a = 0.
Решите уравнения (4—9).
4. (МИФИ, 1980 г.). (х—1)(х—2)(х —3)(х—4) = 15.
5. (КГУ, 1978 г.). (x4-a)(x4-2a)(x-|-3a)(x4-4a) = b‘.
в. (МЭСИ, 1980 г.). ^-1=1; = ^.
7. (МАДИ, 1981 г.). 2£±14-^т = 5.
8. (МТИЛП, 1981 г.).
9. (МТИМБО, 1981 г.). 4-1 = .
2*
35
10*. (МАИ, 1979 г.). Найдите все действительные значения а,
для каждого из которых уравнение j/"x —а(х2 + (14-2а2) х4-2а2)=0
имеет только два различных корня. Запишите эти корни.
11. (МАИ, 1979 г.). Определите все значения n£N, при ко-
ле—8 п
торых уравнение = y не имеет решении.
12*. (БГУ, мехмат, 1979 г.). При каких значениях а уравнение
х44-(1 — 2а)х24-а2—1 =0 а) не имеет решений? б) имеет одно
решение? в) имеет два решения? г) имеет три решения?
13. (МАИ, 1979 г.). При каких действительных значениях а
сумма корней уравнения у 4--^—меньше чем а.3/10?
14. (МАИ, 1979 г.). Решите уравнение
2b2+x2 2х г 1 а
Ь3 —х3 bx+b2+x2 'x—b~
При каких значениях b решение уравнения будет единственным?
15. (МИТХТ, 1979 г.). Найдите все значения а, при которых
неравенство л._а_^_2 < 0 выполняется при всех х из промежутка
1<х<2.
16. (МЭСИ, 1980 г.). Найдите наименьшее целое х, удовлет-
’х—5 . п
воряющее неравенству _ 14 > 0.
17. (МЭСИ, 1980 г.). Найдите целые х, удовлетворяющие не-
равенству х*—Зх®—х-ЬЗ < 0.
2 I 8
х—13 9 *
Найдите наибольшее целое х, удовлетворяющее неравенству
(18—22).
18. (МЭСИ, 1979 г.). < 0.
19. (МЭСИ, 1977 г.),
20. (МЭСИ, 1980 г.). <5^.
21. (МЭСИ, 1980 г.).
22. (МЭСИ, 1977г.). (x-j-1) (х—3)2(х—5)(х — 4)2(х—2) < 0.
23. (ГГУ, мехмат, физфак, 1978 г.). Найдите целые х, удов-
летворяющие неравенству
24. (МАТИ, 1979 г.). Назовем а «хорошим» числом, если для
любого действительного х выполняется неравенство —г~}~2жЛ^ а.
а) Докажите, что число 4 является «хорошим» числом.
б) Найдите все «хорошие» числа.
25. (МИЭТ, 1977 г.). При каких значениях т неравенство
х2—тх—2. . _
•Х2_Зх-1-4 > —1 выполняется при всех х£к?
36
26*. (МГУ, геофизика, 1977 г.). Найдите все значения k, при
I
которых неравенство k ’ выполняется при всех х, удовлет-
воряющих условию — 1 < х < 1.
Рациональные неравенства
Решите следующие неравенства (27—135).
27. (МТИЛП, 1978г.;МИНХ, 1979г.). (х-1) (3-х)(х-2)2>0.
28. (ВЗИИЖТ, 1979 г.). g=|<0.
29. (МИЭТ, 1977 г.). > 0.
30. (МАДИ, 1977 г.). < 0.
31. (ВЗФЭИ, 1980 г.). §=^±р<0.
32. (ВЗФЭИ, 1980 г.). x2j^73 < °-
33. (МТИЛП, 1980 г.). (Х~~1)1(2^2-<О.
34. (МГИ, 1980 г.). gh^±i>0.
35. (МИЭТ, 1977, г.), х4 —5x3-f-4<0.
36. (МАТИ, 1980 г.), х4 — 2х2-63<0.
37. (МИИЗ, 1979 г.). 7=2 <1-
38. (РПИ, 1979 г.). ^<2.
39. (РПИ, 1980 г.).^±3<6.
40. (ЯГУ, 1980 г.).
41. (МИСИ, 1978 г.). 5=7 <2-
42. (МХТИ, 1977 г.). — > 2.
43. (РПИ, 1980 г.). > 4.
44. (МАТИ, 1980 г.). 7=5>у*
45. (МИИЗ, 1979 г.). §q^<l.
46. (МИИЗ, 1977 г.).
47. (МИИЗ, 1977 г.). ^у8<1.
48. (ВЗИТиЛП, 1979 г.).
37
49. (МИХМ, 1980 г.). i^+^=Z<2.
50. (МТИЛП, 1979 г.). ^4х-5 < °- .
51. (ВЗФЭИ, 1980 г.). у2 11,3х1дп < 0.
52. (ВЗФЭИ, 1980 г.). -^f+6<0-
53. (МТИЛП, 1979 г.).
54. (ВЗИТиЛП, 1980 г.), > °*
55. (ВЗИТиЛП, 1980 г.). _^Х^>0.
56. (КПИ, фак. общетехн, дисц., 1979 г.). 2х ~»3gY459> 1.
57. (ЯГУ, 1980 г.). -^~1Т<1.
58. (МХТИ, 1977 г.). -^-^>0.
59. (ВЗЭИС, 1977 г.), > 0.
60. (МАТИ, 1980 г.).
61. (ВЗЭИС, 1978 г.). 17~^72Х2<О-
62. (МСИ, 1977 г.; ПГУ, 1980 г.). Q х*~9 < 0.
63. (МАДИ, 1977 г.). £±?4--*±1>0.
64. (МГИ, 1977 г.). 2х2+у>0.
65. (МИНХ, 1979 г.). ^~6>0.
66. (МИЭТ, 1977 г.). -^*+^<0.
67. (МАДИ, 1977 г.). < 0.
68. (МАДИ, 1977 г.). -/ГТ.8<0.
69. (КишПИ, 1980 г.).
70. (МГИ, 1980 г.). < х.
71. (МГИ, 1979 г.) * < 3
Л |~ JC о
72. (МИИГАиК, 1977 г.). 2|^2<О.
38
73. (МГИ, 1977 г.). -^f~2 Q-< 1.
74. (РПИ, 1980 г.). > 3.
х 7 х3—4x4-5
75. (РПИ, 1980 г.). х2Г3^+^ < 4.
х ’ 7 х2—Зх+З
76. (РПИ, 1980 г.). < 3.
77. (РПИ, 1978 г.). > 2.
78. (МТИПП, 1980 г.). ^tf<-2.
79. (МГИ, 1979
80. (МИНХ, 1977 г.).
81. (РПИ, 1980 г.; БГУ, 1980 г.). ,, < 1.
ох ^х х о
82. (МФТИ, 1977 г.). --215~4*.о < 4.
х ’ 7 х2—-X—12
83. (МИНХ, 1977 г.)
84. (МТИМБО. 1979 г'.) > 0.
85. (МФТИ, 1977, г.; МАИ, 1979 г.). 3JZxl4 < 4.
86. (МФТИ, 1977 г.). ^-^=§^>2.
87. (МАИ, 1979 г.). —°2?т+49о- < 4- •
88. (КишПИ, 1980 г.). >0.
89. (МИИГАиК, 1977 г.).
90. (РПИ, 1980 г.). 2 4—4>-•
91. (РПИ, 1980 г.). l+4n>T-
92. (МИЭТ, 1977 г.). > 0.
93. (МИЭТ, 1977 г.). < 2.
94. (МАИ, 1979 г.).
95, (МАИ, 1979 г.).
90. (МАИ, 1979
97, (БГУ, 1980 г.).г±5 + г±т>±.
89
98. (БГУ, 1980 г.). ._z|;_i|+Aiti<0.
99. (БГУ, 1980 г.). it_3”_4)+JL4+l>0.
100. (МИИГАиК, 1977 г.). > 1.
101. (МИИГАиК, 1977 г.). > 1.
102. (МИНХ, 1977 г.). (х2 + 3х + 1)(х2 + 3х-3)>5.
103. (МИСиС, 1979 г.). (х2-х- 1) (х2— х-7) <-5.
104. (МИФИ, 1979 г.), (х2 —2х) (2х —2) —
105. (МИФИ, 1979 г.). (х2 + Зх)(2х + 3)-16^Ц>0.
106. (МИНХ, 1979 г.). --> 0. +
107. (МИИГАиК, 1977 г.). |х3-1|>1— х.
108. (МТИПП, 1977 г.). j~^j~6<0.
109. (МИХМ, 1979 г.). -ff~7<0.
НО. (МИИЗ, 1977 г.). -^~21 >0.
111. (ЯГУ, 1980 г.). |^| > 1.
112. (ЛГПИ, 1978 г.). |^Ет|>2-
113. (МАИ, 1977 г.).
114. (БГУ, 1980 г.). х2771Хй10<0.
115. (МИНХ, 1979 г.). 1.
116. (МИНХ, 1979 г.). < 1.
117. (МИНХ, 1979 г.). -2,~* < 2.
118. (МАТИ, 1980 г.). —1—<1.
[ Л | — О Z
119. (МИИГАиК, 1978 г.). |1.
120, (МИИГАиК, 1978 г.). | X-^f4 |< 1.
121, (КубГУ, 1980 г.). -^ХТ3!К >2.
122. (БГУ, 1980 г.). — ^^->2х.
123, (МГМИ, 1979 г.). |х|<-.
1 1 X
40
124. (БарнГПИ, матфак, 1981 г.). 1 +-^г <у •
125. (ТашГУ, матфак, 1981 г.), х—17^^.
126. (ТашГУ, физфак, 1981 г.). ^^5^6
127. (ТашГУ, физфак, 1981 г.).
128. (МИСиС, 1981 г.). х<^.
129. (МГПИ, физфак, 1981 г.). х2^7112^0-
130. (МГУ, химфак, 1981 г.). ^=^>25(х + 2).
131. (УЭИИЖТ, 1981 г.). 1 < 3*х7+*+8
132. (МВИМУ, 1981 г.). f'(x)^g'(x), если /(x) = 5-3x-f-
+ g(*) = 3x-7.
133. (МВИМУ, 1982 г.). f'(x)^g'(x), если f(x) = 10x3 —
— 13х2 + 7х, g(x)= Их3 —15х2 —3.
134. (МИИВТ, 1982 г.). ^>3 — х.
135. (МИИВТ, 1982 г.).
§ 6. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
При решении иррациональных уравнений нужно учитывать сле-
дующую теорему. ___
При натуральном п уравнение 2{Zf (х) — <р (х) равносильно
системе
f (х) = (ф(х))2я,
Ф (х) 0.
При решении иррациональных неравенств нужно учитывать
следующие теоремы. ____
При натуральном п неравенство / (х) < ф (х) равносильно
системе неравенств
И(х) <(ф(х))2",
/(*) >0,
Ф (х) > 0.
При натуральном п неравенство f (х) > ф (х) равносильно
совокупности двух систем неравенств
ф(х) < 0, f ф(х) >0,
f(x)>0 И U(x) >(ф(х))2«
41
При натуральном п неравенство
стеме неравенств
У f(x)
ф(*)
> I равносильно си-
Ф(х) > О,
f (х) > (<р (х))2п.
2Т/7~Гл
При натуральном п неравенство < 1 равносильно сово-
Ф \х)
купности двух систем неравенств
ф(х) < О,
Ш >0
' ф (х) > 0,
f(x) >0,
J (х) < (ф (х))2".
Решите следующие уравнения (1 — 118).
1, (МГУ, мехмат, 1980 г.), (х2—1) И2х—1 =0.
2. (МГУ, мехмат, 1980 г.), (х2—4) Их + 1 = 0.
3. (МГУ, мехмат, 1980 г.). (9—х2) И2 —х = 0.
4. (МГУ, мехмат, 1980 г.). (16—х2) У3—х=0.
5. (МЭСИ, 1979 г.). И2х^З-Кх+3 = 0.
6. (ВЗИИЖТ, 1979 г.). j/x+2j/? = 3.
7. (ЛьвГУ, 1980 г.). Ух2— Ух—6 = 0.
8. (МАТИ, 1977 г.; ЛьвГУ, 1980 г.). *+3
У *4-2 о
9. (МВМИ, 1977 г.), у 108- — И10-2х=2.
10. (МФТИ, 1979 г.). /2^7 + -^=Х—= 2.
11. (МФТИ, 1979 г.). -^_2_ Чг2/х+Т=5.
12. (МАТИ, 1979 г.). у^ = х-8.
= 2.
13. (МТИ, 1978 г.). -^=— -------- = 4.
Ух2— 1 |/*+1
14. (БГУ, 1980 г.). /iog^c + v/iog^c = 2.
15. (МТИ, 1979 г.). хКх2+15 —Их р/х2+15 = 2.
16. (МАИ, 1977 г.), + 3 )/|±J = 4.
17, (МЭСИ, 1977 г.). 7ZT -2 =1-
18. (МИИГАиК, 1979 г.). =| •
42
19. (МВМИ, 1978 г.). j/"12^x = x.
20. (МИСиС, 1979 г.). K7zzx = x-1.
21. (МИСИ, 1979 г.). х—Ух+Т = 5.
22. (ВЗИТиЛП, 1979 г.). “21+:J^2x=7 = x.
23. (МВМИ, 1978 г.). 1-КТТбх = х.
24. (МТИМБО, 1977 г.; МГУ, почв. отд. биофака, 1977 г.).
2К* + 5 = х-|-2.
25. (МГУ, почв. отд. биофака, 1977 г.). 4 j/5F+6 = x +1.
26. (МГУ, биофак, 1977 г.). И4+2х —х2 = х —2.
27. (МВМИ, 1978 г.). /37-х2+5 = х.
28. (МГУ, почв. отд. биофака, 1977 г.). ]/б —4х —х2 = х + 4.
29. (МГУ, почв. -отд. биофака, 1977 г.). И 14-4х—х2 = х—1.
30. (МГУ, почв. отд. биофака, 1977 г.). К5—х2 = х—1.
31. (МГУ, почв. отд. биофака, 1977 г.). Кх2 + 8 = 2х+1.
32. (МВМИ, 1977г.). 4+У26 —х2 = х.
33. (МИСиС, 1978 г.). Зх—ф<18х+1 +1 =0.
34. (МАИ, 1979 г.). /бх-х2-5 = 2х-6.
35. (МВМИ, 1978 г.). = 1.
36. (МВМИ, 1978 г.). 1±£2±Н2 = 1ф
Х 4
37. (МВМИ, 1977 г.).
38. (МВМИ, 1977 г.). 2+Ki9-2.t^k
39. (МГУ, эконом, фак., 1979 г.). V13—18 tgx = 6 tg х — 3.
40. (МАТИ, 1980 т.). х2 — 4х-Нб=-И 2х2 — 8х + 12 .
41. (МАТИ, 1978 г.). 2х2 + 3х—5У"2х2 + Зх + 9 + 3 = 0.
42. (МИЭТ, 1980 г.), х2 + /х2 + 2х + 8 = 12 -2х.
43. (МАТИ, 1977 г.). 2х2 + /2х2 —4х+12 = 4х + 8.
44. (МТИПП, 1977г.). Зх2 + 15х +:2/х2 + 5х+1 = 2.
45. (МИИГАиК, 1978 г.). j/16-x3 = 4-x.
46. (МХТИ, 1977 г.). Кх-р= + К2 + х = 0.
47, (МИРЭА, 1977 г.). У9- 5х + ~==.
48. (МИРЭА, 1977г.). ------------1
х+:^х2+х х—]/х2+х х
43
49. (МТИЛП, 1979 г.). /27=3 +/37+Т= 4.
50. (РПИ, 1978 г.). /Зх+Т-/7+4=1.
51. (РПИ, 1978 г.). /27 + 6-/7+Т = 2.
52. (МАТИ, 1980 г.). /7+5-/7=1.
53, (МИСИ, МПИ, 1979 г.). /2Т=4-/Т+5 = 1.
54. (ВЗИИЖТ, 1979 г.). У 27+5 = 8-/7=Т.
55. (МФИ, 1979 г.). /Т+3 + /зТ=2 = 7.
56. (МГИ, 1977 г.). /з7+7—/7+Т=2.
57. (МАДИ, 1977 г.). /4=7 + /5+7 = 3.
58*. (МТИМБО, 1979 г.). /3x2 + 6х + 7 +/572 + 10х + 14 =
= 4 —2х —х2.
59. (МАИ, 1979 г.). /зТ=5 = 3-/7=2.
60, (МИИЗ, 1978 г.). /7+2 + /з=7=3.
(МАТИ, 1979г.). /47+8-/37=2 = 2.
(МИИГАиК, 1980 г.). /27ТЗ + /37+3 = 1.
(МАИ, 1977 г.). /7+4+ /27+6 = 7.
(МГИ, 1977 г.). /зТ=7-/7+Т = 2.
(БГУ, 1979 г.; КишПИ, 1980 г.). /Г5=х + /з=х = 6.
(РПИ, 1979 г.). /7+5-/7=3 = 2.
(РПИ, 1979 г.). 2/7=1+/7+3 = 2.
(БГУ, 1980 г.). Кх + /7+ТТ+/х-/7+ТТ = 4.
69*. (МТИМБО, 1977 г.) /17=7+ /14+7=2.
70, (МИИГАиК, 1980 г.). 3*+1 = 1«
71. (МХТИ, 1977 г.).-/=--?--= -О,
1— yl— X 1+/1— X х
72. (МИНГП, 1979 г.). т/С/Т
4 ’ 7 2—х г 2—х
73. (МАДИ, 1978г.). /1 + х/х?+24 = х +1.
74. (БГУ, 1980 г.). 1+ /1 + х/х2-24 = х.
61,
62.
63.
64.
65.
66.
67,
68.
75. (ЯГУ, 1980 г.). /7 + /х-/Г=7=1.
76. (ВЗИИЖТ, 1979 г.). /7с+Т +/7=3 = 2/7.
77, (МИРЭА; ЛатвГУ, 1980 г.). /Т/Т + /4х"+ 13=/Зх +12.
78, (МАИ, 1979 г.). /7+2-/7с=3 =/47=7.
79. (МАИ, 1979 г.). /7 + /7=3 = /3(х-1).
44
80. (РПИ, 1980 г.). /х-2 + /4-х = /б-х.
81. (ЛатвГУ, 1980 г.), /х + 5 + /2Г-7= 2/7.
82. (ХАИ, 1980 г.). Кх+1+К4х+13 = КЗх+12.
83. (МТИ, 1977 г.). /Зх+1+Кх + 4 = /9— х.
84. (БГУ, 1980 г.)./Зх+4 + |/х-4= 2Кх.
85. (РПИ, 1980 г.). К2х+5 + И5х+6 = К12х+25.
86. (РПИ, 1980 г.). Кх+1+Кх—1 = /Зх-1.
87. (МИЭТ, 1980 г.)./Г/Г-1 = 1^х-К*+8.
88. (МИЭТ, 1977 г.). /х + 3-1 =]/х-/Г=+.
89. (КГУ, 1978 г.). 1?/<12+х 4. ^12+х Ух.
90. (МАДИ, 1979 г.). ^^ + = Кб.
91. (МИЭТ, 1977 г.). ^б-м/б-хМх-з^/х-з =2
' /5—х+/х—3
92. (МИРЭА, 1978 г.). /х2+х+4+/х2+х+1 =/2х2+ 2х+9.
93. (ГГУ, 1979 г.), /х2-4x4-3 +/— х2 + 3х —2 = /х2 —х.
94. (МАИ, 1977 г.). /х + 3 + /х + 4 = /х + 2 + /х + 7.
95. (МИЭТ, 1977 г.). x-/x=2 + )Kх + /Г^2 = 3.
96. (МИФИ, 1980 г.). /х2-2х + 1+Их2 + 2х + 1=2.
97. (МИФИ, 1980 г.). /х2 + 2х + 1—/х2—4х + 4 = 3.
98. (МИЭТ, 1980 г.). х + 2/Г^Т—]/х-2/.П = 2.
99. (МТИ, 1978 г.).)Кх+3—4/Гй+)/х+8—6/ГЛ = 1.
100*. (МИФИ, 1978 г.). х3 + 1=2р/2х—1.
101. (КГУ, ВМК; МАТИ, 1980 г.). 2+* +
„ ’ ' /2+/2+хт
4- 2-*__=-=2/2.
г /2—/2+х _____
102*. (МИФИ, 1977 г.). х + У^а + /х = а.
103*. (МИФИ, 1977 г.), х2—Vа—х=а.
104. (ГГУ, 1978 г.). a]f х—х + 2ах/х2 + 7а2 = 0.
105. (МИФИ, 1980 г.), х2- 4х + 32 = 16 /х.
106. (БГУ, фак. прикладной матем., 1979 г.). (а — 2)//х+4=1.
107. (ГГУ, мехмат, физфак, 1978 г.). 1/~20+х_ 1/~—~х—/б.
г X г X
108. (ТашГУ, 1981 г.). V2(Х+1} =1.
109. (ХАИРЭ, 1981 г.). ^—2 )Л^±1 = 3.
45
ПО. (МФТИ, 1981 г.). ' XL.-+ 1/— = -|.
' ' Vl-j-x т X 2
111. (РИИГА, 1981 г.). Ух + 8 + 2/х + 7 +
+ "У х 4-1 — Кх + 7 = 4.
112. (МТИПП, 1981 г.). /з^ + —£= = /9^.
У 3 — х
113. (МЭИС, 1981 г.). х|/хпУ = 56.
114. (МАДИ, 1981 г.). /х + 5+/х + 5-12 = 0.
115. (МАДИ, 1981 г.). Кбх—5 + К10х-5 = /15х-10.
116. (МТИЛП, 1981 г.). х-1 = Йх/2.
117. (МАИ, 1981 г.). /х2 + 8 = 2х + 1. _
118. (РГУ, физфак, 1977 г.). 2 = 1
У х— 4 У х-}-4
119*. (ЛГУ, 1980 г.). Сколько корней имеет уравнение (най-
дите их) /х2+ 1 -у==== х.
120. (МИСиС, 1979 г.). Найдите корни уравнения
1J3z<512p< 15х—21—К13 15 — 6х = 0, представимые несократимой
дробью а/6, где о —целое число.
Решите следующие неравенства (121—212).
121. (ГГУ, 1979 г.; МИИГАиК, 1980 г.). (х-1)/х2—х—2>0.
122. (МИФИ, 1980 г.), (х2—1)Кх2-х-2>0.
123. (МГМИ, 1979 г.) /(х-2)/(1-2х) > —1.
124. (МИЭТ, 1977 г.). /(Зх-1)/(2-х) > 1.
125. (МВТУ, 1977 г.). (Кх - 3)/(х-2) > 0.
126. (КишПИ, 1980 г.). /Зх-10> |/'б^.
127. (МТИ, 1977 г.). Кх2 + 2х—3< 1.
128. (МИХМ, 1977 г.). i— ^ <-| .
129. (МГМИ, 1980 г.). -Д=—К2^х< 2.
У 2—х
130. (МИХМ, 1977 г.). /2х2+15х-17/(10-х)>0.
131. (МВТУ, 1977 г.; МАДИ, 1977 г.). £££^±£=<0.
v ’ V 19х—х2—78
132. (ЯГУ, 1980 г.). Кх5<х+1.
133. (МТИЛП, 1977 г.; ВТУЗЗИЛ, 1977 г.). 2KxzrT<x.
134. (РПИ, 1978 г.). /7+18 < 2-х.
135. (МИИГАиК, 1978 г.). х> /24-5х.
46
136. (МИИГАиК, 1978 г.). К9х-20 < х.
137. (МГИ, 1979 г.). Ух + 7 < х.
138. (РПИ, 1978 г.). К2х-1 <х-2.
139. (КГУ, 1979 г.). К^+78<х+6.
140. (МИЭТ, 1979 г.). Кб^2х<6х-1.
141. (МИИГАиК, 1978 г.). К* + 61<х+5.
142. (МИТXT, 1977 г.). Пх-6)(1-х) < 3 + 2х.
143. (МИИГАиК, 1978 г.). К2х-х2<5-х.
144. (КГУ, 1979 г.). /2х2-Зх-5 <х-1.
145. (КГУ, 1979 г.). Кх24-3х + 3 < 2х+1.
146. (МАИ, 1977 г.). j/х2 —Зх—10 < 8 —х.
147. (МФТИ, 1977 г.). х + 4 > 2/F^x2.
148. (КишПИ, 1980 г.). |ЛЗх—х2<4 —х.
‘149. (МФТИ, 1977 г.). 3 — х > 3 КТ^^х2-
150. (МФТИ, 1977 г.). х + 4>2К4-х2.
151. (МИЭТ; МФТИ, 1977 г.). 1 - К 13 + 3х2 > 2х.
152. (МИФИ, 1980 г.). х< /2=х.
153. (КГУ, 1978 г.). х + 3<Их+33.
154. (МТИЛП, 1980 г.). УхГ-1>х.
155. (РПИ, 1978 г.). /2х+14>х + 3.
156. (МАТИ, 1978 г.), х—3 < /х^2.
157. (КГУ, 1979 г.). х+2<Кх+Т4.
158. (ВТУЗ ЗИЛ, 1977 г.; МВТУ, 1978 г.). x-l<J<7^x.
159. (МИИГАиК, 1978 г.). J/9x-20>x.
160. (РПИ, 1978 г.). И11-5х>х-1.
161. (РПИ, 1978 г.). Их + 2>х.
162. (МФИ, 1979 г.). Кх*+Т>х-1.
163. (МТИЛП, 1977 г.), /(х + 4) (х + 3)>6-х.
164. (МТИЛП, 1977 г.). К(* + 3) (х-8) > х + 2.
165. (КГУ, 1979 г.). 1-х<Их2-2х.
166. (МИЭТ, 1977 г.). /5^х2>х-1.
167. (МТИЛП, 1980 г.), х-/1 -1 х| < 0.
168. (КГУ, 1980 г.). 4-х < /х2-2х.
169. (КГУ, 1979 г.). х</х2 + х-2.
170. (КГУ, 1979 г.). 4-х<К2х-х2.
47
171. (КГУ, РФФ, 1979 г.), х—3 < /х2 + 4х-5.
172. (МАИ, 1979 г.). 2х + 3 < /х2 + 5х + 6.
173. (МАИ, 1979 г.). /х2-Зх + 2 > 2х-5.
174. (МГУ, биофак, 1980 г.). |/х2 + х>1 —2х.
175. (МГУ, биофак, 1980 г.). J^8 + 2x —х2 > 6 —Зх.
176. (МГУ, биофак, 1980 г.). 2х+3 < К—2-Зх —х2.
177. (МГУ, биофак, 1980 г.). х + 4'<'К—х2-8х-12.
178. (МГУ, биофак, 1980 г.). /—х2 + 6х-5 > 8-2х.
179. (МИХМ, 1977 г.; БГУ, 1980 г.).
180. (КГУ, 1978 г.; МИФИ, 1979 г.). х2> х(2 +И12—2х—х2).
181. (ЛГУ, 1979 г.). К4^-"х2 + ^>0.
182. (МИСиС, 1978 г.). /х-3^2/(/х-2).
183. (АзГПИ, физфак, 1979 г.), х —3 Ух—3— 1>0.
184. (МИФИ, 1979 г.). К« + 4/(1 -а)- 1 <0.
185. (РПИ, 1978 г.). К2Т^Т/(х-2)< 1.
186. (МИХМ, 1977 г.). Их+20/х — 1 < 0.
187. (МФТИ, 1978 г.). /2х2 + 7х-4/(х-|-4) < 1/2.
188. (МИФИ, 1979 г.). (1 -/21-4х-х2)/(х+ 1)>0.
189. (ВильнГУ, физфак, 1979 г.). ]/"4 — У1 — х— К2 — х>0.
190. (МФТИ, 1977 г.), f/r^+l < Кз^х2.
191. (МИФИ, 1979 г.). ЗУх-Ух + 3> 1.
192. (МИФИ, 1979 г.). 3 Ух-/5х + 5 > 1.
193. (ЛГУ, 1979 г.). /х + 3 + Кх+15<6.
194. (МФТИ, 1977 г.). 2 -УТ^ > К^х2.
195. (МИУ, 1979 г.). /х + 3 + /х + 2-|Л2ГЙ>0.
196. (МИФИ, 1979 г.). Ух^6-У 10-х> 1.
197. (ЛГУ, 1977 г.). /ГЙЗ - Кх=Т > К2Г=Т.
198. (ВильнГУ, матфак, 1979 г.). Кх + 3 < Ух^Т + Ух—2.
199. (МИУ, 1978 г.). /Зх2 + 5х + 7-/Зх2 + 5х + 2> 1.
200. (МИЭТ, 1979 г.). Ух + 2У^Т + уГх-2/Г=й>3/2.
201. (КГУ, 1979 г.). Кб + х-К- х -3< 1 +/(х+5) (-х-З)Г
202. (МИФИ, 1980 г.). < 3.
203. (ЛГУ, матмех, 1979 г.). ]/х + 4 + л/'х-?>-.
ж X г х
48
204. (МИФИ, 1980 г.). мКх4-1<1.
205. (МИФИ, 1980 г.). («+ 1) У~2=х < 1.
206. (НГУ, фак. геолого-географ. и естеств. наук, 1981 г.).
4 + 3< V41 —у.
207. (ХАИРЭ, 1981 г.). /х2-4х>х-3.
208. (ЕГУ, мехмат, 1981 г.). —х24-* + 2 + 2х +1 > 0.
209. (МГУ, мехмат, 1981 г.). ?
v ’ ’ ’ logy-(x—4)— I-'
210. (КубГУ, 1980 г.). |x+^±d/1 >0.
211. (ТаджГУ, физфак, 1981 г.). (1/3)г^2 < 3"*.
212*. (МИФИ, 1980г.). х + ^-^=>
у х2 — 1 12
213. (МАДИ, 1981 г.). Найдите середину отрезка, в котором
выполнено неравенство 2х2—7(К*)2=^4.
214. (МТИЛП, 1981 г.). Найдите наименьшее целое положитель-
ное значение х, удовлетворяющее неравенству |/х24-16x4-64 > 20.
215. (МЭСИ, 1977 г.). Найдите целое число, удовлетворяющее
неравенству 2 V 2х 4-1 > 3 К — х2 — х 4- 6.
§ 7. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
Решите следующие системы уравнений (1—77).
( У + х — 1=0,
1. (МИЭТ, 1977 г.). < Г . ’
( |#|—х—1=0.
( х4-3|у|— 1 =0,
2. (МИЭТ, 1977 г.). { ,+!,^ = 0.
1 «/ — 2x4-1 = 0,
3. (МИЭТ, 1977 г.). { ... '
\У — |х| —1 = 0.
( |х — 1 |4-w = 0,
4. (МИНХ, 1979 г.). | 2х-«/=1
I х + 2м —6 = 0,
5. (МИЭТ, 1977 г.). {
1 «4-0 = 2,
6. (МГУ, психфак, 1980 г.). \ ,
' ( |3« —v| = 1.
( и 4- 2v = 2,
7. (МГУ, психфак, 1980 г.). <{ |о о , ,
' ( 12м — Зм I = 1.
1 |х|4-2|м| = 3,
8. (МАТИ, 1979 г,). {
49
9. (МАТИ, 1979 г.).
10. (МИЭТ, 1977 г.).
11. (ВЗПИ, 1978 г.).
12. (МАМИ, 1979 г.).
13. (АЗГПИ, физфак, 1979 г.
I |х —#|= 12#—11,
I #4-1 =2х.
|х—114-|#—2| = 1,
# = 3-|х-1|.
х+у — г = 2,
2х — #4-4г = 1,
— х + 6# + г = 5.
2х + 3у—z = 6,
х —#4-7г = 8,
ч Зх—#-J-2z = 7.
х4-2#—г = 7,
). • 2х —#4-г = 2,
( Зх—5#4-2г =—7.
х#4-х4-#=11,
х2# 4-х#2 = 30.
х#4-4=О,
х4-#=3.
х2—#2 —16,
х4-#=8.
х24-#2 = 41,
у—х = 1.
14. (СимфГУ, матфак, 1982 г).
15. (ЯГУ, 1980 г.).
16. (ЯГУ, 1980 г.).
17. (МГИ, 1980 г.).
{у8 -4- f/2 — 41
*Т у — у-
19. (МИИГАиК, 1980 г.). |
( х2 4- У2 4- 6x4-2# = 0,
20. (МИРЭА, 1980 г.). < , , о а
21. (МАМИ, 1978 г.; БГУ, 1980 г.). # + х 6’
( х4-!/ = 5.
22. (КПИ, 1977 г.). <\ У х “ 6 •
( х2—#2 = 5.
Xs —х#4-#2 = 7,
х4-#=5.
х-]-3 х—• 1 . 16 _л
24. (МЭСИ, 1980 г.). < #=4—’
I Их—3#=1.
23. (РПИ, 1980 г.).
50
25. (МЭСИ, 1980 г.).
26. (МАДИ, 1980 г.).
' Зх + у_х—у _ п
х—1 2у !
чХ —у=4.
'х+у . X—у, 13
. X—у^х+у 6’
+У = 5.
27. (НГУ, фак. геолого-геофиз. и естеств. наук, 1979 г.).
(^+бЫ = 5,
• х—У х+у
.ху=2.
(1—1 = 1,
28. (МАДИ, 1980 г.) { 3* \ 3 ,
(9х2 4у2 Т'
29. (МТИЛП, 1980 г.; МАДИ, 1980 г.).
30. (МГУ, физфак,
1980 г.).
-J- + l=l
х+1ту 3’
1 1 1
(х + 1)2 у2“4*
§_1_ + у=_5,
-2---6.
31. (МГУ, физфак,
32. (МГУ, физфак,
. 2х—у
. 2х+у— ~4'
у - 3
U+2y“ °’
—-----1~х= I»
х—у 1 ’
—^— = —2.
\х—У
1__ J_
У— 1 у+1 — X ’
у3 — х — 5 = 0.
' х+у . х—у _ 5
х—у’’"х+у 6 *
<х3 + у3 = 20.
'2ху-3у=15,
ху + -^=15.
X.
1980 г.).
1980 г.).
33. (МГУ, физфак, 1980 г.).
34. (МАДИ, 1977 г.).
35. (МАТИ, 1977 г.).
36. (МИХМ, 1977 г.).
1
51
/ х 16
I и 3 ’
37. (КИИ, 1978 г.). | У 9
(^-Т=2-
( x1 2 + wa = 20,
38. (РПИ, 1980 г.). {
I *2 + */2 = 68,
39. (БГУ, 1980 г.). < 1С
' ’ ' ( XI/=16.
( x(x + t/)=9,
40. (МИЭТ, 1977 г.). < , , '
(#(х + #) = 16.
1 х2 + ху= 15,
41. (МИЭТ, 1977 г.; ЯГУ, 1980 г.). (^ + ^=ю.
I У2 + х« = 231,
42. (МХТИ, 1977 г.). { * + ^ = 210.
( х2 — ху — 28,
43. (МИРЭА, 1977 г.; БГУ, 1980 г.). < . 1о
v ’ ( у2—ху =—12.
( у2 — ху — 12,
44. (БГУ, 1980 г.). { *
( х2 + у2 = 25 — 2ху,
4S. (МАДИ, 1980 г.). ( s(x+s) = ,0.
1 5(x + «)4-2xw = —19,
46. (МИНХ, 1979 г.).{ 15^+5(х+!/) = -175.
( 5 (х+у) + 2ху = —19,
47. (МАДИ, 1977 г.; МИНХ, 1979 г.). { /_з5.
1 4х2 + у2 — 2ху = 7,
48. (МАДИ, 1980 г.). (
( х+у+ху = 5,
49. (МАТИ, 1977 г.). { х. + у2+ху^
. у ~ 3 ’
х2 + у2= 160.
, 2у2 - 4ху + Зх2 = 17,
51. (МФТИ, 1977 г.). < иг_„2_16
1 х2—xz/+i/2 = 21,
52. (МФТИ, 1977 г.). | г,1_2ед+15 = 0.
53. (НГУ, фак. геолого-геофиз. и естеств. наук, 1978 г.).
j 2х2 + у2 + 8ху=\2,
( 2 (х+у)2—у2= 14.
50. (ВЗИИЖТ, 1979 г.).
52
f х2 +w3—jw= 13,
54. (МАДИ, 1977 г.). { х+у_^Гу=3.
[ 2«24-ху—х2 = 0,
55. (МЭСИ, 1980 г.). { x^xy__y. + 3x + 7y+3==Q,
I ху + Зуг-х+4у-7 = 0,
56. (МГУ, эконом, фак., 1980 г.). •{ 0 , о о . . п
' ’ 'г » / (2ху + у3—2х— 2t/4-l =0.
I 2ху+у2 — 4х—Зу 4-2 = 0,
57. (МГУ, эконом, фак., 1980 г.). \ „2 о .. 1R п
v ’ * ’ ' \ху + 3у2—2х—14i/4-16 = 0.
( Зха + ху—2х + у—5 = 0,
58. (МГУ, эконом, фак., 1980 г.). ( _3х_у_3 =0
( х34-У3==35,
59. (КГУ, мехмат, 1979 г.). { , к
( Х4-^/ = о.
( X —У = 1,
60. (МТИПП, 1977 г.). { г3_„з_7
( 4~ У3 = 7,
61. (РПИ, 1978 г.).( ху{х + у} = _2_
/ «»2
-4- ^-=18,
у 1 х ’
чх4-«/= 12.
г х4 4- V4 = 82
63. (МАДИ, 1977 г.; БГУ, 1980 г.). | = 3
f х3 + и3 = 7,
64. (ЛатвГУ, 1980 г.). { „зиз__8
V л у — °*
( (х24-«2) ху=78,
65. (ЯГУ, 1980 г.). | + Д 97
66. (МФТИ, 1977 г.). ( 155.
rx4-f/4-z= 13,
ха4-#а+2а=91,
^2=xz.
ху
х+У *
-4^ = 2,
62. (МИСиС, 1977 г.).
67. (МИЭТ, 1977 г.).
68. (МИФИ, 1978 г.).
69. (МГУ, мехмат, 1977 г.).
уг о
. У+г
у3 — 9х24-27х-27 = 0,
г3 — 2у3-\-27у—27 = 0,
х? —9z24-27z —27 = 0.
53
71. (МГУ, мехмат, 1977 г.).
(2ys + 2x* + 3x + 3 = 0,
70. (МГУ, мехмат, 1977 г.), j 2г3 + 2y1 2 + 3y+3 = 0,
[2x3 + 2z2 + 3z + 3 = 0.
' у3 — 6х24- 12х —8 = 0,
г3 — 6t/2+ 12у — 8 = 0,
х3— 6z2+12z — 8=0.
( 2х + 3у = 4,
72. (МИСиС, 1981 г.).< _ . ’
v ' I ох + 4у = 3.
73. (КолПИ, отд. физики и механики, 1981 г.).
4х—у+4г — 0,
х4-5«/ — 2г = 3,
_—х4-8г/—2г = 1.
, ( х2у2 — 2х+уъ =0,
74. (МГУ, географ, фак., 1981 г.). ( 2х1_4х+3+^=0.
6х+у3 — г3 — 6,
х2—у—4г = —4,
21х2—2у3+Зу = 22г3.
. х2=(х—а) у,
76. (МИЭМ, 198! г.), j
77. (ТаджГУ, планово-эконом. фак., 1981 г.).
(х2 + 2ху + уа—х—у = 6,
(х—2у — 3.
75. (МФТИ, 1981 г.).
78. (МАИ, 1979 г.). Найдите все значения а, при каждом из
которых система уравнений
1 2x4-2 (а— 1) у=а—4,
I 2|х4-1 |4-а</=2
имеет единственное решение. Найдите это решение.
79*. (МАИ, 1979 г.) Найдите все значения а, при каждом из
которых система уравнений
1 ax-f-(a—l)f/=24-4a»
| 3\х\ + 2у=а— 5
имеет единственное решение. Найдите это решение.
При каких значениях а следующие системы уравнений имеют
решения? Найдите эти решения (80 — 83).
1 х 4- ay = 1,
80. (ОГУ, 1980 г.). < , о
v ’ ’ ( ах+у—2а.
1 (а4-1)я—и=а4-1»
81. (ОГУ, 1980 г.). < , . ' о
' I х4-(а —1)^ = 2.
54
82. (МИФИ, 1980 г.). J ах + у — а, ( х+ау — а2.
83. (МИФИ, 1980 г.). 1 х + ау=1, ( ах 4- у = а2.
При каких значениях а каждая из следующих систем урав-
нений имеет бесчисленное множество решений? (84 — 85).
84. (МЭСИ, 1980 г.). ( Зх 4" ау—3, ( ах4" Зу ~~ 3.
85. (МЭСИ, 1980 г.). 1 (а —2) х4-27у = 4,5, ( 2х4-(а4-1)у = —1.
86. (МАМИ, 1979 г.). При каком значении а сумма квадра-
тов чисел, составляющих решение системы уравнений
| Зх — у = 2—а,
х + 2у=а+ 1,
будет наименьшей?
Решите и исследуйте относительно а следующие системы урав-
нений (87 — 90). ' 2х 4- Зу = 5,
87. (МИРЭА, 1978 г.). х—у = 2,
х + 4у = а.
' —2arccosy + z = 1,
88. (МИФИ, 1979 г.). 5\/rx+arccosy + z = 6a —14,
j/x + arccos I/4-2z = 2а + 1.
89. (МИФИ, 1979 г.). '3-2*4-2# — 3 arcsinz = 7, 2х —у—arcsinz = —6, 5 • 2х — у 4- arcs in z = 6а 4- 2.
90. (МИФИ, 1979 г.). 2)/ tgx4-2ya4-z=-14, ЗИ tgx—«/24~2z = 20 — 4а, , /tgx4-iZ84-2=10.
При каких значениях а для любого b найдется хотя бы одно
с такое, что каждая из нижеследующих систем имеет хотя бы
одно решение? (91 — 94).
91». (НГУ, 1980 г.). <! 2хby = ас2с, bx + 2y — c— 1.
92.* (НГУ, 1980 г.). j х + by = ас24-а, Ьх + 2у = с— 1.
93*. (НГУ, 1980 г.). { 2х+Ьу = с2, Ьх 4- 2у—ас — 1.
55
( bx + y = ac2,
94*. (НГУ, 1980 г.). < , / , .
( x + by = ac+1.
95. (ВильнГУ, 1980 г.). При каких значениях k все решения
системы уравнений
j x-\-ky = 3,
( &x-{-4i/ = 6
удовлетворяют условиям: х> 1, «/> 0?
96. (ЛьвГУ, 1980 г.). Найдите все значения Ь, для которых
х и у, удовлетворяющие системе уравнений
2х —1/ = 5&,
4x + z/ = 3b2-10fc,
удовлетворяют также неравенству х — «/>3.
97. (МАИ, 1977 г.). При каких действительных значениях п
решения системы уравнений
х—2у = п,
2пх—9у =—2
удовлетворяют условиям х> 1/2п, у>0?
98. (КПП, 1977 г.). При каких значениях а числа 1 и а
заключены между числами х0 и у0, где (х0; у0) — решение системы
уравнений
х+у— 1 =2а,
2ху = а? — а>
99. (МАТИ, 1977 г.). Решите систему уравнений
/ 9а 72а а—12
j у х а—6 ’
{9х + 6ау = а3у;
установите, при каких значениях а все решения (х; у) удовлет-
воряют неравенству х + «/>0.
100. (МЭСИ, 1980 г.). Найдите наибольшее значение х, удов-
летворяющее системе уравнений
х3 + у3 = 35,
x2z/+ xt/2 = 30.
101. (МГПИ, матфак, 1979 г.). Назовем матрицей таблицу вида
а Ь\
с d)>
где а, Ь, с, d — действительные числа. Если
, (a b\ R (I т\
d)’ в = \п р)>
то А —В означает, что a = l, b = m, с — п, d — p. Произведением
А-В матриц А и В назовем матрицу
fal-±bn ат-\-Ьр\
\cl-i-dn cm+dp)"
56
. „ . /2 1\ /1 2\
а) Найдите произведение матриц ( j 37 й ( 2 3/•
/1 2\ /4
б) Найдите матрицу X такую, что (9 3 )Х = ( 7
7\
ну-
Системы иррациональных уравнений
Решите следующие системы уравнений (102 — 120).
102. (МОПИ, 1979 г. J Х±У f У = 20’
' '{ х2 +у2 = 136.
103. (МАТИ, 1977 г.). 1
104. (ЛГУ, физфак, 1977 г.).
= 2,
1/ ± = 5
Г х 2 ’
х-(-г/ = 5.
/ У+2
_ x-|j/ = 2.
_।iZV—£
105. (МАТИ, 1977 г.). { V у V х~ 2 •
[ х2 + у2=15.
106. (МИНХ, 1979 г.).
107. (МЭСИ, 1979 г.).<
<х + ^ + %1/ = 9.
К^+У = 5,
У2 — х = 7.
Z х зг/
108. (МЭИ, 1978 г.). 1 4J,_ х =_L6> _
(Кх-/2^=К12-К8.
109. (ВГУ, 1980 г.). ' ^Х~^У = 2,
' ' { ху = 27.
I x-j-y = 9,
ПО. (ПГУ, 1980 г.). < ' , , ’ о
' ’ ’ ( х1/3 + у1'3 = 3.
111. (КишПИ, 1977 г.). / ^х+КУ = 4,
112. (КПИ, 1977 г.). I
__ I V х+УУ= 4.
113. (МИУ, 1978 г), j fX,+/ + !f2jc+^ + 2 = 7’
7 ( 3х + 2у = 23.
114. (МАДИ, 1977 г.). { х^+у ^ХГ"6’
' ’ ' ( х2у + у2х — 29.
57
115. (МИСИ, 1978 г.).
117. (ЛГУ, 1979 г.).
-f = V х + у+У х—у,
^ = Ух-гу—Ух-у.
116. (ЛГУ, 1979 г.; МАДИ, 1980 г.).
/)2 = 3х,
уУ-1)2 = 0.
(х_ и) л. 1/ Х~У - _12_
И У’^ V 2(х+у)-х+у»
Х2-|_уЭ—. J7.
118. (МЭИС, 1981 r.).<
119. (МФТИ, 1981 г.). |
120. (МГУ, психфак, 1981 г.). {
I Л- у Л V •
121. (КГУ, эконом, фак., 1981 г.). При каких значениях а
кривые zf=l+^ и у=4]/гх имеют только одну общую точку?
Системы неравенств с одним неизвестным
122. (МСИ, 1977 г.). Решите систему неравенств
( 2 (Зх-1)< 3 (4x4-1) + 16,
| 4 (24-х) <3x4-8.
123. (МЭСИ, 1980 г.). Найдите наибольшее целое х, удовлет-
воряющее системе неравенств
( 0,5(2х-5)>^4-1,
| 0,2 (Зх —2)4-3 > ^—0,5 (х—1).
124. (МЭСИ, 1980 г.). Найдите натуральные х, удовлетворяю-
щие системе неравенств
J х 4-3 4 4~ 2xt
( 5х — 3 < 4х— 1.
125. (МЭСИ, 1980 г.). Укажите целую часть чисел х, удовлет-
воряющих системе неравенств
( х — 1 2х 4" 3 . х q х —J— 5
"2 3 ‘ 6"^ 2” ’
1 *-|- 5 j 4—х х4~1
1 8 + 2 < 6Х 4 е
58
126. (ВГУ, физфак, 1977 г.). Найдите все значения а, для
которых уравнение
а — 1,5
СОЗХ = 2^0^
имеет решения.
127. (КПИ, 1977 г.). Найдите все значения а, при которых
система неравенств
( х24-2х 4-а^О,
\ х2 — 4х — 6а О
имеет единственное решение.
128*. (ЛГУ, физфак, 1979 г.). При каких а<0 неравенства
2^ах < За —х и x — ]fх/а> 6/а имеют общие решения?
129. (МГУ, геофизика; 1977 г.). Найдите все значения k, при
которых существует хотя бы одно общее решение неравенств
х2 + 4Ь4-3^> 1 +2k и x2-f-2^x<3i2 —8*4-4.
139. (МГУ, геофизика, 1977 г.). Найдите все значения *, при
которых каждое решение неравенства х24-3*2—12>2*(2х—• 1)
является решением неравенства х2—(2х— 1)*4-*2^0.
Решите следующие двойные неравенства (131—133).
131. (МПИ, 1979 г.). 0<|^|<1.
ZX~[~O
132. (МИНХ, 1977 г.). 1
X-j- 1
133. (МИСиС, 1979 г.). 1 < < 2.
Решите следующие системы неравенств (134—141).
I х2—х—6>О
134. (МИНХ, 1979 г.) | ’
Л TLA Ve J
135. (ЯГУ, 1980 г.) <
136. (МАИ, 1979 г.).
137. (МАИ, 1979 г.).
138. (ЯГУ, 1980 г.).
х2 —4<0,
х 1 О,
у—х>0.
1
Зх
4
Зх ’
1,
< 9х2 — 9х +1 < 0.
г и>1,
I |х—1|<3.
59
139. (БГУ, 1980 г.).
140. (БГУ, 1980 г.).
141. (БГУ, 1980 г.).
|х® —4х| <5,
|х+1| <3.
|х- + 5х| < 6,
|х+11< 1.
| х® 4~ 5х | < 6,
|х+11<2.
Системы неравенств с двумя неизвестными
142. (МИЭМ, 1977 г.). Дана система неравенств
J 2х—у>а,
I 3х+2у>3а.
а) При а=0 указать хотя бы одно решение системы.
б) Верно ли, что все решения этой системы удовлетворяют
неравенству 5х -j- у > 4а?
в) Верно ли, что все решения этой системы удовлетворяют
неравенству x4~3z/>2a?
143. (ЛГУ, физфак, 1979 г.). При каком a$R точка (а; а*)
расположена внутри треугольника, ограниченного прямыми
у =sx+l, t/==3 — х, у ——2х?
144. (МГУ, мехмат, 1978 г.). Найдите все значения а, при
которых система неравенств
1 x®4-2xt/—7у®>(1 —а)/(а4-1),
I Зх- 4- Юх«/— 5 г/2 —2
имеет решение.
145. (СимфГУ, матфак, 1982 г.). Изобразите на плоскости
множество точек, координаты которых удовлетворяют уравнению
И + И = 1-
На координатной плоскости хОу штриховкой отметьте мно-
жество точек, координаты которых удовлетворяют следующим
неравенствам с двумя переменными х и у (границу, принадлежа-
щую найденному множеству, изобразите сплошной линией, а не
принадлежащую множеству—штриховой) (146—185).
146. (МИНХ, 1979 г.). Х- — х<_у — ху.
147. (ЯГУ, 1980 г.). |х#|< 1.
148. (КГУ, ВМК, 1978 г.).
149. (КГУ, ВМК, 1978 г.). |x®4-t/2-2|<2(х+у).
150. (КГУ, ВМК, 1978 г.). |4-21х|<х®4-1.
151. (КГУ, ВМК, 1978 г.). x24-!/a<2(]x| + |i/|).
152. (КГУ, ВМК, 1978 г.). 4<х24- if < 2 (| х[ +1у\).
153. (ЯГУ, 1980 г.). £zHL>0.
60
154. (КГУ, ВМК, 1978 г.).
155. (МИНХ, 1979г.). х+у—2<0, 2«/+5х>10, 5х—2у—10^0.
156. (МСИ, 1977 г.). Зх + 2«/+1>0, Зх + 2у-З^О.
157. (ЯГУ, 1980 г.), x + yt^l, — х—1/< 1.
158. (ВЗИТиЛП, 1980г.). х — у^1, х + у<2, «/<2.
159. (МИНХ, 1979 г.). 2#-х<6, 9х + 4г/^56, Зх + 5г/>4.
160. х—3t/-|-130, у-|-55х, 4у + 28^7х.
161. (КГУ, ВМК, 1977 г.). log1/3(2x + ^-2)>log1/3(«/+l),
|/>-2х-3</3-2х.
162. (КГУ, ВМК, 1977 г.). logl/2 (х+у-1) > log1/2 у,
Ку—х—\ < V2 — х.
163. (МСИ, 1977 г.). x2 + z/2>l, x2 + z/2<16.
164. (ЯГУ, 1980 г.). х2 + у2<9, х + у^О.
165. (МИНХ, 1979 г.). #2<4-х2, Зх+2«/-3<0.
166. (МСИ, 1977 г.). x2-4x-i/ + 3<0, 2х—у—2>0.
167. (МАТИ, 1979 г.), у^х2 — 2х—3, у<х+\.
168. (КГУ, эконом, фак., 1977 г.). y^Y \ — х2, г/ + |х|^4.
169. (МИНХ, 1979 г.). 2у — х2<3, х2-у2^0.
170. (МТИПП, 1977; МГИ, 1977 г.), у^х2, t/<4-x2.
171. (МИНХ, 1979 г.). г/>х2-4х + 3, у<х2 + 4х + 3.
172. (МАТИ, 1979 г.). 2у^х2, у^—2х2 + 3х.
173. (МИНХ, 1979 г.). i/-|log2х| > 0, i/-2>0.
174. (САДИ, 1977 г.), уСlog2х, 4х—3у —12<0.
175. (МФТИ, 1977 г.). j/x2-3#2 + 4x + 4<2x+1, х2+у2^4.
176. (МФТИ, 1977 г.). /Зх2 + 3у2-3 >2г/ +1, ^ + 4>2/ 31 х|.
177. (МТИ, 1977 г.), Ух + у^х, г/<2.
178. (МТИММП, 1977 г.). y + x2<0, ^-2х+3>0, у+ 1 <0.
179. (МЭИ, 1978 г.). 2x + y2^Q, х + 2>0, у2-1<0.
180. (ЯГУ, 1980 г.). ху^\, x + y^Q, y — x^Q.
181. (МИНХ, 1980 г.). х2 + у2-4<0, у-х2 + 3<0, х>&
182. (МИФИ, 1980 г.). х2+у2^9, у>х2-3, |х|< 1.
183. (КГУ, ВМК, 1977 г.). log2 (2у-х2 +1) > log2y,
\^у—2х + 4 < Кв — х.
184. (КГУ, ВМК, 1977 г.). |x| + |z/| <4, log2 (2у-х2 + 4) >
> log2 (у+1).
185. (МИФИ, 1980 г.). |x + i/| + |х-у\<4, |х|<1,
y^J^x2—2х+1.
61
§ 8. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И МНОЖЕСТВО ЗНАЧЕНИЙ ФУНКЦИИ
Числовой функцией f называется отображение подмножества D
множества R на подмножество Е множества R. Множество D
называется областью определения, а Е — множеством значений
функции f. Область определения функции f обозначается D(f),
а множество значений — Е (f). Значение f в точке х обозначают f (х).
Число из D(f) обычно обозначают буквой, например х, и назы-
вают независимой переменной или аргументом. Значение функции
обычно также обозначают буквой, например у. Каждому значению
независимой переменной х из области определения D (f) функции f
соответствует определенное значение y = f (х) зависимой перемен-
ной у из множества Е (f) функции f. _____
Пример 1. Областью определения функции у = ^4 — х2 яв-
ляется множество £> = [—2; 2], а множеством значений —мно-
жество £ = [0; 2].
Пример 2. Область определения функции i/ = arccos(2—х)
является множество D = [l; 3], т. е. такое множество значений х,
на котором —1^2 —х^1, а множеством значений — множество
£ = [0; л]. _______
Пример 3. Областью определения функции y = ]f х (2 — х)х
X lg(x—1) является множество £> = ]!; 2], т. е. наибольшее мно-
жество, на котором определены как функция |/х(2—х), так и
функция lg(x— 1).
Пример 4. Областью определения функции у= 4sinx—3cosx
является множество R, а множеством значений —множество
£ = [—5; 5]. В самом деле, положив sin а = 3/5, cos а = 4/5, где
a = arctg (3/4), преобразуем данную функцию к виду
у —5 ^ysinx—-|-cosx) =5 sin (х—а),
т. е. # = 5sin(x—arctg (3/4)), а эта функция принимает все зна-
чения из [—5; 5].
Найдите области определения следующих функций (1—112).
1. (ЯГУ, 1980 г.). у = ]/г2х — х3.
2. (ЯГУ, 1980 г.). i/ = j/’x^T/JF+T.
3. (МТИ, 1978 г.). г/=/х^Т + /б^х.
4. (ЯГУ, 1980 г.). ^ = Кх2—5х + 6.
5. (ЯГУ, 1980 г.).
6. (МИИГАиК, 1977 г.), f (х) = /2^х 4- КТ+х.
7. (МИИГАиК, 1977 г.). I/= К —4х2 4-4х 4-3.
8. (КГУ, 1979 г.). 0 = /б4-7х-Зх2.
9. (ЯГУ, 1980 г.). у = ^ + У2 + х.
62
10. (МСИ, 1980г.). ц= /.
11. (РПИ, 1980 г.), f (x)=/4x-xs.
12. (ЯГУ, 1980 г.), f (x) = j/’3x-x3.
13. (ЯГУ, 1980 г.).
14. (РПИ, 1980 г.). у = '
15. (МАМИ, 1980 г.). y=-^^J7--.
16. (ЯГУ, 1980 г.). f(x) =
17. (ВЗЭИС, 1978 г.; ТартГУ, 1980 г.). у= |Лб-х—у.
18. (УжГУ, 1980 г.), f (х) = /х2-х-20 + |/’б^х.
19. (АзГПИ, физфак, 1979 г.). f (х) = ^х^х~6-.
20. (ВЗЭИС, 1977 г.). у =
21. (МАМИ, 1979 г.). у= .
22. (МИИГАиК, 1978 г.). ^=1/'~2$~2*2 .
23. (МИИГАиК, 1978 г.). w = iZ 7~х --
v У V 4х«—19х+12
24. (ВТУЗ ЗИЛ, 1977 г.; МИИГАиК, 1979г.). ]/
25. (МИИГАиК, 1978 г.; ВЗИИЖТ, 1979 г.) у~ )/.
26. (МИСиС, 1979 г.). ^ = Кх^х2 + 1<Зх-х2-2.
27. (ВЗИИЖТ, 1979 г.). у= ^-х-204- , 1 .
у х2 — 5х —14
28. (МСИ, 1977 г.). + Кх2-х-20.
29. (МИИГАиК, 1980 г.; ЛГПИ, 1980 г.).
_ 1 Г х4—Зх24-х+7 ।
У— у х«_2х3+1 *•
30. (ЯГУ, 1980 г.). f(x) = —5-4——•
' ’ ' ' ' ’ sin*x-|-cos4x
31. (ЯГУ, 1980 г.). f (x) = arcsin3*.
32. (МСИ, 1977 г.), f (х) = (sin х + cos х)2 — 1.
63
33.
34.
35.
36.
(КуйбГУ, физфак, 1977 г.). У = 7==Х.
(МАМИ, 1980 г.).
(МИИЗ, 1980 г.). у=?_|о8;(—
(КуйбГУ, мехмат, 1977 г.). !/= •
37. (МАТИ, 1980 г.). f (х) = У .
у 2х—11
38. (ОГУ, 1980 г.). J^ = log2^.
39. (ЯГУ, 1980 г.). f(x) = lgj±f.
40. (МСИ, 1977 г.). # = Klg(x + l).
41. (ВЗФЭИ, 1980 г.). # = lg((x2 + 8х+7)/(ха + 7)).
42. (МВМИ, 1978 г.). # = /T^x + lg(x +1).
43. (МВМИ, 1977 г.). ^ = /x+T+lg(l-х).
44. (ВЗЭИС, 1977 г.). t/ = lg((x2-3x)(x + 5)).
45. (ВЗЭИС, 1978 г.). г/= |/4х - х2 - log3(х-2).
46. (МИИЗ, 1979 г.). г/ = Кх2 + 4х—5-lg(x+1).
47. (УжГУ, 1980 г.), f (x) = lg(5x2-8x-4) + |/'x=n‘.
48. (МИИЗ, 1979 г.). t/ = /x2 + 4x—51g(х + 5).
49. (МИИЗ, 1979 г.). z/ = (lg(3-2x-x2))//x.
50. (МТИММП, 1980 г.), у = Hg((3-x)/x).
51. (БГУ, 1980 г.). y = V lg((l-2x)/(x + 3)).
52, (ЯГУ, 1980 г.). f(x)= yzx-|x| + lg(x + 2).
53. (ЯГУ, 1980 г.). 9 = 2^£±1.
54. (ВЗИИЖТ, 1979 г.).
55. (КуйбГУ, химико-биолог. фак., 1977 г.). y = prlg((5x—х2)/4).
56. (МАИ, 1977 г.), у = К(х2 —Зх—10) 1g2 (х —3).
57. (ЯГУ, 1980 г.), f (x) = lg(l-/4-x2).
58. (МИНХ, 1980 г.). z/ = lg(5x2-8x-4) + (x + 3)-°-8.
59. (МИСиС, 1980 г.), у = V(1-5*)/(7"*-7).
60. (МТИММП, 1977г.; КГУ, 1979г.). «/=j/4x-x2+lg(x2-1).
61. (МИСИ, 1978 г.). y = /l-lg(x-l) + /(4-x)/(x + 2).
64
62. (МИИГАиК, 1978г.; БГУ, 1980 г.; ЛьвГУ, 1980 г.; ЛатвГУ,
1980 г.; МТИМБО, 1982 г.). «/ = Klog0,3 ((х-1)/(х + 5)).
63. (БГУ, физфак и фак. радиофизики и электроники, 1979 г.).
y = /log0,4 (х—х2).
64. (ВЗИИЖТ, 1979 г.). у = Klog0<3 (х2-5х + 7).
65. (ВЗИИЖТ, 1979 г.), у = / log„,5 (х2-9) + 4.
66. (МАИ, 1977 г.).
67. (ВильнГУ, 1980 г.), f (х) = Кlog0t5 (— х2 + х + 6) + *
68. (ВЗЭИС, 1977 г.; БГУ, 1980 г.). У = Л/ ~logoj3(x~1)..
v ’ * у ]/— л24-2х+8
69. (КГУ, 1979 г.). / (х) = /16х- х5 + log!/8 (х2 - 4).
70. (БГУ, мехмат, 1979 г.), у = jAogi/2 (х/(х2-1)).
71. (МАИ, 1979 г.). / (х) = /4<3*2+2 »)/(*+ з) — 2«*+1’.
72. (МИСиС, 1980 г.). t/ = Klog0,5(3x-8)-log0<5(x2 + 4).
73. (КГУ, 1979 г.), f (x) = /4x-x3 + lg(x2-l).
74. (ВЗИИЖТ, 1979 г.). у = у log4 16-log8 (х2-4х + 3).
75. (МЭИ, 1979 г.), f (x) = log4^2— /х- 2^j=2~)'
76. (МАМИ, 1980 г.).
77. (МЭИ, 1979 г.), f (х) = log/— log1/2 (1 + -ЛЙ— 2^.
\ \ Vх//
78. (ЕГУ, фак. прикладной матем., 1981г.). •
79. (КолПИ, общетехн, фак., 1981 г.). у= у^х
80. (КолПИ, отд. матем. и физики, 1981 г.).
у = V— х2 + 2х + 3 + log3 (х — 1).
81. (КолПИ, отд. физики и механики, 1981 г.). t/=lg(x/(x—2))—
-/^3.
82. (БарнГПИ, матфак, 1981 г.), f (х) =
83. (ЛГПИ, физфак, 1981 г.), f (x) = log3x_3(x2-3x-10).
6 /" 2
84. (МЭИ, 1981г.). f(x)=V 4* + 8^52-22<*-«.
85. (МГУ, 1981 г.). z/ = logi., , где
f (х) = у X3 — у X2—2х + у.
3 В. М. Говоров и др.
65
86. (РГУ, физфак, 1981 г.). у = j/*-go-*!*... 1!..
87. (РГУ, геолого-географ. фак., 1981 г.). t/= х + х2 —2х\
88. (МИИВТ, 1982 г.). z/ = Kx^4-^ + lg(39-х).
89. (МТИМБО, 1982г.). y = lg(l — lg(x2—5х+16)).
90. (ТартГУ, 1980 г.; МСИ, 1980 г.; МИИГАиК, 1980 г.).
У = log0i5 (— log2 ((Зх — 1 )/(Зх + 2)))._________
91. (МЭИ, 1980 г.), у = j/4glgx-lg(4-lgx) — lg3.
92. (ЛГПИ, 1978 г.), у = Klogx_2 (х2-8х+15).
93. (МЭИ, 1978 г.). t/ = lg(|/8-2+Ie^-f/42-IgJC).
94. (ЛПИ, 1980 г.; МИИГАиК, 1980 г.). </ = log10o Д-•
95. (МЭИ, 1979 г.). i/ = log2(-logi/2(l+у=)-1).
96. (МГМИ, 1981 г.). 0 = 1о&х|-42.
97. (МТИМБО, 1979 г.). t/ = Ksinx + K 16—х2.
98. (ТбГУ, мехмат, 1978 г). t/ = Ig(lg2x — 5 lgx + 6).
99. (КолПИ, 1980 г.). у= log1/2 g=±.
100. (МТИМБО, 1977 г.). г/ = 1g sin (х- 3) - И16 -х2.
101. (ВЗИИЖТ, 1979 г.). » = 'g\ =.
' а /х2—2х—63
102. (МТИМБО, 1980 г.). y = arcsin ((х—3)/2) —lg(4 —х).
103. (МТИМБО, 1980 г.). у = Из^+агс5Ш((3-2х)/5).
104. (МИИГАиК, 1980 г.).
у — (*_]_ 0,5) 1Og(0.6 + *) ((*2+2*" 3)/(4Х»-4Х- 3».
105. (МИИГАиК, 1980 г.). «/= logI00 * ((21g х + 2)/(— х)).
106. (МИФИ, 1980 г.). t/ = arccos((2x+l)/2K2x).
107. (МТИМБО, 1980 г.). z/ = arccos (2/(2 -f-sin х)).
108. у = Кз sinx—1.
109. у — j/*2sin(x/2).
НО. z/=l//4 COS X + 1.
Ш. л=к—2 cos2 х + 3 cos х — 1.
112. z/= j/"sin2 х—sin х.
Найдите области определения и множества значений следую-
щих функций (113—120).
113. (МИФИ, 1978 г.). У = ~^-
114. (МСИ, 1980 г.). f(x) = /^F.
115. (ВЗИИЖТ, 1979 г.). ^ = /Зх2-4х + 5.
116. (ВЗИИЖТ, 1979 г.). t/ = lg(3xa—4x4-5).
117. (ВЗИИЖТ, 1979 г.). y = lg(5x2-8x + 4).
118. (МИНХ, 1977 г.). f (x) = K^zrl +2/3^х._
119. (МИФИ, 1980 г.), f (х) = log2 sln *~с0^х+3 /2 .
120. (МИНХ, 1977 г.). f (х) = ^2^х + /Т+х.
121. (МАДИ, 1980 г.). Найдите множество всех х, при кото-
рых не существует ни одна из функций f (x) = log(X_2)/(x+3)2 и
g(x) =Кх2—9.
122*. (МАИ, 1979 г.). При каких действительных значениях
а множество значений функции у = (х— 1)/(а — х24~ 1) не содер-
жит ни одного значения из отрезка [—1; —1/3]?
123*. (МАИ, 1979 г.). При каких действительных значениях а
область значений функции у = (х + 1)/(а+х2) будет содержать
отрезок [0; 1]?
124*. (МАИ, 1979 г.). При каких действительных значениях
а множество значений функции у — (х—1)/(1 — х2 — а) не содер-
жит ни одного значения из отрезка [—1; 1]?
§ 9. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
1°. Основные тождества. Тождества, используемые при реше-
нии показательных и логарифмических уравнений и неравенств
(а > 0, а#= 1):
ах = ау & х = у. (1)
ах -ау = ах+у. (2)
а2 — 1. (3)
ах • Ьх = (а • Ь)х, Ь>0. [(4)
(ах)у = ахУ. (5)
aIoga*=x, Х>0, (6)
logaxy = loga|x| + loga[y|, xz/>0. (7)
logay = loga|x| —logjyl, xy>0. (8)
logoX“ = a logex, x > 0. (9)
loge x2m = 2m loga | x |, x =/= 0, m € M (10)
log.» = g^. x>0, x#=l, 6>0. (И)
(12)
loga x — loga*xft, x>0, k$R, k^=0. (13)
loga»x'® = ^-logaX, x>0; m,k^R, (14)
2°. Показательные уравнения. Если имеем уравнение вида
а/(х) = ^ (а>0), то при
1) Ь<О=Ф>х£0,
3*
67.
2) a) &>0, a =/= 1 => f (x) = loga b, 6) &>0, a=l=^a/w = l,
x£D(f) при b — 1, x C 0 при b =И= 1 •
Рассмотрим примеры решения показательных уравнений.
Пример 1. (ЯГУ, 1980 г.). Решите уравнение 3*г~^+6 = 1.
Решение. Применив тождество (3), имеем х2—5х + б = 0.
Отсюда Xj = 2, х2 = 3.
Ответ. х = 2, х = 3.
Пример 2. (МТИЛП, 1980 г.). (3/7)3*-’ = (7/3)™-s.
Решение. Заметим, что 3/7 = (7/3)-i и перепишем наше
уравнение в виде
(3/7)3х-7 = (3/7)-7х+з.
Применив тождество (1), получим
Зх—7 = —7х + 3, х= 1.
Ответ. 1.
Пример 3. (МИЭТ, 1978 г.). 0,125-42*-8 = (^=)_*.
Решение. Переходя к основанию степени 2, получим
.1.. 22(2х-8) = 2-1/2 ) ~х
или
2~3.22 (2Х-8) __ (2-'2.2*1/2)“*.
Согласно тождеству (2), будем иметь
2“ 3 + 2 (2*-8) (2“2“М)~*.
Пользуясь тождеством (5), запишем
2~ 3+4*-хе __ 22»5*.
Последнее уравнение по тождеству (1) равносильно уравнению
—3 + 4х— 16 = 2,5х,
откуда х = 38/3.
Ответ. 38/3.
Рассмотрим примеры решения показательных уравнений, сво-
дящихся к квадратным.
Пример 4. (МАИ, 1979 г.). 52*-* + 5*+i = 250.
Решение. Применим тождество (2) и запишем исходное
уравнение в виде 52*-5“х + 5*-5 — 250 = 0. Подставив 5* = f>0
в последнее уравнение, получим
1^ + 5/ - 250 = 0.
Отсюда /1 = —50, /2 = 25. Значение = —50 не удовлетворяет
условию />0. Значит, 5* = 25, х = 2.
Ответ. 2.
Пример 5. (МИУ, 1978 г.; МФИ, 1979 г.). 9* + 6* = 2-4*.
Решение. Разделим обе части уравнения на 4х: (9/4)*+
+ (6/4)*—2 = 0, или (3/2)2* + (3/2)* —2 = 0.
68
Обозначим (3/2)* = / (/>0); тогда последнее уравнение запи-
шется так:
i2 + i — 2 = 0, /£ = — 2, /2 = 1.
Значение /£ не удовлетворяет условию t > 0. Следовательно,
(3/2)*= 1, х = 0.
Ответ. 0.
Решение уравнений вынесением общего множителя за скобку
рассмотрим на следующих примерах.
Пример 6. (МИИЗ, 1979 г.). 5*+1-5*~1 = 24.
Решение. В левой части уравнения вынесем за скобку
общий множитель 5*-1: 5*-1 (52—1) = 24.
Получим 5*-1 = 1, откуда х—1=0, х=1.
Ответ. 1.
Пример 7. (КИСИ, 1980 г.). б* + 6*+1 = 2* + 2*+1 + 2*+2.
Решение. После вынесения за скобку в левой части 6*,
в правой 2*, получим 6*(1+6) = 2*(1+2 + 4), или 6* = 2*.
Разделим обе части уравнения на 2*#=0: 3*= 1, х = 0.
Ответ. 0.
3°. Показательные неравенства. При решении показательных
неравенств а./ш>Ь (а>0), если
1) Ь^0, то х£О (/),
2) b > 0, то
f(x) > loga b при a> 1,
f (x) < loga b при 0 < a < 1;
при a=l неравенство равносильно числовому неравенству 1 > b.
Рассмотрим решение некоторых показательных неравенств.
Пример 8. (МГУ, физфак, 1980 г.). 2*+2> (1/4)1/* или
2* + 2 > (2~2)1/*
Решение. По тождеству (5) имеем 2*+2>2-2/*. Так как
основание 2> 1, то х+2>—2/х (знак неравенства сохраняется).
Решив последнее неравенство, получим xg]0, +<»[.
Пример 9. (МЭИ, 1978 г.). (1,25)1“*<(0,64)2 <1+У*).
Решение. Запишем исходное неравенство в виде
(5/4)1"* < (16/25)2 (i+^),
или
(4/5)*-1<(4/5)2-2<1+^).
Так как основание 0 < 4/5 < 1, то последнее неравенство равно-
сильно неравенству х— 1 > 4 (1 + х) (знак неравенства изменился
на противоположный!). Далее имее^м х — 4]/гх — 5 > 0, откуда
(Кх —5) (К*+1) > 0, т. е. )/\>5. Окончательно получим
х > 25.
Ответ*. xg]25, 4~оо[.
4°. Логарифмические уравнения. Рассмотрим наиболее часто
употребляемые методы решения логарифмических уравнений.
1. Решение уравнений, основанное на определении логарифма.
Чэ
Пример 10. (МВМИ, 1977 г.). log3(5 + 41og3(x-l)) = 2.
Решение. Логарифмом числа b по основанию а (а>0,
а#=1) называется показатель степени, в которую надо возвести
число а, чтобы получить число Ь. Следовательно,
5-}-4log3(x— 1) = 32,
или
41ogg(x—1) = 9 — 5, log3(x—1) = 1.
И снова по определению логарифма будем имегь
х—1=31, х = 4.
Проверка, которая является частью решения этого уравнения,
подтверждает правильность полученного результата.
Ответ: х = 4.
2. Решение уравнений потенцированием.
Пример 11. (МВТУ, 1979 г.). log2 (3 —х) +log2 (1 — х) = 3.
Решение. Для нахождения области определения функции,
стоящей в левой части, составим систему неравенств
( 3 —х > 0,
Применив тождество (7), можно записать, что
log2 ((3 —х) (1 — х)) = 3,
а по определению логарифма будем иметь
(3 —х) (1 —х) = 23, или х2 —4х—5 = 0.
Тогда Xj = 5, х2 = —1. Так как первое значение неизвестного не
принадлежит области определения, то окончательно получим
х =— 1.
Ответ. —1.
3. Применение основного логарифмического тождества.
Пример 12. (МТИ, 1979 г.). log2 (9 —2х) = 10^ <3~*>.
Решение. Область определения:
f 9 —2х>0, ( 2х<9, ( x<log29,
< о - о =>) о =>' о =>х<3.
( 3 —х>0, ( х<3, | х < 3,
Применив в правой части тождество (6), будем иметь
log2 (9 — 2х) = 3—х.
По определению логарифма
23-х = 9 — 2х, 23/2Х = 9 — 2х,
22х —9.2х + 8 = 0,
2х = 1, х = 0; 2х=8, х=3 —посторонний корень.
Ответ: х = 0.
4. Логарифмирование.
ТО
Пример 13. (МИНХ, 1979 г.). (х + 1)’е<*+’> = 100(х + 1).
Решение. Область определения: х+1>0=>х>—1.
Прологарифмируем обе части уравнения по основанию 10.
lg (х+ l)lg(x + 1) = lg 100 + lg(x+l).
Обозначим lg(x4-l) = /. Тогда уравнение примет вид t2 — t — 2=0.
Его решения tr =—1, t2 = 2, т. е.
lg(x+l) = —1, х+1 = 1/10, х = — 0,9;
lg(x+l) = 2, х+1 = 100, х = 99.
Ответ: —0,9; 99.
5. Замена переменного.
Пример 14. (МИИЗ, 1979 г.). Решите уравнение (lgx)a—
— lgx3 + 2 = 0.
Решение. Введем переменную t = 1g х, х > 0. Исходное
уравнение примет вид t2 — 3/ + 2 = 0. Его решения /х=1, /а = 2.
Откуда
lgx=l, х=10;
lgx = 2, х=100.
Ответ: 10; 100.
6. Переход к другому основанию.
Пример 15. (МАИ, 1979 г.). 1 + loga(х-1) = logu_x)4.
Решение. Область определения: х>1, х=й=2.
По свойству (11)
10rt л- '°g24 . f2
WKu-i) * log2 (x_ iog2 (x_ j) •
Обозначим log2 (x— 1) = у. Тогда наше исходное уравнение
примет вид i-\-y = 2/y, или у*-\-у — 2 = 0, откуда уг = —2, t/a = l.
loga(x—1) — —2, х—1 = 1/4. хх = 5/4,
loga(x—1) = 1, х—1=2, ха = 3.
Ответ: 5/4, 3.
5°. Логарифмические неравенства. При решении логарифми-
ческих неравенств необходимо помнить, что функция y = logax
(а > 0, а =/= 1, х > 0) является убывающей, если 0 < а < 1, и воз-
растающей, если а> 1. Поэтому неравенство вида
logJW < loga<P(*)
при 0 < а < 1 равносильно системе
f f (х) > Ф (х),
( Ф (х) > 0,
при а > 1 — системе
1 f (*) < Ф (х),
I Нх)>0.
71
Рассмотрим решение некоторых типичных логарифмических
неравенств.
Пример 16. (МИСиС, 1979 г.). log1/6 ((4*4-6)/х) >0.
Решение. Так как logi/51 =;0, то данное неравенство можно
записать так:
logi/5 ((4x4- 6)/х) > logj/51.
С учетом области определения функции это неравенство равно-
сильно системе неравенств
( (4х4-6)/х>0, ((4х 4-6)/х > 0,
\ (4х+6)/х<1, ИЛИ 1(4х + 6)/х-1 <0.
Неравенства решаем методом интервалов
/ 4(х+2')’х>0’ =Л + >0’ =фх€[—2; —3/2[.
( Зх(х+2)<0, ( х(х + 2)<0,
Ответ: х£[—2; —3/2[.
Пример 17. (МТИ, 1978 г.). log^x2 < 1.
Решение, log^+s х2 < log2X+3 (2х 4- 3). Данное неравенство
эквивалентно совокупности систем
Г( 0<2х+3<1, ...
1 х2>2х + 3;
1 2x4-3 > 1,
.1 0 < х2 <2х + 3. 1 '
Решая систему (1), получим
( — 3/2 <х<— 1,
( (х—3) (х4-1) > 0. (3)
Система (3) эквивалентна совокупности двух систем
—3/2 <х< — 1, (4)
х > 3;
—3/2 < / х < —1,
х < —1. (5)
Система (4) не имеет решений. Решение системы (5): хС]—3/2; —1[.
Решая систему (2), получим
( Х>—1, f х>—1,
( (х-3)(х4-1) <о, или1 — 1<х<з,т' е- i; з[.
Ответ: х€]—3/2, —1[U]—1; 3[.
Пример 18. (МАИ, 1979 г.). log(x+4)/2 Qogjy^) <0.
72
Решение. Решением данного неравенства будет объединение
множеств решений таких систем
О < (х + 4)/2< 1,
1 2х— 1 о
bg2 з+Г > °.
2х — 1 Q
3+7 >и’
1 2х—1 . .
bg2-3+7>1;
(2)
Решая систему (1),
получим
0< х 4-4 < 2,
2х— 1 . f —4<х<—2,
г ,г+х =.
fo-l . О. I 3+х >U’
х4-з > ’
—4 < х < —2,
х4-3 <0, => х0—4, — 31.
х—1/2 <0;
Решая систему (2), получим
х > — 2,
2х—1 ,
—гт > Ь
х+З
2(х—1)(х4-3) >0,
^<2-
34-х < ’
( х>— 2,
> 0>
х+3 ’
' (*~4) (х+з) > °-
2х—1 — 2х—6
3+х <U;
х > —2,
х > 4,
х> 1/2;
=£>*€14, +<*>[.
Ответ-. ] — 4, — 3[и]4, 4-оо[.
6°. Системы показательных и логарифмических уравнений.
Рассмотрим решение некоторых систем на примерах.
Пример 19. (МИХМ, 1979 г.). {
Решение. Область определения: %4-t/>0.
Г X 4" У = 2у-х»
1 (х + у)х-У=^2.
73’
Из первого уравнения найдем, что x + z/ = 2*~^ и подставим
во второе уравнение. Тогда
(2^~у)х->'=:2=>2^-^2 = 2=>(х — у)* = 1.
Решением данной системы будет решение совокупности систем
{х—z/=l, (х—у = —1,
х+у=2 и I х + у=^1/2.
Ответ: (3/2; 1/2), (-1/4; 3/4).
Пример 20. (МАТИ, 1980 г.).
1 log3 х + log31/= 2 + log3 2,
I log„ (*+#) = 2/3.
Решение. Область определения: х>0, у > 0.
f log3 X + log3 У = *og3 9 + logs 2.
I log27 (*+#) = 2/3.
В первом уравнении воспользуемся тождеством (7), во втором —
определением логарифма. Получим
f log3 (ху) = logs 18. . / ХУ = 18«
I х + у=(33)г/3. 1 х+{/ = 9.
Решив последнюю систему, получим решение и данной системы.
Ответ: {(6; 3), (3; 6)}.
Показательные уравнения
Решите уравнения (1 — 82).
1. (МВМИ, 1977 г.)
2. (МИЭТ, 1977 г.)
4 ’ ’ 1^5 25
3. (МАИ, 1977 г.). (5/3)*+1-(9/25)*2+2*-11 = (5/3)9.
4. (МГУ, ВМК, 1979 г.). 913*-i 1 = 38*“2.
5. (МТИ, 1979 г.). 23/‘°г«*=1/64.
6. (МИСиС, 1978 г.). 42/х —5-41/х+4 = 0.
7. (МАТИ, 1979 г.). 5х-24 = 25/5*.
8. (ЛьвГУ, 1980 г.). 4*—10-2*~1 = 24.
9. (МВТУ, 1979 г.). 4*2+2—9-2*2+2 + 8 = 0.
10. (МЭСИ, 1978 г.). 4*-г^-12-2*-!-у^^ +8 = 0.
11. (МИНХ, 1979 г.). 64-9* —84-12* + 27-16* = 0.
12. (МАИ, 1979 г., МТИМБО, 1979 г.). 4-22*-б*= 18-32*.
13. (МИНХ, 1979 г.). 7Х+2—у • 7*+1 —14-7*-1 + 2-7* = 48.
14. (РПИ, 1980 г.). З2*-?-9*-1 + 272*/3 = 675.
74
15. (КИСИ, 1980 г.). б^ —7х—52х-35 + 7х-35=0.
16. (МИНХ, 1979 г.),
17. (МАМИ, 1979 г.). 2х+1-5х = 200.
18. (МГМИ, 1980 г.). 3-52х-1 —2-5х-1 = 0,2.
19. (МАИ, 1979 г.). 32х+1 + 10-3* + 3 = 0.
20. (ВЗИИЖТ, 1979 г.). 22х+1-33-2х~1 + 4 = 0.
21. (МТИМБО, 1979 г.). 4-V*+6-Vx=9-i/x
22. (ВТУЗ ЗИЛ, 1979 г.). ((f/27)x/<-^)x^+r^ =//З2.
23. (ЛГПИ, 1979 г.). 22х-3 = 4х*"зх-1.
24. (МТИММП; МИЭТ, 1978 г.). 4*-Зх~1/2 = 3X+V2_22х~».
25. (ВЗПИ, 1978 г.). 7-Зх+1 —5х+2 = Зх+4 —5х+3.
26. (МСИ, 1979 г.). 3- 16х + 2-81х = 5-36х.
27. (МИСиС, 1978 г.). 64i/x-23+3/x +12 = 0.
28. (РПИ, 1980 г.). 22+х —22-х= 15.
29 ., (МТИМБО, 1978 г.). 9х —2х+»’3 = 2х+3’5 — З2*"1.
30. (МЭИ, 1977 г.). (Зх2-7'2х+3-9-9/3)lg(7-x) = 0.
31. (КИСИ, 1980 г.). 312х-1 —9вх-1 —274х-1 + 81зх+1 = 2192.
32. (ЛГУ, эконом, фак., 1980 г.). 52х = 32х + 2-5х + 2-Зх.
33. (МГМИ, 1979 г.). x6Sta3x+2 = l/Kx.
34. (МТИМБО, 1979 г.). г21®4*"1 — 7'84х = 7'84х"1 — 3-4'8 «*.
35. (ПГУ, 1980 г.). 7'8Ж —5'8X+1 =3-5'8—13-7'8Х-*.
36. (МИЭТ, 1978 г.). 15-2х+1 + 15-2-х+2= 135.
37. (МИИГАиК, 1978 г.). 4x+rJr^-5-2х-' + ’/хГ^ = 6.
/ ___1 \ 2
38. (МТИМБО, 1982 г.). \2 (2Г"Х+3) ^_i = 4
39. (МАИ, 1979 г.). 32х+? = Зх+2 + 2.
40. (ВТУЗ ЗИЛ, 1979 г.). =
41. (МИИГАиК, 1978 г.). Гл72х2-5х-6 = (К2)3 '°е»49.
42. (МГИМБО, 1979 г.). 2х2-'-Зх2 = Зх2-'-2х2+2.
43. (МПИ, 1979 г.). 9х2-'-36-Зх2-3+3 = 0.
44. (ВильнГУ, 1980 г.). 34х+8 — 4-32x+3 + 28 = 21og2K2.
45. (МИНХ, 1979 г.). 2-Зх+1-6-Зх-х-Зх = 9.
46. (МИСиС, 1979 г.). 3'8‘s 2-3'sctsx+i = 1.
47. (КГУ, мехмат, 1980 г.). 32х+1 = Зх+ 2 + К1 — 6• 3х + 32(х+<
48. (МЭСИ, 1979 г.). (5/12)х-(6/5)х"1 = (0,3)-1.
49. (МИЭТ, 1979 г.). x2.2x+1 + 2lx-3|+2 = x2-2ix-3i+4 + 2x~I.
50. (МИРЭА, 1978 г.). 5х8^ = 500.
51. (МГМИ, 1979 г.). x‘T"2C0SSX=p/x.
52. (РПИ, 1980 г.). 32<х+5>/<х-7> = 0,25-128<х+1’>/<х-=\
75
53. (ВГУ, матфак, 1980 г.). (4/9)г х = (2,25/ х~*.
54. (ВГУ, ПММ, 1980 г.). 2*-б*"1 = 0,2- Ю2"*.
55. (ЛГУ, 1980 г.). 43+2cos2*—7-41+cos2-,! —41/2 =0.
56. (МИНХ, 1979 г.). (}/5 + J/24 )*+()/"5 —/24 )* = 10.
57. (ТбГУ, физфак, спец, радиофизика и электроника, 1982 г.).
2x2-6-3x'2-« = -^(6x-i)4.
58. (МТИМБО, 1977 г., БашГУ, 1980 г.). 3,og3X+x'oe’x= 162.
59. (МТИМБО, 1981 г.). 0,5*2-22*+2 = 64-1.
60. (МТИМБО, 1981 г.). 92х+4 = 26-32х+3 + 3.
61. (МТИМБО, 1981 г.),
62. (МТИМБО, 1981 г.). 0,125-42*"3 = (-*-/-) •
63. (МТИМБО, 1982 г.). 2sia2 х + 4 • 2<=os2 х = 6.
64. (МТИМБО, 1977 г.).
5х/(/*+2).(о,2)*/О/х+2)= 125-(0,4)('~2)/(г~4\
65. (МТИМБО, 1982 г.), б^’^^ + б'081/4'"1 = ?.
О
66. (МТИМБО, 1979 г.). 3-4*+у-9*+2 = 6-4*+1—~9*+».
67. (МТИМБО, 1979 г.). ^/64-1/2^+12 = 0.
68. (МТИМБО, 1979 г.). 41е*+1-61е*-2-3,8*2+2 =0.
69. (МТИМБО, 1979 г.). 4*-5*+1 = 5-202-*.
70. (МТИМБО, 1979 г.). 3*+1+18-3-* = 29.
71. (МТИМБО, 1979 г.), б’е* —З’^-^З1^*1—б’е*"1.
72. (МТИМБО, 1979 г.). 5*-4 + 5 0,2*-2 = 26.
73. (МТИМБО, 1979 г.). 3-2^2-7-2^4 = 20.
74. (МТИМБО, 1980 г.), x1~~'gx2= ^-2^-.
75. (МТИМБО, 1980 г.), (/х)10^*-1 = 3.
76. (МТИМБО, 1980 г.). х^х= ЮООх2.
77. (МТИ, 1979 г.; МТИМБО, 1980 г.). (0,4),е2*+4 = (6,25)2-'еЛ
78. (МТИМБО, 1980 г.). (О.б^у)*2"12 = (j^)3.
79. (МТИМБО, 1980 г.). 13-Б1^+6-41^ = 0.
1g -У + 5
80. (МТИМБО, 1980 г.), х 3 = 103+'g*.
81. (МТИМБО, 1-980 г.). 2|0^2 • 5!о«зх = 400.
76
82. (МТИМБО, 1980 г.). 9l+log’x —3I+Iog’x — 210 = 0.
83. (МАТИ, 1977 г.). При каком значении р уравнение
р-2хН-2~х = 5 имеет единственное решение?
Показательные неравенства
Решите неравенства (84 — 124).
84. (МГПИ, 1980 г.) 23"вх>1.
85. (МАМИ, 1979 г.). 16* >0,125.
86. (МАМИ, 1979 г.). (0,3)2*2-зх+6 < 0,00243.
87. (МИИГАиК, 1978 г.). (1/3/^ > 3"*.
88. (ЛьвГУ, 1980 г.). 0,14х2-2х-2 <0,12х~3.
89. (МИИЗ, 1979 г.). х+/3>9-
90. (МАТИ, 1980 г.). 8Г^ > 4096.
91. (ВЗЭИС, 1978 г.). ( 2.ye-sx)/(2+6x> < 25/4.
92. (МТИ, 1979 г.). 2Х + 2~Х—3<0.
93. (РПИ, 1978 г.). 4*+1*~4<2.
94. (МГУ, 1977 г.). 4-*+0>5-7-2-*-4 <0.
95. (МИИЗ, 1978 г.). х2-5х-52+х < 0.
96. (МИНХ, 1977 г.). 4Х+1 —16х < 2 log4 8.
97. (КГУ, геофак, 1978 г.). < 2-
98. (МИНХ, 1979 г.),
99. (ВЗЭИС, 1977 г.). 4х — 22 (*-1> + 82 <х-2>/3 > 52.
100. (МТИММП, 1979 г.). (0,3)2+4+3+-+2х > (0,3)72, x£N.
101. (ЛьвГУ, 1980 г.). 22х+1-21-(1/2)2х+3 + 2>0.
102. (МИТХТ, 1979 г.). 3«"зх-35 (1/3)2~3х + 6>0.
103. (МИНХ, 1979 г.). xlg2x-3 Igx+1 > 1000.
104. (МИНХ, 1979 г.). 2х+2-2х+14-2х"1 -2х"2<9.
105. (ЛатвГУ, 1980 г.). 52х+1>5х + 4.
106. (МАДИ, 1979 г.). 2х+2 —2Х+3 —2х+4 > 5х+1 —5х+’.
107. (МАМИ, 1977 г.). З72-(у)* • > 1-
108. (МИЭТ, 1978 г.). 4х—2-52х-10х > 0.
109. (МИСиС, 1978 г.). 25~х-5-х+1> 50.
ПО. (МАДИ; ЛПИ, 1977 г.). 3lgx+2 < 3,gx2+5-2.
111. (МАДИ, 1978 г.). J<9X-Зх+2 > 3х-9.
112. (МИЭТ, 1977 г.). 9-4-Vx + 5-6-1^<4-9-1/x.
ИЗ. (МАИ, 1977 г.). 8-з^>1 + (4)Х.
77
114. (МАМИ, 1979 г.). (у)’°8г > 1.
I *+2 I
115. (МАТИ, 1978 г.), (i)2’'*1 > 9-
116. (МИСиС, 1977 г.). х222* + 9(х + 2)2* + 8х2<(х + 2)22* +
+ 9х22* + 8х + 16.
117. (МИИГАиК, 1977 г.). (l/3)'°g1/3 (3’(1/2)’+5) < 21+*.
118. (ТбГУ, физфак, спец, радиофизика и электроника, 1978 г.).
4* —3<2*+1.
119. (КГУ, ВМК, 1979 г.). (1/3)*+~“ > 1/^27.
120. (КГУ, мехмат, 1980 г.). |/9*+ 3* —2> 9-3*.
121. (МИФИ, 1978 г.). Зг*>2а.
122. (ЛГУ, 1980 г.). 2*4-21*1>2/2.
123. (СимфГУ, физфак, 1981 г.). (0,2) х~2 >5.
2Х+1
124. (СимфПИ, 1981 г.). (ЧУ'* > fvV-
\ О J \ D J
Логарифмические уравнения
Решите уравнения (125 — 261).
125. (МГУ, геофак, 1980 г.). logx_13 = 2.
126. (МИЭТ, 1978 г.). log4 (21og3 (1 + log2 (1 + 31og3 x))) = 1/2.
127. (МВМИ, 1977 г.). log3 (1+log3 (2*-7)) = 1.
128. (МФТИ, 1977 г.). log3 (3* - 8) = 2 - x.
129. (МИНХ, 1979 г.), l0?2^2^ = 1.
130. (ВильнГУ, 1980 г.). log5_A.(x2 —2x-f-65) = 2.
131. (МСИ, 1980 г.). log3 (log,x-|-y4- 9*)=2x.
132. (МХТИ, 1979 r.). log3 (x+ l) + log3 (x + 3) = 1.
133. (МХТИ, 1977 r.). log7(2*-l) + log,(2*-7)=l.
134. (МИИЗ, 1979 г.). lg5 + lg(x+10)-l=lg(2lx-20) —
— lg(2x—1).
135. (МТИММП, 1978 г.). 1-lg5 = y (1gi-4-lg x+-^lg б).
136. (МГУ, почв. отд. биофака, 1977 г.). Igx—-^-Ig^x —
= ig (*+!)•
137. (МТИММП, 1977 г.). 3!oe.’8r*-lgx + lg2x-3 = 0.
138, (ВЗЭИС, 1978 г.). (% —2),82<*-2>+18<х-2)’-12 = 102’«(*-2’.
78
139. (МФТИ, 1976 г.). 91<’е»(1-2х) = 5хг_5.
140. (МИИЗ, 1979 г.). х1+,ех = 10х.
141. (МАТИ, 1979 г.), х2 х = 10х2.
142. (КГУ, геофак, 1978 г.). х^х+^3 = 105+|г*.
143. (ВЗИИЖТ, 1979 г.). х'°г«х = 9.
144. (МСИ, 1980 г.). (Kx),og‘*-1=5.
145. (ТбГУ, мехмат, спец, прикладная матем., 1982 г.).
Xlgx+1 — 1Q\
146. (МТИМБО, 1981 г.). № = 104f*+i.
147. (МТИМБО, 1982 г.). xWr х‘*'2) = 9.
148. (МТИМБО, 1982 г.). ((lgx)/2)’g!x+igx‘-2 = lgVx.
149. (МГУ, физфак, 1980 г.). 3Klog2x — log28x + 1 =0.
150. (МАТИ, 1979 г.). lg2x-31gx = lg(x2)-4.
151. (МАИ, 1979 г.). log1/3 х- ЗИlog1/3x + 2 = 0.
152. (МАИ, 1979 г.). 2(logxK5)2 -3logxj/’5 +1 =0.
153. (УжГУ, 1980 г.). logfx + 21og2/x-2 = 0.
154. (БашГУ, 1980 г.). (aIoe^)2-5xlog» “ + 6 = 0.
155. (МТИМБО, 1979 г.). lg2(100x) + lg2(10х) = 14 + lg(l/x).
156. (СимфГУ, матфак, 1982 г.). log4 (х + 3) —log4 (х—1) =
= 2 —log48.
157. (ТбГУ, мехмат, спец, прикладная матем., 1981 г.).
log4 (х2 — 1) — log4 (х — 1 )2 = log4K(4 —х)2.
158. (ТбГУ, физфак, спец, радиофизика и электроника, 1981 г.).
2 ,ogs 1 = 1О§3 JZTf •
159. (СимфГУ, матфак, 1982г.). 21og4 (4 —х)=4 —log2 (—2 —х).
160. (МАИ, 1979 г.). 3 + 21ogx+13 = 21og3(x+l).
161. (МИИГАиК, 1978 г.). logx(9x2) log|x=4.
162. (МИИГАиК, 1978 г.). log?/2(4x) + log2 (х2/8) =8.
163. (МИТХТ, 1979 г.). log0,5 Хх2 —14 logi6xxs + 401og4A.Kx=0.
164. (МТИМБО, 1982 г., МЭСИ, 1977 г.).
6-(1+4.94-21°g^3)-log7x = logx7, xCQ.
165. (МИИВТ, 1982 г.). logs (4-3*-1) = 2х+ 1.
166. (МИИГАиК, 1978 г.). logs(3*-6) = х-1.
167. (МХТИ, 1979 г.). logs (4х —3)+ log3 (4х—1) = 1.
168. (МАИ, 1979 г.). log3(log?/2x-31og1/2x + 5) = 2.
169. (МГУ, химфак, 1980 г.). log8 =log5 .
170. (МГМИ, 1981 г.). 1 +21og(x+2)5 = log5(x + 2).
171. (МАИ, 1981 г.). logl2<* = 2,0«»4.
79
172. (МВМИ, 1977 г.). log2 (£} =-.
V J log2y-1
173. (МСИ, 1977 r.).
174. (ЛьвГУ, 1980 г.; МТИМБО, 1981 г.). log2 (4-3*-6) —
- log2(9* —6) = 1.
175. (МАДИ, 1977 г.). у lg(5x-4) + lg]/x+T=2 + lgO,18.
176. (МИНХ, 1979 г.). log4 (2Л*“2—1)-(-4 = 2х.
177. (МИИЖТ, 1979 г.). log*/5 + log* (5х)- 2,25 = (log*K5)’.
178. (МИНХ, 1980 г.). lg(lgx) + lg(lgx4-3) = 0.
179. (ВГУ, 1981 г.). log3x-21og1/3x = 6.
180. (МГПИ, 1980 г.). fg|^4)-= 1.
181. (МИТХТ, 1979 г.). 2 log8 (2х) + log8 (х2 +1 - 2х) = 4/3.
182. (МИНХ, 1979 г.). у log2 (х-2)—у = log1/8/3x=5.
183. (МТИ, 1979 г.). 21og3(x-2) + log3(x-4)2 = 0.
184. (МИУ, 1978 г.). /log2(2x2)-log4(16x) = log4x\
185. (МАТИ, 1980 г.). ^^-^ = 21gx+l.
186. (МИЭТ, 1978 г.). =
187. (МИЭТ, 1978 г.). log2 6 - log2 2 = (lg2x-2) log312.
188. (ВЗИИЖТ, 1979 г.). 1—4-lg(2x-l)=4-lg(*-9).
z z
189. (МСИ, 1980 r.).
190. (МГПИ, 1980г.). lg(3x2 + 7)-lg(3x-2) = l.
191. (МИНХ, 1979г.). 4-W2—16x+20)-lg?/7==41g(8-*)-
О О
192. (МАИ, 1979 г.). loge2*+3-loge (3*-2) = х.
193. (ПГУ, 1980 г.). (l+^)lg3 + lg2^1g(27-/3).
194. (МВМИ, 1977г.). 1g(5*"2+ l)=x+lg 13-2lg5+(l -х) 1g2.
195. (КГУ, ВМК, 1980 г.). у lgx+31g/2+^=lg/x(x+2)4-2.
196. (МВТУ, 1979 г.). log2(4*+l) = x + log2(2*+3-6).
197. (МТИПП, 1978 г.).
1 , 21°§0,26 (4~Х)
logs (X 4-3) + log2(3+x)
1.
198. (МЭИ, 1979 г.). log3(9* + 9)^x + log3(28-2-3*).
199. (МПИ, 1979 г.). lg(lgx) + lg(lgx?-2) = 0.
8®
200. (МПИ, 1979 г.; МТИМБО, 1982 г.). logrT(4*-6) —
-logr-(2*-2) = 2.
201. (МВТУ, 1978 г.; МТИМБО, 1982 г.).
log2 (4* + 4) = loga 2* + 10ga(2*+*-3).
202. (МЭСИ, 1977r.).log/-x-j/logx5/5+logz-5/5=-/6.
203. (МСИ, 1977 г.). lg(3*-24"*) = 2-{--l-lg 16—
204. (МСИ, 1977 г.). (iyg!*'Igx = .±. s'gx-i.
205. (МСИ, 1980 г.; МТИМБО, 1981 г.), х lg’ * “ Т ,g*=100^l0.
206. (МСИ, 1980 г.). log2 (25^+3 — 1) = 2-Floga (5*+3 +1).
207. (ПГУ, 1980 г.). log3K 130-7,og*(6~x) = 2.
208. (МСИ, 1977 г.; МТИМБО, 1981 г.). lg2 + lg(4*-* + 9)«
= 1 4-lg(2x-24-1). ___
209. (МГРИ, 1977г.).loga(4^+I + 4)-loga(4*+l) = logiy^/l/8.
210. (МГРИ, 1977 г.), log2 (2х2)-log2 (16х) = 3-logfx.
А
211. (МИНХ, 1979 г.). lg44-(l + ^)lg3 = lg(i/3 + 27).
212. (МИЭТ, 1977r.).lg(x? + 27)-0,51g(x2 + 6x + 9) = 31g/7.
213. (МИИГАиК, 1978 г.). б’е* = 50-х'г5.
214. (МИТХТ, 1979 г.). |х-1 |ig!*-ig*! = | х-113.
215. (МАТИ, 1979 г.), х 'g х~ = j/lO.
216. (МАТИ, 1979 г.). |х- 10|log2(х-3) = 2(х-10).
217. (МИРЭА, 1978 г.; МТИМБО, 1982 г.), log, log, х 4-
+ log2log4x=2.
218. (МАТИ, 1979 г.). (6х-5) | In (2х+2,3) | = 8 In (2x4-2,3).
219. (МИИГАиК, 1976 г.). Klog9 (9х8)• log3 (Зх) = logsх3.
220. (МВТУ, 1977 г.). lg2(100x)-lg2(10x)4-lg2x = 6.
log.,- (*+1) log , (2х’+1)
221. (МАДИ, 1980 г.). 9 ' = 5 '
222. (МФТИ, 1977 г.). lg2(4-x)4-lg(4-x)-lg(x+l) я
•= 21g2 (х 4-у)-
223. (МФТИ, 1977 г.). 21og2^4-log2^-1.
224. (МГУ, эконом, фак., 1979 г.). log3x+7(94-12x4-4x2)4-
4-log2x+3(6x24-23x4-21) = 4.
225. (УжГУ, 1980 г.), lg/1+х4-3 lg/1-х= lg/1-ха.
226. (РИИГА, 1981 г.). = 3.
81
227, (МИИГАиК, 1980 г.). logx2-log4x+-J = 0.
228. (МАРХИ, 1979 г.). 1g (6-5*+ 25-20*) = х +1g 25.
229. (МОПИ, 1980 г.). j/’iog^-0,5 = log2|/'x.
230, (РГУ, 1980 г.). log1/3 (2(l/2)*-l) = log1/3 ((1/4)*-4).
231. (ЛГПИ, 1979 г.). logej/x^2+y log.(х-И) = 1.
232. (МСИ, 1980 г.), logs (з*2-18*+28+|) =log50,2.
233. (КГУ, кибернетика, 1979 г.), log, 2 + log49x = logi/7Fr3.
234. (МИФИ, 1978 г.). (log9taх 2)• (logsin»ха) +1 = 0.
235. (МИФИ, 1976 г.). logr-a-logfl2(j|=^) = l.
236. (МИФИ, 1977 г.). К(log0,04x) +1 + /(log0,2x) + 3=1.
237. (МИФИ, 1978 г.). log3x (3/х) + log| х = 1.
238. (МИФИ, 1977 г.). log*(^a^^ + = —5’
v ’ ' logx2 loge2 log(e’_i) 2
239. (МИФИ, 1977 г.). !^^- + logaxa.log1/a2x = 0.
240. (МИФИ, 1979 г.). log4 (х+12) logx2= 1.
241. (ЛГУ, геофак, 1980 г.). 2^^-* + 2-ri^-2 = 1.
242. (МИФИ, 1978 г.). loge>1 sin 2х + lg cos х — Ig7 = 0.
243. (МТИМБО, 1982 г.). log2 (3-х) -log2 si” g”/4). = 1 +
+ log2 (x + 7).
244. (МТИМБО, 1982 г.). log.(2 + /x + 3) = 2cos(5jt/3).
245. (МТИМБО, 1982 г.). log1/5 (2x+5) = log1/5 (16—x2) +
+ tg (5jt/4).
246. (МТИМБО, 1982 г.). log1/3 Их2 - 2x = sin (11 jt/6).
247. (МТИМБО, 1982 г.). log16x + log4x + log2x = 7.
248. (МТИМБО, 1982 г.), lg 10 +у lg(32 r* + 271) = 2.
249. (МТИМБО, 1982 г.). 21og3x + log3 (x2 —3) = log30,5 +
5log8 (1оИз 8) .
250. (МТИМБО, 1982 г.). log, (3* + 10) + 7,1° = log. (9*+ 56).
251, (МТИМБО, 1982 г.). (log4x-2)-log4x = y(log4x-l).
252. (МТИМБО, 1981 г.). log5x + log25x=logi/5K3.
253. (МТИМБО, 1981 г.). lg(642/2^^) = 0.
254, (МТИМБО, 1981 г.). log2 (9 - 2*) = 3 - х.
255. (МТИМБО, 1981 г.). 2 (lg2—l)+lg(5r*+l)=lg(51~r*+5).
256. (МТИМБО, 1981 г.). logx 3+log3 x=logF- 3 + log^x+±.
82
257. (МТИМБО, 1981 г.). 3^1gx + 21gl^x~1 = 2.
258. (МТИМБО, 1982 г.). % + lg(l+ 2*) = xlg5+lg6.
259. (МТИМБО, 1982 г.). logx(125x)log!5x= 1.
260. (МТИМБО, 1979 г.). log2_^ (2-х*-х*)=2-^—.
261. (МТИМБО, 1979 г.). log3_4^ (9 - 16х«) = 2 4- fog;(3L•
262. (ТбГУ, физфак, спец, радиофизика и электроника, 1977г.).
При каких значениях а уравнение 21og3x—j log3 х 14-а = 0 имеет
четыре решения?
Логарифмические неравенства
Решите неравенства (263—381).
263. (МАТИ, 1979 г.). log1/3(5x-1) > 0.
264. (МИИЗ, 1979 г.). log5 (Зх-1) < 1.
265. (МПИ, 1979 г.). loge>5 (1+2х) >-1.
266. (МИНХ, 1979 г.). log0,5 (х2—5x4-6) > —1.
267. (МЭИ, 1978 г.). log8(х2-4х4-3)< 1.
268. (БГПИ, 1980 г.). lg(xa—5x4-7) < 0.
269. (МИЭТ, 1977 г.). log7 ((2х-6)/(2х-1)) > 0.
270. (МАДИ, 1979 г.). log1>6 ((2х-8)/(х-2)) < 0.
271. (МИСиС, 1979 г.). log3((1 -2х)/х)<0.
272. (МТИЛП, 1979 г.). log1/3 ((2-Зх)/х) >-1.
273. (МИСиС, 1978 г.). log1/4 ((35 - х2)/х) > - 1/2.
274. (МТИ, 1976 г.). logs|3 —4х| > 2.
275. (МАДИ, 1977 г.), log? 5x4-log0 5х-2<0.
276. (МВТУ, 1976 г.). | log3’x| —log3 х —3 < 0.
277. (МИНХ, 1979 г.). log8x<г .
278. (МИСиС, 1978 г.). ?^x.~31g5+3< 1.
279. (МИЭТ, 1978 г.). 4-7—* > 2.
' ' 1-f-lg-x 1— 1g х
280. (БорПИ, 1980 г.). logi/4 (2 —х) > logi/4 (2/(х-[-1)).
281. (МФТИ, 1980 г.). ^-^-<1.
282. (МАИ, 1979 г.). rog4((x+l)/(x4-2)) < >
283. (МАИ, 1979 г.). log3x+5 (9х24-8х4-8) > 2.
284*. (МГУ, эконом, фак., 1979 г.).
logs (х2—4х+11)2—logll(x2—4х—1 1)» >Q
/2—5х—Зх2
285. (ВЗИИЖТ, 1979 г.). log3 ((1 4-2х)/(1+х)) < 1.
286. (МГМИ, 1980 г.). З10^^ <3logs(x“e)4-3.
83
287. (МИЭТ, 1977 г.). log0>2 (х2-х-2) > log0>2 (— х2 + 2х + 3).
288. (УжГУ, 1980 г.). logi/6 (х2-Зх + 2) + 1 < 0.
289. (УжГУ, 1980 г.), log2(х2-2х)-3 > 0.
290. (ВГУ, физфак, 1980 г.). logi/3 (Зх + 4) > logi/a (х24-2).
291. (МАМИ, 1979 г.). (1/2)1ое»<хг-1) > 1.
292. (МВТУ, 1979 г.).
293. (МТМИ, 1980 г.). log0>5/(х-4)/(х+3) < log»,6 2.
294. (МИНХ, 1978 г.). log0,5 (x2-3x + 4)-log0,e (х-1) <—1.
295. (ИГУ, 1980 г.). log,.» (Зх-4) < lg0>6 (х-2).
296. (МГУ, 1977 г.). log„,8 (4-х) >log0,8 2-log0>6 (х-1).
297. (МГПИ, 1980 г.). log0,i (х2 + х-2) > logoд (х + 3).
298. (КГУ, РФФ, 1980 г.). 1 + loga (х-2) > log2 (х2-Зх + 2).
299. (МГУ, химфак, 1977 г.). log1/3 (2*+2 —4*) >-2.
300. (МГУ, химфак, 1978 г.). log1/r-(6*+1 —36*) >-2.
301. (МАТИ, 1976 г.). log1/3 [log, (х2-5)] > 0.
302. (МИРЭА, 1976 г.). log0>6 [loge ((х2+х)/(х + 4))] < 0.
303. (МИРЭА, 1977 г.). log0iI[log2((x24-l)/|x-l |)] <0.
304. (МАДИ, 1978 г.). logx[log9 (3*-9)] < 1.
305. (МИИГАиК, 1980 г.). log0t5 log8 ((х2 —2х)/(х —3)) <0.
1------------------------logo 5 (-*Х)
306. (МГМИ, 1979 г.). — <0.
307. (МГМИ, 1979 г.), < 0-
308. (МИСиС, 1977 г.). > 0.
у 2_Л
309. (КГУ, 1979 г.). Kgi/2 (Fir<0-
310. (МИЭТ, 1980 г.). log3
311. (МИЭТ, 1980г.). logx,((4x-5)/|x-2|)> 1/2.
312. (МИФИ, 1978 г.). 1о§2.(--У—-1} >1.
313. (МИФИ, 1979 г.). log1/3 (х+1) > log8 (2 —х).
314. (МИФИ, 1979 г.). log1/5 (х2-6х +18)+2 log5 (х-4) < 0.
315. (ПГУ, 1980 г.). log1/3 х > logx3—.
316. (БашГУ, 1980 г.). log2 (2*-l)-logi/2 (2*+1-2) >-2.
317. (ЯГУ, 1980 г.). log, (18-2*)-log2 ((18-2*)/8)<-1.
318. (МИФИ, 1978 г.). log5 (х—3)+у log53< 1 log5(2x2—6x4-7).
319. (МГИ, 1979 г.). log2(2x-l)>log1/in?2.
320, (МЭИ, 1977 г.). log4/3(/rb3-Kx)4-log4/» (2/3) >0.
84
321. (МГУ, 1975 г.). 2 log6x—log* 125 < 1.
322. (МИУ, 1978 г.). log5/3x+Tlog*5 > 1.
323. (ТГУ, 1981г.). logax + log^-x + logi/з к < 6.
324» (МИСиС, 1979 г.). (y)'°gl/9 (*’“*+1)<1.
325. (МИСиС, 1979 г.). 1о^,5х + 6>5log0,5x.
326. (ЯГУ, 1980 г.). (1/10)1^-з<*,-«+з)^ 1.
327. (МГМИ, 1980 г.). log£((4x-3)/(4-Зх)) > - 1/2.
328. (МИУ, 1978 г.). kfe* (х2 - 5х + 6) < 1.
329. (МИХМ, 1976 г.). log*(х3-х2-2х) <3.
330. (МТИ, 1978 г.). Iog2*+3X2<1.
331. (МАИ, 1979 г.). log(*_3)(2(x2-10x + 24))>log(*_3) (х2—9).
332. (МАИ, 1979 г.). log(x_rT) ((x + 7)/(x-2))<log(*_y4) 2х.
333. (МАИ, 1979 г.). log(*_4>5) ((х+4)/(2х—6))^ log(*_4(6) (х —5).
334. (МИЭТ, 1979 г.). log, Х|(/9-х?-х-1) > 1.
335. (МИЭТ, 1980 г.). log* 2х < /log* (2х3).
336. (МИТХТ, 1979 г.). logiogs(o.5x)(x2-Юх + 22) > 0.
337. (МАИ, 1979 г.). log(x+ e)/3 (log2 ((х-1)/(2 + х))) > 0.
338. (МИЭТ, 1979г.). log3*/(*2+i>(х2-2,5х+ 1)^0.
339. (МИЭТ, 1980 г.). log*2 (2 + х) < 1.
340. (МГУ, биофак, 1979 г.). log»,»(64-2х-х2)< 1/2.
341. (КГУ, мехмат, 1980 г.). log1/x(2,5х— 1)>-2.
342. (КГУ, мехмат, 1980г.). log„(x+27) —logn(16 —2x)<lognx.
343. (МАМИ, 1979 г.). (1/2) > 1.
344. (МАДИ, 1976 г.). (2/5)Iog«-25 (*’+5Х+8> < 2,5.
345. (ЛГУ, 1980 г.). 2,oe=-*<x2+ex + 15> < 1.
346. (МИИГАиК, 1977 г.). (0,5)’°в. 1о8м (*-<>.») < 1.
347. (МГИ, 1979 г.). (0,5)1о«Л ((*+»)/(*’+ з» > 1.
348. (МИНХ, 1979 г.). (0,5)1Og3'og‘/6 < 1.
349. (МАМИ, 1979 г.). log2 (sin (х/2)) < -1.
350. (МГУ, 1978 г.). log4 (3*-1) log1/4 .
351. (МИТХТ, 1979 г.). log5 x + log* | ~J°g9X).
352. (БашГУ, 1980 г.). logi/2x + log3 х > 1.
353. (РГУ, физфак, 1977 г.; МИФИ, 1978 г.). .
1 »}g2 х Z
354. (КГУ, ММФ, 1977 г.). /log2/2x+41og2/x </2(4—logiex4).
85
355. (РГУ, 1981г.). log(A:+3)/(x_S)4 < 2 (logiZ2 (х — 3) —
— l°gi/-/2 Кх + 3).
356. (МИСиС, 1978 г.). /log2 ((3-2х)/(1-х)) < 1.
357. (МИФИ, 1976 г.). ' “>2.
358. (МИФИ, 1978 г.), log^(5^—1)logrT^^ >2.
359. (МВТУ, 1976 г.). log,?^ log1/3 (2*—5) < 2.
360. (КГУ, 1979 г.). (x/10)Ig*-2 3 < 100.
361. (МАИ, 1976 г Л. .—А-гп<-------?..
V ' logs (х +1) 21og9]/\2+6x-i-9
362. (МТИМБО, 1979 г.). 1g 10lg <*2+2I> > 1 +lgx.
363. (МИТХТ, 1979 г.). loga (x-l)4-logax > 2.
364. (МИФИ, 1978 г.). -31°£а*+.- > 1.
v ' logU+2
365. (МИФИ, 1982г.). 21og5(x—3d+2) —logr-(x+2d-8)<4.
366. (МИФИ, 1980 г.). -f—г------+ -Г-ГГ-<Ь
v ’ ’ 5—logflx 1 14-logaX
367. (СимфГУ, матфак, 1982 г.). lg4x—13 lg2 x36 > 0.
368. (МТИМБО, 1980 г.). log1/2 (log2]-^) >0.
369. (РГУ, мехмат, спец, математика, механика, 1977 г.).
log2 х2 + log^— (х — 1) < logKT 1 ogKT 2.
370. (МИИВТ, 1982 г.). lg2x>lgx-{-2.
371. (РГУ, мехмат, вечери, отд., 1977 г.). logv3x-|-
+ 21og1/9(x—1)< logi/3 6.
372. (МИФИ, 1979 г.). < logs (2х-3).
373. (ЛГУ, 1979 г.). loge (1 -8а~х) > 2 (1 -х) (a£R).
374. (РГУ, физфак, спец, физика, 1977 г.). 21ogi/2 (х — 1)^
< J_______1
3 log^-^e
375. (РГУ, 1980 г.). log2 (4* —5 2*4-2) > 2.
376. (НГУ, мехмат, 1979 г.). logx2+2x_3 lx+*b-|xl >0.
377. (БГУ, мехмат, 1979 г.). (logi/2 х)2—logi/2 х2 > (logi/2 З)2—1.
378. (РГУ, мехмат, спец, математика, механика, 1977 г.).
log2 (х+ 14) -J-2 log* (х + 2) < 2 logi/2 (1/8).
379. (РГУ, мехмат, вечерн. отд., 1977 г.). Iog!/4 (х+1)
— 21ogi/ie 24-logi/« (х24~Зх+8).
380. (РГУ, физфак, спец. радиофизика, 1977 г.).
logi/2 log3 jzr} > 0.
86
381. (МТИМБО, 1981г.). log0,5 log5 (х2 - 4) > log0,51.
382. (РГУ, физфак, спец, физика, 1977 г.). logi/4 х1
+ log(x-1>(l/2)^1°gl/2 2’
383. (МИИВТ, 1982 г.). log2^=^<l.
384. (МТИМБО, 1980 г.). log0>5 (х + 5)2 > log3/2 (Зх-1)2.
385. (МИЭТ, 1980 г.). Известно, что неравенство loga (х2—х—2)>
>loge(—х2 + 2х + 3) выполняется при х = 9/4. Найдите все реше-
ния этого неравенства.
Системы показательных и логарифмических уравнений
Решите системы уравнений (386—427).
386. (МТИМБО, 1982г.). | lg^57/^lg2“^х + 3)’
1 4*+» = 128,
387. (ВЗИИЖТ, 1979г.). | 5зж_2,_8=1
388. (МИХМ, 1979 г.). | 5,+г, = 125. ’
( З2* —2г/ = 77,
389, (МИХМ, 1976 г.). | 3х_2,/2 =7>
( 2* + 2?/= 12
390. (ЯГУ, 1980 г.). < 5 ’
I Х’тУ — °.
1 log, х —log, w = 0,
391. (ЯГУ, 1980 г.) J ё '
v ' ( х2 —5z/24-4 = 0.
1 3-2* + 2-3y = 2,75,
392. (МЭСИ, 1979 г.). | 2х_з* = -0,75.
( 7х- 16г/ = 0,
393. (МАТИ, 1979 г.). < Лх ла ’
' ’ ’ ( 4х —49у = 0.
{4Х/0 —3.4(5»-*)/»= 16
395. (МИУ, 1979 г.). { logy_ 2.
396. (ПГУ, 1980 г.). ( |08.*-1°е»!'-7/6.
' ’ ' ( ху= 16.
1 у— log3x=l,
397. (МСИ, 1978 г.). | ;у = Д
[ x's(' = 2,
398. (МИИЖТ, 1979 г.). ) _9П
87
399.
400.
401.
402.
(МИХМ, 1978 г.).
403.
404.
405. (КазанГУ, физфак, 1978 г.).
407.
( log» х + 2 log» t/ = 3,
(МАТИ, 1979 г.). 2 Г 1?
v ( х2 + 1/ = 16.
г j_.._1___ 2
(ВЗИТиЛП, 1980 г.). I х у “15’
( logs х + log3 г/ = 1 ~Ь logs 5.
( х + у = 4+]/'у2 + 2,
(МЭИ, 1978 г.). I lgx_21g2=lg(l+4.il).
glog, (X-40) — 1 ,
4*-20 — 7.2*- 2^ = 8.
1А-ГО x ) 51og2x = log2^-logr-j2,
(МИХМ, 1978 г.). | iog2y = 8 —logy-jx.
( lg(x2 + ^-l = lgl3,
(МТИММП, 1978г.). { Ы(х + у)_^_л = 31,2.
X , 'у___9
f xa — 8 ’
log2x 4-log^-j Уу = 3.
406. (ХАИРЭ, 1981г.). { !|^,J'|^|Zl1g2.
(МВТУ, 1977 г.). I х +^~4 + ту>
( log3 (х + 2у) + logi/s (х — 2у) — 1.
( 3 • (2/3)2*~« 4- 7 • (г/З)*2*-»)/2 -6 = 0,
(МИУ, 1979г.). { lg(3x_//) + lg(, + x) = 41g2.
( log5x4-3los»*' = 7,
(МИНХ, 1979 г.). | x» = 625s.
f 31ogx 2 _. ylogt g,
410. (ЛГУ, физфак, 1980 г.). < Iog 8 _ iogJ
y. Al “ X •
408.
409.
(xy = a2,
(iSxr+(igi,)-=4(igav.
( 2x-8~y = 2^2,
412. (МИФИ, 1979г.). | lo&l + 0,5 = ±1og.(9!,).
(10’-1s(x-y) = 250,
z V x-У
f log4x—log2y=0,
414. (РПИ, 1980 г.). { X2_2l/2 = 8.
83
415.
416.
417.
418.
419.
420.
/МГЛУМ 1077 1 J logs х + logs 7 • log, у — 1 +log52,
' 3-f-2 log2y = log25 (24-3 log5x).
log2 (х—у) = 5 — log2 (х + у),
Igx—1g 4 _ .
Igy-lg3
| log2 x + log4 у = — 2 logi/2 4,
( log4 x4-log2 y = 51g 10.
( 2(logJ,x+logxy) = 5,
( xy = 8.
I 21og2x—3y=15,
I 3Mog2x = 21og2x + 3!'+I.
(МИЭМ, 1976 г.).
(МИНХ, 1978 г.).
(МИНХ, 1978 г.).
(МИНХ, 1979 г.).
(ЛГПИ, 1979 г.; КГУ, химфак, 1978 г.).
1 log₽x+logxy=2,5,
( ху — 27.
421.
422»
423»
/май mao i J 1о& X-log2 y + log2 (t) + 1) = 1 +log2 3,
(МЭИ, 1980 г.). | 2^-2*-16»=0.
/vrv ж . mon 1 J logs (log2X)+ ^1/3(log1/2!0=l,
(КГУ, физфак, 1980 г.). | Xy* = 4.
( log,, (ху) = log„ X2,
(КГУ, ВМК, 1979 г.). { ^о^=4Д3’
424., (МФТИ, 1981 г.). <
425. (МТИМБО, 1982 г.).
426, (МТИМБО, 1980 г.).
2 log4 (у+ 1) + log2 у= log2 0—2) ,
5 + ^2^-=—^.
10&7
' х У
4Т+~ = 32,
. logs (х - у) = 1 — logs (X+у),
f 0,5-log2x —log4y = 0,
( х2 —5у2 + 4 = о.
427, (МТИМБО, 1979 г.).
3х- 2" = 576,
log/T(#-x) = 4-
$ 10. ПРЕОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Основные формулы.
sin2a-|-cos2a= 1. . (1)
tg2a+l=-ir-, а^^ + пп, n£Z. (2)
ctgsa+l=5^T, a=/=nn, n^Z. (3)
89
sin (a + P) = sin a cos p + cos a sin p. (4)
sin (a — P) =; sin a cos p — cos a sin p. (5)
cos (a + P) = cos a cos p — sin a sin p. (6)
cos (a — P) == cos a cos p + sin a sin p. (7)
*g («+Р) = ’ a, P, a + p^y + лп, n^Z. (8)
tg (a-P) = i^g^g p-, a, P. a-p#=^ + nn, n^Z. (9)
sin2a = 2 sin a cos a. (10)
cos 2a — cos2 a —sin2a = 2 cos2a — 1 — 1—2 sin2a. (11)
fg2«- fi-tgg?a , a, 2a#=| + nn, n$Z. (12)
sin 3a = 3 sin a —4 sin3 a. (13)
Вывод: sin 3a = sin (2a + a) — sin 2a cos a + cos 2a sin a =
=2sina cos2a + (cos2a — sin2a)sina=2sina(l — sin2a) + (1 —2sin2a) x
X sin a = 3 sin a — 4 sin3 a.
cos 3a = 4 cos3 a — 3 cos a. (14)
sin a+sin p = 2 sin cos a~$ . (15)
sin a — sin p =; 2 sin a~ - cos . (16)
cosa + cosp = 2cos—5-^cos —. (17)
cos a — cosp = —2 sin sin — . (18)
sin a cos p = у (sin (a—P) + sin (a + P)). (19)
sinasinp = y (cos(a—P) —cos(a-J-P)). (20)
cos a cos p = у (cos (a — P) + cos (a + P)). (21)
1 + cos 2a = 2 cos2 a. (22)
1 — cos 2a = 2 sin2 a. (23)
« 14-cos 2a cos2 a = — -2 • (24)
. 0 1 —cos 2a Sin2 a — . (25)
1 a I / 1 —cosa |sin 2 |— у 2 (26)
1 al 1 /* 1 + cos a |c°Sy|=]/ . (27)
lx a | t / 1 — cos a , , ~ ~ рёт|= V -l+cosa ’ a^n + 2nra, n£Z. (28)
. 2tg(a/2)
* l+tg2(a/2) ’ a -=f=- л 2лл, ti Z, (29)
90
cos a _ 1-tg2 (a/2) l + tg2(a/2) ’ a =/= л+ ^, n£Z. (30)
sin a 14-cos a * ay= л-}-2лп, n£Z. (31)
. a 1 —cos a sin a ’ a=0= лп, n^z. (32)
| sin a | 1 tg a I a -j 4-nn, n$Z. (33)
/l+tg2a ’
|sina| 1 a=/= nnt n£Z. (34)
14~ctg2a
| cos a J 1 a^y + nn, n£Z. (35)
Kl+tg2a ’
| cos a | [ctg a | Vl+ctg2 a ’ a=7^= лп, tt £ Z • (36)
acosx + bsinx = r 02 + b2sin (x + a), #2 + &2#=o, (37)
где a sin a = , - , у а?+Ь* b fl
уa?+b2
Тождественные преобразования тригонометрических выражений
Докажите тождества (1—60).
1. (ВЗИИЖТ, 1979 г.). .1+sina 1+seca. = tgcc,
v ’ 1 14-cosa 14-coseca b
2. (МИЭТ, 1977 г.). -Sin^?-X = tg3x+ *g2 * + tg x+1.
3. (ВГУ, физфак, 1980 г.). 1 (cos t -J- j/"3 sin t) — cos f .
4. (МИХМ, 1979 г.). s_in_4a+2ty2a^sia-cos4a = cos2a.
5. (МТИММП, 1977 г.). .
4 ’ 7 l+sin2a 1-j-tga
6. (МИЭТ, 1977 г.). -s2 tg2 g) = sin + P)sin (a ~ P) •
7. (БГУ, 1979 r.). tgf^ + a^-^g-2-.
v ’ 7 b \ 4 1 J cos 2a
8. (МАИ, 1977 г.).
sin2 (a + p) — sin2 a — sin2 p = 2 sin a sin P cos (a + P).
9. (МТИММП, 1977 г.). (1 + tg p tg 2p) sin 2p = tg 2p.
10. (МАТИ, 1976 г.).
sin a — sin 2a + sin 3a = 4 cos (3a/2) cos a sin (a/2).
11. (МИХМ, 1977 г.). ъ----sinlfa --—=2 sin a sin 2a.
' ’ ' 2 cos a+cos 3a+cos 5a
12. (МСИ, 1976 r.). sin a + 2sin 3a + sin 5a = 4 sin 3a cos2 a.
13. (МИЭТ, 1977 г.). sin2a+sin4a—sin6a = 4sinasin2asin3a.
91
1 л / л < л т'т я 1Л77 — \ sin а —р- sin Зое —j— sin 5а •
14. (МАТИ, 1977 г.). ——= tg За.
15. (МИЭТ, 1977 г.).
sin2 (45° -г а) — sin2 (30°—а)—sin 15° cos (15° + 2а) == sin 2 а.
16. (МАИ, 1979г.). (sin 2a~sin 6.а)t(c°s42k~c°S 6а) = 2sin2а.
17. (МЭИ, 1979 г.).
+ cos | • cig 4а) sec у а = cosec 4а.
18. (МАТИ, 1977 г.). cos2a — sin22a = cos2acos2a — 2sin2acos2a.
19. (МГПИ, 1978 г.). Sl^ZXt+cTstl = 3x~
20. (МГПИ, 1978 г.).
1 — cos (2x — л) — cos (4x + л) + cos (6x—2 л) = 4cos x cos 2x cos 3x.
21. (МГПИ, 1978 г.) tX^gx = sin2x-
22. (УжГУ, 1980 г.). ^4«^^+cos2a
о а
= COS2 у .
—---------т—4- cos (л — а) = 1.
sin а—cos а tg (а/2) 1 v '
cos а _1
cig2 (а/2) —tg2 (а/2) “ Т Sin а’
25. (ВЗИИЖТ, 1979г.). =
26. (ВГУ, геофак, 1980 г.). (cos а + sina) = cos (-£-«
27. (РПИ, 1980 г.). ^g = ctg-(i + «).
2 (1 —cos а)
sin (я—а)
23. (ВильнГУ, 1980 г.).
24. (МАТИ, 1980 г.).
28. (БГПИ, 1980 г.). sina+_sin5a =t 3
v ' cosa-j-cos5a &
29. (МИХМ, 1977 г.).
. / л) 13 . , „ / 7 \
tg (x — у I COS (y n-|-x j—sin3 ( у n—x )
---------:------г---4-5----5--------- = sin2 X.
COS I X— у 1 tg I у л+*1
30. (МАТИ, 1979 г.). sin® acos® a-]-3 sin2 a cos2 a = 1.
31. (МИХМ, 1977 г.).----т-1 ?=1.
2tg sin2 ^+a)
32. (МИЭТ, 1977 г.), sin2 (-£ + «) — sin2 (-J—a) =-yy-
33. . (МИХМ, .1977 г.). ^ifc- = 2ctg2a.
34. (МЭИ, 1977 г.).
etg a — tg a ,
---i—-/nAO--i o-t ।= cosec a cosec 4a.
2 sin a+c©s (90 -j-3a)sin 5a
93
35. (МАТИ, 1977 г.).
36. (МИТХТ, 1979 г.). cos4a—sin4actg2a = cos2a — 2cos2a.
37. (МАТИ, 1977 г.). 1 + 2 cos7a = sin-^ .
38. (МТИМБО, 1980 г.).
(sin a —sin P) (sin a + sin £) = sin (a—p) sin (a + P).
39. (МИЭТ, 1977 г.). ctga-tga-2 tg2a-4 tg4a = 8ctg8a.
40. (МТИММП, 1977 г.; МТИМБО, 1979 г.).
cos 4a tg 2a—sin 4a t 2 2a
cos 4a ctg 2a + sin 4a »
41. (МТИММП, 1977 г.), g = tg a.
42. (МТИММП, 1977 г.).
sina4-cosa , / я , \ ,i \
cos a—sin a а \ 4 * J * \ 4 /
43. (МАТИ, 1979 г.). 3 — 4 cos 2a + cos 4a = 8 sin4 a.
44. (МИХМ, 1977 г.).
45. (МИХМ. 1977 г.).
46. (МИЭТ, 1977 г.). =clgl'» + "')
v ’ /1+cosa— }^1 — cosa \2 4/
я < a < 2л.
47. (МИЭТ, 1977 г.). 1 —sin 4a + ctg л-2а) cos 4a =0.
48 (МИЭТ 1977 г 1 sln *+c°s x sec2 x-f-2_ _2-
w. v'ihoi, iy//rj. slnx_cosx tg2x—1 tgx-f-1
2sin2f-j-—аД . .
49. (МАТИ, 1979 г.). -Л = ctg + aj .
50. (ЛьвГУ, 1980 г.). cos 2a — cos За — cos 4a Ц-cos 5a =
e= — 4 sin (a/2) sin a cos (7a/2).
51. (ЛьвГУ, 1980 г.). =
52. (ЛатвГУ, 1980г.). 4а~‘S1 “
53. "(МТИМБО, 1980 г.), cos6a—sin6a- (3+cos22a)cos2a
54. (МТИМБО, 1979 г.).
2 (sin6 а + cos6 а) — 3 (sin4 а 4- cos4 а) +1 = 0.
55. (МТИМБО, 1980 г.).
COS <135" + “> “s <315°~“> “ 2 C0S 2а-
56. (МТИМБО, 1979 г.). r^L2±^=lg.tI.
4
93
57. (МТИМБО, 1980г.). 0 “s ° =tg (f-f).
58. (МТИМБО, 1979 г.). ^coh~ =sl"»-
59. (МТИМБО, 1980 г.). 2 cos2 2a+-tjsil2-4a- 1 =sin .
v 7 2 sin2 2а3 sin 4а—1 sin (4а—30)
60. (МТИМБО, 1979 г.). 1— sin4 a —cos4 а = -| sin2 2а.
Упростите следующие выражения (61—79).
61 (МТИМБО 1980 г ) -tg cos (9Р°~а\
Oi. (MiriMDU, itrour.). sin (90°a) ctg (90°—a)tg(90°4-a) ‘
62. (МТИМБО, 1979 г.). —2..(sin2a+2.cg-s2a~1) .
' ’ ' cos a—sin a—cos За-j-sin 3a
63. (МТИМБО, 1980 г.). 3cos2x —4sinxcosx —sin2x—1.
64. (МТИМБО, 1977 г.).
4 cos2(2a—| n) -(-cos (2a — n) + sin - 6a).
(ВЗИИЖТ, 1979 г.).
(МАМИ, 1979 r.).
(МАТИ, 1979 г.).
/т> отлт txtz'T’ 1\ sin За4- sin 5а—]— sin 7а
(ВЗИИЖТ, 1979 г.). cos3tt+cos5a+cos7a-
(МТИММП, 1976 г.). 4cos4a — 2cos2a—-i-cos4a.
(ЛГПИ, 1979 г.).
65.
66.
67,
68.
69.
70.
л , л , 2л , Зл . 4л . 5л . 6л
COS 0 + COS-у-4- COS —+ COS-у- -I-COS-у-+ COS-у-+ COS-у.
71. (МТИММП, 1976 г.).
cos
4 sin (5л —За) cos (а—2л)
72. (МХТИ, 1977 г.).
1 — у sin2 2а
/UVTTI Ш77 \ F 14-sin 4а—cos 4а
73. (МХТИ, 1977 г.). —г—.—т
4 ’ ' 14-cos 4а4“sin 4а
2 cos2 а— 1
74. (МИЭТ, 1977 г.)
75. (КолПИ, 1980 г.).
76. (ОГУ, 1980 г.). !+cosa tg2-^-cos2a.
v ’ 1 1—cos а & 2
94
77. (МТИММП, 1980 г.). tg (Д + %)
\ * / vVD Lfc
78. (РПИ, 1980 г.). sin2a (14--Д—4-ctgaVl
sin ОЬ J
1
sin a
(-ctgal .
______cos 2a______
sin22a(ctg2a—tg^)
79. (МГМИ, 1980 г.).
Вычислите без таблиц (80—105).
80. (МХТИ, 1977 г.). cos67°30' и cos75°.
81. (МЭСИ, 1977 г.). 4(cos24° +cos48° — cos84° — cosl2°).
96 sin 80°4*sin 65° sin 35°
sin 20°4~sin 50°-|-sin 110°
82. (МЭСИ, 1977 г.).
83. (МЭСИ, 1977 г.). 128sin220° sin2 40° sin260° sin2 80.
84. (МГИ, 1977 г.). tg 20° tg 40° tg 80°.
85. (МИИГАиК, 1977 г.).
86. (МИЭТ, 1977 г., МТИМБО, 1979 г.). cos 10°cos50°cos70°.
87. (ТартГУ, 1980 г.). sinl60°cosll0°4-sin250°cos340°4-
4-tg 110° tg 340°.
88. (МИФИ, 1976 г.). tg9° —tg63°4-tg81°—tg 27°.
89. (МЭСИ, 1980 г.). 96 /3sinДcosДcos Д coscosД.
90. (МГМИ, 1980 г.).
91.
. / 7 л o \ /6л \ . 3л
sin (-g--zajcosf-^----al sin a при
(ТбГУ, физфак, спец, радиофизика и электроника, 1978 г.).
sin 110° sin 250°-|-cos 540° cos 290° cos 430°
cos21260° •
92. (ТбГУ, мехмат, спец, прикладная матем., 1980 г.). Про-
1 > 1 4
верьте равенство +
93. (МТИМБО. 1982г.). Проверьте cos у • cos If-. cos = 1.
94. (МТИМБО, 1980 г.). Проверьте cos 20° 4-2 sin2 55°== 1 4-
4-K2sin 65°.
95. (ТбГУ, мехмат, спец, прикладная матем., 1982 г.). Вы-
числите (sin 4a4- 2 sin 2a) cos a, если sin a= 1/4.
96. (ТбГУ, физфак, спец, радиофизика и электроника, 1980 г.).
Дано: 20sin2a-|-21 cos a —24=0, 7 л/4 < a < 2л. Найдите ctg (a/2).
97. (БашГУ, 1980 г.). -д . _5. о , если tga = 0,2.
' ’ ' 64-7 sin 2a ’ ° ’
98. (МХТИ, 1977 г.), sin 2a, если sin (a/2) 4-cos (a/2) = —1/2
и a принадлежит IV четверти.
99. (МХТИ, 1977 г.). tg (Д—2a) , если tga = a.
100. (МАИ, 1979 г.), tg (a—Д) , если cosa=s—9/41, л <a<
< Зл/2.
96
101. (МИИЗ, 1979 г.). cos (а/2), если sin а=—12/13, л<а<Зл/2.
102. (РПИ, 1980 г.), sin(а/2), если sina = —5/13 и л<а<Зл/2.
103. (ГомГУ, прикладная матем., 1980 г.). sin (а/2), если
sin а = 0,8 и 0 < а < л/2.
104. (ЯГУ, 1980 г.). -г-;—у- , если tga = 2.
' sin3a+3cos3a ’ °
105. (ЛьвГУ, 1980 г.). sin6 а + cos6 а, если sina + cosa = m.
Преобразуйте в произведение (106—112).
106. (МЭИ, 1977 г.). sec а—cos а + sec 60° cos 2а sin За—sin 5а.
107. (МТИММП, 1976 г.), sin а + sin 60° +sin (а+ 60°).
108. (МТИ, 1979 г.), sin (5а + р) + sin (За + 0) + sin 2а.
109. (МЭИ, 1978 г.), sin a cos —sin За cos у—
ПО. (МЭИ, 1978 г.). 4cos lla-|-(sin8a—sin 10а —sin 12а -
-J- sin 14a) cosec a cosec 2a.
111. (МЭИ, 1979 г.). tg2a—tg2P—у sin (a—p) sec2asec2p.
112. (МАИ, 1978 г.). etg^afp + Ecos(а-p) sec (a+P) +1]"1.
Обратные тригонометрические функции
Вычислите (113—126).
113. (ВЗИТиЛП, 1979 r.)^arctg l+arccos(—l/2)4-arcsin(—1/2).
114. arcsin (— V2/2) + arccos (—1/2) — arctg (— j/3) +
+ arcctg(—l/j/3).
115. (МЭСИ, 1980 г.). arcctg[tg(—37°)].
116. (МАТИ, 1980 г.). arccos (cos (—/3/2)).
117. (МИФИ, 1979 г.). arctg К2 +arctg(l//2).
118. sin (2 arcsin (3/5)).
119. cos (2 arcsin (2/5)).
120. sin (2 arctg 3).
121. cos (2 arctg 2).
122. sin (y arccos-0.
123. cos (4- arccos ).
124. (МИЭТ, 1976 г.). sin (2 arctg (1/3))+ cos (arctg 2/2).
125. (МТИММП, 1977 г.). sin(arcsin(3/5)-arccos(3/5)).
126. (МАТИ, 1980 г.). tg (arcsinу+ -^).
Докажите (127—132).
127. sin(arcsinx) = x, —l^x^l.
128. cos(arcsinx) = К1—x2, —l^x^l.
96
1
1. 29. cos (arctg х)
у 1 x2
130. tg (arccos х) — ^~Х . —1 x < 0, 0<х^1.
131. arcsin х + arccos х = л/2, —1 sC х 1.
132. arctg х-|-arcctg х = л/2.
Упростите выражения (133—141).
133. sin (arccos 3/5).
134. cos (arcsin 4/5).
135. sin (arctg 2).
136. cos (arctg 2).
137. arcsin (sin (8л/7)).
138. arctg (tg (Юл/7)).
139. arcsin (sin (6л/7)).
140. arctg (tg (6л/7)).
141. arccos (cos (6л/7)).
142. Выразите arcsin (5/13) через значения всех обратных три-
гонометрических функций.
Решите уравнения (143—145).
143. 6 arcsin (х2 — 6х + 8,5) = л.
144. 4 arcsin х 4-arccos х = л.
145. 5 arctg х + 3 arcctg х = 2л.
146. (ГомГУ, 1980 г.). Постройте график у = arcsin(cosх).
147. (РГУ, физфак, спец, радиофизика, 1977 г.). Решите нера-
венство arcsin (sin 5) > х2 —4х.
§ 11. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ,
НЕРАВЕНСТВ И СИСТЕМ УРАВНЕНИЙ
Решение простейших тригонометрических уравнений
Пример 1. sinx = /n, |т|1.
х = (—1)" arcsin т-\-т, n£Z.
Пример 2. cosx = /n, |m|^l.
х= ± arccosт-|-2л/г, n£Z.
Пример 3. tgx = /n, m^R.
х = arctg т + л/г, n^Z.
Пример 4. ctgx = m, tn^R.
х = arcctg tn + л/г, n £ Z.
Замечание 1. В приведенных простейших примерах запись
решений имеет простую и однозначную форму. В более сложных
примерах форма записи множества решений не однозначна, но
идентичность различных форм записи всегда можно доказать при
помощи тождественных преобразований. Различная форма записи
4 В. М. Говоров и дл 97
обычно объясняется различными методами, при помощи которых
решалась данная задача. Например, в задаче 47 было получено
множество решений
— l)n arcsin 4-лп, n£Z.
При проверке правильности ответа задача была решена другим
методом и получили множество решений
-т+(-1)я-Т1 + л«,
Это то же самое множество решений; форма же записи другая. Дей-
ствительно,
. 1 + /3 . /1 1 , У~з 1 \
arcsin r- = arcsin -х- • —— + •-= =
2/2 \2 /2 2 /2 J
=arcsin (sin cos ф- cos sin =
\ 6 4 1 6 4 j
. f • (л t п\\ . / . 5л \ 5л
=arcsin ( sin (-g-4- —Н = arcsin ( sin \ .
Последнее равенство основано на том, что —если
бы это неравенство не выполнялось, необходимо было бы восполь-
зоваться формулами приведения.
При самостоятельном решении задач об этом необходимо по-
стоянно помнить. Если у Вас будет другая форма записи множест-
ва решений, чем приведенная в разделе «Ответы и методические
указания», то необходимо доказать их идентичность. Последнее
само по себе является хорошим упражнением.
Замечание 2. При нахождении решения очень часто мно-
жество решений тригонометрических уравнений записывается при
помощи нескольких формул. Иногда их можно объединить и по-
лучится более простая запись ответа. Например, в задаче 187
первоначально множество решений было записано в форме
лп, (n, k, m^Z).
О о
Это множество решений можно записать и так:
лп, + (n, kez).
Разная форма записи множества решений и здесь часто объясня-
ется различными методами решения предложенного уравнения.
Замечание 3. Если в примерах, приведенных в замечаниях
1 и 2, различные формы записи идентичны и окончательная форма
записи множества решений (с точки зрения правильности реше-
ния) безразлична, то бывает, что одно и то же множество реше-
ний дается несколько раз. В этих случаях необходимо в окон-
98
чательной форме записи эти "повторы исключить. Например, при
решении задачи 76 получены два множества решений
-у + лп, уд+“у" (я, k^Z),
В данном случае все решения, даваемые первым множеством, как
часть входят во второе множество. Действительно, если положить
А = 5/14*2 (ngZ), то из второго множества решений выделяется
первое множество. В этом случае окончательная запись множества
решений будет выглядеть так:
т. е. лишнее надо отбросить.
Замечание 4. В случае, если найденные множества реше-
ний только частично пересекаются, то эта общая часть в записи
окончательного множества решений должна быть приведена лишь
один раз без повторений. Так в задаче 81 (при решении ее не-
которым методом) получено два множества решений
^•4 (1)
Ни одно из этих двух множеств решений не является частью дру-
гого, но если мы положим /1 = 5/п, a k = 2m то получим
и в первом и во втором случае лт. Следовательно, это множе-
ство решений надо в одном из приведенных множеств исключить.
Например, во втором множестве все четные значения k надо исклю-
чить и оставить только k = 21 + 1 (/ £ Z).
Тогда все решения задачи (и при этом каж-
дое решение только один раз) будут записаны
в виде
л (2/ +1)
и At
При другом методе решения эта форма записи
множества решений получается непосредствен-
но. Приведение окончательного множества
решений в виде (1) считается ошибочным.
Замечание 5. Обнаружение пересечения множеств решений
или возможность их объединения легко обнаруживается таким
приемом. Рисуется круг и на нем отмечаются кружочками реше-
ния, принадлежащие одному множеству решений, а крестиками —
другому. На рисунке кружками обозначены решения, принадле-
жащие множеству «2^, а крестиками—решения, принадлежащие
множеству у. Отсчет углов производится от оси L против часо-
вой стрелки. На рисунке видно, что значения 0 и л (и все
отличающиеся от них на период) принадлежат как первому,
так и второму множеству решений. Таким образом, помимо реше-
4* 99
ний, записанных в форме , на круге остались еще две точки
у и (и отличающиеся от них на период). Эти решения можно
записать в виде nl
Решение уравнений разложением на множители
Пример 5. (МАИ, 1979 г.). 2cosxcos2x = cosx.
Решение. Данное уравнение равносильно уравнению
cos х (2 cos 2х — 1) = 0. Это уравнение равносильно совокупности
уравнений
cosx = 0, => * = Т + шг’
cos2x = 1/2, 2x=±4 + 2nfe> т- е- х=±4 + л£, k£Z.
L о О
Ответ: ^-[-яп, ±-g-4~n£ (п, k£Z).
Решение уравнений, сводящихся к квадратным уравнениям
Пример 6. (МАИ, 1979 г.). 3cos2x— 10cosx4-3 = 0.
Решение. Пусть cosx = y. Данное уравнение примет следую-
щий вид: З//2—Юг/4-3 = 0. Решив его, найдем г/1=1/3, у2 = 3.
Значение г/2 = 3 не удовлетворяет условию, так как |cosx|^l.
Следовательно, cosx=l/3; х = ±arccos(1/3) + 2яп, n£Z.
Ответ: ± arccos (1/3) 4~2л/г (n£Z).
Решение однородных и сводящихся к ним уравнений
Уравнения вида
а0 sin" х + sin"'1 х cos х + а2 sin"'2 х cos2 х + ...
... + ^„-1 sin х cos"'1 х + ап cos" х = 0,
где а0, alf ..., ап~ действительные числа, называются однород-
ными относительно sinx и cosx.
Пример 7. (МАМИ, 1979 г.). cos3x + sin3x = 0.
Решение. sin3x = — cos3x. Так как значения х, при кото-
рых cos3x равен нулю, не являются корнями данного уравнения,
то разделив обе части исходного уравнения на cos3x, получим
уравнение, равносильное исходному:
sin Зх cos Зх . о 1
---а-, или t&3x = —1.
cos Зх ’ &
cos Зх
Отсюда Зх =—
Ответ: —~ + п
IZ о
х= — + n£Z.
(n£Z).
100
'Пример 8. (МГМИ, 1980 г.). 6sin2x—sinxcosx — cos2x = 3.
Решение. 6 sin2 х—sin х cos х—cos2x—3 (sin2 х + cos2 х) = 0.
После раскрытия скобок и приведения подобных членов получаем
3sin2x—sin х cos х—4 cos2 x = 0.
Так как значения х = -2- + лп не являются корнями уравнения и
cosx=+0, то разделим обе части уравнения на cos2x:
3 tg2x—tgx—4 = 0,
откуда
tgx =—1, х— — -?~ + лп, n£Z,
и
tgx = 4/3, х = arctg (4/3) +лй, k^Z.
Ответ,'. —-^ + лп, arctg (4/3) + nk (ti, k£Z).
Решение уравнений с помощью введения
вспомогательного аргумента
Пример 9. (МИИЗ, 1979 г.). sinx + cosx = j/"2.
Решение. 2 (—l=sinx~i—cosxA = j/"2,
\ /2 т f 2 /
sinxcos(n/4) + cosxsin (л/4) = 1, sin ^х + у^) = 1>
х + | = у + 2шг (neZ), х = ^-^ + 2лп (n£Z).
Ответ: -^- + 2пп (n£Z).
Пример 10. (МГМИ, 1977 г.). -X^-cosx + ysinx= 1.
Решение, cos (л/6) cosx + sin (л/6) sinx= 1, cos ^х — ^ = 1,
х—~ = 2лп (n£Z), х = -^ + 2лп (n£Z).
Ответ: -2- + 2лп (n£Z).
Решение уравнений преобразованием суммы
тригонометрических функций в произведение
Пример 11. (МАТИ, 1979 г.). cos3x+sin2x—sin4x = 0.
Решение. cos3x + (sin2x—sin4x) = 0.
Преобразовав выражение в скобках по формуле (16) § 10, бу-
дем иметь
cos3x+(— 2sinxcos3x) = 0,
cos Зх(1 — 2sinx) = 0.
101
Последнее уравнение равносильно совокупности уравнений
cos Зх = 0, sin х = 1/2;
следовательно,
Х = ^. + ^П, х=(—l)ft£ + nfe (n, k^Z).
О о О
Множество решений х = (—1)*у + л& (k£Z) целиком содержится
в множестве решений х = у + -^- («€•£). Поэтому только это
множество и остается как множество решений.
Ответ: -£+ ^-п (n£Z).
и о
Решение уравнений преобразованием произведения
тригонометрических функций в сумму
Пример 12. (МАТИ, 1979 г.). sin5xcos3x = sin6xcos2x.
Решение. Применим формулу (19) § 10 к обеим частям урав-
нения:
у (sin 8х + sin 2х) = (sin 8х + sin 4х),
sin 2х—sin 4х = 0.
Применив формулу (16) § 10, получим
—2sinxcos Зх = 0=»
_ ’ sinx = 0, _ х = лп, n£Z,
_cos3x=0, Зх = у + л&, х = ууk, k£Z.
Ответ: лп, -?- + -?•& (n, k£Z).
О о
Решение уравнений с применением формул понижения степени
(формул (24) и (25) § 10)
Пример 13. (МВТУ, 1979 г.). sin2x + sin22х= 1.
Решение. -—х + 1 ~ c^s-4х = 1 =^>cos2x-{-cos4x = 0=>
=>2cos3xcosx = 0. Последнее уравнение равносильно совокупно-
сти двух уравнений
a) cos3x = 0, Зх = -^ + лп х = ^- + ^-п, n£Z.
£ о о
б) cos х = 0, х = у + лк, k$Z.
Множество решений уравнения б) является подмножеством мно-
102
жества решений уравнения а), поэтому в ответе запишем лишь
корни уравнения а).
Ответ: -5- + ^ (ngZ).
О и
Решение уравнений с применением формул
(22) и (23) § 10
Пример 14. (МИЭТ, 1977 г.), cosx— 2 sin2 (х/2) = 0.
Решение. cosx— (1 —cosx) = 0=> 2 cosx— 1 =0=>cos х =
= 1/2==>х—±-g- + 2jin (n^Zj.
Ответ: ±-т + 2лп (n£Z).
О
Решение уравнений с применением формул двойного
и тройного аргументов
(формулы (10)—(14) § 10)
Пример 15. (МГУ, мехмат, 1980 г.), sin 2х—K2cosx.
Решение. Применив формулу (10) § 10 к левой части урав-
нения, будем иметь 2sinxcosх = /*2cosx. Разделить обе части
уравнения на cosx нельзя. Это приведет к потере решений, являю-
щихся корнями уравнения cosx — О. Перенесем K2cosx в левую
часть. Тогда
2sinxcosx —1/*2cosх = 0—>К2cosx (К2sinx— 1) = 0=>
cosx = 0,
К 2 sin x = 1,
х — 4- пп, n£Z,
х==(—l)feJ + nfc, k^z.
Ответ: -^-4-ля, (—l)s-j-4-nA (n, k£Z).
Пример 16. (МИНХ, 1977 г.). 2sin(x/2) cos2 x —
— 2 sin (x/2) sin2 x = cos2 x—sin2 x.
Решение. В левой части уравнения вынесем за скобку общий
множитель 2sin (х/2):
2 sin (х/2) (cos2 х — sin2 х) = cos2 х—sin2 х.
Заменив выражение cos2x—sin2x согласно формуле (И) § 10 на
cos2x, получим
2 sin (х/2) сое 2х <= cos 2х,
103
пли
2 sin (х/2) cos 2x—cos 2x = 0=>cos 2x(2sin (x/2) — 1) = 0=»
' cos2x = 0, x = t + t"’ n€Z>
sin (x/2) = 1/2, x = (~l)ft4 + 2nfe, k£Z.
О
Ответ: n, (— l)fty + 2nfe (n,k£Z).
Решение уравнений с помощью замены переменных
а) Уравнения вида P(sinx±cosx, sinxcosx) = 0, где Р(у, г) —
многочлен, решаются заменой
cosx± sinx = /=> 1 ± 2sinxcosx = /2.
Рассмотрим пример.
Пример 17. (РПИ, 1980 г.). sinx + cosx= 1 4-sinxcosx.
Решение. Обозначим sinx + cosx = (. Тогда
(sinx + cosx)2 = t2, 1 + 2sinxcosx = /2. sinxcosx = (/2—1)/2.
Наше исходное уравнение в новых обозначениях будет выгля-
деть так:
/ = 14-(/2—1)/2 или t2-2/-f-1 =0, (/ — 1)2 = 0, / = 1,
т. е.
:osx=l, К 2 ( —£=- sin х Ч—l=-cosx^ = l,
\ /2 К 2 /
cos (л/4) cosx+ sin (л/4) sinx= 1/К2,
/ л \ V~2
cos lx — j 1 =—j—,
x—^ = ±-^ + 2лл, n^Z,
х = ^±| + 2лл, n$Z.
Ответ: у-(-2лп, 2лп (n£Z).
б) Уравнения вида asinx + fecosx + d, где a, b, d—действи-
тельные числа и а, Ь#=0 решаются заменой
cos*-!+^/2)’ 51пх=ттеж’ х^п+2лп
Пример 18. (МИНХ, 1979 г., СимфГУ, 1982 г.). 3cosx +
+ 4sinx = 5.
Решение.
О 1 - tg2 (х/2) . 2 tg (х/2) -
OH-tg2(x/2)'t-4l+tg2(x/2) J’
3 — 3 tg2 (х/2) + 8 tg (х/2) = 5 + 5 tg2 (х/2),
104
4 tg2 (x/2) -4 tg (x/2) + 1=0, (2 tg (x/2) - I)2 = 0,
tg (x/2) = 1/2, x = 2arctg (1/2)+ 2я«, n£Z.
Ответ: 2arctg (1/2)+ 2я/г (ti£Z).
в) Введением новой переменной решаются многие уравнения.
Пример 19. (МТИММП, 1977 г.). sin4 2x + cos4 2х =
= sin2xcos2x.
Решение, (sin2 2х + cos2 2х)2 — 2 sin2 2х cos2 2х = sin 2х cos2x,
2 sin2 2xcos2 2х+ sin 2xcos 2x— 1=0.
Обозначим sin 2xcos2x = у. Тогда последнее уравнение примет
вид 2у2+у—1=0, или
2(//+1) (//-4) =0-
Перейдем к переменной х и будем иметь
1) sin2xcos2x = — 1, 2sin2xcos2x = —2, sin4x =—2, х£0.
2) sin2xcos2x= 1/2, sin4x=l, 4x = —4-2лм, n£Z,
x = -g+-2-n, ngZ.
Ответ: (n£Z).
Решение тригонометрических уравнений вида f (х) = К <р (х)
Пример 20. (МИНХ, 1978 г.). |/1 — cosx = sinx, хС[л, Зя].
( 1 — cosx/SsO,
Решение. ( _ „
( sinx^O.
При условии, что обе части уравнения неотрицательны, воз-
ведем их в квадрат:
1 — cos х = sin2 х, 1 — cos х = 1 — cos2 x,
cos2x —cos x = 0, cosx(cosx— l) = 0.
1) cosx = 0, x = -^ + nn, n£.Z,
2) cos x = 1, x = 2ak, k£Z.
Но так как sinx^O и хС[я, Зя], то оставляем х = 2я, 5л/2.
Ответ: 2я; 5я/2.
Решение уравнений с использованием ограниченности
функций sinx и cosx
Пример 21. (МИФИ, 1978 г.).
(cos(х/4) —2sinx) sinx + (l +sin(х/4) — 2cosx) cosx = 0.
105
Решение. cos (х/4) sin х— 2 sin2 х + cos х -j- sin (x/4) cos x —
— 2 cos2 x — 0,
sin [x 4- + cos x — 2 (sin2 x + cos2 x) = 0, sin (5x/4) -f- cos x = 2.
Так как функции sin(5x/4) и cosx имеют наибольшее значе-
ние, равное 1, то сумма их равна 2, если sin(5x/4) = 1 и cosx = 1
одновременно, т. е.
( sin(5x/4) = l, ( ^ = ^--г2лп,
< ==> 1 * z
( cosx—1, ( х = 2л& (п, kezy,
п , 2л , 8л , 14- 4м
2л^ = -=- + ^-П, £ =
оо о
Так как k£Z, то п—1-\-5т (m£Z), и тогда х=2л + 8лт,
m£Z.
Ответ: 2л + 8лт, m£Z.
Тригонометрические системы
( sinxcos у = 1/4,
Пример 22. \ о. ,
F Е ( 3tgx = tgi/.
Решение. Преобразуем второе уравнение и получим
3 sin х cos у — sin у cos х = 0.
Теперь подставим в полученное равенство значение произведения
sinxcosz/ из первого уравнения и будем иметь систему
{cosx sin у = 3/4,
sinxcos#= 1/4. (1)
Сложив уравнения системы (1), а затем сделав вычитание из вто-
рого уравнения первого, получим систему, равносильную системе (1):
( sin(x+fO = l,
I sin (х-у) = -1/2,
откуда
( х-Уу = -х- + 2лй,
S л
) х — у = — -g- + 2n/
и
х + у = ^ + 2л£,
106
Из системы (3) найдем
х = -|Н-л (£ + /),
= j + —/).
Из системы (4) найдем
х=—-^-|-л (£ + /),
!/ = -у- + л (fe —/).
Обратите внимание на то,, что целые числа, на которые в (3) умно-
жаются 2л, нужно записать разными буквами (например, k и /),
так как эти множества не связаны между собой. Если эти
множества записать с одной и той же буквой, то это приведет к по-
тере решений.
Решите уравнения (1—245).
1. sinx=l/2. 2. sinx = —1/3.
3. sinx = 0. 4. sinx=l.
5. cosx =1/2. 6. cosx = —1.
7. cosx = 0. 8. tgx = K3.
9. ctgx = —1. 10. sinx = K 2/2.
11. sinx = — КЗ/2. 12. sinx = —1/2.
13. cosx=l. 14. cos2x= 1.
15. cosx = V 3. 16. tgx =—1.
17. tg(x-l) = 7. 18. tg (2x4-3) = KT
i- (л "x \ К 3 19. ctgU-3 20. sin (3x—2) = —1.
21. (МГУ, химфак, 1980 г.).' К 2 cos27x—cos7x = 0.
22. (МВМИ, 1977 г.). 2sinx4- tgx = 0.
23. (МИНХ, 1977 г.). (2 sinx—cosx) (1 + cosx) = sin2x.
24. (ВЗЭИС, 1978 г.). 4cos3x —4cos2x—соэ(л4-х) —1 =0.
25. (МАТИ, 1979 г.). 1 + sinxcos2x = sinx + cos2x.
26. (ВЗИИЖТ, 1979 г.), tg’x-1 +с-т4--3 ctg =3.
27. (МЭИ, 1979 г.), tg 2xsinx + |ЛГ(sinx-KT tg2x) = 3 KT
28. (МВМИ, 1977 r.). sin4 x = 1 — cos1 x.
29. (МАДИ, 1979 г.). КЗ sinx—tgx+tgxsinx —КЗ =0.
30. (МТИМБО, 1981 г.), cos2х + 3sinx = 2.
31. (МАТИ, 1979 г.). ccsx4-secx = 2.
32. (СимфГУ, физфак, 1981 г.). 14-f.osx4-cos2x = 0.
33. (МОПИ, 1976 г.). 6cos2х4-5sinx—7 = 0.
107
34. (ВЛТИ, 1980 г.). cosx + 2cos2x= 1.
35. (МТИПП, 1979 г.). 2cos2x + 4cosx=3sin2x.
36. (МИХМ, 1977 г.). 4sin4x+12cos2x = 7.
37. (МИХМ, 1976 г.). 5 tg4x —sec4x = 29.
38. (МТИМБО, 1981 г.). cos4x + 2cos2x = 0.
39. (МТИМБО, 1982 г.), sin4х + cos4х = cos 4х.
40. (МТИЛП, 1980 г.). sinx + cosx = 0.
41. (ВильнГУ, 1980 г.). cos2x—3sinxcosx= sin(Зл/2).
42. (МАМИ, 1979 г., МТИМБО, 1978 г.).
3 sin2 х—2 sin х cos х — cos2 х = 0.
43. (МАДИ, 1979 г.). cos2x + 2K2 cosxsinx+1 =0.
44. (МИТХТ, 1979 г., МТИМБО, 1978 г.).
sin2x(l + tg x) = 3sin x(cosx — sinx)-}-3.
45. (МТИМБО, 1981 г.). sin3x + sinx = sin2x.
46. (МТИМБО, 1982 г.). 1 — sin2x = cosx — sinx.
47. (БашГУ, 1980 г.), sinx-f-cos х = (1+J/" 3)/2.
48. (МАТИ, 1979 г.). 4sin2x-3sin (2х— у) =5.
49. (МИТХТ, 1979г.). (sin2x+K"3cos 2x)2-5 = cos(y—2x) .
50. (МГРИ, 1979 г.), sin (л — 6х) + Кз sin (у + 6х) = КЗ.
51. (ТбГУ, физфак, спец, радиофизика и электроника, 1982 г.).
cos ^у—Зх^—sin2x = 0.
52. (МТИМБО, 1981 г.). cos2x — cos8x + cos6x= 1.
53. (УжГУ, 1980 г.). sinx + sin2x + sin3x = 0.
54. (МСИ, 1977 г.). sinx + sin2x-f-sin3x + sin4x = 0.
55. (МАТИ, 1978 г.). tg_3x-tgx = 0.
56. (МСИ, 1977 г.), j/3 sin2x-(-cos5x — cos9x = 0.
57. (МСИ, 1977 г.), cos ^y-j-5xj + sinх = 2 cos Зх.
58. (МИИГАиК, 1977 г.).
sin х + sin 2х + sin Зх = cos х 4- cos 2х + cos Зх.
59. (МИИГАиК, 1978 г.). cos3x + sin5x = 0.
60. (МИИГАиК, 1978 г.). cos3x + sin(9x + 2) = 0.
61. (МАТИ, 1976 г.), cos Зх = Ху cosх—ysinx.
62. (МИНХ, 1979 г.), sinх + cosх = К 2sin5x.
63*. (МГИ, 1977 г.).
64. (МТИМБО, 1982 г.).
cos 2х cos х = sin 7х sin 6х + 5 cos (л/2).
65. (МСИ, 1976 г.), cosЗх + sinxsin2х = 0.
66. (МГУ, биофак, 1980 г.). 1 +2cos3xcosx—cos2x = 0.
108
67. (МИСиС, 1978 г.). 2 cos х sin Зх = sin 4x4- 1.
68. (МИИГАиК, 1978 г.). sinxsin7x = sin3xsin5x.
69. (МАТИ, 1976 г.), cosхcosЗх = cos5хcos7х.
70. (МИЭТ, 1978 г.), sinx sin Зх = 1/2.
71. (МТИМБО, 1981 г.). sin2x4~sin22x4-sin23x4~sin24x = 2.
72*. (МФТИ, 1976 г.). cos3x tg5x = sin7x.
73. (МЭИ, 1978 г.).
4 sinxsin I х4--2-) sin
\ о 1
( X + + cos 3x = 1.
\ J
74. (МПИ, 1979 r.). sin 2x sin 6x = cosx cos 3x.
75. (МТИМБО, 1981 г.). sin5x + sinx + 2sin2x= 1.
76. (МИЭТ, 1978 г.), cos22x + cos2Зх = 1.
77. (МИИГАиК, 1978 г.; МТИМБО, 1980 г.).
sin4 (х/3) cos4 (х/3) = 5/8.
78. (КишГУ, 1980 г.). sin4(x/2) — cos4(x/2) = 1/4.
79. (МИЭТ, 1978 г.), sin4х + cos4х = sinxcosx.
80. (МГРИ, 1979 г.). tgx 4-sin (л 4-х) = 2 sin2 (х/2).
81. (МИНХ, 1979 г.). sin2x + sin22x — sin23x — sin24x = 0.
82. (РГУ, мехмат, 1980 г.). sin2x + sin22x4~sin2Зх = (3/2).
83. (МТИПП, 1976 г.).
sin х sin 2х + cos2 х = sin 4х sin 5х + cos2 4х.
84. (МИФИ, 1978 г.). sin2x + sin22x = cos23x + cos24x.
85. (МГУ, геофизика, 1977 г.).
sin2 (2 + 3х) 4*cos2 4-2х) = cos2 (2 — 5x)4~sin2 —6х)
86. (МТИМБО, 1980 г.). sin4x4-eos4x = 3~c4°s6x.
87. (МИЭТ, 1977 г.). 2cos4x—2cos2х = 4cos2х — 1.
88*. (МИИГАиК, 1978 г.). 2cos2x— 1 = sin3x.
89. (МВТУ, 1979 г.), tg (х/2) = 1—cosx.
90. (МАТИ, 1979 г.).
3 sin —х)—4 sin (л 4-х) sin f-y-4-х') 4-8 cos2 -у = 4.
91. (МЭИ, 1978 г.). 3 4-5 sin2х = cos 4х.
92. (МВТУ, 1978 г.). (1 4-cos 4х) sin 2х —cos2 2х.
93. (МАДИ, 1977 г.), sinх —2cos2x= 1.
94. (МАТИ, 1979 г.). ^l-J-sin (у—4х^ sin 4х = cos2 (2х—л).
95. (МИИГАиК, 1976 г.). cos2x — 3 cos х = 4 cos2 (х/2).
96. (МТИММП, 1977 г.). 4 cos х —2 cos 2х —cos 4х= 1.
97*. (МТИМБО, 1982 г.), sin 3x4-sin3 х = Ц^- sin2x.
98*. (МТИМБО, 1979 г.), sin3х —cos3х= 1 4~sin хcosx.
99. (МТИМБО, 1980 г.), sin4х4-cos4х = sin2x — 0,5.
100. (МТИММП, 1977 г.; СимфГУ, 1982 г.; МТИМБО, 1982 г.).
cos3хsinx — sin3xcosx = K2 /8.
109
101. (МИЭТ, 1977 г.), sin 2x = cos2x —sin2x+1.
102. (МИХМ, 1977 г.). (cos2x—1) ctg2x =—3sinx.
103. (МИХМ, 1977 г.). 8cosxcos2xcos4x = sin6x/sinx.
104. (МИНХ, 1977 г.).
sin (x/2) cos 2x + sin? x cos (x/2) = cos2 x cos (x/2).
105*. (МФТИ, 1976 г.). cos3x—cos2x = sin Зх.
106. (МЭИ, 1977 г.). (sin7x + cos7x)2 = 2sin2llx + sin30x.
107. (МГРИ, 1979 г.). sin3x — 4sinxcos2x = 0.
108*. (МТИМБО, 1979 г.).
sin2x tgx + cos2xctgx— sin2x= 1 + tgx-f- tg2x.
109. (МГРИ, 1977 r.). sec2x— tg2x + ctg 0b-f-xj =cos2xsec2x.
ПО. (МИФИ, 1976 г.). sin*x + cos4x—2sin2x-|--|-sin22x = 0.
111. (МТИМБО, 1981 г.). (cos6x—1)ctg3x= sin3x.
112. (МЭИ, 1977 г.), sinx + sin Ji-f-x) = 1 — 0,5 sin2x.
113. (МИИГАиК, 1977 г.).
(1 —sin2x) (cosx—sinx) = 1 — 2sin2x.
114*. (МФТИ, 1976 г.). 2sin3x—Д- = 2cos3x + -?-.
sin X COS X
115. (МТИПП, 1978 г.), sec x + cosec x = 2|/2.
116. (МИЭТ, 1977 г.; МТИМБО, 1979 г.).
, . cos 2х
COS X + sin X — :-Г-s- •
1 1—sin 2x
117. (МГИ, 1979 r.). 4sin(5x + y) + sinl0x=4-
118. (ТбГУ, физфак, спец, радиофизика и электроника, 1981 г.).
3 (cosx—sinx) = 1 +cos2x —sin2x.
119. (МЭСИ, 1980 г.), sinx—cosх=1.
120. (МСИ, 1977 г.). 3sinx = 2 (1 — cosx).
121*. (МФТИ, 1977 г.). cos2x — 2 cos х = 4 sin х—sin2x.
122. (МАТИ, 1977 г.). sin2x-2 У 2 sin (-у—2х) = 3.
123*. (МТИМБО, 1981 г.), tg х+ tg 2х+ tg Зх = 0.
124. (МИФИ, 1978 г.), cos 9х — 2 cos 6х = 2.
125. (МИФИ, 1978 г.).
(4]/cos|-5-^)2 + /r(4 |/cos|-5-^-)-^ = 0.
126*. (МГУ, геофак, 1977 г.).
2 sin (зх + у) — К1 + 8 sin 2х cos2 2х.
127. (МТИМБО, 1979 г.), ctg 2x + ctgx = 8cos2x.
128. (МГМИ, 1979 г.). -|—sin2х = ^9+10&rn2x.
ПО
129. (МГУ, эконом, фак., 1979 г.). К13 — 18 tg х = 6 tg х — 3.
130. (МГМИ, 1979 г.). 4sin3x + 3 = /2sinЗх + 2.
131. (МГМИ, 1980 г.). Кб — sinx—7cos2x4-sinx = 0.
132*. (МТИМБО, 1978 г.). tgx + =2.
у 1 -f-sin 2х
133. (МЭИ, 1979 г.), sin4 х +sin4 (у + у) 4-cos4x = y sin22x.
134. (МИФИ, 1978 г.), cos (л Ух — 4) cos (л К* ) = 1.
135. (МГПИ, 1979 г.). ^у^ = 0.
136. (МТИМБО, 1981 г.), cos2 х + 5 cosх = 2 sin2 х.
137. (МСИ, 1977 г.). sin2x + sin(n —8х) = К2 cos3x.
138. (МИЭТ, 1979 г.). 1 +sin *+costg+sin 2х+с0?-2х- = 0.
139. (МИЭТ, 1978 г.). 4cos26x+16cos23x= 13.
140. (МИЭТ, 1977 г.). tg5x4-2sin 10x = 5sin5x.
141. (МИХМ, 1977 г.). tg3x—tgх = secхsecЗхsinx.
142. (МАТИ, 1977 г.; МТИМБО, 1980 г.).
sin х + sin Зх = 4 cos3 х.
143. (МАДИ, 1980 г.). 2sin22x + 6 sin2x = 5.
И
144. (МГУ, географ, фак., 1980 г.). cos6x — sinex = ycos22x.
145. (МИТХТ, 1979 г.). 4sin4x + sin22x= 1.
146. (МСИ, 1977 г.). 1 4-sin2x = (cos3x + sin3x)2.
147. (МХТИ, 1977 г.). KT-tgx = tg (у—х) .
148. (МВТУ, 1978 г.). ctg2x—tg2x = 8ctg22x.
149. (МВТУ, 1978 г.). cosx+cos4x+cos7x = 0.
150. (МВТУ, 1978 г.). sin5x + cos3x—sinx = 0.
151. (МВТУ, 1979 г.). cos4(x/5) + sin2(x/5) = 1.
152. (МИИГАиК, 1978 г.), sin2 х = sin Зх + cos х (cos х—1).
153. (МИИГАиК, 1977 г.). (3 — ctg2x) sin2x = 2(l +cos2x).
154. (МИИГАиК, 1980 г.). |±!|2E = (sinx + cosx)2.
155. (МИИГАиК, 1980 г.). sinx + sin2x = tgx.
156. (МГИ, 1976 г.), sinx—sin2x4-sin5x + sin8x = 0.
157. (МИТХТ, 1979 г.). 8cos4х — 8cos2х — cosx+ 1 =0.
158. (МГРИ, 1979 г.), tg 3x + cos6x= 1.
159. (МАТИ, 1977 г.; МТИМБО, 1981 г.). tgxtg3x=l.
160. (МТИМБО, 1982 г.).
cos2 у 4- sin2 Зх + cos2 (у+2х) = 3cosy.
161. (МАТИ, 1979 г.).
sin7x + sin9x = 2 (cos2 (у—х)—cos2 (у 4-2х^ .
111
162. (МАТИ, 1980г.). sin9x + K3 cos7х = sin7x + j/'3 cos9x.
163. (МСИ, 1977 г.), sin х + sin 2х = cos х + 2 cos2 х.
164. (МИСиС, 1978 г.).
sin ^2x-f--y^—3cos —х^ = 1 + 2 sinx.
165*. (МИСиС, 1978 г.).
^cos y—sin у + tg x) = sin cos x.
166. (МИЭТ, 1978 г.; МТИМБО, 1980 г.), sin6 х + cos6 х= 7/16.
167. (МИЭТ, 1977 г.). y=(tgx-ctgx) = tg2x + ctg2x-2.
168. (КолПИ, 1980 г.; МТИМБО, 1979 г.).
cos 4x-J-2cos2x = 1.
169. (МАДИ, 1980 г.). sin3x—cos3x = КЗ/2?
170. (ЛьвГУ, 1980 г.; МТИМБО, 1981 г.).
171. (ПГУ, 1980 г.), ctg х—2 sin 2х= 1.
172. (МИХМ, 1977 г.; МТИМБО, 1977г.). 2tgx-cos2x = 2.
173. (МИХМ, 1977 г.), tg (Зх-1) ctg (х+2) = 1.
174. (МГУ, почв. отд. биофака, 1977 г.).
|ctgx| = ctgx + s-^.
175. (МИУ, 1978 г.; МТИМБО, 1980 г.).
2(1— cos 2х) — КЗ tg х.
176. (МТИМБО, 1980 г.). 3cos2x—sin2x — sin2x = 0.
177. (ЛатвГУ, 1980 г.; МТИМБО, 1981 г.).
3 sin2 2х + 7 cos 2х — 3 = 0.
178. (ВЗИИЖТ, 1979 г.).
2 ctg2 х cos2 х + 4 cos2 х — ctg2 x — 2 = 0.
179. (МЭИ, 1978 г.).
4 sinx sin ^x + y^ sin ^x+ 4-cos3x= 1.
180. (МЭИ, 1977 г.).
sinx + Hs sin л —x^ +tgx=K3.
181. (МИЭТ, 1979 г.). 5^x+tglX + 4(1~COSX)==0>
182. (МИУ, 1978 г.). 8sinx = c^ + ^.
183. (МТИММП, 1977 г.). cosx = sinx-l.
184. (МТИМБО, 1982 г.).
cos2 Зх+sin8 (у+5х) — cos8 7х + cos2 9х + cos
112
185. (МГУ, геология, 1977 г.).
sin2(l,5x) 4-sin2 —2,5xj = sin2(5,5x) 4- sin2 —6,5x).
186. (МИЭТ, 1979 г.). tgx4-ctgx —cos4x = 3.
187*. (МИУ, 1978 r.). cosx —/з" sinx = cos 3x.
188. (МГРИ, 1977 г.). ^-1 =-^.
189. (МИРЭА, 1978 г.). 4 sinx 4-cosx = 4.
190. (МИТХТ, 1979 г.). cos5x tg6 |x| + sin5x = 0.
191. (МИФИ, 1979 г.). tg4xcos7x = sin7|x|.
192. (МФТИ, 1977г.). 2 cos 2x 4-2 cosx sin2 x = cosx.
193. (МФТИ, 1977 г.). ---т-t—-= 4cos x).
' • cos x I on \ \4 j
cos (x g-I 4
194. (МФТИ, 1978 г.). 11 ctgx-5 tgx= 16/sinx.
195. (МТИМБО, 1980 г.), cos2 2x 4-cos2 4x — sin26x — sin28x<=0.
196*. (МФТИ, 1979 г.). sinx + sin2x + cos3x = 0.
197. (МФТИ, 1979 г.). cos3x — sin5x — cos7x = sin4x — cos2x.
198. (МФТИ, 1980 г.). 5 sinxx~cos2x —3sin2x.
199. (РПИ, 1980 г.). ctgx + -rzg^- = 2.
200. (МЭИ, 1978 г.). ‘g22x = |^|^.
201. (ВильнГУ, 1980 г.). 2sin2xsin4x —cos2x = sin3x.
202. (РГУ, мехмат, спец, прикладная матем., 1977 г.;
МТИМБО, 1979 г.). 3ctgx-3tgx + 4sin2x = 0.
203. (СимфПИ, 1981 г.). tgx4-ctgx = 2.
204*. (ТбГУ, физфак, спец, радиофизика и электроника, 1977 г.).
sin3 (x/2) — cos® (x/2) _ 1 v
2+sln x — 3 cos x.
205. (МТИМБО, 1982 г.). sin 2х + 2 ctg х = 3.
206. (МИИВТ, 1982 г.). sinxcos xsin2x= 1/8.
207. (МИФИ, 1977 г., МТИМБО, 1982 г.). sin6x + 2 = 2cos4x.
208* . (МИФИ, 1977 г.), tg2 х tg2 Зх tg 4х = tg2 х — tg2 Зх 4-tg 4х.
209. (МИФИ, 1978 г.). 2cos 13x4-3cos3x4-3cos 5х —
_________3 cos х cos^ 4x — 0.
210. (МИХМ, 1979 г.). tg3x — tgx = 2(sin4x — sin 2x).
211. (МИНХ, 1979 г.).
(sin 13°)ct*s*+c,2* = sin2 (2л — x) — cos (л —x) sin (y 4-x).
212. (ВГУ, 1980 r.). 2sin3xsinx + (3/2—l)cos2x = 3.
213. (ПГУ, 1980 г.). ctgx —2sin2x= 1.
214. (ВЗИИЖТ, 1979 г.). tgxsinx —cosx = 0,5secx.
215. (МИУ, 1978г.). sin2x tg x 4-cos2 x ctg x 4-2 sin x cosx =s
« 4/3/3.
216. (МИУ, 1978 г.). tg2xsin2x —3/3ctg2xcos2x = 0.
217. (МИСИ, 1978 г.). sin (3x/2) cos (x/2) = (sin 2x)/2.
113
218. (МТИМБО, 1978 г.). ctg2x-tg2x = ytg4x.
219. (МТИМБО, 1982 г.). sinx4-cosxctg-|- =— КЗ.
220. (ЛГУ, матмех, 1980 г.). cos х cos 2х cos 4х = 1.
221*. (ЛГУ, матмех, 1980 г.). 9 cos12 х 4-cos2 2x4-1 4-2cos2x»
= 6 cos6 х cos 2x 4- 6 cos6 x.
222. (ЛГУ, физфак, 1980 г.), sin 2x(0,1— cosx)=sin2x4-0,2sin3x.
223*. (ЛГУ, физфак, 1980 г.). | cosx | = cos (x-|-a).
224*. (ЛГУ, геофак, 1980 г.).
sin ((2х 4-1 )/х) 4- sin ((2x4-1 )/Зх) - 3 cos2 ((2х 4-1 )/Зх) = 0.
225*. (МИФИ, 1978г.). asin(x/2) — (sinx4~sin(3x/2)) = 0.
226. (НГУ, мехмат, 1980 г.). cos (2 sin х 4-(1 4-1^3) cosx) =*
е= sin ((1 — КЗ) COSX).
227*. (НГУ, мехмат, 1979 г.).
j/’Scos x4-sinx — 24- ctg3x4-sin2x—j- = siny4-^^.
228*. (БГУ, мехмат, 1979 г.). sin4 х 4-cos4 х4-sin 2x4-а = 0.
229. (МЭИС, 1981г.). j/^cos2 2х 4-1 sin ^2х—
/20 \
=соЦт2л; •
230. (МЭИС, 1981 г.). |ctg(2x-^| = c-^-l.
231. (ХАИРЭ, 1981 г.). -2-4-l = sin(n-x)-cosxtg^±i.
232. (КИЦМ, 1981 г.). sin3x — cos3x = 0.
233. (ВильнГУ, матфак, 1979 г.), cos^cos-^-—1 = - cosх.
2 z 2
234. (МГМИ, 1980 г.). _____ =/2cos2x + 2.
у 4 cos 2*+1
235. (КГУ, ВМК, 1979 г.). sin(nx/2 Кз) = х2-2КЗх4-4.
236. (МТИМБО, 1977 г.). sin2x4-tgх = 2.
237. (МТИМБО, 1982 г.), sin2 (^4-= sinx4-sin2 (у—х) .
238. (МИИВТ, 1982 г.). 6sin2х4-sinхcosх —cos2х = 2.
239. (МТИМБО, 1978 г.). ^4-+2 = 0.
240. (ТбГУ, мехмат, спец, прикладная матем., 1978 г.).
sinx—4cosx4-tg х = 4.
241. (МТИМБО, 1980 г.).
8 cos6 х = 3 cos 4х 4- cos 2х 4- 4.
242. (РГУ, мехмат, спец, прикладная матем., 1977 г.;
МТИМБО, 1979 г.). (1 - tg х) (1 4-sin 2х) = 1 + tg х.
243. (ТбГУ, мехмат, спец, прикладная матем., 1981 г.),
sin 3x4-3 sin 4x4-sin5x = 0.
114
244. (МТИМБО, 1982 г.). 2tg2x + 3 = ^.
245. (МТИМБО, 1982 г.). 81’^ + 81СО5!* = 30.
246. (МИТХТ, 1979 г.). Найдите все значения р, при кото-
рых имеет решение уравнение 'Kpcosx — 2sinx = j/2 + K2 — р.
247. (ТбГУ, мехмат, спец, прикладная матем., 1977 г.). Най-
дите все значения а, для которых уравнение cos2x + asinx =
= 2а —7 имеет решение.
248. (МИЭТ, 1977 г.). В интервале (0, л/2) найдите корни
уравнения sin ^2х+^) cos^2x—= —1/4.
249. (МЭСИ, 1977 г.). Найдите (в градусах) решение х урав-
нения 1 + cos 10х cos 6х = 2 cos2 8х + sin2 8х, удовлетворяющее ус-
ловию —20° < х < 80°.
250. (МГУ, физфак, 1980 г.). sin х cos (л/8) 4-cosх sin (л/8) =
= 1/2, х£[—Зл/2, л].
251. (МАТИ, 1979г.). Решите уравнение 4cosx(2 —3 sin2x) +
+ (cos2x+1) = 0. Найдите наименьшее расстояние между его по-
ложительными корнями.
252. (МИНХ, 1979 г.).
cos(n + x)+K3sinx = sin (зх—у) , *€ j
253. (МТИМБО, 1979 г.). 2sin42x — sin22хsin4х = 2sin22х —
— sin 4х, х £ [0; л].
254. (МФТИ, 1978 г.). Проверьте, какие из чисел лп —arctg 3,
где п g Z, являются решениями уравнения
12 tg 2х + —+1 = 0.
° 1 COS X 1
255. (МЭИ, 1980 г.). Найдите все корни уравнения cos4x +
+ = лежащие на отрезке [—Зл/4; л/2].
256. (МЭИ, 1980 г.). Найдите все корни уравнения
(1 — cos2x) sin2x = K3sin2x, лежащие на отрезке [—л; л/3].
257. (МЭИ, 1979 г.). Найдите все корни уравнения sinxtg2x+
+ К 3 (sin х — КЗ tg 2х) = 3 КЗ, удовлетворяющие неравенству
2 + logi/2 х 0.
258. (МИЭМ, 1979 г.). Решите уравнение sin(nx2) —
— sin (л (х2 + 2х)) = 0 и найдите 7-й член возрастающей последо-
вательности его положительных корней.
259. (МИНХ, 1978 г.). Решите уравнение cos4x + 6 = 7cos2x
и найдите сумму его корней на отрезке [0; 314].
260. (МГУ, биофак, 1980 г.). Найдите все те решения урав-
нения 3sin3x — 3cos2x + 7sinx — cos2x+ 1 =0, которые являются
также решениями уравнения cos2x + 3cosxsin2x — 8sinx = 0.
261. (МИНХ, 1979 г.; МТИМБО, 1981г.). Решите уравнение
tg2x = 3tg х, если х€] —2л; 2л[.
115
262. (МФТИ, 1979 г.). Найдите все решения уравнения
sin (4х-{- y) +cos (^x-f- = /2, удовлетворяющие неравенству
cos 2х о - sin ix
cos 2—sin 2
Тригонометрические неравенства
Решите неравенства (263 — 278).
263. sinx > 0.
264. sinx> 1/2.
265. (МАМИ, 1979 г.). log2 (sin(x/2)) <—1.
266. sinx^1/2.
267. sinx^—1. _
268. cosx <—/2/2.
269. tgx>0.
270. tgx<-/3?
271. (ЯГУ, 1980 г.). sinx < cosx.
272. sin3x < sin x.
273. sinx + /3cosx > 0.
274. tg2x — (1 + /3) tgx + /3 <0.
275. sinx (cosx+ =^0.
276. (МИФИ, 1972 г.). 2cos2x + 5cosx + 2i>0.
277. /5 — 2 sin x 6 sin x — 1. _____'
278. (ЛГУ, физфак, 1980 г.). 21^2х y2 — y + ^^i.
Решите системы (279 — 312).
279. (КГУ, +
(cos х <—1/2.
(cos® x — sin3 x = cos 2x,
280. (ЛГУ, 1979г.).|0<х^3я/2
281.
(МИНХ,
(sin2 x 4- sin2 2% = sin2 3x,
1979 г.). < /o . .
7 (—л/2^х^л.
282. (МФТИ, 1979 г.).
283. (МИФИ, 1977 г.).
284. (МВТУ,
1976 г.).
/ . ( л \ / . Зя \ .
sin f x—-j-) —cos ( %4- —1 = 1,
2 cos 7x 2cos2\
< cos 3+ sin 3
sinx sin y= 1/4,
cos x cos z/ = 3/4.
sinx sin z/= 1/4,
ctgxctgr/ = 3.
116
/ sin x +cos z/ = 0,
285. (КГУ, 1978г.). j sin2x-|-cos2y = 1/2,
(0<х<л, 0 < у <л.
t ( y—x = 1/4,
286. (МИФИ, 1976 г.). \
( cos (лх) cos (л//) = V 2/2.
( cos(x — w) = 1/2,
287. (МИФИ, 1978 г.). . ,о
’ 1 cos (х+ «/) = —1/2.
( х+« = Зл/4,
288. (МИФИ, 1979 г.). < , . ’
' 7 (tgx—tg^ = 2.
( sinх-1-cos о = 1,
289. (ЯГУ, 1980 г.). { , „
v ' (х-]-1/ = л/3.
( х + у = 2л/3,
290. (МИФИ, 1975 г.). •! sinx
V sin у
( tg х 4- tg и = 2,
291. (МИФИ, 1975 г.) J . ,о
' ( cosxcosу= 1/2.
( х—у— 13л/2,
292. (МИФИ, 1978 г.). < _ \ 1О .
х ' ( 3cos2x— 12 cos у — — 4.
293. f sin2x + cos2y= 11/16, (УрГУ, 1976 г.). < . .. , * ею v I sin((x + z/)/2)cos((x —1/)/2) = 5/8.
294. f — 1 : =• (3cos2x —6ctg;/4-2)=0, (МГУ, 1977 г.). < V sin
( 18 sin2x—2 tg y — 3 = 0.
295. (МГУ, 1979 г,). 1 4^»-бГ2еозх_5 + 4соз-й ' ’ ' ( cos2x = 0.
296. (6 cos x + 4 cos у = 5, (МФТИ, 1978 г.). <L . , о - n ' (3sinx-|-2sini/ = 0.
f 3tg(y/2)+6sinx = 2sin(w—x),
297*. (МФТИ, 1977 г.). { ' Q . /
' ' ( tg (z//2) — 2 sin x — 6 sin (y + x).
298. (МФТИ, 1978 г.). <! + sinxsin# = cosx,
v ’ ' ( 2sinxctgz/-|-l =0.
299*. (МФТИ, 1978 г.).
300. (КуйбГУ, 1977 г.).
cos 2y-\--cos у—у) (1+2 sin 2x),
sin у (tg3 x -J- ctg3 x) = 3 ctg y.
' tgxtgz = 3,
tgi/tg2 = 6,
yc + y + z = n.
117
„ ( sinx + sin у = sin (х + у),
301. (КуйбГУ, 1977 г.).
l|x| + |i/| = l.
( 4 tg Зх = 3 tg 2y,
302. (МИФИ, 1977 г.). < o , У'
( 2 sinx cos (x—y) — sin y.
{cosx + cosy=a,
x + y = n/4.
, ( tg * + sin у = 2a,
304, (МИФИ, 1978 г.). <L T ’
' ( tgxsini/ = a2—1.
{х+у x—у 1
C°s —cos ——2 ,
COS X COS y= \/4.
( ctgx + sin 2z/ = sin2x,
306. In* • / r \
( 2 sin i/sin (x + t/) = cosx.
307.
(МИФИ, 1976 г.).
sin (x—y) = 3 sin x cos у — 1,
sin (x + y) = —2 cos x sin y.
308.
309.
(МИФИ, 1978 г.).
' tgx + ctgx = 2sin (у—-|* л
tg 1/+ ctg i/= 2 sin
ctg p/x= 1,
cos j/x = — l/j/"2.
ЗЮ f cos//(cosx —cos//) = 2cos ^i^sinysin^^,
I 2y—х = л/2.
[ cosx + cos2x + cos3x = 3,
311. 1 3/ ,04 40
( cos3 (x/2) = cos4 2x.
312. (МГУ, ВМК, 1-977 г.).
I sin2 (—2x)-(3 -K2) tg 5i/ = (3 j/l-1)/2,
I tg2 (5^) + (3 - К 2) sin (—2x) = (3 И2 - 1 )/2.
313. (ЛГУ, эконом, фак., 1980 г.). Найдите все решения сис-
темы уравнений
sin (2x+3t/) + cos (2x-]-3y)=* 1,
< 1Г+18 \ . т/o’ • ( , л+18 > о
cos^x+—j2-0)+]/3sin ^x + -]^-i/J =2,
удовлетворяющие условию | у ] 1.
314. (МГУ, 1976 г.). Найдите все решения системы уравнений
( ctg2(x — y)-(l+K3)ctg(x —1/) + /3 = 0,
( cos ^/ = }^3/2,
удовлетворяющие условиям 0 < х < л, О У 2л.
§ 12. ПРОГРЕССИИ
Арифметическая прогрессия. Числовую последовательность,
каждый член которой, начиная со второго, равен предшествую-
щему члену, сложенному с одним и тем же числом d, называют
арифметической прогрессией. Это число d называют разностью
арифметической прогрессии.
Последовательность {ап} является арифметической прогрессией
тогда и только тогда, когда для любого п > 1 верно равенство
Для арифметической прогрессии имеем:
л zt-L/и 1Ы 2 ai+an „ 2a-j-\-d(n— 1)
— аг “J- \П l)d, % пft,
где d—разность прогрессии, a Sn—сумма ее первых п членов.
Чтобы задать арифметическую прогрессию, достаточно задать
ее первый член и разность прогрессии.
Геометрическая прогрессия. Числовую последовательность, пер-
вый член которой отличен от нуля, а каждый член, начиная со
второго, равен предшествующему члену, умноженному на одно
и то же отличное от нуля число q, называют геометрической
прогрессией. Это число q называют знаменателем геометрической
прогрессии.
Последовательность {Ьп} является геометрической прогрессией
тогда и только тогда, когда для любого п > 1 верно равенство
Для геометрической прогрессии {Ьп} имеем:
Ь=Ь^~\ Sn = -^±- = ^^-t
п 17 ’ » q—1 <? — 1 ’
где q #= 1—знаменатель прогрессии, a S„—сумма ее первых п
членов. При <7=1
—бд/г.
Чтобы задать геометрическую прогрессию, достаточно задать ее
первый член и знаменатель прогрессии.
Сумма бесконечной геометрической прогрессии {Ьп} при |^| < 1
определяется равенством
S= lim Sn9 при этом З-'Дл.
п-* ® 1 я
1. (ВГУ, матфак, 1981 г.). Найдите первый член и разность d
арифметической прогрессии, в которой
J «а + «6 —«з = Ю,
I «® + «» = 17.
119
2. Сумма п первых членов последовательности {ап} определяется
по формуле S„ = 2zi2 + 3n. Докажите, что эта последовательность
является арифметической прогрессией.
3. (ЛатвГУ, 1980 г.). Известно, что при любом п сумма Sn
членов некоторой арифметической прогрессии выражается форму-
лой Sn = 4п2 — 3п. Напишите первые три члена этой про-
грессии.
4. (РПИ, 1980 г.). Найдите сумму 20 членов арифметической
прогрессии, если ее первый член равен 2, а седьмой равен 20.
5. (МАИ, 1976 г.). Определите первый член и разность ариф-
метической прогрессии, если сумма ее первых пяти членов, сто-
ящих на четных местах, равна 15, а сумма первых трех членов
равна (-—3).
6. (КиевГПИ физмат, 1980 г.). Сумма первого и пятого членов
арифметической прогрессии равна 26, а произведение второго и
четвертого ее членов равно 160. Найдите сумму шести первых
членов прогрессии.
7. (МАМИ, 1979 г.). Сумма третьего и девятого членов ариф-
метической прогрессии равна 8. Найдите сумму первых 11 членов
этой прогрессии.
8. (МИФИ, 1980 г.). Сумма квадратов пятого и одиннадцатого
членов арифметической прогрессии равна 3, а произведение вто-
рого и четырнадцатого членов этой же прогрессии равно k. Най-
дите произведение первого и пятнадцатого членов прогрессии.
9. (МХТИ, 1977 г.). В арифметической прогрессии сумма вто-
рого и пятого членов равна 8, а третьего и седьмого равна 14.
Найдите прогрессию.
10. (МАИ, 1977 г.). Сколько членов арифметической прогрес-
сии нужно взять, чтобы их сумма равнялась 91, если ее третий
член равен 9, а разность седьмого и второго членов равна 20?
11. (МАМИ, 1978 г.). Между числами 1 и 1,3 вставьте пять
членов так, чтобы они вместе с данными составили бы арифмети-
ческую прогрессию.
12. (ТартГУ, 1980 г.). Найдите 4 числа между числами 4 и
40 так, чтобы получилась арифметическая прогрессия.
13. (МИФИ, 1978 г.). Найдите сумму всех трехзначных нату-
ральных чисел, которые при делении на 3 дают остаток 2.
14. (МТИММП, 1977 г.). Решите уравнение 52-54-56-...-52* ==
== (0,04)”28.
15. (МВТУ, 1979 г.). Найдите возрастающую арифметическую
прогрессию, у которой сумма первых трех членов равна 27, а
сумма их квадратов равна 275.
16. (КГУ, ЭКФ, 1977 г.). Сумма четырех чисел, образующих
арифметическую прогрессию, равна 1, а сумма квадратов этих чи-
сел равна 0,3. Найдите эти числа.
17. (МВТУ, 1978 г.). В арифметической прогрессии 12 членов;
сумма их равна 354. Сумма членов с четными номерами относится
к сумме членов с нечетными номерами как 32:27. Найдите раз-
ность прогрессии.
120
18. (МИУ, 1977 г.). Произведение третьего и шестого членов
арифметической прогрессии равно 406. При делении девятого члена
этой прогрессии на ее четвертый член в частном получается 2 и
в остатке 6. Найдите первый член и разность прогрессии.
19. (МИНХ, 1979 г.). Первый член арифметической прогрес-
сии а2, а3, ... равен единице. При каком значении разности
прогрессии d величина а±а3 + а2а3 имеет минимальное значение?
20. (МИНХ, 1979 г.). В арифметической прогрессии я7 = 9.
При каком значении разности арифметической прогрессии произ-
ведение 6Zxa2a7 будет наименьшим?
21. (МФТИ, 1975 г.). Две арифметические прогрессии содер-
жат одинаковое число членов. Отношение последнего члена пер-
вой прогрессии к первому члену второй равно отношению послед-
него члена второй прогрессии к первому члену первой и равно 4.
Отношение суммы первой прогрессии к сумме второй равно 2.
Найдите отношение разностей этих прогрессий.
22. (МВТУ, 1979 г.). Все члены арифметической прогрессии —
натуральные числа. Сумма ее девяти последовательных членов,
начиная с первого, больше 200, но меньше 220. Найдите про-
грессию, если ее второй член равен 12.
23. (ВГУ, матфак, 1980 г.). Каждая из двух троек чисел 1gа,
lg ft, Igc и Iga — lg 2£>, lg2fe —lg3c, lg3c —Iga является ариф-
метической прогрессией. Могут ли числа а, &, с служить длинами
сторон треугольника? Если да, то какой это будет треугольник?
Найдите углы этого треугольника, если он существует.
24. (МИСиС, 1979 г.). В арифметической прогрессии четвертый
член равен 4. При каком значении разности этой прогрессии сумма
попарных произведений первых трех членов прогрессии будет наи-
меньшей?
25. (МИНХ, 1977 г.). В арифметической прогрессии шестой
член равен 3, а разность прогрессии больше 0,5. При каком зна-
чении разности прогрессии произведение первого, четвертого и
пятого членов прогрессии будет наибольшим?
26. (МИФИ, 1977 г.). Некоторые числа встречаются в обеих
арифметических прогрессиях 17, 21, ... и 16,21, ... Найдите
сумму первых ста чисел, встречающихся в обеих прогрессиях.
27. (МИСиС, 1976 г.). Три числа образуют арифметическую
прогрессию. Сумма этих чисел равна 3, а сумма их кубов равна 4.
Найдите эти числа.
28. (МОПИ, 1979 г.). Докажите, что числа 1 6 1 о, г 1 о
v ’ logs 2 ’ log6 2 V log12 2
образуют арифметическую прогрессию.
29. (НГУ, мехмат, 1980 г.). При каких значениях параметра а
найдутся такие значения х, что числа 51+* + 5х“*, а/2, 25*+ 25"*
составят арифметическую прогрессию?
30. (ВТИЛП, 1979 г.). Докажите, что последовательность,
общий член которой ап = 2 3п, является геометрической прогрес-
сией и найдите сумму первых восьми членов.
121
31. (РПИ, 1980 г.). Четвертый член геометрической прогрес-
сии больше второго члена на 24, а сумма второго и третьего членов
равна 6. Найдите эту прогрессию.
32. (МАИ, 1979 г.). Разность между четвертым и первым чле-
нами геометрической прогрессии равна 52, а сумма первых трех
членов прогрессии равна 26. Вычислите сумму первых шести членов
этой прогрессии.
33. (МИНХ, 1979 г.). Сумма первых четырех членов геометри-
ческой прогрессии равна 30, а сумма следующих четырех членов
равна 480. Найдите сумму первых двенадцати членов.
34. (МАИ, 1979 г.). Сумма двух первых членов геометрической
прогрессии равна 15. Первый член больше знаменателя этой про-
грессии на 25/3. Найдите четвертый член этой прогрессии.
35. (ЛГУ, 1978 г.). Найдите три числа, образующие геометри-
ческую прогрессию, если их сумма равна 35, а сумма их квадратов
равна 525.
36. (МАМИ, 1980 г.). Последовательность —геометриче-
ская прогрессия, причем &4/fee=l/4, &2 + Ь5 = 216. Найдите bv
37. (МАИ, 1979 г.). Сумма первых трех членов возрастающей
геометрической прогрессии равна 13, а их произведение равно 27.
Вычислите сумму первых пяти членов этой прогрессии.
38. (МГПИ, 1980 г.). Найдите первый член и знаменатель
геометрической прогрессии, сумма первых трех членов которой
равна 10,5, а разность первого и четвертого членов равна 31,5.
39. (МИСиС, 1978 г.). Числа a, b, с, d составляют геометриче-
скую прогрессию. Найдите (а—с)2 + (& — с)2 + (& — d)2 — (a—d)2.
40. (МВТУ, 1979 г.). Сумма первого и третьего членов гео-
метрической прогрессии равна 20, а сумма первых трех ее членов
равна 26. Найдите прогрессию.
41. (МАИ, 1979 г.). Разность между первым и пятым членами
геометрической прогрессии, все члены которой положительные
числа, равна 15, а сумма первого и третьего членов этой прогрес-
сии равна 20. Вычислите сумму первых пяти членов прогрессии.
42. (МИНХ, 1979 г.). Найдите четыре числа, составляющих
геометрическую прогрессию, в которой сумма крайних членов
равна 112, а сумма средних членов равна 48.
43. (МИНХ, 1979 г.). Первый член геометрической прогрес-
сии Ь1г Ьг, Ь3, ... равен единице. При каком значении знаменателя
прогрессии величина 4624-5Ь3 имеет минимальное значение?
44. (КГУ, РФФ, 1977 г.). Сумма трех чисел, образующих гео-
метрическую прогрессию, равна 13, а сумма их квадратов равна 91.
Найдите эти числа.
45. (АзГПИ, матфак, 1980 г.). Числа 5х—у, 2х-(-3# и х-|-2у
составляют арифметическую прогрессию, а числа (у -j-1)2, ху +1,
(х—I)2 составляют геометрическую прогрессию. Найдите х и у.
46. (НГУ, мехмат, 1979 г.). В возрастающей геометрической
прогрессии сумма первого и последнего членов равна 66, произ-
ведение второго и предпоследнего членов равно 128, сумма всех
членов равна 126. Сколько членов в прогрессии?
122
47. (МАДИ, 1979 г.). Сумма первых трех членов геометриче-
ской прогрессии равна 31, а сумма первого и третьего членов
равна 26. Найдите седьмой член прогрессии.
48. (МИЭТ, 1977 г.). Число членов геометрической прогрес-
сии четное. Сумма всех членов прогрессии в 3 раза больше суммы
членов, стоящих на нечетных местах. Найдите знаменатель про-
грессии.
49. (МАИ, 1979 г.). В геометрической прогрессии первый, тре-
тий и пятый члены соответственно равны первому, четвертому и
шестнадцатому членам некоторой арифметической прогрессии. Вы-
числите четвертый член арифметической прогрессии, если ее первый
член равен 5.
50. (РПИ, 1980 г.). Три числа, сумма которых равна 28, об-
разуют геометрическую прогрессию. Если к первому числу приба-
вить 3, ко второму 1, а от третьего отнять 5, то полученные
числа образуют арифметическую прогрессию. Найти эти числа.
51. (РПИ, 1980 г.). Три числа образуют арифметическую про-
грессию. Если к первому числу прибавить 8, получится геометри-
ческая прогрессия с суммой членов 26. Найти эти числа.
52. (МФТИ, 1976 г.). Второй, первый и третий члены ариф-
метической прогрессии, разность которой отлична от нуля, обра-
зуют в указанном порядке геометрическую прогрессию. Найдите
ее знаменатель.
53. (МАИ, 1979 г.). Первый и третий члены арифметической
прогрессии соответственно равны первому и третьему членам гео-
метрической прогрессии, а второй член арифметической прогрессии
превышает второй член геометрической прогрессии на 0,25. Вы-
числите сумму первых пяти членов арифметической прогрессии,
если ее первый член равен 2.
54. (МФТИ, 1977 г.). Найдите четыре числа, из которых первые
три составляют геометрическую прогрессию, а последние три —
арифметическую прогрессию. Сумма крайних чисел равна 14, а
сумма средних равна 12.
55. (КГУ, ВМК, 1979 г.). Найдите четыре числа, первые три
из которых составляют геометрическую прогрессию, а последние
три — арифметическую, если сумма крайних чисел 21, а сумма
средних 18.
56. (МЭСИ, 1977 г.). Три целых числа, сумма которых равна
60, являются тремя последовательными членами арифметической
прогрессии. Если к этим числам прибавить соответственно 2,2; 4;
7, то новые числа составят три последовательных члена геометри-
ческой прогрессии. Найдите наименьшее из первоначально задан-
ных чисел.
57. (КГУ, РФФ, 1977 г.). Сумма первых трех членов геомет-
рической прогрессии равна 6, а сумма первых трех ее членов,
стоящих на нечетных местах, равна 10,5. Найдите знаменатель и
первый член прогрессии.
58. (МВТУ, 1978 г.). Разность третьего и второго членов гео-
метрической прогрессии равна 12. Если к первому члену приба-
123
вить 10, ко второму 8, а третий оставить без изменения, то новые
три числа образуют арифметическую прогрессию. Найдите сумму
пяти первых членов геометрической прогрессии.
59. (МАИ, 1979 г.). Три числа, сумма которых равна 26, со-
ставляют геометрическую прогрессию. Если к этим числам приба-
вить соответственно 1; 6 и 3, то получатся три числа, составля-
ющие арифметическую прогрессию. Найдите эти числа.
60. (МХТИ, 1979 г.). Между числом 3 и неизвестным числом
вставлено еще одно число так, что все три числа образуют ариф-
метическую прогрессию. Если средний член уменьшить на 6, то
получится геометрическая прогрессия. Найдите неизвестное число.
61. (МИФИ, 1976 г.). Три отличных от нуля действительных
числа образуют арифметическую прогрессию, а квадраты этих чи-
сел, взятые в том же порядке, составляют геометрическую про-
грессию. Найдите все возможные знаменатели геометрической про-
грессии.
62. (МФТИ, 1976 г.). Три различных числа х, у, г образуют
в указанном порядке геометрическую прогрессию, а числа х + у,
у + г, z + x образуют в указанном порядке арифметическую про-
грессию. Найдите знаменатель геометрической прогрессии.
63. (МФТИ, 1976 г.). Разность арифметической прогрессии от-
лична от нуля. Числа, равные произведениям первого члена этой
прогрессии на второй, второго члена на третий и третьего на пер-
вый, образуют в указанном порядке геометрическую прогрессию.
Найдите ее знаменатель.
64. (МАДИ, 1976 г.). Три числа составляют геометрическую
прогрессию. Если из третьего числа вычесть 4, то числа составят
арифметическую прогрессию. Если же из второго и третьего членов
полученной арифметической прогрессии вычесть по единице, то
снова получим геометрическую прогрессию. Найдите эти числа.
65. (МИФИ, 1977 г.). Найдите трехзначное число, если его
цифры образуют геометрическую прогрессию, а цифры числа, мень-
шего на 400, — арифметическую.
66. (МИФИ, 1976 г.). ЭВМ решала последовательно несколько
задач. На решение каждой следующей задачи машина затрачивала
в одно и то же число раз меньше времени, чем на решение пре-
дыдущей. Сколько было предложено задач, если на решение всех
задач, кроме первой, ушло 63,5 мин.; на решение всех задач,
кроме последней, —127 мин., а на решение всех задач, кроме
первых двух,— 31,5 минут?
67. (МАТИ, 1977 г.). Даны первые два члена бесконечно убы-
вающей геометрической прогрессии: КЗ, 2/(КЗ+ 1). Найдите зна-
менатель и сумму этой прогрессии.
68. (МИФИ, 1978 г.). Сумма второго и восьмого членов бе-
сконечно убывающей геометрической прогрессии равна 325/128, а
сумма второго и шестого членов, уменьшенная на 65/32, равна
четвертому члену этой же прогрессии. Найдите сумму квадратов
членов этой прогрессии.
124
69. (МИФИ, 1978 г.). Разность между первым и пятым чле-
нами бесконечно убывающей геометрической прогрессии равна 1,92,
а сумма первого и третьего членов той же прогрессии равна 2,4.
Найдите отношение квадрата суммы бесконечно убывающей гео-
метрической прогрессии к сумме квадратов членов той же про-
грессии.
70. (РПИ, 1980 г.). Найдите первые три члена бесконечно
убывающей геометрической прогрессии, сумма которой равна 1,6,
а второй член равен (—0,5).
71. (МИНХ, 1976 г.). Сумма бесконечно убывающей геометри-
ческой прогрессии равна 4, а сумма кубов ее членов равна 64/7.
Найдите шестой член прогрессии.
72. (БашГУ, 1980 г.). Сумма бесконечно убывающей геометри-
ческой прогрессии равна 4, а сумма кубов ее членов равна 192.
Найдите первый член и знаменатель прогрессии.
73. (МИСиС, 1976 г.). При каком иррациональном значении х
три числа 0,(27); х; 0,(72) могут составить прогрессию (арифме-
тическую или геометрическую). Найдите х и сумму четырех членов
этой прогрессии.
74. (МФТИ, 1975 г.). Сумма S бесконечно убывающей гео-
метрической прогрессии на 2 больше суммы первых трех членов
этой прогрессии. Сумма первых шести членов равна 3. Най-
дите S.
75. (МИСиС, 1976 г.). Найдите сумму бесконечно убывающей
геометрической прогрессии, если сумма всех ее членов, стоящих
на четных местах, в три раза меньше суммы всех ее членов, стоящих
на нечетных местах, и сумма первых пяти членов этой прогрес-
сии равна 484.
76. (МИНХ, 1979 г.). Вычислите сумму членов геометрической
прогрессии + axq + arq2 + • • • + a^q^1 + • • •, где есть наиболь-
шее значение функции у = (6х2 — х3 — 16)/8 на отрезке [1; 5], а зна-
менатель прогрессии q= lim (1 — cosx)/x2.
о
77. (ВГУ, эконом, фак., 1981 г.). Первый член некоторой
бесконечно убывающей геометрической прогрессии равен 1, а
сумма ее равна S. Найдите сумму геометрической прогрессии,
составленной из квадратов членов исходной прогрессии.
78. (МАИ, 1976 г.). Сумма кубов членов бесконечно убывающей
геометрической прогрессии относится к сумме квадратов ее членов
как 12:13. Сумма двух первых членов прогрессии равна 4/3.
Найдите эту прогрессию.
79. (МФТИ, 1977 г.). Найдите сумму бесконечно убывающей
геометрической прогрессии, второй член которой, удвоенное про-
изведение первого члена на четвертый и третий член образуют
в указанном порядке арифметическую прогрессию с разностью,
равной 1/3.
80. (МИИЗ, 1977 г.). Найдите три числа, образующие геомет-
рическую прогрессию, если их произведение равно 64, а среднее
арифметическое 14/3.
125
81. (ТбГУ, физфак, спец, радиофизика и электроника, 1981 г.).
Три числа а, Ь, 12 в указанной последовательности составляют
геометрическую прогрессию, а числа а, Ь, 9—-арифметическую про-
грессию. Найти а и Ь.
82. (ТбГУ, мехмат, спец, прикладная матем., 1980 г.). Най-
дите значение х, при котором log2 (5-2*+ 1), log4 (21"* + 1), до-
ставляют арифметическую прогрессию.
83. (МИСИ, 1978 г.). Представьте десятичную периодическую
дробь 7,2(3) в виде обыкновенной дроби.
84. (МГИ, 1977 г.). Вычислите (0,2)'og’z5 (т+Т+1б+- • •) .
85. (КГУ, РФФ, 1977 г.). Найдите сумму бесконечно убыва-
ющей геометрической прогрессии, если сумма первых трех ее чле-
нов равна 3, а сумма первых ее трех членов с нечетными номе-
рами равна 5х/4.
86. (МВТУ, 1979 г.). Сумма бесконечной геометрической про-
грессии равна 243, а сумма ее первых пяти членов равна 275.
Найдите прогрессию.
87. (МХТИ, 1977 г.). Сумма бесконечно убывающей геометри-
ческой прогрессии равна 1,5, а сумма квадратов ее членов равна
1/8. Найдите прогрессию.
88. (МИЭТ, 1977 г.). Сумма членов бесконечно убывающей
геометрической прогрессии равна 3, а сумма кубов всех ее членов
равна 108/13. Напишите прогрессию.
§ 13. РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
1. (УжГУ, 1980 г.). Скорый поезд был задержан у семафора
на 16 мин и ликвидировал опоздание на перегоне в 80 км, идя
со скоростью на 10 км/ч больше, чем по расписанию. Определите
скорость поезда по расписанию.
2. (КГУ, 1978 г.). Лыжнику необходимо было пробежать рас-
стояние в 30 км. Начав бег на 3 мин позже назначенного срока,
лыжник бежал со скоростью, большей предполагавшейся на 1 км/ч,
и прибежал к месту назначения вовремя. Определите скорость,
с которой бежал лыжник.
3. (МГРИ, 1979 г.). Велосипедист проехал 96 км на два часа
быстрее, чем предполагал. При этом за каждый час он проезжал
на 1 км больше, чем ранее предполагал проезжать за 1 ч 15 мин.
С какой скоростью он ехал?
4. (МАИ, 1977 г.). Турист рассчитывал пройти а км за опре-
деленное время. Пройдя b км, турист отдохнул 15 мин и, чтобы
прийти вовремя, увеличил скорость на с км/ч. Определите перво-
начальную скорость движения туриста.
5. (МИНХ/1979 г.). Из пунктов А и В, расположенных на
расстоянии 50 км, навстречу друг другу одновременно вышли два
пешехода. Через 5 часов они встретились. После встречи скорость
первого пешехода, идущего из Л в В, уменьшилась на 1 км/ч, а
скорость второго пешехода, идущего из В в Л, возросла на 1 км/ч.
126
Известно, что первый пешеход прибыл в пункт В на 2 ч раньше,
чем второй пешеход прибыл в пункт А. Определите первоначальную
скорость первого пешехода.
6. (ПГУ, 1980 г.). Найдите скорость и длину поезда, зная,
что он проходил с постоянной скоростью мимо неподвижного
наблюдателя в течение 7 с и затратил 25 с на то, чтобы проехать
с той же скоростью вдоль платформы длиной 378 м.
7. (КГУ, геофак, 1978 г.). Автомобиль проходит расстояние от
пункта А до пункта В с постоянной скоростью. Если бы он уве-
личил скорость на 6 км/ч, то затратил бы на прохождение пути
на 4 ч меньше. А со скоростью, меньшей начальной на 6 км/ч,
он потратил бы на 6 ч больше. Найдите расстояние между пунк-
тами А и В.
8. (КГУ, геофак, 1978 г.). Из пункта Л в 12 ч вышел поезд.
В 14 ч в том же направлении вышел другой поезд. Он нагнал
первый поезд в 20 ч. Найдите средние скорости обоих поездов,
если сумма средних скоростей равна 70 км/ч.
9. (МАИ, 1979 г.). Пешеход и велосипедист отправляются
одновременно навстречу друг другу из городов Л и В, расстояние
между которыми 40 км, и встречаются спустя два часа после от-
правления. Затем они продолжают путь, причем велосипедист
прибывает в Л на 7 ч 30 мин раньше, чем пешеход В. Найдите
скорости пешехода и велосипедиста.
10. (МИНХ, 1980 г.). После встречи двух пароходов один из
них прошел на юг, а другой —на запад. Через два часа после
встречи расстояние между ними было 60 км. Найдите скорость
каждого парохода, если известно, что скорость одного из них
была на 6 км/ч больше скорости второго.
11. (МИНХ, 1979 г.). Первый рыбак должен проплыть на
лодке до места встречи 35 км, а второй —на 313/7% меньше. Что-
бы прибыть к месту встречи одновременно со вторым, первый
выходит на полчаса раньше второго и делает в среднем на 2 км
в час больше, чем второй. Найдите скорость, с какой плыл каж-
дый рыбак и сколько времени каждый был в пути.
12. (БорПИ, 1980 г.). Два велосипедиста выехали одновре-
менно навстречу друг другу из пунктов Л и В, расстояние между
которыми равно 28 км. Через час езды они встретились и, не
останавливаясь, продолжали ехать с той же скоростью. Первый
прибыл в пункт В на 35 мин раньше, чем второй в пункт Л.
Какова скорость каждого велосипедиста?
13. (МЭСИ, 1977 г.). Из Л в В через равные промежутки
времени отправляются три машины. В пункт В они прибывают
одновременно, затем выезжают в пункт С, расположенный на рас-
стоянии 120 км от пункта В. Первая машина прибывает туда
через час после второй, третья машина, прибыв в пункт С, сразу
поворачивает обратно и в 40 км от С встречает первую машину.
Найдите скорость первой машины.
14. (МИНХ, 1977 г.). Из морского порта одновременно отхо-
дят два парохода по двум взаимно перпендикулярным направле-
127
ниям. Спустя 1/2 ч после отплытия пароходов кратчайшее рас-
стояние между ними было 15 км, а спустя еще 15 мин оказалось,
что один из пароходов был от пристани на 4,5 км дальше дру-
гого. Найдите скорость каждого парохода.
15. (БашГУ, 1980 г.). Два судна движутся прямолинейно и
равномерно в один и тот же порт. В начальный момент времени
положения судов и порта образуют равносторонний треугольник.
После того как второе судно прошло 80 км, указанный треуголь-
ник становится прямоугольным. В момент прибытия первого судна
в порт второму остается пройти 120 км. Найдите расстояние
между судами в начальный момент времени.
16. (БашГУ, 1980 г.). По двум прямолинейным дорогам, ве-
дущим в пункт Д, движутся с постоянными скоростями автомо-
биль и велосипедист. В начальный момент времени положения
автомобиля, велосипедиста и пункта А образуют прямоугольный
треугольник. После того как автомобиль проехал 25 км, указан-
ный треугольник становится равносторонним. Найдите расстояние
между автомобилем и велосипедистом в начальный момент вре-
мени, если в момент прибытия автомобиля в пункт А велосипе-
дисту остается проехать 12 км.
17. (МЭСИ, 1979 г.). Из двух городов выехали одновременно
навстречу друг другу два автомобиля. Первый автомобиль за 3 ч
прошел 0,08 всего расстояния между городами, а второй —за 2,5 ч
7/120 этого расстояния. Найдите (в км/ч) скорость второго авто-
мобиля, если до места встречи первый автомобиль прошел 800 км.
18. (МГРИ, 1979 г.). Из пункта А в пункт В выехал мото-
циклист. Через 2 часа из А в В выехал автомобиль, который
прибыл в В одновременно с мотоциклистом. Если бы автомобиль
и мотоциклист одновременно выехали из А и В навстречу друг
другу, то они бы встретились через 1 ч 20 мин после выезда.
Сколько времени провел в пути из Л в В мотоциклист?
19. (ВГУ, физфак, 1980 г.). Трасса велогонок представляет
собой контур прямоугольного треугольника с разностью катетов
в 2 км. При этом его гипотенуза пролегает по проселочной до-
роге, а оба катета —по шоссе. Один из участников прошел отре-
зок по проселочной дороге со скоростью 30 км/ч, а оба отрезка
по шоссе за то же время со скоростью 42 км/ч. Определите про-
тяженность трассы. '
20. (КубГУ, 1980 г.). Две точки движутся по окружности
длиной 1,2 м с постоянными скоростями. Если они движутся в
разных направлениях, то встречаются через каждые 15 с. При
движении в одном направлении одна точка догоняет другую че-
рез каждые 60 с. Определите скорости точек.
21. (МИФИ, 1979 г.). Из пункта А в пункт В одновременно
выехали по одному и тому же шоссе три автомобиля. Второй имел
скорость на 30 км/ч больше первого и прибыл в В на 3 ч раньше
него. Третий прибыл в В на 2 ч раньше первого, причем поло-
вину времени он двигался со скоростью первого, а другую поло-
вину времени —со скоростью второго. Найдите расстояние АВ.
128
22. (МИФИ, 1978 г.). Три пловца должны проплыть из А в
В и обратно. Сначала стартует первый, через 5 с —второй, еще
через 5 с—третий. Некоторую точку С, находящуюся между
пунктами А и В, все пловцы миновали одновременно (до этого
времени ни один из них в В не побывал). Третий пловец, доплыв
до В и повернув назад, встречает второго в 9 м от В, а первого —
в 15 м от В. Найдите скорость третьего пловца, если расстояние
АВ равно 55 м.
23. (МАИ, 1979 г.). Турист выезжает на велосипеде из пункта А.
Проехав 1,5 ч со скоростью 16 км/ч, он делает остановку на
1,5 ч, а затем продолжает путь с первоначальной скоростью.
Через 4 ч после выезда первого туриста вдогонку ему из пункта
А выезжает на мотоцикле второй турист со скоростью 56 км/ч.
Какое расстояние они проедут, прежде чем второй турист догонит
первого?
24. (МИХМ, 1977 г.). Две автомашины выехали одновременно
из одного пункта и едут в одном направлении. Первая автома-
шина едет со скоростью 40 км/ч, а скорость второй составляет
125 % скорости первой. Через 30 мин из того же пункта в том
же направлении выехала третья автомашина, которая обогнала
вторую на 1,5 ч позже, чем первую. Какова скорость третьей
автомашины?
25. (МИСиС, 1980 г.). Из города А в город В вышел пасса-
жирский поезд. В то же время из В в Л вышел товарный поезд.
Скорость каждого из поездов на всем участке движения постоянна.
Через 2 ч после того как поезда встретились, расстояние между
ними составило 280 км. Пассажирский поезд прибыл к месту
назначения через 9 ч, а товарный — через 16 ч после встречи.
Найдите, какое время в пути находился каждый поезд.
26. (ВЗИИЖТ, 1980 г.). Турист проплыл по реке на лодке
90 км и прошел пешком 10 км. При этом на пеший путь было
затрачено на 4 ч меньше, чеэд на путь по реке. Если бы турист
шел пешком столько времени, сколько он плыл по реке, а плыл
по реке столько времени, сколько шел пешком, то эти расстояния
были бы равны. Сколько времени он шел пешком и сколько вре-
мени плыл по реке?
27. (НГУ, геофак, 1979 г.). Два автомобиля едут навстречу
друг другу и встречаются через 6 дней. Если бы первый автомо-
биль ехал 1,8 дня, а второй—1,6 дня, то вместе они бы про-
ехали 520 км. Если бы первый проехал (2/3 пути, пройденного
вторым, а второй—1/3 пути, пройденного первым, то первому
понадобилось бы для этого на 2 дня меньше, чем второму. Сколько
километров за день проезжает каждый автомобиль?
28. (КубГУ, 1980 г.). Два туриста идут друг другу навстречу —
один из пункта Л, другой из пункта В. Первый выходит из А
на 6 ч позже, чем второй из пункта В, и при встрече оказыва-
ется, что он прошел на 12 км меньше второго. Продолжая после
встречи путь с той же скоростью, первый приходит в В через
8 ч, а второй в Л —через 9 ч. Найдите скорости туристов.
В. М. Говоров и др. 129
29. (МИИЖТ, 1979 г.). Два велосипедиста выехали одновре-
менно из пункта А в пункт В. Первый остановился через 42 мин,
не доехав 1 км, а второй —через 52 мин, не доехав 2 км до В.
Если бы первый велосипедист проехал столько же километров,
сколько второй, а второй столько, сколько первый, то первому
потребовалось бы на 17 мин меньше, чем второму. Сколько ки-
лометров между пунктами А и В?
30. (КубГУ, 1980 г.). Два тела, двигаясь по окружности в
одном и том же направлении, сходятся через каждые 56 мин.
Если бы они двигались с теми же скоростями в противоположных
направлениях, то встречались бы через каждые 8 мин. Известно,
что при движении в противоположных направлениях расстояние
по окружности между сближающимися телами уменьшилось с 40
до 26 метров за 24 с. Какова скорость каждого тела?
31. (МИФИ, 1979 г.). Из пункта К в пункт М выехала ма-
шина. Одновременно с ней из пункта М навстречу машине вые-
хал автобус. Когда машина проехала 0,4 пути от К до Л4, авто-
бус находился от нее на расстоянии 4 км. Когда же автобус
проехал половину пути, машина находилась от него на расстоя-
нии 10 км. Найдите отношение времени, которое затрачивает ма-
шина на прохождение пути от /( до Л4, и времени, которое тре-
буется автобусу для прохождения того же пути. Скорости автобуса
и машины постоянны.
32. (МВТУ, 1979 г.). Бак емкостью 2400 м3 наполняется топ-
ливом. При опорожнении этого бака производительность насоса
на 10 м3/мин выше, чем производительность насоса при наполне-
нии. В результате время опорожнения бака на 8 мин меньше
времени заполнения. Определите производительность насоса при
наполнении бака.
33. (КГУ, ЭКФ, 1978 г.). Три каменщика могут совместно
сложить стену за а ч. Первый из них, работая один, может сло-
жить стену вдвое скорее третьего и на 1 ч скорее второго. За
сколько времени каждый из них, работая отдельно, может сло-
жить стену?
34. (РПИ, 1980 г.). Двое рабочих совместно могут выполнить
заданную работу за 12 дней. Если первый рабочий сделает по-
ловину работы, а затем второй — вторую половину, то вся работа
будет закончена за 25 дней. Сколько дней нужно каждому из
рабочих в отдельности для выполнения работы?
35. (МХТИ, 1980 г.). Две трубы, работая одновременно, на-
полняют бассейн за 12 ч. Первая труба наполняет бассейн на
10 ч быстрее, чем вторая. За сколько часов наполняет бассейн
вторая труба?
36. (МХТИ, 1976 г.). Баржа была разгружена с помощью
двух подъемных кранов в течение 15 ч, причем первый кран
приступил к работе на 7 ч позднее второго. Известно, что пер-
вый кран, работая один, может разгрузить баржу на 5 ч скорее,
чем второй. За сколько часов может разгрузить баржу каждый
кран, работая отдельно?
130
37. (МИХМ, 1977 г.). Двое рабочих изготовляли партию оди-
наковых деталей. Когда первый проработал 2 ч, а второй 5 ч,
оказалось, что они выполнили половину работы. После того как
они проработали вместе еще 3 ч, им осталось выполнить 1/20 всей
работы. За какое время каждый рабочий выполнит всю работу?
38. (МИНХ, 1978 г.). Два ученика потратили на подготовку
к школьной викторине 7 ч, считая с момента, когда начал ра-
боту первый ученик; второй приступил к работе на полтора часа
позже первого. Если бы эта работа была поручена каждому
в отдельности, то первому ученику для ее выполнения потребо-
валось бы на 3 ч больше, чем второму. За какое время каждый
из них отдельно мог сделать эту работу?
39. (МИНХ, 1979 г.). Две машинистки вместе напечатали 65
страниц, причем первая работала на один час больше второй.
Однако вторая машинистка печатает в час на две страницы больше
первой, а поэтому она напечатала на 5 страниц больше. Сколько
страниц в час печатает каждая машинистка?
40. (МИЭМ, 1977 г.). Два рабочих должны совместно выпол-
нить некоторую работу. Если бы производительность труда пер-
вого рабочего была в два раза больше, а производительность
труда второго рабочего в полтора раза больше, то время, необ-
ходимое рабочим для выполнения задания, уменьшилась бы на
14/85 части времени, необходимого первому рабочему для выпол-
нения всего задания. У какого из рабочих производительность
труда выше и во сколько раз?
41. (МИНХ, 1979 г.). Двое рабочих заняты на одной и той
же работе. Сначала 1-й рабочий проработал 1/3 того времени,
которое требуется второму для выполнения всей работы, потом
2-й проработал 1/3 того времени, которое потратил бы 1-й на
выполнение всей работы. После этого оказалось, что выполнено
13/18 всей работы. Вычислите, сколько времени потребовалось бы
для выполнения работы каждому рабочему в отдельности, если
вместе они могут выполнить ее за 33/5 ч.
42. (МИНХ, 1979 г.). Соревнуются три бригады лесорубов.
Первая и третья бригады обработали древесины в 2 раза больше,
чем вторая, а вторая и третья в три раза больше, чем первая.
Какая бригада победила в этом соревновании?
43. (МИНХ, 1979 г.). Первый рабочий может выполнить не-
которую работу на 4 ч раньше, чем второй. Вначале они 2 ч
работали вместе, после чего оставшуюся работу выполнил один
первый рабочий за час. За какое время может выполнить всю
работу второй рабочий?
44. (МГРИ, 1979 г.; МИНХ, 1980 г.). Двое рабочих, работая
одновременно, выполнили всю работу за 5 дней. Если бы первый
работал вдвое быстрее, а второй —вдвое медленнее, то работа
заняла бы у них 4 дня. За сколько времени выполнил бы всю
работу один первый рабочий?
45. (МИФИ, 1977 г.). Пять человек выполняют некоторую
работу. Первый, второй и третий, работая вместе, выполняют
5* 131
всю работу за 7,5 ч, первый, третий и пятый —за 5 ч, первый,
третий и четвертый —за 6 ч, четвертый, второй и пятый — за 4 ч.
За какой промежуток времени выполняют эту работу все пять
человек, работая вместе?
46. (МАТИ, 1979 г.). В бассейн проведены две трубы, подаю-
щая и отводящая, причем через первую бассейн наполняется на
2 ч дольше, чем через вторую опорожняется. При заполненном
на 1/3 бассейне были открыты обе трубы и бассейн оказался
пустым спустя 8 ч. За сколько часов, действуя отдельно, первая
труба наполняет, а вторая опорожняет бассейн?
47. (ТбГУ, мехмат, спец, прикладная матем., 1981 г.). Рас-
стояние между двумя городами 220 км. Из этих городов на-
встречу друг другу выезжают два автомобиля. Они могут встре-
титься на середине пути, если первый выедет на 2 ч раньше
второго. Если же они выедут одновременно, то они встретятся
через 4 ч. Найдите скорости автомобилей.
48. (МГПИ, 1980 г.). Бригада рабочих должна была изгото-
вить 360 деталей. Изготовляя ежедневно на 4 детали больше, чем
предполагалось по плану, бригада выполнила задание на 1 день
раньше срока. Сколько дней затратила бригада на выполнение
задания?
49. (МСИ, 1980 г.). Две молотилки обмолачивают собранную
пшеницу за 4 дня. Если бы одна из них обмолотила половину
всей пшеницы, а затем вторая— оставшуюся часть, то вся работа
была бы закончена за 9 дней. Во сколько дней каждая молотилка
в отдельности могла бы обмолотить всю пшеницу?
50. (РПИ, 1980 г.). Моторная лодка, скорость которой в стоя-
чей воде равна 10 км/ч, проехала по течению 91 км и вернулась
обратно. Вычислите скорость течения реки, если лодка провела
в пути 20 ч.
51. (КГУ, геофак, 1978 г.). Расстояние между пристанями
А и В 300 км. Из А в В плывут два катера. Разность во вре-
мени отправления катеров равна 5 ч. К пристани В катера при-
бывают одновременно. Определите время движения каждого ка-
тера, если скорость одного из них на 10 км/ч больше скорости
другого.
52. (МГРИ, 1979 г.). Лодка спускается вниз по течению реки
из пункта А в пункт В, находящийся в 10 км от Л, а затем
возвращается в Л. Если собственная скорость лодки 3 км/ч, то
путь из Л в В занимает на 2 ч 30 мин меньше, чем из В в Л.
Какой должна быть собственная скорость лодки, чтобы поездка
из Л в В заняла 2 ч?
53. (МИФИ, 1978 г.). Катер обеспечивает регулярный перевоз
пассажиров между пунктами Л и В, расположенными вдоль реки.
Если бы собственная скорость катера (в стоячей воде) возросла
в 2 раза, то путь от Л до В и обратно потребовал бы в 5 раз
меньше того времени, которое катер обычно затрачивает на путь
АВ и обратно. Во сколько раз собственная скорость катера
больше скорости течения реки?
132
54. (МСИ, 1979 г.). Расстояние по реке между пристанями
равно 21 км. Отправляясь от одной из этих пристаней к другой,
катер возвращается к первой обратно через 4 ч, затрачивая из
этого времени 30 мин на стоянку. Найдите скорость катера в
стоячей воде, если скорость течения реки 2,5 км/ч.
55. (КубГУ, 1980 г.). Моторная лодка спустилась по течению
на 28 км и тотчас вернулась назад. На путь туда и обратно ей
потребовалось 7 ч. Если бы скорость течения реки была в 2 раза
больше действительной, то на путь туда и обратно потребовалось
бы 11 ч 12 мин. Найдите скорость лодки в стоячей воде и ско-
рость течения реки.
56. (МИНХ, 1979 г.). Для перевозки 60 т груза затребовали
некоторое количество машин. В связи с тем, что на каждую ма-
шину погрузили на 0,5 т меньше, дополнительно было затребовано
еще 4 машины. Сколько машин было запланировано первоначально?
57. (МАИ, 1979 г.). Бригада рыбаков планировала выловить
за некоторое число дней 1800 ц рыбы. Треть установленного
срока бригада ежедневно недовыполняла плановое задание на 20 ц
из-за штормовой погоды. Однако в остальные дни бригада еже-
дневно вылавливала на 20 ц больше дневной нормы, и плановое
задание было выполнено на один день раньше установленного
срока. Сколько центнеров рыбы бригада планировала вылавливать
ежедневно?
58. (МАТИ, 1979 г.). Один совхоз получил средний урожай
гречихи 21 ц с 1 га, а другой, у которого под гречихой было
на 12 га меньше, добился урожая в 25 ц с 1 га. В результате
во втором совхозе было собрано гречихи на 300 ц больше, чем
в первом. Сколько центнеров гречихи было собрано в каждом
совхозе?
59. (МАИ, 1979 г.). Бригада лесорубов должна была по плану
заготовить за несколько дней 216 м3 древесины. Первые 3 дня
бригада ежедневно выполняла установленную планом норму, а
затем каждый день заготовляла 8 м3 сверх плана, поэтому за день
до срока было заготовлено 232 м3 древесины. Сколько кубических
метров древесины в день должна была заготовлять бригада по
плану?
60. (МИНХ, 1977 г.). На заводе для изготовления одного
электродвигателя типа А расходуется 2 кг меди и 1 кг свинца,
на изготовление одного электродвигателя типа В расходуется
3 кг меди и 2 кг свинца. Сколько электродвигателей каждого
типа было произведено на заводе, если известно, что израсходо-
вали 130 кг меди и 80 кг свинца?
61. (РПИ, 1980 г.). В зале было 500 стульев, расположенных
одинаковыми рядами. После реконструкции зала общее число
мест уменьшилось на 1/10; число рядов было уменьшено на 5, но
в каждом ряду можно было разместить на 5 стульев больше.
Сколько рядов и сколько стульев в ряду было вначале?
62. (ПГУ, 1980 г.). Одна мастерская должна сшить 810 ко-
стюмов. Другая за этот же срок должна сшить 900 костюмов.
133
Первая закончила выполнение заказа за 3 дня до срока, а вто-
рая—за 6 дней до срока. По скольку костюмов в день шила
каждая мастерская, если вторая мастерская шила в день на 21
костюм больше первой?
63. (МХТИ, 1977 г.). В соревновании участвуют несколько
команд, причем каждая из них должна провести по одной игре
со всеми остальными. Сколько команд участвовало в соревнова-
нии, если всего было проведено 45 игр?
64. (МИХМ, 1977 г.). Магазин получил 64 чайника двух
разных емкостей, причем меньший из них стоил на 1 руб. дешевле,
чем больший. За большие чайники было выручено 100 руб.,
а за меньшие —36 руб. Сколько было тех и других чайников
и по какой цене они продавались?
65. (МАИ, 1979 г.). Было намечено разделить поровну пре-
мию между наиболее отличившимися сотрудниками предприятия.
Выяснилось, однако, что сотрудников, достойных премии, на 3
человека больше, чем предполагалось. В таком случае пришлось
бы каждому получить на 4 рубля меньше. Администрация нашла
возможость увеличить общую сумму премии на 90 рублей, в ре-
зультате чего каждый премированный получил 25 рублей. Сколько
человек получили премию?
66. (МИНХ, 1979 г.). Сумма квадратов цифр положительного
двузначного числа равна 13. Если из этого числа отнять 9, то
получится число, записанное этими же цифрами в обратном по-
рядке. Найдите это число.
67. (МИФИ, 1978 г.). Квадрат цифры десятков положитель-
ного двузначного числа, сложенный с произведением цифр этого
числа, равен 52, а квадрат цифры единиц, сложенный с тем же
произведением цифр, равен 117. Найдите это двузначное число.
68. (МИНХ, 1979 г.). Найдите два таких числа, чтобы их
сумма, произведение и разность квадратов были равны.
69. (МИФИ, 1978 г.). Найдите трехзначное число, если из-
вестно, что сумма его цифр равна 17, а сумма квадратов его
цифр равна 109. Если из этого числа вычесть 495, то получится
число, записанное теми же цифрами, но в обратном порядке.
70. (МИНГП, 1977 г.). Среднее геометрическое двух чисел
на 12 больше меньшего из них, а среднее арифметическое тех
же чисел на 24 меньше большего из них. Найдите эти числа.
71. (МИФИ, 1977 г.). Найдите пары натуральных чисел, наи-
больший общий делитель которых равен 5, а наименьшее общее
кратное равно 105.
72. (МАИ, 1976 г.). Знаменатель несократимой дроби на 2
больше, чем числитель. Если у дроби, обратной данной, умень-
шить числитель на 3 и вычесть из полученной дроби данную дробь,
то получится 1/15. Найдите данную дробь.
73. (МИХМ, 1976 г.). Какое двузначное число на 19 больше
суммы квадратов его цифр и на 44 больше удвоенного произве-
дения его цифр?
74. (МИФИ, 1977 г.). Произведение натурального числа и
134
числа, записанного теми же цифрами в обратном порядке, равно
2430. Найдите это число.
75. (БГУ, 1978 г.). Найдите два натуральных числа, разность
которых 66, а их наименьшее общее кратное равно 360.
76. (МИФИ, 1976 г.). Найдите пары натуральных чисел, наи-
меньшее общее кратное которых равно 78, а наибольший общий
делитель равен 13.
77. (МИФИ, 1977 г.). Найдите два натуральных числа, сумма
которых равна 85, а наименьшее общее кратное равно 102.
78. (МИФИ, 1977 г.). Найдите пары натуральных чисел, раз-
ность квадратов которых равна 55.
79. (МИФИ, 1979 г.). В трехзначном числе сумма его цифр
равна 11. Если из числа, записанного теми же цифрами, но в
обратном порядке, вычесть 594, то получится искомое число.
Найдите это трехзначное число, если сумма всех попарных про-
изведений цифр этого числа равна 31.
80. (МИФИ, 1979 г.). Сумма квадратов цифр некоторого по-
ложительного трехзначного числа равна 74. В этом числе цифра
сотен равна удвоенной сумме цифр десятков и единиц. Найдите
это число, если известно, что разность между ним и числом, за-
писанным теми же цифрами, но в обратном порядке, равна 495.
81. (МИНХ, 1979 г.). В двузначном положительном числе
сумма квадратов цифр в 2,5 раза больше суммы его цифр и на
единицу больше утроенного произведения этих цифр. Найдите
это число.
82. (ВЗИИЖТ, 1980 г.). Найдите двузначное число, зная, что
цифра единиц искомого числа на 2 больше числа его десятков,
а произведение этого числа на сумму его цифр равно 144.
83. (МИНХ, 1979 г.). Один сплав состоит из двух металлов,
входящих в него в отношении 1:2, а другой сплав содержит те
же металлы в отношении 2:3. Из скольких частей обоих сплавов
можно получить новый сплав, содержащий те же металлы в от-
ношении 17:27?
84. (МИНХ, 1979 г.; ГомГУ, 1980 г.). Два куска латуни
имеют массу 60 кг. Первый кусок содержит 10 кг чистой меди,
а второй —8 кг. Сколько процентов меди содержит первый кусок
латуни, если второй содержит меди на 15% больше первого?
85. (МИФИ, 1980 г.). Сплав меди и олова массой 8 кг содер-
жит р% меди. Какой кусок сплава меди с оловом, содержащий
40% олова, надо сплавить с первым, чтобы получить новый сплав
с минимальным процентным содержанием меди, если масса вто-
рого куска 2 кг?
86. (УжГУ, 1980 г.). Имеются два объема воды, массы кото-
рых отличаются друг от друга на 2 кг. Этим массам придали
одинаковое количество тепла, равняющееся 96 ккал, причем об-
наружилось, что большая масса воды нагрелась на 4° меньше,
чем меньшая. Определите массу воды в каждом из двух объемов.
87. (ЛГУ, физфак, 1980 г.). Два парохода движутся в тумане
навстречу друг другу с одинаковыми скоростями. На расстоянии
135
4 км капитаны включают на 4 мин обратный ход с ускорением
0,1 м/с2, после чего пароходы продолжают движение с достигну-
тыми скоростями. При каких значениях начальной скорости и0
суда не столкнутся?
88. (МИНХ, 1979 г.). Имеются два сплава меди и цинка.
В первом сплаве меди в 2 раза больше, чем цинка, а во втором
меди в 5 раз меньше, чем цинка. Во сколько раз больше надо
взять второго сплава, чем первого, чтобы получить новый сплав,
в котором цинка было бы в 2 раза больше, чем меди?
89. (МИНХ, 1979 г.). Вычислите вес и процентное содержа-
ние серебра в сплаве с медью, зная, что сплавив его с 3 кг
чистого серебра, получат сплав, содержащий 90% серебра, а спла-
вив его с 2 кг сплава, содержащего 90% серебра, получат сплав
84% содержания серебра.
90. (МИНХ, 1979 г.). Два раствора, из которых первый со-
держит 0,8 кг, а второй 0,6 кг безводной серной кислоты, сое-
динили вместе и получили 10 кг нового раствора серной кислоты.
Вычислите вес первого и второго растворов в смеси, если известно,
что безводной серной кислоты содержится в первом растворе на
10% больше.
91. (ПГУ 1980 г.). Из полного бака, содержащего 729 л кис-
лоты, отлили а л и долили бак водой. После тщательного пере-
мешивания отлили а л раствора и снова долили бак водой. После
того как такая процедура была повторена 6 раз, раствор в баке
содержал 64 л кислоты. Найдите величину а.
92. (МИФИ, 1978 г.). В двух сплавах медь и цинк относятся
как 5:2 и 3:4 (по весу). Сколько нужно взять кг первого сплава
и сколько второго, чтобы после совместной переплавки получить
28 кг нового сплава с равным содержанием меди и цинка?
93. (МИФИ, 1978 г.). Имеются две бочки бензина разной це-
ны, объемом 220 л и 180 л. Одновременно из обеих бочек отлили
равное количество бензина и бензин, отлитый из первой бочки,
перелили во вторую, а бензин, отлитый из второй бочки, — в пер-
вую, после чего цена бензина в обеих бочках стала одинаковой.
Сколько бензина было перелито?
94. (МИФИ, 1978 г.). В двух сплавах медь и цинк относятся
как 4:1 и 1:3. После совместной переплавки 10 кг первого
сплава, 16 кг второго сплава и нескольких кг чистой меди по-
лучили сплав, в котором медь и цинк относятся как 3:2. Опре-
делите вес нового сплава.
95. (МГУ, эконом, фак., 1979 г.). Из сосуда, до краев на-
полненного чистым глицерином, отлили 2 л глицерина, а к остав-
шемуся глицерину долили 2 л воды. После перемешивания снова
отлилц 2 л смеси и долили 2 л воды. Наконец, опять после пе-
ремешивания, отлили 2 л смеси и долили 2 л воды. В результате
этих операций объем воды в сосуде стал на 3 л больше объема
оставшегося в нем глицерина. Сколько литров глицерина и воды
оказалось в сосуде в результате проделанных операций?
96. (МГУ, геофак, 1980 г.). Имеются два сплава, состоящие
136
из цинка, меди и олова. Известно, что первый сплав содержит
40% олова, а второй-—26% меди. Процентное содержание цинка
в первом и втором сплавах одинаково. Сплавив 150 кг первого
сплава и 250 кг второго, получили новый сплав, в котором ока-
залось 30% цинка. Определите, сколько кг олова содержится в
получившемся новом сплаве.
97. (КубГУ, 1980 г.). Имеются два сплава с различным про-
центным содержанием свинца. Вес одного 6 кг, вес другого 12 кг.
От каждого из них отрезали по куску равного веса, после чего
сплавили их с остатком другого куска. В результате процентное
содержание свинца в обоих сплавах стало одинаковым. Сколько
весил каждый отрезанный кусок?
98. (МГРИ, 1979 г.). После двух последовательных повыше-
ний зарплата достигла 15/8 частей по сравнению с первоначаль-
ной. На сколько процентов повысилась зарплата в первый раз,
если второе повышение было вдвое больше (в процентном отно-
шении) первого?
99. (БГУ, 1980 г.). Заработная плата рабочего за октябрь
и ноябрь относилась как 1г/2:1Х/3, а за ноябрь и декабрь —как
2:22/3. За декабрь рабочий получил на 40 руб. больше, чем за
октябрь, и за перевыполнение квартального плана ему начислили
премию в размере 40% трехмесячного заработка. Найдите размер
премии. (При решении считать, что число рабочих дней в каждом
месяце одинаково).
100. (МИСИ, 1979 г.). При двух последовательных одинако-
вых процентных повышениях зарплата суммой в 100 рублей обра-
тилась в 125 руб. 44 коп. Определите, на сколько процентов
повышалась зарплата.
101. (МИНХ, 1979 г.). Выработка продукции за год работы
предприятия возросла на 4%, за следующий год она увеличилась
на 8%. Найдите средний ежегодный прирост продукции за этот
период.
102. (МИНХ, 1979 г.). Цена на товар была повышена на
25%. На сколько процентов надо теперь ее снизить, чтобы по-
лучить первоначальную цену товара?
103. (МЭСИ, 1977 г.). Тело двигалось в течение нескольких
секунд и прошло за первую секунду 3 м, а за каждую следую-
щую секунду на 4 м больше, чем за предыдущую секунду. Если
бы тело прошло за первую секунду 1 м, а за каждую следующую
на 8 м больше, чем за предыдущую, то длина пути, пройденного
телом за тот же промежуток времени, была бы длиннее действи-
тельно пройденного им пути более, чем на 6 м, но менее, чем
на 30 м. Определите время движения этого тела (в секундах).
104. (МЭСИ, 1977 г.). Требуется соорудить железнодорожную
насыпь, имеющую в длину 100 м, а в поперечном сечении —равно-
бедренную трапецию с нижним основанием, равным 5 м, верх-
ним основанием, не меньшим 2 м, и углом откоса, равным 45°.
Какую высоту должна иметь эта насыпь, чтобы объем земляных
работ составил не менее 400 м3, но не более 500 м3?
137
105. (КГУ, геофак, 1978 г.). Лодка спускается по течению
реки на расстояние 10 км, а затем поднимается против течения
на расстояние 6 км. Скорость течения реки равна 1 км/ч. В ка-
ких пределах должна лежать собственная скорость лодки, чтобы
вся поездка заняла от 3 до 4 часов?
106. (ЛГУ, физфак, 1979 г.). Ширина реки ам, скорость ее
течения — w м/с, скорость пловца в стоячей воде — v м/с (v < w),
а скорость его движения на суше — и м/с. За какое наименьшее
время пловец может попасть в точку, расположенную на противо-
положном берегу напротив того места, с которого он начинает
переправу? Считайте, что в воде пловец не изменяет выбранного
им в начале движения и что вектор скорости течения реки парал-
лелен ее берегам, которые предполагаются прямолинейными.
107. (МИНХ, 1979 г.). Пункты Л, В, С расположены так,
что | АВ | = 285 км, АВС = 60°. Из А в В выезжает автомобиль
со скоростью 90 км/ч, одновременно из В в С отправляется поезд
со скоростью 60 км/ч. Через какое время расстояние между авто-
мобилем и поездом будет наименьшим?
108. (МИНХ, 1979 г.). Три пункта Л, В и С расположены
в вершинах равностороннего треугольника со сторонами 168 км.
Из пункта Л в пункт В выезжает машина со скоростью 60 км/ч,
из пункта В в пункт С одновременно выезжает машина со ско-
ростью 30 км/ч. Через сколько времени после выезда расстояние
между этими машинами будет наименьшим?
109. (МИНХ, 1979 г.). На реке, скорость течения которой
равна 5 км/ч, в направлении ее течения расположены пристани
Л, В и С, причем В находится посередине между Л и С. От при-
стани В одновременно отходят плот, который по течению дви-
жется к пристани С, и катер, который идет к Л, причем скорость
катера в стоячей воде равна v км/ч. Дойдя до Л, катер разво-
рачивается и движется по направлению к С. Найдите все те зна-
чения у, при которых катер приходит в С позже, чем плот.
ПО. (МИНХ, 1979 г.). Расстояние между пунктами Л и В
равно 120 км. Из пункта Л в пункт В по прямой дороге АВ
начинает двигаться мотоциклист со скоростью 30 км/ч. Одновременно
из пункта В по дороге, перпендикулярной к дороге ЛВ, начинает
двигаться велосипедист со скоростью 10 км/ч. Когда расстояние
между ними окажется наименьшим?
111. (МИНХ, 1979 г.). Пункт В находится на расстоянии
60 км от прямолинейной железной дороги. Расстояние по желез-
ной дороге от пункта Л до ближайшей к пункту В точки С
составляет 285 км. На каком расстоянии от точки С надо по-
строить станцию, чтобы затрачивать наименьшее время на пере-
движение между пунктами Л и В, если скорость движения по
железной дороге равна 52 км/ч, а скорость движения по шоссе
равна 20 км/ч?
112*. (МФТИ, 1979 г.). Пункт N расположен на берегу реки,
ширина которой 1 км, а скорость течения 1 км/ч. Не менее чем
138
на 3 км ниже по течению на другом берегу находится пункт Af.
Из пункта М выходит рыбак и идет вдоль своего берега по на-
правлению к N со скоростью 4 км/ч. Одновременно из пункта М
отплывает на лодке перевозчик, пересекает реку и, дождавшись
рыбака, переправляет его в пункт N. Туда и обратно лодка дви-
галась по прямой, причем направление движения было выбрано
так, что от отплытия до возвращения прошло наименьшее воз-
можное время, равное 9/8 часа. Скорость лодки в стоячей воде
4 км/ч. Найдите расстояние (по течению) между пунктами М и Л\
113. (МЭСИ, 1977 г.). Самоходная баржа должна доставить
срочный груз от речной пристани А к пристани В, расположен-
ной на 24 км выше А по течению, и возможно скорее вернуться
в А за новым грузом. Скорость течения реки равна 6 км/час.
Какова должна быть наименьшая собственная скорость баржи,
чтобы рейс из Л в В и обратно занял (не считая времени, за-
траченного на погрузку и разгрузку) не более трех часов?
114. (МЭИ, 1979 г.). Число 1,25 представьте в виде произве-
дения трех положительных сомножителей так, чтобы произведение
первого сомножителя на квадрат второго равнялось 5 и чтобы
сумма всех трех сомножителей была наименьшей.
115. (МИИГАиК, 1980 г.). Найдите такое число х, чтобы
сумма этого числа и его квадрата была наименьшей.
116. (МЭИ, 1978 г.). При каком уменьшаемом разность будет
наибольшей, если вычитаемое равно удвоенному квадрату умень-
шаемого?
117. (МИНХ, 1979 г.). Разложите число 20 на два слагае-
мых так, чтобы их произведение было наибольшим.
118. (МИЭТ, 1977 г.). Турист идет из пункта Л, находяще-
гося на шоссейной дороге, в пункт В, расположенный в 8 км от
шоссе. Расстояние от А до В по прямой 17 км. В каком месте
туристу следует свернуть с шоссе, чтобы в кратчайшее время
прийти в пункт В, если скорость по шоссе 5 км/час, а по без-
дорожью 3 км/час.
119. (МИФИ, 1980 г.). Тело начинает двигаться в момент вре-
мени t = Q и через 4 с после начала движения приобретает уско-
рение 3 м/с2. Найдите скорость тела через 6 с после начала дви-
жения и величину пути, пройденного телом за это время, если
известно, что скорость тела изменяется по закону и (/) = (/2 +
+ Ь / + 6)м/с и тело движется прямолинейно.
120*. (МФТИ, 1979 г.). Из пунктов А и В навстречу друг
другу вышли одновременно два поезда. Каждый из них двигался i
сначала равноускоренно (начальные скорости поездов равны нулю,
ускорения различны), а затем, достигнув некоторой скорости :
(в разные моменты времени),— равномерно. Отношение скоростей
равномерного движения поездов равно 4/3. В момент встречи
поезда имели равные скорости, а в пункты А и В прибыли одно-
временно. Найдите отношение ускорений поездов.
121. (НГУ, мехмат, 1979 г.). Расстояние между пунктами
А и В равно 120 км. Мотоциклист, двигаясь без остановок, проедет
139
это расстояние за 8 ч, если от А до промежуточного пункта С
он будет ехать со скоростью км/ч, а далее— с ускорением
а км/ч2. Одно и то же время на весь путь ему понадобится, если
от Л до С он будет ехать со скоростью v0 км/ч и от С до В — км/ч
или от А до С со скоростью км/ч и от С до В — км/ч.
Найдите о0, если параметр а по величине равен 2v0 и
§ 14. КОМПЛЕКСНЫЕ ЧИСЛА
В этом параграфе приведены задачи, предлагавшиеся на всту-
пительных экзаменах в МГУ, МИФИ, МФТИ и некоторых других
вузах страны. Комплексные числа будем обозначать буквой z.
z==x + iy, х, у —числа действительные. Число z = x — iy — комп-
лексно сопряженное с числом z.
Представьте в тригонометрической форме следующие комп-
лексные числа (1—16).
1. —1. 2. —I. 3. -/3+1.
4. -/З—i. 5. —3 — 4/.
6. 3 —4i. 7. 5. 8. -J— 9. sin 32°+ i cos 32°.
10. cos 12° —i sin 12°. 11. — sin 110° +i cos 110°.
12. sina — icosa. 13. sina + icosa. 14. — sina—icosa.
15. 1 + itga. 16. 1+ictga.
Выполните указанные действия (17—23).
17. (cos 12° + i sin 12°)?. 18. (— /2 + /2 i)*.
19. (—/3+03. 20. (— l+/3i)3. 21. (1+i)".
22. (1 + cos<p +isinq>)". 23. (1 — cos <p + i sin<p)n.
24. Докажите, что если x+y = 2cosa, то x” + -^- = 2cosna.
25. Применив формулу Муавра, выразите cos За и cos 4a через
cos a, a sin За через sina.
Вычислите (26—30).
26. /Г. 27. j/^T. 28. 29. i-^.
30. /Г.
Решите следующие уравнения (31—32).
31. 2(1 + i)x2 —4 (2 —i)x —5 — 3i = 0.
32.
33. Докажите, что многочлен x3"4-x3ot+1 + x3*+2 делится без
остатка на х2 + х+1, если m, n, fe —любые целые неотрицатель-
ные числа.
140
Укажите точки комплексной плоскости z, удовлетворяющие
уравнениям (34—39).
34. Rez2-0. 35. Imz2 = 0. 36. |z| + z = 0.
37. | z|2 + z = 0. 38. z2 + | Г| = 0. 39. z2+] z\ =0.
40. Докажите, что для любых двух комплексных чисел zx и z2
|г1 + г2|2 + |г1-г2|2 = 2(| zj2 + |z2|2).
41. Докажите, что z + z, zz —действительные числа.
42. Докажите, что
Zj -1— == *~1 —I— Z2,
Н- z2 4* ... 4" zn — zL -}*z2 4~ . zn\ zLz2 = £}Z2;
2jZ2 . . . Zn = ZjZ2. . . Z„, Zn = Z , (Zj/Z2) = Z-JZ^.
43. Пусть Pn(z) = a„z"4-^n_1z"~14-• • • 4-a1z4-a0. Докажите,
что
Pn (г) = a„z”4-oTTJn-14- • • • 4-^z 4-a0.
Если an, an_i, ..., alt a0 — действительные числа, то докажите,
что Ра (г) = Рп (z).
Найдите точки плоскости, удовлетворяющие уравнениям
(44—47).
44. z4-t| = |z4-2|. 45. |z-2|= |z4-2i|.
46. +|-l = l. 47. |-2rt±.|=i.
г+3 I j z—3i I
Найдите точки плоскости, удовлетворяющие следующим нера-
венствам (48—57).
48. |z—l|>|z —i|. 49. | z +2t | < | z—1 |.
50. +4-1 < 1. 51. Iz4-il < 1. 52. I2z — il <2.
г + 1 I ’ 1 1 1 1
53. 1 <|z4-1-«|<2. 54. 1 <|3rz-l|<3.
55. 1//2 <|(14-i)z4-i|<K2 . 56. |z-x|<|z-i|.
57. | z + i | < | z — x | < | z— 1
58. Найдите наименьшее значение, принимаемое функцией
^ = U + 4“| > где. z —комплексная переменная, |z|^2.
Раздел II
НАЧАЛА АНАЛИЗА
§ 1. ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ ПРЕДЕЛЫ.
БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ.
ПРЕДЕЛЫ ФУНКЦИЙ
1. (МЭЙ, 1979 г.). Сумма членов бесконечно убывающей гео-
метрической прогрессии равна наибольшему значению функции
f (х) = х3 + 3х —-9 на отрезке [—2; 3J; разность между первым
и вторым членами прогрессии равна |'(0). Найдите знаменатель
прогрессии.
Найдите пределы (8—59). ______ _______
„ /T/TV in-7'7 X 1- V2fl2+1 —
2. (КГУ, мехмат, 1977 г.), lim —-————-3— .
3. (КГУ, мехмат, 1977 г.), lim + • • • +
4. (ТбГУ, мехмат, спец, прикладная матем., 1978 г.).
.. /. 1 , 1 . (-l)”-i \
Am« V 7 + 49 •••+ 7»-* )•
5. (КГУ, мехмат, 1977 г.).
../1,2, , п— 1 \
„Тш \ «2+1 + «2+1 + + «2 + 1 7 ‘
6. (КГУ, мехмат, 1977 г.). Jim •
7. (КГУ, мехмат, 1977 г.). + f Д”2Дw 2д .
8. (КГУ, мехмат, 1977 г.), lim .
9. lim . 10. lim . 11. lim .
„->*,2" n-> « п 'г"
12. (ТбГУ, мехмат, спец, прикладная матем., 1978 г.).
13. (РГУ, мехмат, спец, физика, 1977 г.).
„™ l+3n + 2n2
142
14. (МИИВТ, 1982 г.), lim
15. (МХТИ, 1979 г.). Vm <4±-)3~64-.
О х
16. lim 0 + *)(1+2х)(1+Зх)-1
х -> О х
17. lim <!+*)52-<1+5*> .
18. lim -Ух~3 .
х_>1 х2-[-х —2
19. (МТИММП, 1977 г.), lim
4 ' —19r—L-0(1
20. (ВЗИИЖТ, 1979 г.), lim -Г~ ,n
-2 x2-t-7x-f-10
x2—2x—15
21. (ВЗИИЖТ, 1979 г.), lim .
x t_3 % 1
22. lim *2~5*+6
x2-8x4-15 *
23. (МТИММП, 1977
г.), lim *3-3*-2
24. (МИХМ, 1978 г.), lim
lim4=3x+2.
x —> 1 X5 —4x4-3
x3 —2x— I
x3— 1
25
26.
lim -hi—s--j-.
_ 1 x—2x— 1
28. lim £+x2+--- J-x»-n
x->- 1 *-l
29. (МФИ, 1979 r.). lim .
X -> 1 ^—1
30. (МГИ, 1977 r.). lim Xх^3 ~3 .
X -> 6 X 6
31. (МТИММП, 1977 г.), lim J/'T+7~1..
0 x
32. (МИУ, 1978 r.). lim ~2 .
x->5 x—5
33. (МИХМ, 1977 г.), lim ±=jf3x~2 .
x -> 2 x“
34. lim yiTg-3 .
x_>4 yx—2
143
or V Vl— X— 3
35. lim —----л y_ - .
*•* -8 2+ v x
36. (МИСиС, 1978 г.), lim
У X —1
Ух — 1
37. (МТИММП, 1977 г.).
УГ-2
38. hm .
х-> 16 ух —4
lim
х -> 9
у/ х— 1 — 2
X—9
39. lim Д1 __________1
0 у/ 1 — у 1 — X
40. (МЭИ, 1979 г.).
.. / 3-/7 ,
lim ( —jr-i--h
х_<Л 9-Х
1
з-/Т
x24-162 \
729—х3 J "
41. (МЭИ, 1979 г.).
Нш ГС-^-Г—
j (Дх2 — X х 1—X3
42. (МЭИ, 1979 г.).
lim
х3—х~1
г3 — 4х \ -1 / х -|- У"2х
х3 —8 ) \ х —2
43. (МТИММП, 1977 г.). Iimxctg3x.
х -> О
*-1
44. (МТИММП, 1977 г.), lim cosW2)~sin <*/2>.
х-0 cosx
46. lim
х-> О
47 ]im sin5x-sin3x
’ Sinx
cosx—cos a
48. hm ----------.
x-+a x~a
49. lim 92sifx+si"x~1| .
x л/6 2 sin2 x—3 sm x+1
51. lim
SUT\X
52. (МФИ, 1979 r.). lim -+3?74.
' 1—5x2
53. (ВЗИИЖТ, 1979 г.), lim (
X-> QD \OX-1 X —j—zx—1
54. (ВЗИИЖТ, 1979 г.), lim ,2x"+?~2.
144
55. (МИХМ, 1979 г.), lim ~4> <.* .
' Х^оо (5х—1)?
56. (МИХМ, 1979 г.), lim '~х .
X -> QO •
57. (МИУ, 1978 г.), lim (х-Кх24-5х).
X +• ®
58. (МИИВТ, 1982 г.), lim
х->-4 Х
х
5 tdt
59. (МИИВТ, 1982 г.), lim °
х-> oxtg(r4-n)
60. Используя определение, покажите, что функция
{xsin(l/x), если х=#0,
О , если х = 0,
непрерывна в точке х = 0.
61. Используя определение, покажите, что функция
£ / \ ( тМ", если х О,
/(*) = |х|
( 1, если х = 0,
разрывна в точке х = 0.
§ 2. Производная. Исследование функций с помощью
производной
1. (МХТИ, 1977 г.). Дана функция f (х) = sin2 2х. Найдите
1 . rw
2 ’ cos 2х ‘ I
2. (МХТИ, 1977 г.). Вычислите f'(x)+f (х) + 2, если f (x)=s
=xsin2x.
3. (МЭИ, 1978 г.). Упростив выражение для f (х), найдите
/'(х), если
_ / 1/"V 9 г 9 \“2 / X—1 \
/^^4-7+2/ G(/r+i)+1)x
4. (МЭИ, 1979 г.). Упростив выражение для /(х), найдите
/'(х), если
f W = (-/.2^Х +34^-Х--------T7-~3^i (2• 310g,‘ х + 3)•
\У 16x4-12 у/к 4-9 2 у/х 4-3/
145
Докажите тождества (5—8).
5. (МТИ, 1978 г.). Г (1)4-/' (—1) = — 4/(0), если f (х)=
=х5 4-х3 — 2х — 3.
6. (МТИ, 1978 г.). f'(x)—2xf(x) + -^f(0)-f’(0) = \, если
f(x) = 3e-v2.
7. (МТИ, 1978 г.). f'(x)4-f(x) + /(y)—у = 0, если/(х)=1пх.
8. (МАИ, 1979 г.). 2f,(x+^'\f(x-^'}=f(Q)-f(2x+^},
где f(x) = cosx.
9. (МАМИ, 1979 г.). Найдите множество значений х, удовлет-
воряющих условию [<р (х)]' + <р (х) = 0, если ф(х) = соэх.
Даны две функции /(х) и g(x). При каких х имеет место
равенство /' (х) = g(х)? (10—13).
10. (МИСиС, 1979 г.). / (х) = sin4 Зх и g(x) = sin6x.
И. (МИСиС, 1979 г.). f(x) = sin32x и g(x) = 4cos2x — 5sin4x.
12. (МИСиС, 1979 г.). f (х) = 2х2 cos2 (х/2) и g(х) = х — х2 sinх.
13. (МИСиС, 1979 г.), f (х) = 4х cos2 (х/2) и g (х) = 8 cos (х/2)—
—3 — 2xsinx.
При каких значениях х производная функции f(x) равна
нулю? (14—16).
14. (КГУ, мехмат, 1977 г.). f(x) = l—sin(n4-*)+
+2 cos ((Зп 4~ *)/2).
15. (КГУ, мехмат., 1977 г.). / (х) — sin Зх—КЗ cos Зх +
4- 3 (cos х—К3 sin х).
16. (КГУ, мехмат, 1977 г.). /(х) = 20cosЗх4- 12cos5x —
—15 cos 4х.
Решите неравенства (17—21).
17. (МВМИ, 1977 г.). /'(х) > g'(х), если f (х) = х3 + х-^2,
g(x) = 3x24~* + K2 •
18. (МВМИ, 1977 г.). /' (х) > g’ (х), если f (х) = 2х3 — х24~КЗ ,
g(x) = x34-T~ КЗ-.
19. (МИИГАиК, 1977 г.). f(x)<g'(x), если f(x) = 2/x,
g(x) = x—х3.
20. (МИЭТ, 1978 г.). /' (х) > g' (х), если f (х) = х-J-In (х — 5),
g (х) = In (х—1).
21. (МИЭТ, 1978 г.). f(x)>g'(x), если f (х) = 52*+1/2,
g(x) = 5*4-4х In 5.
22. (МАМИ, 1978 г.). Найдите все /(х), удовлетворяющие
уравнению /2 (х) 4- 4/' (х) / (х) 4- [/' W]2 = 0.
146
Найдите производные следующих функций (23 — 37).
23. г/ = (х+1)(х + 2)2. ок 1 , 2 . 3 25. у = ——7*Н—г* и X ‘ X2 X3 27. у = ех(х2 — 2х + 2). 29. </ = 1 + -^+ ’ х V х /х 24. z/ = sin(cos2 (tg3x)). 2х 26. У = -г^. 1 —X2 28. # = lg3(x2). 1 у2 1 30. У = 1-1п^—г. 4 х2 -f-1
31. у = — у а2 — х2 32. i/ = ln tg(x/2).
QQ _SiDX —XCOSX О О • 11 — • 34. i/ = ln 1/^Л
J cos x-j-x sin X r 1 4-sinx
35. у = х\/Л +%2. 36. у = sin (sin (sinx)).
37. у = (2—x2)cosx4-2xsibx.
38. (Симф. ГУ, матфак, 1982 г.). Докажите, что ех — х>1,
если х > 0.
Найдите интервалы возрастания и убывания функций (39—43).
39. (МИИВТ, 1982 г.) у = — х(х—2)2.
40. (МАИ, 1977 г.). г/ = 2х3 + Зх2-2.
41. (МИИГАиК, 1978 г.). z/ = -|x3-x2-4x + 5.
’ 42. (МИНХ, 1978 г.), f (х) = 3х4 —8х3 + 6х2+ 1.
43. (МИНХ, 1977 г.). f (х) = (2* —1) (2*-2)2.
Определите точки максимума и минимума и промежутки моно-
тонности функций (44 — 52).
44. (МИСиС, 1978 г.). у = 2х3 — 6х2- 18x4-7.
45. (МСИ, 1977 г.). у = х4 + 4х3-8х2 + 3.
46. (КГУ, геофак, 1977 г.; МСИ, 1977 г.). г/ = х4 —4х3—
— 8х2 + 3.
47. (КГУ, геофак, 1977 г.), у = 4х4- 2х2 + 3.
48. (МИИГАиК, 1978 г.), f (х) = х3/(х2 + 3).
49. (МИИГАиК, 1978 г.). f (х) = (*~2*.Р ~х).
50. (МГУ, почв. отд. биофака, 1977 г.). f(x) = (x — 1)е3х.
51. (МТИМБО, 1980 г.). f(x) = xe~3x.
52. (МТИМБО, 1978 г.; ВЗИИЖТ, 1979 г.). у=х-\пх.
Найдите критические точки функций и исследуйте их на мак-
симум и минимум (53 — 63).
53. у = 2х2 + х + 2.
54. (МИИГАиК, 1978 г.) f (х) = Зх4 — 4х3.
55. (МИИГАиК, 1978 г.). t/ = x4-10х2 + 9.
56. (МИЭТ, 1978 г.). г/= (х —З)2 (х —2)2.
147
57. (МИИГАиК, 1978 г.), у = ух?-4х2.
58. (МАТИ, ,1977 г.). у = х?-х2 + 8.
59. (МИИГАиК, 1978 г.). f(x) = ± + ^.
60. (МТИМБО, 1982 г.). f(x) = g=g±J.
Л —ОЛ “у* А
61. (ТбГУ, физфак, спец, радиофизика и электроника, 1982 г.).
f (х) = ^-—1п(х2 —8).
62. (ВЗИИЖТ, 1979 г.). у = хе*.
63. у = хе~х*.
64. (КГУ, геофак, 1978 г.). Найдите все значения х, при
которых функция i/ = sinx — cos2x — 1 принимает наименьшее зна-
чение. Какое это значение?
65. (МАИ, 1979 г.). При каких действительных значениях а
5а2
и b все экстремумы функции f (х) = -у- х3 + 2ах2 —9х + Ь положи-
тельны и максимум находится в точке х0=>—5/9?
66. (МАИ, 1979 г.). При каких действительных значениях
а и b все экстремумы функции f (х) = а2х3—0,5.ах2 — 2х — b поло-
жительны и минимум находится в точке xQ=> 1/3?
67. (МАИ, 1979 г.). При каких действительных значениях
а и Ь все экстремумы функции f(x)^=a2x3 + ах2 — х + b отрица-
тельны и максимум находится в точке х0 =— 1?
68. (ТбГУ, мехмат, спец, прикладная матем., 1982 г.). Най-
дите постоянную р, при которой функция f (х) = рх2 + —х — 12
имеет максимум в точке х = 9/4.
69*. (ЛГУ, матмех, 1977 г.). В зависимости от р укажите те
значения а, для которых уравнение х3 + 2рх2-|-р = а имеет три
различных действительных корня.
70. (КГУ, РФФ, 1977 г.). Найдите наибольшее значение
функции у 10 + 4х1п9 — 3х"1 — 33“х.
71. (КГУ, РФФ, 1977 г.). Найдите наибольшее значение
функции у = 7 4-2х1п25 —5х"1 —52“х.
72. (КГУ, РФФ, 1977 г.). Найдите наименьшее значение
функции у = Зх4-2-33“х —х1п27 —9.
73. (МИТХТ, 1979 г.). При каком значении х выражение
принимает наименьшее значение?
Найдите наибольшее и наименьшее значения функций (74 — 93).
74. (МИИГАиК, 1977 г.; ВЗИИЖТ, 1979 г.). у = ±х3-4х
на отрезке [0; 2].
148
75. (МХТИ, 1979 г.), f (х) = — х3 + Зх2 + 5 на отрезке [0; 3].
76. (МВТУ, 1979 г.), f (х) = 2х3 —9х2 + 12х на отрезке [0; 3].
77. (МИИВТ, 1982 г.), f (х) = Зх3 - 9х2 + 2 на отрезке [—1; 4].
78. (МИНХ, 1979 г.), f (х) = 2х3 + 3х2 — 12х + 30 на отрезке
[-3; 3].
79. (МАИ, 1977 г.), /(х) = 2х3 + 3х2 — 12х +1 на отрезке
[-1; 5].
80. (КГУ, химфак, 1978 г.), у — х3 — 4х2 + 4х + 3 на отрезке
[-1; 3].
81. (МИИГАиК, 1978 г.). у = х3— Зх2+ 3x^-2 на отрезке
[-2; 2].
82. (МИСиС, 1978 г.). у = х2(2х — 3)— 12 (Зх — 2) на отрезке
[-3; 6].
83. (МХТИ, 1978 г.). г/ = |х3 —Зх2 + 5| на отрезке [0; 3].
84. (МСИ, 1977 г.). /(х) = х4— 8х2 — 9 на отрезке [0; 3].
85. (ВЗИИЖТ, 1979 г.). z/ = x4-8x2-9 на отрезке [—1; 1].
86. (МИИГАиК, 1978 г.). у = х3- — х3 + х-}-2 на отрезке [—1; 1].
87. (МИРЭА, 1979 г.), f (х) = f/х2/(2х- 1) на отрезке [3/4; 2 .
88. (МИТХТ, 1979 г.), f (х) = (2х + 2“х)/1п2 на отрезке [— 1; 2'.
89. (МИТХТ, 1979 г.). / (х) = 2-33*-4-32* + 2-3« на отрезке
[-1; !]•
90. (МИНХ, 1977 г.). f(x) = 2-23*-9-22*+ 12-2* на отрезке
[-1; !]•
91. (КГУ, химфак, 1978г.). f (х) = sinx+cos2x на отрезке[0; л].
92. (КГУ, ЭКФ, 1977 г.). /(x) = cos3x— 15cosх +8 на от-
резке [л/3; Зл/2].
93. (КГУ, ЭКФ, 1977 г.), f (х) = (5 + sinх) cosх + Зх на
отрезке [0; л/2].
94*. (ХГУ, физфак, 1978 г.). Найдите наибольшее значение
функции f (х) = 3fr2 на 0ТРезке [—2; 1] в зависимости от
параметра Ь.
95*. (ХГУ, физфак, 1978 г.). Найдите наибольшее значение
функции f (х) = х4 — 6&х2 + Ь2 на отрезке [—2; 1] в зависимости
от параметра Ь.
96. (КГУ, геофак, 1978 г.). Найдите экстремумы функции
f(x) = 2xsin2x+cos 2х —КЗ на отрезке [—л/2; Зл/8].
97. (МГУ, мехмат, 1977 г.). Докажите, что для функции
f(x) = (cosx)2(sinx) выполняется неравенство
min f(x) > — 7/18.
[-л; л]
98. (МГУ, мехмат, 1977 г.). Докажите, что для функции
/ (х) = (sin х) • (sin 2х) выполняется неравенство max f (х) < 0,77.
[-л; Л]
Составьте уравнение касательной к графику функций (99— 108).
99. (МТИМБО, 1978 г.). г/ = х2 —2х в точках ее пересечения
с осью абсцисс.
149
100. у~— х2—1 в точке х = 2.
101. (ВЗИИЖТ, 1979 г.), у = 2х2 + 1 в точке (1; 5).
102. (МИНХ, 1979 г.). z/ = 4x —х2 в точках пересечения
с осью Ох.
103. (МХТИ, 1979 г.), у = х2 — 2x4-5 в точке ее пересечения
с осью Оу.
104. (МИУ, 1978 г.). У = -£ (ех/2 4-£“х/2) в точке с абсциссой
х = 21п2.
105. (МИНХ, 1977 г.). у = 2~х — 2~2V в точке с абсциссой
х = 2.
106. (МИНХ, 1977 г.). у — Зх4-3“”2х в точке с абсциссой х=1.
107. (МИНХ, 1979 г.). у = (2х— 1) е2 (1“х) в точке ее макси-
мума.
108. (МИНХ, 1979 г.). у = — х2 —2, параллельную прямой
у = 4х 4- 1.
109. (МХТИ, 1977 г.). Касательная к кривой у = 4 — х2
образует с осью Ох угол 75°. Найдите координаты точки ка-
сания.
ПО. (МХТИ, 1977 г.). Найдите значение коэффициента £, при
котором кривая y = x2-\-kx-\-4 касается оси Ох.
111. (МСИ, 1977 г.). На кривой у = х2 — х4-1 найдите точку,
в которой касательная параллельна прямой у = 3х — 1.
112. (МСИ, 1977 г.). На кривой у = 4х2 —6x4-3 найдите
точку, в которой касательная параллельна прямой у = 2х.
113. (МИУ, 1978 г.). На параболе у = х2 взяты две точки
с абсциссами хх=1, х2 = 3. Через эти точки проведена секущая.
В какой точке параболы касательная к ней будет параллельна (
проведенной секущей? Напишите уравнение секущей и этой каса-
тельной.
1Г4*. (МИУ, 1978 г.). Найдите точки, в которых касатель-
ные к кривым y — f (х) = х3 — х— 1 и z/ = <p(x) = 3x2 —4x4-1 парал-
лельны. Напишите уравнение касательных.
115. (МИТXT, 1979 г.). Найдите угол между касательными
к графику функции f (х) = х3 —4х24~3х4- 1, проведенными в точках
с абсциссами 0 и 1.
116. (МИСиС, 1979 г.). Найдите угол между двумя касатель-
ными, проведенными из точки (0; —2) к параболе у = х2.
117. (МИСиС, 1979 г.). Найдите угол между касательными,
проведенными из точки (0; 2) к параболе у = —Зх2.
118. (МИСиС, 1979 г.). Найдите уравнения общих касатель-
ных к параболам у = х2 и у = — х24-3х —2.
119. (СимфГУ, матфак, 1982 г.). Найдите уравнение касатель-
ной к параболе у = х2 — 7x4-3, если эта касательная параллельна
прямой 5x4- у — 3 = 0.
120. (МТИМБО; 1980 г.). В каких точках касательная к гра-
х I 2
фику функции У = ^ образует с осью Ох угол в 135°?
150
121. (РГУ, физфак, спец, радиофизика, 1977 г.). Найдите
точки, в которых касательная к кривой # = х — 0,5 sin 2х—
— 0,5 cos 2х + 16 cosx параллельна оси абсцисс.
122. (МТИМБО, 1978 г.). Найти угол между касательными
к графику функции z/ — x3 —х в точках с абсциссами = — 1
и х2 = 1.
123. (МТИМБО, 1978 г.). В точке М (1; 8) к кривой у=.
= К(5 — х2/3)3 проведена касательная. Найти длину ее отрезка,
заключенного между осями координат.
124. (МИИВТ, 1982 г.). Найдите наибольший объем V конуса
с образующей а.
125. (РГУ, физфак, спец. радиофизика, 1977 г.). Из круга
вырезан сектор с центральным углом а. Из оставшейся части
круга свернута воронка. При каком значении а вместимость
воронки будет наибольшей?
126. (РГУ, физфак, спец, радиофизика, 1977 г.). В равно-
бочной трапеции нижнее основание равно /, угол при основании
равен а. Диагональ трапеции перпендикулярна боковой стороне.
При каком значении а площадь трапеции будет наибольшей?
Найти наибольшую площадь.
127. (РГУ, мехмат, спец, матем., механ., 1977 г.). Основанием
пирамиды служит равнобедренный треугольник с углом а при
основании. Каждый из двугранных углов при основании равен <р.
Радиус шара, вписанного в пирамиду, равен R. Найти объем
пирамиды. При каком значении а объем пирамиды будет наи-
меньшим?
128. (РГУ, физфак, спец, физика, 1977 г.). Конус описан
около шара радиуса R. Угол при вершине в осевом сечении
конуса равен 2а. Найти площадь осевого сечения конуса. При
каком значении а площадь будет наименьшей?
129. (РГУ, физфак, спец, физика, 1977 г). Правильная четы-
рехугольная пирамида объема V описана около полушара так,
что центр основания пирамиды лежит в центре шара. Угол между
боковой гранью пирамиды и плоскостью основания равен а.
Найти объем полушара. При каком значении а объем будет
наибольшим?
130. (МИСиС, 1979 г.). Найдите уравнения общих касатель-
ных к параболам г/ = х2— 5х + 6 и z/ = x2 + x+l.
131. (МАТИ, 1979г.). Докажите, что кривая z/ = x4 + 3x24~2x
не пересекается с прямой у = 2х—1, и найдите расстояние между
их ближайшими точками.
132. (МАМИ, 1979 г.). Открытый кузов грузового автомобиля
имеет вид прямоугольного параллелипипеда с площадью поверх-
ности 2S. Каковы должны быть длина и ширина кузова, чтобы
его объем был наибольшим, а отношение длины к ширине рав-
нялось 5/2.
133. (МИНХ, 1979 г.). Площадь, занимаемая печатным текс-
том, составляет на странице книги 432 см2. Ширина полей вверху
151
и внизу страницы составляет по 2 см, а ширина боковых полей
по 1,5 см. Каковы должны быть ширина и высота страницы,
чтобы количество израсходованной бумаги было наименьшим?
134. (МВТУ, 1978 г.). Представьте число 48 в виде суммы
двух положительных слагаемых так, чтобы сумма куба одного из
них и квадрата другого была наименьшей.
135. (МИНХ, 1978 г.). Определите размеры открытого бас-
сейна с квадратным дном объемом 32 м2 так, чтобы на облицовку
его стен и дна пошло наименьшее количество материала.
136. (РГУ, физфак, спец, радиофизика, 1977 г.), Под каким
углом а нужно провести прямую через точку (х0; у0), чтобы длина
отрезка между осями координат была наименьшей?
137. (РГУ, мехмат, спец, матем., механ., 1977 г.). В основании
пирамиды лежит равнобедренный треугольник, площадь которого
равна S, а острый угол при вершине равен а. Найдите объем
пирамиды, если угол между каждым боковым ребром и высотой
пирамиды равен р. При каком значении а объем будет наименьшим?
138. (МИСиС, 1979 г.). В правильной шестиугольной пира-
миде длина бокового ребра равна 1 см. При какой длине стороны
основания объем пирамиды будет наибольшим?
139. (МИЭТ, 1977 г.). Из трех досок одинаковой ширины
сколачивается желоб. При каком угле наклона боковых стенок
площадь поперечного сечения желоба будет наибольшей?
140. (МИЭТ, 1977 г.). Найдите такой цилиндр, который имел бы
наибольший объем при заданной площади S полной поверхности.
141. (МГМИ, 1980 г.). Объем прямой треугольной призмы
равен V. В основании призмы лежит равносторонний треугольник.
Какова должна быть длина стороны основания, чтобы площадь
полной поверхности призмы была наименьшей?
142. (ЯГУ, 1980 г.). Длина бокового ребра правильной четы-
рехугольной пирамиды равна а. Боковое ребро наклонено к пло-
скости основания под углом а. При каком а объем пирамиды
будет наибольшим?
143. (МВТУ, 1979 г.). Из всех правильных треугольных призм,
имеющих объем V, найдите призму с наименьшей суммой длин
всех ее ребер. Чему равна длина стороны основания этой призмы?
144. (МГМИ, 1980 г.). Из всех прямоугольных параллелепи-
педов с квадратным основанием, вписанных в данный шар, най-
дите тот, который имеет наибольшую площадь боковой поверх-
ности.
145. (МВТУ, 1978 г.). Основаниями правильной призмы слу-
жат квадраты. Одно из оснований призмы принадлежит большому
кругу шара радиуса 7?, а вершины другого лежат на поверхности
этого шара. Определите, какой должна быть длина высоты призмы,
чтобы сумма длин всех ее ребер была наибольшей?
146. (МИНХ, 1979 г.). Консервная банка должна иметь форму
цилиндра, емкостью 1 дм3. Рассчитайте, каким должен быть ра-
диус ее оснований, чтобы площадь жестяного листа, израсходо-
ванного на изготовление банки, была минимальной?
152
147. (МИЭТ, 1979 г.). Найдите высоту цилиндра с наибольшей
площадью боковой поверхности, который может быть вписан в
шар радиуса R.
148. (ЯГУ, 1980 г.). Площадь боковой поверхности конуса
равна S. При каком радиусе основания шар, вписанный в этот
конус, имеет наибольший объем?
149. (МИЭТ, 1979 г.). Дан шар радиуса г. Впишите в него
конус с наибольшей площадью боковой поверхности. Определите
эту площадь.
150. (МВТУ, 1978 г.). В правильной треугольной призме рас-
стояние от центра основания до одной из вершин другого осно-
вания равно Z. При какой длине высоты призмы ее объем будет
наибольшим? Найдите это наибольшее значение объема.
151. (МЭСИ, 1979 г.). Найдите высоту конуса наименьшего
объема, описанного около полушара радиуса = так, чтобы
центр основания конуса совпадал с центром шара.
152. (КГУ, мехмат, 1977 г.). В шар радиуса R вписан прямой
круговой цилиндр высоты Н. Найдите объем этого цилиндра.
При каком Н объем будет наибольшим? Найдите ; этот наиболь-
ший объем.
153. (КГУ, ВМК, 1978 г.). В данный шар вписан цилиндр
с наибольшей плошадью боковой поверхности.'Найдите отношение
радиуса шара к радиусу основания этого цилиндра.
154с (МИЭТ, 1980 г.). В шар вписан цилиндр наибольшего
объема. Во сколько раз объем шара больше объема этого ци-
линдра?
155. (МИУ, 1978 г.). В шар радиуса R вписан цилиндр, имею-
щий наибольшую боковую поверхность. Найдите объем этого ци-
линдра.
156. (КГУ, ВМК, 1978 г.). В данный шар вписан конус наи-
большего объема. Найдите отношение радиуса шара к высоте
этого конуса.
157. (МЭСИ, 1979 г.). Около цилиндра, радиус основания
которого равен а, описан конус наименьшего объема. Плоскости
оснований цилиндра и конуса совпадают. Найдите радиус осно-
вания этого конуса.
158. (ЛьвГУ, 1980 г.). В конус, образующая которого состав-
ляет с плоскостью основания угол величиной 2ф, вписана сфера
единичного радиуса. Найдите площадь боковой поверхности ко-
нуса. При каких значениях <р эта площадь будет наименьшей?
159. (МВТУ, 1979 г.). В сферу радиуса R вписана правиль-
ная четырехугольная пирамида так, что все ее вершины принад-
лежат сфере. Какой должна быть высота пирамиды, чтобы ее объем
был наибольшим? Найдите это наибольшее значение объема.
160. (МВТУ, 1979 г.). В конус с высотой Н и радиусом осно-
вания R вписана правильная шестиугольная призма так, что одно
ее основание лежит в плоскости основания конуса, а вершины
другого основания принадлежат боковой поверхности конуса.
153
Какой должна быть высота призмы, чтобы ее объем был наиболь-
шим? Найдите это наибольшее значение объема призмы.
161. (КГУ, ВМК, 1978 г.). В данный конус вписан цилиндр
с наибольшей боковой поверхностью. Найдите отношение высоты
конуса к высоте этого цилиндра.
162. (КГУ, ВМК, 1978 г.). В данный конус вписан цилиндр
наибольшего объема. Найдите отношение радиуса основания конуса
к радиусу основания этого цилиндра.
163. (МВТУ, 1979 г.). В конус с высотой Н и радиусом осно-
вания R вписан цилиндр так, что одно его основание лежит в
плоскости основания конуса, а окружность другого основания
принадлежит боковой поверхности конуса. Какой должна быть
высота цилиндра, чтобы его объем был наибольшим? Найдите
это наибольшее значение объема.
164. (КГУ, РФФ, 1980 г.). Все ребра треугольной призмы
АВСА1В1С1 имеют равные длины, все плоские углы при вершине А
конгруэнтны. Точки /С и А—середины ребер [ЛЛ/J и [АВ]. Где
на ребре [АС] нужно выбрать точку М, чтобы площадь треуголь-
ника RLM была наименьшей?
165. (ТбГУ, мехмат, спец, прикладная матем., 1980 г.). Через
точку N (2; 4) проведена прямая; отрезок ее с отрезками осей
координат (х>0; у>0) образует прямоугольный треугольник.
Чему должна быть равна длина наибольшего катета, чтобы пло-
щадь треугольника была минимальной?
166. (ТбГУ, мехмат, спец, прикладная матем., 1981 г.). Лодка
находится в точке Q озера, отстоящей от ближайшей точки А на
берегу на 6 км. Лодочник должен попасть в точку В, находя-
щуюся на берегу на расстоянии 11 км от А. Скорость лодки 3 км/ч,
скорость ходьбы лодочника по берегу 5 км/ч. Лодочник подсчи-
тал, что если он сперва доплывет до точки С, которая находится
между А и В, а затем сразу же пешком направится в точку В,
то на путь от Q до В он потратит наименьшее время. Найдите
расстояние от А до С, считая, что лодка движется прямолинейно
и берег озера — прямая линия.
167. (РГУ, мехмат, спец, прикладная матем., 1977 г.). Авто-
мобиль едет из пункта А в пункт С. От пункта А до пункта В,
расположенного между А и С, он едет со скоростью 48 км/ч.
В пункте В он уменьшает свою скорость на а км/ч (0 < а < 48)
и с этой скоростью едет 1/3 часть пути от В до С. Оставшуюся
часть пути от В до С он едет со скоростью, которая на 2а км/ч
превышает первоначальную скорость (48 км/ч). При каком зна-
чении а автомобиль быстрее всего проделает путь от В до С?
§ 3. ГРАФИКИ ФУНКЦИЙ
1. (КГУ, геофак, 1977 г.). Исследуйте функцию у = 3х2—6х+5
и постройте ее график. Каковы наибольшее и наименьшее значе-
ния этой функции в промежутке [0; 2]?
154
2. (МТИПП, 1978 г.). Найдите наибольшее и наименьшее зна-
чения функции f(x) = x3—Зх24-2 на отрезке [—1; 3] и постройте
на этом отрезке ее график.
3. (МИНХ, 1979 г.). Исследуйте функцию у = х3 — 3x4-2 и
постройте ее график.
4. (МАТИ, 1979 г.). Исследуйте функцию у = х3— 4х2—3x4-12
и постройте ее график.
5. (МГРИ, 1977 г.). Дана функция г/= х3—9x4-1- Исследуйте
функцию с помощью производной и постройте график.
6. (МЭИ, 1979 г.). Найдите промежутки монотонности и экстре-
12 1
мумы функции /Дх) = х— ух2— ух3 и постройте ее график.
7. (МЭИ, 1979 г.). Найдите наименьшее и наибольшее значе-
1 9 I
ния функции f(x) = T= х34-пй%2— Vх на отрезке Г—2; 1] и по-
стройте ее график на указанном отрезке.
8. (МЭИ, 1978 г.). Найдите промежутки монотонности и экстре-
____________________5х2__Зх
мумы функции f(x)=^------3---- и постройте ее график.
9. (МАИ, 1979 г.). Исследуйте на монотонность и экстремумы
функцию у = (х3— 4х)/4 и постройте ее график. Вычислите пло-
щадь фигуры, ограниченной графиком этой функции и прямой
у=2 (2 4-х).
10. (МАИ, 1979 г.). Постройте график функции у = х(х2 +
4-3x4-2). Напишите уравнение касательной к графику в точке
с абсциссой хо = 0. Найдите координаты точек пересечения каса-
тельной с графиком функции.
11. (МАИ, 1979 г.). Постройте график функции у = (х24-х)х
х(х—2). Напишите уравнение касательной к графику в точке
с абсциссой хо = 0. Найдите координаты точек пересечения каса-
тельной с графиком функции.
12. (МАМИ, 1979 г.). Исследуйте функцию у = (х*—2х2)/4
с помощью производной и постройте ее график.
13. (МГРИ, 1979 г.). Дана функция г/ = (6х2—х4)/9; иссле-
дуйте функцию и начертите эскиз графика.
14. (МГРИ, МТИММП, 1977 г.). Дана функция у — х^ — 2х24-5;
исследуйте функцию с помощью производной и постройте ее
график.
15. (МГРИ, 1979 г.). Дана функция у = х*—10х24-9; иссле-
дуйте функцию и постройте эскиз графика.
16. (МИНХ, 1978 г.). Дана функция у = (х—1)2(х—2)3.
Исследуйте ход изменения этой функции и постройте ее график.
17. (МГРИ, 1979 г.). Дана функция у = х2/(х—2); исследуйте
функцию и начертите эскиз графика.
18. (МГРИ, 1979 г.). Дана функция z/ = (—х24-3х—1)/х;
исследуйте функцию и начертите эскиз графика.
19. (КГУ, ВМК, 1977 г.). Исследуйте функцию z/=(x3—4)/(х—1)?
и постройте ее график. Сколько корней имеет уравнение
(х3 — 4)/(х— I)3 = с?
155
20. (КГУ, ВМК, 1977 г.)- Исследуйте функцию
у = (х®-|-4)/(х4- О3 и постройте ее график. Сколько решений имеет
уравнение (х3 4- 4)/(х4~ I)3 — с?
21. (КГУ, ВМК, 1977 г.). Исследуйте функцию
у = 8(х3 + х)/(2х—I)3 и постройте ее график. Сколько корней
имеет уравнение 8(х3 + х)/(2х—1)3 = с?
22. (КГУ, ВМК, 1977 г.). Исследуйте функцию
у=8(х34-х)/(2х-|-I)2 и постройте ее график. Сколько корней
имеет уравнение 8 (х3 -|-х)/(2х 4- I)3 = с>
23. (КГУ, ВМК, 1977 г.). Исследуйте функцию
у = (х4—8)/(х+ I)4 и постройте ее график. Сколько корней име-
ет уравнение (х4 —8)/(х+1)4 = с?
Постройте графики функций, проведя полное исследование,
(24—28).
24. y = sin4 x + cos4x. 25. у— (l,3)-2xsin2 х.
26. у = arcsin (2х/(1 4-х2)).
27. (СимфГУ, матфак, 1982 г.), у = |х2—4х4-ЗЦ-2х.
28. (МИИВТ, 1982 г.). у = ^—х2.
29. (МИСиС, 1978 г.). Постройте график функции у = /(х),
ytl____________у — П
где f (х) = Jnn -п, х > 0.
§ 4. ПЕРВООБРАЗНАЯ. ИНТЕГРАЛ.
ПЛОЩАДИ КРИВОЛИНЕЙНЫХ ТРАПЕЦИЙ
Найдите F (х) по данной F' (х) (1—7).
1. (МВМИ, 1977 г.). F'(x) = 4x4-1 и F (—1) = 2.
2. (МВМИ, 1977 г.). F'(x) = 3x2—4х и F(0)= 1.
3. (МХТИ, 1979 г.). F' (х) = 7х2 — 2x4-3, график которой
проходит через точку М. (1; 5).
4. (МХТИ, 1977 г.). F' (х) = 1 4-x4-cos2x, Г(0) = 1.
5. (МХТИ, 1979 г.). F'(x) = sin2x-F3x2, F(0) = 2.
6. (МТИМБО, 1980 г.). F' (х) = l/sin2x, график которой про-
ходит через точку А (л/6; 0)
7. (ТбГУ, мехмат., спец, прикладная матем., 1981 г.). F' (х) =>
=2 sin 5х-|-3 cos (х/2), которая при х = л/3 равна нулю.
Вычислите интеграл (8—10).
Л
р Hy
8. (МИИГАиК, 1978 г.). jc-^.
о
Л/4
9. (КГУ, ЭКФ, 1978 г.). $ ctg22xdx.
л/8
3
10. (МТИМБО, 1981 г.). У [зх"* + (у)а*~Х]^-
о L
156
11. (МГУ, биофак, 1978 г.). Найдите числа Ли В такие, чтобы
функция f(x) = A2x + В удовлетворяла условиям f'(l) = 2,
з
о
12. (ХГУ, физфак, 1978 г.). Найдите все значения а, удов-
2
летворяющие уравнению (/—log2 a) dt =2 log2 .
о
13. (МГУ, мехмат, 1977 г.). Найдите все числа Ь>1, для
ь
которых J (b — 4x)dx^ 6 — 5b.
i
14. (МГУ, мехмат, 1977 г.). Найдите все числа а, для кото-
2
рых J [а2 + (4 — 4а) х + 4х3] dx 12.
1
15. (МВТУ, 1978 г.). Определите, при каких а>0 выпол-
; а
няется неравенство j ех dx > у .
— &
16. (МИСйС, 1978 г.). При каких а<0 выполняется нера-
о
венство (3~2*—2-3-x)dx^0?
Найдите площадь замкнутой фигуры, ограниченной линиями
(17-97).
17. (МИИГАиК, 1978 г.). у = 2х-х\ г/ = 0.
18. (МГУ, физфак, 1977 г.). у = Зх-|- 18 — х2, t/ = 0.
19. (МТИЛП, 1977 г.). у = 4х—х2 и осью Ох.
20. (МИНХ., 1978 г.). t/=14-x2, у = 2.
21. (МСИ, 1977 г.). i/ = 0, t/ = 2x24-l, х = —1, х= 1,
сделайте рисунок.
22. (МФИ, 1979 г.). у=х2 и у = х-\-2.
23. (МГУ, почвенный фак, 1978 г.). у = х-—х, у = 3х.
24. (МИНХ, 1979 г.). 1/ = х2—2x4-3, у = 3х — 1.
25. (МИНХ, 1979 г.). у = ^х2-2х + 4, у=10-х, сделайте
О
рисунок.
26. (МАМИ, 1979 г.). у = х, у = 2х — хг.
27. (МВТУ, 1978 г.). у = 7х-2х\ х + у = 7/2.
28. (МИИГАиК, 1977 г.). г/ = х2, у = 0, х = 3.
29. (МВТУ, 1979 г.). у = ^—х + 2, у = х; х = 0, сделайте
рисунок.
30. (МВТУ, 1979 г.). г/ = 2(1—х), у= 1—х2, х = 0, сделайте
рисунок.
31. (МХТИ, 1977 г.). t/ = x2, у = 2—х, у = 0.
32. (МГМИ,' 1979 г.). у = 0, ^ = 4 (х-2), z/ = (x-l)2.
157
33. (МГМИ, 1979 г.). х = 0, у = —2х + 4, осью Ох и у = х24- 1-
34. (МГМИ, 1979 г.). у = 0, х = 0, у=— х-j-l, у = 2 —х2.
35. (МИНХ, 1977 г.). г/ = х2, г/=14-|-х2.
36. (МИЭТ, 1978 г.). t/ = x2, t/ = 2x —х2.
37. (МИЭТ, 1978 г.). г/ = х2-2х4-2, у = 2 + 4х-х2.
38. (МИТХТ, 1979 г.). у = хг + 2, t/=l-x2, х = 0, х=1.
39. (МГРИ, 1977 г.). г/ = х3-3х2—9x4-1, х = 0, г/ = 6(х<0).
40. (МГРИ, 1979 г.). у= (6х2 —х4)/9, у=1.
41. (МГРИ, 1979 г.). у = х4— 10х24-9, осью Оу и осью Ох.
42. (МИХМ, 1981 г.). х2 = 4у, х + у = 3.
43. (МТИМБО, 1980 г.), г/2 = 8х, 2х-Зг/4-8 = 0.
44. (МИИВТ, 1982 г.; МТИМБО, 1982 г.). # = cosx, z/ = 0,
х = Зл/4, х =—л/4.
45. (МТИМБО, 1982 г.). xz/ = 2, х 4-2//-5 = 0.
46. (РГУ, физфак, спец, физика, 1977 г.), у — — х2, у = 2ех,
х = 0, х — 1.
47. (СимфГУ, физфак, 1981 г.). г/ = х2, г/ = Зх-|-4.
48. (МТИМБО, 1979 г.). у = 4/х2, х=1, у = х — 1.
49. (ТбГУ, физфак, спец, радиофизика и электроника, 1981 г.).
у = х2 — 2х-|-3, «/=4— 2х.
50. (МТИМБО, 1979 г.), у=е*, у = 0, х-2.
51. (МТИМБО, 1982 г.). у = х, у = — х и касательной к кри-
вой у — Ух2 — 5 в точке М (3; 2).
52. (МТИМБО, 1981 г.). г/ = х3, у~Ух.
53. (МТИМБО, 1981 г.). у=1/х, х = 1, х = 2, г/ = 0.
54. (МТИМБО, 1982 г.). t/=l/x2, у = 0, х=1/2, х = 2,5.
55. (МТИМБО, 1982 г.). i/ = sin((nx)/2), у = х2.
56. (МГРИ, 1977 г.). z/ = x4 —2х24-5, г/= 1, х = 0, х=1.
57. (МИЭТ, 1978 г.; МТИМБО, 1982 г.). у = 5/х, «/ = 6-х.
58. (МИХМ, 1977 г.). х«/ = 3, х + у = 4.
59. (МГМИ, 1979 г.). t/ = 5-x, г/ = 6/х.
60. (МИТХТ, 1979 г.). у = §1х, у — 3 — х, х = 6.
61. (МВТУ, 1979 г.). у=1/х, у — х, х — 2, сделайте рисунок.
62. (МИНХ, 1979 г.). z/ = 9/x, у — х, х = 9, у — 0.
63. (МГРИ, 1979 г.). t/ = x2, у = 0, х = 4, у = х2/(х-2).
64. (МГРИ, 1979 г.). t/ = ~x2+3x~1., х=1, х = 2 и осью Ох.
65. (МАДИ, 1977 г.). у = 2Ух, б-у = 0, х = 0.
66. (МГМИ, 1979 г.). t/ = 0, у = — х4-2, у=Ух.
67. (МИСиС, 1978 г.). г/ = х2, у = 2У2х.
68. (МИИГАиК, 1978 г.). г/ = х2, у=Ух.
69. (МИЭТ, 1978 г.). у = Ух, у=У+-Зх, у=0.
158
70. (МИИГАиК, 1977 г.). z/=sinx, г/ = 0, причем О^х^л.
71. (МАМИ, 1979 г.). z/ = sin6x, х = 0, х = л и осью абсцисс.
72. (МВТУ, 1979 г.). t/=sin2x, у=1, х = 0 (х^О), сделайте
рисунок.
73. (МВТУ, 1978 г.). r/ = cosx, г/=1+^-х, х = у.
74. (МИИГАиК, 1978 г.). z/= l/cos2x, z/ = 0, х = 0, х = л/4.
75. (КГУ, РФФ, 1977 г). z/ = 4sin2x(l + cos2x) на промежутке
[—л; л] и осью абсцисс.
76. (КГУ, РФФ, 1977 г.). y = 2cos2x(l+sin2x) на проме-
жутке [0; 2л] и осью абсцисс.
77. (КГУ, РФФ, 1977 г.). t/= 8 sin4 х+4cos 2х на промежутке
[0; л] и осью абсцисс.
78. (КГУ, мехмат, 1977 г.). t/ = |4 —х2|/4 и у = 7 — |х|.
79. (КГУ, мехмат, 1977 г.). у = 2 —12 — х| и х/ = 3/|х|.
80. (КГУ, мехмат, 1977 г.). у = 4—ртрту и </ = | —х + 2|.
81. (КГУ, мехмат, 1977 г.). у = 3 —13—х| и у — 6/|х+ 11.
82. (ХГУ, мехмат, 1978 г.). х = — 1, х = 2,
и осью абсцисс.
83. (МГУ, биофак, 1977 г.). z/ = 0,5x2 —2х-|-2 и касатель-
ными к ней в точке (1; 1/2): у = — х-]- 1,5, и в точке (4; 2): у—
= 2х —6.
84. (КГУ, физфак, 1977 г.). у = 2х2 — 8х, касательной к этой
параболе в ее вершине и осью ординат.
85. (КГУ, физфак, 1977 г.). г/2 = — х—16 и касательными
к этой параболе, проведенными из начала координат.
86. (КГУ, физфак, 1977 г.). г/ = х2+10 и касательными к
этой параболе, проведенными из точки (0; 1).
87. (МВТУ, 1979 г.). у = х2 — 2х-}-2, касательной к этой
линии, проведенной в точке пересечения ее с осью ординат, и
прямой х = 1.
88. (МГМИ, 1979 г.). у = 2х2, осью Ох и касательной к кри-
вой у = 2х2 в точке А (х0; у0), где х0 = 2.
89. (МГМИ, 1979 г.). у = х2 + 3, осями координат и каса-
тельной к кривой t/ = x2-j-3 в точке А (х0; у0), где х0 = 2.
90. (МГМИ, 1979 г.). х = —1, у — 0, у — х2 + х+1 и каса-
тельной к кривой у = х2 + х+\ в точке Л(х0; у0), где х(, = 1.
91. (МИНХ, 1979 г.), у—1/х, х=1 и касательной к линии
г/= 1/х, проведенной в точке х = 2.
92. (МГМИ, 1979 г.). г/ = 0, х = 6, у = 4/х и касательной к
кривой у = 4/х в точке А (х„; у0), где х0 = 2.
93. (МИЭТ, 1978 г.). В некоторой точке графика функции у—
е= Кх касательная наклонена к оси абсцисс под углом 45°. Вы-
159
числите площадь фигуры, ограниченной этой касательной и пря-
мыми «/ = 0, х== 1/4.
94. (МГРИ, 1979 г.). у = х2 —х + 2 и касательной к кривой
у = In х + 3 в точке с абсциссой х=1.
95. (МИЭТ, 1979 г.). у = езх, х = 3 и прямой, являющейся
касательной к линии у = езх в точке с абсциссой х = 0.
96. (МИЭТ, 1979 г.). y = sinx(0 л/2), у = 0, у=Л и
прямой, являющейся касательной к линии у = 1g х в точке с
абсциссой х=1.
97. (МИЭТ, 1979 г.), у = cosx (0^х^л/2), у = 0, х = 0 и
прямой, являющейся касательной к линии z/ = cosx в точке х =
= л/4.
Найдите площади фигур, заданных на координатной плоско-
сти неравенствами (98—103).
98. (КГУ, ВМК, 1978 г.). |у| + у<И1-|х|.
99. (КГУ, ВМК, 1978 г.). |
100. (КГУ, ВМК, 1978 г.). |х2 + у2 -21 < 2 (х + у).
101. (КГУ, ВМК, 1978 г.). |«/| + 2|х|<х2 + 1.
102. (КГУ, ВМК, 1978 г.), х2 + у2 < 2 (| х | +1 у |).
103. (КГУ, ВМК, 1978 г.). 4 <х2 + у2 < 2 (|х | + |у|).
104. (МИЭТ, 1978 г.). Через точку пересечения кривой у =
= 2х2 + 4х — 3 с осью ординат проведена касательная к этой
кривой. Вычислите площадь фигуры, ограниченной этой касатель-
ной и прямыми л/ = 0, х = 0.
105. (МАТИ, 1979 г.). Обозначим через S(k) площадь, заклю-
ченную между параболой z/ = x2 + 2x — 3 и прямой y = kx+\.
Найдите S(—1) и вычислите наименьшее значение S (k).
106. (МИЭТ, 1978 г.). На плоскости задана точка М (1/2; 1).
Проходящая через точку прямая образует с положительными
полуосями координат треугольник. Какое минимальное значение
может принимать площадь этого треугольника?
107. (КГУ, мехмат, 1978 г.). Фигура ограничена линиями
у = х2 + 1, у = 0, х = 0, х=1. В какой точке (х0; у0) графика
функций z/ = x2+l надо провести касательную к нему так, чтобы
она отсекала от фигуры трапецию наибольшей площади?
108. (КГУ, мехмат, 1978 г.). Фигура ограничена линиями
z/=l/x, z/= 0, х=1, х = 2. В какой точке (х0; yQ) графика функ-
ции у=\/х надо провести касательную к нему так, чтобы она
отсекала от фигуры трапецию наибольшей площади?
109. (МГУ, общая геология, 1977 г.). Найдите значение пара-
метра р (р < 0), при котором площадь фигуры, ограниченной
параболой у = (1 +р2)2х2 + р и прямой г/= 0, достигает наиболь-
шего значения.
ПО. (КГУ, мехмат, 1978 г.). Фигура ограничена линиями
^ = (х-[-3)2, у = 0, х = 0. Под какими углами к оси Ох надо про-
160
вести прямые через точку (0; 9), чтобы они разбивали фигуру на
три равновеликие части?
111. (КГУ, мехмат, 1978 г.). Фигура ограничена линиями
= |sin (лх/2) |, z/ = 0, х =—1. Под какими углами к оси Ох надо
провести прямые через точку (0; 0), чтобы они разбивали фигуру
на три равновеликие части?
112. (МЭСИ, 1977 г.). Равносторонний треугольник со сторо-
ной 10 см вращается около внешней оси, параллельной стороне
треугольника и отстоящей от нее на расстоянии, равном половине
высоты треугольника. Найдите объем тела вращения.
113. (МИХМ, 1977 г.). Сумма катетов прямоугольного тре-
угольника равна 9 см. При вращении треугольника вокруг одного
из катетов образуется конус максимального объема. Найдите
площадь боковой поверхности этого конуса.
Раздел III
ГЕОМЕТРИЯ И ВЕКТОРНАЯ АЛГЕБРА
В этом разделе представлены задачи по элементам векторной
алгебры, изучаемым в средней школе, и геометрии. Задачи по
элементам векторной алгебры направлены на то, чтобы прове-
рить знание таких понятий как вектор, координаты вектора в
данной системе координат, скалярное произведение векторов. Эти
задачи носят, как правило, вычислительный характер. Однако
отметим, что понятия и методы векторной алгебры часто можно
эффективно использовать и при решении чисто геометрических
задач.
Остановимся подробнее на задачах по геометрии. Часто гео-
метрическая задача является наиболее трудоемкой частью пись-
менного вступительного экзамена, так как задача по геометрии
всегда многопланова. Здесь нужно выполнить построение необхо-
димых элементов фигуры (прямых, сечений и т. д.), сделать
чертеж, дать доказательство необходимых соотношений между
данными и построенными элементами фигуры (перпендикуляр-
ность, параллельность прямых и плоскостей и т. п.) и, основы-
ваясь на этих соотношениях, провести вычисления искомых в
задаче величин. При этом основным моментом при решении гео-
метрической задачи является четкое обоснование необходимых
соотношений между элементами фигуры, основанное на теоремах
курса геометрии. Здесь проверяется знание теоретического мате-
риала, умение применить его к решению задач. Именно поэтому
задачи на доказательство, а также небольшое количество задач
на построение выделены в отдельные параграфы. Хотя эти задачи
в «чистом виде» довольно редко встречаются в вариантах вступи-
тельных работ, но, как уже отмечалось, они являются неотъем-
лемой частью решения всякой геометрической задачи. Кроме того,
решение этих задач, несомненно, будет способствовать углублению
знания теоретического курса геометрии и окажет неоценимую
помощь при подготовке к устному экзамену по математике.
§ 1. ВЕКТОРНАЯ АЛГЕБРА
Вычислить скалярное произведение векторов (1—4).
1. а = {2; 4; 1} и &={3; 5; 7}.
2. (МИИГАиК, 1978 г.). а = {—2; 3; 11}, й-{5; 7; —4}.
3. (МЭСИ, 1975 г.). a = 2Z + 3/-4£, b = i-2J + k.
162
4. (РГУ, мехмат, 1977 г.). (2а + 3/1) • (4а — 6/8), где а, fl—
единичные взаимно перпендикулярные векторы.
5. (МТИМБО, 1980 г.). Разложить вектор rf = {l; 1; 1} по
трем некомпланарным векторам о={1; 1; —2}, Ь = {1; —Г, 0} и
с={°; 2; 3Ь
6. (МТИМБО, 1981 г.). При каком значении а векторы а =
{2, 3, —4} и 6 = {а; —6; 8} параллельны?
7. (МТИМБО, 1982 г.). При каком значении а векторы а =
₽а{1; а; —2} и 6 = {а; 3; —4} взаимно перпендикулярны?
8. (РГУ, мехмат, спец, прикладная матем., 1977 г.). Зная,
что | а | = 2, | b | = 5, (а, 6) = 2л/3, найдите, при каком значении
а векторы р = аа+176 и q = 3a — b перпендикулярны.
9. (МТИМБО, 1982 г.). При каком значении а векторы I =»
»{6; а; —8} и т — {—3; —1; 4} параллельны?
10. (МИИВТ, 1982 г.). Векторы а и b образуют угол в 120°,
|а| — 3, |6| = 5. Определите \а — 6|.
11. (МТИМБО, 1982 г.). Найдите угол между векторами а =
«{—1; 2; —2} и 6 = {6; 3; —6}.
12. (МТИМБО, 1980 г.). Найдите косинус угла между векто-
рами а — Ь и я + 6, если а = {1; 2; 1} и 6 = {2; —1; 0}.
13. (МИЭТ, 1977 г.). Даны три силы Л1 = (3; —4; 2}, № =
«{2; 3; —5} и Р—{—3; —2; 4}, приложенные к одной точке.
Вычислите, какую работу производит равнодействующая этих трех
сил, когда точка приложения равнодействующей, двигаясь пря-
молинейно, перемещается из положения 3; —7) в положе-
ние М$ (4; —1;—4).
14. (МИИГАиК, 1978 г.). При каких значениях х векторы
а = 3; 4} и 6 = {5; 6; 3} перпендикулярны?
15. (МИИГАиК, 1978 г.; РГУ, физфак, 1977 г.). Даны три
вектора а, b и с. Докажите, что вектор (Ь-с)а — (а-с)Ь пер-
пендикулярен вектору с.
16. (МИИГАиК, 1978 г.). Даны векторы а = {2; 3; —5},
6={3;0; 1} и с — {4; —3; 2}. Найдите координаты и длину вектора
<1 = За\Ь— с.
17. (МЭСИ, 1979 г.). Найдите (в градусах) угол между век-
торами a = 21 + 5/—k и b = i—j-3k.
18. (МГИ, 1977 г.). Найдите угол между векторами 2а и 6/2,
если я = {—4; 2; 4), 6 = {К2; — К2; 0}.
19. (ХГУ, мехмат, 1978 г.). Векторы а и b образуют угол
Ф = 2л/3. Зная, что |я| = 3, |6| = 4, вычислите (За —26) (а+ 26).
20. (МИИГАиК, 1977 г.). Даны четыре точки А (—2; —3; 8),
В (2; 1; 7), С (1; 4; 5), D (—7; —4; 7). Будут ли коллинеарны
векторы АВ и CD?
21. (МВМИ, 1977 г.). Найдите вектор а, коллинеарный век-
тору 6 = {3; 6; 6} и удовлетворяющий условию а-Ь = 27.
22. (МИИГАиК, 1978 г.). Найдите вектор а, коллинеарный
вектору 6 = {2; —Г, 0}, если а Ь = 10.
23. (МИЭТ, 1977 г.; МТИМБО, 1981 г.). Найдите координаты
6*
163
вектора х, коллинеарного вектору a = 2i +J—k и удовлетворяю-
щего условию х-а = 3.
24. (МВМИ, 1977 г.). Найдите вектор а, коллинеарный век-
тору & = {1; —3; 1} и удовлетворяющий условию а-Ь — 22.
25. (МИХМ, 1977 г.). Найдите вектор Ь = {х\ у, г}, коллине-
арный вектору а = {2]^2; —1; 4}, если |&| = 10.
26. (МЭСИ, 1977 г.). Найдите вектор с, зная, что он пер-
пендикулярен векторам а = {2; 3; —1}, б = {1; —2; 3} и удов-
летворяет условию c (2i—= —6.
27. (МЭСИ, 1977 г.). Вектор Ь, коллинеарный вектору а =
« {8; —10; 13}, образует с осью Oz острый угол; зная, что
| Ь | = К37, найдите его координаты. В ответе запишите сумму
координат вектора b с точностью до 0,01.
28. (МИИГАиК, 1977 г.). Найдите вектор Ь, зная, что он
удовлетворяет условиям: скалярное произведение дс = 3, где с =
= {1; —1; 2}, вектор b перпендикулярен а и d, где а —
= {-2; —1; 1}, d = {3; 5; —2}.
29. (МИЭТ, 1977 г.). Найдите косинус угла между векторами
р и q, удовлетворяющими системе уравнений
/ 2p + q = a,
I
если известно, что в прямоугольной системе координат векторы
а н b имеют вид а = {1; 1}, д = {1; —1}.
30. (МИЭТ, 1977 г.). Даны три вектора а = {3; —1}, b = {1; —2},
с — \—1, 7}. Определите разложение вектора р = а-\-Ь-\-с
по векторам а и Ь.
31. (МАТИ, 1979 г.). Даны векторы а = {1; —1; 3}, Ь =
,с={3;—5; 6}. Вычислите np(a+&)(2a —6).
32. (МИЭТ, 1979 г.). Вектор х, перпендикулярный векторам
a = 3i + 2J+2k и b=\8i — 22j—5k, образует с осью Оу тупой
угол. Найдите его координаты, зная, что длина вектора х рав-
на 14.
33. (МИЭТ, 1977 г.; МТИМБО, 1982 г.). Вектор х удовлет-
воряет следующим условиям: а) х коллинеарен вектору а = 67 —
—8j — 7,5fe; б) х образует острый угол с осью Ог; в) | х | = 50.
Найдите координаты вектора х.
34. (МИЭТ, 1979 г.). Даны два вектора « = {—1; 1; 1} и Ь=
= (2; 0; 1}. Найдите вектор х, если известно, что он компланарен
плоскости векторов а и Ь, перпендикулярен вектору b и ах=1.
35. (МИСиС, 1978 г.). В пространстве даны два вектора а=
е={ 1; 1; 2} и 6s={—1; 3; 1}. Найдите единичный вектор, лежащий
в плоскости векторов а и Ь и образующий угол а = л/4 с век-
тором а.
36. (МИЭТ, 1978 г.). Даны три ненулевых вектора а, Ь, с,
каждые два из которых неколлинеарны. Найдите их сумму, если
a~vb коллинеарен с, ib + c коллинеарен вектору а.
37. (МАМИ, 1979 г.). Даны вершины треугольника А (3; 2;—3);
164
В (5; 1; —1); С (1; —2; 1). Найдите его внутренний угол при
вершине А.
38. (МИТХТ, 1979 г.). Докажите, что точки А (—2; —3),
В (—3; 1), С (7; 7), D (3; 0) служат вершинами трапеции. Най-
дите длину средней линии трапеции.
39. (МАИ, 1979 г.). Треугольник задан координатами своих
вершин А (3; 2; —3), В (5; 1; —1) и С (1; —2; 1). Вычислите
величину внешнего угла треугольника при вершине А и коорди-
наты вектора а, «(направленного с вектором АВ и имеющего
длину вектора АС.
40. (МИНХ, 1979 г.). Даны три последовательные вершины
параллелограмма А (—3; —2; 0), В (3; —3; 1) и С (5; 0; 2).
Найдите его четвертую вершину D и угол между векторами АС
и BD.
41. (МАИ, 1979 г.). Треугольник задан координатами своих
вершин А (2; 1; 2), В (1; 0; 0) и С (1 +1/3; /3; — /б). Вычис-
лите величины углов треугольника и длину медианы т, прове-
денной к стороне ВС.
42. (МИСиС, 1978 г.). В треугольнике АВС точка А (—1; 2; 3) —
вершина прямого угла. Найдите координаты вершин В и С, если
известно, что В и С лежат на прямой (MN), где М (—1; 3; 2),
Af(l; 1; 3) и ДВС = 30°.
43. (МИЭТ, 1977 г.). В трапеции ABCD вектор BC = XAD.
Докажите, что вектор р = AC -[-BD коллинеарен AD (а значит
и ВС), и в записи /? = aAD найдите коэффициент а.
44. (РГУ, мехмат, спец, матем., механ., 1977 г.). Дан треугольник
АВС. Длины векторов СВ, СД, АВ равны соответственно а, Ь,
с. Найдите скалярное произведение векторов СА и СО, где
[СО] —медиана треугольника АВС.
45. (МТИМБО, 1979 г.) Докажите, что сумма векторов, сое-
диняющих центр правильного треугольника с его вершинами,
равна нулю.
46. (ТбГУ, физфак, 1978 г.). Через вершину С квадрата ЛВСО
проведена прямая, параллельная диагонали [ВО], которая пере-
секает прямую [ДО] в точке £; Q —точка пересечения диагона-
лей квадрата. Выразите через векторы ОС и CQ сумму векто-
ров АВ и СЕ.
47. (МТИМБО, 1980 г.). Какой угол образуют единичные
векторы а и Ь, если известно, что векторы с = а-[-2Ь и d
^Ьа — ^b взаимно перпендикулярны.
48. (РГУ, физфак, 1977 г.). Дан параллелограмм ABCD.
—> —> —>
Длины векторов ДВ, ДО, ВО равны соответственно а, Ь, с. Най-
дите скалярное произведение векторов АС и AD.
165
49. (РГУ, мехмат, 1977 г.). Дан параллелограмм ABCD.
Длины векторов АВ, AD, АС равны соответственно а, Ь, с. Най-
дите скалярное произведение векторов DB и АВ.
50. (МТИМБО, 1979 г.). Зная векторы р и q, на которых
построен параллелограмм, выразите через них вектор, совпадаю-
щий с высотой параллелограмма, перпендикулярной к стороне р.
51. (РГУ, мехмат, 1977 г.). Дана трапеция ABCD. Длина
основания [AD] в три раза больше длины основания [ВС]. Дли-
ны векторов АВ, ВС, АС равны соответственно а, Ь, с. Найдите
скалярное произведение векторов ВА и AD.
52. (РГУ, мехмат, 1977 г.). В треугольнике проведены меди-
аны [ЛО], [ВС], [СВ]. Вычислите ВС- ADA-CA-BEA- AB-CF.
53. (МИЭТ, 1977 г.). Дан параллелограмм Л BCD ([ЛО]|| [ВС],
[AB]||[CD]). На стороне [ЛО] выбрана точка К, а на [ЛС] —
точка L так, что | АК | = | AD |/5, | AL | = | АС |/6. Докажите, что
векторы KL и BL коллинеарны, и в записи KL = 7.BL найдите
коэффициент пропорциональности %.
54. (МИЭТ, 1977 г.). Пусть Л BCD —параллелограмм, причем
[ЛО]||[ВС], /( — середина [ВС], L — середина [DC]. Обозначим
АК = а, AL — b. Выразите векторы BD и АС через а и Ь.
55. (МИЭТ, 1978 г.). Дан правильный шестиугольник ABCDEF,
М — середина [DB], У —середина [ЛМ], В —середина [ВС]. Раз-
ложите вектор NP по векторам ЛВ и AF.
56. (МИНХ, 1979 г.). В треугольнике ЛВС известны длины
сторон |ЛВ | = 6, |ЛС| = 8 и угол Л = 90°; [ЛАГ] и [В/V] — бис-
сектрисы углов Л и В. Найдите косинус угла между векторами
AM и ВАГ.
57. (МИЭТ, 1978 г.). На сторонах [ВС], [СЛ] и [ЛВ] тре-
угольника ЛВС вне его построены квадраты с центрами Ait Bt
и Ct соответственно. Найдите ЛЛ1 + ВВг-{-СС1.
58. (МИЭТ, 1977 г.; РГУ, 1977 г.). В треугольнике ЛВС
через М обозначена точка пересечения медиан. Докажите, что
МА +МВ + МС = о.
59. (МИЭТ, 1977 г.; СимфГУ, матфак, 1982 г.). Длина гипо-
тенузы АВ прямоугольного треугольника ЛВС равна с. Найдите
сумму АВ-АС А-ВС-ВА + С А-СВ.
60. (МИЭТ, 1978 г.). В треугольнике ЛВС точка М — центр
вписанной окружности. Найдите вектор аМЛ+рМВ + уЛ1С, если
а = | ВС|, ₽ = |СЛ |, ? = | ЛВ|.
61. (МИРЭА, 1979 г.). Точка О —центр окружности, описан-
ной около треугольника ЛВС. Докажите, что ОА sin 2Л+
А~ОВ sin 2В + ОС sin 2С= о.
166
62. (МАИ, 1979 г.). Дана прямоугольная система координат
с началом в точке О. Прямая пересекает ось абсцисс в точке С,
ось ординат в точке А так, что ОСА=а и а > л/4. Точка D —
середина [АС], а точка At симметрична точке А относительно
прямой (OZ?). Определите длины сторон треугольника ACAif если
известны координаты точки С (1; 0).
63. (МАИ, 1979 г.). Дана прямоугольная система координат
с началом в точке О. Прямая пересекает ось абсцисс в точке С,
ось ординат —в точке А так, что ОСА—а и а > л/4. Точка D—
середина [АС], а точка Af симметрична точке А относительно
прямой (OD). Найдите отношение площадей &ODC и ДОСАР
64. (МАТИ, 1979 г.). Доказать, что точки А (5; 0), В (0; 2)
и С (2; 7) являются вершинами прямоугольного треугольника.
Найдите его площадь и укажите все перемещения плоскости,
переводящие его в треугольник с вершинами (—5; 0), (0; —2)
И (-2; —7).
65. (МАТИ, 1979 г.). Доказать, что точки А (3; 0), В (0; 1),
С (2; 7) и D (5; 6) являются вершинами прямоугольника ABCD.
Вычислите его площадь и укажите все перемещения плоскости,
при которых он переходит в себя.
66. (МАТИ, 1979 г.). При каких х и у точки с координатами
А (2; 0), В (0; 2), С (0; 7) и D (х\ у) являются последователь-
ными вершинами равнобочной трапеции ABCD7 JIjir каждой из
этих трапеций найдите площадь и укажите все перемещения
плоскости, переводящие ее в трапецию с вершинами (2; 0), (7; 0),
(0; —7) и (0; —2).
67. (МИЭТ, 1979 г.). К вершине куба приложены три силы,
равные по величине 1, 2, 3 и направленные по диагоналям гра-
ней куба, пересекающихся в этой вершине. Найдите величину
равнодействующей этих трех сил.
68. (МИЭТ, 1978 г.). Дан куб ABCDA^fiJ)^ о нижним
основанием ABCD, верхним — A 1BlC1Di и боковыми ребрами А Ай
BBit CCf, DD}. Докажите, что на прямой (MAIJ, где М и Мг—
соответственно центры граней ABCD и Aнайдется точка О
такая, что ОА-}-ОВ-\-ОС + OD =— OMt. Покажите, что Л1О=
и найдите X.
69. (ХГУ, физфак, 1978 г.). Найдите сумму скалярных про-
изведений векторов, начала которых находятся в центре грани
куба, а концы —в вершинах (таких векторов 8). Длина ребра
куба равна Ь.
70. (МИНХ, 1978 г.). В правильной треугольной пирамиде
ABCS плоский угол при вершине —прямой. Точки D и £ —сере-
дины ребер АС и SB соответственно. Найдите угол между век-
торами SD и ЕС.
71. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху на кривой у = х2 —4x4-5 заданы точка А (хх; у А
167
G абсциссой Xf = l и точка В (х-2, с ординатой г/а=1. Най-
дите скалярное произведение векторов ОА и ОВ.
72. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху на части кривой у — х2— 2x4-3, лежащей в первой
четверти, заданы точка A (х£; yj с абсциссой xf=l и точка
В (х2; у2) с ординатой t/a=ll. Найдите скалярное произведение
векторов ОА и ОВ.
73. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху на кривой t/=2x2 —3x4-5 заданы точка X(xi; уг)
с абсциссой Xi = 1 и точка В—точка пересечения этой кривой
с кривой z/ = 2x2— 2x4-3. Найдите скалярное произведение век-
торов О А и ОВ.
74. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху на кривой у = хг заданы две точки А и В такие,
что OA-i=l и OB-i = —2, где / — единичный вектор оси Ох.
Найдите длину вектора 20А — ЗОВ.
75. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху на кривой у=2х+2 заданы две точки А и В такие,
что OA-i = — 1 и 0В-1 = 2, где I—единичный вектор оси Ох.
Найдите длину вектора —ЬОАА-ОВ.
76. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху на кривой г/ = 6/х заданы две точки А и В такие,
что ОА-1 =—2 и 0В1 = 3, где /—единичный вектор оси Ох.
Найдите длину вектора 2OA-j-3OB.
77. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху к кривой 1/ = х24-х4-Ю проведена касательная
в точке А (ха; у0), гдех0= 1, и эта касательная пересекает ось Ох
' > ' >
в точке В. Найдите скалярное произведение векторов О А и АВ.
78. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху к кривой t/=2j/x проведена касательная в точке
Л(х0; у0), где х0=1, и эта касательная пересекает ось Ох в точ-
ке В. Найдите скалярное произведение векторов АВ и ОА.
79. (МГМИ, 1979 г.). В декартовой прямоугольной системе
координат Оху к кривой у = 8/х2, проведена касательная в точке
А (х0; Уо), где х2 = 2, и эта касательная пересекает ось Ох в точ-
ке В. Найдите скалярное произведение векторов АВ и ОВ.
80. (МАМИ, 1979 г.). Напишите уравнение образа параболы
у = х2 — 2x4-1 при параллельном переносе р = 1+-3].
§ 2. ПЛАНИМЕТРИЯ. ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО
1. Докажите, что угол С треугольника АВС будет прямым’в том
и только в том случае, если длины сторон этого треугольника
связаны равенством | АВ (2 = | АС |24-1 ВС j2.
168
2. (ЯГУ, 1980 г.). У двух выпуклых четырехугольников сов-
падают середины сторон. Докажите, что площади этих четырех-
угольников равны.
3. Докажите, что в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда суммы длин противо-
положных сторон этого четырехугольника равны.
4. Вокруг трапеции описана окружность. Докажите, что это
возможно тогда и только тогда, когда данная трапеция равно-
бочная.
5. Около окружности описана равнобочная трапеция ABCD.
Точки Е и /С —точки касания этой окружности с боковыми сто-
ронами [АВ] и [СО]. Докажите, что отрезок [£7<] параллелен
основаниям трапеции.
6. (ЛатвГУ, 1980 г.). Через концы дуги окружности, содер-
жащей 120°, проведены касательные, и в фигуру, ограниченную
этими касательными и данной дугой, вписана окружность. Дока-
жите, что длина этой окружности равна длине исходной дуги.
7. (МТИЛП, 1978 г.). Докажите, что в прямоугольном ^тре-
угольнике сумма длин катетов равна сумме диаметров вписанной
и описанной окружностей.
8. В равнобедренном треугольнике с основанием а и боко-
вой стороной b угол при вершине равен 20°. Докажите, что |я|3+
+ |&|3 = 3|а||Ь|2.
9. В треугольнике длины сторон а, b и с связаны равенством
I а |2 +1 b |2 = 5 | с |2. Докажите, что медианы к сторонам а и b
взаимно перпендикулярны.
10. Две окружности касаются внешне друг друга в точке С.
К ним проведена общая внешняя касательная (АВ), где А и В —
точки касания. Докажите, что АСВ = л/2.
11. (ЯГУ, 1980 г). Докажите, что радиус г вписанного в мно-
гоугольник круга равен 2S/P, где S и В —соответственно пло-
щадь и периметр многоугольника.
12. Внутри параллелограмма ABCD взята точка О. Дока-
жите, что сумма площадей А О АВ и /\OCD постоянна при любом
выборе точки О.
13. ABCD — квадрат. На стороне [СО] взята точка М, К—
точка пересечения стороны [ВС] с биссектрисой угла ВАМ. Дока-
жите, что | МА | = |вЛ j + |О2И |.
14. В прямоугольном ДАВС угол В прямой, [ВО] —высота,
опущенная на гипотенузу [АС]. Докажите, что | BD | равна сумме
радиусов окружностей, вписанных в ДАВС, Д ADB и /\CDB.
15. Каждая сторона выпуклого четырехугольника пересекается
некоторой окружностью в двух точках, причем длины отрезков
сторон, лежащих внутри окружности, равны. Докажите, что в дан-
ный четырехугольник можно вписать окружность.
16. Величина одного из углов треугольника равна 30°. Дока-
жите, что длина стороны, противоположной этому углу, равна
радиусу описанной окружности.
169
17. Докажите, что середины сторон выпуклого четырехуголь-
ника являются вершинами параллелограмма.
18. Докажите, что сумма длин медиан треугольника больше
его полупериметра, но меньше его периметра.
19. В треугольнике центры вписанной и описанной окружно-
стей совпадают. Докажите, что этот треугольник равносторонний.
20. Докажите, что если прямая, соединяющая середины осно-
ваний трапеции, перпендикулярна основаниям, то трапеция —
равнобочная.
21. Докажите, что прямая, соединяющая середины оснований
трапеции, и продолжения боковых сторон трапеции пересекаются
в одной точке.
22. Докажите, что линия центров двух пересекающихся окруж-
ностей делит пополам их общую хорду.
23. Докажите, что общие внешние касательные двух окруж-
ностей пересекаются на линии центров или параллельны ей; общие
внутренние касательные пересекаются на линии центров.
24. Докажите, что в равнобедренном треугольнике сумма рас-
стояний от любой точки основания до боковых сторон постоянна.
25*. Через центр правильного треугольника проведена пря-
мая. Докажите, что сумма квадратов расстояний от вершин тре-
угольника до этой прямой не зависит от выбора прямой.
26. Докажите, что прямые, соединяющие последовательно
центры квадратов, построенных на сторонах параллелограмма и
примыкающих к нему извне, образуют квадрат.
27. Дан равнобедренный треугольник ABC, R и г —радиусы
описанной и вписанной окружностей. Докажите, что расстояние
между центрами окружностей равно R(R — 2г).
28. Докажите, что расстояние от любой точки окружности,
описанной около правильного треугольника, до одной из его вер-
шин равно сумме расстояний от этой точки до двух других вер-
шин.
29. Докажите, что если стороны одной трапеции равны соот-
ветствующим сторонам второй трапеции, то эти трапеции равны.
30. Докажите, что в трапеции, диагонали которой служат
биссектрисами углов при одном из оснований, длины трех сторон
равны.
31. Пусть а и b (а> Ь) — длины оснований трапеции. Дока-
жите, что отрезок, соединяющий середины диагоналей трапеции,
параллелен основаниям трапеции, а его длина равна (а —Ь)/2.
32. Через точку О пересечения диагоналей трапеции прове-
дена прямая, параллельная основаниям трапеции. Докажите, что
точка О делит пополам отрезок, отсекаемый от прямой боковыми
сторонами трапеции.
33. Докажите, что биссектриса внутреннего угла треугольника
делит противоположную сторону на отрезки, пропорциональные
прилежащим сторонам. Докажите, что верно и'^обратное утверж-
дение, т. е. если прямая, проходящая через вершину, делит про-
170
тиволежащую сторону на отрезки, пропорциональные прилежащим
сторонам, то эта прямая—биссектриса.
34. Пусть т, р, h — соответственно медиана, биссектриса и
высота треугольника, проведенные к одной и той же стороне
треугольника. Докажите, что точка пересечения биссектрисы
с этой стороной лежит между точками пересечения медианы и
высоты с этой стороной (или ее продолжением). Докажите, что
эти точки совпадают в том и только в том случае, если треуголь-
ник равнобедренный.
35. Пусть а, о, с —длины сторон треугольника АВС, лежащих
против углов Л, В и С соответственно, р = (а + & + с)/2 — полу-
периметр, S —плошадь, R и г — радиусы описанной и вписанной
окружностей. Докажите, что справедливы следующие соотношения:
v a b с к-»
1) —- =—- =—- = 27? — теорема синусов;
sin Л sin В sin С
2) а2 = Ь2 + с2 — 2bc cos А — теорема косинусов;
3) S = -i-bcsinА;
4) S = У р (р — а) (р — Ь) (р — с) — формула Герона;
5) S — pr,
6)
7) если та, Рд, ha — длины медианы, биссектрисы и высоты,
проведенных из А, то
та = 1 К2са + 2&2-а2;
о __ sin В ас л
~ sin (Л/2) Ь+с ’
ha = ~ (Р~Ь)(Р-С).
36. Через точку А, лежащую вне круга, проведены две пря-
мые, одна из которых касается окружности, служащей границей
круга, в точке В, а другая пересекает эту окружность в точках
С и D. Докажите, что | ЛО|| ДС| = | АВ\2 (теорема о касательной
и секущей).
37. (БашГУ, 1980 г.) В треугольнике высота и медиана, про-
веденные из одной вершины, делят угол при этой вершине на
три равные части. Докажите, что углы этого треугольника по
величине равны 30°, 60° и 90°.
38. (МИФИ, 1980 г.). В трапеции сумма углов при большем
основании равна 90°. Докажите, что длина отрезка, соединяю-
щего середины оснований, равна полуразности длин оснований.
39. Докажите, что при пересечении биссектрис внутренних
углов параллелограмма, не являющегося ромбом, получается пря-
моугольник, длины диагоналей которого равны разности смежных
сторон параллелограмма.
40. Докажите, что если в трапеции хотя бы одна из диаго-
171
налей в точке пересечения с другой делится пополам, то эта
трапеция — параллелограмм.
41. Докажите, что если отрезок, соединяющий/середины двух про-
тивоположных сторон четырехугольника, равен полусумме двух
других сторон, то этот четырехугольник —трапеция.
42. Докажите, что если длины двух медиан треугольника
равны, то треугольник равнобедренный.
43. Докажите, что если длины двух высот треугольника рав-
ны, то треугольник равнобедренный.
44* . Докажите, что ограниченная фигура не может иметь два
центра симметрии.
45. Докажите, что если выпуклый четырехугольник имеет ось
симметрии, то либо около него можно описать окружность, либо
в него можно вписать окружность.
46. Докажите, что если четырехугольник имеет центр 'сим-
метрии, то этот четырехугольник —параллелограмм.
47. Докажите, что в треугольнике биссектриса делит пополам
угол между высотой и радиусом описанного круга, проведенным
в ту же вершину.
48. В круге диаметра d проведены две взаимно перпендику-
лярные хорды [ДВ] и [СО]. Докажите, что | ДО|2 + |СВ|2 = б!2.
49. На диаметре круга радиуса 1, как на стороне, построен
равносторонний треугольник. Докажите, что площадь части тре-
угольника, находящейся вне круга, равна (ЗКЗ — л)/6.
50. Даны три равных приложенных друг к другу квадрата
ABCD, DCEF, FEPQ. Докажите, что CAD + EAF-\-PAQ = 90°.
51. Докажите, что биссектрисы внутреннего и прилежащего
к нему внешнего углов треугольника взаимно перпендикулярны.
Докажите, что верно и обратное утверждение: прямая, проходя-
щая через вершину треугольника перпендикулярно биссектрисе
внутреннего угла при этой вершине, является биссектрисой внеш-
него угла.
52. Дан равнобедренный треугольник. Из произвольной точ-
ки Р основания восставлен перпендикуляр. Докажите, что сумма
длин отрезков от точки Р до точек пересечения перпендикуляра
с боковыми сторонами или их продолжениями не зависит от вы-
бора точки Р на основании.
53. В ромб, не являющийся квадратом, вписан квадрат. Дока-
жите, что его стороны параллельны диагоналям ромба.
54. Докажите, что в любом треугольнике имеет место нера-
венство R^2r (R и г —радиусы описанного и вписанного кругов),
причем равенство R = 2r имеет место только для правильного
треугольника.
55. (МИРЭА, 1978 г.). Докажите, что для всякого треуголь-
ника АВС справедливо неравенство cos А + cos В + cos С 3/2.
56. Пусть а, Ь, с и d — длины последовательных сторон четы-
рехугольника, S —его площадь. Докажите, что
1) (a + c)(/? + d)^4S,
172
2) ac + bd^2S,
3) ab + cd 2S,
4) ad-\-bc^2S.
57. Через точку M, взятую внутри круга, проведена хорда
(АВ) (точки А и В лежат на окружности). Докажите, что вели-
чина | AM | • | МВ | постоянна для всех таких хорд.
Следующие задачи на нахождение геометрических мест точек
(т. е. множества всех точек, удовлетворяющих какому-либо тре-
буемому свойству) тесно связаны с задачами на доказательство.
При решении этих задач часто бывает удобно использовать коор-
динатный метод.
Конечно, задачи на отыскание геометрических мест точек
можно решать и чисто геометрическими методами, используя те
или иные геометрические теоремы.
58. (КГУ, мехмат, 1977 г.). На плоскости даны две взаимно
перпендикулярные прямые. Найдите множество всех точек пло-
скости, сумма расстояний от которых до данных прямых равна
сумме величин, обратных данным расстояниям.
59. На плоскости даны две точки, расстояние между кото-
рыми равно 1. Найдите множество точек, расстояния которых до
двух данных точек относятся как т:п.
60. (КГУ, мехмат, 1977 г.). На плоскости даны две взаимно
перпендикулярные прямые. Найдите множество всех точек пло-
скости, 1) произведение расстояний от которых до данных прямых
равно модулю разности этих расстояний; 2) модуль разности рас-
стояний от которых до данных прямых равен модулю разности
величин, обратных к данным расстояниям.
61. На плоскости даны прямая и не лежащая на ней точка.
Найдите множество точек, равноудаленных от данной прямой и
данной точки.
62. Найдите множество точек, разность квадратов расстояний
которых до двух данных точек А и В постоянна.
63. Найдите множество точек, сумма расстояний от которых
до двух пересекающихся прямых равна постоянной величине.
64. Найдите множество точек, разность расстояний от кото-
рых до двух пересекающихся прямых равна постоянной величине.
65. Даны два непараллельных отрезка [ЛВ] и [СО]. Найдите
множество точек 7И, для которых площади ДЛЛ4В и ДСЛЮ
равны.
66. Найдите множество середин хорд, проходящих через дан-
ную точку внутри данной окружности.
67. Концы отрезка длины а скользят по сторонам данного
прямого угла. Найдите множество точек, пробегаемых серединой
данного отрезка.
68. Найдите геометрическое место таких точек плоскости, что
касательные, проведенные из этих точек к данной окружности,
образуют между собой угол ос.
173
§ 3. ПЛАНИМЕТРИЯ. ЗАДАЧИ НА ПОСТРОЕНИЕ
Все построения данного параграфа (если специально не ого-
ворено противное) проводятся только циркулем и односторонней
линейкой без делений. Другими словами, мы можем построить
окружность, радиус которой равен длине заданного отрезка, с цент-
ром в данной точке (циркуль) и через любые две данные точки
провести прямую (линейка). Более сложные построения осно-
ваны на различных соотношениях между элементами фигур, ко-
торые надо построить, и вытекающих из аксиом и теорем пла-
ниметрии, и последовательном выполнении указанных двух эле-
ментарных построений. Проведем простейшие построения, ука-
зывая те теоремы курса планиметрии, на которых они основаны.
Пример 1. Даны прямая I и точка М. Проведите прямую Г,
проходящую через точку М перпендикулярно прямой I.
Построение, а) Рассмотрим сначала случай, когда М £ I
(рис. 1).
1) Построим окружность с центром в точке М С I какого-либо
радиуса г>0. Пусть точки А1£ и М —точки пересечения этой
окружности с прямой Z. Тогда точка М — середина отрезка [A^AIJ.
2) Построим окружности одного и того же радиуса R > г
с центрами в точках и М2. Пусть М' — одна из двух точек
пересечений этих окружностей. По построению точка М' равно-
удалена от точек А1£ и М.2, следовательно, она лежит на пер-
пендикуляре, проведенном через середину отрезка [AI£A1^], т. е.
через точку А1.
3) Через точки М и М' проводим искомую прямую По-
строение закончено.
Таким образом, в данном случае мы воспользовались теоре-
мой о перпендикуляре к середине отрезка и, кроме того, что
важно отметить, неявно пользуемся теоремой о единственности
перпендикуляра к данной прямой, проведенного через данную
точку.
174
б) Пусть теперь M(£l (рис. 2).
1) Построим окружность с центром в точке М достаточно
большого радиуса R (радиус окружности таков, что она пересе-
кает прямую / в двух точках). Пусть и ЛЦ—-точки пересечения
прямой I с этой окружностью. По построению точки М± и
равноудалены от точки М и, следовательно, точка М лежит на
серединном перпендикуляре к отрезку [AfjAfJ.
2) Построим окружности одного и того же радиуса > R
с центрами в точках Л4Х и М2. Пусть ЛГ —одна из точек пере-
сечения этих окружностей. Тогда, по построению, Мг также
равноудалена от и М2 и, следовательно, также лежит на сере-
динном перпендикуляре к отрезку [Л41Л12].
3) Через точки М и М' проводим искомую прямую
Здесь мы вновь воспользовались теоремой осерединном перпен-
дикуляре, единственностью этого перпендикуляра. Кроме того,
в обоих случаях мы неявно опирались на аксиомы планиметрии,
которые нам гарантируют возможность выполнения наших двух
элементарных построений (например то, что через две данные точки
можно провести и притом единственную прямую). Далее это за-
мечание мы делать больше не будем.
Пример 2. Даны прямая Z и точка M(£l. Через точку Л1
проведите прямую 1( параллельно прямой Z.
Построение (рис. 3).
1) Из точки М опустим на прямую Z перпендикуляр Пусть
Mt — точка пересечения прямых I и 1±.
2) Из какой-либо точки М2 С Z, не совпадающей с точкой Мь
восставим перпендикуляр 12 к прямой Z.
3) Проведем окружность с центром в точке Л12, радиус кото-
рой равен Пусть точка ЛГ — точка пересечения этой
окружности с прямой Z§, лежащая в той же (относительно пря
мой Z) полуплоскости, что и точка Л1. Тогда по построению точ
ки М иЛГ равноудалены от пря-
мой Z и лежат в одной полу-
плоскости. Следовательно, (тео-
рема!) прямая, проходящая че-
рез точки Л1 и ЛГ, параллельна
прямой Z.
4) Проводим через точки М
и Мг искомую прямую Г.
При проведенном построении
V Mr , ,т
7 - - , If h
и 1 MZ
Рис. 3.
мы помимо теорем, использован-
ных в предыдущей задаче, опирались
в третьем пункте на тео-
рему, которую можно рассматривать как «признак параллело-
грамма». В самом деле, отрезки [ЛШХ] и [ЛГЛ!^] параллельны
(так как они перпендикулярны прямой Z) и равны по длине.
Следовательно, четырехугольник ММгМ2М' — параллелограмм.
Отсюда следует, что Z'||Z.
Пример 3. Данный отрезок [ЛВ] разделите пополам.
175
Построение (рис. 4). Фактически это построение содер-
жится в задаче 1.
1) Проводим окружности, радиус которых равен | АВ\, с цент-
рами в точках А и В, Пусть и М$ — точки пересечения этих
окружностей. Они равноудалены от концов отрезка [ЛВ] и, сле-
довательно, обе лежат на серединном перпендикуляре к отрез-
ку [ЛВ].
2) Через точки Мт и проводим прямую /х. Их точка пере-
сечения С и является искомой точкой.
Пример 4. Даны: прямая /,
точка О С I и угол Л. От дан-
ной прямой I отложите угол,
конгруэнтный углу А, так, чтобы его вершина совпала с точкой О,
а одна из сторон была направлена вдоль прямой Z.
Построение (рис. 5). 1) Из вершины Л данного Л прове-
дем окружность какого-либо радиуса /?>0. Пусть и —
точки пересечения этой окружности со сторонами угла.
2) Строим окружность того же радиуса R с центром в точке О.
Пусть одна из (двух) точек пересечения этой окружности и
прямой Z. Проводим окружность с центром в /Q, радиус которой
равен IMjMgl- Пусть — точка пересечения этой окружности и
окружности радиуса R с центром в точке О (опять какая-либо
одна из двух).
3) Соединяем точки О и К& имеем
|О^| = |ОК§| = | ЛД41| = | ЛМ2|, |= | |
по построению. Следовательно, ДМ1ЛЛ4^ конгруэнтен
Поэтому построенный угол конгруэнтен данному в условии углу.
Отметим, что мы построили один из четырех углов, удовлет-
воряющих условию задачи. Вместе с построенным углом условию
удовлетворяет угол, симметричный относительно прямой I дан-
ному углу, и углы, центрально симметричные этим углам относи-
тельно точки О. Кроме того, отдельно следует рассмотреть случай,
когда данный угол равен двум прямым. В этом случае сама пря-
мая I с данной на ней точкой О и будет давать требуемое по-
строение.
176
Пример 5. Даны отрезок [ЛВ] и Д. Постройте множество
всех точек С таких, что АСВ конгруэнтен данному Д.
Построение (рис. 6).
1) Пусть Z — прямая, проходящая через точки Л и В. От пря-
мой I в точке Л отложим угол ВАМ, конгруэнтный данному Д, и
пусть — прямая, проходящая через точки А и М.
2) Восставим серединный перпендикуляр 13 к отрезку [ЛВ]
(О —середина отрезка [ЛВ]) и перпендикуляр Ц к прямой lt
в точке Л. Пусть точка О—точка пересечения этих перпенди-
куляров (если угол Д был прямым, то точка О совпадает с D).
3) Проведем окружность с центром в точке О и радиусом
длины | О А |; рассмотрим дугу ЛВ, лежащую в той же полуплос-
кости (относительно прямой /), что и точка О, с выколотыми
точками Л и В и симметричную ей относительно I дугу. Объеди-
нение этих двух дуг окружностей и даст нам искомое множество
точек. В самом деле, взяв произвольную точку С, принадлежа-
щую построенному множеству, мы получим, что АСВ измеряется
половиной дуги ЛВ, на которую он опирается (вписанный угол),
и угол ВАМ также измеряется половиной той же дуги (как угол
между касательной к окружности и хордой [ЛВ], проведенной
из точки касания). Следовательно,
углу Д. Если же взять точку С,
не принадлежащую построенному
множеству, то условие задачи выпол-
нено не будет (проверьте самостоя-
тельно).
В проведенном построении, как
мы видим, использовано много теорем
планиметрии. Здесь, помимо теорем
ранее разобранных задач, мы вос-
пользовались теоремой о вписанном
в окружность угле, о касательной и
хорде, теоремой о касательной и ра-
диусе, проведенном в точку касания
(а именно, мы использовали то, что
прямая lt будет касательной к окруж-
ности с центром в точке О радиуса
|ОЛ |). Отсюда мы видим, что ре-
шение задач на построение способ-
ствует активному овладению теоре-
АСВ конгруэнтен данному
К
тическим материалом, что принесет ощутимую пользу и при
решении «стандартных» конкурсных задач по геометрии.
Рассмотрим еще одну простейшую задачу на построение, опи-
рающуюся на теорему о подобии треугольников.
177
Пример 6. Даны отрезки [ДВ] и [СО]. Постройте отрезок
[МЛ/], длина которого равна среднему геометрическому длин дан-
ных отрезков, т. е. = ДВ|-|СО|.
Построение (рис. 7). Данное соотношение между длинами
отрезков можно переписать в эквивалентном виде
| АВ | _ | MN |
| A12V| | CD | ’
поэтому эту задачу иногда называют задачей о построении сред-
него пропорционального двух данных отрезков.
1) На какой-либо прямой I отложим отрезок [ДВ] и отрезок
[В/С], конгруэнтный [СО]. Пусть О —середина отрезка [Д/С]. По-
строим окружность с центром в точке О и радиуса | ОК | = | Д/С 1/2 ==я
= (| ДВ 1 + 1 СО |)/2.
2) Из точки В восставим перпендикуляр к прямой I. Пусть
Е—одна из точек пересечения этого перпендикуляра с построен-
ной окружностью. Тогда [ВВ] искомый. Это следует из подобия
ДДВВ и &ЕВК (проведите рассуждения).
Приведем примеры решения более сложных задач на построе-
ние, указав некоторые применяемые при решении таких задач
Пример 7. Постройте трапецию, если заданы ее диагонали,
угол между диагоналями и одна из боковых сторон.
Построение (рис. 8). Проведем анализ решения задачи.
Пусть ABCD — искомая трапеция, у которой заданы [ДС], [ВО] —
диагонали, [СО]—одна из боковых сторон, ДОО —угол между
диагоналями. Продолжим сторону [ДО] и отложим отрезок [ОО'],
конгруэнтный отрезку [ВС]. Тогда в Л ACD' заданы две стороны
[ДС] и [СО'] (так как отрезок [СО'] конгруэнтен [ВО]) и угол
между ними. Построив этот треугольник и зная отрезок [СО],
найдем положение точки О на [ДО']. Затем проведем через точку С
прямую, параллельную прямой (ДО'). Имея отрезок [ВО] и точку
Og [ДО'], находим положение точки В. Таким образом, мы по-
строили все четыре вершины искомой трапеции. Мы проследили
при анализе задачи все основные этапы построения. Провести
построение в деталях теперь не представляет труда. Отметим, что
при решении мы использовали прием —параллельный перенос эле-
мента фигуры, а именно, вместо [ВО] мы вначале рассматриваем
[СО'], получаемый из [ВО] параллельным переносом.
178
Пример 8. Дан угол А и точка М, лежащая внутри угла.
На стороне угла А найти точки К и N таким образом, чтобы
периметр /\KMN был наименьшим.
Построение (рис. 9). Пусть точки Л41 и симметричны
данной точке М относительно * сторон данного угла. При любом
выборе точек N' и К' на сторонах угла периметр Л K’MN’ будет
равен длине ломаной М^'К'М2. Эта длина будет наименьшей,
если точки Л' и Л/' лежат на прямой Таким образом,
в качестве точек К и N мы должны взять точки пересечения пря-
мой со сторонами угла. Соответствующие построения не
представляют труда. Отметим, что при решении этой задачи ис-
пользован прием отражения элемента (в данном случае точки)
относительно прямой.
Рис. 9. Рис. 10.
Пример 9. Дан угол А и точка М, лежащая внутри угла.
Постройте окружность, проходящую через данную точку М и
касающуюся сторон данного угла.
Построение (рис. 10). Отметим, что центры всех окруж-
ностей, касающихся сторон данного угла, лежат на биссектрисе
этого угла. Пусть / — биссектриса угла А. Возьмем точку 0^1
и построим окружность с центром в этой точке, касающуюся сто-
рон угла А. Пусть М' и ЛГ' —точки пересечения этой окружности
с прямой (AM). Через точку М проводим прямые, параллельно
отрезкам [ОЛТ] и [ОМ'], и пусть и /С2“точки пересечения
этих прямых с биссектрисой угла А. Эти точки /Q и и яв-
ляются центрами искомых окружностей (проведите самостоятельно
полное доказательство и все необходимые построения). При реше-
нии этой задачи мы использовали прием преобразования гомотетии
с центром в данной точке.
В треугольнике АВС буквами а, &, с обозначаются стороны,
лежащие против А, В и С соответственно; та, тъ, Шс-пшы,
ha, —высоты, —биссектрисы, проведенные к соот-
179
ветствующим сторонам; Р — отрезок, длина которого равна пери-
метру данного ДД5С; R и г—радиусы описанной и вписанной
окружностей.
Постройте ДДВС по следующим элементам1) (1—40).
1. а, А, В. 2. а, Ь, А. 3. а, В, ha. 4. a, A, ha.
5. a, A, hb. 6. а, В, hb. 7. a, ha, hb. 8. a, hb, hc.
9. a, b, та. 10. а, b, тс. 11. а, А, та. 12. а, А, ть.
13. а, В, тс. 14. а, В, ть. 15. а, та, ть. 16. а, ть, те.
17. та, ть, тс. 18< а, В, |3С. 19. а, В, |36. 20. а, рй, 0С.
21. а, А и точке М^а, через которую проходит (За.
22. Р, А, В. 23. Р, А, г. 24. a, hb, та.
25. а, та, |fe|/|c[, где |£>|—длина отрезка b (т. е. предпола-
гается, что заданы какие-либо два отрезка, длины которых отно-
сятся как |&|:|с|).
26. А, г и радиусу одной из вневписанных окружностей.
27. а, А и отрезку длины ||£>|2— |с|2|.
28. A, ha и отношению длин отрезков, на которые высота ha
делит основание а.
29. a, ha и углу, величина которого равна разности величин
В и С.
30. йа, ша, Ра.
31. Вершине В, центру описанного круга и центру тяжести
(т. е. точке пересечения медиан).
32. hb, hc, tna. 33. a, b-\-c, А. 34. а, bA-с, В.
35. а, ЪА-с, ВА-С. 36. а, Ь—с, А. 37. а, Ь—с, В.
38. Центру тяжести и серединам двух средних линий.
39. Центру тяжести, центру описанного круга и одной из
вершин.
40. Точкам пересечения высот с описанной окружностью.
41. Постройте прямоугольный треугольник по гипотенузе и
сумме катетов.
42. Постройте прямоугольный треугольник по гипотенузе и
медиане катета.
43. Постройте равнобедренный прямоугольный треугольник по
его периметру.
44. Постройте трапецию, зная ее основания и боковые стороны.
45. Постройте параллелограмм, у которого середины трех сто-
рон лежат в заданных точках.
46. Постройте квадрат, три вершины которого лежат на трех
данных параллельных прямых.
1) Предполагается, что данные таковы, что соответствующие построения
выполнимы.
180
47. Постройте четырехугольник ABCD, зная все его стороны
и угол между продолжениями сторон [ЛВ] и [СО].
48* В данный треугольник впишите квадрат.
49. В данный треугольник впишите прямоугольник а) с за-
данной диагональю, б) с наименьшей диагональю.
50. В данный треугольник впишите другой треугольник, сто-
роны которого параллельны трем данным прямым.
51. В данный выпуклый четырехугольник впишите параллело-
грамм.
52. Дан угол и точка М внутри него. Через точку М прове-
дите прямую так, чтобы ее отрезок между сторонами угла делился
данной точкой в отношении 2:3.
53. Дан угол и точка М9 лежащая вне него. Через точку М
проведите прямую так, чтобы она отсекала от данного угла тре-
угольник данного периметра.
54. Дан круг. Постройте его центр.
55. Даны две окружности. Постройте их общие касательные.
56* . Постройте окружность данного радиуса, 1) касающуюся
двух данных прямых; 2) касающуюся данной прямой и данной
окружности; 3) касающуюся двух данных окружностей.
57. Даны две окружности и их общая внешняя касательная.
На касательной найдите точку так, чтобы сумма углов, под ко-
торыми видны окружности из этой точки, была равна данному
углу.
58. Даны отрезки^длины о и Ь. Постройте отрезки, длины
которых равны а) Уab\ б) Кл2—ab-\-b2*, в) У а2—4а& + 7Ь2.
59. Дан круг и точка внутри него. Проведите через данную
точку хорду заданной длины.
60* . Даны две окружности. Проведите общую секущую таким
образом, чтобы части ее, заключенные внутри окружностей, были
равны данному отрезку.
61. В окружность впишите прямоугольный треугольник,
зная его острый угол и точку, через которую проходит один из
катетов.
62. Даны две концентрические окружности. Через данную
точку проведите окружность, касающуюся данных концентриче-
ских окружностей.
63* . Даны три концентрические окружности. Постройте равно-
сторонний треугольник, вершины которого принадлежат этим ок-;
ружностям.
64. На данной окружности найдите точку М так, чтобы рас-.:
стояния от М w сторон данного угла относились как 2:3.
65* . Через точку пересечения двух данных окружностей про-
ведите прямую так, чтобы окружности высекали на этой прямой
равные хорды.
66* . Дан треугольник и точка, принадлежащая одной из его
сторон. Через данную точку проведите две прямые так, чтобы
они разбили треугольник на три равновеликие части.
181
67. В угол величины а радиан вписана окружность радиуса R.
Между вершиной угла и центром круга проводится касательная
к этой окружности так, что отсекаемый ею от угла треугольник
имеет наибольшую площадь. Выполните построение и вычислите
площадь отсеченного треугольника.
68. Дан треугольник. Постройте равновеликий ему квадрат.
69. В ДЛВС проведите секущую (£>£) так, чтобы |Л£)1 =
=|DE|=|EC| (D€[4B}, EG [SC]).
70*. Впишите в остроугольный треугольник А АВС треуголь-
ник, стороны которого были бы перпендикулярны сторонам дан-
ного. Докажите, что таких треугольников два.
71*. Рассеките трапецию прямой, параллельной основаниям,
так, чтобы отрезок ее внутри трапеции делился диагоналями на
три равные части.
72. Впишите квадрат в данный сегмент так, чтобы одна его
сторона лежала на хорде.
73. Постройте квадрат так, чтобы две его вершины лежали
на данной прямой, а две другие—на данной окружности.
74. Дана прямая (CD) и две точки Л и В, не лежащие на ней.
Найдите на прямой такую точку М, что 1) АМС = BMD;
2) 2AMC = BMD.
75. Около равностороннего треугольника опишите квадрат так,
чтобы обе фигуры имели общую вершину.
76. Даны три луча, выходящие из одной точки. Проведите
прямую, проходящую через данную точку так, чтобы длины от-
резков, отсекаемых на ней лучами, относились как 3:5.
Выполните следующие построения с ограниченными возмож-
ностями (77 — 81).
77. С помощью одного циркуля разделите данный отрезок
пополам.
78. Дан «египетский» треугольник с длинами сторон 3, 4 и
5 см. С помощью одного циркуля впишите в него окружность.
79. Пользуясь только двусторонней линейкой, разделите дан-
ный угол пополам.
80. Дан угол в 19°. С помощью одного циркуля постройте
дугу в 7°.
81. Разделите циркулем и линейкой угол в 54° на три рав-
ные части.
§ 4. ПЛАНИМЕТРИЯ. ЗАДАЧИ НА ВЫЧИСЛЕНИЕ
Приведем основные «вычислительные» формулы и некоторые
утверждения, часто используемые при решении планиметрических
задач (см. также задачи § 2).
I. Пусть а, Ъ, с —длины сторон ДЛВС, лежащих, соответст-
венно, против углов А, В, С; р = (а + Ь-\-с)/2 — полупериметр,
182
S —площадь, R и г —радиусы описанной и вписанной в этот тре-
угольник окружностей, ha9 tnat — длины высоты, медианы и
биссектрисы, проведенных к стороне, противолежащей углу Л. Спра-
ведливы следующие утверждения.
1) Теорема синусов: —== —^ = 2R.
sin A sin В sin С
2) Теорема косинусов: а2 = &2 + с2 —2bccosА. В частности, если
А прямой, то получаем теорему Пифагора.
3) Формулы для вычисления площади треугольника:
S = у aha\ S = ^ab sin С;
S = \/'p(p — a) (p — b) (p—с) —формула Герона;
о с abc
S = pr, S = w.
4) Три медианы треугольника пересекаются в одной точке,
лежащей строго внутри треугольника (центр тяжести). Точка пе-
ресечения делит медианы на отрезки, длины которых относятся
как 2:1, считая от соответствующей вершины.
та = j/^+ с2 — ас cos В\ та — j/*2c2 + 2&2—а2.
5) Три биссектрисы треугольника пересекаются в одной точке,
лежащей строго внутри треугольника. Точка пересечения бис-
сектрис равноудалена от сторон треугольника (центр вписанной
окружности).
Биссектриса при пересечении делит сторону на отрезки, про-
порциональные прилежащим сторонам треугольника.
о __ sin В ас
а sin (A/2) ь + с'
6) Три высоты треугольника пересекаются в одной точке (орто-
центр).
ha = bsmC\ ha = ^- = ^]/'p(p — a) (p — b) (р—с).
7) Три перпендикуляра, восставленные к серединам сторон
треугольника, пересекаются в одной точке. Эта точка равноуда-
лена от вершин треугольника и является центром описанной ок-
ружности.
ту aba в ту а b с *
К уо” , А 1 /ч '— = 7Г >
* 2 sin А 2 sin В 2 sin С
г = [у(р—а)(р-6)(р-с)]1/а.
183
II. Пусть а, Ь — длины смежных сторон параллелограмма ABCD,
А — величина угла между этими сторонами, ha— высота, опущен-
ная на сторону длины a, и d$—длины диагоналей, S —пло-
щадь параллелограмма. Справедливы следующие утверждения.
1) ha = b sin А.
2) S = aha = ab sin А.
3) di = a24-b2—2а&созД.
dl = а2 + b2 + 2ab cos А.
dt+dl = 2(a2 + b2).
4) Точка пересечения диагоналей параллелограмма является
центром симметрии параллелограмма. Отсюда, в частности, сле-
дует, что диагонали делятся точкой пересечения пополам.
5) Параллелограмм можно вписать в окружность в том и только
в том случае, если он является прямоугольником.
6) В параллелограмм можно вписать окружность в том и только
в том случае, если он является ромбом.
III. Пусть а и Ь — длины оснований трапеции, с и d—длины
ее боковых сторон, h — высота, S —площадь трапеции. Справед-
ливы следующие утверждения.
1) S = ±-(a + b)h.
2) В трапецию можно вписать окружность в том и только
в том случае, если a + b = c + d.
3) Трапецию можно вписать в окружность в том и только в том
случае, если она равнобочная.
IV. Пусть, наконец, 7? —длина радиуса некоторого круга,
S—его площадь, /-—длина окружности, являющейся границей
данного круга. Тогда l=^2nR, S = 3tR2.
1. (МЭСИ, 1979 г.). Длина одного из катетов прямоугольного
треугольника больше длины другого на 10 см, но меньше длины
гипотенузы на 10 см. Найдите длину гипотенузы этого треугольника.
2. (МИНХ, 1977 г.). В треугольнике ABC [BD] — медиана,
|ВО| = |ДВ|Кз/4, a DBC = n/2. Найдите величину угла ABD.
3. (МХТИ, 1977 г.). В треугольнике длина основания на 4 см
меньше длины высоты, а площадь этого треугольника равна 96 см2.
Найдите длины основания и высоты треугольника.
4. (МИЭТ, 1977 г.). Длины сторон треугольника равны И см,
13 см и 12 см. Вычислите длину медианы, проведенной к большей
стороне.
5. (МИЭТ, 1977 г.). Длина основания равнобедренного тре-
угольника равна а, а величина угла при вершине—а. Найдите
длину биссектрисы, проведенной к боковой стороне.
6. (МГИ, 1977 г.). В равнобедренном треугольнике величина
угла при вершине равна а, а площадь его равна S. Найдите длину
основания треугольника.
184
7. (МЭСИ, 1979 г.). В прямоугольном треугольнике длины
медиан острых углов равны К156 и [^89 см. Найдите длину ги-
потенузы треугольника.
8. (МИЭТ, 1977 г.). Длины катетов прямоугольного треуголь-
ника равны а и Ь. Найдите длину биссектрисы прямого угла
этого треугольника.
9. (МЭСИ, 1979 г.). Биссектриса угла N треугольника MNP
делит сторону [Л4Р] на отрезки, длины которых равны 28 и 12.
Определите периметр треугольника MNP, если | MN | — | NP | = 18.
10. (МАИ, 1977 г.). В треугольнике АВС известны отношения
длин сторон [ВС] и [АС] к радиусу описанной окружности, рав-
ные, соответственно, 2 и 1,5. Найдите отношение длин биссектрис
внутренних углов Ви С.
11. (МАИ, 1975 г.). В треугольнике АВС длина стороны [АВ]
равна 2 см. Из вершины В к стороне [АС] проведена медиана [ВО],
длина которой равна 1 см. Найдите площадь треугольника АВС,
если ВО А = 30°.
12. (БашГУ, 1980 г.). Найдите углы треугольника, в котором
высота и медиана, проведенные из одной вершины, делят угол
при этой вершине на три равные части.
13. (МИНХ, 1977 г.). В ромбе ABCD точки М и N — середины
сторон [ВС] и [СО] соответственно. Найдите MAN, если ВАО=60°.
14. (МЭСИ, 1977 г.). Периметр ромба равен 48, а сумма длин
диагоналей равна 26. Найдите площадь этого ромба.
15. (МАИ, 1979 г.). Найдите величину угла между диагона-
з
лями прямоугольника с периметром 2р и площадью
16. (МИНХ, 1978 г.). В квадрате ABCD точка М — середина
[ВС], а О —точка пересечения [ОМ] и [АС]. Найдите величину
угла МОС.
17. (МИНХ, 1979 г.). Средняя линия трапеции равна 10 см и
делит плошадь трапеции в отношении 3:5. Найдите длины осно-
ваний этой трапеции.
18. (МАИ, 1977 г.). В равнобочной трапеции ABCD длина бо-
ковой стороны [АВ] и меньшего основания [ВС] равны 2 см и
[ВО] I [АВ]. Вычислите площадь этой трапеции.
19. (МВМИ, 1977 г.). В параллелограмме ABCD величина угла
BAD равна л/3, а длина стороны [АВ] равна 3 см. Биссектриса
угла А пересекает сторону [ВС] в точке Е. Найдите площадь
треугольника АВЕ.
20. (ЛьвГУ, 1980 г.). Параллелограмм с периметром 44 см раз-
делен диагоналями на 4 треугольника. Разность между перимет-
рами двух смежных треугольников равна 6 см. Определите длины
сторон параллелограмма.
21. (МИЭТ, 1977 г.). Дан параллелограмм, в котором величина
острого угла равна 60°. Найдите отношение длин сторон парал-
лелограмма, если отношение квадратов длин диагоналей равно 1/3.
185
«ей
22. (МАИ, 1979 г.). В трапеции длины оснований равны 5 см
и 15 см, а длины диагоналей — 12 см и 16 см. Найдите площадь
трапеции.
23. (МИЭТ, 1977 г.). Длины оснований трапеции равны а и Ъ.
Найдите длину отрезка прямой, соединяющего середины ее диа-
гоналей.
24. (МИЭТ, 1977 г.). Найдите площадь равнобедренной трапе-
ции, зная длину ее диагонали I и величину угла а между этой
диагональю и большим основанием.
25. (МФТИ, 1977 г.). В равнобедренной трапеции ABCD
([ДД]||[ВС]) расстояние от вершины А до прямой (CD) равно длине
боковой стороны. Найдите величины углов трапеции, если
| AD |:| ВС | = 5:1.
26*. (БГУ, 1980 г.). Непараллельные стороны трапеции про-
должены до взаимного пересечения и через полученную точку
проведена прямая, параллельная основаниям трапеции. Найдите
длину отрезка этой прямой, ограниченного продолжениями диа-
гоналей, если длины оснований трапеции равны а и Ь.
27. (МФТИ, 1977 г.). В прямоугольной трапеции отношение
длин оснований равно 4, а отношение длин диагоналей равно 2.
Найдите величину острого угла трапеции.
28. (МГУ, геолог, фак. 1975 г.). Дана равнобедренная трапе-
ция ABCD. Известно, что |ДВ|=10см, | ВС | = 2 см, |ДВ| =
=| CD |=5 см. Биссектриса угла BAD пересекает луч [ВС) в точке Д’.
Найдите длину биссектрисы угла АВК. в треугольнике АВК.
29. (МГУ, геофак, 1977 г.). В прямоугольном треугольнике
АВС биссектриса [ДО] острого угла А делится центром О вписан-
ной окружности в отношении | АО |:| OD | = (|/"3-f- 1):(КЗ — 1).
Найдите величины острых углов треугольника.
30. (МГУ, географ, фак., 1977 г.). В треугольнике АВС сто-
рона [ДВ] имеет длину 3 м, высота [СО], опущенная на сторону [ДВ],
имеет длину КЗ м. Основание О высоты [СО] лежит на стороне [ДВ],
длина отрезка [ДО] равна длине стороны [ВС]. Найдите длину
стороны [ДС].
31. (МГУ, биофак, 1977 г.). Длина диагонали [ВО] трапеции
ABCD равна т, а длина боковой стороны [ДО] равна п. Найдите
длину основания [СО], если известно, что длины основания, диа-
гонали и боковой стороны трапеции, выходящих из вершины С,
равны между собой.
32. (МГУ, биофак, 1977 г.). В выпуклом четырехугольнике
MNLQ углы при вершинах А и L — прямые, а величина угла при
вершине М равна arctg (2/3). Найдите длину диагонали [7VQ],
если известно, что длина стороны [LQ] вдвое меньше длины сто-
роны [Af/V] и на 21 м больше длины стороны [СА].
33. (МГУ, биофак, 1980 г.). Площадь треугольника АВС равна
IS'HSm2. Величина угла ВАС равна 120°. Величина угла АВС
больше величины угла АСВ. Расстояние от вершины А до центра
Г86
окружности, вписанной в треугольник ЛВС, равно 2 м. Найдите
длину медианы треугольника ЛВС, проведенной из вершины В.
34. (ХГУ, физфак, 1978 г.). Дан квадрат ABCD со стороной
длины единица. Точка К принадлежит стороне [CD] и | С/С |/| RD | =з
= 1/2. Найдите расстояние от вершины С до прямой (Л/С).
35. (МГУ, мехмат, 1980 г.). В трапеции углы при одном из
оснований имеют величины 20° и 70°, а длина отрезка, соединяю-
щего середины оснований, равна 2. Найдите длины оснований
трапеции, если длина средней линии этой трапеции равна 4.
36. (МИФИ, 1976 г.). Одно из оснований трапеции служит
диаметром окружности радиуса /?, а другое отсекает от окруж-
ности дугу в а радиан (0<а<л). Определите площадь тра-
пеции.
37. (МИНХ, 1979 г.). Величина угла при основании равно-
бедренного треугольника равна ср. Найдите отношение длины ра-
диуса вписанной в данный треугольник окружности к длине ра-
диуса описанной окружности.
38. (МИНХ, 1979 г.). В равнобедренном треугольнике длина
основания равна 24 см, а боковой стороны—15 см. Определите
радиусы вписанной и описанной окружностей.
39. (МАИ, 1977 г.). В круге радиуса 12 см длина хорды [ЛВ]
равна 6 см, а хорды [ВС] —4 см. Найдите длину хорды, соеди-
няющей концы дуги АС.
40. (МЭСИ, 1977 г.). На сторонах [ЛВ] и [ЛС] угла ВАС, рав-
ного 2л/3, как на диаметрах построены полуокружности. В общую
часть двух образованных полукругов вписана окружность макси-
мального радиуса. Найдите радиус этой окружности, если | ЛВ |« 4,
| ЛС| = 2.
41. (МИФИ, 1978 г.). В треугольнике ЛВС заданы |ЛС|==&,
ЛВС = а. Определите радиус окружности, проходящей через центр
вписанного в треугольник ЛВС круга и вершины Л и С.
42. (ЛатвГУ, 1980 г.). В окружности радиуса г проведена
хорда длины г/2. Через один конец хорды проведена касательная
к этой окружности, а через другой —секущая, параллельная ка-
сательной. Найдите расстояние между касательной и секущей.
43. (ЛатвГУ, 1980 г.). Через концы дуги окружности, содер-
жащей 120°, проведены касательные и в фигуру, ограниченную
этими касательными и данной дугой, вписана окружность. Вычис-
лите длину этой окружности, если радиус исходной окружности
равен R.
44. (КГУ, ВМК, 1977 г.). Две окружности радиусов R и г
касаются внешне в точке С. К ним проведена общая внешняя
касательная [ЛВ], где Л и В —точки касания. Вычислите длины
сторон треугольника ЛВС.
45. (КГУ, ВМК, 1977 г.). Две окружности радиусов R и
г (R > г) касаются внешним образом. Найдите радиусы окружно-
стей, касающихся обеих данных окружностей и их общей внеш-
ней касательной.
187
46. (КГУ, ВМК, 1977 г.). Две окружности радиусов и г
касаются внешне в точке А. На окружности радиуса г взята точка
В, диаметрально противоположная точке А, и в этой точке по-
строена касательная /. Найдите радиус окружности, касающейся
двух данных окружностей и прямой I.
47. (КГУ, ВМК, 1977 г.). Точки и 0^ — центры окруж-
ностей Kt и /^2» касающихся внешне. Радиусы этих окружностей,
равны соответственно и г*. На отрезке [ОГО2] как на1
диаметре построена окружность К3. Вычислите радиус окружно-
сти, касающейся внешне окружностей и Къ и внутренне —ок-
ружности /<3.
48. (МГУ, мехмат, 1980 г.). В треугольнике PQR величина
угла QRP равна л/3. Найдите расстояние между точками каса-
ния со стороной [Q/?] окружности радиуса 2, вписанной в тре-
угольник, и окружности радиуса 3, касающейся прямых (PQ) и
(PR)-
49. (МЭСИ, 1979 т.). Дан треугольник АВС, длины сторон
которого равны: | АВ | = 15, | ВС | = 12, | АС | = 18. Центр вписанной
окружности О делит биссектрису угла С на две части [СО] и [ОО].
Во сколько раз длина [СО] больше длины [OD]?
50. (МЭИ, 1976 г.). В угол величины а радиан вписана ок-
ружность радиуса R. Между вершиной угла и центром окружно-
сти проведена к этой окружности касательная, перпендикулярная
биссектрисе данного угла. Определите площадь отсеченного тре-
угольника.
51. (МИЭТ, 1977 г.). Найдите площадь прямоугольного тре-
угольника, если известно, что радиус вписанного в треугольник
круга равен г, а описанного— R.
52. (МИЭТ, 1977 г.). Окружность касается большего катета
треугольника, проходит через вершину противолежащего острого
угла и имеет центр на гипотенузе. Найдите ее радиус, если длины
катетов треугольника равны 3 и 4.
53. (МИЭТ, 1977 г.; МТИМБО, 1977 г.). В треугольник с
длинами сторон а, Ь, с вписан полукруг, диаметр которого лежит
на стороне длины с. Найдите радиус этого полукруга.
54. (МИЭТ, 1977 г.). В равнобедренном треугольнике величи-
на угла при основании равна л/6. Длина высоты, опущенной на
основание, больше радиуса вписанного круга на 2. Найдите длину
основания этого треугольника.
55. (МСИ, 1977 г.). Около круга радиуса г описана прямо-
угольная трапеция, меньшая из сторон которой равна Зг/2. Вы-
числите площадь этой трапеции.
56. (МИСиС, 1978 г.). Площадь равнобочной трапеции, опи-
санной около круга, равна S. Найдите длину средней линии тра-
пеции, если величина острого угла при ее основании равна а.
57. (МИЭТ, 1977 г.). В окружность радиуса R вписана тра-
пеция, у которой боковая сторона конгруэнтна меньшему осно-
ванию, а угловая мера дуги, стягиваемой этим основанием, равна
а. Найдите площадь трапеции.
188
58. (КГУ, геофак, 1978 г.). В правильный треугольник G дли-
ной стороны 10 см вписан Kpyi. В этот круг вновь вписан пра-
вильный треугольник, в него —снова круг и т. д. Найдите сум-
му площадей всех кругов, образованных в результате последова-
тельного вписывания.
59. (КуйбГУ, 1980 г.). Величины углов треугольника отно-
сятся как 2:3:7. Длина наименьшей стороны равна а. Найдите
радиус окружности, описанной около этого треугольника.
60. (ОГУ, 1980 г.). В равнобедренный треугольник вписана
окружность радиуса г. Высота, проведенная к основанию, делится
окружностью в отношении 1:2. Найдите площадь треугольника.
61. (МГУ, психфак, 1980 г.). В прямоугольном треугольнике
АВС угол А прямой, величина угла В равна 30°, а радиус опи-
санной окружности равен К3. Найдите расстояние от вершины
С до точки касания вписанной окружности и катета [АВ].
62. (МГУ, психфак, 1980 г.). В квадрат ABCD со стороной
длины а вписана окружность, которая касается стороны [CD]
в точке Е. Найдите длину хорды, соединяющей точки, в кото-
рых окружность пересекается с прямой (АВ).
63. (МГУ, эконом, фак., 1980 г.). В прямоугольный треуголь-
ник, периметр которого равен 36 см, вписана окружность. Точка
касания с окружностью делит гипотенузу в отношении 2:3. Най-
дите длины сторон треугольника.
64. (МГУ, эконом, фак., 1980 г.). В прямоугольный треуголь-
ник вписана окружность. Точка касания с окружностью делит
один из катетов на отрезки длины 6 см и 10 см, считая от вер-
шины прямого угла. Найдите площадь треугольника.
65. (МТИМБО, 1978 г.). На большем катете как на диаметре
описана полуокружность. Определите ее длину, если меньший катет
равен 30 см, а хорда, соединяющая вершину прямого угла с точ-
кой пересечения гипотенузы с полуокружностью, равна 24 см.
66. (МГУ, химфак, 1980 г.). В параллелограмме ABCD диа-
гональ [АС] перпендикулярна стороне [АВ]. Некоторая окруж-
ность касается стороны [ВС] параллелограмма ABCD в точке Р
и касается прямой, проходящей через вершины А и В этого же
параллелограмма, в точке А. Через точку Р проведен перпенди-
куляр [PQ] к стороне [АВ] (точка Q—основание этого перпен-
дикуляра). Найдите величину угла АВС, если известно, что пло-
щадь параллелограмма ABCD равна 1/2, а площадь пятиуголь-
ника QPCDA равна S.
67. (КГУ, ВМК, 1978 г.). Вокруг трапеции с высотой длины
Н описана окружность. Основания трапеции видны из центра
окружности под углами аир. Найдите радиус окружности и
площадь трапеции.
68. (ХГУ, мехмат, 1978 г.). Круг радиуса 13 см касается двух
смежных сторон квадрата, длина стороны которого равна 18 см.
На какие два отрезка делит круг каждую из двух других сто-
рон квадрата?
189
69. (МГУ, физфак, 1980 г.). В треугольнике АВС заданы:
ВАС = а, ВСА=$, | АС\ = Ь. На стороне [ВС] взята точка О так,
что \BD | = 3| DC |. Через точки В и D проведена окружность,
касающаяся стороны [ЛС] или ее продолжения за точку А. Най-
дите радиус этой окружности.
70. (МГУ, физфак, 1980 г.). На стороне угла с вершиной А
взяты точки С и D (С между А и D) так, что | АС | = 21 CD |.
Через точки С и D проведена окружность, касающаяся другой
стороны угла в точке В. Между точками А и В взята точка Е.
Известно, что DAE = a, DEA—$, |ЛВ| = k. Найдите радиус ок-
ружности.
71. (МГУ, мехмат, 1977 г.). Длины боковых сторон трапеции
равны 6 и 10. Известно, что в трапецию можно вписать окруж-
ность. Средняя линия делит трапецию на две части, отношение
площадей которых равно 5:11. Найдите длины оснований трапеции.
72. (МГУ, мехмат, 1977 г.). Длина средней линии равнобоч-
ной трапеции равна 5. Известно, что в трапецию можно вписать
окружность. Средняя линия делит трапецию на две части, отно-
шение площадей которых равно 7:13. Найдите длину высоты
трапеции.
73. (МГУ, мехмат, 1980 г.). Окружность радиуса 3, вписанная
в треугольник АВС, касается стороны [ВС] в D. Окружность
радиуса 4 касается продолжения сторон [ЛВ] и [ЛС], а также
стороны [ВС] в точке Е. Найдите | ED |, если величина угла ВС А
равна 2л/3.
74. (МТИМБО, 1980 г.). Треугольник задан координатами
своих вершин Л (3; —2; 1), В(3; Г, 5), С (4; 0; 3). Вычислите
длину медианы JBBJ и величину угла В.
75. (МИФИ, 1980 г.). Определите площадь равнобедренной
трапеции, у которой длины оснований равны 10 см и 26 см,
а диагонали перпендикулярны боковым сторонам.
76. (МТИМБО, 1978 г.). Вычислите площадь прямоугольной
трапеции с основаниями длины 7 см и 3 см и острым углом в 60°.
77. (ТбГУ, физфак, 1981 г.). Дана трапеция MNPQ с осно-
ваниями [А4 Q] и [МВ]. Прямая, параллельная основаниям, пере-
секает боковую сторону [ДНУ] в точке Л, а сторону [PQ] —в точ-
кеВ. Sanpq-Smabq = 2:7. Найдите |ЛВ|, если |2VP| = 4, |Л4Q| = 6.
78. (МТИМБО, 1979 г.). В равнобедренном треугольнике с бо-
ковой стороной длины 4 см проведена медиана к боковой сторо-
не. Найдите длину основания треугольника, если длина медианы
равна 3 см.
79. (ТбГУ, физфак, 1980 г.). Длины катетов прямоугольного
треугольника равны 12 см и 5 см. Найдите расстояние между
центрами вписанной и описанной окружностей.
80. (МТИМБО, 1981 г.). В прямоугольный треугольник с ка-
тетами а и b вписан квадрат, имеющий с треугольником общий
прямой угол. Найдите периметр квадрата.
190
81. (ТбГУ, физфак, 1977 г.). В треугольнике АВС величины
углов А, В, С составляют арифметическую прогрессию. Наимень-
шая сторона в 4 раза меньше наибольшей стороны. Найдите
тангенс наименьшего угла.
82. (МТИМБО, 1981 г.). Длины сторон треугольника пропор-
циональны числам 5, 12, 13. Наибольшая сторона треугольника
превосходит наименьшую на 1,6 м. Определите периметр и пло-
щадь треугольника.
83. (ТбГУ, физфак, 1981 г.). В равнобедренном треугольнике
синус угла при основании в 3 раза больше косинуса угла при вер-
шине. Найдите синус угла при основании.
84. (СимфГУ, матфак, 1982 г.). Найдите длины сторон пря-
моугольного треугольника, если R =15 см, г = 6 см, где Я и г —
радиусы описанной и вписанной окружностей соответственно.
85. (МТИМБО, 1978 г.). Даны две стороны b и с треуголь-
ника и его площадь S = 2&c/5. Найдите третью сторону треуголь-
ника.
86. (СимфГУ, физфак, 1981 г.). Найдите угол между медиа-
нами катетов равнобедренного прямоугольного треугольника.
87. (ТбГУ, мехмат, 1981 г.). В треугольнике АВС из точки Е
стороны [ВС] проведена прямая, параллельная высоте [ВО], ко-
торая пересекает сторону [ЯС] в точке F. Отрезок [BF] делит
треугольник АВС на две равные по площади фигуры. Найдите
длину | EF |, если |ВО| = 6 см, | ЛО|:|ОС| = 2:7.
88. (МТИМБО, 1977 г.). В прямоугольный треугольник впи-
сан полукруг так, что его диаметр лежит на гипотенузе и центр
его делит гипотенузу на отрезки длиной в 15 см и 20 см. Най-
дите длину дуги полуокружности, заключенной между точками
касания ее с катетами.
89. (ТбГУ, мехмат, 1980 г.). Дан треугольник, длины сторон
которого 10 см, 12 см, 18 см. Проведена окружность, касающая-
ся двух меньших сторон, а центр находится на большей стороне.
Найдите ее радиус.
90. (МТИМБО, 1981 г.). Из одной точки проведены к окруж-
ности две касательные длиной в 12 см, а расстояние между точ-
ками касания 14,4 см. Определите радиус окружности.
91. (ТбГУ, физфак, 1982 г.). Из точки А к окружности с
центром в точке N проведены две касательные, которые касают-
ся окружности в точках В и М. Хорда [ВЛ4] пересекает отрезок
[ЛМ] в точке К. Длина отрезка | | в 13/4раза меньше длины
отрезка |/<Д|; | АВ | = 4 см. Найдите площадь треугольника ВАК.
92. (МТИМБО, 1981 г.). Около круга описана равнобедренная
трапеция, у которой средняя линия имеет длину 5 см. Опреде-
лите периметр и длину боковой стороны трапеции.
93. (ТбГУ, мехмат, 1982 г.). В трапеции MPQF длины осно-
ваний | MF | и | PQ | равны 24 см и 4 см соответственно. Высота
трапеции имеет длину 5 см. Точка N делит боковую сторону на
отрезки [Л4У] и [Л/Д]. Длина отрезка |Л4Л71 в 3 раза больше
длины отрезка |ЛД|. Найдите площадь треугольника NQF.
191
94. (МТИМБО, 1981 г.). В ромб, который своей диагональю
делится на два равносторонних треугольника, вписана окружность
с радиусом длины 2 см. Найдите сторону ромба.
95. (ТбГУ, мехмат, 1977 г.). В прямоугольном треугольнике
АВС на высоте [С/С] как на диаметре построена окружность,
которая пересекает катеты [СД] и [СВ] соответственно в точках М
и 2V; | СМ | = 12 см, \CN | = 18 см. Найдите | С А | и |СВ|.
96. (МТИМБО, 1978 г.). Около круга радиуса R описан рав-
нобедренный треугольник с углом 120°. Определите стороны тре-
угольника.
97. (ТбГУ, мехмат, 1978 г.). В равнобедренной трапеции ABCD '
большее основание [ДО] имеет длину 12 см, | АВ | = 6 см. Най-
дите расстояние от точки О пересечения диагоналей до точки /<
пересечения продолжений боковых сторон.
98. (МТИМБО, 1977 г.). Найдите диагональ и боковые сто-
роны равнобедренной трапеции с основаниями длиной в 20 см и
12 см, если известно, что центр описанной окружности лежит на
большем основании трапеции.
99. (ЛГУ, биол.-почв, фак., 1980 г.). Окружность радиуса г
касается изнутри двух окружностей радиусов Rt и R^, причем
центры всех трех окружностей лежат на одной прямой. Найдите
радиус окружности, касающейся всех трех данных.
100. (ЛГУ, геофак, 1980 г.). На катете [ДО] равнобедренного
прямоугольного треугольника АВС выбрана точка Р так, что по-
луокружность, построенная на отрезке [ВС] как на диаметре,
касается гипотенузы [ДВ]. В каком отношении полуокружность
делит отрезок [РВ]?
101. (МЭИ, 1979 г.). При каком значении длины высоты пря-
моугольная трапеция с острым углом в 45° и параметром 4 см
имеет наибольшую площадь?
102. (МИСиС, 1978 г.). Сумма длин двух сторон треугольни-
ка равна а, а величина угла, заключенного между ними, равна
30°. Каковы должны быть длины сторон треугольника, чтобы его
площадь была наибольшей?
103. (МИХМ, 1977 г.). Сумма длин диагоналей параллело-
грамма равна 8 см. Найдите минимум суммы квадратов длин всех
сторон параллелограмма.
104. (МЭСИ, 1977 г.; МТИМБО, 1980 г.). В равнобедренный
треугольник с длиной основания 20 см и высотой 8 см вписан
прямоугольник, одна из сторон которого лежит на основании
треугольника. Какова должна быть длина высоты прямоугольника,
чтобы он имел наибольшую площадь?
105. (МИХМ, 1977 г.). В равнобедренный треугольник с уг-
лом в 120° при вершине и длиной основания 8 см вписан прямо-
угольник наибольшей площади, две вершины которого лежат на
основании. Найдите площадь этого прямоугольника.
106. (МИХМ, 1979 г.). В треугольник, длина основания ко-
торого равна а, а высота —Л, вписан прямоугольник наибольшей
192
площади (основание прямоугольника лежит на основании тре-
угольника). Найдите длины сторон этого прямоугольника.
107. (МИТХТ, 1979 г.). Две стороны параллелограмма лежат
на сторонах данного треугольника, а одна из его вершин при-
надлежит третьей стороне. При каких условиях площадь парал-
лелограмма будет наибольшей?
108. (МИЭТ, 1978 г.; МИУ, 1978 г.). Боковая сторона рав-
нобочной трапеции конгруэнтна ее меньшему основанию, длина
которого равна а. Какова должна быть длина большего основа-
ния трапеции, чтобы ее площадь была наибольшей?
109. (МИЭТ, 1980 г., КуйбГУ, 1980). На окружности радиу-
са дана точка Л. На каком расстоянии от точки А нужно
провести хорду [ВС], параллельную касательной к окружности
в точке Л, чтобы площадь треугольника АВС была наибольшей?
ПО. (ЛГУ, матмех, 1980 г.). Боковые стороны трапеции пер-
пендикулярны. Какое наибольшее значение может иметь площадь
треугольника, образованного диагоналями и средней линией тра-
пеции, если известно, что длины оснований! трапеции равны а и Ь?
111. (МТИМБО, 1980 г.). Из всех прямоугольников, вписан-
ных в окружность радиуса /?, найдите прямоугольник наиболь-
шей площади.
112. (МТИМБО, 1980 г.). Из всех прямоугольников с пло-
щадью 9 дм2 найдите тот, у которого периметр наименьший.
113. (МТИМБО, 1979 г.). В прямоугольный треугольник с
гипотенузой в 24 см и углом в 60° вписан прямоугольник, осно-
вание которого лежит на гипотенузе. Каковы должны быть длины
сторон прямоугольника, чтобы его площадь была наибольшей?
114. (МТИМБО, 1979 г.). Найдите длины сторон прямоуголь-
ника наибольшей площади, вписанного в прямоугольную трапе-
цию с длинами оснований 24 см и 8 см и длиной высоты 12 см.
115. (МТИМБО, 1979 г.). Найдите длины сторон прямоуголь-
ника наибольшей площади, вписанного в прямоугольный тре-
угольник со сторонами длиной 18 см, 24 см и 30 см и имеющего
с ним общий прямой угол.
116. (МТИМБО, 1982 г.). В равнобедренный треугольник со
сторонами длиной 15 см, 15 см и 18 см вписан параллелограмм
наибольшей площади так, что угол при основании у них общий.
Найдите длины сторон параллелограмма.
117. (МТИМБО, 1979 г.). В какой круг можно вписать пря-
моугольник наибольшей площади с периметром, равным 56 см?
118. (МТИМБО, 1978 г.). Гипотенуза прямоугольного тре-
угольника равна с. Каковы должны быть катеты этого треуголь-
ника, чтобы площадь его была наибольшей?
§ 5. СТЕРЕОМЕТРИЯ. ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО
1. Сколько имеется плоскостей, равноудаленных от четырех
данных точек, не лежащих в одной плоскости?
2. Докажите, что если три прямые в пространстве обладают
тем свойством, что любые две из них пересекаются, то либо они
7 В. М. Говоров и др. 193
проходят через общую точку, либо все лежат в одной плоско-
сти.
3. В пространстве даны точки Л, В, С и D, причем [ЛВ] I
±[CD], [ЛС]±[ВР]. Докажите, что [ЛО]±[ВС].
4. В пространстве рассматриваются два отрезка [ЛВ] и [СО],
не лежащие в одной плоскости. Пусть [АШ]— отрезок, соединяю-
щий их середины. Докажите, что | ЛС| + |ВО| > 2[Л4ЛА|.
5. Наклонная образует равные углы с тремя попарно непа-
раллельными прямыми, лежащими в одной плоскости. Докажите,
что наклонная перпендикулярна плоскости.
6. На двух параллельных плоскостях расположены отрезки
[ЛВ] и [СО]. Концы этих отрезков являются вершинами некото-
рой треугольной пирамиды. Докажите, что объем этой пирамиды
не будет меняться, если отрезки перемещать в этих плоскостях
параллельно самим себе.
7. Докажите, что прямая, пересекающая две грани двугран-
ного угла, образует с ними равные углы тогда и только тогда,
когда точки пересечения одинаково удалены от ребра.
8. Докажите, что всякий выпуклый четырехгранный угол мож-
но пересечь плоскостью так, что в сечении получится паралле-
лограмм.
9. Всегда ли можно трехгранный угол пересечь плоскостью
так, чтобы в сечении получился правильный треугольник?
10. Докажите, что если у выпуклого трехгранного угла
все двугранные углы острые, то и все плоские углы также
острые.
11. Сколько плоскостей симметрии может иметь треугольная
пирамида?
. 12. Докажите, что две треугольные пирамиды равны или сим-
метричны, если их соответствующие ребра равны.
13. Докажите, что следующие четыре условия равносильны:
1) боковые ребра пирамиды равны;
2) боковые ребра одинаково наклонены к плоскости основа-
ния пирамиды;
3) боковые ребра образуют одинаковые углы с высотой пира-
миды;
4) около основания пирамиды можно описать окружность, а
высота пирамиды проходит через центр этой окружности.
14. Докажите, что следующие три условия равносильны:
1) высоты боковых граней пирамиды равны;
2) высота пирамиды образует одинаковые углы с боковыми
гранями;
3) боковые грани пирамиды наклонены к плоскости основания
под одним углом (заметим, что при этом двугранные углы при
основании пирамиды могут оказаться различными!).
15. Докажите, что двугранные углы при основании пирамиды
равны тогда и только тогда, когда в основание пирамиды можно
вписать окружность и высота пирамиды проходит через центр этой
окружности.
194
16. Докажите, что если все двугранные углы некоторой тре-
угольной пирамиды равны, то и все ребра этой пирамиды
равны.
17. Докажите, что если в треугольной пирамиде сумма длин
противоположных ребер одна и та же для любой пары таких ре-
бер, то вершины этой пирамиды являются центрами четырех
шаров, попарно касающихся друг друга.
18. Докажите, что в треугольной пирамиде высота проходит
через точку пересечения высот треугольника, лежащего в осно-
вании, в том и только в том случае, если противоположные ребра
пирамиды перпендикулярны.
19. Все ребра одной пирамиды соответственно меньше ребер
другой. Можно ли утверждать, что объем первой из них также
меньше объема второй?
20. Дана правильная треугольная пирамида. Из произвольной
точки Р ее основания восставлен перпендикуляр к плоскости
основания. Докажите, что сумма длин отрезков от точки Р до
точек пересечения перпендикуляра с плоскостями граней не зави-
сит от выбора точки Р на основании.
21. Какие правильные многоугольники могут получиться при
пересечении куба плоскостью?
22. Докажите, что если все диагонали параллелепипеда рав-
ны по длине, то он прямоугольный.
23. Докажите, что если все грани параллелепипеда — равные
между собой параллелограммы, то они являются ромбами.
24. Существует ли многогранник, все грани которого явля-
ются параллелограммами и попарно параллельны, но который,
однако, не является призмой?
25. Докажите, что объем правильной усеченной пирамида
равен V = y/7(S14-Sg + KS1S2), где Я —ее высота, aSx и Sj —пло-
щади оснований.
26. Докажите, что все касательные к шару, проведенные из
одной точки, имеют одинаковую длину.
27. Докажите, что треугольную призму можно вписать в шар
в том и только в том случае, если эта призма прямая.
28. Докажите, что во всякую треугольную пирамиду можно
вписать шар и вокруг этой пирамиды можно описать шар. При
этом 1) все биссекторные плоскости двугранных углов пирамиды
пересекаются в одной точке и эта точка и является центром впи-
санного шара; 2) все плоскости, проведенные через середины ре-
бер данной пирамиды перпендикулярно этим ребрам, пересека-
ются в одной точке, и эта точка и является центром описанного
шара.
29. Докажите, что если противоположные ребра тетраэдра
попарно равны, то вписанный в тетраэдр и описанный вокруг
него шары концентричны.
30. Пусть ABCD — треугольная пирамида; Sf, S§, S3 и S4 —
площади четырех ее граней, г —радиус вписанного в пирамиду
7* 195
шара. Докажите, что объем V этой пирамиды можно вычислить
по формуле V = (Si + Sg + S3 + S4).
31. Шар называется вневписанным в треугольную пирамиду,
если он касается одной из граней пирамиды и плоскостей всех
других ее граней. Докажите, что у всякой треугольной пирамиды
имеется четыре вневписанных шара.
32*. Пусть г-—радиус вписанного, /?3 и —радиусы
вневписанных в треугольную пирамиду шаров. Докажите, что
-2=-L+ 1 + 1 +J_.
33. Докажите, что для того чтобы вокруг пирамиды можно
было описать сферу, необходимо и достаточно, чтобы вокруг осно-
вания этой пирамиды можно было описать окружность.
34. В трехгранный угол с вершиной S вписана сфера с цент-
ром в точке О. Докажите, что плоскость, проходящая через три
точки касания, перпендикулярна прямой (OS).
35. Докажите, что в прямоугольном параллелепипеде
ABCDA'B'C'D' квадрат площади сечения A'BD в 8 раз меньше
суммы квадратов площадей граней.
36. Докажите, что если все ребра тетраэдра касаются одного
шара, то суммы длин всех пар противоположных ребер одинаковы.
37. Какую наибольшую боковую поверхность может иметь
прямоугольный параллелепипед, длина диагонали которого равна а?
Докажите, что наибольшую боковую поверхность будет иметь куб.
38. В пирамиде все двугранные углы при основании равны по
величине а. Докажите, что площадь боковой поверхности и пло-
щадь основания этой пирамиды связаны соотношением S0CB =
=sS6oK cos а.
39. В пространстве даны две пересекающиеся плоскости аир.
На линии их пересечения взята точка А. Докажите, что из всех
прямых, лежащих в плоскости а и проходящих через точку А,
наибольший угол с плоскостью (3 образует та, которая перпен-
дикулярна к линии пересечения плоскостей аир. Чему равен
этот угол?
40. В треугольной пирамиде SABC известны плоские углы при
вершине S: BSC = 90°, Л SC = Л SB = 60°. Вершины Л, S и сере-
дины ребер [SB], [SC], [ЛВ] и [ЛС] лежат на поверхности шара.
Докажите, что ребро [5Л] является диаметром этого шара.
41. Сфера касается трех сторон основания треугольной пира-
миды в их серединах и пересекает боковые ребра в их серединах.
Докажите, что пирамида правильная.
42« Сфера касается всех боковых граней треугольной пирамиды
в центрах описанных около них окружностей. Плоские углы при
вершине этой пирамиды равны. Докажите, что пирамида правильная.
43. Докажите, что если в призму (не обязательно прямую)
вписан шар, то 1) высота призмы равна диаметру шара; 2) точки
касания шара с боковыми гранями лежат на сечении призмы
196
плоскостью, проходящей через центр шара перпендикулярно бо-
ковым ребрам.
44. Докажите, что если в призму можно вписать прямой кру-
говой цилиндр, то эта призма прямая, длина ее бокового ребра
равна длине образующей цилиндра и в основание призмы можно
вписать круг.
45. Если призма вписана в прямой круговой цилиндр, то она
прямая, ее высота равна образующей цилиндра и основание призмы
является вписанным многоугольником. Докажите.
46. Шар вписан в усеченный конус. Докажите, что площадь
поверхности шара меньше площади боковой поверхности конуса.
47. Вокруг сферы описана четырехугольная усеченная пира-
мида. Докажите, что объемы пирамиды и шара относятся как их
полные поверхности.
§ 6. СТЕРЕОМЕТРИЯ. ЗАДАЧИ НА ВЫЧИСЛЕНИЕ
Приведем формулы, которые могут потребоваться при вычис-
лении площадей поверхностей и объемов пространственных фигур.
Sj=S cos а, (1)
где 3 —площадь данной плоской фигуры, a Sj —площадь ее ор-
тогональной проекции на другую плоскость, а — угол между плос-
костями.
S = Pl, (2)
где 3 — площадь боковой поверхности призмы, Р — длина пери-
метра ортогонального сечения, /—длина образующей призмы.
где 3 и Sj—площади параллельных сечений пирамиды, а и —
длины сходственных элементов сечения, h и /^ — расстояния сече-
ний от вершины пирамиды или расстояния каких-либо сходствен-
ных элементов сечений от вершины пирамиды.
S = ™, (4)
где 3 — площадь боковой поверхности правильной пирамиды, Р —
длина периметра основания, h—апофема боковой грани.
3 = 2nRh, St = 2nR (R + h), (5)
где 3 —площадь боковой поверхности прямого цилиндра, Sf —
площадь полной поверхности цилиндра, 7?—длина радиуса окруж-
ности основания, h—длина высоты цилиндра.
S = iiRl, Si = nR(R + l), (6)
где 3 — площадь боковой поверхности прямого конуса, 3£—пло-
щадь полной поверхности конуса, 7?—длина радиуса окружности
197
основания конуса, / — длина образующей конуса.
S = n(R + r)l, (7)
где S — площадь боковой поверхности прямого усеченного конуса,
R и г—длины радиусов оснований усеченного конуса, / — длина
образующей.
S — 2nra=2nRh (рис. 1), (8)
где S —площадь поверхности вращения отрезка [ЛВ] длины а
(рис. 1) около оси (ab), не пересекающей отрезка, г—расстояние
середины отрезка от оси вращения,
h — длина проекции [об] отрезка
[ЛВ] на ось вращения, R — длина
радиуса окружности с центром на
оси вращения и касающейся от-
резка [ЛВ] в его середине, а —
длина отрезка [ЛВ].
S = 2nRh (рис. 2), (9)
Рис. 1.
ности (точка А
где S —площадь поверхности вра-
Рис. 2. щения дуги ЛВ окружности ра-
диуса длины R вокруг оси (ab),
на которой лежит центр окруж-
или В или обе могут лежать на оси вращения),
h — длина проекции дуги ЛВ на ось вращения.
S=AnR\
(Ю)
где S —площадь поверхности шара (площадь сферы), R — длина
радиуса шара.
V = abc, (И)
где V—объем прямоугольного параллелепипеда, а, Ь, с, — длины
его сторон.
V=S-h, (12)
где V —объем призмы, S —площадь многоугольника, лежащего
в основании призмы, /г —длина высоты призмы.
V = Sl, (13)
где V —объем наклонной призмы, S —площадь перпендикулярного
сечения к образующей призмы, /—длина бокового ребра призмы.
V=±Sh, (14)
О
где V—объем пирамиды, S —площадь многоугольника, лежащего
в основании пирамиды, ft —длина высоты пирамиды.
V=4(S + s + /S?)ft, (15)
198
где V — объем усеченной пирамиды, S и s —площади ее основа-
ний, h—длина высоты усеченной пирамиды.
У=лЯ%, (16)
где V—объем кругового цилиндра, 7?—длина радиуса круга,
лежащего в основании цилиндра, Л—длина высоты цилиндра.
У=ул7?2/г, (17)
где V—объем кругового конуса, 7?—длина радиуса круга, ле-
жащего в основании конуса, h—длина высоты конуса.
(18)
где V—объем кругового усеченного конуса, R и г—длины ра-
диусов кругов, лежащих в основании конуса, Л—длина высоты
конуса.
V=^nR2h (рис. 3), (19)
где V—объем шарового сектора с центром на оси вращения (ab),
7?—длина радиуса шарового сектора, h—длина высоты шарового
Рис. 3.
Рис. 5.
пояса, служащего основанием шарового сектора (точка А или В
или обе могут лежать на оси вращения (ab)). На рис. 3 изобра-
жено лишь сечение сектора осевой полуплоскостью.
V^nR3, (20)
где V—объем шара, R—длина радиуса шара.
V = (рис. 4), (21)
где V—объем кольца с центром на оси вращения (ab), l—pflwa
хорды [ЛВ] кольца, h—длина проекции [об] хорды [ЛВ] на ось
вращения (точка Л или В или обе могут лежать на оси вращения
(ab)). На рис. 4 изображено лишь сечение кольца осевой полу-
. 199
плоскостью.
Ve-i-n/i3 + yjt(r? + zi)ft (рис. 5), (22)
где V—объем шарового слоя с центром на оси вращения (ab),
rt и Га — расстояния точек Л и В от оси вращения (ab) (гх и —
длины радиусов кругов, ограничивающих слой), h—длина высоты
шарового пояса, служащего основанием шаровому слою (точка А
или В или обе могут лежать на оси вращения). На рис. 5 изо-
бражено лишь сечение шарового слоя осевой полуплоскостью.
У = |А($ + 4^ + з), (23)
где V—1) объем любого многогранника, у которого основания —
различные неправильные многоугольники, расположенные в парал-
лельных плоскостях, а боковая поверхность образована треуголь-
никами или трапециями, вершины которых совпадают с верши-
нами многоугольников, лежащих в основании; 2) объем цилиндра,
3) объем конуса, 4) объем шарового слоя; S и з —площади фигур,
расположенных в параллельных плоскостях (оснований), —
площадь сечения тела плоскостью, параллельной основаниям и
находящейся от них на равных расстояниях; ft—длина высоты
(расстояние между основаниями).
1. (ХГУ, физфак, 1978 г.). Найдите угол между двумя
скрещивающимися прямыми Lj и Lj, если расстояние между точками
А € Ц и В С й, равноотстоящими от оснований С С и D С В2
общего перпендикуляра к этим прямым, равно 21, a I DC | = | АС |=
»| BD | = I.
2. (ХГУ, физфак, 1978 г.). Даны две скрещивающиеся под
углом а прямые и L$. Расстояние между точками A^Lt и
В С 7.2, равноотстоящими от оснований С £ Lt и общего
перпендикуляра к этим прямым, равно т. Найдите расстояние
между прямыми, если | АС | = | BD | = I.
3. (МЭСИ, 1979 г.). Длина высоты прямоугольного треуголь-
ника АВС, опущенной на гипотенузу [ДВ], равна 9,6. Из вер-
шины С прямого угла восставлен к плоскости треугольника АВС
перпендикуляр [СМ], |СМ| = 28. Найдите расстояние от точки М.
до гипотенузы [ДВ].
4. (МИФИ, 1980 г.). Точки А, В, С, принадлежащие окруж-
ности, |делят длину окружности в отношении 1:2:2 (АС = ВС).
Найдите расстояние от центра окружности О до плоскости у,
если известно, что плоскость у отстоит от точек Д и В на рас-
стояние d, а от точки С—на расстояние Ь.
5*. (МИФИ, 1980 г.). Даны ромб ABCD и плоскость р. Най-
дите расстояние от вершины D до плоскости Р, проходящей через
вершину А, если расстояния от точек В и С до плоскости Р равны,
соответственно, b и с.
200
6. (МВТУ, 1978 г.). Через каждую вершину единичного куба
проведены плоскости, перпендикулярные одной и той же диаго-
нали куба. На какие части делится диагональ этими плоскостями?
7. (ХАИ, 1980 г.). Центр верхнего основания куба соединен
с серединами сторон нижнего основания. Определите боковую по-
верхность полученной пирамиды, если длина ребра куба равна а.
8. (ЛатвГУ, 1980 г.). Диагонали боковых граней прямоуголь-
ного параллелепипеда составляют с плоскостью основания
углы аир. Найдите угол между диагональю параллелепипеда и
плоскостью основания.
9. (КГУ, химфак, 1978 г.). Плоскость пересекает прямоуголь-
ный параллелепипед с квадратным основанием по ромбу с острым
углом а. Под каким углом пересекает эта плоскость боковые
ребра параллелепипеда?
10. (МЭИ, 1978 г.). В прямоугольном параллелепипеде
ABCDAfBjCiDt диагонали основания [АС] и [ВО] пересекаются
в точке М, АМВ = а. Определите площадь боковой поверхности
параллелепипеда, если | BtM | = b, ВМВ± = $.
11. (МВТУ, 1979 г.). Основания параллелепипеда —квадраты
со стороной Ь, а все боковые грани —ромбы. Одна из вершин
верхнего основания одинаково удалена от всех вершин нижнего
основания. Найдите объем параллелепипеда.
12. (МИНХ, 1979 г.). В параллелепипеде ABCDA^-fiJ^
грань ABCD — квадрат со стороной 5 см; длина ребра [AAJ также
равна 5 см, и это ребро образует с ребрами [АВ] и [АО] углы,
равные 60°. Найдите длину диагонали [ВО*].
13. (МЭИ, 1979 г.). Диагональ прямоугольного параллелепи-
педа равна I и образует с плоскостью основания угол а. Найдите
площадь боковой поверхности параллелепипеда, если площадь его
основания равна S.
14. (БГУ, 1980 г.). Найдите площадь боковой поверхности и
объем прямого параллелепипеда, зная, что его высота равна /г,
диагонали его составляют с основанием углы а и (J, а его осно-
ванием служит ромб.
15. (МАИ, 1979 г.). Основанием прямого параллелепипеда
служит ромб. Площади диагональных сечений равны и S2.
Найдите площадь боковой поверхности параллелепипеда.
16. (МЭИ, 1978 г.). Основанием прямой призмы служит ромб
с острым углом а. Определите объем призмы, если ее большая
диагональ имеет длину I и образует с плоскостью основания
угол р.
17. (МГРИ, 1979 г.). Через сторону нижнего основания пра-
вильной треугольной призмы и противоположную вершину верх-
него основания проведена плоскость, наклоненная к плоскости
основания под углом а. Площадь сечения призмы этой плоско-
стью равна S. Найдите объем отсеченной пирамиды.
18. (МИНХ, 1979 г.). В основании прямой призмы лежит
равносторонний треугольник. Плоскость, проходящая через одну
201
из сторон нижнего основания и противоположную вершину верх-
него, наклонена к плоскости нижнего основания под углом <р.
Площадь этого сечения равна Q. Найдите объем призмы.
19. (МЭИ, 1980 г.). Основанием прямой призмы служит рав-
нобедренная трапеция с острым углом а. Боковая сторона тра-
пеции и ее меньшее основание имеют равные длины. Найдите
объем призмы, если диагональ призмы равна а и образует с пло-
скостью основания уголр.
20. (КуйбГУ, 1980 г.). В основании прямой призмы лежит
равнобочная трапеция, у которой диагональ равна а, а угол меж-
ду диагональю и большим основанием равен а. Диагональ призмы
наклонена к основанию под углом р. Найдите объем призмы.
21. (МАТИ, 1980 г.). Определите объем прямой призмы, у ко-
торой основанием служит прямоугольный треугольник с острым
углом а, если боковое ребро призмы имеет длину I и составляет
с диагональю большей боковой грани угол р.
22. (КуйбГУ, 1980 г.). Основанием прямой призмы служит
прямоугольный треугольник с гипотенузой длины с и острым
углом в 30°. Через гипотенузу нижнего основания и вершину
прямого угла верхнего основания проведена плоскость, образую-
щая с плоскостью основания угол 45°. Определите объем тре-
угольной пирамиды, отсеченной от призмы плоскостью.
23. (КГУ, географ, фак., 1977 г.). Прямая призма: имеет
в основании равносторонний треугольник. Плоскость, проходящая
через одну из его сторон под углом а к плоскости основания,
отсекает от призмы треугольную пирамиду объема V. Определите
площадь сечения.
24. (МИНХ, 1979 г.). Каждое ребро наклонной треугольной
призмы равно 2, одно из боковых ребер составляет со смежными
сторонами основания углы в 60°. Найдите площадь полной по-
верхности призмы.
25. (КГУ, ВМК, 1978 г.). Основанием прямой призмы слу-
жит прямоугольный треугольник с периметром 2р и острым
углом а. Найдите боковую поверхность призмы, если известно,
что в нее можно вписать шар.
26. (МГИ, 1980 г.). Длина диагонали правильной четырех-
угольной призмы равна I, диагональ образует с плоскостью осно-
вания угол, величина которого равна а. Найдите объем призмы.
27. (КПИ, 1979 г.). В правильной четырехугольной призме
через середины двух смежных сторон основания проведена плос-
кость, пересекающая это основание под углом а и три боковых
ребра призмы. Определите площадь полученного сечения и его
острый угол, если сторона основания призмы равна Ь.
28. (МТИМБО, 1977 г.). Определите объем правильной четы-
рехугольной призмы, если ее диагональ образует с боковой
гранью угол а, а сторона основания по длине равна а.
29. (ТбГУ, мехмат, спец, прикладная матем., 1981 г.). Осно-
вание призмы —правильный треугольник, длина стороны кото-
рого 4 см. Одна из боковых граней, перпендикулярная плоско-
202
сти основания,— ромб, длина диагонали которого равна 6 см.
Найдите объем призмы.
30. (МТИМБО, 1979 г.). Основанием прямой призмы служит
ромб с острым углом а; угол между меньшей диагональю ромба
и меньшей диагональю призмы равен |3. Определите объем призмы,
если меньшая диагональ ромба равна d.
31. (РГУ, физфак, спец, радиофизика, 1977 г.). Основанием
прямой призмы является равнобедренный треугольник, основа-
ние которого имеет длину а и угол при основании а. Найдите
объем призмы, если площадь ее боковой поверхности равна сумме
площадей оснований.
32. (МТИМБО, 1980 г.). Самая большая диагональ правиль-
ной шестиугольной призмы, имеющая длину d, составляет с бо-
ковым ребром призмы угол а. Определите объем призмы.
33. (ТбГУ, физфак, спец, радиофизика и электроника, 1977 г.).
Основание призмы — равнобедренный прямоугольный треуголь-
ник с катетом длины а см. Боковое ребро, противоположное ги-
потенузе, с катетами составляет острые углы аир, Длина бо-
кового ребра &см. Найдите объем призмы.
34. (МТИМБО, 1978 г.). Площадь полной поверхности пра-
вильной треугольной пирамиды равна S. Зная, что угол между
боковой гранью и основанием пирамиды равен а, найдите сторону
основания.
35. (МТИМБО, 1977 г.). В правильной треугольной пирамиде
сторона основания равна а. а плоский угол при вершине а.
Определите объем пирамиды.
36. (МТИМБО, 1978 г.). Найдите угол между апофемой бо-
ковой грани правильной треугольной пирамиды и плоскостью
ее основания, зная, что разность между этим углом и углом, ко-
торый составляет боковое ребро пирамиды с плоскостью основа-
ния, равна а.
37. (ТбГУ, мехмат, спец, прикладная матем., 1978 г.). Длина
стороны основания правильной треугольной пирамиды равна 10 см,
двугранный угол при основании равен 30°. Найдите объем пи-
рамиды.
38. (МТИМБО, 1982 г.). Боковое ребро правильной треуголь-
ной пирамиды имеет длину I и составляет с плоскостью основа-
ния угол а. Найдите объем пирамиды.
39. (МТИМБО, 1978 г.). Найдите объем правильной треуголь-
ной пирамиды, у которой плоский угол при вершине равен а,
а кратчайшее расстояние между боковым ребром и противопо-
ложной стороной основания равно d.
40. (МТИМБО, 1979 г.). Постройте сечение правильной тре-
угольной пирамиды плоскостью, проходящей через центр основа-
ния параллельно одной из боковых граней пирамиды. Найдите
площадь сечения, если боковая грань пирамиды наклонена к осно-
ванию под углом а, а сторона основания пирамиды равна а.
41. (ТбГУ, мехмат, спец, прикладная матем., 1980 г.). Осно-
вание пирамиды —прямоугольный треугольник с катетом длины а
203
и противолежащим углом а. Боковые ребра наклонены к пло-
скости основания под углом 0. Найдите площадь боковой грани,
проходящей через меньший катет основания, если tga = 3/2,
tg (3 = 2/3, а = 8см.
42. (МТИМБО, 1979 г.). Основанием пирамиды служит пря-
моугольный треугольник АВС, у которого катет | AC J = b и В = 0.
Боковые грани пирамиды, проходящие через катеты [ДС] и [ВС],
перпендикулярны к плоскости основания, а третья боковая грань
образует с основанием угол а. Найдите объем пирамиды.
43. (ТбГУ, мехмат, спец, прикладная матем., 1982 г.). Дана
пирамида SACB с вершиной в S, ее основание —прямоугольный
треугольник АСВ. В этом треугольнике [ДВ] —гипотенуза, ее
длина 2К3 см. Боковое ребро [ВД] перпендикулярно к плоскости
основания. Двугранный угол, составленный боковыми гранями
ВДС и ВДВ, равен 30°. Длина высоты пирамиды —4 см. Найдите
площадь боковой поверхности.
44. (МТИМБО, 1978 г.). Найдите объем пирамиды, основа-
нием которой служит прямоугольный треугольник с гипотенузой
длины с и острым углом а, если боковые ребра наклонены к пло-
скости основания под углом |3.
45. (ТбГУ, мехмат, спец, прикладная матем., 1977 г.). Осно-
вание пирамиды —равнобедренный прямоугольный треугольник,
длина гипотенузы которого равна 5 см. Все боковые ребра накло-
нены к плоскости основания под углом а. Найдите площадь пол-
ной поверхности пирамиды.
46. (МТИМБО, 1982 г.). В основании треугольной пирамиды
лежит равнобедренный треугольник, у которого площадь равна В,
а угол при вершине равен а. Найдите объем пирамиды, если
угол между каждым боковым ребром и высотой пирамиды равен (5.
47. (МТИМБО, 1979 г.). Основанием пирамиды служит равно-
бедренный треугольник, у которого угол между равными сторо-
нами равен а, а противоположная ему сторона имеет длину а.
Боковые грани пирамиды наклонены к основанию под углом 0.
Найдите полную поверхность пирамиды.
48. (МТИМБО, 1982 г.). Определите объем пирамиды, имею-
щей основанием треугольник, два угла которого равны а и 0,
а радиус описанного около основания круга имеет длину R.
Боковые ребра наклонены к плоскости основания под углом <р.
49. (БашГУ, 1980 г.). В правильной треугольной пирамиде
длина стороны основания равна а, а двугранный угол между бо-
ковыми гранями равен а. Найдите объем пирамиды.
50. (МЭИ, 1980 г.). Угол между высотой правильной тре-
угольной пирамиды и апофемой равен а, длина бокового ребра
пирамиды равна I. Найдите объем пирамиды.
51. (ВЗЭИС, 1978 г.). Плоский угол при вершине правильной
треугольной пирамиды равен а, радиус окружности, вписанной
в боковую грань, равен г. Найдите боковую поверхность пира-
миды.
204
52. (ТартГУ, 1980 г.). Сторона основания правильной тре-
угольной пирамиды равна а, двугранный угол при основании ра-
вен 45°. Определите объем пирамиды.
53. (КГУ, геофак, 1978 г.). Найдите высоту правильного те-
траэдра, объем которого равен V.
54. (КГУ, геофак, 1978 г.). Найдите объем правильного те-
траэдра, высота которого равна Н.
55. (КГУ, химфак, 1978 г.). В правильной треугольной пира-
миде, объем которой равен V, боковые грани наклонены к плоско-
сти основания под углом а. Определите полную поверхность пира-
миды.
56. (МИТХТ, 1979 г.). Найдите объем и боковую поверхность
правильной треугольной пирамиды, зная, что плоскость, про-
ходящая через сторону основания и середину высоты пирамиды,
наклонена к основанию под углом <р, а сторона основания равна а.
57. (МАТИ, 1980 г.). Найдите объем правильной треугольной
пирамиды, у которой боковое ребро наклонено к плоскости основа-
ния под углом а и удалено от середины противоположной стороны
на расстояние d.
58. (МИНХ, 1980 г.). Правильная треугольная пирамида рас-
сечена плоскостью, перпендикулярной основанию и делящей две
стороны основания пополам. Определите площадь сечения пирами-
ды этой плоскостью, если известно, что сторона основания равна а,
а высота пирамиды равна Н.
59. (КПИ, 1979 г.). В правильной треугольной пирамиде, сторо-
на основания которой равна а, а боковое ребро — 2а, через сере-
дину бокового ребра, перпендикулярно к нему, проведена плоскость.
Определите площадь образовавшегося сечения.
60. (МИТХТ, 1979 г.). Через вершину С основания правильной
треугольной пирамиды SABC проведена плоскость перпендикуляр-
но боковому ребру [SAL Эта плоскость составляет с плоскостью
основания угол, косинус которого равен 2/3. Определите косинус
угла между боковыми гранями пирамиды.
61. (МТИМБО, 1977 г.; МИТХТ, 1979 г.). Через вершину пра-
вильной треугольной пирамиды и середины двух сторон основания
проведено сечение. Найдите площадь сечения и объем пирамиды,
зная, что длина стороны основания равна а, а угол между сечением
и основанием равен а.
62. (КишПИ 1980 г.). Высота правильной треугольной призмы
равна Н. Через одно из ребер нижнего основания и противополож-
ную ему вершину верхнего основания проведена плоскость. Най-
дите площадь сечения, если угол образовавшегося треугольника
при заданной вершине призмы равен а.
63. (КГУ, физфак, 1977 г.). Найдите объем правильной тре-
угольной пирамиды, если плоский угол при вершине равен а,
а радиус окружности, описанной около боковой грани, равен /?.
64. (КПИ, 1979 г.). Боковое ребро правильной треугольной
пирамиды равно а, а плоский угол при вершине равен 2а. Найдите
площадь поверхности шара, описанного вокруг пирамиды.
205
65. (МТИПП, 1978 г.; ОГУ, 1980 г.). Боковые ребра и две сто-
роны основания треугольной пирамиды равны между собой и рав-
ны I. Угол между равными сторонами треугольника, лежащего в
основании, равен а. Найдите объем пирамиды.
66. (ПГУ, 1980 г.). Основанием пирамиды служит равнобедрен-
ный треугольник, у которого боковая сторона равна а, а угол при
вершине равен а. Все боковые ребра пирамиды наклонены к плос-
кости основания под углом 0. Найдите объем пирамиды.
67. (МЭИ, 1977 г.). Боковая грань правильной треугольной
пирамиды образует с плоскостью основания угол а, сумма длин
высоты пирамиды и радиуса окружности, вписанной в основание
пирамиды, равна а. Найдите объем пирамиды.
68. (ВЗИИЖТ, 1979 г.). Боковые ребра треугольной пирамиды
взаимно перпендикулярны и каждое из них равно Ь. Найдите объем
пирамиды.
69. (МИНХ, 1979 г.). В тетраэдре ABCD найдите угол между
прямыми (AD) и (ВС), если | АВ| =|ЛС| и DAB=DAC.
70. (МИНХ, 1978 г.). Стороны треугольника, лежащего в ос-
новании пирамиды, равны 13, 14 и 15 см. Двугранные углы при ос-
новании пирамиды равны по 45°. Найдите боковую поверхность пи-
рамиды.
71. (КПИ, 1979 г.). В треугольной пирамиде боковые ребра
равны, а в основании ее лежит прямоугольный треугольник, вы-
сота которого, опущенная из вершины прямого угла, равна h.
Двугранные углы, образованные гранями пирамиды, пересекающи-
мися по катетам основания, равны а и 0. Найдите объем пирамиды.
72. (МИСиС, 1979 г.). В основании пирамиды лежит равнобед-
ренный треугольник с углом <р при вершине. Все боковые ребра
пирамиды равны по длине а. Определите объем пирамиды, если
длина радиуса вписанной в основание окружности равна г.
73. (МИСиС, 1979 г.). В основании пирамиды лежит равнобед-
ренный треугольник с углом при вершине, равным по величине а.
Все двугранные углы при основании пирамиды равны 0. Определи-
те объем пирамиды, если радиус окружности, описанной около
основания, равен
74. (МАТИ, 1979 г.). Основанием пирамиды служит равнобед-
ренный треугольник, равные стороны которого имеют длину b и
составляют угол величины а. Боковые ребра пирамиды образуют
с высотой пирамиды угол 0. Определите объем пирамиды.
75. (МАИ, 1979 г.). В треугольной пирамиде SABC две равные
боковые грани Л SB и BSC перпендикулярны плоскости основания,
а грань ASC наклонена к плоскости основания под углом 0. Найдите
радиус шара, описанного около пирамиды, если радиус окружности,
описанной около основания, равен г и АВС=а.
76. (ВильнГУ, матфак, 1980 г.). Сторона основания правильной
треугольной пирамиды равна т, а двугранный угол между боковыми
гранями пирамиды равен 2а. Через одну из сторон основания прове-
206
дена плоскость, перпендикулярная боковому ребру. Найдите
объем части пирамиды, лежащей ниже плоскости.
77. (ЛатвГУ, 1980 г.). Боковая поверхность треугольной пира-
миды равна В, каждое из боковых ребер равно I. Найдите плоские
углы при вершине пирамиды, зная, что они образуют арифметиче-
скую прогрессию с разностью, равной л/4.
78. (КазанГУ, физфак, 1978 г.). Гранями треугольной пирамиды
являются равные равнобедренные треугольники. Основание и про-
тиволежащий ему угол каждого такого треугольника равны а и а
соответственно. Найдите объем пирамиды.
79*. (КазанГУ, физфак, 1978 г.). В основании пирамиды лежит
правильный треугольник со стороной а. Одна из боковых граней
перпендикулярна к основанию, а площади двух других равны
Р и Q соответственно. В каком отношении высота пирамиды делит
сторону основания?
80*. (КазанГУ, физфак, 1978 г.). В основании пирамиды ле-
жит равнобедренный прямоугольный треугольник. Боковая грань,
опирающаяся на гипотенузу, перпендикулярна плоскости основа-
ния. Площади двух других граней равны S и Т соответственно.
Найдите длину гипотенузы основания, если известно, что она
делится высотой пирамиды в отношении 1 : р.
81. (КПИ, 1979 г.). Найдите радиус вписанного в треугольную
пирамиду шара, если все ее углы при вершине прямые, а длины
боковых ребер равны а, b и с.
82*. (КПИ, 1979 г.). Найдите объем треугольной пирамиды,
если площади ее граней равны So, St, S2 и S3, а двугранные углы,
прилежащие к грани с площадью So, равны между собой.
83*. (НГУ, мехмат, 1980 г.). SABC — правильный тетраэдр
с ребром длины единица, О — центр шара радиуса )/2, касающе-
гося ребер (ЛВ), (АС) и (АВ) (или их продолжений). Найдите дли-
ну отрезка [ОК], где К — середина ребра [ВС].
84*. (НГУ, мехмат, 1980 г.). В тетраэдре ABCD ребра [ЛС1,
[ВС] и [DC] взаимно перпендикулярны. Точка М лежит в плоско-
сти ЛВС и одинаково удалена от ребер [ЛВ1, [ВС] и [CD]. Точка К
лежит в плоскости BCD и одинаково удалена от тех же ребер. Най-
дите \MN I, если | ВС 1 = 1 CD |=/3, 1 ЛС 1=3.
85. (ВЗИИЖТ, 1979 г.). В правильной четырехугольной пира-
миде длина высоты равна 3 см, а бокового ребра — 5 см. Найдите
объем пирамиды.
86. (МГИ, 1980.). Найдите объем правильной четырехугольной
пирамиды, если длина стороны ее основания равна а, а величина
двугранного угла при основании равна а.
87. (МИСиС, 1979 г.). Плоский угол боковой грани при вер-
шине правильной четырехугольной пирамиды равен по величине <р.
Найдите величину угла между боковым ребром и плоскостью ос-
нования.
88. (МИТХТ, 1979 г.). В правильной четырехугольной пира-
207
миде двугранный угол при боковом ребре равен а. Найдите плоский
угол при вершине пирамиды.
89. (КПИ, 1979 г.). Основанием пирамиды служит прямо-
угольник, две боковые грани ее перпендикулярны основанию, две
другие боковые грани образуют с основанием углы аир соответ-
ственно. Определите объем пирамиды, если длина наибольшего
из боковых ребер равна /.
90. (КПИ, 1979 г.). Высота правильной четырехугольной пира-
миды равна Н, двугранный угол при основании равен <р. Найдите
радиус вписанного в пирамиду шара.
91. (МИТХТ, 1979 г.). Угол между боковым ребром и основанием
правильной четырехугольной пирамиды равен 60°, длина бокового
ребра равна а. Через середину одного из боковых ребер, перпен-
дикулярно к нему, проведена плоскость. Найдите площадь сечения.
92. (ПГУ, 1980 г.). Высота правильной четырехугольной пира-
миды равна h и составляет с боковой гранью угол а. Через сторону
основания пирамиды проведена плоскость, перпендикулярная про-
тиволежащей грани. Найдите объем пирамиды, отсекаемой этой
плоскостью от данной пирамиды.
93. (КПИ, 1979 г.). Сторона основания правильной четырех-
угольной пирамиды равна а, двугранный угол при основании ра-
вен а. Найдите площадь сечения пирамиды плоскостью, делящей
пополам двугранный угол при основании.
94. (НГУ, мехмат, 1980 г.). Длина каждого ребра правильной
четырехугольной пирамиды SABCD равна 1. Точка М лежит в
основании ABCD пирамиды и одинаково удалена от ребер [AS]
и IDS], a IA1SI — 1Л4С1. Точка N лежит на грани BSC и также оди-
наково удалена от тех же ребер, причем |MS| = 1Л7С1. Найдите пло-
щадь треугольника BMN.
95. (МАИ, 1979 г.). Основанием пирамиды служит ромб, дли-
ны диагоналей которого равны 6 м и 8 м. Высота пирамиды прохо-
дит через точку пересечения диагоналей ромба и имеет длину 1 м.
Найдите площадь боковой поверхности пирамиды.
96. (МИНХ, 1978 г.; МИТХТ, 1978 г.). Основанием пирамиды
служит ромб со стороной а и острым углом а. Две боковые грани
перпендикулярны основанию, а две другие образуют с ним угол
величиной р. Определите объем пирамиды и площадь боковой по-
верхности.
97. (МГРИ, 1979 г.). Основанием пирамиды служит равнобоч-
ная трапеция, у которой боковая сторона равна а, а острый угол
равен а. Все боковые грани образуют с основанием пирамиды
угол р. Найдите объем пирамиды.
98. (МГРИ, 1977 г.; МТИМБО, 1979 г.). Основанием пирамиды
служит прямоугольник с углом а между диагоналями. Боковые
ребра образуют е плоскостью основания угол р. Найдите объем
пирамиды, если радиус описанного около нее шара равен R.
99. (КГУ, физфак, 1977 г.). Найдите объем правильной четы-
рехугольной пирамиды, если угол при основании боковой грани
равен а, а радиус окружности, которая вписана в эту грань, равен R.
208
100. (КПИ, 1979 г.). Высота правильной четырехугольной усе-
ченной пирамиды равна Н, боковое ребро и диагональ боковой
грани пирамиды наклонены к плоскости основания под углами а
и р. Найдите боковую поверхность пирамиды.
101. (МЭИ, 1980 г.). В правильной шестиугольной пирамиде
угол между боковым ребром и смежным ребром основания равен а,
сумма радиусов окружностей, вписанной в основание и описанной
около основания, равна т. Найдите площадь боковой поверхности
пирамиды.
102. (ХГУ, мехмат, 1978 г.). Апофема правильной шестиуголь-
ной пирамиды равна т. Двугранный угол при основании равен а.
Найдите полную поверхность пирамиды.
103. (МИНХ, 1979 г.). Высота правильной усеченной четырех-
угольной пирамиды равна 3 см, объем ее равен 38 см3, а площади
оснований относятся как 9 : 4. Определите боковую поверхность
усеченной пирамиды.
104. (КПИ, 1979 г.). Площади оснований усеченной пирамиды
равны St и S2. Найдите площадь S сечения пирамиды плоскостью,
которая параллельна основаниям и равноудалена от них.
105. (МТИМБО, 1977 г.). Площадь полной поверхности пра-
вильной четырехугольной пирамиды равна S, а плоский угол бо-
ковой грани при вершине равен а. Найдите высоту пирамиды.
106. (РГУ, физфак, спец, радиофизика, 1977 г.). Разность
между длиной апофемы и длиной высоты правильной четырехуголь-
ной пирамиды равна т, а угол между ними равен а. Найдите объем
пирамиды.
107. (МТИМБО, 1978 г.). В правильной четырехугольной пи-
рамиде длина высоты равна h. Через диагональ основания пирамиды
и середину противолежащего ребра проведено сечение, образую-
щее угол а с диагональной плоскостью, проведенной через ту же
диагональ основания. Найдите площадь сечения.
108. (МТИМБО, 1982 г.). Найдите плоский угол при верши-
не правильной четырехугольной пирамиды, если этот угол ра-
вен углу между боковым ребром и плоскостью основания пи-
рамиды.
109. (ТбГУ, физфак, спец, радиофизика и электроника, 1978 г.;
МТИМБО, 1977 г.). Основание пирамиды — прямоугольник, пло-
щадь которого равна 12 см2. Две боковые грани пирамиды перпен-
дикулярны к основанию, а две другие составляют с основанием углы
в 30° и 60°. Найдите площадь полной поверхности пирамиды.
ПО. (МТИМБО, 1982 г.). Основанием четырехугольной пира-
миды служит ромб со стороной длины а и острым углом р. Каждая
боковая грань наклонена к плоскости основания под углом у.
Найдите полную поверхность пирамиды.
111. (МТИМБО, 1982 г.). Основанием четырехугольной пира-
миды служит ромб, меньшая диагональ которого имеет длину d,
а острый угол равен а.. Каждая боковая грань наклонена к плос-
кости основания под углом р. Вычислите полную поверхность пи-
рамиды.
209
112. (ТбГУ физфак, спец, радиофизика и электроника, 1980 г.).
Основание пирамиды — параллелограмм с тупым углом а. Две
боковые грани перпендикулярны к плоскости основания, а осталь-
ные две составляют с плоскостью основания углы |3 и у. Найдите
площадь меньшей боковой грани, если меньшее боковое ребро имеет
длину 8 см, sin Р = 1/3, sin Т=7б, tga=— 73.
113. (МТИМБО, 1982 г.). Длина стороны основания правильной
четырехугольной пирамиды равна а, боковая грань составляет
с плоскостью основания угол а. Найдите радиус описанного шара.
114. (МТИМБО, 1979 г.). Длина стороны основания правильной
треугольной пирамиды равна а, плоский угол при вершине пира-
миды равен а. Найдите длину радиуса вписанного в пирамиду шара.
115. (МТИМБО, 1979 г.). Найдите радиус шара, вписанного
в правильную треугольную пирамиду, у которой высота по длине
равна //, а угол между боковым ребром и плоскостью основания
равен а.
116. (МТИМБО, 1978 г.). В конус вписана правильная тре-
угольная пирамида, боковое ребро которой наклонено к основанию
под углом а. Определите объем конуса, если сторона основания пи-
рамиды имеет длину а,
117. (МТИМБО, 1979 г.). В конус, образующая которого по
длине равна I и наклонена к основанию под углом а, вписана пира-
мида, в основании которой прямоугольник с острым углом 2а
между диагоналями. Найдите расстояние от основания высоты до
боковой грани, проходящей через меньшую сторону основания.
118. (СимфГУ, матфак, 1982 г.). В усеченный конус вписан шар
радиуса длины а. Образующая конуса наклонена к плоскости ос- ,
нования под углом а. Найдите объем усеченного конуса.
119. (МТИМБО, 1978 г.). Объем конуса равен v. В конус впи-
сана пирамида, в основании которой лежит равнобедренный тре- ।
угольник с углом а между боковыми сторонами. Найдите объем
пирамиды.
120. (РГУ, мехмат, спец, прикладная матем., 1977 г.). В конус
вписан цилиндр, высота которого равна радиусу основания конуса.
Найти величину угла между осью конуса и его образующей, зная,
что площадь полной поверхности цилиндра относится к площади
основания конуса как 3 : 2.
121. (МТИМБО, 1982 г.). Найдите объем и полную поверх-
ность конуса, если в его основании хорда длины а стягивает дугу а,
а угол между высотой и образующей конуса равен (J.
122. (СимфПИ, 1981 г.). Определите площадь полной поверх-
ности цилиндра, осевое сечение которого есть квадрат и боковая
поверхность равна S.
123. (МТИМБО, 1982 г.). Через вершину конуса проведена
плоскость под углом а к основанию конуса. Эта плоскость пересекает
основание конуса по хорде длины а, стягивающей дугу (5. Найдите
объем и боковую поверхность конуса.
124. (МТИМБО, 1979 г.). Через две образующие конуса прове-
дена плоскость, отсекающая в основании дугу в 120Q. Определите
210
площадь сечения, если радиус основания конуса по длине равен R
и плоскость сечения составляет с плоскостью основания' угол а.
125. (ТбГУ, физфак, спец, радиофизика и электроника, 1981 г.).
Треугольник Л ВС вращается вокруг стороны [BCJ, Л=120<>. Найдите
площадь той поверхности, которая получается вращением ломаной,
составленной из сторон [СЛ1 и [ЛВ] если |AB|=2V3, |ВС1=5.
126. (МТИМБО, 1977 г.). В шар вписан конус. Площадь осе-
вого сечения конуса равна S. Угол между его высотой и образую-
щей равен а. Найдите объем шара.
127. (РГУ, мехмат, спец, прикладная матем., 1977 г.). Конус
и цилиндр имеют общее основание, а вершина конуса находится
в центре другого основания цилиндра. Найдите величину угла
между осью конуса и его образующей, если известно, что площадь
полной поверхности цилиндра относится к площади полной поверх-
ности конуса как 7:4.
128. (МТИМБО, 1979 г.). Образующая конуса наклонена к
плоскости основания конуса под углом <р. Площадь сечения конуса
плоскостью, проходящей через центр вписанного в конус шара
параллельно основанию, равна Q. Найдите объем конуса.
129. (РГУ, физфак, спец, физика, 1977 г.). В прямой конус,
осевым сечением которого является прямоугольный треугольник,
вписан цилиндр (нижнее основание цилиндра лежит в плоскости
основания конуса). Отношение площади боковой поверхности кону-
са к площади боковой поверхности цилиндра равно 4 J/2. Найдите
величину угла между плоскостью основания конуса и прямой,
проходящей через центр верхнего основания цилиндра и произ-
вольную точку окружности основания конуса.
130. (МТИМБО, 1977 г.). Определите боковую поверхность
конуса, зная длину радиуса R описанного вокруг него шара и
угол а, под которым из центра шара видна образующая конуса.
131. (РГУ, физфак, спец, физика, 1977 г.). В конус вписан
цилиндр, высота которого равна диаметру основания конуса.
Площадь полной поверхности цилиндра равна площади основания
конуса. Найдите величину угла между образующей конуса и плос-
костью основания.
132. (МТИМБО, 1982 г.). Около шара радиуса R описан пря-
мой круговой конус, в котором угол между образующей и плоско-
стью основания равен а. Определите полную поверхность и объем
конуса.
133. (МТИМБО, 1982 г.). В шар радиуса R вписан конус, в
этот конус вписан цилиндр с квадратным осевым сечением. Най-
дите полную поверхность цилиндра, если угол между образующей
конуса и плоскостью основания равен а.
134. (МТИМБО, 1978 г.). В конус вписан шар. Радиус круга
касания поверхности шара и боковой поверхности конуса по длине
равен г. Прямая, соединяющая центр шара с произвольной точкой
окружности основания конуса, составляет с высотой конуса угол,
равный а. Найдите объем конуса.
211
135. (МИНХ, 1979 г.). Радиус основания цилиндра равен 26 см,
длина образующей 48 см. На каком расстоянии от оси цилиндра
следует провести сечение, параллельное оси цилиндра, чтобы оно
имело форму квадрата?
136. (ХАИ, 1980 г.). В цилиндре параллельно его оси на расстоя-
нии а от нее проведена плоскость, которая отсекает от окружности
основания дугу в а радиан. Площадь сечения равна S. Определите
объем цилиндра.
137. (БГУ, 1980 г.). Плоскость, проведенная параллельно оси
цилиндра, делит окружность основания в отношении т : п. Пло-
щадь сечения равна S. Найдите боковую поверхность цилиндра.
138. (КГУ, мехмат, 1978 г.). Высота конуса, равная h, является
диаметром сферы, которая делит боковую поверхность конуса в от-
ношении т : п (считая от вершины). Найдите радиус основания
конуса.
139*. (МГУ, физфак, 1980 г.). Два равных конуса с общей вер-
шиной А расположены по разные стороны от плоскости Р так, что
только одна образующая каждого конуса ([ДВ] для одного конуса
и [АС] для другого) принадлежит плоскости Р. Известно, что
ВАС=0, а угол между высотой и образующей каждого конуса ра-
вен <р. Найдите угол между линией пересечения плоскостей основа-
ний конусов и плоскостью Р.
140*. (МГУ, физфак, 1980 г.). Точка О — общая вершина двух
конгруэнтных конусов, расположенных по одну сторону от пло-
скости а так, что только одна образующая каждого конуса ([ОД] для
одного конуса и [ОВ] для другого) принадлежат плоскости а. Из-
вестно, что величина угла между высотами конусов равна 0, а ве-
личина угла между высотой и образующей каждого конуса равна
<р, причем 2ф<0. Найдите величину угла между образующей
(ОД) и плоскостью основания другого конуса, которой принадле-
жит точка В.
141. (БГУ, 1980 г.). Диагонали осевого сечения усеченного ко-
нуса точкой пересечения делятся в отношении 2:1, считая от
большего основания. Угол между диагоналями, обращенный к ос-
нованиям конуса, равен а. Длина диагонали равна I. Найдите объем
усеченного конуса. _
142. (МТИММП, 1980 г.). Шар радиуса jZ2 см равновелик
прямому конусу, боковая поверхность которого в три раза больше
площади основания. Найдите высоту конуса.
143. (КПИ, 1979 г.). В шаре радиуса R из точки его поверх-
ности проведены три равные хорды под углом а друг к другу.
Определите их длину.
144*. (КПИ, 1979 г.). Четыре сферы радиуса г расположены
так, что каждая из них касается трех других. Найдите радиус сфе-
ры, которая касается каждой из данных сфер.
145*. (КГУ, мехмат, 1978 г.). На плоскости помещено четыре
шара: два шара радиуса а и два одинаковых шара неизвестного ра-
212
диуса х так, что каждый шар касается трех других и плоскости.
Найдите радиус х.
146. (КПИ, 1979 г.). Сфера, центр которой находится в вер-
шине конуса, касается его основания. Найдите угол при вершине
в осевом сечении конуса, если сфера делит конус на части равных
объемов.
147. (КГУ, мехмат, 1978 г.). Сфера с центром в вершине конуса
делит конус на две равновеликие части. Найдите радиус этой сферы,
если радиус основания конуса равен а, а величина угла при вер-
шине его осевого сечения равна а.
148* . (КПИ, 1979 г.). В конус, у которого угол осевого сече-
ния при вершине равен а, вписан шар радиуса /?. Найдите объем
части конуса, расположенной над шаром.
149. (МСИ, 1980 г.). Расстояние от центра вписанного в конус
шара до вершины конуса равно а. Угол между образующей и пло-
скостью основания конуса равен а. Найдите объем конуса.
150. (ВильнГУ, физфак, 1980 г.; МГРИ, 1979 г.). В конус впи-
сан шар, площадь большого круга которого равна Q. Найдите
полную поверхность конуса, если угол при вершине его осевого
сечения равен 2а.
151*. (КГУ, ВМК, 1980 г.). Сфера вписана в прямой круговой
конус с углом а при вершине осевого сечения. В эту сферу вписан
конус с таким же углом при вершине осевого сечения. Найдите
величину угла а, если отношение объема первого конуса к объему
второго конуса равно 27.
152. (ЛПИ, 1980 г.). Центр сферы совпадает с центром основания
конуса, а ее радиус равен радиусу этого основания. Высота конуса
больше радиуса основания конуса. Через окружность, по которой
сфера пересекается с боковой поверхностью конуса, проведена
плоскость. Каким должен быть угол при вершине осевого сечения
конуса, чтобы эта плоскость делила конус на две одинаковые по
объему части?
153. (ЯГУ, 1980 г.). Шар касается всех граней куба. Найдите
отношение площадей поверхности и отношение объемов этих фигур.
154. (МАМИ, 1979 г.). Площадь поверхности шара, вписанного
в конус, равна Q. Определите площадь полной поверхности конуса,
если наибольший угол между его образующими равен а.
155. (МГМИ, 1979 г.). Найдите отношение площади полной
поверхности прямого кругового конуса, вписанного в шар, к пло-
щади поверхности этого шара, если известно, что угол при верши-
не осевого сечения конуса равен а и а>л/2.
156. (МГУ, филфак, 1977 г.). В прямой круговой конус с углом
в 60° при вершине осевого сечения вложено три одинаковых шара
радиуса г так, что каждый из них касается двух других, основания
и боковой поверхности конуса. Найдите радиус основания конуса.
157. (КПИ, 1979 г.). В конус вписан шар радиуса г. Найдите
объем конуса, если известно, что плоскость, касающаяся шара и
перпендикулярная к одной из образующих конуса, отстоит от вер-
шины конуса на расстоянии d.
213
158. (МГМИ, 1979 г.). Найдите отношение объема шара к объе-
му прямого кругового цилиндра, вписанного в этот шар, если извест-
но, что меньший угол между диагоналями осевого сечения цилиндра
равен а и диаметр основания больше высоты цилиндра.
159. (МЭИ, 1980 г.). В цилиндр помещен конус так, что основа-
ние конуса совпадает с нижним основанием цилиндра, а вершина
конуса совпадает с центром верхнего основания цилиндра. Образу-
ющая конуса наклонена к плоскости основания под углом а. Най-
дите объем цилиндра, если площадь полной поверхности конуса S.
160. (КПИ, 1979 г.). В конус, радиус основания которого ра-
вен г, а угол, составленный высотой и образующей, равен а, впи-
сан цилиндр так, что его боковая поверхность относится к боковой
поверхности конуса как т: п. Найдите объем цилиндра.
161. (МИХМ, 1979 г.). В конус вписан полушар так, что боль-
шой круг полушара лежит в плоскости основания конуса, а шаро-
вая поверхность касается поверхности конуса. Найдите площадь
полной поверхности полушара и его объем, если образующая ко-
нуса равна I и составляет с плоскостью основания угол р.
162. (МИСиС, 1978 г.). В конус, у которого площадь боковой
поверхности равна S, а угол наклона образующей к плоскости ос-
нования равен ф, вписана треугольная пирамида, имеющая основа-
нием прямоугольный треугольник с острым углом а. Определите
объем пирамиды.
163. (МГРИ, 1980 г.). Угол между плоскостью основания и бо-
ковой гранью правильной четырехугольной пирамиды равен ф.
Площадь поверхности сферы, вписанной в пирамиду, равна S.
Найдите площадь боковой поверхности пирамиды.
164*. (КГУ, геофак, 1978 г.). В треугольную пирамиду, все
ребра которой имеют длину а, вписан шар. В один из трехгранных
углов пирамиды вновь вписан шар так, что он касается первого.
Найдите -объем второго шара.
165. (КГУ, эконом, фак., 1980 г.). Высота правильной четырех-
угольной пирамиды и радиус описанной сферы равны соответст-
венно h и г {r^.h). Найдите площадь основания пирамиды.
166. (МТИМБО, 1979 г.; БашГУ, 1980 г.). В правильную четы-
рехугольную пирамиду вписан шар. Расстояние от центра шара
до вершины пирамиды равно а, а угол наклона боковой грани пира-
миды к плоскости основания равен а. Найдите площадь боковой
поверхности и объем пирамиды.
167. (КГУ, ВМК, 1980 г.). Сторона основания правильной четы-
рехугольной пирамиды равна а, двугранный угол при основании
равен а. В пирамиду вписан шар, к шару проведена касательная
плоскость, параллельная основанию пирамиды. Определите
площадь боковой поверхности полученной усеченной пирамиды. ’
168. (ЛьвГУ, 1980 г.). В конус, образующая которого наклоне- :
на к плоскости основания под углом а, вписана пирамида. Основа- !
нием пирамиды служит прямоугольный треугольник с катетами
а и Ъ. Найдите объем пирамиды.
169, (МГУ, географ, фак., 1980 г.). В правильную шестиуголь-
214
ную пирамиду вписан прямой конус и около нее описан прямой ко-
нус. Длина высоты пирамиды равна Н, а радиус основания опи-
санного конуса равен R. Найдите разность объемов описанного
и вписанного конуса.
170. (МАИ, 1979 г.). Радиус основания конуса равен г, а обра-
зующая наклонена к плоскости основания под углом <р. Около этого
конуса описана пирамида, имеющая в основании прямоугольный
треугольник с острым углом 2<р. Определите объем пирамиды.
171. (МЭИ, 1979 г.). Определите площадь боковой поверхности
конуса, вписанного в правильную треугольную пирамиду, если
длина бокового ребра пирамиды равна I и боковая грань пирамиды
образует с плоскостью основания угол а.
172. (МГРИ, 1979 г.). В правильную четырехугольную пира-
миду вписан цилиндр с радиусом основания г. Высота цилиндра
в два раза меньше высоты пирамиды. Плоский угол пр» вершине
пирамиды равен а. Найдите объем пирамиды.
173. (БГУ, 1980 г.). В цилиндр вписан параллелепипед, диаго-
наль которого образует с плоскостью основания угол а, а с боль-
шей боковой гранью—угол р. Найдите объем цилиндра, если сто-
рона основания большей боковой грани параллелепипеда равна в.
174. (МСИ, 1980 г.). Основанием прямой призмы служит ромб
с острым углом а и меньшей диагональю d. Плоскость, проходящая
через эту диагональ и вершину второго основания призмы, накло-
нена к плоскости основания под углом 0. Найдите объем цилиндра,
вписанного в призму.
175*. (ЛГУ, геофак, 1980 г.). В основании правильной призмы
лежит треугольник, вершины которого являются серединами ребер
основания правильной пирамиды. Какая часть объема призмы на-
ходится вне пирамиды, если известно, что высота пирамиды в-3 раза
меньше высоты призмы?
176*. (НГУ, мехмат, 1980 г.). SABC — правильный единичный
тетраэдр. Сфера касается ребер [ЛВ], [ЛС], [АВ] и проходит через
середину ребра [ВС]. Найдите радиус сферы, если известно, что
ее центр лежит внутри тетраэдра.
177*.: (НГУ, физфак, 1980 г.). Сфера касается бокового ребра
[ЛЛ'1 и непараллельных ребер оснований [ЛВ] и [Л'О'] единичного
куба ABCDA'B'C'D' и проходит через точку М ребра [CC'J, при-
чем |СЛ1|=Х/». Найдите радиус сферы.
178*.: (КГУ, мехмат, 1978 г.). Внутри цилиндра высотой За
помещено три одинаковых шара радиуса а так, что каждый шар
касается двух других и боковой поверхности цилиндра, причем
два шара касаются нижнего основания, а третий — верхнего.
Найдите радиус основания цилиндра.
179. , (МТИМБО, 1982 г.). Образующая конуса равна I и сос-
тавляет с плоскостью основания угол <р. При каком значении <р
объем конуса будет наименьшим? Чему равен этот объем?
180. (МТИМБО, 1980 г.). В полушар радиуса R вписан конус
так, что вершина его находится в центре полушара. Найдите радиус
основания конуса, при котором объем его будет максимальным.
215
181. (РГУ, мехмат, спец, матем., механ., 1977 г.). Основание
пирамиды — прямоугольный треугольник с площадью Q и острым
углом а. Боковая грань, проходящая через катет, который про-
тиволежит данному углу, перпендикулярна к плоскости основания,
две другие грани образуют с основанием углы, равные 0. Найдите
объем пирамиды. При каком значении а объем будет наибольшим?
182. (МТИМБО, 1980 г.). Найдите отношение высоты к радиусу
основания цилиндра, который при заданном объеме имеет наимень-
шую полную поверхность.
183. (МТИМБО, 1979 г.). В полушар радиуса 7? вписан цилиндр
так, что плоскость основания цилиндра совпадает с плоскостью,
ограничивающей полушар. Найдите высоту цилиндра наибольшего
объема.
184. (МТИМБО, 1981 г.). Бак цилиндрической формы должен
вмещать v литров воды. Какими должны быть его размеры, чтобы
поверхность без крышки была наименьшей?
185. (РГУ, мехмат, вечерн. отд., 1977 г.). Конус объема v описан
около шара. Угол между образующей конуса и плоскостью основа-
ния равен а. Найдите объем шара. При каком значении а объем
будет наибольшим?
186. (МТИМБО, 1980 г.). Около цилиндра (радиус основания
которого равен г, а высота — h) опишите конус наименьшего объема,
если плоскость основания цилиндра и основания конуса совпадают.
Определите объем этого конуса.
187. (ЛГУ, матмех, 1980 г.). Через ребро L4В] правильной пира-
миды SABC с вершиной 3 проведено плоское сечение, имеющее на-
именьший периметр. Найдите площадь этого сечения, если известно,
что высота пирамиды равна h, |ЛВ|=а.
188. (КГУ, мехмат, 1980 г.). Основание пирамиды SABC —
треугольник АВС, у которого АВС=90°, ВАС=ц>, | АС\=Ь. Бо-
ковые ребра пирамиды одинаково наклонены к плоскости основания,
а угол между гранью SBC и плоскостью основания равен а. Опре-
делите объем пирамиды. При каком значении <р объем пирамиды на-
ибольший?
189. (МИФИ, 1980 г.). В прямой круговой конус с радиусом
основания R вписан шар радиуса г. Через вершину конуса проведе-
на плоскость, пересекающая этот шар. Найдите площадь сечения
конуса этой плоскостью, если известно, что эта площадь имеет на-
ибольшее из всех возможных значений.
190. (МИФИ, 1980 г.). В правильную четырехугольную пира-
миду, длина высоты которой равна Н, а угол наклона бокового ребра
к плоскости основания равен 0, вписан конус. Через апофему бо-
ковой грани пирамиды проведена плоскость, пересекающая кони-
ческую поверхность. Найдите площадь сечения конуса этой плоско-
стью, если известно, что эта площадь имеет наибольшее из всех
возможных значение.
191. (МГМИ, 1979 г.). Найдите отношение площади поверхно-
сти, полученной при вращении ромба вокруг большей диагонали,
216
к площади поверхности, полученной при вращении этого ромба
вокруг меньшей диагонали, если известно, что меньший угол между
сторонами ромба равен а.
192. (МГМИ, 1979 г.). Найдите отношение объема тела, полу-
ченного при вращении прямоугольника вокруг большей стороны,
к объему тела, полученного при вращении этого прямоугольника
вокруг меньшей стороны, если известно, что в этом прямоугольнике
меньший угол между диагоналями равен а.
193. (БашГУ, 1980 г.). Прямоугольный треугольник с катетом
длины а и прилежащим к этому катету острым углом а вращается
вокруг прямой, проходящей через вершину данного угла и перпен-
дикулярной к биссектрисе этого угла. Найдите объем тела вращения.
194. (МЭИ, 1979 г.). Длина меньшей стороны параллелограмма
равна а, острый угол параллелограмма равен а, угол между мень-
шей диагональю и большей стороной равен 0. Найдите объем тела,
полученного вращением параллелограмма вокруг его большей сто-
роны.
195. (МЭИ, 1978 г.). Дан треугольник АВС, причем |ВС|=а,
АВС=а, ДСВ=90°4~а. Определите объем тела, полученного вра-
щением этого треугольника вокруг его высоты, опущенной из вер-
шины А.
196. (МЭИ, 1978 г.). Площадь прямоугольной трапеции ABCD
равна S, длина высоты [ДВ] равна h, величина острого угла ADC
равна а. Найдите объем тела, полученного вращением четырехуголь-
ника ABED вокруг прямой (ДВ), если точка Е — середина отрез-
ка [СВ].
197. (МТИМБО, 1982 г.; РГУ, мехмат, 1977 г.). Основанием
пирамиды служит ромб с острым углом а. Все боковые грани сос-
тавляют с плоскостью основания один и тот же угол 0. Найдите
радиус шара, вписанного в пирамиду, если объем пирамиды равен
V. При каких значениях 0 радиус шара наибольший?
198. (РГУ, мехмат, вечерн. отд., 1977 г.). Конус описан около
полушара радиуса R так, что центр основания конуса лежит в
центре шара. Угол при вершине в осевом сечении конуса равен а.
Найдите объем конуса. При каком значении а объем будет наимень-
шим?
Р а з д е л IV
ЗАДАЧИ И ВОПРОСЫ УСТНОГО ЭКЗАМЕНА
ОБ УСТНОМ ЭКЗАМЕНЕ
Во всех высших учебных заведениях страны устные экзамены
проводятся в строгом соответствии с программой по математике
для поступающих в высшие учебные заведения (вариант А для по-
ступающих в высшие учебные заведения страны печатается ниже).
На устном экзамене поступающему предлагается два-три теоретиче-
ских вопроса и дается необходимое время для подготовки обстоя-
тельного ответа на эти вопросы. Как правило, вопросы теории фор-
мулируются так же, как они сформулированы в программе по мате-
матике для поступающих в высшие учебные заведения. Предлага-
ются, обычно, также две-три задачи. Задачи на устном экзамене
могут быть предложены одновременно с вопросами теории, или в
ходе ответа на вопросы теории, или после ответа. Задачи могут
иметь самый разнообразный характер. Для ознакомления чита-
телей с этим материалом мы публикуем отдельные билеты устных
экзаменов некоторых вузов и более четырехсот задач, предлагав-
шихся на устных вступительных экзаменах ряда вузов страны.
§ 1. ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ
I. (МИФИ, 1982 г.).
1. Натуральные числа. Простые и составные числа. Делитель,
кратное. Общие делители. Общее наименьшее кратное. Признаки
делимости на 2, 3, 5, 10.
2. Признак параллельности плоскостей.
II. (МИСиС, 1978 г.).
1. Понятие первообразной. Теорема об общем виде всех пер-
вообразных данной функции. Интеграл.
2. Существование окружности, описанной около трехугольника.
III. (МИЭТ, 1978 г.).
1 .; Свойства функции y=k!x и ее график.
2 , Формула площади правильного многоугольника (через ра-
диус описанной около него окружности).
Дополнительные вопросы:
1, Найдите область существования функции z/=lg(x?—6х+6).
2, Если данная функция — периодическая, найдите наимень-
ший период Т: f(x)=10 sin Зх.
3. Может ли композиция двух поворотов, имеющих разные
центры, быть параллельным переносом?
218
IV. (МИИГАиК, 1979 г.).
1. Числовые функции. График числовой функции. Возрастание
и убывание функции; периодичность, четность, нечетность.
2. Векторы. Операции над векторами. Коллинеарные векторы.
Компланарные векторы.
3. Производная сумма двух функций.
V. (МАРХИ, 1977 г.).
1. Векторы. Операции над векторами. Коллинеарные векторы.
Компланарные векторы.
2. Из 3 пирамид и 10 кубов должна быть составлена композиция,
насчитывающая 7 тел. Сколькими способами может быть составлена
композиция, если в нее должна входить хотя бы одна пирамида?
3. Вычислить площадь фигуры на отрезке [0; л], ограниченном
осью Оу, прямой х=п и кривыми t/=sin х и t/=lcos х|.
VI. (МТИММП, 1980 г.).
1. Выражение стороны правильного многоугольника через ра-
диус вписанной в него окружности.
2. Решите уравнение sin x+sin 3x=0.
3. Векторы и действия над ними.
Пример. Вычислите длину вектора 4а+36, если а =
= (1; 1; —1), *=(2; 0; 1).
VII. (МИНГП, 1980 г.).
1. Площадь поверхности и объем цилиндра.
2. Тригонометрические функции половинного аргумента.
3. Производная функции w=log„x.
VIIL (МГМИ, 1979 г.).
1. Теорема косинусов.
2. Разложение квадратного трехчлена на линейные множители.
IX. (МГРИ, 1079 г.).
1. Формула n-го члена и суммы п первых членов арифметиче-
ской прогрессии.
2. Свойство середины диагонали параллелепипеда.
3. Производная функции «/=tg х.
X. (МТИЛП, 1978 г.).
1. Логарифм произведения, степени, частного.
2. Признак параллельности плоскостей.
3. Найдите предел lim
X -> 00
X2 — х-[-1
2x2-f-x
XI. (МТИПП, 1978 г.).
1. Производная произведения двух функций.
2. Сумма углов треугольника.
3. Решите неравенство -Дп ^х~ Р_е > 0.
г Зх2 — 4х+75
4. Найдите наибольшее и наименьшее значения функции
t/ = 2x—Ух на промежутке [0; 4].
XII. (МПИ, 1979 г.).
1. Свойства показательной функции.
2. Формулы площади поверхности и объема цилиндра.
219
3. Решите уравнение sinxsin 3x=sin 2х sin 4х.
4. Найдите наименьшее и наибольшее значение функции у~
=х? —3х-+3 на отрезке [1; 3].
XIII. (МИСИ, 1979 г.).
1. Тригонометрические функции двойного и половинного аргу-
мента.
2. Существование окружности, описанной около треугольников.
3. Определите промежутки монотонности функции у=хг-—Зх.
4. Решите неравенство log2x<log2x2.
XIV. (МАМИ, 1979 г.).
1. Производная функции z/=cosx.
2. Решите неравенство log0<3(x?—1)^0.
3. Разложение квадратного трехчлена на линейные множители.
4. Теорема о трех перпендикулярах.
XV. (МИИЗ, 1980 г.).
1. Свойства функции у=ах$+Ьх+с и ее график.
2. Признак параллельности прямой и плоскости.
3. Решите уравнение 5лг+1 + 5лг= 150.
4. Упростите выражение + : (у-2 + f ) .
XVI. (МФИ, 1979 г.).
1. Достаточное условие экстремума функции. (Докажите.)
2. Свойство средней линии трапеции. (Докажите.)
3. Решите неравенство log0,8 (х+1)>—1.
4. Вычислите по определению производную функции у = ]/~х+1.
XVII. (РПИ, 1980 г.).
1. Логарифмическая функция, ее свойства и график.
2. Пирамида. Формулы поверхности и объема пирамиды.
3. Решите неравенство 1g (3x2+1)—1g (Зх—2)<1.
4. Упростите выражение _C0S_^M~~?ZP )—।—sinjp+270_)_.
sin2 (а+90°)~1 cos2 (а—90°)— 1
5А. Найдите наибольшее и наименьшее значения функции
X 9.
У = $+— на отрезке [1; 6].
5В. Решите уравнение ^27—3ctg2x+l~0.
XVIII. (ВЗПИ, 1980 г.).
1. Функция. Определение. Способы задания функции.
2. Признак перпендикулярности двух плоскостей.
3. Найдите производную от функции y=ctg3 х.
XIX. (ВТУЗ ЗИЛ, 1980 г.).
1. Сумма бесконечно убывающей геометрической прогрессии.
2. Свойства точек, равноудаленных от концов отрезка.
3. sin (а—у) =—у, а€[Зл/2; 2л]. Найдите tg2a.
XX. (ВЗИТиЛП, 1979 г.).
1. Свойства функции y=k/x и ее график.
220
2. Выведите формулу для вычисления площади сферы.
3. Вычислите arctg l+arccos(—1/2)+arcsin(—V2).
XXI. (ВЗИИЖТ, 1979 г.).
1. Производные функций i/=sin х, y=cosx, y=tg х,
y=logax.
2. Свойство точек, равноудаленных от концов отрезка.
3. Найдите предел Пт .
У=ах,
XXII. (ВЗЭИС, 1978 г.).
1. Производная функции t/=sin х.
2. Существование окружности, описанной около треугольника.
3. Решите уравнение sin x+cos 2х=1.
XXIII. (МВМИ, 1981 г.).
1. Решение уравнений вида sin х=а; cos х=а; tg х=а.
2. Свойства показательной функции.
3. Центр симметрии параллелограмма.
4. Решите уравнение cos x+sin 2х=0.
§ 2. ЗАДАЧИ УСТНОГО ЭКЗАМЕНА
1. (МТИМБО, 1981 г.). Докажите, что дробь (14n+3)/(21n+4)
несократима (n С Z).
2. (МФТИ, 1981 г.). Может ли число n4+4 (п £ N) быть простым?
Если да, то найдите эти простые числа.
3. (МФТИ, 1981 г.). Пусть р и q — два последовательных про-
стых числа. Может ли их сумма быть простым числом?
4. (НЭТИ, 1981 г.). Покажите, что всякое нечетное число можно
представить в виде разности квадратов двух целых чисел.
5. (КИЦМ, 1981 г.). Определите сумму всех четных чисел от 12
до 82.
Сравните числа (6—7).
6. (ТашГУ, 1981 г.), a) sin 3 и cos 3; б) у^З* и У 2.
7. (ВГУ, ПММ, 1981 г.). Л = 4+| + 4-+-|г4-^-, В = 4 +
8. (МФТИ, 1981 г.). Докажите, что ]/*2-J-p^3 — число иррацио-
нальное.
9. (МГУ, ВМК, 1981 г.; МФТИ, 1981 г,). Докажите, что 3<л<4.
10. (ВГУ, хим., географ., биол.-почв. фак. 1981 г.). Сокра-
ти (х_________П2
тите дробь 1 7 •
Упростите выражения (11 —13).
11. (ПГУ, 1980 г.). а1/2+а~1/а.
х ' 14-а1/2 а—1
12. (НЭТИ, 1981 г.). Йо/ар/а...51|/а.
221
13. (МФТИ, 1981 г.). х4-2х2+3х3+. . .+пхп. 1
Докажите, что для любого натурального п (14—16). I
14. (КГУ, мехмат, физфак, 1977 г.). 1
(1-П (1 п (1 1 у Л п=«_+1.
\ 4 J \ 9 J \ 16 J \ n2 J 2п 1
15. (МИФИ, 1977 г.). tL + 5L + 51-4+... +-^2-^.
16. (МИФИ, 1977 г.). 12 + 22 + з2 +. .. + П2= -^--|(2ft+.
17. (ДГУ, 1978 г.). Сколько различных нечетных пятизнач- i
ных чисел с неповторяющимися цифрами можно составить из цифр 5
О, 1, 3, 4, 5?
18. (ДГУ, 1978 г.). Сколько существует телефонных номеров,
содержащих комбинацию 12, если номер состоит из 5 цифр?
19. (КГУ, мехмат, физфак, 1977 г.). Сколько существует пяти- J
значных чисел, в записи которых каждая последующая цифра ;
больше предыдущей? ]
20. (МИФИ, 1977 г.). Сколько диагоналей в выпуклом п- ;
угольнике? j
21. (КГУ, мехмат, физфак, 1977 г.) Прямые 13, 13 парал- ;
лельны и лежат в одной плоскости. На взято т точек, на 13
взято п точек, на 13 взято k точек. Сколько существует треу-
гольников с вершинами в этих точках?
22. (МТИПП, 1978 г.). Коэффициент при х во втором члене
разложения ^х2 — yj” равен 31. Найдите п. '
Постройте графики функций (23 — 67).
23. (КГУ, 1981 г.). г/ = (|х + 11-|х-11)/2.
24. (МИФИ, 1981 г.). у = \х- 11-х.
25. (МАРХИ, 1979 г.). у = \х- 1 | + |х-2| + х.
26. (ЯГУ, 1980 г.). у = |х2-х|.
27. (ВГУ, эконом, фак., 1979 г.). у = х]х — 3|.
28. (ВГУ, хим., биол.-почв. фак. 1979 г.). t/=(x-|-l)3—(х—I)3.
29. (МАТИ, 1980 г.). t/ = /(x24- I)2 —4х2.
30. (ЯГУ, 1980 г.). j/ = /1-|x|.
31. (МИРЭА, 1978 г.). г/ = х2-21х+1|-1.
32. (МАТИ, 1980 г.). z/ = x|x|-4x-5.
33. (БГУ, 1980 г.). t/=(| 1-х| + 2)(х+1).
34. (ЛГУ, 1980 г.). i/ = |2x2 —Зх + |х-1||.
35. (МФИ, 1979 г.). у = 1^4 (х24-3).
36. (МИХМ, 1979 гЛ. z/==x(x —З)2.
37. (ЯГУ, 1980 г.). '«/= 1/|х|.
38. (ЯГУ, 1980 г.). z/ = (x4-3)/(x—1).
39. (МИФИ, 1981 г.). у=(2х4-1)/(х-1).
40. (МАТИ, 1978 г.). у= (21х |- 1)/(х-3).
41. (ЛатвГУ, 1980 г.), t/^2^'4-1.
42. (МАТИ, 1980 г.). у= 2^х^/х.
222
43. (МИФИ, 1981 г.), у = | sin х f/sin х.
44. (ЯГУ, 1980 г/, ТашГУ, 1981 г.). у = — 2"<*1.
45. (МИРЭА, 1977 г.). у^2^~х'.
46. (ЯГУ, 1980 г.), у = 3-2х-2.
47. (МИФИ, 1981 г.). г/= 211ое**1.
48. (ТашГУ, 1981 г.). у = log2|х— 11— 1.
49. (МТИ, 1981 г.) у = |logi/4(x/4)|.
50. (МАТИ, 1978 г.), у = log* Ух.
51. (МАТИ, 1980 г.). «/ = lg|x| — 1g х2.
52. (МИФИ, 1981 г.). i/ = log2 (4х —х2).
53. (МИФИ, 1981 г.). z/ = log2 (2-х).
54. (МИФИ, 1981 г.). у = logI/2(l -х).
55. (МИФИ, 1981 г.). y=|log2x|/log2x.
56. (НЭТИ, 1981 г.). z/ = log2(x2 — 2х+1).
57. (КГУ, мехмат, 1981 г.). z/=logI/2 [.
58. (МАТИ, 1980 г.). У=^^2)-
59. (ТашГУ, 1981 г.). t/ = sin|2x|.
60. (ЯГУ, 1980 г.). z/ = sin2x.
61. (ЯГУ, 1980 г.). # = x4-sinx.
62. (МАТИ, 1978 г.). y = cos /| х| +у) /sin х.
63. (НЭТИ, 1981 г.; МИФИ, 1981 г./ z/ = logi/2sinx.
64. (МАТИ, 1980 г.). t/ = lgtgx-|-lgctgx.
65. (МГУ, ВМК, 1980 г.), х/= log,а1пж। (1/2).
66. (КГУ, мехмат, физфак, 1979 г.).
J 4* — 1, если х < 0;
()/"4х — х2, если х > 0.
67. (КГУ, мехмат, физфак, 1979 г.).
pl 1 —У 1—х2, если х<11;
( 14~logi/2x, если х> 1.
Изобразите на плоскости (х; у) множество точек (68—73).
68. (КГУ, мехмат, физфак, 1979 г.).
{(х; #)|x24-t/2 —2х —2z/4-l=0}.
69. (УрГУ, 1977 г.).
{(х; у)|(х-|х|)24-(1/-Ы)2<4}.
70. (МИФИ, 1981 г.).
{(х; r/)||* + fH + li'—
71. (КГУ, мехмат, физфак, 1977 г.).
{(х; у) | log( । х |_о,5) (х2 4-г/2) < log( । х|-о,5>4}.
72. (МИФИ, 1981 г.).
{(х; y)|cos(x4-i/) = cos(x — у)}.
73. (МИФИ, 1981 г.), {(х; y)\s>m2x = s\n2y\.
223
Линейные и квадратные уравнения и неравенства
74. (МИРЭА, 1978 г.). При каких значениях х функция z/ =
= |х—11 +1 х—3| имеет наименьшее значение? Найдите это зна-
чение.
75. (ВГУ, хим., биол.-почв, фак., 1979 г.). Решите уравнение
х|х| + 2х+ 1 = 0.
76. (МТИ, 1978 г.). Найдите наименьшее значение, принимае-
мое z, если z = x2 + 2xz/ + 3z/24-2x + 6«/4-4.
Решите неравенства (77 — 80).
77. (МТИ, 1981 г.). 9х-14-х2 > 0.
78. (БарГПИ, 1981 г.). х2-5|х| + 4<0.
79. (ЛГПИ, 1981 г.). |х2-4х|> 1.
80. (КиевГПИ, 1981 г.). 2х2-51 х | + 3 > 0.
81. (ТашГУ, 1981 г.). Докажите, что корни квадратных урав-
нений ах2 + Ьх + с = 0 и сх2 + Ьх-}-а — 0 взаимно обратны.
82. (КуйбГУ, мехмат, 1977 г.). Докажите, что если значение
квадратного трехчлена ах2 — 6х-фс является целым числом при
Xj = 0, xg == 1 и х3 = 2, то при любом целом х значение данного
трехчлена является целым числом.
83. (МФТИ, 1981 г.). Докажите, что если ах2 + Ьх + с С Z
при всех x£Z, то a,b,cfzZ.
84. (ВГУ, физфак, 1981 г.). В уравнении ах2 — 5х + 6 = 0
определить а, если отношение его корней х1/х3 = 2/3.
85. (ВГУ, эконом, фак., 1981 г.). Известно, что для у =
=гах2 + &х + с имеет место у(—1) >—4, 1/(1) <0, у (3) > 5.
Определите знак коэффициента а.
Уравнения высших степеней. Теорема Безу. Рациональные
неравенства. Решение неравенств методом интервалов
Решите уравнение (86 — 87).
86. (ДнепрГУ, 1981 г.). (х2-6х)2 —2(х-3)2 = 81.
87. (МФТИ, 1981 г.). 6х4-13х3+12х2-13х + 6 = 0.
88. (МФТИ, 1981 г.). Найдите остаток от деления многочлена
х? + 2х2—2х + 5 на х?—1, не производя операции деления.
89. (КГУ, мехмат, физфак, 1977 г.). Сколько корней имеет
уравнение х4 = 5х-ф2ц в зависимости от а?
90. (КГУ, мехмат, физфак, 1977 г.). Сколько корней в зави-
симости от а имеет уравнение x3 + ax-j-2 = 0?
91. (МФТИ, 1981 г.). Докажите, что у многочлена Р(х) =
— ax34-&x2 + cx-f-d не могут быть все корни целыми, если Р(0)
и Р(—1) нечетные.
92. (ЛГПИ, 1981 г.). Решите уравнение f (x) = g' (х), если
/ (х) = 3 + 2х2, g (х) = Зх2 - (5х - 3) (2—х).
224
Решите неравенства (93 — 99).
93. (ВГУ, хим., географ., биол.-почв, фак., 1981 г.), х +
4--<0.
1 х
94. (МГПИ, географ, фак., 1979 г.). ^у>2.
95. (МИИЗ, 1981 г.). *2±L-<0.
96. (МИФИ, 1981 г.). ~ < -.
97. (ЛГПИ, матфак, 1979 г.). |^=р|> 2.
98. (ТашГУ, 1981 г.) *-~g-~hl2>0.
99. (МВИМУ, 1981 г.).
x-f-l
Иррациональные уравнения и неравенства
Решите уравнения (100 — 101).
100. (МАТИ, 1978 г.). /х-/Г^З=1.
101. (КГУ, 1981 г.). =о.
' ' уч + х2 /1—Л2
Решите неравенства (102 — 106).
102. (КГУ, мехмат, физфак, 1981 г.). И4 —х2^> 1/х.
103. (ВГУ, хим., биол.-почв. фак., 1977 г.). 1 — х +
+ /2х + 3 < 5.
104. (МИФИ, 1981 г.), х + 1 </11-х.
105. (МФТИ, 1981 г.). 8X2 < Ь
106. (УрГУ, физфак, 1977 г.). У5х« + а2> —Зх.
Системы уравнений и неравенств
Решите системы уравнений (107 — 112).
107. (ВГУ, хим., биол.-почв. фак., 1979 г.).
108. (КГУ, 1981 г.).
* + «/ + * = 0,
2х«/ — г2 = 4.
1* + 1И = 1,
1*1 + 11/1 = 1.
109. (МИРЭА, 1978 г.).
ПО. (МИРЭА, 1978 г.).
' 2х + 3«/ = 5,
х— г/ = 2,
x + 4z/ = a.
rx + 2i/ = 3,
ах — ty — —6,
х-\-у=Л.
8 В. М. Говоров и др.
225
111. (ПГУ, 1980 г.). + “ 9’ „
| х1'3 Н-г/1'3 =3.
( т/"2*~ 1 I чЛ у + 2 — О
112. (ЛГУ, физфак, 1977 г.). ! V у-\-2 V 2х—1 ’
( х-\-у = 12.
113. (КГУ, мехмат, физфак, 1977 г.). Сколько решений имеет
„ ( |x| + |t/|= 1,
система уравнении < 1
J (х2 + </2 = а2?
114. (КГУ, 1981 г.). При каких значениях а система урав-
нений
х —у = а(1 4-хг/),
%+х+у-\-ху = 0
имеет только одно решение?
Логарифмические и показательные уравнения,
неравенства и системы
Упростите выражения (115 — 119).
115. (НЭТИ, 1981 г.). logi/4(log23-log34).
116. (ЯГУ, 1980 г.), а) б'г5^25; б) log2lgl00.
117. (БарГПИ, матфак, 1981 г.). log364-logs (1/27).
118. (ВГУ, хим., биол.-почв, фак., 1979 г.).
(log3 4 + log29)2 — (log34 — log29)2.
119. (ХАИРЭ, 1981 г.). 0,8-(1 4-9log»8)los««5.
120. (ХАИРЭ, 1981 г.). lg tg 3° lg tg 6°lg tg 9°.. .lg tg 87°.
Определите знак числа (121 —122).
121. (ВГУ, хим., биол.-почв, фак., 1979 г.). log34 — log43.
122. (НЭТИ, 1981 г.). logt30,4-logi/40,4.
123. (МИФИ, 1981 г.). Вычислите log59,8, если 1g 2 = a, 1g 7=6.
124. (МГУ, ВМК, 1980 г.). Вычислите loge40, если 1g 15 = а,
log2050 = 6.
Найдите область определения функции (125—131).
125. (ХАИРЭ, 1981 г.). г/= К2* — 3*.
126. (ХАИРЭ, 1981 г.). у=-------lg*
127. (ЛГПИ, 1981 г.), f (x) = /9^x2-|-lg(x-l)-/x.
128. (МТИИП, 1981 г.). z/ = log3log1/2x.
129. (ЛГПИ, физфак, 1981 г.). f (х) = log2x-5 (хг —Зх— 10).
130. (ВГУ, эконом, фак, 1981 г.). у= 1g (Кх2 — 5х—24—х—2) .
131. (КиевГПИ, 1979 г.). z/ = log2sinx.
Решите уравнения (132 — 154).
132. (ЯГУ, 1980 г.). 3±±|^ = 2.
133. (ЛГПИ, 1981 г.). 6-9°-5*-2Ч-2-3*-« = 56.
226
134. (КИЦМ, 1981 г.). (0,25)2"х = §7^ .
135. (МИИЗ, 1981 г.). lg(5 —x)4-lg(3 —х)= 1.
136. (ЯГУ, 1980 г.) log3log4log2х = 0.
137. (ЯГУ, 1980 г.). log2|x-l|=l.
138. (МТИПП, 1979 г.). 1g (Зх—2)-2 =у 1g (х 4- 2) — 1g50.
139. (ПГУ, 1980 г.). 1g (3 4-2 lg (1 +х)) = 0._
140. (БарГПИ, матфак, 1981 г.). lgj/x — 3 + lg|/*2x— 1 =
= lg/Зх + З.
141. (КуйбГУ, 1977 г.). 32х2 —2-Зх2+х+64-32 <х+6> = 0.
142. (ЯГУ, 1980 г.). 25i“2 * + 4 • 2cos2 * = 6.
143. (КиевГПИ, 1979 г.), у-т + п , 3<Q , ,ч=0.
v ’ ' 1—logs (2x4-3) 5—logs (2x4-3)
144. (ДнепрГУ, 1981 г.). log2(4*4-4)-log2(2x+1 —3) = х.
145. (ЯГУ, 1980 г.). Iog8x4-log|x4-log|x+ ... = 1/2.
146. (КГУ, мехмат, физфак, 1979 г.). log3cosx +
+ logi/з (1—sinx) = 0.
147. (КГУ, 1981 г.). logasinх-f-logi/2(—cosx) = 0.
tg ( x—y') sil>s ( X—тЛ /cos 2*
148. (МИРЭА, 1978 r.). 2 V 4' -2-0,25 < 4Jl +
4-1=0.
149. (КуйбГУ, физфак, 1977 г.). log2sinx—log2cosx —
—log2 (1 — tgx) — log2(l 4-tgx)= 1.
150. (ДнепрГУ, 1981 г.). loga<x — log^x4-logex = 0,75.
151. (МИИЗ, 1981 г.). x'e*-3 = 0,01.
152. (МТИПП, 1978 г.), х’ех~3 = 10’s’1 °/3)"1.
153. (ДГУ, 1978 г.). (/x)log*11-2 = 11.
154. (МАРХИ, 1979 г.). 5’s* =50-х^5.
155. (КГУ, мехмат, физфак, 1979 г.). При каких а уравнение
3xlgx = 14-й 1g х имеет: а) одно решение; б) два решения?
156. (КГУ, мехмат, физфак, 1979 г.). Сколько корней в за-
висимости от а имеет уравнение х2е2~|ЛГ| = 4а?
Решите следующие система уравнений (157—160).
1 log2x4-log2y= 1,
157. (ЯГУ, 1980 г.). { \
( х 4-Z/ — о.
( log3(xw) = 3,
158. (ЯГУ, 1980 г.). { . „ .
v ’ ( 1о&/з (x/z/) = 1.
I (Зх + у)х~У = 9,
159. (МАРХИ, 1979 г.). ( 18х,±
( 32К х-V у ~81
160. (ВГУ, эконом, фак., 1981 г.). | 1ёКху= 14-lg3.
Решите неравенства (161 — 186).
161. (ЯГУ, 1980 г.). 2х4-3х >2.
162. (ЯГУ, 1980 г.). 2-2х<Зх“1.
163. (МАТИ, 1978 г.). 4х-5-2х- 1
0.
8*
227
164. (МТИ, 1981 г.). log015((2—х)/3) < 0.
165. (ТашГУ, 1981 г.), logv»^’—2х + 4) > — 2.
166. (ВГУ, 1980 г.), logj/5 (х+4) < 2.
167. (КИЦМ, 1981 г.). logf/3 (х- 1)-log17s (2х-3) < 0.
168. (МИИЗ, 1981 г.). log0 5 (Зх- 1) > log0 6 (3—х).
169. (МИИЗ, 1980 г.). log2|x| < 3.
170. (МИИЗ, 1980 г.). | logs х | < 2.
171. (МИРЭА, 1978 г.). i^< 1.
172. (МИФИ, 1981 г.). lqStlog,(l-x)>-l.
173. (МТИПП, 1979 г.). (1/2)108«<х’-2х-з) > L
174. (МИФИ, 1981 г.). logI/3log2(x8 —8)^—1.
175. (МАРХИ, 1979 г.). logx2-log2x2-log24x> 1.
176. (ПГУ, 1980 г.). lg(6/x) > 1g (х+5).
177. (ВГУ, матфак и ПММ, 1979 г.). logx_3 (х—4) < 2.
178. (ДГУ, физфак, 1978 г.). log*_3 (х — 1) < 2.
179. (КиевГПИ, 1979 г.), log*. (2 + х) < 1.
180. (ВГУ, ПММ, 1981 г.). loge^>0, 0<а< 1.
181. (ВГУ, ПММ, 1981 г.). logx+0 g2<logx4.
182. (МИФИ, 1981 г.). log2x+3x2< 1.
183. (МФТИ, 1981 г.). log*£H> 1.
184. (МФТИ, 1981 г.), logj/j (2“х—100sinx) < х.
185. (УрГУ, 1977 г.). loge(l-x«)>l.
186. (КГУ, 1981 г.). |х—2|1ое‘<*+2>-1ой«< 1.
187. (УрГУ, 1977 г.). Решите систему неравенств logi72 cos х <
<logt,2tgx, 0^х<л.
188. (КГУ, 1981 г.). При каких значениях а уравнение
xln| х| = а имеет один корень?
Преобразование тригонометрических выражений
Выясните, какое число больше (189 — 191).
189. (КиевГПИ, 1981 г.), sin 1980® или cos 1980°?
190. (ПГУ, 1980 г.), tg 1 или arctg 1?
191. (КИЦМ, 1981 г.), sin 2 или'cos 3?
Вычислите (192 — 214).
192. (МИИЗ, 1977 г.), arcsin (- 1) + 2arctg (-/З).
193. (МТИММП, 1977 г.), sin (arcsin (3/5) — arccos (3/5)).
194. (ЛГПИ, 1981 г.), tg (arccos (1/2)+arcsin (J^3/2)).
195. (ВЗИТиЛП, 1979 г.). arctg 1 + arccos (—1/2) +
+ arcsin (—1/2).
196. (МИФИ, 1979 г.), arctg K2-arcctg(l/K2).
197. (МИФИ, 1978 г.), sin (2 arctg 2).
198. (МИФИ, 1978 г.), cos arccos
228
199. (МИФИ, 1978 г.), sin arctg
200. (МИФИ, 1978 г.), arcsin (sin (8л/7)).
201. (МИФИ, 1978 г.), arccos (cos (8 л/7)).
202. (МИФИ, 1978 г.), arctg (tg-^b).
203. (МТИЛП, 1979 г.), sina, если sin (a/2) + cos (а/2) = 7/5.
204. (ЯГУ, 1980 г.), sin 2а, если sina + cosa = &.
205. (ВЗИТиЛП, 1979 г.), sin 2а, если ctga = — 7.
206. (МТИЛП, 1979 г.). > если tga = 3.
207. (ЯГУ, 1980 г.). 3 sinQa 3- , если tga = 2.
v ’ ' sm8a+3cos3a’ °
208. (ЯГУ, 1980 г.). tg2a + ctg2a, если tga + ctga = a.
209. (КиевГПИ, 1979 г.). ctg(a/2), если sina = — (3/5).
210. (МИФИ, 1981 г.), tg (а/2), если cos а = — 3/5, л/2 < а < л,
211. (ТашГУ, 1981 г.), tg (а/2), если sin 2а = 0,6; 0 < а < л/4.
212. (ПГУ, 1980 г.). 65 cos (В — А), если sin А = — 4/5,
Зл/2<А<2л; cos В = 5/13, 0<В<л/2.
213. (КИЦМ, 1981 г.), sina, cosa, ctga, если tga=12/5,
л < а < Зл/2.
214. (МИИЗ, 1981 г.), sin 2а и sin (а/2), если tga = 5/12,
л < а < Зл/2.
215. (НЭТИ, 1981 г.). Преобразуйте в произведение
216. (ЯГУ, 1980 г.). Докажите, что если а + р = л/4, то
(l + tga)(l + tgp) = 2.
217. (КуйбГУ, мехмат, 1977 г.). Докажите, что если а, р,
у —углы треугольника, то sin a sin Р — cos у = cos a cos р.
218. (ЯГУ, 1980 г.). Упростите выражение
sin a 4-sin 2a—sin (л 4- 3a)
2 cos a +1 ’
Докажите следующие тождества (219 — 223).
219. (МАРХИ, 1981 г.), sin4 a cos2 a = i—^5 cos 2a—icos 4a 4-
lu oz 10
+ ± cos 6a.
oZ
220. (ДнепрГУ, 1981 г.). 2 (sin* a + cos’a) — 3 (sin4 a + cos4 a) +
+ 1=0.
221. (ВГУ, ПММ, 1981 r.). tg2a— sin2a — tg2a sin2a.
229
222. (БарнГПИ, матфак, 1981 г.). т^-. г^ = tg
223. (мфти, 1981 г.). t;+cosx1);!+cos;x;=^^.
' ’ ' (1-j-sinx) (1—cos 2х) 1—COSX
Тригонометрические уравнения и неравенства
Решите следующие уравнения (224 — 234).
224. (МИИЗ, 1981 г.). sin5x — sin3x = 0.
225. (ТашГУ, 1981 г.), sin3 х 4-sin2 х = 1 4-sinx.
226. (МТИММП, 1981 г.)./3sinx4-cosx= 1.
227. (НЭТИ, 1981 г.), sin а = sin 2а.
228. (ПГУ, 1980 г.), cosx —cos2x4-cosЗх = 0.
229. (ЯГУ, 1980 г.), tg2 ЗЗх = cos 2х -1.
230. (МАТИ, 1978 г.). 6cos2x4~ И sinx—10=0.
231. (МФТИ, 1981 г.). sin3x4~cos4x—4sin7x = cos 10x4-
4- sin 17 х.
232. (МТИПП, 1981 г.), sin4 х 4-cos4 х — cos2 2x4-0,25.
233. (КиевГПИ, 1979 г.), sinхcosxcos2х = —1/2.
234. (КГУ, мехмат, физфак, 1977 г.), tg | х| = (tg х|.
235. (НЭТИ, 1981 г.). Имеет ли решения уравнение 4sin2x-f-
4- cos х = 5?
236. (НЭТИ, 1981 г.). Решите уравнение f- (0) =f- (х), если
f (х) = 5 sin х 4- 3 cos х.
237. (МФТИ, 1981 г.). При каких а уравнение 1 4-sin2ax = cosx
имеет единственное решение?
238. (МИРЭА, 1977 г.). Сколько корней имеет уравнение
log(6Jl/2)X = COSX?
Решите неравенства (239 — 240).
239. (КиевГПИ, 1979 г.), sin
240» (КуйбГУ, 1977 г.). 2sin2 (х--у) —5 sin (х-3-) 4-2 > 0.
241. (МИФИ, МФТИ, 1981 г.). Найдите максимальное зна-
чение функции /(x) = 3sinx-|-4cosx.
Прогрессии
242. (МАРХИ, 1979 г.). Числа а2, Ь2, с2 образуют арифмети-
тт 111
ческую прогрессию. Докажите, что числа также
образуют арифметическую прогрессию.
230
243. (ЯГУ, 1980 г.). Сумма бесконечно убывающей геометриче-
ской прогрессии равна 12, а сумма квадратов ее членов 48. Най-
дите сумму первых десяти членов этой прогрессии.
Пределы
244. (КГУ, мехмат, физфак, 1977 г.). Будет ли монотонной
П2— «+ 1 -
последовательность ап = дг_р'дф1, п С N?
Вычислите пределы (245 — 266).
245. (КИЦМ, 1981 г.), lim т-^-2, n$N.
П->оо 1
246. (НЭТИ, 1981 г.). n^N.
247. (ЯГУ, 1980 г.). n^N‘
248. (КиевГПИ, 1979 г.), lim J-_£——J-, n^N.
П-*- GO
249. (ХАИРЭ, 1981 г.), lim f1 + -U.. .
250. (КГУ, 1981 r.). lim gig, «CAT-
251. (МИФИ, 1981 г.). Jim n^N.
252. (ВЗПИ, 1980 г.), lim
253. (ЯГУ, 1980 r.).
254. (ПГУ, 1980 r.). Jim^t.3)-
255. (МТМИ, 1981 r.). lim £2+5*76.
x-> 1 x x
256. (МТИПП, 1981 г.), lim
x->-2/3 6x x *
257. (ПГУ, 1980 r.). lim ---
«-> —з у X-H — 1
258. (МТИ, 1981 r.). lim K6±5- ^6~x .
% -> 0 x
259. (ВГУ, матфак, 1981 г.), lim -2~^x~3:
x->7 x ~4У
260. (ХАИРЭ, 1981 г.), lim
«->—1 У 2
23*
261. (МИХМ, 1981 г.), lim
х -> 2
262. (МИРЭА, 1978 г.), lim
х -> 64 у х — 4
263. (ЯГУ, 1980 г.), lim
х-> О zx
264. (ЕГУ, 1981 г.), lim ££^x-cos_6x
х о sm2 °*
3 г- ' * з /___________
265. (ЯГУ, 1980 г.).
х -► О х
266. (МИРЭА, 1978 г.), lim
267. (ВГУ, матфак, ПММ, 1979 г.). Через точку А под углом
в 30° проведены два луча. На одном из них на расстоянии а
от точки А взята точка В. Из нее опущен перпендикуляр на
другой луч, из его основания опущен перпендикуляр на [АВ]
и т. д. Найдите длину полученной бесконечной ломаной.
Производная. Исследование функций с помощью производной
Найдите производные функции (268 — 271).
268. (ВЗПИ, 1980 г.), a) ctg3x; б) sinKx.
269. (МТИ, 1981 г.). log§ (2х2 —3x4-1).
270. (КИЦМ, 1981 г.). (2х3—5)tgx.
271. (МГМИ, 1981 г.), a) Kin х; б) Ksin 2х; в) (sin 2x4-8)*.
Найдите производную функцию в указанной точке (272 —275).
272. (ТашГУ, 1981 г.). t/ = ln(2-K2x+T), г/'(0) = ?
273. (ВЗПИ, 1980 г.). i/ = (4x4-5)2, /(0) = ?
274. (ХАИРЭ, 1981 г.). Дх) = -^=^-р f£(0) = ?
275. (ХАИРЭ, 1981 г.), f (х) = sin4хcos 4х, /г (jt/3) = ?
Найдите интервалы возрастания и убывания функции
(276-280).
276. (МАТИ, 1979 г.). f(x) = 2x + ^.
277. (ЯГУ, 1980 г.), f (x) = x-Mn(1 -4х).
278. (МИФИ, 1981 г.). /(х) = х2е“\
279. (ЯГУ, 1980 г.). /(х) = х/1пх.
280. (МТИ, 1981 г.). 1/=3 + 8х4-4х*.
232
Докажите возрастание функций (281 — 283).
281. (МАТИ, 1978 г.). ^ = ^-1-4-2 при х>0.
282. (КГУ, мехмат, физфак, 1977 г.). /(х) = -|-х®—хв4-2№ —
— Зх24-6х—1 при x£R.
283. (ХАИРЭ, 1981 г.). z/==2x4-sinx при x£R.
Определите, при каких значениях а функция возрастает на
всей числовой оси (284 — 286).
284. (КГУ, мехмат, физфак, 1977 г.). / (х) = а ^-1 х- 4-
4-(а — 1)х84-2х4~1.
285. (КГУ, 1979 г.), f (х) = 2е*—ае~* + (2а +1) х-3.
286. (КГУ, 1981 г.). # = sinx—asin2x—-ysin3x4-2ax.
287. (КГУ, 1981 г.). При каких значениях а функция
у = {а 4- 2) х3 — Зах2 4- 9ах — 1 монотонно убывает на всей число-
вой оси?
Найдите критические точки функции (288 — 289).
288. (ЯГУ, 1980 г.), f (х) = (х2 —4)10.
289. (МИРЭА, 1978 г.), у = -у + 2х2 -5х 4- 4.
290. (ХАИРЭ, 1981 г.). Найдите экстремум функции t/=x2—
— 1п(14-2х).
291. (КГУ, 1981 г.). При каких значениях а точки экстре-
мума функции у = х3 — Зах2 4- 3 (а2 — 1) х 4-1 лежат в промежутке
]-2; 4[?
Найдите наибольшее и наименьшее значение функции (292 — 296).
292. (ДГУ, физфак, 1978 г.), f (х) = cos2 х4~ cosx 4-3.
293. (НЭТИ, 1981 г.), f (х) « 4х2 4-у на [1/4; 1].
294. (ЯГУ, 1980 г.), f (х) = Их-2^х на [0; 100].
295. (ЯГУ, 1980 г.). f (х) = ех2~4х+3 на [-5; 5].
296. (МТИПП, 1981 г.). г/ —2х—К х на [0; 4].
297. (КГУ, 1979 г.). При каких значениях а функция
f (х) = х3 + 3 {а — 7)х2 4- 3 (а2—9) х — 1 имеет положительную точку
максимума?
298. (КГУ, 1979 г.). Пусть xt и х^—соответственно точка
максимума и точка минимума функции f (х) = 2х®—9ах2 4- 12а2х4- !•
При каких а справедливо, что Xi = x2?
299. (КГУ, 1979 г.). При каких а функция f(x) = ~x? 4-
<5
4- (a 4-2) х24-(«— 1)х4~2 имеет отрицательную точку минимума?
233
300. (УрГУ, 1977 г.). Найдите все значения параметра а, при
которых точки минимума функции у=14-а2х —х3 удовлетворяют
х24-хЦ-2 п
неравенству
301. (КГУ, 1981 г.). В какой точке промежутка ]0; л/2[
функция у= (tg х+ l)2/tg х принимает наименьшее значение?
302. (МТИПП, 1979 г.). Найдите число, которое в сумме со
своим квадратом дает наименьшую сумму.
303. (МТИПП, 1979 г.). Найдите положительное число, ко-
торое будучи сложенным с обратным ему числом, даст наимень-
шую сумму.
304, (НЭТИ, 1981 г.). Среди равнобедренных треугольников
с данной длиной а боковой стороны найдите треугольник наи-
большей площади.
305. (ВГУ, матфак, ПММ, 1979 г.). Найдите угол при вер-
шине равнобедренного треугольника наибольшей площади, впи-
санного в окружность радиуса R.
Касательные к кривым
306. (НЭТИ, 1981 г.). Найдите угловой коэффициент каса-
тельной, проведенной к графику функции z/=tgx в точке
с абсциссой х0 = л/4.
307. (ЛГПИ, 1981 г.). На кривой у = 4х2 — 6x4-3 найдите
точку, в которой касательная параллельна прямой у = 2х.
308. (ХАИРЭ, 1981 г.). Под каким углом синусоида
г/=—^=-sin3x пересекает ось абсцисс в начале координат?
309. (ВГУ, 1980 г.). К графику функции у = 1пх? постройте
касательную, параллельную прямой у = — х.
Напишите уравнение касательной к графику кривой в ука-
занной точке (310 — 315).
310. (ВГУ, матфак, ПММ, 1979 г.). i/ = sin2x в точке х=л/12.
311. (МИРЭА, 1978 г.), у — х? в точке х = 2.
312. (ХАИРЭ, 1981 г.). у = х2е~х в точке х=1.
313. (ВГУ, физфак, 1981 г.), у — sinx4-1 в точке х = л/2.
314. (ЛГПИ, 1981 г.). у = х2 — 4 в точке пересечения ее
с осью ординат.
315. (КиевГПИ, 1979 г.). у — 2х1 — 4х в точках пересечения
этого графика с осью абсцисс.
316. (МГМИ, 1981 г.). Напишите уравнение касательной
к кривой у = х2 — 7х 4- 3, которая параллельна прямой 5x4-У — 3 = 0.
317. (ЯГУ, 1980 г.). Докажите, что касательная к гиперболе
у — а2/х образует с осями координат треугольник постоянной
площади.
234
Разные задачи
318. (МАРХИ, 1977 г.). Почленным дифференцированием
тождества sin 2х = 2 sin х cos х докажите тождество cos 2х =
= cos2x—sin2x.
319. (МАРХИ, 1977 г.). В каких точках производная функ-
ции у = х3 совпадает со значением самой функции?
320. (ЯГУ, 1980 г.). Касается ли прямая х + 4г/—4 = 0 ги-
перболы у=1/х?
321. (МВИМУ, 1981 г.). На какой промежуток отображает
производная функции у = у/х3 промежуток [1/16; 81]?
322. (МГМИ, 1981 г.). Является ли четной или нечетной
функция: a) f (х) = 2х + 2~х; б) f (х) = К1 Н-хф-х2 — К1 — х + х2;
в) f (х) = lg}~.
323. (МГМИ, 1981 г.). Найдите f (g(x)) ng’(f(x)), если f (х) = 2х,
g(x) = x2.
324. (МГМИ, 1981 г.). Найдите квадратичную функцию f (х),
если f(0) = 1, /(1) = 0, f(3) = 5.
325. (МГМИ, 1981 г.). Найдите функцию, обратную функции
г/ = х2—1, х£] — оо; 0].
326. (ВГУ, матфак, ПММ, 1979 г.). Через какую точку А
на кривой у =— х2 + 2х должна проходить касательная к этой
кривой, чтобы трапеция, образованная касательной и прямыми
х = 0, z/ = G, х=1, имела наименьшую площадь?
Первообразная. Интеграл.
327. (МИРЭА, 1978 г.; ЛГПИ, 1981 г.). Найдите первообраз-
ную функции у — 2/sin2 Зх, график которой проходит через точку
(л/12; 1).
328. (НЭТИ, 1981 г.). Найдите первообразную F (х) функции
f (х) = cos 4х, если F (л/24) = 1.
329. (КГУ, мехмат, физфак, 1977 г.). При каких значениях
х обращается в нуль та из первообразных функции f (х) = я sin лх 4-
+ 2х—4, которая при х=1 имеет значение 3?
330. (МГМИ, 1981 г.). Найдите первообразную функции
(sin (х/2) + cos (х/2))2.
Вычислите интегралы (331—338).
л/2
331. (МИРЭА, 1978 г.). $ sin2xdr.
о
Л/4
332. (МТИ, 1981 г.), j 8cos3xdx.
о
2
333. (ЯГУ, 1980 г.).
235
2е
334. (ЯГУ, 1980 г.). J
О
л
335. (ЯГУ, 1980 г.). $cos2xdx.
О
л/2
336. (ЯГУ, 1980 г.). § sinxcosxdx.
о
л/2
337. (ДнепрГУ, 1980 г.). j | sinx| dx.
-Л/2
Л
338. (КиевГПИ, 1979 г.). § sinxcos3xdx.
о
Найдите площадь фигуры, ограниченной линиями (339 — 349).
339. (ВЗПИ, 1980 г.). г/ = х2, у = 0, х=5.
340. (МТИПП, 1980 г.). у = х2 — 2х + 5, {/ = 0, х = 2,
341. (ЯГУ, 1980 г.). t/ = x3, {/ = 27, х = 0.
342. (ЯГУ, 1980 г.). {/ = х3, у2 = х.
343. (ЯГУ, 1980 г.). {/ = sinx, у — 2х/п.
344. (ТашГУ, 1981 г.). {/ = sinx, {/ = 2х/л, 0^х^л/2.
345. (МИРЭА, 1978 г.). у=*£-—1, у=2—х.
346. (МТИ, 1981 г.). {/ = (х—I)2, {/ = 0, х = 2, х=3.
347. (КГУ, мехмат, физфак, 1977 г.). {/ = 2 + sinx, у=. 1 + cos2x,
х = 0, х = л.
348. (ДГУ, физфак, 1978 г.). р = —Зх2 —|х| + 2, y-Q.
349. (УрГУ, физфак, 1977 г.). |{/|=1—х?.
350. (УрГУ, мехмат, 1977 г.). Верно ли, что площадь фигуры,
ограниченной линиями у = е*~*, у = 0, х — 2, х = 0, меньше 2?
351. (КиевГПИ, 1979 г.). Вычислите площадь фигуры, огра-
ниченной графиком функции {/ = х2 +1 и касательными, прове-
денными к этому графику в точках с абсциссами х = 0 и х = 2.
352. (КиевГПИ, 1979 г.). Через начало координат проведите
прямую, делящую криволинейный треугольник с вершиной в
начале координат, ограниченный линиями у = 2х—х2, {/ = 0, х= 1,
на две равновеликие части.
353. (ТашГУ, 1981 г.). При каком k площадь фигуры, огра-
ниченной линиями {/=х2—3 и y = kx-\-2 будет минимальной?
Вычислите эту площадь.
354. (КГУ, мехмат, физфак, 1977 г.). Вычислите объем про-
странственной фигуры, образованной вращением вокруг прямой
у = 1 плоской фигуры, ограниченной графиком функции {/= 1 + cos2x
на промежутке [—л/2; л/2] и этой прямой.
236
355. (ВГУ, ПММ, 1981 г.). Найдите все положительные а,
а
удовлетворяющие условию J (Зх2 4- 4х — 5) dx = а3 — 2.
о
356. (МВИМУ, 1981 г.). Найдите все значения а, для которых
а
выполняется неравенство х dx а + 4.
о
Векторная алгебра
357. (МТИПП, 1980 г.). Вычислите длину вектора 2« + 3&,
если а = (Г, 1;—1), 6 = (2; 0; 0).
358. (ЯГУ, 1980 г.). При каком значении k длина вектора
а = (—2; 2; 4£) вдвое меньше длины вектора 6 = (3; 36; 0)?
359. (МГМИ, 1981 г.). Вычислите длину вектора а, если Ь —
= (3; —2; 1), a b = 7, а||6.
360. (ЯГУ, 1980 г.). Найдите угол между векторами а = (3; 1; —2)
и Ь = (—2; 3; 4;).
361. (ЯГУ, 1980 г.). Определите, при каком значении т век-
торы a = 2i + mj—3k и b = i—2J+k перпендикулярны.
362. (ТашГУ, 1981 г.). При каком значении а угол между
векторами x = i+j + k и y^=ai-}-j—k равен arccos (1/2К3)?
363. (МИФИ, 1981 г.). Вектор а перпендикулярен векторам
ft = (l; 2; 3) и с = (—2; 4; 1) и удовлетворяет условиям
а (/ — 2/+ k) = —6. Найдите а.
364. (КГУ, мехмат, физфак, 1977 г.). Найдите длины диаго-
налей параллелограмма, построенного на векторах a — 5p-\-2q и
b=p—3q, если известно,что 1 = 2^2, |</| = 3 и (p,q) = n/4.
365. (КГУ, 1981 г.). Известно, что |а| = |6| = |г| = 1 и а 4-
+ b + с = о. Докажите, что ab + Ьс + са = —3/2.
366. (МТИ, 1981 г.). С помощью векторов докажите, что сред-
няя линия треугольника параллельна третьей стороне и ее длина
равна половине длины третьей стороны.
367. (ЛГПИ, 1981 г.). Дан треугольник АВС и М —произ-
вольная точка на стороне АВ. Прямая, проведенная через точку
М параллельна медиане ССЬ пересекает (С А) в точку Р, а (СВ) —в
точке О. Докажите, что РМ -|-О7И = 2СС1.
368. (ЛГПИ, 1981 г.). Докажите, что в любом четырехуголь-
нике ABCD имеет место соотношение МР = -^ (AD-\-BC), где М
и Р — середины отрезков АВ и CD соответственно.
Планиметрия
369. (ЯГУ, 1980 г.). Постройте прямоугольный треугольник
по гипотенузе и высоте, опущенной на гипотенузу.
370. (МИФИ, 1981 г.). Даны отрезки а, Ь. Постройте отре-
зок V ob.
237
371. (МИФИ, 1981 г.). По двум сторонам и медиане, выхо-
дящей из общей вершины данных сторон, постройте треуголь-
ник.
372. (МИФИ, 1981 г.). Дана окружность С и точка Л, ле-
жащая вне круга, ограниченного окружностью С. Постройте пря-
мые, проходящие через точку Л, касательные к окружности С.
373. (КГУ, мехмат, физфак, 1977 г.). Можно ли из отрезков,
равных медианам треугольника, построить треугольник?
374. (ЛГПИ, 1981 г.). В круг вписаны две трапеции с соот-
ветственно параллельными сторонами. Докажите, что диагонали
этих трапеций равны.
375. (ТашГУ, 1981 г.). Докажите, что если соединить сере-
дины сторон выпуклого четырехугольника, то получится парал-
лелограмм. Когда этот параллелограмм будет ромбом? Квадратом?
376. (МИФИ, 1978 г.; ЯГУ, 1980 г.; КГУ, 1981 г.). Дока-
жите, что если в многоугольник можно вписать окружность, то
r — S/p. где г — радиус окружности, S —площадь, а р —полупе-
риметр многоугольника.
377. (МИФИ, 1981 г.). Докажите, что в прямоугольном тре-
угольнике сумма длин катетов равна сумме длин диаметров впи-
санной и описанной окружностей.
378. (КГУ, мехмат, физфак, 1977 г.). Докажите, что отноше-
ние суммы квадратов длин медиан треугольника к сумме квад-
ратов длин его сторон равно 3/4.
379. (МГУ, ВМК, 1980 г.). Докажите, что площадь треуголь-
ника меньше единицы, если длины всех биссектрис меньше
единицы.
380. (КГУ, мехмат, физфак, 1977 г.). Докажите, что сумма
квадратов длин всех сторон и всех диагоналей правильного мно-
гоугольника равна п2г2, где п — число сторон многоугольника, а
г —радиус описанной окружности.
381. (ЯГУ, 1980 г.). Прямая, параллельная основанию тре-
угольника, делит его площадь пополам. В каком отношении она
делит его боковые стороны?
382. (ЯГУ, 1980 г.). Найдите углы ромба, в котором диаго-
наль равна стороне.
383. (ВГУ, матфак, ПММ, 1979 г.). Определите длины сторон
треугольника, если они выражаются целыми числами, образуют
арифметическую прогрессию, а периметр треугольника равен 15.
384. (МИФИ, 1981 г.). Найдите углы треугольника, в кото-
ром центры вписанной и описанной окружностей симметричны
относительно одной из сторон треугольника.
385. (КГУ, 1981 г.). Найдите острый угол между медианами
равнобедренного прямоугольного треугольника, проведенными из
вершин его острых углов.
386. (КГУ, 1981 г.). Вычислите площадь равнобедренной тра-
пеции, если ее высота равна й, а боковая сторона видна из
центра описанной окружности под углом а.
387. (ТашГУ, 1981 г.). Квадрат со стороной а повернут вок-
238
руг центра на 45°. Найдите площадь общей части «старого» и
«нового» квадратов.
388. (НЭТИ, 1981 г.). Имеется квадрат и равновеликий ему
круг. Что больше, длина окружности или периметр квадрата?
, 389. (ВГУ, мехмат, ПММ, 1981 г.). Существует ли треуголь-
ник, все высоты которого меньше 1 см, а площадь больше или
равна 10 см2?
390. (ЛГПИ, 1981 г.). Найдите радиус сектора, если его пло-
щадь равна 144 см2, а дуга содержит 4/9 радиана.
391. (ТашГУ, 1981 г.). Периметр кругового сектора равен I.
Найдите величину центрального угла сектора, при котором его
площадь будет наибольшей.
Стереометрия
392. (ЯГУ, 1980 г.). Радиус сферы увеличился на 50%. На
сколько процентов увеличилась площадь поверхности сферы?
393. (УрГУ, физфак, 1977 г.). Найдите объем параллелепи-
педа с ребрами а, Ь, с, образующими друг с другом углы л/2,
а, а.
394. (МАРХИ, 1979 г.). Полная поверхность правильной че-
тырехугольной пирамиды равна S, а плоский угол боковой гра-
ни при вершине равен а. Найдите высоту пирамиды.
395. (БарГПИ, 1981 г.). Объем правильной четырехугольной
пирамиды равен V, а ее высота Н. Определите длину апофемы
пирамиды.
396. (КГУ, 1981 г.). Плоский угол при вершине правильной
четырехугольной пирамиды равен а. Найдите двугранный угол
между боковой гранью и основанием пирамиды.
397. (МВИМУ, 1981 г.). Найдите угол между непересекающи-
мися ребрами правильной треугольной пирамиды.
398. (ВГУ, эконом, фак. 1981 г.). Куб с ребром а срезан по
углам плоскостями так, что от каждой грани остался правильный
восьмиугольник. Определите объем полученного многоугольника.
399. (ВГУ, эконом, фак. 1981 г.). В конус с высотой Н и
радиусом основания R вписан цилиндр с высотой h. Найдите ра-
диус основания цилиндра.
400. (ДГУ, физфак, 1978 г.). В шар вписана правильная тре-
угольная пирамида с плоским углом а при вершине. Найдите
отношение объема шара к объему пирамиды.
Разные задачи
401. (КГУ, 1981 г.). Пусть f(x) = ln|^. При каких а и b
выполняется равенство f (a)+f (b)=f (утр^)?
402. (КГУ, 1981 г.). Вычислите x* + xl, где xt и х*—корни
уравнения Зх2—5х—1 = 0.
239
Решите уравнения (403—413).
403. (КГУ, 1981 г.). 3*+1—13*—l| = 21ogs|6—х|.
404. (КГУ, 1981 г.). |х— 1 pg!*-'g^ = |x— 1|3.
405. (КГУ, 1981 г.). 2ncosx = |x|—|х—л|.
406. (МАРХИ, 1981 г.). lg(2* + x—41) = х(1 — lg5).
407. (МАРХИ, 1981 г.).
cos х + cos 2х + cos Зх + cos 4х + cos 5х = 0.
408. (УЭИИЖТ, 1981 г.). /5— log2x = 3— log2x.
409. (МАИ, 1981 г.). cos3x+sin (2х —= —2.
410. (ТашГУ, 1981 г.). Сколько корней уравнения
cos2 х + ^2^— sin х—— 1 = 0
лежит в отрезке [—л; л]?
Сколько корней имеет уравнение (411—413).
411. (КГУ, 1981 г.). х4+х3=10?
412. (КГУ, 1981 г.). З'х||2—|х||=1?
413. (КГУ, 1981 г.), х2—2х—log2|l—х| = 3?
414. (КГУ, 1981 г.). При каких значениях а уравнение х3 +
+ сх + 2 = 0 имеет три корня?
415. (КГУ, 1981 г.). При каких значениях а уравнение х-ех =
— а имеет три корня?
416. (КГУ, 1981 г.). При каких а уравнение | 1пх|—ах = 0
имеет три корня?
417. (УЭИИЖТ, 1981 г.). Найдите решение уравнения cos2 х = 1,
для которых х2^20.
418. (УЭИИЖТ, 1981 г.). Найдите sin 2а, если cos а удовлет-
воряет уравнению 25 cos2 а 5 cos а—12 = 0 и л/2 < а < л.
Решите неравенства (419—423).
419. (КГУ, 1981 г.). / 25—х2<12/х.
420. (КГУ, 1981 г.). log<i+^/2|x|(5-x2)>0.
421. (МАРХИ, 1981 г.). 0,11 <<4*-1’/(3л+2)> > 1.
422. (МАРХИ, 1981г.). 3/6 + х—х2> 4х—2.
423. (УЭИИЖТ, 1981
Найдите пределы (424—425).
424. (МАРХИ, 1981 г.), lim .
425. (МАРХИ, 1981 г.). lim -^2~ 2-.
Найдите участки монотонности и точки экстремума функции
(426—427).
426. (КГУ, 1981 г.). у = хе~зх.
427. (КГУ, 1981 г.). z/ = x/lnx.
240
428. (КГУ, 1981 г.). Докажите, что функция y = 3xi—4х*-|-
+ 6x2 + ax + b при любых а и b имеет только одну точку экстре-
мума.
429. (КГУ, 1981 г.). Для каких значений функция у =
— (K”3ctgx-f-а2)3 tgx достигает наименьшего значения на про-
межутке ]0; л/2[ в точке х = л/3?
430. (КГУ, 1981 г.). При каких значениях а минимальное
значение функции у=х2 — 4ах—а* принимает наибольшее зна-
чение?
431. (КГУ, 1981 г.). Используя геометрический смысл интег-
2
рала, вычислите J ]/ 2х — х2 dx.
о
з
432. (УЭИИЖТ, 1981 г.). Вычислите интеграл ^(Зх — x2)dx
о
и объясните его геометрический смысл.
433. (УЭИИЖТ, 1981 г.). Точка движется по закону s(/) =
= — 2t2-f-8t 4-7 до тех пор, пока ее скорость не обратится в нуль.
Найдите пройденный при этом путь.
434. (МАРХИ, 1981 г.). Найдите наибольший объем треуголь-
ной пирамиды МАВС, в основании которой лежит равнобедрен-
ный прямоугольный треугольник АВС (| АВ| = |ВС)), если
[МВ] .]_ (АВС) и |МЛ| = /37
435. (МАРХИ, 1981 г.). Вычислите объем фигуры, получен-
ной при вращении вокруг оси абсцисс плоской фигуры, ограни-
ченной кривой z/=cosx и осью абсцисс, х£[ — л/2; л/2].
436. (КГУ, 1981 г.). Если точка (х; у, г) лежит на плоскости
x4-z/4-z = 3, то х24-//24~22^ 3. Докажите это.
437. (МАИ, 1981 г.). Пирамида задана координатами вершин
S (0; 0; 2), А (0; 0; 0), В(1;0;0), С (0; Г, 0). Найдите координаты
точки М, лежащей на оси Oz, и координаты точки N, лежащей
в плоскости (SBC), если известно, что MN = (1/3; 1/3; 0).
438. (УЭИИЖТ, 1981 г.). Даны точки А (2; 1; —1),
В(3; 2; —1) и С(3; 1; 0). Найдите величину угла между век-
торами АВ и АС.
§ 3. ПРОГРАММА ПО МАТЕМАТИКЕ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ
В ВУЗЫ
ОБЩИЕ УКАЗАНИЯ
На экзамене по математике поступающий в высшее учебное заве-
дение должен показать: а) четкое знание математических опреде-
лений и теорем, предусмотренных программой, умение доказывать
эти теоремы; б) умение точно и сжато выражать математическую
241
мысль в устном и письменном изложении, использовать соответ-
ствующую символику; в) уверенное владение математическими зна-
ниями и навыками, предусмотренными программой, умение приме-
нять их при решении задач.
Программа по математике для поступающих в высшие учебные
заведения в 1983 году состоит из трех разделов. Первый из них
представляет собой перечень основных математических понятий и
фактов, которыми должен владеть поступающий (уметь правильно
их использовать при решении задач, ссылаться при доказательстве
теорем). Во втором разделе указаны теоремы, которые надо уметь
доказывать. Содержание теоретической части экзаменов должно
черпаться из этого раздела. В третьем разделе перечислены основ-
ные математические умения и навыки, которыми должен владеть
экзаменуемый.
Вопросы, отмеченные звездочкой, должны опускаться при экза-
меновке лиц, не обучавшихся все 10 лет по новой школьной про-
грамме.
I. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ФАКТЫ
Арифметика, алгебра и начала анализа
I. Натуральные числа. Простые и составные числа. Делитель,
кратное. Общие делители. Общее наименьшее кратное.
2. Признаки делимости на 2, 3, 5, 10.
3. Рациональные числа, их сложение, вычитание, умножение
и деление. Сравнение рациональных чисел.
4. Действительные числа, их представление в виде десятичных
дробей. Сравнение действительных чисел. Сложение, вычитание,
умножение и деление действительных чисел.
5. Числовые промежутки. Модуль действительного числа, его
геометрический смысл.
6. Числовые выражения. Выражения с переменными. Тождест-
венно равные выражения. Формулы сокращенного умножения.
7. Степень с натуральным показателем. Определение и свойства
арифметического корня.
8. Степень с рациональным показателем. Понятие о степени
с иррациональным показателем.
9. Одночлен и многочлен. Стандартный вид многочлена.
10. Многочлен с одной переменной. Корень многочлена.
И. Понятие функции. Способы задания функции. Область опреде-
ления, множество значений функции. Функция, обратная данной.
12. График функции. Возрастание и убывание функции; пери-
одичность, четность, нечетность.
13*. Достаточное условие возрастания (убывания) функции на
промежутке. Понятие экстремума функции. Необходимое условие
экстремума функции (теорема Ферма). Достаточное условие экст-
ремума. Наибольшее и наименьшее значения функции на проме-
жутке.
242
14. Определение и основные свойства функций: линейной, квад-
ратичной у = ах2 + Ьх + с, степенной у — ахп показательной
у = ах, а > О, логарифмической, тригонометрических ^функций
(у = sinx; у = cosx; у = tgx), арифметического корня у = {/x(n С N).
15. Уравнение. Множество решений уравнения. График урав-
нения с двумя переменными. Равносильные уравнения.
16. Неравенства. Множество решений неравенства. Равносиль-
ные неравенства.
17. Системы уравнений и неравенств. Решение системы. Мно-
жество решений системы. Равносильные системы уравнений.
18. Арифметическая и геометрическая прогрессии. Формула
n-го члена и суммы первых п членов арифметической прогрессии.
Формула n-го члена и суммы первых п членов геометрической про-
грессии, Сумма бесконечно убывающей геометрической прогрессии.
19. Синус и косинус суммы и разности двух аргументов (фор-
мулы).
20. Преобразование в произведения сумм sina±sin|J, cosa±
zb cos р.
21* . Определение производной. Ее физический и геометриче-
ский смысл.
22* . Производные функций у = ах, z/ = logax. Правило нахож-
дения производной сложной функции.
Геометрия
1. Прямая, луч, отрезок, ломаная; длина отрезка. Угол, вели-
чина угла. Вертикальные и смежные углы. Окружность, круг.
Параллельные прямые, направление.
2. Перемещения. Виды перемещений. Осевая и центральная
симметрии. Параллельный перенос. Поворот.
3* . Векторы. Операции над векторами. Коллинеарные векторы.
Компланарные векторы.
4. Выпуклые фигуры. Многоугольник, его вершины, стороны,
диагонали. Оси и центры симметрии многоугольников.
5. Треугольник. Его медиана, биссектриса, высота. Виды тре-
угольников. Средняя линия треугольника.
6. Четырехугольники: параллелограмм, прямоугольник, ромб,
квадрат, трапеция. Средняя линия трапеции.
7. Окружность и круг. Центр, хорда, диаметр, радиус. Каса-
тельная к окружности. Дуга окружности. Сектор.
8. Центральные и вписанные углы.
9. Вписанные и описанные многоугольники. Правильные мно-
гоугольники. Выражение стороны правильного многоугольника
через радиус описанной около него окружности.
10. Площадь многоугольника. Формулы площади: треугольника,
прямоугольника, параллелограмма, ромба, квадрата, трапеции,
правильного многоугольника (через радиус описанной около него
окружности).
243
11. Длина окружности и длина дуги окружности. Радианная
мера угла. Площадь круга и площадь сектора.
12. Подобие. Подобные фигуры. Отношение площадей подобных
фигур.
13. Плоскость. Параллельные и пересекающиеся плоскости.
14. Параллельность прямой и плоскости.
15. Угол прямой с плоскостью. Перпендикуляр к плоскости.
16. Двугранные углы. Линейный угол двугранного угла. Пер-
пендикулярность двух плоскостей.
17. Многогранники. Их вершины, ребра, грани, диагонали. Пря-
мая и наклонная призмы; пирамида. Правильная призма и пра-
вильная пирамида. Параллелепипед. Прямоугольный параллелепи-
пед. Куб.
18. Фигуры вращения: цилиндр, конус, сфера, шар. Центр,
диаметр, радиус сферы и шара. Плоскость, касательная к сфере.
19. Площадь поверхности и объем многогранников и фигур
вращения.
20. Формулы площади поверхности и объема призмы.
21. Формулы площади поверхности и объема пирамиды.
22. Формулы площади поверхности и объема цилиндра.
23. Формулы площади поверхности и объема конуса.
24. Формула объема шара.
25. Формула площади сферы.
II. ОСНОВНЫЕ ФОРМУЛЫ И ТЕОРЕМЫ
Алгебра и начала анализа
1. Свойства функции у = ах-\-Ь и ее график.
2. Свойства функции y = k/x и ее график.
3. Свойства функции у = ах2 + Ьх-\-с и ее график.
4. Формула корней квадратного уравнения.
5. Теорема Виета (прямая и обратная).
6. Разложение квадратного трехчлена на линейные множители.
7. Свойства числовых неравенств.
8. Логарифм произведения, степени, частного.
9. Определение и свойства функций у = sinx и у = cosx их
графики.
10. Определение и свойства функции z/ = tgx и ее график.
11. Решение уравнений вида
sinx = a, cosx = o:, tgx = a.
12. Формулы приведения.
13. Зависимости между тригонометрическими функциями одного
и того же аргумента.
14. Формулы тангенса суммы и разности двух аргументов.
15. Тригонометрические функции двойного и половинного аргу-
мента.
16* . Производная суммы двух функций.
17* . Производная произведения двух функций.
244
18*. Производная частного двух функций.
19*. Производные функций i/ = sinx, i/ = cosx, #=tgx,
у = хР(р^Р).
Геометрия
1. Свойства равнобедренного треугольника.
2. Свойство точек, равноудаленных от концов отрезка.
3. Признаки параллельности прямых.
4. Сумма углов треугольника. Сумма внутренних углов выпук-
лого многоугольника.
5. Свойства средних линий треугольника и трапеции.
6. Центр симметрии параллелограмма.
7. Признаки параллелограмма.
8. Свойство серединного перпендикуляра к стороне прямоуголь-
ника.
9. Существование окружности, описанной около треугольника.
10. Существование окружности, вписанной в треугольник.
11. Свойство касательной к окружности.
12. Измерение угла, вписанного в окружность.
13. Признаки подобия треугольников.
14. Теорема Пифагора.
15. Теорема косинусов.
16. Теорема синусов.
17. Формулы площадей параллелограмма, треугольника, тра-
пеции.
18. Признак параллельности прямой и плоскости.
19. Признак параллельности плоскостей.
20*. Разложение вектора по трем некомпланарным векторам.
21. Признак перпендикулярности прямой и плоскости.
22. Теорема о трех перпендикулярах.
23. Признак перпендикулярности двух плоскостей.
III. ОСНОВНЫЕ УМЕНИЯ И НАВЫКИ
Экзаменующийся должен уметь!
1. Производить арифметические действия над числами, задан-
ными в виде десятичных и обыкновенных дробей; с требуемой точ-
ностью округлять данные числа и результаты вычислений, про-
изводить приближенную прикидку результата; пользоваться таб-
лицами для производства вычислений.
2. Проводить тождественные преобразования многочленов,
дробей, содержащих переменные, выражений, содержащих степен-
ные, показательные, логарифмические и тригонометрические функ-
ции.
3. Строить графики линейной, квадратичной, степенной, пока-
зательной, логарифмической и тригонометрических функций.
4. Решать уравнения и неравенства первой и второй степени,
уравнения и неравенства, приводящиеся к ним; решать системы
245
уравнений и неравенств первой и второй степени и приводящиеся
к ним. Сюда, в частности, относятся простейшие уравнения и
неравенства, содержащие степенные, показательные, логарифми-
ческие и тригонометрические функции.
5. Решать задачи на составление уравнений и систем урав-
нений.
6. Изображать геометрические фигуры на чертеже и произво-
дить простейшие построения на плоскости.
7. Использовать геометрические представления при решении
алгебраических задач, а методы алгебры и тригонометрии— при
решении геометрических задач.
8* . Проводить операции над векторами (сложение и вычитание
векторов, умножение вектора на число) и пользоваться свойствами
этих операций.
9* . Пользоваться понятием производной при исследовании функ-
ций на возрастание (убывание), на экстремумы и при построении
графиков функций.
ОТВЕТЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Раздел I
§ 1
1. 24. Решение. Пусть х—число десятков искомого числа. Тогда
искомое число можно записать в виде 10x4-*/. В этих предположениях задача
сводится к решению системы уравнений
( х4-х/ = 6,
I 10x4-*/4"18= 10i/4-x,
решая которую, получаем х = 2, у = 4.
2. 45. Решение» Запишем искомое число в виде 10x4-*/, где х—цифра
в разряде десятков, у—цифра в разряде единиц десятичной записи числа.
Условие задачи запишем в виде системы уравнений
f (1Ох+^)(х+0) = 4О5,
1 (10f/+x)(x+z/) = 486,
откуда (10х+р)/(10#4~х) = 5/6, или х = 4г//5. Подставив это х в первое урав-
нение системы, получим у2 = 25, у=5 (у = —5 не удовлетворяет условию
задачи). Далее находим х = 4.
3. 8,5; 10; 11,5. 4. 3; 12. 5. 49; 1. 6. 6; 54. 7. 24. 8. 63.
9. 24. Решение. Искомое число запишем в виде 10x4-где х—цифра
в разряде десятков, у— цифра в разряде единиц десятичной записи числа.
По условию задачи
Г 10х + г/ = Зхг/,
1 10х+г/ + 18= 10г/+х.
Решив систему уравнений и отбросив постороннее решение (х =—1/3; # = 5/3),
получим 24.
10. 32. 11. 27.
12. 64. Указание. Пусть х—цифра в разряде десятков, у—цифра
в разряде единиц искомого числа. По условию задачи
J 10x4-r/ = x2~H/2-|-12>
( 10x4-i/ = 2xz/+16.
Вычитая из первого уравнения второе уравнение системы, получаем (х—г/)2 = 4,
откуда х—у = 2 и х—#=—2. Решая каждое из этих уравнений совместно,
например, со вторым уравнением системы и отбрасывая посторонние решения,
получим х = 6, у=4.
13, 13; 31. Решение. Запишем искомое число в виде 10x4-У, где
х, У £ N. По условию задачи
( х2+у2 = 10,
1 (Юх-Н) (10г/4-х) = 403.
247
Второе уравнение системы можно переписать, учитывая первое уравнение,
в виде ху = 3, Система уравнений принимает вид
| х2+//2 = 10, ( (* + */)2=16,
I ху = 3, I ху = 3.
Последняя система эквивалентна двум системам
f *+у=4, ( х+г/ = —4,
I ху=3, 1 ху = 3.
Первая из этих систем имеет решения 1) х=1, у=3 и 2) х = 3, у=1. Вторая
система имеет решения 3) х = —1, у ——3 и 4) х ——3, у=—1. В множестве
целых неотрицательных чисел решениями будут лишь решения первой системы.
14. 23. Указание. Запишем искомое число в виде 10х+#, гдех—цифра
в разряде десятков, у—цифра в разряде единиц. По условию задачи
Г 10х+^=4(х+у) + 3,
( 10х+у=Зху-|-5.
Решая систему, получаем х = 2, г/=3.
15. 91. 16. 64. 17. 72. 18. 71. 19. 32. 20. 15; 95. 21. 7; 8. 22. Знаменатель
равен 9. 23. 3/5. 24. 4/15. Указание. Искомую дробь запишем
пЦгг2, — 1), где п—целое число, п £ 0. По условию задачи
п + 2 1
п2+1 3 *
эту систему неравенств и учитывая, что п—целое число, п 0, полу-
дроби
в виде
Решая
чаем п = 4.
25. 13; 63. Указание. Пусть х—цифра в разряде десятков, у—цифра
в разряде единиц. По условию задачи 10х + 2/ = х2+ху+^2, 10(х+5)+^ =
= (х+5)2+(х+5)у+у2, или
Г 10х+у=х2+ху+г/2,
( 25—4у=х2+ху+у2.
, Решая систему уравнений и отбрасывая посторонние решения, получаем х = 1,
У = 3.
26. 1210. Решение. Число можно записать в виде 4«+1, где л=3, 4,
5, ♦.., 24 (всего таких чисел 22). Эти числа образуют арифметическую про-
грессию, первый член которой равен 13, а последний равен 97. Сумма всех
чисел $ = ^-±^-22=110-11 = 1210.
27. 99270. 28. 676. 29. 49500. 30. 45; 54.
31. (7; 2), (9; 6), (23; 22). Решение. Пусть п и/и —искомые нату-
ральные числа. По условию задачи п2—/и2 = 45= 1-3-3-5, или
(«-—т) 1-3-3-5. (1)
Так как п и т — натуральные числа, п-\-т > 0, правая часть равенства —
число положительное, то п—т—число натуральное, при этом п + т > п—т9
п—т и n+m являются делителями правой части равенства (1). Учитывая
сказанное, для определения п и т получаем системы уравнений:
{п— т=1, ( п—т = 3, ( п—т = 5,
n+/n = 45, 1 л + /тг=15, I «+/и = 9.
Решая эти системы, получим пары чисел (23; 22), (9; 6), (7; 2).
248
32. 156. 33. 34; 51. 34. 5 и 105; 15 и 35.
35. 144 и 864. Решение. Пусть х и у—искомые числа. По условию
x/y = 6k, где k £ N. Так как х и у трехзначные числа, то равенство х/£/ = 6&
возможно лишь при 6=1 и, таким образом, x=6gr. Далее, по условию,
х4-£/ = 504т, где m£Nt при этом т может принимать лишь значения 1,
2, 3, так как 504m < 2000. Решая систему уравнений х4-у = 504m, х—Ъу, полу-
чаем у = 72т. При т=1: £/ = 72, х = 432 не удовлетворяют условию задачи;
при т = 2: £/=144, х — 864 — решение задачи; при т = 3: £/ = 216, х=1296 не
удовлетворяют условию задачи.
36. 19 = 33—23. Указание. Разложив левую часть равенства m3 —п3=19
на множители и воспользовавшись тем, что 19 простое число, можно доказать
что такое представление единственно.
37. (2; >/3; 9), (1/у^2; —y^9/2 ; у^З/2) . У к а з а н и е. Пусть
х, У, г—искомые числа. По условию задачи x3=xyz + 2, tfi—xyz—3,
z3 = x£/z + 3. Перемножив левые и правые части этих равенств и обозначив
хуг через /, для определения t получаем уравнение 2/2—9/—18 = 0.
38. 52. Решение. Запишем искомое число в виде 1 Ox-\-yt где х—цифра
в разряде десятков, у—цифра в разряде единиц. По условию задачи
х +У^7, (1)
х2+у2<30, (2)
10x+y^2(\Qy+x),
или
8х^19у. (3)
Из (3) следует, что у может принимать значения 0, 1, 2, 3 (так как х^9).
Если £/ = 0, то из (1) следует х^7. Эти числа не удовлетворяют неравенст-
ву (2). Если £/=1, то из (I) следует, что х^6. Эти числа не удовлетворяют
неравенству (2). Если у = 2, то х^5. Числа % = 5, у=2 удовлетворяют всем
неравенствам. При у=2, х > 5 неравенство (2) не выполняется. Пусть £/ = 3.
Из (3) следует х^8. Такие числа не удовлетворяют неравенству (2). Таким
образом, больше решений нет.
39. 2573. Решение. Запишем искомое число в виде lOOOx-J-lOOr/ +
+ 10z-|- tt где х, £/, z, t цифры в разрядах тысяч, сотен, десятков и единиц
соответственно, причем х 0. По условию задачи
( х+г/+г=14,
< г/+г + «=15,
( г=* + 4,
поэтому f = x-J-l, г=х+5, £/ = 9—2х. По условию задачи нужно найти такие
значения х, £/, z, t, чтобы x2+^2 + z2+^2=*2 + (х+1)2 + (х+5)2+(9—2х)2 =
= /(х) принимало наименьшее значение. Так как z^9, то из равенства
z=x4~5 следует, что х может принять лишь значения 1, 2, 3, 4. Вычисляя
/(1), f (2)> /(3), f (4) и сравнивая их, получаем /(2)</(1), / (2) < / (3).
/(2) < /(4). Поэтому х = 2, £/ = 5, г = 7, / = 3.
40. 1738. 41. Доказательство. Пусть a = n2+(n+m)2, где л, т—на-
туральные числа. Тогда 2а = 2л2 + 2 (п2 + 2т/г + т2) = (2/г+т)24-/и2« 42. 300.
[25. 26. 27. 28. 29. 301
43в (9 9 10* 11’ 12’ 13’ 14J * * *
249
§ 2
1. 113/15. 2. 2111/990. 3. I. 4. x=30. 5. 8. 6. 6. 7. 7. 8. 1.
9. 0. Решение. l-J-sec 20°— У 3 ctg 40°=sec 20° + ==*
ОЛО 2 (sin 60° • cos 40°—cos 60° sin 40°) пло sin 20°
= Sec2a--------2 sin26°~cos~26°--==Sec2fr~sin20°'"cor205=s
= sec 20° — sec 20° = 0.
10. 100. 11. 1. 12. 1/4. 13. —3/2. 14. 1. 15. 1. 16. 0. 17. 2. 18. /6/2.
19. / 3. 20. 10. 21. /2/2. 22. 1. 23. 3/2. 24. 1. 25. 5. 26. —9/2.
27. 10. 28. 4. 29. 1. Указание. Преобразуйте заданное выражение к виду
а-Ь. 30.0. 31. —10. У к а з а н и е. Если а С Z, то а2 £ Z. 32. (2+ /2- V б)/4.
33. J^2 /3+ / 2 Кр/з— /2 И44-2 у/9+3 j/3 .
34. а < Ь. 35. Доказательство. Так как Ь < с, то
2Ь < Ь+с. (1)
Так как
Ъ+с<а+1, (2)
то по закону транзитивности из (1) и (2) следует
26<а+1. (3)
Так как 1 < а, то
1+а<2а. (4)
По закону транзитивности из (3) и (4) следует 2Ь < 2а, т. е. 6 < а,
36. logs Ю8 > log6 375. Решение,
logs 108=3+log3 4 > 4j (1)
logs 375=3+log6 3< 4. (2)
Из (1) и (2) следует, что logs 108 > log5 375. 37. 0; In (7/5); /ОД 0,9186.
38. 0,37; tg 33°; 1; 65/63; 61/59; tg (-314°). У к а з а н и e. tg (— 314°) = tg 46°=
l+tgl° _l + tg(n/180) 1 + 1/60 ,61 _cos 571’,
1— tg 1° “1 — tg (л/180) > 1—1/60 “59’ . °’02, °’85* 5713
/3/2; /о,762; 1. 40. Указание. Дoкaжитei что последние цифры
десятичной записи чисел Б358 и 33^ равны 3, 41. (л2+2п+2) (л2-—2п-{-2)*
42. (1+п+«2)(1—п+па)(1+/3л+п2)(1 —/Зп+п2).
43. (1+х)^1—-х+ х2^ ^1+ 1 Решение. 1+х?=
= (1 +х) (1 -х+х2-х«+х4)=(1 +х)X2 (л2 + -L- (х +1) + 1) =
-('+*> =/Н)-НН=
„ , . ,( ,1 1+/5V , 1 1—/Д
= (1+х)х2^х+------Г~дх+т---------~Г
= (1 + X) (х2-1±^ х+1) (х2+-Ц^1 х+1) .
44. аЫ(а+Ь). 45. 0. 46. —а4/(а2+62), 47. 4 (а—6)/с6. 48. 2/(а+*).
49. т—п. 50. 1. 51. /2. 52. 1/26с. 53. а (а— Ь—с)/2. 54. 1. 55. —1.
250
56. —(ХуГ(Д,у)Р2)' • 57- 12/(а4-2). 58. — За/(а— 1). 59. 2<?+3. 60. У 2.
61. ab. 62. (a -Z>)/(a+&). 63. 1/а. 64. а"1в9/б° 6"31/30. 65. l/j/^.66. 1.
67. 1. 68. 2/(1—х). 69. 2. 70. У а. 71. УТ^а. 72. 2. 73. (х— 1)Ух.
74. 1. 75. —1. 76. 2/(а—1). 77. 0. 78. 1. 79. х—1. 80. 2—3}<2 t/1/5+9</2/6.
81. —2г/. 82. 1, если а> 0 и 6 > 0; —1, если а < 0, b < 0.
83. Уьх/(У~Ь+-Ух). 84. 1. 85. 1. 86. 2аЪ. 87. У&^Л + а*— 1.
88. 1/10. 89. 4/(/’х+Ку). 90. (1— а)1У~а. 91. У~а/(У"а— У~b). 92. 1.
93. 1. 94. 2 (/а+/д). 95. — УУь. 96. 1 + ^-^. 97. 1 . 98. а (а-f-1).
а — и за
99. У а+У ь- I00- «+1- «И- fl2/S- *02. 2Ь/Уа2 — Ьг. 103. 1/а (а1"" — Ь1'т).
3 У~ з У~~
104. 2/(1 — а). 105. 0. 106. у Ь— / а. 107. 2. 108. —4. 109. a2+ab-{-b2.
НО. (х—а)/х. Решение.
(х(х2—-а2) 1/2 4-1) /х—(х2 — а2)х/2 \ ~1
а(х—£z)“1/24-(x—а)1^ \ я2(х4-а)1/2 /
__(х-[-]/~х2—а2) Ух— а (х— Ух2 — а2) (х2— (х2— а2)) 1
Ух2—а2(а+(х—а)) а2Ух±а ~~ (х~]-а)-х-а2 ~~х2-[-ах 9
После этого преобразования исходное выражение переписывается в виде
(Т—(~ТТ-------------h(x24-ox)-"1^ =
\х2— а2) \х24-я* /
_ (х—а)(х4-п) . / 1 . 1 \__(х— а) (х4-«)-2_х—а
~~ 2 \ х(х4-а) х(х4-а) J ““ 2х (х-j-а) ~~ х *
111. У~а/(У'а—У~Ь).
Пг.З^.Решение/2-^1/--^.)'1
\ За /
3_Га _( (У^-(У-ЬГ
2У а+У Ь\У а(У а—У b)
а^-Ь»'ъ а — Ь \
а_а1/2р/2 у~а+Уь)~
\у-а-у-Ь)^
_ 3|<а / а+УаЬ + Ь__
~ 2 У~а+ У~Ь \ У~а ~~
113. 0.
а^Ь. 116.
а+УаЬ + Ь—а+УаЬ_ЗУ а(2У а+У b) У b „ г-
r~b' У~а ~ ^y-a-^yi^y-a V
114. 0. 115. 1, если а > 0, b > 0, а Ь\ —1, если а < 0, b < 0
а2.
у а + У b
О Г> (Ух— У у)3 + у У у+2х*-.у х , ЗУхи—Зц
х^х + у/ у _ X—у
хУ х—ЗхУ y + зу ху—уУ у+уУ у+2хУ х . 3/~ у ( ]/~х—У~у) _
хУ^+уУ1 Х~У ~
__ЗхУ х—ЗхУ y-f-ЗуУ х . ЗУ у _____
~^Ух+У^
_ ЗхУ х — ЗхУ у+ЗуУх-1-Зу-у(х—Уху-1-у) ЗхУх-]-ЗуУ~у = 3
х|< х-\-уУ~у хУ~х + уУ^
118. — У х. 119. 1. 120. (1+а2/®)2/(1—а1/3). 121. 1/(1—х2). 122. ху.
123. 1. 124.3()<а— У1)1(У~а+Уь). 125. ^/а/(/’а+1), 126. 2^/F/55'.
251
127. 1. 128. 1/(х2—1). 129. уЛп—p/n. 130. 2. 131. V а, если
> У 6 За 0; — а, если \/ b > У~а^0.
132. 2/Г&“. Решение. - ь =
__ Ь3—1________Ь2-1 т/-т_^ + г>+1 &—1! у-^=
ьУ^(ь—1) bt/"b(b+i) ьу~ь ьУ"ь
b2+2—b2 2
• — bf/~b ь у"ь
133, 2(a+4)/a. 134. 2. 135. 1. 136. У^+Уб. 137. 1. 138. —3/2.
139. {/~b. 140. 11У~а. 141. — j/atb. 142. (a+l)/4. 143. x1/3 .
144. р/^+Уб. 145. (Уа+У&)/2. 146. 3. 147. 148. УаЬ. 149.-25,
если а > 0, | а ] > | b | > 0; 25, если а < 0, | а | > | b | > 0. 150. 1. 151. 6—4а
при а^[0; У2]; 2(а—I)2 при a^]V"2; +<»[. 152. —1. 153. 1.
154. У1 —х2. Решение.
vх2-1 , , = ( 1 + УП^___ 1-У1=7 Vх2—1 _
2 “Г \yi—х(1 + УЬ=^)'+’ УГ+х(У1+х—1) / 2 I"
/ 1 1 \2х2— 1 , , (УТ+х— УГ=х)2 х2— Ij,
Дут=7 ут+i; 2 + - (У1=72)2 2 1 -
2—2У1 —х2+, = _j + 1 = УТТГ7.
/ 1+У1-* 1-У1+х У
X 1— —X l-J-X—yrl-]-x /
155. a+b. 156. 1/n. 157. —2b. 158. 1) 2b (a—b); 2)2b(a—b).
159. 2, если | a | < 1; —2, если 1 < | a | У 2. 160. 1 + V^c.
161. l/a&p/J. 162. —2/(а+Уа); (Уб—5)/10. 163. a2+ab+b2-, 2,52.
164. a(b—a)/(a+&); 15/4. 165. f (x, y)=y+V^y, f (9; 0,04) = 0,64.
167. D(jO = J—4; 0[(JI0; +«[; y=—4. _ ________
168. Доказательство. x2-f-p/Z x4y24*V^ x2y4=
-/УИУ^+Уй+/
У У5+/?(У?+УЛ-(У5+У7-),Л-а.
Отсюда следует х2/3+#2/з = а2/3.
169. пР/т21. 170. Область определения: a>0, b > 0, a^b; Л = 0 при
а > Ь; А = У а— У~Ь при а < Ь.
§ 3
2. Доказательство. 1) Проверим справедливость предложения при
л = 1: 41 +15-1 —1 = 18 = 9-2, следовательно, А (1) истинно. 2) Допустим, что
при n = k, где k—натуральное число,
4«+15Л—l=9m, (1)
252
где т — натуральное число, т. е. A (k) истинно. При п = 64-1, учитывая (1)
имеем
4*+14~15 (64-1)—1=4-4*4-606—4 — (45/fe—18) = 4 (4^+15^— 1)—9(56—2) =
= 4*9/п—9 (56—2) = 9.(4/п—564~2)=9р,
где р = 4/п—564~2—число натуральное. Обе части доказательства проведены,
поэтому на основании принципа математической индукции предложение спра-
ведливо при всех натуральных п.
4. Замечание. Эта задача более просто решается без применения ме-
тода математической индукции. Разложим данное выражение на множители:
п3— п = (п—1)п(п4-1). По условию число п—нечетное; следовательно, п—1
и n-Н—четные числа; из двух последовательных четных чисел одно делит-
ся на 2, а другое на 4; кроме того, из трех последовательных целых чисел
п — 1, п, «4-1 по крайней мере одно делится на 3. Таким образом, и3—п
делится на 2-4-3=24.
4
6. Доказательство. 1) При n = 1 предложение справедливо 1—р==
- -3-3.
2) Допустим, что при п=6, где k£N, равенство имеет место, т. е.
(1_1)
(1)
При n = 6-f-l, учитывая (1), будем иметь
(1-т) (,_4)-‘,(I“(26=ip) (1-(Wip)3’
_ 14-26 / 4 \_14-26 (264-1)2—4__
"1-26 Д (264-1)2/~1—26 ’ (264-1)2 “
_(26—1)(264-3)_ 14-2 (64-1) 1+2(64-1)
(1—26) (26+1) —1—26 “Ч—2(6+1)'
Обе части доказательства проведены, поэтому на основании принципа мате-
матической индукции предложение справедливо при всех n£N. Замеча-
ние. Доказательство можно провести и не прибегая к принципу математи-
ческой индукции. Действительно, для любого 6£ЛГ имеем
1 4 -(2fe-»)2~4 .(26-3) (26+1)
(26—1)2 (26—1)2 — (26—1)2 ‘ W
поэтому, давая 6 в формуле (2) значения 1, 2, п и перемножая резуль-
таты, получим
(‘ 1)0 э)(1 (2n-ip)-
_(—1-3) (1-5) (3-7).. .((2n—3)(2n+l))
~~ 1-32-52... (2n—1)2 =*
_ -1.1.32.52.. ,(2n—3)2.(2n—1)(2«+1) _-l-(2n+l) l+2n
, I.32.б2...(2n— I)2 ~ 2/i—1 — Г^2л'
11. x=4. 12. x=ll. 13. x = 5. 14. x = 7. 15. x = 8. 16. x=4.
17. x=5. 18. x=10. 19. x=8. 20. x = 9. 21. x = 3. 22. n = 6, m=3.
23. x = 7. Указание. Решая задачу, получаем уравнение
(х4-3) (*4-2) (х4-1) = 720. На множестве натуральных чисел функция f (х) =
253
— (*+3) (х4-2) (х4~1) возрастающая. Натуральный корень полученного урав-
нения легко найти подбором.
24. х = 3. Указание. Решая задачу, получаем уравнение
120
6(х+3)-х(х+1)=г^2,
x£N. Так как правая часть уравнения при xg/V
положительна, то 6 (х4-3)—х (x+l)C7V, 6 (х4~3)— (x-f-l)x > 0, следовательно,
1«^х<8, причем 120 должно делиться на x-j-2 без остатка, поэтому
х # 5, х / 7. Поэтому корни полученного уравнения нужно искать среди
чисел: 1, 2, 3, 4, 6.
25. 13. 26. 10. 27. (п4“2)2й”1. Решение. Обозначим данное выра-
жение через S:
S = C“+2CA+3C2+...+(«+l)C£ (1)
учитывая, что Сп = С%~\ выражение (1) запишем в виде
S = Сп~^пСп~[~(п—1) Сп~|“««*Н“2Сп 1-|-Сл’ Р)
Сложив равенства (1) и (2), имеем
2S = (п-|-2) (Си4-0/14-0/24“...-]-С”) = (л4~2) 2nt
откуда следует <$ = («+2) 2ZZ~1.
28. {0; 1; 2; 3; 4; 5}. 29. {11; 12; 13; 14; 15; 16; 17; 18}. 30. {6; 7; 8; 9}.
31. п > 14, n£N. 32. {5; 6; 7; 8; 9; 10}.
33. х^2, x£N. Решение. Так как 0^71 = Cx+i = Х > то данное
(х4-1)* ^3 2 . Q п
неравенство имеет вид -—» или * -г*—3 > 0, т. е.
х^] —оо;—(]<134-1)/2[(J](/'13—1)/2; 4~оо[, но по условию задачи x£N, сле-
довательно, х^2—целое число.
34. {1; 2; 3; 4; 5}. 35. {12; 13; 14; ...}. 36. {2; 3; 4; 5; 6; 7; 8; 9}.
37. {8; 9; 10; ...}. 38. Три. 39. Четыре. 40. xf = — 63/4; х2 = — 23/8. 41. mnk.
42. 2«(^5)2 = 2-020)2 способами. Решение. Существует только один
способ рассадить девочек и мальчиков — через одного. При этом девочек можно
посадить Р5 способами и мальчиков— Р5 способами. Кроме того, мальчиков
и девочек можно поменять местами. Поэтому всего будет 24Р5)2 способов.
43. 2-(Рб)2 = 2-7202 способами. 44. Л?о=72О способами. 45. а) Л10 =
— 40-39=1560; б) 4ОС39. 46. С|— 126 способов. 47. C^+k-i способами.
48. 26250 вариантов. Указание. Либо в какой-то урне 3 шара и в
9 урнах —по 1 шару, либо в каких-то двух урнах по 2 шара и в 8 урнах —
по 1 шару.
49. (С|—б) Р3Р5 = 36000 способов. 50. 2187 способами. 51.31. 52. Л|-Л^=
= 720. 53. 125. 54 . 5274 . 55. Лд = 15120. 56. 576.
57. 45-105. Решение. Рассмотрим 10 последовательных семизначных
чисел
aitf2a3a4a5n6l,
Л1Я2а3я4я5я69,
где ai, а2, #31 «4» а5, Яб“~какие“то цифры. Как видим, из этих Ю чисел по-
ловина, т. е. 5 имеет четную сумму цифр. Первая цифра а± может принимать
9 различных значений; каждая из цифр а2, a3t а±, а5, ае может принимать
254
10 различных значений; последняя цифра я7 может принимать лишь 5 раз-
личных значений, при которых сумма всех цифр будет четная. Итак, суще-
ствует 9* 105-5= 45-105 семизначных чисел, сумма цифр которых четная.
58 . 4 - 73= 1372. Решение. По условию задачи в записи четырехзнач-
ного числа обязательно встречается цифра 1 и притом только один раз.
Остальные три цифры могут принимать любое из 7 значений 2, 3, 4, 5, 6, 7, 8.
Заданная цифра 1 может стоять на 1-м, 2-м, 3-м или 4-м месте. Следовательно,
всего чисел, удовлетворяющих условиям задачи, будет 4*7-7-7 = 4-73 = 1372.
59. С?-25 = 672.
во. с} (с|р3-4+с1с1сХ)+сКс|р3+5-зс|р2+сГзс1р2+5-зс|с23) =
= 294840 чисел. У Казани е. Либо среди цифр нет нуля, либо есть. В пер-
вом случае либо какая-то цифра стоит на трех местах, либо имеется два «дуб-
лера». Во втором случае одно из четырех: либо нуль занимает три места,
либо какая-то другая цифра занимает три места, либо нуль занимает одно
место и есть два «дублера», либо нуль занимает два места и есть один «дублер».
61. 4373. Итак, искомыми будут числа 12, 21, ..., 199999992. Для удобства
счета мы все их будем считать девятизначными и обозначать
дописывая нужное количество нулей впереди данного числа. Запишем три по-
следовательных девятизначных числа
Cl4Cl2Cl3Cl4Cl^Cl9Cl7ClgQ,
ci j ci 2d 4a g ci 7 cig 2,
где at может принимать одно из двух значений 0 или 1, каждая из цифр а2,
я3, ^4» а5, fl6, аз может принимать любое из трех значений 0, 1,2. Из этих
чисел надо потом исключить число, для которого 0 = аг = а2 = а3 = а4 — а5 =
= а6 = а7 — а8 = а9. Для того чтобы допустимое условиями задачи девятизначное
число делилось на 3, сумма его цифр ai +
должна делится на 3. Сумма первых восьми цифр может быть равна или
Зя — 2, или Зя —1, или Зя. В каждом случае а9 можно выбрать из 0, 1, 2
лишь единственным образом, чтобы сумма всех девяти цифр была Зя. Итак,
всего чисел, удовлетворяющих условиям задачи, будет 2-З7-1—1=4374—1=4373.
62. 576. Решение. Условию задачи удовлетворяет случай, когда четы-
рехзначное число записано при помощи одной цифры, таких чисел Cj, так как
0 не может быть этой цифрой. Условию задачи удовлетворяет также случай,
когда четырехзначное число записано при помощи двух различных цифр.
Предположим, что одна из них 0, тогда другую можно выбрать С* = 9 спосо-
бами. На первом месте нуль стоять не может, это место занимает вторая
выбранная цифра; следовательно, если в записи числа 0 встречается только
один раз, то таких чисел CJ, если в записи числа 0 встречается два раза, то
таких чисел и, наконец, если 0 встречается три раза, то таких чисел С3.
Итак, чисел, удовлетворяющих условию задачи, и в записи которых встре-
чается хотя бы один нуль, Cj(С3 + CI4-C3) = 9• (3-|-3-f-1) = 63. Последняя
возможность: число записано двумя различными цифрами, среди которых нетО.
Две цифры из 9 можно выбрать способами. Если цифры уже выбраны, то
при записи числа 1-я цифра может встретиться 1 раз, а 2-я—3 раза, таких
255
чисел CJ; 1-я цифра может встретиться 2 раза и 2-я также 2 раза, таких чи-
сел С?2; наконец, 1-я цифра может встретиться 3 раза, а 2-я — 1 раз, таких
чисел С%. Следовательно, всего различных четырехзначных чисел, записанных
только двумя различными числами, среди которых нет 0, будет С% (Cl-J-Cl-}-
+ С?) = 36»(44-64-4) — 36-14 = 504. Итак, условию задачи удовлетворяет
CJ+CJ (C|+C|+C|)+d (C14-Cl+Cj) = 9+63 +506 = 576
чисел.
63. 261972. Решение. Букет может быть составлен из 3, 4, ..., 18
различных цветов. Это можно сделать A = Ci84~£is4~«-«4"£il различными спо-
собами. Учитывая, что Ci84-C’i84_^is4_^i8+---+^i8=::218, т. е.
14-184-153 4-Л = 262144,
получим Л = 262144—172 = 261972.
64. 766. Решение. Итак, искомые числа 1, 2, И, 12,21, 22,...
..., 122222222. Подсчитаем их число. Однозначных чисел, записанных цифрами
1, 2, будет Сг = 2. Двузначных чисел, записанных двумя цифрами 1, 2, будет
С2 4"£2С2 = 24~Ь2 = 4. Трехзначных чисел, записанных двумя цифрами 1, 2,
будет Сг + ^2 (Сз4-Сз) = 24“Ь(34~3) = 8. Четырехзначных чисел, записанных
двумя цифрами 1, 2, будет Cl-J-Cl (Cl4-C14-C4) = C14-(24-CS--d) =
= 2-|-24—2 = 24= 16. Пятизначных чисел, записанных цифрами 1, 2, будет
Cl 4-d (Cl+Cl+Cl+Cl) = 24- (2*—С?—Cl) = 24-2? —2 = 25=32. Шестизнач-
ных чисел, записанных цифрами 1, 2, будет Сг4-£2 (с14-^б+^б+^в+^б)=
= 26 = 64. Семизначных чисел, записанных цифрами 1, 2, будет Ca+^i (С?4-
4- С74-С?4"С?4“С|4-С?) = 27= 128. Восьмизначных чисел, записанных циф-
рами 1, 2, будет 28 = 256. Так как все искомые числа меньше 2-108, то все
девятизначные числа начинаются с 1, и, следовательно, их столько же, сколь-
ко и восьмизначных, т. е. 256. Итак, всего чисел, меньших 2108 и записан-
ных двумя цифрами 1, 2, будет 24-44-84” 164-324-644-1284-2564-256=766.
65. (С^СНсМ-Сз+фСв-Сз-Сз) (С1+С*-Сз+С1с£.с2)+
+ (c|.ct+ci-c25.cj+ctctc13.cl)(c}+ci.cl+c14.c23+c^c|-c21) +
+ (C^+Ctcid+C^CiCa1) (cl+clcJ+CiCjcJ) =
= 1900-46+950-61+950-36 = 87 400 +57950+3420= 179 550. Указание.
При выборе трех нечетных цифр возможны случаи: I) все три выбранные не-
четные цифры одинаковы, II) две выбранные нечетные цифры одинаковы,
а третья от них отлична, III) все три выбранные нечетные цифры различны.
При выборе трех четных цифр надо различать две возможности: 1) среди четных
цифр нет 0,2) среди четных цифр есть 0. Случай 1) подразделяется на три возмож-
ных подслучая: а) все три выбранные четные цифры одинаковы, б) две выбранные
четные цифры одинаковы, а третья от них отлична, 3) все три выбранные четные
числа различны. Случай 2) подразделяется на четыре подслучая: г) все три выбран-
ные четные цифры есть 0, д) две выбранные четные цифры есть 0, а третья четная
цифра отлична от 0, е) одна выбранная четная цифра есть 0, а две других
четные цифры одинаковы и отличны от 0, ж) одна из выбранных четных цифр
есть 0, а две другие—различные четные цифры, отличные от 0. Каждый из
случаев I, II, III может сочетаться € каждым из случаев а), б), в), г), д), е),
256
ж), причем в случаях а), б), в) нечетные цифры можно помещать на любые
из 6 мест шестизначного числа, а в случаях г), д), е), ж) либо одну из нечет-
ных цифр надо поместить в начале, а две другие на любое из оставшихся
5 мест, либо одну отличную от нуля четную цифру поместить в начале,
а остальные размещать произвольно.
66. 840. 67. 45* 104. Указание. См. решение задачи 50. Всего шести-
значных чисел с четной суммой цифр и нечетной суммой цифр равное коли-
чество. Всего же шестизначных чисел 9*105.
68. 13 участников, 156 партий.
69. С?2 = 924. 70. 20х~3/2.
71. п=11. Решен не. Сд—-С„ = 44, т. е. ”- ——п = 44, откуда п4=
=11, п2 ——8. Условию задачи удовлетворяет п=11.
72. Т4 = 70. Решение. Искомый ичлен разложения = (1/х)*;
х8-лх-л=до) откуда 8—26 = 0, & = 4. Т4 = у у 70.
73. Т8 = С?7.
74. Т4 = 35х2. Решение. Искомый член разложения 7\=С*(х~ 2/®)?-*х*=
= С;х2, откуда ^^+* = 2, А = 4;Т4 = ф2=35х2.
75. Т1=14а’/®.
76. T3=165z14. Решение. C^+Ci+,..+C^ = 2'>=2048 = 2«, /1 = 11;
7’з=С?1 (г2)8 (г~ 2/3)3 = 165z14.
77. х=9. Решение. - Дч,/ =4- ,или6-4-6ж/3 = 6->.
С£“в(21/З)6(3“'1/З)*“в 6
откуда х = 9.
78. Шестой. 79. Третий. 80. Тв = 5005.
81. п = 32. Решение. .-1=31, я(ге-~1)=31, щ- = 32, й2 = -3).
10
Условию задачи удовлетворяет п = 32.
82. 7’4 = 1120х4. Решение. (?т—2С^+4С„=97, 1— 2т-}-2т(т—1)=97,
т4=8, лг2 =— 6. Условию удовлетворяет т=8. Далее2 (8—k)—£ = 4, откуда
k = 4, Т4 = С| (х2)4 (— 2/х)4= 1120х4.
83. 380.
84. xi = -I, х2=2. Решение. Cg~2+Off"1+<?%=12 +
4-/п+1 =22, /п=б. Т2+7’4=135, или30.2*+60-2-* = 135, х4 = —1, х2=2.
85. Х1 = 10-4, х2=10. Решение. T3 = C?x3/2(lg х+ =200,
1 3
20х 4 2 08*+») =200, (1 + ^-(ig /+,}) lg х = 1; 1g х = - 4,1g х = .; х,- = 10 ~ 4,
х2 = 10.
86. х = —1/3.
87. х=1. Решение, т (т~1)/2 —20 = m, т2—3/и—40 = 0, mi = 8,
Щ — —5. Условию задачи удовлетворяет т = 8.Далее, Т3—Т5 = 56, или
56 (2х—2-2~х) = 56, или 22-^—2х—2 = 0; 2X1 = 2,xf = 1; 2Xi = —1, х2£0-
88. Х£=10"6/3, х2=10. Решение. Т2 = СбХ«х2|8* =10’, х3х21®* =105;
9 В. М. Говоров и др. 257
(2Igx-f-3) lgx = 5, 21g2x-j-31gx—5=0; lgx= —5/2, Xf=10_5/2; lgx=l,
х2=Ю.
89. Xf=l, x2 — 2. Решение. Шестое слагаемое разложения степени
бинома является пятым членом бинома
Т5 = С|22 logf ** Х+7.2“1о&2 (3*"Х+1)==84,
7,6.21о&2 (э*“х+7).2-1«» (зх“1+1)==§41
g-i±l==4, (3*-1)2-4-3*-I +3=0,
(3JC-1— 1) (ЗЛ7-1—3) = 0; Зх“х=1, хг= 1; 3*-i = 3; х2 = 2.
90. Указание. Данное неравенство равносильно неравенству
(1\и ( \\п
1 -|-) < п. Докажите, что (14— ) <3.
Л j \ tb J
( х 2 \п 1
91. п=13. Указание. Так как I -f-4'Т’ ) (х+2)”# то задачу
\ о О У Ъп
следует решить для (х+2)".
92. Максимальным по модулю является Т^-С^Ь^З1*. Решение.
^=-. Легко убедиться, что |Тk/T> 1
Отношение
при /г< 18 и | Tk!Tk^ I > 1 при £^18. Следовательно, &=18 и Тц будет
наибольшим по модулю членом разложения.
93. п=6; х=±1/2. 94. (х1^ — х~ 1/2)10, T4 = Cfc. 95. Тв=84.
§4
1. {4/3}. 2. {-—9/2; 13/4}. 3. Всех ^[2; + ©о[. Решение. Рассмотрим
три случая: 1) х^О; 2) 0 < х < 2; 3) х^2.
1-й случай: х«с0. В этом случае уравнение равносильно системе
I — х+(х—2) = 2,
множество решений которой пусто.
2-й с л у ч а й: 0 < х < 2. В этом случае уравнение равносильно системе
J0 < х < 2,
{х+(х-2)=2,
множество решений которого пусто.
3-й случай: х^2. В этом случае уравнение равносильно системе
Г х^2,
( х—(х—2) = 2,
множеством решения которого являются все х£[2; + ©о[.
4. {-О-
5. J—оо; —3] U [—У 3/3; 1/2]. Указание. Данное уравнение равно-
сильно уравнению
| я2х4~1 |+1 я3+а2х | = я2х+1 — (а?+«2х).
Уравнение |и|+|о| = м—v равносильно системе
( и^О,
( 0.
При а Ф 0 рассмотрите случаи 0 < а < 1, — 1 < а < 0, а = —1 и а< — I.
258
6. J2; 3[. Peme н и e. Заданное неравенство равносильно неравенству
|2х—5| < 1, которое равносильно двойному неравенству — 1 < 2х—5 < 1,
или 4 < 2х < 6, или 2 < х < 3.
7, ]—оо; 1/6] (J [3/2; + оо[. Указание. Заданное неравенство равно-
сильно совокупности двух неравенств: Зх—2,5 «С—2 и Зх—2,5 2.
8. [ 1; + оо [. Указание. Рассмотрите три случая: 1) х 2; 2) —4 < х < 2;
3) х<;—4. Неравенство можно также решить графически, построив графики
функций #=|х+4[ и у—\х—2|.
9. ]5/3; 3[. Указание. Заданное неравенство равносильно системе не-
равенств
( х—1 >0,
{ 1—х < 2х—4 < х—1.
10. ]—оо; —2[ (J J 2; + оо[. Указание. Рассмотрите два случая:
1) х< — 1; 2) х^—1.
11. ] 9/2; Н-оо [. Указание. Рассмотрите три случая: 1) х«С—2;
2) — 2<х < 1; 3) х^1.
12. ]— оо; —2[ (J ]5; + оо[, х = 6. 13. х = — 1. 14. £= —50.
15. {—4}. Решение. Заданное уравнение запишем в виде |х|2 —
— 21 х |—8 = 0, или (| х |—4) (| х | + 2) = 0. Учитывая, что | х |+2 0, полу-
чаем |х| = 4, откуда находим xi = — 4; х2 = 4. В область определения функ-
ции У 5—2х входит лишь xf=—4.
16. {—2; —1/9}. 17. {1}. 18. {—5/3}. Указание. При решении урав-
нения учтите, что ха=|х|2.
19. {—2; 1}. Решение. 1) Если х2+4х+2^0, то уравнение равно-
сильно системе
( х2+4х+2^0,
( Зх2+7х—10=0,
решая которую, находим х=1.
2) Если х2+4х+2 < 0, то уравнение равносильно системе
( х2+ 4х+ 2 < О,
( Зх2+17х+22=0,
решая которую, находим х2=—2.
Графическое решение состоит в том, что построив графики функций
у=|х2+4х+2| и у=^Хнайдем координаты х$ и х2 точек пересечения
о
этих графиков, которые и будут корнями заданного уравнения.
20- {1; 4}. 21. {2; 5}. 22. {3; 6}. 23. {0; 1}. Решение. Рассмотрим два
случая: 1) х^1, 2) х < 1.
1-й случай. При х^ 1 уравнение равносильно системе
f х^ 1,
( х2+х—2 = 0,
решая которую, находим xj = l.
2-й случай. При х < 1 уравнение равносильно системе
f х < 1,
( х2—х = О,
решая которую, находим х2 = 0.
9*
259
24. {—20,5; 10}. Указание. При упрощении уравнения учтите, что
коэффициенты при х в квадратных трехчленах образуют арифметическую
прогрессию с разностью, равной 1, а свободные члены—арифметическую про-
грессию с разностью, равной 2.
25. {2+/4^а}, если а<— 4; {2—/<+а; 2+ ]/~4+а; 2+/4^а},
если — 4<а < 0; {0; 4}, если а=0; {2— /4+а}, если а > 0. 26. а=20 ± б)/"5.
27. k1 = — 22/3; 62 = 2. 28. а = 4. 29. При всех /ng] 1/4; +00 [• 30. При
всех /ng]— оо; — 1/2[ U ]1 /2; +оо[. 31. При всех /ng]— оо; —1/7 [ (J ]1; -f-оо[.
32. При всех eg ]2; 4[. 33. k= 13. 34. « = ± 2.J 35. а = ± 10. 36. k = ±4.
37. 28х2—20x4-1=0. Решение. Запишем искомое уравнение в виде
х2+/«+<7=0. (1)
Его корни
1 104-/72 54-3
*1—10—/72 ~ 28 14
_ 1 10—6><~2 5—3/2 ,
** 10+6/2 ~ 28 14 ’
... 5 5+3/~2 5-3/2 1
/, = -(xi+x2)=-T; <7 = —------------1Т-=28*
Подставляя полученные значения р и q в уравнение (1), находим искомое
уравнение.
38. ]— 3; 5[. 39. [0; 1/2[. 40. 6 = 3. 41. 6 = 3. 42. «1 = —2; «2=1.
43. При всех ng] — оо; —2] (J [0; +°°[-
44. При всех a g ]—6; 3[. Указание. Нужно найти значения «, при
которых уравнение (а—6)х2—2 = 2«х4-1 не имеет действительных корней.
45. {—4; — 3; 3; 4}.
46. а=—4. Решение. По условию задачи корни Xf и х2 уравнения
связаны равенством x2 = 2xi. Применяя теорему Виета для определения Xf,
получаем систему уравнений
J Xi 4- 2xi== 1 ~~~ 2п$
( 2х1 = о2+2,
из которой для определения а получаем уравнение а24-8а4-16=0. Отсюда
« =—4.
47. af= —3/2; «2 = 6. 48. «1 = 2; «2 = 9/2. 49. {2; 18} при «=6;
{2/19; 18/19} при « = —6/19. 50. «f = — 125/8; «2 = 27/8. 51. р=± 7.52.6 =
= ±3}Г5. 53. «1 = 3/2; «2 = 3. 54. 6 = - 13.
55. р=0. Решение. Пусть х$ и х2—корни данного уравнения. По
условию задачи и теореме Виета
( х?+х!=1б,
I *1+*2 = 4.
Возводя в квадрат второе уравнение системы и учитывая первое уравнение
системы, получим Xix2 = 0 и p=xix2 = 0.
56. « = 2. Решение. Пусть Xf и х2—корни данного уравнения. Приме-
няя теорему Виета для определения х± и х2, получим систему уравнений
{Xi—х2 — (а—1)/2,
х14-х2 = (<?4-1)/2,
260
откуда Xi==a/2, х2 = 1/2. Подставив в уравнение любой из полученных корней,
получим значение а.
57. «1=1/2; а2~ 1. 58. рх = 0, <7i = 0; p2=L <72 = —2.
59. а — — 2. Решение. Первое уравнение имеет действительные корни,
если а2 — 4^0, т. е. если а£]—ос; —2[ (J [2; —|—©о[. Второе уравнение
имеет действительные корни, если 1 — 4а0, т. е. еслиа£] — со; 1/4]. Таким
образом, данные уравнения могут иметь общий корень, если а£] — со; —2].
Пусть х0— общий корень. Тогда будут верными числовые равенства
Xq + CLXq 1 — 0 и xo-f-Хо —0. (1)
Вычитая из первого равенства второе, получаем (а — 1) х0-|-(1—а) = 0, или
ло = (а—1)/(а—1) = 1 (в области [ — со; —2] деление на а—1 правомерно).
Подставив х0 в любое из равенств (1), находим а = — 2.
60. т = — 2. Решение. Найдем корни первого уравнения х^ =
1 — Vе 1 —4m l + K 1—4m
=------, x2=— л-----------------, а также корни второго уравнения
х3=------, х4 = - гg------------------• Корни будут действительными при
условии 1/12. Если 0 < 1/12, то ]/* 1 — 12m < У 1 —4m < 1, и, сле-
довательно, все четыре корня положительны, причем (т 0) 0 < хг < х'3 <
< х4 < х2. Отсюда видно, что х3 2х2 и х4 Ф 2х2. Надо исследовать две
оставшиеся возможности: a) x3 = 2xj или б) x4 = 2xi, т. е.
± —— — 1 — У1—4m=> 1 ± y'l — 12т = 2—2V1—4т=»
=$>2У 1—4т=1 Т /Ч —12т=ф
=Ф4(1—4т) = 1 Т 2/1 —12т+1 — 12т => 1—2т=Т V1 —12т.
В левой части равенства стоит 1—2m > 0, следовательно, и в правой части
должно стоять положительное число, т. е. + У1 — 12m, т. е. возможность
б) отпадает: х4 # 2хх. Возведем правую и левую часть равенства 1 — 2m =
= У1— 12m в квадрат; тогда получим после преобразований m24-2m = 0,
откуда т~—2, так как т Ф 0, но мы рассматриваем случай 0 < m < 1/12,
т. е. пришли к противоречию и в случае а), т. е. х3 Ф 2хх.
Рассмотрим случай m < 0; тогда 1 < У1—4m < У1 — 12m и, следова-
тельно, хх < 0, х3 < 0, х4 >0, х2 > 0, причем х3 < хх < 0 < х2 < х4. Отсюда
видно, что х3 Ф 2х2 и х4 # 2хх. Надо исследовать две оставшиеся возможности
а) х4 = 2х2 и б) х3 = 2хх. Тогда
! 12т = 1 ± V1—4m =ф 1 ± V1 —12т = 2 ± 2^1—4т =ф
=ф ± /1 —12т=1 ± 2V1—4т. (1)
В случае верхних знаков (это случай а)) возводим правую и левую части
в квадрат: 1 — 12т= 1+41^1—4т+4 (1—4т) => т—1 = ]Л1—4т. Здесь
слева т—1 < 0, а справа У1 — 4т > 0; пришли к противоречию. Следова-
тельно, х4 Ф 2х2. В случае нижних знаков в (1) (это случай б)) производим
261
преобразование
2 К Г—4m = 1 + К1 —12m =Ф
-£4(1—4/72) = 14-2)/' 1 —12m-f-l —J2m=*>
=> 1 —2m = — 12m => 1 —4m4~4m2= 1 — 12m =ф m2 = —2m
и так как m О, то отсюда следует m = —2. Следовательно, х3 = 2х£ при
m = — 2.
61. с < 0. Решение. Трехчлен f (x) — ax2-\-bx-\-c не имеет действитель-
ных корней, следовательно, f (к) при любых x£R имеет один и тот же знак,
но f (1) = а4"^+с < 0; следовательно, 0>/(0) = с.
62. xl+xt=3pq—р3. 63. ^+4 = а(а2—18а+9)/27. 64. 215/27.
„ 1 , 1 27а34-36а _ „ D
65. —^4—5-=-----х----. Решение, На основании теоремы Виета
х? х! 8
имеем x14-x2=3a/2^ xix2=—1; тогда
(Х14-*2)3 = 27а3/8=Ф Х14“*24-3*1*2 (*1+*г) = 27а3/8=Ф
, 3 , 3 27а3 о/ 1Y За 8 . з 27а34-36а
=Ф*14-*3 = ~§-----3 (— 1) • у =фХ!4-*2 =--.
„ 1.1 4+4 27а34-36а
Вычислим —тт-4——т~ё- =------------ё-------
*1 *2 4 4 8
66. При всех а£]2; 17/4[. 67. При всех р£[3; 15/4]. 68. При всех
а£]— оо; —6{. 69. При всех а£]6; 4~°°1- 70. При всех а£]5/3; + «>[.
71. k = b.
72. ] —оо; —(а+l^a2—-4а)/2[ (J ] (Vа2—4а—а)/2; 4-оо[ при всех
а£] — °о; О] (J [4; 4-а>[: ] — 00; +«| при всех а£]0; 4(.
73. При всех т£ ]1; + <ю[. 74. При всех а£ J11/9; +°°[- 75. х2 — (а24~1) *+
4-4 = 0. 76. 4х2—8х—4а2—11=0. 77. При всех а£[1/2; 4~°о[. 78. При
всех а£]0; 1[ (J |1; 6/5[. 79. При всех а£] —1/2; 0[ 1J ]0; 5/5f.
80. При всех а£] 0; 1/3 [. Решение. Рассмотрим два возможных
случая: 1) За а4-3; 2) За > а + 3.
1) За а4~3 а 3/2. В этом случае заданное неравенство выполняется
на интервале ]3а; а4-3[. Чтобы оно выполнялось ври всех х£[1; 3J, необ-
ходимо и достаточно, чтобы имела непустое множество решений система не-
равенств
( За < 1, ( а < 1/3,
{а+3>3, ^{а>0 ^°<а<’/3-
Так как при этом а< 3/2, то при всех а£]0; 1/3[ задача имеет решение.
2) За > а4~3 =Ф а > 3/2. В этом случае заданное неравенство выполняется»
на интервале ]а4-3; За[. Чтобы оно выполнялось при всех х£[1; 3J, необхо-
димо и достаточно, чтобы имела непустое множество решений система нера-
венств
f а4-3 < 1, ( а < — 2,
( За > 3, ** ( а > 1.
Мы пришли к противоречивой системе, поэтому в данном случае задача не
имеет решений.
81. &g] — оо; 0] U {!}• Решение. Перепишем неравенства в виде
(х—3k)2 > 4 (k — I)2 и (х—2k)2^k. Из второго неравенства видим, что при
^€1 — °°; 0] оно выполняется для любого действительного х. Остается иссле-
262
довать случай, когда ££]0; 4-оо{. Из первого неравенства получаем
3£—2| £—11 [ (J J3AJ-4-2 | ^—11; 4-оо[.
Из второго неравенства получаем
xg] — со; 2k— y~k] и [2Й+/1; +«1.
Если найдутся такие значения k > 0, что выполняется или неравенство
3^4-2 |£—1 [<26-/1, (1)
или неравенство
2fe+]/“A<3£—2|fe—1|, (2)
то для этих значений k любое действительное х будет являться решением
хотя бы одного из данных неравенств. Неравенство (1) можно переписать
так: &+ / k-\-21 k— 1 |<0, где k > О, j/- Лг > 0, | k— 1 | О, следовательно,
неравенство (1) противоречиво. Перепишем неравенство (2) в виде
2|й—11. (3)
Рассмотрим два случая: 6g[l; 4~°°1 и 6£]0; Ц. В первом случае неравен*
ство (3) перепишется так: Y k <2—k, и, следовательно, если оно выпол-
няется, то только для некоторых из &£[1; 2{. Для этих 6, возведя в квадрат
правую и левую части, получим после преобразований неравенство k2—564"
+ 4^0. Это неравенство справедливо только для — оо; 1]Щ4; + оо[.
Из всех этих значений условию 2[ удовлетворяет лишь одно значение
6=1. Рассмотрим теперь случай £00; 1[. В этом случае неравенство (3)
перепишем так y~k^3k—2, и, следовательно, если оно и выполняется, то
только для некоторых из 6£]2/3; Ц. Для этих k, возводя в квадрат правую
и левую части, получим после преобразований неравенство 962—1364-4^0.
Это неравенство справедливо только для 6g]—оо; 4/9](J[l; + 00 [• Так как
4/9 < 2/3, то ни одно из этих значений k не удовлетворяет условию
6g] 2/3; 1 [. Объединяя все полученные результаты, находим, что задача
имеет решение лишь при 6 g]—оо; 0](]{!}•
82. ag] —1/4; 1 [. Решение. Находим корни уравнения
х2—2х —а24-1=0; (1)
это будут Xf=l — | а Ь х2= 144 а 1> Находим корни уравнения
х2—2(а+1)х + а(а—1) = 0; (2)
это будут х3=а4-1— 4-За, jq«sa4-l + /14-За, Корни уравне-
ния (2) будут действительными при условии, что —1/3^ а. Требуется найти
такое а, чтобы выполнялись неравенства
а+1 — VX+&K 1—| а К 14-] aj < а4-14- /Т+За. (3)
Рассмотрим случай a < 0; тогда неравенства (3) примут вид а4“1— V 14~За <
< 14~а«С 1—а < а4-14~ V14-За. В этом случае надо удовлетворить лишь
неравенству 1—а < a 4-14- V 14“3а, или —2а < К 14~3а, где —2a > 0; воз-
водя в квадрат правую и левую части неравенства, получим после преобра-
зований неравенство 4a2—За—1 < 0, которое выполняется для ag] —1/4; Ц.
Так как у нас a < 0, то поставленная задача имеет решение для ag]—1/4; 0 [.
Пусть теперь а 0; тогда неравенство (3) можно переписать так: a4-1 —
— /14-За < 1—а< 14-а < а+14-/14-За. В этом случае надо удовлетво-
263
рить лишь неравенству <7 4-1— У 1 —[—За < 1 — а, или 2а< У1 4“3я, где 2а ^>0;
возводя в квадрат правую и левую части неравенства, получим после преобра-
зований неравенство 4я2 — За—1 < 0, которое выполняется для ag] — 1/4; 1 [.
Так как в рассматриваемом случае а^О, то поставленная задача имеет реше-
ние для а00; 1 (. Итак, корни первого уравнения лежат между корнями
второго уравнения, если «€1 — 1/4; 1[.
83. 0. 84. [1; 4/3]. 85. 0. 86. ] —2/3; 3[. 87. ] — оо; 4-оо[.
88. ] —оо; —1 [(J 1 15; 4-оо [. 89. [—2; 1].
90. ] —3; —2 [ U ] 2; 3 [. Решение. Заданное неравенство равносильно
неравенству (| х | — 2) (] х | — 3) <0, откуда 2 < | х | < 3. При х > 0 получаем
2 < х < 3, а при х < 0 получаехм 2 < —х < 3, или —3 < х < —2.
91. ] —оо; —2]U[2; 4-оо [. Решение. Заданное неравенство равносиль-
но неравенству (| х |4~ 1) (| х | — 2)^0, которое равносильно неравенству | х | ^2
(так как |х|4-1 >0 при всех х£/?). Раскрывая модуль, при х^О получаем
х>2, а при х < 0 получаем —х^2, или х«С—2.
92. ] —1; 5 [. Указание. Неравенство | х2—2х | < 5 равносильно двой-
ному неравенству —5 < х2—4х < 5, равносильному системе неравенств
( х2—4х—5 < О,
I х2—4x4-5 > О,
решая которую, получим —1 < х < 5.
93. ] — (1+У21)/2; —1)/2[. 94. ] —1; 2 [U] 3; 6[.
95. ]1; 3[. Указание. Заданное неравенство равносильно системе не-
равенств
( х > О,
( — х < х2 — 2х < х.
96. ]2; 5[. 97. ]1— 2— У~2[.
98. ] 2; 4 [. Решение. Следует рассмотреть два случая: 1) х^4; 2) х < 4.
1) При х^4 заданное неравенство равносильно системе неравенств
( х^4,
1 (х—4)2 < О,
которая имеет пустое множество решений.
2) При х < 4 заданное неравенство равносильно системе неравенств
( х < 4,
( х2—6x4-8 < О,
решая которую, получаем 2 < х < 4.
99. ]—5; 3+2 V 2[. 100. ] 1; 3 [. 101. ] —оо; 1 [U13; +оо [.
102.
103.
104.
105.
106.
107.
- оо; (4 - V 2)/2] и [(5+ V 3)/2; + оо [.
-оо; (4—K19)/3[U](4+V19)/3; +оо[.
— оо; —5—VT9[U]/"2—2; +оо[.
-оо; (5-l<5h/2[U](5+><57)/2; +оо[.
-оо; -1 [U1 2; +оо [.]
1; 3 [. Указание. Заданное неравенство равносильно неравенству
| х—6| > х2—-5x4-9, так как х2—5x4-9 > 0 при всех x£R.
108. ]—7; —2[U] 3; 4 [. Указание. Рассмотрите три случая: 1) х^—2;
2) —2 < х < 1; 3) х^1.
264
109. ]—оо; 2 1^2 (U] 2+2'/'З; + оо [. Реш е н и е. При х«^0 неравен-
ство выполняется, что очевидно. Так как х2—2х—8 = (х—4) (х+2), то при
х > 0 следует рассмотреть два случая: 1) 0 < х < 4; 2) х^4.
1) При 0 < х < 4 заданное неравенство равносильно системе неравенств
( 0 < х < 4,
( х2—8 < 0,
решая которую, получаем 0 < х < 2 ]/" 2.
2) При х-^4 заданное неравенство равносильно системе неравенств
( х^4,
( х2—4х—8 > 0,
решая которую, получаем х > 2+2 V* 3. Объединяя полученные решения,
находим приведенное выше выражение.
110. k =15. 111. ]— /2; l[u [К2; 4- ОО [. 112. at=l — У~2, а2=5-[-
+ КТО. 113. а < 0.
§ 5
1. {Кз—2; КЗ —1; КзЧ-1; Кз+2}. 2. {-3, 3}.
4. {(5—К2Г)/2; (5+К21)/2}. Указание. Представьте уравнение
в виде (х2—5х + 4) (х2 — 5х+6)~ 15 и положите х2—5х+4=у.
5. {(_ 5а ± Кба2 ± 4 Va*+^)l2}, если | а | Ss 21Ь |/КЗ;
{(—5а±Кба2+4 К«4+&4)/2}, если |а| < 2]6|/Кз. Указание. Пред-
ставьте уравнение в виде (х2+5ах+4а2) (х2+5ах+6а2) = 64 и положите
х2 + 5ах+4а2 = #. 6. 0. 7. {—1; 1/2}. 8. {1/2}. 9. {2}.
Ю. х±—а, х2 =—1 при всех а£]— оо; —1 [; xi = a, х3 =—2а2 при всех
а£]—1/2; 0[. Решение. Решая данное уравнение, найдем три значения
Xi = a, х2 =—1, х3 = —2а2, которые обращают в нуль или первый, или второй
множитель данного уравнения. Заметим, что при а^О х2—хх < 0,х3—х± < О,
т. е. х2—а < 0, х3—а < 0, т. е. если при а^О в уравнения вместо х под-
ставить х2 или х3, то множитель —а не имеет смысла. Следовательно,
при а^О данное уравнение имеет лишь один корень xf = a. Будем считать
a < 0. При а — —1 имеем х/=х2 > х3, т. е. х8—xf=x3—а < 0; итак, х3 — —2a2
не является корнем уравнения при а — —1; уравнение имеет два совпавших
корня xf = x2, что не удовлетворяет условию задачи. При а =—2а2, т. е. при
а ——1/2, х2—а ——1 + 1/2 =—1/2 < 0, т. е. х2 =—1 не является корнем
уравнения; уравнение имеет два совпадающих корня xf = x3, что не удовлет-
воряет условию задачи. Рассмотрим теперь три случая 1) ag] — оо; —1 (,
2) ag] — 1; —1/2 [, 3) a£J—1/2, 0 [. В случае 1) имеем —2a2 < а < —1, т. е.
х3 < Х1 < х2- Следовательно, х3—хх = х3—а < 0 и х3 не является корнем
уравнения, а х2—xj = x2—а > 0 и, следовательно, х2 является корнем урав-
нения, т. е. при а£] — оо, —1[ уравнение имеет только два различных
корня Xi и х2. В случае 2) имеем—1<а и а<—1/2, т. е. а2> —а/2
или —2а2 < а. Следовательно, в этом случае х2—хг = х2—а < 0 и х3—хх =
= х3—а < 0, т. е. ни х2, ни х3 не являются корнями данного уравнения;
уравнение имеет при а£]—1; —1/2[ только один корень Xf = a. В случае 3)
имеем а > —1/2, следовательно, —2a2 > а > —1, т. е. х2 < xi < х3; в этом
случае х3—Xi = x3—а > 0, а х2—xi = x2—а < 0. Таким образом, х3 является
265
корнем уравнения, а х2 не является. Уравнение при а^} —1/2, 0[ имеет два
различных действительных корня х± — а и х3 = — 2а2. Итак, данное уравне-
ние имеет только два различных действительных корня х^-а и л2 = —1 при
ag]— оо; —1 [ и два действительных различных корня х^=^а и х3 = — 2а2
при ag] —1/2; 0 [.
11. {3; 4; 5; 6; 7; 10}.
12. а) Уравнение не имеет решений при ag] — оо; —HUJ5/4; 4-оо [;
б) уравнение имеет одно решение при а = — 1; в) уравнение имеет два реше-
ния при ag]—1; 1[|J {5/4}; г) уравнение имеет три решения при а=1.
Решение. Корни данного уравнения имеют вид
а) Из рассмотрения выражения (1) видно, что уравнение не имеет ни
одного корня, если 5/4 < а, т. е. ag]5/4; +оо [, или а«с5/4, но а—-у +
.1/5 ~ -,/5 1
+ у ——а < О, т. е. I/ — — а<—— а; это неравенство может выпол-
няться только при а < 1/2; возводя в квадрат правую и левую части нера-
венства, получим (после преобразования) a2 > 1, или |а| > 1; учитывая, что
а < 1/2, получаем отсюда a <—1, т. е. ag]—оо; —1[. Итак, уравнение не
имеет ни одного решения, если ag]—оо; —HU15/4; +<»[« б) Уравнение
имеет только одно решение х = 0, если а—
— а=0, т. е.
5 1
——а=— — а. Это равенство возможно лишь при условии, что a <1/2.
Возводя в этом равенстве правую и левую части в квадрат, получим после
преобразований а2=1, т. е.
Итак, при a=—1 уравнение
жении (1)
а=—1 (а=1 > 1/2, а должно быть а < 1/2).
имеет только одно решение, в) Если в выра-
и а—у — J/ —a < 0, или а=5/4, (2)
то уравнение имеет только
два решения. Преобразуем неравенство (2)
,/~5 г>
у ——а. Второе из этих неравенств выпол-
няется для всех а «С 1/2 и для а > 1/2, для которых a2 < 1, т. е. 1/2 < а < 1,
т. е. второе неравенство из (2) выполняется для всех ag]—оо; 1 [. Первое нера-
венство из (2) выполняется для всех 5/4 а 1/2 и для а < 1/2, для кото-
рых a2 < 1, или —1 < а < 1/2, т. е. первое неравенство из (2) выполняется
для всех ag]—1; 5/4 [. Таким образом, уравнение имеет два решения, если
одновременно выполняются оба неравенства из (2), т. е. при всех ag]—1; 1 [,
или a=5/4. г) Уравнение имеет три решения, если выполняются условия
I . 1/5
а-—4-|/ ——а>0
а=0.
(3)
И
Первое из этих условий выполняется для всех а£]—1; 5/4 [ (см. п. в)). Вто-
1 5
рое условие эквивалентно равенству а—— = у ——а, т. е. а^ 1/2. Воз-
266
водя в квадрат правую и левую части этого равенства, получим после преобра-
зований а2=1, т. е. | а | = 1; так как а > 1/2, то получаем о=1; это значе-
ние удовлетворяет и первому из условий (3). Следовательно, уравнение имеет
только три решения при а==1. д) Если agjl; 5/4(, то уравнение имеет четыре
решения.
13. При всех «С]0; 1[U]1; 5— /15 [(J]5+ /15; +<»[.
14. x = b/2. Решение существует и единственно при b Ф 0.
15. а^]—1/2; 3[. Решение. -—? <002 ?ф7- < 0 02 <
х —я4~2 х+2—а
< -5±.7-
х 4-2—а
Последнее неравенство должно выполняться при всех 1^х^2;
при этих значениях х числитель x-f-7 < О, следовательно, для выполнения
неравенства
х+7
х4~2—а
(I)
знаменатель х-{-2—а должен быть положителен, т. е. x-f-2—а > 0, или
а < x-f-2 для всех 1«^х<:2, следовательно, а < 3. Неравенство (1) перепи-
шем так (учитывая, что 1«Сх^2)
*4-2—а
х+7
Оу > 1
с 4-5 «4-5 £
*4-7 ” х + 7 2
Оа+5 > >— у-
Итак, неравенство (1), а значит, и заданное в условии задачи, будет выпол-
нено для всех «€1—1/2; 3[.
16. х = —6. 17. х = 2. 18. х = —4. 19. х=1. 20. х=2. 21. х=2.
22. х = —2. 23. {11; 12; 14; 15}. 24. б) Все «€(11/4; +»|. а) Следует из б).
25. лг€]-7; 1[.
26. &€[(74-3 1^5)72; 4~°°[- Решение. Запишем неравенство в виде
х2—kxA-l^—66
&(6+х)
(1)
Дискриминант квадратного трехчлена
х2—Ь'4-F—6£
(2)
равен 3k (8—&). Он отрицателен при k <0 и k > 8. При этих значениях k
числитель дроби (1) положителен, поэтому множество решений неравенства (1)
при k < 0 будет ] — оо; —6[, а при k > 8 будет ]— 6; 4-00!» Следовательно,
все k > 8 удовлетворяют условию задачи, а все k < 0 условию задачи не удов-
летворяют.
При k — О неравенство (1) не определено.
При k = 8 неравенство (1) имеет вид
< х < 1.
f(x-4)2
8(6+х)
^Ои выполняется при все»
2 <
2
—1
Рассмотрим 0 < k < 8. В этом случае квадратный трехчлен (2) имеет два
k — V3k(8—k) k 4- V3k(8—k)
корня Xj =-------x2 = —5---------------причем xf < x2 при всех
О < k < 8. В самом деле, неравенство > —6 при 0 < k < 8 равносильно
неравенству &4“12 > )/*3&(8—k)t которое равносильно неравенству fc24~24fe +
267
4- 144 > 24£—3&2, или 4£2-f-144 > 0. Так как х2 > 0 при всех 0 < k < 8, то
при данных значениях k задача имеет решение лишь при т. е. если
k 1, или k—2^УЗА?(8—&), которое может выполняться
лишь при 2 < k^8 и при всех 2 < k < 8 равносильно неравенству (k—2)2^
^>ЗА(8 — А?). Решая систему неравенств
J 2 < k < 8,
1 (A?—2)2^ЗА?(8—k)t
получаем множество решений [(7+3 УЗ)/2; 8[. Объединяя полученные ре-
зультаты, находим ££[(7-{-3 /б)/2;
27. }1; 2[Щ2; 3[. 28. J-1/4; 5/6[. 29. ]-оо; 3/2[U]7/3; -(-oof.
30. J— оо; + оо[. 31. 12; 3[. 32. ]-3; 1[. 33. ]— оо; — 2[(JJ—2; —HUP; + »[.
34. }- оо; —2 [U]-2; -1/2 [UJ1; +<»[• 35. ]-2; -1[UP; 2[. 36. [-3; 3].
37. ]- оо; 2(UJ6; -f-oof. 38.]—оо; 1 [U]3/2; +оо[. 39. ]— оо; 5/2[ U [33/8; + оо[.
40. ]-6; 3[. 41. ]— со; 0[U]4; +оо[. 42. ]—7; —3[. 43. ]—17/25; —3/8f.
44. ]_ оо; —5[(JJ5; -f-oo[. 45. ]— оо; 1[U]4; +оо. 46. ]—3; 1[.47. ]— оо; 0[U
U]3; +оо[. 48. ]—оо; 3[(J]4; 4-оо[. 49. ]—оо;-(-оо[. 50. ]—1; 5[. 51. ]5/2; 8[.
52. ]2; 3[. 53. ]—оо;—l(UJ5;4-oo[. 54.Ц— ос; — l[UP/3; -f-oo[. 55. ]—1/2;2[.
56. ]—оо; —20(UJ23; 4-оо[. 57. ]—2; 4-оо[. 58. ]—1; 0[U]4; -f-oof.
59. 1-5; -2[Ul-2/3; +оо[. 60. ]—оо; (2— /22)/3[U] (2+1<22)/3; 5/2[-
61. J-17/2; —3[UP; +<»[. 62. ]-оо;-3[U]3; 4-оо[. 63. [1; 3](J]5; + оо[.
64. ]-оо; —l/|/l[U]0; +«>[. 65. 1—оо; 6[Щ—2; 0[(J [3; 4-оо[.
66. ]2; 3[UJ5; 6[. 67. ]1; 7[. 68. ]—6; 3[. 69. ]—5; 1[U{3}. 70. ]—1; -|-ool.
71. ]-9/2;-2[U]3; Н-оо[._72. ]-1; HUJ4; 6[.
73. ]-(1 + 1<21)/ 2; (Г2Т- 0/2 [. 74. ]1/2; 3[. 75. ]— оо; - 1(U]4; -(-oof.
76. J—оо; -5/21U1-2; 8[. 77. J3/4; HUJ7; + «>[. 78. J-l; 0[UJO; If.
79. J—5; 1[. 80. ]—оо; — 4[U1~3; 3[(J]6; 4-оо[.
81. ]_oo;-]<7[U]-2; Vjl U [8/3; +оо[.
82. ]-оо;-3[UJ-/7/2; J^7/2[U]4; +оо[. 83. [£; 2[(J]3; 4].
84. ]-/2; - 1[U]-1; /2 {U [3; 4[. 85. ] —’оо; -/ 7/2 [UJ—Н /^/2 [ U
UJ4/3; +оо[. 86. ]—(ll + K737)/28; 4/7[U](/737—11)/28; 1[.
87. -/iO[U]-l/2;2/5[U] /10; -}-оо[. 88. J— оо; -2[Ш-1; 4f.
89. ]—оо; —HUP; +<»[• 90. ]—оо; —2[U]-1; 0[UP/2; -f-oo[.
91. J—оо; 0[U]l; 2[U]3; +оо[. 92. J-oo; -5[UP; 2[U]6; -f-oof.
93. ]—оо; —l[U]0; 1/2(U]1; +«>[. 94. ]—oo; 0[UP; 6[.
95. JI; 2[U]7; 4-oo[l 96. ]-оо; -3[UJ—2; 3[.
97. ]-/2; 0[UP; /2[U]2; +«[. 98. ]-5; 1[U]2;3[.
99. J—оо; —2[U1—1; 3[U]4; +<»[• «». ]—оо; —7[U]—4; -2[.
101. )—oo; -3[U1-2; -H- 102. J-oo;-4]U[-2; -IJUlh +«>{.
103. 1-2; — HU]2, 3|. 104. ]—oo; - 1JU]O; 1JUJ2; 3].
105. [-4; - 3[Ut—3/2; 0[U[l; +oo(. 106. J-oo;— | a | [U 1 |a
если а Ф 0; ]—oo; 0[U]0; 1[U1U +°°[, если я = 0.
107. ]— oo;7—1JU[0; +oo[. 108. ]2; 3[. 109. J—7; —4[U]—4; Ц. 110. J2; +oo|.
111. ] 2; 4 [ (J ] 4; 6 [. Указание. Заданное неравенство равносильно
системе неравенств |х—4 | < 2, х Ф 4.
268
112. ] 3/4; 1 [U]l;+°°[- Указание. Данное неравенство равно-
2х__________________________________1 2х— 1
сильно совокупности двух неравенств --"-у > 2 и <—2.
113. ]— оо; —2 [ U ] — 1; +°о [. Указание. Так как х2Ц-х4~1 > О
при всех х £ R, то заданное неравенство равносильно | х2—Зх—1|<
< 3 (х24~х+1), или —3 (х24-х+1) < х2—Зх— 1 < 3 (х24-х-|-1), или
( —3 (х2+*+1) < х2—Зх—1,
1 X2—Зх—1 < 3(х24-х+1).
114. ] —5; —2[ U ] 2; 3 [ U ]3; 5[. 115. ] — 5; —2 [ (J ] —U 4" <*> I.
116. ] —оо; —2[ U ] —1/2; +оо[.
117. ] — оо; 0[ (J ] 1; +<ю [. Указание. Неравенство можно записать
в виде | х-{-2 |/х <3. 118. ]— оо; —5 [ (J ]—3; 3 [ (J ] 5; +00 [ •
119. ] — оо; —4] U [—1; 1] U [4; +оо[. Указание. Данное нера-
Зх
венство равносильно двойному неравенству ——4 11/111 системе
120. [0; 8/5] U [5/2; 4-оо[.
121. [3/2; 2[. Указание. Так как х2—5х-)-6 = (х—2) (х—3), то при
х > 3 данное неравенство равносильно неравенству 1/(х—2)^2, а при х < 3
равносильно неравенству 1/(2—х)^2.
122. ] — оо; 3 [. 123. ] — К— я; 0 [ при а < 0; ] 0; Y & [ при а > 0;
0 при я = 0. 124. ]3; 4[. 125. [-3, 0 [ U [ 20; 4~ со [.
126. ]-оо; —3[ U J—2; 4-оо [. 127. ] —со; —1 [ U 1 1; 3].
128. ] — оо; —1 ] (J J 5; 6]. 129. ] — со; —3 [ (J [ 1; 4 [.
130. ] —00; —1, 4] и ] 2; 2,6]. 131. [1; 6]. 132. [2; 3]. 133. [—1; 7/3].
134. ] —2; —1 [ U 12’ +°°Ь _
135. ] —2; (3- V 17)/2 ] U ] 0; 2[ U [ (3+ 17>/2; + « [.
§ в
1.{1/2; 1}; 2. (-1; 2}. 3. {—3; 2}. 4. {-4; 3}. 5. {6}. 6. {—27/8; 1}.
7. {-8; 27). 8. {8; 27}. 9. {3}. 10. {!}. И. {3}- ,2- {9>- 13- {—h 81-
14. {2}. Решение. Положив logax = l, получаем уравнение I3-}-!2—
— 2 = 0, или Р—1+/2—1=0, или (1—1)(/2+<+1)+(/ —1)(/4-1)=0, или
(/ —1) (Z2+2/+2)=0, откуда 1=1, т. е. iogax=l,x=2.
15. {—1}. 16. {—3/2; 1/2}. Указание. Положите V(3—х)/(2+*) = 1.
17. {5/2}. 18. {5/3}. 19. {3}. 20. {3}. 21. {8}. 22. {28}. 23. {0}. 24. {4}. 25. {19}.
26. {3}. 27. {6}. 28. {—1}. 29. {3}. 30. {2}. 31. {1}. 32. {5}. 33. {0; 4/3}.
( 9 12 I
34. {34-±'_2Д . 35. л}. 36. {4}. 37. {2}. 38. {5}. 39. <!arctg-=-+лл|п £ Z >.
[ О J io I
40. {2}. У к а за н и е. Положите х2—4х-}-6==£.
41. {—9/2; 3}. Указание. Положите Y2х2—4х+9=у. 42^ {—4; 2}.
Указание. Положите рЛ2х2—4х +12 = г/. 43. {1—р^З; 1 + Р^З }.
44. {—5; 0}. 45. {2}. 46. {2/3}. 47. {-3}. 48. {—1; 9/16}. 49. {2}. 50. {5}.
269
51. {—1; 15}. 52. {4}. 53. {20}. 54. {10}. 55. {6}. 56.{—1; 3}. 57. {—5; 4}.
58. {—1}. Решение. Заметим, что
V Зл24-6х+7 = КЗ(х+1)24-4 Ss УТ = 2,
V5х2+ 10х+14 = У%(х+ l)2+9Ss У9 =3, 4—2х—х2=5—(х+1)2<5.
Следовательно, левая часть уравнения 5 при любых х £ /?, а правая часть
уравнения «С 5 при любых х £ R. Равенство между ними возможно лишь при
условии, что обе части уравнения равны 5 при одном и том же значении х,
У нас правая и левая части уравнения равны 5 при х = — 1.
59. {3}. 60. {—1, 2}. 61. {2; 34}. 62. ;{—!}. 63. {5}. 64. {8+4 VI}.
65. {—1}. 66. {4}. 67. {1}. 68. {5}.
69. {—15; 13}. Решение, У12—х+у^ 14+х=2=Ф]/12—х=
= 2—У 14+х=> 12—х=8—12 У 14+х+6 У(14+х)2—14—х=»
=$>б(У 14+х)2 —12 14+х—18=0=$>(у^ 14+х)2—2 У 14+х—3=0=>
=3> У 14+х= 1 ± У 1+3= 1 ± 2 => У 14+х =—1 или У 14+х=3; если
У 14+х =—1, то 14+х=—1 и х ——15; если У 14+х=3, то 14+х=27
и х= 13.
70. {(3—У73)/4; 0; 3/2; (3+/73)/4 }. Указание. Положите
/2х2—Зх+1 = «/. 71. {1/4}. 72. {0; 16/9}. 73. {0; 5}. 74. {7}. 75. {16/25}.
76. {4}. 77. {—1}. 78. {2}. 79. {4}. 80. {12/5; 4}. 81. {4}. 82. {—1}. 83. {0}.
84. {4}. 85. {2}. 86. {1}. 87. {8}. 88. {22/9; 6}. 89. {12/127}. 90. {12}. 91. {3; 5}.
92. {0; —1}. Указание. Положите х24-х4-4 = г/. 93. {1}. Указание.
Найдите область определения уравнения. 94. {—47/24}. 95. {73/32}.
96. {[—1; 1]}. Указание. Запишите уравнение в виде /(х— I)2 -[-
+ У+Ж=2. или ]х—1 | + [х+1 ( = 2, затем рассмотрите три случая:
1) х < —1; 2) — 1 «Сх^ I; 3) х > 1. Убедитесь в том* что при —1 <х< 1
уравнение выполняется тождественно.
97. {[2; +оо [}. 98. {[2; 4»оо [}. 99. {[5; 10]}.
100. {(— 1—/5~)/2; (/б"—1)/2; 1}. Р е ш е н и е. Положим1 —у\
тогда 2х— 1=^ #34-1 = 2х. Получаем систему уравнений
( х34-1 = 2//,
} ^4-1 = 2х,
откуда следует х3 —г/3 = 2 (у—х), или (х—^}(х24-х^4-^2>4-2(х—^) = 0.
Отсюда получаем 1) х—у=0; 2) х24-х#4"!/2=—2. Последнее уравнение
(1 \ а з
4*"j'^a + 2=0. Эго уравнение не имеет
решений. Возвращаясь к неизвестному х, первое уравнение запишем в виде
у/2х—1 =х, или х3—2х4“1 = 0, или х3 — 1 — 2(х—1) = 0, или (х—1)х
Х(х24-х—1) = 0. Решая это уравнение* получаем х=1* х = (—1 ± /б)/2.
101. {—2; 14-/5}.
102. х £ 0, если a Q — оо; х={0}, если а = 0;
х={ (2а-1 - /4^^3)/3 }* если а £ Р; 4"00 I • Решение. Так как х нахо-
дится под знаком квадратного радикала, то х^0, левая часть уравнения
х4-/а4- /х 0, следовательно, а 0, кроме того, поскольку а есть сумма
270
х и неотрицательной величины У а-]~Ух, то х^а. Таким образом, из рас-
смотрения самого уравнения мы приходим к выводу, что при ag]—оо; 4){
уравнение действительных решений не имеет. Будем считать а^О. Тогда
х-}-Уа-\-У х = а ==>Уа~[~Ух = а—х =>
а 4“ У* — °2—2ах-|-х2 =Ф а2-(2х4-1) а+*2— Ух =0 =ф>
=Ф а — (2*+1 £ У4х24~4х4~1 —4х24~4 Ух )/2
=£ а ==(2x4-1 £ К4x4-4 Ух 4~ 0/2 =Ф> « — (2x4-1 £ (2 Ух 4-1))/2 =$>
=>а =х4- Ух £ 1 или а=х—Ух»
Рассмотрим первую возможность а = х-}- Ух 4-1; учитывая, что в правой
части сумма трех неотрицательных слагаемых, один из которых равен 1,
получаем, что если 0^а< 1, то написанное уравнение решений не имеет.
Будем рассматривать случай а^1; тогда
а = х£- Ух 4-1 х + Ух +1 — а = 0 Ух =(—1 £ У1—44"4tz)/2 =>
=-> рг7 = (-14-У4^=3)/2, или КГ = -(14-1<43^3)/2,
но Ух ^0,а^ 1, поэтому второй случай невозможен; итак,
Ух —(У4а—3 —1)/2=> х = (2а —1— У 4а—3)/2 при а^1.
Рассмотрим теперь случай а = х—Ух ; здесь а может быть любым неотрица-
тельным числом, тогда
а = х—Ух =£> х—Ух —а=0=> Ух =(1 £ У1 + 4а)/2.
Заметим, что соотношение }/х’ = (1 — У14~4а)/2 0, и, следовательно, воз-
можно только при а = 0; тогда х = 0. В случае Ух = (1 £- У 14"4а)/2 х =
= (2а4" 1 +У4а£- 0^2 > а, что невозможно. Объединяя все результаты,
получаем, что х g 0, если а g]— 00 *, 0 [ (J 1 0; 1[, х = {0} при а=0 и
х = {(2а— 1 — У 4а—3)/2 } при а £ [1; 4-°°[*
103. х £ 0, если ag] — 00; —1/4 [, х = {(— 1 £ У4а-±-1)/2 }, если
a g [—1/4; 0]; х={(— 1 — У4а4-1)/2 }, если ag]0; 1[; х =
= {(—1—У4а+1)/2;(1 + У4а—3)/2 }, если a g [1; £-оо{. Решение.
1-й способ. Этим способом решим уравнение подробно. Из рассмотрения
уравнения замечаем, что х<:а<:х2. Тогда
х2 — У а — х=а => х2—а= У а—х==>х4— 2х2а-{-а2=а—х
=> а2—(2х2+ 1) а-|-х4-х4 —0 =>
=>а = (2х24-1 £ У4х44~4х24-1 — 4х—4х4)/2 =£
=Ф>а=(2х24-1 £ (2х —1))/2 => а = х2 + х или а=х2—х£-1.
Итак
а=х24-х или а = х2—х4-1* (1)
В случае а = х24~х пригодны лишь х^0, так как а^х2. Решаем уравнение
х2+х_a = 0==> х=(—1 £ У&+Т)/2. Следовательно, данное уравнение при
а < —1/4 решений не имеет, при a g (—1/4; 0] оно имеет множество решений
х = {(—1 £ У4а4~1)/2 }, при ag ]0;4-°° [ решением будет лишь множество
х= {(—1 — У4а+1)/2}, так как при а>0 выражение х =
= (—14" У4а-±-1)/2 > 0, что в данном случае невозможно. В случае
271
а = х2—х+1 пригодны лишь х^1, таи как а^х2 при этом а^1, ибо
о = 1Ц-х (х—1). Решаем уравнение
х2—х-}-1—а = 0=фх = (1 ± У 1—4+4а)/2 х = (1 ± У 4а— 3)/2.
При 1 выражение (1 — У 4а—3)/2с0, тогда как х в этом случае 1.
Следовательно, решением в этом случае будет лишь х = (14-У"4я— 3)/2,
которое при также 1. Итак, объединяя результаты, получим
х £ 0, если а £ ] —°°; —1/4 [;
х={(-1 ± К4МЛ)/2}, если а £ [—1/4; 0];
х={(-—1 — У 4а-]- 1)/2 }, если a £ ] 0; 1[;
х= {(—1 — /4а+Т)/2; (1 + Vla^3)l2 }, если а £ [1; +<ю I.
2-й способ. Запишем исходное уравнение в виде
1 г_____ 1 / 1 \ 2
-с2—х+-£=(а—х)+^а—х+—&\х—-) =
= х+у) х—у=± *+•§)• <2)
Освобождаясь в уравнениях (2) от иррациональности, получаем уравнения (1).
3-й способ. Положив Уа—х = у и учитывая, что с—х = у2, для опре-
деления хну получаем систему уравнений
{х2—у = а>
У*+х-а. (3)
Вычитая из первого уравнения системы (3) второе уравнение системы, имеем
х2—у2—у—х=0^ (х—У—1) (х-)-г/) = 0
х—у—1=0, Гх— l — l/'a — х,
=> ФФ ___
_х-]-г/ = 0, [х=—У а—х.
Решим уравнение х—1 = У а—х. Это уравнение равносильно системе, состоя-
щей из одного уравнения и одного неравенства
х2—х+1—а = 0,
х—1^0,
Решим уравнение
_ 1 ± V4а—3
2
Х^ 1,
( i + V4a-3
«Н 2 , =>
( 1.
1 + У4а-3
2
при а^ 1.
х = — У а—х»
(4)
Это уравнение равносильно системе, состоящей
из одного уравнения и одного
неравенства
Корень х — — (У’ЧаН-1 +1)/2 удовлетворяет уравнению (4) при всех а ^-—1/4
(и только при этих а).
272
Система, состоящая из одного уравнения и одного неравенства
О,
имеет решение лишь при —1/4<й<0, поэтому корень х = (]/г4а +1 —1)/2
удовлетворяет уравнению (4) при всех —1/4<п<0 и только при этих зна-
чениях а. Объединяя все результаты, найдем все корни исходного уравнения.
104. х = {0}. Решение. Если а < 0, то в левой части уравнения стоят
два выражения а и —УГх-}-2ах Ух2 + 7а2 «С 0, сумма которых равна
нулю; это возможно лишь при условии, что каждое из них равно нулю,
а это возможно, только если х=0. Если а — 0, то уравнение принимает вид
— Ух =0, которое удовлетворяется лишь в случае х = 0. Если а > 0, то
перенеся второй радикал в правую часть уравнения и возведя в квадрат,
получим после преобразований уравнение х(а2—1 —2а Ух24-7а2) = 0, корнем
которого является х = 0. Если есть другие корни, то они удовлетворяют
уравнению а2—1 — 2а У х2-\-7а2, из которого видим, что а2 > 1. Освобож-
даясь от радикала и преобразуя, получим 4а2х2+27а4 + 2а2 —1=0, что
невозможно. Итак, при любых а уравнение имеет единственный корень х = 0.
105. {4}. Указание. Преобразуйте уравнение к виду (х—4)2 +
+ (2fx-4)2 = 0. 106. {а2—-4а} при а > 2; 0 при а<2. 107/0. 108. {—2}.
109. {-4/3}. 110. {1/3}. 111. {2}. 112. {-3}. 113. ^о}. 114. {76}. 115. {!}.
116. {2}. 117. {1}. 118. {5}.
119. Один; х = —4/3. Решение. Предположим, что уравнение имеет
корни; тогда (учитывая, что х2 > 5/3)
^х3+1=х2 + _^+_1__=Фх2_|=2х =»
x4-|*2-S =0 *2=4 ± т =»*’=¥нли *2=—г
Возможен лишь первый результат х2 —16/9, откуда х = 4/3 или х = —4/3.
Проверка показывает, что корнем является лишь один х = —4/3.
120. {11/6}. Указание. Областью определения левой части уравнения
является отрезок [7/5; 5/2], поэтому 7/5 < а/6 < 5/2, т. е. 9 < а < 15.
121. [2; 4-оо [. 122. ]—оо; — 1] U [2; 4~оо [. 123. ] 1/2; 2]. 124. J 3/4; 2 [.
J25. [0; 2 [ и 19;+«О [. 126. ]4; «]. 127. ]—1 — ]<5; — 3] (J [1; V5— 1 [.
128. ]—6/5; —1] U [2; 3 [. 129. ] — оо;1[. Указание. Положите
У2—х=/ и учтите, что ZS&O. 130. ] —оо; —17/2] U П; 101. 131. ] 6; 8].
132. ] —1/2; Н-оо I. 133. ]1; 2( U 12; +оо[.
134. [—18; —2[. Указание. Неравенство Vf (х) < ф (х) равно-
сильно системе неравенств
ф (х) > 0,
f (х) < ф2 (х).
273
135. ]3; 24/5]. 136. [20/9; 4 [U] 5; Н-оо[. 137. ](1 +/*29)/2, +оо[.
138. J5; 4-оо]. 139. ]3; 4~оо[. 140. ]1/2; 5/2[. 141. ]3; 4>оо[. 142. [1; 6].
143. [0; 2]. 144. [5/2; 3[. 145. J2/3; 4-оо[. 146. ]— оо; —2](J[5; 74/13[.
147. [—2; —8/5[UJ0; 2]. 148. [О, 3]. 149. £—1; 0 [ U]3/5; 1]. 150. £—2; —8/5[(J
U]0; 2]. 151. ]— оо; —2[.
152. J—оо; 1[. Указание. Неравенство <р(х)<У7(х) равносильно
совокупности двух систем неравенств
(<p(x)<0, r<p(x)S&0,
и \f(x) ^0,
(<р2(х) < /(х).
153. ]—33; 3[. 154. J—оо; —1]. 155. [—7; If. 156. [2; (7+Уб^/2[.
157. [—14; 2[. 158. ]— оо; 3[. 159. ]4; 5[. 160. ]— оо; 2[. 161. [—2; 2[.
162. ]—оо; 4-оо[. 163. J24/19; + оо[. 164. J—оо; —3]. 165. [2; + «(.
166. ]—Уб; 2[. 167. [—1; (Уб—1)/2[. 168. 18/3; + оо[. 169. [—оо; — 2JU
U12; Ч-оо[. 170. 0. 171. ]—оо; —5]U[1; +»[. 172. ]-оо; —3JU
и]-2;(КТЗ—7)/б[. 173. ]—оо; l](j[2; (17+/Тз)/б[. 174. ](5—У13)/6;+оо[.
175. 11; 4]. 176. [—2; (Уб"— 1б)/Ю[. 177. [—6; УГ—4[. 178. J3; 5J.
179.]1;2КЗ/3]. 18О.[—1—УТЗ;0]и[(1 + УТ7)/2; УТз— 1]. 181.[—УЗ;0[и
U10; 2J. 182. [0; 1]U[4; 1«]. 183. [3; 4[(J 17; +«[. 184. [—4; (3—У2Т)/2[и
UH; +®Ь *85. [1/2; 2[UJ5; +оо[. 186. [—20; 0[(JJ5; +оо[. 187. 1—оо; —4(U
U[1/2;' 8/7[. 188. ]— 2— 2 Уб; —1[ц[—2+2Уб; З]. 189. ](У13—б)/2; 1}«
190. [—1; — УТ/2[и]У^/2; 1]. 191. J1; +оо[. 192. 14; +оо[. 193. [—3; 1[.
194. [—1; — У15/4[и]У15/4; 1]. 195. [—2; +оо[. 196. [(16+ Ут)/2; Ю].
197. [1; 3/2[. 198. ]гУ21/3; +оо[. 199. J—2; — 1J (J [—2/3; 1/3[. 200. [1; +оо[.
201. [—5; 2 У Уб—2—4[.
202. [—1/2; 0[U]0; 1/2]. Указание. Областью определения неравен-
ства является множество чисел [—1/2; 0[(J ]0; 1/2[. Преобразуйте неравенство
к виду
1 —(1—4х2) _ 4х
—;---< 3, ИЛИ ---------------7==г < 3,
х(1+У1 —4х2) 1 + У1 — 4х2
или 4х<3+зУ1—4х2 и докажите, что это полученное неравенство выпол>
няется во всей области определения.
203. [^5/4; +оо[. 204. [—1; +оо[, если 00 —оо; 0J; £—1;
если а£]0; +оо[. 205. ]—оо; 2], если ag]—оо; —1]; js—• если
a€i—*;+оо[. 206. 1—оо;0[ U [1;+“[. 207. ]—оо;0] (J J9/2; + оо(.
208. ]—(3+У29)/10; 2]. 209. {5}и]4+У2; +оо[. 210. [—1; УЦ.
211. [—2; 2[. 212. ]1; 5/4 £ (J 1 5/3; + оо [. 213. 2.
214. 13. 215. х=2.
§7
1. {(0; 1)}. 2. {(—5; 2), (—-2; —1)}. Решение. Нужно рассмотреть два
возможных случая: 1) 2) у > 0.
274
1) При у^О заданная система уравнений равносильна системе* состоящей
из двух уравнений и одного неравенства
{лг—3#=1,
х+у = —3, (1)
//<0.
Решая систему уравнений
( х—3у= 1,
получаем х=—2, у=—1. Это решение удовлетворяет неравенству у^ 0 и,
таким образом, является решением системы (1).
2) При у > 0 заданная система уравнений равносильна системе, состоящей
из двух уравнений и одного неравенства
( х-^3у= 1,
I х-*гУ = —$1 (2)
V У>0.
Решая систему уравнений
<х+3у=1,
——3,
получаем: х = —5, у= 2. Это решение удовлетворяет неравенству у > 0 и,
таким образом, является решением системы (2).
3. {(2; 3)}. 4. {(0; -1)}. 5. {(0; 3), (4; 1)} 6, «1/4; 7/4), (3/4; 5/4)}.
7. {(4/7, 5/7), (8/7; 3/7)}. 8. {(—11/19; 23/19), (1; —1)}. 9. «24/25; 23/25)}.
10. {(с; 4—с)}, если с£ [1, 2]; {(с; с-(-2)}, еслис£[0; 1];0 при остальных
значениях с. Решение. При заданная система уравнений равно-
сильна системе двух уравнений и одного неравенства
\У—2|=х,
у=2+х, (1)
х< 1.
Если у < 2, то система уравнений (1) запишется в виде
у=2—х,
Система (2) не имеет решения, так как решение системы двух первых урав-
нений х=0г у=2 не удовлетворяет неравенству у < 2.
Если у ^2, то система (1) запишется в виде
^=2+^
у=2+^
х< 1,
,У^2.
(3)
Пара чисел х=с, у=2+с при любом с< 1 является решением системы (1),
а следовательно, и заданной системы уравнений.
При х > 1 заданная система уравнений равносильна системе двух уравне-
ний и одного неравенства
1^-21=2-*.
^=4—хл (4)
275
да/трИ у <_2 система (4) запишется в виде
( У = Х,
У = 4—х,
(5)
Система (5) не имеет решений, так как решение системы двух первых урав-
нений х=2, у = 2 не удовлетворяет неравенству у < 2.
Если у^2, то система (4) запишется в виде
С у=4—х,
(У^—х,
х^1, (6)
t/2s2.
Пара чисел х—с, у = 4—с при любом с£[1; 2J и только при этих с является
решением системы (6), а следовательно, и заданной системы уравнений.
II. {(1; 1; 0).} 12. {(2; 1; 1)}. 13. {(2; 3; 1)}.
14. {(1; 5); (5; 1); (2; 3); (3; 2)}. Решение. Полагаем х-}-у=и, xy=v.
Тогда система уравнений принимает вид
Г «4-у= 11,
\ пу = 30,
решения которой w = 5, у = 6 и w=6, у = 5. Тогда относительно х и у получим
две системы
fx+^ = 6, | х+# = 5,
( ху=Ъ, [ х# = 6;
решениями первой системы будут (5; 1) и (1; 5), решениями второй системы
будут (2; 3) и (3; 2). Решения найдены с использованием теоремы Виета.
15. {(4; —1); (-1; 4)}. 16. {(5; 3)}. 17. {(—5; -4); (4; 5)}.
18. ((4; 5), (5; 4)}. 19. {(1; 6), (6; 1)}.
20. {(—6; -2), (—4; -4)}. 21. {(3; 2), (2; 3)}. 22. ((-3; -2), (3; 2)}.
23. {(2; 3), (3; 2)}. 24.] 0. 25. {(5; 1)}. 26. {(-5; -1), (5; 1)}.
Указание. Положите (х—y)l(x-\-y) = t-, чогж (х-}-у)/(х—y)=\/t,
27. {(-2; —1), (2; 1), (-/~6; -/б73), (/б; /‘б/З)}. 28. {(8/13; 12/5.)}
Указание. Введите новые неизвестные, положив 1/Зх=п, 1/2у=о.
29. {(11/13; —24/5)}. 30. {(—7/4; —3), (-7/6; —2)}. 31. {(—1; 9/4), (4; —9)}.
32. {(-7; 3), (7/3; —1)}. 33. {£—1; —3/2), (2;_3)}. 34. {(4; -3), (4; 3)}.
35. {(—з/“2; —К2), (-3/2; /Г), (3/2; — /’2), (з/~2; У~2)}.
36. {(-6; -2), (6; 2)}. 37. {(—2; -3), (2; 3)}. 38. {(—2; -4), (-4; —2), (2; 4), (4; 2)}.
39. {2; 8), (8; 2), (—2; —8), (-8; —2)}. 40. {(—9/5; —16/5), (9/5; 16/5)}.
41. {(—3; —2), (3; 2)}. Указание. Сложив уравнения, получим (х+г/)2 = 25
и т.д. 42. {(—Ю; —11), (10; 11)}. 43. {(—7, —3), (7; 3)}.
44. {(7}^2/5; —3^2/5), (—71/*2/5; Зуг2/5)}Г> У к а з а н и е. Умножив
первое уравнение на 7, а второе на —3 и сложив полученные уравнения,
находим 7у2—4ху—Зх2 = 0, откуда у = х и у = —Зх/7 и т.д.
45. {(—3; -2), (3; 2)}. 46. {(-3; 4), (4; -3)}. 47. {(-3; 4), (4; -3)}.
48. {—1; —3), (3/2; 2), (—/7/2; 0), (К7/2; 0)}.
49. {(1; 2), (2; 1)}. Указание. Сложив оба уравнения, получим квад-
ратное относительно х-\-у уравнение (х-^у)2-\-(х~\-у)—12 = 0.
50. {(-5-/55; —5+/55), (—5+/55; —5— /55), (4; 12), (12; 4)}.
276
51. {(—3; -—5), (—5/3; —13/3), (5/3, 13/3), (3; 5)}. Указание. Вычтите
из первого второе уравнение системы.
52. {(—4; —5), (—3 /3; — /3), (3 /3; /3), (4; 5)}. Указание.
Умножив первое уравнение на 5, а второе на 7, после сложения получите
4
уравнение 5х2— 19хг/-]-12#2 = 0, решая которое, найдете х = 3у и х=-^у.
53. {(-1; -2), (-/2;_-/2), 0; 2), (/2; /2)}._
54. {(1; 4), (4; 1),(2—/3; 24-/3), (24-|СЗ; 2—/з)}. Указание.
Положите х-\-у=и, y~xy — v.
55. ((1; —1). (3; —3), (/157—13; (/157—13)/2),
(—13—V 157;— (134-/157)/2)}. Указание. Решая первое уравнение
системы, получите у=— х и х = 2у.
56. {(2; —3), (г, 1) | c£R}. Решение. Умножив первое уравнение на —2
и сложив полученное уравнение со вторым уравнением системы, после упро-
щений получим уравнение y2Jp2y—3 = 0, откуда Ух=1, г/2 =—3. При у=\
оба уравнения системы выполняются тождественно при всех x£R. При у = —3
х=2.
57. {(-1; 3), (с; 2) [ 58. {(2; -1), (-1; с) | c£R}.
59. {(2; [3), (3; 2)}. Указание. Учитывая, что х-]-г/ = 5, преобразуем
первое уравнение системы (х —f/) (х2—хг/-[-г/2) = 35 к виду х2—ху-\-у2 = 7.
В результате получаем систему уравнений
( х2-хг/4-г/2 = 7,
V +«/=5.
60. {(—1; —2), (2; 1)}. 61. {(—1; 2); (2; —1)}. Указание. Умножьте
второе уравнение на 3 и сложите^ первым уравнением системы. 62. {(4; 8), (8; 4)}.
63. {(—3; —1), (—1; —3), (1; 3), (3; 1)}. Указание. Из второго уравнения
системы находим: // = 3/х; исключая у из первого уравнения системы, получаем
квадратное уравнение относительно х4.
64. {(2; —1), (—1; 2)}. Указание. Положите x3 = u, y3 = v.
65. {(—3; —2), (—2; —3), (2; 3), (3; 2)}. Указание. Из первого урав-
нения системы находим х2-\-у2 = 78/ху. Возведя обе части этого уравнения
в квадрат и учитывая второе уравнение системы, получаем 974-2 (ху)2=782/(ху)2.
66. {(—3; —2), (-2; —3), (2; 3), (3; 2)}. 67. {(1; 3; 9), (9; 3; 1)}.
68. {(12/7; 12/5; —12)}.
69. {(3; 3; 3)}. Решение. Сложив уравнения системы, получим
(х—3)34-(Z/~ 3)34“(^—З)3 =0. (I)
Тройка (3; 3; 3) является решением уравнения (1). Проверка показывает, что
она также является решением системы. (Заметьте: без проверки этого утверж-
дать нельзя!) Покажем, что других решений система не имеет. Из первого
уравнения системы имеем i/3 = 9x2—27х4~27. Дискриминант квадратного трех-
члена 9х2—27х+27 отрицателен. Поэтому, если (х0; у0; z0) —решение системы,
то t/o > 0* Следовательно, yQ > 0. Аналогично, из второго и третьего уравнений
получаем Zo > 0 и х0 > 0. Из первого уравнения системы имеем
(Уо—3) Q/о+Зг/о4-9) = 9х0 (х0—3). (2)
Так как х0 > 0 и г/о4"3^о4"9 > 0, из (2) вытекает, что числа у0~-3 и х0—3
не могут иметь разных знаков. Аналогично, из второго уравнения следует,
277
что числа z0 — 3 и у0—3 тоже не могут иметь разных знаков. Таким образом,
если х0 > 3, то yQ > 3 и z0 > 3; если же х0 < 3, то уь < 3 и г9 < 3. Решение
(хв; у0; г0) системы является также решением уравнения (1), а для (1) ни
> 3, у0 > 3, Zo > 3, ни х0 < 3, у0 < 3, ze < 3 не годятся. Значит, хв=3,
Уо = 3, Zq = 3.
70. {(-1; — 1; —1)}. 71. {(2; 2; 2)}.
72. {(—1; 2)}. 73. {(1; 0; —1)}. 74. {(1; —1)}. Решение. Данная система
уравнений равносильна системе
J у2 = 2х/(14-х2),
\ 2 (х —1)24-1+//3 = 0.
Так как 2х/(14~х2) «С 1 при всех x£R, то из первого уравнения системы (1)
следует —1 у С 1. Из второго уравнения системы следует у<^—1. Значит,
У = — 1, х=\.
75. {(1; 1; 1), ((-5 ± /Т1)/2; (10 Т /П)/2; (4 Т /ГГ)/2)}. Указа-
н и е. Прибавьте к третьему уравнению первое, умноженное на 2, и второе,
умноженное на 3.
76. {(с; с)}, c£R при а = 0; {(За/2; 9а/2), (За/4; —9а/4)} при
77. {(3; 0), (-1/3; -5/3)}.
78. {((4а—а2)/(2а—4); (а—4)/(а—2))}, если а£[2/3; З—Уз];
{((а2—12а+8)/(6а—4); а/(3а—2))}, если ag]3— УЬ; 2].
79. {(0; 1—2 /3")} при а = 7—4 /”3; {(0; 1+2 /З)} при а=7+4 /3.
'Решение. Данная система при х^0 имеет вид
J ах+(а—1)у=24-4а,
(Зх4-2у = а—5,
. а2—14а 4-1 , а2—17а—6 _ . Л
i ее решение 3 —’ # =---------а^З~~ ’ ^ак как то
й2_14д + 1 (а—7+4 УЗ) (а—7—4 Уз)
--------—^0 при ~----------------------- —--—-^0; применяя метод
а—о---------------------------------------а—о
! интервалов, получим ag[7—4 У 3; 3[ U [74-4 У3; 4-оэ[э При х^0 данная
, система имеет вид
< ах4-(а—1)у = 24-4а,
}-3%4-2z/ = a—5, w
а2—14а4~1 а24-7а4-6 „ а2— 14а 4-1
ее решение х =----=---, у — —?------------— . Так как х<0, то —=-тг—
г ба—3 5а—3 5а—3
^0; применяя опять метод интервалов, получим а£[7—4 3; 3/5[(J
U [74-4 КЗ; 4-оо[. Нам надо найти такие а, при которых заданная система
имеет единственное решение, независимо от того, будут ли или х«с0.
Следовательно, нам надо найти такие а, при которых выполняются равенства
( а2—14а4-1___ а2— 14а4~1 1
а~$ 5а—3 ’
4 а2_17а—б_ а2+7а+6
ч а—3 5а—3 *
Из первого уравнения получаем
М2 14a+l)f 1 4- 1 \ 0=i>(a-7-4K3)(a-7+4/3)6(a-l)
(a I4a-r I) ^a_3+5a_3J -О =$> (а-3)(5а-3) “°’
278
т. е. значения х, найденные из систем (1) и (2), будут одинаковыми при а=1,
а —7—4 Y 3, о=7—1-4 1^3. Подставим найденные значения а во второе урав-
нение системы (3). При а=1 получим —11=7, что невозможно, т.е. данная
система при а=Л имеет два решения (6; —11) и (6; 7). При а=7—4 Y 3
. «»»» части (7-4/Г)+-17(7-4/з)-5 !_2Кз, „ , пра.
.ой (7-4 /3)47 (7^4X3)+? _ ,_2 , е. /3-
5(7— 4}<3)-3 '
ная система имеет единственное решение (0; 1 — 2^3). При й = 74-4/ 3
в левой части получаем———-4 = 1_|_2|/гзГ, а в пра-
.ой (7+4 /з)-+7(7+4 /з)+6= гКЗ „7+4/Гз.д.к.
5(7+4/3)-3
ная система имеет единственное решение (0; 1-J-2 }^3).
80. {((1—2а2)/(1 — а2), а/(1 —а2))}, если а != ±1; 0, если а=±1.
81. {((а2+1)М2; (а+О/а2)}, если а # 0; 0, если а = 0.
82. {(0; а)}, если аф ±1; {(c-j-1; с) | c£R}t если а =— 1; {(с, 1 — с) | c£R]t
если а= 1.
83. {((14-а4-а2)/(1+«); — а/(1-|-а))} при ар ±1; {(с; 1 —с) leg/?} при
а=1; 0 при а — — 1.
84. а = 3. 85. а = —7. 86.а=1/17. 87. {(11/5; 1/5)}, если а=3; 0,еслиа/3.
88. {((а—З)2; cos (а—2); 3)}, если ag[3; 24-л]; 0, если а^[3; 2-j-л].
89. [{(Iog2 (а+1); 5; sin (а+2))}, если eg]—*1; (л—4)/2]; 0, если
а^]—1; (л—4)/2]. 90. {(arctg (а—3)2-|-лп; ± ]/"а-|-1; 6) |n^Z}t если ag
€(~1; 3]; 0; если [-1; 3].
91. ag[—1; 0|. Решение. Данная система при b Ф 2 и b —2 и при
А 2ас24“ 2с—bc-\- b
любых а и с имеет единственное решение х==>----4__.fr2——1 У=
2с—2—ab(?—Ьс „ , а
=-------—-------. Если Ь = 2, то данная система имеет вид
(2х+2у=ос2,
{ 2г+2г/=с— 1.
Чтобы эта система имела решения, должно выполняться условие ос24-е=с—1,
т. е. ас2=—1. Рассматривая последнее соотношение как уравнение относи-
тельно с, замечаем, что оно разрешимо при любых ag]—с»; Of. Если 6=—2,
то система имеет вид
( 2х—2y=ac^-\-ci
{ —2х-{-2у=с— 1.
Чтобы эта система имела решения, должно выполняться условие 0^4-6?=—h
т. е. ас2-^2с—1=0. Рассматривая последнее соотношение как уравнение отно-
сительно с, замечаем, что оно имеет решения, если l-f-я^ 0, т. е. ag(—1;+оо[.
Таким образом, при ag[—1; 0[ всегда найдется такое с, что при любом зна-
чении b заданная система имеет по крайней мере одно решение.
92. ag[—(3 уг2+4)/8; (3 У2—4)/8]. У к’а з а н и е. При b & ± У 2
система имеет единственное Грешение. При д=}^2 заданная система имеет
279
решения при выполнении условия ас2 уг2+(}/Г2—1)с4-1=0. Это уравнение
относительно с имеет решения, если а£]—оо; (3 /2—4)/8]. При 6=—К 2
система имеет решения при выполнении условия ас2 ]/п24~(У"2+1) с—1=0.
Это уравнение относительное имеет решение, если а£[—(3 }^2~|- 4)/8; +оо[.
Ср. с решением примера 91.
93. Для любого а£] — оо; —2](J[2; +оо[. Указание. См. решение
примера 91.
94. Для любого а0 —оо; —4](J[4; —[~оо[. Указание. См. решение
примера 91.
95. При всех £0—2; 2[(J]2; 4f.
96. При всех &g](35— /Ю09)/б; (35+/1009)/б[.
97. При всех ng]—(2+/22)/б; 0[ (J ](/22—2)/6; 9/4[.
98. При всех а 00; 5[.
99. {(9а4-54; а3—36а)} при а £. 6, а 5^ 12; {(8с; с) | c£R] при а=12; 0
при а = 6; х-f-i/> 0, где х=9(а-{-6), у—а(а~6) (а+6) при а£]—6; 3[(J
UJ3; 6[U]6; 12[U]12; +оо[.
100. xHaH6. = 3. 101. а) (7 J); б) X=(1 102. {(6; 10). (10; 6)}.
103. {(1; 4), (4; 1)}. Указание. Решите первое уравнение системы, положив
/^=t 104. {(5/3; 1/3)}. _____
105. {(—/15/17; —4/75/17), (—4/15/17, — /75/17),
(/15/17; 4/75/17), (4 /15/17; / 15/17)}. 106. {(—9; —9/4), (4; 1)}.
107. {(-6; —1), (—3; 2), (9; —4) (2; 3)}. 108. {(12;{4)}. 109. {(—1; —27), (27; 1)}.
ПО. {(1; 8), (8; 1)}. 111. {(1; 27), (27; 1)}. 112. {(1; 81), (81; 1)}.
113. {(—9; 25), (5; 4)}. 114. {(1; 4), (4; 1)}.
115. {(5; 4)}. Указание. Умножьте левые и правые части уравнений
системы.
116. {(-2; -1), (-1; -2), (1; 2), (2; 1), (0;_с) | с £*}.
117. {(—/59/2;—3/2), (—/59/2;3/2), (5//2;3//2), (5//2; —3//2)}.
Указание. Рассмотрите два случая: 1) х-\-у > 0, х—у^0‘, 2) х-\-у < 0,
х—у<0.
118. {(1; 8), (8; 1)}. 119. {(2; 2)}. 120. {(4; 2), (4/3; —2/3)}. 121. При
а =1/3 и всех а < 0. 122. ]—7/2; 0[. 123. х=8. 124. х=1. 125. 0; 1.
126. [—1; 7/3]. 127. а£ = 0; а2 = 1.
128. а £ [—2/3; 0[. Решение. Так как а < 0 по условию задачи,
а ах>0, то х<0. В правой части первого неравенства стоит За—х > 2)/~ах>0,
следовательно, х < За. Аналогично из второго неравенства х—(Ъ/а) > У х/а
видим, что 6/а < х. Решаем первое неравенство:
2 У~ах < За—х=^х2—10ах+9а2 > 0=>х £ ] — оо; 9а[ (J ]я; 0|‘,
но мы установили, что х < За, следовательно, х g ]— оо; 9а[. Решаем второе
неравенство:
36
а2
> 0=>
=>х £ ] —оо; 9/а{ U ]4/а; 0[;
но мы установили, что для второго неравенства х > 6/а, следовательно,
х £ ]4/а; 0[. Чтобы оба неравенства имели общие решения, интервалы
280
] — оо, 9а[ и ]4/я; 0[ должны иметь общие точки, т. е. 4/а«С9а=£4/9;>а2=ф
=£> —2/3 <;а < 0. Таким образом, при а £ [—2/3; 0[ два заданные нера-
венства при а < 0 имеют общие решения.
129. Все £ £ ] —оо; 1/2[ U J3/2; 4-оо[. 130. Все k £ [—1; +оо[.
131. ]1/3; 6[. 132. [0; 1/2]. 133. ]—оо; —3[ (J ]2; 4-оо[. 134. [3; 4[.
135. ]—1; 1/2[. 136. ]—оо; -(3+ /5)/2] U ]0; 6]. 137. [2/3; (3+ /*Т)/6[.
138. ]—2; —1] U [к 4[. 139. ]-1; 2[. 140. J—2; 0]. 141. ]—2; 1[.
142. а) х=1; # = 1; б) да; в) нет. 143. При всех а£] — (14~)^"13)/2; —2[.
144. а<—1. Решение. Предположим сначала, что данная система
имеет решения. Тогда имеет решения и неравенство, полученное сложением
первого неравенства данной системы, умноженного на —2, и второго ее нера-
венства: (*+3#)2*С—4/(а+1). Значит, а<—Ь Пусть теперь
Оо < 1. Тогда (1—Оо)/(ао+0<Поэтому, если имеет решения система
уравнений
( х2+2хг/—7г/2 = -1,
1 Зх2-НОлт/—5у2= —2,
то имеет решения и данная система неравенств. Но система (1) имеет реше-
ние—например, (—3/2; 1/2). (Найти указанное решение можно, умножив
первое уравнение на —2 и сложив со вторым.)
145.
148.
281
151
152.
153.
282
166.
167.
168.
283
179.
§ 8
1. О(у) = [0; 2]. 2. O(i/) = [-l; 1]. 3. О(у) = [1;6]. 4. D (у) = ]- co; 2]U
U [3; +oo[. 5. O(i/) = [-3; 5]. 6. О (/) = [-!; 2]. 7. O(i/) = [-l/2; 3/2].
8. O(i/) = [-2/3; 3]. 9. D(y) = [-2; Ц U JU +«>(. «О- O(y) = ]- co; -1/2Ц]
U]3;+«[. 11. £>(/)=]—oo;—2]U[0; 2]. 12. D (/)=]-oo; -}<3]u[0; /з].
13. 0(i/) = ]-oo; 1[ U ]1; +°o[- 14. O(i/) = ]-4; 1]. 15.0(1/) =
= [7/3; 63[ U 163; +oo[. 16. [-3; 0[ (J ]0; 2[ U ]2; 4]. 17. D (y) = J-oo; 0[ (J
U [2; 3]. 18. D(f) = ]- co; -4] (J [5; 6]. 19. O(f) = ]-oo; -3] (J ]2; + ooj.
20. O(y) = ]-3; 3[ (J ]3; 4]. 21. D ({/) = [-2; 1[ U IB 2]. 22. D ($,)=]-3; 1].
23. О ({/) = ] —oo; 3/4[ U H; 7]. 24. O(y) = ]-oo; -1((J[4; +«[.
25. O(//) = ]-«; -4[U 1-2; 2] U [3; +oo[. 26. O(i/) = {1}. 27. O(t/) =
= ]-«; -4] U Г; +«]. 28. O(i/) = [5; 7[. 29. O(t/) = [-2; - 1[UJ—В HU
|J]1; 3]. 30. O(/) = J —co; 4-oof. 31. О (i/) = ]—oo; 0]. 32. O(/) =
= {[rai; л(2п-Н)/2]|п € 33. О (t/) = ]-l/6; л/3] (J [5л/3; 6[. 34. D (y) =
U ]-^+2лп; ^гл+2лп n £ zj-. 35. D(y) =
= ]3; 30[ U ]30; +oo[. 36. D (i/) = [-5; 8[ (J ]8; 9[. 37. D(f) = [4; ll/2[ U
и 311/2; 4-oo|. 38. 0(1/) = ]—oo; -2| U 12; +«>]. 39. 0(i/) = ]-oo; -3] U
U]-l;+oo|. 40. 0(1/) = [0; +oo]. 41. О(1/) = ]— oo; -7[ U ]-l; +«|
42. O(f/) = ]-l; 1[. 43. О(}/) = [-1; Ц. 44. O(y) = ]-5; 0[ (J ]3; 4-oo[.
45. O(y) = ]2; 4]. 46. O(j/) = [1; +<»[. 47. O(f) = ]2; +«[. 48. O(ji) = [l; 4-oo|.
49. O(t/) = ]0; 1|. 50. O(ji) = ]0;3/2]. 51. O(t/)=]-3;-2/3]. 52. O(f) = [0; H-oof.
53. O(i/) = ]-co; —11] (J J-И; —10[ (J 1—10; -9] U 1-9; 2] U 13; 4-co|.
284
54. D (у) = ]9j_-оо[. _55. £>(</) = [!; 4]. 56. D (y) = [5; + oo[. 57. £>(/) =
= [—2; -/з[ U ]K3; 2]. 58. D (y)=J—3; -2/5] U ]2; 4-oo[. 59. D(y) =
= J-oo; -1[ U [0 ; +oo[. 60. D(f/) = ]1; 4]. 61. £>(y) = ll; 4[. 62. D (y) =
= JI; +co[. 63. P(//) = ]0; 1[. 64. D(j/) = [2; 3]. 65. £(y) = |-5; -3£J]3; 5].
66. D(y) = }\\ 6[ U]6; +oo[. 67. Dtf) = ]-2; (l-/21)/2]u[(l + /2T)/2; 3[.
68. £>(«/) = [2; 4]. 69. £>(/) = ]—oo; —2]. 70. D (y) = [(l - /5)/2; 0[ U
U [(l+/5)/2; +oo[. 71. D(f) = ]-oo; -7] U 1-3; +«>[. 72. D(«/) =
= ]8/3; 4-oo[. 73. D (/) = ]- oo; -2] U JU 2]. 74. D ({/) = [-!; 1[ U 13; 5].
75. £>(/) = [0; 1[. 76. ] —oo; (1 — /65)/4[(j[0; (1 + /бб)/4[. 77. D(f)=]O; 16].
78. D ({/) = [!; 2[ U ]2; 5]. 79. D(y) = ]-oo; 2] U 13; + «>(. 80. D (y) = jl; 3].
81. D(y) = [3; 4-oo[. 82. D(/) = ]2; +oo[. 83. D(/) = ]5; +oo|. 84. D(/) =
= [3; +«[. 85. D(t/) = ]-oo; -1[ Ul-1; 4[. 86. D (t/) = [l; 2[ U ]2; 3].
87. D(jr) = ]-oo; -1/2] (J [0; 1]. 88. D(«/) = [4; 5[ U ]5; 39]. 89. D(y) = j2; 3[.
90. D(t/) = ]l/3; +oo[. 91. D(y) = [103; 10*|. 92. D(y) = [4-V2; 3[ (J
u[4+ к2; +oo[. 93. D (i/) = ] 100; + oo[. 94. D (y) = ]0; 10-2w]10-2; 10-1/2[.
95. D (i/) = ]0; 1[. 96. D (y) = ]-oo; -5[ U J—5; —4[ U 14; 5[ U J5; +oof.
97. D(y) = [—4; -л] (J [0; л]. 98. Z>(«/) = ]0; 102[ (J J103; + «o|. 99. D(y) =
= j — oo; —5/3] U P; +»[. 100. D(j/) = ]3—2л ;3—л[ ]J ]3; 4]. 101. D(y) =
= ]9; +oo[. 102. D (y)= [1; 4[. 103. D(t/) = [-l; 3]. 104. Г»(у) = ]-1/2; 1/2] U
U 31/2; 1[ U 13/2; + oo[. 105. D (y) = JO; 10~2[ U jlO"2; 10~^. 106. £>(y) =
= {1/2}. 107. D (у) = {[2лп; n(2n+l)J | n £ Z}.
108. D (y) = {[2nn+arcsin (1/3); л(2п4-1)—arcsin (1/3)] | n £ Z}.
109. O(t/) = {[4nn; 2л(2п-Н)] I « € 2}-
110. D (у) ={]л (2n—l)4-arccos (1/4); л (2n-}*l)—arccos (l/4)[ | n £ Z}.
111. D (y) = {[л (6n—1)/3; л (6«4-l)/3] | n £ Z}.
112. Р(у) = {л(4п+1)/2|п€-Л U{[n(2m+1); 2л(m+1)] | m g Z}.
113. D(y) = ]-oo; 0] U 10; +«>[, E(y)={-1; 1}. 114. П(/) = [0; 1],
£(/) = [0; 1/2]. 115. D(y)=]-oo; +«>[, E (jr) = [l<ll/3; +oo[. 116. D(y) =
= ] —oo; +«[, £(y) = [lg(11/3); +«[. 117. D(y) = ]-co; 4-oo[, E(y) =
= (lg(4/5); +<»[• 118- = 3], £tf)=|y 2; /10]. 119. D(f)=]-oo; 4-oo[,
E (f)=[l; 2]. 120. D (/) = [—!; 2], E(fi = [/3; / б]. 121. x£]- 3; 2].
122. a£J-o°; —1/4[. Решение. Пусть —k [—1; —1/3]. Если
в некоторой точке х функция # = —& (1/3*С&«С1), то
a^+i-==-fe=»y-T=-fl+^-1=»^-T^-°-1+T=o=»
х== к ± V 4^~т+1+а± V (!-^)2+a •
Следовательно, чтобы функция не содержала ни одного значения из отрезка
[—1; —1/3], необходимо, чтобы ((26—1)/2k)2 + а < 0 при любом k £ [1/3; 1],
т. е. а <— ((2k—1)/2&)2. Функция—((2k—1)/2&)2 при 2k—1=0, т. е. при k =1/2,
принимает свое наибольшее значение 0; наименьшие значения на отрезке
1/3^6^ 1 эта функция принимает на концах отрезка: при k = 1 и &=1/3
имеем — ((26—1 )/2k)2= —1/^. Следовательно, при любых — оо; —1/4{
множество значений заданной функции не содержит ни одного значения из
отрезка [—1; —1/3].
285
123. а£]—оо; —1[ U ]—1; 5/4]. Решение. При а — — 1 функция
принимает вид у=(х—1)/(х2—1). Она определена всюду, кроме точек х — ±1.
Если исключить из рассмотрения эти точки, то можно переписать функцию
в виде у= 1/(х+1). Эта функция может принимать любые значения, кроме
y — Q. Следовательно, функция у=(х-]-1)/(а-0х2) при а = —1 не может при-
нимать значения у = 0. Если а < 0 и а —1, то при х —> ± 1^1 а| значение
у—> ± оо. Рассмотрим функцию у = (х-{-\)/(а-\-х2) на участке [—1; —| а |{,
если —1 <—|а|; на этом промежутке х4-1 ^0, х24-« > 0 и, следовательно,
у^О. В точке х =—1 функция у=0, при возрастании х от —1 до —| а |
функция у возрастает от 0 до 4"00 и область значении функции содержит
отрезок [0; 1]. Если а < 0 и —|а| < —1, то на участке ]—|а |; —1] будут
выполнены неравенства *4-1 <:0, х2-\-а < 0, следовательно, и при
изменении х от —1 до —| а | функция у возрастает от 0 до 4*00» следова-
тельно, и в этом случае область значений функции содержит отрезок [0; 1].
Если а^О, то функция у— (х-\-\)1(х2-\-а) принимает значения не при
любых а. Найдем допустимые значения а. Потребуем, чтобы
(х4~1)/(х2 Ч- 1 =$>х4-1 х24~я=>х2—х4-а—1<0=>
=Фх g[(l — У5=4а)/2; (1 + /5=4Н)/2].
Следовательно, чтобы нашлись точки х, в которых необходимо, чтобы
5—4а 0 —> а 5/4. Итак, при х =—1 функция у=0; далее при возраста-
нии х функция у будет возрастать, причем если а *с5/4, то вершина графика
функции будет находиться выше у=1, т. е. область значений функции со-
держит отрезок [0; 1].
124. а £ 0. Решение, у (1) = 0 при всех а, за исключением таких а,.
при которых знаменатель равен нулю. При х=1 знаменатель обращается
в нуль лишь при а=0. Но при а = 0 —(х—1)/(х2—1) =—1/(х4-1). Эта
функция имеет значения, принадлежащие отрезку [—1; 1]. Таким образом, при
всех а заданная функция имеет значения, принадлежащие отрезку [—1; 1].
§ 9
1. {2}. 2. {—1}. 3. {—7/2; 2}. 4. {2/7}. 5. {2"1/2}. 6. {!}. 7. {2}.
8. {3}. 9. {—1; 1}. 10. {9/4; 3}. 11. {1; 2}. 12. {-2}. 13. {0}. 14. {3}.
15. {0}. 16. {-2}. 17. {2}. 18. {0}. 19. 0. 20. {—2; 3}. 21. {1°ё(Г-_1)/а (3/2)}.
22. {10}. 23. {2—1/7/2; 2+У7/2}. 24. {3/2}. 25. {—1}. 26. {0; 1/2}.
27. {3 loge 2; 3}. 28. {2}. 29. {3/2}. 30. {1/5; 6}. 31. {1/4}. 32. {1}.
33. {л (6n— (— 1)п)/18|я С Z}. 34. {25}. 35. {100}. 36. {—1; 2}. 37. {3/2}.
38. {9}. 39. {—2}. 40. {1}. 41. {—3/2; 4}. 42. {— /З; Уз}.
43. {— У 2; —1; 1; /2}. 44. {—3/2; —1}. 45. {1}. 46. {arctg 10+лл | tt£Z}.
47. {log8 (2+/Ti/З)}. 48. {-2}. 49. [3; +ool (J {-1/2; 1/2}.
50. {3}. Решение. Так как данное уравнение содержит множитель
8*"х, то х £ N. Возводим правую и левую части уравнения в степень х;
тогда после преобразований получим 5*2-23*“3*=5?*«22*. Прологарифмируем
при основании 5 правую и левую части данного соотношения; после преобразо-
вания уравнение будет иметь вид (х—3) (x4-log5 2) = 0. Отсюда х = 3 и
х =— log52. Второе решение не удовлетворяет условию —log52£W и, сле-
довательно, решением будет только х = 3.
286
Замечание. Если бы данное уравнение было записано в виде
5*.8**-1^*=500, то х £ R. В этом случае уравнение имело бы своими кор-
нями и х = 3, и х =— log5 2.
51. {л/9; 1; л (6k ± 1)/91 k С N}. 52. {10}. 53. {4}. 54. {1}.
55. {л (3k ± 1)/3( k € Z}. 56. {-2; 2}. 57. {1; 3}.
58. {1/9; 9}. Решение, з'^3 *4-xlog’*= 162 =^з'°^ *)loga х =
— 162зф З108* Чз’°гз Х= 162=> 3 °ез * = 34 =^> log2x=4 =4> log3x=2, или
log3x=—2=фх=9, или х=—1/9. 59. {—2; 4}. 60. {—1}. 61. {2}. 62. {6}.
63. {л(2й+1)/2|й€^}. 64. {9}. 65. {1/16; 1}. 66. {—1/2}.
67. {3}. Замечание. В данном примере х £ N, поэтому второе полу-
ченное значение x = 3/log26 является корнем уравнения 641/*—2(зх+$)/х
+ 12=0; но не данного.
68. {10-2}. 69. {!}.
70. {log32—1; 2}. Решение. 3*+1+18-3-* = 29=»3-(3*)2—29-3*4-
+ 18=0=ф 3(3*—9) (з*—Х)=0. Следовательно, 3*=9=фх=2 и 3* =
= 2/3=^x = log32—1.
71. {100}. 72. {1; 3}. 73. {4}.
74. {10~1/2; 102}. Р ешение, Так как х—основание показательной
функции, то х > О. Тогда
1—7ls«* 1 lgx~(lgx)»
К 8 = .*__=» 10 8 = 10"2/з=>
у/100
=ф 21g2 х—31g х-2=0 =£> 2 (1g х—2) (1g х-{-Х) = 0=ф
=^lgx = 2 или Igx——1/2=фх = 2 или х=—1/2.
75. {1/3; 9}. 76. {1/10; 1000}. 77. {10; 105}. 78. {—5/2; 3}. 79. {—1; 1}.
80. [{10-5; 103}. 81. {9}. 82. {5}. 83. р£{0; 25/4}. 84. оо; 1/2(.
85. |-3/4; + oof. 86. I-оо; l/2f U 11; +«>1. 87. J2; + «>[. 88. х € R.
89. х £ 0. Решение. Так как *+1 £ N, то с учетом этого замечания
имеем
*+У"з > 9=фЗ^*+1> > 32=ф 1/(х-М) > 2=$>
=» 7X7-2 > 0=» < о=фх € 1-1; —1/21.
Таким образом, если задача имеет решения, то х £ ]—1; —1/2[, но х может
быть равно только числам 0; 1; 2; ...; ни одно из этих чисел интервалу
1—1; —1/2J не принадлежит, следовательно, данное неравенство ни при каком
х £ No не выполняется. Замечание. Если бы исходное неравенство было
задано в виде 31/<Х+1) > 9, то здесь х £ и найденный выше интервал
и был бы решением этого неравенства.
90. J4/3; +oof. 91. J — оо; —2[ U 1—1/2; + оо[. 92. J0; Ц. 93. [1/2; If.
94. 1-2; +оо[. 95. J—5; 5[. 96. 1 — со; 0[ U Pogi3; -f-oof. 97. х £ R.
98. j —оо; 0[ (J [1; +<*>!• 99. ]3; 4-оо[. 100. {1; 2; 3; 4; 5; 6; 7}.
101. [(log23—2)/2; +оо[. 102. ) —оо; 1 — (log3 5)/3[. 103. J103; +оо[.
104, 1 — оо; 2]. 105. ]0; +оо[. 106. J0; +оо[. 107. [0; 64[. 108. j — оо; Iog0,42f.
287
109. ]—oo; —log6 10]. 110. J10-2; + «o[. 111. ]-2; + «f. 112. J—1/2; Of.
113. ]0; log2/3(l/3)[. 114. ]-K2; -1[ U ]1: K2[- 115. J2; 6[. 116. [-1; 0] (J
U [2; 3]. 117. jlog23; +«>[. 118. ] —«; log23]. 119. |-oo; -If U ]0; 2f.
120. [log3 (83/19); +<*>[• 121. x £ ]a2 logs2; +«>[ при a £ [0; 4-oof.
x € P; +«[ при a £ ] — eo; Of. 122. ]-oo, log2 (/2— 1)] fj [1/2; + «f.
123. ]5/3; 2[. 124. ]1; 4[. 125. {1+/ 3}. 126. {2}. 127. {4}. 128. {2}.
129. {0}. 130. {—5}. 131. {1/3}. 132. {0}. 133. {3}. 134. {3/2; 10}.
135. {16/j/5}. 136. {1}. 137. {100}. 138. {2+10"’; 3; 102}. 139. {—2—/Тб}-
140. {10-1; 10}. 141. {y^lO1-^; }^101+У1 }. 142. {10~5; 103}.
143. {3~У\ 3Г7}. 144. {1/5; 25}. 145. {10“3; 102}. 146. {10-*; 10).
147. {5}. 148. {IO-3; 10}. 149. {2; 16}. 150. {10; 10*}. 151. {1/81; 1/3}-
152. {Кб; 5}. 153. {1/4; 2}. 154. {2loga6; 3,ogab}, a > 0, a £ 1, b > 0, b ф 1.
155. {KlO^ 10}. 156. {5}. 157. {з+/"б}. 158. {—5}. 159. {—4}.
160. {— (3— У"3)/3; 8}. 161. {1/9; 3}. 162. {2“’; 2}. 163. {l//^; 1; 4}.
164. {7}. 165. {—1; 0}. 166. {2}. 167. {!}. 168. {1/16; 2}. 169. {3}.
170. {—9/5; 23}. 171. {2}. 172. {1/2; 128}. 173. {1//T6; ^Ц)}. 174. {1}.
175. {8}. 176. {2}. 177. 5}. 178. {10}. 179. {9}. 180. {4}. 181. {2}.
182. {3}. 183. {3; 34-/”2}. 184. {16}. 185. {10-в/3; 102}. 186. {48}.
187. {lO-1"3; 10^}. 188. {13}. 189. {29}. 190. {1; 9}. 191. {—3}.
192. {logs 4}. 193. {1/2}. 194. {0}. 195. {98}. 196. {0}. 197. {3}. 198. {—1; 2}.
199. {10}. 200. {2}. 201. {2}. 202. {1/5}. 203. {3}. 204. {10~2; 102}.
205. {10-*; 10}. 206. {—2}. 207. {2}. 208. {2; 4}. 209. {0}. 210. {2-2/8; 16}.
211. {1/4; 1/2}. 212. {1; 2}. 213. {100}. 214. {10-*; 2; 103}. 215. {10-2/3; 102/3}.
216. {13/4; 10}. 217. {16}. 218. {—13/20; 13/6}. 219. {з(* + з >^)/*o}t
220. {10-s; 10}. 221. {0; 2}. 222. {O; 7/4; (3+2 /’б)/2}. 223. {—17}.
224. { — 1/4}. Реш’ен ие. Основания логарифмов 3x4-7 и 2х4~3 должны
быть больше нуля и отличны от 1. Тогда, учитывая сказанное,
log3x+7 (94-12x4-4x2)4-log2x+3 (6х24-23x4-21) = 4 =ф
1°£зл;+7 (2x4-3)24“log2jc + з (2x4-3) (Зх4~7) = 4
=Ф 2 log3x+7 (2х4-3)4-14-log2je+3 (3x4-7) = 4
=»2 log3jc+7(2х +3) + ——-L-p^ - 3 = 0 =ф
=Ф 2 (Iog3A.+7 (2х4-3))2—3 log3x+7 (2х4-3)4-1 =0э$>
=Ф (log3*+7 (2x4-3) —1) (2 log3je+7 (2x4-3) —1) = 0=ф
=Ф log3x+7 (2x4-3) = 1 или 2 log3x+7 (2х-}-3) = 1 =0
=>2х4-3 = Зх4-7 или (2х4-3)2 = Зх-|-7.
Первая из полученных возможностей приводит к х =—4, но при этом зна-
чении 2х-}-3 = —5 < 0, что противоречит условию 2х-(-3> 0. Вторая возмож-
ность дает 4х24~9х4-2 = 0, откуда х = —2 или х =—1/4; но’при х =—2 осно-
вание логарифмов 2x4-3 = —1 < 0, что опять противоречит условию. Значение
х =—1/4 удовлетворяет всем условиям.
225. {0}. 226. {2; 3}. 227. {2-2/3; 8}. 228. {log2 (3/5); log2 (2/5)}. 229. {2}.
230. {—log23}. 231. {14}. 232. {3; 10}. 233. {1/12}.
288
234. {(-1)” arcsin 2-r~(logs o)/2+nn | n£Z, 0 < a < 1}.
235. x£0 при ag] —oo; O](J{1; 2}; x = a+2 при a£]0; 2 (U{3};
x = a ± 2 при ] 2; 3 [ (J]3; + 00L Решение. Так как Ух и а2 являются
основаниями логарифмов, то х Ф 1, а 1; неизвестное х, входит в выраже-
ние Ух, следовательно, х > 0; а > 0, так как логарифмы берутся только от
положительных чисел; кроме того, 0 < (а2—4)/(2а—х) < + оо и, следовательно,
а Ф 2, х Ф 2а и х > 2а при 0 < a < 2 и х < 2а при а > 2» Заметим, что при
этих условиях
log^z—a = 2/logax
и
loga2 ((a2—4)/(2a—х)) = 0,5 loga ((a2—4)/(2a —х))
и заданное уравнение можно записать в виде
Iogola^=IogaX=^l^=7=X=?>x2—2ajc+a2—4 = °=^* = a ± 2.
Так как при ag ] 0; 1 [ (J ] 1; 2 [ мы имеем х > 2a, то из двух найденных решений
этому условию удовлетворяет только х — а-\-2. При a > 2 величина х < 2а и,
следовательно, этому условию удовлетворяют оба решения, кроме а = 3,
так как в этом случае х = а—2 = 1, что исключено из значений х, следова-
тельно, при а = 3 имеем для х лишь одно решение х = а-|-2 = 5. Объеди-
няя все результаты, мы и получим записанное выше решение.
236. {25}. 237. {З-2; .1; 3}. 238. х£0 при а£] —оо; 1]; х = а± 1 при
ag] I’» У % [U] /2 ; 2 [U1 2; +оо[; х = а-}-1 = 3 при a = 2. Решение.
Из рассмотрения уравнения заключаем, что х>0, х # 1, a > 0, a ?= 1,
а2—1 > 0, т. е. | а | > 1, а так как а > 0, то отсюда следует, что а > 1;
а2—1 5^ 1, т. е. а2 2 или а Ф У 2; и наконец, 2а—х > 0, т. е. х < 2а. Сле-
довательно, для неизвестного х получим границы 0 < х < 2a, х?Н. Записывая
данное уравнение при основании всех логарифмов, равном 2, получим
log2 (2a—x)4-log2x = log2 (a2—1) => (2a—x)x = a2—1 =£
=$>x2—2ax+a2— 1 = 0 => (x—a)2— 1 => x — a ± 1.
Всем перечисленным выше условиям найденные решения удовлетворяют, кроме
условия х # Г, действительно, при а = 2 получаем два значения для х, одно
из которых, х = а+1=3, удовлетворяет всем условиям, а второе, х=1, ре-
шением не является. .Объединяя все результаты, мы получим записанное
выше решение.
239. {а2|а=1/}<2; а # 1). 240. {4}. 241. {(2+ ^3)1о®‘ <2+*Т)}
242. {arcsin (l/14)+2nn | ti^Z}. 243. {1}. 244. {!}. 245. {—1}. 246. {—1:3}.
247. {16}. [248. {9}. 249. {2}. 250. {1; log3 2}. 251. {2; 64}. 252. {l/j/з}.
253. ;{4; 36}. 254. {0; 3}. 255. {9}. 256. {1/3; 9}. 257. {10; 104}. 258. {1}.
259. {5-4; , 5}. 260. {—1/2; 1/2}. 261. {—1/2; 1/2}. 262. При всех
ag] — «о; [0(U]0; 1/8[. 263. 11/5; 2/5[. 264. ] 1/3; 2 [. 265. J —1/2; 1/2[.
266. )1; 2Ц_|]3; 4[. 267. [—1; 1[U]3; 5]. 268. ]2; 3[. 269. ]-<»; 1/2[.
270. J4; 6[. 271. [1/3; 1/2[. 272. [1/3; 2/3[. 273. [—7; —}<35[U15; ^351.
274. ] —оо; —3/2[(J]3; +«[. 275. [1/2; 4]. 276. ]1//27; 4-оо[.
277. JO; 1/2JU1 2; 4]. 278. ]0; 10[. 279. ]0,1; 1 [{J 1 1;
' 280. 1—1; 0[[J]l; 2[. 281. [logs0,9; 2[. 282. ]—1; 4-оо[.
Ю В. М. Говоров и др. „ 289
283. 1—4/3; —17/22[.
284. ]—2; 2—У15[. Решение. Так как анаменатель дроби всегда > О,
то и числитель должен быть ^0, чтобы выполнялось неравенство. Трехчлен.
2 —5х—х2 > 0 при х£]—2; 1/3[, и только при этих значениях знаменатель
имеет смысл. Трехчлен х2—4х-|-11 = (х—2)2+7^7 при любых и при
этом log5 (х2—4x4-11)2 > 0. Трехчлен х2—4х—11 принимает неотрицательные
значения при х£] — оо; 2—У 15[(J ]24" У 4~оо[ и лишь при этих значе’
ниях logn (х2—4х—II)3 имеет смысл. Итак, чтобы левая часть неравенства
имела смысл, необходимо, чтобы выполнялись оба неравенства, т. е. чтобы
х£]—2; 2—У 15[. На этом интервале 7 (х) = logn (х2—4х—11) < 0. Дейст-
вительно, f (—2) = logn I3 == 0, /(2—У15) = logn 0 =—оо. [Минимального
значения трехчлен х2—4х—11 достигает при х = 2. При изменении х влево
от х = 2 значения трехчлена постоянно растут, при х = 2—У15 его значение
равно нулю, при х=+2 это значение равно 1; таким образом, /(х) при
изменении х от 2— У15 до —2 монотонно возрастает, оставаясь все время
отрицательной. Следовательно, числитель дроби в левой части неравенства
при х£]—2; 2—У 15[ положителен и неравенство справедливо при этих
значениях.
285. J-oo; —2[(J]—1/2; +<»[. 286. ]6; 4-оо[. 287. 12; 5/2[.
288. ]-оо; —1[U№ +<»[. 289. ]-оо; —2[UH; +«>[.
290. J—4/3; (3—/17)/2[[J](3+/T7)/2; +«>[.291. ]-УТ;-1[иЛ; /2[.
292. ]—1; 0[Ull; + «>[. 293. ]—16/3; —3[.294. ]1;2[U]3; +«>[. 295. ]2; +«>[.
296. ]1; 2]u[3; 4[. 297. ]— /5; — 2[U]1; /5[. 298. ]2; 3[. 299. ] — oo; 2(.
300. J —oo; 0]U[loge5; 1[. 301. ]-3; -/6[U]/6; 3[.
302. J—4; —3[U]8; + oo[. 303. ] —oo; —1 —/2 [UJ —1 + /2; I [(J ] 1;+ oo[.
304. jlogs 10; +co[. 305. ]3; 4[UJ6; + oo[. 306. j—1/2; 0]. 307. J—1/2; —1/3[.
308. JO; 1/2[(J]2; 3[. 309. ]-oo; -2[[J]-/2l -1[U]1; /2[[J]2; +«>[.
310. j-oo; —2/3]U[1/2; 2]. 311. [/6—1; 2[U]2; 5]. 312. ]log2 (2/3); 0[U]0;+oof.
313. ]—1; (l-/5)/2[Ul(l + /5j/2; 2[. 314. ]4;+«>[. 315. ]0; l[U]/3; 9[.
316. jlog2(5/4); log23[. 317. [log214; 4]. 318. J3; 10[. 319. J5/8; +oo[.
320.,'[0;25/48]. 321. ]0; l/5[(J]1; 5/5[. 322. ]1;4[. 323. |0;27[. 324. [0;l/3[U]3;10/3].
325. ]0; 1/8] [J [1/4; +co[. 326. [2+/2; 4[. 327. ]3/4; 4/3[.
328. 30; 1/2[(J]1; 2[UJ3; 6[. 329. ]2; +oo[. _ _
330. ]—3/2; —1[U1—Il 0[U]0; 3[. 331. ]10— /43; 4[U]10+/43; +oo[.
332. 12; /2+l[U[3,5; +oo[. 333. ]5; 5,5[U[6,5; +oo[.
334. [-/8; —1[ U ]1; (/4T—1)/5]. 335. ]0; 1] [J ]2; +oo[.
336. ]3; 5—/3[U]7; +oo[. 337. ]-6; —5[U]-3; —2[.
338. ]0; (3—/5)/2[(J[5/2; (3+/5)/2[.
339. ]—2; -HUJ-1; 0[U]0; 1[U]2; +oo[.
340. ]1 -/7;- 1[(JJ —1/3; 0[U]0; 1/3[U]2; l + /7[.
341. [l/2;l[U[2;+oo[.342J3;4,5[U]8; + oo[. 343J-/2;-l[U]l;/2 [.
344. [—4; —1]. 345. ]—4—/2; —5[(J]—3; —4+/2[(J]l; 2[. 346. ]0,7; 1[.
347. ]—1; 2[. 348. ]—1; — 2//5[U]2//5; 1[.
349. ]4nn; n(12n+D/3[U]n(12n+5)/3; 2«+4nn[(n^Z).
290
350. ]0; 1[U[3; 4-oo[. 351. ]0; l/]<5 [(J]l; 3[. 352. ]0; 10(,g 0>s,lg 3)/Ig I>5[.
353. 10; 1/2[U[K2; +*>[• 354. ]0, 1/4]U[h 4[. 355. ]3; 9]. 356. [2; + «[.
357. ]0; 1/4] U ]4; + oo [. 358. ]log6 (1 + V 2); log5 3[. 359. ]log2 5; 3[ U ] log214; + oo [.
360. JI; 103[. 361. ]—1; 0]. 362. ]0; 3[ U ]7; +»k
363. x^Jl; (1 + Kl + 4a2)/2 [при a£]0; i[;
xC] (1 Ч-F l+4a2)/2; +oo[ при a^]!; +oo[.
364. x£]a4; «-1[ при a£]0; 1[; x^]a-1; a4[ при xg]l; 4-oo[.
365. x£[(202—53d)/24; -J-oo] при d£] —oo; 2[; x£[4; -}-oo[ при d=2;
x£[3d—2; 4-oo[ при d£]2; H-oo[.
366. «6)0; a5[U]«3; a2]U]«-1; +оо[при a£]0; 1[;
x£]0; в-'ШН; a3[UHs; +«[ при a£]l; +»[.
367. ]0; 10-s[(J]10-2; lO^UPO3; + «o[. 368. ]—oo; —2[. 369. ]1; 2[.
370. ]0; 10-1](J[102; +«>[•
371. [3; -|-oo[. Решение. Выражения в левой части имеют смысл при
х£]1; Н~оо[. Тогда, учитывая, что logi/3y—убывающая функция, имеем
logi;s*+21ogi/e(x— l)<log1/36 =ф logvsCx2—x)<logi/36 => ж2—х5&6 =5>
=>ж<—2, или жй=3. Так как, кроме того, ж£]1; Н-оо[, то первое полу-
ченное неравенство отпадает и заданное неравенство выполняется только при
*£[3; +оо[.
372. ]3; 4[.
373. x€[loge (4+У 16+а2); 3 loga2 [ при а£]0; 1[;
*€[loga (4+ V 164-а2); + оо[ при а£]1; + <»[.
374. [2; +оо[. 375. ]—l+log2 (5+ КЗЗ); +оо[.
376. ] — 1 — Кб; -3[U] Кб— 1; 5[. 377. ]0; 1/6[(J]3/2; + оо[.
878. ]—2; 2[. 379. ]—1; + «[. 380. [2; + °о[. 381. ]—3; —К1Й11]К5: 3[.
382. ]1; 2[. 383. ]1/3; 1[. 384. ]—оо; —5[U]—5; — 1[U]3; +оо[. 385. ]2;5/2[.
386. {1}. 387. {(2; 3/2)}. 388. {(1; 2), (2; 1)}. 389. {(2; 2)}. 390. {(2; 3), (3; 2)}.
391. {(4; 2), (1; 1)}. 392. {(—2; 0)}. 393. {(—2; 1/784)}. 394. {(12; 4)}.
395. {(5; 2)}. 396. |{(8; 2)}. 397. {(27; 4), (1/81; —3)}. 398. {(2; 10), (10; 2)}.
399. {(2^2; р^в)}. 400. {(3; 5)}. 401. {(5; 1/2)}. 402. {(5; 1)}. 403. {(4; 16)}.
404. {(9; 7)}. 405. {(4; 2), (2; 4)}. 406. {(10/3; 20/3), (—10; 20)}. 407. {(2; 1/2)}.
408. {(2; 2)}. 409. {(625; 3), (125; 4)}.
410. {(г*/ *082 7/10g’5; 3Z1O45/1^ 7) }. 411. {(аз. д-X). (а-1. а3) I а>0}.
412. {(2; 1/6)}. 413. {(20; 16)}. 414. {(4; 2)}. 415. {(2; 5)}. 416. {(6; 2)}-
417. {(4, 16)}. 418. {(2; 4), (4; 2)}. 419. {(512; 1)}. 420. {(3; 9), (9; 3)}.
421. {(5; 5)}. 422. {(64; 1/4)}. 423. {(2; 1/4), (2+К7; 2+К 7)}.
424. {(4; 1)}, (16; 2)}.
425. {2; 1}. Решение. Первое уравнение системы можно переписать
так (ху 0):
22(^2+i/2)w=25s^?J^i^=5==:> 2—+— =5=> 2 (—Y —5 fi^+2 =
*У У х/ у \у J \у J
8= 0 => —2^ х^2у или z/ = 2x.
10*
291
x = 2yt
х2—у2 = 3,
х—у > 0,
х+у > 0,
ху # 0;
Решая совместно два уравнения из
(2; 1) и (—2; —1). Первое из этих
второе не удовлетворяет третьему и
Таким образом, исходная система уравнений сводится к двум системам
( x = 2yt ( У=*2х,
] log3(x—y) = l — Iog3(x+^), •! log3(x—y) = l —log3(x+^),
( xy 0; \ xy 0.
Из второго уравнения системы замечаем, что х—у > 0 и х-[-у > 0. Системы
можно переписать так:
f у=2х,
х2 — у2 = 3,
ч х—у > 0,
х+У> 0,
. ху^О,
первой системы, получаем два решения:
решений удовлетворяет всем условиям, а
четвертому условиям. Подставляя у = 2х
из первого уравнения второй системы во второе уравнение, получаем проти-
воречивое равенство —3#2 = 3; следовательно, вторая система решений не
имеет. Итак, данная система имеет единственное решение (2; 1).
426. {(1; 1)}. 427. {(2; 6)}.
§ Ю
К2 sin ^2а-|~^
61. —1. 62.
1/sin а = cosec а. 63. 2
64. 32 sin2 а cos4 а.
65. 1. 66. tga. 67. 2. 68. tg5a. 69. 3/2. 70. 1, 71. cos 2а. 72. 0. 73. tg2a.
74. _1/2. 75._ (sin 4a)/2. 76. sin2 a. 77. 1. 78. sin 2a. 79. 1/4. JO. /2— У 2/2,
(/6—/ 2)/4. 81. 2. 82. 42. 83./4,5. 84. /3. 85..?(3— У 3)/2. 86. У 3/8.
87. 0. 88. 4. ,89- 9. 90. У 2/8. 91. —1. 95. 225/128. 96. ctg(a/2)=— 3 или
ctg(a/2) = — У15/3. 97. 65/113. 98. —3 99. (1— a2—2a)/(l — a2+2a).
100. 31/49. 101. —2//13. 102. 5//26. 103. 1//5. 104. 10/11.
105. (4—3 (m2—1)2)/4, |m|</2. 106. /2 tgasln (y-f-a).
107. 2/3 cos sin f/x-H—'j . 108. 4 cos a sin cos —
109. sin (a-15°)cos (a+15°). 110. 4/2sin (j—Ila).
nt a»/ • ^""HP—60° a+P+60° 0 90
111. 2 sin (a — p) sin —-----cos —-------sec2 a sec2 P.
112. 0,5 cos (a—p) sec a seep. 113. Зл/4. 114. 17л/12. 115. 127°.
116. /3/2. 117. л/2. 118. 24/25. 119. 17/25. 120. 3/5. 121. —3/5. 122. 2/3.
123. 3/4. 124. 14/15. 125. —7/25. 126. —3/4. 133. 4/5. 134. 3/5. 135. 2//5^
136. 1//5. 137. —л/7. 138. Зл/7. 139. л/7. 140. —л/7. 141. 6л/7.
142. arccos (12/13) = arctg(5/12) = arcctg (12/5). 143. {2; 4}. 144. 1/2. 145.1
146. Л
147. Х02—/9—2л; 2+/9—2л(.
292
§ 11
1. х = (—1)"n£Z.
2. х= (—1)л arcsin (-l/3)4-nn = (—l)w+x arcsin (1/3) +лп, n£Z.
3. х — (—1)”arcsinО-|-лп = лл, n£Z.
4. х = (—1)" arcsin 1-|-лп = (—1)"лп, n£Z. Полагая n = 2k и
л
п = 2&4“1, получаем в обоих случаях х = k£Z,
тг тг
8. х=—+лл, n£Z. 9. *=—£4-лл, >£Z. 10. л (4n+(—1)")/4 (n£Z).
о 4
11. л (Зл—(—1)4/3 (n£Z). 12. л(4л—1)/2 (ngZ). 13. [2nn(n£Z).
14. пл (л£2Г). 15. 0. 16. л (4л—1)/4 (n£Z). 17. arctg 7-|-1-|-лп (n£Z).
18. (л(Зл+1)~9)/6 (n^Z). 19. л (12л—1)/4 (n£Z). 20. (л (4л—1)4-4)/3
(n£Z). 21. л(8л±1)/28, л(2А4-1)/14 (n,k^Z). 22. лл, 2л (ЗА ± 1)/3
(л, A£Z). 23. л+2лл, л(6А4-(—1)4/6 (л, A£Z). 24. 2лл (fl£Z).
25. л(4л+1)/2, nk (п, k£Z). 26. л(4л—1)/4, л(ЗА±1)/3 (Л. 'fi£Z).
27. л(3л—1)/6 (n£Z). 28. лл/2 (n£Z). 29. л(4л-|-1)/2, л (ЗА—1)/3
(n.A^Z). 30. л(4л4-1)/2, л (6А+(—1)*)/6 (л, A£Z).’ ' 31. 2лл (ngZ).
32. л(2л+1)/2, 2л(3л1±1)/3 (n,m£Z). 33. (—l)narcsin (1/3)-f-лл,
л(6А-|-(—1)*)/6 (л, A£Z). 34. л-|-2лл, ± arccos (3/4)4-2лА (л, AgZ).
35. ± arccos ((/Т9—2)/5)4-2лл (л£Z). 36. л(2л4-1)/4 (n£Z). 37. л(3л±1)/3
(n£Z). 38. л(2л4-1)/4, л(3т±1)/3 (л, m£Z). 39. лл/2 (n^Z). 40. я(4м—1)/4
(n£Z), 41. arctg 2+лл, [л (4^+1)/4 ,(л, k£Z). 42. л(4п-|-1)/4,
arctg(—1/3)4-лА (л, A£Z). 43. arctg (—/2 )4-лл (n£Z). 44. л(4А—1)/4,
л(3л±1)/3 (л, A£Z). 45. лл/2, л(6А±1)/3 (л, A£Z). 46. 2лл, л(4лг—1)/2,
л(4А4-1)/4 (л, т, k£Z).
47.----—р(— 1)” arcsm —1 __
4 2/2
f-лл (лgZ) л (12л — 34-5 (—1)4/12
(n£Z). 48. (л (4л-|-1)—2arccos (4/5))/4 (n£Z). 49. л (12л—5)/12 (ti£Z).
50. лл/3, л (6А-|-1)/18 (л, A^Z). 51. л(2л4-1)/5, 2лА (л, A(=Z). 52. лл/3,
л(2А4~1)/8 (n, k^Z). 53. лА/2, 2л (Зл ± 1)/3 (л, A^Z). 54. 2лл/5, л (2А4~1)/2,
л(2л:4-1) (л, A, m^Z). 55. лл (n^Z). 56. лл/2, л (ЗА—(—1)*)/21 (л, A£Z).
57. л(2л4-1)/6, л (4А—1)/4 (л, k^Z). 58. 2л (Зл ± 1)/3, л (4А-{-1)/8 (л, AgZ).
59. л (4л—1)/4, л(4А4-3)/16 (л, A£Z). Указание. sln5x=cos —5х).
60. ((4л—1) л—4)/12, ((2А—1) л—4)/24 (n,A£Z). 61. л (12л—1)/24,
л (12А4-1)/12 (n,A£Z). 62. л(8л4-3)/24, л(8А4-2)/16 (n.k^Z).
63. arctg (2 ±/3)4-лл « л (6л-)- (—1)«)/12 (n^Z). 64. л(2л4-1)/16,
л (2А4-1)/10 (л, AgZ). 65. л(2л4-1)/4, л(2А4-1)/2 (л, A^Z). 66. л(2л4-1)/4
(n^Z)- 67. л (4л4~1)/4 (n^Z). 68. лл/4 (n£Z). 69. лл/8 (n^Z). 70. л (2л4-1)/4,
л(6А±1)/6 (л.А^г). 71. л(2л4-1)/10; л(2А4-1)/4 (л, AgZ). 72. лл;
л(2А4-1)/20 (n,k^Z). 73. л(4л4-1)/6, 2лА/3 (л, A£Z). 74. л(2л4-1)/10,
л(2лг4-1)/6 (л, m£Z). 75. л (6л4-(—1)4/18, л(2А4-1)/4 (л, A^Z).
76. л(2А4-1)/10 (л, ACZ). 77. л(3л ± l)/2fa£Z). 78. 2лл ± arccos (—1/4)
(W£Z).
293
79. л(4л+1)/4 (n£Z). Решение. sin4 х+cos4 х=sinx cos х=>
(1—cos 2x\2 . /1-4-cos 2x\2 1 , n . 9 n , л > . , .
--------2---) + \~'~~2----} ==^'2sln^xz=^ 1+cos2 2x = sin2x=$> 1 + 1 —
— sin22x=sln 2x=|> sin2 2x+sin 2x = 2. Это соотношение возможно лишь при
sin2x=l, откуда 2х=-^-+2лм =t> х=-~-+лп. Итак, х=л(4п+1)/4.
80. л(4п+1)/4, 2л& (n,£gZ). 81. лп/5; л (2&+1)/2 (ntk£Z).
82. л (2п+1)/8, л (3k ± 1)/3 (и, k£Z). 83. лп/3, 2 л 6, л (2т+1)/11 (n, k, m£Z).
84. л(2&+1)/4, л(2т+1)/10 (m, k£Z). 85. л(2п+1)/16, (л (4&+1) — 8)/4,
(л (4/n4-l)4-8)/12 (л, &, m£Z). 86. л (2n+l)/10 (n£Z).87. л(3л ± l)/3(n£Z).
88. л (4Aj-f-l)/10 (k£Z). 89. л(4л+1)/2, 2л£ (n,££Z). 90. л(2и+1)/2 (n£Z).
91. л(6п—(—1)«)/12 (n£Z). 92. л (2«+1)/4, л (6fc+(—1)*)/12 (n, k£Z).
93. л (4л—1)/2, (—1)* arcsin (3/4)+лЛ (л, &£Z). 94. л(4л+1)/4,
л(66+(—1)*)/24 (л, k£Z). 95. 2л(3л±1)/3 (n£Z). 96. 2лл, л (26+0/2
(л, k£Z). 97. лп/2, л(126± 1)/6 (и, k£Z). 98. л (4n+l+( —1)")/4 (n£Z).
99. л (4л+1)/2 (n£Z). 100. л (4л+(— \)п/\3 (n^Z). 101. лл+arctg (—1 ± К 3)
(n£Z). 102. л (6л+(—1)«)/б (n£Z). ЮЗ. л (2л+1)/14 (n£Z). 104. л (2л+1)/4»
л (46+0/2 (л, 6£Z).
105. л(4л—1)/4,2лт, Л (46—1)/2, л (4Z+1 +(—1/]/ 2<arcsin ( j/ 2/4))/4
(п, mt k, l£Z), Решение. Так как cos3x=cos3x—3cosxsin2x, sin3x =
= 3cos2xsinx—sin3x, cos2x = cos2x—sin2x, то данное уравнение перепи-
сывается так:
cos3 x+sin3x—3 cos х sin x (cos x+sin x) —(cos x+sin x) (cosx—sin x) = 0
или
(cos x+sin x) (cos2 x+sin2 x—4 sin x cos x+sin x—cos x) = 0.
Тогда или
1) cosx+sinx=0, или 2) l—2sin 2x+sinx—cosx = 0.
В случае 1) tgx=—1 и х = л(4и—-l)/4 (ngZ). В случае 2) положим
sinx—cosx=у; (!)
тогда r/2 = (sin х—cos х)2 = 1 — sin 2х и, следовательно,
sin2x=l— у2. (2)
Подставляя эти значения в уравнение, получим 1 — 2 (1 — у2)+# = 0 или
2*/2+#-—1 = 0. Корни этого уравнения—1 и L/2. Тогда для нахождения х
получим уравнения
a) sinx—cosx = —1 и б) sinх—cosх= 1/2.
(Заметим, что если воспользоваться соотношением (2), найти значение х проще,
но при этом могут появиться посторонние корни, так как уравнения (1) и (2)
не эквивалентны. Из (1) следует (2), но не наоборот.) В случае а) уравнение
перепишем так:
sin х +1 — cos х = 0.=ф 2 sin (x/2) cos (Jv/2)+2 sin2 (x/2) =>
=^> 2 sin2 (x/2) (etg (x/2) +1) =x 0 => sin (x/2) =0 или etg x = — 1 =4>
=>х = 2лт, х = л(4£—1)/2 (m, fegZ).
В случае б) правую и левую части уравнения умножим на Y 2/2 и перепи-
шем его в виде
sin х cos (л/4)—cos х sin (л/4) = >/”2/4»
£94
или
откуда
*=+Н~О1 У-i.arcsin (/£Z).
106. л(2п + 1)/22, л(6*+(—1)*)/48 (п, k^Z).
107. л/г, л (66 ± 1)/6 (n, k£Z). Решение, sin Зх₽— 4sin xcos 2х = 0=>
=>3sin xcos2x—sin3x—4 sin xcos2x = 0 =£> sin x ^3- CgS %X—-——
— 4 cos 2x) =0 => sin x (1 — 2 cos 2x) = 0 => sin x = 0 или 1—2cos2x — 0=$>
=^х = л/г, 2x = ± 4г-|-2л£ (n,k^Z). Таким образом, корнями данного урав-
«5
нения будут ли, л(6&± 1>/6 (/г, k£Z).
108. л (6/1-4-(—1)")/12 (n£Z). Решение. sin2xtgx+cos2xctgx —
. « 1.4 .4 -sin4 х-4-cos4 х , п , . sin2x+cos2x
— sin 2х = 1 Ч-tg x-J-ctg х =>—-—!----sin 2х=Н------:!-------=ф
* ‘ ь sin X COS X 1 sin X COS X
2 2
=> ——-----sin 2x—sin 2x= 1-]—-—=ф—2 sin 2x== 1 => sin 2x —— 1/2. От-
sin 2x 1 sin 2x
куда х = л(6п+(—1)”)/12 (n^Z).
109. лп, л(4*-}-1)/4 (n,k£Z). 110. ^^arcsin (4—2}<3)+-y« (n^Z).
111. 2л (3« ± l)/9 (n£Z). 112. л (4n+l)/2, л+2л* (n, k£Z). 113. л (4n-M)/2, 2л*,
л(4т+1)/4 (n, k, m£Z). 114. л (4«+l)/4 (ti£Z). 115. л (8*+1)/4,
л (8/i4~3)/12 (n, k£Z). 116. 2л/г, л (4k—l)/4, л(4т—1)/2 (n, k, m£Z).
117. л(12п—3-4-2 (—1)«)/60 (n^Z). 118. л(4п+1)/4 (n^Z). 119. л (4n-|-l)/2,
л (26-4-1) (n, k^Z). 120. 2л/г, 2 arctg (3/2)+2л& (n, k£Z).
121. л/г—arctg (—1/2) (ngZ). Решение. Переписываем данное уравне-
ние в виде
cos2x—2 (1 — sin х) cos х—4 sin х=0.
Это квадратное уравнение относительно cosx. Решаем его:
cosx = 1—sinx ± У1—2sinx+sin2x+4sin х==
«1—sin х ± Y1+2 sin x+sin2 х— 1 — sin х ± (1 + sin х).
В случае верхнего знака получаем cosx = 2, этот случай надо отбросить.
В случае нижнего знака получаем cosx = — 2sinx или tgx = — 1/2, откуда
х = — arctg (1/2) + яп (n£Z). Если решать данное уравнение, выразив все
функции через tg (х/2), то придем к уравнению
3 tg4 (х/2) —12 tg3 (х/2)—2 tg2 (х/2) - 4 tg (х/2) — 1 = 0г
которое можно разложить на два сомножителя
(tg2 (х/2)—4 tg (х/2) — 1) (3 tg2 (х/2) + 1) = 0.
Второй сомножитель нулю не равен ни при каком значении х£/?, а пер-
вый обращается в нуль при tg (х/2) = 2 ± V* 5, т. е. при х = 2 arctg (2 ± У 5) +
+ 2лп (n^Z). Это другая форма записи решения. Легко показать, что если
tg (х/2) = 2 ± У 5, то отсюда следует, что tgx = —1/2. Верно и обратное.
Таким образом, обе записи решения эквивалентны.
295
122. ji«+arctg(3—2/2) (n£Z).
123. лп/3, nk ± arctg (l/y~2)s&nk ± 0,5 arccos (1/3) (n, k£Z). P e ш e н и e.
Заметим, что tg2x = 2tg x/(l—tg2x), a tg 3x = (3 tg x—-tg3 x)/(l — 3 tg2 x),
причем x Ф л (2Z—|—1)/4, x л (2/n4~l)/6 (Z, m£Z). При подстановке этих зна-
чений и преобразований заданное уравнение примет вид
tg х (2 tg4x—7 tg2x+3) = 0,
откуда следует две возможности:
tgx = 0, 2tg4x~7tg2x+3 = 0.
Первая возможность дает х==лр (p£Z). Вторая возможность flaeTtgx=±}^ 3
и tgx=± 1/К' 2 и, следовательно,
х=±4г-1~ят (mgZ), х=± arctg (1/У~2)Ц-л<! (k£Z).
О
Ранее полученное решение х = лр и решение х = л(3т± 1)/3 можно объеди-
нить и записать х = т/3 (n£Z). (Прип = 3рмы получим лр, а прил = 3/п ± 1
получим л(3т±1)/3.) Итак, все решения можно записать так: лл/3,
nfe±arctg(l/K2) (n, kgZ). Легко доказать эквивалентность этой формы
записи решения другой, приведенной выше.
124. л(2п-Н)/6, 2л(3£±1)/9 (n, k^Z). Указание. Введите новую
переменную Зх=р. 125. 4лп (n£Z).
126. л (24л4-1)/12, л (24&—7)/12 (n, k^Z). Решение. Для того чтобы
данное уравнение имело решение, должны выполняться условия
1) sin ^Зх+-2-)^0 и 2) l + 8sin2xcos22x^0. При этих условиях возводим
в квадрат правую и левую части
4 sin2 ^Зх-(--^-^ = 1Ч~8 sin 2х (1 —sin2 2х) => 2^1 — cos ^бх-f—=
= 14-8sin 2х—8sin32х =ф 24-2sin 6х= 14~8sin 2х—8sin3 2х =ф>
=^> 24-2 (3 sin 2х—4 sin3 2х) = 14~8sin 2х—8sin32x=>
=ф> l=2sin2x=>x = -^-4”^ и x=-^'4~Jim tn£Z).
1^2 1 £
Проверим, будут ли все найденные значения х удовлетворять условиям 1) и 2).
Подставим х=-у™--| л/ в первое условие
sin ^3x4-^=sin ^-^-4“Зл/4—=sin ^Зл/4--^-^ ^cos Зл/,
cos3nZ=l > 0 при I четном и cosЗлZ = — 1 < 0 при Z нечетном. Для выпол-
нения первого условия полагаем Z = 2n, тогда х =-или sin х= 1/2.
Это значение х подставляем во второе условие. Тогда имеем
14-8sin 2хcos2 2х= 14-8 •-j • |=4 > 0,
т. е. второе условие также выполнено, т. е. х — л (24«4- 0/12 является реше-
нием данного уравнения. Подставим теперь х=-у^4~шп в первое условие;
296
получим
sin =sin ^sin ^Др4~3шп^ =— cos Зл/n,
— cos Зл/n = — 1 < 0 при четном т и —cos Злт = 1 > 0 при т нечетном.
Для выполнения первого условия полагаем в этом случар m — 2k—1; тогда
7 л
х —---1у4-2л&. Так как и в этом случае sin 2х — 1 /2, то второе условие
также выполнено, следовательно, х — л (24&—7)/12 является решением данного
уравнения.
127. л(2п4-1)/2, л(6$ + (-1)*)/24 (и, k£Z). 128. л (6п — (—1)")/12
(n£Z). 129. arctg (2/3)4-лм (n£Z). 130. л (6n— (—1)")/18 (n£Z).
131. лп—(—l)rt arcsin (1/3) (n£Z). 132. лп-[-arctg ± , л& +
+ arctg 1 ±^13' (n,k£Z). 133. л(8п —1)/4 (n£Z). 134. 4. 135. 0.
136. лп ± arccos (1/3) (n£Z). 137. л (2п+1)/6, л (4*+(—1)*)/20 (п, k£Z).
138. 2л(3п±1)/3 (n^Z). 139. л(6п±1)/18 (n£Z). 140. лп/5,
(2л* ± arccos (1/4))/5 (п, k£Z). 141. лп, л (6k ± 1)/3 (п, k£Z). 142. л (2п-|-1 )/2,
л(4*+1)/4 (п, k£Z). 143. л(2п+1)/4 (n£Z). 144. я (2k +1)/4, л (6п ± 1)/6
(п, k£Z). 145. л(6п± 1)/6, (n£Z). 146. лп/2, л(2*+1)/8 (п, k£Z). 147. лп,
л(3*+1)/3 (п, *£Z). 148. л (2п + 1)/4, л (6* ± 1)/6 (п, k£Z). 149. л (2п+1)/8,
л(3*±2)/9 (п, k£Z). 150. л(2п+1)/6, л(6*—(—1)*)/12 (п, *gZ). 151. 5лп,
5л(2*+1)/2 (п, k^Z). 152. 2лп/3, л(4*+1)/4, л(4m—1)/4 (п, k, m£Z).
153. arctg(—1/3)+лп, л(4*+1)/4, л(2т+1)/2 (п, k, tn£Z). 154. лп,
л(4*—1)/4 (п, k£Z). 155. лп, n(6*± 1)/3 (п, k£Z). 156. лп/3, л(2*+1)/7
(п, k£Z). 157. 2лп, 2л(3*± 1)/3 (п, k£Z). 158. лп/3, л (4*+1)/12 (п, k£Z).
159. л(2п+1)/8 (ngZ). 160. л(2п+1)/2, л(6* ± 1)/15 (n,k£Z).
161. л(2п+1)/Н. 2л*/5, л(2т-[-1)/2 (п, k, m£Z). 162. лп, л(6*+1)/48
(п, k£Z). 163. л(4п+1)/4, 2л (3* ± 1)/3 (п, k£Z). 164. лп, л (6*+(—1)*)/6
(п, k£Z). 165. л (4п+(—1)")/4 (n£Z). 166. л (Зп ± 1)/6 (ngZ). 167. л (2п+1)/4,
n(3k—1)/6 (п, k£Z). 168. л(2п+1)/6 (n^Z). 169. л (12*4-3+4 (—1)*)/36
(*£Z). 170. л(6п+(—1)«)/6 (n^Z). 171. л(4п—1)/4, л(4т+1)/8 (п, m£Z).
172. л(4п+1)/4 (n^Z). 173. (лп + 3)/2 (n£Z). 174. 2л(Зп+1)/3 (n^Z).
175. лп, л(3*+(—1)*)/6 (п, *£Z). 176. л(4п—1)/4, n*+arctg3 (п, k^Z).
177. л(2п+1)/4 (n£Z). 178. л(2п+1)/4 (n^Z). 179. 2лп/3, л(4*+1)/6
(п, *£Z). 180. л(Зп + 1)/3, л+2л* (n,*gZ). 181. ± arccos (1/4)+2лп (n£Z).
182. л(6п+1)/6, л (6k ± 1)/12 (п, k£Z). 183. л+2лп, л (4* + 1)/2 (п, k£Z).
184. лп/12 (n^Z). 185. лп/4,'л (4*+ 1)/32 (п, k£Z). 186. arcsin +
+ -2-п, я(4*+1)/4 (п, *£Z). 187. лп, л (3*+(—1)*)/6 (n,*£Z).
188. л (4п+1)/4 (n^Z). 189. л (4п+1)/2, 2 arctg(3/5)+2л* (п, k£Z). 190. лп/11,
лт (n.£N0, m£N). 191. лп/3, л*/11 (п = 0, 1,2, ...; —*£Л1). Г92. л (2п+1)/4
(n^Z). 193. л(4п+1)/4, л (4*—(—1)*)/8 (п, k^Z). 194. ± arccos ( — 1/4) +
+2лп (n£Z). 195. л(2п+1)/20, л(2*+1)/8 (п, k£Z).
196. л(4п—1)/4, (л(4* —1)—4(—l)*arcsln((/~2—2)/2))/4 (n,k£Z),
Указание. Данное уравнение равносильно уравнению
sin х (l-f-sin x)4-cos х (1 —sin2 x) = 0.
297
Уравнение sin x4-cos х—sin х cos х=0 равносильно уравнению (sin x4-cos х)2 —
— 2 (sin x+cos х)—1 = 0.
197. л(6л4-(—1)")/12, л (4*4-1)/14, л (4m 4" 0/6 (л, k, m%Z\.
198. л (6л—(—1)л)/6 (л€^). 199. л(6£+(—1)*)/6 (k£Z). 200. 2лл/5,
2л*/3 (л, k£Z).2W. л(4л+1)/6, л(6£—(—1)*)/18 (ntk£Z).2Q2. л (Зл ± 1)/3
(л£2Г). 203. л(4л+1)/4 (л£2Г). 204. л(4л+1)/2 (n£Z). 205. л(4л+1)/4
(n£Z). 206. л(6л±1)/12 (n£Z). 207. лл/2, л(66—(—1)*)/12 (n,k£Z).
208. лл/4, (л£2Г). 209. лл/4, л (3k ± 1)/12 (л, k£Z). 210. лл/2, л (2k +1)/12
(л, k£Z). 211. лл/4 (л #: 4m, m£Z). 212. л (8п ± 1)/8 (n£Z). 213.>(4л+1)/8,
л(4*4"3)/4 (л, k£Z).
214. л (Зл ± 1) /3 (л £Z). Указание. Так как cos х / 0, то уравнение
разделите на cosx и примените формулу (2) § 10.
215. л(Зл+(—1)«)/6 (n£Z). 216. л(Зл+1)/6 (n£Z). 217. лл (л£Г).
218. л (Зл ± I) /12 (n£Z).
219. л (6л—1) /3 (n£Z). 220. 2лл (n£Z).22\. -~4-лл, 2л* ± arccos 2/3,
2лт4~л ± arccos у^2/3 (л, k, m£Z). 222. лл, 2л* ± arccos ((—3+ К5) /6),
2лт ± arccos((—3—К 5)/6) (m, k, n£Z).
223. Если а=2лл (n£Z), то
{[л (4*- 1) /2; л (4*4-1) /2] | k£Z}-,
если а = (2л4-1) я (n£Z), то
{[л (4*4-1)/2; л (4*4-3)/2]\k£Z}\
если л£]4лл, (4л4-1)л[ (ti^Z), то
{(л (8*4-7 ± 1) — 2a)l4\k£Z}-i
если аС](4л-Н)л, (4л+2)л[ (n£Z), то
{(л (8>fe4-5 ± 1) — 2а) /41 k^Z}}
если (4л-|-2) л, (4л4-3)л[ (n^Z), тъ
{(л (8k+3 ± 1)—2а) /4 ] k£Z}i
если а£] (4л4-3) л, (4л4-4)л[ (n£Z), то
{(л (86-4-1 ± 1)—2а)/4 lk£Z}.
224. 2/(Зл(2л4-1)—4), 1/(3(л*4-(— 1)*arcsin(3/4))—2) (k, n£Z).
225. 2лл; ± 2arccos ((—14-К4о4-3)/4)4-4л^ при а£[—5/4;5];
±2arccos((—1—У*4а4~3)/4)4-4л/л при 5/4; 1] (л, k, m£Z).
226. (— l)ra+1 arcsin (л/8) -f- л (Зл—1) /3, (— 1)л агозт(л/4 К 2)4-л (4k—1)/4
(л, k£Z).
227. л (24л 4" 13) /6 (n^Z). Указание. Y 3cosx4- sinx—2 =
= 2 cos х—— 1 .
\ \ Ь / )
228. х= [(—1)л arcsin (1 — V^2a-\-3)-\-nk]/2 (k^Z) при ag[—3/2; 1/2].
229. л (2л4-1) /4 (n£Z). 230. лл/2, л (4k ± 1)/8 (л, k£Z). 231. л(2л+1),
л (4*4-1)/4 (л, k£Z). 232. л(4л4-1)/4 (n^Z). 233. л (12л ±5)/6 (n£Z).
234. л(6л±1)/6 (n£Z). Решение. Для решения данного уравнения
требуется, чтобы 4 cos 2х > — 1, т. е. cos 2х > —1/4 (2 cos 2x4-2^ 0 при лю-
бых x£R). Тогда, умножая на Vе4 cos 2x4-1, возводя в квадрат и преобра-
298
зуя, получим уравнение
8 cos2 2*4-10 cos 2*—7 = 0
или
(4 cos 2x4-7) (2 cos 2х— 1) — 0.
В этом выражении 4 cos 2*4-7 >0 при любых x£R> поэтому 2cos2x=l й
х = я(6/г i 1)/6 (n£Z).
235. К 3.
2 t$z x
236. л (4n 4~ D/4 Решение, sin 2*4~tg* = 2 1 4- tg'2~x~*~ x ~
= 2 —> tg3 x—2tg2*4-3tgx—2 = 0 —> (tg x — 1) (tg2 x—tg *4-2) = 0. Второй
множитель ни при каком xCR не может обращаться в нуль. Поэтому данное
уравнение при условии, что х # л (2/4-1)/2 (/£Z), эквивалентно уравнению
tgx—1=0, откуда х = л(4л4"1)/4 (n£Z).
237. л/г, л(86± 1) /4 (/i, k£Z}. 238. л/г4-arctg (3/4), л(4£—1)/4 (n, k£
£Z). 239. я(3п±1)/3 (n£Z). 240. л (2/14-1), я/и4-агс^4 (/г, т g Z).
241. л (4/14~ 1) /4, л (26 4-1) /2 (n, k£Z).
242. л (4/г—1)/4, лб (/г, k£Z). Решение. Выражения, стоящие в ле-
вой и правой части данного уравнения, имеют смысл при условии, что х £
Ф л (2/4-1) /2 (/£Z). Так как 1 — tg x = (cos х—sin х) /cos х, 14~sin2x =
= (cos x4-sin х)2, 14-tg x = (cos x4~sin x)/cos x, причем cos x 0, то уравне-
(cosx—sin x) (cos x+sin x)2 , . , .
ние принимает вид ----------cosx----------— ’ 4~tgx =£>
=£> (cos2 x—sin2x) (cos *4-sin *) /cos x = 14-tg x =5>
—>cos 2x-(14-tg x) = (l 4-tg x) =£ (1 4- tgx) (cos 2x—l) = 0 =S>
==>tgx= —1 или cos 2x = 1 => x — л (4/г—1)/4, или х=я6, где nt k£Z.
243. я/г/4 (n£Z).
244. 2л/г (n^Z). Решение.
2tg2x4-3=—— =^>2sec2Jt+l-------- = 0^>2 (—— V—3 f—1—^+1 =
cosx cosx \cos x/ \cosx/
=o=> (—!—1} (——i^o.
\cosx / \COSX J
Заметим, что уравнение имеет смысл лишь при условии cos х 0. Второй
множитель полученного произведения ни при каких x£R нулю не равен.
Первый множитель равен нулю, если cosx=l# т. е. х = 2лп (ngZ).
245. л(6п±1)/6, л(3/п i 1)/3 (/и, n£Z). Решение. Обозначим
gjsm2x_^. тогда gjcos2x__g|i-sm2x_g| ^_3 и уравнение после преобразований
принимает вид у2—30//4-В1=0, корнями этого уравнения будут // = 3иу —27.
Тогда 81sin2* = 3 или 81S1I,2,V = 27. Первое из них можно переписать 34SH12x =
= 3 =ф4 sin2x = l =t> sinx= ± 1/2=Ф х= ±-g-4-лп (n£Z). Второе уравнение
дает 81’1п‘х=27 =*>34sIn2x = 33 =>4sin2x = 3=>sinx= ±V 3/2=£х= +
О
4-лт (m^Z). Следовательно, решениями данного уравнения будут множества
л (6/г ± 1) /6, л(3/п± 1)/3 (n, m^Z). Это множество решений можно записать
и в другой форме: л (30п-|-15 ± 4)/60 (ngZ).
246. 1; 2J. 247. «€[2;. 6]. 248. 7л/18. 249. 0°. 250. — 31л/24;
299
л/24; 17л/24. 251. л (2/n-f-1)/2, л (6n ± 1)/3, 2л& ± arccos (—2/3) (m, n,k£Z).
Наименьшее расстояние между положительными корнями равно л/6.
252. —5л/6; —2л/3; 0; л/6; л/3. 253. 0; л/8; л/4; л/2, 5л/8; Зл/4; я.
254. л (2&-}-1)—arctg 3 (k£Z)t т. е. все числа, для которых п — число нечет-
йое. 255. —7л/12; л/12; 5л/12. 256. — л; —5л/6; —2л/3; —л/3; 0; л/6.
257. л (Зп— 1)/6 (п = 3, 4, ...). 258. п, (—1 ± ]Лз"+41)/2 (n£Z; 6 = 0, 1,
2, ...), х7 = (— 1 + ^23)/2. 259 . лп (n.£Z), 4950л. 260. лп4~(—1)” arosin (1/3)
(n£Z). 261. лп (n = —1, 0, 1); л (66-4-1) /6 (6 = —2, —1, 0, 1); л (6m— 1)/6
(т = — 1, 0, 1, 2). 262. л(8п-|-5)/8 (n£Z). 263. ]2лп; л-|-2лп[, n£Z.
264. ]л (12n+1) /6; л(12п+5)/6[, n£Z.
265. ]4лп, n(12«+l)/3f (J ]л(12га+5)/12, 2л4-4лп[, n^Z.
266. [л(12п—7)/6; л (12п4-1)/6], n£Z. 267. л(4п— 1)/2, n£Z.
268. ]л (8/Н-З)/4; л(8п4-5)/4[, n£Z. 269. ]яп; л(2п4-1)/2[, n£Z.
270. ]л(2п—1)/2; л (Зп—1) /3[, n^Z. 271. ]л(8п—3)/4; л(8п-}-1)/4[,
n£Z.
272. ]л (8п — 1) /4; 2лп [ (J ] л (8п 4- 1) /4; л (8п 4- 3) /4[ (J
U ]л-}- 2лп; л (8л 4-5)/4[, n£Z. 273. ]л (6п— 1) /3; 2л (Зп4-1)/3[, n£Z.
274. ]л(4п4-1)/4; л(Зп4-1)/3[, n£Z.
275. [2л (Зп4-1) /3, л4-2лп] (J [2л (Зп— 1)/3; 2яп], n£Z.
276. [2л (Зп—1)/3; 2л (Зп-Ь 1)/3], n£Z. 277. [л(12п— 7)/6; л (12п4-1)/6],
n£Z. 278. {(лп, 1/2) \n£Z}. 279. я+2яп, л (126 ±5)/6 (п, k£Z). 280. 0;
л/4; л/2; 5л/4. 281. —л/2; —л/6; 0; л/6; л/2; 5л/6; л. 282. л(8п4~3)/4
(n£Z).
283. {(л(6п4*66—1)/6, л (6п—6k—1)/6), (л (6п4-6^4-1)/6, л(6п — 6k 4-
4-1)/6)} (п, k£Z).
284. {(л(66-|-6/п—1)/6, л (6k—6т— 1) /6), (л (664-6/4-1) /6, л(66-6/-[-
4-1)/6)} (k, т, l£Z).
285. {(л/6; 2л/3), (5л/6; 2л/3)}. 286. {(п, (4п-|-1)/4), ((4п— 1)/4, п)}
n£Z.
287. {(л(664-6п± 1) /6; л (26 — 2п ± 1) /2), (л(264-2п± 1)/2; л (66—6п±
± 1)/6)} (6, n£Z). Замечание. Здесь кратко записаны четыре группы
значений; верхнему знаку в формуле для х соответствует верхний же знак
в формуле для у, а нижнему знаку в формуле для х соответствует нижний
знак в формуле для у. Этим правилом удобно пользоваться и при различных
вычислениях.
288. {(— л (12п—5) /12; л (Зп 4- 1) /3), (— л (12п — 1) /12; л (Зп 4- 2) /3)}
(«€*)• _________________________ ___________________________________
289. -^((—l)tt arcsin]/2— У 3—~(-яп, ^-—(—l)"arcsinV 2— V3—nn)j-
(n£Z).
290. {(л(2п-|-1)/2; — л(6п— 1)/6)} (n£Z).
291. {(л (4m4*l)/4; л (8п—4пг4-1)/4)} (п, m£Z).
292. л4-агссоз (('/57—б)/3)-|-2лп, arccos (("/57—б)/з) -|- 2лп^;
л—arccos ((рл57—6)/3)4-2лп, — arccos ((J^57—6)/3)-|-2лп )} (n£Z).
293. {(л (6п4-(—1)")/6, (—1)*arcsin (3/4)4-лб)} (п, 6£Z).
294. {(л (8п — 1)/4; arctg 3-)-л6)} (п, 6£Z).
гоо
295. {(л (8п ± 3) /4; я (66+(—!)*)/6)} (n, k^Z).
296. {(arocos (3/4) 4“ 2л&; — arccos (1/8) 4“ 2лп); (— arccos (3/4) -f- 2л&;
arccos (1/8)-}-2лп)} (n, k£Z). Решение. Из первого уравнения 6 cosх =
= 5—4 cos у, из второго 6sinx=—4 sin у. Возводя в квадрат и складывал,
получаем cos у= 1/8 или у— ± arocos (1/8)-}-2лп (n£Z). Тогда из первого
уравнения системы cosx = 3/4, или х — ± arccos (3/4)-{-2nk (k£Z). Так как
при возведении в квадрат мы могли получить посторонние корни, то непо-
средственной подстановкой найденных значений во второе уравнение, убежда-
емся, что из четырех комбинаций знаков годятся только две:
xt— arccos (3/4)4-2л^, yi = — arccos (1/8)4~2лп,
х2 =— arccos (3/4)4-2л£, у2 = arccos (1/8)4-2лп.
297. {(л/п; 2лп); (2л/п—arccos (1/7); 2л (Зп4-1) /3); (2л/п-[-arccos (1/7);
2л (Зп— 1) /3)} (nz, n£Z). Указание. Перемножив уравнения почленно,
после преобразований получим уравнение
tg2 (У/2) =4 sin2 у.
Оно имеет три серии решений
2 л 2 л
У1=2лп, у2 = -~—[~2лп, уз —----—}-2лп (ngZ).
О о
Каждое из найденных значений у подставим в оба уравнения исходной сис-
темы.
Для yi = 2nn получим
sinx=0 и Х1 = л/и.
тт 2л , о
Для у2 = -^—получим систему
( У* 3 cosx—5 sin х = 3 У~3,
\ 3 У~3 cos х—sin х— V 3,
откуда
cosx =1/7, sirix=—4 У"3/7, т. е. —л/2 < х < 0, х2=2лт—arocos (1/7).
тт 2л . о t
Для у3 =---з—}-2л/ аналогично получим
cosx =1/7, sinx = 4 У*3/7,
т. е. О < х <—•, следовательно, х3 = 2л/n 4~ arccos (1/7).
298. {(л (6п4-1) /3; л(6/п—1)/3); (л (6п — 1) /3; л (6/п4-1) /3)} (/п, ngZ),
299. ((л (4/n-f-1) /4; л (6п ± 1) /3);
((л/п-}-(—1)от arcsin У*2/3)/2; 2лп ± arccos V 2/3);
((пт—(—I)"1 arcsin 2/3)/2; 2лп ± (л—arccos 1^2/3))} (т, n£Z).
Решение. Так как cos 2у = 2 cos2 у—1, то первое уравнение данной сис-
темы перепишем так:
(4cos2y— l) = (2cosy— 1) (14~2sin2x) =Ф(2созу—1) (2cosy-}-l —1 — 2sin 2х) =
= 0=£> 2cosу—1=0 или cosy—sin2x=0.
В первом случае cos у= 1/2 =фу= л (6n ± 1)/3 (n£Z). Подставляя это зна-
чение у во второе уравнение системы, получим
i/""q / 1 \ ч 1
± V Vg3x + t^H±^^t^X+t^ = 2=^(tg3x)2--2(tg3x)4-1^
= 0=4>tg3x=l =4>tgx=l =ф х=л (4/п4~1) (mgZ).
301
Итак, решением системы является множество
(л (4/n+1) /4; л (6n ± 1) /3) (л, m£Z).
Во втором случае cos у — sin 2х. Тогда второе уравнение системы принимает
вид
sinyfS1'nVCO3s6^=3^^>
\ sin3xcos3x J sin у
=> ,sin2 у ((sin6 х + 3sin4 х cos2 x-]-3sin2 х cos4 x+cos6 x)—
—3sin2xcos2x (sin2x+cos2x)) = 3cosу(sinxcos x)3 =>
(1—cos2#) ((sin2x4-cos2x)3—3 (sinx cos x)2) ==
== 3cos у (sin x cos x)3 => (1 — sin2 2x) 1 ——1^
— 3sin 2x -ngfe =ф 3„sin4 2x— 14sin2 2*+8=0 =ф
О
=>(sin22x—4) (3sin2 2x—2) = 0.
Первый сомножитель sin22x—4 $£ 0 при x£Z?. Второй сомножитель прирав-
ниваем нулю, тогда ___
3sin22x = 2 =Ф sin2x= ± У”2/3.
В случае sin2x=j/’2/3—>х=(л/л-}-(—l)w arcsin 2/3) /2 (m£Z), а так как
cos#=sin2x = ]/ 2/3, то у=лп ± arccos У 2/3 (n£Z), Аналогично, в случае
sin2x= — V*2/3 получаем х— (л/л—(—1)от arcsin У"" 2/3) /2 и #=лл±(л —
— arccos У 2/3) (т, n£Z).
300. {х==л (4& ± 1)/4, у— £ arctg2+лл, ?=л—х—у} (п, k£Z). За-
мечание. Верхнему знаку у х соответствует верхний знак у у; нижнему —
нижний.
301. (х; #)£{(1/2; —1/2), (—1/2; 1/2), (1; 0), (-1; 0), (0; 1); (0; -1)}.
302. {(л/л; л/)} (т, l£Z).
303. J (~-arccos- а----[-2лл; -S-Uarccos- а------— 2лп\
\^8 У2+]Г2 8 /2+Г2 J
(-^--{-arncos а------^ — arccos °---------— SjwAl
У 2+ / 2 8 У2+У2 j]
(n£Z), а£[- К21-
304. {(arctg (а—1) + лл; (—1)* arcsin (а+1)4~л£)} (л, k£Z) при 2,0],
{(arctg (а+ 1) + лп; (—1)*arcsin (а—1) + л&)} (л, k£Z) при а£[0; 2].
305. {(л(6л± 1)/3; л (6/и+ 1) /6), (л (6л ± 1)/6; л(6/и— 1)/3)} (л, m£Z).
306. {(л (1—2 (л—т)) /2; лл/2), (л (6 (т—2/) + 3 ± 4) /6; л (3/ Т 1) /3)}
(л, /л, l^Z), Замечание. В формулах надо брать или верхние знаки,
или нижние.
307. ^(—1)" arcsin-|-+(—l)w arcsin-^-+л (л + /л)^;
•??((—I)”arcsin—(—1)OTarcsin4* + л(л—/л))^> (л, tn^Z),
2 \ о о / J
308. {(л(8я+1)/4; л(8*+5)/4)} (п, k£Z). 309. {(л(8n—3)/4)\
310. {(л (8й+ 1)/2; л(4й+1)/2)} (k^Z). 311. {4лй} (fe£Z)-
312. {(л (4m— (— 1)п)/8; (лп—arctg (1/1^2))/5}} (п, m^Z).
313. {((л(8п+1)—6)/4; 1} (n^Z). 314, {(л/3; л/6); (5л/12; л/6);
(л/12; 11 л/6)}.
302
§ 12
1. «1=13, d= —1. Решение. Для арифметической прогрессии «п =
= «i+d(n — 1). Выразив слагаемые через а± и получим
J «i4~3d = 1(\
1 2«i -f- 9d = 17.
Из первого уравнения «f=10—3d. Тогда 2 (10—3d)4-9d= 17 =Ф d = — 1,
«i=13.
2. Доказательство. S„=2n2—Зя, Sn_f —2 (п—1)2 + 3 (n — 1) =
= 2я2—я — 1; «n = S„—S„_i = 4n+ 1, «n_j = 4 (я —1)4-1 =4n—3; d—an —
— «п-1 = 4«4"1 — (4я—3) = 4 постоянна, следовательно, эта последователь-
ность— арифметическая прогрессия.
3. 1; 9; 17. 4. 610. 5. «! = —2; d=I. 6. 69; 87. 7. 44. 8. (1166 —
— 39)/90. 9. ai =—1; d=2. 10. 7. 11. 1,05; 1,1; 1,15; 1,2; 1,25. 12. 11,2;
18,4; 25,6; 32,8. 13. 164850. 14. 7. 15. «f = 5, d = 4. 16. 0,1; 0,2; 0,3; 0,4*
17.5. 18. «1 = 4, d=5 или «i = —79/7, d = —37/14. 19. d=—5/4. 20. d =
= 33/20. 21. 26. 22. «1 = 8. d=4.
23. Могут; тупоугольный; A = arccos (—29/48) = л—arccos (29/48), § =
= arccos (61/72), d=arccos (101/108). Решение. По условию задачи имеем
(а, Ь, с > 0)
{21g 6 = 1g «4-lg с, ( Ь2=асг
2(lg26—Ig3c) = lg3c-lg26 ИЛИ 1 2b=3c.
Решая последнюю систему относительно а и Ь, получим «=9с/4, Ь — Зс/2.
Итак, тройка чисел, удовлетворяющая условиям задачи, будет 9с/4, Зс/2,
с (с Ф 0). Для того чтобы отрезки длиной «=9с/4, 5 = Зс/2 и с могли образо-
вать треугольник, достаточно проверить выполнение условий 1) а 4- b > с,
2) Ь+с > «, 3) а-^с > Ь. Но так как «4-Ь= 15с/4 > с, 6-|-с = 5с/2 > 9с/4 =
= « и «4-с= 13с/4 > Зс/2 = Ь (с > 0), то треугольник с длинами сторон «, Ь, с
существует, и так как «2 > &24-с2, то он тупоугольный. Для нахождения
углов этого треугольника воспользуемся теоремой косинусов, откуда
5» &24-с2— «2 29 б а2+с2—Ъ* 61
cos 4 =—------±=f——, cosB=—Цг-----
2bc 48 ’ 2ас 72*
л а2+&2_с2 101
cosC = —2аГ...= 108*
Таким образом, учитывая, что 4, Д', (Г—углы треугольника, получаем
4=arccos (—29/48) = л—arocos (29/48), В=arccos (61/72),
£=arccos (101/108).
24. d = 24/H. 25. d=12/5. 26. 101100. 27. (б— Кб)/6; 1; (б-J- /~б)/6.
29. «£[12; 4-оо[. 30. 19680. 31. 1/5; 1; 5; 25.
32. 728. Решение. Из условия
J ^4_Z?i = 52, __ ( 6i^ —&i=52,
1 bi 4~ ^2 4” =26f j 6i4-M4-W=26,
( ^1(д2-1) = 52, ( bi(q^l)(q^+q+l)^52,
1 bitt+q+q2)^,^} bi(l+q+q*)^%>.
Поделим левые и правые части уравнений и получим^—1=2, q — З. Подста-
вим значение q в первое уравнение. Получим&t=2. Так как Sn=&i (?”—!)/(<?— 1),
то Se=2.(3«—1)/(3—1) = 728.
33. 8190. 34. 8/3 или 5000/3. 35. 5; 10; 20. 36. 12 или 108/7. 37. 121.
38. bi = 3,5; q = — 2. 39. 0. 40. 2; 6; 18 или 18; 6; 2. 41. 31. 42. 4; 12;
36; 108. 43. —2/5.
44. 1; 3; 9. Решение. По условию задачи 13 и bf-j-bl-}-
-|- б| = 91, т. е. имеем систему двух уравнений
f 51(1+<? + 92) = 13.
1 &2i(1+<72+?4) = 91.
Возведем левую и правую части первого уравнения системы в квадрат, тогда
получим
*1 (1+?+<72)2= 169 =» b\ (1 + <?2+?4)-F262! q (1-Н+?2)= 169=»
=»62 (1+92+<74)+2М-*1 (1+9+?2)=169=»91+2М-13=169 =»
=> bYq = 3 Ьг = 3q/.
Подставляя bi = 3/q в первое уравнение системы, после преобразований полу-
чим 3<72—10^4-3 = 0. Решая это уравнение, находим q = 3 илид = 1/3. Тогда
соответствующие значения bt будут = l или bi = 9. Следовательно, искомая
прогрессия в первом случае будет 1; 3; 9, а во втором 9; 3; 1. Искомые числа
в обоих случаях 1; 3; 9.
45. 0; 0 или 10/3; 4/3 или —3/4; —3/10. 46. 6. 47. 1/625 или 15625.
48. 2. 49. 5 или 20. 50. 4; 8; 16. 51. 10; 6; 2 или -6; 6; 18. 52. —2.
53. 22,5 или 2,5. 54. 2; 4; 8; 12 или 12,5; 7,5; 4,5; 1,5. 55. 75/4; 45/4; 27/4;
9/4 или 3; 6; 12; 18. 56. 12,2 (заданные числа 27,8; 20; 12,2 или 17; 20; 23).
57. &i = 8; д = —0,5 или Ь^ 24/19; ? = 3/2. 58. 186. 59. 2; 6; 18. 60. 27
или 3. 61. 1; 3—2 Y*2; 3+2 К 2- 62. —2 или 1. 63. —2. 64. 1; 3; 9 или
1/9; 7/9; 49/9. 65. 931. 66. 8 задач; 127,5 мин. 67. 1 — 1 /"З; 3. 68. 100/3.
69. (3 ± ]<5)/2. 70. 2; —1/2; 1/8. 71. 1/16. 72. &х = 6; ? = — 1/2. 73. Если
прогрессия геометрическая, то х=± 2 Y 6/11; 54 = (3 ± 2 V б)/3; если про-
грессия арифметическая, то х = 1/2; S4 = 27/ll. 74. 4. 75. 486. 76. 4.
77. S2/(2S —1). 78. bi=l; g = l/3. 79.9/8. 80. 2; 4; 8. 81. а = 3; b = 6 или
а = 27; д = 18. 82. х= 1— log25. 83.217/30. 84. 4. 85. 8/3, 86. дх = 405
0 = —2/3. 87. di = 3/19; ?= 17/19. 88. дх = 2; <? = 1/3.
§ 13
1. 50 км/ч. Решение. Пусть v км/ч—скорость поезда до остановки.
Тогда (v+10) км/ч —скорость на перегоне в 80 км после остановки. По рас-
писанию поезд должен проехать этот перегон за 80/v ч, а затратил на самом
деле 80/(у+ 10) ч. Из условия
80 80 ^16
v и+10 60 ’
Преобразуя последнее уравнение, получим и2+ 10у—3000 = 0, откуда v = 50км/ч.
2. 25 км/ч. 3. 16 км/ч. 4. (—1?+ Y с2+16ас — 16Ьс)/2, если а > Ь,
5. 6 км/ч. Решение. По условию задачи пешеходы встретились через
5 часов. Следовательно, за час они проходили 50:5=10 км. Если и v2 —
304
скорости пешеходов, то Ут4-У2=Ю. Первый пешеход прошел до в^тречи'бУ! км,
а второй прошел этот путь за 5z71/(v2 —f— 1) ч. Второй пешеход прошел до встречи
5у2 км, а первый прошел этот путь за 5у2/(у1-*-1) ч. Так как второй шел после
встречи на 2 ч дольше, то
5и/ 5у2 _2
у2+1 t'l-l
Имеем систему уравнений
( ^1+^2= 10,
1 5t>1 5l/2 ~ 2
V и2+1 у1"“1
Решив ее, получим Ух = 6.
6. 75,6 км/ч, 147 м. Указание. Если /м—длина поезда, то Z/7 =
= (378+Z)/25. 7. 720 км.
8. 30 км/ч, 40 км/ч. Решение. Если vt и v2—скорости поездов, то Ух+
4-v2 = 70; в 14 ч расстояние между поездами равно 2У1 км. Каждый час это
расстояние уменьшается на (v2—Ух) км (у2 > Ух). Так как второй поезд догонял
первый 20 —14 = 6ч, то 2v1 — S(v2—v1). Имеем систему уравнений
J ^1 + ^2 = 70,
I 2ух = 6(у2—Ух);
отсюда Ух = 30км/ч, у2 = 40км/ч.
9. 4 км/ч; 16 км/ч. 10. 18 км/ч, 24 км/ч. 11. Ух=10км/ч, /х=3,5ч;
v2 — 8 км/ч; /2 = 3 ч или Ух = 14 км/ч, /х = 2,5 ч; v2 = 12 км/ч, t2 = 2 ч. 12. 12 км/ч,
16 км/ч.
13. 30 км/ч. Решение. Пусть Ух, у2, у3—скорости машин. Тогда, исходя
из условия, что три машины отправляются из пункта А через равные проме-
жутки времени, можем записать
|ЛВ| |ЛВ|_|ЛВ| /АВ)
Ух у2 “ у2 Уз
Так как вторая машина прибыла в С на 1 ч раньше первой, то получим второе
уравнение
120-120^1
У1 у2 ““
Из условия следует, что третья машина прошла 120-|-40—160 км за то же
время, за которое первая машина прошла 120—40 = 80 км. Поэтому третье
уравнение получаем такое:
160_80
у3 У! ‘
Итак, получим систему уравнений
(]АВ\ |ЛВ|^|ЛВ| |Л£|
Ух У2 Уа У3 1
120 120 ,
УХ У2
160 80
V у3 ““ Vi *
Решив ее, получим ух = 30 км/ч.
14. 18 км/ч; 24 км/ч. 15.240 км. 16. 20 }/"3 км. 17. 35 км/ч. 18. 4 ч.
305
19. 24 км.
20. 0,03 м/с; 0,05 м/с. Указание. В задачах на движение тел по окруж-
ности нужно иметь в виду следующее. Если два тела начали двигаться из одной
точки в одном направлении с разными скоростями, то тело с большей скоро-
стью может догнать другое тело, если разница между пройденными расстояниями
будет равна длине окружности. В данной задаче пусть vf и и2—скорости точек
и Vi > v& Тогда
( 60^1—60и2= 1,2,
I 15014-15^2= 1,2.
Решив систему, получим trf = 0,03 м/с; о2 = 0,05 м/с.
21. 180 км, 22. 1 м/с. 23. 56 км. 24. 60 км/ч. 25. /п = 21 ч, /т=28 ч.
26. 2 ч шел, 6 ч плыл. 27. 1—200 км, II—100 км. 28. 4 км/ч; 6 км/ч.
29. 15 км. 30. 20 м/мин; 15 м/мин.
31. (14- 3)/2, (2 Т V~2)/2. Указание. Обозначив ] КМ | через s, а
/м//а=оа/ом=А:| из условия задачи получим
( s— (0,4s4-0,4s«х) 1=4,
После преобразований система сводится к уравнению
Решив его, получим
х=(1 + Кз)/2, х = (2 т К"2)/2.
32. 50 м3/мин.
33. I—(5а—2— V 25а2+4а+4)/4 ч,
II —(5а4-2+ /25а2+4а+4)/4 ч, III—(5а—2+/25а2+4а+4)/2 ч.
34. 20 дн., 30 дн.
35. 30 ч. Решение. Пусть первая труба наполняет бассейн за х ч,
тогда за 1 ч она наполнит 1/х часть бассейна, а вторая труба— 1/(х4~ 10) часть
бассейна. Так как по условию обе трубы наполняют в 1 ч 1/12 часть, то
! , 1 _ 1
x+x4-P0“12*
Отсюда х=30 ч.
36. 20 ч; 25 ч. 37. 12 ч; 15 ч. 38. 11ч; 14 ч. 39. 5; 7. 40. Производи-
тельность труда второго рабочего в 1,5 раза выше, чем первого. 41. 6 ч; 9 ч
или 9 ч; 6 ч.
42. III бригада. Решение. Обозначим через х9 у и г—производитель-
ности I, II и III бригад соответственно. По условию
f x+z=2j/, |'Л+1=2.^,
I 2 Z
< или <
У+г=Зх, ±+1=з.±.
\ \ 2 - 2
Решая эту систему, получим x/z=3/5, г//г=4/5, т. е. х:</:г=3:4:5. Итак, по-
бедила третья бригада.
43. 8. 44. 10 дн.
306
45. 3 ч. Решение. Пусть х, у, 2, и и v—производительности 1, II, П1>
IV, и V рабочего соответственно. Из условия следует, что
В полученной системе пять неизвестных, а уравнений четыре. Но не сле-
дует искать каждое неизвестное. В задаче требуется найти сумму' f-—|—L-f-
• \ х У
+ • Способов решения такой системы много. Укажем, например,
такой. Левую и правую части четвертого уравнения умножим на 2, а затем
сложим левые и правые части всех уравнений; получим
o/I,l,l.I.I\i I , I , 1 , 1 , I I
3 I —I--L——-1_— 1 = 1 т. е. —-j---------------I-—=-5- в
\х 1 у 1 z ' и ' v J х у * z 1 и 1 v 3
46. 8 ч; 6 ч. 47. 27,5 (3— Y 5) км/ч; 27,5 (/~5— 1) км/ч. 48. 9 дн. 49. 6 дн;
12 дн. 50. 3 км/ч. 51. 10 км/ч; 15 км/ч. 52. 4 км/ч.
53. Y3/2. Решение. Пусть г>к—скорость катера в стоячей воде и —
скорость течения реки. Из условия задачи имеем
| ЛВ | , | ЛВ | = 1 / | ЛВ ] | ЛВ| \
2uK4-vT‘ 2ик—- ,т“ 5 \ t>K+vT * ук~ут/
или
\АВ\, 1 1 1 1 \
( 2 I 1 2 __1 ) ( — I 1 _1 )
\ ит ' ит / \ От”’" ит /
Разделив обе части на | ЛВ |/от, получим уравнение с неизвестным ок/от, от-
куда vK/vT= / 3/2.
54. 12,5 км/ч. 55. от=3 км/ч; ол==9 км/ч. 56. 20. 57. 100. 58.3150;
3450. 59. 24. 60. Л— 20; В— 30. 6L Рядов—20, стульев—25. 62. 54; 75.
63. 10. 64. 40 по 2,5 руб. и 24 по 1,5 руб. 65. 18. 66.32. 67. 49.
68. (34- /”5)/2 и (1 + ]/~5)/2 или (3—/”5)/2 и (1— /3)/2. 69. 863. 70. 6
и 54. 71. 5 и 105 или 15 и 35. 72. 3/5. 73. 72. 74. 54 и 45. 75. 90 и 24.
76. 78 и 13 или 26 и 39.
77. 51 и 34. Р е ш е н и е. Пусть эти числа а и b, d — их общий наиболь-
ший делитель; тогда a=axd, Ь — Ь^сК Наименьшее общее кратное чисел а и b
есть a1b1dt причем а± и bt не имеют общих множителей. Тогда ayb^d—102 =
= 1-2*3• 17, + d = 85== Ь5* 17. Следовательно, d== 1 или</=17. В первом
случае аВ= 102, о4-6 = 85 и числа а и b не целые. Во втором случае a^bi = 6,
0x4-61 = 5, ах = 3, 6Х = 2 или Ох = 2, 6Х = 3, тогда данные числа равны 51и34.
78. 28 и 27 или 8 и 3. 79. 137.
80. 813. Решение. Пусть х, у, г—цифры данного трехзначного числа.
Тогда 100x4-10^4-2—данное число, a 100z4~ W+*—число, записанное этими
цифрами в обратном порядке.
307
По условию
( *2+У2+z2=74, 1
<{ х4-2 = 2у, я
V (100x4-10//4-z)~(100f+10f/+x)=495. I
Решив систему, найдем х = 8; у—\\ г=3, 1
81. 13 или 31. 82. 24. 83. 3 и 7. 84. 25%. 85. 2 кг при р > 60, а кг, |
где а 00; 2], при р = 60, 0 кг при 0 < р < 60. 86. 6; 8. 87. [0; 20] м/с. 1
88. В 2 раза, 89.^2,4 кг или 80%. 90. 4 кг, 6 кг. 91. 243 л. 92. I—7 кг, !
П — 21 кг. 93. 99? 94. 35. |
95. 0,5 л глицерина и 3,5 л воды. Решение. Если через v л обозначить |
объем сосуда, то после первой операции (замена двух литров глицерина водой) j
глицерин займет (v—2)/и-ю часть сосуда. Отлив 2 литра смеси, получим (v—2) X I
v—2 . |
X v - л глицерина в сосуде и после доливания воды глицерина будет зани- |
/ у______2 \ а
мать ( —} -ю часть сосуда. После третьей операции глицерин займет 1
fv—2\3 I
( ——\ -ю часть сосуда, а количество глицерина в сосуде будет равно |
(у 2\з а
— j л. По условию задачи воды в сосуде на 3 л больше, т. е. |
Складывая эти количества, получаем уравнение
откуда
аЗ—9у24_24у~16 = 0;
левую часть этого уравнения разложим на множители
(о—1) (у—4)2 = 0,
Отсюда v — 4 л (и=1 л не подходит по смыслу задачи), значит, объем глице-
рина равен
fv—2V пс
v I ---I =0,5 л.
k * J
96.170 кг. 97.4кг. 98.25%. 99.166 р. 100.12%. 101.(12 /78—100)%.
102. 20%. 103. 4 с. 104. Высота h£[1; (5— V 5)/2]. 105. цл € [4; (8+ /бТ)/3].
106. (а/’(«4-^)2—v2/uv) с. 107. t — 2 ч, если | ВС 120 км, / = |ВС|/60,
если 0 < |ВС| < 120 км. 108. 2 ч. 109. 5; 15f в км/ч. ПО. Через3,6 ч.
111. 25 км.
112. 3,75 км.
308
113. 18 км/ч. 114. Xi=l,25; х2 = 2; х3 = 0,5. 115. —0,5. 116. 0,25
117. %1=х2 = 10. 118. 9 км от А, 119. 12 м/с; 28 м.
120.7/9. Решение. Введем обозначения. Поезд, вышедший из пункта Л,
имел ускорение ах; через /х ч он достиг скорости v1 = a1t1, с которой и про-
должал двигаться, пока не прибыл в пункт В\ в пути первый поезд, так же
как и второй, находился 4 ч. Второй поезд, вышедший из пункта В, имел
ускорение а2 Ui (для определенности будем считать а2 < alf в противном
случае решение будет такое же, только поменяются роли первого и второго
поезда), через 4 он достиг скорости v2 = a24, с которой и продолжал дви-
гаться, пока не прибыл в пункт Л. Обозначим a2/ai = x < 1. По условию за-
дачи при встрече (этот момент обозначим 4) поезда имели равные скорости.
Это возможно лишь при условии, что к моменту встречи один из поездов (тот,
у которого ускорение было больше, у нас это первый поезд) двигался уже
равномерно с постоянной скоростью (у нас ^i = «i4), а другой еще продолжал
равноускоренное движение (и имел в момент 4 скорость а24). По условию
задачи эти скорости равны, т. е. а2^з —^14, откуда
4=4/*. (1)
Скорость равномерного движения первого поезда Vi=fli4, а второго поезда
у2 = «ч4 > Vi, по условию задачи v2 = 4vx/3 => fl2/2 = 4ai4/3, и, следовательно,
4 = 44/3*. (2)
Путь, пройденный вторым поездом до момента встречи, 51 = а2^з/2, это путь,
пройденный первым поездом после момента встречи, т. е. s1 = y1(/4—4) =
— fli4 (4—4). Следовательно,
—2-- = «i4 (4 — 4)»
или, учитывая соотношение (1) и то, что а2 —получим
так как 4 # 0, то отсюда получаем
4 = 34/2%. (3)
По условию задачи расстояние между Л и В поезда прошли за одно и то же
время 4- Подсчитаем этот путь для первого и второго поездов отдельно. Для
первого поезда
। v h f\— t\___
------------2“*
Для второго поезда
_ 8а24 . 4/х / 3ti 4/i \ __ 2a2tl 8a2ti 10а2/? 10а,/?
9х* 2 + 2 ’ Зх \ 2х Зх J" х2 9х2 ~ 9х2 ~ Эх '
Приравнивая эти значения и деля правую и левую часть на о,/,, получим
2__________________1^10 27__ 20=J_ _2_^2
2х 2 Эх 18х 18х 2 ~^х~~ at'
309
121. 10 км/ч. Решение. Если |ЛС|»хкм, то
х . 120—х х . 120—
и0 1 01 01 00
Если t—время, необходимое мотоциклисту, движущемуся со скоростью и0 км/ч,
для преодоления расстояния | АС [, то
vel = 60, М8-0+й'8~—==60.
Учитывая условия n = 2v0> получаем
ио —15уо+50 = 0,
v0 —5 не удовлетворяет условию, так
уже 12 часов. Итак, по=1Окм/ч.
и0 = 5 или v0 = 10.
как тогда на преодоление | АС | уйдет
14
§
1. cos(tt+2n£) + *sin (л4-2л&),££2Г.2. cos^2n£—-у)
3. 2
л
+ *sin ^2л&4-ул^ j , k£Z.
+ i sin (2nfe+^+arctg (4/3))), k£Z.
+ isin (2л&—arctg (4/3))), k£Z.
cos
5.
5 (cos (2n£-{-rc4-arctg (4/3)) 4-
6. 5 (cos (2л&—arctg (4/3)) +
7. 5 (cos 2nk 4- i sin 2л&), k £ Z.
, k£Z. 9. cos(360°A’+58°) +
+ i sin (360° *4-58°), k£Z. 10. cos (360° 6— 12°)4~i sin (360°*—12°), k£Z.
11. cos (360°k+200°)4-isin (360°k+200°), k£Z. 12.cos^2nJfe—y4-a^ +
4-isin ^2n&—y4~a) » k£Z. 13. cos ^2л&4-у — +*sin ^2л&4~у — a^ ,
k^Z. 14. cos ^2л&4--^“—“a)+J*sin ^2n£4-^—» k^Z.
(cos (2n^4"a)+t sin (2л^4"а))» если 2лл —у < a < 2лп4~j-;
-р^ур (cos(2nfe4~^+a) + J Sin (2л^4-л4-а)), если 2лп4-'^ < а < 2лп4-^-;
kt n£Z.
16.
15.
если 2лп < а <
I / / '
< я (2п+1): (cos l2nft+’
л(2п4"0 < а < 2л («4-1); n, k£Z.
17. (1 +i/"3)/2. 18. —16. 19. 8i. 20. 8. 21. —21®.
22. 2п cos" (ф/2) (cos (лф/2)4-* sin (лф/2)).
23. 2"sin" (ф/2) (cos(n (л—ф)/2)4-гsin (п (л—ф)/2)).
25. cos За = 4 cos3 а—3 cos a, cos 4а = 8 cos4 а—8cos2a4-l, sin За =
= 3 sin а—4 sin3 а.
г 2 /2 .
2 ’ 2 ‘ 2
—а
если
26.
27, 2 2 : 2 2 ’
— а
— а
2
310
28‘ 2 + 2 ’ *’ 2 2 • 29, 2 ' 2 ’ 2'2’ 22’
1/^ i
----g*. 30. cos (2^/n)4-i sin (2л/?//г), &=0, 1,2, . ..,n — 1.
31. {_ (bj_i)/2; (3—5£)/2}. 32. {ctg(£jt/n)|£==l, 2, n—1}.
33. Указание. Достаточно доказать, что корни многочлена х2+х +1
являются корнями многочлена x3"+x3OT+1+x3ft+2’
34. Прямые г/=±х. 35. Прямые г/=0 и х = 0.
36. Луч у=0, х<0. 37. {—1, 0}. 38. {0; —t; /}.
39. {0; —t; /}. 44. Точки прямой г/=2х+(3/2). 45. Точки прямой */= —х.
46. Точки прямой х =—1/2. 47. Точки прямой г/=1.
48. Точки плоскости, расположенные над прямой у=х (удовлетворяющие
неравенству у > х).
49. Все точки плоскости, расположенные под прямой 2х4-4#4-3 = 0.
50. Точки х > 0, т. е. все точки правой полуплоскости.
51. Точки открытого круга с центром в точке (0; —1) и радиуса 1.
52. Точки открытого круга с центром в точке (0; 1/2) и радиуса 1.
53. Точки открытого кольца, ограниченного окружностями с радиусами,
равными 1 и 2 и центром в точке (—1; 1).
54. Точки открытого кольца, ограниченного окружностями с радиусами,
равными 1/3 и 1 и центром в точке (0; —1/3),
55. Точки открытого кольца, ограниченного окружностями с радиусами,
равными 1/2 и 1 с центром в точке (—1/2; —1/2).
56. Все точки плоскости, расположенные под параболой #=(х2-]-1)/2.
57. Все точки плоскости вне прямой х = 1, расположенные под параболой
г/=—(ха4-1)/2.
58. 3/2.
Раздел II
§ 1
1. ? = 2/3. 2. V 2— 1. 3. 1/2. 4. 7/8. 5. 1/2. в. 1. 7. 4/3. 8. 0. 9. 0. 10. 0.
11. 0. 12. —2/5. 13. 1/2. 14. —4/7. 15. 48. 16. 6. 17. 10. 18. 4/3. 19. 1/8.
20. —5/3.21.8/13.22. —1/2.23.3/4.24.0. 25. 1. 26. 1/3. 27. т/п. 28. п (п-|-1)/2.
29. 1/4. 30. 1/6. 31. 1/2. 32. 1/4. 33. 1/16. 34. 4/3. 35. —2. 36. 2/3. 37. 1/12.
38. 1/4. 39. 3/2. 40. —2/9. 41. 3. 42. 1/2. 43. 1/3. 44. 1. 45. 5. 46. 1/2. 47. 2.
48. — sina. 49. —3. 50. /2. 51. —1/2. 52. —1/5. 53. 6/5. 54. 0. 55. 5~®.
56. 0. 57. —5/2. 58. —1/4. 59. 1/2.
§2
1. 2sin2x. 2. 2х cos 2х-|-(14-х) sin 2х-|-2. 3. /(х) = 4/(ха—4), /'(х) =
= —8х/(ха—4)2. 4. /(х) = 3, f'(x)*=0. 9. л(4п4-1)/4, n£Z. 10. х = тл/6,
m£Z, х = {(± arccos (2/3)4-2лп)/6| ngZ}. И. х = {л (2п-[-1)/4; (лт-|-
4- (—1)“ arcsin (l/3))/2|n, m£Z}. 12. х = {0; 2л(3/п ± l)/3|m£Z}. 13. х =
= {2л(6л± l)/3|n£Z}. 14. х={2л(2п4-1)/3|п€^}.
15. х={л(4т4-1)/8; л (12&4-1)/12 | т, k£Z}.
16. х = {лт/4; л (6n ± 1)/3 | т, n£Z}.
17. х0—оо, о[UJ2, 4-«о[. 18- 0[ш 1; 4-«Ь 19. х=»[-1; 0[.
зп
20. x6J5;_+»r. 21. *€]0; +<Ю[. 22. yi^Ci-e^ a~^x, C^R, y2=>
= C2.e-(K 3+2)\ C^R. 23. (x+2) (3x+4). 24. (2tg»x)X
Xcos(cos2(tg3x)). 25. — (x24-4x4-9)/x4. 26. 2(14-x2)/(l—x2)2. 27. xM.
28. (61g2 (x2))/x In 10. 29. —(64-3Kx4-2 ^/^/бх2. 30. x/(x4—1).
31. a2/(a2—x2)3/2. 32. 1/sinx. 33. x2/(«os x-f-xsin x)2. 34. —1/cosx.
35. пн-гх^/^Г+х2.
36. cos x - cos (sin x) • cos (sin (sin x)). 37. x2 sin x.
38. Д ок аз ател ьство. Рассмотрим функцию f(x) — ex—х—1. Так
как /(0) = 0, f (х) — непрерывная функция, ff (х) — ех—1>0 при х > 0, то
при всех х > 0 функция f (х) возрастает; поэтому f (х) > f (0) при всех х > 0,
т. е. ех—х — 1 > 0 при всех х > 0.
39. Функция убывает при х£] —оо; 2/3[U] 2; +оо[ и возрастает при
xg] 2/3; 2[.
40. Функция убывает при х£]—1; 0[ и возрастает при
х0-оо; —1 [U]0, +<»[.
41. Функция убывает при х£] — 1; 2[ и возрастает при
x€]-o>;-l[U]2; +оо[.
42. Функция убывает при х£] — оо; 0[ и возрастает при х£]0; 4~оо[.
43. Функция убывает при х£] log2 (4/3); 1[ и возрастает при
*€]-оо; log2 (4/3) [U] 1; +оо[.
44. Локальный максимум при х = —1, локальный минимум при х=3.
Функция убывает при х^] — 1; 3[ и возрастает прих^]— оо; —1 [(J] 3; +оо[.
45. Локальные минимумы при х =—4 и х=1, локальный максимум при
х = 0. Функция убывает при х£] — оо; —4 [(J ] 0; 1[ и возрастает при
-4; 0[U]l; +оо[.
46. Локальные минимумы при х — ~ 1 и х = 4, локальный максимум при
х = 0. Функция убывает при х£] — оо; —1 [U] 0; 4[ и возрастает при
1; 0[U]4; +оо[.
47. Локальные минимумы при х =—1/2 и х=1/2, локальный максимум
при х = 0. Функция убывает при х£] — оо; —1/2 [(J]0; 1/2[ и возрастает при
*0-1/2; 0[U]l/2; 4-о°[.
48. Функция возрастает при х£] — оо; 4-оо[.
49. Локальный максимум при х = 16/5, точка разрыва при х = 0. Функ-
ция убывает при х£] — оо; 0 [(J] 16/5; -)-оо[ и возрастает при х£]0; 16/5[.
50. Локальный минимум при х = 2/3. Функция убывает при хе]—оо; 2/3[
и возрастает при хе]2/3; +°°Е*
51. Локальный максимум при х=1/3. Функция убывает при хе] 1/3; 4-оо[
и возрастает при xei — оо; 1/3[.
52. Минимум при х==1. Функция убывает при хе] 0; 1[ и возрастает
при хе]1; оо[.
53. Минимум при х =—1/4.
54. Критические точки х = 0 и х=1; минимум при х=1.
55. Минимум при х=±У 5, локальный максимум при х = 0.
56. Минимум при х = 2 и х = 3, локальный максимум при х = 5/2.
57. Локальный максимум при х = 0 и локальный минимум при х = 1.
58. Локальный максимум при х = 0 и локальный минимум при х= р/215.
312
59. Максимум при х = ~ 3, минимум при х = 3.
60. Максимум при х = -/2, минимум при х = V 2.
61. Минимумы при х=±5.
62. Минимум при х = —1.
63. Минимум при х =—1/V* 2 и максимум при х—1/У 2.
64. у — —9/4 при х£{л (12/z— 1)/6, л(12/п—5)/61 л, m£Z}.
65. При я = —9/5 и 6g] 36/5; +°°[ и ПРИ «=81/25 и 6g]400/243; +<»[.
Решение. Так как коэффициент при х3 положителен, то максимум, если
он существует, расположен левее минимума. Для нахождения экстремальных
точек найдем производную данной функции, приравняем ее нулю и найдем
корни квадратного уравнения; это будут хх =—9/(5п) и х2=1/0. Если а < 0,
то х2 < хх и» следовательно, х2 = х0, т.е. 1/0 =—5/9 => а = — 9/5. Тогда
хх =—9/(50) = 1. В этой точке f (х) имеет локальный минимум, который должен
быть > 0. Имеем / (1) = — ^4" 6 >0, т. е. b > 36/5. Если а > 0, то хх < х2
о
и, следовательно, хх=х0, т.е. —9/50 =—5/9 =£>0 = 81/25. Тогда точка мини-
мума х2= 1/д = 25/81. В этой точке f (25/81) = — ^4~6 > 0, т. е. b > 400/243.
Итак, экстремумы f (х) будут положительны при 0 =—9/5 и 6036/5; -)-оо[
и при а = 81/25 и 6g] 400/243; +оо[.
66. При 0 = —2 и 6g] —оо; —11/27[ и при 0 = 3 и 6g] — оо; —1/2[.
67. При а — —1/3 и 6g]—оо; —5/9[ и при 0=1 и 6g] — оо; —1[.
69. Если р > 0, то 0g]p; (32р34-27р)/27[; если р = 0, то 0g0; если
р < 0, то 0g](32p3-f-27p)/27; р[. Решение. Для того чтобы уравнение
х3+2рх2+р=0 имело три действительные корня, функция f (х)=х3+2рх2+р—а
должна иметь локальный максимум и локальный минимум, причем f (xmax) > 0,
a f (xmin) < Так как коэффициент при х3 положительный, то xmax < xmin.
Найдем экстремумы этой функции f (х) = 3х24-4рх. Производная обращается
в нуль при хх = 0 и х2 = —4р/3. Здесь возможны три случая. Если р > 0, то
32
х2 < хх и, следовательно, / (x2)z=^ р34-р—а > 0, а /(хх) = р—0 < 0, откуда
р < а < (32р3 4-27р)/27. Если р = 0, то хх=х2 и функция экстремумов не имеет:
/' (х) всюду, кроме х = 0, положительна и функция монотонно возрастает.
Таким образом, в этом случае нет таких значений 0, при которых данное
уравнение имело бы три действительных корня. Если р < 0, то хх < 0 и,
32
следовательно, / (хх)=р —0 > 0, a f (х^=^ р3+р—а < 0, откуда (32р3+
4- 27р)/27 < а < р.
70. г/=241пЗ при х=3. 71. р=14-81п5 при х = 2. 72. ^ = 6(1 —1пЗ)
при х = 2. 73. При х=0.
74. у (1) = — 8/3 = min/(х), у (2) = 8/3 = max f (х).
[0, 2] [0, 2]
75. min/(х) = /(0) = /(3) = 5, max f (х)=f (2) = 9.
[0; 3] [0; 3]
76. min f (x)—f (0) = 0, max f (x) = f (3) = 9.
[0; 3] [0, 3]
77. min /(x)=/(—1) =—10, max / (x)=/(4) =50.
I-1;4] [-U4]
78. min / (x) = /(1) = 23, max / (x)=/(3) = 75.
313
79. min f(x)=/(!) =-6, max f (x) = f (5) ==266.
1-1:5] 1-1:5]
80. min f(x)=f(—1) = —9, max /(x)=/(3)=6.
1-1:3] 1-1:3]
81. min f(x)=f(—2) = — 24, max f(x)=/(2)=4.
[-2:2] [-2:2]
82. min /(x)=/(3) = —57, max f (x) = f (6) = 132.
[-3:6] 1-3; 6]
83. min/(x)=/(2)= 1, max / (x)=/(0)=/(3) = 5.
[0; 3] [0, 3]
84. min f (x)=/(2) = —25, max/(x)=/(3)=0.
[0.3] [0;3]
85. min /(%) = /(—1) = /(!) = —16; max f (x) = f (0) = —9.
1-1:1] [-1:1]
86. min f(x) = f (—1)=1, max /(*)=/(1) = 3.
1-1:1] [-1:1] ___
87. min f(x)=f(l)=\, max f (x)=f (2) = У 4/3.
[3/4; 2] [3/4; 2] v
88. min /(x) = /(0) = 2/ln2, max f (x) = / (2) = 17/(4 In 2).
[-1;2] [-1;2]
89. min 7(x) = 7 (0)=0, max 7 (x) = 7 (1) = 24.
bl; 1] НИЦ
90. min 7 (x)=/ (—1) =/ (1) = 4; max /(*)=/ (0) = 5.
91. min f (x) — f (л/2) = 0, max / (x) = f (arcsin (1/4)) =
[0, л] (4), л]
= f (л—arcsin (1/4)) = 9/8.
92. min 7 (x)=7 (л/3) = —1/2, max f(x)—f (— л) = 22.
(л/3; Зл/2] (л/3; Зл/2] __
93. min f (х)=f (л/2) = Зл/2, max f (х) =/ (arcsin (( >^57— 5)/4))) =
[0; л/2] ___________ (0;л/2(
= (154- /57) И10 /57-66/164-3 arcsin ((/57—5)/4).
94. max / (х)=7 (—2)=—1/(362—86 + Ю) при 2]; max f(x) =
£-2;i] 1-2; 1]
= /(0) = —1/362 при &£[2; +оо[.
Решение. Замечаем, что f (+а) = 7 (—а). Чтобы найти наибольшее зна-
чение f (х) на отрезке [—2; 1], найдем критические точки. Для этого находим
' w“~(262x2—х4—362)2* ' '
Если b < 0, то х2—b > 0 при любых x£R. Поэтому /'(х) = 0 только при
х = 0, причем для х < 0 производная /' (х) < 0, а для х > 0 производная
/' (х) > 0. Следовательно, в точке х = 0 функция f (х) имеет минимум и наи-
большего значения достигает на левом конце (учитываем симметрию и то, что
|—2 | > 1). Следовательно, наибольшее значение функции в этом случае будет
7 (—2) = — 1/(362—86+16). При 6 = 0 имеем f (х) — — 1/х4, при х < 0 функ-
ция убывает, при х > 0—возрастает. Следовательно, в этом случае наи-
большее значение функция принимает при х=—2, а именно 7 (—2) =
= —1/(362—86 + 16) = —1/16. При 6 > 0 производная имеет три критические
точки xi =—у2_6, х2 = 0, хз=Уь. Проверка показывает,_что f (х) < 0 при
*€]-«•; -/б[U10; /б| и/'(х)>0 при ХС1-/&; 0[и 1 /F, 4-®>Ь
Таким образом, при х = 0 мы имеем локальный максимум 7(0) = —1/362. Для
того чтобы это значение было наибольшим, надо потребовать, чтобы
3&2—864-16^ 3ft2 3ft2—8ft 4-16 "3ft2
=i>362—8&4-16<362=^>—8&4-16<0=> ft 5г2.
314
Итак,
max f (x)—f (0) =—I/ЗЬ2 при 6£[2; +oo[,
1-2; il
max / (x)=f (—2) =—1/(364— 8&+16) при 6£]-<ю; 2].
[-a; i]
95. max f (x)=f (-2) = 16 - 246 + 62 при 6£J— oo; 2/3],
[-2; i]
max f(x)=/(0) = 62 при 6£[2/3;+«>[.
[-2; i] _
96. min f (x)—f (—л/2) = —1—T^3,
[-Л/2; ЗЛ/8)
min f (X)=t (3л/8) = ((3л-4) /2-4/3)/4.
[-л/2; зл/8]
97. min /(*) = —2 ]<3/9 >—7/18.
[-л; л]
98. max f (х) = 4 УЗ /9 < 0,77.
[-л; л]
99. у=—2х, у=2х—4. 100. у——4х+3. 101. //=4х+1. 102. у=4х,
у= — 4х+16. 103. у=— 2х+5. 104. </ = (Зх+10—61п 2)/8. 105. у = — (2х—7)/16.
106. //=((25 In 3) х+28 —25 In 3)/9. 107. у= 1.108. //=4х+2.
109. (-(2+/3)/2; (9—4 ]/~3)/4). ПО. й=±4. 111. (2; 3). 112. (1; 1).
113. (2; 4); уравнение касательной 0=4х—4; уравнение секущей
t/ = 4x—3.
114. На второй кривой 0=ф(х) в точке ((&+4)/6; (£2—4)/12) касательная
y = kx—(k2+8k+2)/12 параллельна касательной y—kx Т 2 ((&+1)/3)3,2 в точ-
ках (± ]/*(&4-1)/3; —1 ± ({k—2) |/3 (Z?4-l)/9) первой кривой y = f(x) при
любом &£[—1; 4-оо[. Решен и е. Будем искать уравнение касательной в виде
y—yx=k (х—Xi), где £/i)—точка на кривой,, в которой проведена касательная,
угловой коэффициент которой k. Координаты,точки касания найдены из уравне-
ний yt=f (xi), /' (хх) = ^для первой кривой и из уравнений у2 — ф (х2),ф' (x£ — k
для второй кривой. Для кривой y=f(x) имеем y\_—ff (xx) = 3xi— \ = k, откуда
видим, что —1, т. е. если зададимся значением—оо; —1[, то на кри-
вой y—f(x) нет ни одной точки, в которой касательная имела бы такой угло-
вой коэффициент. Для второй кривой 0=ф(х) имеем #2 = ф'(х2) = 6х2-—4 = 6
и k может принимать любые значения. Итак, будем:считать, что££[—1; +°°[.
Тогда для кривой y—f(x) для данного k получим xj — ± 1)/3, а из
уравнения кривой 0i=?=--l ± (&—2) 1^3 (k +1Й/9 и уравнение касательной в
точках (± УЬ+й&. —1 ± (6-2) О (6+0/9) будетy = kx Т 2(К(6+1)/3)8.
Для кривой 0 = ф(х) для того же значения k получим х2 = (&+4)/6 и у2 —
= (£2—4)/12 и уравнение касательной в точке ((&+4)/4; (k2—4)/12) будет
y—kx—(k2-\-8k^-2)!X2. Касательные в найденных точках параллельны для
любого &£[—1; +<эо[.
115. Острый угол между касательными равен arctg (1/7}. 116. я—2 arctg У8.
117, »-2»е1г ГЯ. >18.
Z О Z О
119. у=2—5х. 120. (0; —1), (4; 3). 121. (6я; (26л—1+32(—1)*)/2), kgZ.
122. 0°. 123. 5 У 5. 124. Г = 2ла3/9 У 3. 125. а=2л (1 — ^2/3). 126. а = л/3,
S = 3/2 У 3/16. 127.
/?3tg<ptg»a
3tg3(<p/2) tg(a/2>
а=
я
315
„о № _2/?»a+sina)a______л
. 0 f л a \ . sin 2a 6
tg It—2)tga
129. (nV sin2 a cosa)/2, a = arctg )/" 2 = arccos (1/1^ 3). 130. t/ = — (3x—5)/9.
131. 1//5? 132. /53/3, Уг43715. 133. 21 см и 28 см. 134. 16/3 и 128/3.
135. a = 4 м и Л = 2 м.
136. Тривиальное решение: а = arctg (f/0/x0), если точка (х0; yQ) лежит в
первом или третьем квадранте и а = л-}-arctg G/o/*o), если точка лежит во
втором или четвертом квадранте; длина отрезка при этом равна 0. Нетри-
виальное решение: а=л—arctg j/"у0/х0, если точка лежит в первом или
третьем квадранте, и а =—arctg у/yo/xQt если точка лежит во втором или
четвертом квадранте. Решение. Для определенности будем считать х0 > 0,
Уо > 0. Другие случаи разбираются аналогично. Уравнение прямой у =
= £/o+&(х“*(>)• Эта прямая пересекает оси координат в точках (0; г/О“^о)
и о). Квадрат длины отрезка, соединяющего эти точки,
«*=(*<>— у) -НУо—х^)2 = (Уо—*<Л)2 •
Очевидно, что s и s2 достигают минимального значения при одних и тех же
условиях. Поэтому находим (s2)' и приравниваем производную нулю; тогда
получаем
(S*)'= -2(1/0-^) (xo+g)=0.
Следовательно, имеются две критические точки (не считая значений k = Q и
k=- 00,—это случаи горизонтальной и вертикальной прямой, когда s2= 00): k =
= tga ==//0/^0 и £=tga = — jZу0/х0. Первое значение a = arctg (у0/х0) соот-
ветствует тривиальному случаю: s = 0. Второе значение а=л—arctg ydxo
соответствует локальному минимуму.
<37. *
6 J^sin a cos (а/2) tg £ 3
138. "/*2/3. 139. 2л/3. 140. Цилиндр, у которого диаметр основания равен
высоте. 141. 142. a = arctg (]/r2/2). 143. (4V)1/3/v/<3. 144. Параллеле-
пипед, у которого длина стороны основания равна радиусу описанного шара
R, а высота— 1?}^ 2. 145. R/3. 146. (2л) “V3 дм. 147. y~2R.
148. Ks (/2— 1)/л. 149. 8 ]^ЗлЯ2/9. Радиус основания конуса относится к
радиусу шара как 2 V* 2:3. 150. l/V3, Z3/2. 151.3. 152. У = л(4/?2—Я2) Т//4,
Утах = 4лЯ3/3 У~3 при H = 2R/V'3. 153. /2. 154. В /3 раз. 155. л/?3//2.
156. 3/4. 157. За/2.
158. л ctg2 ф/cos 2ф. Наибольшее значение площадь боковой поверхности
будет принимать при ф = 0,5 arccos (У 2—1), т. е. соз2ф=}/п2—1. Это
значение будет равно л (У 2-|-1)2.
159. 4Я/3, 64Я3/81. 160. 77/3, 2R2H / 3/9. 161. 2. 162. 3/2. 163. /7/3,
4л/?2/7/27. 164. На середине ребра [ЛС]. 165. 8. 166. 4,5 км. 167. а= 12км/ч.
316
§ 3
>• 2.
317
13.
318
c-vy,-/;
iff "
о
17.
Один корень при с С
£]—-оо ; 4/9 [ у ] 4; +<»[; два
корня при с £ {4/9; 1; 4}; три
корня при с 04/9; 1 [U] 1; 4[.
20.
Один корень при eg
С]—00; 4/9 [U] 4; +оо[; два
корня при eg {4/9; !, 4}; три
корня при eg]4/9; 1 [U] 1; 4[.
Ни одного корня при е= 1; один ко-
рень при eg]—°о; 16/27 [и
U]16/25;1[U]1; +оо[; два
корня при eg{16/27; 16/25}; три
корня при eg] 16/27; 16/25[.
320
22.
Ни одного корня при с= 1; один ко-
рень при —оо; 16/27 [ U
U1 16/25; 1 [U] 1; +«>[; Два
корня при с£ {16/27; 16/25}; три
корня при [16/27; 16/25[.
Ни одного корня при с£]8;4-оо[;
один корень при с^{1; 8}, два
корня при оо; 1[(J] 1» 8[.
11 В. М. Говоров и др.
321
у=(143)-«* (1—cos 2х)/2.
26.
322
§ 4
7 о
1. F (x) = 2x1 2+x+l. 2.F(x)=x3—Зл24-1. 3. F (x)=4^-xa+3x+4.
о 3
y2 1 ,—
4. F(x)=x+%-4-ySin2x-|-1.5. F(x) = —0,5cos2x+x3 *4-2,5. 6. /3—ctgx.
9 14
7j 6sin (x/2)— 4-cos5x—£. 8. 5tg(n/5). 9. (4—л)/8;. 10. 1066/243 ln3.
0 0
11. Л=1/1п2, В = 7(In22— 1)/(3 In2 2). 12. a > 0. 13. 6 = 2. 14. a=3.
15. a>ln2. 16. a<—1. 17. 4/3. 18.121,5. 19. 32/3. 20.4/3. 21.10/3.
22. 9/2. 23. 32/3. 24. 9/2. 25. 81/2. 26. 1/6. 27. 9. 28. 9. 29. 4/3. 30. 1/3.
31. 4,5. 32. 2/3. 33. 7/3. 34. (8 /"2—3)/6. 35. 8/3. 36. 1/3. 37. 9. 38. 5/3.
39. 7/4. 40. 16 V 3/15. 41. 88/15. 42. 64/3. 43. 4/3. 44. 2. 45. (15—16 In 2)/4.
46. (6e—5)/3. 47. 125/6. 48. 3/2. 49. 4/3. 50. e2—1. 51. 5. 52. 1/3. 53. In 2.
54. 8/5. 55. (6—л)/3л. 56.53/15. 57. 12—5 In 5. 58.4—3 In 3. 59. 2,5—6 In (3/2).
60. 5In(6/5)— 0,5. 61. 1,5—ln2. 62. 4,54-91n3. 63. 14,54-41n2. 64. l,5-ln2.
65. 18. 66. 7/6. 67. 8/3. 68. 5/12. 69. 8/9. 70. 2. 71. 1/3. 72. (л—2)/4.
73. (3л—4)/4. 74. 1. 75. 5л. 76. 5л/2. 77. Зл. 78. 16. 79. (4—31n3)/2.
80. 11 —6 In 3. 81. 90,5—6 In 2. 82. 16/3. 83. 9/8. 84. 16/3. 85. 128/3. 86. 18.
87. 1/3. 88. 4/3. 89. 61/24. 90. 7/6. 91. In 2—5/8. 92.4 In 3—2. 93. 1/8. 94. 4/3.
95. (2e«—101)/6. 96. (In 10—n+4)/2. 97. (4/2—16-{-л/"2)/16. 98. 5/6.
99. 2—2 In 2. 100. 2л+4. 101. 4/3. 102. 4л+8. 103. 8.104. 9/8.105. S (—1)=
= 125/6, minS(£) = S(2)=32/3. 106. S = l. 107. x0=l/2, j/0=5/4. 108. x0 =
=3/2, t/0=2/3. 109. p=—1. 110. a! = arctg (27/2), =arctg (27/4^ 111. ar =
= л4-arctg (4/3n), «2 = n+arctg (8/3n). 112. 625л cms. 113. 18 /5 л см2.
Раздел III
§1
9 Ч Ч
1. 33. 2. —33 . 3. —8; 4. —10. 5. d=-^a+-£ O-j-g-C. e. —4. 7. —2.
8. 40. 9. 2. 10. 7. И. arccos (4/9). 12.- arccos (1/11). 13. 13. 14. —6.
16. d={5; 12; —16}, |d| = 5/T7. 17. 90°. 18. Зл/4. 19. —61. 20. Да.
21; а = {1; 2; 2}. 22. а = {4; —2; 0}. 23. {1; 1/2; —1/2}. 24. а={2; —6; 2}.
25. 0f={4 /2; —2; 8}, &a = {—4 2; —8}. 26. с={—3; 3; 3}.
27. & = {8/3; —10/3; 13/3}, 3,66... 28. & = {9/16; 3/16; 21/16}. 29. cosa=
= —4/5. 30. р=2а—30. 31. —22//133. 32. х={—4; —6; 12}.
33. х={—24; 32; 30}. 34. х={—3/2; 5/2; 3}.
35. {(1 ± У~2)/3/6; (5 Т 7/1) /3/30; (10 ± /2)/3/30}. В этой
записи надо всюду взять или верхние или нижние знаки.
Решение. Пусть искомый* вектор есть с = {х; у\ г}. Тогда |с ]2=х24-г/2 +
далее, cos(a?^) = cosn/4=l/‘|/’2==^a*c/(|a|’|c|)=(x4-y +
•4-2г)/рг"б== х-}-£/4-22== Так как вектор с лежитв плоскости
векторов а и Ь, то вектор с можно разложить по векторам а и Ь: с ъ
= ka-}-lb x = k—lt y=k-}-3lt z = 2k+l. Исключая из последнихсоотношу
ний k и /, получим 5х-|-3#—4z = 0. Итак, : надо совместно, решить систему;
11* 32?
уравнений
f*2+*/2+z2=b
5х-|-Зу—4г = 0,
х+у+2г= /З?
Из второго и третьего уравнений находим
_ 3 v 3 5 V 3 _ ,п
x=5z---L—,yes—L--------7г‘ (1)
Подставляя эти значения х и у в первое уравнение, получим после преобра-
зований 150г2—100 ]Лз Z-}- 49 = 0, откуда
г_ 1 , 1 _(Ю±/^)/3
/Т*^- 30 (2)
Подставляя эти два значения для z в соотношения (1), мы получим, соответ-
ственно, по два значения для х и у.
..__!_ , 1 _(1 ± /2) /3 1 7 (5Т7 К2)/3
~2/3* /6 6 ’ *2 КЗ 5/6 30
(3)
Заметим, что в записи соотношений (2) и (3) верхнему знаку у г соответст-
вует верхний знак у х и у, а нижнему—нижний.
36. о. 37. arccos (4/9). 38. Зрг34/2. 39. л— arccos (4/9), а = 2ЛВ =
= {4; —2; 4}. 40. D (— 1; 1; 1), (AC, BD) = 2л/3.
л V"3+V~2 — 1 в 1-/2
41. cos А , cos 5 =--— ,
V 9+2 /6 -2/3 V 6
а 2/3+/"2—1 ,/•--—-----—
cos с = ,/• —, «8=2 V 9+2 / 6-2 /3.
V 18+4 /6-4 / 3
42. В ((2 КЗ—1)/3; (7—2/3)/3; (7+/ОДЗ),
С (-(3+2 /3)/9; (21+2 / 3)/9; (21 — / 3)/9), или
В (- (1+2 / 3)/3; (7+2 / 3)/3; (7- /3 )/3),
С ((2 /3—3)/9; (21—2 / 3)/9; (21 + / 3 )/9). 43. а=1+%.
44. (а2+362—с2)/4. Решение. Известно, что CD = (CA-\-CB)/2. Иоэто-
му СО • СД = (СЛ+СВ) • Й/2 = (СД2+СВ. СД)/2=(62+а6 cos (СВ, СД))/2. Для
—> —>
отыскания cos (СВ, СА) используем теорему косинусов с2 = а2+&2 —
— 2ab cos (С А, СВ), откуда cos (С А, СВ) = (а2-{-Ь2—c2)/2ab. Следовательно,
CD • СА = (Ь2+(а2 + Ь2—с2)/2)/2 = (а2+ЗЬ2 - с2)/4.
45. Доказательство. Допустим, что сумма векторов, соединяющих
центр правильного n-угольника (в частности, треугольника) с его вершинами
есть некоторый вектор х. Тогда повернем n-угольник вокруг его центра на
угол 2л/п; при этом вся фигура, все рассматриваемые на ней векторы, в том
числе и вектор х, повернутся на угол 2л/я. Пусть х занял положение х*. Но
при повороте на угол2л/п рассматриваемый n-угольник совместится с перво-
начальным, и, следовательно, все векторы, идущие от центра к вершинам,
324
в совокупности остались прежними, а значит, и сумма их, т. е. вектор х,
осталась неизменной, но два вектора х и х*, повернутые друг по отношению
к другу на угол 2л/л, могут совпадать лишь в случае, если х = х‘ = о.
46. ЛВ+С£ = — (CD4-2CQ).
47. л/3. Решение. Обозначим (а?Ь) = а. Тогда 0 = C‘d = (a + 26)«
• (5а — 45) = 5а2 + Юаб — 4аЬ—8Ь2=5+10 cos а—4 cos а—8=6cos а—3,
откуда cos а =1/2 и а==л/3.
48. (а2+362—с2)/2. 49. (За2+*2—с2)/2.
50* ± ’ Решение- Для определенности будем считать
вектор, совпадающий с высотой, направленным от вершины к стороне р.
Тогда (см. рисунок) ВЕ—ВА-\-АЕ (если угол BAD тупой, то точка Е лежит
* >
вне отрезка [Л/)]). Вектор АЕ коллинеарен с век-
тором р, следовательно, АЕ — kp (знак k определит
положение точки Е), В А —— q. Тогда скалярное
произведение векторов BE и AD равно нулю, т. е.
0 = ВЕ-ЛЕ = (-^+^)./? = —^+^2,
и
А
с
откуда k~{pq)!p2 и, следовательно, ВЕ =
р. Если бы мы рас-
сматривали вектор ЕВ, знаки были бы противоположные, что и записано
выше.
51. 3(а2+62—с2)/2. 52. 0. 53. X =—1/5. 54. ЛС = 2(а+5)/3, BD = 2(b~а).
55. NP=^AB—^-AF. 56. cosа = —1//Т(Г. 57. о. 59. с2. 60. о.
62. | ЛС] = 1/cos а, |ЛЛх| = 281па, | С Лх | == | cos 2а |/cos а. Решение.
Из условия задачи следуют две возможности расположения точки Л: на по-
ложительной или отрицательной полуоси ординат. Для
определенности мы остановимся на случае, когда точка
Л расположена на отрицательной полуоси ординат (см.
рисунок). Другое расположение будет симметрично от-
носительно оси Ох, и поэтому длины сторон треуголь-
ника ЛСЛХ в обоих случаях будут одинаковыми. Най-
дем координаты точек Л и Лх (х; у). Из треугольника
ЛОС, учитывая, что |ОС[ = 1 и 0СЛ = а, получаем
|0Л| = (£а, следовательно, Л(—tga; 0). Длина
|ЛС]= 1/cos а. Достраиваем треугольник О АС до
прямоугольника. В нем |ЛВ| = 1, ЛВ0 = а; тогда | АК | == sin а. Длина
]ЛЛх| = 281па. Точка Лх лежит в четвертом квадранте, так как a > л/4.
х = про* ОЛХ = прОд?(ОЛ 4-ЛЛХ) = 0+1 ЛЛХ | sin a =
= 2 sin a-sin a = 2 sin2 a= 1 —cos 2a,
npoy OAi = npoy (CA+ААЦ = — tg a+| Л Лх | cos a =
= •—tg a+2 sin a cos a = tg a-cos 2a.
325
Итак, А (1 —cos2а; tg a cos 2а). Отсюда 1
] СЛг|« y’cos2 2аЦ-tg2 a cos2 2а « | cos 2а |/cos а.
63. l:sinaa. 64. 29/2. 65. 20. 66. D(2; О), 5=14 или D(7; О), 5=22,5.
67. 5. 68. Х= 1/4. 69. 1252. 70. arccos /2/5“. 71. 4. 72. 26. 73. 30. 74. 2/4Г.
75. 10. 76. 5. 77. —148. 78. —6. 79. 3. 80. у=*2—4*4-7.
§2
2. Воспользуйтесь тем, что соединив середины последовательных сторон
выпуклого четырехугольника, получите параллелограмм, площадь которого
равна половине площади исходного четырехугольника.
3. Докажите, что для любого выпуклого четырехугольника можно построить
окружность, касающуюся любых трех его сторон или их продолжений. Затем про-
ведите касательную к окружности, параллельную четвертой стороне. Сравните
периметры построенного и данного четырехугольников и воспользуйтесь тео-
ремой о касательных к окружности, проведенных из одной точки.
4. Докажите, что перпендикуляр к середине основания трапеции будет
в этом случае осью симметрии трапеции.
5. Воспользуйтесь тем, что перпендикуляр к середине основания трапе-
ции в этом случае является осью симметрии для окружности и трапеции.
6. Вычислите длину вписанной окружности, обозначив радиус исходной
окружности через /?.
7. Пусть а, b—длины катетов, с—длина гипотенузы прямоугольного тре-
угольника, г и R— радиусы вписанной и описанной окружностей. Докажите,
что 2R — c, 2г = а-[-Ь—с, используя теорему о равенстве длин касательных,
проведенных к окружности из одной точки.
8. Имеем | а [=21 b | sin 10°. Подставьте в равенство и воспользуйтесь
формулой для синуса тройного угла.
9. Воспользуйтесь формулой для вычисления длины медианы через длины
сторон треугольника и тем свойством, что медианы делятся точкой пересече-
ния в отношении 1:2.
10. Используйте тот факт, что радиус окружности, проведенный в точку
касания, перпендикулярен касательной, и то, что прямая, соединяющая центры
касающихся окружностей, проходит через точку касания.
12. Докажите, что сумма площадей указанных треугольников не меняется
при переносе точки О параллельно стороне параллелограмма. Отсюда полу-
чите, что эта сумма всегда равна половине площади параллелограмма.
13. Поверните Л АВК на угол в 90° так, чтобы точка В совместилась
с точкой D (поворот вокруг точки А). Покажите, что сторона (В К) пойдет
по стороне (CD) ,и что Л AM К' равнобедренный (К'—точка, в которую пере-
ходит точка К),
14. Воспользуйтесь формулой для вычисления площади треугольника
через радиус вписанной окружности и полупериметр.
15. Докажите, что центр вписанной окружности совпадает с центром дан-
ной окружности, а точками касания будут середины отрезков сторон, лежа-
щих внутри данной окружности.
16. Используйте теорему синусов.
17. Докажите, что отрезок, соединяющий середины смежных сторон вы-
пуклого четырехугольника, параллелен соответствующей диагонали, а его
длина равна половине ее длины.
326 „
18. Пусть: a, b, с—длины сторон треугольника, та—медиана к сто-
роне а. Докажите, что b—0,5а < та < (Ь-{-с)/2. Напишите такие же нера-
венства для медиан к другим сторонам.
19. Пусть А, В, С—вершины Л АВС, О—центр вписанной и описанной
окружностей. Покажите, что ОАС = ОСА*=ОАВ = ОВА.
20. Покажите, что эта прямая является осью симметрии трапеции.
21. Пусть О—точка пересечения боковых сторон трапеции, Oi и О2—
середины оснований. Покажите, что точки О, Oi и О2 лежат на одной прямой.
Используйте то, что [ООХ] и [ОО2]—медианы подобных треугольников.
22. Докажите, что линия центров является осью симметрии для двух
окружностей.
23. Используйте указание к предыдущей задаче.
24. Докажите, что сумма этих расстояний равна длине высоты к боковой
стороне треугольника.
25. Пусть Л АВС—данный правильный треугольник, О—центр симмет-
рии Л АВС, | ОД| = 7?— радиус описанной окружности, а—угол между (ОД)
и данной прямой. Докажите, что искомая сумма квадратов равна
R2 £sinaa4-sin2 a^+sin2 =4 Я2.
26. Соедините центры квадратов с вершинами параллелограмма и рас-
смотрите образовавшиеся треугольники. Из равенства этих треугольников
получите, что стороны рассматриваемого, четырехугольника равны и взаимно
перпендикулярны.
27. Используйте то, что искомое расстояние; равно также \h — (7?4-г)|,
где h—высота к основанию. Выразите R в г через h и, величину угла при
основании и. проверьте соответствующее равенство.
28. Пусть R — радиус окружности, описанной около правильного Л АВС,
точка О лежит на окружности (например* между вершинами В и С), О АС —а.
Тогда, используя теорему синусов,, получаем | ОС [=27? sin a, |0В| = 2/?Х
Xsirt —оЛ и [ О А | = 27? sin . Отсюда | О А |=±=[ОС|4-| ОВ |.
V о J \ 1
29. Докажите равенство соответствующих углов трапеций.
30. Пусть ABCD—данная трапеция ([ВС] || [ Д£>]). Докажите, что Л АВС
и ДВСП равнобедренные.
31. Пусть ABCD—данная трапеция, |Д2)|^=а, |ВС[ = 0. Через точку С
проведите прямую, параллельную диагонали [В£>]. Пусть D'—точка пересе-
чения этой прямой с (AD), Вычислите длину средней линии Л ACD' и отсюда
найдите расстояние между центрами диагоналей трапеции.
32. Пусть ABCD—данная трапеция, [M7V] — отрезок прямой, проходящей
через точку пересечения диагоналей—точку О. Воспользуйтесь подобием тре-
угольников Л ABD и Л 7ИВО; Л ACD и Л OCN.
33. Пусть Д ЛВС—данный треугольник. Прямое утверждение хорошо
известно. Для доказательства обратного утверждения рассмотрим точку £)£[ЛС]
такую, что | AD |:| ЛВ[ = |С7) |:| СВ| и воспользуемся теоремой синусов.
Получим
sin ЛвЬ sin Жв, sln6BS=4^Lsin6BS»
327
Так как sin ADB = sin CDB, то sin ABD—sin CBD, а отсюда следует равен-
ство ADB и CDB,
34. Пусть A ABC—данный треугольник; m, 0, h—медиана, биссектриса
и высота, проведенные к стороне [ЛС]; М, N и /С—точки пересечения ме-
дианы, биссектрисы и высоты с [ЛС] (или продолжением). Пусть [ЛВ |^г| ЛС|.
Докажите, что B^^BNIC^BNC ^ВКС — л/2. Отсюда получите требуемое
утверждение.
38. Используйте результат задачи 21.
39. Воспользуйтесь тем, что биссектрисы смежных углов параллелограмма
взаимно перпендикулярны, а биссектрисы противоположных углов парал-
лельны.
40. Пусть ABCD—данная трапеция, О—точка пересечения диагоналей,
| ЛО| = | ОС |. Докажите, что Л A0D = &СОВ.
41. Приведем краткое решение. Пусть ABCD—данный четырехугольник,
М и N—середины сторон [ЛВ] и [ОС] соответственно. Проведем через точки
М и С прямую (МС) и отложим на ней отре-
зок [М/С] так, что |МК| = |МС|. Соединим
точку К с точками Л и О (см. рисунок). Тогда
А АМК= A ВМС—> (КА) J (ВС) и | КА | = | ВС|.
Но [МАГ] —средняя линия Л KCD —> | MN | =
= \KD |/2 ^(| ВС | + l AD |)/2; знак равенства
возможен в том и только в том случае, если точ-
ки К, Л и О лежат на одной прямой. Но тогда
(ВС) || (КА) Р (AD)t т. е. ABCD—трапеция.
42. Пусть Д АВС—данный треугольник, [ЛА/] и [СМ]—медианы к сто-
ронам [ВС] и [ВЛ] соответственно, О—точка пересечения медиан. Докажите,
что Д ЛОМ = А CON.
43. Пусть А ЛВС—данный треугольник, [AN] и [СМ]—высоты к сто-
ронам [ВС] и [ВЛ]. Докажите, что Д ANC = &CMA.
44. В качестве иллюстрации проведем решение этой задачи с помощью
координатного метода (см. конец § 2). Пусть О и Ох—центры симметрии фи-
гуры Ф. Проведем через точки О и Of прямую, выберем на ней масштаб так,
чтобы 1 OOi | = 1. Ось Оу проведем через точку О перпендикулярно (OOj) (см.
рисунок). Пусть М£Ф и имеет в построенной системе координат координаты
Уо)- Рассмотрим точку Mf (2—х0; —Уо), симметричную точке М относи-
тельно Of, затем М2(х0—2; уо), симметричную Mf относительной, затем
М3 (4—х0; —yQ), симметричную М2 относительно Of, и т. д. Все эти точки Мк
принадлежат нашей фигуре Ф. С другой стороны, расстояние 1OM2k_i | =
328
= |OAf2fe| равно V (х0—2£)2+^o , т. е. неограниченно возрастает с увели-
чением номера k. Следовательно, фигура Ф не может быть ограниченной.
45. Докажите, что ось симметрии либо пересекает две противоположные
стороны выпуклого четырехугольника в их серединах и в этом случае четы-
рехугольник— равнобочная трапеция, либо ось симметрии проходит через две
противоположные вершины и делит четырехугольник на два симметричных
треугольника.
47. Опишите вокруг треугольника окружность, продолжите биссектрису
и серединный перпендикуляр к соответствующей стороне до пересечения
с описанной окружностью. Докажите, что они пересекаются в одной точке.
Далее воспользуйтесь тем, что высота и соответствующий серединный перпен-
дикуляр параллельны.
48. Пусть AD и СВ—дуги между точками А и £>, С и В. Докажите, что
сумма длин этих дуг равна л/?, т. е. половине длины окружности. Далее
соедините точки Л, В, С и D с центром О окружности и из Л AOD и Л СОВ
по теореме косинусов вычислите нужную величину.
49. Докажите, что площадь искомой части треугольника равна половине
площади всего треугольника минус площадь одной шестой части круга.
50. Докажите, что Л САЕ оэ’д СР А и что ‘CAEJrCEA = 45\
52. Докажите, что сумма длин этих отрезков равна удвоенной длине вы-
соты, проведенной к основанию треугольника.
53. Докажите сначала, что диагонали квадрата проходят через центр
симметрии ромба. Проведите диагонали и опустите из центра квадрата пер-
пендикуляры на стороны ромба. Воспользуйтесь равенством полученных
прямоугольных треугольников.
54. Воспользуйтесь результатами задач 27 и 19, предварительно доказав
следующее утверждение. Пусть Л АВС вписан в окружность радиуса /?.
Пусть основание [ЛС] этого треугольника фиксировано, а вершина В пере-
мещается по дуге окружности. Тогда радиус вписанной в Л АВС окружности
будет наибольшим в том случае, если Л АВС равнобедренный.
55. Приведем решение, основанное на вычислении максимума функции.
Пусть в Л АВС величина угла С фиксирована: С = а, а углы А и В ме-
няются. Положим Л = х; тогда В~п—а—х. Рассмотрим функцию /(*) =
= cos A-f-cos /?+cos £ = cos *+cos a-j-cos (л—a—x). Исследуя эту функцию
на максимум-минимум при х£]0, л[, получаем, что максимум достигается
при х = (л—а)/2, т. е. в том случае, если А АВС равнобедренный (А—В).
Пусть теперь Л АВС равнобедренный, А = В=х. Тогда С = л—2х. Рассмот-
рим функцию f (х) =cos A-|-cos В-4-cos С = 2 cos x+cos (л—2х). Исследуя эту
функцию на максимум при х£]0, л/2[, мы получим, что f (х) достигает мак-
симума при х = л/3, т. е. в случае равностороннего треугольника. Таким
образом, сумма косинусов углов треугольника достигает наибольшего значе-
ния для равностороннего треугольника и равна в этом случае 3/2.
56. Для доказательства первого и третьего соотношений используйте фор-
_ ab
мулу для вычисления площади треугольника S = — sin а, где а—величина
угла между сторонами треугольника. Для доказательства второго соотноше-
329
ния постройте равновеликий данному четырехугольник с теми же длинами
сторон, но такой, чтобы стороны длины а и с, b и d были смежными.
57. Проведите через точку М диаметр (CD) и докажите, что |АЛ4[*|Л4В| =
= ]CM |.[AW |.
58. Решение. Выберем систему прямоугольных координат, взяв в ка-
честве начала этой системы точку пересечения данных прямых, а сами эти
прямые в качестве координатных осей, выбрав на них положительные направ-
ления и указав единицы масштаба (см. рисунок). Тогда расстояние от любой
~ точки М с координатами (х; у) до данных прямых будет равно |х | и |//|
соответственно. Следовательно, точка М (х; у) принадлежит искомому гео-
метрическому месту точек в том и только в том случае, если |^|+|^/| =
= А+А • Тогда 0(0; 0) не может принадлежать искомому множеству,
Iх! IУI
поэтому |х |+| у | 9^ 0, и, следовательно, написанное уравнение равносильно
уравнению |х||г/| = 1. Графиком данного уравнения будет объединение гра-
фиков функций у=1/х и г/=—1/х, т. е. две гиперболы. Таким образом, мы
построили искомое множество точек.
59. Решение. Воспользуемся вновь координатным методом. Пусть дан-
ные точки О и А. Рассмотрим прямоугольную систему координат Оху, начало
. которой совпадает с точкой О, ось Ох содер-
жит отрезок [ОЛ]. Можно считать, что точ-
- ка А имеет координаты (1; 0) (см. рисунок).
X/ I Воспользовавшись формулой > для вычисле-
. < / |- ния расстояния между двумя точками на
^1 & ’MJJ) . L & плоскости с заданными координатами, мы
получим | ОЛ1[ = Vх2+У2 > I AM | =
= У (х—1)2+$/2 , где М (х; у)—любая точка плоскости. Таким образом, точ-
ка М (х; у) принадлежит искомому геометрическому месту точек в том и
только в том случае, если У\2-\-у2 : (х—1)2+у2 =/и:п, т. е.
п2 (х2+^) = т2 [(х~ 1)2+у2].
Преобразуем полученное соотношение
(п2—т2) x2+2m2x+(n2—т2) у2=т2.
Если /г = /п, то мы получаем х=1/2, т. е. искомое геометрическое место то-
чек будет прямой, проходящей через середину отрезка [ОД] перпендикулярно
330
этому отрезку. Таким образом,
перпендикуляре! Пусть теперь
дальнейшие преобразования:
2 о т2
х2—-2—5---Г
т2—п2
{ т2 \
х
при m = n мы получаем теорему о серединном
п Ф т, можно считать т > п > 0. Выполним
*4-у2
т2— п2
т2
т2
т2—п2 9
2 __т4 т2
f “ (т2 — п2)2 т2—п2 *
« / тп \2
х
m2—n2J -^m2_n2 J •
Последнее уравнение определяет окружность с центром в точке 2V (/n2/(m2—л2); 0)
радиуса тп/(т2—п2). Таким образом, мы показали, что искомое геометриче-
ское место точек при т = п (т. е. при равенстве расстояний от искомой точки
до двух данных) есть серединный перпендикуляр к отрезку с концами в двух
данных точках, а при т Ф п это некоторая окружность с центром на пря-
мой, проходящей через данные точки. Укажем на тесную связь построенного
множества точек М с внутренней и внешней биссектрисами /\0МА (см. ри-
сунок). Пусть К £ [ОД] и L £ [ОД]—точки пересечения данной окружности
с прямой (ОД). Тогда [Л4/С]—биссектриса внутреннего ОМ% треугольника
ОЛ4Д, так как прямая (М/Q делит сторону [ОД] на части, пропорциональные
сторонам [ОЛ4] и [ДМ] (см. задачу 33 этого параграфа). Так как прямая (ML)
перпендикулярна биссектрисе (МЛ), то (ML)—биссектриса внешнего угла
при вершине М треугольника ОМА (см. задачу 51 этого параграфа).
60. Искомые множества точек описываются уравнениями
1) |х|1г/|=1И-1</11. 2) |р|—
Постройте соответствующие множества на плоскости.
61. Парабола с осью симметрии, проходящей через данную точку Ff
перпендикулярно данной прямой I. Вершина параболы расположена на оси
симметрии на равном расстоянии от данной прямой и данной точки. Ветви
параболы удаляются от данной прямой. Если ось параболы принять за ось
Оу, причем за положительное направление принять направление от Z к F,
вершину—за начало координат О, прямую, проходящую через вершину
перпендикулярно Оу—за ось Ох, расстояние от данной точки до данной
прямой обозначить р, то уравнение параболы примет вид х2 = 2ру.
62. Обозначим середину отрезка [ДВ] через О, а заданную постоянную
через а2. Тогда искомым геометрическим местом являются две прямые, пер-
пендикулярные прямой (ДВ) и отстоящие от точки 0 на расстоянии а2/2|ДВ|.
63. Воспользуйтесь результатом задачи 24 этого параграфа.
64. Пусть А—точка, лежащая на стороне угла и удаленная от другой
стороны на данное расстояние. Проведите через А прямую, параллельную
биссектрисе. Тогда часть прямой, лежащая внутри угла, удовлетворяет усло-
виям задачи. Рассмотрите все возможные случаи.
65. Прямые, проходящие через точку пересечения прямых (ДВ) и (CD),
расстояние от точек которых до (ДВ) и (CD) обратно отношению [ ДВ |:| CD(
(исключая саму точку пересечения этих прямых).
66. Окружность, построенная на отрезке, соединяющем данную точку
с центром окружности, как на диаметре.
331
67. Часть окружности с центром в вершине данного прямого угла и ра-
диуса а/2.
68. Окружность, концентричная данной и радиуса /? = r/sin (а/2), где
г —радиус данной окружности.
§4
1. 50 см. 2. л/6. 3. 12 см, 16 см. 4. 9,5 см. 5. —.. .
sin ((л+За)/4)
6. 2 УS tg (а/2) . 7. 14 см. 8. ab V17(a+b). 9. 85.
Д 10. 7(УТ—1)/9/Т. Решение. Обозна-
чим длины сторон [ЛВ], [ВС], [СЛ] через с, а,
Ь* Тогда по условию a]R = 2, &/7? = 3/2, т. е.
/а = 2/?, b — 37?/2. С другой стороны, a= 2R sin Л,
следовательно, sin Л=1, т. е. угол Л прямой. В
прямоугольном треугольнике ЛВС найдем третью
сторону | АВ | =с = У a2—b2 = V\R2 —9/?2/4 = /?рг7/2. Биссектрисы (см.
рисунок)
рь = |ВО|=У|ДВ|2+|ЛР I2 , Рс = |СВ|=У|ДС|2+|4В|2 .
। j n I_। дг । I А& I__I АЕI______I АВ I__। ।_____*£_
|ДР|-|ДС| | ЛВ|_|_|ВС) — а+с > |ЛВ|_|ЛВ| |ЛС| + |ВС| а+&.
Тогда
1ДП|_ 3R-RУ 7 _ 3R/7 л _ 3R-R/7 3R/7
1 l-2.2(2R+R/7/2)_2(4+Г7)’ * 1 * * * У 1 2-2-(2R+3R/2)~ 14 •
_ Г7Ri I 9-7-R2 /7Я2(16+8У 7+7+9)
Рь-|/ 4 't'4(4+|<7)2 |/ 4(4+1<7)2 “
f 7R2(32+81/~7) __ У 77? /~8(4+Т/~7) _ У 77? У 2
У 4 (4+У 7)2 2 У (4+К7)2 У'4+уг1=Я
_ У 77?-2 _ 27? У 7 27? У 7
""Кв+г/Т ]/74-2/7+1 К 7+1 ’
о ,/9R2 , 9-77?2_37? -,/77T_3R-2/2 37?У2
Рс~ У 4 4-7а 2 У *+7"~ 2У7 ~ У 7 ‘
Искомое отношение
2R/7 У7 _ _14£(У7-0 _7(У7-1) ,
Рс (У7+1)ЗЯ-У2 (7— 1) 3R У 2 9У 2
11. У 3(У 5+1)74. 12. л/6, я/3, я/2. 13. arccos (13/14). 14. 25.
15. 2 arctg (1/3). 16. arccos (1/У10). 17. 15 см, 5 см. 18. ЗУЗсм2.
19. (9УЗ/4)см2. 20. 14 см, 8 см.
21. 1. Решен ие. Пусть стороны параллелограмма а и bt меньшая диа-
гональ dlf а большая d2. Тогда 2a2-\-2b2 = df -j-dl, но по условию di=3d?, по-
этому a24-62=2di. По теореме косинусов d? = a24-b2—2ab cos 60° = 2d*—ab,
т. е. ab = df. Следовательно, a2-j-b2~l-2ab = 2di^-2di = 4dii или (a+6)2 = 4djf
332
t. e. a-\-b = 2di. Получили систему
( a b s= f
t a6 = d?,
ее решение a = b = di, т. e. a/b—X.
22. 96 cm* 2. 23. | a—b |/2. 24. Z2 sin a cos a. 25. 0,5 arcsin (4/5),
л—0,5 arcsin (4/5).
26. 2ab/\ a—b |. Решение. Пусть | AD | > | ВС [ (см. рисунок); для оп-
AD=a, ВС = Ъ. Тогда —1^£1—=
|КС|_ Ь _
|KD| а ~
b 1^с1
ределенности будем считать
_ b | LC | _ b
~ а+Ь | ЛС| — а+Ь ’
|КС|
|КГ>|—|КС|
|КС|_|АГС| 6
|СО| |ЛС|
I ЛС| _а+Ь
\LC\~ Ь
|А^1
| AL | \AL\ + \LC\~
M К N
b
a—b | CD | a—b
Перемножая пропорции
a—b ’
\NC\_
|ЛС| ,
Ь
----g , получим
| ГС 14-1 АТС | __ 2а
' |£С|
41.
45.
47.
А
| LN | _ 2а
|LC| а—Ь —' [ТС] а—Ь "г | LC | — а— Ь’
| LN I |Л1ЛМ 2а . . 2аЬ „ А , .
Н0 | £ё| 1=5 | ВС | '"а—6 ’ откУда I МАГ | = ^—& . Если бы было а < Ь, то
при выводе их роли поменялись и мы получили бы | MN \—2abl{b—а).
27. arctg (2/3). 28. У 5/2 см. 29. л/6 и л/3. [30. V 7 м. 31. У/п2,4-л2/2.
32. 21 УТЗсм. 33./91 м. 34. 1/У13. 35. 2 и 6. 36. Я2 cos (а/2) (l+sin(a/2)).
37. tg (ф/2) sin 2<p. 38. 4 см; 12,5 см. 39. (УГб’Ц-УЗб) см. 40. (3—У7)/2.
6/(2 cos (а/2)). 42. г/8. 43. 2л/?/3. 44.2/Rr,2RVr/(r-\-R), 2rVR!(r^-R).
RrKVR+V^^, R^/(V"R—Vr~r)i(R>r). 46. r(r+R)/R, r^R.
rir2/2(ri+r2). 48. Уз. 49. В 2 раза. 50. 27?2 (1 — sin (a/2))2/sin a.
2Rr-\-r2. 52. 15/8. 53. ^-руУр(р—a)(p—6)(p—с), где p=(a-HH-c)/2.
2 (34-2УЗ). 55. 9r2/2. 56. (S/sin a)V2. 57. 2R2sin3 * * * * 8 a. 58. 100л/9см2.
a. 60. ЗУЗ/-2. 61. У24—6У 3/2. 62. 2a/У 5. 63. 9 см, 12см, 15см.
64. 240 см2. 65. 20л см. 66. 0,5 arccos (3—8S) (1/4 < S < 3/8).
67. Пусть 0< P<a< л; /7/(2 sin ((a—₽)/4) sin ((a+P)/4)) и 772ctg((a—P)/4)t
если основания трапеции расположены по одну сторону от центра окружности,
/7/(2 cos ((а—₽)/4) cos ((а-(-₽)/4)) и Н2 tg ((a-f-P)/4), если основания трапеции
расположены с разных сторон от центра окружности.
68. 1 см и 17 см. 69. ± 6 . 70. k sinP(5-2y6cosa)
8 sin Р sm (a-f-0) 6 sin a sin (a-[-P)
71. 2 cm, 14 cm. 72. 4 см. Решение. Так как , то , т. е.
□ 2 13 0-J-4Z 13
7а—13& = 30. С другой стороны, а-\-Ь—10. Следовательно, я = 8, Ь = 2. Боко-
вая сторона IПоэтому высота Н2 — 12 — (s=s25 — 9 =16,
т. е. /7 = 4 см.
51.
54.
59.
333
73. 3V3. 74. |ВВ1|=/'53/2> B = arc«os (11У 6/30). 75. S = 216 cm8.
76. 20/"3 cm2. 77. | AB | = 2/46/3. 78. /Тбcm. 79. /65/2. 80. P =
= 4ab/(a-]-b). 81. tg a = /~3/7, где a — наименьший угол треугольника. 82.6 м,
6/5 м2. 83. sin a = (1-/ '/73)/12, где a—угол при основании треугольника.
84. 18 см, 24 см, 30 см. 85. Yb2-\-c2 ± §bcfi). 86. arccos(4/5) или л—arccos(4/5).
К7. \EF [ = 9/2/7 см. 88. 6лсм. 89. 40/2/11 см. 90. 9см. 91. 16/7/11 см2.
92. 20см, 5 см. 93. 45/2 см2. 94. %! У Зсм. 95. |СД|=вь39 см, |СВ| = 26см.
96. Боковые стороны 2R (2-|-/ 3)//3, основание 2R (2-|-/"3). 97. |О/С| =
= 5/14 см. 98. 8/ 5 см, 4/5* см. 99. /?х—г, R2—rt г (7?х—г) (R2—r)/(R1R2—r2).
100. 1:4 (3-2/2). 101. 2 (/2—1) см. 102. а/2, а/2. 103. 32см2. 104.4 см.
105. 8//Зсм2. 106. а/2, Л/2. 107. h — H/2, где h и Н—высоты параллело-
грамма и треугольника соответственно. 108. 2а. 109. 37?/2.
ПО. (а—Л)3/16а> b. 111. Квадрат со стороной R/2, Smax = 27?2.
112. Квадрат со стороной Здм. 113. 12смиЗ/Зсм. 114. 12см и 9см. 115. 9 см
и 12см. 116. 9см и7,5см. 117. В круг радиуса 7/*2 см. 118. с/У 2 и с!/~2.
§ 5
1. 7. Указание. Рассмотрите случаи, когда по разные стороны плос-
кости лежат по две вершины и одна и три вершины.
2. Если прямые не проводят через одну точку, то покажите, что они ле-
жат в плоскости, проходящей через три точки их пересечений.
3. Рассмотрите тетраэдр ABCD и покажите, что вершина D проектируется
в точку пересечения высот Л АВС. Воспользуйтесь теоремой о трех перпен-
дикулярах.
4. Через [ЛВ] проведите плоскость, параллельную [CD]. Через точку А
в этой плоскости проведите прямую, параллельную [CD], и отложите на ней
отрезок4j4D'.J,-равный [CD]. Рассмотрите £±D'DB, покажите, что |Л4Л | равна
.длине медианы £± D'DB и отсюда получите требуемое неравенство.
5. Пусть I—наклонная, Zx, /2 и Z3—три данные прямые. Докажите, что
наклонная I перпендикулярна биссектрисам углов между прямыми Zx и 12 и
прямыми Zx и Z3. Отсюда следует, что Z перпендикулярна плоскости, в которой
лежат Zx, 12 и Z3.
6. Достройте треугольную пирамиду до треугольной призмы с основаниями,
лежащими в данных плоскостях. Докажите, что объем призмы не будет ме-
няться при параллельном перемещении отрезков, а объем данной треугольной
пирамиды равен трети объема построенной призмы.
8. Рассмотрите сечение четырехгранного угла плоскостями, перпендику-
лярными линии пересечения плоскостей, проходящих через его противополож-
ные ребра.
9. Нет. Указание. Рассмотрите трехгранный угол, у которого два
плоских угла прямые, а третий не более л/3.
10. Докажите, что если а—величина плоского угла при вершине данного
трехгранного угла, то величина не прилежащего к нему двугранного угла
больше а.
11. 0, 1, 3 и 6.
334
16. Приведем решение, основанное на теореме о связи площади основания
и боковых граней. Пусть величина всех двугранных углов пирамиды равна а;
Si, S2, S8> S4—площади граней. Получаем
' Si = cos a (S2+S8+S4)r
S2 = cos а (51+5з+54),
S8 = cos а (Si+S2+S4),
\ S4 = cos ос (Sf+S2+S3).
Отсюда Si = S2 = S3 = S4 и cos а = 1/3. Кроме того, в этом случае высоты
пирамиды проектируются в центры вписанных в грани пирамиды окружностей.
Отсюда легко получить, что апофемы боковых граней равны (если одна из
граней принята за основание). Но тогда и длины стороны основания равны.
Повторяя эти рассуждения для каждой грани, получим равенство всех ребер
пирамиды.
17. Приведем решение. Обозначим цифрами 1, 2, 3 и 4 вершины пира-
миды; 6112, «1з, «14, «23, «24, а34—длины ребер, соединяющих соответствующие
вершины; 7?i, /?2, и Т?4—радиусы шаров с центрами в соответствующих
вершинах. Тогда решение задачи сводится к вопросу о разрешимости системы
^1+^2 = **12»
#1 + #3 ==<213>
7?1 ~{“/?4 = «14>
^2 + ^3 = а23>
^2~Ь^4:==а24>
/?з + ^4 = Л34
при условии «12+^34 = ^13+^24 = ^11+^23 = ^, данная величина. Тогда
выписанная система равносильна следующей;
' ^1 + ^2 = а12<
₽i+^s = 6Z13,
/?1 + /?4 = «14,
< Ri + ^2+^з + ^4=^*
Отсюда находим
Ri = (#12+^1з+«14—*0/2 > О,
/?2= («12'~Н*^_-~*^13-а14)/% > О,
/?з = («1з+*/—«12—«к)/2 > О,
/?4 = («!<+*/—«12—«1з)/2 > О,
т. е. мы доказали, что такие шары существуют и указали их радиусы (то,
что J?/ > 0 при- * = 1, 2, 3, 4, докажите, используя соотношения между дли*
нами сторон треугольника).
18. Проведите' плоскость через высоту пирамиды и боковое ребро и рас-
смотрите линию пересечения этой плоскости с основанием пирамиды.
19. Нет. Постройте соответствующий пример.
20. Докажите, что эта величина равна 37/, где Н—высота пирамиды. Для
этого из точки Р опустите перпендикуляры на стороны основания и докажи-
те, что сумма их длин постоянна и равна длине h высоты основания, а иско-
мая величина равна fttga, где a—величина двугранного угла при основание
пирамиды.
21. Треугольник, квадрат, шестиугольник.
335
24. Существует. Например, рассмотрите многогранник, который получит-
ся, если поставить друг на друга два равных наклонных параллелепипеда
так, чтобы совместились их основания.
26. Пусть М—данная точка, /х и /2—касательные к шару, К и М—точки
касания и /2 с шаром. Проведите плоскость через точки М, К и N и вос-
пользуйтесь теоремой о касательных к окружности.
29. Пусть О—центр описанного вокруг пирамиды шара. Рассмотрите
четыре пирамиды, вершины которых совпадают с точкой О, а основаниями
являются грани исходного тетраэдра. Докажите, что они равны между собой.
Отсюда будет следовать, что точка О равноудалена от плоскостей граней,
т. е. является и центром вписанного в тетраэдр шара.
32. Пусть —длина высоты пирамиды, проведенная к грани площади
вневписанный шар радиуса касается этой грани. Докажите, что —-=s
1 2
=------— , Далее воспользуйтесь равенством = г (S14-S24-S3“|-S4)=3V.
г nk
Отсюда получаем
________________VI _____________V
/ г \ •514-524-5з+54/
2S3 \ । 1(. 2S4 \ _ 2_
+ г \ •$1+‘52+*$з+54/ г
33. Для доказательства достаточности покажите, что центр описанной
сферы будет совпадать с точкой пересечения перпендикуляра к основанию,
восставленного из центра описанного вокруг основания круга, и плоскости,
перпендикулярной отрезку, соединяющему вершину пирамиды с любой верши-
ной основания, проведенной через его середину.
34. Пусть М, N и К—точки касания сферы с гранями трехгранного
угла. Рассмотрите пирамиду SMNR, Докажите, что | SM | = | SN | = | SK |.
Отсюда следует, что высота пирамиды проходит через центр окружности,
описанной около основания. Используя это, покажите, что продолжение вы-
соты пройдет через точку О, т. е. центр данной сферы.
36. Воспользуйтесь теоремой о равенстве длин касательных, проведенных
к данной сфере из одной точки (см. задачу 26).
39. Докажите, что указанный угол по величине равен двугранному углу,
образованному - плоскостями а и 0.
40. Пусть точки Mt N, К и L—середины сторон [SB], [SC], [ДС] и [ДВ[
соответственно, точка О—середина [S4]. Докажите, что четырехугольник
MNKL—прямоугольник, а Д5ДС и Л 5ЛВ— равносторонние. Далее дока-
жите, что точка О одинаково удалена от точек М9 N, К, L, S и А. Отсюда
получите, что О—центр данной сферы.
41. Рассмотрите сечения данного шара плоскостью основания и плос-
костью, проходящей через середины боковых ребер пирамиды. Так как круг,
подученный в сечении шара основанием пирамиды, касается сторон основа-
ния в их серединах, то докажите, что в основании пирамиды лежит равно-
сторонний треугольник. Рассмотрите прямую, проходящую через центры
полученных в сечениях кругов, и докажите, что она перпендикулярна основа-
нию. Далее покажите, что длины боковых ребер пирамиды равны между собой.
46. Пусть 2а—величина угла при основании осевого сечения данного
конуса, Z—длина образующей этого усеченного конуса. Тогда 7?i = rctga>
336
^a=ztga, l—Ri+Rz, где г—радиус вписанного шара, Ri и /?2-^РаДиУсы
оснований данного конуса. Воспользовавшись формулой для площади боковой
поверхности усеченного конуса, получаем
•^бок. усеч. кон.== 2 Л (^?1+^?2) Z/2= ЛГ2 (tg a~j-ctg а)2.
Далее, так как tga+ctga^2 (0 < a < л/2), то Вбок. усеч. кон. 4лг2 = В,
где В—площадь поверхности вписанного шара.
§6
1. 2л/3. Указание. Через точку CQLi проведите прямую £а||£а, а че-
рез точку B£L2—прямую £J||(C£>). Пусть В'—точка пересечения L' и LJ.
Рассмотрите треугольник В'СЛ.
2. Ут2—4Z2 sin2 (a/2) либо Ут2—4l2 cos2 (a/2j в зависимости от вза-
имного расположения точек А и В на прямых Lt и L2.
3. 29,6. Указание. Воспользуйтесь теоремой о трех перпендикулярах.
4. 1) (d4-Z>cos (л/5))/(1+соб (л/5)), если точки А, В и С лежат по одну
сторону от плоскости у;
2) | d—b cos (л/5) |/(1+cos (л/5)), если точки А и В лежат по одну сто-
рону от у, а точка С—по другую сторону; 3) b cos (n/5)/(l+cos (л/5)), если
А и В лежат по разные стороны от у.
5. 1) | с—b |, если В и С лежат по одну сторону от плоскости ₽; 2) b-]-ct
если В и С лежат по разные стороны от плоскости 0.
6. На три равные части длины /”3/3 каждая. 7. За2/2.
8. arcctg Уctg2a+ctg20. 9. arcsin tg (a/2) (0 < a < л/2). 10. 2}/~2б2Х
Xsin2psin ((2а+л)/4). 11. b3//2. 12. |ВП1|=5/3’см. 13.2Zsin a/2B+Z2cos2a.
14. V=h3 (ctg a ctg P)/2, S=2/i2/ctg2 a+ctg2 ₽. 15.
16. P sin ₽ cos2 ptg(a/2)/2. 17. S$/2 sin aK /Зсоза/з. 18. Q3/2sin<pK pTcos <p.
19. a3 (sin a sin P cos2 P)/2. 20. a3 (sin 2a tg P)/2. 21. Z3 (sin 2a tg2 p)/4. 22. ^/32.
23. У 3(V ctg a)2/3 sec a. 24. 4+6У 3. 25. 4p2 sin 2a/(l +sin a+cos a).
26. Z3 (sin 2a cos a)/4. 27. 7Z>2/(8 cos a), 2 arctg (cos a). 28. a3/cos 2a/sin a.
29. б/2Гсм. 30. d3 (tg p ctg (p/2))/2. 31. a3(tgatg(a/2))/8. 32. ЗсР(8ййа81па)/16.
33. a2/?/sin2 a—cos2 p/2. Задача имеет решение, если sin a > cos Р,
34. К28 cos а/ /”з/cos (a/2).
35. a3/3ctg2(a/2)—1/24 (a < 2л/3).
36. arctg ((1 ± У1 —8 tg2 a)/2 tg a). Задача имеет решение при tg2 a^l/8.
37. 125 /3/9 см3.
38. Z3 (sin 2a cos a) / 3/8. 39. сР/(3 sin (a/2) (3—4 sin2 (a/2))).
40. a2 У 3/(27 cos a). 41. 32 /133/27 cm2. 42. d3 (cos3 p tg a)/(6 sin p).
43. (12+13/ 3)/2 cm2. 44. c3 (sin 2a tg p)/3.45. 25 (2+2 tg a+ /2+4 tg2a>/8.
46. S ctg P/2S sin a/(6 sin a cos (a/2)). 47. a2 (1+cos P)/(4 cos P tg (a/2)).
48. 2/?3 sin a sin P sin (a+ P) tg qp. 49. a3 cos (a/2)/(12 /4 sin2 (a/2)— 1).
50. /3Z3tg2a(l+4tg2a)“3/2. 51. 6r2 (1+sin coseca. 52. ^/24.
53. 2-3”1/6 54, #3/3/8. 55. /3 ^^—(ЗИctga)2^. 56. (a3 tgqp)/12,
337
a2]/r3(I4-4tg4<p)/4. 57. 4d»/(9 /3 sin a sin 2a). 58. ЗаЯ/16. 59. 2aa K15/49.
60. 1/7. 61. V’3a2/(48cosa), (a3tga)/48. 62. №sina/(4cos a—2).
63. R3 sin3 a У 3 ctg2 (a/2) —1/3. 64. Злв2/(1 +2 cos 2a). 65. Z>ssin(a/2)X
xKl + 2cosa/6 (0<a<2n/3). 66. a3 (sin (a/2) tg P)/6. 67. y'&^tga/O+tga)3.
68. 63/6. 60. rt/2. 70. 84 cm2.
71. h3 (tg2a+tg2p)3/a/(12tgatg 0). P ешение. Так как все ребра
равны, то равны и их проекции на основание; следовательно, вершина 5
(см. рисунок) проектируется в центр D описанной вокруг треугольника АВС
окружности. Треугольник прямоугольный, поэтому точка D—середина гипо-
тенузы. Пусть [SK] JLr#C] и Г51]±МС], S/<D=a, SLD = p, |£>Я| = | AC |/2,
DL | .== | ВС |/2. Тогда H = [ SD [ = J?cHg« = „I ffPJ.jgP.; положим | AC |=
== k tg (3 и |BC| = £tga, где k некоторый коэффициент, который позднее
будет найден. Тогда Н=(k tg a tg р)/2. Искомый объем V = 5-==
о 2
ЬЗ fgp2 & tgr2 Л
=------№-----• Площадь треугольника S = (| АВ | h)2 = | АС [ • | ВС |/2. Из
этого соотношения найдем k. Действительно, | АВ | = У | ЛС|2+|ВС |2=
= k Уtg2a+tg2($, поэтому yrtg2a4-tg2P == k2 fg a tg p, откуда k =
==&y4g2a-|-tg2P/tg atg fl. Тогда объем пирамиды
R2(/tg2a+tg2p)2 tg2a tg2 fl Л3 (/tg2a+ tg2p)2
tg2atg3p * 12 12tgatgp
к- ба.чФд)с1«'(2Т2)
и-
74. b3 (sin (a/2) tg p)/6. 75. г У1 + cos* (a/2) tg2 p.
76. m3 ctg а УЗ—ctg2 a/24 (л/6«са).
77. Обозначим a=arosin (2S(/2—l)//2). Тогда, если л/4 < a< л/3, то
искомые углы a—(л/4), а, а+(л/4); если л/3 < а < л/2, то искомые углы
а—(л/4), а, а+(л/4) или (Зл/4)—а, л—а, (5л/4)—а.
78. а8 У cos а/(12 sin (а/2)). Решение. Пусть | АВ |==| CD |*ADB ==
= ЛСБ = РЛС=/5вС=а (см. рисунок). Через [DC] проведем плоскость,,
перпендикулярную стороне [ЛВ], она пересечет эту сторону в точке К такой,
что | ЛЛ| = |ХВ |. Тогда объем пирамиды равен 4-|ЛВ[5сок. Из прямо-
о
338
угольного треугольника ADK находим |DK| = | Л/CI-ctg (а/2) = а/(2 tg (а/2)).
Из прямоугольного треугольника DKM находим
л2
|“|‘-|ю|’-|М|~пйгй-т" _
a* 2 (cos2 (а/2) —sin2(a/2))_ a2 cos а .|Л.М| «/cos a
----------------4Sin2(a/2j=?>|KAfl-2sta((x/2)' <°<“<я/2).
4 sin2 (а/2)
Тогда
и искомый объем пирамиды равен а3 У cos а/(12 sin (а/2)) (0 < а < л/2).
79. [За4—16 (Р2—Q 2) ]: [За4+16 (Р2 - Q2)]. -
80. 1) 2 j/|^±l||S2-Т2| прир#1;
2) при р=1 длина гипотенузы может принимать любое значение из .
интервала ]0, 2 (при этом S = T).
8t_______________abc
ab + Ьс+ас -f- Y (afe)2-(-(ac)2-f-(M2 *
82. 1 /So • |/ 1-(у)2 S * * * (s~2Si) (5-2S2)(S-2Ss), где S=Si+
. + Sa+s3.
83.5/3/6. 84. 7. 85.32 см3. 86. (a9 tg a)/6. 87. arccos (/2 sin (ф/2)).
88. 2 arccos (1/ ]/ 1 —cos а) (а>л/2). Решение. Проведем )ВЛ4] и
.(DM] (см. рисунок), перпендикулярные ребру [SC]. Тогда BMD=a. Иско-
мый угол BSC=p. Обозначим | ВС | = а, | SB|==
= Z; тогда | BN | = а ]/"2/2. Вычислим sin (₽/2):
sin (8/2)= 1^| а
'р/ ' |5j5| 2/ t |£М| 2|BW|
=sin P-sin • —=•
2 У2
Итак,
sin (Р/2) = /2 sin (₽/2) cos (Р/2) sin (a/2),
откуда
cos (Р/2) = 1/( У2 sin (a/2)) = 1/ — cos a (a > л/2)
или
P==2arocos (l/yrl — cos a) (a > л/2).
89. P (ctg a ctg ₽)/3 (1 +ctg2 a+ctg^ P).
389
90. H cos <p/(i + cos <p) s' H ctg ф tg (ф/2).
91. а2 /З/б.
92. —4ft3 cos2acos2a/3 (л/4<:а < л/2). При 0 < а < л/4 указанная
плоскость не пересекает пирамиду.
93. a2 sin2 a cos (a/2)/sin2 (За/2).
94. Указание. Докажите, что точка М совпадает с центром
основания пирамиды, а точка N—с центром круга, описанного около грани
BSC.
95. 26 м2. 96. a3 (sin2 a tg (J)/3, a2 sin а (1 -}-sin P)/cos р. 97. a3 (sin2atg Р)/6.
98. 27?3 (sinatg Psin32P)/3. 99. 4r3 ctg3 (a/2) cos 2а/(3 cos a)=4r3 ctg3 (a/2) X
X /tg2a—1/3 (л/4 < a < л/2).
100. 2Я2 — /2 ctg2 P—ctg2 a. 10L 6 (7—4 /з) m2 tg a.
102. 4 /3m2 cos a cos2 (a/2). 103. 10 V19 cm2. 104. (V§'i+
105. /(S cos a)/2(l-|-sin a — cos a). 106. m3 (sin2 a cos a)/6sin6 (a/2).
107. 0,5-ft2tga/cosa. 108. 2arcsin ((/Тб—/2)/4). 109. 12 (2+/з) см2.
110. 2a2sin Psln2(v/2)/cosy. 111. dctg(a/2)sin2(P/2)/cosp. 112. 384 /10/169 cm2.
113. a (1+ cos2 a)/2 sin 2a.
114. (л/6)/(/3-tg (a/2))/(/3+tg(a/2)). 115. tf(/4 tg2a+l-l)/4tga.
116. (na3tga)/9/3.117./ cos2 a /3+cos2 2a/2 sin a. 118. 2na3(3+cos2a)/3sin2a.
119. 2t> (cos (a/2) sin a)/n. 120. arcctg 2. 121. ла3 ctg p/(24 sin3 (a/2)),
ла2 (1 + sin P)/(4 sin P sin2 (a/2)). 122. 3S/2.
123. ла3 (cos (P/2) tg a)/(24 sin3 (P/2)),
ла2 Vl + cos2(p/2)tg2a/(4 sin2 (P/2)).
124. fl2 /3/(4 cos a). 125. 15л (5+2 /3)/Кз7+ 10 /З.
126. /(2S/sin 2a)3/(8 cos3 a).
127. 2arctg /1/3. Решение. Пусть ABCD—осевое сечение цилиндра,
a ASD—осевое сесение конуса. Величину угла между осью конуса и его
образующей обозначим а, 0 < а < л/2. Длину радиуса общего основания
конуса и цилиндра обозначим г. Площадь полной поверхности цилиндра равна
5ц = 2лг24-2лг«г ctg а = 2лг2 (1 +ctg а),
а площадь полной поверхности конуса
SK = лг2 + лг • r/sin а=лг2 (1 -J-sin a)/sin а.
По условию задачи <$ц:SK = 7:4, т. е.
2 (1-4-ctg a) sin a_7
1 +sin a 4 ’
Так как l-J-sina^O при 0 < a < л/2, то умножением на 1 +sin а данное
уравнение приводится к уравнению sin a+8 cos a = 7. Далее, учитывая, что
sin a=2 sin (a/2) cos (a/2), cos a=cos2 (a/2)—sin2 (a/2), l=cos2 (a/2)4~sin2 (a/2),
приведем данное уравнение к виду
15 sin2 (a/2) —2 sin (a/2) cos (a/2)—cos2 (a/2) = 0,
Деля это уравнение почленно на cos2 (a/2) 0, получим
15 tg2 (a/2) — 2 tg (a/2) — 1= 0,
340
которое имеет два корня tg (а/2) = 1/3 и tg (а/2) = —Г/5. Так как по усло-
вию задачи а > 0, то второе решение .надо отбросить. Итак, tg (а/2) = 1/3 =$>
=р а = 2 arctg (1/3).
128. 8Q tg ф cos6 (<р/2) /Q/л. 129. arctg ((2 ± ^2)/4). 130. 2л/?2 sin а X
Xsin (а/2). 131. arctg (4/(4—/б)). 132. л/?2 ctg2 (а/2) (1-}-cos a)/cos а, л/?3Х
X (ctg3 (а/2) tg а)/3. 133. 24л/?2 sin4 a/(2-)-tg а)2. 134. — лг3 tg 2а/8 cos6 а.
135. 10 см. 136. лаЗ/sin а (0 < а < л). 137. nS/sin (лт/(т-\-п)) (т<п).
138. h (У>+(»/«)—1)1/2. 139. arctg (sin (₽/2) ctg<p).
. 12sin2 (p/2)—cos2ф I tt d
140. arcsin ---------------— . Указание. Через точку В проведите
в плоскости а прямую, параллельную прямой (ОЛ), и вычислите угол между
этой прямой и плоскостью основания другого конуса. __________
141. 7л/3 (sin (а/2) sin а)/54. 142. 4 см. 143. 27? /14-2cos а//3.
144. г(/б—2)/2, г(/б4-2)/2. 145. а (2— /з), а(2-|-/з).
146. 2 arccos((14~/17)/8). 147. 0,5а j/ctg (а/2)/sin2 (а/4).
«ла л7?3 Г .а а а\2/ а\1
148. -у- cos4^ cosec—— ( 1 — sin -75- I 2-|-sin -5- .
о l ~ ~ \ ~ / \ г J
149. ла3 ((1 cos a)3 ctg2 a)/3. 150. Q ((14-sina)/sina)3 tg2 a.
151. 2arcsin ((ЗЦ- р^з)/б) или 2arcsin((3—/з)/б). 152. arccos (l/p^l*).
153. Отношение площади поверхности шара к площади поверхности куба
равно л/6, отношение их объемов равно л/6.
1М 2-0 eta2 (1 + sin (a/2) Q (1 4~sin (a/2))3
4 4 g \ 4 /sin (a/2) 2 cos (a/2) sin a *
155. sin3 a (1 + cosec (a/2))/4. 156. 5/7/3.
157. лг2 (Vr*+(d+r)*+r)3/3 (d + r)\
лг2(/‘/'2+(^-г)2 + г)3/3 (d-r)\
158. 4/3 sin a cos (a/2). 159. -2=
у л
S cos a \ 3/2
1 + cos a J
tga.
160. r3———( 1 ± 1/ 1---------— ) (параметры m9 n и a должны
4 nsina\ V ncosa/ ' r
удовлетворять условию n cos a 2m).
161. 3л (/2 sin2 2p)/4, л (/3 sin3 2₽)/12.
162. S3/2 sin 2a sin ф /cos ф/(Зл3/2).
163. S ctg2 (a/2)/(л cos a). 164. ла3 /6/1728. 165. 2A(2r —h).
I66, ^sin2^ +C0S a)2~ C0S a Ct£2 У a3 ct^2 a + cosa^’
167. a2/cos4 (a/2). 168. ab tg a /а24~Г2/12. 169. л/?2Я/12.
170. г3 (1 “Ь tg ф) [1-|”Ctg ((л—4ф)/4)]/6. 171. n/2cosa/(l+3cos2a).
172. 32r3 ]/"cosa/(3 sin (a/2)).
173 3X03_______tg a cos3 p________ла3 cos2 a sin a
4 /cos3 (a + P) cos3 (a — P) 4 /(cos2 a—sin2 p)3*
174. nd3 (cos2 (a/2) ctg (a/2) tg P)/8. 175. 29/36 или 1.
176. 1/2/2. Указание. Докажите, что сфера касается всех ребер
тетраэдра в их серединах, а ее центр совпадает с центром описанной около
тетраэдра сферы.
341
177. 3<5/3. 178. c(3/2+4)/4. 179. При <p=arcctg У% объем конуса
2л/3/9 КЗ. 180. Л У2/3.
181. Q tg (а/2) tg р y~2Q ctg а/3, а=л/3. Решение. Пусть в данной
пирамиде ЛВС == л/2, SBC [ АВС, ВАС=а, двугранные углы при сторонах
[ЛВ] и [ЛС] равны Р, соответствующие линейные
/7 . углы на рисунке SBC=SED=fi, причем [SD]—высо-
Л та пирамиды, [SB] | [ЛС], [DB] | [ЛС], [SB] [ [ЛВ].
/|\ Заметим, что | BD | = | SD | ctg Р = | DE |, |SB|==
Z 1 \ = | SD (/sin Р = | SE |. Легко показать, что | ЛВ | =
// I \ = | ЛЕ| иВЛ£) = ВЛЕ=а/2. Так как | ВС] = | ЛВ | tga,
//I \ то площадь треугольника ЛВС
// { \ Q = l^|.|BC| = l|4S|3tga,
/ / д I \ откуда
/ I I = / 2Qctga.
Следовательно, высота пирамиды | SD | = | BD | tg р =
= | ЛВ | tg (a/2) tg р = tg (a/2) tg p У2Q ctg a. Тогда
объем пирамиды равен
V = Q tg (a/2) tg p У 2Q ctga/3,
где по смыслу задачи на углы аир накладываются ограничения: 0 < a <
< л/2, 0 < Р < л/2. Найдем наибольшее значение функции V (а); для этого
достаточно найти наибольшее значение функции
f (a) = tg (a/2) /"ctg a, 0 < a < л/2.
Тогда
= J^ctga__________tg (a/2) _ sin a (2 cos a— 1)
2 cos2 (a/2) 2 p^ctg a sin2 a 4 cos2 (a/2) sin2 a У ctg a*
На интервале ]0, л/2[ производная f (a)=0 тогда и только тогда, когда
cosa=l/2, т. е. при а = л/3. Если а£]0, л/3[, то fr (а) > 0, если а£
£]л/3, л/2[, то /' (а) < 0. Следовательно, при а = л/3 функция f (а), а следо-
вательно, и V (а) принимает наибольшее значение.
182. 2. 183. Л/У'З. 184. Высота цилиндра должна равняться радиусу
3/“—
круга основания и равняться у v/n.
185. 4о tg3 (a/2)/tg a, a=arccos (1/3).
186. Длина радиуса основания конуса равна Зл/2, 9лг2Л/4,
187. 1) (3a2/i)/4/a2+3/i2 при h> а]]/б;
2) (а/2) У^+(а^/12) при 0 < h^a/Уб.
188. b3 (tg a sin 2ф cos <р)/24. Наибольшее значение объем пирамиды при-
нимает при (p=arcctg У~2.
189. 1) 2г£3/(/?2—г2) яри г < R < (1 + /2) г;
2) Я2 ((/?2 + г2)/(/?2—г2))2/2 при ₽ > (1 + J/2) г.
190. 1) (Я2 ctg Р)//2 при arctg (/2/2) <Р < л/2;
2) Я2 (14-sin2 р)/(4 sin2 Р) при 0 < Р < arctg (1^2/2).
342
191. tg (a/2). 192. tg (a/2). 193. ^cos”»Si° ,94’ па?5Ш2аХ
Xsin (a+P) cosec p. 195. no? (sin 2a sec2 2a)/6.
196. л [16S2+6SA2ctg2a4-/i«ctg4al/24/i.
197. /би sin a ctg p tg (P/2)/2, p = arccos (1/3).
198. jv/?3/(3cos2 (a/2) sin (a/2)), a=2arcctg /2.
Раздел IV
§ 2
2. Да. 5. Указание. Воспользуйтесь тем, что п4+4 = (п2+2п+2) X
X (п2—2л+2).
3. Да, если одно из них—число 2.
4. Решение. Так как любое нечетное число можно представить в виде
2т+1, где т £ Zt то справедливость утверждения следует из равенства
2m-j-1 = (m+l)2—m2.
5. 1692. 6. a) sin3 > cos3; б) j/^3 > }Г2 (так как (j/^з)в= 9,
(И2)* = 8). 7. A > В.
8. Указание. Так как (/Т+/У)а = 5 + 2/б, то для доказатель-
ства утверждения достаточно доказать, что /б—число иррациональное.
> 9. Указание. Сравните площадь круга единичного радиуса с пло-
* щадью правильного вписанного 12-угольника и площадью описанного квадрата.
10. —1 при х < 1; 1 при х > 1. 11. 2/(1—а).
12. а511/б12. 13. п (п+1)/2 при х= 1; (х—(п+1)х»+х+пх«+2)/(1—х)2
при х 5^ 1. Решение. При х=1 заданная сумма равна 1 + 2+3+<*.
...+ п=л(п+1)/2. При х#1 сумма
х+2х2+Зх3 + ... + пх" =
=х (1 + 2х+Зх2+, „+пх'1-*)=х (х+х2+х3 +. t,+х«)'=
_ /х-—Х” + 3Л'___ 1— (п+1)х" + пх”+1>
1— X ) ~х (1—х)2 •
. . — —, « 1 Д?—“1 ^+1 . _
14. Решение. Так как 1—тт==—т— • —г—, k С Z, то
ял к я
Ю(-4ЖЬ.(-^)=
___L. (п—1), n+i= 1 в n+i_n+i
2 2 3 3*4 4 ‘* п * п 2 * п 2п ’
15. Решение. Так как при любых й#0 имеет место равенство
1 1 1 _
k *4-1 * ТО
1 , 1 , 1 , , 1 __
Г2‘Ь2.3-Г3-4'1 *« (n+ I)3®
— 1 1 j_ 1 1_i_1 ’ к _l ’ ’ __ «
i “1 22 3 + 3 4+***+n n+1 n+1" п+Г
16. Указание. Докажите методом математической индукции.
17. 3-3 Ps=54. 18. 3970. 19. С|=126.
343
20. п(п—3)/2. Указание. Число отрезков, соединяющих вершины
выпуклого n-угольника, равно Си, из них диагоналей С2п—п (остальные от-
резки—стороны многоугольника). Задачу можно решить и другими способами.
Например. Каждая вершина соединена диагоналями с п — 3 вершинами. Так
как вершин л, то получаем п (п—3); но при этом каждая диагональ счита-
лась дважды (диагональ соединяет две вершины многоугольника и мы ее
считали выходящей как из первой вершины, так и из второй). Поэтому раз-
личных диагоналей будет п(п—3)/2.
21. Не более, чем С^+я+£——Сп — С&.
22. п = 32. Решение. Этот коэффициент равен С2 - —=31, т. е.
344
31.
32.
33.
345
34$
347
348
349
74. */наим = 2 ПРИ всех х £ [1; 3]. Указание. Рассмотрите функцию
при х < 1; при 1 <; х <; 3; при х > 3.
75. {1—j/lF}. Указание. При х^О данное уравнение равносильно
системе
( х2+2х+1=0,
I х^О,
а при х < 0 оно равносильно системе
{х2—2х—1=0,
х < 0.
76. гнаим=1 при х=0, у=—1. Справедливость утверждения следует из
тождества
2=xa+2xi/+3^+2x+6i/+4^(A:+i/+l)2+2(r/+l)2+l.
77. J 2; 7[. 78. J-4; —1 [ U ] 1; 4{.
79. J —оо; 2—/5 [UJ2—/Т; 2-{-/3 [Щ 24-/5; -{-oof.
80. ] —оо; —3/2] U [—1; 1] U [3/2; -f-oo [.
82. Указание. Из условия задачи следует, что с, а—b-f-с, 4а—2Ь+с—
целые числа, поэтому с, а—bt 2а, 2Ь, а-^-Ь—числа целые. Далее, учитывая
сделанный вывод, рассмотрите отдельно случай четного х и случай нечетного х,
84. а=1. Указание. Из условия задачи следует, что Xi4-x2=5/a,
xxx2=6/a, xi=2x2/3. Решая эту систему, получаем ав|,
85. а > 0. Решение. По условию
a~Z?+c>—4, (1)
fl+b-f-c < 0=$> —a—6—с > 0^ (2)
9а+364-с > 5. (3)
Сложив (1) и (2), получим
—2/?>—4. (4)
Сложив (2), (3), (4), получим 8а > 1 =>а > 0.
86. {З—2/5; 3; 3-{-2/5}. Р е ш е н и е. Перепишем уравнение так:
((ж2—6*+9)—9)2—2 (х—3)2=81
или
((X—З)2—9)2—2 (х—3)2=81,
т. е*
(х—3)4—20(х—3)2=0
ИЛЗ
(х—3)»(х—3+/20) (х—3— /20) =0,
откуда
Xj = 3*~~2 "j/-5 > х2=3, х3=3+2 5 •
87. {3/2; 2/3}. Указание. Преобразуйте уравнение к виду
6 (х8+4-)-13 (*+т)+12=°’
положите х4~=/ и Учтите, что х2-|--^-=/2—2.
88. 7—х. Указание. 1-й способ. Проведите группировку х®4"2ха—
— 2х+5 = (х®—х)+(2х2—2)—х+7=(х2—1)(х+2)—х4-7. 2-й способ.
Учитывая, что остаток от деления многочлена на х2—1 имеет вид ах+&»
примените теорему Безу.
350
89. Ни одного корня,'если а < — 15^ю/16; один корень, если а=
= —15 К)/16; два корня, если а > —15 у^1о/16. Решение. Рассмотрим
функциюг/=х4—5х—Значения х, при которых г/—0, являются корнями
заданного уравнения. График данной функции имеет две симметричные
ветви, направленные от вершины в сторону возрастания у. Таким образом,
в вершине (х0; t/0) функция принимает свое наименьшее значение. Найдем
х0 и yQ. Для этого найдем ^'=4х3—5 и приравняем производную 0. Тогда
4x0—5 = 0, Ло = 5/4, x0=j/Z I0/2, а, следовательно,
Уо —хо(хо—5)—2а=—15 W—2a.
Следовательно, если у0 > 0, т. е. а<—15 р/ю/16, то вершина расположена
выше оси Ох и график функции ось Ох не пересекает, следовательно, задан-
ное уравнение не имеет корней. Если Уо = ®, т. е. а=— 15 у/ ю/16, то график
функции касается оси Ох и заданное уравнение имеет один корень: х0 = у/ю/2.
Если а > —15^10/16, то вершина расположена ниже оси Ох, и график
функции пересекает ось Ох в двух различных точках; следовательно, задан-
ное уравнение имеет два корня.
90. Один при а> —3; два при а = — 3; три при а < — 3. У к аз ан ие.
Рассмотрите функцию т/=х3-}-ах-|-2. Если функция экстремумов не имеет,
то'корень один. Если функция имеет максимум и минимум и в точке макси-
мума у > 0, а в точке минимума у < 0, то корней—три, и т., д.
92. {13/12}. 93. 1 —оо; 0 [. 94. ]— 1;Q[. 95. J —4; —3 [.
96. 1 —6; —2 [(J ] 0; 31[. 97. J — оо; — 1 [ (J ] — 1; 1/2 [. Указание.
При решении следует учесть, что данное неравенство равносильно совокуп-
ности двух неравенств; (2х—4)/(х+1) > 2 и (2х—4)/(х-{-1) < —2.
98. [3; 4 [ U 1 4; + оо [. 99..] —1; 0] (J {!}. Ю0. {4}. 101. {0}.
102. [—2; о[ (J [/2—/3; |/’2+/з]. Р е ш е и и е. Областью опреде-
ления неравенства ^является множество чисел 2; 0[Щ0; 2]. Все
х £ Xi = [—2; 0[ являются решениями неравенства, так как при этих значе-
ниях х лева^ часть неравенства неотрицательна, а правая—отрицательна.
Если х £ J0; 2], то обе части неравенства неотрицательны, поэтому в этом
множестве чисел данное неравенство равносильно системе неравенств
{0<х^2, Г0<х<2,
или <
4— х2^= ух\ Д х4—4x2-f-l «^0;
откуда
{0<х<2,
(х+/2+ 1^3 ) G+K2-/3) (х-Иг—/з) (х-/2+Уз) < о.
Решением системы является множество чисел Х2=[1^2—У~3 24-Уз ]•
Решением заданного неравенства является множество Xt U Х2.
103. [—3/2; 1]. Решение. Областью определения неравенства является
множество чисел [—3/2; 1J. Обе части неравенства положительны при всех х
из области определения, поэтому обе части неравенства -можно возвести
351
в квадрат. После соответствующих преобразований получаем неравенство
2 j/2*+3 < 21— х,
обе части которого неотрицательны в области определения* Освобождаясь от
иррациональности, получаем неравенство 9х2—38x4-429 > 0, которое выпол-
няется при всех х Следовательно, заданное неравенство выполняется
во всей области определения. Замечание. В области определения
]Л1—х <»<1+3/2<2, j/*2x +3< р^б < 3, поэтому для всех х из области
определения У'1—х4~ V 2x4-3 < 5.
104. ] — ©о; 2 [. Указание. Данное неравенство равносильно совокуп-
ности двух систем неравенств
( х4-1 <0, г 11—х^О,
I 11—х^О и \ *4-1^0,
I (х4-1)2 < 11-х.
105. [— У 2 /4; 0 [ (J ] 0; 1 /3 [. Решение. Областью определения нера-
венства является множество чисел [—]/Т/4; 0 [ (J ] 0; У 2 /4 ]. Так как
1—У1—8х2^ 0, то для всех х £ [— У 2 /4; 0[ исходное неравенство выпол-
няется. Пусть xg]0; У 2 /4 ], тогда исходное неравенство равносильно нера-
венству
1—2х < У1 —8х2, (1)
причем 1—2х > 0 для рассматриваемых значений х. Возводя в квадрат обе
части неравенства (1), получим после преобразования неравенство Зх2—х < 0,
или Зх—1 < 0, т. е. х < 1/3. Следовательно, неравенство выполняется при
всех х £ [- }<2 /4; 0 [ (J ] 0; 1/3 [ .
106. [а/2; 4-ос [ при а < 0; [— а{2\ 4"00 [ при 0- Решение. Если
х^0, то неравенство выполняется. При х<0 данное неравенство равно-
сильно неравенству (^бх2 4~а2)2 (—Зх)2 или неравенству х2«^а2/4, или
| х | | а ]/2. Таким образом, неравенство выполняется также при всех
|—|а|/2^х<0. Объединяя полученные результаты, получаем приведенные
выше промежутки.
107. {(с; 1 —с)} при 0<с*С1; {(с; — 1 — с)} при —1^с«^0. Указание.
Решите систему графически.
108. 0.
109. {(11/5; 1/5)} при а=3; 0 при а 3. Решение. Решением си-
стемы двух первых уравнений является пара чисел х — 11/5; г/= 1/5. Эта пара
чисел является решением третьего уравнения заданной системы лишь
при а=3.
ПО. {(-1; 2)} при а=-2; 0 при а # 2. 111. {(1; 8), (8; 1)}. 112. {(5; 7)}.
113. 0, если 1а}<У2/2 или | а | > 1; четыре, если | а |= У 2)2 или
| а | = 1; восемь, если У 212 < | а | < 1. Указание. Решите задачу графи-
чески. При этом следует учесть, что х24-#2 = я2 при а ^0 есть уравнение
окружности радиуса |aj; при а=0 уравнению удовлетворяют координаты
точки 0(0; 0); при |а| < 0 это уравнение не имеет решений. Уравнению
х |4-1 у | = 1 удовлетворяют координаты точек сторон квадрата с вершинами
в точках (—1; 0), (0; 1), (1; 0), (0; —1).
114. а=±1, а=±2/К5 • Р е ш е н и е. Из второго уравнения системы
находим 14-ху=— (14~х+*/)’ Исключив 14“*!/ из первого уравнения си-
352
стемы, получаем уравнение
(а+1) х+(а—1) у = —а.
При а—1, х = —1/2, У — — 3; при а= —1, у= —1/2.
выражаем у из уравнения (1):
а , яЦ-1
y=z-----1
1 —а ‘ 1 —а
0)
х = —3, при а ±1
Исключая у из второго уравнения заданной системы, получаем для опреде-
ления х уравнение
х2
а+2
<Н-1
а—2
а+Т
О,
дискриминант которого равен нулю при а= ±2/VTT. При каждом из этих
значений а система уравнений также имеет единственное решение.
115. —1/2. 116. а) /Т. б) 1. 117. —18. 118. 16. 119. 4. 120. 0.
121. Положительный. 122. Отрицательный.
too «+2/7 — 1 n , no 1g 9,8 1g (98/10)
1-Л 65 1g 5 1g (10/2)
_ lg24-2 lg7—lg 10_a+26 — 1
lg 10— lg 2 1—a '
124. (5 — b)/(2ab-\-2a—46+2). Решение. Так как log2050 = 6, то
lg (100/2)
lg 20
2—lg2
1+Ig2
6=»lg2 =
2—b
1+6’
(1)
Так как lg 15 = a, то lg3+lg5 = a=£>lg3+lg(10/2) = a=$lg3—lg2=a—1 =J>
=2>lg3 = lg2+a—1. Учитывая (1), находим
lg3
2—6
1 + 6
a— 1.
(2)
Учитывая (1) и (2), получаем
logg 40 =
l+21g2_ 5 — 6
2 lg 3 2a6+2a—46+2
125. D («/) = ]- oo; 0]. 126. D (y) = [2; 3 [ U 1 3; 4 ]. 127. D (/) = } 1; 3].
128. £>(0=]O; 1]. 129. D (/) = ] 5; +oo [.
130. D(y) — ] — oo; —3]. Указание. Для нахождения области опре-
деления заданной функции следует решить неравенство р+2—5х—24 > х+2,
которое равносильно совокупности двух систем неравенств
( х2—5х—24SsO, ( Xs—5х+24^0,
1 _L П И 1 X+23s0,
I х+2 <0 ( х2—5х—24 > (х+2)2.
131. D (#) = {] 2лп; л (2« + 1) [ | п £ Z}.
132. {1/2}. 133. {6}. 134. {1/3}. 135. {4—^ТТ}. 136. {16}. 137. {—1;3}.
138. {2}. 139. {—9/10}. 140. {5}.
141. {—2; 3}. Указание. Умножьте уравнение на 3”2х~12 и поло-
жите Зх2“*~6== t. Для определения t получите квадратное уравнение.
142. {л (2п+1)/2 | п g Z}. Указание. Преобразуйте уравнение к виду
28ш2*_|_8-2~81п2х = 6 и положите 2sin2х = t Для определения t получите
квадратное уравнение.
12 в. М. Говоров и др. " 36®
143. {—7/5; 61}. Указание. Для упрощения выкладок положите
logs (2х -{- 3) = /.
144. {2}. Указание. Для упрощения выкладок положите 2х = t.
145. {2}. У к аз а н ие. Считая | log8х [ < 1, левую часть уравнения
запишите в виде (log8x)/(l—log8x).
146. {2л£ \k £ Z}. 147. {л (8n+3)/4 | n £ Z}.
148. 0. Решение. Данное уравнение не имеет смысла, если cos 2х=0,
т. е. если х = л(2&+1)/4, k g Z. Заметим, что
Л ( Л \
\ 4 /__________V____4 / 1 “"sin %х (sin х—cos х)2
cos 2х 2 cos 2х 2 cos 2х —2 (sin2 х—cos2 х)
sin х—cos х ___ tg х— 1 ________1_. f л\
6=2—2 (sin cos x) 2(l+tgx)~’ 2 \ 4/*
tg (*-•7)
Исходное уравнение при этом имеет вид 2 =1. Решением последнего
уравнения являются х = л (4/г-[-1)/4, я £ Z, но все эти числа исключены из
рассмотрения (они получаются при k — 2n). Следовательно, данное уравнение
не имеет решений.
149. {2nn+arctg ((/17—1)/4) | п £ Z} = {2лп 4-0,5 arctg 4 | п £ Z\.
150. {а} при а £ ] 0; 1 [ (J 1 1; +<» В 0 при a g j —оо; 0] U {1}.
151. {10; 100}. Решение. Применив основное логарифмическое тожде-
ство, данное уравнение запишем в виде 10lgx(Ig^"?) = 10-2=^>lg2x—31gx+
+ 2 = 0=фlgx= 1, lgx=2; хх—10, х2= 100. Замечание. Можно решить
уравнение, прологарифмировав обе части уравнения по основанию 10, и т. д.
152. {1; 100}.
153. {1/11}. Указание. Прологарифмируйте обе части уравнения по
основанию х.
154. {100}. 'Указание. При решении примера следует учесть, что
а°^ь с— clogb а При а > о, Ь > 0, с > 0, b Ф I. В самом деле, применяя основ-
ное логарифмическое тождество, имеем
a10gb с = (dlog& а) 10gb = (?og& 9 1og& fl= clogb e.
155. а) При всех ag ]—-oo; 0]; б) при всех aC]0;+oo[.
156. Один корень при а = 0; два при а=1; четыре при 0 < а < 1; 0 при
а < 0 и а > 1. Указание. Решите задачу графически: постройте графики
функций у=х2е2”1 х * и у = 4а и определите, сколько общих точек имеют
графики этих функций при различных значениях а.
157. {(1; 2), (2; 1)}. 158. {(—3; —9), (3; 9)}.
159. {(—1/4; —9/14), (5/4; —3/4)}. Указание. Учитывая первое урав-
нение системы (Зх-{-у)х-У = $, преобразуйте второе уравнение системы
3241/(х“ 0=2 (3x4-г/)2 =ф324=2^->'.(3х+г/)2 <»-У> =ф 324=81 -2Х~У =$>х—у=2.
Для определения х и у получите систему уравнений
( х—у=2,
1 (Зх+у)2 = 9.
160. {25; 36}. 161. [0; 4-оо[. 162. ]log8/26; 4-оо[.
354
163. ]loga((5+У29)/2); +<»[. 164. ]— oo; —1[. 165. ]0;2[. 166. [— 15/4;+оф
167. ]3/2; 2[. 168. ]l/3; 1[. 169. ]—«; 0[(J ]0; 8[; 170. ]l/9; 9[.
171. ]0; 1[ U ]3; + oo[. Решение. ------1 < 0, или < q
1 1 1 logs* log8x •
или
logax—1 „ [logsx < 0, „ Г0 < x < 1,
log3x > U°g3*>l. L x > 3.
172. ]—8; 0[. Решение. logi/2 log3(l— x) > — 1 4^0 < log3 (1— x) <
< (1/2)-1 4Ф 1 < 1 —x < 9 <=> — 1 > x— 1 > -9Ф-8 < x < 0.
173. ]1 —/Г; —1[ U ]3; 1 + /б[. Решение (1/2),0^<*’-2*-3) > 1 &
«lol, («"-2.-3) < о e { <!: ®
1 (x-f-1) (x—3) >0, _ (l-уь <X<-1,
l(x-l + K5)(x-l—Кб) <0, (3 <x< 1 + УТ.
174. [-4; —3[ (J ]3; 4].
175. ]2~^2 ; l/2[ U ]1; . Указание. Переведите логарифмы косно-
ванию 2, обозначьте log2x = Z, полученное неравенство решите методом ин-
тервалов.
176. ]0; 1[.
177. ]4; 4-оо[. Указание. Так как в области определения неравенства
основание логарифма больше единицы, то заданное неравенство равносильно
системе неравенств
( х—4 > 0,
( х—4 < (х—З)2.
178. ]3; 4[ U ]5;+оо[. Указание. При потенцировании рассмотрите
два случая: 1) 0 < х—3 < 1; 2) х—3 > 1.
179. ]—2; —1[ U ]—1; 0[ U ]0; И U ]2; + оо[. Указание. При потен-
цировании нужно рассмотреть два случая: 1) 0 < х2 < 1; 2) х2 > 1.
180. [7; 4-оо[. _
181. ]0; (3—/5)/10[и](3+/5)/10; 4/5[ U ]1; +»Ь Решение. Пре-
образуем неравенство
logx+0,2 2 < logx4
аа 1 - 2 а logax—21oga(x+0,2) Q
logs (х+0,2) 14 logax log2x-log2 (x-f-0,2)
logs (;+о,2)2' ’log2 x-log2(x+°>2) < °; (О
log2x меняет знак при переходе х через точку Xf»!; log2 (х+0,2) меняет
знак при переходе х через точку х2 = 4/5; log2
х
(х+0,2)2
меняет знак при пе-
реходе х через точки х3 = (3 — yT")/10, х4 = (3+1^5 )/10. Больше нет точекв
при переходе х через которые левая часть неравенства (1) меняла бы знак.
Нанеся эти точки на ось Ох, учтя, что при х^0 неравенство не определено,
а при х > 1 левая часть неравенства отрицательна, методом интервалов легко
найти множество решений.
182. ]—3/2; —1 [ U ]—1; 0[ U ]0; 3[. Указание. При потенцировании
рассмотрите два случая: 1) 0 < 2х+3 < 1; 2) 2х+3 > 1.
12*
355
183. JI; 3[. Указание. Так как х > 1, то заданное неравенство равно-
сильно системе неравенств (х—[—3)/(х — 1) > х и х > 1.
184. {J(2n— 1) л; 2nn[|ngZ}. Указание. Данное неравенство равно-
сильно неравенству 2~х — 100 sin х > 2~х & —100 sin х > 0 sin х < 0.
185. ]—1; —и 1[ при 0 < а < 1; 0 при остальных
значениях а.
186. ]1; 2[ U ]3; +«>[. Указание. Неравенство определено при х£
€10; 2[UJ2; + °°[. В этой области неравенство равносильно неравенству
bg4 • 1о& IX—21 < 0.
Функция в левой части последнего неравенства меняет знак при переходе х
через точки Xf=l, х2=2, х3 = 3. Неравенство можно решить методом интер-
валов с учетом области определения.
187. ]0; arcsin ((У”5 — 1 )/2)[. Указание. Заданная система неравенств
равносильна системе неравенств
cosх> tgx, (cos2х> sinx, fsin2x4-sinx—1 <0,
tg;v>0,
0 х<; л, 10 < х < л/2, I 0 < х < л/2.
188. [а| > 1/е. 189. sin 1980°. 190. tg 1. 191. sin2. 192. —7л/6.
193. —7/25. Решение sin (arcsin (3/5)—arccos (3/5)) =sin (arcsin (3/5)) X
3 3 /* 9~
Xcos (arccos (3/5))—cos (arcsin (3/5)) sin (arccos (3/5)) = 1/ 1 — X
О О г 20
X V 1 25 — 25 ’
194. — V3 . 195. 3n/4.
196. л/2. Решение, arctg (1/1^2 )=arcctg 2 , arctg ]/"2 4-arcctg }Z2==
= л/2, так как при любых x£R
arctg х 4-arcctg х== л/2.
197. 4/5. Решение. sin (2 arctg 2) = 2 sin (arctg 2) *cos (arctg 2) —
_2._2_._J____________=
/’14-4 V14-4 5 *
.ЛО о/л n ( 1 1 \ -i /" 14-cos (arccos (1/8))
198. 3/4. Решение, cos I — arccos-5- )== 1/ —!---— --” =
\ 2 о j r 2
< 14-1/Г- 3
“ V 2 4 •
199. 1/У 5 . Решение, sin (J-arctg 1/^-!—cos_arctgj(4/3)_ __
\ 2 о у г 2
= т/А 1. ~г~—__
Г 2 2 у 2 2-5“F 10~/5 •
200. —nil. Решение, arcsin (sin (8 л/7)) = arcsin ^sin^n — -=
_ л
“”“7 ’
356
201. 6л/7. Решение, arccos
f 6л X 6л
= arccos ( cos -у- ) =— •
202. л/7. Решен ие. arctg Гtg -ybj =arctg
arccos
203. 24/25. Решение.
( . а , а X 2 49 . . 49
^1п_+со8-^ =25-=»Sina + l=2g-
204. b2— 1, если | b | < 'У 2 ; 0, если | д | > У~2 .
205. —7/25. Решение.
7
“ 25 ’
. __ 2 sin а cos а __ 2 ctg а __________
sin 2а- sin2ay_cos2a— 14-Ctg2a “
14
50
ЛЛЛ гл cos4 а+sin3 a cos a cos4 a+sin3 a cos а
206. 7/9. Решение. --
sin2 2а 4 sin2 a cos2 а
_ l+tg3a _ 1+27.— 7
4 tg2 а “ 4*9 ~ ,9, *
207.
208.
209.
1Л/11 Г» sin а 8 cos2 а
10/11. Решение. -т-з—r-z-ч—=—гтч—Го—в
' sin3 а+3 cos3 a tg3 а+3
__ tg а (1+tg2 а) _ 10
~ tg3 а+3 — 11 *
а2—2, если | а |2; 0, если |п| <2.
—3 или —1/3. Указание. Учтите, что
2 sin (a/2) cos (a/2) _ 2 ctg (a/2)
sin2 (a/2)+cos2 (a/2) l+ctg2(a/2)
210. 2.
211. /Тб*—3. Решение. Так как 0 < a < л/4, то cos2a =
л о ч Л 1+cos 2a 3 , a f1— cos a
= /1-(0,6)- =0,8;cosa = ]/ -----; tgy= j/ =
-=i/~=K(yrIo'—з)2 = укГ—3.
у /ю +3
212. —33. 213. sina =—12/13; cos a = —5/13; ctga=5/12.
214. sin2a =120/169, sin (a/2) =5//26 . 215. 1/2sin2 (a/2).
216. Указание. Преобразуйте выражение tg (a-(-P) = tg (л/4).
217. Доказ ательство. sin a sin Р — cos у = sin a sin P — cos (л—(a+P)) =
= sin a sin P+cos (a+P) — sin a sin P+cos a cos P — sin a sin P = cos a cos p.
1 ~| cos 2P
218. sin 2a. 219. Указание. Примените формулы cos2 p = - -- ,
Sin*P = 1-C2OS?A,
220. Доказательство. 2 (sin6 a+cos6 a)—3 (sin4 a+cos4 a)+l =
=2 (sin6 a+3 sin4 a cos2 a+3 sin2 a cos4 a+ cos6 a)—2-3 sin2 a cos2 a (sin2 a +
+ cos2 a)—3 (sin4 a+2 sin2 a cos2 a+cos4 a)+3 -2 sin2 a cos2 a+1 = 2 (sin2a+
+ cos2 a)3—6 sin2 a cos2a—3 (sin2 a+cos2 a)2+6sin2acos2a+l =2—3+1=0.
357
_ (1 Л-cos х) (1+cos2x) (14-cos x) 2 cos2 x
223. Решение. ++—:—++---------=+ =++—:—чл . -о— —
(l~r"Sinx)(l—cos2x) (1 +sin x) 2 sin2 x
_ (1 + cos x) (1 — sin x) (1 -j-sinx) 1 —sin x
— (l + sinx)(l— cosx) (I-}-cosx) 1 — cosx
224. {лл, л (26+ l)/8 I n, k£Z}.
225. {л (2л+1)/2| л^}.
226. {2лл; 2л (3&+1)/31 л, k£Z}. Решение. 1-й способ.
]/" 3 sin х = 1 — cos x <=> 2 У~3 sin (x/2) cos (x/2) =
= 2 sin2 (x/2) ФФ 2 sin (x/2) (sin (x/2)— V~3 cos (x/2)) = 0 => sin (x/2) = 0,
х = 2лл; tg(x/2) = yr3 , х = 2л (3&+l)/3, ft, k£Z.
Л « J' 3 , f 1 I у. X . Л . Л 1 z x
2-и способ. —sin x +—cosx =~ Ф> sin-тг sin x+ cos — cosx——
2 2 2 3 3 2
& cos ^x — у)=“-ФФх — y=± у4~2ли, n£Z.
227. {лл; л(6&± l)/31 л, k£Z}.
228. {л(2л4-1)/4; л (6£± 1)/3 | k, n£Z}.
229. {лл|л^}. Решение. tg233x = cos2x—1 Ф> tg233x + 2 sin2 х = 0Ф>
{sinx = 0, , --
tg 33x^0,
230. {л(6л+(—1)«)/6| n£Z}.
231. {лл/7; л (4&4“3)/2 | л, k£Z}. Решение. sin3x4-cos4x—4sin7x =
= cos 10x+sin 17x ФФ (sin Зх—sin 17x) + (cos 4x — cos lOx)—4 sin 7x=0 <=>
Ф>—2 sin 7xcos 10x4-2 sin 3x sin 7x—4 sin 7x = 0 ФФ—2sin 7x(cos lOx —sin3x +
+2) = 0, откуда sin7x=0, х=лл/7, ft^Z; или
in . o , л f COS lOx — —I, ...
cos 1 Ox—sin 3x+2 = 0 ФФ < 01 (1)
1 sin зх — 1.
Решим систему (1). Сначала решим второе уравнение системы (1):
sin3x=l, Зх = л (4лг+1)/2, х— л (4fn-j~ 1)/6.
Из этих чисел выберем те, которые удовлетворяют первому уравнению си-
стемы (1), ,
cos (Юл (4m+l)/6) = cos (5л (4/n-f-1)/3) = — 1. (2)
Равенство (2) имеет место при яг = 2+3&. Следовательно, системе уравнений (1)
удовлетворяют числа х = л (4&+3)/2, k^Z. Объединяя полученные результаты,
находим х£{лл/7; л (4&4”3)/2 | л, k^Z}.
232. {л(2л4-1)/8| л£7}. Решение. Применяя формулы cos2 а =
= (14-cos 2а)/2, sin2a=(l — cos 2а)/2, имеем:
( 1—cos2x\2 / 14-cos2x\2 1
(—2—) +(“^—J =cos-2x+t°
4=> 2 cos2 2x = 1 ФФ 1 + cos 4x = 1 cos 4x — 0, x = л (2л + 0/3, ft C Z.
233. 0. 234. {]— л(2^+1)/2; —л£] U № л (2^+l)/2[ | k£N}.
235. He имеет. Решение. Уравнение 4 sin 2x+cos х=5 равносильно
системе уравнений
( sin2x= 1,
[ cos х = 1.
35$
Уравнению cosx=l удовлетворяют числа 2л&, k£Z. Ни одно из этих чисел
не удовлетворяет первому уравнению системы.
236. {2 л/г; 2л&—2arctg (3/5) | n, k£Z}. Решение. 5 cos х — 3 sin х = 5 <=>
10 sin2 (х/2) 4-6 sin (х/2) cos (х/2) = 0Ф£ 2 sin (х/2) (5 sin (х/2) 4-3 cos (х/2)) = 0=>
=£>sin (х/2) = 0, х = 2лп, n£Z;
5 sin (х/2) 4-3 cos (х/2) = 0 <=> tgr (х/2) = —3/5,
х — —2 arctg (3/5) 4-2лД k£Z.
Объединяя полученные результаты, находим искомое решение.
237. При иррациональных значениях а. Указание. Рассмотрите от-
дельно уравнение при а рациональных и а иррациональных.
238. Три. Указание. Определите число точек пересечения графиков функ-
ций у — log3n/2х и у = cosx.
239. {] л (24&4- 0/12; л (24А;4-17)/12[ | k£Z}. Замечание. Заданное
. ( л\ 1
неравенство равносильно неравенству sin ( х —— 1 >—у .
240. {] л (12/г—5)/6; л (4п4“1)/2[ | n£Z}. Указание. Заданное нера-
. / л \
венство равносильно совокупности двух неравенств sin I х—-у j > 2, которое
не имеет решений, и sin ^х —< V2, которому удовлетворяют —-^4“ 2 лл <
< x—j < 4+2яи> n^z-
241. /max (*) =5.
242. Доказательство. По условию
Ь2—а2 —с2—Ь2. (])
Нужно доказать, что *
1_______= ____________!_
с-[-а Ь-[-с а-[-Ь с-[-а * * ; '
или
b—а с—b ______п
9
или
(/>2~а*)-^-62) „
(a+c)(b+c)(a+b) 9 ™
Из равенства (1) следует справедливость равенства (3), а следовательно,
и равенства {2).
243. 3069/256. 244. Да. Решение. При любых n£N
(и4-1)2—(«+П + 1 л2—-/г-]-!
a»+i ап— па+«+1 ~
__ п24-л+1 и2—л-{-1 2(/г24-л—1)
~~п24-3л4-3 л24-«+1 ~ (п24-п+1)(л24-3и+3) >Ов
п2 1
245, —1/9. Решение, lim -—lira -----------=*
П °° А---П + со i q
п2
359
246. 0. 247. 1/4.
248. 1. Решение.
lim
tl -* aa
4-+i+4+-+f
4+и+з
2 (1+2+3+... +«) _
n™» n2+4«+12 ~
n (n+1)
e= hm t'tc-
n -* <» rt2-j-4ra-f-12
249. 1/2.
2». 1. Решение. Ita <±g-_ Ikn
n - ~ Зга4-5Л a <» (3/5)«+1
0+1 -j
0+1 -l
251. 5.
„„ , _ x2—5x+6 (x—3)(x—2) .. . o. ,
252. 1. Решение, hm -—=btn -=hm (x—2)=1.
x-з x—3 x-,3 x—3 x->8'
253. 6/5. 254. 1/4. 255. —7. 256. 13/5.
ft r, x+3 (x+3)(/x+4+0
257. 2. Решение. hm --- hm '—1—————I— =
x -» -3 у x-[-4—1 x -» -a (x+4)—1
= lim (K*+4+0 = 2.
X-> — 3
258. V 6/6. 259. —1/56.
t _ v Vr2x+3— 1
260.4. Решен иe. lim ,---=
X--1 К 5+x—2
lim ((2x+3)-l) (/5+x+2)_
x--i ((54-x)-4)(K2x+3+l)
2 Iim Г5+х+2
— & 11 m —----:—
x-*-i ><2x4-34-1
4_
2
=4.
261. — /3/24.
262.
в z*-
3. Решение. Положим у x = t, t—*2 при x—>64. Тогда
('-2)(/2+2^+4)__q
*2-4 “ZT2 (/-2) (/+2)
lim ---------= lim
c-*64 p/x—4 /->2
263.
264.
3/2.
2/5. Решение.
„ .. sinx .. 5x 1
= 2 lim-------- lim g— • -ё-==-Е-
x x->osin5x 5 5
cos 4x—cos 6x
lim -----—5-^-----== lim
x -> 0 sin 5x x -> 0
2
2 sin 5x sin x
sin2 5x
noe «zn о т i/l+sinx—j/l—sinx
265. 2/3. Решение, lim ---!---------------=;
x -> 0 x
___________________(14-sin x) —(1—sin x)
** 0 x (]/(l-J-sin x)2+}/ 1+sinx у/1 — sinx+ ]/(1—sin x)2)
= 2 lim . lim 4 - -—~ ——4 . _=
x у (14-sin x)2+у 1—sin2x4-y (1—sinx)2
360
z2-^+8
lim ——--=
t -> 4 VI— 2
266. 8. Решение. Положим 2х — t, t—>4 при x—>2. Тогда
2^ + 2з-^—6 t
11 m -—4-;----= 11 m -:----zr
K-* 2 У^2~х-2l~x * -> 4 1 _
ут *
_ (Г7+2)<1-2)(,-4) = Иш (/7+2)(,_2) = 8.
/ -> 4 Г 4: t -> 4
t — 4
267. a(a+V3). Указание. Длины последовательных звеньев по-
строенной бесконечной ломаной образуют убывающую геометрическую прогрес-
сию. Под длиной бесконечной ломаной подразумевается сумма этой прогрессии.
268 a) 3ctS2*- б) C0S 269 4х~3
' sin2* ’ °' 2 К? ‘ 2 9’ (2*2—3*+1) 1п 2 *
270. Gx2tgx+?^-~. 271. а) ------^=г; б) -£gs2*-- ;
~ c°s2* 2х p^ln* ]<sin 2*
в) 6(sin ,2x4” В)2 cos 2х.
272. —1. 273. 40. 274. 1/8. 275. —2.
276. Функция возрастает на интервалах ]—оо; —1[ и J1; +°°[, убывает
на интервалах ]—1; 0[ и ]0; 1[.
277. Функция возрастает на интервале [—оо; —3/4[, убывает на интер-
вале ]—3/4; 1/4[. Замечание. Не забудьте учесть область определения
функции.
278. Функция возрастает на интервале ]0; 2[ и убывает на интервалах
]— оо; 0[ и ]2; + °°1*
279. Функция возрастает на интервале ]е; 4~°°[ и убывает на интервалах
J0; 1[ и ] 1; е[. Замечание. Не забудьте учесть область определения
функции.
280. Функция возрастает на интервале ]—1/|/ 2; 4-оо[ и убывает на
интервале ]— оо; —\Ц/ 2[.
282. Доказательство. /'(х) = 6(х8— х2 4- х2— х 4- 1) =
/ /х2 \ / IV / у V
=6х2(хв—хзJ4.3*24.6х4-1 )=6х2(х3 — 4-Зх24-б(~1 j >
>0 при всех x£R.
284. Решение. /' (х) = (а2—1)х24~2(а—1)х4-2. Дискриминант квад-
ратного трехчлена
D = 4 (а— I)2—8 (а2— 1) = —4 (а — 1) (а4-3)
отрицателен при всех а£]—оо; —3[U]1’» +°°[’ Так как при всех этих зна-
чениях а коэффициент при х2 положителен, то квадратный трехчлен положи-
телен при всех х£Я. При а= 1 имеем /' (х)=2 > 0. При а — — 1 имеем /' (х)==
=-4x4-2, f (х)<0 при х^ 1/2. При —1 < а < 1 коэффициент при х2 меньше
нуля, поэтому при каждом из этих значений а существуют х, при которых
Г (х) < 0. При а = — 3 имеем /'(х) = 2(2х—1)2 = 0 только при х= 1/2. При
—3 < а < —1 квадратный трехчлен имеет два различных действительных корня
Xf и х2. Если хх < х2, то /' (х) < 0 для всех x£]xi; х2[. Из изложенного сле-
дует, что f' (х) > 0 при всех x^R при любом оо; —3]U[1; 4"°°1 и
только при этих значениях а.
285. При всех а 0. Замечание. f! (х) = е~х (е*4“а) (2е*4" D > 0 ПРИ
всех а^0.
361
286. При всех ag[l; + «>[• Решение. y' = cosx—2acos2x—cos3x +
+ 2а = 4а sin2 х + 2 sin х sin 2х — 4а sin2 х + 4 cos х sin2 х = 4 sin2 х (a+cos х).
При а^ 1 имеем у' > 0 при всех х, исключая точки х = лл, ngZ, в которых
у’ =0. Поэтому функция возрастает при всех а^=1.
287. При всех ag]—оо; —3]. 288. х± =—2, х2 —0, х3 = 2. 289. Xf = —5;
х2= 1.
290. х= 1/2—точка минимума, у (1/2) = (1—41п2)/4.
291. ag]—1; 3[. Решение. у' = 3(х2—2ax+a2—1) = 3(х—а+1)Х
X (х—а— 1). Для того чтобы корни трехчлена принадлежали интервалу ]—2; 4[,
необходимо и достаточно, чтобы выполнялись неравенства a—1 > —2, a-f-1 <4,
следовательно, чтобы a€J-1; 3[.
292. /наиб = 5;/наим = 11/4. 293. /наиб —/ (l) = 6j /найм = /0/2) = 3.
294. /наиб = 7(Ю0) = 10—2/10; /наим = / (1) =—1. 295. /наиб = / (—5) = е48;
/найм — / (2) == 1/^* 296. {/наиб ~У (4) = 6; {/найм ==1/0/16) =—1/8.
297. При всех ag]—оо;—3[ (J ]3; 29/7[. Решение. /' (х) = 3(х2 +
+ 2 (а—7)х+а2—9). Для того чтобы в точке Х{ функция / (х) имела макси-
мум, нужно, чтобы при переходе х через точку xt в порядке возрастания функ-
ция /'(х) меняла свой знак с плюса на минус. Поэтому квадратный трехчлен
х2+2(а—7)х+а2—9 (1)
должен иметь два действительных корня xi и х2. Если xf < х2, то Xf—точка
максимума, так как /' (х) > 0 при х < xi, а при Xf < х < х2 производная
/' (х) <0. Так как (по условию задачи) точка максимума должна быть поло-
жительной, то оба корня квадратного трехчлена (1) должны быть положитель-
ными (при этом Xi < х2). Это будет тогда и только тогда, когда
/ (д—7)2—(а2—9) > 0,
1 а—7 < 0, (2)
\ а2—9 > 0.
Решая систему (2), получаем ag]—оо; —3 [(J]3; 29/7[.
298. а=2. Замечание. Из условия задачи следует /'(х) = 6(х—2а)Х
X (х—а). Корни Хх и х2 трехчлена х2—Зх+2а2 должны быть действительными
и различными, при этом, если хх < х2, то х±—точка максимума, х2—точка
минимума.
299. При всех ag]l; +оо[. Замечание. Из условия задачи следует
/' (х) = ах2+2 (а+2)х+а— 1.
Нужно рассмотреть три случая: а = 0, а > 0, а < 0. При а > 0 и при а < 0
нужно рассматривать те значения а, при которых оба корня действительны^
при этом если х* < х2, то при a > 0 минимум в точке х2, а при a < 0 минимум
в точке xj.
300. а с]—3 УЪ —2 Кз[и]2 УЗ; 3/з[. Р е ш е н и е. Решим неравен-
ство
х24-х+2 х2+х+2
"о-ТЪ -ТТ“^0, ИЛИ 7—, , от<0.
х2+5х+6 (х+3) (х+2)
Так как х2+х+2 = ^x+^J +4" > ® ПРИ то неравенство выполняется,
если (х+2) и (х+3) будут разных знаков, т. е. х+2 < 0 и х+3 > 0 или
х < —2 и х > —3. Следовательно, неравенство выполняется для всех xg
g]~3; —2[. Найдем критические точки функции у= 1+а2х—х3. Находим
362
у' = а2—Зх2 и приравниваем ее нулю, получаем две критические точки xt =
= — I а |/1^3 их2 = | а\/У" 3. Произвольная у' на интервалах ]—оо; —| а|/"Кз[
и ]| а |/У^З; +°°[ отрицательна, а на интервале ]—[ а |/У' 3; |а[/)^ 3[ поло-
жительна; следовательно,гхх =—| а |/ У 3 есть точка минимума функции и она
должна удовлетворять неравенству
_3 < — |a< —2, или 2 /3 < |а| < 3 ]/"3.
Итак, условиям задачи удовлетворяют все ag]—3]/" 3; — 2Уз[ц]2У 3; 3]/"з[<
301. х = л/4.
302. —1/2. Решение. Пусть х—искомое число. Нужно найти точку
минимума функции f (х)=х4~х2. Так как /' (х)=2х4~1, то х = —1/2—точка
минимума функции f (х). 303. 1.
304. Треугольник со сторонами а, а, аУ~2 и площадью а2/2. Решение.
Пусть b—длина основания треугольника, S— площадь треугольника. Так как
S = -|-V4a2—62=3 (&), TO
S' = (2а2—b2)/2 У~4а2—Ь2; S' (b) = 0 => b = a V 2, Smax = a212.
305. ji/3. Решение. Пусть/—длина боковой стороны, a — длина осно-
вания, h—высота, S— площадь треугольника. Тогда / = 2/? cos (a/2), h —
= 2R cos2 (a/2) = R (1 4“ cos a), a/2 — 2R cos (a/2) sin (a/2) = R sin a, S = ah/2 =
= R2 (1+cos a) sin a. Найдем максимум функции S (a). Имеем S(O) = S(jt)=O,
S(a)>0 при 0 < a < л. Далее S'(a) = /?2 (cos a-f-cos2 a—sin2 a) =
= R2 (cos a-}-cos 2a) ~2R2 cos (a/2) cos (3a/2). На интервале [0; л] находятся
критические точки х = л и х = л/3; отбросив посторонние решения, найдем
а=л/3.
306. 2. 307. (1; 1). 308. л/3. 309. у=—х—2+2 In 2. 310. 0=у +
+ Vr3^x— ^) . 311. z/=12x—16. 312. у—х/е. 313. у=2. 314. > = —4.
315. у——4х, у=4х—8. 316. у=— 5x4-2. 317. Решение. Пусть х0—
абсцисса точки касания прямой и гиперболы. Ординатой точки касания будет
#о=а2/хо, а уравнением касательной уравнение
Найдем координаты точек пересечения касательной с осями координат. Поло-
жив х=Х1=0, получаем f/1 = 2a2/x0, (0; 2a2/x0). Положив г/ = г/2 = 0, полу-
, чаемх2 = 2х0, /И2(2х0; 0). Площадь прямоугольного треугольника /И1ОЛ12 равна
1 1 2a2
у1ОМ111 ОМ21 =± -g_. 2 |х01 = 2а2.
319. Xf = 0, х2=3.
320. Да. Решение. Найдем координаты точек пересечения прямой и
гиперболы. Для этого решим уравнение
1 4—х
»(х—2)2=о=фхо=2, 1/0 = 1/2.
X 4г
Так как прямая и гипербола имеют при этом только одну общую точку, то
прямая касается гиперболы.
363
321. [1/4; 3/2]. 322. а) Четная; б) и в) нечетные. 323. 2*2; 22х,
7 13
324. /(%)=—х2—f-я+Ь Указание. Запишите функцию в виде
о о
/ (х) = ах24-^х4~с.
325. x=-KFH- +<»[•
326. Л (1/2; 3/4). Решение. Пусть х0, yQ— координаты точки Л. Так
как у' (х0) = 2—2х0, то уравнением касательной к параболе в точке Л будет
у=Хо + (2 — 2х0) х. Координаты точек пересечения касательной с прямыми
х=0 их=1 будут: *1 = 0, yi = xo; х2=1, г/2 = хо—2х04~2. Площадь трапеции
5=Ц^.1=х?-х0+1.
Тогда S'==2x0 — 1. Заметим, что S' < 0 при х0 < 1/2; S' > 0 при х0 > 1/2,
следовательно, в точке х0=1/2 площадь S имеет минимум. Таким образом
*0=1/2, у0 = 3/4.
327. у = (5—2ctg3x)/3.
328. F(x) = (2sin4x4-7)/8.
329. х=2. Решение. F (х) =—созлх-|-х2 — 4*+С, Г(1) = — cos л 4*1—
—44~С = 3 => С = 5. Решим уравнение
F (х) = 0ФФ — cos лх4-х2—4x4-5 = 0 <=>
{Y__о — П
sin(nx/2)=0,
330. х—COSX4-C. 331. 1. 332. 4/Т/З. 333. 3/8. 334. 2In (е4-1).
335. л/2. Указание. Примените формулу cos2 x = (14~cos 2х)/2.
336. 1/2. Указание. Примените формулу sin х cos х = (sin 2х)/2.
л/2 л/2
337. 2. Указание. J |sinx[dx = 2 J sinxdx.
-л/2 0
338. 0. Указание. Примените формулу sin a cos (3 = (sin (а — 0)+
+ sin (а 4* РЖ
339. 125/3. 340. 50/3. 341. 243/4. 342. 5/12. 343. (4 —л)/2. 344. (4—л)/4.
345. 64/3. 346. 7/3. 347. (44-л)/2.
348. 44/27. Указание. Так как фигура, ограниченная кривой у —
= —Зх2—|х|4-2 и прямой t/=0, симметрична относительно оси Оу, то сле-
дует вычислить площадь фигуры, расположенной’ в первом квадранте и огра-
ниченной кривой у =—Зх2—х4~2 и прямыми х = 0 и £/=0, а затем получен-
ный результат удвоить.
349. 8/3. Указание. Так как фигура симметрична относительно осей
Ох и Оу, то достаточно вычислить площадь фигуры, расположенной в первом
квадранте, ограниченной кривой у=1—х2 и прямыми х = 0 и у = 0, и полу-
ченный результат умножить на 4.
350. Нет, так как площадь фигуры равна е—~ > 2,7—>2.
351. 2/3.
352. у=2х/3. Решение. Площадь криволинейного треугольника
1
S = J (2х—x2)dx=y .
о
3*4
Искомая прямая y=kx отсекает от криволинейного треугольника прямоуголь-
ный треугольник, площадь которого S/2=l/3, а основание равно 1, следова-
тельно, другой его катет—высота треугольника —равен 2/3 и, следовательно,
^ = 2/3.
353. £ = 0. Площадь равна 20]/'5/3. Указание. Постройте графики
функций у—%2—3 и г/ = /?х4"2. Геометрически докажите, что площадь фигуры,
ограниченной параболой # = х2—3 и прямой у = 2,— наименьшая. При этом
площадь
/Г УТ
S = 2 J (2—(х2—3))dx = 2 J (5-x2)dx= 2Q^5 .
о о
354. Зл2/8. Решение.
Л/2 Л/2 л/2
У=л у cos4*dK = 2n; j cos4xdx = 2ji j f -a
-Л/2 О 0
л/2
л Р / 14-cos4x\ , Зл2
=т j 11+2 cos 2х+^5—г = -8- •
о
355. «1=1/2, «2 = 2- 356. При всех «61—2; 4]. 357. 6 У2. 358. ^^0.
359. У14/2. Указание. Так как а || Ь, то а = Хд = (ЗЛ; — 2Л; X).
360. л—arccos (11/^406). 361. /п = —1/2. 362. «=]<273.
363. а = (5; 7/2; —4). Указание. Положив а — (х\ у\ z), для опреде-
ления х, у, z получаем систему уравнений x4~2*/4~3z = 0, —2х-{"4#-|-г=0,
х—2y+z = “6-
364. |а+Ь| = 15, |а—Ь| = У”б93.
365. Указание. Преобразуйте выражение (а4“^+^)2 = 0- 373. Да.
374. Указание. Докажите, что если а—длина стороны треугольника,
вписанного в окружность радиуса 7?, лежащая против угла а, то я = 2/? sin а,
и воспользуйтесь этим результатом.
375. Ромб, когда диагонали исходного четырехугольника перпендику-
лярны. Квадрат, когда они вдобавок равны.
378. Указание. Примените векторную алгебру. 381. (j/"2 —1):1.
382. л/3; 2л/3. 383. 3 , 5, 7; 4, 5, 6; 5, 5, 5. 384. 36°, 36°, 108°.
385. arccos (4/5). Указание. Примените векторную алгебру.
386. h2 ctg (а/2). Указание. Пусть а и Ь — длины оснований трапеции.
Постройте чертеж и докажите, что («4“^)/2 —h ctg (а/2).
387. 2 (1<2" — 1) а2.
388. Периметр квадрата. 389. Да. 390. 18 У 2 см. 391. 2 радиана.
392. На 125%.
393. abc У—cos 2а; л/4 < а < Зл/4. 394. У$ (ctg (а/2) — 1 )/2.
395. У(4Н3 + ЗГ)/4/7. 396. arccos (tg (а/2)) = arcsin (/"cos а/cos (а/2))в
397. 90°. Указание. Примените теорему о трех перпендикулярах.
398. 7 (/2 — 1)а3/3. 399. R (Н—ЩН, 0 < h < И.
400. о -ь-;3^3*-------400 401- ПРИ всех а£]-1; 1[, b£]-1; Ц.
2 sin2 (а/2) (14-2 cos а)2 r 1
365
402. 943/81. Решение. Так как хх4-х2 = 5/3, ххх2 = —1/3, то
(хх4-х!) = (х2 4-*a)2 —2x1x1= ((хх4-х2)2—2ххх2)2— 2 • — —
_ /Л5V . 2 V2 2 __943
\\ 3 ) ф 3 ) 9 — 81 *
403. {1; 11}. Решение. Рассмотрим два случая: 1) х^О, 2) х < 0
1) х^О. Заданное уравнение запишется
3* + 1 _(3* — 1) = 2 log5 ] 6-х » 1 = log51 6-х | <-> | х-61 = 5»
=£>ХХ=1, х2=11.
2) х < 0. Заданное уравнение запишется в виде
3*+14-(3х-1) = 2 logs (6-х) 4^ 3х = log5 (6-х).
Это уравнение не имеет корней при х < 0, так как при х < 0, 3* < 1, а
log5 (6—х) > 1.
404. {1/10; 2; 1000}.
405. {—2л/3; л/2; —2л (3n=F 0/3, л (66 ± 1)/3 | л, k£N). Решение. Рас-
смотрим 3 случая: 1) х < 0; 2) 0<:х<: л; 3) х > л. 1) х < 0. Уравнение
запишется в виде
2 л
2лсозх = —х—(л—х) О cos х =—1/2 =£> х = ± —-----2лл, n£Z.
О
Условию х<0 удовлетворяют числа —2л(3п±1)/3, n£N, и —2л/3.
2)0аСх«Сл. Уравнение [запишется в виде 2лсовх=х—(л—х) = 2х—л.
Графики функций у=2лсозх и 'у=2х—л на отрезке [0; л] пересекаются
только в одной точке с абсциссой х = л/2. Следовательно, на отрезке [0; л]
уравнение имеет один корень х=л/2. 3) х > л. Уравнение запишется в виде
1 л
2ncosx = x—(х — л) = Л 4^ COS X = 75-=:>X=± [~2л£, k£Z.
Z о
Условию х > л удовлетворяют числа ± -2-]-2л#, k£N.
о
406. {41}. У к а з а н ие. Запишите х (1 — lg5) = x (1g 10—lg5) = x Ig2 = lg2x.
407. {л (2&+0/6, 2лп ± arccos ((—1± Y 5)/4) [&, n£Z}. Указание.
Проведите следующие преобразования:
cos х-4-cos 2x-(-cos 3x4-cos 4x4-cos 5x=
= 2 cos 3x cos 2x4-2 cos 3xcos x4-cos 3x =
=cos 3x (2 cos 2x4-cos x4-l) = cos 3x (4 cos2 x4- cos x—1).
408. {2}. 409. {л(6&4"1)/3 fk^Z], Указание. Данное уравнение равно-
сильно системе уравнений
{cos Зх=—1,
/о 7л X
cos I 2х-g- 1 = — 1.
410. 4.
411. 2. Указание. Постройте график функции ^=х4+х3 —16 и най-
дите количество точек его пересечения с осью Ох.
412. 4. Указание. Постройте графики функций */ = |2—|х|| и
и найдите число их точек пересечения. 413. 4. Указание. По-
366
стройте графики функций у=х2—2х—3 и {/ = log2| 1—х| и найдите число их
точек пересечения.
414. а < —3. Указание. Чтобы уравнение имело три корня, нужно,
чтобы функция = имела минимум и максимум; если х±— точка
максимума, а х2—точка минимума функции, то xt > х2, у (xi) > 0, а у (х2)<0.
415. О < а < 4/е2. 416. О < а < 1/е. 417. {—л; 0; л}. 418. —24/25.
419. ]0; 3] U [4; 5]. Указание. Данное неравенство равносильно си-
стеме неравенств х > 0, 25—х2^0, 25—х2 С 144/х2.
420. [—2; — 1[UJ—1; l[U]h 2]. Указание. При всех х 0,
| х ] Ф 1 имеем (14~х2)/(2 [ х |) > 1.
421. ]1/4; 3[. 422. [—2; 2[. Указание. Неравенство равносильно сово-
купности двух систем неравенств: 1) 6+*—х2^0, 4х—2 < 0; 2)6-(-х—х2^0,
4х—2^0, 9(б4-х—х2) > (4х—2)2.
423. ] —со; —5[UJ1; +«>[.
424. 2. 425. 2 sin 2. 426. На ]—оо; 1/3[ возрастает, на ]1/3; 4~оо[ убы-
вает, х= 1/3—точка максимума.
427. Промежутки убывания ]0; 1| и ]1; х = е —точка минимума,
]е; + оо[—промежуток возрастания.
428. Указание. Так как у' = 12х(х2—х+ 1) + а, то нужно доказать,
что уравнение 12х (х2—х+1) + а = 0 имеет только один корень Xf, при этом
при переходе х через Xf производная у' меняет знак. Если я = 0, то корень
один: х = 0. При а^О значение х = 0 не является корнем. Представьте урав-
нение в виде х2—x-f-l=a/(12x) и докажите, что графики функций у = а/(12х)
и у — х2—х+1 пересекаются в одной точке.
429. 430. а=0. 431. л/2. 432. 4,5. 433. 15. 434. 1/3. 435. л2/2.
437. М (0; 0; 2/3), N (1/3; 1/3; 2/3). Указание. Вектор MN параллелен
биссектрисе первого координатного угла плоскости хОу. 438. л/3.
ПРИЛОЖЕНИЕ
Здесь собран материал справочного характера.
I. АЛГЕБРА И ТРИГОНОМЕТРИЯ
Натуральные числа (У={1, 2, 3, ...» я, Всякое натуральное чис-
ло п единственным образом раскладывается в произведение простых сомно-
жителей
Л = ^ ...
где pt, .—простые делители числа п, a ki, ..., km—кратности этих
делителей (ki, • • •» € AQ.
Для вычисления наибольшего общего делителя двух натуральных чисел
нужно каждый их простой общий делитель возвести в степень, равную мень-
шей из кратностей, с которыми этот делитель входит в разложение данных
чисел на простые множители, и все полученные числа перемножить.
Для вычисления наименьшего общего кратного двух натуральных чисел
нужно каждый простой делитель, входящий в разложение хотя бы одного
из этих чисел, возвести в степень, равную большей из кратностей, с кото-
рыми этот делитель входит в разложение данных чисел на простые множи-
тели, и все полученные числа перемножить.
Если я0—цифры в разряде единиц, а±—цифра в разряде десятков и т. д.
натурального числа п, то это число записывается в виде
n = ... а1а0 = а^- 10й-)-..• -{-^1 • 10-|-ао.
Признаки делимости. Число п делится:
1) на 2 (на 5) тогда и только тогда, когда а0 делится на 2 (на 5);
2) на 4 тогда и только тогда, когда число ар 10-f-а0 делится на 4;
3) на 3 (на 9) тогда и только тогда, когда сумма всех цифр этого числа
делится на 3 (на 9).
Рациональные числа (Q). Всякое рациональное число —- (p£Z—целое
число, q£N—натуральное число) представимо в виде бесконечной периодиче-
ской десятичной дроби (возможно с нулевым периодом)
•—• == dz a, <Xf, • •., ап (PiP2* • *0z»)*
368
Справедливо и обратное представление:
± а, а± ... ап (PiP2 ... РОТ)=±Д±О, «1 • «п(Р1Р2 ••• &»)==
. . а1 • • • алР1 Р2 *•* Pzzt ai ••• an
= ± a ±----------99.179-0 "ТО--------‘
т л '
Действительные числа (Q). Числа, представимые всевозможными десятич-
ными дробями, называются действительными числами.
Формулы сокращенного умножения. Для любых чисел a, b£Q справед-
ливы равенства
(a+b)2 = a2+2ab + b2’t
(a—b)2 = a2—2ab + b2;
(а+b)3 = a34-3a26 4-3a&24-3&3;
(а — Ь)3 = а3—3a2b-\-3ab2—ЗЬ3*,
a*—b2 = (a—b) (а-\-Ь)*9
а3—Ь3~(а — b) (a2-\-ab-}-b2)\
a3-}-b3 = (a-}-b) (a2-ab-\-b2).
Справедливы также общие формулы того же типа:
(а+Ь)п = Сппап+С^«-16+... . -j-C^b»
— формула бинома Ньютона*,
ап— bn — (a—b) (aw“1+a"-2&+... +ап-*Ь*+...
a2n+i-}-b2n+1 = (a-}-b) (a2n~a2n~lb-}-. ,»—-ab2n“i-}-b2n).
Свойства биномиальных коэффициентов С%.
я! = 1-2* ... «п, 0! = 1 (по определению).
В частности,
0! = 1, 1! = 1, 21=2, 3! = 6,
4! =24, 5! = 120, 6! = 720 и т. д.
С"= й! (n—k)l <°<*<«)•
В частности,
cj=i, cj=5, ci=io, (4= ю, с|=5, Cs=l
Справедливы следующие равенства (Q^k^n):
Ck гуП — k I +
П = Ьп , = Cn + 1,
<4+CA+...+C«+.,.+C«=2*.
Модуль действительного числа.
। , J а, если
1 a I I— а, если a < 0.
|a+&|<|a|+|bl, 11 a|—16 11 I a—61.
369
Арифметический корень. Неотрицательное число bt такое, что Ьп = а
(п^ 2 натуральное), называется арифметическим корнем п-й степени из чи-
сла а и обозначается а. В частности, ]/'с2 = |с[.
Корень п-й степени. Число b называется корнем п-й степени из числа а,
если Ьп = а.
Например, числа 2 и —2 — корни четвертой степени из числа 16; число
—3—корень кубический из числа —27. В то же время арифметический ко-
рень четвертой степени из числа 16 только один, а именно, число 2. Ариф-
метического корня третьей степени из числа —27 не существует.
Квадратное уравнение. Уравнение вида
ах2+Ьх+с=0 (а 0) (*)
называется квадратным уравнением. Величина!) — /?2—$ас называется дискри-
минантом квадратного уравнения. Тогда:
1) если D^O, то уравнение имеет два действительных корня
-b-VD
1— 2а ’ 2~ 2а
(при D = 0 корни совпадают);
2) если D < 0, то уравнение действительных корней не имеет. Справед-
ливы следующие утверждения:
а) если xi и х2—корни квадратного уравнения (*), то: Xf+x2^ —
xj.x2=y (теорема Виета);
б) ах2 + Ьх+с=а (х—Xi) (х—х2) — формула разложения квадратного
трехчлена на множители.
Решение квадратичных неравенств
ах2+Ьх-\-с > 0 (а 0). (**)
1) Если D > 0, то уравнение (*) имеет два различных действительных
корня Xi < х2. Тогда
а>О=фх0 — оо; xi[U]a:2; +оо[;
а < 0=>х£] xj; х2|.
2) Если D = 0, то уравнение (*) имеет два равных действительных корня
Х£=х2. В этом случае
а > 0=$>х^] —оо; xi [U]xf; +оо[;
а < О=фх£0.
3) Если D < 0, то уравнение (*) корней не имеет. В этом случае
а > 0=>х£] —оо, +оо[;
а < О=^>х£0.
Аналогично решается неравенство ax2-f-bx-\-c^0.
370
Теорема Безу. Если число с является корнем многочлена
Р (х) = ОоХк+aixn -14-... + ап,
то этот многочлен делится на (х—с) без остатка.
Свойства степени. Пусть а > О, b > 0, а, Тогда:
1) #о=1 (по определению); 4) (#а)₽ = аа’р;
2) #а./ = аа+Э; 5) аа-Ьа =(а.Ь)а;
3) а“:/ = а“-₽; 6) аа:6а= (у)“.
Свойства логарифмов. Логарифмом положительного числа х по основанию
а (а > 0, а # 1) называется число, равное показателю степени, в которую
нужно возвести а, чтобы получить х.
Обозначения: loga х; logi0 х = lg х, loge х ss In х. По определению а1°ёа
1) logaxrx2 = loga |xi | + log^ | х21, Х1.х2 > 0;
2) loga ^-=loga | Xi |—loga I x21, xx-x2 > 0;
x2
3) loga X/’ = P loga X, *>°;
loga X2" = 2n loga I x I, n£N, X / 0;
4) loga X=J^ X > 0, — b > 0, b £ 1.
’ &a logb a ' r
Решение простейших показательных и логарифмических уравнений.
ах — Ь (а > 0, а Ф 1) logtfx=&
1) ^<o=>xg0, ъ
2) b>0=>x = loga/>. Х
Решение простейших показательных и логарифмических неравенств.
ах < b (а > 0, а 7^ 1) logfl х < b
1) Ь«^0=>хб 0, 1) а> 1=>0<х<а&,
2) & >0, а>1=£»х< loga 2) 0 < а < 1 => х > аь.
Z? > 0, 0 < а < 1 => х > loga
Аналогично решаются неравенства со знаками
Решение простейших тригонометрических уравнений.
sin х—а
1) |#| > l=»xg0,
2) j а | < 1 =$>
=>х = (—1)^ arcsin а+ши, mgZ.
tgx = а
x = arctg а + лД
cos х = а
1) |я| > 1 =£>*(; 0,
2) |а|<1=ф
=> х = ± arccos + 2лп,
ctg х=а
x = arcctg a-\-nk9 k£Z.
Основные тригонометрические формулы.
1) sin2 а + cos2 а= 1.
2) sin (а Ц-Р) = sin а cos Р +cos а sin р.
3) sin (а—P) = sinacosP — cos а sin р.
4) cos (a + P) = cos a cos Р—sin a sin р.
5) cos (а—P) = cos acos p + sin asin р.
6)tg(a+p) = j^i^p a, p, a + P^-J+nn.nCZ.
371
7) sin 2a=2 sin a cos a.
8) cos 2a=cos2 a —sin2 a = 2 cos2 a—1 = 1 —2 sin2 a.
9) sin3a=3sina—4 sin3 a.
10) cos 3a = 4 cos3 a—3 cos a.
11) sin a + sin £=2 sin sin .
12) sin a—sin p = 2 sin cos .
13) cos a+cos P = 2 cos cos a .
14) cos a—cos P = — 2 sin sin .
15) sin a cos P = y[sin (a—P)+sin (a+P)].
16) sin asin P = ~- [cos (a—p)—cos (a + P)].
® 17) cosacos p = -i-[cos (a — рЦсоз (a+P)]
(см. также формулы на стр. 89—91).
Формулы приведения
1) sin (nn + a) = (— l)wsin a, sin (лп~ a) = (— I)**1 sin a.
2) cos (лп ± a) = (— 1)" cos a.
3. ) sin лп ± a)=(—l)”cosa.
4) cos ^y+nn + a^ =(—!)"sin a, cos 0^+л/г—a^ ==(—!)« sin a.
Обратные тригонометрические функции. Арксинус числа х£[—1, +1]
(обозначается arcsin х)—такое число •5-1, синус которого ра-
I £ £ J
вен х.
Арккосинус числа х£[—1, 1] (обозначается arocos х) —такое число у£ [0, л],
косинус которого равен х.
Арктангенс числа x£R (обозначается arctg х)—такое число у^
]л л Г
—о » » тангенс которого равен х.
Z £ L
Основные тождества:
1) sin (arcsin х) = х,
arcsin (sin х) —х,
2) cos (arccos х) =х,
arccos (cos х) = х,
3) tg (arctg х) = х4
arctg (tgx)=x,
4) arcsin x +arccos x==-2-,
xec-1; +1];
_ Г л л "1
2-]!
*€[-1; 4-1];
x£[0, л];
x£R;
-1 л л Г
т[5
*€[-1, 4-Ц.
372
Таблица значений тригонометрических функций
а® а (радианы) sin а tga ctg а cos а
0 0 0 0 00 1 1,571 90
1 0,017 0,017 0,017 57,29 1,000 1,553 89
2 0,035 0,035 0,035 28,64 0,999 1,536 88
3 0,052 0,052 0,052 19,08 0,999 1,518 87
4 0,070 0,070 0,070 14,30 0,998 1,501 86
5 0,087 0,087 0,087 11,43 0,996 1,484 85
6 0,105 0,105 0,105 9,514 0,995 1,466 84
7 0,122 0,122 0,123 8,144 0,993 1,449 83
8 0,140 0,139 0,141 7,115 0,999 1,431 82
9 0,157 0,156 0,158 6,314 0,988 1,414 81
10 0,175 0,174 0,176 5,671 0,985 1,396 80
11 0,192 0,191 0,194 5,145 0,982 1,379 79
12 0,209 0,208 0,213 4,705 0,978 1,361 78
13 0,227 0,225 0,231 4,331 0,974 1,344 77
14 0,244 0,242 0,249 4,011 0,970 1,326 76
15 0,262 0,259 0,268 3,732 0,966 1,309 75
16 0,279 0,276 0,287 3,487 0,961 1,292 74
17 0,297 0,292 0,306 3,271 0,956 1,274 73
18 0,314 0,309 0,325 3,078 0,951 1,257 72
19 0,332 0,326 0,344 2,904 0,946 1,239 71
20 0,349 0,342 0,364 2,747 0,940 1,222 70
21 0,367 0,358 0,384 2,605 0,934 1,204 69
22 0,384 0,375 0,404 2,475 0,927 1,187 68
23 0,401 0,391 0,424 2,356 0,921 1,169 67
24 0,419 0,407 0,445 2,246 0,914 1,152 66
25 0,436 0,423 0,466 2,145 0,906 1,134 65
26 0,454 0,438 0,488 2,050 0,899 1,117 64
27 0,471 0,454 0,510 1,963 0,891 1,100 63
28 0,489 0,469 0,532 1,881 0,883 1,082 62
29 0,506 0,485 0,554 1,804 0,875 1,065 61
30 0,524 0,500 0,577 1,732 0,866 1,047 60
31 0,541 0,515 0,601 1,664 0,857 1,030 59
32 0,550 0,530 0,625 1,600 0,848 1,012 58
33 0,576 0,545 0,649 1,540 0,839 0,995 57
34 0,593 0,559 0,675 1,483 0,829 0,977 56
35 0,611 0,574 0,700 1,428 0,819 0,960 55
36 0,628 0,588 0,727 1,326 0.809 0,942 54
37 0,646 0,602 0,754 1,327 0,799 0,925 53
38 0,663 0,616 0,781 1,280 0,788 0,908 52
39 0,681 0,629 0,810 1,235 0,777 0,890 51
40 0,698 0,643 0,839 1,192 0,766 0,873 50
41 0,716 0,656 0,869 1,150 0,755 0,855 49
42 0,733 0,669 0,900 1,111 0,743 0,838 48
43 0,750 0,682 0,933 1,072 0,731 0,820 47
44 0,768 0,695 0,966 1,036 0,719 0,803 46
45 0,785 0,707 1,000 1,000 0,707 0,785 45
cos а Ctg а tg а sin а а (радианы) а®
373
Комплексные числа.
z=a+bit t2 = —1, a, b£R;
r = | z |= Уа2-)- b2 — модуль числа z.
Величина угла ф£]—л, л], удовлетворяющего системе уравнений
J cos у> = а/Уа2 + Ь2,
[ sin у = Ь/Уа2+Ь2,
называется главным аргументом числа z, а ф4-2ля (п£2Г) —аргументами
числа z.
г = | z ] (cos <р + i sin <р) — тригонометрическая форма записи комплексного
числа.
(fll + ^10 ± («2+^2Г) = («1 ± я2) + (^£ ± ^2) И
(а1 + М (я2+/?20 == (axfl2— ^1^2) + (а1^2Ч“а2^1) 9
(а‘+м (a2~M’
Число z—a—bi называется комплексно сопряженным с числом z=a-\-bi.
z-7=[ z|2 = a2+&2.
Умножение и деление комплексных чисел в тригонометрической форме.
Если
Zf = Ti (cos Ф1+* sin фг),
z2 = r2 (cos ф2+< sin ф2),
то
2i-z2 = ri.r2 [cos (Ф1+ф2) + * Sin (ф£+ф2)Ь
Zi:z2 = ri/r2 [cos (ф1—ф2) + * sin (epi—ф2)Ь
Формула Муавра.
[г (cos ф + i sin ф)]" = rn (cos пф + i sin пф).
Решение квадратных уравнений
Если D^O, то корни действительные
Если D < 0, то корни—комплексные числа, вычисляемые по формулам
b + iV^D _f—b — iV^D
Xi-------2а ’ Xi-------------2а *
Справедливо утверждение (теорема Гаусса): любой многочлен степени я имеет
ровно п корней (с учетом их кратностей).
374
II. НАЧАЛА АНАЛИЗА
Последовательности. Если имеется правило, которое каждому натураль-
ному числу п ставит в соответствие некоторое действительное число ап, то
говорят, что задана числовая последовательность a±t а2, • ап, »•<
В частности, если для всех п an+1 — an-]-d, где d—фиксированное
число, то такая последовательность называется арифметической прогрессией.
Если же an+i = an*q, где q—также фиксировано, то последовательность на-
зывается геометрической прогрессией (см. стр. 119).
Число а называется пределом последовательности (а„), если для любого
числа 8 > 0 существует число N (зависящее от числа 8), такое, что для
всех членов последовательности с номерами п> N справедливо неравенство
рп—а| < 8.
Обозначение: а= lim ап.
П-Ж>
В частности, lim qn = Q (при |g| < 1)>
П->00
lim
П-> 00
(определение числа е).
Предел функции. Пусть функция /(х) определена на множестве
и пусть точка а такова, что в любой ее окрестности лежит бесконечно много
точек множества D(f) (точка сгущения или предельная точка множества
Число b называется пределом функции f (х) в точке а, если для любого
числа 8 > 0 существует такое (зависящее от, 8) число б > 0, что для всех
и удовлетворяющих условию 0 < [х—а| < б справедливо неравен-
ство
l/W-ь 1 < 8.
Обозначение: b= lim / (х).
х->_а
В частности, lim ^-^=1.
о х
Функция / (х) называется непрерывной в точке a£D (/), если lim f (х) = f(a).
х-+ а
Функция непрерывна на множестве если она непрерывна в каждой
точке этого множества. Сумма, разность и произведение двух непрерывных
на одном и том же множестве функций также непрерывны на этом множестве.
Если знаменатель дроби не обращается в нуль на множестве, то и частное
двух непрерывных на этом множестве функций также непрерывно. В частно-
сти, многочлен непрерывен на всей числовой оси, а дробно рациональная
функция непрерывна во всех точках оси, где знаменатель отличен от нуля.
Определение производной.
/-(«)- Ит fK+W-W.
375
Правила дифференцирования.
1) (f (x)+g(x)Y—l' W + g' (x).
2) (C/(x))' = C/'(x) (С—постоянная).
3) (f (x)-g(x)y=f (x) g (x) +/ (x) g’ (x).
., ,f ,w f (x) g (x) — f (x) g' (x)
4) (/ <*)/g W) --------------------•
Производные некоторых функций.
1. (C') = 0. 2. (xay=ax “-1 («€«)•
3. (sin x')=cos x. 4. (cos x)' = • —sinx.
5. (tgx)' =—V- . v 7 COS2X 6. (ctgx)'=- 1 sin2 x ’
7. (a*)' = a* In a, 8- flogax)z = 1 x In a ’
(ex)’=ex. dnx)’=4
9. (arcsin x) =-^r===-. 10. (arccos x)' __ 1 /T^x2 *
11. (arctg x)'=j-p^2 . 12. (arcctg x)' = 1 l + x2‘
Геометрический смысл производной. Г (х)—угловой коэффициент каса-
тельной к графику функции y=f (х) в точке (х; f (х)).
Уравнение касательной к графику функции y=f (х) в точке (х0; f (х0)): у=
= /(хо)+Г(*о) (к-*о).
Если f'(x)>Q(<Q) на интервале ]а; Ь[, то функция f (х) возрастает
(убывает) на этом интервале.
Точка x0£D(f) называется точкой максимума (минимума) функции /(х),
если для всех x£D (/) из некоторой окрестности точки х0 выполняется неравен-
ство f(x)<,f(xQ) (f (х)>/(х0)). Точки максимума и минимума называются
точками экстремума функции.
Критическая точка функции —точка из области определения функции,
в которой производная равна нулю или не существует.
Необходимое условие экстремума (теорема Ферма). Если дифференцируе-
мая в точке х0 функция / (х) имеет в этой точке экстремум, то /' (хо) = О.
Достаточное условие экстремума. Если при переходе через критическую
точку х0 производная функции меняет знак с « + » на «—», то х0—точка
максимума; если производная меняет знак с «—» на « + », то х0—точка
минимума этой функции; если производная не меняет знака, то х0 не является
точкой экстремума.
Интеграл. Функция F (х) называется первообразной для f (х) на проме-
жутке, если F- (x) = f (х) на этом промежутке. Все первообразные функции
f (х) запишутся в виде F (х)-\-С, где С—всевозможные постоянные.
Если F (х) и G (х) — первообразные функций / (х) и g(x), то F(x)4-G(x),
aF(x), lF(fex+^-первообразные функций /(x) + g(x)? a/(x), f(kx-[-b)
&
376
соответственно. Первообразные некоторых элементарных функций легко по-
лучить из таблицы производных, приведенной выше.
ь
Интеграл от функции f (х) на отрезке [а, Ь] (обозначается f (х) dx)—
а
предел интегральных сумм f (сг) bxr+f (с2) Дх2+ ... +/ (сп) кхп при условии,
’гго длина наибольшего из отрезков [x^-i, х^] стремится к нулю. Здесь
а=х0 < хх < ... <x„=Z?, Axfe = Xfe—Xfe-i, ck^[xk^; xk].
Формула Ньютона—Лейбница. Если F (х) —первообразная/ (х) на [я, dj, то
ь
J f (х) dx = F (b)—F (а),
а
Площадь криволинейной трапеции с основанием [а, Ь], ограниченной
сверху графиком неотрицательной функции f (х), равна
&
5 = р (х) dx.
а
Объем тела вращения, образованного вращением вокруг оси Ох криво-
линейной трапеции a^x^b, (х), равен
ь
V = л р2 (х) dx.
Векторы. Вектором называется направленный отрезок. Длиной вектора
называется длина этого отрезка. Векторы называются равными, если их
длины равны и они сонаправлены.
Обозначения вектора: а, АВ (если А —начало, а В —конец вектора);
|а|, |~АВ |—обозначение длины вектора. Если |а| = 0,тоа — нулевой вектор.
Для любой пары векторов а и Ь определены их сумма а-}-Ь и разность
а—Ь. Любой вектор а можно умножить на любое число k^R.
Ненулевые векторы называют коллинеарными, если они лежат на парал-
лельных прямых, и компланарными, если они параллельны одной плоскости.
Нулевой вектор считается коллинеарным любому вектору; любые три вектора,
среди которых есть нулевой, считаются компланарными.
Если р, q и г —три некомпланарных вектора, то любой вектор а пред-
ставим в виде a = xp-\-yq-\-zr. [Это представление называется разложением
вектора а по базису pt q, г; числа х, у, z называются координатами век-
тора а в базисе р, q, г. Запись: а = {х; у, г].
377
Если в данном базисе ai = {xi; yi, zj, а2 = {х2; у2\ z2}, то в том же ба-
зисе ai+a2={*i+*2; #i+#2*, zi+zj, ka1={kx1\ kx2; kx3}.
> —>
Отложим от произвольной точки О векторы а = ОА и Ь = ОВ. Углом
между ненулевыми векторами а и Ъ называется угол между лучами О А и ОВ.
Обозначение (а, Ь).
Скалярное произведение векторов а и Ъ определяется равенством
= &) = | а 11 b ] cos (a^b).
Если хотя бы один из векторов нулевой, то скалярное произведение считается
равным нулю по определению. Скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Если Z, j и k—базис из ортогональных векторов, по длине равных еди-
нице (координатные векторы), и в этом базисе а = {хх; г/х; zx}, b = {х2; #2‘> z2}> то
(a, b)=xx-x2+fZi.«/24-zi-z2;
cos(0)=77=^±^±^==-.
КXi+yl+zl V
Справочный материал по геометрии см. в разделе III данного пособия.
список
ВЫСШИХ УЧЕБНЫХ ЗАВЕДЕНИЙ СТРАНЫ
(С УКАЗАНИЕМ СОКРАЩЕННЫХ НАЗВАНИЙ,
ПРИНЯТЫХ В ДАННОМ СБОРНИКЕ), МАТЕРИАЛЫ
КОТОРЫХ ИСПОЛЬЗОВАНЫ В СБОРНИКЕ ЗАДАЧ
АзГПИ—Азербайджанский ордена Трудового Красного Знамени государ-
ственный педагогический институт им. В. И. Ленина.
АзГУ—-Азербайджанский ордена Трудового Красного Знамени государст-
венный университет им. С. М. Кирова.
АзПИ—Азербайджанский политехнический институт им. Ч. Ильдрыма.
АрГПИ —Архангельский государственный педагогический институт
им. М. В. Ломоносова.
БарГПИ—Барнаульский государственный педагогический институт.
БашГУ—Башкирский государственный университет им. 40-летия Октября.
БГПИ — Благовещенский государственный педагогический институт
им. М. И. Калинина.
БГУ — Белорусский ордена Трудового Красного Знамени государственный
университет им. В. И. Ленина.
БорПИ—Борисоглебский педагогический институт.
ВГУ—Воронежский ордена Ленина государственный университет им. Ле-
нинского комсомола.
ВЗИИЖТ—Всесоюзный заочный институт инженеров железнодорожного
транспорта.
ВЗИТиЛП—Всесоюзный заочный институт текстильной и легкой про-
мышленности.
ВЗПИ—Всесоюзный заочный политехнический институт.
ВЗФЭИ—Всесоюзный заочный финансово-экономический институт.
ВЗЭИС—Всесоюзный заочный электротехническй институт связи.
ВильнГУ — Вильнюсский ордена Трудового Красного Знамени и ордена
Дружбы Народов государственный университет им. В. Капсунаса.
ВЛТИ—Воронежский ордена Дружбы Народов лесотехнический институт.
ВолгПИ—Волгоградский ордена Трудового Красного Знамени политехни-
ческий институт.
ВТИЛП—Витебский технологический институт легкой промышленности.
ВТУЗ ЗИЛ—Завод-втуз при Московском автомобильном заводе
им. И. А. Лихачева.
ГГУ — Горьковский ордена Трудового Красного Знамени государственный
университет им. Н. И. Лобачевского.
379
ГомГУ — Гомельский государственный университет.
ДГУ—Дальневосточный государственный университет.
ДнепрГУ — Днепропетровский ордена Трудового Красного Знамени госу-
дарственный университет им. 300-летия воссоединения Украины с Россией.
ДонГУ — Донецкий государственный университет.
ЕГУ —Ереванский ордена Трудового Красного Знамени государственный
университет.
КазанАИ — Казанский ордена Трудового Красного Знамени авиационный
институт им. А. Н. Туполева.
КазанГУ — Казанский ордена Ленина и ордена Трудового Красного Зна-
мени государственный университет им. В. И. Ульянова—Ленина.
КГУ — Киевский ордена Ленина государственный университет нм.
Т. Г. Шевченко.
КиевГПИ — Киевский государственный педагогический институт им.
А. М. Горького.
КирГПИ —Кировский государственный педагогический институт им.
В. И. Ленина.
КИСИ — Киевский инженерно-строительный институт.
КИЦМ—Красноярский ордена Трудового Красного Знамени институт
цветных металлов им. М. И. Калинина.
КишГУ — Кишиневский ордена Трудового Красного Знамени государст-
венный университет им. В. И. Ленина.
КишПИ—Кишиневский политехнический институт им. С. Г. Лазо.
КолПИ—Коломенский педагогический институт.
КПИ — Киевский ордена Ленина политехнический институт им. 50-летия
Великой Октябрьской социалистической революции.
КрГУ — Красноярский государственный университет.
КубГУ — Кубанский государственный университет.
КуйбГУ — Куйбышевский государственный университет.
ЛатвГУ — Латвийский ордена Трудового Красного Знамени государствен-
ный университет.
ЛГПИ — Ленинградский ордена Трудового Красного Знамени государст-
венный педагогический институт им. А. И. Герцена.
ЛГУ—Ленинградский ордена Ленина и ордена Трудового Красного Зна-
мени государственный университет им. А. А. Жданова.
ЛПИ—Ленинградский ордена Ленина ' политехнический институт им«
М. И. Калинина.
ЛФЭИ —Ленинградский ордена Трудового Красного Знамени финансово-
экономический институт им. Н. А. Вознесенского.
ЛьвГУ—Львовский ордена Ленина государственный университет им.
Ивана Франко.
МАДИ—Московский ордена Трудового Красного Знамени автомобильно-
дорожный институт.
МАИ — Московский ордена Ленина и ордена Октябрьской Революции
авиационный институт им. Серго Орджоникидзе.
МАМИ—Московский автомеханический институт.
МарПИ — Марийский политехнический институт им. А. М. Горького.
МАРХИ — Московский ордена Трудового Красного Знамени архитектур-
ный институт.
380
МАТИ — Московский авиационный технологический институт им.
К. Э. Циолковского.
МВИМУ— Мурманское высшее инженерное морское училище им. Ленин-
ского комсомола.
МВМИ — Московский вечерний металлургический институт.
МВТУ — Московский ордена Ленина, ордена Октябрьской Революции и
ордена Трудового Красного Знамени высшее техническое училище им.
Н. Э. Баумана.
МГИ—Московский ордена Трудового Красного Знамени горный институт.
МГМИ—Московский ордена Трудового Красного Знамени гидромелиора-
тивный институт.
МГПИ — Московский ордена Ленина и ордена Трудового Красного Зна-
мени государственный педагогический институт им. В. И. Ленина.
МГРИ — Московский ордена Трудового Красного Знамени геологоразве-
дочный институт им. Серго Орджоникидзе.
МГУ — Московский ордена Ленина, ордена Октябрьской Революции и
ордена Трудового Красного Знамени государственный университет им.
М, В. Ломоносова.
МИИВТ—Московский институт инженеров водного транспорта.
МИИГАиК—Московский ордена Ленина институт инженеров геодезии,
аэрофотосъемки и картографии.
МИИЖТ—Московский ордена Ленина и ордена Трудового Красного Зна-
мени институт инженеров железнодорожного транспорта.
МИИЗ—Московский институт инженеров землеустройства.
МИНГП—Московский ордена Трудового Красного Знамени институт
нефтехимической и газовой промышленности им. И. М. Губкина.
МИНХ—Московский ордена Трудового Красного Знамени институт на-
родного хозяйства им. Г. В. Плеханова.
МИРЭА—Московский институт радиотехники, электроники и автоматики.
МИСИ—Московский ордена Трудового Красного Знамени инженерно-
строительный институт им. В. В. Куйбышева.
МИСиС—Московский ордена Октябрьской Революции и ордена Трудового
Красного Знамени институт стали и сплавов.
МИТХТ—Московский ордена Трудового Красного Знамени институт тон-
кой химической технологии им. М. В. Ломоносова.
МИУ—Московский ордена Трудового Красного Знамени институт управ-
ления им. Серго Орджоникидзе.
МИФИ — Московский ордена Трудового Красного Знамени инженерно-
физический институт.
МИХМ —Московский ордена Трудового Красного Знамени институт хи-
мического машиностроения.
МИЭМ—Московский институт электронного машиностроения.
МИЭТ—Московский институт электронной техники.
ММИ—2-й Московский ордена Ленина государственный медицинский
институт им. Н. И. Пирогова.
МОПИ—Московский областной педагогический институт им. Н. К. Круп-
ской.
МордГУ—Мордовский государственный университет им. Н. П. Огарева.
МПИ — Московский полиграфический институт.
381
МСИ—Московский ордена Трудового Красного Знамени станко-инстру-
ментальный институт.
МТИ—Московский ордена Трудового Красного Знамени текстильный
институт им. А. Н. Косыгина.
МТИЛП—Московский ордена Трудового Красного Знамени технологи-
ческий институт легкой промышленности.
МТИМБО—Московский технологический институт Министерства бытового
обслуживания населения РСФСР.
МТИММП—Московский технологический институт мясной и молочной
промышленности.
МТИПП—Московский ордена Трудового Красного Знамени технологи-
ческий институт пищевой промышленности.
МФИ—Московский финансовый институт.
МФТИ—Московский ордена Трудового Красного Знамени физико-техни-
ческий институт.
МХТИ—Московский ^ордена Ленина и ордена Трудового Красного Зна-
мени химико-технологический институт им. Д. И. Менделеева.
МЭИ—Московский ордена Ленина и ордена Октябрьской Революции
энергетический институт.
МЭИС—Московский ордена Трудового Красного Знамени электротехни-
ческий институт связи.
МЭСИ—Московский экономико-статистический институт.
НГУ—Новосибирский государственный университет им. Ленинского ком-
сомола.
НЭТИ—Новосибирский электротехнический институт.
ОГПИ—Одесский государственный педагогический институт им.
К. Д. Ушинского.
ОГУ—Одесский ордена Трудового Красного Знамени государственный
университет им. И. И. Мечникова.
ОмГУ—Омский государственный университет.
ОПИ—Одесский ордена Трудового Красного Знамени политехнический
институт.
ПГУ—Пермский ордена Трудового Красного Знамени государственный
университет им. А. М. Горького.
РГУ—Ростовский ордена Трудового Красного Знамени государственный
университет.
РИИГА—Рижский Краснознаменный институт инженеров гражданской
авиации им. Ленинского комсомола.
РПИ—Рижский ордена Трудового Красного Знамени политехнический
институт.
САДИ—Сибирский ордена Трудового Красного Знамени автомобильно-
дорожный институт.
СГУ—Саратовский ордена Трудового Красного Знамени государственный
университет им. Н. Г. Чернышевского.
СимфГУ—Симферопольский государственный университет.
ТаджГУ—Таджикский государственный университет им. В. И. Ленина.
ТартГУ — Тартусский ордена Трудового Красного Знамени государствен-
ный университет.
382
ТашГПИ—Ташкентский государственный педагогический институт
им. Низами.
ТашГУ —Ташкентский ордена Трудового Красного Знамени государствен-
ный университет им. В. И. Ленина.
ТашПИ —Ташкентский ордена Дружбы Народов политехнический инсти-
тут им. Бирун и.
ТбГУ—Тбилисский ордена Трудового Красного Знамени государственный
университет.
ТГУ—Томский ордена Октябрьской Революции и ордена Трудового
Красного Знамени государственный университет им. В. В. Куйбышева.
ТИАСУиР—Томский институт автоматизированных систем управления и
радиоэлектрон ик и.
ТРТИ—Таганрогский радиотехнический институт им. В. Д. Калмыкова.
УжГУ—Ужгородский государственный университет.
У ПИ—Уральский политехнический институт/
УрГУ—Уральский ордена Трудового Красного Знамени государственный
университет им. А. М. Горького.
УЭИИЖТ—Уральский электромеханический институт инженеров желез*
нодорожного транспорта.
ХАИ—Харьковский ордена Ленина авиационный институт им. Н. Е. Жу-
ковского.
ХАИРЭ—Харьковский институт радиоэлектроники.
ХГУ—Харьковский ордена Трудового Красного Знамени и ордена
Дружбы Народов государственный университет им. А. М. Горького.
ЯГУ—Ярославский государственный университет.
ЯПИ—Ярославский политехнический институт.
Валерий Михайлович Говоров
Петр Тимофеевич Дыбов
Николай Васильевич Мирошин
Серафима Федоровна Смирнова
СБОРНИК КОНКУРСНЫХ ЗАДАЧ
ПО МАТЕМАТИКЕ
(с методическими указаниями и решениями)
Редактор А. Ф. Лапко
Технический редактор С. Д. Шкляр
Корректор М. Л. Медведская
ИБ № 11933
Сдано в набор 06.04.83. Подписано к печати 02.08.83.
Формат 6OX9Ol/ie- Бумага тип. № 2. Литературная
гарнитура. Высокая печать. Условн. печ. л. 24. Уч.-изд.
л. 30,41. Тираж 400 000 экз. (1-й завод 1—200 000 экз.).
Заказ № 1577. Цена 1 р. 20 к.
Издательство «Наука*
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции и ордена Трудового
Красного Знамени Первая Образцовая типография имени
А. А. Жданова Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии и книж-
ной торговли. Москва, М-54, Валовая, 28
НЕКОТОРЫЕ ИЗ ОПЕЧАТОК
Страницы Строка Напечатано Следует читать
369 4 СВ. Q R
369 6 СВ. Q R
371 4 СВ. R R
371 12 св. xvx2 (хгх2)
371 16 св. -Ь>0 Ь>0
371 10 сн. arccos arccosа
371 1 сн. а, Р, ,а, Р,
372 11 св. —cos(ot+|3) + cos(ot + p)
372 10 и 9 сн. Э е
373 11 св. 0,999 0,990
374 11 сн. г\1г2 (ri/r2)
378 2 св. кх2; } кУь ^1}