Автор: Доннелли-мл. Р. А.
Теги: теория статистики статистические методы статистика математическая статистика статистический анализ
ISBN: 5-17-040812-9
Год: 2007
Текст
Полное
руководство
Книги серии
Шаг за шагом» -
лучший способ
достичь
немедленных
результатов
Статистика
♦ Исчерпывающее введение
в описательную статистику
и статистику вывода
♦ Незаурядные решения
нудных вероятностных задач
♦ Краткое и доступное
руководство
по проверке гипотез
Роберт А. Доннелли-мл.
Предисловие
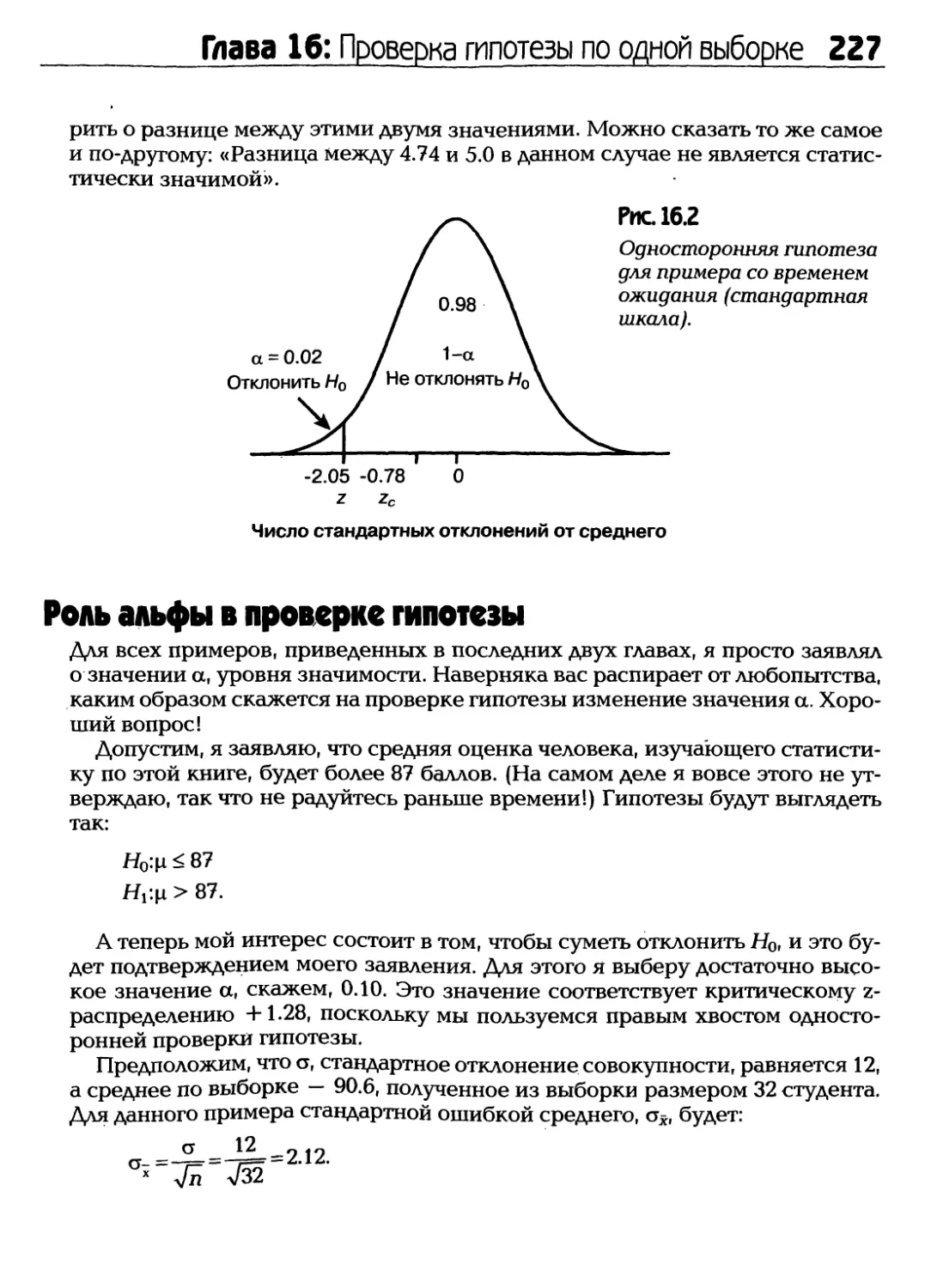
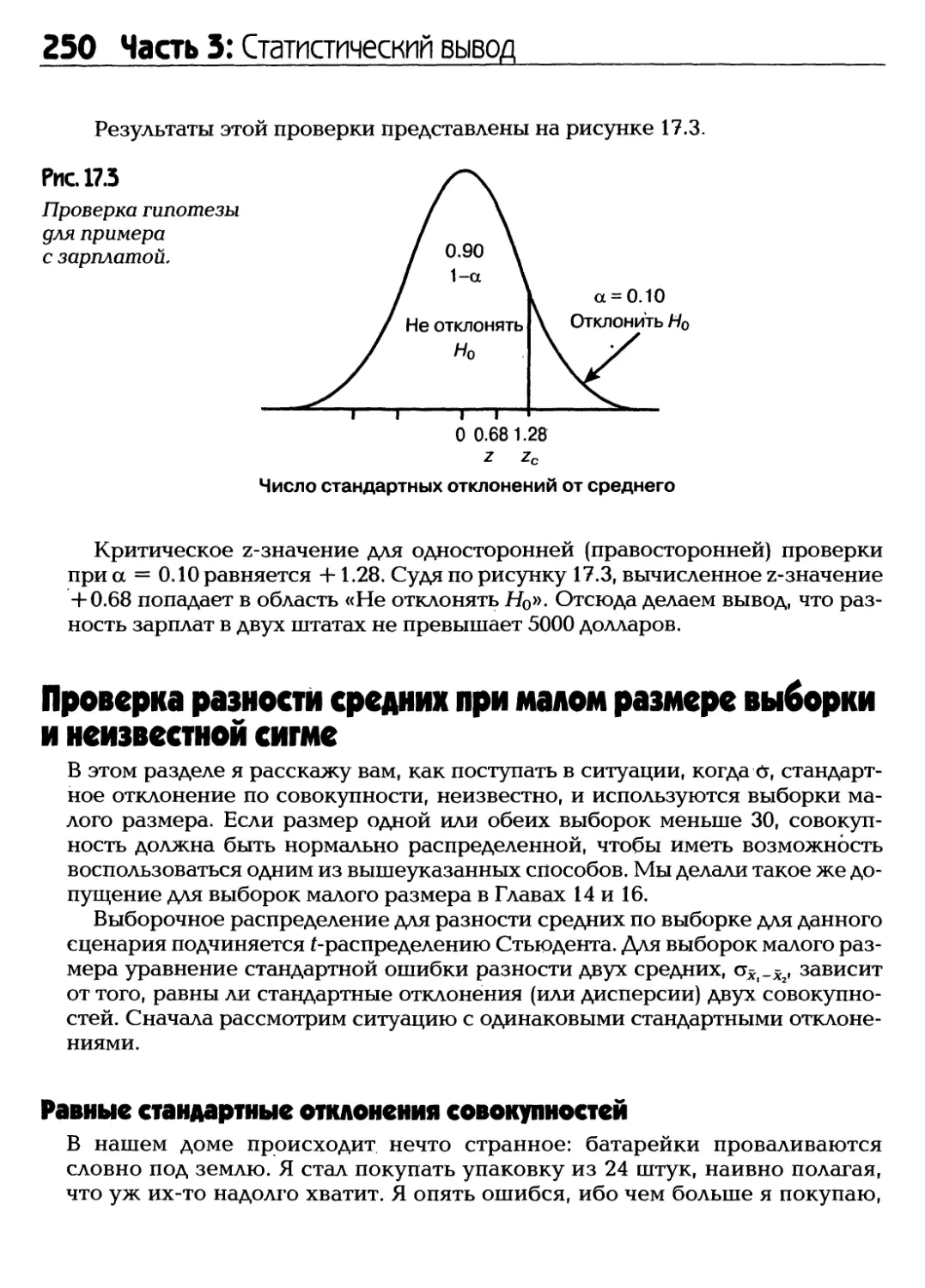
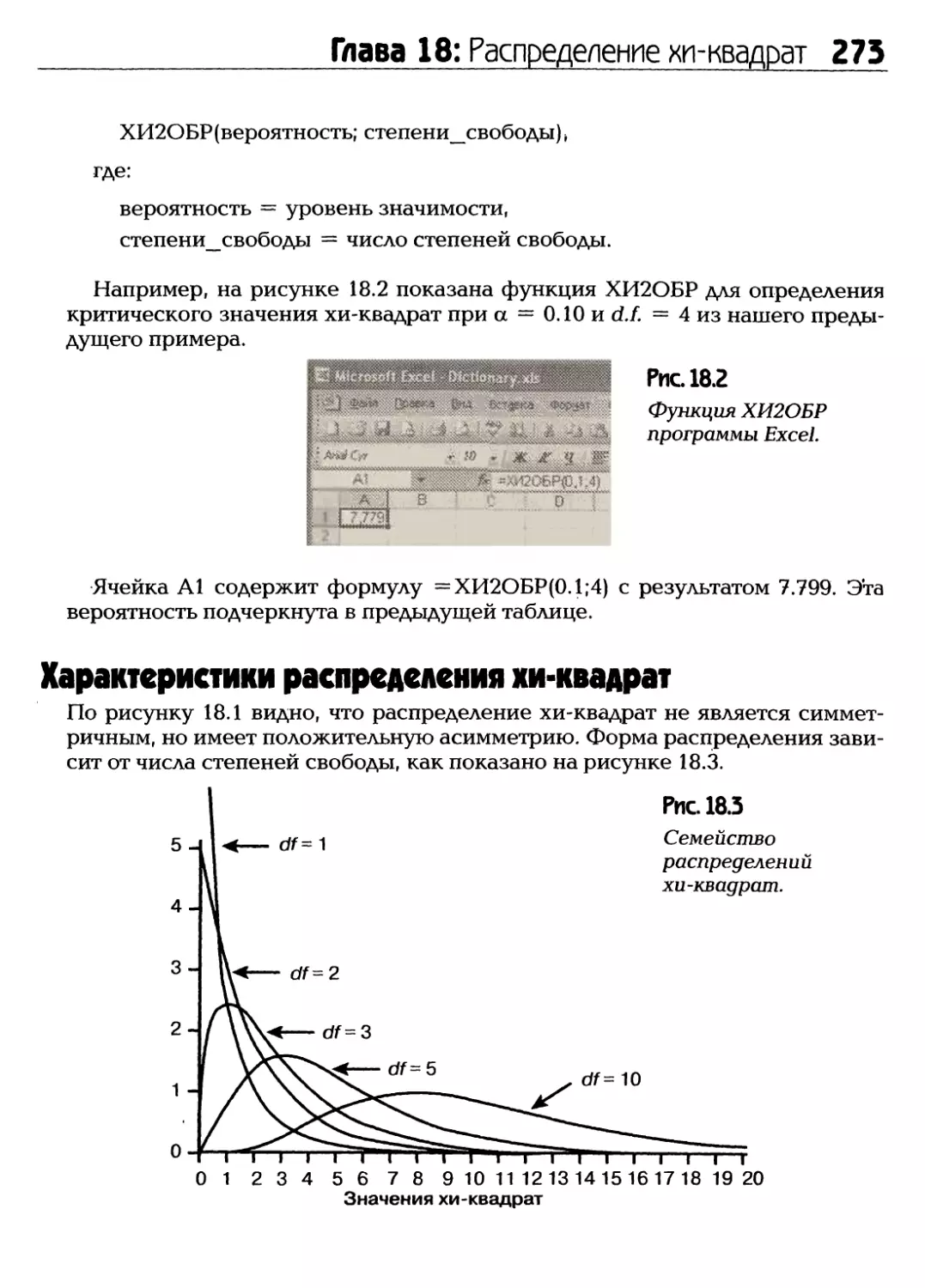
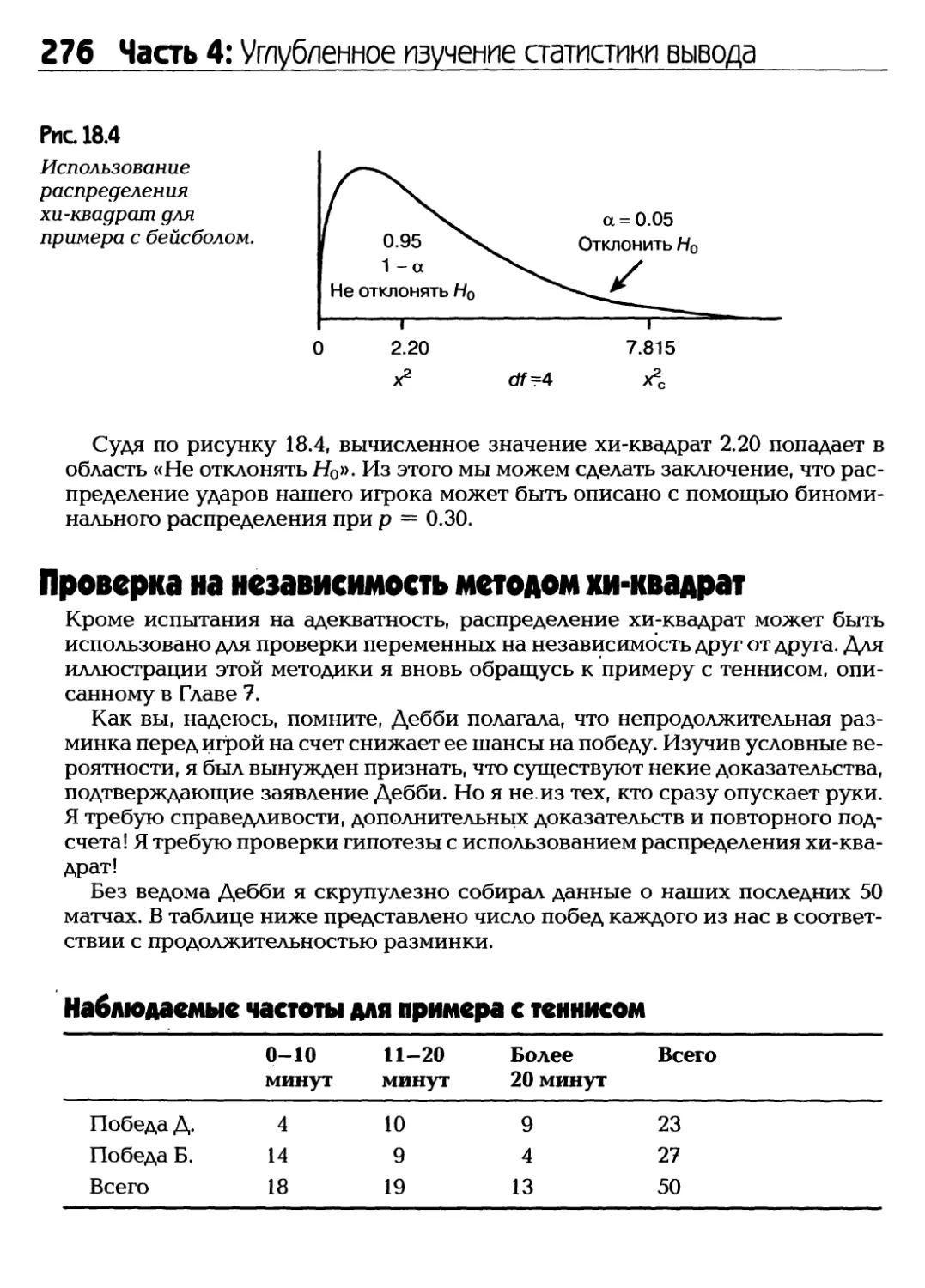
Статистика, статистика повсюду, но мы ровным счетом ничего о ней не
знаем! На самом деле понимание статистики — это крайне необходимый навык,
которым мы все должны овладеть в это непростое время. Каждый день нас
буквально заваливают информацией о политике, спорте, бизнесе, фондовом
рынке, здоровье, финансовом секторе и по многим другим вопросам.
Большинство из нас не обращают никакого внимания на массу получаемой
статистики, но страшнее то, что мы не понимаем, что нам делать со всеми этими
цифрами, коэффициентами и процентами, о которых слышим ежедневно.
Чтобы узнать, что же скрывается за всеми этими числами, мы должны
выяснить, о чем в действительности говорят нам полученные данные. Нам
необходимо определить, не пристрастна ли эта информация или же цифры
являются отражением реальной ситуации. Это и есть одна из причин, по которой
вам совершенно необходимо прочесть эту книгу.
Статистику как направление трудно назвать популярнейшим школьным
предметом. На самом деле многие идут на все, лишь бы отказаться изучать
этот предмет. Причина заключается в том, что статистику часто
воспринимают как математический курс, нечто очень количественное, и это
отпугивает многих учащихся. Другие люди, одолевшие математику, не обладают
необходимым терпением, чтобы узнать, о чем же говорят нам цифры. Они
сильно сомневаются, что статистические данные могут корректно
использоваться для выяснения реального положения дел. Независимо от того,
идет ли речь о важных демографических тенденциях, среднем уровне
заработной платы или безработицы, сходствах или различиях цен на фондовом
рынке, статистика на практике является крайне необходимой входной
информацией для принятия жизненно важных решений. Понимание того, как
получать статистические данные и истолковывать их с целью принятия
конкретного решения, может определить, будет ли это решение
правильным или нет.
К примеру, предположим, что вы хотите продать дом. Для этого вам
необходимо определить продажную цену. Средняя продажная цена на дома в
вашем районе составляет 250* тысяч долларов, так что вы вполне можете
назначить цену 265 тысяч долларов. Вероятно, 250 тысяч долларов — это средняя
цена из диапазона от 200 до 270 тысяч долларов. Тем не менее среднее
значение 250 тысяч может быть получено из следующих цен на дома: 175, 150, 145,
100 и 780 тысяч долларов. Попадание одной высокой цены в пятерку
представленных чисел приводит к резкому росту среднего значения, и в этом слу-
* При подготовке перевода книги был оставлен без изменения формат оформления
десятичных дробей с использованием точки в качестве разделителя дробной и целой частей.
Однако следует учитывать, что при вводе данных в формулы вычисления, в частности
аргументы статистических функций, в качестве разделителя целой и дробных частей используется
запятая (,), как того требует русскоязычная версия спецификации формата десятичных дробей
для этих функций. — Примеч. ред.
Предисловие xi
чае получается, что вы назначили завышенную цену. Поэтому необходимо
понять, что же скрывается под выражением «среднее значение».
Другая причина, по которой нам всем необходимо изучать статистику, —
это то, что мы живем в обществе, движимом таким понятием, как качество.
Вся сегодняшняя жизнь завязана на «улучшении качества», «качественном
рабочем месте», «процессах улучшения качества». Многие компании
стараются повысить качество своей продукции и персонала, используя для
достижения и измерения качества такие методики, как «непрерывное улучшение
качества» или «методику 6 сигма». Даже самый обычный потребитель
слышал об этих понятиях и хочет понимать их, чтобы быть «продвинутым»
заказчиком или клиентом. И вновь понимание статистики может помочь вам в
принятии мудрых решений в отношении своего покупательского поведения.
Поскольку мы находимся в процессе перехода от информационного века
к веку знаний, нам крайне важно хотя бы понимать, а лучше даже получать в
свое распоряжение и грамотно использовать статистические данные. Боб
Доннелли выполнил большую и необходимую работу, представив статистику
в этой книге так, что вы можете улучшить свои навыки в плане оценки и
понимания получаемых ежедневно данных. Долгие годы преподавания
статистики наделили Боба Доннелли феноменальными способностями объяснять
сложнейшие статистические понятия. Даже самые неискушенные
пользователи очень быстро постигнут все тонкости и мощь статистики.
Кристин Кидд
Введение
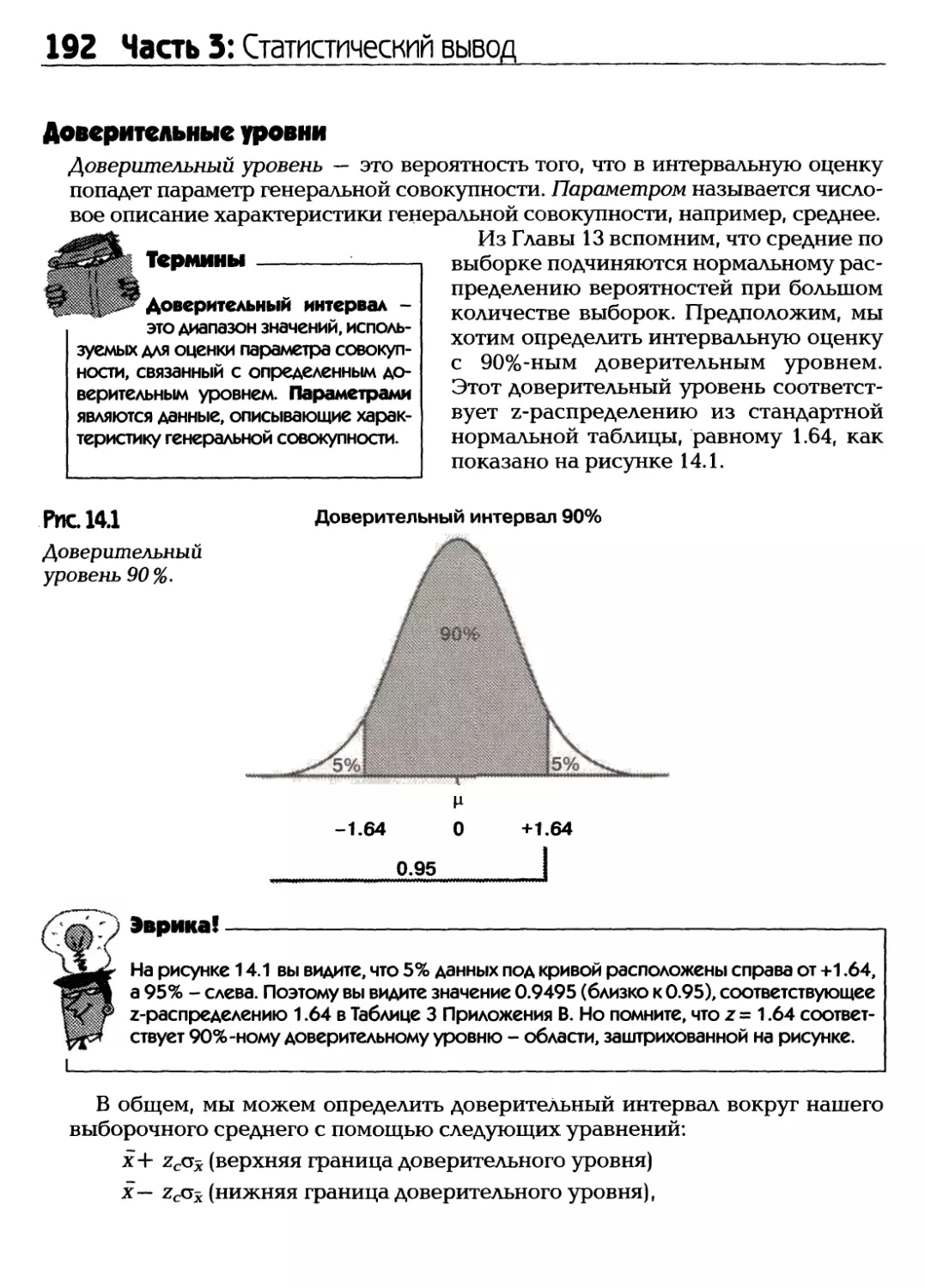
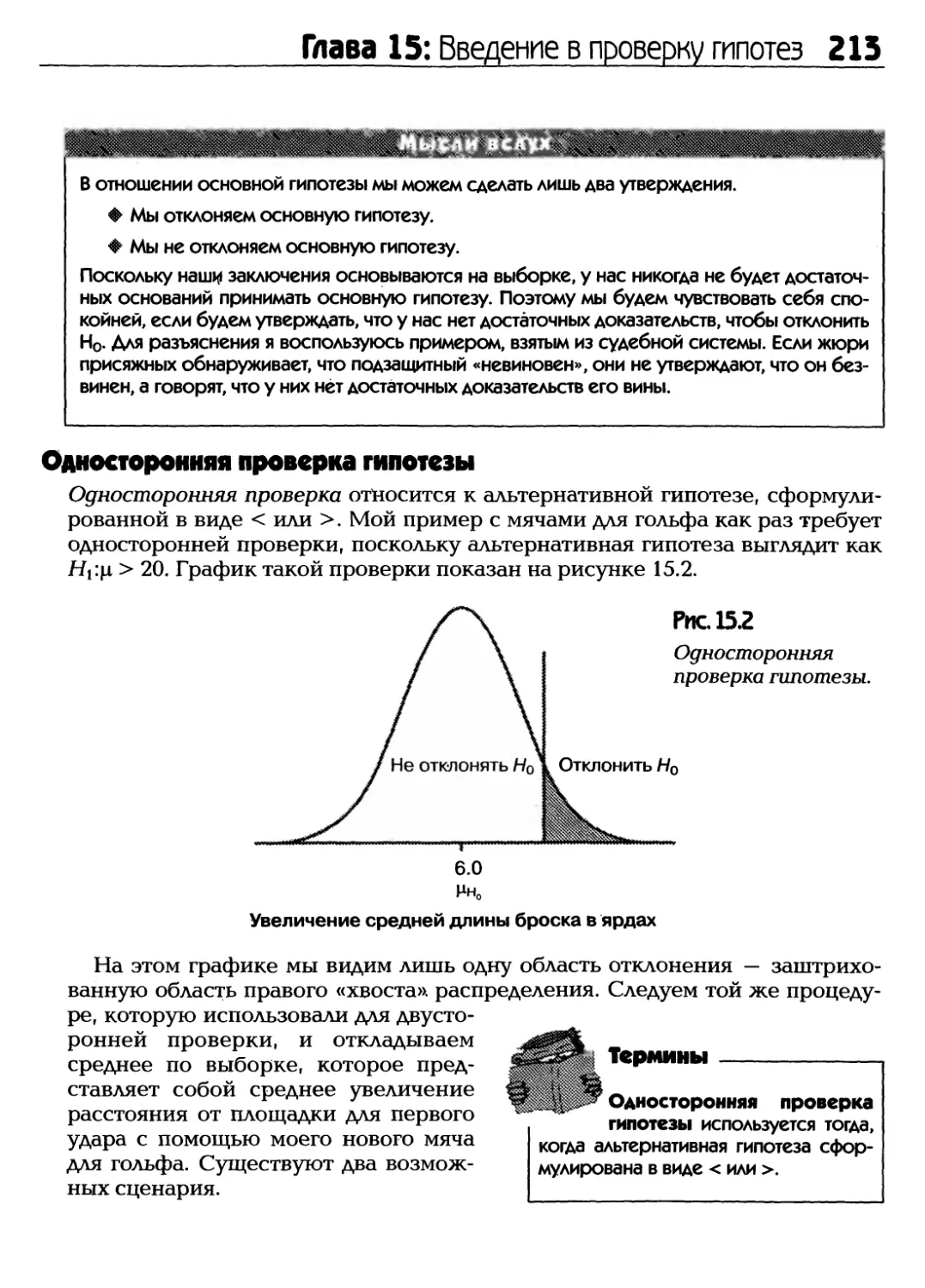
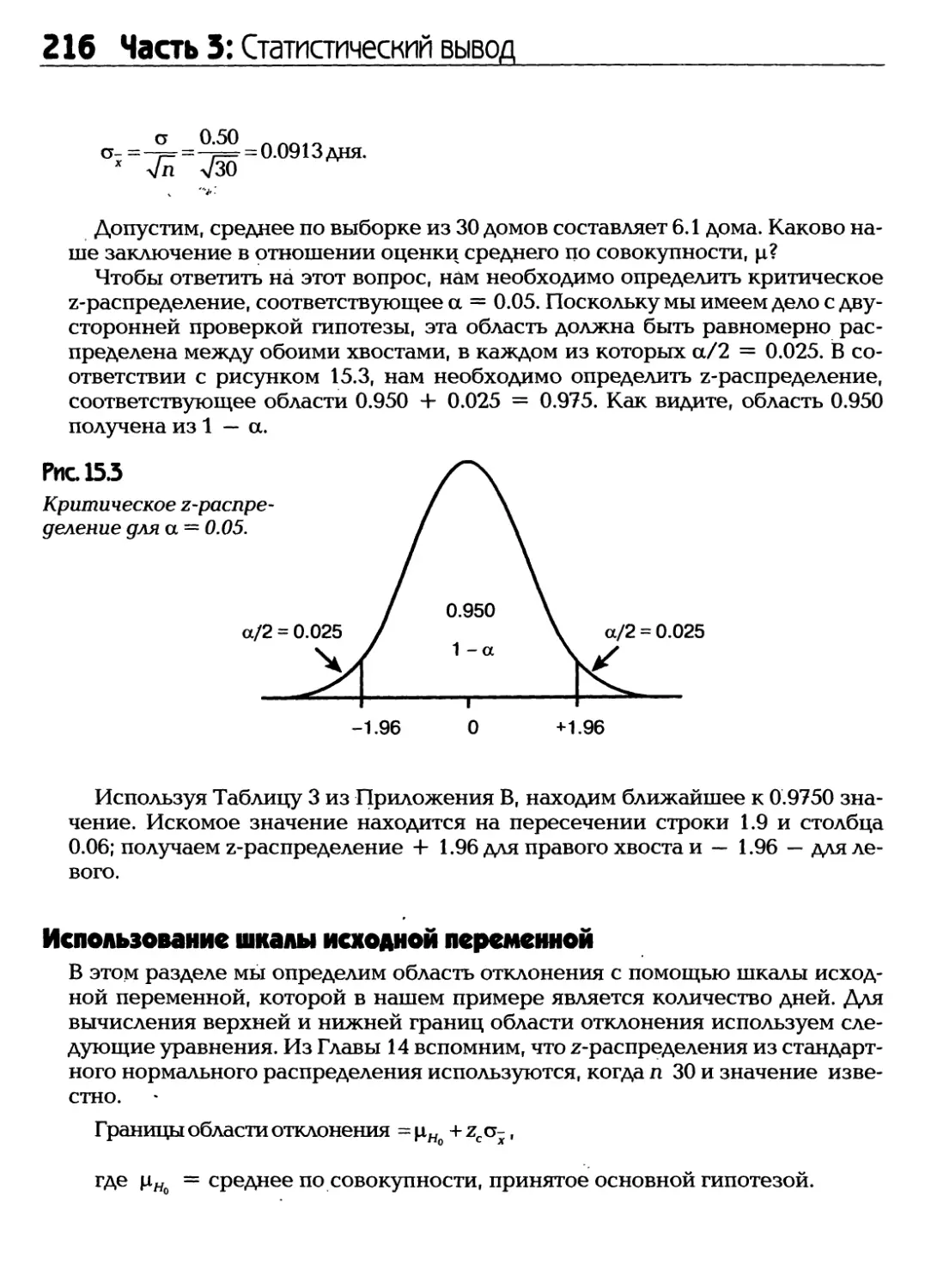
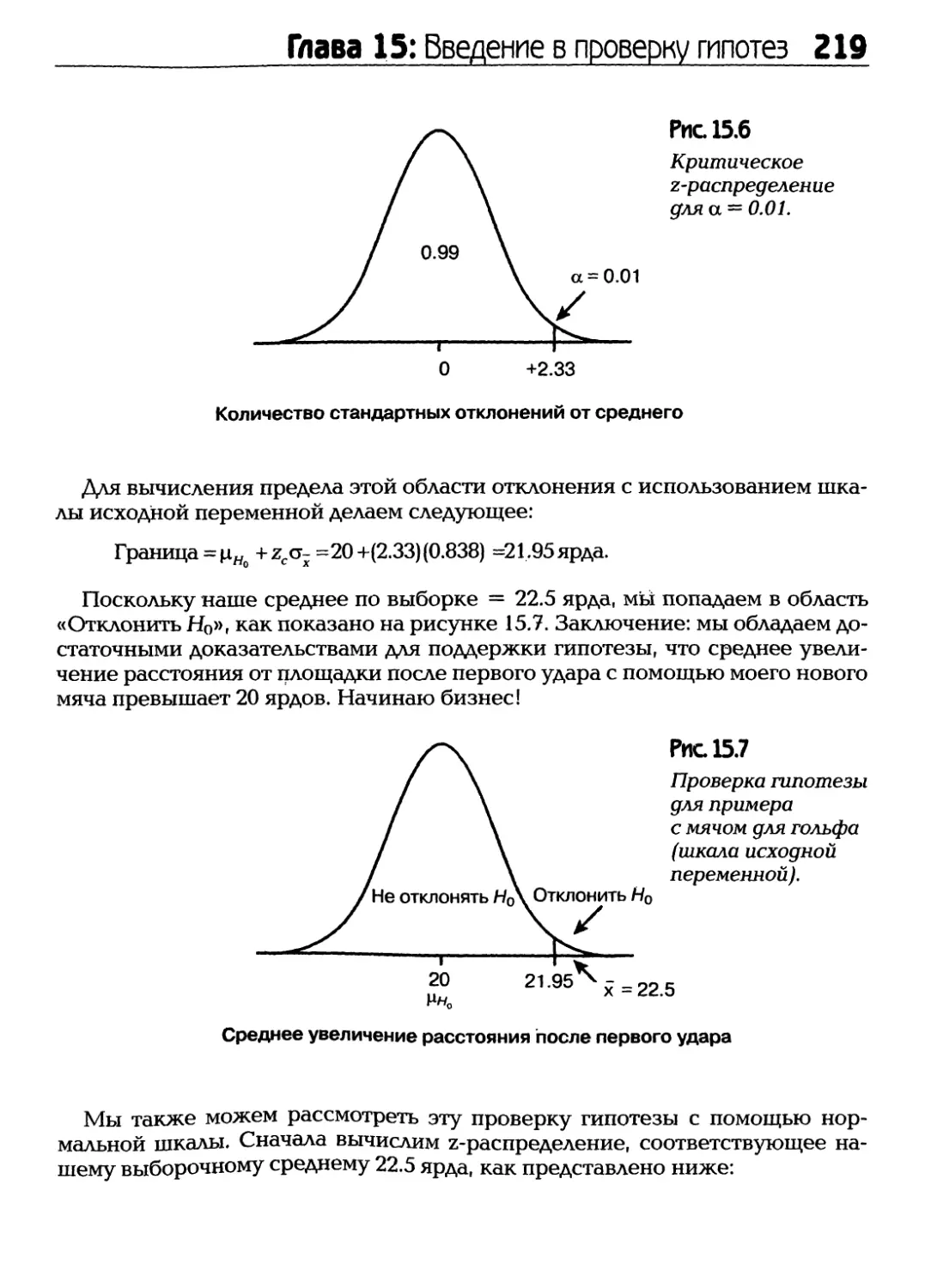
Статистика. Почему это слово так пугает нынешних студентов? Даже
упоминание о статистике в классе вызывает остекленевшие и оцепеневшие
взгляды. В той или иной форме статистика в течение многих сотен лет причиняла
студенту страдания. Наверняка вы думаете, что слово «статистика»
произошло от латинских слов «ста» в значении «Почему» и «тистика» в значении «я
должен изучать этот никому не нужный предмет?». Но на самом деле не так
страшен черт, как его малюют. Понятие «stat» совершенно необязательно
должно ассоциироваться в головах учеников с неприличным словом.
Читая этот абзац, вы наверняка ломаете голову, думая, зачем вам вообще
читать эту книгу. Ну, хотя бы потому, что она написана человеком (то есть
мной), который а) прекрасно помнит, как сам когда-то был студентом (хотя и
в прошлом веке); б) отлично представляет, какую дилемму вам необходимо
сейчас разрешить (я чувствую вашу боль и страдания), и в) кое-чему
научился за долгие годы преподавания (учебные занятия не прошли для меня
даром). Богатый опыт позволяет мне поделиться с вами самыми разными
способами изучения непростых концепций, которые, как правило, кажутся
студентам непостижимыми и непреодолимыми. Взяв на вооружение
многочисленные методики и способы из примеров, детально описанных в этой книге,
вы наверняка обнаружите, что задача постижения статистики уже не
кажется такой устрашающей, какой казалась на первый взгляд.
К сожалению, такие непонятные термины, как статистический вывод,
дисперсионный анализ и проверка гипотез, уже могут привести к тому, что многие
ученики побегут от статистики без оглядки. Я поставил себе цель показать вам,
что эти сложные термины на деле используются для описания самых
ординарных и простых вещей. Применяя большинство этих методик к повседневным (и
зачастую смешным) ситуациям, я попытался доказать, что статистика — это не
только предмет, который под силу одолеть буквально любому, но и наука,
которая может принести реальную пользу при решении самых разных задач.
Для оказания дополнительной поддержки тем, кто в ней действительно
нуждается, я разработал сайт для этой книги; он находится по адресу:
www.stat-guide.com. На этом сайте вы найдете дополнительные задачи с
вариантами решений, а также ссылки на другие полезные ресурсы в Интернете.
Если у вас сложилось определенное мнение об этой книге, которым вы
хотите поделиться, пишите мне на электронный адрес, который найдете на сайте.
Так что держитесь крепче, мы готовы совершить увлекательное
путешествие в мир чисел, неравенств и конечно же многочисленных непонятных
символов. Вы столкнетесь с большим количеством уравнений, которые на
первый взгляд покажутся вам китайской грамотой, но их, оказывается, можно
объяснить вполне понятным языком. Пошаговое объяснение каждой
проблемы поможет вам разбить весь процесс на части. Проработав каждый
представленный пример, вы обретете необходимую уверенность, разовьете
свои способности и научите обращать сухие цифры в полезную
информацию. И, представьте себе, именно так и рождаются статисты!
Как устроена эта книга
Книга разбита на четыре части:
В Части 1 «Постигаем основы» мы начнем с самого начала, считая, что вы
обладаете нулевыми знаниями в области статистики. После небольшого
экскурса в историю, который заставит вас начать слегка шевелить мозгами, мы
окунемся в мир данных и узнаем о различных типах данных и системах
измерений. Мы также научимся отображать данные графически, как вручную,
так и с помощью программы Microsoft Excel. В завершении первой части мы
узнаем, как рассчитывать описательную статистику выборки, в частности,
среднее и стандартное отклонение.
В. Части 2 «Изучаем вероятность» мы откроем врата в устрашающий
мир теории вероятности. Как и в первой части, я предполагаю, что вы не
обладаете никакими знаниями в этой области (а если и обладаете, то я
надеюсь на то, что эти знания зарыты глубоко в вашем подсознаний и вы
рассчитывали на то, что никогда не придется их ворошить). Небезынтересным
вопросом в этом разделе будет изучение того, как рассчитывать число
событий, и эти знания помогут вам постигнуть тонкости игры в покер. После
изучения основ мы плавно перейдем к распределению вероятностей,
рассмотрев, в частности, нормальное и биномиальное распределения. Как
только мы одолеем эти вопросы, будем считать, что подготовлена база для
изучения Части 3.
В Части 3 «Статистический вывод» мы узнаем о том, как отбираются и
ведут себя выборки с точки зрения статистики. К тому моменту, как эти
понятия будут нами рассмотрены и осознаны, мы сможем считать себя
настоящими статистами, делая оценку совокупностей с использованием
доверительных интервалов. К этому времени вы изменитесь так, что собственная мать
узнает вам с трудом! Венцом Части 3 станет изучение милой сердцу любого
статиста темы — проверки гипотез. С использованием этого мощнейшего
инструмента вы можете производить смелые сравнения мужского
населения с женским. Эту задачу я поручу вам.
В Части 4 «Углубленное изучение статистики вывода» мы продолжим
изучение раннее рассмотренных вопросов и узнаем о дисперсионном
анализе, весьма популярной методике сравнения более двух совокупностей
друг с другом. Мы также познакомимся с критерием хи-квадрат,
позволяющим определить, являются ли две переменные взаимозависимыми. В
завершении мы узнаем, как линейная регрессия (иногда ее называют
простой, но на самом деле она не так проста, иначе ей бы не посвящалась
последняя глава книги) описывает мощность и направление связи между
двумя переменными. Изучив все эти вопросы, вы станете совершенно другим
человеком, и из ваших уст будут сыпаться такие слова, что друзья будут
только диву даваться.
xiv Введение
Термины -
Под этим названием вы
найдете определения
жаргонных словечек, но на вполне понятном
нормальному человеку языке. Эти
определения помогут вам постичь
важные понятия. Не пугайтесь этих
словечек: не так страшен черт, как его
малюют.
Это предупреждение о том,
что впереди вас может ждать не
совсем приятный сюрприз. Изучив эти
заметки, вы уже не наступите на те же
грабли, которые набили немало
шишек на лбах ваших
предшественников.
Эврика! -
Здесь вы найдете советы и
рекомендации, кропотливо
собранные мной в течением
многих лет преподавательской
практики. Цель этих заметок
следующая: вас должна осенить гениальная
мысль, в результате чего вы
непременно воскликнете: «Эврика!»
Мысли вслух
Здесь представлены мои наблюдения
по текущему вопросу, которые
представляются мне (надеюсь, и вам тоже)
небезынтересными. Статистика
буквально кишит малоизвестными
фактами, которые помогут вам значительно
облегчить изучение какой-либо темы.
Что еще вы найдете в этой книге
Изучая книгу, вы встретите на полях различные заметки, которые, я
надеюсь, сослужат вам добрую службу и помогут разобраться со сложными
вещами. Многие из них основаны на моем личном преподавательском опыте и
посвящены вопросам, которые вызывают у студентов наибольшие сложности.
Торговые марки
Все термины, известные как торговые марки, выделены заглавными
буквами. Издательство Alpha Books and Penguin Group (USA) Inc. не несет
ответственности за точность и достоверность этой информации. Использование
подобных терминов и понятий в этой книге никоим образом не влияет на
законность и достоверность товарных знаков.
€№¥lt
Постигаем основы
Ключом к успешному изучению статистики является солидный багаж
базовых знаний. Чтобы в полной мере осознать вопросы высокой
сложности (а таких будет немало), необходимо как следует разобраться в
концепциях, представленных в этой части. После небольшого
исторического экскурса мы сосредоточим свое внимание на данных, которые
являются основой любого метода, используемого в статистике. Вас
наверняка удивит, как мало мы знаем о данных и их свойствах. Мы рассмотрим
различные типы данных, способы их сбора, отображения и
использования с целью вычисления среднего значения и стандартного отклонения.
разница мещу стандартным и средним
(не яр/ыющимсд стандартным) отклонением
состоит р том, что первое яшется
нормой, а второе - понятием не слишком
хорошим*1
1 Используется игра слов. В английском mean
подлый, слабый». — Примеч. пер.).
не только «среднее», но и «плохой,
Гла
Начало работы
В этой главе
Ф Назначение статистики — зачем вам ее изучать?
Ф История возникновения и становления статистики — кто
это все придумал?
Ф Краткий обзор науки статистики
Ф Этическая сторона статистики
Как часто вы задавались вопросом: а зачем вообще вам изучать
эту статистику? Думаю, вы не одиноки. Очень часто студенты
погружаются в самую бездну математических теорий и
концепций и никогда не догадаются обозреть «картину сверхур
прежде, чем осуществить это погружение. Цель настоящей
главы состоит в том, чтобы представить вашему вниманию
самую широкую и общую перспективу и убедить вас в том, что
статистика — это мощнейший и полезнейший инструмент, так
необходимый в наше время. Можно даже сказать, что это ваш
спасательный круг. Так держитесь же за него крепче!
В сегодняшнем мире технологий нас заваливают тоннами
данных и информации, получаемых из источников, которые
убеждают нас что-то приобрести или согласиться с чьей-то
точкой зрения. Когда по телевизору нам говорят, что по
результатам опросов какой-то политик занимает лидирующее
положение, а потом где-то мелкими буквами приписано -I- или —
4 Часть 1: Постигаем основы
4 процента, то как это понимать? Когда новое лекарство рекомендовано
четырьмя из пяти врачей, задаем ли мы себе вопрос, насколько объективны их
заявления (иными словами, не заплатили ли врачам за рекламу препарата) ?
Статистика может оказывать сильнейшее воздействие на наши чувства,
мнения и даже принимаемые решения. Так что будет совсем нелишним
научиться пользоваться этим мощным инструментом.
Где используются статистические данные?
В словаре Funk and Wagnalls Dictionary, который я обнаружил на своей
книжной полке, приводится следующее определение понятия «статистика»:
это наука о сборе, сопоставлении и систематической классификации
количественных данных, используемых в качестве основы для выводов и
заключений. Ну и завернули! Говоря простыми словами, я воспринимаю статистику
как способ получения различных чисел и их преобразования в полезную
информацию, на основе которой могут быть приняты грамотные решения.
Эти решения способны серьезно повлиять на течение нашей жизни.
Например, для оценки эффективности нового медицинского препарата
проводятся многочисленные исследования и тесты. Статистические данные
создают основу для принятия объективного решения о том, является ли данный
препарат более эффективным, чем другие средства. Очень часто политика
правительства опирается на результаты статистических исследований и
способ их представления.
Крупнейшие международные
корпорации принимают серьезные решения,
основываясь на статистическом анализе.
В 80-х годах прошлого века компания
Marriot провела широкомасштабное
исследование среди своих потенциальных
клиентов на предмет их отношения к
тому, какие услуги предлагают отели и
гостиницы. После тщательного анализа
полученной информации был запущен
проект Courtyard by Marriot, принесший
немалую славу и деньги компании.
Федеральное правительство
неслучайно проводит национальную перепись
населения каждые 10 лет. Ее проводят с
целью определения размеров
финансирования для различных категорий
граждан страны. Статистический анализ, проводимый на основе данных
переписи населения, служит далеко идущим целям, например, для составления
различных социальных программ как на государственном, так и на федеральном
уровнях.
Внимание!
Неверное истолкование
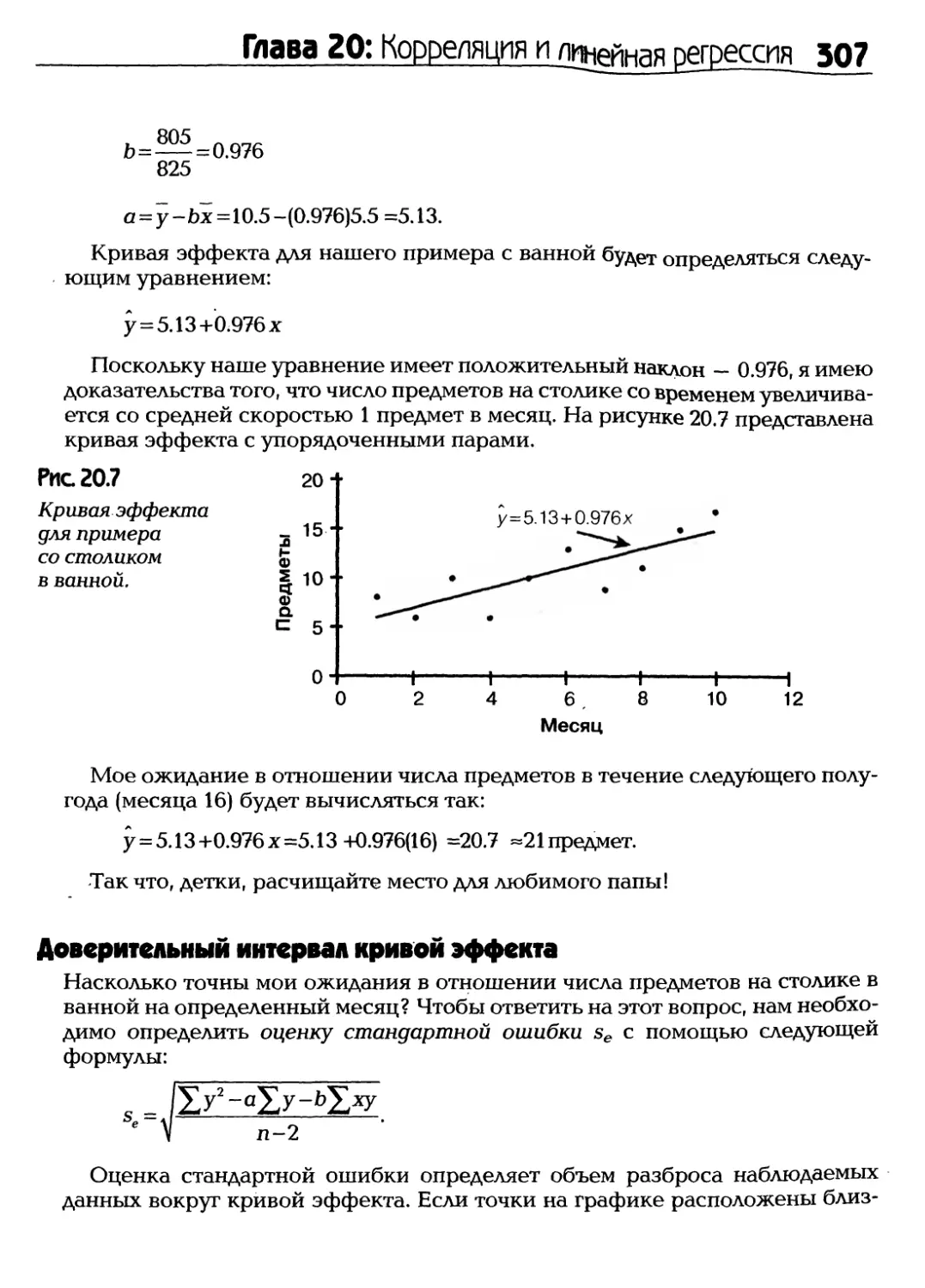
статистических данных может привести к
весьма печальным последствиям. В
1985 году компания Coca-Cola
провела широкомасштабное
социологическое исследование и,
основываясь на его результатах, решила
изменить свой флагманский напиток
Соке. Этот шаг вызвал такую волну
негодования среди потребителей
продукта, что корпорация была
вынуждена отказаться от
нововведений и вернуть на рынок
полюбившийся напиток. Ну и конфуз вышел!
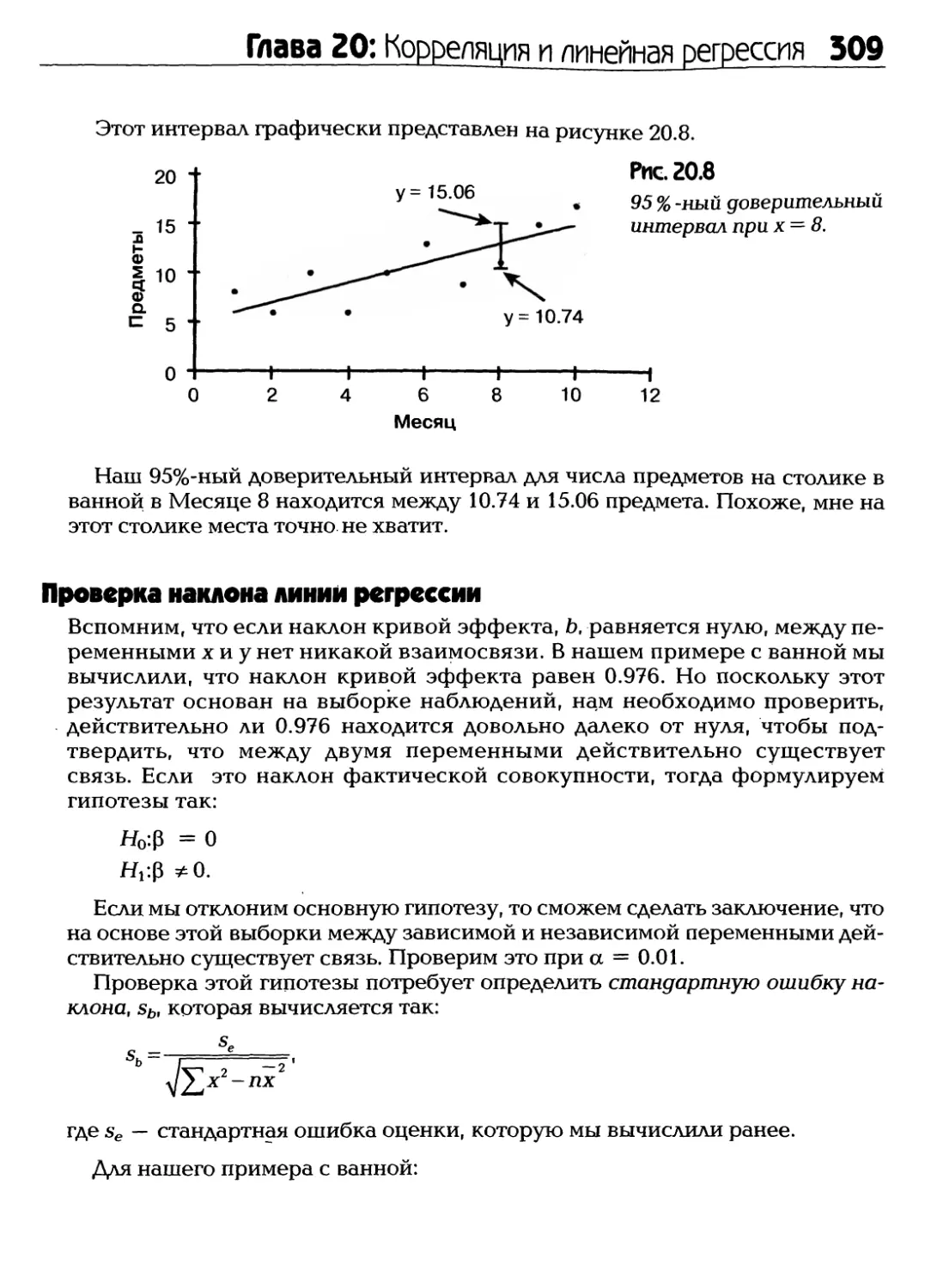
Глава 1: Начало работы 5
Спортивная индустрия напрямую и полностью зависит от статистики. Вы
можете себе представить бейсбол, футбол или баскетбол без
статистического анализа? Вы бы никогда не узнали, кого считают лучшими игроками, кто
наиболее востребован, а кто не пользуется популярностью. Без
статистических данных разве посмели бы игроки требовать такие баснословные суммы
за свое участие в играх?
Всеми вышеперечисленными примерами я хочу донести до вас мысль о
том, что мы окружены статистикой и что если бы ее не существовало, все в
мире было бы совершенно иначе. Так что статистику с полным правом
можно назвать полезным, а в некоторых случаях даже крайне необходимым
инструментом в нашей повседневной жизни.
Кто придумал статистику?
Статистика уходит своими корнями в далекое прошлое. Первым шагом в
историческом развитии этой науки в том виде, какой мы знаем ее теперь,
стали опросы населения. Если верить Библии, первая перепись населения
была проведена в Римской Империи более двух тысяч лет тому назад.
Само слово «статистика» происходит от латинского слова «status»,
означающего «состояние». Эта этимологическая связь отражает самое раннее
назначение статистики: она использовалась для измерения таких вещей, как
общее количество субъектов (облагаемых налогом) в Империи или
количество субъектов, которых необходимо направить на покорение соседних
территорий.
Пионеры статистики
Основу статистики заложили европейские математики. В 1532 году сэр
Уильям Петти представил миру свой первый отчет об уровне смертности в
Лондоне и стал делать это еженедельно. С этого самого момента страховые
компании начали проявлять нездоровый интерес к статистике смертности.
В начале 17-го века математик из Швейцарии Джеймсу Бернулли
рассчитал вероятность последовательности событий, известных как «независимые
испытания». Выбор слов оказался весьма неудачный: на протяжении
нескольких веков студенты с немалым трудом осваивали эту концепцию и
ощущали себя так, будто испытания проводятся над ними самими. Вы наверняка
помните свои попытки разрешить проблему вычисления вероятности
выпадения 7 «орлов» при подбрасывании монетки 10 раз. Так что можете
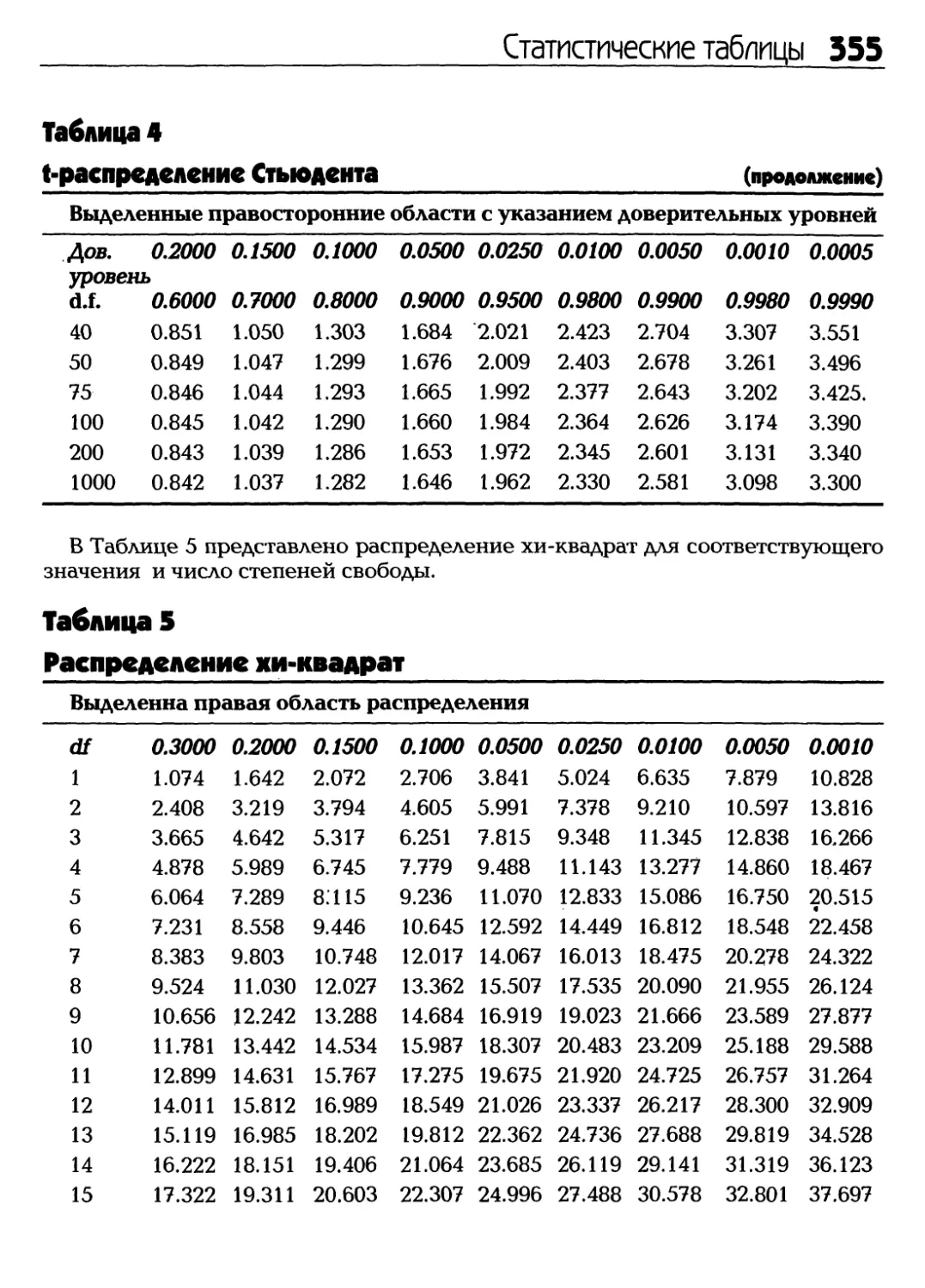
поблагодарить господина Бернулли за то, что он придумал, как разрешить эту
непростую задачу. В Главе 9 вы найдете детальное описание независимых
испытаний Бернулли и тогда сможете справиться с этим испытанием
самостоятельно.
В начале 18-го века английский математик Томас Байес разработал понятия
теории вероятности, которые также сослужили добрую службу науке-статис-
6 Часть 1: Постигаем основы
тике. Байес использовал статистику
событий прошлого для предсказания
вероятностей будущих событий. С тех пор
концепция вывода очень широко
используется при описании статистических методик.
В Главе 7 вы узнаете об этом понятии,
составляющем основу «теоремы Байеса».
Другие известные статисты
Лишь в начале 20-го века статистика стала развиваться достаточно быстрыми
темпами и стала такой, какой мы знаем ее сегодня. Уильям Госсет разработал
знаменитый «f-критерий» на базе ^-критерия Стьюдента, и сделал он это,
когда работал в пивоварне Guinness в Дублине, Ирландия.
Так что когда приступим к изучению изысканий господина Госсета в
Главе 14, не забудем поднять за него свои бокалы.
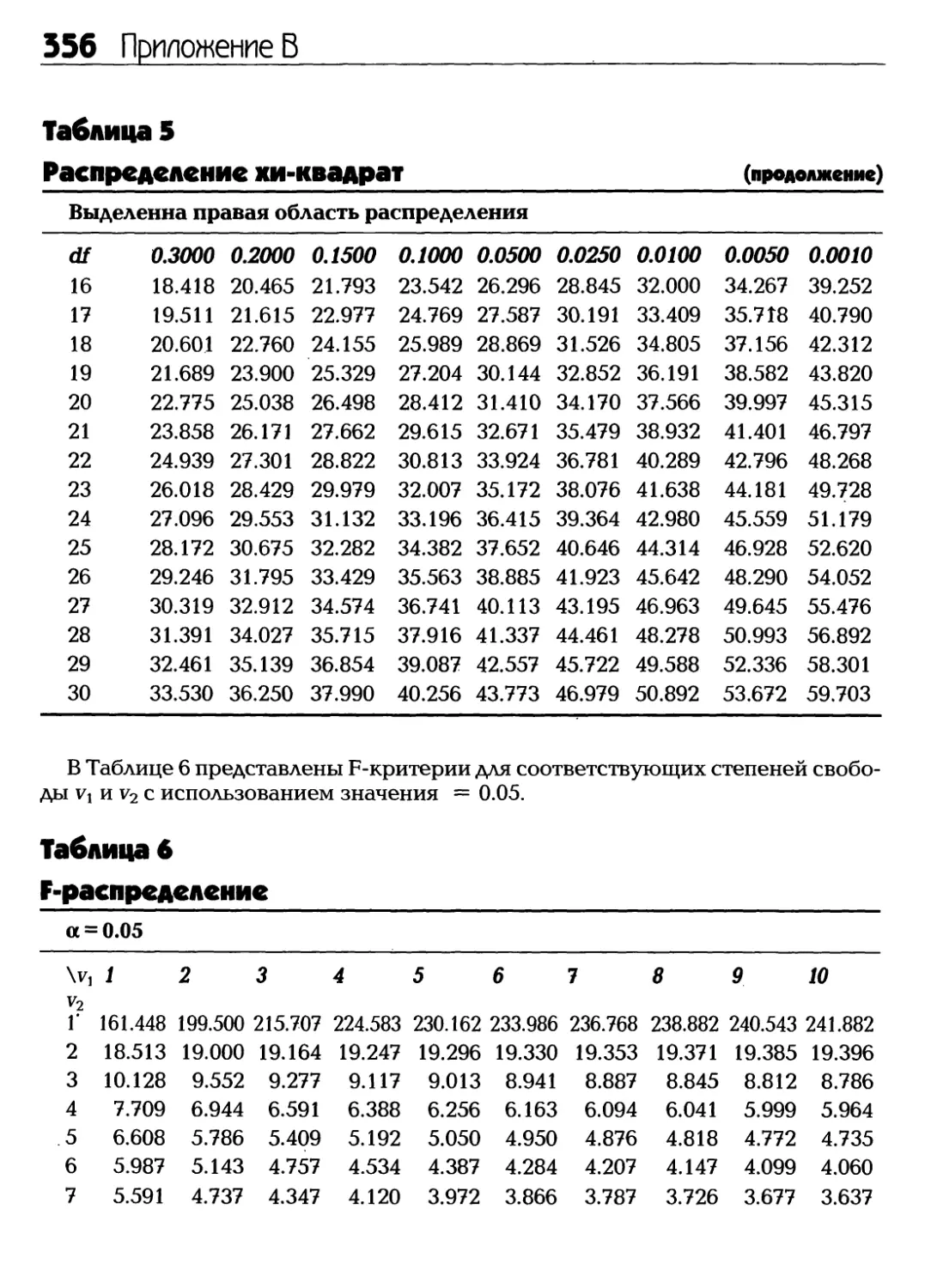
Уильям Эдвард Деминг известен тем, что произвел слияние статистики и
контроля качества в производственной сфере. В 50-х и 60-х годах прошлого
столетия господин Деминг провел немало времени в Японии, пропагандируя идею
статистического контроля качества для промышленных предприятий. Данная
методика опирается на карты контроля качества при наблюдении над
производственным процессом, а также на использовании статистики при
определении качества данного процесса. В течение 70-х годов прошлого века японская
автомобильная индустрия заполучила лакомый кусок рынка США благодаря
превосходному качеству продукции. Вот и судите о силе и мощи статистики!
философия Деминга приняла форму знаменитых «14 пунктов». Эта концепция оказалась
прямо-таки бесценной для организаций, желающих использовать статистику для
повышения эффективности своих производственных процессов. Благодаря усилиям господина
Деминга, статистика заняла почетное место в мире бизнеса. Если вас заинтересовала его
теория, вы можете прочесть книгу The Deming Management Method
Статистика сегодня
Наука статистика развивалась по двум направлениям, образовав
описательную статистику и статистику вывода. Поскольку описательная статистика в
целом более доступна для понимания, ее можно символически назвать
«низшей лигой»; что же касается статистики вывода, то ее изучение потребует от
вас весьма значительных усилий, поэтому назовем ее «высшей лигой».
Сегодня в работе со статистическими данными огромную роль играют
компьютеры и различные программы. Компьютеры способны обрабаты-
Тсрмины
Термин вывод является
ключевым в статистике при
обобщении имеющихся фактов.
Глава li Начало работы
Термины
вать гигантские объемы
данных и информации, а
программы вроде SAS и SPSS
позволяют производить
сложнейшие статистические
операции без особого труда и
применять их в своей работе.
В этой книге я
продемонстрирую вам, как выполнять
самые разные статистические
операции с использованием
программы . Microsoft Excel,
предустановленной на
практически любом современном
компьютере (эта программа
включена в пакет программ
Microsoft Office).
Excel представит вашему вниманию многообразие возможностей работы
со статистическими данными, которые помогут вам сэкономить немало
времени и усилий. Если от этих слов у вас вдруг кровь застыла в жилах (не
волнуйтесь, передо мной не стояла задача написать книгу о компьютерных
программах)., постарайтесь успокоиться. Вы можете беспрепятственно
пропустить разделы! содержание которых вас вряд ли заинтересует. Материал,
представленный в этой книге, является самодостаточным, так что даже если
вы пропустите какие-то главы или разделы, такой шаг никоим образом не
отразится на вашем понимании статистики. И потом, я могу вас заверить, что
на экзамене этого не будет!
Назначение описательной
статистики состоит в том,
чтобы суммировать или отображать
данные так, чтобы оперативно
получать общую картину, так сказать,
обзор. Статистический вывод
позволяет делать умозаключения о какой-
либо совокупности на основе
выборки данных из этой
совокупности. Совокупность представляет
собой все возможные исходы или
измерения, представляющие для нас
интерес. Выборка - это
подмножество совокупности.
Описательная статистика - низшая лига
Основная задача описательной статистики состоит в сборе и отображении,
данных и информации. Описательная статистика сейчас в большом почете;
такое положение дел объясняется огромными объемами данных, в
буквальном смысле выскакивающих из-под наших пальцев. Имея самый
простенький компьютер и выход в Интернет, мы можем за несколько секунд получить
доступ к огромному количеству информации. Способность грамотно
суммировать эти разрозненные данные, чтобы получить общую картину, и
представить их в графическом или числовом виде — это и есть основные задачи
описательной статистики.
Я могу привести множество примеров описательной статистики, самым
распространенным из которых можно с уверенностью назвать среднее
значение. Предположим, я хочу вычислить среднее время фиксации внимания
моего любимого Лабрадора. Каждый раз, фиксируя его внимание, я засекаю
время с помощью секундомера и записываю результаты. В таблице ниже
8 Часть 1: Постигаем основы
представлены результаты наших тренировок; исчисление времени
производится в секундах:
Наблюдение
Время в секундах
1
2
3
4
5
6
7
8
9
4
8
5
10
2
4
7
12
7
Используя методы описательной статистики, я могу вычислить среднюю
продолжительность фиксации внимания, как показано ниже:
4+8 + 5+10+2+4+7+12+7
= 6.6 секунды
Описательная статистика также позволяет представлять данные в
графическом виде, как показано на следующем рисунке. Ну и славный же у меня пес!
Рис 1.1
График
продолжительности
фиксации внимания.
х12
секунда
00 о
00
of 6
о. 4
00
2
0
4 5 6
Наблюдения
Самое пристальное внимание описательной статистике будет уделено в
Главах 3 и 4. А пока посмотрим, что же происходит в высшей лиге.
Глава 1: Начало работы 9
Статистический вывод - высшая лига
Описательную статистику с уверенностью можно назвать цифродробилкой —
так быстро она умеет обрабатывать числовые данные. Но чего мы
действительно ждем с нетерпением, так это изучения статистики вывода. Данная
категория включает огромное количество различных методов, суть которых
сводится к тому, чтобы делать выводы и умозаключения о совокупности
данных на основании выборки. Например, мне пришла в голову идея определить
в целом, кто способен дольше фиксировать на чем-либо свое внимание: лаб-
радоры или подростки. (Основываясь на собственном опыте, я должен
признаться, что знаю ответ на этот вопрос, но оставлю свои предположения при
себе.) Измерить продолжительность фиксации внимания всех лабрадоров и
подростков не представляется возможным, так что HaMv необходимо сделать
выборку из каждой совокупности и измерить параметры этой выборки.
Пришло время определить понятия генеральной совокупности и выборки.
Понятие «совокупности» (или «генеральной совокупности») используется в
статистике для выделения полного собрания объектов, представляющих для
нас интерес. Под «выборкой» понимается часть генеральной совокупности,
представляющая собой группу репрезентативных единиц, специальным
образом отобранных из этой совокупности.
В нашем примере совокупностями являются все подростки и все лабрадо-
ры. Мне необходимо сделать Выборку подростков и лабрадоров, отбирая ре-
презентационные образцы каждой из совокупностей. На основании
результатов каждой из выборок я могу сделать заключение о средней
продолжительности фиксации внимания каждой совокупности в целом и определить,
кто же победил в этой нелегкой борьбе.
На следующей странице показано отношение выборки к генеральной
совокупности.
Рис 1.2
Отношение выборки
к генеральной*
совокупности.
Несколько примеров статистического вывода.
Ф Основываясь на самой последней выборке, я на 95% уверен, что средний
возраст моих заказчиков составляет от 32 до 35 лет.
Ф По результатам случайным образом проведенного опроса, средняя
заработная плата мужчин, занимающих определенную должность, по стране
выше, чем заработная плата женщин в этой же должности.
10 Часть 1: Постигаем основы
Ф В первом квартале 2003 года еженедельный заработок граждан среднего
достатка упал на 1,5%. Печально! (журнал Time, за 26 мая 2003 года,
страница 46).
В каждом из представленных выше случаев результаты основывались на
выборке из совокупности; при этом полученные результаты приписываются
всей генеральной совокупности.
Основное различие между описательной статистикой и статистическим
выводом состоит в том, что описательная статистика предоставляет отчеты
лишь на основании подручных наблюдений и ничего иного. Статистический
вывод подразумевает заключение о целой совокупности на основании
результатов исследования выборки, отобранной из этой совокупности.
Чувствую, что должен сообщить вам следующее известие: статистический
вывод — это та область статистики, освоение которой доставляет студентам
большинство хлопот. Чтобы научиться делать заключения на основании
выборок, необходимо использовать мате-
Эврика! матические модели теории вероятности.
Страшно? Тогда сделайте глубокий вдох
и медленно досчитайте до 10. Так-то
лучше. Понимая, что именно эта тема
является камнем преткновения для многих из
вас, я посвятил теории вероятности
немало страниц в этой книге.
Глубокое понимание
вероятностных концепций - это базовый
трамплин для освоения
статистики. Часть 2 этой книги полностью
посвящена теории вероятности.
Этика и статистика - действительность коварна и опасна
Статистика довольно часто используется для убеждения кого-либо принять
чью-то точку зрения. Мотивом подобного убеждения может служить желание
что-нибудь продать вам или заручиться вашей поддержкой. Подобная
мотивация может привести к нечистоплотному применению статистических данных.
Одним из наиболее частых примеров некорректного использования
статистики являются выборки, параметры которых соответствуют желаемым, вместо
того, чтобы отобрать действительно репрезентативные элементы совокупности,
представляющей для нас интерес. Такие выборки называются некорректными.
Предположим, что я — политик, заинтересованный лишь в том, чтобы
привлечь внимание своих избирателей. Я хочу предложить, чтобы Конгресс
учредил национальный праздник гольфа. В этот замечательный день все
государственные учреждения и коммерческие организации будут закрыты, и мы все
отправимся загонять маленький белый мячик в крохотные лунки с помощью
клюшек, намеренно изготовленных так, чтобы сделать эту задачу
невыполнимой. Смешно, правда? Но моя задача как политика состоит в том, чтобы
продемонстрировать, что любой средний американец поддержит меня в этом
вопросе. И вот в чем состоит гениальность моего плана: вместо того чтобы про-
Глава 1: Начало работы И
водить опрос среди всех
американцев, я раздаю свои анкеты только в
гольф-клубах. Содержание моего
шедевра будет примерно следующим:
Мы хотим учредить национальный
праздник гольфа. В этот день каждый
получает выходной и целый день играет
в гольф (такое заявление означает, что
вам не надо будет спрашивать
разрешения у своей второй половины).
Поддерживаете ли вы это предложение?
A. Да, полностью поддерживаю.
Б. Конечно, почему бы и нет.
B. Нет, я предпочитаю провести целый день на работе.
P.S. Если вы выбираете вариант В, мы лишаем вас всех привилегий игры в
гольф повсеместно и пожизненно. Все очень серьезно.
А теперь я могу со спокойной совестью передать в Конгресс отчет с
результатами проведенного опроса: все участники опроса высказались в
поддержку нового праздника. И самое интересное состоит в том, что Конгресс,
скорее всего, поверит мне.
Другой способ злоупотребления статистикой — это увеличение разницы
результатов путем обманчивого представления данных в графической
форме. Раз уж я заговорил о гольфе, то я использую в качестве примера
результаты игры в гольф. Предположим, что в мае я в среднем набрал 98 очков,
играя в гольф. Взяв несколько уроков, я улучшил свои показатели, набрав в
июне 96 очков. (Для непосвященных: в гольфе чем меньше очков, тем лучше
результат.) По рисунку 1.3 понятно, что мои успехи не настолько хороши,
чтобы ими хвастаться.
Конечно, мне очень неприятно, что я зря потратил деньги на уроки гольфа.
Чтобы сгладить это неприятное ощущение, я могу представить свои
результаты, используя иную шкалу измерений, как показано на рисунке 1.4.
Изменив шкалу измерений, я создал впечатление, будто сильно
поднаторел в игре в гольф, хотя на самом деле прогресс весьма незначительный.
Другой пример неграмотного использования статистики — это
многочисленные опросы, проводимые через Интернет. На самых разных сайтах
вы найдете объявления с предложением проголосовать за вопрос дня.
Результаты этих неформальных опросов трудно назвать достоверными,
поскольку организаторы опросов не контролируют, кто оставляет свой голос
и сколько раз голосует один и тот же посетитель сайта. Как указывалось
ранее, для грамотного проведения опроса мнения необходимо создать
репрезентативную выборку из представляющей интерес совокупности.
Термины
Выборка с пристрастием -
образец
нерепрезентативного представительства свойств
генеральной совокупности, что может
привести к искажению полученных
данных. Необъективный выбор может
произойти или преднамеренно или
неумышленно.
12 Часть 1: Постигаем основы
Рис 1.3
На этом графике
показана реальная
разница между
моей игрой в мае
и июне.
120
РИС 1.4
На этом графике
разница между
количеством
очков за май
и июнь
преувеличена.
со
о
т
О
о
со
&
0)
т
S
е;
s
0)
X
0)
а
О
03
о
т
о
о
со
н
о
а>
т
S
с;
о
а)
0)
х
а>
а
О
100^
80
60
40
20
99
98
97
96
95
Май Июнь
Месяцы
Май Июнь
Месяцы
Такие условия создать просто невозможно, если каждый бороздящий
просторы Интернета имеет возможность принять участие в опросе. И хотя
организаторы подобных опросов заявляют, что полученные результаты не
являются высокоточными, человеческая природа такова, что люди почему-то
склонны им доверять.
Мораль такова: мы все является потребителями статистических данных.
Нас постоянно окружает информация, предоставляемая теми, кто пытается
оказать на нас воздействие или заполучить наше доверие и поддержку.
Знание статистики поможет нам отвратить от себя мошенников, пытающихся
извратить правду. Начиная со следующей главы, мы начнем наше путешествие
к этой цели... и конечно же подготовимся к сдаче экзамена по статистике.
Глава 1: Начало работы 13
Ваша очередь
Определите, в каких примерах используется описательная статистика, а в
каких — статистический вывод:
1. В 2001 году 72.7% азиатско-американских семей в США владели
компьютером (The News Journal, 21 мая, 2003 года, страница А1).
2. Вероятность того, что семьи с детьми до 18 лет (62%) имеют выход в
Интернет выше, чем бездетные семьи (53%). («A Nation Online»,, февраль
2002 года, www.ntia.doc.gov/ntiahome/dn/index/html.)
3. Средняя бэттинг-результативность Барри Бонда составляет .295
(www.espn.com).
4. Средний балл за Стэндфордский экзамен на уровень овладения
знаниями студентов, поступающих в местный колледж в 2002 году, составлял
550.
5. По результатам последнего опроса, 67% американцев положительно
отзываются о президенте Джордже У. Буше (журнал Time, 7 апреля, 2003
года, страница 40).
Повторение - мать учения
Ф Статистика является необходимым инструментом для предоставления
организациям информации при принятии грамотных решений.
Ф Первые шаги в области статистики были сделаны европейскими
математиками в 17-м веке.
Ф Задача описательной статистики состоит в сборе и отображении данных
так, чтобы нашему вниманию предстала общая картина ситуации.
Ф Статистический вывод базируется на выводах и заключениях о
совокупности, сделанных на основании выборки данных из этой
совокупности.
# Все мы пользуемся статистическими данными и должны относиться к
ним крайне внимательно и осторожно, чтобы не стать жертвами
мошенников, использующих статистику в своих интересах.
Глен
Данные, данные повсюду,
как же выбрать нужные?
В этой главе
■Ф Чем отличаются данные от информации
Ф Откуда можно получить данные?
# Какие типы данных можно использовать?
Ф Различные способы измерения данных
# Программа Excel и статистический анализ
Данные являются основой статистики. Достоверность
любого статистического исследования самым теснейшим образом
связана с достоверностью данных, причем с самого начала
вашего исследования. Многие вещи могут оказаться
сомнительными, например, точность данных или их источника. Без
надежной основы ваши усилия по получению качественного
анализа окажутся тщетными.
Все, что связано со сбором данных, может оказаться на
редкость сложным и запутанным. Странно, не так ли? Ведь мы
говорим о числах? Что же здесь может быть затруднительного?
Оказывается, многое. Данные могут классифицироваться
несколькими способами. Необходимо различать количественные
и качественные данные и способ использования каждого из
Глава 2: Данные7 повсюду данные7 как же выбрать нужные? 15
этих типов. Существуют различные способы измерения данных. Выбор
способа измерения данных в самом начале нашего исследования определит,
какие статистические методики мы будем применять.
Важность данных
Данные можно довольно просто определить как значение, присвоенное
определенному наблюдению или измерению. Если я собираю данные о том,
как храпит моя супруга, я могу делать это по-разному. Например, я могу
посчитать, сколько раз Дебби всхрапнула в течение 10-минутного периода. Я
могу посчитать продолжительность каждого храпа в секундах. Я также могу
измерить громкость храпа с помощью описаний вроде «Это похоже на
медведя, только что вышедшего из берлоги после зимней спячки», «Вот это да!
Это было похоже на крик аляскинской чайки, зовущей своих птенцов». (Как
подобный звук мой издавать человек, который носит джинсы второго
размера и может при этом еще и дышать, я никогда не смогу понять.)
В каждом случае я записываю данные об одном и том же событии, но в
различной форме. В первом случае я измеряю частоту, или количество случаев.
Во втором примере я измеряю продолжительность, или временной отрезок.
А в последнем случае я описываю событие по громкости с использованием
слов, а не цифр. Каждый из представленных случаев демонстрирует, как
можно использовать данные.
Если вы еще не обратили на это внимание, люди, посвятившие себя
статистике, любят использовать в своей речи жаргонные словечки. Так что вот вам еще
пара терминов. Данные, используемые для описания интересующего аспекта
совокупности, называют параметром. Если же данные используются для
описания выборки из данной совокупности, речь идет о показателе выборки.
Например, предположим, что нас интересует совокупность в,виде дошкольной группы
трехлетних детишек, в которой работает моя супруга. Положим, нам
необходимо посчитать, сколько раз в день эти маленькие чертенята пользуются туалетом
(по словам Дебби, они делают это чаще, чем это физически возможно).
Мы можем посчитать среднее количество посещений туалета ребенком, и
тогда полученная цифра будет параметром, поскольку в наших расчетах
будет задействована целая совокупность. Однако, если мы хотим рассчитать
среднее количество посещений туалетной комнаты в день трехлетним
ребенком нашей страны, тогда группа Дебби будет нашей выборкой. Среднее
число, полученное в результате расчетов по этой дошкольной группе, будет
показателем выборки, если мы хотим с его помощью оценить по этому
параметру всех трехлетних детишек в нашей стране.
Данные являются основным компонентом всех статистических
исследований. Вы можете нанять самых высокооплачиваемых, известных
статистов, предоставить в их распоряжение самое современное компьютерное
оборудование и программное обеспечение, но если данные, с которыми
они работают, будут неточными или несоответствующими проводимому
16 Часть 1: Постпгаем основы
Термины .
Данные являются значением, присвоенным наблюдению или измерению, и
представляют собой основные элементы статистического анализа. Множественное
число - это данные, а единственное - данное (или данная величина), используемое в
отношении отдельного наблюдения или измерения.
Данные, описывающие характеристику совокупности, называются параметром. Данные,
описывающие характеристику выборки, называют статистикой выборки. Информацией
называют данные, преобразованные в полезные факты, которые можно использовать с
определенной целью, например, для принятия решения.
статистическому исследованию, полученные результаты будут
совершенно бесполезными.
Однако данные сами по себе тоже не представляют особой ценности. По
определению данные — это всего лишь голые факты и цифры, имеющие
отношение к определенному измерению. С другой стороны, информация
получается из фактов с целью принятия решений. Одна из основных задач
статистики состоит в том, чтобы преобразовывать данные в информацию.
Например, представленная ниже таблица показывает объем ежемесячных продаж
для небольшого розничного магазина.
Данные об объеме ежемесячных продаж
Месяц Объем продаж (в долларах)
Январь 15 178
Февраль 14 293
Март 13 492
Апрель 12 287
Май 11321
Используя методы статистического анализа, мы можем получить
небезынтересную информацию типа «Стоп! Ты совершаешь ошибку. При таком
уровне падения объема продаж тебе придется закрыть магазин уже в начале
следующего года!». Используя эту ценную информацию, мы можем принять
некоторые важные решения и попытаться избежать грядущих
неприятностей, нависших над бизнесом.
Источники данных - откуда вообще берутся данные?
Источники данных можно разделить на две большие категории — первичные
и вторичные. Вторичными данными являются данные, собранные другими
го использования. Вторичными
считаются данные, собранные кем-то
другим, которые вы используете в своих
целях.
Глава 2: Данные, повсюду данные, как же выбрать нужные? 17
людьми и предоставленные для ши- ^ЙЙЙЯк
рокого пользования. Например, Жщт —Термины
правительство США очень любит Й^ЙМЩ
собирать и публиковать всякого ро- ЧЫР^ Первичными являются данные,
^ - J л. I собранные вами для собственно-
да любопытную информацию, ' ^
лишь бы хоть кто-нибудь проявлял
к ней интерес. Министерство
торговли США имеет дело с данными
переписи населения, а
Министерство труда осуществляет сбор
огромного количества данных о статистике труда. Министерство внутренних
дел предоставляет самые разнообразные данные о ресурсах США. Например,
вам известно о том, что в США водятся 250 видов белок? Если вы мне не
верите, то зайдите по адресу www.npwrc.usgs.gov/resource/distr/mammals/squir-
rel.htm, и вы можете стать настоящим экспертом по части белок.
Правительство Канады использует мощную систему предоставления
статистических данных для самого широкого применения. В отличие от США,
где каждое министерство отвечает за сбор и оплату соответствующих
данных, в Канаде для этого существует государственное статистическое
агентство Statistics Canada (www.statcan.ca/start.htm). Его можно сравнить с
магазином, в котором статисты могут приобрести все, что им необходимо.
Агентство имеет замечательный сайт, который превращает изучение различных
данных в настоящее удовольствие.
Основным недостатком вторичных данных является тот факт, что вы не
имеете возможности контролировать способ сбора этих данных. Человеку
свойственно верить всему напечатанному. (Вы ведь верите мне, не правда
ли?) Достоинством вторичных данных является их дешевизна (порой их
можно заполучить вообще бесплатно) и доступность. Такие данные служат
незамедлительным подтверждением соответствующих домыслов и предпосылок.
Первичными являются данные, собранные человеком, который сам будет
их использовать. Получение таких данных стоит недешево, зато это будут
ваши собственные данные, и вам некого будет винить, кроме самого себя, если
они будут собраны неверно.
Интернет стал одним из важных источников получения данных для целей статистики,
публикуемых различными отраслями экономической деятельности. Если вы можете потратить
свой день на изучение тысяч сайтов, выданных самым обычным поисковым сервером,
возможно, вам и удастся найти прелюбопытнейшую информацию. Однажды я обнаружил в
Интернете японское исследование о влиянии фторида на зародышей жаб (www.fluoride-jour-
nal.com/1971 .htm). До прочтения этого материала я и не подозревал, что у жаб есть зубы,
и был совершенно далек от мысли о том, что и их мучает кариес. С нетерпением жду того
момента, когда смогу поделиться этой сногсшибательной новостью со своими друзьями.
18 Часть 1: Постигаем основы
При сборе первичных данных вы непременно захотите удостовериться в
том, что результаты не искажены их неграмотным сбором. Существует
множество способов сбора первичных данных, такие как непосредственное
наблюдение, эксперименты и опросы.
Непосредственное наблюдение - я буду следить за вами
Как правило, данный способ означает сбор данных об интересующих
объектах в их естественной среде, когда они и не подозревают, что происходит
вокруг них. Примерами таких исследований могут служить наблюдение за
дикими животными, выслеживающими свою жертву в лесу, или за
подростками, сбивающимися в кучу каждый пятничный вечер (а может, это один и тот
же пример?). Очевидным достоинством этого способа является то, что
объекты не оказываются под влиянием сбора данных, поскольку не
подозревают об этом.
Одна из методик непосредственного наблюдения — это фокус-группы, в
которых объекты наблюдения знают о том, что с их помощью производится
сбор данных. В бизнесе фокус-группы используются для сбора информации
рядом респондентов, управляемых модератором. Как правило,
респондентов, которым оплачивают потраченное на опрос время, просят предоставить
комментарий по определенному вопросу.
Эксперименты - кто используется в качестве подопытных кроликов?
Это еще более прямая методика, чем наблюдение, поскольку объекты сами
принимают участие в эксперименте, цель которого — определить
эффективность чего-либо. Примером может послужить использование нового
медицинского препарата. В ходе эксперимента создаются две группы. Одна из
них является экспериментальной; ее представителям дают новый препарат.
Вторая группа является контрольной; ее представители думают, что
получают новый препарат, хотя на самом деле над ними не производится никакого
медикаментозного лечения. По результатам эксперимента производится
измерение и сравнение реакций обеих групп, после чего осуществляется
оценка эффективности препарата.
Заявления, подтвердить которые и призваны экспериментальные
исследования, должны быть четкими и конкретными. Совсем недавно я прочел
статью о чудодейственной травке под названием «гинкго билоба». В статье
написано, что люди, продающие эти травки с целью заработать, заявляют,
что гинкго билоба поможет вам сохранить острый ум. Похоже, что все
именно этого и хотят. А теперь вернемся к моему утверждению. Данное
заявление довольно трудно подтвердить. Что значит «сохранить острый ум»?
И потом, как измерить остроту ума? Так что грамотное проведение
статистического эксперимента — не такая уж простая и вовсе не тривиальная
задача.
Глава 2: Данные, повсюду данные, как же выбрать нужные? 19
Очевидными плюсами экспериментов является возможность для статиста
контролировать различные факторы, которые могут повлиять на результаты
эксперимента, например, пол, возраст и образование участников. Проблема
сбора информации с помощью экспериментов состоит в том, что на ответы
участников может повлиять факт их участия в исследовании. Разработка
экспериментов для статистического исследования — это весьма сложная тема,
выходящая за рамки этой книги.
Опросы - это ваш окончательный ответ?
Данная методика сбора данных подразумевает, что респонденту напрямую
задают ряд вопросов. Анкета должна быть составлена таким образом, чтобы
избежать уклонения от ответов (см. Главу 1) и не запутать анкетируемых.
Проблемы могут также появиться в части влияния опроса на ответы
участников. Некоторые участники отвечают так, так того, по их мнению, требует
опрос. Это очень похоже на то, как заложники стараются выполнять
требования своих захватчиков. Опрос может проводиться по электронной или
обычной почте или по телефону. Особенно мне нравятся телефонные опросы,
когда звонки застают меня за обедом, в душе или тогда, когда мне наконец-то
удалось взяться за написание очередной главы.
Эврика! ■ .
Исследования показали, что ответы участника опроса могут зависеть от того, как
заданы вопросы. Вопрос, который звучит положительно, скорее всего, вызовет
положительные эмоции и такой же ответ, и наоборот. Целесообразно протестировать анкету
на небольшой группе людей, прежде чем делать ее достоянием общественности.
Какую бы методику вы ни использовали, прежде всего, вы должны
позаботиться о том, чтобы выборка была репрезентативным образцом
интересующей вас совокупности.
Типы данных
Есть и еще один способ классификации данных: количественные или
качественные.
Ф Количественные данные используют численные значения для
описания интересующего нас объекта. Примером может служить возраст
Дебби, который я обязался хранить в строжайшем секрете, подписав
юридический документ, и не указывать в книге, даже в качестве
ответа на один из вопросов, указанных в приложении (намек: см.
страницу 49).
20 Часть 1: Постпгаем основы
Ф Качественные данные используют описательные выражения для
измерения или классификации интересующего нас объекта. Примером
качественных данных может послужить имя респондента, участвующего в
опросе, и его/ее уровень образования. Далее представлена более
детальная информация о качественных данных.
Типы шкал измерения - вопрос немаловажный
Разве кто-нибудь из вас мог хоть на секунду представить, что данные
можно рассматривать с такого количества точек зрения? Не забудем сказать и о
том, что классифицировать данные можно с помощью различных способов
их измерения. Выбор способа измерения данных имеет огромное значение,
поскольку определяет, какие методы статистического анализа мы будем
применять к интересующим нас данным. Каждый из способов измерения
подробно описан в следующих разделах.
Номинальный уровень измерения8
Номинальный уровень измерения используется исключительно с
качественными данными. Явления соотносятся с определенными, заранее заданными
категориями. Примером может служить пол респондента, тогда категориями
будут «мужской» и «женский». Другой пример: данные, обозначающие тип
соседских собак. Категориями для этих данных будут являться различные
породы собак: Лабрадор, терьер, глупые дворняжки, которые постоянно
тревожат мой сон своим воем на луну. Этот тип данных не позволяет нам выполнять
какие-либо математические операции, например, сложение или умножение.
У нас не получится упорядочить такой список от максимума до минимума
(хотя я бы поставил Лабрадора на высшую ступень). Такой тип относится к
самому низкому уровню данных и налагает значительные ограничения на
выбор метода статистического анализа.
На номинальном уровне измерения могут также использоваться числа. Но
даже к такому случаю применимы все те же правила номинальной шкалы.
Примером могут служить почтовые индексы или номера телефонов, которые
никак нельзя сложить или расположить в порядке возрастания или
убывания. Несмотря на то что в качестве данных используются числа, такие
данные считаются качественными.
Порядковый уровень измерения3
Порядковый уровень чуть выше номинального; он предоставляет нам более
детальную информацию о явлении. Этот уровень характеризуется всеми
Автор вторгается в область теории измерений, где более употребим термин шкала
наименований, по крайней мере, в отечественной литературе. — Примеч. ред.
3 В теории измерений это шкала порядка. — Примеч. ред.
Глава Z: Данные, повсюду данные, как же выбрать нужные? 21
особенностями номинального плюс возможность ранжировать значения от
максимального до минимального. Например, вы решили провести
состязание между косильщиками лужаек. Результирующий порядок получился
такой: Скотт, Том и Боб. Мы по-прежнему не можем осуществлять
математических действий над этими данными, зато можем сказать, что косилка
Скотта более шустрая, чем косилка Боба, но не можем сказать, насколько она
шустрее. Порядковые данные не позволяют нам осуществлять измерения
внутри категорий и утверждать, например, что косилка Скотта работает в два
раза быстрей, чем косилка Боба (на самом деле это не так).
Порядковые данные могут быть как качественными, так и
количественными. Примером количественных данных может служить ранжирование
кинофильмов с помощью 1,2,3 или 4 звездочек. Однако этот способ не дает нам
никаких оснований заявлять, что 4-звездочный фильм в четыре раза лучше
фильма с одной звездочкой.
Интервальный порядок измерения4
Двигаясь вверх по шкале данных, мы добрались до интервального уровня,
применяемого исключительно к количественным данным. И вот теперь мы
можем обратиться к математическим операциям сложения и вычитания при
сравнении значений. Для этого типа данных мы можем измерить разницу
между различными категориями с помощью реальных чисел, получив весьма
полезную и точную информацию. Типичным примером может служить
температура, измеряемая в градусах по Фаренгейту. Например, 70 градусов —
это на 5 градусов теплее, чем 65 градусов. Что же касается умножения и
деления, то эти операции нельзя применить к интервальным данным. Почему?
Да потому, что температура 100 градусов — это вовсе не в два раза теплее,
чем 50 градусов.
Относительный порядок измерения5
Это высшая ступень типов данных. На этой ступени вам предоставляется
масса возможностей оперировать с данными. Вы можете выполнять все
четыре математические операции для сравнения значений данных, не
испытывая при этом никаких угрызений совести. Примерами таких данных могут
являться возраст, вес, рост и заработная плата.
Относительные данные обладают всеми характеристиками интервальных
данных плюс истинное нулевое значение. Понятие «истинного нулевого
значения» означает, что данные со значением 0 — это отсутствие объекта, над
которым производится вычисление. Например, заработная зарплата со
значением 0 — это отсутствие заработной платы.
4 В теории измерений это шкала интервалов. — Примеч. ред.
5 В теории измерений это шкала отношений. — Примеч. ред.
22 Часть 1: Постигаем основы
Внимание!
Данные на интервальной шкале
не обладают истинным нулевым
значением. Например, О градусов по
Фаренгейту вовсе не означает отсутствия
температуры, хотя на первый взгляд
именно так и может показаться. Если
хотите заполучить еще один пример,
попробуйте испечь пирог при
температуре, вдвое превышающей
рекомендованную, за время, вдвое меньше
необходимого. Вот смеху-то будет!
Имея в наличии истинное значение О,
вы можете сравнивать значения данных
с помощью правил умножения и
деления. Таким образом, мы можем сказать,
что человек ростом 6 футов в два раза
выше, чем человек ростом в 3 фута, или
что 20-летний юноша в два раза моложе
40-летнего мужчины.
Различие между интервальным и
относительным уровнями совсем
небольшое. Чтобы правильно выбрать шкалу
измерения, воспользуйтесь правилом «в
два раза больше». Если эта фраза в
точности описывает отношения между
двумя значениями, различающимися
числом, кратным двум, тогда эти данные являются относительными.
Можно привести множество примеров относительных данных.
Рассмотрим скорость печати в количестве слов в минуту. Что касается меня, то я
печатаю довольно плохо. И хотя я неоднократно обращался за помощью к
специальным программам, выходит все равно очень плохо. Хорошим днем
считается тот, когда мне удается напечатать 20 слов в минуту. А мой 15-
летний сын Джон, напротив, принадлежит к хвастунам, которые
печатают, даже не глядя на клавиатуру, и умудряются напечатать за минуту до 60
слов. Поскольку я могу с уверенностью сказать, что Джон печатает в три
раза быстрее, чем я, скорость печати можно отнести к относительным
данным.
На рисунке ниже вы увидите схему, демонстрирующую различие между
шкалами измерения данных и отношения между ними. По мере изучения
различных статистических методик мы будем возвращаться к этой схеме.
Очень скоро вы узнаете, что определенные методики требуют работы с
определенными типами данных.
Рпс.2.1
Схема шкал
измерения
данных.
Типы данных
Качественные
Количественные
Номинальные
Порядковые
Интервальные Относительные
Глава 2: Данные, повсюду данные, как же выбрать нужные? 23
Как компьютеры приходят нам на помощь
В Главе 1 сказано, что мы обратимся к работе с программой Excel для
решения некоторых статистических задач. Если у вас нет никакого желания
изучать программу в таком разрезе, просто перейдите к следующему разделу.
Обещаю, что не обижусь. Цель последнего раздела этой главы состоит в
том, чтобы ознакомить вас с тем, как использовать компьютер для решения
статистических задач в целом, а также убедиться, что ваш компьютер
отвечает всем требованиям для обработки статистических данных.
Роль компьютеров в статистике
Когда в 70-е годы прошлого века я был студентом технического вуза, слова
«персональный компьютер» были для меня пустым звуком. Все вычисления
производились с помощью хитроумного устройства под названием «счетная
логарифмическая линейка». Для тех из моих читателей, кого в ту пору еще и
на свете не было, я решил изобразить этот чудный прибор на рисунке 2.2,
представленном ниже.
■ Рис. 22
I Счетная
1 логарифмическая
линейка образца
I 1975 года.
Вы сами видите, что это устройство напоминает линейку, откормленную
стероидами. Оно умеет выполнять самые разнообразные математические
действия, но его трудно назвать эргономичным и удобным. Во времена
первого года моего обучения в колледже я приобрел свой первый ручной
калькулятор, модель производства компании Texas Instruments, который мог
выполнять только основные математические действия. По размеру он вполне мог
сойти за кассовый аппарат.
В то время глубокий и серьезный статистический анализ мог
осуществляться только на универсальных вычислительных машинах и только людьми,
обладающими значительными навыками в области программирования. Эти
люди отличались от нас, простых смертных. К счастью, те дремучие времена
остались в прошлом, а мы получили в свое распоряжение превосходные
эргономичные компьютеры, доступные многим. Тем из нас, кто ничего не
понимает в компьютерном программировании, достались такие замечательные
и мощные программы, как SAS, SPSS, Minitab и Excel. С их помощью мы
имеем возможность осуществлять мудреные операции статистического анализа.
В некоторых главах этой книги вы найдете описание применения
определенных статистических методик с использованием программы Excel. Если вы
24 Часть 1: Постигаем основы
решили пропустить эти части, это никак не отразится на изучении
материала книги. Это всего лишь дополнительная информация, демонстрирующая,
как статистический анализ связан с компьютером. Я полагаю, что вы
обладаете базовыми знаниями работы с программой Excel.
Установка средств анализа данных
Прежде всего, необходимо убедиться в том, что на вашем компьютере
установлены необходимые инструменты для осуществления анализа данных.
Чтобы это сделать, откройте приложение Excel и щелкните левой кнопкой
мыши на меню Tools (Сервис), как показано на рисунке 2.3. С этого момента
под словом «кликнуть» я буду иметь в виду «щелкнуть левой кнопкой мыши».
Рис 23
Меню Tools (Сервис)
программы Excel.
:■;;.,:;■■
1J w
|: k'i* ,_Nr
BRmhiqihui
,
1»f~
1
:
в
1
■,-■••-
Обратите внимание, что на рисунке в меню выделен пункт Data Analysis
(Анализ данных). В вашем меню программы этот пункт может отображаться
или не отображаться. Если он отображается, пропустите оставшуюся часть
этого абзаца и следующие два и приступите к абзацу, начинающемуся со
слов «щелкните левой кнопкой мыши по Data
Analysis (Анализ данных)».
Если пункта Data Analysis (Анализ данных) в
меню не видно, вам необходимо добавить его туда. Для
этого в том же меню щелкните Add-Inns
(Надстройки). Если и этот пункт в меню не представлен,
распахните меню с помощью все той же двойной
стрелки. Щелкнув на Add-Inns (Надстройки), вы увидите
на экране окно, представленное на рисунке 2.4.
В этом окне вы увидите список всех доступных
надстроек программы. Установите флажок
Analysis ToolPak, а затем щелкните ОК. А теперь
Мысли
Если меню Tools (Сервис)
выглядит иначе, чем на
рисунке выше, это может
означать, что вам видны не
все доступные пункты
меню. Чтобы увидеть все
доступные опции, щелкните
по двойной стрелке в
нижней части меню.
Глава 2: Данные, повсюду данные, как же выбрать нужные? 25
Рис 2.4
Диалоговое окно
Add-Inns (Надстройки)
программы Excel.
-fib» надстройки]
FJ Мастер годстаисиаж
strep суммирования
:
lO^W^^CT е ftepo
:Г }ГЫСГ Р9ШЙМЯЯ
Щ] Понощии* гю Интернету
5
2
Згхеиа
!
онагизеш*
ц, {
оты пакага знапю-з
Мысли вслух
Не впадайте в истерику, если на вашем экране появится такое сообщение: Microsoft Excel can't
run this add-in. This feature is not currently installed. Would you like to install it now? (Microsoft Excel
не удается запустить это приложение. Компонент не установлен. Установить его?) Для
установки Analysis ToolPak вам необходимо иметь при себе фирменный диск Microsoft Office.
Щелкните Yes (Да) и следуйте инструкциям на экране. После установки необходимого компонента в
меню Tools (Сервис) появится долгожданный пункт Data Analysis (Анализ данных).
снова откройте меню Tools (Сервис) — в нем должна появиться опция
Data Analysis (Анализ данных).
Щелкните Data Analysis (Анализ данных) в меню Tools (Сервис) — на
экране появится диалоговое окно, представленное на рисунке 2.5.
>*к трукймчы аиаякм
I :"»OJfrtb»« Ди<П«»«*'«ъЙ «НИМ С повторения*
1 Гнстргздяил
Рис 2.5
Диалоговое окно
Data Analysis
(Анализ данных).
Теперь ваша программа Excel полностью готова к демонстрации всех
чудес статистики, и мы будем активно ею пользоваться при изучении
различных статистических методов. А пока щелкните Cancel (Отмена) и закройте
26 Часть 1: Постигаем основы
приложение Excel. Когда вы вновь обратитесь к этой программе,
инструментарий для анализа данных будет в вашем полном распоряжении.
Ваша очередь
Проклассифицируйте следующие данные по следующим уровням:
номинальный, порядковый, интервальный и относительный. Объясните свой
выбор.
1. Среднемесячная температура в градусах по Фаренгейту по городу
Уилмингтону в течение года.
2. Среднемесячное выпадение осадков в дюймах по городу Уилмингтону
в течение года.
3. Образовательный уровень участников опроса
Уровень Количество респондентов
Общеобразовательная школа 168
Степень бакалавра 784
Степень магистра 212
4. Семейное положение участников опроса
Семейное положение Количество респондентов
Не женат/не замужем 28
Женат/замужем 189
Разведен (а) 62
5. Возраст участников опроса
6. Пол участников опроса
7. Год рождения участника опроса
8. Политические предпочтения участников опроса по следующей
классификации: республиканец, демократ, не определившийся
9. Расовая принадлежность участников опроса: белый, афроамериканец,
азиат, иное
10. Оценка производительности сотрудников компании по шкале:
превосходит ожидания, отвечает ожиданиям, не отвечает ожиданиям
11. Номер формы каждого участника спортивной команды
12. Список выпускников школы по классу
13. Результаты выпускного экзамена по статистике моего класса по шкале
от 0 до 100
14. Условия проживания участников опроса
Глава 2: Данные, повсюду данные, как же выбрать нужные? 27
Повторение - мать учения
Ф Данные являются структурными элементами любого статистического
анализа.
Ф Данные могут быть качественными или количественными.
Ф Номинальные данные относят к заранее заданным категориями;
математические сравнения между наблюдениями не предусмотрены.
Ф Порядковые данные обладают всеми характеристиками номинальных
данных плюс возможность упорядоченного распорложения
наблюдений.
Ф Интервальные данные обладают всеми характеристиками порядковых
данных плюс возможность вычисления разницы между наблюдениями.
Ф Относительные данные обладают всеми характеристиками
интервальных данных плюс возможность выражения одного наблюдения в
качестве множителя другого.
Мл
Представление
описательной статистики
В этой главе
Ф Как определять распределение частот
Ф Как представить распределение частот с помощью
гистограммы
Ф Как создать представление «ствол и листья»
Ф Как использовать секторную, линейчатую и графическую
диаграммы
Ф Как работать с Мастером диаграмм программы Excel для
построения диаграмм
В Главе 2 я представил вашему вниманию описание
различных типов данных, используемых для статистического анализа.
В этой главе мы рассмотрим способы представления данных.
Имея дело с данными в их первозданном виде, мы наверняка
будем испытывать сложности при определении их
структурной организации по той простой причине, что человеческий
мозг не слишком хорошо справляется с обработкой длинных
списков цифр. Нам гораздо проще воспринимать данные,
представленные в уже суммированной форме в виде таблиц и
графиков.
Глава 5: Представление описательной статистики 29
В следующих разделах мы рассмотрим множество способов
представления данных в виде, удобном для того, кто проводит анализ. С помощью этих
методик мы сможем получить весьма развернутое представление о том, о чем
говорят нам данные. И уж поверьте мне, в мире существует великое
множество данных, готовых поведать нам интереснейшие истории. Идем дальше.
Распределение часто?
Одним из наиболее популярных способов графического представления
данных является распределение частот. Проще всего описать использование
данного способа на конкретном примере.
С самого детства я считаю себя
ярым фанатом Pittsburgh Pirates —
бейсбольной команды из высшей лиги.
Не знаю, почему я все еще болею за
этих парней: с 1992 года они не
одержали ни одной победы. Как бы то ни было,
ниже представлена средняя бэттинг-
результативность игроков этой
команды в сезоне 2002 года. Я не стал
снабжать эти результаты именами игроков,
дабы не дискредитировать команду.
Термины
Распределением частот
называется таблица,
демонстрирующая некоторое количество
измерений данных для определенных
интервалов значений.
Средняя бэттинг6 - результативность игроков команды Pittsburgh
Pirates
в 2002 году
.160 .300 .077 .246 .283
.264 .264 .252 .250 .294
.234 .119 .232 .216 .206
.125 .175 .264 .233
.244 .308 .121 .100
.190 .154 .150 .298
Источник: www.espn.com
Глядя на эти данные, представленные в виде таблицы, вы вряд ли сможете
понять, насколько сложным оказался 2002 год для моей любимой команды.
Преобразование данных в распределение частот поможет ответить на этот вопрос.
Бэттинг-результативность Количество игроков
.000 до .049
.050 до .099
.100 до. 149
0
1
4
6 Бэттер (бьющий) — игровое амплуа в бейсболе. — Примеч. ред.
30 Часть 1: Постигаем основы
Бэттинг-результативность Количество игроков
.150 до. 199 5
.200 до .249 7
.250 до .299 8
.300 до .349 2
Вы видите, что распределение частот — это всего лишь таблица, в которой
некоторые значения данных сгруппированы в интервалы значений. В
данном примере этими интервалами являются данные средней бэттинг-резуль-
тативности игроков в первом столбце таблицы. Количество значений данных —
это количество игроков, попадающих в каждых из интервалов; они
представлены во втором столбце. Что ж, этот сезон не удался, может, в следующем все
получится.
Интервалы распределения частот называют группами, а количество
наблюдений в каждой группе — частотой попадания в группу. В следующем
разделе вы узнаете, как организовывать эти группы.
Как вычислять распределение частот
Порой при определении распределения частот необходимо принимать
важные решения. Чтобы вы поняли важность этих решений, обратимся к
примеру, понятному всем, — с мобильными телефонами. Мой сын Джон и я
пользуемся специальным «семейным тарифом», то есть он получает в
распоряжение максимальное количество минут разговора, а я пользуюсь телефоном с 3
ночи до 6 утра через субботу. В таблице ниже указано ежедневное
количество звонков, сделанных и принятых Джоном за месяц май.
Количество звонков в день
3
3
6
2
3
1
1
• 9
4
5
0
8
2
1
9
5
1
6
1
4
13
2
2
9
1
2
15
7
7
4
Источник: очень загадочный телефонный счет, в содержании которого под силу разобраться
лишь большому специалисту в области метафизической коммуникации.
Используя эти данные, я составил следующее распределение частот.
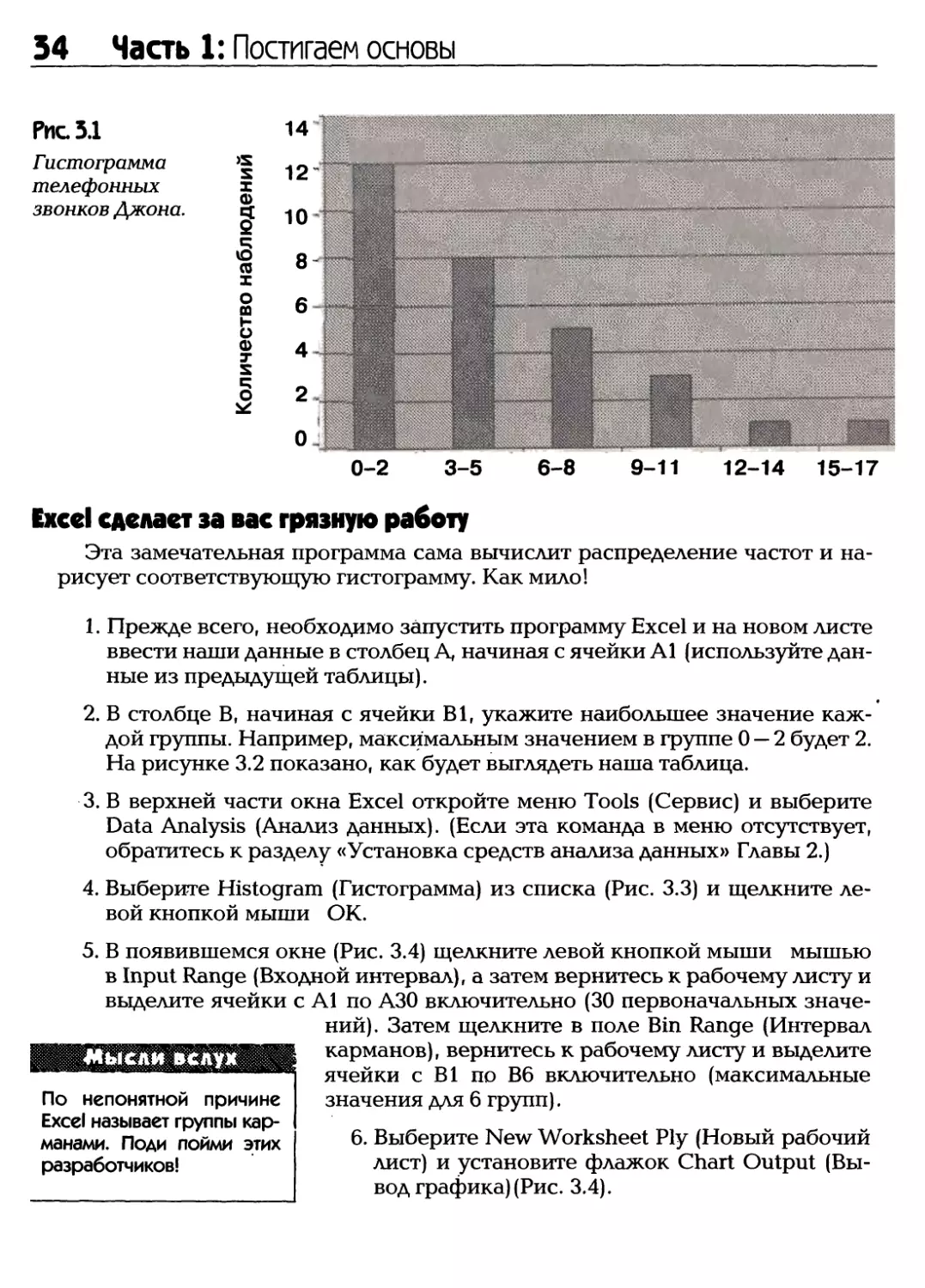
Глава 3: Представление описательной статистики 31
Распределение частот
Количество звонков в день Количество дней
0-2 12
3-5 8
6-8 5
9-11 3
12-14 1
15-17 1
При организации этих групп я следовал следующим правилам:
1. Группы должны быть одного размера. В данном случае я использовал 3
значения данных для каждой группы. Примером группы является 0-2;
эта группа включает в себя количество дней, в которые было сделано 0Г
1 или 2 звонка.
2. Все группы должны быть взаимоисключающими, то есть не должны
пересекаться. Например, я не стал создавать две группы со
значениями 3 — 5 и 5 — 7, поскольку значение 5 звонков оказалось бы сразу в
двух группах.
3. Постарайтесь, чтобы количество групп было не менее 5 и не более 15.
Слишком маленькое или большое количество групп делает свойства
распределения частот менее очевидными.
4. По возможности постарайтесь избежать неограниченных групп
(например, от 15 и более).
5. Все значения данных из первоначальной таблицы должны быть
включены в группы. Иными словами, группы должны быть исчерпывающими.
Слишком малое или большое
количество групп усложнит
структурную организацию распределения
частот. Одной крайностью является
ситуация, когда групп так много,
что в каждую из них попадает лишь
одно наблюдение. Есть и другая
крайность: выделена лишь одна
группа, в которую попадают все
наблюдения. От такого распределения
частот толку никакого не будет!
Зш^, Термины .
* IP? Группы считаются взаимоис-
. ключающими, если каждое из
наблюдений попадает только в одну
| группу. Например, группы по
половому признаку «мужской» и «женский»
являются взаимоисключающими,
поскольку человек не может
принадлежать сразу к обеим группам.
32 Часть 1: Постигаем основы
Термины
Распределение относительных (выборочных) частот
Еще один способ представления
подобных данных — использование
распределения относительных частот. Вместо
представления количества наблюдений в
каждой группе эта методика опирается
на расчет процентного отношения
наблюдений в каждой группе путем
деления частоты каждой группы на общее
количество наблюдений. Я могу
представить данные о телефонных звонках Джона в виде распределения
относительных частот, которую вы видите в таблице ниже.
Распределение
относительных* частот отображает
процентное отношение наблюдений в
каждой группе к общему числу
наблюдений.
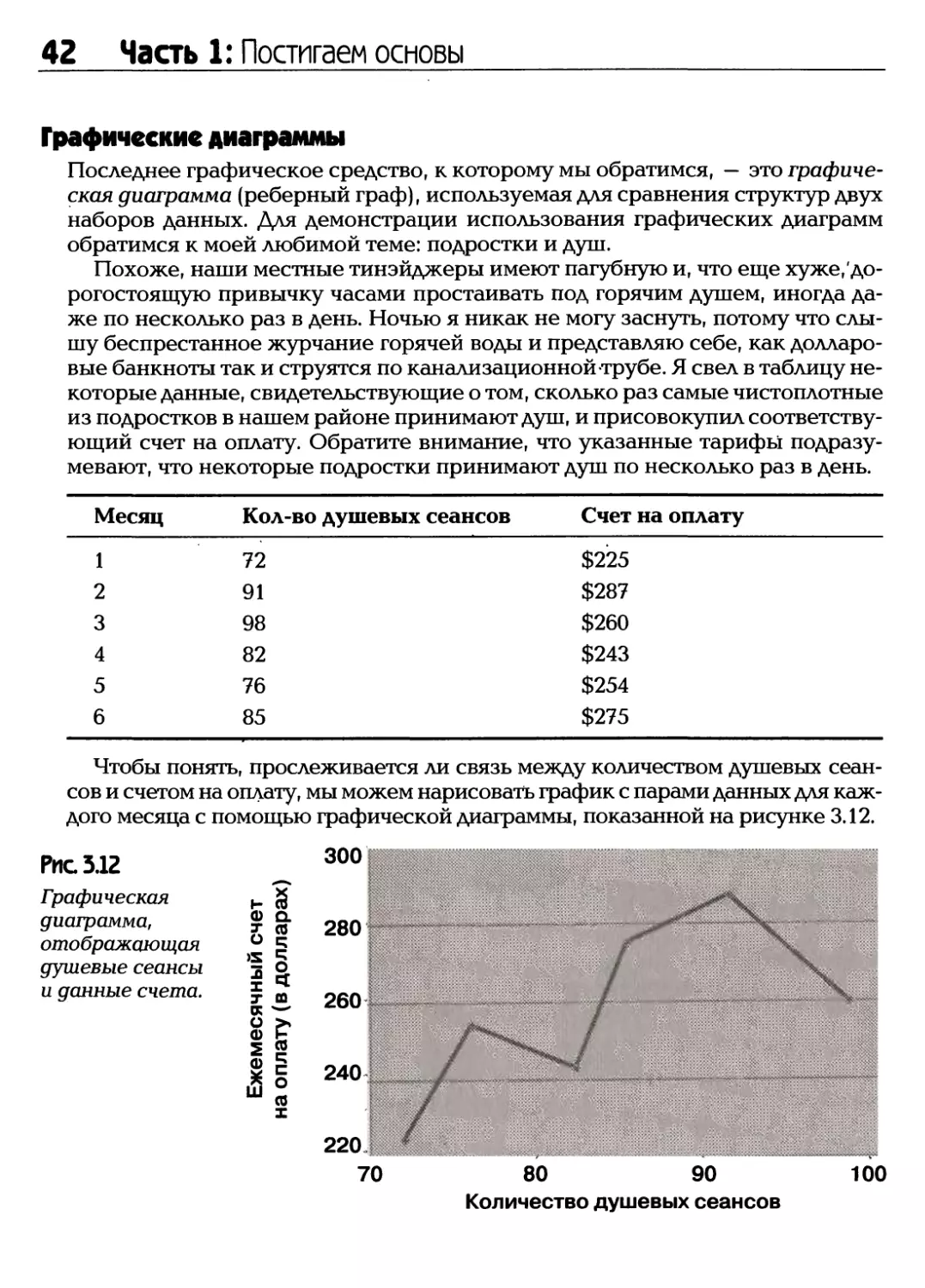
Распределение относительных частот
Количество звонков в день Количество дней Процентное отношение
0-2
3-5
6-8
9-11
12-14
15-17
12
8
5
3
1
1
Всего: 30
12/30 = 0.40
8/30 = 0.27
5/30 = 0.17
3/30 = 0.10
1/30 = 0.03
1/30 = 0.03.
Всего: 1.00
В соответствии с этой таблицей, Джон пользуется мобильным телефоном
от 3 до 5 раз в 27% дней в месяц.
Общее процентное отношение распределения относительных частот
должно равняться 100 или около 100 (в пределах 1% с учетом неточности при
округлениях).
Распределение интегральных частот
Термины
;; 1
* Распределение
интегральных частот определяет
процент наблюдений, количество
которых меньше или равно количеству
наблюдений в данной группе.
Этот «неразлучный друг»
распределения относительных частот просто
суммирует процентные доли каждой
группы по мере движения вниз по
столбцу. Эта методика предоставляет
в ваше распоряжение процент
наблюдений, количество которых мень-
Глава 5: Представление описательной статпстпкп 53
ше или равно количеству наблюдений в интересующей нас группе. Ниже
представлено полученное в результате статистического анализа
распределение интегральных частот.
Распределение интегральных частот
Кол-во звонков
вдень
0-2
3-5
6-8
9-11
12-14
15-17
Кол-во дней
12
8
5
3
1
1
Всего:
30
Процент
12/30 = 0.40
8/30 = 0.27
5/30 = 0.17
3/30 = 0.10
1/30 = 0.03
1/30 = 0.03
Всего: 1.00
Интегральный
процент
0.40
0.67
0.84
0.94
0.97
1.00
Значение 0.67 в последнем столбце получено в результате сложения 0.40 и
0.27. Из этой таблицы можно сделать вывод, что Джон пользовался
телефоном не более 8 раз в день в 84% дней в месяц. .
Если распределение частот вычислено правильно, оно представляет собой
отличный способ извлечения полезной информации из вроде бы никчемных
данных. В следующем разделе вы узнаете, как изобразить распределение
частот графически.
Графическое представление распределения частот
с помощью гистограммы
Гистограмма — это диаграмма, показывающая количество наблюдений в
каждой группе в виде бруска соответствующей высоты. На рисунке 3.1
представлена гистограмма звонков Джона. Для построения этого графика
я воспользовался Мастером диаграмм Excel. Чуть ниже в этой главе я
продемонстрирую вам, как им
пользоваться (см. раздел «Мастер диаграмм
Excel»).
Термины _ , Этот график явно демонстрирует нам,
что Джон пользуется мобильным
телефоном достаточно разумно. Самый
высокий брусок — это представление
группы, соответствующей 0 — 2 звонкам
ежедневно. Все могло бы обстоять гораздо
хуже.
Гистограмма - это диаграмма,
отражающая количество
наблюдений в каждой группе в виде
призмы соответствующей высоты.
34 Часть 1: Постигаем основы
Рис 5.1
Гистограмма
телефонных
звонков Джона.
>s
S
X
ф
3
ё
СО
X
о
DQ
Б
О
т
S
е;
о
14
12
10
0-2
3-5
6-8
9-11 12-14 15-17
Excel сделает за вас грязную работу
Эта замечательная программа сама вычислит распределение частот и
нарисует соответствующую гистограмму. Как мило!
1. Прежде всего, необходимо запустить программу Excel и на новом листе
ввести наши данные в столбец А, начиная с ячейки А1 (используйте
данные из предыдущей таблицы).
2. В столбце В, начиная с ячейки В1, укажите наибольшее значение
каждой группы. Например, максимальным значением в группе 0 — 2 будет 2.
На рисунке 3.2 показано, как будет выглядеть наша таблица.
3. В верхней части окна Excel откройте меню Tools (Сервис) и выберите
Data Analysis (Анализ данных). (Если эта команда в меню отсутствует,
обратитесь к разделу «Установка средств анализа данных» Главы 2.)
4. Выберите Histogram (Гистограмма) из списка (Рис. 3.3) и щелкните
левой кнопкой мыши ОК.
5. В появившемся окне (Рис. 3.4) щелкните левой кнопкой мыши мышью
в Input Range (Входной интервал), а затем вернитесь к рабочему листу и
выделите ячейки с Al по АЗО включительно (30 первоначальных
значений). Затем щелкните в поле Bin Range (Интервал
карманов), вернитесь к рабочему листу и выделите
ячейки с Bl по В6 включительно (максимальные
значения для 6 групп).
Мысли вслух
По непонятной причине
Excel называет группы
карманами. Поди пойми этих
разработчиков!
6. Выберите New Worksheet Ply (Новый рабочий
лист) и установите флажок Chart Output
(Вывод графика) (Рис. 3.4).
Глава 3: Представление описательной статистки 35
ВИНЯ
Ij&falCyr
57
■
1
2
j
1 * ■ 3
1
|11; е
4
Ш|
. :
1 1в ^
:.
ш
6
3:
Я
17;
-J
1 ГотвЁЭ
.. .,..,
*•
Рис 3.2
Необработанные
данные для вычисления
распределения частот.
| Деух4»йктор*1ЬЙ лис«вклюкнь*> г>*$ пи* с го&горе«х<аи« ..'.
-лторяый дисгавйиониып а«зпиэ бел гк**тс>{*зни« :
| Описательная статистика
: te лог: ■:
Г07*С©Н&
Рис 3.3
Диалоговое окно
Data Analysis
(Анализ данных).
7. Щелкните левой
кнопкой мыши ОК для
создания распределения
частот и построения
гистограммы (Рис. 3.5).
Вы видите, что в
столбцах А и В представлено
распределение частот,
вычисленное программой.
Мысли вслух
Для отображения гистограммы я предпочитаю
использовать в своей работе Мастер диаграмм, а не
средство анализа данных. Мне кажется, что в этом
случае график получается более наглядным. Мастер
диаграмм предоставляет вам больше возможностей
для определения внешнего вида гистограммы.
Дополнительную информацию о Мастере диаграмм вы
найдете в разделе «Мастер диаграмм Excel».
36 Часть 1: Постигаем основы
Рис 3.4
Диалоговое окно
Гистограмма.
Рис 3.5
Распределен ие
частот
и гистограмма.
Входной «ктервап. [$А$1ф&$30
; HgtejM [$»И *Ш
:;. i %£кс>ДнОи НХ?*р&&К
1 О Мо#«л рабочей «o*r а
иго (о-п:орт>^<овани&« гйст0фа»ц$
1 ш iiiMiiiMuiiuiai шп шин
ш
^ j 1
I Ortfena j j
f gftp& 1
'■i?.1.1"11 чаУ
I j ; 3$£№£
■
7
А !
Щ
6
6 ;Еще_
11
2 Ж
хг D
Гистограмма
К*ф*лн
[«Частота]
**!\.Л«'
Здорово! А вот гистограмма выглядит так, словно на нее сверху уселся
слон. Щелкните на гистограмме и потяните мышью за ее нижнюю границу
вниз, чтобы распахнуть ее. Должно получиться так, как представлено на
Рисунке 3.6.
Распределение частот и гистограммы — это очень удобный способ
получения четкой картины того, о чем пытаются поведать нам данные, на первый
взгляд кажущиеся такими разрозненными. С помощью гистограммы я
понял, что данные шепчут мне на ушко: «Заполучи побольше минут разговора в
месяц с помощью семейного тарифа». Прекрасно!
Глава 3: Представление описательной статистики 37
| ' ►-.'),•.>" •■•-.:-•>'.•-• •',
' :
S j
1Г;:
!
■1
Гистограмм*
* 4-р
«7 . { ):,:
| ' ^ л>ц
5 ?•• 5 11
Кари.ч*
«
СЭ-!-: т:-;'«
<
I Рис.3.6
Вот как выглядит
окон нательная
гистограмма.
Мощный инструмент статистики - иерархическое
древовидное представление
Древовидное представление — это еще один способ графического
представления данных. Идея создания этого метода принадлежит статисту Джону
Тьюки, разработавшему его в 70-х годах XIX века. Основное достоинство
данного подхода состоит в том, что все первоначальные данные
представлены на экране.
Для демонстрации работы этого метода я воспользуюсь результатами игры
в гольф моего сына Брайана. В таблице ниже представлены очки,
полученные за последние 24 раунда. Как правило, Брайан для отчетности
предоставляет более обнадеживающие результаты, но мы, статисты, должны быть
непредвзятыми и точными.
Результаты игры в гольф Брайана
81
79
84
86
83
79
78
84
80
80
95
83
81
85
79
82
88
87
92
80
84
90
78
80
Рис. 3.7 показывает, как выглядят полученные в ходе игры очки в
древовидном представлении.
38 Часть 1: Постигаем основы
88999
00001123344445678
025
Рис 3.7
Древовидное
представлен ие.
«Стволом» в данном представлении является первая колонка цифр,
обозначающая первую цифру результатов игры. «Листья» — это вторая цифра
результата, по одной цифре на каждый результат. Поскольку Брайан 5 раз
набрал больше 70 очков, справа от цифры 7 стоят 5 цифр.
При желании мы можем дробить данное представление и дальше,
добавляя дополнительные стволы. Этот подход проиллюстрирован на рисунке 3.8.
Термины
*т^ Древовидное представление
разбивает значения данных на
листья (последняя цифра в значении) и
стволы (все остальные цифры в
значении). Указав все листья справа от
каждого ствола, алы можем графически
представить, как распределяются
данные.
Здесь ствол, обозначенный 7 (5),
содержит все набранные очки от 75 до 79. Ствол
8 (0) содержит все очки от 80 до 84.
Внимательно изучив это представление данных,
я вижу то, что скрыто от меня на рисунке
3.7: оказывается, чаще всего Брайан
набирает немногим больше 80 очков.
Отличным источником информации о
данном подходе является статистический
портал Канады по адресу: www.statcan.ca/
english/edu/power/ch8/plots.htm.
Рис 3.8
Более развернутое
древовидное
представлен ие.
7(5)
8(0)
8(5)
9(0)
9(5)
88999
000011233444
5678
02
5
Представление статистических данных в виде графиков
Графики — это еще один эффективный способ выделения и представления
структурных особенностей набора разрозненных данных. В этом разделе я
поведаю вам о различных типах графиков, которые помогут нам
разобраться, о чем же говорят полученные нами данные.
Какая у вас любимая секторная диаграмма?
Секторные (круговые) диаграммы, как правило, используются для описания
данных, полученных из распределения относительных частот. Этот тип
графика представляет собой круг, поделенный на сектора, каждый из которых
по размеру соответствует относительной частоте попадания в группу. Чтобы
проиллюстрировать использование секторных диаграмм, предположим, как
какой-то анонимный профессор представил следующее распределение
финальных баллов.
Глава 3: Представление описательной статистики 39
Финальные баллы
Оценка Кол-во студентов Распределение относительных частот
А
В
С
D
9
13
6
2
Всего:
30
9/30 = 0.30
13/30 = 0.43
6/30 = 0.20
2/30 = 0.07
Всего: 1.00
Это распределение относительных частот можно представить в виде
секторной диаграммы, показанной на рисунке 3.9. Этот график построен с
помощью Excel — об этом я расскажу чуть позже.
В
43%
Эврика!
Секторные диаграммы идеально
подходят для разноцветного
представления данных из
распределения относительных частот. Если
использование разных цветов не
представляется возможным, вы можете
разнообразить свои секторные
диаграммы с помощью текстур и узоров.
Рис 3.9
Секторная диаграмма,
демонстрирующая
распределен ие
полученных студентами
оценок.
Как видите, такая диаграмма
гораздо наглядней и приятней для глаза, чем
колонки цифр в таблице. Должно
быть, этот профессор неплохо
смыслит в статистике!
Чтобы построить секторную
диаграмму вручную, необходимо, прежде
всего, вычислить центральный угол для
каждой доли диаграммы, как показано
на рисунке ниже.
40 Часть 1: Постигаем основы
Рис 310
Центральный угол
секторной диаграммы.
А
В
С
D
9/30 = 0.30
13/30 = 0.43
6/30 = 0.20
2/30 = 0.07
Всего: 1.00
Для вычисления центрального угла умножьте относительную частоту
группы на 360 (количество градусов в круге). Результаты представлены в
таблице ниже.
Центральный угол для построения секторной диаграммы
Оценка Относительная частота Центральный угол
0.30*360 = 108 degrees
0.43*360 = 155 degrees
0.20*360 = 72 degrees
0.07*360 = 25 degrees
С помощью любого приспособления для измерения углов, например,
транспортира, вы можете поделить свою диаграмму на доли
соответствующего размера. При условии, конечно, что вы уже овладели навыком рисовать
круги.
Линейчатые диаграммы
Линейчатые диаграммы хороши при необходимости изображения
отдельных значений данных рядом друг с другом. Для рассмотрения данного типа
диаграмм, одна из которых представлена на рисунке 3.11, воспользуемся
данными из следующей таблицы. Эти данные представляют собой
месячный баланс кредитной карты безымянной супруги безымянного человека,
пишущего книгу по статистике. (Если она увидит это, меня ждут большие
неприятности!)
Глава 3: Представление описательной статпстпкп 41
Баланс анонимной кредитной карты
Месяц
Баланс (в долларах)
1
2
3
4
5
6
375
514
834
603
882
468
Источник: безымянный сейф для хранения документов
1000
Рис. 3.11
Линейчатая
I диаграмма для
I представления
I баланса чьей-то
{кредитной карты.
Сейчас вы вполне можете сказать себе: «Погодите-ка, где-то я это уже видел!» Говоря
«это», я имею в виду тип диаграммы, а вовсе не кредитную историю моей супруги.
Гистограмма, представленная чуть выше в этой главе, является особым типом линейчатой
диаграммы; она имеет дело с частотами, а не с реальными значениями данных.
Я уверен, что все ваше существо вопрошает: «Что выбрать, секторную
диаграмму или линейчатую?» Если вы ставите себе целью сравнить
относительные размеры каждой груцпы, используйте секторную диаграмму.
Линейчатые диаграммы больше подходят для сравнения реальных значений
данных.
42 Часть 1: Постигаем основы
Графические диаграммы
Последнее графическое средство, к которому мы обратимся, — это
графическая диаграмма (реберный граф), используемая для сравнения структур двух
наборов данных. Для демонстрации использования графических диаграмм
обратимся к моей любимой теме: подростки и душ.
Похоже, наши местные тинэйджеры имеют пагубную и, что еще хуже,
дорогостоящую привычку часами простаивать под горячим душем, иногда
даже по несколько раз в день. Ночью я никак не могу заснуть, потому что
слышу беспрестанное журчание горячей воды и представляю себе, как
долларовые банкноты так и струятся по канализационной трубе. Я свел в таблицу
некоторые данные, свидетельствующие о том, сколько раз самые чистоплотные
из подростков в нашем районе принимают душ, и присовокупил
соответствующий счет на оплату. Обратите внимание, что указанные тарифы
подразумевают, что некоторые подростки принимают душ по несколько раз в день.
Месяц Кол-во душевых сеансов Счет на оплату
$225
$287
$260
$243
$254
$275
Чтобы понять, прослеживается ли связь между количеством душевых
сеансов и счетом на оплату, мы можем нарисовать график с парами данных для
каждого месяца с помощью графической диаграммы, показанной на рисунке 3.12.
Рис 3.12 3001
- ~7^~У\
1
2
3
4
5
6
72
91
98
82
76
85
Графическая
диаграмма,
отображающая
душевые сеансы
и данные счета.
нЙ
О Q.
о =;
>s 5
is
X 0Q
2 а
а> 5
X
. .
280
260
240
220
70
80 90 100
Количество душевых сеансов
Глава 3: Представление описательной статистики 43
Я решил разместить количество сеансов по оси х (горизонтальная), а
данные счета — по оси у (вертикальная). Судя по тому, что линия,
объединяющая точки, имеет тенденцию все время подниматься вверх, я понял, что мои
подозрения вполне подтвердились: чем больше времени проводят в душе
наши лягушата, тем больше сумма в счете.
Графические диаграммы очень хороши в тех случаях, когда вам
необходимо проследить взаимосвязь между двумя различными типами данных.
Подойдут они и тогда, когда вы хотите показать большое количество точек на
одном графике.
Мастер диаграмм Excel
Как и было обещано, в последнем разделе я продемонстрирую вам, как
создавать профессиональные графики посредством всего нескольких щелчков
мыши. Поможет нам в этом программа Excel.
Поскольку сложней всего построить вручную секторную диаграмму, я
покажу вам, как построить график распределения оценок, подобный тому, к
которому мы уже обращались выше.
1. Запустите программу Excel и на новом рабочем листе введите данные
распределения относительных частот, как показано на рисунке 3.13.
I РИС 3.13
Введите данные
о распределении оценок.
А
ft
Р .<
■0.43
**ьн*я частота г>э*од.ан** 8 групп* ■
2. Запустите Мастер диаграмм
Excel, снабженный
пошаговыми инструкциями. Для этого
откройте меню Insert (Вставка)
(оно находится между меню
View (Вид) и Format (Формат))
и выберите Chart (Диаграмма).
3. Когда на экране появится
окно Мастера диаграмм,
выберите в списке Chart Туре
Вы также можете запустить Мастер диаграмм
с помощью стандартной панели
инструментов, нажав кнопку Chart Wizard (Мастер
диаграмм). Кнопка напоминает крохотную
гистограмму. Также обратите ваше внимание на
то, что если вы перед запуском Мастера
диаграмм выделите ячейки, которые хотите
отобразить на диаграмме, вам не нужно
выполнять шаг 4 описываемой процедуры.
44 Часть 1: Постигаем основы
(Тип) Pie (Круговая), а затем щелкните Next (Далее) в нижней части
окна (Рис. 3.14).
Рис 3.14
Выберите тип
диаграммы.
KU ,•■;. н«^{№ 1HHJ 1*«. ,*,«.* ^*
• -
4. Если программа Excel не выбрала автоматически те данные, которые вы
хотите отобразить на диаграмме, щелкните мышью в поле Data Range
(Диапазон), чтобы там оказался курсор. Затем на рабочем листе
щелкните ячейку А1 и тяните мышью вниз по диагонали до ячейки В5, как
показано на рисунке 3.15.
Рис 5.15
Укажите источник
данных.
;№:№•; : -1) К£<0Ч»4М( ОДИН** ИМ
\ Дж*к»&м Д***»*
£эдм£:
Глава 5: Представление описательной статистки 45
5. Убедитесь, что включена опция Series in: Columns (Ряды в: столбцах).
Затем щелкните Next (Далее), чтобы перейти к другим свойствам
диаграммы (Рис. 3.16).
t¥K*4«H«*K
•«""-< *^^?»
• '•• ММ >ил к.х.-:я*«*1»а« | цм|.
Рис 3.16
Введите необходимую
информацию для
построения диаграммы.
6. На вкладке Title (Заголовки) вы можете указать заголовок своей
диаграммы. Пусть поработает ваша фантазия.
7. Чтобы указать на диаграмме процент для каждой группы, перейдите на
вкладку Data Labels (Подписи данных) и установите флажок Percentage
(Доли) в группе Label Contains (Включить в подписи), как показано на
рисунке 3.17.
:-(дд»чки Докных
тДр
Рис 3.17
На этой вкладке
вы можете включить
в подписи доли.
8. Щелкните Next (Далее), чтобы вернуться к шагу 4. В появившемся окне
вы можете указать размещение вашей диаграммы. При выборе As new
sheet (отдельном) диаграмма будет размещена на отдельном рабочем
листе в текущем файле Excel; при выборе As object in (имеющемся) она
будет расположена на уже имеющемся листе, который вы укажете.
9. Щелкните Finish (Готово), и все! Excel нарисует для вас диаграмму.
46 Часть 1: Постигаем основы
Видите, это очень просто, и лучше всего то, что вам не придется рисовать
круги.
Ваша очередь
1. В таблице ниже представлены результаты экзамена 36 студентов одного
класса, в котором я, возможно, преподавал. Вычислите распределения
частот из 9 групп от 56 до 100.
Экзаменационные баллы
60
81
99
79
75
78
95
99
82
88
91
79
75
89
62
98
86
83
84
58
86
72
81
85
85
66
85
72
96
92
74
98
99
72
86
68
2. Используя решение Задачи 1, постройте гистограмму.
3. Используя данные из Задачи 1, вычислите распределение
относительных и интегральных частот.
4. Используя данные из решения Задачи 1, постройте круговую диаграмму.
5. Используя данные из Задачи 1, создайте представление «ствол и
листья», взяв по 1 листу для результатов до 60, 70, 80, 90 и 100 баллов.
6. Используя данные из Задачи 1, создайте представление «ствол и листья».
Повторение - мать учения
Ф Распределение частот, или частота попадания в группу, — это
эффективный способ суммирования данных путем учета количества
наблюдений и их размещения в группы.
Ф Гистограммы позволяют графически представить данные
распределения частот.
Ф Представление «ствол и листья» позволяют не только графически
представить распределение данных, но и содержат реальные значения
интересующих нас данных.
Ф Секторные (круговые), линейчатые и графические диаграммы — это
эффективные средства представления данных в различных формах.
Ф Мастер диаграмм Excel — это мощный инструмент, предоставляющий
пользователю возможность создавать множество различных
представлений данных.
Г' fiSffl> J888&. 888888b
жав
Ore SOtxewo mow
Вычисление описательных
статистик: центральная
тенденция(среднее,
медиана и мода)
В этой главе
Ф Что представляет собой центральная тенденция
Ф Как вычислять среднее, взвешенное среднее, медиану и
моду выборки и совокупности
Ф Как вычислять среднее распределения частот
Ф Как использовать Excel для вычисления центральной
тенденции
Содержание Главы 3 имело своей целью
продемонстрировать вам различные способы графического представления
данных так, чтобы вниманию наших мозговых клеток предстала
картина в целом. Успешно решив поставленную задачу, мы
можем смело переходить к следующему шагу — рассмотрению
способов числового суммирования данных. После изучения
48 Часть 1: Постигаем основы
этой главы мы сможем разбрасываться словечками типа «медиана», «мода»,
причем мы даже будем знать, что они значат!
Как уже было указано в Главе 1, описательная статистика составляет
основу практически любого статистического анализа. Если вычисления
описательной статистики неверны, финальный результат анализа может
оказаться противоположным реальному положению дел. А всем известно, что
статисты не любят вводить остальных в заблуждение. Поэтому цель настоящей
главы состоит в том, чтобы научиться вручную выполнять вычисления
описательной статистики и подтверждать их достоверность с помощью нашего
хорошего друга — программы Excel.
Это первая глава в книге, в которой вы увидите математические формулы
с забавными буквами греческого алфавита, которые могут запросто
повергнуть вас в шок. Не путайтесь. Мы будем уничтожать этих демонов одного за
другими с помощью доходчивых объяснений, и в конечном итоге победа
будет в наших руках. Вперед!
Меры центральной тенденции
Существуют две основные и широко используемые категории описательной
статистики. Первая из них, центральная тенденция (определяет положение
центра распределения), описывает центральную точку нашего набора
данных с помощью одного значения. Эта методика позволяет нам суммировать
разрозненные данные с помощью одного числа. Вторая категория, рассеяние
(разброс данных), детально рассмотрена в Главе 5. Существует множество
показателей центральной тенденции наших данных — ниже вы узнаете о
том, что они собой представляют и как ими пользоваться.
Среднее
Наиболее распространенным
показателем центральной тенденции является
среднее (арифметическое), которое
вычисляется путем сложения всех
значений нашего набора данных и деления
полученной суммы на количество
наблюдений. Математическая формула
для вычисления среднего несколько
варьируется в зависимости от того,
вычисляете ли вы среднее по выборке или
среднее по совокупности
(математическое ожидание). Вычисление
выборочного среднего выполняется по следующей
формуле:
Термины
Центральная тенденция -
мера описывает точку
концентрации набора данных. Дисперсия -
мера описывает, как далеко значения
данных отклонились от среднего.
Среднее или усредненное - самая
общая мера центральной тенденции и |
вычисляется суммированием всех
значений данных в нашей выборке с
последующим делением этого
результата на число наблюдений.
Глава 4: Вычисление описательной статистики 49
2>,
х=^—,
л
где:
х — среднее по выборке,
х{ — значения выборки (xt — значение первого аргумента выборки,
х2 — значение второго аргумента выборки и так далее),
п
Z*. = сумма всех значений данных выборки,
п — количество значений данных выборки
f:0%:) Эврика!
Не впадайте в панику; увидев выражение ... £х,.7 которое всего лишь означает сумму х
при /' .= от 1 до п. Если наша выборка содержит значения 5, 8 и 2, тогда п = 31х1 = 5,х2 = 8,
з
х3 = 27 в результате чего получаем выражение ^xi=x1+x2+x3= 5+8+2 = 15.
Формула для вычисления среднего по совокупности выглядит так:
N
"-It-
где:
ц = среднее по генеральной совокупности (произносится довольно
забавно — «мю»),
N
Y,xt = сумма всех значений данных совокупности,
N = количество значений данных совокупности.
Чтобы показать вам, как вычисляются меры центральной тенденции, я
воспользуюсь следующим примером. Во многих семьях, в которых
проживают подростки, привычным развлечением являются видеоигры. Брайан и
Джон любят вовлечь меня в игру, а потом обнулить счетчик моих очков. У
меня закралось подозрение, что Джон подсунул мне «неисправный» пульт
управления, потому что он сильно тормозит, создавая 10-секундную задержку
между нажатием кнопки и откликом на экране. Оказалось, что задержка на
самом деле происходит между моими мозгами и пальцами. Как бы то ни
было, ниже представлен набор данных, представляющий собой количество
часов, проводимых за видеоиграми в нашей семье каждую неделю.
3749546 17 47
50 Часть 1: Постигаем основы
Поскольку эти данные представляют собой выборку, мы можем вычислить
среднее по выборке:
Е*,
3+7 + 4+9+5+4+6+17+4+7
10
■■'— =6.6 часа.
Похоже, что стоит серьезно попрактиковаться, прежде чем тягаться со
своими сыновьями.
Взвешенное среднее
При расчете среднего количества часов в предыдущем примере каждому
значению присваивался один и тот же вес. Взвешенное среднее — это
средняя величина, которой необходимо посидеть на диете. Шуткаt Просто хотел
удостовериться, что вы читаете внимательно. Взвешенное среднее позволяет
вам приписывать некоторым значений больший вес, а другим — меньший.
Предположим, ваша оценка по статистике в этом семестре будет
складываться из экзаменационной оценки, оценки за домашнюю работу и финальный
проект. Каждому компоненту финальной оценки присваивается вес в
соответствии со следующей таблицей:
Тип
Результат
Вес (Процент)
Экзамен 94
Проект 89
Домашнее задание 83
50
35
15
Эврика!
Выражение Xw«*x/
означает сумму произведении
w и х. Каждая пара сначала
перемножается, а затем результат
суммируется.
Мы можем рассчитать вашу
финальную оценку, воспользовавшись
следующей формулой расчета взвешенного
среднего. Обратите внимание, что здесь
мы делим на сумму присвоенных весов, а
не количество значений данных.
п
Iiyrx*xt)
У = —
где:
w( = вес каждого значения данных х„
п
Hwi = сумма весов.
Глава 4: Вычисление описательной статистики 51
Предыдущее уравнение можно представить в виде следующей таблицы,
чтобы вам была понятна процедура:
Тип Результат Вес Вес X Результат (и>*дс)
Экзамен 94 0.50 47.0
Проект 89 0.35 31.2
Домашнее задание 83 0.15 12.4
£иг,=1.0 £(w,.*x,.)=90.6
i=i /=i
Тот же результат может быть получен путем вставки чисел
непосредственно в формулу расчета взвешенного среднего:
__ (0.50* 94)+(0.35 *89) +(0.15 *83)
0.50+0.35+0.15
_ 47.0+31.2+12.4 пл_
х=—-■ = 90.6.
1.00
Поздравляю! Вы заслужили высшую оценку.
Эврика!
Сумма весов во взвешенном среднем не обязательно должна равняться единице, как в
приведенном выше примере. Предположим, я хочу получить взвешенное среднее
своих двух последних результатов игры в гольф, 90 и 100. Причем я хочу, чтобы вес
результата в 90 очков в два раза превышал вес результата в 100 очков, мотивировав это тем,
что игра, в результате которой я получил 90 очков, была значительной трудней, чем та, в
которой я получил 100 очков. Тогда взвешенное среднее будет вычисляться по такой формуле:
^_(2*90)+(1*Ю0)_поо
х = = 93.3.
3
Поскольку меньшему значению присвоен больший вес, полученный результат ниже
фактического среднего значения в 95 очков. На этом, я полагаю, мы закончим с понятием взвешенного
среднего.
Среднее значение распределения частот группы данных
Пришло время узнать кое-что страшно любопытное. Оказывается, вы
можете вычислить среднее значение группы данных распределения частот.
Воспользуемся данными из Главы 3, имеющими отношение к звонками
Джона. Эти данные представлены в таблице ниже.
52 Часть 1: Постигаем основы
Количество звонков в день
3
3
6
2
3
1
1
9
4
5
0
8
2
1
9
5
1
6
1
4
13
2
2
9
1
2
15
7
7
4
В следующей таблице вы видите те же данные в виде распределения
частот; группой является «Количество звонков в день».
Распределение частот
Количество звонков в день Количество дней
0-2 12
3-5 8
6-8 5
9-11 3
12-14 1
15-17 1
Для вычисления среднего значения этого распределения необходимо,
прежде всего, определить среднее значение по каждой группе с помощью
следующей формулы:
_ Минимальное значение+Максимальное значение
Среднее значение по группе =
Например, среднее значение в последней группе таблицы будет
вычисляться так:
^ 15+17^с
Среднее значение по группе= =16.
Таблица, представленная ниже, поможет нам в вычислениях:
Группа Середина (jc) Частота (/*)
0-2 1 12
3-5 4 8
6-8 7 5
Глава 4: Вычисление описательной статистики 53
Группа
9-11
12-14
15-17
Середина U)
10
13
16
Частота (/*)
3
1
1
После определения среднего значения по каждой группе мы можем
приступить к вычислению среднего значения распределения частот, используя
следующее уравнение, которое по своей сути является формулой
вычисления взвешенного среднего:
*=—п ■
/=1
где:
xt = середина каждой группы при / = от I до л,
f( = количество наблюдений (частота) каждой группы при / = от 1 до л,
п = количество групп в распределении.
Среднее значение данного распределения частот будет определяться
следующим образом:
__(12*1)Ц8*4)+(5*7)+(3*Ю)+(1*\3)Ц1*Щ =463DOnKa
12+8+5+3+1+1
В соответствии с полученным средним значением данного распределения
частот, Джон в среднем совершает по 4.6 звонка в день.
Внимание! . .
Среднее значение распределения частот, когда данные помещены в группы,
является всего лишь приближенным значением средней величины первоначального набора
данных, из которого оно было получено. Это происходит потому, что мы исходим из
предположения, что значения данных расположены примерно в середине каждой группы, а на
самом деле это не всегда так. Точное значение 30 первоначальных значений данных в
примере с мобильным телефоном составляет 4.5 звонка в день, а не 4.6.
Если группы распределения частот представляют собой не интервал
данных, а лишь одно значение, среднее вычисляется так, словно распределение
является взвешенным средним. Например, предположим, что
представленная ниже таблица отображает количество дней, на протяжении которых в од-
54 Часть 1: Постигаем основы
ной скобяной лавке наблюдался спрос на какую-то особую модель молотка.
Данные представлены за период в 65 рабочих дней магазина.
Спрос по дням (х)
0
1
2
3
4
5
Количество дней (/)
10
15
12
18
6
4
Всего: 65
Например, за последние 65 дней было 15 дней, в течение которых в
магазине был спрос на 1 молоток в день. Каков средний ежедневный спрос на
этот товар за 65 дней?
*=—п
^_(10*0)+(15*1)+(12*2)+(18*3)+(6*4)+(4*5)
10+15+12+18+6+4
_ 137
х= =2.1 молотка в день.
65
Став настоящими экспертами по части вычисления среднего значения
всеми возможными способами, мы можем переходить к методам
определения других составляющих центральной тенденции.
Медиана
Среднее значение — это не единственная мера центральной тенденции.
Медианой называется такое значение набора данных, по отношению к
которому половина наблюдений имеют большее значение, а половина — меньшее.
Для определения медианы необходимо расположить значения данных по
возрастанию и найти центральное значение.
Вернемся к примеру с видеоиграми и выстроим наши данные в порядке
возрастания.
3444567779 17
Глава 4: Вычисление описательной статистики 55
Термины
Поскольку мы имеем четное
количество значений (10), медиана
является центральным значением двух
точек, расположенных в середине
нашей последовательности. В нашем
случае это значения 5 и 6, а
медианой будет значение 5.5 часов в
неделю, посвященных видеоиграм.
Обратите внимание на то, что мы имеем 4
значения данных (3, 4, 4 и 4) слева от
центральных точек и 4 значения (7,
7, 9 и 17) справа от них.
Чтобы показать, как вычисляется
медиана для нечетного количества значений данных, уберем из нашей
последовательности число 17 и повторим наш анализ.
Медианой называется мера
центральной тенденции,
представляющая собой такое значение в
последовательности данных, по
отношению к которому половина
наблюдений имеют большее значение, а
половина - меньшее. При четном
количестве значений данных медианой
является среднее арифметическое двух
центральных точек.
Сейчас в нашем распоряжении осталась только одна центральная точка —
5. Поэтому медианой для данной последовательности будет 5 часов видеоигр в
неделю. И снова мы имеем 4 значения слева и 4 значения справа от
центральной точки.
Мода
Наконец, мы рассмотрим последнюю меру центральной тенденции — моду.
Модой является наблюдение, встречающееся в наблюдении чаще всего.
Определим моду для нашего примера с видеоиграми.
3444567779 17
Модой является 4 часа видеоигр
еженедельно — это значение встречается в нашей
последовательности 3 раза.
Вот мы и закончили со способами
вычисления мер центральной тенденции. Однако один
вопрос остался без ответа.
Чему отдать предпочтение?
мтмт***
Один набор данных может
иметь более одной моды в
случае, если более одного
значения встречается в
последовательности чаще
всего.
Уверен, вы никогда не подозревали о том, что вашему вниманию будет
предложено такое количество способов вычисления основной тенденции.
Это все равно что оказаться в магазине с 30 сортами мороженого. Попробую
помочь вам в выборе. Если вы считаете, что все данные в вашей
последовательности одинаково важны и существенны, лучшим выбором будет среднее
значение. Для этой меры имеют значение количество и величина ваших дан-
56 Часть 1: Постигаем основы
ных. Если же значения данных слишком велики или малы, они могут оказать
весьма существенное влияние на среднее арифметическое, особенно если
размер выборки невелик. Если это вас беспокоит, советую остановить свой
выбор на медиане. Медиана не столь чувствительна к большим или
маленьким числам.
Возьмем набор данных, полученных в примере с видеоиграми.
3444567779 17
Число 17 значительно превышает все остальные значения
последовательности. Среднее значение этого набора данных — 6,6, а медиана — 5,5. Если вы
считаете, что 17 — это нетипичный представитель полученного набора
данных, то лучшим способом измерения центральной тенденции будет медиана.
А вот бедная-несчастная мода имеет весьма ограниченное число
применений. Как правило, она используется для описания данных по номинальной
шкале, то есть данных, сгруппированных в описательные группы, такие как
пол. Если 60 процентов наших респондентов — мужчины, тогда модой наших
данных будет мужской пол.
Использование Excel для вычисления
центральной тенденции
Всего за несколько щелчков мыши программа Excel вычислит для вас
среднее значение, медиану и моду. Я покажу вам, как это делается, на примере
все тех же домашних видеоигр.
1. Откройте чистый рабочий лист Excel и введите данные, как показано на
рисунке 4.1.
Рис 4.1
Введите данные
из примера
с видеоиграми.
Mktwtiiuxt 1Ы*йог;.- г
& ия&*
Глава 4: Вычисление описательной статистики 57
2. Откройте меню Tools (Сервис) в верхней части листа (оно находится
между меню Format (Формат) и Data (Данные)) и щелкните Data Analysis
(Анализ данных). (Если в меню эта команда отсутствует, вернитесь к
разделу «Установка средств анализа данных» в Главе 2.) Выбрав
вышеуказанную команду, вы увидите на экране диалоговое окно,
представленное на рисунке ниже (Рис. 4.2).
I Рис. 4.2
I Диалоговое окно
I Data Analysis
(Анализ данных).
■EZ3
4
9
5:
4
17
: Корреляция
■«..„....... ,..: •■■.■■■
3. Выберите Descriptive Statistics (Описательная статистика) и щелкните
ОК. Вы увидите на экране окно, показанное на рисунке 4.3.
^Ма^шШ^^И^^^ШШ^ рис 4.з
5г
■
I Диалоговое окно
Descriptive Statistics
(On исательная
статистика).
4. Для ввода данных в поле Input Range (Входной интервал) выделите
мышью ячейки с А! по А10 включительно; для ввода данных в поле Output
Range (Выходной интервал) щелкните по ячейке С1. Установите флажок
Summary (Итоговая статистика) и щелкните ОК.
i
5. Немного раздвинув границы столбцов С и D, чтобы на экране были
" представлены все данные, вы увидите то, что показано на рисунке 4.4.
58 Часть 1: Постигаем основы
Рис 4.4
Показатели
центральной
тенденции
для примера
с видеоиграми.
' \
т\
17;
Cfottrt&q*
Стандартная ошибка
Медизиз
Мод*
■•■■ ■
Эксцесс
Асиммн
Минимум.
Щ
Щ
1606218
14
Как видите, среднее арифметическое составляет 6.6 часа, медиана
5.5 часа, а мода — 4.0 часа. Очень просто!
Ваша очередь
1. Вычислите среднее, медиану и моду для следующего набора данных: 20
15 24 10 8 19 24 12 21 6
2. Вычислите среднее, медиану и моду для следующего набора данных: 84
82 90 77 75 77 82 86 82
3. Вычислите среднее, медиану и моду для следующего набора данных: 36
27 50 42 27 36 25 40 29 15
4. Вычислите среднее, медиану и моду для следующего набора данных: 8
И 6 2 И 65 6 10
5. Одна компания подсчитала количество своих сотрудников в каждой из
следующих возрастных категорий. Каков средний возраст сотрудников
компании?
Возрастной диапазон
20-24
25-29
30-34
35-39
40-44
45-49
Количество сотрудников
8
37
25
48
27
10
Глава 4: Вычисление описательной статистики 59
6. Вычислите взвешенное среднее следующих значений с
соответствующими весами.
Значение Вес
118 3
125 2
107 1
7. Одна компания подсчитала количество своих сотрудников, распределив
их по уровню, соответствующему количеству лет работы на компанию.
Каково среднее количество лет работы в данной компании?
Количество лет работы
1
2
3
4
5
6
Количество сотрудников
5
7
10
8
12
3
Повторение - мать учения
Ф Среднее (арифметическое) набора данных рассчитывается путем
сложения всех значений и деления полученного результата на количество
значений.
Ф Медианой набора данных является центральное значение
последовательности данных, если значения расположены в порядке возрастания
или убывания.
Ф Медианой является единственное центральное значение
последовательности данных, если количество значений этой последовательности
нечетное. Медиана — это среднее арифметическое двух центральных
значений последовательности, если количество значений этой
последовательности четное.
Ф Модой набора данных называется наиболее часто используемое
значение. В наборе данных может быть более одной моды.
.-. :х*й*й$
на
Вычисление описательной
статистки:
меры рассеяния
В этой главе
Ф Вычисление размаха выборки
Ф Вычисление дисперсии и стандартного отклонения
выборки и совокупности
Ф Использование эмпирического правила и теоремы Чебы-
шева для прогнозирования распределения значений
данных
Ф Использование мер относительного положения для
определения выбросов
Ф Использование программы Excel для вычисления мер
рассеяния
В Главе 4 мы научились рассчитывать меры центральной
тенденции путем суммирования нашего набора данных в одно
значение. Но следует признать, что при этом мы можем
потерять из виду полезную информацию. Если в примере с
видеоиграми я сообщил бы вам только то, что среднее значение рав-
Глава 5: Вычисление описательной статистики: меры рассеяния 61
няется 6.6 часа, вы не узнали бы, находятся ли все значения в промежутке
между 6 и 7 или они разбросаны в промежутке между 1 и 12 часами. Чуть
позже вы поймете, что эта разница может сыграть весьма значительную роль.
Поэтому мы обратим свое внимание на вторую категорию описательной
статистики — меру рассеяния, определяющую, насколько отдельные
значения отдалены от средней величины. Разделы ниже содержат информацию о
различных способах измерения рассеяния.
Размах
Размах — это простейшая мера рассеяния, представляющая собой разницу
между самым большим и самым малым значениями набора данных. Чтобы
показать вам, как вычисляется широта, я воспользуюсь следующим
примером. Одним из особых качеств Дебби является ее любовь к приготовлению
пищи на гриле. Набор данных, представленный ниже, показывает, сколько
раз Дебби готовит пищу на гриле каждый месяц:
7 9 8 И 4.
Размах данной выборки будет определяться следующим образом:
Размах =11—4 = 7 раз.
Вычислив размах, мы можем дешево и
сердито получить представление о
разбросе набора данных. И все же размах
описывает лишь две точки нашей
выборки, тем самым ограничивая наше
представление о ней. Вычисление размаха не
подразумевает использование других
значений выборки.
Термины
Размах выборки
вычисляется путем вычитания
самого маленького значения из самого
большого.
Дисперсия
Одной из наиболее используемых мер рассеяния в статистике является
дисперсия, вычисляемая путем суммирования возведенного в квадрат
отклонения каждого значения данных от средней величины. Формула для
вычисления дисперсии представлена ниже:
где:
Е(х,--х)2
s2=^ ,
Л-1
s2 = дисперсия выборки,
х = среднее значение выборки,
Термины
Дисперсия - это мера
рассеяния, описывающая
сравнительное отклонение между значениями
данных и средней величиной. Эта мера
широко используется в статистике вывода.
62 Часть 1: Постигаем основы
п = размер выборки (количество значений данных),
(х, -х) = отклонение от средней величины для каждого значения набора
данных.
Первым шагом при вычислении дисперсии является определение
среднего значения выборки, которое в примере с грилем равняется 7,8 раза в месяц.
Остальные вычисления можно облегчить с помощью следующей таблицы.
(*г*)
(XfXf
7
9
8
11
4
7.8
7.8
7.8
7.8
7.8
-0.8
1.2
0.2
3.2
-3.8
0.64
1.44
0.04
10.24
14.44
I(x,.-x)2 =26.80.
Финальная фаза вычисления дисперсии
выглядит так:
26.8
5-1
=6.7.
Для тех, кто любит производить все
вычисления за один раз, уравнение будет
выглядеть следующим образом:
Внимание!
Обратите внимание, что
в таблице выше квадрат
отрицательного значения является
положительным числом. Поэтому
все значения в четвертом
столбце являются
положительными числами.
2_(7-7.8)2+(9-7.8)2+(8-7.8f +(ll-7.8f ч-(4-7.8f
5-1
Использование метода «сырого счета» (пример с грилем)
Существует более эффективный способ вычисления дисперсии,
известный как метод «сырого счета». Хотя с первого взгляда уравнение может
показаться весьма громоздким, на самом деле оно не такое уж страшное.
Можете в этом удостовериться, а потом и решите, какой метод вам больше
нравится.
?*?
I*,
п-1
Глава 5: Вычисление описательной аашапкп: меры рассеянпя 65
где:
л
Sxf = сумма каждого значения данных после возведения в квадрат,
г2-
/=1
= квадрат суммы всех значений данных.
W
Не теряйте рассудок прямо сейчас. Позвольте представить все это в виде
таблицы, и тогда вы увидите, что вычислений здесь меньше, чем в
предыдущем примере. '
Xi лг2
7
9
8
И
4
49
81
64
121
16
2>,=39 Zx2=331
(М
£xi) (39) 1521 ^U» Если вы вычисляете
дисперсию вручную, я советую вам
1521 yKW пощадить свои руки и каль-
331 — 331-304.2 ?Р кУ^тоР и воспользоваться
s2 = s2 = ——=6.7 | методом «сырого счета».
Эврика! ■
Как видите, результат получился тот же, что и при использовании
предыдущего метода. Достоинства данного метода становятся очевидными по мере
роста размера выборки (п).
Дисперсия генеральной совокупности
Пока мы рассмотрели только дисперсию в рамках выборки. Хорошая
новость состоит в том, что дисперсия совокупности рассчитывается так же, как
и дисперсия выборки. Есть и плохая новость: мне необходимо ввести новый
символ греческого алфавита — сигму. Выражение для вычисления
дисперсии генеральной совокупности представлено ниже:
1(х,-ц)2
а2=^-
N
64 Часть 1: Постигаем основы
где:
о2 = дисперсия генеральной совокупности (произносится как «сигма в
квадрате»),
х( — исчисление каждого значения генеральной совокупности,
|и = средняя величина генеральной совокупности,
N = размер совокупности.
Внимание!
Удостоверьтесь, что
уравнение для вычисления дисперсии
генеральной совокупности
нормализуется на N, а при вычислении
дисперсии выборки - на п -1.
Уравнение по методу «сырого счета»
выглядит следующим образом:
,2_М ' N
N
Хотя процедура вычисления дисперсии по совокупности идентична
определению дисперсии выборки, позвольте обратиться еще к одному примеру.
Положим, мой класс является совокупностью, а возрастные категории,
представленные ниже, — измерением. (Можете предположить, какое из этих
чисел является моим возрастом? Дам подсказку: благодаря моему возрасту
дисперсия приобретает некоторую изюминку.)
21 23 28 47 20 19 25 23
Я воспользуюсь методом «сырого счета», где размер совокупности (N)
будет равняться 8 (хотел бы я иметь класс из такого количества студентов!)
*i
21
23
28
47
20
19
25
23
441
529
784
2209
400
361
625
529
2>,=206
£xf=5878
Глава 5: Вычисление описательной статистики: меры рассеяния 65
(£х,1 = (206)2=42 436
42 436
5 878-
2_ 8
с =
2 5 878-5304.5
с = = 71.7
Благодаря одному пожилому юноше дисперсия совокупности
получилась 71.7.
Стандартное отклонение
Это довольно просто. Стандартным отклонением называется квадратный
корень из дисперсии. Равно как и для дисперсии, стандартное отклонение
существует и у выборки, и у совокупности, как показано ниже.
Стандартное отклонение выборки:
Стандартное отклонение
генеральной совокупности:
Термины
Стандартное отклонение - это
квадратный корень из дисперсии.
оЧи2=\^
И*-?)2
N
Для вычисления стандартного отклонения необходимо сначала рассчитать
дисперсию, а затем извлечь из нее квадратный корень. Вспомните, как» в
предыдущих разделах мы рассчитывали дисперсию из примера с грилем и
получили значение 6.7. Стандартное отклонение будет вычисляться следующим
образом:
s = V? = >/б?7 =2.6 раза.
А теперь вспомните дисперсию для примера с классом, равную 71,7.
стандартное отклонение возраста для данной совокупности будет
рассчитываться так:
а = л/о5" = л/7Г7 =8.5 лет.
66 Часть 1: Постигаем основы
На самом деле стандартное отклонение приносит больше пользы, чем
дисперсия, поскольку исчисляется в единицах первоначального набора данных. Для
примера: единицы дисперсии для примера с грилем — 6.7 возводимых в квадрат
раз, а для примера с возрастом студентов — 71.7 возводимых в квадрат лет. Не
знаю, как вы, но мне бы не хотелось, чтобы мой возраст равнялся 2 209 годам.
Вычисление стандартного отклонения
для сгруппированных данных
Представленное ниже уравнение показывает, как вычислять стандартное
отклонение сгруппированных данных распределения частот.
g(x,-x)2/;
V n-l
где:
/,- = количество значений данных в каждой группе распределения,
т = количество групп,
т
п = Е^ = общее количество значений в наборе данных.
Таблица ниже представляет собой распределение частот с указанием
количества раз, когда каждый ребенок в группе Дебби отпрашивается в туалет.
Количество посещений туалета в день (дс,) Количество детей (/5)
2 1
3 4
4 12
5 8
6 5
В этом примере т = 5, а п = 30. В Главе 4 мы узнали, как вычислять
среднее распределения частот, и у нас получилось вот что:
*=i=4—
т
¥
_ (1х2)+(4хЗ)+(12х4)+(8х5)+(5х6) л А
х= — — -1 — =4.4 раза в день на каждого ребенка
1 + 4+12+8+5
Глава 5: Вычисление описательной сгатпсгпкп: меры рассеяния 67
В таблице ниже представлены суммированные вычисления стандартного
отклонения.
*,
/>
(хгх)
(х,-х?
(xrxff,
2
3
4
5
6
т
И*,
/=1
1
4
12
8
5
-xffr-
4.4
4.4
4.4
4.4
4.4
=31.20
-2.4
-1.4
-0.4
0.6
1.6
5.76
1.96
0.16
0.36
2.56
5.76
7.84
1.92
2.88
12.80
Z(x,-x)24
г-4 М
f/-*) *( /31.20 /
= А —-— = л/1.08 =1.04 раза в день на реб<
л-1 V30-1
>енка.
Распределение частот для этого примера имеет среднюю величину,
равную 4.4 раза в день на ребенка, а стандартное отклонение — 1.04 раза в день
на ребенка. Должно быть, такая частота не оставляет Дебби ни одной
свободной минутки.
Эмпирическое правило:
определение стандартного отклонения
Значения большинства наборов данных, как правило, группируются вокруг
среднего или медианы так, что распределение данных на гистограмме
напоминает по форме симметричный колокол. В таких случаях эмпирическое правило
(звучит как постановление императора) гласит, что примерно 68% всех значений
данных находятся в пределах 1 стандартного отклонения от средней величины.
Предположим, что средний результат экзамена по статистике в моем
классе составляет 88 баллов,
стандартное отклонение — 4 балла, а
распределение представлено в виде
симметричного колоколообразного
графика, в центре которого расположена
средняя величина, как показано на
рисунке 5.1. Поскольку на 1
стандартное отклонение увеличение
средней величины будет равняться
92 (88 + 4), а на 1 стандартное
отклонение уменьшение средней величи-
Тсрмины
В соответствии с эмпирическим
правилом, если распределение
данных представлено в виде
колоколообразного симметричного графика, в
центре которого находится средняя
величина, примерно 68%, 95% и 99,7%
значений окажутся в пределах 1, 2 и 3
стандартных отклонений соответственно.
68 Часть 1: Постигаем основы
ны — 84 (88-4), эмпирическое правило свидетельствует о том, что примерно
68% результатов экзамена окажутся в промежутке между 84 и 92 баллами.
о
&
0)
т
s
с;
о
Рис 5.1
Одно стандартное
отклонение
от среднего.
ЩщЩ f г ■ .у.тду, г
88 92 96 100 104
Результаты экзамена
Согласно эмпирическому правилу, примерно 95% значений данных будет
располагаться в пределах 2 стандартных отклонений от среднего. В нашем
случае 2 стандартных отклонения будут равняться 8 баллам (2*4). Двумя
отклонениями выше среднего значения будет число 96 (88 + 8), а ниже — 80 (88 — 8).
На рисунке 5.2 показано, что примерно 95% результатов экзамена попадут в
интервал между 80 и 96 баллами.
m
о
н
X
о
о
т
н
о
0)
т
s
§
л
Рис 52
Два стандартных
отклонения
от средней величины.
\
72 76 80 84 88 92 96 100 104
Результаты экзамена
И наконец, эмпирическое правило свидетельствует о том, что при
указанных условиях примерно 99.7% значений данных окажутся в пределах трех
Глава 5: Вычисление описательной статистики: меры рассеяния 69
стандартных отклонений от средней величины. На рисунке 5.3 показано, что
практически все результаты экзамена окажутся в пределах 12 баллов (2*4)
выше или ниже средней величины, равной 88 баллов. Иными словами, все
они будут расположены в промежутке между 76 и 100 баллами.
Рис 5.3
Три стандартных
отклонения
от средней величины.
со
е
х
ф
5
о
о
00
Б
Ф
Т
S
с;
о
100 104
Результаты экзамена
В целом мы можем воспользоваться следующим уравнением для
выражения значений в пределах к стандартных отклонений от средней величины:
ц ± КС
В последующих главах мы вновь обратим свое внимание на эмпирическое
правило.
Теорема Чебышева
Теорема Чебышева представляет собой математическое правило, сходное с
эмпирическим, но применимое к любому распределению, а не только к
симметричным колоколообразным графикам. Теорема Чебышева гласит, ч,то для
любого числа к больше 1 по меньшей мере
1
1—^*100%
процентов значений попадут в к стандартных отклонений от средней
величины. Используя это выражение, мы можем сделать ряд предположений:
Ф Как минимум 75% всех значений данных окажутся в пределах двух
стандартных отклонений от средней величины, если в уравнении Чебышева к = 2.
Ф Как минимум 88.9% всех значений данных окажутся в пределах трех
стандартных отклонений от средней величины, если в уравнении
Чебышева к = 3.
70 Часть 1: Постигаем основы.
Термины
Теорема Чебышева
может применяться к
любому распределению данных, но
для значений к больше 1.
Ф Как минимум 93.7% всех значений данных
окажутся в пределах четырех стандартных
отклонений от средней величины, если в
уравнении Чебышева к = 4. Выражение
для последнего примера выглядит просто.
1
*100%=93.7%
Проверим, как же работает теорема Чебышева на практике. В таблице
ниже представлено число хоумранов7 основных 40 игроков высшей
бейсбольной лиги за сезон 2002 года.
Количество хоумранов основных 40 игроков за 2002 год
57
38
33
29
52
38
32
29
49
37
31
29
46
37
31
28
43
35
31
28
42
34
30
28
42
34
30
28
41
34
30
28
39
33
29
27
39...
33
29
27
Источник: www.espn.com.
Гистограмма, представленная ниже, свидетельствует о том, что это
распределение несимметрично и не имеет колоколообразнои формы, поэтому
эмпирическое правило здесь неприменимо (Рис. 5.4). Нам необходимо
воспользоваться теоремой Чебышева.
18'
РИС 5.4
Гистограмма
хоумранов
за 2002 год.
m
о
о
а
о
со
н
о
а>
т
S
с;
о
23-27 28-32 33-37 38-42 43-47 48-52
Число хоумранов
53-57
7 Показатель активности игрока в бейсболе. — Примеч. ред.
Глава 5: Вычисление оппсательноп статистики: меры рассеяния 71
Среднее для данного распределения равно 34.7 хоумранов, а стандартное
отклонение — 7.2. Следующая таблица суммирует различные интервалы по
отношению к средней величине с процентным отношением значений в
пределах этих интервалов.
к
2
3
4
И
34.7
34.7
34.7
о
7.2
7.2
7.2
|i + to
49.1
56.3
63.5
ц,- ко
20.3
13.1
5.9
% по Чебышеву
75.0%
88.9%
93.7%
Фактический %
95.0%
97.5%
100.0%
Эта таблица подтверждает теорему Чебышева, в соответствии с которой как
минимум 75% значений окажутся в пределах двух стандартных отклонений от
средней величины. Из указанного набора данных видно, что 95%
действительно попадают в интервал между 20.3 и 49.1 хоумранов (38 из 40). То же
объяснение используется в отношении 3 и 4 стандартных отклонений от среднего.
Меры относительного положения
Рассеяние данных также может рассматриваться с точки зрения мер
относительного положения, описывающих процент данных ниже определенной
точки. В разделах ниже вы узнаете, каковые эти меры и как ими пользоваться.
Квартили
Квартили делят организованный в порядке возрастания набор данных на 4
равных сегмента. Примерно 25% значений окажутся ниже первого квартиля,
Qx. Примерно 50% значений окажутся ниже второго квартиля, Q2. И
наконец, примерно 75% значений будут ниже третьего квартиля, Q3. Чтобы
продемонстрировать, как определять значения Qlf Q2 и Q3, воспользуемся
следующим набором данных.
9 5 3 10 14 б 12 7 14
Шаг 1: расположите данные в порядке возрастания.
3 5 6 7 9 10 12 14 14
Шаг 2: определите медиану набора
данных. Это и будет Q2-
Термины
q2 = 9 illlllifP^ Квартили измеряют
относительное положение значений
данных после деления всею набора
данных на 4 равных сегмента.
Шаг 3: определите медиану меньшей
части набора данных (в скобках). Это и
будет Qle
72 Часть 1: Постигаем основы
(3 5 6 7) 9 10 12 14 14
€>г = 5.5
Q2 = 9
Шаг 4: определите медиану большей части набора данных (в скобках). Это
и будет Q3.
3 5 6 7
Q1 = 5.5
Q2 = 9
ОЗ = 13
(10 12 14 14)
Мсжквартильный размах
После вычисления квартилей мы можем без особого труда определить меж-
квартильный размах (IQR). Он определяет разброс центральной половины
набора данных и вычисляется путем вычитания первого квартиля из
третьего, как показано ниже.
IQR = Q3 - Qi
IQR = 13 - 5.5 = 7.5
Термины
Мсжквартильный размах -
мера разброса центральной
половины набора данных, которые
являются флуктуацией и должны быть
отброшены перед анализом.
Межквартильный размах
используется для определения выбросов, которые
являются «черными овцами» нашего
набора данных. Это экстремальные
значения, чья точность находится под
вопросом и которые могут привезти к
искажению результатов статистического
анализа. Любые значения больше:
ОЗ + 1.5IQR = 24.25
13 + 1.5(7.5) = 24.25
или меньше:
Ql - 1.5IOR
5.5 + 1.5(7.5) = - 5.75
должны быть отброшены.
Теперь, когда мы истерли все пальцы до костей, высчитывая все эти
премудрости, посмотрим, как программа Excel упрощает все эти процедуры.
Глава 5: Вычисление описательной статистики: меры рассеяния 73
Использование Excel для вычисления мер рассеяния
Excel предлагает рассчитать для вас широту, дисперсию и стандартное
отклонение выборки при помощи опции Data Analysis (Анализ данных) в меню
Tools (Сервис). Шаги, которые необходимо выполнить для расчета этих
составляющих, точно такие же, как при вычислении мер центральной
тенденции, описанных в Главе 4. Если выполнить эти шаги (см. раздел
«Использование Excel для вычисления центральной тенденции») для примера с грилем из
этой главы, то получим результат, представленный на рисунке 5.5.
Рис 5.5
Меры рассеяния
для примера с грилем.
.
^^s^s^'
'?:"■•.-
»&э
M«;ai!M3
Mftftl
имемт :
■■
■•'■
: Слоям
:
'"X...
#Vfl
"
'
А
1'
Из рисунка выше видно, что размах
выборки равен 7, дисперсия — 6.7, а
стандартное отклонение — 2.6.
Обратите внимание, что представленный набор
данных не имеет моды, поскольку ни
одно из значений не встречается более
одного раза.
На этом мы завершаем рассмотрение
различных способов описания мер
рассеяния.
Термины
Значения для дисперсии и
стандартного отклонения,
указанные в Excel, вычислены для
выборки. Если ваши данные
представляют собой генеральную
совокупность, вам необходимо вновь вычис^
лить результаты, используя в кач'естве
знаменателя N, а не п - 1.
Ваша очередь
1. Вычислите дисперсию, стандартное отклонение и широту для
следующей выборки: 20 15 24 10 8 19 24.
2. Вычислите дисперсию, стандартное отклонение и широту для
следующей совокупности: 84 82 90 77 75 77 82 86 82.
3. Вычислите дисперсию, стандартное отклонение и широту для
следующей выборки: 36 27 50 42 27 36 25 40.
74 Часть 1: Постигаем основы
4. Вычислите квартили и границы выбросов для следующего набора
данных: 8 И 6 2 11 6 5 6 10 15.
5. Одна компания подсчитала количество сотрудников в каждой из
следующих возрастных групп. Б соответствии с данным
распределением, каково стандартное отклонение для возраста сотрудников
компании?
Возрастной
20-24
25-29
30-34
35-39
40-44
45-49
интервал
Количество сотрудников
8
37
25
48
27
10
6. Одна компания подсчитала количество сотрудников на каждом уровне,
соответствующей количеству лет работы на компанию. В соответствии с
данным распределением, каково стандартное отклонение для
количества лет работы сотрудников на компанию?
Количество лет работы
1
2
3
4
5
6
Количество сотрудников
5
7
10
8
12
3
7. Набор данных с симметричным колоколообразным распределением
имеет среднее значение, равное 75, а стандартное отклонение — 10.
Данные с таким отклонением и расположенные вокруг среднего
значения будут представлять 95% точек данных?
8. Набор данных с несимметричным распределением имеет среднее
значение, равное 50, а стандартное отклонение — 6. Каков минимальный
процент значений, попадающих в интервал между 38 и 62?
Повторение - мать учения
Ф Широта набора данных — это разность между самым большим и самым
малым значениями.
Глава 5: Вычисление описательной статпопкп: меры рассеяния 75
Ф Дисперсия набора данных суммирует возведенное в квадрат
отклонение каждого значения от средней величины,
Ф Стандартное отклонение набора данных определяется как квадратный
корень из дисперсии и выражается в тех же единицах, что и
первоначальные значения данных.
Ф Эмпирическое правило гласит, что если распределение можно
представить в виде симметричного колоколообразного графика, в центре
которого расположено среднее 3Ha4eHHet примерно 68, 95 и 99,7% значений
данных окажутся в пределах 1, 2 и 3 стандартных отклонений от
среднего значения соответственно.
Ф Межквартильныи размах измеряет разброс центральной половины
набора данных и используется для определения выбросов, которые
должны быть отброшены перед проведением статистического анализа.
Часи
Изучаем
вероятность
Связь между описательной статистикой и статистическим
выводом базируется на понятии вероятности. Мне известно, что
теория вероятности делает немилым свет для большинства
студентов, и все же это чрезвычайно важная тема для
проникновенного понимания статистики. Тема вероятности играет роль
необходимого звена между описательной статистикой и
статистикой вывода. Без четкого осознания вероятностных
концепций статистический вывод будет представляться вам
совершенно вражеским языком. Именно поэтому Часть 2 предназначена
для того, чтобы помочь вам в преодолении этого препятствия.
я хочу понять теорию еброятности,
НО, ВЗГ/ЫНУР НА ДАННЫб, Я ПОНЯЛ,
ЧТО, 06РОЯТНО, ОТКАЖУСЬ от этой
ЗАТбИ.
Гла
Введение в вероятность
В этой главе
Ф Различия между классической, эмпирической и
субъективной вероятностями
Ф Использование распределения частот для вычисления
вероятности
Ф Изучение основных свойств вероятности
Ф Демонстрация пересечения и объединения простых
событий с помощью диаграммы Венна
Покидая счастливый мир описательной статистики, вы
можете испытывать такое чувство, будто вы уже готовы
приступить к освоению статистического вывода. Но прежде чем
войти в царство статистики вывода, нам необходимо вооружиться
теорией вероятности. Возможность с точностью
предсказывать, с какой вероятностью произойдёт то или иное событие,
имеет широкую сферу применений. Например, в игровой
индустрии теория вероятности используется в лотереях,
карточных играх и спортивных событиях.
Цель настоящей главы состоит в том, чтобы начать изучение
основ вероятности, после чего мы плавно перейдем к освоению
более сложных понятий — этому посвящены Главы 7 и 8. Мы
рассмотрим различные типы вероятнрстей и научимся
вычислять вероятность простых событий. Мы будем опираться на
80 Часть 2: Изучаем вероятность
данные распределений частот для изучения вероятности комбинации
простых событий. Так что устраивайтесь поудобней, и давайте кинем кости!
Что такое вероятность?
В жизни нас повсюду окружают понятия теории вероятности. Когда в
сводке погоды сообщают, что вероятность выпадения осадков в виде дождя
завтра составляет 80% (а именно завтра я собираюсь поиграть в гольф) или когда
моя любимая команда выигрывает всего 40% игр в этом году (таков же был их
результат в прошлом и позапрошлом годах), существует 65%-ный шанс, что я
буду пребывать в дурном расположении духа.
Говоря простыми словами, вероятность — это возможность реализации
какого-либо события, например, дождя или выигрыша в игре. Но прежде чем
мы отправимся дальше, нам необходимо ознакомиться с очередной порцией
жаргона. Когда речь идет о вероятности, часто используются
соответствующие термины.
Ф Эксперимент. Процесс измерения или наблюдения за действием с
целью сбора данных. Примером является кидание костей.
Ф Исход. Определенный результат эксперимента. Пример — выпадение
троек при кидании костей.
Ф Выборочное пространство. Все возможные исходы эксперимента.
Выборочное пространство для нашего эксперимента — это числа {2, 3, 4, 5, 6,
7, 8, 9, 10, 11 и 12}. Статисты любят окружать значения выборочного
пространства скобками, видимо потому, что считают, что это очень круто.
Ф Событие. Один или несколько исходов, которые представляют интерес
для эксперимента и которые являются подмножеством выборочного
пространства. Примером является выпадение. двоек, троек, четверок
или пятерок обеих костей.
Чтобы правильно определить вероятность, необходимо решить, о каком
типе вероятности идет речь.
Классическая вероятность
Классическая вероятность применима к ситуациям, когда нам известно
число возможных исходов определенного события и можем вычислить
вероятность этого события с помощью следующего уравнения:
Количество возможных исходов реализации События А
. ' Общее количество возможных исходов в выборочном пространстве
где:
Р[А] = вероятность того, что произойдет событие А.
Глава 6: Введение в вероятность 81
Например, если Событие А = выпадение на обеих костях суммы 2, 3, 4 или
5, нам необходимо определить выборочное пространство для данного
эксперимента, показанное в таблице ниже.
{1.1}
{1-2}
{1-3}
{1,4}
{1-5}
{1,6}
{2,1}
{2,2}
{2,3}
{2,4}
{2,5}
{2,6}
{3,1}
{3,2}
{3,3}
{3,4}
{3,5}
{3,6}
{4,1}
{4,2}
{4,3}
{4,4}
{4,5}
{4,6}
{5,1}
{5,2}
{5,3}
{5,4}
{5,5}
{5,6}
{6,1}
{6,2}
{6,3}
{6,4}
{6,5}
{6,6}
Существует 36 возможных исходов данного эксперимента, имеющих
одинаковую вероятность. Подчеркнуты исходы, соответствующие Событию А;
всего их 10. Таким образом:
Р[А] =
10
36
=0.28.
Чтобы воспользоваться
классической вероятностью, вам необходимо
иметь представление о происходящем
событии, чтобы оценить количество
его исходов. Вы также должны суметь
сосчитать общее число событий в
данном выборочном пространстве. Скоро
вы убедитесь в том, что сделать это не
всегда возможно.
Термины
- „Щ
Классическая вероятность
требует, чтобы вы знали
количество исходов, соответствующих
определенному событию. Вам также
необходимо знать общее количество
возможных исходов в данном
выборочном пространстве.
Эмпирическая вероятность
Когда мы не обладаем достаточной
информацией о происходящем и не
можем определить число возможных
исходов интересующего нас события,
мы можем воспользоваться
эмпирической вероятностью. Этот тип
вероятности определяет количество
реализаций события эмпирическим путем и
вычисляет вероятность с помощью
распределения относительных частот.
Получаем следующее уравнение:
Р[А] =
Частота События А
Термины
Эмпирическая вероятность
требует, чтобы вы
определили частоту, с которой происходит
событие, эмпирическим путем и
вычислили вероятность с помощью
распределения относительных частот.
Общее количество наблюдений
82 Часть 2: Изучаем вероятность
Примером эмпирической вероятности можно с уверенностью назвать
старый как мир вопрос: какова вероятность того, что Джон проснется утром и
отправится в школу после первого звонка будильника? Поскольку мне никак
не понять, почему подросток никак не желает выбираться из постели раньше
2 часов пополудни, мне придется опереться на эмпирическую вероятность. В
таблице ниже представлено количество звонков будильника, которые
понадобились Джону за последние 20 дней, чтобы пробудиться.
Количество звонков будильника Джона
(за предыдущие 20 школьных дней)
2433124331
42 33132434
Мы можем суммировать эти данные и представить их в виде
распределения относительных частот.
Распределение относительных частот для звонков будильника
Джона
Кол-во звонков Кол-во наблюдений Процент
1 3 3/20 = 0.15
2 4 4/20 = 0.20
3 8 8/20 = 0.40
4 5 5/20 = 0.25
Всего: 20 ,
На основании этих наблюдений следует: если Событие А = Джон покинет
постель по первому звонку будильника, тогда Р[А] = 0.15.
Используя предыдущую таблицу, мы можем также определить
вероятность и других событий. Предположим, Событие В = Джону требуется более
2 звонков, чтобы выбраться из постели. Тогда Р[В] = 0.40 4- 0.25 = 0.65.
Этому парню следует ложиться спать пораньше!
Если я проведу еще один эксперимент
по изучению поведения Джона за 20
Термины , дней, результаты, вероятнее всего, будут
иными, чем в предыдущем случае. А если
бы мне пришлось изучить его поведение
в течение 100 дней, относительные
частоты почти сравнялись бы с
классическими вероятностями. Такой сценарий
получил название закона больших чисел.
Закон больших чисел гласит,
что когда эксперимент
проводится большое число раз,
эмпирическая вероятность этого процесса
стремится к классической.
Глава б: Введение в вероятность 85
Чтобы продемонстрировать вам действие этого закона, предположим, что
я трижды подбросил монетку, и каждый раз она выпадала «орлом» вверх. Для
данного эксперимента эмпирическая вероятность выпадения орла равняется
100%. Но если бы я подбросил монету 100 раз, эмпирическая вероятность
оказалась бы гораздо ближе к классической вероятности в 50%.
Субъективная вероятность
Субъективная вероятность используется тогда, когда классическую и
эмпирическую вероятности применить невозможно. В этом случае при оценке
вероятности мы вынуждены полагаться на опыт и интуицию.
Примерами субъективной вероятности могут служить следующие
вопросы: «Какова вероятность того, что мой сын Брайан попросит мою новую
машину с шестиступенчатой коробкой передач, чтобы отправиться на
школьный бал?» (97%) или «Какова вероятность того, что я получу назад свою
машину со всеми 6 работающими передачами?» (18%). Эти вероятности
основываются на моих личных наблюдениях, когда во время поездки на машине
я слышал подозрительные шумы в области коробки передач, от которых я
весь похолодел и которые до сих пор преследуют меня в ночных кошмарах. В
подобной ситуации я вынужден прибегать к субъективной вероятности, ведь
моя бедная машина не пережила бы нескольких подобных экспериментов.
Основные свойства вероятности
Следующий наш шаг — это ознакомление с основными правилами теории
вероятности.
Ф Если Р[А] = 1, то Событие А точно произойдет. Пример События А =
Дебби в этом месяце купит пару туфель.
Ф Если Р[А] = 0, то Событие А произойдет врядли. Пример События А =
Боб, наконец, закончит в подвале ремонт, начатый три года назад.
Ф Вероятность События А должна быть между 0 и 1.
Ф Сумма всех вероятностей событий выборочного пространства должна
равняться 1. Например, если экспериментом является подбрасывание
монеты при Событии А = орел и Событии В = решка, то А и В
представляют собой все выборочное пространство. Мы также знаем, что Р[А] +
Р[В] = 0.5 + 0.5 = 1.
Ф Дополнение События А определяется как все исходы в пределах
выборочного пространства, которые не являются частью События А, и
обозначается А\ Используя это определение, мы можем утверждать
следующее: Р[А] + Р[А'] = 1 или Р[А] = 1 - Р[А'].
Например, если экспериментом является подбрасывание одной шестисто-
ронней кости, то выборочное пространство показано на рисунке 6.1.
84 Часть 2: Изучаем вероятность
Рис 6.1
Выборочное пространство
для эксперимента с одной
• • •
костью.
Если Событие А = выпадение 1, тогда Событие А' = выпадение 2, 3, 4, 5
или 6. Получаем следующее:
Р[А]=-=0.167
Р[А'] = 1 - 0.167 = 0.833.
До настоящего момента все примеры в этой главе были случаями простой
вероятности, определяемой как вероятность единичного события. В
следующих разделах все понятия будут применяться к более чем одному событию.
Пересечение событий
Порой интерес для нас представляет вероятность комбинации событий, а не
единичного события. В целях демонстрации данной методики я составил
таблицу, представленную ниже, в которой вы увидите распределение частот
оценок 50 студентов моего класса.
Оценка
Количество студентов
А
В
С
18
22
10
Всего: 50
Следующая таблица, называемая факторной, разбивает распределение
оценок по половому признаку.
Факторная таблица дм распределения оценок
Оценка
Мужской
Женский
Всего
А
В
С
Всего
8
14
6
28
10
8
4
22
18
22
10
50
Глава 6: Введение в вероятность 85
Факторные таблицы показывают фактическую или относительную
частоту двух типов данных одновременно. В данном случае типами данных
являются мужской и женский пол.
Предположим, студент выбирается из этой группы случайным путем, то
есть все студенты имеют равные шансы быть выбранными. Будем исходить
из предположения, что в моей группе нет «любимчиков». Определим
События А и В.
Ф Событие А = выбранный студент получил высшую оценку
Ф Событие В = выбранный студент оказался студенткой.
Воспользуемся предыдущей таблицей для вычисления простой
вероятности того, что выбранный студент получил высшую оценку:
18
Р[А] = —=0.36.
J 50
Вероятность того, что будет выбрана студентка, рассчитывается так:
22
Р[В]=—=0.44.
1 J 50
Какова же вероятность того, что выбранный студент окажется
представительницей прекрасного пола и получил высшую оценку? Такое событие
называется пересечением Событий А и В и обозначается А В. Количество
студенток, получивших высшую оценку, исходя из нашей факторной таблицы,
равняется 10, поэтому:
Р[А и В] = Р[А пВ] = —= 0.20.
Вероятность пересечения двух событий называется суммарной
вероятностью.
Пересечение Событий А и В можно также описать с помощью рисунка 6.2,
известного как диаграмма Венна.
Термины :
Факторная таблица показывает число наблюдений, распределенных в
соответствии с двумя переменными. Пересечением Событий А и В называется
количество одновременных реализаций Событий А и В (то есть один и тот же студент является
представителем прекрасного пола и получает высшую оценку). Вероятность
пересечения двух событий - это суммарная вероятность. Диаграмма Венна изображает две
или более пересекающихся окружностей, отражающих отношение между несколькими
событиями.
86 Часть 2: Изучаем вероятность
Круг, обозначающий Событие А, представляет 18 студентов, получивших
«пятерки», а круг, обозначающий Событие В, — 22 студентки.
Заштрихованная область пересечения кругов представляет 10 студентов, которые
одновременно принадлежат к слабому полу и получили высшую оценку.
Рис 6.2
За штр ихованная
область — это
пересечение
Событий А и В.
Объединение событий: брак, заключенный на небесах
Объединение Событий А и В — это все реализации либо События А, либо
События В, либо обоих событий одновременно. Обозначается А В. В
соответствии с предыдущим примером, таблица ниже показываем 4 группы
студентов, которые либо являются студентками, либо получили высший балл.
Оценка
Пол
Количество студентов
А
А
В
С
Male
Female
Female
Female
8
10
8
4
Всего: 30
Термины
Объединением Событий А и В
называется количество реализаций
Событий А или В (то есть количество
студентов, которые либо принадлежат к женскому
полу, либо получили высшую оценку).
Эврика!
Вероятность пересечения двух
событий никогда не может превышать
вероятность объединения двух
событий. Если ваши вычисления
свидетельствуют об обратном, значит, вы
допустили ошибку!
Таким образом, вероятность того,
что выбранный студент окажется
студенткой или получит высшую оценку,
вычисляется следующим образом:
Р[А или В] = Р[А иВ] = — =0.60
ои
, Объединение Событий А и В
может также быть представлено с
помощью диаграммы Венна, показанной
на рисунке 6.3.
Заштрихованные области
представляют либо студентов,
получивших высшую оценку (Круг А), или
студенток (Круг В). О том, как
вычислять вероятность объединений и
пересечений, вы узнаете в Главе 7.
Глава б: Введение в вероятность 87
Рис 6.3
Заштрихованные
области являются
объединением
Событий А и В.
Ваша очередь
1. Определите тип вероятности: классическая, эмпирическая или
субъективная.
a. Вероятность того, что бейсболист Самми Coca сделает успешный
удар во время своего хода.
b. Вероятность выпадения туза из колоды карт.
c. Вероятность получения мной менее 90 очков во время следующего
раунда игры в гольф.
d. Вероятность выигрыша в следующем тираже государственной
лотереи.
e. Вероятность выхода из строя ременной передачи моей
газонокосилки этим летом (она действительно вышла из строя).
f. Вероятность того, что я успею завершить написание этой книги до
установленного срока.
2. Определите, какие из представленных ниже вариантов являются
вероятностями.
a. 65%
b. 1.9
c. 110%
d. - 4.2
e. 0.75
f.O
3. Среди 125 семей был проведен опрос относительно наличия доступа в
Интернет из дома. Семьи сгруппированы по признаку расовой
принадлежности. Ниже представлена таблица факторов.
Расовая принадлежность Есть доступ Нет доступа Всего
Европейская 15 22 37
Азиатско-американская 23 18 41
Афроамериканская 14 33 47
Всего: 52 73 125
88 Часть 2: Изучаем вероятность
4. Произведен случайный выбор семьи из опроса. Дадим определение.
Событие А: выбранная семья имеет дома выход в Интернет.
Событие В: выбранная семья принадлежит к азиатско-американской расе.
a. Определите вероятность того, что выбранная семья имеет доступ в
Интернет.
b. Определите вероятность того, что выбранная семья принадлежит к
азиатско-американской расе.
c. Определите вероятность того, что выбранная семья имеет доступ в
Интернет и принадлежит к азиатско-американской расе.
d. Определите вероятность того, что выбранная семья имеет доступ в
Интернет или принадлежит к азиатско-американской расе.
Повторение - мать учения
Ф Классическая вероятность требует знания о происходящем процессе с
целью подсчета количества возможных исходов интересующего
события.
Ф Эмпирическая вероятность опирается на исторические данные,
полученные из распределения частот, для определения возможности
реализации события.
Ф Закон больших чисел гласит, что когда эксперимент проводится
большое количество раз, эмпирическая вероятность процесса стремится к
классической вероятности.
Ф Пересечение Событий А и В представляет собой количество
одновременных реализаций Событий А и В.
Ф Объединением Событий А и В называется количество реализаций
События А или События В.
Глав
И снова о вероятности
В этой главе
Ф Вычисление условных вероятностей
Ф Различия между зависимыми и независимыми событиями
Ф Использование правила умножения вероятностей
Ф Определение взаимоисключающих событий
Ф Использование правила сложения вероятностей
Ф Использование теоремы Байеса для вычисления условных
вероятностей
Добравшись до второй из трех глав, посвященных понятиям
вероятности, мы готовы к решению новых непростых задач.
Для этого нам необходимо вооружиться понятиями,
освоенными в Главе 6, и пустить их в ход, чтобы подняться на одну
ступеньку вверх по лестнице знаний. Не уподобляйтесь мне и не
пугайтесь высот, просто смотрите вперед!
В этой главе речь пойдет об умелом обращении с
вероятностями различных событий. По мере поступления новой
информации о событиях мы будем возвращаться к полученным ранее
данным и извлекать из них еще большую пользу. Порой это
приводит к самым неожиданным результатам, и в этом вы
скоро сами убедитесь!
90 Часть 2: Изучаем вероятность
Условная вероятность
Условной называется вероятность События А при условии, что Событие В
уже произошло. Для наглядности воспользуемся следующим примером.
Дебби — большая любительница тенниса, и мы частенько играем друг против
друга. Но взгляды на игру у нас совершенно разные. Супруге нравится
проводить длительную разминку перед началом самой игры, и мне всегда приходится
ломать голову над тем, кто выигрывает и какой счет. Мое представление о
разминке иное: затянуть пояс, зашнуровать кроссовки и морально подготовиться к
игре. Я расцениваю каждый теннисный турнир как испытание моей мужской
силы, и разминка не имеет ничего общего с триумфом побед и горечью
поражений. Ничего не могу с собой поделать; должно быть, это типичное мужское
поведение, сформировавшееся в ходе многовековой истории. А Дебби
утверждает, что без основательной разминки ей не удается хорошо сыграть. А я говорю,
что такие заявления безосновательны, и сейчас я это докажу. В таблице ниже
представлены результаты последних 20 игр с указанием типа разминки.
Факторная таблица для результатов игры в теннис
Время разминки Выигрыши Дебби (А) Выигрыши Боба (А') Всего
Менее 10 минут (В) 4 9 13
10 и более минут (В') 5 2 7
Всего 9 11 20
Для нас интерес представляют определенные события.
Ф Событие А = Дебби одерживает победу в игре.
Ф Событие В = разминка длится менее 10 минут.
Ф Событие А' = Боб одерживает победу в игре.
Ф* Событие В' = разминка длится 10 или более минут.
Не имея никакой дополнительной информации, мы можем рассчитать
простую вероятность следующим образом:
Р[А] =—=0.45 Р[В] =—=0.65
20 20
Р[А] =—=0.55 Р[А] =—=0.35.
20 20
Поскольку подобные вероятности мы еще никак ранее не обозначали, я
припас для вас название для них. Вероятности, полученные из информации,
имеющейся в наличии в текущий момент, носят название априорных.
Глава 7: И снова о вероятности 91
Термины
Простая, или априорная,
вероятность всегда базируется
на общем количестве наблюдений. В
предыдущем примере это 20 матчей.
Вы можете задаться вопросом: «О
какой друтой информации говорит этот
человек?» Предположим, мне
известно, что разминка продолжалась менее
10 минут. Обладая этой информацией,
могу ли я рассчитать вероятность того,
что Дебби выиграет? В этом случае
речь идет об условной вероятности
События А с учетом того, что Событие В уже произошло и нам об этом известно.
Взглянув на предыдущую таблицу, мы увидим, что Событие В произошло
13 раз. Поскольку Дебби одержала победу в 4 из этих матчей (А), вероятность
События А при известном значении В вычисляется так:
Р[А/В]=—=0.31.
Дебби не сильно обрадуется, увидев такой результат.
Мы также можем рассчитать вероятность выигрыша Дебби при
продолжительности разминки 10 или более (практические целая вечность) минут. Если
следовать данным, представленным в предыдущей таблице, такие марафонские
разминки имели место 7 раз, а Дебби выиграла 5 из таких матчей. Поэтому:
Р[А/В']=-=0.71.
Шансы Боба выглядят не слишком обнадеживающе. Надо бы припрятать
эту главу от своего корректора.
И вновь я введу в обиход жаргонное словечко. Условную вероятность
иногда называют апостериорной. Можно сказать, что она является
переработанным вариантом априорной вероятности с учетом дополнительной
информации. Например, априорная вероятность выигрыша Дебби составляет
Р[А] = 0.45. Но имея на руках
информацию о том, что разминка
продолжалась 10 или более минут, мы
пересчитываем вероятность выигрыша моей
супруги и получаем Р[А/В'] = 0.71.
Условная вероятность необходима
для расчета вероятностей составных
событий, в чем вы и убедитесь после
изучения следующих разделов.
Термины
Русловная вероятность - это
вероятность События А, если
известно, что Событие В уже
произошло. Условную вероятность также
называют апостериорной.
Независимые и зависимые события
События А и В считаются независимыми друг от друга, если реализация
События В никак не влияет на Событие А. Используя условную вероятность,
получаем, что События А и В независимы друг от друга, если:
92 Часть 2: Изучаем вероятность
Р[А/В]= Р[А]
Если События А и В не являются независимыми друг от друга, они
считаются зависимыми событиями.
В примере с теннисом События А и В зависят друг от друга, поскольку
вероятность выигрыша Дебби напрямую зависит от того, продолжается ли
разминка 10 или более минут. Наглядная демонстрация моего заявления
подтверждается следующими вычислениями:
Р[А]=— =0.45 и Р[А/В] = — =0.31.
20 13
Полученные вероятности
свидетельствуют о том, что в целом Дебби выигрывает
45% игр, а при короткой разминке — всего
31% игр. Поскольку эти вероятности не
равны, События А и В являются зависимыми.
Примером двух независимых событий
является результат выброса 2 костей.
Термины
9 События А и В считаются
независимыми друг от друга,
если Событие В происходит, не
оказывая влияния на вероятность
События А. Если События А и В не
являются независимыми друг от друга,
тогда они считаются зависимыми.
# Событие А: выпадение «4» на первой
из двух костей.
Ф Событие В: выпадение «6» на второй
кости.
Простая вероятность для этих событий рассчитывается так:
Р[А] =-=0.167 и Р[В] =- = 0.167.
6 6
Даже если мы знаем, что на первой кости выпадает «4», вероятность
выпадения «6» на второй кости никоим образом не зависит от этого, поскольку
кости, как правило, не обладают особыми умственными способностями и не
интересуются тем, что происходит вокруг. С учетом этого получаем следующее:
Р[В/А] = Р[В]=-=0.167.
6
Таким образом, События А и В являются независимыми друг от друга.
Правило умножения вероятностей
Правило умножения вероятностей используется для вычисления суммарной
вероятности двух событий. Другими словами, мы вычисляем вероятность
этих событий, происходящих одновременно. В Главе 6 это называлось
пересечением двух событий. Для двух независимых событий правило умножения
выглядит следующим образом:
Глава 7: И снова о вероятности 93
Р[АиВ] = Р[А]*Р[В]
Вспомните из предыдущей главы, что выражение Р[А и В] называется
суммарной вероятностью Событий А и В.
Например, мы можем использовать правило умножения для вычисления
суммарной вероятности выпадения «1» на каждой из двух костей.
Определяем события.
Ф Событие А = выпадение «1» на первой кости.
Ф Событие В = выпадение «1» на второй кости.
Поскольку эти события точно являются независимыми, мы можем
рассчитать вероятность того, что они выпадут одновременно:
Р[Аи В] =
■I I-
6 б"
36'
Термины
Для зависимых событий
правило умножения гласит, что Р[А и
В] = Р[А/В] * Р[В]. Если события
являются независимыми, правило
умножения упрощается: Р[А и В] = Р[А] * Р[В]
Если два события являются зависимыми, правило умножения выглядит
следующим образом:
Р[АиВ] = Р[А/В]*Р[В].
Продемонстрируем, как выглядит
правило умножения для зависимых
событий. Для этого вернемся к
примеру с теннисом и вычислим
вероятность Р[А и В] того, что Дебби одержит
победу при разминке
продолжительностью менее 10 минут (из
полученных ранее результатов):
Р[В] =0.165 и Р[А/В] =0.31
Р[А и В] =0.65* 0.31
Р[А/В] =0.2. ^jr Правило умножения может быть
изменено алгебраически для
вычисления условной
вероятности События В при реализации
Событии А. Уравнение будет
выглядеть так:
Р[В]
Эврика!
Мы можем подтвердить этот
результат, вернувшись к
первоначальной факторной таблице, в которой
увидим, что из 20 матчей Дебби
одержала победу в четырех при короткой
разминке. Таким образом:
Р[АиВ]=—=0.20.
1 J 20
Возможно, Дебби где-то права, выражая недовольство. Интересно, она
когда-нибудь устает от собственной правоты ?
94 Часть 2: Изучаем вероятность
Взаимоисключающие события
Два события считаются взаимоисключающими, если в рамках одного
эксперимента они не могут происходить одновременно. Предположим, что
эксперимент состоит в том, чтобы кинуть одну кость, а интересующие нас события
определим просто.
Ф Событие А: выпадение «1».
Ф Событие В: выпадение «2».
Поскольку эти события ни при каких обстоятельствах не могут происходить
одновременно, они считаются взаимоисключающими. Диаграмма Венна,
представленная ниже, показывает взаимоисключающие События А и В (Рис.7.1).
Рис 7.1
События АиВ
являются
взаимоисключающими.
Термины
w Два события являются
взаимоисключающими, если в
рамках эксперимента они не могут
происходить одновременно.
События, которые могут происходить
одновременно, соответственно, не
являются взаимоисключающими. В примере
с теннисом События А и В не являются
взаимоисключающими, поскольку Деб-
би может выиграть матч (А) при
разминке продолжительностью менее 10 минут
(В) в одном и том же эксперименте. Представленная ниже диаграмма Венна
показывает События АиВ, которые не являются взаимоисключающими
(Рис.7.2).
Рис7.2
События АиВ
не являются
взаимоисключающими.
Область пересечения двух кругов свидетельствует о том, что События А и
В могут происходить одновременно.
Правило сложения вероятностей
Правило сложения вероятностей используется для вычисления вероятности
объединения событий, то есть вероятности того, что произойдет Событие А
Глава 7: И снова о вероятности 95
или Событие В. Для двух
взаимоисключающих событий правило сложе- ||§' ^ Термины
ния выглядит так:
Р[АилиВ] = Р[А] + Р[В].
Выберем взаимоисключающие
события для примера с одной костью.
Ф Событие А: выпадение «1».
Ф Событие В: выпадение «2».
^Для взаимоисключающих
событий правило сложения
гласит, что Р[А или В] = Р[А] + Р[В]. Если
события не являются
взаимоисключающими, правило сложения меняется
следующим образом: Р[А или В] =
Р[А] + Р[В]-Р[АиВ].
Простые вероятности вычисляются следующим образом:
Р[А] =-=0.167 и Р[В]=-=0.167.
6 6
Вероятность выпадения «1» или «2» вычисляется так:
Р[А или В] = Р[А] + Р[В] = 0.334.
Для событий, не являющихся взаимоисключающими, правило сложения
выглядит так:
Р[АилиВ] = Р[А] + Р[В] - Р[АиВ].
Вернемся к примеру с теннисом.
Ф Событие А = Дебби одерживает победу в матче.
Ф Событие В = разминка продолжается менее 10 минут.
Вспомним, что:
Р[А] = 0.45 Р[В] = 0.65
Р[А и В] = 0.2.
Таким образом, вероятность выигрыша Дебби или непродолжительной
разминки получается следующей:
Р[А или В] = Р[А] + Р[В] - Р[А и В]
Р[АилиВ] =0.45 + 0.65 - 0.2= 0.90.
Смысл вычитания Р[А и В] в правиле сложения состоит в том, чтобы
избежать двойных расчетов. Наглядно это представлено в таблице ниже, в
которой распределение частот преобразовано в распределение
относительных частот.
96 Часть 2: Изучаем вероятность
Распределение относительных частот для примера с теннисом
Время разминки
Менее 10 минут
10 и более минут
Всего
Выигрыши Дебби Выигрыши Боба Всего
4/20 .= 0.20 9/20 = 0.45 12/20 = 0.65
5/20 = 0.25 2/20 = 0.10 7/20 = 0.35
9/20 = 0.45 11/20 = 0.55 20/20 = 1.00
Объединение Событий А и В представлено на рисунке 7.3.
Рис 7.3
Объединение
Событий АиВ
Эврика!
Время разминки Выигрыши Дебби Выигрыши Боба Всего
Менее 10 минут
10 и более минут
Всего
0.20
0.25
0.45
0.45
0.65
0.10
0.55
0.35
1.00
Преобразуя частоты в
относительные частоты с
помощью факторных таблиц,
всегда делите каждое число в
таблице на общее
количество наблюдений. В предыдущем
примере это 20 матчей.
Вероятность выигрыша Дебби (Событие
А) представлена прямоугольником в
первом столбце. Вероятность
непродолжительной разминки (Событие В) представлена
прямоугольником в первой строке.
Складывая Р[А] + Р[В], то есть первый столбец
плюс первая строка на рисунке 7.3, мы тем
самым дважды вычисляем Р[А и В] = 0.20 и
поэтому должны вычесть эту сумму в
правиле сложения для событий, не
являющихся взаимоисключающими.
Суммируем подученные сведения
Прежде чем переходить к последнему разделу по вероятности в этой главе,
давайте вернемся назад и посмотрим, каких результатов мы уже достигли.
На рисунке 7.4 представлены простые, суммарные и условные вероятности
распределения относительных частот для примера с теннисом.
Обратите внимание на определение событий.
Ф Событие А' = Боб одерживает победу.
Ф Событие В' = разминка продолжается 10 или более минут.
Условные вероятности раскрывают секрет моего успеха на корте.
Вероятность моего выигрыша после непродолжительной разминки, Р[А'/В],
составляет 0.69, а вероятность выигрыша моей соперницы после длительной
разминки, Р[А'/В'], составляет 0.29. Воистину я должен был избрать другой
пример для этой главы.
Глава 7: И снова о вероятности 97
Время разминки Выигрыши Дебби Выигрыши Боба Всего
(А) (А')
Менее 10 минут (В)
10 и более минут (В
Всего
Суммарные
вероятности
р[А и В] = 0.20
р[А и В] = 0.45
р[АиВ'] = 0.25
р[А' и В'] = 0.10
Простые
вероятности
р[А] = 0.45
р[А] = 0.55
р[В] = 0.65
р[В'] = 0.35
Р[А/В]=
Р[А'/В]=
Р[А/В']=
Р[А'/В']=
Условные
вероятности
,Р[АиВ] 0.20
Р[В] ~0.65
Р[А'ИВ]=0.45
"0.65
0.25
= 0.31
:0.69
Р[В]
Р[АиВ1=г:^
Р[В'] 0.35
Р[А'иВ'] 0.10
Р[В'] 0:35
г=0.29
Рис 7.4
Суммируем
вероятности
для примера
с теннисом.
Теорема Байеса
Томас Байес (1701—1761) вывел формулу, позволяющую вычислить Р[В/А],
исходя из информации о Р[А/В]. Теорема Байеса гласит:
Р[В/А]=
Р[В]Р[А/В]
(Р[В]Р[А/В]+Р[В] Р[А7В'])
где:
Р[В'] = вероятность дополнения События В,
Р[А/В'] = вероятность События А при том, что дополнение к Событию В
уже произошло.
На первый взгляд это уравнение локажется чересчур громоздким, но
давайте применим его к нашей задаче с теннисом, и все прояснится. С
помощью теоремы Байеса мы можем рассчитать Р[В/А], то есть вероятность того,
что разминка продолжалась менее 10 минут, зная, что Дебби одержала
победу. Используем полученные в предыдущем примере значения:
98 Часть 2: Изучаем вероятноаь
Р[В/А]=
Р[В/А]=
Р[В/А]=
0.650.31
(0.65 0.31)+(0.35 0.71)
0.20
0.20+0.25
0.20
0.20+0.25'
Зная, что Дебби одержала победу, мы можем
сказать, что существует 44%-ная вероятность, что
разминка длилась менее 10 минут.
Убедимся в правильности полученного
результата с помощью первоначальной факторной таблицы.
Поскольку Дебби выиграла 9 матчей, из которых в
4 случаях была проведена разминка, не
превышающая по времени 10 минут, получаем:
Р[В/А]=-=0.44.
Вот так вот! Я рассчитываю на продолжительные аплодисменты.
Томас Байес был не только
великим математиком.
Будучи пресвитером
использовал математические
методы в изучении религии.
Ваша очередь
Телефонный опрос 260 человек ставил своей целью узнать, насколько народ
приветствует предлагаемый законопроект. Все опрошенные были разделены
на демократов и республиканцев. Результаты опроса представлены в
факторной таблице ниже.
Партийная принадлежность
За
Против Всего
Республиканцы
Демократы
Всего
98
79
177
54
29
83
152
108
260
Один из опрошенных выбирается случайным образом.
Ф Событие А: выбранный участник опроса одобряет новый законопроект.
Ф Событие В: выбранный участник опроса — республиканец.
1. Определите вероятность того, что выбранный участник опроса
одобряет новый закон.
2. Определите вероятность того, что выбранный участник опроса
является республиканцем.
Глава 7: И снова о вероятности 99
3. Определите вероятность того, что выбранный участник опроса не
одобряет нового закона.
4. Определите вероятность того, что выбранный участник опроса
является демократом.
5. Определите вероятность того, что выбранный участник опроса
одобряет новый закон, если нам известно, что он республиканец.
6. Определите вероятность того, что выбранный участник опроса не
одобряет нового закона, если нам известно, что он республиканец.
, 7. Определите вероятность того, что выбранный участник опроса
одобряет новый закон, если нам известно, что он демократ.
8. Определите вероятность того, что выбранный участник опроса
одобряет новый закон и является республиканцем.
9. Определите вероятность того, что выбранный участник опроса
одобряет новый закон и является демократом.
10. Определите вероятность того, что выбранный участник опроса
одобряет новый закон или является республиканцем.
11. Определите вероятность того, что выбранный участник опроса
одобряет новый закон или является демократом.
12. С помощью теоремы Байеса вычислите вероятность того, что
выбранный участник опроса был республиканцем, если нам известно, что он
одобрил новый закон.
Повторение - мать учения
Ф Условной^азывается вероятность События А, если известно, что
Событие В уже произошло.
Ф События А и В считаются независимыми друг от друга, если произошедшее
Событие В никоим образом не влияет на Событие А. если События А и В не
являются независимыми друг от друга, тогда они считаются зависимыми.
Ф Для зависимых событий правило умножения гласит, что Р[А и В] =
Р[А/В] * Р[В]. Если события являются независимыми, правило
умножения упрощается до: Р[А и В] = Р[А] * Р[В].
Ф Два события считаются взаимоисключающими, если в течение
эксперимента они ни при каких условиях не могут происходить одновременно.
Ф Для взаимоисключающих событий правило сложения гласит, что Р[А
или В] = Р[А] + Р[В]. Если события не являются взаимоисключающими,
правило сложения выглядит так: Р[А или В] = Р[А] + Р[В] — Р[А и В].
Ф Теорема Байеса позволяет вычислить Р[В/А] на основе информации о
Р[А/В] с помощью следующей формулы:
Р[В]Р[А/В]
Р[В/А]=
(Р[В]Р[А/В]+Р[В'] Р[А/В'])
Впив мм хйЪь \»\\
■на
Принципы счета
и распределение
вероятностей
В этой главе
Ф Использование фундаментального принципа счета
Ф Различие между перестановками и комбинациями
Ф Определение случайной переменной и распределение
вероятностей
Ф Вычисление среднего и дисперсии дискретного
распределения "вероятностей
Что ж, мы добрались до последней из трех глав, посвященных
общим вероятностным понятиям. Эта глава создаст основу для
последних трех глав Части 2, в которых речь пойдет об
определенных типах распределений вероятностей. А уж после этого мы
с чистой совестью приступим к изучению статистики вывода.
Эта глава также научит вас счету. Но этот счет не имеет
практически ничего общего с тем, что вы видели на Улице
Сезам. Счет событий — это важный шаг при вычислении
вероятностей и поэтому должен осуществляться особенно тщательно.
Глава 8: Принципы счета и распределение вероятностей 101
Принципы счета
Классическая вероятность, с которой мы познакомились в Главе 6, требует
умения подсчитывать количество интересующих нас событий, а также
общее число событий, которые могут произойти в определенном выборочном
пространстве. Для простых событий вроде кидания одной кости количество
возможных исходов (всего их 6) очевидно. Но для более сложных событий,
примером которых является розыгрыш государственной лотереи, нам
придется положиться на особые методики, известные как принципы счета. В
следующих трех разделах речь пойдет именно об этих методиках.
Фундаментальный принцип счета
В жаркий полдень после непростого матча по гольфу Брайан, Джон и я
решаем восстановить утраченные силы посредством посещения магазина
мороженого, расположенного по дороге домой. Не успел я зайти в магазин,
как уже теряюсь в догадках, какой из 4 наполнителей и какую из 3 обливок
выбрать. Сколько существует возможных комбинаций наполнителя и
обливок мороженого? И тут мне на помощь приходит фундаментальный
принцип счета, который гласит, что если одно событие (выбор наполнителя
мороженого) может иметь т вариаций, а второе (выбор обливки) — п
вариаций, то общее количество вариаций обоих событий, происходящих вместе,
равно т * п. В моем случае это 4*3= 12 комбинаций наполнителя и
обливок, способных пустить коту под хвост
всю мою диету. (Оставлю эту тему для
другой главы.)
Этот принцип распространяется и на
большее количество событий. Помимо
наполнителей и обливок, мне
предстоит сделать выбор между маленькой и
большой порцией. Таким образом, я
получаю в свое распоряжение просто
невероятное количество комбинаций,
равное 4 * 3 * 2 = 24, которые
суммированы в таблице прямо после списка
вариантов.
В — ванильное
К — клубничное
Кф — кофейное
Термины
В соответствии с
фундаментальным принципом счета,
если одно событие может иметь т
вариаций, а второе - п вариаций, общее
количество вариаций обоих событий,
происходящих одновременно,
равняется т * п. Этот принцип применим и к
большему количеству событий.
Наполнители мороженого
Ш — смерть от шоколада
102 Часть 2; Изучаем вероятность
Обливки
СП — сливочная помадка
БС — баттерскотч (ирис из сливочного масла и жженого сахара)
КК — карамельные крошки
Размер
М — маленький
Б — большой
Список комбинаций (наполнитель-обливка-размер)
Ш-СП-Б
Ш-СП-М
Ш-БС-Б
Ш-БС-М
Ш-КК-Б
Ш-КК-М
В-СП-Б
В-СП-М
В-БС-Б
В-БС-М
В-КК-Б
В-КК-М
К-СП-Б
К-СП-М
К-БС-Б
К-БС-М
К-КК-Б
К-КК-М
Кф-СП-Б
Кф-СП-М
Кф-БС-Б
Кф-БС-М
Кф-КК-Б
Кф-КК-М
Попробуйте догадаться, на чем остановил свой выбор любитель шоколада?
Еще один пример использования фундаментального принципа счета —
это вычисление количества уникальных комбинаций государственных
автомобильных номерных знаков. Предположим, что номерной знак состоит из 3
букв, за которыми следуют 4 цифры. Цифра «0» и буква «О» не
используются, поскольку их схожий внешний вид может ввести в заблуждение.
Поскольку английский алфавит содержит 25 букв (без «О») и мы имеем 9 цифр
(без «0»), общее количество уникальных комбинаций рассчитывается
следующим образом:
Первая
буква
25*
Вторая
буква
25*
Третья
буква
25*
Первое
число
9*
Второе
число
9*
Третье
число
9*
Четвертое
число
9 =
Всего получаем 102 515 625 возможных комбинаций!
Перестановки
Перестановками называется количество различных способов расположения
объектов. Каждая перестановка встречается только один раз. Количество
перестановок п отдельных объектов равняется п! (читается как п факториал) и
вычисляется следующим образом:
л! = л*(л-1)*(л-2)*(л-3)*---*4*3*2*1
Глава 8: Прпнцппы счета и распределение вероятностей 103
По определению 0! = 1. Например,
6! = 6*5*4*3*2*1 = 720. В качестве
примера: существует 6 перестановок для
чисел 1, 2, 3, которые показаны ниже:
123 132 213 231 312 321.
Поскольку:
3! =3*2*1 = 6.
Термины
Перестановки-размещения -
это количество различных
способов представления объектов в
различном порядке. Количество
перестановок л объектов, взятых г за раз,
рассчитывается как:
лРг=
п\
(п-г)\
Перед началом профессионального
баскетбольного матча первые 5
игроков объявляются по 1 за раз. Сколько
существует способов объявления игроков? Количество перестановок
составляет 5! = 5*4*3*2*1 = 120.
Предположим, мы хотим выбрать отдельные объекты из группы.
Количество перестановок п объектов, взятых г за раз, определяется так:
пРг=-
п\
(п-г)\
Эврика! -
Проще вычислять количество перестановок-размещений с помощью такой формулы:
лРг=-
л!
(л-г)!
=л*(л-1)*(л-2) *•••*{ л-г+1).
• Эта формула действует потому, что каждое значение в знаменателе (нижняя часть
дроби) сводит на нет множество значений в числителе (верхняя часть дроби).
Но вернемся к нашему примеру с бейсболистами. Если всего в команде 12
игроков, сколько существует способов представления любых 5 игроков «
начале игры? В этом случае л = 12, а г = 5, поэтому количество перестановок
получится следующее:
Р =
12 г5
12! 12 *11 *10 *9 *8 *7 *6 *5 *4 *3 *2 *1
(12-5)!
7 *6 *5 *4 *3 *2 *1
Р =
12*5
12!
(12-5)!
-=12*11*10*9*8=95040.
Я очень рад, что не мне решать, кого объявлять первым!
Иногда порядок событий не имеет особого значения. Такие случаи
рассматриваются в следующем разделе.
104 Часть 2: Изучаем вероятность
Термины
Комбинациями называют
количество различных способов
представления объектов без учета
порядка. Количество комбинаций п
объектов, взятых гза раз, определяется таю
ЯС=-
л!
(л-г) г!
Комбинации
Комбинации подобны перестановкам с
тем лишь исключением, что порядок
объектов здесь не имеет значения.
Количество комбинаций п объектов, взятых г
за раз, определяется так:
с =?—.
п г (п-г)г\
Эврика!
Проще вычислять количество комбинаций с помощью такой формулы:
_ л! _л*(л-1)*(л-2)*---*(л-г+1)
п т~(п-г)г\~ г! *
Логика та же, что и в формуле с перестановками.
Например, в покере из колоды в 52 карты случайным образом выбирают 5
карт. Сколько существует комбинаций из пяти карт?
52^-5 —
52!
52*51*50*49*48
(52-5)!5! 5*4*3*2*1
=2598960
Сколько существует перестановок из пяти карт?
52!
52*5 :
(52-5)!
= 52*51*50*49*48=311875200
Перестановок из пяти карт получается больше, поскольку следующие
карты на руках в покере считаются двумя различными перестановками, но
считаются одной комбинацией, поскольку это те же самые карты, но
расположенные в другом порядке:
Набор карт 1
Пиковый туз
Червовая дама
Десятка пик
Десятка бубен
Тройка треф
Набор карт 2
Пиковый туз
Десятка пик
Червовая дама
Десятка бубен
Тройка треф
Глава 8: Прпнцппы счета и распределение вероятностей 105
Теперь, когда мы знаем общее количество комбинаций из пяти карт в
колоде из 52 карт, мы можем вычислить вероятность флэша, то есть все 5 карт
одной масти (пики, трефы, бубны или червы). Сначала нам необходимо
вычислить количество флэшей одной масти, например, бубен. Поскольку в
колоде количество карт бубновой масти равняется 13, количество выпадений
по 5 карт будет рассчитываться так:
г
13^-5
13!
13*12*11*10*9
(13-5)!5! 5*4*3*2*1
=1287
Поскольку в колоде 4 масти, общее количество вариантов флэш из пяти
карт любой масти будет равняться: 1287*4 = 5148. Следовательно,
вероятность сдачи флэша в наборе из 5 карт будет:
Р[Флэш] = 5148 =0.002.
2598960
То есть примерно дважды на 1000 раздач при игре в покер. Готовы сдавать
Эврика! . каРты?
С помощью комбинации удобно
вычислять вероятность выигрыша в
лотерее. При участии в обычной
лотерее вам необходимо выбрать 6 чисел
из возможных 49. Поскольку порядок
расположения чисел не играет роли,
мы пользуемся формулой для
вычисления комбинаций, а не
перестановок. Количество шестизначных
комбинаций из 49 возможных чисел
получается так:
В других книгах вы можете
встретить иное обозначение
о
Статисты обожают обзаводиться не
сколькими обозначениями одного и то
го же понятия!
г =
49^-6
49! _ 49*48*47*46*45*44
(49-6)!6! ~ 6*5*4*3*2*1
:13983816.
Поскольку всего существует около 14 миллионов возможных
шестизначных комбинаций, вероятность выигрыша вашей комбинации будет
рассчитываться следующим образом:
Р[выигрыш в лотерее 6 из 49] =
1
13983816
-=0.00000007.
106 Часть 2: Изучаем вероятность
^^г .Внимание!
Вероятность не обладает памятью. Это значит, что 6 чисел, выпавших в розыгрыше
лотереи на прошлой неделе, имеют ту же вероятность выпадения на этой неделе. Это
объясняется тем, что два розыгрыша являются независимыми событиями и совершенно не
влияют друг на друга. Поэтому выбор 6-значного номера лишь по причине его невыпадения за
последнее время нисколько не увеличивает ваши шансы на выигрыш. Простите, если с
моей подачи рухнули ваши надежды на скорый выигрыш.
С такими шансами на победу вам, право, не стоит пока отказываться от
честного заработка.
Использование Excel для вычисления перестановок и комбинаций
У меня для вас хорошая новость: вместо того чтобы возиться со всеми
этими факториалами, мы можем использовать Excel для вычисления
количества перестановок и комбинаций. В одном из приведенных выше
примеров мы подсчитали, что 12Рб = 95 040. Подтвердим этот результат с
помощью встроенной функции ПЕРЕСТ со следующими
характеристиками:
ПЕРЕСТ(п, г)
На рисунке 8.1 показано, как выглядит функция ПЕРЕСТ для 12Ps.
Ячейка А1 содержит формулу программы Excel = ПЕРЕСТ(12,5) с
результатом — 95 040.
А теперь попробуем с помощью Excel посчитать количество комбинаций.
Вспомним, что 49^6 — 13 983 816. Используем функцию ЧИСЛКОМБ со еле-
дующими характеристиками:
- ЧИСЛКОМБ(п,г)
На рисунке 8.2 показана функция ЧИСЛКОМБ для 49^6-
Глава 8; Принципы счета и распределение вероятностей 107
Рис 8.2
Функция ЧИСЛКОМБ
программы Excel.
1 Гг'а'' 1 Ё
I; V 1 у:?Щ]Ц
1 2
t:
$1& :;; 86 Л?.--* : Л<^Г
-■
.&****.
л
1 *•
Ячейка А1 содержит формулу программы Excel = ЧИСЛКОМБ(49,6) с
результатом — 13 983 816. Вот видите, я говорил, что новость будет хорошая.
Шансы выиграть в лотерее так ничтожно малы, что трудно даже определить вероятность
выигрыша. Пример с лотереей «6 из 49»: если бы я покупал лотерейный билет каждый день в
течение целого .года, вероятность моего выигрыша составляла бы один раз за 38 312 лет.
Заметим, что 38 000 лет тому назад люди жили в пещерах каменного века, и я не уверен, что
мне хотелось бы ждать выигрыша столько времени, сколько бы денег я ни получил.
На этом мы завершаем разговор о принципах счета. Многие из вас,
должно быть, удивлены тем, как сложно считать события. Обращу ваше внимание
на то, что это очень важное понятие в статистике, к которому мы еще
обратимся в Главе 9.
Распределения вероятностей
Этот раздел Главы 8 подготовит вас к изучению последних трех глав Части 2.
Нам необходимо проделать некоторую предварительную работу в
отношении распределения вероятностей, прежде чем мы перейдем к обсуждению
определенных типов вероятностей, описанных в Главах 9, 10 и 11.
В общем, распределение вероятностей — это перечень всех возможных
исходов эксперимента вместе с относительной частотой или вероятностью
каждого исхода. В качестве примера рассмотрим следующий: дважды подбросить
монетку и зафиксировать количество «орлов» (О). Выборочное пространство
для данного эксперимента представлено в таблице ниже (решка — Р).
Количество «орлов»
2
1
1
0
Первая монета
О
О
Р
Р
Вторая монета
О
Р
О
Р
108 Часть 2: Изучаем вероятность
В представленной ниже таблице показано распределение относительных
частот для количества «орлов».
Количество «орлов»
Частота
Относительная частота
0
1
2
1
2
1
Bcei
х> = 4
1/4 = 0.25
2/4 = 0.50
1/4 = 0.25
Всего = 1.00
Эврика!
Распределения вероятностей
играют весьма значительную
роль в статистике вывода.
Четкое понимание этого вопроса
является неотъемлемой частью
успешного понимания статистики.
В предыдущей таблице представлено
распределение вероятностей для
количества «орлов» дважды подброшенной
монетки. Так, вероятность выпадения
двух «орлов» в результате двух
подбрасываний равняется 25%.
Перед тем как перейти к детальному
изучению распределений вероятностей,
нам необходимо ввести несколько
основных терминов.
Случайные переменные
В Главе 6 мы говорили о проведении экспериментов с целью получения данных.
Примерами экспериментов было кидание костей и игра в теннис с супругой.
Исходы этих экспериментов считаются случайными переменными. По
определению, эти исходы неизвестны нам с точностью до момента проведения
эксперимента. Но с помощью теории вероятности и статистики мы зачастую можем
делать предположения относительно вероятности определенных исходов. На-
Термины
У ^
Случайная переменная - это
исход, приобретающий
численное значение в качестве
результата эксперимента. До момента
проведения эксперимента значение нельзя
предугадать. Значение случайной
переменной часто обозначается х.
Например, в случае с киданием одной
кости получаем:
P[x = lJ = i.
О
пример, я не могу с точностью
предугадать результат кидания кости, но я знаю,
что вероятность выпадения «1»
составляет 1/6. В этом случае случайной
переменной является число, которое выпадет.
Все случайные переменные
создаются неравнозначными. Первый тип носит
название непрерывных случайных
переменных, являющихся результатом
измерения на непрерывной числовой
прямой. Например, каждое утро, когда я
делаю глубокий вдох и встаю на весы в
ванной, чтобы взвеситься (сделав
глубокий вдох и задержав воздух, я чувствую,
как мой вес становится больше), я с ужа-
Глава 8: Принципы счета п распределение вероятностей 109
сом и недоверием взираю на непрерывную случайную переменную.
(Возможно, мне следовало бы остановить свой выбор на маленькой порции
мороженого.) Примером значений для непрерывной случайной переменной
этого типа являются 180, 180.5, 183.2 и т.д. (На этом я, пожалуй,
остановлюсь.) Поскольку это и есть непрерывная случайная переменная, мой
утренний вес может принять бесчисленное количество возможных значений, и
это весьма печально.
Второй тип случайной переменной — дискретная. Дискретные случайные
переменные являются результатом подсчета исходов, а не их измерения.
Такие переменные могут принять определенное количество целых значений в
пределах интервала. Примером дискретной случайной переменной является
результат моей игры в гольф для следующего раунда, поскольку это значение
получено в результате подсчета общего количества моих ударов по лункам.
Очевидно, это значение должно быть целым числом, например, 94,
поскольку частичные удары посчитать
невозможно (хотя порой мои удары
кажутся именно такими).
Другими примерами непрерывных
случайных переменных являются
следующие:
Ф Количество местных осадков в
виде дождя, в дюймах
Ф Количество времени,
необходимого для обслуживания клиента в
магазине
Ф Скорость автомобиля,
измеряемая радаром
Другими примерами дискретных случайных переменных являются:
Ф Количество дней в месяце, в которые шел дождь
Ф Количество клиентов, стоящих в очереди на кассу в магазине
Ф Количество автомобилей, которые двигались со скоростью,
превышающей разрешенную
Непрерывные случайные переменные будут подробно рассмотрены в
Главе 11. Оставшаяся часть этой главы, а также Главы 9 и 10, посвящены
исключительно дискретным случайным переменным.
Дискретные распределения вероятностей
Перечень всех возможных исходов экспериментов для дискретной
случайной переменной вместе с относительной частотой или вероятностью каждо-
Термины
И
Случайная переменная
считается непрерывной, если она
может принимать только числовые
значения в пределах определенного
интервала, полученные в результате
измерения Исхода эксперимента. Случайная
переменная считается дискретной,
если она может принимать только опре- !
деленные целые значения в результате
подсчета исхода эксперимента.
ПО Часть 2: Изучаем вероятность
го исхода называется дискретным распределением вероятностей. Для
иллюстрации этого понятия я воспользуюсь следующим примером.
Моя старшая дочь Кристин в период с 7 до 13 лет была очень хорошей
пловчихой. Этот талант достался ей явно не от меня. В таблице ниже
представлено распределение относительных частот с перечнем
финишировавших первыми, вторыми, третьими, четвертыми и пятыми в 50 заплывах.
Место Количество заплывов Относительная частота (вероятность)
27/50 = 0.54
12/50 = 0.24
7/50 = 0.14
3/50 = 0.06
1/50 = 0.02
Всего
Если в качестве случайной переменной определим х = место, которое
заняла в заплыве Кристин, предыдущая таблица будет дискретным
распределением вероятностей для переменной х. Исходя из этой таблицы, мы можем
вычислить вероятность того, что Кристин займет первое место:
Р[х = 1] = 0.54.
Вероятность того, что Кристин займет первое или второе место,
получается так:
Р[х = 1 или* = 2] = 0.54 4- 0.24 = 0.78.
На рисунке 8.3 показано графическое представление дискретного
распределения вероятностей для х.
1
2
3
4
5
27
12
7
3
1
Всего
Рис 8.3 °-6*
Дискретное 0.5 -
распределение £
вероятностей g 0.4
для заплывов х
Кристин. g u,°
&0.2
m
0.1
3
Место
Глава 8: Принципы счета и распределение вероятностей 111
Правила дискретных распределении вероятностей
Любое дискретное распределение вероятностей должно отвечать ряду
требований.
Ф Любой исход распределения должен быть взаимоисключающим, то есть
значение случайной переменной не может попадать в более чем одну
группу распределения частот. Например, Кристин не может
одновременно занять первое и второе места.
Ф Вероятность каждого исхода Р[х] должна находиться в интервале от 0 до 1,
то есть 0 < Р[х] < 1 для всех значений х. В предыдущем примере Р[х = 3] =
= 0.14, то есть как раз между 0 и 1.
Ф Сумма вероятностей всех исходов распределения должна равняться 1,
п
то есть ]>]Р[х,]=1. В примере с плаванием:
. '=1
Р[х = 1] + Р[х = 2] + Р[х = 3] -I- Р[х = 4] +Р[х = 5] =
= 0.54 + 0.24 Н- 0.14 -h 0.06 4- 0.02 = 1.00
Среднее значение дискретного распределения вероятностей
Среднее значение дискретного распределения вероятностей — это
взвешенное среднее (см. Главу 4), вычисленное с помощью следующей формулы:
п
где:
ц = среднее значение дискретного распределения вероятности,
Xj = значение случайной переменной для i-ro исхода,
P[Xi] = вероятность i-ro исхода,
п = количество исходов распределения.
В таблице ниже представлено переработанное распределение
вероятностей.
Место х4 Вероятность P[xJ
1 0.54
2 0.24
3 0.14
4 0.06
5 0.02
112 Часть 2; Изучаем вероятность
Среднее значение дискретного распределения вероятностей получается
следующим:
ju = £x,. *P[x,]=i(10.54) + (2-0.24) + (3-0.14) + (4-0.06) + (5-0.02)
ц = 1.78.
Полученный результат говорит нам о том, что среднее место, которое
занимает Кристин в заплыве, — 1.78! Как ей это удается? Конечно, полученное
число не может быть результатом ни одного заплыва. Оно представляет
собой усредненный результат множества заплывов. Среднее значение
дискретного распределения вероятностей не обязательно должно быть целым
значением (в нашем случае это 1, 2, 3, 4 или 5).
Другим термином для описания среднего значения распределения
вероятностей является математическое ожидание — Е[х]. Таким образом:
Щх] = ц = £Х'*РМ-
/=1
Кажется, я уже упоминал о том, что
статисты часто используют различные
обозначения одного и того же понятия!
Дисперсия и стандартное отклонение дискретного
распределения вероятности
Только вы подумали, что можно расслабиться, как на сцене появляется еще и
дисперсия! Что ж, если вы знакомы с одним способом вычисления
дисперсии, значит, вы знакомы и со всеми остальными способами. Дисперсия для
дискретного распределения вероятности рассчитывается так:
а2=£(х,-^)2*РМ.
где:
а2 = дисперсия дискретного распределения вероятности.
Для вас не будет секретом, что стандартное отклонение распределения
выглядит так:
' а = л/?.
Для демонстрации этих уравнений обратимся к распределению
предыдущего примера с плаванием Кристин. Вычисления представлены в таблице
ниже.
Термины
(Р^ Математическое ожидание -
это средняя величина
распределения вероятности.
Глава 8:
Принципы счета и распределение вероятностей
113
X. Р[Х|
1 И х, - ц (Xj-ц)2 (х,-ц)2Р[;
fj
1
2
3
4
5
0.54
0.24
0.14
0.06
0.02
1.78
1.78
1.78
1.78
1.78
-0.78
0.22
1.22
2.22
3.22
0.608
0.048
L.488
4.928
10.368
0.328
0.012
0.208
0.296
0.208
a2 = £(x,-nf*P[Xi]=1.052.
1=1
Стандартное отклонение данного распределения вычисляется так:
a = >/a5" = Vi:052=1.026.
Существует и более эффективный способ вычисления дисперсии
дискретного распределения вероятности:
*2=[1Х*рм]-ц2.
В таблице ниже представлены соответствующие вычисления для примера
с плаванием.
.*i РМ х? *?»РМ
1 0.54 1 0.54
2 0.24 4 0.96
3 0.14 9 1.26
4 0.06 16 0.96
5 0.02 25 0.50
£х?*Р[х,] = 4.22
V »=1 )
a2 = 4.22 - (1.78)2
a2 = 1.052
Как видите, результат тот же самый, но приложено меньше усилий!
114 Часть 2: Изучаем вероятность
Ваша очередь
1. Посетителю ресторана предлагается меню, содержащее 3 аперитива, 8
главных блюд, 4 десерта и 3 вида напитков. Сколько различных
вариантов блюд можно заказать?
2. Тест содержит 10 вопросов, к каждому из которых прилагаются 4
варианта ответов. Какова вероятность того, что студент, отвечая на каждый
вопрос методом «случайного тыка», выполнит весь тест правильно?
3. Команды НБА с 13 худшими результатами в конце сезона принимают
участие в лотерее с целью определить порядок, в котором они будут
отбирать новых игроков на следующий сезон. Сколько существует
различных вариантов порядка отбора для этих 13 команд?
4. В заплыве участвует 8 пловцов. Сколько существует вариантов того, что
пловцы займут первое, второе и третье места?
5. Сколько существует различных способов ранжирования 10 новых
кинолент критиками на получение первого и второго мест?
6. Замок с цифровой комбинацией имеет 40 чисел и откроется при
правильном выборе 3-значной комбинации. Сколько возможных
комбинаций существует?
7. Я хотел бы выбрать 3 книги в бумажной обложке из списка 12 книг, чтобы
взять с собой на отдых. Сколько различных наборов книг я могу выбрать?
8. 12 присяжных должны быть выбраны из 50 человек. Сколько разных
присяжных можно выбрать?
9. Был проведен опрос с участием 450 семей с целью выяснить, сколько
кошек имеет каждый из респондентов. В таблице ниже представлены
результаты опроса.
Количество кошек Количество семей
0 137
1 160
2 112
3 31
4 10
Постройте распределение вероятностей для этих данных и вычислите
среднее значение, дисперсию и стандартное отклонение.
Повторение - мать учения
Ф Фундаментальный принцип счета гласит, что если одно событие может
иметь т вариаций, а второе — п вариаций, то общее количество вариа-
Глава 8: Принципы счета и распределение вероятностей 115
ций обоих событий, происходящих одновременно, равно т*п. Этот
принцип может применяться к более чем 2 событиям.
Ф Перестановки — это количество различных способов расположения
объектов в порядке. Комбинации — это количество различных способов
представления объектов с учетом того, что порядок не имеет никакого
значения.
Ф Распределение вероятностей — это перечень всех возможных исходов
эксперимента вместе с относительной частотой или вероятностью
каждого исхода,
Ф Случайная переменная — это исход, который принимает числовое
значение как результат эксперимента. Значение невозможно определить с
точностью до момента проведения эксперимента.
Ф Случайная переменная является непрерывной, если она может
принимать любое числовое значение как результат измерения исхода
эксперимента. Случайная переменная считается дискретной, если она может
принимать лишь ограниченное число целых значений как результат
подсчета исхода эксперимента.
Ф Среднее значение дискретного распределения вероятности
рассчитывается по формуле:
Л
ц=2>,*Р[х,].
1=1
Ф Дисперсия дискретного распределения вероятности вычисляется по
формуле:
о*=2>,-Ц)2*Ч*]-
Г* 88& ЯЯКь :■:■:■'.:■:■.
Янк и£389 ИЭВ
Биноминальное
распределение
вероятностей
В этой главе
Ф Описание характеристик биноминального эксперимента
Ф Вычисление вероятностей биноминального распределения
Ф Определение вероятностей с помощью биноминальной
таблицы
Ф Определение биноминальных вероятностей с помощью
Excel
Ф Вычисление среднего значения и стандартного
отклонения биноминального распределения
Наше обсуждение дискретного распределения вероятностей
пока ограничивалось произвольными распределениями,
основанными на предварительно собранных данных. Но
существуют и теоретические распределения вероятностей,
рассчитанные по математической формуле, а не основанные на
существующих данных. В этой главе мы рассмотрим первое из них —
биноминальное распределение вероятностей.
Глава 9: Биноминальное распределение вероятностей 117
Есть целый круг задач, при решении которых мы заинтересованы в
определении вероятности повторяющегося события. Классическим примером
является вопрос, которым в течение многих лет преподаватели мучают
студентов: Какова вероятность выпадения «орла» семь раз при 10-кратном
подкидывании монеты? Закончив изучение этой главы, вы сможете без труда
ответить на этот каверзный вопрос.
Характеристики биноминального эксперимента
Если ваша память вам не изменяет, то вы должны вспомнить, что в Главе 6
мы определили эксперимент как процесс измерения или наблюдения за
каким-либо процессом с целью сбора данных. Предположим, нас интересует
эксперимент, подразумевающий выполнение профессиональным
баскетболистом трех штрафных бросков. Каждый штрафной бросок считается
испытанием для эксперимента. Для данного конкретного эксперимента
существуют два возможных исхода для каждого испытания: либо штрафной бросок
попадает в корзину (успех), либо не попадает (неудача). Поскольку
возможны только два исхода для каждого испытания, эксперимент считается
биноминальным.
Положим,- речь идет о Майкле
Джордане, который за всю свою
баскетбольную карьеру забросил 80% всех
штрафных бросков. Таким образом,
вероятность (р) попадания в корзину
мяча с любого штрафного броска
составляет 0.80. Поскольку существует
всего два возможных исхода,
вероятность непопадания (д) составляет 0.20.
Для биноминального эксперимента
значения р и q должны быть
постоянными для каждого испытания
эксперимента. Поскольку в биноминальном
эксперименте может быть лишь два
исхода, получаем: р = 1 — д.
Наконец, в биноминальном
эксперименте каждое испытание должно
быть независимым от других. Иными
словами, вероятность успеха второго
броска не зависит от того, был ли
успешным первый бросок. Примерами
биноминальных экспериментов
являются следующие:
Ф Проверка запчасти на предмет
неисправности после производства
Термины
Биноминальный эксперимент
обладает следующими
характеристиками: (1) Эксперимент состоит
из фиксированного количества
испытаний, обозначаемых гг, (2) Каждое
испытание имеет два возможных исхода:
успех или неудача; (3) Вероятность
успеха и вероятность неудачи
являются постоянными величинами в рамках
эксперимента; (4) Каждое испытание
является независимым от других
испытаний эксперимента.
Мысли вел
Биноминальные эксперименты также
называют процессом Бернулли, по
имени швейцарского математика
Джеймса Бернулли, жившего в 17-м
веке. Многократное повторение
процесса Бернулли - это испытания
Бернулли. Эта мысль преследует
студентов уже сотни лет!
118 Часть 2; Изучаем вероятность
Ф Наблюдение за количеством правильных ответов в тесте с
множественным выбором
Ф Вычисление количества американских семей, имеющих выход в
Интернет
Изучив основные правила биноминальных экспериментов, мы можем
смело переходить к освоению биноминальных вероятностей.
Биноминальное распределение вероятностей
Биноминальное распределение вероятностей позволяет нам вычислить
вероятность определенного количества успехов для определенного количества
испытаний. То есть случайной переменной для данного распределения будет
количество успехов, за которыми мы ведем наблюдение. Чтобы
продемонстрировать вам, что представляет собой биноминальное распределение, я
обращусь к следующему примеру.
Дебби научила нашу собаку Кейли выполнять немыслимый трюк. Каждое
утро, когда супруга выпускает нашего четвероногого друга через заднюю
дверь погулять, та как молния несется по нашей довольно длинной
подъездной дорожке, хватает газету, бежит обратно к двери и аккуратно кладет
газету на ступеньку. За эту рутинную, но так необходимую работу она получает
две чашки сухого собачьего корма. Вы скажете, что это просто чудо. Но это
еще не все. Надо отметить, что Кейли совсем неглупа. Она сделала
удивительный вывод: 2 завтрака лучше, чем один. В результате она при каждой
возможности рыскает по всем соседям в поисках газет, которые можно
положить на ступеньки. А однажды она приволокла огромную телефонную
книгу, наивно полагая, что получит дополнительную порцию. Мы отчаянно
пытались научить собаку возвращать обратно эти газеты, но собачьи мозги,
оказывается, отказываются работать в обратном направлении.
Поэтому во второй половине дня я всегда занят тем, что незаметно
возвращаю украденную прессу в надежде, что соседи не заметят собачьих
слюней на своих газетах трехдневной давности. Как бы то ни было,
предположим, что в определенный день существует 30%-ная вероятность, что
Кейли вернет газету хозяину, и 70%-ная — что она этого не сделает. Положим,
что в день она может вернуть не более одной газеты. Такой сценарий
представляет собой биноминальный
эксперимент, каждый день в котором
является испытанием Бернулли с р = 0.30
(вероятность успеха) ид = 0.70
(вероятность неудачи). Мы можем вычислить
вероятность г успехов в п испытаниях с
помощью биноминального
распределения, воспользовавшись следующей
формулой:
Эврика!
Из Главы 8 вспомним, что
п!
{п-г)\г\
-=„СГ
- количество комбинаций п объектов,
взятых г за раз.
Глава 9: Биноминальное распределение вероятностей 119
Р[г,л]=—^_pV"r
(п-г)\г\
С помощью этого уравнения мы можем определить вероятность того, что
в течение следующих 5 дней Кейли вернет 3 газеты.
Р[3,5] =—-—(0.3)3(0.7)5^
1 J (5-3)!ЗГ
P[3,5] = f—)(0.027)(0.49) =0.1323
Существует 13%-ная вероятность, что в течение следующих 5 дней наша
воришка вернет истинным владельцам их почту. Мы можем также определить
вероятность того, что она вернет 0, 1, 2, 4 или 5 газет за следующие 5 дней.
Для г = 0:
Р'0,5'" ^-niini'0'3'0'0,7' i*L*r Из Главы 8 вспомним, что О! = 1.
(5-0)!0!
P[0,5]=f^-l(l)(0.1681) =0.1681
Эврика!
Также х° = 1 для любого значе-
™_
ниях.
Для г = 1:
5! —М,П^5Ч
рП51= :—(0.3)!(0.7)
L J (5-1)!1Г
P[l,5]=f—1(0.3)(0.2401) =0.3601
Дляг = 2
РГ2,51= -—(0.3)2(0.7)
L J (5-2)!2!
,5-2
Р [2,5]=(—1(0.09) (0.343) =0.3087
Дляг = 4
p[4,5l=—-—{OSftO.J)5^
L J (5-4)!4Г
*5Кш)
1(0.0081) (0.7) =0.0283
120 Часть 2: Изучаем вероятноаь
Дляг = 5
Р[5Г5]=
5!
(5-5)\5\
(0.3)5(0.7)5
Р.[*5]=-
5!
-(0.3)5(0.7)5
(5-5)!5!
В таблице ниже представлены все полученные выше вероятности.
г Р[#\ 5]
0
1
2
3
4
5
0.1681
0.3601
0.3087
0.1323
0.0283
0.0024
Всего = 1.0
Эта таблица представляет собой биноминальное распределение
вероятностей для г успехов в 5 испытаниях с вероятностью успеха 0.30. Обратите
внимание, что сумма всех вероятностей равна 1 — это требование для всех
распределений вероятностей. На рисунке 9.1 распределение вероятностей
представлено в виде гистограммы.
Рпс9.1
Биноминальное
распределение
вероятностей.
о
о
х
о
о.
ф
ш
0.4
0.3
0.2
0.1
2 3 4
Количество успехов
Глава 9: Биноминальное распределение вероятностей 121
Из этого рисунка понятно, что наиболее вероятное количество газет,
которые Кейли вернет в течение следующих пяти дней, — это всего 1
газета.
Наконец, мы можем определить вероятность сложных событий для
данного распределения. Например, вероятность того, что за следующие 5 дней
Кейли утащит по крайней мере 3 газеты, определяется так:
Р[г>3] = Р[3, 5] + Р[4, 5] + Р[5, 5]
Р[г>3] = 0.1323 + 0.0283 + 0.0024 = 0.163.
Вероятность того, что за следующие 5 дней Кейли утащит не более 1
газеты, определяется так:
Р[/<1] =Р[0,5] +Р[1,5]
Р[/<1] = 0.1684 + 0.3601 = 0.528$.
Наши соседи были бы в ужасе при виде полученных результатов!
Биноминальные таблицы вероятностей
По мере увеличения количества испытаний в вашем биноминальном
эксперименте вычисление вероятностей с помощью предыдущих формул
приведет к тому, что откажут не только батарейки ваших калькуляторов, но и
ваши мозги. Существует более простой способ определения этих
вероятностей — биноминальные таблицы вероятностей, представленные в
Приложении В этой книги. Ниже приведен отрывок из этого приложения, в котором
подчеркнуты вероятности, имеющие отношение к нашему предыдущему
примеру.
Таблица вероятностей организована по количеству п — общему числу
испытаний. Строки таблицы представлены количеством успехов (г), а
столбцы — вероятностями успеха (р). Обратите внимание, что сумма
каждого блока вероятностей для определенного значения составляет 1.
Значения р
п г 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
40 0.6561 0.4096 0.2401 0.1296 0.0625 0.0256 0.0081 0.0016 0.0001
2 0.0486 0.1536 0.2646 0.3456 0.3750 0.3456 0.2646 0.1536 0.0486
3 0.0036 0.0256 0.0756 0.1536 0.2500 0.3456 0.4116 0.4096 0.2916
4 0.0001 0.0016 0.0081 0.0256 0.0625 0.1296 0.2401 0.4096 0.6561
122 Часть 2: Изучаем вероятность
Значения р
п г 0.1 0.2 0.3 0.4 0.5
0.6
0.7
0.8
0.9
50
1
2
3
4
5
0.5905
0.3280
0.0729
0.0081
0.0005
0.0000
0.3277
0.4096
0.2048
0.0512
0.0064
0.0003
01681 0.0778 0.0313 0.0102 0.0024 0.0003 0.0000
0.3601 0.2592 0.1563 0.0768 0.0284 0.0064 0.0005
0.3087 0.3456 0.3125 0.2304 0.1323 0.0512 0.0081
0.1323 0.2304 0.3125 0.3456 0.3087 0.2048 0.0729
0.0283 0.0768 0.1563 0.2592 0.3601 0.4096 0.3281
0.0024 0.0102 0.0313 0.0778 0.1681 0.3277 0.5905
Биноминальные таблицы имеют одно существенное ограничение: вы
можете использовать только те значения р, которые представлены в таблице.
Например, предыдущая таблица не подойдет для р = 0.35. В других
учебниках по статистике вы можете найти более развернутые биноминальные
таблицы, чем в Приложении В.
Использование Excel для вычисления
биноминальных вероятностей
Весьма удобно рассчитывать биноминальные вероятности с помощью
нашего старого друга — программы Excel — и встроенной в эту программу
функции БИНОМРАСП со следующими характеристиками:
БИНОМРАСП (г, п, р, интегральная)
где:
интегральная = ЛОЖЬ, если вы хотите, чтобы число успехов в
точности равнялось г
интегральная — ИСТИНА, если вы хотите, чтобы число успехов не
превышало г
Например, на рисунке 9.2 показана функция БИНОМРАСП для
вычисления вероятности того, что в течение следующих 5 дней Кейли вернет ровно
2 газеты.
В ячейке А1 содержится формула = БИНОМРАСЩ2; 5; 0,3; ЛОЖЬ) с
результатом 0.3087.
С помощью Excel мы также можем вычислить вероятность того, что в
течение следующих 5 дней Кейли вернет не более 2 газет, как показано на
рисунке 9.3.
В ячейке А1 содержится формула = БИНОМРАСП(2; 5; 0,3; ИСТИНА) с
результатом 0.8369. Тот же результат можно получить вручную по формуле:
Глава 9: Биноминальное распределение вероятностей 125
Рис 9.2
Функция БИНОМРАСП
для вычисления числа
успехов, в точности
равного г.
Рис. 9.3
Функция БИНОМРАСП
для числа успехов
не более г.
Р[г<2] = Р[0, 5] + Р[1, 5] + Р[2, 5]
Р[г<2] = 0.1681 + 0.3601 + 0.3087 = 0.8369.
Другими словами, существует 83%-ная вероятность, что в течение
следующих 5 дней Кейли окажется у нашей задней двери с 0, 1 или 2 не
принадлежащими нам газетами. Эта собака не оставляет мне ни минуты
отдыха!
Преимуществом использования Excel для вычисления биноминальных
вероятностей является то, что вы не ограничены значениями р,
представленными в Приложении В. Функция БИНОМРАСП позволяет нам использовать в
качестве р любое значение от 0 до 1.
Среднее значение и стандартное отклонение
биноминального распределения
Среднее значение биноминального распределения вероятностей может
быть определено по следующей формуле :^
jii = пр,
где:
п = число испытаний,
р = вероятность успеха.
124 Часть 2: Изучаем вероятность
Для примера с Кейли среднее значение распределения будет следующим:
ц = пр = (5) (0.3) = 1.5 газеты.
Другими словами, каждые 5 дней Кейли приносит в среднем по 1,5 газеты.
Стандартное отклонение биноминального распределения вероятностей
вычисляется по следующей формуле:
o = y]npq,
где:
q = вероятность неудачи.
Для нашего примера стандартное отклонение распределения получается
следующим:
а = yfnpq = ^/(5) (0.3) (0.7) =1.02 газеты.
Вот мы и закончили изучение биноминального распределения
вероятностей. Но не печальтесь. Мы снова встретимся с этим распределением в
следующих главах.
Ваша очередь
1. Какова вероятность выпадения в точности 7 «орлов» при 10-кратном
подбрасывании монеты?
2. Колледж Goldey-Beacom College ежегодно принимает 75% студентов из
подавших заявление о поступлении. Какова вероятность того, что будут
приняты точно 3 из следующих 6 подавших документы на поступление?
3. Майкл Джордан выполняет 80% всех штрафных бросков. Какова
вероятность того, что он выполнит как минимум 6 из следующих 8 штрафных
бросков?
4. Студент методом «случайного тыка» отвечает на 12 вопросов теста, в
котором каждый вопрос имеет 5 вариантов ответа. Какова вероятность
того, что студент ответит правильно точно на 6 вопросов?
5. Статистика свидетельствует о том, что 5% посетителей определенного
сайта что-либо приобретают на нем. Какова вероятность того, что их
следующих 7 посетителей не более 2 сделают покупки на сайте?
6. В течение сезона 2002 года средняя бэттинг-результативность Барри
Бондза, игрока Высшей Лиги Бейсбола, составила 0.370. Постройте
биноминальное распределение вероятностей для числа успехов (ударов) за
5 официальных игр сезона?
Глава 9: Биноминальное распределение вероятностей 125
Повторение - мать учения
Ф Биноминальный эксперимент имеет лишь 2 возможных исхода д,ля
каждого испытания.
Ф Для каждого биноминального эксперимента вероятности успеха и
неудачи являются постоянными величинами.
Ф Каждое испытание биноминального эксперимента не зависит от других
испытаний данного эксперимента.
Ф Вероятность г успехов в п испытаний при биноминальном
распределении вычисляется по формуле:
L J (п-г)\г\ Ч
Ф Среднее значение биноминального распределения вероятностей
вычисляется по формуле: ц = пр.
Ф Стандартное отклонение биноминального распределения вероятностей
вычисляется по формуле:
o = \Jnpq.
Распределение
вероятностей Пуассона
В этой главе
Ф Описание характеристик процесса Пуассона
Ф Вычисление вероятностей с помощью уравнений Пуассона
Ф Использование таблиц вероятностей Пуассона
Ф Использование программы Excel для вычисления
вероятностей Пуассона
Ф Использование уравнения Пуассона для
приблизительного вычисления биноминального уравнения
Разобравшись с биноминальным распределением
вероятностей, мы можем смело переходить к следующему шагу —
дискретному теоретическому распределению, распределению
Пуассона. Это распределение вероятностей названо в честь
Симеона Пуассона, французского математика, работавшего над
распределением в начале 19-го века.
Распределение Пуассона применяется для вычисления
вероятности того, что определенное событие произойдет в течение
определенного периода времени. Такое распределение может
быть использовано для определения вероятности того, что в
течение следующего часа в магазин войдут 10 покупателей или
Глава 10: Распределение вероятностей Пуассона 127
что в течение следующего месяца на оживленном перекрестке произойдут
два автомобильные аварии. Так давайте возьмем несколько тонких
французских блинчиков и круассанов и окунемся в мир французской математики.
Характеристики процесса Пуассона
В Главе 9 мы определили биноминальный эксперимент, также известный под
названием процесса Бернулли, как подсчет числа успехов в определенном
количестве испытаний. Результатом каждого испытания является успех или
неудача. Процесс Пуассона подсчитывает число реализаций события за
определенный период времени, в определенной области, расстоянии или
любой другой тип измерения.
Процесс Пуассона может иметь любое количество исходов в пределах
выбранной единицы измерения. Например, число покупателей, которые зайдут
в местный круглосуточный магазин в течение следующего часа, может
равняться 0, 1, 2, 3 и т.д. Случайной переменной распределения Пуассона будет
фактическое количество реализаций; в данном случае — количество покупа-.
телей, которые зайдут в магазин в течение следующего часа.
Среднее значение распределения Пуассона — это среднее количество
реализаций, ожидаемых в пределах единицы измерения. Для процесса
Пуассона среднее значение должно быть одинаковым для каждого интервала
измерения. Например, если среднее число покупателей, заходящих в магазин
каждый час, равняется 11, это среднее значение должно применяться к
каждому одночасовому приращению.
Последняя характеристика процесса Пуассона: число реализаций в течение
одного интервала не зависит от числа реализаций в других интервалах. Иными
словами, если в первый час работы магазина его посетят 6 покупателей, это
никоим образом не скажется на количестве покупателей второго часа работы.
<J^ Термины
Щ|; ^ Процесс Пуассона обладает следующими характеристиками: (1) Эксперимент
подразумевает подсчет числа реализаций событий за период времени, в определенной
области, расстоянии или любую другую единицу измерения. (2) Среднее значение
распределения Пуассона должно быть одинаковым для каждого интервала измерения. (3)
Количество реализаций в течение одного интервала не зависит от количества реализаций в другие
интервалы.
Примерами случайных переменных, следующих распределению
вероятностей Пуассона, являются:
Ф Количество машин, прибывающих в городскую тюрьму в течение
определенного промежутка времени
128 Часть 2: Изучаем вероятность
# Количество типографических ошибок, обнаруженных в манускрипте
Ф Количество студентов, отсутствующих на моем уроке по статистике,
проводимом по понедельникам
Ф Количество профессиональных футболистов, еженедельно
размещаемых в списке травмированных
Теперь, когда мы разобрались с основными понятиями процесса
Пуассона, давайте перейдем к вычислению вероятностей.
Распределение вероятностей Пуассона
Если случайная переменная подчиняется модели, соответствующей
распределению вероятностей Пуассона, мы можем вычислить вероятность
определенного числа реализаций события за определенный промежуток времени.
Для осуществления подобных вычислений нам необходимо знать среднее
количество реализаций события за этот период. Чтобы показать распределение
вероятностей Пуассона в действии, я воспользуюсь следующим примером.
История, которую я собираюсь вам поведать, действительно имела место.
Имена не изменены, поскольку невинных в этой истории нет. Не то чтобы
какая-то из предыдущих историй была ложной, но эта правдива от начала до
конца. Каждый год Брайан, Джон и я совершаем паломничество любителей
гольфа на Мертл Бич, что в Южной Каролине. В одну из таких поездок, а
именно в последний вечер перед отъездом домой, мы бродили по
магазинчику, торгующему различными принадлежностями для гольфа. Каким-то непо-
. стижимым образом Брайану удалось убедить меня в необходимости
приобретения бывшей в употреблении, но весьма симпатичной брендовой
клюшки. Он клялся и божился, что без этой самой клюшки ему не раскрыть
полностью своего потенциала как игрока в гольф. Эта весьма подержанная
клюшка стоила больше, чем любая новая, которую мне доводилось покупать в
своей жизни. Подростки обладают особым даром пренебрегать любой
рациональной логикой взрослого человека в тех случаях, когда они уже приняли
решения и не намерены от него отступать.
На следующее утро мы встали пораньше, упаковали свои вещички,
выписались из гостиницы и отправились на наш последний раунд в гольф, весьма
предусмотрительно запланированный мной прямо по дороге домой. На
первой метке Брайан извлекает свое новое подержанное приобретение и делает
короткий удар влево, при котором обычно мяч улетает далёко в кусты. Я
нервно улыбаюсь и убеждаю себя в том, что следующим удар выйдет у
Брайана значительно лучше. Но косые удары продолжаются, и я уже с трудом
удерживаю сына от того, чтобы забросить свое новое подержанное
приобретение в озеро.
После завершения раунда я возвращаюсь в тот магазин, чтобы вернуть
клюшку обратно, добавив еще час к нашему и без того 10-часовому путеше-
Глава 10: Распределение вероятностей Пуассона 129
ствию. Продавщица в магазине радостно сообщает мне, что готова принять
назад клюшку, но мне необходимо предъявить для этого... чек. И только
теперь я смутно припоминаю, что положил его в какое-то особое место на
случай, если он мне пригодится, но после всех сборов, выезда из гостиницы и
игры в гольф, я скорее нашел бы панацею от рака, чем вспомнил, куда я
запихнул этот клочок бумаги.
Но я не из тех, кто сдается без боя, поэтому я направляюсь к машине и
начинаю перерывать все наши вещи. Через некоторое время, когда я уже
разбросал все свое нижнее белье и носки по стоянке, из магазина появляется та же
милая женщина и сообщает, что готова вернуть мне деньги за клюшку без
чека, но при условии, что я быстренько соберу все свои вещи обратно в машину.
Таким образом, я обнаружил весьма мощный способ, которыми/хочу с
вами поделиться. Представьте, что это бонус, вознаграждающий вас за изуче-.
ние этой книги. Если я не могу найти чек, необходимый для возврата денег, я
складываю грязную одежду в чемоданчик и повторяю ту же сцену, что и
перед тем магазинчиком. Действует безотказно.
Как бы то ни было, предположим, что в течение раунда в гольф Брайан
обычно выполняет 5 ударов, попадающих в цель, а именно в фарвей. Фар-
вей — коротко выстриженная лужайка вокруг лунки, куда, по мнению
людей, придумавших эту игру, и должны попадать мячи. Предположим, что
фактическое количество фарвеев, на которые попадает Брайан в течение
раунда, подчиняется распределению Пуассона.
Внимание! .
Откуда я знаю, спросите вы, что число фарвеев, на которые попадет Брайан в
течение первого раунда, подчиняется распределению Пуассона? В данный момент я не могу
этого утверждать. Чтобы удостовериться, что мое утверждение истинно, мне необходимо
записать количество фарвеев, на которые попадал мяч Брайана на протяжении нескольких
раундов, а потом выполнить «испытание на адекватность», чтобы узнать, соответствуют ли
эти данные модели распределения Пуассона. Обещаю, что мы вместе выполним это
испытание в Главе 18, так что наберитесь терпения.
А сейчас мы можем воспользоваться распределением Пуассона для
вычисление вероятности того, что Брайан поразит своим мячом х фарвеев в
течение следующего раунда:
их-е~и
х!
где:
х = количество интересующих нас реализаций за определенный
промежуток времени,
150 Часть 2; Изучаем вероятность
\х = среднее количество реализации за определенный промежуток
времени,
е = математическая константа, равная 2.71828,
Р[х] = вероятность в точности х реализаций за определенный
промежуток времени.
Теперь мы можем вычислить вероятность того, что Брайан попадет точно
на 7 фарвеев в течение следующего раунда. При = 5 получаем следующее
уравнение:
(57)(2.71838'5)
РР1="
7!
(78125)(0.006738)=01044
7*6*5*4*3*2*1
Иными словами, вероятность того, что Брайан поразит точно 7 фарвеев,
немногим больше 10%.
Мы также можем вычислить суммарную вероятность того, что Брайан
поразит не более 2 фарвеев с помощью следующего уравнения:
Р[х<2] = Р[х = 0] + Р[х = 1] + Р[х = 2]
(5^(2^^
1 J 0! 1
p[x = 1] = (5-)(2.71838-)J5)(0.006738)=00337
оос5
Р[* = 2]=(5 )(2J1838 > J25H00Q6738) =о,о842
1 J 2! 21
Р[х<2] = 0.0067 + 0.0337 + 0.0842 = 0.1246.
Эврика!
В некоторых учебниках по
статистике вы можете увидеть
символ к (произносится «лямбда»)
для обозначения средней
величины распределения
вероятностей Пуассона. Обозначение иное, а
уравнение то же самое.
То есть есть 12.6%-ная вероятность, что
Брайан попадет мячом не более чем на 2
фарвея в течение следующего раунда.
В предыдущем примере средняя
величина распределения вероятностей
Пуассона оказалась целым числом (5). Но так
бывает далеко не всегда. Предположим,
число студентов, отсутствующих на
моем уроке по статистике в понедельник,
подчиняется распределению Пуассона
Глава 10: Распределение вероятностей Пуассона 131
со средним значением 2,4. Вероятность того, что в следующий понедельник
будут отсутствовать 3 студента, вычисляется так:
Р[х = 3] =
(2.43)(2.71838"
3!
Эврика!
3*2*1
Есть еще одна любопытная
особенность распределения Пуассона:
дисперсия распределения равняется
среднему значению. То есть:
а2 = jli.
Это означает, что вам не придется
производить муторные вычисления для этого распределения, с которыми мы
имели дело в предыдущих главах.
Из Главы 8 вспомним, что 0! = 1.
Также х° = 1 для любого
значения х.
Таблицы вероятностей Пуассона
Подобно биноминальному распределению вероятностей, распределение
вероятностей Пуассона имеет таблицу, в которой вы можете найти
вероятности для определенных средних значений. Таблица распределения Пуассона
представлена в Приложении В этой книги. Ниже представлен отрывок из
этого приложения, в котором подчеркнуты значения для нашего примера с
магазинчика, торгующего клюшками для гольфа.
Значения ц
X
0
1
2
3
4
5
6
7
8
3.2
0.0408
0.1304
0.2087
0.2226
0.1781
0.1140
0.0608
0.0278
0.0111
3.4
0.0334
0.1135
0.1929
0.2186
0.1858
0.1264
0.0716
0.0348
0.0148
3.6
0.0273
0.0984
0.1771
0.2125
0.1912
0.1377
0.0826
0.0425
0.0191
3.8
0.0224
0.0850
0.1615
0.2046
0.1944
0.1477
0.0936
0.0508
0.0241
4.0
0.0183
0.0733
0.1465
0.1954
0.1954
0.1563
0.1042
0.0595
0.0298
4.2
0.0150
0.0630
0.1323
0.1852
0.1944
0.1633
0.1143
0.0686
0.0360
4.4
0.0123
0.0540
0.1188
0.1743
0.1917
0.1687
0.1237
0.0778
0.0428
4.6
0.0101
0.0462
0.1063
0.1631
0.1875
0.1725
0.1323
0.0869
0.0500
4.8
0.0082
0.0395
0.0948
0.1517
0.1820
0.1747
0.1398
0.0959
0.0575
5.0
*0.0067
0.0337
0.0842
0.1404
0.1755
0.1755
0.1462
0.1044
0.0653
132 Часть 2: Изучаем вероятность
дг
9
10
11
12
13
14
15
3.2
0.0040
0.0013
0.0004
0.0001
0.0000
0.0000
0.0000
3.4
0.0056
0.0019
0.0006
0.0002
0.0000
0.0000
0.0000
3.6
3.8
00.0076 0.0102
0.0028
0.0009
0.0003
0.0001
0.0000
0.0000
0.0039
0.0013
0.0004
0.0001
0.0000
0.0000
4.0
0.0132
0.0053
0.0019
0.0006
0.0002
0.0001
0.0000
4.2
0.0168
0.0071
0.0027
0.0009
0.0003
0.0001
0.0000
4.4
0.0209
0.0092
0.0037
0.0013
0.0005
0.0001
0.0000
4.6
0.0255
0.0118
0.0049
0.0019
0.0007
0.0002
0.0001
4.8
0.0307
0.0147
0.0064
0.0026
0.0009
0.0003
0.0001
5.0
0.0363
0.0181
0.0082
0.0034
0.0013
0.0005
0.0002
Таблица вероятностей построена исходя из значений \i, среднего числа
реализаций. Обратите внимание, что сумма каждого блока вероятностей для
определенного значения равна 1.
Как и в биноминальных таблицах, недостаток таблицы вероятностей
Пуассона состоит в том, что вы ограничены только теми значениями ц, которые
представлены в таблице. Например, мы не сможем воспользоваться этой
таблицей для \х = 0,45. В других учебниках по статистике могут быть
представлены более развернутые таблицы Пуассона, чем в Приложении В этой книги.
Распределение Пуассона для ц = 5 графически представлено на
следующей гистограмме. Вероятности, показанные на рисунке 10.1, взяты из
последнего столбца предыдущей таблицы.
Рис 10.1
Распределение
вероятностей
Пуассона.
0.2
0.16'
б
о
X
к
о
а
а>
0.12-
0.08 т
[I
0.04
4 6 8 10 12
Количество реализаций
14
Обратите внимание, что наиболее вероятное число реализаций для
данного распределения — это 4 и 5.
Глава 10; Распределение вероятностей Пуассона 155
А вот другой пример. Предположим, что месячное количество
автомобильных аварий на оживленном перекрестке, по которому я следую по дороге на
работу, подчиняется распределению Пуассона со средним значением 1,8
аварии в месяц. Какова вероятность того, что в следующем месяце произойдет 3
или более аварий? Получаем следующее уравнение:
Р[х>3] = Р[х = 3] + Р[х = 4] + Р[х = 5] + Р[х = 6] + ... + Р[х = оо]
Технически распределение Пуассона не имеет верхнего ограничения по
числу реализаций в течение определенного интервала. В таблицах
Пуассона вы увидите, что вероятность большого количества реализаций
практически равняется 0. Поскольку мы не имеем возможности сложить все
вероятности неопределенного количества реализаций (если у вас это получится,
можете считать, что вы великий статист!), мы должны вычесть из 1
дополнение к Р[х 3], то есть:
Р[х>3] = 1 - Р[х<3],
поскольку:
Р[х = 0] + ...Р[х = 1] 4- Р[х = 2] + Р[х = 3] + Р[х = 4] + Р[х = 5] + ...
+ Р[х = оо] = 1.0.
Таким образом, чтобы определить вероятность 3 или более аварий,
выполним следующее:
Р[х>3] = 1 - (Р[х = 0] 4- Р[х = 1] + Р[х = 2])
Используя вероятности, подчеркнутые в таблице ниже (похоже, я куда-то
засунул свой калькулятор), получаем следующее:
Значения ц
х 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0
0 0.3329 0.3012 0.2725 0.2466 0.2231 0.2019 0.1827 0.1653 0.1496 0.1353
1 0.3662 0.3614 0.3543 0.3452 0.3347 0.3230 0.3106 0.2975 0.2842 0.2707
"I 0.2014 0.2169 0.2303 0.2417 0.2510 0.2584 0.2640 0.2678 0.2700 0.2707
3 0.0738 0.0867 0.0998 0.1128 0.1255 0.1378 0.1496 0.1607 0.1710 0.1804
, 4 0.0203 0.0260 0.0324 0.0395 0.0471 0.0551 0.0636 0.0723 0.0812 0.0902
5 0.0045 0.0062 0.0084 0.0111 0.0141 0.0176 0.0216 0.0260 0.0309 0.0361
6 0.0008 0.0012 0.0018 0.0026 0.0035 0.0047 0.0061 0.0078 0.0098 0.0120
7 0.0001 0.0002 0.0003 0.0005 0.0008 0.0011 0.0015 0.0020 0.0027 0.0034
8 0.0000 0.0000 0.0001 0.0001 0.0001 0.0002 0.0003 0.0005 0.0006 0.0009
9 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0001 0.0002
154 Часть 2: Изучаем вероятность
Р[х>3] = 1 - (0.1653 + 0.2975 + 0.2678)
Р[х>3] = 1 - 0.7306 = 0.2694
Иными словами, существует 27%-ная вероятность того, что в следующем
месяце на этом перекрестке произойдет 3 или более аварий. Похоже, мне
следует найти более безопасный маршрут!
Использование Excel для вычисления
вероятностей Пуассона
Вероятности Пуассона можно с легкостью вычислить с помощью нашей
любимой программы Excel. Встроенная функция ПУАССОН имеет следующие
характеристики:
ПУАССОН(х; ц; интегральная)
где:
интегральная' = ЛОЖЬ, если вы хотите получить вероятность в
точности х реализаций
интегральная = ИСТИНА, если вы хотите получить вероятность не
более х реализаций
Например, на рисунке 10.2 показана функция ПУАССОН для вычисления
вероятности того, что в следующем месяце на этом опасном перекрестке
произойдет ровно 2 аварии.
Рис юг НИШЮм''|||Ш1ш^Ш:г^ДН
Функция ПУАССОН
для х реализаций.
Ячейка А1 содержит формулу Excel =ПУАССОН(2; 1,8; ЛОЖЬ) с
результатом 0.2678. Эта вероятность подчеркнута в таблице выше.
С помощью Excel мы также можем вычислить суммарную вероятность
того, что в следующем месяце на перекрестке произойдет не более 2 аварий,
как показано на рисунке 10.3.
Ячейка А1 содержит формулу = ПУАССОН(2; 1,8; ИСТИНА) с
результатом 0.7306, вероятность, которую вы видели в предыдущем вычислении и
которая является суммой подчеркнутых вероятностей в предыдущей таблице.
Глава 10: Распределение вероятностей Пуассона 135
шштшшттшштштшттттттмтщщаяшт
м
шя
•••
\г~г
ны
1
1 II
Рис 10.3
Функция ПУАССОН
для не более х
реализаций.
Преимуществом использования Excel для вычисления вероятностей
Пуассона является то, что вы не ограничены значениями, представленными в
таблице Приложения В. Функция ПУАССОН позволяет вам использовать любое
значение ц.
Использование распределения Пуассона как
приближение к биноминальному распределению
Не знаю, как вы, но я, имея под рукой два способа сделать что-либо, всегда
выбираю тот, который требует меньше усилий. Если вы не согласны со мной,
можете опустить этот раздел. А если согласны, обязательно прочтите его!
Мы можем использовать распределение Пуассона для вычисления
биноминальных вероятностей при выполнении следующих условий:
Ф Если число испытаний, л, больше или равно 20 и...
Ф Если вероятность успеха, р, меньше или равна 0.05...
Тогда формула Пуассона будет выглядеть следующим образом:
Р[х] =
(пр)х*ё
х\
■ш
Эврика!
Если вам необходимо
вычислить вероятности при числе
испытаний, /7, больше или равным
20, и вероятности успеха, д
меньше или равной 0.05, вы
можете использовать уравнение для
распределения Пуассона для
приблизительного определения
биноминальных вероятностей.
где:
п = количество испытаний,
р = вероятность успеха.
Сейчас вы наверняка спрашиваете
себя, для чего вам вообще это делать. Ответ
таков: формула Пуассона подразумевает
меньшее количество вычислений, чем
формула биноминальных вероятностей,
а при соблюдении указанных выше
условий распределения получаются очень
похожими друг на друга.
136 Часть 2: Изучаем вероятность
Если вы проживаете в штате Миссури, то следующий пример должен быть
для вас показательным. Предположим, в моем городе 20 светофоров и для
каждого из них существует 3%-ная вероятность, что в определенный день
они не будут работать. Какова вероятность того, что сегодня не будет
работать точно 1 из 20 светофоров? Это биноминальный эксперимент с п = 20,
г = 1, р — 0.03. Из Главы 9 мы помним, что биноминальная вероятность
рассчитывается так:
Р[Г,Л] =
л!
(п-г)\г\
Р[1,20] =
20!
(20-1)!1!
tf<T
(O.O^O^f
Р[1,20] = (20) (0.03) (0.560613) = 0.3364.
Аппроксимация Пуассона получается следующая:
(пр)х*е-{пр)
РМ=-
х\
Поскольку пр = (20) (0.03) = 0.6,
(О.б^е"106*
Р[Ц=-
1!
Р[1] = (0.6) (0.548812) = 0.3293.
Даже если вы из Миссури, вы должны согласиться с тем, что вычисления
Пуассона значительно проще, а результаты весьма схожи. Но если вам
нужны еще доказательства...... Рисунки 10.4 и 10.5 показывают гистограммы
каждого распределения для этого примера.
Рис 10.4
Бином инальное
распределение
вероятностей
при п = 20,р = 0.03.
<
Z1/ Z2
Z3 /z4
Z5/Z6
m
>
Z7/ Z8
Глава 10: Распределение вероятностей Пуассона 137
Z2 /
/z3
'Z1
m
- ■>
Рис 10.5
Распределение
вероятностей
Пуассона со средним
значением = 0.6.
Даже для самого завзятого скептика эти два распределения покажутся
весьма схожими. Так что я советую вам использовать уравнение Пуассона,
если вам необходимо вычислять биноминальные вероятности при п 20 и р 0.05..
На этом завершается наше обсуждение дискретных распределений
вероятностей. Надеюсь, вам было так же интересно, как и мне!
Ваша очередь
1. Месячное количество дождливых дней в определенном городе
подчиняется распределению Пуассона со средним значением, равным 6 дней.
Какова вероятность того, что в следующем месяце будет 4 дождливых дня?
2. Количество посетителей одного магазина подчиняется распределению
Пуассона со средним значением 7.5 посетителей в час. Какова
вероятность того, что в течение следующего часа магазин посетят 5 человек?
3. Количество электронных сообщений, получаемых мной ежедневно,
подчиняется распределению Пуассона со средним значением, равным
4.2 письма в день. Какова вероятность того, что завтра я получу больше
2 сообщений?
4. Количество сотрудников, позвонивших в понедельник в офис компании и
сказавшихся больными, подчиняется распределению Пуассона со
средним значением, равным 3.6. Какова вероятность того, что в следующий
понедельник по этой причине в офис позвонят не более 3 сотрудников?
5. Количество нежелательных сообщений, получаемых мной ежедневно,
подчиняется распределению Пуассона со средним значением 2.5.
Какова вероятность того, что завтра я получу в точности 1 нежелательное
сообщение?
6. Статистика свидетельствует о том, что 5% посетителей определенного
сайта покупает что-либо на нем. Какова вероятность того, что в
точности 2 посетителя из следующих 25 приобретут что-либо на сайте?
Используйте распределение Пуассона для приблизительного вычисления
биноминальной вероятности.
138 Часть 2: Изучаем вероятноаь
Повторение - мать учения
Ф Процесс Пуассона считает число реализаций события за определенный
период времени, в определенной области, расстоянии или любую
другую единицу измерения.
Ф Среднее распределения Пуассона — это среднее количество
реализаций, ожидаемых за единицу измерения, которое должно быть
одинаковым для каждого интервала измерения.
Ф Число реализаций в течение одного интервала процесса Пуассона не
зависит от количества реализаций в других интервалах.
Ф Если х —' это случайная переменная Пуассона, вероятность х
вероятностей за определенный промежуток равна
х\
Ф Если число биноминальных испытаний больше или равно 20 и
вероятность успеха меньше или равна 0.05, вы можете использовать уравнение
для распределения Пуассона для получения приблизительных значений
биноминальных вероятностей.
Нормальное
распределение
вероятностей
В этой главе
# Изучение свойств нормального распределения вероятностей
Ф Использование стандартной нормальной таблицы для
вычисления вероятностей нормальной случайной переменной
Ф Использование Excel для вычисления нормальных
вероятностей
Ф Использование нормального распределения для
приблизительного вычисления биноминального распределения
Мы закончили наше путешествие по дискретным
распределениям вероятностей и переходим к следующему непростому
этапу. Наш очередной пункт назначения — непрерывные
случайные переменные и непрерывное распределение
вероятностей, известное также как нормальное распределение.
Возможно, вы помните, что в Главе 8 мы определили непрерывную
случайную переменную как переменную, которая может
принимать любое числовое значение в пределах интервала как ре-
140 Часть 2: Изучаем вероятность
зультат измерения исхода эксперимента. Примерами непрерывных
случайных переменных являются вес, расстояние, скорость или время.
Нормальное распределение — это основополагающий инструмент
статиста. Такое распределение является основой для многих типов статистики
вывода, которыми мы пользуемся сегодня. Мы будем часто обращаться к этому
распределению в оставшихся главах книги.
Характеристики нормального распределения вероятностей
Непрерывная случайная переменная, которая подчиняется нормальному
распределению вероятностей, обладает некоторыми особыми свойствами.
Предположим, месячная норма дождевых осадков в дюймах в выбранном
городе подчиняется нормальному распределению со средним значением 3.5
дюйма и стандартным отклонением 0.8 дюйма. Распределение вероятностей
для такой случайной переменной представлено на рисунке 11.1.
РИС 11.1
Нормальное
распределен ие
со средним значением
3.5, стандартным,
отклонением 0.8.
I I I'Tfl I 1 1 1 I t I I V П ГТ1"|"1 \ ГТч ми
Среднее значение = 3.5
Стандартное отклонение = 0.8
Из этого рисунка мы можем сделать следующие наблюдения
относительно нормального распределения:
Ф Средняя величина, медиана и мода имеют одинаковое значение; в
данном случае это 3.5 дюйма
Ф Распределение имеет форму колокола и симметрично относительно
медианы
Ф Общая область под изгибом равняется 1
Ф Правый и левый «хвосты» нормального распределения вероятностей
имеют неограниченную протяженность, никогда не касаясь
горизонтальной оси
Стандартное отклонение играет немаловажную роль в форме изгиба. Если
посмотреть на предыдущий рисунок, то можно заметить, что практически
Нормальное распределение
вероятностей
Глава 11: Нормальное распределение вероятностей 141
все измерения месячного нормы дождевых осадков попадают в интервал от
1,0 до 6,0 дюймов. А теперь взгляните на рисунок 11.2, на котором
представлено нормальное распределение с той же медианой 3.5 дюйма, но со
стандартным отклонением всего 0.5 дюйма.
Нормальное распределение
вероятностей
Рис 112
Нормальное
распределен ие
со средним значением
3.5, стандартным
отклонением 0.5.
Медиана = 3.5 дюйма,
стандартное отклонение = 0.5 дюйма
Здесь вы видите, что изгиб
значительно плотней прилегает к среднему
значению. Почти все месячные
измерения осадков попадают в интервал
от 2.0 до 5.0 дюймов.
На рисунке 11.3 показано, как
смещается изгиб при изменении средней
величины нормального
распределения до 5.0 дюймов при том же
значении стандартного отклонения 0.8.
Эврика!
Небольшое значение стандартного
отклонения выражается в более
«тощей» и высокой кривой, плотно
прижимающейся к среднему
значению. Чем больше стандартное
отклонение, тем «толще», ниже и
растянутее получается кривая.
Нормальное распределение
вероятностей
Среднее = 5.0,
стандартное отклонение -
PnclL3
Нормальное
распределение
со средним значением
= 5.0, стандартным
отклонением = 0.8.
0.8
142 Часть 2: Изучаем вероятноаь
Для каждого из вышеуказанных рисунков характеристики нормального
распределения вероятностей оказались истинными. В каждом случае
значения (средней величины) и (стандартного отклонения) полностью описывают
форму распределения.
Функция вероятности для нормального распределения имеет весьма
угрожающий вид, а именно:
/M=-4=e-(1/2)[(x^)/o12.
а>/2я
Обещаю, что больше подобных монстров не будет. К счастью, у нас есть
иные способы вычисления вероятностей для данного распределения,
которые выглядят более прилично. О них мы узнаем в следующем разделе.
Вычисление вероятностей для нормального распределения
Существует несколько подходов к вычислению вероятностей для
нормальной случайной переменной. Их применение я продемонстрирую на
следующем примере.
Произошла эта история несколько дней назад. Тем утром Дебби
позвонила мне на мобильный, пока я бегал по делам, и произнесла два слова,
услышать которые я боялся весь последний год. «Они вернулись», — сказала
она. «Хорошо», — ответил я печально, отключился и направился прямиком
в хозяйственный магазин. Задача передо мной стояла непростая, но я не
собирался сдаваться без боя. Мне была объявлена война, и я ехал домой,
полностью подготовленный к битве. Конечно, я говорю о моей ежегодной
борьбе с самым мерзким и подлым существом на планете — японским
хрущиком.
К моменту моего приезда домой из хозяйственного магазина половина
нашего прекрасного сливового дерева стала похожей на швейцарский
сыр. Я немедля нанес контрудар, распылив по дереву самый
сильнодействующий химический препарат, который можно купить за деньги.
Наконец, когда токсичный спрей рассеялся, я стоял один, хозяин своей
территории.
Но вернемся к нашей теме. Предположим, что каждый год объем
расходуемого мной спрея подчиняется нормальному распределению со средним
значением 60 унций и стандартным отклонением 5 унций. Это значит, что
каждый год во время борьбы с этими демонами я использую наиболее вероятный
объем спрея в 60 унций, но каждый год этот объем несколько различается.
Вероятность других объемов, больше или меньше 60 унций, уменьшается в
соответствии с симметричным колоколообразным графиком. Вооруженные
этой информацией, мы готовы приступить к вычислению вероятностей
разнящихся каждый год объемов потребления спрея.
Глава 11: Нормальное распределение вероятностей 145
Вычисление х-распредслсния
Поскольку общая область под изгибом нормального распределения равняется
1 и изгиб является симметричным, мы можем утверждать, что вероятность
использования мной 60 и более унций спрея составляет 50%, равно как и
вероятность использования 60 или меньше унций. Это показано на рисунке 11.4.
Рис 11.4
Нормальное
J распределение
со средним = 60,
стандартным
отклонением = 5.0.
45 50 55 60 65 70 75
Унции токсического спрея
Как вычислить вероятность использования мной 64.3 и менее унций спрея
в год? Я рад, что вы задали этот вопрос. Для этого нам необходимо определить
стандартное нормальное распределение, а именно нормальное
распределение сц = 0ио= 1.0, как показано на рисунке 11.5.
Рпс.11.5
Стандартное
нормальное отклонение
со средним = 0
и стандартным
отклонением —1.0.
Количество стандартных отклонений
Это стандартное нормальное распределение является основой для всех
вычислений нормальных вероятностей и часто используется в этой главе.
144 Часть 2: Изучаем вероятность
Термины
Стандартное нормальное
распределение - это
нормальное распределение со
средним значением, равным О, и
стандартным отклонением, равным 1.0.
Следующим шагом мы определим, на
сколько стандартных отклонений отстоит
значением 64,3 от среднего значения 60, и
покажем это значение на графике
стандартного нормального распределения. Мы
сделаем это с помощью следующей формулы:
z =
x-\i
где:
х = нормально распределенная случайная переменная,
\i = среднее значение нормального распределения,
а = стандартное отклонение нормального распределения,
z = количество стандартных отклонений между х и ц, известное как
стандартное Z-распределение.
Для данного примера стандартное z-распределение получается следующим:
64.3-60
•Zcrfo "
= 0.86.
Теперь я знаю, что значение 64.3 находится в 0.86 стандартного
отклонения от среднего значения 60 в моем распределении.
Использование стандартной нормальной таблицы
Рассчитав стандартное z-распределение, я могу использовать следующую
таблицу, чтобы определить вероятность использования 64.3 или менее унций
спрея в следующем году. Таблица представляет собой часть таблицы из
Приложения В и показывает область стандартной нормальной кривой,
включающей определенные значения z. Поскольку в нашем примере z = 0.86, мы
находим строку 0.8 и столбец 0.6, которые пересекаются на значении 0.8051 (в
таблице оно подчеркнуто).
Вторая цифра %
Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359
0.1 0.5398 0.5438 0.5478 0,5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753
0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141
0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480. 0.6517
0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879
Глава 11: Нормальное распределение вероятностей 145
Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.5 0.6915
0.6 0.7257
0.7 0.7580
0.8 0.7881
0.9 0.8159
1.0 0.8413
0.6950
0.7291
0.7611
0.7910
0.8186
0.8438
0.6985
0.7324
0.7642
0.7939
0.8212
0.8461
0.7019
0.7357
0.7673
0.7967
0.8238
0.8485
0.7054
0.7389
0.7704
0.7995
0.8264
0.8508
0.7088
0.7422
0.7734
0.8023
0.8289
0.8531
0.7123
0.7454
0.7764
0.8051
0.8315
0.8554
0.7157
0.7486
0.7794
0.8078
0.8340
0.8577
0.7190
0.7517
0.7823
0.8106
0.8365
0.8599
0.7224
0.7549
0.7852
0.8133
0.8389
0.8621
Эта область графически представлена на рисунке 11.6.
М=1 Рис.11.6
Заштрихованная
область представляет
вероятность того,
что z будет меньше
или равно 0.86.
0 0.86
Количество стандартных отклонений
Вероятность того, что стандартное z-распределение будет меньше или
равно 0.86, является 80.51%. Поскольку:
P[z<0.86] = Р[х<64.3]= 0.8051.
То есть, существует 80.51%-ная вероятность, что в следующем году я
распылю на этих отвратительных японских хрущиков 64.3 или менее унций
спрея. Это показано на рисунке 11.7.
Рис 117
Заштрихованная
область представляет
вероятность того,
что х будет меньше
или равен 64.3 унции.
60 64.3
Унции токсичного спрея
146 Часть 2: Изучаем вероятность
Внимание!
С помощью непрерывных случайных переменных мы не сможем определить
вероятность использования точно 64.3 унции спрея, поскольку такая вероятность будет ничтожно
мала. Это потому, что существует неопределенное количество объемов, которые я могу
распылить в определенный год. В один год я могу распылить 61.757 унций спрея, а в
другой - 53.472 унции. Поэтому с помощью непрерывных случайных переменных мы можем
вычислять только вероятности определенных интервалов, например, менее 64.3 унции или
от 50.5 до 58.1 унции. Сравните эту особенность с дискретными случайными переменными
из предыдущих глав. Для таких переменных существует ограниченное число значений,
поэтому мы можем вычислить в точности х реализаций или гуспехрв.
А какова вероятность того, что в следующем году я использую более 62.5
унций спрея? Поскольку стандартная нормальная таблица содержит только
те вероятности, которые меньше или равны z-распределению, нам
необходимо дополнение этого события.
Р[х>62.5] = 1 - Р[х<62.5]
Тогда Z-распределение получается следующим:
62.5-60 ___
zfi9,= = 0.50.
В соответствии с нашей нормальной таблицей:
P[z<0.50] = 0.6915.
Но нам необходимо получить:
P[z>0.50] = 1 - 0.6915 = 0.3085.
Эта вероятность графически представлена на рисунке 11.8.
Рис 11.8
За штр ихованная
область представляет
вероятность того,
что z будет больше 0.50.
0 0.5
Количество стандартных отклонений
Глава 11: Нормальное распределение вероятностей 147
Поскольку:
P[z > 0.50] = Р[х > 62.5] = 0.3085.
То есть существует 30.85%-ная вероятность, что в следующем году я
использую более 62.5 унций спрея. Ну, жуки, берегитесь!
А какова вероятность того, что я использую более 54 унций спрея? И
снова мне необходимо дополнение, а именно:
Р[х>54] = 1 - Р[х<54].
Z-распределение получается следующим:
54 5
Отрицательное результат означает, что мы находимся слева от среднего
значения распределения. Обратите внимание, что в таблице представлены
только положительные значения z. Но здесь никаких проблем не возникнет,
поскольку распределение симметрично. На рисунке 11.9 видно, что
заштрихованная область слева от — 1.20 стандартных отклонений от среднего — это
то же самое, что и заштрихованная область справа от + 1.20 стандартных
отклонений от среднего.
/~\ Рис 11.9
/ \ Заштрихованные
области равны.
-1.2 1.2
Количество стандартных отклонений
Мы можем определить область справа от + 1.20 стандартных отклонений:
P[z>+ 1.2] = 1 - P[z< + 1.2] = 1 - 0.8849= 0.1151.
Таким образом, область слева от —1.20 стандартных отклонений от
среднего также равна 0.1151. Теперь мы можем вычислить область справа от
—1.20 стандартных отклонений от среднего.
P[z>- 1.2] = 1 - P[z< - 1.2] = 1 - 0.1151 = 0.8849.
Поскольку:
Р[х > 54] = P[z > - 1.2] = 0.8849.
148 Часть 2: Изучаем вероятность
То есть существует 88.49%-ная вероятность, что я распылю более 54 унций
спрея. Эта вероятность графически представлена на рисунке 11.10.
Рис 11.10
За штр ихованная
область — это
вероятность того,
что х будет больше
54 унций.
а = 5 / N
0.1151
54 60
Унции токсичного спрея
Эврика!
В краткой форме предыдущий пример можно представить таю
P[z>- 1.20] = P[z< + 1.20]
P[z>- 1.20] =0.8849.
В целом вы можете использовать следующие два отношения для любого значения а,
когда речь идет об отрицательных z-распределениях:
P[z>-a] = P[z< + а]
P[z<-a] = 1 - P[z< 4- а].
Наконец, давайте рассчитаем вероятность того, что я использую от 54 до
62.5 унции в следующем году. Эта вероятность графически представлена на
рисунке 11.11.
РИС.1Ш ;:?
о — э
Заштрихованная
область — это
вероятность того,
что х окажется в
интервале от 54
до 62.5 унции. 0.1151
60 62.5
Унции токсичного спрея
Глава 11: Нормальное распределение вероятностей 149
Из предыдущего примера мы знаем, что область слева от 54 унций — это
0.1151, а справа от 62.5 унции — 0.3085. Поскольку общая область под кривой
распределения равна 1:
Р[54<х<62.5] = 1 - 0.1151 - 0.3085 = 0.5764.
Существует 57.64%-ная вероятность того, что я распылю от 54 до 62.5
унции ядовитого спрея в следующем году. Никак не могу этого дождаться.
И снова эмпирическое правило
Помните, как в Главе 5 мы обсуждали эмпирическое правило? Оно гласило,
что если распределение можно представить в виде колоколообразного
симметрического графика, сконцентрированного вокруг среднего, то примерно
68, 95 и 99.7% значений окажутся в пределах 1, 2 и 3 стандартных отклонений
от среднего значения соответственно. Я рад сообщить вам, что теперь у нас
есть возможность продемонстрировать эти результаты на практике.
Заштрихованная область на рисунке 11.12 показывает процент
наблюдений, которые по нашим ожиданиям должны оказаться в пределах 1.0
стандартного отклонения от среднего значения.
Рис 11.12
Заштрихованная область —
это вероятность того, что
х окажется в диапазоне от
— 1.0 до + 1.0 стандартного
отклонения от средней
величины.
-1 1
Количество стандартных отклонений
Откуда появились эти 68%? Давайте посмотрим в таблице вероятность того,
что наблюдение будет менее 1.0 стандартного отклонения от средней величины.
P[z< +1.0] = 0.8413.
Таким образом, область справа от 4- 1.0 стандартного отклонения равна:
P[z> +1.0] = 1 - 0.8413 = 0.1587.
Благодаря симметрии, область слева от — 1.0 стандартного отклонения
также равна 0.1587. Получается, что область от —1.0 до + 1.0 равна:
Р[- 1.0<z< + 1.0] = 1 - 0.1587 - 0.1587 = 0.6826.
0.1584
0.1584
150 Часть 2: Изучаем вероятноаь
Та же логика используется для подтверждения вероятностей 2.0 и 3.0
стандартных отклонений от среднего значения. Попробуйте проверить их
сами.
Вычисление нормальных вероятностей с помощью Excel
И снова мы обращаемся к Excel с просьбой выполнить за нас рутинную
работу. Прежде всего, рассмотрим встроенную функцию НОРМРАСП,
обладающую следующими характеристиками:
НОРМРАСП(х; среднее; стандартное__откл; интегральный)
где:
интегральная = ЛОЖЬ, если мы хотим получить вероятность
распределения частот (мы ее не хотим получить)
интегральная = ИСТИНА, если мы хотим получить суммарную
вероятность (она-то нам и нужна)
Например, на рисунке 11.13 показана функция НОРМРАСП,
используемая для вычисления вероятности того, что в следующем году я распылю
менее 64,3 унции спрея на этих мерзких жуков.
РИС 11.13
Функция
НОРМРАСП
для менее 64.3 унции.
В ячейка А1 содержится формула = НОРМРАСЩ64.3; 60.5; ИСТИНА) с
результатом 0.8051. Эта вероятность подчеркнута в предыдущей таблице.
В Excel также есть функция НОРМСТОБР со следующими
характеристиками:
НОРМСТОБР(вероятность)
Вы предоставляете в распоряжение этой функции вероятность от 0 до 1, а
она возвращает соответствующее z-распределение. На рисунке 11.14
показана функция НОРМСТОБР, вернувшая z-распределение для вероятности
значения 0.8413, расположенного в 1.0 стандартном отклонении от средней
величины.
Глава 11: Нормальное распределение вероятностей 151
Рис 11.14
Функция
НОРМСТОБР
для стандартного
отклонения 1.0.
В ячейке А1 содержится формула = НОРМСТОБР(0.8413) с результатом
0.9998 (близко к 1.0). Если вернуться к рисунку 11.12, то вы увидите, что
область слева от 1.0 стандартного отклонения от средней величины в сумме
составляет 0.8413. Вы также найдете это значение в стандартной нормальной
таблице рядом с z = 1.0.
Использование нормального распределения
как приближение биноминального распределения
Помните, сколько проблем может доставить нам биноминальное
распределение? Что ж, нормальное распределение сможет помочь нам в эти
непростые моменты при определенных условиях. Вспомним из Главы 9, что
биноминальное уравнение позволяет
вычислить вероятность г успехов в п
испытаниях при р = вероятность успеха
для каждого испытания, a q =
вероятность неудачи. Если пр > 5 и nq > 5,
мы можем использовать нормальное
распределение для получения
приближения биноминального
распределения.
Пример: предположим, что в моем
классе по статистике 60% — девушки.
Если я случайным образом выберу 15
студентов, какова вероятность того,
что в полученной группе окажется 8,
9, 10 или 11 девушек? В этом примере
п = 15, р = 0.6, q = 0.4, г = 8, 9, 10 и
И. Мы можем использовать
нормальное распределение, поскольку пр =
150.6 = 9 и nq = 150.4 = 6. (Уж
простите меня, парни, я никак не хотел
этим сказать, что, выбрав вас, меня
ждет неудача!)
Эврика!
Даже если вам не слишком
интересно, как можно использовать
нормальное распределения для
получения приближенного
биноминального распределения, я
очень советую вам проработать
пример, предложенный в этом разделе. В
любом случае вы сможете
попрактиковаться в вычислении вероятностей для
нормального распределения. А мы все
знаем, что повторение - мать учения!
Термины
Нормальное распределение
может быть использовано
для получения приближения
биноминального распределения, если пр>5
и nq>5.
152 Часть 2: Изучаем вероятность
Нам понадобится биноминальная таблица, представленная в Приложении В.
Ниже вы видите часть этой таблицы, где подчеркнуты интересующие нас
вероятности.
Значения р
п г
15 0
1
2
3
4
5
6
7
8
9
10
11
0.1
0.2059
0.3432
0.2669
0.1285
0.0428
0.0105
0.0019
0.0003
0.0000
0.0000
0.0000
0.0000
0.2
0.0352
0.1319
0.2309
0.2501
0.1876
0.1032
0.0430
0.0138
0.0035
0.0007
0.0001
0.0000
0.3
0.0047
0.0305
0.0916
0.1700
0.2186
0.2061
0.1472
0.0811
0.0348
0.0116
0.0030
0.0006
0.4
0.0005
0.0047
0.0219
0.0634
0.1268
0.1859
0.2066
0.1771
0.1181
0.0612
0.0245
0.0074
0.5
0.0000
0.0005
0.0032
0.0139
0.0417
0.0916
0.1527
0.1964
0.1964
0.1527
0.0916
0.0417
0.6
0.0000
0.0000
0.0003
0.0016
0.0074
0.0245
0.0612
0.1181
0.1771
0.2066
0.1859
0.1268
0.7
0.0000
0.0000
0.0000
0.0001
0.0006
0.0030
0.0116
0.0348
0.0811
0.1472
0.2061
0.2186
0.8
0.0000
0.0000
0.0000
0.0000
0.0000
0.0001
0.0007
0.0035
0.0138
0.0430
0.1032
0.1876
0.9
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0003
0.0019
0.0105
0.0428
Также вспомним из Главы 9, что среднее значение и стандартное
отклонение этого биноминального распределения получаются так:
ц = пр = (15) (0.6) = 9
а = yfnpq=V(15)(0.6)(0.4) =1.897.
Вероятность того, что в группе из 15 студентов окажется 8, 9, 10 или 11
девушек, получается следующим образом:
Р[г = 8, 9, 10 или 11] = 0.1771 + 0.2066 + 0.1859■+ 0.1268' = 0.6964.
А теперь давайте решим эту проблему с помощью нормального
распределения и сравним полученные результаты. На рисунке 11.15 показано
нормальное распределение с ц = 9 и а = 1.897.
Обратите внимание, что заштрихованная область простирается от 7.5
до 11.5, а не от 8 до 11. Не беспокойтесь, ошибки здесь нет. Я вычел 0.5 из
8 и добавил 0.5 к 11, чтобы компенсировать то, что нормальное
распределение является непрерывным, а биноминальное — дискретным.
Прибавление и вычитание 0.5 называется поправкой на непрерывность. Для
больших значений л, например, 100 или более, вы можете игнорировать эту
поправку.
Глава 11: Нормальное распределение вероятностей 155
11 = 9
а =1.897
Рис 11.15
Приближение
нормального
распределен ия
к биноминальному.
7.5 9 11.5
Количество девушек
Теперь нам необходимо вычислить z-распределение.
_х-ц_11.5-9
Z-J с
а
х-\х
1.897
7.5-9
1.897
- = +1.32
= -0.79
В соответствии с нормальной таблицей:
P[z< +1.32] = 0.9066.
Эта область заштрихована на рисунке 11.16.
и = о /%
с=1 т \
Рис 11.16
Вероятность того,
что z< +1.32
стандартных
отклонений от
среднего значения.
0 +1.32
Количество стандартных отклонений
Благодаря симметрии кривой нормального распределения мы также
знаем, что:
P[z< - 0.79] = 1 - P[z< + 0.79].
В соответствии с таблицей:
P[z< +0.79] = 0.7852.
154 Часть 2: Изучаем вероятность
Следовательно:
P[z< - 0.79] = 1 - 0.7852 = 0.2148.
Эта вероятность показана на заштрихованной области рисунка 11.17.
РИС 11.17
Вероятностыпого, что
z< — 0.79 стандартных
отклонений от средней
величины.
-0.79 0
Количество стандартных отклонений
Вероятность для интересующего нас примера — это область между z-pac-
пределениям — 0.79 и + 1.32. Чтобы вычислить эту область, выполним
следующие вычисления:
Р[- 0.79 <z< +1.32] = P[z<+ 1.32] - P[z<- 0.79]
Р[- 0.79<z< + 1.32] = 0.9066 - 0.2148 = 0.6918.
Эта вероятность представлена на заштрихованной области рисунка 11.18.
Рис 11.18
Вероятность того,
что- 0.79<z< +1.32
стандартных отклонетий
от среднего значения.
-0.79 0 +1.32
Количество стандартных отклонений
Используя нормальное распределение, мы определили вероятность того,
что в моей группе из 15 студентов окажется 8, 9, 10 или 11 девушек, — 0.6916.
Как видите, эта вероятность очень близка к результату, полученному нами из
биноминальной таблицы, — 0.6964.
Глава 11: Нормальное распределение вероятностей 155
На этом завершается глава, посвященная нормальному распределению
вероятностей. Чувствую, что я как следует подготовился к очередной
встрече со своим заклятым врагом — японским хрущиком. Пожелайте мне
удачи.
Ваша очередь
1. Скорость машин, проезжающих через пункт контроля, подчиняется
нормальному распределению с|и = 62.6 миль в час и а = 3.7 миль в час.
Какова вероятность того, что следующая машина будет двигаться со
скоростью:
а. Превышающей 65.5 миль в час?
в. Превышающей 58.1 миль в час?
с. От 61 до 70 миль в час?
2. Продажная цена различных домов в районе подчиняется нормальному
распределению сц = $176 000 и а= $22 300. Какова вероятность того,
что следующий дом будет продан за цену:
а. Менее $176 000?
в. Менее $158 000?
с. От $150 000 до $168 000?
3. Возраст покупателей одного розничного магазина подчиняется
нормальному распределению сц = 37.5 лет и а = 7.6 лет. Какова
вероятность того, что возраст следующего покупателя, вошедшего в магазин,
будет:
а. Больше 31 года?
в. Меньше 42 лет?
с. От 40 до 45 лет?
4. Монету подбросили 14 раз. Используйте нормальное распределение как
приближение к биноминальному для вычисления вероятности
выпадения 4, 5 или 6 «орлов». Сравните полученный результат с
биноминальной вероятностью.
Повторение - мать учения
Ф Нормальное распределение имеет колоколообразную и симметричную
кривую, сконцентрированную вокруг среднего значения.
Ф Общая область под кривой нормального распределения равна 1.0.
Ф Таблицы нормального распределения основываются на стандартном
нормальном распределении с ц=0ио= 1.0.
156 Часть 2: Изучаем вероятность
Ф Количество стандартных отклонений между нормально распределенной
случайной переменной (х) и носит название z-распределения и может
рассчитываться по формуле:
а
Ф Программа Excel имеет две встроенные функции, с помощью которых
вы можете выполнять вычисления, связанные с нормальным
распределением: НОРМРАСП и НОРМСТОБР.
Ф Нормальное распределение может быть использовано для примерного
вычисления биноминального распределения, еслипр>5ипд>5.
Статистический
вывод
А теперь мы можем взять все те замечательные понятия, которыми
загрузили свои бедные мозги благодаря Частям 1 и 2, и заставить их
работать с помощью слов с вполне статистическим звучанием, вроде
доверительного интервала и проверки гипотезы. Статистический
вывод позволяет нам делать предположения о генеральной
совокупности на основе результатов случайной выборки из этой
совокупности. Например, с помощью статистического вывода можно точно
предугадать, кто станет победителем на выборах, задолго до выборов,
с помощью результатов сравнительно маленькой, но грамотно
отобранной выборки. Это весьма любопытно!
Я СД6/1А/1 СЛУЧАЙНУЮ РЫЮРКУ ИЗ
СОВОКУПНОСТИ И ОЙНАРУЖИ/1, ЧТО Ш
ГРА)КДАН /1Ю5ЯТ МО/ЮКО, 8Г/о -
СМОТРИТ Т6/16РИЗОР и лоо% -
ненАрцдят социо/югические опросы.
Выборка
В этой главе
Ф Причина, по которой измеряется выборка, а не совокупность
# Различные методы отбора случайной выборки
Ф Определение ошибок выборки
Ф Последствия применения неверных выборочных методик
Наша первая глава по долгожданной теме статистики вывода
посвящена выборке. Если вы еще способны припомнить то, о
чем мы говорили в Главе 1, то речь шла о генеральной
совокупности, представляющей все возможные исходы или измерения,
представляющие интерес, и о выборке, подмножестве
совокупности. В этой главе вы побеседуем о том, почему в статистике
имеют дело с выборками и каковы могут быть последствия их
неправильного отбора.
Практически все статистические результаты основываются
на измерении выборки, взятой из генеральной совокупности.
Судьбоносные решения часто принимаются на основе
информации, полученной из выборок. Например, рейтинги Артура
Нельсона формируются на основании собранной информации у
небольшой выборки граждан, а на их основе делаются заключения
в отношении телевизионной аудитории всей страны. Будущее
вашего любимого телевизионного шоу находится в руках этой
небольшой группки граждан! Грамотный отбор выборки — это
решающий шаг, влияющий на точность статистических выводов.
160 Часть 3: Статпстическпй вывод
Почему выборка?
Большинство статистических исследований опираются на выборку, взятую
из генеральной совокупности. Отношения между выборкой и генеральной
совокупностью показаны на рисунке 12.1 (а также описаны в Главе 1).
Рис 12.1
Отношения
между выборкой
и генеральной
совокупностью.
Почему бы не измерить всю генеральную совокупность вместо того, чтобы
полагаться на выборку? Хороший вопрос! В зависимости от исследования
измерение генеральной совокупности может стоить слишком дорого или
вообще представляться невозможным. Если я захочу измерить
продолжительность жизни одного из видов назойливых москитов (кстати, их жизнь очень
коротка), то мне вряд ли удастся произвести
[наблюдение за всеми москитами в
совокупности. Мне придется положиться на
выборку генеральной совокупности москитов,
измерить продолжительность их жизни, а
затем сделать предположение относительно
продолжительности жизни всей
генеральной совокупности. В этом и состоит
основополагающая идея статистического вывода!
К сожалению, выполнить то, о чем я только
что сказал, куда сложней, чем просто
написать об этом. И этому посвящена
оставшаяся часть книги.
Даже если бы мы могли измерить всю
генеральную совокупность целиком, такой
шаг мог бы оказаться совершенно
бесполезным. Если выборка отобрана грамотно и
анализ произведен правильно, мы можем
сделать довольно точные выводы и оценку всей
совокупности. Нет смысла выходить за
пределами выборки и измерять все, что
окажется в поле зрения. Измерение всей генраль-
ной совокупности зачастую оборачивается
впустую потраченными временем и
деньгами — ресурсами весьма дефицитными.
Компания Nielsen Media Research
проводит опросы среди 5000 семей по
всей стране, чтобы сделать выводы о
телевизионных пристрастиях
миллионов граждан. Поскольку результаты
этих опросов частенько являются
основой для принятия решений об
отмене шоу или в отношении доходов от
рекламных роликов, вы уж поверьте,
что эта компания весьма осторожна и
внимательна при отборе выборки.
Эврика!
Часто измерить всю
совокупность целиком не
представляется возможности. Но даже
если такая возможность
существует, измерение целой
совокупности может оказаться
впустую потраченными временем и
деньгами и мало что прибавит к
измерению выборки.
Глава 12: Выборка 161
Подобное решение было принято в колледже Golden-Beacom College, где я
сейчас преподаю. Я также являюсь председателем комитета кодекса чести
студентов и поэтому был вовлечен в проект, ставивший своей целью собрать
информацию об отношении наших студентов к честности и
добросовестности. Мы вполне могли бы опросить всех студентов колледжа, но благодаря
статистике вывода в этом не было необходимости.
Наконец, мы приняли мудрое решение и отобрали лишь часть студентов,
чтобы сделать выводы обо всей совокупности.
Случайная выборка
Термин случайная выборка относится к процедуре отбора, при котором все
представители совокупности имеют равные шансы быть отобранными. Цель
случайной выборки — удостовериться, что финальная выборка, подлежащая
измерению, является репрезентативной в отношении всей совокупности, из
которой она была взята. Если же это не так, то мы имеем дело с выборкой с
пристрастием, измерение которой можем привести к неверным
результатам. Вспомните, в Главе 1 мы уже
обсуждали пристрастную выборку,
когда говорили об опросе в отношении
курса по гольфу. Грамотный отбор
выборки является решающим для
точности статистического анализа.
Существует несколько способов
отбора случайной выборки. Для их
демонстрации я воспользуюсь
следующим примером.
По большей части я считаю Дебби
человеком вполне разумным (в конце
концов, она же замужем за мной). Но
в последнее время у меня зародились
некоторые опасения в отношении ее поведения в связи с тем, что она
достигает определенной вехи раньше меня. Мне не разрешено разглашать,«что это
за веха такая (под страхом того, что она больше не будет вычитывать
написанные мною главы). Скажу лишь, что оно имеет отношение к делению 100
на 2 (вы же математики!).
Как бы то ни было, недавно, когда мы с женой прогуливались по
универмагу, она вдруг подбежала к прилавку, где продавались небольшие шиньоны
в виде конских хвостиков. Никогда в жизни я не видел ничего подобного, и
мне никогда в голову и идея такая не пришла бы. Дебби же, напротив,
считала эту идею просто превосходной. В ту же секунду из ниоткуда появилась
какая-то незнакомка, и, прежде чем я успел сказать, что это моя жена,
незнакомка быстренько уложила волосы Дебби и пристроила ей на затылок
конский хвостик, немного напоминающий маленькое волосатое животное.
Термины
' Случайной выборкой
называется процедура выборки, при
которой все представители
совокупности имеют равные шансы быть
отобранными. Выборка с пристрастием -
это выборка, не являющаяся
репрезентативной по отношению к совокуп- I
ности; ее использование может
привести к искажению результатов.
162 Часть 3: Статистический вывод
Дебби, в восторге от своего «нового облика», повернулась ко мне и
спросила моего совета. Поскольку в этот день была как раз годовщина нашей
свадьбы, я тихонько пробормотал, что выглядит она прекрасно, и протянул
незнакомке кредитку. (Я немного торможу в таких вопросах, но я отнюдь не
глупец.) Остаток дня Дебби скакала по всему универмагу со своим
симпатичным волосатым животным на голове. Когда я свыкся с этой идеей, я был
вынужден признать, что смотрится этот пучок совсем неплрхо.
Допустим, мы хотим организовать опрос мнений относительно нового
облика Дебби. Вы, дорогой читатель, можете сообщить мне свое мнение, лишь
взглянув на рисунок 12.2, а затем отправив мне по почте сообщение на адрес
с сайта этой книги www.stat-quide.com.
Если я сочту моей совокупностью всех посетителей универмага, мне
необходимо решить, как отбирать случайную выборку тех, чье мнение мне
хотелось вы узнать. В следующих разделах мы узнаем, что существуют четыре
способа отбора случайной выборки: простая случайная, систематическая,
групповая и расслоенная.
Простая случайная выборка
Простая случайная выборка — это выборка, в которой все представители
совокупности имеют равные шансы быть отобранными. Но проще сказать, чем
сделать. В примере с универмагом я могу случайным образом выбирать лю-
Глава 12: Выборка 165
Термины
дей и спрашивать их мнение. Но в
моем отборе могут быть пристрастия.
Например, если я увижу некоего типа
угрожающего вида с татуировкой
«Смерть всем статистам», вряд ли я
выберу его, чтобы узнать, что он
думает о новом облике моей супруги. Но
тогда я поступлю необъективно.
Допустим, я могу избавить себя от выборки с пристрастием, тогда приме
ром простой случайной выборки будет рисунок 12.3.
Выборка является простой
случайной, если все
представители совокупности имеют равные
шансы быть отобранными.
Магазин 3
©
Магазин 2 х
Магазин 1
©
Магазин 4
©
© х ©
х
©
Магазин 5
Магазин 6
Магазин 7
Рис 12.3
Простая
случайная
выборка.
Каждый «X» — это покупатель, а каждый «X», обведенный кругом, —
покупатель, вошедший в мою выборку.
Есть и другие способы отбора простой случайной выборки для опроса в
колледже, упомянутого ранее в этой главе. Я мог бы случайно отобрать
студентов с помощью таблицы случайных чисел. (Это просто таблица с
совершенно случайными числами.) Ниже показана часть такой таблицы. *
57245
42726
82768
97742
48332
26700
66156
64062
39666
58321
32694
58918
38634
40484
16407
10061
18545
59267
62828
33317
20510
28341
57395
01923
50534
72742
19097
34192
09198
25428
86230
29260
57654
53968
09877
06286
56256
08806
47495
32771
25519
63679
32093
39824
04431
98858
13908
71002
35477
54095
23518
74264
22753
04816
97015
58132
71309
56563
08654
01941
20944
16317
58225
58646
12212
09820
64815
95810
95311
94928
82255
69089
98911
86291
19894
26247
29515
05512
01956
63694
164 Часть 5: Статистический вывод
24713 95591 26970 37647 26282 89759 69034 55281 64853 50837
90417 18344 22436 77006 87841 94322 45526 38145 86554 42733
Положим, наша генеральная совокупность состоит из 1000 студентов, из
которых нам необходимо отобрать выборку в 100 человек. (Позже мы
обсудим размер выборки.) Пронумеруем этих студентов от 0 до 999. В
соответствии с таблицей случайных чисел будет отобран студент 572, затем студент 427
и так далее, пока не будут отобраны 100 студентов.
Используя такую методику, я произведу совершенно случайную выборку
студентов.
Случайные числа также можно сгене-
рить с помощью функции СЛЧИС()
программы Excel. Пример ее использования
показан на рисунке 12.4.
Ячейка А1 содержит формулу
= СЧИС(), которая предоставляет
случайное число от 0 до 1. Благодаря этому
случайному числу для выборки будет
отобран студент 435.
Эврика!:
При каждом изменении Excel
автоматически пересчитывает
все функции и формулы; в
результате для каждой функции
СЛЧИЛО генерируется новое
случайное число.
Рис 12.4
Генератор
случайных чисел
Excel.
Термины
Систематическая выборка
Один из способов избежать пристрастности при случайном отборе людей —
это использование систематической выборки. Эта методика подразумевает
отбор каждого к члена совокупности, который и будет представлен в
выборке. Значение к зависит от размера выборки
и генеральной совокупности. В примере с
колледжем при размере совокупности в 1000
студентов и выборке 100 студентов к = 10.
Из списка всей совокупности я буду
отбирать для выборки каждого десятого
студента. В целом, если N = размер генеральной
совокупности, п = размер выборки, тогда:
При систематической
выборке будет отобран
каждый /с-ый член генеральной
совокупности. При этом значение к будет
приблизительно равно
N
Глава 12: Выборка 165
Мы также можем применить эту методику к примеру с универмагом. На
рисунке 12.5 показано, что каждому третьему посетителю универмага будет
задан вопрос по поводу нового облика Дебби, даже если этот посетитель
будет обладателем угрожающей татуировки.
И снова «X» — посетитель, а «X», обведенный крутом, — посетитель,
вошедший в выборку.
Магазин 3
Магазин 2
Магазин 1
©
©
Магазин 4
х х Qm
Магазин 5
Магазин 6
Магазин 7
Рис 12.5
Систематическая
выборка.
©
Преимуществом использования систематической выборки является
простота ее проведения по сравнению с простой случайной выборкой — такая
выборка часто требует меньших затрат времени и средств. Недостаток —
опасность отбора пристрастной выборки, если в совокупности
прослеживается поведение, сопоставимое со значением к. Например, предположим, что
я провожу опрос в кампусе, спрашивая студентов, сколько часов в неделю
они посвящают учебе, и для сбора данных я выбираю каждую четвертую
неделю. Поскольку в колледже семестр длится 8 недель, каждая четвертая
неделя может оказаться неделей зачетов и тестов, требующей более
серьезного погружения в учебу, чем обычно (во всяком случае, мне хотелось бы так
думать!).
Групповая выборка
Если генеральную совокупность можно разделить на группы, тогда простая
случайная выборка может быть произведена из этих групп для
формирования финального варианта выборки. В примере с комитетом кодекса чести в
качестве групп могут выступать учебные группы, которые мы будем
отбирать случайным образом для участия в опросе. В каждой из выбранных групп
все студенты будут включены в выборку.
166 Часть 3: Статистический вывод
Термины
Групповой называется
простая случайная выборка групп
совокупности. Каждый представитель
отобранной группы будет включен в
выборку.
Опрос в универмаге тоже можно
провести с использованием групповой выборки.
Группами могут стать магазинчики в
генеральной совокупности всего универмага.
Магазинчики могут быть отобраны
случайным образом, а каждому посетителю
выбранных магазинов будет задан вопрос
о прическе Дебби. На рисунке 12.6
графически представлена групповая выборка.
Рис 12.6
Групповая
выборка.
ф Магазин зф
| ©
X
Man
^^ Магазин 4 Qy
©
XXX
азин 2
© !
Магазин 1
©
X
X
X
х I
Магазин 5
X
Магазин 6
X
Магазин 7
В соответствии с предыдущим рисунком, Магазины 1, 3 и 4 выбраны для
участия в опросе.
Чтобы групповая выборка была эффективной, каждая группа, отобранная
для участия в ней, должна быть репрезентативной по отношению ко всей
совокупности. На самом деле каждая группа является уменьшенной версией
целой совокупности. При грамотном использовании групповая выборка
может быть весьма экономически целесообразным способом отбора случайной
выборки из генеральной совокупности. В примере с универмагом мне
достаточно посетить три магазина для проведения в них опроса, чем я очень
сэкономлю себе время в годовщину своей свадьбы.
Споенная выборка
Слоенная выборка подразумевает деление совокупности на
взаимоисключающие группы (слои) и случайную выборку из каждой из этих групп. В нашем
примере с универмагом слоями могут быть представители мужского и
женского полов. Использование слоенной выборки гарантирует, что в моей
конечной выборке будет равное количество мужчин и женщин. Такое
расслоение графически представлено на рисунке 12.7.
Глава 12: Выборка 167
Существует множество различных
способов поделить генеральную
совокупность на слои. В примере со
студенческим комитетом кодекса чести
слоями могут быть студенты и аспиранты.
Если 20% нашей студенческой
совокупности представлены аспирантами,
я могу использовать слоенную
выборку, и в финальной выборке 20% будут
тоже аспиранты. Другими примерами
критериев расслоения выборки могут
быть возраст, доход или занятие.
Термины
Слоенной называется
выборка, подразумевающая деление
совокупности на
взаимоисключающие группы (слои) и случайную
выборку из каждой из этих групп.
/р\ Магазин 3
Man
© м
азин 2
Магазин 1
F
М
F
(jjj) Магазин 4 ^
F
®
(м)
F
\и
Магазин 5
Магазин 6
М |
Магазин 7
Рис 12.7
Слоенная
выборка.
Слоенную выборку особенно целесообразно использовать тогда, когда мы
хотим, чтобы финальная выборка обладала определенными
характеристиками целой совокупности. Если бы в примере с универмагом мы использовали
простую случайную выборку, в финальной выборке не была бы соблюдена
необходимая пропорция мужчин и женщин. Это может привести к
пристрастной выборке в том случае, если у мужчин окажется совершенно иной
взгляд на новый облик Дебби, чем у женщин.
Ошибки выборки
Пока мы рассматривали лишь плюсы отбора выборки из генеральной
совокупности, предпочитая именно выборку измерению всех представителей
совокупности. Однако в статистике, как и в жизни, не существует бесплатного
сыра. Полностью полагаясь на выборку, мы включаем «зеленый свет»
ошибкам, которые могут привести к неточным выводам в отношении генеральной
совокупности.
168 Часть 5: Статистический вывод
Любой статист больше всего беспокоится по поводу ошибок выборки,
которые происходят, когда измерение выборки отличается от измерения
совокупности. Поскольку генеральная совокупность целиком измеряется крайне
редко, невозможно совершенно точно вы-
Термины числить ошибку выборки. И все-таки с
помощью статистики вывода мы
научимся определять вероятности некоторого
количество ошибок выборки (Глава 15).
Ошибки выборки случаются тогда,
когда мы производим неудачный отбор
выборки, не соответствующей своей
генеральной совокупности. Если
большинству посетителей универмага очень
понравилась новая прическа Дебби, но нам
Ошибка выборки
происходит тогда, когда свойства
выборки существенно отличаются от
свойств генеральной совокупности.
Это случается при отборе выборки,
не соответствующей совокупности, из
которой она была получена.
случилось выбрать тех, кто не способен ценить красоту, тогда Дебби,
возможно, уже не придется носить свой прелестный конский хвостик.
К ошибкам выборки следует быть готовым: они являются своего рода
платой за то, что нам не приходится обрабатывать всю совокупность целиком.
Одним из способов уменьшения вероятности ошибки выборки
статистического исследования является увеличение размера выборки. В целом, чем
больше размер выборки, тем меньше вероятность ошибки. Если вы увеличите
размер выборки до размера генеральной совокупности, то ошибка выборки
будет равна нулю. Но таким образом вы лишитесь всех достоинств выборки.
Примеры использования ошибочных выборочных методик
Выборочные методики широко используются в политике. Но используются
они не всегда грамотно. Одна из самых известных неудач при
осуществлении выборки произошла во время президентской гонки 1936 года, когда
Литературный Дайджест предсказал, что Альф Лэндон одержит победу над
Франклином Рузвельтом. Даже если вы не очень сильны по части истории,
вы наверняка поняли, что кое-кто после выборов оказался в весьма
неприятном положении. Литературный Дайджест отобрал выборку из телефонных
книг и регистрационных книг автомобилистов. Но проблема состояла в том,
что в 1936 владельцами телефонов и автомобилей являлись в основном
состоятельные республиканцы, выборка которых не являлась репрезентативной
для всей совокупности избирателей.
Другая политическая ошибка подобного рода была допущена в 1948 году,
когда во время президентской гонки Институт Гэллапа предсказал, что Томас
Дьюи одержит победу над Гарри Труменом. На рисунке 12.8 показан
ликующий Трумен, который держит в руках утренний выпуск газеты Chicago
Tribune с заголовком «Дьюи одерживает победу над Труменом».
Неудача Института Гэллапа состояла в том, что в их выборке оказалось
большое количество неопределившихся избирателей. Было сделано невер-
Глава 12: Выборка 169
Рис 12.8
Дьюи одерживает
победу над Труменом.
~-~*ч Внимание!
Вы когда-нибудь принимали участие в опросе online на спортивном или новостном
сайте с возможностью просмотреть результаты? Эти опросы могут быть весьма забавными
и любопытными, но к результатам необходимо относиться критически. Это потому, что
респонденты выбирают себя сами, а это значит, что выборка не является случайной.
Результаты подобных опросов считаются пристрастными, поскольку их участники не являются
репрезентативными по отношению к совокупности в целом. Например, те, у кого нет выхода
в Интернет, не могут быть включены в выборку, а могли бы ответить на вопросы иначе, чем
те, у кого есть доступ в Интернет.
ное предположение о том, что эти избиратели являются репрезентативной
выборкой определившихся избирателей, поддерживающих Дьюи. Трумен
без труда выиграл на выборах, набрав 303 голоса против 189 голосов у Дьюи.
Как видите, для статистики вывода грамотный отбор выборки является
решающим шагом. Даже большой размер выборки не способен скрыть ошибок
отбора выборки, не являющейся репрезентативной в отношении
совокупности в целом. История показала, что большие размеры выборок вовсе не
обеспечивают точности. Например, Институт Гэллапа предсказал, что Никсон
получит 43% голосов на президентских выборах 1968 года, а он получил 42,9%. В
данном случае Институт Гэллапа опирался на размер выборки всего в 2
тысячи человек, в то время как Литературный Дайджест опросил 2 миллиона
человек. (Источник: www.personal.psu.edu/facu!ty/g/e/gec7/Sampling.htm)
Ваша очередь
1. Систематическая выборка должна быть произведена из телефонной
книги, содержащей 75 тысяч фамилий. Если должна быть выбрана
каждая к фамилия из книги, то какое значение к необходимо выбрать для
отбора выборки размером 500?
170 Часть 5: Статистический вывод
2. Генеральная совокупность определена как все сотрудники одной
компании. Как можно использовать групповую выборку для отбора выборки
для участия в опросе по поводу удовлетворенности сотрудников работой
в компании?
3. Генеральная совокупность определена как все сотрудники одной
компании. Как можно использовать слоенную выборку при отборе выборки
для участия в опросе по поводу удовлетворенности сотрудников работой
в компании?
Повторение - мать учения
Ф Простая случайная выборка — это выборка, в которой все
представители совокупности имеют равные шансы быть отобранными.
<# В систематической выборке каждый к член совокупности отбирается
для выборки, причем значение к приблизительно равно
N
п
$ Групповой называется простая случайная выборка групп совокупности.
Каждый представитель выбранных групп будет включен в финальную
выборку.
Ф Слоенная выборка получается путем деления совокупности на
взаимоисключающие группы (слои) и случайной выборки из каждого из этих
слоев.
Ф Ошибка выборки случается тогда, когда измерение на выборки
отличается от измерения на генеральной совокупности. Это происходит при
отборе выборки, не соответствующей генеральной совокупности, из
которой она была получена.
Выборочные
распределения
В этой главе
Ф Использование выборочных распределений среднего и
доли
Ф Работа с центральной предельной теоремой
Ф Использование стандартной ошибки среднего и доли
В Главе 12 мы пели дифирамбы выборкам, используемым в
статистическом анализе, и рассуждали о том, что это гораздо
проще и эффективней, чем измерять всю совокупность
целиком. В этой главе вы обсудим еще одно достоинство выборок —
выборочные распределения.
Выборочные распределения описывают поведение средних
по выборке. Вы наверняка удивитесь, узнав, что ведут они себя
очень хорошо, даже лучше, чем совокупности, из которых они
были получены. Хорошее поведение означает, что мы можем
достаточно точно предугадать будущие значения средних по
выборке, обладая весьма скудной информацией. Пока это
звучит несколько туманно, но к концу главы вы будете в
полнейшем изумлении качать головой.
172 Часть 3: Статпстпческпп вывод
Что такое выборочное распределение?
Положим, я хочу провести исследование с целью узнать, сколько миль
обычный человек проезжает в день на машине.
Поскольку я не могу измерить модели поведения за рулем всех членов
совокупности, я случайным образом отбираю выборку размером 10 (п = 10)
квалифицированных лиц и фиксирую, сколько миль они вчера проделали. Затем я
выбираю еще 10 водителей и фиксирую ту же информацию. Сделав то же
самое еще три раза, я помещаю все данные в таблицу, представленную ниже.
Номер выборки Среднее число миль (среднее по выборке)
1 40.4
2 76.0
3 58.9
4 43.6
5 62.6
Как видите, каждая выборка имеет свое собственное среднее значение,
и это значение всегда разное. Мы можем продолжить этот эксперимент,
отбирая многочисленные выборки и наблюдая за поведением средних по
выборке. Такое поведение средних по выборке представляет выборочное
распределение для количества миль, ежедневно проделываемых средним
водителем.
Распределение среднего по выборке
Распределение из предыдущего примера представляет распределение
среднего по выборке, поскольку интересующим нас измерением было среднее
каждой выборки. Такое распределение имеет ряд любопытных свойств,
которые я проиллюстрирую следующим примером.
Во время моего последнего отпуска на курорте мой 15-летний сын Джон
обратил внимание на рекламу турнира по пинг-понгу. Надо отметить, что у него
достаточно навыков, чтобы разгромить своего старика отца. Я научил его
играть в настольный теннис, когда ему еще
т приходилось вставать на кулер, чтобы ви-
■^ i деть, что происходит на столе. Мы играли
друг с другом, и мне частенько
приходилось довольствоваться ничьей. С трудом
сдерживая в себе дух соперничества, я
отбивал мяч с видом человека, у которого
случился эпилептический припадок, и
мяч летел прямо в сетку. И все-таки я за-
Распределение среднего по
выборке имеет отношение к
поведению средних в выборке при
отборе выборок из генеральной
совокупности.
Глава 13: Выборочные распределения 173
платил сравнительно небольшую цену: гордыня Джона была вполне
удовлетворена, а я сэкономил себе остаток недели отпуска. На что только мы не идем
ради детей.
В общем, мы используем мячики для пинг-понга для описания поведения
средних по выборке. Предположим, у меня в ящике 100 мячей, причем 20 из
них отмечены цифрой 1, 20 — цифрой 2, 20 — цифрой 3, 20 — цифрой 4 и
20 — цифрой 5.
В таблице ниже представлено распределение вероятностей этой
совокупности.
Номер мяча
Частота Относительная частота Вероятность
1
2
3
4
5
20
20
20
20
20
20/100
20/100
20/100
20/100
20/100
0.20
0.20
0.20
0.20
0.20
Это называется дискретным прямоугольным распределением
вероятностей, поскольку каждое событие имеет одинаковую вероятность, как
показано на рисунке 13.1
0.25
РИС 13.1
Дискретное
прямоугольное
распределение
вероятностей.
Номер мяча
Среднее и дисперсия дискретного прямоугольного распределения
вычисляются следующим образом:
174 Часть 5: Статистический вывод
Термины
Дискретным прямоугольным
называется распределение, в
котором каждому дискретному (его
можно посчитать) событию
приписывается одна и та же вероятность.
li=-(a+b)
12
где:
a = минимальное значение
распределения,
Ь = максимальное значение
распределения.
Для совокупности мячей для пинг-понга:
ц=|(1+5)=3.0
ст2=—(5-lf =—=1.33.
12 12
Запомните эти результаты. Мы вернемся к ним чуть позже в этой главе.
А теперь о выборочном распределении. Смешав все мячи, я выбираю один
мячик, записываю его номер, помещаю его обратно в ящик, выбираю второй
мяч и делаю с ним то же самое. Это моя первая выборка размером 2 (п = 2).
Проделав эту процедуру 25 раз, я вычисляю среднее каждой выборки и
представляю результаты в таблице ниже.
Распределение среднего (я = 2) по выборке
Выборка Первый мяч
Второй мяч Среднее по выборке х
1
2
3
4
5
6
7
8
9
10
11
1
2
2
1
4
1
1
3
2
1
3
3
1
1
1
2
3
2
1
5
3
3
2.0
1.5
1.5
1.0
3.0
2.0
1.5
2.0
3.5
2.0
3.0
Глава 13: Выборочные распределения 175
12
13
14
15
16
17
18
19
20
21
22
23
24
25
4
5
3
1
4
2
2
1
2
1
5
3
5
2
2
2
1
4
4
2
2
1
5
2
5
2
5
1
3.0
3.5
2.0
2.5
4.0
2.0
2.0
1.0
3.5
1.5
5.0
2.5
5.0
1.5
Здесь я должен признаться вам кое в
чем. Я и не собирался покупать 100
мячей и нумеровать их. Номера из
предыдущей таблицы были получены с
помощью функции случайного числа Excel,
которую мы обсуждали в Главе 12.
Мы можем преобразовать эту
таблицу в распределение относительных
частот, как показано в таблице ниже.
Внимание!
Студенты часто путают размер
выборки (п) и количество выборок. В
предыдущем примере размер
выборки равняется 2 (л = 2), а количество
выборок - 25. Другими словами, у нас
есть 25 выборок размером 2.
Среднее по выборке Частота Относительная частота Вероятность
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
3
4
7
2
3
3
1
0
2
3/25
4/25
7/25
2/25
3/25
3/25
1/25
0/25
2/25
0.12
0.16
0.28
0.08
0.12
0.12
0.04
0.00
0.08
Предыдущая таблица представляет собой выборочное распределение
среднего для эксперимента с пинг-понгом при п = 2. Это распределение
графически представлено на рисунке 13.2.
176 Часть 5: Статистический вывод
А сейчас я слышу, как вы громогласно вопрошаете: Что произойдет с
борочным распределением, если увеличить размер выборки? Отличный
прос, ответ на который вы найдете в следующем разделе.
вы-
во-
РИС13.2
Выборочное
распределение
среднего при п = 2.
л
\-
о
о
X
о
а
0)
со
0.251
0.15
0.05
2 2.5 3 3.5 4
Средние по выборке
Центральная предельная теорема
Я уже говорил ранее, что средние по выборке ведут себя по-особому. В
соответствии с центральной предельной теоремой, при увеличении размера
выборки (п) средние по выборке начинают подчиняться нормальному
распределению вероятностей, независимо от распределения совокупности, из
которой была получена выборка. Удивительно, скажете вы.
Глядя на рисунок 13.2, вы наверняка думаете о том, что представленное
на нем распределение совершенно не похоже на нормальную кривую,
которая должна быть колоколообразной и симметричной. И вы абсолютно
Эврика!
По моему скромному
убеждению, центральная предельная
теорема является самым
мощным инструментом
статистического вывода. Она формирует
основу для множества статистических
моделей, используемых нами сегодня.
Я вам настоятельно советую дружить с
этой теоремой.
правы, поскольку выборка размером 2
слишком мала, чтобы на нее
распространялось действие центральной предельной
теоремы.
Давайте удовлетворим ваше
любопытство и повторим эксперимент, собрав 25
выборок, каждая из которых состоит из 5
мячей (л = 5). Я рассчитал среднее каждой
выборки и представил их на рисунке 13.3.
Обратите внимание, каким образом
увеличение размера выборки влияет на форму
выборочного распределения. Оно начина-
Глава 13: Выборочные распределения 177
ет принимать колоколообразную и
симметричную форму. А теперь
взглянем на размеры выборок 10 и
20, представленные на рисунках
13.4 и 13.5 соответственно.
Термины
4
I-
О
О
X
I-
к
о
о.
Q)
ю
В соответствии с центральной
предельной теоремой, при
увеличении размера выборки (л) средние по
выборке начинают подчиняться
нормальному распределению вероятностей и
концентрироваться вокруг среднего
значения гегнеральной совокупности. Это
утверждение оказывается верным
независимо от распределения совокупности,
из которой была получена выборка.
Рис 13.3
Распределение
среднего по выборке
при п = 5.
1.0 1.5
2 2.5 3 3.5 4 4.5
Средние по выборке
5.0
0.61
0.51
0.41
0.31
0.2 J
0.1 J
о|
Рис 13.4
Распределение
среднего по выборке
при п = 10.
1.0 1.5
2 2.5 3 3.5 4 4.5
Средние по выборке
5.0
178 Насть 3: Статистпческий вывод
РИС 13.5 0.4
Распределение 0.35
среднего по выборке
при л = 20. 0.3
t 0.25
О
JE 0.2
R 0.15
ф
m 0.1
0.05
0
1.0 1.5 2 2.5 3 3.5 4 4.5 5.0
Средние по выборке
Обратите внимание, что по мере увеличения размера выборки
выборочное распределение становится похожим на нормальное распределение
вероятностей. Не знаю, как вы, но меня эта метаморфоза весьма впечатляет,
учитывая тот факт, что совокупность, из которой были получены эти выборки,
даже близко не напоминает нормальное распределение. Вспомните,
совокупность мячей для настольного тенниса подчинялась прямоугольному
распределению, показанному на рисунке 13.1.
Также заметьте, что по мере роста размера выборки средние по выборке
начинают сосредотачиваться вокруг среднего генеральной совокупности,
значение которого, как вы помните, равно 3.0. Это еще одна важная
особенность центральной предельной теоремы.
Верите или нет, но центральная предельная теорема обладает еще одним
важным свойством, речь о котором пойдет в следующем разделе.
Стандартная ошибка среднего
Обратите внимание, что на последних четырех рисунках по мере увеличения
размера выборки выборочные распределения становились все более
похожими друг на друга. Иными словами, по мере роста размера выборки
уменьшалось стандартное отклонение средних по выборке. В соответствии с
центральной предельной теоремой (снова она!), стандартное отклонение средних
по выборке вычисляется таким образом:
а
Глава 13: Выборочные распределения 179
где:
о* = стандартное отклонение средних по выборке,
ст = стандартное отклонение генеральной совокупности,
л = размер выборки.
Стандартное отклонение средних по выборке называется стандартной
ошибкой среднего.
Вспомните, как чуть ранее в этой главе, в разделе «Распределение
среднего по выборке» мы определили, что
дисперсия совокупности мячиков для
пинг-понга составляется 1.33.
Следовательно:
Термины
а = >/? = л/ГзЗ=1.15.
Теперь мы можем вычислить
стандартную ошибку среднего при п = 2 в
нашем примере:
1.15
сь =
л/л >/2
=0.813.
Стандартной ошибкой
среднего называется стандартное
отклонение выборочного Среднего. В
соответствии с центральной
предельной теоремой, стандартная ошибка
среднего рассчитывается по формуле:
<Ь =
VJT
Эврика!
Студенты часто путают о и а*. Символ а (стандартное отклонение генеральной
совокупности) измеряет вариации в пределах генеральной совокупности - мы обсуждали
это понятие в Главе 5. Символ а* (стандартная ошибка) измеряет вариации средних по
выборке и уменьшается по мере увеличения размера выборки.
В таблице ниже показано, как меняется стандартная ошибка при
изменении размера выборки в нашем примере с мячами пинг-понга.
Стандартная ошибка изменяется по мере изменения
размера выборки
Размер выборки
Стандартная ошибка
2
5
10
20
0.813
0.514
0.364
0.257
180 Часть 3: Статистический вывод
Почему работает центральная предельная теорема?
В этом разделе я объясню, почему центральная предельная система
действует именно так. Если этот вопрос вас не интересует, можете переходить к
следующему разделу. Обещаю, что не обижусь на вас.
Вернемся к первому эксперименту с размером выборки п = 2. В таблице
ниже показаны все возможные комбинации с 2 мячами с указанием
выборочного среднего.
Выборка Первый мяч Второй мяч Среднее по выборке х
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
2
2
2
2
3
3
3
3
3
4
4
4
4
4
5
5
5
5
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1.0
1.5
2.0
2.5
3.0
1.5
2.0
2.5
3.0
3.5
2.0
2.5
3.0
3.5
4.0
2.5
3.0
3.5
4.0
4.5
3.0
3.5
4.0
4.5
5.0
Глава 13: Выборочные распределения 181
Мы можем преобразовать эту таблицу в распределение относительных
частот, как.показано ниже.
Среднее по выборке х Частота Относительная частота Вероятность
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
1
2
3
4
5
4
3
2
1
1/25
2/25
3/25
4/25
5/25
4/25
3/25
2/25
1/25
0.04
0.08
0.12
1.16
0.20
0.16
0.12
0.08
0.04
В предыдущей таблице представлено теоретическое выборочное
распределение среднего, поскольку здесь показаны все возможные комбинации
выборок с соответствующими вероятностями. Графически это
распределение представлено на рисунке 13.6.
Средние по выборке
По рисунку видно, что чаще всего встречается среднее выборки 3.0, а
средние по выборке 1.0 и 5.0 встречаются реже всего. Это потому, что
комбинаций выборок из 2 мячей со средним 3.0 (а именно 5) больше, чем
комбинаций выборок из 2 мячей со средним 1.0 или 5.0 (а именно 1). Иными словами,
182 Часть 3: Статистический вывод
Термины
Теоретическое
распределение среднего по выборке
отображает все возможные средние
по выборке вместе с их
классическими вероятностями. Если вы забыли, что
такое классическая вероятность,
перечитайте Главу 6.
вероятность вытащить выборку из 2
мячей со средним 3.0 в 5 раз больше, чем
средние по выборке 1.0 или 5.0.
Когда мы увеличиваем размер
выборки до 5, 10 и 20, вероятность
вытащить выборку со средним 1.0 или 5.0
уменьшается, а вероятность вытащить
выборку со средним 3.0 увеличивается.
Это объясняет, почему по мере
увеличения размера выборки становится
больше выборок, сконцентрированных
вокруг 3.0, и меньше тех, что сконцентрированы вокруг 1.0 и 5.0.
Как заставить центральную предельную теорему работать
Я вижу, что вам не терпится испробовать в действии новый превосходный
инструмент. Не будем медлить с этим.
Если мы знаем, что средние по выборке подчиняются нормальному
распределению вероятностей, а также нам известны среднее и стандартное
отклонение этого распределения, мы можем предсказать вероятность того, что
средние по выборке будут больше или меньше определённых значений.
Например, возьмем наш эксперимент с мячиками для пинг-понга при п =
20. Следуя центральной предельной теореме, мы знаем, что средние по
выборке подчиняются нормальному распределению при:
\х = 3.0
а ^ 1.15
л/л~л/20
=0.257.
Какова вероятность того, что наша следующая выборка из 20 мячей будет
иметь среднее по выборке не более 3.4? Распределение выборочного
среднего показано на рисунке 13.7; заштрихованная область — это интересующая
нас вероятность.
Как и в Главе 11, нам необходимо вычислить z-распределение. Уравнение
выглядит несколько иначе, поскольку мы работаем со средними по выборке,
но на самом деле это то же самое уравнение, что и в Главе 11.
z =
х-ц
3.4-3.0
0.257
= 1.56.
Используя стандартную z-таблицу из Приложения В, получаем:
Р[х <3.4] = P[z< 1.56] = 0.9406
Глава 13: Выборочные распределения 185
Выборочное распределение среднего
при п = 20
ц = 3.0
ст* = 0.257
3.0 3.4
Средние по выборке
Эта вероятность показана на рисунке 13.8.
Выборочное распределение среднего
при п = 20
ц = 3.0
ах = 0.25~
Рис 157
Вероятность того,
что наше следующее
среднее по выборке
будет не более 3.4.
Рис 13.8
Вероятность того,
что следующее
среднее по выборке
будет не более 1.56
стандартных
отклонений
от среднего
по совокупности.
0 +1.56
Количество стандартных отклонений
В соответствии с заштрихованной областью, вероятность того, что наша
следующая выборка из 20 мячей будет иметь среднее по выборке не более
3.4, приблизительно равна 94%.
Использование центральной предельной теоремы при неизвестном
среднем совокупности
В нашем эксперименте с мячиками мы узнали, что среднее совокупности
равно 3.0. А что делать, если среднее совокупности неизвестно? Мы можем
взять среднее от средних по выборке и использовать его как приближение к
среднему по совокупности.
184 Часть 5: Статистический вывод
В таблице ниже показаны 25 средних по выборке из нашего эксперимента
при размере выборки 20 (п = 20).
Средние по выборке из 35 выборок мячей
Выборка Средние по выборке Выборка Средние по выборке
1
2
3
4
5
6
7
8
9
10
11
12
13
2.35
3.30
3.50
2.90
2.70
3.45
3.00
3.20
3.30
2.40
2.25
3.10
3.15
14
15
16
17
18
19
20
21
22
23
24
25
2.90
3.55
2.60
3.15
2.70
3.35
2.70
2.95
2.50
3.40
3.30
2.65
Если сложить средние по выборке и поделить полученную сумму на 25, мы
получим общее среднее:
- _ Сумма средних по выборке _ 74.35
*~ 25 25 '
Если следовать центральной предельной теореме, среднее по
совокупности приблизительно равно этому общему среднему:
Возвращаясь к нашему примеру, в котором мы вычисляли вероятность
того, что наше следующее среднее по выборке будет не меньше 3,4, получаем:
x-ix 3.4-2.97
z34 = -= =1.67.
34 а5 0.257
Воспользуемся z-таблицей из Приложения В:
Р[х<3.4] = P[z< 1.67] = 0.9527.
Полученная вероятность несколько выше, чем в предыдущем примере,
потому, что это приближенное значение среднего совокупности.
Глава 15: Выборочные распределения 185
Потенциал центральной предельной теоремы состоит в том, что для ее
применения достаточно небольшого объема информации о распределении
совокупности. Средние по выборке будут вести себя превосходно до тех пор,
пока размер выборки достаточно велик. Это многоцелевая теорема, которая
имеет бесчисленное количество реальных приложений. Уверен, вы будете
потрясены.
Распределение доли в выборке
Среднее по выборке — это не единственная мера, которую можно
определить. А что, если я хочу определить процент подростков, которые согласятся
со следующим высказыванием: «Я часто обращаюсь к своим родителям за
советом, когда речь идет о судьбоносном вопросе». Поскольку каждый
респондент имеет только два варианта ответа (согласен или не согласен), данный
эксперимент подчиняется биноминальному распределению вероятностей,
описанному в Главе 9.
Вычисление доли в выборке
Меня интересует доля подростков для выборки размером п, которые
согласны с вышеуказанным утверждением. Выборочная доля, р, вычисляется
следующим образом:
_ Количество успехов в выборке
s= п *
Поскольку мне не известна доля по совокупности, р, тех, кто согласен с
данным утверждением, мне необходимо собрать данные из выборок и найти
приблизительное значение доли по совокупности так же, как я вычислял ее в
примере со средними тю выборке.
Я хочу, чтобы размер моей выборки был достаточно велик, для применения
нормального распределения вероятностей вместо биноминального
распределения. Вспомните, что в Главе 11 мы говорили о том, что если пр > 5 и щ > 5,
мы можем использовать нормальное распределение для приблизительного
вычисления биноминального распределения (q = 1 — р, вероятность
неудачи). Надеюсь, что р будет хотя бы 5%
(хотя бы небольшое количество
подростков слушают советов родителей),
поэтому я выбираю п = 150. Тогда:
пр = (150) (0.05) = 7.5
nq = (150) (0.95) = 142.5.
Предположим, я отобрал 10
выборок, каждая из которых имеет размер
Помните, что значение доли, р
или Р& должно попадать в интервал от
О до 1. Студенты часто допускают
такую ошибку: узнав, что доля
составляет 10%, они пишут р = 10. На самом
деле в таком случае р = 0.10.
186 Часть 5: Статистический вывод
150, и зафиксировал число согласий (успехов) в каждой выборке в
нижеследующей таблице.
Выборка
Количество успехов ps
Выборочная доля
1
2
3
4
5
6
7
8
9
10
26
18
21
30
24
21
16
28
35
27
26/150 = 0.173
18/150 = 0.120
21/150 = 0.140
30/150 = 0.200
24/150 = 0.160
21/150 = 0.140
16/150 = 0.107
28/150 = 0.187
35/150 = 0.233
27/150 = 0.180
Затем я вычисляю среднее выборочных долей, чтобы приблизительно
определить долю по совокупности, р:
0.173 + 0.12 + 0.14 + 0.02+0.16+0.14 + 0.107 + 0.187+0.233+0.18
P*PS=-
10
= 0.164.
Вычисление стандартной ошибки доли
Теперь мне необходимо определить стандартное отклонение этого
распределения в выборке, которое носит название стандартной ошибки доли,
обозначается р и вычисляется по формуле:
Термины
Стандартной ошибкой доли
называется стандартное
отклонение выборочных доль. Она
вычисляется по формуле:
->-F?-
р V 150
Вот сейчас я готов ответить на вопрос:
Какова вероятность того, что из
следующей выборки в 150 подростков не более 20% согласятся с известным
утверждением? Заштрихованная область на рисунке 13.9 показывает эту
вероятность, отображающую выборочное распределение доли для нашего
примера.
Глава 15: Выборочные распределения 187
Распределение доли в выборке
р = 0.164 М
ctd= 0.030 Д
Рис 13.9
Выборочное
распределение
доли.
0.164 0.20
Выборочные доли
Поскольку размер выборки позволяет нам использовать нормальное
распределения для приблизительного вычисления биноминального распределения, мы
можем вычислить z-распределение доли с помощью следующего уравнения:
z =
Ps-P
0.20-0.164
0..030
:+1.20.
Обратимся к стандартной z-таблице из Приложения В:
P[ps< 0.20] = P[z< 1.20]= 0.8849.
Эта вероятность графически представлена на рисунке 13.10 в виде
заштрихованной области.
Распределение доли в выборке
р = 0.164
= 0.030
0 +1.20
Выборочные доли
Рис 13.10
Вероятности того,
что следующая
доля в выборке
будет не более 1.2
стандартных
отклонений от доли
по совокупности.
188 Часть 5: Статистическим вывод
Полученные результаты говорят нам о том, что существует 88.49%-ная
вероятность того, что не более 20% подростков из следующей выборки
размером 150 согласятся с нашим утверждением. Что ж, возможно, когда они
повзрослеют, они смогут постичь мудрость своих родителей.
Ваша очередь
1. Вычислите стандартную ошибку среднего при:
a. а = 10, п = 15
b. а = 4.7, л = 12
c. а = 7, п = 20
2. Совокупность имеет среднее значение, равное 16.0, и стандартное
отклонение, равное 7.5. Вычислите следующее, если размер выборки
равен 9.
а.Р[х<17]
Ъ.Р/х> 18]
с.Р[14.5<х<16.5]
3. Вычислите стандартную ошибку доли.
a. р = 0.25, п = 200
b. р = 0.42, п = 100
c. р = 0.06, п = 175
4. Доля по совокупности приблизительно равна 0.32. Вычислите
следующее, если размер выборки равен 160.
a. P[ps < 0.30]
b. P[ps > 0.36]
c.P[0.29<ps<0.37]
Повторение - мать учения
Ф Распределение среднего по выборкам имеет отношение к поведению
средних по выборке при отборе выборок из совокупностей.
Ф В соответствии с центральной предельной теоремой, при увеличении
размера выборки (п) средние по выборке начинают подчиняться
нормальному распределению вероятностей.
Ф В соответствии с центральной предельной теоремой, при увеличении
размера выборки (п) средние по выборке начинают концентрироваться
вокруг среднего по совокупности.
Глава 13: Выборочные распределения 189
Ф Стандартная ошибка среднего — это стандартное отклонение средних
по выборке. В соответствии с центральной предельной теоремой,
стандартная ошибка среднего определяется по формуле.
а
Ф Стандартной ошибкой доли называют стандартное отклонение долей по
совокупности; стандартная ошибка доли вычисляется по формуле:
гт IEEE
Доверительные
интервалы
В этой главе
Ф Толкование значения доверительного интервала
Ф Вычисление доверительного интервала для среднего при
больших и малых выборках
Ф Введение в ^-распределение Стьюдента
Ф Вычисление доверительного интервала доли
#> Определение размеров выборки для получения
определенного уровня погрешности
Мы научились осуществлять отбор случайной выборки и
узнали, как при определенных условиях ведут себя средние по
выборке и доли. А теперь мы заставим эти выборки работать на
нас с помощью доверительных интервалов.
Одна из наиболее важных ролей статистики сегодня состоит
в том, чтобы получать информацию из выборки и использовать
эту информацию, чтобы делать выводы о совокупности, из
которой была получена выборка. Мы используем выборки в
качестве оценок совокупности. Но какую оценку предлагает нам
сделать выборка? На этот вопрос нам помогут ответить
доверительные интервалы.
Глава 14: Доверительные интервалы 191
Доверительные интервалы для среднего
при больших выборках
В этом разделе мы узнаем, как определить доверительный интервал для
среднего по генеральной совокупности, используя выборку большого размера. Под
большим размером мы понимаем п > 30. Первый шаг на пути к определению
доверительного интервала для совокупности подразумевает обсуждение оценок.
Оценки
Простейшая оценка совокупности — это точечная оценка, а самая
распространенная из точечных оценок — среднее по выборке. Точечная оценка — это
единичное значение, лучше всего описывающее интересующую нас
совокупность. Я поясню это понятие на следующем примере.
Мне кажется, что мою жену похитили и подменили похожей на нее
женщиной, которая является большой поклонницей телевизионного канала,
предлагающего произвести покупки на дому. Никому и ничему в нашем
доме не удалось избежать влияния товаров, обнаруженных Дебби на ее
любимом телевизионном канале. Она уже приобрела товары для автомобиля,
кухни, собаки, кожи, волос и так далее и тому подобное.
Неожиданно главным праздником в нашем доме стала неделя «Diamonique
Week». Я не уверен, что хорошо
представляю себе, что это за Diamonique,
но подозреваю, что это что-то вроде
«доступно в течение ограниченного
времени». Как только я включаю дома
телевизор, на экране появляется
назойливая личность, умоляющая меня:
«Позвонить прямо сейчас! Осталось
всего три штуки!»
Как бы то ни было, я хочу оценить
среднее значение стоимости заказа для
совокупности любителей канала
покупок на дому. Если бы мое среднее по
выборке оказалось равным 78.25 доллара, я мог бы использовать это значение как
точечную оценку для всей совокупности любителей делать покупки на дому.
Преимуществом точечной оценки является простота ее вычисления и
понимания. Однако есть и недостаток: я не представляю себе, насколько эта
оценка точна.
Чтобы покончить с этой неопределенностью, мы можем использовать
интервальную оценку, представляющую диапазон значений, лучше всего
описывающих совокупность. Для вычисления интервальной оценки нам
необходимо познакомиться с доверительными интервалами, чем мы и займемся в
следующем разделе.
Термины
Точечная оценка - это
единичное значение, лучше всего
описывающее интересующую нас
совокупность; чаще всего в этом
качестве выступает среднее по выборке.
Интервальная оценка предоставляет
диапазон значений, лучше всего
описывающих совокупность.
192 Часть 5: Статистическим вывод
Термины
Доверительные уровни
Доверительный уровень — это вероятность того, что в интервальную оценку
попадет параметр генеральной совокупности. Параметром называется
числовое описание характеристики генеральной совокупности, например, среднее.
Из Главы 13 вспомним, что средние по
выборке подчиняются нормальному
распределению вероятностей при большом
количестве выборок. Предположим, мы
хотим определить интервальную оценку
с 90%-ным доверительным уровнем.
Этот доверительный уровень
соответствует z-распределению из стандартной
нормальной таблицы, равному 1.64, как
показано на рисунке 14.1.
Доверительный интервал -
это диапазон значений,
используемых для оценки параметра
совокупности, связанный с определенным
доверительным уровнем. Параметрами
являются данные, описывающие
характеристику генеральной совокупности.
PncW.1
Доверительный
уровень 90%.
Доверительный интервал 90%
-1.64 0
0.95
+1.64
j
Эврика!
На рисунке 14.1 вы видите, что 5% данных под кривой расположены справа от +1.64,
а 95% - слева. Поэтому вы видите значение 0.9495 (близко к 0.95), соответствующее
z-распределению 1.64 в Таблице 3 Приложения В. Но помните, что z = 1.64
соответствует 90%-ному доверительному уровню - области, заштрихованной на рисунке.
В общем, мы можем определить доверительный интервал вокруг нашего
выборочного среднего с помощью следующих уравнений:
х+ zcGx (верхняя граница доверительного уровня)
х— zcGx (нижняя граница доверительного уровня),
Глава 14: Доверительные интервалы 193
где:
х = среднее по выборке,
zc = критическое z-распределение — количество стандартных
отклонений на основе доверительного уровня,
о* = стандартная ошибка среднего (Глава 13).
Выражение zcgx носит название уровня погрешности, Е, и часто
используется в опросах.
Возвращаясь к нашему примеру с покупками на дому, предположим, что в
выборке из 32 заказчиков средняя стоимость заказа составляет 78.5 доллара, а
стандартное отклонение совокупности —
37.0 доллара. Мы можем вычислить наш ^S^^SL Термины
90%-ный доверительный уровень
следующим образом: ^РИДРР Доверительным уровнем
Hair = 78.5 доллара i зывается вероятность того,
п = 32
а = 37.0 доллара
zr = 1.64
а $37.50
а-;/г-ж~=$6-63-
что интервальная оценка включит в
себя параметр генеральной
совокупности, например, среднее. Уровень
погрешности, Е, определяет широту
доверительного интервала и
вычисляется по формуле z<Bx •
Верхняя граница = х + 1Ыах = $78.25 + 1.64($б.бЗ) = $89.12.
Нижняя граница =х - 1.64о* = $78.25 - 1.64($6.63) = $67.38.
В соответствии с полученными результатами, наш 90%-ный доверительный
уровень для случайной выборки домашних покупателей находится между 67.38
и 89.12 доллара или ($67.38; $89.12). Этот интервал показан на рисунке 14.2.
Интервальная оценка для среднего долларового "ТК. 14.2
значения заказа домашнего покупателя. Интервальная оценка
I | I для среднего долларового
I I ! I значения заказа
$67.38 $78.25 $89.12 домашнего покупателя.
Будьте внимательны при анализе доверительного интервала!
В предыдущем разделе было сказано, что доверительный интервал является
диапазоном значений, используемых для оценки параметра совокупности,
связанным с определенным доверительным уровнем. Доверительный
интервал должен быть описан в контексте нескольких выборок. Если мы отберем
194 Часть 3: Статистическим вывод
10 выборок из нашей совокупности любителей покупок на дому и построим
90%-ные доверительные интервалы вокруг каждого из средних по выборке,
тогда теоретически 9 из 10 интервалов будут включать истинное среднее
совокупности, которое остается неизвестным. На рисунке 14.3 показано, о чем
я говорю.
Рис 14.3
Толкование определения
доверительного
интервала.
Толкование 90%-ного доверительного интервала
Этот интервал
не включает ц
/
Как видите, выборки с 1 по 9 имеют доверительные интервалы,
включающие истинное среднее по совокупности, а выборка 10 его не включает.
Довольно просто ошибиться с определением доверительного интервала.
Например, неверно утверждать, что «существует 90%-ная вероятность того, что истинное
среднее по генеральной совокупности попадает в пределы интервала ($67.38;
$89.12)». Правильно будет звучать утверждение о том, что «существует 90%-ная
вероятность того, что любой доверительный интервал из случайной выборки будет включать
в себя среднее по совокупности».
Поскольку существует 90%-ная вероятность того, что любой
доверительный интервал будет содержать истинное среднее совокупности, остается
10%-ная вероятность того, что этого не
произойдет. Это 10%-ное значение носит
название уровня значимости,
обозначаемого а, представленного на рисунке
14.4 в виде белых «хвостов» кривой.
Вероятность доверительного уровня
является дополнением к уровню значи-
Тсрмины
Уровень значимости (а) - это
вероятность допущения
ошибки первого рода.
Глава 14: Доверительные интервалы 195
Уровень значимости
Рис 14.4
Уровень значимости.
мости. Например, уровень значимости для доверительного уровня 95%
составляет 5%; уровень значимости для доверительного уровня 99% составляет
1% и так далее. В целом доверительный интервал (1 —а) имеет уровень
значимости, равный а.
В дальнейших главах мы еще раз коснемся темы уровня значимости.
Что происходит при изменении доверительных уровней
Пока мы рассмотрели лишь 90%-ный доверительный интервал. Но
доверительные уровни могут быть разными, в зависимости от наших требований. В
таблице ниже представлен наш эксперимент с покупкой на дому с
доверительными уровнями 90, 95 и 99%.
Доверительные интервалы с различными
доверительными уровнями
Доверительный
уровень
90
95
99
Zc
1.64
1.96
2.57
<*х
$6.63
$6.63
$6.63
Средние
по выборке
$78.25
$78.25
$78.25
Нижняя
граница
$67.38
$65.26
$61.21
Верхняя
граница
$89.12
$91.24
$95.29
Из таблицы видно, что
увеличение доверительного
уровня означает, что наша
интервальная оценка истинного
среднего генеральной
совокупности становится менее
точной. Это очередное
доказательство того, что в статистике
^ Эврика!.
Я советую вам самостоятельно
подтвердить значения z-распределений в этой
таблице, сверившись с Таблицей 3
Приложения В. Повторение - мать учения! При
необходимости обратитесь к Главе 11.
196 Часть 3: Статистический вывод
бесплатного сыра не бывает. Если мы хотим быть уверенными в том, что наш
доверительный интервал будет включать истинное среднее по совокупности,
нам придется смириться с тем, что доверительный интервал станет шире.
Что происходит при изменении размера выборки
И все-таки есть один способ уменьшить ширину нашего доверительного
интервала, сохранив тот же доверительный уровень. Мы можем увеличить
размер выборки. И снова статистика доказывает, что бесплатного сыра не
существует: увеличение размера выборки имеет свою цену. Скажем, мы
увеличиваем размер выборки до 64 любителей покупок на дому. Изменения
коснутся нашей стандартной ошибки:
а $37.50
Нашим новым 90%-ным доверительным интервалом для первоначальной
выборки будет:
х = $78.25
п = 64
а* = $4.69.
Верхняя граница = х + 1.64а* = $78.25 + 1.64($4.69) = $85.94.
Нижняя граница = х - 1.64а* = $78.25 - 1.64($4.69) = $70.56.
Увеличение размера выборки с 32 до 64 уменьшило доверительный
интервал с ($67.38; $89.12) до ($70.56; $85.94) — получился более точный интервал.
Определение размера выборки для среднего
Мы также можем вычислить минимальный размер выборки при
необходимости получения определенного уровня погрешности. Какой размер выборки
нам понадобится для 95%-ного доверительного интервала, имеющего уровень
погрешности $8.00 (Е = $8.00) для нашего примера с домашними покупками?
Е = 7X5*
/— ZG
4fJ
Глава 14: Доверительные интервалы 197
п J (1.96)(37.50) Y 844,85
I, $8.00 )
Следовательно, для получения 95%-ного доверительного интервала от
$78.25 - $8.00 = $70.25 до $78.25 + $8.00 = $86.25 нам потребуется выборка
размером в 85 любителей домашних покупок.
Вычисление доверительного интервала при неизвестном значении
Этот раздел не доставит вам особых сложностей (наконец-то!). Во всех
наших предыдущих примерах подразумевалось, что нам известно значение а,
стандартное отклонение генеральной совокупности. А что делать, если это
значение неизвестно? Не паникуйте, пока п > 30 мы можем заменить а,
стандартное отклонение генеральной совокупности, значением s, стандартным
отклонением выборки, и выполнить описанную выше процедуру. Для
иллюстрации этой методики изучите следующую таблицу, в которой представлен
размер заказа в долларах 30 любителей домашних покупок.
Выборка любителей домашних покупок (п = 30)
75 109 32 54 121 80 96 47 67 115
29 70 89 100 48 40 137 75 39 88
99 140 112 87 122 75 54 92 89 153
С помощью программы Excel подтверждаем, что:
х = $84.47 и s = $32.98.
99%-ным доверительным интервалом вокруг этого выборочного среднего
будут:
х = $84.47
п =30
s = $32.98
zc = 2.57
у/п л/30
Мы используем о*1* ДЛЯ обозначения того, что мы примерно вычислили
стандартную ошибку среднего, используя s вместо а. Нам, статистам, очень
нравится ставить над буковками черточки.
Верхняя граница = х 4- 2.57аи5 = $84.47 + 2.57($6.02) = $99.94.
198 Часть 3; Статистический вывод
Нижняя граница = х - 2.57а^ = $84.47 - 2.57($6.02) = $69.00.
Видите! Совсем недурно.
Использование функции ДОВЕРИТ программы Excel
Программа Excel имеет в своем составе встроенную функцию,
позволяющую вычислять доверительные интервалы. Функция ДОВЕРИТ обладает
следующими характеристиками:
ДОВЕРИТ(альфа;станд_откл; размер),
где:
альфа = уровень значимости доверительного уровня
станд_откл = стандартное отклонение совокупности
размер = размер выборки.
Например, на рисунке 14.5 показана функция ДОВЕРИТ, используемая
для вычисления доверительного интервала для нашего примера с домашними
покупками.
Рис 14.5
Функция ДОВЕРИТ для
примера с домашними
покупками.
В ячейке А1 содержится формула =ДОВЕРИТ(0.1; 37.5; 32) с результатом
10.90394. Это значение представляет уровень погрешности, или величину,
добавляемую или вычитаемую из выборочного среднего:
$78.25 + $10.90 = $89.15
$78.25 + $10.90 = $67.35.
Этот доверительный интервал несколько отличается от ранее
вычисленного в этой же главе из-за округления чисел.
Глава 14: Доверительные интервалы 199
Доверительные интервалы для среднего
при малых выборках
Пока в этой главе мы рассматривали примеры с п 30. Уверен, что теперь вы
задаетесь вопросом, как определить доверительный уровень для выборки
размером меньше 30. Что ж, здесь все зависит от обстоятельств.
При малом размере выборки мы лишаемся работы с нашим другом —
центральной предельной теоремой и вынуждены принять допущение, что
совокупность является нормально (или приблизительно нормально)
распределенной во всех случаях. Сначала мы рассмотрим случай, когда нам известно о,
стандартное отклонение совокупности.
Когда значение известно
Когда значение известно, процедура та же, что и при большом размере
выборки. Мы можем делать так потому, что приняли допущение о том, что
совокупность является нормально распределенной. Давайте определим 95%-ный
доверительный интервал из следующей выборки любителей домашних
покупок размером 10.
75 109 32 54 121 80 96 47 67 115
Выборка любителей домашних покупок (п =10)
х = $79.60
Мы обладаем следующей информацией:
$79.6
п = 10
s = $37.50 (из первоначального примера)
zc = 1.96
а $37.50
G-=—r== т=— =$11.86.
х >fc Vio
Верхняя граница = х+ 1.96с* = $79.60 + 1.96($11.86) = $102.85.
Нижняя граница = х - 1.96с* = $79.60 + 1.96($11.86) = $56.35.
Обратите внимание, что при малом размере выборки мы получаем
широкий доверительный интервал. И снова мы принимаем допущение, что
совокупность, из которой получена выборка, является нормально
распределенной, и это первое подобное допущение, принятое нами в этой главе.
200 Часть 3: Статистический вывод
Когда значение а неизвестно
Чаще всего значение о нам не известно. Здесь мы делаем небольшую
корректировку, к которой уже обращались ранее, и заменяем а, стандартное
отклонение генеральной совокупности, s, стандартным отклонением выборки.
Но из-за малого размера выборки эта замена вынуждает нас использовать
новое распределение вероятностей, известное как ^-распределение Стью-
дента (названное в честь вас, студентов).
t-распределение является непрерывным распределением вероятностей, с
присущими им свойствами.
Мысли вслух
f-распределение Стьюдента было
выведено Уильямом1 Госсетом (1876-1937)
во время работы на ирландскую
пивоваренную компания Guinness Brewing
Company. Он опубликовал свое
открытие под псевдонимом «Студент». Теперь
редко когда встретишь такого
скромного ирландского статиста!
Термины
Степени свободы - это
количество значений, которые
могут свободно варьироваться, при
условии, что известна информация
вроде выборочного среднего.
Ф Имеет колоколообразную форму и
симметрично расположено вокруг
среднего.
Ф Форма кривой зависит от степеней
свободы (d.f.), которые при
выборочном среднем равны п — 1.
Ф Область под кривой равна 1.
Ф t-распределение более плоское,, чем
нормальное. При увеличении числа
степеней свободы форма t-paenpe-
деления становится похожа на
нормальное распределение, как
показано на рисунке 14.6. Если степеней
свободы (выборка размером 30 и
более), оба распределения являются
практически идентичными.
Рис. 14.6
t-распределен ие
Стьюдента
в сравнении
с нормальным
распределением.
{-распределение в сравнении
с нормальной кривой
d.f. = 15
Стандартная нормальная кривая
0
Глава 14: Доверительные интервалы 201
Студенты часто испытывают трудности, связанные с этим понятиям,
которое представляет собой число оставшихся после принятия какого-либо
решения (например, определения выборочного среднего) свободных альтернатив.
Например, если я знаю, что моя выборка размером 3 имеет среднее, равное 10,
я могу варьировать только 2 значения (п — 1). После определения мной 2
значений я не могу выбирать третьего значения, поскольку мое среднее по выборке
должно быть равно 10. В данном случае я обладаю двумя степенями свободы.
А теперь мы можем определить доверительные интервалы для среднего,
используя выборку малого размера:
х + tсаих (верхняя граница доверительного интервала)
х — tc^x (нижняя граница доверительного интервала),
где:
tc = критическое f-значение (их вы найдете в Таблице 4 Приложения В),
Gli-=—j= — оцененная стандартная ошибка среднего.
х л/п
Для иллюстрации этой процедуры примем допущение, что совокупность
любителей домашних покупок подчиняется нормальному распределению и
отобрана следующая выборка размером 10.
Выборка любителей домашних покупок из нормального распределения
(л = 10)
29 70 89 100 48 40 137 75 39 88
Не зная значения а, мы можем построить 95%-ный доверительный
интервал вокруг выборочного среднего.
Чтобы определить значение tc для данного примера, мне необходимо
вычислить число степеней свободы. Поскольку п = 10, в моем распоряжении
п — 1 = 9 степеней свободы. Это соответствует tc = 2.262, значению,
подчеркнутому в таблице ниже, взятой из Таблицы 4 Приложения В.
t-распрсдсленис Стьюдснта
Выбранные области правого «хвоста» с доверительными уровнями
Дов.ур. 0.2000 0.1500 0.1000 0.0500 0.0250 0.0100 0.0050 0.0010 0.0005
d.f. 0.6000 0.7000 0.8000 0.9000 0.9500 0.9800 0.9900 0.9980 0.9990
1 1.376 1.963 3.078 6.314 12.706 31.821 63.657 318.31 636.62
2 1.061 1.386 1.886 2.920 4.303 6.965 9.925 22.327 31.599
3 0.978 1.250 1.638 2.353 3.182 4.541 5.841 10.215 12.924
4 0.941 1.190 1.533 2.132 2.776 3.747 4.604 7.173 8.610
202 Часть 3: Статистическим вывод
Выбранные области правого «хвоста» с доверительными уровнями
Дов.ур. 0.2000 0.1500 0.1000 0.0500 0.0250 0.0100 0.0050 0.0010 0.0005
d.f. 0.6000 0.7000 0.8000 0.9000 0.9500 0.9800 0.9900 0.9980 0.9990
5
6
7
8
2.
10
И
12
0.920
0.906
0.896
0.889
0.883
0.879
0.876
0.873
1.156'
1.134
1.119
1.108
1.100
1.093
1.088
1.083
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
5.893
5.208
4.785
4.501
4.297
4.144
4.025
3.930
6.869
5.959
5.408
5.041
4.781
4.587
4.437
4.318
Далее нам необходимо определить среднее по выборке и стандартное
отклонение, которые получаются следующими (Excel):
х = $71.50 и s = $33.50.
Теперь мы можем приблизительно вычислить стандартную ошибку
среднего:
оЦ s $33^50
х JR <Ло
и выстроить наш 95%-ный доверительный интервал.
Верхняя граница = x+tcG»x = $ 71.50 + 2.262($ 10.59) = $95.45.
Нижняя граница = x-tco^ = $71.50 - 2.262($10.59) = $47.55.
Ну вот и все!
Термины
(-распределение может использоваться, когда выполнены все нижеуказанные
условия:
Ф Совокупность подчиняется нормальному (или приблизительно нормальному)
распределению.
Ф Размер выборки не превышает 30.
#■ Стандартное отклонение по генеральной совокупности а неизвестно и должно быть
приблизительно вычислено с помощью s - стандартного отклонения выборки.
Глава 14: Доверительные интервалы 205
В таблице ниже суммирована вся информация, представленная в этой
главе вплоть до этого момента, чтобы вы могли решить, какой метод
использовать для построения доверительного интервала вокруг среднего.
Сводная таблица доверительных интервалов среднего
Условия
п > 30, а известно, любая совокупность
л > 30, о неизвестно, любая совокупность
п < 30, ст известно, норм, совокупность
л < 30, а неизвестно, норм, совокупность
Доверительный интервал
X ± zco*
X =±= ZcGx
X =t ZcGx
X ± tcG»x
На этом мы завершаем обсуждение доверительных интервалов среднего.
Следующие в нашем меню — доли!
Доверительные интервалы для долей
при больших выборках
Мы можем также определить долю по совокупности, построив
доверительный уровень из выборки. Из Главы 13 вспомним, что данные о долях
подчиняются биноминальному' распределению, которое можно приблизительно
вычислить с помощью нормального распределения при соблюдении
следующих условий:
цр > 5 и nq > 5,
где:
р = вероятность успеха по совокупности,
g = вероятность неудачи по совокупности (q = 1 — р).
Допустим, я хочу вычислить долю любителей домашних покупок
женского пола на основе выборки. Из предыдущей главы вспомним, что
выборочную долю можно определить следующим образом:
_ Число успехов в выборке
Вычисление доверительного интервала для доли
Доверительный интервал вокруг выборочной доли рассчитывается
следующим образом:
204 Часть 5: Статистическим вывод
ps + zccp (верхняя граница доверительного интервала)
ps — zcgp (нижняя граница доверительного интервала),
где ар — стандартная ошибка доли (то есть стандартное отклонение
выборочных долей) при:
Хвала тем, кто уже видит, какая перед нами возникает проблема. Мы
пытаемся оценить р, долю по совокупности, но нам необходимо значение для р
для задания доверительного интервала. Наше решение состоит в том, чтобы
оценить стандартную ошибку, используя выборочную долю как
приближенное значение для доли по совокупности:
*-.-№*.
Теперь мы можем построить доверительный уровень вокруг выборочного
среднего:
ps + zca^x (верхняя граница доверительного уровня)
ps — ZcC^x (нижняя граница доверительно уровня).
Заставим эти уравнения работать на нас. Пытаясь оценить долю женщин
среди любителей домашних покупок, я отобрал выборку из 175 случайных
покупателей, из которых 110 — женщины. Теперь я могу вычислить ps,
выборочную долю:
_ Количество успехов в выборке _ 1Ю Л90
Ps~ п ~175~ '
Стандартная ошибка доли получается следующей:
а,_ =л/МД=((^29)(0.371)=0()365
х V 175 V 175
Теперь мы готовы построить 90%-ный доверительный интервал вокруг
нашей выборочной доли (zc = 1.64).
Верхняя граница = ps + 1.64ар = 0.629 4- 1.64(0.0365) = 0.689
Нижняя граница = ps- 1.64ар = 0.629 - 1.64(0.0365) = 0.569
Наш доверительный интервал для доли женщин среди лкэбителей
домашних покупок — (0.569; 0.689). Дебби должна оказаться как раз в этом
интервале!
Глава 14: Доверительные интервалы 205
Определение размера выборки для доли
Мы почти закончили. Мы уже делали подобное со средним, а теперь мы
можем определить необходимый размер выборки для получения необходимого
уровня погрешности. Каким должен быть размер выборки для 99%-ного
доверительного интервала, имеющего уровень погрешности 6% (Е = 0.06) в
нашем примере с домашними покупками? Вот формула для вычисления л,
размера выборки:
п=мЬ) ■
Обратите внимание, что нам нужны значения р и q. В случае отсутствия
предварительной оценки значений определим р = q = 0.50. Поскольку
половина совокупности — это женщины, мне кажется, что я выбрал правильную
стратегию.
\2
n = (0.50)(0.50)| ^j|j =459.
Следовательно, для получения 99%-ного доверительного интервала,
обеспечивающего уровень погрешности не более 6%, нам понадобится выборка
размером 459 любителей домашних покупок.
«ькл* вецух
Причина, по которой мы используем р= q= 0.50 в случае отсутствия оценки доли
совокупности, состоит в том. что эти значения обеспечивают наибольший размер выборки по
сравнению с другими комбинациями р и д. Это вроде наказания за отсутствие информации
о вашей совокупности. В этом случае вы можете быть уверены в том, что ваша выборка
будет большого размера, независимо от доли совокупности.
Ваша очередь
1. Постройте 97%-ный доверительный интервал вокруг выборочного
среднего 31.3, взятого из ненормально распределенной совокупности со
стандартным отклонением 7.6, используя размер выборки 40.
2. Какого размера должна быть выборка для получения уровня
погрешности 5 для 98%-ного доверительного интервала, взятого из ненормально
распределенной совокупности со стандартным отклонением
совокупности, равным 15?
3. Постройте 90%-ный доверительный интервал вокруг выборочного
среднего 16.3, взятого из ненормально распределенной совокупности со
стандартным отклонением совокупности 1.8, используя выборку
размером 10.
206 Часть 5: Статистический вывод
4. Следующая выборка размером 30 была получена из ненормально
распределенной совокупности:
10 4 9 12 5 17 20 9 4 15
11 12 16 22 10 25 21 24 9 8
14 16 20 18 8 10 28 19 16 15
Определите 90%-ный доверительный интервал вокруг среднего.
5. Следующая выборка размером 12 была получена из ненормально
распределенной совокупности со стандартным отклонением совокупности
12.7:
37 48 30 55 50 46 40 62 50 43 36 66
Определите 94%-ный доверительный интервал вокруг среднего.
6. Следующая выборка размером 11 была получена из ненормально
распределенной совокупности:
121 136 102 115 126 106 115 132 125 108 130
Определите 98%-ный доверительный интервал вокруг среднего.
7. Следующая выборка размером 11 была получена из ненормально
распределенной совокупности:
87 59 77 65 98 90 84 56 75 96 66
Определите 99%-ный доверительный интервал вокруг среднего.
8. Была протестирована выборка из 200 лампочек, 11 из которых оказались
с дефектом. Вычислите 95%-ный доверительный интервал вокруг этой
выборочной доли.
9. Какого размера должна быть выборка для построения 96%-ного
доверительного интервала вокруг доли явки избирателей на следующих
выборах для обеспечения уровня погрешности 4%? Примем допущение, что
доля по совокупности оценена в 55%.
Повторение - мать учения
Ф Доверительный интервал — это диапазон значений, используемых для
оценки параметра совокупности и связанных с определенным
доверительным уровнем.
Ф Доверительный уровень — это вероятность того, что оценка интервала
будет включать параметр совокупности, например, среднее.
Глава 14: Доверительные интервалы 207
Ф Увеличение доверительного уровня приводит к тому, что
доверительный интервал становится более широким и менее точным.
Ф Увеличение размера выборки уменьшает широту доверительного
интервала, но увеличивает его точность.
Ф Используйте (-распределение для построения доверительного
интервала, когда совокупность подчиняется нормальному (или приблизительно
нормальному) распределению, размер выборки — меньше 30 и
неизвестно а, стандартное отклонение по совокупности.
Ф Используйте нормальное распределение для построения
доверительного интервала вокруг выборочной доли, когда пр>5ипд>5.
Введение в проверку
гипотез
В этой главе
Ф формулировка основной и альтернативной гипотез
Ф Различия между односторонней и двусторонней
проверкой гипотез
Ф Ошибки первого и второго рода
Ф Определение границ области отклонения проверки
гипотезы
Ф Заключение проверки гипотезы
Теперь, когда мы умеем производить оценку параметра
совокупности, например, среднего, с помощью выборки и
доверительного интервала, мы готовы приступить к изучению
краеугольного камня статистики вывода — проверке гипотез.
Статисты любят делать предположения относительно
параметра совокупности, отбирать выборку из этой совокупности,
измерять выборку и объявлять, было ли первоначальное
предположение подтверждено выборкой. Это я вам в двух словах
рассказал, что представляет собой проверка гипотезы. Читайте
дальше, и вы узнаете массу любопытных деталей, без которых
у меня получилась бы всего одна коротенькая главка!
Глава 15: Введение в проверку гипотез 209
Цель этой главы состоит в том, чтобы кратко ознакомить вас с основами
проверки гипотез. В последующих двух главах эта тема представлена более
подробно, и вы узнаете, каково практическое применение этой методики.
Оставайтесь с нами!
Проверка гипотез - основы
В мире статистики гипотезой называется предположение о параметре
генеральной совокупности. Примерами гипотез являются предположения:
# Средний взрослый в среднем выпивает 1,7 чашки кофе ежедневно.
Ф 12% студентов после окончания университета отправятся сразу в
аспирантуру.
Ф Не более 2% товаров, продаваемых нашим заказчикам, окажутся с
дефектом.
В каждом случае мы сделали предпо
ложение относительно совокупности, Шг -^ I Терцины
которое может оказаться истинным или
тт т л ~ ^лДЬ~^гопотеза - это предположе-
ложным. Цель проверки гипотезы — w-^ш- *"-«
у^^гиэхи. м^ю np^o^rv* ние в отношении параметра
сделать статистический вывод о при- совокупности,
нятии или отклонении этих
предположений. Для более детального
разъяснения этого понятия я обращусь к следующей истории.
Мне хватает мужества признаться в том, что я страшно боюсь змей.
Поэтому я тут же запаниковал, узнав, что Сэм, старший сын Дебби, поймал
змею и принес ее домой (и Дебби великодушно разрешила ему поселить
рептилию в спальне Сэма).
На следующее утро мой самый страшный ночной кошмар стал
действительностью. Змея проскользнула сквозь прутья клетки и теперь блуждала по
дому. Вероятно, Сэм никогда не слышал о змее-матери, которая ради
спасения своего малыша умудрилась приподнять малолитражку Volkswagen.
Не буду называть имен, но чья-то супруга предложила подложить в
комнату Сэма мышку, которая послужила бы приманкой и своим запахом
привлекла змею к себе. Я воспринял этот совет как хорошую шутку, но лишь до того
момента, как в комнате Сэма появился белый грызун, используемый в
качестве приманки для змеи.
В ту ночь я не сомкнул глаз (один глаз был все время открыт, а ушки были
на макушке), а моя супружница спокойно посапывала рядышком.
На следующее утро я обнаружил, что вчера были только цветочки. А
наутро пошли и ягодки: мышь прогрызла дырочку в своей коробке и тоже
разгуливала по дому. Теперь в моих излюбленных местах, где я вкушаю пищу,
сплю и смотрю телевизор, шастают два диких животных. Уже с утра я начал
лихорадочно изучать телефонную книгу, пытаясь найти место, где находят
210 Часть 5: Статистический вывод
свой приют змеи и мыши. Дебби же считала, что я «слишком близко принял
сложившуюся ситуацию к сердцу».
В ту ночь я принял позу зародыша, чтобы защитить свои внутренние
органы, а также руки и ноги со стороны кровати, а моя супружница снова
спокойно посапывала рядышком.
А теперь попытаемся связать эту научную фантастику с проверкой
гипотез. Положим, моя гипотеза состоит в том, что понадобится в среднем б дней,
чтобы поймать змею. Другими словами, я хочу проверить свое
предположение, что среднее по генеральной совокупности, ц, равно 6 дням. Для этого я
сделаю выборку людей, по домам которых расползлись змеи, и вычислю
среднее число дней, необходимых для ловли рептилий. Допустим, среднее по
выборке равно 6.1 дня. Проверка гипотезы скажет мне, действительно ли
6.1 дня значительно отличаются от 6.0 дней или эта разница сугубо случайна.
Далее последуют детали, не переключайтесь!
Основная и альтернативная гипотезы
Каждая проверка гипотезы подразумевает наличие основной (нулевой) и
альтернативной гипотез. Основная (нулевая) гипотеза, обозначаемая Н0,
неизменна и высказывает предположение, что среднее по совокупности .>, =
или < определенного значения. Основная гипотеза считается истинной, если
нет явного доказательства противоположного. В нашем примере основная
гипотеза будет выглядеть следующим образом:
Н0: u= 6.0.
Альтернативная гипотеза,
обозначаемая Hi, содержит утверждение,
противоположное утверждению основной
гипотезы, и считается верной, если
основная гипотеза оказывается ложной.
Альтернативная гипотеза всегда утверждает,
что среднее по генеральной
совокупности <, * или > определенного значения. В
нашем примере моя альтернативная
гипотеза гласит, что:
НьЦ^б.О.
В таблице ниже показаны три фактических сочетания основной и
альтернативной гипотез.
Основная гипотеза Альтернативная гипотеза
Н0:|и = 6.0 Н,:ц*6.'0
Я0:ц>6.0 Н^^Кб.О
Н0:|Л<6.0 Hl:\i> 6.0
Термины
Основная гипотеза»
обозначаемая Н0% представляет
собой статус-кво и содержит
предположение, что среднее по совокупности
<, = или > определенного значения.
Альтернативная гипотеза,
обозначаемая Нл, заявляет обратное и считает- \
ся верной, если основная гипотеза
оказывается ложной.
Глава 15: Введение в проверку гипотез 211
В некоторых учебниках используется правило, гласящее, что основная гипотеза всегда
формулируется в виде = и никогда не использует < или >. Какой бы методикой для
формулировки гипотезы вы не воспользовались, это никак не скажется на статистическом анализе.
Просто всегда придерживайтесь однажды выбранной позиции.
Обратите внимание, что альтернативная гипотеза никогда не
использует <, = или >. Выбору правильной комбинации посвящен следующий
раздел.
Формулировка основной и альтернативной гипотез
Будьте предельно внимательны при формулировке основной и
альтернативной гипотез. Ваш выбор будет зависеть от характера проверки и мотивации
человека, ее проводящего.
Если целью является проверка того, что среднее по совокупности равно
определенному значению, например, как в примере со змеями, назначьте
такое утверждение основной гипотезой. В результате получим
следующее:
Н0:ц = 6.0
Н^ц^б.О.
Часто проверка гипотезы проводится исследователями с целью доказать,
что их открытие существенно улучшает существующие продукты или
процедуры. Например, если я изобрел мяч для гольфа и утверждаю, что он летит
дальше обычных мячей более чем на 20 ярдов, моя гипотеза будет выглядеть
следующим образом:
Я0:ц < 20
Hl:\i>20.
Обратите внимание, что я использовал альтернативную гипотезу для
формулировки утверждения, которое я хочу доказать статистически, с целью
заработать себе состояние на продаже этих мячей отчаявшимся игрокам в
гольф вроде меня. Поэтому альтернативная гипотеза также носит название
исследовательской, поскольку представляет позицию, которую хочет
утвердить и закрепить исследователь.
Двусторонняя проверка гипотезы
Двусторонняя проверка гипотезы используется в случае, если
альтернативная гипотеза сформулирована как ф. В нашем примере со змеями
двусторонняя проверка как раз уместна, поскольку альтернативная гипотеза выглядит
212 Часть 3: Статистический вывод
как: Нх\\х * 6.0. Эта проверка графически представлена на рисунке 15.1,
который, как вы видите, изображает кривую двусторонней проверки.
Рис 15.1
Двусторонняя
проверка
гипотезы.
Двусторонняя проверка гипотезы
Отклонить Н0
Отклонить Н0
Среднее количество дней, требуемое для ловли змеи
График на рисунке представляет выборочное распределение среднего для
количества дней, необходимых для ловли змеи. Среднее по генеральной
совокупности, которое в соответствии с основной гипотезой должно равняться
6.0, является средним выборочного распределения и обозначается цНо.
Процедура выглядит просто.
Ф Отобрать выборку размером п и вычислить выборочный показатель — в
данном случае среднее по выборке.
Ф Отложить среднее по выборке на оси х кривой выборочного
распределения.
Ф Если среднее пр выборке оказывается в пределах белой области, мы не
отклоняем Н0. То есть, у нас нет достаточных доказательств для
поддержки Hi, альтернативной гипотезы, утверждающей, что среднее по
совокупности не равно 6.0 дням.
Ф Если среднее по выборке попадает в одну из заштрихованных
областей, называемых областями отклонения гипотезы, мы отклоняем Н0.
То есть мы обладаем необходимым доказательством для поддержки Hi
и убеждены, что истинное среднее по совокупности не равняется 6.0
дней.
Поскольку на рисунке присутствуют две заштрихованные области, мы
имеем дело с двусторонней проверкой гипотезы. Скоро мы научимся
определять границы областей отклонения гипотез.
Глава 15: Введение в проверну гипотез 213
Мыглй irc/rpf
В отношении основной гипотезы мы можем сделать лишь два утверждения.
$ Мы отклоняем основную гипотезу.
Ф Мы не отклоняем основную гипотезу.
Поскольку наши заключения основываются на выборке, у нас никогда не будет
достаточных оснований принимать основную гипотезу. Поэтому мы будем чувствовать себя
спокойней, если будем утверждать, что у нас нет достаточных доказательств, чтобы отклонить
Н0. Для разъяснения я воспользуюсь примером, взятым из судебной системы. Если жюри
присяжных обнаруживает, что подзащитный «невиновен», они не утверждают, что он
безвинен, а говорят, что у них нет достаточных доказательств его вины.
Односторонняя проверка гипотезы
Односторонняя проверка относится к альтернативной гипотезе,
сформулированной в виде < или >. Мой пример с мячами для гольфа как раз требует
односторонней проверки, поскольку альтернативная гипотеза выглядит как
Hx\\i > 20. График такой проверки показан на рисунке 15.2.
Рис. 152
Односторонняя
проверка гипотезы.
Увеличение средней длины броска в ярдах
На этом графике мы видим лишь одну область отклонения —
заштрихованную область правого «хвоста», распределения. Следуем той же
процедуре, которую использовали для
двусторонней проверки, и откладываем
среднее по выборке, которое
представляет собой среднее увеличение
расстояния от площадки для первого
удара с помощью моего нового мяча
для гольфа. Существуют два
возможных сценария.
Односторонняя проверка
гипотезы используется тогда»
когда альтернативная гипотеза
сформулирована в виде < или >.
214 Часть 5: Статистический вывод
Ф Если среднее по выборке попадает в
рамки незаштрихованной области,
мы не отклоняем Н0. То есть, у нас
нет достаточных доказательств для
поддержки Hi, альтернативной
гипотезы, утверждающей, что
изобретенный мною мяч увеличивает
расстояние от площадки ти более чем
на 20 ярдов, а значит, мое состояние
летит коту под хвост.
Ф Если среднее по выборке
оказывается в пределах области
отклонения, мы отвергаем Н0. То есть мы обладаем достаточными доказательствами
для поддержки Нх, утверждающей, что мой новый мяч увеличит расстояние
от ти более чем на 20 ярдов. Так что пора уходить на пенсию и зарабатывать
на новом изобретении!
Освоив основы проверки гипотез, мы переходим к ошибкам, которые
могут возникнуть при осуществлении выборки.
Ошибки первого и второго рода
Помните, что цель проверки гипотезы состоит в подтверждении
утверждения относительно совокупности на основе одной выборки. Поскольку мы
полагаемся на выборку, то подвергаем себя риску, что наши выводы о
совокупности могут оказаться ошибочными.
Используя пример с мячами для гольфа, положим, что моя выборка
попадает в область «Отклонить Н0» на последнем рисунке. То есть, в
соответствии с выборкой, мой мяч увеличит дистанцию более чем на 20 ярдов. А что,
если истинное среднее по совокупности на самом деле значительно меньше
20 ярдов? Это может произойти в результате ошибки выборки, которую мы
обсуждали в Главе 12. Тип ошибки, когда мы отклоняем Н0, а на самом деле
эта гипотеза является истинной, называется ошибкой первого рода.
Вероятность совершения ошибки первого рода определяется уровнем значимости,
о котором речь шла в Главе 14, и обозначается .
При проверке гипотезы может произойти и другого рода ошибка.
Предположим, выборка с мячом для гольфа оказалась в пределах области «Не
отклонять Н0» на последнем рисунке. То есть, в соответствии с выборкой, мой мяч
увеличивает дистанцию не более чем на 20 ярдов. Но что, если истинное
среднее по совокупности на самом деле больше 20 ярдов? Тип ошибки, когда
мы не отклоняем Н0, а на самом деле она является ложной, называется
ошибкой второго рода. Вероятность совершения ошибки второго рода
называется мощностью гипотезы и обозначается р.
В таблице ниже представлены оба типа ошибок проверки гипотезы.
Эврика!
Для проверки односторонней \
гипотезы область отклонения
будет всегда соотноситься с
ориентацией Нл. При Нл :\х > 20
область отклонения будет
располагаться в правом хвосте
выборочного распределения. При Нл-.ул < 20
область отклонения будет находить- |
ся слева. i
Глава 15: Введение в проверку гипотез 215
#о истинна Н0 ошибочна
Отклонить Н0 Ошибка первого рода Правильный исход
Р[ошибка первого рода] = а
Не отклонять Н0 Правильный исход Ошибка второго рода
Р[ошибка вт. рода] =р
Как правило, при проверке гипотезы
мы определяем значение а, которое
находится в пределах от 0.01 до 0.10, и
происходит это до отбора выборки. Тогда
можно вычислить значение р, но эта
тема не входит в задачи этой книги.
Скажите мне «спасибо» за это, потому что
это понятие — весьма сложное!
А теперь давайте заставим эти
понятия работать на нас и проведем
настоящую проверку гипотезы!
В идеале значения аир должны быть по возможности маленькими. Однако для
определенного размера выборки уменьшение значения а приведет к увеличению значения р. Обратное
тоже верно. Единственный способ уменьшить сразу аир- это увеличить размер выборки.
Как только размер выборки достигает размера генеральной совокупности, значения аир
становятся равными 0. Но, как мы уже обсуждали в Главе 12, делать этого не рекомендуется.
Пример двусторонней проверки гипотезы
Гипотезы для примера со змеями выглядят следующим образом:
H0:|li = 6.0
Нх\\х *6.0,
где jii = среднее количество дней, необходимых для отлова в доме змеи.
Допустим, мне известно, что стандартное отклонение по совокупности, ,
равно 5.0 дням, а размер выборки для проверки гипотезы, л, составляет 30
домов. (Не спрашивайте, где я возьму 30 домов, по которым свободно ползают
змеи. Я сочиняю историю прямо на ходу, так что не придирайтесь к словам.)
Определим а = 0.05, и это означает, что я допускаю, что существует 5%-ная
возможность совершения ошибки первого рода.
Прежде всего, вычислим стандартную ошибку среднего, а*. Если помните
содержание Главы 13, то уравнение выглядело так:
Термины
Ошибка первого рода
происходит тогда, когда основная
гипотеза отклоняется, а на самом деле
является истинной. Ошибка второго
рода происходит тогда, когда
основная гипотеза принимается, а на самом
деле является ложной.
216 Часть 3: Статистический вывод
х л/К л/30
Допустим, среднее по выборке из 30 домов составляет 6.1 дома. Каково
наше заключение в отношении оценки среднего по совокупности, ц?
Чтобы ответить на этот вопрос, нам необходимо определить критическое
z-распределение, соответствующее а = 0.05. Поскольку мы имеем дело с
двусторонней проверкой гипотезы, эта область должна быть равномерно
распределена между обоими хвостами, в каждом из которых а/2 = 0.025. В
соответствии с рисунком 15.3, нам необходимо определить z-распределение,
соответствующее области 0.950 + 0.025 = 0.975. Как видите, область 0.950
получена из 1 — а.
Рис 153 /~\
Критическое z-pacnpe- / \
деление для а = 0.05. I \
/ 0.950 \
а/2 = 0.025 / \ а/2 = 0.025
ч/ 1а \у
-1.96 0 +1.96
Используя Таблицу 3 из Приложения В, находим ближайшее к 0.9750
значение. Искомое значение находится на пересечении строки 1.9 и столбца
0.06; получаем z-распределение + 1.96 для правого хвоста и — 1.96 — для
левого.
Использование шкалы исходной переменной
В этом разделе мы определим область отклонения с помощью шкалы
исходной переменной, которой в нашем примере является количество дней. Для
вычисления верхней и нижней границ области отклонения используем
следующие уравнения. Из Главы 14 вспомним, что z-распределения из
стандартного нормального распределения используются, когда п 30 и значение
известно.
Границы области отклонения = |iHo + zca-,
где |иНо = среднее по совокупности, принятое основной гипотезой.
Глава 15: Введение в проверку гипотез 217
Для нашего примера со змеей:
Верхняя граница =цНо +zco- =6.0 +(1.96)(0.0913) =6.18 дня
Нижняя граница = \xHq + zca- =6.0 +(-1.96) (0.0913) = 5.82 дн я.
Поскольку наше среднее по выборке равно 6.1 дня, мы попадаем в область
«Не отклонять Н0», как показано на рисунке 15.4. Отсюда делаем вывод, что
разница между 6.1 и 6.0 днями — это исключительно дело случая и у нас есть
подтверждение, что среднее по совокупности равняется 6.0 дням.
Рис 15.4
Проверка гипотезы
для примера со змеями
(шкала исходной
переменной).
Отклонить Н0
\
5.82
6.18
6.0 6.1
Среднее количество дней, требуемое для ловли змеи
Использование стандартизованной нормальной шкалы
Мы можем получить то же самое заключение, установив границы области
отклонения с помощью нормальной шкалы. Для этого вычисляем
z-распределение, соответствующее выборочному среднему, как показано ниже:
Г = *-*Ч = 6.1-6.0
о- 0.0913
= + 1.09.
Эврика!
Убедитесь, что вы понимаете разницу между вычисленным и критическим z-pacnpe-
делением. Вычисленное z-распределение, z, представляет собой количество
стандартных отклонений между выборочным средним и ц^, средним по совокупности,
согласно основной гипотезе. Критическое z-распределение, zc, основывается на
уровне значимости, а, и определяет границу области отклонения.
На рисунке 15.5 полученный результат представлен графически.
Поскольку вычисленное z-распределение, равное 4-1.09, находится в пределах
области «Не отклонять Н0», заключения по обоим вариантам совпадают.
218 Часть 3: Статистический вывод
Рис 15.5
Проверка гипотезы
для примера со змеями
(нормальная шкала).
Отклонить Но /Не отклонятьН0 МЭтклонитьН0
Пример односторонней проверки гипотезы
Поскольку альтернативная гипотеза в примере с мячом для гольфа
формулируется как 20г мы имеем дело с односторонней проверкой гипотезы.
Гипотезы для данного примера выглядят так:
Я0:ц < 20
Hj:n>20,
где ц = среднее увеличение расстояния в ярдах от первой площадки.
Положим, мне известно, что стандартное отклонение совокупности, а,
равно 5.3 ярда, а размер моей выборки (п) для проверки гипотезы составляет
40 игроков в гольф. Для данного примера установим а = 0.01. Стандартная
ошибка среднего, а*, будет равна:
а- = —7= = —f= = 0.838 ярда.
х V^ V40 т
Допустим, среднее по выборке из 40 игроков — 22.5 ярда. Каково наше
заключение относительно оценки среднего по совокупности, ц?
И снова нам необходимо определить критическое z-распределение,
соответствующее а = 0.01. Поскольку речь идет об односторонней
проверке гипотезы, вся область должна находиться в одной стороне отклонения
в правой части распределения. В соответствии с рисунком 15.6, нам
необходимо определить z-распределение, соответствующее области 0.99, или
1 - а.
Используя Таблицу 3 из Приложения В, находим ближайшее к 0.9900
значение и получаем критическое z-распределение, равное 2.33.
Глава 15; Введение в проверку гипотез 219
Рис 15.6
Критическое
z-распределение
для а = 0.01.
а = 0.01
0 +2.33
Количество стандартных отклонений от среднего
Для вычисления предела этой области отклонения с использованием
шкалы исходной переменной делаем следующее:
Граница = ц„о + zcg-= 20+(2.33) (0.838) =21.95 ярда.
Поскольку наше среднее по выборке = 22.5 ярда, мы попадаем в область
«Отклонить Н0», как показано на рисунке 15.7. Заключение: мы обладаем
достаточными доказательствами для поддержки гипотезы, что среднее
увеличение расстояния от площадки после первого удара с помощью моего нового
мяча превышает 20 ярдов. Начинаю бизнес!
Рис 15.7
Проверка гипотезы
для примера
с мячом для гольфа
(шкала исходной
переменной).
f Не отклонять Н0\ Отклонить Н0
/
х = 22.5
Среднее увеличение расстояния после первого удара
Мы также можем рассмотреть эту проверку гипотезы с помощью
нормальной шкалы. Сначала вычислим z-распределение, соответствующее
нашему выборочному среднему 22.5 ярда, как представлено ниже:
220 Часть 3: Статистический вывод
Должно быть, вы задаетесь вопросом: «Если среднее по выборке равно 21.0 ярду, разве
это не исчерпывающее доказательство того, что мой новый мяч увеличивает длину
первого удара за 20 ярдов?» В соответствии с предыдущим рисунком, ответ на этот вопрос
отрицательный. Поскольку наше решение основывается на выборке, среднее 21 слишком
близко к 20, чтобы подтвердить мое утверждение. Среднее по выборке должно равняться
21.95 или более ярдам, чтобы полностью отклонить основную гипотезу.
z = -
*-цНо 22.5-20
о- ~ 0.838
= +2.98.
На рисунке 15.8 показано, что вычисленное z-распределение находится в
пределах области «Отклонить Н0» и соответствует нашим предыдущим
изысканиям.
Рпс.15.8
Проверка гипотезы для
примера с мячом для
гольфа (нормальная
шкала).
Не отклонять \ Отклонить Н0
z = +2.98
Количество стандартных отклонений от среднего
Эврика! •
Я советую вам при выполнении
проверки гипотезы изображать
выборочное распределение с
областями отклонения. Лаже в
статистике один рисунок стоит
тысячи слов!
Я еще раз вернусь к этому примеру в
Главе 17 и продемонстрирую вам, как
выполнять проверку гипотезы при
сравнении среднего двух совокупностей с
зависимой выборкой. Оставайтесь с нами!
В таблице ниже показаны z-распреде-
ления для различных уровней а.
Альфа
Хвост
Критическое z-распределение
0.01
0.01
Один
Два
=2.33
=2.57
Глава 15: Введение в проверку гипотез 221
Альфа Хвост Критическое z-распределение
0.02
0.02
0.05
0.05
0.10
0.10
Один
Два
Один
Два
Один
Два
±2.05
±2.33
±1,64
±1.96
±1.28
±1.64
Также обратите внимание на то, что критические z-распределения для
правого хвоста выборочного распределения всегда имеют положительные
значения, а критические z-распределения для левого хвоста — всегда
отрицательные значения.
Я уже упоминал ранее, что целью этой главы является ввести основные
понятия проверки гипотез. В следующих двух главах эта же тема
рассматривается более подробно. Так что готовьтесь, пока мы только разминаемся!
Ваша очередь
1. Сформулируйте гипотезу для следующего утверждения: Средний
взрослый в среднем выпивает 1.7 чашки кофе ежедневно. Выборка из
35 взрослых выпила в среднем 1.95 чашки кофе за день.
Предположим, что стандартное отклонение по совокупности составляет
0.5 чашки. При а = 0.10 проверьте свою гипотезу. Каково ваше
заключение?
2. Сформулируйте гипотезу для следующего утверждения: Средний
возраст наших заказчиков составляет менее 40 лет. Была отобрана выборка
из 50 человек, средний возраст которых составлял 38.7 лет.
Предположим, что стандартное отклонение совокупности — 12.5 лет. При а = 0.05
проверьте свою гипотезу. Каково ваше заключение?
3. Сформулируйте гипотезу для следующего утверждения: Средняя
продолжительность работы наших лампочек составляет 1 000 часов.
Средняя продолжительность работы выборки из 32 лампочек составила 1 190
часа. Предположим, что стандартное отклонение совокупности
составляет 325 часов. При а = 0.02 проверьте свою гипотезу. Каково ваше
заключение?
4. Сформулируйте гипотезу для следующего утверждения: Среднее время
доставки составляет менее 30 минут. Среднее время выборки из 42
доставок составило 26.9 минуты. Предположим, что стандартное
отклонение совокупности составляет 8 минут. При а = 0.01 проверьте свою
гипотезу. Каково ваше заключение?
222 Часть 3: Статистический вывод
Повторение - мать учения
Ф Основная гипотеза, Н0, является неизменной и утверждает, что
среднее по совокупности <, = или > определенного значения.
Ф Альтернативная гипотеза, Hi, утверждает обратное основной гипотезы
и является истинной, если основная гипотеза оказывается ложной.
Ф Двусторонняя проверка гипотезы используется тогда, когда
альтернативная гипотеза сформулирована как *, а односторонняя гипотеза
используется, когда альтернативная гипотеза сформулирована как < или >.
Ф Ошибка первого рода происходит тогда, когда основная гипотеза
отклоняется, а на самом деле она является истинной. Вероятность этой
ошибки обозначается а — уровень значимости.
Ф Ошибка второго рода происходит, когда основная гипотеза
принимается, а на самом деле является ложной. Вероятность этой ошибки
обозначается р — мощность проверки гипотезы.
Проверка гипотезы
по одной выборке
В этой главе
Ф Проверка среднего по совокупности с использованием
выборки большого и малого размеров
Ф Обсуждение роли альфы (а) при проверке гипотезы
Ф Использование р-значения для проверки гипотезы
Ф Проверка доли по генеральной совокупности с
использованием выборки большого размера
В Главе 15 я ввел понятие проверки гипотезы, чтобы возбудить
ваш интерес. В этой главе речь пойдет о проверке гипотезы в
рамках одной совокупности, а Глава 17 посвящена проверке
гипотезы, при которой производится сравнение двух совокупностей.
Проверка гипотезы по одной совокупности подразумевает
подтверждение утверждений о том, что среднее по совокупности
равно определенному значению. Этот тип проверки гипотезы
имеет множество различных случаев, которые мы и рассмотрим в
следующих разделах. В Главе 16 вы встретите уже знакомые вам
понятия, представленные в Главах 14 и 15. Это сделано для того,
чтобы вы могли свободно оперировать новыми понятиями до
глубокого и проникновенного погружения в материал этой главы.
224 Часть 5: Статистический вывод
Проверка гипотезы для среднего при больших выборках
Когда размер выборки, используемой нами для проверки гипотезы,
достаточно велик (п > 30), мы можем положиться на центральную предельную
теорему, описанную в Главе 13. При этом у нас остается еще два случая для
рассмотрения: когда а, стандартное отклонение совокупности, известно и когда
оно неизвестно.
Когда сигма известна
Для иллюстраций этого случая обращусь к следующему примеру.
Одной из самых страшных фраз, которую муж может услышать от своей
жены, является следующая: «Дорогой, давай вместе сядем на диету». У меня
должны были возникнуть подозрения относительно мотивации Дебби,
предложившей сесть на низкоуглеводную диету, особенно потому, что она носит
брюки 2 размера. Но я решил, что вполне смогу перенести потерю
нескольких фунтов, поэтому, немного поколебавшись, согласился. В конце концов, я
представлял себе, что мы можем превратить эту затею в соревнование, чем
сделаем свою жизнь более интересной.
По прошествии нескольких мучительных дней без моих любимых
углеводов (кто бы мог подумать, что взрослый мужчина может мечтать о сырных
снеках!) мне стало любопытно, как удается Дебби так хорошо себя
чувствовать, сидя на такой беспощадной диете. Ответ на эту загадку я нашел в ее
машине — наполовину пустая коробка булочек с корицей! Полагаю, в этом
соревновании я одержал по.беду. О, сладость победы!
А теперь к делу. Предположим, что составители этой диеты утверждают,
будто средний возраст человека, готового подвергнуть себя подобной пытке,
составляет менее 40 лет. Формулируем гипотезы:
H0:\i > 40 лет
Нх\\\ < 40 лет.
Составляем выборку из 60 человек, сидящих на этой диете, и
обнаруживаем, что средний возраст составляет 37.5 лет. При а, стандартном отклонении
совокупности, равным 16 годам, проверяем гипотезы при а = 0.05.
/^7) Эврика! '■ .
^£лшг Вспомним из Главы 15, что а, уровень значимости, представляет собой вероятность
(ШЯ совершения ошибки первого рода, которая происходит тогда, когда мы отклоняем
^^Р Н0, а она на самом деле является истинной. В этом случае ошибка первого рода озна-
||р чает, что мы верим в утверждение о том, что средний возраст человека, сидящего на
• диете, составляет менее 40 лет, а в действительности это заявление ложно. В нашем
примере существует 5%-ная вероятность ошибки первого рода.
Глава 16: Проверка гипотезы по одной выборке 225
Поскольку размер выборки более 30 и нам известно значение а,
вычисляем z-распределение из нормального распределения, как мы это проделывали
в Главе 15.
z-
х~»н0
а-
Для нашего примера стандартная ошибка среднего, х, вычисляется так:
о- = —j= = -т==2.07 года.
х 7n V60
Теперь определяем z-распределение:
х-цНй 35.7-40
z=-
2.07
= -2.08.
Вновь обратимся к Главе 15: критическое z-распределение, определяющее
границы области отклонения, равно — 1.64 для однохвостовой
(левосторонней) проверки при = 0.05. На рисунке 16.1 эта проверка представлена
графически.
/ 0.95
а = 0.05 / 1-а
Отклонить Н0 / Не отклонять
1 I 1
-2.08 -1.64 0
Z Zc
Hq \
Рис 16.1
Односторонняя проверка
гипотезы для примера
с диетой (стандартная
шкала).
Число стандартных отклонений от среднего
На рисунке видно, что вычисленное z-распределение — 2.08 попадает в
область «Отклонить Н0», из чего мы можем заключить, что заявление о том, что
средний возраст человека для этой диеты составляет менее 40 лет, истинно. Я
чувствовал, что слишком стар для таких опытов над собственным организмом!
В целом мы отклоняем Н0, если |z| > |zc|, где |z| = «абсолютное значение» z.
Например, |-2.08| = 2.08.
226 Часть 3: Статистический вывод
Когда сигма неизвестна
Во многих случаях нам не известно значение а, стандартного отклонения
генеральной совокупности. Но если размер нашей выборки не менее 30, мы
можем подставить s, стандартное отклонение выборки, вместо а. Покажу это
на примере.
Не знаю, как обстоят дела у вас, но лично я провожу немало времени,
вися на телефоне и выжидая, когда же мне удастся услышать голос живого
представителя службы поддержки клиентов. Положим, одна из компаний
заявляет, что среднее время ожидания заказчика на телефоне составляет
менее 5 минут. Допустим, нам не известно значение а. В таблице ниже указано
время ожидания в минутах для случайной выборки из 30 клиентов.
Время ожидания в минутах
6.2
3.2
5.5
3.8
2.7
4.7
1.3
4.0
6.5
5.4
7.3
7.1
4.7
3.6
4.4
4.4
4.9
5.2
4.6
0.5
6.1
5:0
2.9
7.4
6.6
2.5
4.8
8.3
5.6
2.9
С помощью Excel определяем, что х = 4.74 минуты, a s = 1.82 минуты. С
первого взгляда кажется, что утверждение этой компании верно. Но давайте
проведем проверку гипотезы при а = 0.02, чтобы в этом удостовериться.
Наши гипотезы выглядят следующим образом:
HQ:\i > 5.0 минут
Hx:\i < 5.0 минут
Из Главы 15 мы знаем, что критическое z-распределение для однохвосто-
вой (левосторонней) проверки гипотезы при а = 0.02 равно — 2.05.
Как и в Главе 14, мы можем приблизительно вычислить стандартную
ошибку среднего:
ац- = ~т= = —т==0.332 минуты
х л/л >/30 У
Вычисленное z-распределение для данного примера будет равняться:
Z=*Z14= 4.74-5.0
ац- 0.332
На рисунке 16.2 эта проверка проиллюстрирована графически.
В соответствии с этим рисунком, мы не отклоняем основную гипотезу.
Другими словами, у нас нет достаточных доказательств для поддержки
заявления компании о том, что среднее время ожидания составляет менее 5
минут. Даже несмотря на то, что среднее по выборке на самом деле меньше 5
минут (4.74 минуты), это значение слишком близко к 5 минутам, чтобы гово-
Глава 16: Проверка гипотезы по одной выборке 227
рить о разнице между этими двумя значениями. Можно сказать то же самое
и по-другому: «Разница между 4.74 и 5.0 в данном случае не является
статистически значимой».
>^ Рис 16.2
/ \ Односторонняя гипотеза
I \ для примера со временем
I 0 98 ■ \ ожидания (стандартная
I \ шкала).
а = 0.02 / 1-а \
Отклонить Н0 I Не отклонять Н0 \
\У \
-2.05 -0.78 0
z zc
Число стандартных отклонений от среднего
Рель альфы в проверке гипотезы
Для всех примеров, приведенных в последних двух главах, я просто заявлял
о значении а, уровня значимости. Наверняка вас распирает от любопытства,
каким образом скажется на проверке гипотезы изменение значения а.
Хороший вопрос!
Допустим, я заявляю, что средняя оценка человека, изучающего
статистику по этой книге, будет более 87 баллов. (На самом деле я вовсе этого не
утверждаю, так что не радуйтесь раньше времени!) Гипотезы будут выглядеть
так:
H0:\i < 87
Hj-.n > 87.
А теперь мой интерес состоит в том, чтобы суметь отклонить Н0, и это
будет подтверждением моего заявления. Для этого я выберу достаточно
высокое значение а, скажем, 0.10. Это значение соответствует критическому z-
распределению +1.28, поскольку мы пользуемся правым хвостом
односторонней проверки гипотезы.
Предположим, что а, стандартное отклонение совокупности, равняется 12,
а среднее по выборке — 90.6, полученное из выборки размером 32 студента.
Для данного примера стандартной ошибкой среднего, о*, будет:
а 12 -2 12
228 Часть 3; Статистическим вывод
Отсюда получаем вычисленное z-распределение:
х-
±4_9O6-87=+1J0
о- 2.12
Судя по рисунку 16.3, я достиг поставленной цели, отклонив Н0, поскольку
вычисленное z-распределение оказалось в заштрихованной области.
Похоже, моя шутка с книгой удалась!
Рис 16.3
Проверка гипотезы
для примера с оценкох
при а = 0.10.
а = 0.10
ОТКЛОНИТЬ Н0
Число стандартных отклонений от среднего
Но я должен признать, что выбрал слишком большое значение а = 0.10,
чтобы доказать свое заявление. То есть я готов принять, что существует 10%-
ная вероятность ошибки первого рода. Проверка будет куда более
впечатляющей, если задать более низкое значение а, например, равное 0.01. Зато это
значение значительно ближе к реальному положению дел. Уровень
значимости соответствует критическому z-распределению +2.33. На рисунке 16.4
показано, как это отразится на области отклонения.
Рис 16.4
Проверка гипотезы
для примера с оценкой
при а = 0.01.
1 Л-г* \
а = 0.01
Отклонить Н0
Число стандартных отклонений от среднего
Глава 16: Проверка гипотезы по одной выборке 229
Как видите, заштрихованная область, к моему вящему ужасу, уже не
включает вычисленное z-распределения +1.7. Следовательно, я не отклоняю
Н0 и не могу утверждать, что средняя оценка тех, кто будет учиться
статистике по моей книге, превысит 87 баллов. В целом проверка гипотезы,
отклоняющей Н0, более впечатляющая при низком значении а.
Введение уровня р-значимости
Термины
Только вы подумали, что теперь можно окунуться в воду, как на горизонте
появляется еще одна акула. Думаю, сейчас самое время познакомить вас еще
с одним понятием. Ворчите? Что же, ничего удивительного, но потом вы
будете меня благодарить.
Уровнем р-значимости называется
самый маленький уровень значимости,
при котором будет отвергнута основная
гипотеза при допущении, что основная
гипотеза является истинной. Иногда
уровень р-значимости называют
наблюдаемым уровнем значимости. Знаю, пока
все эти слова кажутся вам
бессмысленными, но иллюстрация этих понятий на
примере поможет разъяснить их.
Наблюдаемый уровень
значимости - это самый
маленький уровень значимости, при котором
основная гипотеза будет отвергнута
при допущении, что она является
истинной. Это понятие также носит
название уровня р-значимости.
Уровень р-значимости для односторонней проверки гипотезы
На примере предыдущей задачи с баллами (более 87 при успешном
изучении этой книги) на рисунке 16.5 показан уровень р-значимости,
соответствующий заштрихованной области справа от вычисленного z-распределения
+ 1.7.
Рис.16.5
Уровень р-значимости
для примера с баллами.
0.9554
Уровень р-значимости
0.0446
Число стандартных отклонений от среднего
250 Часть 5: Статистический вывод
Эврика! Используя нашу стандартную
нормальную z-таблицу (Таблица 3
Приложения В), мы можем подтвердить, что
заштрихованная область в правом
хвосте равна P\z >+1.7] = 0.0446.
Поскольку уровень р-значймости
0.0446 больше значения (0.01), мы не
отклоняем Я0. Большинство
статистических программных продуктов
Вспомним, что P[z> +1Л] = 1 -
P[z< +1 Л] = 0.0446. Если
хотите освежить свою память
относительно использования этой
таблицы, вернитесь к Главе 11.
(включая Excel) позволяют получить р-значения с соответствующим
анализом.
Еще один способ описать это уровень р-значимости — это сказать голосом
прилежного ученика: наши результаты являются значимыми на уровне
0.0446. Это означает, что пока значение не ниже 0.0446, мы будем отклонять
Н0, а это хорошие новости для исследователей, старающихся подтвердить
свои открытия.
Термины
Мы можем использовать уровень р-значимости для принятия решения о том,
отклонять основную гипотезу или нет. В целом.
Ф Если уровень р-значимости < а, мы отклоняем основную гипотезу.
Ф Если уровень р-значимости > а, мы не отклоняем основную гипотезу.
Вычисление уровня р-значимости для двусторонней проверки гипотезы
несколько отличается от только что рассмотренного; о том, как это делается,
вы узнаете в следующем разделе.
Уровень р-значимости для двусторонней проверки гипотезы
Вспомним, что двусторонняя проверка гипотезы проводится, когда
основная гипотеза представляет собой равенство. Например, давайте проверим
заявление о том, что среднее количество миль, которое ежегодно
проделывает пассажирский автобус, составляет 11 500 мили. Наши гипотезы
выглядят так:
H0:\i = 11 500 мили
Hv:\x ф\\ 500 мили.
Предположим, а = 3 000 миль, и мы хотим установить а = 0.05. Отбираем
80 водителей и определяем, что среднее число пройденных миль составляет
11 900 мили. Каков уровень р-значимости и какие мы делаем заключения в
отношении наших гипотез?
Глава 16: Проверка гипотезы по одной выборке 251
Для данного примера стандартная ошибка среднего, о*, получается
следующим образом:
3000
о-=-
= 335.41 мили.
* у/п л/80
Получаем вычисленное z-распределение:
x-[iHo 11900-11500
335.41
= -Ы.19.
Критическое z-распределение для двусторонней проверки при а = 0.05
составляет 1.96. На рисунке 16.6 показано р-значения для данной проверки в
виде заштрихованной области.
Уровень р-значимости для двусторонней
проверки гипотезы
Рис.16.6
Уровень р-значимости
для примера с милями.
Уровень р-значимости
= 0.117 + 0.117 = 0.234
Уровень р-значимос- /
ти равняется сумме /
заштрихованных /
областей /
"^ 1 1
0.766
1 \ !
-1.96 -1.19
0.8830
+1.19 +1.96
z zc
В соответствии с Таблицей 3 Приложения В, P[z < +1.19] = 0.8830. Это
означает, что заштрихованная область в правом хвосте рисунка 16.6 это
P[z> + 1.19] = 1 — 0.8830 = 0.117. Поскольку мы имеем дело с двусторонней
проверкой, нам необходимо умножить эту область на 2, чтобы получить
уровень р-значимости. Судя по рисунку, уровень р-значимости — это общая
область обеих заштрихованных областей, которая равняется 2 х 0.117 = 0.234.
Поскольку р > а, мы не отклоняем основную гипотезу. Полученные данные
подтверждают заявление о том, что среднее количество миль, пройденных в
год пассажирским автобусом, равняется 11 500.
В целом чем меньше уровень р-значимости, тем выше наша уверенность в
необходимости отклонения основной гипотезы. В большинстве случаев
исследователь пытается найти подтверждение альтернативной гипотезы.
Низкий уровень р-значимости обеспечивает необходимую поддержку и дарует
радость исследователям.
232 Часть 5: Статистический вывод
Проверка гипотезы для среднего при малых выборках
В Главе 14 говорилось, что при малых размерах выборки центральная
предельная теорема уже не действует, и мы вынуждены допускать, что
совокупность является нормально распределенной во всех случаях. Сначала
рассмотрим ситуацию, когда нам известно а, стандартное отклонение по
генеральной совокупности.
Когда сигма известна
Если известна о, проверка гипотезы осуществляется так же, как при
больших размерах выборки. Мы можем делать так потому, что приняли
допущение, что совокупность является нормально распределенной.
Продемонстрируем эту процедуру на следующем примере.
В последнее время изучение счета мобильного телефона требует
действительно крепких нервов. Устало вскрывая конверт, я с ужасом думаю, какие
сюрпризы ждут меня на этот раз. Поскольку мы пользуемся семейным
тарифом, я всегда думаю о том, что кто-то из домочадцев обнаружил новую
функциональную возможность, не имеющую ничего общего с общением по
телефону с другим человеком, и постоянно ею пользуется. Время от времени я с
замиранием сердца просматриваю бесчисленные страницы, сплошь
покрытые номерами и кодами, и с облегчением вздыхаю, воздавая хвалу Господу.
Но в течение многих месяцев я завершал свой просмотр счета ударами себя
в грудь и душераздирающими воплями. Это вроде мягкой формы русской
рулетки с телефонной компанией.
Предположим, телефонная компания заявляет, что средний месячный
счет за пользование мобильным телефоном выставляется на сумму 92
доллара (хорошо бы!). Проверим это заявление с помощью следующих гипотез:
H0:[i = 92 доллара
Н\\\х, фШ доллара.
Допустим, что а = 22.50 доллара и генеральная совокупность удовлетворяет
нормальному распределению. Случайным образом отбираем 18 телефонных
счетов и определяем среднее по выборке —107 долларов. Каков вывод мы
можем сделать при о = 0.02?
Для данного примера стандартная
ошибка среднего, о*, составляет:
Термины
Вспомним из Главы 14, что
поскольку нам известно значение
а и мы допустили, что совокупность
является нормально распределенной, мы
можем использовать z-распределения
из нормального распределения
вероятностей для проверки этой гипотезы.
а $22.50
а- = —j= = —р=— = $5.30.
х Лг >/18
Отсюда вычисляем z-распределение:
z = ^4=$107-$92=+283
а- $5.30
Глава 16: Проверка гипотезы по одной выборке 233
Критическое z-распределение для двусторонней проверки при а = 0.02
равняется +2.33. На рисунке 16.7 эта проверка представлена графически.
Судя по рисунку 16.7, вычисленное z-распределение +2.83 находится в
пределах области «Отклонить Н0». Следовательно, мы можем сделать вывод,
что средний счет на использование мобильной связи выставляется вовсе не
на 92 доллара. А я никогда так и не думал!
Рис 16.7
Проверка гипотезы для
примера с телефонными
счетами.
а/2 = 0.01
Отклонить Н0
к/
—^-1 i гт^
-2.33 0 +2.33 +283
zc Zc Z Zc £
Число стандартных отклонений от среднего
Когда сигма неизвестна
В Главе 14 при неизвестной а и малом размере выборки, взятой из
нормально распределенной совокупности, мы использовали ^-распределение Стью-
дента. Это распределение позволяет нам подставлять s, стандартное
отклонение выборки, вместо а.
Пример: предположим, мой сын Джон заявляет, что средний результат его
игры в гольф составляет меньше 88 баллов. Не будем ставить его слова под
сомнение, а просто проверим это утверждение с помощью следующих гипотез:
Н0:\х > 88
Я,:ц<88.
Предположим, что нам неизвестна а и результаты игры Джона
подчиняются нормальному распределению. Ниже представлена случайная выборка
10 результатов игры Джона.
Результаты игры Джона
86 87 85 90 86 84 84 91 87 83
С помощью Excel определяем, что для данной выборки х = 86.3, a s = 2.58.
Из Главы 14 вспомним, что мы можем приблизительно определить
стандартную ошибку среднего с помощью следующего уравнения:
а/2 = 0.01
Отклонить Н0
234 Часть 3: Статистический вывод
s z58=0816
" л/Л л/Ш
Затем мы можем вычислить f-результат с помощью следующего
уравнения:
f=^4=86.3-88=_208
Gx 0.816
Проверим эту гипотезу при = 0.05. Чтобы найти соответствующий
критический f-результат, воспользуемся Таблицей 4 Приложения В, отрывок из
которой представлен в таблице ниже.
t-распрсдсленис Стьюден та
Выбранные области правого «хвоста» с доверительными уровнями
Дов. ур. 0.2000 0.1500 0.1000 0.0500 0.0250 0.0100 0.0050 0.0010 0.0005
d.f. 0.6000 0.7000 0.8000 0.9000 0.9500 0.9800 0.9900 0.9980 0.9990
1 1.376 1.963 3.078 6.314 12.706 31.821 63.657 318.31 636.62
2 1.061 1.386 1.886 2.920 4.303 6.965 9.925 22.627 31.599
3 0.978 1.250 1.638 2.353 3.182 4.541 5.841 10.215 12.924
4
5
6
7
8
9
10
0.941
0.920
0.906
0.896
0.889
0.883
0.879
1.190
1.156
1.134
1.119
1Л08
1.100
1.093
1.533
1.476
1.440
1.415
1.397
1.383
1.372
2.132
2.015
1.943
1.895
1.860
1.833
1.812
2.776
2.571
2.447
2.365
2.306
2.262
2.228
3.747
3.365
3.143
2.998
2.896
2.821
2.764
4.604
4.032
3.707
3.499
3.355
3.250
3.169
7.173
5.893
5.208
4.785
4.501
4.297
4.144
8.610
6.869
5.959
5.408
5.041
4.781
4.587
Из Главы 14 вспомним, что нам необходимо определить число степеней
свободы, которое равняется п — 1 = 10— 1 =9 для данного примера.
Поскольку мы имеем дело с односторонней (левосторонней) проверкой
гипотезы, смотрим столбец а = 0.05 и получаем критическое f-значение, равное —
1.833 (в таблице выше это значение подчеркнуто). Эта проверка графически
представлена на рисунке 16.8.
Судя по рисунку, вычисленное f-значение — 2.08 попадает в
заштрихованную область «Отклонить Я0». Таким образом, мы можем сделать заключение,
что средний результат игры в гольф моего сына действительно ниже 88. Это
вполне объясняет, почему он частенько обыгрывает меня. В целом мы
отклоняем Н0, если \t\ > \tc\.
Глава 16; Проверка гипотезы по одной выборке 255
а = 0.05
Отклонить Н0
Рис 16.8
Проверка гипотезы
для результатов Джона.
fc = -2.08 tc =-1.833
Давайте обратимся к другому
примеру, чтобы показать, как проверяется
двусторонняя гипотеза с помощью
^-распределения. Я хочу проверить заявление о
том, что средняя скорость машин,
проезжающих по определенному участку
перекрестка, составляет 65 миль в час.
Гипотезы для данного примера выглядят
следующим образом:
H0:jli = 65 миль в час
Hi'.ii ф 65 миль в час.
Допустим, значение нам не известно
и скорости подчиняются нормальному
распределению. Ниже представлена
случайная выборка скорости 7 автомобилей.
Скорости автомобилей
62 74 65 68 71 64 68
С помощью Excel определяем, что х =
66.9 миль/час и s = 4.16 миль/час для
данного примера. Мы можем
приблизительно определить стандартную ошибку
среднего.
5 4.16
\fh~~ л1?
Термины
Поскольку пример с
результатами Джона - это
односторонняя проверка в левой части
распределения, мы получили отрицательное
критическое t-значение. Если бы речь шла
о правосторонней проверке, мы бы
получили положительное значение.
Эврика! -
Невозможно определить
уровень р-значимости для
проверки гипотезы с помощью таблицы
t-распределения Стьюдента,
представленной в Приложении В.
Но многие статистические программы
включают определение уровня
р-значимости как часть стандартного
анализа. Об этом мы узнаем позже.
—j= = —W- = 1.57 миль/час
А теперь вычисляем f-значение:
236 Часть 3: Статистический вывод
t,x=paL=6R9-65 =
с"- 1.57
X
Проверим эту гипотезу при а = 0.05. Чтобы найти соответствующее
критическое f-значение, воспользуемся Таблицей 4 из Приложения В. Ниже
показана часть этой таблицы.
t-распределение Стьюдснта
Выбранные области правого «хвоста» с доверительными уровнями
Дов. ур. 0.2000 0.1500 0.1000 0.0500 0.0250 0.0100 0.0050 0.0010 0.0005
d.f. 0.6000 0.7000 0.8000 0.9000 0.9500 0.9800 0.9900 0.9980 0.9990
1 1.376 1.963 3.078 6.314 12.706 31.821 63.657 318.31 636.62
2 1.061 1.386 1.886 2.920 4.303 6.965 9.925 22.327 31.599
3 0.978 1.250 1.638 2.353 3.182 4.541 5.841 10.215 12.924
4
5
6
7
0.941
0.920
0.906
0.896
1.190
1.156
1.134
1.119
1.533
1.476
1.440
1.415
2.132
2.015
1.943
1.895
2.776
2.571
2.447
2.365
3.747
3.365
3.143
2.998
4.604
4.032
3.707
3.499
7.173
5.893
5.208
4.785
8.610
6.869
5.959
5.408
Количество степеней свободы для данного примера равняется п — 1 = 7 —
1=6. Поскольку это двусторонняя проверка гипотезы, нам необходимо
поделить а = 0.05 на две равные части, одна — в правой части распределения,
а другая — в левой. Затем смотрим столбец а/2 = 0.025 и получаем
критический ^-результат, равный 2.447 (подчеркнут). Эта проверка графически
представлена на рисунке 16.9.
РИС 16 9 Двусторонняя проверка гипотезы
Проверка гипотезы для
примера со скоростью.
а/2 = 0.025 / \ а/2 = 0.025
Отклонить Н0 / Не отклонять Н0 \ Отклонить Н0
Глава 16: Проверка гипотезы по одной выборке 237
По рисунку видно, что вычисленное f-значение +1.21 попадает в область
«Не отклонять Н0». Таким образом, мы можем заключить, что средняя
скорость пересечения этого участка перекрестка составляет 65 миль в час.
Использование функции СТЬЮДРАСПОБР программы Excel
Мы можем получать значения ^-распределения с помощью функции СТЬЮ-
РАСПОБР программы Excel, которая имеет следующие характеристики:
СТЬЮДРАСПОБР(вероятность; степени__свободы)
где:
вероятность = уровень значимости, а, для двусторонней проверки
степени__свободы = число степеней свободы
Например, на рисунке 16.10 показана функция СТЬЮДРАСПОБР,
используемая для определения критического f-результата для а = 0.05 и d.f. = 6 для
нашего предыдущего примера — двусторонней проверки.
Рис 16.10
Функция
СТЬЮДРАСОБР
для двусторонней
проверки.
Ячейка А1 содержит формулу = СТЬЮДРАСПОБР(0.05; 6) с результатом
2.447. Эта вероятность подчеркнута в предыдущей таблице.
Односторонняя проверка выглядит несколько иначе. Нам необходимо
умножить вероятность функции СТЬЮДРАСПОБР на два, поскольку этот
параметр базируется на двусторонней проверке. На рисунке 16.11 показана
функция СТЬЮДРАСПОБР для определения критического f-результата для
а = 0.05 и d.f. = 9 из нашего примера с результатами игры Джона.
РИС 16.11
Функция
СТЬЮРАСОБР
для односторонней
проверки.
Ячейка А1 содержит формулу = СТЬЮДРАСПОБР(2*0.05; 9) с
результатом 1.833, соответствующим результату из нашего предыдущего примера.
• ...: -; ■ ; ■■
ы
'с \ *
■
'_._., А;.,;
238 Часть 5: Статишческпй вывод
Проверка гипотезы для доли при больших выборках
Проверка гипотезы может выполняться для доли совокупности при большом
размере выборки. Из Главы 13 вспомним, что данные доли подчиняются
биноминальному распределению, которое может быть приблизительно
вычислено с помощью нормального распределения при выполнении следующих
условий:
пр > 5 и ng > 5,
где:
р = вероятность успеха по совокупности,
q = вероятность неудачи по совокупности (д = 1 — р).
Рассмотрим одностороннюю и двустороннюю проверку гипотез для доли.
Односторонняя проверка гипотезы для доли
Допустим, мы хотим проверить гипотезу о том, что более 30 семей в США
имеют доступ к Интернету. Гипотезы будут выглядеть следующим образом:
Н0: р < 0.30
Ht:p> 0.30,
где р = доля семей США, имеющих доступ к Интернету.
Отбираем выборку из 150
американских семей и обнаруживаем, что 38% из
них имеют доступ к Интернету. Каковы
наши заключения при а = 0.05?
Сначала вычислим р, стандартную
ошибку доли, описанную в Главе 13, с
помощью следующего уравнения:
Будьте внимательны: не путайте
определение р и уровень р-значимос-
ти, о котором мы говорили чуть раньше.
р~\ п '
где рНо = доля, допускаемая основной гипотезой. В нашем примере:
--1
/(0.30) (1-0.30)
150
=0.037
Теперь определяем вычисленное z-распределение:
_ Р~Рип
Глава 16: Проверка гипотезы по одной выборке 239
где р = выборочная доля. Для нашего примера:
р-рНо 0.38-0.30
z = -
0.037
= +2.16.
Критический z-результат для односторонней проверки при а = 0.05
составляет + 1.64. Эта проверка гипотезы графически представлена на
рисунке 16.12.
/ 0.95 V
/ 1~а \
/ Не отклонять Н0 К
Рис 1612
Проверка гипотезы
для примера с доступом
в Интернет.
а = 0.05
Отклонить Н0
0 1.64 2.16
Число стандартных отклонений от среднего
Судя по рисунку 16.12, вычисленный z-результат -I- 2.16 попадает в область
«Отклонить Н0». Следовательно, мы можем заключить, что доля
американских семей, имеющих доступ в Интернет, превышает 30%.
Уровень р-значимости для данной проверки представлено графически на
рисунке 16.13.
Уровень
р-значимости
0.0154
Рис 16.13
Уровень р-значимодти
для примера
с Интернетом.
Число стандартных отклонений от среднего
сяо Часть 3: Статистический вывод
Используя нашу стандартную нормальную таблицу (Таблица 3
Приложения В), мы можем подтвердить, что заштрихованная область в правом хвосте
равна:
P[z> +2.16] = 1 - P[z< +2.16]
P[z > +2.16] = 1 - 0.9846 = 0.0154.
Таким образом, наши результаты являются значимыми на уровне а > 0.0154.
Пока а > 0.0154, мы сможем отклонять Н0.
Двусторонняя проверка гипотезы ДЛЯ ДОЛИ
Завершим эту главу еще одним примером двусторонней проверки. Сейчас
мы хотим проверить гипотезу для компании, заявляющей, что 50% ее
заказчиков являются мужчинами. Наши гипотезы выглядят следующим
образом:
Н0 : р = 0.50
Нх : р * 0.50
Случайным образом отбираем 200 заказчиков и обнаруживаем, что 47% из
них — мужчины. Какие можем мы сделать выводы при а = 0.05?
Нам необходимо определить ар, стандартную ошибку доли:
= К(1-Ря0) = J\
(0.50) (1-0.50)
200
=0.035.
Далее определяем вычисленный z-результат:
z =
Р~Рн0 = 0.47 -0.50
<тп 0.035
=-0.86.
Эврика!
В целом мы отклоняем Н0, если
\z\ > \zc\ или \t| > |fc|. Мы не
отклоняем Н0, если \z\ < \zc\ или
М<|Ц
Критическое z-значение для
двусторонней проверки при а = 0.05
составляет 1.96. Эта проверка гипотезы
графически представлена на рисунке
16.14.
Судя по рисунку 16.14, вычисленное z-
значение — 0.86 попадает в область «Не
отклонять Н0». Таким образом, мы
делаем вывод, что доля заказчиков мужского
пола составляет 50% для данной
компании.
Глава 16: Проверка гипотезы по одной выборке 241
а/2 = 0.025 J
Отклонить Н0 /
Vf
-1.96
zc
1 0.95 \
/ 1~а \
Не отклонять Н0
—т- 1
-0.86 0
z
Рис 1614
Проверка гипотезы
для примера с процентом
заказчиков-мужчин.
< а/2 = 0.025
\ Отклонить Н0
К/
+1.96
Zc
Число стандартных отклонений от среднего
Уровень р-значимости для данной проверки графически представлено на
рисунке 16.15.
Рис 16.15
Уровень Р-значимости
для примера с процентом
заказчиков-мужчин.
Уровень р-значимости
равняется сумме
заштрихованных
областей
Уровень р-значимости =
= 0.1685 + 0.1685 = 0.337
-1.96 -0.86
Zc Z
0.8315
0 +0.86
J
+1.96
Zc
Используя нашу стандартную нормальную таблицу (Таблица 3
Приложения В), мы можем подтвердить, что заштрихованная область в левом хвосте
равняется:
P[z< -0.86] = 1 - P[z< + 0.86]
P[z< -0.86] = 1 - 0.8315 = 0.1685
Поскольку это двусторонняя проверка, уровень р-значимости будет
равняться 2X0.1685 = 0.337, то есть общая площадь обеих заштрихованных областей.
242 Часть 3: Статпстпческии вывод
Ваша очередь
1. Проверьте заявление о том, что средний результат сдачи Стэндфордско-
го экзамена на уровень овладения знаниями студентами, окончившими
среднюю школу, равен 1100. Была отобрана случайная выборка из 70
студентов; оказалось, что средний результат составлял 1035. Допустим,
а = 310, а = 0.10. Каков уровень р-значимости для данной выборки?
2. Небольшой бизнес-колледж заявляет, что средний размер класса
составляет 35 студентов. Проверьте это утверждение при а = 0.02 с
помощью следующей выборки размеров класса:
42 28 36 47 35 41 33 30 39 48
Предположим, совокупность является нормально распределенной, а а
неизвестна.
3. Проверьте утверждение о том, что среднее потребление бензина
автомобилем в США составляет более 7 литров в день (метрическая система
мер). Используйте показанную ниже выборку, представляющую собой
ежедневное потребление бензина одной машиной:
9 6 4 12 4 3 18 10 4 5
3 8 4 И 3 5 8 4 12 10
9 5 15 17 6 13 7 8 14 9
Предположим, совокупность является нормально распределенной,
неизвестна. При а = 0.05 определите уровень р-значимости для данной выборки.
4. Проверьте заявление о том,- что доля избирателей-республиканцев в
одном городе составляет менее 40%. Была отобрана случайная выборка из
175 избирателей; оказалось, что процент республиканцев — 30%. При
а = 0.01 определите уровень р-значимости для этой выборки.
Повторение - мать учения
Ф Чем меньше значение а, уровеня значимости, тем сложней отклонить
основную гипотезу.
Ф Мы отклоняем Н0, если \z\ > \zc\ или \t\ > \tc\.
Ф Уровень р-значимости — это самый маленький уровень значимости,
при котором основная гипотеза будет отклонена при допущении, что
основная гипотеза является истинной.
Ф Если уровень р-значимости < а, мы отклоняем основную гипотезу. Если
уровень р-значимости > а, мы не отклоняем основную гипотезу.
Ф t-распределение Стьюдента используется для проверки гипотезы, если
п < 30, значение а неизвестно, а совокупность является нормально
распределенной.
Проверка гипотезы
по двум выборкам
В этой главе
Ф Построение выборочного распределения для разности
средних
Ф Проверка разности средних по совокупностям с
использованием выборок большого и малого размеров
Ф Различие между независимыми и зависимыми выборками
# Использование Excel для выполнения проверки гипотезы
Ф Проверка разности долей совокупностей
Научившись так хорошо выполнять проверку гипотезы по
одной выборке, вы со спокойной душой можете переходить к
следующему этапу — проверке гипотезы по двум выборкам.
Подобная проверка, как правило,.осуществляется с целью
обнаружить различие между двумя отдельными совокупностями.
Например, я мог бы провести проверку с целью сравнить
результаты игры в гольф Джона и Брайана. Но я опытный
родитель, а потому делать этого не буду.
Поскольку понятия, с которыми вы познакомитесь в этой
главе, во многом схожи с понятиями Главы 16, удостоверьтесь,
что как следует изучили предыдущУ10 главу, прежде чем
погружаться в изучение этой.
244 Часть 3: Статистический вывод
Концепция сравнения двух совокупностей
Многие статистические исследования подразумевают сравнение
определенного параметра, например, среднего, двух различных совокупностей.
Ф Существует ли разница между результатами Стэндфордского экзамена
у мужчин и женщин?
Ф Действительно ли «долговечные» лампочки превышают по сроку
службы обычные лампочки?
Ф Отличается ли средняя продажная
цена дома в Ньюмарке от средней
Термины , цены дома в Уилмингтоне?
Распределение по выборке
для разности средних
описывает вероятность наблюдения
различных интервалов для получения разнсн-
сти двух средних по выборке.
Чтобы ответить на эти вопросы, нам
необходимо ознакомиться с новым
распределением по выборке. (Обещаю, это
последнее.) У этого распределения самое
причудливое щля: распределение по
выборке для разности средних.
Распределение по выборке для разности средних
Лучше всего распределение по выборке для разности средних может быть
описано с помощью рисунка 17.1
Рис 17.1
Распределен ие
по выборке для
разности средних.
Совокупность 1
<*1
Совокупность 2
а2
Hi
т—
Распределение по Распределение по
выборке для среднего выборке для среднего
(Совокупность 1) (Совокупность 2)
3>
<*х2/4
fe
Распределение по выборке
для разности средних
Н-Х1-Х2
Глава 17: Проверка гипотезы по двум выборкам 245
В качестве примера рассмотрим проверку разницы между результатами
экзамена у мужчин и женщин. Сдающие экзамен женщины будут
представлены Совокупностью 1, а мужчины — Совокупностью 2. График 1 на
рисунке 17.1 представляет собой распределение результатов экзамена для женщин
со средним 1 и стандартным отклонением 1. На графике 2 показаны те же
параметры для мужчин.
График 3 представляет собой выборочное распределение для среднего для
женщин. Этот график получился так: отобрали выборки размером п и
начертили распределение средних по выборке. Помните, мы обсуждали
распределение средних по выборке в Главе 13. Среднее этого распределения будет
определяться так:
Это соответствует центральной предельной теореме, речь о которой шла в
Главе 13. Так же был получен график 4 — для мужчин.
График 5 на предыдущем рисунке — это распределение, представляющее
собой разность средних по выборке из двух совокупностей. Это выборочное
распределение для разности средних, которое в свою очередь имеет
следующее среднее:
Иными словами, среднее распределения, показанного на графике 5, — это
разность средних графиков 3 и 4.
Стандартное отклонение графика 5 носит название стандартной ошибки
разности средних и вычисляется следующим образом:
о. - -НА
Л,"Х2 г' Л, п,
где: $Щ$Ф\ Термины
G2ltol = дисперсия
Совокупностей 1 и 2,
nlt п2 = размер выборки соответ-
•2 = аиш^ии ^ив^уигг^ щ$д*$зг Стандартная ошибка разно-
сти двух средних описывает
дисперсию разности двух средних по
ственно из
Совокупностей 1 и 2.
выборке и вычисляется по формуле:
А теперь я продемонстрирую вам, как
использовать эти понятия на практике.
Проверка разности средних для выборок
большого размера
Если размеры выборок из обеих совокупностей превышают 30, мы можем
обратиться к центральной предельной теореме и использовать нормальное
246 Часть 5: Статистический вывод
распределение для приблизительного вычисления выборочного
распределения для разности средних. Эту методику я продемонстрирую вам с помощью
следующего примера;
Были проведены исследования в отношении эффектов стимуляции на
мозговое развитие крыс. Думаю, что эти исследования следовали такой
логике: что хорошо для крыс, не может быть плохим для людей. Из одной
совокупности крыс отобраны две случайные выборки.
Представители первой выборки, которую мы назовем
«крысы-везунчики» (Совокупность I), были окружены неслыханной роскошью. Я
представляю себе атмосферу загородного клуба, курс гольфа, теннисные корты и
пятизвездочный ресторан, где наши крысы могут полакомиться
импортным сыром и французским вином за обсуждением состояния крысиной
экономики.
Представители второй выборки «менее везучих грызунов» (Совокупность 2)
никак не могут похвастаться условиями своего существования. Их закрыли в
скучной клетке, заставили поедать консервированный сыр и смотреть
повторение реалити-шоу. Активисты, выступающие за права животных, были
против этого эксперимента, заявляя, что насильственное применение
консервированного сыра — это негуманно.
По истечений трех месяцев проживания в указанных условиях
ученые-садисты измерили размер мозга каждой крысы на вес. Не буду вдаваться в
подробности того, как это осуществлялось, но мышонок Харви мистическим
образом не объявился на своем восьмичасовом утреннем чае, и его группа
отправилась без него.
В таблице ниже представлены результаты этого страшного эксперимента.
Итоговые данные эксперимента с крысами
Совокупность
Везунчики (1)
Менее везучие
(2)
Средний
вес мозга
(в граммах)
2.4
2.1
Стандартное
отклонение
выборки
0.6
0.8
Размер
выборки
50
60
Для этой проверки гипотезы примем допущение, что две выборки
являются независимыми друг от друга. Иными словами, между крысами везучей и
невезучей выборок не существует никакой взаимосвязи.
Наши гипотезы будут выглядеть так:
Н0:Ц1< Ц2
Hi:jii>fi2.
Глава 17: Проверка гипотезы по двум выборкам 247
где:
\xi = средний вес мозга крысы из везучей совокупности,
ц2 = средний вес мозга крысы из невезучей совокупности.
Гипотезы также могут выглядеть следующим образом:
^i^i - ц2>0.
Альтернативная гипотеза поддерживает заявление о том, что у
крыс-везунчиков вес мозга будет больше. Мне кажется, что для самих крыс это не
слишком-то хорошо, но это уже совершенно иная история. Проверим эту
гипотезу при а = 0.05.
Если Gi или а2 неизвестны, тогда мы можем использовать sl или s2,
стандартные отклонения выборок Совокупностей 1 и 2, в качестве приближения,
пока п > 30 для обеих совокупностей, как показано ниже:
Принимая во внимание данное допущение, мы можем приблизительно
вычислить стандартную ошибку разности двух средних:
xt-x2
Поскольку значения Qj или о2 нам неизвестны, устанавливаем:
аЦ1 = Si и аи2 = s2
(o.6)2f(a8f =0134rpaMMa
50
60
Теперь мы готовы определить
вычисленное z-значение с помощью
следующего уравнения:
(ъ-Х2)-(111-Ц2)н0
z = -
Для нашего примера с крысами
это значение равняется:
^ Jx\-x2)--(14-14)h0 = (2.4-2.1)-0 = |224
ац- - 0.134
Эврика!
Понятие (|1Ж - ц2)Но носит
название гипотетической разности
средних двух совокупностей.
Если в ходе проверки основной
гипотезы выясняется, что разности
средних двух совокупностей не
существует, тогда (д, - ДгЦ равно нулю.
Результаты проверки гипотезы представлены на рисунке 17.2.
248 Часть 3: Статистический вывод
Критический z-результат для односторонней проверки гипотезы
(правосторонней) при а = 0.05 равняется -I-1.64. Судя по рисунку 17.2, это z-значе-
ние +2.24 попадает в область «Отклонить Н0». Отсюда делаем вывод, что
везучие крысы имеют больший вес мозга, чем невезучие.
Рис 17.2
Проверка гипотезы
для примера с крысами,
а = 0.05
Отклонить Н0
Число стандартных отклонений от среднего
Термины
Сформулируем условия, необходимые для проверки гипотезы для разности
средних при большой размере выборки.
Ф Выборки являются независимыми друг от друга.
Ф Размер каждой выборки должен быть не меньше 30.
Ф Если стандартные отклонения по совокупности неизвестны, для приблизительного их
вычисления могут быть использованы стандартные отклонения выборок.
; Уровень р-значимости для данной выборки может быть определено с
помощью нормальной таблицы z-результатов из Приложения В:
P[z > +2.24] = 1 - P[z< + 2.24]
P[z> +2.24] = 1 - 0.9875 = 0.0125
Эврика!
Подобная методика может также примениться к выборкам размером менее 30, но
при соблюдении определенных условий.
Ф Обе совокупности должны быть нормально распределенными.
Ф Должны быть известны стандартные отклонения обеих совокупностей.
Глава 17: Проверка гипотезы по двум выборкам 249
Результаты нашего крысиного опыта способны улучшить жизнь многих.
Если в одно прекрасное субботнее утро супруг подлавливает ваС| КОгда вы
крадетесь на урок по гольфу, вы можете спокойно объяснить, что просто
пытаетесь улучшить состояние своих мозгов. Теперь у нас есть статистические
данные, чтобы поддержать вас в ваших действиях. Но не забывайте о том, что
дополнительный вес мозга может вылиться для вас в дополнительные
проблемы.
Проверка разности, отличной от нудя
В предыдущем примере перед нами стояла задача лишь определить,
существует ли разница между двумя совокупностями. Мы также можем определить,
не превышает ли эта разница определенного значения. В качестве примера
предположим, что мы хотим проверить заявление о том, что средняя
зарплата математика в Нью Джерси превышает среднюю зарплату математика в
Вирджинии более чем на 5000 долларов. Имеем следующие гипотезы:
Н0- Hi - Ц2 ^ 5000
Ht: \ii - из > 5000.
где:
Hi = средняя зарплата математика в Нью Джерси,
|л2 = средняя зарплата математика в Вирджинии.
Предположим, что ai = $ 8 100, a2 = $ 7 600, и проверим эту гипотезу при
а= 0.10.
Были отобраны две выборки:
Ф 42 математика из Нью Джерси со средней зарплатой 51 500 долларов;
Ф 54 математика из Вирджинии со средней зарплатой 45 400 долларов.
Стандартная ошибка разности двух средних получается так:
- - -J^1
Xl *2 V 42 * 54
Получаем вычисленный z-результат:
z=(Xl-X2)'(lil-[i2)
G- -
х,-х2
_($51500-$45 400)-($5 000) _^^
$1622.3
250 Часть 3: Статистическим вывод
Результаты этой проверки представлены на рисунке 17.3.
Рис 17.3
Проверка гипотезы
для примера
с зарплатой.
z zc
Число стандартных отклонений от среднего
Критическое z-значение для односторонней (правосторонней) проверки
при а = 0.10 равняется +1.28. Судя по рисунку 17.3, вычисленное z-значение
+ 0.68 попадает в область «Не отклонять Н0». Отсюда делаем вывод, что
разность зарплат в двух штатах не превышает 5000 долларов.
Проверка разности средних при малом размере выборки
и неизвестной сигме
В этом разделе я расскажу вам, как поступать в ситуации, когда ст,
стандартное отклонение по совокупности, неизвестно, и используются выборки
малого размера. Если размер одной или обеих выборок меньше 30,
совокупность должна быть нормально распределенной, чтобы иметь возможность
воспользоваться одним из вышеуказанных способов. Мы делали такое же
допущение для выборок малого размера в Главах 14 и 16.
Выборочное распределение для разности средних по выборке для данного
сценария подчиняется ^-распределению Стьюдента. Для выборок малого
размера уравнение стандартной ошибки разности двух средних, сг^.^, зависит
от того, равны ли стандартные отклонения (или дисперсии) двух
совокупностей. Сначала рассмотрим ситуацию с одинаковыми стандартными
отклонениями.
Равные стандартные отклонения совокупностей
В нашем доме происходит нечто странное: батарейки проваливаются
словно под землю. Я стал покупать упаковку из 24 штук, наивно полагая,
что уж их-то надолго хватит. Я опять ошибся, ибо чем больше я покупаю,
а = 0.10
Отклонить Н0
О 0.681.28
Глава 17: Проверка гипотезы по двум выборкам 251
тем быстрей они исчезают. Возможно, их исчезновение связано с некими
подростками, которые любят в предрассветные часы слушать музыку по
плееру при умопомрачительной громкости. Но это только мои догадки.
Поэтому как только до меня доходят слухи о новых долговечных
батарейках, у меня сразу ушки на макушке. Допустим, какая-то компания
заявляет, что ее батарейки более долговечны, чем любые другие. Гипотезы
выглядят так:
Н0: щ < \х2
где:
Hi = средний срок работы долговечных батареек,
ji2 = средний срок работы обычных батареек.
Проверим эту гипотезу при а = 0.01. Ниже суммированы данные о
продолжительности срока работы в часах батареек обоих типов:
Данные для примера с батарейками
Долговечные батарейки (Совокупность 1):
51 44 58 36 48 53 57 40 49 44 60 50
Обычные батарейки (Совокупность 2):
42 29 51 38 39 44 35 40 48 45
С помощью Excel суммируем эти данные в следующую таблицу:
Суммированные данные для примера с батарейками
Совокупность
часов
Долговечные (1)
Обычные (2)
Средние
по выборке
49.2
41.1
Станд. откл.
выборки
6.40
7.31
Размер
выборки 4
12
10
В данном примере мы допускаем, что ах = а2, но значения этих
параметров неизвестны. При таких условиях мы вычисляем совместную оценку
стандартного отклонения с помощью уравнения:
sp-x\ л^-2
252 Часть 3: Статистический вывод
Термины
Совместная оценка стандартного отклонения объединяет 2 выборочные
дисперсии в одну и вычисляется по формуле:
= \(nrl)sf+{n:
Y П]+П2~
-IK
2
Не впадайте в панику. Это уравнение выглядит куда как лучше, когда в нем
указаны конкретные числа.
= 1(пг1)5|2+(лг-1)^= /(12-l)(7.3lf +(10
\ л1+л2-2 V 12+10-
-I
l)(6.40f
2
956,44^^
20
А теперь мы можем приблизительно вычислить стандартную ошибку
разности двух средних:
1 1
ои- - =sD — +-
Сейчас мы можем определить вычисленное z-значение с помощью
следующего уравнения:
о""- - =sD /—+—=(6.92U—+—
л''*2 p\i\ п, У 112 10
стм- - = (6.92)V0.1833 =2.96 часа.
Определяем количество степеней свободы для данной проверки:
f Jxi-^Hft-feb/, = (49.2-41.1) -0 = [273
стц- - 2.96
х1-х2
d.f. = Л! + л2 - 2 = 12 + 10 - 2 = 20.
Критический f-результат, взятый из Таблицы 4 Приложения В, для
односторонней (правосторонней) проверки при а = 0.10 и 20 степенями свободы
равен + 2.528. Проверка этой гипотезы графически представлена на рисунке
17.4.
Глава 17; Проверка гипотезы по двум выборкам 253
Рис. 17.4
Проверка гипотезы
для примера
с батарейками.
а = 0.01
Отклонить Н0
7"Х
: 2.528
t = 2.73
Судя по рисунку 17.4, наше вычисленное t-значение +2.73 попадает в
область «Отклонить Н0». Из этого мы заключаем, что срок работы долговечных
батареек действительно больше, чем у обычных. Я уже отправился их покупать.
Термины :
Проверка гипотезы для разности средних при малых размерах выборки требует
выполнения нескольких условий.
Ф Выборки являются независимыми друг от друга.
Ф Совокупность должна быть нормально распределенной.
Ф Если О! и оа известны, используйте нормальное распределение для определения
области отклонения.
Ф Если ал и <jfc неизвестны, вы можете приблизительно вычислить их с помощью 5Л и s* и
использовать t-распределение Стьюдента для определения области отклонения.
Эта процедура основывалась на допущении, что стандартные отклонения
обеих совокупностей равны. А что, если это допущение неверно? Я рад, что
вы спросили.
Неравные стандартные отклонения совокупностей
Рассмотрим эту ситуацию на том же примере с батарейками, но при
допущении, что ах * а2. Процедура практически не отличается от предыдущей, за
исключением двух нюансов.
Первое отличие касается стандартной ошибки разности двух средних. В
данном случае используется следующее уравнение:
п, п0
254 Часть 5: Статистический вывод
Для примера с батарейками получаем следующий результат:
_ lW£+W£^ (4.45)+(4.10) =2.92.
Х'Х2 V 12 10 V
Теперь определяем вычисленное z-значение с помощью уравнения:
fJxi-X2)-(m-m)H0 J49.2-41.1)-0 = |27?
аи- - 2.92
х,-х2
Второе отличие касается способа определения числа степеней свободы
для f-распределения Стьюдента.
\2
^2_
П0
d.f.=-
s2
+
{* f i^
[п. j [п2
-+-
Hj-l л2-1
Пока вам не стало плохо, я поспешу доказать вам, что не так страшен черт,
как ее малюют. Прежде всего, определим, что:
£L«=4.45Hi-=(^=4.io.
п{ 12 я, 10
Теперь вставим полученные значения в вышеуказанное уравнение:
df_[(4.45)+(4,10)]2_ 73.10 _Ш92
(4.45)2+(4.10)2 1.80+1.87
И + ~~ 9~"
Поскольку количество степеней свободы должно быть целым числом,
округляем этот результат до 20. Критический f-результат, взятый из Таблицы 4
Приложения В, для односторонней (правосторонней) проверки при а = 0.01
с 20 степенями свободы равняется + 2.528. Поскольку t > tcx мы отклоняем Н0.
Программа Excel выполнит за вас черновую работу
Эта программа умеет выполнять разные проверки гипотез, описанных в этой
главе. Я покажу вам, как решить предыдущую задачу с батарейками с
помощью этой разносторонней программы. Выполните предлагаемые шаги,
1. Откройте чистый рабочий лист и введите данные из примера с
батарейками в столбцы А и В, как показано на рисунке 17.5.
2, В меню Tools (Сервис) выберите Data Analysis (Анализ данных). Из
списка выберите t-Test: Two-Sample Assuming Unequal Variances (Двухвыбо-
Глава 17: Г^ове^ка гипотезы по двум выборкам 255
?г
рочный t-тест с различными дисперсиями). (Если опция Date Analysis
(Анализ данных) отсутствует в меню Tools (Сервис), обратитесь к
разделу Главы 2 «Установка средств анализа данных».)
Hi
ж
35
40
-
Рис 17.5
Ввод данных
для примера
с батарейками.
Г в*«брлиля CSV/ -iitrHtstX ч**»л
тшж®
рае .-■■ ■ j
3. Щелкните ОК.
4. В окне t-Test: Two-Sample Assuming Unequal Variances (Двухвыборочный
t-тест с различными дисперсиями) выберите ячейки В1:В12 в поле
Variable 1 Range (Интервал переменной 1) и ячейки А1-.А10 в поле
Variable 2 Range (Интервал переменной 2). Установите значение
Hypothesized Mean Difference (Гипотетическая средняя разность)
равное 0, Alpha (Альфа) а = 0.01, a Output Range (Выходной интервал) —
ячейка D1, как показано на рисунке 17.6.
Рис 17.6
Диалоговое окно*
«Двухвыборочны и
t-mecm с различными
дисперсиями».
I—Щ
-::-^^:С^ :;: ••::::;-:;:Г:': -:■;*:; ;г../-
Г*
1 •
43
44
г*'""--IM"
256 Часть 3: Статистический вывод
5. Щелкните ОК. На экране будет представлен t-тест, как показано на
рисунке 17.7.
Рис 17.7
Выход t-mecma.
ад
4=
Судя по рисунку 17.7, вычисленное t-значение 2.758 обнаружено в ячейке
Е9, и это значение несколько отличается от того; что мы получили в
предыдущем разделе (2.77) в силу округления чисел. Уровень р-значимости, равный
0,006, указан в ячейке ЕЮ. Поскольку уровень р-значимости < а, мы
отклоняем основную гипотезу.
Проверка разности средних при зависимых выборках
До этого момента в этой главе мы обсуждали независимые друг от друга
выборки. Выборки считаются независимыми, если они никоим образом не
связаны друг с другом. Им противостоят зависимые выборки, где каждое
наблюдение одной выборки связано с наблюдением в другой.
Примером зависимой выборки может быть исследование по потере веса.
Каждый испытуемый взвешивается в
начале (Совокупность 1) и в конце
(Совокупность 2) программы. Изменения в
весе каждого человека определяется путем
вычитания весов Совокупности 2 из
весов Совокупности 1. Каждое
наблюдение из Совокупности 1 сравнивается с
наблюдением. Совокупности 2.
Зависимые выборки тестируются отлично от
независимых.
Чтобы показать вам, как проверяются зависимые выборки, я вернусь к
примеру с мячом для гольфа, который мы обсуждали в Главе 15. Если вы
помните, я размечтался, что изобрел мяч, позволяющий увеличить расстояние
от площадки ти более чем на 20 ярдов. Для проверки моего заявления
предположим, что 9 игроков били по моему мячу, а потом по обычному мячу для
Термины
В зависимых выборках
данные из одной выборки
связаны с данными из другой выборки. В
независимых выборках наблюдения
никак не связаны.
Глава 17: Проверка гипотезы по двум выборкам 257
гольфа. В таблице ниже представлены полученные результаты. Буква d
означает разность между моим мячом и обычным мячом.
Расстояние в ярдах для примера с мячом для гольфа
Игрок 12 3 4 5 6 7 8
9
Мой мяч 215 228 256 264 248 255 239 218 239
Другой мяч 201 213 230 233 218 226 212 195 208
d 14 15 26 31 30 29 27 23 31
d2 196 225 676 961 900 841 729 529 961
Для будущих вычислений нам понадобится:
£d = 14 + 15 + 26 + 31 + 30 + 29 + 27 + 23 + 31 = 226
£d2 = 196 + 225 + 676 + 961 + 900 + 841 + 729 + 529 + 961 = 6018.
Расстояния, достигнутые с использованием моего мяча, будут
составлять Совокупность 1г а расстояния, достигнутые с использованием другого
мяча, — Совокупность 2. Поскольку в каждом случае игрок ударяет по
обоим мячам, представленные в таблице выборки являются зависимыми.
Гипотезы будут выглядеть так:
Н0:щ - ц2< 20
H\V\ - ц2>20,
где:
Ц! = среднее расстояние, достигнутое с помощью моего нового мяча,
ц2 = среднее расстояние, достигнутое с помощью другого мяча.
Но поскольку нас интересует только разность двух совокупностей, мы
можем переписать данное утверждение как единую выборочную
гипотезу:
H0:|id< 20
Ht:|id>20,
где d — это среднее разности двух совокупностей.
Проверим эту гипотезу при а = 0.05.
Далее мы вычислим разность средних, d и стандартное отклонение
разности, sd, двух выборок:
d = ^=—= 25.11ярда
п -9
258 Часть 5: Статистический вывод
I*2
(24
п-\
|(6.0Ш,-«
8
-I
342.89
8
=6.55 ярда.
Уравнение для вычисления sd — это то же уравнение для определения
стандартного отклонения, которое мы рассмотрели в Главе 5.
Если обе совокупности следуют нормальному распределению, мы
используем ^-распределение Стьюдента, поскольку размеры обеих выборок
меньше 30 и o~i и ст2 нам неизвестны. Вычисленное f-значение получается
следующим образом:
t =
d-\id 25.11-20 5.11
^
6.55
"л/9
2.18
= +2.34
Количество степеней свободы для данной проверки равняется:
d.f. = п - 1 = 9 - 1 = 8
Критическое f-значение, взятое из Таблицы 4 Приложения В, для
односторонней (правосторонней) проверки при а = 0.05 и d.f = 8 равняется
+ 1.86. Проверка этой гипотезы графически представлена на рисунке 17.8.
Рис 17.8
Проверка гипотезы
для примера с мячом
для гольфа.
а = 0.05
Отклонить Н0
7"х
1.86
t = 2.34
Судя по рисунку 17.8, наше вычисленное f-значение +2.34 попадает в
область «Отклонить Н0». Отсюда делаем заключение, что мой мяч увеличивает
расстояние от ти более чем на 20 ярдов. Жаль, что это только мои грезы!
Глава 17: Проверка гипотезы по двум выборкам 259
Проверка разности долей при независимых выборках
Проверка гипотезы может проводиться с целью определения разности долей
двух совокупностей при большом размере выборки. Из Главы 13 вспомним,
что данные долей подчиняются биноминальному распределению, которое
можно приблизительно определить с помощью нормального распределения
при выполнении следующих условий:
пр > 5 и nq > 5,
где:
р = вероятность успеха по совокупности,
q = вероятность неудачи по совокупности (q = 1 — р).
Предположим, я хочу проверить утверждение о том, что доля мужчин и
женщин в возрасте от 13 до 19 лет, пользующихся программами обмена
мгновенными сообщениями с помощью Интернета, равна. Гипотезы будут
выглядеть так:
Н0: Р\ = р2
Н1:р1*р2,
где:
Pi — доля парней в возрасте от 13 до 19 лет, еженедельно использующих
эти программы,
р2 = доля девушек в возрасте от 13 до 19 лет, еженедельно
использующих эти программы.
В таблице ниже сведены данные их наших выборок:
Зммированные данные для выборок пользователей программ
>мена мгновенными сообщениями
Совокупность Количество успехов (х) Размер выборки (п)
Парни 207 300
Девушки 266 350
Каково наше заключение при а = 0.10?
Выборочная доля парней, р1г и девушек, р2, использующих программы
обмена мгновенными сообщениями, может быть вычислена так:
- хх 207 л_п - х, 266
р,=—L = = 0.69 и п =—= =0.76.
л, 300 п, 350
260 Часть 3: Статистический вывод
Для определения вычисленного z-результата нам необходимо знать
стандартную ошибку разности долей (ну уж, это чересчур!), а^-^, которая
определяется по формуле:
а- - =
РгРг
PlP-Pl) , Р7^~Р2)
Но проблема состоит в том, что нам неизвестны значения ргир2,
фактические Доли юношей и девушек по совокупности. Далее нам необходимо
определить оценку стандартной ошибки разности двух долей, аи^ _р2, с помощью
следующего уравнения:
aVp2=>4d-p"
1 1
—+-Г-
где:
рц, оценка доли двух совокупностей, определяется по формуле:
лМ_х1 + х2_207+266=()728
щ+щ 300+350
Для нашего примера оценка стандартной ошибки разности двух долей
получается следующей:
о»- - = 1(0.728)(1-0.728)(—+— ] =0.035.
' и-* V Л300 350 J
А теперь мы, наконец, можем вычислить z-результат:
(Pi-ftHfl-Ak
z = -
Рх-Рг
zJPi-P2)-(Pi-P2)H0 = (0.69+0.76)-0 = 2Ш
&1- г 0.035
Р\-Рг
Термины
Понятие (р1-рг)Но носит название
гипотетической разности долей
двух совокупностей. Если проверка
основной гипотезы показывает, что разности
между долями совокупностей не
существует, тогда значение (Pi-p2)H0 равно нулю.
Критическое z-значение для
двусторонней проверки при а = 0.10
равняется 1.64. Проверка этой
гипотезы графически представлена на
рисунке 17.9.
Судя по рисунку 17.9,
вычисленное z-значение — 2.00 попадает в
область «Отклонить Н0». Таким
образом, мы делаем вывод, что доли
юношей и парней в возрасте от 13
Глава 17; Проверка гипотезы по двум выборкам 261
Проверка гипотезы для разности долей
/ 0.90 \
а/2 = 0.05 / !_« \ а/2 = 0.05
Отклонить Н0 / \ Отклонить Н0
У\
1
-2.0-
z
Не отклонять Н0
| —f 1
ч^
1.64 0 +1.68
Zc Zc
Рис 17.9
Проверка гипотезы
для примера
с пользователями
программ мгновенных
сообщений.
Число стандартных отклонений от среднего
до 19 лет, использующих программу обмена мгновенными сообщениями,
не равны.
Термины
Стандартная ошибка разности двух долей описывает изменения разности между
долями двух выборок и вычисляется по формуле:
о- = &ё
-й) fP2(!-ft)
Ъ
Оценка стандартной ошибки разности двух долей приблизительно определяет
изменения разности долей двух выборок и вычисляется по формуле:
*«-^хм(й)
Оценка доли двух совокупностей - это взвешенное среднее долей двух выборочных
долей, вычисляемое по формуле:
рЦ- Х1 +Х2
П1+Л2*
Уровень Р-значимости для этих выборок можно найти с помощью
нормальной z-таблицы в Приложении В:
2(P[z> +2.00]) = 2(1 - P[z< + 2.00])
2(P[z> +2.00]) = 2(1 - 0.9772) =^0.0456.
Этот результат также подтверждает, что мы отклоняем Я0, поскольку
уровень р-значимости < а.
262 Часть 5: Статистический вывод
На этом мы завершаем наше удивительное путешествие по стране
проверки гипотез. Но не печальтесь. Мы вновь обратимся к этим методикам в
Части 4 этой книги «Углубленное изучение статистики вывода». Уверен, вы с
нетерпением этого ждете.
Ваша очередь
1. Проверьте гипотезу о том, что средние результаты экзамена по
математике у студентов из Пенсильвании и Огайо различаются. Были отобраны
две выборки: у 45 студентов из Пенсильвании средний результат был
равен 552, а у 38 студентов из Огайо — 530. Предположим, что стандартные
отклонения по генеральной совокупности для Пенсильвании и Огайо
составляют 105 и 114 соответственно. Осуществите проверку при а = 0.05.
Каков уровень р-значимости для этих выборок?
2. Компания отслеживает уровень удовлетворенности заказчиков
различными магазинами по шкале от 0 до 100. Представленные ниже данные —
это оценка заказчиков из Магазинов 1 и 2.
Магазин 1:
90 87 93 75 88 96 90 82 95 97 78
Магазин 2:
82 85 90 74 80 89 75 81 93 75
Допустим, что стандартные отклонения по совокупности равны, но
неизвестны, а совокупность является нормально распределенной.
Осуществите проверку при = 0.10.
3. Создатели новой диеты утверждают, что по завершении программы ее
участники потеряют более 15 фунтов веса. Представленные ниже
данные — это вес 9 участников до и после программы. Проверьте это
утверждение при а = 0.05.
До 221 215 206 185 202 197 244 188 218
После 200 192 195 166 187 177 227 165 201
4. Проверьте гипотезу о том, что доля владельцев квартир во Флориде
превышает национальную долю при = 0.01. Используйте следующие
данные:
Размер выборки Совокупность Число успехов
Флорида 272 400
Национальный уровень 390 600
Каков уровень р-значимости для данных выборок?
Глава 17: Проверка гипотезы по двум выборкам 263
Повторение - мать учения
Ф Нормальное распределение используется при проверке гипотезы для
разности средних, когда п > 30 для обеих выборок.
Ф Нормальное распределение используется при проверке гипотезы для
разности средних, когда п < 30 для любой выборки, если ох и о2
известны и обе совокупности являются нормально распределенными.
Ф ^-распределение Стьюдента используется при проверке гипотезы для
разности средних, когда п < 30 для любой выборки, если аг и о2
неизвестны и обе совокупности являются нормально распределенными.
Ф В зависимых выборках наблюдение из одной выборки связано с
наблюдением из другой. В независимых выборках наблюдения выборок не
имеют друг к другу никакого отнбшения.
Углубленное
изучение
статистики вывода
В первых трех частях книги мы узнали много интересного.
Неужели осталось еще что-то, что осталось за рамками нашего изучения?
В последних главах представлены более продвинутые методики
статистики вывода (не волнуйтесь, вы и с ними справитесь) вроде
критерия хи-квадрат, дисперсионного анализа и линейной
регрессии. Вооруженные этим знанием, мы сможем определять, связаны
ли две категориальные переменные (хи-квадрат), сравнивать три
или более совокупностей (дисперсионный анализ) и описывать
мощность и направление взаимосвязи между двумя переменными
(линейная регрессия). Когда вы овладеете всеми этими знаниями,
считайте, что вы допрыгнули до самой высокой планки!
Я ХОТЫ НАЙТИ КРИТЕРИЙ хи-квадрат,
но не обнаружил его р. меню
МЕСТНОГО КИТАЙСКОГО ресторана,
Распределение
хи-квадрат
В этой главе
Ф Проведение испытания на адекватность с
распределением хи-квадрат
# Выполнение проверки независимости с распределением
хи-квадрат
Ф Использование факторных таблиц для отображения
распределения частот
В последних трех главах мы открыли для себя удивительный
мир проверки гипотез. Мы сравнивали средние и доли одной и
двух совокупностей и делали обоснованные заключения
применительно к собственным заявлениям. Теперь, когда эти
методики стали частью нашего опыта, мы готовы к более
значительным свершениям.
В этой главе мы узнаем, как сравнивать две или более долей
с помощью еще одного типа распределения: хи-квадрат. С
помощью этого теста мы сможем подтверждать, подчиняется ли
набор данных определенному распределению вероятностей,
например, биноминальному или Пуассона. (Помните, что это
за распределения? Они вернулись!) Мы можем также исполь-
268 Часть 4: Углубленное изучение статистики вывода
зовать это распределение для определения того, являются ли две переменные
статистически независимыми. На самом деле все это довольно любопытно, и
вы в этом очень скоро сами убедитесь!
Обзор шкал измерения данных
В Главе 2 мы обсуждали различные типы шкал измерения данных:
номинальную, порядковую, интервальную и относительную. Освежим вашу память
кратким описанием каждой из них.
Ф Номинальный уровень измерений имеет дело исключительно с
количественными данными. Наблюдениям просто присваиваются
определенные категории. Пример: пол респондента с категориями «мужской» и,
«женский».
Ф Порядковый уровень измерения находится на одну ступень выше.
Он обладает всеми свойствами номинального уровня плюс
возможность ранжировать значения от максимального до минимального.
Пример: оценить фильм как отличный, хороший, приличный или
слабый.
Ф Интервальный уровень измерения имеет дело не только с
качественными данными. Здесь мы можем использовать математические операции
сложения и вычитания для сравнения значений. Разница между
различными категориями может измеряться с помощью числовых значений, а
также предоставлять смысловую информацию. Типичный пример:
измерение температуры в градусах по Фаренгейту.
# Относительный уровень — это самая точная шкала измерений. Здесь
мы можем выполнять все 4 математические операции для сравнения
данных. Примерами такого типа данных являются возраст, вес, рост и
зарплата. Относительные данные обладают всеми характеристиками
интервальных данных плюс «истинное нулевое значение», которое
означает, что данные с нулевым значением — это отсутствие измеряемого
объекта.
При проверке гипотезы, которую мы рассматривали в последних трех
главах, использовались строго интервальные и относительные данные. А
распределение хи-квадрат, о котором пойдет речь в .этой главе, позволит нам
выполнять проверку гипотез с использованием
Термины номинальных и порядковых данных.
Две основные методики, о которых
мы узнаем в этой главе, используют
распределение хи-квадрат для
выполнения испытания на адекватность и
проверки независимости двух
переменных. Начнем!
Распределение хи-квадрат
используется для выполнения
проверки гипотезы с номинальными и
порядковыми данными.
Глава 18: Распределение хи-квадрат 269
Испытание на адекватность хи-квадрат
Одним из многочисленных способов использования распределения
хи-квадрат является испытание на адекватность, использующее выборку для
проверки того, соответствует ли распределение частот ожидаемому распределению.
Пример: предположим,, новый фильм, находящийся в процессе создания,
имеет ожидаемое распределение оценок, представленное в таблице ниже.
Ожидаемое распределение оценок фильма
Количество звезд Процент
5 40%
4 30%
3 20%
2 5%
1 5%
Всего 100%
После премьеры фильма были опрошены 400 кинозрителей. Результаты
представленных ими оценок показаны в таблице ниже.
Наблюдаемое распределение оценок фильма
Количество звезд Количество наблюдений
5 145
4 128
3 73
2 32
1 22
Всего 400
Можем ли мы заключить, что ожидаемые рейтинги фильма действительно
основываются на наблюдаемых рейтингах, предоставленных 400 кинозрителями?
Формулировка основной и альтернативной гипотез
Основная гипотеза испытания на адекватность хи-квадрат содержит
утверждение о том, что выборка наблюдаемых частот поддерживает заявление об
ожидаемых частотах. Альтернативная гипотеза содержит утверждение о том, что
270 Часть 4: Углубленное изучение статистики вывода
Термины
Испытание на адекватность
использует выборку для
проверки того, соответствует ли
распределение частот ожидаемому
распределению.
поддержка заявления об ожидаемых
частотах отсутствует. Для примера с
фильмом формулировка гипотезы будет
выглядеть следующим образом:
Н0: Фактическое распределение
рейтингов может быть описано с
помощью ожидаемого
распределения.
Hf. Фактическое распределение рейтингов отличается от ожидаемого
распределения.
Проверим эту гипотезу при а = 0.10.
Наблюдаемые и ожидаемые частоты
Эврика! -
Общее число ожидаемых
(Е) частот должно равняться
общему числу
наблюдаемых (О) частот.
Проверка методом хи-квадрат в основном
сравнивает наблюдаемые (О) и ожидаемые
(Е) частоты для определения того, существует
ли между ними статистически значимая
разница. Для нашего примера с фильмом
наблюдаемыми частотами являются количество
наблюдений, собранных для каждой
категории нашей выборки. Ожидаемые частоты —
это ожидаемое число наблюдений для каждой
категории, вычисляемые в таблице ниже.
Термины
Наблюдаемые частоты - это число фактических наблюдений, отмеченных для
каждой категории распределения частот в рамках анализа методом хи-квадрат.
Ожидаемые частоты - это число наблюдений, ожидаемых для каждой категории наблюдений с
допущением об истинности основной гипотезы в рамках анализа методом хи-квадрат.
Таблица ожидаемых частот
Рейтинг
фильма
Ожид.
процент
Размер
выборки
Ожид.
частота (О)
Набл.
частота (Н)
5
4
3
2
40%
30%
20%
5%
400
400
400
400
0.40(400) = 160
0.30(400) = 120
0.20(400) = 80
0.05(400) = 20
145
128
73
32
Глава 18:
Распределение хи-квадрат 271
Рейтинг
фильма
1
Всего
Ожид.
процент
5%
100%
Размер
выборки
400
400
Ожид. Набл.
частота (О) частота (Н)
0.05(400) = 20 22
400
Теперь мы готовы вычислить статистику хи-квадрат.
Вычисление статистики хи-квадрат
Статистика хи-квадрат определяется по следующей формуле:
где:
О = число наблюдаемых частот для каждой категории,
Е = число ожидаемых частот для каждой категории.
Вычисления с применением этого уравнения представлены в таблице
ниже.
Вычисление значения хи-квадрат для примера с фильмом
Рейтинг
фильма
5
4
3
2
1
Всего
О
145
128
73
32
22
Е
160
120
80
20
20
Ю-Е)
-15
8
-7
12
2
Ю-Е)2
225
64
49
144
4
Е
1.41
0.53
0.61
7.20
0.20
t.j&f.^
Определение критического значения распределения хи-квадрат
2
Критическое значение распределения хи-квадрат, % с, зависит от числа
степеней свободы, которое для данной проверки будет равняться:
d.L = А - 1,
где к равняется числу категорий распределения частот. Для примера с
фильмом существует 5 категорий, поэтому d.L =к — 1=5— 1 = 4.
272 Часть 4: Углубленное изучение статистики вывода
Критическое значение хи-квадрат можно найти в Таблице 5 Приложения
В этой книги. Здесь приведена часть этой таблицы.
Критические значения распределения хи-квадрат
Выделенные области правого хвоста
d.f. 0.3000 0.2000 0.1500 0.1000 0.0500
1 1.074 1.642 2.072
2 2.408 3.219 3.794
3 3.665 4.642 5.317
4 4.878 5.989 6.745
5 6.064 7.289 8.115
6 7.231 8.558 9.446
2.706
4.605
6.251
7.779'
9.236
10.645
3.841
5.991
7.815
9.488
11.070
12.592
0.0250
5.024
7.378
9.348
11.143
12.833
14.449
0.0100
6.635
9.210
11.345
13.277
15.086
16.812
0.0050
7.879
10.597
12.838
14.860
16.750
18.548
0.0010
10.828
13.816
16.266
18.467
20.515
22.458
При а = 0.10 и d.f. = 4 критическое значение хи-квадрат %2С (подчеркнуто
в таблице выше). На рисунке 18.1 представлены результаты этой проверки.
Рис 18.1 1
Использование
распределения
хи-квадрат для примера
с фильмом.
1 0.90 Xs
/ 1-а
/ Не ОТКЛОНЯТЬ #о
оТ=4
а = 0.10
Отклонить Н0
^/
| j
7.779 9.95
А.
X
Судя по рисунку 18.1, вычисленное значение хи-квадрат 9.95 попадает в
область «Отклонить Н0», из чего мы можем сделать заключение, что
фактическое распределение частот оценок фильма отличается от ожидаемого
распределения. Пока X с < X2 мы всегда будем отклонять Я0.
Поскольку вычисленное значение хи-квадрат для испытания на
адекватность может быть только положительным значением, проверка гипотезы
всегда будет областью с одним хвостом отклонения в правой части.
Использование функции ХИ20БР программы Excel
У вас все еще нет под рукой таблицы распределения хи-квадрат? Не
отчаивайтесь. Мы можем генерировать критические значения хи-квадрат с
помощью функции ХИ20БР программы Excel, которая имеет две
переменные.
Глава 18: Распределение хи-квадрат 273
ХИ20БР(вероятность; степени_свободы) ■,
где:
вероятность = уровень значимости,
степени_свободы = число степеней свободы.
Например, на рисунке 18.2 показана функция ХИ20БР для определения
критического значения хи-квадрат при а = 0.10 и d.f. = 4 из нашего
предыдущего примера.
■
Ячейка А1 содержит формулу =ХИ2ОБР(0.1;4) с результатом 7.799. Эта
вероятность подчеркнута в предыдущей таблице.
Характеристики распределения хи-квадрат
По рисунку 18.1 видно, что распределение хи-квадрат не является
симметричным, но имеет положительную асимметрию. Форма распределения
зависит от числа степеней свободы, как показано на рисунке 18.3.
Рис 18.2
Функция ХИ20БР
программы Excel.
274 Часть 4: Углубленное изучение статистки вывода
По мере увеличения числа степеней свободы форма распределения хи-
квадрат становится более симметричной.
Испытание на адекватность с биноминальным
распределением
В предыдущих главах мы порой принимали допущения, что совокупность
подчиняется определенному распределению, например, нормальному или
биноминальному. В этом разделе мы узнаем, как подтверждать такие
заявления.
В качестве примера предположим, что определенный игрок Высшей
бейсбольной лиги заявляет, что вероятность совершения им удачного удара в
любое определенное время составляет 30%. В таблице ниже представлено
распределение частот количества ударов за игру с учетом последних 100 игр.
Предположим, в каждой игре он отбил мяч 4 раза.
Данные о бейсболисте
Количество ударов Количество игр
0 26
1 34
2 30
3 7
4 3
Всего 100
Иными словами, в 26 играх он не отбил мяч ни разу, в 34 — 1 раз и т.д.
Проверим заявление о том, что это распределение подчиняется биноминальному
распределению при р = 0.30 и а = 0.05.
Формулировка гипотезы будет выглядеть следующим образом:
Н0: Распределение ударов игрока может быть описано с помощью
биноминального распределения вероятностей при р .= 0.30.
Я,: Распределение отличается от биноминального при р = 0.30.
Прежде всего, вычислим распределение частот для ожидаемого числа
ударов за игру. Для этого нам необходимо заглянуть в Таблицу 1 Приложения В
при п = 4 (количество испытаний за игру) и р = 0.30 (вероятность успеха).
Эти вероятности вместе с вычислениями ожидаемых частот представлены в
таблице ниже.
Глава 18: Распределение хи-квадрат 275
Вычисление ожидаемых частот для бейсболиста
Кол-во ударов за игру Бином, вер-ть Число игр Ожид. частота
О
1
2
3
4
Всего
0.2401
0.4116
0.2646
0.0756
0.0081
1.0000
100 =
100 =
100 =
100 =
100 =
24.01
41.16
26.46
7.56
0.81
100.00
Эврика!
Ожидаемые частоты не
обязательно должны быть целыми
числами, поскольку они
представляют лишь теоретические
значения.
Прежде чем продолжить, нам
необходимо сделать одно уточнение
относительно ожидаемых частот. При
использовании проверки хи-квадрат нам
необходимо как минимум 5
наблюдений в каждой из категорий
ожидаемых частот. Если наблюдений меньше
5, нам придется объединить категории.
В предыдущей таблице мы объединим
3 и 4 удара за игру в одну категорию, чтобы соответствовать этому требованию.
Теперь мы готовы определить вычисленное значение распределения
хи-квадрат с помощью следующей таблицы:
Вычисленное значение распределения хи-квадрат для примера
с бейсболом
Удары
0
1
2
3-4
Всего
*7 + 3 = 10
" 7.56 + 0.81
О
26
34
30
10*
1 = 8.37
Е
24.01
41.16
26.46
8.37**
(О-Е)
1.99
- 7.16
3.54
1.63
(О-Е)2
3.96
51.27
12.53
2.66
(О-Щ2
Е
0.16
1.25
0.47
0.32
В соответствии с Таблицей 5 Приложения В, критическое значение хи-
квадрат при а = 0.05 и d.f. = к = 4 — 1 = 3 равняется 7.815. Эта проверка
представлена на рисунке 18.4.
276 Часть 4; Углубленное изучение статистики вывода
Рис 18.4
Использование
распределения
хи-квадрат для
примера с бейсболом.
С
f 0.95 \ч
1-а
Не отклонять Н0
I ? . .,
) 2.20
х2
df-
=4
а = 0.05
Отклонить Н0
7.815
х2
л с
Судя по рисунку 18.4, вычисленное значение хи-квадрат 2.20 попадает в
область «Не отклонять Н0». Из этого мы можем сделать заключение, что
распределение ударов нашего игрока может быть описано с помощью
биноминального распределения при р = 0.30.
Проверка на независимость методом хи-квадрат
Кроме испытания на адекватность, распределение хи-квадрат может быть
использовано для проверки переменных на независимость друг от друга. Для
иллюстрации этой методики я вновь обращусь к примеру с теннисом,
описанному в Главе 7.
Как вы, надеюсь, помните, Дебби полагала, что непродолжительная
разминка перед игрой на счет снижает ее шансы на победу. Изучив условные
вероятности, я был вынужден признать, что существуют некие доказательства,
подтверждающие заявление Дебби. Но я не из тех, кто сразу опускает руки.
Я требую справедливости, дополнительных доказательств и повторного
подсчета! Я требую проверки гипотезы с использованием распределения
хи-квадрат!
Без ведома Дебби я скрупулезно собирал данные о наших последних 50
матчах. В таблице ниже представлено число побед каждого из нас в
соответствии с продолжительностью разминки.
Наблюдаемые частоты для примера с теннисом
0-10
минут
11-20
минут
Более
20 минут
Всего
Победа Д.
Победа Б.
Всего
4
14
18
10
9
19
9
4
13
23
27
50
Глава 18: Распределение хп-квадрат 277
Такая таблица носит название факторной; в ней представлены
наблюдаемые частоты двух переменных. В данном случае переменными являются
продолжительность разминки и игрок в теннис. Таблица организована в виде г
строк и с столбцов. Для нашей таблицы г = 2, а с = 3. Пересечение строки и
столбца называется ячейкой. Факторная таблица имеет тс ячеек; в нашем
случае пересечением является значение 6
Проверка хи-квадрат на независи- <^SiPk\ Термины
мость определит, одинакова ли доля {
побед Дебби для всех трех случаев w >д.. Таблица исходов показывает
разминки. Если исход проверки гипо- , наблюдаемые частоты двух
тезы покажет, что эти Доли
неодинаковы, мы заключим, что
продолжительность разминки сказывается на
результате игры. Но у меня есть
некоторые сомнения.
Для начала сформулируем гипотезы:
Я0: Качество игры не зависит от продолжительности разминки
Н\: Качество игры зависит от продолжительности разминки
Проверим эту гипотезу для а = 0.10.
переменных. Ячейка - пересечение
строки и столбца факторной таблицы,
факторная таблица имеет гх с ячеек.
Далее определим ожидаемую частоту каждой ячейки в факторной
таблице при допущении, что две переменные являются независимыми. Делаем это
с помощью следующего выражения:
сумма строки г х сумма столбца с
£? — f
общее число наблюдений
где ETiC = ожидаемая частота ячейки на пересечении строки г и столбца с.
В таблице ниже вышесказанное применено к нашему примеру с теннисом.
Строка/столбец
г = 1
г = 2
с = 1
с = 2
с = 3
Категория
Деб побеждает
Боб побеждает
0—10 минут разминки
11—20 минут разминки
Разминка более 20 минут
Общее число
наблюдений
23
27
18
19
13
Общее число наблюдений для этого примера = 50; это мы можем
подтвердить, сложив 23 •+- 27 или 18-1-19+13. Теперь определяем ожидаемые
частоты для каждой ячейки:
278 Часть 4: Углубленное изучение статистики вывода
11 50 ^2 50
*,.,= <») =9.72 4.2=(27И19)
=8.74 Ц, ='
=10.26 Ця
(23)(13)
50
(27)(13)
=5.98
50 ' 50 " 50
В таблице ниже эти вычисления суммированы.
=7.02
Ожидаемые частоты для примера с теннисом
Победа Деб
Победа Боба
Всего
0-10
минут
8.28
9.72
18
11-20
минут
8.74
10.26
19
Более
20 минут
5.98
7.02
13
Всего
23
27
50
Эврика!
Обратите внимание, что
ожидаемые частоты для таблицы
исходов сводятся к суммам строки и
столбца из наблюдаемых частот.
Теперь необходимо вычислить
значение хи-квадрат:
Эти вычисления суммированы в
таблице ниже.
Использование метода хи-квадрат для примера с теннисом
(О-Е)2
Строка
1
1
1
2
2
2
Столбец
1
2
3
1
2
3
О
4
10
9
14
9
4
Е
8.28
8.74
5.98
9.72
10.26
7.02
(О-Е)
- 4.28
1.26
3.02
4.28
- 1.26
- 3.02
(О-Е)2
18.32
1.59
9.12
18.32
1.59
9.12
Е
2.21
0.18
1.53
1.88
0.15
1.30
Для определения критического значения хи-квадрат нам необходимо
знать число степеней свободы, количество которых для независимой
проверки будет равно:
Глава 18: Распределение хи-квадрат 279
А/. = (г - 1)(с - 1)
В нашем случае мы имеем (г — 1)(с — 1) = (2 — 1)(3 — 1) = 2 степени свободы.
В соответствии с Таблицей 5 Приложения В, критическое значение хи-
квадрат при а = 0.10 и d./. = 2 равно 4.605. Эта проверка графически
представлена на рисунке 18.5.
Рис 18.5
Использование метода
хи-квадрат для примера
с теннисом.
0 4.605 7.25
df=2 х^ х2
Судя по рисунку 18.5, вычисленное значение хи-квадрат 7.25 попадает в
область «Отклонить Н0». Из этого мы заключаем, что существует зависимость
между продолжительностью разминки и качеством моей игры и игры Дебби.
Безобразие — Дебби опять оказалась права! А у вас дела обстоят иначе?
Но у меня остается одно утешение. Проверка независимости хи-квадрат
позволяет лишь узнать, существует ли связь между двумя переменными, но
не дает никакого представления о направлении этой связи. Иными словами,
со статистической точки зрения Дебби не может утверждать, что при
короткой разминке она оказывается в неравных условиях. Она лишь может
заявлять, что продолжительность разминки сказывается на ее игре. Мы,
статисты, всегда находим выход из неприятных ситуаций!
Ваша очередь
1. Компания считает, что распределение прихода заказчиков в течение
недели следующее:
День недели Ожидаемый процент заказчиков
Понедельник 10
Вторник 10
Среда 25
Четверг 15
Пятница 20
Суббота 30
Всего 100
0.90
1-а
Не отклонять Н0
а = 0.10
Отклонить Н0
/
280 Часть 4: Углубленное изучение статистпкп вывода
Случайным образом была взята неделя и подсчитано ежедневное число
заказчиков. Результаты получились следующими: понедельник — 31,
вторник — 18, среда — 36, четверг — 23, пятница — 47, суббота — 60.
Используйте эту выборку для проверки ожидаемого распределения при а = 0.05.
2. Сайт электронной торговли желает проверить гипотезу о том, что
число посещений сайта в минуту подчиняется распределению Пуассона при
X = 3. Были собраны следующие данные:
Количество посещений
страницы сайта
в минуту 0
Частота 22
1
51
2 3
72 92
4
60
5
44
6
25
7 или более
14
Проверьте эту гипотезу при а = 0.01.
3. Про'фессор английского языка хочет выявить взаимосвязь между
оценкой по английскому языку и количеством часов, посвящаемых
студентом предмету еженедельно. Было опрошено 500 студентов. Результаты
опроса представлены в таблице ниже.
Кол-во часов чтения
в неделю
Менее 2
2-4
Более 4
Всего
А
36
27
32
95
В
75
28
25
128
Оценка
С
81
50
24
155
D
63
25
6
94
F
10
10
8
28
Всего
265
140
95
500
Проверьте эту гипотезу при а = 0.05.
Повторение - мать учения
Ф Распределение хи-квадрат несимметрично, но отличается
положительной асимметрией. По мере увеличения числа степеней свободы форма
распределения хи-квадрат становится более симметричной.
Ф Распределение хи-квадрат позволяет выполнять проверку гипотезы с
номинальными и порядковыми данными.
Ф Распределение хи-квадрат* может применяться для выполнения
испытания на адекватность, с использованием выборки для проверки
соответствия полученного распределения частот ожидаемому
распределению.
Глава 18:_Распределенпе хи-квадрат 281
Ф Проверка методом хи-квадрат на независимость выявляет наличие или
отсутствие взаимосвязи между двумя переменными, но не определяет
направление этой связи.
Ф Факторная таблица показывает наблюдаемые частоты двух
переменных. Пересечение строки и столбца факторной таблицы носит название
ячейки.
Дисперсионный анализ
В этой главе
Ф Сравнение трех или более средних по совокупности с
использованием дисперсионного анализа
Ф Использование распределения Фишера
(F-pacnpeделения) для выполнения проверки гипотезы для
дисперсионного анализа
Ф Использование программы Excel для выполнения одно-
факторного дисперсионного анализа
Ф Сравнение пар средних по выборке с помощью критерия
Шеффе
В Главе 17 мы познакомились с проверкой гипотез и
научились сравнивать средние двух различных совокупностей
с целью узнать, существует ли между ними разница. А что,
если нам необходимо сравнить средние трех или более
совокупностей? Тогда вы оказались в нужное время в нужном
месте, потому что эта глава посвящена как раз этой
проблематике.
Для выполнения этого типа проверки нам необходимо
ввести понятие еще одного распределения вероятностей,
называемого F-pacnpe делением. Проверка, которую мы будем
осуществлять, имеет весьма впечатляющее название —
дисперсионный анализ. Этот тип проверки настолько специфичен, что
а
_jfoaga_19: Дисперсионный анализ 283
имеет собственную аббревиатуру — ANOVA. Звучит как что-то
космическое. Читайте дальше, чтобы узнать, что скрывается под этим словом.
Однофакторный дисперсионный анализ
Если вы хотите сравнить средние трех или более совокупностей, тест
ANOVA — как раз для вас. Допустим, я заинтересован в определении того,
существует ли разница между степенью удовлетворенности покупателей
тремя сетями фаст-фуда. Для этого мне необходимо отобрать выборку
оценок удовлетворенности каждой из сетей и определить, существует ли
значительная разница между выборочными средними. Допустим, в моем
распоряжении есть следующие данные:
Совокупность Сеть фаст-фуда Оценка среднего в выборке
1 McDoogles 7.8
2 Burger Queen 8.2
3 Windy's 8.3
Формулировка гипотез будет выглядеть следующим образом:
Нх\ не все равны.
Моя задача состоит в том, чтобы определить, связаны ли вариации оценок
покупателей из предыдущей таблицы с сетью фаст-фуда или они носят
исключительно случайный характер. Иными словами, видят ли покупатели
разницу между тремя сетями фаст-фуда? Если я отклоню основную гипотезу, я
смогу лишь заключить, что разница все же существует. Дисперсионный
анализ не позволяет сравнивать средние по совокупности между собой и
определять, какое из них больше остальных. Решение подобного вопроса требует
проведения дополнительного анализа.
Эврика! — 1
Для использования однофакторного ANOVA-анализа должны соблюдаться
некоторые условия.
Ф Интересующие нас совокупности должны быть нормально распределены.
Ф Выборки должны быть независимыми друг от друга.
Ф Все совокупности должны иметь одинаковую дисперсию.
Фактор в ANOVA-анализе описывает причину вариаций данных. В
предыдущем примере фактором будет сеть фаст-фуда. В данном случае речь идет
284 Часть 4: Углубленное изучение статистики вывода
об однофакторном дисперсионном анализе, поскольку рассматривается
только один фактор. Более сложные типы дисперсионного анализа могут
описывать несколько факторов.
Уровень дисперсионного анализа описывает число категорий внутри
интересующего нас фактора. В нашем случае мы имеем 3 уровня, основанных
на трех разных рассматриваемых сетях фаст-фуда.
. Чтобы показать вам, как выполняется дисперсионный анализ на практике,
я обращусь к следующему примеру. Я должен признать, к досаде Деб, что я
совершенно неумело обращаюсь с нашей лужайкой. Мой девиз: Если
лужайка зеленого цвета, значит, все в порядке. Что касается Деб, то она
совершенно точно знает, какие удобрения использовать и когда. Я же терпеть не могу
раскидывать удобрения по лужайке, потому что с ними трава растет
значительно быстрей, а значит, мне приходится чаще ее стричь.
Ситуация ухудшается тем; что мой сосед Билл вечно стыдит меня за
ненадлежащий уход за состоянием лужайки. Мистер «Совершенная Лужайка»
каждый выходной тщательнейшим образом подстригает свои владения,
отчего его лужайка становится похожа на поле Национальной ассоциации
боулинга на траве. От этого Деб страдает «лужаечной завистью». Билл даже
обзавелся маленькой симпатичной тележкой, которую он прицепляет позади
своего тягача. Я спросил Деб, не заиметь ли и
нам такую тележку, но она парировала,
что с моими знаниями в области ухода за
лужайками я смогу только пораниться.
Как бы то ни было, существует
несколько различных типов
дисперсионного анализа, для рассмотрения которых
мне понадобилось бы написать отдельную
книгу. В оставшейся части книги я буду
пользоваться вышеописанным примером
с лужайкой для иллюстрации основной
процедуры дисперсионного анализа.
Термины
Фактор в дисперсионном
анализе описывает причину
вариаций данных. Есди рассматривается
лишь один фактор, процедура носит
название однофакторного
дисперсионного анализа. Уровень
дисперсионного анализа описывает число
категорий интересующего нас фактора.
Полностью рандомизированный дисперсионный анализ
Термины
Простейший вид ANOVA-ана-
лиза - это полностью
рандомизированный однофакторный
дисперсионный анализ,
подразумевающий случайный независимый отбор
наблюдений для каждого уровня
фактора.
Простейший тип дисперсионного
анализа носит название полностью
рандомизированного однофакторного ANOVA-ана-
лиза, подразумевающего независимый
случайный отбор наблюдений для
каждого уровня фактора. Ну и завернули,
однако! Чтобы помочь вам в этом разобраться,
допустим, я хочу сравнить
эффективность трех типов удобрений для нашей
лужайки. Предположим, я выбрал 18 слу-
Глава 19: Дисперсионный анализ 285
чайных участков нашей лужайки и применил к каждому из них Удобрение 1, 2
или 3. Через неделю я скашиваю мои участки и взвешиваю срезанную траву.
Фактором в нашем случае является удобрение. У нас есть 3 уровня,
соответствующие трем типам удобрений. В таблице ниже представлен вес
срезанной с каждого участка травы в фунтах. В таблице также указаны среднее
и дисперсия.
Данные дм скошенной травы
Среднее
Дисперсия
Удобрение 1
10.2
8.5
8.4
10.5
9.0
8.1
9.12
1.01
Удобрение 2
11.6
12.0
9.2
10.3
10.3
12.5
10.92
1.70
Удобрение 3
8.1
9.0
10.7
9.1
9.1
9.5
9.48
0.96
Данные для каждого типа удобрения будут выборкой. Судя по
предыдущей таблице, мы имеем 3 выборки, каждая из которых состоит из 6
наблюдений. Гипотезы будут сформулированы следующим образом:
Н\. не все одинаковы,
где 1, 2 и 3 — фактические средние по совокупности фунтов скошенной
травы для каждого типа удобрения.
Разбиение суммы квадратов
Проверка гипотезы для дисперсионного анализа сравнивает два типа
вариаций из выборок. Сначала нам необходимо признать, что общая вариация
данных наших выборок может быть разделена, или, как мы, статисты, любим
выражаться, «разбита», на две группы.
Первая группа — это вариация внутри каждой выборки, называемая
суммой квадратов внутри выборки (SSW) и вычисляемая по формуле:
SSW = £to-l)s?,
где к = число выборок (или уровней).
286 Часть 4: Углубленное изучение статистики вывода
В примере с лужайкой к = 3 и:
s^l.01 s*=0.96 s*=1.70
щ = 6 n2 = 6 n3 = 6.
Сумма квадратов внутри выборки вычисляется так:
SSW = (6 - 1)1.01 + (6 - 1)1.70 + (6 - 1)0.96 = 18.35.
В некоторых учебниках это значение может называться суммой квадратов
ошибки (SSE).
Вторая часть — это вариация между выборками, называемая суммой
квадратов между выборками (SSB) и рассчитываемая по формуле:
где х = общее среднее, или среднее значение всех наблюдений. Для нашего
примера:
5г, = 9.12 х2 = 10.92 . х3 = 9.48.
щщсл##*мц
В некоторых учебниках по
статистике значение SSB также
носит название суммы квадратов
между испытаниями (SSTR).
Теперь мы определяем значение общего
среднего:
х =
_£
N
где N = общее число наблюдений из всех выборок.
Для примера с удобрением:
= 10.2+8.5 +8.4 +10.5+ -+10.7 +9.1+10.5 +9.5
х = -
18
=9.83
Теперь мы можем вычислить сумму квадратов между выборками:
к /~ =\2
55Б = £л,. I*'-*)
ANOVA-анализ не требует,
чтобы все выборки были
одинакового размера, как в
примере с удобрениями.
Примеры неравных по размеру
выборок представлены в Задаче
1 раздела «Ваша очередь».
55В = 6(9.12 - 9.83)2 + 6(10.92 - 9.83)2 +
+ 6(9.48 - 9.83)2 = 10.86.
Наконец, полная вариация всех наблюдений
носит название полной сумы квадратов (SST) и
рассчитывается:
SST = SSW + 55В.
Для нашего примера:
55Г = 18.35 + 10.86 = 29.21.
Глава 19: Дпеперспонный анализ 287
Обратите внимание, что мы можем вычислить дисперсию
первоначальных 18 наблюдений, s2, следующим образом:
s2=OT1 = 29:21=172
N-1 18-1
Полученный результат можно подтвердить, используя уравнение для
вычисления дисперсии, которое мы обсуждали в Главе 4, или программу Excel.
Определение F-критерия
Для проверки гипотезы для дисперсионного анализа нам необходимо сравнить
вычисленный и критический критерии значимости с помощью распределения
Фишера (F-распределения). F-критерий можно вычислить по формуле:
F= MSB
MSW'
где MSB = средний квадрат между выборками, определяемый как:
к-1
MSW = средний квадрат внутри выборки, определяемый как:
N-k
Теперь применим эти понятия к нашему примеру:
mB=ssBJ™6=5A3
к-1 3-1
N-k 18-3
_ MSB 5.43
F = = = 4.45.
MSW 1.22
Эврика!
Средний квадрат между выборками (MSB) - это измерение вариации между
выборочными средними. Средний квадрат внутри выборки (MSW) - это измерение вариации
внутри каждой выборки. MSB-вариация, значительно превышающая MSW-вариацию,
означает, что средние по выборке не очень близки по значению. Это приведет к
получению большого значения F, вычисленного F-критерия. Чем больше значение F, тем больше
вероятность, что оно превысит критический F-критерий (скоро мы научимся его определять),
из чего можно сделать заключение, что между средними по совокупности существует разница.
288 Часть 4: Углубленное пзученпе статистики вывода
Если вариация между выборками (MSB) значительно превышает
вариацию внутри выборки (MSW), мы, вероятнее всего, отклоним основную
гипотезу и заключим, что между средними по совокупности существует разница.
Завершим мы нашу проверку гипотезы введением F-распределения в
следующем разделе.
Определение критического значения F-критерия
F-распределение используется для определения критического значения
F-критерия, который при проверки гипотезы ANOVA-анализа сравнивается
с вычисленным F-критерием. Критическое значение F-критерия, F,k-l,N-kt
зависит от двух различных степеней свободы, определяемых так:
Vj = /с — 1 v2 = N — k
Для нашего примера:
v, = 3 - 1 = 2 v2 = 18 - 3 = 15
Критическое значение F-критерия можно получить из таблицы
F-распределения в Таблице 6 Приложения В этой книги. Ниже приведена часть этой таблицы.
Таблица критических F-критериев
а = 0.05
v212 345678 9 10
1 161.448 199.500 215.707 224.583 230.162 233.986 236.768 238.882 240.543 241.882
2 18.513 19.000 19.164 19.247 19.296 19.330 19.353 19.371 19.385 19.396
3 10.128 9.552 9.277 9.117 9.013 8.941 8.887 8.845 8.812 8.786
4 7.709 6.944 6.591 6.388 6.256 6.163 6.094 6.041 5.999 5.964
5
6
7
8
9
10
И
12
13
14
15
6.608
5.987
5.591
5.318
5.117
4.965
4.844
4.747
4.667
4.600
4.543
5.786
5.143
4.737
4.459
4.256
4.103
3.982
3.885
3.806
3.739
3.682
5.409
4.757
4.347
4.066
3.863
3.708
3.587
3.490
3.411
3.344
3.287
5.192
4.534
4.120
3.838
3.633
3.478
3.357
3.259
3.179
3.112
3.056
5.050
4.387
3.972
3.687
3.482
3.326
3.204
3.106
3.025
2.958
2.901
4.950
4.284
3.866
3.581
3.374
3.217
■ 3.095
2.996
2.915
2.848
2.790
4.876
4.207
3.787
3.500
3.293
3.135
3.012
2.913
2.832
2.764
2.707
4.818
4.147
3.726
3.438
3.230
3.072
2.948
2.849
2.767
2.699
2.641
4.772
4.099
3.677
3.388
3.179
3.020
2.896
2.796
2.714
2.646
2.588
4.735
4.060
3.637
3.347
3.137
2.978
2.854
2.753
2.671
2.602
2.544
Глава 19: Дисперсионный анализ 289
а =
Ух
16
17
18
0.05
1
4.494
4.451
4.414
2
3.634
3.592
3.555
3
3.239
3.197
3.160
4
3.007
2.965
2.928
5
2.852
2.810
2.773
6
2.741
2.699
2.661
7
2.657
2.614
2.577
8
2.591
2.548
2.510
9
2.538
2.494
2.456
10
2.494
2.450
2.412
Обратите внимание, что эта таблица приведена только для а = 0.05.
Другие значения потребуют другой части таблицы. Для vt = 2 и v2 = 15
критическое значение F-критерия выделенно в предыдущей таблице
подчеркиванием. На рисунке 19.1 представлен результат проверки нашей гипотезы.
Рис19.1
Пример
ANOVA-анализа
с удобрением.
0.95
1-а
Не отклонять Н0
а = 0.05
Отклонить Н0
v2=15
Судя по рисунку 19.1, вычисленный F-критерий 4,45 попадает в область
«Отклонить Н0». Отсюда делаем вывод, что средние по совокупности
неодинаковы. Пока Faik_ltN_k < F, мы всегда будем отклонять Н0.
Эврика!
F-распределение обладает набором характеристик.
Ф Оно несимметрично, но имеет положительную асимметрию.
Ф Форма F-распределения зависит от степеней свободы, указанных значениями
V! и v2.
# По мере увеличения значений v-i и v2 форма F-распределения будет
становиться более симметричной.
Ф Общая площадь под кривой равняется 1.
# Среднее значение F-распределения примерно равняется 1.
Наше финальное заключение состоит в том, что одно из испытанных нами
удобрений ускоряет рост травы сильней, чем остальные. Похоже, это
заключение только прибавит мне хлопот.
290 Часть 4: Углубленное изучение статистики вывода
Т"1
Несмотря на то что мы отклонили основную гипотезу Н0 и пришли к заключению,
что средние по генеральной совокупности неодинаковы, ANOVA-анализ не позволяет
нам сравнивать средние между собой. Иными словами, у нас нет достаточных
доказательств того, что Удобрение 2 усиливает рост травы больше, чем Удобрение 1. Для
этого нам понадобится еще одна проверка, называемая парным сравнением, о которой
речь пойдет чуть ниже в этой главе.
А сейчас мы узнаем, как программа Excel поможет нам выполнить все эти
непростые вычисления.
Использование функции 1РАСПОБР программы Excel
И снова мы будем генерировать критические F-критерии с помощью
функции FPACnOBP со следующими характеристиками:
РРАСПОБР(вероятность; степени_свободы1; степени_свободы2),
где:
вероятность = уровень значимости,
степени_свободы1 = vt = к — 1
степени_свободы2 = v2 = N — к.
Например, на рисунке 19.2 показана функция FPACIIOBP для
определения критического F-критерия при а = 0.05, V!=3— 1=2hv2 = 18 — 3=15
из нашего предыдущего примера.
Рис 192
Функция FPACnOBP.
'
|Г'гГ
1 7
1,31
•
,3|Щ
:.: ■
Ячейка А1 содержит формулу = FPACnOBP(0.05; 2; 15) с результатом
3.682. Эта вероятность подчеркнута в предыдущей таблице.
Глава 19: Дисперсионным анализ 291
Использование Excel дня выполнения однофакторного
дисперсионного анализа
Уверен, вы убедились в том, что выполнять ANOVA-анализ вручную требует
немало усилий. Думаю, вас удивит, с какой легкостью программа Excel
выполнит такую массу вычислений.
1. На чистом рабочем листе, в столбцы А, В и С, введите данные из нашего
примера с удобрениями.
2. Откройте меню Tools (Сервис) и щелкните Data Analysis (Анализ
данных). (Если эта команда отсутствует в меню Tools (Сервис), обратитесь к
разделу «Установка средств анализа данных» Главы 2.)
3. В появившемся окне Data Analysis (Анализ данных) выберите Anova:
Single Factor (Однофакторный дисперсионный анализ), как показано на
рисунке 19.3, и щелкните ОК.
Рис. 19.3
Выбор однофакторного
дисперсионного анализа
Plf в Excel.
^Ofifyiwy* 1 ,
4. Укажите требуемые значения в окне однофакторного дисперсионного
анализа, как показано на рисунке 19.4.
РИС 19.4
I Диалоговое окно Anova:
Single Factor
(Однофакторный
дисперсионный анализ).
Si
хр}
—
292 Часть 4: Углубленное изучение статпапкп вывода
5. Щелкните ОК. На рисунке 19.5 показаны результаты дисперсионного
анализа.
Рис 19.5
Окончательные
результаты
однофакторного
дисперсионного
анализа.
14-
1
1'
i
1
1
i!
\ *
.•.'.■'.• Cv,.v vV*««* <':■■<- *уС*#У.;У
■
б
Полученные результаты соотносятся с тем, что мы так долго и старательно
определяли в предыдущих разделах. Обратите внимание, что уровень р-зна-
чимости = 0.0305, а это значит, что мы отклоняем Н0, поскольку
уровень р-значимости < а. Как вы помните, при формулировке гипотез мы
установили значение а = 0.05.
Парные сравнения
Термины
Отклонив основную гипотезу с помощью дисперсионного анализа, мы
можем определить, какие средние по выборке отличаются от остальных, и
сделаем мы это с использованием проверки Шеффе. Эта проверка сравнивает
каждую пару средних по выборке из
процедуры дисперсионного анализа. Для нашего
примера с удобрениями мы будем
сравнивать хх и хъ хх и х3, х2 и х3, чтобы узнать,
существует ли между ними разница.
Сначала вычисляем критерий проверки
Шеффе, F, для каждой пары средних по
выборке:
Отклонив Н0 с помощью
ANOVA-анализа мы
можем определить среднее
выборки, используя проверку Шеффе.
F=-
(Ха-Хь^
SSW
2>-Ч
1 1
— + .—
пп пн
где:
ха, хь = сравниваемые средние по выборке,
SSW = сумма квадратов внутри выборок, взятая из процедуры
дисперсионного анализа,
JMig 19j_flncnepcnoHHbin аналпз_293
ла, Пь = размеры выборок,
к = число выборок (или уровней).
Сравнивая xt и х2, получаем:
Е=-
(Ха-Хь^
(9.12-10.92)2
SSW
I(n-i)Ln- Пь
1 1
— + —
18.35
5+5 + 5
1
-I]
F=-
3.24
=8.048
1.22[G.33]
Сравнивая Iti и х3г получаем:
(9.12-9.48)2 0.13
F=-
18.35
1 1
- + --
6 6
1.22[0.33J
=0.323
5+5+5L
Сравнивая х2 и х3, получаем:
(10.92-9.48)2 _ 2.07
F=-
18.35
5+5+5
1 1
-+-
6 б
1.22[0.33]
=5.142
Затем определяем критическое значение критерия Шеффе, Fsc, умножив
критическое значение F-критерия из дисперсионного анализа на к — 1, как
показано ниже:
Fsc = (1с - \)Fa,k-l,N-k.
Для нашего примера с удобрениями получаем:
^0.05,2,15 = 3.682
^sc = (3 - 1) (3,682) = 7.364.
Если Fs < Fsc, мы заключаем, что разница между выборочными средними
отсутствует; если больше, то присутствует. В таблице ниже суммированы
полученные результаты.
Итого проверки Шеффе
Парная выборка
Fs
Fsc
Заключение
Xi и х2 8.048 7.364 Разница есть
294 Часть 4: Углубленное изучение статистики вывода
Парная выборка
х2их3
Fs
0.323
5.142
Fsc
7.364
7.364
Заключение
Разницы нет
Разницы нет
В соответствии с полученными результатами, статистически значимая
разница присутствует только между Удобрением 1 и Удобрением 2. Если
Удобрение 2 окажется более эффективным с точки зрения роста травы, чем
Удобрение 1, я приложу все усилия, чтобы Дебби никогда не узнала об этом удобрении.
Ваша очередь
1. Группа потребителей проверяет расход бензина трех различных
моделей автомобилей. Несколько машин каждой модели проделали по 500
миль, и был зафиксирован их расход, как показано ниже:
Машина 1 Машина 2 Машина 3
22.5
20.8
22.0
23.6
21.3
22.5
18.7
19.8
20.4
18.0
21.4
19.7
17.2
18.0
21.1
19.8
18.6
Обратите внимания, что для выполнения дисперсионного анализа
размеры выборок не обязательно должны быть одинаковыми.
Проверьте разницу между выборочными средними при а = 0.05.
2. Выполните парное сравнение для средних по выборке из Задачи 1.
3. Вице-президент компании желает определить, существует ли разница
между средним числом покупателей в день 4 разных магазинов,
используя следующие данные.
Магазин 1
36
48
32
28
31
Магазин 2
35
20
31
22
19
Магазин 3
26
20
38
32
37
Магазин 4
26
52
37
36
18
Глава 19: Дисперсионный аналпз_295
Магазин 1 Магазин 2 Магазин 3 Магазин 4
55 42 15 30
29 21
Обратите внимания, что для выполнения дисперсионного анализа
размеры выборок не обязательно должны быть одинаковыми.
Проверьте разницу между выборочными средними при а = 0.05.
Повторение - мать учения
Ф Дисперсионный анализ, ANOVA, сравнивает средние трех или более
совокупностей.
Ф Фактор, выделенный,дисперсионным анализом, описывает причину
вариаций данных. Если рассматривается только один фактор, процедура
носит название однофакторного дисперсионного анализа.
Ф Уровень ANOVA-анализа описывает число категорий внутри
интересующего нас фактора.
Ф Самый простой тип дисперсионного анализа называется полностью
рандомизированный однофакторный дисперсионный анализ,
подразумевающий независимый случайный отбор наблюдений для каждого
уровня одного фактора.
Ф Для осуществления проверки гипотезы для ANOVA-анализа нам
необходимо сравнить вычисленный критерий значимости с критическим с
использованием распределения Фишера.
Ф Отклонив основную гипотезу с помощью дисперсионного анализа, мы
можем определить, какие из средних по выборке являются отличными
от других с помощью критерия Шеффе.
Корреляция и линейная
регрессия
В этой главе
Ф Различия между независимыми и зависимыми
переменными
Ф Определение корреляции и кривой эффекта для данных
упорядоченных пар
Ф Вычисление доверительного интервала для кривой эффекта
Ф Выполнение проверки гипотезы для кривой эффекта
Ф Использование Excel для выполнения анализа линейной
регрессии
На протяжении последних нескольких глав мы применяли
статистику вывода для заключений в отношении одной, двух
или более средних и долей по совокупности. Я знаю, что вам
было весело, но нам пора переходить к другому типу
статистики вывода, которая будет не менее любопытной. (Если вы
можете себе представить что-то еще более увлекательное!)
В последней главе речь пойдет о том, как переменные могут
быть связаны друг с другом. С помощью корреляции и
линейной регрессии мы сможем, во-первых, определять, существует
ли связь между первой и второй переменной, а во-вторых, опи-
Глава 20^ор£ел^^
сывать природу этой связи в математических терминах. Надеюсь, это
занятие покажется вам не менее увлекательным, чем предыдущие!
Независимые и зависимые переменные
Допустим, я хочу определить, существует ли связь между количеством часов,
посвященных студентом изучению статистики, и финальной
экзаменационной оценкой. В таблице ниже представлены выборочные данные о б
случайным образом отобранных студентах.
Данные для экзамена по статистике
Количество часов учебы Экзаменационная оценка
3 86
5 95
4 92
4 83
2 78
3 82
Очевидно, количество часов напрямую отражается на финальной оценке.
Переменная «Часы изучения»
считается независимой переменной (х),
поскольку она приводит к наблюдаемой
вариации переменной
«Экзаменационная оценка», которая в нашем случае
считается зависимой переменной (у).
Данные из предыдущей таблицы
считаются упорядоченными парами (х,у)
значений, такими как (3.86) и (5.95).
«Причинная связь» между
зависимыми и независимыми переменными
существует только в одном направлении:
Независимая переменная (х) ~>
Зависимая переменная (у)
В обратном направлении эта связь
не работает. Например, мы с трудом
можем себе представить, что
переменная оценки может быть причиной
более продолжительного изучения
предмета студентом.
Термины ^
Независимая переменная (х)
является причиной вариации
зависимой переменной (у).
Будьте внимательны,
определяя, какая из переменных является
зависимой, а какая - независимой.
Изучите связь между ними в обоих
направлениях, чтобы понять, какая из
этих связей более логична. Неверный
выбор направления приведет к
бессмысленным результатам.
298 Часть 4: Углубленное изучение статпстпкп вывода
Другие примеры зависимых и независимых переменных представлены в
следующей таблице.
Примеры зависимых и независимых переменных
Независимая переменная
Зависимая переменная
Размер телевизора
Уровень рекламы
Размер оплаты игроков
Цена телевизора
Объем продаж
Число побед
В следующем разделе речь пойдет о связи между переменными х и у с
использованием статистики вывода.
Корреляция
Корреляция измеряет мощность и направление связи между х и у. На
рисунке 20.1 представлены различные типа корреляции в виде графиков
рассеяния упорядоченных пар (х,у). По традиции переменная х размещается на
горизонтальной оси, а у — на вертикальной.
у у Рис 20.1
Различные типы
' ' корреляции.
(А) Положительная
линейная корреляция
(В) Отрицательная
линейная корреляция
(С) Отсутствие корреляции
(D) Нелинейная
корреляция
График А на рисунке 20.1 являет собой пример положительной линейной
корреляции: при увеличении х также увеличивается у, причем линейно. График
В показывает нам пример отрицательной линейной корреляции, на котором при
Глава 20: Корреляция и лпнепная^ресспя 299
увеличении х у линейно уменьшается. На графике С мы видим отсутствие
корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.
Наконец, график D — это пример нелинейных отношений между
переменными. По мере увеличения х у сначала уменьшается, потом меняет
направление и увеличивается.
Оставшаяся часть главы посвящена линейным взаимосвязям между
зависимой и независимой переменными. С нелинейными переменными дело
обстоит гораздо сложней, поэтому мы не будем обсуждать их в рамках этой книги.
Коэффициент корреляции
Коэффициент корреляции, г, предоставляет нам как силу, так и направление
связи между независимой и зависимой переменными. Значения г находятся
в диапазоне между — 1.0 и + 1.0. Когда г имеет положительное значение,
связь между х и у является положительной (график А на рисунке 20.1), а
когда значение г отрицательно, связь также отрицательна (график В).
Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что
между х и у связи не существует (график С).
Сила связи между х и у определяется близостью коэффициента
корреляции к — 1.0 или + 1.0. Изучите рисунок 20.2.
. г = +1.0
г = -1.0
Рис 20.2
Сила связи
между переменными.
г = +0.60
г = -0.60
.х.
График А показывает идеальную положительную корреляцию между х и у
при г = + 1.0. График В — идеальная отрицательная корреляция между х и у
при г = — 1.0. Графики С и D — примеры более слабых связей между
зависимой и независимой переменными.
300 Часть 4: Углубленное изучение статистики вывода
Термины
|| |>^ Коэффициент корреляции, г, определяет как силу, так и направление связи между
зависимой и независимой переменными. Значения г находятся в диапазоне от - 1.0
(сильная отрицательная связь) до + 1.0 (сильная положительная связь). При г = 0 между
переменными х и у нет никакой связи.
Мы можем вычислить фактический коэффициент корреляции с помощью
следующего уравнения:
"2>-£*)0»
Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение
непонятных символов, но прежде чем ударяться в панику, давайте применим
к нему наш пример с экзаменационной оценкой. Таблица, представленная
ниже, поможет нам разбить это уравнение на несколько несложных
вычислений и сделать их более управляемыми.
Часы изучения
X
3
5
4
4
2
3
2>21
Экзамен
У
86
95
92
83
78
82
2>
= 516
Оценка
ху
258
368
475
332
156
246
]Гху = 1835
х2
9
25
16
16
4
9
1У=79
у2
7 396
8 464
9 025
6 889
6 084
6 724
£у2 =44582
Используя эти значения и п = 6 (число упорядоченных пар), получаем:
6(1835)-(21)(516)
г =
>/[б(79)-(21)2][б(44582)Ч516)2 ]
Глава 20: Корреляция и линейная регрессия 301
174
г=-= =0.862.
V(33)(1236)
Как видите, между числом часов, посвященных изучению предмета, и
экзаменационной оценкой существует весьма сильная положительная
корреляция. Преподаватели будут весьма рады узнать об этом.
Внимание! __
Вам необходимо различать ^х2 и (Xх)2. В первом случае J^x2 мы сначала возводим
каждое значение х в квадрат, а затем складываем полученные квадраты. Во втором случае
(£х)2 мы сначала складываем все значения х, а затем возводим полученный результат в
квадрат. Результаты очень разнятся!
Какова выгода устанавливать связь между подобными переменными?
Отличный вопрос. Если обнаруживается, что связь существует, мы можем
предугадать экзаменационные результаты на основе определенного количества
часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем
точнее будет наше предсказание. Мы научимся делать подобные
предварительные оценки уже в этой главе, когда перейдем к теме линейной регрессии.
Проверка значимости коэффициента корреляции
Мы можем осуществить проверку гипотезы для определения того,
существенно ли отличается коэффициент корреляции совокупности, р, от 0 на основе
значения вычисленного коэффициента корреляции, г. Формулируем гипотезы:
Н0: р < 0
Нг.р > 0
Таким образом мы проверяем, существует ли положительная корреляция
между х и у. Я мог бы также воспользоваться двусторонней проверкой и
определить, существует ли корреляция вообще (положительная или
отрицательная), сформулировав гипотезы следующим образом: Н0:р = 0 и Нх\р ф 0.
Критерий значимости для коэффициента корреляции использует £-рас-
пределение Стьюдента:
Vn-2
где:
г = вычисленный коэффициент корреляции упорядоченных пар,
л = число упорядоченных пар.
502 Часть 4; Углубленное пзученпе статпстикп вывода
Для примера с экзаменационной оценкой вычисленный f-критерий
вычисляется так:
t =
0.862
/l-r2 /l-(0.8
Vn-2 V б-:
-(0.862)2
2
.= "£2.-1401.
V
257
4
Критический f-критерий базируется на d.f. =п — 2. Если выбрать а = 0.05,
то tc = 2.132 из Таблицы 4 Приложения В для односторонней проверки.
Поскольку t > tc, мы отклоняем основную гипотезу и делаем заключение, что,
действительно, между количеством часов изучения предмета и финальной
оценкой существует положительная корреляция. И снова статисты
доказывают, что в мире все устроено правильно!
Использование Excel дня вычисления коэффициентов корреляции
Я уверен, что, взглянув на эти ужасные вычисления коэффициентов
корреляции, вы испытаете истинную радость, узнав, что программа Excel может
выполнить за вас всю эту работу с помощью функции КОРРЕЛ со
следующими характеристиками:
КОРРЕЛ (массив I; массив 2),
где:
массив 1 = диапазон данных для первой переменной,
массив 2 = диапазон данных для второй переменной.
Например, на рисунке 20.3 показана функция КОРРЕЛ, используемая при
вычислении коэффициента корреляции для примера с экзаменационной оценкой.
РИС 20.3
Функция КОРРЕЛ
на примере
с экзаменационной
оценкой.
•
*Д.-
,;ft ■"
1
Часы
4
S
А
|
Оцанкз |
86
93
«5
€9
аг
>сн
iLiia
303
Ячейка А1 содержит формулу =КОРРЕЛ (А2:А7; В2:В7) с результатом
0.862.
Линейная регрессия
Метод линейной регрессии позволяет нам описывать прямую линию,
максимально соответствующую ряду упорядоченных пар (х,у).
Уравнение для прямой линии, известное как линейное уравнение, представлено
ниже:
у = а+Ьх,
где:
Термины
у ~ ожидаемое значение у при
заданном значении х,
х = независимая переменная,
а = отрезок на оси у для прямой
линии,
Ь = наклон прямой линии.
На рисунке 20.4 это понятие представлено графически.
Метод линейной регрессии
позволяет нам описывать
прямую линию, максимально
соответствующую ряду упорядоченных пар
(х,У).
у=2 + 0.5х
Рис 20.4
Уравнение для прямой
линии.
. подъем линии .1 п с
£>= = —= и.5
длиналинии 2
На рисунке выше показана линия, описанная уравнением у=2+0.5х.
Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2.
Наклон линии, Ь, отношение подъема линии к длине линии, имеет значение
0.5. Положительный наклон означает, что линия поднимается слева направо.
Если Ь = 0, линия горизонтальна, а это значит, что между зависимой и
независимой переменными нет никакой связи. Иными словами, изменение
значения х не влияет на значение у.
Студенты часто путают у и у. На рисунке 20.5 показаны 6
упорядоченных пар точек и линия, в соответствии с данным уравнением
у=2+0.5х.
504 Часть 4: Углубленное изучение статистики вывода
Рис 20.5
Различие между
у и у.
у+О.Ьх
На этом рисунке показана точка, соответствующая упорядоченной паре
х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии
с линией при х = 2 является у. Мы можем подтвердить это с помощью
следующего уравнения:
у=2+0.5х=2+0.5(2)=3.
Значение у представляет собой фактическую точку, а значение у — это
ожидаемое значение у с использованием линейного уравнения при заданном
значении х.
Следующий шаг — определить линейное уравнение, максимально
соответствующее набору упорядоченных пар.
Метод наименьших квадратов
Метод наименьших квадратов — это математическая процедура
составления линейного уравнения, максимально соответствующего набору
упорядоченных пар, путем нахождения значений для а и Ь, коэффициентов в
уравнении прямой. Цель метода
наименьших квадратов состоит в миними-
Термины , зации общей квадратичной ошибки
между значениями у и у. Если для
каждой точки мы определяем ошибку у,
метод наименьших квадратов
минимизирует:
Метод наименьших
квадратов - это математическая
процедура составления линейного
уравнения, максимально
соответствующего набору упорядоченных пар, путем
нахождения значений для а и Ь,
коэффициентов в уравнении прямой.
Цель метода наименьших квадратов
состоит в минимизации общей
квадратичной ошибки между значениями у и
у. Линия регрессии - это линия,
максимально соответствующая данным.
t(y.-r,t
где п ■= число упорядоченных пар
вокруг линии, максимально
соответствующей данным.
Это понятие проиллюстрировано на
рисунке 20.6.
Глава 20: Корреляция и линейная регрессия 305
6-
5"
4-
з-
2-
1-
0-
—1—1—hH—I—t-
Уз "Уз
■У4-У/
Рпс20.б
Минимизация ошибки.
0 12 3 4 5 6
х
Судя по рисунку 20.6, линия, максимально соответствующая данным,
линия регрессии, минимизирует общую квадратичную ошибку четырех точек
на графике. Я покажу вам, как определять это уравнение регрессии с
помощью метода наименьших квадратов на следующем примере.
В последнее время в ванной комнате нашего дома разгорелась нешуточная
молчаливая война, о которой я хочу вам поведать. Конечно же речь идет о
месте на длинном столе в ванной, который Деб и я по неписанному соглашению
должны быть «использовать совместно». За последние несколько месяцев я
внимательно следил за тем, с какой скоростью увеличивается число
предметов на ее части стола, увеличивается куда быстрей, чем растет дефицит
федерального бюджета. Меня потихоньку вытесняют с моей части стола емкости
с загадочными названиями вроде «мусс для укладки, увеличивающий
объемность волос» или «соевый комплекс». Конечно, я мог бы просто вскинуть на
плечо свое белое полотенце и гордо направиться в ванную детей, комнату, в
которую я поклялся не входить, потому что... ну, от описания царящего там
беспорядка я вас, так уж и быть, избавлю.
Как бы то ни было, в таблице ниже представлено число предметов Деб на
столике в ванной, накопившихся за последние несколько месяцев.
Данные о содержимом столика в ванной
Месяц Число предметов
Месяц
Число предметов
1
2
3
4
5
8
6
10
6
10
6
7
8
9
10
13
9
11
15
17
Поскольку своей целью я определил задачу узнать, увеличивается ли со
временем число предметов, «Месяц» будет независимой переменной, а
«Число предметов» — зависимой.
306 Часть 4: Углубленное изучение статистики вывода
С помощью метода наименьших квадратов определяем уравнение,
максимально соответствующее данным, путем вычисления значений а, отрезка на
оси у, и Ь, наклона линии:
а = у~Ьх,
где:
х = среднее значение х, независимой переменной,
у = среднее значение у, зависимой переменной.
В таблице ниже суммированы необходимые для этих уравнений
вычисления.
Вычисления отрезка на оси у и наклона линии
Месяц
X
1
2
3
4
5
6
7
8
9
10
2>
X-
Ь =
-55
_55_
~10~
_i£
5.5
ху-
У
8
6
10
6
10
13
9
И
15
17
2>=
- 105
£»G»
Число
105
=10.5
предметов
ху
8
12
30
24
50
78
63
88
135
170
Z*y=
= 658
10(658)-(55) (105)
х2
1
4
9
16
25
36
49
64
81
100
]Гх2=385
у2
84
36
100
36
100
169
81
' 121
225
289
1>2=1221
п1>2-(2»2 Ю(385)-(55)2
Глава 20: Корреляция и линейная регресспя^ 507
Ь=^ = 0.976
825
а = у -Ьх=10.5 -(0.976)5.5 =5.13.
Кривая эффекта для нашего примера с ванной будет определяться
следующим уравнением:
у=5.13 +0.976 х
Поскольку наше уравнение имеет положительный наклон — 0.976, я имею
доказательства того, что число предметов на столике со временем
увеличивается со средней скоростью 1 предмет в месяц. На рисунке 20.7 представлена
кривая эффекта с упорядоченными парами.
Рис 20.7
Кривая эффекта
для примера
со столиком
в ванной.
у=5.13 + 0.97В-
Мое ожидание в отношении числа предметов в течение следующего
полугода (месяца 16) будет вычисляться так:
у = 5.13+0.976х=5.13-Ю.976(16) =20.7 -21предмет.
Так что, детки, расчищайте место для любимого папы!
Доверительный интервал кривой эффекта
Насколько точны мои ожидания в отношении числа предметов на столике в
ванной на определенный месяц? Чтобы ответить на этот вопрос, нам
необходимо определить оценку стандартной ошибки se с помощью следующей
формулы:
s =
п-2
Оценка стандартной ошибки определяет объем разброса наблюдаемых
данных вокруг кривой эффекта. Если точки на графике расположены близ-
508 Часть 4; Углубленное изучение статистки вывода
ко к кривой эффекта, оценка стандартной ошибки будет сравнительно
низкой и наоборот. Для нашего примера с ванной:
_ \Ъу2-(1Ъу-'ЬЪхУ _ /(1221)-5.13(105) -0.976(658)"
л-2
-I
10-2
-J¥-**
Теперь мы можем вычислить доверительный интервал (Глава 14) среднего
у вокруг определенного значения х. В Месяце 8 (х = 8) у Деб на столике
находится И предметов (у = 11). Из линии регрессии ожидаем, что:
у=5.13+0.976х=5.13 +0.976(8) =12.9 предмета.
. В целом, доверительный интервал вокруг среднего у при определенном
значении х находится по формуле:
Термины
Стандартная ошибка оценки,
Se, измеряет объем разброса
наблюдаемых данных вокруг кривой
эффекта.
CI = y±tcse |- +
(х-х)2
Ъ*Уа*1'
где:
tc = критический ^-критерий из £-рас-
пределения Стьюдента,
se = стандартная ошибка среднего,
п = число упорядоченных пар.
Сейчас мы применим это уравнение к нашему примеру. Положим, мы
хотим получить 95%-ный доверительный интервал для среднего у Месяца 8. Для
определения критического f-критерия мы открываем Таблицу 4 Приложения
В. В нашем случае л — 2= 10 — 2 = 8 степеней свободы, то есть tc = 2.306 из
Таблицы 4 Приложения В. Тогда наш доверительный интервал:
CI = y±tcse 1+-
(x-xf
G>2)-
О»
п
С7 = 12.9±(2.306)(2.24) I—+ (8 5>5) ?
110 ,оос, (Hf_
10
(385)-^
CI = 12.9 ± (2.306) (2.24) (0.419) = 12.9 ± 2.16
CI = 10.74 и 15.06.
Глава 20: Корреляция п линейная регрессия 309
Этот интервал графически представлен на рисунке 20.8.
20 +
Рис 20.8
95 % -ный доверительный
интервал прих = 8.
Наш 95%-ный доверительный интервал для числа предметов на столике в
ванной в Месяце 8 находится между 10.74 и 15.06 предмета. Похоже, мне на
этот столике места точно не хватит.
Проверка наклона линий регрессии
Вспомним, что если наклон кривой эффекта, Ь. равняется нулю, между
переменными х и у нет никакой взаимосвязи. В нашем примере с ванной мы
вычислили, что наклон кривой эффекта равен 0.976. Но поскольку этот
результат основан на выборке наблюдений, нам необходимо проверить,
действительно ли 0.976 находится довольно далеко от нуля, чтобы
подтвердить, что между двумя переменными действительно существует
связь. Если это наклон фактической совокупности, тогда формулируем
гипотезы так:
Н0ф = 0
J4V.P *0.
Если мы отклоним основную гипотезу, то сможем сделать заключение, что
на основе этой выборки между зависимой и независимой переменными
действительно существует связь. Проверим это при а = 0.01.
Проверка этой гипотезы потребует определить стандартную ошибку
наклона, sb, которая вычисляется так:
VI?1
— 2
пх
где se — стандартная ошибка оценки, которую мы вычислили ранее.
Для нашего примера с ванной:
510 Часть 4: Углубленное изучение статистки вывода
Внимание!
2.24
Наличие статистически
значимой связи между двумя переменными
еще не означает существования
причинной связи между ними. Такая
математическая связь может быть результатом
чистого совпадения. Поэтому при
принятии подобных решений потребуется
ваш здравый смысл и трезвый расчет.
sh=-
2.24
пх
у]385-Щ5.5)2
=0.247.
Критерий значимости для данной
гипотезы будет рассчитываться так:
где рНо — это значение наклона по совокупности в соответствии с основной
гипотезой.
Для нашего примера вычисленный ^-критерий будет такой:
,Ь-Рн0 _0.976-0
t~
0.247
=3.951.
Критический г-критерий получим из {-распределения Стьюдента при
л — 2=10 — 2 = 8 степенях свободы. При двусторонней проверке а =0.10
tc = 3.355 в соответствии с Таблицей 4 Приложения В. Поскольку t > tc, мы
отклоняем основную гипотезу и заключаем, что между месяцем и числом
предметов на столике действительно существует связь. Я так и думал!
Коэффициент смешанной корреляции
Еще один способ измерения силы связи носит название коэффициента
смешанной корреляции, г2. Это процент вариации у, выраженный линией
регрессии. Это значение вычисляется простым возведением г, коэффициента
корреляции, в квадрат. Для нашего примера с ванной коэффициент корреляции
определяется следующим образом:
г-
^1*Ч2>)2][<>2У-(!>?]
г =
г=
Щ658)-(55)(105)
^[l0(385) -(55)2][l0(1221) -(105)2 ]
805
^/(825) (1185)
=0.814.
Глава 20: Корреляция и линейная регрессия 511
Тогда получаем коэффициент
смешанной корреляции:
г2 = (0.814)2 =0.663.
Термины
Коэффициент смешанной
корреляции, г2, - это доля
вариации у, отраженная в линии
регрессии.
Иными словами, 66.3% вариации в числе предметов на столике
объясняется переменной Месяца. Если г2 = 1, вся вариация у объясняется переменной
х. Если г2 = 0Г переменная х вообще не объясняет вариаций у.
Использование Excel для определения линейной регрессии
А теперь, когда наши калькуляторы уже погорели на всех этих мудреных
вычислениях, я покажу вам, как проделать все это с помощью программы
Excel.
1. Введите данные нашего примера с ванной в столбцы А и В чистого
листа.
2. Откройте меню Tools (Сервис) и щелкните Data Analysis (Анализ
данных). (Если эта опция отсутствует в меню Tools (Сервис), обратитесь к
разделу «Установка средств анализа данных» в Главе 2.)
3. В появившемся окне Data Analysis (Анализ данных) выберите Regression
(Регрессия), как показано на рисунке 20.9, и щелкните ОК.
Рис 20.9
Выбор линейной
регрессии в Excel
4. Установите необходимые параметры регрессии в окне Regression
(Регрессия), как показано на рисунке 20.10.
512 Часть 4: Углубленное изучение статистки вывода
Рпс 20.10
Диалоговое окно
Regression (Регрессия).
(С
| i S
й
-•^/Ww
мшмшмшш
...
■
5. Щелкните ОК. На рисунке 20.11 показаны полученные результаты.
Рис 20.11
Финальные результаты
регрессионного анализа
в Excel.
шШЬфюж
&1Т
|ЦйддИЙЙЙ --
Gggmgf
ЕД|ДГШСИРИ»«8 «*»ак»
(*
5S
.&SS3£151S:
MB
£ 1
ХГ«у f:
5э^ш>: :
i
j Месяц
Эти результаты соответствуют тем, которые мы получили путем
самостоятельных вычислений в предыдущих разделах. Поскольку мы видим, что
уровень р-значимости для независимой переменной «Месяц» равен 0.00414, а это
меньше а = 0.01, мы можем отклонить основную гипотезу и сделать вывод, что
связь между переменными существует. Теперь-то Деб придется поверить мне!
Пример линейной регрессии с отрицательной корреляцией
В обоих примерах, приведенных в этой главе, речь шла о положительной
связи между х и у. Пример, который я сейчас приведу, венчает наши усилия по
определению линейной регрессии, но уже с отрицательной связью.
Совсем недавно у меня была возможность поспорить с моим сыном
Брайаном по поводу покупки его первого автомобиля на 16-летие. Брайан
конечно же мечтал о «Мерседесе» или «БМВ», а я думал о «Хонде» или «Тойоте».
Глава 20; Корреляциям линейная регрессия 313
После многочисленных «обсуждений» этого вопроса мы остановились на
автомобиле «Фольксваген Джетта» 1999 года. Но Брайан выдвинул два требования.
Ф Машина должна быть черного цвета.
Ф Машина должна иметь современный дизайн.
Очевидно, кому-то в «Фольксвагене» пришла в голову замечательная идея
слегка изменить дизайн «Джетты» прямо в процессе производства
автомобиля. Лично я никогда не заметил бы никакой разницы. Что касается Брайана, то
он категорически отказывался водить машину старого дизайна и отмел
добрую половину подержанных автомобилей. Но я не опускал рук и перерыл все
возможные варианты, вопрошая каждого продавца: «Это автомобиль нового
дизайна?» Вот оно, счастье быть родителем! Как бы то ни было, ниже
представлена таблица с пробегом в милях 8 автомобилей нового стиля с указанием
цен, названных продавцом. В оставшейся части этой главы будут
использоваться именно эти данные для иллюстрации методик корреляции и регрессии.
Данные для примера с автомобилем
Пробег
21800
34 000
41700
53 500
Цена
$16 000
$11500
$13 400
$14 800
Пробег
65 800
72 100
76 500
84 700
Цена
$10 500
$12 300
$8 200
$9 500
В таблице ниже вы найдете данные (в тысячах), необходимые нам для
осуществления различных вычислений.
Пробег
X
21.8
34.0
41.7
53.5
65.8
72.1
76.5
84.7
£х = 450.
Цена
У
16.0
11.5
13.4
14.8
10.5
12.3
8.2
9.5
£у = 96.2
ху
348.80
391.00
558.78
791.80
690.90
886.83
627.30
804.65
£ху = 5100.1
х2
475.24
1 156.00
1 738.89
2 862.25
4 329.64
5 198.41
5 852.25
7 174.09
£х2 =28 786.8
у2
256.00
. 132.25
179.56
219.04
110.25
151.29
67.24
90.25
Y,y2 =1205.9
514 Насть 4: Углубленное изучение статистки вывода
- 450 гс-г
х= =56.3
8
~у=^=12.0.
Коэффициент корреляции определяется так:
n2>-Q>xXy)
|*Х*ЧХ*)]ИУ-(Ху)2]
8(5100.1)-(450.1) (96.2)
г =
г =
^[8(28 786.8) -(450)2][8(1205.9) -(96.2)2 ]
-2 498.82
^(27 794.4) (392.76)
= -0.756.
Отрицательная корреляция означает, что по мере увеличения пробега (х)
цена (у) падает, как и положено. Смешанный коэффициент корреляции равен:
г2 = (-0.756)2 = 0.572
То есть, примерно 57% вариации цены объясняется вариацией пробега.
Теперь определим кривую эффекта:
-Ь=
пХ^~(ХхХЕу)_3(5100.1)-(450.1)(96.2)
-249а82=-0.0902
8(28786.8)-(450.1)2
27704.39
а = у-Ьх = 12.025-(-0.0902)56.26 =17.100.
Линию регрессии можно описать следующим уравнением:
у = 17.1 -0.0902 х
Это уравнение графически представлено на рисунке 20.12.
Рис 20.12
Линия регрессии для
примера с машиной.
$20 000 т
>
ф
3
$15 000-
$10 000-
$5 000-
$0-
t^-^
♦
1 1
= 17.10-
♦
^"**5**
1
- 0.0902 х
1 1
20000 40000 60000 80000 100000
Пробег (х)
Глава 20: Корреляция и линейная регрессия 315
Какова ожидаемая цена автомобиля с пробегом 45 тысяч миль?
у = 17.1-0.0902(45.0) =13.041
Кривая эффекта предсказывает, что машина с таким пробегом будет
стоить 13 041 долларов. Каков будет доверительный интервал при х = 45 000?
Стандартная ошибка оценки вычисляется так:
4
_ ((1205.9) -17.1(96.2) -(-0.0902Н5100.1)
S'~J 8-2
g = 1(1205.9)-(1645.02) ч{450.03) _{Ш
Критический f-критерий для п — 2 = 8 — 2 = 6 степеней свободы, а 90%-
ный доверительный интервал равен tc = 1.973 из Таблицы 4 Приложения В.
Тогда наш доверительный интервал равен:
а-у±гл \U *-#-
0>')-2£
а = 13.041±(1.934)(1.867) \U (45 56-g|
«В (28786.8)-1—^~
С/=13.04±(1.934)(1.867)(0.402) = ±1.452
С1= 11.589 и 14.493.
90%-ный доверительный интервал для автомобиля с пробегом 45 000 миль
находится между 11 589 и 14 493 долларами.
Является ли связь между пробегом и ценой статистически значимой при
а— 0.10? Формулируем гипотезы:
Н0ф = 0
Н0:р* 0.
Стандартная ошибка наклона, sbl вычисляется так:
516 Часть 4: Углубленное изучение статистики вывода
se 1.867
sb= "£L =0.0317.
л/3465.3
Вычисленный критерий значимости для данной гипотезы равен:
^6^-0.0902-0^,.
sb 0.0317
Критический t-критерий получаем из t-распределения Стьюдента при
п — 2 = 8 — 2 = 6 степеней свободы. Для двусторонней проверки при
а = 0.10, tc = 1.943 в соответствии с Таблицей 4 Приложения В.
Поскольку \t\ > \tc\, мы отклоняем основную гипотезу и делаем вывод, что существует
связь между переменными пробега и цены. Мы используем абсолютные
значения, поскольку вычисленный f-критерий находится в левой части
^-распределения двусторонней проверки гипотезы.
Допущения для линейной регрессии
Чтобы все эти результаты были действительными, нам необходимо
убедиться, что не нарушаются допущения линейной регрессии.
Ф Индивидуальные различия между данными и кривой эффекта (у, — у(),
являются независимыми друг от друга.
Ф Наблюдаемые значения у являются нормально распределенными
вокруг ожидаемого значения, у.
Ф Вариация у вокруг кривой эффекта равняется всем значениям х.
К сожалению (или к счастью), методики для проверки этих допущений не
входят в рассмотрение этой книги.
Линейная и множественная регрессии
Линейная (простая) регрессия ограничивается рассмотрением связи между
зависимой переменной и только одной независимой переменной. Если в
связи присутствует более одной независимой переменной, тогда нам
необходимо обратиться к множественной регрессии. Уравнение для такой регрессии
выглядит так:
y = a+blxl+bzx2+- + bnxn.
Как вы понимаете, тут все очень сложно, и эта тема выходит за рамки этой
книги. Оставлю эту тему для «Статистика. Первые шаги. Часть 2». Ой-ой,
кажется, Деб упала в обморок.
Глава 20: Корреляция и линейная регрессия 317
Ваша очередь
1. В таблице ниже представлена оплата 10 команд Высшей бейсбольной
лиги (в миллионах) за 2002 год с указанием числа побед за этот год.
Оплата Победы Оплата Победы
$171
$108
$119
$43
$58
103
75
92
55
56
$56
$62
$43
$57
$75
62
84
78
73
67
Вычислите коэффициент корреляции. Проверьте, не равняется ли
коэффициент корреляции нулю при а = 0.05.
2. Используя данные из Задачи 1, ответьте на предлагаемые вопросы.
a) Какова кривая эффекта, максимально соответствующая данным?
b) Является ли связь между оплатой и победами статистически
значимой при а = 0.05?
c) Каково ожидаемое число побед при оплате 70 миллионов долларов?
d) Каков 90%-ный доверительный интервал вокруг среднего числа
побед при оплате 70 миллионов долларов?
e) Какой процент вариации побед объясняется оплатой?
Повторение - мать учения
Ф Независимая переменная (х) вызывает вариации зависимой переменной (у).
Ф Коэффициент корреляции, г, указывает на мощность и направление
связи между зависимой и независимой переменными.
Ф Линейная регрессия позволяет нам описывать прямую линию,*
максимально соответствующую набору упорядоченных пар (х,у).
Ф Метод наименьших квадратов — это математическая процедура для
определения линейного уравнения, максимально соответствующего
набору упорядоченных пар, путем нахождения значений а, отрезка на оси у,
и Ь, наклона прямой.
-Ф Стандартная ошибка оценки, se, измеряет объем разброса наблюдаемых
данных вокруг линии регрессии.
Ф Коэффициент смешанной корреляции, г2, представляет собой процент
вариации у, объясняемый кривой эффекта.
Ответы на вопросы
раздела «Ваша очередь»
Глава 1
1. Статистический вывод, поскольку опросить каждую ази-
атско-американскую семью в стране весьма
проблематично. Эти результаты будут основаны на выборке
совокупности и использованы для целой совокупности.
2. Статистический вывод, поскольку опросить каждую
семью в стране весьма проблематично. Эти результаты
будут основаны на выборке совокупности и использованы
для целой совокупности.
3. Описательная статистика, поскольку средняя бэттинг-ре-
зультативность Барри Бондза основывается на всей
совокупности, то есть на каждом ударе, сделанном за время его
карьеры.
4. Описательная статистика, поскольку средний результат за
экзамен основывается на целой совокупности, то есть
потоке студентов первого курса 2002 года.
5. Статистический вывод, поскольку опросить каждого
американца в стране весьма проблематично. Эти результаты
будут основаны на выборке совокупности и использованы
для целой совокупности.
Отеетш1а_вопросы раздела «Ваша очередь» 519
Глава 2
1. Интервальные данные, температура в градусах по Фаренгейту не
содержит истинной нулевой точки.
2. Относительные данные, месячное количество осадков в виде дождя
имеет истинную нулевую точку.
3. Порядковые данные, поскольку степень магистра выше степени
бакалавра или диплома об окончании средней школы. Тем не менее мы не
можем утверждать, что степень магистра в два или три раза
превышает остальные.
4. Номинальные данные, поскольку мы не можем расположить
категории в каком-либо порядке.
5. Относительные данные, поскольку возраст имеет истинную нулевую
точку.
6. Определенно номинальные данные, если, конечно, вы не готовы
вступить в спор о том, какой из полов меньше!
7. Интервальные данные, поскольку разница между годами имеет
смысловую нагрузку, но не имеет истинной нулевой точки.
8. Номинальные данные, так как я не готов утверждать, что одна
политическая партия стоит выше другой.
9. Номинальные данные, поскольку это просто неупорядоченные категории.
10. Порядковые данные, поскольку мы можем указать, что «Превосходит
ожидания» находится выше по шкале производительности, чем 2
остальных высказывания, но не можем прокомментировать разницу
между этими категориями.
11. Номинальные данные, поскольку мы не можем заявлять, что человек,
который носит 10-й размер, чем-то лучше того, кто носит 4-й размер.
12. Порядковые данные, поскольку мы не можем определить разницу в
производительности студентов. Два студента, стоящих на высшей ступени,
могут иметь сильно отличные оценки, а результаты работы студентов,
стоящих на второй и третьей ступенях, могут быть весьма схожи.
13. Относительные данные, поскольку эти экзаменационные результаты
имеют истинную нулевую точку.
14. Номинальные данные, поскольку не существует порядка в категориях
штатов.
Глава 3
1.
Экзаменационная оценка Число студентов
56-60 2
61-65 1
66-70 2
520 Приложение А
Экзаменационная оценка
Число студентов
71-75
76-80
81-85
86-90
91-95
96-100
6
3
8
5
3
6
56-60 61-65 66-70
к Г
71-75 76-80
Гистограмма для
экзаменац ионных
оценок.
86-90 91-95 96-100
Экзаменационная оценка
3.
Экзам. оценка Число студентов Процент Совок, процент
56-60
61-65
66-70
71-75
76-80
81-85
86-90
91-95
96-100
2
1
2
6
3
8
5
3
6
Всего = 36
2/36 = .06
1/36 = .03
2/36 = .06
6/36 = .17
3/36 = .08
8/36 = .22
5/36 = .14
3/36 = .08
6/36 = .16
.06
.09
.15
.32
.40
.62
.76
.84
1.00
Ответы на_воп^у^зз^ла_!<Ваша очередь» 321
Круговая диаграмма
для примера
с экзаменационной
оценкой.
17%
Ш 56-60 1
О 61-65
1*66-70
| Ш 71-75
■ 76-80
I #81-85
! Ш 86-90
] «91-95 !
| * 96-100 |
21%
5.
Древовидное
представление
для примера
с экзаменационной
оценкой.
6.
Древовидное
представление
для Задачи 6.
5
6
7
8
9
88999
0268
222455899
1123455566689
125688999
Древовидное представление
для Задачи 5
5(5)
6(0)
6(5)
7(0)
7(5)
8(0)
8(5)
9(0)
9(5)
8
02
66
2224
55899
11234
55566689
12
5688999
Древовидное представление
А>
\я
Задачи 6
Глава 4
1. Среднее = 15.9, медиана = 17, мода = 24.
2. Среднее = 81.7, медиана = 82, мода = 82.
3. Среднее = 32.7, медиана = 32.5, мода = 36. .
4. Среднее = 7.2, медиана = 6, мода = 6.
322 Приложение Л
5 -_ (22х8}+(27х37) +(32 х25) +(37 х48) +(42 х27) +(47 хЮ)
8+37+25+48+27+10
года.
6 -=(3х118)+(2х125)+(1х107)=11£5
3+2+1
„ - (5х1)+(7х2)+(10x3)+(8x4)+ (12x5)+ (3x6) ос
7. х=- — — — — —- =3.5 года службы.
5+7+10+8+12+3 У
Глава 5
L
х4 х2
20
15
24
10
8
19
24
400
225
576
100
64
361
576
|>,=120 |>?=2302
I*
\2
= (120)2 =14400
&
Т*?-—
С2=-!У_
2 302-i44^-
л 7
п-1
s = V408=6.4
Размах = 24 - 8 = 16.
=40.8
Xi
84 7 056
82 6 724
90 8 100
Ответы на вопросы раздела «Ваша очередь» 323
Xi
77
75
77
82
86
82
5 929
5 625
5 929
6 724
7 396
6 724
2>,=735
£x*=60 207
]Гх,. = (735)2 =540 225
N
_2 ,=1
С) —
1
a = >/202=^
Размах = 7
/л/ у
^ 60207-^^
N 9
V 9
1.5
5 - 50 = 25.
=20.2
3. Размах = 25, дисперсия = 75.4, стандартное отклонение = 8.7
4.2 5 6 6 6 8 10 11 11 15
Ох = 5,5 02 = 7 03 = 11
Обратите внимание, что медиана набора данных подчеркнута.
£к**)
__fcJ (8x22)+(37x27) +(25x32) +(48x37) + (27 х42) +(10 х47)
lA
8+37 + 25+48+27+10
Xi
(Xj-X)
(Xi-X)2
(x4-x)2ft
22
27
32
8
37
25
34.5
34.5
34.5
-12.5
-7.5
-2.5
156.25
56.25
6.25
1 250.00
2 081.25
156.25
324 Приложение Л
Xj fj X (Xj-X) (Xj-X)2 (Xi-X)2fj
37 48 34.5 2.5 6.25 300.00
42 27 34.5 7.5 56.25 1518.75
47 10 34.5 12.5 156.25 1562.50
n = ^=155 ]Г(х,.-х)2( =6 868.75
л-1 V 155-1
Y(f.xx)
~_ ы * _(5xl)+(7x2)+(10x3)+(8x4)+(12x5)+(3x6) =35
yf " 5+7 + 10+8+12+3
Xj fi X (Xj-X) (Xj-X)2 (Xi-X)2fi
1
2
3
4
5
6
Л1
i=i
5
7
10
8
12
3
= 45
3.5
3.5
3.5
3.5
3.5
3.5
-2.5
-1.5
-0.5
0.5
1.5
2.5
zfr-
i=l
-3<
6.25
2.25
0.25
0.25
2.25
6.25
= 97.25
31.25
15.75
2.50
2.00
27.00
18.75
m-*i
M*'-*M /9725 .
= A -M = ,p^ =>/Z21 =1.49 года.
V л-l V45-1
7. С помощью эмпирического правила определяем, что 95% значений
попадают в пределы к = 2 стандартных отклонений от среднего.
ц = /со- = 75 + 2(10) =95, ц = ка = 75 - 2(10) = 55
Таким образом, 95% значений данных попадают в интервал от 55 до 95.
Ответы на вопросы раздела «Ваша очередь» 325
8. Значения 38 и 62 являются 2 стандартными отклонениями от среднего
50. Это можно выразить в виде следующих уравнений:
ц + key = 762, ц + ко = 38
А=62-ц = 62-50=2Д * = _(38VL -f3^Uo.
С помощью теоремы Чебышева определяем, что по крайней мере
fl~lxl00% = fl-4-l><100%=75%
значений данных попадают в интервал от 38 до 62.
Глава 6
1а. Эмпирическая, поскольку мы имеем дело с историческими данными о
спортивных достижениях Самми Coca.
lb. Классическая, поскольку нам известно число карт и тузов в колоде.
1с. Если у меня есть данные о результатах последних раундов игры в
гольф, тогда эмпирическая; в противном случае — субъективная.
Id. Классическая, поскольку мы можем вычислить вероятность на основе
правил розыгрыша лотереи.
1е. Субъективная, поскольку я не буду собирать данные для этого
эксперимента.
If. Субъективная, поскольку я не буду собирать данные для этого
эксперимента.
2а. Да.
2Ь. Нет, вероятность не может быть больше 1.
2с. Нет, вероятность не может превышать 100%.
2d. Нет, вероятность не может быть меньше 1.
2е. Да.
2г.Да.
За. Р[А]= — = 0.42
L J 125
3b. P[Bl=—=0.33
L J 125
24
Зс. Р[АиВ]=Р[АпВ]= = 0.18
3d. Таблица ниже показывает общее число семей для объединения
Событий А и В.
326 Приложение А
Раса Интернет Число семей
Азиатско-американская
Азиатско-американская
Белая
Афроамериканская
Да
Нет
Да
Да
23
18
15
14
Всего = 70
70
Р[АИЛИВ]=Р[АиВ]=—-=0.56
Глава 7
177
1. РГА1= = 0.68
L J 260
2. Р[В]= —=0.58
L J 260
З.Р[А']=—=0.32
L J 260
4. P[B']=—=0.42
L J 260
198
5. P[A/B]= —= 0.64
6. P[A7B]= —= 0.36
7. P[A]= —= 0.42
L J 125
8. P[A]= —= 0.42
L J 125
9. P[A]= —= 0.42
L J 125
52
10.P[A]= = 0.42
L J 125
n Р[АилиВ']=Р[А]+Р[В']-Р[АИВ]=0.68+0.42 -0.31 =0.79
Ответы на вопросы раздела «Ваша очередь» 327
12. РГВ/АЬ р[в]-р[а/в]
L J (Р[В]Р[А/В])+(Р[В']Р[А/В'])
(05В)(0-64) = 0-37 =0 м
L J (0.58).(0.64) +(0.42). (0.73) 0.37+0.31
Глава 8
1.3 8 4 3 = 288 различных приемов пищи.
2. Существует 4444444444=1 048 576 различных способов
представить ответ на экзамене. Если хоть одна из этих последовательностей
является правильной, существует вероятность, равная 1/1048576 =
0.00000095, что студент угадает правильную последовательность.
3. 13! = 6 227 020 800 различных способов упорядоченных расположений
имен игроков.
4. 8Р3= 8! ч =8-7-6=336
8 3 (8-3)!
10!
10 2 (10-2)!
6. 40Р3=7-^-г = 40-3938=59280
40 3 (40-3)!
12 3 (12-3)!3! 3-2 1
8- .0,- 5°! =50-49-48-47.46.45.44.43.42.41-40.39 =121399651100
50^2 (50-12)!12! 12 -11 • 10 -9 -8 -7 -6 5 -4 -3 2 1
Число кошек Число семей Вероятность х2 х?-Р[х,.]
0
1
2
3
4
Всего
137
160
112
31 .
10
137/450 = 0.304
160/450 = 0.356
112/450 = 0t249
31/450 = 0.069
10/450 = 0.022
0
1
4
9
16
0
0.356
0.996
0.621
0.352
Jx2P[xI]=2.325
528 Приложение А
ц=£*,-р[*,1 = (°х °-304) +(1x0.356) +(2x0.249) -КЗ х 0.069) +(4 х 0.0 22) =1.149
а2=[£хгР[х,]]-^ =2.325 -(1.149)2 =1.005
a = VoJ = Vl.005 =1.002
Глава 9
1. Поскольку л = 10, г = 7, р = 0.5
Р[7,10]= Ш! .0.57-0.510-7 =10'9'8'7'6<5'4(0.0078)(0.125) =0.117.
(10-7)!7! 7654-3.2-1
Здесь также может быть использована биноминальная таблица из
Приложения В.
2. Поскольку л = 6, г = 3, р = 0.75
Р[3,6]=— 0.7530.256"3 =6'5'4(0-4219)(0.0156) =0.1316.
1 J (6-3)!3! 3-2 1
3. Вероятность удачного совершения 6 из следующих 8 штрафных бросков
составляет Р[6,8] + Р[7,8] + Р[8,8], поскольку л = 8, р = 0.8
Р[6,8]=—?! 0.86-0.28-* =^{0.2621) (0.04) =0.2936.
(8-6)!6! 21
Р[7Г8]=—- 0.87-0.28-7 =(8) (0.2097) (0.2) =0.3355.
Р[8,8]=—^—-0.88-0.28"8 =(1)(0.1678)(1) =0.1678.
(8—8)!8!
Таким образом, вероятность совершения 6 из 8 штрафных бросков
составляет 0.2936 + 0.3355 4- 0.1678 = 0.7969.
4. Поскольку п = 12, г = 6, р = 0.2
io| 19 11 10 Q Я 7
Р[6,12]= = 0.26-0.812^ = (0.000064)(0.2621) =0.0155.
(12-6)!6! 65-4-3-2 4
5. Вероятность того, что не более 2 из 7 посетителей магазина что-то
приобретут, рассчитывается так: Р[0,7] + Р[1,7] + Р[2,7]. Поскольку л = 7, р = 0.05
Р[0,7]=— 0.05° -0.957"0 =(1)(1)(0.04) =0.6983
-QlgglbLHgjfonpocbi раздела_«Ваша очередь» 329
Р11,71=]7^)Ш 005' ■(Ш74 =(7)(0.05)(0.7351) =0.2573
Р[2'7] = (7^)!2! °°52'°-957""2 =Ц(0.0025)(0.7738) =0.0406.
Таким образом, вероятность того, что не более 2 из 7 посетителей
магазина что-либо приобретут, равняется 0.6983 + 0.2573 + 0.0406 = 0,9962.
6. Поскольку п = 5, р = 0.37
Р[0,5]= Д[о[-0.37°-0.63" =(1)(1)(0.0992) =0.0992
41-5] = ^^ 0.37' 0.6354 =(5)(0.37)(0.1575) =0.2914
Р12.5] = ^^у0.3720.635-2 4Ц1(0.1369)(0.2500) =0.3423
Р[3,5]= - 0.373 0.63" =
1 (5-3)!3!
f5-4-3\ft
(О-1
0507)(0.3969) =0.2010
Р[4,5]= 0.37" 0.63м =(5)(0.0187)(0.63) =0.0590
Р[5,5]=— 0.375 0.635"5 =(1)(0.0069)(1) =0.0069.
Р[гг51
0
1
2
3
4
5
Глава 10
1 РГ41 =
(64)(2.71838
0.0992
0.2914
0.3423
0.2010
0.0590
0.0069
Всего = 1.0
^)(1296)(.002479)
4! 24
330 Приложение А
(7.55)(2.7183875) J23 730.469) (0.0005531) =Q ^
2- М 5! 120
3. Р[х>2]=1-Р[х<2]=1-(Р[х=0]+Р[х=1]+Р1х=2])
(4.2°)(2.71838-42) (1)(.0150) =
11 О! 1
(4.2')(2.71838-42) J4.2)(.015Q)
1 1! 1
(4.22)(2.71838-42) =(17.64)(0-0150) =0 1323
2! 2
Р[х>2]=1-(0.0150+0.0630 +0.1323) =0.7897
4. Р[х<3] = (Р[х=0]+Р[х=1]+Р[х=2]+Р[х=3])
(3.6°)(2.71838-аб) =(1)(.027324) =()0273
О! 1
(3.6')(2.71838-36) (3.6)(0.027324)
И 1! 1
р (3.62)(2.71838-36) =(12.96)(0.027324)
2! 2
(3.63)(2.71838-36) J46.656)(0.027324)
1 3! 6
Р[х<3] =(0.0273+0.0984+0.1771+0.2125) =0.5152
(2.5')(2.71838-25) =(2.5)(0.082085)
5. N j, j
6 Р[х]=^ , л = 25, р = 0.05, пр = 1.25
х!
Jl.25f.e~™ =(1.5625)(0.286505)
2! 2
Ответынавстдхкыраздела<<Вашаочередь» _351
Глава 11
65.5-62.6 п_0 „,
la. zKS= — =+0.78, P[z>+o.781=l-P[z< + 0.78J = l-0.7834 = 0.2166
58.1-62.6 . 00 _,.
lb. *»i = — =-1.22, P[z>-1.22] =P[Z^+1.22] =0.8880
70-62.6 _. 61-62.6
lc. zw =——— =+2.0, z61 =——— =-0.43,
P[-0.43<z<+2.0] =P[x<+2.0] -P[zS-0.43],
P[-0.43 < z < +2.0] = 0.9772 - 0.3327 =0.6445
2a. zm = 19°~176 = +0.63, P[z<+0.63] =0.7349.
158—176
2b. zm = = -0.81, P[z<-0.81] =1 -P[ z<+0.81] =0.2098
168-176 „oc 150-176
P[-1.17<z<-0.36] = P[z<-0.36] -F[z<-IA7\
P[z<-0.36]=l-P[z<+0.36] =0.3599, P[z<- 1.17] = 1 -P[z<+ 1.17]=0.1218
P[-1.17<z<-0.36] =0.3599-0.1218 =0.2381
3a. z31 = 31~375 = -0.86, P[z>-0.86] = P[z<+0.86] =0.8038
7.6
47-T7 5
3b. z42 = = +0.59, P[z<+0.59] =0.7231
42 76
3,z„,*L|L5.+0.99. fc.«^. + 0a
7.6 7.6
P[ + 0.99 < z < + 0.33] = P[z < 4- 0.99] - Pfz< + 0.33] = 0.8381 -0.6289=0.2092
4. Для данной задачи n = 14, p = 0.5, и g = 0.5. Мы можем использовать
нормальное приближение, поскольку лр = nq = (14) (0.5) = 7.
Биноминальные вероятности из биноминальной таблицы следующие:
Р[г= 4, 5 или 6] = 0.0611 + 0.1222 + 0.1833 = 0.3666. Также и ц = пр -
532 Приложение А
= (14)(0.5) = 7 и o = Jnpq = ^(14) (0.5) (0.5) =1.871. Нормальное
распределение будет: Р[3.5 < х < 6.5].
6.5-7 ___ 3.5-7
zfi, = = -0.27, з., = = -1.87
65 1.871 ^5 1.871
P[-1.87<z<-0.27] = P[z<-0.27] -P[z<-1.87]
Р [z <-0.27] =1-P[z<+0.27] =0.3946, P[ z<-1.87] =1 -P[ z<+1.87] =0.0307
P[-1.87<z<-0.27] =0.3946 -0.0307 =0.3639
Глава 12
n 500
2. Если каждый сотрудник принадлежал к определенному отделу, для
опроса могли быть выбраны те отделы, представителям которых было бы
предложено принять участие в опросе. Другие ответы также возможны.
3. Если каждого сотрудника можно определить в класс менеджеров или
не-менеджеров, удостоверьтесь, что выборочная доля каждого типа
схожа с долей менеджеров и не-менеджеров в компании. Другие ответы
также возможны.
Глава 13
1а. а_ * ™ =2.58
х yfn л/15
lb. а-=-£=-=-¥1 = 1.36
* yfn Vl2
1с. CT-=-4=- = -iL = 1.57
* V^ х/20
2а. a_ = -iL=l£=2.5, z17 = 17~16 = +0.40, P[z<+0.40] =0.6554
* VH л/9 17 2.5 l
2b. z18=18~16 = +0.80, P [z >+0.80] =1-P[z<+0.80] =1-0.7881 =0.2119
14.5-16 л„л 16.5-16 л '
2c- ^145= Q<- = -0-60, z165 = =+0.20
Ответы на вопросьцзаздела «Вашарчередь» 535
P[z<+0.20] = 0.5793, P[z<-0.60]=l-P[z<+060] =0.2743
P[14.5<x<16.5] = P[-0.60<z<0.20] =0.5793-0.2743 =0.3050
За. ар=ШШ=ШШ =0.0306
р V л V 200
3b.op=JE-/^(1-0.42)
р V л V loo
зс. qp-JSErt jo-Peg-Мб) =0Ш79
р V п V 175
4а „ И-Р) /0-32(1-0.32) 0.30-0.32
°р =ГТ~ =V 160 =а0369' Zo30 =~0l3i9- =Ч)-54
P[z<-0.54]=l-P[z<+0.54] =0.2946
4b- zo3e =0^6~^:32=+108, P[z>+1.08J =1-P[z^ + 1.08] =1-0.8599 =0.1401
0.0369
0.29-0.32 _Qi 0.37-0.32 f _
4c. z02g = = -0.81, z037 = = +1.36
029 0.0369 037 0.0369
P[z< +1.36] =0.9131, P[z<-0.81] =1 -P[ z<+0.81] =0.2090
P[0.29<ps <0.37] =P[-0.81 <z<+l.36] =0.9131-0.2090 =0.7041
Глава 14
La-=-^L = -^t = 1.20, z=2.17
x yfn V40
Верхняя граница =x+zca- =31.3 +2.17(1.20) =33.90.
Нижняяграница =x~zca- =31.3 -2.17(1.20) =28.70.
Z _fzaV_f(2.33)(15)Y
■■(f)-P
5 ;
=48.9 «49
3. Это вопрос с подвохом! Размер выборки слишком мал, чтобы
представлять ненормально распределенную совокупность. Этот вопрос выходит
за рамки этой книги. Чтобы ответить на него, вам придется прибегнуть к
помощи статиста.
334 Приложение А
4. С помощью Excel мы можем вычислить х = 13.9 и s = 6.04.
a- = -^L =-^1 = 1.20, zc=2.17.
х л/л л/40
Верхняя граница =х+гса^- =13.9 +1.64(1.10) =15.70.
Нижняяграница =x-zcaA1- =13.9 -1.64(1.10) =12.10.
5. С помощью Excel мы можем вычислить х = 46.92.
a = 12.7, zc=1.88, и a- = -^L =Ц2, =3.67.
л/л \/12
Верхняя граница =x + zca-=46.92 +1.88(3.67) =53.82.
Нижняя граница = х- zca- =46.92 -1.88(3.67) = 40.02.
6. С помощью Excel мы можем вычислить х = 119.64 и 5 = 11.29.
5 11.29
a - =~7=г= .— =3.40
х л/К л/П
Для 98%-ного доверительного интервала при п —1 = 11 — 1 = 10
степенях свободы гс = 2.764.
Верхняя граница = х + tco\ =119.64 +2.764(3.40) = 129.04.
Нижняя граница = х- £саи- = 119.64 - 2.764(3.40) = i ю.24.
7. А это еще один вопрос с подвохом! Размер выборки слишком мал, чтобы
представлять ненормально распределенную совокупность. Этот вопрос
выходит за рамки этой книги. Чтобы ответить на него, вам придется
прибегнуть к помощи статиста.
8. ps=—=0.055.
s 200
Поскольку nps = (200) (0.055) = 11 nnqs = (200) (0.945) = 189, мы можем
использовать нормальное приближение.
Верхняя граница =ps +zcap =0.055 +1.96(0.0161) = 0.087.
Нижняяграница =р5- zcap =0.055-1.96(0.0161) = 0.023.
_Отеетьт^^
9. n = P?\jj =(0.55)(0.45)^j =650
Глава 15
1. Н0:ц = 1.7
Нх:\х* 1.7
о. <* 0.50 .л
л = 35, а = 0.5 чашек, ст- = -^ = -= = 0.0845 чашки, zc ±1.64
Верхняя граница = цНо + zcCT; =1.7 +(1.64) (0.0845) = 1.84 чашки.
Нижняя граница = цЯо - zcg- =1.7 - (1.64) (0.0845) = 1.56 чашки.
Поскольку х = 1.95 чашки, мы отклоняем основную гипотезу и делаем
вывод, что среднее по совокупности не равно 1.7 чашки в день.
2. Н0 : ц > 40
Hi:n<40 ^ 125
л = 50, о = 12.5 лет, ст- = -т= = ~г== = 1768 года,
л/л V50
zc = — 1.64 (левый хвост распределения)
Нижняя граница = juHo + zcg- =40 +(-1.64) (1.768) =37.1 года.
Поскольку х = 38.7 года, мы не отклоняем основную гипотезу и делаем
вывод, что у нас нет достаточных доказательств для подтверждения
заявления о том, что средний возраст составляет менее 40 лет.
3. Н0 : ц < 1000
Н> .41 > 1000 ^ з25
л = 32, ст = 325 часов, ст- = -^ь = —== = 57.45часа,
а/л л/32
zc = + 2.05 (правый хвост распределения)
Верхняя граница = \xHq + zcg- =1000 +(2.05)(57.45) =1117.8 часа.
Поскольку х = 1190 часов, мы отклоняем основную гипотезу и
заключаем, что средняя продолжительность службы лампочки превышает 1 000
часов.
4. Н0 : ц > 30
Ht:n<30 ^ 8()
л = 42, ст = 8.0 минут, ст- = -^ = -^^ = 1.23 минуты,
л/л v42
»36 Приложение Л
zc = —2.33 (левый хвост распределения)
Нижняя граница = [iHo + zcc- =30 +(-2.33) (1.23) =27.13 минуты.
Поскольку х = 26.9 минуты, мы отклоняем основную гипотезу и
заключаем, что среднее время доставки составляет менее получаса.
Глава 16
1. H0:[i = 1100
Нх : ц*1100
Л = 70, а = 310, а- =-^==Щ2= =37.05, zc =±1.64,
х 4п л/70
_*-Ц„о ^1035-1100, 1?5
а- 37.05
X
Уровень р-значимости = (2)(P[z< - 1.75]) = (2)(1 - P[z < + 1.75]) =
(2)(1 - 0.9599) = 0.0802.
Поскольку уровень р-значимости = а, мы отклоняем основную
гипотезу и делаем вывод, что средний результат экзамена не равняется
1 100.
2. Н0 : \i < 35
Нх : ц > 35
- s 6 74
x = 37.9,s = 6.74„n=10,d/. =л-1 =9, о; = -==-^==2.13, L =±2.821,
л/л VIO
( = ^4=37;9Z35= + 136
Ox 2.13
Поскольку t < tc, мы не отклоняем основную гипотезу и делаем вывод,
что средний размер класса равняется 35 студентов.
3. Н0 : ц < 7
Нх : и > 7
- s 4 29
x = 8.2,s = 4.29,n = 10,d/. =л-1 =9, о* =-£= =-=^£ =0.78, zr =+1.64
Vn л/30
х-Д„ 8.2-7
z = . ° =^^-1=+1.54
Ох 0.78
Уровень р-значимости = P[z > + 1.54] = 1 — P[z < + 1.54] = 1 —
0.9382 = 0.0618.
Ответы на вопросы раздела «Ваша очередь» 337
Поскольку z<zc или уровень р-значимости, мы не отклоняем основную
гипотезу и делаем вывод, что средний расход топлива в США не
превышает 7 литров на машину в день.
4. Н0 : р > 0.40
Нх:р< 0.40
Р„о0-Р*о) ЩШ-^0) z =Ь^ ^30^-0.40 =
р V п V 175 ар 0.037
Уровень р-значимости = P[z< - 2.70] = 1 - P[z< + 2.70] = 1 - 0.9965
= 0.0035, zc= - 2.33.
Поскольку уровень р-значимости а, мы отклоняем основную гипотезу
и делаем вывод, что доля республиканцев составляет менее 40%.
Глава 17
1. Н0:щ = |и2
ffj : jii ^ jli2, Пенсильвания = 1, Огайо = 2
CT.. = E5=«+(iiiL=24.22i Zr=±1.,
*'-*2 \щ щ V 45 38
(x,-I2)-(m-H2)Ho (552-530)-0
z = = = +и.У1
а- - 24.22
XI -XI
Поскольку z < zc, мы не отклоняем основную гипотезу и делаем вывод,
что у нас нет достаточных доказательств для подтверждения разницы
между 2 штатами.
Уровень р-значимости = (2)P[z> + 0.91] = (2)(1 - P[z< + 0.91]) = 2(1 -
0.8186) = 0.3628
2. Н0: ц, = jli2
Hj : щ * \х2, хг = 88.3, st = 7.30, х2 = 82.4, s2 = 6.74,
96
/(A-l^+K-l)^2 |(10)(7.30)2+(9)(674)Г ^лу1
S'=V „+л2-2 =V ПТТ^ = 704
I—+— = (7.04U—+— =(7.04)л/Ь.1909 = 3.08
^п, п2 VII 10
сг- - =sn
X] -Х2 Р
^(до-хгНц-й^ _ (88.3-82.4)-0 =
а". - 3.08
538 Приложение А
А/. = пг + л2 - 2 = 11 + 10 - 2 = 19, fc = ± 1.729
Поскольку t > tc, мы отклоняем основную гипотезу и заключаем, что
оценки удовлетворенности клиентов двумя магазинами разные.
3. Н0 : |nd < 15
Нх : ца < 15, £d = 21 +23+ 11 + 19+ 15 + 20+ 17 + 23+17= 166
Y,d2 = 441 +529+ 121+361+225 + 400 + 289 + 529 + 289 = 3 184
d = ^ = l^ = 18.44,
л 9
&^:_^£.ш„
* = ^^ = 18'^/5=—= +2.64» d/.=n-l=9-l=8, tc =+1.860
sd_ Ml 1.30
jn n/9
Поскольку t > tc, мы отклоняем основную гипотезу и делаем вывод, что
заявление о программе потери веса является действительным.
4. Н0 : Pj < р2
Н\ : Pi >Р2, Совокупность 1 = Флорида, Совокупность 2 = Нация
- х, 272 - *2 390 ц *i+x2 272+390 _„.
р, = — = = 0.68, р9 =—= =0.65, рц = = =0.662
л, 400 л2 600 Л!+Л2 400+600
0305
* V, =^-Р^~) =|0.662),1-0.662)^+4) =°
zJpl-p2)-(p,-ft)HoJ0.68-0.65)-0= +
о*- - 0.0305
Р\~Р2
Поскольку z < zc, мы не отклоняем основную гипотезу и делаем вывод,
что у нас нет достаточных доказательств для подтверждения заявление
о том, что доля владения квартирами во Флориде больше, чем по стране.
Уровень р-значимости = P[z> + 0.98] = 1 - P[z< + 0.98] = (1 - 0.8365) =
0.1635
Ответы на вопросы^аздела «Ваша очередь» 339
Глава 18
1.Я0:Пр
де,
Нх\ Процесс прибытия отличается от ожидаемого распределения.
1. Я0: Процесс прибытия можно описать с помощью ожидаемого
распределения.
Размер выборки = 215 покупателей
День Ожид. Размер
процент выборки
Пон.
Вт.
Ср.
Чт.
Пт.
Сб.
Всего
День
Пон.
Вт.
Ср.
Чт.
Пт.
Сб.
Всего
10%
10%
15%
15%
20%
30%
100%
О
31
18
36
23
47
60
Е
21.50
21.50
32.25
32.25
43.00
64.50
215
215
215
215
215
215
(О-Е)
9.50
- 3.50
3.75
- 9.25
4.00
- 4.50
Ожид.
частота (Е)
0.10(215) =
0.10(215) =
0.15(215) =
0.15(215) =
0.20(215) =
0.30(215) =
215
(О-Е)2
90.25
12.25
14.06
85.56
16.00
20.25
= 21.5
= 21.5
= 32.25
= 32.25
= 43
= 64.5
(O-Ef
Е
4.20
0.57
0.44
2.65
0.37
0.31
ха=£
Набл.
частота (О)
31
18
36
23
47
60
215
[- ^-=8.54
Е
При а = 0.05 и d.f. = к - 1 = 6 - 1 = 5, X2 = 12.592. Поскольку Х2С > X2
мы не отклоняем основную гипотезу и делаем вывод, что распределение
прибытия совпадает с ожидаемым распределением.
Н0: Процесс может быть описан с помощью распределения Пуассона
при X = 3.
Hi'. Процесс отличается от распределения Пуассона при X = 3.
Приложение А
Размер выборки = 380 заходов
Число Вер-ти Число Ожид.
посещений/мин Пуассона посещений частота
0
1
2
3
4
5
6
7 и более
Всего
0.0498
0.1494
0.2240
0.2240
0.1680
0.1008
0.0504
0.0336
1.0000
380 =
380 =
380 =
380 =
380 =
380 =
380 =
380 =
18.92
56.77
85.12
85.12
63.84
38.30
19.15
12.77
380.00
Посещений/мин
0
1
2
3
4
5
6
7 и более
Всего
О Е
22 18.92
51 56.77
72 85.12
92 85.12
60 63.84
44 38.30
25 19.15
14 12.77
(О - Е) (О - Е)2
3.08 9.46
-5.77 33.32
-13.12 172.13
6.88 47.33
-3.84 14.75
5.70 32.44
5.85 34.19
1.23 1.52
(O-Ef
Е
0.50
0.59
2.02
0.56
0.23
0.84
1.79
0.12
При а = 0.01 и d.f. = к - 1 = 8 - 1 = 7, X2 = 18.475. Поскольку X2 > X2
мы не отклоняем основную гипотезу и делаем вывод, что процесс
соответствует распределению Пуассона при X = 3.
3. Н0: Оценки не зависят от времени изучения.
Hi: Оценки зависят от времени изучения.
Вычисления ожидаемой частоты в выборке:
(265) (128)
(265И95)=5035
1,1 500
500
= 67.84 Ц,
(265) (155)
500
= 82.15.
Ответы на вопросы раздела «Ваша очередь» 341
Строка
2
2
2
2
2
3
3
3
3
3
Столбец
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
О
36
75
81
63
10
27
28
50
25
10
32
25
24
6
8
Е
50.35
67.84
82.15
49.82
14.84
26.60
35.84
43.40
26.32
7.84
18.05
24.32
29.45
17.86
5.32
Всего
(О-Е)
- 14.35
7.16
- 1.15
13.18
- 4.84
0.40
- 7.84
6.60
- 1.32
2.16
13.95
0.68
- 5.45
- 11.96
2.68
(О-Е)2
205.92
51.27
1.32
173.71
23.43
0.16
61.47
43.56
1.74
4.67
194.60
0.46
29.70
140.66
7.18
-Ef
—'- = 34.38
Е
(О-Е)2
Е
4.09
0.76
0.02
3.49
1.58
0.01
1.72
1.00
0.07
0.60
10.78
0.02
1.01
7.88
1.35
При а = 0.05 и d.f. = (г - 1)(с - 1)... = (3 - 1)(5 - 1) = 8,12с = 15.507.
Поскольку X2 > X2 мы отклоняем основную гипотезу и делаем вывод,
что между оценкой и временем изучения есть связь.
Глава 19
1. Я0: |л, = ца = |л3 *i = 22.12 х2 = 19.67 х3 = 18.94
Нх : не все jj, одинаковы. s\ = 0.98 s\ = 0.98 s2 = 0.98
N = 17 щ = 6 п2 = 6 п3 = 6
к
SSW = y£(ni -\)sf = (6- 1)0.98 + (6-1)1.45+(5- 1)2.36 = 21.59
/=i
= Ух 22.5+ 20.8+ 22.0 +23.6+...+ 18.0 + 21.1 + 19.8+ 18.6
х = ^~ = : =20.32
N 17
к /_ =ч2
SSB^nAXi -х) = 6(22.12-2-.32)2 + 6(19.67-20.32)2 + 5(18.94-20.32)2 = 31.50
SSB = 3L50 MW=^=^=1.54,
k-l 3-1 N-k 17-3
42 Приложение А
= MSB_ = 15J5 = = = =3 73д
MSW 1.54 a,*l,N* .05.2.14
Поскольку F > Fc, мы отклоняем основную гипотезу и делаем вывод, что
между выборочными средними есть разница.
(*а~хь) _ (22.12-19.67)2
2. Для хх и хъ F = -
SSW
Длях,их3, F =
/=i
(Xa-Xb^
1
|_n0
+
1
nbJ
21.59
5+5+4
1 1
- + -.
.6 6
= 11.70
(22.12-18.94)2
SSW
1 1
-+ -
Длях2их3, F =
(xa-Xb^
21.59
5+5+4
1 1
+ -.-
6 6
= 19.71
(19.67 -18.94)2
SSW
1 1
-• + -
ZK-i)i
Fsc=(b-№*-w-k =(3-l)(3.739) =7.478
21.59 Г1 ll
5+5+4|.6" + 6j
= 1.04
Выборочная пара
Заключение
Xl их2
X, их3
х2их3
11.70
19.71
1.04
7.478
7.478
7.478
Разница есть
Разница есть
Разницы нет
Мы заключаем, что существует разница между пробегом Машин 1 и 2, а
также Машин 1 и 3.
3. Н0: |д, = ц2 = Цз *i = 38.33 х2 = 28.29 х3 = 31.43
Я, : не все р, равны. s\ = 115.47 s\ = 72.57 s\ = 132.62
N = 17 щ = 6 п2 = 7 п3 = 7
SSW= (6 - 1)115.47 + (7 - 1)72.57 + (6 - 1)86.8 + (7 - 1)132.62 = 2242.49
: Ух 36 + 48+32+28+...+36+18+30+21 П4
= ***— = =31.;
N
26
38
Ответы на вопросы раздела «Ваша очередь» 343
SSB = 6(38.33 - 31.38)2 + 7(28.29 - 31.38)2 + 6(28 - 31.38)2 + 7(31.43 -
31.38)2 = 425.22
SSB 425.22 SSW 2242.49
MSB = ^ = = 141.74, MSW =^— = ******* =ioL93
F =
к-\ 4-1
MSB 141.74
MSW 101.93
: 1.391, F
N-k 26-4
F = F =3 049
raM-lN-k f053.22 ^.W*^
Поскольку F < Fc, мы не отклоняем основную гипотезу и делаем вывод,
что между выборочными средними нет разницы.
Глава 20
1.
Оплата
х
Победы
У
ху
х2
У2
171
108
119
43
58
56
62
43
57
75
2> = 745
103
75
92
55
56
62
84
78
73
67
2> = 792
17613
8100
10948
2365
3248
3472
5208
3354
4161
5025
]Гху = 63 494
29241
11664
14161
1849
3364
3136 .
3844
1849
3249
5625
£х2=77 982
10609
5625
8464
3025
3136
3844
7056
6084
5329
4489
£у2=57 661
- 792 - 745
х = = 79.2, у = = 74.5, г
10 ' 10
"I*y-g*XI»
г =
l^2-(^)2][nZf-(Ty1]
10(63,494) -(792) (745) 44,900
^/[10(77 982)-(792)2][l0(57 661) -<745)2 ] #52 556)(21 585)
=0.782
Н0 : р = 0
Нх : р ф 0
344 Приложение А
г О 7R9
t = . = , = 3.549, d/. = л-2 =10 -2 =8, *с =2.306
1-г2 1-(782)2
п-2 V Ю-2
Поскольку t > tc, мы отклоняем основную гипотезу и заключаем, что
коэффициент корреляции не равен нулю.
2а ь=л1^-(1хХХу)_10(63494)-(792)(745) _ 44900
nZ*2-(Zx)2 10(77 982)-(792)2 152556
а = у-Ьх= 74.5- (0.294)79.2 =51.21, у = 51.21+0.294х
2Ь. Н0 : Р = 0
Я, : Р * 0
= /Xy2-QZy-bZ^^ /с
/Zy2-QI>-bZ*y = /(57661)-51.21(745) -(0.294) (63"494f = ш 2б
10-2
sb=, ** = , 10Д6 =0.0831, f=^.0^ = 3.538
d./. = л — 2 = 10 — 2 = 8, fc = 2.306, поскольку £ > £С1 мы отклоняем
основную гипотезу и делаем вывод, что между оплатой и победами
существует связь.
2с. у = 51.21 +0.294* =51.21 +0.294(70) = 71.79
2d. CI = y±tcse I- + ^-^ =-
d.f. = п - 2 = 10 - 2 = Мс = 3.355
С/= 71.79 ±(3.355) (10.26) I— + (7° 792) 9
'10 (77982)-^2
10
С1 = 7179 ± (3.355) (10.26) (0.325) = 71.79 ± 11.19, (60.60, 82.98)
2е. г2 = (0.782)2 = 0.612 или 61.2%.
Приложени
Статистические таблицы
Источник: мистер Карл Шварц, www.staf.sfu.ca/~cschwarz.
Использовано с его разрешения.
Таблица 1 представляет вашему вниманию вероятность в
точности г успехов в п испытаниях для различных значений р.
Таблица 1
Биноминальное распределение вероятностей
Значения р
п т
2 0
1
2
3 0
1
2
3
4 0
1
2
3
4
0.1
0.8100
0.1800
0.0100
0.7290
0.2430
0.0270
0.0010
0.6561
0.2916
0.0486
0.0Q36
0.0001
0.2
0.6400
0.3200
0.0400
0.5120
0.3840
0.0960
0.0080
0.4096
0.4096
0.1536
0.0256
0.0016
0.3
0.4900
0.4200
0.0900
0.3430
0.4410
0.1890
0.0270
0.2401
0.4116
0.2646
0.0756
0.0081
0.4
0.3600
0.4800
0.1600
0.2160
0.4320
0.2880
0.0640
0.1296
0.3456
0.3456
0.1536
0.0256
0.5
0.2500
0.5000
0.2500
0.1250
0.3750
0.3750
0.1250
0.0625
0.2500
0.3750
0.2500
0.0625
0.6
0.1600
0.4800
0.3600
0.0640
6.2880
0.4320
0.2160
0.0256
0.1536
0.3456
0.3456
0.1296
0.7
0.0900
0.4200
0.4900
0.0270
0.1890
0.4410
0.3430
0.0081
0.0756
0.2646
0.4116
0.2401
0.8
0.0400
0.3200
0.6400
0.0080
0.0960
0.3840
0.5120
0.0016
0.0256
0.1536
0.4096
0.4096
0.9
0.0100
0.1800
0.8100
0.0010
0.0270
0.2430
0.7290
0.0001
0.0036
0.0486
0.2916
0.6561
346 Приложение В
Таблица 1
Биноминальное распределение вероятностей
(продолжение)
Значения р
п г
5 0
1
2
3
4
5
6 0
1
2
3
4
5
6
7 0
1
2
3
4
5
6
7
8 0
1
2
3
4
5
6
7
8
9 0
1
0.1
0.5905
0.3280
0.0729
0.0081
0.0005
0.0000
0.5314
0.3543
0.0984
0.0146
0.0012
0.0001
0.0000
0.4783
0.3720
0.1240
0.0230
0.0026
0.0002
0.0000
0.0000
0.4305
0.3826
0.1488
0.0331
0.0046
0.0004
0.0000
0.0000
0.0000
0.3874
0.3874
0.2
0.3277
0.4096
0.2048
0.0512
0.0064
0.0003
0.2621
0.3932
0.2458
0.0819
0.0154
0.0015
0.0001
0.2097
0.3670
0.2753
0.1147
0.0287
0.0043
0.0004
0.0000
0.1678
0.3355
0.2936
0.1468
0.0459
0.0092
0.0011
0.0001
0.0000
0.1342
0.3020
0.3
0.1681
0.3601
0.3087
0.1323
0.0283
0.0024
0.1176
0.3025
0.3241
0.1852
0.0595
0.0102
0.0007
0.0824
0.2471
0.3177
0.2269
0.0972
0.0250
0.0036
0.0002
0.0576
0.1977
0.2965
0.2541
0.1361
0.0467
0.0100
0.0012
0.0001
0.0404
0.1556
0.4
0.0778
0.2592
0.3456
0.2304
0.0768
0.0102
0.0467
0.1866
0.3110
0.2765
0.1382
0.0369
0.0041
0.0280
0.1306
0.2613
0.2903
0.1935
0.0774
0.0172
0.0016
0.0168
0.0896
0.2090
0.2787
0.2322
0.1239
0.0413
0.0079
0.0007
0.0101
0.0605
0.5
0.0313
0.1563
0.3125
0.3125
0.1563
0.0313
0.0156
0.0938
0.2344
0.3125
0.2344
0.0938
0.0156
0.0078
0.0547
0.1641
0.2734
0.2734
0.1641
0.0547
0.0078
0.0039
0.0313
0.1094
0.2188
0.2734
0.2188
0.1094
0.0313
0.0039
0.0020
0.0176
0.6
0.0102
0.0768
0.2304
0.3456
0.2592
0.0778
0.0041
0.0369
0.1382
0.2765
0.3110
0.1866
0.0467
0.0016
0.0172
0.0774
0.1935
0.2903
0.2613
0.1306
0.0280
0.0007
0.0079
0.0413
0.1239
0.2322
0.2787
0.2090
0.0896
0.0168
0.0003
0.0035
0.7
0.0024
0.0284
0.1323
0.3087
0.3601
0.1681
0.0007
0.0102
0.0595
0.1852
0.3241
0.3025
0.1176
0.0002
0.0036
0.0250
0.0972
0.2269
0.3177
0.2471
0.0824
0.0001
0.0012
0.0100
0.0467
0.1361
0.2541
0.2965
0.1977
0.0576
0.0000
0.0004
0.8
0.0003
0.0064
0.0512
0.2048
0.4096
0.3277
0.0001
0.0015
0.0154
0.0819
0.2458
0.3932
0.2621
0.0000
0.0004
0.0043
0.0287
0.1147
0.2753
0.3670
0.2097
0.0000
0.0001
0.0011
0.0092
0.0459
0.1468
0.2936
0.3355
0.1678
0.0000
0.0000
0.9
0.0000
0.0005
0.0081
0.0729
0.3281
0.5905
0.0000
0.0001
0.0012
0.0146
0.0984
0.3543
0.5314
0.0000
0.0000
0.0002
0.0026
0.0230
0.1240
0.3720
0.4783
0.0000
0.0000
0.0000
0.0004
0.0046
0.0331
0.1488
0.3826
0.4305
0.0000
0.0000
Статистические таблицы 547
Таблица 1
Биноминальное распределение вероятностей
(продолжение)
Значения р
п г
2
3
4
5
6
7
8
9
10 0
1
2
3
4
5
6
7
8
9
10
11 0
1
2
3
4
5
6
7
8
9
10
11
0.1
0.1722
0.0446
0.0074
0.0008
0.0001
0.0000
0.0000
0.0000
0.3487
0.3874
0.1937
0.0574
0.0112
0.0015
0.0001
0.0000
0.0000
0.0000
0.0000
0.3138
0.3835
0.2131
0.0710
0.0158
0.0025
0.0003
0.0000
0.0000
0.0000
0.0000
0.0000
0.2
0.3020
0.1762
0.0661
0.0165
0.0028
0.0003
0.0000
0.0000
0.1074
0.2684
0.3020
0.2013
0.0881
0.0264
0.0055
0.0008
0.0001
0.0000
0.0000
0.0859
0.2362
0.2953
0.2215
0.1107
0.0388
0.0097
0.0017
0.0002
0.0000
0.0000
0.0000
0.3
0.2668
0.2668
0.1715
0.0735
0.0210
0.0039
0.0004
0.0000
0.0282
0Л211
0.2335
0.2668
0.2001
0.1029
0.0368
0.0090
0.0014
0.0001
0.0000
0.0198
0.0932
0.1998
0.2568
0.2201
0.1321
0.0566
0.0173
0.0037
0.0005
0.0000
0.0000
0.4
0.1612
0.2508
0.2508
0.1672
0.0743
0.0212
0.0035
0.0003
0.0060
0.0403
0.1209
0.2150
0.2508
0.2007
0.1115
0.0425
0.0106
0.0016
0.0001
0.0036
0.0266
0.0887
0.1774
0.2365
0.2207
0.1471
0.0701
0.0234
0.0052
0.0007
0.0000
0.5
0.0703
0.1641
0.2461
0.2461
0.1641
0.0703
0.0176
0.0020
0.0010
0.0098
0.0439
0.1172
0.2051
0.2461
0.2051
0.1172
0.0439
0.0098
0.0010
0.0005
0.0054
0.0269
0.0806
0.1611
0.2256
0.2256
0.1611
0.0806
0.0269
0.0054
0.0005
0.6
0.0212
0.0743
0.1672
0.2508
0.2508
0.1612
0.0605
0.0101
0.0001
0.0016
0.0106
0.0425
0.1115
0.2007
0.2508
0.2150
0.1209
0.0403
0.0060
0.0000
0.0007
0.0052
0.0234
0.0701
0.1471
0.2207
0.2365
0.1774
0.0887
0.0266
0.0036
0.7
0.0039
0.0210
0.0735
0.1715
0.2668
0.2668
0.1556
0.0404
0.0000
0.0001
0.0014
0.0090
0.0368
0.1029
0.2001
6.2668
0.2335
0.1211
0.0282
0.0000
0.0000
0.0005
0.0037
0.0173
0.0566
0.1321
0.2201
0.2568
0.1998
0.0932
0.0198
0.8
0.0003
0.0028
0.0165
0.0661
0.1762
0.3020
0.3020
0.1342
0.0000
0.0000
0.0001
0.0008
0.0055
0.0264
0.0881
0.2013
0.3020
0.2684
0.1074
0.0000
0.0000
0.0000
0.0002
0.0017
0.0097
0.0388
0.1107
0.2215
0.2953
0.2362
0.0859
0.9
0.0000
0.0001
0.0008
0.0074
0.0446
0.1722
0.3874
0.3874
0.0000
0.0000
0.0000
0.0000
0.0001
0.0015
0.0112
0.0574
0.1937
0.3874
0.3487
0.0000
0.0000
•0.0000
0.0000
0.0000
0.0003
0.0025
0.0158
0.0710
0.2131
0.3835
0.3138
348 Приложение В
Таблица 1
Биноминальне распределение вероятностей
(продолжение)
Значения р
п г
12 0
1
2
3
4
5
6
7
8
9
10
11
12
13 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14 0
1
2
3
0.1
0.2824
0.3766
0.2301
0.0852
0.0213
0.0038
0.0005
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.2542
0.3672
0.2448
0.0997
0.0277
0.0055
0.0008
0.0001
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.2288
0.3559
0.2570
0.1142
0.2
0.0687
0.2062
0.2835
0.2362
0.1329
0.0532
0.0155
0.0033
0.0005
0.0001
0.0000
0.0000
0.0000
0.0550
0.1787
0.2680
0.2457
0.1535
0.0691
0.0230
0.0058
0.0011
0.0001
0.0000
0.0000
0.0000
0.0000
0.0440
0.1539
0.2501
0.2501
0.3
0.0138
0.0712
0.1678
0.2397
0.2311
0.1585
0.0792
0.0291
0.0078
0.0015
0.0002
0.0000
0.0000
0.0097
0.0540
0.1388
0.2181
0.2337
0.1803
0.1030
0.0442
0.0142
0.0034
0.0006
0.0001
0.0000
0.0000
0.0068
0.0407
0.1134
0.1943
0.4
0.0022
0.0174
0.0639
0.1419
0.2128
0.2270
0.1766
0.1009
0.0420
0.0125
0.0025
0.0003
0.0000
0.0013
0.0113
0.0453
0.1107
0.1845
0.2214
0.1968
0.1312
0.0656
0.0243
0.0065
0.0012
0.0001
0.0000
0.0008
0.0073
0.0317
0.0845
0.5
0.0002
0.0029
0.0161
0.0537
0.1208
0.1934
0.2256
0.1934
0.1208
0.0537
0.0161
0.0029
0.0002
0.0001
0.0016
0.0095
0.0349
0.0873
0.1571
0.2095
0.2095
0.1571
0.0873
0.0349
0.0095
0.0016
0.0001
0.0001
0.0009
0.0056
0.0222
0.6
0.0000
0.0003
0.0025
0.0125
0.0420
0.1009
0.1766
0.2270
0.2128
0.1419
0.0639
0:0174
0.0022
0.0000
0.0001
0.0012
0.0065
0.0243
0.0656
0.1312
0.1968
0.2214
0.1845
0.1107
0.0453
0.0113
0.0013
0.0000
0.0001
0.0005
0.0033
0.7
0.0000
0.0000
0.0002
0.0015
0.0078
0.0291
0.0792
0.1585
0.2311
0.2397
0.1678
0.0712
0.0138
0.0000
0.0000
0.0001
0.0006
0.0034
0.0142
0.0442
0.1030
0.1803
0.2337
0.2181
0.1388
0.0540
0.0097
0.0000
0.0000
0.0000
0.0002
0.8
0.0000
0.0000
0.0000
0.0001
0.0005
0.0033
0.0155
0.0532
0.1329
0.2362
0.2835
0.2062
0.0687
0.0000
0.0000
0.0000
0.0000
0.0001
0.0011
0.0058
0.0230
0.0691
0.1535
0.2457
0.2680
.0.1787
0.0550
0.0000
0.0000
0.0000
0.0000
0.9
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0005
0.0038
0.0213
0.0852
0.2301
0.3766
0.2824
0.0000
0.0000
0.0000
0.00Q0
0.0000
0.0000
0.0001
0.0008
0.0055
0.0277
0.0997
0.2448
0.3672
0.2542
0.0000
0,0000
0.0000
0.0000
Статистические таблицы 549
Таблица 1
Биноминальное распределение вероятностей (продолжение)
Значения р
п г
4
5
6
7
8
9
10
И
12
13
14
15 0
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
0.1
0.0349
0.0078
0.0013
0.0002
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.2059
0.3432
0.2669
0.1285
0.0428
0.0105
0.0019
0.0003
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.2
0.1720
0.0860
0.0322
0.0092
0.0020
0.0003
0.0000
0.0000
0.0000
0.0000
0.0000
0.0352
0.1319
0.2309
0.2501
0.1876
0.1032
0.0430
0.0138
0.0035
0.0007
0.0001
0.0000
0.0000
0.0000
0.0000
0.0000
0.3
0.2290
0.1963
0.1262
0.0618
0.0232
0.0066
0.0014
0.0002
0.0000
0.0000
0.0000
0.0047
0.0305
0.0916
0.1700
0.2186
0.2061
0.1472
0.0811
0.0348
0.0116
0.0030
0.0006
0.0001
0.0000
0.0000
0.0000
0.4
0.1549
0.2066
0.2066
0.1574
0.0918
0.0408
0.0136
0.0033
0.0005
0.0001
0.0000
0.0005
0.0047
0.0219
0.0634
0.1268
0.1859
0.2066
0.1771
0.1181
0.0612
0.0245
0.0074
0.0016
0.0003
0.0000
0.0000
0.5
0.0611
0.1222
0.1833
0.2095
0.1833
0.1222
0.0611
0.0222
0.0056
0.0009
0.0001
0.0000
0.0005
0.0032
0.0139
0.0417
0.0916
0.1527
0.1964
0.1964
0.1527
0.0916
0.0417
0.0139
0.0032
0.0005
0.0000
0.6
0.0136
0.0408
0.0918
0.1574
0.2066
0.2066
0.1549
0.0845
0.0317
0.0073
0.0008
0.0000
0.0000
0.0003
0.0016
0.0074
0.0245
0.0612
0.1181
0.1771
0.2066
0.1859
0.1268
0.0634
0.0219
0.0047
0.0005
0.7
0.0014
0.0066
0.0232
0.0618
0.1262
0.1963
0.2290
0.1943
0.1134
0.0407
0.0068
0.0000
0.0000
0.0000
0.0001
0.0006
0.0030
0.0116
0.0348
0.0811
0.1472
0.2061
0.2186
0.1700
0.0916
0.0305
0.0047
0.8
0.0000
0.0003
0.0020
0.0092
0.0322
0.0860
0.1720
0.2501
0.2501
0.1539
0.0440
0.0000
0.0000
0.0000
0.0000
0.0000
0.0001
0.0007
0.0035
0.0138
0.0430
0.1032
0.1876
0.2501
0.2309
0.1319
0.0352
0.9
0.0000
0.0000
0.0000
0.0002
0.0013
0.0078
0.0349
0.1142
0.2570
0.3559
0.2288
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0003
0.0019
# 0.0105
0.0428
0.1285
0.2669
0.3432
0.2059
550 Приложение В
В Таблице 2 представлены вероятности в точности х числа реализаций для
различных значений ц.
Таблица 2
Распределение вероятностей по Пуассону
Значения \л
х 0.1 0.2
0 0.9048 0.8187
1 0.0905 0.1637
2 0.0045 0.0164
3 0.0002 0.0011
4 0.0000 0.0001
5 0.0000 0.0000
6 0.0000 0.0000
Значения ц
х 1.1 1.2 -
0 0.3329 0.3012
1 0.3662 0.3614
2 0.2014 0.2169
3 0.0738 0.0867
4 0.0203 0.0260
5 0.0045 0.0062
6 0.0008 0.0012
7 0.0001 0.0002
8 0.0000 0.0000
9 0.0000 0.0000
Значения \л
X '
0
1
2
3
4
5
6
2.1
0.1225
0.2572
0.2700
0.1890
0.0992
0.0417
0.0146
2.2
0.1108
0.2438
0.2681
0.1966
0.1082
0.0476
0.0174
2.3
0.1003
0.2306
0.2652
0.2033
0.1169
0.0538
0.0206
2.4
0.0907
0.2177
0.2613
0.2090
0.1254
0.0602
0.0241
2.6
0.0743
0.1931
0.2510
0.2176
0.1414
0.0735
0.0319
2.7
0.0672
0.1815
0.2450
0.2205
0.1488
0.0804
0.0362
2.8
0.0608
0.1703
0.2384
0.2225
0.1557
0.0872
0.0407
2.9
0.0550
0.1596
0.2314
0.2237
0.1622
0.0940
0.0455
3.0
0.0498
0.1494
0.2240
0.2240
0.1680
0.1008
0.0504
0.3
0.7408
0.2222
0.0333
0.0033
0.0003
0.0000
0.0000
0.4
0.6703
0.2681
0.0536
0.0072
0.0007
0.0001
0.0000
0.6
0.5488
0.3293
0.0988
0.0198
0.0030
0.0004
0.0000
0.7
0.4966
0.3476
0.1217
0.0284
0.0050
0.0007
0.0001
0.8
0.4493
0.3595
0.1438
0.0383
0.0077
0.0012
0.0002
0.9
0.4066
0.3659
0.1647
0.0494
0.0111
0.0020
0.0003
1.0
0.3679
0.3679
0.1839
0.0613
0.0153
0.0031
0.0005
1.3
0.2725
0.3543
0.2303
0.0998
0.0324
0.0084
0.0018
0.0003
0.0001
0.0000
1.4
0.2466
0.3452
0.2417
0.1128
0.0395
0.0111
0.0026
0.0005
0.0001
0.0000
1.6
0.2019
0.3230
0.2584
0.1378
0.0551
0.0176
0.0047
0.0011
0.0002
0.0000
1.7
0.1827
0.3106
0.2640
0.1496
0.0636
0.0216
0.0061
0.0015
0.0003
0.0001
1.8
0.1653
0.2975
0.2678
0.1607
0.0723
0.0260
0.0078
0.0020
0.0005
0.0001
1.9
0.1496
0.2842
0.2700
0.1710
0.0812
0.0309
0.0098
0.0027
0.0006
0.0001
2.0
0.1353
0.2707
0.2707
0.1804
0.0902
0.0361
0.0120
0.0034
0.0009
0.0002
m
p
си
cu
ьч
Щ
г i
\0 о
CD
CN
О
d
00
00
О
о
со
CO
о
о*
О)
со
о
о
00
Ч-Н
о
о
О)
о
о
о
о
со
00
о
о
о
00
СО
о
о
о"
ю
СО
о
о
о
о
о
о
00
о
о
о
00
СО
о
о
о
ю
о
о
о
о
о
о
00
со
о
о
о
со
о
о
о
о
о
о*
о
о
о
о
о
о
о
о
о
Г**
CN
о
о
о
CN
CN
о
о
о
00
о
о
о
о
о
о
о
о
о*
О)
о
о
о
о
о
о
о
о
СО
о
о
о
о*
о
о
о
о
со
о
о
о
о
00
о
о
о
о
СО
о
о
о
о*
СО
о
о
о
о
о
о
о
о
со
о
о
о
о*
о
о
о
о
о
о
о
о
о
о
о
о*
о
о
о
о
о
8
о
о
о
о
о
CN
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о"
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о ^
[^ 00 05 ^ и
3
г
я
т
О
Ю*
00
^*
СО
СО
О
О
о
CN
00
о
о
о
о
о
со
со
о
о
О)
со
о
о
CN
СО
о
CN
00
о
о
00
О)
о
о
со
СО
о
о
о.
г**
«о
о
со
СО
со
о
о
CN
00
о
ю
00
ю
«о
о
Ч-Н
о
CN
CN
СО
о
00
О)
со
о*
со
CN
со
о
о
СО
о
о
СО
00
о
со
ю
СО
о
о
о
о
о
о
о
со
СО
со
о
о
о
со
о
о
CN
о
00
о
о
о
о
00
о
CN
00
о
о
о
СО
о
о
о
3
о
о
со
о
о
о
СО
CN
о
о
о
О)
о
о
со
о
о
о
8
о
о
о
о
о
о
ю
о
о
о
о
со
о
о
о
о
о
о
о
CN
о
о
о
о
о
о
о
о
о
о
о
^ о о о о о
СООСОРО^Г^^СОСОСТ)
CN^CO^t^COCOC^CNO
^ОО^н^^н^^ООО
^ О О О* о о о о о о о
OOCOCNTtCOCOCOOOO
lOCOCNiO^CO^OOCOCO
^СОСООООСО^СОСО'-н
CNOO^^h^^^OOO
^'0000000000000
CN C^
CD со
8 8
о о
l> CN
о о
о о
о
о
о
О)
о
о
о
ю ~ о
о о о
о о о
о о о
odd
СО н о
о о о
о о о
о о о
odd
COCOiO^^COCNiOOOCNCOa)CO.CN^O
ООСОСОЮЮСО^ОФСОЮ^ОООО
^н i> ^ о av со оюс^^ ~
ООО^^^^^ООО
О
о
о о
о о о о
о о о о
о о о о
^О^Ю^Г^ЮСОн^ФСО^нОО
CS lO и Tf Tf t^
CN 00 CO О О) т*
О О ^ CN *-< -^
СОО^ОСО^-нОООО
OJiOCN^OOOOOO
оооооооооо
оооооооооооооооо
СО
Tt^incNc^coin^Hcocoa>co^oo
00l>CN'-Hl>CNCNa^l>CNOOOOO
^ ~ — — — ^^-.ооооооо
ооооооооо
N ст> г^ <-н ст> со со
СО О О "-ч CN ^н -
7со О* О* О О* О*
о
о
^ Ю G1 Ю СО ^
СО СО CN 00 СО СО
СО <-н О *-< СО CN
^ О н ^н CN и гн
СО о о о* о о*
СО
00 00 СО О) со
t ^ Ю н о
со ^ о о о
о о о о о
о о о о о о о
00
о
о
о*
Гк CO *-<
00 CN 00
О CN |>
CN CN *-н
о* о*
00 00
О 1>
СО CN
О О
dodo
X О ^ CN СО т* lO
н О СО ^t
«-< *г ^ о
^ о о о
о о о о
о" о о* о*
О <-<
СО 1>» 00 CD ч-Н ч-Н
CN О
О о
о о
о о
о о
^н О
о о
о о
о о
о* о
о о
о о
о о
о о
о о
о о
о о
о о
о о
о о*
CN СО ^ Ю
о
г*^
00
СО
СО
СО
8
О
о
о*
Ч-Н
о
о
о
о
о
о"
со
о
о
о
СО
г*-,
о
о
о
о
CD
о
о
о*
со
CN
CN
о
о
00
«о
CN
о
о
СО
CD
CN
О
о
CN
ю
о
о
00
о
о"
CN
ю
СО
о
о*
CN
5?
о
о
CN
CD
о
о
со
о
о
CN
о
О)
со
о
о
CN
ч—1
о
Гк со О СО CN 1>.
н О ^ CN (О СО
О *н СО 1> ^ ^*
^ О О О О *н ^
СО О О О О* о о
о со о СО О) О)
CN CS CJ) О ^ Tt
О ^ СО 00 CN Ю
CN О О О О ^ ^
СО о о о о о о
о
СО
00
ю"
СО
lO
Tf
lO
CN
lO
lO
CN
О
о
о
о
со
о
о
о
со
о
о
о
о
о
о
ю
СО
о
о
о*
О)
о
о
СО
о
о*
о
8
о*
CN
о
о
1>
00
CN
о
о
СО
о
о
О)
о
СО
о
о
о
00
ю
о
о
О)
СО
СО
о
о
СО
о
о
CN
О)
00
о
о
СО
00
О)
о
о
CN
00
о
о*
СО
00
о
со
О).
CN
о
О)
со
со
о
00
CN
о
о
о
о
СО
о
00
СО
о*
СО
о
СО
о
СО
ю
СО
о
О)
СО
о
00
CN
1>.
о
00
о
X О ^ CN CO ^ СО
552 Приложение В
Таблица 2
Распределение вероятностей по Пуассону (продолжение)
Значения ц
6 0.1515 0.1555 0.1584 0.1601 0.1606 0.1601 0.1586 0.1562 0.1529 0.1490
7 0.1125 0.1200 0.1267 0.1326 0.1377 0.1418 0.1450 0.1472 0.1486 0.1490
8 0.0731 0.0810 0.0887 0.0962 0.1033 0.1099 0.1160 0.1215 0.1263 0.1304
9 0.0423 0.0486 0.0552 0.0620 0.0688 0.0757 0.0825 0.0891 0.0954 0.1014
10 0.0220 0.0262 0.0309 0.0359 0.0413 0.0469 0.0528 0.0588 0.0649 0.0710
11 0.0104 0.0129 0.0157 0.0190 0.0225 0.0265 0.0307 0.0353 0.0401 0.0452
12 0.0045 0.0058 0.0073 0.0092 0.0113 0.0137 0.0164 0.0194 0.0227 0.0263
13 0.0018 0.0024 0.0032 0.0041 0.0052 0.0065 0.0081 0.0099 0.0119 0.0142
14 0.0007 0.0009 0.0013 0.0017 0.0022 0.0029 0.0037 0.0046 0.0058 0.0071
15 0.0002 0.0003 0.0005 0.0007 0.0009 0.0012 0.0016 0.0020 0.0026 0.0033
16 0.0001 0.0001 0.0002 0.0002 0.0003 0.0005 0.0006 0.0008 0.0011 0:0014
17 0.0000 0.0000 0.0001 0.0001 0.0001 0.0002 0.0002 0.0003 0.0004 0.0006
18 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0001 0.0002 0.0002
В Таблице 3 представлена область слева от соответствующего z-результата
для стандартного нормального распределения.
Таблица 3
Нормальное распределение вероятностей
Вторая цифра z
z ом от от ом ом о.об ом от ом ом
0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359
0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753
0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141
0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517
0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879
0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224
0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549
0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852
0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133
0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389
Статистические таблицы 553
Таблица 3
Нормальнее распределение вероятностей (продолжение)
Бторая цифра z
z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621
1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830
1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015
1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177
1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319
1.5 0.9332 0.9345 0,9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441
1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545
1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633
1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706
1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767
2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817
2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857
2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890
2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916
2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936
2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952
2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964
2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974
2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981
2.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986
3.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990
3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 Ь.9993
3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995
3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997
3.4 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998
3.5 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998
Таблица 4 предлагает вашему вниманию f-критерий для соответствующего
значения альфы или доверительного интервала и число степеней свободы.
354 Приложение В
Таблица 4
t-распрсдслснис Стьюдснта
Выделенные правосторонние
Дов.
0.2000
уровень
d.f. 0.6000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1.376
1.061
0.978
0.941
0.920
0.906
0.896
0.889
0.883
0.879
0.876
0.873
0.870
0.868
0.866
0.865
0.863
0.862
0.861
0.860
0.859
0.858
0.858
0.857
0.856
0.856
0.855
0.855
0.854
0.854
0.1500
0.7000
1.963
1.386
1.250
1.190
1.156
1.134
1.119
1.108
1.100
1.093
1.088
1.083
1.079
1.076
1.074
1.071
1.069
1.067
1.066
1.064
1.063
1.061
1.060
1.059
1.058
1.058
1.057
1.056
1.055
1.055
0.1000
0.8000
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
1.333
1.330
1.328
1.325
1.323
1.321
1.319
1.318
1.316
1.315
1.314
1.313
1.311
1.310
области с указанием доверительных уровней
0.0500
0.9000
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
1.740
1.734
1.729
1.725
1.721
1.717
1.714
1.711
1.708
1.706
1.703
1.701
1.699
1.697
0.0250
0.9500
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
2.110
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
0.0100
0.9800
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
2.567
2.552
2.539
2.528
2.518
2.508
2.500
2.492
2.485
2.479
2.473
2.467
2.462
2.457
0.0050
0.9900
63.657
9.925
5.841
4.604
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
2.921
2.898
2.878
2.861
2.845
2.831
2.819
2.807
2.797
2.787
2.779
2.771
2.763
2.756
2.750
0.0010
0.9980
318.31
22.327
10.215
7.173
5.893
5.208
4.785
4.501
4.297
4.144
4.025
3.930
3.852
3.787
3.733
3.686
3.646
3.610
3.579
3.552
3.527
3.505
3.485
3.467
3.450
3.435
3.421
3.408
3.396
3.385
0.0005
0.9990
636.62
31.599
12.924
8.610
6.869
5.959
5.408
5.041
4.781
4.587
4.437
4.318
4.221
4.140
4.073
4.015
3.965
3.922
3.883
3.850
3.819
3.792
3.768
3.745
3.725
3.707
3.690
3.674
3.659
3.646
Статпстческпе таблицы 355
Таблица 4
t-раСПрСДСАСНИС СтЬЮДСНТа (продолжение)
Выделенные правосторонние области с указанием доверительных уровней
Лов.
0.2000
уровень
йЛ. 0.6000
40
50
75
100
200
1000
0.851
0.849
0.846
0.845
0.843
0.842
0.1500
0.7000
1.050
1.047
1.044
1.042
1.039
1.037
0.1000
0.8000
1.303
1.299
1.293
1.290
1.286
1.282
0.0500
0.9000
1.684
1.676
1.665
1.660
1.653
1.646
0.0250
0.9500
2.021
2.009
1.992
1.984
1.972
1.962
0.0100
0.9800
2.423
2.403
2.377
2.364
2.345
2.330
0.0050
0.9900
2.704
2.678
2.643
2.626
2.601
2.581
0.0010
0.9980
3.307
3.261
3.202
3.174
3.131
3.098
0.0005
0.9990
3.551
3.496
3.425.
3.390
3.340
3.300
В Таблице 5 представлено распределение хи-квадрат для соответствующего
значения и число степеней свободы.
Таблица 5
Распределение хи-квадрат
Выделенна правая область распределения
df
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0.3000
1.074
2.408
3.665
4.878
6.064
7.231
8.383
9.524
10.656
11.781
12.899
14.011
15.119
16.222
0.2000
1.642
3.219
4.642
5.989
7.289
8.558
9.803
11.030
12.242
13.442
14.631
15.812
16.985
18.151
0.1500
2.072
3.794
5.317
6.745
8.115
9.446
10.748
12.027
13.288
14.534
15.767
16.989
18.202
19.406
0.1000
2.706
4.605
6.251
7.779
9.236
10.645
12.017
13.362
14.684
15.987
17.275
18.549
19.812
21.064
0.0500
3.841
5.991
7.815
9.488
11.070
12.592
14.067
15.507
16.919
18.307
19.675
21.026
22.362
23.685
0.0250
5.024
7.378
9.348
11.143
12.833
14.449
16.013
17.535
19.023
20.483
21.920
23.337
24.736
26.119
0.0100
6.635
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.666
23.209
24.725
26.217
27.688
29.141
0.0050
7.879
10.597
12.838
14.860
16.750
18.548
20.278
21.955
23.589
25.188
26.757
28.300
29.819
31.319
0.0010
10.828
13.816
16.266
18.467
20.515
22.458
24.322
26.124
27.877
29.588
31.264
32.909
34.528
36.123
15 17.322 19.311 20.603 22.307 24.996 27.488 30.578 32.801 37.697
356 Приложение В
Таблица 5
Распределение хи-квадрат
(продолжение)
Выделенна правая область распределения
df
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0.3000
18.418
19.511
20.601
21.689
22.775
23.858
24.939
26.018
27.096
28.172
29.246
30.319
31.391
32.461
33.530
0.2000
20.465
21.615
22.760
23.900
25.038
26.171
27.301
28.429
29.553
30.675
31.795
32.912
34.027
35.139
36.250
0.1500
21.793
22.977
24.155
25.329
26.498
27.662
28.822
29.979
31.132
32.282
33.429
34.574
35.715
36.854
37.990
0.1000
23.542
24.769
25.989
27.204
28.412
29.615
30.813
32.007
33.196
34.382
35.563
36.741
37.916
39.087
40.256
0.0500
26.296
27.587
28.869
30.144
31.410
32.671
33.924
35.172
36.415
37.652
38.885
40.113
41.337
42.557
43.773
0.0250
28.845
30.191
31.526
32.852
34.170
35.479
36.781
38.076
39.364
40.646
41.923
43.195
44.461
45.722
46.979
0.0100
32.000
33.409
34.805
36.191
37.566
38.932
40.289
41.638
42.980
44.314
45.642
46.963
48.278
49.588
50.892
0.0050
34.267
35.718
37.156
38.582
39.997
41.401
42.796
44.181
45.559
46.928
48.290
49.645
50.993
52.336
53.672
0.0010
39.252
40.790
42.312
43.820
45.315
46.797
48.268
49.728
51.179
52.620
54.052
55.476
56.892
58.301
59.703
В Таблице 6 представлены F-критерии для соответствующих степеней
свободы Vi и v2 с использованием значения = 0.05.
Таблица 6
F-распределение
<х =
\v,
V2
1*
2
3
4
5
6
7
0.05
1
161.448
18.513
10.128
7.709
6.608
5.987
5.591
2
3
199.500 215.707
19.000
9.552
6.944
5.786
5.143
4.737
19.164
9.277
6.591
5.409
4.757
4.347
4
224.583
19.247
9.117
6.388
5.192
4.534
4.120
5 6
7
230.162 233.986 236.768
19.296 19.330
9.013 8.941
6.256 6.163
5.050 4.950
4.387 4.284
3.972 3.866
19.353
8.887
6.094
4.876
4.207
3.787
8
9
10
238.882 240.543 241.882
19.371
8.845
6.041
4.818
4.147
3.726
19.385
8.812
5.999
4.772
4.099
3.677
19.396
8.786
5.964
4.735
4.060
3.637
Статистические таблицы 357
Таблица 6
F-распрсдслснис
а =
\v,
v2
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
0.05
1
5.318
5.117
4.965
4.844
4.747
4.667
4.600
4.543
4.494
4.451
АЛЫ
4.381
4.351
4.325
4.301
4.279
4.260
4.242
4.225
4.210
4.196
4.183
4.171
4.160
4.149
4.139
4.130
4.121
4.113
4.105
4.098
4.091
2
4.459
4.256
4.103
3.982
3.885
3.806
3.739
3.682
3.634
3.592
3.555
3.522
3.493
3.467
3.443
3.422
3.403
3.385
3.369
3.354
3.340
3.328
3.316
3.305
3.295
3.285
3.276
3.267
3.259
3.252
3.245
3.238
3
4.066
3.863
3.708
3.587
3.490
3.411
3.344
3.287
3.239
3.197
3.160
3.127
3.098
3.072
3.049
3.028
3.009
2.991
2.975
2.960
2.947
2.934
2.922
2.911
2.901
2.892
2.883
2.874
2.866
2.859
2.852
2.845
4
3.838
3.633
3.478
3.357
3.259
3.179
3.112
3.056
3.007
2.965
2.928
2.895
2.866
2.840
2.817
2.796
2.776
2.759
2.743
2.728
2.714
2.701
2.690
2.679
2.668
2.659
2.650
2.641
2.634
2.626
2.619
2.612
5
3.687
3.482
3.326
3.204
3.106
3.025
2.958
2.901
2.852
2.810
2.773
2.740
2.711
2.685
2.661
2.640
2.621
2.603
2.587
2.572
2.558
2.545
2.534
2.523
2.512
2.503
2.494
2.485
2.477
2.470
2.463
2.456
6 ■
3.581
3.374
3.217
3.095
2.996
2.915
2.848
2.790
2.741
2.699
2.661
2.628
2.599
2.573
2.549
2.528
2.508
2.490
2.474
2.459
2.445
2.432
2.421
2.409
2.399
2.389
2.380
2.372
2.364
2.356
2.349
2.342
1
3.500
3.293
3.135
3.012
2.913
2.832
2.764
2.707
2.657
2.614
2.577
2.544
2.514
2.488
2.464
2.442
2.423
2.405
2.388
2.373
2.359
2.346
2.334
2.323
2.313
2.303
2.294
2.285
2.277
2.270
2.262
2.255
8
3.438
3.230
3.072
2.948
2.849
2.767
2.699
2.641
2.591
2.548
2.510
2.477
2.447
2.420
2.397
2.375
2.355
2.337
2.321
2.305
2.291
2.278
2.266
2.255
2.244
2.235
2.225
2.217
2.209
2.201
2.194
2.187
(продолжение)
9
3.388
3.179
3.020
2.896
2.796
2.714
2.646
2.588
2.538
2.494
2.456
2.423
2.393
2.366
2.342
2.320
2.300
2.282
2.265
2.250
2.236
2.223
2.211
2.199
2.189
2.179
2.170
2.161
2.153
2.145
2.138
2.131
10
3.347
3.137
2.978
2.854
2.753
2.671
2.602
2.544
2.494
2.450
2.412
2.378
2.348
2.321
2.297
2.275
2.255
2.236
2.220
2.204
2.190
,2.177
2.165
2.153
2.142
2.133
2.123
2.114
2.106
2.098
2.091
2.084
358 Приложение В
Таблица 6
F-распрсдслснис
а =
\ух
V2
40
41
42
43
44
45
46
47
48
49
50
а =
\Vi
v2
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
0.05
1
4.085
4.079
4.073
4.067
4.062
4.057
4.052
4.047
4.043
4.038
4.034
0\05
тг
2
3.232
3.226
3.220
3.214
3.209
3.204
3.200
3.195
3.191
3.187
3.183
12
3
2.839
2.833
2.827
2.822
2.816
2.812
2.807
2.802
2.798
2.794
2.790
1з~
242.983 243.906 244.690
19.405
8.763
5.936
4.704
4.027
3.603
3.313
3.102
2.943
2.818
2.717
2.635
2.565
2.507
2.456
2.413
2.374
19.413
8.745
5.912
4.678
4.000
3.575
3.284
3.073
2.913
2.788
2.687
2.604
2.534
2.475
2.425
2.381
2.342
19.419
8.729
5.891
4.655
3.976
3.550
3.259
3.048
2.887
2.761
2.660
2.577
2.507
2.448
2.397
2.353
2.314
4
2.606
2.600
2.594
2.589
2.584
2.579
2.574
2.570
2.565
2.561
2.557
ТГ
5
2.449
2.443
2.438
2.432
2.427
2.422
2.417
2.413
2.409
2.404
2.400
1б~
6
2.336
2.330
2.324 .
2.318
2.313
2.308
2.304
2.299
2.295
2.290
2.286
1б~
7
2.249
2.243
2.237
2.232
2.226
2.221
2.216
2.212
2.207
2.203
2.199
W
245.364 245.950 246.464 246.918
19.424
8.715
5.873
4.636
3.956
3.529
3.237
3.025
2.865
2.739
2.637
2.554
2.484
2.424
2.373
2.329
2.290
19.429
8.703
5.858
4.619
3.938
3.511
3.218
3.006
2.845
2.719
2.617
2.533
2.463
2.403
2.352
2.308
2.269
19.433
8.692
5.В44
4.604
3.922
3.494
3.202
2.989
2.828
2.701
2.599
2.515
2.445
2.385
2,333
2.289
2.250
19.437
8.683
5.832
4.590
3.908
3.480
3.187
2.974
2.812
2.685
2.583
2.499
2.428
2.368
2.317
2.272
2.233
8
2.180
2.174
2.168
2.163
2.157
2.152
2.147
2.143
2.138
2.134
2.130
W
(продолжение)
9
2.124
2.118
2.112
2.106
2.101
2.096
2.091
2.086
2.082
2.077
2.073
If
10
2.077
2.071
2.065
2.059
2.054
2.049
2.044
2.039
2.035
2.030
2.026
20
247.323 247.686 248.013
19.440
8.675
5.821
4.579
3.896
3.467
3.173
2.960
2.798
2.671
2.568
2.484
2.413
2.353
2.302
2.257
2.217
19.443
8.667
5.811
4.568
3.884
3.455
3.161
2.948
2.785
2.658
2.555
2.471
2.400
2.340
2.288
2.243
2.203
19.446
8.660
5.803
4.558
3.874
3.445
3.150
2.936
2.774
2.646
2.544
2.459
2.388
2.328
2.276
2.230
2.191
Статистические таблицы 359
Таблица 6
Г-распрсдслснис
а = 0.05
\vt 11 12 13
v2
19 2.340 2.308 2.280
20 2.310 2.278 2.250
21 2.283 2.250 2.222
22 2.259 2.226 2.198
23 2.236 2.204 2.175
24 2.216 2.183 2.155
25 2.198 2.165 2.136
26 2.181 2.148 2.119
27 2.166 2.132 2.103
28 2.151 2.118 2.089
29 2.138 2.104 2.075
30 2.126 2.092 2.063
31 2.114 2.080 2.051
32 2.103 2.070 2.040
33 2.093 2.060 2.030
34 2.084 2.050 2.Q21
35 2.075 2.041 2.012
36 2.067 2.033 2.003
37 2.059 2.025 1.995
38 2.051 2.017 1.988
39 2.044 2.010 1.981
40 2.038 2.003 1.974
41 2.031 1.997 1.967
42 2.025 1.991 1.961
43 2.020 1.985 1.955
44 2.014 1.980 1.950
45 2.009 1.974 1.945
46 2.004 1.969 1.940
47 1.999 1.965 1.935
48 1.995 1.960 1.930
49 1.990 1.956 1.926
50 1.986 1.952 1.921
14 15 16
2.256 2.234 2.215
2.225 2.203 2.184
2.197 2.176 2.156
2.173 2.151 2.131
2.150 2.128 2.109
2.130 2.108 2.088
2.111 2.089 2.069
2.094 2.072 2.052
2.078 2.056 2.036
2.064 2.041 2.021
2.050 2.027 2.007
2.037 2,015 1.995
2.026 2.003 1.983
2.015 1.992 1.972
2.004 1.982 1.961
1.995 1.972 1.952
1.986 1.963 1.942
1.977 1.954 1.934
1.969 1.946 1.926
1.962 1.939 1.918
1.954 1.931 1.911
1.948 1.924 1.904
1.941 1.918 1.897
1.935 1.912 1.891
1.929 1.906 1.885
1.924 1.900 1.879
1.918 1.895 1.874
1.913 1.890 1.869
1.908 1.885 1.864
1.904 1.880 1.859
1.899 1.876 1.855
1.895 1.871 1.850
(продолжение)
17 18 19 20
2.198 2.182 2.168 2.155
2.167 2.151 2.137 2.124
2.139 2.123 2.109 2.096
2.114 2.098 2.084 2.071
2.091 2.075 2.061 2.048
2.070 2.054 2.040 2.027
2.051 2.035 2.021 2.007
2.034 2.018 2.003 1.990
2.018 2.002 1.987 1.974
2.003 1.987 1.972 1.959
1.989 1.973 1.958 1.945
1.976 1.960 1.945 1.932
1.965 1.948 1.933 1.920
1.953 1.937 1.922 1.908
1.943 1.926 1.911 1.898
1.933 1.917 1.902 1.888
1.924 1.907 1.892 1.878
1.915 1.899 1.883 1.870
1.907 1.890 1.875 1.861
1.899 1.883 1.867 1.853
1.892 1.875 1.860 1.846
1.885 1.868 1.853 1.839
1.879 1.862 1.846 1.832
1.872 1.855 1.840 1.826
1.866 1.849 1.834 1.820
1.861 1.844 1.828 1.814
1.855 1.838 1.823 1.808
1.850 1.833 1.817 1.803
1.845 1.828 1.812 1.798
1.840 1.823 1.807 1.793
1.836 1.819 1.803 1.789
1.831 1.814 1.798 1.784
Глоссарий
Альтернативная гипотеза — обозначается Яь содержит
утверждение, обратное утверждению основной гипотезы, и
считается истинным, если основная гипотеза оказывается
ложной.
Биноминальное распределение вероятностей — используется
для вычисления вероятности определенного числа успехов для
определенного числа испытаний.
Биноминальный эксперимент — эксперимент, который имеет
только два исхода для каждого испытания. Вероятности успеха
и неудачи являются константами. Все испытания
эксперимента являются независимыми друг от друга.
Вероятность — возможность того, что произойдет
определенное событие.
Взаимоисключающие события — когда два события не могут
произойти одновременно в рамках одного эксперимента.
Взвешенное среднее — величина, вычисляемая с различным
весом отдельных компонент (больший вес одних значений и
меньший — других).
Вторичные данные — данные, собранные другими людьми и
предоставленные для широкого пользования.
Выборка — подмножество генеральной совокупности.
Глоссарий 561
Выбросы — экстремальные значения в наборе данных, которые должны
быть отброшены перед проведением анализа.
Генеральная совокупность — представляет все возможные исходы или
измерения, представляющие для нас интерес.
Гипотеза — предположение относительно параметра совокупности.
Гистограмма — график, демонстрирующий число наблюдений в каждой
группе в виде призмы определенной высоты.
Графическая диаграмма — представление данных, при котором точки
упорядоченных пар данных соединены между собой линией.
Групповая выборка — простая случайная выборка групп из генеральной
совокупности. Каждый член выбранной группы будет частью финальной выборки.
Группы — интервалы распределения частот.
Данные — значения, приписываемые наблюдению или измерению,
основной элемент статистического анализа.
Двусторонняя проверка гипотезы — используется, когда альтернативная
гипотеза сформулирована в виде *.
Дискретное распределение вероятностей — список всех возможных
исходов эксперимента для дискретной случайной переменной вместе с
относительной частотой или вероятностью.
Дисперсионный анализ (ANOVA) — процедура проверки разности двух или
более средних на генеральной совокупности.
Дисперсия — измерение разброса, описывающего относительное расстояние
между значениями данных из набора и средним значением из набора данных.
Доверительный интервал — диапазон значений, используемый для оценки
параметра совокупности и связанный с определенным доверительным уровнем.
Доверительный уровень — вероятность того, что интервальная оценка будет
включать заданный параметр совокупности.
Древовидное представление — отображает распределение частот путем
деления значений данных на стебли (последняя цифра значения) и стволы
(оставшиеся цифры значения).
Зависимая переменная — переменная, обозначаемая у в уравнении
регрессии, на которое оказывает влияние независимая переменная.
Зависимые выборки — наблюдаемые данные из одной выборки связаны с
данными из другой выборки.
Закон больших чисел — гласит, что когда эксперимент проводится
большое число раз, эмпирические вероятности процесса стремятся к
теоретическим.
362 Приложение С
Измерение центральной тенденции — описывает центральную точку
нашего набора данных с помощью одного значения.
Интервальная оценка — обеспечивает диапазон значений, максимально
описывающих совокупность.
Интервальный уровень измерения — тип данных, позволяющий
использовать сложение и вычитание при сравнении данных, но с произвольной
нулевой точкой.
Испытание на адекватность — использует выборку с целью проверки,
соответствия распределения частот фактическому распределению.
Исход — определенный результат эксперимента.
Качественные данные — используют описательные средства для измерения
или классификации объектов, представляющих интерес.
Квартили - измеряют относительное положение значений данных путем
деления набора данных на 4 равных сегмента.
Классическая вероятность — это ситуация, в которой нам известно число
возможных исходов события.
Количественные данные — используют числовые значения для описания
объектов, представляющих интерес.
Комбинации — число различных способов расположения объектов
безотносительно порядка их расположения.
Коэффициент корреляции — указывает на силу и направление линейной
связи между зависимой и независимой переменными.
Коэффициент смешанной корреляции (г2) — процент вариации у,
объясняемый линией регрессии.
Критерий — значения, описывающие характеристику выборки.
Критерий значимости — величина, взятая из выборки, используемое для
принятия решения об отклонении или принятии основной гипотезы.
Линейная регрессия — процедура, описывающая прямую линию,
максимально соответствующую набору упорядоченных пар (х,у).
Линейчатая диаграмма — представление данных, при котором значение
наблюдения пропорционально высоте призмы на графике.
Медиана — значение из набора данных, по отношению к которому
половина наблюдений имеют большее значение, а половина — меньшее.
Межквартильный размах — измеряет протяженность центральной
половины набора данных и используется для определения выбросов.
Мера относительного положения — описывает процент данных ниже
определенной точки.
Глоссарш 363
Метод наименьших квадратов — математическая процедура, используемая
для определения линейного уравнения, максимально соответствующего
набору упорядоченных пар, путем нахождения значений а, отрезка на оси у, и
Ь, наклона прямой. Цель этого метода состоит в минимизации общей
квадратичной ошибки между значениями у и у.
Мода — наблюдение в наборе данных, встречающееся чаще всего.
Наблюдаемые частоты — число фактических наблюдений, отмеченных для
каждой категории распределения частот методом хи-квадрат.
Наблюдаемый уровень значимости — самый маленький уровень
значимости, при котором нулевая гипотеза будет отклонена. Также носит название
уровень р-значимости.
Независимая переменная — переменная, обозначаемая х в уравнении
регрессии; предполагается, что она влияет на зависимую переменную.
Независимые выборки — данные из одной выборки не связаны с
наблюдаемыми данными из другой выборки.
Независимые события — реализация События В никоим образом не влияет
на реализацию События А.
Непрерывная случайная переменная — переменная, которая может
принимать любое числовое значение в пределах заданного интервала в результате
наблюдения за исходом эксперимента.
Номинальный уровень измерения — тип данных для определения группы
или категории использующий имена объектов.
Общая сумма квадратов — общая вариации в дисперсионном анализе,
получаемая путем сложения суммы квадратов между выборками [SSB) и суммы
квадратов внутри выборок (SSW).
Объединение — реализация по крайней мере одно из возможных событий.
Односторонняя проверка гипотезы — используется, когда альтернативная
гипотеза сформулирована с помощью операций сравнения < или >.
Однофакторный ANOVA-анализ — дисперсионный анализ,
предусматривающий анализ одного фактора.
Ожидаемые частоты — число наблюдений, ожидаемых для каждой
категории распределения частот с принятым допущением, что основная гипотеза
является истинной с помощью анализа методом хи-квадрат.
Описательная статистика — используется для суммирования или
представления данных так, чтобы мы могли получить быстрый обзор ситуации-
Опросы — сбор данных, подразумевающий прямые вопросы респонденту.
Основная (нулевая) гипотеза — обозначается Н0, является неизменной и
утверждает, что среднее по совокупности <, = или > определенного значения.
364 Приложение С
Относительный уровень измерения — уровень данных, позволяющий
использовать все 4 математические операции для сравнения данных, с учетом
абсолютной нулевой точки.
Ошибка второго рода — когда основная гипотеза принимается, а на самом
деле является ложной.
Ошибка выборки — когда измерение на выборке отличается от измерения
на генеральной совокупности.
Ошибка первого рода — когда основная гипотеза отклоняется, хотя на самом
деле является истинной.
Параметр — характеристика совокупности.
Первичные данные — данные, собранные тем, кто будет в дальнейшем их
использовать.
Пересечение — два или более событий происходят одновременно.
Перестановки — число различных способов упорядочивания представления
объектов.
Персентиль — измеряет относительное положение значений данных путем
деления набора данных на 100 одинаковых сегментов.
Полностью рандомизированный однофакторный дисперсионный анализ —
процедура дисперсионного анализа, подразумевающая независимый
случайный отбор наблюдений для каждого уровня фактора.
Порядковый уровень измерения — обладает всеми свойствами
номинального уровня плюс возможность ранжировать значения в порядке возрастания
или убывания.
Правило сложения вероятностей — определяет вероятность объединения
двух или более событий.
Правило умножения вероятностей — определяет вероятность пересечения
двух или более событий.
Пристрастная выборка — выборка, не являющаяся репрезентативной по
отношению к соответствующей генеральной совокупности, и может привести
к искаженным выводам.
Проверка Шеффе — используется для определения, какие средние по
выборке являются отличными от других после отклонения основной гипотезы с
помощью дисперсионного анализа.
Простая случайная выборка — выборка, отобранная из любых элементов
генеральной совокупности.
Пространство выборки — все возможные варианты исхода эксперимента.
Прямое наблюдение — сбор данных в момент нахождения интересующих
нас объектов в естественных условиях.
Глоссарий 565
Размах — результат вычитания самого наименьшего измерения из самого
наибольшего измерения выборки.
Распределение вероятностей Пуассона — используется для вычисления
вероятности того, что за определенный промежуток времени произойдет
определенное число событий.
Распределение относительных частот — представляет процент наблюдений
каждой группы в отношении к общему числу наблюдений.
Распределение разности средних в выборке — описывает вероятность
наблюдения различных интервалов разности двух средних по выборке.
Распределение среднего в выборке — поведение средних по выборке при
отборе выборок из генеральной совокупности в целом.
Распределение частот — возможные исходы эксперимента с указанием
относительной частоты или вероятности каждого исхода.
Распределение частот — таблица, отражающая число наблюдений данных,
попадающих в определенные интервалы.
Секторная диаграмма — используется для описания данных распределения
относительных частот с помощью окружности, разделенной на сегменты,
площадь которых пропорциональна распределению относительных частот.
Систематическая выборка — выборка, в которой каждый к член
совокупности отбирается для выборки, причем значение к приблизительно равно N/n,
где N равняется размеру совокупности, an — размеру выборки.
Слоенная выборка — выборка, получаемая путем деления совокупности на
взаимоисключающие классы (слои), и случайный отбор из каждого такого
класса.
Случайная переменная — переменная, принимающая числовое значение в
результате произвольного эксперимента.
Событие — один или более исходов, представляющих интерес для
эксперимента и являющихся подмножеством выборочного пространства.
Совместная оценка стандартных отклонений — взвешенное среднее двух
дисперсий выборки.
Совокупное распределение частот — процент наблюдений, меньший или
равный текущей группе.
Среднее — вычисляется путем сложения всех значений набора данных и
деления полученного результата на число наблюдений.
Средний квадрат внутри выборки (MSW) — измерение вариации внутри
каждой выборки.
Средний квадрат между выборками (MSB) — измерение вариации между
выборочными средними.
566 Приложение С
Стандартная ошибка доли — стандартное отклонение выборочных доль.
Стандартная ошибка оценки, sc, — измеряет величину разброса
наблюдаемых данных относительно линии регрессии.
Стандартная ошибка разности двух средних — описывает вариацию
разности двух средних.
Стандартная ошибка среднего — стандартное отклонение средних по
выборке.
Стандартное отклонение — вариация, вычисляемая путем извлечения
квадратного корня из дисперсии.
Статистика — наука сбора, распределения и систематической
классификации количественных данных, используемых в основном для выводов и
заключений.
Статистический вывод — используется для того, чтобы делать заявления и
выводы применительно к генеральной совокупности на основе выборки
данных из этой совокупности.
Степени свободы — число значений, которые могут свободно
варьироваться, если известна определенная информация, например, среднее по выборке.
Субъективная вероятность — вероятности, оцениваемые на основе личного
опыта и интуиции.
Сумма квадратов внутри выборки (SSW) — вариация в пределах выборок в
рамках дисперсионного анализа.
Сумма квадратов между выборками (SSB) — вариация между выборками в
рамках дисперсионного анализа.
Суммарная вероятность — вероятность пересечения двух событий.
Теорема Байеса — теорема, используемая для вычисления Р[В/А] на основе
информации о Р[А/В]. Понятие Р[А/В] нрсит название вероятности События
А при условии, что Событие В произошло.
Точечная оценка — единое значение, точнее всего описывающее
интересующую нас совокупность; чаще всего в этом качестве используется среднее.
Уровень — число категорий в пределах интересующего нас фактора в
процессе дисперсионного анализа.
Уровень значимости () — вероятность совершения ошибки первого рода.
Уровень погрешности — определяет широту доверительного интервала и
вычисляется с помощью zc а*.
Уровень р-значимости — самый маленький уровень значимости, при
котором будет отклонена основная гипотеза при допущении, что основная
гипотеза является истинной.
Глоссарий 367
Условная вероятность — вероятность События А при том, что Событие В
уже произошло.
Фактор — описывает причину вариации данных для дисперсионного
анализа.
Факторные таблицы — показывают фактическую или относительную
частоту двух типов данных одновременно, в одной таблице.
Фокус-группы — методика наблюдения, когда участникам известно о том,
что происходит сбор данных. Фокус-группы обычно используются в бизнесе
для сбора информации в групповом окружении, контролируемом
модератором.
Фундаментальный принцип счета — гласит, что если одно событие может
иметь т вариаций, а второе — л вариаций, то общее число вариаций обоих
событий, происходящих вместе, равно т* п.
Центральная предельная теорема — теорема гласит, что по мере увеличения
размера выборки (п) средние по выборке стремятся следовать нормальному
закону распределения вероятностей.
Эксперимент — процесс измерения или наблюдений за действием с целью
сбора данных.
Эмпирическая вероятность — тип вероятности, определяющий число
реализаций события с помощью эксперимента и вычисляющий вероятность из
распределения относительных частот.
Эмпирическое правило — если распределение подчиняется колоколообраз-
ной симметричной кривой, сконцентрированной вокруг среднего, примерно
68, 95 и 99,7% значений попадут в пределы 1, 2 и 3 стандартных отклонений от
среднего соответственно.
Содержание
Часть 1: Постигаем основы 1
1 Начало работы 3
Где используются статистические данные? 4
Кто придумал статистику? 5
Пионеры статистики 5
Другие известные статисты 6
Статистика сегодня 6
Описательная статистика — низшая лига 7
Статистический вывод — высшая лига 9
Этика и статистика — действительность коварна
и опасна 10
Ваша очередь 13
Повторение — мать учения 13
2 ДАННЫЕ, ДАННЫЕ ПОВСЮДУ, КАК ЖЕ ВЫБРАТЬ НУЖНЫЕ? 14
Важность данных 15
Источники данных — откуда вообще берутся
данные? 16
Непосредственное наблюдение — я буду следить
за вами 18
Эксперименты — кто используется в качестве
подопытных кроликов? 18
Опросы — это ваш окончательный ответ? 19
Типы данных 19
Типы шкал измерения — вопрос немаловажный .20
Номинальный уровень измерения 20
Порядковый уровень измерения 20
Интервальный порядок измерения 21
Относительный порядок измерения 21
Как компьютеры приходят нам на помощь 23
Роль компьютеров в статистике 23
Установка средств анализа данных 24
Ваша очередь 26
Повторение — мать учения 27
3 ПРЕДСТАВЛЕНИЕ ОПИСАТЕЛЬНОЙ СТАТИСТИКИ 28
Распределение частот 29
Как вычислять распределение частот 30
ii Содержание
Распределение относительных (выборочных) частот 32
Распределение интегральных частот 32
Графическое представление распределения частот
с помощью гистограммы 33
Excel сделает за вас грязную работу 34
Мощный инструмент статистики —■ древовидное
представление 37
Представление статистических данных в виде
графиков 38
Какая у вас любимая секторная диаграмма? 38
Линейчатые диаграммы 40
Графические диаграммы 42
Мастер диаграмм Excel 43
Ваша очередь 46
Повторение — мать учения 46
4 ВЫЧИСЛЕНИЕ ОПИСАТЕЛЬНЫХ СТАТИСТИК:
ЦЕНТРАЛЬНАЯ ТЕНДЕНЦИЯ (СРЕДНЕЕ, МЕДИАНА И МОДА) 47
Меры центральной тенденции 48
Среднее 48
Взвешенное среднее 50
Среднее значение распределения частот группы данных.. .51
Медиана 54
Мода 55
. Чему отдать предпочтение? 55
Использование Excel для вычисления центральной
тенденции 56
Ваша очередь 58
Повторение — мать учения 59
5 ВЫЧИСЛЕНИЕ ОПИСАТЕЛЬНОЙ СТАТИСТИКИ:
МЕРЫ РАССЕЯНИЯ 60
Размах 61
Дисперсия ,61
Использование метода «сырого счета» (пример с грилем)". .62
Дисперсия генеральной совокупности 63
Стандартное отклонение 65
Вычисление стандартного отклонения для
сгруппированных данных 66
Эмпирическое правило: определение стандартного
отклонения 67
Теорема Чебышева 69
Содержание Hi
Меры относительного положения 71
Квартили 71
Межквартильный размах 72
Использование Excel для вычисления мер
рассеяния . 72
Ваша очередь 73
Повторение — мать учения 74
ЧАСТЬ2 ИЗУЧАЕМ ВЕРОЯТНОСТЬ ;„J7
6 ВВЕДЕНИЕ В ВЕРОЯТНОСТЬ 79
Что такое вероятность? 80
Классическая вероятность 80
Эмпирическая вероятность ..: 81
Субъективная вероятность 83
Основные свойства вероятности 83
Пересечение событий .84
Объединение событий: брак, заключенный
на небесах 86
Ваша очередь 87
Повторение — мать учения 88
7 И СНОВА О ВЕРОЯТНОСТИ 89
Условная вероятность 90
Независимые и зависимые события 91
Правило умножения вероятностей 92
Взаимоисключающие события 94
Правило сложения вероятностей 94
Суммируем полученные сведения 96
Теорема Байеса 96
Ваша очередь 98
Повторение — мать учения 99
8 ПРИНЦИПЫ СЧЕТА И РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ 100
Принципы счета 101
Фундаментальный принцип счета 101
Перестановки 102
Комбинации 104
Использование Excel для вычисления перестановок
. и комбинаций 106
Распределения вероятностей 107
Случайные переменные 108
iv Содержание
Дискретные распределения вероятностей 109
Правила дискретных распределений вероятностей 111
Среднее значение дискретного распределения
вероятностей 111
Дисперсия и стандартное отклонение дискретного
распределения вероятности 112
Ваша очередь 114
Повторение — мать учения 114
9 БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ 116
Характеристики биноминального эксперимента 117
Биноминальное распределение вероятностей 118
Биноминальные таблицы вероятностей 121
Использование Excel для вычисления биноминальных
вероятностей 122
Среднее значение и стандартное отклонение
биноминального распределения 123
Ваша очередь 124
Повторение — мать учения 125
10 РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ПУАССОНА 126
Характеристики процесса Пуассона 127
Распределение вероятностей Пуассона 128
Таблицы вероятностей Пуассона 131
Использование Excel для вычисления вероятностей
Пуассона 134
Использование распределения Пуассона как
приближение к биноминальному
распределению 135
Ваша очередь 137
Повторение — мать учения 138
11 НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ 139
Характеристики нормального распределения
вероятностей 140
Вычисление вероятностей для нормального
распределения 142
Вычисление z-распределения 143
Использование стандартной нормальной таблицы 144
И снова эмпирическое правило 149
Вычисление нормальных вероятностей с помощью Excel .. 150
Использование нормального распределения как
приближение биноминального распределения .151
Содержание v
Ваша очередь 155
Повторение — мать учения 155
ЧАСТЬЗ СТАТИСТИЧЕСКИЙ ВЫВОД 157
12 ВЫБОРКА 159
Почему выборка? 160
Случайная выборка 161
Простая случайная выборка 162
Систематическая выборка 164
Групповая выборка 165
Слоенная выборка 166
Ошибки выборки 167
Примеры использования ошибочных выборочных
методик 168
Ваша очередь 169
Повторение — мать учения 170
13 ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ 171
Что такое выборочное распределение? 172
Выборочное распределение среднего 172
Центральная предельная теорема 176
Стандартная ошибка среднего 178
Почему работает центральная предельная
теорема? 180
Как заставить центральную предельную теорему
работать 182
Использование центральной предельной теоремы
при неизвестном среднем совокупности 183
Выборочное распределение доли .185
Вычисление выборочной доли 185
Вычисление стандартной ошибки доли 186
Ваша очередь 188
Повторение — мать учения 188
14 ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ 190
Доверительные интервалы для среднего при больших
выборках 191
Оценки 191
Доверительные уровни 192
Будьте внимательны при анализе доверительного
интервала! 193
vi Содержание
Что происходит при изменении доверительных уровней .. 195
Что происходит при изменении размера выборки 196
Определение размера выборки для среднего 196
Вычисление доверительного интервала при неизвестном
значении s , .197
Использование функции доверит программы Excel 198
Доверительные интервалы для среднего при малых
выборках - 199
Когда значение s известно .... 199
Когда значение s неизвестно 200
Доверительные интервалы для долей при больших
выборках 203
Вычисление доверительного интервала для доли 203
Определение размера выборки для доли 205
Ваша очередь 205
Повторение — мать учения 206
15 ВВЕДЕНИЕ В ПРОВЕРКУ ГИПОТЕЗ 208
Проверка гипотез — основы 209
Основная и альтернативная гипотезы 210
Формулировка основной и альтернативной гипотез 211
Двусторонняя проверка гипотезы 211
Односторонняя проверка гипотезы 213
Ошибки первого и второго рода 214
Пример двусторонней проверки гипотезы 215
Использование шкалы исходной переменной 216
Использование стандартизованной нормальной
шкалы 217
Пример односторонней проверки гипотезы 218
Ваша очередь 221
Повторение — мать учения 222
16 ПРОВЕРКА ГИПОТЕЗЫ ПО ОДНОЙ ВЫБОРКЕ 223
Проверка гипотезы для среднего при больших
выборках 224
Когда сигма известна 224
Когда сигма неизвестна 226
Роль альфы в проверке гипотезы 227
Введение р-значения . . . 229
Уровень р-значимости для односторонней проверки
гипотезы 229
Уровень р-значимости для двусторонней проверки
гипотезы 230
Содержание vii
Проверка гипотезы для среднего при малых
выборках 232
Когда сигма известна 232
Когда сигма неизвестна 233
Использование функции СТЬЮДРАСПОБР программы
Excel 237
Проверка гипотезы для доли при больших
выборках 238
Односторонняя проверка гипотезы для доли 238
Двусторонняя проверка гипотезы для доли 240
Ваша очередь 242
Повторение — мать учения 242
17 ПРОВЕРКА ГИПОТЕЗЫ ПО ДВУМ ВЫБОРКАМ 243
Концепция сравнения двух совокупностей 244
Выборочное распределение для разности средних . . . .244
Проверка разности средних для выборок большого
размера 245
Проверка разности, отличной от нуля 249
Проверка разности средних при малом размере
выборки и неизвестной сигме 250
Равные стандартные отклонения совокупностей 250
Неравные стандартные отклонения совокупностей 253
Программа Excel выполнит за вас черновую работу . . .254
Проверка разности средних при зависимых
выборках 256
Проверка разности долей при независимых
выборках 259
Ваша очередь 262
Повторение — мать учения 263
ЧАСТЬ 4 УГЛУБЛЕННОЕ ИЗУЧЕНИЕ СТАТИСТИКИ ВЫВОДА 265
18 РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ 267
Обзор шкал измерения данных 268
Испытание на адекватность хи-квадрат 269
Формулировка основной и альтернативной гипотез 269
Наблюдаемые и ожидаемые частоты 270
Вычисление статистики хи-квадрат 271
Определение критического значения хи-квадрат 271
Использование функции ХИ20БР программы Excel 272
Характеристики распределения хи-квадрат 273
viii Содержание
Испытание на адекватность с биноминальным
распределением 274
Проверка хи-квадрат на независимость 276
Ваша очередь 379
Повторение — мать учения 380
19 Дисперсионный анализ 282
Однофакторный дисперсионный анализ 283
Полностью рандомизированный дисперсионный
анализ , 284
Разбиение суммы квадратов 285
Определение вычисленного F-критерия 287
Определение критического значения F-критерия 288
Использование функции FPACIIOEP программы Excel 290
Использование Excel для выполнения однофакторного
дисперсионного анализа 291
Парные сравнения 292
Ваша очередь 294
Повторение — мать учения 295
20 КОРРЕЛЯЦИЯ И ЛИНЕЙНАЯ РЕГРЕССИЯ 296
Независимые и зависимые переменные 297
Корреляция 298
Коэффициент корреляции 299
Проверка значимости коэффициента корреляции 301
Использование Excel для вычисления коэффициентов
корреляции 302
Линейная регрессия 303
Метод наименьших квадратов 304
Доверительный интервал кривой эффекта 307
Проверка наклона кривой эффекта 309
Коэффициент смешанной корреляции 310
Использование Excel для определения линейной
регрессии 311
Пример линейной регрессии с отрицательной
корреляцией 312
Допущения для линейной регрессии 316
Линейная и множественная регрессии 316
Ваша очередь 317
Повторение — мать учения 317
Содержание ix
ПРИЛОЖЕНИЯ 318
ПРИЛОЖЕНИЕ А: ОТВЕТЫ НА ВОПРОСЫ РАЗДЕЛА
«ВАША ОЧЕРЕДЬ 318
Глава 1 318
Глава 2 319
Глава 3 • 319
Глава 4 321
Глава 5 322
Глава 6 325
Глава 7 326
Глава 8 327
Глава 9 328
Глава 10 329
Глава 11 331
Глава 12 v 332
Глава 13 332
Глава 14 333
Глава 15 335
Глава 16 336
Глава 17 337
Глава 18 339
Глава 19 341
Глава 20 343
ПРИЛОЖЕНИЕ В: СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ 345
Таблица 1 345
Биноминальное распределение вероятностей 345
Таблица 2 350
Распределение вероятностей по Пуассону 350
Таблица 3 352
Нормальное распределение вероятностей 352
Таблица 4 354
t-распределение Стьюдента 354
Таблица 5 355
Распределение хи-квадрат 355
Таблица 6 356
F-распределение 356
ПРИЛОЖЕНИЕ С: ГЛОССАРИЙ 360
УДК 311
ББК 60.6
Д67
Настоящее издание представляет собой
авторизованный перевод издания
«The complete idiot's guide to Statistics»
Опубликовано совместно с Alpha Books
членом Penguin Group (USA) INC.
Подписано в печать 22.10.2006. Формат 70x90/16.
Гарнитура BalticaC. Бумага газетная. Усл. печ. л. 2В.1.
С: CIG. 2000 экз. Заказ № 4145.
С: ШзШ. 2000 экз. Заказ № 4144.
Общероссийский классификатор продукции
ОК-005-93, том 2; 953000 — книги, брошюры
Санитарно-эпидемиологическое заключение
№ 77.99.02.953.Д.003857.05.06 от 05.05.2006 г.
Все права защищены. Ни одна часть данной публикации не может быть воспроизведена
ни в какой форме, включая электронное и фотокопирование без предварительного
письменного разрешения правообладателя.
Доннелли-мл., Р.
Д67 Статистика/ Роберт А. Доннелли-мл.; пер. с англ. Н. А Ворониной. —
М.: Астрель: ACT, 2007. - XIV, 367,[3] с: ил.
ISBN 5-17-040812-9 (ООО «Издательство ACT»)(CIG)
ISBN 5-271-15808-Х (ООО «Издательство Астрель»)
ISBN 5-17-040811-0 (ООО «Издательство АСТ»)(ШзШ)
ISBN 5-271-15809-8 (ООО «Издательство Астрель»)
ISBN 1-59257-199-9 (англ.)
Книга знакомит с основными законами статистики, их применением в различных
ситуациях выбора. Вы научитесь формулировать гипотезы, выбирать критерии и
принимать решения, опираясь на законы статистики. Эта книга может оказаться
подспорьем в различных ситуациях принятия решения в вашей жизни.
УДК 311
ББК 60.6
ISBN 5-17-040812-9 (ООО «Издательство ACT») (CIG)
ISBN 5-271-15808-Х (ООО «Издательство Астрель»)
ISBN 5-17-040811-0 (ООО «Издательство ACT»)(ШзШ)'
ISBN 5-271-15809-8 (ООО «Издательство Астрель»)
ISBN 1-59257-199-9 (англ)
Copyright © 2004 by Robert A. Donnelly Jr., Ph. D
© ООО «Издательство Астрель», 2006
Роберт А. Доннелли-мл.
СТАТИСТИКА
Перевод с английского Н. А. Ворониной
Дизайн обложки студии «Дикобраз»
Зав.ред. Я. Г. Гершович
Ответственный редактор А. А. Подщеколдин
Художественный редактор И. С. Островская
Технический редактор Т. П. Тимошина
Корректор И. Н. Мокина
Компьютерная верстка Е. М. Илюшиной
ООО «Издательство Астрель»
129085, Москва, пр. Ольминского, д. ЗА
ООО «Издательство ACT»
170002, г. Тверь, пр-т Чайковского, д. 27/32
Наши электронные адреса:
www.ast.ru
E-mail: astpub@aha.ru
Отпечатано в ОАО ордена Трудового Красного Знамени
«Чеховский полиграфический комбинат».
142300, г. Чехов Московской области,
тел./факс (501)443-92-17, (272)6-25-36.
E-mail:marketing@chpk.ru
Конечно же вы не глупы.
Но сидя на занятиях по статистике, вы порой
испытываете дискомфорт. При толковании всех этих
чисел в таблицах, новостных статьях, отчетах вам
кажется, что у вас никогда ничего
не выйдет...
Но теперь вы лишитесь этого неприятного ощущения!
Книга «Статиаика» предоаавитвам уникальный шанс
улучшить свои знания и сохранить ясное понимание
предмета не только во время занятий,
но и после них. В этой книге вы найдете:
♦ Советы различного уровня сложноаи
о том, как с помощью программы Excel
облегчить свою работу.
♦ Доступное для всех введение в вычисление
центральной тенденции и параметров рассеяния.
♦ Профессиональные инарукции о том,
что предаавляют собой секторные, линейчатые
диаграммы и графики.
♦ Понятную всем информацию о свойавах
и облааях применения
распределений вероятноаей
♦ Доступное введение в более углубленное
изучение разделов аатиаики, в чааности
корреляции и анализа регрессии.
Из этой книги
вы узнаете о:
+ Распределениях частот
♦ Среднем, медиане и моде
♦ Размахе, дисперсии
и стандартном отклонении
♦ Вероятности
♦ Биноминальном
распределении
♦ Распределении Пуассона
♦ Нормальном распределении
♦ Доверительных интервалах
♦ Проверке гипотез
♦ Тесте хи- квадрат
♦ Корреляции
♦ Анализе линейной регрессии
Независимых и зависимых
отбытиях
♦ Параметрах относительного
положения
♦ Роли компьютеров
в статистике
ISBN 5-17-040811-0
III
78В17ПИ4П81 1fi