Author: Романков П.Г. Павлов К.Ф. Носков А.А.
Tags: процессы и оборудование химической технологии в целом химическая технология
Year: 1987
Similar
Text
|_п
1 I
для
высшей
школы
К.Ф.Павлов, П.Г.Ромашов
АЛЛосков
Примеры
и задачи
по курсу
процессов
и аппаратов
химической
технологии
Издание десятое,
переработанное и дополненное
Под редакцией чл.-корр. АН СССР
П. Г. Ромаыкова
Допущено Министерством высшего и среднего специального
образования СССР в качестве учебного пособия для студентов
химико-технологических специальностей
высших учебных заведений
Ленинград - „ХИМИЯ"
Ленинградское отделение
1987
6П7.1
П12
УДК 66.02 (076.1)
Рецензент: д-р техи. наук проф. 5. Я. Кисельникоз
УДК 66.02 (076.1)
Павлов К. Ф.> Романков П. Г., Носков А. А.
Примеры и задачи по курсу процессов и
аппаратов химической технологии. Учебное пособие для
вузов/Под ред. чл.-корр. АН СССР П. Г. Роман-
кова. — 10-е изд., перераб. и доп.—Л.: Химия,
1987. — 576 с.» ил.
Задачи и примеры составлены иа основе многолетнего опыта
преподавания курса в Ленинградском технологическом институте
им. Ленсовета. В книгу вошли разделы: основы прикладной гидравлики,
иасосы, вентиляторы и компрессоры, гидромеханические методы раз*
деления, теплопередача в химической аппаратуре, выпаривание и
кристаллизация, основы массопередачи, перегонка, ректификация и
абсорбция, адсорбция, экстрагирование, сушка умеренное и глубокое
охлаждение. В начале каждой главы приведены основные расчетные
формулы, необходимые для решения примеров и контрольных задач.
По сравнению с прекыдущдо 9-м иац,ан.нем (,1981 г.) внесены
изменения в главы 2—10, расширен круг примеров решения иижеиериыя
задач е помощь»® ЭВМ.
Для студентов химико-технологическнх вузов, а также вуаов
и факультетов химического машиностроения.
Табл. 141. Ил. 218. Бнблиогр. список: 182 назв.
2801020000-049 © Издательство «Химия», 1981
п 050701)-87 7 © Издательство «Химия», 1987,
с изменениями
ОГЛАВЛЕНИЕ
Предисловие к десятому изданию ^
Основные условные обозначения и единицы измерения ?
Вводные методические указания * *
Глава 1. Основы прикладной гидравлики 12
Основные зависимости н расчетные формулы 12
Примеры 29
Контрольные задачи 58
Глава 2. Насосы. Вентиляторы. Компрессоры 65
Основные зависимости и расчетные формулы 65
Примеры 71
Контрольные задачи 86
Пример расчета центробежного насоса 90
Глава 3. Гидромеханические методы разделения. Гидродинамика
взвешенного слоя. Перемешивание в жидкой среде 93
Основные зависимости h расчетные формулы 93
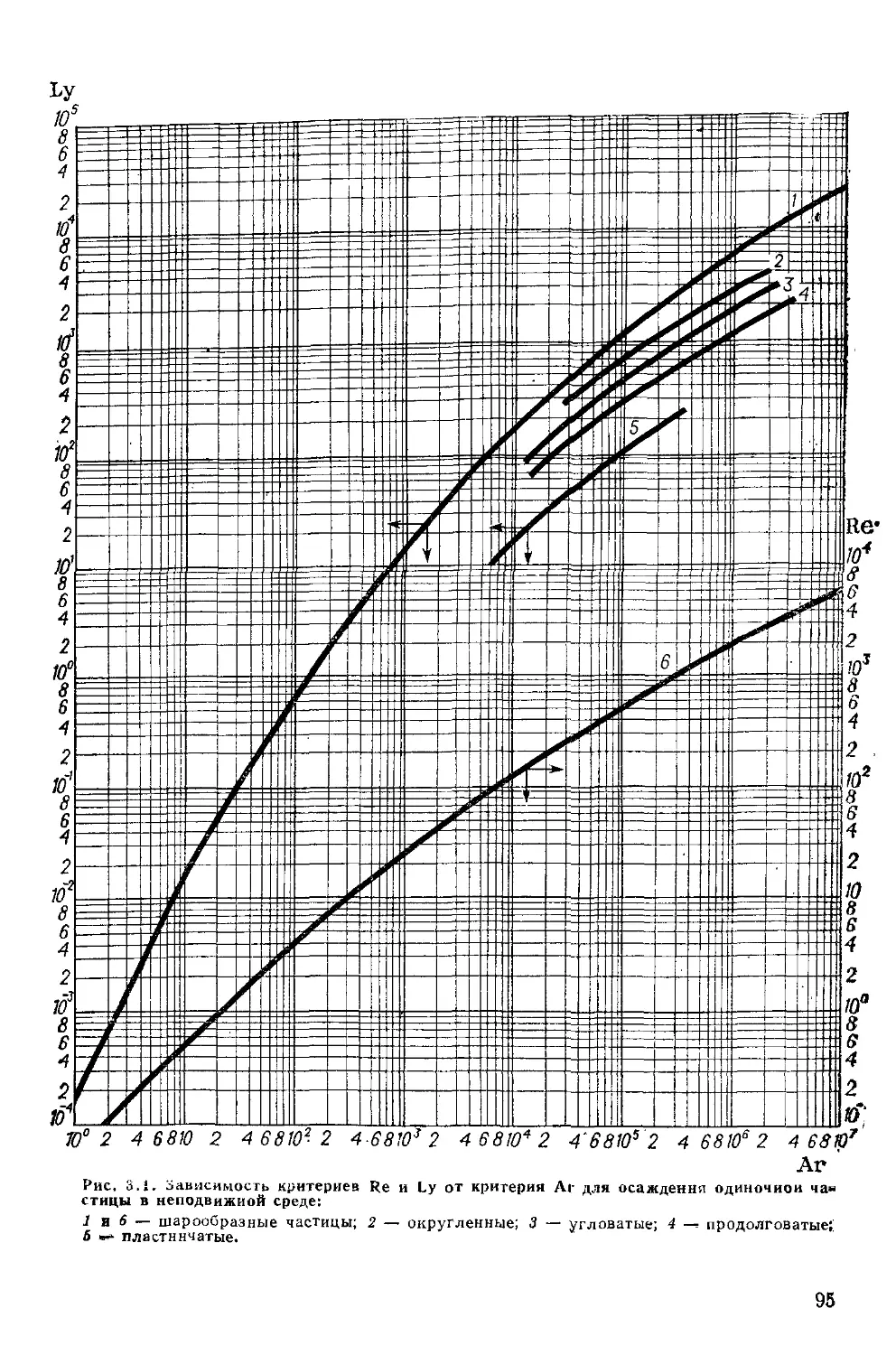
Осаждение 93
Фильтрование 98
Центрифугирование ' 101
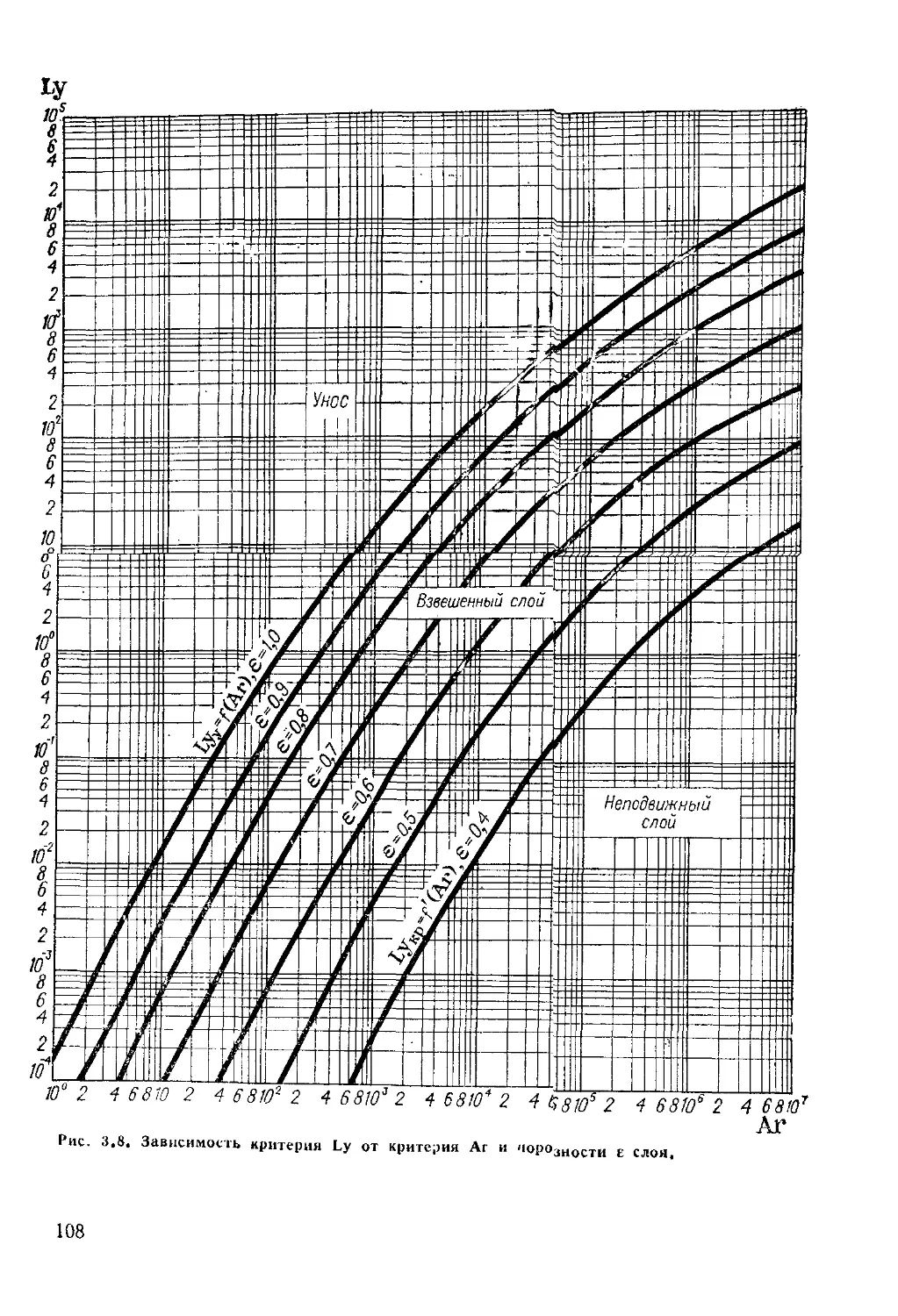
Гидродинамика взвешенного слоя 104
Перемешивание в жидкой среде 109
Примеры ПО
Осаждение ПО
Фильтрование 115
Центрифугирование ; 121
Взвешенный слой 127
Перемешивание в жидкой среде 131
Контрольные задачи 137
Пример расчета батарейного циклона 142
Пример расчета пенного газопромывателя для очистки газа от пыли ... 143
Пример расчета барабанного вакуум-фильтра 147
Глава 4. Теплопередача в химической аппаратуре 149
Основные зависимости и расчетные формулы 149
Теплопроводность 149
Теплоотдача 150
Теплопередача в поверхностных теплообменниках 168
Теплопередача при непосредственном соприкосновении потоков . . . 170
Ориентировочные значения коэффициентов теплоотдачи и
теплопередачи 171
Примеры 171
Контрольные задачи 205
Примеры расчета теплообменников 213
1*
3
Глава 5. Выпаривание. Кристаллизация . , 247
Основные зависимости и расчетные формулы ,.,..... 247
Примеры 255
Контрольные задачи * . •* 269
Пример расчета трехкорпусной выпарной установки 276
Глава 6, Основы массопередачи. Абсорбция 282
Основные зависимости и расчетные формулы . 282
Примеры , 295
Контрольные задачи 314
Глава 7. Перегонка и ректификация 319
Основные зависимости и расчетные формулы 319
Йримеры 325
Контрольные задачи 347
Пример расчета тарельчатой ректификационной колонны 351
Глава 8, Экстрагирование 361
Основные зависимости н расчетные формулы 361
Примеры 374
Контрольные задачи . , . . . 400
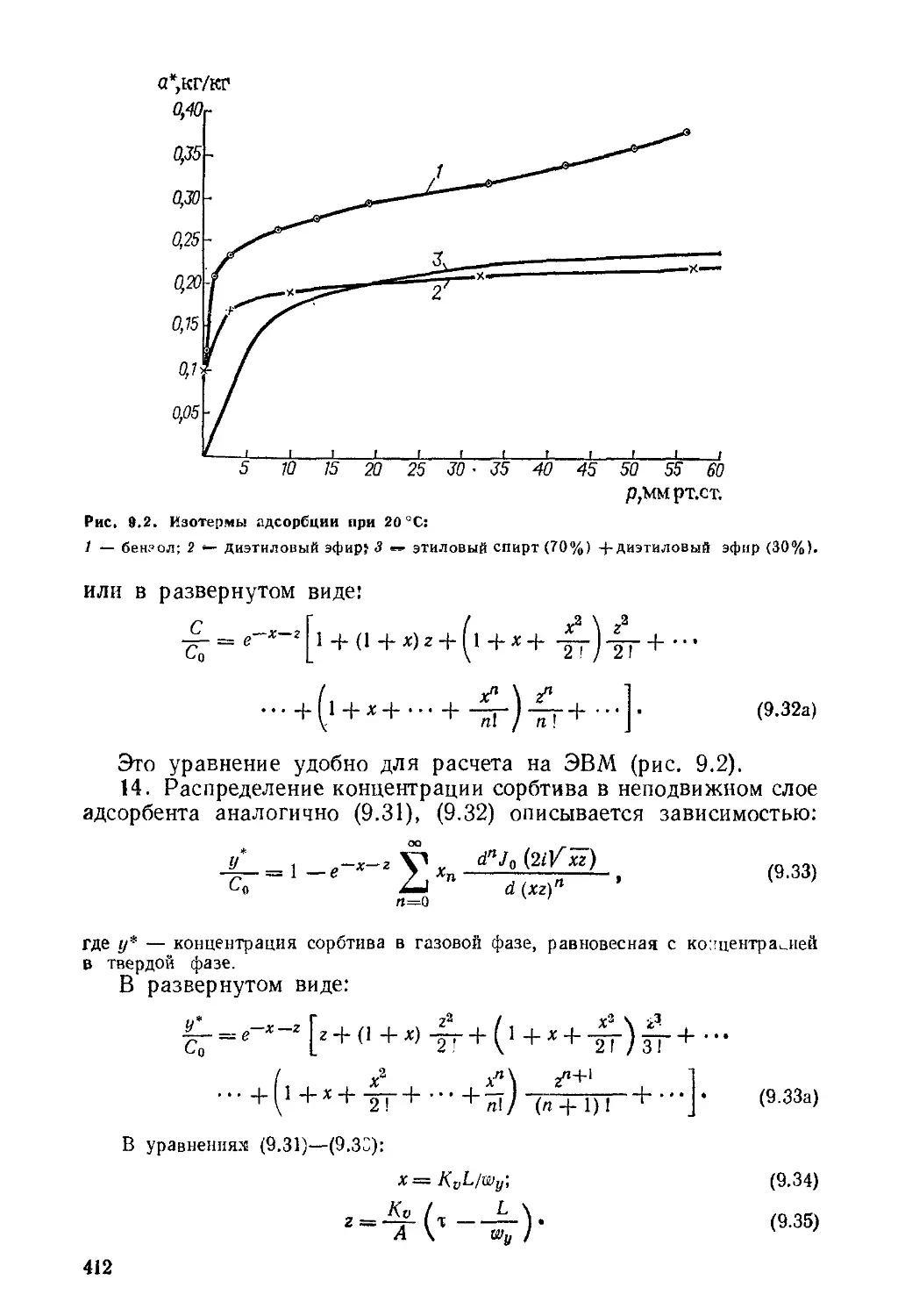
Глава 9. Адсорбция 403
Основные зависимости и расчетные формулы 403
Примеры . . 414
Контрольные задачи 422
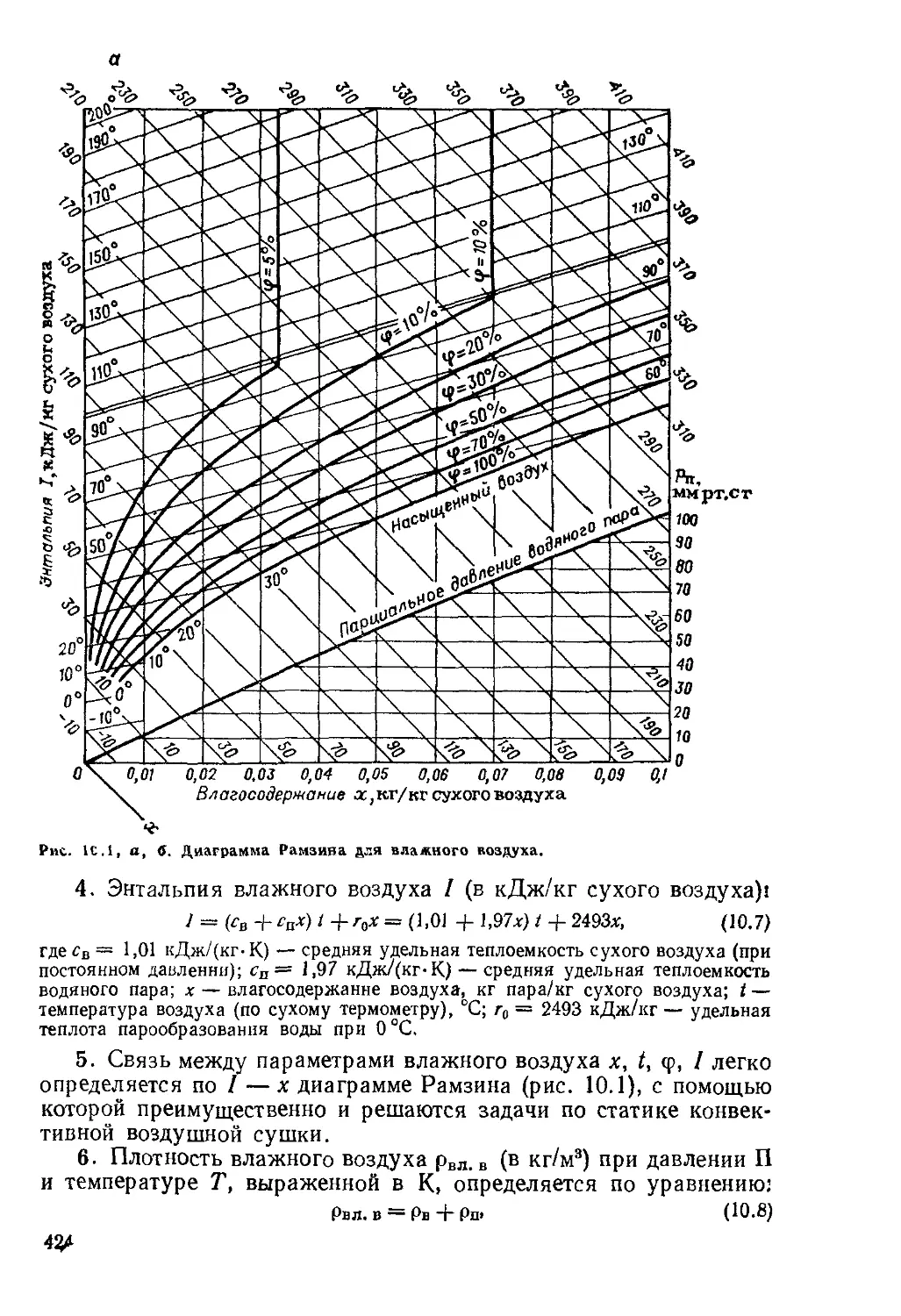
Глава 10. Сушка 423
Основные зависимости и расчетные формулы 423
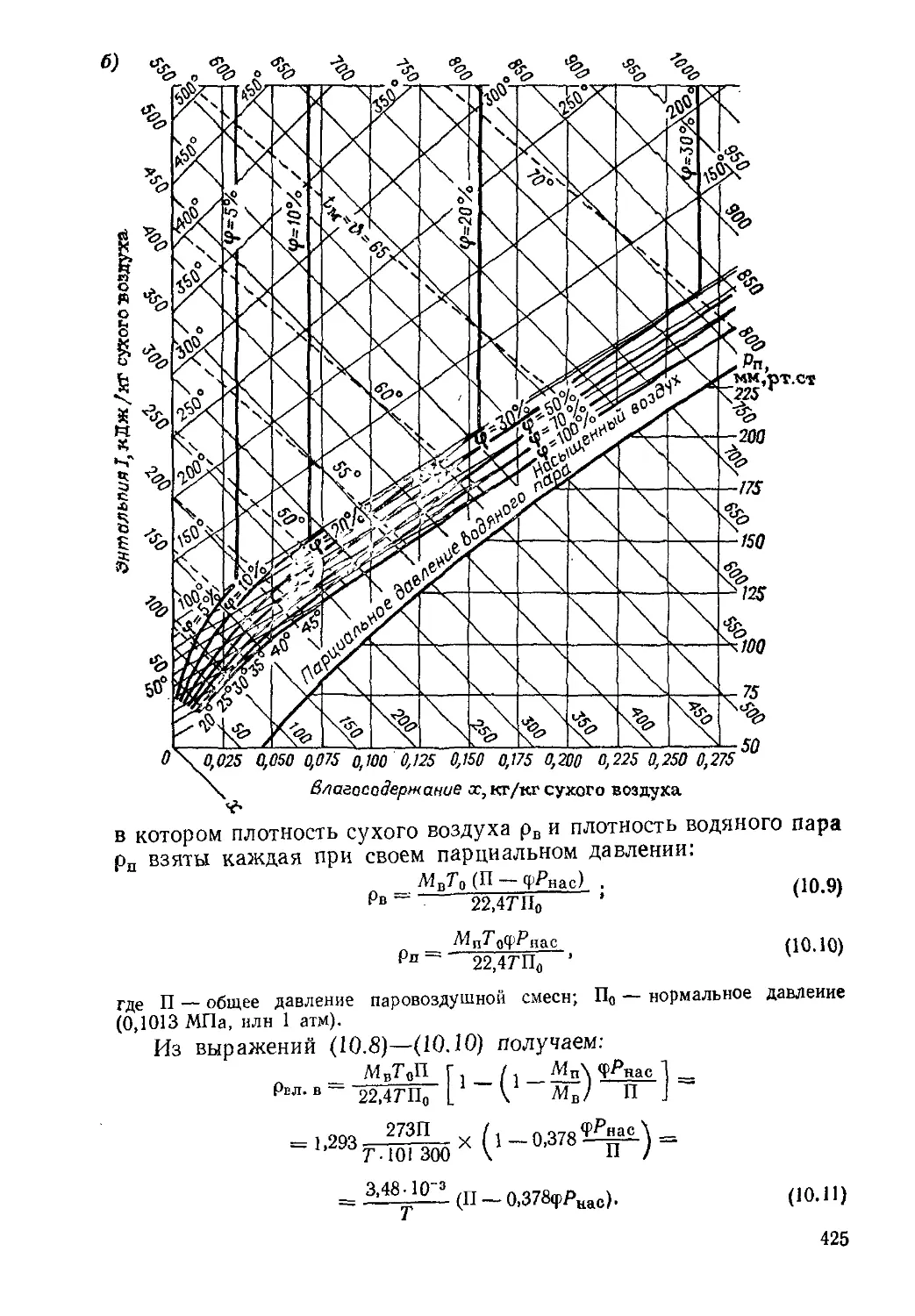
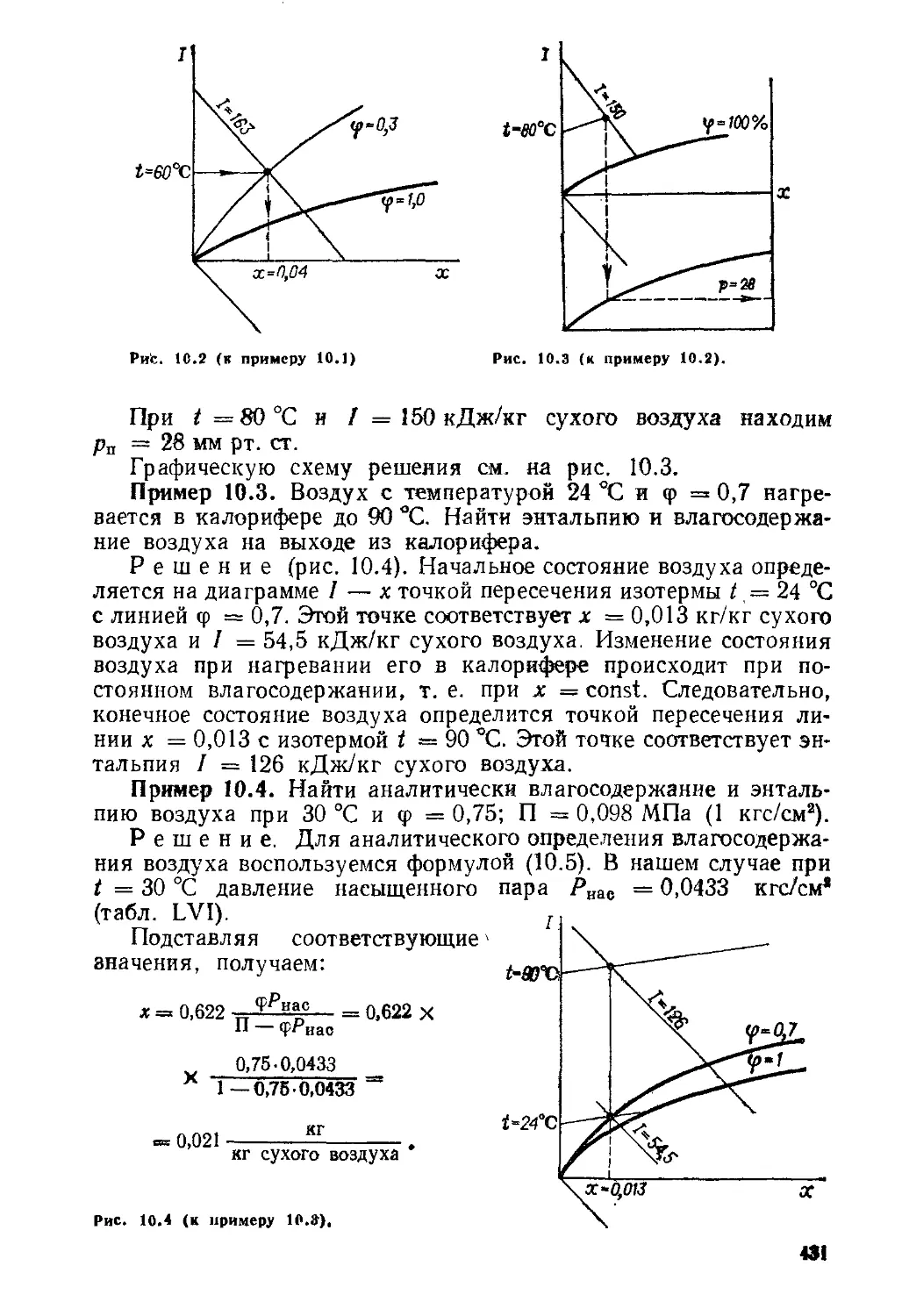
Примеры 430
Контрольные задачи 451
Пример расчета сушилки кипящего слоя для сушки хлористого калия 456
Пример расчета вальцовой сушилки 463
Глава П. Умеренное и глубокое охлаждение 465
Основные зависимости и расчетные формулы . 465
Примеры 470
Контрольные задачи 491
Ответы на контрольные задачи 495
Библиографический список 502
Приложение 510
ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
Курс «Процессы и аппараты химической технологии» является
ведущим в общеинженерной подготовке студентов и играет важную
роль в освоении ими специальных дисциплин. В своем
непрерывном развитии наука о процессах и аппаратах, обобщая
теоретические и экспериментальные методы исследования основных
процессов, является генератором новых идей, ускоряющих научно-
технический прогресс -химической технологии. В
Постановлении ЦК КПСС об основных направлениях экономического и
социального развития СССР на 1986—1990 годы и на период до
2000 года отмечается необходимость приоритетного расширения
и углубления фундаментальных исследований, а также таких форм
интеграции науки, техники и производства, которые позволяют
обеспечить быстрое прохождение научных идей от зарождения
до широкого применения на практике. Эти задачи успешно
решаются высшей школой при подготовке квалифицированных
инженерных кадров в соответствии с последними постановлениями
Партии и Правительства «Основные направления перестройки
высшего и среднего специального образования в стране».
В освоении учебной дисциплины «Процессы и аппараты
химической технологии», являющейся фундаментальной для химико-
технологического образования, существенное значение имеют
практические занятия по расчетной части курса. С этой целью
на кафедре процессов и аппаратов ЛТИ им. Ленсовета было
создано настоящее учебное пособие, которое от издания к изданию
обновляется. Книга служит естественным дополнением к
известному учебнику А. Г. Касаткина, подготовленному кафедрой
процессов и аппаратов МХТИ им. Д. И. Менделеева, и к ряду
современных монографий по отдельным разделам курса (в
соответствии с утвержденной Минвузом СССР программой).
Кроме того, кафедрой процессов и аппаратов ЛТИ им.
Ленсовета в развитие курса были созданы монографии
«Гидромеханические процессы химической технологии», «Теплообменные
процессы химической технологии», «Массообменные процессы (системы
с твердой фазой)».
Десятое издание отличается от предыдущего тем, что в него
внесены новые расчетные примеры основных типов аппаратов
(теплообменников, массообменных аппаратов) с применением ЭВМ.
5
Программы составлены на легко адаптируемом для различных
систем ЭВМ языке (ФОРТРАН-IV). Переработке подвергались
также главы 2—10. В новом издании особое внимание уделено
вопросам стандартизации.
В подготовке нового издания большая работа была
выполнена М. И. Курочкиной. За ценные советы по обновлению
информационного материала в отдельных главах этого учебного
пособия выражаю благодарность Н. В. Озеровой, А. А. Медведеву
и другим преподавателям нашей кафедры.
Выражаю признательность В. Н. Кисельникову за сделанные
замечания и высказанные пожелания.
П. Г. Ромашов
ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
И ЕДИНИЦЫ ИЗМЕРЕНИЯ
Величина
Обозначение
Вес
Влагосодержание воздуха
Влажность воздуха
относительная
Влажность материала
Время
Высота
Вязкости коэффициент-
динамический
кинематический
Давление, парциальное давление
Давление насыщенного пара
Давление смеси газов общее
Диаметр
Диффузии коэффициент
Длина
Концентрация (доля):
мольная
массовая
мольная относительная
массовая относительная
Концентрация объемная:
мольная
массовая
Масса мольная
Массоотдачи коэффициент
Массопередачи коэффициент
Местного сопротивления
коэффициент
Мощность
Напор:
скоростной
статический
Объем
Объем удельный
Объемного расширения
коэффициент
Р
X
Ф
U, tt*
т
/г, л
и
V
р
р
П
Z>, d
D
L, I
x, у
x, g
X, Y
X. 7
С
с
м
Рх> Ру
кх> ки
i
ы
- иск
ст
V
р
Единицы измерения
н
кг/кг
кг/кг
с, ч
м
Па* с
м*/с
Па
Па
Па
м
м*/с
м
кмоль/м3
кг/м3
кг/кмоль
кг/[м?*с(ед. дв. силы)];
кмоль/[м?-с (ед. дв. силы)]
кг/[м?-с(ед. дв. силы)];
кмоль/[м?*с (ед. дв. силы)]
Вт
м
м
М3, ДМ3, Л
м3/кг
к-1
Продол же н и е
Величина
Обозначение
Периметр
Плотность
Площадь поперечного сечения
Площадь поверхности
Полезного действия коэффициент
Порозность слоя
Производительность насоса,
вентилятора
Радиус
Расход:
массовый
объемный
Расхода коэффициент
Скорость
Скорость угловая
Температура
Температу ропровоДности
коэффициент
Теплоты расход
Теплоемкость удельная
Теплонапряжение, удельная
тепловая нагрузка
Теплоотдачи коэффициент
Теплопередачи коэффициент
Теплопроводности коэффициент
Теплота парообразования
удельная
Трения коэффициент
Флегмы число
Холодильный коэффициент
Частота вращения
Ширина
Энтальпия удельная
Единицы измерения
п
р
/, s
F
Ц
8
Q
R, г
G, L, М, W
V
а
w
(0
г, /, е
а
Q
с
я
а
К
1
г
к
R
8
п
В, Ь
Л i
м
кг/м3
м2
м?
м3/с. мз/ч
м
кг/о
м3/с
м/с
рад/с
К, °С
м2/с
Вт
Дж/(кг^К)
Вт/м2
Вт/(м2- К)
Вт/(м2-К)
Вт/(м-К)
Дж/кг
об/с, c~i
м
Дж/кг
ВВОДНЫЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Целевой установкой практических занятий по курсу процессов
и аппаратов является обучение студентов методике расчета и
проектирования химической аппаратуры путем рассмотрения
примеров и решения конкретных задач.
При расчете аппаратов приходится применять различные
физические величины, пользоваться данными о физических
свойствах веществ (плотность, вязкость, теплопроводность и т. п.).
Все эти величины могут быть измерены и выражены в тех или иных
единицах.
В СССР с 1 января 1980 г. принята для всех областей науки,
техники и народного хозяйства Международная система единиц
(СИ), основными единицами которой являются: длины — метр (м),
массы — килограмм (кг), времени — секунда (с), силы
электрического тока — ампер (А), температуры — Кельвин (К), силы
света — кандела (кд), количества вещества — моль. Кроме того,
стандартом предусмотрены две дополнительные единицы:
единица плоского угла — радиан (рад) и единица телесного угла —
стерадиан (ср).
Остальные единицы-производные образуются на базе
основных. Размер производных единиц определяется с помощью
физических уравнений, выражающих связь между
величинами.
Сопоставление важнейших единиц системы СИ с единицами
других систем и внесистемными дано в Приложении —
табл. LVIII.
Приступая к решению задачи, следует изобразить схему
устройства, обозначить на ней все размеры и величины, отметить
стрелками направления движения потоков и разобраться в
условиях работы установки.
Затем следует выписать все данные задачи, написать основные
расчетные уравнения, наметить путь решения, разбив задачу на
ряд частных вопросов, выписать нужные численные значения
различных физических свойств.
Подставив в расчетные уравнения числовые значения,
проверить правильность подстановки, после чего приступить к
арифметическим вычислениям.
9
Ответ следует подвергнуть критике с точки зрения соответствия
полученного результата практическим условиям работы
рассчитываемой установки или аппарата.
Полезно решить задачу в общем виде и исследовать
результаты, выясняя влияние тех или иных факторов, входящих в
условия задачи.
Во время групповых занятий студенты должны научиться
пользоваться основными справочниками, объединяющими опыт
большого числа исследователей и проектировщиков (Справочник
химика, Справочник физико-химических и технологических
величин Технической энциклопедии, Справочник механика
химического завода), а также ГОСТами и каталогами.
Выработка навыков к ведению технического расчета является
главной задачей расчетных упражнений по курсу. Погрешность
обычного инженерного расчета ~5%.
Применение персонального компьютера или
логарифмической линейки является обязательным. Несколько задач следует
решить с применением ЭВМ (составить программу) — см.
примеры расчетов в гл. 4, 7, 10.
Для более четкой проработки курса далесообразно иметь две
тетради: одну для групповых занятий, другую для
самостоятельной домашней работы — решения задач и зарисовки эскизов
главных аппаратов и нх деталей.
Отчетливое изложение, систематический ход вычислений,
аккуратность записи — условия, несоблюдение которых ведет к
непроизводительной трате времени студента и преподавателя.
В заключение рассмотрим несколько примеров на
установление единиц измерения и соотношений между ними.
1. Найти единицу измерения динамического коэффициента
вязкости в СИ.
Уравнение Ньютона для силы трения Р между параллельно
движущимися слоями жидкости имеет вид;
~ dw
где ц — динамической коэффициент вязкости; F — площадь трения; dmfdy —
градиент скорости.
Решив это уравнение относительно р, получаем следующую
единицу измерения р:
Pdy I Н-с-м Н-с „ кг-м^с кг
* ' - — = Па-с= —
w-[tS]-
м2 • м м2 с3 • ма м. с
2. Найти единицу измерения коэффициента теплопроводности
в СИ.
Для установления теплового потока Q через однородную
плоскую стенку можно написать:
10
где к — коэффициент теплопроводности; б — толщина стенки; F —
поверхность, через которую передается теплота; А* — разность температур по обе
стороны стенки.
Решив это уравнение относительно Я, получим:
Дж
m - \MJ\ - с М Вт_
1Л]" IF M У~" м2-К " м-К '
3. Найти соотношение между единицами измерения
динамического коэффициента вязкости в системах СИ и СГС;
1Па-с ~1-?-« *?00г ю ю —Е— д юп = 1000сП;
м-с 100-см-с см-с
1 сП= 10-3Па.с=э 1мПа-с.
4. Установить соотношение между единицами измерения коэф-
А ккал Вт
фициента теплопроводности м q ос и -jj7]r:
, ккал 4190Дж , 100 Вт
м-ч-°С м*3600-с-К ' м-К #
5, Исходя из того, что 1 английский фунт = 0,454 кг и 1 °С *=«
= 1,8 °F, установить соотношение между BTU (британской
тепловой единицей), ккал и Дж; 1 BTU—это количество теплоты,
которое нужно затратить, чтобы нагреть 1 фунт воды на 1 °F.
Удельная теплоемкость воды в британской системе единиц с —
— 1 вти
— * lb-°F"
Искомое соотношение найдем G помощью известной формулы:
Q«cAf (*, — *!),
где Q — количество теплоты, затраченное на нагревание М кг воды; с —
удельная теплоемкость воды; t±. и t% — начальная и конечная температуры.
Из уравнений
Q «1 ^Т0р 1 lb. 1 °F ~1 BTU
и
Q = 1 ™* о,454 кг -rV °C - 0,252 ккал
КГ * V_* 1 j О
следует, что 1 BTU = 0,252 ккал.
Так как 1 ккал = 4190 Дж. то 1 BTU = 0,2524190 Дж =
= 1055 Дж.
RTII
6. Выразить коэффициент теплопередачи К = 50f,2 . ор в
Вт
Поскольку 1 BTU = 1055 Дж; 1 ft = 0,305 м; 1 °F = 0,56 К, то.
К~50 пс f^f лш/ = 50.5,6 Д^.Ш Вт
(0,305м)2-3600 с-0,56К ' м2.оК ~ м2-К
11
Глава 1
ОСНОВЫ ПРИКЛАДНОЙ ГИДРАВЛИКИ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Удельный вес (вес единицы объема) у и плотность (масса
единицы объема) р связаны зависимостью:
Y^pg. (l.l)
где g — 9,81 м/с2 — ускорение свободного падения.
Так как в СИ за единицу массы (кг) принята масса некоторого
эталона, а в технической системе (МКГСС) за единицу силы (кгс)
принят вес этого же эталона, то плотность в единицах СИ (кг/м3)
численно равняется удельному весу в единицах системы МКГСС
(кгс/м3).
Относительной плотностью (относительным удельным весом) Д
называется отношение плотности (удельного веса) вещества к
плотности (удельному весу) воды:
Д «- Р/Рв « Y/Yb- (1.2)
В интервале температур от 0 до 100 °С плотность воды рв с
достаточной для технических расчетов точностью можно считать
равной рв ~ 1000 кг/м3.
Плотность смеси жидкостей, при смешении которых не
происходит существенных физико-химических изменений, приближенно
можно рассчитать, принимая, что объем смеси равен сумме объемов
компонентов:
1 - *г +4г-+..м (1.3)
PCM Pi Рй
где Jet, х2, ... — массовые доли компонентов смеси; pCMl pf, р2, ... —
плотности смеси и ее компонентов.
По аналогичной формуле
1 * +1РА (1-4)
Ро Ртв Рж
рассчитывают плотность суспензии рс.
Здесь х —массовая доля твердой фазы в суспензии; ртв и рж — плотности
твердой и жидкой фаз.
12
2. На основании уравнений Клапейрона *, плотность р любого
газа при температуре Т и давлении р может быть рассчитана
по формуле:
где р0 = Л1/22,4 кг/м3 — плотность газа при нормальных условиях**; М —
мольная масса газа, кг/кмоль; Т — температура, К.
Давление р и р0 должны быть выражены в одинаковых
единицах.
Плотность смеси газов:
Рем = УФ1 + УгРъ + • • ¦»
где #1, #2» • •• —объемные доли компонентов газовой смесн; р{, ра, *.. —
соответствующие плотности компонентов.
3. Давление р столба жидкости высотой h при плотности
жидкости р равняется:
P = pgfc. (1.6)
Здесь р выражено в Па; р — в кг/м3; g — в м/с?; h — в м.
Исходя из этого уравнения, получаем следующие соотношения
между единицами давления:
1 атм = 760мм рт. ст. = pgft = 13 600-9,81-0,76 = 1,013-10$ Па =
= 1,033* 10* мм вод. ст. = 1,033-10* кгс/м2 = 1,033 кгс/см2;
1 кгс/см2 = 104 кгс/м2 = 9,81 • 104 Па =735 мм рт. сг. = 104 мм вод. ст.
4. Основное уравнение гидростатики:
P = Po + №h> (1.7)
где р — гидростатическое давление на глубине h (в м) от поверхности
жидкости, Па; р0—давление на поверхность жидкости, Па.
Сила давления жидкости на плоскую стенку Р (в Н);
P = (Po + Pghc)F, (1.8)
где А) — давление иа поверхность жидкости, Па; /?с — глубина погружения
центра тяжести стенки под уровнем жидкости, м; р — плотность жидкости,
кг/м5; F — площадь поверхности стенки, м2; g= 9,81 м/с? — ускорение
свободного падения.
* В уравнении Клапейрона для I кмоль газа pv =» RT газовая постоянная
о__ Ро^о 760-133,3.22,4 .... _ ,. ...
а = -х~ «=• %=% = 8310 Дж/(кмоль'К).
¦/ о Но
** Т. е. при Г0 = 0 °С = 273,15 К н р0 = 760 мм рт. ст. = 1,013' 105 Па.
13
ста *:
коэффидие)
г . Не „ кг .
г — кгсс
иммкгес — j^2—•
Г 1 ДИН-С Г „
1ц]гГГ = з— = = II (пуаз).
^ CI с см2 см.с \ j /
Соотношение между обычно применяемыми единицами
измерения \i:
Кинематический коэффициент вязкости v (в м*/с) связан с
динамическим коэффициентом вязкости \i соотношением:
v = p/p (1.9)
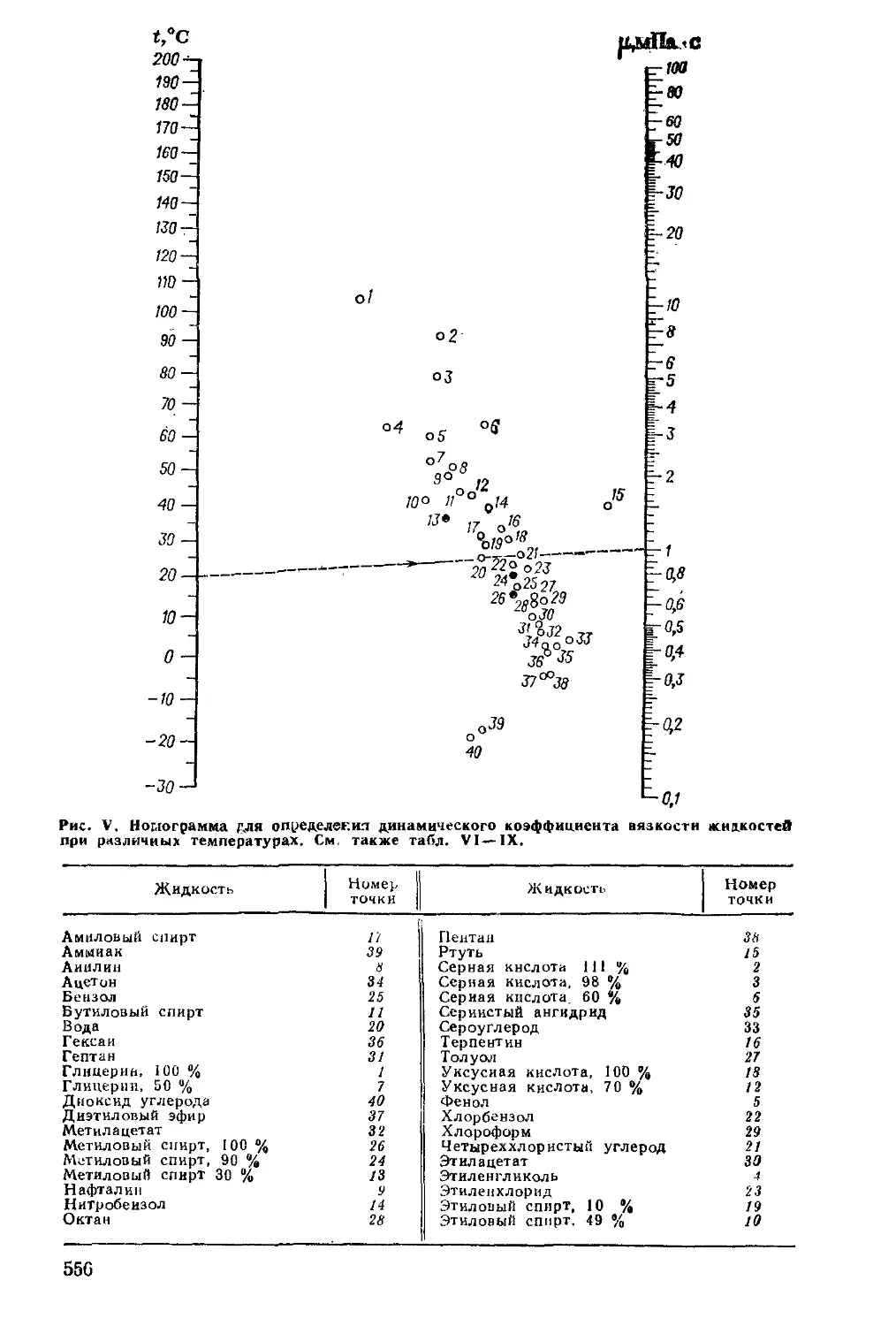
6 . Значения \i для жидкостей при различных температурах
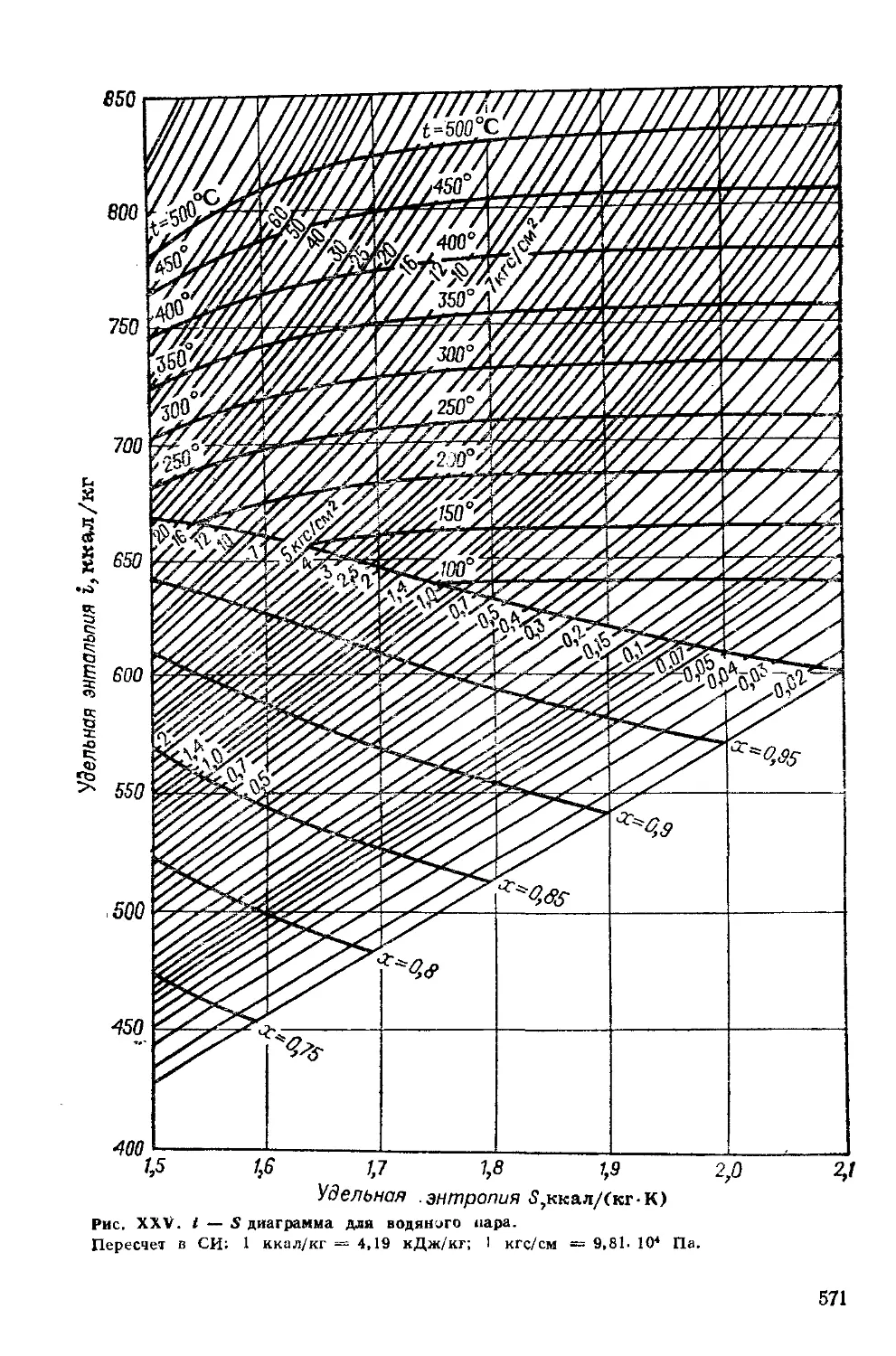
можно определить по номограмме, приведенной на рис. V (см.
Приложение).
При отсутствии экспериментальных данных динамический
коэффициент вязкости многих органических жидкостей (при
20 °С) приближенно может быть вычислен по следующей
эмпирической формуле:
lg(lgH) = QM*-f Sp)-^—2>9* <110>
где ц — динамический коэффициент вязкости жидкости при атмосферном дав-
лении и 20 °С, мП; р — плотность жидкости, кг/м3; М—мольная масса,
кг/кмоль; А — число одноименных атомов в молекуле органического
соединения; п — численное значение атомной константы; р — поправка на
группировку атомов и характер связи между ними.
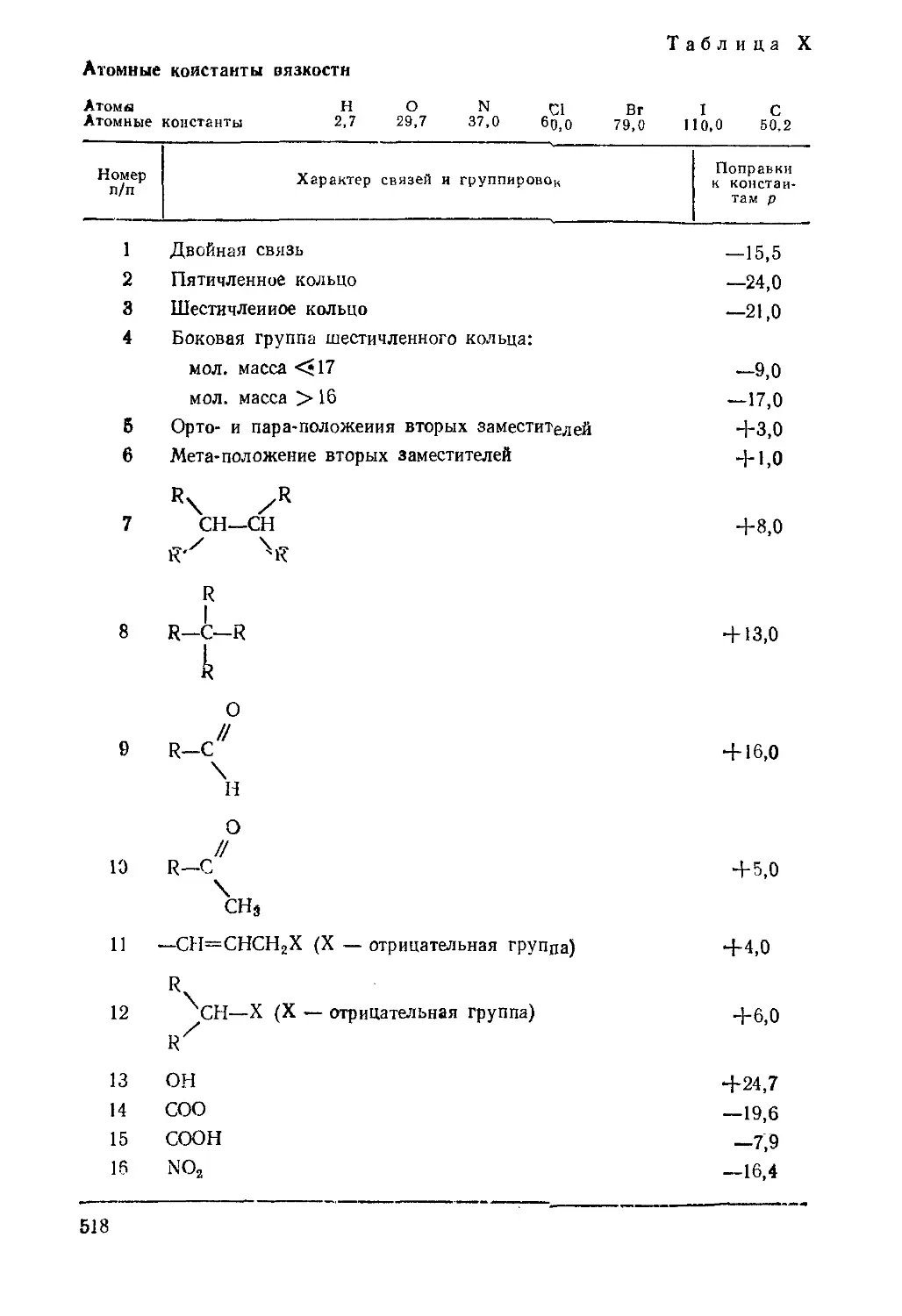
Атомные константы п и численные значения поправок р
приведены в табл. X (см. Приложение).
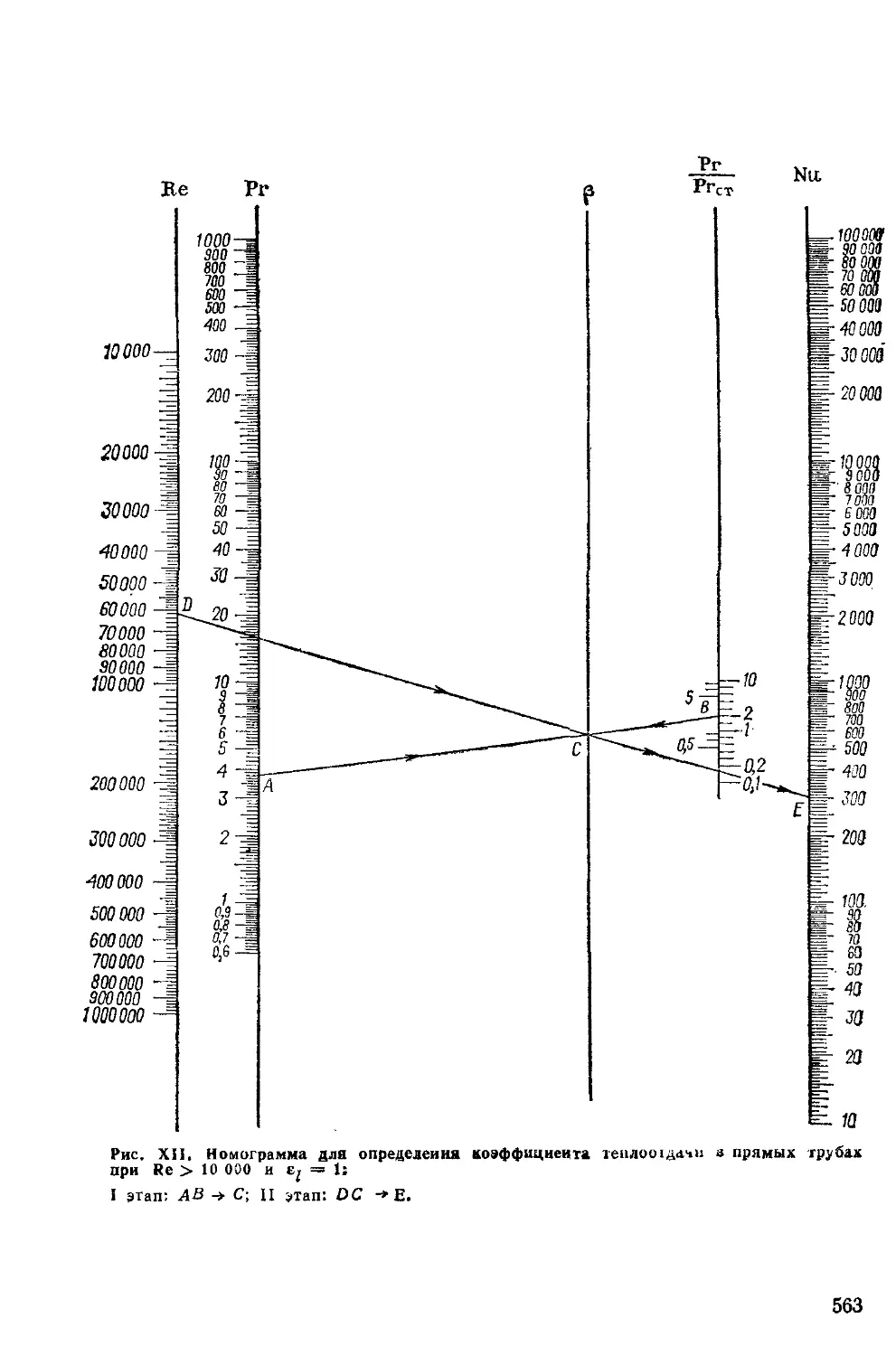
Для определения \х по уравнению (1.10) удобна номограмма
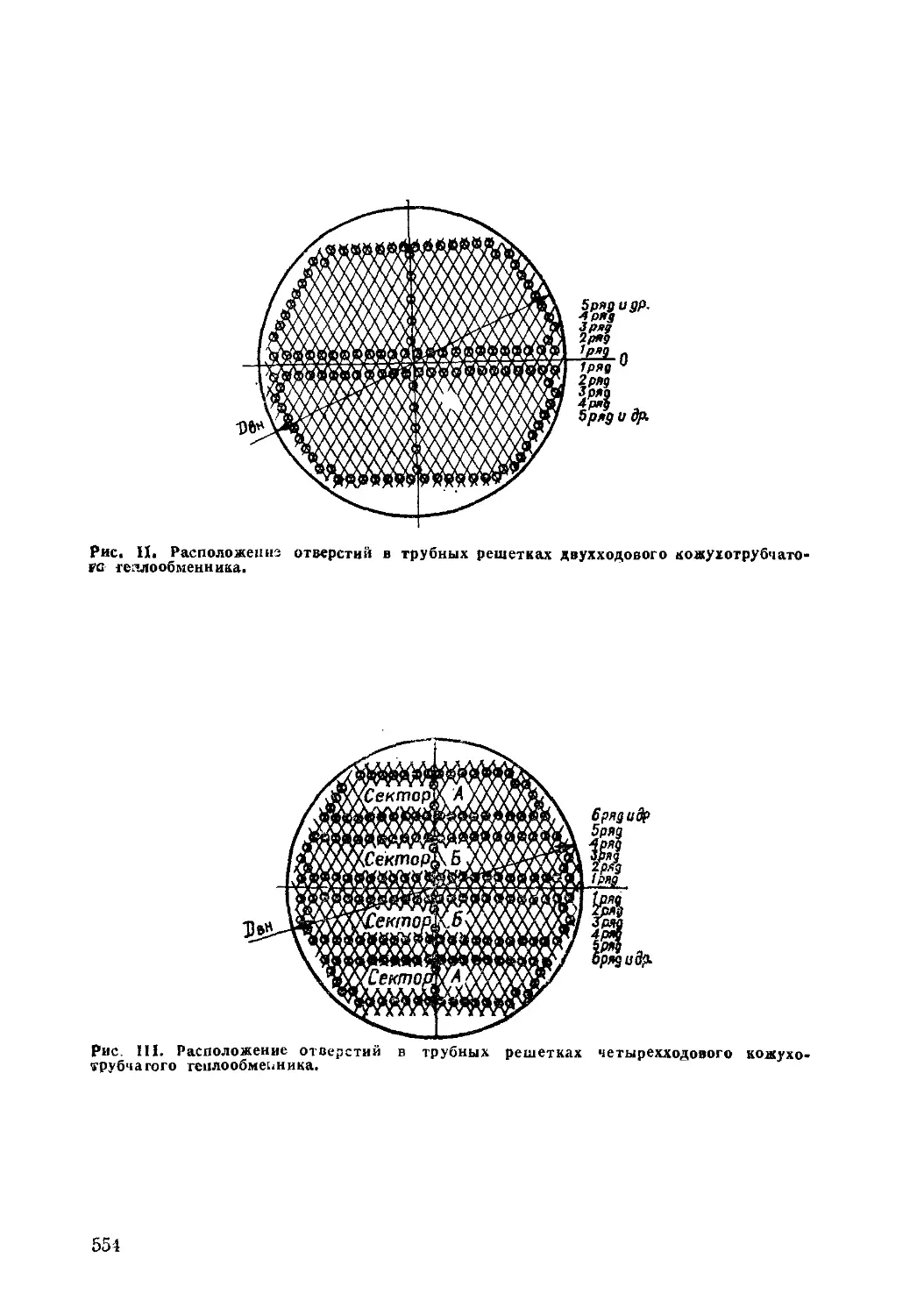
(рис. I, стр. 553), на которой величина lg (lg \i) обозначена через у.
Если у — величина положительная, следует пользоваться правой
шкалой, при отрицательном значении у — левой. Каждому
значению у соответствует значение \i — динамический коэффициент
вязкости жидкости при 20 °С.
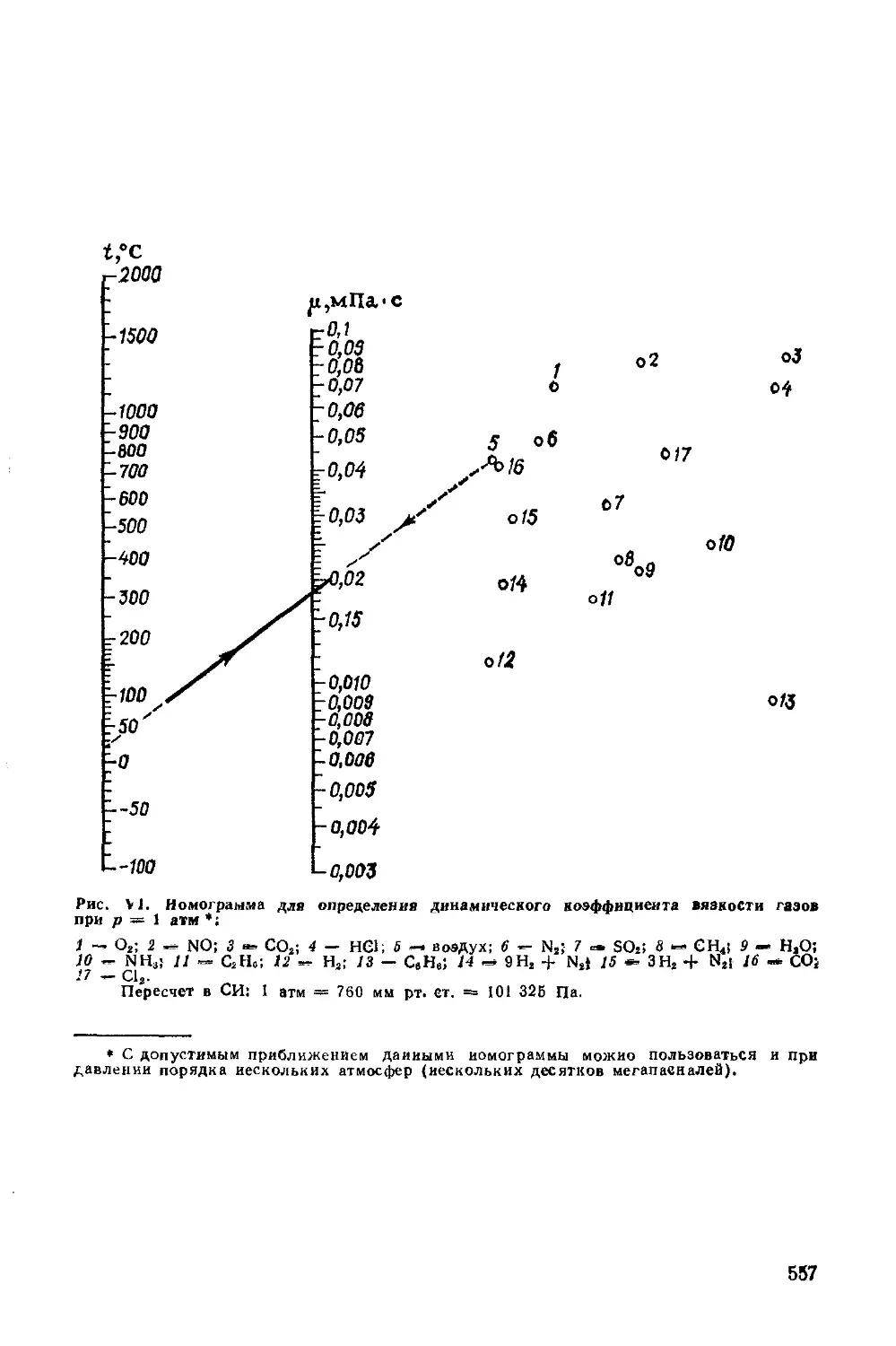
7. Для определения динамического коэффициента вязкости
газов при различных температурах можно использовать
номограмму, приведенную на рис. VI.
* Часто динамический коэффициент вязкости сокращенно называют просто
вязкостью.
И
Динамический коэффициент вязкости газовых смесей может
быть вычислен по приближенной формуле:
jES!LteJ?i^ + jM!5.+ ...t (1.11)
Цсм Ц1 йа
где Мсш> Mf, М2, ..., — мольные массы смесн газов н отдельных компонентов;
Иом' f*i» 14. ...—соответствующие динамические коэффициенты вязкости;
i*i* У%> -•• — объемные доли компонентов в смесн.
Для вычисления р.см для газов применяется также следующая
эмпирическая формула, проверенная на ряде газовых смесей
(коксовый газ, генераторный газ и др.) при атмосферном
давлении:
УМ УМгТкр + y2\h VM2TKV + ...
Цсм г У * • <1Л2>
Ух V МХА Крг +ЙК м*1 кр
2
Здесь цом — динамический коэффициент вязкости смеси при температуре i;
jij, ца, ... — динамические коэффициенты иязкостн компонентов при
температуре t\ tfi, y2, .*., — объемные доли компонентов; Afjf AfSt.»« — мольные массы
компонентов; Г , Т , ... — критические температуры компонентов, К#
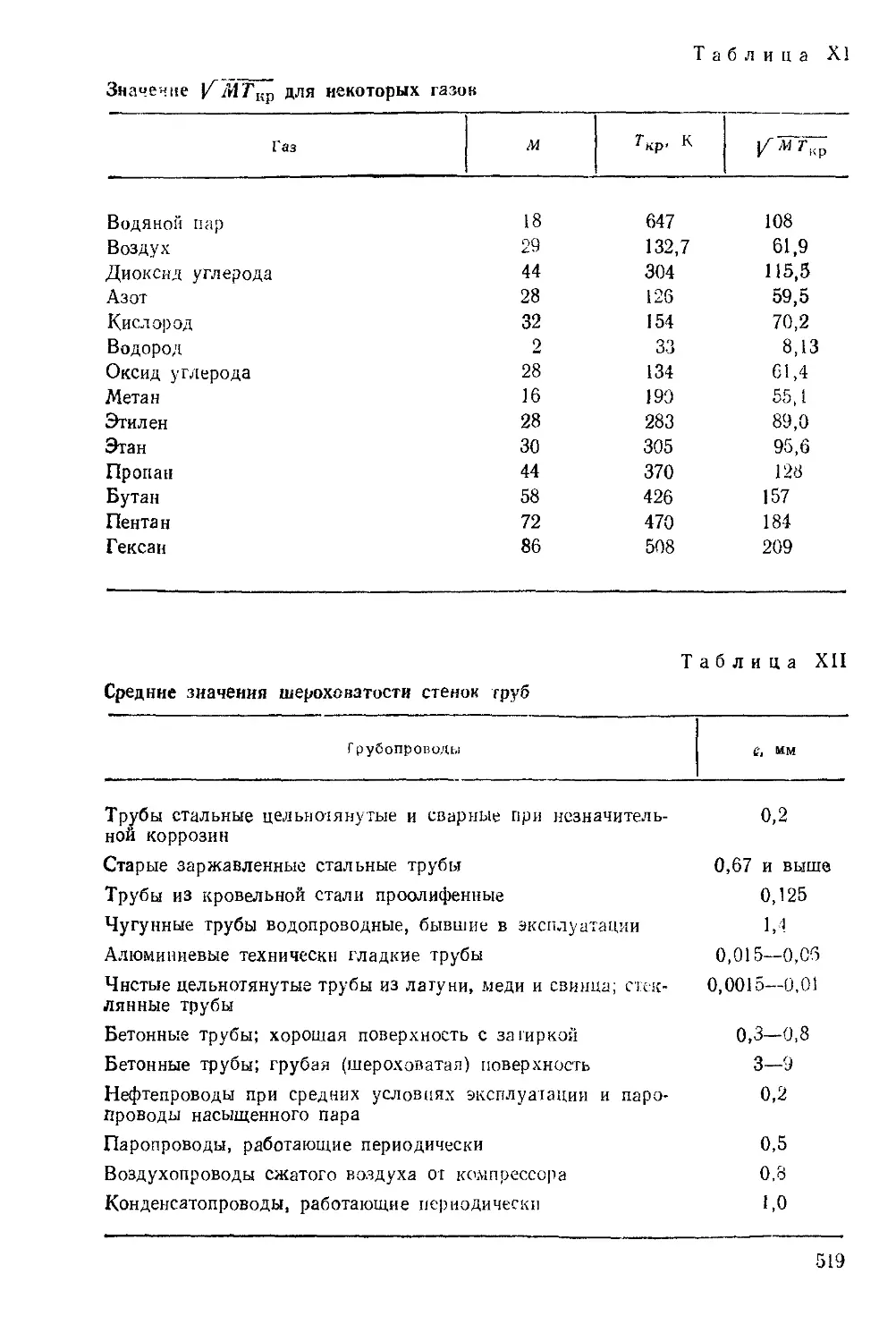
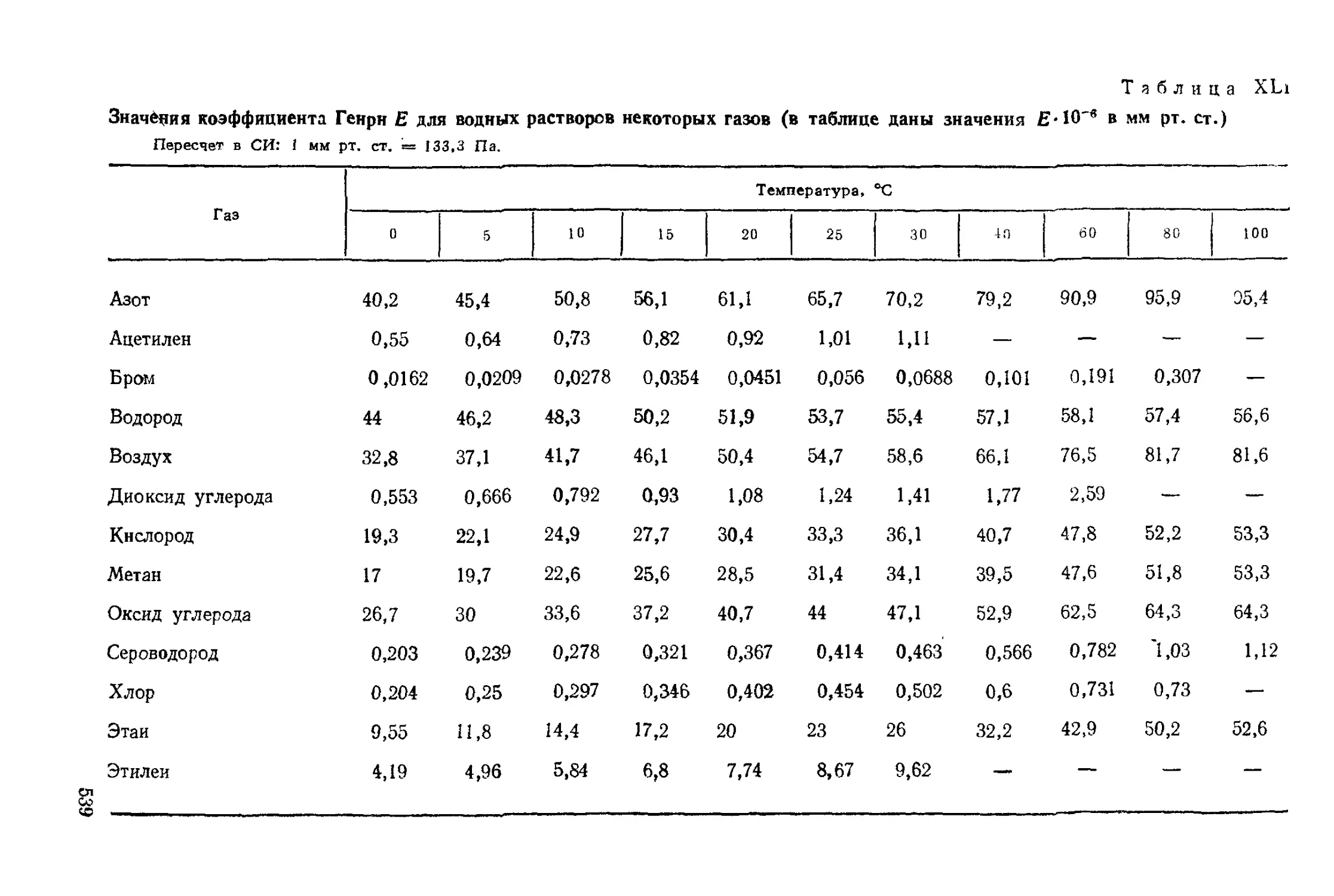
В табл. XI^ приведены значения ^MTKV для различных
газов.
Изменение динамического коэффициента вязкости газов с
температурой выражается формулой:
273 +С / Г \3/2
Р'"** Т + С V"273") ' (1ЛЗ)
где Мю — динамический коэффициент вязкости при О °С; Г — температура, К;
С — постоянная Сатерленда [13, т. 1J—см. табл. V.
8. Для смеси нормальных (неассоциированных) жидкостей
значение ц,оМ может быть вычислено по формуле:
крсм=*Ч tem +*2 igfia + •••» (Ы4)
где щ, ц2, .,.—динамические коэффициенты вязкости отдельных компонентов;
Ч* хъ> ••• — мольные доли компонентов в смесн.
В соответствии с аддитивностью текучестей компонентов
динамический коэффициент вязкости смеси нормальных жидкостей
определяется уравнением:
i х* х*
*- + -ТГ-+"-» O-Ua)
И~СМ ^1 Ц2
где xyj, x0a, ... — объемные доли компонентов в смеси.
Динамический коэффициент вязкости разбавленных суспензий
ц0 может быть рассчитан по формулам:
прн концентрации твердой фазы менее 10% (об.)
Не = Цж U + 2,5<р); (1.15)
15
при койцёнтрации твердой фазы до 30% (об.)
_ 0,59
Цс-Цж (0(77__ф)2 > И-™)
Здесь цж — динамический коэффициент вязкости чистой жидкости; <р —
объемная доля твердой фазы в суспензии.
9. Для нахождения динамического коэффициента вязкости
жидкости по динамическому коэффициенту вязкости эталонного
вещества может быть применено правило линейности однозначных
химико-технологических функций, установленное К. Ф.
Павловым. На основании правила линейности получаем *:
e^'Ze1*' =ft = const, (i.i6)
где t„ и t„ — температуры жидкости; @ц и В — температуры эталонного
вещества, при которых его динамические коэффициенты вязкости равны
соответствующим динамическим коэффициентам вязкости жидкости щ и ц2.
Для многих жидкостей зависимость между lg \i и 1/77
практически линейна:
lgfi = a + ^r-, (1.16а)
где а и Ь — индивидуальные константы жидкости; Т — температура, К.
Как следует из последнего уравнения, будет линейна и
зависимость между логарифмами динамических коэффициентов
вязкости двух жидкостей А и В (при одинаковых температурах):
^а.г.-ЧИа.г. =const>
При приближенном расчете динамических коэффициентов
вязкости жидкостей по правилу линейности результаты будут тем
надежнее, чем ближе по своей физико-химической природе две
сопоставляемые жидкости (водные растворы солей — вода,
предельные углеводороды — гептан и т. п.).
10. Уравнения расхода.
Объемный расход жидкости или газа V (в m*/c)s
V**wf. (1.17)
Массовый расход жидкости или газа М (в кг/с):
M = Vp = wfp. (1,18)
Здесь / — площадь поперечного сечения потока, м?; w — средняя скорость
потока, м/с; р — плотность жидкости или газа, кг/м8.
Для трубопровода круглого сечения уравнение (1.17)
принимает вид:
V = 0J85d*w,
где d — внутренний диаметр трубы, м.
* Это соотношение экспериментально было найдено А, Портером.
16
Таблица 1.1
Поток
w, м/с
Газы при естественной тяге 2—4
Газы при атмосферном или близком к нему давлении в вентиляцион- 5—20
ных газоходах и трубопроводах
Жидкости при движении самотеком 0,1—0,5
Жидкости в напорных трубопроводах 0,5—2,5
Водяной пар при абсолютном давлении рабс:
>4,9.104 Па (0,5 кгс/см2) 15—40
(1,96-4,9). 10* Па (0,2—0,5 кгс/см2) 40-60
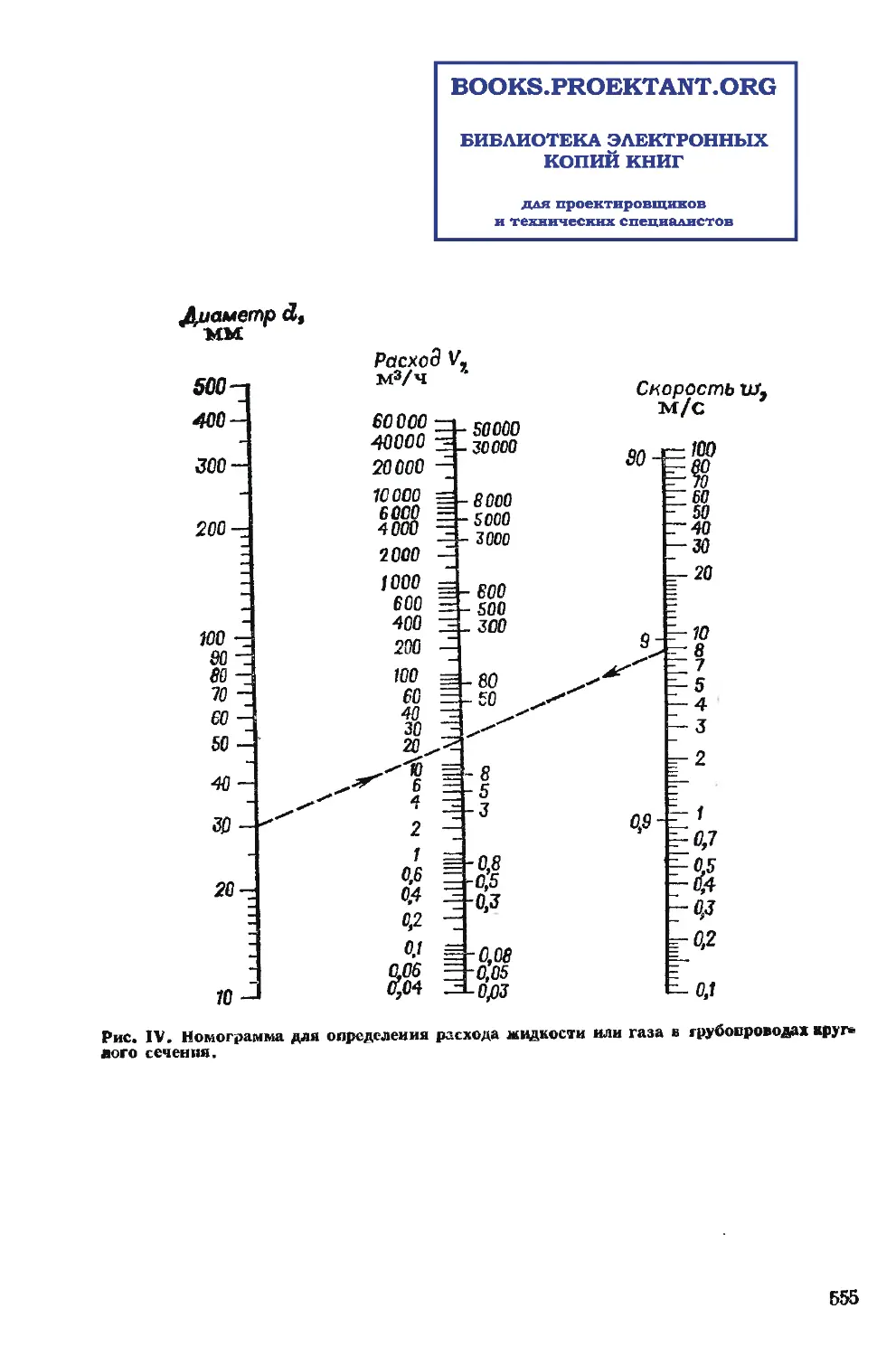
При заданном расходе V и принятой скорости w диаметр
трубопровода определяется по уравнению:
По этому уравнению построена номограмма (рис. IV).
Ориентировочные значения скоростей, принимаемых при
расчетах внутризаводских трубопроводов, приведены в табл. 1.1.
Уравнение неразрывности (сплошности) для несжимаемой
жидкости, протекающей по трубопроводу переменного сечения:
V = wjx = wj2 = w3fs = ... (1.20)
II. Основные критерии гидродинамического подобия потоков,
протекающих по трубам и каналам.
Критерий Рейнольде а, характеризующий
гидродинамический релшм и являющийся мерой отношения сил инерции
и внутреннего трения в потоке:
Re « wdp/ц = wd/v, (1.21)
где w — средняя скорость потока, м/с; d — диаметр трубопровода, м; р —
плотность жидкости, кг/м3; ц—динамический коэффициент вязкости, Па*с; v —
кинематический коэффициент вязкости, м2/с.
Для потоков, проходящих по прямым трубам, характерны
следующие значения критерия Рейнольдса:
Ламинарное течение Re<3 2300
Переходная область 2300<3 Re<3 10 000
Развитое турбулентное течение Re> 10 000
Для потоков, проходящих по изогнутым трубам (змеевикам),
критическое значение ReKp выше, чем в прямых трубах, и зависит
от отношения d/D, где d — внутренний диаметр трубы змеевика,
D — диаметр витков змеевика. Эта зависимость представлена
на рис. 1.1.
Для потоков некруглого поперечного сечения в выражение
для Re подставляется эквивалентный диаметр, равный
учетверенному гидравлическому радиусу.
17
8000
Рис. 1.1. Зависимость Re в
змеевиках от отношения d/D.
Гидравлический
радиус гг представляет собой
отношение площади
поперечного сечения' потока
/ к омываемому потоком
О—ioi 0,02 0,03 0,04 0,05 ofie 0,07 (смоченному) периметру П:
d/D
гг = //П. (1.22)
Для трубы круглого сечения, сплошь заполненной жидкостью:
iuP __ d
(1.23)
Следовательно, для потоков некруглого сечения вместо
диаметра можно применять эквивалентный диаметр:
<f,« 4гг = 4//П. (1.24)
Критерий Фруда, являющийся мерой отношения сил
инерции и тяжести в потоке:
ш2
Fr =
в*
(1.25)
где g — ускорение свободного падения, м/с?.
Критерий Эйлера, являющийся мерой отношения сил
давления и инерции в потоке:
Еи =
рад2
(1.26)
где Др — разность давлений (потеря давления, затраченного на преодоление
гидравлического сопротивления), Па.
12. Уравнение Бернулли для невязкой (идеальной)
несжимаемой жидкости:
2l +
Pi
+
w\
= г2 +
Р2
+
Wi
Для вязкой (реальной) несжимаемой жидкости!
Pi . w'i и - . Р2
(1.27)
*i +
+
2g
— hu = гг +
+
w\
(1.27а)
9ё Ч ~ " ' 9g ' 2g
Здесь г— геометрический (высотный) напор, м; pj{pg) — пьезометричесиий
(статический) напор, м; w2/(2g) — скоростной (динамический) напор., м; Лп—
напор, потерянный на преодоление сопротивлений, м.
S3. Зависимость между средней скоростью w и максимальной
(осевой) скоростью &'макс в трубопроводе:
а) при ламинарном режиме w = 0,5шмакс;
б) при турбулентном режиме отношение w/wMaK0 зависит от
величины критерия Re = wmKGdp/\i (рис. 1.2).
Приближенно при турбулентном режиме w — (0,84-0,9) йУМакс*-
* При больших значениях Re отношение w/wMaKQ может быть и выше 0,9.
18
Рис. 1.2. Зависимость отношения w/wMaK0 qg
or критерия Re. '
Л
14. Скорость истечения жид- ^ о,7
кости w (в м/с) из малого от- ">
верстия в дне или в стенке со- °>s ~
суда при постоянном уровне д5
жидкости в сосуде:
W
= Ф^2#Я, (1.28)
где (р — коэффициент скорости, безразмерный; g — ускорение свободного
падения, м/с2; Н — высота уровня жидкости над центром отверстия, м.
Если давление на поверхности жидкости в сосуде (/?0, Па)
и давление в пространстве, куда вытекает струя (/?, Па),
неодинаковы, то в формулу (1.28) вместо Н надо подставить величину
Я' = Н + Ро~~р , где р — плотность вытекающей жидкости,
го
кг/м3.
Объемный расход жидкости V (в м3/с), вытекающей через
отверстие площадью /0 (в м2), при постоянном уровне жидкости
в сосуде и при р0 = р составляет:
V~ahV2gH. (1.29)
Здесь а — безразмерный коэффициент расхода, представляющий собой
произведение коэффициента скорости q> и коэффициента сжатия струи е:
а = ф8. (1.30)
15. Время опорожнения т (в с) открытого сосуда, имеющего
постоянную площадь поперечного сечения /, через отверстие
площадью /0 может быть подсчитано по уравнению:
2/ Уй
где Н — начальный уровень жидкости над отверстием, м.
16. Измерение расхода жидкости или газа нормальной
диафрагмой (рис. 1.3).
Объемный расход жидкости или газа V (в м3/с):
V = akU V2-J~= ^о УЧИ *2=2- • (1.32)
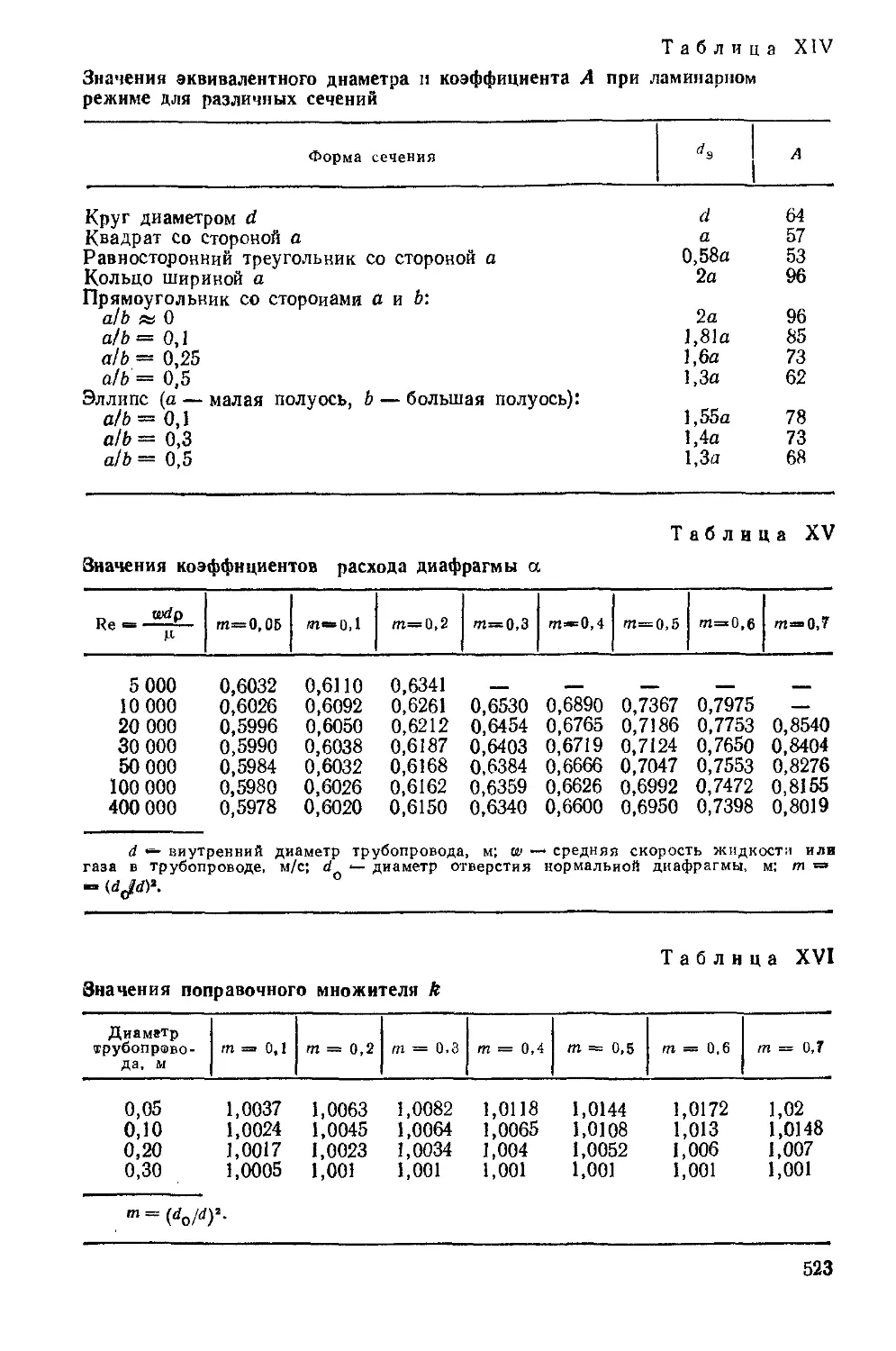
где а — коэффициент расхода нормальной диафрагмы в гладком
(нешероховатом) трубопроводе (табл. XV); к— поправочный множитель, учитывающий
-шероховатость стенок трубопровода (средние значения к для трубопроводов
приведены в табл. XVI; для гидравлически гладких трубопроводов к~ 1);
/о == 0,785rfg — площадь отверстия диафрагмы, м'2; dQ — диаметр отверстия, м;
Н — разность уровней жидкости в дифманометре, присоединенном к диафрагме, м;
рм — плотность жидкости в дифманометре, кг/м3; р — плотность жидкости
(или газа), протекающей по трубопроводу, кг/м3.
19
г-
I-
.J ll.jh. .!¦—.!.
Рис. 1,3, Схема измерения расхода с помощью диафрагмы.
Рис. 1.4. Схема измерения скоростного давления с помощью трубы Пито—Прандтля*
Так как коэффициент расхода диафрагмы а зависит от Re =
= t?)d/v, а значение. Re заранее неизвестно, то при измерении
расхода У следует принять по табл. XV среднее значение а для
данного т. Затем, вычислив V, определяют значение Re,
уточняют величину а и, если нужно, корректируют расчет.
17. Измерение расхода жидкости или газа с помощью пневмо-
метрической трубки Пито — Прандтля (рис. 1.4).
Трубку Пито — Прандтля устанавливают точно по оси
трубопровода и при помощи присоединенного к ней дифманометра
находят величину Ар = Н (рм — р) g — Д/?Ск. Затем
рассчитывают максимальную (осевую) скорость потока аймаке —
.= V^2gH (pM — р)/р, определяют величину Re = wMaKCdp/\i и по
графику (рис. 1.2) находят отношение ш/шмакс, из которого
вычисляют среднюю скорость w.
Расход жидкости или газа определяют по формуле (1.17):
где f — площадь поперечного сечения трубопровода, м2.
18. Мощность N (в кВт), потребляемая двигателем насоса
(или вентилятора), рассчитывается по формуле:
V Ар VpgHn
N
(1.33)
1000т) Ю0ОП
Здесь V — объемный расход жидкости или газа, м3/с; Др — повышение
давления, сообщаемое насосом (вентилятором) перекачиваемому потоку и равное
полному гидравлическому сопротивлению сети*, Па; Нн — напор, создаваемый
* Сетью называется та система трубопроводов и аппаратов, через которую
насос (вентилятор) прокачивает жидкость (газ). Давление, полученное жидкостью
от насоса, полностью расходуется на преодоление всех гидравлических
сопротивлений сети.
20
насосом, м; р — плотность жидкости, кг/м3; g = 9,81 м/с2 — ускорение
свободного падения; г\ — общий к. п. д. насосной (вентиляционной) установки —
см. формулу (2.4).
При перекачивании жидкостей насосами уравнение (1.33)
справедливо при любых Ар, а для газов лишь при Ар < 0,981 X
X I04 Па, или 0,1 кгс/см2 (вентиляторы). Если для газов Ар ?>
6> 0,981 -104 Па (газодувки, компрессоры), то расход энергии
подсчитывается по термодинамическим формулам — см. гл. 2.
При расчете по уравнению (1.33) мощности, потребляемой
насосом или вентилятором, величину Ар, равную полному
гидравлическому сопротивлению сети, подсчитывают как сумму
следующих слагаемых:
АР = АРик + Артр + ЛРм. с + АрПод + Ард0п. С1-34)
где Арск — затрата давления на создание скорости потока на выходе из сети
(скорость в пространстве всасывания равна нулю); Дртр — потеря давления на
преодоление сопротивления трения; &pMi 0 — потеря давления на преодоление
местных сопротивлений; Арпод = pghn0R — затрата давления на подъем
жидкости; Ардоп = р2 — рг — разность давлений в пространстве нагнетания (р2)
и в пространстве всасывания (pt),
19. Затрата давления на создание скорости потока:
АРск-^Р/2, (1.35)
где w — скорость потока в трубе, м/с; р — плотность жидкости (газа), кг/м3.
20. Потеря давления на трение в прямых трубах и каналах.
А. Изотермический поток (рис. 1.5 и 1.6).
Температура протекающей по трубе жидкости (газа) постоянна.
Расчетная формула:
Ар^^Х — ^-9 (1.36)
или в критериальной форме (для данной шероховатости стенки
трубы):
Eu = CRemr. (1.37)
В этих формулах к — коэффициент трения, безразмерный (его значение
в общем случае зависит от режима течения и шероховатости стенки трубы е)\
dg —эквивалентный диаметр, м (для трубы круглого сечения d^ = d)'f L —
длина трубы, м; w — скорость потока, м/с; р — плотность жидкости или газа,
кг/м3; Ей — Дртр/(рша); Re = wd9pl\i\ Г — Шэ.
Значение коэффициента трения К определяют по данным
рис. 1.5 * и 1.6 или по нижеследующим формулам.
/. Ламинарное течение (Re < 2300). Коэффициент К не
зависит от шероховатости стенки трубы, а зависит только от Re:-
для труб круглого сечения
b = 64/Re; (1.38)
* На рис. 1.5 пунктиром показана граница так называемой автомодельной
области, в которой коэффициент трения X не зависит от критерия Re и
определяется только величиной отношения djet
21
//. Турбулентное течение (Re t> 2300). 1. Гидравлически
гладкие трубы (стеклянные, медные, свинцовые):
X = 0,316/Re0.254 (1<40)
Формула (1.40) действительна при Re < 100 000.
2. Гидравлически шероховатые трубы (стальные, чугунные).
Безразмерной геометрической характеристикой
гидравлически шероховатых труб кроме отношения L/dQ является
относительная шероховатость, т. е. отношение средней высоты выступов
(бугорков) е на стенках трубы к ее эквивалентному диаметру йэ:
&=e/dQ. (1.41)
Применяется также и обратная величина (dje).
Ориентировочные средние значения шероховатости стенок труб
е (в мм) приведены в табл. XII.
Формула для расчета коэффициента трения К в шероховатых
трубах
применима и для автомодельной области, если второе слагаемое
в квадратных скобках приравнять нулю.
Б. Неизотермический поток.
При неизотермическом течении, когда протекающая по трубе
жидкость нагревается или охлаждается (температура стенки
трубы отличается от температуры жидкости), следует правые части
формул (1.38) и (1.40) умножать на безразмерные поправочные
коэффициенты х [4.1]:
для ламинарного режима
'-(-?а-П'+¦•»№)"•*
для турбулентного режима в технически гладких трубах
*-(-№
где Иеж, Ргж, Gr^ — критерии Рейнольдса, Прандтля и Грасгофа (см. стр. 151),
вычисленные для средней температуры жидкости; Ргст — критерий Прандтля,
вычисленный для жидкости при температуре стенки трубы.
Так как для газов значение критерия Рг с изменением
температуры практически остается постоянным, то поправочный
коэффициент х по формуле (1.44) для газов равен единице.
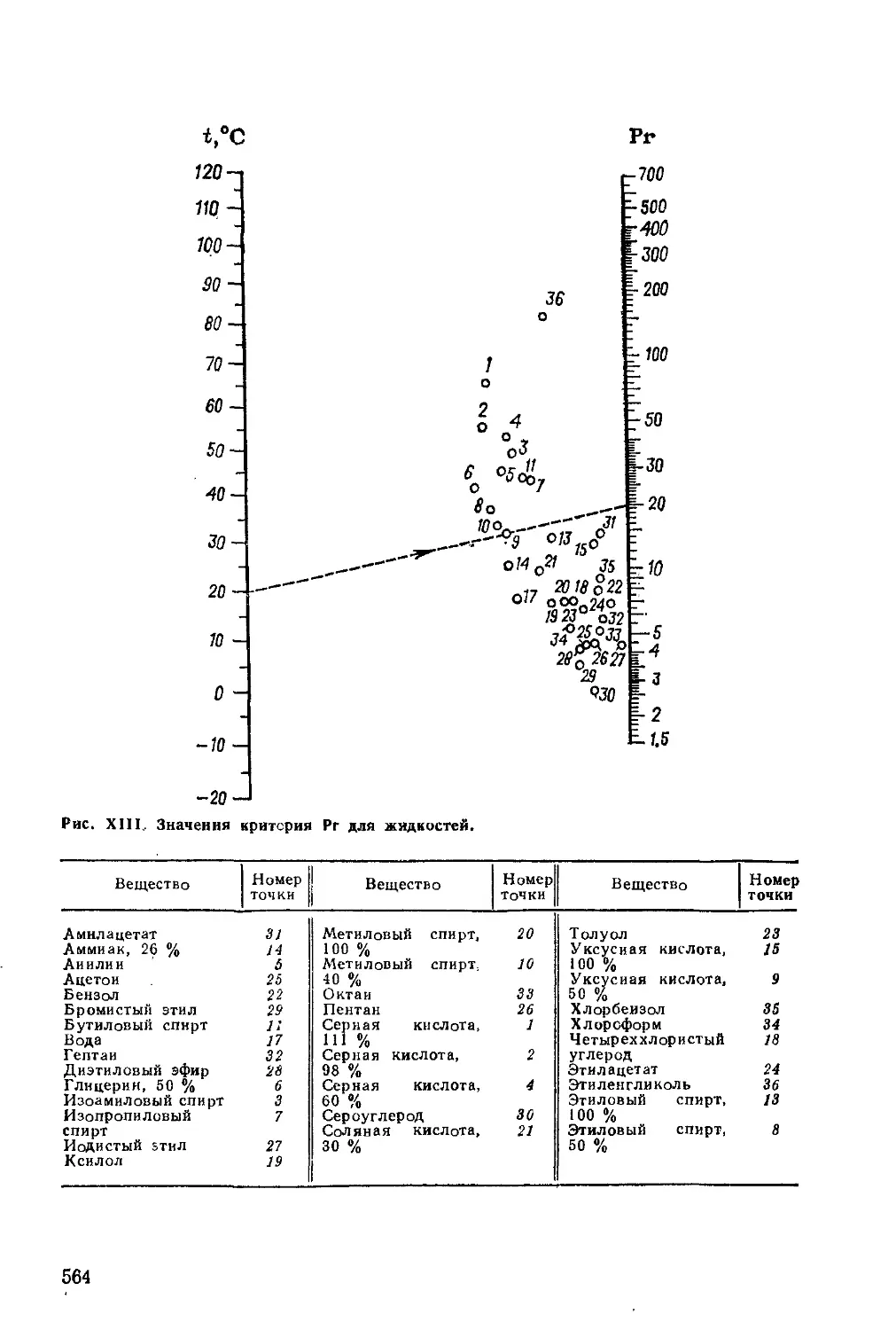
С повышением температуры у капельных жидкостей значения
критерия Рг уменьшаются (рис. XIII), поэтому поправочный
коэффициент (Ргст/Ргж)'/3 при охлаждении жидкости (/ст< ^ж)
больше единицы, а при нагреве жидкости (/ст ?> /ж) меньше
единицы.
21. Потеря давления на трение в изогнутой трубе (змеевике)
Д/?зм больше, чем в прямой трубе А/?пр;
АРвм = ДРпрФ- 0*45)
24
Безразмерный поправочный коэффициент -ф ?> 1 вычисляют
по формуле:
^= I +3,54-g-, (I.46)
где d — внутренний диаметр трубы; D — диаметр витка змеевика (см. рис. 1.1).
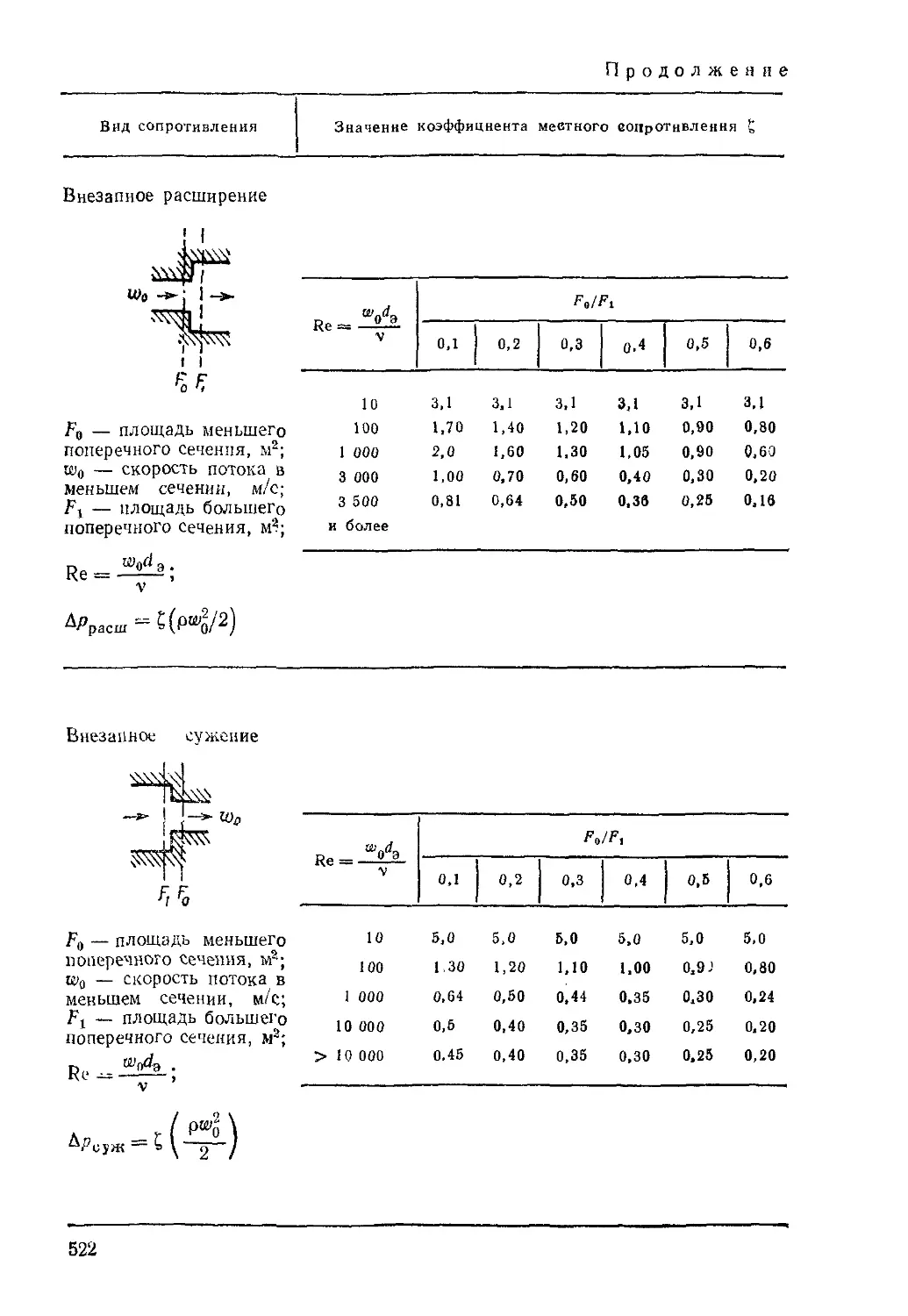
22. Потеря давления на преодоление местных сопротивлений
(колена, диафрагмы, запорные приспособления, внезапные
расширения или сужения и т. п.).
Потеря давления в каждом местном сопротивлении является
суммой двух потерь: на трение и дополнительной потери,
вызванной изменением направления или площади поперечного сечения
потока. Так как при расчете сопротивления трения А/?тр
учитывают всю длину трубопровода L (включая местные
сопротивления), то А/?м. с в уравнении (1.34) представляет собой сумму этих
дополнительных потерь давления.
Расчет потерь давления на местные сопротивления
осуществляется по формуле:
Лрм.с = 2?"^> (1'47)
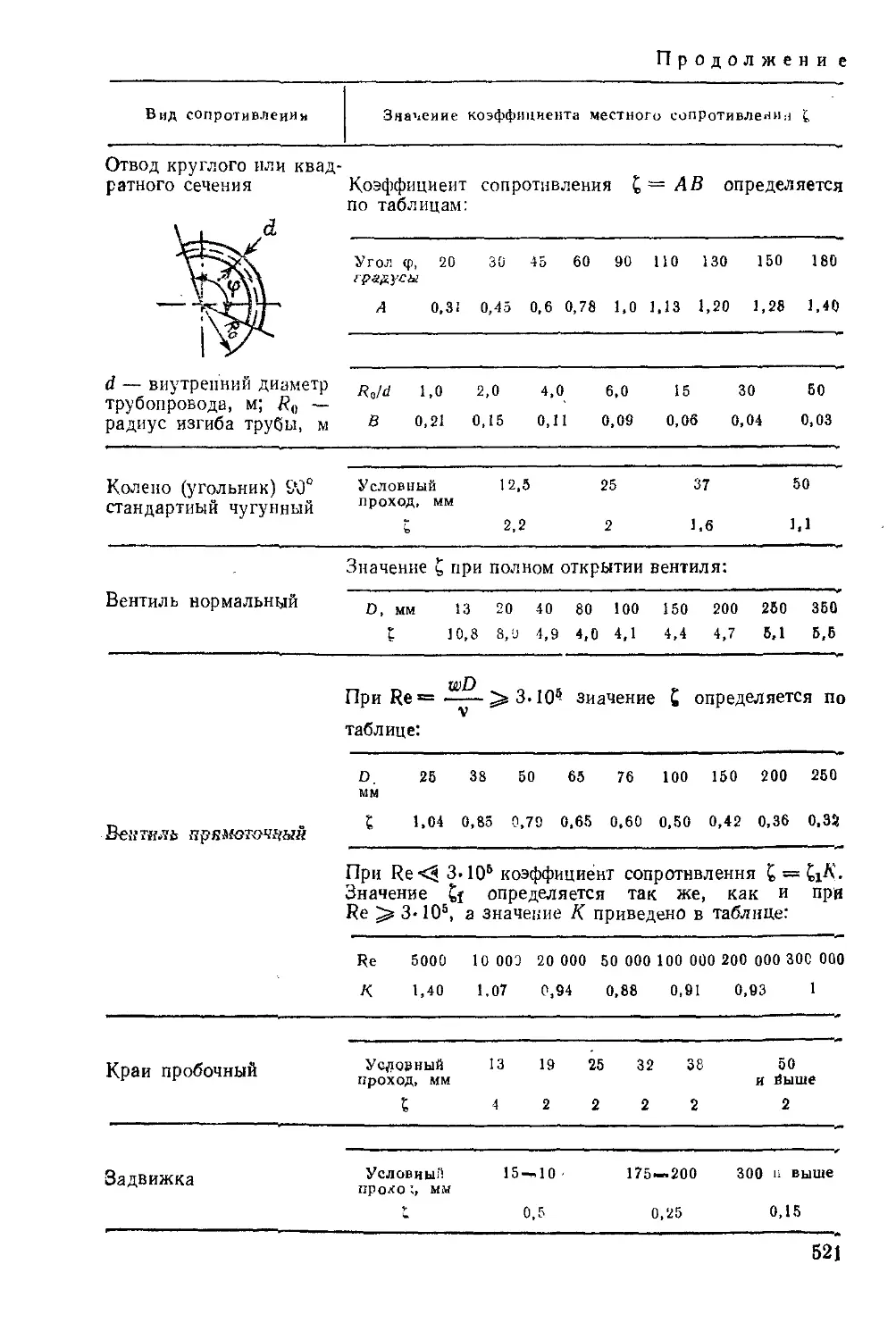
где ? — коэффициент местного сопротивления, безразмерный (его значения
для некоторых местных сопротивлений приведены в табл. XIII).
Иногда применяется другой способ расчета, по которому
потеря давления в местном сопротивлении приравнивается
гидравлическому сопротивлению прямой трубы эквивалентной длины:
Здесь L9 = nd — эквивалентная длина прямой трубы, имеющей такое же
гидравлическое сопротивление, как и данное местное сопротивление; п
—коэффициент (безразмерный), значения которого приводятся в справочниках
(например, для вентиля нормального л = 100—120, для вентиля прямоточного л —
== 10-Н20).
23. Если сеть представляет собой трубопровод постоянного
поперечного сечения, то скорость жидкости (газа) постоянна по
длине трубопровода и полное гидравлическое сопротивление сети
А/?с в соответствии с уравнением (1.34) будет равно
АРс - "^ (l + -^~ + U) + Р^под + 0>2 - Pi) (1.49)
или при втором способе расчета потерь на местные сопротивления:
АЛ, ¦= -^ [ 1 + ML4SL9)] + 9gh*°* + ip2 " Pl)' (L50)
24. Гидравлическое сопротивление пучков труб при
поперечном омывании их потоком.
26
Таблица 1.2
Ф° 90 80 70 60 50 40 30 10
b 1 1 0,95 0,83 0.69 0,53 0,38 0,15
Коридорные пучки:
Ей = Ь (3 + 4,5л») ^ДЛ"°'23 Re'0'26. (1.51)
Шахматные пучки:
d ^ d
Ей = Ь (2 + 3,3m) Re"0'28; (1.52)
при-^
En = & (2,7 + IJm) Re"0'28. (1.53)
В этих формулах Ь — поправочный коэффициент, зависящий от угла атаки ф
(угол между осью трубы и направлением движения потока) и определяемый
по табл. 1.2; т — число рядов труб в пучке в направлении движения потока;
d—наружный диаметр трубы; s3 и s2 — поперечный и продольный шаги.
Скорость потока подсчитывают по самому узкому сечению
пучка; значения физико-химических свойств берут для средней
температуры потока. Критерий JRe рассчитывается по наружному
диаметру трубы.
25. Гидравлическое сопротивление кожухотрубчатых
теплообменников.
Для трубного пространства теплообменника, а также для
межтрубного пространства без поперечных перегородок (см.
рис. 1.21):
д' = ЧНг + 11^ с-54)
где L — длина одного хода, м; п — число ходов. Остальные обозначения те же,
что н в предыдущих формулах.
Для коэффициентов местных сопротивлений ? в
кожухотрубчатых теплообменниках принимают следующие значения:
Трубное пространство
Входная или выходная камера 1,5
Поворот на 180° между ходами или секциями ... 2,5
Вход в трубы или выход из них 1,0
Межтрубное пространство
Вход в межтрубное пространство или выход из него 1,5
Поворот на 180° через перегородку в межтрубном
пространстве 1,5
Поворот на 90° в межтрубном пространстве 1,0
26
При наличии поперечных перегородок в межтрубном
пространстве (см. рис. 4.4) гидравлическое сопротивление в нем
определяют по формулам (1.51)—{1.53) *.
Скорости жидкости (газа) в штуцерах обычно близки к
скоростям в трубах или в межтрубном пространстве. Если же скорость
в штуцерах больше, то потери давления при входе в
теплообменник и выходе из него рассчитывают по скорости в штуцерах.
26. Гидравлическое сопротивление скрубберных насадок.
Сопротивление слоя сухой (неорошаемой) насадки высотой Я:
Н wlP
где X — коэффициент сопротивления при прохождении газа через слой
насадки, безразмерный; Н — высота слоя насадки, м; rfg —эквивалентный
диаметр, м; wv —скорость газа в свободном сечении иасадки (действительная), м/с;
р — плотность газа, кг/м3.
Эквивалентный диаметр можно выразить через
характеристики насадки — свободный объем VCB м3/м3 (численно равный
свободному сечению в м2/м2) и удельную поверхность о м2/м3:
d9 = 4f/n=:4VCB/o. (1.56)
Действительная скорость газа wv связана с фиктивной
скоростью w (отнесенной к полному поперечному сечению аппарата)
зависимостью:
wr = w/VCB. (1.57)
По данным Н. М. Жаворонкова, для неупорядоченной насадки
из колец (навалом):
при Rer < 40 к = 140/Rer; {1.58)
при Rer>40^s=16/Re0'2i (1.59)
где Rer = wT d$i\i = Awpi{o\x).
Расчет гидравлического сопротивления орошаемых насадок
более сложен — см. формулы и графики, приведенные в [6.1
и 6.3].
27. Гидравлическое сопротивление тарельчатых колонных
аппаратов.
Сопротивление барботажной тарелки Ар рассчитывают как
сумму трех слагаемых:
Ар = ЛрСуХ + &Ро + Аргж. (1.60)
* Применяется также формула
?-3m/Re0'2,
где m — число рядов труб в направлении движения потока,
27
Рис, 1.7, Схема колпачковой тарелки.
Здесь Арсух — сопротивление сухой
тарелки; кр0 — сопротивление,
вызываемое силами поверхностного натяжения;
Дргж — сопротивление газожидкостного
слоя на тарелке.
Сопротивление сухой тарелки:
Д^сУк = С
»5р,
(1.61)
где w0 — скорость газа в прорезях колпачка или в отверстиях тарелки, м/с;
рг — плотность газа, кг/м3; Q — коэффициент сопротивления, равный:
Для колпачковых тарелок 4,5—5,0
Для ситчатых тарелок:
со свободным сечением отверстий 7—10% . . 1,82
» » » » 11—25% . 1,45
Для решетчатых провальных тарелок 1,4—1,5
Сопротивление, вызываемое силами поверхностного
натяжения:
APa = 4o/d9l (1-62)
Здесь о—поверхностное натяжение, Н/м; dg —эквивалентной диаметр
отверстия, м. Для колпачковых тарелок d9 = 4//П (/ — площадь свободного
сечения прорези, П — периметр прорези), для ситчатых и дырчатых
провальных тарелок d9 равен диаметру отверстия, а для решетчатых провальных
тарелок — удвоенной ширине щели.
Сопротивление газожидкостного слоя (при тех скоростях газа,
которые применяются в тарельчатых массообменных колоннах —
см. гл. 6 и 7):
а) на колпачковой тарелке
ДРгж = U3kPm (/ + -L + д/i) g,
(1.63)
где g — ускорение свободного падения, м/с2; k — относительная плотность
газожидкостного слоя (пены) [при расчетах принимают приближенно ft =0,5];
рж — плотность жидкости, кг/м3; /— расстояние от верхнего края прорезей
до сливного порога, м (рис. 1.7); е — высота прорези; м; Ah — высота уровня
жидкости над сливным порогом, м;
б) на ситчатой тарелке
ДРгж = 1,3?/фж (hn + ДЛ), (1.64)
где hn — высота сливного порога, м (см. рис. 7.18).
Величина А/г определяется по формуле истечения через
водослив с учетом плотности пены:
\ 1,8511ft / >
(1.65)
где Vm — объемный расход жидкости, м^с; П — периметр слива, м; k =0,5
(см. выше).
28
ПРИМЕРЫ
Пример 1.1. Относительный удельный вес нефти 0,89.
Определить плотность нефти в СИ и в системе МКГСС.
Решение. 1) СИ. Согласно уравнению (1.2), А — р/Рв—
— y/Vb) поэтому
р = Дрв « 0,S9-1000 = 890 кг/м3.
2) МКГСС:
Y = Д-ув = 0,89-1000 = 890 кгс/м3.
По уравнению (1.1)
р = y/g = 890/9,81 = 90,6 кгсс2/м4.
Пример 1.2. Определить в СИ плотность диоксида азота при
Ризб = Ю кгс/см2 и / = 20 °С. Атмосферное давление 760 мм рт. ст.
(1,03 кгс/см2; 101,3 кПа).
Решение. По уравнению (1.5)
М 273/7 46-273.11,03 „ - . ,
^22,4 7>0 " 22,4.293.1,03 =*>***'*.
Пример Ь3« Определить плотность воздуха при вакууме (т. е.
разрежении) 440 мм рт. ст. (58,6 кПа) и температуре —40 °С.
Атмосферное давление в данном случае принять равным
750 мм рт. ст. (99,97 кПа).
Решение. Мольная масса воздуха (79% азота и 21%
кислорода по объему):
М = 0,79-28 + 0,21 -32 = 28,8 кг/кмоль.
По формуле (1.5)
М 273р 28,8.273(750-440) Q fil-__..
Р" 22,4 1% 22,4.233-760 0,615 кг/м .
Пример 1.4§ По трубам одноходового кожухотрубчатого
теплообменника (число труб п — 100, наружный диаметр труб 20 мм,
толщина стенки 2 мм) проходит воздух при средней температуре
50 °С и давлении (по манометру) 2 кгс/см2 со скоростью 9 м/с.
Барометрическое давление 740 мм рт. ст. Определить: а) массовый
расход воздуха; б) объемный расход воздуха при рабочих
условиях; в) объемный расход воздуха при нормальных условиях.
Решение. Плотность воздуха при нормальных условиях
р0 = 1,293 кг/м3 (табл. V).
Рабочее давление (абсолютное):
Р = Рбар + Рман = 740.133,3 + 98 100*2 = 294800 Па,
ИЛИ
Р = Рбар + Рман = 740 + 735-2 = 2210 мм рт. ст.
Соотношения между единицами измерения см. табл. LVIII.
Плотность воздуха при рабочих условиях;
29
или
Р = Ро~^-~= 1.293
2210-273
= 3,18 кг/м3.
р0Г 760(273+50)
Массовый расход воздуха по уравнению (1.18):
М = Vp = wfp « wn-0J85d*p = 9-100-0,785.0,01б2-3,18 =*= 0,57 кг/с.
Объемный расход воздуха при рабочих условиях:
V = М/р = 0,57/3,18 « 0,18 м3/с
Объемный расход воздуха, приведенный к нормальным
условиям: VQ = M/pQ = 0,57/1,293 = 0,44 м*/с
Пример 1.5. В открытом резервуаре находится жидкость с
относительной плотностью 1,23. Манометр, присоединенный в
некоторой точке к стенке резервуара, показывает давление /?Изб =
= 0,31 кгс/см2. На какой высоте над данной точкой находится
уровень жидкости в резервуаре?
Решение. Высота уровня жидкости в резервуаре над
точкой присоединения манометра определяется уравнением (1.7):
Рй
По условию: р — р„=^ 0,31 кгс/см2 = 0,31-Ю4-9,81 Па.
Плотность жидкости: р = 1,23.1000= 1230 кг/м3.
0,ЗЬ10*.9,81
Отсюда
А«
1230-9,81
= 2,52 м.
Пример 1.6. Вакуумметр на барометрическом конденсаторе
показывает вакуум, равный 60 см рт. ст. Барометрическое
давление 748 мм рт. ст. Определить: а) абсолютное давление в
конденсаторе в Па и в кгс/сма; б) на какую высоту Н поднимается
вода в барометрической трубе (рис. 1.8).
Решение. Абсолютное давление в
конденсаторе:
0 = 748 — 600 =148 мм рт. ст. = 148.133,3= 19700 Па;
Ю700 А ОЛ1 , >
р=-9ЖТог = 0'201кгс/см"-
Высоту столба воды в барометрической
трубе найдем из уравнения:
Откуда
АЛЛ. 1ЯЯ Я
= 8,16 м.
и = l**v ~~р — 600*133'3
р?
Рис. 1.8 (к примеру 1,0).
1000.9,81
S0
Рис. 1.9 (к примеру 1.7),
Пример 1.7. К двум
точкам горизонтального
трубопровода присоединен
Сообразный стеклянный ди-
фманометр, заполненный
ртутью. Разность уровней
ртути в дифманометре
h = 26 мм. Какова
разность давлений в этих точках, если по трубопроводу проходит:
а) вода; б) воздух при 20°С и атмосферном давлении?
Решение. Из условия равенства давлений на уровне а — а
слева и справа (рис. 1.9)
Pi + htpg = p2 + h&g + ftpMg
находим, заменяя h2 через (ht—Л):
Pi — Ps^^ipM — Р)?>
где р — плотность жидкости в трубопроводе (и в
ках); рм — плотность жидкости в дифманометре.
присоединительных труб-
По условию задачи h = 0,026 м, рм = 13 600 кг/м3.
а) Для воды:
р = 1000 кг/м»,
Pl — р% = 0,026 (13 600— 1000) 9,81 = 3220 Па.
б) Для воздуха:
29-273
Р =
1,2 кг/м3;
22,4-293
Pi —р2 = 0,026(13 600— 1,2)9,81 ^0,026.13 600-9,81 =3470 Па.
Из последнего равенства следует, что при измерении разности
давлений в газовых потоках жидкостными дифференциальными
манометрами поправкой на плотность газа можно пренебречь,
так как плотность газа (при давлениях, близких к атмосферному)
очень мала по сравнению с плотностью жидкости.
Пример 1.8. Колокол мокрого
газохранилища (газгольдера) для азота
диаметром 6 м весит с
дополнительным балластом 2900 кгс (рис. 1.10).
Пренебрегая потерей в весе
погруженной вводу части колокола,
определить избыточное давление газа
в наполненном газохранилище.
Решение. Площадь
горизонтальной проекции колокола:
0,785.б2 = 28,2 м3.
дбООО
77777777777,
77777,
777777777777.
Рис. 1.Ю (к примеру 1.8).
31
Давление в газохранилище:
2900-9,81 ._,_ _
Ризб = 281— ^ ° ° Пй|
или
1010
0,01 кгс/см2.
9,8Ы04
Пример 1.9. Определить кинематический коэффициент
вязкости диоксида углерода при / = 30 °С и /?абс = 5,28 кгс/см2.
Решение. Пренебрегая зависимостью динамического
коэффициента вязкости от давления, находим по графику (рис. VI)
для диоксида углерода при 30 °С: \х = 0,015 сП = 0,015-10-3 Пас.
Определяем плотность диоксида углерода:
44.273-5,28
Р== 22,4.303-1,033 -9.°5""VH».
Кинематический коэффициент вязкости;
v = pi/p = 0,015-10~3/9,05 = 1,66. Ю-6 м2/с
Пример 1.10. Предполагая отсутствие экспериментальных
данных, вычислить приближенно динамический коэффициент вязкости
нитробензола (QH5N02) при 20 °С.
Решение. Воспользуемся эмпирической зависимостью (1.10).
Мольная масса нитробензола 123 кг/кмоль; плотность 1200 кг/м3
(табл. IV). Вычисляем сумму атомных констант 2 An (табл. X)i
? Лп = 6-50,2 + 5-2,7+ 1-37 + 2.29,7 = 411,1.
Вычисляем сумму структурных поправок ?р по пунктам 1, 3f
4 и 16 табл. X:
Sp = 3 (-15,5) + 1 (-21,0) + 1 (-17,0) + 1 (-16,4) = -100,9.
Тогда
/С= ? Лл+ ? /7 = 411,1—100,9 = 310,2.
Далее
'g(^)~* 1^-^-310,2 1(ff%3 -2,9 = 0,126.
По номограмме (рис. I) находим \х — 2,15 сП = 2,15-10-8 Па-с,
что совпадает с экспериментальными данными (рис. V).
Пример 1.11. Определить динамический коэффициент вязкости
топочных газов, имеющих состав: С02 — 16%, 02 — 5%, N2 — 79 %
(по объему). Температура газов 400 °С, давление /?абс — 1 кгс/см2.
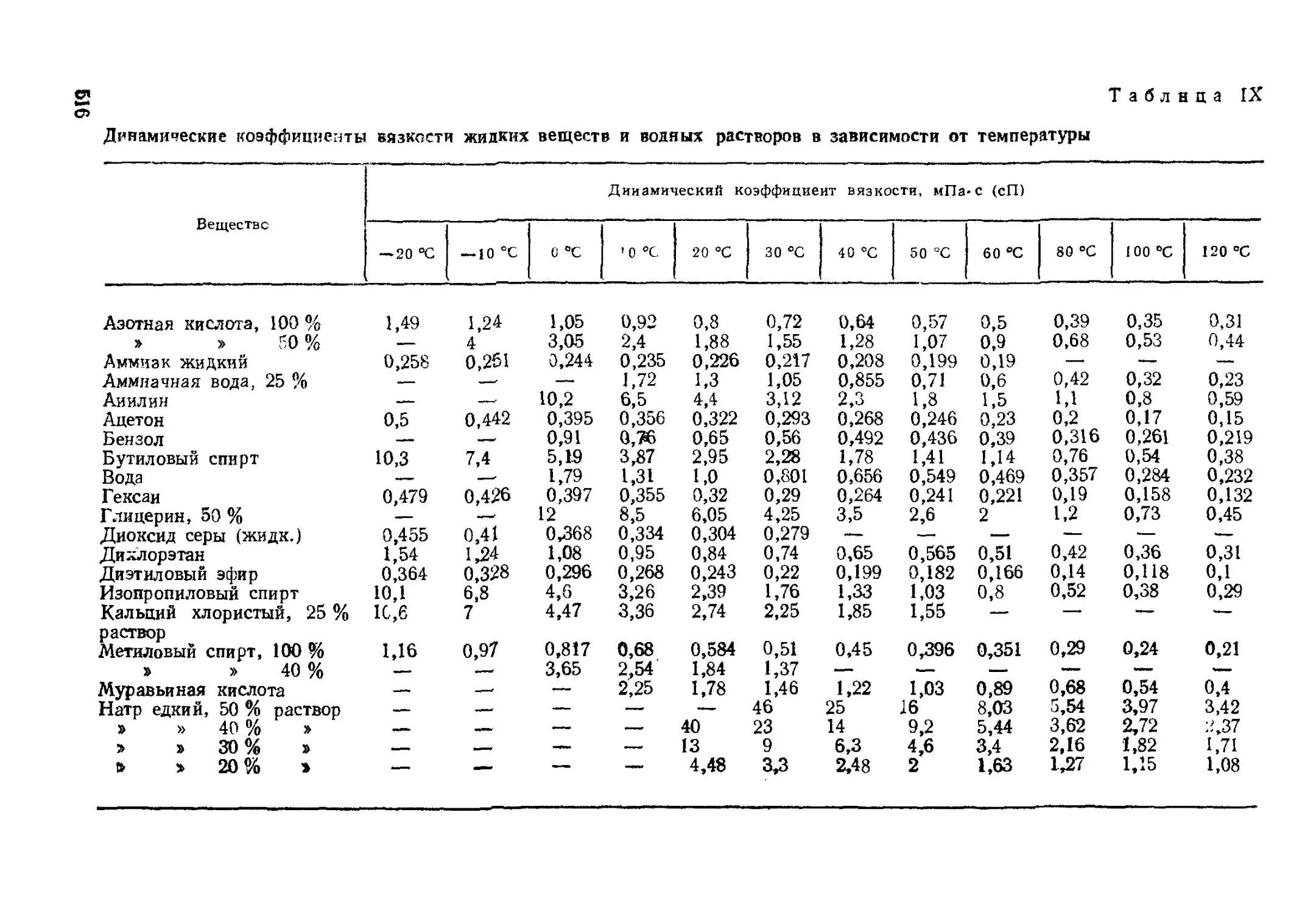
Решение. По номограмме (рис. VI) находим динамические
коэффициенты вязкости отдельных компонентов смеси. При 400 °G
|4,со =0,035, \i0 —0,039 и (j,N = 0,0335 мПа-с.
Расчет динамического коэффициента вязкости смеси сделаем
по формуле (1.11):
Мсм 0,16-44 0,05.32 0,79-28 _
Нем 0,035 О'О39 0,0335
32
Мольная масса смеси!
Мсж = 0,16-44 + 0,05-32 + 0,79-28 = 30,8 кг/кмоль.
Динамический коэффициент вязкости смеси:
цсм = 30,8/902 = 0,034 мПа-с «= 0,034- Ю~3 Пас.
Пример 1.12. Определить кинематический коэффициент
вязкости жидкости, имеющей состав: 70% (мол.) кислорода и 30%
(мол.) азота при 84 К и /?абс = 1 кгс/см2 (~0,1 МПа).
Решение. Считая, что жидкие кислород и азот
принадлежат к классу нормальных жидкостей, динамический коэффициент
вязкости смеси вычислим по формуле (1.14). При 84 К для жидкого
кислорода \ix = 22,6 10"5 Па-с, а для жидкого азота ^2 = 11,8х
X Ю-5 Па с. Тогда
«вИом = *i IgfH + «a lg |ia == 0.7 lg (22,6-10"*) + 0,3 lg (Ilf8- I0"*J = 6,2694,
откуда |iCM = 18,6• Ю-5 Па-с
Массовые доли компонентов в смеси:
- 0,7-32 - 0,3-28
х~ 0,7.32 + 0,3.28 -и.'^'>*2- 0,7.32 + 0,3.28 ~u'z/0-
Плотность жидкого кислорода рх = 1180 кг/м3, жидкого азота
р2 = 780 кг/м3. Плотность смеси по уравнению (1.3):
рсм = (0,727/1180)+ (0,273/780) ^ 103° кг/м8-
Кинематический коэффициент вязкости смеси:
vCM = Исм/Рсм =18,6-10--/1030 « 0,18. Ю-' м2/с
Пример 1.13. Вычислить динамический коэффициент вязкости
суспензии бензидина в воде, если в чаи загружено на 10 м3 воды
.1 т бензидина. Температура суспензии 20 °С, относительная
плотность твердой фазы 1,2.
Решение. Объем твердой фазы:
"- т - ттияг - »¦»» -•
Объемная концентрация твердой фазы в суспензии!
о язя
4= 10 + 0.833 - 0.077 мз/мз.
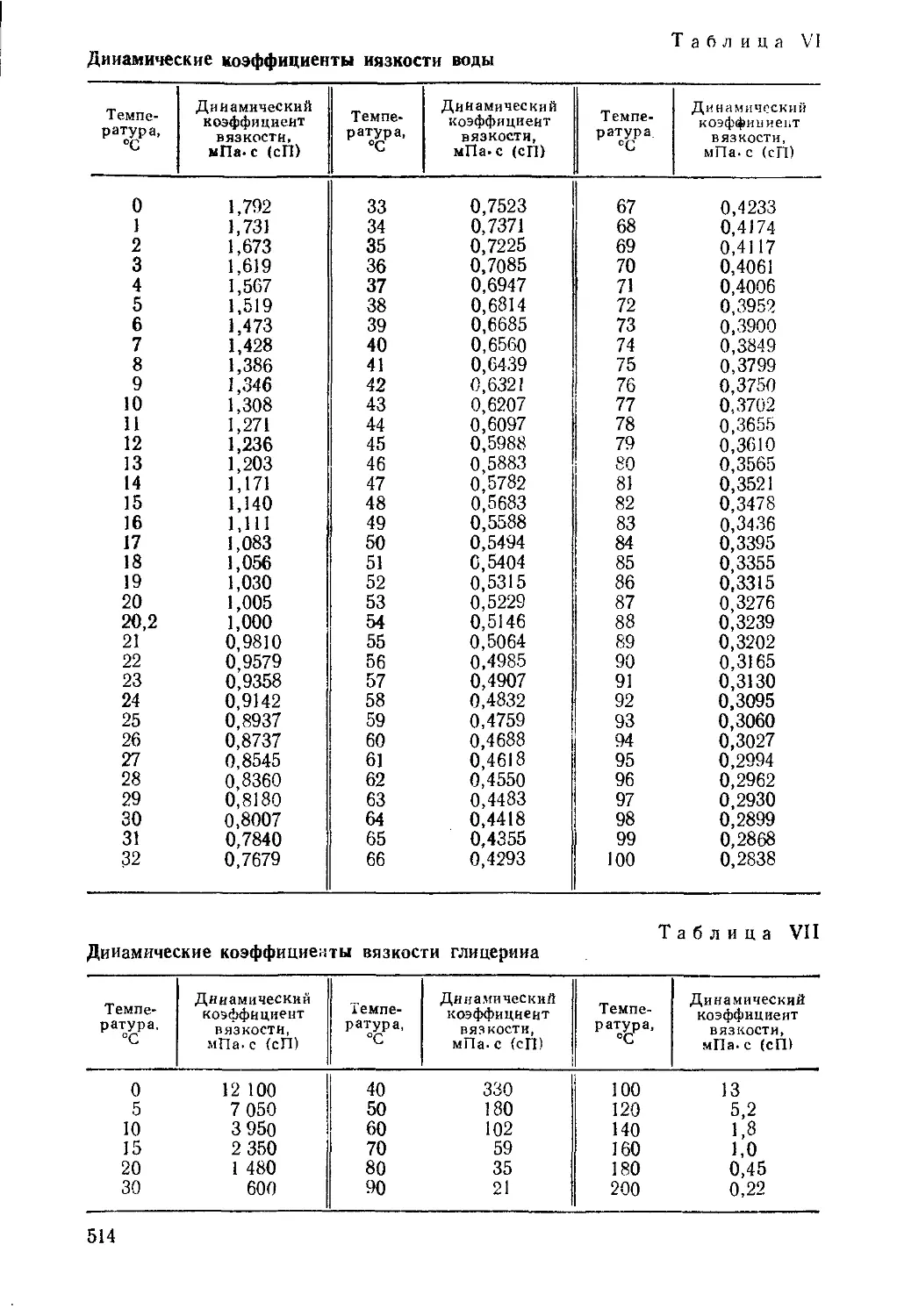
При 20 °С динамический коэффициент вязкости воды равен
] мПа с, или 1 сП (табл. VI). Динамический коэффициент
вязкости суспензии по формуле (1.15):
tAc=H*(l +2,5ф) = 1 (1 + 2,5-0,077) = 1,19 сП = 1,19-10"3 Па-с.
По формуле (1.15а):
"° = "*lo^V = W=W = 1'23 сП = '-23'1ГЗ Па'с-
2 Павлов К. Ф. и др. 33
Пример 1.14* Известно, что динамический коэффициент
вязкости хлорбензола при 20 °С равен 0,9 сП, а при 50 °С 0,6 сП. Найти
пользуясь правилом линейности, динамический коэффициент вяз
кости хлорбензола при 70 °С.
Решение. В качестве эталонной жидкости возьмем воду
Находим температуры эталонной жидкости, при которых ее дина
мический коэффициент вязкости равен 0>9 и 0,6 сП.
Для воды динамический коэффициент вязкости 0,9 сП соответ
ствует температуре 25 °С, а 0,6 сР — температуре 45 °С (табл. VI)
Следовательно, константа уравнения (1.16)
/< =
^2 *1*1
Да (Я;
50 — 20 __ 30
45 — 25 ~ 20
= 1,5.
Далее находим температуру воды, при которой ее
динамический коэффициент вязкости равен динамическому коэффициенту
вязкости хлорбензола при 70 °С, из уравнения
70 — 20
1,5 =
е
Дз
25
откуда 9Цз = 58,4 °С. При этой температуре находим для воды
М-з — 0>48 сП. Следовательно, динамический коэффициент
вязкости хлорбензола при 70 °С равен 0,48 сП.
Если для сравнения обратимся непосредственно к номограмме
(рис. V), то найдем \х = 0,46 сП = 0,46-Ю-3 Па с.
Пример 1.15. Динамический коэффициент вязкости некоторой
жидкости составляет:
При *= 34 °С 0,554 Па-с
» t= 28 °С 0,934 »
» /— 25 °С 1,42 »
» t = 20 °С 2,09 »
Определить динамический коэффициент вязкости этой
жидкости при / = 16 °С.
Решение. Воспользуемся правилом линейности, взяв
в качестве стандартной жидкости глицерин. Зависимость
динамического коэффициента вязкости
глицерина от температуры р,гл =
= / (в) дана на рис. 1.11 (кривая
АБ). По этой кривой находим
температуры глицерина в:
При ftrjl= 0,554 Па. с 32 °С
» Цгл *= 0,934 » 26 °С
» Игл = Ь42 » 21 °С
» (дгл = 2,09 » 16 °С
Построив зависимость
температуры жидкости t от температуры
Рис. 1.11 (к примеру 1.15),
34
глицерина в при одинаковых значениях вязкости, получаем
прямую ВЛ Далее находим, как показано пунктиром, что искомый
динамический коэффициент вязкости жидкости при / = 16 °С,
равный динамическому коэффициенту вязкости глицерина при
Э = 11 ?С, составляет 3,46 Па-с.
Пример 1.16. Теплообменник изготовлен из стальных труб
диаметром 76 X 3 мм *. По трубам проходит газ под атмосферным
давлением. Требуется найти необходимый диаметр труб при работе
с тем же газом, но под давлением риз& = 5 кгс/см2, если требуется
скорость газа сохранить прежней при том же массовом расходе
газа и том же числе труб.
Решение. Под давлением /?изб = 5 кгс/см2 (~0,5 МПа)
плотность газа в соответствии с формулой (1.5) будет в 6 раз
больше, чем при атмосферном давлении. Так как массовый расход
газа
G = Vp = wfp
должен быть сохранен неизменным, то
t^j^i •0,785rffp1 = w2n2-0J85dlp.2t
Подставляя w2 = wx> п2 = nlt p2 = 6pi, dx = 0,07 м,
получаем; 0,072 = 6d|, откуда
d2 =* l/*0,072/6 = 0,0286 м & 29 мм.
Пример 1.17. Определить режим течения жидкости в
межтрубном пространстве теплообменника типа «труба в трубе» (рис. 1.12)
при следующих условиях: внутренняя труба теплообменника
имеет диаметр 25 X 2 мм, наружная 51 X 2,5 мм; массовый
расход жидкости 3730 кг/ч, плотность жидкости 1150 кг/м3,
динамический коэффициент вязкости 1,2-10~3 Па*с.
Решение. Скорость жидкости из уравнения расхода:
__ V 3730 п
W~ f ~ 1150-3600-0,785(0,0462 —0,0252) -и»//м/с-
Эквивалентный диаметр кольцевого сечения по формуле (1.24):
где D — внутренний диаметр наружной трубы, м; d — наружный диаметр
внутренней трубы, м.
Динамический коэффициент вязкости жидкости \х = 1,2 X
X Ю-3 Па-с. Критерий Рейнольдса:
0,77-0,021-1150 ^
^
1,2-Ю-3 ^FvJJ
* Первое число обозначает
наружный диаметр трубы, второе —
толщину стенки.
Рис. 1.12 (к примеру 1.17),
2* 35
Следовательно, режим турбулентный.
Пример 1.18, Найти критическую скорость в прямой трубе
диаметром 51 X 2,5 мм: а) для воздуха при 20 °С и раб0 = 0,1 МПа;
б) для нефтяного масла, имеющего \х = 35 мПа»с и
относительную плотность 0,963.
Решение. Критическая скорость будет иметь место при
ReKp =2300; следовательно, из уравнения (1.21)
2300м-
а) Для воздуха:
о-кр =
2300-0,018.10-»
= 0,75 м/с,
0,046-1,2
где 0,018 — динамический коэффициент вязкости воздуха при 20 °С (по рис. VI),
мПа*с; 1,2 кг/м3 — плотность воздуха при 20 °С и Рабо г== 0,1 МПа по
формуле (1.5).
б) Для нефтяного масла г
2300-35.10-»
Щ<р =
= 1,8 м/с.
0,046-963
Пример 1Л9. На трубопроводе с внутренним диаметром 200 мм
имеется плавный переход на диаметр 100 мм (рис. 1.13). По
трубопроводу подается 1700 м3/ч (при нормальных условиях) метана
при 30 °С. Открытый в атмосферу U-образный водяной манометр,
установленный на широкой части трубопровода перед сужением,
показывает избыточное давление в трубопроводе, равное
40 мм вод. ст. Каково будет показание такого же манометра на
узкой части трубопровода? Сопротивлениями пренебречь.
Атмосферное давление 760 мм рт. ст.
Решение. Считая приближенно плотность метана на
участке трубопровода между точками присоединения манометров
постоянной (что проверим в конце расчета), составляем уравнение
Бернулли для несжимаемой жидкости:
откуда находим:
Wl — W\
Pl—P2= " о Р-
Определяем скорости метана в сечениях / и //, принимая, что
j j давление в трубопроводе
приблизительно равняется атмосферному:
1700-303
Шх —
3600- 273- 0,785- 0,2*
= 16,7 м/с.
По уравнению (1.20)
200 \2
w2 = wt
b -,6-' №)' - *¦ *
Рис. 1.13 (к примеру 1.19),
36
Вычисляем плотность метана*
р*=
мт<
16-273
г = 0,645 кг /м3.
22t4T *~ 22,4-303
Находим разность давлений;
_.(ш% —ш?)Р (бб,^ - 16,7а) 0,645
1354 Па,
Pi — Р2 = g ~ ~~ ~~ 2
или 1354/9,81 = 138 мм вод. ст., откуда
Рг^Р\~~ № = 40— 138 = —98 мм вод. ст.,
т. е. давление в сечении //будет меньше, чем в /, на 138 мм вод. ст.,
и манометр в сечении // будет показывать вакуум, равный
98 мм вод. ст. (961 Па).
Абсолютное давление в сечении h
10 330 + 40= 10 370 мм вод. ст. = 1,037 кгс/см3 = 0,1017 МПа;
в сечении П\
10 330—98= 10 232 мм вод. ст. = 1,023 кгс/см3 = 0,1003 МПа.
Принимая при вычислении скоростей и плотности метана
постоянство давления в трубопроводе, мы допустили погрешность,
не превышающую
100 «1,4 ?
1,037—1,023
1,023
Пример 1.20* На рис. 1.14 изображен так называемый сосуд
Мариотта, представляющий собой закрытый резервуар, из кото-
рого жидкость может вытекать через трубку А. Трубка Б вверху
открыта в атмосферу. При вытекании по трубке А жидкости из
резервуара в его верхней части образуется вакуум, причем через
трубку Б засасывается атмосферный воздух. Вследствие этого
в резервуаре на уровне Н пад трубкой А давление всегда будет
равно атмосферному, независимо от количества жидкости в ре-
аервуаре, и истечение жидкости будет происходить под постоянным
напором до тех пор, пока уровень ее не опустится ниже Я. По
указанным на рис, 1Л4 размерам
(в мм) определить скорость
течения воды и время, за которое
уровень ее снизится от начального
(1400 мм) до величины Н =300 мм.
Коэффициент скорости ф = 0,82.
Коэффициент сжатия струи
е =1.
Решение. По формуле (1.28)
при р0 «р:
о
W-*
=Ф^2?#^0,82^2*9,8Ь0,3==1,98м/с.
Риъ. 1.14 (к примеру 1.20).
0800
37
Объем воды, который вытечет из сосуда при снижении уровня
от 1400 до 300 мм, составляет:
V = 0,785- 0,8* (1,4 — 0,3) = 0,553 м*.
Время истечения:
0,553
569 с « 9,5 мин.
0,785-0,025М,98
Пример 1.21. Цилиндрический бак диаметром 1 м наполнен
водой на высоту 2 м. Отверстие для истечения в дне имеет диаметр
3 см. Определить время, необходимое для опорожнения бака.
Решение. Воспользуемся формулой (1.31):
X =
а/о V4 *
где / — площадь сечения сосуда, м2; /0 — площадь отверстия, м2; Н —
начальная высота уровня, м; а — коэффициент расхода (для отверстия с незакруглея-
ными краями можно принять а = 0,61).
Подставляя заданные величины в формулу, находим*
2-0,785-12 ^2
т = г = 1J80 с да 20 мин
0,6Ь0,785*0,032К2.9,81
Пример 1.22. По горизонтальному гидравлически гладкому
трубопроводу с внутренним диаметром 152 мм протекает вода при
температуре 20 °С со средней скоростью 1,3 м/с. В трубопроводе
установлена нормальная диафрагма, диаметр отверстия которой
равен 83,5 мм. Определить показание ртутного дифманометра
диафрагмы (см. рис. 1.3).
Решение. Расход воды:
V = wf=* 1,3-0,785-0,1523 = 0,0236 м3/с.
Критерий Рейнольдса:
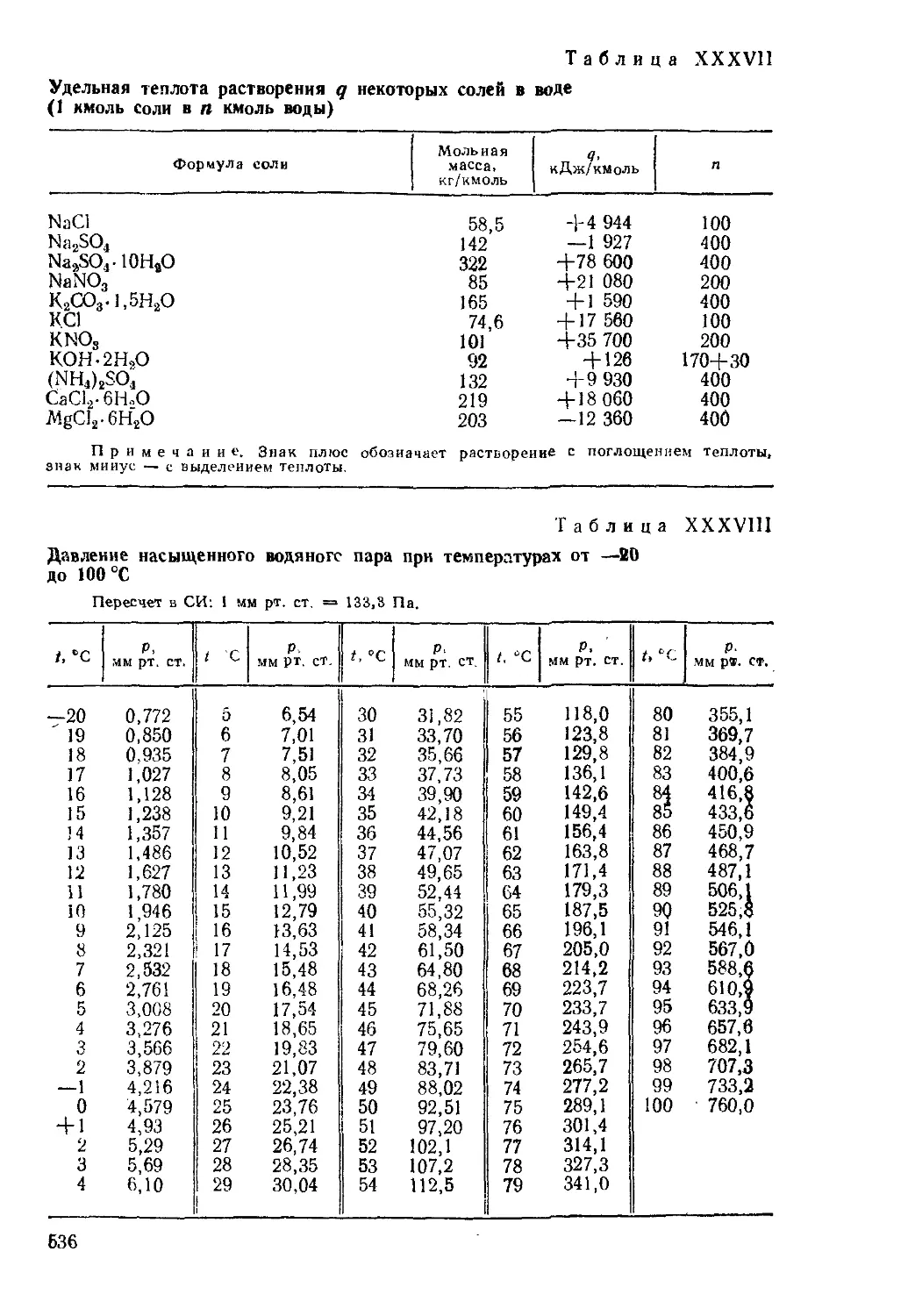
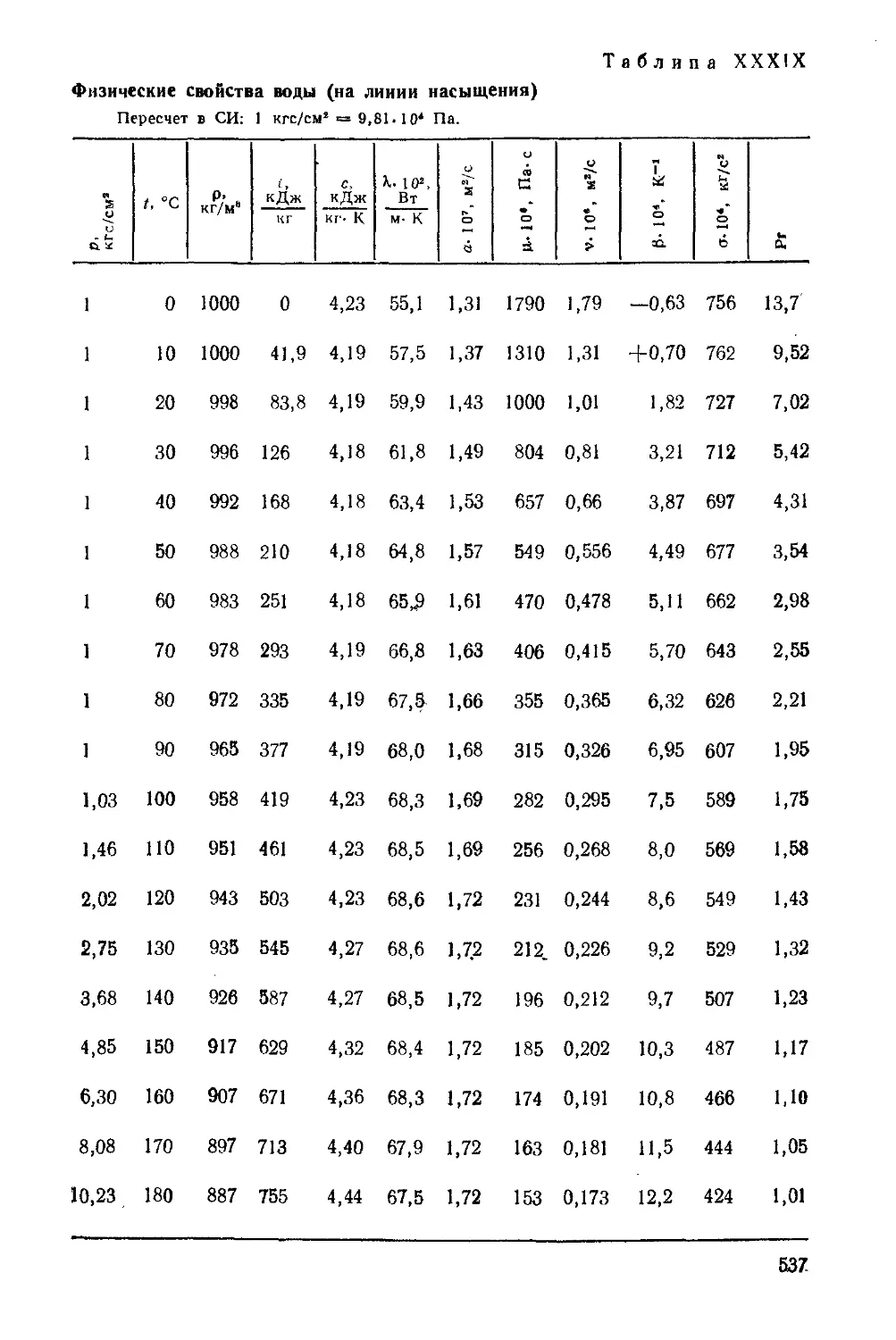
где v — кинематический коэффициент вязкости воды при 20 °С (табл. XXXIX),
м2/с.
Определяем коэффициент расхода диафрагмы а, который
зависит от величины критерия Re и от значения т = {d0/df =
= (83,5/152)2 ^ 0,3. По табл. XV находим а ж 0,635.
Исходя из формулы (1.32) и принимая k = 1, получаем;
V 0,0236
Ун~
o/ol/ %g— ~ 0,635.0,785-0,083521/2-9,81
13 600—J 000
1000
« 0,432,
откуда Н =0,188 м = 188 мм.
Пример 1.23. Показание водяного дифманометра трубки
Пито — Прандтля (см. рис. 1.4), установленной по оси гор и зон-
38
тального воздухопровода, составляет 13 мм. Определить расход
воздуха, если температура его 40 °С, диаметр трубопровода 159 х
X 6 мм, а перед трубкой имеется прямой участок длиной 7 м.
Давление воздуха атмосферное.
Решение. Плотность воздуха при 40 °G
р= 1,293(273/313) = 1,13 кг/мз.
Максимальная (осевая) скорость воздуха определяется из
выражения:
о-макс = ^2 Дрск/р = 1/2.13.9,81/1,13= 15,07 м/с.
&гой скорости соответствует значение критерия Рейнольдса
пР _ <%ако <*р _ , 15,07-0,147.1,13
Re- -0)019.1(ГЗ ~ 132000.
Длина прямого участка стабилизации потока до трубки Пито —
Прандтля должна быть не менее 40 диаметров: 40-0,147 = 5,9 м.
&го условие соблюдено, так как имеется прямой участок
трубопровода протяженностью 7 м По рис. 1.2 для Re = 132 000
отношение средней скорости к максимальной со/шмакс ~ 0,85.
Средняя скорость:
ш = 0,85-15,07= 12,8 м/с.
Расход воздуха;
V =0,785.0,1472-12,8 «0,217 м3/с = 780 ма/ч.
Пример 1.24. Дымовые газы из печной установки,
расположенной в Ленинграде, отводятся через дымовую трубу высотой
19 м. Состав газов: С02 — 12,7%, 02 — 4,9%, N2 — 77,5%,
Н20 — 4,9% (по объему). Площадь поперечного сечения дымовой
трубы равна площади поперечного сечения горизонтального
газохода. Средняя температура газов в газоходе и дымовой трубе
250 °С. Найти скорость газов, если сумма коэффициентов
сопротивлений газохода и дымовой трубы:
+ -T- + Et = 27,3f
da d
где Хс и Хт — коэффициенты трения; Lc — длина газохода; йэ — эквивалентный
диаметр газохода; d — внутренний диаметр дымовой трубы; Н — высота трубы;
Е С — сумма коэффициентов местных сопротивлений.
Решение. Плотность газа при нормальных условиях:
Ро = 15Т = "2?4" <44'0'127 + 32-0,049 — 28.0,775 + 18-0,049) = 1,328 кг/м^.
Плотность газа при 250 РС:
Т 273
Рг = Ро -/- = 1,328 273 250 » 0,693 кг/мз.
39
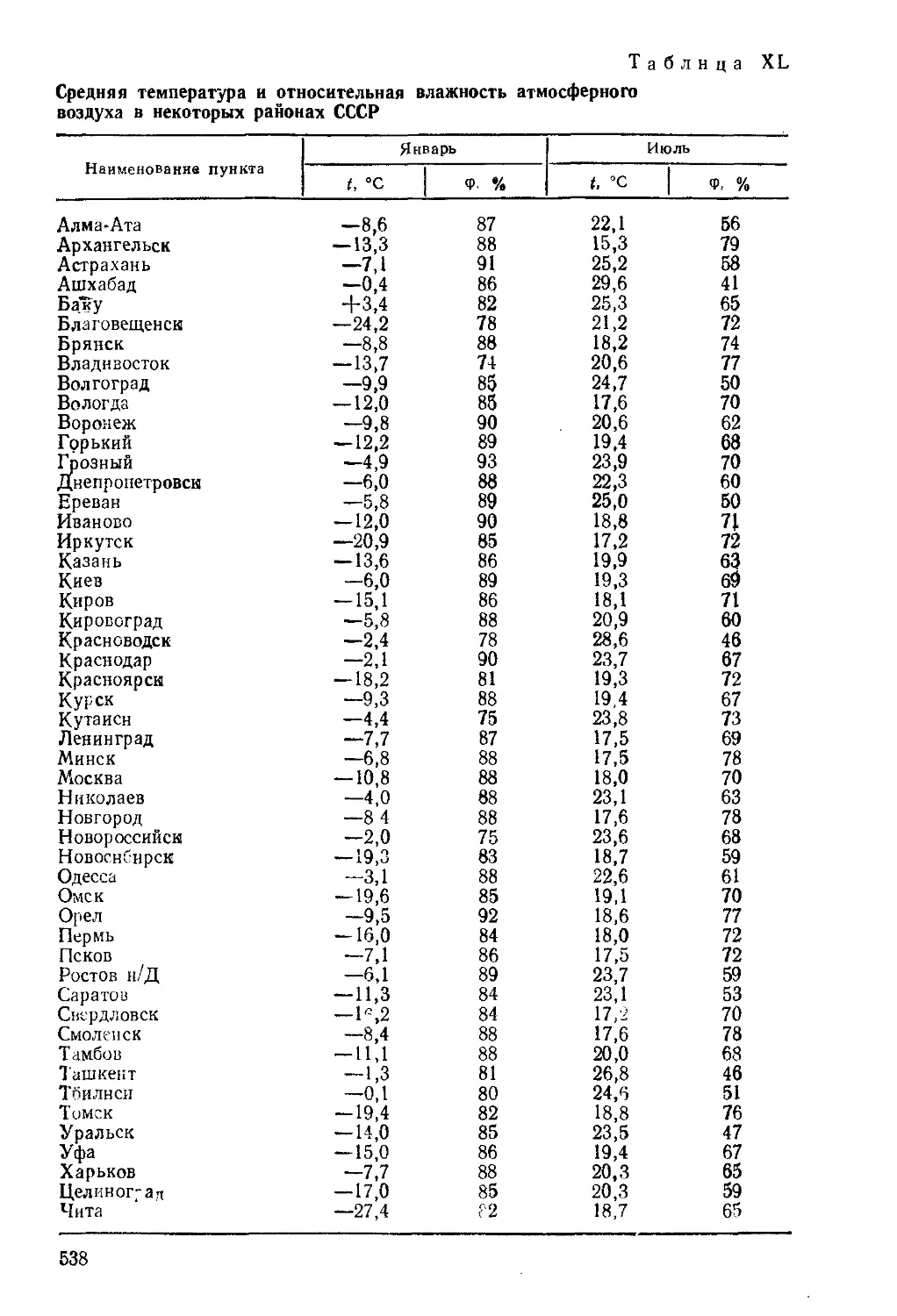
В летних условиях средняя температура воздуха в Ленинграде
17,5 °С (табл. XL). Плотность воздуха при этой температуре;
274
р,-1,293 273+17>5 -1,216 кг/*.
По уравнению Бернулли (при плоскости отсчета, проведенной
на уровне газохода):
^бар' + "^2" = Рбар» + -*V" + 9^Н + АРП0Т»
где рбар, — барометрическое давление на уровне горизонтального газохода;
Рбар" ~~ барометрическое давление у верхнего края дымовой трубы; w —
скорость газа; Н — высота дымовой трубы; Арпот — суммарные потери давления
(суммарное сопротивление газохода и дымовой трубы).
В левой части уравнения Бернулли рассматривается сечение,
проведенное через начало газохода, в правой — через верхний
край дымовой трубы.
Барометрическое давление на уровне горизонтального
газохода:
Подставляем это значение в уравнение Бернулли и получаема
ДРиот = (Рв — Pr)gH-
Сопротивление газохода и дымовой трубы:
ApL0T = ( «I + is|L + д) .??. „ 27,3 *f .
Следовательно,
Подставляем численные значения:
27,3 0,6^3ш2 = (1,216 - 0,693) 9,81.19.
Отсюда находим скорость газа в газоходе и дымовой трубе
в летних условиях:
w=s 3,2 м/с.
Аналогично может быть подсчитана скорость газа в зимних
условиях (для Ленинграда средняя температура —7,7 °С). В
зимних условиях w = 3,5 м/с.
Пример 1.25. Определить потерю давления на трение в
змеевике (рис. 1.15), по которому проходит вода со скоростью 1 м/с.
Змеевик сделан из бывшей в употреблении стальной трубы
диаметром 43 X 2,5 мм. Диаметр витка змеевика 1 м. Число
витков 10. Средняя температура воды 30 °С.
Решение. Потерю давления на трение находим по формуле
(1.36) для прямой трубы, а затем вводим поправочный коэффи-
40
Рис. 1. 15 (к примеру 1.25).
циент для змеевика по формуле (1.46).
Предварительно определяем режим течения.
Динамический коэффициент вязкости воды при
30 °С равен 0,8 мПа-с (табл. VI). Критерий
Рейнольдса:
Re =
wdp
is?L=«»
Для цельнотянутой стальной трубы с
незначительной коррозией е = 0,2 мм
(табл. XII). Тогда отношение dje = 38/0,2 =
= 190. По графику (рис. 1.5) при Re =47 500 и dje
находим К =0,0316. Приближенно длина змеевика равна:
L = nDn = 3,14.Ы0 = 31,4 м.
Потеря напора на преодоление трения в прямой трубе:
»
190
Арпп = Я,
d
pw2
= 0,0316
31,4 1000-12
= 13 100 Па.
2 0,038 2
По формуле (1.46) находим поправочный коэффициент;
*р = 1 + 3,54-^- = 1 + 3,54 -2^*1 = 1,134.
Следовательно, для змеевика:
дРзм = дРпрг|* =* 13 100.1,134= 14 800 Па = 1510 мм вод. ст.
Пример 1.26. оО т/ч нитробензола при 20 °С перекачиваются
насосом из бака с атмосферным давлением в реактор, где
поддерживается избыточное давление 0,01 МПа (рис. 1.16).
Трубопровод выполнен из стальных труб диаметром 89 X 4 мм с
незначительной коррозией. Длина всего трубопровода, включая
местные сопротивления, 45 м. На трубопроводе установлены:
диафрагма (d0 = 51,3 мм), две задвижки и четыре отвода под углом
90° с радиусом изгиба 160 мм.
Высота подъема жидкости 15 м.
Найти мощность, потребляемую
насосом, приняв общий к. п, д. его
равным 0,65.
Решение. Массовый
расход нитробензола:
М = 30 000/3600 = 8,34 кг/с.
Объемный расход:
V = М/р = 8,34/1200 = 0,00695 м3/с,
где р — 1200 кг/м3 — плотность
нитробензола (табл. IV).
5
*€
1
Ъ
Рис. 1,16 (к примеру 1.26)
41
Скорость нитробензола!
V 0,00695 , Qr ,
Ш=гТ= 0,785-0,081'а !'35м/с'
Критерий Рейнольдса:
Re- «** - Ь35-0,081-1200 .^
где fi — динамический коэффициент вязкости нитробензола (рис. V).
Определяем коэффициент трения. По табл. XII шероховатость
стальных труб с незначительной коррозией г = 0,2 мм. По рис. 1.5
для die = 0,081/0,0002 = 405 и Re = 62 500 находим К = 0,0257.
Коэффициенты местных сопротивлений, взятые из табл. XIII*
сводим в табличку:
Вид сопротивления
2?
Вход жидкости из бака в трубопровод (труба с острыми края- 0,5
ми)
Диафрагма \т= (51,3/81)?= 0,4] 8,25
Задвижка (? = 0,5) 2-0,5= 1,0
Отвод (при ф= 90° и K0/d= 160/81 « 2):
? = АВ= 1-0,15= 0,15 4-0,15= 0,6
10,35
Общее гидравлическое сопротивление трубопровода (сети) по
уравнению (1.49):
Ар = -^f-(* + — + St) + PghnoR + дРдоп =
- 120°2'-35- (1+.W+,Q,35) + 1200.9,81.15 +
+ 0,1 - 9,8Ы04 = 215 000 Па.
Потребляемая насосом мощность по уравнению (1.33):
N - "ToOOrJ - 1000-0,65 ~ 2>6 KbT-
Пример 1.27. Воздух с температурой 50 °С подается
вентилятором в установку, где имеется избыточное давление 35 мм вод. ст.
Трубопровод выполнен из стальных труб диаметром 102 X 6 мм
с незначительной коррозией. Длина всего трубопровода, включая
местные сопротивления, 70 м. На трубопроводе установлены\
диафрагма (d0 = 49,3 мм), две задвижки и четыре отвода под
углом 90° с радиусом изгиба 300 мм. Электродвигатель
вентилятора потребляет мощность 1,35 кВт; к. п. д. электродвигателя
42
VT]9 = 0,95. Показание водяного дифманометра, присоединенного
к диафрагме, 400 мм. Определить к. п. д. вентилятора.
Решение. Плотность воздуха при 50 °С:
Р = Ро (Т0/Т) = 1,293 (273/323) = 1,09 кг/м3.
Коэффициент расхода диафрагмы определяем по табл. XV.
При m = (49,3/90)2 = 0,3 принимаем среднее значение а л; 0,64.
Расход воздуха по формуле (1.32) при k = 1 (табл. XVI):
V = а/0 \T2gH (9м — 9)19 = 0,64-0,785-0,04932 1^2-9,81 -0,4 (988 ~ 1,09)/1,09 =
= 0,103 м3/с.
Скорость воздуха в трубопроводе:
V °>103 ,йо /
»в 0,785^ = 0,785¦0,09*" = 16'2 М/С'
Критерий Рейнольдса, определяемый по диаметру
трубопровода:
Рр "Ф 16,2-0,09-1,09
^е = = — — = «I 000.
|я 0,0196-10 6
Динамический коэффициент вязкости воздуха \i =0,0196 X
X 10"3 Па-с определен по рис. VI.
Проверяем принятое значение а. По табл. XV для m = 0,3
и Re = 81 000 находим а =0,637, что практически совпадает
с принятым значением.
Определяем коэффициент трения. По табл. XII средняя
шероховатость стальных труб с незначительной коррозией е — 0,2 мм.
По рис. 1.5 для die = 90/0,2 = 450 и Re = 81 000 находим к ж
ж 0,025.
Коэффициенты местных сопротивлений, взятые из табл. XIII,
сводим в табличку:
Вид сопротивления
2^
Вход воздуха в трубопровод (труба с закругленными краями)
Диафрагма (m ~ 0,3)
Задвижка (? = 0,5)
Отвод (при ф = 90° и RJd = 300/90 = 3,3):
С= ЛВ= 1-0,13= 0,13
) 0,2
18,2
2-0,5 =
4-0,13 =
19,92 *»
1,0
0,52
20
Общее гидравлическое сопротивление трубопровода (сети);
Др = 4-(1 + ^ + ^)+А^п =
_ J^ (, + 1^- + 20) + 35.9,81 = 6030 Па.
43
Рис, 1*17 (к примеру 1,28),
К. п. д. вентилятора:
___ V Ар 0,103-6030
Г)ВРНТ —
WOO^N 1000.0,95-1,35
да 0,48.
Пример 1.28. Жидкость,
имеющая плотность 1200 кг/м3 и
динамический коэффициент вязкости
2 мПа-с, из бака с постоянным
4 уровнем 1 самотеком поступает в
реактор 2 (рис. 1.17).*
Определить, какое максимальное количество жидкости (при полностью
открытом кране) может поступать из бака б реактор. Уровень
жидкости в баке находится на 6 м выше ввода жидкости в реактор.
Трубопровод выполнен из алюминиевых труб с внутренним
диаметром 50 мм. Общая длина трубопровода, включая местные
сопротивления, 16,4 м. На трубопроводе имеются три колена
и кран. В баке и реакторе давление атмосферное.
Решение. Напишем уравнение Бернулли для
установившегося потока жидкости, взяв первое сечение по уровню жидкости
в баке, а второе — по концу трубопровода на выходе потока
в реактор!
*+^+
ЧХОТ
г2 +
№
+
и>1
ч
Так как рх = рг и wx < Щ, то
zi — га
щ
2g
W:
+ ^ПОТ — "оТ + ^ТР + ^М. О
2?
ИЛИ
Hpg =
0У2р
(i+i-Jr + к)
(а)
Напор Hpg расходуется на все гидравлические сопротивления
трубопровода.
В последнем уравнении две неизвестные величины: w
и к.
Решение может быть найдено путем последовательных
приближений.
По табл. XII для алюминиевых технически гладких труб
принимаем шероховатость е = 0,06 мм. Тогда die = 50/0,06 =
= 840. Зададимся (с последующей проверкой) величиной к =
= 0,022.
44
Коэффициенты местных сопротивлений, взятые из табл. XIII»
сводим в табличку:
Вид сопротивления
St
Вход жидкости в трубопровод 0,5
Кран 2,0
Колено (С« 1,1) 3-1,1 = 3,3
5,8
Исходное уравнение (а) принимает вид:
6.1200.9.81 =-^(,+^^1 + 5,8),
откуда w = 2,9 м/с.
Расход жидкости (при полностью открытом кране)!
V « wf = 2,9-0,785.0,052 = 0,0057 м3/с = 20,5 м3/ч.
Проверим значение к. Имеем:
Re = -2*L - 2'9-0°-°5-1200- = 87000.
\х 2-Ю"3
По рис. 1.5 для Re = 87 000 и die = 840 находим к = 0,022,
что совпадает с принятым значением.
Пример 1.29. Минеральное масло в количестве 40 м8/ч
перекачивается по трубопроводу диаметром 108 X 4 мм в бак,
помещенный на высоте 20 м. Длина горизонтального участка
трубопровода 430 м.
Вычислить необходимую мощность насоса, если перекачка
производится: а) при 15 °С и б) при 50 °С. При этих температурах
относительная плотность масла составляет 0,96 и 0,89,
динамический коэффициент вязкости 3,43 и 0,187 Па-с, соответственно.
Экономично ли подогревать до 50 °С масло перед перекачкой,
если 1 кВт-ч электроэнергии стоит 4 коп., а 1 т греющего
(отбросного) пара (/?аб0 =0,1 МПа) 2 руб. и если общий к. п. д.
насосной установки равен 0,5?
Решение. Скорость масла:
40
W" 0,785¦ 0,Р.3600 =1'414 м/с.
Критерий Рейнольдса:
при 15°С
при 50 °С
Re° °'Мз,434'960 -39=
0,Ы,414-890
Re ~ оТТвт - 67°-
45
Следовательно, в обоих случаях имеет место ламинарный
режим.
Потерю давления на трение определяем по формуле (1.39):
при 15 °С
дРтр = 32(430+20П.414.3,43 =7010000 Па, или 71,5 кгс/см-
при 50 °С
0 187
Лртр= 7 010 000-^^- = 383 000 Па, или 3,9 кгс/см3.
Затрата давления на подъем жидкости [формула (1.34) h
при 15 °С
АРпод = 20'9бО-9,81 = 188400 Па, или 1,92 кгс/см3;
при 50 °С
Дриод = 20-890-9,81 = 174 600 Па, или 1,78 кгс/см2.
Затрата давления на создание скорости [формула (1.35)]:
Дрск = 960-1,4142/2 = 960 Па.
Этой величиной а данном случае пренебрежем так же, как
и потерей давления на преодоление местных сопротивлений.
Тогда необходимая мощность по формуле (1.33):
при 15°С
_ 40(7 010 000+188 400) _
Л — 3600-1000-0,5 "IWKH'
при 50 СС
40(383 000+174 600)
Л - 3600-1000^0,5 = U>6 КЬТ*
Следовательно, при перекачке холодного масла требуется
дополнительный расход мощности 160 — 12,3 = 147,7 кВт. В
условиях задачи стоимость дополнительной электроэнергии на
перекачку составит: 147,7-0,04 =5,9 руб./ч
Расход теплоты на подогрев масла от 15 до 50 °С при удельной
теплоемкости масла с = 1,68-108 Дж/(кг*К):
Q= 40.960.1.68^(50-15) ^6250()0 ^
Удельная теплота конденсации отбросного пара (/?абс =
=^0,1 МПа) r^2260-10:J Дж/кг.
Расход пара на подогрев масла:
° = Т" = -2260°№ = °'276 КГ/С w 100° КГ/Ч'
Стоимость 1 т пара 2 руб. Следовательно, предварительный
подогрев масла при данной стоимости пара и электроэнергии
безусловно выгоден.
Пример 1.30. Вывести обобщенную расчетную формулу для
коэффициента трения в трубах по следующим экспериментальным
данным.
46
Таблица 1.3
Жидкость
Нефть
м/с
0,85
1,21
1,54
1,91
2,32
W2,
(и/у
0,723
1,46
2,37
3,65
5,38
Др
Па
738
1300
2060
3020
4050
Aw2
0,0522
0,0458
0,0445
0,0424
0,0386
Жидкость
Вода
м/с
о,п
0,16
0,22
0,26
(м/с)*
0,0121
0,0256
0,0484
0,0676
Др,
п*
105
201
238
455
. Др
Х~ Aw*
0,0433
0,0392
0,0348
0,0337
1. При перекачке нефти относительной плотности 0,9 по
стальному трубопроводу с внутренним диаметром 300 мм на прямом
участке длиной 13 м были получены следующие величины потери
давления в зависимости от скорости нефти:
Скорость, м/с ... 0,85 1,21 1,54 1,91 2,32
Потеря давления, Па . . . 738 1300 2060 3020 4050
2. Аналогичные экспериментальные данные для воды при
перекачивании ее по прямому стальному трубопроводу с внутренним
диаметром 60 мм, длиной 24 м;
Скорость, м/с ... 0,11 0,16 0,22 0,26
Потеря давления, Па . , . 105 201 238 455
Решение. Вычислим значения коэффициентов трения X для
нефти и воды по формуле (1.36).
Предварительно определим постоянные (в наших опытах)
величины А = Lp/(2d). Для нефти! А = 13-900/(2-0,3) = 19 500.
Для воды: А =24-1000/(2-0,06) =200 000.
Дальнейший расчет сведен в табл. 1.3.
Как следует из табл. 1.3, коэффициент трения X уменьшается
с возрастанием скорости потока.
Если нанести зависимость коэффициента трения от скорости
на график (рис. 1.18), получим две различные кривые. На
логарифмической сетке, т. е. в координатах lg ш — lg %, получаются
две прямые линии, приближенные уравнения которых:
для нефти
JgA, = —1,31— 0,25 Igay А
или А, = 0,049ау-°'25; щ
для воды
lgX = —1,65 — 0,3 lg цу
или Х = 0,0224 иГ0'3. W4
Таким образом, мы
получили две различные
0,03
Рис, 1.18 (к примеру 1.30): *
1 — нефть; 2 — вода. С09М/С
¦2
^
4NL
^^-
•
•
47
эмпирические формулы, каждая из которых действительна лишь
в тех условиях, при которых она была получена Последняя
формула, например, пригодна для вычисления коэффициента
трения только для воды при протекании ее по трубе внутренним
диаметром 60 мм со скоростью 0,1—0,3 м/с (и при той же
температуре воды, при которой проводились опыты).
Получить по имеющимся экспериментальным данным для
нефти и воды общую расчетную формулу, пригодную не только
для нефти или волы, но также и для других жидкостей при других
скоростях, других диаметрах труб и других температурах, можно
с помощью теории подобия.
Для потери давления на трение в трубах теория подобия дает
зависимость (1.37) в критериальной форме: Ей = ф (Re, Г).
Для труб с данной шероховатостью стенок в турбулентной
(доавтомодельной) области коэффициент трения к зависит только
от величины критерия Re — см. уравнения (1.38), (1.40) (1.42)з
Х-/(Re).
Следовательно, для получения обобщенного уравнения мы
должны найти зависимость коэффициента трения не от скорости,
как это было сделано выше, а от критерия Re.
Значения кинематического коэффициента вязкости при опытах
были: для нефти v = 0,8* 10~4 м2/с, для воды v = 10'6 м2/с.
В табл. 1.4 сопоставлены значения Re и kt вычисленные по
вышеприведенным экспериментальным данным.
Если построить график зависимости к от Re,то получим одну
кривую, на которую укладываются все точки для нефти и воды.
В логарифмических координатах получим прямую линию
(рис. 1.19). На этом графике по оси абсцисс отложены величины
х = [g Re — 3,5, а по оси ординат — величины у = lg к + 2.
Уравнение полученной прямой линии: у = —0,254х + 0,71,
или lg к + 2 = —0,254 (lg Re — 3,5) + 0,71; lg к = —0,0254 X
XlgRe —0,4, откуда к = 0,398/Re0-254.
Таблица 1.4
Жн^кооть
Нефть
Вода
W. М/С
0,85
1,21
1,54
1,91
2,32
0,11
0,16
0,22
0,26
„ wd
Re=*_
3 190
4 530
5 780
7 160
8 700
6 600
9 600
13 200
15 600
л
0,0522
0,0458
0,0445
0,0424
0,0386
0,0438
0,0392
0,0348
0,0337
lg Re
3,50
3,66
3,76
3,85
3,94
3,82
3,98
4,12
4,19
iff*
2,72
2,66
2,65
2,63
2,59
2,64
2,59
2,54
2,53
48
Рис. 1.1ft (к примеру 1Л0):
• — нефть; О -*¦ вода.
Полученная формула и
представляет собой общую зависимость,
которой можно пользоваться для
расчета коэффициента трения в
трубах не только для нефти и
воды, но и для любых других
жидкостей в пределах значений
критерия Re = 3000—16 000.
Следует добавить, что эта формула
пригодна лишь для труб с такой
же относительной шероховатостью
стенок, какая была при опытах.
Так как экспериментальные
данные укладываются на одну
прямую (рис. 1.19), то можно
о
<И
0,2 0,4 0,6
cc-lg-Re-J,5
считать, что относительная шероховатость стенок eld в опытах с
нефтью и с водой была примерно одинаковой.
Эту относительную шероховатость можно найти, если на
график (рис. 1.5 или 1.6) нанести экспериментальные данные из
табл. 1.3 и 1.4, представив их в виде % = / (Re) или Eu/Г = / (Re).
Пример 1.31. Для экспериментального изучения в
лабораторных условиях некоторого производственного процесса
изготовлена геометрическая модель промышленного аппарата в масштабе
1 : 10. В производственном аппарате рабочее вещество —
горячий воздух (100 °С, атмосферное давление), движущийся со
скоростью 3 м/с. В лабораторной модели предполагается применить
в качестве рабочего вещества воздух атмосферного давления с
температурой 22 °С.
Возможно ли при этих условиях получить полное
гидродинамическое подобие промышленного аппарата и модели, и какова
должна быть скорость воздуха в модели?
Решение. Для соблюдения гидродинамического подобии
необходимо при подобных граничных условиях равенство
критериев Рейпольдса и Фруда (критерий Эйлера в данном случае
не является определяющим) в модели и в производственном
аппарате, т. е. должно быть:
Rei = Re2; "ЫФх ^ »APt ,
(а)
Ff! - Fr2;
ОУТ
w\
eh gl\
(б)
В этих уравнениях индекс «1» относится к промышленному
аппарату, индекс «2» — к модели.
49
Имеем:
Wi =3 м/с; i8 = 0,lff;
Pi = 1,293 (273/373) = 0,945 кг/ма;
pa = 1,293 (273/295) = 1,19 кг/м3;
(ij = 0,0235 мПа-с; fi2 *= 0,0185 мПа-с.
Подставляя эти значения в уравнение (а), находим!
3ir0,945/0,0215 = ^.0,1^. 1,19/0,0185,
откуда
3.0,945-0,0185 ОЛ _ ,
^ = 0,1.0,0216-1.19 " 2°'5 М/°*
Подстановка в уравнение (б) дает:
3V/i«»i/(0,Wi),
откуда
ау3 = ]^(р = 0,946 м/с.
Полученные результаты показывают, что соблюдение полного
гидродинамического подобия, т. е. одновременного подобия сил
трения и сил тяжести, в модели и в промышленном аппарате при
заданных условиях невозможно. Придется ограничиться
приближенным моделированием процесса, как это в большинстве случаев
на практике и делается, т. е. ограничиться соблюдением только
одного условия (либо Re = idem, либо Fr — idem) в зависимости
от того, какое из этих условий является более существенным. Если,
например, в нашем случае большее значение имеют силы трения,
т. е. критерий Re, то скорость воздуха в модели должна быть
взята 20,5 м/с.
Выясним, при каких условиях возможно получение
одновременного подобия сил трения и сил тяжести в модели и в
промышленном аппарате.
Из условия Re = idem, т. е. w1tl/v1 = w2l2/v2, где v —
кинематический коэффициент вязкости, следует, что wjw2 =*V\hl(vd>d'
Из условия Fr = idem, т. е. wV(gh) = wlj(gl2), находим:
Оба условия (Re = idem и Fr = idem) будут соблюдены, если
vihltyth) = Ci/Wl/2. т- е. Vv2 = (/i/'a)3/2.
Последнее равенство и выражает требуемое условие
одновременного подобия сил трения и сил тяжести.
Пример 1.32. Найти диаметр трубопровода для
транспортирования водорода при массовом расходе его 120 кг/ч. Длина
трубопровода 1000 м. Допускаемое падение давления А/? =
= 110 мм вод. ст. (1080 Па) Плотность водорода 0,0825 кг/м3.
Коэффициент трения к = 0,03.
50
Решение. В длинных магистральных газопроводах
давление расходуется главным образом на преодоление трения, поэтому
приравниваем заданную потерю давления А/? = А/?тр.
Так как скорость потока — величина неизвестная, то выразим
ее через объемный расход V и искомый диаметр трубопровода,
а затем подставим в уравнение (1.36):
V
W =
0,785tf2
Тогда
XL V2p
Ар~ d 2-0,7852d4 *
Решая это уравнение относительно диаметра, получаем;
-cf
Tv*$
Ар '
ъ г ^
где С = у "о~т§52^7( В нашем случае
У о,оз
С== V 0,785*.2 ~0'48'
Секундный объемный расход водорода:
Так как кр = 110-9,81 = 1080 Па, то
J/0,0825-0,405М000 пп
d-wy [обо = °'2м*
Пример 1.33. Определить начальное давление газа,
достаточное для передачи его по трубопроводу на расстояние 100 км, при
следующих условиях: расход газа 5000 кг/ч, плотность газа
0,65 кг/м3 (при нормальных условиях), средняя температура газа
18 °С. Диаметр трубопровода 0,3 м, коэффициент трения % =
= 0,0253. Давление газа при выходе из трубопровода должно
быть рабс = 1,5 кгс/см2 (~0,15 МПа).
Решение. Как и в предыдущем примере, считаем, что
давление в трубопроводе расходуется лишь на преодоление
трения. В случае дальних газопроводов формулу (1.36) для
определения потери давления на трение следует применять, исходя
из дифференциального выражения, так как плотность и скорость
газа по длине трубопровода меняются *:
к ау2р
* Знак минус поставлен потому, что с возрастанием длины трубопровода
давление в нем падает.
51
где переменные плотность р и скорость w — функции давления
газа, падающего по мере продвижения его по трубопроводу.
Однако произведение шр, т. е. массовая скорость потока, остается
по длине трубопровода постоянным.
Выразим р и w через соответствующие характеристики газа
при нормальных условиях
и подставим их в уравнение для потери давления!
Принимая температуру Т постоянной по длине трубопровода,
сведем все постоянные величины * в общий коэффициент!
_ Xpo^oPoZL
С " 257^
Тогда
—pdp = CdL,
Интегрируя это уравнение в соответствующих пределах
ркон 1*
— [ pdp = C \dLt
получаем:
Рнач О
Т- (ри*ч ~ Ркон) = CL ИЛИ Йач - Ркон = 2CL-
2
В условиях задачи скорость газа при О °С и 760 мм рт. ст.
составляет:
[5000
W° ~~ 0,65.3600-0,785.0,32 ~" ^U М/С'
Следовательно,
п 0,0253-0,65-302-101 300.291
С " 2-6,3-273 ~ 266> 10 '
Подставим заданные и найденные величины в полученное
уравнение: р\лч — (14,7-104)2 = 2-266-104-105 Отсюда находим,
что начальное давление газа в сети должно быть:
Рнач = 71 ¦ Ю* Па, или 7,3 кгс/см2.
Пример 1.34. Определить экономически наивыгоднейший
диаметр трубопровода для транспортировки 6000 м3/ч (считая при
0 °С и 760 мм рт. ст.) метана на расстояние 4 км. К. п. д.
нагнетателя с электродвигателем 0,5. Стоимость электроэнергии 4 коп.
* Коэффициент трения X является постоянным по длине трубопровода
так же, как и критерий Re, поскольку wp = ш0р0 = const.
52
за 1 кВт-ч. Стоимость амортизации трубопровода 2,4 руб. в год
на 1 м длины и 1 м диаметра. Стоимость ремонта (эксплуатации)
трубопровода 1,8 руб. в год на 1 м длины и 1 м диаметра.
Решение. Примем ориентировочно, что коэффициент
трения к — 0,03 и что потери на местные сопротивления составляют
10% от потерь н# трение.
Сделаем расчет для условной температуры 30 °С, принимая
(с последующей проверкой), что падение давления в трубопроводе
невелико и среднее давление приближенно можно считать равным
атмосферному.
Объемный расход метана:
Тогда
.. 6000-303 , я- ,.
У в 3600.273 -*>85м3^
V __ 1,85 __ 2,36
w "~ 0,7854* *~ 0,785# Ф М/С*
Пренебрегая затратой давления на создание скорости,
получаем по формуле (1.34) для горизонтального газопровода при
д/>доп = 0:
Др = Лртр + Лрм, с = 1,1 Лртр,
т. е.
lt\KLw2p _ 1,1.0,03*4000.2,36».0,64 __ 235 „
где плотность метана
16-273. пал / ч
р в -22^303- " 0'64кг'м3'
В соответствии с принятым допущением подсчитаем
расходуемую нагнегателем мощность при Др <$0,1 кгс/см2 по формуле
(1.33):
V Lp 1,85-235 0,87 „
ЮООп 1000.0,5d* t$
1 кВт*год стоит 0,04-24-330 = 316 руб., принимая 330 рабочих
дней в году.
Таким образом, годовая стоимость электроэнергии в
зависимости от диаметра трубопровода гложет быть выражена формулой!
Э = 0,87-316/^ = 275/rf5 руб./год.
Подобным же образом выразим годовую стоимость
амортизации трубопровода
А = 2t4Ld = 2,4.4000rf = 9600d руб./год.
и реконта (эксплуатации) его:
Р « lt8U = 7200d руб./год.
63
Суммарная годовая стоимость как функция диаметра
выразится уравнением:
Э + А + Р = (275/d*) + \6 800d руб./год.
Для отыскания минимума берем производную и приравниваем
ее нулю:
д
dd
(Э + А + Р) = — 5-275сГв + 16 800 = 0.
Вторая производная положительна.
Из последнего уравнения находим- d = 0}66 м. Это и будет
экономически наивыгоднейший диаметр газопровода.
Проверим величину Др в трубопроводе диаметром 0,66 mj
Ар = 235/rf5 = 235/0,бб5 = 1890 Па, или 0,0193 кгс/см2,
т. е. меньше 0,1 кгс/см2, как и было принято выше.
Пример 1.35. При тепловом расчете теплообменника для
нагрева некоторого раствора был выбран по каталогу четыреххо-
довой кожухотрубчатый теплообменник (рис. 1.20), в котором
раствор проходит по трубному пространству со скоростью 0,3 м/с.
Определить гидравлическое сопротивление трубного пространства.
Характеристика теплообменника: общее число труб 90, трубы
стальные диаметром 38x2 мм с незначительной коррозией,
высота трубного пространства 2 м, штуцеры для раствора имеют
диаметр 159x4,5 мм. Средняя температура раствора 47,5 °С,
динамический коэффициент вязкости 0,83 мПа-с, плотность
1100 кг/м3.
Решение. Критерий Рейнольдса для раствора:
оф 0,3-0,034-И00
Re =
f*
0,83-I0~3
= 13 500.
В этом примере требуется определить потерю давления для
неизотермического турбулентного потока. Но поскольку здесь
мы имеем нагревающийся поток капельной жидкости, то
приближенно рассчитываем гидравлическое сопротивление как для
потока изотермического, делая при этом
ошибку в сторону преувеличения потери
давления, т. е. в сторону запаса. Для расчета
применяем формулу (1.54).
Определяем потерю давления на
преодоление трения в трубах.
По табл. XII для стальных труб с
незначительной коррозией шероховатость е =
« 0,2 мм. При этом die = 34/0,2 = 170. По
рис. 1.5 для Re = 13 500 и die = 170
находим к = 0,035.
Рис. 1.20 (к примеру 1.35).
54
Скоростное давление в трубах:
АРск = Р^2/2= 1100-0,32/2==49,5 Па.
Потеря давления на преодоление трения в грубах!
дРтр « % (nL/d) Дрск » 0,035 (4-2/0,034) 49,5 = 407 Па,
где п = 4 — число ходов по трубному пространству.
Определяем потери давления на преодоление местных
сопротивлений теплообменника (рис. 1.20) по следующей табличке:
Вид.сопротивления
Ь
2^
Входная и выходная камера 1,5 1,5-2= 3
Вход в трубы я выход из них 1 1-8=8
Поворот на 180° из одной 2,5 2,5-3=7,5
секции в другую
Скорость раствора в штуцерах:
wm = w (ndyd^) = 0,3 (90 : 4-0,0342/0,152) = 0,346 м/с.
Скоростное давление в штуцерах:
Ьр'Ск = ри^/2 = ИО0-О,34б'2/2 = 66 Па.
Скорость в штуцере больше скорости в трубах, поэтому потери
давления для входной и выходной камер находим по скорости
в штуцерах, а потери при входе и выходе из труб и при поворотах
из одной секции в другую — по скорости в трубах:
Арм. с = 3-66 + (8 + 7,5) 49,5 = 966 Па.
Общее гидравлическое сопротивление трубного пространства
теплообменника:
Ар =* 407 + 966 « 1373 Па = 140 мм вод. ст.
Пример 1.36. По межтрубному пространству кожухотрубчатого
теплообменника (рис. 1.21) параллельно осям труб проходит
анилин со скоростью 0,5 м/с. Теплообменник состоит из 19
стальных труб диаметром 26x2,5 мм, длиной 2,7 м. Внутренний диаметр
кожуха 200 мм. Средняя шероховатость труб е = 0,2 мм. Анилин
в теплообменнике охлаждается водой от 100 до 40 °С
Определить потерю давления на трение для анилина: а) считая
поток изотермическим; б) для неизотермического потока при
средней температуре стенки труб 25 °С.
Решение, а) Для изотермического потока потерю
давления на трение рассчитываем по формуле (1.36) при средней
температуре анилина, равной (100 + 40)/2 = 70 °С.
55
Рис, 1 .21 (к примеру 1.36).
Эквивалентный диаметр межтрубного
пространства теплообменника:
<*э-
4/ _ D2 — nd?
П ~~ D + nd
2002 —19.262
200+19-26
= 39,2 мм,
где D — внутренний диаметр кожуха, мм; d—
наружный диаметр трубы, мм; п — число труб.
Определяем значение критерия Рейнольдса:
wdp 0,5-0,0392.1040
Re =
Р
1,4-10'3
= 14 600.
И
Здесь 1040 кг/м3 — плотность анилина; 1,4-10~3
Па-с—динамический коэффициент вязкости анилина
при 70 °С (рис. V).
Коэффициент трения определяем по рис. 1.5. Для Re = 14 600
die =39,2/0,2 = 196 находим к =0,034.
Потеря давления на трение:
KL w2Q 0,034-2,7-0,52-1040
&Р
= 304 Па.
d 2 ~" 0,0392-2
б) Если поток неизотермический (температура стенки
отличается от температуры жидкости), то значение Д/>тр для
изотермического потока необходимо умножить на поправочный
коэффициент, который определяем, как и для гидравлически гладких
труб, по уравнению (1.44):
где Ргст — критерий Прандтля для протекающей жидкости прн температуре
стенки трубы; Ргж — критерий Прандтля для протекающей жидкости при ее
средней телшературе.
Значения критерия Прандтля для анилина находим по
номограмме (рис. XIII): для /ст =25°С Рг =47, для /ж = 70 °С
Рг = 16,5.
Потеря давления на трение для неизотермического
(охлаждающегося) турбулентного потока анилина:
Дртр = 304 (47/16,5)1/3 = 430 Па,
что значительно выше, чем для потока изотермического.
Пример 1.37. Для определения коэффициента продольного
перемешивания Ev в насадочной колонне для газовой фазы были
проведены опыты по получению выходной кривой отклика на
импульсный (мгновенный) ввод индикатора в газовой поток на
входе в колонну. Высота слоя насадки 6 м. Скорость газа в
колонне (фиктивная) 0,8 м/с. Полученные результаты приведены
в табл. 1.5 и на рис. 1.22. Найти величину ?г.
56
Таблица 1.5
(
0
1
2
3
4
С
0
0
0,7- Ю-4
0,0621
1,792
т
5
6
7
8
с
7,972
10,87
6,511
2,151
X
9
10
11
12
с
0,450
0,0657
0,0072
0,0006
т — время от момента ввода индикатора, с; С — концентрация
индикатора на выходе, г/м3.
Решение.
Находим среднее время пребывания в колонне частиц (струек)
газового потока:
оо /со
ЬСр~
о / о
Вычисляем интегралы по формуле трапеций.»
оо 12 / П—1 \
0 0 \ «=1
= 1 (0,0003 + 29)86) = 29,86 г-с/м3;
оо 12 / /г—I
J
0
тСйт
j
iC d% « Лт
tjv^n
+
2 **<?,
0 \ i—1
= 1 (0,0036 + 179,7) = 179,7 г-с2/м3;
тср = 179,7/29,86 = 6,018 с
Определяем дисперсию Cr/u3
оо
оо
a2 = \т*Сс1тПСс1т:
о /о
оо 12 /
/ т2 С
] т'2С d% & т2С d% zz Дт —^-^- +
0 0 ^
п-\ \
+ J] T?Ci = ! (°>0432 +П18) =
= Ш8г-с3/м3;
а2 = 1118/29,86= 1,230 с».
В безразмерных единицах:
°е = а'"АсР = 1,230/36,22 = 0,03396.
Рис. 1.22 (к примеру 1.37),
о
Ю 20 S0 АО 50
57
Находим значение модифицированного критерия Пекле для
продольного перемешивания Ре ~wH/ED из уравнения
°е = -^-(Ре-1+е-Ре).
Решая это уравнение методом последовательных приближений,
имеем:
Ре = 57,8.
Находим действительную скорость газа в колонне:
w « #/тср = 6/6,018 = 0,997 м/с.
Коэффициент продольного перемешивания:
Ег = wH/Pe = 0,997.6/57,8 = 0,103 м2/с.
КОНТРОЛЬНЫЕ ЗАДАЧИ*
1.1. Найти мольную массу и плотность водяного газа при
/ =s 90 °С и рабс = 1,2 кгс/см2 (~0,12МПа). Состав водяного газа:
На — 50 %, СО — 40 %, N2 — 5 %, С02 — 5 % (по объему).
1.2. Определить плотность диоксида углерода при / — 85 °С
и Риаб = 2 кгс/см2 (~0,2 МПа). Атмосферное давление
760 мм рт. ст.
1.3. Состав продуктов горения 1 кг коксового газа (в кг):
С02 — 1,45; N2 - 8,74; Н20 — 1,92. Найти объемный состав
продуктов горения.
1.4. Разрежение в осушительной башне сернокислотного
завода измеряется U-образным тягомером, наполненным серной
кислотой плотностью 1800 кг/м3. Показание тягомера 3 см.
Каково абсолютное давление в башне, выраженное в Па, если
барометрическое давление составляет 750 мм рт. ст.?
1.5. Манометр на трубопроводе, заполненном жидкостью,
показывает давление 0,18 кгс/см2. На какую высоту h над точкой
присоединения манометра поднимается в открытом пьезометре
жидкость, находящаяся в трубопроводе, если эта жидкость;
а) вода, б) четыреххлористый углерод (рис. 1.23)?
1.6. Высота уровня мазута в резервуаре 7,6 м (рис. 1.24).
Относительная плотность мазута 0,96. На высоте 800 мм от дна
в резервуаре имеется круглый лаз диаметром 760 мм, крышка
которого прикрепляется болтами диаметром 10 мм. Принимая
для болтов допустимое напряжение на разрыв 700 кгс/см2,
определить необходимое число болтов. Определить также давление
мазута на дно резервуара.
1.7. На малый поршень диаметром 40 мм ручного
гидравлического пресса (рис. 1.25) действует сила 589 Н (60 кгс).
Пренебрегая потерями, определить силу, действующую на прессуемое тело,
если диаметр большого поршня 300 мм.
* Ответы к контрольным задачам даны на стр. 495.
58
I
i
i-
M
le
^
Рис. 1.23 (к контрольной задаче 1.5).
~~1
Рис. 1.24 (к контрольной задаче 1.6),
1.8. Динамический коэффициент вязкости жидкости при 50 °0
равняется 30 мПа-с. Относительная плотность жидкости 0,9.
Определить кинематический коэффициент вязкости.
1.9. Найти динамический коэффициент вязкости при 20 СС
и атмосферном давлении азотоводородной смеси, содержащей
75% водорода и 25% азота (по объему).
1.10. Известно, что динамический коэффициент вязкости
льняного масла при 30 °С равняется 0,331 П, а при 50 °С 0,176 П.
Чему будет равен динамический коэффициент вязкости этого
масла при 90 °С? (Воспользоваться правилом линейности,
приняв за стандартную жидкость, например, 100%-ный
глицерин).
1.11. Холодильник состоит из 19 труб диаметром 20x2 мм
(рис. 1.21). В трубное пространство холодильника поступает вода
по трубопроводу диаметром 57x3,5 мм. Скорость воды в
трубопроводе 1,4 м/с. Вода идет снизу вверх. Определить скорость
воды в трубах холодильника.
1.12. По трубам теплообменника, состоящего из 379 труб
диаметром 16X1,5 мм, проходит азот в количестве 6400 м3/ч
(считая при 0 °С и 760 мм рт. ст.) под давлением ризб = 3 кгс/см2
(~0,3 МПа). Азот входит в теплообменник при 120 °С, выходит
при 30 °С. Определить скорость азота в трубах теплообменника
на входе и на выходе.
1.13. Холодильник состоит из двух
концентрических стальных труб
диаметром 29x2,5 мм и 54X2,5 мм. По
внутренней трубе протекают 3,73 т/ч
рассола плотностью 1150 кг/м3. В
межтрубном пространстве проходит 160 кг/ч
газа под давлением рабс = 3 кгс/см2
(~0,3 МПа) при средней температуре
Рис. 1.2:> (к контрольной задаче 1.7).
59
О °С. Плотность газа при О °С и 760 мм рт. ст. равна 1,2 кг/м3.
Найти скорости газа и жидкости в холодильнике.
1.14. Определить необходимый диаметр наружной трубы в
условиях предыдущей задачи, если газ пойдет под атмосферным
давлением, но при той же скорости и при том же массовом
расходе.
1.15. Вычислить в общей форме гидравлический радиус при
заполненном сечении для кольцевого сечения, квадрата,
прямоугольника и равностороннего треугольника.
1.16. Определить эквивалентный диаметр межтрубного
пространства кожухотрубчатого теплообменника (рис. 1.21),
состоящего из 61 трубы диаметром 38x2,5 мм. Внутренний диаметр
кожуха 625 мм.
1.17. Определить режим течения воды в кольцевом
пространстве теплообменника типа «труба в трубе» (рис. 1.12). Наружная
труба — 96x3,5 мм, внутренняя — 57x3 мм, расход воды 3,6 м3/ч,
средняя температура воды 20 °С.
1.18. Определить режим течения этилового спирта: а) в
прямой трубе диаметром 40x2,5 мм; б) в змеевике, свитом из той
же трубы. Диаметр витка змеевика 570 мм. Скорость спирта
0,13 м/с, средняя температура 52 °С.
1.19. Определить местную скорость по оси трубопровода
диаметром 57x3,5 мм при протекании по нему уксусной кислоты
в количестве 200 дм3/ч при 38 °С.
1.20. В середине трубопровода с внутренним диаметром 320 мм
установлена трубка Пито—Прандтля (рис. 1.4),
дифференциальный манометр которой, заполненный водой, показывает разность
уровней Н = 5,8 мм. По трубопроводу проходит под
атмосферным давлением сухой воздух при 21 °С. Определить массовый
расход воздуха.
1.21. Из отверстия диаметром 10 мм в дне открытого бака,
в котором поддерживается постоянный уровень жидкости
высотой 900 мм, вытекает 750 дм3 жидкости в 1 ч. Определить
коэффициент расхода. Через сколько времени опорожнится бак, если
прекратить подачу в него жидкости? Диаметр бака 800 мм.
1.22. В напорный бак с площадью поперечного сечения 3 м?
притекает вода. В дне бака имеется спускное отверстие. При
установившемся течении расход через отверстие равен притоку
и уровень воды устанавливается на высоте 1 м. Если прекратить
приток воды, уровень ее будет понижаться и через 100 с бак
опорожнится. Определить приток воды в бак.
1.23. По горизонтальному трубопроводу с внутренним
диаметром 200 мм протекает минеральное масло относительной
плотности 0,9. В трубопроводе установлена диафрагма (рис. 1.3)
с острыми краями (коэффициент расхода 0,61). Диаметр
отверстия диафрагмы 76 мм. Ртутный дифманометр, присоединенный
к диафрагме, показывает разность уровней 102 мм. Определить
скорость масла в трубопроводе и его расход.
60
Рис. 1.26 (к контрольной за- i
даче 1.24). ]
¦
1.24. На трубопроводе
диаметром 160x5 мм
установлен расходомер «труба
Вентури» (рис. 1.26),
внутренний диаметр узкой
части которой равен 60 мм.
По трубопроводу проходит
этан под атмосферным
давлением при 25 °С.
Показание водяного дифманометра трубы Вентури Н = 32 мм.
Определить массовый расход этана, проходящего по трубопроводу
(в кг/ч), приняв коэффициент расхода 0,97.
1.25. Определить потерю давления на трение при
протекании воды по латунной трубе диаметром 19x2 мм, длиной 10 м.
Скорость воды 2 м/с. Температура 55 °С. Принять шероховатость
трубы е = 0,005 мм.
1.26. Определить потерю давления на трение в свинцовом
змеевике, по которому протекает 60%-ная серная кислота со
скоростью 0,7 м/с при средней температуре 55 °С. Принять
максимальную шероховатость свинцовых труб по табл. XII.
Внутренний диаметр трубы змеевика 50 мм, диаметр витка змеевика
800 мм, число витков 20. Длину змеевика определить
приближенно по числу витков и их диаметру.
1.27. По стальному трубопроводу внутренним диаметром
200 мм, длиной 1000 м передается водород в количестве 120 кг/ч.
Среднее давление в сети 1530 мм рт. ст. Температура газа 27 РС.
Определить потерю давления на трение.
1.28. Найти потерю давления на трение для пара в стальном
паропроводе длиной 50 м, диаметром 108x4 мм. Давление пара
рабс = 6 кгс/см2 (~0,6 МПа), скорость пара 25 м/с.
1.29. Как изменится потеря давления на трение в газопроводе,
по которому проходит азот, если при постоянном массовом
расходе азота: а) увеличить давление (абсолютное) подаваемого
азота с 1 до 10 кгс/см2 при неизменной температуре; б) повысить
температуру азота от 0 до 80 °С при неизменном давлении.
1.30. По водопроводной трубе проходит 10 м3/ч воды. Сколько
воды в 1 ч пропустит труба удвоенного диаметра при той
же потере напора на трение? Коэффициент трения считать
постоянным. Течение турбулентное.
1.31. По прямому горизонтальному трубопроводу длиной 150м
необходимо подавать 10 м3/ч жидкости. Допускаемая потеря
напора 10 м. Определить требуемый диаметр трубопровода,
принимая коэффициент трения к = 0,03.
1.32. Как изменится потеря давления на трение, если при
неизменном расходе, жидкости уменьшить диаметр трубопровода
61
Рис. 1.27 (к контрольной задаче 1.33),
Рис, 1.23 (к контрольной задаче 3,84),
V7/////////}/;y///V//h/////77?
КЕ-~Ч-2
вдвое? Задачу решить в двух вариантах: а) считая, что оба
режима (старый и новый) находятся в области ламинарного течения;
б) считая, что оба режима находятся в автомодельной области.
1.33. Жидкость относительной плотности 0,9 поступает
самотеком из напорного бака, в котором поддерживается атмосферное
давление, в ректификационную колонну (рис. 1.27). Давление
в колонне 0,4 кгс/см2 (~40 кПа) по манометру (/>Изб)- На какой
высоте х должен находиться уровень жидкости в напорном баке
над местом ввода в колонну, чтобы скорость жидкости в трубе
была 2 м/с. Напор, теряемый на трение и местные
сопротивления, 2,5 м. Применить уравнение Бернулли.
1.34. 86% раствор глицерина спускается из напорного бака /
в аппарат 2 по трубе диаметром 29x2 мм (рис. 1 28). Разность
уровней раствора 10 м. Общая длина трубопровода 110 м.
Определить расход раствора, если относительная плотность его 1,23, а
динамический коэффициент вязкости 97 мПа -с. Местными
сопротивлениями пренебречь. Режим течения принять ламинарным (с
последующей проверкой). Уровень раствора в баке считать постоянным.
1.35. 20 т/ч хлорбензола при 45 °С перекачиваются насосом
из реактора / в напорный бак 2 (рис. 1.29). В реакторе над
жидкостью поддерживается разрежение
200 мм рт. ст. (26,66 кПа), в напорном
баке атмосферное давление.
Трубопровод выполнен из стальных труб с
незначительной коррозией диаметром 76 х
X 4 мм, общей длиной 26,6 м. На
трубопроводе установлены 2 крана,
диафрагма (d0 = 48 мм) и 5 отводов под
углом 90° (Rjd = 3). Хлорбензол
перекачивается на высоту # = 15 м.
1
^
г
•ft
62
Рис. 1.29 (к контрольной задаче 1,35)»
Найти мощность, потребляемую насосом, приняв общий к. п. д.
насосной установки 0,7.
1.36. Кожухотрубчатый теплообменник (рис. 1.21) состоит
из 187 стальных труб с незначительной коррозией (е = 0,2 мм)
диаметром 18x2 мм, длиной 1,9 м. Кожух выполнен из трубы
426X12 мм. По межтрубному пространству параллельно осям
труб проходит 3000 м3/ч азота (считая при нормальных условиях)
под атмосферным давлением при средней температуре —10 °С.
Диаметр входного и выходного штуцера 250 мм. Определить
гидравлическое сопротивление межтрубного пространства»
1.37. В теплообменнике типа «труба в трубе» (рис. 1.12),
состоящем из двух концентрических труб (внутренней диаметром
44,5X3,5 мм и наружной диаметром 89x5 мм), охлаждается от
70 до 30 °С толуол в количестве 1900 кг/ч. Толуол проходит по
кольцевому пространству между наружной и внутренней трубой;
по внутренней трубе протекает охлаждающая вода,
нагревающаяся от 14 до 21 °С. Определить потерю давления на трение на
1 м длины трубы для толуола и для воды, принимая, что стальные
трубы имеют незначительную коррозию. Средняя температура
стенки внутренней трубы 25 °С.
1.3S. Привести формулу (1.39) к критериальному виду.
1.39. Какой должен быть взят геометрический масштаб
модели, если в промышленном аппарате рабочая жидкость — нефть,
а в модели — вода, кинематический коэффициент вязкости
которой в 50 раз меньше, чем у нефти? Какую скорость надо дать воде
в модели, если скорость нефти в промышленном аппарате 1 м/с?
Моделируются одновременно силы трения и силы тяжести.
1.40. Определить мощность, расходуемую при перекачке
насоса 4,6 м3/ч холодильного рассола (25% раствор СаС12) из
холодильной установки в конденсатор, расположенный над
ректификационной колонной. Высота подъема 16 м, динамический
коэффициент вязкости рассола 9,5 мПа-с, плотность 1200 кг/м5,
диаметр трубопровода 32x2,5 мм, общая длина 80 м. Стальные
трубы имеют незначительную коррозию. На линии установлены
6 отводов под углом 90° (RJd = 4) и 4 прямоточных вентиля.
Общий к. п. д. насоса с электродвигателем 0,5.
1.41. По горизонтальному трубопроводу перекачивается
жидкость. Во сколько раз возрастет расход энергии на перекачку,
если через трубу будет проходить удвоенное количество
жидкости? Коэффициент трения считать постоянным, Ардоп = 0.
1.42. По стальному трубопроводу внутренним диаметром 75 мм
требуется перекачивать 25 м3/ч жидкости плотностью 1200 кг/м3,
с динамическим коэффициентом вязкости 1,7 мПа-с. Конечная
точка трубопровода выше начальной на 24 м. Длина
трубопровода 112 м. На нем установлены 2 прямоточных вентиля и 5
прямоугольных отводов с радиусом изгиба 300 мм. Трубы имеют
незначительную коррозию. Найти потребляемую мощность, если
общий к. п. д. насосной установки 0,6.
63
Рис. 1.30 (к контрольной задаче 1.43).
1.43. Вода при 10 °С подается из
реки насосом в открытый резервуар
(рис. 1.30). Верхняя точка на 50 м
выше уровня воды в реке. Трубопровод
стальной с незначительной коррозией,
внутренний диаметр его 80 мм,
расчетная длина (собственная длина плюс
эквивалентная длина местных
сопротивлений) 165 м. Насос подает 575 дм3/мин.
Какова расходуемая насосом мощность, если к. п. д. насосной
установки 0,55?
1.44. По прямому воздухопроводу прямоугольного сечения
400x600 мм, сделанному из кровельной стали, надо подавать
14 400 кг/ч воздуха при 27 °С и атмосферном давлении. Длина
воздухопровода 60 м. Найти требуемую мощность
электродвигателя, если его к. п. д. 0,95, а к. п. д. вентилятора 0,4.
1.45. По трубопроводу с внутренним диаметром 100 мм
подается диоксид углерода под давлением 2 кгс/см3 (по манометру)
при средней температуре 75 °С с массовой скоростью 30 кг/(м2.с).
Шероховатость трубы е = 0,7 мм. Определить гидравлическое
сопротивление горизонтального трубопровода при длине его
90 м и при наличии четырех колен под углом 90° и задвижки.
Определить также мощность, потребляемую газодувкой для
перемещения диоксида углерода, если ее к. п. д. составляет 50 %.
!.46. 40%-ный этиловый спирт спускается из бака по трубе
диаметром 33,5x2,8 мм. На трубе имеются кран и 2 колена под
углом 90°. Общая длина трубопровода 49 м. Определить скорость
спирта в трубопроводе (при разности высот 7,2 м). Коэффициент
трения принять приближенно равным 0,025. Найдя скорость
спирта, проверить значение коэффициента трения. Температура
спирта 35 °С.
1.47. По трубопроводу диаметром 26,8x2,5 мм стекает
нитробензол с температурой 44 °С. Начальная точка трубопровода выше
конечной на 200 мм. Длина горизонтальной части трубопровода
242 м. Учесть только сопротивление трения. Найти массовый
расход нитробензола и проверить принятый режим его движения.
1.48. В аппарат, работающий под давлением ра0с = 0,2 МПа,
надо подавать насосом воду из открытого резервуара по
трубопроводу внутренним диаметром 70 мм. Верхняя точка
трубопровода выше уровня воды в резервуаре на 5 м. Расчетная длина
трубопровода (собственная длина плюс эквивалентная длина
местных сопротивлений) 350 м. Коэффициент трения к = 0,03.
Найти зависимость между расходом воды, протекающей по
трубопроводу, и потерей давления на преодоление всех сопротивлений
трубопровода (найти уравнение характеристики сети).
64
Рис, 1.31 (к контрольной задач* 1.52).
Воздух.
Кислота
8-В
1.49. Центробежный насос имеет
следующую паспортную характеристику:
Расход воды, м3/ч 12 18 24 30
Создаваемый напор, м 38 36 32 26
Сколько воды будет подавать этот
насос, если поставить его работать на сеть
контрольной задачи 1.48? (Найти рабочую
точку) .
1.50. Вентилятор подает воздух,
засасывая его из атмосферы. Подача
вентилятора 12 500 м3/ч. Какое массовое количество воздуха подает
вентилятор зимой (t = —15 °С) и летом (t =* 30 °С)?
1.51. Определить давление, развиваемое вентилятором,
который подает воздух из атмосферы при температуре 18 °С в
пространство с избыточным давлением 43 мм вод. ст. Потери давления
в трубопроводе 275 Па, скорость воздуха в нем 11,5 м/с.
1.52. Какое абсолютное давление (в кгс/см2) должен иметь
воздух, подаваемый в монтежю (рис. 1.31) для подъема серной
кмглсгы относительной плотности 1,78 т высоту 21 ы?
Гидравлическими потерями пренебречь.
1.53. Скорость струи на выходе из диффузора горизонтального
водоструйного насоса (см. рис. 2.10) 2,35 м/с. Вода выходит из
диффузора под атмосферным давлением. Диаметр выходного
отверстия диффузора 62 мм, диаметр отверстия сопла (сечение /)
30 мм. Пренебрегая потерями, определить теоретическую
высоту Н: на которую может быть поднята откачиваемая вода из
открытого резервуара.
1.54. Определить гидравлическое сопротивление слоя сухой
насадки высотой 3 м, состоящей из керамических колец 15x15 X
X 2 мм. Через насадку просасывается воздух при 20 °С и
атмосферном давлении со скоростью 0,4 м/с (скорость фиктивная).
Глава 2
НАСОСЫ, ВЕНТИЛЯТОРЫ. КОМПРЕССОРЫ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Полный напор, развиваемый насосом (рис. 2.1),
определяется уравнением
Н== PVgPl +Я' + Й* (2.1)
идентичным уравнению (1.49).
3 Павлов К. Ф. н др. 65
Рис. 2.1.
coca.
Схема установки центробежного на-
Здесь Н — полный напор, развиваемый
насосом, в метрах столба перекачиваемой
жидкости; р2 и pi —давления в
пространстве нагнетания и в пространстве всасывания,
Па; р — плотность перекачиваемой
жидкости, кг/м3; Ht — геометрическая высота
подъема жидкости, м; hn — напор,
затрачиваемый на. создание скорости и на
преодоление треиия и всех местных сопротивлений
во всасывающей и нагнетательной линиях, м;
% = 9,81 м/с2 — ускорение свободного
падения.
Этот же полный напор Н может
быть рассчитан и по другому
уравнению:
wj Рн РВС I ж/ I
И- + //„ +
W1 —Wl„
И ВС
(2.2)
^fmJD^-^^-r^z-
где рд — давление в нагнетательном
трубопроводе на выходе жидкости из насоса, Па;
Рве — давление во всасывающем трубопро-
~_' __ *. воде на входе жидкости в насос, Пя; #0—
— вертикальное расстояние между точками
измерения давлений рн и рвс, м; wH — скорость жидкости в нагнетательном
трубопроводе, м/с; wBC — скорость жидкости во всасывающем трубопроводе, м/с
Если скорости wH и швс близки и расстояние #0 мало, то
уравнение (2.2) упрощается:
Ял
Рн — Рве
Р?
(2.2а)
Формулы (2.1) и (2.2) получаются из уравнения Бернулли,
составленного для соответствующих сечений потока. Формула (2.2)
применяется при испытании действующих насосов» а формула
(2.1) — при проектировании насосных установок.
2. Мощность N (в кВт), потребляемая двигателем насоса:
QpgH
N =
lOOOri
(2.3)
Здесь Q — объемная производительность (подача) насоса *, м3/с; р —
плотность перекачиваемой жидкости, кг/м3; g ~ 9,81 м/с2 — ускорение свободного
падения; И — полный иапор, развиваемый насосом, в метрах столба
перекачиваемой жидкости; т] — общий к. п. д. насосной установки, представляющий
собой произведение к. п. д. насоса т]н, к. п. д. передачи т]д и к. п. д. двигателя т1д:
'П = Лн'ПпЛл- (2*4)
С запасом на возможные перегрузки двигатель к насосу
устанавливается несколько большей мощности Л/уст, чем
потребляемая мощность:
* В учебникам по насосным и вентиляторным установкам объемный расход
жидкости (газа), подаваемой насосом (вентилятором), обычно обозначают через Q.
66
Таблица 2 J
Температура.
N, кВт
N. кВ?
В
1—5
2—1,5
1,5-1,2
5-50
50
1,2—1,15
1,1
Таблица 2.2
2 0
30
40
50
60
70
80
90
100
Давление
насыщенного пара hf.
м вод. ст.
кПа
0,09 0,12 0,24 0,43 0,75 1,25 2,02 3,17 4,82 7,14 10,33
0,88 1,18 2,36 4,22 7,36 12,26 (9,82 31,1 47,3 70,04 101,3
Коэффициент запаса мощности (3 берется в зависимости от
величины N (табл. 2.1).
3. Теоретическая высота всасывания поршневого насоса Яв0
(в м) определяется выражением (рис. 2.2):
#вс<Л-/1*-51/1, (2.5)
где А — атмосферное давление; ht — давление насыщенного пара всасываемой
жидкости при температуре перекачивания t; % h — потери высоты всасывания,
включающие затрату энергии на сообщение скорости потоку жидкости и
преодоление инерции столба жидкости во всасывающем трубопроводе, а также
на преодоление трения и местных сопротивлений во всасывающей линии; с
увеличением частоты вращения (числа оборотов) насоса ? h возрастает.
Все величины: Л, ht, ? h — выражены
в метрах столба перекачиваемой жидкости.
Атмосферное давление А зависит
от высоты места установки насоса
над уровнем моря (табл. XIX).
Давление насыщенного пара
всасываемой жидкости ht определяется
ее температурой. Для воды
зависимость величины h% от температуры
представлена в табл. 2.2.
Практически для определения
допускаемой высоты всасывания (вм)
при перекачивании воды
поршневыми насосами рекомендуется
пользоваться данными табл. XX.
о
¦Tr-f
Г
Г
--в
Рис. 2.2, Схема поршневого насоса,
3*
67
и
Рис. 2.3. Характеристики центробежного
coca (при п — const) и сети.
на-
4. Производительность
поршневого насоса Q (в м3/с):
а) простого действия и
дифференциального
Q-Tb-^sr: (2.6)
60 »
б) двойного действия
(2F — /) sn
Q = %
60
(2.7)
Здесь if]v — коэффициент подачи, величина которого в среднем составляет
0,8—0,9; F — рабочая площадь (площадь поперечного сечения) поршня
(плунжера), м2; / — площадь поперечного сечения штока; м2; s — ход поршня, м;
п — частота вращения, т. е. число двойных ходов поршня в 1 мин.
5. Напор и производительность центробежного насоса при
данной частоте вращения зависят друг от друга. Если на график
этой зависимости, называемый характеристикой насоса, нанести
кривую характеристики сети (рис. 2.3), то пересечение обеих
кривых даст так называемую рабочую точку, определяющую
напор и производительность насоса при работе его на данную сеть.
К. п. д. центробежного насоса меняется при изменении
напора и производительности.
При изменении в небольших пределах частоты вращения п
центробежного насоса изменения его подачи Q, напора Н и
потребляемой мощности N определяются следующими
соотношениями;
Q2
J5l
По
EL
Н2
(2.8)
Высота всасывания центробежного насоса Яве (в м)
рассчитывается по формуле:
"вс ^ А — п% — nUt EC -— «кав»
где Л — атмосферное давление; h% —давление насыщенного пара всасываемой
жидкости; hGi EC — гидравлическое сопротивление всасывающей линии,
включая затрату энергии на сообщение скорости потоку жидкости; Акав — кавита-
ционная поправка (уменьшение высоты всасывания во избежание кавитации),
зависящая от производительности насоса Q (в м^с) и частоты вращения п
(в об/мин); /гнав.= 0,00125 (Q/i2)0'67,
Все величины: Л, ht, hm ВС) Лкав — выражены в метрах столба
перекачиваемой жидкости.
6. Давление (точнее — повышение давления), создаваемое
вентилятором * при подаче воздуха (рис 2.4):
ДР = (ра — Pi) + (ДРвс + ДРн) +
w2p
(2.9)
* Это давление в учебниках по вентиляционным установкам иногда
называют полным напором вентилятора и обозначают буквой Н»
68
UJ)H
ДР= I Рот. hH 2
t-H
Рст. bc +
8Й
ее
P
(2: Ю)
гл? Pi — давление в пространстве, из которого вентилятор забирает воздух, Па;
Pi — давление в пространстве, куда вентилятор подает воздух, Па; Д/?вс и
Др„ — потери давления во всасывающей и нагнетательной линиях, Па; w —
скорость воздуха на выходе из сети, м/с; рСт.н и рст. Ес —статические
давления непосредственно после вентилятора и до него, Па; wH и о>Ве —скорости
воздуха в нагнетательном и всасывающем трубопроводах, м/с; р — плотность
воздуха, кг/м3.
Уравнение (2.9) идентично уравнению (2.1) для насоса и
уравнению (1.49). Уравнение (2.10) идентично уравнению (2.2)
для насосов.
Если вентилятор подает не воздух, а другой газ,
отличающийся по плотности от окружающего воздуха, то в предыдущих
формулах р — плотность газа, а к правой части уравнения (2.9)
добавляется величина;
ДРпод — (Р — Рвовд) №
Здесь г — разность высот мест нагнетания и всасывания, м.
Мощность N (в кВт), расходуемая вентиляторной установкой:
'V Ю00г| * {гА1)
где Q — подача вентилятора, ntVc; Д/? — повышение давления, создаваемое
вентилятором, Па; т] = т]Ет]пт]д — общий к. п. д. вентиляционной установки —
см. уравнение (2.4).
7* Так же как и для центробежного насоса, графическая
характеристика центробежного вентилятора меняет свое
положение при изменении частоты вращения.
При этом зависимость между старыми и
новыми параметрами работы центробежного
шп
4000 6000
8000 10000
12000 14000
Рнс, 2,4, Схема установки вентилятора.
Рнс, 2.5. Характеристика центробежного вентилятора.
69
вентилятора при изменении частоты вращения в небольших
пределах определяется формулой (2.8).
На рис. 2.5 показана примерная характеристика
центробежного вентилятора при разных частотах вращения.
8- Теоретическая величина работы Lm (в Дж/кг),
затрачиваемой одноступенчатым компрессором при адиабатическом (изоэн-
тропическом) сжатии 1 кг газа, может быть подсчитана по
формуле:
Г fe-i "|
k { р2 \ k . k
i-ад —
k — 1
«r« [(*)**'
1
(2.12)
ИЛИ
^ад === h — H-
(2-13)
Температура газа в конце процесса адиабатического сжатия
определяется уравнением:
Г2 _ / Р2 \ &
Tt"\Pi)
(2.14)
В этих формулах k — показатель адиабаты, равный отношению Cp!cv\ pi
и р2 — начальное и конечное давление газа, Па; vt — удельный объем газа
при начальных условиях, т. е. при давлении рг и температуре Т+, м3/кг; if
и U — начальная и конечная энтальпия (теплосодержание) газа, Дж/кг; R —
газовая постоянная, равная 8310/Ж Дж/(кг-К); М — мольная масса газа.
Мощность N (в кВт), потребляемая двигателем
одноступенчатого компрессора, сжимающего G кг газа в 1 ч от начального
давления рг до конечного давления р2» рассчитывается по
формуле:
N
(2.15)
3600-10001] 3600.1000т) '
где г\ — общий к. п. д. компрессорной установки.
9. Производительность Q (в м3/с) поршневого компрессора
простого действия определяется по уравнению:
Fsn
Q = X
60
(2.16)
где X — коэффициент подачи, безразмерный; F — площадь поршня,
длина хода поршня, м; п — частота вращения, об/мин.
м2: s
Коэффициент подачи:
Х,= (0,8 -т- 0,95) V
Здесь Хф — объемный к. п. д. компрессора, равный:
Хо==1~8ч("рг)'П ~1Г (2Л7)
где в0 — отношение объема вредного (мертвого) пространства цилиндра к
объему, описываемому поршнем; m — показатель политропы расширения сжатого
газа, оставшегося во вредном пространстве.
70
10. Теоретическая величина работы ?ад (в Дж/кг),
затрачиваемой многоступенчатым компрессором при адиабатическом
сжатии 1 кг газа от начального давления рх до конечного
давления Ркон, определяется по формуле:
Г fe-i
Г k-l
k
nRTt
_k / Ркон \ kn __ .
-1 1Л Pi I
ИЛИ
*-ад = Д'1 + Д'а Н V Д*п-
(2.18)
(2.19)
Здесь п — число ступеней сжатия; Д/f, Д(2... — разности энтальпий газа
для 1, 2, ... ступени [формула (2.13)].
Потребляемая многоступенчатым компрессором мощность
рассчитывается по формуле (2.15). Для воздушных компрессоров
иногда пользуются также уравнением:
# =
1.69GL,a
3600-1000
1 ,№GRTX In -^25.
Pi
3600-1000
(2.20)
где N — мощность, кВт; 1,69 — установленный практически коэффициент,
учитывающий отличие действительного процесса сжатия воздуха в компрессоре
от изотермического.
Производительность многоступенчатого поршневого
компрессора определяется производительностью первой ступени.
Пренебрегая потерей давления между ступенями,
приближенно число ступеней сжатия п находят из уравнения:
(2.21)
л
х = Ркон/Pl»
откуда
п =
lg Ркон — lg Pi
lg*
Где х — степень сжатия в одной ступени.
ПРИМЕРЫ
Пример 2.1. Манометр на нагнетательном трубопроводе насоса
(см. рис. 2.1), перекачивающего 8,4 м3 воды в 1 мин, показывает
давление 3,8 кгс/см2 (~0,38 МПа). Вакуумметр на всасывающем
трубопроводе показывает вакуум (разрежение) 21 см рт. ст.
(~28 кПа). Расстояние по вертикали между местом присоединения
манометра и местом присоединения вакуумметра 410 мм. Диаметр
всасывающего трубопровода 350' мм, нагнетательного — 300 мм.
Определить напор, развиваемый насосом.
Решение. Применяем формулу (2.2).
71
Скорость воды во всасывающем трубопроводе:
W™ = 8,4.0,785.0,ЗУса1>45м/С|
Скорость воды в нагнетательном трубопроводе:
W«~ 60.0,785-0^ -Ь98^
Давление в нагнетательном трубопроводе (принимая
атмосферное давление равным 1,013-105 Па, или 760 мм рт. ст.):
Рп == (3,8 + 1,013) 91 • 10* я* 474 000 Па.
Давление во всасывающем трубопроводе:
Рве = (°Д6 — 0.21) 133,3.1000 = 73 300 Па.
Напор, развиваемый насосом:
474 000 — 73300 , п Ai , 1,98я — 1,45»
Н ~ шли п 01 Г °.4l +
1000-9,81 ' ' 2-9,81
= 40,8+ 0,41+ 0,09 = 41,3 м вод. ст.
Пример 2.2. Поршневой насос, делающий 150 об/мин, должен
перекачивать воду, нагретую до 60 °С. Предварительные подсчеты
показали, чт<? затрата энергии на создание скорости, инерционные
потери и гидравлические сопротивления всасывающей линии
составляют в сумме 6,5 м вод. ст. Среднее атмосферное давление
в месте установки насоса 736 мм рт, ст. На какой высоте над
уровнем воды должен быть установлен насос?
Решение. Величина А — ht — %h [формула (2.5) 1 в
данном случае равняется:
0,736-13 600 ОЛО е г , .Q
— юоо 2,02 —6,5= 1,48 м,
где hf = 2,02 м взято из табл. 2.2.
Следовательно, теоретическая высота всасывания не может
быть больше 1,48 м. Практически, по данным табл. XX, высота
всасывания в этом случае (п = 150 об/мин) равна нулю, т. е.
насос должен быть установлен ниже уровня жидкости («под
заливом»).
Пример 2.3. Поршневой насос двойного действия (рис. 2.6)
подает 22,8 м3/ч жидкости. Частота вращения насоса 65 об/мин,
диаметр плунжера 125 мм, диаметр штока 35 мм, радиус
кривошипа 136 мм. Определить коэффициент подачи насоса.
Решение. Объем, вытесняемый плунжером за один оборот:
(2F — f)s = (2.0,785.0,12s2 —0,785.0,035а) 0,272 = 0,00637 м3,
где 0,272 м — длина хода плунжера, равная удвоенному радиусу кривошипа,
Теоретическая подача насоса при 65 об/мин:
0,00637-65 = 0,413 м3/мин.
72
М feL
VM//)
й№?
и*
1 Г Тйшя
h
Рие. 2.6 (к примеру 2»Я).
Действительная подача:
22,8/60 = 0,38 м3/мин.
Коэффициент подачи:
т}0 — 0,38/0,413 = 0,92.
Пример 2.4. Поршневым
насосом простого действия (см.
рис. 2.2) с диаметром поршня
160 мм и ходом поршня
200 мм необходимо подавать
430 дм3/мин жидкости
относительной плотности 0,93 из
сборника в аппарат, давление в котором ризб = 3,2 кгс/см2
(~0,32 МПа). Давление в сборнике атмосферное. Геометрическая
высота подъема 19,5 м. Полная потеря напора во всасывающей
линии 1,7 м, в нагнетательной — 8,6 м. Какую частоту вращения
надо дать насосу и какой мощности электродвигатель установить*
если принять коэффициент подачи насоса 0,85 и коэффициенты
полезного действия: насоса 0,8, передачи и электродвигателя по 0,95?
Решение. Из формулы (2.6) находим:
Q-60
п =
i)vFs
В нашем случае:
430
е«
1000-60
= 0,00717 м3/с; F = 0,785-0,16* = 0,0201 ма?
п =
0,00717-60
0,85.0,0201-0,2
= 126 об/минл
Напор, развиваемый насосом, определяем по формуле (2.1):
3,2-9,8Ы04
# =
930-9,81
+ 19,5+ 10,3 = 64,2 м.
Мощность, потребляемую электродвигателем насоса,
рассчитываем по формуле (2.3):
0,43.930-9,81.64,2
60-1000-0,72 ~~Ь^ КЬТ*
# =
где 0,72 — общий к. п. д. насосной установки
Л = ЛнПпЛд = 0,8.0,95-0,95 = 0,72.
В соответствии с данными табл. 2.1 необходимо установить
(с запасом на перегрузки) электродвигатель мощностью
5,82-1,17 = 6,8 кВт.
73
Пример 2.5. Центробежный насос, делающий 1200 об/мин,
показал при испытании следующие данные:
Qt дм3/с. . . 0 10,8 21,2 29,8 40,4 51,1
Я, м . . . . 23,5 25,8 25,4 22,1 17,3 11,9
Л', кВт. . . 5,16 7,87 10,1 11,3 12,0 18,5
Перекачивался раствор относительной плотности 1,12.
Определить к. п. д. насоса для каждой производительности и построить
графическую характеристику насоса.
Решение, К. п. д. насоса определяем из уравнения:
QpgH
N =
откуда
I)
ЮООт] '
QpgH
По
насоса:
1000/V
этой формуле вычислены следующие значения к. п. д.
Q, дм3/с 0 10,8 21,2 29,8 40,4 51,1
т) 0 0,39 0,587 0,643 0,637 0,36
Характеристика насоса представлена на рис. 2.7.
Пример 2.6. Требуется подавать 115 м3/ч раствора
относительной плотности 1,12 из бака в аппарат на высоту 10,8 м, считая
от уровня жидкости в баке. Давление в аппарате ртб = 0,4 кгс/см2
(~40 кПа), давление в баке атмосферное. Трубопровод имеет
диаметр 140X4,5 мм, его расчетная длина (собственная длина
плюс эквивалентная длина местных сопротивлений ) 140 м. Можно
ли применить центробежный насос предыдущего примера, если
принять коэффициент трения в трубопроводе Я равным 0,03?
Решение. Определяем необходимый напор, который
должен давать насос.
Скорость жидкости:
115
w =
Скоростной
3600-0,785-0.1312
напор:
2,37 м/с.
h
ск
хаз1
2,372
2-9,81
30
А/,КВТ
н
*= 0,286 м,
Потеря напора на
трение и местные
сопротивления:
h
тр+м. с
Я (L + Ц)
d
h
ск
0,03.140
0,131
0,286 = 9,16 м.
Чдм7с
Рис. 2,7 (к примерам 2,5 и 2.6)*
74
Таблица 2.3
пг= 1200 об/мин ft, дмя/с 21,2 29,8 40,4
Hv м 25,4 22,1 17,3
п2= 1260 об/мин (?2. Дм3/с 22,3 31,3 42,5
#2, м 28,0 24,4 19,1
Требуемый полный напор насоса вычисляем по формуле (2.1):
Н= °'4,,1200009°8Г +Ю.8+ 9,16+ 0,286-23,8 „¦
Требуемая производительность насоса:
п 115-1000 00 _.
Q = 3600 в 32 дм3/с-
Обращаясь к рис. 2.7, мы видим, что точка А с координатами
Q = 32 дм3/с, Н — 23,8 м лежит выше кривой характеристики
насоса, и, следовательно, данный насос при пх = 1200 об/мин не
сможет обеспечить требуемую производительность (при Н =
= 23,8 м насос может подавать только 26 дм3/с). Однако, если
несколько увеличить частоту вращения, то насос окажется
пригодным. Пользуясь соотношением (2.8)
Q2 п2 Н2 \ п2 / *
можно подобрать необходимую новую частоту вращения п2.
Если, например, взять п2 = 1260 об/мин и пересчитать
данные примера 2.5 по формулам (2.8) на эту новую частоту
вращения, то получим следующие результаты (табл. 2.3).
Вычертив по данным табл. 2.3 кривую характеристики насоса
при п2 = 1260 об/мин (рис. 2.8), мы увидим, что при этой частоте
вращения насос сможет обеспечить требуемые подачу (32 дм3/с)
и напор (23,8 м).
Мощность, потребляемую насосом при новой частоте
вращения, определяем по формуле
1000*1 '
считая приближенно, что к. п. д. насоса г\ не изменился *.
Значение его берем по данным примера 2.5, в котором было найдено,
что для Q = 30-4-40 дм3/с к. п. д. насоса г\ ж 0,64.
Мощность, потребляемая насосом при п2 ?= 1260 об/мин:
32.1120-9,81.23,8
N- 1000-1000.0,64" S=13J KBT-
Пример 2.7. Определить коэффициент подачи шестеренчатого
насоса (рис. 2.9), делающего 440 об/мин. Число зубьев на ше-
* Мощность можно подсчитать также по формуле N* = Л\ ( -тк™ ) , °зяв
значение Nx по графику (рнс. 2.7).
75
20 30 40
Цдм3/с
Рис. 2,8 (к примеру 2.6).
Рис. 2.9 (к примеру 2.7).
стерне 12, ширина зуба 42 мм, площадь сечения зуба,
ограниченная внешней окружностью соседней шестерни, 960 мм2. Насос
подает 0,312 м3/мин.
Решение. Производительность шестеренчатого насоса Q
(в м3/с) определяется по формуле:
2fbzn
<2 = %,
60
где r\v — коэффициент подачи; / — площадь сечения зуба, ограниченная
внешней окружностью соседней шестерни, м2; Ь — ширина зуба, м; г — число зубьев
на шестерне; п — частота вращения в 1 мин.
Теоретическая подача в нашем случае:
QT = 2fbzn/60 = 2-0,00096.0,042.12.440/60 = 0,00708 м*/о.
Действительная подача:
Q = 0,312/60 = 0,0052 м8/с.
Отсюда коэффи ци ент пода чи:
i)v = Q/Qt = 0,0052/0,00708 = 0,735.
Пример 2.8. Определить (пренебрегая потерями) теоретическое
разрежение, которое может быть создано рабочей струей воды в
камере А водоструйного насоса (рис. 2.10). Давление на выходе из
диффузора атмосферное (1,013.10* Па,
или 760 мм рт. ст.), скорость струи
в этом месте 2,7 м/с. Диаметр струи в
сечении / 23 мм, в сечении// 50 мм,
Решение. Напишем,
пренебрегая потерями, уравнение Бернул-
ли для сечений струи / и //:
*1 +
Pi
+
w{
= z2 +
Рг
PS
+
Рис, 2,10 (к примерам 2.8 и 2.9).
76
При горизонтальном расположении насоса:
Далее имеем:
Wi
7ГШа==(~1г) 2'7 = 12>8м/с-
Из уравнения Бернулли находим:
Р1 = Ра+Л^1р = 7бо.1зз,з+2-7а712'8а10оо^
= 101 300 — 78 300 = 23 000 Па.
Теоретическое разрежение, следовательно, составляет:
101 300 — 23 000
9.8Ы0*
= 0,8 кгс/см2 & 80 кПа.
Пример 2.9. Водоструйный насос (рис. 2.10) поднимает 7,8 м3/ч
перекачиваемой жидкости относительной плотности 1,02 на
высоту Н ~ 4 м. Расход рабочей (напорной) воды при этом
составляет 9,6 м3/ч. Напор рабочей воды перед насосом Яр = 22 м.
Определить к. п. д. водоструйного насоса.
Решение. Производимая насосом полезная работа
(мощность):
#пол = 7,8.1020-9,81 -4/3600 = 86,7 Вт.
Затрачиваемая насосом мощность:
N = 9,6'1000-9,8] (22 — 4)/3600 = 471 Вт.
Отсюда к. п. д. водоструйного насоса:
Пример 2.10. Определить давление, развиваемое вентилятором
(см. рис. 2.4), который подает азот (р = 1,2 кг/м3) из
газохранилища в установку. Избыточное давление в газохранилище
60 мм вод. ст., в установке 74 мм вод. ст. Потери во всасывающей
линии 19 мм вод. ст., в нагнетательной линии 35 мм вод. ст.
Скорость азота в нагнетательном трубопроводе 11,2 м/с.
Решение. Давление, развиваемое вентилятором, находим
по формуле (2,9).
Разность давлений в местах нагнетания и всасывания:
Рй ~ Pi = (74 — 60) 9,81 = 137 Па, или 14 мм вод. ст.
Общие потери во всасывающем и нагнетательном
трубопроводах:
Арвс + АРн = О9 + 35) 9,81 = 530 Па, или 54 мм вод. ст.
Скоростное давление на выходе из трубопровода:
w*f>/2= 11,2s. 1,2/2 = 76 Па, или 7,7 мм вод. ст.
Давление, создаваемое вентилятором:
Ар = 137 + 530 + 76 = 743 Па, или 76 мм вод. ст.
77
Пример 2.11. Во всасывающем трубопроводе перед
центробежным вентилятором имеется разрежение 15,8 мм вод. ст.; манометр
на нагнетательном трубопроводе после вентилятора показывает
избыточное давление 20,7 мм вод. ст. Расходомер аоказывает
подачу воздуха 3700 м3/ч. Всасывающий и нагнетательный
трубопроводы имеют одинаковый диаметр. Частота вращения в 1 мин
равна 960. Вентилятор расходует 0,77 кВт. Определить давление,
развиваемое вентилятором, и к.п.д. вентилятора. Как изменится
производительность вентилятора, если увеличить частоту его
вращения до 1150 об/мин, и какая мощность будет расходоваться
при новой частоте вращения?
Решение. Давление, развиваемое вентилятором, находим
по формуле (2.10). Так как всасывающий и нагнетательный
трубопроводы имеют одинаковый диаметр, то скоростные давления
одинаковы. Тогда
Др = Рст- н — Рст. в = 20,7-9,81 — (—15,8-9,81) = 354 Па.
Секундная подача вентилятора:
Q = 3700/3600= 1,03 мя/с.
Теоретический расход мощности:
iVT « 1,03-354/1000-0,368 кВт.
К. п. д. вентилятора:
ц = Nr/N « 0,368/0,77 = 0,48.
Подачу вентилятора при п2 = 1150 об/мин определяем по
формуле (2.8):
Q2 = Qi (rta/«i) = 3700 (1150/960) = 4430 м»/ч.
Расходуемая мощность при новой частоте вращения:
A^JVj (tt2/rt])3 = 0,77 (1150/960)»= 1,33 кВт
Пример 2,12. При испытании центробежного вентилятора о
частотой вращения в 1 мин п = 1440 получены следующие данные:
Q, м3/ч 100 350 700 1000 1600 2000
Л /Па 449 424 432 427 387 316
ар мм вод. ст 45,8 43,2 44,0 43,5 39,5 32,2
Сколько воздуха будет подавать этот вентилятор при работе
на некоторую сеть (с той же частотой вращения, что и при
испытании), если расчет сопротивления сети показал, что при
прохождении через нее 1350 м3/ч воздуха получаются следующие
величины потерь давления:
дрск = 85 Па, или 8,7 мм вод. ст.
Дртр -f Дрм. с — 288 Па, или 29,4 мм вод. ст.
Разность давлений в пространстве нагнетания и в пространстве
всасывания для рассчитываемой сети составляет:
Д/;дои = Р% — pi = 128 Па, или 13 мм вод. ст.
78
О 400 800 1200 WOO 2000
V,M3/4
Рис. 2.11 (к примеру 2.12).
Решение. Для решения
этой задачи необходимо найти
рабочую точку на пересечении
характеристик вентилятора и сети.
Характеристика сети
выражается параболой, в уравнении
которой
др = flQ2 + Ь
первое слагаемое правой части aQ2
равно сумме потерь давления
А/?Ск + А/?тр + А/?м. с и
изменяется пропорционально квадрату
расхода, а второе слагаемое Ь не зависит от расхода и
представляет собой разность давлений в пространстве нагнетания и в
пространстве всасывания, т. е. А/?доп; а — постоянный
коэффициент.
Вычислим по имеющимся данным несколько точек этой
параболы (табл. 2.4).
Нанесем на общий график (рис. 2.11) характеристику
вентилятора по данным его испытания и характеристику сети по
вычисленным точкам.
Точка пересечения обеих характеристик показывает, что при
работе на заданную сеть вентилятор будет подавать 1170 м3/ч
воздуха.
Пример 2.13. Сравнить теоретическую затрату работы на
сжатие 1 м3 воздуха от /?абс = 9,81 - Ю4 Па: а) до /?абс = 10,8 X
X 104 Па и б) до /?абс = 49,1.104 Па. Рассчитать затрату работы
как по термодинамической формуле для адиабатического сжатия,
так и по гидравлической формуле (т. е. считая воздух
несжимаемым).
Решение, а) рх = 9,81. Ю4 Па; /?2 =* 10,8.104 Па.
Таблица 2.4
Г\ 1 1
Q, м3/ч
1350
1350/1,5= 900
1350/2 = 675
1350/2,5 = 540
0
При меча ни
ст.).
aQ2
38,1
38,1/1,52= 16,9
38,1/22= gj5
38,1/2,52= 6,1
0
е. Значение Ъ во всея
Па
501
293
221
187
128
' случаях
Ар
128 I
мм вод. ст
51,4
29,9
22,5
19,1
13
1а (13 мм вод.
79
По формуле (2.12), если отнести работу сжатия в
компрессоре к 1 м3 газа (при условиях всасывания), получаем (в Дж/ма):
k
La* ~~ k-l
Pi
к*)
1
Для воздуха k = 1,4 (табл. V). Тогда
( ^- \
\\Л 1-4 — 1 / = 9520 Дж/м*.
^«¦SjWi.io»
Расчет по гидравлической формуле Lt = Q Ар дает при Ар =
10,8.10* — 9,8Ы04 = 9,9.103 Па:
Lr = 1-9,9.103 = 9900 Дж/м3,
б) /?! = 9,8Ы04 Па; р% = 49,1.104 Па.
По термодинамической формуле:
LaTI =449,81.104
-ад
0,4
G^'-l)-
201 000 Дж/м3.
По гидравлической формуле при Ар = 49,1.104 — 9,81.10* =
«= 39,3.10* Па:
Lr = 1.39,3-10* = 393000 Дж/м3.
Сравнивая варианты а) и б), мы видим, что в первом случае
результаты, полученные по термодинамической и по
гидравлической формулам, различаются всего на 3%. Этот случай (p2/Pi ~
= 1,1) соответствует предельной степени сжатия воздуха
вентиляторами, для которых расчет потребляемой мощности
производится, как мы видели выше, по гидравлической формуле.
Во втором случае {pjpx = 5), который соответствует'сжатию
воздуха в компрессоре, результаты, полученные по формуле
адиабатического сжатия и по гидравлической формуле, расходятся
на 100%. Для расчета мощности, потребляемой компрессором,
всегда применяются термодинамические формулы (2.12) и (2.13).
На теоретической
индикаторной диаграмме
поршневого компрессора (рис. 2,12)
ясно видно, что площадь аЬсе
(представляющая собой
затрачиваемую работу
адиабатического сжатия при р% =
= 1,1 кгс/см2) приблизительно
равна площади abde, но
площадь afge (для р2 = 5 кгс/сма)
далеко не равна площади afhe.
Рис. 2.12 (к примеру 2.13).
Пример 2.14. Определить мощность, потребляемую
одноступенчатым поршневым компрессором, который сжимает 460 м3/ч
(считая при 0 °С и 760 мм рт. ст.) аммиака от рабс = 2,5 кгс/см2
Д° Рабс ^ 12 кгс/см2. Начальная температура аммиака—10 °С;
к. п. д. компрессора 0,7. Определить также температуру аммиака
в конце сжатия.
Решение. Определяем теоретическую работу компрессора
по формуле (2.12) для адиабатического сжатия.
Для аммиака по табл. V находим: k — 1,29, R = 8310/17 =
«= 489 Дж/(кг-К). Тогда
0,29
12
1 2Q
/ 12 \ 1,29 , _
Л 2,5 ;
240 000 Дж/кг.
Эту же величину вычислим теперь по формуле (2.13). По
диаграмме Т — S для аммиака (рис. XXVI) находим для точки /
уг = — Ю °С; р1 = 2,5 кгс/см2) 1г = 1440 кДж/кг. Проведя из
этой точки вертикальную прямую (S = const) до пересечения
с изобарой р% — 12 кгс/см2, находим точку 2, для которой /2 =
== 1673 кДж/кг. Тогда по формуле (2.13)
Laa = 1 673 000 — 1 440 000 = 233 000 Дж/кг,
что близко к найденному выше (расхождение около 3%).
Массовый расход аммиака:
G = 460-0,76 = 350 кг/ч.
Здесь 0,76 кг/м3 — плотность аммиака при нормальных
условиях:
р0 = Л1/22,4 = 17/22,4 = 0,76 кг/м3.
Потребляемую компрессором мощность находим по формуле
(2.15):
350.240 000
™~ 3600-1000-0,7 ~^4кт-
Температуру в конце сжатия вычисляем по уравнению (2.14):
0,29
Га==26з/~-) 1,а9 =374К = ЮГС.
Если определить зту температуру непосредственно по Г — S
диаграмме, то найдем в точке 2\ /2 — 104 °С.
Пример 2.15. Требуется подавать сжатый воздух под
давлением /?изб = 4,5 кгс/см2 в количестве 80 кг/ч. Пригоден ли будет
для этой цели одноступенчатый поршневой компрессор простого
действия, имеющий диаметр цилиндра 180 мм, длину хода поршня
200 мм и делающий 240 об/мин? Вредное пространство составляет
5% от объема, описываемого поршнем. Показатель политропы
расширения принять равным 1,25.
61
1/vwWf
V
Рис. 2.13 (к примеру 2.16):
Р0 — 1 кгс/см2; Pt e 1,26 кгс/см ; рг
— 5,5 кгс/смя.
Решение. Определим по
формуле (2.16)
производительность компрессора.
Предварительно необходимо найти объемный
к. п. д. компрессора %0.
По уравнению (2.17) находим:
Яе = 1 — 0,05 Цб"7^ — 1) = 0,854.
Примем коэффициент подачи:
Я = 0,85Я0 = 0,85-0,854 = 0,725.
Производительность компрессора:
= 0.725.0,1^.3 14.0.2.240 = ^ = и
4-ЬО
Считая, что компрессор всасывает атмосферный воздух с
температурой ~20 °С, имеющий плотность 1,2 кг/м3, получим
массовую производительность компрессора: 53*1,2 = 63,6 кг/ч.
Следовательно, компрессор не обеспечит заданной
производительности (80 кг/ч). Однако требуемая массовая
производительность при использовании данного компрессора все же может быть
достигнута, если увеличить частоту вращения с 240 до (80/63,6) X
X 240 = 302 об/мин или если дать компрессору, не меняя частоты
вращения, наддув установленной перед ним воздуходувкой,
которая будет сжимать воздух от атмосферного давления до
давления (абсолютного), равного 80/63,6 = 1,26 кгс/см2, и с
этим давлением подавать воздух на всасывание компрессора
(рис. 2.13).
В обоих случаях специальным расчетом должна быть
проверена динамика компрессора.
Пример 2.16. В одноступенчатом поршневом компрессоре,
предназначаемом для сжатия метана, вредное пространство
составляет 8,5% от объема, описываемого поршнем. Считая процесс
расширения сжатого газа из вредного пространства
адиабатическим, определить, при каком предельном давлении нагнетания
производительность компрессора станет равной нулю. Давление
всасывания атмосферное.
Решение. Производительность компрессора станет равной
нулю, когда равным нулю сделается его объемный к. п. д., т. е.
Ао — 1 — е0
Л pi /
0.
82
Согласно условию, расширение газа из вредного пространства
считаем адиабатическим, т. е. вместо показателя политропы т
берем показатель адиабаты к, равный для метана 1,31 (табл. V).
Вредное пространство е0 = 0,085. Давление всасывания pt =*
= 1 кгс/см2. Тогда
1 —0,085 Ц1'31 — 1 / = °-
Из этого уравнения находим: pt'763 = 12,8, откуда р2 ж
ж 28 кгс/см2.
Следовательно, производительность компрессора будет равна
нулю при давлении нагнетания ра&с =:
28 кгс/см2.
Пример 2.17. Сравнить температуру в конце сжатия,
теоретическую затрату работы и величину объемного к. п. д. при сжатии
воздуха от давления (абсолютного) 1 до 9 кгс/см2: а) в
одноступенчатом поршневом компрессоре, б) в двухступенчатом
компрессоре с промежуточным охлаждением между ступенями. Начальная
температура воздуха и температура его после холодильника
20 °С. Объем вредного пространства составляет 8% от объема,
описываемого поршнем.
Решение, а) Одноступенчатое сжатие.
Температуру в конце сжатия определяем по формуле (2.14).
Для воздуха k = 1,4 (табл. V):
0,4
Г2 = 293-9 м =293-1,88 = 551 К = 278°С.
Теоретическую затрату работы вычисляем по формуле (2.12).
Для воздуха по табл. V находим:
R = 8310/29 = 287 ДжДкг-К).
Следовательно,
?ад = -Id-287-293 (1,88—1) = 260 000 Дж/кг.
Объемный к. п. д. компрессора находим по уравнению (2.17),
принимая, что расширение воздуха из вредного пространства
происходит по адиабате:
к0=*\— 0,08 U"1^" — 1 / = 0,7.
б) Двухступенчатое сжатие.
Степень сжатия в каждой ступени находим по уравнению
(2.21)! х2 = 9, откуда х = 3.
Температура в конце сжатия в каждой ступени!
Г2 = 293-3 м = 293-1,37 = 402 К = 129°С.
Суммарную теоретическую затрату работы в обеих ступенях
вычисляем по формуле (2.18)i
83
1ад =2*287.293—\Ь88"Г^])«218000Дж/кг,
k—l
где 1,88 s* (Лсон'л) * •
Объемный к. п. дл
Я0 = 1 — 0,08 \3~ — 1) == 0,905.
Сопоставим полученные результаты для одноступенчатого и
двухступенчатого сжатия:
Число ступеней сжатия 1 2
Температура в конце сжатия Г2, °С 278 129
Теоретическая затрата работы ?ад> Дж/кг . . . 260 000 218 000
Объемный к. п. д. Х0 0,7 0,905
Приведенное сопоставление ясно показывает преимущества
двухступенчатого сжатия. Чем больше отношение pmJpu тем
сильнее проявляются преимущества многоступенчатого сжатия.
Пример 2.18. Компрессор должен подавать 210 м3/ч метана
(считая при 0 °С и 760 мм рт. ст,), сжатого до давления /?абс =
== 55 кгс/см2. Начальное давление атмосферное, начальная
температура 18 °С. Определить: а) число ступеней сжатия и
распределение давлений по ступеням; б) расходуемую мощность,
принимая к. п. д. компрессора 0,7; в) расход воды в холодильниках
компрессора при нагревании ее на 10 °С.
Решение, а) При допускаемой степени сжатия в одной
ступени ~4 требуемое число ступеней, согласно уравнению (2.21),
будет равно:
я = Ig55/)g4 = 2,9»3.
Пренебрегая потерей давления между ступенями, уточним
степень сжатия в каждой ступени трехступенчатого компрессора
(рис. 2.14): _
Таким образом, приближенное распределение давлений по
ступеням:
Рнач Ркон
I ступень 1 3,8
II » 3,8 J 4,45
III » 14.45 55
hm—I РЯ—I—Р71—;="
гзя^шцжт:
ЧлллМ
Рис, 2.14 (к примеру 2.18),
84
Рис. 2,15 (к примеру 2.18).
б) Теоретический расход
работы определяем по формуле (2.18).
Для метана по табл. V находим:
ft = 1,31; R = 8310/16 = 519 Дж/(кг< К);
р0 = 0,72 кг/м3 (при 0е С и
760 мм рт. ст.).
Принимая, что в промежуточных холодильниках метан охла
ждается до 30 °С, получаем:
/ 0.31 \
1ад = 3.519-303-^\551,31"3 -1/ =
746 000 Дж/кг.
Расходуемую мощность вычисляем по формуле (2.15)з
210.0,72.746 000
3600.1000-0,7 «.о квт.
в) Для определения расхода воды в холодильниках
компрессора найдем температуру в конце сжатия в ступенях II и III,
принимая, как уже было сказано, что в промежуточных
холодильниках после I и II ступеней метан охлаждается до 303 К
(рис. 2.15). В цилиндре I ступени компрессора температура в конце
сжатия будет несколько ниже, так как в I ступень метан
засасывается не при 30 °С, а при 18 °С.
По уравнению (2.14) имеем:
0,31
Га = 303-3,8 1>31 = 416 К = 143° С.
Принимая приближенно удельную теплоемкость метана при
абсолютных давлениях 3,8; 14,45 и 55 кгс/см2 одинаковой и
равной 2,22 кДж/(кг*К), находим, что в трех холодильниках
компрессора (после I, II и III ступеней) охлаждающая вода всего
должна отнимать теплоты:
Q = 3.210.0,72-2,22. JO3 (J43 —30)/3600 = 31 700 Вт.
Это же количество теплоты может быть подсчитано другим
путем, как теплота, эквивалентная работе сжатия:
Q = Lwy0p0 = 746000.210-0,72/3600 = 31 300 Вт.
При нагревании воды на 10 °С расход ее составит!
Q 31 700
°в~ c(/t-/x)
" 4,19-103'10
0,756-3600
= 0,756 кг/с нлн V
в
J 000
= 2,71 м3/ч.
Здесь с= 4,19 «10s Дж/(кг-К) — удельная теплоемкость воды.
85
Пример 2.19. При помощи поршневого вакуум-насоса в
аппарате должен быть создан вакуум (разрежение) 0,9 кгс/см2. Считая
процесс сжатия воздуха в вакуум-насосе политропическим (с
показателем политропы 1,25), определить теоретический расход
работы: а) в тот момент, когда достигнут вакуум 0,1 кгс/см2, т. е.
остаточное давление в аппарате стало равным 0,9 кгс/см2; б) когда
давление в аппарате стало равным 0,3 кгс/см2; в) когда достигнут
требуемый вакуум, т. е. остаточное давление в аппарате стало
равным 0,1 кгс/см2.
Решение. Подсчитываем теоретический расход работы на
1 м3 засасываемого газа (т. е. в Дж/м3) по формуле (2.12):
т
Pi
т— 1
т—1
(?)" -
где т — показатель политропы сжатия.
рг _ 9,81-10* _^L__i^__5- т~1 -02-
; Pt "~ 8,83-10* '' т - 1 ~ 0,25 ~" °* т ~~ ' '
б)
Рз
в)
L = 5.8,83-104 (l,H0*2 — 1) = 9720 Дж/м3.
Q О 1 1 Л4
= '» °д "1Л. = 3,33; L = 5-2,94.104 (3,330'2 — l) = 40 000 Дж/м3.
~= 09ЗДЬ10* = 10: ^ = 50,981 - JO4 (100'2 — 1) = 28 600 Дж/м3.
Мы видим, что расход работы, затрачиваемой вакуум-насосом,
проходит через максимум. На этот максимум и рассчитывается
мощность двигателя вакуум-насоса.
КОНТРОЛЬНЫЕ ЗАДАЧИ
2.1. Насос перекачивает 30%-ную серную кислоту.
Показание манометра на нагнетательном трубопроводе 1,8 кгс/см2
(~0,18 МПа), показание вакуумметра (разрежение) на
всасывающем трубопроводе перед насосом 29 мм рт. ст. Манометр
присоединен на 0,5 м выше вакуумметра. Всасывающий и
нагнетательный трубопроводы одинакового диаметра. Какой напор развивает
насос?
2.2. Насос перекачивает жидкость плотностью 960 кг/м3 из
резервуара с атмосферным давлением в аппарат, давление в
котором составляет рш6 = 37 кгс/см2, или ~3,7 МПа (см. рис. 2.1).
Высота подъема 16 м. Общее сопротивление всасывающей и
нагнетательной линий 65,6 м. Определить полный напор,
развиваемый насосом.
2.3. Определить к. п. д. насосной установки. Насос подает
380 дм3/мин мазута относительной плотности 0,9. Полный напор
30,8 м. Потребляемая двигателем мощность 2,5 кВт.
86
Рис. 2Л6 (к контрольной задаче 2.6).
2.4. Производительность
насоса 14 дм3/с жидкости
относительной плотности 1,16.
Полный напор 58 м. К. п. д. насоса
0,64, к. п. д. передачи 0,97,
к. п. д. электродвигателя 0,95.
Какой мощности двигатель надо
установить?
2.5. Поршневой насос (см. _^
рис. 2.2) установлен на заводе,
расположенном на высоте 300 м
над уровнем моря. Общая потеря высоты всасывания составляет
5,5 м вод. ст. Геометрическая высота всасывания 3,6 м. При
какой максимальной температуре воды еще возможно всасывание?
2.6. Определить производительность дифференциального
поршня насоса (рис. 2.16), который имеет больший диаметр
ступенчатого плунжера 340 мм, меньший — 240 мм. Ход плунжера
480 мм, частота вращения 60 об/мин. Коэффициент подачи 0,85.
Определить также количество жидкости, подаваемой каждой
стороной ступенчатого плунжера.
2.7. Поршневой насос двойного действия (см. рис. 2.6)
наполняет бак диаметром 3 м и высотой 2,6 м за 26,5 мин. Диаметр
плунжера насоса 180 мм, диаметр штока 50 мм, радиус
кривошипа 145 мм. Частота вращения 55 об/мин. Определить
коэффициент подачи насоса.
2.8. Центробежный насос, делающий 1800 об/мин, должен
перекачивать 140 м3/ч воды, имеющей температуру 30 °С. Среднее
атмосферное давление в месте установки насоса 745 мм рт. ст.
Полная потеря напора во всасывающей линии составляет 4,2 м.
Определить теоретически допустимую высоту всасывания.
2.9. Центробежный насос при перекачке 280 дм3/мин воды
создает напор Н = 18 м. Пригоден ли этот насос для перекачки
жидкости относительной плотности 1,06 в количестве 15 м3/ч
по трубопроводу диаметром 70 X 2,5 мм из сборника с
атмосферным давлением в аппарат с давлением /?ЛЗб = 0,3 кгс/см2?
Геометрическая высота подъема 8,5 м. Расчетная длина трубопровода
(собственная длина плюс эквивалентная длина местных
сопротивлений) 124 м. Коэффициент трения в трубопроводе К = 0,03.
Определить также, какой мощности электродвигатель потребуется
установить, если к. п. д. насосной установки составляет 0,55.
2.10. Центробежный насос для перекачки воды имеет
следующие паспортные данные: Q = 56 м3/ч, Н — 42 м, N = 10,9 кВт
при п = 1140 об/мин. Определить: 1) к. п. д. насоса, 2)
производительность его, развиваемый напор и потребляемую мощность
при п = 1450 об/мин, считая, что к. п. д. остался
неизменным.
87
2.11. При испытании центробежного насоса получены
следующие данные:
Q, дм8/мин 0 100 200 300 400 500
Я, м 37,2 38,0 37,0 34,5 31,8 28,5
Сколько жидкости будет подавать этот HacoG по трубопроводу
диаметром 76 х 4 мм, длиной 355 м (собственная длина плюс
эквивалентная длина местных сопротивлений) при геометрической
высоте подачи 4,8 м? Коэффициент трения % «= 0,03; А/?ДОп = 0.
(Построить характеристики насоса и трубопровода и найти
рабочую точку.)
Как изменится производительность насоса, если
геометрическая высота подачи будет 19 м?
2.12. Определить производительность шестеренчатого
насоса (см. рис. 2.9) по следующим данным: частота вращения
650 об/мин, число зубьев на шестерне 12, ширина зуба 30 мм,
площадь сечения зуба, ограниченная внешней окружностью
соседней шестерни, 7,85 см2, коэффициент подачи 0,7.
2.13. Требуется выкачивать 215 дм3/мин раствора относительной
плотности 1,06 из подвального бака водоструйным насосом
(см. рис. 2.10). Высота подъема 3,8 м. Давление воды перед
насосом ршб = 1,9 кгс/см2 (~0,19 МПа). К- п. д. насоса 0,15. Сколько
кубометров воды будет расходовать в 1 ч водоструйный
насос?
2.14. Какой мощности электродвигатель необходимо
установить к вентилятору производительностью ПО м3/мин при полном
напоре 834 Па (85 мм вод. ст.)? К. п. д. вентилятора 0,47.
2.15. Центробежный вентилятор, делающий 960 об/мин, подает
3200 м3/ч воздуха, потребляя при этом 0,8 кВт. Давление
(избыточное), создаваемое вентилятором, 44 мм вод. ст. Каковы будут
у этого вентилятора подача, давление и затрачиваемая мощность
при п = 1250 об/мин? Определить также к. п, д. вентилятора.
2.16. Какое количество воздуха будет подавать вентилятор
примера 2.12 при работе на сеть, у которой при расходе 1000 м3/ч
сумма (Арск + Артр + Арм. с) составляет 265 Па, а разность
давлений в пространстве нагнетания и в пространстве всасывания
равняется 20 мм вод. ст.?
2.17. Сколько воздуха будет подавать вентилятор примера 2.12
в сеть, у которой при расходе 1350 м3/ч сумма (Д/?Ск + &Ртр +
+ &Ри, с) составляет 167 Па, а Д/?ДОп равно 128 Па?
2.18. Какую частоту вращения надо дать вентилятору
примера 2.12, если он должен подавать 1500 м3/ч воздуха в сеть,
полное сопротивление которой при этом расходе 422 Па?
2.19. Определить аналитическим путем и по диаграмме Т — S
температуру воздуха после адиабатического сжатия его от
начального давления (абсолютного) 1 кгс/см2 до конечного давления
3,5 кгс/см2. Начальная температура 0 °С Определить также
затрату работы на сжатие 1 кг воздуха.
88
2.20. Определить шщность, потребляемую углекислотным
поршневым компрессором производительностью 5,6 м3/ч (при
условиях всасывания). Компрессор сжимает диоксид углерода
от 20 до 70 кгс/см2 (давление абсолютное). Начальная температура
—15 °С. К. п. д. компрессора принять равным 0,65. Задачу решить
как аналитическим путем, так и с помощью диаграммы Т — S
для углерода (рис. XXVII).
2.21. Определить объемный к. п. д. компрессора предыдущей
задачи, если вредное пространство составляет 6% от объема,
описываемого поршнем, а показатель политропы расширения
m = 1,2.
2.22. Определить производительность и расходуемую
мощность для одноступенчатого поршневого компрессора по
следующим данным: диаметр поршня 250 мм, ход поршня 275 мм, объем
вредного пространства 5,4% от объема, описываемого поршнем,
частота вращения 300 об/мин. Компрессор сжимает атмосферный
воздух до /?абс = 4 кгс/см2. Показатель политропы расширения
на 10% меньше показателя адиабаты. Начальная температура
воздуха 25 °С Общий к. п. д. компрессора 0,72.
2.23. Как изменяется производительность и потребляемая
мощность компрессора предыдущей задачи, если дать ему
воздуходувкой наддув до /?113б = 0,4 кгс/см2 (см. рис. 2.13). Конечное
давление (абсолютное) 4 кгс/см2.
2.24. При каком давлении нагнетания объемный к. п. д.
одноступенчатого поршневого компрессора, сжимающего этилен,
упадет до 0,2? Давление всасывания 1 кгс/см2. Расширение газа
из вредного пространства считать адиабатическим. Объем вредного
пространства составляет 7% от объема, описываемого поршнем.
2.25. Исходя из условия, что компрессорное смазочное масло
допускает без заметного ухудшения смазки температуру в
цилиндре не выше 160 °С, определить предельное значение давления
нагнетания в одноступенчатом поршневом компрессоре: а) для
воздуха, б) для этана. Давление всасывания 1 кгс/см2. Начальная
температура 25 °С. Процесс сжатия считать адиабатическим.
2.26. По данным примера 2.17 определить для
одноступенчатого и двухступенчатого компрессоров теоретическую затрату
работы по формулам (2.13) и (2.19).
2.27. Определить требуемое число ступеней поршневого
компрессора, который должен сжимать азот от 1 до 100 кгс/см2
(давление абсолютное), если допускаемая температура в конце сжатия
не должна превышать 140 °С. Процесс сжатия считать
адиабатическим. Начальная температура азота 20 °С.
2.28. Определить теоретическую затрату работы на сжатие
водорода от 1,5 до 17 кгс/см2 (давление абсолютное) при
одноступенчатом и двухступенчатом сжатии. Начальная температура
водорода 20 °С.
2.29. Компрессор при испытании нагнетал атмосферный
воздух в баллон объемом 42,4 дм3. За 10,5 мин давление в баллоне
89
повысилось от 0 до 52 кгс/см2 (давление избыточное), а
температура воздуха в баллоне поднялась от 17 до 37 °С. Определить
производительность компрессора в м3/ч (при нормальных
условиях).
2.30. Определить потребляемую мощность и расход воды на
холодильники поршневого компрессора, который сжимает 625 м3/ч
(при нормальных условиях) этилена от давления (абсолютного)
9,81 * 10* до 176,6-104 Па. К. п. д. компрессора 0,75. Охлаждающая
вода нагревается в холодильниках на 13 °С. Начальная
температура газа 20 °С.
ПРИМЕР РАСЧЕТА ЦЕНТРОБЕЖНОГО НАСОСА
Центробежный насос необходимо установить на высоте 5 м над уровнем
открытого водоема для перекачки 45 м^ч воды в реактор, работающий под
избыточным давлением 0,1 МПа. Геометрическая высота подъема воды 20 м.
Температура воды 20 °С. На линии нагнетания (LH = 35 м) расположены 2
отвода под углом 90° и 5 отводов под углом 110°, а также 2 нормальных вентиля
и 1 прямоточный. На линии всасывания (LBC = 15 м) установлено 2
прямоточных вентиля и 3 отвода под углом 90° (в обоих случаях отношение радиуса
изгиба к внутреннему диаметру трубопровода равно 4). Следует выбрать насос
(по напору и мощности).
Решение. I. Выбор диаметра трубопровода проведем, приняв скорость
воды во всасывающей и нагнетательной линиях одинаковой и равной 1,5 м/с;
d = VVliOJSbw) = ^45/(3600.0,785-1,5) = 0,103 м.
Выбираем стальной трубопровод с незначительной коррозией,
2. Расчет потерь на трение и местные сопротивления.
Определим режим течения воды:
Re=wdp/|A= 1,5-0,103.998/(1,005.1(Г9)= 153 420.
Режим турбулентный.
Среднее значение абсолютной шероховатости стенок труб е = 0,2 мм
(табл. XII). Относительная шероховатость dje = 103/0,2= 515. По графику 1.5
находим значение коэффициента трения Я — 0,0235.
Сумма коэффициентов местных сопротивлений для всасывающей линии:
2 ?вс -=- Ci + К, + ЗЕз = 0,5+ 2-0,5 + 3-0,11 - Ь83,
где ^1= 0,5— вход в трубу (с острыми краями); ?,= 0,5 — прямоточный
вентиль (для d = 100 мм и Re > 3- Щ; t,3~ АВ = ll0-0.ll = 0,11 — отвод
под углом 90° (табл. XIII). Тогда
АРвс=(Я-^+2?вс)
= (0,0235 0 тз~ + Ь83\ 998.1,5'2/2 = 5894Па.
Потери напора на всасывающей линии:
¦ #п. вс = ApBC/(pg) = 5894/(998-9,81) = 0,60 м.
Сумма коэффициентов местных сопротивлений для нагнетательной линии:
2 Ен «= ti + 2t« + 5?а + 2Ь + Е6« 1+2-0,11 +5.0,12 + 2.4,1 + 0,5 =* 10,52,
90
где ?, — 1 —выход из трубы; ?2 — /42Я<> = 1,0-0,11 =0,11 —отвод под углом °'0°;
?з = /43В3 = 1,13-0,11 = 0,12 — отвод под углом 110°; ?4 = 4,1 — норыгмь-
ный вентиль (при d= 100 мм); С5=0,5— прямоточный вентиль (при Re :>
> 3-105). Тогда
Лри - (о,0235 -~^ + 10,52) "821,52 = 20 777 Па.
Потери напора на нагнетательной линии:
Ян = bPnKpg) = 20 777/(998-9,81) = 2,12 м.
Общие потери напора:
#П = Явс + Ян = 0,60 + 2,12 = 2,72 м.
3. Выбор насоса.
По формуле (2.1) рассчитаем полный напор, развиваемый насосом:
Полезная мощность насоса:
N = VpgH = 45-998-9,81 -32,93/3600 = 4030 Вт = 4,03 кВт.
Для центробежного насоса средней производительности примем г\ =
= 'Пп'ПдПн ~ 0,6. Тогда мощность, потребляемая двигателем насоса:
#дв = 4,03/0,6 = 6,7 кВт.
По табл. 2.5 устанавливаем, что по заданным производительности и напору
следует выбрать центробежный насос марки Х45/54, для которого при
оптимальных условиях работы производительность Q= 1,25*10"? mVc, напор Н = 42 м»
к. п. д. насоса г\п = 0,6. Насос снабжен двигателем А02-62-2 номинальной
мощностью 17 кВт (г\д ~ 0,88, частота вращения вала п = 48,3 об/с).
4. Предельная высота всасывания.
Для центробежных насосов запас напора, необходимый для исключения
кавитации, рассчитывают по формуле:
Якав =0,3 (Qn2)2/3 = 0,3 (0,0125-48,32)2/3 =2,84 м.
По формуле (все слагаемые выражены в метрах перекачиваемой жидкости)
ЯПр. вс ^ А — hf — Явс — Якав, где А — атмосферное давление, ht —
давление насыщенного пара при соответствующей температуре,
Явс < 10,25 — 0,24 — 0,60 — 2,84 = 6,57 м.
Здесь А = 10,25 (табл. XIX), ht — 0,24 м при 20 °С (табл. 2.2).
Таким образом, расположение насоса на высоте 5 м над уровнем водоема
вполне допустимо.
91
Таблица 2.5
Марка
насоса
Х2/25
Х8/18
Х8/30
Х20/18
Х20/31
Х20/53
X 45/21
Х45/31
X45/54
X90/I9
Х90/33
X 90/49
X90/85
X160/29/2
X160/49/2
X160/29
Q, м8/с
4,2-КГ4
2f4*10"8
2,4-10"*
5,5-10"*
5,5. Ю~3
5,5. Ю~3
1,25-10"*
1,25-10*8
1,25-10"2
2,5-10"?
2,5-10"*
2,5- Ю'в
2,5-10"?
4,5-10"?
4,5.10"?
4f5.10"3
и,
м столба
жидкости
25
11,3
14,8
18
17,7
24
30
10,5
13,8
18
18
25
31
34,4
44
53
13,5
17,3
21
19,8
25
31
32,6
42
54
13
16
19
25
29,2
33
31,4
40
49
56
70
85
20
24
29
33
40,6
49
29
п.
об/с
50
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
48,3
24,15
Чн
—
0,40
0,50
0,60
0,55
0,50
0,60
0,60
0,60
0,70
0,70
0,70
0,65
0,65
0,75
0,60
Электро;
тип
АОЛ-12-2
А02-31-2
ВАО-31-2
А02-32-2
ВАО-32-2
А02-31-2
ВАО-31-2
А02-41-2
ВАО-41-2
А02-52-2
ВАО-52-2
А02-51-2
ВАО-51-2
А02-52-2
ВАО-52-2
А02-62-2
А02-71-2
А02-72-2
А02-51-2
А02-52-2
А02-62-2
А02-62-2
А02-71-2
А02-72-2
А02-71-2
А02-72-2
А02-81-2
А02-81-2
А02-82-2
А02-91-2
ВАО-72-2
А02-72-2
А02-81-2
А02-81-2
А02-82-2
А02-91-2
А02-81-4
(питатель
/V
кВ
1,1
3
3
4
4
3
3
5,5
5,5
13
13
10
10
13
13
17
22
30
10
13
17
17
22
30
22
30
40
40
55
75
30
30
40
40
55
75
40
Ч
—_
—
0,82
—
0,83
—
0,82
0,87
0,84
0,89
0,87
0,88
0,87,
0,89
0,87
0,88
0,88
0,89
0,88
0,89
0,88
0,88
0,90
0,90
0,88
0,89
—
_~
—
0,89
0,89
0,89
_
_^
_
0,89
_
Примечания. 1. Насосы предназначены для перекачивания химичеоки
активных и нейтральных жидкостей без включений (или о твердыми включениями с
размером частиц до 0,2 мм при концентрации их до 0,2 %).
2. Каждый насос может быть изготовлен с тремя различными диаметрами колеса,
что соответствует трем различным напорам (в области оптимального значения г\ \.
92
Глава 3
ГИДРОМЕХАНИЧЕСКИЕ МЕТОДЫ РАЗДЕЛЕНИЯ*
ГИДРОДИНАМИКА ВЗВЕШЕННОГО СЛОЯ*
ПЕРЕМЕШИВАНИЕ В ЖИДКОЙ СРЕДЕ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
Осаждение
Осаждение под действием силы тяжести (пылевые камеры,
отстойники),
1. Для описания в критериальной форме процесса осаждения
шарообразной частицы в неподвижной неограниченной среде
могут быть применены критерии подобия! Архимеда Аг, Лященко
Ly и Рейнольдса Re.
Наиболее удобной формой критериальной зависимости
является Ly = / (Аг).
2. При так называемом ламинарном режиме осаждения, когда
критерии имеют значения Аг < 3,6; Ly < 2- 1(Г3; Re < 0,2,
Сгоксом теоретически получегга следующая формула для скорости
осаждения woc (в м/с) шарообразной частицы *i
w°c=—щг0—• (ЗЛ)
Для осаждения частицы в газовой среде формула (3,1)
упрощается:
-6с - ¦§*, (3-2)
так как в этом случае величиной рс можно пренебречь.
В формулах (3.1) и (3,2): d — диаметр шарообразной частицы м; р —
плотность частицы, кг/м3; Рс_— плотность среды, кг/м3; ^с — динамический
коэффициент вязкости среды, Па*с, т. е. Н»с/м?, или кг/(м*с),
3. Определение скорости осаждения шарообразной
одиночной частицы в неподвижной неограниченной среде по обобщенному
методу, пригодному при любом режиме осаждения, осуществляют
следующим образом.
Определяют критерий Архимеда;
Afa8Ga^-asJ^-eZlPca,,^P"Pe)Pcg> <8Л)
Рс Fr рс Мо
где Ga = Re2/Fr — критерий Галилея.
Для осаждения в газовой среде-
Аг = d3ppcg/ii%
* Практически возможно применение формулы Стокса и при более высоки»
значениях критериев Архимеда и Лященко,
93
По найденному значению критерия Аг определяют критерий
Re или критерий Ly (рис. 3.1):
Аг р —рс Ис (Р — Рс) ЙГ
либо (если среда — газ)
w* р2
Ly = -^1. (3.4а)
VcgP
Далее вычисляют скорость осаждения:
Рс"
или
W
= |Ду |ас (р - рс) g/p*. (3.5а)
Для частицы неправильной формы скорость осаждения
определяют тем же путем из критерия Лященко, но с подстановкой
в критерий Архимеда вместо d величины da-
Эквивалентный диаметр d3 частицы неправильной формы
вычисляют как диаметр условного шара, объем которого V равен
объему тела неправильной формы:
4 = Y^VJk= 1,24 у"АТ7р, (3.6)
где М —масса частицы, кг.
4. Диаметр осаждающейся шарообразной частицы при
известной скорости осаждения находят обратным путем, т. е.
вычисляют сначала критерий Лященко
12? О2
Ly =
f^c (Р — Pc)g
и по найденному значению Ly определяют критерий Аг (рис. 3.1);
из последнего по формуле (3.3) вычисляют диаметр шарообразной
частицы.
5. Эквивалентный диаметр частицы твердого тела
неправильной формы при известной скорости осаждения определяют таким
же путем. Сначала определяют критерий Ly по формуле (3.4),
затем находят значение критерия Аг из рис. 3.1 для частицы
соответствующей формы и вычисляют ее эквивалентный диаметр!
Аг Lip
9 V (Р — Рс)Рс?
6. Площадь осаждения Foc (в м2) пылеосадительной камеры
или отстойника для суспензий (взвесей) определяется по формуле:
^оС = V/w'n, (3.8)
где V — объемный расход газа (жидкости), проходящего через аппарат
параллельно поверхности осаждения, м3/с; w'0Q — средняя расчетная скорость
осаждения частиц, м/с,
94
by
8
b
4
2
ю4
8
6
4
2
id
8
6
4
2
if
8
в
4
2
Mf
8
6
4
2
1(f
8
в
4
2
ю"
8
в
4
2
ю2
8
в
4
2
ю3
я
и
S
4
2
Ю4
¦
——
_
—___
=
— —
в
'- +
J..I II 1.1,
_
L 1___
—
= : :
_^~—
I .
hfrf
—.—
—i—
_—
---¦>—
¦рг —?
r=Z
1 1
- - - ¦ ——
_Дц ——
—\
- - -
... 4-
Т""Т -Г
—Az?
^гГ
^—^—f—"~~
--i-. -
y-\~z
гтуи'"-^
5,
¦
ТТ7 ~"
—
—i ^
1
——-<
. '
1
-^ <¦ —
S* **
| \ \ -
—| 1-|
6*'*
i
¦
к—
Mil "
__-_
|
1 —j
_4р
3 ^^Р*
I
н
U
--Ч* h
—л— ,_. _
2- —
Г
_—_
= =::=i
i j ¦¦)-+-
- f*
•
"--¦
-
R
1С
^
7
1С
— 8
- - - *?
... о
0
k
-л8
¦ 4
9
л,
16
ft
... tf
... >?
"Г
?
...ffl
^
<>
- ¦ ^
to
Ar
Рис. 3.i. Зависимость критериев Re и Ly от критерия Ai- для осаждении одиночной чая
стицы в неподвижной среде:
J и 6 — шарообразные частицы; 2 — округленные; 3 — угловатые; 4 -^ продолговатые;:
6 ** пластинчатые.
95
Слав
Начальная.
Суспензия
сЬ
Рис. 3,».
ствия.
Отстойник непрерывного дей-
Отношение средней расчетной
скорости стесненного осаждения
частиц Woe к скорости осаждения
¦ л одиночной частицы woc зависит от
\ Сгущенная суспензия ? ^
;^ объемной концентрации суспензии.
При ориентировочных расчетах, учитывая приближенно
отличие реальных условий осаждения от теоретических (стесненность
осаждения, форма частиц, движение среды), среднюю расчетную
скорость осаждения часто принимают равной половине
теоретической скорости осаждения одиночной шарообразной частицы:
woc = 0,5b;,
ОС"
7. В применении к отстойнику непрерывного действия для
отстаивания суспензий (рис. 3.2) формула (3.8) принимает вид:
'н
''ос —
\ сСГ)
9cw
(3.9)
с ос
ИЛИ
Е- ^0 (ХСГ
Г оС : Г-
*н)
«ЪЛг
(ЗЛО)
Здесь Foc — площадь осаждения отстойника, м2; GH — массовый расход
начальной (разбавленной) суспензии, кг/с; сн — массовая концентрация твердой
фазы в начальной суспензии, кг/кг; ссг— массовая концентрация твердой фазы
в сгущенной суспензии (шламе), кг/кг; рс — плотность
осветленной жидкости, кг/ма; V0 — объемный расход
жидкой фазы, содержащейся в начальной суспензии, ма/с;
хн и хст — концентрации начальной суспензии и шлама,
кг твердой фазы
кг жидкой фазы'
Осаждение под действием центробежной
силы (циклоны)
8. Основные размеры циклона (рис. 3.3)
определяются обычно в зависимости от его
диаметра D. Для распространенных циклонов
НИИОГАЗ (Научно-исследовательский
институт по промышленной и санитарной очистке
газа) эти размеры (в долях D) даны в табл. 3.1.
Отличительной особенностью циклонов
НИИОГАЗ является наклонный патрубок для
поступающего газа.
Рис, 3.3. Циклон НИИОГАЗ,
&
ц
96
Таблица 3.1
Характеристика циклона
ЧИП !лИКЛОЬЗ
ЦН-24
ЦН-15
цн-п
Диаметр выходной трубы Di 0,6 0,6 0,6
Ширина входного патрубка Ь 0,26 0,26 0,26
Высота входного патрубка hx 1,11 0,66 0,48
Высота выходной трубы h2 2,11 1,74 1,56
Высота цилиндрической части h3 2,11 2,26 2,08
Высота конической части h4 1,75 2,0 2,0
Общая высота циклона Н 4,26 4,56 4,38
Коэффициент сопротивления ?0 60 160 250
Широко применяются три типа этих циклонов:
1) с углом 24° (ЦН-24); этот тип обеспечивает повышенную
производительность при наименьшем гидравлическом
сопротивлении; предназначен для улавливания крупной пыли;
2) с углом 15° (ЦН-15); этот тип обеспечивает хорошую степень
улавливания при сравнительно небольшом гидравлическом
сопротивлении;
3) с углом 11° (ЦН-11); этот тип обеспечивает повышенную
эффективность и рекомендуется в качестве унифицированного
пылеуловителя.
9. Диаметр циклона D определяют по условной скорости газа
оУц, отнесенной к полному поперечному сечению цилиндрической
части циклона;
где V — объемный расход газа, проходящего через циклон, мя/с.
Скорость оУц определяется по формуле (3.12). При этом
предварительно задаются отношением Д/?/р (см. пример ЗЛО).
По данным [3.1 ] значения wn принимают равными 2,5—
4 м/с.
10. Гидравлическое сопротивление Ар (в Па) циклона
рассчитывают по уравнению:
а>цр
Др = ?о-у-. (3.12)
где ?у — коэффициент сопротивления циклона, безразмерный; р — плотность
газа, проходящего через циклон, кг/м3.
11. Степень улавливания пыли ц в циклоне зависит,
помимо свойств пыли, от диаметра циклона, а также от
4 Павлов К. Ф. и др.
97
100 200 300 400 500 600 700 §00
А мм
Рис. 3.4» Степень улавливания пыли в циклоне
ЦН-15
Значения d (в мкм)*, I *-• 16; 2 * 10; 3 — 6.
скорости газа шц, т. е. от
отношения Ар/р в соответствии с формулой
(3.12).
На рис. 3.4 показана
зависимость степени улавливания ц от
диаметра циклона D при
различных диаметрах частиц пыли d.
График составлен для пыли с
плотностью 2300 кг/м3 при Д/?/р =
= 740 м2/с2.
Фильтрование
12. При А/? — const объем фильтрата V, прошедшего через
1 м2 фильтрующей поверхности за время т, и продолжительность
фильтрования т связаны
уравнением:
(3.13)
где С — константа фильтрования, характеризующая гидравлическое
сопротивление фильтрующей перегородки (ткани), м3/м2; К — константа фильтрования,
учитывающая режим процесса фильтрования и физико-химические свойства
осадка и жидкости [см. формулу (3.15) J, м2/с; т — продолжительность
фильтрования, с.
Константы К и С определяются опытным путем.
13. Скорость фильтрования [в м3/(м2-с)] в данный момент
определяется по уравнению:
К
dV
d% 2(V+Cy
(3.14)
По этому уравнению может быть рассчитана и скорость
промывки осадка промывной жидкостью, если вязкость промывной
жидкости равна вязкости фильтрата и если промывная жидкость
проходит через фильтр тем же путем, что и фильтрат. При этих
условиях скорость промывки равняется скорости фильтрования
в конечный момент.
Видоизмененное уравнение (3.14)
* 2 к +
dV
К
2С
К
выражающее прямолинейную зависимость между величинами
dxtdV и V, применяется для определения констант С и К по
экспериментальным данным. Для этой цели откладывают по оси
абсцисс измеренные значения VXf V2, ...» а по оси ординат —
соответствующие измеренные значения Axj/AVi, Ат2/АК2, ... Проведя
98
по экспериментальным точкам прямую (рис. 3.5), находят затем К
и С из уравнений:
14. Константа фильтрования К (в м2/с), отнесенная к 1 м2
фильтрующей поверхности, при А/? = const связана с удельным
сопротивлением осадка уравнением [ЗЛО];
2Др
К
\icr
(3.15)
где Ар — перепад давлений на фильтре, Па; fi — динамический коэффициент
вязкости фильтрата, Па*с; г — удельное сопротивление осадка (в расчете на I кг
содержащегося в нем твердого сухого вещества), м/кг; с — масса сухого твердого
вещества, отлагающегося на фильтре при прохождении через фильтрующую
поверхность 1 м3 фильтрата, кг/м3.
15. Величина с (в кг/м3) может быть выражена через
концентрацию фильтруемой суспензии х следующим образом (см.
пример 3.11):
- 9Х (3.16)
I
тх
Здесь р — плотность фильтрата, кг/м3; х — массовая концентрация твердой
фазы в суспензии, кг!кг; т — масса влажного осадка в расчете на 1 кг
содержащегося в нем сухого вещества, кг/кг.
При подстановке значения с в уравнение (3.15) получаем
следующую формулу для константы К (в м2/с):
2 Ар (I — тх)
К
\ХГХС)
(3.17)
Если известна константа фильтрования К, то удельное
сопротивление осадка г может быть найдено из уравнения (3.15), ре-
(в —« \,
\ кг сухого осадка/
шенного относительно г в
кг сухого осадка
2Ар (1 — тх)
Кцхр
(3.18)
16. Константа фильтрования С (в м3/м2), характеризующая
сопротивление фильтрующей перегородки (ткани) и отнесенная
к 1 м2 поверхности фильтра, при A/? =const определяется
следующим выражением [3.10]:
С =
' ТК
ГС
(3-19) §
или в соответствии с уравнением (3.16):
гхр
где /-тк —удельное сопротивление фильтрующей
ткани (на 1 м2 поверхности), м/ма; г — удельное
сопротивление осадка, м/кг.
Рис, 3,5. Зависимость Дт/ДК от К.
4*
Следовательно, если значение константы фильтрования С
(в м3/м2) известно, то удельное сопротивление ткани может быть
вычислено по формуле:
Гти« J^SL. (3.21)
1 — тх
17. Концентрация промывной воды в любой момент времени
от начала основного (диффузионного) периода промывки * может
быть вычислена по уравнению!
с-с*-*-. (3'22)
Здесь Ci — концентрация промывной воды в начале процесса; е —
основание натуральных логарифмов (е = 2,718); К — коэффициент, учитывающий
физико-химические свойства осадка и промывной воды, а также режим промывки
(находится экспериментальным путем); w — удельная интенсивность промывки
или скорость прохождения промывной воды, м3/(м?*с); т — продолжительность
промывки, с; 6 — толщина слоя осадка, м.
Уравнение (3.22) после логарифмирования принимает вид!
т2 — Ti 2,3ft
lg Ct - h C2 Kw
(3.23)
где тх и т2 — время начала и конца наблюдений в любой период процесса
диффузионной промывки; С] и С2 — соответствующие концентрации промывной
воды.
Из уравнений (3.22) и (3.23) может быть найдена
продолжительность промывки т, т. е. время, необходимое для заданного
изменения концентрации вымываемого вещества в осадке, а также
величина коэффициента /(.
18. Количество сухого вещества G (в кг) в осадке» получаемом
на фильтре, зависит от количества собранного фильтрата V,
плотности фильтрата р, массовой доли твердой фазы в суспензии х,
влажности осадка (выражаемой массовым отношением т) и может
быть вычислено по формуле:
G = Vc~V л рХ . (3.24)
1 — тх v '
19. Концентрация твердой фазы в суспензии х в зависимости
от плотности суспензии рс выражается формулой;
,а (Po-rtPT.. (3.25)
(Ртв —Р)Рс
Плотность суспензии:
Рс - /+Д - P(1+")P™ . (3.26)
__L 4- — р + ртвП
Ртв Р
* Во время основного периода промывки идет процесс диффузии
растворимого вещества в промывную воду и удаления его с водой. Во время же начального
периода промывки происходит лишь вытеснение фильтрата промывной водой из пор
осадка.
100
В этих формулах к — массовая концентрация твердой фазы в суспензии, кг/кг;
Sq — плотность суспензии, кг/м8; р — плотность жидкой фазы, кг/м3; ртв —
лотность твердой фазы, кг/м8; п — масса жидкой фазы в суспензии на единицу
массы твердой фазы (Т : Ж — 1 • л).
По формуле (3.26) можно вычислить и плотность влажного
осадка, рассматривая его как концентрированную суспензию.
20. Расчет рукавных фильтров для газов сводится к
определению требуемой поверхности F (в м2) фильтра по формулез
F = VfVyJV (3.27)
где V — объемный расход запыленного газа; Куд — удельный объемный расход
эапыленного газа в расчете на 1 м? поверхности ткани.
Величину Ууд принимают обычно равной 0,2—1 м3/(м2-мин),
а при улавливании крупной пыли до 2,5 м3/(м2-мин).
Центрифугирование
21. Центробежная сила С (в Н), развиваемая при
центрифугировании, определяется по уравнению:
С = Mn2/R = Мсо2Я s* 4QMn*R я* 20Mri*D. (3.28)
Здесь M—масса осадка и жидкости, находящихся в барабане
центрифуги, кг; со — угловая скорость, с"1; D = 2R—диаметр барабана, м; п —
частота вращения центрифуги, с"*.
Давление фильтрования (в Па) при центрифугировании!
приближенно
Д/?Ц = С/Л (3.29)
где С — центробежная сила, рассчитываемая по уравнению (3.28); F= nDH —
средняя поверхность фильтрования, м2; D — внутренний диаметр барабана
центрифуги, м; Н — высота барабана (в центрифугах периодического и
полунепрерывного действия) или длина зоны фильтрования (в центрифугах
непрерывного действия), м;
более точно
APlx « 20pcn2 (*§ - R\) = 5рсп2 {D\ - D% (3.30)
где рс — плотность суспензии, кг/м3; Dx = 2RX — диаметр внутреннего слоя
жидкости, м; D2 — 2R* — внутренний диаметр барабана, м; п — частота
вращения центрифуги, с-*1.
22. Фактором разделения в центрифугах называется
отношение ускорения центробежной силы к ускорению силы тяжести;
/ = с/Р = (o2R/g ъ 20Fr;, (3.31)
где R — радиус барабана, м; со — угловая скорость, с"*.
* Фактор разделения представляет собой видоизмененный критерий Фруда
(центробежный);
?тц - Dn4g.
101
23* Скорость фильтрования при центрифугировании может?
быть выражена в форме общего гидравлического закона:
dV _ Д/7Ц
d% " Rn *
Здесь Дрд — перепад давлений при центрифугировании; Rn = R0G + i?TK—
общее сопротивление при центрифугировании, равное сумме сопротивлений
осадка и фильтрующей перегородки.
Величины сопротивлений Roc и RTK могут быть рассчитаны по
уравнениям фильтрования или определены экспериментальным
путем.
24. Глубина воронки h (в м) жидкости, образуемой при
вращении барабана центрифуги, рассчитывается ориентировочно
по формуле:
h = 2n?R\ (3.32)
где п — частота вращения барабана, с"1; R — радиус барабана, м.
По этой же формуле приближенно может быть рассчитана
глубина воронки и в аппаратах с мешалкой.
25. Расход мощности в пусковой период для центрифуг
периодического действия вычисляется по следующим формулам
а) Мощность, расходуемая на преодоление инерции барабана
и загрузки.
Работа Т1 (в Дж), затрачиваемая на преодоление инерции
барабана в пусковой период:
Тг = т1мб/2, (3.33)
где w2 — установившаяся по достижении заданной частоты вращения окружная
скорость вращения барабана (на внешней поверхности его с радиусом R9), м/с;
Mq — масса барабана, кг.
Работа Т2 (в Дж), затрачиваемая на преодоление инерции
загрузки в пусковой период (объем загруженного материала
принят равным половине полного объема барабана):
Г2 = 0,75^рК/4. (3.34)
Здесь wx — окружная скорость вращения на внутреннем радиусе
барабана Rf9 м/с; р — плотность загруженного материала, кг/м3; V — полный объем
барабана центрифуги, равный nRlHt м3.
Мощность Nx (в Вт), расходуемая на преодоление инерции
барабана и загрузки во время пускового периода:
Nx = (7\ + Г2)/т, (3.35)
где т — продолжительность пускового периода, с.
По практическим данным т обычно составляет 1—3 мин.
102
Рис» 3.6. Схема действующих сил в барабане
центрифуги.
б) Мощность N2 (в Вт),
расходуемая на трение вала в
подшипниках:
N2=%MwBg, (3.36)
где \ — коэффициент трения, равный 0,07—
0,1 *; М —масса всех вращающихся
частей центрифуги вместе с загрузкой, кг;
wn — окружная скорость вращения цапфы
вала, м/с.
в) Мощность N$ (в Вт), расходуемая на трение стенки барабана
о воздух:
No == 2,94- 10-3р^рВ) (3.37)
где рв — плотность воздуха, кг/м3; Р — коэффициент сопротивления, равный
в среднем 2,3.
г) Полный расход мощности #т (в Вт) для центрифуги
периодического действия в пусковой период:
iVT = iVt + Л/2 + iV8. (3.38)
С учетом к. п. д. передаточного устройства цп расходуемая
мощность:
N = N7fr\n. (3.39)
Установочную мощность электродвигателей для центрифуг
следует выбирать с запасом в 10—20%.
26. Расчет толщины стенки барабана центрифуги или проверка
стенки на прочность могут быть сделаны по уравнению:
Са + С2
/<2 =
2/
(3.40)
Здесь Kz — допускаемое напряжение материала стенки барабана на
разрыв, Па, / — площадь сечения стенки барабана, м? [так как действующее
усилие воспринимается обеими частями сечения барабана, то общая площадь
сечения равна 2/ (рис. 3.6)]; Сх — центробежная сила полукольца стенки
барабана, Ы; С2 — центробежная сила полукольца загрузки, Н.
Величины Сх и С2 рассчитываются по уравнению (3.28). При
этом расстояние R (в м) от центра тяжести вращающегося
полукольца до оси вращения определяется по формуле:
/?«
Зя
4 - *?
>2 г>2
(3.40а)
Щ - *-,
где Rx и R2 — внутренний и наружный радиусы полукольца, м.
27. а) Производительность V (объемный расход поступающей
суспензии) отстойной центрифуги с ножевым съемом осадка типа
* Для обыкновенных подшипников с кольцевой смазкой, Для
шарикоподшипников К = 0,03,
103
АОГ (в м8/с) при ламинарном режиме осаждения определяется
по видоизмененному уравнению (3.8)!
V^F'wr\. (3.41)
Здесь F' = 2n/?0L — поверхность зеркала суспензии в барабане, м?; /?« —
внутренний радиус кольцевого слоя суспензии, м; L —длина барабана, м; w =
= wocf — скорость осаждения частиц под действием центробежной силы, m/cj
шое — скорость осаждения частиц под действием силы тяжести, м/с; / — фактор
разделения, определяемый по радиусу /?0; Ч — коэффициент, учитывающий
отношение действительной и теоретической производительности центрифуги, который
при отсутствии опытных данных можно принимать равным 0,4—0,5; он зависит
от скольжения жидкости относительно барабана, а также учитывает наличие
вихрей, затрудняющих осаждение.
Формула (3.41) может быть приведена к удобному для расчетов
виду (применение см. в примере 3.23)i
V^4=25,3riLn2^ocfe, (3.42)
где k — отношение времени подачи суспензии (время собственно
центрифугирования) к общему времени работы центрифуги.
б) Производительность V (в м3/ч) по суспензии центрифуги
НОГШ (непрерывнодействующей отстойной горизонтальной со
шнековой выгрузкой осадка) определяется по уравнению:
V - 3,5 \р1лЬсл (р - рс) dV]Ai, (3.42а)
где Dcn и 1сл —диаметр и длина «сливного цилиндра», м; р и рс — плотность
частиц и среды, кг/м3; d — крупность разделения (диаметр наименьших
осаждаемых частиц)» м; п— частота вращения ротора, об/мин; р. — динамический
коэффициент вязкости среды, Па-с.
28. Производительность V (в м3/с) трубчатой сверхцентрифуги
(по питанию) определяется из следующего выражения:
V^wVm/h, (3.43)
где w — скорость осаждения частиц в центробежном поле, м/с; Vm = 0,785 (D2 —
— Dl) L — объем жидкости в барабане, м3; h — глубина потока в барабане, м;
L — длина рабочей части барабана, м; D — внутренний диаметр барабана, м;
D0—диаметр сливного порога, м.
Условием хорошей работы сверхцентрифуги (без уноса частиц)
расчетного диаметра является наличие ламинарного режима
движения потока в барабане (Re < 350). При больших значениях
критерия Re необходимо увеличивать длину барабана.
Гидродинамика взвешенного слоя
29. Для неподвижного слоя твердых частиц порозность» т. е.
относительная доля объема, не занятого твердой фазой:
В том случае, когда плотностью среды между частицами можно
пренебречь по сравнению с плотностью самих частиц:
е0= 1 —(Рнас/Р)- (3.44а)
Здесь V и Унас — объем, занимаемый частицами, и объем слоя, м3; р и pHac~
плотность частиц и плотность слоя (так называемая насыпная), кг/м^.
104
Практически порозность неподвижного насыпанного
(неупорядоченного) слоя шарообразных частиц одинакового диаметра
колеблется в пределах 0,38—0,42; в расчетах принимается среднее
значение 0,40.
Для взвешенного слоя твердых частиц порозносты
* = lVca-V)/Vw (3.45)
где Vcn — объем взвешенного слоя, м3.
30. Условием перехода неподвижного слоя твердых частиц
во взвешенное состояние является равенство силы давления со
стороны среды (проявляющейся в наличии перепада давления по
высоте слоя) и веса слоя, приходящегося на единицу площади
его поперечного сечения.
Основной гидродинамической характеристикой взвешенного
слоя (при неизменном количестве материала в нем) является
постоянство Дрсл:
АЯсл = <W«S = const, (3.46)
гДе бсл — вес материала в слое, Н; S — площадь поперечного сечения, м?.
Перепад давления (в Па) для потока, проходящего через
взвешенный слой твердых частиц, определяется по уравнению;
ДРсл = (Р " Рс) g 0 — ») ^ = (р — Рс) 8 (1 - Ч) Ао, (3.47)
где h и Л0 — высота взвешенного и неподвижного слоев, м; р и рс — плотность
твердых частиц и среды, кг/м3.
Если средой является газ, то рс < р, и приближенно:
АРсл = Р? (1 — «) h = pg (1 — во) Ао. (3,47а)
Перепад давления (в Па) в газораспределительной решетке
можно определить по уравнению:
АРреш ~ °.503^оРо 0 - <Р2У С'- (3.48)
Здесь ф — доля живого сечения решетки; эта величина часто принимается
равной 0,03—0,05; w0 = шДр — скорость потока в отверстиях решетки» м/с;
w — скорость потока, отнесенная к полному сечению аппарата, м/с; С •—
коэффициент сопротивления решетки, зависящий от отношения й01Ь и
определяемый по графику (рис. 3.7); d0 —
диаметр отверстия решетки, м; б —
толщина решетки, м.
31. Скорость потока, при
которой сопротивление слоя
становится равным весу слоя,
приходящегося на единицу
площади поперечного сечения,
и при которой частицы
неподвижного слоя переходят во
Рис. 3.7. Коэффициент сопротивления
решеток;
i, — данные Г. Хьюмарка и X. О* Коинела;
2 » данные Д. И. Орочко н др,
ел
S
%0,9Г
s
14»
О
S 0}7
о
2 4 6 8
d0 _ диаметр отверстия
$ ~ толщина решетки
Ю
105
взвешенное состояние, называется критической скоростью или
скоростью псевдоожижения. Критическая скорость для слоя
сферических частиц одинакового диаметра определяется из
уравнения [3.15]:
__Аг _
"1400 + 5,22Уаг~ '
Re*p = — ___,- . (3.49)
Это уравнение выведено для средней порозности неподвижного
слоя е0 = 0,4 и дает погрешность ±20%. В нем
ReKp
=
==
tf>
wKvd
v0 '
(p —Pc)g
vcPc
Re2(P
Ar = ft-
Pr
d3pc (p —
— Pc)
9c
Pc)S
где tjyKp — критическая скорость потока, отнесенная к полному сечеиию
аппарата, м/с; d — диаметр частиц, м; р и рс — плотность частиц и среды, кг/м3;
vc — кинематический коэффициент вязкости среды, м2/с; \х — динамический
коэффициент вязкости среды, Па*с.
Для газа (ре <^ р):
d*pg
Аг =
vcPo
Для частиц неправильной формы критическую скорость потока
можно определить с учетом фактора формы:
Ф = 0,207S/V2/3, (3.50)
где V — объем частицы, м3; S — поверхность частицы, м2-.
При этом принимается, что эквивалентный диаметр d9 (в м)
равен:
где dm—диаметр шара (в м), объем которого равен объему частицы (dm =
= 1,24 ?v).
Для полидисперсного слоя, состоящего из частиц разного
диаметра:
п
rf3
-St-
Здесь п — число фракций; dt — средний ситовой размер /-й фракции (т. е.
среднее между размерами проходного и иепроходного сит); xi — массовое
содержание 1-й фракции в долях единицы.
32. При увеличении скорости потока w происходит
расширение (т. е. увеличение высоты и порозности) взвешенного слоя.
Высота взвешенного слоя h (в м) связана с высотой неподвижного
слоя h0 соотношением:
106
Порозность взвешенного слоя может быть подсчитана по
формуле:
e=(18Re+A°;36Re2r. (353)
Отношение рабочей скорости газа, отнесенной к полному
сечению аппарата, к критической скорости называют числом
псевдоожижения:
/Сю = да/даКр* (3.54)
Действительная скорость потока в свободном (живом) сечении
между частицами слоя определяется выражением:
а>д = а>/е. (3.55)
33. Скорость потока, при которой одиночная частица
переходит во взвешенное состояние, называется скоростью витания.
Она приближенно соответствует началу разрушения
монодисперсного взвешенного слоя. При этом е = 1. Скорость витания может
быть определена по формуле:
18+ 0,61 у Аг
где ReBHT = давит фс/Ис-
34. На рис. 3.8 представлен график зависимости Ly =*= / (Аг, г)
для взвешенного (кипящего) слоя от е0 = 0,4 до е = 1,0. График
позволяет определять скорость потока ш, необходимую для
достижения заданной порозности взвешенного слоя, состоящего
из частиц известного диаметра d, или решать обратную задачу.
35. Среднее расходное время пребывания т0 (в с) частиц
твердого материала в аппарате со взвешенным слоем (одиночным):
т0 = M/L. (3.57)
Здесь М —масса материала, находящегося в слое, кг; L — расход твердого
материала, кг/с.
Ввиду интенсивного перемешивания материала во взвешенном
слое время пребывания в слое отдельных частиц значительно
отличается от среднего расходного времени пребывания твердого
материала в слое т0. Если известно среднее расходное время т0
и задано некоторое время т (например, продолжительность какого-
либо процесса, проводимого во взвешенном слое), то долю х
частиц, имеющих время пребывания в слое, не меньшее чем т,
можно определить по уравнению:
х = е~х/х°, (3.58)
где е=- 2,718.
Для получения более равномерного распределения частиц
по времени пребывания применяют несколько последовательно
расположенных взвешенных слоев. Доля хп частиц материала,
107
10° 2 4 68Ю2 46810*2 4 6810я 2 4 6810* 2 4 Шь 2 46810s 2 468Ю7
Ar
Рис. 3,8, Зависимость критерия Ly от критерия At и чорозности ? слоя<
108
имеющих в многослойном аппарате время пребывания, не меньшее
чем т, для аппарата с п взвешенными слоями составит:
Перемешивание в жидкой среде
36. Критерии гидродинамического подобия для процесса
перемешивания определяются следующим образом.
Критерий Рейнольдса (центробежный):
Reu = pntfVn- (3.60)
Критическое значение этого критерия: Кец. кр & 50.
Критерий мощности *:
N
^""^Г' (3'61)
Критерий Фруда (центробежный):
Fru *= пЧ/g. (3.62)
В этих критериях: N— мощность, потребляемая мешалкой, Вт; р —
плотность жидкости, кг/м3; ц — динамический коэффициент вязкости жидкости, Па-с;
л — частота вращения мешалки, с'1; d — диаметр мешалки, м; g = 9,81 m/g2 —
ускорение свободного падения,
37, Критериальное уравнение для расчета мощности*
потребляемой мешалкой, в общем виде:
Kn = f (R&n> Р*ц> Го» Тъ, Г#0, ...),
Обычно влиянием силы тяжести пренебрегают. Тогда
K^ = <P(Reu> Го, Г*, Г//0> ...),
где Г = Dld\ Tb = bid; TH = HQ/d — симплексы геометрического подобия,
характеризующие конструкцию мешалки, влияние высоты слоя жидкости и
другие геометрические факторы; d — диаметр мешалки, м; D — диаметр сосуда, м;
Ъ — ширина лопасти мешалки, м; #0 — высота слоя жидкости, м.
Для геометрически подобных аппаратов с мешалками
обобщенное критериальное уравнение принимает вид:
Км^с/Яе™, (3.63)
где с и m — постоянные величины (для данной конструкции мешалки и для
определенного режима перемешивания),
Данные расхода энергии на перемешивание приведены в
литературе [3.22]. Значения постоянных величин си/пв общем
уравнении (3.63) для различных мешалок приведены в табл. XXI;
на рис. VII дана зависимость /Cjv = / (Кед) для тех же мешалок.
* В литературе иногда называется центробежным критерием Эйлера и
обозначается Еиц,
109
ПРИМЕРЫ
Осаждение
Пример 3.1, Найти верхний предел (т, е, наибольший диаметр
частиц) применимости формулы Стокса к частицам кварца
плотностью 2650 кг/м3, осаждающимся в воде при 20 °С.
Решение, Формула Стокса строго применима при Аг <
< 3,6. Поэтому наибольшая частица кварца, осаждение которой
может быть рассчитано по формуле Стокса, должна иметь диаметр:
Пример 3.2. Найти скорость осаждения в воде частиц
кварцевого песка шарообразной формы диаметром 0,9 мм, если плотность
песка 2650 кг/м3, а температура воды 20 °С.
Решение. Определяем критерий Аг;
Лг___ <*Э(Р — Pc)Pcg _
\&
0,9М0-е(2650— Ю00) 1000-9,81 t 10 tn.
= 12,10-а = 1,18-10*,
где для воды д0 — \-\0"° Па-с (табл. VI),
По значению Аг — 1,18-104 из рис. 3.1 находим Re = 140.
Скорость осаждения частиц кварцевого песка шарообразной
формы диаметром 0,9 мм определяем из выражения:
Reuc 140-1-10^ Л]_ ,
w™ в -2ЙГ в 0,0009-1000- = °'15 м/с'
Пример 3.3. Определить размер наибольших шарообразных
частиц мела, которые будут уноситься восходящим потоком воды,
идущим со скоростью 0,5 м/с. Температура воды 10 °С, плотность
мела 2710 кг/м3.
Решение. Определяем критерий Ly по формуле (3.4):
г __ Д&РЬ 0,5М0002-1рз _ , 03
У Не (р — рс) g ~ 1,3 (2710 — 1000) 9,81 * *' '
где для воды при 10 °С \xG = 1,3- I0~s Па-с.
По найденному значению Ly = 5,72-103 из рис. 3.1 находим
Re = 1750; затем по формуле (3.5) определяем максимальный
диаметр частиц мела, которые будут уноситься водой:
- Refic 1750-1,3.10-3 __
d = ее. = — 1Алл- — 4'55' Ю 3 м = 4,55 ми.,
^осРс 0,5-1000
Пример 3.4. Найти скорость осаждения в воде при 20 °С
частицы свинцового блеска угловатой формы с d3 = 1 мм. Плотность
свинцового блеска 7560 кг/м3.
ПО
Решение. Скорость осаждения частиц неправильной формы
найдем из критерия Ly, предварительно определив значение
критерия Аг:
. 4 (Р - Рс) Peg __ I3-10-" (7560 - 1000) 10*.9,81 а AA
АГ — -^ lMO-e ~~ °* *
где \хс = Ы(Г3 Па-с (табл. VI).
По графику (рис. 3.1) находим для частиц угловатой формы
Ly = 3,Ы02.
Скорость осаждения по формуле (3.5а):
И>ос
= ^У »*с (Р — Рс) «/Й =
= у'3,1 • Ю2-1 • 10"» (7560 — 1000) 9,81/ЮОО2 = 0,271 м/с.
Пример 3.5. Определить размеры продолговатых частиц угля
(р2 = 1400 кг/м3) и плоских частиц сланца (р2 = 2200 кг/м3),
оседающих с одинаковой скоростью ш00 = 0,1 м/с в воде при
20 °С.
Решение. Размеры частиц dB следует рассчитать по
формуле (3.7)
4=*^ Аг*2
(р —Рс)рс? '
предварительно определив значение критерия Аг по критерию Ly
из графика (рис. 3.1) для частиц соответствующей формы.
Для частиц продолговатой формы;
Lv "&Pc ю-мо« 2,5
У1~ fic(Pi~Pc)? ~Ы0"3-0,4-103.9,81-^°'
где ц.с = МО"3 Па-с (табл. VI); рс = 1000 кг/м3.
Для частиц пластинчатой формы:
^осРс КГМО6
У2 МР»-Рс)* I- Ю-»- 1,2-103-9,81 ~85'
Значению Lyx = 255 соответствует Агх = 9 -104 для
продолговатых частиц. Значению Ly2 = 85 соответствует Аг2 = 7 • 104 для
частиц пластинчатой формы.
Эквивалентный диаметр частиц угля:
,3/ Аг]^ Y Э-ЮММО"8
^ = V (Pl-Pc)Peg " V 9,81.04.103.10» = 2'82"10" М = 2'82 »"
Эквивалентный диаметр частиц сланца:
/ Аг2^с -шУ 7^104.12-10-« , _ _ „
мм.
, / АгоЦ? з/- 7-104-12-10"в
*--К (рй-Рс)Ре^У 9^1.1,2.103-Юз-Ь8Ь Ю-з м^Ь81
111
Рис, 3.9 (к примеру 3,6).
ь Пример 3.6. Какую
высоту надо дать слою газа
между полками пылевой
камеры (рис, 3.9), чтобы
осели частицы
колчеданной пыли диаметром 8 мкм
при расходе печного газа
0,6 м3/с (при нормальных
условиях)? Длина камеры
4,1 м, ширина 2,8 м,
общая высота 4,2 м. Средняя
температура газа в камере
427 °С. Вязкость газа при
этой температуре 0,034-Ю-3 Па-с, плотность пыли 4000 кг/м3,
плотность газа 0,5 кг/м3.
Решение. Определяем расход газа при заданных условиях:
V = 0,6 (273 + 427)/273 « 1,54 м3/с
Линейная скорость газа (пренебрегая толщиной полок):
^г = 1,54/(2,8-4,2) = 0,131 м/с.
Время пребывания газа в камере:
т =L/a;r = 4,1/0,131 =31,3 с.
Теоретическая скорость осаждения шарообразных частиц
(величиной рс пренебрегаем) по формуле (3.1):
1 (8-10"6)2 4000-9,81
woc =
18
0,034-Ю"3
= 0,0041 м/с.
Действительную скорость осаждения принимаем равной 0,5 X
X 0,0041 == 0,002 м/с.
Находим расстояние между полками:
h = w'x = 0,002-31,3 « 0,06 м =* 60 мм.
ОС
Проверяем правильность применения формулы (3.1):
К цс 0,034.10'3 ~ ufuuuw.
Так как Re = 0,00048 < 0,2, то применение формулы Стокса
допустимо.
Пример 3.7, Определить размер наименьших частиц,
осаждающихся в газоходе квадратного сечения длиной 16 м и высотой 2 м
при линейной скорости газа 0,5 м/с. Вязкость газа 0,03-Ю-3 Па-с,
плотность газа 0,8 кг/м3, плотность частиц 4000 кг/м3.
Решение. Газ проходит канал в течение
т = 16/0,5 = 32 о.
112
За это время успеют полностью осесть только те частицы,
действительная скорость осаждения которых не меньше, чем
woc = 2/32 = 0,062 м/с.
Определим диаметр шарообразных частиц, теоретическая
скорость осаждения которых вдвое больше, т. е. равна 0,124 м/с.
Вычислим значение критерия Ly по формуле (3.4а):
т. ШосРс 0>124з.0,82
ygSS~Wg"a О.ОЗ.Ю-з.4000-9,81 ^ОЗВ-Ю*.
По графику (рис. 3.1) находим значение Re = 0,14, откуда-
А RefAc 0,14-3-10-2- Ю-3 ,0. 1А . ...
d = —^ г ,пл по = 4,24-10 § м = 42,4 мкм.
^осрс 0,124-0,8
Пример 3.8. Определить диаметр отстойника (см. рис. 3.2) для
непрерывного осаждения отмученного мела в воде.
Производительность отстойника 80 т/ч начальной суспензии, содержащей
8% (масс.) СаС03. Диаметр наименьших частиц, подлежащих
осаждению, 35 мкм. Температура суспензии 15 °С. Влажность
шлама 70%. Плотность мела 2710 кг/м3.
Решение. Чтобы определить диаметр отстойника, надо
вычислить необходимую площадь осаждения по формуле (3.9),
для чего предварительно находят скорость осаждения:
w „_gjPr-Pc)g__ 3,5M0-" (2710-1000) 9,81
°С " ЩГо 18-1,14-10-3 = °'001 м'с'
где fAc= 1,14-Ю-3 Па-с (тябл. VI).
Проверим значение критерия Re:
Re = ^сФс. = ыо-'-у -ш-моз = 0)0307 < 0>2>
Действительная скорость осаждения:
woc = 0,5-0,001 =0,5. Ю-8 м/с.
Площадь отстойника:
, -Ч'-g-) м-№('-ж) 325м,
ЗбООр^ 3600-103.0,5.10-3 -<W> м'
Диаметр отстойника:
?> = V 32,5/0,785 = 6,4 м.
Пример 3.9. Определить высоту отстойника (см. рис. 3.2), если
известно, что для уплотнения суспензии в зоне' сгущения
необходимо 16 ч. Относительная плотность твердой фазы 2,6. Среднее
разбавление в зоне сгущения Т : Ж = 1 : 1,5. Диаметр отстой-
пика 10 м. Суточная производительность отстойника 24,2 т
твердой фазы. Жидкая фаза — вода.
113
Решение. Находим относительную плотность суспензии
в зоне сгущения по формуле (3.26), разделив ее на р:
Дтв(л + 1) _ 2,6(1,5 + 1) _10о
Лс~ Дтвп + 1 ~~ 2,6-1,5+1 ~l'aZf
где п— Ж : Т= 1,5.
Массовая концентрация суспензии в зоне сгущения:
1 Л . кг твердой фазы
х = , , , , «0,4
1+1,5 кг суспензии
Таким образом, 1 м3 сгущенной суспензии содержит твердой
фазы:
Т = 1320-0,4 = 630 кг.
По условию задачи, в течение суток на 1 м2 осаждается твердой
фазы:
24 2
_gJ_ = 0,308T/(M».cyTKH).
Следовательно, в зоне сгущения за 16 ч пройдет 0,308 -щ =
= 0,205 т твердой фазы на 1 ма площади осаждения.
Выше было найдено, что суспензия в зоне сгущения содержит
0,530 т твердой фазы на 1 м3; поэтому высота этой зоны:
h2 = 0,205/0,530 = 0,387 м.
Высота зоны питания принимается 0,45—0,75 м. Для
разбавленной суспензии (Т : Ж ~ 1 : 10) можно принять ее равной
hx = 0,6 м.
Высота зоны отстойника, в которой вращаются гребки, зависит
от наклона лопастей к дну отстойника. Примем ее равной 0,146 и
на 1 м радиуса отстойника. Следовательно,
/i3 = 0,146.5 = 0,73 м.
Таким образом, общая высота отстойника:
Н = hx + h2 + /i3 = 0,6 + 0,387 + 0,73 = 1,717 м ^ 1,72 м.
Пример 3.10. Рассчитать циклон для выделения частиц сухого
материала из воздуха, выходящего из распылительной сушилки,
по следующим данным: наименьший размер частиц 80 мкм, расход
воздуха 2000 кг/ч, температура 100 °С.
Решение. Для улавливания частиц материала размером
80 мкм выбираем циклон типа ЦН-15.
Принимая А/7/рР = 740, диаметр циклона найдем по формуле
v_
t7H5wa'
114
°-v*
предварительно определив условную скорость газа в
цилиндрической части циклона шц из уравнения, &р/рг = ?0ш*/2, где ?0 —
= 160 (стр. 97):
wn = V740-2/160 = 3,04 м/с.
Плотность воздуха: рр = 1,293 (273/373) =» 0,95 кг/м3.
Следовательно,
., l/ 2000 ллаг
° = V 0,95.3600-0,785.3,04 ° °Л% М'
Принимаем диаметр циклона равным 0,5 м.
Гидравлическое сопротивление циклона:
Apu = t0(pX)/2=160(0,95.3,042)/2 = 703 Па, т. е. 72 мм вод. ст.
Фильтрование
Пример 3.11. Вывести формулу (3.16), дающую зависимость
между массой сухого осадка на 1 м3 фильтрата, плотностью
фильтрата, концентрацией суспензии и влажностью осадка.
Решение. Уравнение материального баланса процесса
фильтрования:
"СУСП === ^ф ~Г ^ЕЛ- ОС»
где Gcycn> Сф и Gjijj, ос — масса суспензии, фильтрата и влажного осадка,
соответственно.
Разделим это уравнение на Gcyx— массу сухого вещества,
содержащегося в суспензии:
^суса ^ф , ^вл. ос
G "О +~G ' (364)
ucyx ucyx ucyx
Массу фильтрата заменим произведением объема фильтрата
на его плотность:
Введем обозначения:
__ ^вл. ос Кг влажного осадка
"~ ^сух кг сухого вещества '
__ ^сух кг сухого вещества #
^сусп кг суспензии '
— ,^с>* кг сухого вещества
™~ Уф м3 фильтрата
Тогда уравнение (3.64) можно переписать так:
X С
115
откуда
с,—. 1
1 —тх
Пример 3.12* Определить продолжительность фильтрования
10 дм3 жидкости через 1 м2 фильтра, если при предварительном
испытании фильтра с 1 м2 было собрано фильтрата; 1 дм3 через
2,25 мин и 3 дм3 через 14,5 мин после начала фильтрования.
Решение. По опытным данным находим
экспериментальные константы К и С в уравнении фильтрования:
V2 + 2VC = /Ст.
Для этого составляем два уравнения с двумя неизвестными:
I2 + 2-Ь С = #-2,25; З2 + 2-3-С = /С-ИД
откуда К — 0,77 дмб/(м4-мин) и С = 0,37 дм3/м2.
Для определения искомой продолжительности фильтрования
полученные значения констант и заданный объем фильтрата
подставляем в уравнение фильтрования:
102 +2-10.0,37 = 0,77т,
откуда с — 140 мин или 2 ч 20 мии.
Пример 3,13. В условиях предыдущего примера определить
длительность промывки осадка, если количество промывной воды
составляет 2,4 дм3/м2 и промывка идет по линии основного
фильтрата.
Решение. Пренебрегая различием в динамических
коэффициентах вязкости фильтрата и промывной воды, будем считать,
что скорость промывки равна скорости фильтрования в конечный
момент.
Скорость фильтрования в конечный момент определим по
уравнению (3.14) с использованием данных предыдущего примера:
dV К 0,77
dx 2(V +C) 2(10 + 0,37)
Продолжительность промывки:
= 0,037 дм3/(м2-мин).
Тпп — их! i j \ == л ъгъ~ = "О МИН.
пр (dV/dx)np 0,037
Пример 3.14. Во время опытного фильтрования водной
суспензии с содержанием 13,9% карбоната кальция при 20 °С на
лабораторном фильтрпрессе с F = 0,1 м2 и толщиной осадка 50 мм
были получены данные, приведенные в табл, 3.2,
Определить константы фильтрования: К (в м2/ч) и С (в м3/м2).
Решение, Численные значения констант фильтрования
найдем из уравнения (3.13):
У2 + 2VC = Кт.
116
При избыточном давлении
Па
кгс/см2
Собрано
фильтрата, дм''
Таблица 3.2
Время от начала
опыта,
3,43-104
10,3.10*
0,35
1,05
2,92
7,80
2,45
9,80
146
888
50
660
При избыточном давлении 3,43-10* Па (0,35 кгс/см2)
результаты опытов дают:
Vi
2,92
1000-0,1
2,92.10-2 м3/м3; Tj =--
146
3600
= 0,0405 ч;
П =
7,8
1000-0,1
7,8*10"2 м3/м2;
12 = 1600 = °'246 Ч'
Подставляем пересчитанные величины в уравнение (3.13)
и решаем систему уравнений:
(2,92 • 10"8)2 + 2 • 2,92.10~2С « К • 0,0405;
(7,8-10"3)2 + 2-7,8.10'2С = #-0,246,
откуда К = 278-Ю-4 м2/ч; С = 4,7-КГ8 м3/м2.
Аналогичным образом вычисляем константы К и С для
избыточного давления 10,3-10* Па (1,05 кгс/см2). Получаем следующие
значения констант фильтрования: К — 560• 10~4 м2/ч; С ~ 3,78 X
X Ю-3 м3/м2.
Пример 3.15. В условиях предыдущего примера рассчитать
удельное сопроти вление осадка карбоната кальция.
Дополнительно известно, что влажность осадка при /?а = 3,43* 104 Па
(0,35 кгс/см2) равнялась 37%, а при р2 = 10,3-10* Па
(1,05 кгс/см2) — 32% от массы влажного осадка.
Решение. Удельное сопротивление осадка рассчитываем
по формуле (3.18).
Давление фильтрования Ар = рх = 3,43-10* Па.
Плотность фильтрата р = 1000 кг/м3.
Динамический коэффициент вязкости фильтрата при 20 °С:
ц = з^о 10~3 ^ 27,8'10"8 кг/(м'ч>*
Константа фильтрования (при давлении рг = 3,43-10* Па) К =
= 278 10~4 м2/ч.
Массовая доля твердой фазы в суспензии х = 0,139.
117
Массовое отношение влажного осадка к сухому т =
- 1/(1—0,37) - 1,59.
Количество фильтрата на 1 кг суспензии 1 — тх = 1 —
~ 1,59-0,139 - 0,779.
Найденные величины подставляем в формулу (3.18):
_2Ар(1 — тх) 2-3,43-104 -0,779
Т K\ipx ~ 278.10~4.27(8-10-«.1000-0,139 ~*
« 5- 10м .
кг сухого осадка
При давлении фильтрования 10,3-10* Па, т. е. 1,05 кгс/см2,
имеем:
К-560.10"4 м2/ч; m = _L-_«ll47;
1 — mx = 1 — 1,47.0,139 = 0,795.
Остальные величины имеют те же значения, что и при рх =
= 3,43-10* Па, т. е. 0,35 кгс/см2.
Новое удельное сопротивление осадка можно найти путем
подстановки численных значений этих величин в формулу (3.18)
или из соотношения:
r2 ApzKi{l —mx)t _ 10,3-104-278- 1Q-*.0,795
П AptKzll—mx)^ 3,43.104-560-10"*-0,779 =1>52>
откуда
г2= 5-1010-1,52 = 7,6-1010 м/кг сухого осадка.
Следовательно, при увеличении давления фильтрования
в 3 раза удельное сопротивление осадка карбоната кальция
увеличилось лишь на 52%.
Пример 3,16. Чему равно удельное сопротивление ткани при
фильтровании суспензии карбоната кальция в условиях
примеров 3.14 и 3.15?
Решение. Удельное сопротивление ткани (в м/м2)
вычисляем по формуле (3.21):
гтк — Сгрх/(] — тх).
При рг = 3,43-104 Па, т. е. 0,35 кгс/см2:
гтк = 4,7-10"3- 5- Ю10-1000-0,139/0,779 = 4,2.1010 м/м2.
При р2 = 10,3-104 Па, т. е. 1,05 кгс/см2:
гтк = 3,78. Ю-з.7,6- K)io. 1000*0,139/0,795 = 5- 10й м/м3.
При изменении давления в 3 раза удельное сопротивление
ткани изменилось лишь на 19%.
Пример 3.17. Необходимо отфильтровать суспензию на
рамном фильтрпрессе и за 3 ч получить 6 м3 фильтрата. Опытное
118
фильтрование этой суспензии на лабораторном фильтрпрессе
при том же давлении и той же толщине слоя осадка показало,
что константы фильтрования, отнесенные к 1 ма площади фильтра,
имеют следующие значения: К = 20,7*10'* м2/ч и С~ 1,45 X
X 10~3 м3/м2. Определить требуемые размеры фильтрпресса.
Решение. Находим по уравнению фильтрования (3.13)
производительность 1 м2 фильтрпресса:
V1 + 2.0,145- 10~2К = 2QJ-lO~*-3,
откуда
V = — 0,145-10-2+ ^ (0,145-10'2)2 + 62,1 -10~* =
= — 0,145- 10"2 + 7,88-КГ2 = 7,73-10~3 м3/м*
за цикл фильтрования, т. е. за 3 ч.
Следовательно, для заданной производительности необходима
поверхность фильтрования:
F = 6/0,0773 = 77,5 м2.
По каталогу выбираем ближайший больший фильтрпресс с/г==
== 83 м2, имеющий 42 рамы размером 1000 X 1000 мм.
Примечание. Поверхность фильтрования можно определить также
непосредственно нз уравнения (3.13), составленного для всего фильтра с поверхностью F
н производительностью Vf м3 фильтрата за цикл фильтрования,
VF + WFFC = KF2t;
б2 + 2-6-1,45- Ю-з/7 = 20J. 1<Г*.ЗЯ.
откуда F = 77,4 м2.
Пример 3.18.- На барабанный вакуум-фильтр непрерывного
действия (рис. ЗЛО) подается 8,5 м3/ч водной суспензии,
содержащей 17,6% твердой фазы. Желательная конечная влажность
осадка 34%. Предполагаемый вакуум на заводе 600 мм рт. ст.
Во время опытного фильтрования на лабораторной модели при
вакууме 510 мм. рт. ст. было установлено, что необходимая
влажность осадка достигается за
32 с работы зоны фильтрования.
При этом константы
фильтрования, отнесенные к 1 м2,
оказались равными: К =
= 11,2 дм6/(м4-с) и С =
= 6 дм3/м3. Плотность
суспензии 1120 кг/м3. Определить
требуемую поверхность
фильтра и частоту его вращения.
Решение. Пересчитаем
константу фильтрования/С для
Рис. 3.10 (к примеру 3.18),
119
вакуума 600 мм рт. ст., принимая приближенно, что К
пропорционально А/? *:
К!К' «600/510 = 1,17,
откуда
К= 11,2-1,17 « 13,1 дмв/(м*.с).
Определяем удельную производительность зоны фильтрования
из уравнения (3.13), приняв время фильтрования % = 32 с (по
заданию):
V2 + 2VC = Kvt V2 + 2V-6 = 13,1 -32;
V = — 6 + /36 + 420 = — 6 + 21,4 = 15,4 дм3/м2 за 32 с.
Следовательно, удельная производительность зоны
фильтрования в 1 с: 15,4/32 = 0,482 дмУ(ма-с).
Пересчитываем заданную производительность по суспензии
на производительность по фильтрату.
При влажности осадка 34% массовое соотношение влажного
и сухого осадка:
т= 1/(1— 0,34)= 1,52.
Массовая доля твердой фазы в суспензии х = 0,176; расход
суспензии Gc = Ксрс = 8,5-1120= 9500 кг/ч; масса влажного
осадка Goc = Gcxm = 9500-0,176-1,52 = 2540 кг/ч; масса
фильтрата Сф = Gc — Goc == 9500 — 2540 = 6960 кг/ч. При плотности
фильтрата р = 1000 кг/м3 объемный расход фильтрата составляет
6960 дм3/ч.
Таким образом, заданная производительность по фильтрату:
6960/3600= 1,93 дм3/с.
Следовательно, необходимая поверхность в зоне фильтрования:
/^=1,93/0,482=4,0 м2.
Так как обычно в барабанных вакуум-фильтрах поверхность
зоны фильтрования составляет ~35% от общей поверхности, то
общая поверхность фильтра:
F = 4,0/0,35= 11,43 м2.
По каталогу подбираем ближайший тип барабанного вакуум-
фильтра с F = 12 м2. Диаметр фильтра/) = 2,1 м, длина фильтра
L = 1,8 м.
Частота вращения фильтра в 1 мин, необходимая для
обеспечения заданного времени фильтрования т = 32 с, определится
из пропорции
32 — 0,35
60— л,
* На самом деле это не совсем так — см. пример 3.14»
120
откуда
п = 60*0,35/32 = 0,655 об/мин.
Пример 3.19. Сколько времени необходимо отмывать осадок
на фильтрпрессе от NaCl, чтобы достигнуть концентрации 5 г/дм3,
допустимой в иромывной воде? Промывка ведется чистой водой.
Интенсивность промывки 0,33 м3/(м2«ч). Толщина слоя осадка
35 мм. Константа промывки К = 520 см^дм3* В начальный
момент промывки концентрация NaCl в промывной воде 143 г/дм8.
Решение. Воспользуемся уравнением (3.23), подставив
в него заданные величины в соответствующих единицах измерения:
б = 0,035 м; w = 0,33 м3/(м2-ч); К = 520-0,001 м3/м3. Тогда*
* = 5202o'oofo,33 <* 1«_1вБ)- 0,683 ч _ 41 мин.
Пример 3.20. В условиях предыдущего примера рассчитать
концентрацию NaCl в промывной воде через 50 мин после начала
основного периода промывки.
Решение. Концентрацию соли в промывной воде найдем
по формуле (3.22):
520.0,001.0,33-50
С2 - изГ °'035,60 = 143е-4'08*
Логарифмируя это выражение, получаем:
lg С2 = lg 143 ~4х " 2'156""!>75 в °'406-
Следовательно, С2 = 2,53 г/дм3.
Центрифугирование
Пример 3.21. Определить технологический тип и наметить
конструкцию центрифуги для отделения поташа от маточного
раствора, исходя из того, что концентрация твердого вещества в
суспензии составляет 75%; для осадка (кристаллического) требуемая
остаточная влажность 3%; промывка осуществляется водой,
отбелка — паром; как маточный раствор, так и осадок имеют
щелочную реакцию.
Процесс разделения следует механизировать, так как
центрифуга должна обеспечить большую производительность.
Решение. Для разделения системы жидкость — твердое
тело в случае грубых суспензий пригодны центрифуги
технологического типа 1-а.
Согласно заданию, процесс должен быть механизирован. Этому
заданию отвечают центрифуги полунепрерывного (класс Б) и
непрерывного (класс В) действия. Учитывая необходимость
промывки осадка водой и отбелки паром, останавливаемся на
центрифугах полунепрерывного действия. Механизация процесса может
быть обеспечена путем автоматизации управления. К классу Б
121
относятся две конструктивные группы центрифуг: горизонтальные
и вертикальные. Из числа центрифуг полунепрерывного действия
получили наибольшее распространение горизонтальные
центрифуги, поэтому останавливаем свой выбор на центрифуге
горизонтального типа.
Пример ¦ 3,22. Центрифуга периодического действия имеет
барабан с внутренним диаметром 1200 мм, высотой 550 мм,
толщиной стенок 10 мм и массой 120 кг. Число отверстий в стенке
барабана по вертикали 12, диаметр отверстий 5 мм. На барабан
надеты три стальных обруча сечением 15 X 30 мм2 каждый.
Материал барабана — сталь с временным сопротивлением на разрыв
4500 кгс/см2. Масса загрузки 400 кг, толщина слоя 200 мм. Найти
предельно допустимую частоту вращения центрифуги, если запас
прочности не должен быть менее 5.
Решение. Для данной стали допускаемое напряжение на
разрыв:
Кг = 4500-9,81 -104/5 = 8,83-107 Па, или 900 кгс/см2.
Площадь сечения стенки барабана и обручей за вычетом
отверстий:
/ = 55.1 — 12-1.0,5 + 3.3.1,5 = 62,5 см- » 6,25-1 (Г3 м2.
Из формулы (3.40) следует, что максимально допустимая
центробежная сила:
С,+С2 = 8,83.10^.2.6,25.10-3= \y\.\w н.
Расстояние от центра тяжести полукольца стенки барабана
до оси вращения находим по формуле (3.40а):
4 / 0,61» — 0,6» \ г. ад_
*б "~ F3^4 W.6l»-0,6»; ™Мй7 и"
Центробежная сила, развиваемая половиной барабана,
согласно уравнению (3.28):
d = 0,011 -60-0,387/г3 « 0,253n2 H.
Расстояние от центра тяжести полукольца загрузки до оси
вращения:
Центробежная сила, развиваемая полукольцом загрузки:
С2 = 0,011.200-0,32wa = 0,697/г2 Н.
Общая центробежная сила:
С± + С% = 0,253п2 + 0,697л2 = 0,950n2 H.
Выше было найдено, что центробежная сила не должна
превышать 1,110е Н. Следовательно, максимально допустимая
частота вращения центрифуги:
п = /1,1.108/0,950 = 1070 об/мин = 17,8 об/с.
122
Пример 3.23, Определить часовую производительность (по
питанию) автоматической осадительной центрифуги АОГ-800 при
работе ее на водной суспензии гидроксида магния. Плотность
частиц р = 2525 кг/м3. Температура суспензии 30 °С.
Наименьший диаметр частиц 3 мкм. Характеристика центрифуги:
диаметр барабана 800 мм; длина барабана 400 мм; диаметр борта
570 мм; частота вращения 1200 об/мин. Цикл работы центрифуги
составляет 20 мин; из них 18 мин — подача суспензии, 2 мин —
разгрузка осадка.
Решение. Производительность определяем по формуле
(3.42):
Скорость осаждения частиц находим по формуле Стокса:
w ^(P-Pc)g ^ 3» (2525 - 1000) 9,81 0935.10- ,e
ос" 18мо Ю12-18-0,8. Ю-з - "&° ш м'с'
Динамический коэффициент вязкости воды при 30 °С ис =
= 0,8-10"3 Па-с.
Определяем скорость осаждения под действием центробежной
силы:
Яо"2 лпог ,л-5 0,285-12002 . _ft 1Л_3 /
ш==Шос ~Ш~== °'935*10 900 = 4,26.10 3 м/с.
Проверяем режим осаждения:
wd9o _ 4,26-lQ-»-3-lQ-«-10» , ш_2
т. е. режим ламинарный.
Далее находим:
?= 18/20 = 0,9.
Производительность центрифуги, принимая ц = 0,45;
V, = 25,3-0,45-0,4-12002.0,2852-0,935-10~5.0,9 = 4,46 м3/ч.
Пример 3.24. Определить, какую производительность может
обеспечить трубчатая сверхцентрифуга СГО-150 с трехлопастной
крыльчаткой, работающая на осветлении минерального масла.
Плотность масла рс = 900 кг/м3. Динамический коэффициент
вязкости масла при температуре центрифугирования 3-10-3 Па с.
Плотность твердых частиц р = 1400 кг/м3. Диаметр частиц 1 мкм.
Техническая характеристика центрифуги: внутренний диаметр
барабана 150 мм, диаметр сливного порога 50 мм, длина барабана
750 мм, частота вращения 13 000 об/мин.
Решение. Производительность определяем по формуле
(3.43).
123
Так как частицы очень малы, то режим осаждения их будет,
вероятно, ламинарным. Воспользуемся формулой Стокса G
последующей проверкой режима осаждения:
<*2(Р — 9с) g I2 (1400 —900)9,81 ЛЛС 1Л.Й ,
Woc= Wc - 10^-18.3.10-3 ^.06-Ю »м/а.
Скорость осаждения под действием центробежной силы:
w = wocf = 9,06-10-8.4700 = 4,26-10"4 м/с.
Здесь
/ = n*RQ/900 = 132-106.0,025/900 = 4700.
Проверяем режим осаждения:
^ wdpc 4,26-1.900 __ 1,42
цс 104- 10в-3-10"3 104 *
Найдем полезный объем барабана центрифуги:
Vx = FL = 0,785 (D2 — D2) L = 0,785 (0,152 — 0,052) 0,75 = 0,0118 м*.
Глубина потока в барабане:
й=О-^=А15-0Д)5_=0)05м_
Тогда
V ^ Л!%* 3600 = 4-^°'°А18 3600 = 0,368 м»/ч.
п 10*-0,05
Проверяем режим потока в барабане центрифуги:
Do — Wn0T d99 •
Кепот — »
И*
*"« = T = w-0,0157 e°'0067 M/c; V = 1600"= Тог м3/с;
F = 0,785 (D2 — D2) = 0,785 (0,152 — 0,052) = 0,0157 м2.
Для центрифуги с трехлопастной крыльчаткой:
_ F _ 4л (Р« - Pg) _ л (Ра - Pg) 3,14(0,15^ — 0,05^) ЛЛО|С „.
3 П " 4(nP + 6ft) ~ nD + 6A - 3,14.0,15 + 6-0,05 -u>uolJM»
RenoT=0'00673°ff:5-900-164<350,
т. е. режим ламинарный.
Пример 3.25. Выбрать тип фильтрующего аппарата для геля
кремниевой кислоты и определить необходимое число аппаратов
на основании следующих данных: 1) начальная концентрация
твердой фазы в суспензии 4,7 %, относительная плотность
суспензии 1,1; 2) суточное задание 9 т влажного осадка; 3) осадок должен
иметь наименьшую влажность, так как в дальнейшем идет на
сушку (в вакуум-сушилку); 4) осадок аморфный, плохо
фильтрующийся.
124
Характеристика
Площадь фильтрования, ма
Толщина слоя осадка, мм
Продолжительность:
фильтрования
промывки щелочью и водой
общая
Профильтровано суспензии, дм^
Остаточная влажность осадка, %
Вакуум, мм рт. ст.
Таблица 3.3
Отсосный
фильтр
Центрифуга
1
60
1 ч
2 ч
3 ч
170
85
400
0,3
30
45 мин
33 мин
1,3 ч
108
78
__
Предварительные опыты фильтрования геля на отсосном
фильтре (нутч-фильтре) и на центрифуге дали результаты,
приведенные в табл. 3.3.
Барабан центрифуги имел D — 400 мм, Н = 250 мм, п =
= 800 об/мин.
Решение. 1. Определение давления фильтрования.
Отсосный фильтр
Ар = 400/760 = 0,525 кгс/см2 = 5.15.104 Па.
Центрифуга
При коэффициенте заполнения барабана центрифуги во время
ее работы <р = 0,5 имеем объем суспензии (рабочий объем
барабана):
Vc = 0,785D2//(p = 0,785.0,42-0,25-0,5 = 0,0157 м3.
Давление фильтрования при центрифугировании определяем
по формуле (3.29):
яШ/?я2 0tQUMRn* 0,011-0,0157-ПОО.0,2-8002
Ар
900F
F 0,3
= 8,Ы04 Па, или 0,83 кгс/см2.
Следовательно, давление при центрифугировании было в
полтора раза больше, чем при фильтровании на отсосном фильтре.
2. Определение удельной производительности.
Отсосный фильтр
Профильтровано 170 дм3 суспензии с начальной
концентрацией 4,7 %, т. е. собрано геля, считая на сухое вещество:
0 = 0,170.1100.0,047 = 8,8 кг.
Продолжительность всей операции 3 ч (без учета времени на
разгрузку), следовательно, удельная производительность:
_— = ' = 2,94 кг сухого геля/(м2-ч).
Считая на влажный гель (при влажности 85 %):
2,94/0,15 = 19,5 влажного геля/(м2-ч).
125
Центрифуга
Профильтровано 108 дм3 суспензии, следовательно, получено
осадка, считая на сухое вещество:
G = 0,108.1100-0,047 = 5,54 кг.
Соответственно, удельная производительность:
G 5 54
-р~- =лЛ х = 14,3 кг сухого геля/(м2-ч).
Считая на влажный гель (при влажности 78%):
14,3/0,22 = 65 кг влажного геля/(м2«ч).
3. Сопоставим, насколько больше надо удалить воды при сушке
влажного геля после отсосного фильтра по сравнению с гелем,
отжатым на центрифуге
Влажность осадка на отсосном фильтре 85%, а на центрифуге
78%, следовательно, центрифуга удаляет воды больше, чем
отсосный фильтр, на 2120 кг;
1000 1000 кг воды
0,15 0,22 кг сухого геля"
Сопоставляя опытные и расчетные данные по фильтрованию
геля, можно констатировать следующее.
Центрифуга, работая с давлением фильтрования в 0,83/0,525 =
= 1,6 раза большим и при толщине слоя осадка в 2 раза меньшей,
чем в случае отсосного фильтра, дает производительность
в 14,3/2,94 ^ 5 раз большую, чем отсосный фильтр (считая на
сухой гель; в пересчете на влажный осадок производительность
центрифуги больше в 65/19,5 = 3,3 раза).
Центрифуга, по сравнению с отсосным фильтром, дает
меньшую остаточную влажность и тем самым облегчает работу
сушилки, освобождая ее от испарения 2,12 т воды (считая на 1 т
сухого геля).
При суточной производительности 9 т геля с влажностью 78%
и удельном расходе пара на сушку, равном 1,5 кг/кг испаренной
влаги, экономия пара за сутки составит:
/>п = 9.0,22.2,12-1,5 = 6,3 т.
Большая удельная производительность центрифуги, меньшая
остаточная влажность осадка и, следовательно, существенная
экономия пара при сушке геля заставляют в данном случае отдать
предпочтение центрифуге, несмотря на ее более высокую
стоимость.
4. Определим ориентировочно число промышленных
центрифуг, необходимых для выполнения суточного задания (9 т
влажного геля).
При таком сравнительно большом задании целесообразно
остановиться на центрифуге полунепрерывного действия с
механической выгрузкой осадка и автоматическим управлением. По ката-
126
логу выбираем горизонтальную центрифугу со следующей
характеристикой: D = 1600 мм, Н = 700 мм, п — 500 об/мин, полезный
объем 500 дм8.
Поверхность фильтрования этой центрифуги:
F = 3,14-1,6-0,7 = 3,5 м2.
Развиваемое давление фильтрования по формуле (3.29):
Др = 0,011-0,5.1100*0,8.5002/3,5 = 34,6.104 Па, или 3,5 кгс/см2,
Таким образом, промышленная центрифуга развивает
давление фильтрования в 3,5/0,83 = 4 раза больше, чем опытная.
Ориентировочно производительность фильтров
пропорциональна ]/A/?, следовательно, можно ожидать увеличения удельной
производительности центрифуги почти в 2 раза, т. е. до 65*2 —
— 130 кг влажного геля/(м2-ч).
Так как фильтрование и промывка осадка занимают около 75%
общего времени работы центрифуги полунепрерывного действия,
то средняя часовая производительность ее равна 130-0,75 —
- 97 кг/(м2-ч).
Следовательно, суточная производительность одной
центрифуги, принимая для нее 20 рабочих часов в сутки, составит 97 X
х 3,5-20 = 6800 кг влажного осадка.
Для обеспечения всей заданной суточной производительности
необходимо установить 9000/6800 — 1,32, т. е. две центрифуги,
а с резервом — три.
Взвешенный слой
Пример 3.26. В аппарате имеется взвешенный слой силика-
геля, ситовой состав которого следующий:
Фракция, мм —2,0+1,5 —1,5+1,0 —1,0+0,5 —0,5+0,25
Содержание, 43 28 17 12
% (масс.)
Насыпная плотность силикагеля рнас — 650 кг/м3, плотность
частиц р = 1100 кг/м3. Температура воздуха 150 °С. Число
псевдоожижения Kw = 1,6.
Определить критическую, рабочую и действительную (в
свободном сечении между частицами) скорость воздуха.
Решение. Подсчитываем величину критерия Аг и по
рис. 3.8 находим соответствующее значение LyKp.
С этой целью определяем эквивалентный диаметр частиц
силикагеля.
Среднеситовые диаметры фракций:
, 2,0+ 1,5 , тс , 1,5+ 1,0 , ос
dx — ^—-—= 1,75 мм; d2 — —¦—^ = 1,25 мм;
1,0 + 0,5 л__ А 0,5 + 0,25 л,_
dz = i = 0,75 мм; d& — ——~ — 0,37 мм.
127
Тогда эквивалентный диаметр по формуле (3.51):
*Э Д "У^Т = "О^З 0,28 0,17 0,12^1>0ММ'
La dt 1,75 + 1,25 + 0,75 + 0,37
Динамический коэффициент вязкости воздуха при 150 °С (см,
рис. VI): \i = 0,024-10-^ Па-с.
Плотность воздуха:
27Я
Р= 1>Ш273+150==: °>т Кг/м3'
Следовательно,
а
3
РРС? lMO-M.LlO3-0,835.9,81
АГ = ^= "'" ММОпГ— -1.566.10».
Значению Аг = 1,565-104 соответствует LyKp = 3-10-2.
Отсюда
w
кр
^-.зАУкрИоре _ з/^З. 10-^.0,024. Ю-з. 1,1.103.9,81 _
~ J/ ^2 J/ р35^ ™и""* М/С'
Определяем рабочую скорость воздуха:
ш = К^оУкр = 1,6-0,224 = 0,358 м/с.
Найдем порозность взвешенного слоя. При Kw = 1,6:
Ly = /C*,LyKp = 1,63-3.10"2= 1,23-10-*.
По^рис. 3.8 приЬу= 1,23.10-1иАг= 1,565-10* имеем е = 0,47.
Действительная скорость воздуха в свободном сечении слоя:
оуд = w/в = 0,358/0,47 = 0,762 м/с.
Пример 3.27. По данным предыдущего примера определить
размеры и гидравлическое сопротивление аппарата.
Производительность 2,5 т/ч силикагеля при среднем времени пребывания его
в аппарате т0 = Ю мин. Расход воздуха в рабочих условиях
4300 м3/ч. Живое сечение решетки 0,015, диаметр отверстий 0,8 мм,
толщина решетки 2 мм.
Решение. Определяем диаметр аппарата. Секундный
расход воздуха;
V = 4300/3600 =1,195 мз/с.
Площадь сечения аппарата:
S = V/w = 1,195/0,358 = 3,34 м2*
Диаметр аппарата:
D = j/TS/л == J/4.3,34/3,14 = 2,06 м.
Определяем высоту слоя в аппарате. Масса силикагеля в
аппарате;
М = Ltu = 2500-10/60 = 417 кг.
128
Объем неподвижного слоя силикагеля:
У с « М/Рнас = 417/650 = 0,642 м3.
Высота неподвижного слоя:
hQ = Vc/S = 0,642/3,34 = 0,192 м.
Порозность неподвижного слоя:
во * 1 — (Рнас/Р) = 1 — (650/1100) = 0,41.
Высота взвешенного слоя при Kw = 1,6:
Рассчитаем гидравлическое сопротивление аппарата.
Сопротивление слоя:
АРсл = р (1 — е0) gft0 = 1100 (1 — 0,41) 9,81 -0,192 = 1200 Па.
Скорость воздуха в отверстиях решетки при живом сечении
Ф = 0,015:
w0 = оу/ф = 0,358/0,015 = 23,9 м/с.
Диаметр отверстий решетки d0 «= 0,0008 м, толщина решетки
6 = 0,002 м. При d0/6 = 0,4 по рис. 3.7 находим С = 0,63.
Сопротивление решетки:
ЛРреш = 0>503-23,92.0,835 (I — 0,0152)/0,632 == 605 Па.
Сопротивление аппарата:
Ар = Арсл + Арреш = 1200 + 605= 1805 Па, т. е. 184 мм вод. ст.
Пример 3.28. Определить диаметр шарообразных частиц
кварцевого песка плотностью 2640 кг/м8*, которые начнут переходить
во взвешенное состояние при скорости потока воздуха 1 м/с и
температуре 20 °С.
Решение. Диаметр шарообразных частиц песка определяем
из критерия Аг, предварительно найдя значение критерия LyKp:
Lv <рр' 1М>2052 зп
Р" Hi? ~ 0,018.9,81-2640-10~3
где рс = 1,293 (273/293) = 1,205 кг/м3; \ic = 0,018-10"3 Па-с.
Значению LyKp = 3,14 соответствует, по рис. 3.8, Аг — 9-Ю5.
Искомый диаметр частиц песка:
d= \/ = 1/ —п,лл , nrtr , П1——0,0021 м=2,1 мм.
У PPcff ' 2640-1,205-9,81
Пример 3.29. Во взвешенном слое содержится 1000 кг твердого
материала; расход материала через слой (скорость ввода и вывода
частиц) составляет 4000 кг/ч. Определить: 1) какая доля частиц
будет находиться в слое в течение времени, большего чем среднее
расходное время пребывания материала в слое; 2) сколько таких
взвешенных слоев необходимо соединить последовательно, чтобы
5 Павлов К. Ф. и др, 129
доля частиц, находящихся в аппарате в течение времени,
меньшего чем среднее расходное время пребывания материала в одном
слое, не превышала 10%.
Р е ш е н и е. Вычисляем среднее расходное время
пребывания материала в одном слое. При М = 1000 кг, L = 4000 кг/ч
т0 = M/L = 1000/4000 = V« ч = 900 с.
Определяем долю материала, находящегося в одном
взвешенном слое в течение времени т ^ т0:
хх = е~т/т° в е-9оо/9оо _ е-\ в ош
Таким образом, только 37 % материала находится в слое
больше 15 мин, и, следовательно, для материала, находящегося
в слое, менее 15 мин, составит:
1 —xx = 0,63, т. е. 63%.
Для того чтобы найти число взвешенных слоев, которые должны
быть соединены последовательно, определим по формуле (3.59)
для аппарата с двумя, тремя и т. д. слоями долю материала, время
пребывания которой в слоях меньше т0.
а) Для двухслойного аппарата:
* - ( 1 + i) е~^ - (I +|?) *-9~ - ^ -W " °.™:
1 ~х2 = 0,264.
Следовательно, в аппарате с двумя последовательно
соединенными взвешенными слоями 26% материала будет находиться
в слоях меньше 15 мин.
б) Для трехслойного аппарата:
'>=['+i+i(i)'k'"-
-['+w+i(S)!)]<-*ww=i^-^
J — Яд = 0,08-
Таким образом, в аппарате с тремя слоями только 8% мате
риала будет находиться в слоях менее 15 мин. Следовательно,
трехслойный аппарат удовлетворяет требуемым условиям.
Среднее расходное время пребывания материала в трехслойном
аппарате составит:
тср = 3M/L «= 3000/4000 =* 3/4 ч ^ 45 мин.
Сравним этот трехслойный аппарат с таким однослойным,
в котором количество материала в слое такое же, как и во всех
слоях трехслойного (3000 кг). Среднее расходное время
пребывания твердого материала в таком однослойном аппарате также
составит:
тср = 3000/4000 = 3/4 ч = 45 мин.
130
Рис. 3.11.. (к примеру 3.30).
Но доля материала, находящегося в
слое менее 15 мин, будет уже больше:
1 _е-т/т0 = 1 —е-15/45 = 0,285, т. е. 28,5 %.
Отсюда видно преимущество
секционированного (трехслойного) аппарата.
Перемешивание в жидкой среде
Пример 3.30. Смесь кислот
(плотность 1600 кг/м3, динамический
коэффициент вязкости 2-10~2Па-с)
приготовляют в аппарате без перегородок
(диаметр 1200 мм, высота 1500 мм), заполненном на 0,75 объема.
Исходные кислоты перемешивают пропеллерной мешалкой с
частотой вращения 3,5 об/с (рис. 3.11). Определить требуемую
установочную мощность электродвигателя.
Решение. Находим диаметр нормализованной мешалки:
rf = D/3 = 1,2/3 = 0,4 м.
Определяем режим перемешивания по формуле (3.60):
Reu =
pnd2 1600-3,5-0,42
= 44 800.
\х 20-10"3
Режим — турбулентный.
Определяем значение критерия мощности по графику (рис. VII)*.
KN = 0,27.
Рассчитываем мощность, потребляемую мешалкой при
установившемся режиме, по уравнению (3.61):
iVp = KNpriMb = 0,27-1600-3,5».0,45 = 200 Вт = 0,2 кВт.
Мощность в пусковой момент обычно в 2—3 раза превышает
рабочую:
^пуск = 2Л^р=:0,4 кВт.
Определяем установочную мощность, принимая к. п. д.
электродвигателя с передачей 0,95 и запас мощности в 20%:
Л\-Сг = 0,4-1,2/0,95 я^0,5 кВт.
Пример 3.31. Электродвигатель мощностью 16,5 кВт с
приводом, понижающим частоту вращения до 240 об/мин, приводит
в действие открытую турбинную мешалку с шестью лопатками;
мешалка интенсивно размешивает реакционную массу (р ==
= 1200 кг/м3, \х = 1,6 Па-с) в сосуде диаметром 1630 мм с
перегородками. Какой должен быть диаметр мешалки?
Решение. Поскольку обусловлено интенсивное
перемешивание, можно считать режим развитым турбулентным. По рис. VH
находим: KN = 6,9.
5* 131
м.
По формуле (3.61):
d~V К^-У 6,9.1,2.103-43 -У*Ш 10 -0'5
Проверим отношение Did:
D/d= 1,63/0,5 = 3,26.
Пример 3.32. Теоретический анализ и результаты опытов
показывают, что мощность, затрачиваемая на перемешивание жидкости
(N), зависит от динамического коэффициента вязкости (|я) и
плотности (р) жидкости, ускорения свободного падения (g), частоты
вращения мешалки (п), ее диаметра (dM) и других геометрических
характеристик (диаметра аппарата, высоты заполнения его
жидкостью, высоты размещения мешалки над дном сосуда). Требуется
найти общий вид критериальной зависимости, связывающей
перечисленные переменные.
Решение. Для геометрически подобных систем
функциональная зависимость между переменными записывается так:
N =/ (ц, р, g, л, dM). (a)
В соответствии с л-теоремой искомая критериальная
зависимость должна иметь вид
ф (Ль Л2, Л3) = 0 ИЛИ Л! = / (Л2, Л3),
где ль л2, л3 — неизвестные пока безразмерные выражения (критерии подобия).
Предполагая, как обычно, что связь, существующую между
переменными, в некотором диапазоне изменения переменных с
достаточной точностью можно описать уравнением типа степенного
одночлена, перепишем исходную зависимость (а) так:
№ = Cln]a\p]blg]e{n]eldu]f. (б)
Далее, подставляя единицы измерения соответствующих
величин, получим уравнение связи основных единиц:
Сопоставляя затем показатели степени у одноименных единиц
измерения, придем к системе из трех уравнений, содержащей пять
неизвестных:
а + 2с + е = 3; (г)
а + 3& —с —/ = —2. J
Полученную неопределенную систему уравнений (г) можно
решить относительно трех любых величин, принимая две
остальные величины заданными. Общее число вариантов решений
определяется числом сочетаний, которые могут быть составлены из
всех неизвестных, входящих в систему, по числу выбираемых
заданными, т. е. в данном случае числом сочетаний из пяти по два:
5-4
1-2
кг-м2 1
= С
Cg = ^-=10.
132
Такими сочетаниями будут:
ab, ас, ае, aft
be, be, bf,
се, cf,
ef.
Элементарный анализ системы уравнений (г) позволяет
установить, что при выборе заданными величин а и Ъ решить систему
невозможно * и, таким образом, число вариантов решений
уменьшается до девяти.
Решим систему уравнений (г), считая заданными величины а
и с (показатели степени у \х и g)
6=1 — а; е = 3 — а — 2с; f = 5 — 2а — с.
Перепишем уравнение (б), используя найденные значения Ь,
е и /:
Группируя величины с одинаковыми буквенными
показателями, получим:
P/zVm \ \Х } \ g )
или
т. е. получим систему безразмерных переменных, в которой только
по одному разу и каждая только в один какой-то критерий входят
физические характеристики \х и g.
Таким же путем, принимая заданными
b не, получим: KN Reu = С Ref( ?т~с\
а не, . /<^Fr3=C2Ga-aFreu;
b не, , /<^ReuFru = CGa^2Frf;
с*е, . /^Re^CGa'Re*;
.2 \а
Re7
«¦Л , KNVr{=C[^p\Fv{y
bHft . KNRenFrl^cl^)bFr{9
Fr^
с и /,
^Re'=c2(ff)CRe-
в и Л . K3N К Fru = С3 (|^-)в Ga'.
* Следует подчеркнуть, что невозможность решения системы (г) при выборе
заданными величин а и b не случайна, а отражает физическую особенность
реальных жидкостей — вязкость и плотность являются свойствами, которые
независимо изменять нельзя.
133
1_J
Рис. 3.12 (к примеру 3.33).
Таким образом, для описания процесса
TJ-3' |'с— перемешивания жидкости можно использо-
/ • \. вать девять принципиально совершенно
р равноценных, но различных по форме крите-
J т риалъных уравнений.
Различие уравнений обусловливается
теми физическими величинами,
характеризующими изучаемое явление (в данном случае
двумя величинами), которые входят в
определяющие критерии только по одному разу
и каждая только в один какой-то критерий.
Все уравнения легко могут быть преобразованы одно в другое,
поскольку численные значения показателей степени определяются
уравнениями связи.
Выбор того или иного критериального уравнения определяется
обычно либо стремлением использовать традиционные формы
обобщенных переменных (в данном случае критерии Рейнольдса и
Фруда), либо удобством обработки экспериментальных данных.
Численные значения коэффициента С и показателей степени могут
быть определены только опытным путем.
Пример 3.33. В реакторе (рис. 3.12) диаметром 1000 мм,
заполненном на высоту 1000 мм реакционной массой, имеющей при
температуре ведения процесса \х == 150-10"3 Па*с и рс ~ 1200 кг/м3,
необходимо обеспечить равномерное распределение твердых частиц
катализатора с наибольшим размером 1,3 мм и плотностью
2450 кг/м3; Т : Ж = I : 4.
Какую мешалку целесообразнее использовать —
пропеллерную трехлопастную (рис. 3.13, а) с шаговым отношением 1 или
турбинную (рис. 3.13, б) закрытого типа с восемью
лопастями?
Решение. 1. Определяем диаметр нормализованной
мешалки:
1М
(0,25 ~ 0,3) D = (0,25 ~~ 0,3) 1 = 0,3 м.
2. Для нахождения требуемых значений критерия Иец и
величины определяющей частоты вращения воспользуемся
обобщенным уравнением:
Reu « С Ga*S'Г?П.
В этом уравнении:
Для пропеллерной мешалки
» турбинной » . .
т
0,105 0,6 0,8 0,4 1,9
0,25 0,57 0,37 0,33 1,16
134
а
Рис. 3.13 (к примерам 3.33 и 3.34).
г&гчислием значения критериев и симплексов подобия:
/3„?
Ga =
_ duPc2 33.К)-*-i,28-i0«-9tfr
F
1,5*. 10"8
-.1,7-10»;
Sp-
p4 2,45-103
p0 ~~ i,2.jo» -04;
rd
4
lM
1,3.10'3
= 3-10-x "4'33-10->;
z?
1,0
^"^"TIP""3'33'
Найденные величины критериев и симплексов подобия лежат
в пределах приложимости уравнения.
Находим значения критерия ReQ и определяющей частоты
вращения для пропеллерной мешалки:
Нец-0(105Са0'650р'8Г0^9 « 1,05.10-Ч,70'б.104'2.2,040'8 X
X 4,33м • Ю^'^З.ЗЗ'^^^.юЗ.
и 4,5Ь 10». 1,5-10*1
Рой
м
1,2-J03-3a-I0~3* 6|^6 об/с = 376 об/мин.
135
Находим значения критерия Reu и определяющей частоты
вращения для турбинной мешалки:
Re„ = 0,25Ga0'57SO-37ro.33ri.i5==2)6.10^.b7o.57.103,99.2)04o137 х
X 4,330,33-10"0,99.3,331,15 = 2,85.103;
п0 = Reu -L = 2;82'|оз'.змо°аХ = 3>96 o6/G = 238 об/мии-
3. Определяем мощность, затрачиваемую непосредственно на
перемешивание.
Из графика KN = f (Re) [2] находим для пропеллерной
мешалки: Kn ~ 0,32; для турбинной мешалки: Kn ~ 1>3.
Вычисляем постоянный множитель:
Мощность, потребляемая пропеллерной мешалкой:
N « K^ngPcd5M = 3,2-КГ1 -6,263-2,91 = 227 Вт « 0,23 кВт.
Мощность, потребляемая турбинной мешалкой:
N » Ка^3Рс4 — 1.3-3.963-2,91 =234 Вт ж 0,23 кВт.
Так как в данном случае мощность, затрачиваемая на
перемешивание, одинакова, выбираем турбинную мешалку, работающую
при меньшей частоте вращения.
Пример 3.34. Опыты по окислению сульфида аммония в
тиосульфат кислородом, проведенные в модельном аппарате
диаметром 500 мм с четырьмя отражательными перегородками,
показали, что при перемешивании закрытой турбинной мешалкой
диаметром 125 мм, с частотой вращения 6 об/с и при удельном расходе
кислорода ии = 3,5-10"? м^ 02/(м3-с) обеспечивается поглощение
1,04 дм3 кислорода на 1 м3 реакционной среды в 1 с — удельная
производительность ku = 1,04-10"3 м3 02/(м3-с).
На основании результатов модельных опытов проектируется
промышленный аппарат диаметром 2 м с мешалкой диаметром
0,5 м, геометрически подобный модельному (rD = Did = 4).
Необходимо рассчитать частоту вращения мешалки в
промышленном аппарате, при которой будет обеспечена такая же удельная
производительность, как и в модельных условиях. Расход
кислорода в промышленном аппарате ип — 3,6*10"3 м3 02/(м3-с);
физические свойства реакционной среды в модельном и в
промышленном аппаратах близки к свойствам воды. Температура реакции
80 °С.
Решение. Для расчета промышленных аппаратов, в
которых ReQ ^ 1,8 *105, можно воспользоваться уравнением:
D1 = С Re°'09 Fr°u'165K°/5r?0'167 , (a)
где Di = kin — критерий Дьяконова; Ки " и/п — критерий распределения.
136
Если при переходе от модели к промышленному аппарату
свойства реагирующих фаз не изменяются, уравнение (а) приводится
к виду:
л0,67^1,015^0,75
А = С* ^67 *
Вычисляем значение критерия Рейнольдса (центробежного)
для модельного аппарата:
_ pndl _ 972.6-0,125*
Кец--у - 3,56-10-* -2'bb ° > ,Ь Ш'
Таким образом, результаты опытов могут быть использованы
для моделирования.
По опытам на модели определяем коэффициент Сх для
рассматриваемого процесса:
k D°'Q7 1 (\л 1Л—3 лс0,67
г Дм м 1,04-10 -0,5 . й
*°и'67 К)м01Ч*75 в^^.олгб^^Чз^.ю-3)0'75 ~ * '
Подставив в уравнение характеристики промышленного
аппарата и найденное значение Си рассчитаем частоту вращения
мешалки:
пп =
An*#e7 \°'67 / 1,04.Ю-3.2°.^ \0'67
с\ (^м)п'°15"п75 / V 1.15-КГ1-0,51-016(3,5-1(Г3)0'75
^= 2,85 об/с.
Принимаем скорость вращения мешалки па = 3 об/с.
Проверяем значение критерия Рейнольдса для промышленного
аппарата:
972-3.0,5* _2QiW
К ц 3,56-10-* *
Поскольку значение критерия Рейнольдса для промышленного
аппарата также лежит в пределах приложимости уравнения (а),
выбранная частота вращения обеспечит заданную
производительность.
КОНТРОЛЬНЫЕ ЗАДАЧИ
3.1. Найти соотношение диаметров частиц свинцового блеска
(р — 7800 кг/м3) и кварца (р = 2600 кг/м3), осаждающихся с
одинаковой скоростью: а) в воздухе; б) в воде, считая, что осаждение
происходит при Re < 0,2.
137
3.2. С какой скоростью будут осаждаться шарообразные
частицы кварца (р = 2600 кг/м3) диаметром 10 мкм; а) в воде при
15 °С; б) в воздухе при 15 и 500 °С?
3.3. Какой должна быть скорость воздуха в вертикальной
трубе пневматической сушилки, чтобы обеспечить перемещение
кристаллов плотностью 2000 кг/м3 с наибольшим диаметром 3 мм?
Температура воздуха 60 °С. Скорость воздуха должна быть на
25% больше скорости витания частиц.
3.4. Рассчитать скорость восходящего потока воздуха в
воздушном сепараторе, необходимую для отделения мелких (d <
< 1 мм) частиц апатита от более крупных. Температура воздуха
20 °С. Плотность апатита 3230 кг/м3.
3.5. Каким должно быть расстояние между полками пылевой
камеры (см. рис. 3.9), чтобы в ней оседали частицы колчеданной
пыли диаметром более 15 мкм? Остальные условия такие же, как
в примере 3.6.
3.6. Через пылевую камеру (см. рис. 3.9) с расстоянием между
полками 100 мм проходят 2000 м3/ч запыленного газа плотностью
1,6 кг/м3 (расход и плотность даны при нормальных условиях).
Температура газа 400 °С. Динамический коэффициент вязкости
газа при этой температуре 0,03• 10"^ Па*с. Плотность пыли
3700 кг/м3. Длина камеры 4,55 м, ширина 1,71 м, высота 4 м.
Какого размера частицы пыли будут улавливаться в камере, если
считать, что действительная скорость осаждения вдвое меньше
теоретической?
3.7. Доказать идентичность формул (3.9) и (3.10) для расчета
площади отстойника непрерывного действия.
3.8. Определить диаметр отстойника (см. рис. 3.2) для
непрерывного уплотнения водной суспензии мела, имеющей
температуру 35 °С. Остальные условия такие же, как в примере 3.8.
3.9. Как изменится производительность отстойника, если
температуру водной суспензии повысить с 15 до 50 °С? В обоих
случаях Re < 0,2.
3.10. Подобрать циклон типа НИИОГАЗ (см. рис. 3.3 и
табл. 3.1) по следующим данным: расход запыленного воздуха
5100 м3/ч (0 °С и 760 мм рт. ст.), температура воздуха 50 °С.
Плотность пыли 1200 кг/м3. Частицы пыли имеют наименьший диаметр
15 мкм. Определить также гидравлическое сопротивление
циклона.
3.11. Вывести формулу (3.25), исходя из условия, что объем
суспензии равен сумме объемов жидкой и твердой фаз.
3.12. Рассчитать плотность водкой суспензии, содержащей
10% (масс.) твердой фазы. Относительная плотность твердой фазы
равна 3.
3.13. Определить скорость осаждения в воде при 25 °С
продолговатых частиц угля (р == 1400 кг/м3) и пластинчатых частиц
сланца (р = 2200 кг/м3), имеющих эквивалентный диаметр
2 мм.
138
3.14. Определить диаметр частиц свинцового блеска угловатой
формы, осаждающихся со скоростью 0,25 м/с в воде при
температуре 15 °С. Плотность свинцового блеска 7500 кг/м3.
3.15. Какое количество влажного осадка будет собрано на
фильтре в результате фильтрования 10 м3 суспензии
относительного удельного веса 1,12, содержащей 20% (масс.) твердой фазы?
Влажность осадка 25%.
3.16. В результате фильтрования водной суспензии с
содержанием 20% (масс.) твердой фазы собрано 15 м3 фильтрата.
Влажность осадка 30%. Сколько получено осадка, считая на сухое
вещество?
3.17. Фильтрпресс имеет 26 рам размером 62x62 см. Толщина
рам 25 мм. Время фильтрования до заполнения рам 2 ч. Промывка
ведется водой в количестве 10% от объема фильтрата. Давление
во время фильтрования и промывки одинаково и постоянно.
Сколько времени требуется на промывку? Осадок однородный
несжимаемый, объем его составляет 5% от объема фильтрата.
Расчет вести по уравнению (3.13), полагая С = 0.
3.18. Время фильтрования 20 м3 раствора на рамном фильтр-
прессе 2,5 ч. Найти ориентировочное время промывки осадка 2 м8
воды, полагая приближенно, что скорость промывки в 4 раза
меньше скорости фильтрования в конечный момент.
Сопротивлением ткани пренебречь. Динамические коэффициенты вязкости
фильтрата и промывной воды одинаковы.
3.19. Как изменится время промывки осадка в условиях
предыдущей задачи, если \л фильтрата 1,5-10~8 Па-с, а промывной
воды 1 • 10~3 Па*с.
3.20. Найти теоретическое время промывки осадка на фильтре
при следующих условиях: интенсивность промывки 6 дм8/(м2*мин);
толщина лепешки 30 мм; начальная концентрация отмываемой
соли в фильтрате промывной воды 120 г/дм8, конечная — 2 г/дм3.
Константа скорости промывки /(, по опытным данным, равняется
350 см3/дм3.
3.21. Определить константу скорости промывки К при
следующих условиях: интенсивность промывки 10 дм3/(м2-мин);
толщина лепешки 25 мм; начальная концентрация соли в фильтрате
промывной воды 40 г/дм3, конечная — 0,5 г/дм3; время промывки
1 ч 40 мин.
3.22. Как изменится производительность фильтра, если:
1) вдвое увеличить фильтрующую поверхность; 2) вдвое увеличить
давление (при однородном несжимаемом осадке); 3) вдвое
увеличив концентрацию твердого вещества в фильтруемой суспензии;
4) вдвое уменьшить (повышая температуру) 'вязкость фильтрата;
5) вдвое увеличить время полного оборота фильтра (т. е.
увеличить толщину слоя осадка)?
3.23. Показать ориентировочно, как влияет изменение частоты
вращения барабанного вакуум-фильтра (см. рис. 3.10) на его про-
139
изводительность (например, при увеличении частоты вращения на
50 %). Воспользоваться уравнением (3.13), полагая С = 0.
3.24. Определить технологический тип и наметить
конструкцию центрифуги для отделения n-нитроанилина от раствора после
перекристаллизации, учитывая следующие данные: 1)
концентрация твердого вещества в суспензии 35%; 2) растворитель —
вода; 3) осадок кристаллический; 4) требуемая остаточная
влажность 5%; 5) кристаллизация идет периодически.
3.25. Требуется выделить хлопковое масло из промывных вод
(соапстока) после щелочной очистки. Определить технологический
тип и наметить конструкцию центрифуги, учитывая следующие
данные: 1) характер смеси — эмульсия; 2) относительная
плотность масла 0,9; 3) относительная плотность водного раствора
соли (добавленной для разрушения эмульсии) 1,05.
3.26. Определить удельное давление на стенки барабана
центрифуги, если толщина слоя жидкости, 10 см, внутренний диаметр
барабана 1 м, частота вращения 500 об/мин. Плотность жидкости
1100 кг/м3.
3.27. Найти частоту вращения центрифуги, если известно, что
высота барабана Н — 0,5 м. Давление у стенок барабана должно
быть 5 кгс/см2 (~0,5 МПа). Загружено 400 кг суспензии.
3.28. Показать приближенно, что при допускаемом
напряжении на разрыв для стали Кг = 88,3-10е Па, т. е. 900 кгс/см2,
окружная скорость барабана центрифуги не должна превышать
60 м/с. Исходя из этого условия, определить наибольший
допустимый диаметр барабана: а) для фильтрующей центрифуги,
делающей 1100 об/мин; б) для трубчатой сверхцентрифуги, делающей
14 000 об/мин.
3.29. Вывести формулу, по которой можно вычислить скорость
центрифугирования твердых шарообразных частиц, исходя из
закона Стокса. Частота вращения измеряется в об/с.
3.30. Во сколько раз быстрее произойдет осаждение одних и
тех же частиц в центрифуге, чем в отстойнике, если барабан
центрифуги имеет D = 1 м и п = 600 об/мин? Режим осаждения
в обоих случаях ламинарный.
3.31. Определить приближенно, пренебрегая трением вала
в подшипниках и трением стенки барабана о воздух, время
разгона центрифуги, в которую загружено 300 кг влажной соли.
Внутренний диаметр барабана 1 м, его масса 200 кг. Рабочая частота
вращения 800 об/мин. Мощность электродвигателя 6 кВт, общий
к. п. д. агрегата 0,8. Высота барабана 780 мм, коэффициент
заполнения барабана 0,5.
3.32. В услъвиях предыдущей задачи найти требуемую
мощность электродвигателя (с учетом трения), если период разгона
центрифуги принять равным 2,5 мин. Диаметр вала 70 мм;
подшипники — шариковые; толщина стенки барабана 10 мм.
3.33. Определить необходимое число центрифуг
периодического действия с размерами барабана D= 1200 мм, Н = 500 мм
140
для фильтрования 50 т суспензии в сутки. Суспензия содержит
40% (масс.) твердой фазы. Относительная плотность жидкой фазы
1,1, твердой— 1,8. Продолжительность одной операции 25 мин.
Число рабочих часов в сутках принять равным 20. Коэффициент
заполнения барабана 0,5.
3.34. Как изменится производительность фильтрующей
центрифуги, если увеличить частоту ее вращения вдвое? Осадок
однородный несжимаемый. Сопротивлением фильтрующей ткани
пренебречь.
3.35. Отстойная горизонтальная автоматическая центрифуга
АОГ-1800 должна работать на водной суспензии мела.
Определить производительность центрифуги по питанию, если
температура суспензии 40 °С. Размер наименьших частиц мела 2 мкм.
Техническая характеристика центрифуги: диаметр барабана
1800 мм, длина барабана 700 мм, диаметр борта 1300 мм, частота
вращения п = 735 об/мин; к. п. д. принять равным 0,45.
3.36. Во сколько раз производительность промышленной
фильтрующей центрифуги типа АГ больше производительности
лабораторной модели, геометрически ей подобной? Размеры
промышленной центрифуги больше размеров лабораторной в три раза.
Работа ведется на одной и той же суспензии, с одинаковой частотой
вращения и при одинаковом времени заполнения барабана осадком.
3.37. Определить производительность шнековой осадительной
центрифуги НОГШ-600, работающей на водной суспензии гипса
при температуре 50 °С. Наименьшие частицы гипса в суспензии
имеют диаметр 2 мкм. Техническая характеристика центрифуги:
диаметр сливного цилиндра 480 мм; длина зоны осаждения 350 мм;
частота вращения барабана п = 1400 об/мин.
3.38. Осаждение частиц какого диаметра обеспечит
центрифуга НОГШ-230, если на разделение подавать 3 м3/ч водной
суспензии каолина при 35 °С? Техническая характеристика центрифуги:
диаметр сливного цилиндра 180 мм; длина его 164 мм; частота
вращения барабана 1600 об/мин.
3.39. Определить скорость воздуха, необходимую для начала
образования взвешенного слоя частиц гранулированного алюмо-
силикагеля при следующих условиях: температура воздуха 100 СС;
плотность алюмосиликагеля (кажущаяся) р = 968 кг/м3; диаметр
частиц 1,2 мм. Каково будет гидравлическое сопротивление, если
высота неподвижного слоя 400 мм?
3.40. В условиях предыдущей задачи определить порозность и
высоту взвешенного слоя, если скорость воздуха превышает
критическую в 1,7 раза.
3.41. Определить наибольший диаметр гранулированных
частиц угля, начинающих переходить во взвешенное состояние в
воздухе при скорости его в аппарате 0,2 м/с. Температура 180 РС.
Определить также объемную концентрацию частиц, если скорость
воздуха повысится до 0,4 м/с. Плотность угля (кажущаяся)
660 кг/м3.
141
8.42. Бак диаметром 900 мм и высотой 1100 мм, снабженный
мешалкой, заполнен на 3/4 цилиндровым маслом (р = 930 кг/м3,
[д. = 18 Па-с). Какой мощности надо установить электродвигатель
для трехлопастной пропеллерной мешалки с частотой вращения
180 об/мин?
3.43. Для получения разбавленного раствора минеральная
соль интенсивно размешивается с водой при 64 °С посредством
лопастной мешалки. Какова частота вращения мешалки, если
диаметр ее 0,5 м, а мощность, потребляемая электродвигателем,
0,8 кВт? Физические характеристики для разбавленного раствора
принять такие же, как и для воды.
3.44. Лопастная мешалка размером^ =-О/З заменена на
меньшую с d2 = D/4. Размешивание в обоих случаях производится
в условиях ламинарного режима. Как изменится частота вращения
мешалки при той же мощности электродвигателя?
3.45. Каков должен быть диаметр пропеллерной мешалки для
интенсивного перемешивания технического глицерина (р =
= 1200 кг/м3, \х = 1,6 Па-с) в баке диаметром 1750 мм при л =
= 500 об/мин и расходе мощности 17 кВт?
ПРИМЕР РАСЧЕТА БАТАРЕЙНОГО ЦИКЛОНА [3.1]
В батарейном циклоне (рнс. 3.14) требуется очищать от пылн 7800 м3/ч газа
при температуре 310 °С. Плотность газа (при 0 ^С н 760 мм рт. ст.) 1,3 кг/м3.
Барометрическое давление 99 300 Па {745 мм рт. ст.). На входе в батарейный
циклов газ находится под разрежением 294 Па (30 мм вод. стЛ. Гидравлическое
сопротивление батарейного циклона не должно превышать 392 Па (40 мм вод. ст.).
Плотность пыли 2450 кг/м8. Запыленность газа 32 г/м3 (при 0 °С н 760 мм -рт. ст.).
Пыль слабо слипающаяся.
Решение. Характеристики циклонных элементов типа БЦ с розеточ-
ным направляющим аппаратом в случае улавливания слабо слипающейся ныли
с плотностью 2300 кг/м3 при Др/р = 736 м2/с2 (или Ар/у = 75 м) приведены
в табл. 3.4. На основании даииых этой таблицы выбираем циклонные элементы
диаметром 150 мм (допускаемая запыленность газа до 35 г/м3).
Определим плотность газа при рабочих условиях;
273(745--^-)
Р-1-293 .(т + т)тт>'-<>-**«/*¦
По условию потеря давления Ар не должна превышать 392 Па (40 мм вод. ст).
Соотношение Дэ/р = 392/0,595 = G00 мг/са (или Ар/у = 40/0,595 = 67,2 м)
не выходит нз рекомендуемых пределов 540—736 м2/с2 (или 55—75 м).
Таблица 3.4
Диаметр
элемента мм
Наибольшая
допускаемая
запыленность
газа, г/м3 (прн
ОХ и 760 мм рт.
от.)
Степень улавливания
пылн (в %) при диаметре
частиц
5 мкм
10 мкм
15 мкм
Коэффициент
гидравлического
сопротивления
to при угле наклона
лопастей
25°
30е
250 75 72 84 93
150 35 78 88 95 90 65
100 15 82 91 96
142
Рис. 3.14. Батарейный циклон.
Для направляющего аппарата типа розетки с
углом наклона лопастей к горнзонтали 25°
коэффициент гидравлического сопротивления ?0 = 90.
Скорость газа в цнлнндрнческой части
циклонного элемента шд определяем из формулы (ЗЛ2):
—УЪ-У
392-2
90-0,595
= 3,84 м/с.
Расход газа на один элемент батарейного
циклона:
Уг = 0,785О2-3600шд = 0,785-0,1502-3600-3,84 «
= 244 м3/ч.
Требуемое чксло элементов:
п = 7800/244 = 32.
Располагаем их в четыре ряда по ходу газа
(восемь элементов в каждом ряду).
ПРИМЕР РАСЧЕТА ПЕННОГО
ГАЗОПРОМЫВАТЕЛЯ ДЛЯ ОЧИСТКИ ГАЗА
ОТ ПЫЛИ [3.9]
Определять основные размеры пенного
газопромывателя для очистки от пыли 50 000 м^/ч
газа при 80 °С. Запыленность газа на входе в
аппарат свх = 0,01 кг/м3 (при нормальных условиях),
степень очистки 0,99.
Решение. Поскольку скорость газа в
полном сеченни аппарата является основным
фактором, от которого завнсит хорошее пеиообразование
и, следовательно, эффективность очнстки, важно
правильно выбрать расчетную скорость. Верхннм
пределом допустимой скорости газа является такая
его скорость, при которой резко усиливается унос воды в виде брызг. По
экспериментальным данным в газопромывателях, имеющих слой пены высотой
30—100 мм, струйный прорыв газа, вызывающий разрушение пены я сильный
брызгоунос, начинается при скоростях газа в полном сечеиии аппарата (под
решеткой) от 2,7 до 3,5 м/с.
Чем выше слой пены на решетке и чем больше свободное сеченне решетки,
тем большая скорость газа возможна без брызгоуноса. Уменьшение диаметра
отверстнй (при сохранении постоянного свободного сечения решетки) также
способствует уменьшению брызгоуноса. Обычно верхннм пределом является
скорость газа под решеткой ~3 м/с.
Нижним пределом скорости газа для пенного аппарата являе ся такая
скорость, при которой сильно уменьшается пеиообразование.
Для пениых газопромывателей с большим свободным сечеиием решетки и
большим диаметром отверстий ннжним пределом является такая скорость газа,
при которой большая часть жидкости протекает через отверстия, в результате
чего высота пены становится ннчтожно малой. Для обычных условий нижним
пределом расчетной скорости можно считать 1 м/с.
Примем среднюю скорость газа w — 2,3 м/с. Определяем площадь
поперечного сечения аппарата:
/= 50000 бы-
Лыль
143
а Газ
Рис. 3.15. Пенный газопромыватель.
* Утечка
Газопромыватель может быть круглого или
прямоугольного сечения. В круглом аппарате
обеспечивается более равномерный поток газа, в
прямоугольном — лучшее распределение
жидкости.
Примем аппарат прямоугольного сечения
размером 3X2 м с подачей воды посередине
(рис. 3.15). Для лучшего распределения газа по
площади аппарата ввод газа осуществляется
Слив через диффузор.
Расчет количества подаваемой воды
проводится различно, в зависимости от
температуры поступающего газа. Для холодного газа
наибольшее влияние на расход воды оказывают
гидродинамические факторы, для горячего газа
расход воды определяется тепловым
балансом.
При очистке от пыли газов, имеющих температуру ниже 100 °С, расчет
количества подаваемой воды проводят, исходя из гидродинамики процесса и
материального баланса газоочистки. В обычных условиях для сохранения достаточной
равномерности ценообразования по всей решетке необходимо, чтобы через
отверстия протекало не больше 50 % подаваемой воды, так как слишком сильная
утечка создает неравномерность высоты слоя воды на решетке.
Расход воды в газопромывателе складывается нз расхода воды, идущей
в утечку, н расхода воды, идущей на слив с решетки.
Испарением воды при заданной температуре газа можно пренебречь.
Количество воды, протекающей через отверстия решетки, определяется
массой уловленной пыли и заданным составом суспензии, а затем подбирается
решетка с таким свободным сечением, диаметром отверстии и прочими данными,
чтобы обеспечить установленную утечку.
При заданной степени очистки ц концентрация пылн в газе после
газопромывателя свых определяется по формуле *:
Свых=^вх(1~ Л) = 0>01 (1—0,99) = 0,0001 кг/м3.
Количество улавливаемой пыли:
Сул =*= М<?вх--<W) == 50 000
273
273 + 80
(0,01 —0,0001) =363 кг/ч.
Если известна концентрация суспензии с = Т : Ж (в кг/кг), то утечка Lyt
т. е. объем воды, необходимый для образования суспензии (в м3/ч), определяется
по уравнению:
*- юоос '
где К — коэффициент распределения пыли между утечкой и сливной водой,
выраженный отношением количества пыли, попадающей в утечку, к общему
количеству уловленной пыли; обычно К = 0,6-~0,8,
Концентрация суспензии, как правило, находится в пределах отношения
Т : Ж = (I : 5) -i- (1 : 10). Получение суспензии с Т : Ж> 1 : 5 может вызвать
забивание отверстий решетки (особенно мелких). Получение суспензии с Т : Ж <j
< 1 : 10 нерационально ввиду ее слишком больших объемов.
*
Концентрация пылн свых отнесена к объему газа перед аппаратом К0,
приведенному к нормальным условиям. Она незначительно отличается от
запыленности газа (в кг/м3) после аппарата, так как количество газа после аппарата
увеличивается на 1—2 % за счет испарения воды в газопромывателе.
144
Примем с= 1 : 8 = 0,125 кг/кг и К — 0,7. Тогда
0,7-383 ol. а/
L^ 1000-0,125 ^2'Им/ч
на всю решетку или
2,14/6 = 0,36 м3/(м2-ч)
на 1 м2 решетки.
Вследствие трудности определения параметров решетки по заданной утечке,
а также учитывая частичное испарение воды после ее протекания через решетку,
возьмем коэффициент запаса ~1,5, т.е. примем /,у = 1,5-2,14 «3,3 м3/ч,
или 0,55 м3/ м2-ч).
Количество сливной воды определяется по формуле:
где i — интенсивность потока на сливе с решетки, м3/'м-ч); Ь — ширина решетки
перед сливом, равная длине сливного порога, м.
Принимая i— 1 м3/(М'Ч), находим для выбранного типа аппарата (слив на
обе стороны):
1сл = 1.2-2 = 4 мз/ч.
Общий расход воды:
L = 3,3 + 4 = 7,3 м3/ч.
Удельный расход воды:
?уд = 7300/50 000 = 0,146 дм3/м3 газа.
Утечка составляет от общего расхода воды L:
Ly = (3,3/7,3) 100 = 45 %,
что приемлемо (должно быть L ^ 2Ly).
Основные характеристики решетки (диаметр и шаг отверстий) подбирают,
исходя нз необходимой утечки.
Установлено, что утечка воды возрастает с увеличением диаметра отверстий
do и высоты исходного слоя * жидкости на решетке hQ,
Утечка сильно возрастает при уменьшении скорости газа в отверстиях ниже
4—6 м/с (в зависимости от dQ н hQ) и резко снижается при увеличении скорости
газа выше 13—15 м/с, что может вызвать забивание решетки пылью. Кроме того,
повышение скорости газа в отверстиях при небольшом слое воды (пены) на
решетке, характерном для газопромывателей, приводит к струйному прорыву газа
и сильному брызгообразованию.
Для обеспечения нормальной работы газопромывателя скорость газа w0
в крупных отверстиях решеток следует выбирать в пределах 8—13 м/с, а для
решеток с более мелкими отверстиями в пределах 7—10 м/с, в зависимости от
исходной запыленности газа, возможных колебаний газовой нагрузки и других
условий.
Учитывая значительную концентрацию пылн в газе (10 г/м3 при нормальных
условиях) и относительно большую легкость изготовления решеток с крупными
отверстиями (меньше отверстий и легче сверловка их), устанавливаем решетку
с крупными отверстиями, для которых рекомендуются расчетные скорости газа
8—13 м/с. Считая, что колебания в нагрузке аппарата по газу будут
происходить, в основном, в сторону снижения (обычные условия), выбираем скорость
газа w0 = 12 м/с.
Тогда отношение площади свободного сечения решетки /0 к площади сечеиня
аппарата f составит:
Ulf = w/(wQz) « 2,3/(12- 0,95) = 0,2,
* Исходным слоем называется высота слоя невспеиениой жидкости, идущей
на образование слоя пены данной высоты.
145
Рис. 3.16. Размещение отверстий на решетке.
т i
где г = 0,95— коэффициент, учитывающий, что 5 %
площади свободного сечения занимают опоры решетки,
? переливные стенки и т. д.
Г При разбивке отверстий решетки по
шестиугольнику с шапш t заштрихованная площадь на рнс. 3.16
равняется:
S = tx = t-2 V? - (*а/4) « 1,73*а.
На эту площадь приходится два отверстия
диаметром d0. Площадь отверстий;
S0 = 2-0,785d§ =l,57djj.
Как было найдено выше, отношение SjS должно составлять 0,2:
1,5748/(1,73/*) =0,2,
откуда
t « 1^1,57^8/(1,73.0,2).
При диаметре отверстий d$ — 5 мм:
t = ^"0,91-25/02 = 10,7 ^11 мм.
Высота порога егн сливе с решеткяг устанавливается нз расчета создания
слоя пены перед сливом высотой 60—100 мм (в зависимости от заданной степени
очистки).
Подсчитаем, какова должна быть высота слоя п^ны на решетке, чтобы
обеспечить заданную степень очистки г\ = 0,99.
Коэффициент скорости пылеулавливания
Кп = 2г|Ш/(2 — л) = 2.0,99-2,3/(2-0,99) = 4,5 м/с.
Связь между коэффициентом /Сп и высотой слоя пеиы Н при улавлнвании
гидрофильной пыли со средним размером частиц 15-—20 мкм выражается
эмпирической формулой:
Н=Кп— 1,9501+0,09 = 4,5— 1,95-2,3 + 0,09 = 0,1 м.
С другой стороны, для пылеуловителей
Н = 0,806в»°'?Л8'в,
где hQ — высота исходного слоя воды на решетке, м.
Отсюда
^ ™ V0,806^'V " \ 0,806*2,30'5 / - 0,°13 м"
Высота исходного слоя жидкости /i0 связана с ннтенсивностью потока на
сливе i н с высотой порога /in эмпирической зависимостью:
Ао = Ф Y& + 4%,
где ф — коэффициент, характеризующий водослив; для производственных
расчетов с достаточной точностью можно принять ф = 3; Ч*" — степень подпора
жидкости порогом, которая может значительно изменяться в зависимости от условий
пенообразовании; для рабочих условий газопромывателей Ф" ж 0,4.
Таким образом, высоту порога (в мм) можно рассчитать по формуле;
/1Д = 2,5/10 — 7,5^.
146
В нашем случае: w~ 2,3 м/с, i =* i м3/(м*ч). Тогда высота порога:
hn = 2,5-13 — 7,5^Т* = 25 мм.
Для обеспечения работы аппарата при колебаниях его режима примем
высоту порога 30 мм.
Общая высота газопромывателя складывается из высот отдельных частей
его: надрешеточной hlt подрешеточной h2 и бункера /15. Эти высоты определяются
конструктивное hx — в зависимости от брызгообразования и размеров брызго-
уловителя, /i2 — в зависимости от конструкции подвода газа, h§ — в зависимости
от свойств суспензии.
ПРИМЕР РАСЧЕТА БАРАБАННОГО ВАКУУМ-ФИЛЬТРА
Рассчитать барабанный вакуум-фильтр (см. рис, 3.10) производительностью
2,8 т/сутки сухого осадка гидрата закиси ннкеля по следующим данным: 1)
вакуум 53,3* 10^ Па (400 мм рт. ст.); 2) среднее удельное сопротивление осадка
г—43,21-1010 м/кг сухого осадка; 3) удельное сопротивление фильтрующей
ткани (диагональ) атк = 11,43-1010 м/м2; 4) масса твердого вещества,
отлагающегося на фильтре при получении 1 м3 фильтрата, с— 207,5 кг/м3; 5) заданная
толщина слоя осадка 6 = 5 мм *; 6) объем влажного осадка, получаемого при
прохождении через фильтр 1 м3 фильтрата, 0,680 мэ/м3; 7) плотность влажного
осадка 1220 кг/м3 (при влажности 75,2%), плотность фильтрата 1110 кг/м3;
8) общее число секций фильтра z = 24 (по аналогии с применяющимися барабан-
нымн фильтрами); 9) динамический коэффициент вязкости фильтрата (прн
температуре фильтрования 50 °С) (л = 1,5Ы0_3 Па-с; 10) время просушки осадка
на фильтре тс = 1,5 мин; 11) концентрация исходной суспензии 10,67%.
Решение. Расчет вакуум-фильтра сводится к определению необходимой
поверхности фильтрования и к подбору фильтра по каталогу.
Поверхность фильтрования F (в м2) можно определить из выражения:
где У0бщ — производительность фильтра по фильтрату, м3/ч; V —
производительность 1 м* фильтра по фильтрату, равная vn, м3/(м2-ч); v—
производительность 1 м2 фильтра за один оборот, м3/м'2; п — частота вращения фильтра, об/ч.
Определяем производительность фильтра по фильтрату.
Производительность фильтра по сухому осадку должна составить
2,8 т/сутки, или 117 кг/ч. В пересчете иа влажный осадок (влажность 75,2%)
это будет (117'110)/24,8= 472 кг/ч.
Количество суспензии, поступающей на фильтрование, при концентрации ее
10,67% составит (117* 100)/10,67 = 1096 кг/ч. Тогда выход фильтрата будет
равен 1096— 472= 624 кг/ч илн, при плотности фильтрата 1110 кг/м3, 624/1110==
= 0,56 м3/ч, т. е. 13,4 м3/сутки.
Таким образом, У0бщ = 0,56 ь^/ч.
Для определения V надо знать производительность I м2 фильтра за один
оборот, т. е. за время прохождения зоны фильтрования т, и частоту вращения
фильтра в 1 ч.
Известно, что объем влажного осадка, отлагающегося на фильтре при
прохождении 1 м3 фильтрата, равен 0,686 м3/м3. При заданной толщине слоя осадка
5 мм необходимая поверхность зоны фильтрования на 1 м3 фильтрата 0,686/0,005—
= 137,5 м2/м3. Очевидно, через поверхность зоны фильтрования в 1 м2 пройдет
объем фильтрата:
v = 1/137,5 = 0,00728 м8/ма.
* Такая толщина слоя объясняется аморфной структурой осадка; для
кристаллических оса,',ков толщина слоя обычно больше (15—20 мм)*
147
Для определения частоты вращения фильтра надо знать время
фильтрования т (время, за которое образуется осадок толщнной 5 мм), Для этого
воспользуемся основным уравнением фильтрования (3.13);
К* + 2VC = Кт,
где К= 7,28-10-3 м3/м2.
Константу К определим по уравнению (3.15):
2Ар 2-53300 л_ ,л л ,,
К -_ ?1 __ л 7<). Ю"в м2/с
л Исг 1,5Ы0-з.207,5.43,21-1010 -и'/у lu м/с'
где
Ар = 53 300 Па = 400 мм рт. ст.; ц = 1.5Ы0-3 Па-с;
с = 207,5 кг/м3; г = 43,21 • 1010 м/кг.
Константу С определим по уравнению (3.19):
гт„ _ 11,43-10» _
С-"7Г- 43,2Ы0».207,5 -1'28103 м 'м •
Тогда
7,282.10-в + 2-7,28. КГ*. 1,28. КГ» П1 , со
Для определения частоты вращения барабана необходимо найти угловую
скорость вращения фильтра по формуле:
360 — ф'
(О —
т + т0
где т = 1,52 мии — время фильтрования; т0 = 1,5 мнн — время подсушки
осадка; ф' — угол, занимаемый зоно:4. съема осадка и мертвой зоной [принимаем
его равным 1,23 рад, или 70° (на основании практических данных)]. Тогда
2л— 1,23 , й_
(о = ^-g2— = 1.67 рад/мин,
или
360 — 70 пй 0 ,
0) = ¦ тгцо = 96»2 град/мни.
Общая продолжительность рабочего цикла, или продолжительность одного
оборота барабана:
т0б = 2я/1,67 = 360/96,2 ъ 3,8 мин.
Частота вращения фильтра в 1 ч:
п = 60/3,8 =15,8 об/ч.
Время просушкн, съема осадка и пребывания в мертвых зонах!
тсуш = 3,8—1,52 = 2,28 мин.
Число секцнй, одновременно находящихся в зоне просушки, в зоне съема
осадка и в мертвых зонах:
г = 2,28-24/3,8 ж 14.
В зоне фнльтровання находится 10 секций (24—14),
Необходимая поверхность фильтра:
F = К°бщ = ^ = 4 86 м2
^й 0,00728.15,8 '°° м "
Принимаем вакуум-фильтр с поверхностью фнльтровання 5 м3,
148
Глава 4
ТЕПЛОПЕРЕДАЧА В ХИМИЧЕСКОЙ АППАРАТУРЕ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
Теплопроводность
1. Уравнение теплопроводности для установившегося
теплового потока через однослойную плоскую стенку:
,= «_ = jL=is. = _*L(/p_/x)l (4.1)
где q—удельный тепловой поток (удельная тепловая нагрузка), Вт/м2; Q —
тепловой поток (расход теплоты), Вт; F—площадь поверхности стенки, м8;
*г н ^к — температуры горячей н холодной поверхности стенки, К нли °С; г =
= Ь/к г— термнческое сопротивленне стенки, (м2«К)/Вт; 6 — толщина стенки, м;
к— коэффициент теплопроводности, Вт/(м-К).
Уравнение теплопроводности для установившегося теплового
потока через многослойную плоскую стенку:
(4-2)
/7 -
q —
Q tr — tx *г — 'х
F ~ Zr " «i + б* +...
xt k2
2. Для цилиндрической однослойной стенки средняя площадь
поверхности определяется по формуле:
FCP - iHtepL - " № "/> L , (4.3)
где di н d2 — внутренний и наружный диаметры; L — длина цилиндра, м. ¦
Уравнение теплопроводности для установившегося теплового
потока через однослойную цилиндрическую стенку:
Q = 4 </Р - /ж) Fcp « *b(tr-tjL 9 (4 4)
Здесь б = (rf2 — <*i)/2.
Если da/di < 2, то вместо вычисления по формуле (4.3) можно
с достаточной точностью принимать для средней площади
поверхности однослойной цилиндрической стенки величину
Fср = я (dj + йж) 1/2. (4.5)
Уравнение теплопроводности для установившегося теплового
потока через многослойную цилиндрическую стенку:
2nHtr-tx) 2nL(tr-tx)
> _. In " __ in —i- + T- In —- + • • •
Lj к dB ki dx k2 d2 '
Здесь dB н da — внутренний и наружный днаметры каждого
цилиндрического слоя,
149
3. При отсутствии экспериментальных данных коэффициент
теплопроводности жидкости Я [в Вт/(м-К) ] при температуре
~30 °С может быть рассчитан по формуле:
где с—удельная теплоемкость жидкости, Дж/(кг*К); р — плотность
жидкости, кг/м3; М — мольная масса жидкости, ;:г/кмоль; А — коэффициент,
зависящий от степени ассоциации жидкости, м3-кмоль"1',3-с~1.
Для ассоциированных жидкостей (например, воды) А —
= 3,58-10"8, для неассоциированных (например, бензола) А =
- 4,22-10"8.
Коэффициент теплопроводности жидкости при температуре t
определяется по формуле:
Я(=Я30[1-е(г-30)], (4.8)
где е — температурный коэффициент. Значения е*103 (в °С~1):
Анилин 1,4 Метиловый спирт . . 1,2 Хлорбензол . .
Ацетон 2,2 Нитробензол .... 1,0 Хлороформ . .
Беизол 1,8 Пропиловыи спирт . 1,4 Этилацетат . .
Гексан 2,0 Уксусная кислота . 1,2 Этиловый спирт
1,5
1,8
2,1
1,4
Коэффициент теплопроводности водного раствора при
температуре t определяется по формуле:
где Л.р и Яв — коэффициенты теплопроводности раствора и воды.
4. Коэффициент теплопроводности газа [в Вт/(м-К)1 при
невысоких давлениях может быть вычислен по формуле:
к=*Всф. (4.10)
Здесь ц — динамический коэффициент вязкости газа, Па*с; В = 0,25 X
X (9k — 5); k — cp/cD — показатель адиабаты; ср и с0 — удельная теплоемкость
газа при постоянном давлении и при постоянном объеме,
соответственно, Дж/(кг»К).
Так как для газов данной атомности отношение cp/cv есть
величина приблизительно постоянная, то для одноатомных газов В =
= 2,5, для двухатомных В = 1,9, для трехатомных В = 1,72.
Для расчета коэффициента теплопроводности смеси газов
правило аддитивности в общем случае неприменимо. Приближенный
расчет к смеси газов см. в примере 4.6.
Теплоотдача
5. В табл. 4.1 дан перечень основных случаев теплоотдачи и
соответствующих расчетных уравнений.
6. Основные критерии подобия, входящие в критериальные
уравнения конвективной теплоотдачи:
Критерий Нуссельта:
Nu = a//A. (4.11)
150
Таблица 4.1
Вид теплоотдачи
Номер
уравнения
A. Конвективная теплоотдача, не сопровождающаяся
изменением агрегатного состояния
/. Вынужденное движение
1. Течение в трубах и каналах:
а) развитое турбулентное течение
б) Re< 10 000
2. Поперечное обтекание пучков труб:
а) гладких
б) оребреиных
3. Течение вдоль плоской поверхности
4. Отекание жидкости пленкой по вертикальной поверхности
б. Перемешивание жидкостей мешалками
//. Свободное движение (естественная конвекция)
Б. Теплоотдача при изменении агрегатного состояния
1. Пленочная конденсация пара
2. Кипение жидкостей
B. Теплоотдача при тепловом излучении твердых тел
(4.17)—(4.22)
(4.23)—(4.28)
(4.29)-(4.35)
(4.36)—(4.37)
(4.38)—(4.40)
(4.41)—(4.44)
(4.45)
(4.4б)-(4.48)
(4.49)-
(4.60)-
(4.66)-
-(4.59)
(4.65)
(4.71)
Критерий Прандтля:
Pr = c\ifk = v/a.
Критерий Рейнольдса:
Re = wlp/ii = wl/\.
Критерий Галилея:
Ga = Rea/Fr = #/3ра/и2 = gl*/v\
Критерий Грасгофа:
Gr = Gap Д* =
va
рлл
Критерий Пекле:
Ре = RePr = wl/a = wlcp/k.
(4.12)
(4.13)
(4.14)
(4.15)
(4.16)
Эти критерии учитывают, соответственно, влияние физических
свойств теплоносителя и особенностей гидромеханики его
движения на интенсивность теплоотдачи.
Величины, входящие в выражения для критериев подобия, и
их единицы измерения приведены в табл. 4.2.
Физико-химические свойства жидкости (газа), входящие в
критериальные уравнения, необходимо брать при так называемой
определяющей температуре. Какая температура * принимается за
определяющую, указывается для каждого частного случая
теплоотдачи.
6. Приближенные значения критерия Рг для капельных
жидкостей можно определить по номограмме (рис. XIII). Для воды
значения критерия Рг даны в табл. XXXIX.
151
Таблица 4.2
Величина
Наименование
Единица
измерения
в СИ
а
а
р
V
Л/(ф)
g
г
At
W
Коэффициент теплоотдачи
Коэффициент объемного расширения
Коэффициент теплопроводности
Динамический коэффициент вязкости
Кинематический коэффициент вязкости
Плотность
Коэффициент температуропроводности
Удельная теплоемкость (при постоянном давлении)
Ускорение свободного падения
Определяющий геометрический размер (для
каждой формулы указывается, какой размер является
определяющим)
Теплота парообразования (испарения) удельная
Разность температур стенки и жидкости (или
наоборот)
Скорость
Вт/(м2.К)
к-*
Вт/(м-К)
Па-с
м2/с
кг/м3
м2/с
Дж/(кг.К)
м/с2.
м
Дж/кг
К
м/с
У капельных жидкостей с возрастанием температуры величина
критерия Рг уменьшается — см. рис. XIII. Следовательно, для
капельных жидкостей при нагревании Рг/Ргст > 1, а при
охлаждении Рг/Ргст < 1. На этом основании при проектировании
теплообменников в расчете коэффициентов теплоотдачи для
нагревающихся жидкостей можно принимать (Рг/Ргст)0'25 = 1, допуская
небольшую погрешность в сторону уменьшения коэффициента
теплоотдачи, т. е. в сторону запаса. Для охлаждающихся жидкостей,
когда Pr/PrCT ^ 0,5, с достаточной точностью можно принимать
среднее значение (Рг/Ргст)0,25, равное 0,93.
7. Во многие критериальные уравнения конвективной
теплоотдачи входит множитель (Рг/Ргст)0,25, учитывающий направление
теплового потока и близкий к единице, когда температуры
жидкости и стенки не сильно отличаются. При вычислении критерия
Ргст значения физико-химических свойств жидкости надо брать
по температуре стенки.
Для газов Рг/Ргст — 1 как при нагревании, так и при
охлаждении, поскольку для газа данной атомности (при невысоких
давлениях) критерий Рг является величиной приблизительно
постоянной, не зависящей от температуры и давления.
Приближенные значения критерия Рг для газов,
рекомендуемые для расчетов:
Одноатомные газы 0,67 Трехатомные газы 0,8
ДЬухатомные газы 0,72 Четырех- и многоатомные газы 1,0
8. Теплоотдача при развитом турбулентном течении в прямых
трубах и каналах (Re > 10 000).
Расчетная формула:
Nu = 0,02l8f Re°'8Pr°'43(Pr/PrCT)0'25. (4.J7)
152
По уравнению (4.17) построена номограмма (рис. XII),
рекомендуемая для расчетов.
Выражения для критериев Nu, Re, Pr — см. уравнения (4.11)
и следующие, а также табл, 4.2.
Определяющая температура — средняя температура жидкости
(газа), определяющий геометрический размер / — эквивалентный
диаметр аэ:
<*Э = 4//П, (4.18)
где / — площадь поперечного сечения потока, а П — полный периметр
поперечного сечения потока, независимо от того, какая часть этого периметра участвует
в теплообмене.
Для труб круглого сечения dB = d.
Значения поправочного коэффициента еь учитывающего
влияние на коэффициент теплоотдачи отношения длины трубы L к ее
диаметру dt приведены в табл. 4.3.
Для изогнутых труб (змеевиков) полученное по формуле (4.17)
значение а умножают на коэффициент х, учитывающий
относительную кривизну змеевика:
азм = ха; (4.19)
d
#= 1-f 3,54
D
(4.20)
где d — внутренний диаметр трубы змеевика; D — диаметр витка змеевика.
Для газов расчетная формула (4.17) упрощается, так как в этом
случае Рг/Ргст = 1, а Рг зависит только от атомности газа:
Nu = Ce? Re0*8. (4.21)
Например, для воздуха:
Nu = 0,01881 Re0,8- (4.22)
9. Теплоотдача в прямых трубах и каналах при (GrPr) <
<8-10б и Re < 10 000 для вертикального или горизонтального
расположения труб (см. табл. 4.4).
a) Re < 2300:
Ц \ 0,14
Nu = l,55ei (Re-LY/3(.
Мет
)
(4.23)
Таблица 4.3
Значения коэффициента е;
Значение
критерия
Re
Отношение L/d
10
20
30
40
50 и более
ью4
2-Ю4
5-Ю4
Ы0&
ЬЮ»
1,23
1,18
1,13
1,10
1,05
1,13
1,10
1,08
1,06
1,03
1,07
1,05
1,04
1,03
1,02
1,03 1
1,02 1
1,02 1
1,02 1
1,01 1
153
Nu
Рис. 4.1. Зависимость
Nu
Pr°'*3(Pr/Pr0T)0**5
от
30
26
22
18
И
10
6
О
1
—.
1/
1/
критерия Re при значении (GrPr) < $* Ю8.
Коэффициент et (et ^ 1)
вводится, если перед обогреваемым
участком трубы нет участка
гидродинамической стабилизации. Величина В;
обычно близка к единице и для
приближенных расчетов может не
учитываться. Остальные обозначения —
см. уравнения (4.11)—(4.16) и
табл, 4.2. Для газов (ц/цСт) не
учитывается.
Определяющая температура: t =
/
ж. ор
в 0,5 (/ст + /ж.ср), где
= и;0 (^ж.нач ~г *ж. кон)-
Формула (4.23) выведена при
значениях 0,00067 < (|л/|ДСт) и 20 <
<(р4)-
При значениях (Ре т) ^ 20 величина Nu асимптотически
стремится к предельному значению
в
в ю
Яе-Ю'3
Nu & 3,66.
(4.24)
б) 2300 < Re < 10 000. В этой области надежных расчетных
формул нет. Приближенно расчет (с запасом) можно выполнять
по графику (рис. 4.1).
10. Теплоотдача в прямых трубах и каналах при (GrPr) >
> 8-10* и Re < 10 000 (табл. 4.4).
Определяющая температура t = 0,5 (/ст + tni. Cp)»
а) Горизонтальное расположение труб (Re < 3500):
Nu
= 0,8 (
ре ^»'VPr)o,i (.
^
^ст
)
0,14
(4.25)
Обозначения — см. в уравнениях (4.11)—(4 16) и табл. 4.2.
Для газов (и./|хст) не учитывают.
Формула (4.25) выведена при значениях 20 < (Ре — \ <: 120;
10е < (GrPr) < 1,3-10»; 2 < Рг < 10.
При ( Ре -j-j <: 10 значение Nu определяют по уравнению:
Nu
-0,5 (ft-г)-
(4.26)
154
Таблица 4.4
Указатель формул для расчета коэффициентов теплоотдачи в прямых
трубах и каналах при Re < 10 000
Значение
GrPr
<8-10*
Ра положение
прямых труб
Пределы применения
Номер
формулы
или
рисунка
20 <
(*4)
(4.23)
Любое
Re < 2 300
("¦т)
20
(4.24)
2 300 < Re < 10 000
Рис. 4.1
>8-10ь
Горизонтальное
Re < 3 500
20<(Ре-|Л<120 (4.25)
<ю
(4.26)
Re > 3 500
(4.27)
Вертикальное
при
несовпадении
свободной и
вынужденной
конвекции
250 < Re < 10 000
(4.28)
б) Горизонтальное расположение труб (Re > 3500):
Nu = 0,022 Re°'8Pr0'4 0i/(iCT)n, (4.27)
где п =0,14 при нагревании, п = 0,25 при охлаждении.
Формулы (4.25) и (4.27) выведены на основании
экспериментальных данных при (GrPr) < 13-10е. Для приближенных
расчетов эти формулы можно применять и при (GrPr) > 13-10е.
в) Вертикальное расположение труб при несовпадении
свободной и вынужденной конвекции (движение жидкости в
вертикальной трубе снизу вверх при охлаждении и сверху вниз при
нагревании):
Nu = 0,037 Re0*75 Рг0'4 Oi/-xc,)n, (4.28)
где п = 0,11 при нагревании, п = 0,25 при охлаждении.
Формула (4.28) выведена при значениях 250 < Re < 10 000;
1,5-10е < (GrPr) < 12-10е. Для приближенных расчетов эту
формулу можно применять и при (GrPr) > 12-10е.
г) Вертикальное расположение труб при совпадении свободной
и вынужденной конвекции (движение жидкости в вертикальной
трубе снизу вверх при нагревании и сверху вниз при охлаждении).
Коэффициенты теплоотдачи при такой схеме движения теплонсси-
155
телей значительно ниже коэффициентов теплоотдачи при
горизонтальном расположении труб и при вертикальном расположении
при несовпадении вынужденной и свободной конвекции. Поэтому
аппараты с такими направлениями движения теплоносителей
применять не рекомендуется и расчетная формула не приводится.
Сводка расчетных формул при Re<10 000 приведена в табл. 4.4.
11. Теплоотдача при поперечном обтекании пучка гладких труб.
а) Аппараты с однократно-перекрестным движением жидкости.
Пример — межтрубное пространство аппарата, изображенного
на рис. 4.2. Течение жидкости по В—В.
При Re < 1000 для коридорных и шахматных пучков:
Nu ^ 0,56еф Re0'5 Pr0,36 (Pr/PrCT)0'25. (4.29)
При Re > 1000 для коридорных пучков:
Nu = 0,22еф Re0'65 Pr°>36 (Pr/PrCT)0'25; (4.30)
для шахматных пучков:
Nu = 0,4еф Re0'6 Pr0,36 (Pr/PrCT)0'25. (4.31)
Определяющая температура — средняя температура жидкости,
определяющий размер — наружный диаметр трубы. Расчет
скорости w ¦— см. формулу (4.35).
Коэффициентом ел учитывается влияние угла атаки <р (рис. 4.3).
Значения еф приведены в табл. 4.5.
По формулам (4.29)—(4.31) находят значения коэффициентов
теплоотдачи для третьего и последующих рядов труб в пучке. При
м достаточно большом числе
рядов эти значения
приближенно можно считать
средними для всего пучка.
Для газов формулы
упрощаются, так как Рг/Ргст =
= 1, а Рг зависит только от
В
В
t
Рис. 4.2. Схема аппарата с однократно-перекрестным движением жидкости.
Рис. 4.3, Угол атаки.
156
Таблица 4.5
Ф
-Ф
90
1
80 70 60
1 0,98 0,94
50 40 30 20 10
0,88 0,78 0,67 0,52 0,42
атомности газа. Для воздуха при Re > 1000 и шахматном
расположении труб:
Ки = 0,356ефКе°>6. (4.32)
б) Аппараты с многократно-перекрестным движением жидкости.
Пример — межтрубное пространство кожухотрубчатых
теплообменников с поперечными перегородками (рис. 4.4); течение
жидкости по В—В.
Применительно к кожухотрубчатым теплообменникам с
поперечными перегородками (рис. 4.4) в формулах (4.29)—(4.31)
принимают коэффициент еф = 0,6, учитывая, что теплоноситель в
межтрубном пространстве лишь часть пути движется поперек труб и
при угле атаки, меньшем 90°; кроме того, он может протекать через
щели между перегородками и кожухом или трубами.
Расположение входного штуцера и сегментных перегородок
для одно- и двухходового кожухотрубчатых теплообменников
показано на рис. II и III.
Поперечные перегородки в
межтрубном пространстве часто
размещают на таком расстоянии друг от
друга, чтобы живое сечение
продольного потока в сегментном вырезе
перегородки было равно живому
сечению поперечного потока у края
перегородки.
При соблюдении этого условия,
например, для стрелки сегмента & =
= 0,25Z)BH расстояние между
перегородками / будет равно:
' = Т4ТЙГ- <4-33>
где ф — коэффициент, зависящий только от
наружного диаметра d и шага t труб:
^ = t^W- (4'34)
Расчетная скорость потока:
w = V/Sc, ж. (4.35)
Рис. 4.4. Кожухотрубчатый теплообменник с сег*
ментными поперечными перегородками.
t
157
SO
50
40
30
20
10
15 25 35 45 55 65 75 а
Рис. 4.5. Труба с поперечными ребрами.
Рис. 4.&. Зависимость а от а.
Здесь V—расход жидкости, м3/с; 5С. ж — площадь проходного сечения
межтрубного пространства, между перегородками, м3. Для стандартных
теплообменников в ГОСТах приводятся площади проходных сечений.
12. Теплоотдача при обтекании пучка труб с поперечными
ребрами.
Расчетная формула имеет вид:
Nu = С (d/t)-°M (/i/0~°'14 RenPr°'\ (4.36)
В этой формуле (рис. 4.5): d— наружный диаметр несущей трубы м; t —
шаг ребер, м; h = (D —d)l2 высота ребра, м.
Для коридорных пучков: С = 0,116, п — 0,72; для шахматных
пучков: С = 0,25, п = 0,65.
Определяющая температура — средняя температура жидкости,
определяющий размер — шаг ребер t.
Формула (4.36) применима при значениях Re = 3000—25 000
и 3 < (dlt) < 4,8.
По вычисленному из уравнения (4.36) коэффициенту
теплоотдачи определяют по графику (рис. 4.6) так называемый
приведенный коэффициент теплоотдачи апр, который и подставляют в
формулу для коэффициента теплопередачи (отнесенного к полной
площади наружной поверхности FH):
К-—, . I „. , (4.37)
+
1 FH
апр аа ^в
+
2jrOT
где FH — площадь полной наружной поверхности оребрениой трубы на единицу
длины, включая поверхность ребер; FB — площадь внутренней поверхности
несущей трубы на единицу длины; <х2 — коэффициент теплоотдачи для потока,
проходящего внутри трубы, Вт/(м2-К); Е ^ст —сумма термических
сопротивлений стенки и загрязнений.
13. Теплоотдача при течении вдоль плоской горизонтальной
поверхности.
Расчетные формулы:
a) Re < 5 -105
Nu = 0,66 Re0*5 Pr0'33 (Рг/Ргст)0,25; (4.38)
158
6) Re > 5-105
Nu = 0,037 Re0*8 Pr0'43 (Pr/PrCT)0'25. (4.39)
Определяющая температура — средняя температура жидкости,
определяющий размер — длина обтекаемой стенки по направлению
движения потока.
Для расчетов по формуле (4.39) можно использовать
номограмму (рис. XII), умножая полученное значение критерия Nu
на величину 0,037/0,021 - 1,76.
Для газов формулы упрощаются. Для воздуха уравнение (4.39)
приводится к виду:
Nu = 0,032 Re0'8. (4.40)
14. Теплоотдача при стенании жидкости пленкой по
вертикальной поверхности.
а) При турбулентном стекании пленки (Re > 2000):
Nu = 0,01 (GaPrRe)1/3. (4.41)
б) При ламинарном стекании пленки (Re < 2000):
Nu « 0,67 (Ga2Pr3Re)1/9. (4.42)
Определяющая температура — средняя температура
пограничного слоя, равная 0,5 (/от + ^»р. ж)-
В уравнениях (4.41) н (4.42):
Nu = a#/X; Ga » tf3p2g/[i2; Re = wd^/p. = 4Г/ц, (4.43)
где Н — высота поверхности, м; d3 — 4//П — эквивалентный диаметр пленки, м;
/ — площадь поперечного сечения пленки, м2; П — омываемый пленкой
периметр, м; Г — G/(ndn) = G/U — линейная плотность орошения, кг/(м-с).
При Re < 1500 толщина пленки Ь определяется теоретическим
уравнением:
15. Теплоотдача при перемешивании жидкостей мешалками *.
Коэффициент теплоотдачи в аппаратах со змеевиками,
рубашками и мешалкой можно рассчитать по уравнению:
Nu = CRem Pr0*33 ((i/fiox)0,14 Г"1, (4.45)
где Nu == adjX; Re = pnd^/[L\ Г — D/dM\ D — диаметр сосуда; п — частота
вращения мешалки; dM — диаметр окружности, ометаемой мешалкой; fiCT —
динамический коэффициент вязкости жидкости при температуре стенки рубашки
или змеевика; fi — динамический коэффициент вязкости жидкости при средней
температуре 0,5 (/ср. ж + /от).
Значения остальных физических констант надо брать при
средней температуре жидкости в сосуде /ср. ж.
* См, также [3.22], и [3.23].
159
Для аппаратов с рубашками: С = 0,36, т = 0,67; для
аппаратов со змеевиками: С = 0,87, т = 0,62.
Формула (4.45) дает удовлетворительные результаты для
турбинных, пропеллерных и лопастных мешалок с Г = D/dM = 2,5 ч-
-т-4 в аппаратах диаметром до 1,5 м.
16. Теплоотдача при свободном движении (при естественной
конвекции).
Расчетные уравнения:
А. Теплоотдача снаружи горизонтальных труб при 103 <
< GrPr < 10э:
Nu = 0,5 (GrPr)0'25 (Pr/PrCT)0,25. (4.46)
Определяющая температура — температура окружающей
трубу среды; определяющий размер — диаметр трубы.
Б. Для вертикальных поверхностей, плоских и
цилиндрических:
а) при 103 < GrPr < 109
Nu = 0,76 (GrPr)0*25 (Рг/РГст)0,25; (4-47)
б) при GrPr > 109
Nu = 0,15 (GrPr)0'33 (Pr/PrCT)0*25. (4.48)
Определяющая температура — температура окружающей
среды; определяющий размер для вертикальных поверхностей —
высота.
17. Теплоотдача при пленочной конденсации пара.
А. Пленочная конденсация чистого насыщенного пара любых
веществ, не содержащих неконденсирующихся газов (воздуха,
инертных газов).
1. Обобщенная расчетная формула теплоотдачи в модели
Нуссельта с преимущественным термическим сопротивлением
в пленке конденсата:
Nu = С (GaPr Кф)п, (4.49)
Здесь С, п — постоянные; Nu = Ш/Х; Ga = gfipVn; Pr = \icp/k; Кф —
= г 1(СрЫ)\ а—среднее значение искомого коэффициента теплоотдачи при
конденсации пара; /—характерный линейный размер, равный высоте Я для
вертикальных поверхностей теплоотдачи и диаметру d для поверхностей
горизонтальных труб; Я,, р, \i, cp, g—соответственно, величины коэффициента
теплопроводности, плотности массы, динамической вязкости, изобарной
теплоемкости и ускорения свободного падения для пленки конденсата при средней
определяющей температуре ее /пл ~ 0,5 (*КОид + *ст)> равной полусумме
температуры конденсации ^Конд и температуры стенки ?ст; г—теплота фазового
превращения при /Копд:
Дг = ^конд — 'ст*
С = 0,728 — при конденсации на поверхности одиночных горизонтальных труб;
С ~ 0,94 — при конденсации на поверхности вертикальных стенок (пучка труб)
в приближении ламинарного режима стекания пленки конденсата; С= 1,15 —
то же, но с поправкой в 21 % на волнообразование в стекающей плеике
конденсата; п = 0,25,
160
а) Среднее значение коэффициента теплоотдачи [в Вт/(м2-К)1
на поверхности пучка вертикальных труб высотой Н:
где К {К g* /". И. д^1 Я — для пленки конденсата при /пл = 0,5 (/копд — /ст)
в единицах СП.
б) Среднее значение коэффициента теплоотдачи [в Вт/(м2-К)]
на наружной поверхности одиночной горизонтальной трубы
диаметром d\
2. Коэффициенты теплоотдачи при пленочной конденсации
в скорректированной модели Нуссельта.
Коррекция модели состоит в выборе определяющей
температуры для вычисления физических свойств пленки конденсата.
Принимая в качестве определяющей температуры *КОнд» в
соотношения (4.49) вводим поправочную функцию zt по формуле [4.1,
с. 134]:
-№)'-?]"¦
Индекс tCT означает, что Kt и \i определяют при
температуре поверхности стенки, соприкасающейся с пленкой конденсата.
Значение е, может быть весьма существенным для вязких
конденсатов при больших At. Для воды величину et в первом
приближении принимают равной единице.
Скорректированным моделям (4.49) посредством соотношений
(4.50) и
г^аАШНп/G (4.51)
часто придают более простой для проектных расчетов вид,
используя для этого данные о массовом расходе конденсирующегося
пара G и общем числе теплообменных труб п.
а) В случае конденсации на пучке п вертикальных труб
высотой Н диаметром d среднее значение коэффициента теплоотдачи
[в Вт/(ма-К)1:
Где значения величин А,, р, \i берут при /Конд-
В частности, в этом случае для водяного пара, полагая et = 1:
а = 2,04—44^. (4.52а)
Значения функций Bt и At для воды приведены в табл. 4.6
при /К0НД, где Bt = Xp2^/\i1^.
6 Павлов К. Ф. и др. 161
Таблица 4.6
"емпература конденсации
водяного пара /
конд>
=С
100
по
20
140
160
18Э
At
6960
1010
7100
1040
7240 7420 7490 7520
1070 1120 1150 1170
б) В случае конденсации на наружной поверхности пучка
горизонтальных труб длиной L при определении среднего значения
коэффициента теплоотдачи а помимо функции е, вводят еще
поправочный множитель е, учитывающий влияние числа труб по
вертикали. Тогда осредненный по всему пучку коэффициент
теплоотдачи а [в Вт/(м2'К)1:
а
-••™- if tSu-
(4.53)
где ? зависит от пв (рис. 4.7).
Число труб пв можно определить по ГОСТ 15118—79 (см.
табл. 4.14).
Для водяного пара в случае конденсации на пучке
горизонтальных труб при ?/ = 1:
аср= 1,28е.Л4/(<*Д*)0,26. (4.54)
Значения At и Bt — см. табл. 4.6.
При технических расчетах в тех случаях, когда второй
коэффициент теплоотдачи значительно ниже, для конденсирующегося
водяного пара можно принимать приближенно осионд = 10 000 ч-
4-12 000 Вт/(м2-К).
в) Подставляя в формулы для аиопд значение д /коид = <7/оско,.д
(где q — удельная тепловая нагрузка, Вт/м2), получаем:
для вертикальных поверхностей
аконд
-¦»ЧО-)в^
\
1
(4.55)
Рис. 4.7. Зависимость усредненного для всего гучка коэффициента е о. чис.^я труб по
вертикали п
ЖСИУ1И TpyG.
веотикали лт> » порядок определения п„ дли коридорного (/) ;i шахматного (2) расколо-
1S В
162
для одиночных горизонтальных труб
аконд = 0,645^ {^jLy^q-W. (4.56)
г) Конденсация пара внутри горизонтальных труб и
змеевиков.
Общая критериальная зависимость для случая конденсации
водяного пара приводится к виду 14.21 ]:
ссКонд= l,36^°'5L°'35d-0'26 (4.57)
или
«ковд = 1.85Л2 Д/конд^0,7^'5, (4.58)
где Л — коэффициент, объединяющий физико-химические константы воды и пара
(его значения в зависимости от температуры конденсации приведены на
рис. 4.8); q—удельная тепловая нагрузка, Вт/м2; L — длина трубы, м; d —
внутренний диаметр трубы, м.
При конденсации пара в змеевиках длина змеевика не должна
быть очень большой, так как в нижней части длинных змеевиков
скапливается конденсат, что ухудшает теплоотдачу; кроме того,
уменьшается давление пара, что приводит к снижению полезной
разности температур.
По практическим данным, для паровых змеевиков начальная
скорость пара в змеевике не должна превышать ~30 м/с. При
средней разности температур Д/ср = 304-40 К предельное
наибольшее отношение длины змеевика к диаметру трубы Lid в
зависимости от давления пара рабс составляет:
МПа 0,49 0,29 0,15 0,78
кгс/см* 5 3 1,5 0,8
(^)макс 2?5 225 175 125
При других значениях д tcp для паровых змеевиков
приведенные значения Lid следует умножать на коэффициент 6/-/Д?ор.
Б. Конденсация пара, содержащего неконденсирующийся газ
(например, воздух).
Если пар содержит воздух или другой неконденсирующийся
газ, то теплоотдача при конденсации сильно ухудшается. На
рис. 4.9 приведены полученные опытным путем значения
отношения гг = ав/аконд в зависимости от концентрации Y воздуха в паре.
Здесь ссКОнд — коэффициент теплоотдачи при конденсации чистого пара»
рассчитываемый_по приведенным уравнениям; ссв — то же при содержании
воздуха в паре; У — относительная массовая концентрация воздуха в паре,
кг воздуха/кг пара [или % (масс.)].
В. Конденсация чистого перегретого пара.
а) Если температура стенки выше температуры насыщения, то
конденсации нет и теплоотдачу рассчитывают как для
охлаждающегося газа.
6*
163
-А
S
8)
7
5
1 1
1
1
!
i
-
1,0
0,8
0,6
0,4
0,2
А
\
1*
1
II
1
100 ПО 140 1S0 W
200
Ь,°С
О Г 2 3 4 5 6 7 8
iVc. 4.8. Значение коэффициента А [формулы (4.57; (4.58)1.
Рис. 4.9, Зависимость поправочного коэффициента е от концентрации воздуха в паре*
б) Если температура стенки ниже температуры насыщения, то
расчет теплоотдачи ведут по формулам (4.52) и (4.58), но вместо
теплоты конденсации г подставляют сумму теплот конденсации
и перегрева:
г'= г + спЦп—^ш?> (4.59)
где сп — теплоемкость перегретого пара, Дж/(кг-К); in—начальная
темперы ура перегретсго пара, К; ^Конд— температура конденсации, К.
За Д/ в формулах (4.52) и (4.58) при конденсации перегретого
пара принимается также разность температуры конденсации пара
и температуры стенки.
18. Теплоотдача при кипении жидкостей.
Уравнения теплоотдачи при кипении жидкостей существенно
различаются в зависимости от вида термомеханического режима
этого энергоемкого гетерогенного процесса, сопровождающегося
фазовым превращением. По характеру и интенсивности кипения
различают три основных режима процесса: 1) пузырьковый; 2) пу-
зырчато-пленочный и 3) пленочный, причем наибольшее
применение в химической технологии нашел первый режим, который
в расчетной практике оценивают указанием области изменения
удельной тепловой нагрузки (днгк0 < q < дГфг х).
Современные модели кипения в пузырьковом режиме опираются
на представления о турбулизующем влиянии пузырьков паровой
фазы, лимитирующем кинетику этого процесса, что позволяет
значительно сократить его описание и выразить коэффициент
теплоотдачи а без прямого обращения к методам статистики через
обобщенный критерий Нуссельта Nu посредством модифицированного
критерия Рейнольдса Re и критерия Прандтля Рг:
Nu =* CRe"1 Pr"%
(4.60)
т
# * * * #
где С, /if, п2—постоянные; Nu = а/А; Re — w l/ц; I—характерный
(модифицированный) линейный размер процесса теплоотдачи, являющийся
параметрической функцией критического лапласовского радиуса пузыря /?кр,
выраженного через ссиовные физические свойства кипящего теплоносителя
(изобарную теплоемкость ср> плотности масс паровой рп и жидкой рж фаз,
поверхностное натяжение о, теплоту фазового превращения ги и температуру
* " #
кипения Тшш); w — средняя скорость движения паровой фазы (w = а»п), опре-
деляется по удельной тепловой нагрузке q и объемной теплоте фазового
превращения.
Используя явный вид такси зависимости, например, по
Д. А. Лабунцову, в области Ю-2 < Re < 104, когда С = 0,125;
пх = 2/3; п2 — '/;{, т. е. из уравнения
Nu = 0,125Re2/3PF1/3, (4.61)
*
можно определить критерий Nu и найти из него среднее значение
коэффициента теплоотдачи а при пузырьковом режиме кипения
жидкости.
В пределах пузырькового режима кипения жидкостей в
условиях свободного или вынужденного движения в трубах и
продольных иекруглых каналах можно использовать преобразованное
уравнение (4.60), которому придают упрощенный вид, удобный
для определения осредненного значения коэффициента
теплоотдачи а [в Вт'(лг-К)] через удельную тепловую нагрузку q или
движущую силу процесса ДТ|;,Ш:
.BtCT:Bt, ^у. (4.62,
Здесь величины коэффициента теплопроводности %, плотности теплового
потока qy кинематической вязкости v, поверхностного натяжения о,
температуры кипения ТК11ПУ движущей силы процесса теплоотдачи АГКИП = (Т'от—
— ^кип) выражают в единицах СИ (табл. 4.2).
Численные значения безразмерной функции bt
апробированной на множестве опытных данных по кипению различных
жидкостей на поверхностях из нержавеющей стали, бронзы, никеля,
меди и серебра, можно найти из графика зависимости Ь от
отношения плотности жидкости рж к плотности ее пара рп (рис. 4.10).
При составлении этого графика использовано уравнение вида:
Ь = 0,075 + 0,75 ( Bs У/3. (4.62а)
V Рж ~ Рп /
Отклонения экспериментальных данных по величине Ь =
— а \/ —7~—, найденной в соответствии с обратным соотноше-
/ * VO* НИИ
нием (4.62), от численных значений ?>, рассчитанных по формуле
(4.62а), составили iL35% из-за влияния на интенсивность
теплоотдачи материала теплопередающих труб и чистоты поверхности
нагрега.
165
0,13
0,11
0,09
0,07
j
i
i I
¦¦¦i
i
i
I
——i—
^t
—*_
Jn -_
.^—
\
1
Рис, 4.Ю. Значение коэффициента Ъ в
формуле (4.62).
Преобразованная формула
(4.62) относительно абсолютного
давления П (в кгс/см2)
применительно к определению
коэффициента теплоотдачи кипящей воды
имеет вид [4.1 ]:
3.4П0'18
а
\ _ 0,0045П
А.63)
2
J
Щ
4
О
i тт
Кроме приведенных выше
расчетных формул (4.61) и (4.62) для
аь*пн можно использовать формулы
других авторов (см. пример 4.22).
Величина критической тепловой нагрузки qHP,x при кипении
жидкости па горизонтальных трубах в большом объеме
определяется уравнением (при рж > рп):
<7кр. i = 0, Ur Vp~n YVZPZ, (4.64)
где г — теплота парообразования, Дж-'кг.
Отклонения экспериментальных данных от рассчитанных по
формуле (4.64) также лежат в пределах ±35%.
Для приближенного расчета коэффициента теплоотдачи при
пузырьковом кипении жидкости в большом объеме на внешней
поверхности пучков труб и в вертикальных испарителях в области
умеренных тепловых нагрузок (до 0,4^) и давлений /?абс —
= 0,2^-10 кгс/см2 можно применять формулу:
акип = 2)72фрОЬ4у7> <4-65)
где ф—множитель, учитывающий физические свойства жидкости; paf)C
выражено в кгс/см2.
«-л.
экспериментально найденные значения <р (для кипения на
поверхности труб из цветных металлов):
Бензол 0,31 9 % водный раствор NaCl . . . 0,86
Газолин 0,27 24 % водный раствор NaCl . . 0,62
Гептан 0,46 10 % водный раствор Na2S04 . . 0,91
Вода 1 Керосин 0,31—0,50
Метиловый спирт 0,36
Этиловый спирт 0,45
26 % водный раствор глице- 0,83
рпна
25 % водный раствор сахара . 0,57
19. Теплоотдача при тепловом излучении твердых тел.
Количество теплоты, переходящей от более нагретого тела
к менее нагретому посредством лучеиспускания, определяется по
уравнению:
**-с*-*р[{тУ-(тУ'.
(4.LC)
168
Здесь (?л — количество теплоты, передаваемой лучеиспусканием в
единицу времени, Вт; F — площадь поверхности излучения, м2; Ci_2 —
коэффициент излучения, Вт/(м2-К4); 7\ — температура поверхности более нагретого
тела, К; Т2 — температура поверхности менее нагретого тела, К; Ф—угловой
коэффициент, безразмерный.
Коэффициент излучения Сх.2 зависит от взаимного
расположения и степени черноты е излучающих поверхностей, имеющих
температуры Тг и Т2.
а) Если одно тело, площадь поверхности излучения которого
равна Fl9 расположено внутри полого тела с площадью
поверхности излучения F2i то F = Flt угловой коэффициент ф= 1 и
Ci F2 \ С2 Сч I
(4.67)
где Ci — ггСч — коэффициент лучеиспускания меньшего тела; С2 = е2Сч —
коэффициент лучеиспускания большего (охватывающего) тела; Сч =
= 5,7 Вт/(м2-К4)— коэффициент излучения абсолютно черного тела; е% и е2 —
степени черноты поверхности меньшего и большего тела.
Значения е для некоторых материалов:
Алюминий 0,05—0,07 Краска масляная .... 0,78—0,96
Асбест 0,96 Лак 0,8—0,98
Вода 0,93 Медь . .0,57—0,87
Гипс 0,78—0,9 Свинец 0,28
Дерево строганое 0,9 Стекло 0,94
Железо (сталь) окислен- Чугун шероховатый окис-
ное 0,74—0,96 ленный 0,96
Кладка кирпичная 0,93 Штукатурка 0,93
б) Если площадь F2 очень велика по сравнению с Fx (например,
аппарат в цехе), т. е. отношение Fx/F2 близко к нулю, то
коэффициент излучения Сх_2 = С\-
в) Если Fx — Рг (две параллельные бесконечно большие
поверхности), то
Сиг = — J — . (4.68)
Cj Cg Ctj
Суммарный коэффициент теплоотдачи лучеиспусканием и
конвекцией:
а = ал + ак, (4.69)
где
а Qn .С"[ЙМм)1 (470)
ак—коэффициент теплоотдачи конвекцией, определяемый по соответствующим
формулам для свободного или вынужденного движения.
167
Для расчета тепловых потерь аппаратов» находящихся в
закрытых помещениях, при температуре поверхности аппарата до
150 °С можно пользоваться приближенной формулой:
а = 9,74 + 0,07Д*, (4.71)
где а — суммарный коэффициент теплоотдачи лучеиспусканием и конвекцией,
Вт/(м2*К); Д*—разность температур поверхности аппарата и окружающего
воздуха, К.
Теплопередача в поверхностных теплообменниках
Основную группу теплообменных аппаратов, применяемых
в промышленности, составляют поверхностные теплообменники,
в которых теплота от горячего теплоносителя передается
холодному теплоносителю через разделяющую их стенку. Другую группу
составляют теплообменники смешения, в которых теплота
передается при непосредственном соприкосновении горячего и
холодного теплоносителей.
20. Уравнение теплопередачи:
Q^KFAtcv. (4.72)
Здесь Q — тепловой поток (расход передаваемой теплоты), Вт; К —
коэффициент теплопередачи, Вт/(м2*К); F — площадь поверхности теплопередачи,
м2; Д/Ср — средняя разность температур горячего и холодного теплоносителя, К«
Удельная тепловая нагрузка (удельный тепловой поток):
q=Q/F = KAtcv. (4.73)
Для плоской поверхности коэффициент теплопередачи К в
формулах (4.72) и (4.73) равняется:
К - —, ^ г-, (4.74)
- + 2/СТ+ —
где аг и ах — коэффициенты теплоотдачи для горячего и холодного
теплоносителя, Вт/(м2-К); S гс? — сумма термических сопротивлений всех слоев,
из которых состоит стенка, включая слои загрязнений, (м2,К)/Вт.
Уравнения (4.72)—(4.74) с достаточной точностью можно
применять и для расчета теплопередачи через цилиндрическую стенку,
если dBH > 0,5dHap.
Площадь поверхности теплопередачи трубчатых аппаратов
Fanu (B м2) определяют по формуле:
^апп *= я<*срл?. (4-75)
Здесь dcp = dBH, если анар > авн; dcp = 0,5 (dHap + dBH), если анар <
^ авн; п — число труб; L — длина труб, м.
Для трубчатого теплообменника, состоящего из п труб длиною
каждая L (в м), уравнение теплопередачи может быть представлено
в виде:
Q = KLnLAtcv. (4.76)
168
Здесь коэффициент теплопередачи на 1 м длины Kl [в Вт/(м> К) ]
равен:
я
Kl = —j ^—i и 1 vT~7 * <4,77)
1 |- у _ 1п^?-+—JL—+ у гаагр
где X — коэффициент теплопроводности материала стенки, Вт/(м-К).
Тепловая проводимость загрязнений на стенках (1/гРагр)
зависит от рода теплоносителя, его температуры и скорости, а также
от материала стенки, температуры нагревающей среды и
длительности работы аппарата без очистки, т. е. в конечном счете от рода
осадка или продукта коррозии. Точные данные о гзагр можно
получить только опытным путем.
Ориентировочные значения тепловой проводимости
загрязнений приведены в табл. XXXI.
При редких чистках аппарата или сильной коррозии значение
l/'sarp может уменьшаться до 500 Вт/(м2-К) и ниже.
21. Средняя разность температур Д/ср, входящая в
уравнение теплопередачи, определяется следующим образом.
а) Для противотока и прямотока:
__ At6 — AiM _ At6-AtM „7™
а'°* ~ In Wt/Atu) 2,3 lg (Д/б/Д/м)» (*'7а>
где Д/g и Д/м — большая и меньшая разности температур на концах
теплообменника.
Следует отметить, что из уравнения (4.78) вытекает: если
Д/б = 0 или Д*м = 0, то и Д/ср = 0; если Д/б = Д*м, то Д/Ср =
= Mfs = Д/м.
Если отношение (Д*б/Д/М) < 2, то с достаточной точностью
вместо уравнения (4.78) можно применять уравнение
Л*ср = (Л'б + Л'м)/Й. (4.79)
Формулы (4.72), (4.78) и (4.79) применимы при условии, что
в теплообменнике значения коэффициента теплопередачи К и
удельной теплоемкости с для каждого из теплоносителей можно
считать постоянными вдоль всей поверхности теплообмена.
В тех случаях, когда вдоль поверхности теплообмена
значительно меняется величина коэффициента теплопередачи К (или
величина с), применение уравнений (4.72) и (4.78) становится
недопустимым.
В этих случаях определение поверхности теплопередачи
выполняют по дифференциальному уравнению теплопередачи
методом графического интегрирования — см. пример 4.26.
б) Для смешанного тока в многоходовых теплообменниках
и для перекрестного тока:
Д*ср = ед* Д'пр> (4.80)
где ед^ — поправочный коэффициент к средней разности температур А^ПР)
вычисленной для противотока.
169
Значение коэффициента B\t берется из специальных графиков
[13, 4.1 i. Примеры таких графиков даны на рис. VIII.
В многоходовых теплообменниках с простым смешанным
током (один ход в межтрубном пространстве и четное число ходов
в трубном — см. рис. 4.15 и 4.20) среднюю разность температур
можно рассчитать по формуле [13]:
А'«- ^ТТ^ГГ' (4'81)
ср
2,3 lg
Л*б + 'м — А
где A/q и Д/м — большая и меньшая разности температур на концах
теплообменника при противотоке с теми же начальными и конечными температурами
теплоносителей; А = КбТ2 + ^2; &Т = Гнач — Гкон — изменение
температуры горячего теплоносителя; 6/ — /нон—/нач—изменение температуры
холодною теплоносителя.
22. Определение средних температур теплоносителей.
В большинстве критериальных уравнений теплоотдачи
значения физико-химических констант теплоносителя отнесены к его
средней температуре, которая находится следующим образом.
Для того теплоносителя, у которого температура изменяется
в теплообменнике на меньшее число градусов, средняя температура
определяется как средняя арифметическая между начальной и
конечной:
<ср|«('нИ|+'кон1)/2- (4'82)
Для второго теплоносителя среднюю температуру находят по
формуле:
Это уравнение справедливо и тогда, когда температура
первого теплоносителя постоянна вдоль поверхности теплообмена.
Теплопередача при непосредственном соприкосновении потоков
23. Обобщенное уравнение для определения коэффициента
теплопередачи от охлаждающегося ненасыщенного газа к жидкости
в колонных аппаратах с насадками:
Ki = 0,01 Re°'7 Re^7 PrJ*33. (4,83)
Здесь Ki = Kd3/kr— критерий Кнрпичева; Rer = 4Шфр|/(оцг) —
критерий Рейнольдса для газа; Rem = 4/,/(ацж) — критерий Рейнольдса для
жидкости; Ргг = CpfXjAr — критерий Прандтля для газа; К — коэффициент
теплопередачи от газа к жидкости, Вт/(м2,К); d^ = WCJ° — эквивалентный
диаметр насадки, м; VCB — свободный объем насадки, м^/м3; о — удельная
поверхность насадки, м2/м3; Шф — фиктивная скорость газа в аппарате (отнесенная к
полному поперечному сечению аппарата), м/с; L — плотность орошения,
кг/(м2-ё); ?tr—коэффициент теплопроводности газа, Вт/(м-К); Мт
—динамический коэффициент вязкости газа, Па-с; рг—плотность газа, кг/м3; [хж —
динамический коэффициент вязкости жидкости, Па-с.
Формула (4.83) получена по экспериментальным данным для
охлаждения воздуха от 80 до 2 °С при удельном орошении водой,
равном 3,5—10 м3/(м2,ч).
170
24. Обобщенное уравнение для коэффициента испарения с
поверхности жидкости в турбулентный газовый поток при
вынужденном его движении:
Nur = 0,027 Re^'8(Pr;)
0,33
(4.81)
где Nuj; = $d/Dr — диффузионный критерий Нуссельта; Pr^ = \/Dr —
диффузионный критерий Прандтля для газа; р — коэффициент испарения, м/с;
Dr — коэффициент диффузии, м2/с; vr — кинематический коэффициент вязкости,
м2/с.
Для случая охлаждения воздухом воды, стекающей пленкой
внутри каналов, по которым проходит воздух (Pi> = 0,63):
Nur = 0,019 Re
0,83
г
(4.85)
Ориентировочные значения коэффициентов теплоотдачи
и теплопередачи
В табл. 4.7 приведены приближенные значения коэффициентов
теплоотдачи (с округлением) для воды и воздуха, вычисленные по
вышеприведенным формулам для основных случаев конвективной
теплоотдачи, а в табл. 4.8 — ориентировочные значения
коэффициентов теплопередачи, полученные практически для
различных случаев теплообмена.
Таблица 4.7
Ориентировочные значения коэффициентов теплоотдачи [в Вт/(м2-К)]
Вид теплоотдачи
Примечание
Вынужденное
турбулентное течение;
а) в трубах и
каналах
1200-
-56С0
35—60
d — 30 мм.
Приведенные значения а
соответствуют скоростям:
воды — от 0,2 до
1,5 м/с, воздуха —
8—15 м/с
С) ii^u поперечном
обтека шп Tpyfi
Св<yficji(iо** дв пже!iне
Кипение ^оды
Ko:ir:UTr':ai;,MH пап 1-
mej;-;cro гс^.гпюго :ui-
p:i на наружно-"! по-
п;_-;)Х';' . > :i ГОрпЗ:),-
та.'Н ;: ,'Л TpV("i,i
3I00--
230-
2000-
&:(()-
-ЮО0О
-900
-24 000
-1 b 000
70-
3-
-I00
-9
Шахматный пучок;
*ф= *
Давление
атмосферное. Значения а
соответствуют Ы — 5-е
-15 К
Давление н?сьтщенно-
ного пара (збс.)
0,4 МПа; rf= 30 мм.
Значения а
соответствуют Д? = 35-т-5 К
171
Таблица 4.8
Ориентировочные значения коэффициентов теплопередачи [в Вт/(м2*К)]
Вид теплообмена
Вынужденное
движение
От газа к газу (при невысоких давлениях)
От газа к жидкости (газовые холодильники)
От конденсирующегося пара к газу
(воздухоподогреватели)
От жидкости к жидкости (вода)
От жидкости к жидкости (углеводороды, масла)
От конденсирующегося пара к воде
(конденсаторы, подогреватели)
От конденсирующегося пара к органическим
жидкостям (подогреватели)
От конденсирующегося пара органических
веществ к воде (конденсаторы)
От конденсирующегося пара к кипящей
жидкости (испарители)
10—40
10—60
10—60
800—1700
120—270
800—3500
120—340
300—800
Свободное
движение
4—12
6-20
6—12
140—340
30—G0
300—1200
60—170
230—460
300—2500
ПРИМЕРЫ
Пример 4.1. Аппарат диаметром 2 м и высотой 5 м покрыт
слоем теплоизоляции из асбеста толщиной 75 мм. Температура
стенки аппарата 146 °С, температура наружной поверхности
изоляции 40 °С. Определить потери теплоты (тепловой поток)
через слой изоляции.
Решение. Средняя площадь, через которую проходит
теплота:
FCp = n /#ср/,+ 2-^Л = 3,14 (2,075-5+ 0,5-22)= 38,8 м*.
Коэффициент теплопроводности асбеста К = 0,151 Вт/(м-К)
находим по табл. XXVIII.
Тепловой поток через изоляцию:
Q = 4";(^~^)Fcp = "S (146_40)38'8==8280 Вт'
Пример 4.2. Рассчитать коэффициент теплопроводности
жидкого нитробензола при 120 °С по формуле (4.7).
Решение. Удельная теплоемкость нитробензола (табл.
XXVI) с= 1380 Дж/(кг-К).
Плотность нитробензола при 30°С р де 1200 кг/м3 (табл. IV).
Коэффициент теплопроводности нитробензола при 30 °С по
формуле (4.7):
Ь30 == Аср Ур/М = 4,22-10~8-1380-1200 ^1200/123 = 0,149 Вт/(м-К),
где А = 4,22-Ю"8 для неассоциированных жидкостей; М = 123 кг/кмоль —
мольная масса нитробензола.
Коэффициент теплопроводности нитробензола при 120 °С по
формуле (4.8):
U=ho П — е (^ — 30)] =0(149 [1 — 1,0-10"3 (120 — 30)] =0,136 ВтДм-К).
По экспериментальным данным (рис. X) Kt — 0,137 Вт/(м>К).
172
Пример 4.3, Рассчитать коэффициент теплопроводности 25 %
водного раствора хлористого натрия при 80 °С. Плотность 25%
раствора хлористого натрия р == 1189 кг/м3.
Р е ш е н и е. По номограмме (рис. XI) удельная теплоемкость
25% раствора хлористого натрия при 30 °С равна с =
- 3390 Дж/(кг-К).
Мольная масса раствора:
М = 0,907.18 + 0,093-58,5 = 21,7 кг/кмоль.
лпПО 25/58,51
где 0,093 = ,9г/г-я Ъ _l <7*>/]R\ — мольная доля хлористого натрия в
растворе.
Коэффициент теплопроводности 25% раствора хлористого
натрия при 30 °С по формуле (4.7):
Ь30 = 3,58-10~8-3390.1189 ^1189/21,7 = 0,548 Вт/(м-К).
Коэффициент теплопроводности раствора при 80 °С по формуле
(4.9):
1т = 0,548 (0,674/0,615) = 0,60 Вт/(м-К),
где 0,674 и 0,615 Вт/(м-К)— коэффициенты теплопроводности воды при 80
и 30 °С (рис. X).
Пример 4.4. Вычислить коэффициент теплопроводности для
жидкого метана при t= —160,6 °С и сопоставить полученное
значение с экспериментальным.
Решение. Жидкий метан относится к неассоцнироваиным
жидкостям.
I = Acp Y&M = 4,22.10-8-3,47.103-423 ^423/Тб = 0,184 Вт/(м-К),
где А = 4,22-10"^ для неассоциированных жидкостей; с = 3,47-103 Дж/(кг-К)—
удельная теплоемкость жидкого метана при Т = 112,6 К; р = 423 кг/кг —
плотность жидкого метана; М — 16 кг/кмоль — мольная масса метана.
По справочнику [4.15] коэффициент теплопроводности
жидкого метана при t = —160,6 °С равен 0,194 Вт/(м«К). Погрешность
при вычислении по формуле (4.7) составляет:
0,194-0,184
0,184 Ю0 = 5,40/0.
Пример 4.5. Рассчитать коэффициент теплопроводности сухого
воздуха при 300 °С.
Решение. По формуле (4.10):
I =г Bcv\i = 1,9-0,748.103-2,97. 10"6 = 0,0422 Вт/(м-К).
Здесь В = 1,9 для двухатомных газов; cv—удельная теплоемкость при
постоянном объеме, определяется из отношения cJcv = 1,4:
cv = cpJ\ ,4 = 1,05-103/1А = 0,748-103 Дж/(кг- К);
ср — 1,05-103 Дж/(кг-К) — удельная теплоемкость сухого воздуха при 300 °С;
fi = 2,97 * 10" 5 Па-с — динамический коэффициент вязкости воздуха при 300 °С.
173
Пример 4.6. Вычислить коэффициент теплопроводности при
О °С для газовой смеси состава; Н2 — 50%, СО — 40%, N2 — 10%
(по объему).
Решение. Правило аддитивности неприменимо.
Приближенно можно определить коэффициент теплопроводности смеси
газов по формуле (4.10). Выпишем значения физико-химических
свойств для отдельных компонентов смеси:
Н2
СО
0,09
1,25
1,25
10.14
0,75
0,75
1,41
1,4
1,4
Находим массовый состав газовой смеси:
0,00842
0,0166
0,017
н2
со
N2
50
40
10
50-0,09= 4,5
40-1,25= 50,0
10-1,25= 12,5
6,7
74,6
18,7
Итого
100
67,0
100,0
Вычисляем сь для смеси газов:
с0 = 0,067. Ю, 14. Ю3 + 0,746-0,75-Ю3 4-0,187-0,75-103« 1,379-10* Дж/(кг-К).
Находим динамический коэффициент вязкости газовой смеси
по формуле (1.12) и по табл. XI:
__ .(0,5-8,13.0,00842 4- 0,4-61,4-0,0166+ 0,1-59,5-0.017)-10~3
Исм "~ 0,5-8,13 + 0,4-61,4 + 0,1-59,5 ^
= 0,0156-10'3 Па.с.
Вычисляем коэффициент В в формуле (4.10):
5=0,25(9.1,4-5) = 1,9.
Определяем коэффициент теплопроводности газовой смеси:
Ьсм*=Ясу1см« 1,9* 1,379.10^0,0156* КГ3 = 0,041 Вт/(м-К).
Если рассчитать коэффициент теплопроводности газовой смеси
по правилу аддитивности, воспользовавшись данными табл. XXX,
то получим:
для аддитивности по объему
Ьем- 0,0926 Вт/(м-К);
по массе
^см = 0,0317 ВтДм-К).
174
Пример 4.7. Стенка печи состоит из двух слоев: огнеупорного
кирпича (бг = 500 мм) и строительного кирпича (б2 — 250 мм).
Температура внутри печи 1300 °С, температура окружающего
пространства 25 °С. Определить: а) потери теплоты с ! м2
поверхности стенки и б) температуру tB на грани между
огнеупорным и строительным кирпичом. Коэффициент теплоотдачи от
печных газов к стенке ах = 34,8 Вт/(м2-К); коэффициент
теплоотдачи от стенки к воздуху а2 = 16,2 Вт/(м2-К). Коэффициент
теплопроводности огнеупорного кирпича %i = 1,16 Вт/(м-К);
коэффициент теплопроводности строительного кирпича А2 =
= 0,58 Вт/(м-К).
Решение. Схема процесса теплопередачи через стенку
печи изображена на рис. 4.11.
а) Коэффициент теплопередачи:
К« Ц = * = 1,05 Вт/(м».К).
<*i ^ ^2 ct2 34,8 "*" 0,16 ~*~ 0,58 ~*~ 16,2
Потери теплоты с 1 м2 поверхности стенки:
q = K(t1 — t5) = 1,05(1300 — 25) = 1340 Вт/м2.
б) Температура 4 на грани между огнеупорным и
строительным кирпичом может быть найдена из соотношений
Я - (>i- У / (~ + y[) ; f = «i d ~/а> = ТГ ('2""/з)'
Отсюда
^-^300-^1261'С;
Строительный кирпич может применяться до 800 °С.
Следовательно, температура на внутренней поверхности
строительного кирпича 4 — 684 °С допустима.
Пример 4.8. Определить температуры внутренней t2 и
наружной ?3 поверхностей стенки теплообменника, а также температуру
ti наружной поверхности изоляции, которой покрыт аппарат.
Температура жидкости в теплообменнике t1 — 80 °С, температура
наружного воздуха th = 10 °С. Теплообменник сделан из стали;
толщина стальной стенки бст = 5 мм, толщина изоляции биз =
= 50 мм. Коэффициент теплоотдачи от жидкости к стенке аппарата
а1 ~ 232 Вт/(м2-К), коэффициент теплоотдачи от поверхности
изоляции к воздуху а2 = 10,4 Вт/(м2-К), коэффициент
теплопроводности изоляции Киз = 0,12 Вт/(м-К).
Р е hi е н и е. На рис. 4.12 дан схематический разрез стенки
аппарата, покрытого изоляцией.
175
ti*130Q°C
ti*80°C
ts«ro°c
Рис. 4.11 ^к примеру 4,7).
Коэффициент теплопередачи:
J
Рис, 4.12 (к примеру 4.8),
/< =
J
1 . ^ст | °из I 1
. _|_ j_ . _j
Cti Лет Лдз &2
1 0,005 t 0,05 , 1
0,12 ^ 10,4
232 ' 46,5
= 1,86 Вт/(м2.К),
где Яст = 46,5 Вт/(м-К) (табл. XXVIII).
Удельный тепловой поток:
q=, /С (^ — у «1,86 (80— 10)= 130 Вт/м2.
Температуры t2, ts и 4 определяются из соотношения:
9 = «I Ci — ^Я) = ТГ2- ^ — *з) = «2 (*4 — У-
б
ст
Температура внутренней поверхности стенки аппарата:
h = * i — — = 80
а*
130
232
= 79,4 °С.
Температура наружной поверхности стенки аппарата;
6ПЧ. „ . 130-0,005 7Q ог
-от 46,5
Температура наружной поверхности изоляции:
<' = i + ^-mr + 10=22'4°c-
Как видим, при наличии изоляции термическим сопротивлением
стальной стенки можно пренебречь (t2tt t3).
Пример 4.9. Определить среднюю температуру стенки в
паровом подогревателе, в котором водяным паром (/?абс = 0,4 МПа)
подогревается: а) воздух при атмосферном давлении; б) вода.
Средняя температура как воздуха, так и воды 30 °С. Толщина
стенки стальных труб бот = 4 мм. Коэффициенты теплоотдачи
для пара* воздуха и воды взять приближенно по средним данным
табл. 4.7 (турбулентное течение в трубах). Учесть наличие
ржавчины на обеих сторонах стенки. Тепловая прсводимость одного
Слоя ржавчины: 1/грж = 2320 Вт/(м2-К). Обозначение темпера-
Фур — см. на рис. 4.13.
176
Рис, 4,13 (к примлру 4.9).
Решение. Температуры
поверхностей стенки t2 и tB найдем из
соотношения:
Я = ОС! (ti — У = СС2(/3 — ti)-
Температура конденсации
водяного пара при /?абс = 4 кгс/см2
равняется 143 ЬС (табл. LVII).
а) Паром нагревается воздух.
Коэффициент теплопередачи:
к-
Воздух
или
вода
=J0°C
1 , ! 6
~ -г Лрж -г т—
Ст J_r _i_ J-
1
1
+
1
, 0,004 t
Л лс с ~Г
1
13 300 ^ 2320 ^ 46,5 ^ 2320 ^ 46,4
+
1
= 44,3 Вт/(м2-К).
Здесь коэффициент теплоотдачи для конденсирующегося пара
ах = 13 300 Вт/(м2-К), для воздуха а3 = 46,4 Вт/(м2-К),
коэффициент теплопроводности стали (табл. XXVIII) KQT =
= 46,5 Вт/(м-К).
Удельный тепловой поток:
q = K (h — ti) = 44,3 (143 — 30) = 5010 Вт/м3.
Температура ?2:
^2 = ^_J-=143-1^-=142,60G.
аг 13 300
Температура t3:
,3 = ,4+4- = зо+ 501°
а2
46,4
= 138 «XX
Средняя температура стенки:
б) Паром нагревается вода.
Коэффициент теплопередачи:
/С =
1
бет
1
а! +Лрж + 1^+Лрж+"^
1
1
г ooon T /ic с Т ооо/л 1
= 761 Вт/(м*.К).
13 300 ^ 2320
46,5
2320 ' 3420
Здесь коэффициент теплоотдачи для воды аа = 3420 Вт/(ма-К).
177
Удельная тепловая нагрузка:
q^K (f4 — /4) = 761 (143 —30) = 86000 Вт/м2.
Температура t2:
q 86 000
/2^г1-^7==14о~1ззоо =136*5 с'
Температура t3:
Средняя температура стенки:
'ср == (к + /з)/2 = (136,5 4- 55,2)/2 « 96 °С,
Пример 4Л0. В противоточный трубчатый конденсатор
поступает 200 кг/ч аммиака под давлением рабс =1,19 МПа при
температуре 95 °С. Конденсатор охлаждается водой, поступающей
при температуре 15 °С. Жидкий аммиак выходит из аппарата при
температуре конденсации.
Какое количество воды надо подавать в конденсатор, если
наименьшая разность температур аммиака и воды в конденсаторе
допускается в 5 К; какую температуру будет иметь вода на
выходе из конденсатора?
Решение. По Т—S диаграмме для аммиака (рис. XXVI)
или по табл. XLVIII находим, что температура конденсации
аммиака под давлением /?абс = 1,19 МПа равняется 30 °С.
Следовательно, входящий в конденсатор с температурой 95 °С аммиак
находится в состоянии перегретого пара. Для охлаждения его при
постоянном давлении р^с = 1,19 МПа от 95 °С до начала
конденсации, т. е. до 30 °С, необходимо отнять теплоты:
п 200(1647-103-Н67.10")
Cl== збоо я ООООВт'
где (1647-Ш3— 1467-Ю3) Дж/кг — разность удельных энтальпий паров
аммиака при давлении Рабс — 1»19 МПа и температурах 93 и 30 °С — см. диаграмму
T—S (рис. XXVI).
Для того чтобы затем сконденсировать пар аммиака в
жидкость, необходимо отнять теплоты:
Q2 ^ 200 (1467-103 — 323- 1С3)/3600 = 63 600 Вт,
где 323-10я Дж/кг— удельная энтальпия жидкого аммиака при раос =
= 1,Ш МПа и t= 30 °С.
Таким образом, водой должно быть отнято теплоты:
Q = Qj 4- Q2 = 10 000 + 63 600 = 73 600 Вт.
Изменение температуры аммиака в конденсаторе в
зависимости от количества отданной им теплоты изображено на рис. 4.14.
17«
Рис, 4.И (к примеру 4.10).
Исходя из условия, что
разность температур аммиака и
воды в любом сечении
конденсатора не должна быть меньше
5°С = 5 К.принимаем
температуру воды в том сечении
конденсатора, где начинается
конденсация аммиака и имеется
наименьшая разность
температур, равной 30 — 5 = 25 °С.
Удельная теплоемкость воды
при 0—100°С равна 4,19-Ю3 Дж/(кг-К). Тогда необходимый
расход воды может быть найден из уравнения теплового баланса
участка конденсации:
63 600 = GB.4,19*103(25— 15),
откуда GB = 1,515 кг/с.
Температуру воды на выходе из конденсатора tt определим из
уравнения теплового баланса конденсатора:
73 600= 1,515.4,19- Юз (^_ 15)|
откуда
и=*
73 600
1,515-4,1^-Юз
-f 288-299,6 K^^^C.
Пример 4.11, Теплота крекинг-остатка используется для
подогрева нефти. Определить среднюю разность температур в
теплообменнике между обогревающим крекинг-остатком и нагреваемой
нефтью, если крекинг-остаток имеет температуры (Нач = 300 °С,
'иоп ^ 200 °С, а нефть /1|ач = 25 °С, /кон = 175 °С.
Решение. Рассмотрим два случая [см. формулу (4.78)1.
/ случай. Прямоток — обе жидкости движутся в одном
направлении:
300 —*¦ 200
25—* 175
Мь = 275
М
м
25
At
м
275
25
> 2.
Следовательно,
Л/Ср =
275 — 25
« 104 °С == 104 К.
2,3 lg (275/25)
2 случай. Противоток — жидкости движутся в
противоположных направлениях:
300 —*• 200
175^— 25
М
б
Д/м= 125 Д/б«175* М
м
175
125
<2.
179
Рис» 4.15 (к примеру 4.12)»
Следовательно,
Д/ср=(125+175)/2=150°С==: 350 К.
Если рассчитать среднюю
разность температур для противотока
как среднюю логарифмическую,
получим 149 °С = 149 К.
Из приведенного расчета следует,
что при прочих равных условиях
средняя разность температур при
противотоке больше, чем при
прямотоке.
Необходимо отметить, что в
случае противотока обогреваемая
жидкость (нефть) может быть нагрета до
температуры, гораздо более высокой,
чем 175 °С (например, до 290 °С), а
крекинг-остаток может быть
охлажден много ниже 200 °С. Это является
основным преимуществом
противотока.
Пример 4.12. Определить среднюю разность температур в
многоходовом теплообменнике, имеющем один ход в межтрубном
пространстве и два хода в трубном (рис. 4.15):
Начальная температура горячего теплоносителя 7\ = 80 °С
Конечная » » » Г2 — 40 °С
Начальная » холодного теплоносителя tt — 10 °С
Конечная » » » to = 34 °С
Решение. Воспользуемся формулой (4.81), откуда
А = V8T'2 + Ы% « V 402 — 242 » 46,6.
Температурная схема при противотоке:
80-¦ 40
34 *- 10
Д*б « 46 Д/м = 30 •
Средняя разность температур в многоходовом теплообменнике:
А 46,6
м
ср
2,3 lg ¦*'«+*« + * 2,3 1gi|±|^±4M
= 32 °С = 32 К.
Д*б+Д*м—4
46 -f 30 — 46,6
Сделаем расчет по формуле (4.80):
А^ор *= еД/ д^пр-
180
Вычислим среднюю разность температур для противотока:
Д/пр = (46 + 30)/2 ~ 38 °С » 38 К.
Найдем величины Р и R (см. рис. VIII):
,,_,, 34-10
^~Tl — t1 ~~ 80-10 "" ' '
Г1-Г2 80-40
*~ ,,_,, ~ 34— 10 -1'66'
По графику (рис. VIII, а) определяем значение поправочного
коэффициента sAt. При Р = 0,34 и R = 1,66 находим едг — 0,9.
Следовательно, средняя разность температур в многоходовом
теплообменнике:
Atcp = eAt Д/Пр = 0,9-32 = 28,8 ^ = 28,8 К.
Пример 4.13. Вычислить коэффициент теплоотдачи для воды,
подогреваемой в трубчатом теплообменнике, состоящем из труб
диаметром 40x2,5 мм. Вода идет по трубам со скоростью 1 м/с.
Средняя температура воды 47,5 °С. Температура стенки трубы
95 °С; длина трубы 2 м.
Решение. Определяем режим течения:
D wdp Ь0,035-989 RA0„n
Re = ~ir^ 0,57.10-3 -60800'
где 0,57-10"3 Па-с — динамический коэффициент вязкости воды лри 47,5 °С
(табл. VI); р = 989 кг/м3 — плотность воды при 47,5 °С (табл. XXXIX).
Значение Re > 10 000. Коэффициент теплоотдачи определяем
по номограмме (рис. XII), построенной по формуле (4.17):
Nu =0,021e; Re°.8pro,43 (ргд>Гст)о.25(
Здесь ег = 1 для L/d = 2000/35 = 57 (табл. 4.3); Рг/Ргст =
= 3,74/1,85 = 2,02, где Рг - 3,74 при /ср. ш = 47,5 °С; Ргст =
- 1,85 при *от = 95 °С (табл. XXXIX).
По номограмме находим Nu = 300, откуда
а== —~ 0,035 ^551° *'<*'*>•
где к = 0,643 Вт/(м-К) — коэффициент теплопроводности воды паи 47,5 °С
(табл. XXXIX).
Пример 4.14. В трубах кожухотрубчатого теплообменника
нагревается бензол. Внутренний диаметр труб 53 мм, длина труб
3 м, скорость бензола в трубах 0,08 м/с, средняя температура
бензола 40 °С, температура поверхности загрязнения стенки,
соприкасающейся с бензолом, 70 °С. Определить коэффициент
теплоотдачи бензола.
181
Решение. Определяем режим течения бензола при / =
- 40 °С:
wdp 0,08-0/53-?58 „„ЛЛ 1ЛЛЛЛ
Re = ^T= 0,492-Ю-з - 7400 < 10 000.
Здесь \i = 0,492-Ю-3 Па-с— динамический коэффициент вязкости бензола
при 40 СС (табл. IX); р= 858 кг/м3 — плотность бензола при 40 °С (табл. IV).
Для выбора расчетной формулы при Re < 10 000 определяем
критерии Gr, Рг и Re при определяющей температуре t =
- 0,5 (/ж.ср + /ст) = 0,5 (40 + 70) - 55 °С:
d»p8PA/g _ 0,0533-8413-0,0394.9,81 _ ооп
°Г- j? - 0,413--10-ь -^-Ш ;
* ф 1800.0,413-]0'3 , 01 D даф 0,08-0,053-841 Q._rt
Pr==aX = 0Л4 ==°'3,; Кев"7"В 0,413-Ю-з -8630>
где р — 841 кг/м3 — плотность бензола при 55 °С (табл. IV); рА^ = (у2 —
— y^/oj, = (Pl — р2)/р2 =г (858 — 825,5)/825,5 = 0,0394; р2 = 858 и р2 =
= 825,5 кг/м3 — плотности бензола при 40 и 70 °С; ^ — 0,413-Ю"3 Па-с —
динамический коэффициент вязкости бензола при 55 °С (табл. IX); с =
= 1800 Дж/(кг * К) — удельная теплоемкость бензола при 55 СС (рис. XI); к =
— 0,14 Вт/(м-К) — коэффициент теплопроводности бензола при 55 иС (рис. X).
Произведение (GrPr) - 239-106-5,31 = 12,7-108. При
значениях 106 < (GrPr) < 12-Ю6 и Re ?> 3500 применяются для
горизонтальных труб формула (4.27), а для вертикальных —
формула (4.28). В нашем случае (GrPr) ?> 12-106. Однако для
приближенного расчета используем эти же формулы.
Горизонтальное расположение труб [формула (4.27)]:
Nu =* 0,022 Re0'* Pr°'! v^/M-ct)0'14 = 0,022-8630u«s.5,310'4 (0,413/0,36)°'!4 = 61,6.
Здесь u0T = 0,36-10"3 Па-с — динамический коэффициент вязкости
бензола при /0Т = 70°С (табл IX).
arop = NuW= 01,6-0,14/0,053= 162,7 Вт/(м2-К).
Вертикальное расположение труб [формула (4.28)]:
Nu =* 0,037 Ren*7-"1Pr°»4(p,/nCT)0'11 = 0.037-86300*7 -5,31°** (0,4I3/0,36)r-!1 = 65,6;
«верт = Nu X/d = 65,6-0,14/0,053 = 173 Bt/'(m2-K).
Пример 4.15. В трубном пространстве теплообменника
нагревается толуол. Внутренний диаметр труб 21 мм, длина труб 4 м.
Скорость толуола 0,05 м/с. Средняя температура толуола 30 °С.
Температура поверхности стенки, соприкасающейся с толуолом,
50 °С. Определить коэффициент теплоотдачи толуола.
Решение. Определяем режим течения толуола при его
средней температуре 30 °С:
Ыр 0,050,021-856 ,_ол
Re = — = —5Т522'-Ш^~ = {120>
где р = 856 кг/м3— плотность толуола при 30 °С (табл. IV); и, = 0,5*>2 X
X 10"3 Па -с — динамический коэффициент вязкости толуола при 30 СС
(табл. IX).
182
Для выбора расчетной формулы при Re < 10 000 рассчитываем
критерии Gr, Рг и Re при средней температуре / — 0,5 (30 +
+ 50) - 40 °С:
„ dVpA^g 0,021з.8472.1,И-Ю-3 (50 — 40)9,81 „ QQ 1Аб
Gr- j?-^-- 0,466»-Ю-» ~d,*M0.
Здесь р — 847 кг/м3 — плотность толуола при 40 °С (табл. IV); Р =
= 1,11'Ю"3 К-1 — коэффициент объемного расширения толуола при 40°С
(табл. XXXII); (я = 0,466-10"3 Па-с — динамический коэффициент вязкости
толуола при 40 °С (табл. IX).
Рг = сц/к = 1718-0,466- Ю-з/0,14 = 5,72,
где с = 1718 ДжУ(кг-К)—удельная теплоемкость толуола при 40 °С
(рис. XI); X = 0,14 Вг/(м-К)—коэффициент теплопроводности толуола при
40 °С (рис. X).
\i 0,466*10 3
Произведение (GrPr) - 3,33-106-5,72 = 19.10е >8-105.
Расчетные формулы:
а) Для горизонтальных труб при Re < 3500 [формула (4.25)]:
_ 0,8 (,900.5,72 Ш-)" ,19-10-)».' (^-f- ».П.
Здесь Ре — RePr = 1900-5,72; цст = 0,42-10"3 Па-с —динамический
коэффициент вязкости толуола при 50 ~С (габл. IX).
Таким образом,
arop = Nutyd = 21,75-0,14/0,021 = 145 Вт/(м2-К).
б) Для вертикальных труб при несовпадении свободной и
вынужденной конвекции (при движении жидкости сверху вниз при
нагревании) [формула (4.28)]:
Nu = 0,037Re°'75PrM (ц/цСт)0,11 = 0,037-1900°'75-5,720*4 (0,466/0,42)°'п =
= 21,17,
где цст = 0,42-Ю"3 Па-с — динамический коэффициент вязкости толуола
при 50 °С (табл. IX).
Следовательно,
ОЕверт = N" Я-Д/= 21,17-0,14/0,021 = 141 Вт/(м2-К).
Пример 4.16. Через трубное пространство кожухотрубчатого
теплообменника прокачивается рассол хлористого кальция
концентрации 24,7% (масс.) при средней температуре /ср.р = —20 °С
со скоростью 0,1 м/с. Внутренний диаметр труб 21 мм, длина
труб 3 м. Средняя температура поверхности загрязнения стенки,
соприкасающейся с рассолом, /ст = —10 °С.
183
Определить коэффициент теплоотдачи хлористого кальция.
Решение. Критерий Рейнольдса при средней температуре
рассола /ср,р = —20 °С [при концентрации ~25% (масс.)]:
Не ~ ~]Г" 99,96-10-* 2Ы}
где р = 1248 кг/м3—плотность рассола при /ср, р = —20 °С (табл. IV); \i =
— 99,96-10"4 Па-с — динамический коэффициент вязкости рассола при /ср р =
== — 20 °С (табл. LI).
Для выбора расчетной формулы при Re < 10 000 находим
критерии Gr, Pr и Re при определяющей температуре / =
= 0,5(/от+ /ср.р) = 0,5 [(-10) + (-20)] - —15 ОС-
d3paP Atg 0,021з. 12462-0,0036b 9,81 _ А 77 1л4
Ur~ |? ~ 81,32". Ю"8 -и,//-ш,
D __ ф 2861-81,32-lQ-^ wdp _ 0,1-0,021-1246 __ „00
1Г~"Т_ М67 ~4УА Ке ? 81,32.10"* ~бггш
Здесь р= 1246 кг/м3—плотность рассола при /=—15 °С (табл. IV);
РД* = (у2 — их)/»! = (pi — р2)/р2 = (1248 — 1243,5)/1243,5 = 0,00361; Pl =
= 1248 и р2 = 1243,5 кг/м3 — плотности рассола при /ср. р = —20^ и tCT =
= —10 °С (табл. IV); JA — 81,32-Ю"4 Па-с — динамический коэффициент
вязкости рассола при t = —15 °С (табл. LI); с = 2861 Дж/(кг°К) — удельная
теплоемкость рассола при t=—15 °С (табл. LII); % = 0,467 Вт/(м-К) —
коэффициент теплопроводности рассола при t=—15 °С (табл. LI).
Произведение (GrPr) - 0,77• 104-49,8 = 3,84.10е <Г 8-105 —
расчетная формула как для горизонтальных, так и для
вертикальных труб (4.23):
= 1,55.91,31/3.1,3°'14= 1,55.4,5.1,037 = 7,24,
где |^ст = 62,69-Ю"4 Па-с — динамический коэффициент вязкости рассола при
tCT = —10 °С (табл. LI).
Коэффициент теплоотдачи рассола:
а = Nutyd = 7,24-0,467/0,021 = 161 Вг/(м2К).
Пример 4.17. В условиях предыдущего примера рассчитать
коэффициент теплоотдачи рассола при его скорости 1,24 м/с.
Решение. Определяем режим течения раствора
хлористого кальция:
wdp _ 1,24.0,021.1246
Re - ~ " 81,32.10-* °°°*
При значении (GrPr) = 3,84-105 <8-105 в пределах 2300 <
< Re = 4000 < 10 000 приближенный расчет (с запасом)
коэффициента теплоотдачи осуществляем по графику (рис. 4.1). При
Re = 4000 находим:
Рг°>43 (Рг/Ргст)0'25
184
откуда
Nu = 12Pr0'43 (Pr/PrCT)0'25 = 12-49,80'43 (49,8/37,77)0'25 - 69.
Здесь PrrT = 2874-62,69-10~4/0,477 = 37,77 при tCT = —10 °C (табл, LI
и LII).
Следовательно,
a = Nutyd = 69-0,467/0,021 «= 1535 Bt/(m3-K).
Пример 4Л8. Определить коэффициенты теплоотдачи воздуха
для двух случаев: а) однократное поперечное обтекание под углом
90° многорядного пучка шахматно расположенных труб (рис. 4.2};
скорость воздуха в наиболее узком сечении 12 м/с; б) движение
воздуха через межтрубное пространство (с поперечными
перегородками) кожухотрубчатого теплообменника; расчетная скорость
12 м/с (рис. 4.4). В обоих случаях наружный диаметр труб
44,5 мм, средняя температура воздуха 200 °С, давление
атмосферное.
Решение, а) Однократное обтекание пучка труб.
Критерий Рейнольдса:
wdp __ 12-0,0445.0,745
Re-"1T" - 0,026-Ю-з ~ 1530°'
973
где р = 1,293 -~ = 0,745 кг/м3 — плотность воздуха при 200 СС; ц = 0,026 X
X 10~? Па*с— динамический коэффициент вязкости воздуха при 200°С
(рис. VI).
По формуле (4.32):
Nu = 0,356еф Re0»6 = 0,356-1.15 ЗОО0,6 = 115.
Здесь еф = 1 (табл. 4.5),
Коэффициент теплоотдачи:
а = NuK/d = 115-0,0395/0,0445 = 102 Вт/(м3.К),
где % = 0,0395 Вт/(м • К) — коэффициент теплопроводности воздуха прн 200 °С
(табл. XXX).
б) Течение воздуха в межтрубном пространстве
теплообменника с поперечными перегородками в кожухе.
Если задана расчетная скорость, то расчет аналогичен
предыдущему, но в формулы для определения Nu или а вводится
коэффициент еф = 0,6 (см. стр. 157):
ефсс = 0,6-102 = 61 Вт/(м2-К).
Пример 4.19. В вертикальном кожухотрубчатом
теплообменнике, состоящем из 61 трубы диаметром 32x2,5 мм и высотой
1,25 мм, стекает сверху тонкой пленкой по внутренней
поверхности труб 13 м3/ч четыреххлористого углерода. Средняя
температура четыреххлористого углерода 50 °С, температура
внутренней поверхности труб 24 °С.
185
Определить коэффициент теплоотдачи от четыреххлористого
углерода к стенке в двух случаях: а) четыреххлористый углерод
стекает тонкой пленкой по внутренней поверхности труб; б)
четыреххлористый углерод проходит по трубам, заполняя все их
поперечное сечение.
Решение, а) Стекание пленкой. В зависимости от режима
течения коэффициент теплоотдачи будем определять по одной
из формул (4.41) или (4.42). В обеих формулах значения физико-
химических констант надо брать при температуре пограничного
слоя (пленки):
tnx = Сер. ж + >ст)/2 « (50 + 24)/2 - 37 "С.
Критерий Рейнольдса (формула (4.43)]:
Rp _ 4G 4.13-1560
Re *= Imf - 3600.3,14.0,027.61-0,77.10-* = 5660>200°-
Здесь fi в= 0,77'Ю"3 Па-с — динамический коэффициент вязкости
четыреххлористого углерода при 37 °С (табл. IX).
Стекание пленки турбулентное. Применим формулу (4.41):
_ HVg __ 1,25М560*-9,81 _
Ga—v?~~~олмо^"75,6'10 '
При 37 °С находим по номограмме (рис, XIII) Рг = 6. Тогда
Nu = 0,01 (GaPrRe)1'3 = 0,01 (78,6-1012-6-5660)1/3 » 13 900,
откуда
апл = Nu Я/tf = 13 900.0,109/1,25 = 1210 Вт/(м2.К),
где X = 0,109 Вт/(м3-К)—коэффициент теплопроводности четыреххлористого
углерода при 37 СС.
б) Сплошное заполнение труб. Скорость течения
четыреххлористого углерода:
W== 61-0,785.0,027*-3600 ==0'103 м/с*
Критерий Рейнольдса:
Re « wdp/ц ^ 0,103-0,027.1536/(0,65-10'3) = 6570,
где 1536 кг/м3—плотность четыреххлористого углерода при 50 °С (табл. IV);
0,65-Ю"3 Па*с—вязкость четыреххлористого углерода при 50 °С (табл. IX).
Критерий Рейнольдса Re = 6570, следовательно, режим
движения соответствует переходной области.
Из графика (рис. 4.1) для Re = 6,6-103 имеем:
Nu ^ 22,6Рг0»43 (Рг/Ргст)0'25 = 22,6-5,40'43 (5,4/6,6)0'25 = 40.
Здесь Рг = 5,4 — критерий Прандтля для четыреххлористого углерода при
50 °С (рис, XIII); Рг = 6,6 —то же при 24 °С (рис. XIII).
186
Коэффициент теплоотдачи при полном заполнении трубок
жидкостью:
а= NuVd = 40.0,10/0,027 « 150 Вт/(м2-К),
где X =0,10 Вт/(м2-К) — теплопроводность четыреххлористого углерода при
50 СС (рис. X).
Отношение апл/а = 1210/150 л* 8.
Таким образом, в условиях данного примера коэффициент
теплоотдачи при стекании четыреххлористого углерода тонкой
пленкой в 8 раз больше коэффициента теплоотдачи при сплошном
заполнении всех трубок теплообменника жидкостью.
Пример 4.20. Изопропиловый спирт нагревается в баке в
условиях свободной конвекции горячей водой, подаваемой насосом
через ряд горизонтальных труб наружным диаметром 30 мм.
Определить коэффициент теплоотдачи для изопропилового спирта,
если его средняя температура 60 °С, а средняя температура
наружной поверхности труб 70 °С.
Решение. Коэффициент теплоотдачи при свободном
движении жидкости около горизонтальных труб рассчитываем по
формуле (4.46):
Nu = 0,5 (GrPr)0'25 (Рг/Ргст)0-25.
Значения констант, входящих в критерий Gr = d3p-$At g/\i%,
для определяющей температуры 60 °С: р = 752 кг/м3 (табл. IV);
\х = 0,8 -Ю-3 Па-с (табл. IX). Величину [ЗА/ находим по
уравнению:
f>At = (vt2 — vtj)/vtv
где Vi — удельный объем изопропилового спирта при 70 °С; vt — то же
при 60 °С.
Удельные объемы можно рассчитать по уравнению:
wj = ii0(l + а/ + W2 +4*h
В справочнике [13, т. П для изопропилового спирта даны
следующие значения коэффициентов (округленно): а ~ 1,043 X
X 1б-3; b - 0,443-10-в; с* = 2,73-1(Г8. Тогда
р м a(k-t\) + b(t?-t\)-\-c{q-tb
р ill — : ; ; ГТ ; —
' 1 -г at] -j- bt-} +ct{
- J '°il?Ji^liZ^ — CO) f 0,443-10-° (703 — 602) 4- 2,73-10~8 (703~- 603) _
I - !7W3-i6-8-60 -f- 0,443-10^-60' -ь2(/3-10"8-603 "
= 0,0135.*
J/ ч ]-• i
X\j, I: i i ¦ > • A [J ttL . s.' ,r t!..
r.. n-v^Mfs 0,03B-75ff-P,0135-9,81 q ,_ |M
Сi -- 1(5— = (O^To^ - = 3,16.И*.
* Wo -'^". .-ллП \>^ l,Il>.10-:t К"1 и Э Л/= 0,0112.
187
По номограмме (рис. XIII) находим для изопропилового
спирта: при 60 °С Рг = 19; при 70 °С Ргст = 16,5. Следовательно,
Nu - 0,5 (GrPr)0'25 (Pr/PrCT)0'25 = 0,5 (3, J6- JO6- 19)u'25(19/16,5)0'25 = 46.
Коэффициент теплопроводности изопропилового спирта при
60 °С находим по формуле (4.8):
h =М1 — в (^ — 0)] = 0,154 [(1 — 1,4- 10~3-60)J = 0,141 Вт/(м-К),
где л0 — 0,154 Вт/(м-К)— коэффициент теплопроводности изопропилового спирта
при0°С [13, т. 1]; е= 1,4-10"3 (принимаем как для пропилового спирта).
Коэффициент теплоотдачи;
а = Nuk/d * 46-0,141/0,03 = 216 (Вт/(м2- К).
Пример 4.21. Определить коэффициент теплоотдачи от
конденсирующегося насыщенного пара бензола к наружной
поверхности пучка вертикальных труб при атмосферном давлении.
Температура стенки трубы 75 °С. Высота трубок в
конденсаторе 4 м.
Решение. Коэффициент теплоотдачи при конденсации
насыщенного пара бензола находим по формуле (4.52):
Физические свойства жидкого бензола при температуре
конденсации 80,2 °С: К = 0,13 Вт/(м-К) (рис. X); р - 815 кг/м3
(табл. IV); |.i - 0,316-Ю-3 Па-с (табл. IX); г = 384 кДж/кг
(табл. XLV). Значение гг принимаем равным 1 —см. пояснение
к формуле (4.50). Следовательно,
оА,-14/^133-8152-384-103 11п0 D „ , „ч
*-2>04У 0,316.10-3.5,2.4 ~1102 ВтЛ»-Ю*
где 5,2 К = 5,2 °С — разность температуры конденсации и температуры стенки
80,2 — 75).
Пример 4.22. В вертикальных трубах испарителя (куб
ректификационной колонны) кипит толуол с небольшим содержанием
бензола при средней температуре 110°С. Температура
конденсирующегося водяного пара (в межтрубном пространстве) 136 °С.
Диаметр труб 25x2 мм.
Определить коэффициент теплопередачи.
Принять коэффициент теплоотдачи от конденсирующегося
водяного пара к стенке аг = 10 000 Вт/(м2-К), температуру
поверхности стенки, соприкасающейся с толуолом, /ст, 2 =
= 128,5 °С. Влияние примеси бензола на теплоотдачу не
учитывать.
188
Решение. Коэффициент теплоотдачи от стенки к кипящему
толуолу по формуле (4.62):
м ЧЫ^кип)2
«2 = «КИП == Ь3 -
jiTOi Кцп
0,0933.0,1162-777 (128,5—ПО)2
0,251.ИГ3-18,35-10"8 (273 + 110)
1630 Вт/(м2-К).
Здесь физические свойства жидкого толуола при /КИП=110°С: рт =
= 777 кг/м3 (табл. IV); Хт = 0,116 Вт/(м-К) (рнс. X); (iT = 0,251 -КГ3 Пас
(табл. IX); о = 18,35-10 3 Н/м — поверхностное натяжение толуола при 110СС
92 1¦273
(табл. XXIV). Плотность паров толуола рП = оо л /07Q > ini ~ 2^ кг/м3
(92,1 кг/кмоль — мольная масса толуола). Движущая сила процесса: А7"КИП =
= 128,5—110= 18,5 °С= 18,5 К. Коэффициент Ь = 0,093 (из рис. 4.10).
Принимаем тепловые проводимости загрязнений стенки со
стороны пара и толуола по 1/г = 5800 Вт/(м2-К) (табл. XXXI).
Коэффициент теплопроводности стали к = 46,5 Вт/(м-К)
(табл. XXVIII). Тогда
1 1
*"" KQAA 1 АС С 1
2580 Вт/(м2-К).
5800 ' 46,5 ' 5800
Коэффициент теплопередачи:
К = —j 1 j— = 910 Вт/(м2-К).
1 OCQA t
10000^ 2580 ' 1630
Средняя разность температур при кипении: А/ср = 136 —
— ПО — 26 °С = 26 К. Тогда плотность теплового потока:
q = К А/Ср = 910-26 = 23 600 Вт/м2.
Для определения коэффициента теплоотдачи от стенки к
кипящей в большом объеме жидкости можно также использовать
следующие формулы:
1) по С. С. Кутателадзе [4.2],
NuHcn = 7,0- Ю"4 (Re Kpf>7 Pr0'35,
#. * *
где Nu = аШТ11!к Re = qlpml(rgnvmyt Kp = plla\ Pr = vw/aw = \lcp/K; I =
= V°/lg(Pw — Pn)] — определяющий линейный размер (см, стр. 165).
Для плотности теплового потока q = 20 000 Вт/м2:
* 1,555-10"3-777 . с,й 1А_3
Re^^ 362,5.10^2,9.0,251.10-^ ==4-578-10<?;
/ 18,35-Ю-з _
У 9,81 (777-2,9)-1'555'10 м'
/Ср= 1,013- Юб-1,555-10-3/18,35-10'3 = 8584;
рг _ 0,251-10-»-0,45-4190
где ср = 0,45-4190 Дж/(кг-К).
189
Тогда NuHCn — 15,34, откуда
_^ИогЛ _ 15,34-0,116 _
«кип = * 1,555-10~3 ~ ьт/(м ¦ К).
2) По А. М. Кутепову [4.5],
^Лcп = c(P<•63^'5)', и^ Nu„cn = av,
где /V = РеК°'63Л'°'\
Пои .V "^ 107 С == 3,2-Ю-5 и л = 0,7, при 10s < ЛГ < 107'
С = 0,101 и п = 0,25.
*
* * л/ *
Здесь NuHCn = а//?.>к; Ре = —- = RePr;
гржа
Рж Рж — Ри срТа gVo/lg(pm—pa)\ ' а g ]/~o/[g (рш—рп) 1
Для <? = 20 000 Вт/м2:
Re - 4,578-10-3.20000 = 91,56; Ре = RePr =^ 91,56-4,08 = 373,6;
2,9 2,9 362,5.103
Ki~ 777 777 —2,9 0,45-4190(273+ ПО) Х
X г 362-5103 = =174; *?.«-25,76;
9,81 Kl8f35-10-3/L9,8l (777 — 2,9)] *
К Г 362,5-10* 23 79 10я-
а~йГо/1,{рт-Ы\~ $ "9,81-1,555-10- -*"» Ш>
/С^5 = 4,877-10*;
N = Ре/С?'63/^'5 « 373,6-25,76-4,877-103 = 4,68-107.
Для этих значений N: С = 3,2 ¦ 10~5; /г = 0,75. Тогда
Nuncn = Ctf" =3,2.10"5-565 800 = 18,106,
откуда
-=^1^ 18,106 , *'и* ^ 1350 Вт
кип- * - -> — 1,555-10-» ^ мз.к •
Расхождение расчетных данных по приведенным формулам
±20 %.
Пример 4.23. Метиловый спирт (100 %) нагревается в трубном
пространстве одноходового кожухотрубчатого теплообменника от
15 до 40 °С. Противотоком в межтрубном пространстве течет вода,
которая охлаждается от 90 до 40 °С. Теплообменник состоит из
111 стальных труб диаметром 25x2 мм. Скорость метилового
спирта в трубах 0,75 м/с.
190
Определить необходимую поверхность теплопередачи
теплообменника и длину трубчатки, если принять коэффициент
теплоотдачи от воды к стенке 840 Вт/(м2-К), суммарную тепловую
проводимость обоих загрязнений стенки 1700 Вт/(м2-К) и среднюю
температуоу загрязнений поверхности стенки со сторон л спирта
38 °С.
Решение. Средняя разность температур:
90 —* 40
40^-15
At6 = 50 Д/м = 25.
Отношение A/G/A/M = 50/25 = 2, следовательно, можно
принять среднюю аоифметическую оазность температур А^ср =
= 0,5(50 + 25) = 37,5 К.
Средняя температура спирта;
/2==0,5(40+ 15)= 27,5 °С.
Массовый расход спирта:
G.2 = n.0,785d!«/.2p.2= Ш-0,785-0,0212-0,75-785 = 22,6 кг/с,
где р2 = 785 кг/м3 — плотность метилового спирта при 27,5 °С (табл. IV).
Количество передаваемой теплоты:
Q = G2c2 (*кон. 2 — .'нач. 2) == 22,6-2520 (40 — 15) = 1,424-106 Вт,
где с2 = 2520 Дж/(кг-К) — удельная теплоемкость спирта при 27,5 °С
(рис. XI).
Критерий Рейнольдса для спирта:
Re2=^^^°-7n5y,2'3785 ^23 000.
^2 0,53-10 3
Здесь ц9 = 0,53'10"3 Пас— динамический коэффициент вязкости спирта
при 27,5 °С (табл. IX).
Критерий Прандтля для спирта:
Рг = с3(хгАя = 2520-0,53-10"3/0,212 = 6,3,
где Х2 = 0,212 Вт/(м-К)— коэффициент теплопроводности спирта при 27,5°С
(рис. X).
Режим течения спирта турбулентный, поэтому принимаем для
расчета формулу (4.17), полагая гг = 1:
Nu2 = 0,021Re^8Pr^43(Pr2/PrCT)°'25 = 0,021-23 000°'8.6,30»43 (6,3/5,94)0'25 =
= 145.
Здесь
PrCT = (c2lu2A2)cr = 2589-0,48- Ю-з/0,209 = 5,94,
где c2t (i2 и ^2 определены при /ст = 38 °С.
191
Тогда
Nu«b 145-0,212
^^-Л"* 0,021 =1460Вт/(м"-К).
Коэффициент теплопередачи:
1
/С-
1 . ^ст , V , 1
+-F^ + 2>мгп + -
«1 ^ст ^ загР ^ а2
--1 0,002 | 1—-г-400 IW-K),
840 + 46,5 + 1700 + 1460
где Хст = 46,5 Вт/(м ¦ К) — коэффициент теплопроводности стали (табл, XXVIII).
Поверхность теплообмена;
Q 1,424-10° _ ле 2
Г ~ KAtcp " 400-37,5 -уй м '
Длина трубчатки по среднему диаметру труб:
, F 95
/т*ср ~~ 111-3,14.0,023 -п'там-
Здесь rfcp = (0,025 + 0,021)/2 = 0,023 м.
По ГОСТ 15122—79 для теплообменника с кожухом 400 мм
и числом труб 111 трубчатка имеет длину 2; 3; 4 и 6 м. Чтобы
обеспечить запас поверхности теплообмена, принимаем 5 аппаратов
с трубчаткой длиной 3 м.
Запас поверхности теплообмена будет равен:
Для принятых теплообменников L/d = 3000/25 = 120 > 50.
Следовательно, величина гг = 1 принята правильно.
Пример 4.24. Воздух подогревается в трубном пространстве
двухходового кожухотрубчатого теплообменника с 2 до 90 °С
при среднем давлении (абсолютном) 810 мм рт. ст. Объемный
расход воздуха при нормальных условиях (0 °С и 760 мм рт. ст.)
составляет v0 = 8290 м3/ч. Общее число труб — 450, на один ход
трубного пространства — 225. Диаметр труб равен 38x2 мм.
В межтрубное пространство подается насыщенный водяной пар
под давлением (абсолютным) 2 кгс/см2 (~0,2 МПа).
Определить необходимую поверхность теплообмена и длину
трубчатки. Принять коэффициент теплопередачи равным
коэффициенту теплоотдачи воздуха.
Решение. Массовый расход воздуха:
52 = ^оРо/3600 = 8290-1,293/3600 =* 2,98 кг/с,
где ро = 1,293 кг/м3 — плотность воздуха при нормальных условиях (табл. V).
192
Средняя разность температур:
А . (119,6-2)-(П9,6-90) _ 88 __ ?д 0Q
д^р- 001 119,6 — 2 "" 2,3 \g 3,973 "" '
2>3 >fi 119,6-90
Средняя температура воздуха:
'ср. 2 = 'кокд - Д'ср = 119,6 — 63,79 & 55,8 °С.
Плотности воздуха при средних рабочих условиях:
<* = *>!&= ! '293 760 (827°3 +355,8) " 1>Ш ^
Объемный расход воздуха при средних рабочих условиях:
1>2 = 52/р2 = 2,98/1,144 = 2,6 м3/с.
Скорость воздуха в трубах:
Ю« = f = 225.0.78560.034^ = 12,76 М/С'
где /2 — площадь поперечного сечения труб (на один ход).
Критерий Рейнольдса для воздуха при 55,8 °С:
w2d2p2 12,76-0,034.1,144
^""""й" oWW* = 24800'
Здесь fi2 = 0,02* 10"3 Па-с — динамический коэффициент вязкости для
воздуха. ир*\ 55,врС (jhsc. УЦ.
Режим движения воздуха турбулентный [формула (4,22) h
Nu2 = 0,018Re§'8e, = 0,018-24 800м.1 = 59.
Следовательно,
аг = NuaA,a/d2 = 59*0,0284/0,034 = 49,3 Bt/(m2-K).
Здесь А-2 = 0,0284 Вт/(м • К) — коэффициент теплопроводности воздуха
при 55,8°С (табл. XXX). Величину е принимаем равной 1, предполагая, что
Lid будет больше 50.
Количество передаваемой теплоты:
Q = Q& ('кон. 2 — 'нач. 2) = 2,98-1006 (90 — 2) = 263 800 Вт,
где с2 = 1006 Дж/(кг-К) — удельная теплоемкость воздуха при 55,8°С
(табл. XXVII).
Поверхность теплообмена (по заданию К & а2):
р - Q _ 263 800 _ а
УГдЦ" 49,3-63,79 -б^ум*
Ввиду того, что коэффициент теплоотдачи для воздуха много
меньше коэффициента теплоотдачи для пара (а2 <^ осх), расчет-
7 Павлов К- ф- и ДР. *^3
ную поверхность определяем по внутреннему диаметру труб
d - 0,034 м.
Длина трубчатки по расчету:
= 3,49 м.
225- и -0,034 225-3,14-0,034
По ГОСТ 15121—79 длины трубчатки для двухходового ко-
жухотрубчатого теплообменника с диаметром кожуха 800 мм и
числом труб 450/225 составляют 2; 3; 4 и 6 м. Принимаем L =
= 4м.
Запас поверхности теплообмена:
Ф^ 4~ У9 100^15%.
Проверка принятой величины ег:
Ljd = 4000/34 « 117 > 50.
Таким образом, величина ег = 1 была принята правильно.
Пример 4.25. В выпарном аппарате со стальными трубами
высотой 4 м и толщиной стенок 5 = 2 мм кипит под разрежением
0,64 кгс/см2 при средней температуре 80 °С 20% водный раствор
аммиачной селитры. Греющий пар имеет давление (абсолютное)
1,1 кгс/см2 (—0,11 МПа).
Определить удельную тепловую нагрузку и коэффициент
теплопередачи.
Решение. Температура конденсации греющего пара 101,7 °С
(табл. LVII). Средняя разность температур:
Д/ор = 101,7 — 80 « 21,7 °С - 21,7 К.
Коэффициент теплоотдачи для конденсирующегося греющего
водяного пара находим по формуле (4.55):
».=''»(-^)|,з'-"э-
Физико-химические свойства конденсата взяты из табл.
XXXIX. Для 20% раствора аммиачной селитры при 80 °С
[5.1]: А, = 0,445-1,16=* 0,517 Вт/(м-К); 9т = Ю51 кг/м3; ц «
= 41-10-6-9,81 = 0,402-Ю-8 Па-с; а= 65,3-10"3Н/м (принимая
I о 974 ft 4fi
такое же изменение ас температурой, как у воды); рд = ' ' ' =
= 0,224 кг/м3 (где р0 = М/22,4 = 18/22,4).
194
Коэффициент теплоотдачи для кипящего раствора находим по
формуле (4.62):
av^b
( KW
1/3
\ Н^кип
,2/3 _
Здесь значение коэффициента Ь — 0,078 определено при pmfpu =
1051/0,224 = 4700 по формуле (4.62а):
6 = 0,075[. + ,0(-^-,)-2/3].
Сумма термических сопротивлений стенки и загрязнений
(табл. XXVIII и XXXI):
ст = "5 \- Лзагр. 1 + гзагр. 2 я
2-
0,002
I СОЛЛ I
3,88-ИГ4 (м2.К)/Вт,
46,5 ' 5800 ' 5800
где Кст = 46,5 Вт/(м-К) — коэффициент теплопроводности стали (табл. XXVIII).
Коэффициент теплопередачи:
t
К =
+ 7 .'ст +
1
«л ¦ ?J "' ' «р 2,17.10V0,33
Удельная тепловая нагрузка:
21,7
1
+ 3,88.10-4 +
1
2,43,?
,0,67
Откуда
^ — /С Д/Ср — 04бь ,0-5о.зз + 3)88. io*-4 + 0.412?-°'67
0,461 - 10-У'^ + 3,88- ЮЛ + 0,412<у0'33 — 21,7 - 0.
Это уравнение решаем графически, задаваясь значениями q
(рис. 4.16), у — левая часть уравнения. При */= 0 находим
q = 21 000 Вт/м*.
Коэффициент теплопередачи: У
/С = ^ср« 21 000/21,7 = 968 Вт/(м2-К).
Пример 4.26. Определить
поверхность противоточного теплообмен- 3
ника, в котором горячая жидкость
(поглотительное масло) в количестве ;
3 т/ч охлаждается от 100 до 25 °С
холодной жидкостью, нагревающейся °
от 20 до 40 °С, Известно, что коэф- ~>
Рис. -".16. Графическое опре ..сленне q (к
примеру 4.25), -J
2,2 2,6 3,0
U7
195
фициент теплопередачи следующим образом изменяется с
температурой масла:
Г, °С 100 80 60 40 30 26
/С, Вт/(м2-К) 354 350 342 308 232 166
Удельная теплоемкость масла 1,67-103 Дж/(кг-К).
Решение. По условию задачи коэффициент теплопередачи
сильно меняется вдоль поверхности теплообмена, поэтому
среднюю логарифмическую разность температур применить нельзя.
Воспользуемся уравнением теплопередачи в дифференциальной
форме:
GrcT dT = — К (Т — t) dFt
откуда
т т
•u& J жг-о гг J K(T-t)>
т t
н J к
где 7\ / — температура горячей и холодной жидкости соответственно,
т
н
Интеграл [ „ __ . решаем графическим путем.
Предварительно найдем данные, необходимые для построения
графика с ординатой к {т^*\ и абсциссой — температурой
горячей жидкости 7\ Сначала из уравнения теплового баланса
Grcr (Гн - Т) = Gxcx (*н - ()
определим отношение:
<Vr tK-~tn 40 — 20
Gxcx Гн~ /к 100 — 25
Следовательно,
= 0,267.
f = /„ - -^- (Гв — Г) « 40 - 0,267 (100 - Г).
GA
Задаваясь значениями Г, находим по этому уравнению
соответствующие температуры холодной жидкости t. Полученные
данные сводим в табл. 4.9.
По данным табл. 4.9 строим график (рис. 4.17). Площадь под
Гн
кривой S= \ к iT _ t) определяем приближенно по формуле
в
трапеции:
<; — Гн"~г« /Уо±Уп , (1 , „ , . „ \
5 _ ^ _ ЬУ1~гУъ+л" -гУп-г)
196
Таблица 4.9
т
100
80
60
40
30
25
t
40,0
34,7
29,3
24,0
21,3
20,0
Т <ш t
60,0
45,3
30,7
16,0
8,7
5,0
К
354
350
342
308
232
166
., 1 Л*
K(T-t) -10
0,47
0,63
0,95
2,30
4,96
12,07
Примем п — 10 и составим табл. 4.10, взяв из графика
значения ординат у. По данным табл. 4.10 находим:
Тя-Тк ( Уо + Уп +я?у
s =
п
=
100 — 25 /12,07 + 0,47
10
(
+ 12,2) 10~4 = 138-104 (ма.К)/Вт.
Требуемая площадь поверхности теплообмена:
F = Grc
г*т
j
к
dT
3000
К (T — t)~~ 3600
1,67.10М38-10-* —19,2 м2.
Если определить площадь под кривой более точно
(планиметрированием), получим F = 18,9 м2.
Для сравнения рассчитаем требуемую поверхность теплообмена,
если принять постоянным значение коэффициента теплопередачи К
(при средней температуре) и применить среднюю логарифмическую
разность температур:
100
40*
-25
20
Д*пп =
Д*б = 60 А(ы = 5;
60 — 5
= 22,2°С =
ср~ 2,3 lg (60/5)
=> 22,2 К.
Средняя температура
охлаждаемой жидкости:
^ср = *©р + Д'ср = 30 + 22,2 = 52,2 °С.
При этой температуре К =
= 329 Вт/(м2-К).
Рис» 4,17 (к примеру 4,26),
Г
KU-Q
12
10
8
6
4
2
Ю4
Уа
0 10 20 30 40 50 60 70 60 90 !00
Т,°С
197
Таблица 4.10
7\°С
Н©мер
ординаты
К { Т ~ t)
)04
Т, PC
Номер
ординаты
У —
К ( Г - t)
in*
25
32,5
40
47,5
55
62,5
0
1
2
3
4
5
12,07
3,85
2,30
1,60
1,13
0,85
70
77,5
85
92,5
100
6
7
8
9
10
0,74
0,65
0,58
0,50
0,47
Расход передаваемой теплоты:
3000
Q
3600
1,67-103 (100 — 25) =- 104 500 Вт.
Площадь поверхности теплообмена:
Q 104 500
F =
КМ
ср
329-22,2
= 14,3 м2.
В
Как видим, расчет по этому методу дает большую ошибку
сторону уменьшения требуемой поверхности теплопередачи.
Пример 4*27. Толуол (горячая жидкость) в количестве Ог =
= 1400 кг загружен в сосуд, в котором имеется змеевик. Через
змеевик пропускается вода (холодная жидкость). Толуол
охлаждается от температуры 7\ = 105 до Т2 = 25 °С в течение т ч.
Вода повышает свою температуру от tt ~ 13 °С до t. Конечная
температура воды в периодическом процессе все время
уменьшается по мере понижения температуры толуола. В конце процесса
охлаждения толуола черезт чтемпература /станет равной ^(<Т2).
Сколько времени т потребуется для охлаждения толуола и
каков будет общий расход воды Gx, если поверхность теплопередачи
змеевика F = 3,2 м2, а значение коэффициента теплопередачи
принять постоянным и равным К = 255 Вт/(м2К)?
Решение. Схема процесса:
в сосуде (толуол охлаждается): 7\ = 105 °С, через т ч Т2 = 25 °С:
U
?
в змеевике (вода нагревается): tx = 13 С, через т ч
Принимаем t2 = 18 °С.
Уравнение теплопередачи:
Q = KF Л/Ср. охл^-
Средняя разность температур для периодического процесса
охлаждения жидкости в сосуде [11:
At
ср. охл
in
7\
\А In A/
105
Т2 -
25 / 1,714-1
ш
-13 \1,
105
25-ЛЗ"
714 In 1,714
) = 30,36 °С = 30,36 К.
198
Величина А постоянна для всего процесса охлаждения. Для
любого момента времени, когда температура охлаждаемой
жидкости равна Т:
При расчете поверхности теплообмена принимаем Т = Т% =*
*= 25 °С:
л г3-^_ 25-13 m
Тъ—t* 25—18
Средняя конечная температура охлаждающей жидкости (воды):
^2ср = Д^ср. охл In А + h == 30,36 In 1,714 + 13 = 29,35 °С.
Количество теплоты, отдаваемое толуолом воде:
Q = Grcr (Тх — Г2) = 1400-1,8-103 (105 — 25) = 2016-105 Дж.
Здесь сг = 1,8-Ю3 Дж/(кг-К) — удельная теплоемкость толуола при
средней температуре 65 °С (рис. XI).
Время охлаждения толуола:
Т ""^Л^ср.охл" 255-3,2.30,36 °Ш с ~ г>^ ч'
Общий расход охлаждающей воды:
Q 2016-105
M^cp-'i) " 4190(29,35-13)
Gx ~ —— — — ,,лгх ,п„ л^ г^- = 2943 кг.
Пример 4.28. Бутиловый спирт (холодная жидкость) в
количестве Gx = 1800 кг загружен в сосуд, в котором имеется
змеевик. Через змеевик пропускается вода (горячая жидкость).
Бутиловый спирт нагревается от температуры tx = 20 до t2 = 60 °С
в течение т ч. Вода понижает свою температуру от 7\ = 90 °С
до 7V Конечная температура воды в периодическом процессе
все время увеличивается по мере повышения температуры спирта.
В конце процесса нагревания через т ч температура станет
равной Т2 (>*а).
Сколько времени т потребуется для нагрева спирта и какой
должен быть общий расход горячей воды Gr, если поверхность
теплопередачи змеевика F = 4,3 м2, а значение коэффициента
теплопередачи принять постоянным и равным К = 280 Вт/(м2*К)?
Решение. Схема процесса:
в сосуде (бутиловый спирт нагревается): tx = 20 °С через т ч
U = 60 °С;
в змеевике (вода охлаждается); 7\ = 90 °С через т ч Тг = ?
Принимаем Т2 = 70 °С.
Уравнение теплопередачи:
Q = KF Д/ср< нагрт*
199
Средняя разность температур для периодического процесса
нагрева жидкости в сосуде [1]:
а/ - '«-'! (А~— \-
Д'ср. нагр - Tt _ h {^-й Л J
Tt-tt
60 — 20 /3—1
. 90 — 20
In
(4Й)=28'65°(:=28'65К-
90 — 60
Величина А постоянна для всего процесса нагрева. Для
любого момента времени, когда температура нагреваемой жидкости
будет равна t:
Tt — t 90 — 60 30 _ з
А ~~Т2 —1~ 70 — 60 "10
При расчете поверхности теплообмена определяют А для t~
= /2 = 60 °С.
Средняя конечная температура горячей воды:
T2cv = Тх - Д/Ср. нагр 1п А « 90 - 28,65 Ш 3 = 58,52 °С.
Количество теплоты, отдаваемое водой спирту:
Q = Cxcx(/2 — /х)= 1800-2,56.103 (60 —20)= 1843.10§ Дж.
Здесь сх = 2,56 • 103 Дж/(кг ¦ К) — удельная теплоемкость бутилового спирта
при средней температуре 40 °С (рис. XI).
Время нагрева спирта:
х» « = 1843-10- =5343 с - 1,48 ч.
К/'Л'ср.нагр 280-4,3.28,65
Общий расход горячей воды:
Gr= 3 = "ИЗ-"» - = 1397 кг.
cr (7\ — Ггср) 4190 (90 — 58,&2)
Пример 4.29. Определить потерю теплоты лучеиспусканием
поверхностью стального аппарата цилиндрической формы,
находящегося в помещении, стены которого выкрашены масляной
краской. Размеры аппарата: Н = 2 м; D = 1 М. Размеры помещения:
высота 4 м; длина 10 м; ширина 6 м. Температура стенки аппарата
70 °С, температура воздуха в помещении 20 °С.
Определить также общую потерю теплоты аппарата
лучеиспусканием и конвекцией.
Решение. Потерю теплоты излучением вычислим по
формулам (4.66) и (4.67):
QjI==Cl-2fl[(loo) -(тШ J;
Ci_2 —
JL+ (J L\Jl
ct ^ \ c% c4) F%
200
В нашем случае:
Т± = 273 + 70 = 343 К; Т2 = 273 + 20 = 293 К;
Ft = nDH + 2-0J85D2 = 3,14-1 -2 + 2-0,785-12 = 7,85 м2;
F2 = 2 (4-6 + 4.10 + 6-10) = 248 м2.
Так как площадь F2 велика по сравнению с площадью Flt то
коэффициент излучения Сх_2 & Сг.
Для окисленной стали среднее значение степени черноты 8 =
= 0,85 [см. формулу (4.67)]. Следовательно, Сг = 5,7*0,85 =
= 4,84 Вт/(м2.К4).
Потеря теплоты лучеиспусканием:
<?л = CtFi [ (J±)* - (-Щ-)4] = 4,84-7,85 (3,43* - 2,93*) = 2490 Вт.
Общую потерю теплоты лучеиспусканием и конвекцией найдем
по формуле;
Q = &Fi (^ст — ^возд)»
Здесь а — суммарный коэффициент теплоотдачи лучеиспусканием и
конвекцией — определяется по формуле (4.71):
а = 9,74 + 0,07 М = 9,74 + 0,07 (70 — 20) = 13,2 Вт/(м2. К).
Общая потеря теплоты аппаратом:
Q = 13,2-7,85 (70 — 20) = 5200 Вт.
Пример 4.30. Определить необходимую толщину слоя
изоляции аппарата, внутри которого температура 154 °С, Изоляционный
материал — совелит. Температура наружной поверхности
изоляции не должна быть выше 40 °С.
Решение. Примем температуру окружающего воздуха
/0 = 20 °С и определим суммарный коэффициент теплоотдачи
в окружающую среду лучеиспусканием и конвекцией по
уравнению (4.71):
а = 9,74 + 0,07 М = 9,74 + 0,07 (40 — 20) = 11,1 Вт/(м2-К).
Удельный тепловой поток:
q = а (/Ст — /0) = П, 1 (40 — 20) = 222 Вт/м2.
Принимая приближенно, что все термическое сопротивление
сосредоточено в слое изоляции, можно написать
х
Я = К (*вн — *0) » -§- ('вн — *o)f
откуда толщина слоя изоляции:
6-~-(/вн~д===^г(154~20)=0,059м'
где Я = 0,098 Вт/(м-К)— коэффициент теплопроводности совелита (табл.
XXVIII).
201
Пример 4.31. Вдоль плоской стенки аппарата продувается
воздух со скоростью 3 м/с при средней температуре 90 °С и
давлении 900 мм рт. ст. Снаружи аппарат покрыт слоем теплоизоляции
(совелит) толщиной 40 мм. Определить количество теплоты q,
теряемое с 1 м2 стенки аппарата.
Длина стальной стенки 5 м, толщина 5 мм; температура
воздуха в помещении 20 °С. Учесть загрязнение внутренней стенки
аппарата.
Решение. Находим коэффициент теплоотдачи от горячего
воздуха к стенке [расчетная формула (4.40)]. Значение критерия
Нуссельта:
NU! = 0,032Re0'8 = 0,032 (9,07-10*)0'8 => 1867.
wLpi 3-5.1,149 n/V7 1Afi , оно 900-273
Здесь Re--^- ^^ -9,07-10»; Pi-l,»^^^^
= 1,149 кг/м3 — плотность воздуха при рабочих условиях; щ = 0,019 X
X 10~3 Па-с — динамический коэффициент вязкости воздуха при 90 °С
(рис. VI).
Следовательно,
ах = Nu^/I » 1867-0,0316/5 « 11,8 Bt/(m2-K),
где ^ = 0,0316 Вт/(м-К) — коэффициент теплопроводности воздуха при 90 °G
(табл. XXX).
Суммарный коэффициент теплоотдачи лучеиспусканием и
конвекцией от наружной поверхности изоляции в окружающую среду:
а3 = 9,74 + 0,07 (/ст., — /возд).
Ввиду того, что /ст. 2 — температура наружной поверхности
изоляции — неизвестна, для первого приближения принимаем
Оя « 10 Вт/(м2.К).
Тепловую проводимость загрязнения внутренней поверхности
стенки принимаем по табл. XXXI для теплоносителя — воздуха:
1/'«Гр.1 = 2800Вт/(м3.К).
Коэффициент теплопередачи (ориентировочный):
1 1 0,005 0,04 1
~г оолл "Г л с г "Г л i\c\o Т" 1 л
11,8 ' 2800 ' 46,5 ^ 0,098 ' 10
= ! р- = 1,685 Вт/(ма • К)^
0,4934 + —
Здесь коэффициент теплопроводности совелита А. — 0,098 Вт/(м-К), для
стали Яст = 46,5 Вт/(м-К) — см. табл. XXV1I1.
Уточнение а2:
Д'2 « 'ст. 2 — ^возд =» К Д^ср/а* = 1,685.(90 — 20)/10 = 11,8 К;
а2 = 9,74 + 0,07.11,8 =10,57 Вт/(ма. К).
202
Уточненное значение коэффициента теплопередачи:
*= 0.4934 + (1/10,57) =1.7Вт/(м»-К).
Удельные потери теплоты:
q^K А^ср= 1,7 (90 — 20)= 119 Вт/м2.
Пример 4.32. Цеолит NaX подвергается десорбции —нагреву
в токе горячего воздуха в непрерывнодействующем аппарате со
взвешенным слоем цеолита. Средняя температура воздуха 190 °С.
Цеолит поступает в аппарат с начальной температурой 20 °С
Диаметр зерна цеолита 4 мм, плотность его 1100 кг/м3, удельная
теплоемкость 870 Дж/(кг- К), коэффициент теплопроводности
0,24Вт/(м.К). Число псевдоожижения * 4. Определить время,
необходимое для нагрева зерна цеолита от 20 °С до средней
температуры 185 °С.
Решение. Прогрев зерна цеолита представляет собой
нестационарный процесс теплопроводности в твердом теле. Решение
уравнения нестационарной теплопроводности (при. постоянстве
теплофизических характеристик нагреваемого тела)
дх
совместно с граничными и начальными условиями приводит [4.21
к уравнению
^о. с — 'и
= /(Bi, Fo), (a)
правая часть которого — сложная функция критериев Био (Bi)
и Фурье (Fo).
Для зерна, имеющего форму шара радиусом R:
Bi«4^; fo=: ax *тТ
fvj> A C^Pq,I\
2 '
В последних уравнениях tu, tn> t0t c — начальная и конечная
температуры нагреваемого тела, температура окружающей среды; а — коэффициент
теплоотдачи от окружающей среды к поверхности нагреваемого тела; Ят, ст
рт — коэффициент теплопроводности, удельная теплоемкость и плотность
твердого тела; а — коэффициент температуропроводности твердого тела (зерна),
На рис. 4.18 приведен график уравнения (а) для шара [4.1,
4.12].
Определяем коэффициент теплоотдачи а от воздуха к
поверхности зерна цеолита во взвешенном слое. Предварительно
найдем значение критерия Архимеда по уравнению (3.3):
л,_ *РтРс* 0,004М100-0,763-9,81
Л!- = 25JM0-» ~8'10'
* Отношение рабочей скорости воздуха к критической (скорости псевдо-
ожижеиня).
203
*к~*н
Рис. 4.18 (к примеру 4,32).
где р0 = 0,763 кг/мэ и \ic = 25,7 х
X Ю"8 Па-с—плотность и
динамический коэффициент вязкости среды
(воздуха) при 190 °С [4.1].
По графику (рис. 3.8) находим
при Аг = 8.106 и е = 0,4
критерий Лященко LyKp = 2,75. Отсюда
по уравнению (3.4а) определяем
критическую скорость
псевдоожижения:
W
кр
= Т^Ьукр^с^Рт/рс =
= У2.75.25,7-10-6-9,8ЫЮ0/0,7632 =
= 1,09 м/с.
Рабочая скорость воздуха (отнесенная к полному поперечному
сечению аппарата):
w = 4цукп = 4-1,09 = 4,36 м/с.
'кр
По этой скорости рассчитываем критерий Лященко
4,363.0,7632
Ly =
w39l
= 174
licpTg 25,7-10*6'П00-9,81
и по рис. 3.8 при Аг = 8.105 находим порозность взвешенного
слоя 8 = 0,67.
Критерий Рейнольдса для потока воздуха:
wdpc 4,36-0,004-0,763
Re-
ем с
0,67-25,7-Ю"6
773.
Критерий Прандтля Рг = сф = 1020.25,7. Ю'70,0385 - 0,681.
Определяем критерий Нуссельта по уравнению [lh
Nu = 0,4Re°'67Pr0,33 = 0f 4.7730*67-0,6810'33 = 30,2.
Коэффициент теплоотдачи от воздуха к поверхности зерна:
a =r NuA,c/d= 30,2-0,0385/0,004 «= 290 Вт/(м2-К),
где Яс = 0,0385 Вт/(м-К) — коэффициент теплопроводности воздуха при 190 °С
[4.1].
Критерий Био:
Bi = aRfkT « 290-0,002/0,24 « 2,42.
Симплекс разностей температур:
*к —/н 185 — 20
t
о. с
•н
190 — 20
0,97.
По этим данным находим по графику (рис. 4,18) значения
критерия Fo = 1, откуда время прогрева зерна цеолита:
T = FocTpTtf2AT = 1.870*1100-0,0022/0,24^ 16 с.
204
КОНТРОЛЬНЫЕ ЗАДАЧИ
4.1. Во сколько раз увеличится термическое сопротивление
стенки стального змеевика, свернутого из трубы диаметром 38 х
Х2,5 мм, если покрыть ее слоем эмали толщиной 0,5 мм? Считать
стенку плоской. Коэффициент теплопроводности эмали 1,05
Вт/(м.К).
4.2. Паропровод длиной 40 м, диаметром 51x2,5 мм покрыт
слоем изоляции толщиной 30 мм; температура наружной
поверхности изоляции /а = 45 °С, внутренней tx = 175 °С. Определить
количество теплоты, теряемое паропроводом в 1 ч. Коэффициент
теплопроводности изоляции Я = 0,116 Вт/(м«К)«
4.3. Стальная труба диаметром 60x3 мм изолирована слоем
пробки толщиной 30 мм и сверху еще слоем совелита (85 %
магнезии + 15% асбеста) толщиной 40 мм. Температура стенки
трубы —110°С, а наружной поверхности изоляции 10 °С.
Вычислить часовую потерю холода с 1 м длины трубы.
4.4. Как изменится потеря холода в условиях предыдущей
задачи, если внутренний слой сделать совелитовым (б = 40 мм),
а наружный — пробковым (б = 30 мм)?
4.5. Найти температуру внутренней поверхности обмуровки
аппарата (рис. 4.19), если температура на наружной поверхности
ее 35 °С. Толщина обмуровки 260 мм. Термометр, заделанный на
глубину 50 мм от наружной поверхности, показывает температуру
70 °С.
4.6. Вычислить коэффициент теплопроводности для: а)
жидкого хлороформа при / = 20 °С; б) сернистого газа при t = 160 СС
и абсолютном давлении 1 кгс/см2 (~0,1 МПа); в) 25% водного
раствора хлористого кальция при t = 30 °С.
4.7. Необходимо испарять 1600 кг/ч жидкости, кипящей при
i = 137°С и поступающей в испаритель при этой температуре,
Удельная теплота испарения жидкости г = 377.108 Дж/кг.
Температура греющего пара должна быть не ниже 150 °С. Определить
расход греющего пара: а) сухого насыщенного, /?иаб *= 4 кгс/см2
(~Q,4 МПа); б) перегретого до 250 °С, pas6 = 4 кгс/смя
(~0,4 МПа); в) перегретого до 250 °С, /?ИЗб *= 3 кгс/смя
(~0,3 МПа). Удельная теплоемкость перегретого пара 2,14.103
Дж/(кг.К).
Изобразить процессы изменения состояния греющего пара на
диаграмме Т — S. Конденсат греющего пара отводится при
температуре конденсации.
4.8. До какой температуры будут нагреты
глухим паром 2 т раствора хлористого кальция,
если расход греющего пара (рабс = 2 кгс/см2,
т. е. ~0,2 МПа) за 2,5 ч составил 200 кг, а
расход теплоты на нагрев аппарата и потери
Рис, 4.19 (к контрольной задаче 4.6),
205
теплоты в окружающую среду составляют в среднем 2030 Вт?
Начальная температура раствора 10 °С. Удельная теплоемкость
раствора 2,5 X 103 Дж/(кг-К).
4.9. Определить количество передаваемой теплоты в противо-
точном конденсаторе, в котором конденсируется 850 кг/ч пара
сероуглерода под атмосферным давлением. Пар сероуглерода
поступает в конденсатор с температурой 90 °С. Жидкий
сероуглерод выходит из конденсатора при температуре на 8 °С ниже
температуры конденсации. Удельная теплоемкость пара сероуглерода
0,67.10* Дж/(кг-К).
4.!0. В кожухотрубчатый конденсатор поступает 120 кг/ч
сухого насыщенного пара диоксида углерода под давлением
Рабе = 60 кгс/см3 (~6,0 МПа). Жидкий диоксид углерода
выходит из конденсатора под тем же давлением при температуре
конденсации. Принимая разность температур диоксида углерода
и воды на выходе воды из конденсатора 5 К, определить
необходимый расход воды, если она поступает в конденсатор с
температурой 10 °С.
4.11. Колонна для ректификации жидкого воздуха покрыта
слоем тепловой изоляции из шлаковой ваты толщиной 250 мм.
Температура жидкости внутри колонны —190 DC, температура
воздуха в помещении 20 СС. Какое количество теплоты может
проникать из окружающего воздуха в колонну через 1 м2
поверхности, если пренебречь термическими сопротивлениями со
стороны жидкости, окружающего воздуха и металлической стенки
колонны?
4.12. Как изменится коэффициент теплопередачи в аппарате,
если заменить стальные трубы диаметром 38x2,5 мм на медные
такого же размера: а) в паровом калорифере для воздуха,
в котором ссвояд = 41 Вт/(м8.К), агр. пара = 11 600 Вт/(м2-К);
б) в выпарном аппарате, в котором otilHn раств = 2320 Вт/(м2-К),
агр. пара — 11600 Вт/(ма-К)? Загрязнений поверхности не
учитывать.
4.13. Как изменится величина коэффициента теплопередачи
в теплообменном аппарате, выполненном из стальных труб
толщиной 3 мм, если на поверхности труб отложится слой накипи
(водяного камня) толщиной 2 мм; а) в водяном холодильнике для
газа, в котором агапа = 58 Вт/(м2-К), аводы = 580 Вт/(м2-К);
б) в выпарном аппарате, в котором аиип раств = 2780 Вт/(м8.К),
аРр.иаРа =11600 Вт/(м».К)?
4.14. Какая наибольшая удельная тепловая нагрузка
(в Вт/м2) может быть в испарителе толуола, если стальные трубы
испарителя толщиной 4 мм с обеих сторон покрыты ржавчиной?
Толщина одного слоя ржавчины 0,6 мм. Испаритель обогревается
насыщенным паром (ртб = 3 кгс/сма, т. е. ~0,3 МПа). Толуол
кипит под атмосферным давлением. Считать, что термическое
сопротивление стенки и двух слоев ржавчины значительно больше
суммы остальных термических сопротивлений.
206
Ю6°С
зо°с
Рис. 4.20 (к контрольной задаче 4.16).
4.15. Горячий концентрированный
раствор, выходящий из выпарного аппарата
с температурой 106 °С, используется для
подогрева до 50 °С холодного
разбавленного раствора, поступающего на
выпарку с температурой 15 °С
Концентрированный раствор охлаждается до 60 °С.
Определить среднюю разность температур
для прямоточной и противоточной схем.
4.16. В многоходовом кожухотрубчатом
теплообменнике, имеющем четыре хода в
трубном пространстве и один ход в
межтрубном (рис. 4.20), толуол охлаждается
водой от 106 до 30 °С. Вода, проходящая по трубам, нагревается
от 10 до 34 °С. Определить среднюю разность температур в
теплообменнике.
4.17. 1930 кг/ч бутилового спирта необходимо охлаждать от
90 до 50 °С в противоточном теплообменнике поверхностью 6 м2.
Охлаждение производится водой с начальной температурой \8 °С
Коэффициент теплопередачи в теплообменнике 230 Вт/(м2 • К);
Д/Ср считать как среднюю арифметическую. Сколько кубических
метров воды в 1 ч надо пропускать через теплообменник?
4.18. На складе оборудования имеется кожухотрубчатый
теплообменник, состоящий из 19 латунных труб диаметром 18x2 мм,
длиной 1,2 м. Достаточна ли его поверхность для конденсации
350 кг/ч насыщенного пара этилового спирта, если принять
коэффициент теплопередачи раЕным 700 Вт/(м2-К), начальную
температуру воды 15 °С, а конечную 35 °С? Конденсация спирта
предполагается при атмосферном давлении, жидкий спирт отводится
при температуре конденсации.
4.19. Кожухотрубчатый противоточный теплообменник
(рис. 4.21) перед контактным аппаратом на сернокислотном заводе
300°С
560*С
Рис. 4,21 (к контрольной задаче 4,1»)*
207
имеет поверхность теплообмена 360 м2. Очищенный газ
колчеданных печей поступает в межтрубное пространство
теплообменника при 300 °С, выходит при 430 С. Горячий газ из контактного
аппарата входит в трубы теплообменника при 560 °С. Расход
газа 10 т/ч, удельная теплоемкость газа в среднем 1,05 X
х 103 Дж/(кг-К). Потери теплоты через кожух теплообменника
составляют 10% от количества теплоты, полученного
нагревающимся газом. Определить коэффициент теплопередачи в
теплообменнике.
4.20. Определить коэффициент теплопередачи в спиральном
теплообменнике по следующим данным: поверхность теплообмена
48 м2; в аппарате подогревается 85,5 т/ч воды от 77 до 95 °С;
нагревание производится насыщенным паром при /?ИЗб = 23 кПа.
4.21. Определить необходимую поверхность противоточного
теплообменника при охлаждении 0,85 м3/ч сероуглерода от
температуры кипения под атмосферным давлением до 22 °С.
Охлаждающая вода нагревается от 14 до 25 °С; otcs2 =270 Вт/(м2-К);
ан2о =720 Вт/(м2-К). Толщина стальной стенки 3 мм. Учесть
наличие загрязнений — ржавчины и накипи, приняв ? гбаГ[) =
= 0,00069 (м2-К)/Вт. Определить также расход воды.
4.22. Требуется конденсировать 10 т/ч насыщенного пара
я-гексана при 70 °С. Охлаждение конденсатора может быть
осуществлено: а) водой, нагреваемой от 16 до 36 °С; б) воздухом,
нагреваемым от 25 до 48 °С. Коэффициент теплоотдачи для
конденсирующегося пара гексана в обоих случаях принять равным
1700 Вт/(м2*К). Коэффициенты теплоотдачи для воды и воздуха
взять ориентировочно (средние значения) по табл. 4.7, для воды—
при турбулентном течении по трубам, для воздуха — при
поперечном обтекании труб. Жидкий гексан отводится при температуре
конденсации. Термические сопротивления стенки и загрязнений
не учитывать. Удельная теплота конденсации гексана 33,3 X
X 104 Дж/кг. Определить расходы воды и воздуха (в м3/ч) и
требуемые поверхности теплообмена.
4.23. Метан под избыточным давлением 5 кгс/см2 (~0,5 МПа)
проходит по межтрубному пространству кожухотрубчатого
теплообменника параллельно трубам со скоростью 4,6 м/с. Средняя
температура метана 75 °С. Теплообменник состоит из 37 стальных
труб диаметром 18X2 мм, заключенных в кожух, внутренний
диаметр которого 190 мм. Определить коэффициент теплоотдачи.
4.24. 3700 кг/ч метилового спирта подогреваются от 10 до
50 °С, проходя по трубному пространству теплообменника,
состоящего из 19 труб диаметром 16X2 мм. Определить
коэффициент теплоотдачи, если принять температуру стенки 60 °С.
4.25. В кожухотрубчатом теплообменнике по трубам
диаметром 46x3 мм проходит со скоростью 0,7 м/с вода, которая
нагревается. Определить коэффициент теплоотдачи, если средняя
температура поверхности стенки, соприкасающейся с водой, 90 9С,
а средняя температура воды 46 9С.
208
Рис. 4.22
4.27).
(к контрольной задаче
4,26. Определить
коэффициент теплоотдачи для
воздуха, охлаждаемого под
абсолютным давлением
2 кгс/см2 (-0,? МПа) от
90 до 30 °С в межтрубном
пространстве кожухотруб-
чатого теплообменника с
поперечными
перегородками. Трубы диаметром 25 X
Х2 мм расположены по
ходу газа в шахматном
порядке. Скорость воздуха
в вырезе перегородки
Воздух
t
Воздук
узком
Конденсат
сечении
пучка
(в самом
труб) 8 м/с (рис. 4.22, б).
4.27. Воздух атмосферного давления нагревается насыщенным
водяным паром в кожухотрубчатом конденсаторе с трубками
диаметром 25x2 мм. Средняя температура воздуха 60 °С. Сравнить
коэффициенты теплопередачи для двух случаев: 1) воздух
проходит по трубам со скоростью 10 м/с (Lld> 50), греющий пар
конденсируется в межтрубном пространстве (рис. 4.22, а); 2)
воздух проходит по межтрубному пространству, снабженному
поперечными перегородками. Скорость воздуха в вырезе
перегородки (в самом узком сечении пучка труб) 10 м/с (рис. 4.22, б),
греющий пар конденсируется в трубах. Принять коэффициент
теплоотдачи пара 11 600 Вт/(м2-К).
4.28. При теплообмене двух турбулентных потоков (Re >
> 10 000) у первого потока ах =230 Вт/(м2-К), У второго а% =
= 400 Вт/(м2'К). Во сколько раз увеличится коэффициент
теплопередачи, если скорость первого потока возрастет в 2 раза,
а скорость второго — в 3 раза (при прочих неизменных условиях)?
Термическое сопротивление стенки не учитывать.
4.29. Определить коэффициент теплоотдачи для 98 % серной
кислоты, проходящей по кольцевому (межтрубному) пространству
горизонтального теплообменника типа «труба в трубе» со скоростью
0,9 м/с. Средняя температура кислоты 72 °С, средняя температура
Стенки 58 °С. Наружная труба теплообменника имеет диаметр
54X4,5 мм, внутренняя —26x3 мм.
4.30. Четыреххлористый углерод нагревается в трубном
пространстве горизонтального кожухотрубчатого теплообменника.
Средняя температура четыреххлористого углерода 26 °С, скорость
его в трубах 0,15 м/с. Средняя температура поверхности
загрязнения труб, соприкасающейся с четыреххлористым углеродом,
34 9С. Диаметр труб 25x2 мм. Определить коэффициент
теплоотдачи четыреххлористого углерода.
209
4.31. Через трубное пространство кожухотрубчатого
теплообменника прокачивается раствор хлористого кальция (23,8 %),
который нагревается при средней температуре —20 °С. Скорость
рассола в трубах 0,5 м/с, средняя температура поверхности стенки,
соприкасающейся с раствором, —10 °С. Коэффициент объемного
расширения рассола 0,35* 10~3 К"1, внутренний диаметр труб
0,021 м, длина труб 4 м. Определить коэффициент теплоотдачи
для рассола.
4.32. Раствор хлористого натрия [21,2 % (масс.)]
нагревается в трубном пространстве кожухотрубчатого
теплообменника от —15 до —12 °С. Внутренний диаметр труб 21 мм, длина
труб 3 м. Скорость рассола в трубах 0,3 м/с. Средняя температура
поверхности загрязнения стенки, соприкасающейся с рассолом,
tCT = —6,5 °С. Определить коэффициент теплоотдачи от рассола
к стенке. Коэффициент объемного расширения рассола |J =*
-0,35-10-3 К'\
4.33. Этилацетат охлаждается в трубном пространстве
горизонтального кожухотрубчатого теплообменника. Внутренний
диаметр труб 21 мм, длина труб 3 м. Средняя температура
охлаждаемого этилацетата fcp = 50 °С, средняя температура поверхности
загрязнения стенки со стороны этилацетата /ст =40°С. Скорость
этилацетата 0,04 м/с. Определить коэффициент теплоотдачи от
этилацетата к стенке. Коэффициент теплопроводности % =
-0,1128 Вт'(м-К).
4.34. Бензол охлаждается в трубах горизонтального
кожухотрубчатого теплообменника. Внутренний диаметр труб 21 мм,
длина труб 4 м. Средняя температура охлаждаемого бензола 50 °С»
средняя температура поверхности загрязнения стенки со стороны
бензола tCT = 30 С. Скорость бензола 0,05 м/с. Определить
коэффициент теплоотдачи от бензола к стенке.
4.35 В вертикальном кожухотрубчатом теплообменнике
бензол прокачивается через трубы снизу вверх при охлаждении от 70
до 30 °С. Внутренний диаметр труб 21 мм, высота труб 4 м.
Скорость бензола 0 05 м/с. Средняя температура поверхности
загрязнения стенки со стороны бензола 30 °С. Определить коэффициент
теплоотдачи от бензола к вертикальной поверхности стенки.
4.36. Вода нагревается в условиях свободного движения.
Наружный диаметр горизонтальных труб 76 мм. Определить
коэффициент теплоотдачи, если температуру поверхности трубы
принять равной 45 °С Средняя температура воды 25 °С.
4.37. В условиях свободной конвекции охлаждается толуол.
Средняя температура толуола 50 °С. Диаметр горизонтальных
труб 38x2 мм. Температура наружной поверхности загрязнения
труб, соприкасающейся с толуолом 30 °С. Определить коэффицент
теплоотдачи толуола.
4.38. Вертикальный кожухотрубчатый теплообменник состоит
из 91 трубы диаметром 57x3 мм, высотой 4 м. По внутренней
поверхности труб стекает пленкой вода в количестве 52 м3/ч,
210
которая нагревается от 18 до 25 °С. Средняя температура
внутренней поверхности труб 26 °С. Определить коэффициент
теплоотдачи.
4.39. По вертикальной стенке пленочного холодильника
стекает пленкой 60% серная кислота в количестве 2,1 дм3/с на 1 м
ширины стенки. Высота холодильника 5 м. Средняя температура
поверхности стенки 24 °С, средняя температура кислоты 50 °С.
Вычислить коэффициент теплоотдачи для кислоты, если
коэффициент теплопроводности ее равняется 0,43 Вт/(м-К).
4.40. Вычислить коэффициент теплоотдачи кипящего под
атмосферным давлением 20 % водного раствора хлористого натрия.
Разность температур греющей поверхности и кипящего раствора
10 К- Для кипящего раствора % =0,658 Вт/(м-К).
4.41. В кубе ректификационной колонны под атмосферным
давлением внутри вертикальных труб высотой 4 м кипит толуол
с небольшим содержанием бензола (наличие бензола не учитывать).
Диаметр труб 25x2 мм. Определить коэффициент теплоотдачи
к кипящему толуолу. Принять температуру поверхности
загрязнения стенки со стороны толуола 125,3 °С. -
4.42. В межтрубном пространстве вертикального
кожухотрубчатого теплообменника, состоящего из 261 трубы диаметром
25x2 мм, конденсируется под атмосферным давлением 4 т/ч
насыщенного пара метилового спирта. Определить коэффициент
теплоотдачи.
4.43. Насыщенный водяной пар конденсируется на наружной
поверхности пучка горизонтальных труб. Наружный диаметр
труб 38 мм. Расположение труб шахматное. Расчетное число труб
по высоте 11. Температура конденсации 160 °С. Определить
средний коэффициент теплоотдачи, приняв температуру наружной
поверхности труб 152 °С. Пар содержит 0,5 относительных %
воздуха.
4.44. Метиловый спирт (100%) нагревается в трубном
пространстве одноходового кожухотрубчатого теплообменника от
15 до 42 °С. Противотоком в межтрубном пространстве течет
вода, которая охлаждается от 90 до 40 °С. Теплообменник с
кожухом 400 мм состоит из 111 стальных труб диаметром 25x2 мм.
Скорость метилового спирта в трубах 0,75 м/с. Коэффициент
теплоотдачи для воды 840 Вт/(м2*К), суммарная тепловая проводимость
стенки и обоих загрязнений стенки 1700 Вт/(м2-К), средняя
температура поверхности загрязнения, соприкасающейся со спиртом,
38 °С. Определить требуемую площадь поверхности теплообмена.
4.45. Воздух подогревается в трубном пространстве
одноходового кожухотрубчатого теплообменника с 20 до 90 °С при
среднем абсолютном давлении 810 мм рт. ст. Расход воздуха,
считая при нормальных условиях, составляет 7770 м3/ч. В
теплообменнике 197 труб диаметром 38x2 мм. В межтрубное
пространство подается насыщенный водяной пар под абсолютным
давлением 2 кгс/см2 (~0,2 МПа). Коэффициент теплоотдачи пара
211
10 000 Вт/(ма-К), суммарная тепловая проводимость стенки и обоих
ее загрязнений 1700 Вт/(м2-К). Определить требуемую площадь
поверхности теплообмена.
4.46. Воздух атмосферного давления в количестве 5200 м3/ч
(при нормальных условиях) нагревается в трубном пространстве
кожухотрубчатого теплообменника с 2 до 90 °С. Число труб 111.
Диаметр труб 38x2 мм. Абсолютное давление греющего водяного
пара 2 кгс/см2 (~0,2 МПа). Определить требуемую длину труб
и расход греющего пара, если его влажность 6%. Принять К «
^ ^возд*
4.47. По змеевику проходит 1,5 т/ч толуола, охлаждающегося
от 90 до 30 °С. Охлаждение (противотоком) проводится водой,
нагревающейся от 15 до 40 °С. Труба змеевика стальная
диаметром 57X3,5 мм; аводы =580 Вт/(м2-К). Диаметр витка
змеевика 0,4 м. Определить необходимую длину змеевика и расход
воды. Термическое сопротивление стенки и ее загрязнений
принять равным 0,0007 (м2-К)/Вт, а отношение Рг/Ргст для толуола
равным 0,75.
4.48. В теплообменнике типа «труба в трубе», состоящем из
двух концентрических труб: внутренней диаметром 44,5X3,5 мм
и наружной диаметром 89x5 мм, охлаждается от 70 до 30 9С
толуол в количестве 1900 кг/ч. Толуол проходит по кольцевому
пространству между наружной и внутренней трубой; по
внутренней протекает охлаждающая вода, нагревающаяся от 14 до 21 РС.
Средняя температура поверхности загрязнения со стороны толуола
26 °С, со стороны воды 20 °С. Определить коэффициент
теплопередачи. Учесть термические сопротивления загрязнений стенки
со стороны толуола и со стороны воды (среднего качества).
Расчет сделать- а) без учета влияния Рг/Ргст; б) с учетом
влияния Рг/Ргст.
4.49. Вертикальная стенка выпарного аппарата покрыта слоем
изоляции [X =0,12 Вт/(м-К)] толщиной 45 мм. Температура
кипящего раствора 120 °С, температура воздуха в помещении 20 РС.
Определить потерю теплоты излучением и конвекцией с 1 м^
в 1 ч, принимая температуру поверхности стенки,
соприкасающейся с кипящим раствором, равной температуре последнего.
4.50. По горизонтальному паропроводу диаметром 51 Х2,5 мм,
длиной 50 м проходит насыщенный пар под давлением рабс =
= 4 кгс/см2 (~0,4 МПа). Определить количество конденсата,
образующегося в течение суток в неизолированном трубопроводе.
Температура воздуха в цехе 15 °С.
4.51. Во сколько раз уменьшится потеря теплоты, если
паропровод, рассматриваемый в предыдущей задаче, покрыт
теплоизоляционным слоем толщиной 40 мм с коэффициентом
теплопроводности 0,093 Вт/(м-К).
4.52. Аппарат изолирован слоем шамотного кирпича толщиной
125 мм [к =0,68 Вт/(м*К)] и слоем изоляционной массы [К ==
— 0,12 Вт/(м-К)]. Температура наружной поверхности металли-
212
ческой стенки аппарата 500 °С. Найти достаточную толщину
изоляционного слоя, чтобы температура его наружной
поверхности не превышала 50 °С при температуре воздуха в цехе
25 °С
4.53. В сушилке, вдоль ее плоской стенки длиной 6 м,
проходит со скоростью 2,5 м/с горячий воздух атмосферного давления,
имеющий среднюю температуру 85 °С. Стальная стенка сушилки
толщиной 5 мм изолирована снаружи слоем теплоизоляции
толщиной 30 мм. Температура воздуха в помещении 18 °С.
Определить количество теплоты, теряемой в I ч с I м2 стенки сушилки
путем конвекции и излучением. Учесть тепловую проводимость
загрязнения внутренней стенки сушилки.
ПРИМЕРЫ РАСЧЕТА ТЕПЛООБМЕННИКОВ
Аппараты теплообменные кожухотрубчатые с неподвижными трубными
решетками и кожухотрубчатые с температурным компенсатором на кожухе
применяются в тех случаях, когда нет необходимости в механической очистке
межтрубного пространства (очистка от осадка возможна только для трубного
пространства). Поэтому в трубное пространство подают ту жидкость (воду
или водные растворы), которая прн нагревании или выпаривании может
выделять нерастворимый осадок на стенках труб, а в межтрубное пространство
подают чистую жидкость или конденсирующийся пар.
Конечную температуру охлаждающей воды не следует принимать выше
45—50 °С во избежание значительного образования накипи.
Кожухотрубчатые теплообменные аппараты с неподвижными трубными
решетками и с поперечными перегородками в межтрубном пространстве,
применяемые в химической, нефтяной и других отраслях промышленности,
обозначаются индексами и классифицируются:
— по назначению (первая буква индекса): Т — теплообменники; X —
холодильники; К—конденсаторы; И—испарители;
— по конструкции (вторая буква индекса): Н — с неподвижными трубными
решетками; К — с температурным (линзовым) компенсатором на кожухе;
— по расположению (третья буква индекса): Г — горизонтальные; В —
вертикальные.
Основные сведения о кожухотрубчатых теплообменных аппаратах с
неподвижными трубными решетками по ГОСТам 15119—79, 15120—79, 15121—79
и 15122—79 для труб 25X2 мм из стали марок 10 и 20 приведены в табл. 4.11,
4.12, а также в Приложении (табл. XXXIV и XXXV).
Размещение отверстий под трубы в трубных решетках и основные размеры—
см. ГОСТ 15118—79. Примеры размещения отверстий в трубных решетках
приведены на рис. II и III (см. Приложение).
Кожухотрубчатые теплообменные аппараты с неподвижными трубными
решетками типа ТН, ХН, КН, ИН можно применять только в тех случаях,,
когда разность температур кожуха (/к) и труб (/т) будет меньше максимальной,
приведенной в табл. XXXV.
Если разность fK и tT окажется больше максимально допустимой, то
используют кожухотрубчатый теплообменпый аппарат с линзовым компенсатором
типа ТК, КК, ХК, ИК или с плавающей головкой (ГОСТ 14246—79).
Кожухотрубчатые теплообменные аппараты с неподвижными трубными
решетками, предназначенные для аммиачных и углеводородных холодильных
установок (ГОСТ 22485—77 и 22486—77), в этом пособии не приводятся.
Пример 4.1. Рассчитать теплообменный аппарат для охлаждения 1,1 кг/с
диэтилового эфира от -(-25 до —10 °С рассолом — раствором хлористого
кальция [23,8 % (масс.)], поступающим из холодильной машины. Рассол нагревается
от —15 до —12 °С. Давление в линиях эфира и рассола менее 0,3 МПа. Со-
213
Таблица 4.11
Применение кожухотрубчатых теплообменных аппаратов со стальными
трубами
Рраб "~ предельные рабочие давления, зависящие от характеристики и температуры
среды; 1 кгс/см2 » 0,1 МПа
Тип -аппарата
Применение и нормы
в кожухе
в трубах
Теплообменники
ТН и ТК
(ГОСТ 15122—79)
Конденсаторы КН
и КК
(ГОСТ 15121—79)
Холодильники
ХН и ХК
(ГОСТ 15120—79)
Испарители ИН
и ИК
(ГОСТ 15119—79)
Нагревание и охлаждение жидких и газообразных сред
Температура теплообменивающихся сред от —70 до + 350 °С
Русл Для ТН от 6 до 25 кгс/см2 Русл от 6 до 16 кгс/см?
для ТК от 6 до 16 кгс/см2
Конденсируемая среда
Температура от 0 до + 350°С
Русл Для КН от 6 до 25 кгс/сма
для КК от 6 до 16 кгс/см2
Охлаждаемая среда
Температура от —20 до + 300°С
Русл Для ХН от 6 до 40 кгс/см2
для X К от 6 до 16 кгс/см2
Греющая среда
Температура греющей и испаряемой среды от —30 до
+350*4:
Русл Для ИН от 6 до 40 кгс/см2 Русл от 6 до 10 кгс/смЗ
для И К от 6 до 16 кгс/см2
Охлаждающая среда
Вода или другая
нетоксичная и невзрыво"
и непожароопасиая
среда
Температура от —20
до +60 °С
РуСЛ яо 6 кгс/cw*
Испаряемая среда
поставить несколько вариантов аппаратов, отличающихся гидродинамическим
режимом течения теплоносителей.
Решение. Общая часть. 1. Определим расход теплоты н расход рассола.
Примем индекс «Ь для горячего теплоносителя (диэтилового эфира), индекс
«2» — для холодного теплоносителя (рассола).
Предварительно найдем среднюю температуру рассола:
t2 = 0,5 [—15 + (—12)] = —13,5 °С;
среднюю температуру дизтилового эфира:
*, = ** + Д/Ср = —13,5 + 16 = +2,5°С;
где Д/Ср — средняя разность температур, равная при противотоке теплоиосителеЙ
16 К.
+25
эфир
10
рассол
_12 « 15
Д*б = 37
Д*б — Д*м
37 — 5
Л'ср 1п(Д*б/Д*м) "In (37/5)
= 16 К.
214
Основные характеристики теплообменников ТН и ТК и холодильников ХН и ХК с трубами 25X2 мм
(ГОСТ 15118—79, ГОСТ 15120—79, 15122—79)
Таблица 4.12
пр — число рядов труб по вертикали для горизонтальных аппаратов
по ГОСТ 15118 —79; h ~* расстояние м^жду перегородками
Диаметр
кожуха
внутренний
D, мм
Число
труб п
1,0
Длина труб /, м
1,5
3,0
3.0
4,0
6,0
9,0
Поверхность теплообмена F, м*
Проходное сечение, м*
S.108
т
V102
SB. „• l*f
159 *
273 *
325 *
400
600
800
1000
1200
325*
400
600
800
1000
1200
600
800
1000
1200
600
800
1000
1200
* Наруж*
13
37
62
111
257
465
747
1083
56
100
240
442
718
1048
206
404
666
986
196
384
642
958
шй диаметр
W
3,0
—¦
—
—,
—
—
—¦
_
—
—
—
__
—
_
__
—
кожуха.
1,5
4,5
7,5
_
__
__
—
6,5
—
—
—
__
—
_.
__
—
—~
~__
—
2,0
6,0
10,0
1?
40
73
9,0
16,0
38
69
32
63
31
60
Одноходовые
Sfi
9,0
14,5
26
61
109
176
—
13,0
24,0
57
104
169
—
Ч
49
95
157
—
]
46
90
151
—.
—
—
19,5
35
81
146
235
340
—
—
—
52
121
219
352
510
Д в узе ход
17,5
31,0
75
139
226
329
е ты р
65
127
209
310
—
47
113
208
338
494
е х х о
97
190
314
464
—
—
—
_
—
329
528
765
овне
_
—
_
312
507
740
ДОБЫ
—_
285
471
697
Шести ходовые
61
121
202
301
91
181
302
451
__
271
454
S77
С,5
1,3
2,1
3,8
8,9
16,1
25,9
37,5
1,0
1,7
4.2
7,7
12,4
17,9
1,8
3,0
5,5
8,4
м
2,2
3,6
5,2
0,8
1,1
2,9
3,1
5,3
7,9
14,3
17,9
1,5
2,5
4,5
7,0
13,0
16,5
4,5
7,0
13,0
16,5
4,5
7,0
13,0
16,5
0,4
0,9
1,3
2,0
4,0
6,9
10,6
16,4
1,3
2,0
4,0
6,5
10,6
16,4
4,0
6,5
10,6
16,4
3,7
7,0
10,2
14,2
п.
h, мм
5
7
9
11
17
23
29
35
8
10
16
22
28
34
14
20
26
32
14
20
26
32
100
130
180
250
300
350
520
550
180
250
300
350
520
550
300
350
520
550
300
350
520
550
С учетом потерь холода в размере 5 % расход теплоты:
Q = 1,050^ (t1H - /1к) == 1,05-1,1-2140 [25 - (-10)] = 86 500 Вт;
расход рассола:
Q 86 500
2 " с2 (t2K - t2H) ~ 2900 [-12 -(-15)] ~у>Укг'с>
где Cf = 2140 Дж/(кг-К) и с2 = 2900 Дж/(кг*К) — удельные теплоемкости
эфира и рассола при их средних температурах ?1=s_jl2,50C и t2=— 13,5°C
(рис. XI и табл. LI1)*.
Объемные расходы эфира и рассола:
^«Gt/p!» 1,1/733 = 0,0015 м3/с;
K2 = G2/p2 = 9,9/1220 = 0,0081 м3/с,
где pf = 733 кг/м3 и р2» 1220 кг/м3— плотность эфира (рис. XI) и рассола
(табл. LII).
2. Наметим варианты теплообменных аппаратов.
Для этого определим ориентировочно значение площади поверхности
теплообмена, полагая д0р = 250 Вт/(м2-К) по табл. 4.8, т. е. приняв его таким же, как
и при теплообмене от жидкости к жидкости для углеводородов и масел:
F Q - 86 50° ~ 22 и2
F°P - /(op *'ср ~ 250Л6 ~ 22 М •
Из величины F0p = 22 м2 следует, что проектируемый холодильник
может быть: а) теплообменником типа «труба в трубе»; б) элементным, т. е.
составленным из нескольких кожухотрубчатых аппаратов меньшей площади,
соединенных последовательно; в) одиночным кожухотрубчатым аппаратом. Как
следует из табл. 4.13, можем использовать как аппараты типа ХН, так и типа ТН.
Для обеспечения интенсивного теплообмена попытаемся подобрать аппарат
с турбулентным режимом течения теплоносителей. Рассол направим в трубное
пространство, так как он дает загрязнения, эфир — в межтрубное
пространство.
В теплообменных трубах 025X2 мм холодильников по ГОСТ 15120—79
скорость течения рассола при Re2 > 10 000 должна быть более
Re#2 10 000-7,165.10-3
^яТйа 0,02Ы220 ~2'8М/С>
где ц2 = 7,165-Ю"3 Па-с — вязкость рассола при t% =—13,5°С (табл. LI).
Проходное сечение трубного пространства при этом должно быть менее
SJ = V2jwr, = 0,0081/2,8 = 0,289.10~2 м2.
Кожухотрубчатый холодильник наименьшего диаметра 159 мм с числом
труб 13 имеет ST = 0,5-10~2 м2 (табл. 4.12). Следовательно, турбулентное
течение рассола можно обеспечить только в аппарате с меньшим сечением
трубного пространства, т. е. в теплообменнике «труба в трубе».
Вариант L Теплообменник «труба в трубе» (ГОСТ 9930—78).
1.1. Рассмотрим аппарат, изготовленный из труб 89X4 мм (наружная труба)
и 57X3,5 мм (внутренняя труба). Скорость рассола в трубах для обеспечения
турбулентного течения должна быть более w'2:
10000^2 10000-7,165.10"8 . 17 .
2== rf2p3 " 0,05-1220 вв1,17 М/С*
w2 =
* Теплофизические свойства эфира приведены в табл. IV, IX, X, XXXIII
и иа рис. XI и XIII, свойства рассола — в табл. XXXIII, LI, LII.
216
Число параллельно работающих труб 57X3,5 мм, при этом
Уг 0,0081
л'
0,785^2 0,785- 0,053-1,17
= 3,53,
Примем л = 2. Определим скорость и критерий Рейнольдса для рассола:
V% 0,0081
w2 =
OJSSdin 0,785-0,05^2
2,07 м/с;
Re2 e 5йр, = i^^iM0_el7660i
Для эфира:
а»1
1^2
0,0015
7,165-10"3
0,0015
Sx 0,785 (D3 — (P) n 0,785 (0,081*—0,0572)-2
= 0,27 m/cj
Rex =
MaPi 0,27-0,024-733
^i
0,28-1(Г3
= 16960,
где эквивалентный диаметр d3 — D — d = 0,081 — 0,057 = 0,024 м,
1.2. Составим схему процесса теплопередачи (рис. 4.23). По табл. 4.1
находим, что теплоотдача для обоих потоков описывается уравнением (4.17)|
Nu » 0,0216/ Re°'8Pr°'43 (Pr/PrCT)0'25.
Коэффициент е^ примем равным 1, полагая, что Lid > 50 (табл. 4.3).
Ввиду того, что температуры стенок со стороны эфира /Ст. I и рассола /ст. i
пока неизвестны, примем сомножитель (Рг/РгСт)0'25 равным единице для обоих
потоков [это позволяет сделать сама форма уравнения (4.17)],
а) Коэффициент теплоотдачи для эфира.
Критерий Прандтля для эфира при _j_2,5°C:
Pri = CijAiAi = 2140-0,28.10"8/0,136 = 4,4,
где ^i = 0,136 Вт/(м-К) — коэффициент теплопроводности эфира (рис. Х),ч
Критерий Нуссельта для эфира:
Nu; = 0,021 - Ы6 960м.4,4°>43.1 = 94,8.
Коэффициент теплоотдачи от эфира к стеике:
а{ = NuXt/dt = 94,8-0,136/0,024 = 537 Вт/(м2.К).
б) Коэффициент теплоотдачи для рассола.
Критерий Прандтля для
рассола при —13,5 °С:
Рг2 = с^2/Х2 = 2900-7,165х
Xl0"2/0,473 = 44,
где Яа= 0,473 Вт/(м • К) —
коэффициент теплопроводности
рассола (табл. LI).
Рис. 4,23 (к первому варианту
расчета примера 4,1).
Qepup
t^ + 2,5°C
*ст.1е"й7вС "I
^Загр,1
Рассоп
*ст.2—//,2вС
* Ц=5920Ът/ы*
at*526BT/(M2-№W | а2*2550Вт/(м*-К)
-—^эагр.2
217
Критерий Нуссельта:
Nua = 0,021 • 1 • 17 6500'8 -440'43.1 = 262.
Коэффициент теплоотдачи от стенки к рассолу:
о? = NuaXa/da = 262-0,473/0,050 = 2480 Вт/(м3-К).
Термическое сопротивление стеики и загрязнений (табл. XXXI):
1 , 0,0035
s
ГСт =
5800
+ ieT + 58oo = 4'2-10"4Ma-K/BT-
что
Коэффициент теплопередачи:
К'ш.- =^ г=-1 1 —=373 Вт/(м».К).
¦W + lir"+-b 537 + 4'2 • 10"4 + 2480
Поверхностная плотность теплового потока:
q' « К' А/Ср = 373-16 = 5970 Вт/ма.
1.3. Определим ориеитировочио значения *ст. J и /ст. 2, исходя нз того,
где сумма
Найдем:
q' = К' А/ср = «I А/; = —^— A/J = а? М'г%
Д/, == (/'/«; = 5970/537 = 11,1 К;
ДС = <?' И гст= 5970-4,2.10-" = 2,5 К;
л.- - * 5970 ..,.
Д'2=<? "5Г = 2480 = 2Л К-
Проверка: сумма Д/j, Д^ и А/ст равна Д*ср:
ПА + 2,5+ 2,4= 16 К = 16°С
Отсюда
Ci = 'i — A*I =2,5—11,1 = — 8,6 °С;
'ст.2 = ^ + л4 = ~13'5 -Ь 2,4 = —11,1 °С.
Введем поправку в коэффициенты теплоотдачи, определив (Рг/Ргот)0|25<
Критерий Прандтля для эфира при tCTt t — —8,6 °С:
Ргст.1 = ^ст.^стаАст.г = 2050-0,322-10-3/0,137 = 4,85.
Критерий Прандтля для рассола при tCTt г = —11,1°С:
Ргст.3 =сст.2(хст.2ДСТ(3 = 2900*6,2.10'3/0,475 =38.
Коэффициенты теплоотдачи;
для эфира
а, = а[ (PrjyPrc-r.i)0'25 = 537 (4,4/4,85)0'25 = 537.0.9080'25 =
==537-0,98 = 526 Вт/(м2.К);
218
для рассола
а2 = а,: (Рг2/Ргст.2)0'25 = 2480 (44/38)0'25 = 2480* 1,1 б0*25 =
= 2480-1,03 = 2550 Вт/(ма-К).
Исправленные значения Kt <?, tCTt i, /ст> 2:
к = ! = 370 Вт/(м2.К);
526 + *>2-^ + §550
q = К Д^ср == 370 -16 = 5920 Вт/м2;
'сти = ^—^- = 2.5-^ = 2,5-11,2 =-8,7°С;
*ст.3 = /, + J- = -13,5 + SS! = -13,5 + 2,3 - —11,2 "С.
2
2550
Дальнейшее уточнение alt aa и других величии не требуется, так как
расхождение между а[у ал и а2» а2 и ДР- ие превышает 5 %.
1.4. Расчетная площадь поверхности теплопередачи:
Fp = Qft = 86 500/5920 = 14,6 ма.
С запасом 10%: Fp = 16,1 ма.
Площадь поверхности теплообмена одного элемента длиной 6 м?
Fia=jK*cpL« 3,14-0,0535.6 «1,01 м2.
Число элементов в каждой из двух секций (ветвей):
* - тпт " §тогe 8 "•
Общее число элементов nN = 2-8 = 16 шт. Масса аппарата «труба в
трубе» — 1600 кг. — см. каталог «Теплообменники ТТ. Емкостная сварная
аппаратура». М., ЦИНТИХИМНЕФТЕМАШ, 1968.
Вариант 2. Кожухотрубчатый холодильник диаметром 159 мм с трубами
25X2 мм (ГОСТ 15120—79).
2.1. Скорость и критерий Рейиольдса для рассола:
__ V2 Уг 0,0051
Щ~~$^~ 0,785ш*! ~0,785.0,0213.13 ~^ lf81 M/C;
Re2 ^ i^^ = 14^^^° = 6500;
[г2 7,165-10 а
скорость и критерий Рейиольдса для эфира:
Vi 0,0015
Щ= Х" 0,8.10- bWi*;
Рг _ MiPi 0,187-0,025.733
Ке1-"7Г~= 0,28-10-^ e12300'
где Sf = 0,8-Ю"2 м2 — проходное сечение межтрубного пространства между
перегородками по ГОСТ 15120—79; щ = 0,28-10~3 Па -с — вязкость эфира
при +2,5 °С (табл. IX); dx = 0,025 м — наружный диаметр труб, определяющий
линейный размер при поперечном обтекании.
2.2. Для расчета процесса теплопередачи в этом случае (как и в предыдущих)
необходимо знать температуры /ст, t и /вт. г- Для потока в трубах при Re2<
219
<С 10 000 значение /ст. 3 влияет на выбор вида расчетной формулы через
посредство произведения GrPr. Зададимся значениями tCTt i и tCTt 2» исходя из
того, что tx > tCTr j > /ст> 2 > *2, например, примем ^ 1 = —10 °C; *;Ti 2 =
= —11°C (с последующей проверкой).
а) Коэффициент теплоотдачи для эфира (Re; = 12300).
При поперечном омывании потоком трубного пучка при Re > 1000
рекомендуется соотношение (4.31):
Nu = 0,4еф Re°*6Pr0'36 (Рр/Ргст)0'25.
Примем еф = 0,6 (см. с. 157). Критерий Прандтля для эфира при ^от. % = —10 °С;
Рг'ст.1 *= (qi/X)* „, , = 2070-0,328-10"3/0,136 = 5,0.
Тогда
Nui = 0,4-0,6-12 300°'6.4,40'36 (4,4/5,0)0*25 = 105;
а[ = Nu^i/d! = 105.0,136/0,025 = 570 Вт/(м2-К).
б) Коэффициент теплоотдачи для рассола (Re2 = 6500).
Для выбора расчетной формулы определим произведение (GrPr) при
определяющей температуре—средней температуре пограничного слоя (см. с. 154):
?2 = 0,5 (tCT *+**) = 0,5 [—11+ (—13,5)] = —12,25 °С.
Физические свойства рассола при t2 = —12,25 °С: р2 = 1220 кг/м3; Щ =
= 6,7-10~3 Па-с; bft = 0,475 Вт/(мК) — табл. LI; с2 = 2902 Дж/(кг-К) —
табл. LII; Ра«0,35-10"-3 К'1—табл. XXXIII;
Рг' = ^3Д3 = 2902-6,7-10-3/0,475 = 40,9;
G.' = ifl р д,,_ 5!«W^o,35. Ю- t_H _ (_13,5)] = 2,4.10,
(Gr'PO = 2,4.10М0,9 « 9,8-10*,
Для определения Nu2 при (Gr2Pr2) < 8-10& воспользуемся рис. 4.1, При
Ке-=б500:Рг°ЛЗ(р?/рГст)о,5-^ о^да
NU2- 22Рг^43(Рг/РрЗДв 2)°'25 = 22.440'43 (44/38)0'25 = 115
(где Ргст. 2 = 38 при /Ст. 2 = — И °Q;
а2 = NuJ^/d, = 115-0,473/0,021 « 2590 Bt/(m2-K).
Коэффициент теплопередачи:
К = -j г- = 390 Вт/(м*.К).
570 +4,2.10- + ш
Поверхностная плотность теплового потока;
q' = К Д?ст = 390.16 = 6240 Вт/м2-
2,3. Уточним значения /ст. i и /ст, 2-
п 694-П
<oi.i-'i-A/i-/i—^--+2,б-~--8.5ЧС;
a 6940
/ст. 2 = ^+^2--^+-^«-13,5 + ^==-11,ГС.
220
Имеем существенное расхождение между /Ст. i и /Ст. i (—10 °С и —8,5 °С),
однако это не влияет на коэффициент теплопередачи aj, так как критерий
Прандтля эфира при —8,5 °С равен 4,9, что близко к Рг^т< 1 « 5,0 при — 10 °С,
Итак, окончательно /0т. j = —8,6 °С, tCT 2 =»—11,1 °С.
2.4. Расчетная площадь поверхности теплопередачи:
Fp = Q/q = 86 500/6240 = 13,85 ма.
С запасом 10%: Fp = 15,2 м2.
Принимаем к установке аппараты длиной 3 м (ГОСТ 15120—79), Площадь
поверхности теплообмена одного аппарата по среднему диаметру труб;
F « ndCpnL = 3,14-0,023.13-3 = 2,81 ма.
Необходимое число аппаратов:
N = Fp/F = 15,2/2,81 =5,4.
Примем N = 6, Запас поверхности составляет при этом
FN — F',
2.8Ь6-13,85 100 = 21>3%,
F' 13,85
Масса одного аппарата диаметром 159 мм с трубами длиной 3 м равна Mf =»
= 255 кг (ГОСТ 15120—79), масса элементного теплообменника, состоящего
из N аппаратов:
М = МгЫ « 255-6 =» 1530 кг.
Аппараты по варианта^ 1 и 2 имеют высокую металлоемкость (~100 кг/м*
поверхности теплообмена) •** в этом их общий недостаток. Кроме того, оба
варианта отличаются большим числом элементов и фланцевых соединений, что
неудобно для обслуживания (замена прокладок, проверка герметичности и т* п.).
Поэтому целесообразно в качестве варианта рассмотреть кожухотрубчатый теп*
лообменник большего диаметра, например аппарат D = 273 мм или 325 мм«
Вариант 3. Кожухотрубчатый холодильник диаметром D = 273 мм С
Трубами 25X2 мм (ГОСТ 15120—79).
3.1, Скорость и критерий Рейнольдса для рассола:
V* У2 0,0081 _ йок .
Щ " -5Г " ТТ8^Г - 0,785.0,021».37 = °'635 M/G'
где п = 37 — число труб (ГОСТ 15118—79);
Re =M)8rfapft ^ 0,635-0,021-1220 _8Q
2 щ 7,165- Ю"3
Скорость и критерий Рейнольдса для эфира:
Vt 0,0015 n IQA .
^в1Г"ТП5=г-°'13вм/с;
Re _w&Pt _,0,136-0,025-733
Re* = ~7Г 0,28.10-» = 10000'
где Sf = 1,1 -10"2 м2 — проходное сеченне межтрубного пространства
(ГОСТ 15120—79).
3.2. Для теплового расчета ориентировочно примем t0Tt i = —10 °С, /ст< t =*
а) Коэффициент теплоотдачи для эфира.
При Rej = 10 000 применим соотношение (4.31):
Nul = 0,4-0,6.10 000°'6.4,40'36 (4,4/5,0)°>25 = 97,5;
а[ eNuJ^/di =97,5-0,136/0,025 = 530 Вт/(м3-К).
б) Коэффициент теплоотдачи для рассола.
221
Для выбора расчетного соотношения при Re8 «= 2280 определим
произведение Ре -р (табл. 4.4) при средней температуре пограничного сл°я h
h = 0,5 (/,+ W a) =0,51-13,5+ (-11)] =-12,25 °С
и максимальной длине труб L = 3 м:
d __ и-'rffp rf 0,635-2900- 1220-0,021 0,021 _ ^
е L ~~ к L - 0,47 3
При Ре — > 20 применима формула (4.23):
Примем гг = 1; вязкость рассола: Ист~ 6,35-Ю"3 при ?ст. 2 = —И °Q
а'2 = Nu2X,/d, = !4,0-0,470/0,02! = 313 Bt/(m*.K).
Коэффициент теплопередачи:
К' =¦—] vT V =~\ " Т~ = 181 Вт^м2-К^
Поверхностная плотность теплового потока:
q' = К1 Д/Ср = 181 • 16 = 2900 Вт/м3.
Проверка значений /Ст. i и ^ст.а:
'от. i = *i—^- = +2>5~w = 2'5-5-5 = -з°с;
<от. •-<• + -?- =-13.5+ |^«-4,2 °С.
При этих значениях /ст. j и /от. a сделаем новый расчет. Введение поправки
в коэффициент теплоотдачи для эфира не требуется, так как сомножитель
(Рг/Ргст)0'25 в новых условиях близок к таковому в предыдущем расчете.
Для рассола определяющая температура
h = 0,5 (/, + /Ст. t) « 0,5 [-13,5 + (-4,2)] = -8,85 °С.
Физические свойства рассола при ?3 = — 8,85°С: р = 1220 кг/м3; с2 =
= 2910 Дж/(кг-К); ^3 = Б/7-НГ* Пас; Ь = 0,48 Вт/(м*К). Тогда
Ре = wdcQ/k = 0,635-0,021 -2910-1220/0,48 = 99 000;
ре JL _ 99 000^1 = 690-
Как следует из сравнения произведений Ре -у- Для рассматриваемых
значений tCTi2 также близки и поэтому введение поправки в а2 не требуется.
Расчет теплопередачи окончен.
3.4. Расчетная площадь поверхности теплопередачи:
Fp « Q/g = 86 500/2900 = 29,8 м\
222
С запасом 10 94: Fp = 32,7 м2.
Площадь поверхности теплопередачи одного аппарата с трубами L = 3 м:
Fj = ж*Срл/,= 3,140,023-37,3 = 8 мя.
Необходимое число аппаратов:
/V' =Fp/F1 = 32,7/8 = 4,1.
Принимаем N = 4. Запас:
iVF-Fp 4-8 — 29,8
с' 29,8
р
100 = 7,4%.
Масса одного аппарата ?> = 273 мм с трубами L = 3 м равна Л^х = 553 кг.
Масса всех аппаратов:
М = MtiV =5534 = 2212 кг.
Из расчета следует, что дальнейшее уменьшение скорости рассола приведет
к еще большему снижению коэффициента К и росту поверхности теплопередачи.
Однако, учитывая то обстоятельство, что в более крупных аппаратах расход
металла на единицу площади теплообмена меньше, чем в мелких аппаратах,
выполним расчет одноходового аппарата D = 400 мм с трубами 25X4 мм.
Другим направлением может быть применение многоходовых аппаратов
(см. вариант 6).
Вариант 4> Кожухотрубчатын аппарат D — 400 мм одноходовый
(ГОСТ 15122—79).
Расчет аналогичен предыдущему. Приведем здесь лишь окончательные
результаты. В аппарате с трубами длиной L = 6 м для эфира: ш$ = 0,0425 м/с;
Ret = 2790; ах = 292 Вт/(м2- К); для рассола: w2 = 0,261 м/с; Re2 = 930; а2 =
= 197 Вт/(м2-К).
Коэффициент теплопередачи: К =112 Вт/(м2*К).
Поверхностная плотность теплового потока: q = 1790 Вт/м2.
Расчетная площадь поверхности теплопередачи:
Fp ==86 500/1790 = 48,4 м2.
С запасом 10 %: Fp = 53 м2.
Площадь поверхности теплообмена одного аппарата:
Fj = ndcpnL = 3,14-0,023* 111-6=: 48,2 м2.
Из сравнения F\ и Fp следует, что от аппарата с трубами L = 6 м придется
отказаться, так как при его применении нет запаса поверхности теплообмена
(при использовании аппарата с D = 400 мм, L = 6 м придется прибегнуть
к более холодному рассолу, чтобы повысить q за счет Лт'ср)-
Вариант 5. В аппаратах с трубами L = 4 м: аг = 292 Вт/(м*-К); а2 =
= 242 Bt/(ms-K); К — 125 Вт/(м2-К). Площадь поверхности теплообмена:
Fp = 43,4 м2; с запасом 10 %: Fp = 47,7 м2. Для одного аппарата F\ =32,2 м2.
Число аппаратов: /V = 47,7/32,2 = 1,48. Принимаем N = 2. Запас
поверхности составит—' . '—100=48,5%. Как видим, запас поверхности в этом
случае неоправданно велик.
Вариант 6. Кожухотрубчатын холодильник диаметр 325 мм с трубами
25X2 мм двухходовый (ГОСТ 15120—79).
6.1. Проверим возможность и целесообразность применения многоходового
аппарата, вычислив среднюю разность температур смешанного тока,
воспользовавшись соотношениями (4.80) и (4.81).
223
а) По формуле (4.80) Д/Ср = ед,Л^ср пр, где e = f (P, R):
P-JlZlU-^ (-12)-(-15) ^A^QQS-
г ~ г, - <, 25 - (-15) 40 U'U6'
Т-,-7-, 25-(-10) 35
R~ t,-tt ~ (-12) -(-15) ~ 3 ~'2'
На рис. VIII зависимость для /? = 12 отсутствует, что делает невозможным
определение ед по формуле (4.80).
б) По (4.81):
А/ср~0 Д<б + А*м + Л " ., 37+5 + 3572-^ 14,5 К'
J^lg дгб + Дгм-Л "* g 37+5-35,2
где Д^ = 37; Д^м = 5 (см. расчет AtCv при противотоке);
А = КоТ^+б^ ^ ^[25 — (—10)]2 + [(-12) - (—15)]* = К353 + З2 = 35,2.
Применение многоходового аппарата в нашем случае будет сопровождаться
небольшим снижением Д/Ср (с 16 К до 14,5 К, т. е, в 1,1 раза). Следовательно,
многоходовой аппарат применим.
6.2. По ГОСТ 15118—79 число труб одного хода пх — 26 шт., общее —
п = 52 шт. Сечение одного хода трубного пространства ST = OJSfaP/ii =
= 1-1(Га м3, проходное сечение межтрубного пространства (между
перегородками) SMT= 1,5-10~2 м2 (ГОСТ 15120-79).
Скорость и критерий Рейнольдса для эфира:
Dft М1Р1 0,0935-0,025-733,6
*е1ввПч~в 0,29.10-» = '
где Uf и pj; взяты при средней температуре эфира tx = t2 4- Д/С1) — —13,5 4-
+ 14,5 = 1 °С.
Скорость и критерий Рейнольдса для рассола:
V2 0,0081 л 01 ,
^2 - -с2- » r-TT^i = 0,81 м/с;
Sa 1-10
д^м0,81-0^
2 Щ 7,165-10 J
6.3. Для теплового расчета примем /CTt j = —6 °С, /ст, 3 = —8 °С»
а) Коэффициент теплоотдачи для эфира. По формуле (4.31):
Nux = 0,4.0,6.5920°'6.4,50'36 (4,5/4,8)0'25 = 74,5;
аг = Nu! Vrfi =74,5.0,136/0,025 «=405 Вт/(м2-К).
б) Коэффициент теплоотдачи для рассола. По рис. 4.1:
Nu2 « 6Pr°'43 (Pr2/PrCTi 2)0'25 « 6-440'43 (44/33)0'25 = 32,7;
а3 = Nu2V^2 = 32,7-0,473/0,021 =736 Вт/(м2-К).
Коэффициент теплопередачи:
К=*—. ! р-^235 Bt/(m2-K).
_ + 4,2-10- + ^
224
Поверхностная плотность теплового потока:
q » К Д/Ср *= 235> 14>5 «= 3400 Вт/м2.
Проверка значений *ст. i и /ст. 2;
Д/, » <?/«! = 3400/405 = 8,4 К = 8,4 °С;
/ст> t — ^ —8.4 = J —8.4 — -7,4 °С;
Д*3 « 9/а2 = 3400/736 « 4,6 К = 4,6°С;
'ст. з = —13*5 + 4>6 « — 8>9 К.
Введение поправки в расчет щ, аг, /С и q не требуется.
Площадь поверхности теплопередачи:
Fp = 86 500/3400 = 25,4 м2.
С запасом 10 %: Fp = 27,9 м2.
Площадь поверхности теплопередачи одного аппарата по среднему диаметру
Труб при L = 4 м:
/^ 3,24.0,023-52*4 = 15 м2.
Число аппаратов:
N' = F plF\ = 27»9/15 ~ 1,86.
Принимаем N = 2 шт. Запас:
2-15 — 25,4
25,4
100= 18%,
Масса двух аппаратов: М = 2*820= 1640 кг.
Вариант 7. Кожухотрубчатый аппарат диаметром 400 мм с трубами 20X2 мм
двухходошй.
7.1- Аппараты с трубами.20X2 мм обладают большей площадью поверхиосга
теплообмена при тех же габаритных размерах, что, вероятно, позволит нам
обойтись одним аппаратом. В аппарате D = 400 мм, ST = 1,7-10'* м, 5адт = 3,0 X
X 1(Г2 м2 (ГОСТ 15120—79). Число труб одного хода 83, общее 166
(ГОСТ 15118—79).
Для эфира:
„< = -?- = |^ = 0,0467 м/с;
abddh 0,ОШ-0,020.733,6
1 ~ ТГ~ ~ 0,29-Ю-з ~ гШ-
Для рассола:
V, 0,0081 п _ ,
^=^=Т7Ло^~0'477м/с>-
_ МаР» 0,477-0,016-1220
"' ~ "7Г~ = 7,165.10-3 = 130°-
7.2. Для теплового расчета примем /ст- х = —6 °С, <от< : = —8 "С.
а) Коэффициент теплоотдачи для эфира:
а, - -Ь- Nut = ^|0,4.0,6.2370»'6.4,5^б ^у.25 = ^ ^.^
8 Пацлов К. Ф. и др. 22&
б) Коэффициент теплоотдачи для рассола.
Определим Ре -р при ?2 — 0»5 (U + 'ст. г) — °»5 [—13,5 + (—6)]
=—10 °С и длине труб L = 6 м:
L ^2 L 0,48 6
^ = М8 .М4]1/3 /^lO^y.".^ Вт/(м2.К).
1 d2 0,016 \ 5,0-10 3 /
Коэффициент теплопередачи:
к в _^ ! _ 125 Вт/(мя • К).
§86 + ^-^+542
7.3. Площадь поверхности теплопередачи:
F> <? - 86 50° - 47 8 м*
С запасом 10 %: fp = 52,5 м2.
Площадь поверхности теплообмена одного аппарата (D = 325 мм, L =
= 6000 мм):
Ft « nrfcprtL = 3,14-0,018-166-6 = 56,5 м2.
Запас:
F*~FP _ 56.5-47,8 ,
р ^ 100 = 17,8%.
р
Масса аппарата: Мх = 1890 кг.
Сопоставление вариантов аппарата для охлаждения диэтилового эфира
рассолом выполним по показателям, приведенным в табл. 4.13 *.
Наименьшую стоимость имеет аппарат типа «труба в трубе», однако ои
обладает существенным гидравлическим сопротивлением (по рассолу 10 Па),
громоздок. Поэтому предпочтение следует отдать кожухотрубчатым аппаратам:
элементному, состоящему из двух аппаратов D = 325 мм и L = 4 м или
одиночному аппарату D = 400 мм, L = 6 м с трублми 20X2 мм.
Пример 4.II. Рассчитать два варианта горизонтального кожухотрубчатого
теплообменного аппарата для нагреза 20 т/ч толуола от 21 до 98 °С. Греющий
водяной насыщенный пар имеет абсолютное давление р = 1,6 кгс/см2. В
водяном паре содержится 0,5 % воздуха.
1-й вариант; турбулентное течение толуола в трубном пространстве,
2-й вариант: ламинарное течение толуола в трубном пространстве.
Решение. Ввиду того, что в трубах нагревается толуол, а не вода и
температура в трубах выше 60 °С, используем аппараты типа ТН или ТК.
Принимаем для межтрубного пространства индекс «1», для трубного—«2».
Температура конденсации водяного пара /Конд — 112t7 СС (табл. LV1I).
Температурная схема*.
112,7—112,7
21 —у 98
Д*б = 91,7 А^м= 14,7.
* Цены взяты по «Прейскуранту № 23—03. Оптовые цены на оборудование
химическое. Часть 1. Стандартизованное химическое оборудование. Кн. 1».
М.: Прейскурантиздат, 1981. — 348 с.
226
Таблица 4.13
Холодильники для охлаждения эфира рассолом
Аппарат
Количеотро
N, шт.
Масса
1 шт.,
кг
Цена 1 шт.,
руб.
Цена
N шт., руб.
Металлоемкость,
кг/мЕ
Теплообменник «труба в трубе» (ГОСТ 9930-
16 100 —100 1600—1700
Трубы
89X4 мм
57X3,5 мм
-78)
99,5
Кожухотрубчатые холодильники одноходовые
(ГОСТ 15120—79)
D = 159 мм,
L = 3 м,
d= 25X2 мм
D = 273 мм,
L = 3 м,
d= 25X2 мм
255
553
345
600
2070
2400
91,0
69,5
Кожухотрубчатые теплообменники
(ГОСТ 15122—79)
jD =
L =
rf =
jD =
L =
d =
400 мм,
6 M,
25X2mm
400 мм,
4 м,
25X2 мм
1
**
1750
1290
1530
1200
1530
2400
36,5
40,3
Кожухотрубчатые холодильники двухходовые
(ГОСТ 15120—79)
D = 325 мм, 2 820
L = 4 м,
d = 25X2 мм
D =* 400 мм, 1 1890
L = 6 м,
d = 20Х 2 мм
900
1800
1800
1800
54,7
33,5
* Нет запаса поверхности теплопередачи.
** Запас слишком велик ( — 48 %).
Средняя разность температур:
л / — A/fl А?м _ 91,7— 14,7 _ ло I °г — 49 1 К
Л?СР - 2,3 К; (Д/б/Д/м) -2,3 lg (91,7/14,7) ~ ^Л ^ ~ ^'1 *<•
Средняя температура толуола:
/2 *= ^ — А/Ср = 112,7-42,1 л;70оС.
Расход толуола:
G2 « 20000/3600 » 5,56 кг/с; Ка = G2/p2 = 5,56/820 = 0,00678 м3/о.
Здесь р2 — 820 кг/ма—плотность толуола при 70 °С (табл. iV),
8!
227
Расход теплоты на нагрев толуола:
Q = G2c2 (tm — tm) » 5,56-1800 (98 — 21) = 771 000 Вт,
где с2= 1800 Дж/(кгК) — средняя удельная теплоемкость толуола (рис. XI),
Расход сухого греющего пара с учетом 7 % потерь теплоты:
. 1.07Q 1,07-771000
Gi = -т- = 2227.103 = 0,37 кг/с,
где /- = 2227-103 Дж/кг— удельная теплота конденсации водяного пара
(табл. LVI1).
Ориентировочно определяем максимальную величину площади поверхности
теплообмена. По табл. 4.8 минимальное значение коэффициента теплопередачи
для случая теплообмена от конденсирующегося водяного пара к органическим
жидкостям (подогреватели /СМив = 120 Вт/(м2К)). При этом
Q 771000
^мин^ср "" 120-42,1
П V ' ' 1 WU ._Л g
Расчет первого варианта (Rea > 10 000).
Составляем схему процесса теплопередачи (по типу рис. 4.23).
Для обеспечения турбулентного течения толуола при Re2 > 10 000
скорость в трубах должна быть больше w'2:
10000а2 10000.0,36.10-3 оло
W>" Th = 0.021-820 = °'209 М/С'
где |Л2 = 0,3610~3 Па-с — динамический коэффициент вязкости толуола при
70 °С (табл. IX).
Число труб 25X2 мм, обеспечивающих объемный расход толуола при Re2 —
= 10 000:
0,785<%>>2 0.785-0.0212-0,209
Условию л < 93,7 и F< 150 ма удовлетворяют (табл. 4.12) два
теплообменника;
а) четырехходовый диаметром 600 мм с числом труб на один ход трубного
пространства л — 52,5 (общее число труб 210);
б) шестиходовый диаметром 600 мм с числом труб на один ход трубного
пространства я =.33 (общее число труб 198).
Выбираем четырехходовый аппарат, как более простой.
I. Коэффициент теплоотдачи для толуола.
Уточняем значение критерия Re2:
Re2 = 10 000 (riln) = 10 000 (93,7/52,5) « 17 850.
Критерий Прандтля для толуола при 70 °С:
Prs = с2ц2А2= 1800-0,36-10-3/0,1248 = 5,19.
Здесь Х2 = 0,1248 Вт/(м К) — коэффициент теплопроводности толуола при
70 °С (рис. X).
Расчетная формула (4.17):
Nu2 = 0,021 • Re°'8Pr?'43 (Pr^/Pr^ 2)°'2bei = °>021'17 ti5°M •5» I9°'43 *
X 1,05-1 = 112,7.
228
Отношение (Pr2/PrCT. 2)0'25 принято равным 1,05 (с последующей проверкой).
Таким образом,
а2 =Nu3X2/d3= 112,7-0,1248/0,021 =669 Вт/(м2.К).
II. Коэффициент теплоотдачи при конденсации водяного пара на пучке
горизонтальных труб.
Расчет осуществляем приближенно (бе^ учета влияния поперечных
перегородок) по формуле (4.54):
В нашем случае известно G\ = 0,37 кг/с и п — 210. Поэтому используем
зависимость а, = f (n, L, G) с учетом влияния примеси воздуха (0,5 %):
а1 = 2,02еегБ( (n/G^^L4* = 2,02.0,62-0,6-1048 (210/0,37) 1/8LV* = 65201/'%
где е— коэффициент [см. формулу (4.53)], для шахматного расположении труб
в пучке и при числе рядов труб по вертикали пв = 14 (табл, 4.12) е = 0,62
(рис. 4.7); 8р — коэффициент, зависящий от содержания воздуха в паре (рис. 4.9),
ер= 0,6; Bt = 1048 (табл. 4.6).
Надо задаться длиной труб (по табл. 4.12 длины труб 2; 3; 4 и 6 м).
Задаемся L = 3 м. Если по окончании расчета будет принята другая длина труб,
то расчет необходимо скорректировать (с увеличением L при Gx = const
величина аСр возрастает). Имеем:
сех = 6520.37s = 9400 Вт/(м2-К).
Принимаем тепловую проводимость загрязнений со стороны греющего пара
1/гз^гр. х « 5800 Вт/(м2-К), со стороны толуола 1//загр.2 » 5800 Вт/(м2 К)
(табл. XXXI). Коэффициент теплопроводности стали %'ат = 46,5 Вт/(м-Ю
(табл. XXVIII). Тогда
^=_L- + Mk,_L- = 2580 Вт/(м2-К)'
5800 "*" 46,5 "*" 5800
Коэффициент теплопередачи:
yc = -j ~ г = —i Г Г" =503 Вт/(м3"К)-
"^"+2jr°T +~^Г "940СГ + "2580" + ~669"
Поверхностная плотность теплового потока:
?» УС Д/0р = 503-42,1 =21 180 Вт/м*.
Проверяем принятое значение (Рг2/Ргст> 2)0,25- Определяем
М2 = д/а2 = 21 180/669 « 32 К » 32 °С;
'ст. 2 = h + Д'а = 70 + 32 =* 102 °С;
Ргст. 2 =* сст. зМст в Act. з = 1885-0,27.10^/0,1163 » 4,38.
Здесь сст1=1885 Дж/(кгК) (рис. XI); |i0T а = 0,27-10"* Пас
(табл. IX); Лст'.3 = 0,1163 Вт/(м-К) (рис. X).
229
Следовательно,
(Pr2/PrCT. 2)0'25 « (5,19/4,38)».» *= 1,043.
Было принято (Рг2/Ргст. 2)0>2Ь = i-05. Разница ~0,7 %. Расчет К закончен.
Расчетная площадь поверхности теплообмена:
„ Q __ 771000 og ,
fp~ КД/Ср " 503-42,1 ~~ **'* м "
Коэффициент теплоотдачи ссг = 9440 > а2 = 664 Вт/(м2-К), поэтому
расчетным диаметром при определении поверхности труб следует принять о2 =*
= 0,021 м.
Аппарат с L « 3 м имеет площадь поверхности теплообмена:
F = JGrf2/iL = 3,14-0,021*210-3 =* 41,56 м2.
Запас площади поверхности теплообмена: — о„ л—— 100 = 14,2 %*
36,4
Запас площади поверхности теплообмена достаточен.
Принимаем один четырехходовый кожухотрубчатый теплообменник с
внутренним диаметром кожуха 600 мм, числом труб 52,5/210 и длиной труб L = 3 м.
Ввиду того, что общая разность температур А/Ср =42,1 К близка к
допускаемой разности (/к— ^т)макс — 40 К (табл. XXXV), принимаем аппарат тила
ТН.
Определяем tGTt %:
A/g = q/a2 =* 21 180/669 = 31,659 К = 31,659 °С;
/ст> 2 = 70,6 -f 3J,659 « J 02,3 °С.
На схему процесса теплопередачи типа рис. 4.23 нужно нанести уточненные
еначения /Ст. 1> *ст.2» аг> а2> Я-
Расчет второго варианта (Re2 < 2300).
вставляем схему процесса теплопередачи по типу рис. 4.23.
Для течения толуола при Re^ < 2300 скорость в трубах должна быть
меньше w'2:
2300яа_ 2300-0,36-10-3
*ae"5S" 0,021-820 ==0>048м/с»
а число труб иа один ход трубного пространства должно быть больше n,j
У* _ 0>00678
й,7ЪЬйЫг 0,7850,021*0,048 ~
Условно п > 408 и F < 150 м- удовлетворяет одноходовый кожухотруб»
чатый аппарат с внутренним диаметром кожуха 800 мм, площадью поверхности
теплообмена от 74 до 226 м2 и общим числом труб п = 473 (табл. 4.12).
I. Коэффициент теплоотдачи для толуола.
Уточняем величину критерия Рейнольдса:
Re2 = 2300 (пЧп) = 2300 (408/473) = 1984.
Находим ориентировочное значение произведения критериев (Gr2Pr2). В
величину критерия Gr3fl а также в выражение определяющей температуры
входит величина А^2 — *Ст. 2— h- Однако /ст. 2 определяется только в конце
расчета, поэтому величиной Д/2 надо задаваться.
Коэффициент теплоотдачи при конденсации водяного пара значительно
больше коэффициента теплоотдачи при нагреве толуола (табл. 4.7), поэтому
принимаем ориентировочно (с последующим уточнением):
разность температур
Д/2= 0,75 Д*ср = 0,75-42,1 ^ 32 К ~32СС;
230
определяющую» температуру
/ = г» + (Д^з/2) = 70 + (32/2) ~ 90 °С;
температуру стенки
'ст. 2 = к 4- А^2 = 70 + 32 = 102 °С.
Ориентировочное значение (Gr2pF2) яри 90 °С для толуола (физические
величины по табл. IV, IX, XXXII):
<С*,Рг,> _ РГг = о,295М(Г» 4,93=13,4-10*
Зйесь
Рг2 = 2023-0,295.10"3/0,121 =4,93,
где с3= 2023 Дж/(кг-К); Я.2= 0J21 Вт/(м-К).
При (Gr2Pr2) > 8-I05 и Rea<3500 применима формула (4.25). Принимаем
длину трубы L = 3 м. Тогда
Nu2 = 0,8 (Ре2 АуЛ (Gr2Pr2*>l (^)°'М = 0,8 (72)М (13,4- Ю')М X
X (-§§-)0,Н = 0,8.5,53-6,5.1,014 = 29,2,
где Ре2 -J- *=Re2Pr2 -j- = 1984-5,19 Ml1 = 72; fxCT. 2 = 0,266-Ю-3 Па-с
при 'ст. 2= 102 °С.
Таким образом,
а2 = Nu2k2/d2 = 29,2-0,1248/0,021 = 173 Вт/(м2. К).
П. Коэффициент теплоотдачи при конденсации водяного пара.
В первом варианте расчета аппарата при п = 210, е ^ 0Г62 было
определено clx = 9400 Вт/(м2-К). Во втором варианте п = 473. Число рядов труб
по вертикали пв = 32 (табл. 4,14), чему соответствует е ^ 0,57 (рис. 4.7),
При той же длине труб L = 3 для второго варианта:
ai = 9400Т§" ("Яг)73 = 9400-0.92-1>31 - И 400 Вт/(м*.К).
Коэффициент; теплопередачи при L = 3 м (предварительный):
/(t=3 = —j y Г" = 16° Вт/(м2'К>'
7Т400 + "2500" + 173
где вСт/Яст = 1/250О.
Уточнение принятых величин:
а) разнос гь температур Д/2 по расчету
М2 = К Мср/а2 » 160-42Л/173 =39 К = 39 °С;
б) определяющая температура
f =.70+(Э9/2) я*90°С
(расчетное значение определяющей температуры совпало с принятым 90 °С);
в) уточнение а2 за счет того, что расчетное значение Ы2 оказалось больше
принятого
ct2 = 173(39/32)^ = 173-1,02 = 176 Вт/(м2-К);
231
г) уточненное значение коэффициента теплопередачи при L = 3 м
*|>« = —1 \ — - 162 Вт/(м«.К).
11 400 + 2500 +17б"
Расчетная площадь поверхности теплообмена при L = 3 м:
р 771000 ll0 a
Коэффициент теплоотдачи «i > ct2) поэтому за поверхность теплообмена
аппарата следует принять внутреннюю поверхность труб [формула (4.75)].
Так, одноходовый теплообменник с внутренним диаметром кожуха 800 мм при
длине труб 3 м имеет площадь поверхности теплообмена F = л-0,021 X
X 473*3 = 93 м2, что недостаточно.
Рассмотрим два варианта: а) длина труб 4 м, F = л-0,021 -473*4 = 125 ы2\
б) длина труб 2 м; два аппарата с общей площадью поверхности 125 м2«
а) Теплообменник с трубами 4 м:
ccj « 11 400 ^4/3)1/я в И 400-1,1 » 12500 Вт/(м2.К);
аа « 176 (3/4)0-4 » 176-0,89 = 157 Вт/(м2-К).
Kl=4 = j !j j— = 146 Вт/(ма.К).
i2 500 + ToOO + "IsT
Расчетная- площадь поверхности теплообмена при Z. = 4 м:
771000 3
/Ч="- 146-42,1 -U5>4 M-
Площадь поверхности теплообмена недостаточна, так как нет запаса,
б) Два теплообменника с трубами длиной по 2 м:
а2= 176 (3/2)о.* «176-1,176 «207 Вт/(м2-К);
KLm,2 « — \ — « 188 Вт/(м2-К).
12 500 + 2500 +~20Г
Поверхностная плотность теплового потока (удельная тепловая нагрузка)
q= К Д^ср = 188-42,1 = 7915 Вт/м2. Расчетная площадь поверхности
теплообмена при L = 2 м:
^L-2 = Q/<7 = 771 000/7915 « 97,4 м2.
Принимаем два одноходовых теплообменника с внутренним диаметром
кожуха 800 мм и длиной труб по 2 м.
125 97 4
Запас площади поверхности теплообмена: Q .. ' 100 — 28 %. Запас
у/,4
площади поверхности теплообмена достаточен.
Определение /от. г и tCTt a для принятого варианта:
A'i = <7/«i — 7915/12 500 = 0,633 К *» 0,633 °С;
Wi= П2,7 —0,633= 112,067 °С;
Д'а = <?/сеа = 7915/207 « 38,237 К « 38,237 °С;
/ст. 2 — 70,6 + 38,237 = 108,837 °С.
232
Вт
' м2-К
"г^Ёк
<2=Ш0=Вт/м*
Рис. 4.24. Схема процесса
теплопередачи (к примеру 4,III).
На схему процесса
теплопередачи нужно нанести
уточненные значения /от> %, /0т. 2,
Пример 4. III, Рассчитать
кожухотрубчатый теплообмен ¦
ник для охлаждения в
межтрубном пространстве 1240 м3/*]
(считая при нормальных
условиях) азота от 76 до 31 °С.
Абсолютное давление азота
1,5 кгс/см2 (~0,15 МПа). Вода
поступает в трубное
пространство прн 16 С,
Решение. Для данного
расчета можно использовать
кожухотрубчатые аппараты
типов ХН или ХК.
Составляем схему процесса
теплопередачи (рис. 4.24). Принимаем для азота индекс «1* для воды (в
трубах) — индекс «2», конечную температуру воды 26 °С.
Температурная схема теплообмена при противотоке:
76 —*• 31
26 «— №
Д*« = 15.
fcCT.2-2ff,54°C
ie—
50- 15
А/б = 50
Средняя разность температур:
А/б ~ А*м
а(°Р 2,3 lg (А/в/А/м) 2,3 lg (50/15)
Средняя температура воды:
/3=(26+16)/2=21°С.
Средняя температура азота:
/i = /я + А/Ср = 21 + 29 =* 50 °С.
Количество теплоты, передаваемое от азота к воде:
= 29°С = 29К.
Q
v
oi
3 600
Poici {ha — ^ik)
1240
.3600
1,25-1050 (76 — 31) = 20 300 Вт,
где Poi= 1,25 кг/м3— плотность азота при 0 °С и 760 мм рт. ст. (табл. V);
сг= 1050 Дж/(кг- К) — средняя удельная теплоемкость азота (табл. XXVII).
Расход воды:
G9 =
Q
20 300
М'гк-'гн) 4190(26—16)
0,485 кг/с.
Ориентировочно определяем максимальную величину площади поверхности
теплообмена. По табл. 4.7 принимаем для случая поперечного обтекания
воздухом пучка труб, расположенных в шахматном порядке, аВОЯп = К =
= 70 Вт/(м2-К). Тогда д
Q 20300=10м*.
макс
/Смян А/
ЗЛ1
чатый аппарат с числом труб 37.
70-29
МИБ "*Ср
Условию F < 10 м2 удовлетворяет (табл. 4,12) одноходовый кожухотруб-
233
Основные данные: 1) площадь проходного сечения по трубам
ST = 37-0,785-0,0212= 0,0128 м2;
2) площадь проходного сечения в вырезе перегородки S0. ж = 0,013 ма:
3) расстояние от диагонали до хорды сегмента /ii = 40 мм (табл. XXXV).
Рассчитаем площадь поверхности теплообмена.
1) Межтрубное пространство.
Размер стрелки сегмента:
*«-5|Э hx = _ipL_40s==90 мм>
Р асстоявие межд^ перегородками 1форм^ ла (4.3&) V.
^ТлЩ^ТлШ^т^ мм'
где л|) [формула (4.34))
. 1-WQ 1-(25/32)
^ 1—0,9 (d//)8 1 — 0,9 (25/32)2 и»*°°-
Расчетная скорость азота в межтрубном пространстве [формула (4.35)]:
k>j *= Vi/Sc. ж =0,28/0,013 = 21,5 м/с,
1240.323-1,033 ЛОО з/ л
где Ух — п : =0,28 м7с—объемный расход азота при рабочих
условиях.
Критерий Рейнольдса для азота:
Rei__]ir~ 0,019-Ю-з— —43 300,
273-15
где рэ = 1,25 ona I a'qq — 1»53 кг/м*— плотность азота при рабочих условиях;
о2о* J ,0оо
|j,i =* 0,019- Ю~3 Па-с — динамический коэффициент вязкости азота при 50 °G
(рис. VI).
Расчетная формула (4.32):
Nut = 0,356Не?',;еф = 0,356-43 300°'6'.0,6 = 130,
где ?ф = 0,6 — коэффициент (см. стр. 157).
Тогда
л ЫщКг 130.0,0267 ^^
где Я, = 0,0267 Вт/(м* К) — коэффициент теплопроводности азота при 50 °С
(табл. XXX).
2) Трубное пространство.
Скорость воды:
С2 0,485
Щ " "557 = 998.0,0128 = °>°38 м/С*
Критерий Рейнольдса:
Re ._ «М« _ 0,038-0,021 0|Y1^lnQnn
Re2___ _____ = 809 < 10 000,
где v2 = 0,986'10~6 м2/с— кинематический коэффициент вязкости воды прн
21 °С (табл. XXXIX). F
Находим ориентировочное значение произведения (Gr2Pra),
234
При расчете теплоотдачи в случае Re-< 10 000 определяющая температура
% = 0,5 (/ст> 2 + /2). Ввиду того, что температура ^ст. 2 будет определена только
в конце расчета, необходимо задаться величиной Л/2.
В данном примере теплопередачи от газа к жидкости следует учесть, что
коэффициент теплоотдачи от газа к стенке обычно значительно меньше
коэффициента теплоотдачи от стенки к жидкости, поэтому примем At2 ~ 0,25 Д^ст> —
= 0,25-29,5 а; 8 К^ 8 °С. У
При этом ?ст 2 = t2+ А^2 = 21 + 8 = 29 °С, и за определяющую
температуру прнмем V = 0,5 (fCT> 2 + h) = 0,5 (29 + 21) = 25 °С.
При этих допущениях:
Юг Рг ) - МЫЫ- Рг 0,0213-9972-2,52-Ю-".8-9,81 _
1 2 2> jl| РГг ~ 0.9022.10-е 6-22 - И-10 .
Значения р2, р2, (i2 и Рг2 для воды взяты по табл. XXXIX.
Произведение (Gr2Pr2) — 14-10* > 8-106; следовательно, для
горизонтального аппарата расчетная формула (4.25):
Nu2 = 0,8 (Ре2-4-)°'4 (Gr2Pr2)M (^J''4-
Принимаем по табл. 4.12 теплообменник с максимальной длиной труб L —
= 3 м. Тогда
(Pe2-^-)=Re2Pr2^- = 809-6,22-^4^-= 35,2;
Nu2 = 0,8 (35,2)М (о,14.10»)М (-^|§-)°'М = 0,8-4,16-4,12-1,01 =* 13,85,
где \iCT. я ~ 0,825- 10г3 Па-с — динамический коэффициент вязкости воды при
'ст. 2= 29 °С (табл. XXXIX).
Следовательно,
а2 = NuaX2/d2 = 13,85-0,608/0,021 = 401 Вт/(м2-К),
где Я2 = 0,608 Вт/(м- К) — коэффициент теплопроводности воды при 25 СС
(табл. XXXIX).
Примем тепловую проводимость загрязнений стенки со стороны азота
равной 2800 Вт/(м2 • К) (табл. XXXI), коэффициент теплопроводности стали
46,5 Вт/(м* К) (табл. XXVIII), тепловую проводимость загрязнений стенки со
стороны воды среднего качества 2400 Вт/(м** К) (табл. XXXI). Тогда
^=i^tw—:г:-1220 Вт/(м2-К)-
2800 -*" 46,5 "** 2400
Коэффициент теплопередачи:
К = — 1 — =95,2 Вт/(м2.К).
"l39~ + 1220 + ~4Ш~
Поверхностная плотность теплового потока:
q = К Atcp = 95,2-29 = 2760 Вт/ма.
Проверим применимость формулы (4.25) и уточним расчет. Расчетное значение Д/й.
Д/2 = q/a2 = 2760/401 = 6,88 К = 6,&8 °С.
235
Уточненное значение (Gr2Pra):
(Gr8Pr2) = 0,14-10'(6,88/8)°Д« 0,14-Ю'.0,988« 1,38.10*.
Формула (4.25) применена верно, так как (Gr2Pr2) > 10е и (Ре2-~Л > 20,
Расчетное значение определяющей температуры t = /2 + —тг-~ 21 +
+ —~ = 24,44, а было принято *— 25 °С.
Расчет q произведен правильно.
Расчетная площадь поверхности теплообмена:
F « Q/q » 20 300/2760 = 7,35 м*.
Принимаем один одноходовый кожухотрубчатый теплообменник с
внутренним диаметром кожуха 273/259 мм и длиной труб 3 м.
Площадь поверхности теплообмена по среднему диаметру труб:
F =* rofCprtL = 3,14.0,023.37-3 » 8,02 ма.
Запас площади поверхности теплообмена: —-——-ё ' 100= 9,1 %. Запас
. 7,Зо
площади поверхности теполообмена недостаточен.
Теплообменников с тем же числом труб, но с большей длиной труб по
ГОСТу нет.
Для увеличения запаса площади поверхности теплообмена, учитывая, что
с уменьшением длины трубчатки возрастает величина а, иместо одного
теплообменника с L = 3 м принимаем два теплообменника с L = 1,5 м, соединяемых
последовательно.
Коэффициент «j не изменится, а величина а2 возрастет;
а2 = 401 (3/1,5)М = 529 Вт/(м».К).
Коэффициент теплопередачи увеличится:
К=*—г 1 j—«101 Вт/(м2.К).
1W + Т220" + ~529~
Поверхностная плотность теплового потока:
q ** К Мср = 101 -29 = 2930 Вт/м«;
Уточнение значении /ст. 2:
А/8 « Я/а2 = 2930/529 = 5,54 К = 5,54 °С;
'от. 2 = ** + Д'а = 21 + 5,54 = 26,54 °С.
Было принято /ст# 2 ~ 29 °С. Разница незначительная.
Расчетная площадь поверхности теплообмена:
F = 20 300/2930 = 6,93 м2.
О ЛО f* ПО
Запас площади поверхности теплообмена: —-— ¦¦-'— 100 = 15,73 %. Запас
0,Уо
площади поверхности теплообмена достаточен.
Проверка допустимости применении аппарата типа ХН.
236
Определение температуры наружной поверхности труб /Т(Н:
Ч = r3arp>1 ' 29,3U- 1/2800 '
/т, н = 27,85 К = 27,85 °С.
Определение температуры внутренней поверхности труб /т# в:
/т,в — 26,54 ,
1/2400 '
д-_ /т. В 'СТ. 2
2930
''загр. в
tTt в = 27,77 К =* 27,77 °С.
Средний температура стенок труб:
*т = 0,5 (27,85 + 27,77) = 27,81 °С.
Средняя разность (/к — tT) = 50 — 27,81 — 22,19 °С = 22,19 К*
Величина (tH — tT) больше 20 К (табл. XXXV), поэтому принимаем аппарат
типа ХК.
Пример 4. IV. Рассчитать вынесенную греющую камеру выпарного аппарата.
Выпарная установка работает при кипении раствора в трубах при оптималм
ном уровне. При расчете выпарного аппарата принята высота труб Н = б ы.
При расчете установки определены: тепловая нагрузка Q = 1 100 000 Вт;
средняя температура кипения раствора хлористого натрия (20%) /кип« 90 °С;
температура конденсации сухого насыщенного водяного пара /конд = 116,3°С.
Для кипящего раствора X = 0,65 Вт/(м* К).
Решение. Составляем схему процесса теплопередачи (рис, 4.25),
Средняя разность температур:
iXto.r\ — *wnwrr — *
ср
конд
кип
116,3 — 90 = 26,3 °С = 26,3 К.
Находим коэффициент теплоотдачи от конденсирующегося водяного пара
к поверхности вертикальных труб по формуле (4.52а):
аконд = 2,04 (Н д/к^д)о,25 - 2,04 -??- (Д*кондГ0'25 = 9800 (Д/Н0ВДГ».«».
5°^
Следовательно,
Q = а А/ = 9800 А*0,75
^конд аконд а'конд уоии а'конд*
Конденсир ующийся
пар
tcT.i = W,250C
Of
конд'
7424
м2-К
Кипящая жидкость
кип
90°С
^ у*22300Ът/м*
«кип ^2071
ВТ
м**К
:»rW2
Рис. 4.25. Схема процесса теплопередачи (к примеру 4.IV).
237
Коэффициент теплоотдачи от стенки труб к кипящему раствору [формула
(4.62)]:
h ( *'Р \1/а V. лл^о/ 0,65М115 \У,д,Л _
акип e * V"]^7 ) g/a-°>074 0,51.10-^67,7-10-3.363 ) * e
где Ь = 0,075 [1 + 10 (рп/рж)*'»] = 0,075 [1 + 10 (0,424/1 II5)'/зJ = 0,079.
Физические величины для 20 % раствора хлористого натрия определены
по табл. IV, IX, XXIV.
Принимаем тепловую проводимость загрязнений стенкн со стороны
греющего пара ~ 5800 Вт/(м2-К) и со стороны кипящего раствора ~2900 Вт/(м2*К)
(табл. XXXI). Тогда
1 Х ^ 1785 Вт/(м2-К),
ст
1
1 °'002 ¦
1
2900
5800 ' 46,5
где %ст = 46,5 Вт/(м- К) — коэффициент теплопроводности стали (табл. XXVIII).
Ввиду того, что <*конд = /j (Д*коид) и акип = /2 (^кип) = /> (Д/щш)» Для
расчета коэффициента теплопередачи принимаем метод последовательных
приближений.
Для определения исходного значения КИСХУ учитывая: что при
установившемся режиме теплопередачи дшп = <?коид» выражаем акип через ?Конд:
«кип = 2.61?^ - 2,61^вд = 2,61 (9800 Д47„д)!/з = 1195 Д&5ВД.
Затем рассчитываем исходные значения /СИсх и <7иех» принимая Д/КОнд ^
= 1 К:
Кисх = —-л i г— = 667 Вт/(м2. К);
1
+
1
+
1
9800 "г 1785 ' 1195
<7исх = Ктх Д/Ср = 667-26,3 =17 540 Вт/м2.
Находим значение (A/K0Hn)x = <7ИОЯ/9800 = 17 540/9800= 1,79 К = 1,79 °С.
Составляем расчетную таблицу 4.14, в которую записываем исходные
данные *конд, гкип, (А^конд)ъ 1^? гот и результаты последующих расчетов.
Таблица 4.14
Приближения
и
поверочный
расчет
Конденсация греющего пара
^КОНД'
°С
СТ. 1'
°С
^^конд* К
д,0,25
конд
аконд»
Вт/(м2. К)
^КОИД'
Вт/м2
1
11
III
116,3
116,3
116,3
114,5
114
113,29
1,79
2,38
3,01
1,156
1,24
1,32
8472
7900
7424
15 160
18 800
22 300
Приближения
и
поверочный
расчет
Стенка н ее
загрязнения
7 2'ст-
ВтДТГ2. к)
А/
ст-
К
1
п
III
1785
1785
1785
8,5
10,53
12,52
t
ст. 2»
°С
Кипение раствора
t
КИП'
°С
\t
кип
К
а
КИП'
ВтДм*. К)
106,01
103,47
100,77
90
90
90
16,01
13,47
10,77
1600
1846
2071
Вт/м2
25 600
24 870
22 300
238
I. Первое приближение:
Сет. i)l -=¦ >конд - (А'коед)1 = 116,3—1,79= 114.51 °С;
(««нд)1 - 9*00 (*<конд)Г0'25 - "T^Sr - -?Щ- - 8472 Вт/С". К);
(?ковд)1- (<*конд)1 (А'конд)1 = 8472-1,79 - 15 160 Вт/м*;
(A'ct)i = 1] 'от <<7конД)1 « 15 160/1785 « 8,5 К = 8,5 °С;
Сет. a)l = Сет. i)l - (д^ст)1 = П4,51 - 8,5 = 106,01 °С;
(A'mm)l = Сет. 2)l - 'кип = Ю6.01 - 90 = 16,01 °С = 16,01 К;
(ак-л)л - 2>61 (^сяд)!'1 - 2,61 • 15,160*'* - 2,61 -612,5 «
= 1600 Вт/(м2'К);
fowm)l = (a™nh(A'wra)l = 1600.16,01 « 25 600 Вт/м2.
В первом приближении (^конд)г < (?кип)т-
II. Второе приближение.
Рассчитываем по первому приближению Ку
Кг « —, i — = 767 Вт/{м2.К)(
8472 + 1785 + 1600
тогда
Я1 = Ki Mcv = 767-26,3 = 20 180 Вт/м2.
Величину (Д*КОНд)и определяем, принимая (^коНд)ц = qi при (aK0H„)r =
= 8472Bt/(m2-K):
(^конд)и = <7i/C*k<Wi = 20 180/8472 = 2,38 К = 2,38 °С.
Затем выполняем аналогичный расчет (см. строку II в табл. 4.14).
24 870—18 800 1ЛП
Расхождение с/конд и дКип по второму расчету: Т$Щ 10° =
= 32% > 5%.
По результатам расчетов первого и второго приближения строим график
Я ~ f Сет. i)- Полагая, что при малых изменениях*гемпературы поверхностные
плотности у'конд и 9Кип линейно зависят от /ст. * (или от Д/КОНд)» графически
определяем Сст, i)ni~ 113,29 °С (рис. 4.26, точка Л).
III. Поверочный (третий) расчет (см. табл. 4.14).
22 350-22 300 1ЛЛ _ „ 00 0/ ^ _ ..
Расхождение ?коНД и ?КШ1: ^^ 100= 0,22 % < 5 %.
На рис. 4.26 наносим значения (</конд)ш н (<7кип)И1 и проводим через точки
I, II, Ill-го расчетов линии зависимости <7КОпд=* h Сст. i) и <7иип — /а Сот.l)-
Как видим, они нелинейны.
Расчет <7 закончен.
239
qC/O^Bf/M»
114 M,5
Рис. 4.26. Графическая зависимость * * =*/(?> (к примеру 4.IV).
На схему процесса теплопередачи (рис. 4.25) наносим из таблицы значения
'от. i» *ст. ?> аконд» акиш <7- По даииым последнего приближения определяем
коэффициент теплопередачи;
К =
1
аконд
+
S
ст
+
а
кип
7424
+
1
1785
+
2071
= 848 Вт/(м2-К).
Площадь поверхности теплопередачи:
Q 1,ыов
KAtCp 848(116,3 — 90)
= 50 ма.
Принимаем аппарат с площадью поверхности теплопередачи 65 м2 [5.4],
т. е. с запасом —^-— 100 — 30 %.
оО
В связи с необходимостью применения метода последовательных
приближений расчет процесса теплопередачи в греющей камере выпарного аппарата
рекомендуется выполнять с помощью ЭВМ. Ниже представлен алгоритм такого
расчета в виде блок-схемы и программа, записанная на языке ФОРТРАН-IV
применительно к ЭВМ «Искра-1256». В расчете коэффициентов теплоотдачи
использованы соотношения (4.52) при е^ = 1 и (4.62). Критическая плотность теплового
потока определена по уравнению (4.64). Значение А^конд №Я последующего
приближения определяется по данным предыдущего прнолижения на основе
того, что средняя рязность температур потоков (А/Ср ~ *конд — *кип)
распределяется по участкам: конденсация пара — стенка — кипение жидкости
пропорционально их термическим сопротивлениям.
240
/Ввод
/ ^кип»
/ гкчп*
J
( н
*КОНД
Лж> рж
П,дст т
ачлло }
1 ¦
,М>
.***,'
Acr,Q
т~
г -I
p,f*,At
О» рп.
|С)ш
I r7 {V
конд /
/
/
J
Блок-схема
чета примера 4.
М^-)
т
л _ «,чГ *ж рж 1
* ~
?Уст = Глагр.1 +-гзагр.2+(^ст/Асг)
I
±
tct. 2 s tcr.! ~3 к<энд ? 1*ег
г
¦А ^ ки п -1 ст. 2 *" ^ кип
I
Нет
*=
Чконд~Чнип
«Злонд
клнд
Да
Нет
<Jcp -0>5(<}конд + ^Кип)
Да
Печать лконд,<*кип.
К =
(7/ак.онд)ч-ОЛ*-кип)+?Усг
I
/ Печать7
[ F-9/[K(tK0HA-trtHn)J
I —
I Печать K,F,c[kP
Идентификаторы к расчету кипятильника с обогревом паромГ
Исходные данные
а) Конденсация пара.
Величина
Идентификатор
б) Кипение
Величина
Идентификатор
в) Аппарат.
Величина
Идентификатор
Величина
Идентификатор
Величина
Идентификатор
'конд
Т1
жидкое™
'ьип
Т2
Q
Q
Л b
А В
Sep
QSR
г
R1
I.
Рж
R02
И
Н
* Р Iх д'конл
LI ROl MU1 DT1
Pd ^ж Иж ° гкио
ROP2 L2 MU2 SIGMA R2
°ст ^ст гзагр. 1 гзагр. $ 8
DST LSI RZ1 RZ2 EPS
Рассчитываемые величины
С
С
</кр
QKR
аконд аьип ^ст. 1 'ст. 2 <?нонд 9кив ^
AL1 AL2 TS1 TS2 Ql Q2 R
2>ст А'кип 6 /( f
RST DT2 DKLTA К F
242
Программа расчета:
PROGRAM
COMMENT РАСЧЕТ КИПЯТИЛЬНИКА С ОБОГРЕВОМ
COMMENT ПАРОМ
REAL LI, MU1, L2, MU2, LST, К
READ (5) Tl, Rl, LI, ROl, MU1, DT1
READ (5) Т2, R02, ROP2, L2, MU2, SIGMA, R2
READ (5) Q, H, DST, LST, RZ1, RZ2, EPS
COMMENT РАСЧЕТ КОЭФФИЦИЕНТОВ ТЕПЛООТДАЧИ
A=,2.04*(SQRT(SQRT(((L1 * *3)*(R01 * *2)*
R1)/(MU1 *H))))
B=0.075*(1.+ 1O./((RO2/ROP2— 1.)* * 0.667))
C=(B* *3)*((L2* *2)*R02/(MU2*SIGMA*(T2
+ 273.)))
RST=RZ1+RZ2+DST/LST
1 AL1 = A/SQRT(SQRT(DT1))
Q1 = AL1*DT1
TS1=T1— DTI
TS2=TS1—Q1*RST
DT2=TS2—T2
IF (DT2<=0.) GO TO 2
AL2=C*(DT2* *2)
Q2=AL2 * DT2
DELTA=ABS((Q1— Q2)/Q1)
IF (DELTA<=EPS) GO TO 4
COMMENT ЗНАЧЕНИЕ DTI ДЛЯ СЛЕДУЮЩЕГО
COMMENT ПРИБЛИЖЕНИЯ
R=l./ALl-fl./AL24-RST
DT1=(T1—T2/R/AL1
GO TO 3
2 DT1 = DT1*0.5
3 GO TO I
COMMENT ПРОВЕРКА РЕЖИМА КИПЕНИЯ
4 QKR=0.14 *R2 *SQRT(ROP2) *SQRT(SQRT(
SIGMA *9.81 *R02))
QSR = (Ql + Q2)/2.
IF (QSR>QKR) GO TO 7
WRITE (6,5) AL1, AL2, Ql, Q2,TS1, TS2,
DELTA
б FORMAT (10X, 'AL1 = ', F7.1, 2X, 'AL2=\ F7.1
/10X, 'Ql-', F7.0, 2X, JQ2=\ F7.0/10X,
»TSl = \ F7.2, 2X, 'TS2=\ F7.2/15X, 'DELTA
= \ F8.4)
COMMENT КОЭФФИЦИЕНТ ТЕПЛОПЕРЕДАЧИ И
COMMENT ПЛОЩАДЬ ПОВЕРХНОСТИ ТЕПЛОПЕРЕДАЧИ
K=1./(1./AL1+1./AL2+RST)
F=Q/(K*(T1—T2))
WRITE (6,6) К, F, QKR
6 FORMAT (10X, 'K=\ F7.1/10X, 'F=\ F8.1/
10X, 'QKR=\ F15.0)
GO TO 9
7 WRITE (6,8) QSR, QKR
8 FORMAT (2X, 'QSR=\ F15./0, JQKR=\ F15.0,
'ПЛЕНОЧНОЕ КИПЕНИЕ —СЛЕДУЕТ ИЗМЕНИТЬ
РЕЖИМ РАБОТЫ АППАРАТА')
9 STOP
END ®®
Пример 4.V. Рассчитать змеевик для периодического нагрева
в баке (в условиях свободной конвекции). Ксилол в количестве 1600
быть нагрет от 16 до 80 °С в течение 1 ч. Нагрев производится паром, имеющим
давление рабс = 2 кгс/см2 (0,2 МПа). Стальной змеевик выполнен из трубы
диаметром 53 X 2 мм.
Решение. Температура конденсации греющего пара 119,6 °С (табл. LVII).
Так как она постоянна, то среднюю разность температур за время иагрева можно
рассчитать по формуле:
Д/„ач-А/коя __ ЮЗ.6-39,6 = 66)6 сс ^ 66?6 К)
где
А'ср 2,3 lg (Д*Нач/Л'кон) ~ 2,3 lg (103,6/39,6)
Д'нач = П9,6— 16= 103,6 °С = 103,6 К;
А^кон « *19>6 — 80 = 39,6 °С = 39,6 К.
Средняя температура ксилола:
'к = <конд - А*ср « 119,6 - 66,6 « 53 °С.
Средний расход передаваемой теплоты:
1600
Ц — ^кск ('кон ' *нач)
3600
1840(80— 16) = 52 300 Вт,
где Си = 1840 Дж/(кг-К) —средняя удельная теплоемкость ксилола (рис. XI).
Термическое сопротивление стальной стенки и загрязнений (табл. XXV11I
и XXXI):
6 . 1 0,002 . 1
2_ , б , 1 , 0,002 ,
'ст - 'загр. 1 + -J— + 'загр. 2 - 58оо + -Jglf +
5800
,ст 5800
» 0,0004 (ма-К)/Вт.
Коэффициент теплоотдачи для ксилола рассчитываем по уравнению (4.46),
принимая с запасом (Рг/Ргст)0,25 = 1 для нагревающейся жидкости:
Nu « 0,5 (GrPr)0'25 - 0,5 (S^P Pr)°'25<25 -
- 0 S ^8-0,053з.837М, 15-ИГ»-4,5 \°'25Л/о,25 _ 36 6 Л/*'25
— \ 0,43*. 10"в / к — ^°'ьдгк »
гдер — 837 кг/м3 — плотность ксилола при 53 °С(табл. IV); и = 0,43- 10г3Па-с —
динамический коэффициент вязкости ксилола [4J5]; Рг = 4,5 — критерий
Прандтля для ксилола при 53 °С (рис. XIII);
R — ^2 — ^i Pi — P2 837 — 778
Р~ v-s.M "~ р2Д* ™ 778(119,6 — 53)
= 1,15-10-» К"1,
Р —- средний коэффициент объемного расширения ксилола в интервале температур
53—119,6 °С; Д/к- *ст.2-/к (рис. 4.27).
Коэффициент теплоотдачи для ксилола:
NuX _ 36,6-0,128 аЛЗ>25
i ~~ 0,053
Ксилол
%
конд
ак =
и.
88,4 Д*?'25,
где Я = 0,128 Вт/(м- К) — коэффициент
теплопроводности ксилола при 53 °С (рис. X).
Так как коэффициент теплоотдачи для
ксилола много меньше, чем для
конденсирующегося водяного пара,
последний без расчета можно принять равным
Рис. 4.27. Схема процесса теплопередачи (к
примеру 4.V).
244
~ Ю ООО Вт/(м2* К). Далее можно написать следующую систему уравнений:
q = ап Д*п = „ от ¦ « «к А'к; д'ср = А'п + Д'ст + А'к#
где Д/п = ^К0Нд — ^ст. г\ А/Ст — /ст, 1 /ст. 2-
Подставляя численные значения, будем иметь:
10000 Мп = Д*сТ/0,0004 = 88,4 Д^25; 66,6 » Д/п + Мст + Д/к.
Из этой системы уравнений получаем:
0,0442 Д^'25 + Мк — 66,6 = 0.
Решая последнее уравнение (графически), находим:
Дгк = 59,3°С = 59,ЗК.
Тогда
q = сск Д/к = 88.4.59.31'25 = 14 550 Вт/м2.
Требуемая площадь поверхности теплообмена:
F^Qjq = 52 300/14 550 = 3,62 м2.
Длина змеевика:
, F _ 3,62
" Ш^ ~ 3,14-0,051 - ^,D M*
С запасом*.
L = 22,6-1,15^26 м.
Расход греющего пара с учетом 5 % потерь теплоты:
г b°5Q 1,05-52 300 _П9.0
Оп - -^ - 2208.10з,0,95 " °'0262 Кг/с*
где г = 2208» 103 Дж/кг (табл. LVII); х = 0,95 — принятая степень сухости
греющего пара.
По практическим данным для нормальной работы парового змеевика
начальная скорость пара должна быть не более 30 м/с, а отношение Lid должно быть
ие более
4--с 6
где С зависит от давления конденсирующегося пара и для ра$с = 2 кгс/см2
равняется — 190 — см, «Теплоотдача при конденсации насыщенного пара»
(стр. 163).
Проверим начальную скорость пара:
__ Gn 0,0262 19А
Шнач " рп.0,785^ - 1,107.0,785.0,049^ ~ 1ДЬ м/с'
где рл = 1,107 кг/м8 — плотность пара (табл. LVII).
Наибольшее допустимое отношение Lid:
(~) =190 в д140>
\ d /макс ^66,6
Следовательно, длина змеевика должна быть не более
L= 140^ = 140-0,049 = 6,9 м.
Принимаем число параллельно работающих змеевиков п = 4. Длина
каждого змеевика 26/4 = 6,5 м.
246
Блок-схема алгоритма решения примера 4.V:
(ачало
I
Э
А ?<нач ~ А^ояд—46нач
I
4?ср =
ЛЬнач - AtitoH
2,3lg
ЛЙН
ач
4t^oH
I
t^ - t конд ~Л?с(>
I
W -6гкСк(?кон~?нач)
ZrcT
*
- 1..., .* , .„' .
тзагр.1 г3агР/2
I
= Р1"Р2
р2-4?ср
^(*р-*Г
Т
Решение уравнения
aAtfc25+bAtK + c=0
методом
пропорциональных частей,где
а - 5 -~^-, 6 = 7, с ~~А tcp
Т
r_abs(At(K5>- &42>)
Да ,,
Нет
1
AtK =М(КЪ)
U
Г _?WQ
1
Gn
Гиач~ pn. 0,755 сГ|
1
^ **в / макс
, б
' V4tcp'
\
Ьм&кс - л макс оГв
*
Определение
V^MaKC /
k
/ -М-
±
^ Конец ^
Глава 5
ВЫПАРИВАНИЕ, КРИСТАЛЛИЗАЦИЯ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Уравнения материального баланса процесса выпаривания:
Gm*~Ghoh+W; (5.1)
Здесь GHaq, GK0H — массовые расходы начального (исходного) раствора
и конечного (упаренного) раствора, кг/с; дгнач» хкоа — массовые доли
растворенного вещества в начальном и конечном растворе; W — массовый расход
выпариваемой воды, кг/с;
W=GHa4(l 5SXL.). (5.3)
2. Уравнение теплового баланса выпарного аппарата:
Q + ^нач^нач^нач = ^цонскон*кон + ^'вт + Фпот ± Фд, (5.4)
где Q — расход теплоты на выпаривание, Вт; сшч, скон — удельная теплоемкость
начального (исходного) и конечного (упаренного) раствора, ДжУ(кг'К); ^нач»
^кон — температура начального раствора на входе в аппарат н конечного на выходе
из аппарата при верхней разгрузке, °С; /вт — удельная энтальпия вторичного
пара на выходе его из аппарата, Дж/кг; Qn0T — расход теплоты на компенсацию
потерь в окружающую среду, Вт; QA — теплота дегидратации, Вт.
3. Расход теплоты на выпаривание.
Из уравнения (5.4) получаем:
Q === ^начАшч ('кои чяач) -(- ™ Ubt — св*кош -\~ Упот> (°-5)
где св — удельная теплоемкость воды- при /кОН» Дж/(кг-К).
Если раствор поступает в выпарной аппарат в перегретом
состоянии (?Haq > *кон), то QHarp = GHaqcHa4(ifB0H — *нач) имеет
отрицательный знак, и расход теплоты в выпарном аппарате
сокращается, так как часть воды испаряется за счет теплоты,
выделяющейся при охлаждении поступающего раствора от tna4 до
?кои. Величина GHU4cuai4 (tH9i4 — tK0R) носит название теплоты
самоиспарения.
Расход теплоты на компенсацию потерь в окружающую среду
Qaor ПРИ расчете выпарных аппаратов принимают в размере 3 —
5% от суммы (Quarp + Qncn)- Величину Qn0T можно подсчитать
по уравнению:
Qiiot =3 а^нар (*ст — ^возд)* (5*6)
Здесь а — ал -J- ак — суммарный коэффициент теплоотдачи
лучеисиуеканием и коявекцией, Вт/(м2*К); FBap — площадь наружной поверхности теило-
нзолнрованного аппарата, м2; tCT — температура наружной поверхности
изоляции,, С или К; *возд — температура окружающего воздуха, СС или К.
В общем случае в тепловом балансе выпарного аппарата
должна учитываться еще затрата теплоты на дегидратацию
растворенного вещества, но обычно эта величина по сравнению с дру-
247
гими статьями теплового баланса мала и ею можно пренебречь
(см. пример 5.5).
Расход греющего пара GP. п (в кг/с) в выпарном аппарате
определяют по уравнению;
где Г — удельная энтальпия сухого насыщенного пара, ДжУкг; i' — удельная
энтальпия конденсата при температуре конденсации, Дж/кг; х — паросодержа-
ние (степень сухости) греющего пара; гь-п — удельная теплота конденсации
греющего пара, Дж/кг.
Удельный расход пара на выпаривание d представляет собой
отношение расхода греющего пара Gr,^n к расходу испаряемой
воды W:
d-GbdW. (5.8)
4. Теплоемкость раствора.
Удельная теплоемкость раствора может быть вычислена по
общей формуле:
с = с^ + с2х2 + с3х3 + ..., (5.9)
где си c2t c3i ... — удельные теплоемкости компонентов;^, x2t *з* • ¦• — массовые
доли компонентов.
Для расчета удельной теплоемкости двухкомпонентных
(вода + растворенное вещество) разбавленных водных растворов
(х <& 0,2) пользуются приближенной формулой:
с =4190(1 — х). (5.10)
Здесь 4190 Дж/(кг- К) — удельная теплоемкость воды; х—концентрация
растворенного вещества, масс. доли.
Для концентрированных двухкомпонентных водных растворов
(х > 0,2) расчет ведут по формуле;
с = 4190(1— x) + clX, (5.11)
где сх — удельная теплоемкость безводного растворенного вещества, Дж/(кг» К).
Удельную теплоемкость химического соединения при
отсутствии экспериментальных данных можно ориентировочно
рассчитать по уравнению:
Мс = ' гСх + п2С2 + п3С9 + ... , (5.12)
где М — мшгекулярная масса химического соединения; с — его массовая
удельная теплоемкость, Дж/(кг« К); пг, л2» п9, ... — число атомов элементов, входящих
в соединение; Q, C2, CSf ... — атомные теплоемкости, Дж/(кг-атом' К).
При расчетах по формуле (5.12) применяются значения
атомных теплоемкостей, приведенные в табл. 5.1.
5. Температурный режим однокорпусной вакуум-выпарной
установки (рис. 5.1).
248
Таблица 5.1
Элемент
Атомная теплоемкость
элементов для химических
соединений,
кДж/( кг- атом- К)
в твердом
состоянии
В ЖИДКОМ
СОСТОЯНИИ
Элемент
Атомная теплоемкость
элементов для химических
соединений,
кДж/(хг-атом. К)
в твердом
состоянии
в жидком
состоянии
с
н
в
Si
о
7,5
9,6
11,3
15,9
16,8
11,7
18,0
19,7
24,3
25,1
F
Р
S
Остальные
20,95
22,6
22,6
26,0
29,3
31,0
31,0
33,5
Обозначения температур и давлений»
Барометрический конденсатор
Паровое пространство сепаратора
Кипение раствора в сепараторе
Кипение в трубках (среднее значение)
Греющий пар
Разбавленный раствор, поступающий в
выпарной аппарат
^> 'кип ^> *
Рь к
Pi* *кон
Pcj» 'кип
Рг. п» 'г. п
U
Енач
нон
к > t0.
Соотношение температур: tPtU
Определение и расчет tup.
t0 — температура вторичного пара в барометрическом
конденсаторе. Определяется как температура насыщения при давлении /?0.
/j —температура вторичного
пара в сепараторе выпарного
аппарата. Определяется как
температура насыщения при
давлении рг\
>i = *o + А'г. о (5-13)
где А/Г>с — гидравлическая
депрессия, или изменение
температуры вторичного пара на
участке сепаратор —
барометрический конденсатор,
вызванное падением давления пара
из-за гидравлического
сопротивления паропровода
вторичного пара Л/?г-с. Это
сопротивление может быть подсчитано
по уравнению [см. формулу
(1.49)].
Рис. 5.1. К определению р„ -.
ср
1 — греющая камера; 2 — сепаратор; в ^~
циркуляционная труба; 4 — водомерное
стекло; 5 — барометрический конденсатор.
кои
РгРа*ДРт.0
н-
VP.
249
Давление pt определяется как
Pi = Po + APr.c> (5.I4)
и величина гидравлической депрессиях
Afr. с «-** — <*- (5.15)
Величину &fr с принимают по практическим данным равной
0,5—2,5 К.
Температура 4он — это температура кипения раствора в
сепараторе выпарного аппарата, при которой упаренный (конечный)
раствор выводится из аппарата:
'кон = h + д*депр- (5.16)
Здесь Д*депр — температурная депрессия, выражающая поввгазение
температуры кипения раствора по сравнению с температурой киаения чистого
растворителя (воды) при том же давлении, К:
А'депр=== (*рает» ^воды)р- (^-17)
В выпарных аппаратах непрерывного действия с естественной
или принудительной циркуляцией концентрация кипящего
раствора близка к яанетаой, поэтому А/дащ> в этях аппаратах берут
для раствора конечной концентрации лгкон<
При периодическом процессе выпаривания, когда исходный
раствор полностью заливается в аппарат до начала выпаривания,
Д'деар определяют при средней концентрации раствора.
В табл. XXXVI приведена температура кипения водных
растворов некоторых солей при атмосферном давлении, а на
рис. XIX — значения Д^пр*
6. Расчет температуры кипения растворов и других
жидкостей при давлениях, отличных от атмосферного.
Первый способ. Если известны две температуры
кипения данного раствора или органической жидкости при
соответствующих давлениях, можно воспользоваться уравнением
lgJ4-lgPB, ~C (5Л8)
и номограммой (рис. XIV).
Здесь pAi и pBt —давления насыщенного* пара дцух жидкостей при одной
и той же температуре tt\ рА и рв — давления иасыц^ешого пара этих жидко*
стей при температур* ?2; С — постоянная.
Температура кипения жидкости может б*лть также найдена по
правилу линейности химико-технических функций *i
Рх Рг = К, (5.19)
ер.-вР,
* Это соотношение экспериментально было найдено Дюрингом.
250
Таблица 5.2
0,«
0,8
Отношение р/р0
0,7
0,6
0,5
Давление р, мм рт ст.
0,4
0,3
Поправка,
=ьД*, К
100 200 400 450 500 550 650 0,9
— 50 200 350 450 500 550 1,8
— — 100 275 300 350 400 2,6
— — — 150 200 250 300 3,6
где tut — температуры кипения жидкости (раствора или
индивидуального вещества) при двух давлениях рх и р2', в и врэ — температуры кипения
воды или другой эталонной жидкости * при тех же давлениях (рис. XV и XV0.
Второй способ. Если для какого-либо раствора
известна только одна температура кипения при одном давлений,
то можно определить температуру кипения этого раствора при
другом давлении, воспользовавшись правилом Бабо
(p/Poh =* const (5.20)
с поправкой В. Н. Стабникова для концентрированных водных
растворов, кипящих под вакуумом (табл. 5.2).
Здесь р — давление пара раствора; р0 — давление насыщенного пара чистого
растворителя при той же температуре.
Если теплота растворения положительна (теплота выделяется
при растворении), то поправка берется со знаком плюс, если
отрицательна, то со знаком минус **.
Если давление в аппарате р Ф 1 кгс/см2, то значения А/деПр,
найденные по табл. XXXVI, пересчитывают на соответствующее
давление (см. пример 5.8).
7. Температура tKvin — это средняя температура кипения
раствора в трубах:
*КИП ™ *КОН "Г" Д*Г. 9фэ (5.21)
где А/г. Эф — гидростатическая депрессия, или повышение температуры
кипения раствора вследствие гидростатического давления столба жидкости в аппарате
(гидростатический эффект).
Температура кипения раствора в выпарном аппарате переменка
по высоте труб. Обычно среднюю температуру кипения определяют
* При определении по правилу линейности температур кипения
органических соединений, нерастворимых в воде, в качестве эталонной жидкости обычно
берут гексаи. Зависимость давления его насыщенного пара от температуры дана
на рис. XVII.
** Изменение энтальпии при образовании водных растворов — см.
Справочник химика. Т. III. M.—Л*: Химия, 1965, с. 612.
25!
на середине высоты греющих труб с учетом гидростатического
давления.
Давление в среднем слое выпариваемого раствора (см. рис. 5.1)i
?сР = Pi + O.Bppgtfyp = Pi + &рг. 9ф, (5.22)
где А^г> 0ф — повышение давления в жидкости на глубине Яур/2 от поверхности
(так называемый гидростатический эффект); рр — плотность раствора.
Гидростатическая депрессия Д/Р. 9ф, связанная с величиной
А/?Р. 9ф, зависит от высоты уровня раствора #ур, определяемой
по водомерному стеклу, и от плотности раствора. Оптимальная
высота уровня при выпаривании водных растворов в выпарных
аппаратах с естественной циркуляцией раствора может быть
рассчитана по формуле [5.1]:
//опт « [0,26 + 0,0014 (рр - рв)| Ятр. (5.23)
Здесь //опт (//ур) — оптимальная высота уровня по водомерному стеклу, м;
//тр — рабочая высота труб, м; рр и рв — плотности раствора конечной
концентрации (табл. IV) и воды (табл. XXXIX) при температуре кипения, кг/м3.
При отсутствии данных для /кип можно принять, что
(Рр - Pb)w ~ (Рр - Рь)/-ао«с- (5-24>
Величина Д?г. эф определяется по уравнению?
А'г. *Ф «='ср —'i> (5-25)
где *ср — температура кипения воды при давлении рор.
Средняя температура кипения раствора:
*кип ~ ^кон *b А/г. 9ф == ^о + Д^г.с + А^деПр Н- А^г. эф — ^о + 2j А?Пот»
(5.26)
где сумма температурных потерь ?А^П0Т
J] А/пот ^ А*г. с + А/депр + Д'р""эф. (5.27)
Порядок расчета /кип — см. пример 5.11.
8. Общая и полезная разность температур. Площадь
поверхности теплопередачи.
Разность между температурой конденсации греющего пара tv,a
и температурой конденсации вторичного пара в барометрическом
конденсаторе t0 называют общей разностью температур
А^общ = ^г. и — 'о» (5.28)
а разность между температурой конденсации греющего пара /г. п
и температурой кипения раствора /кип — полезной разностью
температур:
А?пол — *г. п — 'кап — Агобщ — 2j А'пот- (5.29)
252
Площадь поверхности теплопередачи выпарного аппарата —
см. формулу (4.72);
F = тЛг- = 1П$—> <530>
где А/пол — средняя движущая сила Д*Ср.
9. В многокорпусных выпарных установках Д/0бщ — разность
между температурой конденсации греющего пара первого
корпуса и температурой конденсации вторичного пара последнего
корпуса; JJ д^пот = д^депР + д*г. эф + Д^г. о — сумма
температурных потерь во всех корпусах.
Распределение полезной разности температур между
отдельными корпусами производится:
а) в случае расчета на минимальную общую площадь
поверхности всех корпусов — пропорционально y^QIK
б) в случае расчета на равную площадь поверхности
корпусов — пропорционально отношению Q//C
А// = MuonQtfKi I 2*1г; (5,32)
где Qf —тепловая нагрузка корпуса; Ki — коэффициент теплопередачи в
корпусе.
10. Масса образовавшихся кристаллов GKp (в кг) определяется
из уравнения материального баланса кристаллизатора;
Gt (x2 — Xj) — Wx2
где Gf — количество исходного раствора, кг; Хл—концентрация исходного
раствора по безводной соли, массовые доли или %; х2 — концентрация по
безводной соли маточного раствора после кристаллизации, массовые доли или %;
W — количество испаренного растворителя, кг; хкр=М/Мкр—отношение
мольных масс безводного растворенного вещества в кристаллогидрата.
Если вещество кристаллизуется в безводной форме, то *кр =1.
При изогидрической кристаллизации (без удаления части
растворителя при W = 0):
Окр-°;(Х1~;г). (5.34)
U. Удельную теплоту растворения qp (в Дж/кг) твердых
веществ, обладающих небольшой растворимостью, можно
определить по формуле:
19,2.10» Ig^-
м(тг -тг)
Здесь сг и с2 — растворимость вещества при температурах 7\ и Т% (в К);
М — мольная масса растворенного вещества, кг/моль.
263
Окр = - - , (5.3J)
Удельную теплоту плавления qnn (в Дж/кг) при отсутствии
экспериментальных данных можно вычислять по следующим
приближенным зависимостям;
а) для неорганических соединений
Ля-25,МО»-^L; (5.36)
б) для органических соединений
^«41.9-10»-^, (5.37)
гДе Лзл — температура плавления, К; М — мольная масса соединения, кг/моль.
Количество теплоты Q (в Дж), выделяющейся при
кристаллизации без испарения части растворителя, определяется из
уравнения теплового баланса кристаллизатора:
Q^Gtcih-h)^ GKp(7, (5.38)
где Gi — количество исходного раствора, кг; с — удельная теплоемкость
исходного раствора, Дж/(кг« К); tx и t2 — начальная и конечная температуры раствора,
СС или К; йцр — количество образовавшихся кристаллов, кг; q — удельная
теплота кристаллизации, Дж/кг.
12. Удельную теплоту парообразования жидкости г (в Дж/кг)
при давлении р можно определить по уравнению:
г"~г&т"7и
(-тУ-Зг- <^>
В формуле (5.39) г и гэт — удельная теплота парообразования искомой и
эталонной * жидкостей при одном и том же давлении р% Дж/кг; М и М9Т —
мольные массы этих жидкостей, кг/моль; Т и в — их температуры кипения при
давленнн р, К; d&, dT — дифференциалы температур кипення эталонной
жидкости и жидкости, для которой определяется теплота парообразования (на
основании правила линейности отношение дифференциалов замеииют отношением
разностей температур кипения при двух давлениях).
Удельная теплота парообразования неполярных жидкостей г
(в Дж/кг) при атмосферном давлении может быть вычислена по
формуле Кистяковского:
г-19,2.10»-J^ (1,91+ |g Г), (5.40)
где Т — температура кипения, К; М — мольная масса жидкости, кг/кмоль.
13. Расход воды на конденсатор GB (в кг/с) определяется из
уравнения теплового баланса конденсатора:
GB = У(Г-П _ Г г + сж (t0 - tw) ^ (ЪА{)
с ('в. кон ^в. аач) с (^в. кон — ^в. нач)
где W — расход вторичного пара, поступающего в конденсатор, кг/с; F —
удельная энтальпия этого пара, Дж/кг; i' — удельная энтальпия конденсата при вы-
* См. сноску к формуле (5.20), Зависимость удельной теплоты
парообразования гексана от температуры приведена на рнс. XVIII.
254
коде из конденсатора, Дж/кг; /в. нач, tB. Нон ~ начальная и конечная
температуры охлаждающей воды, °С или К; с, сж — средние удельные теплоемкости
воды и конденсата, Дж/(кг-К); г — теплота конденсации» Дж/кг; *0, ^ —
температура конденсации и конечная температура конденсата, СС или К.
В конденсаторах смешения температура конденсата равна
конечной температуре охлаждающей воды. Поэтому в
конденсаторах смешения:
GB - W '"-^в*он ш (5 42)
с \1в. ион 'в. нач/
Количество воздуха, откачиваемого вакуум-насосом из
барометрического конденсатора, GB03n (в кг/с) определяют по
эмпирической формуле:
СВозд = 0,000025 (№ +GB) -г-0,0Ш. (5.43)
Объем насыщенного водяным паром воздуха V (в м3/с),
откачиваемого из противоточного барометрического конденсатора:
у = ^возд'возд __ 278ТВо3дС/Возд ,g 44)
^возд(П-Рп) П-рп
Здесь Гнозд—температура воздуха (в К), откачиваемого из
барометрического конденсатора; определяется по приближенной эмпирической формуле
Т'возд — 273 -f [^в. нач + 0,1 (/в. нов — ^в. нач) + 4]; (5.45)
'в. нач и *в. hoH — начальная и конечная температуры воды, СС (конечную
температуру воды /в# ион принимают не менее чем на 3 СС ниже температуры
конденсации вторичного пара); П — давление (абс.) в барометрическом конденсаторе,
Па; рп — давление насыщенного водяного пара при температуре Гвозд. Па*
Высота барометрической трубы Я (в м) зависит от величины
вакуума (разрежения) в конденсаторе и равняется:
Я = Яй + //г.с + 0,5, (5.46)
Где Я0 = 10,33——; Ъ — вакуум в конденсаторе, мм рт. ст.; НГш с — -?—х
X f 1 -Ь X, —J--T- 1.6 J; w — скорость воды в трубе, м/с; Я — коэффициент
трения; d — диаметр трубы, м.
ПРИМЕРЫ
Пример 5.1. Исходный (начальный) раствор гидроксида
натрия содержит 79 г/л воды. Плотность упаренного раствора при
30 °С равна 1,555 г/см3. Это соответствует концентрации 840 г/л
раствора. Определить количество выпаренной воды на 1 т
исходного раствора.
Решение. Массовая доля растворенного вещества в
начальном растворе:
1000 + 79
*нач = т^г-т-^ = 0,0733.
255
В конечном растворе:
Хкон = 840/1555=: 0,54.
Количество выпаренной воды на 1 т исходного раствора:
*=G™ О -?г) -100° О -W-) -865 кг-
Пример 5.2, Найти удельную теплоемкость 25 % водного
раствора натриевой соли салициловой кислоты.
Решение. Так как концентрация раствора больше 20%*
то удельную теплоемкость раствора рассчитаем по формуле (5.11),
Предварительно определяем у дельную теплоемкость сх сухой
натриевой соли салициловой кислоты по формуле (5.12),
воспользовавшись данными табл. 5.1. Химическая формула соли
C6H4(GH)CGGNa; M = 160. Имеем:
Cl = (7,5-7 + 9,6-5 + 16,8-3 + 26,0)/160 =1,11 кДж/(кг-К).
Удельная теплоемкость 25% раствора:
с =4190 (1-х) +cix« 4190-0,75+ 1110.0,25 = 3420 Дж/(кг-К).
Пример 5,3. Определить, пользуясь правилом линейности,
температуру кипения анилина под вакуумом 0,08 МПа, т. е.
при остаточном абсолютном давлении 0,02 МПа. Известно, что
при температуре 160 °С давление насыщенного пара анилина
равняется 390 мм рт. ст., а при атмосферном давлении
температура кипения анилина 184 °С.
Решение. Возьмем в качестве эталонной жидкости гексан.
По диаграмме (рис, XVII) находим для гексана:
При рх = 390 мм рт. ст. в* = 49,2 °С
» р2 — 760 мм рт. ст. 82 = 69 °С
Тогда
К - '"J ~ '* - 160~184 _ | 01
A-ePi-ePa~ 49,2-69 ~I,ZI<
При абсолютном давлении р = 0,02 МПа, т. е. 0,2-735 =
= 147 мм рт. ст., температура кипения гексана 24,5 °С (рис. XVII).
Следовательно,
49,2-24,5 "J,/1'
откуда f = 130,1 °С.
Если решать эту задачу с помощью диаграммы линейности,
составленной с применением воды в качестве эталонной жидкости
(рис. XV), то получим: температура кипения воды при
абсолютном давлении р =s 0,2 кгс/см2 равна ~6G °С (табл. LVII). По
диаграмме линейности находим точку пересечения ординаты 60 °С
(для воды) с линией 12 (для анилина). Этой точке пересечения
256
соответствует на шкале абсцисс температура кипения анилина,
равная 130 °С.
Пример 5.4. Вычислить с помощью правила линейности
теплоту парообразования анилина при абсолютном давлении
0,2 кгс/см2.
Решение. Воспользуемся уравнением (5.39), взяв в
качестве эталонной жидкости гексан. Температура кипения анилина
при р.= 0,2 кгс/см2 равна 130 °С (см. предыдущий пример).
Температура кипения гексана при р = 0,2 кгс/см2 равна 24,5 °С.
Удельную теплоту парообразования гексана при 24,5 °С находим
по графику (рис. XVIII): г = 366 • 103 Дж/кг.
Отношение dQ/dT находим по данным предыдущего примера.
Так как зависимость между Т и в при одинаковом давлении
прямолинейна, то dQ/dT — величина постоянная. Следовательно,
dB - 1 - l -0 82fi
Подставляя все эти значения в формулу (5.39), получаем:
Мэт / Т \2 dS „дд 1П. 86 / 273 + 130 \2 оос
Г=8^ТГ(Т) ИТ = 366-1° Ж (273 +24,5 )°'826==
= 515 000 Дж/кг.
Если в качестве эталонной жидкости взять не гексан, а воду,
то получим следующие данные.
Для воды при абсолютном давлении р — 0,2 кгс/см3
температура кипения равна 59,7 °С, а удельная теплота парообразования
(по табл. LVII) г = 2358-103 Дж/кг.
Отношение dQjdT находим по рис. XV как тангенс угла
наклона линии 12:
dB 110-20.
dT ~ 200-80 -и''°*
Подставляя в формулу (5.39), получаем:
г « 2358- Юз _^|_ (J№_.yQj5 e 503 000 Дж/кг.
Пример 5.5. Определить расход греющего насыщенного
водяного пара в одиночном выпарном аппарате при непрерывном
концентрировании раствора NaOH. Расход начального раствора 2 т/ч,
его концентрация 14,1% (масс), конечная концентрация 24,1%
(масс). Температура греющего пара 150 °С. Давление вторичного
пара в аппарате атмосферное. Тепловые потери выпарного
аппарата составляют 58 000 Вт.
Расчет произвести для трех вариантов: а) раствор поступает
на выпаривание с начальной температурой 20 °С; б) раствор
поступает на выпаривание при температуре кипения в аппарате;
в) раствор поступает в выпарной аппарат перегретым до 130 °С.
Решение. Если давление вторичного пара в аппарате
атмосферное, то конечная температура раствора, выводимого из
аппарата, должна равняться — 111 °С (табл. XXXVI).
9 Павлов К. Ф. и др. 25.7
в
а) Количество теплоты, передаваемое от греющего пара к
кипящему раствору [формула (5.5)]:
Чг. п — "начинай ('коп *нач) т* ™ ('вт. п св*кон) *г VhoT»
Для всех вариантов расчета вторые и третьи слагаемые оди-
наковй. Определяем второе слагаемое:
829
^0'вт.п~^кон) = -зёоо"(2677"4'23,1И)103==508 кВт'
гдеГ=Онач (\-Л**2) =2000 (l-ilij) = 829 кг/ч; с
= 4,23 кДж/(кг-К)—теплоемкость воды при П1 С (табл, XXXIX); <вт# п =
= 2677 кДж/кг — удельная энтальпия водяного пара при абсолютном давлении
1 кгс/см2.
Определяем расход теплоты на нагревание раствора.
Подсчитываем удельную теплоемкость начального раствора.
Удельная теплоемкость твердого NaOH по формуле (5.12):
ct «-(16,8 + 9,6 + 26,0)/40 = 1,31 кДж/(кг- К).
Удельная теплоемкость 14,1% водного раствора NaOH:
с= 1,31-103.0,141 + 4,19-103-0,859 = 3780 Дж/{кг-К).
Подсчитываем расход теплоты на нагревание раствора для
каждого варианта:
а) начальная температура раствора 20 °С
- 2000-3,78. Ю3 /1П __. iQKnnnn
QHa. p = 360 (111 — 20) *= 195 000 Вт;
б) начальная температура равна температуре кипения
Чнагр == Oi
в) раствор поступает в выпарной аппарат перегретым до
130 °С
Рнагр = -^щ^ (1П - 130) » - 35 700 Вт.
Подсчитаем расход теплоты на дегидратацию NaQH, чтобы
получить представление о величине этой статьи расхода в
тепловом балансе выпарного аппарата.
По Справочнику физико-химических величин Технической
энциклопедии (т. VII) находим, что теплота образования NaOH
в растворе с п молями воды составляет:
п 3 5 7 9 13,5
Теплота образования 456,6 465,5 469,1 469,5 470,23]
NaOH, кДж/моль
Подсчитываем количество молей воды, приходящихся на 1 моль
NaOH.
Начальный раствор:
258
количество молей NaOH в 1 кг раствора
141/40-3,52;
количество молей воды в 1 кг раствора
(1000— 14!)/18 = 47,^.
количество молей воды на 1 моль NaOH
47,7/3,52= 13,5.
Конечный раствор:
количество молей NaOH в 1 кг раствора
241/40 = 6,02;
количество молей воды в 1 кг раствора
(1000 —241)/18 = 42,1;
количество молей воды на 1 моль NaOH
42,1/6,02=7,0.
Следовательно, теплота дегидратации:
470,23 — 469,1 = 1,13 кДж/моль NaOH.
Общая теплота дегидратации:
Зд = 3,52-2000.1130/3600 = 2220 Вт.
Составим сводную таблицу расхода теплоты (в Вт) в выпарном
аппарате для всех трех вариантов (табл. 5.3).
Из табл 5 3 следует, что расход теплоты на дегидратацию
составляет малую величину, которой мо^кно пренебречь.
Определяем расход греющего пара. П0 табл. LVI:
Iй = 2753-103 Дж/кг; V = 633. юз Дж/кг;
i" — i' = 2753 — 633 = 2120 кдж/КГ4
Таблица 5.3
Статьи расхода
На испарение воды
На дегидратацию
Теплопотери
На нагревание раствора
Итого
а
508 000
2 220
58 000
195 000
763 220
^Црианты
б
508 000
2 220
58 000
0
5(38 220
в
508 000
2 220
58 000
—35 700
532 520
9*
259
Таблиц а 5.4
Концентрация х, % (масс;) 5 10 20 30 40 50
Температура кипения, °С Цшп» 55 56 60 67 76 95
Коэффициент теплопередачи при ки- 2150 1740 ИЗО 740 490 280
пении К; Вт/(м2-К)
Следовательно, по формуле (5.7):
а) 0Г. „ - jAjr = 2Т^таб " °'36 КГ/С " 1296 КГ^:
б^- = ЖТ55о = °'268кг/с = 965кг^
в) 0,п = 2-|^ = 0,25! кг/с = 904 кг/ч.
Пример 5.6. В вакуум-выпарной аппарат периодического
действия, имеющий площадь поверхности нагрева 40 м2, заливается
20 т слабого раствора с концентрацией хнач = 5% (масс).
Начальная температура слабого раствора 20 °С. Раствор
выпаривается до концентрации хнон *= 50% (масс.;. Зависимость
температуры кипения раствора и коэффициента теплопередачи в аппарате
от концентрации раствора дана в табл. 5.4. Абсолютное давление
пара в аппарате 0,15 кгс/см2, чему соответствует температура
насыщения fHac = 53,6 °С.
Коэффициент теплопередачи для периода нагрева слабого
раствора до начала кипения Кх *= 350 Вт/(мг-К). Температура
греющего насыщенного водяного пара 120 °С.
Определить расход греющего пара, принимая влажность его
5%, и продолжительность процесса выпаривания.
Решение. Количество выпариваемой воды:
^==Снач (l— -j5^) = 20 000(l— -|Л «18000 кг.
Первый период. Нагрев раствора от 20 °С до температуры
кипения 55 °С (без учета потерь теплоты в окружающую среду):
Qr. п = Сначснач (tmn - *нач) « 20 000-4,19.0,95 (55 — 20) « 2 790 000 кДж,
где 0,95.4,19 — теплоемкость начального (5%) раствора, кДж/(кг« К).
Расход греющего пара за I период с учетом потери теплоты
в окружающую среду в 3%:
G - Qr.n-I,03,_ 2790000.1,03 _ _
Г* ° " 'г. п-0,95' " 2207-0,95 " w/0 КГ'
Здесь гГш п = 2207 кДж/кг — удельная теплота парообразования
насыщенного водяного пара при 120 °С (табл. LVI); 0,95 — сухость греющего пара.
2бЬ
Продолжительность I периода (нагрев до 55 °С)
т Qr.n 2 790 000-10»
Tl = Ki (A<cp)l F = 350-82.5-40 = 2415 с = 0,67 ч,
где (A^cp)i — средняя (по времени) разность температур в I периоде
120 120
20 —> 55
Д*б = 100 Д/м = 65 .
Так как (Д*б/Д/М) < 2, то
(Д/Ср)1 = (ЮО + 65)/2 = 82,5 К
Второй период (выпаривание).
1. Тепловой баланс за весь цикл.
Подводимая теплота: Qr, п — теплота конденсации греющего
пара; GHa4cB&4t'Ha4 — теплота, вносимая начальным раствором
при 55 °С.
Отводимая теплота: GK0HcH0HfH0H — теплота, отводимая с
упаренным раствором при *кип = 95 °С; WilT. п — теплота, выносимая
вторичным паром при температуре насыщения fBT. D = 53,6 °С
Тепловой баланс:
%. п + СначСнач'нач = Gkohckoh'koh + Wi0rib>
Заменял GK0VcKQHtK0H = Оначсна,^0н — WcBtR0B, получаем:
«г. о = СнаЛа, ('нон ~ >нач) + W (<5, 15 ~ *Лов) в
= 20 000.4,19.0,95(95 — 55) + 18 000(2596 — 4,19-95) =
= 3 184 400 +39 563 000 = 42,7-10е кДж,
где i'o is ~ 2596 кДж/кг — удельная энтальпия вторичного пара при р=*
= 0,15'кгс/см2 (табл. 1ЛЧ1).
Расход греющего пара за II период с учетом потери теплоты
в окружающую среду в 3%:
42,7-106-1,03
2207-0,95
Gr, П = :п I = 21 000 кг.
2. Продолжительность II периода (выпаривания).
В этом периоде концентрация кипящего раствора я, его
температура кипения t и величина коэффициента теплопередачи К
непрерывно изменяются — см. табл. 5.4.
Уравнение теплопередачи для бесконечно малого отрезка
времени d%
dQ=z KF(T — t)dx
содержит только две постоянные величины: температуру
конденсации греющего пара Т = 120 °С и площадь поверхности
теплообмена F = 40 м2.
261
Таблица 5.5
х, % 5 10 20 30 40 50
2 W, кг 0 10 000 15 000 16 700 17 500 18 000
?Q.10-10 Дж 0 2,37 3,56 3,96 4,15 4,27
{Т — /), К 65 64 60 53 44 25
1 10е 7 8,9 UJ 25,4 46,3 142,8
/С (Г — /)
Из последнего уравнения получаем:
к (Т - о
Интегрирование правой части уравнения
Q( dQ
о
может быть выполнено графически.
Необходимые для графического интегрирования величины
получают расчетным путем:
а) К(Т_{) определяют, используя данные табл. 5.4;
например, для х = 20%
к (т-1) = -wkw =14'7-,0_s и т- д-;
б) 2 Q; например, для х = 20%
? Q ^ 0нагр + QHa4 = 20 000-4190.0,95 (60-55) +
+ 15000(2596 — 4,19-60)-103 = 398-106+35 175-Ю6 = 3,56-1010 и т. д.
Полученные расчетным путем данные сведены в табл. 5.5.
Принимаем масштаб для оси абсцисс: 1 мм = 2*10^ Дж.
» » » » ординат: 1 мм = ЫО"6 м2/Вт,
Единица подынтегральной величины:
1 мм2 = 2.108 Дж-ЫО"6 м2/В' =200 m2-c.
Если по данным расчетов, приведенным в табл. 5.5, построить
график (рис. 5.2), то, определяя на нем величину заштрихованной
площади (например, по правилу трапеций), найдем:
Q=4,27.!01C
J
dQ = Ft2 = -Щ^~ 200 = 550 000 м2 ¦ с8
откуда
тп = 550 000/40 = 13 755 с = 3,82 ч.
262
J
K(T~t)
150* W6
100-?0~* -
50-Ю
-e
0
i-S
,-s
7-10~° № Ю
\\\ЧЧЧ\Ч\ЧЧЧЧЧЧЧ\ЧЧЧ\Ч\ЧЧ\ЧЧЧ^
143-Ю
-8
427-Ю'*
1-20
ю
2-Ю
ю
3-Ю
ю
4-Ю10
Рис, 5.2 (к примеру 5.6).
3. Общая продолжительность процесса
% = Tl + тп = 0,67 + 3,82 я* 4,5 ч.
Пример 5.7. Сравнить теоретический расход энергии для двух
случаев: а) при откачке вторичного пара вакуум-насосом из
выпарного аппарата, работающего под вакуумом 0,7 кгс/см3; при
конденсации вторичного пара в конденсаторе и откачке насосом
конденсата. Производительность выпарного аппарата 1000 кг/ч
испаренной воды.
Решение, а) Примем, что сжатие вторичного пара в
вакуум-насосе адиабатическое. В этом случае расходуемая работа
определится по уравнению (2.13). Энтальпии находим по
диаграмме /—5 для водяного пара
(рис. 5.3 и XXV):
L = i2 — it = 2840-103 — 2620-103 =
= 220-103 Дж/кг.
Требуемая теоретическая
мощность (без учета к. п. д.
вакуум-насоса):
Л/т = 220-103 -1000/3600 =
«= 62,7-103 Вт = 62,7 кВт.
б) При откачке насосом
жидкости (конденсата) необхо-
Рис» 5,3 (к примеру 5.7).
Б 1г=2840-10*Дж/к?
2620-10°Дж/кт
263
дшлую теоретическую мощность насоса (без учета его к. п. д.)
определим по уравнению:
VAp 1000-68,7.103 nnin _
N* = Тобо" в 3600-Ю00.103 = °>019 кВт>
г* V- З6О0Т0ОО «35» М3/С: А'= °'7 кгс/см^68,7.103Па.
Из данного примера видно, что откачивать вторичный пар
вакуум-насосом нецелесообразно, так как это требует большого
расхода энергии (в 62,7/0,019 = 3300 раз больше, чем при откачке
конденсата). Поэтому вторичный пар никогда не откачивают,
а всегда конденсируют.
Пример 5.8. Определить, пользуясь правилом Бабо,
температурную депрессию А/Деир для 25% водного раствора хлористого
кальция при абсолютном давлении над раствором рх = 0,36 кгс/см2.
Решение. 1. Определение температуры кипения раствора
при наличии абсолютного давления над раствором рх =
= 0,36 кгс/см2.
По табл. XXXVI находим, что 25% водный раствор хлористого
кальция под атмосферным давлением (1,033 кгс/см2) кипит при
температуре 107,5 °С. При этой температуре давление
насыщенного пара воды (табл. LVI) р'ъ = 1,345 кгс/см2.
Отношение давлений пара над раствором р[ и воды р'в при
одной и той же температуре 107,5 С:
(Р^Котл"1-033/1-345-0,77.
Согласно правилу Бабо [уравнение (5.20)1, это отношение
сохраняет постоянное значение при всех температурах кипения
раствора.
Для искомой температуры кипения раствора при рх =
= 0,36 кгс/см2:
<Pi/PBJt = 0,36/pB = 0,77,
откуда
рв = 0,36/0,77 = 0,467 кгс/см2 = 343 мм рт. ст.,
чему соответствует по табл. XXXVIII температура кипения воды
79,2 °С. Эту же температуру кипения будет иметь и раствор
хлористого кальция (25%) при давлении над раствором 0,36 кгс/см2.
2. Определение А/Депр-
Температура кипения воды при давлении 0,36 кгс/см2 =
= 264,6 мм рт. ст. (табл. XXXVIII) равна 72,9 °С.
Температурная депрессия раствора [формула (5.17)]:
Л'дапр = 'р- >в =- 79,2-72,9 = 6,3° С = 6,3 К.
Учтем поправку Стабникова. По табл. 5Л при (рр/рв) — 0,77
и рр = 0,36 кгс/см2 = 264,6 мм рт. ст. поправка At = —0,9 К.
Поправка со знаком минус, потому что теплота растворения
хлористого кальция отрицательная (Справочник химика. Т. III,
1965, с. 613). Таким образом,
^депр = 6,3^0,9 = 5,4К.
264
Пример 5.9. Вычислить гидростатическую депрессию Д/к Эф
при выпаривании 25% водного раствора хлористого кальция под
вакуумом в выпарном аппарате с оптимальным уровнем раствора
в трубах. Рабочая высота труб #Тр = 4 м, абсолютное давление
над поверхностью раствора рг = 0,36 кгс/см2 (см. рис. 5.1).
Решение. При рх = 0,36 кгс/см2 температура воды ix =
= 72,7 °С (табл. LVII).
Оптимальная высота уровня по водомерному стеклу
определяется по формуле (5.23):
яопт = [0,26 + о,0он (рр - pB)i tfTp.
Так как плотности рр и рв надо брать при температуре кипения
раствора, пока неизвестной, приходится ею задаваться. Примем
'нип = 85 °С. Тогда
Яонт = [0,26 + 0,0014 (1197 — 969)] 4 = 2,3 м.
Здесь рр = 1197 кг/м8 — по табл. IV; рв = 969 кг/м3 — по табл. XXXIX.
Гидростатическое давление рСр в середине высоты труб при
И
11 от*
П ^ 11Q7 Q R] 9 4
Pep = Pi + 0,5PpgtfonT - 0,36 + 9,81 10* ' = °'5 КГС/СМ2'
Температура кипения воды при 0,5 кгс/см2 (табл. LVII) /ср =
= 80,9 °С.
Гидростатическая депрессия [формула (5.25)]:
Л'г. аф = 'ср - h = 80.9 - 72,7 - 8,2° С = 8,2 К.
Пример 5.10. Вторичный пар из выпарного аппарата поступает
в барометрический конденсатор по паропроводу диаметром 150 мм.
Скорость пара в паропроводе 50 м/с. Давление в конденсаторе
(абс.) Ро = 0.3 кгс/см2. Длина паропровода 14 м. Коэффициент
трения Я = 0,03. На паропроводе имеются три поворота на 90 °С
(? = 0,2). Определить гидравлическую депрессию Atr. c.
Решение. По уравнению (5.15):
При р0 = 0,3 кгс/см2 t0 = 68,7 °С (табл. LVII). Для
определения температуры tx необходимо найти давление на поверхности
выпариваемого раствора р19 равное р0 + Лрг.с (см- Рис» 5.1),
где
Сумма коэффициентов местных сопротивлений;
Вход в трубу .... 0,5 (табл. XIII)
Выход из трубы ... 1,0
Повороты 3-0,2= 0,6
ЕС =2,1
2Й
Дополнительное сопротивление сепаратора не учитываем.
Следовательно,
. 502-0,188 /, , 0,03-14 , П1\ .ооп п.
АРг. с = 2 \ 0,15 1" 2,1 j — 1390 Па,
где рп = 0,188 кг/м3 — плотность пара, считая его насыщенным (табл. LVII).
Тогда
1390
Pi = Ра + АРг. с = 0,3 + Q 81,104 ~ °>314 кгс/см2.
По табл. LVII при р, - 0,314 кгс/см2 ^ - 69,6 °С.
Гидравлическая депрессия:
д/г с = tx — /0 = 69,6 — 68,7 = 0,9 °С = 0,9 К.
Пример 5.11. Определить необходимую поверхность нагрева
вакуум-выпарного аппарата (рис. 5.1) и расход греющего
насыщенного водяного пара для выпаривания раствора хлористого
кальция от 15 до 25%. Производительность по исходному
(разбавленному) раствору 20 000 кг/ч. Абсолютное давление греющего
пара 1,4 кгс/см2, влажность его 5%. Абсолютное давление в
барометрическом конденсаторе р0 = 0,345 кгс/см2. Слабый раствор
поступает в аппарат при tu.d4 — 75 °С.
Коэффициент теплопередачи принять равным 1000 Вт/(м2.К),
а тепловые потери — в размере 5% от полезно затрачиваемой
теплоты.
Решение. 1. Температурный режим.
Температура вторичного пара в сепараторе выпарного
аппарата [формула (5.13)1:
*! = /0 + А/г. с =* 71,7 + 1 = 72,7 °С (при Рх = 0,36 кгс/см2).
Здесь /0—71,7°С — температура насыщенного водяного пара при р0 =
= 0,345 кгс/см2 (табл. LVII); Mv с — гидравлическая депрессия. Принимаем
А/г. с = 1 °С.
Конечная температура расавора (температура кипения
раствора в сепараторе) [формула (5.16) ]:
'кон = h + А'депр = 72,7 + 5,4 = 78,1 °С,
где А/децр—температурная депрессия. В примере 5.8 определено А*де1Ш =
= 5,4 °С.
Средняя температура кипения раствора в трубах [формула
(5.21)1:
^кип = 'кон -Ь &*г. эф — 78»! + 8,2 = 86,3 °С,
где А^г. Эф — гидростатическая депрессия (гидростатический эффект). В
примере 5.9 определено А^г. эф= 8,2 °С.
2. Количество выпариваемой воды [формула (5.3)]:
*пя* \ 20 000 /. 15
w с tx *пач \ 20 000 /. 15 \ п по ,
w=Gmv -i^r) =-w I1 -it) =2*22 кг/с-
266
3. Количество теплоты, передаваемой от греющего пара к
кипящему раствору {формула (5.5)):
Vp. о — ^нач^нач (^кон ' ^нач) Н" ™ (*вт. п св^кон) "Ь Упот
Здесь сиач — теплоемкость разбавленного раствора [формула (5.10)]:
свач = 4190 (1 — хпач) = 4190 (1 — 0,15) = 3560 Дж/(кг- К);
'вт. п == 2496 кДж/кг — удельная энтальпяя пара пря температуре ^ = 72,7 °С,
Следовательно, с учетом тепловых потерь в 5%;
Qr.n=l,05 [^^-3560(78,1-75)4-2,22(2496.103-4190.78,1)] =
= 5120-103 Вт.
4. Расход греющего пара [формула (5.7)1:
G - <?»° г, 5120'1()3 2 1 кг/с
г'п~ 'г. и* 2237.103.0,95 ~ А4 КГ/С'
где гг> п — 2237-103 Дж/кг —. удельная теплота парообразовавия греющего
пара при Рабе" М кгс/см2 (табл. LVII).
Удельный расход греющего пара [формула (5.8)1:
GP, п 2,4 кг греющего пара
W 2,22 кг испаренной воды
5. Общая [формула (5.28) 1 и полезная [формула (5.29)1
разность температур;
Д/общ = 'p. d — 'о = Ю8,7— 71,7= 37ЭС = 37 К;
А'пол = 'г. п - /кии = Ю8.7 - 86,3 =* 22,4 °С = 22,4 К,
где /Р, п= 108,7 °С при давлении насыщения раб0 — 1,4 кгс/см? (табл. LVII),
Проверка:
2 Д'пот ** А'р. о + А^депр + А/г. 9ф * 1 + 5,4 + 8,2 « 14,6 °С;
А^пол = А/общ - S Д^от — 37—14.6=- 22,4 °С = 22,4 К.
6. Площадь поверхности нагрева выпарного аппарата
[формула (5.30)1:
Q _ [5120-10» оос>5м,
f " КА/П0Л ~ 1000-22,4 -228,5 м.
Пример 5.12. Сколько кристаллов выделится в
кристаллизаторе при охлаждении 10 т насыщенного водного раствора поташа
от 80 до 35 СС без испарения воды? Поташ кристаллизуется g двумя
молекулами воды.
267
Решение. Применим формулу (5.34). По кривой
растворимости поташа (рис. XX) находим концентрацию его насыщенных
водных растворов:
гт оЛог ,„ МОЛЬ К2С03
ПРи8° С 10 -ТООО г воды
» 35 °С 8,15
Мольная масса К2С03 равняется 138 кг/кмоль. Следовательно,
Ю-138 п« / 8,15-138 __ -о кг/кг-
*« в ЮОО + ЮЛЖ в 0'И КГ/КГ; *** - 1000 + 8.15.13» - °'53 КГ/КГ'
М/Мкр= 138/174 = 0,795,
где 174 — мольная масса К3СОз*2Н30, кг/моль.
Подставляя эти значения в формулу (5.34), находим:
10 000(0,58-0,53) ^ 1900 кг
кр 0,793 — 0,53
Пример 5.13. Определить количество теплоты, которое
необходимо отводить в кристаллизаторе непрерывного действия для
охлаждения от 90 до 40 °С 5000 кг/ч водного раствора NaN08l
содержащего при 90 °С 16 моль NaN03 на 1000 г воды. Учесть, что
в кристаллизаторе при охлаждении раствора одновременно
испаряется вода в количестве 3% от исходного количества раствора.
Решение. По кривой растворимости NaN03 (рис. XX)
находим, что концентрация насыщенного раствора NaN03 при
40 °С составляет 12,3 моль на 1000 г воды.
При охлаждении раствора до 40 °С будет выделяться GKp
(в кг/с) кристаллов [формула (5.33)]:
°кр = ' _х •
*2 лКр
Пересчитываем концентрации в массовые доли:
Xl = looo+^as ~ °'576 кг/кг: х*" юооУ'й-аз - °'511 кг/кг-
Здесь 85 — мольная масса NaN03, кг/кмоль.
Величина хкр = I, так как NaN08 кристаллизуется в
безводной форме. Имеем:
. 5000(0,511 -0,576) -0,03»5000-0,511
GKp 3600(0,511-1) °>Л2У КГ/0'
Количество теплоты, которое надо отводить, подсчитаем по
формуле:
где W — расход испаряющейся воды, кг/с; г — удельная теплота парообразо*
вания воды, Дж/кг.
Удельную теплоту кристаллизации NaNOs q примем равной
21000.10» Дж/кмоль (табл. XXXVII).
'268
Удельную теплоемкость раствора с определяем по уравнению
(5.11), для чего предварительно находим удельную теплоемкость
твердой соли сх по уравнению (5.12):
d = (26,0 + 26,0 + 3-16,8)/85 = 1,2 кДж/(кг*К).
Тогда при х— 57,6%:
с = 4190-0,424 + 1200-0,576 = 2470 Дж/(кг-К).
Количество отводимой теплоты:
Q=^0 2,47.103(90-40)+0,229 21Ш-1<Р 0,03.5000.2345-103
3600 ' v ' -г-,— 85 3600
= 130 000 Вт,
где 2345-103 Дж/кг — удельная теплота парообразования воды при средней
90 -4- 40
температуре, равной ^ = 65 °С (табл. LVI).
Пример 5.14, В условиях предыдущего примера определить
требуемую площадь поверхности охлаждения и расход воды
в кристаллизаторе. Коэффициент теплопередачи принять равным
100 Вт/(м2.К). Вода поступает в охлаждающую рубашку при
15 СС и выходит при 20 °С Охлаждение противоточное.
Решение. Площадь поверхности охлаждения определяем
по формуле:
Р <?
К А/ср *
В условиях задачи температурная схема:
90 —> 40
20 <— 15,
откуда
д,ср _ (90-20)-(40-15) = 36.2 «С = 36,2 К.
Следовательно,
F^_ Дзоооо
F - 100.36,2 =36М'
Расход воды:
°° - 4,19.103з0(20-15) " 6'33 КГ/С = 2240° КГ/Ч-
КОНТРОЛЬНЫЕ ЗАДАЧИ
5.1. Рассчитать удельный расход сухого насыщенного
водяного пара при выпаривании воды под атмосферным давлением
и под вакуумом (разрежением) 0,8 кгс/см2. Абсолютное давление
269
греющего водяного пара в обоих случаях райс = 2 кгс/см2.
Вода поступает на выпарку; а) при температуре 15 °С; б)
подогретой до температуры кипения.
5.2. Производительность выларного аппарата по исходному
раствору 2650 кг/ч. Концентрация исходного раствора 50 г/л
воды. Концентрация выпаренного раствора 295 г на 1 л раствора.
Плотность выпаренного раствора 1189 кг/м3. Найти
производительность аппарата по выпаренному раствору.
5.3. Как изменится производительность выпарного аппарата,
если на стенках греющих труб отложится слой накипи толщиной
0,5 мм? Коэффициент теплопередачи К для чистых труб равен
1390 Вт/(м2.К). Коэффициент теплопроводности накипи X =
- 1,16 Вт/(м.К).
5.4. Производительность выпарного аппарата, обогреваемого
насыщенным водяным паром с избыточным давлением ртб =
= 1,5 кгс/см2, необходимо повысить с 1200 до 1900 кг/ч (по
разбавленному раствору). Выпаривание производится под
атмосферным давлением, температура кипения раствора в аппарате 105 °С,
раствор подается на выпарку подогретым до температуры
кипения. Определить, какого давления греющий пар надо подавать
в аппарат. Тепловые потери не учитывать, коэффициент
теплопередачи считать неизменным, так же как и конечную
концентрацию раствора.
5.5. Сколько надо выпарить воды из 1500 кг раствора
хлористого калия, чтобы изменить его концентрацию от 8 до 30% (масс)?
5.6. Какое количество воды надо выпарить из 1 м3 серной
кислоты с плотностью 1560 кг/м3 [65,2% (масс.)], чтобы
получить кислоту с плотностью 3840 кг/м3 [98,7% (масс.)]. Какой
объем займет полученная концентрированная кислота?
5.7. В выпарной аппарат поступает 1,4 т/ч 9% раствора,
который упаривается под атмосферным давлением до конечной
концентрации 32% (масс). Разбавленный раствор поступает на
выпарку с температурой 18 °С. Упаренный раствор выводится
из аппарата при 105 °С. Удельная теплоемкость разбавленного
раствора 3800 Дж/(кг-К). Расход греющего насыщенного водяного
пара с избыточным давлением ризб = 2 кгс/см2 составляет
1450 кг/ч. Влажность греющего пара 4,5%. Определить потерю
теплоты в окружающую среду.
5.8. Определить удельную теплоемкость холодильной смеси,
состоящей из 2 л воды, 8 кг льда и 5 кг поваренной соли.
5.9. Раствор состоит из 0,7 м3 серной кислоты (100 %),
400 кг медного купороса (CuS04-5H20) и 1,4 м3 воды. Определить:
а) удельную теплоемкость раствора; б) количество сухого
насыщенного водяного пара с абсолютным давлением /?абс = 2 кгс/см2,
необходимое для нагревания раствора от 12 до 58 °С. Потери
теплоты аппаратом за время нагревания раствора составляют
25 100 кДж. Удельную теплоемкость серной кислоты и медного
купороса определить по формуле (5.12).
270
-н=
Рис. 5.4 (к контрольной задаче 5.13):
1 — выпарной аппарат; 2 —
теплообменник.
5.10. В выпарном аппарате
подвергае-1Ся упариванию под
атмосферным давлением 2,69 т/ч
7% водного раствора.
Начальная температура раствора 95 °С,
конечная 103 °С Средняя
температура кипения в аппарате
105 °С. Избыточное давление
греющего насыщенного
водяного пара ризб — 2 кгс/см2.
Площадь поверхности теплообмена
в аппарате 52 м2, коэффициент
теплопередачи 1060 Вт/(м2-К).
Тепловые потери аппарата в
окружающую среду составляют
110 000 Вт.
Определить: а) конечную
концентрацию раствора; б)
расход греющего пара при
влажности его 5%.
5.11. В выпарном аппарате с площадью поверхности
теплообмена 30 м2, работающем под атмосферным давлением,
непрерывно концентрируется раствор хлористого калия от 9,5 до
26,6 % (масс). Начальная температура раствора 18 °С,
избыточное давление греющего насыщенного водяного пара ризб =
= 2 кгс/см2. Производительность аппарата вначале была 900 кг/ч
(разбавленного раствора), но через некоторое время снизилась
до 500 кг/ч из-за образования накипи. Пренебрегая тепловыми
потерями аппарата в окружающую среду, определить толщину
образовавшегося слоя накипи, приняв для накипи к = 1,4 Вт/(м- К).
Гидростатическим эффектом пренебречь.
5.12. В условиях примера 5.7 определить расход энергии
при откачке вторичного пара вакуум-насосом и при откачке
конденсата насосом, если вакуум в аппарате равен 0,95 кгс/см2.
5.13. В непрерывнодействующий однокорпусной выпарной
аппарат подается 12,5% раствор сернокислого аммония, который
упаривается под атмосферным давлением до 30,6% (масс).
Концентрированный раствор выходит из аппарата в количестве
800 кг/ч. Разбавленный раствор, поступающий на выпарку,
подогревается в теплообменнике вторичным паром от 24 до 80 °С.
Остальное количество вторичного пара идет на обогрев других
производственных аппаратов (рис. 5.4). Тепловые потери
выпарного аппарата составляют 6% от полезно используемого
количества теплоты, т. е. от суммы QHarD + Qncn- Принять Д/р, с «=
1 К.
271
Определить: а) расход греющего насыщенного водяного пара
(с избыточным давлением ризб = 2 кгс/см2), принимая его
влажность 5%; б) количество вторичного пара, отбираемого на
обогрев производственных аппаратов; в)требуемую площадь
поверхности теплообмена (подогревателя), принимая величину
коэффициента теплопередачи в нем К = 700 Вт/(м2.К).
5.14. Дифенил (СвН5)2 кипит под атмосферным давлением при
255 °С. Вычислить удельную теплоту испарения, а также
удельную теплоемкость жидкого дифенила.
5.15. 48% водный раствор едкого натра кипит под давлением
760 мм рт. ст. при 140 °С, а под абсолютным давлением рабс «
= 0,2 кгс/см2 — при 99 °С. Определить удельную теплоту
испарения воды из этого раствора при давлении 0,8 кгс/см2, а также
удельную теплоемкость раствора.
5.16. Определить температуру кипения бромбензола под
абсолютным давлением рабс — 0,1 кгс/см2 по диаграмме линейности
и по номограмме XIV. Определить также удельную теплоту
испарения бромбензола при этом давлении.
5.17. Определить давление насыщенного пара бензальдегида
при 120 °С, пользуясь диаграммой линейности.
5.18. Воспользовавшись правилом Бабо и табл XXXVI,
определить температуру кипения 42,5% водного раствора
азотнокислого аммония при абсолютном давлении рабс = 0,4 кгс/см2.
5.19. В вакуум-выпарной аппарат (рис. 5.1) поступает 10 т/ч
8% водного раствора азотнокислого аммония при температуре
74 °С. Концентрация упаренного раствора 42,5%. Абсолютное
давление в среднем слое кипящего раствора рср = 0,4 кгс/сма.
Избыточное давление греющего насыщенного водяного пара риаб =
— 1 кгс/см2. Принять А^,. 9ф = 6,1 К- Коэффициент
теплопередачи 950 Вт/(м2. К). Потери теплоты составляют 3% от суммы (QHarp +
+ Qncn)- Определить площадь поверхности нагрева выпарного
аппарата.
5.20. По данным предыдущей задачи определить абсолютное
давление в барометрическом конденсаторе, если гидравлическая
депрессия А/г с = 1 К, а гидростатическая депрессия Д?г эф =
- 6,1 К.
5.21. 2200 кг/ч разбавленного водного раствора упариваются
от 7 до 24% (масс.) под атмосферным давлением. Разбавленный
раствор подается в выпарной аппарат при 19 °С. Температурная
депрессия 3,5 К, гидростатическая 3,0 К, гидравлическая 1,0 К.
Избыточное давление греющего насыщенного водяного пара
Ризб — 2 кгс/см2. Коэффициент теплопередачи 1100 Вт/(м2.К).
Определить требуемую поверхность теплообмена в аппарате и
расход греющего пара, принимая потери теплоты в окружающую
среду в размере 5% от суммы (Qliarp + QHCn) и влажность
греющего пара 5%.
5.22. Как изменится производительность выпарного аппарата,
работающего под атмосферным давлением, при обогреве насыщен»
272
ным водяным паром с избыточным давлением рт$ = 1,2 кгс/см5,
если в аппарате создать вакуум 0,7 кгс/ем2, а обогрев перевести
на пар с избыточным давлением 0,6 кгс/см2? Гидростатический
эффект для среднего слоя Дрг.Эф ~ 9,81 -103 Па; в обоих
случаях считать температурную депрессию 4 К; раствор поступает
на выпарку подогретым до температуры кипения в аппарате.
Коэффициент теплопередачи считать неизменным. Тепловыми
потерями пренебречь.
5.23. В выпарном аппарате концентрируется водный раствор
от 14 до 30% (масс). Греющий насыщенный водяной пар имеет
давление (абсолютное) 0,9 кгс/см2. Полезная разность
температур 11,2 К. Гидростатическая депрессия Д?г. эф = 3 К.
Определить часовой расход разбавленного раствора, поступающего
в аппарат, если площадь поверхности теплообмена в нем 40 ма,
а. коэффициент теплоотдачи составляет 700 Вт/(м2-К).
Разбавленный раствор поступает в аппарат подогретым до температуры
кипения. Среднее давление в аппарате (абсолютное) 0,4 кгс/см2.
Тепловыми по!ерями пренебречь.
5.24. Определить расход греющего насыщенного водяного
пара (абсолютное давление 2 кгс/см2) и площадь поверхности
нагрева выпарного аппарата, в котором производится упаривание
1,6 т/ч раствора от 10 до 40 % (масс). Среднее давление в аппарате
(абсолютное) 1 кгс/см2. Разбавленный раствор поступает на
выпарку при 30 °С. Полезная разность температур 12 К.
Гидростатическая депрессия Д/г. эф = 4 К. Коэффициент теплопередачи
900 Вт/(м2-К). Тепловые потери принять равными 5 % от полезно
используемого количества теплоты QHarp + Qncn-
5.25. Раствор поташа упаривается от 8 до 36% (масс.) под
вакуумом 0,2 кгс/см2. Начальное количество раствора 1500 кг/ч.
Определить количество воды, подаваемой: а) в барометрический
конденсатор; б) в поверхностный конденсатор, принимая
температуру отходящего конденсата на 5 °С ниже температуры
конденсации. Вода в обоих случаях нагревается от 15 до
35 °С.
5.26. В выпарном аппарате производится концентрирование
водного раствора от 12 до 38% (масс.) под вакуумом (в
конденсаторе) 600 мм рт. ст. (см. рис. 5.1). Расход охлаждающей воды
в барометрическом конденсаторе 40 м3/ч, вода нагревается от 14
до 30 °С. Определить часовую производительность выпарного
аппарата по разбавленному и концентрированному раствору.
Температуриой депрессией пренебречь. Атмосферное давление
747 мм рт. ст.
5.27. Вакуум в выпарном аппарате над раствором 0,7 кгс/сма.
Расход разбавленного водного раствора, поступающего на
выпарку, 2,4 т/ч, его концентрация 12% (масс). Конечная
концентрация 32 % (масс). В барометрический конденсатор подается
38,6 м3/ч холодной воды с температурой 12 °С. Определить
температуру воды на выходе из барометрического конденсатора.
27$
Гидравлическим сопротивлением паропровода и температурной
депрессией пренебречь.
5.28. В трехкорпусиой выпарной батарее, работающей по
прямоточной схеме (см. рис. 5.7), подвергается упариванию
1300 кг/ч водного раствора с начальной концентрацией 9% (масс.)
до конечной концентрации 43% (масс). Вычислить
концентрации раствора по корпусам, если известно, что в каждом следующем
корпусе выпаривается воды на 10% больше, чем в предыдущем.
5.29. Какое предельное число корпусов может быть в
многокорпусной выпарной установке, если избыточное давление
греющего насыщенного водяного пара в первом корпусе ризб =
= 2,3 кгс/см2, остаточное давление в конденсаторе 147 мм рт. ст.
Сумму температурных потерь во всех корпусах принять равной
2]А^пот = 41 К. Допустимая полезная разность температур в
каждом корпусе должна быть не меньше 8 К.
5.30. В двухкорпусной установке, работающей по
прямоточной схеме, упаривается 1000 кг/ч водного раствора
азотнокислого натрия. Начальная концентрация 10% (масс), конечная
после первого корпуса 15% (масс), конечная после второго 30%
(масс). Конечная температура раствора после первого корпуса
103 °С, после второго 90 °С. Определить, сколько воды испарится
во втором корпусе за счет самоиспарения и какой это составит
процент от общего количества воды, испаряющейся во втором
корпусе.
5.31. В двухкорпусную выпарную установку, работающую
по прямоточной схеме, поступает 1000 кг/ч водного раствора
хлористого магния. Начальная концентрация раствора 8% (масс).
Концентрация раствора после первого корпуса 12% (масс).
Абсолютное давление над раствором в первом корпусе 1 кгс/см2,
во втором корпусе 0,3 кгс/см2. Конечная температура раствора
после первого корпуса 104 °С, после второго 77 °С. Определить,
до какой конечной концентрации упаривается раствор во втором
корпусе, если обогрев второго корпуса осуществляется за счет
вторичного пара первого корпуса (отбора экстра-пара нет).
Тепловыми потерями пренебречь.
5.32. Во второй корпус двухкорпусной установки,
работающей по прямоточной схеме без отбора экстра-пара, поступает из
первого корпуса 500 кг/ч 16% водного раствора углекислого
натрия с температурой 103 °С. Абсолютное давление над кипящим
раствором в первом корпусе 1 кгс/см2, во втором корпусе
0,6 кгс/см2. Концентрированный раствор, выходящий из II
корпуса с температурой 89 °С и концентрацией 28% (масс),
используется в противоточном теплообменнике для подогрева
разбавленного раствора, поступающего на выпарку. Пренебрегая
тепловыми потерями и депрессией, определить: а) концентрацию
разбавленного раствора, подаваемого на выпарку; б) на сколько
градусов будет подогрет разбавленный раствор в теплообменнике,
если концентрированный раствор выходит из теплообменника с тем-
274
Рис. 5.5 (к контрольно i задаче 5.33).
Рис. 5.6 (к контрольной задаче 5.34).
')
I
I
t
¦т
I
A-Jr
пературой 32 °С. Удельная теплоемкость концентрированного
раствора 3,35-103 Дж/(кг-К).
5.33. В двухкорпусную выпарную установку, работающую
по прямоточной схеме, поступает 1000 кг/ч водного раствора
хлористого кальция. Начальная концентрация раствора 8 % (масс),
конечная 30% (масс). В первом корпусе абсолютное давление
вторичного пара 1 кгс/см2 > во втором 0,3 кгс/см2. Конечная
температура раствора после первого корпуса 104 °С, после второго
78 °С. В первом корпусе образуется 400 кг/ч вторичного пара.
Часть этого пара (рис 5.5) отбирается на сторону (зкетра-пар).
Пренебрегая тепловыми потерями, определить, какое количество
экстра-пара отбирается.
5.34. В однокорпусный выпарной аппарат (рис. 5.6),
работающий с тепловым насосом (сжатие вторичного пара в
турбокомпрессоре), поступает разбавленный водный раствор с концентрацией
5% (масс). Из аппарата выходит 550 кг/ч раствора с
концентрацией 15% (масс). Температурная депрессия 2,5 К.
Гидростатическим эффектом и гидравлическим сопротивлением пренебречь.
Турбокомпрессор сжимает вторичный пар от 1 до 2 кгс/см2.
Тепловые потери составляют 5% от (QHarp + Qiicn)- Начальная
температура разбавленного раствора 70 °С. Определить: а) сколько
приходится добавлять греющего насыщенного водяного пара
(пар сухой насыщенный, избыточное давление /?изб = 2 кгс/см2);
б) какую мощность потребляет турбокомпрессор, если общий
к. п. д. его равен 0,72.
5.35. До какой температуры надо охладить горячий 40%
водный раствор калиевой селитры, чтобы после охлаждения и
выпадения кристаллов концентрация маточного раствора стала вдвое
меньше исходной?
5.36. Сколько килограммов кристаллов выделится при
охлаждении от 30 до 15 °С 4,2 т раствора соды, содержащего 2,5 моль
275
соды на 1000 г воды? Сода кристаллизуе^я с 10 молекулами воды.
5.37. Определить необходимую площадь поверхности
охлаждения противоточного кристаллизатора, в котором охлаждается
от 85 до 35 °С 10 000 кг/ч раствора, содержащего 7,0 моль
сернокислого аммония на 1000 г воды. При охлаждении испаряется
вода (5% от массы начального раствора). Коэффициент
теплопередачи 127 Вт/(м2-К). Охлаждающая вода нагревается от 13
до 24 °С. Определить также ее расход.
ПРИМЕР РАСЧЕТА ТРЕХКОРПУСНОЙ ВЫПАРНОЙ УСТАНОВКИ
Рассчитать трехкорпусную прямоточную выпарную установку с
естественной циркуляцией раствора (рис. 5.7) для концентрирования 5 т/ч 12 % водного
раствора азотнокислого натрия. Конечная концентрация раствора 40 % (масс.).
Раствор поступает на выпарку подогретым до температуры кипения в выпарном
аппарате. Абсолютное давление греющего насыщенного водяного пара 4 кгс/см2.
Высота греющих труб 4 м. Вакуум (разрежение) в барометрическом конденсаторе
0,8 кгс/см2.
Решение*. 1. Количество воды, выпариваемой в трех корпусах
установки:
W
5000
3600
(l — -ig-) = 3500 кг/ч *= 0,97 кг/с.
2. Распределение нагрузки по корпусам.
Сделаем это распределение иа основании практических даииых, приняв
следующее соотношение массовых количеств выпариваемой воды по корпусам:
I : И : III = 1,0: 1,1 : 1,2.
* В литературе описано несколько методов расчета многокорпусных
выпарных установок. Все они включают те или иные допущения, снижающие точность
окончательного результата. Один из подобных упрощенных методов расчета
использован в настоящем примере.
| Квакуум*
| насосу
-н
л,
Вода
Х7
л
Конденсат
Рис. 5,7. Схема трехкорпусной выпарной установки.
276
Eft
Следовательно, количество выпариваемой воды;
в • «*¦*« ^ - aeoodTui1+.,2) -°-295кг/°
Во " » г"-1шёг=°'324кг/0
Итого It7 = 0,97 кг/с
3. Расчет концентраций раствора по корпусам.
Начальная концентрация раствора дгнач = 12%. Из I корпуса во II
переходит раствора:
°1в°на*-^1=-|§йб 0,295 =1,39-0,295-1,09 кг/с.
Концентрация раствора, конечная для I корпуса и начальная для II, будет
равна:
w _ ^начхнаq 1,од- \1 ^ _ „
Ч~ Онач-»7! ~ 1,39-0,295 ~'0,//°-
Иа И корпуса в Ш переходит раствора
G2 = 0Нач — U^j — W^jz = 1,39 — 0,295 — 0,324 «0,77 кг/о
с концентрацией
х2= 1,39.12/0,77=. 21,6%.
Из III корпуса выходит раствора
<?«оа == Снач - W а 1,39 - 0,97 - 0,42 кг/0
о концентрацией
Jtob-1,39-12/0.42-40%,
что соответствует заданию.
4. Распределение перепада давлений по корпусам.
Разность между давлением греющего пара (в I корпусе) и давлением пара
в барометрическом конденсаторе:
Др « 4,0 — 0,2 = 3,8 кгс/см2.
Предварительно распределим этот перепад давлений между корпусами
поровну, т. е. иа каждый корпус примем:
Ар = 3,8/3 «= 1,27 кгс/см2.
Тогда абсолютные давления по корпусам будут;
В III корпусе р3 — 0,2 кгс/сма (задано)
Во II » р8 = 0,2+ 1,27 =« 1,47 кгс/сма
В I » Pt = 1,47 + 1,27 = 2,74 кгс/см*
Давление греющего пара:
р = 2,74 + 1,27 я» 4 кгс/сма.
По паровым таблицам находим температуры насыщенных паров воды и
удельные геплоты парообразования для принятых давлении в корпусах:
Удельная
Температура теплота па-
насыщенного рообразовгГ-
пара, °С ния> кДж/kf
В I корпусе 129,4 2179
Во II * 110,1 2234
В III * 59,7 2357
Греющий пар (из котельной) 143 2|41
Эти температуры и будут температурами конденсации вторичных паров по
корпусам.
5. Расчет температурных потерь по корпусам.
От депрессии
В справочных таблицах (например, табл. XXXVI) находим температуры
кипения растворов при атмосферном давлении:
вдяН№?5Ро,". Температура Депрессия,
% кипения, G ?С или К
В I корпусе 15,2 102 2,0
Во II » 21,6 103 3,0
В III » 40,0 107 7,0
Для упрощения расчета не уточняем температурную депрессию (в связи
с отличием давления в корпусах от атмосферного).
Следовательно, по трем корпусам:
^депр=2 + 3 + 7=12°С=12К.
От гидростатического эффекта
По справочнику * плотность раствора NaNOa при 20 °С:
Концентрация NaNOa, % 15,2 21,6 40,0
Плотность, кг/м3 1098 1156 1317
Эти значения плотностей примем (с небольшим запасом) и для температур
кипения по корпусам.
Расчет ведем для случая кипения раствора в трубках при оптимальном
уровне [формула (5.23)].
I корпус. Яопт = [0,26 + 0,0014 (рр —рв)] И =
= [0,26 + 0,0014 (1098 — 1000)j 4 =* 1,589 м;
. пе о «,- , 0,5.1098.9,8Ь1,589 0 007 , .
Рст, = Pi 4- 0,5рр^Яопт = 2,74 + — 9,8Ы0« в ' кгс/см2-
При Pl = 2,74 кгс/см2 /кип= 129,4 °С; при рср = 2,827 кгс/см? /кип = 130,6 °С.
^г.эф= 130,6—129,4= 1,2QC« 1,2 К.
II корпус. Яопт = [0,26 -(-0,0014 (1156 — 1000)] 4 = 1,91 и;
. „, ( 0,5.1156-9,81.1,91 л CQ . о
Рср«1.47 + —= 98),104 = 1,58 кгс/см2.
* Справочник химика, 2-е изд., пер, и доп. Т. III, — М.—Л,: Химия, 1965,
с. 544.
278
При Pl= 1,47кгс/см2 fHIIII = 110.1 °C; при рср = 1,58кгс/с» /КИп == П2,3°С.
Д'г. эф= 112,3— ПО,I = 2,2°С = 2,2 К.
III корпус. Иоат = 10,26 + 0,0014(1317— 1000)] 4= 2,81 м;
л 0 , 0,5-I317-9,8I.2,81 n QCr , 2
Рср = 0.2 + 9,81-104 ^ ' КГС/Ш
При рср = 0,385 кгс/см2 *кип = 74,39 °С; при рл = 0,2 кгс/см2 /кип = 59,7 °С.
д*р>эф = 74,39—59,7 = 14,69 иС= 14,69 К.
Всего ? Д*г.аф= 1,2 + 2,2+ 14,69= 18,09 °С = 18,09 К.
От гидравлических сопротивлений
Потерю разности температур на каждом интервале между корпусами
принимаем в 1 К. Интервалов всего три (I—II, II—III, III — конденсатор),
следовательно,
AfPiC = Ь3=3 К.
Сумма всех температурных потерь для установки в целом:
2] Д'пот = 12 + 18,09 + 3 = 33,09 К.
6. Полезная разность температур.
Общая разность температур 143 — 59,7— 83,3 °С — 83,3 К; следовательно,
полезная разность температур:
Л/пол = 83,3 — 33,09 = 50,21 К-
7. Определение температур кипения в корпусах:
В III корпусе /а = 59,7+1 + 7 + 14,69 = 82,4 °С
Во II « /2= 110,1 + 1 +3 + 2,2=116,3 °С
В I « /1==129,4 + 1 +2+ 1,2 = 133,6 °С
8. Расчет коэффициентов теплопередачи по корпусам.
По найденным температурам кипения и концентрациям растворов в
корпусах подбираем в справочниках расчетные константы — физические
характеристики растворов (плотность, теплопроводность, теплоемкость, вязкость).
Далее задаемся диаметром труб и их длиной (в зависимости от типа выпарного
аппарата).
По этим данным рассчитываем коэффициенты теплоотдачи для
конденсирующегося пара и кипящего раствора и коэффициенты теплопередачи (примеры
таких расчетов даны в гл. 4). При этом следует учесть слой накипи порядка
0,5 мм.
На основании таких предварительных расчетов примем:
Для I корпуса Кг = 1700 Вт/(м2. К)
» И » К2= 990 »
» III » /С3= 580 »
Ориентировочное соотношение коэффициентов теплопередачи по корпусам
при выпаривании водных растворов солей К\ ' К2 '• Кв = 1 • 0.58 : 0,34.
9. Составление тепловых балансов по корпусам.
Для упрощения приближенного расчета составляем тепловые балансы без
(учета тепловых потерь и принимаем, что из каждого корпуса в последующий
раствор поступает при средней температуре кипения.
По условию раствор подается на выпарку подогретым до температуры
кипения в I корпусе,
279
Тогда расход теплоты в I корпусе:
Qj = WVl = 0,295-2179.10* = 643 000 Вт.
Раствор приходит во II корпус перегретым, следовательно, QHarp
отрицательно (теплотд самоиспарения) и расход теплоты во II корпусе
Qu = Wur2 — Glcx(tl — t2) = 0,324-2234.103 —
— 1,09-4190.0,848(133,6—116,3) = 657 000 Вт.
Количество теплоты, которое даст вторичный пар I корпуса при
конденсации, составляет Ш\гг= 643 000 Вт. Расхождение прихода и расхода теплоты
в тепловом балансе II корпуса меньше 1 %.
Расход теплоты в III корпусе:
Qui = ^икз — <Va ('2 — h) =
= 0,351-2357-103 — 0,77-4190.0,784(116,3 — 82,7) =743000 Вт.
Вторичный пар II корпуса дает теплоты при конденсации (приход теплоты
в III корпусе):
Wur2 = 0,324-2234-103 = 724000 Вт.
10. Расход греющего пара в I корпусе:
г 643.000 .
г* п ~~ 2 141 Ю3 "~ КГ
Удельный расход пара:
d = Gr, n/W = 0,3/0,97 = 0,31 кг/кг.
11. Распределение полезной разности температур по корпусам.
Распределение полезной разности температур по корпусам сделаем в двух
вариантах: из условия равной площади поверхности и из условия Зминимальвой
общей площади поверхности корпусов, т. е. пропорционально QlK и
пропорционально V"Q/K.
Найдем факторы пропорциональности:
Отношение
Vi
643 000 „„ „,.
I корпус ,700 = 378 615
„ 657 000
11 » 990 =664 815
.„, , _™<™ 1280 ИЗ.
ooU
V-^- = 2322 V|/-|- 103 = 2561
280
Полезные разности температур по корпусам:
Вариант равной площади
поверхности корпусов
_ 50,21-378 _ Q17/l
Д/1 2322 8'174
Вариант минимальной общей
площади поверх ностй корпусов
Д/х
= 50,21*615 =
2561
12,057
А/2 =
50,21-664
2322
= 14,358
., 50,21-815 __.__
А/, =
50,2Ы280
2322
27,682
Е А':
пол
50,21 К
в 50,21.1131 =
S А^пол = 50,21 К
12. Определение площади поверхности нагрева:
Вариант равной площади
поверхности корпусов
Л =
F, =
/ч =
643 000
1700-8,174
657 000
990-14,358
743 000
580-27,682
= 46,27
« 46,22
= 46.28
EF= 138,8 м2
Вариант минимальной общей
площади поверхности корпусов
/ч =
*.=
^¦ =
643 000
1700-12,057
657 000
990-15,978
743 000
580.22,174
¦• 31,37
41,53
57,77
?F= 130,7 м?
Следовательно, при равных площадях поверхностей корпусов общая
площадь поверхности нагрева больше лишь на 6%.
Принимаем поэтому вариант равной площади поверхности корпусов,
обеспечивающей однотипность оборудования.
Проверим температуру вторичного пара и давление по корпусам:
Корпус
Температура кипения, °С
t
кип
t
Р П "*ПОЛ
Температура конденсации
вторичного пара, °С
о кип
пот
Давление
Рабо.
кгс/см1
I
II
III
143,0— 10,1 = 132,9
129,3— 17,6= 111,7
106,7 — 33,4= 73,3
132.9 — 3,59= 129.3
111,7 — 4,96= 106,7
73,3 — 13,32= 60
2,7
1,31
0,2
После этого необходимо, исходя из найденных площадей поверхностей
корпусов, произвести уточненный расчет установки, в котором учесть потери
теплоты в окружающую среду и несколько изменившееся распределение температур
и давлений по корпусам.
281
Глава 6
ОСНОВЫ МАССОПЕРЕДАЧИ. АБСОРБЦИЯ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Способы выражения состава фаз двухкомпонентных систем
жидкость — газ (пар) представлены в табл. 6'Л.
Формулы для пересчета концентраций (в жидкой фазе) даны
в табл. 6.2. Для газовой (паровой) фазы справедливы те же
соотношения, но с заменой обозначений х на у, X иа У, Сх на Су.
2. Концентрация компонента в газовой фазе может быть
выражена также через его парциальное давление. На основании
уравнений Клапейрона и Дальтона мольная (объемная) доля
у любого компонента смеси идеальных газов равняется:
у = Р/п, (6.1)
где
компонента газовой
П
р — парциальное давление компонента газовой смеси; U = рА + рв -\-
+ рс + ... — общее давление смеси газов или паров, равное сумме
парциальных давлений всех компонентов.
3. Законы межфазного равновесия для идеальных растворов,
а) Закон Генри:
р* — Ех,
(6.2)
где /?* — парциальное давление компонента в газовой фазе над равновесной с
газом жкдкостыо; х — мольная доля компонента в жидкости; Е — коэффициент
Генри, зависящий от температуры и от природы газа и жидкости.
Таблица 6.1
Концентрация
Обозначение концентрации
компонента А
в жидкой
фазе
в газовой или
паровой фазе
Мольная доля,
Массовая доля,
кмоль А
кмоль (А + В)
кг А
кг (А + В)
Относительная мольная концентрация (доля),
«моль А
кмоль В
X
X
У
У
Y
Относительная массовая концентрация (доля),
Объемная мольная концентрация,
Объемная массовая концентрация,
кг А
кг В
кмоль А
м3 (А + В)
кг А
X
м3 (А + В)
'X
'X
'У
'У
282
Таблица 6.2
283
Выражение
концентрации
компонента А
X
X
X
X
Сх
сх
Для
Р
мв.
смес!
П
RT
X
Ма*
Л*см
X
1 —х
Мах
Мв(\-
рх
Мсм
рМл*
Мсм
и Af ., — мо.
см
i идеалоных
пг0
22,4П0Г
X)
пьные
газов
X
хМСи
МА
или
xlMA
X 1 —X
МЛ ' Мв
—
хМв
МА(\-х)
Z
1 — х
рх
МА
рх
массы компонент
•
•
X
X
1+Х
мАх
мАх + мв
—
мАх
мв
рх
мАх + мв
МАрХ
МАХ + Мв
ов и смеси, кг/км<
X
мвх
мвх + мА
X
1+Х
МВХ
МА
—
рХ
МА (X + 1)
Сх
схмсм
р
или
схмв
Р + СХ(МВ - МА)
рх
Х+ 1
злы Мш = МАХ + Мв
мАсх
р
мвсх
р — МлСх
МаСх
Р — МАСХ
—
МаСх
(1 — х)\ р *« плотное
Сх
схмсм
рМл
или
схмв
рМА+Сх(Мв-МА)
Сх
р
мвсх
МА(р-Сх)
сх
Р — Сх
сх
МА
ть смеси, кг/м3.
Значения Е для водных растворов некоторых газов даны
в табл. XLI.
Подставляя в уравнение (6.2) значение /?* = у*П по
уравнению (6.1), получаем:
у* = тх. (6.3)
Здесь у* — мольная доля компонента в газовой фазе, равновесной с
жидкостью; т = Е/П — безразмерный коэффициент (коэффициент распределения) t
постоянный для данной системы газ — жидкость при /= const и П = const.
Если, применительно к двухфазной трехкомпонентной системе
(газовая фаза: А + В, жидкая фаза: А + С), подставить в
уравнение равновесия (6.3) значения х и у* для компонента А,
выраженные через его относительные концентрации X и Y*% X и Y*
(табл. 6.2), получим:
v* х
— т . , v ; (6.4)
1 + К* I + Х '
V* х
= т
Y + Мв Л+ МС
(6.5)
где МА — мольная масса распределенного между фазами компонента А; Мв —
то же второго компонента бинарной газовой смеси; Mq — то же второго
компонента бциариой жидкой смеси.
При малых концентрациях распределенного компонента в газе
и в жидкости, когда Y* < 1 и X <^ 1, в знаменателях уравнения
(6.4) величинами К* и X можно пренебречь, и оно получает
вид:
Аналогично при
получим:
Y* = тХ.
г*«#-*«тЙ-
?*-т М° X.
(6.6)
из уравнения (6.5)
(6.6а)
мв
б) закон Рауля:
р* = Рх, (6.7)
где р* — парциальное давление компонента в парогазовой смеси иад жидкостью
в условиях равновесия; Р — давление насыщенного пара чистого компонента —
одиозиачиая функция температуры; Р — f (t)\ x — мольная доля компонента
в жидкости.
При подстановке в уравнение (6.7) значения р* = у*П из
уравнения (6.1) получаем:
где у* — мольная доля компонента р парогазовой фазе, равновесной с жидкостью.
284
Для двухкомпонентной. смеси, когда оба ее компонента следуют
закону Рауля, уравнение (6.8) приводится к виду:
ахА
'*-1+(.Л),А- (6-9)
Здесь а = Рд/Рв *~ коэффициент относительной летучести; Рд —
давление насыщенного дара более летучего (низкокипящего) компонента при той же
температуре; Рв — давление насыщенного пара менее летучего (высококипя-
щёго) компонента при той же температуре.
4. Многочисленные экспериментальные данные о равновесных
составах жидкости и пара для различных растворов имеются
в справочнике [6.7]. Для некоторых бинарных смесей данные о
равновесных составах жидкости и пара при П = const приведены
в табл. XLVII и на рис. XXI и XXII.
5. Причиной (движущей силой) процесса массопередачи —
перехода какого-либо компонента из одной фазы в другую
(например, из жидкой фазы Ф^. с мольной концентрацией
переходящего компонента х в газовую фазу Фу с мольной концентрацией у)
является неравновесность соприкасающихся фаз, их отклонение
от состояния динамического равновесия. В химической
термодинамике устанавливается, что величина этого отклонения, при
равенстве температур и давлений фаз, определяется разностью
химических потенциалов переходящего компонента (\ix — \iy),
которая и является движущей силой процесса массопередачи.
При равновесии фаз потенциалы \ix и \iy равны.
Заменяя потенциал \ix равным ему потенциалом равновесной
газовой смеси \iy, получим для движущей силы процесса
массопередачи выражение
Аналогично, заменяя потенциал iiy равным ему потенциалом
равновесной жидкой фазы |ij, получим:
Из последних равенств следует, что движущая сила процесса
(У* — Цу) может быть выражена двумя способами: либо как
разность химических потенциалов, взятых по газовой фазе, либо как
разность потенциалов, взятых по жидкой фазе. При этом
необходимо помнить, что газовая фаза с потенциалом \х,у и концентрацией
у*, так же как и жидкая фаза с потенциалом \il и концентрацией
х*, — фазы гипотетические, в реальном процессе массопередачи
отсутствующие — см. рис. 6.1.
В технических расчетах применяют не химические потенциалы,
а более простые, легко определяемые величины — концентрации,
с помощью которых также может быть охарактеризовано
отклонение фаз Фх и Фи от состояния равновесия. Однако, в отличие от
разности химических потенциалов (\ix — \iy)t которая равна нулю
при равновесии фаз, разность концентраций (х— у), в общем
285
х,У
-^-
I
Ряс. 6.1. Схема процесса массопередачи:
00 — граница раздела фаз.
случае не равная нулю при
равновесии *, не может
служить мерой отклонения фаз от
равновесного состояния, т. е.
движущей силой процесса
массопередачи. При технических
расчетах движущую силу
процесса массопередачи —
отклонение системы от состояния
равновесия — выражают
поэтому как разность
концентраций (у*—у) или (х — х*). Так
как концентрации могут быть
выражены в различных
единицах, то движущая сила про-
— см.
цесса массопередачи может иметь различные значения
пример 6.3.
6. В соответствии с двумя возможными способами выражения
движущей силы процесса массопередачи — по газовой фазе
(Ау = у* — у) или по жидкой фазе (Ах = х — л:*) — уравнение
массопередачи, аналогичное уравнению теплопередачи, может
быть написано в двух видах:
Л*« KybycvF (6.10)
или
М = Кх A*cp^.
(6.11)
Здесь М — расход компонента, переходящего из одной фазы в другую,
кмоль/с; F — площадь поверхности массопередачи,
м
2.
Ку — коэффициент
массопередачи, отнесенный к движущей силе ау, выраженной через мольные
доли компонента в газовой фазе, кмоль/(м2-с) **; Кх — коэффициент
массопередачи, отнесенный к движущей силе Ах, выраженной через мольные доли
компонента в жидкой фазе, кмоль/(м2-с); Д#ср и A*Cp — соответствующие
средние для всего процесса движущие силы (см. ниже).
В последних уравнениях вместо мольных расходов и
концентраций могут быть массовые, а вместо Д#ср могут быть AYCV;
АСУ и Д/?Ср> соответственно, вместо Axcv могут быть АХ,
ср
или АС
хср'
. 7. При определенных допущениях (отсутствие диффузионного
сопротивления при переходе компонента через поверхность
раздела фаз, существование равновесия на этой поверхности, линей-
* См., например, данные о равновесных концентрациях в табл, XLVII.
„* ,, _ кмоль кмоль
Иногда пишут
м2-с(Д#= 1)
или
ма-с
кмоль
кмоль
286
ность уравнения равновесия у* = тх или* У* = тх + Щ
получаются следующие зависимости между коэффициентами массопере-
дачи Ку и Кх и фазовыми коэффициентами массоотдачи $у и РЛ:
к, = -г^Г; (6Л2)
My Px
х,= , ' , . (6-,3>
"Фи fte
где m — тангенс угла наклона линии равновесия- Коэффициенты массоотдачи
и массопередачи выражены в кмоль/(м2-с).
Знаменатели последних уравнений представляют собою
общее диффузионное сопротивление, равнее сумме диффузионных
сопротивлений газовой и жидкой фаз.
Когда основное диффузвонное сопротивление сосредоточено
в газовой фазе, т. е. при-о—-С б-,
Рх Ру
Когда основное диффузионное сопротивление сосредоточено
в жидкой фазе, т. е. при —q-<^-q-,
ffiPy Px
Из уравнений (6.12) и (6.13) следуем» что
Ку = Кх/т. (6-16)
8. Основные диффузионные критерии подобия
установившихся процессов массоотдачи.
Диффузионный критерий Нуссельта:
Nu' = p//D. (6-17)
Диффузионный критерий Пекле:
Ре' =mi//D. (6-18)
Диффузионный критерий Пр'андтля:
Рг' = Pe'/Re = v/D. (6-19)
_ а , / «МОЛЬ КГ
Здесь р — коэффициент массоотдачи, м/с / • или
п кмоль „ кг
/ — характерный линейный размер, м; D — коэффициент молекулярной диффу-
еии, м7с; ш — скорость газа или жидкости, м/с; v — кинематический
коэффициент вязкости, nt/c.
287
Таблица 6.3
Атомный объем, см7атом
В
с
С1
н
N в первичных аминах
N во вторичных аминах
N с двумя насыщенными
связями
О с двумя насыщенными
связями
О в альдегидах и кетонах
О в сложных эфирах
О в простых эфирах
О в высших простых и
сложных эфирах
О в кислотах
О в соединениях с S, Р, N
S
27,0
14,8
24,6
3,7
10,5
12,0
15,6
7,4
7,4
9,1
9,9
11,0
12,0
8,3
25,6
Мольный объем.
1
н2
о2
N2
Воздух
СО
со2
so2
NO
NaO
NH3
н2о
H2S
COS
Cl2
Br2
I2
смУмоль
37.0
14,3
25,6
31,2
20,9
30,7
34,0
44,8
23,6
36,4
25,8
18,9
32,9
51,5
48,4
53,2
71,5
Структурные постоянные*
Бензольное кольцо
Нафталиновое кольцо
Антраценовое кольцо
—15
—30
—47,5
9. При отсутствии экспериментальных данных коэффициент
диффузии (молекулярной) газа А в газе В (или газа В в газе А)
может быть вычислен по формуле:
4,3. Ю~7Т^2 1/ 1 , Г
у "**— + -п— * (62°)
Dn =
Р № + «#*)
1/3\2
МА
М
в
давление
— моль-
где Dr — коэффициент диффузии, м2/с; Т — температура; К; р •
(абсолютное), кгс/см3; М и A1R — мольные массы газов А и В; v. и t
ные объемы газов А н В, определяемые как сумма атомных объемов элементов,
входящих в состав газа — см. пример 6.6 (атомные объемы некоторых элементов
и мольные объемы некоторых газов приведены в табл. 6.3).
Как следует из формулы (6.20), если известно значение
коэффициента диффузии Dx при температуре 7\ и давлении ри то
значение его D2 при температуре Т2 и давлении рг можно найти из
уравнения:
Ръ \Т\ I
D2 = DX
(6.21)
Значения коэффициентов диффузии в'воздухе для некоторых
газов и паров приведены в табл. XLII.
* При расчете мольного объема химического соединения величину соответствую.
щей структурной постоянной надо прибавить к сумме атомных объемов.
28$
10. Коэффициент диффузии в жидкости Dm при 20 °С можно
вычислить по приближенной формуле:
°ш = лв кjl (^/з + ^/з)2 У "ЖГ + "Щ"' (6>22)
где Ож — коэффициент диффузии, м3/с; ^—динамический коэффициент
вязкости жидкости, мПа*с; vA и vB — мольные объемы растворенного вещества и
растворителя; М^ и Мв — мольные массы растворенного вещества и
растворителя; А и В — коэффициенты, зависящие от свойств растворенного вещества и
растворителя.
Значения коэффициентов А для некоторых веществ,
растворенных в воде:
Для газов 1
» этилового спирта 1,24
» метилового спирта 1,19
» уксусной кислоты 1.27
Коэффициент В равен:
Для воды 4,7
» этилового Спирта 2,0
» метилового спирта 2,0
» ацетона 1,15
» неассоцкировакнык жидкостей Ц0
Коэффициент диффузии газа в жидкости Dt (при температуре
/) связан с коэффициентом диффузии D20 (при.температуре 20 °Q
следующей приближенной зависимостью
Dt = D20 [j + ? (/ — 20)], (6.23)
в которой температурный коэффициент b может быхь определен
по эмпирической формуле:
Ь = 0,2 Vv/Vp> (6.24)
где \i —динамический коэффициент вязкости жидкости при 20 °С,, мПа-с; р —
плотность жидкости, кг/м3.
Значения коэффициентов диффузии некоторых газов в воде
приведены в табл. XLIII.
Коэффициент диффузии в разбавленных растворах может быть
вычислен также по формуле;
Вж = 7,4-10"» (РАУ—• (6-25)
Здесь Dm — коэффициент диффузии, м3/с; М — мольная масса
растворителя; v — мольный объем диффундирующего вещества; Т — температура, К;
(1 — динамический коэффициент вязкости растворителя, мПа-с; р — параметр,
учитывающий ассоциацию молекул растворителя и равный:
Для воды 2,6
» метилового спирта 1,9
» этилового спирта 1,5
» бензола, эфира, гептана 1
11. Материальный баланс абсорбера (рис. 6.2).
Ю Павлов К. Ф. и др. 269
G,V
Рис. 6.2. Схема абсорбера.
*»Х
Рис. 6.3. Рабочая и равновесная линии абсорбера;
АВ — рабочая линия прн расходе поглотителя L; АС_-*- рабочая линия при расходе
поглотителя ?мин; ОС —- равновесная линия К* = f (X)>
При расчете абсорбера с нелетучим жидким поглотителем
массовые {ът жшьные} расколы шглотетеля н наертаого.» аераство-
ряющегося в жидкости газа будут постоянными по высоте
абсорбера. Выражая концентрации поглощаемого компонента в газе
и жидкости в относительных массовых (или мольных) единицах,
получим уравнение материального баланса (в массовых единицах):
М
(6.26)
где М — расход поглощаемого компонента, кг/с; G н L — расходы инертного
газа и жидкого поглотителя, кг/с; Кы и YB — концентрации поглощаемого_ком-
понента в газе в низу и на верху абсорбера, кг/кг инертного газа; Хн и Хв —
то же в жидкости в низу и на верху абсорбера, кг/кГ жидкого поглотителя.
В координатах Y—X уравнение (6.26), при постоянных^ G
и L, выражает ojpe30K прямой, проходящей через точки В lXHt
Yu] и А [Хъ, Рв] —см. рис. 6.3.
Уравнение этой прямой — рабочей линии:
~(Х~ХН)
(6.27)
или
? = УВ + -±~(Х-ХЪ),
(6.28)
где Y и X — переменные по высоте колонны концентрации поглощаемого
компонента в контактирующих неравновесных потоках газа н жидкости в данном се-
чеиин абсорбера — рис. 6.2.
Расход жидкого поглотителя:
(6.29)
290
Здесь <р> 1 — коэффициент избытка поглотителя; LMnB —теоретически
минимальный расход поглотителя, определяемый графическим (см. рис, 6.3)
или аналитическим путем:
М
МИн ™ -=п — • (6-3())
XR — л в
Степенью поглощения (или извлечения) называется величина
Са в КнГКв - Уа.ГКв . (6.30а)
Кн ун
12. Средняя движущая сила в абсорбере с непрерывным
контактом фаз.
В общем уравнении массопередачи
м
F = —-=— (6.31)
Ку АКср
где F—поверхность массопередачи в абсорбере, м2; М —
расход поглощаемого компонента, кг/с; Kg — коэффициент массо-
кг \
передачи, ма.с 51 ) средняя движущая сила ДКсропре-
кг инертного газа/
деляется следующим образом.
Если в пределах от Хъ до Хн (рис. 6.3) линия равновесия
прямая, то
ДКср = —ДКн ~-АК - , (6.32)
р 2,3 lg (ДКа/ДКв)
где ДКН и ДКВ — концевые движущие силы; ДКн = Кн — Кн — в иизу
абсорбера при X — Хн\ ДКв — Уъ — Кв — на верху абсорбера при X =Х в-
Когда отношение ДУ"ни АКВ находится в пределах
0,5 < AYJAYB < 2,
среднюю движущую силу в абсорбере можно рассчитывать по
более простой формуле:
дкср » (ДКН + дкв)/2. (б.ЗЭ)
Если же линия равновесия не прямая, то
ДКср = Кн~Кв . (6.34)
J
dY
Т7 77*
Y — Y
Y
в
Величину интеграла в знаменателе последнего уравнения
находят графическим построением или методом графического
интегрирования. Другой метод расчета при криволинейной линии
10* 291
равновесия: разбивают равновесную линию на участки,
принимаемые приближенно за отрезки прямых, и для каждого участка в
отдельности определяют среднюю движущую силу по уравнению
(6.32) или (6.33).
При расчетах абсорберов движущую силу часто выражают
в единицах давления — см. пример 6.9.
13. Определение диаметра насадочного абсорбера.
Диаметр абсорбционной колонны D (э м) рассчитывают по
уравнению расхода для газового потока:
D
У^ШГ' (6'35)
где V — расход газа, проходящего через абсорбер, mVc; w ~ скорость газа,
отнесенная к полному поперечному сеченяю колонны (фиктивная), м/с.
Скорость газа w находят следующим путем.
Сначала рассчитывают фиктивную скорость газа ш3 в точке
захлебывания (инверсии) по уравнению (при рж > рг):
Здесь а — удельная поверхность насадки, м^м3; # — ускорение свободного
падения, м/с2; Ксв — свободный объем насадки, м3/м3; рс и рж — плотяости газа
и жидкости, кг/м3; цж — динамический коэффициент вязкости жидкостя, мПа-с;
L и G- массовые расходы жидкости и газа, кг/с; А = 0,022 для насадки из
колец или спиралей [6.3], для ректификации А =*—0,125.
Затем определяют рабочую скорость газа w (фиктивную),
принимая для абсорберов, работающих в пленочном режиме
w = (0,75 + 0,9) ш8. (6.37)
14. Определение высоты насадочного абсорбера,
а) Через высоту единицы переноса (ВЕП),
Поверхность контакта фаз в абсорбере при пленочном режиме
работы:
F = Ян5а-ф, (6.38)
где #н — высота слоя насадки, м; S = nD*/4 — площадь поперечного сечения
колонны, м2; D — диаметр колонны, м; о — удельная поверхность сухой насадки,
mVm3; i|>— коэффициент смоченности насадки, безразмерный —расчет вели*
чины этого коэффициента см. [6.3].
Высота слоя н асадки:
^н
#я =
G Г dV
f ™
J V-Y* ~ КуЧу' (6-3S)
KySoty J у — У
у
в
Здесь G — постоянный по высоте колонны расход инертного газа, кг/с или
кмоль/с; Ки — средний коэффициент массопередачи, кг/ { м2*с )
у I \ кг инертного газа/
или кмоль/(м2'С ); /ifl„ — высота единицы переноса, м:
т / \ кг инертного газа/ оу F
292
fyy — общее число единиц переноса:
я
п
Off
-J
dV
У— У'
(6.40а)
в
Из уравнения (6.34) следует:
Поу = (Кн-Кв)/ДР0*- (6.41)
При прямолинейной равновесной зависимости среднюю
движущую силу АУсо рассчитывают по уравнению (6.32) или (6,33),
при криволинейной равновесной зависимости число единиц
переноса п0у находят графическим построением или методом
графического интегрирования — см. пример 6.10.
Объемным коэффициентом массопередачн Куу называют
величину
К „у = КуоЦ = Куа, (6.42)
где а= аф—удельная смоченная (активная) поверхность насадки, м?/^; при
i|>= i a= о.
Применяя объемный коэффициент массопередачн,
для высоты единицы переноса:
G G
п0у —
получаем
(6.43)
KySoy KyVS
б) Через высоту, эквивалентную теоретической тарелке
(ВЭТТ).
Высота слоя насадки Нн может быть рассчитана также по
уравнению:
Нн = Мт» (6.44)
где Лд — высота, эквивалентная теоретической тарелке (ВЭТТ) или
теоретической ступени (ВЭТС), м (определяется по экспериментальным данным); пт —
число теоретических тарелок (ступеней изменения концентрации)»
Число теоретических тарелок — у* у
ступеней изменения концентрации в y'i
абсорбере определяют обычно гра- _
фическим путем (рис. 6.4). На этом Ун
рисунке АВ — рабочая линия,
построенная по уравнению (6.27) или
(6.28), ОС — равновесная линия.
15, Критериальные формулы для
расчета коэффициентов массоотдачи
в насадочных абсорберах с
неупорядоченной насадкой (навалом) при
пленочном режиме.
/7-const
Т- const
Рис. 6.4. Графическое определение числа
ступеней изменения концентрации (теоретических
тарелок) в абсорбере.
293
а) Для газовой фазы:
Nu; = 0,407 Re?'655 (Pr,')0'33. (6.45)
Здесь Nu: =-2^-; Rer = -^; Рг; = -^-; Рг — коэффициент мае*
кмоль м _ . , ,.
соотдачи для газа, = —; Dr — коэффициент диффузии поглоща-
о КМОЛЬ С
М2-С —
м8
еиого компонента в газе, м2/с. Остальные обозначения — см. формулы (6.36) и
(6.38).
Уравнение (6.45) справедливо при значениях Re^ от 10 до
10 000.
б) Для жидкой фазы:
Nt4 « 0,0021 Re0/5 (Pr^)0'5, {6.46)
где Nu' = -НИ-ПР; Rem ¦=¦» . ; Рг^ = ^ff-; Рж — коэффициент массоот.
дачи для жидкости, м/с; опп = —-— — так называемая приведен-
Р \Рж8 )
ная толщина жидкой пленки, м; Dm — коэффициент диффузии поглощаемого
компонента в жидкости, м2/с; L — массовый расход жидкости, кг/с.
Выражение для критерия 1?еж получено следующим путем.
Обозначения — см. уравнения (6.36) и (6.38).
Омываемый жидкостью периметр сечения абсорбера находим
из уравнения (6.38):
П = F/Iih = Soyp. (6.47)
Скорость течения пленки жидкости через насадку;
L _ L
ржПб ~~ Рж5а1р6 *
где б — средняя толщина пленки, м.
Эквивалентный диаметр жидкой пленки:
dnjl = 4П6/П = 4о\ (6.49)
Подставляя эти значения в выражение для критерия Reao
получаем:
R6ffi = Ц'ж.шАлРж =.*L-. (6.50)
16. Определение диаметра и высоты тарельчатой
абсорбционной колонны проводится так же, как и для тарельчатых
ректификационных колонн — см. гл. 7. Диаметр тарельчатого абсорбера
рассчитывают по уравнениям (7.16) и (7.17). Высоту тарельчатой
части абсорбера Ят определяют по уравнению (7.18). Требуемое
число тарелок находят графически с применением кинетических
зависимостей для расчета коэффициентов массопередачи или
294
»ж. пл = Т—7ТТ = „ е-.,.*1 * <6'48)
ВЕП. При приближенных расчетах для определения числа
тарелок находят графически число ступеней изменения концентрации
(рис. 6.4) и затем число тарелок п по уравнению (7.19).
ПРИМЕРЫ
Пример 6.1. Жидкая смесь содержит 58,8% (мол.) толуола
и 41,2% (мол.) четыреххлор истого углерода (ч. х. у.). Определить
относительную массовую концентрацию толуола X (ъ толуол-\
и его объемную массовую концентрацию Сх (в кг/м3).
Решение. Относительная массовая концентрация толуола:
х =
MjQJlX
Мч.х.у{1~х)>
где Л4Т0Л — мольная масса толуола (92 кг/кмоль); МЧт х< у — то же четырех-
жлористого углерода (354 кг/кмоль); х — мольная доля толуола.
Имеем:
^ 92-0,588 кг толуола
154-0,412 кг ч. х. у
Чтобы рассчитать объемную массовую концентрацию толуола
Сх, необходимо знать плотность смеси рсм. Для расчета плотности
предварительно найдем массовую долю толуола х.
По табл. 6.2:
- * 0,в53 ....
х _ _ _ ¦ = 0,461.
Далее по табл. IV находим: плотность толуола ртоя =
= 870 кг/м3, плотность четыреххлористого углерода рЧ1? =
= 1630 кг/м3.
Считая, что изменение объема при смешении не происходит,
т. е. объем смеси равен сумме объемов компонентов, находим
объем 1 кг смеси
°'461+0^9=0(862.10.3MSf
870 ' 1630
откуда плотность смеси:
рсм== 0,862-Ю-з ~ И60*г/"'-
Можно рассчитать рсм и так:
1 + Х 1 + 0,853
1.Х" 1 ^0,853
! -+- Л. 1-1- V,000 пел , •
Рсм « : =— = г-2- тго&г- = Ибо кг/м».
о +1Г- I630 ~*~ 870
Объемная массовая концентрация толуола:
Сх = рх = 1160-0,461 = 535 кг/м8.
296
Пример 6.2. Воздух атмосферного давления при температуре
34 °С насыщен водяным паром. Определить парциальное давление
воздуха,- объемный и массовый % пара в воздушно-паровой смеси
и его относительную массовую концентрацию, считая оба
компонента смеси идеальными газами. Атмосферное давление
745 мм рт.' ст. Определить также плотность воздушно-паровой
смеси, сравнить ее с плотностью сухого воздуха.
Решение. По табл. XXXVIII находим, что при / = 34 QQ
давление насыщенного водяного пара составляет 39,9 мм рт. ст.
Это давление является парциальным давлением водяного пара рп
в воздушно-паровой смеси, а парциальное давление воздуха
равняется:
рв = П — ри в= 745 — 39,9 » 705 мм рт. ст.
Мольная (объемная) доля водяного пара в смеси:
у = рп/П = 39,9/745 = 0,0535.
Массовая доля пара:
а - М»у - 18-0,0535 _ Q 0 _
* Миу + Мв (1 — а) ~ 18-0,0535 + 29-0,9465 ~~ и'иода'
Относительная массовая концентрация:
Y = ' = °S-- 0,0351 КГПЗра .
1 — У 0,9661 кг воздуха
Плотность воздушно-паровой смеси рассчитываем как сумму
плотностей компонентов, взятых каждая при своем парциальном
давлении:
Рсм - Рв + Рп - 22/4ГП0 + 22,4ГП0 " 22,4ГП0 (Л*вРв + МпРа) ~
97Я
- 22,4-307-760 (29'705 + 18"39'9) я 1>105 КГ/Л
Можно рассчитать плотность смеси иначе.
Мольная масса смеси:
Мсм = Мы/ + мь(\ — у) = 18-0,0535 + 29-0,9465 = 28,4 кг/кмоль.
Плотность смеси при П = 745 мм рт. ст. и / = 34 °С:
D . Л*смПГ0 _ 28,4-745-273 ,.
Рсм"~ 22,4П0Г ~ 22,4.760-307 " !>IW> КГ/М "
Плотность сухого воздуха при тех же давлении и температуре:
__ МВПТ0 __ 29-745-273
Рс" в " 22,4ГП0 " 22,4-307-760 ~ 1,ld КГ/М *
Пример 6.3. При температуре 25 °С приведены в
соприкосновение: воздух атмосферного давления, содержащий 14 % (об.)
ацетилена (С2Н2), и вода, содержащая растворенный ацетилен
296
is количестве: а) 0,29'10~? кг на 1 кг воды; б) 0,153-10~3 кг на
1 кг воды. Определить: 1) из какой фазы в какую будет
переходить ацетилен; 2) движущую силу этого процесса перехода в
начальный момент времени (в относительных мольных
концентрациях). Атмосферное давление 765 мм рт. ст. Равновесные
концентрации ацетилена в газовой и в жидкой фазах определяются
законом Генри.
Решение. Закон Генри [уравнение (6.2)]:
р* = Ex.
По табл. XLI находим, что при t = 25 °С коэффициент Генри
Е = 1,0Ы0в мм рт. ст.
Парциальное давление ацетилена в воздухе по уравнению
(6.1):
р=:(/Г1 = 0,14-765 = 107 мм рт. ст.
ч »* V- /\ пл 1Л-3 кг ацетилена
а) Мольная доля ацетилена в воде при л = 0,29*10 *— ¦
кг воды
(табл. 6.2):
* 0,29.10-3 18.0,29.10-3
X + Jl^L o,29.10-» +-=г
Ответы на вопросы примера могут быть получены двумя
путями.
I. В условиях равновесия парциальное давление ацетилена
в газовой фазе над жидкостью с х. = 0,2-10~3 по закону Генри
должно составлять:
р* = ?х= 1,0Ы0в-0,2.10-3:=202 мм рт. ст.
Имеющееся в действительности над этой жидкостью
парциальное давление ацетилена меньше: р = 107 мм рт. ст. Чтобы в
процессе массопередачи система газ—жидкость приближалась к
состоянию равновесия, парциальное давление ацетилена в газовой
фазе должно увеличиваться, т. е. он будет переходить из воды
в воздух.
Движущая сила этого процесса перехода (отклонение от
состояния равновесия) в начальный момент времени будет равна:
в единицах парциального давления ацетилена
Ар = р* — р = 202 — 107 = 95 мм рт. ст.;
в мольных долях
209
Ду = у* - у = ¦— — 0,14 = 0,264 - 0,14 - 0,124;
в относительных мольных концентрациях
у* у 0,264 0,14
ЛУ « К* — К =
\—у* 1—У 1—0,264 1—0,14
кмоль ацетилена
= 0,359 — 0,163 = 0,196
кмоль воздуха
297
II. В условиях равновесия с газовой фазой, в которой
парциальное давление ацетилена равняется 107 мм рт. ст., вода по
закону Генри должна иметь концентрацию ацетилена (в мольных
долях):
^=^=тет-==0-106-10-3-
Имеющаяся в действительности мольная доля ацетилена в воде
больше: х — 0,2* 10~3. Для того чтобы в процессе массоперехода
система приближалась к состоянию равновесия, мольная доля
ацетилена в воде должна уменьшаться, т. е. ацетилен будет
переходить из воды в воздух.
Движущая сила этого процесса перехода в начальный момент
времени (считая ее по концентрации в жидкой фазе):
в мольных долях
Ах = х — х* = 0,2.1(Г8 — 0,106-10~8 = 0,094-10"8;
в относительных мольных концентрациях
1 —X 1 — X*
Так как в данном примере х и х* оба много меньше единицы,
то в знаменателях последнего уравнения ими можно пренебречь
и
ДХ = х - х* = 0,094. Ю-з -КМ°ЛЬ аце™а
кмоль воды
б) Мольная доля ацетилена в воде:
х ж 18-0,153.10-3/26 = 0,106-Ю"3.
Перехода ацетилена из одной фазы в другую не будет, так как
соприкасающиеся фазы находятся в равновесии:
х = ** = 0,106-10~8, у = у* = 0,\4.
Пример 6.4. В массообменном аппарате, работающем под
давлением /?абс = 3,1 кгс/см2, коэффициенты массоотдачи имеют сле-
. ft I fY7 КМОЛЬ о по КМОЛЬ
дующие значения: р„=1,07 м,,ч(Дув1), Р* = 22 ^ч(Ах=1).
Равновесные составы газовой и жидкой фаз характеризуются
законом Генри р* = 0,08-10* х. Определить: а) коэффициенты мас-
сопередачи Ку и Кх\ б) во сколько раз диффузионное
сопротивление жидкой фазы отличается от диффузионного сопротивления
газовой фазы:
Решение. Приведем уравнение равновесия к виду у* = тх:
р* 0,08.10»
У П 3,1-735 *-JV*.
298
Находим коэффициенты массопередачи:
1 1 1
*»-
V ~~ J_4--fL 1 ,35,1 0,935+1,595
Pff + Р* 1,07 + 22
кмоль
0,396
Кх =
м2.ц(Д^= 1) •
1 1 1
1 _!__ " 1 1 0,0266 + 0,0455
"Гц ос 1 1 Л7 т
т$у • {5Х 35,Ы,07 1 22
кмоль
13,9
м^ч(Д* = 1)
Проверка:
/Cx/ZCy = 13,9/0,396 = 35,1 = m.
Отношение диффузионных сопротивлений жидкой н газовой
фаз при движущей силе Ау:
т 1 1,595
Рх ' $у 0,935
= 1,71.
Такое же отношение будет и при движущей силе Ах.
Диффузионное сопротивление жидкой фазы в 1,71 раза больше
сопротивления газовой фазы.
Пример 6.5. В массообменном аппарате — абсорбере коэффи-
г/ 1Л . КМОЛЬ тл /
циент массопередачи Ку = 10,4 = . Инертный газ (не пе-
м2-ч—=—
м8
реходящии в жидкость) — азот. Давление /?абс в аппарате
760 мм рт. ст., температура 20 °С. Определить значения коэффи-
|у 1 \ КМОЛЬ
циента массопередачи Ку в следующих единицах: 1) М2, /д^^ п'
9\ кмоль . о\ кг
/ ИДИ _ II _ *«м Пт |-"т- ' /
м^-ч-мм рт. ст. ' „ кг
м2-ч
кг инертного газа
Решение. Напишем равенства:
М = ку АС/ - ^ А^ = *; ApF,
где УИ — мольный расход переходящего в жидкость компонента, кмоль/ч.
Отсюда:
1) КуАСу = КуАу, т. е.
Из табл. 6.2:
C<J- Мсм У 22,4П0Г »•
299
В данном примере П = П0 и
лс1_ « п/* = ft 2/в = о,041б;
^y 22,4Г 22,4.293
\Сп к моль
2) /С;Д^= /С;Др.
По уравнению (6.1):
у = р/П; Д# == Др/П;
,Г-к" Д^ -.(L-bi3! _569.]0-4___™^
КУ-КУ~К?~~ П ~ 760 _t>' ° м»-ч.мм рт. ст. '
5,69-10"4 , ,„ 1Л_9 кмрль
или збоо-13з,з =1'Ш-10'1ШГ-
3) Из равенств
(где W — массовый расход переходящего компонента, кг/ч)
находим:
К'у~ = К'уМк
По табл. 6.2:
к =
Л*и.Р(1-уГ
Здесь Мк и Ми< г — мольные массы переходящего компонента и
инертного газа. При малых значениях у:
У & АЛ У'
Отсюда
к;г = к:, Мн*у =к:ма О = о,4зз.28 = 12,1 кг
а' м3 • ч
кг инертного газа
Пример 6.6. Вычислить коэффициент диффузии сероводорода
в воде при 40 °С.
Решение. Сначала вычислим коэффициент диффузии при
20 °С по формуле (6.22):
D мо"' лГ 1 ,_.,. *
20 ABV^{vl^ + vff г Мл мв •
300
Для сероводорода Для воды
А = 1 В « 4,7
иЛ « 2-3,7 + 25,6 = 33,0 (табл. 6.3) \i = 1 сП =
= 1 мПа-с
JMA= 34 t>B=* 2-3,7 +
+ 7,4 = 14,8
Мв= 18
Подставляем эти значения в формулу (6.22):
D"= 4,7.1(14X33^ Уж + ж = ^°->-*¦
Вычисляем температурный коэффициент & по формуле (6.24)j
ft = 0,2 V^IVp « 0,2 KF/VTooo = 0,02.
Искомый коэффициент диффузии по формуле (6.23) равняется!
Д40 « 1,93.10-» [1 + 0,02 (40 — 20)] = 2,7-10"» м»/с
Для сравнения рассчитаем коэффициент диффузии
сероводорода в воде при 40 °С по формуле (6.25):
п 7,4-10-12(2,6-18)°'5.313 7,4. Ю-12.6,83.313
/? — ; ^ — — 2,96-10 8 ма/о.
0.656-330'6 0,656-8,15
Здесь 0,656 мПа-с — динамический коэффициент вязкости воды при 40 °С
(табл. VI).
Пример 6.7. Определить расход серной кислоты для осушки
воздуха при следующих данных. Производительность скруббера
500 м3/ч (считая на сухой воздух при нормальных условиях).
Начальное содержание влаги в воздухе 0,016 кг/кг сухого
воздуха, конечное содержание 0,006 кг/кг сухого воздуха.
Начальное содержание воды в кислоте 0,6 кг/кг моногидрата, конечное
содержание 1,4 кг/кг моногидрата. Осушка воздуха производится
при атмосферном давлении.
Решение. Массовый расход воздуха:
6 = 500.1,293 = 646 кг/ч,
где 1,293 кг/м3 — плотность воздуха при нормальных условиях.
По уравнению (6.26) расход серной кислоты (моногидрата):
l-Qg>-j>-646 °^6~п?°6 -«.Иг/*,
Ха-Хв 1,4-0,6
Пример 6.8. Скруббер для поглощения паров ацетона из
воздуха орошается водой в количестве 3000 кг/ч. Средняя
температура в скруббере 20 °С. Через скруббер пропускается под
атмосферным давлением смесь воздуха с парами ацетона, содержащая
6% (об.) ацетона. Чистого воздуха в этой смеси содержится
1400 м3/ч (считая на нормальные условия). В скруббере
улавливается 98% ацетона.
301
Уравнение линии равновесия:
К*= 1.68Х.
Здесь X н Y* выражены в киломолях ацетона на 1 кмоль второго
компонента, т. е. воды нлн воздуха.
Найти диаметр и высоту скруббера, заполненного
керамическими кольцами размером 25x25x3 мм. Скорость газа принять
на 25% меньше скорости захлебывания.
Коэффициент массопередачи Ку = 0,4 кмоль ацетона/ (м2-ч X
кмоль ацетона \ лг , ,
X \ Коэффициент смоченности насадки принять
равным единице.
Решение. Количество поглощаемого ацетона:
ял ^и. ?У\\съ.
- (1_Ун)22,4 "
1400-0,06-0,98
0,94-22,4
3.9 кмоль/ч,
где са = 0,98 — степень поглощения.
Начальная концентрация ацетона в воде, подаваемой на верх
скруббера, Хп = 0.
Конечная концентрация ацетона в воде4 вытекающей внизу
из скруббера:
M* _ 3,9 _qq^3j кмоль ацетона
Хн =
L/M
в
3000/18
КМОДЬ ВОДЫ
Начальная концентрация ацетона в воздухе внизу при входе
в скруббер:
^а =
Ун
1— Ун
0»06 __ q 0639 кмоль ацетона
0,94 ' кмоль воздуха "
Конечная концентрация
ацетона в воздухе, выходящем из
скруббера:
= 0,0012^
кмоль
кмоль
0,06-0,02
0,94
ацетона
воздуха
ОуОЮ Q,(H5 (JfiSO
У .кмоль ацетона
9 кмоль воды
По этим Точкам на диаграмме
Y—X (рис. 6.5) нанесена рабочая
линия; ниже проведена
равновесная линия По уравнению F* =
= 1.68Х.
Рис, 6,5 (к примеру 6.8).
802
Находим движущую силу абсорбции в низу скруббера;
кмоль ацетона
&*в = ^н - У. = °>°639 - 0,0393 = 0,0246 кмоль воздуха •
Значение YI находим по уравнению равновесной линии для ХЯ9
соответствующего низу скруббера:
К* в 1>68Х в 1,68-0,0234 = 0,0393 КМ0ЛЬ аЦ6Т0На .
н н кмоль воздуха
Движущая сила абсорции на верху скруббера:
кмоль ацетона
ДК = X — X* == 0,00128 — 0 = 0,00128
в в в » - кмоль воздуха
Средняя движущая сила:
... ДХН —ЛХВ 0,0246 — 0,00128 кмоль ацетона
у 0 Q , ДХН 0 - . 0,0246 кмоль воздуха
iid[g~KYZ 2,31ё"0Ж28
Требуемую поверхность массопередачи находим по уравнению:
KyAYCv - 0,4-0,0079 - 1AW м '
Объем слоя керамических колец, необходимый для создания
найденной поверхности, при г|? = 1 [см. уравнение (6.38)]:
К = tfHS = F/a = 1230/204 = 6 м3,
где а~ 204 м2/м3 — удельная поверхность насадки (табл. XVII).
Определим сечение скруббера.
По уравнению (6.36) вычисляем фиктивную скорость газа в
точке инверсии, пренебрегая небольшим содержанием ацетона
в жидкости и газе.
Значения входящих в уравнение величин:
Т 973
I = 3000 кг/ч; рг = р0 -^- = 1,293 —^ =~ 1,2 кг/м*;
G = 1400*1,293 = 1810 кг/ч; рж = 1000 кг/м3;
L/G = 3000/1810 = 1,66; рг/рж « 1,2/1000 =* 0,0012;
*1Ж = 1 мПа-с; Ксв = 0,74 м^/м8 (табл. XVII).
Подставляем эти значения в формулу (6.36):
/«Й.204.0,0012 . \ . „- п m
\g{ 981.0748—* ' ) = 0,022- 1.75-1,66°'25.0,00120'123
или
lgOf0616w*^ = —0,825,
откуда шв = 1,56 м/с.
По условию берем рабочую фиктивную скорость газа w на
25% меньше:
w ** 0>75йУ3 = 0,75-1,56 « 1,17 м/о.
Площадь поперечного сечения скруббера:
*- 360(topr ~ 3600-1,17.1,2 гаи^м-
Отсюда диаметр скруббера:
D = j/"0,358/0,785 = 0,675 м.
Требуемая высота насадки:
Ян = V/S = 6/0,358 = 16,8 м.
Пример 6.9. Определить коэффициент массопередачи в водяном
скруббере при поглощении из газа диоксида углерода по
следующим данным. В скруббер поступает 5000 м3/ч газовой смеси,
считая при атмосферном давлении и при рабочей температуре. На
скруббер подается 650 м3/ч чистой воды. Начальное содержание
диоксида углерода в газе 28,4% (об.), конечное (в верху
скруббера) 0,2% (об.). Давление в скр.уббере рабс = 16,5 кгс/см2.
Температура 15 °С. В нижнюю часть скруббера загружено 3 т
керамических колец 50x50x5 мм. Выше загружено 17 т колец
35x35x4 мм. Коэффициент смоченности считать равным единице.
Решение. Вычислим суммарную поверхность всех колец.
Поверхность колец 50x50x5 мм:
, Gj зооо
h^ — a g30" 87,5 = 495 м^,
где рЛ = 530 кг/м3 — насыпная плотность насадки из колец 50X50X5 мм; at =*
= 87,5 м2/м3 — удельная поверхность насадки (табл. XVII).
Аналогично вычисляем поверхность колец 35 X 35 X 4 мм:
, G2 17000 ..Л л_,_ .
/2==^аз=-505-140==4717м-
Суммарная поверхность всех колец:
F = h + /а = 495 + 4717 = 5212 м2.
Определим количество диоксида углерода, поглощенного водой.
Начальное количество диоксида углерода в газе (в низу
скруббера):
^нсо2 - ^нсмУн = 5000-0,284 « 1420 м»/ч.
Количество диоксида углерода в выходящем газе (в верху
скруббера):
v v и ^ои-^исо, ,. 5000-1420АЛП0
"всо8 = ^ввмУв = y=Jb У* = 1 - 0,002 °'002 = 7'2 м 'ч'
804
Поглощается водой:
Уаогл - ^нсоя - ^вСо2 = 142° - 7'2 = 1412'8 м3/4 (Р = 1 кг*/сма>
илн —0,1 МПа, н * = 15° С)
ИЛИ
Спогл - Уп0тТ° Ро Д273+153 1 *976 = 263° КГ/Ч'
т. е. 2630/44 = 60 кмоль/ч.
Здесь 1,976 кг/м3 — плотность С02 при нормальных условиях; 44 кг/кмоль —
мольная масса С02.
Находим движущую силу процесса абсорбции в низу
скруббера.
Парциальное давление диоксида углерода на входе в скруббер:
Рн = Щн в °>284' 162° = 46° кПа>
где 1620= 16,5*98,1 кПа—общее давление в скруббере.
Мольная доля С02 в воде, вытекающей из скруббера:
х <W^CQ2 2630/44
%" G™ G„ л ~ 2630 . 650000 - U'W1W>-
'со2 , ^н,о
_l_ _ 44 -г
^7^^7 44 18
Коэффициент Генри Е для диоксида при 15 °С равен 0,93 К
X 10е мм рт. ст. (табл. XLI), или 0,124-106 кПа; отсюда
парциальное давление диоксида углерода в газе, равновесном с
жидкостью, вытекающей из скруббера [уравнение (6.2)]:
р» =?*H = 0,00166-0,124.106 = 206 кПа.
Движущая сила процесса абсорбции в низу скруббера:
Дрн = рн — р* = 460 — 206 = 254 кПа.
Определяем движущую силу процесса абсорбции на верху
скруббера.
Парциальное давление диоксида углерода в газе, выходящем
вверху из скруббера:
Ръ = Пг/В = 1620-0,002 = 3,24 кПа.
Так как вода на орошение скруббера подается чистая, то
парциальное давление диоксида углерода в равновесном с водой газе
равно нулю; отсюда движущая сила процесса абсорбции на верху
скруббера:
Ари = рв-р1= 3,24 - 0 = 3,24 кПа.
Средняя движущая сила для всего процесса!
2^4 3 24
АР*Р в 2,3 lg (254}з,24) " Ь?Л *П*'
305
Таблица 6.4
х,
кмоль аммиака
кмоль воды
кмоль аммиака
кмоль инертного' газа
X,
кмоль аммиака
КТГОЛЬ ВОДЬ!
Y*,
кмоль аммиака
кмоль инертного газа
0
0,005
0,010
0,0125
0
0,0045
0,0102
0,0138
0.015
0.020
0,023
0.0183
0,0273
0,0327
Коэффициент массопередачи:
м 2630
Кд. =
Д*~~ FApcv 5212-57,4
0,0088
кг
ма-ч-кПа
Если коэффициент массопередачи отнести к разности давлений
Д/?, выраженной в мм рт. ст., то получим следующее его значение:
КА =
2630
Др 5212(57,4/0,133)
0,0012
кг
М^'Ч.ММ рТ. СТ.
Пример 6.10. В скруббере аммиак поглощается водой из газа
под атмосферным давлением. Начальное содержание аммиака
в газе 0 03 кмоль/кмоль инертного газа. Степень извлечения равна
90 %. Вода, выходящая из скруббера, содержит аммиака
0,02 кмоль/кмоль воды. Путем отвода теплоты в скруббере
поддерживается постоянная температура.
Данные о равновесных концентрациях аммиака в жидкости
и газе при температуре поглощения приведены в табл. 6.4.
Определить требуемое число единиц переноса nQy: 1)
графическим построением; 2) методом графического интегрирования.
Решение, 1) По данным табл. 6.4 на рис. 6.6 построена
равновесная линия АВ. На этом же графике нанесена рабочая
линия CD. Она проходит через точку С с координатами Хь = 0,
YB = 0,03 (1 — 0,9) = 0,003 (верх скруббера) и точку D с
координатами Хн = 0,02, YH = 0,03 (низ скруббера).
Число единиц переноса nQy находим следующим путем.
Отрезки ординат между рабочей и равновесной линиями разделены
пополам; через середины их проведена вспомогательная
пунктирная линия. Затем, начиная от точки С, построение выполнено
таким образом, что для каждой ступени ab = be. Каждая из
полученных ступеней представляет собой единицу переноса, т. е.
каждой ступени соответствует такой участок аппарата, на котором
изменение рабочей концентрации (Уг — Y2) равно средней движущей
силе на этом участке (Y — ^*)Ср-
Всего получено 5,82 ступени (последняя неполная ступень
равна отношению отрезков Ddief = 0,82):
п
оу
5,82.
306
Рис, 6,6 (к примеру 6.10).
Рис, 6.7, Определение числа единиц переноса методом графического интегрирования
(к примеру 6,10).
Как следует из графика, на нижнем участке кривой
равновесия, где ее наклон меньше наклона рабочей линии, единица
переноса меньше ступени изменения концентрации; на верхнем
участке равновесной линии, где ее наклон больше наклона рабочей
линии, наблюдается обратная картина.
2) Для определения числа единиц переноса методом
графического интегрирования по данным табл. 6.4 и рис. 6.6
составляем табл. 6.5.
По данным последней таблицы строим график l/(Y — Y*) =
= / (Y) — рис. 6.7. Подсчитываем на этом графике отмеченную
штриховкой площадь (например, методом трапеций) (см. пример
Таблица 6,5
X
0
0,005
0,010
0,0125
0,015
0,020
Y
0,003
0,0097
0,0165
0,0200
0,0234
0,0300
у*
0
0,0045
0,0102
0,0138
0,0183
0,0273
V —V*
0,003
0,0052
0,0063
0,0062
0,0051
0,0027
Y — Y*
333
193
159
161
196
371
307
4.26). Величина этой площади (5,83) дает значение интеграла
ув=о,оз
J
dY
Y_y*, т. е. число единиц переноса п0у.
Ув=0,003
Пример '6.11. Определить теоретически минимальный расход
жидкого поглотителя с мольной массой 224 кг/кмоль,
необходимый для полного извлечения пропана и бутана из 1000 м8/ч
(считая при нормальных условиях) газовой смеси. Содержание
пропана в газе 15% (об.), бутана 10% (об.). Температура в абсорбере
30 °С, абсолютное давление 3 кгс/см2 (294 кПа).
Растворимости бутана и пропана в поглотителе характеризуются законом
Рауля.
Решение. Максимальная концентрация (мольная доля)
пропана в поглотителе, вытекающем из скруббера (равновесная
с входящим газом), определяется по уравнению (6.8):
П 9Q4
*" " Т5Г*П = "98Г°'15 ~ °'045»
где Ри — 981 кПа (10 кгс/см2) —давление насыщенного пара пропана при 30 °С<
Количество содержащегося в газовой смеси пропана, которое
требуется поглощать:
Gn = Vyn/22t4 » 1000*0,15/22,4 = 6,7 кмоль/ч.
Минимальный расход поглотителя для поглощения пропана
определяется из уравнения:
LMHH П п
= О,
1~*п
* — ^ш
откуда
Gu(X~xn) 6,7-0,955
*-мин = Y* = О045— = И2 КМ0Ль/ч*
'п
или 142-224 = 31 800 кг/ч.
Наибольшая возможная концентрация бутана в поглотителе,
вытекающем внизу из скруббера:
П 294
*б== 15^6 = ^0,1 =0,11,
где Pq = 265 кПа (2,7 кгс/см2) — давление насыщенного пара бутана при 30 °С,
Количество поглощаемого бутана:
Gq = Кг/б/22,4 = 1000.0,1/22,4 = 4,47 кмоль/ч.
Минимальный расход поглотителя для поглощения бутана:
^-мин^ббО—*б)/*б = 4,47-0,89/0,11 =36,1 кмоль/ч.
Минимальный расход поглотителя для полного поглощения
бутана значительно меньше, чем для поглощения пропана, следо-
308
вательно, найденным выше количеством поглотителя (142 кмоль/ч)
бутан будет полностью уловлен.
Пример 6.12. Определить коэффициент массоотдачи для
газовой фазы в насадочном абсорбере, в котором производится
поглощение диоксида серы из инертного газа (азота) под
атмосферным давлением. Температура в абсорбере 20 °С, он работает в
пленочном режиме. Скорость газа в абсорбере (фиктивная) 0,35 м/с.
Абсорбер заполнен кусками кокса (а = 42 м2/м3, 1/св = 0,58 м3/м3).
Решение. По уравнению (6.45):
Nup = 0,407 Re°'655 (Pr^)0'33,
где
Кег~" ацг ~~ 42.0,0175-10"» "" 1Ш>
ро 974
рг~ 22 4-293" в1,16кг/м>; ^ = 0,175.10-3 Па-с (рис. VI).
Коэффициент диффузии Z)p принимаем такой же, как в воздухе.
Имеем:
DrS=10,3.10"6(293/273)b5 = ll,45.10-6M2/c (табл. XLII);
„ ftr _. 0,0175.10-3
кгг pvDp 1,16.Н,45-10-в ~ ^^^
Диффузионный критерий Нуссельта:
Nu; =* tyjD, « 0,407-22100'655. 1,320'33 = 69.
Эквивалентный диаметр:
d9 = 4VCB/o = 4-0,58/42 = 0,055 м.
Коэффициент массоотдачи:
Рр = Nu;Dr/da = 69-11,45.10"6/0,055 ** 144- 1<И м/с.
Пример 6.13. Из критериального уравнения (6.45) вывести
расчетную формулу для определения высоты единицы переноса
по газовой фазе.
Решение. Из уравнения (6.12)
1 \ т
Ку Ру Рх '
в котором Ку, ру, и ря выражены в кмоль/(м2-с), получаем
G G mG L
-г
KySa $ySo ' L f>xSo
или в соответствии с уравнением (6.43) при г{? = 1
hoy ^ ku ¦+¦ "7~ х*
809
Здесь G и L — мольные расходы газа и жидкости, кмоль/с; S — поперечное
сечение абсорбера, м2; а *— удельная поверхность насадки, м2/м3; hy — G/(py«So) —
высота единицы переноса для газовой фазы, м; hx — Lf{fixSo) — то же для жидкой
фазы, м.
В критериальном уравнении (6.45)
Nu; = 0,407 Re0/65" (РГ;)0^
», . Вр^я о КМОЛЬ /
где Nu' = Hi, , коэффициент массоотдачи рг выражен в — м/о«
р Dr ' ^ пк КМОЛЬ
г м2*с —
м3
Соотношение между Ру и р„ находим из уравнения:
откуда
Тогда
Ру - Рг -^- = Рг -д^- (см. табл. 6.2),
6 __ СЛ4СМ _ а; о/
"У
Р„5а РгРг^а рга гг hyo
где ю = #^ — фиктивная скорость, м/с.
Подставляя найденное значение (Зр в выражение для
диффузионного критерия Нуссельта, получаем:
, ^ аи^грг _ шрг ftr 4? ___ **егРгЛ
ur ^aDr[XrPr ацг D(Pr hy 4Ay
и из уравнения (6.45):
Пример 6.14. В скруббере с насадкой из керамических колец
50x50x5 мм (навалом) производится поглощение диоксида
углерода водой из газа под давлением /?аГ;С = 16 кгс/см2 (1,57 МПа)
при температуре 22 °С. Средняя мольная масса 20,3 кг/кмоль,
динамический коэффициент вязкости газа при рабочих условиях
1,31 -Ю-5 Па-с, коэффициент диффузии С02 в инертной части газа
1,7-Ю-6 м2/с. Средняя фиктивная скорость газа в скруббере
0,041 м/с, плотность орошения (фиктивная скорость жидкости)
0,064 м3/(м2-с). Определить общую высоту единицы переноса h0llt
принимая коэффициент смоченности насадки ф равным единице.
Решение. Общая высота единицы переноса (см.
предыдущий пример):
и и I mG и
"0(/ = hy Н ?~ hx-
Находим hy — высоту единицы переноса для газовой фазы:
A,«0,615^Re°'M5(Pr;)0'".
310
Характеристики насадки VCB = 0,785 м3/м3 и а= 87,5 м2/м*
берем из табл. XVII. Таким образом,
R.r-iaL- "•"'¦¦f-l, -.920.
ацг 87,5-1,31-10 ^
Здесь
_ МГПТ0 20,3.16-273 |0 л
р» ~ 22,4П0Т " " 22,4-295 ~ W'4 КГ/М ;
ИГг" PrD» ~ 13,4.1,7-10-* -°'&7&-
Высота единицы переноса для газовой фазы:
hy = 0,615-0,0359.1920°'345.0,5750'67 » 0,205 м.
Находим Лж — высоту единицы переноса для жидкой фазы по
формуле
^="96прКе^(Ргж)°>5,
полученной из уравнения (6.46) так же, как в предыдущем
примере из уравнений (6.45) получено выражение для hy.
Значения физико-химических свойств для воды при 22 °С:
рж = 1000 кг/м3; |лж= 0,958-Ю-8 Па-с (из табл. VI); DiK =•
- 1,87. Ю-9 м2/с (табл. XLIII).
Приведенная толщина жидкой пленки:
А / И& Y/3 / 0,958а. 10-е ч 1/3
пр=№; ~v ку-9,81 ) =4.55-10§м-
По условию плотность орошения:
= 0,064 мЗ/(м2-с),
^т
$Рж
где Lm — массовый расход жидкости, кг/с.
Массовая плотность орошения:
Lm/S « 0,064рж = 64 кг/(м2-с).
По уравнению (6.50):
Re 4Lm - 4'64 -3060-
Кеж~ SaihiHc - 87,5-0,958- 10-« ~ Л№0'
Рг' ^ 0.958-10-»
Кж" ржОж " 1000 1,87*10-°
Высота единицы переноса для жидкой фазы:
Нх = 119.4,55-10—3-3060°*255120*5 =0,91 м.
311
Находим отношение мольных расходов газа и жидкости G/L.
Из уравнения расхода для газа w = GM9/(pvS) получаем:
G/S == шрг/Л4Р = 0,041 • 13,4/20,3 = 0,0271 кмоль/(м2-с).
Для жидкости:
~5~ = SM ~ ~W ~ *^6 кмоль/(м2-с).
Отсюда
G/L = 0,0271/3,56 = 0,00761.
Коэффициент распределения т в уравнении (6.12):
Е 1,144.10е ... /с_.
m = -=- е= — ^— = 97,3 — см. уравнение (6.3),
где коэффициент Генрн Е = 1,144- 10е мм рт. ст. (при 22 °С) получен
интерполяцией данных табл. XLI.
Общая высота единицы переноса:
h6y = hy + -^±- hx = 0,205 + 97,3-0,00761 -0,91 = 0,205 + 0,675 = 0,68 и.
Пример 6.15. По данным примера 6.8 определить число
единиц переноса в абсорбере с учетом обратного (продольного)
перемешивания.
Решение. Число единиц переноса для условий идеального
Еытеснения, т. е. без учета обратного перемешивания, составляет:
п0у = {Ун — Кв)/ДКср = (0,0639 — 0,00128)/0,0079 = 7,93.
Искомое число единиц переноса с учетом обратного
перемешивания nhy находим из уравнения
_J 1 l_
в котором поправка на обратное перемешивание яобр равняется:
Л In Л
"обр - -XZTT Ф + Репр.
л L л . 0,05 /А \0.5
Значение критерия Per'iP вычисляют по уравнению:
1 + '
Репр ^/гРем. г fmPtM. ж
Здесь f - П^ + 6'8А°'Ъ . f _ % + 6'7Л0,5. ре' _ WrH
Рем. ж = шж^^ж — модифицированные критерии Пекле для газа и жидкости;
шг, о»ж — скорости потоков газа и жидкости, м/с; Ег, ?ж — соответствующие
коэффициенты обратного перемешивания, м2/с; Н — рабочая длина аппарата —
высота слоя насадки, м,
312
По данным примера 6.8 находим:
П ПП 19Я
= 2,67.
I' Уп — Ув 0.0639 — 0,00128
G' Хп — Хв 0.0234 — 0
Примем предварительно пЬу = 9. Тогда
9 + 6,8.1.59^ ^ 9 + 6,8.1.590^ =
9 + 6.8-1.591'5 9 + 6,8.1,59-0-5
Для определения скоростей газа и жидкости (wp и wm)
необходимо найти доли поперечного сечения абсорбера, занимаемые
каждым потоком в отдельности. Долю объема насадки б,
занятую жидкостью, рассчитаем по уравнению [6.3]:
б^4,83.10-4аГ0'435/^'24,
в котором
r='fe-== 3600-03,°3°58.204 ==0'0114 КГ^С'М>;
dd = 4fCB/a = 4-0,74/204 ^ 0,0145 м.
Подставляя эти значения, находим:
6 = 4,83-10~4.204^ а0114°*435/0,01450'24 = 0,039.
Скорость течения жидкости в слое насадки:
__ _Lq 3000 0
Шж " Рж^5 ~~ 3600.1000-0,358-0,039 " ' 6 М/С'
Скорость газа:
Gc 1810
Шг~ Рг5(Ксв-6) ~~ 3600.1,2-0,358(0,74-0,039) -1'67 м/с.
Величины коэффициентов обратного перемешивания Еж и Е9
находят опытным путем — см. пример 1.37. Для ориентировочного
их определения в насадочном абсорбере воспользуемся
критериальными уравнениями,
Для жидкой фазы:
ж
Для газовой фазы:
В этих уравнениях;
-0.2 ln-0,002Rem
Rem в 4^-; Rer = duG°
где da — номинальный размер элементов насадки, м,
313
В нашем случае:
0,025-3000
кеж- 3600*0,358-МО"» —ов'
Re 0,025.1810 1330
*г~ 3600.0,358.0,0182.10"» "~
Для жидкой фазы:
Мн/^ж = 7,58.10-3.58°*Г03 = 130-Ю-3.
Коэффициент обратного перемешивания в жидкой фазе:
?-н< = &уж^н/0,13 = 0,06-0,025/0,13 = 0,0116 м2/с;
Рем. ж в *>жН/Еж = °'06* 16'8/°>0116 = 87-
Для газовой фазы:
^н_= 2Д 2.4
?r Re°'2-10o'002Re>K 1930°-2.100'002-58
Коэффициент обратного перемешивания в газовой фазе:
Ег = a)rrfH/0,403 = 1,67-0,025/0,403 = 0,104 м2/с;
"Рем. р = «>вН1Ег = 1,67-16,8/0,104 = 270.
Приведенный критерий Пекле:
Ре- =| ! + _ >
пр l AfT Ре;. г /ж Ре;
ж м.ж
V 1,59-0,78-270 + 1,22-87 ) = 80,5;
Ф=1 ^9|_(4-Г-1--^(-^Г- 1-0,007 «0.993.
(РепР) V л0у / 80,5°'2° V У /
Поправки на обратное перемешивание:
A-2,3 1gA ^ 3,59-2,3 lg 1,59
«ofp ^ JZTj Ф-~Репр = ^59 0,993 + 80,5 = 81,7.
Число единиц переноса с учетом обратного перемешивания:
что близко к значению п'оУ — 9, принятому в начале расчета.
КОНТРОЛЬНЫЕ ЗАДАЧИ
6.1. Смешаны два равных объема бензола и нитробензола.
Считая, что объем жидкой смеси равен сумме объемов
компонентов, определить плотность смеси, относительную массовую кон-
314
центрацию X нитробензола и его объемную мольную
концентрацию Сж.
6.2. Состав жидкой смеси: хлороформа 20%, ацетона 40%,
сероуглерода 40%. Проценты мольные. Определить плотность
смеси, считая, что изменения объема при смешении не
происходит.
6.3. Воздух насыщен паром этилового спирта. Общее давление
воздушно-паровой смеси 600 мм рт. ст., температура 60 СС.
Принимая оба компонента смеси за идеальные газы, определить
относительную массовую концентрацию Y этилового спирта в смеси
и плотность смеси.
6.4. Газ состава: водород 26%, метан 60%, этилен 14%
(проценты мольные) имеет давление /?абс = 30 кгс/см2 и температуру
20 СС. Считая компоненты смеси идеальными газами, определить
их объемные массовые концентрации Су (в кг/м3).
6.5. Показать, что в формуле
при любых значениях Мв и МА у не может быть отрицательным.
6.6. В условиях примера 6.3 (а) определить движущую силу
процесса массоперехода в начальный момент времени по газовой
и по жидкой фазе в объемных концентрациях, мольных и
массовых.
6.7. Пар бинарной смеси хлороформ — бензол, содержащий
50% хлороформа и 50% бензола, вступает в контакт с жидкостью,
содержащей 44% хлороформа и 56% бензола (проценты мольные).
Давление атмосферное. Определить: а) из какой фазы в какую
будут переходить хлороформ и бензол; б) движущую силу
процесса массопередачи по паровой и по жидкой фазе на входе пара
в жидкость (в мол. долях). Данные о равновесных составах см.
в табл. XLVII.
6.8. Смесь воздуха с паром четырех хлор истого углерода,
сжатая до абсолютного давления 10 кгс/см2, охлаждается в трубчатом
водяном холодильнике. При 40 °С начинается конденсация че-
тыреххлористого углерода. Определить: а) массовый процент
его в воздухе в начальной смеси и б) степень выделения из
газовой смеси после охлаждения ее до 27 °С. Давление
насыщенного пара четыреххлористого углерода — см. рис. XIV или
XXIV.
6.9. Газовая смесь, содержащая 0,8% (об.) октана, сжимается
компрессором до /?абс = 5 кгс/см2 и затем охлаждается до 25 °С.
Определить степень выделения октана. Как изменится степень
выделения, если охладить сжатую газовую смесь холодильным
рассолом до 0 °С? Давление насыщенного пара октана — см.
рис. XIV, точка 31.
315
6.10. Рассчитать коэффициенты молекулярной диффузии под
атмосферным давлением: а) пара бензола в паре толуола при
температуре 100 °С; б) пара этилового спирта в водяном паре при
температуре 92 °С.
6.11. Определить коэффициент массопередачи в орошаемом
водой абсорбере, в котором &у = 2,76-10-3 кмоль/(м2-ч-кПа),
а рж = 1,17-10~4 м/с. Давление в аппарате /?аб0 = 1,07 кгс/сма.
Уравнение линии равновесия в мольных долях: у* = 102*.
6.12. Определить среднюю движущую силу и общее число
единиц переноса щу при поглощении из газа паров бензола маслом.
Начальная концентрация бензола в газе 4% (об.); улавливается
80% бензола. Концентрация бензола в масле, вытекающем из
скруббера, 0,02 кмоль бензола/кмоль чистого масла. Масло,
поступающее в скруббер, бензола не содержит. Уравнение
равновесной линии в относительных мольных концентрациях:
К* = 0,126Х.
Движущую силу выразить в единицах концентрации Y (кмоль
бензола/кмоль инертного газа).
6.13. В скруббере поглощается водой диоксид серы из
инертного газа (азота) под атмосферным давлением (760 мм рт. ст.).
Начальное содержание диоксида серы в газе 5% (об.). Температура
воды 20 °С, ее расход на 20% больше теоретически минимального.
Извлекается из газа 90% S02. Определить: 1) расход воды на
поглощение 1000 кг/ч сернистого газа; 2) среднюю движущую
силу процесса; 3) общее число единиц переноса nQy. Линия
равновесия может быть принята за прямую; координаты двух ее
точек: 1) парциальное давление S02 в газовой фазе р = 39 мм рт. ст.,
~? = 0,007 кг S0.2/Kr воды; 2) р = 26 мм рт. ст., X = 0,005 кр
502/кг воды.
6.14. В насадочном абсорбере производится поглощение пара
метилового спирта водой из газа под атмосферным давлением
при средней температуре 27 СС. Содержание метилового спирта
в газе, поступающем в скруббер, 100 г на 1 м3 инертного газа
(считая объем газа при рабочих условиях). На выходе из скруббера
вода имеет концентрацию 67% от максимально возможной,
т. е. от равновесной с входящим газом. Уравнение растворимости
метилового спирта в воде в относительных мольных
концентрациях: F* — 1,15а". Извлекается водой 98% от исходного
количества спирта. Коэффициент массопередачи: Кх = 0,5 кмоль
спирта /(м2-ч- кмоль спиРта \ расход инертного газа 1200 м3/ч
г / \ кмоль воды / г
(при рабочих условиях). Абсорбер заполнен насадкой из
керамических колец с удельной поверхностью 190 м2/м3. Коэффициент
смачивания насадки ty = 0,87. Фиктивная скорость газа в
абсорбере w = 0,4 м/с. Определить расход воды и требуемую
высоту слоя насадки.
316
6.15. В скруббер диаметром 0,5 м подается 550 м3/ч (при
760 мм рт. ст. и 20 СС) воздуха, содержащего 2,8% (об.) аммиака,
который поглощается водой под атмосферным давлением. Степень
извлечения аммиака 0,95. Расход воды на 40% больше
теоретически минимального. Определить: 1) расход воды; 2) общее число
единиц переноса щу\ 3) высоту слоя насадки из керамических
колец 50Х50X5 мм. Коэффициент массопередачи: Ку =
г\ лл1 // 2 кмоль аммиака \ и ....
= 0,001 кмоль аммиака /( w-с- ). Данные о рав-
' / \ кмоль воздуха / ^
новесных концентрациях жидкости и газа взять из примера 6.10.
Коэффициент смоченности насадки ty = 0,9.
6.16. Вывести формулу для определения высоты единицы
переноса в насадочном абсорбере для жидкой фазы hx из
критериального уравнения (6.46).
6.17. Воздух с примесью аммиака пропускается через
орошаемый водой скруббер, заполненный насадкой из колец с удельной
поверхностью 89,5 м2/м3. Свободный объем насадки 0,79 м3/м3.
Температура абсорбции 28 СС, абсолютное давление 1 кгс/см2.
Среднее содержание аммиака в газовой смеси 5,8% (об.).
Массовая скорость газа, отнесенная к полному сечению
скруббера, 1,1 кг/(м2*с). Определить коэффициент массоотдачи для
газа, считая, что скруббер работает при пленочном
режиме.
6.18. Рассчитать коэффициент массоотдачи от жидкой фазы
в насадочном абсорбере, в котором производится поглощение
диоксида углерода водой при температуре 20 °С. Плотность
орошения 60 м3/(м2-ч). Насадка — керамические кольца 35х35х
Х4 мм навалом. Коэффициент смоченности насадки ty = 0,86.
6.19. Определить коэффициент массоотдачи для газа в
скруббере при поглощении пара бензола из коксового газа по следующим
данным: насадка хордовая из реек 12,5X100 мм с расстоянием
между рейками b = 25 мм (для такой насадки d3 = 2b = 0,05 м);
скорость газа, считая на полное сечение скруббера, 0,95 м/с;
плотность газа 0,5 кг/м3; динамический коэффициент вязкости газа
0,013 мПа-с; коэффициент диффуьии бензола в газе 16-10~в м2/с.
Режим считать пленочным.
6.20. Определить диаметр и высоту тарельчатого абсорбера
для поглощения водой аммиака из воздушно-аммиачной смеси при
атмосферном давлении и температуре 20 СС. Начальное
содержание аммиака в газовой смеси 7% (об.). Степень извлечения 90%.
Расход инертного газа (воздуха) 10 000 м3/ч (при рабочих
условиях). Линию равновесия считать прямой, ее уравнение в
относительных массовых концентрациях: Р* = 0,61|Х. Скорость газа
в абсорбере (фиктивная) 0,8 м/с. Расстояние между тарелками
0,6 м. Средний к. п. д. тарелок 0,62. Коэффициент избытка
поглотителя ф = 1.3.
6.21. По условиям предыдущей задачи определить: 1) высоту
насадочного абсорбера с насадкой из керамических колец 50Х
317
х50х5 мм, приняв /ig —высоту слоя насадки, эквивалентную
теоретической тарелке (ВЭТТ), равной 0,85 м; 2) величину
коэффициента массопередачи в этом насадочном абсорбере Ку кр
Ко кг аммиаках -,
м*. с ___ \ 9 считая коэффициент смоченности
насадки г|) равным 0,9.
6.22, По данным контрольных задач 6.20 и 6.21 определить
высоту слоя насадки через общее число единиц переноса nQy и
высоту единицы переноса (ВЕП) /г0у.
6.23. Абсорбер для улавливания паров бензола из
парогазовой смеси орошается поглотительным маслом с мольной массой
260 кг/кмоль. Среднее давление в абсорбере /?абс — 800 мм рт. ст.,
температура 40 °С. Расход парогазовой смеси 3600 м3/ч (при
рабочих условиях). Концентрация бензола в газовой смеси на входе
в абсорбер 2% (об.) извлекается 95% бензола. Содержание
бензола в поглотительном масле, поступающем в абсорбер после
регенерации, 0,2% (мол.). Расход поглотительного масла в 1,5 раза
больше теоретически минимального. Для расчета равновесных
составов принять, что растворимость бензола в масле
определяется законом Рауля. При концентрациях бензола в жидкости до
X = 0,1 кмоль бензола/кмоль масла равновесную зависимость
У* = / {X) считать прямолинейной.
Определить: 1) расход поглотительного масла в кг/ч; 2)
концентрацию бензола в поглотительном масле, выходящем из
абсорбера; 3) диаметр и высоту насадочного абсорбера при скорости
газа в нем (фиктивной) 0,5 м/с и высоте единицы переноса (ВЕП)
Ку = 0,9 м; 4) высоту тарельчатого абсорбера при среднем к. п. д.
тарелок 0,67 и расстоянии между тарелками 0,4 м.
6.24, В насадочном абсорбере диаметром 1 м диоксид серы
поглощается водой из воздуха. Начальное содержание S02 в
поступающей смеси 7% (об.). Степень поглощения 0,9. На выходе
из абсорбера вода содержит 0>0072 кг Б02/кг воды. Коэффициент
массопередачи в абсорбере Ку =[0,005 кг SQ2^M2-c-Kr ^духа/'
Насадка из керамических колец 50x50x5 мм. Коэффициент
смоченности насадки i|> = I. Высота единицы переноса hQy = 1,17 м.
Определить расход воды в абсорбере.
6.25. В абсорбере под атмосферным давлением при
температуре 20 °С поглощается из парогазовой смеси 300 кг бензола в 1 ч.
Начальное содержание пара бензола в парогазовой смеси 4%
(об.). Степень извлечения бензола 0,85. Жидкий поглотитель,
поступающий в абсорбер после регенерации, содержит 0,0015 кмоль
бензола/кмоль поглотителя. Фиктивная скорость газа в абсорбере
0,9 м/с. Уравнение линии равновесия: Y* = 0,2А^, где У* и X
выражены соответственно в кмоль бензола/кмоль инертного газа
и кмоль бензола/кмоль поглотителя. Коэффициент избытка
поглотителя ф = 1,4. Определить диаметр абсорбера и концентрацию
бензола в поглотителе, выходящем из абсорбера.
Глава 7
ПЕРЕГОНКА И РЕКТИФИКАЦИЯ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
ls Уравнение простой перегонки:
, ±- 7_*_ (7Л)
in w J у* — х у
xw
где F — начальное количество перегоняемой смесн; W — остаток жидкости в кубе
после перегонки; у* и х — равновесные концентрации легколетучего (низко-
кипящего) компонента в паре и в жидкости; хр — содержание легколетучего
компонента в начальной смесн; xw — содержание легколетучего компонента
в остатке после перегонки.
Средний состав перегнанной жидкости:
v ¦- Fxf~Wxw /7.2)
Расчет по уравнениям (7.1) и (7.2) проводят, применяя либо
мольные количества и мольные концентрации, либо массовые
количества и массовые концентрации.
2. При перегонке нерастворимых в воде жидкостей с водяным
паром (или инертным газом) расход пара рассчитывают по
уравнению:
г ^ Мв(П-Р) 7
Здесь GB — количество водяного пара, уходящего с паром перегоняемой
жидкости, кг; G — количество перегоняемой жидкости, кг; Мв и М — мольные
массы воды и перегоняемой жидкости; Р — давление насыщенного пара
перегоняемой жидкости при температуре перегонки; П — общее давление смеси паров;
Ф — коэффициент, учитывающий неполноту насыщения водяного пара паром
перегоняемого вещества (при ориентировочных расчетах принимают <р == 0,7 -*-
+ 0,8).
3. Уравнения материального баланса ректификационной
колонны непрерывного действия * (рис. 7.1):
Gf = GD + Gw\ (7.4)
GFXF-GDXD + GWXW, <7*5)
где G/г, Gd, Gyp — массовые илн мольные расходы питания, дистиллята и
кубового остатка; хр, xD, xw — содержание легколетучего (низкокипящего)
компонента в питании, дистилляте и кубовом остатке, массовые или мольные доли.
* Приводимые ниже уравнения справедливы для ректификационной
колонны, обогреваемой глухим паром. При ректификации водных смесей с подачей
р колонну острого пара уравнения материального баланса и рабочей линии
нижней част колонны изменяются — см. пример 7.16.
319
Gv-G^+Gs
Рис. 7.1. Схема ректификационной ко»
лонны.
4. Уравнения рабочих
линий (при питании колонны
кипящей смесью):
а) верхней (укрепляющей)
части ректификационной
колонны
у
R
х +
XD
(7.6)
Я + 1 " ' Я + 1
б) нижней (исчерпывающей)
части колонны
R + F
1
Конденсат
У~~ R + l X~~ R + l V- VJ>
В ректификационной
колонне принимают на основании
теоретических предпосылок
постоянными по высоте колонны
общие мольные расходы пара
и жидкости. В соответствии с
этим в уравнениях (7.6) и (7.7)
применяются мольные расходы
Gw7Xw и концентрации.
В верхней части колонны, выше ввода исходной жидкой смеси,
постоянный по высоте колонны мольный расход жидкости равен
GRt в нижней части колонны он равен (GR + GF) —см. рис. 7.1.
Постоянный по высоте мольный расход пара Gv одинаков в
верхней и в нижней части колонны.
В уравнениях (7.6) и (7.7): у и х — переменные по высоте колонны
неравновесные концентрации (мольные доли) легколетучего компонента в паре и в
жидкости в данном сечении колонны. Для тарельчатых колонн: у — мольная доля
легколетучего компонента в паре, входящем снизу на тарелку; х — мольная доля
легколетучего компонента в жидкости, стекающей с этой тарелки; R — GRfGp —
число флегмы; F
= 2л
Go
XD XW
xF — xw
— относительный (на 1 кмоль
дистиллята) мольный расход питания.
При применении относительных мольных расходов уравнения
материального баланса колонны (7.4) и (7.5) получают вид:
F^i+W; (7.8)
где W =
G
w
G
хр xf
ху XW
— относительный мольный расход кубового
остатка; #„, *D, xw — мольные доли легколетучего компонента в питании,
дистилляте, кубовом остатке.
5. Минимальное число флегмы Л*мин в ректификационной
колонне непрерывного действия» когда кривая равновесия не имеет
точек перегиба (впадин), определяют по уравнению:
В - *D ~" У*р (7.10)
А Мин — ^ .— » х '
мин — „%
W — *¦
где jtD — мольная доля легколетучего компонента в дистилляте; хр — то же
в исходной жидкости (питании) колонны; t/p — то же в паре, равновесном с
жидкостью питания.
Рабочее (действительное) число флегмы:
Я = фЯмин- (7-11)
Здесь ф > 1 — коэффициент избытка флегмы.
При расчетах ректификационных колонн рабочее число флегмы
часто определяют по формуле:
/? = 1,3/?МИн + 0>3. (7 Л 2)
Об экономически оптимальном флегмовом числе см. [6.1].
Если на кривой равновесия имеется впадина, то величину
определяют графическим путем — см. пример 7.16.
6. Расход теплоты в кубе-испарителе ректификационной
колонны непрерывного действия определяют из уравнения
теплового баланса колонны с дефлегматором-конденсатором (рис. 7.1):
Он +<Vf в QA + GD{D + GW(W + <2пОТ, (7- 13)
где QK — расход теплоты, получаемой кипящей жидкостью от конденсирующегося
греющего пара в кубе-испарителе, Вт; <2Д — расход теплоты, отнимаемой
охлаждающей водой от конденсирующихся в дефлегматоре паров, Вт; QU0T — тепловые
потери колонны в окружающую среду, Вт; Gp, Go, Gyp — массовые расходы
питания, дистиллята, кубового остатка, кг/с; ip, «д, % — соответствующие
удельные энтальпии, Дж/кг.
Из уравнения (7.13) получаем:
«« - Qd + Wd + Ww - <Wf + Опот, (7- (4>
где cD, cw, cF —средние удельные теплоемкости, Дж/(кг*К); tD, tw> tp —
соответствующие температуры, °С.
Расход теплоты, отдаваемой охлаждающей воде в
дефлегматоре;
«д-^О + Я)'!,. (7-15)
Здесь R — число флегмы; rD — удельная теплота конденсации паров в
дефлегматоре, Дж/кг,
7. Определение диаметра тарельчатой ректификационной
колонны производится по уравнению:
где V — расход проходящего по колонне пара, mVc; w — скорость пара,
отнесенная к полному поперечному сечению колонны, м/с,
11 Павлов К* Ф. н др. 321
Рекомендуемую скорость пара в колонне рассчитывают по
формуле
» = С V (рж - Рп)/Рш (7.17)
в которой С — коэффициент, зависящий от конструкции тарелок*
расстояния между тарелками» рабочего давления в колонне,
нагрузки колонны по жидкости; рж и рп — плотности жидкости и
пара, кг/м3.
Когда рж >
™ = С ^Рж/Рп- (7.17а)
На рис. 7.2 по данным, приведенным в 17.2], представлены
в зависимости от расстояния между тарелками h значения
коэффициента С для ректификационных колонн, работающих при
атмосферном давлении и средних нагрузках по жидкости.
После определения по уравнению (7.16) диаметра колонны его
уточняют в соответствии с имеющимися нормалями.
8- Определение высоты тарельчатой ректификационной
колонны (расстояния Ят между верхней и нижней тарелками)
проводится по уравнению:
Ят = {п— \)h, (7.I8)
где п — число тарелок в колонне; h — расстояние между тарелками.
Расчет требуемого числа тарелок п ведут графическим путем,
используя кинетические закономерности — уравнение массопере-
дачи и расчетные зависимости для коэффициентов массоотдачи
(или чисел единиц переноса) в паровой и жидкой фазах на тарелке
[7.2].
При приближенных расчетах применяют теоретически менее
обоснованный, но более простой метод определения числа тарелок
с помощью так называемого среднего к. п. д. тарелок (к. п. д.
колонны):
п = лт/ть (7.19)
где пт — число теоретических тарелок — ступеней изменения концентрации,
которое находят графическим построением между равновесной и рабочими
линиями на у — х диаграмме — см. рнс. 7.3.
Величина среднего к. п. д. тарелок г), который вводят для учета
реальных условий массообмена на тарелках, зависит от многих
переменных величин (конструкция и размеры тарелки,
гидродинамические факторы, физико-химические свойства пара и
жидкости). Значения т| определяют по опытным данным, большей частью
они находятся в пределах 0,3—0,8.
На тарелках с перекрестным током пара и жидкости с
увеличением длины пути жидкости по тарелке массообмен улучшается,
величина среднего к. п. д. г\ возрастает.
На рнс. 7.4 приведены значения среднего к. п, д. тарелок,
полученные по опытным данным для промышленных, ректификацнон-
322
U,IU
OfiS
0,06
Qfi4
QfiZ
"a
jS*
j
^r
J^
^p
8,
\^b
Ш 200 300 400 500 600 700
/lfMM
Phc. 7.2. Значение коэффициента С:
А, Б — к-олпачковые тарелки а круглыми колпачками; В — ситчатые тарелка.
Рис. 7.3. Графическое определение числа ступеней изменения концентрации
(теоретических тарелок) в ректификационной колонне;
АВ —• рабочая линия верхней части колонны; АС — рабочая линия нижней чаетн но-
лонва.
ных колонн сравнительно небольшого диаметра. По оси абсцисс
на этом графике отложены произведения коэффициента
относительной летучести разделяемых компонентов а [см. уравнение
(6.9)1 на динамический коэффициент вязкости жидкости питания
\х (в мПа-с) при средней температуре в колонне.
При определении среднего к. п. д. тарелок в колоннах
большого диаметра (с длиной пути жидкости / ?> 0,9 м) рекомендуют
к значениям, найденным по рис. 7.4, давать поправку Д:
ru = Л (!+*)¦ (7.20)
Значения поправки А для смесей с a^i = 0,1-г-1,0 приведены
на рис. 7.5.
0,1 42 0,3 0$ 0,5 0,7 1,0 2,0 3,0 4,0 5,0 7,0 Ю,0
ар,
Рис. 7,4. Диаграмма для приближенного определения среднего к. п. д. тарелок.
11* 323
А
OJQ
0,25
0,20
0,15
0,10
0,05
О
Рнс. 7,5. Зависимость поправки А
длины пути жидкости иа тарелке /.
от
9. Коэффициентом
обогащения (коэффициентом полезного
действия) отдельной тарелки
называют величину:
^о =
Уг — У\
У* — У\
(7.21)
г,м
где У\ — мольная доля легколетучего
компонента в паре, поступающем
снизу на тарелку; г/2 —т0 же Б паРе>
уходящем с тарелки; у\ — то же в
паре, равновесном с жидкостью,
стекающей с тарелки.
Если жидкость на тарелке
полностью перемешивается, то
г/1 — мольная доля
легколетучего компонента в паре,
равновесном с жидкостью на тарелке.
10. Определение диаметра и высоты насадочной
ректификационной колонны проводится так же» как и абсорбционных наса-
дочных колонн — см. гл. 6.
Диаметр насадочной колонны рассчитывается по уравнению
(6.35). Фиктивную скорость пара в точке захлебывания wQ при
Рж > Рп находят по уравнению (6,36), но с другим значением А.
Для ректификационных колонн А = —0,125.
Высоту слоя насадки Яи при пленочном режиме работы
колонны находят отдельно для верхней и для нижней части колонны
по уравнению
Ян-
G
У2
F J v*
dy
KySoi
аналогичному уравнению (6.39).
У
— ™вупоу>
(7.22)
В уравнении (7.22): G — постоянный по высоте колонны мольный расход
пара, кмоль/с; Ку — коэффициент массопередачи, кмоль/(м2*с»Лг/~ 1); S~
— я?)2/4 — площадь поперечного сечения колонны, м2; о — удельная
поверхность иасадки, м2/м3; tf> — коэффициент смоченности насадки, безразмерный;
у* ну — равновесная и рабочая концентрации (мольные доли) легколетучего
компонента в паре.
Для насадочных ректификационных колонн, работающих в
режиме эмульгирования, эквивалентная высота насадки Лэ (в точке
инверсии) может быть определена из уравнения [6.1]:
h
э
d*
-»«*¦ (f r m"
lg
mG
1 — т
G
(7.23)
324
где d^ = 4VCB/a — эквивалентный диаметр насадки, м; Ren — 4шрп/(а(л п) —
критерий Рейнольдса; G/L — отношение потоков пара и жидкости (в верхней
G R+1 . #_i_i
части колонны —г- = =т-—¦, в нижней части колонны GIL = - ' _ —
L R R -\- F
см. уравнения (7.6) и (7.7); т — тангенс угла наклона равновесной линии.
Высоту слоя насадки находят по уравнению (6.44).
ПРИМЕРЫ
Пример 7.1. Вычислить состав равновесной паровой фазы при
50 °С для жидкости, состоящей из смеси гексана и воды,
предполагая их полную взаимную нерастворимость.
Решение. Давление насыщенного пара гексана при 50 °С
равняется 400 мм рт. ст. (рис. XVII). Давление насыщенного пара
воды при 50 °С составляет 92,5 мм рт. ст. (табл. XXXVIII). При
полной взаимной нерастворимости компонентов парциальное
давление р каждого компонента равняется давлению его насыщенного
пара Р.
Общее давление смеси паров:
П = рв + рс = Рв + Рг = 400 + 92,5 = 492,5 мм рт. ст.
Мольную долю гексана в паровой фазе найдем по уравнению
(6.1):
Уг = Рг/П = 400/492,5 = 0,812.
Мольная доля воды:
Ув = Рв/П = I — Уг = 0,188.
Пример 7.2. Определить температуру кипения при
атмосферном давлении жидкой смеси толуола и воды, учитывая их полную
взаимную нерастворимость.
Решение. Данная смесь будет кипеть при такой
температуре, при которой сумма давлений насыщенных паров толуола и
воды будет равна 760 мм рт. ст.
Из диаграммы (рис. XXIV) следует, что пересечение кривой
давления насыщенного пара толуола с кривой давления
насыщенного пара воды (отложенного от 760 мм рт. ст. сверху вниз)
происходит при 84 °С. Так как точка пересечения этих кривых
соответствует такой температуре, при которой сумма давлений
насыщенных паров равна 760 мм рт. ст., то эта температура и будет
температурой кипения смеси.
Пример 7.3. Вычислить состав равновесной паровой фазы при
60 °С для жидкой смеси, состоящей из 40% (мол.) бензола и 60%
(мол.) толуола, считая, что данная смесь характеризуется
законом Рауля. Найти также, какого состава жидкая смесь бензола
и толуола кипит при 90 °С под давлением 760 мм рт. ст.
Решение. Давление насыщенного пара бензола и толуола
при 60 °С определяем по рис. XXIV: для бензола Ро = 385 мм
рт. ст.; для толуола РТ ~ 140 мм рт. ст.
325
Парциальные давления бензола и толуола определяем по
формуле (6.7):
рб = P$xq «я 385-0,4 = 154 мм рт. ст.;
рт == Ртхт = Рт (1 — лгб) = 150 (1 — 0,4) = 84 мм рт. ст.
Общее давление:
П = рб + рт = 154 -f 84 = 238 мм рт. ст.
Состав паровой фазы определяем по формуле (6.1):
У в — Рб/П « 154/238 = 0,648.
Итак, равновесный пар содержит 64,8% (мол,) бензола и
35,2% (мол.) толуола.
Для определения состава жидкости, кипящей под давлением
760 мм рт. ст. при 90 °С, напишем уравнение
П = Р(5*б + рт*г ^й 760 « 1013Х& -Ь 408 (1 — хб),
откуда Хб — 58,3%; л:т = 41,7%.
Здесь 1013 и 408 — давления насыщенного пара чистых бензола и толуола
при 90 °С, мм рт. ст.
Пример 7.4. Вычислить равновесные составы фаз и построить
диаграммы равновесия в координатах t— х, у и у* — х для бен-
зольно-толуольной смеси при атмосферном давлении, считая, что
смесь характеризуется законом Рауля.
Решение. Для вычисления равновесных составов фаз
воспользуемся уравнениями (6.7):
Рв = Рбх; рт « Рт (1 —х).
По закону Дальтона:
П = Рб + Рт « Р& + ^т (1 — *)t
откуда
П —рт
х~ р6-рт '
По формуле (6.8):
* рб
y*=-jj-x.
Здесь х и у*— мольные доли бензола в жидкости и в равновесном с ним паре.
Весь расчет помещен в табл. 7,1.
Полученные данные нанесены в виде кривых в координатах
t— х, у (рис. 7.6) и в координатах у* — х (рис. 7.7).
Пример 7.5. С помощью диаграммы t—х, у (рис. 7.6)
определить состав равновесного пара и температуру кипения для
жидкости, содержащей 55% (мол.) бензола и 45% (мол.) толуола.
Решение. Проведя на рис. 7.6 линию ABCD, находим:
а) температура кипения равна ~91 °С;
326
Таблица 7.1
t, °с
'б.
мм рт. ст
ммрт. ст.
п.
мы рт. ст.
X =
П~Рт
У*
п
80
84
№
92
96
100
104
108
ПО
760
852
957
1078
1204
1344
1495
1659
1748
300,0
333,0
379,5
432,0
492,5
559,0
625,5
704,5
760,0
760
760
760
760
760
760
760
760
760
1
760-333
852—333
760—379,5
957—379,5
760—432
1078—432
760—492,5
1204-
760-
-492,5
-559,0
1344-
760-
-559,0
-625,5
1495-
760-
-625,5
-704,5
1659-
-704,5
О
852
0,823
0,659
0,508
0,376
0,256
0,155
0,058
760
957
760
1078
760
1204
760
1344
760
1495
760
1659
¦ 0,823 =
-0,659 =
¦ 0,508 =
0,376 =
¦ 0,256 =
-0,155 =
0,058 =
; 0,922
= 0,830
= 0,720
= 0,596
•¦ 0,453
= 0,304
= 0,128
О
б) состав равновесного пара:
Бензол 75 % (мол.)
Толуол 25 % (мол.)
Пример 7.6, 2500 кг загрязненного скипидара перегоняются
в токе насыщенного водяного пара под атмосферным давлением
(760 мм рт. ст.). Исходная смесь
содержит 88% (масс.) скипида- У
ра, 12% (масс.) воды и подается 1>°
в аппарат при 30 °С. Внешнего
подогрева нет.
I*
по
100
W
1
1
1
1
I
^s?
Is
J
I
1 *J
0
0.2
0,4 A 0M D0? W q
0?
Dfi
0,4
O^
Ц*.
V
*s
/
j
?,?/
0,2
0,4 Ofi 0лд fy0
a:
Рис, 7,6 (к примеру 7,4 и 7.5),
Рис, 7.7 (к примеру 7.4),
32/
Для перегонки применяют насыщенный пар с давлением (в
паропроводе) /?абс = 1,5 кгс/см2. Степень-насыщения водяного пара
скипидаром ф = 0,7.
Определить: а) расход пара на перегонку; б) массовый и
мольный состав отгоняемых паров; в) парциальные давления скипидара
и воды в смеси паров. Потери теплоты в окружающую среду
принять в размере 10% от полезно затрачиваемой теплоты.
Физические характеристики для скипидара: мольная масса 136 кг/кмоль;
удельная теплоемкость жидкого скипидара 1,76-103 Дж/(кг-К);
удельная теплота испарения 310 • 103 Дж/кг.
Решение. Определяем по рис. XXIV температуру
перегонки и давление насыщенного пара скипидара. Температура
перегонки 96 °С; Рсн = 115 мм рт. ст.
Количество водяного пара, уходящего вместе с паром
скипидара, находим по формуле (7.3)
0в = Оск *¦ <" ~ Р°*> - 2500.0,88 18,^-'175) - 2330 кг.
L" Мск^скФ 136-115-0,7
Массовая доля в парах:
скипидара
Gnu 2500-0,88
У™ = GCK + GB "" 2500-0,88 + 2330 ™ °'485;
ЕОДЫ _
У* = 1 — Уск = 1 — 0,485 = 0,515.
Мольная доля:
а Уон/^ск 0,485/136 0,00356
Усн У в " 0>485 0,515 ~ 0,00356 + 0,0286 ~и>1Ш'
Мск ^в 136 + 18
Ув ~= 1 — 9с к = 1 — 0,11 « 0,89.
Парциальные давления в смеси паров при общем давлении
П = 760 мм рт, ст.:
Рек = %ск — 760-0,11 = 84 мм рт. ст.;.
рв = П — pcii = 760 — 84 = 676 мм рт. ст.
Расход теплоты:
а) на подогрев исходной смеси от 30 °С до температуры
перегонки 96 °С.
Скипидар!
Сс^сн^пер —^ач)-= 2500-0,88-1,76-10^(96—30) = 256000-103 ДЖ.
Вода:
GiACnep—'нач) «= 2500• 0,12-4,19-103 (96 — 30) = 83000-103 Дж;
<?нагр = (256 + 83) 10е = 339-10» Дж.
б) на испарение перегоняемого скипидара
<?исп = ^ск^ск = 2 500-0,88.310.103 = 682 000-103 Дж.
328
в) на компенсацию потерь теплоты в окружающую среду
QnoT«0(l (<?нагр + <?исп) = (339000 + 682 000) 108-0,1 = 102 000-103 Дж.
Общий расход теплоты:
<?обш = <?нагр + <?исп + <?пот - (339 000 + 682 000 + 102 000) 10» =
= 1 123 000-Ю3 Дж= 1123-103 кдж.
Определяем расход пара. Абсолютному давлению насыщенного
пара в трубопроводе (1,5 кгс/см2) соответствует температура
110,7 °С (табл. LVII); уходит с перегоняемым скипидаром 2330 кг
пара при температуре перегонки 96 °С. Следовательно* этот
уходящий пар охлаждается от 110,7 до 96 °С, причем выделяется
теплоты:
<?Быд = ^Б.п(^-^ер) = 2330.1,97-10» (110,7- 96) -
= 67 900.103 Дж г* 67 900 к Дж,
где 1,97* 103 — 35,5« 10V18 — удельная теплоемкость водяного пара, Дж/(кг< К) —
табл. XXVII.
Остальное количество теплоты
Qoct = <?обш - <?выд = 0 123000 - 67 900) 103 « 1055.10» кДж
должно быть подведено за счет конденсации некоторого
добавочного количества подаваемого пара и охлаждения получившегося
конденсата до температуры перегонки.
Расход конденсирующегося (греющего) пара:
О _ Qqct _ 1055 000-103
^конд- ,*_., "(2700-402) 10» ~ 4bU Кг
где 2700-103 Дж/кг — удельная энтальпия насыщенного водяного пара при
1,5 кгс/см2; 402• 103 Дж/кг — удельная энтальпия воды при 96 °С.
Общий расход пара:
Gn « 2320 + 460 я. 2790 кг.
Пример 7.7. В простом перегонном кубе производится
разгонка 1000 кг смеси, содержащей 60% (масс.) этилового спирта и
40% (масс.) воды. После отгонки в кубовом остатке содержится 5%
(масс.) спирта. Определить состав дистиллята, его массу и массу
кубового остатка. Данные о равновесных составах приведены
в табл. 7.2, в которой х обозначает массовую долю этилового
спирта в жидкости, у* — массовую долю этилового спирта в
равновесном паре.
Решение. Для решения используем уравнение (7.1):
1п
F f dx
W
х3
f dx
J у* — х
329
Рис. 7,& {к примеру 7,7>.
Аналитически выполнить
интегрирование невозможно, так
как аналитическая форма
зависимости у* от х неизвестна; поэтому
решаем интеграл графически. Для
этого строим график зависимости
I
^_ . ОТ X ДЛЯ С0ИрТО-ВОДНОИ
смеси (рис. 7.8).
Принятый масштаб:
о
0,2 0,4 0,6 _0>8
X
По оси абсцисс
» » ординат
I ьщз^ 0,02.0,2 = 0,004
1 мм = 0,02
1 мм = 0,2
Значение интеграла в пределах от xt = 0,6 до х2 = 0,05
изображается заштрихованной площадью. Эта площадь равна 403 мм3.
Отсюда
0,6
j
у'
— = 403-0,004 = 1,612*.
х
0,05
Следовательно,
In-?-«2.3 !*-?--1,61% 4--5,01.
По условию, F = 1000 кг. Масса кубового остатка:
W = 1000/5,01 = 200 кг,
откуда масса дистиллята:
D = F — W » 1000 — 200 = 800 кг.
Таблица 7.2
V
«V
0,025
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
й*
а
0,225
0,360
0,516
0,600
0,655
0,690
0,710
0,728
0,740
Г? * >.- Y
У ¦--' Л
0,200
0,310
0,416
0,450
0,455
0,440
0,410
0,378
0,340
i
у* - х
5,00 1
3,22 :
2,40
2,22
2,20
2,27
2,44
2,64
2,9*
V
\
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
й*
и
0,754
0,767
0,778
0,789
0,800
0,810
0,835
0,855
II* •— V
jf • А.
0,304
0,267
0,228
0,189
0,150
о,ио
0,085
0,055
i
у* — х
3,29
3,74
4,38
5,29
6,66
9,09
11,75
18,20
*
Приближенно значение интеграла может быть найдено по формуле
трапеций — см. пример 4.2G.
330
Количество спирта в остатке после перегонки:
Gw » Wxw =* 200-0,05 = 10 кг.
Количество спирта, перешедшего в дистиллят:
GD = FxF — Gw= 1000-0,6 — 10 = 590 кг.
Массовый процент спирта в дистилляте:
^ = ^-100 = 100^ = 73,7.
Пример 7.8. В условиях предыдущего примера найти для
процесса перегонки расход греющего пара (рлее = 2.кгс/см2).
Перегоняемая смесь подается в куб нагретой до температуры начала
кипения. Потери теплоты в окружающую среду принять в
размере 10% от полезно затрачиваемого количества теплоты.
Влажность греющего пара 5%. По диаграмме t—х, у найдено, что
температура начала перегонки, когда кипящая смесь содержит 60%
(масс.) спирта, равняется 81 °С, а температура конца перегонки,
когда кипящая смесь содержит 5% (масс.) спирта, 94,9 °С.
Решение. Средняя температура перегонки;
Расход теплоты на нагрев исходной смеси от 81 до 88 °С:
Qi = (1000-0,6.3,35.103 + 1000-0,4-4,19-103).(88— 81) =25800- Ю3 Дж,
pie 3,35* Ш3 л 4,19-Ю3 Дж^кг-К)—удельные теплоемкости спирта и воды
(ряс. XI).
Расход теплоты на испарение при 88 °С:
& -=590-855-103 + (800 — 590) 2290-10» = 985000-10* Дж.
Здесь 855* I©3 и 2290* 10* Дж/кг — удеяьяые теолога парообразования спирта
и воды.
Расход теплоты на нагревание остатка от 88 до 94,9 °С:
Q8 = (200.0,05-3,35-103 + 200-0,95-4,19-10е)-(94,9— 88) =»5700• 103 Дж.
Общий расход теплоты с учетом потерь:
Q = (25 800 + 985 000 + 5700) 103-1,1 = 1 120000-10» Дж.
Расход греющего пара:
1 120 000-103 - „
°г'п " 2206- ДО- 0,95 -й*>*г»
где 2208-103 Дж/кг — удельная теплота конденсации водяного пара при рабс =¦
== 2 кгс/см2.
Пример 7.9. При расчете ректификационной колонны g кол-
пачковыми тарелками принято расстояние между тарелками
300 мм. Через колонну проходит 3200 м*/ч пара. Плотность пара
1,25 кг/м3 (расход и плотность пара — при нормальных условиях).
Плотность жидкости 430 кг/м3. Абсолютное давление в колонне
331
1,2 кгс/см2 и средняя температура —40 °С. Определить требуемый
диаметр колонны.
Решение. Для определения диаметра колонны необходимо
найти допустимую рабочую скорость пара в ней.
По уравнению (7.17а)
w = С V'p^Jpv = 0,0315 1^430/1,75 = 0,495 м/с.
Плотность пара при рабочих условиях:
рп~ Тр0 - 233-1,033 " 1>'0КГ1М'
Значение С — 0,0315 определено по рис. 7.2.
Объемный расход пара в колонне при рабочих условиях:
У0ТРо __ 3200.233-1,033
7>-3600 ~ 273-1,2.3600 ~ и,0<" M '
Требуемая площадь поперечного сечения колонны:
S = V/w = 0,632/0,495 = 1,28 ма,
откуда диаметр колонны:
D = ^5/0,785 » ^1,28/0,785 = 1,275 м.
По каталогу-справочнику «Колонные аппараты» [7.11]
принимаем D = 1200 мм.
Пример 7.10. Определить число тарелок в ректификационной
колонне непрерывного действия для разделения смеси метиловый
спирт—вода под атмосферным давлением. Содержание
метилового спирта в питании колонны 31,5% (мол.). Дистиллят требуется
получать с содержанием спирта 97,5% (мол.), в кубовом остатке
допускается содержание спирта 1,1% (мол.). Коэффициент
избытка флегмы 1,77. Число тарелок, эквивалентное одной ступени
изменения концентрации, 1,7. Колонна обогревается глухим
паром.
Решение. Расчет числа тарелок проводим графически.
Для этого по данным табл. XLVII для смеси метиловый спирт—
вода при Пабс = 760 мм рт. ст. строим кривую равновесия в
координатах у*—х (рис. 7.9).
Определяем минимальное число флегмы по формуле (7.10):
Р хв-уг _ 0,975-0,675 _ft
*мин ~~ ур-хг ~ 0,675-0,315 ~и,бЛ'
где значение ур = 0,675 найдено по равновесной кривой (рис. 7.9).
Действительное (рабочее) число флегмы:
/? = ф/?мин=* 1.77-0.835 «1,48.
Уравнение рабочей линии верхней части колонны:
1,48 , 0,975
Ув 1 ла . Г-Х +
1,48 + 1 ' 1,48+ 1
332
У*У
1,0
а
о
8
0,8
0,5
0,4
о
-и*=
У
У 1
L* г
Щ
0в75
и^и/о
/У
t
/
' /
У /
У /
1 S
\а
¦
S
•
-"
у-
S
л
у^В
1 1
0,1 0,2 0,3 0,4 0,5 Oft 0J 0,8 0,9 1ft
Рис. 7.9 (к примеру 7.10).
или
$/ = 0,598* + 0,393.
Отложив по оси ординат 0,393, наносим рабочую линию АВ
для верхней части колонны. Через точки А и С проводим
рабочую линию для нижней части колонны.
Выполнив на диаграмме построение ломаной линии (начиная
от точки В), находим необходимое число ступеней изменения
концентрации: в верхней части колонны оно составляет ~7, в
нижней ~4; всего 11.
Число действительных тарелок: в верхней части колонны 1,7 X
X 7 « 12; в нижней 1,7-4 ж 7, всего 19 тарелок.
Пример 7.11. Построить кривую равновесия для смеси четы-
реххлористый углерод (СС14) — двуххлористая сера (SC12) при
давлении 760 мм рт. ст.
Решение. При отсутствии экспериментальных данных
кривую равновесия строим, исходя из допущения, что смесь следует
закону Рауля.
Давления насыщенного пара СС14 в зависимости от
температуры приведены в табл. 7.3.
Для SC12 имеются две точки: температура кипения при
давлении 760 мм рт. ст., равная 59 °С, и температура кипения при
400 мм рт. ст., равная 41 °С.
333
Таблица 7.3
U "С
40
50
65
*
ширт.
214
ЗГ5
580
ст.
.
t, °С
70
75
80
Л
мм рт. ст.
©1
715
843
Для нахождения давления насыщенного пара SC12 при других
температурах воспользуемся правилом линейности.
Вычислим постоянную Я для SC12 и воды» взятой в качестве
стандартной жидкости;
59—41
К =
100 — 83
-1,06,
где 83 °С — температура кипения воды при 400 мм рт. ст. (табл. XXXVIII)
Температуры кипения SC12 при разных давлениях могут быть
определены из уравнения:
59 — ; = 1,06(100 — 9),
откуда
f « 1,06в —47.
Здесь t — температура кипения SC12, СС; 0 — температура кипения воды
при том же давлении, °С.
В табл. ТА приведены вычисленные по последней формуле
значения t при разных давлениях.
На рис. 7.10 по данным табл. 7.3 и 7.4 нанесены давления
насыщенных паров SC12 и ОС14 в зависимости от температуры.
Имея данные о давлении насыщенных паров чистых
компонентов при разных температурах, можно построить диаграмму
равновесия, применив закон Рауля. Методику построения см. в
примере 7.4. На рис. 7.11 дана диаграмма равновесия в координатах
У*—х.
Пример 7.12, В периодическидействующей тарельчатой
ректификационной колонне разгоняется под атмосферным давлением
жидкая смесь четыреххлористого углерода СС14 и двухлористой
Т а б л и а з 7.4
Р, MM pT, GT
760
880
1030
О "С
106
104,2
108,7
и °с
59
63,5
68,2
Р, мм рт,
П75
1320
1470
ст
е, °о
U2J
116,3
119,6
U °е
72,5
76,3
79,8
334
Рис* 7.10 {к примеру 7.11). ?>?ММ*рТ.ПР:
ism
серы SC12, содержащая 50%
(мол.) SC12. Дистиллят
должен содержать 90% (мол.), а
кубовый остаток после
ректификации — 15% (мол.)
SCIS.
Определить необходимое
число тарелок, если на одну
ступень изменения
концентрации приходится i ,7
тарелки. Определить также
отношение минимальных чисел
флегмы в конце и в начале
разгонки.
Решение.
Воспользуемся данными о
равновесии смеси четырех хлористый
углерод — двухлористая сера^ полученными в предыдущем
примере.
Находим по формуле (7.10) минимальное число флегмы #мия
для конечного момента разгонки, когда кубовая жидкость содер-
У*У
%0
0,8
9,6
0,4
U?
',
_——-
г
.
ms
0
9j
V
/\
/ \
1
1
J
.1
а
7/
д/\>
2
6/
4 ,
V
У
,
¦
й-
¦
¦¦
r_V^
о
/
Л
/
-
.
4
•$/
{ /
//
/
¦¦
п
$У
V
А
//
\
Я
2
$
^
S
¦
t—'¦ )
1
(91
]s*
Jf
Г
'
¦
?
s
¦
—
1
!
11
Ряс. 7.21 U щшшфш ?.Л т 7Л*Ь
X
335
жит 15% SC12 (в этот момент существуют наиболее трудные
условия разделения);
хр-УР ^ 0,9-0,25
yp-xF 0,25 — 0,15
АМИН — ..* - ""- r\ n& л ir — D»°.
Здесь 0,25 — мольная доля SCI2 в парах, равновесных с кубовым остатком,
содержащим 15 % SC12,— определяется по диаграмме равновесия.
Для действительного процесса принимаем число флегмы на
20% больше /?мин'
# = 1,2-6,5 = 7,8.
Уравнение рабочей линии (7,6) для конечного момента
перегонки:
7,8 , 0,9
7,8+1 ' 7,8+1
или у = 0,887л: + 0,102.
Строим рабочую линию и определяем графически число
ступеней изменения концентрации. Как следует из рис. 7.11, числу
флегмы R — 7,8" соответствуют 11 ступеней.
Число действительных тарелок, требуемое для разгонки:
я» 1,7-11 « 19.
Для начального момента разгонки, когда хР ~ 0,5,
минимальное число флегмы:
d- 0,9-0,64 Rft
*«ин= 0,64-0,5 ~h*>*
где Ур = 0,64 найдено по диаграмме равновесия (рис. 7.11).
Отношение минимальных чисел флегмы в конце и в начале
разгонки:
^мин/^ин = 6,5/1,86 = 3,5.
Таким образом, в процессе разгонки флегмовое число меняется,
достигая максимального значения R = 7,8 в конце процесса.
Пример 7.13. Построить диаграмму /—х в области насыщения
для смеси СН4—N2 при /?абс = 10 кгс/см3.
Решение. Методику построения и применения диаграммы
У—х см. [6.1 ].
Для определения равновесных соотношений системы СН4—Na
воспользуемся экспериментальными данными.
По диаграмме состояния / — lg p для N2 и СН4 определяем
энтальпии чистых компонентов на 1 кмоль пара и жидкости в пре*
делах температур существования системы СН4—N2 при 10 кгс/см3
(табл. 7.5).
Строим сетку диаграммы: по оси абсцисс откладываем
содержание Na, по оси ординат — энтальпию в кДж/кмоль (рис. 7Л2).
Далее наносим энтальпии чистых газообразных N2 и СН4
(табл. 7.5) на оси ординат для температур 170; 160 и 150 К, Соеди-
336
т. к
Пар
;СН4
кДж/кмоль
'и.
кДж/кмоль
Таблица 7.5
Жидкость
;СН4
кДж/кмоль
'N,
кДж/кмоль
170
160
150
145
140
135
130
125
120
115
ПО
105
100
11 100
10 700
10 270
—
—
_
——
—
—
—
—
-^_
—
9420
9100
8800
8640
8480
8330
8160
7990
7810
7630
7420
7210
—
4690
3930
3310
3040
2820
2550
2310
2050
1830
1580
1360
—
¦¦ ¦
—
—
—
—
—
—
—
—
—
3460
3160
2890
2610
няя эти точки прямыми, получаем соответствующие изотермы.
Предполагаем, что теплота смешения равна нулю.
Ниже температуры 150 К газообразный метан при 10 кгс/см2
не существует. Однако мы экстраполируем энтальпию СН4 и ниже
этой температуры, считая, что Д//Д71 в области экстраполяции
имеет то же значение, что и выше 150 К. В результате получаем
изотермы пара вплоть до 100 К, т. е. до температуры конденсации
чистого азота при 10 кгс/см2. На рис. 7.12 показано несколько
изотерм пара, построенных таким образом, начиная с изотермы 145 К.
Далее, пользуясь равновесными данными для системы СН4—N2,
определяем температуры начала конденсации различных паровых
смесей и наносим соответствующие точки на диаграмму /—х.
Соединяя найденные точки, получаем линию конденсации.
Изотермы жидкости строятся по тому же принципу, что и для
газа. Дело осложняется тем, что часть температур равновесия
лежит выше критической температуры азота (126 К), вследствие
чего энтальпию жидкого азота при этих температурах снять не
представляется возможным. В этом случае можно поступить
следующим образом: вычислить среднюю теплоемкость жидкого азота
в интервале, скажем, ПО—120 К и считать условно, что и далее,
при температурах выше критической, теплоемкость азота в смеси
остается такой же. Часть построенных таким образом изотерм
жидкости на рис. 7.12 показана пунктиром (в области насыщения).
Принятое допущение не может привести к большим ошибкам,
так как для изотерм высоких температур (выше 125 К) ошибка
смягчается тем, что эти изотермы пересекаются кривой кипения
при большом проценте метана, энтальпии которого сняты без
всяких допущений. Поэтому отклонение, вызванное неточностью
в определении энтальпии азота, влияет незначительно вследствие
337
л
кДнг
КМОЛЬ
12000
10000
В 000
6000
4000
тот
О 0}1
сн4
0,2 0,3 0,4 0,5 0,6 0,1 0,8 0,9 1,0
Рис. 7.12 (к примеру 7Л8)
малой его доли. Для изотерм низких температур (ниже 125 К)
энтальпии жидкого азота сняты без допущений.
По данным фазового равновесия системы СН4—N2 наносят на
диаграмму точки начала кипения для жидких смесей разного
состава и после соединения этих точек получают линию кипения
диаграммы /—х. В области насыщения проводят соединительные
изотермы (соединяют составы жидкости на кривой кипения с
равновесными составами пара на линии конденсации). На этом
заканчивается построение диаграммы /—х.
Пример 7.14. В ректификационную колонну непрерывного дей*
ствия подается смесь, состоящая из 30% (мол.) СН4 и 70% (мол.)
338
N2. Смесь поступает в количестве 1000 м3/ч в парообразном
состоянии при /?абс = Ю кгс/см2 и температуре насыщения. Здесь
и далее в этом примере все объемные расходы (в м*/ч) указаны
при нормальных условиях.
В результате разделения в колонне получаются газообразные
продукты: фракция метана с содержанием 3% N2 и фракция азота
с содержанием 5% СН4.
Требуется, пользуясь диаграммой /—х, определить: а)
количество получаемых фракций; б) минимальное число флегмы /?МИн1
в) число ступеней изменения концентрации при коэффициенте
избытка флегмы 1,25; г) количество теплоты, передаваемой в
дефлегматоре колонны; д) количество теплоты, передаваемой в кубе
(в случае вывода из куба колонны метановой фракции в жидком
состоянии).
Решение. Используем диаграмму равновесия системы
СН4—N2 при 10 кгс/qm2 в координатах /—х, построенную в
предыдущем примере.
а) Для определения количества получаемой фракции строим
на диаграмме вверху (рис. 7ЛЗ) прямую линию ///—/—//; точка /
характеризует исходную смесь (70% N2), точка // — азотную
фракцию (95% N2) и точка /// — метановую фракцию (3% N2).
Количество получаемой метановой фракции на 1 кмоль
исходной смеси, как следует из уравнения материального баланса
хв" xf Gw I — // 0,95 — 0,7
___ e _ раВно отношению отрезков 77J-jj - Q>95_0>03-
Коли чество метановой фракции:
Исн4 = ¦§§-100° - т *'4'
Коли чество азотной фракции:
VNt = 1000 — 272 = 728 м»/*.
б) Определяем /?мин. Точка М представляет собой состояние
исходной смеси, поступающей на разделение. Она должна лежать
на главной прямой, соединяющей полюсы укрепляющей и исчер-*
пывающей части колонны. Для определения наинизшего
положения полюса колонны укрепления яу, соответствующего RMhh?
необходимо совместить главную прямую с изотермой, проходящей
через точку М (линия МО). Продолжая эту линию до
пересечения с вертикалями, проведенными из значений концентраций
получаемых фракций, найдем полюсы яу и яи, соответствующие
Амин-
Отношение отрезков:
ММ' _ пуМ' _ /?мия
ОК пуК Ямвн + 1 '
В нашем случае:
ММ' 0,95-0,7 .
ОК " 0,95 — 0,217 — и1Л11 Ямин-^&Ю.
339
ь
кмолъ
И 000
120Q0
10000
еооо
еооо
4QQ0
2000
0,7 0,8 0,3 хаЮ
от
Рис. 7,13 (к примеру 7.14у»
По условию, действительное число флегмы:
R = 1,25/гмин « 1,25-0,518 = 0,647.
Определим положение действительного полюса п'У} соответ-
ствующего числу флегмы R = 0,647.
Для этого из соотношения
MM' R
i г/ /
О'К
R + 1
340
t isf
находим величину отрезка О'К
о-К' « мм- *±L = <Ms-o.7)i,647 =
/< 0,647
а затем абсциссу точки О':
0,95 — 0,637 = 0,313.
Проведя прямую через точки М и О' до пересечения ее с
вертикалями, абсциссы которых xD и л:^, получим главную прямую для
R = 0,647- Точки пересечения главной прямой с вертикалями —
действительные полюсы п'у и п'и.
в) Далее определяем графическим путем число ступеней
изменения концентрации. Для этого находим состав жидкости,
равновесный с паром, содержащим 95% N2 (точка N). Это будет точка /,
соединенная с точкой N изотермой. Далее проводим луч 1 — Лу.
Пересечение этого луча с кривой пара дает точку 2. Из точки 2
повторяем построение. Получив точку 5 на кривой жидкости левее
главной прямой, дальнейшее построение ведем с помощью
нижнего полюса Пи. Число таких переходов дает число ступеней
изменения концентрации. В результате получаем: в укрепляющей части
(выше питания) две ступени (несколько больше); в исчерпывающей
части (ниже питания) четыре ступени (несколько меньше).
г) Количество теплоты, отводимой в дефлегматоре, определяется
разницей энтальпий в точках л'у и N, т. е.
<?д = 12 230 — 7330 = 4900 кДж/кмоль.
Так как при разделении получается 728 м3/ч азотной фракции,
то общее количество теплоты, передаваемое в дефлегматоре;
<?д = 4900 -Ш^. = 159 000 к Дк/ч =* 159^'°' = 44 200 Вт.
д) Количество теплоты, передаваемой в кубе колонны, q$ при
отводе фракции метана в газообразном состоянии определяется
разницей энтальпий в точках Р и п'и. При отводе метановой
фракции в жидком виде отсутствует затрата теплоты на испарение
фракции; в этом случае теплота qK определяется разницей
энтальпий в точках L и Пи> что составляет 5150 кДж на 1 кмоль
метановой фракции.
Общее количество теплоты, передаваемой в кубе колонны:
л 5150-103 272 _„__ _
^-"збоо-^Г^17300^
Пример 7.15. Определить высоту и диаметр верхней
(укрепляющей) части насадочной ректификационной колонны для
разделения смеси метиловый спирт — вода под атмосферным
давлением.
В колонну подается 1550 кг/ч исходной смеси, состоящей из
40% спирта и 60% воды. Концентрация дистиллята 97,5% спирта.
В кубовом остатке содержится 2% спирта (проценты мольные).
341
Число флегмы R = 1,48. В качестве насадки применены кольца
25x25x3 мм. Колонна работает в режиме эмульгирования.
Обогрев глухим паром.
Решение. При работе насадочной ректификационной
колонны в режиме эмульгирования скорость пара в ней находим из
уравнения (6.36). А = —0,125.
( Ы*ИЦ№* \ , L 4 0,25 / рп v 0.I25
В нашем случае: а= 204 м2/м3 (табл. XVII); VCB = 0,74 м3/м3.
Средний состав жидкости:
*сР = (xf + xd)/2 в <*° + ш>ъ)& = 70 % <мол-) ^«Р^;
рш » 840 кг/ы3; ji^ да 0,5-10"3 Пас;
Mw = 32-0,7 + 18-0,2 = 26,0.
Средний состав пара:
#ср = (#*• + ^d)/2 = <63 + 97>5)/2 = 80 % (мол.)сшфта.
Здесь */F = 63% (мол.) — содержание спирта в паре,
поступающем в верхнюю часть колонны (рис. 7.9; в примере 7.10
рабочая линия Еерхней части колонны занимает такое же положение,
как и в нашем случае). Средняя температура в верхней части
колонны ~72 °С. Имеем:
о - [л^ср + Мв(1-Уср)]ГоР (0,8.32 + 0,2-18)273-1,033
Ри ИАТ^ ~ 22,4-345.1 = 1.03кг/н\
|лп«1,1Ы0-5 Па-с.
Отношение массовых расходов жидкости и пара равно (при
близких значениях Ми и Мч<):
R Мж 1,48
G R + 1 Мп ~ 2,48
= 0,6.
Подставляя эти значения в формулу (6.36), получаем:
igV ^,81.0,743.840 ) =-^25-1,75.0,6*.** (w ) t
]g<0,0565a>2) = —0,7?8,
откуда w = 1,7 м/с.
342
Эквивалентную высоту насадки /гэ рассчитываем по уравнению
(7.23):
L
(Ci \СЬ35 / п \0»2 ь mft
4) (-Й-) —
_ mG
L
R
, a 4KCB / 4c^ y^/ ^+1\°'35/ Рж V'2 gm(J?-f I)
e&' о \o|Ib J \ R ) \9n) » mjR + i)
R
5>2-4-0,74 / 4-1.7-1.03 \a*2/ 2,4& \0'35/ 840 \0»2 g 0,45-2,48 ^
204 V 204-l,ii-l(r& / 4 1,48/ ^ 1,03 / , 0,45 **
0,6
= G,86 м.
Как следует из рис. 7.9, т = 0,45, число ступеней изменения
концентрации в пределах от xD = 0,975 до xF = 0,4 составляет
6,4 *. Следовательно, требуемая высота насадки по уравнению
(6.44):
На = hQnT = 0,86*6,4 = 5,5 м.
Для определения диаметра колонны найдем предварительно
расход дистиллята. Мольный расход питания:
Gf = хРМеш +(l~xF)MB = 0,4-32+ 0,6-18 = ет'6 КМ0ЛЬ/Ч-
Из уравнений материального баланса колонны
GD + Gw = 63,6; 0,975GD + 0&2GW = 0,4-63,6
находим расход дистиллята GD = 25,3 кмоль/ч.
Объемный расход пара в верхней части колонны:
„ G/>(*+1)22,47' 25,3(1,48+1)22,4.345 А ,по
" 7V3600 "" 273-3600 -и.*« м/с-
Требуемый диаметр колонны:
г
п Л/ V ЛГ Q>493 n Г1
D==F STojSs^ К I^ojSs-e°'61 м'
Принимаем колонну стандартного диаметра /)к = 0,6 м.
Пример 7.16. В ректификационной колонне непрерывного
действия разделяется под атмосферным давлением смесь этиловый
спирт—вода, содержащая 25% (мол.) этилового спирта. Требуемая
концентрация дистиллята 80% (мол.), допускаемое содержание
спирта в кубовом остатке не выше 0,1% (мол.). В куб колонны по-
* При более точном построении в большом масштабе число ступеней
изменения концентрации получается немного больше 7.
343
Рис. 7,14 (к примеру 7.16),
дается острый пар. Определить
рабочее число флегмы и относительные
мольные расходы питания, подаваемого
острого пара и кубового остатка на 1 кмоль
дистиллята. Нанести рабочие линии на
диаграмму у — х.
Решение. На рис. 7.14 дана
схема материальных потоков
(относительных мольных расходов) в
ректификационной колонне, в куб которой
подается острый пар. Из уравнений
материального баланса колонны
F + V = 1 + W\ FxF = xD + Wxw\ V
W = F + R
R + \
при
получаем:
F =
XD + R*W
w=
XD + RXF
Xf — Xyp Xf — Xyp
Уравнения рабочих линий:
верхней части колонны
R . хо
y~R + l X + R + 1
нижней части
колонны
R + F
У =
R + 1
х —
R + F
R + 1
xw>
В этих уравнениих: F = Gf/Ge>', W = Gw/Gq; V ¦= Gy/G/э; Gf, Go» G^,
Gy — мольные расходы питания, дистиллята, кубового остатка, подаваемого
пара, кмоль/с.
Рабочая линия верхней части колонны такая же, как и при
обогреве колонны глухим паром — см. уравнение (7.6), она
пересекает диагональ диаграммы у — х при х= xD и ось ординат при
= х°
у Я
Нерабочая линия нижней части колонны пересекает ось абсцисо
при х = xw Обе рабочие линии пересекаются при х = xF.
Кривая равновесия, построенная по данным [7.5], имеет
впадину (рис. 7.15), Для определения 7?мин из точки А проводим
касательную АВ к кривой равновесия. Касательная АВ отсекает на
оси ординат отрезок, равный 37,5. Отсюда
__ 0,8-0,375
"•мин — *~
XD
Rmkh + 1
0,375 и
0,375
1,13.
Рабочее число флегмы (по уравнению (7.12):
Я=1,3/?мин + 0,3 = 1,3.1,13 + 0,3 = 1,77.
344
Отрезок, отсекаемый рабочей линией верхней чаети колонны
на оси ординат при R — 1,77:
Х° °'8 =0,289.
R+X 1,77+1
Наносим рабочие линии на диаграмму — рис. 7.15 (на рисунке
точка xw на оси абсцисс нанесена не в масштабе). Находим
относительные мольные расходы:
с_ xD+Rxw _ 80+1,77-ОЛ ,п,.
xF-xw ™" 25-0,1 -°»zl»
xD + Rx,^to+l977-X
х/? —х^ 24,9
у := Я + 1 = 1 77 + 1- 2,77.
Проверка материального баланса:
F Ч- V -= 1 -Ь W;
3,21 +2,77 = 1 + 4,98.
Расход подаваемого в колонну острого пара следует проверить
по уравнению теплового баланса колонны, которое имеет
следующий вид:
Gv'n + GFcFiF ^®д+ GDCDfD + GWCWfW + $пот .
Здесь Gy, Gf, Gd, Gw— массовые расходы пара, исходной смеси, дистил-
лита, кубового остатка, кг/с; G'w ~G'V + G^— G'D' cFt cDy cw —
соответствующие удельные теплоемкости, Дж/(кг-К); tp, to, ^w — температуры, °С;
*n — удельная энтальпия пара, Дж/кг; Q% — расход теплоты, отдаваемой
охлаждающей воде в дефлегматоре, Вт [уравнение (7.15)], QnoT — тепловые
потери в окружающую среду, Вт.
Пример 7.17. Определить число тарелок ректификационной
колонны, необходимое для разделения смеси метиловый спирт—
вода под атмосферным давлением. Содержание метилового спирта
в питании xF = 0,3, в дистилляте xD — 0,9, в кубовом остатке
xw = 0,05 (мольные доли), Флегмовое число R = 2. Зависимость
коэффициента обогащения rj от состава жидкости приведена
в табл. 7.6.
Решение. Для определения числа тарелок используем
метод кинетической кривой, позволяющей учесть зависимость
коэффициента обогащения от состава [1].
По данным табл. XLVII строим для смеси метиловый спирт—
вода кривую равновесия в координатах у—х (рис. 7.16). Наносим
на диаграмму рабочие линии (порядок их определения — см.
пример 7.10): у = 0,67* + 0,3 и у = 1,8л:— 0,04.
Для построения кинетической кривой — линии, координаты
точек которой (у и х) представляют собой составы пара и жидкости,
покидающих тарелки, необходимо:
345
Рис. 7.i5 (к примеру 7.16).
Рис. 7.16 (к примеру 7.17;4
а) наметить на рабочих линиях ряд точек Аъ Аг> ..., Ait
отвечающих нескольким сечениям колонны;
б) определить в выбранных сечениях предельное изменение
состава пара у* —у, изображаемое отрезками АьВи
в) определить по соотношению (7.21) действительное изменение
состава пара Ау в выбранных сечениях колонны, т. е. иайти
отрезки AfCt:
г) нанести на диаграмму отрезки Лг-С* и соединить точки С-г
плавной линией — кинетической кривой.
Этапы построения кинетической кривой следует отразить
в таблице 7.6.
Таблица 7.6
х 0,05 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90
1} 0,40 0,43 0,48 0,53 0,55 0,53 0,52 0,51 0,49 0,47
tf—tj 0,25 0,28 0,25 0,17 0,16 0,15 0,12 0,10 0,08 0,06
&У или ц (у* — у) 0,10 0,12 0,12 0,09 0,09 0,08 0,06 0,05 0,04 0,03
Примечание, Вместо значений у* —• у и Ц (у* — у) в таблицу можно вносить
непосредственно пропорциональные им длины отрезков А>В,, А.С± в мм; Т) :sssAtCtjAiBi
Построив ступени между кинетической кривой и рабочей линией» определим, число
ступеней раздельно для верхней и нижней части колонны. Число ступеней дает число
рабочих тарелок. Получаем: число тарелок нижней части колонны п =* 4 шт., верхней «
п =ав 7 шт. Тарелка питании — четвертая fnp» счете снизу).
346
КОНТРОЛЬНЫЕ ЗАДАЧИ
7.1. Крезол (СН3СеН4ОН) перегоняется с водяным паром
а) под атмосферным давлением, б) под давлением 300 мм рт. ст.
Определить: температуру перегонки; массовый состав
получаемой смеси; объемный процент крезола в паре и его парциальное
давление. Принять ф = 0,8. Давление насыщенного пара
крезола— см. рис. XIV (,и-крезол).
7.2. Глицерин очищается перегонкой с перегретым водяным
паром при 230 °С под вакуумом 590 мм рт. ст. Степень насыщения
водяного пара глицерином 0,75. Определить расход пара,
уходящего с 1 т глицерина. Сырой глицерин подается при температуре
перегонки. Аппарат имеет внешний обогрев. Как изменится состав
паровой смеси, если повысить вакуум до 620 мм рт. ст.?
Температура кипения чистого глицерина под давлением 760 мм рт. ст.
равняется 290 °С, а под давлением 50 мм рт. ст, 205 °С.
Воспользоваться правилом линейности, взяв в качестве стандартной
жидкости воду (табл. XXXVIII).
7.3. Смесь бензола и толуола кипит при 95 °С под давлением
760 мм рт. ст. При 95 °С давление насыщенного пара бензола Р$ =
= 1167 мм рт. ст.; давление насыщенного пара толуола Рг =
= 480 мм рт. ст. Найти состав кипящей жидкости, считая, что
смесь характеризуется законом Рауля.
Если жидкость будет содержать в два раза меньше толуола, то
под каким давлением она будет кипеть при той же температуре?
7.4. Определить равновесные составы жидкости и пара для
смеси метиловый спирт — вода при температуре 50 °С; а) под
давлением 300 мм рт. ст., б) под давлением 500 мм рт. ст., считая, что
смесь характеризуется законом Рауля.
Объяснить полученный для случая б) результат.
7.5. Построить кривую равновесия х—у* при общем давлении
2 кгс/см2 для смеси гексан —гептан, считая приложимым закон
Рауля. Давления насыщенных паров чистых компонентов взять
по номограмме (рис. XIV).
7.6. Определить состав равновесного пара над жидкой смесью,
состоящей из 10% (мол.) воды, 50% (мол.) уксусной кислоты и
40% (мол.) ацетона при i~ 80 °С, считая, что компоненты смеси
следуют закону Рауля.
7.7. 1000 кг бинарной смеси бензол —толуол, содержащей
30% (масс.) бензола, подвергают простой перегонке под
атмосферным давлением. Определить количество и состав дистиллята, если
содержание бензола в кубовом остатке равно 18% (масс.)
Воспользоваться данными табл. 7.1.
7.8. 2600 кг смеси уксусной кислоты и воды подвергают простой
лерегонке под атмосферным давлением. Исходная смесь содержит
10% (мол.) уксусной кислоты, остаток — 50% (мол.) уксусной
кислоты. Определить массу остатка и дистиллята и состав
дистиллята. Данные о равновесных составах см. в табл. XLVII.
347
7.9. В ректификационную колонну непрерывного действия
поступает жидкость с 24% (мол.) легколетучего компонента.
Концентрация дистиллята 95% (мол.), концентрация кубового остатка
3% (мол.) легколетучего компонента. В дефлегматор поступает
850 кмоль/ч пара, в колону из дефлегматора поступает 670 кмоль/ч
флегмы. Сколько получается кубового остатка?
7.10. Определить аналитически абсциссы точек пересечения
рабочих линий ректификационной колонны с диагональю
диаграммы у—х и друг с другом.
7.11. В ректификационной колонне непрерывного действия
разгоняется смесь этилового спирта и воды. Уравнение рабочей
линии нижней части колонны: */= 1,28л* — 0,0143. Определить
массовый процент спирта в кубовом остатке. Колонна обогревается
глухим паром.
7.12. Колонна непрерывного действия перерабатывает смесь
бензола и хлороформа. При ректификации получается дистиллят,
содержащий 95% (масс.) легколетучего компонента. Питающая
жидкость содержит 40% этого компонента. Найти тангенс угла
наклона рабочей линии верхней части колонны, если известно,
что рабочее число флегмы в 2 раза больше минимального. Данные
о равновесных составах см. в табл. XLVII.
7.13. В ректификационной колонне непрерывного действия
разгоняется под атмосферным давлением 340 кмоль/ч смеси вода—
уксусная кислота. Ордината точки пересечения рабочих линий
0,48. Уравнение рабочей линии верхней части колонны у = 0,84х +
+ 0,15. Количество пара, поступающего в дефлегматор,
550 кмоль/ч. Определить количество кубового остатка (в кг/ч) и
массовую концентрацию уксусной кислоты в нем.
7.14. В ректификационную колонну непрерывного действия
подается 1000 кмоль/ч смеси, содержащей 30% (мол.) пентана и
70% (мол.) гексана. Верхний продукт содержит 95% (мол.) пен.
тана, нижний — 90% (мол.) гексана. Определить количество верх
него и нижнего продуктов (в кг/ч), а также количество пара,
конденсирующегося в дефлегматоре, если известно, что тангенс угла
наклона рабочей линии верхней (укрепляющей) части колонны
равняется 0,75.
7.15. Из ректификационной колонны выходит 1100 кг/ч
дистиллята с содержанием 98,5% (масс.) легколетучего компонента
и 3650 кг/ч кубового остатка с содержанием 96,6% (масс.) второго
компонента. Число флегмы 2,94. Определить: а) массовый
процент легколетучего компонента в питании колонны; б) количество
пара (в кг/ч), поступающего из колонны в дефлегматор.
7.16. На одной из тарелок ректификационной колонны в
верхней (укрепляющей) ее части кипит смесь азота и кислорода.
Концентрация азота в жидкости, стекающей с тарелки, 50% (мол.).
Найти состав жидкости, стекающей сверху на данную тарелку,
если одна ступень изменения концентрации соответствует
одной тарелке. Число флегмы 2,3. Верхний продукт при-
348
нять за чистый азот. Данные о равновесных составах см. в
табл. XLVII.
7.17. На одной из тарелок верхней части ректификационной
колонны находится жидкость, содержащая 65% (мол.)
легколетучего компонента. Колонна работает при флегмовом числе R —
= 2,5. Дистиллят содержит 98% легколетучего компонента.
Определить составы пара, приходящего на указанную тарелку
и уходящего с нее, если коэффициент обогащения тарелки ц0 =
= 0,75, смесь следует закону Рауля, коэффициент относительной
летучести а = 2,5. Жидкость на тарелке полностью
перемешивается.
7.18. В ректификационной колонне непрерывного действия
xD = 90% (мол.), xF = 30% (мол.), xw = 3% (мол.), R = 8.
Определить состав пара, приходящего на тарелку, где жидкость
содержит: а) 75 и б) 15% (мол.) легколетучего компонента.
7.19. В ректификационной колонне непрерывного действия
получается 200 кг/ч уксусной кислоты с концентрацией 70% (мол.)
Перерабатывается смесь уксусной кислоты с водой, смесь поступает
в колонну при температуре кипения. Содержание уксусной
кислоты в исходной смеси 31% (мол.). С верха колонны отгоняется
вода, содержащая 8% (мол.) уксусной кислоты. Давление в
колонне атмосферное. Определить число ступеней изменения
концентрации при числе флегмы 4. Определить также расход в кубе
колонны греющего пара (рабс = 4 кгс/см2), имеющего влажность
5%. Тепловые потери составляют 4% от полезно затрачиваемой
теплоты. Данные о равновесных составах см. в табл. XLVII.
7.20. В ректификационную колонну поступает 5000 кг/ч смеси,
состоящей из 29% (масс.) метилового спирта и 71% (масс.) воды.
Уравнение рабочей линии верхней (укрепляющей) части колонны;
у = 0,73л; + 0,264. Кубового остатка получается 3800 кг/ч.
Определить: а) массовый процент метилового спирта в кубовом остатке;
б) количество пара (в кг/ч), поступающего из колонны в
дефлегматор; в) расход воды в дефлегматоре, если она нагревается в нем
на 12 К.
7.21. Уравнения рабочих линий ректификационной колонны
для разделения смеси бензола и толуола под атмосферным
давлением: # = 0,723*+0,263; #= 1,25* —0,0188. В колонну
подается 75 кмоль/ч смеси при температуре кипения. Греющий пар
в кубе колонны имеет избыточное давление 3 кгс/см2. Определить
требуемую поверхность нагрева в кубе колонны и расход
греющего пара, имеющего влажность 5%. Коэффициент теплопередачи
К = 580 Вт/(м2К). Тепловыми потерями пренебречь.
Температуру кипения жидкости в кубе принять как для чистого толуола.
7.22. В ректификационную колонну непрерывного действия
подается смесь вода—этиловый спирт, содержащая 10% (масс.)
спирта. Определить расход теплоты в кубе колонны и количество
отводимой теплоты в дефлегматоре на 1 кг дистиллята,
содержащего 94% (масс.) спирта, если кубовый остаток практически не
349
содержит спирта. Исходная смесь вводится в колонну при
температуре 70 °С. Укрепляющая часть колонны работает с числом
флегмы 4. Тепловыми потерями пренебречь. Обогрев глухим
паром.
7.23. Производительность ректификационной колонны для
разделения смеси метиловый спирт — вода составляет 1500 кг/ч
дистиллята. Колонна работает под атмосферным давлением.
Поверхность теплообмена дефлегматора 60 м2, коэффициент
теплопередачи в нем 810 Вт/(м2-К). Определить число флегмы и расход
охлаждающей воды в дефлегматоре, если она нагревается от 15
до 35 ГС.
7.24. Определить требуемую поверхность и расход воды в
дефлегматоре ректификационной колонны для разделения бекзоль-
но-толуольной смеси при следующих условиях; количество
верхнего продукта 6С0 кг/ч; число флегмы 3,75; начальная и конечная
температурь? охлаждающей воды 20 и 45 °С; коэффициент
теплопередачи 700 Bt/(m'z-K). Считать верхний продукт за чистый
бензол. Давление в колонне атмосферное.
7.25. Определить необходимое число тарелок в
ректификационной колонне периодического действия для разгонки смеси
хлороформ — бензол иод атмосферным давлением. Исходная смесь
содержит 38 % (мол.) хлороформа, дистиллят должен содержать 97%
(мол.), кубовый остаток после перегонки— 10% (мол.).
Коэффициент избытка флегмы 2. Данные о равновесных составах см.
в табл. XLVII. На одну ступень изменения концентрации
приходится 1,4 тарелки,
7.26. В ректификационной колонке непрерывного действия
разгоняется 5000 кг/ч смеси метиловый спирт—вода. Массовая
концентрация метилового спирта в питании 20%, в верхнем
продукте 90%. Коэффициент избытка флегмы 1,8. Расход воды на
дефлегматор 40 м3/ч» нода в нем нагревается от 20 до 40 °С.
Определить количество метилового спирта, уходящего с кубовым
остатком.
7.27. Для обогрева куба ректификационной колонны, в
которую полается на разделение 6 т/ч бензолы-ю-толуолы-юп смеси,
имеется в распоряжении пар с абсолютным давлением 0,1 МПа.
Концентрация исходной смеси 32% бензола. Требуемая
концентрация дистиллята 97% бензола, кубового остатка — 95%
толуола . Проценты массовые.
Определить: а) массовые расходы получаемого дистиллята и
кубового остатка; б) давление в колонне; в) требуемое количество
тарелок при числе флегмы 3,1 и при среднем к. п. д. тарелок г\ =
= 0,71; г) расход греющего пара и расход воды в дефлегматоре
грп нагреве воды в нем на 15 К. Влажность греющего пара 5%.
Смесь характеризуется законом Рауля. Тепловые потери
принять в размере 3% от полезно затрачиваемой теплоты. Питание
подается в колонну при температуре кипения. Принять разность
температур в кубе колонны 10 К.
350
7.28. Определить диаметр и высоту тарельчатой колонны для
разделения смеси метиловый спирт—вода под атмосферным
давлением. Расход исходной смеси 3 т/ч (0,84 кг/с). Содержание
метилового спирта в питании 40% (мол.), в дистилляте 95% (мол.),
в кубовом остатке 5% (мол.). Скорость пара в колонне 0,8 м/с,
расстояние между тарелками Н = 300 мм. Зависимость
коэффициента обогащения ц от состава жидкости:
х 10
ц 0,45
20
0,55
30
0,63
40
0,69
50
0,75
60
0,78
70
0,80
90
0,80
ПРИМЕР РАСЧЕТА ТАРЕЛЬЧАТОЙ РЕКТИФИКАЦИОННОЙ КОЛОННЫ
Рассчитать ректификационную колонну непрерывного действия с ситчатыми
тарелками для разделения под атмосферным давлением 10 т/ч жидкой смеси,
содержащей 50% (масс.) бензола и 50 % (масс.) толуола. Требуемое содержание
бензола в дистилляте 96 % (масс), требуемое содержание толуола в кубовом
остатке 98 % (масс.)- Исходная смесь перед подачей в колонну подогревается
до температуры кипения. Греющий пар имеет давление /?ИЗб = 3 кгс/см2 (0,3 МПа),
В расчет входит определение расходов дистиллята, кубового остатка, флег-
мового числа, греющею пара, охлаждающей воды и определение основных
размеров колонны — D и Я. Определение числа тарелок выполи-ить: а) графически —
методом теоретической тарелки; б) аналитически ~- методом от тарелки к
тарелке — с помощью ЭВМ. Составы пара и жидкости на тарелках колонны вывести
иа печать.
Схема ректификационной установки дана па рис. 7.17.
I. Материальный баланс.
Обозначим массовый расход
дистиллята через Go кг/ч,
кубового остатка через Gyp кг/ч.
Из уравнений
материального баланса (7.4) и (7.5)
GD + GW= 10000;
Go-0,96 + ^.0,02» 10000-0,5
находим Gp — 5110 кг/ч, Gy —
= 4890 кг/ч. '"°Р
Для дальнейших расчетов л-1г
выразим концентрации питания,
дистиллята и кубового остатка
в мольных долях (в
соответствии с табл. 6.2). Коыдетрт
Питание
А
Исходная
смесь
f\M
Xf~
х/Мб
J
Дистиллят
хр , 100 — х/?
-j—
50/78
50 . 60
-г
= 0,542.
Н
78
92
^*— Пар
3-*-Конденсат
Вода
Рис. 7.17. Схема ректификационное
установки.
тЛуйиый
Ъ
осттоК
351
Дистиллят:
*о 100-*о" - _96_ 4_ - 0>965'
Мб + Мт 78 + 92
Кубовый остаток:
^__%/Мб _ . 2/78 _
xw Юр — дг^7 2 98
Мб "^ Мт 78 + 92
Относительный мольный расход питания:
v xd — Xw 0,965 — 0,023
xf—xw 0,542 — 0,023
= 1,82.
Кривая равновесия (рис. 7.7) * точек перегиба не имеет.
Определяем минимальное число флегмы по уравнению (7.10):
ХР—УЪ ^0,965 — 0,74
Ур — хР ""0,74 — 0,542
^МИН — ™Т~ " — ТГ^Гл л г-лл — 1» l°°t
где у^г = 0,74 — мольную долю бензола в паре, равновесном с жидкостью
питания, определяем по диаграмме у * — дг.
Рабочее число флегмы по уравнению (7,12):
R = 1,ЗЯМИН + 0,3 = 1,3-1,135 + 0,3 = 1,78.
Уравнения рабочих линий;
а) верхней (укрепляющей) части колонны
„^ R , , *Р _. Ь78 0,965,
у "" /? + 1 * ^ # + 1 - 2,78 х ~г 2,78 '
# = 0,64*+ 0,347;
б) нижней (исчерпывающей) части колонны
* --д+Т Я+Т *^ ~ gj8 * 2J^°'023'
у« 1,3г — 0,0068.
П. Определение скорости пара и диаметра колон-
и ы.
Средние концентрации жидкости:
а) в верхней части колонны
*сР = (xf + xd)/2 = (°-542 + °,965)/2 = °'754;
б) в нижней части колонны
*ср = (*р + V)/2 = <0'542 + °'023)/2 = °>283*
Средние концентрации пара находим по уравнениям рабочих линий:
а) в верхней части колонны
у* = а, 64л' + 0,347 = 0,64-0,754 + 0,347 = 0,829;
*
В технических расчетах используют обычно экспериментальные данные
о фазовом равновесии [6.7]. В этом примере использованы равновесные
зависимости, полученные расчетным путем на основании закона Рауля, которые для
системы бензол—толуол близки к экспериментальным данным.
352
б) в ннжией части колонны
0jp « J ,3x'cp = 0,0068 = 1,3-0,283 — 0,0068 «0,361.
Средние температуры пара определяем по диаграмме t — к, у (рис. 7,6):
а) при у'ср = 0,829 йр = 88 °С,
и _ ."
б) при ^Gp =0,361 *Gp = 103 °С.
Средние мольные массы и плотности пара:
а) Мер = 0,829<78+ 0,17Ь92 = 80,3 кг/кмоль;
^срГо 80,3-273
СР "" 22,47' 22,4-361
2,71 кг/м3;
б) Мер = 0,361*78+ 0,639-92 = 87 кг/кмоль;
^ср^о 87-273
СР 22.4Г' 22,4-376
^р
2,82 кг/м3.
Средняя плотность пара в колонне:
Рп = (Pep + Pip)/2 ~ <2*71 + 2>32)/2 - 2,77 кг/м3.
Плотности жидких бензола и толуола близки. Температура в верху колонны
при yD = 0,965 равняется 82 °С, а в кубе-испарителе при xw — 0,023 она равна
109 °С (рис. 7.6).
Плотность жидкого бензола при 82 °С pg — S13 кг/м3, а жидкого толуола
при 109 °С рт = 783 кг/м3 [4,15].
Принимаем среднюю плотность жидкости в колонне
рж = (813 + 783)/2 » 800 кг/м*.
Определяем скорость пара в колонне по уравнению (7.17). По данным
каталога-справочника «Колонные аппараты» принимаем расстояние между
тарелками h = 300 мм. Для ситчатых тарелок по графику (рис. 7.2) находим С = 0,032.
Скорость пара в колонне по уравнению (7.17а):
w
= С\/~Рж!Рп = 0,032^800/2,77 = 0,54 м/с.
Объемный расход проходящего через колонну пара при средней температуре
в колонне /ср = (88+ 103)/2 да 96 °С
С0(^ + 1)22,4ГсвРо 5110(1,78+1)22,4.369-1,033
AZ07V36OOp ~" 78,5-273.3600-1 " ' ' '
где М$ — мольная масса дистиллята, равная
MD = 0,965-78 + 0,035-92 = 78,5 кг/кмоль.
Диаметр колонны:
° = 1^1^ = }/ЖЖ==1'89м-
По каталогу-справочнику «Колонные аппараты» берем D = 1800 ммш Тогда
скорость пара в колонне будет:
V 1,52 пл
W = 0,785D* = 0.7Й6.1.8» == М М/С'
12 Павлов К. Ф. и др. 363
til
ша
Рис. 7,18. Схема сетчатой тарелки.
III. Гидравлический расчет
тарелок.
Принимаем следующие размеры ситчатой
тарелки: диаметр отверстий dn ~ 4 мм, высота
сливиой перегородки hn ~ 40 мм. Свободное
сечение тарелки (суммарная площадь отверстий)
8 % от общей площади тарелки. Площадь,
заиимаемаи двумя сегментными переливными
стаканами, составляет 20 % от общей площади
тарелки.
Рассчитаем гидравлическое сопротивление
тарелки в верхней и в нижней части колоивы
по уравнению (1.60):
Ар = Арсух + Ара + Арпт.
а) Верхняя часть колонны.
Гидравлическое сопротивление сухой
тарелки:
АРсух * ?<Рп/2= 1,82.7,53.2,71/2 = 138 Па,
где ? = 1,82 — коэффициент сопротивления
неорошаемых ситчатых тарелок со свободным
сечением 7 — 10 %; w0 = 0,6/0,08 = 7,5 м/с —
— скорость пара в отверстиях тарелки.
Сопротивление, обусловленное силами
поверх ностного натяжения:
Ар0 =i 4a/rf0 = 4.20,5* 10-8/0,004 = 20,5 Па,
где a = 20,5' 10~3 И/м — поверхностное
натяжение жидкости при средней температуре в верхней
части колонны 88 °С [4.16] (у бензола и толуола практически одииаковсе
поверхностное натяжение); d2 = 0,004 м — диаметр отверстий тарелки.
Сопротивление парожидкостдаго слоя иа тарелке:
Арпда = \>3hmi<Pmngk-
Высота парожидкостного слоя (рис. 7.18):
/1пж = ^п + Ah.
Величину Ah—высоту стоя над сливной перегородкой рассчитываем по
формуле:
_/ Уж У'»
где Vm — объемный расход жидкости, м8/с; П — периметр сливиой перегородки,
м; & = рпн</рж— отношение плотности парожидкостного слоя (пены) к плотности
жидкости, принимаемое приближенно равным 0,5.
Объемный расход жидкости в верхней части колонны:
ОрДМср 5110.1.7881,4
ж" МоР*Г~ 3600-78,5-800 - и>и(ШЙ м'с'
где МСр= 0,7^4-78 + 0,246-92= 81,4— средняя мольная масса жидкости,
кг/кмоль.
Периметр сливной перегородки П (рис. 7.18) находим, решая систему
уравнений:
А/1
0,1яЯ2 = 2/3Ш>,
354
где /? = 0,9 м — радиус тарелки; 3/3Ш — приближенное значение площади
сегмента.
Решение дает; П = 1,32 м; Ъ = 0,289 м. Находим АА:
a/'°(i,85°:58o,5)v,-0'0193m-
Высота парожидкостного слоя на тарелке:
Лщк = Ап + ДА = 0,04 + 0,0193 = 0,0593 м.
Сопротивление парожидкостного слоя;
Дрпж= ЬЗАджйрн^» 1,3-0,0593.0,5-800-9,81 =302 Па.
Общее гидравлическое сопротивление тарелки в верхней части колонны:
Ар' « Арсух + Аро + Арпж = 138 + 20,5 + 302 = 461 Па.
б) Нижняя часть колонны:
1,82-7,52-2,82 ... ^ . 4.18,8-10-
Арсух = 2 ^ Ш Па; Ар0 ^ Щ4 = 18>8 Па
(18,8-10~3 Н/м — поверхностное натяжение жидкости при tcp = 103 °С);
(A/F = 0,542-78 + 0,458-92 = 84,4 кг/кмоль; МСр = 0,283-76 +
+ 0,717-92 = 88 кг/кмоль);
Адж = 0,04 + 0,0325 = 0,0725 м
ЛрШх = 1,3-0,0725-0,5.800-9,81 =369 Па.
Общее гидравлическое сопротивление тарелки в нижней части колонны;
Ар" = 144+ 18,8 + 369 = 532 Па.
Проверим, соблюдается ли при расстоянии между тарелками А = 0,3 м
необходимое дли нормальной работы тарелок условие
Ар
А>1,8
Рж?
Для тарелок нижней части колонны, у которых гидравлическое
сопротивление Ар больше, чем у тарелок верхней части;
1.W 1,8-532 =0)122м_
Рж? 800-9,81
Следовательно, вышеуказанное условие соблюдается:
Проверим равномерность работы тарелок—рассчитаем минимальную
скорость пара в отверстиях ш0, ыин, достаточную для того, чтобы ситчатая тарелка
работала всеми отверстиями:
a R7 ТАР^пж . fi7 if 9,81.800-0,0725
Wo. мин-0,67 J/ _—— «0,67 у i)82.2,82 ** 7'05 М/С'
Рассчитанная скорость цу0> мин = 7,5 м/с; следовательно, тарелкн будут
работать всеми отверстиями.
12* 355
У*,УЖ
wo
0\ 20
ЮО«с,%
Рис. 7Л9. Определение числа сту,
пеней изменения концентрации.
IV. Определение
числа тарелок и высоты
колонны.
а) Наносим на диаграмму
у — х рабочие линии верхней и
нижней части колонны (рис. 7.19)
н находим число ступеней
изменения концентрации лт. В
верхней части колонны п'т « 7, в
нижней части л* « 8, всего 15
ступеней.
Число тарелок рассчитываем
по уравнению (7-19):
П = Пт/Т].
Для определения среднего
Хс=54,2 Хп*9&5' WW определении средшпи
и к. п. д. тарелок tj находим
коэффициент относительной летучести разделяемых компонентов а= Pq/Pt h
динамический коэффициент вязкости исходной смеси \1 прн средней температуре в
колонне, равной 96°С.
Прн этой температуре давление насыщенного пара бензола Pg= 1204 мм
рт. ст., толуола Ят = 492,5 мм рт. ст. (табл. 7.1), откуда а = 1204/492,5 = 2,45.
Динамический коэффициент вязкости бензола прн 96 °С равен 0,27 сП,
толуола 0,29 сП. Принимаем динамический коэффициент вязкости исходной смеси
\х= 0,28 сП= 0,28-10-8 Па-с.
Тогда
а^= 2,45-0,28= 0,685.
По графику (рис» 7.4) находим rj = 0,53. Длина пути жидкости на тарелке
(рнс. 7,18)
/ = ?> — 2Ь= 1,8 — 2-0,289= 1,22 м.
По графику (рис. 7.5) находим значение поправки иа длину пути А = 0,105,
Средний к. п. д. тарелок по уравнению (7.20):
цг = п (1 + Л) = 0,53 (1 +0,105) = 0,59.
Для сравнения рассчитаем средний к. п. д. тарелки т|0 по критериальной
формуле, полученной путем статистической обработки многочисленных опытных
данных для колпачковых н ситчатых тарелок:
Ло = 0,068/С?'1-Ке*11&<
В этой формуле безразмерные комплексы:
Кг = §^п рг
Кп
«Лпрп \1ж Ип
'СВ
Иш
whupn
$с вМ-п Рж^ж И ж *^с вРж^ж
я2 = 4|2-рг:
Vi
We
ж
wh„o
VxVn
О
v>k Vnp^Ktiy2 /in/)»v* аурж^ж '
356
Рис. 7.20. К потарело чному расчету колонны:
I, i + * -* номера сечений( между которыми
находится тарелка о номером i.
Лен
где w — скорость пара в колонне, м/с; 5СВ —
относительная площадь свободного сечеиия
тарелки; /in—высота сливиой перегородки, м;
рп и Рж — плотности пара и жидкости, кг/м3;
?)ж — коэффициент диффузии легколетучего
компонента в исходной смеси, определяемый
по формуле (6.25), м2/с; о— поверхностное
натяжение жидкости питания, Н/м.
Физико-химические константы отнесены к средней температуре в колонне.
Предварительно рассчитаем коэффициент диффузии DH<:
-12
?>ж = 7,4-10->
(РИ)°'5Г
В нашем случае: р=1; ц-ж — 0,28 сП =* 0,28-10"? Па-с; М = MF
84,4 кг/кмоль; и = 6-14,6 + 6-3,7 — 15 = 96; Г = 96 + 273 == 369 К,
Коэффициент диффузии:
7,4.](Г12-84,40>5.369
*>ж = — ^о-ш^ =* 5,8- Ю-8 м2/с
0,28-960'6
Безразмерные комплексы:
К,:
whnPn __ 0,6.0,04-2,77 _
К,
а
19,7-10"3
0,6-800-5,8- 1(рв
=5-= 0,71.10*.
а>рж0ж
Средний к. п. д. тарелки:
Л0 « 0.068К?*' К§И1Й = 0,068 (1,79- Ю5)0'* (0,71 • 104)0'115 = 0,63,
что близко к найденному значению Цг.
Число тарелок:
в верхней части колонны
в инжиеи части колонны
п'=* п'т/г\г =* 7/0,59 =* 12;
Л" =^/^ = 8/0,59=* 14.
Общее число тарелок п — 26, с запасом а = 30, нз них в верхней части
колонны 14 н в иижией части 16 тарелок.
Высота тарельчатой части колонны:
Ят = (п - 1) h = (30 - 1) 0,3 « 8,7 м.
Общее гидравлическое сопротивление тарелок:
Лр= Др'пв + Лр"пн=:=46Ы4 + 532-16= 14 950 Па » 0,15 кгс/см*.
б) Система уравнений, позволяющая аналитически определить число тарелок,
з также составы пара н жидкости разделяемой смесн беизол — толуол,
покидающих каждую из тарелок, включает в себя уравнение равновесия (6.9), уравнение
рабочих линий частей колонны (7.6) и (7.8), выражение для коэффициента
обогащения (7.21).
Расчет состоит в последовательном определении в сечениях колонны между
тарелками составов пара и жидкости (г/г-» ¦*/)¦
Нижние индексы у составов пара и жидкости отвечают номеру сечения.
Номер тарелки совпадает с номером расположенного под нею сечения (рис, 7,20),
357
Принимай» что 1 коэффициент стиосительной ле^У460™ постоянен? 2)
коэффициент обогащения"^-постоянен; 3) куб-испарнтель* не обладает разделяющим
действием, т. е. выходящий из него пар имеет тот же состав» что и кубовый
остаток (iff «= Хф)-
Блок схема расчета:
/
СНачало]
ocF,x0>xW)R,F,af7j
I
yp = RxF/(«+7)txB/(R+t)
I ~
I —
l»f
i
УГ=Л=С,-/[ос?(<1-7)+71
^t+t = tViM(R+^)+(/r~0^w]/(rR+
3
/——1
——<fVt+7>*D \
Нет
x
. ¦
]
_=з 1
Печать- эс^х^ХэдчК^сЦД I
f Конец j
ИдеитифнкатоРы к примеру расчета колоииы П01аРелочиым методом!
Исходные данные
Величина
ИдентификзТ0Р
XF
XF
XD
XW
R
R
а
ALFA
11
KPD
368
Рассчитываемые величины
Величина
Идентификатор
F
F
Ур
YF
х1
Х(1)
YR(I)
У (1+ 1)
п
N
Программа расчета:
PROGRAM
COMMENT ПОТАРЕЛОЧНЫЙ РАСЧЕТ КОЛОННЫ
R E AL KPD
DIMENSION Х(200), Y(200), YR(200)
READ (5) XF, XD, XW, R, ALFA, KPD
F=(XD—XW)/(XF— XW)
YF=R/(R+1.)*XF+XD/(R+1.)
X(1)=XW
Y(I)=XW
WRITE (6,1)
1 FORMAT (6X, T, 5X, 'X(I)', 5X, JY(I+1)')
2 1=1+1
N=I
YR(I)=ALFA*X(I)/(X(I)*(ALFA—l.)+l.)
Y(I+I)=Y(I)+KPD*(YR(I)—Y(I))
WRITE (6, 3) I, X(I), Y(I+1)
3 FORMAT (5X, 13, 2X, F8.5, 2X, F8.5)
IF(Y(I+1)>=YF) GO TO 4
X(I+1)=(Y(I+1)*(R+1.)+(F-1.)*XW)/(R+F)
GO TO 2
4 IF (Y(I+1)>=XD) GO TO 5
X(I+1)=(Y(I+I)*(R+1.)—XD)/R
GO TO 2
5 WRITE (6, 6) N
6 FORMAT (5X, 'ЧИСЛО ТАРЕЛОК N=', 13)
STOP
END®®
Результаты расчета даиы в табл. 7.7.
Таблица 7.7
Составы жидкости и пара, покидающих тарелки колонны
xF » 54,2; xD « 96,5; х^ = 2,3; ^ = 69.42; Я — 1,78; F =» 1,82; а = 2.45;
Т) = 0,59.
Номер
тарелкн
1
2
3
4
5
6
7
8
9
10
11
12
х, %
2,30
3,7366
5,7977
8,6559
12,443
17,177
22,702
28,682
34,681
40,287
45,214
49,331
у, %
4,1604
6,8294
10,531
15,434
21,565
28,720
36,464
44,232
51,492
57,873
63,204
67,486
Номер
тарелкн
13
14
15
16
17
18
19
20
21
22
23
х. %
52,638
56,395
61,177
66,286
71,496
76,577
81,330'
85,611
89,345
92,514
95,145
у, %
70,821
73,883
77,154
80,490
83,744
86,787
89,528
91,919
93,948
95,562
97,006
359
V. Тепловой расчет- установки* -
Расход теплоты, отдаваемой охлаждающей воде в
дефлегматоре-конденсаторе, находим по уравнению (7.15):
^110в
<2д » 0D (1 + R)rD = -щ^ (1 + 1,78) 392-10»- 1550000 Вт.
Здесь
rD = */Уб + (1 — */>) 'т = 0,96-392,4.103 + 0,04.377,8-103 = 392-103 Дж/кг.
где го и /-т — удельные теплоты конденсации бензола и толуола при 82 QC.
Расход теплоты, получаемой в кубе-испарителе от греющего пара, находим
по уравнению (7.14):
Qk — Сд + GDcDtD + G-^c^tw — GfCf(f + QnoT e
- 1,03 (^1 550000 + -~- 0,46.4190-82 + -|™§- 0,45.4190-109 —
10000
3600
0,455.4190.91,5^ = 1 615000 Вт.
Здесь тепловые потери С?Пот приняты в размере 3% от полезно затрачиваемой
теплоты; удельные теплоемкости взяты соответственно при *?> — 82 °С, % =
— 109 °С и tf = 91,5 °С; температура кипения исходной смеси tp = 91,5 °С
определена по рис. 7.6.
Расход теплоты в паровом подогревателе исходной смеси:
Q= \l05GFcF(tF-tHai4)= 1,0511—0,425-4190(91,5— 18) =: 382000 Вт.
Здесь тепловые потери приняты в размере 5%, удельная теплоемкость
походной смеси ср = (0,5-0,43 + 0,5-0,42) 419С Дж/д;г*К) взята при средней
температуре (91,5 + 18)/2 ъ 55 °С.
Расход теплоты, отдаваемой охлаждающей воде в водяном холодильнике
дистиллята:
Q - GDcD (tD - /кон) = -|j~jJ-0,43-4190 (82 - 25) = 145 500 Вт,
где удельная теплоемкость дистиллята cD = 0,4?- 4190 Дж/(кг- К) взята при
средней температуре (82 + 25)/? «? 54 °С.
Расход теплоты, отдаваемой охлаждающей воде в водяном холодильнике
кубового остатка:
4890
Q = Gwcw (% - *кон) = -gggg-0,425-4190 (109-25) = 203000 Вт,
где удельная теплоемкость кубового остатка 'w= 0,425**190 Дж/(кг«К) взята
при средней температуре (109+ 25)/2 = 67 °С.
Расход греющего пара, имеющего давление рабс ^ 4 кгс/см2 и влажность 5%:
а) в кубе-испарителе
г QK 1615000 nftlrr/p
г'п~"^~~ 214Ы03-0,95 "~и,й КГ/С|
где /у. п — 2141 «'О3 Дж/кг — удельная теплота коидеисации греющего пара;
б) ь подогревателе исходной смеси
п 382000 А lft ,
°г-=2Т4ьЖоЖ = ОЛ9кг/с-
Всего: 0,8+ 0,19= 0,9о кг/с или 3,6 т/ч*
360
Расход охлаждающей воды при нагреве ее на 20 °Cf
а) в дефлегматоре
Од 1 550 QQQ nmfr з
ввсв(/коИ-ЫРв" 4190-20.1000 -0>0185м/с:
б) в водяном холодильнике дистиллята
^=41Э104205°Ю00=0'00174м8/6;
в) в водяном холодильнике кубового остатка
^ = 41Ш0200010000°0-00242ц8/°-
Всего 0,0227 м3/с, или Ь2 м3/ч,
Глава 8
ЭКСТРАГИРОВАНИЕ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
Экстрагированием называется процесс извлечения одного или
нескольких компонентов из смеси, находящейся в твердом или
жидком состоянии, путем обработки растворителем (экстраген-
том), избирательным по отношению к отдельным компонентам.
Для последующего выделения целевого компонента из смеси с экс-
трагентом применяют выпаривание или ректификацию.
Целесообразность применения жидкостной экстракции
определяется: 1) невозможностью разделения смеси ректификацией
вследствие образования азеотропных смесей, нелетучести или
недостаточной термической стойкости компонентов; 2) экономией
теплоты, если затраты на ректификацию исходной смеси вследствие
близости температур кипения составляющих компонентов, малых
концентраций или других причин больше, чем расходы на
экстракцию и отгонку растворителя из продуктов разделения.
Задачи по статике экстрагирования решаются
преимущественно графическим путем — с помощью треугольной или
прямоугольных диаграмм.
1. Особенности треугольной диаграммы:
а) вершины треугольника (рис. 8.1) соответствуют чистым
компонентам А, В и С, стороны треугольника АВ, ВС и АС — двух-
компонентным смесям Л и В, В и С, Л и С, точки внутри
треугольника — трехкомпонентным системам [например, точка g является
фигуративной, т. е. характеризующей следующий состав смеси:
70% (масс.) А, 20% (масс.) В и 10% (масс.) С];
361
-*-А,%(масс.)
Рис 8.1. Треугольная диаграмма. Рис. 8.2. Правило рычага
б) лучи Аа, Bby Сс, проведенные из вершин треугольника,
являются геометрическим местом фигуративных точек смесей с
постоянным отношением содержаний двух других компонентов Хв/хс,
Ха1%с> ха/хв соответственно;
в) линии dd, ее, //, параллельные сторонам треугольника АС,
ВС, АВ, являются геометрическим местом фигуративных точек
смесей с постоянным содержанием компонентов В, А, С
соответственно.
2. Правило рычага (частный случай правила центра тяжести):
при смешении двух растворов, составы которых характеризуются
на диаграмме любыми точками а и Ь> общий состав смеси
выражается точкой с, лежащей на прямой ab, соединяющей эти точки;
отрезки ас и be обратно пропорциональны количествам взятых
растворов (рис. 8.2)
причем ха + Хь ф хс.
Тогда
Gaac = ОъЬс; GJbc ~ Съ/ас*, 1
0сас = 0ъаЬ\ \ (8.1)
ОсЬс == Gaab\ Ос/аЬ = Gb/ac — Gafbc- i
Здесь Ga, Gb, Gc — масса компонентов смеси а, Ь и с, кг; ха, хь> хс —
содержание любого компонента (А, Р и С) в смеси а, Ъ и с, % (масс).
Эти же соотношения действительны при расслаивании смеси о
на две сосуществующих фазы х и Ъ,
3. Типовые тройные системы, имеющие наибольшее значение,
представлены на рис. 8.3 и 8.4. Здесь вершина треугольника А
соответствует первичному растворителю (твердое тело или
жидкость), вершина В — экстрагируемому компоненту (твердое тело
362
Рис. 3.3. Система жидкость—жидкость с одной (а) н с двумя (б) парами частично раство*
римых друг в друге компонентов (при t *» const).
или жидкость), вершина С — вторичному растворителю или экс-
трагенту (жидкость).
На рис. 8.3: линия abcdKd'c'b'a — пограничная (бинодальная)
кривая; поле внутри этой кривой — область смесей,
расслаивающихся на две сосуществующие фазы, состав которых выражается
точками на кривой; поле вне пограничной кривой — область не-
расслаивающихся (гомогенных) растворов; точка К —
критическая точка; левая часть пограничной кривой — ветвь рафинатов
(остатка первичного растворителя после извлечения из него
экстрагируемого вещества); правая часть пограничной кривой — ветвь
экстрактов; отрезки ЬЬ*', ее', dd't соединяющие фигуративные точки
сосуществующих фаз, — хорды равновесия (конноды) *.
На рис. 8.4: линия abede — пограничная кривая; поле слева—
область трехкомпонентиых гетерогенных смесей; поле справа —
область расслаивания; сторона треугольника ВС характеризует
составы верхнего потока (раствор экстрагируемого вещества в
растворителе); пограничная кривая характеризует составы
нижнего потока (гетерогенная смесь твердого нерастворимого
вещества экстрагируемого
компонента и растворителя,
удерживаемого в порах твердого
вещества); хорды равновесия
bb'y cc', dd' при своем
продолжении проходят через вершину
треугольника А,
* Описание графической
интерполяции хорд равновесия иа
треугольной диаграмме см. в примере 8.1.
Рис» 8.4. Система твердое тело—жидкость
(при t = const). А
363
4. Коэффициент распределения экстрагируемого компонента
В между фазами экстракта и рафината выражается соотношением:
Ув/Хв> k
I.
(8.2)
где ув — содержание экстрагируемого компонента В в фазе экстракта, % (масс);
хв — равновеснее содержание экстрагируемого компонента В в фазе рафината,
% (масс).
Обычно коэффициент распределения зависит от концентраций,
поэтому аналитические расчеты [8.1] дают только приближенный
результат.
5. Прямоугольные диаграммы.
Если взаимной растворимостью первичного (А) и вторичного
(С) растворителей можно пренебречь, для графического расчета
используют более удобную прямоугольную диаграмму в
координатах х'в — у в (массовые относительные доли). При этом
*„ =
в
в~ 100 — х
в
кг экстрагируемого компонента , ,
- — в фазе рафината:
кг первичного растворителя
Ув кг экстрагируемого компонента ,
Ун — т™ — в фазе экстракта.
а 100 — ув кг вторичного растворителя
(8.3)
6. Прямоугольные диаграммы используют также в тех случаях,
когда из-за скученности линий треугольная диаграмма не дает
достаточной точности.
По оси ординат откладывают отношение содержания одного
из компонентов тройной системы к сумме содержаний двух других
компонентов, а по оси абсцисс — отношение содержания другого
компонента к этой же сумме. Часто используются, например,
следующие координаты:
а) Координаты X, Y—z, Z и X — Y * для системы жидкость —
жидкость (рис. 8.5; обозначения те же, что на рис. 8.3):
х =
У =
г =
1 =
"В
"в
кг В
ХА + ХВ
Ув
Уа+Ув
хс
ХА+ХВ
Ус
Уа + Ув
100 — д:с кг (A-J-В)
У в кг В
в фазе рафината;
в фазе экстракта;
100 - ус кг (А + В)
1^1F(IW B фазе рафииата:
Ус кг С
100-ус кг(А + В) Вфазе экстРак™-
(8.4)
* Вспомогательная диаграмма для нахождения хорд равновесия.
364
Рис* 8*6* Система жидкость—жидкость с одной (а) и с двумя (б) парами частично
растворимых друг в друге компонентов (при t = const).
Формулы для обратного пересчета:
1-Х \—Y _ X У
*' Уа — i+z ' *в ~ 1 + г' Ув e 1 + Г
г Z
i+z
хс —ПГТ' ус ~*
1+г
1 + Z •
(8.4а)
б) Координаты Л"', К'—г , Z для системы твердое тело —
жидкость (рис. 8.6; обозначения те же, что на рис. 8.4):
X' =
У =
г'=-
7' —_
ХВ
хв * хс
Ув
Ув+Ус
ХА
ХВ "Г хс
Уа
хв
100 — хА
Ув
ЮО - уА
ХА
100 - х.
А
Уа
кг В
кг (В + С)
кг В
кг(В+С)
кг А
кг (B-fC)
кг А -
Ув + Ус " т-УА КГ(В+С)
в иижием потоке;
в верхнем потоке;
в нижнем потоку
в верхнем потоке.
(8.5)
363
Г\т'
хт,У
Рис, 8.6. Система твердой тело-^жндкость (при
t «* const).
В этих формулах: хА, хВ1
xQ—содержание компонентов А, В, С в фазе рафииата
(в нижнем потоке), % jviacc); yA1 ув, ус —
равновесное содержание компонентов А, В,
С в фазе экстракта (в верхнем потоке), %
(масс),
7. Жидкостная экстракция в
перекрестном токе.
Уравнение общего материального
баланса п-й ступени
экстрагирования * (рис. 8.7, а):
Gr, n-i + 08ш п - Or, n + G?, n. (8.6)
Уравнение материального баланса n-й ступени по
экстрагируемому компоненту:
Gfi, n-A-X + G8, аУз - СЛ, пХп + GB, n V W
В случае, когда взаимной растворимостью первичного
растворителя и экстрагента можно пренебречь, для расчета применяют
прямоугольную диаграмму в координатах х'—у'.
Количество первичного растворителя А (в кг или кг/с) в
исходной смеси:
О a ~Gf
ЮО — д:
F
100
(8.8)
или
* Значения индексов: F—исходная смесь; S — вторичный растворитель
экстрагент; R — рафинат; Е — экстракт.
^^-ад
Xj'^R ^2 **/
OCq —JCfe f\
Рис. 8 7. Жидкостная экстракция в перекрестном токе.
366
Количество вторичного растворителя Сп (в кг или кг/с) в
экстракте:
г 100 — д9
GgnE °8 100 ' (8'9>
Уравнение рабочей линии n-й ступени:
у'п - - -^- к - *;-о+й. <*• jo
Угол наклона рабочей линии а характеризуется соотношением:
tga = G^/G9n. (8.1I)
Число ступеней изменения концентрации (число ступеней
экстрагирования) определяется числом рабочих линий на диаграмме
(рис. 8.7, б).
В случае частичной взаимной растворимости первичного
растворителя и экстрагента для расчетов пользуются треугольной
диаграммой (рис. 8.7, в).
Положение точки Мп, характеризующей общий состав смеси
на п-й ступени, определяется по правилу рычага из соотношения
потоков Cflln-i/Cstn-i.
Составы рафината хп и экстракта уп, выходящих с n-й ступени,
определяются концами хорды равновесия (Rn и Еп), проведенной
через точку Мп. Количества рафината и экстракта определяются
также по правилу рычага.
Необходимое число теоретических ступеней экстрагирования
определяется числом хорд равновесия EnRnJ вмещающихся при
построении на диаграмме до достижения заданного состава
рафината xR.
Состав и количество экстрактов или рафината после отгонки
растворителя определяются точкой пересечения луча,
проведенного через вершину треугольника С и фигуративную точку сырого
экстракта или рафината, со стороной АВ.
Порядок расчетов и графических построений см. в примерах
8.2 и 8.3.
8. Противоточная жидкостная экстракция.
Уравнение общего материального баланса n-ступенчатой
экстракционной установки (рис. 8.8, а):
GF + GS~GR + GE. (8.12)
Уравнение материального баланса по экстрагируемому
компоненту:
gfxf + °&8 = Gn*R + °еУе- <8-13)
В случае, когда взаимной растворимостью первичного
растворителя и экстрагента можно пренебречь, количество чистых
растворителей первичного GA и вторичного Gc по всем ступеням уста-
367
flf
fe-fitf
Gp'GRfi
1
J>$2
G*,1 ,
a
Рис* 8.8. Противоточная жидкостная экстракция»
новки будут одинаковыми. Тогда уравнение материального
баланса по экстрагируемому компоненту:
Уравнение рабочей линии:
Угол наклона рабочей линии а (рис. 8.8, б) определяется из
соотношения:
¦„ О a yh — y's /я ,А,
*ав^в"3?=3$-' (8Л6)
Необходимое число теоретических ступеней экстрагирования
определяется графически так же, как при абсорбции и
ректификации.
В случае расчета процесса с помощью треугольной диаграммы
(рис. 8,8, в) количества потоков выражаются положением точки
Mt характеризующей фиктивный (условный) общий состав смеси
в экстракционной установке, и определяются по правилу рычага
из соотношений
Gf -t- Gs = GR + Gb = Gm;
GF/Gs = MCfFM; GB/GR = MR/ME. (8.17)
Необходимое число теоретических ступеней экстрагирования
определяется числом хорд равновесия EnRni вмещающихся при
построении на диаграмме до достижения заданного состава рафи-
ната xR.
Точка Р, называемая полюсом экстрагирования, является
точкой пересечения прямых, проведенных через точки F и Et R и С,
Rn и Еп+и и служит для отыскания фигуративных точек
экстрактов на экстрактной ветви пограничной кривой *. Порядок
расчетов и графических построений см. в примере 8.4.
9. Противоточная жидкостная экстракция с возвратом **.
Общий материальный баланс экстракционной установки
(рис. 8.9, а):
(здесь и в дальнейшем принято, что потоки GSt0i Gs_x и Gs,n+1
представляют собой чистый растворитель С, а потоки Ge, G^ не
со дер жат р аствор ите ля).
Материальный баланс по экстрагируемому компоненту В:
* Полюс экстрагирования может находиться как справа, так и слева от
треугольника.
** В зависимости от условий может применяться возврат как одного, так
и обоих продуктов.
369
Минимальные коэффициенты возврата экстракта Re1gm и ра-
фината Rr определяются (рис. 8.9, б) точками пересечения
Ремш и Pr (полюсы экстрактной, или укрепляющей, и рафннат-
ной,или исчерпывающей, частей колонны) хорды равновесия ab,
проходящей при своем продолжении через точку F, с ординатами,
проведенными через фигуративные точки ?" и R':
(8.20)
Минимальным возвратам соответствует бесконечно большое
необходимое число ступеней экстрагирования. Рабочие
коэффициенты возврата:
Rr - Р#кмин - PrR/REu*v
(8.21)
где Р — коэффициент избытка возврата, всегда больший единицы.
Количества потоков и расход растворителя рассчитываются
путем последовательных вычислений:
С, , = С* z :
Qe-ge+ Gs~i = GH* + ze)\ (8-22>
^к, о = ReGe;
gr.o+ge-gbV + *e) = g'eV+*b)(1+Rs):
Gs* •= cT+t,°* (z* i - **>=G* (*+**) $*>¦ ~ ^); (8,23)
Ge, i = GSl о + (GR, 0 + Ge) и т. д.; (8.24)
Gs,«+ieG/Ai;
GK = G* + GS, „+i - GJj (I + 8b);
gK,„+i = *kGr=V?«(,+*k);
GC,*+i = №k ит* Д- <8-25>
Здесь Gct n+l — количество растворителя С в рафииате GRf n+j,
направляемом в смеситель.
Общее количество циркулирующего растворителя:
Необходимое число теоретических ступеней экстрагирования
определяется графически с помощью диаграмм Х^ Y—z, Z и X—Y
(рис. 8.9, б). Методика построения описана в примерах 8.10 и 8.11.
370
мии
Рнс. 8.0. Противоточная жидкостная экстракция с возвратом;
I ** гкетрактор; 2, 2* *** аппараты для отгонки растворителя; 3 «* смеситель,
10, Экстрагирование из твердого тела (выщелачивание) с
периодической сменой растворителя*.
Уравнения материальных балансов n-й ступени те же, что и
для жидкостной экстракции в перекрестном токе [рис. 8.10, а и
уравнения (8.6) и (8.7)].
* Схема процесса аналогична жидкостной экстракции в перекрестном токе
371
а
%,3
Ч5.П.
&
<97
'7*,<>7 .,.,'*
*«..
^,2
%»
<v
Vi
Уг
Уз
•
'Vn
°*
*я
Рис. 8*10. Экстрагирование из твердого гела с периодической сменой растворителя.
В случае если обработка производится чистым растворителем
С, степень «недоизвлечения» экстрагируемого вещества
(отношение количества экстрагируемого вещества в остатке к количеству
его в исходном материале) можно вычислить по формуле:
Gr, пхп I
<Р =
GFXF
<1+а1)(1+ая)<1+а.)...(1+а|)...(1+ап)
(8.27)
(8.28)
где at — G? {/0'^ t — отношение потоков: массы тделяемого раствора к массе
раствора, удерживаемого твердым веществам (можно использовать и отношение
объемов растворов); CU ^= Gn ;(1 —хЛ— м:хса компонентоБ В и С,
Если отношение потоков постоянно, т. е. аг = 0% = а3 — • • • =
= ап = const, то формула упрощается:
1
<р =
(l+a)
где пс — число ступеней экстрагирования.
Расчет с помощью треугольной диаграммы аналогичен расчету
для жидкостной экстракции в перекрестном токе (рис. 8.10, б).
11. Противоточное экстрагирование из твердого тела.
Уравнения материальных балансов те же, что и для противо-
точной жидкостной экстракции [рис. 8.11, а и уравнения (8.12) и
(8.13)].
В случае, если отношение потоков для всех ступеней, кроме
первой, постоянно, т. е. а% = а3 =...= а = const, ступень
недоизвлечения экстрагируемого компонента можно определить
по формуле:
Ф=.
1 _j_ Ql (1 + в + а2 + ... + а""1) —
Gsy8
GR, пХП
[1 + ах (1 + а + а2 + •. .а"~2)]
(8.29)
372
При применении чистого растворителя (ys — 0) это выражение
упрощается:
Ф = т 5 г"тг • (8.30)
Если, кроме того, поступающий твердый материал уже
содержит такое же количество раствора, как и между ступенями, т. е.
ах = а, получим:
Ф =
1
(8.31)
1 + а + а2 + ... + ап
Необходимое число теоретических ступеней экстрагирования
пс при постоянном отношении потоков а2 = а3 ~ ... = а = const
можно определить по формуле:
лс — 1 = lg
R
ys
Х1 — У2
lg
У% — У& _^ Ч — У2
X
-lg
R
XR-yS
к
ii
R
Ч%-Ув
(8.32)
Это число можно определить графически, так же как для
бинарной системы, на прямоугольной диаграмме в координатах у — х',
где х = y^
в
т. е. масса твердого нерастворимого вещества
в расчете не участвует. Уравнение линии равновесия в этом случае
у * = х'\ уравнения рабочих линий легко выводятся из
уравнений материальных балансов.
В общем случае расчет можно проводить с помощью
треугольной диаграммы (рис. 8.11, б) или прямоугольной диаграммы в
координатах X', V — z\ Z' (рис. 8.11, в). Методика расчета
аналогична расчету для противоточной жидкостной экстракции.
ft
Рис# 8»|t. Противоточное экстрагирование из твердого тева.
373
ПРИМЕРЫ
Пример 8.1. Построить треугольную диаграмму фазового
равновесия для системы вода—ацетон—хлорбензол. Необходимые
данные взять из табл. 8.1. Определить по диаграмме: а)
содержание воды и хлорбензола в водном слое с концентрацией ацетона
45% (масс); б) состав равновесного с ним слоя хлорбензола; в)
количество ацетона, при добавлении которого перестанет
расслаиваться смесь 0,П кг хлорбензола и 0,09 кг воды.
Решение. Вычерчиваем равносторонний треугольник
(рис. 8.12). Находим на стороне АС точки / и /', соответствующие
первой строке табл. 8.1. Внутри треугольника находим точки 2 и
2', соответствующие второй строке таблицы, и соединяем их
отрезком прямой 2—2'. При отыскании точек внутри треугольника
сначала откладываем на стороне АВ содержание ацетона в
растворе, а затем параллельно стороне АС—содержание хлорбензола.
После нахождения всех точек соединяем их плавной кривой.
а) Через точку а на стороне АВ проводим прямую аЪ
параллельно стороне АС. Отрезок аЪ является геометрическим местом
точек, характеризующих смеси с содержанием ацетона 45% (масс).
На пересечении отрезка аЪ с левой ветвью бинодальной кривой
находим точку с, характеризующую состав водного слоя: 52,8%
(масс.) воды, 2,2% (масс.) хлорбензола.
б) Для определения состава сосуществующей фазы через
точки 2, 2', 3t 3\ ..., 7, 7' проводим прямые, параллельные
боковым сторонам треугольника, и точки их пересечения 2", 3", ..., 7"
соединяем плавной кривой. Затем через точку с проводим прямую,
параллельную стороне ВС, до пересечения с соединительной
кривой в точке с", а из точки с" — прямую, параллельную стороне АВ,
до пересечения с бинодальной кривой. Точка с' является искомой.
Состав слоя: 54,9% (масс.) ацетона, 4,3% (масс.) воды, 40,8%
(масс.) хлорбензола.
Таблица 8.1
Равновесные составы сосуществующих фаз [в % (масс.)]
вода
Водный слой
ацетон
хлорбензол
вода
Слой хлорбензола
ацетон
хлорбензол
99,89
89,79
79,69
69,42
58,64
46,28
27,41
25,66
0
10
20
30
40
50
60
60,58
0,11
0,21
0,31
0,58
1,36
3,72
12,59
13,76
0,18
0,49
0,79
1,72
3,05
7,24
22,85
25,66
0
10,79
22,23
37,48
49,44
59,19
61,07
60,58
99,82
88,72
76,98
60,80
47,51
33,57
15,08
13,76
374
Ацетон
В
Хлорбензол
Рис. 8.12 к примеру 8.1).
в) Находим на стороне АС точку dy характеризующую общий
состав заданной смеси 0 09 L_0 и 100 = 45% (масс.) воды и 55%
(масс.) хлорбензола]. При добавлении к этой смеси ацетона
общий состав ее будет изменяться по линии dB, на пересечении
которой с бинодальной кривой найдем искомую точку е. Необходимое
количество ацетона найдем из соотношения отрезков Be и ed:
Gd/GB = Be/ed; GB = (0,09 + 0,11) 53,5/33 = 0,325 кг.
Пример 8.2. Ацетон экстрагируется хлорбензолом из 50%
водного раствора. Остаток должен содержать не более 2% (масс.)
ацетона. Пользуясь диаграммой, построенной в предыдущем при-
375
мере, определить количество растворителя, необходимое для
обработки 100 кг исходной смеси, если экстрагирование
производится в одну ступень. Определить также выход рафината, выход
и состав экстракта после удаления из него растворителя.
Решение. Через точку R (рис. 8.13), характеризующую
состав остатка, проводим хорду равновесия RE* Точку F,
характеризующую состав исходной смеси, соединяем с вершиной
треугольника С. Точка пересечения М линий FC и RE определяет
состав смеси исходного раствора с растворителем, необходимый для
получения рафината заданного состава. Требуемое количество
растворителя находим из соотношения
Gs/Gf = FM/MC; Gs = 100-81,5/5 = 1630 кг.
Масса полученной смеси:
Gm= 1630 + 100= 1730 кг.
Количество экстракта находим из соотношения
Ge/Gm = RM/RE; GE = 1730-94,4/97 «= 1682 кг.
Масса рафината:
GR = GM — GE = 1730 — 1682 = 48 кг.
Количество экстракта после удаления из него растворителя
G'R &GE — Gs= 1682—1630 = 52 кг,
так как растворимостью хлорбензола в остатке в данном случае
можно пренебречь.
Состав экстракта после удаления из него растворителя
определяется точкой пересечения Е' стороны АВ с лучом, проведенным
из вершины С через точку Е: содержание ацетона 95,5% (масс),
воды 4,5% (масс).
Пример 8.3. В условиях предыдущего примера определить
необходимое количество растворителя, состав и выход продуктов и
число ступеней экстрагирования, если на каждой ступени
экстрагирование производится свежим растворителем в количестве,
равном массе обрабатываемой смеси.
Решение. При смешении равных количеств исходного
раствора и хлорбензола положение точки Мх (рис 8.14),
характеризующей общий состав смеси, определится из соотношения
FMi/MxC = 100/100 = 1; FM± = MtC.
Через точку Мх проводим хорду равновесия RXEX. Точки Rx и
Ех характеризуют составы и количества рафината и экстракта
первой ступени. Рафинат первой ступени отделяется и вновь
смешивается с равным ему по массе количеством растворителя.
Положение точки М2, определяющей состав смеси во второй ступени,
находится из соотношения
GRi JGs = MUC/R±MU = 1; RtMu = МйС.
376
Рис. 8.13 (к примеру 8.2),
Рис. ВЛ4 (к примеру 8.3)
Через точку М2 вновь проводим хорду равновесия и т. д.
Построение продолжаем до тех пор, пока не будет достигнут
требуемый состав рафината. В настоящем примере для этого необходимы
четыре ступени экстрагирования. Определяем количества
рафината и растворителя по ступеням:
Gs.*=GRli-i; Gr.«=- 2-63,5.37,5/86,5 = 55,1 кг;
Gs, 3 = 55,1 кг;
GSi i « Gfl( 0 = Gf « 100 кг; GRiS «2.55,1.44/93 = 52,1 кг;
GRi i = 2 -100 • 23,5/74 = 63,5 кг; G8t 4 = 52,1 кг;
Gs, 2 = 63,5 кг; GR.4 = 2-52,1-45/96 = 49,0 кг.
Общее количество растворителя:
Gs«EGSiI-« 100 +63,5 +55,1 +52,1 = 270,8 кг.
Общее количество экстракта:
Ge^Gf + Gs — Gr, , = 100 + 270,8 — 49,0 = 321,8 кг.
После удаления растворителя останется:
G'E =G^ — GS =321,8-270,8 = 51 кг.
Средний состав экстракта ~96% (масс.) ацетона.
Пример 8.4. В условиях примера 8.2 определить состав и
выход продуктов, а также число теоретических ступеней
экстрагирования, если экстракция производится противотоком при
соотношении потоков 1:1.
Решение. Через точку R (рис. 8.15), характеризующую
состав рафината, и точку М, определяющую общий фиктивный
состав смеси исходного раствора со всем растворителем (так как
GF : Gs — 1, FM ~ МС), проводим прямую до пересечения с
правой ветвью бинодальной кривой в точке Е, соответствующей
составу экстракта. При продолжении отрезков FE и RC они
пересекаются в точке Р (полюсе); Полюс является общей точкой
пересечения всех лучей, проходящих через точки, характеризующие
состав рафината на любой ступени и состав экстракта на
последующей ступени. Линии /—/', 2~2\ ..,, 4—4' являются хордами
равновесия; число их определяет число теоретических ступеней
экстракции. Таким образом, число ступеней определяется
графически, путем последовательного проведения линий: FC, RME ()'),
FEP, RCP, t'—l, 1—Р, 2'—2, 2—Р, Зг—3, 3—Р, 4'—4 (R). В
данном случае пс = 4.
Количество экстракта находим из соотношения;
Ge/Gm = GeI(Gf + Gs) = RM/RE;
GE = (100 + 100) 64/85 = 150,5 кг.
378
Рис, 8.1й (к примеру 8,4),
Таблица 8.2
Аарактериетика процесса
Перекрестный ток
Противоток
Число ступеней
Расход растворителя, кг
Выход рафииата, кг
Выход экстракта, кг
Выход экстракта после удаления
растворителя, кг
Содержание ацетона в экстракте после
удаления растворителя, % (масс.)
1
1630
48
1682
52
95,5
4
270,8
49
321,8
51
96
4
100
49,5
150,5
50,5
97,5
После удаления из экстракта растворителя масса его
составляет:
G'E*=* 150,5—100 = 50,5 кг.
Состав конечного экстракта характеризуется точкой ?":
ацетона 97,5% (масс); воды 2,5% (масс).
Количество рафината:
0'R^GR^GM—GE^ 200 — 150,5 = 49,5 кг.
Результаты примеров 8.2, 8.3 и 8.4 сведены для сравнения
в табл. 8.2,
Исходные данные: смесь состоит из воды (А), ацетона (В) и
хлорбензола (С); xF = 50% (масс); xR =* 2% (масс); у8 — 0;
GF = 100 кг.
Из таблицы следует, что противоточная экстракция имеет
в данном случае большие преимущества (меньший расход
растворителя, большая чистота экстракта и др.).
Пример 8.5. Оценить приблизительно целесообразность
использования экстракции в примере 8.4, если удаление
растворителя из экстракта производится непрерывной ректификацией;
допустимое содержание хлорбензола в дистилляте 10% (масс),
ацетона в кубовом остатке 1 % (масс) Коэффициент избытка флегмы
принять в обоих случаях равным 2.
Решение. Экстракт, поступающий на перегонку, считаем
для упрощения бинарной смесью. Минимальное число флегмы и
число теоретических тарелок определяем по равновесным данным
обычными методами (расчет не приводится). Полученные данные
сводим в табл. 8.3.
Из сопоставления результатов делаем вывод, что экстракцию
в данном случае использовать целесообразно, но экономия, если
учесть стоимость оборудования и эксплуатационные расходы,
будет незначительной. Для окончательного решения вопроса
необходим более подробный анализ.
380
Пример 8,6, Бинарная смесь 1,4-диоксана g водой не может
быть разделена ректификацией при атмосферном давлении
вследствие образования нераздельно кипящей смеси. Для извлечения
диоксана используется экстракция его из водного раствора
бензолом с последующей ректификацией смеси диоксан—бензол.
Определить конечное содержание диоксана в воде, если 150 кг
20% раствора диоксана обрабатываются последовательно пятью
порциями бензола по 100 кг каждая. В свежем растворителе
содержится 2% (масс.) диоксана. На каждой ступени
экстрагирования достигается равновесие. Взаимной растворимостью воды и
бензола пренебречь.
Данные по растворимости диоксана в воде и бензоле при 25 °С:
Содержание диоксана в воде, % (масс,)
6,1
5,2
18,9
22,5
25,2
32,0
Равновесное содержание диоксана в бензоле, % (масс.)
Решение. Переводим массовые проценты в массовые
относительные доли.
Содержание диоксана в воде:
х кг диоксана
100 —х кг воды
Равновесное содержание диоксана в бензоле:
у кг диоксана
У
100 — г/ кг бензола
При этом получаем:
х\ кг диоксаиа/кг воды
(/', кг диоксаиа/кг бензола
0,0537
0,0548
0,233 0,337
0,291 0,471
Таблица 8.3
Характеристика процесса
Ректификация смеси
ацетои-воДа
Экстракция
ацетона
и последующая
ректификация
смеси ацетои-
хлообензол
Содержание ацетона в исходной смеси, %:
масс.
мол.
Содержание ацетона в дистилляте, %:
масс.
мол.
Содержание ацетона в кубовом остатке, %*
масс.
мол.
Число флегмы:
*?мнн
R
Число теоретических тарелок
Отношение расходов теплоты на ректификацию
Яг '</?!+ 1)
Я% г(/?а+1)
50
23,7
97,5
92,4
2
0,63
0,38
0,76
10
0,76+ 1
0,32 + 1
32,5
47,8
90
94,5
1
1,9
0,16
0,32
7
= 1,33
381
Содержание диоксана в исходной смеси:
20 л пс кг диоксана
Хр = -ттт^ ™ = 0,25
¦F— 100 — 20 ' кг воды *
Содержание диоксана в свежем растворителе:
,/ — 2 == 0 022 "* диоксана
Vs— loo — 20 ' кг бензола "
Количество воды GA в исходной смеси GF можно определить
по формуле:
г г {00~xf 150(100-20)
GA = GF ш = ioo = 120 кг.
Количество бензола Gc, приходящееся на Gs = 100 кг свежего
растворителя, можно найти так:
г г т~Ув 100(100-2)
gg = gs—шо— = т ==98кг*
Тангенс угла наклона рабочих линий [формула (8.16)]
tg<* = GAIGc = i 20/98 = 1,225.
На рис. 8.16 через точку / с координатами x'f и y's проюдим
с наклоном 1,225 : 1 прямую до пересечения с линией равновесия.
Координаты точки пересечения характеризуют составы экстракта
у[ и рафината х\ первой ступени. Через точку 2 с координатами
х\ и y's вновь проводим прямую с наклоном 1,225 : 1 до
пересечения с равновесной кривой и т. д. Содержание рафината на
последней ступени:
ХЯ ^ хъ я= 0,022 кг диоксана/кг воды
ИЛИ
0,022-100 01,.. .
xR » хъ = } , 0 Q22 = 2,15 % (масс.) диоксана.
Пример 8.7. В противоточном экстракторе непрерывного
действия обрабатываются чистым бензолом сточные фенольные воды
с целью очистки воды и извлечения фенола. Определить
необходимое количество растворителя и число теоретических ступеней
экстрагирования, если в 1 ч обрабатывается 10 м3 воды. Содержание
фенола в воде: начальное 8 кг/м3, конечное 0,5 кг/м3, конечное
содержание фенола в бензоле 25 кг/м3, температура жидкостей 25 °С.
Решение. Данные по равновесию берем из «Справочника
химика» [13]:
Содержание фенола в воде съ г-экв/л 0,0272 0,1013 0,3660
Равновесное содержание фенола в бензоле с2, г-экв/л 0,062 0,279 2,978
Пересчитываем концентрации в кг/м3: х ж 15,686^; у' &
ж 15,686с2. При этом получаем:
Содержание фенола в воде х\ кг/м3 0,426 1,59 5,74
Равновесное содержание фенола в бензоле (/', кг/м3 0,974 4,37 46,7
382
о
Ч
и
а
4
я
ы
^в»г* уИЯ—1—i
0,4
^
Рис, 8.16 (к примеру 8.6).
г кгдиоксана
кг воды
Необходимое количество бензола найдем из уравнения
материального баланса:
^=3600 25~-°05 - 0^083 мз/с;
Gs = 0,00083-879 = 0,73 кг/с.
Число теоретических ступеней находим графически: наносим
на диаграмму равновесия, построенную по приведенным данным
(рис. 8.17), рабочую линию, проходящую через точки с
координатами Хн, у'к и Хк, t/н, и вписываем между рабочей линией и
равновесной кривой ступени изменения концентрации. В данном случае
требуется семь ступеней.
Пример 8.8. По равновесным составам сосуществующих фаз
[в % (масс.)], приведенным в табл. 8.4, построить фазовые
диаграммы равновесия для системы вода (А) — уксусная кислота
(В) — диэтиловый эфир (С) при 25 °С в координатах: а) X, Y—zt
Z; б) X—Y.
383
О К 1
х
3 f 4 5
t кг ФЕНОла
8
М3 ВОДЫ
Рис. 8.17 (к примеру 8.7)
Решение. Проведем пересчет концентраций
(8.4)]:
[формулы
х =
к =
в
кг уксусной кислоты
хл + xR кг (вода -}- уксусная кислота) '
кг уксусной кислоты
1А ' ~В
Ув
г —
Z =
уд -j- yB кг (вода -J- уксусная кислота) '
хс кг диэтилового эфира
ха ~^~ хв кг (вода "+- УксУсная кислота) '
Ус
кг диэтилового эфира
уА -\-Ув кг (вода -f- уксусная кислота)
Полученные данные сводим в табл. 8.5.
Таблица 8.4
Водный слой
вода
уксусная
кислота
диэтнловый
эфир
Эфирный елой
вода
уксусная
кислота
диэтиловый
эфир
93,3
88,0
84,0
78,2
72,1
65,0
55,7
0
5,1
8,8
13,8
18,4
23,1
27,9
6,7
6,9
7,2
8,0
9,5
11,9
16,4
2,3
3,6
5,0
7,2
10,4
15,1
23,6
0
3,8
7,3
12,5
18,1
23,6
28.7
97,7
92,6
87,7
80,3
71,5
61,3
47,7
384
Таблица 8.5
Водный слой
X
0
0,055
0,095
0,150
0,204
0,263
0,333
Z
0,072
0,074
0,078
0,087
0,105
0,135
0,196
Эфирный слой
Y
0
0,514
0,593
0,635
0,635
0,610
0,549
z
42,55
12,53
7,14
4,07
2,51
1,58
0,913
Построение диаграмм ведем обычным порядком (рис. 8.18).
На диаграмму X, Y—г, Z хорд равновесия не наносим — для
отыскания их при расчетах служит вспомогательная диаграмма X—Y.
Пример 8.9. Определить наибольшую достижимую
концентрацию экстракта для системы вода—уксусная кислота—диэтиловый
эфир при 25 °С, если экстракция ведется в противотоке: а) для
15%-ной исходной смеси; б) для 5%-ной исходной смеси (по
кислоте) *.
Решение. По диаграмме X—Y (рис. 8.18) находим, что
с исходной смесью X = 0,15 находится в равновесии экстракт
с содержанием уксусной кислоты Y — 0,635; с исходной смесью
X = 0,05 равновесен экстракт с Y = 0,46. Таким образом, в
первом случае максимальная концентрация уксусной кислоты в
экстракте (после отгонки растворителя) составит 63,5% (масс), во
втором случае — 46% (масс); в реальных условиях наибольшие
достижимые концентрации будут несколько меньше.
Пример 8.10. Рассчитать необходимое число ступеней и
количество растворителя для экстрагирования уксусной кислоты из
водного раствора диэтиловым эфиром (t = 25 °С), если
концентрация исходной смеси 5% (масс), а концентрация экстракта после
отгонки растворителя 60% (масс). В 1 ч перерабатывается 1000 кг
исходного раствора; эфир из рафината и экстракта отгоняется
полностью; содержание кислоты в остатке не более 1% (масс).
Решение. Так как заданной концентрации экстракта
обычным противоточным экстрагированием достичь невозможно (см.
пример 8.9), применяем процесс с возвратом части экстракта
(рис 8.19).
Определяем минимальный коэффициент возврата экстракта.
Проводим хорду равновесия через точку F (рис. 8.18), характери-
* Экстракцию уксусной кислоты из воды целесообразно проводить прн
не слишком больших концентрациях, так как температура ее кипения 118,1 С
и для выделения ректификацией небольшого количества кислоты придется
испарять значительное количество воды, равное (G/r — G^) (R + 1), где Gw — масса
концентрированной кислоты; R — число флегмы,
13
Павлов К. Ф. н др. 385
24?r
Рис. 8.18 (к примерам 8.8 8.9 и
8.10).
зующую исходную смесь
(XF - 5/100 = 0,05; *F =
= 0), до пересечения с
вертикалью, проведенной
через точку Е (Хя=60/100 =
= 0,6; ZE = 0),
соответствующую конечному
экстракту.
Так как в нашем
случае растворитель
удаляется полностью, имеем
[формула (8.20)]:
Re
G
R, о
Ре
мин^1
мин
мин
У у
^Е, 1 ?П, О
19 — 6,7
6,7—0
= 1,835.
Принимаем
коэффициент избытка возврата
р = 3:
/??•« 1,835-3 = 5,51.
Определяем координату
полюса укрепляющей
части установки ZPjE:
5,51 ~ 6,7-0 *
2Р,д«43,6.
Через точки РЕ и F
проводим прямую до
пересечения с вертикалью,
проведенной через точку R
, (XR - 1/93,3^0,01; гд =
* - 6,7/93,3 = 0,072),
характеризующую состав
конечного рафината (до
удаления растворителя). Полученная точка является полюсом
исчерпывающей части установки.
Далее определяем число ступеней экстрагирования,
последовательно проводя хорды равновесия и лучи и подсчитывая число
386
о
V
0,2 0,3 0,4 Ofi 0,6 0J
X
Рис. а. 19 (и примеру 8.10).
хорд. Порядок построения: ExRl9 RiPe> E%R2, PRR%EB и т. д. до
получения заданной концентрации рафината.
Для построения хорд равновесия пользуемся вспомогательной
диаграммой X—У, позволяющей по заданному значению X
определять равновесную концентрацию Y (или наоборот). В данном
случае требуется шесть ступеней экстрагирования. Питание
подается на вторую ступень. На рис. 8.18 показано, как определять
число ступеней по диаграмме X—Y (следует учитывать, что
рабочие линии в этом случае не являются прямыми).
Величины потоков рассчитываем из уравнений материальных
балансов.
Баланс компонентов А и В:
GF = GH + G?-
Баланс компонента В:
xfgf =* xrg'k + xege.
Решаем систему уравнений:
1000 = G^ + GJ,;
0,05-1000 = 0,01G^ + 0,6%
Масса экстракта: Gh = Ge — 68 кг. Масса рафината: 0% =
= 932 кг. Отсюда
GR = G'R (1 + гд) = 932 (1 + 0,072) = 1000 кг.
Масса эфира в рафинате: 1000 — 932 =68 кг. Масса
возвращаемого экстракта: GR}Q = GERE = 68*5,51 ==375 кг. Масса
удаляемого в отделителе растворителя: G$ о = (Gs + GR 0)ZSt г =
= (68 + 375) 6,7 = 2970 кг.
13* 387
Общий баланс установки:
Of + Os — Ge + ^s, 0 + Gr;
1000 + Gs = 68 + 2970 + 1000,
откуда необходимое количество растворителя: Gs = 3038 кг.
Пример 8.11. В противоточном экстракторе непрерывного
действия экстрагируется стирол из 38% раствора его в этилбензоле
диэтиленгликолем. Производительность экстрактора по исходной
смеси 100 кг/ч. Так как обычное противоточное экстрагирование
требуемой чистоты разделения дать не может, применяется
экстрагирование с возвратом части экстракта и рафината. Экстракт и
рафинат содержат соответственно 95 и 3% (масс.) стирола после
отгонки от растворителя. Определить необходимое количество
растворителя, состав и количество экстракта, рафината и
возвратов, а также необходимое число теоретических ступеней
экстрагирования, приняв, что возврат экстракта в 1,5 раза больше
минимального.
Таблица 8.6
Продукт
Исходная смесь
Растворитель,
направляемый в смеситель
Сырой экстракт
Экстракт-продукт
Экстракт-возврат
Рафинат-продукт
Рафинат-возврат
Раствор из смесителя
Добавляемый
растворитель
Растворитель после
отгонки экстракта
Полюс укрепляющей
части:
минимальный
рабочий
Полюс исчерпывающей
части:
минимальный
рабочий
Обозначение
фигуративной
ТОЧКИ
F
S*
Ег
Е
Ro
R
Rn+t
E-n+i
—-
1
S0*
мин
Ре
Р
^мин
Pr
Обозначение
потока
Gf
G8
Ge>i
Ge
Or,0
Or
Gr, n+i
Ge, п+г
AGs
Gs, о
—
—
—
—
Состав (координаты)
Х.(У)
кг В
кг (А + В)
0,38
—
0,95
0,95
0,95
0,03
0,03
0,03
—
—
0,95
0,95
0,03
0,03
z(Z),
кг С
кг (А + В)
0
со
2,95
Q **
Q **
0,007 3*
0,007 3*
8,65
оо
ОО
3,3
43,5
—20
—26,2
Расход^
кг/ч
100
1805,5
2418
38
575
62,5
190
1995,5
0,5 4*
1805
—
—
—_
——
* На диаграмме фигуративная точка отсутствует.
** Очистка производится полиостью в одной колонне.
й* Очистка нецелесообразна.
4* Имеет место унос растворителя с рафинатом-продуктом.
388
Рис* 8.20 (к примеру 8.11).
Решение. После
составления схемы процесса * и
построения фазовых диаграмм, X, Y — г,
Z и X — Y (равновесные данные
здесь не приводятся) определяем
состав продуктов и наносим на
диаграмму (рис. 8.20)
соответствующие им точки. Данные по
мере их нахождения сводим в
табл. 8.6. Так как рафинат на
любом участке рафинатной кривой
содержит весьма малые количества
растворителя, установка
рафинатной и второй экстрактной
отгонной колонны в данном случае
нецелесообразна.
Координаты полюсов
укрепляющей и исчерпывающей частей
экстракционной колонны,
соответствующие минимальным
возвратам, определяем, проводя через
точку F прямую, совпадающую с
коннодой, до пересечения с
вертикалями, проходящими через
точки Е и R. Число ступеней
экстрагирования будет при этом
бесконечно большим.
Минимальный возврат:
GE ZE, 1~ZE,X
33 ~2'95 =10,35;
2,95 — 0
Gr, n+i R Р>ймин
GA ZE, n+2 - ZR
0,007 + 20
""8,65 —0,007" *
При полном возврате экстракта
и рафината в экстрактор!
* См. рис. 8.9, а. Аппарат для
отгонки растворителя, отмеченный т схеме
звездочкой, в данную установку не входит.
т. е. лучи превращаются в параллельные вертикальные прямые.
Этому соответствует минимальное число ступеней
экстрагирования.
Находим координаты полюсов при |3 =1,5:
Z2,95~2095 в 10'35* * '5; 1р> в ~ 43'53-
Количество экстракта по правилу рычага:
XF~XR\GF
| Хе— Xr 1 »
GR Ge
GF (XF - XR) 100 (0,38-0,03)
0? _ ______ _ 0j95_003 - ^8,0 кг/ч.
Возврат экстракта:
Gr, о — 10,35-2-38,0 _ 575 кг/ч.
Количество рафината (с уносимым растворителем):
AGS + GR _ (GF - GE) (1 + гй) = (100 - 38,0) (1 + 0,007) _. 62,5 кг/ч.
Возврат рафината:
ZP. ?w„„ — ;:Я. В 33 -f 26,2
== oz.o —r-—- ——-
мин
?я, п+1 = GR —V= -— «= 62,5 __-^^_ w 190 кг/ч.
Количество циркулирующего в течение 1 ч растворителя:
Количество добавляемого при этом растворителя (равное
потерям с рафинатом-продуктом):
AGS *= GR2R « 62-0,007 « 0,5 кг/ч.
Производительность по сырому экстракту (перерабатываемому
отгонной колонной):
GE% i=GRyQ + GE-{~Gsto-= 575 + 38 + 1805 = 2418 кг/ч.
Расход раствора, выходящего из смесителя:
Ge, п+1 = GS + GR, n+J - 1805,5 + 190 = 1995,5 кг/ч.
Расход растворителя, подаваемого в смеситель:
Gs == GSt 0 + AGs « 1805,5 кг/ч.
Необходимое число ступеней экстрагирования ввиду слияния
лучей и коннод удобнее определять по диаграмме X — Y
Проводим из рабочих полюсов ряд лучей до пересечения с
пограничными кривыми (точки Ent Rn, ... , Ет, Rm, ...), а на диаграмме
X — Y находим точки с координатами Х%, Y\y ... , Хе, Y%, ...
390
После проведения через эти точки плавной кривой (являющейся
рабочей линией) вписываем между рабочей и равновесной
линиями ступени и подсчитываем их число. В данном случае
необходимы 23 ступени экстрагирования; исходная смесь подается на
12-ю сверху ступень.
Пример 8.12. В вертикальном отстойнике с коническим дном
находятся осадок и 7 м3 раствора, содержащего 2 т NaOH. После
отстаивания сливается прозрачная часть в количестве 6 м3,
отстойник доливается чистой водой, и суспензия перемешивается.
После повторного отстаивания снова сливается 6 м3 чистого
раствора. Три слитых с осадка раствора смешиваются и направляются
на выпарку. Определить: а) количество NaOH, остающееся в осадке
(шламе); б) процент извлечения NaOH; в) процентное содержание
NaOH в растворе, поступающем на выпарку.
Решение, а) В отстойнике происходит трехкратное
промывание осадка с отношением объемов удаляемого и удерживаемого
растворов а = 6 : 1 =6. Согласно формуле (8.28), в шламе после
трехкратного промывания остается:
1 1 \
(1 + я)3 ~~ 73 343
от первоначального количества NaOH, или
^NaOH = 2000 = 5,8 кг.
б) Извлекается NaOH:
2000—5,8
2000
100 = 99,7%.
По данным табл. LIV экстрагированное вещество при
трехкратном промывании шестикратным количеством растворителя
составляет 99,71 %.
в) Количество раствора:
Кр = 6.3= 18 м3.
Содержание в нем NaOH:
GNa0H = 2000 — 5,8 = 1994,2 кг,
или
1994 2
18 000 + 1994,2 100~10°/о-
Пример 8.13. С целью извлечения меди колчеданные огарки
подвергаются хлорирующему обжигу с поваренной солью. В
обожженной, массе медь содержится в виде СиС12. Содержание
хлорида меди составляет 11%. Обожженный продукт подвергается
выщелачиванию в противоточной батарее подкисленной водой,
получающейся от промывки отходящих газов. Инертная твердая
391
масса удерживает 2 кг воды на 1 кг твердого вещества. На
каждой ступени достигается равновесие. Сколько ступеней необходимо
иметь в батарее для получения раствора, содержащего 12%
(масс.) СиС12, и извлечения 98% Си из обожженного продукта?
Решение. Поскольку твердая фаза при движении со
ступени на ступень удерживает постоянное количество воды (кроме
первой ступени, так как в эту ступень поступает сухой обожженный
продукт, который уходит из нее, удерживая 2 кг воды на 1 кг
твердой фазы), для определения числа ступеней в установке можно
воспользоваться формулой (8.32).
Примем за основу расчета 100 кг сухого твердого остатка,
свободного от меди, и вычислим количества продуктов и
концентрации.
С обожженной массой поступает CuCl2i
100 -ii-= 12,36 кг.
С остатком уходит: 12,36 (100 — 98)/100 = 0,25 кг. С
экстрактом уходит: 12,36-98/100-12,11 кг.
Определим количество поступающей в установку
подкисленной воды Gs, учитывая, что 200 кг воды уносит твердый остаток,
а остальное уходит с экстрактом:
(Gs —200) 12/88= 12,11,
откуда Gs = 288,8 кг.
Содержание СиС12 в экстракте (в кг на 100 кг воды);
Такое же содержание будет иметь раствор, удерживаемый
твердым веществом при переходе из первой ступени во вторую:
х\ ~ УЕ~ 13,64.
Содержание СиС12 в растворе, уходящем с твердым остатком!
^-~f-ЮО-0,125.
Поступающая в батарею подкисленная вода не содержит
солей меди и у8 — 0.
Содержание хлорида меди у2 в верхнем потоке, переходящем
из второй ступени в первую, определим по балансу СиС12 в
первой ступени. Количество растворителя в верхнем потоке
составляет 288,8 кг. В первую ступень поступает на 100 кг инертной
сухой массы 12,36 кг СиС12 и Л кг с 288,8 кг растворителя из
второй ступени; всего (12,36 + А) кг. Уходит из первой ступени!
с экстрактом 12,11 кг, с раствором нижнего потока - ' ¦ 200 =
= 27,28 кг; всего 12,11 +27,28 =39,39 кг.
392
Баланс первой ступени по СиС12:
12,36 + Л =39,39 кг,
откуда
Л = 39,39 — 12,36 = 27,03 кг.
Содержание СиС12 в верхнем потоке (в кг на 100 кг воды):
у = W 10°в 9'36'
Число ступеней (без первой):
к
\е *'"
g х ¦
1сГ
'& .,
~Уг
-у8
~XR
13,64 — 9,36
«с - 1 = ?—^ « 13,64Q-Q%5Q e 10 СтУпеней<
У<ь~У
s
9,36 — 0
а всего /?с *= 10 + 1 = 11 ступеней.
Пример 8.14. Едкий натр получается по реакции
Na2C03 + СаО + Н20 = СаС03 + 2NaOH.
Продукты реакции поступают в первую ступень непрерывной
противоточной трехступенчатой батареи с содержанием воды 50%
от массы шлама (СаС03). В дальнейшем, при переходе со
ступени на ступень и выходе из батареи, шлам удерживает воды
в 1,5 раза больше собственной массы. Желательно добиться 98%-го
извлечения NaOH. Определить расход воды (на 100 кг сухого
шлама) и концентрации растворов на каждой ступени.
Решение. Для составления материальных балансов по
каждой ступени нет достаточного количества данных.
По табл. LV для достижения 97,5%-го извлечения продукта
при трехступенчатом непрерывном экстрагировании отношение
количеств растворителя и удерживаемого раствора составляет 3.
Остановимся на этих цифрах и составим последовательно балансы,
начиная с третьей ступени. Расчет будем вести на 100 кг сухого
СаСО».
На 100 кг СаС03 в первую ступень вводится 80 кг NaOH. Из
этого количества переходит в экстракт 97 5%, или 80-97,5/100 =
= 78 кг.
Теряется с остаточным раствором: 80 — 78 =2 кг.
100 кг шлама удерживают воды: 100-1,5 — 150 кг.
Содержание NaOH в остаточном растворе (в кг на 1 кг чистого
раствора):
jc^ = 2/150 = 0,0133.
В систему через третью ступень вводится воды в качестве
растворителя: 150-3 =450 кг.
Таким образом, в верхнем потоке по установке идет 450 кг
воды, в нижнем вместе с твердой фазой 150 кг.
393
Содержание NaOH в растворителе: ys = 0. Содержание NaOH
в верхнем потоке, переходящем из третьей ступени во вторую:
03 = ^ = 0,0133 кг/кг.
Неизвестно содержание NaOH в нижнем потоке х2.
Определим его по балансу NaOH в третьей ступени:
450г/5 + 150*2 = 150л:я + 45%»
450-0 + 1504 — 150-0,0133 + 450-0,0133;
1504 = 8> х2 =* 8/150 = 0,0533 кг/кг.
Содержание NaOH в верхнем потоке, поступающем из второй
ступени в первую: у-2 = х'2 = 0,0533 кг/кг.
Неизвестно лишь содержание NaOH в нижнем потоке,
поступающем из первой ступени. Это содержание х\ определяется из
баланса второй ступени:
450г/з + 150*; = 450г/2 + 1504;
450-0,0133+ 1504 =450-0,0533+ 150-0,0533;
1504 + 6 = 24 + 8;
4 = (32— 6)/150 = 26/150 = 0,1733 кг/кг.
Для определения содержания NaOH в экстракте в первой
ступени необходимо Сч>ставить водный баланс этой ступени,
обозначив через А количество воды, уходящее с экстрактом:
Л + 150 = 450 + 50; Л = 350 кг.
Экстракт содержит 78 кг NaOH. Следовательно, содержание
NaOH в экстракте:
Уе= э5о7+78 100==18»2% (масс-)
Пример 8.15. Маслоэкстракциоиная установка перерабатывает
1 т/ч «лепестка» (раздавленные и частично обезжиренные семена
подсолнуха) с содержанием масла 28% и бензина 2,5%.
Поступающий в установку в качестве растворителя регенерированный
бензин содержит 1,5% масла. Количество растворителя,
поступающего в установку, составляет 50% от массы «лепестка». По
опытным данным количество раствора, удерживаемого твердой
фазой, зависит от содержания в нем масла (табл. 8.7).
Твердый остаток после экстрагирования содержит 5% масла.
Определить: 1) количество экстракта и содержание в нем
масла; 2) количество остаточного раствора, удерживаемого
твердой фазой (шротом) и содержание в нем масла; 3) число
ступеней экстрагирования.
Решение. Задача решается графическим методом в пря-
моуюльной системе координат X'—г' (рис. 8.21).
394
Таблица 8.7
Содержание масла,
кг/кг раствора
Количество
удерживаемого
раствора, кг/кг
твердого вещества
0.0 0,500
0.1 0,505
0,2 0,515
0,3 0,530
Содержание масла,
кг/кг раствора
Количество
удерживаемого
раствора, кг/кг
твердого вещества
0,4 0,550
0,5 0,571
0,6 0,595
0,7 0,620
Данные первой графы табл, 8.7 равны отношению X' =
Данные второй графы — массовые количества раствора на
единицу массы твердого вещества — надо пересчитать на обратные
величины; тогда они будут выражать отношения г' = хА/(хв + хс),
т. е. количества твердой фазы на единицу массы раствора (см.
табл. 8.8).
Данные табл. 8.8 представляют собой координаты точек
кривой нижнего потока (рис. 8.21). В верхнем потоке твердого
вещества нет (zf = 0), поэтому линия верхнего потока сливается
с осью абсцисс. После нанесения кривой вычертим на диаграмме
линии материального баланса.
Определим координаты точки Ft отвечающей составу
«лепестка», поступающего на экстрагирование. По условию задачи:
X' - 28 - 0 92- г' 100-28-2,5
Лр 28 ц- 2,5 -и'у/' гР- 28 + 2,5 *= *>и-
Координаты точки S, соответствующей составу растворителя:
xs= 1,5/100 = 0,015; zs = 0.
Точки F и S наносятся на диаграмму, соединяются прямой,
которая делится по правилу рычага точкой М на части,
пропорциональные количествам поступающих продуктов, исключая
нерастворимое твердое вещество (иначе правило рычага на таких
диаграммах применять нельзя). Растворитель поступает в установку
Таблица 8.8
Y' г— s
хв + хс
ХА
*в+ хс
0.0 2.0
0,1 1.980
0.2 1,942
0,3 1.887
¦у/ В
хв + хс
ХА
хв+хс
0,4 1,818
0,5 1J51
0,6 1,681
0,7 1,613
395
р
Рис» 8.21 (к примеру 8.15).
в количестве 50% от массы «лепестка». Если принять эту массу
за единицу, то жидкая часть в нем составит 0,28 + 0,025 = 0,305
единицы массы, а растворитель 0,5 единицы массы. Точка М
лежит на расстоянии 0,305/(0,5 + 0,305) = 0,38 отрезка SF, считая
от S.
Числовых данных для построения линии расхода RE нет.
Известно лишь, что линия RE пересекается с SF в точке М и что
точка R лежит на кривой, а точка Е — на оси абсцисс, так как
ее ордината г'ь = 0. Не располагая координатами точки R, мы все
же можем определить их отношение, так как из условия задачи
известно, что твердый остаток после экстрагирования содержит
5% масла:
1а е- *AR \ *br ~ *ar
^R XBR + XCR I КЫ< + XCR XBR
396
95
= 19.
Прямая, проходящая через начало координат и имеющая
тангенс угла наклона 19, пересечет кривую в точке R. Проведя такую
прямую, засечем точку R на кривой. Соединим точку R с точкой
М и, продолжив прямую до оси абсцисс, найдем точку Е.
Определим по диаграмме абсциссы точек R> M и Е\
X'R = 0,03; Х'м = 0,36; Х'Е = 0,58.
В установку поступает жидкой фазы с «лепестком» и
растворителем:
1000-0,305+ 1000-0,5 = 805 кг/ч.
Это количество делится между остатком и экстрактом
пропорционально отрезкам ЕМ и MR. Для расчета можно
воспользоваться абсциссами концов отрезков:
Количество остаточного раствора составляет 322 кг/ч, а
состав его определяется из предположения, что масло, теряемое в
остатке, содержится в этом растворе. Содержание масла в
остаточном растворе:
Количество экстракта:
GE = 806 — 322 = 483 кг/ч.
Содержание масла в экстракте:
100-0,28—(1000-0,695.5/95)
483
100 = 50,4%,
Для определения числа ступеней через точки F, Е и R, S
проводим два луча до пересечения их в полюсе Р. Так как при
экстрагировании твердых тел в каждой ступени установки имеется
только один раствор с одной концентрацией, то все хорды
равновесия будут вертикальными линиями. Восстанавливаем
перпендикуляр из точки Е — хорду первой ступени — до пересечения с
пограничной кривой. Точку пересечения хорды с пограничной
кривой соединяем лучом сточкой Р. Из точки пересечения этого луча
с осью абсцисс снова восстанавливаем перпендикуляр до
пересечения с пограничной кривой и т. д., пока не попадем в точку R или
не окажемся в непосредственном соседстве с ней.
Число хорд равновесия указывает число ступеней. В данном
случае необходимы семь ступеней экстрагирования.
Пример 8.16, В непрерывнодействующей противоточной
установке производительностью 4,4 т/сутки из руды извлекается
397
озокерит (горный воск) с помощью керосина (или бензина). В
экстракте, выходящем из каскада экстракторов, содержится 5 кг
озокерита в 100 кг чистого растворителя. В исходной руде ~ 25%
озокерита и 75% породы. В рафинате 0,2 кг озокерита на 100 кг
пустой породы. Растворитель содержит 0,05 кг озокерита на 100 кг
керосина. Необходимо определить число теоретических ступеней
для осуществления процесса экстрагирования.
Решение. 1. Составим уравнение материального баланса
по потокам:
GS + GR, rfl'n =» GE, n-l + 0**1
или по извлекаемому компоненту:
Osys + GR>nxn = Gf.n-i^ii-i + GRlxxa'u
где а! — соотношение потоков Ж : Т (количество жидкости, удерживаемое
твердой фазой); Gs — расход свежего растворителя, кг/ч; GR — расход твердой фазы
в рафинате, кг/ч; х — содержание извлекаемого компонента (озокерита) в
рафинате, кг А/кг В; у — содержание озокерита в экстракте, кг А/кг С; п —
любая ступень в каскаде; m — конечная стулеьь, в которую поступает исходный
твердый материал; А — озокерит; В — пустая порода; С — керосин.
Исключив G#, n-1 из балансовых уравнений, получим
уравнение рабочей линии процесса:
GR, т*пап . GSfe-G/M*taI
Уп-Х — 7> ^ ~' , г* ~J~ ~г
Gs — GRt xa\ + GRtna'n Gs — GRj xa\ — GR%na'n
При отсутствии взаимодействия между экстрагентом и пустой
породой, а также при постоянстве потока твердой фазы из одной
ступени в другую уравнение рабочей линии преобразуется к видуз
f Gs -l I a'{ \ - г -и Q^"GRXK
\°Ran an J GRan
При постоянном соотношении потоков Ж \ Т = а' = const
можно упростить уравнение рабочей линии:
А'Уп-1 = A'ys + xn — xlt
где А' — Gs/ GRa).
При условии равновесия концентрации озокерита в экстракте
с концентрацией в рафинате у% =хл.
Тогда
хп — А' (xn_i — ys)-~ хх = 0.
Решение этого уравнения:
г — ГА' " I %х ~ А Уо
где С— константа, котор>ю молено найти из граничного условия; при п = 0
хп = *j=yo-
39$
После упрощения получим уравнение
(а)
которое является вариантом уравнения (8,32) для расчета числа
теоретических ступеней в виде:
m
Ч'+^-'Ч^0)]/1^-
В условиях примера хт =0,05 кг/кг; х0 =0,0005 кг/кг;
х1 =0,001 кг/кг (по опытным данным); GR = 100 кг/ч; Gs =
= 871 кг/ч; а' = 2.
Тогда
Л' =Gs/(GRa') =871/(100-2) =^4,35.
По уравнению (а)
4,35*1—1 0,05 — 0,0005
4,35—1 0,001—0,0005
Отсюда т = 3,96 ж 4 ступени.
Если количество жидкости, удерживаемое твердой фазой при
переходе из ступени в ступень изменяется, то для расчета числа
теоретических ступеней следует использовать графические методы
(с помощью треугольной или прямоугольных диаграмм).
2. При расчете комплекса Л' расход растворителя
определялся из балансовых соотношений озокерита в потоках:
25
1) количество озокерита в руде: 100 -=? = 33,33 кг/ч;
2) количество озокерита в растворителе: 0,00056$ кг/ч;
3) количество озокерита в рафинате: 100-0,002 =0,200 кг/ч;
4) количество озокерита в экстракту (Gs — 200) 0,05 ==
^ 0,05GS — 10;
5) полный выход озокерита: 0,05GS — 9,80 кг/ч. Отсюда:
33,33 + 0,0005GS = 0,05GS — 9,80 кг/ч.
Расход керосина (растворителя): Gs =871 кг/ч.
С учетом того, что в отработанной твердой фазе (рафинате)
остается 200 кг/ч керосина, в концентрированном экстракте
содержится 871 — 200 = 671 кг/ч. Озокерита в этом экстракте
содержится 671-0,05 =33,55 кг/ч.
Концентрация озокерита в потоке экстракта, поступающем во
2-ю ступень, равна его концентрации в сливе из первой ступени —
0,05 кг озокерита/кг керосина. Следовательно, содержание
озокерита в экстракте, поступающем во вторую ступень: 200-0,05 =
= 10 кг/ч. Содержание озокерита в потоке, идущем из 2-й ступени
в 1-ю (из баланса 1-й ступени): 10 + 33,55 — 33,33 = 10,22 кг/ч.
Отсюда концентрация: у% = 10,22/871 >= 0,0117 кг/кг; ys *=»
*= 0,0005 кг/кг; х{ = 0,05 кг/кг; л;* = y*R =0,2/200 =0,001 кг/кг.
399
По уравнению (8.32):
х\ — Уг \ х1 — кн
Q,QQ1—Q.QQQ5 J 0,0117 — 0,Q005 __ g
g 0,05-0,0117 I g 0,05-0,001
Полное число теоретических ступеней:
КОНТРОЛЬНЫЕ ЗАДАЧИ
8.1. Построить треугольную диаграмму равновесия для
системы вода — уксусная кислота — этиловый эфир при 25 °С,
пользуясь данными табл. 8.4. Сравнить полученную диаграмму с
диаграммой X, Y — z, Z (см. пример 8.8).
8.2. Определить состав и количество сосуществующих фаз, на
которые расслаивается смесь 10 кг воды, 5 кг этилового эфира и
5 кг уксусной кислоты. При удалении какого количества этилового
эфира эта смесь перестанет расслаиваться? *
8.3. Уксусная кислота экстрагируется из водного раствора,
содержащего ее 15% (масс.) при 25 °С Масса исходной смеси
1200 кг. Определить состав и количество конечных продуктов
после отгонки растворителя, если экстракция производится чистым
эфиром в перекрестном токе. Процесс ведется в две ступени при
отношении массы растворителя к массе обрабатываемой смеси
1,5 *.
8.4. Уксусная кислота экстрагируется в противотоке
этиловым эфиром из водного раствора, содержащего 20% (масс.) кис*
лоты. Определить необходимое количество растворителя на
1000 кг/ч исходной смеси и число теоретических ступеней
экстрагирования, если экстракт должен содержать 60% (масс), а ра-
финат — не более 2% (масс.) кислоты (после отгонки
растворителя).
8.5. Бензойная кислота экстрагируется из водного раствора
с содержанием ее 1,5 кг на 1 м3 воды, последовательной промывкой
бензолом, содержащим 0,2 кг бензойной кислоты на 1 м8 бензола,
при отношении объемов воды и бензола Vt/V$ = 4. Определить,
сколько понадобится промывок, если конечное содержание бензола
в воде 0,2 кг/м3. Определить также составы получающихся
экстрактов. Равновесные данные при рабочей температуре:
Концентрация бензойной кислоты в воде, кг/м3 0,104 0,456 0,707 1,32 1,56
Концентрация бензойной кислоты в бензоле, 0,182 2,45 6,12 18,2 24,5
кг/м3
8.6. В противоточном экстракторе экстрагируется 1,4-диоксан
из 25% водного раствора бензолом, содержащим 0,5% (масс.) диок-
* Для решения воспользоваться треугольной диаграммой, построенной
в контрольной задаче 8Д.
400
Таблица 8.9
вода
98,1
97,1
95,5
91,7
84,4
71,1
58,9
45,1
37,1
В одн ы й ел о й
уксусная
кислота i ;
0,69
1,41
2,89
6,42
13,30
25,50
36,70
44,30
46,40
изопропило-
вый эфир
1,2
1,5
1,6
1,9
2,3
3,4
4,4
10,6
16,5
вода
0,5
0,7
0,8
1.0
1,9
3,9
6,9
10,8
15,1
Эфирный слой
уксусная
кислота
0,18
0,37
0,79
1,93
4,82
11,40
21,60
31,10
36,20
изопрогсило-
ВЫЙ эфир
99,3
98,9
98,4
97,1
93,3
84,7
71,5
58,1
48,7
сана. Конечное содержание диоксана в воде 2% (масс).
Определить: 1) минимальное количество растворителя на 100 кг
исходной смеси; б) необходимое число теоретических ступеней
экстрагирования; в) состав экстракта, приняв количество растворителя
в 1,5 раза больше минимального. Равновесные данные см. в
примере 8.6.
8.7. Построить фазовые диаграммы равновесия в координатах
X, Y — z, Z и X — Y для системы вода — уксусная кислота —
изопропиловый эфир при 20 °С, пользуясь данными о
равновесных составах сосуществующих фаз [в % (масс.)], приведенными
в табл. 8.9. Соединительные линии на диаграмме X, Y — г, Z
проводить не следует. Определить максимальные концентрации
экстракта при работе противотоком для составов исходных слесей
5 и 10% (масс).
8.8. Определить минимальное количество возврата экстракта
и соответствующее ему минимальное количество растворителя на
100 кг исходной смеси вода — уксусная кислота с содержанием
последней 10% (масс), если экстракция производится диэтиловым
эфиром при 25 °С. Экстракт после отгонки растворителя должен
содержать 75% (масс) уксусной кислоты, а рафинат 1% (масс);
растворитель отгоняется полностью *.
5.9. Решить задачу 8.8 приняв количество возврата двойным
против минимального. Определить также число теоретических
ступеней экстрагирования *.
8.10. Построить фазовые диаграммы равновесия в
координатах X, Y — z, Z для системы гептан — метилциклогексан —
анилин при 25 °С. Данные о равновесных составах
сосуществующих фаз [в % (масс)] взять из табл. 8.10. Определить, какой
концентрации продукты можно получить, обрабатывая 40%
раствор метилциклогексана в гептане чистым анилином при обычной
* При решении задачи использовать диаграмму равновесия, построенную
по данным примера 8.8 (рис. 8.18),
401
Таблица 8.10
Рафинатный слой
X
г
Экстрактный слой
У
0 0,064 0 15,7
0,085 0,064 0,160 13,8
0,216 0,070 0,365 11,2
0,445 0,078 0,623 8,2
0,525 0,079 0,700 7,33
Рафииатиый слой
X
г
Экстрактный слой
Y
Z
0,610 0,087 0,770 6,68
0,730 0,099 0,870 5,67
0,810 0,105 0,920 6,10
0,885 0,117 0,960 4,80
1,0 0,124 1,0 4,70
противоточной экстракции. Определить также минимальное число
ступеней экстрагирования (при полном возврате экстракта и
рафината), если экстракт содержит 98% (масс), а рафинат 1%
(масс.) метилциклогексана (после отгонки от растворителя).
8.11. Метилциклогексан экстрагируется анилином из 40%
раствора его в гептане при 25 °С в экстракционной установке с
возвратом части экстракта и рафината. Экстракт содержит 98% (масс),
а рафинат 1% (масс.) метилциклогексана (исключая
растворитель). Отношение количеств возврата экстракта и
экстракта-продукта принять в 1,615 раз больше минимального. Определить
число ступеней экстрагирования, состав и количество рафината,
экстракта, возвратов и растворителя на 100 кг/ч исходной смеси.
8.12. В батарею из трех отстойников противоточного действия,
объемом по 7 м3 каждый, поступают 2 т раствора NaOH в 1 м3 воды
вместе с осадком СаС03 и отбираются 6 м3 прозрачного
концентрированного раствора на выпарку. С другой стороны, в батарею
подается в качестве растворителя 6 м3 чистой воды на 2000 кг
NaOH. Осадок СаС03 при переходе со ступени на ступень и при
удалении из батареи удерживает 1 м3 раствора. Определить:
а) количество NaOH в шламе; б) степень извлечения NaOH;
в) процентное содержание NaOH в растворе, поступающем на
выпарку.
8.13. Определить число ступеней экстрагирования в условиях
примера 8.12, если степень извлечения NaOH равна 0,98.
8.14. Определить число ступеней экстрагирования в условиях
примера 8.13, если содержание СиС12 в экстракте будет равно 9%
(масс), а степень извлечения меди 92%.
8.15. Завод перерабатывает в сутки 10 т сульфида бария с
соответствующим количеством соды и 35 т воды с целью получения
карбоната бария и раствора сульфида натрия. Переработка
ведется в пятиступенчатой противоточной батарее. Осадок карбоната
бария во время процесса удерживает двойное (по массе)
количество воды. В результате переработки получается 10% раствор
сульфида натрия. Желательно добиться 98%-го извлечения
сульфида натрия. Определить: а) потерю сульфида натрия в остатке; б)
количество воды, которое необходимо добавить в качестве
растворителя; в) концентрации в каждом сгустителе.
402
8.16. В противоточной экстракционной батарее экстрагируется
едкий натр из продуктов реакции
Na2C03 + СаО+НаО = СаС03 + 2NaOH.
Поступающая в батарею смесь содержит воды 50% от массы
осадка (СаС03). Из этой смеси в батарее извлекается 95% NaOH,
причем получается 15% раствор. Сколько воды в качестве
растворителя должно поступать в батарею и сколько ступеней должно
быть в батарее, если из опытных данных известно, что осадок
удерживает раствор в следующих количествах, зависящих от
содержания в нем NaOH:
Содержание
NaOH,
% (массJ
Удерживается
раствора на 1 кг
осадка, кг
0 1,39
5 1,72
10 2,04
Содержание
NaOH,
% (масс.)
Удерживается
раствора на 1 кг
осадка, кг
15 2,70
20 3,85
Глава 9
АДСОРБЦИЯ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. В процессе адсорбции предельным состоянием для каждого
поглощаемого вещества является состояние равновесия между
содержанием в адсорбенте (так называемой статической
активностью) Oq и парциальным давлением р (или концентрацией Су)
адсорбируемого вещества в парогазовой или жидкой смеси.
Кривая равновесия при постоянной температуре а$ — f (р)
носит название изотермы адсорбции и служит основной
характеристикой статики процесса. При относительно высоких парциальных
давлениях р содержание адсорбируемого вещества а$
приближается к постоянной величине ато, характеризующей состояние
максимально возможного насыщения адсорбента при данной
температуре.
Между концентрацией Су (в кг/м3) адсорбируемого вещества
в газовой смеси и его парциальным давлением р, согласно
уравнению Клапейрона, существует прямая пропорциональность:
где R — газовая постоянная, Дж/(иг«К).
403
2. Наиболее полными уравнениями изотерм адсорбции, не
имеющих в координатах aj — р точек перегиба, учитывающими
к тому же структурные особенности сорбентов, являются
уравнения Дубинина, полученные на основе теории объемного
заполнения микропор.
Для микропористых сорбентов, обладающих однородной
микропористой структурой (синтетические цеолиты), это уравнение
имеет вид:
—в
Т% ( Ps \2
v
аЪ^^Лг М v " . (9-2)
Для адсорбентов со сложными микропористыми структурами
(мелкопористые силикагели, активные угли):
Г / Р$\2
а-*вГв'^'-' +
+ J^e '"'l"-'. (9-3)
Здесь а* — величина адсорбции, ммоль/г; W0 и Bt Wol и Ви W02 и В1—
константы, характеризующие адсорбент; Т — температура, К; Р — коэффициент
аффинности пара адсорбтива по отношению к стандартному веществу; pjp —
отношение давления насыщенного пара поглощаемого компонента к его
парциальному давлению.
3. Согласно теории Эйкена и Поляни, располагая изотермой
адсорбции пара стандартного вещества для температуры Tl9
можно вычислить изотерму адсорбции другого пара при
температуре Т2.
Для вычисления величин адсорбции служит формула:
где #,* — ордината изотермы стандартного вещества (обычно бензола), кг/кг или
ммоль/г; а\ — ордината определяемой изотермы, кг/кг или ммоль/г; V\ и Vz —
мольные объемы стандартного и исследуемого веществ (в жидком состоянии),
м3/кмоль.
Мольные объемы определяются по формуле:
V« Л1/р. (9.5)
Здесь М — мольная масса, кг/кмоль; р — плотность жидкости, кг/м^.
Давления вычисляются по формуле:
' 2 Pi
где pi и р% — парциальные давления стандартного и исследуемого веществ, мм
рт. ст.; ps% i — давление насыщенного пара стандартного вещества при
температуре 7\ (выраженной в К), мм рт. ст.; pSt 2 — давление насыщенного пара
исследуемого вещества при температуре Т2 (выраженной в К), мм рт. ст.; Р —
коэффициент аффинности, равный отношению мольных объемов
Р - Уг/Уг. (9.7)
404
Таблица 9.1
Вещество
Метиловый спирт
Бромистый метил
Этиловый спирт
Муравьиная кислота
Сероуглерод
Хлористый этил
Пропан
Хлороформ
Ацетон
Бутан
3
0,40
0,57
0,61
0,61
0,70
0,76
0,78
0,86
0,88
0,90
Вещество
Уксусная кислота
Бензол
Циклогексан
Четыреххлористый
углерод
Диэтиловый эфир
Пентан
Толуол
Хлорпикрин
Гексан
Гептан
3
0,97
1,00
1,03
1,05
1,09
1.12
1,25
1,28
1,35
1,59
В табл. 9.1 приведены коэффициенты аффинности Р для ряда
веществ. В качестве стандартного вещества принят бензол.
При расчете точек изотермы исследуемого пара координаты
а* и ру берутся по кривой стандартного вещества, значения /?S|1,
/7S)2 — из таблиц давления насыщенного пара, р2 — вычисляется
по формуле (9.6).
4. Теплота адсорбции складывается из теплоты конденсации и
теплоты смачивания. Практически можно принять, что величина
теплоты адсорбции органических веществ не зависит от
температуры. Зависимость удельной теплоты адсорбции q (в Дж/кг угля)
от количества поглощенного пара (для веществ, отмеченных
звездочкой в табл. LIII) определяется формулой [9.31:
q^man, (9.8)
гдэ а — количество адсорбированного пара, дм3/кг угля; тип — кокстаиты,
значения которых представлены в табл. 9.2.
Таблица 9.2
Вещество
Формула
а
т- 1От*
Бензол
Бромистый этил
Диэтиловый эфир
Йодистый этил
Метиловый спирт
Сероуглерод
Хлористый этил
Хлороформ
Четыреххлористый углерод
Этиловый спирт
Этилформиат
свнв
С2Н5Вг
(С2Н5)20
С2Н51
снчон
CS2
С2Н5С1
СНС13
СС14
с2н5он
НСООС2Н5
0,959
0,900
0,9215
0,956
0,938
0,9205
0,915
0,935
0,930
0,928
0,9075
3,24
3,77
3,84
3,10
3,11
3,15
3,06
3,47
3,74
3,65
3,96
405
При адсорбции водяного пара углем теплота адсорбции зави
сит от температуры следующим образом:
Температура, °С
Теплота адсорбции <7* 10"3,
Дж/кмоль
— 15 10 40 80 128 187
46 500 41 900 39 000 34 800 30 900 21 800
При отсутствии опытных данных величина теплоты адсорбции
(отнесенной к 1 кмоль газа) определяется по приближенной
формуле, аналогичной правилу Трутопа:
qiV 7\<ип = const,
(9.9)
где q — теплота адсорбции, Дж/кмоль газа; Ттп — температура кипения адсорб-
тива при атмосферном давлении, К.
Величина константы зависит от природы адсорбента;
например, для активного угля она равна 2180.
Теплоту адсорбции (в Дж/кмоль) можно также вычислить по
формуле:
'-«•"*Шт;-т;)'
(9.10)
Здесь plt p2 — равновесные давления адсорбтива над адсорбентом при темпе
ратурах Т} и Тъ выраженных в К-
5. На практике поглощение газов и паров, как правило,
производится в динамических условиях — из потока газа-носителя.
В этом случае слой сорбента характеризуется величиной
динамической адсорбционной емкости (активности) ад — количеством
поглощенного вещества (сорбтива) слоем сорбента до момента
появления за слоем проскока сорбтива:
ад = С0шт,
(9.11)
где ад—динамическа:: адсорбционная емкость слоя сорбента, кг/м3; С0 —
исходная концентрация сорбтнпа в газовом потоке, кг/м3; w — скорость
парогазовой смеси, отнесенная к полному сечению аппарата, м/с; т — время защитного
действия, с.
Степень использования равновесной адсорбционной емкости
т] = aja$ (а$ —равновесная статическая адсорбционная емкость
слоя сорбента, кг/м3) микропористых сорбентов в процессе
динамического опыта при высоте слоя 30—50 см, скоростях
паровоздушного потока от 0,3 до 0,5 м/с и исходных концентрациях
сорбтива 10—20 г/м3 составляет обычно 0,8—0,9.
6. Процесс адсорбции в динамических условиях можно
охарактеризовать кинетическим уравнением, согласно которому
скорость адсорбции (или количество вещества, адсорбируемого в
единицу времени единицей объема адсорбента) прямо
пропорциональна коэффициенту массоотдачи и движущей силе процесса!
^«Р^С-С*), (9Л2)
406
где С — концентрация адсорбируемого вещества в парогазовой смеси, кг/м3
инертного газа; С*—концентрация адсорбируемого вещества в парогазовой смеси,
равновесная поглощенному единицей объема адсорбента количеству вещества,
кг/м3 инеотного газа; (Зу — кинетический коэффициент (коэффициент массоот-
дачи), с"1.
Для ориентировочных расчетов коэффициента массоотдачи ру
при адсорбции на активном угле (d =1,74-2,2 мм, w потока
0,3 — 2 м/с) пользуются уравнением (при условии, что изотерма
адсорбции описывается уравнением Лангмюра):
Nu' = i,6 Re0'54. (9.13)
Здесь Nil' = $у dz/D; Re = w dh\ d — средний диаметр частиц адсорбента,
м; D — коэффициент диффузии адсорбтива в газе при температуре процесса, м2/с;
w — скорость потока парогазовой смеси, рассчитанная иа свободное сечение
аппарата, м/с; v — кинематический коэффициент вязкости парогазовой смеси, м2/с.
7. Процесс адсорбции в динамических условиях можно также
охарактеризовать временем, прошедшим от начала пропускания
парогазовой смеси через слой адсорбента до момента появления
проскока (индицируемой концентрации) сорбтива за слоем
адсорбента. Этот промежуток времени т называется временем
защитного действия слоя поглотителя и определяется из уравнения
Шилова:
т = К(Я—А), (9.14)
в котором Kh ~ т0.
Следовательно,
т = КЯ-т0, (9.15)
где К — коэффициент защитного действия слоя сорбента, с/м; Н — высота слоя
сорбента, м; h — высота неиспользованного слоя сорбента в условиях
динамического опыта, м; т0 — кинетический коэффициент, или потеря времени защитного
действия слоя сорбента, с.
Коэффициент защитного действия слоя можно вычислить по
формуле;
К = а07(юСо), (9.16)
где aj — равновесная адсорбционная емкость, кг/м3; w — скорость парогазовой
смеси, отнесенная к полному сечению аппарата, м/с; С0 — начальная
концентрация адсорбируемого вещества в парогазовой смеси, кг/м3.
8. Для одних и тех же адсорбента и поглощаемого вещества
при постоянных концентрации и температуре парогазового
потока, имеют место следующие соотношения, называемые
динамическими характеристиками В± и В2:
В± — К1Щ = K^w2 = K/Cq = const; (9.17)
Здесь К — коэффициент защитного действия слоя, с/м; w — скорость
парогазового потока, м/с; т0—потеря времени защитного действия слоя, с; d3 —
средний диаметр зерен сорбента, м.
407
Таблица 9.3
С/С0
0,005
0,01
0,03
0,05
0,1
ь
1,84
1,67
1,35
1,19
0,94
С/Со
1 0,2
0,3
0,4
0,5
0,6
ь
0,63
0,42
0,23
0,09
-0,10
cic
0,7
0,8
0,9
b
—0,27
—0,46
—0,68
9. Продолжительность адсорбции при периодическом процессе
определяется путем решения системы уравнений, состоящей из
уравнения баланса поглощенного вещества, уравнения кинетики
адсорбции и уравнения изотермы адсорбции.
Изотерма адсорбции делится на три области: первая
характеризуется отношением p/ps <0,17 (по бензолу), для второй
p!ps ^0,17 4-0,5, а для третьей p/ps > 0,5.
При определении продолжительности процесса по изотерме
адсорбции и заданной концентрации исходной паровоздушной смеси
Со находят al и устанавливают, к какой области изотермы
относится величина Со. Затем вычисляют коэффициент массоотдачи
РУ по формуле (9.13).
В зависимости от положения величины С0 на изотерме
применяют один из следующих трех методов определения
продолжительности адсорбции [9.3 ].
а) Для первой области, где изотерма адсорбции считается
прямолинейной и приближенно отвечает закону Генри, пользуются
фор мулой:
/т = У aZl(wCt) VH - ЬУ а*0/{$уС0), (9.19)
где т—продолжительность адсорбции, с; w—скорость парогазового потока,
отнесенная к полному сечению аппарата, м/с; Н — высота слоя активного угля,
м; С'а — начальная концентрация адсорбируемого вещества в парогазовом потоке,
кг/м3, <?* — количество адсорбированного вещества, равновесное с концентрацией
потока С0, кг/м3 (берется по изотерме адсорбции в кг/ki и умножается на
насыпную плотность угля в кг/м3); р,7 — коэффициент массоотдачи, с-1.
Величина коэффициента Ь берется для ряда значений С/С0 из
табл. 9.3 (С — содержание адсорбируемого вещества в газовом
потоке, выходящем из адсорбера, кг/м3).
б) Для второй области изотермы адсорбции пользуются
уравнением:
т = ^-
wCq
Н —
W
р
У
р
In
(*-')
+ 1п-^
С
1
(9.20)
Здесь Р = CjC*\ С* — содержание вещества в газовом потоке, равновесное
с половинным количеством от максимально адсорбируемого данным адсорбентом,
'I. е. равновесное с аоо/2, кг/м3.
408
в) Для третьей области изотермы адсорбции;
а;
*
wC0
н- w
Р
у
Чт-)]
(9.21)
10. Весьма важной кинетической характеристикой процесса
адсорбции является высота зоны массопередачи (высота
работающего слоя) /г0, которая рассчитывается на основании
выходных кривых (кривых отклика) по уравнению:
к = н ,Тна0Г,!!пр—гт-' (9-22)
тнас — I1 — и 1тнас — %щ)
где Н — высота слот, сорбента; тнао — время до равновесного насыщения; тпр —
время защитного действия при минимальной индицируемой проскоковой
концентрации; / — неиспользованная равновесная адсорбционная емкость сорбента
в условиях динамического опыта в зоне массопередачи (для микропористых
сорбентов в зоне массопередачи f яз 0,5).
11. Непрерывные адсорбционные процессы осуществляются
в адсорбционных аппаратах с движущимся сверху вниз слоем
поглотителя *, причем парогазовая смесь идет ему навстречу
(противотоком). Расчетом определяются минимальная скорость
движения и сорбента (скорость, при которой степень использования
равновесной адсорбционной емкости сорбентов в условиях
динамического опыта составляет 0,95—0,98 и обеспечивается заданная
глубина очистки или осушки паровоздушных потоков) и рабочая
высота слоя в гиперсорбционном аппарате Я0.
Скорость движения слоя и рассчитывается по формуле:
и = i/К « (С0 - Спр) wjal, (9.23)
где w — скорость газового потока, отнесенная к полному сечению аппарата; К —
коэффициент защитного действия слоя; С0 — начальная концентрация
адсорбируемого вещества в парогазовой смеси; Спр — постоянная индицируемая проско-
ковая концентрация адсорбируемого вещества в парогазовом потоке за слоем
сорбента.
В процессах тонкой осушки или очистки газовых потоков Спр
изменяется от 0,025 до 0,008% в зависимости от величины С0 (когда
С0 меняется от 20,0 до 10,0 г/м3). Поэтому в данном случае в
уравнении (9.23) постоянной индицируемой проскоковой
концентрацией можно пренебречь.
Рабочая высота слоя в гиперсорбционном аппарате
рассчитывается по формуле:
#0 = yh0. (9.24)
Здесь 7 — коэффициент, характеризующий отношение насыпной плотности
с вибрационным уплотнением слоя к плотности без уплотнения (в среднем 7 —
— 1>4); /*о— высота зоны массопередачи неподвижного слоя.
* При гиперсорбции или текучем слое,
409
12. Высота слоя адсорбента может быть рассчитана по
общему методу через число единиц переноса:
// =
Со
Vr с dC
J T:-C* ~K
гп,
(9.25)
где Vr — расход парогазовой смеси; 5 — площадь поперечного сечения слоя;
Ру — коэффициент массоотдачи; С,, и Ci — концентрация парогазовой смеси при
входе в адсорбер и при выходе из него; С* — равновесная концентрация
адсорбируемого вещества в парогазовой смеси по изотерме.
Разность концентраций С — С* определяет движущую силу
процесса. Примером такой разности может служить отрезок DE
на рис. 9.1, у которого абсцисса точки/? равна С, а точки Е—С*.
Отношение Vv/(S$y) выражает высоту слоя поглотителя,
эквивалентную одной единице переноса, и обозначается через /гэ, а инте-
с*
грал J .—— представляет собой общее число единиц переноса
с,
и обозначается через т. Для определения Н надо найти величину
Со
интеграла 1 — —. Делается это графическим методом.
Располагая данными С0, ат и Clt ад1, наносят на диаграмму
изотермы адсорбции обе эти точки и, соединяя их прямой,
получают рабочую линию Л/С. Затем в координатах С
кривую (аналогичные расчеты см. в гл. 6 и 7).
Со
Bi dC
место такого определения интеграла -
с-с
— строят
с —с*
можно вос-
Ci
пользоваться более простым графическим методом. Начав от точки
А (рис. 9.1) на рабочей линии (точки входа парогазовой смеси
в адсорбер), строят между равновесной кривой и этой линией
ступени изменения
концентрации до точки К (точки выхода
парогазовой смеси из
адсорбера).
Число единиц переноса,
соответствующее одной ступени,
обозначается через т0. Если
число ступеней равно п и все
они одинаковы, то т = т0п и
высота слоя
Я = h^rn = Нътф, (9.26)
С с; 25
50 _ 75 100
С, КГ/М 3
П5 • Ю~
Рис. 9 1. Определение числа ступеней изме*
иеиия концентрации.
410
Такой случай возможен лишь на прямолинейном участке
изотермы. В общем же виде формула для расчета высоты слоя имеет
следующий вид:
п
н = лэ К + тЪ} + • • • + <)=нэ 2 то- (9-27>
Для каждой ступени изменения концентрации число единиц
переноса т0 вычисляется отдельно по формуле:
Снач — Скон 2 уСпач —' Скон/ ,д поч
1(Снач — Снач) + (СКон — Скон/1/2 Снач — Скон
где Снач — концентрация иа входе парогазовой смеси в ступень, например
абсцисса точки А; Скон — концентрация на выходе парогазовой смеси из ступени,
например абсцисса точки D; Снач — равновесная концентрация, например абс-
цисса точки В, причем Скон = СНач; Скон — равновесная концентрация,
например абсцисса точки Е.
На прямолинейном участке изотермы для определения высоты
слоя можно воспользоваться также формулой
Н = ~ . (9.29)
Sp^ACcp
Здесь G — количество вещества, адсорбируемого в единицу времени; АСср —
средняя движущая сила адсорбции, которую можно вычислить как среднюю
логарифмическую
лу; АСо — ЛСх Qm
АСср = .--¦,¦ t (9.30)
Р 1п (АСо/АСг)
где ЛС0 — большая движущая сила на одном конце слоя (С0 — CJ); АС1 —
меньшая движущая сила на другом конце слоя (С{ — С*).
13. Адсорбция в неподвижном слое адсорбента является
неустановившимся процессом, что затрудняет определение
изменения концентрации целевого компонента по высоте слоя, а также
расчет времени защитного действия.
Связь между концентрацией в газе, высотой слоя адсорбента и
временем для первой (линейной) части изотермы адсорбции
описывается уравнением:
* -1-е-*-У dnj«W**) . (9.31,
Q> й{кг)п
где С и С0 — концентрация сорбтива в газовой смеси в момент времени т на
высоте слоя L и на входе в адсорбер, соответственно; J0 — функция Бесселя первого
рода нулевого порядка; х — безразмерное приведенное расстояние или высота
слоя; г — безразмерное приведенное время контакта адсорбента с газовой смесью
(без учета газа, находящегося в слое перед началом процесса).
В результате преобразований уравнения (9.31) получим:
со k
*-* iii" " ж * ^ь • X
-Х-г V V
г
k
С0 ?J uJ тп\ k\
(9.32)
411
а*кг/кг
5 Ю 15 20 25 JO ¦ «75 40 45 5Q 55 60
р,ммрт.ст.
Рис. 9.2. Изотермы адсорбции при 20 С:
/ — бен-°ол; 2 — диэтнловый эфир? 3 *=¦ этиловый спирт (70%) + Диэтиловый эфир (30%).
или в развернутом виде:
с
Сс
~Х—2
1 + (1 + х)г + [1+х +
Х*\ г2
+ 1 + Ж+...+
I п\
2\ 21
+
+
(9.32а)
Это уравнение удобно для расчета на ЭВМ (рис. 9.2).
14. Распределение концентрации сорбтива в неподвижном слое
адсорбента аналогично (9.31), (9.32) описывается зависимостью:
оо
У
с,
= 1 — е
—ж—2
2*-
/1=0
dnJ0 (2iVxz)
d (xz)n
(9.33)
где у* — концентрация сорбтива в газовой фазе, равновесная с концентрацией
в твердой фазе.
В развернутом виде:
Со ~6
[
г2
27
*+(l+*)^+(l+* + -ff)?- +
3!
В уравнениях (9.31)—(9.33):
)!
+
(9.33а)
x=^KvL/wy\
А \ wy I
(9.34)
(9.35)
412
Таблица 9.4
с/с„
0,005
0,010
0,020
0,030
0,040
0,050
z
Z
Z
ц
Z
Z
Z
10
1,5
0,15
2,0
0,20
2,6
0,26
3,0
0,30
3,3
0,33
3,6
0,36
20
6,6
0,33
7,6
0,38
8,7
0,44
9,5
0,48
10,0
0,50
10,5
0,53
Прр
30
13,0
0,43
14,3
0,48
15,8
0,53
16,8
0,56
17,5
0,58
18,2
0,61
[ значениях х
50
27,1
0,54
29,0
0,58
31,1
0,62
32,5
0,65
33,5
0,67
34,5
0,69
100
66,4
0,66
69,3
0,69
72,6
0,73
74,7
0,75
76,3
0,76
77,6
0,78
150
108
0,72
112
0,75
116
0,77
119
0,79
121
0,80
122
0,82
200
151
0,76
166
0,78
161
0,80
164
0,82
116
0,83
168
0,84
Здесь Kv — объемный коэффициент массопередачи; L — высота слоя
адсорбента; wy — скорость газовой фазы, рассчитанная на общее сечение адсорбера;
% — продолжительность процесса адсорбции; А — константа из уравнения
изотермы адсорбции: А = у*/а (а— величина адсорбции).
Кривые распределения концентраций (см. рис. 9.2) сорбтива
в твердой фазе представлены в литературе [1 ] в соответствии
с данными, рассчитанными по уравнению (9.33а). Практически
такие графики используют редко, так как для условий проскока
представляют интерес малые значения С/С0 или г//С0, которые
трудно определить по рисунку из-за мелкого масштаба.
Для расчета времени защитного действия с помощью ЭВМ
удобно пользоваться данными табл. 9.4.
В табл. 9.4 приведены значения z и г\ (г\ — коэффициент
полезного действия адсорбционной емкости адсорбента при
проскоке). При низких значениях C/CQ коэффициент полезного
действия адсорбционной емкости т] приближенно равен отношению
комплексов zlx.
После экспериментального определения С/С0 и г\ из табл. 9.4
находят значения х и г. Из величин х и г по формулам (9.34) и
(9.35) рассчитывают коэффициент массопередачи Kv и
соотношение равновесных концентраций между фазами C/CQ или у/Сй.
Для единичного объема газовой смеси (при г =.const) в отрезке
высоты слоя Llx (равном высоте единицы массопередачи)
концентрация Сх изменяется в С2 по зависимости:
dC
\
С~?/ =
= 1.
Таким образом, комплекс х представляет собой число единиц
массопереноса.
413
ПРИМЕРЫ
Пример 9.1. Определить требуемое количество активного угля,
высоту слоя адсорбента и диаметр адсорбера периодического
действия для поглощения паров бензина из смеси его с воздухом.
Расход паровоздушной смеси 3450 м3/ч. Начальная концентрация
бензина С0 = 0,02 кг/м3. Скорость паровоздушной смеси w ~
= 0,23 м/с, считая на полное сечение аппарата, динамическая
активность угля по бензину 7% (масс), остаточная активность после
десорбции 0,8% (масс), насыпная плотность угля риао =500 кг/м3.
Продолжительность десорбции, сушки и охлаждения адсорбента
составляет 1,45 ч.
Решение. Для поглощения бензина за 1,45 ч необходимо
адсорбента:
г 3450-1,45 -0,02
G= 0,07-0,008 -1612кг-
При заданной скорости паровоздушной смеси 0,23 м/с и
расходе 3450 ма/ч диаметр адсорбера должен быть равен:
D = у п^л V^, „ пп = 2,3 м.
3450
3600-0,785 0,23
Высота слоя адсорбента:
U 1612 ло
Н~ 500-0,785-2^ **°'8м'
Пример 9.2. По опытным данным, продолжительность
поглощения паров хлорпикрина (С0 = 6,6 г/м3) слоем активного угля
высотой Н = 0,05 м и площадью поперечного сечения S = 0,01 м3
при объемной скорости V =0,03 м3/мин составляет т =336 мин.
По изотерме хлорпикрина активность угля а$ =222 кг/м3.
Диаметр частиц угля d3 = 1,5 мм. Определить: а) коэффициент
защитного действия слоя /С; б) потерю времени защитного действия
<г0; в) величину динамических характеристик Вх и В2.
Решение. По формуле (9.16):
К = aj/U'Co).
Величины al и С0 заданы, а линейная скорость паров
вычисляется по объемной скорости и поперечному сечению адсорбера:
w = VfS = 0,03/0,01 = 3 м/мин.
После подстановки получаем:
К » 222/(3-0,0066) = 11 200 мин/м я* 187 ч/м.
Потеря времени защитного действия определяется по
уравнению (9.15):
т0 « /(Я — т = 11 200-0,05 — 336 « 224 мин.
414
Динамические коэффициенты Вх и В2 определяются по
формулам (9.17) и (9.18):
Вг = Kw « 11 200 - 3 = 33 600;
В2 = Te^S/de = 224 1^ 3/0,0015 == 259000.
Пример 9.3. Если в условиях предыдущего примера скорость
потока паровоздушной смеси w ~ 6 м/мин, то как при этом
изменяется: а) коэффициент защитного действия слоя; б) потеря
времени защитного действия; в) продолжительность поглощения
для слоя высотой Н( =0,1 м?
Решение. Так как коэффициент Вг — величина постоянная,
/(' = Kwlw' = BJw' = 33 600/6 = 5600 мин/м.
Из формулы для коэффициента В2 определим:
/ п а нт 259000-0,0015
tJ — B2djy w = — лг 159 мин.
V 6
Продолжительность поглощения определим по уравнению
Шилова:
т' •=/С'Я' — т^ « 5600-0,1 — 159 = 401 мин.
Пример 9.4. Через адсорбер периодического действия за один
период проходит 2000 м3 паровоздушной смеси с концентрацией
диэтилового эфира С0 = 0,006 кг/м3. Температура процесса 20 °С,
давление атмосферное, скорость потока паровоздушной смеси w =
— 13 м/мин, концентрация смеси после выхода из адсорбера С =
= 3«10"5 кг/м3. В качестве поглотителя применяется активный
уголь марки АГ-5 с диаметром зерен d3 = 0,004 м и насыпной
плотностью 500 кг/м3. Высота слоя угля Я — 0,7 м.
По изотерме бензола для 20 °С на том же угле построить
изотерму адсорбции диэтилового эфира из воздуха при 20 °С.
Пользуясь этой изотермой, определить количество активного угля,
необходимое на одну загрузку, диаметр адсорбера и
продолжительность поглощения до проскока.
Решение. Ординаты и абсциссы точек изотермы
диэтилового эфира вычисляются по формулам (9.4) и (9.6):
а;«аГ-?ц lgP2 = lgp8.2-P^Mg^,
У г 1 2 Pi
где а± и а2 — концентрации адсорбированных бензола и эфира, кг/кг; V\ n V2 —
мольные объемы бензола и эфира в жидком состоянии, м3/кмоль; рг и р2 —
парциальные давления паров бензола и эфира, мм рт. ст.; pS) х и pSi2 — давления
насыщенных ааров бензола и эфира при 20 °С, мм рт. ст.; 7\ и Т2 —
температуры бензола и эфира при адсорбции (в данном случае Т% = Тг= 293 К); Р —
коэффициент аффинности.
Мольные объемы бензола и эфира:
Ул а М1/р1 = 78/879 = 0,0887 м3/кмоль;
У2 = М2/р2 = 74/714 = 0,1036 м3/кмоль.
415
Таблица 9.5
Изотерма бензола
-*
Qj , КГ/КГ
Ру, ММ рТ. СТ.
Изотерма днэтилового эфнра
Р2» мм рт. ст.
0,0202
0,0501
2,82
10,1
32,2
56,9
88,2
169,2
224,5
275,0
Коэффициент аффинности:
р = V%iVx = 0,1036/0,0887 =1,17.
На изотерме бензола (рис. 9.2) берем ряд точек.
Первая точка', а* = 0,2€2 кт/м, pi =8 тшрт.ст. Bwraoraw
координаты соответствующей точки на изотерме диэтилового
эфира:
0,103
0,122
0,208
0,233
0,202
0,276
0,294
0,318
0,338
0,359
0,105
0,223
1
3
8
13
19
33
42
50
0,0837
0,0992
0,169
0,190
0,212
0,224
0,24
0,258
0,273
0,292
at
at
а\ = 0,262/78 кмоль/кг;
0,262 0,0887
= 0,00287 кмоль/кг =
V2 78 0,1036
= 0,00287-74 кг/кг ==0,212 кг/кг;
9Q3 7^
lgp2=Ig 442-1,17^ lg —= 1,50822; р2 - 32,2 мм рт. ст.
По этому методу вычисляем ординаты и абсциссы для
остальных точек и полученные данные сводим в табл. 9.5.
По найденным точкам строим изотерму диэтилового эфира для
20 °С (кривая 2 на рис. 9.2).
Определим с помощью изотермы статическую активность угля
по диэтиловому эфиру при концентраций паровоздушной смеси
С0 = 0,006 кг/м3.
Предварительно необходимо рассчитать парциальное давление,
соответствующее С0» по формуле (9.1):
р0^Со^Г=,0,006^293~^==1,4 ммрт. ст.
По диаграмме, абсциссе р0 =1,4 ммрт. ст. соответствует
ордината aj = 0,132 кг/кг.
Количество активного угля на одну загрузку составляете
Gi = 2000-0,006/0,132 = 91 кг или 91/500 «=0,182 nt*.
416
Диаметр адсорбера вычисляется из равенства
nD2a
—/-Я = 0,182 м3,
откуда
,/ 0,182-4 ,/0,182-4
Р'~К пн - V 5ЛЩ7~°'69 м-
Так как на изотерме точка, соответствующая исходной
концентрации паровоздушной смеси С0 = 0,006 кг/м3, находится в
первой (прямолинейной) области, то продолжительность процесса
вычисляется по формуле (9.19):
где Г = а%/С0= 0,132.500/0,006= 11000; w = 13 м/мин — скорость газового
потока; Н = 0,7 м — высота слоя угля; b — функция, определяемая по табл. У.З
(для С/С0 = 0,00003/0,006 = 0,005 значение b = 1,84); (*у — коэффициент массо-
отдачи, который вычисляется по формуле (9.13), приведенной к расчетному виду:
ft 1 * Dw°^
Находим кинематический коэффициент вязкости воздуха. Так
как по рис. VI (х = 0,018-Ю-3 Па»с, то
v = ц/р = 0,018-10-3/1.2 = 0,15-10"4 м2/с
Тогда
v°'54 = (0,15. Ю-4)°'51 = 0,248-10"*-
Диаметр частиц угля d3 = 0,004 м. Следовательно,
4'46 = 0,004м6 = (0,40. Ю-2)1'46 = 0,3154- Ю"3.
Скорость w — 13 м/мин = 13/60 м/с, поэтому
(ш/60)0'54 = (13/60)0'54 = 0,438.
Коэффициент диффузии при 0 РС для системы диэтиловый
эфир — воздух:
D0= 0,028 м2/ч =0,0778.10-4 м2/с
Для температуры 20 РС коэффициент диффузии вычисляем по
формуле:
0-*•*(?)''•-••»»-и~-К?Г-
= 0,0778-10-*-1,П = 0,0864-10"4 м2/с.
]4 Павлов К. Ф. н др. 4!7
После подстановки получаем объемный коэффициент массоот-
дачи:
R 1,6*0,0864.10"«-0,438 _ -
Ру~ 0,248.10-*.0,3154-10"» ~ ' ° '
Определяем продолжительность процесса:
Г5_/^^-1Д4/1^-1«8,1-69.4-118.7;
т =^ 118,7* = 14 090 с =* 234,9 мин = 3,9 ч.
Определим количество паровоздушной смеси, проходящей
через адсорбер за это время:
У=< T=3.1W13,234)9=и42м3
4 4
По условиям примера, за один период через адсорбер должно
пройти 2000 м3. Следовательно, диаметр адсорбера следует
увеличить;
л 1 /2000-4 т/ 2000-4
а Г яат г 3,14-13-234,9
Необходимо также увеличить количество активного угля на
одну загрузку:
—?^-Я'500=0,785.0,833-500.0,7= 190 кг.
Пример 9.5, Пользуясь изотермой адсорбции смеси паров
этилового спирта и диэтилового эфира (кривая 3 на рис. 9.2),
определить продолжительность адсорбции этой смеси слоем активного
угля высотой Я = 1,0 м. Начальная концентрация смеси С0 =
= 0,072 кг/м3; средняя концентрация на выходе из адсорбера
С = 0,0001 кг/м3; скорость парогазовой смеси, отнесенная к
полному сечению адсорбера, w = 12 м/мин; диаметр частиц
активного угля ds — 0,004 м; насыпная плотность рцао = 500 кг/м3;
температура адсорбции 20 °С; давление атмосферное.
Решение. По изотерме адсорбции (рис. 9.2) определяется
а$, соответствующая концентрации Со = 0,072 кг/м3. Мольная
масса смеси Мсм = 0,3-46 + 0J7-74 = 65,6 кг/кмоль.
Давление, соответствующее С0:
р0 = C0RT = 0,072 ~ 293 —- = 20 мм рт. ст.
По изотерме а5 = 0,20 кг/кг = 0,2-500 = 100 кг/м3. Эта точка
находится в третьей области изотермы; поэтому
продолжительность поглощения определяется по формуле (9.21):
wCn I
Р» V с
418
Для расчета по этой формуле необходимо вычислить только
коэффициент массоотдачи ру для смеси.
Коэффициент диффузии эфира в воздухе при 0 9&
Dq = 0,028 м2/ч = 0,0778- Ю-4 ы2/с.
Коэффициент диффузии этилового спирта в воздухе при 0 °С:
D0 = 0,0367 мУч = 0,1019-10~4 м2/с.
Для расчета примем меньший коэффициент диффузии (для
эфира) и пересчитаем его на температуру 20 °Ci
»-«?(?)¦"-««-г (ИГ-
= 0,0312 м2/ч = 0,0866-10"* м2/с
Кинематический коэффициент вязкости рассчитываем по
воздуху (см. предыдущий пример): v = 0,15-10"* м2/с
Рассчитаем значения v0'54, о/**54 и d*'46:
v0'54 = (0,15. Ю^4)0'54 =* 0,248- Ю-2;
(ш/60)°'5*= (12/60)0,54 = 0,42;
d\AQ = 0.0041*46 = 0,3154.10"3.
После подстановки найденных величин получим коэффициент
массоотдачи:
— Ьб-0,0866-10-^.0,42 _s
Р*> "~ 0,248-10'2.0,3154.10^ ~ М с '
Продолжительность поглощения составляет:
100-60 г Л 12 ПЛ1 / 0,072
* =
12-0,072
[^-б&^'НоТШ—1)] =5900 с = 1 ч 38 мии-
Пример 9.6, Через адсорбер непрерывного действия диаметром
D = 0,32 м проходит в 1 ч 120 м3 парогазовой смеси.
Поступающий в зону адсорбции активный уголь содержит ах = 4 кг/м8
адсорбируемого компонента; при выходе из нее содержание
адсорбируемого компонента доходит до ап =30 кг/м3. Концентрация
парогазовой смеси, поступающей в адсорбер С0 — 0,105 кг/м3» по-
кидающей адсорбер С\ = 0,0065 кг/м3. Коэффициент массоотдачи
адсорбируемого компонента в условиях работы адсорбера (Зу =
= 5 с"1. Изотерма адсорбции известна (рис. 9.1). Определить
скорость движения и высоту слоя активного угля.
Решение. Скорость движения угля находим по формуле
(9.23);
14* 419
Определим линейную скорость парогазовой смеси!
VA 120-4
Ш~ ЗбООяЯ2 ~ 3600-3,14.0.322 = и'410 м'с-
Подставив найденное значение w в формулу (9.23),
определим скорость движения угля:
0,105-0,415 ЛЛЛ]„0 ,
и — _ _ 0,00128 м/с.
От:
Для расчета высоты слоя на диаграмму изотермы наносим
рабочую линию (рис. 9.1) по координатам ее начальной точки А
(Со = 0,105 кг/м3 иад =30 кг/м3) и конечной К (C~i = 0,0065 кг/м3
и ах = 4 кг/м3).
От начальной точки рабочей линии к конечной строим ступени
изменения концентрации. Получается пять ступеней. Для каждой
ступени определяем число единиц переноса т0 по формуле (9.28):
mi 2 <5о - 5i) _ 2(0.105 — 0.0815) _
Шо== С0-С*2 ~ 0,105-0,053 ~0'905'
„Л 2(0,0815-0,053) ,„ 2(0,053-0,028)
Шо ~ 0,0815-0,028 ™ 1ДК*' то ~ 0,053-0,0115 ~ 1|АК>*
IV _ 2(0,028-0,0115) _ у __ 2(0,0115 -0,0065) _
то ~ 0,028-0,0065 ~ 1,0*>; то ~~ 0,0115-0,004 ~ 1,АК>"
Высоту слоя активного угля находим по формулам (9.25) и
(9.27):
v v
Я==^"2то==Т"2то=== ^Т^" (0'905+ 1'065 + 1,2°5 + 1-535+1,335)=
Spyi-J Py I
0,083.^,045^0,5 м-
Пример 9.7. Определить количество теплоты, которое
выделяется за один период (т = 133 мин) при адсорбции паров
этилового спирта активным углем. Диаметр адсорбера 2 м, высота
слоя В = 1,0 м.
Скорость паровоздушной смеси w = 25 м/мин; начальная
концентрация С0 =0,029 кг/м3; концентрация смеси на выходе из
адсорбера Сх = 0,0002 кг/м3; насыпная плотность слоя рнас =
=* 500 кг/м3.
Решение. Площадь поперечного сечения аппарата:
S = nD2/4 = 3,14.22/4==3,14 Mat
За один период через адсорбер проходит парогазовой смеси:
V = wSt = 25-3,14.133= 10 400 м3.
Адсорбируется пдров этилового спирта:
Gcn = 10 400 (29 — 0,2)/1000 = 300 кг.
420
или
Gcn » 300/46 ж 6,52 кмоль.
В адсорбер загружается активного угля*
5Ярйас = 3,14.1,0-500 ¦= 1570 кг,
что составляет
1570/6,52^240,8 кг угля/кмоль.
Воспользоваться данными табл. LIII здесь нельзя, так как она
составлена из расчета поглощения 1 кмоль на 500 кг угля.
Теплоту адсорбции можно рассчитать по формуле (9.8)!
q = тап-
Количество адсорбированного пара а на 1 кг угля составляет
а = 6,52-22,4.1000/1570 *» 93 л/кг.
Числовые значения тип берутся из табл. 9.2: т = 3,65* Ю3#
л = 0,928.
По формуле (9.8) на 1 кг угля выделяется теплоты!
<7*= 3,65-93°'928 =245 кДж/кг.
Всего за один период выделяется теплоты
qx = 245.1570 = 385 000 кДж.
Эта теплота расходуется на нагревание угля и аппаратуры, на
тепловые потери и в основном на нагревание парогазовой смеси.
Если предположить, что вся выделившаяся теплота расходуется
только на нагревание парогазовой смеси, и считать удельную
теплоемкость и плотность ее как для воздуха (с = 1,01 • 103 Дж/(кг> К)»
р = 1,2 кг/м3), то температура смеси повысится на
., 385 00(Ы0а олк гг
Л' ~ 10400.1,2.1,01-Юз ~ dU|5 *'
Пример 9.8. Определить длину зоны массопередачи
неподвижного слоя цеолита типа NaA (с1э = 0,002 м) и рабочую высоту
колонного аппарата для процесса глубокой осушки газов (Спр =з
= 2,94'10~? кг/м3) при следующих условиях* высота
неподвижного слоя 0,26 м, С0 =0,01 кг/м3, скорость паровоздушного
потока, отнесенная к полному сечению аппарата, 0,5 м/с, тнао =
= 190 мин, тпр — 110 мин.
Решение. Высота зоны массопередачи рассчитывается по
формуле (9.22)!
^нас тпр
tin = п
тнас — (1 — /) (тнас — ^пр)
__n9fi 190—110 26-80
-U|Z0 190 — (1 — 0,5) (190 — 110) ~~ 150 ~[*аск-
421
Здесь h0 — высота зоны массопередачи, см; Н — высота слоя сорбента, см;
тнас — время для равновесного насыщения слоя, мии; тпр—время защитного
действия ирн минимальной индицируемой проскоковой концентрации, мин; f —
неиспользованная часть адсорбента в зоне массопередачи.
Рабочая высота слоя в аппарате рассчитывается по формуле:
#о= yhQ = 1,4-13,8 = 19,3 см,
где у — коэффициент, характеризующий отношение гравиметрической плотности
с вибрационным уплотнением слоя к гравиметрической плотности без уплотнения
(V= 1,4).
КОНТРОЛЬНЫЕ ЗАДАЧИ
9.1. Определить количество загружаемого активного угля,
диаметр адсорбера и продолжительность периода поглощения
100 кг паров октана из смеси с воздухом при следующих данных:
начальная концентрация паров октана С0 =0,012 кг/м3, скорость
w = 20м/мин, активность угля по бензолу 7%, насыпная плотность
угля раас = 350 кг/м3, высота слоя угля в адсорбере Я = 0,8 м.
9.2. Определить продолжительность поглощения до проскока
т и потерю времени защитного действия т0 для адсорбции паров
четыреххлористого углерода слоем активного угля высотой Н = ,
= 0,10 м. Скорость парогазовой смеси w = 5 м/мин: диаметр
частиц угля d3 = 2,75 мм, динамические коэффициенты Вх —
- 14 500 и В2 = 52 945.
9.3. По изотерме адсорбции бензола при 20 °С (рис. 9.2)
построить изотерму адсорбции паров этилового спирта при 25 °С.
9.4- Пользуясь изотермой адсорбции бензола (рис. 9.2),
определить скорость и высоту слоя активного угля при непрерывной
адсорбции парогазовой смеси с начальной концентрацией С0 =
= 0,11 кг/м3, скоростью прохождения смеси w = 20 м/мин и
коэффициентом массоотдачи ру = 4 с-1. Уголь в процессе
адсорбции насыщается до 80% своей статической активности.
Остаточная активность угля после десорбции составляет 14,5% от
первоначальной статической активности. Парогазовая смесь должна
быть очищена до концентрации не более Сх = 0,01 кг/м3.
9.5. В вертикальный адсорбер диаметром 3 м со стальной
трубой днаметроы 0,35 м поступает 170 м*/мнн парогазовой смеси,
содержащей С0 = 0,02 кг/м3 паров этилового спирта.
Концентрация этилового спирта в отходящем газе Сх = 0,0002 кг/м*; высота
слоя активного угля в адсорбере Н = 1,5 м; насыпная плотность
угля рнас = 500 кг/м3; продолжительность одного периода
поглощения 4 ч 37 мин. Определить количество теплоты, выделяющейся
в адсорбере за первый период,
9.6. Определить минимальную скорость движения цеолита
типа NaA в колонном аппарате при глубокой осушке воздуха при
следующих данных: С0 =0,01 кг/м3, Спр = 2,94-10~6 кг/м3,
d3/.= 0,002 м, Оо = 170 кг/м3. Скорость газового потока,
отнесенная к полному сечению аппарата 0,5 м/с.
422
Глава 10
СУШКА
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Влажность материала может быть выражена в процентах
либо от общей массы влажного вещества (и), либо от массы
сухого вещества (и') Величины и и и' связаны соотношениями г
КЮи 100и' /1Л п
U = 100-гг ; U==lQQ + W <Ю1)
2. Количество влаги W, удаляемое из материала в процессе
сушки» при изменении влажности материала от иа до ию
равняется:
где Ga и ин — начальная масса и влажность материала, поступающего на сушку;
GK и ик — конечная масса н влажность высушенного материала.
Если влагосодержаме материала дано в процентах от массы
сухого вещества и', то
и'п — ик
WaG'y* 1QQ ' <10'3>
Здесь Gcyx — производительность сушилки по абсолютно сухому материалу.
3. Паросодержание парогазовой смеси х (в кг пара/кг сухого
газа):
Х = Л?"-^Й (Ю.4)
МР П — рп '
где Мп и МГ — мольные массы пара и газа; П — общее давление парогазовой
смесн; рп—парциальное давление пара.
Влагосодержание паровоздушной смеси х (в кг водяного
пара/кг сухого воздуха):
х = от *p'y . (ю.5)
11 — Waste
Здесь 0,622 — отношение мольных масс водяного пара и воздуха; <р —
относительная влажность воздуха:
Ф^РпАРнас; (Ю.6)
Ра — парциальное давление водяного пара в воздухе (при температуре сухого
термометра); Рвае — давление насыщенного водяного пара при той же
температуре (табл. XXXVIII и LVI) *.
* Если температура влажного воздуха выше температуры насыщения водя-
423
ного пара при давлении И, то Р^ас = П и х = 0,622 -т-~
Рис. 1С.1, а, б. Диаграмма Рамзина а-ля влажного воздуха.
4. Энтальпия влажного воздуха / (в кДж/кг сухого воздуха)!
]=*(св + сах) t+rQx= (1,01 + 1,97х) t + 2493*, (JO.7)
где св — 1,01 кДж/(кг- К) — средняя удельная теплоемкость сухого воздуха (при
постоянном давлении); са = i,97 кДж/(кг-К) — средняя удельная теплоемкость
водяного пара; х — влагосодержанне воздуха, кг пара/кг сухого воздуха; t —
температура воздуха (по сухому термометру), СС; г0 = 2493 кДж/кг — удельная
теплота парообразования воды при 0°С.
5. Связь между параметрами влажного воздуха х, t> cp, / легко
определяется по / — х диаграмме Рамзина (рис. 10.1), с помощью
которой преимущественно и решаются задачи по статике
конвективной воздушной сушки.
6. Плотность влажного воздуха рвЛ. в (в кг/м3) при давлении П
и температуре Г, выраженной в К, определяется по уравнению:
Рвл.в = Рв + Рш (Ю.8)
42А
мм.рт.с?
I IX У1 \v I \_ I XI V ^ IX „ __
0\0f025 0,050 0,075 0,Ю0 0,!25 0,150 0,175 0,200 0,225 0,250 0,275
влааосодермание ос, кг/кг сухого воздуха
SO
в котором плотность сухого воздуха рв и плотность водяного пара
рп взяты каждая при своем парциальном давлении:
Л1кГ0 (П-фРнас) . (10.9)
22,4ГП0
МпГ0фРдас
22,4ГП0 '
'в
Ря^
(10.10)
где П — общее давление паровоздушной смесн; П0 — нормальное давление
(0,Ю13 МПа, илн 1 атм).
Из выражений (10.8)—(ШЛО) получаем:
МВГ0П [1 /, __ Л^п\ ф?нас_ 1 _.
Рвл.в- 22,4ГП0 L \ мв) П -
= .«JE,x
Г-101 300
3,48-10"3
(l -0,378 ^р) -
(П~0,378фРнас).
(10.11)
425
7. Удельный объем влажного воздуха (приходящийся на 1 кр
сухого воздуха) ауд (в м3/кг) рассчитывается по формуле:
П-фРнас '
Руд-" тт !п . (10-12)
где /?в — газовая постоянная для воздуха, равная 287 Дж/(кг-К); Т —
температура воздуха, К, П — общее давление паровоздушной смеси, Па; Ф^нас — Рп —
парциальное давление водяного пара, Па.
8. Расход сухого воздуха в сушилке L (в кг/с)!
L = WL (10.13)
Здесь W—производительность сушилки по испаряемой влаге, кг/с; / —
удельный расход сухого воздуха, кг/кг испаряемой влаги:
I" , ' ; со.14)
¦*2 — л0
л*0 и л*2 — начальное и конечное влагосодержание воздуха.
9. Расход теплоты в калорифере Q (в Вт) при нормальном
(основном) варианте процесса сушки:
Q«L(/i-/0)> (Ю-15)
где /0 н 1Х — энтальпии воздуха на входе в калорифер и на выходе из него, Дж/кг
сухого воздуха.
Из теплового баланса сушильной установки для нормального
сушильного варианта следует:
Q = L(/3-/0) + 2] Q, (10.16)
где /3 — энтальпия воздуха на выходе из сушилки; Е Q — сумма расходов теп--
лоты на нагрев материала, нагрев транспортных устройств, потери в окружающую
среду (см. ниже).
Пренебрегая величиной 2 Q по сравнению с L (/3 — /в) —
основным расходом теплоты на испарение влаги и нагрев воздуха
и пара, — получаем уравнение для теоретической сушилки:
QT = L(/2-/0). (10.17)
10. Удельные расходы теплоты q (в Дж/кг испаряемой влаги)
в действительной сушилке:
<-ТГ~ёЕ?-'<'х-'.>; (юле,
в теоретической сушилке при том же конечном состоянии
воздуха:
Ag Ад
426
Разность удельных расходов теплоты в действительной и в
теоретической сушилке
q-Qt= l1"1* =Д (Ю.20)
Л2 — ^0
при отсутствии дополнительного подогрева в сушильной камере
равна:
л ?Q , ^л (10.21)
= —w = ^мат **"Ятр "*"<?яот ~" н*
Здесь
пот
<7мат ™г ск ($к — "Н)*; #тр — ^, ^тр (fy; — Фн); #п0т — —v#— .
?к» гтр» с— удельные теплоемкости высушенного материала, транспортных
устройств, воды, Дж/(кг'К); #н» #к— температуры начальная (поступающего в
сушилку влажного материала) и конечная (высушенного материала, выходящего из
сушилки), СС.
11. Тепловой к. п. д. сушилки:
4 = r/q, (10.22)
где г — удельная теплота парообразования воды, определяемая по температуре
материала при сушке (температуре мокрого термометра), Дж/кг; q~ удельный
расход теплоты в сушилке, Дж/кг.
12. При измерении психрометром относительной влажности
движущегося воздуха парциальное давление водяного пара в нем
может быть рассчитано по психрометрической формуле:
Рп = Р'нас - ^ ('~ <м ) П. (10.23)
где Рвас — давление насыщенного водяного пара при температуре мокрого
термометра; /—*м — разность температур сухого и мокрого термометров; П —
барометрическое давление; А — коэффициент, зависящий от ряда факторов, из
которых основным является скорость воздуха.
При w > 0,5 м/с:
А = 0,00001 / 65 + —¦) . (10.24)
Приближенное определение по показаниям психрометра
относительной влажности воздуха на / — х диаграмме Рамзина — см.
пример 10.12.
13. Скорость испарения воды с влажной поверхности
материала (в первом периоде сушки) G [в кг/(м2-ч)] может быть
рассчитана по эмпирическому уравнению:
G = 0,04075оЛ8Д/>, (10.25)
где w — скорость воздуха над материалом, м/с; Др = (Рнас — Рп) — разность
давлений насыщенного пара в пограничном слое воздуха у поверхности влажного
материала и парциального давления пара в проходящем воздухе, мм рт. ст.
* Омат = <Vk#k — <Vh#h — Окся (#к — #н) — Wc$w
427
Значение Рнае берется по паровым таблицам для температуры
мокрого термометра; рп определяется по формуле (10.23) или по
диаграмме Рамзина (рис. ЮЛ).
14* Продолжительность сушки при постоянных условиях (по
воздуху) может быть определена по приближенным уравнениям!
а) для периода постоянной скорости
б) для периода падающей скорости
X2^<l^2)3lg!^^9 (Ю.27)
Здесь N — скорость сушки в первом периоде, выражаемая числом
килограммов влаги (на 1 кг сухого вещества), испаряемой за 1 с; и'н, и' , и'<г и' —
начальное, критическое, конечное и равновесное влагосодержание материала (считая на
сухое вещество).
Общая продолжительность сушки:
т == хг + т2.
Вследствие неравномерного омывания материала созду хом,
наличия «мертвых» зон и других причин в теоретические формулы
(10.26) и (10.27) приходится вводить поправочный коэффициент,
равный 1,5—2. Приближенное уравнение для определения
продолжительности сушки (без учета равновесного влагосодержания)
имеет вид:
f ' Г г
t=""~"kp +-^g-2.3 lg АВ-. (Ю.28)
15. Движущая сила процесса сушки (в первом периоде)
может быть выражена следующим образом.
а) Как разность температур воздуха / и поверхности
влажного материала, которая принимается равной температуре мокрого
термометра tM:
x*=t — tM. (10.29)
Величину х называют также потенциалом сушки.
б) Как разность влагосодержаний воздуха насыщенного д'пас
(в поверхностном слое) и ненасыщенного х (в ядре воздушного
потока)!
Д* — *нас — *• (10.30)
Средняя движущая сила определяется по уравнениям;
*р-зтает- (1031)
и
^-^Йвд- <10-32>
где %! = *i — fM; к2 = t2 — /м; kxi = хшс — хх\ ^x2 = *нас — *а.
428
Обозначения температур и влагосодержаний — см. пример 10.14.
16. Скорость сушки N в первом периоде может быть
определена либо опытным путем, либо через коэффициент массоотдачи.
Так как количество испаренной влаги (в кг/с)
V = Р/^ср.
(10.33)
ТО
N = tt?/Gcyx - PFA*cp/Gcyx = Р/Д*ср- (Ю.34)
Здесь Р—коэффициент массоотдачи в газовой фазе, кгДма«с — );F— пло-
дь поверхнос
сухого воздуха;
mVki\
щадь поверхности испарения, м2; Ад:ср — средняя движущая сила, кг пара/кг
i; j = FfGGy% — удельная поверхность (на кг сухого вещества),
17. Коэффициент массоотдачи р может быть определен из
критериального уравнения:
^; = ЛКе?(Рг;)0'33аи0»135,
(10.35)
где Nu'= P//D; Re = wlh\ Pr:= v/Z>,
Определяющим размером при вычислении критериев NuJ и
Rep является длина поверхности испарения / в направлении
движения сушильного агента.
Параметрический критерий Гухмана Gu — (Тс — Ты)/Тс, где
Тл и Т
м
температуры сухого и мокрого термометров, К.
Величины А и п в уравнении (10.35) зависят от критерия Rep
(табл. 10.1).
Следует отметить, что при интенсивном процессе сушки
значение коэффициента массоотдачи может быть выше рассчитанного
по уравнению (10.35).
18. Продолжительность сушки и размеры противоточной
сушилки при переменных условиях (по воздуху и материалу) могут
быть определены с помощью уравнений (10.36) и (10.38). Для
первого периода сушки в противоточной сушилке необходимо
обеспечить площадь поверхности материала (в м2);
Fx = -L in *нас ~" Ч
(10.36)
Rer
1—200
200—6 000
6 000-70 000
А
0,9
0,87
0,347
Т
а б л и ц а 10.1
п
0,5
0,54
0,65
429
F2 = ^ * =—^ -' (1°-37)
Для второго периода сушки в сушилке необходимо развить
площадь поверхности материала (в м2):
^*п Г dx
(Хна* — х) Ги* — -тг- (*х — хи)
Правая часть уравнения (10.37) может быть
проинтегрирована, так как переменным является только х.
В результате интегрирования получаем следующее выражение:
г _ »КР Ум 1п (*8аС в) '
Р и.\К„ Г и. У.. V (Ю-38)
нас
В сушилке должна быть развита общая площадь поверхности
материала:
В уравнениях (10.36)—(10.38) приняты следующие обозначения: L—рас-
код сухого воздуха, проходящего через сушилку, кг/ч; VM — расход материала,
проходящего через сушилку (считая на сухое вещество), м3/ч; Р — коэффициент
массоотдачи, определяемьш экспериментальным путем, кг/(м2-ч—); и* —
содержание избыточной (свободной) влаги в материале (ы* = и' — и' н) в момент
времени т после начала периода падающей скорости, кг влаги/м3 сухого
материала; и* —содержание избыточной (свободной) влаги в материале в
критической точке, кг влаги/м3 сухого материала; х9—влагосодержание
воздуха, входящего во вторую зону противоточнон сушилки, кг/кг воздуха (см.
рис. 10.13); хг — влагосодержание воздуха, уходящего из второй зоны
сушилки и входящего в первую зону, кг/кг воздуха; хг— влагосодержание
воздуха, выходящего из сушилки, кг/кг воздуха; хиас — влагосодержанае
насыщенного воздуха, кг/кг воздуха.
ПРИМЕРЫ
Пример 10.1. Определить по / — х диаграмме Рамзина
(рис. ЮЛ) энтальпию и влагосодержание воздуха при 60 °С и
Ф = 0,3.
Решение. Как показано на рис. 10.2, находим: / =
= 163 кДж/кг сухого воздуха; х = 0,04 кг/кг сухого воздуха.
Пример 10.2. Определить парциальное давление водяного
пара в паровоздушной смеси при 80 °С и / =150 кДж/кг сухого
воздуха.
Р е ш е н и е. По диаграмме Рамзина (рис. 10.1) находим точку
пересечения изотермы 80 °С с линией / = 150 кДж/кг сухого
воздуха и эту точку проектируем на линию парциального давления
водяного пара, которая находится внизу диаграммы; полученную
точку проектируем направо на ось ординат, на которой нанесены
парциальные давления водяного пара (в мм рт. ст.).
430
t=60°C
t-eo°c
Ри1с. 1С.2 (к примеру 10.1)
Рис. 10.3 (к примеру 10.2).
При f = 80 °С и / = 150 кДж/кг сухого воздуха находим
рп = 28 мм рт. ст.
Графическую схему решения см. на рис. 10.3.
Пример 10.3. Воздух с температурой 24 °С и <р =0,7
нагревается в калорифере до 90 °С. Найти энтальпию и влагосодержа-
ние воздуха на выходе из калорифера.
Решение (рис. 10.4). Начальное состояние воздуха
определяется на диаграмме / — х точкой пересечения изотермы / = 24 °С
с линией ф = 0,7. Этой точке соответствует х =0,013 кг/кг сухого
воздуха и / = 54,5 кДж/кг сухого воздуха. Изменение состояния
воздуха при нагревании его в калорифере происходит при
постоянном влагосодержании, т. е. при х = const. Следовательно,
конечное состояние воздуха определится точкой пересечения
линии х = 0,013 с изотермой t = 90 °С. Этой точке соответствует
энтальпия / = 126 кДж/кг сухого воздуха.
Пример 10.4. Найти аналитически влагосодержание и
энтальпию воздуха при 30 °С и ф = 0,75; П = 0,098 МПа (1 кгс/ш2).
Решение. Для аналитического определения влагосодержа-
ния воздуха воспользуемся формулой (10.5). В нашем случае при
t = 30 °С давление насыщенного пара Риае = 0,0433 кгс/см*
(табл. LVI).
Подставляя соответствующие
значения, получаем: t-SDX>
Ф^нас
0,622
X
П — фРнас
0,75-0,0433
1—0,75.0,0433
= 0,622 X
0,021
кг
i~24°Q
кг сухого воздуха
Л,
ф
ч.
X-0,013
X
Рис. 10.4 (к примеру 10.9),
431
Энтальпия воздуха подсчитываете я по уравнению (10.7).
Подставляя соответствующие величины, имеем:
/ = (1,01 + 1,97*)/ + 2493*=» (1,01 + 1,97-0,021)30 +
+ 2493-0,021 =83 кДж/кг сухого воздуха.
Пример 10.5, По данным предыдущего примера определить
удельный объем влажного воздуха, приходящийся на 1 кг сухого
воздуха, т. е. на (1 + х} кг воздушно-паровой смеси.
Решение. Удельный объем влажного воздуха находим по
формуле (10.12):
_ RBT 287-303
VW -' ц _ фрнао — 9,81 • 10* - 0,75-0,0433.9,81.10*
— 0,92 м3/кг сухого воздуха.
Пример 10,6. Найти парциальное давление водяного пара,
плотность и влагосодержание воздуха, если его температура 60 °С,
давление Паб0 = 380 мм рт. ст. и <р — 0,4.
Решение. Из табл. XXXVIII находим Рнао —149,4 мм рт. ст.
По уравнению (10.6) парциальное давление водяного пара:
рп = Рнасф = 149,4-0,4 = 59,8 мм рт. ст.
Плотность влажного воздуха по уравнению (10.11):
- 1 OQQ гоП Л 0,378ФРнас\ _
. опо 273-380 /, 0,378-59,84 лк , _
вв1'293 "333^60- V 380—)=^5кг/мЗ.
Влагосодержание воздуха по уравнению (10.5):
х « 0,622 -^ = 0,622 *9'* а = 0,116 КГ
п~Рп * 380 — 59,8 ' кг сухого воздуха *
Пример 10.7, Определить относительную влажность воздуха
при t = 150 °С и П — 760 мм рт. ст., если его влагосодержание
х = 0,07 кг/кг сухого воздуха.
Решение. Под атмосферным давлением насыщенный
водяной пар не может иметь температуру выше 100 °С. Поэтому при
температуре воздушно-паровой смеси выше 100 РС РНао = П.
Тогда по уравнению (10.5):
х - о 622 фП - О 622 ф
т. е. при данном влагосодержании х относительная влажность <р
является постоянной величиной, не зависит от температуры. В
нашем случае:
0,07 = 0,622 J-3L,
откуда ф я^ 0,1 == 10%.
482
Пример 10.8. Найти влагосодержанне влажного воздуха при
/ = 60 °С и ф =50%, если барометрическое давление П =
= 765 мм рт. ст., и определить ошибку при расчете этого влаго-
содержания с помощью диаграммы Рамзина, построенной для
П = 745 мм рт. ст.
Решение. По табл. XXXVIII для t =* 60 °С находим PHdiG =
= 149,4 мм рт. ст. Тогда
, = 0.622 -S%^- = 0,622 7 "^'f* =
П — фРнас 765 — 0,5 * 149,4
= 0,0672 кг пара/кг сухого воздуха.
По диаграмме Рамзина (рис. 10.1) при t = 60 °С й ф =50%
находим х = 0,0695 кг/кг.
п 0,0695 — 0,0672 1ЛП 0 Ал.
Погрешность составляет: -—» Q6-' 100 = 3,4%.
Пример 10.9. Определить расход сухого воздуха и теплоты
В теоретической сушилке для удаления из влажного материала
100 кг/ч влаги, если начальное состояние воздуха (до
калорифера): tQ = 15 °С, ф0 =0,8, а на выходе из сушилки: t2 = 44 °С,
ф3 =s= 0,5.
Решение. По диаграмме / — х находим: х0 = 0,009 кг/кг;
х% —0,03 кг/кг. По уравнению (10.14) определяем удельный
расход сухого воздуха:
/=__J «. „ ' ,-47,6
Н — Ч 0»03 — 0,009 ' кг испаряемой влаги
Удельный расход теплоты находим по уравнению (10.19),
предварительно сняв значения энтальпий по диаграмме / — л:. В
условиях данного примера /3 = 121,5 кДж/кг; /0, = 40 кДж/кг.
Удельный расход теплоты:
h—h 121,5 — 40 OQQ„ u t
Я - -^Г^ " 0,03-0,009 ~ 388° кДж/КГ испаРяем™ влага-
Расход сухого воздуха по уравнению (10.13)j
L « Wl « 100-47,6 = 4760 кг/ч.
Расход теплоты:
Q = Wq = 100-3880/3600 = 108 кВт.
Пример 10» 10* В калорифер вводится смесь свежего воздуху
(t0 = 25 РС; ф0 = 0,5) и отработанного (*а « 50 °С; ф2 = 0,8)
в массовых отношениях 1 \ 3 (счнтая на сухой воздух). Найти
параметры смеси перед калорифером и после подогрева ее в
калорифере до 80 °С.
Решение. По диаграмме / — х определяем влагосодержа-
ще и энтальпию свежего й отработанного воздуха при заданных t
и ф. При t0 =25°C и ф0 =0,5: х0 =0,01 и /0 = 50 кДж/кг.
433
При (2 = 50 X, и ф, = 0,8: х3 = 0,069 и /2 = 228 кДж/кг.
Следовательно, влагосодержание смеси будет равно:
*см = 0,25-0,01 + 0,75-0,069 = 0,0542 кг/кг,
а энтальпия
/см = 0,25.50 + 0,75-228= 183,5 кДж/кг.
Далее находим на диаграмме точку с координатами х = 0,0542
и / = 183,5. Этой точке соответствуют 4м = 45 °С и <pCw — 0,85.
Нагревание смеси в калорифере происходит при х = const.
Следовательно, точка пересечения линии х = 0,0542 кг/кг с
изотермой 80 °С даст нам состояние смеси после калорифера. Этой точке
соответствуют: /см = 147 кДж/кг и Фсм =0,018.
Пример !0.11. Найти точку росы для воздуха, имеющего
t = 40 °С и ф = 0,8.
Решение. Точка росы соответствует той температуре, при
которой паровоздушная смесь с данным влагосодержанием
становится насыщенной водяным паром. При охлаждении влажного
воздуха ниже этой температуры происходит конденсация водяного
пара. Для определения точки росы необходимо на диаграмме / — х
найти точку, соответствующую заданному состоянию воздуха,
затем опуститься по линии х = const до пересечения с кривой ф = ],
т. е. до линии насыщения. В нашем случае х = 0,039 кг/кг и точка
росы соответствует температуре t = 36 °С {см. схему решения на
рис. 10.5).
Пример 10.12, Показания психрометра: по сухому термометру
t = 40 °С, по мокрому ^м = 35 °С. Определять приближенно по
диаграмме / — х Рамзина относительную влажность воздуха.
Решение. Находим на диаграмме точку пересечения
изотермы fM с линией ф «= 100% (точка А на рис. 10.6). Из этой точки,
двигаясь по линии постоянной температуры мокрого термометра
434
*- тХ
tz=50°C
ta=22°C
4
И
-4
0
отг=
^<м
Рис» 10.7 (к примеру 10ЛЗ).
0-0^x^^0/25 *Haceft<W
Рис. 10.8 (к примеру 10. Н),
(^м = const)*, доходим до пересечения с изотермой ^. В точке
пересечения В находим искомое значение ср.
Если на диаграмме Рамзина для упрощения ее линии /м —
= const не нанесены, как на рис. 10.1, а, то искомую
относительную влажность воздуха приближенно можно определить, двигаясь
из точки А по линии / = const до пересечения ее с изотермой t.
Линии /м = const и / = const близки, и при небольших значениях
разности (t — /м) погрешность при таком приближенном
определении невелика.
В нашем случае при t = 40 °С и tK = 35 °С находим по линии
/ = const: ф -70%.
Пример 10.13. Найти температуру материала, выходящего из
сушилки, если его влажность выше критической и воздух на
выходе из сушилки имеет t2 = 100 °С и х2 = 0,0135 kf/кг.
Решение. В первом периоде сушки температура влажного
материала равна температуре мокрого термометра ?м. Ее
находим (рис. 10.7), двигаясь от точки А по линии / = const до
пересечения с линией ф = 1 в точке Вг через которую проходит
изотерма /м = 60 °С.
Пример 10.14. Найти движущую силу процесса сушки Длгср и
иср для теоретической сушилки при следующих условиях: ^0 =
= 22 °С; U = 50 °С; Фо = 0,75; щ = 0,45.
Решение. По диаграмме / — х (рис. 10.8) находим: хг =
= 0,0125 кг/кг; х2 =0,037 кг/кг; лгнао =0,043 кг/кг; Ф « 37 °С.
Следовательно,
Axt — Д*а (0,043 — 0,0125) — (0,043 — 0,037)
Ах
ср
2-3 * Ш
Нср —
щ — у%
0,043-0,0125
' g 0,043 — 0,037
(Ш— 37) — (50 — 37)
= 0,0152 кг/кг;
2.3 Ig
2,3 ig
1 11—37
50 — 37
= 35СС = 35К.
* На рис* ЮЛ, б линии /м = const нанесены пунктиром.
435
Пример 10.15. Определить по показаниям психрометра
относительную влажность воздуха, покидающего сушилку, если
температура сухого термометра t = 85 РС, температура мокрого
термометра <м = 68 °С, барометрическое давление П = 750 мм рт. ст.,
а скорость воздуха w — 1 м/с.
Решение. Относительная влажность воздуха!
По табл. LVI находим, что при t — 85 °С давление
насыщенного пара Рнас = 0,59 кгс/см2. Затем определяем парциальное
давление водяного пара ра по формуле (10.23)!
Находим по табл. LVI давление насыщенного пара при
температуре *м мокрого термометра* Р'нас = 0,2912 кгс/см2.
Коэффициент А определяем по формуле (10.24);
00072.
А = 0,00001 (б5 + 2*р) « 0,
Затем находим:
Ф = Г 0,2912 — 0,00072 (85 — 68) ~^1 /о,59 = 0,47,
Пример ЮЛ6. Определить расход воздуха, а также расход и
необходимое давление греющего пара для непрерывнодействую-
щей противоточной сушилки, работающей по нормальному
сушильному варианту.
Производительность сушилки по Gn — 350 кг/ч
влажному материалу
Начальная влажность материала ын == 42 %
Конечная влажность материала "к" И %
Температура материала, поступающе- Ф$ — 18 °С
го на сушку
Температура материала, выходящего $2 = 47 °С
из сушилки
Характеристика состояния воздуха:
до калорифера tQ =* 15 °С, <р0 = 70%
после сушилки t2 =* 45 °С, ф2 = 60 %
Удельная теплоемкость высушенного ск = 2,35-103 Дж/(кг-К)
(ик = 11 %) материала
Масса транспортирующего устройства GTp = 600 кг
(стальной транспортер)
Тепловые потери сушилки и калори- Qn0T =*= 12 % от суммы всех
фера в окружающую среду остальных слагаемых
теплового баланса
Влажность греющего пара 6 %
Решение. Количество испаренной в сушилке влаги
определим по уравнению:
1Г = ^ж^ = 350-ж=тгг=122кг/ч-
436
По диаграмме / — х находим влагосодсржание и энтальпию
воздуха до калорифера и воздуха, выходящего из сушилки; х^ =
= 0,0077; х2 =0,038; /0 =35 кДж/кг; /2 = 145 кДж/кг.
Расход сухого воздуха в сушилке на испарение W кг/ч влаги*
^ = -^" = 0,38 -0,0077 = 403° КГ/Ч-
Расход теплоты в теоретической сушилке;
QT = L (/а — /0) = i звОО = i23000 Вт'
В действительной сушилке теплота расходуется еще на
подогрев материала;
СкСк «,, _ <ц . (350-.22) 2,35.03(47-,8) _ ^ ^
а также на нагрев транспортирующих устройств:
г ,« ч ч 600-0,5-103 {47— 18) О,ол _
<VTp («8 - «l) = —Ш = 2420 ВТ'
где 0,5-103 — удельная теплоемкость стали, Дж/(кг- К) — табл. XXV,
Из общего количества теплоты, которое необходимо подать
в сушилку, надо вычесть количество теплоты, вносимое влагой,
находящейся во влажном материале:
IFVb = 122-18-4,19.103/3600 = 2560 Вт.
Тогда общее количество теплоты, которое должно быть
подведено в калорифер, с учетом потерь в окружающую среду,
составит:
0 =* (123 000+ 4300+ 2420 — 2560) 1,12= 142 500 Вт.
Сравнивая расходы теплоты в теоретической и действительной
сушилке, можно видеть, что в последней расход теплоты выше
па 15%.
Так как
Q = L (/j — /0) = 142 500 Вт,
ТО
. . Q 142 500-3600 __„_ 1Л, Дж
L 403Q кг сухого воздуха
Следовательно,
кДж
1% = 127,5 + /0 = 127,5 + 35 = 162,5
кг сухого воздуха
Этому значению 1Х соответствует температура воздуха после
калорифера tx « 138 °С (по диаграмме / — х).
437
Принимаем разность температур греющего пара и воздуха на
выходе из калорифера:
Д' = 'г.д— 'i= 10°С= 10 К.
Тогда
/г.ц= 138 + 10= 148 °С,
чему соответствует необходимое давление греющего пара ра6с &
& 0,461 МПа, или 4,7 кгс/см2 (табл. LVI).
Расход греющего пара:
п Q 142 500 ЛЛ,,е , OCT .
С* ¦ = W- e 2122.103.0,94 " °'°715 КГ/С " Ш КГ/Ч'
где г = 2122 кДж/кг — удельная теплота конденсации греющего пара при 148 °С
(табл. LVI); к' — паросодержание греющего пара.
Удельный расход греющего пара:
, __ GTt п _ 257 __ _ кг греющего пара
"~ W "~722"~ ' кг испаряемой влаги *
Пример 10.17. Определить средний коэффициент
теплопередачи (относя его к разности температур греющего пара и
высушиваемого материала) в опытном элементе паровой трубчатой
сушилки для торфа по следующим данным:
Производительность элемента сушил- ^сух" *1»2 кг/ч
ки (считая на абсолютно сухой торф)
Начальная влажность торфа (считая и'п — 0,57 кг/кг
на сухое вещество)
Конечная влажность торфа и'к = 0,148 кг/кг
Температура торфа, поступающего на Ф1=20°С
сушку
Температура торфа, выходящего нз 03 — 52 °С
сушилки
Удельная теплоемкость абсолютно су- с= 1,26-10s Дж/(кг-К)
хого торфа
Характеристика состояния
продуваемого воздуха:
до сушилки t0 — 22 °С, ф0 == 0,34
после сушилки /а ~ 82 °С, ф3 = 0,37
Барометрическое давление П *= 773 мм рт. ст.
Температура греющего пара /= 100 °С
Площадь поверхности нагрева трубы F — 2,18 ма
Решение. Средний коэффициент теплопередачи определим
по уравнению:
Q
К =
F&tcv
Здесь Q — расход теплоты, проходящей через поверхность нагрева; Д*ср
средняя разность температур.
438
Расход теплоты, передаваемой через греющую поверхность!
Q = Qi + Q3 + Qs.
где Qi — теплота, пошедшая на испарение влаги и иа нагрев воздуха; Qa—
теплота, пошедшая на нагревание торфа; Q3— потери теплоты в окружающую среду.
Расход испаренной влаги [формула (10.3)}:
W = Gcyx (иа — ик) = 13,2 (0,57 - 0,148)/3600 = 0,0013 кг/с.
Определяем начальное и конечное влагосодержание воздуха
по формуле (10.5):
^-°^Г017°-003420,0270 ^ °.0057 кг/кг;
,^0,622 -01°;3:-^>5233^0,146 кг/кг.
Энтальпия воздуха до поступления в сушилку [формула
(10.7)]:
/0 = (1,01 • 103 + 1,97-103-0,0057) 22 + 2493-103-0,0057 = 36,5- 10s Дж/кг,
а по выходе из сушилки:
/2 =(1,01.103 + Ь97.103-0Л46) 82+ 2493-103-0,146= 470-Ю3 Дж/кг.
Тогда
Ql e W h^JjL e 0,0013 ^,14°;-S03 = 4050 ВТ;
к% — х& 0,146 — 0,0057
Здесь /а и iQ — энтальпии сыходящего и входящего в сушилку, торфа (считая
на 1 кг сухого торфа):
/2 = (1,26- /О3- J -)~4J9.JO3.0,f48)52^97,8.IO3 Дж/кг;
с0 « (U26- Ш3.1 + 4,19-Ю3'0,57) 20 = 73-103 Дж/кг.
Следовательно,
Qa = ~|- (97,8- Ю3 - 73-103) = 77 Вт.
Потери теплоты в окружающую среду Q3 примем равными 10%
от Qv Тогда общее количество теплоты:
Q == 4050 + 77 + 405 = 4532 Вт.
Средняя разность температур в сушилке:
Atcp = [(100 — 20) + (100 — 52)J/2 = 64 °С = 64 К-
Коэффициент теплопередачи:
439
Таблица 10.2
0
2,5
Время
от начала
сушки, ч
Влагосо- 104,0 84,0 79,1
держание
материала, % на
сухое
вещество
6 8 10 12 14 16 18 20
63,9 53,9 43,9 32 21,9 14,0 8,0 5 3 1,5
Пример 10.18. Определить к. п. д. теоретической воздушной
сушилки при следующих условиях: процесс сушки идет при / =
= 115 кДж/кг, состояние воздуха меняется от <р0 = 0,8, tQ — 20 °С
до ф2 = 0,6, t2 = 40 °С.
Решение. С помощью диаграммы / — х Рамзина (рис. 10.1)
находим по формуле (10.19) удельный расход теплоты в сушилке
на испарение 1 кг влаги: q = 3820 кДж/кг. По табл. LVI для tK =
= 33 °С при / = 115 кДж/кг удельная теплота парообразования г
равна 2420 кДж/кг. Следовательно, к. п. д. сушилки по формуле
(10.22):
2420
ц = —=
3820
100 = 63,3%.
Пример 10.19. Паста красителя высушивалась в камерной
сушилке с рециркуляцией воздуха. Анализ проб на влажность дал
следующие результаты (табл. 10.2).
Определить скорость сушки в зависимости от времени; по
полученным данным построить кривую и найти критическое влаго-
содержание материала.
Решение. Составляем табл. 10.3. По данным этой таблицы
строим кривую в координатах скорость сушки — время сушки
(рис. 10.9) и находим, что критическое влагосодержание
материала достигается через б ч после начала сушки. Ему
соответствуют 43,9% влаги, считая на абсолютно сухое вещество, или
43,9-100 Qnc0/
100 J--43 9 = 30,6% влаги,
считая на общую массу продукта.
Пример 10.20. Для сушки
влажного материала с 33 до 9%
влагосодержания (считая на
абсолютно сухое вещество) в
промышленной сушилке
потребовалось 7 ч. Критическое
влагосодержание материала было
Рис. 10,9 (к примеру 10.19).
440
Таблица 10.3
Время
от начала
сушкн т, ч
Скорость сушки
AW
(считая на сухое вещество),
Время
от на^ала
сушкн ** ч
Скорость сушки
Аи*
Ах
(считая на сухое вещество)
%/ч
2
2,5
4
5
6
8
104 — 84
84
79,1 •
2
— 79,1
0,5
-63,9
1,5
10
:9,8
10,14
63,9 — 53,9= 10
53,9 — 43,9 = 10
43,9—32
= 5,95
10
12
14
16
18
20
32 — 21,9
2
21,9—14
2
14 — 8
2 "
8 — 5
2 "
5 — 3
2
3,0—1,5
= 5,05
= 3,95
= 3,0
1.5
'1,0
= 0,75
16%, а равновесное 5%. Требуется определить время,
необходимое для сушки этого материала от 37 до 7% влажности, если
условия сушки остаются без изменения. Начальным пусковым
периодом можно пренебречь.
Решение. Определим N — скорость сушки в первом периоде.
Продолжительность первого периода сушки [уравнение (10.26) 1з
*1 = ("'н - «кр)/Л - (0,33 -0,16)/N = 0,17/Л.
Продолжительность второго периода [уравнение (10.27) ]з
Ь2
цкр-"р оот„ "кр-"р 0,16-0,05 OQ1^0,16 —0,05 0.111
~ N W lg ,/ _ ,/ ~ N " ' lg 0,09 - 0,05 " ~'
и — и
к р
Общая продолжительность сушки была 7 ч. Следовательно,
7 0,17 , 0,111 0,281
Ъ + Ч — 7 = -jj- +
N
N
N '
откуда N =0,0402 кг/(кг«с).
При новых условиях начальной и конечной влажности
материала:
0,37 — 0,16
Ti =
0,0402
= 5,22 ч;
v 0,16-0,05 ... 0,16-0,05
Та== 0,0402 2'3 lg 007^005 д 4'66 Ч*
Общее время сушки составит:
т = 5,22+ 4,66 = 9,9 ч.
441
Пример 10,21. Определить время сушки кристаллов
салициловой кислоты (частицы угловатой формы) в воздушной
пневматической сушилке и необходимую длину сушилки при следующих
условиях; производительность GK = 250 кг/ч высушенного
продукта, эквивалентный диаметр частиц d^ = 1 мм, плотность
материала рмат = 1480 кг/м3.
Характеристика состояния воздуха:
до калорифера
после калорифера
на выходе нз сушилки
Температура кристаллов при входе
Температура кристаллов при выходе
Удельная теплоемкость сухих
кристаллов
Влагосодержаиие кристаллов (считая
на абсолютно сухое вещество):
начальное
конечное
*„= 15 °С, Фо= 0,7
tx = 90 °С
tt = 50 °С
#!= 15 °С
#2 = 40 °С
ск = 1,16-Ю3 Дж/(кг-К)
«i= 15%
и
к
* 1%
о
Решение. Время сушки можно определить из уравнения
теплоотдачи:
Q
т =
aFr. At
ср
Для определения расхода воздуха и теплоты на сушку
производим построение сушильного процесса иа / — х диаграмме
(рис. 10.10).
В теоретической сушилке при 1Х =111 кДж/кг процесс сушки
шел бы по линии постоянной энтальпии ВС' и удельный расход
теплоты #i равнялся бы
дт ~-т— - Ql023-0,0075 ==50Ш ******* испаРяем<>и Вла™,
*2
"0
tt~90°C
tz~5Q°C
tu~32'C
t,«75°C
Xo'0,0075
Ъ
'0,021
где x'2 = 0,023 — влагосодержаиие
воздуха в точке С.
В действительной
сушилке конечное влагосодержаиие
воздуха Х2 (в точке С) будет
меньше хЬ. Его значение
находим следующим образом.
Из уравнения линии
реального процесса сушки ВС
I = It — Д (х — x0)t
задаваясь произвольным
значением xt находим /,
предварительно рассчитав расход
испаряемой влаги W и
поправку А для реального
процесса сушки.
Рис, ГОЛО (к пример* 10.21),
442
По уравнению (10.3)з
W e Gc*x """нхЛ = 25° ¦0,99 (0Л5 ~~ °,01) в 34,6 КГ/Ч'
По уравнению (10.21) при <7тР =0*
Д *= <7мат + <7пот — <#i5
4мат «<VK (дя — $i)/№ = 250-1,16-10я (40 - 15)/34,6 =
= 209,5.10' Дж/кг испаряемой влаги.
Примем удельную потерю теплоты ^п0т в размере 5,5% от q?t
<7пот =0,055-5000 =275 кДж/кг испаряемой влаги. Тогда
А = <7мат + <7пот — <#t = 2°9.5 + 275 - 4,19-15 =
= 421,7 кДж/кг испаряемой влаги.
Задаемся х =0,016 и находим:
/ = /, — Д (х — х0) « 111 —421,7(0,016 — 0,0075) = 107,4 кДж/кг.
Проведя через точки В и D (xD =0,016; ID = 107,4) прямую
линию до пересечения с изотермой (г = 50 СС, получаем точку С»
для которой находим х2 = 0,021 кг/кг.
Расход сухого воздуха на сушку;
W 34,6 ОСЙп ;
— 2560 кг/ч.
х2 -х0 0,021—0,0075
Расход теплоты, передаваемой воздуху в калорифере:
Q^Li^ — /0) = 2560 (ПЬЮ3 — 33,5- 10я)/3600 = 55200 Вт.
Коэффициент теплоотдачи а от горячего воздуха к частицам
материала, подвергающимся сушке в трубе-сушилке, может быть
определен приближенно по рис. 10.11, на котором представлена
зависимость Nu = / (Аг), полученная по опытным данным
И. М. Федорова.
Критерий Нуссельта
Nu = adQ/k.
Критерий Архимеда:
Ar = 4W2/(vcPc)>
где Uq — Ю-3 м — диаметр частицы; X = 0,0285 Вт/(м- К) — коэффициент
теплопроводности воздуха при его средней температуре (90 + 50)/2 = 70 °С; рмат =
= 1480 кг/м3 — плотность материала; ре = 1,03 кг/м8 — плотность воздуха при
70 °С; vc = 2-10"$ м2/с — кинематический коэффициент вязкости воздуха.
Подставляя эти значения, получаем:
ю-мш.9,81 4. ^v, _328
™ 2е -10"1» -1,03 ~" * ""
По рис. 10.11 находим Nu = 10, откуда
а = Ntu/4, = 10-0,0285/0,001 = 285 Вт/(м2- К)-
443
J 4 5 6 78910
20 30 40 50 60708090100
Рис. 10.11. Зависимость критерия Nu от критерия Аг (к примеру 10.2П.
Число частиц материала, проходящих через сушилку за 1 ci
G
П *=в
И/6)рмат*3600 '
Они дают общую площадь поверхности;
Fc ^ nnd9 = 4рмат.3600 = 0,001.1480-3600 ** °'281 м*/с"
Среднюю разность температур приближенно * определяем
следующим образом:
гп Воздух
60 *-
Материал
oZ —'¦>
50
40
Д/-П =
Д/б = 58
58—10
ср " 2,3 |g (58/10)
Д>М=Ш'
27,3° С = 27,3 К.
Расход теплоты, получаемой в сушилке материалом от горя-
чего воздуха, складывается из следующих слагаемых (принимая
приближенно, что вся влага испаряется при tM = 32 °С).
* Не учитывая кратковременного начального периода подогрева материала,
его начальную температуру здесь можно принять равной температуре мокрого
термометра, т. е. 32 °С (см, рис, 10,10),
1) Нагрев влажного материала!
/250 , ,„ . 34,6
Qt e (fllAl + Wc) (/м - <Ы - (J^ 1,16 + gg 4,19) (32 - 15) - 2,05 кВт.
2) Испарение влагш
Qa _ТГг - |i? 2420 « 23,25 кВт.
3) Нагрев высушенного материала!
250
3600
250
Qs - <%<*(*• - *м) в ^ U6 (40- 32) - 0,65 кВт.
Всего:
Q *= Qi + Q2 + Qs = 2>05 + 23,25 + 0,65 = 25,95 кВт.
Продолжительность сушки:
Q _ 25,95.103 ,
aFcAtCv ~ 285-0,281.27,3 — "^ u
Длина сушилки может быть найдена из следующего равенства!
1s= l/(W — W0C),
где /— длина трубы, м; w — скорость воздуха в сушилке, м/с; woc — скорость
осаждеиия (витания), м/с; шос находим по рис. ЪЛ, иа котором дана зависимость
Ly sbl f (Аг) для частиц угловатой формы.
Для Аг = 3,52-104 находим Ly = 205, откуда
woc = у/Ту УсРмат^/Рс *= J/*205.2.10-5.1,48.103-9,81/1,03 = 3,86 м/с.
Обычно принимают ш = (1,1 -г- 1,25) w0G. Примем w =
= 3,86-1,2 =4,64 м/с. Тогда
/ = т (w — woc) — 11,9 (4,64 — 3,86) s= 9,28 м.
В действительности время пребывания частиц в трубе-сушилке
больше, чем получается по расчету, так как в расчете не
учитывается время на разгон частиц, только после которого
устанавливается режим движения; это подтверждается экспериментальными
данными.
Дополнительная длина /р трубы для частиц размером 0,2—1 мм
и скорости воздуха 15—50 м/с может быть определена по
эмпирической зависил- ^ти:
/р = wd,
где w — скорость воздуха, м/с; d— диаметр частицы, мм.
Для нашего примера /р = 4,64-1 = 4,64 м. Тогда необходимая
длина трубы-сушилки:
L= 9,28+4,64» 14 м.
445
В 140°С
Рис. (0.12 (к примеру 10.22).
Д и аметр тр у бы-су ши л ки
определяется из уравнения
расхода;
D
-г*
2560
1,03-3600
785&У *
= 0,69 мз/с;
&0Э95 0,02525 QJQJ47 QJH1
Пример 10.22. Определить
расход воздуха и теплоты
при высушивании 1 т
влажного материала от ин = 50%
до ип = 6% (считая на
общую массу) в теоретической
х сушилке, работающей: а) по
нормальному сушильному
варианту; б) по варианту с
промежуточным подогревом
(считая, что воздух в калориферах подогревается до 100 °С); в)
по варианту с рециркуляцией 80% отработанного воздуха.
Сравнить также потенциалы сушки для этих вариантов. Параметры
атмосферного воздуха: tQ = 25 °С; х0 = 0,0095 кг/кг сухого
воздуха. Параметры отработанного воздуха: /а = 60 °С; х2~ 0,041 кг/кг
сухого воздуха.
Решение. Определяем количество испаренной при сушке
влаги;
W = GH
"п ~ «
к
= 1000
50
100 — 6
= 468 кг/ч.
100 — н,,
а) Нормальный сушильный вариант (ABC на рис. 10.12).
Удельный расход сухого воздуха:
1 1
*2 —*о 0,041—0,0095
Общий расход сухого воздуха:
= ЗЬ8
кг
кг испаряемой влаги
L = № = 31,8-468 = 14 900 кг/ч.
Удельный расход теплоты:
q » I (/, — /0) = 31,8 (167 — 46) = 3860 кДж/кг испаряемой влаги.
Значения энтальпий находим, пользуясь / — х диаграммой
Рагозина (рис. ЮЛ).
Общий расход теплоты:
Q = Wq=* 468-3860/3600 = 502 кВт.
446
б) При ведении процесса сушки с промежуточным подогревом
(АВ'С'С'С на рис. 10.12) необходимы два калорифера для
подогрева воздуха в каждом до 100 °С. При этом в первой зоне
сушилки влагосодержание воздуха повышается до 0,02525 кг/кг
сухого воздуха и удельный расход сухого воздуха составляет:
V e п пп_ ' п _г = 63,6
0,02525 — 0,0095 ' кг испаряемой влаги
Но так как в первой зоне сушилки испаряется только половина
всей влаги, т. е. 468/2 = 234 кг/ч, то часовой расход сухого
воздуха:
L = /' -у- = 63,6*234 = 14 900 кг/ч.
Во второй зоне сушилки происходит испарение остальной влаги
тем же воздухом, но подогретым до 100 °С в промежуточном
калорифере.
Теплота на подогрев воздуха затрачивается в двух
калориферах, и расход его равен:
c-/'('i-'o)T-+/'(/»-/»)T—f^C*-7»).
но так как Г/2 = /, то
Q^Wl (/2 - /0) = ijgg 31,8 (167 - 46) = 500 кВт.
в) Для сушильного процесса с возвратом 80% отработанного
воздуха (АМВ"С на рис. 10.12) определяем характеристики смеси,
поступающей в калорифер:
*см = О>2*0 + 0Д*2 = 0,2-0,0095 + 0,8-0,041 =
= 0,0347 кг влаги/кг сухого воздуха;
'см = 0,2/0 + 0,8/2 = 0,2-46 + 0,8-167= 143 кДж/кг сухого воздуха.
Тогда удельный расход сухого воздуха:
Г = Ь-Хои ~* 0,0*1 - 0,0347 e 159 КГ/КГ ВЛЗГИ'
а расход воздуха (смеси), поступающего в сушилкуз
Г = Щ" « 468-159 = 74 500 кг/ч.
Расход атмосферного воздуха (20%):
L = 74 500-0,2 = 14 900 кг/ч.
Удельный расход теплоты:
„ U - /см 467-143 ооол п i
4 = **-*с* = 004ГЗШ4Г = 382° кДж/кг влаги'
447
Расход теплоты!
Q = Wq = Ш6 382° = 495*кВт'
Из сравнения расходов воздуха и теплоты на сушку по трем
рассмотренным вариантам видно, что при одних и тех же
начальных и конечных параметрах воздуха (точки Л и С на рис. 10.12)
эти расходы одинаковы.
Сравним средние потенциалы сушки:
2,3 lg -1 ?¦ 2,3 lg
'i-'м о ч . HQ-4Q
h — tu ?щ g 60 — 40
б) х,^100-35^^-35^ 41.8-С-413 К;
2'3 8^0^40"
кср = (41,8 + 36,5)/2 = 39,15 °С = 39,15 К;
«* * (75 - 40) - (60 - 40) 9fi7cr_9fi7[f
в) хср = у-5 _ 4Q = 26,7 L = Д>,7 К.
2-3 '§ -60-^40-
Из сравнения потенциалов сушки видно, что наименьшее
значение потенциала (наиболее мягкие условия сушки), получено
в варианте с возвратом части отработанного воздуха, а
наибольшее — при нормальном сушильном варианте.
Пример 10.23. Некоторый материал высушивается в противо-
точной сушилке непрерывного действия от 50 до 3,5% влаги,
.считая на общую массу. Производительность сушилки по влажному
материалу 2260 кг/ч. Плотность сухого материала 640 кг/м8. На
1 кг сухого материала приходится 0,0615 м2 поверхности
испарения.
При предварительном опытном высушивании было найдено,
что критическое влагосодержание материала составляет 20%,
а равновесное — 1,5% от общей массы. В первом периоде
сушки, когда поверхность материала насыщена влагой, скорость
сушки составляла 2,44 кг влаги с 1 м2 в 1 ч, Применявшийся
в этом случае воздух имел влагосодержание 0,0306 кг/кг.
Влагосодержание насыщенного воздуха при температуре материала
было д;нас = 0,0495 кг/кг. По этим данным определен коэффициент
массоотдачи:
2 44
»- 0,0495 10,0306=129КГ/(М2-Ч-А*=1)-
Определить необходимую продолжительность сушки.
448
оона
сс2 = 0,0294
сс,=
и
хпъс~0>0495
Материал
Езона
0,0124
Воздух
х0=0,0075
и
кр
и.
Рис» 10.13 (к примеру 10.23).
Решение (рис. 10.13). Определим по уравнению (10.36)
длительность первого периода сушки, в котором вся поверхность
материала насыщена влагой. По заданным параметрам: /0 = 20 °С;
ф0 =0,5; /х = 140 °С и t2 = 63 °С, находим х0 =0,0075 и х2 —
= 0,0294. Затем обычным расчетом, который здесь не приводится
находим, что часовой расход сухого воздуха L = 49 700 кг/ч; хх —
= 0,0124 кг/кг; xHaG =0,0495 кг/кг. Тогда по уравнению (10.36)1
2,3-49 700, 0,0435 — 0,0124
12У
lg
= 237 м3.
0,0495 — 0,0294
При заданной производительности сушилки часовая подача
материала соответствует поверхности испарения
2260-0,5.0,0615 = 69,5 м*/ч.
Таким образом, первая зона сушилки, соответствующая
первому периоду сушки, должна содержать количество материала»
загруженного в течение 237/69,5 = 3,41 ч, т. е. длительность
первого периода сушки 3 ч 25 мин.
Переходя к определению длительности второго периода сушки,
находим:
а) объем сухого материала:
VM » 2260-0,5/640 = 1,77 м»/ч;
б) критическое влагосодержание
и = 20-640/80 а 160 кг/м8 сухого материала;
в) равновесное влагосодержание
и = 1,5-640/98,5 =9,75 кг/м3 сухого материала.
Содержание свободной влаги в критической точке!
мкр ~ икр ~~ ир — 160 — 9,75 = 150,25 кг/м3 сухого материала.
15 Павлов К.. Ф, и
Др.
449
Требуемую площадь поверхности испарения для второй зоны
сушилки F2 находим по уравнению (10.38), в котором
u*VJL = 150,25-1,77/49 700 = 0,0054;
Л«
150,25
1,77
X In
129 0,0495 + 0,0054 — 0,0124
(0,0495 — 0,0075)0,0054
(0,0495 — 0,0124) ^0,0075 + 0,0054 — 0,0124)
х
-= 120 ма,
т. е. вторая зона сушилки, соответствующая второму периоду
сушки, должна содержать количество материала, загруженного
в течение 120/69,5 = 1,73 ч. Следовательно, длительность второго
периода сушки будет 1 ч 44 мин.
Общая продолжительность сушки:
т = 3 ч 25 мин + 1 ч 44 мии = 5 ч 9 мин.
Пример 10.24. В сушилке, работающей по нормальному
сушильному варианту, удаляется из материала влаги 1000 кг/ч.
Атмосферный воздух (/0 — Ю СС, ф0 =78%) нагревается в паровом
калорифере, давление греющего пара в котором 4 кгс/сма
(~ 0,4 МПа) по манометру. Психрометр на воздухопроводе после
сушилки показывает t2 = 50 °С, tM = 37,5 °С. Приняв удельный
расход теплоты на 13% больше, чем в теоретической сушилке,
определить; производительность вытяжного вентилятора, расход
греющего пара, имеющего влажность 5%, и площадь поверхности
нагрева калорифера, если коэффициент теплопередачи в нем равен
30 Вт/(м2.К).
Р е ш е н и е. По диаграмме Рамзина находим: х0 = 0,006 кг/кг
сухого воздуха; /0 = 25,1 кДж/кг; х2 =0,037 кг/кг сухого
воздуха; /2 = 146,6 кДж/кг; рп =41,5 мм рт. ст. (рис. 10.14).
Удельный расход сухого
воздуха по уравнению (10.14)з
в"*в —*о * 0,037 — 0,006 в
= 32,3 кг/кг испаряемой влаги.
Расход сухого воздуха:
L = ^« 1000-32,3 «32 300 кг/ч.
Удельный объем
влажного воздуха по уравнению
(10.12):
t-wx
Uyl! =
R*t
287 (273 + 50)
*= (745 — 41,5) 133,3 ~
= 0,988 м3/кг сухого воздуха.
Рис, to.И (к примеру 10.24).
450
Производительность вытяжного вентилятора:
V « Lcya = 32 300-0,988 « 31 900 м3/ч.
Удельный расход теплоты в теоретической сушилке по
уравнению (10.19):
4Т *= Ii^zJjl « i </2 __ /0) = 32,3 (146,6 — 25,1) =
= 3920 кДж/кг испаряемой влаги.
Для реальной сушилки:
<7 = 1,13<?т = 1,13-3920 = 4430 кДж/icr испаряемой влаги.
Из уравнения (10.18)
А2 Л0
находим:
!г = /0 + -1- = 25,1 + —|- - 162,1 кДж/кг.
Этому значению 1± в точке В соответствует температура tx
144 °С
Расход теплоты в калорифере:
Q = Wq = ^^- 4430 = 1230 кВт.
Расход греющего пара:
G* - - 4- - -2IT7W - °'613 КГ/С " 2'2 Т/Ч-
Средняя разность температур в калорифере»
151,1 151,1
Ю —> 144
А/б = 141,1 A*M*=7,i;
йГ°Р" 2.3 18(А<б/А'н) ~ 2,3 lg (141,1/7,1) -4i)b-4^-
Площадь поверхности нагрева калорифера:
/С А/Ср i*0-45
КОНТРОЛЬНЫЕ ЗАДАЧИ
10.1. Во сколько раз больше придется удалить влаги из 1 кг
влажного материала при высушивании его от 50 до 25%, чем при
высушивании от 2 до 1% влажности (считая на общую массу).
В обоих случаях поступает на сушку 1 кг влажного материала.
10.2. Найти влагосодержание, энтальпию, температуру
мокрого термометра и точку росы для воздуха, покидающего сушилку
при t = 50 °С и ф =0,7.
.15*
451
10.3. Температура воздуха по сухому термометру 60 ?С, по
мокрому 30 °С. Найти все характеристики воздуха.
10.4. Найти влагосодержание и относительную влажность
паровоздушной смеси при 50 СС, если известно, что парциальное
давление водяного пара в смеси 0,1 кгс/см2.
10.5. Найти содержание водяного пара в смеси: а) с воздухом,
б) с водородом, в) с этаном (считая на I кг сухого газа)
при t = 35 °С и ф = 0,45. Общее давление (абсолютное) П =
- 1,033 кгс/см2.
10.6. Сопоставить удельный расход воздуха и теплоты в
сушилке для летнего и зимнего времени (в условиях Ленинграда),
если в обоих случаях воздух, уходящий из сушилки, будет иметь
/2 = 40 °С и ф2 = 0,6. Сушилка теоретическая, нормальный
сушильный вариант. Характеристики состояния воздуха в
различных районах в разное время года см. в табл. XL.
10.7. Общее давление (абсолютное) паровоздушной смеси при
150 °С и относительной влажности ср = 0,5 составляет 745 ммрт. ст.
Найти парциальное давление водяного пара и воздуха и
влагосодержание воздуха.
10.8. Влажный воздух с температурой 130 °С и ф =0,3
находится под давлением Р^с= 7 кгс/см2 (~ 0,7 МПа). Определить
парциальное давление воздуха, его плотность и влагосодержание.
10.9. Какое количество влаги удаляется из материала в
сушилке, если воздух поступает в сушилку в количестве 200 кг/ч
(считая на абсолютно сухой воздух) с tx =¦ 95 СС, q^ =5%,
а уходит из сушилки с /2 = 50 °С и ср2 = 60%? Определить также
удельный расход воздуха.
10.10. Влажный воздух с температурой 130 °С и ф = 1
находится под абсолютным давлением П = 7 кгс/см2 (~ 0,7 МПа).
Найти парциальное давление водяного пара, плотность влажного
воздуха и его влагосодержание.
Сравнить результаты задач 10.10 и 10.8.
10.11. Определить производительность вытяжного вентилятора
для сушилки, в которой из высушиваемого материала удаляется
100 кг/ч влаги при следующих условиях: tQ = 15 °С, ф0 =0,8,
1г = 45 °С, ф2 = 0,6, П = 750 мм рт. ст.
10.12. Воздух перед поступлением в сушилку подогревается
в калорифере до 113 °С. При выходе из сушилки температура
воздуха 60 °С и ср.. = 0,3. Определить точку росы воздуха,
поступающего в калорифер. Процесс сушки идет по линии / = const,
10.13. Определить часовой расход атмосферного воздуха и
теплоты, а также температуру воздушной смеси перед калорифером
в сушилке с рециркуляцией части отработанного воздуха при
следующих условиях:
Характеристика воздуха (считая на
сухой воздух):
атмосферного /0 = 50 кДж/кг; ср0 = 0,7
отработанного /2 = 260 кДж/кг; <р2 = 0,8
452
Количество возвращаемого воздуха 80 % (от выходящего из
сушилки)
Влажность материала (считая на
общую массу);
начальная ии = 47 %
конечная ик — 5 %
Производительность сушилки (по GH = 1,5 т/ч
влажному материалу)
10.14. Найти необходимый расход воздуха в сушилке и расход
теплоты на калорифер при следующих условиях:
Характеристика воздуха:
атмосферного х0 — 0,01; t0 = 20 °С
отработанного х2 = 0,028; /2 == 34 °С
Влажность материала (считая на
общую массу);
начальная «н — 50 %
конечная ык — 13 %
Производительность сушилки по аб- Gc = 1 т/ч
солютно сухому материалу
Потери теплоты ? Q с материалом, 15 % от общего количе-
транспортиым устройством и в окру- ства теплоты
жающую среду (за вычетом теплоты,
вносимой влагой)
10.15. Определить к. п. д. теоретической сушилки, если
состояние воздуха в ней меняется от ф0 = 0,7 и t0 =20 СС до ср2 = 0,6
и t2 = 50 СС. Влага испаряется при температуре мокрого
термометра.
10.16. Найти средний потенциал сушки в теоретической
сушилке при t0 = 20 °С, ф0 = 0,7 и t2 = 50 °С, ф2 = 0,4.
Испарение идет при температуре мокрого термометра.
10.17. В теоретическую сушилку поступает воздух из
калорифера с температурой 85 °С, при этом потенциал сушки составляет)
43 СС. Потенциал сушки воздуха, покидающего сушилку, 8 °С.
Найти парциальное давление водяного пара в воздухе, уходящем
из сушилки, и объемный процент водяного пара в нем, если
давление в сушилке (абсолютное) П = 750 мм рт. ст.
10 18. Влажный материал с начальной влажностью 33%,
критической 17% и равновесной 2%, высушивается при постоянных
условиях сушки до 9% влажности в течение 8 ч. Определить
продолжительность сушки до 3% влажности в тех же условиях.
Влажность дана в процентах от массы абсолютно сухого вещества.
10.19. Определить поверхность нагрева вальцовой вакуум-
сушилки производительностью 200 кг/ч (по высушенному
материалу). Начальная влажность 50%, конечная 5% (считая на общую
массу). Коэффициент теплопередачи 350 Вт/(м2-К); температура
сушки 60 СС; удельная теплоемкость сухого материала
1,26" 108 Дж/(кг-К); начальная температура материала 20 9С;
давление греющего пара Рабс = 1,5 кгс/см2. Потери теплоты
составляют 10% от общего количества теплоты, отдаваемого греющим
паром.
453
10.20. Найти течку росы и относительную влажность воздуха,
выходящего из сушилки, по показаниями психрометра: /е =50 °С,
10.21. Найти, температуру влажного материала в
теоретической сушилке (в первом периоде сушки), если атмосферный воздук
поступает в калорифер при t0 = 15 °С я ср0 = 0,8 и нагревается
в нем до tx =123 °С.
10.22. В сушилке производительностью 1 т/ч (до влажному
материалу) высушивается материал от 55 до 8% влажности (ка
общую массу). Атмосферный воздух имеет параметры t0 = 20 °С,
ф0 =0,75 и нагревается в калорифере до tx = НО °С Потенциал
сушки на выходе из сушилки х2 = 10 °С. Определить расход
воздуха и греющего пара, если давление пара PA$G = 0,25 МПа,
а степень сухости его 95 %.
10.23. В сушилке производительностью 500 кг/ч (па абсолютно
сухому продукту) высушивается материал от 42 до 9% влажности
(на абсолютно сухое вещество). Температура воздухаг
поступающего в калорифер, tQ = 20 °С, а его точка росы tv = 8 °С. Процесс
сушки в теоретической сушилке шел бы при / = 125 кДж/кг.
Температура воздуха на выходе из сушилки t2 = 45 °С.
Нормальный сушильный вариант. Определить расход греющего пара и
поверхность нагрева калорифера, если давление (абсолютное)
греющего пара 0,2 МПа и влажность 5%, а коэффициент
теплопередачи К = 32 Вт/(м2- К). Сумма всех потерь теплоты
составляет 15% от расхода теплоты в теоретической сушилке.
10.24. Воздух с / = 60 °С и ф =0,2 охлаждается холодной
водой в трубчатом противоточном теплообменнике до точки росы.
Охлаждающая вода нагревается от 15 до 25 °С Определить расход
охлаждаемого воздуха, парциальное давление водяного пара и его
объемный процент в воздухе, а также расход охлаждающей воды,
если поверхность теплообменника 15 м2, а коэффициент
теплопередачи К ~ 46 Вт/(м2- К).
10.25. Найти температуру и влагосодержание гоздуха,
уходящего из теоретической сушилки, если средний потенциал сушки
кср =41вС. Воздух поступает в калорифер при ^ = 15 °С н
Ф =70%. Энтальпия воздуха, поступающего из калорифера
в сушилку, / = 144,2 кДж/кг. Определить также температуру
влажного материала (в первом периоде сушки).
10.26. Определить температуру поступающего в теоретическую
сушилку воздуха, если средняя движущая сила сушильного
процесса Ахср =0,0136 кг/кг, температура уходящего из сушилки
воздуха t2 — 45 °С, а его относительная влажность ф2 =60%,
10.27. Определить расход воздуха, расход греющего пара и
требуемое его давление для противоточной воздушной сушилки,
работающей по нормальному сушильному варианту.
Производительность сушилки 600 кг/ч влажного материала, начальная
влажность которого 50% (считая на общую массу), а конечная 9%.
Воздух, поступающий в калорифер, имеет t0 = 10 °С, ф0 =80%;
454
воздух, выходящий из сушилки, имеет t2 = 50 °С, ср2 =50%.
Температуру греющего пара выбрать. Влажность греющего пара 6%,
Расчет произвести; а) для теоретической сушилки, 6) для
действительной сушилки, принимая в ней температуру материала на
входе 16 °С, на выходе 55 °С. Удельная'тешюемкостъ высушенного
материала 1,68 кДж/(кг- К). Масса транспортного устройства
{стальной транспортер), несущего часовую загрузку сырого
материала, 450 кг. Потери теплоты сушилкой в окружающую среду
составляют 10% от количества теплоты, передаваемого воздуху
в калорифере.
10.28. В теоретическую сушилку, работающую с
промежуточным (ступенчатым) подогревом воздуха, поступает 1800 кг/ч
влажного материала с начальной влажностью 39%. Конечная
влажность 8% {считая на общую массу). Воздух на выходе из сушилки
имеет температуру 45 °С. Температура атмосферного воздуха 20 °С.
Всего в сушильной установке три калорифера, в каждом из
которых воздух нагревается до 70 °С После каждого калорифера
воздух в сушилке насыщается водяным паром до «р = 0,7.
Определить расход сухого воздуха и греющего пара. Давление греющего
пара Яабс = 0,3 МПа, влажность его 5%. Дать схему процесса
на диаграмме Рамзина,
30.29. Расход пара в калорифере сушилки при давлении Ризб =
= 0,2 МПа и влажности 10% составляет 200 кг/ч. Расход
теплота на 10% больше расхода теплоты в теоретической сушилке.
Площадь поверхности нагрева калорифера 41 м2. Атмосферный
воздух имеет t0 — 25 °С и точку росы ?р = 10 °С Процесс сушки
идет при /2 = 100 кДж/кг. Парциальное давление водяного пара
в воздухе, покидающем сушилку, 25 мм рт. ст.
Определить коэффициент теплопередачи в калорифере и
производительность сушилки по влажному материалу, если
поступающий в сушилку материал имеет влажность 60%, а выходящий из
сушилки 10% (считая на общую массу).
10.30-В сушилке производительностью 500 кг/ч {по
высушенному материалу) высушивается материал от 70 до 10% (считая на
общуюмассу). Показания психрометра атмосферного воздуха 15 и
20 °С. Из сушилки воздух выходит с температурой 45 СС и
относительной влажностью 50%. Потери теплоты в сушилке и в
калорифере составляют 8% от расхода теплоты в теоретической сушилке.
Определить площадь поверхности нагрева калорифера и
расход греющего водяного пара, если он имеет давление Яабс =
= 0,2 МПа и влажность 5%. Коэффициент теплопередачи в
калорифере 35 Вт/(м2-К).
10-31. 1000 кг/ч влажного материала с начальной влажностью
50% высушивается до конечной влажности 8% (считая на общую
массу). Высушивание производится: а) в вакуум-сушилке при
температуре материала во время сушки 40 °С; б) в атмосферной
воздушной сушилке при той же температуре материала (в первом
периоде). Атмосферный воздух имеет t0 = 20 °С, ф0 =0,7; ухо-
455
дящий из сушилки воздух имеет t2 = 55 °С. В обоих случаях
влажный материал поступает в сушилку при 15 °С, а выходит
при 40 °С. Удельная теплоемкость высушенного материала
1,26-108 Дж/(кг« К). Пренебрегая потерями теплоты в окружающую
среду и на нагрев транспортирующего устройства, определить
удельные пасходы теплоты в обеих сушилках.
10.32. В теоретической сушилке производительностью 600 кг/ч
абсолютно сухого материала высушивается материал от
влажности 35 до 8% (считая на общую массу). Показания психрометра,
установленного в помещении, из которого поступает воздух в
калорифер: t0 = 18 °С, /м = 15 °С. Выходящий из сушилки воздух
имеет /2 = 40 °С и ф2 = 0,65.
Определить расход греющего пара в калорифере и площадь
поверхности нагрева, если давление пара Рабс =0,2 МПа и
коэффициент теплопередачи К = 33 Вт/(м2*К).
10.33. Определить расход воздуха, расход греющего пара,
требуемое его давление и поверхность калорифера для сушилки,
производительность которой равна 600 кг/ч влажного материала
с начальной влажностью 50у6 и конечной 9% (считая на общую
массу). Показания психрометра для воздуха, поступающего в
калорифер, 10 и 5 °С- Воздух на выходе из сушилки имеет t2 = 50 °С,
ф2 = 50% Температуру греющего водяного пара принять на
15 °С выше температуры воздуха на выходе из калорифера.
Влажность греющего водяного пара 6%. Расход теплоты на 10% больше
расхода теплоты в теоретической сушилке. Коэффициент
теплопередачи в калорифере 35Вт/(м2-К).
10.34. Определить производительность по высушенному
материалу, поверхность иагрева калорифера и долю возвращаемого
воздуха в теоретической сушилке с рециркуляцией части
отработанного воздуха. Расход свежего атмосферного воздуха
6000 кг/ч, его энтальпия 50 кДж/кг, парциальное давление
водяного пара в нем 12 мм рт. ст. Начальная влажность материала
40%, конечная 7% (на общую массу). Параметры воздушной смеси
на входе в калорифер: х =0,034; t = 40 °С. В калорифере воздух
нагревается до 88 °С. Коэффициент теплопередачи в калорифере
47Вт/(м2-К). Давление греющего водяного пара Р„аД =0,2 МПа.
ПРИМЕР РАСЧЕТА СУШИЛКИ КИПЯЩЕГО СЛОЯ
ДЛЯ СУШКИ ХЛОРИСТОГО КАЛИЯ
Данные для расчета.
Производительность (по высушенному материалу) GK — 20 т/ч
Влажность соли (на общую массу):
начальная ип — 10 %
конечная ин — 0,5 %
Средний диаметр частиц d= 0,25 мм (duaKQ = 0,5 мм,
<*мин—0»! мм)
Температура соли, поступающей на сушку дх = 20 С
Удельная теплоемкость сухой соли см = 0,712-103 Дж/(кг-К)
Плотность соли Рмат — 2* Ю3 кг/м3
456
Для сушки использовать топочные газы. Тепловые потери принять разными
15 % от расхода теплоты на нагрев материала и испарение влаги. В качестве
топлива используется мазут марки М-100 состава: Ср — 80,8 % ; Нр = 9,8 % ; Np —
= 0,46 % ; Sp = 0,64 % ; Ор = 0,28 % ; Ар = 0 %; Wp - 8 % . Коэффициент
избытка воздуха а— 1,25.
Тепловые потери в топке принять равными 5 % от теплоты сгорания твердого
топлива. Параметры воздуха на входе в топку: t0 = 20 °С; х0 = 0,01 кг/кг.
Значения коэффициентов для расчета теплоемкостей различных компонентов
при заданных температурах даны в табл. 10.4.
Выбор конструкции сушилки и условий ее работы.
Факторы, влияющие на выбор конструкции сушилки:
1) состояние высушиваемого материала — сыпучий, комкующийся во
влажном состоянии;
2) материал выдерживает нагревание до высокой температуры (?пл~ 770 °С)}
3) отношение максимального размера частиц к минимальному dMaHQ/dMHH =
= 0,5/0,1 = 5;
4) подлежит удалению в основном поверхностная влага;
5) решетку выбираем (рекомендуемую при сушке солей) с диаметром отверстий
d0TB= 5 мм;
6) допускается некоторая неравномерность высушенного материала по
конечному влагосодержанию, поскольку при хранении все частицы соли приобретут
одинаковую влажность.
Фактор 3) позволяет предварительно выбрать однокамерный сушильный
аппарат с вертикальными стенками.
Для обеспечения лучших гидродинамических условий выбираем аппарат
круглого сечеиия.
Высоту кипящего слоя в аппарате принимаем в 4 раза больше высоты зоны
действия струй — зоны гидродинамической стабилизации [10,7]. Последняя
определяется из соотношения;
h
стр
20^отв = 20-5= 100 мм;
h = 4/iCTp = 4-100 = 400 мм.
Температуру разбавленных воздухом топочных газов, поступающих под
решетку, принимаем равной ^=800°С, температуру выходящих газов /а =
= 125 °С, что позволит исключить конденсацию паров в пылеулавливающей
аппаратуре (циклоны, фильтры). Температуру выгружаемой соли приближенно можно
принять равной температуре отходящих газов, т. е. йР = 125 °С.
Подачу комкующейся влажной соли для обеспечения равномерного «кипения»
следует производить с помощью разбрасывателей, равномерно распределяющих
материал по поверхности слоя.
Выгрузку соли из аппарата рекомендуется производить непосредственно
у решетки для вывода из аппарата комков.
Расчет. 1, Количество влажного материала:
100 — «„ 0,995
G„ = G
'и
к
100
—2S- = 20 000 -?р = 22 100 кг/ч = 6,15 кг/о.
Гвз
Таблица 10.4
Коэффициенты для расчета с = / (f)
со2
н2о
N2
so2
ог
Воздух
0,3805
0,3569
0,3092
0,3805
0,3119
0,3150
0,2221
0,0532
0,0240
0,2221
0,0506
0,0310
—0,0473
—0,0014
—0,0007
—0,0473
—0,0231
—0,0027
457
2. Количество испаряемой влаги:
W = GH — GK = 22 WO — 20 000 = 2100 кг/ч « 0,584 кг/с
3. Расход теплоты:
«=1,15 {0,584 [2490-108+1,97-108 (125 —20)]+5,56-0,712.10« (125—20}]} =
»2280.103 Вт.
Удельный расход теплоты:
9 « Q/r = 2280/0,584 = 3900 кДж/кс влаги.
4. Расчет расхода и состава сушильных газов.
Так как этот расчет связан с большим объемом вычислений, то оя проводится
на ЭВМ.
Блок-схема алгоритма расчета:
—1 '
/в*(в,в9Ср+26^Нр-3,330,*)(|+/15»в)
^=0,75сь f°+O,0Np; ^=0,7Sp; /s=0,2fK°(cl-f)
— 1
k=i
22,4
*c*f
*«7
i
r-
?[* t г
i
,, a-w<?H + y%«,6)*4
Lr S2
Нэт
Vcm — ^r
S2tr-S3ti
[c{-2,s)(bXo)+x0-^6c^,2)]tr[c(^6)(7-Xo)+x0-J,6c(4>2)]^
I
V(2)=V(2)+^-Vf3)=V(3)+0,7S^CM;V(5)=Vir5)+0,2^c„
I
»
Xj=
QJVz+Wa&M~22$
1
5-Sl 273 .
r1"SY(275HJ)1
- St 8 273
29 .
SV^SV+KCM ; Sl=Sl + ^M^-;S3=S3+C(2e)K;M;S4=S4+c(3(6>K;M
45Й
Условные обозначения к блок-схеме расчета: Q|j — теплота сгорания
твердого топлива (низшая, с учетом диссоциации продуктов сгорания); У« — расход
воздуха на горение; V0 — количество воздуха, теоретически необходимого для
горения; V(k)— объемы отдельных составляющих продуктов горения; УУ^у —
объем топочных газов после топки; c(l- k)—теплоемкости компонентов газа при
заданных температурах; t'r — температура горения газов; VCM — расход воздуха
на смешение; В — расход топлива на горение; хх — влагосодержаппе на входе
в сушилку; Lx — расход сушильных газов на входе в сушилку; L2—расход
сушильных газов на выходе из сушилки; рг — средняя плотность газа на входе
в сушилку; р2 — средняя плотность газа на выходе из сушилки; у^у
—объемные доли компонентов газа; ф — тепловые потери в топке;: х0 — влагосодержание
воздуха на входе в топку; а — коэффициент избытка воздуха.
Таблицы идентификаторов:
Индекс i соответствует: 1 — температуре газов на выходе из топкп; 2 — тем-
пературе газов на входе в сушилку (после смешения); 3 — температуре газов на
выходе из сушилки; 4— температуре воздуха, поступающего на смешение*
Индекс k соответствует: 1 — С02; 2 — Н20; 3 — N2; 4 — SOb; 5 — 02.
И сходные дан ные
Вели- /г tx t2 /0 М(к) Ср Нр Np Sp Op
чина
Иденти- Т(1) Т(2) Т(3) Т(4) М(К) Х(1) Х(2) Х(3) Х(4) Х(5)
фикатор
Величина
Идентификатор
Х(б) AL W
Рассчитываемые величины
Величина
Идентификатор
0Р V0 V t
QRN V0 VA T1
Q a(k) b(k)
Q TK(K, 1) ТК(К, 2)
VSM В U L2 XI
d(k) i
ТК(К, 3) I
Pi P2
ROI R02
k
К
V(K)
Программа расчета:
PROGRAM
DIMENSION Х(б), М(5), V(5), С(4,6), TK(6,3), T(4), Y(5)
REAL LI, L2, М
READ(5) X, Т, М, W, Q, AL
READ(5) ((TK(KJ), K= 1,6) 1=1,3)
QRN-(340. * X(J)+1256. * Х(2)—109, * (Х(5)—Х{4))— 25. * (9. * X(2)-fX(7)))
* 10Е4
V0X(8.89* X(l)+26,5 * Х(2)—3.33 * Х(5)) * 1.016
VA=AL*V0
SV=0S1 = 0
V(t)=1.85*X(l)
V(2)=l 1.2 * X(2) + 1.24 * X(7)+0. 016 * .AL *V0
V(3)-0.79* AL * V0+0.8 * X(3)
V(4)=0.7*X(4)
V(5)=0.21»(AL—1)*V0
459
DO 1 K=l,5
SV-SV+V(K)
1 S1=S1+(V(K)/22.4)*M(K)
DO 2 1=2,4
DO 2 K=l,6
2 С(1Д)=(ТК(К,1)+ТК(К,2)»Т(1)+ТК(К,3)*Т(1)* *2)*4190
3 S2-0
DO 4 K=l,6
С(1,К)=(ТК(К,1)+ТК(К,2)»Т(1)+ТК(К,3)*Т(1)* *2)*4I90
4 S2=S2+C(1,K)*V(K)
Tl=(0,95*QRN+V0*C(4,6)*T(4))/S2
IF (ABS(T(1)—Tl)<5) GO TO 5
T(1)=T1 GO TO 3
5 T(1)=T1
S3=0 S4=0 S5-0 S6-0
DO 6 K=l(5
S3-S3+C(2,K)*V(K)
S4=,S4+C(3,K)*V(K)
S5^S5+C(2,K) *22.4/M(K)
6 SG=S6+C(3,K)*22.4/M(K)
VSM=(S2*T(i)—S3* T(2))/((C(2,6)* 0.984+0.016 »C(2,2))*T(2)—
(C(4,6) * 0.984+0.016 *C(4,2)) *T(4))
V(2)=V(2)+W/B
V(3)=V(3)+0.79*VSM
V(5)=V(5)+0.21*VSM
SV=SV+VSM
Sl=Sl + VSM*29./22.4
S3=S3+C(2,6)*VSM
S4=S4+C(3,6)*VSM
DO 7 K=l,5
7 Y(K)=V(K)/SV
B=Q/(T(2)*S3—T(3)*S4)
Ll=B*Sl
XI=(0.8*V(2)+VSM*0,013)/L1
R01=(Sl/SV) *(273./(273. + T(2)))
L2-L1+W
R02=(Sl + W/B)/(SV+1.24 * W/B) * (273./(273.+T(3)))
WRITE(7,8) QRN, V0, VA, TI, VSM, Y(l), Y(2), Y(3), Y(4),
Y(5), B, XI, LI, L2, ROl, R02
8 FORMAT (5X, 'QRN', 10X, 'V0\ 10X, 'VA', I0X, 'Tl\ 10X, 'VSM7
2X, 5E11.4/5X, 'Yd)', 10X, 'Y(2)\ 10X, *Y(3)\ 10Xf 'Y(4)\
10X, 'Y(5)72X, 5E11.4/5X, 'В', 10Х, 'ХГ, 10X, 'Ll\ 10X,
'L2', 10X, 'R0172X, 5E11.4/5X, 'R0272X, 5ЕП.4)
STOP
END®®
Программа реализована на ЭВМ «Искра-1256».
В результате расчета получены следующие данные: Q{J — 37,42-Ю3 кДж/кг;
х== 0,6168 кг/кг; #2 = 0,707; V0 « 9,927 м3/кг *; Lx = 2,969 кг/с; #3 = 1,805;
Ка = 12,41 м3/кг *; Ц = 3,555 кг/с; у4 = 0,0003; 7\ = 1668 °С; fa = 0,329 кг/м3;
#б = 0,323; VCM = 17,95 м3/кг *; р8 = 0,8067 кг/м3; S = 0,0737 кг/с; ^ = 0,113.
5, Расчет динамических коэффициентов вязкости сушильных газов.
* При 0°С и давлении 0,1013 МПа (760 мм рт. ст.).
460
Значения динамических коэффициентов для каждого компонента при
заданной температуре находим по номограмме (рис, VI):
5
Мсы= 2 0ftA*ft = O,113.44+0,707-18 + 1,805.28 +
+ 0,0003-64 +0,323-32 = 78,59 кг/кмоль;
и - Мсм ...
И-1 — —5 -
^ УкМк
78,59
0,113-44 0,707-18 1,805-28 0,0003-64 , 0,323-32
+ О ЛК 1Л~5 1/1Й.1А-6 1 Л Г1.1Л-6 *
5-10"5 ^ 3,45-Ш'6 ""*" 4,8-10~б "^ 4,0-Ю'6 ^ 5,6-Ю-*
= 4,606-10"5 кг/(м-с);
„ - М™ - -
А=1
78,59
н2
0,113-44 0,707-18 1,805-28 0,0003-64 0,323-32
2,05.10"$ + 1,4-10'8 + 2,2.10-6 + 1,7-10-» + 2,6-10~б
= 2,043-10*6 кг/(м-с).
6. Скорость газов.
Предварительно рассчитываем критическую скорость псевдоожижения для
частиц среднего размера, пользуясь графиком Ly=f (Аг) для температуры в слое,
которую можно считать равной температуре уходящих газов, т. е. 125 °С,
Критерий Архимеда:
дг <*сРРмат?Р2 2,53.10-^.2.103.9,8Ь0,8067 Q9
Й " 2,0432.10-ю "*№'10 "
Критическое значение критерия Лященко: LyKp = 10~4. Критическая
скорость псевдоожижения:
о>кр = >^Укр1Ч?Рмат/Р1 = ^10-«.2,043.10~»-9,8l -2-10»/0 80672 -
= 0,039 м/с.
Рабочее значение критерия Ly выбираем при порозности кипящего слоя
8 = 0,75, так как для процессов сушки, идущих в первом периоде, интенсивность
пропесса тем выше, чем больше скорость газов.
При 8= 0,75 находим Ly = 3,4-10~1 (рис. 10.15). Тогда число
псевдоожижения:
Kw ^ у Ly/LyKp = УЗ,4.10-1/Ю-4 = 15.
Скорость газов (считая на полное сечение решетки):
w = Кы>Мщ> = 15-0,039 = 0,585 м/с.
Скорость газов непосредственно у решетки больше из-за более высокой
температуры. Эта скорость равна:
2?3 + >i лсо, 273 + 800 , __ t
W*" e W -mft = °'585 273 + 125 = 1 ^ М/С'
461
Dcm=J800
5,67-10*
Ю7
Ar
Рис. 10.15. Определение критерия Ly.
Рис. 10.16. Эскиз сушилки.
Если площадь живого сечения решетки принять равной 10% от всей ее
площади, то скорость газа в отверстиях решетки будет равна: w0TB = 10* 1,58 =
15,8 м/с. Эта скорость достаточна для псевдоожиженного слоя не только с
частицами наибольшего диаметра (dMaKC = 0,5 мм), но и с более крупными
образованиями (комками), что видно из следующего расчета.
Если принять число псевдоожижения для укрупненных частиц небольшим,
лишь достаточным для их перемещения {например, &ш = Щ* ™ критическая
скорость псевдоожижения для этик частиц будет
w
кр (отв) = Щтв/Kw — 15,8/3 = 5,27 м/с.
Тогда
^Укр <отв* —
3 "2
_ шкр<отв)Р1 __
5,273-0,3292
МгЯРмат
4,606-10-5.9,8Ь 2-103
= 1,75-10.
Значению LyKp = 1,75* 10 соответствует Ar = 107. Тогда диаметр
укрупненных частиц (комков):
ном ~~ У Pua.gPi ~ У 2.103.9,81-0,329 -°>Ш4У м
Таким обр-азом, у отверстий решетки в состоянии перемещаться даже комки
соли диаметром ^15 мм.
7. Размер решетки сушилки.
Полную площадь решетки определим из выражения:
Рек/ 0,8067-0,585
= 7,533 м2.
Диаметр решетки:
О
реш
]Лчоеш/0,785 = /7,533/0,785 = 3,098 м.
8. Сепарационное пространство.
Высоту сепаращшнного пространства прлыимаем в 4 раза больше высоты
кипящего слоя:
йсеп = 4-400= 1600 мм.
Общая высота аппарата (над решеткой):
h + hceQ = 400 + 1600 = 2000 мм.
462
Проверим, будут ли выноситься из аппарата наименьшие частицы соли (диа
метр ~0,1 мм). Критерий Архимеда:
Дг ?Ррмат?р2 1-10-ц-2. )0'-9,81¦•0,8067 _ - -Q |<v
АГ== & " 2,043». 10-" ~ '
Критерий Лященко, соответствующий уносу частиц, будет равен Ьувит
<С0,16, а скорость витания частиц диаметром 0,1 мм:
ювят = >^ЬувитЦ*Рма1в/Р? = 3/0Л6.2,043- Ю-б.2.10=*.9,81/0,8067» = 0,453 м/с.
Таким образам, аппарат с вертикальными стенками не обеспечит осаждения
в сепарационном пространстве частиц соли диаметром 0,1 мм. Для того чтобы
обеспечить их осаждение, сечение сепарапионного пространства следует расширить
до значения
Здесь коэффициент 1,1 вводится для некоторого снижения скорости потока
по сравнению со скоростью витания, необходимого для обеспечения осаждения
частиц.
Диаметр сепарационного пространства при этом будет равен;
?>сеп = ^сеп/0,785 = V 10,7/0,785 - S,69 M.
Эскиз сушилки дан на рнс. 10.16.
ПРИМЕР РАСЧЕТА ВАЛЬЦОВОЙ СУШИЛКИ
Определить основные размеры двухвальцовой сушилки для сушки пасты
углекислого никеля производительностью 90 кг/ч пасты. Начальная влажность
75%, конечная 10% (на общую массу). Сушилка обогревается глухим паром
(^абс ~ 1 кгс/см2, т. е. ~0,1 МПа). Толщина слоя материала ~1 мм. Толщина
стенки чугунного вальца 10 мм. Над поверхностью материала продувается воздух
со скоростью 1,5 м/с. Температура воздуха 40 °С, ф= 40%.
Решение. Расчет сушилки можно сделать через коэффициент
теплопередачи от пара к воздуху. Процесс передачи теплоты в вальцовой сушилке
происходит следующим образом: от конденсирующегося пара теплота передается стеике
барабана, а от него — высушиваемому материалу. Влага, испаряющаяся на
материале, диффундирует в воздух, унося с собой соответствующее количество
теплоты. Можно подсчитать количество диффундирующей влагн и, исходя из этого
количества, определить эквивалентный коэффициент теплоотдачи.
Примем коэффициент теплоотдачи от конденсирующегося пара к стенке
барабана а = 9280 Вт/(м2-К). Коэффициент теплопроводности чугуна Хч =
= 46,4 Вт/(м-К), средний коэффициент теплопроводности высушиваемого
материала ^мат = 0,8 Вт/(м-К).
Эквивалентный коэффициент теплоотдачи при испарении влаги определяем
из следующего уравнения:
а __ <?исп _ Gr
BCD — д/ — q f t
а[ "мат — *возд
где г — удельная теплота парообразования, Дж/кг.
Так как по уравнению (10.25) удельный расход испаряемой влаги Q
[в кг/(м*ч)] равен
G = 0,04075^°'8Ap,
то коэффициент теплоотдачи аИСп [в Вт/(м2-К)] может быть рассчитан по
уравнению:
0,04075ш0'8 Apr
аисл — "*~
ДЛ3600
463
Зададимся (с последующей проверкой) температурой наружной поверхности
материала #мат = #0 °С (допустимая температура для углекислого никеля не
выше ЬЬ °С). Давление насыщенного водяного пара при 80 °С ЯНао ~ 355 мм
рг. ст.; парциальное давление водяного пара рп в воздухе при t = 40 °С и ф = 0,4
составляе! 22,4 мм рт. ст. Удельная теплота парообразования воды при
атмосферное давлении г~ 2264-103 Дж/кг.
Следовательно, эквивалентный коэффициент теплоотдачи при испарении:
(80 - 40) 3600 294 ВТ/(М 'К)-
Коэффициент теплопередачи от конденсирующегося пара к воздуху;
*- i , о.о' ,'0,001 , Г^^^-
9280 + 46,4 + 0,8 + 294
Удельная тепловая нагрузка:
Я = К (/пара - 'ноэд) = 203 (100 - 40) « 12 180 Вт/м2.
Проверим принятую температуру поверхности материала ФМат по Уравнению:
Д/=<7/аисп = 12 180/294 = 41,4°С = 41,4 К.
Температура поверхности материала*.
*>мат = 'возя + А/ = 40 + 41,4 = 81,4 ПС,
что близко к принятой.
Расход воды, испаряемой в сушилке:
W = G цн~ "к = Q0 75-~10 « 65 кг/ч
^~ан 100-ак 100-10 №КГ/Ч'
Расход теплоты на подогрев материала и на испарение влаги:
90.3,4в.10«(81,4-15)+65.2264.10» „ц^д,,
3600
Необходимая площадь поверхности нагрева вальцовой сушилки:
Q 46 500
f =Т= 12180-0,75 =5.38м*.
где 0,75 — коэффициент, учитывающий фактическую поверхность
соприкосновения материала с греющей поверхностью вальцов.
По нормалям ближайшая двухвальцовая сушилка имеет F — 5,2 м2 (диаметр
вальцов 600 мм, длина 1400 мм). Эту сушилку мы и выбираем, хотя площадь ее
поверхности нагрева немного меньше, чем требуется по расчету. Для обеспечения
заданной производительности потребуется несколько увеличить давление
греющего пара, что легко отрегулировать на практике.
Тепловые потери сушилки должны быть учтены при определении расхода
греющего пара.
Пример расчета камерной сушилки с рециркуляцией воздуха — см, седьмое
издание этой книги, 1970 г.
Примеры расчета барабанной сушилки и вакуум-сушильного шкафа — см,
шестое издание этой книги, 1964 г»
464
Глав а 11
УМЕРЕННОЕ И ГЛУБОКОЕ ОХЛАЖДЕНИЕ
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Для холодильного (обратного) цикла Карно 1—2—3—4,
состоящего из двух изотермических и двух изоэнтропическнх
процессов (рис. 11.1), холодильный коэффициент:
L
Qi
Qi
Т(
Q-Qc
т — т(
(ПЛ)
•к ^д
Здесь Q0 — холодопроизводительность — расход теплоты, получаемой
холодильным агентом (рабочим веществом) от охлаждаемой среды при температуре
Т0, Вт; Q — расход теплоты, отдаваемой хладагентом воде при температуре Т, Вт;
LH — мощность, затрачиваемая в компрессоре при изоэнтропическом сжатии
пара рабочего вещества, Вт; 1д — мощность, получаемая при изоэнтропическом
расширении хладагента в детандере, Вт; L = LH — ?д — Q—Q0 —
теоретическая мощность, затрачиваемая в цикле, Вт.
Как следует из формул (11.1), ек теоретически зависит только
от значений температуры Т и Т0 и не зависит от природы
хладагента.
2. Для реального влажного цикла паровой компрессионной
холодильной установки 1—2—3—4' (рис. 11.2) холодильный
коэффициент-
Q-Qo
U — d
где L — мощность, затрачиваемая компрессором при сжатии пара хладагента, Вт;
(Ь '2> «
з» U"—удельные энтальпии хладагента в соответствующих точках цикла
{рис. П.2), Дж/кг. Остальные обозначения — см. формулу (11.1).
3. Для сухого цикла одноступенчатой паровой компрессионной
холодильной установки (рис. 11.3):
а) без переохлаждения жидкого хладагента (процесс 1—2—
—3—4—4')
е = -г =
б) с
—3—4-
h -*- 11
L
переохлаждением жидкого хладагента (процесс /
~5—6)
(П.З)
—2—
h — te
h — h
(11.4)
В последней формуле: г —
холодильный коэффициент; Q0 = G (^ — *'Б)—
хо одопроизводительиость установки, Вт;
L= Q — QQ= G (i2 — ix) — теоретическая j
мощность, затрачиваемая компрессором, «°
Вт; Q~ G (ia — i5) — расход теплоты,
отдаваемой хладагентом воде в
конденсаторе (включая переохлаждение жидкого
Рис, 11,1. Холодильный цикл Карно.
465
Вода
Т
т
Рассол
Рис. П 2. Влажный цикл.
хладагента), Вт; G — расход хладагента в цикле» кг/с; ilt i2, ... — удельные
энтальпии хладагента в соответствующих точках, цикла, Дж/кг.
На рис. 11.4 сухой цикл одноступенчатой компрессионной
холодильной установки изображен в координатах р — /.
4. Действительная мощность ЛГ (в кВт), расходуемая
компрессионной холодильной установкой:
n = ..,/;„ . (П.5)
lOOOri
где г\ — общий к. п. д., равный
Ц = *U%iex*to%;
О L6)
щ — индикаторный к. п. д. компрессора, которым учитывается отличие
действительного рабочего процесса от теоретического (изоэнтропического) [величина
щ зависит от степени сжатия холодильного агента, т. е. от отношения давления
конденсации р к давлению испарения /?0; ориентировочные значения щ для
аммиачных компрессоров приведены на рис. 11.5]; Ямех— механический к. п. д.
компрессора, учитывающий потери, вызываемые трением; rjn — к. п. д. передачи;
т]д — к. п. д. двигателя компрессора.
При приближенных расчетах обычно принимают;
Ямех = 0.8 + 0,9; г}п = rfo = 0,95.
5. Холодопроизводительность компрессора Q0 (в Вт);
(11.7)
где к— коэффициент подачи компрессора — отношение действительного
секундного объема пара, всасываемого компрессором, к геометрическому объему Vp
(в mVc), описываемому поршнем (для аммиачных компрессоров можно пользо-
Рис. И.8. Сухой цикл.
Рис. И.4. Сухой цикл в координатах р — 1%
466
Рис. U.S. Значения коэффициентов t^ и & для вертикальных прямоточных аммиачных
компрессоров ( ) и дли горизонтальных аммиачных кома рессорой двойного
действия ( — — —),
Рис. 11.6, Идеальный процесс сжижения газа.
ваться значениями коэффициента подачи %t приведенными на рис. 11.5, в
зависимости от отношения давления в конденсаторе р к давлению в испарителе р0);
q0 — объемная холодопроизводительность (в Дж/м3) холодильного агента, равная
* = Pi (<i - *•>; (п-в)
ii и гБ — удельные энтальпии холодильного агента на выходе из испарителя и на
входе в него (см. рнс. 11.3 нли 11.4), Дж/кг; fo — плотность пара, всасываемого
компрессором, кг/м^.
6. При пересчете холодопроизводительности Q0 компрессора на
другие условия (Qq) при неизменной частоте вращения пользуются
формулой:
Ж'Ж <"'9>
Нормальными условиями работы паровой компрессионной
холодильной установки при одноступенчатом сжатии считаются:
температура испарения —10 °С, температура конденсации 25 °С,
температура переохлаждения жидкого хладагента 15 °С.
7. Минимальная работа, необходимая для ожижения 1 кг газа
при идеальном процессе сжижения (рис, 11.6):
-Um - Тх (S, - S0) - (it -tj, (11.10)
где 7\, Si н ii — температура, удельные энтропия и энтальпия газа в начальном
состоянии (точка 1); S0 и i0 — удельные энтропия и энтальпия жидкости (точка 0).
Хотя практически идеальный процесс сжижения неосуществим,
но LMHH имеет значение как масштаб, с которым сравнивают
реальные циклы.
8. Ожижение воздуха с расширением его без отдачи внешней
работы — дросселированием (цикл Линде).
а) Простой регенеративный цикл — см. стр. 477.
467
Удельная холодопроизводительность цикла q (в Дж/кг):
q = ix-tt. (11.11)
Здесь if, is — удельные энтальпии расширенного и сжатого воздуха при
температуре входа в теплообменник, Дж/кг.
Ожижаемая доля воздуха:
и _ Я 9пот __ (Н — h) — Япот /ij jo)
где /0 — удельная энтальпия жидкого воздуха (при давлении расширенного
воздуха ), Дж/кг; <7П0Т — суммарные потерн холода, отнесенные к 1 кг
перерабатываемого воздуха.
б) Цикл с предварительным (аммиачным) охлаждением.
Удельная холодопроизводительность цикла qr (в Дж/кг):
<f = i[ — i* (11-13)
где i[ и i'3— удельные энтальпии расширенного и сжатого воздуха при
температуре входа в основной теплообменник после аммиачного холодильника, Дж/кг»
Ожижаемая доля воздуха:
у- *'.Г^?0Т ¦= ^~р-Япот ш (1, 14)
Удельное количество теплоты qa (в Дж/кг), передаваемой в
аммиачном теплообменнике (считая на 1 кг сжатого воздуха)
Яа=й' — Я + У((1—П)- (П.15)
Здесь q' — удельная холодопроизводительность цикла [формула (11.13)];
q—удельная холодопроизводительность цикла в случае отсутствия
предварительного аммиачного охлаждения [формула (11.11)]; i{ и t[ — см. формулы (11.11)
и (11.13).
в) Цикл с циркуляцией воздуха под давлением — см. стр. 479.
Удельная холодопроизводительность цикла q (в Дж/кг):
<7 = (ia - «"а) + М ((*! -/а), (П. 16)
где /i, /2» 'з — удельные энтальпии расширенного воздуха, сжатого воздуха
среднего давления и сжатого воздуха высокого давления соответственно прн
температуре входа в основной теплообменник, Дж/кг; М — доля воздуха,
дросселируемого до низкого давления (обычно 0,2—0,4).
Ожижаемая доля воздуха:
yz= (t'a —i3) + M(ti-- y — ftiQT (n i7)
Обозначения те же, что и в формуле (11.12).
9. Ожижение воздуха при расширении его с отдачей внешней
работы 'Us детандере.
а) Цикл среднего давления (Клода) — см. стр. 480.
Удельная холодопроизводительность цикла q (в Дж/кг):
4^(h-i2)+M(is-it)t (11.18)
468
где fb i2 — удельные энтальпии расширенного и сжатого воздуха при температуре
входа в основной теплообменник, Дж/кг; /3, t4 — удельные энтальпии сжатого
воздуха при входе в детандер и при выходе из него, Дж/кг; М — доля воздуха,
направляемого в детандер (обычно принимают М= 0,8).
Для воздуха, расширяющегося в детандере, в этом цикле обычно
принимают:
/3 - ^« о,65 А/Й3 = 0,65 ((3 - i&).
Здесь А/из— изменение удельной энтальпии воздуха при изоэнтропическом
процессе; i& — удельная энтальпия воздуха при давлении после детандера и при
той же энтропии, что и (3> Дж/кг.
Ожижаемая доля воздуха:
и = ('1 — 'а) + М (/3 — U) — даот e .j L ig
h — 'о
Обозначения те же, что и в формуле (11.18).
б) Цикл высокого давления (Гейландта) — см. стр. 482.
Удельная холодопроизводительность цикла q (в Дж/кг):
где ilt 1*3 — удельные энтальпии расширенного и сжатого воздуха при
температуре входа в основной теплообменник и в детандер, Дж/кг; iu — удельная
энтальпия воздуха по выходе из детандера, Дж/кг; М — доля воздуха, направляемого
в детаидер (обычно принимают М = 0,45-"-0,5).
В этом цикле можно принять для воздуха, расширяющегося
в детандере:
*3 - U = 0.75 Д(из = 0,75 (19 - /&).
Ожижаемая доля воздуха:
у^_ (ti — h) + M(iz — J4) — qu0T (11.21)
i\ — i0
в) Цикл низкого давления с турбодетандером (Капицы) — см.
стр. 483.
Ожижаемая доля воздуха:
у _.. O'l — У + (1 — ay) (h — U) — да0т (п 22)
где ix, *2 ~ удельные энтальпии расширенного и сжатого воздуха при
температуре входа в основной теплообменник, Дж/кг; i3, i±— удельные энтальпии
сжатого воздуха перед турбодетандером и после него, Дж/кг; а — коэффициент,
учитывающий испарение при дросселировании жидкости от давления конденсации
до атмосферного давления (при давлении конденсации ра6с = °\89-10^ Па =
— (> кгс/см* а ~ 1,25).
Можно принять для воздуха, расширяющегося в турбодетан-
дере:
h - h = 0.8 Мт = 0,8 (fa — /5). (11.23)
Здесь 1Ъ — удельная энтальпия воздуха при давлении после детандера и при
той же энтропии, что и i3, Дж/кг.
469
10 - Потер и холода ^лот складываются из двух ела гаемых:
Quot —Ятп + 9й* с- (If-24)
Потери холода от недорекуперации (в Дж/кг):
<7нед=Ср А/, (11.25)
г, ;, — удельная теплоемкость газа при температуре выхода из теплообменника,
Дж/(кг«К); А^—разность температур сжатого воздуха, входящего в
теплообменник, и расширенного воздуха, выходящего из теплообменника, К.
Потери холода в окружающую среду (через изоляцию) ^0 с
составляют обычно 4—12 кДж на 1 ivr3 (при нормальных
условиях) перерабатываемого воздуха.
ПРИМЕРЫ
Пример 11.1. Определить холодильный коэффициент
компрессионной холодильной установки, работающей по циклу Карно,
если температура в испарителе — 23 °С, а в конденсаторе 27 °С.
Решение. По формуле (11.1) получаем:
Г0 273 — 23
е* -* Г —Г0 (273 + 27)—(27а—23) *
Пример 11.2. Вычислить теоретическую мощность, затрачи"
ваемую холодильной установкой, работающей по циклу Карно и
отводящей в 1 с 17 400 Дж, при —19 °С (температура испарения).
Температура конденсации 15 °С
Решение. Холодильный коэффициент:
Т0 254 Р
Ч~ Г —Г0 "" 268 — 254 ~~7'°*
Теоретическая мощность:
л/ L Qo - 17400
т~~ Г000 екИ0» "~ 7,5-103
2,32 кВт.
Пример 11.3. Найти минимальную (для цикла Карно)
теоретическую мощность компрессора аммиачной холодильной
установки и расход воды в конденсаторе при выработке в 1 ч 500 кг
льда из воды, имеющей температуру 0 °С. Аммиак кипит при
—7 °СТ а конденсируется при 20 °С. Вода в конденсаторе
нагревается от 10 до 15 °С.
Решение. Теплота, выделяющаяся при замерзании воды:
500-339,1-1000 ,7innR
Qo== 3600 -47 100 Вт,
где 339,1 • 103 Дж/кг — удельная теплота з-амерзания воды.
Мощность компрессора (за вычетом работы изоэнтропического
расширения):
t=A = 1Г~Г° Qa= 293~266-47 100 « 4760 Вт.
кк Т0 ° 266
470
Расход теплоты, отводимой воден в конденсаторе!
Q вкфд +1 = 47 100 + 478G « 51 880 Вт » 51,9 кВт.
Расход воды:
51 880 л __в „
<И-Ц) 4.1^1000" e 2j478 w/c-
Пример 11.4. Определить для углекислотыой холодильной
установки, работающей по влажному циклу, удельную холодо-
производительность хладагента, холодильный коэффициент,
количество отводимой в конденсаторе теплоты, количество
циркулирующего хладагента и теоретическую расходуемую мощность, если
температура испарения —30 РС, температура конденсации 20 °С,
температура переохлаждения 16 °С. Требуемая холодопроизводи-
тельность установки 58 150 Вт.
На рис. 11.7 показан цикл в координатах Т — 5. Значения
удельных энтальпий определены с помощью диаграммы Т — S
для диоксида углерода (рис. XXVII). Линия 1—2 — сжатие
в компрессоре, 2—3' — конденсация, 3'—3 — переохлаждение
жидкого хладагента, 3—4 — дросселирование, 4—1 — испарение.
Решение. Удельная холодопроизводительность хладагента!
ix — iA« 590 ¦ 10» — 46ЫО* « 129-103 Дж/кг.
<7t>
Холодильный коэффициента
(590 —461)103
(632 — 590) 103
= 3,h
Количество отводимой в конденсаторе теплоты на 1 кг
циркулирующего диоксида углерода;
q = f, — i, « 632^ Юз __ 461 -103 = 171 -108 Дж/кг.
Расход хладагента, циркулирующего в цикле!
Q0 58150
G
S=5
%
129-103
0,448 кг/с.
Расход теплоты, отводимой в конденсаторе:
Q« 17Ы03.0,448 = 76 900 Вт = 76,9 кВт.
¦30°С
иб23-Ю*Дж/КР
ЯГ ?4,7кгс/смгЧ= 590-/03Дж/КГ
Рис. И.7 <к примеру И.4).
471
Необходимая теоретическая мощность:
Nr = G (i2 — ix) = 0,448 (632-103 _ 590.103) = 0,448-42.103 =
= 18 700 Вт= 18,7 кВт.
Пример 11.5. Определить коэффициент подачи аммиачного
компрессора простого действия имеющего ход поршня 0,32 м,
диаметр цилиндра 0,25 м и частоту вращения 180 об/мин. Цикл
сухой, без переохлаждения. Температура испарения — 10 РС,
температура конденсации 30 °С, холодопроизводительность 93 000 Вт.
Решение. Удельная холодопроизводительность аммиака*
Яо = h — h = (1430 — 324) Юз = \ 106.103 Дж/кг.
Удельные энтальпии определены по диаграмме Т—S для
аммиака (рис. XXVI).
Объемная холодопроизводительность аммиака:
qv = Wl = ПОб-2,39-103 = 2640-103 Дж/м3,
где рг = 2,39 кг/м3 — плотность засасываемого компрессором пара (табл. XLV111).
Объем, описываемый поршнем;
.. nD* n 3,14.0,25* 0 180
Vr = _- s -^ » -i—? 0,32 — = 0,047 м»/с-
Коэффициент подачи по формуле (11.7):
х- «о 93 000
~V^T~ 0,047-2640Л03 ~U'/4D-
Пример 11.6. Аммиачный компрессор марки 3-АВ
(вертикальный) имеет холодопроизводительность Q0 = 174 000 Вт при
нормальных условиях. Какова будет холодопроизводительность этого
компрессора, если он будет работать при температуре испарения
—25 °С, температуре конденсации 30 °С и температуре
переохлаждения 25 °С?
Решение. Для определения холодопроизводительности при
рабочих условиях воспользуемся формулой (11.9)i
Qh = Qo _ ^ •
Как следует из этой формулы, для пересчета
холодопроизводительности компрессора необходимо определить qVt cfVi 1 и 1',
Исходя из определения нормальных условий работы (tma =
= — 10 °С, /конд =s 25 °С, /п =з= 15 °С), находим с помощью
диаграммы T—S (рис. XXVI) и табл. XLVIIIi
Ч9*= <toP = (ij ~ i«) р » (1430-103 — 251 • 103) 2,39 = 2830-103 Дж/м8.
Аналогично находим q'v\
% = («I — Q Р' = (НЮ- Ю3 — 299-103) 1,297 = 1440.103 Дж/м3,
472
Рис. 11.8 (к примеру 11,7)
Г
-20°С
Ш^Дж/кг
~= 1,3 кгс/ш * Т<1г№0.Ю3Дж/КГ
Для определения К
находим отношение давле- +25*с
ний конденсации и испаре- +20°с
ния при нормальных
условиях, т. е. отношение
давления /?,
соответствующего температуре
конденсации 25 °С, и давления р0,
соответствующего температуре испарения —10 °С (табл. XLVIII)!
Р/Ро=~ Ю04/281 =,3,45.
Для этого отношения давлений К =0,82 (см. рис. 11.5).
Аналогично определяем k't исходя из заданных рабочих
условий. Находим отношение давления /?, соответствующего
температуре конденсации 30 °С, и давления р0, соответствующего
температуре испарения —25 °С:
р/р0= 1167/152 = 7,7.
Для этого отношения давлений V = 0,57 (см. рис. 11.5).
Рабочая холодопроизводительиость компрессора;
ffl ,~лппл 1440.10^-0,57
Qo = Q(
= 174 000
= 62000 Вт = 62 кВт.
qvX " 2830-103-0,82
Пример 11.7. Определить размеры цилиндра а также
действительную расходуемую мощность для одноступенчатого аммиачного
компрессора простого действия, работающего на сухом ходу.
Требуемая холодопроизводительиость 290 000 Вт при температуре
испарения —20 °С. Температура конденсации 25 °С, температура
переохлаждения 20 °С. Определить также холодильный коэффициент
установки.
На рис. 11.8 показан цикл, соответствующий заданным
условиям, в координатах Т—S. Линия /—2 — сжатие в компрессоре,
2—3' — охлаждение перегретого пара и конденсация, 3'—3 —
переохлаждение жидкости, 3—4—дросселирование,
4—/—испарение.
Решение. Значения удельных энтальпий аммиака в
различных точках цикла находим на диаграмме Т—S (рис. XXVI).
Удельная холодопроизводительиость аммиака:
q0 = ix — i4 = (1420 — 276) 103 = 1144-108 Дж/кг.
Расход циркулирующего аммиака:
Q0 2Э0 000
= 0,254 кг/с.
q0 1144-103
Объемная холодопроизводительиость аммиака*
<fo =<?oPi = 1144- 10з.1,6 = 1830-10 Дж/м*,
гдерх = 1,6 кг/м3 — плотность засасываемого компрессором пара (табл. XLVIII).
473
Объем, описанный поршнем в 1 с:
V Qo 29QQ0° 0 227 мУс
Vr~ qv\ - 1830.103-0,7 "°-"7м/с-
Отношение plp§ = 10/1,9 =5,3. По рис. 11.5 находим 1 =0,7.
Если принять частоту вращения п = 210 об/мин, то объем
цилиндра:
V .= 0,227-60/210 = 0,065 м3.
Обычно отношение хода поршня s к диаметру D составляет
s/D = 1,1 -i- 1,3. Примем это отношение равным 1,2. Тогда
0,065 =-=?- 1,2D,
откуда D =0,41 м =410 мм; s =410-1,2 =490 мм.
Теоретическая мощность компрессора:
/VT=,G(<3 —у = 0,254(1654— 1420) 103 =59,5-103 Вт =59,5 кВт.
Действительная расходуемая мощность:
N = 3VT/T) = 59,5/0,643 = 92,5 кВт.
Здесь ч — общий к. п. д., равный по формуле (11.6).
Значение индикаторного к. п. д. t\t при pfp$ =5,3 находим по
ряс. 1L5. Для этого отношения давлений щ =0,84.
Принимаем: г]мех =0,85; г|а = 0,95; г|д = 0,95. Тогда
ц = 0,84-0,85.0,95.0,95 = 0,643.
Холодильный коэффициент:
gQ 1144.10s
I л (1654 — 1420) 103
4,88.
Пример 11.8. Определить по условиям предыдущего примера
количество воды, подаваемой в конденсатор, и поверхность
теплопередачи конденсатора (включая переохлаждение жидкого
аммиака), если начальная температура воды 35 °С, конечная 21 °С,
коэффициент теплопередачи для зоны конденсации (включая
охлаждение перегретого пара) К ==2330 Вт/(м2«К), а для зоны
переохлаждения жидкого аммиака К" = 465 Вт/(м2» К).
Решение. Расход теплоты, передаваемой в конденсаторе,
определяем по формуле:
Q = G (i2 — /3) = 0,254 (1654 — 276} 103 = 350-103 Вт = 350 кВт.
Расход теплоты, передаваемой в зоне охлаждения перегретого
пара и конденсации:
Q' = G {it — Га) = 0,2&4 (1654 — 2Щ 10 * = 344. И*» Вт = 344 кВт,
474
Расход теплоты, передаваемой в зоне переохлаждения жидкого
аммиака:
Q" = (350'—344,0) 103 = 6" 10я Вт =г6- кВт.
Расход воды, подаваемой в конденсатор:
Q 350¦Ша
Gn-
= 13,9 кг/с.
в {'юта — WKb. (21 - 15)4,19. квР
Температура воды после зоны переохлаждения жидкого
аммиака:
6- ю3
i = 15 +
= 15.1 °С.
13,9*4,19-i03
Средняя разность температур в зоне конденсации без учета
температуры перегрева аммиака (рис. 11.9):
(25—15,*) —(25 —21)
А'ср
2,3 lg
25 — Ь5.1
"25 — 21
6,5 °С-6,5 К.
Средняя разность температур в зоне переохлаждения жидкого
аммиака:
Д/^р = [(25— 15,1) + (20 — 15)1/2 == 7,4 °С == 7,4 К.
Площадь поверхности теплопередачи в зоне конденсации!
Q' 344-10»
F' -
/с ак
ср
2330-6,5
- = 22,8 м3.
Площадь поверхности теплоотдачи в зоне переохлаждения!
Q" 6-I03
Г*=
*" Д^р
«1,68 м2.
465-7,45
Общая площадь поверхности конденсатора:
F = /?' + F" = 22,8 + 1,68 * 24,5 ма.
Удельная тепловая нагрузка (съем теплоты с 1 м2 теплопере-
дающей поверхности):
др =350-103/24,5 ^ 14,3- Ю3 Вт/м2.
Пример 11.9. В воздухе содержится 5,8% (об.) пара четырех-
хлористого углерода. Если охлаждать эту газовую смесь
под атмосферным давлением t
(760 мм рт. ст.), то при какой
температуре начнется
конденсация четыреххлористого 25°С
углерода? Определить также, ^^
до какого давления необхо-
\
Рис. 11.9 (к пример) 11,8).
Аммиак
ZZZZ71
Вода
25°С
20°С
15°С
Q
344000 35000 Ът
475
димо сжать газовую смесь, чтобы при последующем охлаждении
ее при постоянном давлении до 30 °С сконденсировалось 75% от
содержащегося в воздухе четыреххлористого углерода.
Решение. Конденсация четыреххлористого углерода из
газовой смеси начнется тогда, когда его парциальное давление в
смеси станет равным давлению насыщенного пара.
Парциальное давление четыреххлористого углерода в газовой
смеси:
р = уТ[ = 0,058-760 = 44 мм рт. ст.
По диаграмме зависимости давления насыщенного пара
четыреххлористого углерода от температуры (рис. XXIV) находим, что
давлению 44 мм рт. ст. соответствует температура 8 °С, при
которой, следовательно, и начнется конденсация четыреххлористого
углерода.
Определим давление П, до которого надо сжать исходную
газовую смесь, чтобы после охлаждения до 30 °С сконденсировалось
75% четыреххлористого углерода.
Из 5,8 моль четыреххлористого углерода, содержащихся в
100 моль исходной смеси, по условию должно остаться в газовой
фазе после конденсации 5,8-0,25 = 1,45 моль. Общее число молей
в газовой смеси после конденсации:
(100 — 5,8)+ 1,45=95,65.
Парциальное давление четыреххлористого углерода в газовой
фазе над жидкостью равняется его давлению насыщенного пара
при 30 °С и составляет 145 мм рт. ст. (рис, XXIV).
Общее давление смеси П найдем из пропорции!
1,45— 145
95,65 —П,
откуда
П « 95^5.'14а = 9565 мм рт. ст. = 13 кгс/см2 » 1,275 МПа.
Пример 11.10. Определить по диаграмме Т—S (рис. XXIX)
процент образовавшегося жидкого воздуха после дросселирования
сжатого воздуха с 80 кгс/см2 и 140 К До 1 кгс/см2 (~ 0,1 МПа).
Решение. Находим точку пересечения изобары 80 кгс/см^
с изотермой 140 К и от этой точки по линии i = const опускаемся
до пересечения с изобарой 1 кгс/см2, Беря отношение участка,
лежащего на изобаре 1 кгс/см2 справа от найденной точки до
пограничной линии пара, ко всему отрезку между линией жидкости
и линией пара при р = 1 кгс/см2, получаем, что жидкости в
образовавшейся парожидкостной смеси содержится 33%.
Пример 11.11. Определить, какое количество теплоты
необходимо отнять от 1 кг воздуха для сжижения его при атмосферном
давлении и какую для этого необходимо затратить теоретически
минимальную работу. Начальная температура воздуха 290 К.
476
7
Вода
~HJJ
Компрессор
i—-->¦
Теплообменник
Г=298 К
13=474-!0%Ж/КГ \Ц-510-Ю?р№
¦ Ь-ШОуЦк/аег
ЯСЬ
Рис. П. 10 (к примеру П. 12).
Р е ш е н и е. По диаграмме Г—5 для воздуха (рио. XXIX)
находим, что при р = J кгс/см2
(г - ('ж = 502. Ш3 — 92- Ю3 = 410.10» Дж/кг.
Теоретически минимальную затрату работы для ожижения 1 кг
воздуха находим по формуле (11.10):
imm = Тх (S, - S0) — (h - 'о) = 290 (3,75 - 0) 103 - 410-103 «
= 677-103 Дж/кг-
Значения 5Х и S0 определены по диаграмме Т—S для воздуха.
Таким образом,
Lmm = 677/3600 =* 0,188 кВт- ч/кг.
Пример 1Ы2. Определить количество получаемого в J ч
жидкого воздуха и необходимую для этого затрату мощности при
переработке 200 кг/ч воздуха, сжатого до 200 кгс/см2. Установка
работает по простому регенеративному циклу Линде. Температура
воздуха до и после компрессора (при входе в теплообменник)
25 °С. Воздух дросселируется до 1 кгс/см2. Потери холода в
окружающую среду принять в размере 4,19* 108 Дж на 1 м3 воздуха
(при нормальных условиях). Недорекуперация 5 9С.
Решение. На рис. НЛО даны принципиальная схема
установки и изображение процесса в координатах Т—5. Для расчета
пользуемся диаграммой Т—S для воздуха (рис. XXIX).
Удельную холодопроизводительность цикла определяем по
формуле (11.11):
Ч = tA — t3 = (510 — 474) 103 = 36-103 Дж/кг.
m
Потери холода на 1 кг перерабатываемого воздуха определяем
по формулам (11.24) и (11.25):
а) потери от недорекуперации *
qRen = cvAl = 1,01-103-5 = 5,05-10* Дж/кг;
б) потери в окружающую среду
9о. с = 4,19-103/1,29= 3,25.10» Дж/кг.
Суумарные потери:
<7пот в (5>05 + 3,25) 10» в 8|3. юз джукг.
Ожижаемую долю воздуха определяем по формуле (11.12):
„_ (h-h)~Quo, (36-8,3)10^ _ЛАЙ7
^" /!-/0 " (510-92,1)103 -U'UD'-
Расход ожижаемого воздуха:
Gw =- 200-0,067 = 13,4 кг/ч.
Затрачиваемую на валу компрессора мощность определяем по
формуле (2.20):
tf-I,69Ge*7ln-*-- 1.69-4^-^ 298 In 2°°
Р! ' 3600 1000 1
1,69
0,287.298-2,3 lg 200 «42,5 кВт.
18
Удельный расход энергии на 1 кг жидкого воздуха:
<?уд = 42,5/13,4 «= 3J6 кВт-ч/кг.
Пример 11.13. Определить расход перерабатываемого воздуха
для получения 50 кг/ч жидкого воздуха и затрачиваемую при этом
мощность, если ожижение ведется по циклу с предварительным
(аммиачным) охлаждением воздуха до —35 °С. Давление сжатия
200 кгс/см2, дросселирование до 1 кгс/см2. Начальная температура
ьоздуха 25 °С. Суммарные потери холода в окружающую среду и
от иедор^уперации принять в размере 8,8 кДж/кг,
Решение. Для определения удельных энтальпий
воспользуемся диаграммой Т—5 для воздуха (рис. XXIX).
Удельную холодопроизводительность цикла определяем по
формуле (11.13):
ц' = /; — Г3 «= (449 — 386) 103 = 63- 10я Дж/кг,
где 1\ — удельная энтальпия воздуха прир = 1 кгс/см2 и t = —35 °С; i'3 —
удельная энтальпия воздуха при р = 200 кгс/см2 и /= —35 °С.
Ожижаемую долю воздуха определяем по формуле (11.14)1
У*= i^TJl = (449-92)103 -U«JM'
* Здесь не учитывается уменьшение обратного потока ьоздуха на количество
сжиженного воз&уха,
478
Для получения 50 кг/ч жидкого воздуха необходимо
перерабатывать воздуха:
G = 50/0,153 = 327 кг/ч.
Количество теплоты, передаваемой в аммиачном
теплообменнике, определяем по формуле (11.15):
да ^ q' _ q + у (i} _ q ^ 63-10' — 36- 1(Г + 0,153 (510 — 449) 10я =
= 36-103 Дж/кг,
где (7= 36,0-103 Дж/кг и ^ «= 510-103 Дж/кг (см. пример 11.12).
Определяем мощность на валу воздушного компрессора:
N = I,69Gc/?r In-^- = 1,69 -J^r 287-298-2,3 g 200 = 69,5.103 Вт *= 69,5 кВт.
Мощность, потребляемая аммиачным компрессором?
.. 36,0-327 0 лл „
N*~ 8540-0,66 ~2'"кВт-
Здесь 8540 кДж/(кВт-ч) — теоретическая удельная холодопроизводитель-
*
яость аммиачной холодильной установки при температуре испарения аммиака
—40°С [11.2]; 0,66— принятый общий к. п. д. аммиачного компрессора.
Общая расходуемая мощность:
^«=69,5 + 2,11 =71,61 кВт.
Удельный расход энергии на 1 кг жидкого воздуха!
Nyn = 71,61/50= 1,43 кВт-ч/кг.
Пример 11.14. Определить ожижаемую долю и удельный
расход энергии при получении жидкого воздуха по схеме с
циркуляцией воздуха под давлением. Высокое давление воздуха
200 кгс/см2, среднее давление 50 кгс/см2. Температура воздуха при
входе в теплообменник 20 °С. Доля воздуха, дросселируемого до
низкого давления, М =0,3. Суммарные потери холода от недо-
рекуперации и в окружающую среду составляют 10,5 кДж на 1 м3
воздуха (при нормальных условиях) высокого давления,
поступающего в установку.
Решение. На рис. 11.11 даны принципиальная схема
установки с циркуляцией воздуха под давлением и изображение
процесса в координатах Т—5. Для определения удельных энтальпий
воспользуемся диаграммой Т—S для воздуха (рис. XXIX).
Удельную холодопроизводительность цикла определяем по формуле
(11.16):
Я « (Н - h) + М (г, — /2) = (494 — 467) 103 + 0,3 (505 — 494) 10* =
«30-10s Дж/кг.
* Температура —40°С приняла с учетом А/ = 5 К между температурами
воздуха и аммиака.
479
Т=293 К
^о=92-Ю?ДЖ/КГ 6.
Рис. 11.11 (к примеру 11.14),
Ожижаемую долю у определяем по уравнению (11 Л7)\
„_ U2-i9)-hM(il~i2)~qUOT 30.10* - (10,5-103/1,29) Л ЛСО
У I^^o " (505-92)10^ -*м>ад.
Мощность на валу компрессора определяем по формулам;
N' шш 1,69-^-287.293.2,3 Ig-igjJ--W,5 Вт;
50
N" = 1,69
0,3
287-293.2,3 lg~—= 46,1 Вт;
3600 ' s 1
/V =х (54,5 + 46,1 )/1000 = 0,1 кВт.
Удельный расход энергии на 1 кг жидкого воздуха)
#уд-= 0,1/0,053= 1,89 кВт-ч/кг.
Пример 11.15. При получении жидкого воздуха с отдачей
внешней работы в детандере по циклу среднего давления
затрачивается мощность 110 Вт (на валу компрессора). Сколько
получается килограммов жидкого воздуха в 1 ч, если известно, что
воздух сжимается до 35 кгс/см2? В детандер отводится 80% от
веего количества перерабатываемого воздуха; температура
воздуха перед детандером —110°С, недорекуперация 5 °С. Потери
холода в окружающую среду (через изоляцию) 0,93 кВт. Принять,
что работа, возвращаемая детандером на вал компрессора,
составляет половину от теоретического (изоэнтропического) тепло-
480
Рис» 11.12 (к примерз' 11.15).
падения в детандере. Температура воздуха, поступающего после
компрессора в теплообменник, 25 РС. Определить также удельный
расход энергии на 1 кг жидкого воздуха.
Решение. На рис. 11.12 даны принципиальная схема
установки и изображение процесса в координатах Т—S. Для
определения энтальпий воспользуемся диаграммой Т—S для воздуха
(рис. XXIX).
Удельную холодопроизводительность цикла определяем по
формуле (11.18):
q = (<( — t2) + М Л3 — /4) = (510 — 502) 103 + 0,8-58.103 = 54-108 Дж/кг,
где /3 — U = 0,65 (i9 — jB) » 0,65 (345 — 255) 103 = 58-103 Дж/кг.
Работа, возвращаемая детандером при расширении в нем 1 кг,
воздуха:
/д = 0,5 (345 — 255) 103 » 44,6-103 Дж/кг.
Определяем количество воздуха G (в кг/с), сжимаемого
компрессором, из уравнения:
1= L„ —1д« l,69G/?r.2,3 lg 35 — 0,80.44,6.
По условию L = ПО кВт. Следовательно,
110 =1,696.287.298-2,4 lg 35 — 0,8-44,6 G,
откуда
G = 0,231 кг/с или 0,231-3600*= 835 кг/ч.
16 Павлов К. Ф. и др.
Потери холода определяем по формулам * (11.24) и (11.25)!
QHefl = GcpA* =0,231.1,0Ы0з.5 « 1,17.10s Вт.
По условию Q0 0 = 0,93-103Вт. Общие потери холода
<Эпот = (1.17 + 0,93) 103 = 2,10. Юз Вт
или, считая на 1 кг перерабатываемого воздуха;
qnor = 2,JO- J08/0,231 = 9,1. Ю3 Дж/кг.
Ожижаемую долю воьдуха определяем по формуле (11.19)i
„ - Ci-'«)'+** Сд-Ц —?пот _ (54-9,1) 10* _
У й^, (510 — 92) 10s -U-1U/-
Количество получаемого жидкого воздуха на установке:
Gm = 835-0,107 = 89,3 кг/ч.
Удельный расход энергии на 1 кг жидкого воздуха:
Л'уд = 110/89,3= 1,23кВт-ч/кг.
Пример 11.16. Определить к, п. д. процесса ожижения воздуха
с отдачей внешней работы по циклу высокого давления, если
известно, что воздух сжимается компрессором до 200 кгс/см*.
Начальная температура воздуха 30 °С, в детандер направляется
половина перерабатываемого воздуха. Суммарные потери холода
принять в размере 8,4 кДж на 1 кг перерабатываемого воздуха.
Расширение в детандере производится с 200 до 10 кг/см2, с 10 до
1 кгс/см2 — дросселирование. Возврат работы детандером на вал
компрессора принять как в предыдущем примере.
Решение. На рис. 11.13 даны принципиальная схема
установки и изображение процесса в координатах Т—S. Для
определения удельных энтальпий воспользуемся диаграммой Т—S для
воздуха (рис. XXIX).
Удельную холодопроизводительность цикла определяем по
формуле (11.20):
Я « (h ~ h) + М (is - U) = (515 — 482) 103 +
+ 0,5-119-103 = 93,2-103 Дж/кг,
где i9 — Ц = 0,75 (t3 - t5) = 0,75 (482 - 322) 103 = 119-103 Дж/кг.
Ожижаемую долю воздуха определяем по формуле (11.21):
v_ (*1-*а) + М('8-'«)-9пот ^ (93,2-8,4)10*
у ii — i0 (515 — 92) Ю3 "~
Мощность, затрачиваемая на сжатие воздуха:
WK = 1,69 GCRT In-^-«1,69-^^-287.303-2,3 lg 200 = 216 Вт.
* He учитывается уменьшение обратного потока на ожиженную часть
воздуха.
482
'^r
a
Летандщ
14
i
i
L-515-103}
¦
Компрессор
Теплообменник!
Теплообменники
Ж
Рве. tt.tS (к примеру fLTtfJ.
Мощность, возвращаемая на вал компрессора при расширении
воздуха в детандере:
0,5
N =
д 3600
0,5 (482 — 322) 10*вЦ,1 Вт.
Фактически затрачиваемая мощность на валу компрессора
N « NK - УУД = 216 - 11,1 = 204,9 Вт = 0,205 кВт.
Удельный расход энергии на 1 кг жидкого воздуха!
NуД =0,205/0,2= 1,02 кВт.ч/кг.
К. п. д. процесса ожижения:
0,188
Т] »
1,02
100-= 18,5 %,
где 0,188 кВт-ч/кг —теоретически минимальная работа ожижения 1 кг воздуха
при начальной температуре его 303 К (см. пример 11,11).
Пример 11.17. Определить удельный расход энергии при
ожижении воздуха по циклу низкого давления с турбодетандером
(рис. 11.14). Воздух поступает в установку при 30 °С и
абсолютном давлении 6 кгс/см2. Недорекуперация 5 °С, потери в
окружающую среду 8,4 кДж/м3 (при 0 °С, 760 мм рт. ст.).
Решение. Принимаем температуру воздуха перед
турбодетандером 122 К. Тогда по формуле (11.23):
19 — 1Л = 0,8 ((3 - (В) = 0,8 (325 - 283) Ю* = 33,5-10» Дж/кг.
16* 483
г--*-
w-
Турбокомпрессор
Теплообменник
Отожитепь
ц=51Ш
ц=51Ш
Ь5-283-Ю%ж/К?
Рис. 11.14 (к примеру 11.17).
Удельная энтальпия взята по диаграмме Т—S для воздуха
(рис. XXIX).
Ожижаемую долю воздуха определяем по формуле (11.25);
0 =
8 4-103
(513 —511) 103 +33,5-103(1 — 1,25(/)—^^ 1,0Ы03.5(1-(/)
(513 — 92) 103
откуда у = 0,052.
Работа, возвращаемая турбодетандером, считая на 1 кг
перерабатываемого воздуха:
^д =
(i3 _ ;4) (i __ ay)0,85 33,5-Ю3 (1 — 1,25^0,052) 0,85
3600 3600
= 0,0074 кВт-ч/кг,
где 0,85 — коэффициент отдачи мощности турбо детандера; а = 1,25 — си.
формулу (11.22).
Удельный расход энергии на 1 кг жидкого воздуха при
изотермическом к. п. д. компрессора 0,6:
., / 287-303-2,3 lg6,3 ллл7Л/лл*о i о« и ,
Nm = ( 1000-0,6-3600 0.0074)/0,052 - 1,26 кВт-ч/кг.
УД
Здесь 6,3 — степень сжатия в компрессоре (с учетом гидравлических потерь
установки).
Пример 11.18. При обследовании установки для ожижения
воздуха, работающей с отдачей внешней работы по циклу низкого
484
давления, были измерены перед турбодетандером абсолютное
давление 6 кгс/см2 и температура 120 К. Давление и температура
после турбодетандера были соответственно 1,6 кгс/см2 и 89 К.
Измеренная мощность, отдаваемая турбодетандером, 100 кВт.
Определить количество воздуха, проходящего через турбодетандер,
и термодинамический к. п. д. турбодетандера.
Решение. Определяем действительное и изоэнтропическое
теплопадение в турбодетандере, используя диаграмму Т—S
воздуха (рис. XXIX):
Удельная энтальпия воздуха при б кгс/см3 и 120 К 322-103 Дж/кг
Удельная энтальпия воздуха после нзоэнтропического расшире- 289-103 Дж/кг
ния до 1,6 кгс/см3
Удельная энтальпия воздуха при 1,6 кгс/см3 и 89 К 29 6-103 Дж/кг
Отсюда
Д*д « (322 — 296) 103 = 26,6* 10» Дж/кг;
Д'из = (322 — 289) 103 = 33,3.10» Дж/кг.
Термодинамический к. п. д. детандера:
26,6-10а
11 ^ 33,3-103 '
Определяем приближенно количество воздуха, проходящего
через турбодетандер (пренебрегая потерями энергии):
г 3600/V 360Q.100.10a
°"Д7"- 26,6-Юз =13500 кг/ч.
Пример 11.19. Найти необходимое давление воздуха при
установившемся режиме в установке для получения газообразного
кислорода. Установка работает без предварительного охлаждения
по простому регенеративному циклу. Недорекуперация 5 9С,
потери холода через изоляцию 12,6 кДж на 1 м3 (при 0 °С и
760 мм рт. ст.) перерабатываемого воздуха. Температура воздуха
перед теплообменником 25 °С.
Решение. Потери холода определяем по формулам (11.24)
и (11.28):
Янеп = 1,0Ь 103-5 « 5,05- Ю3 Дж/кг;
</о, о = 12,6- Юз/1,29 = 9,74.10» Дж/кг;
qmT = 5,05.103 + 9,74-103 =* 14,8.103 Дж/кг.
Для покрытия этих потерь 1 кг сжатого воздуха,
дросселируемого в установке, должен дать At = 14,8 кДж.
Эффект дросселирования определяем при 25 °С (температура
входа сжатого воздуха в теплообменник)!
где it — удельная энтальпия воздуха при /?абс — 1 кгс/см2 и 25 °С, равная 510 X
X 103 Дж/кг (по диаграмме Г—S, рис. XXIX).
435
Следовательно,
14,8-Юз = 510-10s —fs#
откуда t3 = 495,2-103 Дж/кг. По диаграмме Т—S находим, что
этой удельной энтальпии воздуха при 25 °С отвечает давление
Лабе = 65 КГС/СМ2.
Пример 11.20. В воздухоразделительной установке,
работающей с отдачей внешней работы по циклу среднего давления,
получается 100 м3/ч (при 0 Си 760 мм рт. ст.) газообразного
кислорода и 25,8 кг кислорода в жидком состоянии; кислород получается
чистотой 99%, Давление сжатия воздуха 40 кгс/см^. Температура
сжатого воздуха перед детандером 160 К. Расширение в
детандере идет до 6 кгс/см2. Термодинамический к. п. д. детандера 0,65. •
Отбросный азот содержит 5% кислорода. Недорекуперация 5 °С.
Температура входящего в установку воздуха 300 К. Потери
в окружающую среду составляют 6,3 кДж на 1 м3 (при 0 °С и
760 мм рт. ст.) перерабатываемого воздуха. Определить долю
воздуха, направляемого в детандер.
Решение. Общее количество получаемого кислорода*
9^ 8
V0f « 100 +-у^ - U8 м*/ч,
где 1,43 — плотность кислорода при нормальных условиях, кг/м3.
Количество (при нормальных условиях) перерабатываемого
воздуха (В) и отбросного азота (А) находим из уравнений
материального баланса:
В= 118+ Л;
0,215 = 0,99-118 + 0,05Л,
откуда В = 695 мя/ч, А = 577 м3/ч.
Определяем потери холода:
от недорекунерации
<7неД = ( 10(М,43-0,92- Ю1 + 577-1,25-1,05-103)/3600 = 1230 Вт = 1,23 кВт;
в окружающую среду
?о. с = 695-6,3-103/3600 = 1210 Вт= 1,21 кВт;
уносится жидким кислородом
Ям. к = 25,8-406- 10V3600 = 2930 Вт *= 2,93 кВт.
Здесь 406*103—разность удельных энтальпий кислорода, газообразного
при 300 К и жидкого (при 1 кгс/см2), Дж/кг.
Итого:
Qno-r = '230 -f- 12Ю -f- 2930 = 5370 Вт = 5,37 кВт.
Холодопроизводительность установки, получаемая за счет
дросселирования:
G Мпр » 695.1,29-8,38-!0*/3600 = 2080 Вт =* 2,08 кВт,
где 8,38-103—разность удельных энтальпий воздуха при 1 и 40 кгс/едг (при
300 К), Дж/кг.
486
Теоретическое (изоэнтропическое) теплопадение в детандере!
Д<иЭ - ',-40 кгс/см* = We кгс/см* = (333 - 283) 10^ = 50.10» Дж/кг.
**=160 К
Действительное теплопадение:
Д*д = 50-103-0,65 « 32,5- Юз дж/Кг.
Количество воздуха, поступающего в детандер, находим из
уравнения
5370 — 2080 = 32,5-103*.
Отсюда
ж «0,1 кг/с = 360 кг/ч.
Доля воздуха, направляемого в детандер!
360
695-1,29
= 0,40.
Пример 11.21. Определить количество выделяющейся влаги
и расход энергии на охлаждение 3000 кг/ч воздуха (считая на сухой
воздух), насыщенного водяными парами при рабс = 6 кгс/сма.
Воздух охлаждается (за счет кипящего аммиака) от 0 до —40 °С.
Холодопроизводительность аммиачной холодильной установки
5130 кДж/(кВт*ч).
Решение. При охлаждении сухого воздуха потребуется
отвести теплоты:
Qi *= <Vp Снач — 'кон) = 3000-1,03- 10s (0 + 40)/3600 = 34 300 Вт.
Здесь Ср — 1,03* 103 Дж/(кг> К) — удельная теплоемкость сухого воздуха при
Рабс =s 6 кгс/см2 в данном интервале температур.
Найдем количество влаги, выпадающей из воздуха при
охлаждении.
Количество влаги в воздухе при входе в холодильник!
G' =00622 фРнас --^3000 °>622-Ь4'6 ^180кГ/-1
^вл ubu'^z П-ФРнас JUUU 6-760-4,6 -ЬЙУКГ/4»
где Рнас = 4,6 мм рт. ст.—давление насыщенного водяного пара при 0 °С
(табл. XXXVIII).
Количество влаги в воздухе, выходящем из холодильника*
°» = 3000-0,622 6,7600,!_90)09 = 0,038 кг/ч,
где Рнас = 0,09 мм рт. ст. — давление насыщенного водяного пара при —40 °С.
Количество влаги, выпадающей в холодильнике!
ввл e °m - °вл = i,89 —0,038 = 1,852 кг/ч.
487
Количество теплоты, выделяющейся при конденсации и
замерзании влаги:
Qz = Свл [r + q + c (tua4 — /кон)] =
= 1,852 [2490- Ю3 + 335.103 + 2,09.103 (0 + 40)]/3600 » 1490 Вт.
Здесь г = 2490-103 Дж/кг — удельная теплота конденсации при 0°С; а=*
= 335-103 Дж/кг — удельная теплота плавления; <?=2,09-10? Дж/(кг*К) —
удельная теплоемкость льда.
Общее количество теплоты, отводимой аммиаком:
Qi + Qz *= 34 300 + 1490 = 35 790 Вт » 35,8 кВт.
Мощность, расходуемая аммиачной холодильной установкой
35,8-3600
Л/ =
5130
= 25 кВт.
Пример 11.22. Определить расход перерабатываемого воздуха
при получении 100 м3/ч кислорода чистотой 99%. Отбросный азот
содержит 4% кислорода.
Решение. Обозначим через х искомое количество воздуха
(в м3). Тогда
0,21* = 100-0,99 + (х — 100) 0,04,
где 0,21 — объемная доля кислорода в воздухе. Отсюда
х = 560 м3/ч.
Пример 11.23. Определить для нижней колонны двухколонного
воздухоразделительного аппарата (рис. 11.15) количество обра-
Дзот 0,754м3
Пар
0,794-0,09=
Кислород,
0,206м*
Азот е
карманах
0,5м*
Возду,
Пар
0,09м3
Жидкость
после
дросселирования
0,4Ы*
0,5мЗ
зующегося в карманах азота и
количество кубовой жидкости,
обогащенной кислородом, считая на
1 м3 поступающего воздуха.
Чистота азота в карманах 98 %,
жидкость куба содержит 40%
кислорода.
Решение. Обозначим через
х количество азота (в м3),
получаемого в карманах, и через у —
количество кубовой жидкости.
Тогда
* + ? = 1
и (по кислороду)
0,02*-f 0,4(/ = 0,2Ы.
Решая эти уравнения
материального баланса, получим:
х = 0,5 м3; у = 0,5 м3 (при 0° С и
760 мм рт. ст.).
Ряс. 11.15 (к примерам 11.23 и И.24),
488
Пример 11 «24, Определить число флегмы и количество
получаемых азота и кислорода (считая на 1 м3 воздуха) в верхней
колонне двухколонного воздухоразделительного аппарата
(рис. 11.15), учитывая данные предыдущего примера и принимая,
что чистота азота 99%, а кислорода 98%.
Решение. Составим уравнения материального баланса.
Обозначим через х количество отходящего азота и через у —
количество отходящего кислорода. Тогда
0,01х + 0,98у = в,21,
откуда х = 0,794 м3; у = 0,206 м3.
Находим отношение количества жидкости L, стекающей по
колонне, к количеству поднимающегося пара G.
Жидкая азотная флегма подается на верх колонны из
карманов нижней колонны, причем, как видно из диаграммы состояния
для азота, при дросселировании жидкого азота с 6 до 1 кгс/см^
образуется ~ 18% пара. В предыдущем примере было найдено,
что в карманах нижней колонны получается 0,5 м3 азота.
Следовательно, количество жидкого азота, попадающего в верхнюю
колонну, составляет:
L = (1 — 0,18)0,5 = 0,41 м*.
Количество пара, поднимающегося по верхней колонне!
G = 0,794 — 0,5-0,18 = 0,704 м3,
где 0,5-0,18 — количество пара, образующегося после дросселирования жидкого
азота из карманов нижней колонны в верхнюю колонну, м3.
Отношение LIG =0,41/0,704 =0,582.
Определяем число флегмы:
-тпт - °'582-
Отсюда R = 1,39.
Пример 11.25. Определить расход энергии при получении 1 м3
газообразного кислорода чистотой 99,5% на установке с двойной
ректификацией, работающей по простому регенеративному циклу
без предварительного аммиачного охлаждения. Отбросный азот
содержит 5% кислорода. Общие потери холода составляют 6,3 кДж
на 1 кг перерабатываемого воздуха. Температура сжатого
воздуха, поступающего в установку (после компрессора), 25 °С.
Решение. Определяем количество воздуха х, необходимое
для получения 1 м3 кислорода:
0,21* = 1-0,995+ (х —1)0,05; х = 5,9м3.
Определяем давление сжатия воздуха при установившемся
режиме, когда потери холода составляют 6,3 кДж/кг:
Ai«f,— /3; 6,3-103 = 510-Юз_г3,
где 510-Ю3 — удельная энтальпия воздуха при 1 кгс/см2 н 25 °С, Дж/кг
(диаграмма Г—S, рис. XXIX).
489
Отсюда
f3 = (510 — 6,3) 103 = 504,7- 103 Дж/кг.
По диаграмме Т—S находим, что этой удельной энтальпии
воздуха при 25 °С соответствует абсолютное давление 60 кгс/см2.
Работу на сжатие 1 кг воздуха с 60 до 1 кгс/см2 определяем
по формуле:
I = 1 >№GRT in -^- « 1,69-1 -287-298-2,3 lg 60 = 590.103 Дж/кг = 590 кДж/кг.
Р\
Для получения 1 м3 кислорода требуется 5,9 м3 воздуха.
Следовательно, затрата энергии иа 1 м3 кислорода составляет!
#уд = 590-5,9.1,29/3600 «1,25 кВт-ч/м3.
Пример 11.26. Через изоляцию резервуара (танка) для
хранения жидкого кислорода проникает из окружающей среды
теплоты 83;8 кДж/(м2-ч) (считая на наружную поверхность).
Внутренний диаметр резервуара шарообразной формы 1200 мм:
Наружный диаметр внешнего кожуха, имеющего цилиндрическую
форму, 1900 мм, высота 2300 мм. Определить, сколько испаряется
в 1 ч кислорода и через какое время испарится весь кислород,
если резервуар был заполнен на 0,75 своего объема. Кислород
хранится под атмосферным давлением.
Решение. Площадь наружной поверхности цилиндрического
кожуха резервуара:
jtO2 3 14.1 Ф
F = 2-^— + nDH = 2 *'14 ь* +3,14-1,9-2,3= 19,34 м2.
Проникает теплоты в резервуар;
G « 19,34 -83,8.103/3600 = 450 Вт =* 0,45 кВт.
Расход испаряемого кислорода:
„ 450-3600
°02 = 213,7-10» = lfi КГ/Ч-
Здесь 213,7» 103 Дж/кг— удельная теплота испарения кислорода под
атмосферным давлением.
Количество кислорода в резервуаре при заполнении его на
0,75 объема:
G = 0,75 ~^- 1100 - 0,75 3'14'1'23 ЦОО = 743 кг,
О О
где 1100 кг/м3— плотность жидкого кислорода.
Время испарения всего кислорода:
^иса = 743/7,6 = 98 ч.
490
КОНТРОЛЬНЫЕ ЗАДАЧИ
11.1. Вычислить холодильный коэффициент и мощность,
потребляемую холодильной установкой, работающей по циклу
Карно, если ее холодопроизводительность 6400 Вт при
температуре испарения —10 °С. Температура конденсации 22 °С.
11.2. Найти минимальную затрату работы (по циклу Карно) и
расход роды в конденсаторе при выработке 100 кг/ч льда из воды,
имеющей температуру 0 °С. Хладагент испаряется при —5 °С,
а конденсируется при 25 °С. Вода в конденсатор подается при 12 °С,
а уходит при 20 °С. Уцелькая теплота замерзания воды 335 кДж/кг.
11.3. Определить удельную холодопроизводительность
хладагента и холодильный коэффициент цикла для: а) аммиака;
б) диоксида углерода и в) дифтордихлорметана CF2C12.
Температура испарения —15 °С, температура конденсации 30 °С. Цикл
сухой, переохлаждение жидкости перед дросселированием
отсутствует.
11.4. Вычислить теоретический холодильный коэффициент уг-
лекислотной холодильной установки, если температура
конденсации 20 °С, а температура испарения —40 °С. Цикл сухой,
переохлаждение жидкости перед дросселированием отсутствует.
11.5. Сравнить теоретические холодильные коэффициенты
аммиачной компрессионной холодильной установки, работающей
при температуре испарения —20 °С и температуре конденсации
30 °С: а) для цикла Карно; б) для реального влажного цикла;
в) для сухого цикла без переохлаждения жидкого аммиака; г) для
сухого цикла с переохлаждением до 25 °С жидкого аммиака после
конденсации.
11.6. По условиям предыдущей задачи сравнить теоретические
холодильные коэффициенты для фреоновой холодильной
установки, пользуясь диаграммой i — lg р (рис. XXVIII).
11.7. В конденсаторе аммиачной холодильной установки 20 м3/ч
воды нагревается на 6 К. Теоретическая мощность, затрачиваемая
компрессором, 23,5 кВт. Определить холодопроизводительность
установки и холодильный коэффициент.
11.8. Определить часовой объемный расход аммиака,
поступающего в компрессор, при следующих условиях:
холодопроизводительность установки 58 200 кВт; температура конденсации 25 °С,
переохлаждения нет; температура испарения —15 °С; цикл сухой.
11.9. 1000 кг/ч этилового спирта необходимо охлаждать от
20 до —15 °С. Охлаждение ведется аммиаком, кипящим при
—25 °С. Определить теоретическую мощность, затрачиваемую
компрессором. Температура конденсации 25 °С. Цикл сухой,
переохлаждение жидкости перед дросселированием отсутствует.
11.10. Аммиачный компрессор типа ГД (горизонтальный) имеет
холодопроизводительность 697 800 Вт при температуре испарения
—15 °С и температуре конденсации 25 °С. Определить
холодопроизводительность этого компрессора, если температура испаре-
491
CF2Cl2
-!4QC
p= Икгс/см2
Рис. П.16 (к контрольной задаче 11.14),
ния будет —5 °С, а температура
конденсации 30 °С.
11.11. Углекислотная
холодильная установка
производительностью 116 300 Вт работает
при температуре испарения
—15 °С, абсолютном давлении в
конденсаторе 75 кгс/см2 и
переохлаждении до 25 °С.
Компрессор имеет сухой ход. Определить холодильный коэффициент и
теоретическую потребляемую мощность.
11.12. Аммиачная холодильная установка холодопроизводи-
тельностью 116 300 Вт с компрессором вертикального типа
работает при температуре испарения —15 °С, температуре конденсации
30 °С и переохлаждении до 25 °С. Компрессор имеет сухой ход.
Определить: давления в конденсаторе и испарителе, холодильный
коэффициент, часовой объем засасываемых компрессором паров,
теоретическую и действительную потребляемую мощность,
температуру аммиака на выходе из компрессора, расход воды на
конденсатор при нагревании воды в нем на 7 °С.
11.13. Аммиачный двухцилиндровый вертикальный
компрессор одноступенчатого сжатия имеет диаметр цилиндров 150 мм,
ход поршня 150 мм и чистоту вращения 400 об/мин. Вычислить
холодопроизводительность этого компрессора при нормальных
условиях, а также при рабочих условиях, когда испарение
производится при рабе = 2 кгс/см2, а конденсация при рабс =
= 12 кгс/см2. Перед дросселированием производится
переохлаждение жидкого аммиака на 6 °С. Вычислить также действительную
расходуемую мощность для рабочих условий.
11.14. В каскадной холодильной установке, работающей с
фреоновым и этановым циклами (рис. 11.16), этан конденсируется при
—14 °С под абсолютным давлением 17 кгс/см2. Количество теплоты,
передаваемой от конденсирующегося этана к кипящему фреону
(хладону), составляет 23 260 Вт. Температура испарения фреона
на 5 °С ниже температуры конденсации этана. Конденсируется
фреон при 30 °С, переохлаждения жидкого фреона нет, цикл
сухой. Определить степень сжатия фреона в компрессоре (отношение
давления конденсации к давлению испарения) и расход воды в
конденсаторе фреона при нагревании ее на 8 °С.
11.15. Сжатый до рабс = 10 МПа воздух охлаждается в
испарителе двухступенчатой аммиачной холодильной установки до
температуры, на 5 °С превышающей температуру испарения
аммиака. После охлаждения сжатый воздух дросселируется до
давления рабс = 0,4 МПа. Определить температуру воздуха после
дросселирования, если аммиак испаряется под давлением рабе =
= 0,042 МПа.
492
11 .16. Определить по диаграмме T—S интегральный джоуль-
томсоновский эффект при дросселировании воздуха до 1 кгс/смаз
а) при начальной температуре воздуха 15 °С и начальном давлении
50 кгс/см2; б) при начальной температуре воздуха —50 °С и
начальном давлении 50 кгс/см2; б) при начальной температуре
воздуха —50 °С и начальном давлении 200 кгс/см2.
11.17. Определить затрату энергии на 1 кг жидкого воздуха,
получаемого по простому регенеративному циклу, при следующих
условиях: а) начальная температура воздуха 15 °С, давление
сжатия 50 кгс/см2; б) начальная температура 15 °С, давление сжатия
200 кгс/см2. Расширение в обоих случаях производится до 1 кгс/см2.
Потери холода от недорекуперации и в окружающую среду не
учитывать.
11.18. Определить ожижаемую долю воздуха и расход энергии
на 1 кг жидкого воздуха в простом регенеративном цикле при
начальной температуре воздуха 30 °С и давлении сжатия рабс =
= 200 кгс/см2. Общие потери холода 10,5 кДж на 1 кг
перерабатываемого воздуха.
11.19. Определить расход энергии на 1 кг жидкого воздуха при
дросселировании воздуха с 200 до 1 кгс/см2 в цикле с
предварительным аммиачным охлаждением до —50 °С. Удельная хо-
лодопроизводительносгь аммиачной холодильной установки
4820 кДж на 1 кВт*ч. Потери холода от недорекуперации и в
окружающую среду не учитывать. Начальная температура
воздуха 15 °С.
11.20. Определить ожижаемую долю воздуха и расход энергии
на 1 кг жидкого воздуха в установке, работающей с циркуляцией
воздуха под давлением. Давление сжатия рабе = 200 кгс/сма;
промежуточное давление ра^с — 50 кгс/см2; низкое давление
1 кгс/см2; М = 0,2; начальная температура воздуха 25 °С. Потери
холода не учитывать.
11.21. Определить потребляемую мощность и количество
жидкого воздуха, получаемого в цикле среднего давления с
отдачей внешней работы, при переработке 300 м3/ч воздуха (при 0 9С
и 760 мм рт. ст.). Воздух сжимается до 40 кгс/см2; температура
воздуха перед детандером —80 °С; температура воздуха после
компрессора (перед входом в теплообменник) 30 °С; доля воздуха,
направляемого в детандер 0,8. Определить также расход энергии
на 1 кг жидкого воздуха. Общие потери холода принять в размере
11,5 кДж на 1 кг перерабатываемого воздуха.
11.22. Определить расход энергии на 1 кг жидкого воздуха
в цикле высокого давления с отдачей внешней работы при сжатии
воздуха до 200 кгс/см2 и давлении после детандера 8 кгс/см2;
М = 0,5. Общие потери холода 14,7 кДж на 1 кг
перерабатываемого воздуха. Начальная температура воздуха 30 РС.
11.23. При испытании турбодетандера установлено, что
воздух в нем расширяется от 4 до 1,2 кгс/см2, причем от
турбодетандера отводилась мощность в 4 кВт и через него проходило 650 кг/ч.
493
Определить термодинамический к. п. д. турбодетандера. Сжатый
воздух поступал в турбодетандер при 114 К.
11.24. Определить расход энергии на 1 кг жидкого воздуха
в цикле низкого давления с турбодетандером, если известно, что
компрессором сжимается 6000 м3/ч воздуха (при нормальных
условиях) до /7абс = 7 кгс/см2. Турбодетандер отдает мощность 55 кВт.
Потери от недорекуперации и в окружающую среду составляют
6,3 кДж на 1 м3 сжимаемого воздуха (при нормальных условиях).
Для компрессора изотермический к. п. д. принять равным 0,7.
Воздух поступает в установку при 35 °С. В турбодетандер
направляется 80% перерабатываемого воздуха. Коэффициент испарения
а = 1,25.
11.25. Сколько кубических метров воздуха необходимо
переработать для получения 200 м3 кислорода 99% чистоты, если
отбросный азот содержит 10% кислорода?
11.26. По практическим данным, потери холода составляют
335 кДж с 1 м2 наружной поверхности кожуха теплоизолирующего
цилиндрического бака, заполненного жидким метаном.
Внутренние размеры бака: D — Н =1,1 м. Бак окружен со всех сторон
изоляцией толщиной 300 мм. Определить время испарения всей
жидкости, если вначале бак был залит полностью. Плотность
жидкого метана 415 кг/м3.
11.27. Определить затрату энергии при получении 1 кг жидкого
метана по простому регенеративному циклу. Метан сжимается до
давления 150 кгс/см2. Температура метана после компрессора
300 К. Диаграмму Т—5 для метана см. [11.8].
11.28. Определить расход энергии при получении 1 кг жидкого
метана в цикле с предварительным аммиачным охлаждением до
—45 °С при давлении сжатия метана 150 кгс/см2. Удельная холо-
допроизводительность аммиачной холодильной установки
4820 кДж/(кВт-ч).
11.29. В установке для получения газообразного кислорода,
работающей по циклу среднего давления с отдачей внешней работы,
давление поступающего воздуха 20 кгс/см2. Недорекуперация
составляет 8 °С, потери холода в окружающую среду 8,38 кДж
на 1 м3 перерабатываемого воздуха. В детандере воздух
расширяется от 20 кгс/см2 (при 140 К) до б кгс/см2, к. п. д. детандера
0,65. Определить долю воздуха, направляемого в детандер,
пренебрегая эффектом дросселирования воздуха от б до 1 кгс/см2.
ОТВЕТЫ НА КОНТРОЛЬНЫЕ ЗАДАЧИ
Глава 1. Основы гидравлики
1.1. М = 15,8; р = 0,616 кг/м3.
1.2. 4,43 кг/м3.
1.3. 7,3% С02; 69,2% N2; 23,5% Н20.
1.4. 0,995-105 Па.
1.5. а) 1,8 м; б) 1,1 м.
1.6. 6 болтов; 0,716-10^ Па или 0,73 кгс/см2*
1.7. 3,31 -10* Н.
1.8. 0,33-10"4 м2/с.
1.9. 1,5-10"6 Па-с.
1.10. 0,07 П = 0,007 Па-с.
1.11. 0,72 м/с.
1.12. wBX — 13,1 м/с; швых = 10,1 м/с*
1.13. ют = 2,0 м/с; wr — 10,4 м/с.
1.14. 73 мм.
1.16. 0,105 м.
1.17. Переходный режим.
1.18. а) Переходный режим; б) ламинарный режим.
1.19. 0,056 м/с.
1.20. 2840 кг/ч.
1.21. т= 1 ч 13 мин; а = 0,632.
1.22. 0,06 м»/с.
1.23. w = 0,47 м/с; G = 47 800 кг/ч.
1.24. 280 кг/ч.
1.25. 2,88-104 Па.
1.26. 1,37-10* Па (е = 0,01 мм).
1.27. 520 Па (е = 0,8 мм).
1.28. 1,15-10* Па (е = 0,2 мм).
1.29. а) Уменьшится в 10 раз; б) изменится в . * раз.
^о-* о
1.30. 56,5 м3/ч.
1.31. 50 мм.
1.32. а) Увеличится в 16 раз; б) увеличится в 32 раза.
1.33. 7,1 м.
1.34. 5,9 л/мнн.
1.35. 1,51 кВт.
1.36. 821 Па.
1.37. Для толуола 15,6 Па; для воды 513 Па.
1.39. Масштаб 1 : 13,6; w = 0,271 м/с.
1.40. 1,43 кВт.
1.41. Увеличится в 8 раз.
1.42. 4,0 кВт.
1.43. 10,2 кВт.
1.44. 4,7 кВт.
1.45. Ар = 3360 Па, N = 0,35 кВт.
1.46. w = 1,7 м/с; к = 0,0255.
1.47. 4,79 *10"2 кг/с; режим ламинарный.
1.49. 21 м3/ч.
1.50. Зимой 1,71-10* кг/ч; летом 1,46-10* кг/ч,
1.51. 776 Па или 79 мм вод. ст.
1.52. 36,7-10* Па или 3,74 кгс/см2.
1.53. 4,84 м.
1.54. 354 Па.
Глава 2. Насосы. Вентилиторы. Компрессоры
2.1. 15,6 м.
2.2. 467 м.
2.3. 0,69.
2.4. 18,3 кВт.
2.5. 43 °С.
2.6. 0,037 ntVc; большой плунжер 0,0184 м*/с; малый плунжер 0,0186 м*/с,
2.7. 0,89.
2.8. Не более 2,2 м.
2.9. 1,86 кВт.
2.10. г, = 0,59; Q =- 71,2 м»/ч; И = 68 м; N = 22,4 кВт,
2.11. Qx = 0,4 mVmhh; <J2 = 0,3 м3/мин.
2.12. 0,257 м3/мин.
2.13. 18,2 м3/ч.
2.14. 4 2 кВт.
2Л5. тГ= 0,48; <? = 4170 м3/ч; Др = 734 Па; N = 177 кВт#
2.16. 940 м3/ч.
2.17. 1650 ма/ч.
2.18. 1800 об/мин.
2.19. 117 °С; 118 кДж/кг,
2.20. 4,6 кВт.
2.21. 0,89.
2.22. 3,25 м3/мин; 13,0 кВт.
2.23. 5,46 м3/мин; 13,2 кВт.
2.24. 20,3-10^ Па или 20,7 кгс/сма.
2.25. 3,62-1№ Па ила 3t69 хгъ'см2 — воздух; 9,20~Ю* Па клк 9,3? кгскм* —
этан.
2.26. Одноступенчатое сжатие: 261 кДж/кг; двухступенчатое сжатие: 220 кДж/кг.
2.27. 4 ступени.
2.28. Одноступенчатое сжатие: 4,28 -103 кДж/кг; двухступенчатое сжатие:
3,54-10^ кДж/кг.
2.29. 10,7 м^ч (при нормальных условиях).
2.30. Двухступенчатое сжатие: N — 83,2 кВт, расход воды 4,13 uVq;
трехступенчатое сжатие: N ~ 80 кВт, расход воды 3,96 м37ч.
Глава 3. Гидромеханические методы разделении. Перемешивание
в жидкой среде
3.1. a) djdx = U73; б) a\ldx = 2,06.
3.2. а) ш00 = 7,65-10-5 м/с; б) при 15°Сш0С = 7,8ft.10"» м/с, при5ОО°Сс0оо =
= 3,93* 10"3 м/с.
3.3. 16,8 м/с.
3.4. 7,63 м/с.
3.5. 226 мм.
3.6. 11,4 мкм.
3.8. 5,14 м.
3.9, В ~2 раза.
ЗЛО. ЦН-15; Ар = 808 Па или 82,4 мм рт. ст.
3.12. 1070 кг/м3,
3.13. а) 0,08 м/с; б) 0,11 м/с,
3.14. 0,93 мм.
3.15. 2990 кг,
3.16. 4200 кг.
3.17. 1 ч 36 мин.
3.18. 2 ч.
3.19. 1 ч. 20 мин.
3.20. 58,5 мин.
3.21. ПО см3/дм3.
3.24. Центрифуга периодического действия вертикальной подвесной конструкции,
3.25. Сверхцентрифуга,
496
3.26. 1,375-105 Па нли 1.40 кгс/сма.
3.27. ~600 об/мин.
Й.28. а) 1,04 м; б) 0.082 м>
3.30. В 200 раз.
3.31. 1 мин 18 с.
3.32. 4,8 кВт.
3.33. 3 центрифуги.
3.34. Увеличится не более чем на 100%.
3.35. 6,53 м8/ч.
3.36. В 27 раз.
3.37. 5,07 ма/ч.
3.38. 6,15 мкм.
3.39. 0,28 м/с; 2279 Па.
3.40. 0,48; 462 мм.
3.41. 1,3 мм; 50%.
3.42. 137 Вт.
3.43. 240 об/мин.
3.44. Увеличится в 1,3 раза»
3.45. 0,58 м.
Глава 4. Теплопередача в химической аппаратуре
4.1. Увеличится в 10 раз.
4.2. 1,75 кДж.
4.3. 136 кДж/ч.
4.4. Увеличится на ~23%.
4 5. 217 °С
А.Ъ. 0,14 Вт/(м-К); 0,017 Вт/(м-К); 0.48 Вт/(м-К).
4.7. 285 кг/ч; 259 кг/ч; 2820 кг/ч.
4.8. 94,7 °С.
4.9. 92 кВт.
4.10. 582 кг/ч.
4.11. 63,8 Вт/м2.
4.12. а) Не изменится; б) увеличится на 9%,
4.13. а) От 52,55 до 50,28 Вт/(м3 -К); б) от I960 до 730 Вт/(м2 -К).
4.14. 28,7 кВт/м3.
4.15. Прямоток 36.7 °С; противоток 50,5 °С,
4.16. 38,4 °С.
4.17. 4,21 м3/ч.
4.18. Поверхность имеющегося теплообменника недостаточна,
4.19. 9,38 Вт/(м2-К).
4.20. 2140 Вт/(м2-К).
4.21. 3,1 м2; 560 кг/ч.
4.22. а) Расход воды: 39,8 м3/ч; F = 18 м2;
б) расход воздуха: 112 000 м3/ч (при нормальных условиях); F
4.23. 112 Вт/(м*-К).
4.24. 1510 Вт/(м3-К).
4.25. 3890 Вт/(м2К).
4.26. 92 Вт/(м3-К).
4.27. 1) 42,3 Вт/(м3-К); 2) 72,3 Вт/(м3-К).
4.28. Увеличится в 1,94 раза.
4.29. 1100 Вт/(м2-К).
4.30. 266 Вт/(м3-К).
4.31. 268 Вт/(м2К).
4.32. 266 Вт/(м2К).
4.33. 156 Вт/(м2-К).
4.34. 117 Вт/(м3-К).
4.35. 141 Вт/(м2К).
4.36. 287 Вт/(м2-К).
4.37. 113,8 Вт/(м3-К).
4.38. 4140 Вт/(м2-К).
4.39. 3080 Вт/(м2К).
4.40. 2340 Вт/(м2 К).
4.41. 1017 Вт/(м2 К).
4.42. 1660 Вт/(м2 К).
4.43. 5035 Вт/(м2 К).
4.44. 98 м2.
4.45. 66 м2.
4.46. 3,61 м; 284,5 кг/ч.
4.47. 40 м; 1512 кг/ч.
4.48. а) 309 Вт/(м2-К); б) 300 Вт/(м2-К)*
4.49. 215 Вт/(м2-К).
4.50. 772 кг/сут.
4.51. Уменьшится в 9,7 раз.
4.52. 166 мм.
4.53. 127 Вт/м2.
Глава 5. Выпаривание. Кристаллизация
5.1. I. а) 1,184 кг/кг; б) 1,023 кг/кг; II. а) 1,152 кг/кг; б) 1,067 кг/кг.
5.2. 0,141 кг/с.
5.3. Уменьшится на 37,5%.
5.4. 3,47-105 Па или 3,54 кгс/см2.
5.5. 1100 кг.
5.6. W = 530 кг; V = 0,56 м3.
5.7. 80 кВт.
5.8. 1995 Дж/(кг-К).
5.9. с = 2768 Дж/(кг-К); GT n = 189 кг.
5.10. х = 33%; Gr.n =* 2530 кг/ч.
5.П. 2,1 мм.
5.12. а) 173 кВт; б) 0,026 кВт.
5.13. а) 1430 кг/ч; б) 980 кг/ч; в) 3,8 м2.
5.14. г = 305 кДж/кг; с = 2080 Дж/(кгК).
5.15. л= 2030 кДж/кг; с = 2810 Дж/(кг-К).
5.16. ?Кип ^ 82 °С; г = 244 кДж/кг.
5.17. 18,1 кПа или 136,1 мм рт. ст.
5.18. 81,5СС.
5.19. 149 м2.
5.20. А) = 0,317 кгс/см2.
5.21. 42 м2; 2150 кг/с.
5.22. Увеличится в 2 раза.
5.23. 932 кг/ч.
5.24. 85 ма; 1494 кг/ч.
5.25. а) 35 м3/ч; б) 32 кгУч.
5.26. Gnaq = 1640 кг/ч; GK0H = 560 кг/ч.
5.27. 35 С
5!28.' 11,8% (масс); 18,0% (масс); 43% (масс).
5.29. 4 корпуса.
5.30. 13,5 кг/ч, т. е. 4,04% от общего количества воды, испарившейся во втором
корпусе.
5.31. 25,9%.
5.32. хнач = 11,3% (масс); At = 20,7 К,
5.33. 88 кг/ч.
5.34. 129 кг/ч; 56 кВт.
5.35. 15 °С.
5.36. 1 3 т
5!37." F ^ 23 м2; GB = 8630 кг/ч.
Глава 6. Основы массопередачи. Абсорбция
6.1. Рсм= 1050 кг/мв; Л = 1,333 кг нитробензола/кг бензола; Сх = 4,86 кмоль
нитробеизола/м3 смеси.
6.2. 1143 кг/м3.
498
0.3. 1,59 кг спирта/кг воздуха; рсм = 1,08 кг/м3.
6.4. 0,634 кг/м3 водорода; 11,59 кг/м3 метана; 4,740 кг/м3 этилена.
6.6. ЛСу = 5,15-Ю-3 кмоль СаНз/м3 газа; АСУ = ^),1340 кг С2П2/^ газа;
&СХ = 5,26-10~3 кмоль С2Н2/м3 жидкости; АСХ = 0,1369 кг СзНа/м3
жидкости.
6.7. Дх = 0,08 кмоль хлороформа/кмоль смеси;
Дг/ = 0,10 кмоль хлороформа/кмоль смеси.
6.8. а) 13,8% (масс); б) 42,5%.
6.9. а) 40,5%; б) 85%.
6.11. 0,00122 кмоль/(м2-ч*кПа).
6.12. ДКср = 0,02 кмоль бензола/кмоль инертного газа; п0у = 1,6.
6.13. L = 175 000 кг/ч; п0и = 6,02. Д/?ср = 5,67 мм рт. ст.
6.14. L = 1475 кг/ч; Ян = 7,2 м.
6.15. L = 760 кг/ч; Нн = 1,93 м; п0и = 4,68.
6.17. 0,038 м/с.
6.18. 2,16 10_в м/с.
6.19. 0,0285 м/с.
6.20. D = 2,15 м; Нт = 5,4 м.
„ „. г, ел с л люп / / 9 кг аммиака \
6.21. #н = 5,1 м; Kv = 0,0132 кг аммиака/ { м2-с 1.
и у / \ кг воздуха /
6.22. 5,1 м.
6.23. L = 12,3 т/ч; Хн = 0,0611 кмоль бензола/кмоль масла; D = 1,59 м;
Ян = 7,02 м; Ят = 4,0 м.
6.24. 30 м3/ч.
6.25. D = 1,03 м; Ха = 0,149 кмоль бензола/кмоль поглотителя.
Глава 7. Перегонка и ректификация
7.1. а) 99 °С; 10,2% (масс.) крезола, 89,8% (масс.) воды; 1,85% (об.) крезола,
14 мм рт. ст.;
б) 74 °С; 7,25% (масс.) крезола, 92,75% (масс.) воды; 1,29% (об.) крезола,
3,9 мм рт. ст.
7.2. а) 94 кг; б) 31,3 кг.
7.3. xq = 0,408; П = 962 мм рт. ст. или 128,3 кПа.
7.4. а) х = 0,675; у* = 0,90;
б) при 50 °С давление не может превышать 400 мм рт. ст.
7.6. 4,2% (мол.) воды; 13% (мол.) уксусной кислоты; 82,8% (мол.) ацетона.
7.7. 465 кг; 43,8% (масс.) бензола.
7.8. W = 22,6 кг; D = 2577,4 кг; xD = 73,6%,
7.9. 608 кмоль/ч.
7.11. 12,1% (масс).
7.12. 0,897.
7.13. 7,2% (масс); 13 000 кг/ч.
7.14. GD = 17 150 кг/ч; Gw = 64 700 кг/ч; Gv = 68 400 кг/ч.
7.15. 25,4% (масс); 4330 кг/ч.
7.16. 68,4% (мол.).
7.17. 74,4% (мол.); 80,3% (мол.).
7.18. а) 76,7% (мол.); б) 17,96% (мол.).
7.19. nG = 9; 720 кг/ч.
7.20. 7,1% (масс); Gv = 4400 кг/ч; Оводы = 97 100 кг/ч,
7.21. 59,2 ма; 2170 кг/ч.
7.22. В дефлегматоре: 4700 кДж/кг; в кубе: 5787 кДж/кг.
7.23. 3,21; 83 т/ч.
7.24. 9,4 м2; 10,75 т/ч.
7.25. ят = 17.
7.26. 190 кг/ч.
7.27. a) GD = 1760 кг/ч; Gw = 4240 кг/ч; б) р = 328 мм рт. ст.; в) пт =» 13 ;
г) Gr п = 1435 кг/ч; GB = 46,5 т/ч.
7.28. D = 800 мм; Ят ч = 3300 мм.
499
Глава 8. Экстрагирование
8.2. *Aj = 62,2; хв% = 24,8; хАя = 18,9; xBg = 25,1% (масс); 1,74 кг.
8.3. G?j = 1940; GE =180 кг; хЕ л* 55% (масс.) (после удаления
растворителя);
GE — 1735; GE = 99 кг; хЕ = 35% (масс.) (после удаления
растворителя);
G^2 — 915; Сд = 850 кг; Хп =4% (масс.) (после удаления
растворителя).
8.4. G8 = 1334 кг/ч; nG = 4.
8.5. nQ = 3; хЕ = 4 г/л; 1,2 г/л; 0,6 г/л.
8-6- Чшн = " w; «о = 8.
8.7. 63% (масс); 70% (масс).
8.8. 38,9 кг; 256 кг.
8.9. 77,8 кг; 450 кг; nG = 7.
8.10. Экстракт 58% (масс); рафинат ~0%; лСмнн = 1Ь
8.11. пс = 18; GSq =: 1718 кг; GSt0 = 1734 кг.
8.12. а) 7,7 кг; б) 99,6%; в) 24,9% (масс).
8.13. п0 = 2.
8Л4. /70 = 6.
8.15. а) 0,1 т или 2%; б) 28,8 т; в) 1 — 10%, 11 — 7,9%, III —6,1%, IV —
4,7%, V-3,6%.
8.16. 565 кг; л0 = 3.
Глава 9. Адсорбция
9.1. 1430 кг; 2,55 м; 1 ч 22 мин.
9.2. т = 225 мин; т0 = 65 мин.
9.4. и = 0,08 м/с; Я0 = 0,4 м.
9.5. д=228 кДж/кг угля; Q^l^l-lO6 кДж.
9.6. 2,94-10*8 м/с.
Глава 10. Сушка
10.1. В 33 раза.
10.2. х = 0,060 кг/кг; / = 209 кДж/кг; tM = 43 °С; /р = 42 °С.
10.3. х == 0,020 кг/кг; / = 105 кДж/кг; tv ^ 24 °С; <р == 0,25; рп = 23 мм рт. ст.
10.4. х = 0,069 кг/кг; <р = 0,8.
10.5. а) 0,0159 кг/кг; б) 0,231 кг/кг; в) 0,0154 кг/кг.
10.6. /э = 36,4 кг/кг; <?з= 4350 кДж/кг; /л= 47,6 кг/кг; <?л = 3710 кДж/кг.
10.7. р = 372,5 мм рт. ст.; Рвозд = 372,5 мм рт. ст.; х = 0,622 кг/кг.
10.8. х = 0,083 кг/кг; рв » 6,173 кгс/см2 или 6,06-106 Па; р = 5,68 кг/м3.
10.9. 4,6 кг/ч; 43,5 кг/кг.
10.10. рп = 2,755 кгс/см2 или 270,3 кПа; р = 5,05 кг/м3; х = 0,404 кг/кг.
10.11. 3230 м3 влажного воздуха/ч.
10.12. 25 °С.
10.13. 9700 кг/ч; 566 кВт.
10.14. 47 200 кг/ч; 910 кВт.
10.15. 71,3%.
10.16. 35,8 °С.
10.17. 7,4 кПа илн 56 мм рт. ст.; 7,4%,
10.18. 16,5 ч.
10.19. 5,81 м2.
10.20. 33 °С; 0,39.
10.21. 38 °С.
10.22. L = 20 800 кг/ч; Gr п = 950 кг/ч.
10.23. 320 кг/ч; 132 м2.
10.24. L = 1710 кг/ч; GB = 1315 кг/ч; рп = 30 мм рт. ст.; 3,95%,
10.25. # = 38 °С, /2 = 53 °С, *2 = 0,035 кг/кг.
600
10.26. 127 °С.
10.27. L = 7400 кг/ч; Gr. п = 590 кг/ч; Рабо ^ 8 кгс/сма.
10.28. ?,= 16 200 кг/ч; Gr п = 960 кг/ч.
10.29. 34 Вт/(м3-К); 156 кг/ч.
10.30. 868 м2; 1865 кг/ч.
10.31. а) 2545 кДж/кг; б) 3685 кДж/кг.
10.32. 150 м2; 401 кг/ч.
10.33. L = 6840 кг/ч; Gr. п = 565 кг/ч; Рабо = Ю кгс/см3; F = 135 ма.
10.34. Скон = 423 кг/ч; F = 70 м2; доля возвращаемого отработанного воздуха
60,8%.
Глава 11. Умеренное и глубокое охлаждение
11.1. 8= 8,22; N = 0,78 кВт.
11.2. L = 1042 кВт; GB = 0,31 кг/с.
11.3. а)<?о= 1110 кДж/кг; е = 4,84; б) ?0 = П9.6 кДж/кг; 8= 1,96; в) q0 =
= 118,5 кДж/кг; е= 4,87.
11.4. 1,89.
11.5. а) 5,06; б) 4,38; в) 4,16; г) 4,27.
11.6. а) 5,06; б) 4,50; в) 4,00; г) 4,13,
11.7. Qo= И6,5 кВт; е= 4,96.
11.8. 99,5 м3/ч.
П.9. 5,82 кВт.
11.10. 1098 кВт.
11.11. 3,08; 37,8 кВт.
11.12. рн = 1166,9 кПа нли 11,895 кгс/см3; рн = 206,4 кПа илн 2,41 кгс/см3;
е = 4,94; V = 189 м3/ч; /VTe0p = 23,6 кВт; N = 36,3 кВт; t = 97 °С;
VB = 14,3 м3/ч.
11.13. Qp = 85 950 Вт, Q' = 53 730 Вт; N = 23,2 кВт.
11.14. р/р0 = 4,75; GB = 3125 кг/ч.
11.15. — 82 °С.
11.16. а) 11 °С; б) 73 °С.
11.17. а) 4,92 кВт-ч/кг; б) 2,10 кВт*ч/кг.
11.18. 0,0545 кг/кг. расход энергии на 1 кг жидкого воздуха 4 кВт-ч/кг.
11.19. 1,084 кВт-ч/кг.
11.20. 0,066 кг/кг; расход энергии на 1 кг жидкого воздуха 1,31 кВт ч/кг.
11.21. N — 46,7 кВт; Gm = 46,6 кг/ч; расход энергии на 1 кг жидкого воздуха
~1 кВт-ч/кг.
11.22. 1,07 кВт-ч/кг.
11.23. 0,69.
11.24. 0,995 кВг-ч/кг.
11.25. 1618 м8.
11.26. 113 ч.
11.27. 2,2 кВтч'кг.
11.28. 1,15 кВтч/кг.
11.29. 0,67.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Общая
1. Касаткин А. Г. Основные процессы и аппараты химической технологии.
9-е изд., пер. и доп. — М.: Химия, 1973, 754 с.
2. Плановский А, Н., Николаев П. И. Процессы и аппараты химической и
нефтехимической технологии. 3-е изд., пер. и доп. — М.: Химия, 1987. 540 с.
3. Цибороеский Я- Основы процессов химической технологин/Пер. с польск.;
Под ред. П. Г. Романкова. — М.: Химия, 1967. 719 с.
4. Гельперин Н. И. Основные процессы и аппараты химической технологии.
Кн. 1, 2 — М.: Химия, 1981. 812 с.
5. Берд Р.у В. Стьюарт, Е, Лайтфут. Явления переноса/Пер. с англ.; Под
ред. Н. М. Жаворонкова и В. А. Малюсова. — М.: Химия, 1974. 687 с.
6. Гухман А. А. Введение в теорию подобия. 2-е изд., пер. и доп. — М.: Высшая
школа, 1973. 295 с
7. Кафаров В. В. Методы кибернетики ь химии и химической технологии.
4-е изд., пер. и доп. — М.: Химия, 1985. 443 с.
8. Бояриноб А. И.у Кафаров В. В. Методы оптимизации в химической
технологии — М.: Химия, 1975. 575 с.
9. Кафаров В. В. и др. Принципы математического моделирования химико-
технологических систем/В, В, Кафаров, В. Л Перов, В. П. Мешалкнн.—
М.: Химия, 1974. 344 с,
10. Кафаров В. В., Дорохов И. Н, Системный анализ процессов химической
технологии = Основы стратегии. — М.: Наука, 1976. 500 с.
11. Протодьяконов И. О. и др. Явления переноса i; процессах химической
технологии/И. О. Протодьяконов, Н. А. Марцулевич, А. В. Марков. — Л.:
Химия, 1982. 272 с.
12. Протодьяконов И. О., Богданов С. Р. Статистическая теория переноса в
процессах химической технологии. — Л.: Химия, 1983. 420 с.
13. Справочник химика/Под ред. Б. Н. Никольского. Т. V. 2-е изд. — М.; Л :
Химия, 1966. С. 354—804
14. Перри Дж. Справочник инженера-хнмпка/Пер. с англ.; По,, ред. Н. М.
Жаворонкова, П. Г, Романкола. Т. 1, 2. — Л.: Химия, 1969. С. 504, 64G.
15. Левсншпиль О. Инженерное оформление химических процессов/Пер. с англ.*
Под ред. и с доп. М. Г. Слинько. — М.: Химия, 1969. 624 с.
16. Беннет К- О., Майерс Дж. Е. Гидродинамика, теплообмен и ма^сообмен/Пер.
с англ.: Под ред. Н. И. Гельперина, И. А. Чарного. — М.: Недра, 1966.
726 с.
17. Бенедск Я., Ласлс А. Научные основы химической технсиогии/Пер. с венг.;
Под ред. П. Г. Романкова, М. И. Курочкиной. — Л.: Химия, 1970. 376 с.
18. Мухленов И. П. Общая химическая технология. Т. 1,2. 4-е изд. — М.; Высшая
школа, 1984. 256+ 263 с.
19. Основы химической технологии/И. П. М_ хленов, А. Е. Горштейн, Е. С, Ту-
маркина, В. Д. Тамбовцева. 3-е изд. — М.: Высшая школа, 1983. 335 с.
20. Кутепов А. М. и др. Общая химическая технологня/А. М. Кутепов, Т. И
Бондарева, М. Г. Беренгартен. — М.: Высшая школа, 1985. 448 с.
21 Романков П. Г., Носков А. А. Сборник расчетных диаграмм по курсу
процессов и аппаратов химической технологии. 2-е изд., испр. — Л.: Химия,
1977. 24 с.
22. Руководство к практическим занятиям в лаборатории процессов и аппаратов
химической технолог и и/Под ред. П. Г. Романкова. 5-е изд., пер. — Л.:
Химия, 1979. 256 с.
23. Цблонспий П. Л., Озерова Н. В. Проектирование тепло- и массообменной
аппаратуры химической промышленности/Под ред. П. Г. Романкова. — Л.:
РИО ЛТИ им. Ленсовета, 1984. 34 с.
502
24. Лащинский А. Д., Толчинский А Р. Основы конструирования и расчета
химической аппаратуры. — Л.: Машиностроение, 1970. 752 с.
25. Машины и аппараты химических производств/И. И. Чернобыльский,
A. Г. Бондарь, Б. А. Гаевский и др.; Под ред. И. И. Чернобыльского. 3-е изд.,
пер. и доп. — М.: Машиностроение, 1975. 456 с.
26. Ставников В. Я. и др. Процессы и аппараты пищевых производств/В. Н. Стаб-
ников, В, М. Лысянский, В. Д. Попов. 4-е изд., пер. и доп. — М.: Агропром-
издаг, 1985. 510 с.
27. Машины а аппараты химических пронзводств=Примеры и задачи/И. В. До-
манекий, В. П. Исаков, Г. М. Островский, А. С. Решанов, В. Н. Соколов;
Под ред. В. Н. Соколова. — Л.: Машиностроение, 1982. 384 с.
28. Соколов В. Н., Доманский И. В. Газожидкостные реакторы. — Л.:
Машиностроение, 1976. "214 с.
29. Ставников В. #., Баранцез В. И. Процессы и аппараты пищевых
производств. 3-е нзд. — М.: Легкая и пищева промышленность, 1983. 328 с.
ГО. Смирное Я. Я., Волжинский Л. И. Химические реакторы в примерах и
задачах/Под ред. П. Г. Ромаикова. 2-е изд. — Л-: Химия, 1986. 224 с.
31. Смирное Я. Я. и др. Расчет и моделирование ионообменных реакторов/
Н. Н. Смирнов А. И. Волжинский, В. А. Константинов, — Л.: Химия,
198'. 223 с.
32. Расчет и ко1 струнрование машин и аппаратов химических производств=
Примеры и задачи/М. Ф. Михалев, Н. П. Третьяков, А. И. Мильченко,
B. В. Зобнин; Под ред. М. Ф. Михалева. — Л.: Машиностроение, 1984. 300 с.
33. Дытнерский Ю. И. Основные процессы и аппараты химической технологии;
Пособие по курсовому проектированию. — М.: Химия, 1933. 272 с.
34. РоАсаккое П. Г., Кцдшшш М. И. Расчетные, ддаг^аммы. а щшпх^аммы. па
курсу «Процессы и аппараты химической промышленности». — Л.: Химия,
1985. 56 с.
35. Ходаков Г. С. Физика измельчения. — М.: Наука, 1972. 307 с.
36. Бородуля В, Д., Гупало Ю. П. Математические модели химических реакторов
с кипящим слоем/Под ред. С. С. Забродского, Ю. С. Рязанцева. — Мн,:
Наука и техника, 1976. 208 с.
37. Еленков Д. Процеси и апаратн в химическая промишленност. — София:
Дзержавнс нздателство Техника 1962. 513 с,
38. Bratu Em. A. Operatii si utilaje in industria chemica. V. 1. — Bucuresti:
Technika, 1960. 629 s.
39 Mc Cabe №., Smith J. Unit Operations of Chemical Engineering. 3-rd ed. —
N.—Y.: Mc Graw—Hill Book Co., 1976. 1028 p.
40. Coulson J. M.t Richardson J. F. Chemical Engineering. V. 1,2, — London;
Pergamon Press, 1968. 980 p.
41. WelQ S.f Romankow P. G., Noskow A. Д., Miiitze- K.-—E Thermische Ver-
fahrenstechnik II. 3 Aufl. — Leipzig: DeutscHer Verlag fur Grundstoffin-
dustrie, 1984. 291 s.
К главе 1. Основы прикладной гидравлики
1.1. Прандтль Л. Гидроазромеханика/Пер. с нем. 2-е нзд. — М.- Л.: ИЛ,
1951. 575 с.
1.2. Лойцянский Л. Г. Механика жидкости и газа- 5-е нзд., пер. — М.: Наука,
1978. 736 с.
1.3. Романков П. Г., Курочкина М. И, Гидромеханические процессы
химической технологии. 3-е нзд., пер. — Л,: Химия, 1982. 288 с.
1.4. Протодьяконов И, О., Сыщиков Ю. В. Турбулентность в процессах
химической технологии. Л.: Наука, 1984. 343 с.
1.5. Протодьяконов И. О., Глинский В. А. Экспериментальные методы
исследования гидродинамики двухфазных систем в инженерной химии. — Л,:
Изд-во ЛГУ, 1982. 192 с.
1.6. Кутателадзе С. С, Стырикович М. Д. Гидравлика газо-жидкостиых
систем. — М.: Энергия, 1976. 296 с.
1.7. Coy Г. Гидродинамика многофазных систем/Пер, с англ, — М,; Мир, 1971.
536 с.
503
1.8. Уоллис Г* Одномерные двухфазные течения/Пер. с англ. — М.: Мир, 1972,
440 с.
1.9. Уилкинсон У. Л. Неньютоновские жидкости—Гидромеханика,
перемешивание и теплообмен/Пер. с англ.; Под ред. А. В. Лыкова. — М.: Мир,
1964. 216 с.
1.10. Идельчик И. ?, Справочник по гидравлическим сопротивлениям, М.; Лл
Госэнергоиздат, 1960. 464 с
1.11. Алътшулъ А Д. Гидравлические сопротивления, — М.: Недра 1S70.
216 с.
1.12. Идельчик И Е. Аэродинамика промышленных аппаратов. —М,; Л.:
Энергия, 1964. 288 е.
1.13. Справочник машиностроители. Т. 2. 3-е изд., испр. н доп. — М.: Машгиз,
196С". 740 с.
К главе 2. Насосы. Вентиляторы. Компрессоры
2.1. Черкасский В. М. Насосы, вентиляторы, компрессоры. — М,: Энергия,
1977. 424 с.
2.2. Калииушкин М. П Вентиляторные установки 7-е изд. — М,: Высшая
школа, 1979. 223 с.
2.3. Старк С. ?. Основы гидравлики, иасосы и воздуходувные машины. Сборник
задач. — М.; Металл у ргиздат, 1961. 458 с.
2.4. Сидоров М. Д. Справочник но воздуходувным и газодувным машинам. —
М.; Л,: Маштиз, 1962. 260 с.
2.5. Центробежные горизонтальные и вертикальные химические насосы с
проточной частью из металла: Каталог.—М.: ЦИНТИхимнефтемаш, 1981.
92 с
К главе 3, Гидромеханические методы разделения. Гидродинамика
взвешенного слоя. Перемешивание в жидкой среде
3 1. Гордон Г. М.у Пейсахов И. Л. Пылеулавливание и очистка газов ^ цветной
металлургии. 3-е изд. — М,: Металлургия, 1977. 456 с.
3.2. Ушаков С, Г., Зверев М. Я. Инерционная сепарация пыли. — М.: Энергия,
1974. 168 с.
3.3. Коузов П. Л. Указании по расчету циклонов (А6— 52): Методические
материалы для проектировании. — М.: ГПИ, Сантехпроект, 1971. 52 с.
3.4. Очистка промышленных газов от пыли/В. Н. Ужов, А. Ю Вальдберг,
Б. И. Мягков, И. К. Решидов, — М.: Химии, 1981. 392 с.
3.5. Страус В. Промышленнаи очистка газов/Пер. с англ. — М.: Химия, 1981.
616 с.
3.6. Лукин В. Д.у Курочкина М* И. Очистка вентиляционных выбросов в
химической промышленное -и/Пол ред. П. Г. Романкова. — Л.: Химия, 1980.
232 с.
3.7. Монтвид Л. Э. Многокамерные сгустители в производстве глинозема. —
М.; Л.: Металлургиздат 1952. 56 с.
3.8. Малиновская Т. Л. Разделение суспензий в промышленности
органического синтеза. — М.: Химии, 1971. 318 с.
3.9. Поэин М. Е. и др. Пенные газоочистители, теплообменники и абсорберы=
Работа и расчет пенных аппаратов/М. Е. Позин, И П. Мухленов.. Э. Я. Та-
рат — Л.: Госхимиздат, 1959. 123 с.
ЗЛО. Жужиков В. А, Фильтрование=Теории и практика разделения
суспензий. 4-е изд., пер. и доп. — М : Химии, 1980. 398 с.
З.П. Олевский В. Л. Конструкции и расчет механических классификаторов и
гидроциклонов. — М.: Госгортехиздат, 1960. 314 с.
3.12. Поваров Л. Я. Гидроциклоны. — М.; Л.: Госгортехиздат, 196U 266 с»
3.13. Соколов В. И. Центрифугирование. — М.: Химия, 1976. 408 с
3.14. Шкоропад Д. Е. Центрифуги дли химических производств. — М.:
Машиностроение, 1975. 246 с.
3.15. Аэров М% Э., Тодес О. М. Гидравлические и тепловые основы работы аппа-
?атов со стационарным и кипищим зернистым слоем, — М»; Л,: Химия,
968. 510 с.
604
8.16, Разумов Я. М Пневмо- и гидротран:порт в химической промышленности.—
М.: Химия, 1979. 245 с.
3.17. Островский Г. М. Пневматический транспорт сыпучих материалов в
химической промышленности. — Л.: Химия, 1984. Но с.
3.18, Гельперин Я. И. и др. Основы техники псевдоожижения/Н, И. Гельпернн,
В. Г. Айнштейн, В. Б. Кваша. — М.: Химия, 1967. 664 с.
3.19. Дэвидсон Дж., Харрисон Д. Псевдоожижение/Пер. с англ.; Под ред*
Н, И. Гельперина. — М,: Химии, 1973. 725 с.
3.20* Забродский С. С. Высокотемпературные установки с кипящим слоем. М.:
Энергия. 1971. 326 с.
3.21. Членов В. Д., Михайлов Я, В. Виброкипящий слой, — М.: Наука, 1972.
343 с.
3.22. Штербачек 3., Тауск П. Перемешивание в химической промышленности/
Пер. с чешек.; Под ред. И. С. Павлушенко. — Л.: Госхимиздат, 1963.
416 с.
3.23. Стренк Ф. Перемешивание и аппараты с мешалками/Пер. с польск,; Под
ред. И. А. Щуплика. — Л,; Химии, 1975. 384 с.
3.24. Брагинский Л. Я. и др. Перемешивание жидких сред=Физические основы
и инженерные методы расчета/Л. Н. Брагинский, В. И. Бегачев, В. М Ба-
рабаш. — Л.: Химия, 1984. 336 с.
3.25. Липатов Я. Я., Новиков О, Я. Саморазгружающиеся сепараторы,—М.:
Машиностроение, 1975. 247 с.
3.26. Куний Д., Левеншпилъ О. Промышленное псевдоожижение/Пер. с англ.;
Под ред. М. Г, Слинько и Г. С. Яблонского. — М.: Химия, 1971, 447 с.
3.27. Васильцов Э. Д., Ушаков В, Г. Аппараты для перемешивания жидких
сред: Справочное пособие. — Л.: Машиностроение, 1979. 271 с.
3.28. Справочник по пыле- и золоулавлнванию/Под ред, А. А. Русанова. — М.:
Энергии, 1975. 296 с.
К главе 4. Теплопередача в химической аппаратуре
4.1. Михеев М. Л.. Михеева Я, М, Основы теплопередачи. — М.: Энергия
1973. 319 с.
4.2. Кутателадзе С. С. Основы теории теплообмена. 5-е изд. — М.: Атомиздат,
1979. 415 с.
4.3. Кутателадзе С. С. Анализ подобии в теплофизике. — Новосибирск: Наука,
1982. 280 с.
4.4. Гухман А. А. Применение теории подобия к исследованию процессов
тепломассообмена=Процессы переноса в движущихеи средах. 2-е изд.,
пер. н доп. — М.: Высшая школа, 1974. 328 с,
4.5. Кутепов А. М. и др. Гидродинамика и теплообмен при парообразовании/
А. М. Кутепов, Л. С. Стерман, Н. Г. Стюшин. — М.: Высшая школа, 1977.
352 с.
4.6. Романко Я. Г,, Фролов В. Ф. Теплообменные процессы химической
технологии. Л.: Химии, 1982. 26S с.
4.7. Хоблер Т. Теплопередача и теплообменники/Пер. с польск,; Под ред,
П, Г. Романкова. — Л.: Госхимиздат, 1961. 812 с.
4.8. Чечеткин А. В. Высскотекшературные теплоносители. 3-е изд., пер. и
доп. — М.: Энергии, 1971. 496 с.
4.9. Долинин Я. Я. Установки для нагрева химической аппаратуры
высокотемпературными органическими теплоносителими. — М.: Машгиз, 1963,
292 с.
4.10. Петухов Б. С. Теплообмен и сопротивление при ламинарном течении
жидкости в трубах. — М.: Энергия, 1967. 411 с.
4.11. Кисельников В. Я. Основы теплопередачи и расчета тепловых аппаратов
химической промышленности. — Иваново: ИХТИ, 1977. 103 с.
4.12. Кутателадзе С. С, Боришанский В. М, Справочник по теплопередаче.—
М.; Л.: Госэнергоиздат, 1959. 414 с,
4.13. Краткий справочник по теплообменным аппаратам/В. А. Григорьев,
Т. А. Колач, В. С. Соколовский, Р. М. Темкии. — М.; Л,: Госэнергоиздат,
1962. 255 с.
Б05
4.14. Исаченко И. П. и др. Теплопередача/И. П. Исаченко, В. А. Осипова,
А. С. Сукомел. — М.: Энергия, 1975. 480 с,
4.15. Справочник по теплофизическим свойствам газов и жидкостей./Под ред,
Н. Б. Варгафтика. 2-е изд., пер, и доп. —М.: Наука, 1972. 720 с.
4.16. Теплопроводность жидкостей и газов: Справочные даниые/Н, Б. Вар-
гафтик, Л. П. Филиппов, А. А. Тарзиманов, Е. Е. ТоцкиЙ. — М.: Изд-во
стандартов. 1S78. 471 с.
4.17. Краснощекое Е. Л., Сукомел А. С. Задачник по теплопередаче. 3-е изд.,
пер. и доп. — М.: Энергия, 1975, 280 с.
4.18. Чиркин В. С, Теплопроводность промышленных материалов Справочное
пособие. 2-е изд., пер. и доп, — М.: Машгиз, 1962. 247 с.
4.19. Тананайко Ю. М., Воронцов Е. Г. Методы расчета и исследования
пленочных процессов. — Киев: Техника, 1975. 312 с.
4.20. Ивановский М. Н. и др. Физические основы тепловых труб/М. Н.
Ивановский, В. П. Сорокин, И. В. Ягодкнн. — М.: Атомиздат, 1978. 256 с.
4.21. Маньковский О. Н. и др. Теплообменная аппаратура химических
производств/О. Н. Маньковский, А. Р. Толчинский, М. В. Александров Под ред.
П. Г. Гоманкова и М, И. Курочкиной. — Л.: Химия, 1976. 307 с.
4.22. Клименко Л. /7., Каневец Г. Е. Расчет теплообменных аппаратов на ЭВМ.—
М,; Л.: Энергия, 1966. 140 с.
4.23. Проектирование и оптимизация теплообменных аппаратов на ЭЦВМ/Под
ред. Г. Е. Каневца. — Ч. 1—3. — Киев: Ин-т кибернетики АН УССР,
1970. С. 134, 176, 232.
4.24. Стандартные кожухотрубчатые теплообмеикые аппараты общего
назначения. Каталог. 3-е изд, — М.: Изд-во ЦИНТИхимнефтемаш, 1982. 32 с.
4.25. Steidl H. et al, Uvod do provdeni tekutin a sdileni tepla. — Praha: Aca-
demia, 1975. 486 s.
К главе 5. Выпаривание. Кристаллизация
5.1. Чернобыльский И. И. Выпарные установки. — Киев: Вшца школа, 1970,
240 с.
5.2. Таубман Е. И. Выпаривание. — М.: Химия, 1982. 328 с.
5.3. Федоткин И. М., Ткаченко С. И. Теплодинамические процессы в выпариыл
аппаратах. — Киев: Техника, 1975. 212 с.
5.4. Выпарные аппараты вертикальные, трубчатые общего назначения: Каталог
УКРНИИхиммаша. — М.: ЦИНТИхимнефтемаш, 1979. 38 с.
5.5. Мапгусевич Л, Н. Кристаллизация нз растворов химической
промышленности. — М.: Химия, 1968. 304 с.
5.6. Гельперин Н. И., Носов Г. А. Основы техники кристаллизации
расплавов. — М.: Химия, 1975. 316 с.
5.7. Тодес О. М. и др. Кристаллизация из растворов/О. М. Тодес, В. А. Себалло,
А Д. Гольцикер. — Л.: Химия, 1984. 232 с.
5.8. Бэмфорт А. В. Промышленная кристаллизация/Пер. с англ. — М.; Химия,
1969. 239 с.
5.9. Удыма П. Г. Аппараты с погружными горелками. 2-е изд., пер. и доп. —
М.: Машиностроение, 1977. 271 с.
5.10. Веривин А. И. и др. Кристаллизация i дисперсных системах/А, Н. Вери-
гин, И. А. Щупляк, М. Ф. Михалев. — Л.: Химия, 1986. 256 с.
5.11. Smith R. Л. Vaporisers. Selection, design and operation. — Burnt Mill,
Harlow Essex: Longman group Ltd., 1986. 25b p.
К главе 6. Основы массопередачи. Абсорбция
6.1. Кафаров В. В. Основы массопередачи. Системы газ—жидкость, пар—
жидкость, жидкость—жидкость. 3-е изд., пер — М,: Высшая школа,
1979. 439 с.
6.2. Романков П. Г. и др. Массообменные процессы химической технологии-
Системы с твердой фазой/П. Г. Романков, Н. Б. Рашковская, В О.
Фролов. — Л.: Химия, 1975. 336 с.
6.3. Рамм Б. М, Абсорбция газов,— М.: Химия, 1976, 655 с.
506
6.4. Хоблер 7\ Массопередача и абсорбция/Пер. с польск.; Под ред. П. Г, Ро-
манкова. — Л.: Химия, 1964. 479 с.
6.5, Рудобашта С. П. Массоперенос в системах с твердой фазой. — М.: Химия,
1980. 248 с.
6.G. Цытнерский Ю. И. Обратный осмос и ультрафильтрация. — М.: Химия,
1978, 352 с,
6.7. Коган В. Б. и др. Равновесие между жидкостью и паром. Кн, 1, 2./В. Б.
Коган, В. М. Фридман, В. В. Кафаров. — М.; Л.: Наука, 1966. 640—
786 с.
6.8. Цытнерский Ю. И. Баромембранные проиессы=Теория и расчет. — М.:
Химия, 1986. 272 с.
6.9. Шервуд Т., Пигфорд Р. Л., Уилпи Ч. Массопередача/Пер с англ. Под
ред, В. А. Малюсова. М.: Химия, 1982. 696 с.
6.10. Treybal R. E. Mass — Transfer Operations. 2-nd ed. — N.—Y,; Mc Graw —
Hill Book Co., 1968. 717 p.
t.ll. Skelland A. H. P Diffusional Mass Transfer. — N,—Y.: Mc Graw—Hill,
Book Co., 1974. 642 p.
К главе 7. Перегонка и ректификация
7.1. Багатуров С. А. Основы теории и расчета перегонки и ректификации.
3-е изд., пер. — М.: Химия, 1974. 439 с.
7.2. Александров Я. А. Ректификационные и абсорбционные аппараты. 3-е изд.,
пер.—М,: Химия, 1978. 280 с.
7.3. Александров И. Л. Массопередача при ректификации и абсорбции
многокомпонентных смесей- — Л.: Химия, 1975. 319 с.
7.4. Платонов В. М., Берго Б. Г..Разделение многокомпонентных смесей=з
Расчет и исследование ректификации н^ вычислительных машинах. — М.:
Химия. 1965. 368 с.
7.5. Ставников В. И, Расчет и конструирование контактных устройств
ректификационных и абсорбционных аппаратов. — Киев: Техника, 1970,
207 с.
7.6. Холланд Ч, Д. Многокомпонентная ректнфикация/Пер. с англ, — М.:
Химия, 1969. 348 с.
7.7. Ziolkowski Z. Destylacja i rekiifikacja w przemysle chemichnym — War-
szawa: WycLwnictwa naukowo-techniczne, 1966. 1044 s.
7.8. Cuuf.de Э. К. и др. Дистилляция/Э. К. Сийрде, Э. Н. Теаро, В. Я- Миккал/
Под ред, П. Г. Роланкова.— Л,: Химия, 1971. 21G с.
7.9. Коган В. Б. Азеотропкая и экстрактивная ректификация. — Л.: Химия,
1971. 432 с.
7.10. Kirschbaum Е. Deslillier — und Rektlfiziertectmik. 4. АллИ. — Berlin;
Springer Verlag, 1969. 494 s.
7.11. Колонные аппараты: Каталог. 2-е изд. — М.: ЦИНТИхимнефтемаш, 1978.
31 с.
К главе 8. Экстрагирование
8.1. Трейбал Р. Жидкостная экстра^цкя/Пер. с англ.; Под ред. С. 3. Кагана,—
М,: Химия, 1966. 724 с.
8.2. Зюлковский 3. Жидкостная экстракция в химической промышленности/
Пер. с польск.; Под ред. П. Г. Романкова. — Л.: Госхимнздат, 1963. 478 с.
8.3 Основы жидкостной экстракции/Под ред. Г. А, Ягодина. — М.: Химия,
1981. 400 с.
8.4. Акссльруд Г. А., Лысянский В. М, Экстрагирование. Система твердое тело—
жидкость. —- Л.: Химия, 1974. 254 с.
8.5. Ромаиков П. Г., Курочкина М, Я. Экстрагирование из твердых
материалов. — Л.: Химия/Н,'83. 256 с.
8.6. Белоглазое И. //. Тнердофазные экстракторы—Инженерные методы
расчета. — Л.: Химия, 1985. 240 с.
8.7. Аксельруд Г. А-, Молчанов А. Д. Растворение твердых веществ. М.: Химия,
1977. 172 с.
507
К главе 9. Адсорбция
9.1. Тимофеев Д. /7. Кинетика адсорбции. — М.: Изд-во АН СССР, 1962. 252 с.
9.2. Романков П. Г.. Лепилин В. п. Непрерывная адсорбция паров и газов.—
Л.: Хнмня, 1968. 227 с.
9.3. Серпионова Е. Н, Промышленная адсорбция газов и паров, 2-е изд. — М.»
Высшая школа, 1969. 414 с.
9.4. Кельцев И. В. Основы адсорбционной техники. — М.: Химия, 1976* 612 с.
9.5. Дубинин М. М. Адсорбция н пористость. — М.: Изд-во Воен. акад. хим»
защиты, 1972. 127 с.
9.6. Лукин В. Н., Анцыпович И. С. Рекуперация летучих растворителей. —
Л.: Химия, 1983. 21G с.
9.7 Протодьяконов И, 04, Сипаров С. В. Механика процесса адсорбции в
системах газ—твердое тело. — Л.: Наука, 1985. 298 с.
К главе 10. Сушка
10.1. Лыков А В. Тепло- и массообмен в процессах сушки, — М.; Л.: Госэнерго-
издат, 1956. 464 с.
10.2. Гинзбург А. С. Расчет и проектирование сушильных установок пищевой
промышленности. — М.: Агропромиздат, 1985. 336 с.
10.3. Лыков М. В. Сушка в химической промышленностн. — М.: Химия, 1976.
432 с.
10.4. Красников В. В. Конвективная сушка. — М.- Энергия, 1973 288 с.
10.5. Плановский А. Н. и dp. Сушка дисперсных материалов в химической
промышленностн/А. Н. Плановский, В. И. Муштаев, В. М. Ульянов. —
М.: Химия, 1979. 287 с.
10.6. Сажин Б. С. Основы техники сушки. — М.: Химия, 1984. 319 с.
10 7, Романков Я. Г., Рашковская И, Б. Сушка во взвешенном состоянии»
3-е изд., пер. и доп, — Л.: Химия, 1979. 272 с.
10.8. Муштаев В. И. и др. Сушка в условиях пиевмотранспорта/В. И.
Муштаев, В. М. Ульянов, А. С. Тимоннн. — М.: Химия, 1984. 230 с.
10.9. Лыков М. B.t Леончик В. И. Распылительные сушилки. —М,:
Машиностроение, 1966. '331 с.
10.10. Сушильные аппараты и установки: Каталог НИИхиммаша» 3-е изд.—
М.: ЦИНТИхимнефтемаш, 1975. 64 с.
К главе 1L Умеренное и глубокое охлаждение
11.1. Холодильные машины/Под ред. Н. Н, Кошкина.—М,: Пищевая
промышленность, 1973. 512 с.
11.2. Комаров И. С, Холод. 5-е изд., пер. и доп. Мв; Гизлегпищепрсм, J 953,
704 с.
11.3. Орехов Я. #., Обрезков В. Д. Холод в процессах химической технологии. —
Л,: Изд-во ЛГУ, 1980. 256 с.
11.4. Теплообменные аппараты холодильных установок/Г. Н. Данилова,
С. Н. Богданов, О. П. Иванов, Н. М. Медиикова. — Л.: Машиностроение,
1973. 328 с.
11.5. Розенфельд Л. М., Ткачев А. Г, Холодильные машины и аппараты, —
М.: Госторгиздат, 1960. 652 с.
11.6. Розенфельд Л. М. и др. Примеры и расчеты холодильных машии и
аппаратов/Л. М. Розенфельд, А. Г Ткачев, Е. С. Гуревнч. — М.:
Госторгиздат, I960. 238 с,
11.7. Проектирование холодильных сооружений: Справочник. — М.: Пищевая
промышленность, 1978. 255 с,
11.8. Справочник по физико-техническим основам глубокого охлаждения/
М. П, Малков, И. Б, Данилов, А. Г, Зельдович и др, — М.; Л.; Госэнерго-
издат, 1963. 415 с.
11.9. Справочник по разделению газовых смесей методом глубокого
охлаждения/Под ред. Н. И. Гельперина, 2-е изд. — М.: Госхимиздат, 1963,
512 с.
508
НЛО. Свердлов Г. 3., Яьнель Б, К. Курсовое и дипломное проектирование
холодильных установок и систем кондиционирования воздуха. — М.:
Пищевая промышленность, 1978, 264 с.
11.11. Теплотехнические основы получения искусствеииого холода;
Справочник/Под ред. И. М. Кальпння. — М.: Пищевая промышленность, 1980.
231 с.
11.12. Теплоэнергетика и теплотехника. Общие вопросы: Справочник^ — Мл
Энергия, 1980. 529 с.
11.13. Холодильные машины: Справочник. — М,: Легкая и пищевая
промышленность, 1982. 223 с.
ПРИЛОЖЕНИЕ
ТАБЛИЦЫ
Таблица I
Атомные массы некоторых элементов по Международиой
таблице 1977 г.
Точность последней цифры =Ь 1 или =ЬЗ, если она выделена мелким шрифтом.
Наименование
Азот
Алюминий
Аргон
Барий
Бериллий
Бор
Бром
Ванадий
Висмут
Водород
Гелий
Железо
Золото
Иод
Кадмий
Калий
Кальций
Кислород
Кобальт
Кремний
Криптон
Ксенон
Литий
Магний
Символ
N
А1
Аг
Ва
Be
В
Вг
V
Bi
Н
Не
Fe
Au
I
Cd
К
Ca
О
Co
Si
Kr
Xe
Li
M«
Атомная
масса
14,0067
26,98154
39,948
137,33
9,01218
10,81
79,904
50,9415
208,9804
1,0079
4,00260
55,847
196,9065
126,9045
112,41
39,0983
40,08
15,9994
58,9332
28,0855
83,80
131,30
6,94!
24,305
Наименование
Марганец
Медь
Молибден
Мышьяк
Натрий
Никель
Олово
Плати на
Радий
Ртуть
Свинец
Серебро
Сера
Стронций
Сурьма
Титан
Углерод
Уран
Фосфор
Фтор
Хлор
Хром
Цинк
Символ
Мп
Си
Мо
As
Na
Ni
Sn
Pt
Ra
Hg
Pb
Ag
S
Sr
Sb
Ti
С
U
P
F
CI
Cv
Zn
Атомная
масса
54,9380
63,54e
95,94
74,9216
22,98977
58,70
118.6g
195,09
226,0254
200,5e
207,2
107,868
32,06
87,62
121,7»
47,90
12,011
238,029
30,97376
18,998403
35,453
51,996
65,38
Таблица П
Плотность твердых материалов
Материал
Плотность,
кг/м8
Насыпная
плотность,
кг/м3
Алебастр 2500 —
Антрацит 1600 —
Апатит 3190 1850
Асбест 2600 —
Материал
Плотность,
кг/м3
Насыпная
плотность,
кг/м3
Бетон 2300 —
Винипласт 1380 —
Гипс кристалли- 2240 1300
ческий
510
Продолжение
Материал
Глина сухая
Гранит
Зола
Земля сухая
Известняк
Каолин
Каучук
Кварц
Керамика
кислотоупорная
Кирпич
обыкновенный
Кокс
Колчедан Серый
Кожа сухая
Литье каменное
Мел кусковой
Мрамор
Парафин
Паронит
Песок сухой
Поташ
Пробка
Резина
Селитра натриевая
Плотность,
кг/м3
_
2700
2200
1800
2650
2200
930
2650
2600
1500
1300
5000
860
3000
2200
2600
900
1200
1500
2260
240
1500
2260
Насыпная
плотность.
кг/м3
1380
—
680
1300
1800
—ш
—
1500
—
—
500
3300
—
1300
—
—
—
1200
—
—
—
1200
Материал
Сода
кристаллическая
Соль каменная
Сосна
Стекло
Текстолит
Уголь древесный
Уголь каменный
Фаолит
Фосфорит
Цемент
Эмаль
Металлы
Сталь
Чугун серый
Медь катаная
Латунь
Алюминий
Свинец
Огнеупоры
Динас
Магнезит
Шамот
Плотность,
кг/м3
1 450
2 350
500
2 500
1 380
1 450
1 350
1 730
—
2 900
2 350
7 850
7 250
8 800
8 500
2 700
11 400
1 900
2 900
1 900
Насыпная
плотность,
кг/м3
800
1020
—
—
—
200
800
—
1600
—
—
—
—
—
—
—
—
—
Таблица III
Плотность некоторых жидкостей при 0—20 °С
Жидкость
Азотная кислота, 92 %
Аммиак, 26 %
Бензин
Глицерин, 100 %
» 80 %
Диэтиловый эфир
Керосин
Ксилол
Мазут
Метиловый спирт, 90 %
» » 30 %
Нафталин (расплавленный)
Нефть
Ргуть
Плотность,
кг/м3
1 500
910
760
1 270
1 130
710
850
880
890—950
820
950
1 100
790—950
13 600
Жидкость
Серная кислота, 30 %
Соляная кислота, дымящая
Уксусная кислота, 70 %
» » 30 %
Хлороформ
Четыреххлористыи углерод
Этилацетат
Этиленхлорид
Этиловый спирт, 100 %
» » 70 %
» » 40 %
» » 10 %
Плотность,
кг/м3
1 220
1 210
1 070
1 040
1 530
1 630
900
1 280
790
850
920
980
511
Т аб л и п а
Плотность жидких веществ и водных растворов в зависимости
от температуры [13 ]
Вещество
Плотность, кг/м3
—20 °С
0 °С
20 °С
40 °С
60 °С
80 °С
100 °С
120°G
Азотная кислота, 100 %
» » 5о %
Аммиак жидкий
Аммиачная вода, 25 %
Анилин
Ацетон
Бензол
Бутиловый спирт
Вода
Гексан
Глицерин, 50 %
Диоксид серы (жидк.)
Дихлорэтан
Диэтиловый эфир
Изопропиловый спирт
Кальций хлористый, 25 %
раствор
л*-Ксилол
Метиловый спирт, 100 %
» » 40 %
Муравьиная кислота
Натр едкий, 50 % раствор
» » 40 % »
» » 30% »
» » 20 % »
» ' э 10% ,
Натрий хлористый, 20 %
раствор
Нитробензол
Октан
Олеум, 20 %
Пропиловый спирт
Серная кислота, 98 %
» » 92 %
»- > 75 %
» » 60 %
Сероуглерод
Соляная кислота, 30 %
Толуол
Уксусная кислота, 100 %
» » 50 %
Фенол (расплавленный)
Хлорбензол
Хлороформ
Четыреххлористый углерод
Этилацетат
Этиловый спирт, 100 %
» » 80 %
» » 60 %
» » 40 %
» » 20 %
1582
_
665
-^
—
835
—
838
—
693
—
1484
1310
758
817
1248
—
828
—
—
—_
—
—
—
—_
—
—
734
—
—
—
1866
1709
1532
1323
1173
902
—
—
—
1150
1563
1670
947
-823
—
—
—
—
1547
1334
639
918
1039
813
900
824
1000
677
1136
1434
1282
736
801
1239
882
810
946
1244
1540
1443
1340
1230
1117
1157
1223
718
1922
819
1857
1845
1689
1515
1293
1161
884
1072
1074
_
1128
1526
1633
924
806
857
904
947
977
1513
1310
610
907
1022
791
879
810
998
660
1126
1383
1254
714
785
1230
865
792
935
1220
1525
1430
1328
1219
1109
1148
1203
702
1896
804
[837
1824
1669
1498
1263
1149
866
1048
1058
1075
1107
1489
1594
901
789
843
891
935
969
1478
1287
580
897
1004
768
858
795
992
641
1116
1327
1224
689
768
1220
847
774
924
1195
1511
1416
1316
1208
1100
1189
1183
686
1870
788
1817
1803
1650
1482
1233
1138
847
1027
1042
1058
1085
1450
1556
876
772
828
878
923
957
1443
1263
545
887
987
746
836
781
983
622
1106
1264
1194
666
752
1210
831
756
913
1171
1497
1403
1303
1196
1089
ИЗО
1163
669
1844
770
1798
1783
1632
1466
1200
1126
828
1004
1026
1040
1065
1411
1517
851
754
813
864
910
946
1408
1238
510
876
969
719
815
766
972
602
1006
1193
1163
640
735
1200
796
736
902
1147
1483
1389
1289
1183
1077
1120
1143
653
1818
752
1779
1765
1614
1450
1165
1115
808
981
1010
102^
1041
1380
1471
825
735
797
849
897
934
1373
1212
462
866
952
693
793
751
958
581
996
1111
1133
611
718
1190
796
714
891
1121
1469
1375
1276
1170
1064
1110
1123
635
1792
733
1761
1744
1597
1434
1125
1103
¦ 788
958
994
1003
1021
1326
1434
797
716
783
835
885
922
1338
1186
390
856
933
665
769
735
943
559
986
1010
1102
576
700
1180
77
—
880
1096
1454
1360
1261
1155
1049
1100
1103
617
1766
711
Г 742
1723
1580
1418
1082
1090
766
922
978
987
995
1280
1390
768
693
768
820
872
910
612
^ Основные фнзнческяе свойства некоторых газов
Пересчет в СИ: 1 мм рт. ст. — 133,3 Па; 1 кгс/см2 = 9,81 • 10* Па.
о
а
Я
•
s
•а
ч**
Сл
Название
Азот
Аммиак
Аргон
Ацетилен
Бензол
Бутан
Воздух
Водород
Гелий
Диоксид азота
Диоксид серы
Диоксид углерода
Кислород
Метан
Оксид углерода
Пентан
Пропан
Пропилен
Сероводород
Хлор
Хлористый метил
Этан
Этилен
ч
О
е
N*
NH8
Аг
С2Н2
свнв
QHio
—
н2
Не
ш2
S02
со2
о«
сн4
со
с6н12
С3Н8
QH,
HaS
С1?
CHgG
с2н6
СзН4
S
ft^«
t=2s
UN
о
Cod.
1,25
0,77
1,78
1,171
—
2,673
1,293
0,0899
0,179
,—
2,93
1,98
1,429
0,72
1,25
•—
2,02
1,91
1,54
3,22
2,3
1,36
1,26
- о;
<я
к
0j <Ч
Is
28
17
39,9
26,0
78,1
58,1
(29,0)
2,02
4,0
46,0
64,1
44,0
32
16,0
28,0
72,2
44,1
42,1
34,1
70,9
50,5
30,1
28,1
Удельная
теплоемкость
при
20 °С
и Рабе те
« 0,1
кДж/(
СР
1,05
2,22
0,53
1,68
1,25
1,92
1,01
14,3
5,28
0,804
0,633
0,838
0,913
2,23
1,05
1,72
1,87
1,63
1,060
0,482
0,742
1,73
1,53
МПа,
кг- К)
rv
0.746
1,68
0,323
L,36
1,140
1,80
0,721
10,140
3,18
0,62
0,503
0,654
0,654
1,70
0,754
1,58
1,65
1,44
0,804
0,355
0,582
1,45
1,26
Сс
Таблица V
^
•??
О)
a
E
ft
bS
« S
Hfts
Л г: С Ci -
Критические
точки
температура,
°C
давление
солютное),
кгс/см2
Вязкость Цо при С °С
н
Рабе
1 к^ссм2
10» Па-с
кон
станта
С урар-
нення
(1.13)
1,40
1,29
1,66
1,24
1.1
1,08
1,40
1,407
1,66
1,31
1,25
1,30
1,40
1,31
1,40
1,09
1,13
U7
1,30
1,36
1,28
1,20
1,20
— 195,8
—33,4
— 185,9
—83,7
(возг.)
+ 80,2
—0,5
—195
—252,8
—268,9
+ 21,2
— 10,8
—78,2
(возг.)
— 133,0
— 161,6
—191,5
+36,1
—42,1
—47J
—60,2
—33,8
-21,4
—88,50
—103,7
199,4
1374
163
830
394
387
197
455
19,5
712
394
574,0
213
511
212
360
427
440
549
306
406
486
482
— 147,1
+ 132,4
— 122,4
+35,7
+ 288,5
+ 152
— 140,7
—239,9
—268,0
+ 158,2
+157,5
+ 31,1
— 118,8
—82,15
-^140,2
197,1
95,6
91,4
100,4
144,0
148
32,1
9,7
33,49
III,5
48,00
61,6
47,7
37,5
37,2
12,80
2,26
100,00
77,78
72,9
49,71
45,6
34,53
33,0
43
45,4
188,9
76,1
66,0
48,85
50,7
17
9,18
20,9
9,35
7,2
8,1
17,3
8,42
18,8
—
11,7
13,7
20,3
10,3
16,6
8,74
7,95 (!8°С)
8,35 (20 °С)
И,66
12,9 (16 °С)
9,89
8,5
9,85
114
626
142
198
—
377
124
73
78
—
396
254
131
1G2
100
—
278
322
—
ЗЯ1
4Г4
2Н7
241
ел
CO KJ ¦—* ¦—*
о о ел о ел о
h*^
— Ю CO-*J «S3
O-f-OJOO-
O 00 СП СЛ СЛ О
о ооо о о
Ю 00 -О О) СП 4*.
оооооо
| .СО
to со сл о со се
— СЛ СО Ю О О
fy^) ¦—1 k_t Had ¦—1 «—t
О00 05*.ЮО
О ООО О О
О О J— — СЛ СО
'О СЛ
и ГС
2 ™ о а
° о к «
_ п с >с
О .Z К л
з-а?к
о*2
м ?
л н ГС
(а ^
2 — О S
о о к s
э н?
Я
S
я
X
0>
о
ж
К
¦е-
¦е-
я
ф
г
я
а
ы
о
а
Я
3
J3
-о
к
г»
ю — ОчОоо--5ст)Сл4^соЮ'-- О0ч00о*^0)сл*»сою»— осооо-^дасп^соЮ"—о
^^ООООСОООООООчСчСчСчСООООО"— ь-1 — ЮКЭЮС0С0СО«й»-е-.СЛСЛСГ)СГ)-^-^
¦vi^ocoD^coco-f-oiNj^ocnoosW"©'- coa^»— ооа*ст>с»сочс--]сосо — to
ОэаэС^СТ>СТ>СТ>аэСЛСЛОЧСПСЛСЛСЛСЛСЛСЛ4^^4^4^4^^
O)cn*»coto>- оа?оо^а^сл^оою'--о^оо-^сг>сл^со^-- Очсоо^аэсл^со
ррроророооорорррооорооороооооороро
4*. ¦fr.V-Tfik 4*. 4^ 4^"ч5ь >?>¦ "*4*. "jb. СгГсл СЛ СЛ 01*01 "сл СЛ СЛ СЛ "сл'сТ) СТ> ОЭ "о "сТ> "СТЭ"сТ> ~ОЪ --J --J -v] --J
чОСЛ — СОСЛ — СОСЛСООООСТ>4»>Ю'— ОСОСОСОСОООСО^ОЮСОС^СО1—' 4*. 00 Ю *<1 Ю
СОСЛООСООООООСОЮ^-Сл^СТЭСОСЛ^^ООСОЮСоОО^^^О?
осо^^^^Ф^^^^ооОооооэооооооаоооос^^^^^--^^-^
оюоо^Фсп-^соЮ'-оюоочазсл^.соЮ'-о Ф оо-д ст> сп^сою —Очсоо-д
о о о о о о о о о о о о о о р о о о роооо ор оро ророра
"Volo ю"ю1о ю*со-со"со"со"соЪэ"со со'со со "со "со соЪэ~сосо"со со'со со со "со co'^V. W-^.
ooooSoM^soaiooiiovDOJOioiO'icftoo'-cio^issotocDo^a)1—-j ф- со
Динамический
коэффициент
вязкости,
ыПа.с (сП)
Температура,
°с
Динамический
коэффициент
вязкости,
мПа-с (сП)
Температура
Динамический
коэффициент
вязкости,
мПа- с (сП)
Т а б л и ц а VII?
Динамические коэффициенты вязкости некоторых водных растворов
Растворенное
вещество
NaOH
NaCl *
NaN03
Na2C03
КОН
KC1
KN03
NH4N03
MgCl2
CaCl2**
* См. та
** См. та
Концентрация, %
(масс.)
5
15
25
5
15
25
10
20
30
10
20
30
10
20
30
5
15
20
5
15
30
10
30
50
10
20
35
10
20
35
кже табл. L.
кже табл. L1
0°С
—
1,86
2,27
3,31
—
__
—
1.7
1,58
1,68
1,58
1,51
2,8
5,3
19,3
2,17
3,14
8,9
Динамический коэффициент
пязкости, мПа.с (сП)
20 СС
1,3
2,78
7,42
1,07
1,36
1,89
1,07
1,18
1,33
1,74
4,02
1,23
1,63
2,36
0,99
1,0
1,02
0,98
0,98
0,96
1,0
1,33
1,5
2,7
10,1
1,27
1,89
5,1
30 °С
1,05
2,10
5,25
0,87
1,07
0,88
1,03
1.3
1,38
2,91
8,35
1,0
1,33
1,93
0,8
0,83
0,85
0,8
0,8
0,89
0,79
0,84
1,14
—
—
40 °С
0,85
1,65
3,86
0,71
0,89
0,72
0,86
1,07
и
2,25
5,6
0,83
1,11
1,57
0,66
0,69
0,72
0,66
0,69
0,66
0,73
0,99
-д.-.—
—
60 °С
—
0,51
0,64
0,54
0,62
0,79
—
и.
0,48
0,52
0,54
0,49
0,51
0,5
0,57
0,77
—
—
17*
515
Таблица IX
Динамические коэффициенты вязкости жидких веществ и водных растворов в зависимости от температуры
Веществе
Динамический коэффициент вязкости, иПа-с (сП)
— 20 °С
10 °С
0 °С
0 °С
20 °С
30 °С
40 °С
50 °С
60 °С
80 °С
100 °С
120 °С
Азотная кислота, 100 %
» > 50 %
Аммиак жидкий
Аммиачная вода, 25 %
Аиилин
Ацетон
Бензол
Бутиловый спирт
Вода
Гексаи
Глицерин, 50 %
Диоксид серы (жидх.)
Дихлорэтан
Диэтиловый эфир
Изопропиловый спирт
Кальций хлористый, 25 %
раствор
Метиловый спирт, 100 %
ъ > 40%
Муравьиная кислота
Натр едкий, 50 % раствор
» » 40 % >
> » 30% »
» * 20% *
1,49
—
0,258
—
—
0,5
10,3
—
0,479
—
0,455
1,54
0,364
10,1
1С,6
1,16
—
—
—
—
—
1,24
4
0,261
—¦
—.
0,442
—¦
7,4
0,426
—.
0,41
1,24
0,328
6,8
7
0,97
—¦
—
—¦
—
—
1,05
3,05
0,244
—
10,2
0,395
0,91
5,19
1,79
0,397
12
0,368
1,08
0,296
4,6
4,47
0,817
3,65
—
—
—
—
—
0,92
2,4
0,235
1,72
6,5
0,356
0,76
3,87
1,31
0,355
8,5
0,334
0,95
0,268
3,26
3,36
0,68
2,54
2,25
—
—
—
—
0,8
1,88
0,226
1.3
4,4
0,322
0,65
2,95
1.0
0,32
6,05
0,304
0,84
0,243
2,39
2,74
0,584
1,84
1,78
—
40
13
4,48
0,72
1,55
0,217
1,05
3,12
0,293
0,56
2,28
0,801
0,29
4,25
0,279
0,74
0,22
1,76
2,25
0,51
1,37
1,46
46
23
9
3^
0,64
1,28
0,208
0,855
2,3
0,268
0,492
1,78
0,656
0,264
3,5
0,65
0,199
1,33
1,85
0,45
1,22
25
14
6,3
2,48
0,57
1,07
0,199
0,71
1,8
0,246
0,436
1,41
0,549
0,241
2,6
0,565
0,182
1,03
1,55
0,396
1,03
16
9,2
4,6
2
0,5
0,9
0,19
0,6
1,5
0,23
0,39
1,14
0,469
0,221
2
0,51
0,166
0,8
—
0,351
0,89
8,03
5,44
3,4
1,63
0,39
0,68
—
0,42
1.1
0,2
0,316
0,76
0,357
0,19
1,2
0,42
0,14
0,52
——
0,29
0,68
5,54
3,62
2,16
1,27
0,35
0,53
—
0,32
0,8
0,17
0,261
0,54
0,284
0,158
0,73
0,36
0,118
0,38
—
0,24
0,54
3,97
2,72
1,82
1,15
0,31
0,44
—
0,23
0,59
0,15
0,219
0,38
0,232
0,132
0,45
0,31
0,1
0,29
—
0,21
0,4
3,42
:i,37
1.71
1,08
Продолжение
г»
Вещество
—20 °С
— ЮвС
о°с
Динамический коэффициент вязкости, мПа-с (сП)
10°С
20 °С
30 °С
40 °С
50 °С
60 °С
80 °С
100 °С
120°С
Натр едкий, 10 % раствор
Натрий хлористый, 20 %
раствор
Нитробензол
Октаи
Олеум, 20 %
Серная кислота, 98 %
» > 92 %
» » 75 %
» » 60 %
Сероуглерод
Соляная кислота, 30 %
Толуол
Уксусная кислота, Г00 %
» » 50 %
Феиол (расплавленный)
Хлорбензол
Хлороформ
Четыреххлористый углерод
Этила цетат
Этиловый спирт, 100 %
» » 80%
» » 60%
» » 40%
» » 20%
—
—
——
0,968
—
—
130
95
20
0,556
—
1,06
—
.—
—
1,48
0,9
1,9
0,79
2,38
—
—
—
—
—
4,08
—
0,829
—
.—
90
50
15
0,488
—
0,9
.—
,—
—
1>24
0,79
1,68
0,67
2,23
—
—
—
—
—
2,67
3,09
0,703
95
55
48
30
10,5
0,433
—
0,768
^
4,35
—
1,06
0,7
1,35
0,578
1,78
3,69
5,75
7,14
5,32
—
1,99
2,46
0,61
60
37
32
20
7,7
0,396
2,1
0,667
—
3,03
—
0,91
0,63
1,13
0,507
1,46
2,71
3,77
4,39
3,17
1,86
1,56
2,01
0,54
36,6
25,8
23,1
13,9
5,52
0,366
1,7
0,586
1,22
2,21
11,6
0,8
0,57
0,97
0,449
1,19
2,01
2,67
2,91
2,18
1,45
1,24
1,69
0,479
28,8
17,1
15,6
10,6
4,08
0,319
1,48
0,522
1,04
1,7
7
0,71
0,51
0,84
0,4
1,0
1,53
1,93
2,02
1,55
1,16
1,03
1,44
0,428
20,8
12,9
11,8
8,1
3,42
0,29
1,3
0,466
0,9
1,35
4,77
0,64
0,466
0,74
0,36
0,825
1,2
1,45
1,48
1,16
0,98
0,87
1,24
0,386
12,8
9,46
8,4
5,9
2,8
0,27
—
0,42
0,79
1,11
3,43
0,57
0,426
0,65
0,326
0,701
0,97
1,13
1,13
0,91
0,91
0,74
1,09
0,35
9 -
7,5
6,7
4,6
2,4
0,25
—
0,381
0,7
0,92
2,56
0,52
0,39
0,59
0,297
0,591
0,79
0,9
0,89
0,74
0,7
0,57
0,87
0,291
5,3
4,1
3,8
2,8
1,5
0,21
—
0,319
0,56
0,65
1,59
0,435
0,33
0,472
0,248
0,435
0,57
0,6
0,6
0,51
0,65
0,46
0,7
0,245
—¦
2,7
2,5
1,9
1,07
0,19
0,271
0,46
0,5
1,05
0,37
0,29
0,387
0,21
0,325
<Г,52
0,45
0,44
0,38
0,6
0,38
0,58
0,208
—
2
1,95
1,45
0,9
0,17
—
0,231
0,37
0,4
0,78
0,32
0,26
0,323
0,178
0,248
0,43
0,34
0,34
0,3
Таблица X
Атомные константы вязкости
8
9
10
11
12
R\ /R
СН—СН
К'У
V
R
R-C-R
1
R—С
О
//
\
Н
О
R-C
//
\
—СН—СНСНгХ (X — отрицательная группа)
R.
R
\
СН—X (X — отрицательная группа)
13
14
15
15
ОН
соо
соон
N02
Атоме
Атомные
Номер
п/п
1
2
3
4
б
6
Н О N ci
константы 2,7 29,7 37,0 6о,0
Характер связей и группировок
Двойная связь
Пятичленное кольцо
Шестнчлеииое кольцо
Боковая группа шестичленного кольца:
мол. масса <«17
мол. масса > 16
Орто- и пара-положеиия вторых заместителей
Мета-положение вторых заместителей
Вг I С
79,0 110,0 50,2
Поправки
к
константам р
— 15,5
—24,0
—21,0
—9,0
—17,0
+3,0
+ 1,0
+8,0
-Ы3,0
+ 16,0
+5,0
+4,0
+6,0
+24,7
—19,6
-7,9
—16,4
518
Таблица XI
Значение УМТК1} для некоторых газов
Газ
]f МТ
кр
Водяной пар
Воздух
Диоксид углерода
Азот
Кислород
Водород
Оксид углерода
Метан
Этилен
Этан
Пропан
Бутан
Пеитан
Гексан
18
29
44
28
32
9
28
16
28
30
44
58
72
86
647
132,7
304
126
154
33
134
190
283
305
370
426
470
508
108
61,9
115,5
59,5
70,2
8,13
61,4
55,1
89,0
95,6
128
157
184
209
Средние значения шероховатости стенок труб
Таблица XII
Трубопроводы
е, мм
Трубы стальные цельнотянутые и сварные при
незначительной коррозии
Старые заржавленные стальные трубы
Трубы из кровельной стали проолифенные
Чугунные трубы водопроводные, бывшие в эксплуатации
Алюминиевые технически гладкие трубы
Чистые цельнотянутые трубы из латуни, меди и свинца;
стеклянные трубы
Бетонные трубы; хорошая поверхность с загиркой
Бетонные трубы; грубая (шероховатая) поверхность
Нефтепроводы при средних условиях эксплуатации и
паропроводы насыщенного пара
Паропроводы, работающие периодически
Воздухопроводы сжатого воздуха от компрессора
Конденсатопроводы, работающие периодически
0,2
0,67 и выше
0,125
М
0,015—0,05
0,0015—0,01
0,3—0,8
3-9
0,2
0,5
0,8
1,0
519
Таблица XIII
Коэффициенты местных сопротивлений
Вид сопротивления
Значение коэффициента местного сопротивления ?
Вход в трубу
С острыми краями: ? = 0,5
С закругленными краями: % — 0,2
Выход из трубы
При расчете Ар по формуле (1.49) это сопротивление
? для выхода из трубы учитывать не надо
Диафрагма (отверстие)
с острыми краями в
Прямой трубе
^LS^ -^
Г
Юл
Wo Ют
db — диаметр отверстия
диафрагмы, м; б —
толщина диафрагмы, м;
К'0— средняя скорость
потока в отверстии, м/с;
w,r — средняя скорость
потока в трубе, м/с; m —
= {-jf) J D —Диаметр
трубы, м
При
6
do
0 -5- 0,015 потеря давления Ар =* ?
Р»?
Значение S определяется по таблице:
m 0,02 0.04 0,06 0,08 0.1 0,12 0,14 0.16 0,18 0,20 0,22
I 7000 1670 730 400 245 165 117 86,0 Ь5,5 51,5 40.0
m 0.24 0,26 0,28 0,30 0,34 0,4 0,5 0,6 0,7 0,8 0,9
Г. 32,0 26,8 22,3 18,2 13,1 8,25 4,00 2,00 0,97 0,42 0,13
Б20
Продолжен и е
Вид сопротивлении
Значение коэффициента местного сопротивлении ?
Отвод круглого или
квадратного сечения Коэффициент сопротивления ? — АВ определяется
по таблицам:
d
Угол ф, 20 30 45 60 90 110 130 150 180
градусы
А
0,31 0,45 0,6 0,78 1,0 1,13 1,20 1,28 1,40
d — внутренний диаметр
трубопровода, м; R0 ~
радиус изгиба трубы, м
Rv/d 1,0
В 0,21
Условный
проход, мм
2,0 4,0
0,15 0,П
12,5
6,0
0,09
25
15
0,06
37
30
0,04
50
0,03
50
Колено (угольник) ?0°
стандартный чугунный
2,2
1,6
1,1
Значение ? при полном открытии вентиля:
¦ -.I i i ¦ — — i i hi — ¦ "¦ "| "ч»
D, мм 13 20 40 80 100 150 200 260 350
10,8 8, U 4,9 4,0 4,1 4,4 4,7 6,1 Б,Б
Вентиль нормальный
L
Вентиль првшт&чуый
При Re*
таблице:
wD
v
> 3.Юь значение ? определяется по
D. 25 38 50 65 76 100 150 200 250
мм
t 1,04 0,85 0,79 0,65 0,60 0,50 0,42 0,36 О.ЗЙ
При Re<3 3-10& коэффициент сопротивления ? == ?j/C.
Значение ?j определяется так же, как и при
Re ^3*105, а значение К приведено в таблице:
Re 5000 10 000 20 000 50 000 100 000 200 000 ЗОС 000
К 1,40 1,07 0,94 0,88 0,91 0,93 1
Край пробочный
Условный
проход, мм
I
13 19 25 32 38
50
и выше
Задвижка
Условный
прохо I, мм
V
W
15 — 10
о,?
175 — 200 300 ii выше
0,25
0,15
521
Продолжение
Вид сопротивления
Значение коэффициента местного сопротивления ?
Внезапное расширение
Wo -*-; i
F0 — площадь меньшего
поперечного сечения, м2;
к>0 — скорость потока в
меньшем сечении, м/с;
Fy — площадь большего
поперечного сечения, м^;
Re
АЯрасш^?(р%2/2)
Ш<А
Re= u J
V
10
100
1 000
3 000
3 500
и более
0,1
3,1
1,70
2,0
1,00
0,81
0,2
3,1
1,40
1,60
0,70
0,64
Fq/Fi
0,3
3,1
1,20
1.30
0,60
0,50
0-4
3,1
1,10
1,05
0,40
0,36
0,5
3,1
0,90
0,90
0,30
0,25
0,6
3.1
0,80
0,60
0,20
0,16
Внезапное сужение
—*- I !—>- го о
V
PJFt
0Л
0,2
0,3
0,4
0.5
0,6
F0 — площадь меньшего
поперечного сечения, мг;
Wq — скорость потока в
меньшем сечении, м/с;
Fj — площадь большего
поперечного сечения, м2;
Re - W^ ¦
V
Арс\ж — ?
2
)
10
100
1 000
10 000
> 10 000
Ь,0
1.30
0,64
0,5
0,45
5,0
1,20
0,50
0,40
0,40
5,0
1,10
0,44
0,35
0,35
5,0
1,00
0,35
0,30
0,30
5,0
0,9 J
0,30
0,25
0,25
5,0
0,80
0,24
0,20
0,20
522
Таблица XIV
Значения эквивалентного диаметра и коэффициента А при ламинарном
режиме для различных сечений
Форма сечения
А
Круг диаметром d
Квадрат со стороной а
Равносторонний треугольник со стороной а
Кольцо шириной а
Прямоугольник со сторонами а и Ь:
alb & О
alb = 0,1
alb « 0,25
alb '= 0,5
Эллипс (а — малая полуось, b — большая полуось):
alb = 0,1
alb = 0,3
alb = 0,5
d
а
0,58а
2а
2а
1,81а
1,6а
1,3а
1,55а
1,4а
1,3а
64
57
53
96
96
85
73
62
78
73
68
Значения коэффициентов расхода диафрагмы а
Таблица XV
Re- "*'
У-1
5 000
10 000
20 000
30 000
50 000
100 000
400 000
т—0,06
0,6032
0,6026
0,5996
0,5990
0,5984
0,5980
0,5978
ffl~0,l
0,6110
0,6092
0,6050
0,6038
0,6032
0,6026
0,6020
/n= G, 2
0,6341
0,6261
0,6212
0,6187
0,6168
0,6162
0,6150
т=0,3
0,6530
0,6454
0,6403
0,6384
0,6359
0,6340
т«0,4
^^н
0,6890
0,6765
0,6719
0,6666
0,6626
0,6600
т=0,Ъ
_
0,7367
0,7186
0,7124
0,7047
0,6992
0,6950
m=«0,6
^^^т
0,7975
0,7753
0,7650
0,7553
0,7472
0,7398
т=0,7
_
—
0,8540
0,8404
0,8276
0,8155
0,8019
d **- внутренний диаметр трубопровода, м; w — средняя скорость жидкости илн
газа в трубопроводе, м/с; d — диаметр отверстия нормальной диафрагмы, м; т =»
\2
(dJdV
Таблица XVI
Значения поправочного множителя к
Диаметр
трубопровода, м
0,05
0,10
0,20
0,30
т « (d0/d]
m — 0,1
1,0037
1,0024
1,0017
1,0005
l2-
т = 0,2
1,0063
1,0045
1,0023
1,001
tn = 0,3
1,0082
1,0064
1,0034
1,001
m = 0,4
1,0118
1,0065
1,004
1,001
tn = 0,5
1,0144
1,0108
1,0052
1,001
tn =* 0,6
1,0172
1,013
1,006
1,001
tn = 0,7
1,02
1,0148
1,007
1,001
523
Таблица XVII
Характеристика скрубберных насадок из колец н кускового материала
Вид насадки
Кольца фарфоровые
» керамические
». »
» »
» »
» стальные
» »
Гравий круглый
Андезит кусковой
Кокс кусковой
» »
» »
» »
Катализатор синтеза
аммиака в кусочках
Катализатор конверсии
СО в таблетках
Катализатор
сернокислотный (ванадиевый) в
таблетках
Размеры
элемента
насадка мм
8X8X1,5
15X15X2
25Х 25Х 3
35X35X4
50X50X5
35X35X2,5
50Х 50Х 1
42
43,2
42,6
40,8
28,6
24,4
6,1
d= 11,5; h^ 6
d= 11; ft= 6,5
. * ' О
ч.йо«
_ (П Я В *
2 ossiKt
Й t- о; К с:
У К i9 Ч о
~ <и»о о <я
1 465 000
250 000
53 200
20 200
6 000
19 000
6 000
14 400
12 600
14 000
15 250
27 700
64 800
5 200 000
1 085 000
1 000 000
Ъ
С? -
О S
1*
0,64
0,70
0,74
0,78
0,785
0,83
0,95
0,388
0,565
0,56
0,545
0,535
0,532
0,465
0,38
0,43
*
А
Is»
570
ззо
204
140
87,5
147
ПО
80,5
68
77
86
НО
120
960
400
415
-п U
? *
- л
600
690
532
505
530
—
430
—
1200
455
585
660
600
2420
1100
614
Характеристика хордовых насадок (деревянные рейки)
Таблица XVIII
Сечение рейки
Размеры
сечений, мм
Расстояние
между
рейками.
мм
Расстояние
между
рядами
Реек,, мм
Удельная
поверхность,
Прямоугольное
Треугольное
12,5X100
12,5X100
12,5X100
ЗОХ ЗОХ 30
25,0
12,5
10,0
30
20
20
20
12,5
50
75
78
Таблица XIX
Зависимость атмосферного давления от высоты над уровнем мори
Пересчет в СИ: 1 м вод. ст. — 9810 Па.
Высота
над уровнем
моря, м
о
о
'-О
I
1
о
о
о
1—¦<
+
о
о
<м
о
о
СО
о
о
¦*
о
о
ю
о
о
'.О
о
о
f-
о
¦ о
оо
о
о
О)
о
о
о
**м
о
о
ю
fM
Атмосфер- 11,3 10,3 10,2 10,1
давление Л,
м вод. ст.
10,0 9,8 9,7 9,6 9,5 9,4 9,3 9,2 8,6
524
Т а б л и ц а XX
Допустимая высота всасывания (в м) при перекачивании воды
поршневыми насосами
Частота
вращения
насоса,
об/мин
БО
60
90
120
150
180
0
7
6,5
5,5
4,5
3,5
2,5
20
6,6
6
б
4
3
2
Температура
30
6
5,5
4,5
3,5
2,5
1,5
40
5,5
5
4
3
2
1
воды, °С
50
4
3,5
2,5
1,5
0,5
0
60
2,6
2
1
0,5
0
0
70
0
0
0
0
0
0
Таблица XXI
Значения постоянных с и т для различных типов мешалок
Тми мешалка
Геометрическая
характеристика
ajd
Did
bid
Значения
повтояииых
т
Примечание
Двухлопастная
»
Двухлопастная с
лопастями под углом 45°
Четырехлопастная
Четырехлопастная с
лопастями, наклонными
вверх под углом 45°
Четырехлопастная с
лопастями, наклонными
вверх под углом 60°
Якорная двухлопастная
»
четырехлопастная
Пропеллерная
двухлопастная с углом наклона
22,5°
Пропеллерная
трехлопастная
Турбинная трехлопаст*
. ная с входным отверстием
37 мм
Турбинная шестилопаст-
ная с направляющим
аппаратом
2
3
3
coco
2
3
3
i
0,36
0,33
0,33
0,33
0,33
111,0
14,35
6,8
4,05
§,52
5,05
1,0
0,31
0,2
0,2
0,2
0,2
Re<3 20
Re=100-r-6.10*
1,11
1,11
0,33 6,30 0,18
1,11
1,П
0,11
0,11
6,2
6,0
3,6 3,8 1
0,25
0,25
0,33 0,985 0,15
230
4,63
1,19
3,90
1,67
0,35
0,15
0,2
0,33
1,78 2,4 0,25 6,98 0,15
Форма
лопасти круглая
Re<3 30
Re <3 3.10s*
Re> 3.109
625
Таблица XXII
Поверхностное натяжение жядкостей
ЖнДкость
Температура,
Поверхностное
натяжение,
а-10я, Н/м
Азот жидкий
Кислород жидкий
Оливковое масло
Парафиновое масло
Скипидар
—196
—183
+20
+25
+ 15
8,5
13,2
32,0
26,4
27,3
Таблица XXIII
Поверхностное натяжение
Растворенное вещество
водных растворов
Температура. °с
Значение О- 10s (и Н/м) при различных
концентрациях [в % (масс.)]
5
10
20
60
Na2S04
NaN03
КС1
KN03
касо3
NH4OH
NH4Ci
NH4N03
MgCl2
18
30
18
18
10
18
18
100
18
73,8
72,1
73,6
73,0
75,8
66,5
73,3
59,2
73,8
75,2
72,8
74,8
73,6
77,0
63,5
74,5
60,1
—
—
74,4
77,3
75,0
79,2
59,3
—
61,6
—
79,8
106,4
67,5
Таблица XXIV
Поверхностное натяжение жидких веществ и водных растворов
в зависимости от температуры
Вещество
Азотная кислота, 100 %
» » 50 %
Аммиак жидкий
Аммиачная вода, 25 %
Анилин
Ацетон
Бензол
Бутиловый спирт
Вода
Гексан
Глицерин, 50 %
Диоксид серы (жидк.)
^20 °С
48,3
-__
38
_
—
28,7
_
28
—
22,6
—
31
По
0 °С
44,8
68,2
27
65,7
_.
26,2
31,7
26,2
75,6
20,5
72,4
26,8
иерхкостиое натяжение <у. Ю*
•20 °е
41,4
65,4
21,2
62,9
42,9
23,7
29
24,6
72,8
18,4
69,6
22,7
40 °С
38,2
62,2
16,8
59,7
40,6
21,2
26,3
22,9
69,6
16,3
66,4
18,8
60 °С
35,2
58,8
12,8
56,3
38,3
18,6
23,7
21,2
66,2
14,2
63
14,8
80 °С
32,4
55,2
_.
52,7
36
16,2
21,3
19,5
62,6
12,1
59,4
——
Н/м
юв°е
29,8
51,5
_.
49
33,7
13,8
18,8
17,8
58,9
10
55,7
¦'
120 °в
27,4
47,5
_
45
31,4
11.4
16,4
16
54,9
7,9
51,7
—
526
Продолжение
«h
Вещество
Диэтиловый эфир
Дихлорэтан
Изопропиловый спирт
Кальций хлористый, 25 %
раствор
Метиловый спирт, 100 %
Муравьиная кислота
Натр едкий, 50 % раствор
» » 40 % »
» » 30% »
» » 20% »
» » 10% »
Натрий хлористый, 20 %
раствор
Нитробензол
Октан
Серная кислота, 98 %
» » 92 %
» » 75 %
» » 60 %
Сероуглерод
Солиная кислота, 30 %
Толуол
Уксусная кислота, 100 %
» » 50 %
Фенол (расплавленный)
Хлорбензол
Хлороформ
Четыреххлористый
углерод
Зтнл ацетат
Этиловый спирт, 100 %
» » 80 %
» » 60%
» » 40 %
» » 20 %
— 20 °С
22
37,8
24,7
89,4
26,6
—
—
—
—
—
—
—
—
25,8
—
63
74,1
77,3
38,3
—
33
—
—.
—
38,4
32,8
31
29,5
25,7
—
—
—
—
Поверхностно? натяжеки,
0 °С
19,5
35
23,2
86,6
24,5
39,8
—
__
—
—
—
82,6
46,4
23,8
55,9
61,9
73,6
76,7
35,3
72,6
30,7
29,7
43
43,1
36
30
29,5
26,9
24
26
28
32
40
20 СС
17
32,2
21,7
83,8
22,6
37,6
130
108
97
85,8
77,3
79,8
43,9
21,8
55,1
60,9
73,1
76,1
32,3
69,8
28,5
27,8
40
40,9
33,6
27,2
26,9
24,3
22,3
25
27
30
38
40 °С
14,6
29,5
20,1
80,6
20,9
35,5
130
108
96,4
85
76,1
76,6
41,4
19,8
54,3
60,9
72,6
75,4
29,4
66,6
26,2
25,8
37
38,8
31,1
24,4
24,5
21,7
20,6
23
25
28
36
60 °6
12,4
26,7
18,5
77,2
19,3
33,3
129
107
95,8
84,7
75
73,2
39
17,9
53,7
60,3
72,1
74,5
26,5
63,2
23,8
23,8
33
36,6
28,8
21,7
22
19,2
19
21
23
26
33
> а.] С,
so °с
10,2
24
17
73,6
17,6
31,2
129
107
95,3
83,2
73
69,6
36,7
15,9
53,1
59,7
71,6
73,6
23,6
59,6
21,5
21,8
30
34,4
26,5
19
19,6
16,8
17,3
20
22
24
31
Н, ,:
100°С
8
21,3
15,5
69,9
15,7
29
128
106
94,4
81,3
70,7
65,9
34,4
13,9
52,5
59,1
71,1
72,7
20,7
55,9
19,4
19,8
27
32,2
24,1
16,3
17,3
14,4
15,5
18
20
22
29
120°6
6,1
18,6
14
65,9
13,6
26,8
128
106
93,6
79,6
69
61,9
32,2
11,9
51,9
58,5
70,6
71,8
17,8
51,9
17,3
18
24
30
21,8
13,6
16,1
12,1
13,4
16
18
19
27
Таблица XXV
Средняя удельная теплоемкость некоторых твердых материалов
при 0—100°С, кДж/(кг.К)
Алюминий
Асбест
Бетой
Броиза
Винипласт
Глина
Дерево (сосна)
Железо
Известняк,
Каолин
известь
0,92
0,84
1,13
0,385
1,76
0,92
2,72
0,50
0,92
0,92
Каменный уголь
Кварц
Кирпич красный
Кирпич огнеупорный
Кокс
Латунь
Лед
Литье каменное
Магнезия
Медь
1,30
0,80
0,92
0,88—1,01
0,84
0,394
2,14
0,84
0,92
0,385
527
Продолжение
Mt-Л
Нафталин
Парафин
Песок сухой
Пробка
Резина
СвннеЦ
Сталь
0,88
1,30
2,72
0,80
1,68
1,68
0,13
0,50
Стекло
Текстолит
Целлюлоза
Цинк
Чугун
Шерсть
Шлак
0,42—0.84
1,47
1,55
0,38
0,50
1,63
0,75
Таблица XXVI
Средняя удельная теплоемкость некоторых жидкостей, кДж/(кг*К)
(отсутствующих на рис. XI)
Азот жидкий
Азотная кислота
Аммиак
Бензин
Гексан
Керосин
2,01
2,77
4,19
1,84
2,51
2,10
Кислород жидкий
Машинное масло
Нитробензол
Серный ангидрид
Скипидар
Фенол
1,68
1,68
1,38
1,34
1,76
2,35
Таблица XXVII
Мольная теплоемкость газов, кДж/(кмоль • К) (при Рабо = * атм) *
Пересчет в СИ: 1 атм =760 мм рт. ст, ¦= 101 325 Па.
Fas
Температура, °G
0
;оо
300
000
Азот, кислород, воздух, оксид
углерода
Аммиак
Водород
Водяной пар
Диоксид углерода и диоксид серы
Метан
Сероводород
Хлор
29,0
35,3
29,1
35,0
38,6
35,7
34,3
36,3
29,3
37,9
29,3
35,5
41,1
39,7
35,8
36,4
30,0
43,2
29,7
36,7
45,7
47,8
38,8
36,7
31,0
50,1
30,4
39,3
54,3
59,8
43,3
37,0
* С допустимым приближением данными таблицы можею пользоваться и при дяв«
йении порядка нескольких атмосфер.
628
Таблица XXVIII
Коэффициенты теплопроводности некоторых материалов ПрН о—100 °С
Материал
'Плотность
(Д^я сыпучих
мйтерналов
Насыпная
плотность),
кг/м*
Коэффициент
теплопроводности,
Вт/(м. К)
Асбест
Бетон
Винипласт
Войлок шерстяной
Дерево (сосна) поперек волокон
» » вдоль волокон
Кладка из обыкновенного кирпича
» » огнеупорного кирпича
» » изоляционного кирпича
Краска масляная
Лед
Литье камекное
Магнезия 6$%' в порошке
Накипь, водяной камень
Опилки древесные
Пенопласт
Песок сухой
Пробковая мелочь
Ржавчниа (окалина)
Совел ит
Стекло
Стеклянная вата
Текстолит
Торфоплиты
Фаолит
Шлаковая вата
Эмаль
Металлы
Алюминий
Бронза
Латунь
Медь
Свинец
Сталь
» нержавеющая
Чугун
600
2 300
1380
300
600
600
1 700
1 840
600
—
920
3 000
2(6
—.
230
30
1500
160
.,,
450
2 500
200
1380
220
1730
260
2 350
2 700
8 000
8500
8 800
И 400
7 850
7 900
7 500
0,151
1,28
0,163
0,047
0,140—0,174
0,384
0,698—0,814
1,05*
0,116—0,209
0,233
2,33
0,698
0,070
1,163—3,49
0,070—0,093
0,047
0,349—0,814
0,047
1,16
0,098
0,698—0,814
0,035—0,070
0,244
0,064
0,419
0,076
0,872—1,163
203,5
64,0
03,0
384
34,9
46,5
17,5
46,5-93,0
* При температуре 800^*1100 °0.
Таблица XXIX
Коэффициенты теплопроводности жидкостей и водных растворов
(не приведенных на рис X)
Вещество
Концентрация,
% (маев.)
21
40
21
42
10
16
30
22
11
29
18
20
40
10
12,5
30
60
90
12,5
26
38
100
100
100
50
50
100
100
100
100
Температура. °С
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
32
0
100
0
0
100
0
100
0
100
Коэффициент
теплопроводности. Вт/(м- К)
ВаС12
КВг
КОН
K2S04
КС!
MgS04
MgCl2
CuS04
NaBr
Na2COa
NaCl
H2S04
HC1
Аммиак жидкий
Дихлорэтан
Уксусная кислота
Хлорбензол
Хлороформ
0,58
0,50
0,58
0,55
0,60
0,58
0,56
0,59
0,58
0,52
0,58
0,57
0,54
0,58
0,58
0,52
0,44
0,35
0,52
0,48
0,44
0,541
0,314
0,1396
0,314
0,477
0,132
0,1128
0,142
0,0919
Таблица XXX
Коэффициенты теплопроводности газов при рабе = 1 атм * [в Вт/(мК)|
Газ
Азот
Аммиак
Водород
Водяной пар
Воздух
Кислород
Метан
Оксид углерода
Диоксид углерода
Этан
Этилен
* Пересчет в СИ и при
0
0,0233
0,0209
0,1628
0,0163
0,0244
0,0244
0,0302
0,0221
0,0140
0,0174
0,0163
мечание см. таС
Температура, °С
50
0,0267
0,0256
0,1861
0,0198
0,0279
0,0291
0,0361
0,0244
0,0186
0,0233
0,0209
»л. XXV11
100
0,0314
0,0314
0,2210
0,0244
0,0326
0,0326
0,0465
—
0,0233
0,0314
0,0267
200
0,0384
—
0,2559
0,0326
0,0395
0,0407
—
—
0,0314
—
—-
530
Таблица XXXI
Среднее значение тепловой проводимости загрязнений стенок
Теплоносители.
Тепловая проводимость
загрязнений стенок
, Вт/<м*. К)
гзагр
Вода загрязненная
» среднего качества
» хорошего качества
» очищенная
» дистиллированная
Нефтепродукты чистые, масла, пары хладагентов
Нефтепродукты сырые
Органические жидкости, рассолы, жидкие
хладагенты
Водяной пар (с содержанием масла)
Органические пары
Воздух
I 400—1 860 *
1 860—2 900 *
2 900—5 800 *
2 900—5 800 *
11 600
2 900
1 160
5 800
5 800
11 600
2 800
* Для поды меньшие значения тепловой прозодимости загрязиеиий соответствуют
более высоким температурам.
Таблица XXXII
Коэффициенты объемного расширения жидкостей при ~20 °С (в К"1)
ЖнДк-оСТ:,
Бензин
Глицерин
Керосин
ж-Ксилол
Масло оливковое
» парафиновое
р. Ю5
125
53
100
101
70
90
Жидкость
Пентан
Раствор СаС12, 6 % *
» СаС12, 41 %
» NaCl, 26 % *
Скипидар
Спирт амиловый
$. 10*
159
25
46
44
94
93
* Значения 3 для рассолов см. Данилова Г. Н. и др. Сборник задач и расчетов
по теплопередаче. — М. -Л.: Госторгиздат, 1961.
Таблица XXXIII
Коэффициент Р объемного расширения жидких веществ м водных
растворов в зависимости от температуры
Вещевгв*
ji. i оя
Q.
О
и
о
о
N
и
о
О
¦*
О
о,
о
чэ
и
о
О
оо
О
о
О
О
.—1
и
о
о
Азотная кислота, 50 %
Аммиак жидкий
Анилин
Ацетон
Бензол
—
1,84
—
1,31
—
0,84
2,15
0,83
1,35
1,18
0,88 0,92
2,42 2,8
0,84 0,86
1,43 1,52
1,22 1,26
0,97
3,2
0,88
1,62
ьз
1,03
4,3
0,91
1,88
1,37
1,09
6,2
0,95
2
1,43
14,5
1,01
2,12
1,57
531
Продолжение
Вещество
о
О
CS
1
1
О
0
о
О
о
о
N
р. ю
о
о
о
•+
а
О
0
о
чэ
О
о
о
00
и
о
О
О
*—*
и
о
а
м
¦"*
Бутиловый спирт
Вода
Гексан
Диоксид серы (жндк.)
Дихлорэтан
Диэтиловый эфир
Изопропиловый спирт
Кальций хлористый, 26 %
раствор
Метиловый спирт
Муравьиная кислота
Натр едкий, 60 % раствор
» » 40% »
* » 30% »
» » 20% ]»
» » 10% »
Натрий хлористый, 20 %
раствор
Нитробензол
Октан
Серная кислота, 98 %
» » 92 %
» » 76 %
» » 60 %
Сероуглерод
Соляная кислота, 30 %
Толуол
Уксусная кислота
Фенол (расплавленный)
Хлорбензол
Хлороформ
Четыреххлористый углерод
Этилацетат
Этиловый спирт
0,83
—
1,16
1,64
1,07
1,46
0,98
0,35
1,09
—
—
—
—
—
—
—
—
1,09
—
0,58
0,68
0,58
1,13
—
1
—
—
0,92
1,18
1,Н
1,2
1,03
0,85
-Ofid
1,22
1,75
1,11
1.51
1,01
0,35
1,14
0,98
0,48
0,47
0,44
0,41
0,34
0,36
0,81
1,11
0,66
0,68
0,61
0,68
1,14
0,62
1,04
1,05
0,76
0,94
1,22
1,18
1,26
1,06
0,88
0,21
1,37
1,92
1,16
1,63
1,05
0,39
1.19
0,99
0,48
0,47
0,46
0,45
0,4
0,41
0,82
1,14
0,48
0,58
0,58
0,56
1,19
0,62
1,07
1,07
0,79
0,97
1,27
1,22
1,35
1,08
0,91
0,39
1,48
2,23
1;21
1,76
1,08
0,43
1,27
1,01
0,47
0,48
0,48
0,48
0,46
0,46
0,84
1,17
0,53
0,57
0,56
0,55
1,28
0,51
1,П
1Д1
0,82
1,0
1,34
1,26
1,46
1,13
0,94
0,53
1,67
2,61
1,26
1,85
1,12
0,46
1,3
1,04
0,47
0,49
0,6
0,61
0,61
0,5
0,86
1,22
0,63
0,66
0,56
0,65
1,41
0,6
1,17
1,14
0,86
1,03
1,43
1,32
1,52
1,22
0,98
0,63
U
3,16
1,31
2,16
1,16
0,49
1,42
1,08
0,47
0,5
0,52
0,55
0,67
0,54
0,88
1,27
0,62
0,56
0,65
0,54
1,6
0,62
1,24
1,18
0,9
1,07
1,53
1,37
1,6
1,33
1,03
0,75
1,86
3,9
1,37
2,6
1,2
0,51
1,61
1,13
0,46
0,61
0,56
0,59
0,63
0,68
0,89
1,34
0,61
0,66
0,65
0,63
1,84
0,66
1,33
1,23
0,96
1,И
1,66
1,6
1,76
1,44
1,09
0,8$
1,97
4,4
1,44
3,1
1,27
0,55
1,81
1,16
0,48
0,62
0,68
0,63
0,69
0,62
0,91
1,42
0,6
0,66
0,54
0,53
2,06
0,6
1,44
1,3
0,99
1,16
1,8
1,62
1,94
1,87
532
Таблица XXXIV
Поверхносгн теплообмена (по tfHap) испарителей ИН н ИК
н кондеисагоров КН н КК с грубамн 25X2 мм по ГОСТ 15119—79
н 15121—79
Диаметр
кожуха
(внутренний), мм
Число труб
общее
на один
ход
Длина труб, м
Площадь повер хноетн теплооб*
меиа, м3 (по <*нар)
Типы
аппаратов
Одноходовые
600
800
1000
1200
1400
261
473
783
1125
1549
261
473
783
1125
1549
40
74
121
—
—
61
112
182
260
358
81
150
244
348
480
Испарители ИН,
ИК
Двухходовые
600
800
1000
1200
1400
600
800
1000
1200
1400
600
800
1000
1200
1400
244
450
754
1090
1508
210
408
702
1028
1434
198
392
678
1000
1400
122 - 57
225 - 106
377 — 175
645 — —
754 - -
Четырехходовые
52,5 — 49
102 — 96
175,5 — 163
267 — —
358,5 — —
Шестиходовые
33 — 46
65,3 — 93
113 — 160
166,6 — —
233,3 - —
76
142
234
338
—
65
128
218
318
62
123
213
314
^^^в
114
212
353
609
706
98
193
329
479
672
93
185
319
471
659
Конденсаторы
КН, КК
633
Таблица XXXV
Количество ходов по трубам К, общее число труб л, площади проходных сечений
одного хода по трубам ST и в вырезе перегородки S-» ж, расстояния по диагонали до хорды
сегмента hj и допускаемая разность температур кожуха (*к) и труб(*т) при Р <1.0 МПа
и t < 250 °С для труб 25 X 2 мм с шагом 32 мм для стали 10 и 20 (исполнение Ml),
Диаметр
кожуха
{внутренний), мм
150
259
325
400
600
800
1000
1200
К
1
1
1
2
1
2
1
2
4
6
1
2
4
6
1
2
4
6
1
2
4
п
13
37
61
52
111
100
261 (279)
244 (262)
210 (228)
198 (216)
473 (507)
450 (484)
408 (442)
392 (426)
783(813)
754 (784)
702 (732)
678 (708)
1125(1175)
1090(1140)
1028 (1078)
ST.10»f м*
0,4
1,4
2.1
0,9
3,8
1,7
9,0
4,2
1,8
1,14
16,7
7,8
3,1
2,2
27,0
13,1
6,0
3,8
39,0
13,9
8,5
^с. ж* Ю»,
0,5
1,3
1,4
2,2
4,9
7,7
12,1
16,8
&!, ММ
25
40
55
68
III
Тбб
166
194
194
250
222
(*к — Омане' к
(для ТН, ХН,
КН, ИН)
Для ХН 20
Для ТН 30
30
40
50
Для ТН 60
60
6 1000(1050) 5,7
305
Примечания: J, В скобках указано общее количество труб для случая, когда
нет отбойников и труЗы добавлены с двух сторон., см. ГОСТ 15118—79.
2. Значения Л, приведены для теплообменников и холодильников.
634
Таблица XXXVI
Концентрации [в % (масс.)] некоторых водных растворов,
кипящих под атмосферным давлением
Растворен-
нив веще»
ство
СаС12
КОН
КС1
К2С08
KN03
MgCl2
MgS04
NaOH
NaCl
NaN03
Na2S04
Na2COa
CuS04
ZnS04
NH4N03
NH4Ci
(NH4)2S04
Растворен»
НО" веще»
QTBO
Ю1
5,66
4,49
8,42
10,31
13,19
4,67
14,31
4,12
6,19
8,26
15,26
9,42
26,95
20,00
9,09
6,10
13,34
125
102
10,31
8,51
14,31
18,37
23,66
8,42
22,78
7,40
11,03
15,61
24,81
17,22
39,98
31,22
16,66
11,35
23,14
Температура
103
14,16
11,97
18,96
24,24
32,23
11,66
28,31
10,15
14,67
21,87
30,73
23,72
40,83
37,89
23,08
15,96
30,65
104
17,36
14,82
23,02
28,57
39,20
14,31
32,23
12,51
17,69
27,53
—
29,18
44,47
42,92
29,08
19,80
36,71
Температура
140 160 180
200
кипения, °С
105
20,00
17,01
26,57
32,24
45,10
16,59
35,32
14,53
20,32
32,43
—
33,86
46,15
34,21
22,89
41,79
107
24,24
20,88
32,62
37,69
54,65
20,32
42,86
18,32
25,09
40,47
—
—
—
42,53
28,37
49,73
кипения, "С
220
240
по
29,33
25,66
—
43,97
65,34
24,41
—
23,08
—
49,87
—
—
—
51,92
35,98
, _
260
115
35,68
31,97
—
50,86
79,53
29,48
—
26,21
—
60,94
—
—
—
63,24
46,95
_
280
120
40,83
36,51
—
56,04
—
33,07
—
33,77
—
68,94
—
—
—
71,26
—
—
300
СаС12 45,80 57,89 68,94 75,85 — — — — — —
КОН 40,23 48,05 54,89 60,41 64,91 68,73 72,46 75,76 78,95 81,63
КС1 _-_-. -___--
К2С03 60,40 — — — _-_„___
KNOa __-_ ______
MgCl2 36,02 38,61 — — — ___ — _
MgS04 — — — — ______
NaOH 37,58 48,32 60,13 69,97 77,53 84,03 88,89 93,02 95,92 98,47
NaCl __ — _ ______
NaN08 — — — — _ _ ____
Na3S04 — — — — — _ _ _ _ _
N a2COa _ _ _ — ______
CuS04 — — — — — — _„__
ZnS04 _ _ _ _ ______
NH4N03 77,11 87,09 93,20 96,00 97,61 98,84 — — - -
NH4C1 ___ — _______
{NH4)2S04 _ _ _ _ _______
Таблица XXXVII
Удельная теплота растворения q некоторых солей в воде
(1 кмоль соли в п кмоль воды)
Формула соли
Мольная
масса,
кг/кмоль
кДж/кмоль
п
NaCl
Na2S04
NaaSO4-10HflO
NaN03
K2C03.1,5H20
КС)
KNOs
KOH-2HsO
(NH4)2S04
СаС12.6Н*0
MgC!2.6H20
Примечание. Знак плюс
знак минус — с выделением теплоты.
обозначает
58,5
142
322
85
165
74,6
101
92
132
219
203
раствор
+ 4 944
—1 927
+78 600
+21 080
+ 1 590
+ 17 560
+35 700
+ 126
+9 930
+ 18 060
—12 360
100
400
400
200
400
100
200
170+30
400
400
400
еиие с поглощением теплоты,
Таблица XXXVIII
Давление насыщенного водяногс пара при температурах от —20
до 100 °С
Пересчет в СИ: 1 мм рт. ст. » 133,S Па.
/, вс
—20
" 19
18
17
16
15
14
13
12
И
10
9
8
7
6
5
4
3
2
—1
0
+ 1
2
3
4
мм рт. ст-
0,772
0,850
0.935
1,027
1,128
1,238
1,357
1,486
1,627
1,780
1,946
2,125
2,321
2,532
2,761
3,008
3,276
3,566
3,879
4,216
4,579
4,93
5,29
5,69
6,10
t с
5
6
7
8
9
10
11
12
13
14
15
16
1 17
18
19
20
21
22
23
24
25
26
27
28
29
1
i
р-
мм рт. ст.
6,54
7,01
7,51
8,05
8,61
9,21
9,84
10,52
11,23
11,99
12,79
13,63
14,53
15,48
16,48
17,54
18,65
19,83
21,07
22,38
23,76
25,21
26,74
28,35
30,04
t, °с
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
р.
мм рт. ст.
31,82
33,70
35,66
37,73
39,90
42,18
44,56
47,07
49,65
52,44
55,32
58,34
61,50
64,80
68,26
71,88
75,65
79,60
83,71
88,02
92,51
97,20
102,1
107,2
112,5
/, °с
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
р»
мм рт. ст.
118,0
123,8
129,8
136,1
142,6
149,4
156,4
163,8
171,4
179,3
187,5
196,1
205,0
214,2
223,7
233,7
243,9
254,6
265,7
277,2
289,1
301,4
314,1
327,3
341,0
и°с
80
81
82
83
й
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
р.
мм рФ. ст.
355,1
369,7
384,9
400,6
416,8
433.6
450,9
468,7
487,1
506,1
525,8
546,1
567,0
588,6
610,9
633,9
657,6
682,1
707,3
733,2
760,0
636
Табл ипа XXXIX
Физические свойства воды (на линии насыщения)
Пересчет в СИ: 1 кгс/см2 = 9,81.10* Па.
5
о
о
/, °с
кг/м"
г,
кДж
кг
с,
кДж
кг- К
*.. ю2,
Вт
м- К
о
2
Г*
О
^н
*
*
Я)
С
*
о
*-м
*
У
^н
*
1
tf
*¦
О
за
(4
О
Ьн
о
^^
*
а,
0 1000 0 4,23 55,1 1,31 1790 1,79 —0,63 756 13,7
10 1000 41,9 4,19 57,5 1,37 1310 1,31 +0,70 762 9,52
20 998 83,8 4,19 59,9 1,43 1000 1,01 1,82 727 7,02
30 996 126 4,18 61,8 1,49 804 0,81 3,21 712 5,42
40 992 168 4,18 63,4 1,53 657 0,66 3,87 697 4,31
50 988 210 4,18 64,8 1,57 549 0,556 4,49 677 3,54
60 983 251 4,18 65^ 1,61 470 0,478 5,11 662 2,98
70 978 293 4,19 66,8 1,63 406 0,415 5,70 643 2,55
80 972 335 4,19 67,5 1,66 355 0,365 6,32 626 2,21
90 965 377 4,19 68,0 1,68 315 0,326 6,95 607 1,95
,03 100 958 419 4,23 68,3 1,69 282 0,295 7,5 589 1,75
,46 ПО 951 461 4,23 68,5 1,69 256 0,268 8,0 569 1,58
2,02 120 943 503 4,23 68,6 1,72 231 0,244 8,6 549 1,43
2,75 130 935 545 4,27 68,6 1,72 212_ 0,226 9,2 529 1,32
3,68 140 926 587 4,27 68,5 1,72 196 0,212 9,7 507 1,23
4,85 150 917 629 4,32 68,4 1,72 185 0,202 10,3 487 1,17
6,30 160 907 671 4,36 68,3 1,72 174 0,191 10,8 466 1,10
8,08 170 897 713 4,40 67,9 1,72 163 0,181 11,5 444 1,05
10,23 180 887 755 4,44 67,5 1,72 153 0,173 12,2 424 1,01
J
X
го
a
X
ч
>o
го
H
S
о
X
а.
а>
-е*
о
о
?
t-
cd
J9
f-
о
о
a:
*
cd
ч
а
с;
cd
За-
ч«
<u о
fcW
ss
у к
О cd
* х
fc! О
Ов?
„ ed
я о.
5 х
6- п
* «j
« х
a ?,
? *
а> т
о. о
U Ш
Июль
Январь
3?
*
-**
*•-
ё-
о
о
•К1
Наименование пункта
ЮГ^10^СОГ^^Г^ЮГ^СОСО^СОЮГ^Г^СОСОГ^Ю^ЮГ^С1ЭГ^СО^
t— C^<MCTiCOOOOOOCO
« CO^CN CO C^CS M<^^C?^CD ^O^C^O<ttCSa^CO^O^<^^C^^ OO 1ЛЮ© —« CD CO^O^CO -^.^C^'-O (¦>.—« >l (?> O^OO^tr CO Ю •* CO CO N
N0O-* CO(N CO GO -f И>ЮОС> С0 0р0>ОЮс0ФО00 00О^00Ю^С0Ю00(»ЮМ00ЮМ^С0ф^^(Х100^ОСЧ1С^00
оооо<^сосог^оог^сосо<^с»<^сосо<^оососососог^<^аэсог^с^
сюо-<
CD CO —' '^'^C^.OO^O^C^O CO C^<?i C^0C^C^<^<^C^^C^^^C4 CO ^ ^OO O^O^Tf O^CO^
схГсо"г^о*соЛ^о6^со"<^с^<^с^^<^ю"с^сГсо"<^^ e\f <?i со cd** o^ со* г-^* со* -^ e" oc
17 1 1+7 17 17 17 I I 1777 17 I I 17 M M7 M 17 17 17 I 177 I
I
I ' I ' I ' I
COCsjrf—-CO—-'^ОО^-О4*
00* —* —** О* СГ)" -d" lO 1>Г Г-Г Г-.'
Ijl^l 1777 I ""
I I I
I I
<
(
s
4
о
CU
и
и
«J
a.
ro
ro
?3
«3'
а
о
Ж
СУ
си
со
о
V
ч
О
к
к
о.
ы
о
н
о
о
Я
ж
го
го
а,
(-
о
и
ч
о
СО
(X
о
о
си
Я со
а. а. о
О о
о
а
о
m
о
о.
F-
CU
к
о
Си
с
си
ас
к
го
я
о
сх
о
a
о
ас
«J
со
о
н
о,
со
CU
3
со
о
сх
о
я
о
сх, сх,
3
Я
о
к
о
«J
о.
сх
«J
<=?
о
к
о
«J
а
и
о.
W
о
к
о
«J
«
и
и.
ЕС
О
S3
го
н
О. CU >. >.
со
a.
с-
-41
К
си
«
о
к
3
1Т1
я
N1
и
О
со
си
го
е;
о
км
о
сх
о
и
я
о
а
о
«Я
о
о
О
я
о
И
о
сх
-41
к
о
я
о
п
с
о
си
CJ CU
я
я
S О
CXtd
1) О
я
о
н
о
о
о
н
го
сх
та
о
я
о
сх
32
о
>^
о
S
Н I-
я
о
Й
о
>^
S
'-О
S
о
я
РЗ
я
о
«
я
сх
сх-в*та
«J
t -
с_
о
к
ч
си
та
00
со
Таблица XLi
Значения коэффициента Генрн ? для водных растворов некоторых газов (в таблице даны значения Е*Ю~в в мм рт. ст.)
Пересчет в СИ: 1 мм рт. ст. '= 133,3 Па.
Газ
Азот
Ацетилен
Бром
Водород
Воздух
Диоксид углерода
Кислород
Метан
Оксид углерода
Сероводород
Хлор
Этаи
Этилен
0
40,2
0,55
0,0162
44
32,8
0,553
19,3
17
26,7
0,203
0,204
9,55
4,19
5
45,4
0,64
0,0209
46,2
37,1
0,666
22,1
19,7
30
0,239
0,25
11,8
4,96
Ю
50,8
0,73
0,0278
48,3
41,7
0,792
24,9
22,6
33,6
0,278
0,297
14,4
5,84
15
56,1
0,82
0,0354
50,2
46,1
0,93
27,7
25,6
37,2
0,321
0,346
17,2
6,8
Температура,
20
61,1
0,92
0,0451
51,9
50,4
1,08
30,4
28,5
40,7
0,367
0,402
20
7,74
25
65,7
1,01
0,056
53,7
54,7
1,24
33,3
31,4
44
0,414
0,454
23
8,67
°с
30
70,2
1,П
0,0688
55,4
58,6
1,41
36,1
34,1
47,1
0,463
0,502
26
9,62
40
79,2
—
0,101
57,1
66,1
1,77
40,7
39,5
52,9
0,566
0,6
32,2
—
60
90,9
—
0,191
58,1
76,5
2,59
47,8
47,6
62,5
0,782
0,731
42,9
—
80
95,9
—
0,307
57,4
81,7
—
52,2
51,8
64,3
"1,03
0,73
50,2
—
100
05,4
—
—
56,6
81,6
—
53,3
53,3
64,3
1,12
—
52,6
—
Таблица XLII
Коэффициеиты диффузии газов и паров в воздухе (при нормальных
условиях)*
Газ
Азот,
Аммиак
Бензол
Водород
Водяной пар
Диоксид серы
» углевода
Диэшловый эфир
Кислород
Метиловый спирт
Серный ангидрид
Сероуглерод
Хлористый водород
Этиловый спирт
D0. 10V mVc
13,2
17,0
7,7
61,1
21,9
10,3
13,8
7,8
17,3
13,3
9,4
8,9
13,0
10,2
О0, м2/ч
0,0175
0,0612
0 0277
0,22
0,079
0,037
0,0497
0,028
0,064
0,0478
0,034
0,0321
0,0467
0,0367
При других температурах и давлениях D =0,
О
Т \3/2
Таблица XL1II
Коэффициеиты диффузии гекоторых газов в воде при 20 °С *
Газ
Азот
Аммиак
Водород
Диоксид углерода, оксид азота
Кислород
Хлор, сероводород
Хлористый водород (при 12 °С)
зота
>°С)
0. 10е, Ма/с
1,9
13
5,3
13
2,1
1,6
2,3
О. 10е, мг/ч
6,9
6,6
19,1
6,4
7,5
5,8
8,3
При других температурах Da =
02О Ь + 0,02 (/ - 20)).
640
Таблица XLIV
Физические свойства некоторых органических Жидкостей
Пересчет в СИ: I мм рт. ст. «= 133,3 Па.
Жидкость
Химическая
формула
За
Г
(С
о
1
НИ
« К
К*
К 4)
Ж К
го
С!
2 Он
2° °
|о .
4*_ О-
«'
Я) ,.
& А)
4»
НИ
Ацетон
Бензин
Бензол
Дихлорэтан
Изопропилацетат
Ксилолы (смесь)
Мети л ацетат
Пропилацетат
Сероуглерод
Скипидар
Спирт бутиловый
» изоамило-
вый
Спирт изобутило-
ВЫЙ
Спирт изопропи-
ЛОВЫЙ
Спнрт метиловый
» пропиловый
» этиловый
Толуол
Углерод четырех-
хлористый
Хлороформ
Этил ацетат
Эфир дпэтиловый
CHsCOCH8
—_
CeHe
СН2С1—СН2С1
СН3СООС5 Н i f
С6Н4(СН3)2
сн8соосн8
CH3COOC3H.
CS2
Ci«Hie
C4H9CH
C*HnOH
C4H9OH
C3H;OH
CH3OH
C3H7OH
C2H5OH
QjHjjCHg
CC14
CHC13
CH8COOCaHe
с2н5ос2н5
58,08
—
78,11
98,97
130,18
106,16
74,08
102,13
76,13
136,1
74,12
88,15
74,12
60,09
32,04
60,09
46,07
92,13
153,84
119,36
88,10
74,12
810
690—760
900
1250
870
860
930
890
1290
56
70—120
80,2
83,7
142,5
136—145
57,5
101,6
46,3
850—880 155—190
810
810
800
785
800
800
790
870
1630
1530
900
710
117,7
132
108
82,4
64,7
97 2
78,3
110,8
76,7
61,2
77,15
34,5
186
—
75
65
6
10
170
25
298
4
4,7
2,2
8,8
32,4
9" J
14,5
44
22,3
90,7
160
73
442
—94,8
——
+5,5
—
—13-f*
>-—48
—
—112
—
-90
—117
—108
-89
—98
—126
—114,5
—95
—22,8
_
—83,6
—116,3
Таблица XLV
Удельная теплота парообразования некоторых веществ (в кДж/кг)
Вещество
Аммиак
Анилии
Ацетон
Беи зол
Бутиловый
спирт
0
1265,4
—_
565,7
448,3
703,9
20
1190,0
¦'¦¦
553,1
435,8
687,2
Температура, °С
60
_
""
519,6
408,5
653,6
100
_
~™
473,5
379,2
611,7
140
435,8
(при 184 °Q
—
346,1
561,5
541
Продолжение
Вещество
Вода
Диоксид углерода
Дизтнлогый эфир
Изопропил^ый спирт
Метиловый спирт
Нитробензол
ПрОИНЛОЕЫН СПНрТ
Сероуглеро!
Толуол
Уксусная кислота
Хладои-12 (фреон-12)
Хлор
Хлорбензол
Хлороформ
Четыреххлорнаый углерод
Этилацетат
Этиловый спирт
Температура, °С
20
60
'00
140
2493,1
235,1
387,6
775,2
1198,3
^™^
812,9
374,6
414,8
¦¦'¦¦'
155,0
266,5
375,8
271,5
218,3
427,4
921,8
2446,9
155,4
366,6
750,0
1173,2
^¦v
791,9
367,0
407,7
1
144, гв
253,1
369,5
263,1
213,7
411,5
013,4
2359,0
—
325,4
699,7
1110,4
"™*
745,8
344,4
338,8
¦ ¦¦¦
132,4
222,0
354,4
247,6
201,9
385,9
879,9
2258,4
—
'282,4
636,9
1013,9
—-
683,0
316,4
368,7
406,4
(при 118 °С)
—
176,8
338,1
23 U
185,6
355,7
?12,9
2149,5
—
228,4
557,3
892,6
331,4
(при 211 °С)
595,0
282,4
344,0
395,5
—
71,23
320,5
—
168,0
317,2
712,3
Таблица XLV1
Температуры кипеннп {в °С) некоторых органических, жидкостей при
давлениях <1 атм
Пересчет ; СИ 1 атм = 760 мм рт. ст — 101 32Г> П
Давление
(абсолютное)
мм рт ст.
10
20
40
60
100
200
400
700
Анилин
69,4
82,0
96,7
106,0
119,9
140,1
161,9
184,4
Глицерин
167,2
182,2
198,0
208,0
220,1
240,0
263,0
290,0
м- Ксилол
28,3
41,1
553
64,4
76,8
95,5
116,7
139,1
Нитробензол
84,9
99,3
115,4
125,8
139,9
161,2
185,8
210,6
Толуол
6,4
18,4
31,8
40,3
51,9
69,5
89,5
110,6
Октан
19,2
31,5
45,1
53,8
65,7
83,6
104,0
125,6
642
Таблица XLVII
Равновесные составы жидкости и пара для некоторых бинарных систем
при Паос = 760 мм рт. ст.
Метиловым спирт — вода
/, °С
% (мол ) мртилойого спирта
в жидкости
в паре
Хлороформ — бензол
и °о
% (мол.) хлороформа
в жидкости
в паре
100,0
96,4
93,5
61,2
87,7
Ы,7
78,0
75,3
73,1
71,2
69,3
67,5
66,0
64,5
0
2
4
6
10
20
30
40
50
60
70
80
90
100
0
13.4
23,0
30,4
41,8
57,9
6*0,5
72,9
77,9
82,5
87,0
91,5
95,8
100
80,6
79,8
79,0
78,2
77,3
76,4
75,3
74,0
71,9
68,9
61.4
0
8
15
22
29
36
44
54
66
79
100
0
10
20
30
40
50
60
70
80
90
100
Вода
t, °С
— уксусная кислота
% (мол.) воды
в жидкости
в паре
т, к
Азот — кислород
% (мол.) азота
в жидкости
в паре
118,1
115,4
113,8
110,1
107,5
105,8
104,4
103,2
102,1
101,3
100,6
100,0
0
5
10
20
30
40
50
60
70
80
90
100
0
9,2
16,7
30,2
42,5
53,0
62,6
71,6
79,5
86.4
93,0
100
90,1
89,5
89
88
87
86
85
84
83
82
81
80
79
78
77,3
0
3,5
6,2
11,5
17,1
22,2
27,7
33,8
40,5
47,8
56,6
66,6
78,4
91,9
100
0
13,0
20,2
30,4
39,7
47,8
55,7
63,1
70,1
76,4
82,3
88,0
93,2
97,8
100
543
I I ! I И 1 I II I +++++
ооооослоспослоооосл
о
Ъ> ^—"to "со "а Ъо о lo "en "oo "to ^— "со Vi "ел "en ~~-i
СЛЮСОСОСЛЬЭСО«а>1**СГ1^*СЛЬОСОСОСО<Х
со ел *— со ел rf*
СЛСТзСПСЛСЛСЛ^^4й-^4й-
СО ^ rf^ tO СО ^ СЛ >*¦
. coco со со to to
СО СО (У) СО и- сО С i
»—*—.— (ососо^сл
о о *— to ф» <д en ^ <о о to s со *— ст> ^- со
"гР* *00 СЛ "С» ~^-"0 "to СЛ "О 00 00"-J 00 "ел"*— "to ~^-
00
Q0 СЮ "О "^ ¦*¦*! С5С5СТ>С»СТ>С»СЛСЛ4*4* СОС0
pi Ы> ОО^СЛ *—С0^СЛСО*—©СЛ ©?Л Ю 00 tO
"ооо"о"о"со Ъ>сл Ъс^ о ©*©"©© VjV
н
ф
г
я
OfD
ГУ»
OS
н
*<
¦о
в>
к
_^)а
5 о »
s 3 к
-о 5
*
зё
SS
? о
^н
ts
"
я я
-3 »
--•о
К Ш
{*-
,
«-
h
С
и»
В
¦ о
о
3
а
* гь ?
?! СЕ Н Ш
па»»
»
-ч
=3
ф
тэ
а>
о
чет
и
п
S
* •
^*
з;
-1
о
г>
S
II
to
Си
—
О
№
я
to
•*<¦>
*
ь
ё
О
а
р
¦
re
"W
' ф
Я
ы
а
?
а>
л
т.
a
«
о
OS
о
St
ств
p
a
p
r>
E
?
n
X
о
-1
о
3
p
43
p
дифтордихлорметан
p
Таблица XL
X
Cnrf^JS'COCOtObO-—
ослослослослосп
J_ I I I I I I I I I I
i О I *— >— tOtOCOCO****-^
>—totococo^j^cn
СЛОСЛОСЯ0010СЛО
О 00 СЛ CO
ОООЧФУ^ОЗЮМ-
о о о о
^к-оо^оою^^^(ок;о^о<^*'сослк;со--^сл^
ЮСЛСГ1СЛСОЮ4^СО^с^--^^-СТ>^-*'^---сггсоСл-—
ЧСЯОСЛСПСПн-и-^-сОСОЮСЙООСГпОО'-СЙО)
СО 00 Ю 00
^^^^C^C^O^O^CftOlCnCn01CnCn^Jb.4^4^4^J^
^СЛЬЭООрСЛСО^—ОООСЗИ^СО^— О ОО -<| СЛ 4*. СО Ю
с^ослюОоооосоосоо^сосооосососпгосост!^
СЛ^-^СООООСЛСООО — CCiOOOi-vlOlHOJWNCn
О О О О OjO ООО ООООрООО ^- — Ю JO
*о"о ©'"Q"'¦¦-,^-"^-"^— ю "to "to "со Хй- ЪгЪ^"мчсо"к;'спо"с^
CTi-^Ccc0^-EOrf»--v]O*'00rf^-— OtO-^iCTi—СЛО —
СОЕОСООТОООСОД^СПСОСОфООООСО — СО СЛ © »— --J
СЛС^С00^004^000СЛ^<0*»---4СЛЬС>0^— СО СЛ О
О О О О О О ОООООООО©ОО О ©О О
"ел СУ*"сл*СЛ &Gb&Ob(2)(2>(2>(2>G3(2><y>(2><y>(2>(2>(2>m<i
WUlCnbOOOWOiSSOwOCTiO^NOOOO
CntOtOOcOSCTiCn^rf^COEOtO
VjVj o~4* oVj~cft^--] oo"-— "Voo'co со
. Cft
слооаоо
j— О О О О
"о oo Ъ> ел "со
ся^ососососо-— сл©слоос?>с^©сосою^©оо
С7> *¦* СД*— »*^СЛ4^00СОСЮК;СОООй^-^ООСОСЛОЮ
ОО^—¦—^- — ^-EOtOtOCOtOtO^COCOCOCOCOJS'J^
СЯ-^ОЬО^О^ОО'—tC4^CTiCc.c0^-tO4i.CTiS00O —
СО OO *- #bCT>QOQOO--lCT>COi -*4*СОСП©й*>00ЮСЭ
•о
2
"О
р
Темпе.
Давление
(абсолютное),
Як
¦«¦о
*
ЖИДКОСТИ
р', кг/дм9
¦о
Ж
«IS
Удельный объем
Плотность
Удель»зя
теплота
•о
а
м
а
л
п
ft
а
а
ш
ft
ш
о
о »
S 2
ш
_ р
5 я
ii ?
-- §
00 -1
¦— Q
5 S
•с
р
Р
S
S
а
р
?!
Р
Г4
Таблица L
Физические свойства водных растворов хлористого иатрия
при низких температурах
оре,
раств
с)
СоДерж
соли в
% (мае
ES
Й-
о ж
X .
ату pa
1НИЯ (
Темпер
замерза
Динамнчеокий коэффнцне
вязкости М"Ю*, Па-с
и
о
О
О
о
1
и
о
о
•—1
1
О
о
LO
7
НТ
— 20 °С
Коэффициент
теплопроводности А
Вт/(м- К)
0
о
и
а
О
7
о
0
о
1
0,1
1,5
2,9
4,3
5,6
7,0
8,3
9,6
11,0
12,3
13,6
14,9
16,2
17,5
18,8
20,0
21,2
22,4
23,1
23,7
24,9
26,1
26,3
100 J
1010
1020
1030
1040
1050
1060
1070
1080
1090
1100
1110
1120
ИЗО
1140
1150
1160
1170
1175
1180
1190
1200
1203
0,0
—0,9
-1,8
—2,6
—3,5
-4,4
-6,4
-6,4
-7,5
—8,6
—9,8
—11,0
—12,2
— 13,6
— 15,1
— 16,6
—18,2
—20,0
—21,2
—17,2
—9,5
-1,7
0,0
17,66
17,85
18,05
18,25
18,44
18,74
19,13
19,62
20,21
20,80
21,48
22,37
23,25
24,33
25,60
26,88
28,25
29,63
30,41
31,39
32,96
34,73
35,02
-—
—
«_
—
—
«_
23,05
23,74
24,43
25,21
26,09
27,17
28,35
29,72
31,20
32,77
34,43
36,40
37,47
38,55
40,71
—
—
—
—
—
—
—
—
—
—
—
—
¦—
33,45
34,92
36,79
38,75
40,81
43,07
45,62
47,09
48,66
—
—
——
—
—
—
—
—
—
—
—
—
—
—
—
—
—
47,77
50,13
52 78
55,82
57,49
59,35
—
—
—
—
—
—
.—
—
—
—
—
—
—
—
—
—
—
—
—
—
68,67
70,44
—
—
.—
—
0,5815
0,5780
0,5757
0,5734
0,5710
0,5687
0,5664
0,5641
0,5606
0,5582
0,5559
0,5536
0,5513
0,5489
0,5466
0,5443
0,5420
0,5408
0,5396
0,5385
0,5361
0,5338
0,5338
—
—-
—
—
_
—
—
—
—
—
—
0,5187
0,5164
0,5140
0,5117
0,5094
0,5071
0,5059
0,5047
0,5036
—
—
—
—
—
—
.—
—
—
—_
—
—
—
—
—
—
—
—
—
—
0,4768
0,4757
.—
—
—
—
Физические свойства водных растворов хлористого кальции
при низких температурах
Таблица LI
ч
SJ ffl
ИЙ"
ев
<3
о
3!
а
к.
и
<0
со
Is
г4 эт
Динамический коэффициент
вязкости |Х- 10* Па.с
U
о
О
U
о
1
и
о
U
о
О
СО
Коэффициент
теплопроводности
Вт/ (м- К)
К
U
о
О
и
о
I
О
о
о
I
U
о
О
СО
0,1
5,9
11,5
16,8
17,8
18,9
19,9
20,9
21,9
22,8
23,8
1000
1050
1100
1150
1160
1170
1180
1190
1200
1210
1220
0,0
-3,0
-7,1
— 12,7
— 14,2
— 15,7
-17,4
—19,2
—21,2
—23,3
—25,7
17,76
19,82
22,96
27,66
28,74
29,92
31,20
32,77
34,43
36,20
38,16
—
—
—
43,65
45,13
46,70
48,46
50,72
53,27
56,11
59,25
—
—
—
—
—
—
—
—
86,13
90,15
94,76
0,5815 - —
0,5675 — -
0,5524 — -
0,5350 0,504 —
0,5303 0,500 —
0,5257 0,497 —
0,5210 0,493 —
0,5164 0,490 —
0,5117 0,486 0,465
0,5071 0,484 0,463
0,5024 0,480 0,450
18 Павлов К. Ф. и др.
545
8*
о о
к ш
а: н —
* о. °
QJ m <i
« ~
О S^o
(Jre; «^
О.
и„
ость
кг/м
я .
&и
с0
с?
о
Г* к
Is
5 щ
S 5
Динамический коэффициент
вязкости Ц.-Ю4, Па-с
О
о
О
и
о
О
1-Х
1
и
о
О
(N
1
и
о
о
СО
1
Продолжение
Коэффициент
?«плопроводности К.
Вт/(м. К)
г ¦*
и
о
О
и
0
о
,_¦
I
и
о
О
С»
1
и
о
О
И
1
24,7
25,7
16,6
27,5
28,4
29,4
29,9
30,3
31,2
QO- 1
33,0
33,9
34,7
35,6
36,4
37,3
1230
1240
1250
1260
1270
1280
1286
1290
1300
1310
1320
1330
1340
1350
1360
1370
—28,3
—31,2
—34,6
—38,6
—43,6
—50,1
—55,0
—50,6
—41,6
—33,9
—27,1
—21,2
—15,6
— 10,2
-5,1
0,0
40,22
42,58
45,22
48,07
51.21
54,94
56,90
58,86
63,37
68,28
73,87
80,15
86,52
93,20
100,9
109,2
62,60
66,81
70,83
75,24
80,25
86,33
90,45
93,29
100,6
108,7
117,3
127,2
138,1
151,9
—
-—
99,96
105,7
111,7
118,5
126,9
137,9
143,9
149,6
161,9
176,3
191,9
210,0
—
—
—
-—
—
148 1
158,9
171,7
188,4
212,9
225,6
238,4
265,9
307,1
.—
.—
—
—
—
——
0,4978
0,4931
0,4885
0,4838
0,4792
0,4745
0,4722
0,4С99
0,4652
0,4605
0,4571
0,4524
0,4478
0,4431
0,4396
0,4350
0,477
0,473
0,470
0,464
0,463
0,459
0,457
0,456
0,452
0,449
0,444
0,441
0,438
0,433
—
—
0,457
0,455
0,452
0,449
0,446
0,444
0,443
0,442
0,438
0,436
0,434
0,431
—
—
—
——
—
0,437
0,436
0,435
0,434
0,433
0,431
0,430
0,429
0,428
—
—
—
—
—
——
Таблица LII
Удельная теплоемкость водных растворов хлористого натрия
и хлористого кальция [в кДж/(кг*К)]
Плотность
при 15°С,
кг/м8
1010
1020
1030
1040
1050
1060
1070
1080
1090
1100
1110
1120
ИЗО
1140
1150
1160
1170
1175
1203
Хлористый в
') OQ
4,077
4,006
3,943
3,884
3,830
3,775
3,725
3,679
3,633
3,591
3,553
3,515
3,478
3,444
3,411
3,377
3,344
3,331
3,251
—10 °С
,
—
—
—
—
™
—
—
—
3,582
3,541
3,503
3,469
3,432
3,398
3,365
3,335
3,323
—
атрий
— 20 °С
.—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
3,323
3,310
—
Плотность
при 15 °С,
кг/м3
1100
1110
1120
ИЗО
1140
1150
1160
1170
1180
1190
1200
1210
1220
1230
1240
1250
1260
1270
1280
1286
1370
о °с
3,503
3,444
3,385
3,331
3,276
3,226
3,176
3,130
3,088
3,046
3,004
2,967
2,933
2,899
2,870
2,841
2,812
2,782
2,757
2,740
2,531
Хлорист
— 10°С
^^
—
—
3,306
3,251
3,201
3,155
3,109
3,063
3,021
2,979
2,941
2,908
2,874
2,845
2,816
2,786
2,757
2,732
2,715
ый кальций
— 20 °С
i .
—
-^
-^
—
-^
—
—
—
—
2,954
2,916
2,883
2,849
2,819
2,791
2,761
2,732
2,707
2,690
— 30 °С
-J__
—
—
—
—
—
—
—
—
—
—
—
—
—
2,795
2,766
2,736
2,707
2,682
2,665
^46
Таблица LIT!
Удельная теплота адсорбции углем некоторых органических веществ
Вещество
Беизин
Бензол *
Бутил хлористый
emop-Бутил хлористый
mpetn-Ъутил хлористый
Днхлорметан
Изопропил хлористый
Метан
Метил хлористый
Пропил хлористый
Сероуглерод *
Спирт метиловый
» пропнловый
» этиловый *
Углерод четыреххлористый *
Хлороформ *
Этил бромистый *
» йодистый *
» хлористый *
Этилформиат *
Эфир диэтиловьш *
Формула
свнв
СН3(СН2)3С1
СН3СНС1С2Н5
(СН3)3СС1
CH2CI2
СН,СНС1СН3
СН4
СН3С1
СН3(СН2)2С1
cs2
СН3ОН
С3Н7ОН
С2Н5ОН
СС14
СНС13
С^Вг
С2Н51
С2Н5С1
нсоос*н5
(С2Н5)20
Теплота
кДж/кмоль
50 280
61 590
65 360
60 340
56 980
51 960
54 890
18 860
38 550
61 170
52 380
54 890
68 720
62 850
64 ПО
60 760
58 240
58 660
50 280
60 760
64 950
адсорбции
кДж/кг
628,5
789,8
706,4
652,4
615,9
611,3
699,3
1230
763,4
779,3
689,3
1715
1145
1366
415,2
508,2
534,6
376,3
779,3
820,8
877,8
Примечания. 1. Величины теплоты адсорбции даны для условий поглощения
I кмоль пара 500 кг угля при 0 °С (за исключением бензина,
для которого соотношение между количествами поглощенного
вещества и угля не указывается).
2. Звездочкой отмечены вещества, для которых теплота
адсорбции рассчитана по формуле (9.8) q = man (в Дж/кг угля)
Таблица LIV
Степень извлечения экстрагируемого вещества при последовательной
обработке одинаковыми порциями свежего растворителя
Отношение
потоков а
1
•j
3
4
5
6
7
8
9
10
степень
извлечения, %
(масс.)
50,00
60,07
75,00
80,(10
83,33
85,71
67,50
88,89
90,00
90,90
1
общий.
объем
растворителя
1
Аш1
> >
,5
4
о
6
7
8
9
10
i
степень
извлечения, %
(масс.)
75,00
88,89
93,75
96,00
97,22
97,96
98,44
98,76
99,00
99,17
Число п
г
общий
объем
растворителя
2
4
6
8
10
12
14
16
18
20
ромывок
4
степень
извлечения, %
(масс.)
87,50
96,30
98,44
99,20
99,54
99,71
99,81
99,86
99,90
99,92
*
общий
объем
растворителя
3
6
9
12
15
18
21
24
27
30
/
степень
извлечения, %
(масс )
93,75
98,76
99,61
99,84
99,92
99,96
99,98
99,98
99,99
99,99
?
общий
объем
растворителя
4
8
12
\$
20
24
28
32
36
40
18*
547
Таблица LV
Степень извлечения [в % (масс.)] экстрагируемого вещества
при обработке твердого материала в противотоке
Отношение
потоков а
1
2
3
4
6
6
7
8
9
10
1
50,00
66,67
75,00
80,00
83,33
85,71
87,50
88,89
90,00
90,90
Члс
2
66,67
85,71
92,31
95,24
96,77
97,67
98,24
98,63
98,90
99,10
ло ступеней экстрагирования пй
3
75,00
93,00
97,50
98,82
99,36
99,61
99,75
99,83
99,88
99,91
^
80,00
96,77
99,17
99,71
99,87
99,94
99,96
99,98
99,99
¦ ¦
ь
83,33
98,42
99,73
99,93
99,97
—
—
—
.—
~
6
85,71
99,21
99,91
—
—
—
—
—
—
~
Таблица LVI
Свойства насыщенного водяного пара в зависимости от температуры
Пересчет в СИ: 1 кгс/см2 = 9,81. 10* Па.
Тем.
пера-
Тура
•С
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
ПО
115
120
125
Давление
(абсолют.
ное),
кгс/см2
0,0062
0,0089
0,0125
0,0174
0,0238
0,0323
0,0433
0,0573
0,0752
0,0977
0,1258
0,1605
0,2031
0,2550
0,3177
0,393
0,483
0,590
0,715
0,862
1,033
1,232
1,461
1,724
2,025
2,367
Ч J _ J*
Удель иый
объем,
Ма/кг
206,5
147,1
106,4
77,9
57,8
43,40
32,93
25,25
19,55
15,28
12,054
9,589
7,687
6,209
5,052
4,139
3,414
2,832
2,365
1,985
1,675
1,421
1,212
1,038
0,893
0,7715
Плотность,
кг/м3
0,00484
0,00680
0,00940
0,01283
0,01729
0,02304
0,03036
0,03960
0,05114
0,06543
0,0830
0,1043
0,1301
0,1611
0,1979
0,2416
0,2929
0,3531
0,4229
0,5039
0,5970
0,7036
0,8254
0,9635
1,1199
1,296
Удельная
энтальпия
жидкости *',
кДж/кг
0
20,95
41,90
62,85
83,80
104,75
125,70
146,65
167,60
188,55
209,50
230,45
251,40
272,35
293,30
314,3
335,2
356,2
377,1
398,1
419,0
440,4
461,3
482,7
504,1
525,4
Удельная
энтальпия
пара i",
кДж/кг
2493,1
2502,7
2512,3
2522,4
2532,0
2541,7
2551,3
2561,0
2570,6
2579,8
2589,5
2598,7
2608,3
2617,5
2626,3
2636
2644
2653
2662
2671
2679
2687
2696
2704
2711
2718
Удель иая
теплота
парообразования г,
кДж/кг
2493,1
2481,7
2470,4
2459,5
2448,2
2436,9
2425,6
2414,3
2403,0
2391,3
2380,0
2368,2
2356,9
2345,2
2333,0
2321
2310
2297
2285
2273
2260
2248
2234
2221
2207
2194
548
Продолжение
Темпера*
тура,
°G
Давление
(абсолют.
ное),
кгс/см2
Удельный
объем,
м*/кр
Плотность,
кг/м3
Удельная
энтальпия
жидкости *',
кДж/кг
Удельная
энтальпия
пара t"t
кДж/кг
Удельная
теплота
парообразо*
ваиия г,
кДж/кг
130
135
140
145
150
160
170
180
190
200
210
220
230
240
250
260
270
280
290
300
310
320
330
340
350
360
370
374
2,755
3,192
3,685
4,238
4,855
6,303
8,080
10,23
12,80
15,85
19,5>
23,66
28,53
34,13
40,55
47,85
56,11
65,42
75,88
87,6
100,7
115,2
131,3
149,0
168,6
190,3
214,5
225
0,6693
0,5831
0,5096
0,4469
0,3933
0,3075
0,2431
0,1944
0,1568
0,1276
0,1045
0,0862
0,07155
0,05967
0,04998
0,04199
0,03538
0,02988
0,02525
0,02131
0,01799
0,01516
0,01273
0,01064
0,00884
0,00716
0,00585
0,00310
1,494
1,715
1,962
2,238
2,543
3,252
4,113
5,145
6,378
7,840
9,567
11,600
13,98
16,76
20,01
23,82
28,27
33,47
39,60
46,93
55,59
65,95
78,53
93,98
113,2
139,6
171,0
322,6
546,8
568,2
589,5
611,3
632,7
654,1
719,8
763,8
808,3
852,7
897,9
943,2
989,3
1035
1082
ИЗО
1178
1226
1275
1327
1380
1437
1498
1564
1638
1730
1890
2100
2726
2733
2740
2747
2753
2765
2776
2785
2792
2798
2801
2803
2802
2799
2792
2783
2770
2754
2734
2710
2682
2650
2613
2571
2519
2444
2304
2100
2179
2165
2150
2125
2120
2089
2056
2021
1984
1945
1904
I860
1813
1763
1710
1653
1593
1528
1459
1384
1302
1213
1117
1009
881,2
713,6
411,5
0
Таблица LVII
Свойства насыщенного водяного пара в зависимости от давления
Пересчет в СИ*. 1 кгс/см2 =* 9,81-10* Па.
Давление
(абсолютное),
кгс/см*
пература,
°С
Удельный
объем,
м3/кг
Плотность,
кг/м3
Удельная
энтальпия
жидкости *',
кДж/кг
Удельная
энтальпия
пара 1",
кДж/кг
Удельная
тепл ота
парообразования г,
кДж/кг
0,01
0,015
0,02
0,025
0,03
0,04
0,05
0,06
6,6
12,7
17,1
20,7
23,7
28,6
32,5
35,8
131,60
89,64
68,27
55,28
46,53
35,46
28,73
24,19
0,00760
0,01116
0,01465
0,01809
0,02149
0,02820
0,03481
0,04133
27,7
53,2
71,6
86,7
99,3
119,8
136,2
150,0
2506
2518
2526
2533
2539
2548
2556
2562
2478
2465
2455
2447
2440
2429
2420
2413
549
Продолжение
Давление
(абсолютное),
к г с/см*
Тем.
пера-
тура.
°С
Удельный
объем,
м*/кг
Плотность,
кг/мя
Удельная
энтальпия
жидкости i*,
кДж/кг
Удельная
энтальпия
пара ia,
к Д ж/кг
Удельная
теплота
парообразования г,
кДж/кг
0,08
0,Ш
0,12
0,15
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,0
1.2
1,4
1,6
1,8
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10
И
12
13
14
15
16
17
18
19
20
30
40
50
60
70
80
90
100
120
140
160
180
200
225
41,1
45,4
49,0
53,6
59,7
68,7
75,4
80,9
85,5
89,3
93,0
96,2
99,1
104,2
108,7
112,7
116,3
119,6
132,9
142,9
151,1
158,1
164,2
169,6
174,5
179,0
183,2
187,1
190,7
194,1
197,4
200,4
203,4
206,2
208,8
211,4
232,8
249,2
262,7
274,3
284,5
293,6
301,9
309,5
323,1
335,0
345,7
355,4
304,2
374,0
1Ъ,45
14,96
12,60
10,22
7,977
5,331
4,072
3,304
2,785
2,411
2,128
1,906
1,727
1,457
1,261
1,113
0,997
0,903
0,6180
0,4718
0,3825
0,3222
0,2785
0,2454
0,2195
0,1985
0,1813
0,1668
0,1545
0,К38
0,1346
0.1264
0,1192
0,1128
0,1070
0,1017
0,06802
0,05069
0,04007
0,03289
0,02769
0,02374
0,02064
0,01815
0,01437
0,01164
0,00956
0,00782
0,00614
0,00310
0,05420
0,06686
0,07937
0,09789
0,1283
0,1876
0,2456
0,3027
0,3590
0,4147
0,4699
0,5246
0,5790
0,6865
0,7931
0,898
1,003
1,107
1,618
2,120
2,614
3,104
3,591
4,075
4,536
5,037
5,516
5,996
6,474
6,952
7,431
7,909
8,389
8,868
9,349
9,83
14,70
19,73
24,96
30,41
36,12
42,13
48,45
55,11
69,60
85,91
104,6
128,0
162,9
322,6
172,2
190,2
205,3
224,6
250,1
287,9
315,9
339,0
358,2
375,0
389,7
403,1
415,2
437,0
456,3
473,1
483,6
502,4
558,9
601,1
637,7
667,9
694,3
718,4
740,0
759,6
778,1
795,3
811,2
826,7
840,9
854,8
867,7
880,3
892,5
904,2
1002
1079
1143
1199
1249
1294
1337
1377
1455
1531
1606
1684
1783
2100
2573
2581
2588
2596
2607
2620
2632
2642
2650
2657
2663
2668
2677
2686
2693
2703
2709
2710
2730
2744
2754
2768
2769
2776
2780
2784
2787
2790
2793
2795
2796
2798
2799
2800
2801
2802
2801
2793
2780
2763
2746
2726
2705
2684
2638
2592
2540
2483
2400
2100
2400
2390
2382
2372
2358
2336
2320
2307
2296
2286
2278
2270
2264
2249
2237
2227
2217
2208
2171
2141
2117
2095
2075
2057
2040
2024
2009
1995
1984
1968
1956
1943
1931
1920
1909
1898
1800
1715
1637
1565
1497
1432
1369
1306
1183
1061
934
799
617
0
550
ДИАГРАММЫ И НОМОГРАММЫ
-у мПя - с
-0,45
1-0,50
0,55
о,13-
0,18-
0,17-
0,f6-
0,15-
0,14
0,13-
0,12-
0,1] - - 0,00
0,10-
0,63- • 0,65
0fi8-
0,07-'°>70
0,00--0,75
0,05-
+у мПа * с
г-4,0
0,2^ '
0,19-
0,18 ~-3,25
0,17
3,75
-3,35
3,0
W:-2,75
0,15-
0,14-
0,13-
0,12-
0,11 - -
-2,55
-2,25
0,07-
2,0
1,90
№§1,80
0,05 - \ Щ
0,08 -" 1,60
-1,50
0,06 -. tfO
0,05- ш
0,04-
0,03-~°>85
0fi2--0,00
0,01--0,35
0±1fl
Рис, I, Номограмма для определения
динамического коэффициента
вязкости органических жидкостей.
1,30
0,04--
0,02'-_. уо
W; - i,os
О ±1.0
§рядидр.
4P*S
far
1ряд
5/>*p У dp.
Рис. П. Расположенно отверстий в трубных решетках двухходового кожухотрубчато-
fc теплообменника.
6ряд и dp
5ряд
Рис. III. Расположение отверстий в трубных решетках четырехходового кожухо-
трубчатого теплообменника.
554
Аиаметр df
500
4Q0
i
№-i
200-4
20-J
10
Расход V,
мз/ч 7
60000
40000
20000
10000
6QO0
4000
2000
1000
50000
30000
8000
5000
3000
Скорость Ш,
м/с '
30
Ей*
100
о
?Z70
El 60
- 50
-30
^-20
9 +
70
8
7
5
4
J
t-2
V
0,2
Рис. IV. Номограмма для определения расхода жидкости или газа в трубопровода! круг*
лого сечения.
200 tl
190-
180-
170-
160-
150—
140-
130 —
/20-
w-
Ю0~
90-
80-
70-
60-
50-
40-
30-
20-
о/
o2
04
o5
o7
oQ
z90
-60
t 50
f-J0
l~20
¦10
¦8
6
5
4
3
10-
0-
-10-
-20-
-30-
9<=>
10° И
98
JZ
On
-»и^5
^2527
2,^8o/5
15
r-2
oo.
J7^J»
о
39
о
40
¦f
¦0,6
0,5
0,4
E-^2
t-0,1
Рис. V. Номограмма &яя определения динамического коэффициента вязкости жидкостей
при различных температурах. См. также табл. VI — IX.
Жидкость
Номер
точки
Жидкость
Номер
точки
Амиловый спирт
Аммиак
Анилин
Ацетон
Бензол
Бутиловый спирт
Вода
Гексаи
Гептан
Глицерин, 100 %
Глицерин, 50 %
Диоксид углерода
Диэтиловый эфир
Метилацетат
Метиловый спирт,
МеТ ИЛОВЫЙ СПИрТ,
Метиловый спирт
Нафталин
Нитробензол
Октан
100 %
90 %
30 %
п
39
8
34
25
11
20
36
31
1
7
40
37
32
26
24
13
9
14
28
Центаы
Ртуть
Серная кислота 111 %
Серная кислота, 98 %
Серная кислота. 60 %
Сернистый ангидрид
Сероуглерод
Терпентин
Толуол
Уксусная кислота, 100 %
Уксусная кислота, 70 %
Фенол
Хлорбензол
Хлороформ
Четыреххлористый углерод
Этилацетат
Этиленгликоль
Этилеихлорид
Этиловый спирт, 10 %
Этиловый спирт, 49 %
ЗН
15
2
3
в
35
33
16
27
18
12
5
22
29
21
30
4
23
19
10
55G
t,°c
¦2000
1500
-1000
-900
-аоо
-700
-600
-500
-WO
rftl
t0,03
-0,06
-0,07
70,06
0,05
r0,04
\0,03 у
t
5 об
o15
o/4
о/г
-o,oo$
-0t008
-0,007
0,006
0,005
-0,004
-0,003
o2
oj
0*
0/7
C7
об
o»
oO
o//
0/3
Рис. VJ. Номограмма для определения динамического коэффициента вязкости газов
при р — 1 атм *;
i ~* 02; 2 -* NO; 3 — СОа; 4 — НС1; 5 — воэДух; tf — N2; 7 «» S02; в — CH4t 9 — Н,0;
J0 - NH3j ii — C2H0; J* - H2; i3 — СвНв; 14 *=* 9Н2 -f Ns* 15 — 3H2 4- N2i itf «* COi
.'7 *- CI,.
Пересчет в СИ; 1 атм — 760 мм рт. ет. =*= 101 32Б Па.
» С допустимым приближением данными номограммы можно пользоваться и при
давлении порядка нескольких атмосфер (нескольких десятков мегапасналей).
557
^Sft&gjMi?
to
5>
<5
6.
в
к
X
X
V
в
«
о
с
at
о
в«
¦а
о
а
«г
ъ
о.
и
В
a
х
a
ta
ы
о
я
о
X
tf
О
?
я
X
а.
v
н
К
a
и
л
н
ь»
О
?
X
?
ва
«J
со
J
а
ь
Рис. VII (продолжение)
i —* открытая турбинная мешалка с шестью прямбши вертикальными Лопатками {b ¦¦
= 0,20rfM; / — 0.25rfM) при D/dM — 3 в с ссуде с четырьмя Перегородками (б dM « 0,17):
2 —- турбинная мешалка типа / при й/^м — 0Л0; S — открытая турбинная мешалка
с шестью изогнутыми вертикальными лопатками (6 *¦ 0,20^, / « 0,25*?м) при А^м *= з
в еоеуде с четырьмя перегородками (В/^ ж 0,10); 4 ^ турбинная мешалка тигк: 1 при
B/dM *= 0 04; 5 — открытая турбнниая мешалка < шестью «трелввндиыми лопатками
(/; = 0,20ffM, I ¦" 0,25rfM) ирй ОД*м « 3 в сосуде с четырьмя иереРвродкаин (B/dM =
= О, Iо), ? — односторонняя раднально-дпековая мешалка о шестью прямыми верти*
шальными лопаткаыи {Ь = Q,l0dM. I = 0,35^) снизу даска прн 0/rfM « 2*5 в сосуде
с четырьмя перегородками (^/^м — 0,25); 7 — радиальная турбинная мешалка -г шевт*
яадцатьго лопатками го статором в сосуде без перегородок; 8 — Двухлопастная мешалка
G прямыми вертикальиыми лопаегями (Ь = 0.2Б4М) при DfdM*= 4.3Б в еоеуде € тревя
перзрородками (В/ам = 0,!'); 9 — восьмилонастная мешалка с пряными лопаегями (Ь ¦=
« 0,25#м) под углом 45° нрг -9/й'м — 3 н сосуде с четырьмя ПерегорвДкамй (B/dM «- 0,10);
?0 -=¦ дв>*> лопастная мешалка гнпа 8 прн ®/dM =» 3 в еоеуде с четырьмя перегородками
(Bid*. — 0,10). Л — закрытая турбинная мешалка с шестью лопатками со ©татором при
D/du =-= 2,4 в еоеуде без перегородок; 12 — турбинная мешалка, входная с типом 11*
при О <.JM = 3в сосуде бел перегородок^ 13 **¦ турбинная мешалка типа 12, без етаторг»
при -9/^м ж 3 s сосуда е четырьмя перегор»Дкзнн (B/d^ =*= 0,10); /4 *- турбинная
мешалка rrina 1 в сосуде без перегоредвк: 15 — трехлопастная првкеллериая мешалка
s — 2dM при 0/^м *= 3 в сосуде е четырьмя перегородками (B/dM в 0,10); /$ — четырек»
лопастная мешалка типа 8 при 0/^м *= 3 з еоеуде без перегородок; 17 *¦• четыреклопаст-
я'-я мешалка «лопаегями (Ь *= 0,25^м) под углем 60° прн D/<?M «= 3 в оосуде без вере*
городок- /? — трехлопаетиая пропеллерная мешалке гпна /5, но яри s = lf33dL. и -9/^м да
¦* lf> в сосуде с гремя перегородками (B/d^ ** 0,06); /5 — четырехлопавтная ^мешалка
тяиа 8 при 0/^м — 5,2 в сосуде без перегородок; 20 — двухлопастная мешалка типа 8
при &/dM =* 3 *¦ сосуде без перегородок: 2J — трехлоиастная пропеллерная мешалка
типа 15 при О riM — 3,3 в сосуде без перегородок; 23 -*¦ четырехлопавтная мешалка типа ?
(такая же, как 19) при 0/«м — 2,4^3,0 в сосуде без перегородок; 23 * трехлопастная
пропеллерная мешал на тиий IS при s = l«04rfM и O/rf = 9,6 в сосуде « тремя перегоред-
камн (В/ам = 0,06); 24 *- то же npi: ь = (^ и О/^ — 3 в еоеуде с четырьмя яерегврвд-
ками (в"*м = 0,10) 25 — то же при $ = b°4dM и ^/^м e 4.S в еоеуде бе» перегородвк;
26 — го же при с = йм и ?>/^м "= 3 в еоеуде без перегородок; .27 •* то же при в « U06^M
в 0/dM «* 2*7 а сосуде без перегородок; 5Л — то жг при и — ^м и D/^M = 3(8 в еоеуде беа
перегородок: 29 — двухлопастная мешалка типа S о узкими лопастями [Ь «* <0Л8ф
¦4-0,17) riM] при ?7^м ~ 1Л с сосуде без перегородок.
Обозначения, принятые для характеристики мешалок: D —¦ диаметр вееуда; #м ¦¦
диаметр мешалки; Ь — ширина лопасти мешалки; ' *^ Длииа лопасти; В ^- ширина
перегородки; s — шаг пропеллерной мешалки.
О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 OjS 0,3 1,0
Р
tPE
5~t
1
Era,»'»
**
0,50 0,1 0,2 0,3 Ofi 0,5 0,6 0,7 0,8 4,9 1,0
P
Рис. VIU. Поправочные коэффициенты е для смешанного тока в мнороходовых кожу*
Хотрубчатых теплообменниках:
а — с одним кодом в межтрубном пространстве в двумя* чесырьмя# шадТь» н более кодамв
а трубном простраиетве; ё ~ с двумя ходами в мыктрубном пространстве в поперечными
перерородквмн и четырьмя йодами в трубном пространстве; р = (/г «* tS/ifi ** *i)I
о^
8
ем
0 200 400 600
800 1000
Рис. IX. Коэффициенты теплопроводности дымовы.ч газ<->в Состав дымовых гячпп'
% (об.); СОа — 13; Оа — 5; (N„ -f H,0) ~ 82. состав дымовых газов,
Содержание еоданого пара (в %): / — 0; 2 — 15; 3 ~ 20
Пересчет в СИ: 1 ккал/(м. ч.°С) = 1,163 ВтДм- К.,,
560
Рис. X. Коэффициенты теплопроводности некоторых жидкостей.
Вещество
Аммиак, 26 %
Аиилни
Ацетон
Бензол
Бутиловый спирт
Вазелиновое масло
Вода
Гекеан
Глицерин безводный
» 50 %
Диэтиловый эфир
Изопропиловый
спнрт
Касторовое масло
Керосин
Ксилол
Номер
линии
31
6
8
и
9
15
16
26
1
25
29
12
5
28
14
Вещество
Метиловый спирт,
100 %
То же, 40 %
Муравьиная
кислота
Нитробензол
Октан
Серная кислота,
98 %
Сероуглерод
Соляная кислота,
30 %
Толуол
Уксусная кислота
Хлористый
кальций, 25 %
Номер
ЛНН0Н
3
32
2
10
33
30
23
27
13
7
17
Вещество
Хлористый
25 %
натрий,
Четыреххлористый
углерод
Этиловый
100 %
Этиловый
80 %
ЭТИЛОВЫЙ
60 %
Этиловый
40 %
Этиловый
20 %
спирт,
спирт.
спирт.
спирт.
спирт,
Номер
лннвн
18
24
4
19
20
21
22
Пересчет в СИ: 1 ккал/(м-ч. °С) = 1,163 Вт/(м- К)
2
о
rfc
•Qfi
2Q0-
150-=
Ю0~
оЗ
о4
^qj
о
8
10
9о°2Э
11
о
°J0
75
Е-44
Ж
/ЗсР о/4
?-0,5
о
13
о
о
/7
24 25
20
о
/5
2'оо22
33 о ° o"oo27^!i-
--* "?""25
J2
о34
-0,7
35
о
3?
о
Qfi
-0,8
—0,9
r-W
о
о
!
с*
-о
?
I
а>
I
6
§
¦о
с;
Рис. XI. Номограмма для определения теплоемкости жидкостей,
Вещество
Амилацетат
Анилин
Ацетон
Бензол
Бромистый этил
Бутиловый спирт
Вода
Гептан
Глицерин
Дифенил
Диэтиловый эфир
Иэобутиловый
спирт
Изопентаи
ИзопропиловыЙ
спирт от 0 до 50 °С
Пересчет в СИ:
Номер
точки
12
14
18
29
1
24
36
18
21
f
17
33
20
32
1 ккалУ
Вещество
ИзопропиловыЙ
спирт (от —50 до
0°С)
Йодистый эт-нл
0- Н .И-К.СНЛОЛ
п- Ксилол
Метиловый спирт
Октан
Пропиловый спирт
Серная кислота,
100 %
Сероуглерод
Соляная кислота,
30 %
Толуол (от —60 до
40 °С)
(кг.°С) = 4,19. 10' Дл
Номер
точки
27
5
9 \
10 !
23
15
25
7
4
26
28
</(кг. К)
Веществ
Толуол (от 40 до
100 °С)
Уксусная кислота,
100 %
Хлорбензол
Хлористый
кальций, 25 %
Хлористый натрий,
25 %
¦ Хлористый этил
Хлороформ
Четыреххлористый
углерод
Этилацетат
Этиленгликоль
Этиловый спирт
_
Номер
точке
Зо
16
6
34
35
11
3
2
13
22
31
562
10000
20000 -1
20000 ¦=
40000
50000
60000
70000
80000
900QO
WO 000
200 OQO -=
JWflOD ^
-ИЮЛЮ
7ДОШ
8000QO
900000
1QQOOOO
100009
90 OQO
80 0№
7в от
600Ш
50 OQO
40 от
зо от
Шг 20000
W
вот
7 от
BOQQ
500(3
4 OOQ
Рис. XII, Номограмма для определения коэффициента теплосмдачи j прямых трубах
при Re > 10 000 и el = U
I этап: АВ -> С; Ц этап: ОС -» Е.
563
t,°c
1201
w-
-
100-
90-
80-
10-
60-
50-
40-
30-
20-
10 -
0 -
-10-
-20-
Pr
^100
-500
r400
YZOO
36
1-20O
0 Г
/
0
2
о 4
V
*0 ^-
JOo -—- ЛЛ
^—-"^ °/j/50o
---¦-* -7 a?Wo22
0?7 №&
29
4?0
~fO0
. _,
—
-50
С
|-20
jpffl
-5
F
|-2
Е.Г.5
Рис. XIII Значения критерия Рг для жидкостей.
Вещество
Амилацетат
Аммиак, 26 %
Аиилин
Ацетон
Бензол
Бромистый этил
Бутиловый спирт
Вода
Гелтаи
Диэтиловый эфир
Глицерин, 50 %
Изоамиловый спирт
Изопропиловый
спирт
Йодистый зтнл
Ксилол
Номер
точки
31
14
5
25
22
29
11
17
32
28
6
3
7
27
19
Вещество
Метиловый спирт.
100 %
Метиловый спирт.
40 %
Октаи
Пентан
Серная кислота,
Ш %
Серная кислота,
98 %
Серная кислота,
60 %
Сероуглерод
Соляная кислота,
30 %
Номер
точки
20
10
33
26
1
2
4
30
21
Вещество
Толуол
Уксусная кислота,
100 %
Уксусная кислота,
50 %
Хлорбензол
Хлороформ
Четыреххлористый
углерод
Этилацетат
Этиленгликоль
Этиловый спирт,
100 %
Этиловый спирт,
50 %
Номер
точки
23
15
9
35
34
18
24
36
13
8
564
t°c
-60 A
-SQ-i
Погексану
±.
-40 4
-30
-20 4
-/0
w
20-1
30-
40.
?0-j
70-1
80-
90-
WO-
110-
no-
w-
HO-
150-
novo-
18Q-
-100^5000 J
1Г р,мм рт. ст.
По воде
Si
/J<
0
/5
/4J
/7
/5
16)
ao.
•50
27
W
00
h200
25(7
w$-3QQ
48
1-2000
.1000
L500
¦40' %
¦30
¦ 200
100
5U
•20
10 -
3^50
54Ы0
20
3-w
I-f
A*
A°G
\--Ю
\~0
10
20
PJ?7
40
~9Q
1Q
80
^90
100
w
¦120
7JO
¦140
¦150
¦160
¦170
¦180
¦19Q
Рис. XIV. Hoiwuграмма для определения давления насыщенного пара и
ьипес ия некоторых жидкостей.
температуры
565
Рнс. XIV. (продолжение).
Вещество
Аллеи
Аммнак
Анилин
Ацетилен
Ацетон
Бензол
Бромбензол
Бромистый этил
се-Бромнафталнн
1,3-Бутадиеи
Бутан
ее-Бутилен
Р-Бутнлен
Бутнленгл:;коль
Иода
Гексан
Гептан
Глицерин
Декалин
Декан
Диоксан
Дифеиил
Номер
точки
6
49
40
2
51
24
35
18
46
10
11
9
12
5S
54
22
28
60
38
36
29
45
Вещество
1,2-Днхлорэтан
Диэтиловый эфир
Изонреи
Иодбензол
ж-Крезол
о-Крезол
ж-Ксилол
азо-Мзсляиая
кислота
Метиламин
Метнлмоносилан
Метиловый спирт
Мети лформа ат
Нафталин
а-Нафтол
3» Нафтол
Нитробензол
Октан
Пентан
Пропан
Номер
точки
26
15
14
39
44
41
34
57
50
3
52
16
43
47
48
37
31
S2 *
17
5
Вещество
Пропилен
Пропиоиовая
кислота
Ртуть
Тетралии
Толуол
Уксусная кислота
Фторбензол
Хлорбензол
Хлористый винил
» метил
» метилен
» этнл
Хлороформ
Четыреххлористый
углерод
Этан
Этилацетат
Этнлеиглнколь
Этиловый спирт
С'Тилфорыиат
Номер
точки
4
56
61
42
30
65
27
33
8
7
19
13
21
23
1
25
59
53
20
Пересчет в СИ: 1 мм рт. ст. = 133,3 Пп.
* По данным разных авторов
01 b 1 1 1 1 1 1 1 1 1 1 Ы
-40 0 40 80 120 160 200
Температура иипения жидкости, °С
Рис. XV. Диаграмма линейности для определения температуры кипения (по воде);
1 — диэтиловый эфир; 2 — сероуглерод; 3 — ацегон; 4 — хлороформ; 5 — четырех»
клористый углерод; 6 — бензол; 7 —¦ толуол; 8 — хлорбензол; 9 — о-ксилол; 10 ¦»«• брок-
i tH30JI* " ~~ бензальдегид; 12 — анилин.
10 20 30 40 50 GO 7Q 80 30 100
Температура кипения жидкости7°С
Рис. XVI. Диаграмма линейности для определения температуры кипения (по гексану)*
3 — диэтнловый эфир; I1 —- сероуглерод; 3 « хлороформ; 4 =* четыреххлористый
углерод; 5 — бензол; 6 — толуол.
А ММ РТ.СТ.
7 л
OVV
700
600
500
450
400
350
WW
30Q
2^0
200
150
120 <
j
А
/
?
J
*
/
г1
Л
s
,
20
30
40
50
60
t,°c
Рис. XVII. Зависимость давления насыщенного пара гексана от температуры*
Пересчет в СИ: 1 мм рт. ст. — 133,3 Па.
70
567
У.ккал/кг
95
60 70
t,°C
Рис. XVIII. Зависимость удельной теплоты парообразования гексана от температуры.
Пересчет в СИ: I ккал/кг = 4,19 кДж/кг
50
40
30
20
10
oU В
*• 7
Си *
р с.
-so 5
4к
—- -"
*
i
/
с>*
А
v/
*
$
-ч
^
^
'С
1°Ч
^
\/
<ь
г
'?
h
г -<
S
Г/
/^
и^>
^
И
г 1
1&
¦- v^<
Ж
/
*
>5
^^
\р
4
&
t\
1
й
^О
V
^.
?-f
•^i
7?
Ю
20 30 40
Ионцентрация, %(масс)
SO
Рис. XIX. Повышение температуры кипения водных растворов (при атмосферном даьле«
нии) в зависимости or концентрации.
568
150
О
о
I
С
100
50
¦
'
?
м
ш
о
от
«3
г;
i
У
№>
\
3
¦*,
/с
f/
i i
-(
J
5
/
t^Z-
<?/
у
•
*'
«oV
\>
^о7
/0
/5
20
Концентрат насыщенного раствора ,моль ББЗР0Дн°и ">*>*
г ^ ? 1000 г воды
Рис, XX, Растворимость некоторых солей в воде в зависимости от температуры*
V
100
90
80
70
60
50
АО
30
20
10
—
I-/
/
1—*-
у/
}
/
/
'
у
/
1^
У
У
^
9*
г
/
йЛт
X
Рис. XXI. Кривые равновесия при П — 760 мм рт. ст.:
I — ацетон—вода; 2— четыреххлорнстый углерод—толуол,
Пересчет в СИ: 760 мм рт, ст. = 1 атм — 101 325 Па.
669
wo
30
80
ТО
во
50
40
30
20
Ю
О
¦
$
1
/
1
г"
—^
А
'/
'у
2
/
,.-.-
?
i
<
/i
i
—f.,—
Ю 20 30 40 50 60 70 80 90 100
cc
Р,ммрт.ст.
800
10
30 50 70 Э€ 110 130
t,°c
Рис. XXII, Кривые равцовесия (c азеотропной точкой) при П = 760 мм рт, ст.З
* — вода ^-муравьиная кислота; :' — метиловый спнрт — бензол.
Пересчет в СИ: 760 мм рт> ст> == j атм — ю! 325 Па.
Рис. ХХШ. Давление н^СЫщенн0Г0 аара некоторых органических жидиостей в зависи<
мости от температуры;
1 — Днэтиловый эфир; 2 =- ацетон, 3 — метиловый спирт; 4 — этиловый спирт; 5 ~*
муравьиная кислота; 6 ^ уксусная кислота.
Пересчет в СИ: 1 мм р>. Ст. — 133,3 Па.
800
760
40 ВО
100 120 140 160 180 200
Рис. XXIV. Давление насыщенного пара органических жидкостей, не смешивающихся
с водой, в зависимости от температуры:
i=- сероуглерод; 2 — ге^саН; з „_ четыреххлорнстый углерод; 4 =• бензол; 5 ™ толуол;
6^~ скипидар; 7 — анилии; $ «. крезол; 9 — нитробензол; 10 =• илтротолуод»
Пересчет в СИ: 1 мм рт, СТ( s 133,3 Па.
570
1JB /f7 %8 1,9
Удельная .энтропия 5,ккал/Осг*К)
Рис. XXV. / — S диаграмма для водяного пара.
Пересчет в СИ: 1 ккал/кг — 4,19 кДж/кг; 1 кгс/см — 9,81. 10* Па.
У
571
Рис. XXVb T— S диаграмма для аммиака
Пейесче-Е а СИ: 1 ккал/кг = 4,1&* Ю*
1 кгс/см' = 9,8Ь ID* Па.
Ц40,9 130 Ц 1,2 ?3
Удельная 'энтропии 5,квад/(кг"К)