БИБЛИОТЕКА ПО АВТОМАТИКЕ
Выпуск 565
И. П. ПАЛЬТОВ
НЕЛИНЕЙНЫЕ МЕТОДЫ
ИССЛЕДОВАНИЯ
АВТОМАТИЧЕСКИХ СИСТЕМ
«ЭНЕРГИЯ»
ЛЕНИНГРАД 1976

б4>б.§
П 14
УДК 62-503.2
Редакционная коллегия
И. В. Антик, Г. Т. Артамонов, А. И. Бертинов, М. А. Боярченков,
А. А. Воронов, Л. М. Закс, В. С. Малов, В. Э. Низе,
Д. А. Поспелов, И. В. Прангишвили, О. В. Слежановский,
Ф. Е. Темников, М. Г. Чиликин, А. С. Шаталов
Рецензент Е. Н. Розенвассер
Пальтов И. П.
П 14 _ Нелинейные методы исследования
автоматических систем. Л., «Энергия», 1976.
128 с. с ил. (Б-ка по автоматике. Вып. 565)
В книге изложены основные методы исследования
непрерывных автоматических систем при учете существенных нелинейностей.
Рассматриваемые вопросы выполнены в доступной широкому кругу
читателей форме. Теоретические методы иллюстрируются
расчетными примерами.
Книга предназначается для инженеров, занимающихся
проектированием автоматических систем, а также для студентов
технических вузов, изучающих теорию автоматического управления.
П 30502-153 128,76 6ф6 5
051(01)-76
© Издательство «Энергия», 1976

ПРЕДИСЛОВИЕ
В настоящее время имеется большое количество
литературы, освещающей вопросы исследования
линейных и нелинейных замкнутых автоматических
систем. Начинающему исследователю зачастую
нелегко выбрать нужный метод исследования,
применимый для конкретной системы, и овладеть теорией,
излагаемой в объемных монографиях. В
предлагаемой брошюре автор сделал попытку изложить
основные вопросы теории автоматического
регулирования нелинейных систем, часто встречающиеся
в инженерной практике и необходимые при
начальном изучении методов исследования нелинейных
автоматических систем.
Первая глава включает в себя основные
вопросы составления структурных схем, их
преобразования, составления уравнений и классификации
нелинейных систем.
Во второй главе рассматриваются точные
методы исследования нелинейных систем: метод при-
пасовывания, графо-аналитический метод решения
нелинейных уравнений (который из-за малости
методической ошибки автором отнесен к точным
методам), метод фазовых траекторий. В этой же главе
рассматриваются теоремы прямого метода А. М.
Ляпунова для исследования устойчивости нелинейных
систем и частотный метод исследования
устойчивости В. М. Попова.
Третья глава посвящается рассмотрению основ
метода гармонической линеаризации, как
приближенного метода исследования нелинейных систем
более высокого порядка (выше второго). Метод
гармонической линеаризации удачно сочетается с
точными методами, применение которых становится
затруднительным (из-за большой трудоемкости
вычислений) в случае систем выше третьего
порядка.
Четвертая глава освещает вопросы
исследований нелинейных систем на основе метода
гармонической линеаризации в случае несимметричных
колебаний и учета внешних воздействий в
автоколебательных системах.
1*
3

В пятой главе рассматриваются методы оценки
качества систем и синтеза корректирующих
устройств в нелинейных автоматических системах с
применением показателя колебательности, как
критерия качества равновесно сходящихся нелинейных
процессов.
Отзывы о книге и замечания просьба присылать
по адресу: 192041, Ленинград, Марсово поле, д. 1,
Ленинградское отделение издательства «Энергия».
Автор

ВВЕДЕНИЕ
Основой теории автоматического регулирования является
изучение движения замкнутых автоматических систем и их
построение с целью обеспечения оптимального в некотором
смысле хода процесса. Реальные системы, как правило,
нелинейны, т. е. имеют нелинейные зависимости в исходных
уравнениях, определяющих их движение. При изучении процессов,
протекающих в замкнутых автоматических системах, движение
систем описывается с помощью уравнений (дифференциальных,
алгебраических, разностных). Этот переход от реальных
процессов il их математическому представлению, естественно, не
может быть сколь угодно точным. Именно с этим переходом
связано деление систем на линейные и нелинейные. В предлагаемой
брошюре рассматриваются наиболее распространенные
непрерывные системы с процессами, описываемыми
дифференциальными уравнениями.
Под линейными непрерывными системами понимаются
такие системы, процессы в которых с достаточной для
практических исследований точностью описываются линейными
дифференциальными уравнениями. К нелинейным системам, в свою
очередь, относят системы, процессы в которых описываются
нелинейными дифференциальными уравнениями. Как видно,
деление автоматических систем на линейные и нелинейные
является условным. Оно отражает методы математического
представления и исследования реальных систем. В первом случае
реальная система для исследования принимается в виде
линейной модели, тогда как во втором — в виде нелинейной, т. е. при
учете основных нелинейностей. Во многих случаях одна и та
же система в первом приближении может быть исследована как
линейная, а при уточнении исследований может
рассматриваться как нелинейная.
Методы линейной теории автоматического регулирования
хорошо разработаны и поэтому могут широко применяться на
первом этапе исследования многих нелинейных систем. Однако
имеются нелинейные системы, например релейные, которые с
самого начала должны исследоваться в качестве нелинейных.
Нелинейные системы имеют свои особенности,
усложняющие их исследование. В таких системах нет подобия процессов
при различных начальных состояниях и различных величинах
внешних воздействий. К ним неприменим принцип
суперпозиции. В переходном процессе в нелинейных системах изменяются
не только амплитуда, но и частота колебаний.
5

Нелинейные системы могут иметь несколько состояний
устойчивого и неустойчивого равновесия. Области устойчивости
в нелинейных системах определяются не только значениями
параметров, но и соотношением между начальными условиями.
Нелинейные системы, в отличие от линейных, могут иметь не
только сходящиеся и расходящиеся процессы, но и устойчивые
собственные периодические движения — автоколебания и
более сложные процессы.
В зависимости от типа проектируемой нелинейной системы,
условий ее работы и предъявляемых требований может
оказаться, что в одних случаях следует иметь устойчивый в
отношении равновесия установившийся режим, а в других-—
автоколебательный режим.
Для автоматических систем с большими подвижными
массами, мощными управляемыми объектами автоколебательный
режим недопустим, так как при таком режиме возникнут
недопустимые перегрузки, будут преждевременно изнашиваться
кинематические передачи, появятся дополнительные ошибки.
В системах с малыми подвижными массами, например в
измерительной аппаратуре, автоколебательный режим зачастую
может быть полезным, так как при этом повышаются
быстродействие системы и чувствительность измерительного прибора
за счет ликвидации зоны застоя.
Поэтому проектирование-нелинейных систем, как и
линейных, должно начинаться с изучения условий работы и
разработки требований на проектирование. Постановка требований на
проектирование часто определяет и методы исследования
нелинейных систем.
Важным этапом проектирования является составление
структурной схемы или математической модели системы. Структурная
схема системы составляется на основании принципиальной или
функциональной схемы, определяемыми назначением и
принципом действия первоначального варианта системы. Одновременно
со структурной схемой системы составляется и
дифференциальное уравнение или система дифференциальных уравнений,
описывающих движение нелинейной системы.
После составления уравнений обычно выполняется
исследование процессов в замкнутой системе. Для нелинейной системы
важно определить возможные виды процессов в зависимости от
значений параметров и начальных условий. После выполнения
такого исследования и выбора параметров системы из условия
обеспечения желаемого вида процесса можно более подробно
исследовать качество процесса на основании решения
дифференциального уравнения или косвенными методами.
По условиям задания на проектирование может оказаться,
что исходная система не способна удовлетворить требованиям
на проектирование. Тогда следует прибегнуть к изменению
исходной структурной схемы с задачей получения требуемого
качества процесса в системе. Чаще всего такая задача решается
введением в систему корректирующих устройств.
Исследование нелинейной системы по ее исходной
структурной схеме, а также синтез корректирующих устройств должны
выполняться методами нелинейной теории, основы которых
излагаются в брошюре.

ГЛАВА ПЕРВАЯ
СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ И УРАВНЕНИЙ
НЕЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
1-1. Нелинейности в автоматических системах
Дифференциальные уравнения, описывающие динамику
процессов в автоматических системах, могут быть нелинейными
вследствие того, что в них некоторые переменные или их
производные по времени входят не в первой степени или имеется
произведение переменных и производных либо иная нелинейная
комбинация. Кроме того, коэффициенты уравнений могут быть
функциями переменных и их производных.
Нелинейные автоматические системы обычно представляют
собой комплекс произвольного конечного числа звеньев, причем
динамика большинства из них описывается линейными
дифференциальными уравнениями, а одно или несколько звеньев
описываются нелинейными уравнениями.
Как линейные, так и нелинейные системы при исследовании
удобно представлять структурными схемами (математическими
моделями). Для примера на рис. 1-1 представлена структурная
схема нелинейной системы, в которой линейные звенья
обозначены передаточными функциями W (р) с соответствующими
индексами, а нелинейное звено представлено в виде некоторой
нелинейной функции х3 = F (х). На схеме через g обозначено
задающее воздействие, через у — выходная величина системы, а
через finf2 — возмущающие воздействия, приложенные к системе.
При рассмотрении нелинейных звеньев следует отличить
понятие нелинейного звена от понятия нелинейности.
Нелинейным звеном называется некоторый элемент системы, который
описывается нелинейным уравнением, например
— безынерционное нелинейное звено (здесь хг и х2 — входная
и выходная величины нелинейного звена);
или уравнением
x2 = F (*i)
(1-D
(1-2)
xt = Fx (х1) = е-Хр F (Xl)
— нелинейное звено с временным запаздыванием.
(1-3)
7

Под знаком нелинейной функции может находиться как
входная, так и выходная переменная нелинейного звена.
Нелинейное звено может описываться уравнением, содержащим как
линейные, так и нелинейные члены, например, уравнением (1-2).
Под нелинейностью понимается нелинейная функция, входящая
в уравнение нелинейного звена.
Рис. 1-1
При применении некоторых методов исследования
нелинейных систем, например метода гармонической линеаризации,
удобно переходить к свернутым структурным схемам, выделяя
нелинейное звено, а все линейные звенья объединяя в единый
структурный блок, называемый линейной частью системы. Так,
нелинейную систему со структурной схемой, изображенной на
рис. 1-1, в свернутом виде можно представить, как показано
на рис. 1-2, а.
а)
6)
Линейная
часть
системы
1-Х XJ
Нелинейное
звено
\х Z
Приведенная
линейная
часть
Нелинейность
Рис. 1-2
Линейная часть системы сама по себе может иметь любую
структуру, в том числе многоконтурную, с различного вида
корректирующими устройствами.
В уравнении нелинейного звена могут находиться линейные
члены, как, например, (Тр + 1) х2 в уравнении (1-2). Поэтому
в нелинейном звене можно выделить нелинейность, т. е.
входящую в это уравнение нелинейную функцию, а оставшуюся
линейную функцию отнести к линейной части, назвав ее при этом
приведенной линейной частью системы. Так, в уравнении (1-2)
нелинейность можно записать в виде
z=F(Xl) (1-4)
и получить линейное уравнение
(Тр + \)х2 = г.
(1-5)
8

При этом, отнеся к линейной части линейное уравнение (1-5),
получим приведенную линейную часть и нелинейность (рис. 1-2,6).
В нелинейных автоматических системах очень часто
нелинейности приходится учитывать в виде статических характери-
Рис. 1-3
стик (статические нелинейности). Эти характеристики могут быть
однозначными нечетно-симметричными, двузначными гистерезис-
ными, однозначными четно-симметричными, двузначными
опережающими и в общем случае любыми несимметричными.
Рис. 1-4
На рис. 1-3 представлены однозначные нечетно-симметрич.
ные нелинейности: а — идеальная релейная характеристика^
б — релейная характеристика с зоной нечувствительности'
в — характеристика с насыщением или ограничением, г — ха!
Рис. 1-5
рактеристика с переменным коэффициентом усиления. Здесь
и далее на статических характеристиках угол наклона
соответствующего участка в целях экономии места обозначается условно
через к вместо arctg k (k есть коэффициент усиления).
Некоторые гистерезисные двузначные статические
характеристики изображены на рис. 1-4: а — релейная характеристика
9

общего вида, б — релейная гистерезисная характеристика
в — характеристика для учета люфта или зазора.
Двузначные опережающие характеристики на рис. 1-5, а—в
соответствуют специально создаваемым нелинейным
корректирующим устройствам.
* Несимметричные статические нелинейности представлены на
рис. 1-6, я, б, в. Четно-симметричная нелинейная
характеристика изображена на рис. 1-6, г.
Рис. 1-6
Учет одной нелинейности в системе представляет более
простую задачу расчета нелинейных автоматических систем. Часто
приходится учитывать несколько существенных нелинейностей.
Кроме статических, в дифференциальные уравнения могут
входить нелинейности от производных переменных нелинейного
звена — динамические нелинейности.
1-2. Классификация и структурные преобразования
нелинейных систем
Проектирование нелинейных автоматических систем обычно
содержит те же этапы, что и проектирование линейных систем:
1) изучение условий работы создаваемой системы и постановка
требований на проектирование; 2) построение структурной схемы
или модели системы; 3) составление дифференциальных
уравнений, описывающих движение системы, и анализ процессов
методами теории регулирования; 4) синтез корректирующих
устройств с последующим изменением структуры системы;
5) проверка результата синтеза путем построения фазовых
частотных характеристик, кривых переходных процессов или
путем моделирования системы; 6) натурные испытания опытного
образца системы.
На стадии изучения условий работы системы
рассматриваются основные функции, выполняемые системой; составляется
ее принципиальная схема; изучается регулируемый или
управляемый объект; выявляются внешние полезные и возмущающие
воздействия; учитываются экономические и эксплуатационные
факторы. Уже на этом этапе выявляются основные
нелинейности, которые надлежит учесть при проектировании системы.
Важным этапом проектирования является построение
структурной схемы системы и выбор метода (аппарата)
исследования.
10

В соответствии с видом нелинейностей и местом их в
структурных схемах примем нижеприведенную классификацию
нелинейных систем.
Нелинейными системами первого класса будем считать
системы, в уравнения которых под знаком нелинейной функции
входит только одна переменная, возможно со своей производной.
Наиболее распространенными нелинейными системами^первого
класса являются системы, содержащие нелинейности вида z =
= F (х) или z = F (Ху рх). С точки зрения структурных схем
нелинейные системы первого класса обычно имеют одно
нелинейное звено или два звена, не разделенных линейной частью
(рис. 1-7). В последнем случае два нелинейных звена могут быть
приведены к одному более сложному нелинейному звену, так
как в результате двух нелинейных операций можно получить
нелинейное уравнение,
непосредственно связывающее входную
величину первого звена с выходной
величиной второго звена.
К нелинейным системам
второго класса относятся такие
системы, в уравнения которых под
знаками нелинейных функций
входят две (или более)
переменные. Так, если в системе имеется
нелинейное звено, описываемое
уравнением
-
Линейная
часть
Нелинейное
Нелинейное
звено I
звено Л
F (х2) рх2 + х2 = k^,
Рис. 1-7
то она относится к первому классу, так как произведение
F (х2) рх2 является нелинейным выражением типа г — F (х2) рх2).
Но'если нелинейное звено описывается уравнением
F(xi) px2 + x2 = k1x1,
то даже без других нелинейностей система будет относиться ко
второму классу нелинейных систем, так как произведение
F (хг) рх2 является нелинейностью типа г = F (хъ px2)t где
Xi и рх2 связаны между собой линейным дифференциальным
уравнением линейной части системы.
К нелинейным системам второго класса также относятся
системы с двумя или несколькими нелинейными звеньями, если
переменные под знаками нелинейных функций разделены
достаточно сложными линейными частями, не описываемыми
одним из простых соотношений:
х2 = kxlt х2 = \грхъ х2 = k
При приведенных простых соотношениях для линейных частей
в большинстве случаев нелинейную систему можно привести
к системе первого класса.
К нелинейным системам второго класса относятся и такие
системы, в уравнения которых под знаками нелинейных
функций входят две или более переменных, связанных между собою
нелинейными дифференциальными уравнениями. Сюда отно-
11

сятся, например, системы со схемой рис. 1-8, когда в
уравнениях обоих нелинейных звеньев под знаками нелинейных
функций стоят либо входные переменные хг и х3, либо выходные
переменные х2 и *4. Эти переменные не могут быть связаны между
собой линейными дифференциальными уравнениями.
Линейная
*1
Нелинейное
часть!
звено!
Нелинейное
Линейная
звено Л
часть П
Рис. 1-8
При расчёте автоматических систем проектируемую систему
обычно представляют в виде развернутой структурной схемы,
где изображается каждое динамическое звено. В линейных
системах каждое звено обладает определенной передаточной
функцией, параметры которой не зависят от состояния соседних
звеньев. Методика преобразования структурных схем с линей-
ньши звеньями хорошо известна.
о)
6)
?2
W, W3
Рис. 1-9
В нелинейных звеньях параметры зависят от величины
входного или выходного сигнала. Преобразования структурных схем
нелинейных систем требуют специального подхода с учетом
свойств нелинейных звеньев.
В том случае когда требуется «свернуть» структурную схему,
преобразования над линейными звеньями можно выполнять,
как обычно. Так, для структурной схемы на рис. 1-1 после
приведения звеньев, охваченных обратной связью, к одному полу-
12

■ы F
UW3Ws
nw3ws
■4
г)
3)
w2
F
У
У
UW5W5
1+W,WS
Рис. 1-10

чим схему, изображенную на рис. 1-9, а. После приведения по*
следовательных линейных звеньев к одному получим схему
(рис. 1-9, б), состоящую из линейной части с соответствующей
передаточной функцией и нелинейного звена с нелинейной
функцией F (х).
При переходе от развернутых к свернутым схемам часто
становятся неявными места приложения внешних воздействий.
Поэтому свернутые схемы удобны для исследования собственных
движений систем, например для определения автоколебаний,
и неудобны для изучения их движения при приложении внешних
воздействий. В том случае когда требуется исследовать
движение нелинейной системы при внешних воздействиях,
структурные преобразования следует выполнять с сохранением
интересующих нас входов и выходов системы.
Рассмотрим пример приведения многоконтурной системы
с одним нелинейным звеном к одноконтурной с сохранением
места приложения входного задающего воздействия и выхода
системы. Исходная структура системы представлена на
рис. 1-10, а. После приведения линейных
встречно-параллельных звеньев Wz и Wb к одному получим схему на рис. 1-10, б.
Выполняя вынос звеньев за пределы соответствующих контуров,
имеем схему, показанную на рис. 1-10, в. Объединив обратные
связи в одно звено, получим схему, изображенную на рис. 1-10,г.
И, накойец, отделив звено W2 от нелинейного элемента F,
получим структурную одноконтурную схему с изолированным
нелинейным элементом (рис. 1-10, д).
При преобразовании структурных схем нелинейных систем
сначала рекомендуется выполнять операции над линейными
звеньями. Так как вид сигнала на выходе нелинейного элемента
существенно зависит от амплитуды входного сигнала, то нельзя
менять местами с нелинейным элементом линейные звенья и
точки суммирования. С линейными звеньями, расположенными
по ту или иную сторону нелинейного элемента, можно
производить любые преобразования.
1-3. Преобразования нелинейных статических
характеристик
Поскольку нелинейности в системах чаще всего учитываются
в виде статических характеристик, целесообразно рассмотреть
методы их преобразования. Такие преобразования обычно
выполняют с целью объединения смежных нелинейных звеньев
для упрощения проводимых исследований. Смежные звенья
с нелинейными статическими характеристиками могут
встречаться в схемах в виде последовательного соединения, согласно-
параллельного соединения и встречно-параллельного
соединения, или обратной связи (рис. 1-11).
При последовательном соединении двух звеньев с
нелинейными статическими характеристиками (рис. 1-11, а) для
результирующей характеристики можно записать:
x2 = F(Xl) = F2[FX (хг)).
Запись означает, что результирующая характеристика
может быть получена как нелинейная функция F2 аргумента, стоя-
14

щего в квадратных скобках, который сам является нелинейной
функцией х = Fx (хх).
Предположим, что первое звено имеет нелинейную
статическую характеристику
х = х\ sign х{,
а второе звено — статическую характеристику
з г-
Ч = у * .
Результирующая характеристика будет
Рис. 1-11
Если последовательно соединенные нелинейности заданы
графически, то также несложно получить результирующую
характеристику. Наиболее просто выполнить такое построение,
если первую из характеристик построить, как обычно, а для
второй характеристики за ось абсцисс принять ось ординат
первой характеристики. При симметричных характеристиках
построения можно выполнять для одной ветви.
В качестве примера рассмотрим графическое построение
результирующей характеристики F (хг) двух последовательно
соединенных звеньев с нелинейными статическими
характеристиками Fx (*i) и F2 (х) (рис. 1-12).
Ветвь первой характеристики строим в первом квадранте.
Ветвь второй характеристики строим во втором квадранте,
принимая за ось абсцисс ось ординат первой характеристики.
Интервал графического решения кхх для переменной хх
выбираем таким, чтобы п дискретных значений переменных с
достаточной точностью определяли исходные и искомую
статические характеристики. Затем для каждого дискретного значения
хг определяются точки ветви результирующей характеристики
F (х±). На рис. 1-12 показан порядок графического решения
для некоторого значения Из точки, соответствующей *lt-,
восстанавливается перпендикуляр и определяется значение х-ь
на характеристике Flt Значение Х{ переносим (как показано
стрелкой) на характеристику F2. Опустив перпендикуляр на
ось абсцисс, получим значение Хф Его переносим на
перпендикуляр, восстановленный из точки лги\ Проделав такое
построение для п значений, получим п точек, принадлежащих одной
ветви статической характеристики F (л^). Вторая ветвь функции

F (хг) строится нечетно-симметричной первой ветви относительно
начала координат.
При согласно-параллельном включении звеньев с
нелинейными статическими характеристиками (рис. 1-11,6) можно
записать:
х2 = F (х{) = x2 + xn2 = Fl (х{) + F2 [х{).
Получение результирующей статической характеристики
здесь сводится к сложению статических характеристик
отдельных звеньев и не представляет никакого затруднения как при
аналитическом, так и при графическом задании нелинейностей.
В случае встречно-параллель-
Хх . ного соединения нелинейных
%[х) \г У**1' звеньев (рис. 1-11, в) можно за-
^\ | / fFtoi) писать:
х2
х2ь
x1i
Рис. 1-12
х2 = F± (х) = F± (х1 ± х0. с),
где знак «+» соответствует
положительной обратной связи, а
знак «—» — отрицательной
обратной связи. Так как
*о. с ^ -^о. с С^г)»
то получим
*2 = М*! ± ^O.cte)]-
Разрешая последнее равенство относительно аргумента,
имеем
*i ± Fo.c{*2)=h (*г)-
гАе fi — обратная функция для функции Fv
Полученное выражение можно записать в виде
Ч = V (х2) = fx (х2) + F0. с (*8). (1-6)
где ¥ (х2) — суммарная функция, учитывающая сигнал прямой
цепи и цепи обратной связи.
В (1-6) знак «—» соответствует положительной обратной
связиг а знак «+» — отрицательной обратной связи.
Результирующая статическая характеристика F (*х) будет обратной
функцией для функции ¥ (х2).
Как видно из (1-6), для получения результирующей
-статической характеристики для нелинейного звена с нелинейной
обратной связью следует найти обратную функцию /х (х2) для
функции Fx (х) основного звена, вычесть для положительной
и прибавить для отрицательной обратной связи нелинейную
функцию обратной связи F0. с (х2), а затем найти обратную
функцию F (хг) для полученной суммарной функции ¥ (х2).
Пусть, например, имеем встречно-параллельное соединение
двух звеньев с нелинейностями, заданными аналитически
16

(рис. 1-13). Согласно (1-6) запишем выражение входной
величины хг для отрицательной обратной связи:
*i = /х (**) + Fo. с (*2) = V~4 sign х% + ]A*7sign х2 =
= 2 Yx% sign *2.
Разрешая полученное выражение относительно х2, получим
результирующую статическую характеристику
x2 = F(x{) = — *f sign*P
Рис. 1-13
Если уравнение (1-6)
трудноразрешимо относительно х2, то можно не
находить аналитического выражения
для результирующей статической
характеристики, а, задаваясь значениями
*2> определять хг и строить
характеристику графически.
Таким же образом к одному звену можно приводить
нелинейное звено, охваченное жесткой линейной связью, или
линейное звено, охваченное жесткой нелинейной связью.
При графическом задании исходных нелинейных
статических характеристик в случае встречно-параллельного
соединения нелинейных звеньев построение результирующей
характеристики эквивалентного звена согласно (1-6) может быть
выполнено в следующем порядке. В координатных осях xlt х2 строится,
а)
/
/
ОС2
Рис. 1-14
как обычно, характеристика основного звена Fx (хг). Затем
строится характеристика звена обратной связи, для которой
переменная х2, откладываемая на оси ординат, является
аргументом, а хг является функцией F0. с (х2). Сложив значения хг
указанных характеристик в дискретных точках, получим
результирующую характеристику для отрицательной обратной
связи. Для положительной обратной связи следует вычесть из
значений хг на характеристике Fx (хг) значения хг на
характеристике обратной связи FQ, с (х2). Полученная характеристика
и будет эквивалентной результирующей х2 = F (хг).
17

В качестве примера рассмотрим получение результирующей
характеристики для основного звена, имеющего статическую
характеристику с зоной нечувствительности при линейном
продолжении (рис. 1-14, а), и звена обратной связи, имеющего
характеристику с ограничением. Характеристику основного звена
i7! (хх) строим, как обычно, на координатной плоскости xlt х2
(рис. 1-14, б), имея в виду, что хг = х в отсутствие обратной
связи. Характеристику F0. с (*г) строим в зависимости от ее
аргумента х2. Сложив значения хг для построенных
характеристик, получим результирующую характеристику F (хг) для
отрицательной обратной связи. Вычтя значения хх для FQ. с из
значений хг для Flt получим характеристику для
положительной обратной связи F' (л^). Причем для кусочно-линейных
характеристик сложение и вычитание достаточно выполнить при
значении х2 = 0, в точках изломов исходных характеристик
и при некотором интересующем нас конечном значении х% (в
нашем примере хг = 0; 1; 3).
1-4. Составление уравнений нелинейных автоматических систем
Составление уравнений нелинейных автоматических систем
обычно выполняется после изображения структурных схем.
Как и при исследовании линейных систем, вначале составляются
уравнения отдельных звеньев, а затем уравнения звеньев
объединяются в уравнение системы. Для некоторых методов
исследования не требуется перехода от уравнений звеньев к
уравнению системы. К таким методам можно отнести графо-аналити-
ческие методы решения нелинейных дифференциальных
уравнений и исследование процессов в нелинейных системах с помощью
моделирующих и вычислительных машин.
Наличие нелинейных звеньев не позволяет получить сразу
единое уравнение нелинейной системы. Как уже говорилось,
обычно вначале составляются уравнения линейных частей и
уравнения нелинейных звеньев. В простейшем случае система
представляется линейной частью с ее линейным
дифференциальным уравнением и нелинейностью, описываемой
нелинейным дифференциальным или алгебраическим уравнением либо
представляемой графиком нелинейной статической
характеристики.
Объединяя линейное уравнение линейной части и
нелинейное уравнение нелинейного звена, можно записать общее
уравнение системы, которое в целом будет нелинейным. Получение
линейного уравнения системы становится возможным лишь
после применения к нелинейностям методов линеаризации. В
дальнейшем будем использовать в основном готовые уравнения и
передаточные функции линейных звеньев, известные из литературы.
К составлению уравнений звеньев будем прибегать лишь в
некоторых случаях при рассмотрении конкретных примеров
замкнутых нелинейных систем.
Составление уравнений линейных частей может выполняться
либо методом исключения переменных, либо с помощью
передаточных функций. Получение же линейного уравнения системы
даже после линеаризации нелинейностей должно выполняться

с соблюдением правил структурных преобразований в
нелинейных системах.
Пусть имеем одноконтурную линейную систему с одним
нелинейным звеном (рис. 1-15), внешним задающим воздействием
g (t) и выходной величиной у (t), для которой требуется
составить уравнение.
Соответственно структурной схеме имеем уравнения звеньев,
входящих в систему:
1. Уравнение датчика рассогласований
2. Уравнение первого звена
(T1p+l)x = k1x1.
(1-7)
(1-8)
Iff
1+Ър
F(x)
*2
итчр
Рис. 1-15
3. Уравнение нелинейного звена
х2= F(x).
4. Уравнение третьего звена
(Т2р + \)ру = k2x2.
5. Уравнение звена обратной связи
(Г4Р+1).01 = МГзР + 1)У.
(1-9)
(1-10)
(1-11)
Найдем уравнение линейной части методом исключения
переменных. Выходной величиной линейной части является
переменная х, и поэтому, начиная с первого звена, ведем
исключение переменных, обходя контур против направления
прохождения сигналов. Заменяя в уравнении (1-8) хх его значением
из (1-7), имеем:
(T1p+l)x = k1g-k1y.
Умножив полученное уравнение на оператор левой части
уравнения (1-11), получим
(TlP + 1) (7> + 1) х = ^ (Г4р + \)g ~ Ms (Tzp + 1) у.
Далее полученное уравнение умножаем на оператор левой
части уравнения (1-10)
(TlP + l)(T2p + l)(T,p+l)px =
= h (Т2Р + 1) (г4р + 1) «-МЛ (т3Р +1) 0-12)
В результате получили дифференциальное уравнение
линейной части с ее выходной величиной х, входной х2 и задающим
19

воздействием g. Нелинейное звено описывается нелинейным урай
нением
x2=F(x).
(1-13)
Объединяя (1-12) и (1-13), получим нелинейное уравнение
замкнутой системы для входной величины нелинейного звена
(TiP + О (Т2р + 1) (7> + 1) рх + kxk2k3 (Т3р + l)F (х) =
Здесь в процессе составления общего уравнения системы
исключилась выходная величина у (f), которая, как правило,
может интересовать при исследовании. После получения
решения уравнения (1-14) для переменной х (t) можно всегда
привести решение к выходной величине системы у (tf), используя
передаточные функции звеньев, разделяющих х (t) и у (t).
Если в нелинейной системе составлять уравнение
относительно выходной величины, то оно, как правило, не разрешается,
так как выходная величина входит в аргумент нелинейной
функции.
Составление уравнений замкнутых систем с использованием
их передаточных функций для разомкнутого состояния системы
широко применяется к линейным системам. В нелинейных
системах из-за наличия нелинейностей и вследствие того, что
общее уравнение составляется относительно выходной величины
линейной части, а не всей системы, зачастую невозможно
пользоваться передаточными функциями для составления
уравнений.
При рассмотрении собственного движения нелинейной
системы уравнение линейной части можно сразу выразить через
ее передаточную функцию. Для рассматриваемого примера при
g (t) — 0, согласно структурной схеме (рис. 1-15), передаточная
функция линейной части будет
{TiP + 1) (Т2Р + О (?> + 1) Р* = МЛ (Т3р + 1)х2, (1-15)
что соответствует (1-14) при g = 0 и учете знака «—»,
необходимого для замыкания системы.
В качестве второго примера составим уравнение
нелинейной системы, имеющей жесткую дополнительную обратную
связь, охватывающую нелинейное звено (рис. 1-16).
Запишем уравнения звеньев системы соответственно их
передаточным функциям:
= кг (T2p + \){T,p + \)pg.
(1-14)
Гл(р) =
p(l + TlP)(l + T2p)(l + T,p) 9
откуда имеем
(Tip + 1) х2 = kxx1$ x^g — y,
х3 = F (x)i
(1-16)
(1-17)
(1-18)
(Ы9)
20

коэффициент kt связывает изменение скорости ру с возмущением
/ (О-
Составим уравнение линейной части, в которую включим
все звенья и узлы системы, кроме нелинейного звена. Для
линейной части выходной величиной является переменная ху а
входной — переменная х3. Из (1-18) имеем
X = Х2 /?о. с У'
Умножив данное уравнение на оператор первого уравнения
(1-16), получим
(Тгр +\)х = Mi - ко. с (ТгР + 1)У
У
ит1Р
<2Н F(x)
Рис. 1-16
или, при учете соотношения замыкания системы хг = g—у,
(TlP +\)x = k1g-[k1 + k0, с (TlP + I)] у.
Полученное уравнение умножаем на оператор левой части
уравнения (1-19):
(TlP + 1) (Т2р + \)px = k1 (Т2р + l)pg-
- №г + k0. с (TlP + 1)] (k2X3 + kff)
или
(TlP + 1) (T2p +l)px = kx (T2p + l)pg-
- k2 [kx + k0. с (T^ + 1)] x3 - kf [k± + k0. с (Тгр + 1)] /. (1-20)
Полученное уравнение линейной части может быть
объединено с уравнением нелинейного звена (1-17) в единое
нелинейное уравнение замкнутой системы
(ТгР + 1) (Т2р + \)рх + к2 [кг + ко. с (ТгР + 1)] F (х) =
= *i (Т2Р + l)pg-kf[k1 + k0. с (Тгр + 1)]/. (1-21)
При наличии нескольких нелинейностей, разделенных друг
от друга непростыми линейными звеньями (см. стр. И),
составляются уравнения для соответствующих линейных частей и
учитываются нелинейные уравнения, связывающие входные и
выходные величины линейных частей. Например, пусть имеем
систему со структурной схемой на рис. 1-17, а, содержащую
две нелинейности. Для исследования собственного движения
систему можно представить состоящей из двух линейных частей
21

с передаточными функциями Wt (р) и tyt (р) и двух
нелинейностей Ft (х) и F2 (х3) (рис. 1-17, б).
Передаточная функция для первой линейной части будет
Щ (р) = *J*» ,
p(l+TlP)(l + T2p)
а дифференциальное уравнение запишется в виде
(TlP + 1) (7> + 1) рх3 = МЛ-
(1-22)
а;
UT,p
и т.
1+ТеР
ш
w2(p)
F2M
Xj
Рис. 1-17
Для второй линейной части передаточная функция будет
Г,(р)= *зМ1 + 7» (
,{1 + тгР + ту){\ + т^)
а соответствующее ей дифференциальное уравнение примет вид
{Т\р2 + Т3р + 1) (Т6р + \)х = k3k4 [Тър + 1) х4. (1-23)
. Выход линейной части W2 (р) связывается со входом
линейной части Wx (р) через нелинейное уравнение хг = F± (*),
а выход линейной части Wx (р) со входом линейной части
^2 (р) — через нелинейное уравнение х4 = F2 (х3)«
ГЛАВА ВТОРАЯ
ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
НЕЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
2-1. Исследование нелинейных систем методом припасовывания
Метод припасовывания заключается в том, что нелинейное
уравнение системы разбивается на ряд линейных уравнений,
соответствующих некоторым участкам движения системы.
Представление нелинейного уравнения несколькими линейными
уравнениями чаще возможно при наличии в системе кусочно^
линейных статических нелинейностей.
22

Полученные линейные уравнения решаются соответственно
участкам статической нелинейности обычным или операционным
методами. При этом конечные значения решения для
предыдущего участка принимаются за начальные значения решения
последующего участка, т. е. участки решения припасовываются
друг к другу.
Рассмотрим применение метода непосредственно на примере
нелинейной системы. Возьмем систему регулирования
температуры с принципиальной и структурной схемами, изображенными
на рис. 2-1, а, б. Регулируемым объектом является некоторый
а)
6)
dt
1+Tof
Рис. 2-1
объем, в котором требуется поддерживать постоянное значение
температуры 6. Измерительным элементом служит термометр
сопротивления ТС, который включается в мостовую схему.
При отклонении температуры от номинального значения
с диагонали моста снимается напряжение и подается в обмотку
управления двухпозиционного поляризованного реле ПР.
Контакты реле управляют двигателем постоянного тока Д.
Последний через редуктор Р приводит в движение регулирующий
орган (например, изменяет положение шторок, регулирующих
отвод тепла от объекта).
Для регулируемого объекта можно записать
дифференциальное уравнение процесса нагрева, как для апериодического
звена первого порядка, в виде
г0^ + е = _*0g+ /(*), (2-1)
at
где 6 — отклонение температуры от номинального значения,
£ — отклонение регулирующего органа, f (t) — внешнее
возмущение (нагрев или охлаждение регулируемого объекта), Т0
и kQ — постоянная времени и коэффициент передачи
регулируемого объекта.
23

Учитывая, что инерционность регулируемого объекта
значительно превышает величины инерционности измерительного
элемента, реле и двигателя, весь регулятор можно принять за
безынерционное звено с нелинейной статической
характеристикой, изображенной на рис. 2-2, а. Причем входной величиной
регулятора будет отклонение температуры 6, а выходной —
dt
скорость отклонения шторок —2-. При принятых допущениях
dt
dt
в
ь
0
ъ
5)
V
f;
д
1
4
в) il
\dt
Рис. 2-2
нелинейное уравнение регулятора, согласно статической
характеристике (рис. 2-2, а), запишется следующим образом:
d%
dt
d%
dt
dt
dt
dt
= с при 0 > b
— — с при 0 < b
= с при 6 > — b
= — с при 9 < — b
когда — > 0;
dt
Логда — < 0.
dt
(2-2)
(2-3)
Будем рассматривать свободное движение системы, полагая
в (2-1) I (t) = 0. Изобразим некоторый переходный процесс в
системе для отклонения температуры 0 (рис. 2-2, б) и скорости
движения регулирующего органа (рис. 2-2, в). Рассмотрим
dt
два участка переходного процесса для произвольного периода:
участок А В и участок BD на рис. 2-2, б.
24

На участке АВ в соответствии со значением скорости
регулирующего органа уравнение регулятора будет -^-= с. Диффе-
dt
ренцируя уравнение объекта (2-1) по времени и подставляя вме-
d£
сто —— его значение с, получим уравнение для определения
dt
процесса на участке АВ
„ d*Q . dQ f /0 „ч
Т0 = —k0c (2-4)
dt* dt
и на участке BD
dt* dt
Решение уравнения (2-4) для скорости изменения
температуры будет
dQ - 4-
-df = c* °-V, (2-6)
откуда получим
0= — Т0Схе Т° —k0ct + C2, (2-7)
где Сх и С2 — постоянные интегрирования.
Для упрощения будем отсчитывать время от начала участка
А В. Тогда начальные условия запишутся в виде
dO
д = Ь, — = 0Л при * = 0,
dt
где 0^ пока неизвестна.
Используя начальные условия из (2-7), определяем
произвольные постоянные по уравнениям
b = — 7\А + Са, 0л = Сг - k0c. (2-8)
В результате получим
Сх = 0д + V, С2 = b + ToCi. (2-9)
Для участка BD, согласно (2-5) и (2-7), имеем
— = C2e r°+V» (2-Ю)
i_
Q=—T0c[e T° +k<ft + C'2. (2-11)
При отсчете времени также от начала участка для
постоянных интегрирования находим
C; = 0B-V> С'2 = -Ь + Т0С[. (2-12)
25

Ёсе остальные участки кривой переходного процесса будут
определяться такими же решениями, но с другими численными
значениями величин Сг, С2, &л, С\, С2, дв.
Как видим, величины 0д и 0^, необходимые для
определения произвольных постоянных, находятся как значения 8 в
конце предшествующего участка. Поэтому, если будет задана
величина 9 в начальной точке первого участка, то все решение
для переходного процесса, искомое пб участкам, будет вполне
определенным.
Задаваясь численными значениями параметров и начальной
скоростью, можно построить по полупериодам переходный
процесс, который в данном случае будет колебательным нелинейным.
Далее можно определить устойчивый периодический режим,
к которому приходит переходный процесс, т. е.
автоколебательный установившийся режим. Для этого, очевидно, нужно, чтобы
в точке D выбранного периода колебаний (рис. 2-2, б)
получались те же значения 6 и 6, какие были в начале его,
т. е. в точке А. Вследствие симметрии статической нелинейной
характеристики (рис. 2-2, а), оба полупериода автоколебаний
должны быть одинаковыми. Поэтому для определения
автоколебаний достаточно рассмотреть только один участок А В и
потребовать, чтобы
ев=-9л. (2-13)
Обозначив период искомых автоколебаний через 2Г, а
длительность участка АВ по времени, следовательно, через Г, из
(2-6) найдем
Т
~*~ т
$в ==- Схе ° — Кс
или, согласно (2-13),
т
То
и, учитывая значение 0^ из (2-8), получим
Сг[\ + е r°) = 2V. (2-Н)
В уравнении (2-14) содержатся две неизвестные Сх и Т.
Величину Т, т. е. длительность участка АВ, можно также
выразить из (2-7), так как известно, что в конце участка 0 = — Ь.
При этом запишем:
Т
— b= — Т^е То — k0cT + С2, (2-15)
и, кроме того, из (2-8) имеем
*=-7\А + С2. (2-16)
26

Вычитая из (2-16) уравнение (2-15), получим
— ToCxG—* То) +к0сТ=г-2Ь, (2-17)
Подставив в (2-17) значение Сх из (2-14), можно записать
т
(2-18)
1 ~е
т
1 —е
т
т.
2Г0 T0k0c
Трансцендентное уравнение (2-18) с неизвестной Т можно
решить графически (рис. 2-3), построив в зависимости от Т
функцию
iV /У2
Уг =
1
и прямую
У 2 = '
1 -
Т
т
То
2Г0 TQkQc
Рис. 2-3
Абсцисса, соответствующая точке пересечения уг с у2, и
будет решением для полупериода колебаний: Т = Тп (рис. 2-3).
Период колебаний, соответственно, Те = 2ТП.
Амплитуда периодического решения ап определяется как
максимальное значение 6 на участке А В путем исследования
(2-7) на максимум.
Для доказательства того, что полученное периодическое
решение представляет собой автоколебания, следует доказать
его устойчивость. В простейшем случае устойчивость
периодического решения оценивается построением двух переходных
процессов: при начальных значениях отклонения и скорости,
превышающих значения их в периодическом решении, и
меньших, чем в периодическом решении. В первом случае
переходный процесс должен затухать, приближаясь к автоколебаниям,
во втором — расходиться, также приближаясь к полученному
периодическому режиму.
2-2. Графо-аналитический метод исследования
нелинейных систем
Графо-аналитический метод решения нелинейных
дифференциальных уравнений в общей его постановке подобен методу
припасовывания. При выполнении графо-аналитического
решения здесь также нелинейности учитываются по частям, от
участка к участку. Методическая погрешность решения мала,
27

и потому метод можно отнести к точным, хотя в литературе его
часто относят к приближенным методам. Возможности
исследования нелинейных систем графо-аналитическим методом шире,
чем при использовании метода припасовывания, так как в этом
случае без особого труда можно выполнять построения процесса
при наличии нескольких нелинейностей, разделенных
линейными частями. Нелинейности могут учитываться в графическом
виде, т. е. без аналитического представления.
В отличие от метода припасовывания здесь не составляется
полное уравнение системы, а берутся уравнения линейных и
нелинейных звеньев (или их статические характеристики) и
выполняется решение по дискретным значениям интервалов
времени для каждого звена системы. В последнем метод не
отличается от метода численного интегрирования, за исключением
того, что интегрирование дифференциальных уравнений
выполняется с помощью графических построений.
Для того чтобы построить переходный процесс в нелинейной
системе графо-аналитическим методом, надо уметь выполнять
построения переходных процессов в линейных и нелинейных
звеньях.
Графо-аналитических методов решения дифференциальных
уравнений имеется несколько. Будем рассматривать только
метод Д. А. Башкирова, обладающий высокой точностью и
наглядностью.
Любая нелинейная система может быть структурно
представлена в виде соединения двух типов элементарных линейных
звеньев (апериодического первого порядка и идеального
интегрирующего) и соответствующих нелинейных звеньев.
Рассмотрим определение переходных процессов
графо-аналитическим методом в простейших линейных звеньях. Для этого
прежде всего следует усвоить две операции: графическое
построение переходного процесса в апериодическом звене первого
порядка и графическое выполнение интегрирования.
Уясним, каким образом можно графически построить
переходный процесс в апериодическом звене первого порядка.
Возьмем уравнение звена
Пусть входная величина будет хг = 1 (t) при начальных
условиях х2 (0) = 0. Аналитическое решение уравнения (2-19)
при принятых условиях дает возрастающую экспоненту
стремящуюся к значению k при t —► оо.
Покажем, каким образом можно построить экспоненту
графически, не прибегая к аналитическому решению. Наносим оси
координат t и х2 (рис. 2-4, а). На основании исходного
уравнения имеем параметры k и Т. Проводим линию, к которой
стремится экспонента, на высоте k. На данной линии откладываем
постоянную времени звена Т. Ось времени разбиваем на отрезки
tat (шаг решения), укладывающиеся целое число раз в отрезке Т.
(Tp+\)x2 = kx1.
(2-19)
(2-20)
28

Из начала координат проведем линию в точку /' (в конец
отрезка Т на высоте k). По свойству экспоненты эта линия есть
касательная к экспоненте в начале координат. Значит, на
малом участке (на первом шаге решения A t) отрезок этой
касательной можно приближенно принять за отрезок экспоненты.
Экспонента обладает свойством равномерности затухания,
заключающемся в том, что проекция касательной в любой точке
экспоненты на ее асимптоту есть величина постоянная, равная Т.
На основании этого свойства полученное решение для первого
шага можно было бы продолжить. Для этого из конца отрезка
первой касательной следует провести линию в точку 2'.
Отрезок этой линии внутри второго шага приближенно будет про-
Рис. 2-4
должением искомой экспоненты. Продолжая решение подобным
же образом, можно приближенно построить экспоненту. Это так
называемый метод касательных.
Нетрудно заметить, что получаемая таким построением
приближенная экспонента из отрезков прямых будет отличаться от
истинной экспоненты. Отрезок первой касательной
принадлежит истинной экспоненте только в одной начальной точке, а
конец его уже не принадлежит ей. В методе касательных
погрешность в ходе построения накапливается, и этот метод является
приближенным.
В графо-аналитическом методе Д. А. Башкирова вместо
касательных используются секущие искомой экспоненты. Для
проведения первой секущей необходимо соединить прямой
начало координат с точкой /, отстоящей от оси х2 на отрезок
Т + Отрезок секущей внутри первого шага как своим
началом, так и своим концом принадлежит искомой экспоненте.
Из конца первого отрезка проводится вторая секущая, в точку 2,
отрезок которой на втором шаге решения опять двумя точками
принадлежит экспоненте.
Подобным же образом решение продолжается. Погрешность
при этом не накапливается. При А£ = Т/2 методическая ошибка
не превосходит 1%.
Если правая часть в уравнении (2-19) не постоянная
величина, а, скажем, любая графически заданная функция, то
решение принципиально ничем не будет отличаться от описанного.
Прямые в этом случае необходимо проводить в точки, отстоящие
29

на те же значения во времени (рис. 2-4, б), но обязательно
принадлежащие функции хг (t), заданной в правой части уравнения.
В этом случае решение получается в виде отрезков различных
экспонент, заменяемых их секущими.
При построении переходного процесса в апериодическом
звене первого порядка его инерционность, как видим,
учитывается тем, что начало отсчета времени для выходной величины
смещается влево от начала отсчета времени входной величины
на величину Т.
Рассмотрим построение переходного процесса в разомкнутой
цепи апериодических звеньев первого порядка. Пусть имеем
три апериодических звена, соединенных последовательно
а)
h
х1
К2
х2
h
ит1Р
1+Тгр
Рис. 2-5
(рис. 2-5, а). На вход первого из них подано внешнее
воздействие g (t). Требуется построить переходный процесс для
выходной величины х3 (/).
Допустим, внешнее воздействие задано в виде единичного
скачка g (t) = 1 (t), который изображаем справа (рис. 2-5, б).
Начало отсчета времени для выходной величины первого звена хх
смещаем влево на величину постоянной времени первого звена Тх.
Так как величина х\ является входной величиной для второго
звена, то начало отсчета для его выходной величины х2 еще
смещаем влево на величину Т2. Начало отсчета для выходной
величины третьего звена x3f являющейся выходной величиной
всех трех последовательно соединенных звеньев, смещаем еще.
на величину постоянной Т3. Смещениями начал отсчета времени
учитывается инерционность всех звеньев. Далее выбираем шаг
решения А/ и по заданной величине g (t) строим хг (t), как для
апериодического звена первого порядка. По хг (t) таким же об»
разом определяем х2 (t), а по х2 (t) графическим построением'
находим х3 (t).
Рассмотрим методику выполнения второй элементарной,
операции — графического интегрирования.
30

Пусть имеется идеальное интегрирующее звено,
описываемое уравнением
Х\
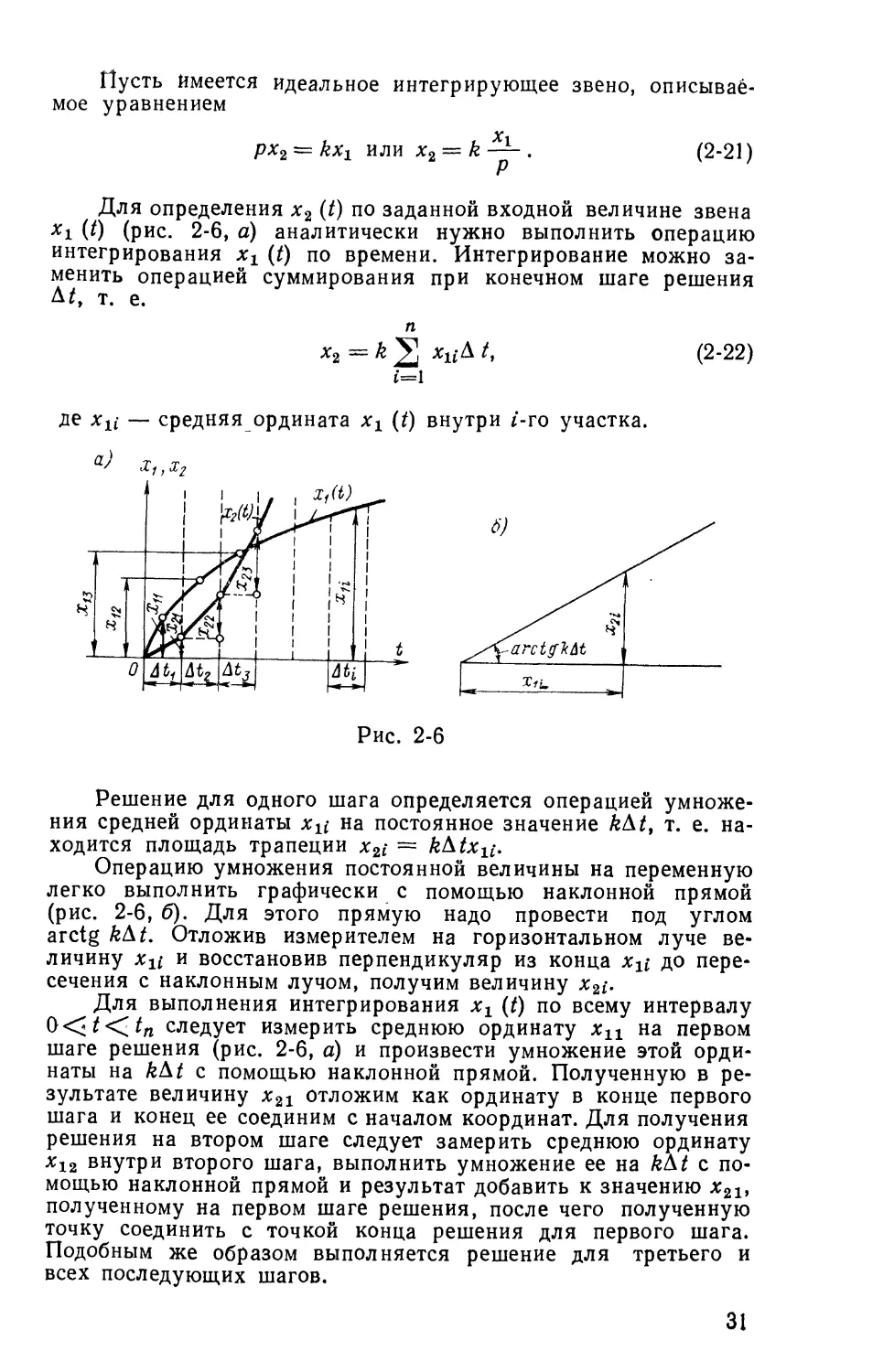
px2 = kxi или x2 = k—b-. (2-21)
Р
Для определения х2 (t) по заданной входной величине звена
xi (0 (рис. 2-6, а) аналитически нужно выполнить операцию
интегрирования хг (t) по времени. Интегрирование можно
заменить операцией суммирования при конечном шаге решения
At*, т. е.
п
x2=k^ xuA t, (2-22)
де xXi — средняя ордината хг (t) внутри i-ro участка.
Рис. 2-6
Решение для одного шага определяется операцией
умножения средней ординаты на постоянное значение kkt, т. е.
находится площадь трапеции x2i = kAtx^.
Операцию умножения постоянной величины на переменную
легко выполнить графически с помощью наклонной прямой
(рис. 2-6, б). Для этого прямую надо провести под углом
arctg kkt. Отложив измерителем на горизонтальном луче
величину xxi и восстановив перпендикуляр из конца xxi до
пересечения с наклонным лучом, получим величину х2(.
Для выполнения интегрирования хг (t) по всему интервалу
0<^t<ltn следует измерить среднюю ординату хХ1 на первом
шаге решения (рис. 2-6, а) и произвести умножение этой
ординаты на kkt с помощью наклонной прямой. Полученную в
результате величину #2i отложим как ординату в конце первого
шага и конец ее соединим с началом координат. Для получения
решения на втором шаге следует замерить среднюю ординату
х12 внутри второго шага, выполнить умножение ее на kht с
помощью наклонной прямой и результат добавить к значению х21>
полученному на первом шаге решения, после чего полученную
точку соединить с точкой конца решения для первого шага.
Подобным же образом выполняется решение для третьего и
всех последующих шагов.
31

Если в цепи звеньев первого порядка имеется
апериодическое звено второго порядка (рис. 2-7, а), описываемое
дифференциальным уравнением
[т\р2 + Тхр + 1) х2 = kxx при Гj > 2Г2, (2-23)
то оно может быть представлено в виде двух последовательно
соединенных звеньев первого порядка с промежуточной
переменной z (рис. 2-7, б).
Уравнение для двух последовательно соединенных звеньев
первого порядка запишется в виде
(7> + 1)(Г4р + l)x2 = kXl. (2-24)
Новые постоянные времени Т3 и Т4 определяются
уравнениями
Г2=Г3Г4, ТХ = Т3 + Т4, (2-25)
полученными приравниванием коэффициентов при одинаковых
степенях р в (2-23) и (2-24).
*) б)
А
*
2
1
1+Т4р
Рис. 2-7
Решение уравнений (2-25) дает
(2-26)
Графическое решение для двух апериодических звеньев
первого порядка выполняется по ранее рассмотренному правилу.
Если в цепи звеньев имеется колебательное звено,
описываемое уравнением
(Т\р2..+ Тхр + I) х2 = кхх при Тг < 2Т2, (2-27)
то его нельзя представить в виде соединения двух
апериодических звеньев первого порядка, так как корни
характеристического уравнения
Т\р2 + Тхр + \ =0 при ТХ<2Т2
будут комплексными.
Вынесем за скобки из первых двух членов уравнения (2-27)
TiP и уравнение запишем в виде
ТгР Р + I ) Ч = кхг - xv (2-28)
32

Введем новую переменную г.
Т2 \
—р- р + 1 j ДР, = г. (2-29)
Тогда (2-28) запишется в виде
Тгр2 = кхх — х2. (2-30)
С помощью уравнения (2-30) будем находить г по заданному
х1у как в интегрирующем звене. Для полученного значения г
в соответствии с (2-29) будем определять x2t как в
апериодическом звене первого порядка.
Результат решения для х2 на первом шаге соответственно
(2-28) должен вычитаться из kxlf т. е. начиная со второго шага
и для всех последующих шагов входной величиной будет
кхх—х2. Решение здесь нельзя выполнять до конца для каждой
переменной в отдельности, а следует вести решение циклично,
шаг за шагом.
При построении переходного процесса в замкнутой
автоматической системе, как и в случае колебательного звена, решение
должно выполняться циклично, с тем чтобы в конце одного шага
решения полученный результат для выходной величины системы
учитывать как исходные данные решения на следующем шаге.
Построение решения в нелинейных звеньях выполняется
согласно нелинейному уравнению, описывающему нелинейное
звено. В простейшем случае наличия статической нелинейности
последняя сразу учитывается при построении процесса в
нелинейной системе, что рассмотрим на конкретном примере.
2-3. Пример на построение переходного процесса
в нелинейной системе графо-аналитическим методом
Пусть требуется построить переходный процесс для
свободного движения в нелинейной автоматической системе со
структурной схемой на рис. 2-8, а графо-аналитическим
методом. Зададимся значениями параметров линейных звеньев:
7\ = 0,1 с; Т3 = 0,05 с; кх = 5; к3 = 10; &4 = 0,1 1/с.
Нелинейным звеном является идеальное релейное звено со
статической характеристикой, изображенной на рис. 2-8, б, при с — 4.
Примем следующие начальные условия: хх (0) =10, х3 (0) = 0,
х, (0) = 0.
Выбираем шаг решения At — Т3 — 0,05 с и наносим
начала отсчета времени, проводим оси ординат для всех
переменных (рис. 2-9, а). Смещение начала отсчета времени для х3
относительно начала отсчета времени для х2 на величину Т3 =
= 0,05 с обеспечивает учет инерционности третьего звена.
Аналогично смещение начала отсчета времени для хх относительно
начала отсчета времени для *4 на величину Тх = 0,1 с
обеспечивает учет инерционности первого звена.
Коэффициенты передачи kx и k3 отнесем к интегрирующему
звену, т. е. для интегрирующего звена считаем коэффициент
передачи к — кхк3к^ = 5-10-0,1 = 5 1/с. Это не повлияет на
результат решения, а только изменит масштабы построения.
2 Заказ Ш 933
33

Построение процесса для апериодических звеньев
выполним по методу секущих, а интегрирование — по методу средних
ординат.
Для интегрирующего звена имеем
x± — k — = k [ x3dt к kAt 2 =
P о i=i
n n
-5 0,05 2 *3t = 0,25 2 x3i.
i=i i=\
Умножение средних ординат x3i на коэффициент, равный
kAt = 0,25, выполним с помощью наклонной линии. Для этого
проводим прямую под углом arc tg 0,25 (рис. 2-9, б).
а)
S)
пт1Р
г
0
Р
х2
Рис. 2-8
Построение начинаем с того, что наносим начальное
значение хх (0) = 10. Этому значению, согласно статической
нелинейной характеристике второго звена, соответствует постоянное
значение х2 = с = 4. Проводим для х2 линию на уровне
указанного положительного значения.
По известному значению х2 находим решение для х3 в
интервале первого шага. Для этого из начала отсчета времени О
для х3 проводим луч в точку alf принадлежащую х2 = с = 4
и смещенную по времени относительно точки О на величину
Ts Н——. Отрезок этого луча в интервале первого шага и есть
искомое решение.
Известную для первого шага переменную х3 интегрируем
по методу средних ординат. Полученное значение х4 откладываем
с обратным знаком (необходимым по принципу работы
замкнутых систем) в конце первого шага (точка а2) и начало координат
для *4 соединяем с полученной точкой.
По известному значению *4 на первом шаге определяем xlt
как для апериодического звена первого порядка, с учетом на-
34

чального значения xt (0) = 10, т. е. проводя луч из точки
*i = 10 в точку а3.
Далее выполняем решение на втором шаге. Для этого из
конца отрезка х3, полученного на первом шаге решения,
проводим луч в точку Ьх. Отрезок этого луча в интервале второго шага
и будет решением. Интегрированием х3 на втором шаге
получаем значение х4 в интервале второго шага. Полученный
результат добавляем с обратным знаком к значению *4 для первого
шага и результат откладываем в конце второго шага (точка Ь2).
По известному х4 находим хх на втором шаге, проводя луч в
точку Ь3. Аналогичным образом выполняем решение для третьего
и последующих шагов до тех пор, пока процесс не установится.
При продолжении решения следует иметь в виду, что когда
переменная хг изменит знак (в нашем примере это происходит
в четвертом шаге), то х2 скачком изменит свое значение,
принимая величину х2 = — с = — 4.
Если изменение значения х2 произошло внутри некоторого
шага, то решение следует выполнить по соответствующим
частям шага, как по целому шагу. При этом следует учесть
изменение значения kAt, используемого в интегрирующем звене,
происшедшее из-за изменения At. Это значит, что наклонную
прямую следует провести для решения по части шага под
меньшим углом arctg&A/', где At' —соответствующая часть At.
В дальнейшем решение следует продолжать по целым шагам.
Из результата решения, представленного на рис. 2-9, а,
видно, что в системе устанавливаются автоколебания.
Переменная #з на выходе нелинейного звена представляет собой
колебания прямоугольной формы, а переменная х3 — колебания,
составленные из отрезков экспонент. Переменные х± и хх
совершают колебания, близкие к гармоническим.
Период колебаний будет одинаковым для всех переменных
и легко определяется из построения.
Для определения амплитуд установившихся колебаний
каждой переменной следует найти масштаб по уравнениям
установившихся значений. Так, для переменной х3 имеем:
Х3 = ^3-^2»
что при учете значений х2 = с = 4 и k3 = 10 дает х3 = 10-4 —
= 40, т. е. уровню х2 = 4 соответствует значение х3 = 40.
Для первого звена в установившемся состоянии имеем
Хх == kxX^y
что при значениях хх = 10, kx = 5 дает
т. е. значению Arx = 10 соответствует значение *4 = 2.
Из выполненного построения для амплитуд имеем: aXi ~ 2,
av « 4, av « 40, ау ж 0,8. Период колебаний Т « 0,5 с,
/ * 2 Гц.
36

2-4. Исследование нелинейных систем
методом фазовых траекторий
Дифференциальное уравнение замкнутой автоматической
системы п-го порядка можно представить в виде совокупности
уравнений первого порядка:
dxx
dx2
dt
-=Ф1(х1, х2, . . . , хп, /, g),
U g),
(2-31)
dxn
dt
Д?2
с начальными условиями хх = х10, х2 = #2о» • • • » *л = хпо
при / ■= 0, где*!, х2, . . . , хп — переменные, являющиеся
искомыми функциями времени, причем хг может обозначать
регулируемую переменную, а х2 ~
■4- хп — другие
вспомогательные переменные; f и g
—возмущающее и задающее
воздействия.
Пусть, например, в
уравнениях (2-31) п = 3 (система
третьего порядка). Переменные
*i» *2> хз могут иметь любой
физический смысл. Но условно
их можно представить как
прямоугольные координаты
некоторой точки М (рис. 2-10).
В реальном процессе в
каждый момент времени хъ х2, х3
принимают вполне
определенные значения. Это соответствует
вполне определенному
положению точки М в пространстве.
С течением времени величины хъ х2, х3 изменяются. Это
соответствует перемещению точки М в пространстве по
определенной траектории. Траектория точки М может служить наглядным
отображением протекания процесса регулирования. Точка М
называется изображающей точкой, ее траектория называется
фазовой траекторией, а пространство (xlt х2, х3) называется
фазовым пространством. Производные координат точки по
времени в (2-31) представляют собой проекции вектора скорости
движения изображающей точки на оси координат.
Следовательно, по значениям правых частей уравнений (2-31) в каждый
момент времени можно судить о движении изображающей точки,
а значит, о поведении всей реальной системы. Начальные
условия процесса регулирования (х10, х20, х30) определяют
Координаты начальной точки фазовой траектории М0 (рис. 2-10).
Если переменных в уравнениях (2-31) будет всего две х{
и х2 (система второго порядка), то изображающая точка будет
Рис. 2-10
37

двигаться не в пространстве, а на плоскости (фазовая плоскость).
Если переменных будет п>3, будем иметь дело с я-мерным
пространством. Фазовые траектории в фазовом пространстве
представляют собой геометрические образы динамических
процессов, протекающих в реальных системах. В этом геометрическом
представлении участвуют координаты и исключается время.
Если уравнения (2-31) составлены в отклонениях хи
*2> • • • » хп и внешние задающее и возмущающее воздействия
равны нулю, то установившееся состояние характеризуется
значениями хх — х2 = . . . = хп = 0. Следовательно,
изображением установившегося состояния служит начало координат
фазового пространства.
Отсюда вытекает, что фазовые траектории устойчивой
линейной системы в ее свободном движении будут асимптотически
приближаться к началу координат. Фазовые траектории
неустойчивой линейной системы будут неограниченно удаляться от
начала координат.
Для нелинейных систем вследствие особенностей их
процессов фазовые траектории могут принимать самые разнообразные
очертания.
В общей своей постановке метод фазовых траекторий может
быть использован для исследования линейных и нелинейных
систем любого порядка. Однако уже начиная с третьего порядка
усложняются представления о пространственных фазовых
траекториях. Здесь при исследовании приходится рассматривать
плоскости сечений фазового пространства.
Наибольшую наглядность и практическое применение
метод фазовых траекторий нашел в случае систем второго порядка,
при этом очень удобно за одну координату фазовой плоскости
принять отклонение регулируемой величины ху а за вторую ~
скорость ее изменения у = . Рассмотрим для этого случая
dt
изображения процессов на фазовой плоскости.
Затухающий колебательный процесс. Начальная точка
процесса (рис. 2-11, а) имеет определенные значения х (0) и у (0) =
= J^L. и на фазовой плоскости (рис. 2-11, б) изобразится
dt
х=о
в виде изображающей точки М0. На участке процесса х (0), 1
dx
величина х увеличивается, а производная у = уменьшается.
dt
Точка / в переходном процессе соответствует точке V на
фазовой плоскости. На участке /, 2 процесс идет с уменьшением
координаты х при отрицательной производной y==:"~~£f' Точке 2
в переходном процессе будет соответствовать точка 2' на
фазовой плоскости. Рассуждая аналогично, далее получим
последующие участки фазовой траектории, соответствующие
участкам переходного процесса. В результате видим, что
сходящемуся колебательному процессу соответствует фазовая
траектория, сходящаяся к началу координат. Начало координат в этом
случае называется устойчивым фокусом.
38

Расходящийся колебательный процесс (рис. 2-12, а)
изобразится в виде спиральной фазовой траектории, удаляющейся от
начала координат (рис. 2-12, б). Начало координат фазовой
плоскости в этом случае называется неустойчивым фокусом.
Рис. 2-11
Монотонные сходящиеся процессы (рис. 2-13, а) на фазовой
плоскости изобразятся в виде кривых (рис. 2-13, б), сходящихся
к началу координат. Начало координат в этом случае называется
устойчивым узлом.
Монотонный расходящийся процесс (рис. 2-14, а)
изобразится в виде фазовой траектории, удаляющейся от начала ко-
Рис. 2-12
ординат (рис. 2-14, б). Начало координат в этом случае
называется неустойчивым узлом.
Периодический процесс (рис. 2-15, а) изобразится на фазовой
плоскости в виде замкнутой кривой (рис. 2-15, б), называемой
предельным циклом. Предельный цикл называется устойчивым,
когда все близлежащие фазовые траектории сходятся извне и
изнутри к предельному циклу (рис. 2-16, а), и неустойчивым —*
когда траектории расходятся от предельного цикла (рис. 2-16, б).
39

В первом случае в системе устанавливаются устойчивые
периодические колебания, называемые автоколебаниями. Во втором
случае имеем неустойчивое периодическое решение. При этом
о системе можно сказать, что она устойчива в малом, т. е.
устойчива при малых начальных значениях отклонения и скорости
В)
/ dt
с
У'
V
J
\
оМ0
Рис. 2-13
х (0) и у (0), и неустойчива в большом, т. е. неустойчива при
больших значениях х (0) и у (0).
В нелинейных системах зачастую одновременно имеется два
предельных цикла: малый — неустойчивый и большой —
устойчивый (рис. 2-17, а). При этом можно сказать, что система
устойчива в малом, неустойчива в среднем и устойчива в большом.
Внешний предельный цикл соответствует автоколебаниям в
нелинейной системе»
Рис. 2-14
Кроме особых линий типа предельного цикла, в нелинейных
системах возможны и другие особые линии, как, например,
особые линии типа отрезка (рис. 2-17,6), характерные для систем
с нелинейными звеньями, обладающими зоной
нечувствительности. Возможны также особые линии более сложного
очертания, не рассматриваемые здесь.
Укажем общие свойства фазовых траекторий на плоскости
dx dx . Л
с координатами х и у — . Так как у = , то при г/>0
dt dt
величина х всегда увеличивается во времени и, следовательно,
40

в верхней полуплоскости изображающая точка М всегда
движется слева направо, а в нижней полуплоскости, при #<0, х
всегда уменьшается во времени и изображающая точка движется
справа налево.
Все фазовые траектории пересекают ось х под прямым
углом, так как при у = 0 имеет место либо максимум, либо
минимум функции х (t).
2-5. Пример исследования нелинейной системы
методом фазовых траекторий
Обратимся к системе регулирования температуры с
поляризованным реле (рис. 2-1, а), переходный процесс в которой
исследовался методом припасовывания. Структурную схему
системы при учете только инерционности регулируемого объекта
изобразим, как показано на рис. 2-18, а.
а)
Регулируемый объект
•5)
1+7,
оР
Чувствительный
элемент и реле
и
ъ
0
ъ
Привод с регулирующим
органом
Рис. 2-18
Уравнение регулируемого объекта для свободного
движения системы запишется в виде
(70р + 1)е= -kQt. (2-32)
Уравнение привода совместно с регулирующим органом,
как для идеального интегрирующего звена, будет
р6 = М- (2-33)
Чувствительный элемент вместе с реле является
нелинейным звеном со статической нелинейностью
u=*F(Q)9 (2-34)
изображенной на рис. 2-18, б.
Объединяя (2-32) и (2-33), получим уравнение линейной
части системы
(7> + 1)рв= — Мх«. (2-35)
42

Учитывая (2-34), получим нелинейное уравнение системы
для ее свободного движения, записанное относительно входной
величины нелинейного звена,
(Т0р + 1).рв= — kfaF (0). (2-36)
Нелинейное уравнение (2-36) соответственно участкам
статической характеристики нелинейного звена (рис. 2-18, б) можно
записать в виде четырех линейных уравнений:
(1) (Т0р + 1) р0 = k0klCl при 0 ^ 6, 0 > О,
(2) (Т0р + 1) р0 = - k0klC при 0 > Ь, 0 > О,
(3) (7>+1)р0 = — k0kxc при 0 > — Ь, 0 <0,
(4) (Т0р + 1) р0 = ko^c при 0 ^ — 6,0 < 0.
7/_
а
Рис. 2-19
Наносим оси координат фазовой плоскости (рис. 2-19)
dx d0
dt ~~ dt
* = 0, y =
и отмечаем характерные значения х = 0 = b и * = 0 = — b,
согласно статической характеристике нелинейного звена.
Определенным «квадрантам» фазовой плоскости будут
соответствовать следующие уравнения (2-37): «квадранту» d, b,
— х — уравнение (1); d, b, х — уравнение (2); е, — b, х — (3);
е, - Ь, - х - (4).
Следовательно, для определения фазовых траекторий на
полуплоскости правее ломаной d, b, — b, е будет справедливо
уравнение
(Гор + 1)р0= —Mi*, (2-38)
43

а для полуплоскости левее ломаной d, Ъу — b, е — уравнение
(T0p + l)pQ = k0k1c, (2-39)
отличающееся только знаком при с от уравнения (2-38).
Запишем уравнение (2-38) в обычной форме
Го — + — = - kokiC (2-40)
dt1 dt
При учете обозначений координат фазовой плоскости
dQ dx
6, у =
(2-40) можно записать в виде
dt dt
То^г + У= - Mi*. (2-41)
at
Для исключения времени в (2-41) разделим все члены урав-
dx
нения на у ~ . В результате получим
dt
dy 1 k0kxc
или
dx TQ T0y
dx== Toydy_^ (2.42)
Выполняя интегрирование, имеем
dy
x = - T0 \y
у + k0kxc
= - Г0 ly In (у + kfac) - J In (у + k0klC) dy] +CX =
= - T0y In \y + k0kxc) + T0(y + kQklC) [In (y + - 1 ] + Ci =
= To^iC In (y + k0klC) — T0y + C2. (2-43)
Соответственно для левой полуплоскости с учетом
изменения знака с получим
* = - Tq№ic 1п [У - *oV) - тоУ + с2- (2-44)
Из (2-43) видно, что при у = — kQkxc х = — оо.
Следовательно, все фазовые траектории для полуплоскости правее
ломаной dy 6, — 6, е, отвечающие различным С2, будут иметь
асимптоту у = — k^kxC Аналогично из (2-44) при у = k^k^c
получим х = оо, т. е. имеем асимптоту для траекторий
полуплоскости левее ломаной d, Ь, — Ь, е, описываемую уравнением у =
44

Для построения фазовых траекторий или, как говорят,
фазового портрета необходимо в (2-43) и (2-44) задаваться
значениями произвольных постоянных интегрирования С2 и С2
и вычислять значения х в зависимости от значений у. Различным
значениям С2 и С2 будут соответствовать свои фазовые
траектории в правой и левой полуплоскости.
Для приближенного анализа процесса в рассматриваемой
системе можно фазовые траектории изобразить, пользуясь их
общим свойством. Положим, что в начальный момент времени
изображающая точка соответствовала большим начальным
значениям х (0) и у (0) и занимала положение М0. По свойству
фазовых траекторий в нижней полуплоскости изображающая
точка с течением времени должна двигаться справа налево,
приближаясь к асимптоте у = — k^kxc. В результате фазовая
траектория, соответствующая уравнению (2-43), изобразится
в виде линии М0 / . Так как фазовые траектории представляют
собой сплошное поле кривых, то в левой полуплоскости найдется
продолжение для траектории М0 1 , определяемое уравнением
(2-44), т. е. некоторая траектория 1'2'. По второму свойству
фазовых траекторий указанная траектория пересечет ось — х
под прямым углом и, двигаясь слева направо в верхней
полуплоскости, должна приближаться к своей асимптоте у — кйкхс.
Для траекторий 1'2' также найдется продолжение в право!"'
полуплоскости и т. д.
Как видим, фазовая траектория с большими начальными
значениями х (0) и у (0) с течением времени приближается к
некоторой области вблизи начала координат.
Аналогично можно проследить ход фазовой траектории с
начальным положением изображающей точки М0 при малых
значениях х (0) и у (0). В этом случае фазовая траектория удаляется
от начала координат, т. е, здесь имеем расходимость процесса
в малом.
Сопоставляя рассмотренные случаи, замечаем, что в
установившемся режиме в системе получим устойчивый предельный
цикл 1, 2, т. е. имеем автоколебательный установившийся режим.
Амплитуду автоколебаний для температуры aQ и для ее скорости
можно оценить непосредственно по предельному циклу
(рис. 2-19).
Кроме того, можно подметить, что амплитуды
автоколебаний для температуры и ее скорости будут увеличиваться с
увеличением коэффициента передачи в системе к^кхс, так как при
этом асимптоты удаляются от оси х.
2-6. Применение метода точечного преобразования
для исследования нелинейных систем
Из приведенного в § 2-5 примера видно, что фазовые
траектории обычно складываются из отдельных кусков,
представляющих решение уравнений по участкам. Пусть, например, гранич-
45

ными линиями Между кусками фазовых траекторий являются
ось х и линии FG и LN (рис. 2-20, а).
Возьмем начальное положение изображающей точки М0 на
полуоси Ох. Первый этап движения системы состоит в переходе
точки М0 в положение Мг на линии FG. На следующем этапе
изображающая точка переходит в положение М2 на полуоси
ОН, затем — в положение М3 на кривой LN, и, наконец,— в
положение Л44 на исходной полуоси Ох.
Каждому положению изображающей точки на полуоси Ох
М0 (х0, О) соответствует определенное положение точки
Mi (xi> Ух) на кривой FG. Это называется точечным
преобразованием полупрямой Ох в кривую FG. Далее следует
преобразование кривой FG в полупрямую ОН, затем ОН — в кривую
Рис. 2-20
LN и, наконец, кривой LN — в полупрямую О*. Весь этот цикл
преобразований в целом называют точечным преобразованием
полупрямой Ох самой в себя, что записывается в виде
определенной зависимости *4 = f (х0) (рис. 2-20, а), где через #4 и х0
обозначены абсциссы точек Л44 и М0.
Если при любом х0 оказывается *4<х0, то в системе будет
затухающий процесс, а если *4 > *0 — расходящийся процесс.
Если же возможно равенство х4 = х0, то на фазовой плоскости
получится либо устойчивый, либо неустойчивый предельный
цикл.
В тех случаях когда общая картина фазовых траекторий
разделяется на две симметричные части, достаточно исследовать
половину всего точечного преобразования.
В нашем случае верхняя полуплоскость симметрична
нижней относительно начала координат. Поэтому достаточно
рассмотреть лишь первую половину преобразования, т. е. точечное
преобразование Ох в полупрямую ОН, и выразить его в виде
зависимости
1*.1=/(*о). *2<0, (2-45)
причем условием наличия предельного цикла будет
I х2 \ =*0 при х2 < 0.
46

Пусть зависимость (2-45) имеет вид кривой, изображенной
на рис. 2-20, б. Проведем на этом графике прямую под углом 45°
к координатным осям. Если она пересечет кривую, то в точке
пересечения получим | х2 | = х0, т. е. условие предельного цикла.
Чтобы определить, к какому типу предельного цикла
относится полученный предельный цикл, надо взять значения х0,
меньшее и большее периодического, х0 ^ ап и проследить ход
точечного преобразования, как это показано стрелками на
рис. 2-20, б. В данном случае процесс сходится с обеих сторон
к точке пересечения. Следовательно, имеем устойчивый
предельный цикл, соответствующий автоколебаниям с амплитудой
#о = ап- Построение, выполненное на рис. 2-20, б, называется
диаграммой точечного преобразования.
Другие возможные диаграммы точечного преобразования
изображены на рис. 2-21. При этом диаграмма на рис. 2-21, а
соответствует неустойчивому предельному циклу.
Случай рис. 2-21, б соответствует двум предельным циклам:
большему — устойчивому и меньшему — неустойчивому.
Диаграмма (рис. 2-21, в) отвечает вырожденному случаю двух
предельных циклов, когда последние сливаются в один
полуустойчивый предельный цикл. На рис. 2-21, г изображена диаграмма
для устойчивой системы с равновесно сходящимся процессом
при любых начальных значениях х0, а на диаграмме 2-21, д —
для неустойчивой системы.
2-7. Исследование нелинейных процессов методом изоклин
Не всегда фазовые траектории можно определить
интегрированием уравнений по участкам. Когда такое интегрирование
затруднено, ход фазовых траекторий, хотя бы качественно,
можно проследить с помощью так называемого метода изоклин.
Изоклиной называется такая линия на фазовой плоскости,
которую фазовые траектории во всех точках пересекают под
одним и тем же углом к оси абсцисс х.
Так, если известно дифференциальное уравнение фазовых
траекторий
4^ С2"46)
ах
то для получения изоклины нужно положить
dx
Уравнение изоклины, следовательно, будет
/ (*, У) = с, (2-47)
причем с обозначает определенный тангенс угла наклона фазовых
траекторий; каждому заданному значению с соответствует своя
изоклина.
48

Пусть, например, имеем нелинейное уравнение второго
порядка
l*L--k(l—x*) — + x = <3\
dt* dt
которое можно привести к уравнению фазовых траекторий.
Учитывая, что
dx
Рис. 2-22
находим
dy
dt
— k(l—x2)y + x = 0.
Поделив все члены последнего уравнения на у, получим
уравнение фазовых траекторий
dy
dx
k (1—— —.
(2-48)
Соответствующее уравнению (2-48) уравнение изоклин будет
6 (1-х2)
: С ИЛИ у■
k(\—x*) — c
(2-49)
49

Задавая различные значения с (при заданном &), будем
всякий раз строить изоклины. Затем на каждую изоклину наносим
стрелочки под углом arc tg с. Из этих стрелочек и составляются
искомые фазовые траектории (рис. 2-22).
2-8. Теоремы прямого метода Ляпунова
для исследования устойчивости нелинейных систем
Рассмотренные выше методы исследования нелинейных
систем были связаны с построением переходных процессов или их
геометрических образов — фазовых траекторий. После
выполнения таких построений становится ясной картина процесса
только для принятых при построении или решении начальных
условий. Часто требуется определить сходимость переходных
процессов в нелинейных системах для некоторой области
расположения начальных отклонений или для любых начальных
условий. Этому вопросу и посвящены теоремы прямого метода
Ляпунова.
Теоремы прямого метода Ляпунова для исследования
устойчивости нелинейных систем базируются на отображении движения
реальной системы посредством фазовых траекторий в фазовом
пространстве. При этом используются понятия
асимптотической и неасимптотической устойчивости. Если фазовые
траектории вблизи начала координат стягиваются к нему, то имеет
место асимптотическая устойчивость. Если же фазовые
траектории вблизи начала координат стягиваются к некоторой
особой линии (например, к особому отрезку, обусловленному
зоной нечувствительности), то будем иметь неасимптотическую
устойчивость.
При рассмотрении прямого метода Ляпунова будем
полагать, что движение нелинейной системы описывается п
уравнениями первого порядка:
—J- = Хх (хъ х2, . . . , хп),
at
(2-50)
dx,
dt
~~ — Хп (хъ х2,
> *я),
где Х1у Х2, . . . , Хп — произвольные функции, содержащие
нелинейности любого вида; xlt x2i . . . , хп — отклонения
переменных в переходном процессе от их значений в новом
установившемся состоянии, соответствующем значениям внешних
воздействий I = f0 (возмущающее воздействие), g = g0 (задающее
воздействие).
Очевидно, что всегда удовлетворяется условие
Хх = Х2 = . . . = Хп = 0 при X) = х2 = . . . = хп = 0, (2-51)
50

Так как в установившемся состоянии все отклонения
переменных и их производные равны нулю по самому определению
понятия этих отклонений.
Для рассмотрения теорем Ляпунова требуется уяснить
вначале понятия о знакоопределенных, знакопостоянных и
знакопеременных функциях.
Пусть имеется функция нескольких переменных
V=V(xu хп). (2-52)
Можно считать, что под знаком нелинейной функции
находятся координаты n-мерного пространства хъ х2, . . . , хп.
В каждой точке -этого пространства функция V будет иметь
определенное значение. В дальнейшем будем рассматривать функ-
Рис. 2-23
ции V (*!, х2, . . . , хп), которые обращаются в нуль в начале
координат (т. е. при хх = х2 = . . . = хп = 0) и непрерывны
в некоторой области вокруг него.
Функция V называется знакоопределенной в некоторой
области, если она во всех точках этой области, исключая начало
координат, сохраняет один и тот же знак и нигде не обращается
в нуль, кроме самого начала координат.
Функция V называется знакопостоянной, если она
сохраняет один и тот же знак, но может обращаться в нуль не только
в начале координат, но и в других точках данной области.
Функция У называется знакопеременной, если она в данной
области вокруг начала координат может иметь разные знаки.
Примеры У-функций:. при п = 2 V = х\-\- х\ — знако-
определенная (положительная) и V — — (*i + *г) — знако-
определенная (отрицательная); при п = 3 V = х\ + х\—
знакопостоянная, так как она может обращаться в нуль при любом
значении х3, если хг = х2 = 0 (рис. 2-23, а). Функция V =
= хх + х2 будет знакопеременной, так как она положительна
для всех точек плоскости справа от прямой х2 — — хх
(рис. 2-23, б) и отрицательна слева от этой прямой.
В некоторых задачах требуется, чтобы функция V
обращалась в нуль не в начале координат, а на заданном конечном
отрезке АВ (рис. 2-23, в). Тогда знакоопределенность функции V
будет означать ее неизменный знак и необращение в нуль в
некоторой области вокруг этого отрезка.
51

Любую функцию V = V (xlt х2) . . . , хп), тождественно
.обращающуюся в нуль при х± = х2 = . . . = хп = 0, будем
называть функцией Ляпунова, если в ней в качестве величин
*i> *2» • • • > хп взять отклонения переменных исследуемой
системы регулирования в переходном процессе:
*i = *i(0> • • . "*/1 = *я(0.4
входящие в уравнения (2-50).
Производная функции Ляпунова по времени будет
dy dV dxx , dx2 , , dV dxn
-77- + — '-IT + • ■ • + — ~• (2-53)
d/ дхг dt ' dx3 d/ ' ' dxn dt
Подставив значения производных из заданных уравнений
(2-50) в (2-53), получим производную функции Ляпунова по
времени в виде
dV dV у , dV у , м дУ У /о *л\
— = —- Л! + — Х2 + . . . + — Хя, (2-54)
d/ d#i их2 дхя
где Хх, Х2, . . . , Хп — правые части уравнений системы (2-50),
представляющие собой заданные функции отклонений.
Следовательно, производная функции Ляпунова по
времени, так же как и сама функция, является некоторой функцией
отклонений:
3V
-— = W (xlt x2t . . . :xn). (2-55)
dt
Функция W, так же как и сама V, тождественно обращается
в нуль при хг = х2 = . . . = хп = 0. Поэтому к ней можно
применять все те же понятия знакоопределенности, знакопо-
стоянства и знакопеременности.
Базируясь на этих предварительных сведениях, дадим
общую формулировку теорем Ляпунова об устойчивости и
неустойчивости нелинейных систем. Теоремы эти справедливы для
любых значений начальных отклонений, для которых
справедливы исходные уравнения. Устойчивость системы при любых
начальных отклонениях называется коротко устойчивостью
в целом.
Теорема Ляпунова об устойчивости нелинейных систем.
Если при заданных в форме (2-50) уравнениях системы л-го
порядка можно подобрать такую знакоопределенную функцию
Ляпунова V (хъ х2, - . . , хп), чтобы ее производная по времени
W (хъ х2, . . . , хп) тоже была знакоопределенной (или
знакопостоянной), но имела знак, противоположный знаку V, то
данная система устойчива. При знакоопределенной функции W
будет иметь место асимптотическая устойчивость.
Проиллюстрируем справедливость теоремы Ляпунова об
устойчивости на наглядных геометрических образах. Возьмем
52

систему третьего порядка (п = 3). Уравнения для нее в общем
виде будут:
dx-% у. f.
~ Л 1Л*1> *2> Х3)>
dt
——- — Х2 #2, х3),
-dt
—~ ~ Хз (*i» х2> хз)-
dt
(2-56)
Возьмем знакоопределенную положительную функцию
Ляпунова в виде
(2-57)
где a, bt с — произвольно заданные вещественные числа.
Будем придавать величине V возрастающие постоянные
значения: V — О, Съ С2, ...» что соответствует уравнениям
о?х\ + tfxi + clx\
О,
а2х\ + b2x\ + с2х\ = CV
а2х\ + Ь2х\ + с2х\ = С2,
Первое из этих уравнений соответствует одной точке хх =
= х2 — х3 = 0 (началу координат фазового пространства), а
остальные— поверхностям эллипсоидов в фазовом пространстве,
причем каждый последующий эллипсоид целиком содержит
предыдущий (рис. 2-24).
Возьмем теперь производную функции Ляпунова по
времени согласно (2-54); получим
dV
= 2а2х1Х1 \(хъ х2) х3) + 2Ь2х2Х2 (хъ х2> х3) +
dt
+ 2сЧ3Х3(хъ х21 х3) = W (*!, x2j x3),
где функции Xlt X2, X3 берутся из заданных уравнений системы
регулирования.
Если получится, что W (xlt х2у х3) окажется знакоопределен-
ной отрицательной, т. е. если
dV
dt
<0
(2-58)
во всех точках исследуемого фазового пространства, кроме
только начала координат, где
dV
dt
= 0 ПрИ = *2 = *3 = 0,
53

t6 при любых начальных условиях изображающая точка М,
согласно (2-58), будет двигаться в сторону уменьшения значения V,
т. е. будет пересекать эллипсоиды, изображенные на рис. 2-24,
извне внутрь.
В результате с течением времени изображающая точка М
будет стремиться к началу координат О фазового пространства.
Это означает затухание всех отклонений xi9 х2, х3 в переходном
процессе с течением времени.
Таким образом установлена справедливость теоремы об
устойчивости для системы третьего порядка. Аналогично
получим справедливость теоремы Ляпунова и для системы /х-го
порядка, где вместо поверхностей эллипсоидов будем иметь ги
перповерхности. Ах*
Если же функция W будет не знакоопределенной, а
знакопостоянной, то траектория изображающей точки М не везде
будет пересекать поверхности V — С, а может их касаться в тех
точках, где W обращается в нуль (помимо начала координат).
Но так как во всех других местах фазового пространства
функция W имеет один и тот же знак, вследствие чего изображающая
точка может перемещаться только извне внутрь поверхности
V — Су то при решении задачи остается лишь проверить, не
остановится ли изображающая точка там, где W = О (это можно
проследить при решении конкретных задач).
Трудность применения метода Ляпунова состоит в том, что
отсутствуют общие правила отыскания функции Ляпунова V,
Поэтому к теореме об устойчивости следует сделать два важных
замечания.
1. В теореме идет речь о подборе функции Ляпунова V (xlt
*2> • • • » хп)- Можно подобрать несколько вариантов
знакоопределенной функции V со знакоопределенной производной
функцией W. Различные варианты функции V могут дать различные
условия устойчивости. При этом одни из них будут шире,
другие уже, последние могут входить в первые как частный случай.
Поэтому теорема Ляпунова, можно сказать, обеспечивает
получение достаточных условий устойчивости, которые не всегда
будут и необходимыми. При выполнении условий теоремы си-
kx2
Рис. 2-24
Рис. 2-25
54

стема наверняка будет устойчивой в некоторой области
параметров, которые охватываются данной подобранной функцией
Ляпунова, однако может быть, что полученные условия не охватят
всей области параметров. Применение теоремы Ляпунова об
устойчивости несколько усложняется указанным
обстоятельством и требует творческого подхода в подборе функции Ляпунова
при исследовании конкретных нелинейных систем.
2. К сформулированной теореме Ляпунова необходимо
добавить, что понятие устойчивости по Ляпунову допускает, что
при знакоопределенной функции V производная ее W не
обязательно знакоопределенная или знакопостоянная, но может быть
и Тождественно равна нулю во всем рассматриваемом фазовом
пространстве. В этом случае изображающая точка М будет
оставаться все время на какой-нибудь из поверхностей V =
= const, куда ее забросили начальные условия. В результате
система не будет асимптотически приближаться к
установившемуся состоянию, но все же будет все время в достаточной
близости от него.
Теорема Ляпунова о неустойчивости нелинейных систем.
Теорема определяет достаточные условия неустойчивости
нелинейной системы и формулируется так: если при заданных
в форме (2-50) уравнениях системы я-го порядка производная
W х2, •■• • ■» хп) какой-нибудь функции Ляпунова V (xlt
х2> . . . , хп) окажется знакоопределенной, причем сама
функция V в какой-нибудь области, примыкающей к началу
координат, будет иметь знак, одинаковый со знаком производной W,
то данная система неустойчива.
Справедливость этой теоремы геометрически иллюстрируется
следующим образом. Пусть для некоторой системы второго
порядка (п = 2) найдена такая знакопеременная функция V (х1у х2),
для которой производная
оказалась знакоопределенной положительной.
Пусть при этом линии V (*!, х2) = const на фазовой
плоскости располагаются, как указано на рис. 2-25, где линии АВ и
CD соответствуют значениям V = 0 и разделяют те области,
внутри которых V > 0 и V < 0.
Возьмем изображающую точку М, как показано на рис. 2-25.
Поскольку там V < 0 и везде
то изображающая точка М с течением времени будет двигаться
и пересекать линии V = С, переходя от меньших значений С
к большим. Она может лишь временно приблизиться к началу
координат, но в конце концов будет неограниченно удаляться
от начала координат. Это соответствует расходящемуся процессу,
т. е. неустойчивости системы.
Аналогично можно показать справедливость теоремы и для
систем /1-го порядка.
dV
dt
dV
дхх
*i(*i> *г) Н *2 (*ь *г) = V х*)
дх2
55

2-9. Частотный метод В. М. Попова
для определения абсолютной устойчивости нелинейных систем
Частотный метод, предложенный румынским ученым
В. М. Поповым, позволяет исследовать абсолютную
устойчивость нелинейной системы с одной однозначной статической
нелинейностью. Под абсолютной устойчивостью понимается
устойчивость в целом при любой форме нелинейности,
удовлетворяющей условиям (рис. 2-26, а):
0^JLM_^k прих^'О, F(0) = 0.
х
Рис. 2-26
Уравнение линейной части системы (рис. 2-26, б) с одной
однозначной нелинейностью z ~ F (х) запишется в виде
Q(p)x= — R(p)z, (2-59)
где
Q (р) = а0рп + alPn-1 + . . . +an_lP + ап>
R(p) = b0pm + b{pm-l+ . . . +bm_lP + &m,
причем обычно удовлетворяется условие m<n.
Пусть нелинейность (рис. 2-26, а) имеет любое очертание,
не выходящее за пределы угла arctg k.
Характеристический полином линейной части Q (р), или
знаменатель ее передаточной функции
w*{p) = tU' <2"60>
имеет все корни с отрицательными вещественными частямилибо
кроме них имеется еще не более двух нулевых корней (т. е.
допускается второй порядок астатизма для линейной части).
Другими словами, допускается, чтобы в
характеристическом полиноме линейной части Q (/?) коэффициенты были ап = О
или ап = 0 и an_i = 0.
56

При указанных условиях приведем формулировку теоремы
В. М. Попова без доказательства»
Для установления устойчивости нелинейной системы
достаточно подобрать такое конечное действительное число я,
при котором при всех со > 0 выполняется неравенство
Ке[(1+/со/1)1Гл(/со)] + 4->0, (2-61)
k
где Wn (/со) — амплитудно-фазовая частотная характеристика
линейной части системы (2-60).
X
jпри п-т>1 ц*
(о
О1=оо Тш-0
В) |
^\при n-m=1 ц*
о) Jcu=Q*
V
м)~оо /
Рис. 2-27
Другая формулировка той же теоремы, дающая удобную
графическую^интерпретацию, связана с введением
видоизмененной частотной характеристики Wn (/со), которая определяется
следующим образом:
Re^(/©) = Re^(/©),
Im UP* (/©) = ©Im №л(/со).
(2-62)
Видоизмененная частотная характеристика Wn (/со) имеет
вид (рис. 2-27, а), аналогичный виду обычной характеристики
№л (/со), когда в выражениях Q (р) и R (р) разность степеней
п—m > 1. Если же п—m = 1, то конец характеристики Wn (/со)
будет на оси мнимых ниже начала координат (рис. 2-27, б).
Преобразуем левую часть неравенства (2-61):
Re [(1+/©Л) УлU©)] + 4" =
k
= Re Гл (/со) — ©Л Im 1Гл (/©) + — -
k
Выполненное преобразование связано с перемножением
комплексных величин, записанных в алгебраической форме!
(«i + jbi) {а2 + jb2) = (аха2 — ЬХЬ2) + / (ахЬ2 + а2Ьг).
Положив
57

и ИСлОльзоаав соотношения (й-бй), получим вместо (2-61) дли
теоремы В. М. Попова условие
6/; (ю) - Л (©> + -!.> о (2-63)
к
при всех © > 0.
Очевидно, что равенство
"л-< + у = 0 (2-64)
Рис. 2-28
при любом действительном h представляет собой уравнение
прямых на плоскости (U*9 jV*), проходящих через точку
(--М-
Отсюда вытекает графическая интерпретация теоремы
В. М. Попова: для установления устойчивости нелинейной
системы достаточно подобрать такую прямую на плоскости ([/*,
JV*), проходящую через точку ^ — , /oj , чтобы вся кривая
(/©) лежала справа от этой прямой.
На рис 2*28, а, б показаны случаи выполнения теоремы,
а на рис. 2-28, в, г — случаи, когда, теорема В. М. Попова не
выполняется.
58

ГЛАВА ТРЕТЬЯ
ОСНОВЫ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
Линейная
часть
9(0
3-1. Гармоническая линеаризация нелинейностей
Метод гармонической линеаризации является
приближенным методом исследования нелинейных автоматических систем.
При сравнительной простоте метод обладает большой
универсальностью в применении к различным нелинейным задачам
и удачно дополняет точные методы исследования нелинейных
систем. Метод гармонической линеаризации дает приемлемую
для практических расчетов точность при исследовании систем
высокого порядка (начиная с третьего) и имеет ограничения
в применении к системам низкого
порядка и при некоторых специфичных
нелинейностях, где задачи
исследования могут быть решены лишь ранее
рассмотренными точными методами.
Основы метода гармонической
линеаризации в общей его постановке
были разработаны Н. М. Крыловым и
Н. Н. Боголюбовым. Применительно
к задачам теории автоматического
регулирования метод был развит Е. П.
Поповым и Л. С. Гольдфарбом.
Пусть имеется нелинейная
замкнутая автоматическая система, которая в простейшем случае
представляется в виде линейной части и нелинейного звена
(рис. 3-1). Уравнение линейной части системы без учета
внешних воздействий, т. е. при g (t) = 0 и / (/) = 0, в общем
случае запишется в виде
нелинейное
звено
Рис. 3-1
Q(p) *i=. —#(р) х2.
(3-1)
Рассмотрим простой случай, когда нелинейным звеном
является безынерционное звено с нелинейной статической
характеристикой
*2 = /•(*!> рхх). (3-2)
Вообще метод гармонической линеаризации применим и
к более сложным случаям наличия динамических
нелинейностей, а также нескольких нелинейностей в системе.
В нелинейных системах часто возникают автоколебания,
т. е. собственное устойчивое периодическое движение. Если
в установившемся режиме в системе возникнут автоколебания,
то для всех переменных, являющихся входными и выходными
величинами звеньев системы, они будут несинусоидальны из-за
наличия нелинейности. Однако на выходе линейной части
системы, или на входе нелинейного звена, эти колебания будут
близки к гармоническим, так как линейная часть обычно
подавляет высшие гармоники (является фильтром низких частот).
Поэтому автоколебания в системе по методу гармонической ли-
59

неаризации приближенно для входной величины нелинейного
звена определяют в гармоническом виде
xi == sin соп/, (3-3)
где ап и соп — амплитуда и частота искомого периодического
решения.
. В, этом состоит первая приближенность метода.
Гармоническая форма входного сигнала нелинейности
принимается и в случае рассмотрения колебаний с медленным
изменением амплитуды вблизи. периодического движения. Кроме
того, нелинейное звено можно рассматривать в отдельности и на
него подавать гармонические воздействия, наблюдая за
изменением выходной величины, как это делается при снятии
частотных характеристик линейных звеньев. Поэтому запись для
входной величины нелинейности в форме (3-3) будет использоваться
только для периодических решений. В общем случае для
гармонической линеаризации нелинейности ее входную величину
будем записывать без индекса <<п» при амплитуде и частоте, в виде
хх — a sin со/. (3-4)
При наличии на входе нелинейного звена гармонических
колебаний на его выходе будем иметь колебания с той же
частотой, но несинусоидальной формы. Периодическую нелинейную
функцию
х2 = F (хг) = F (a sin со/)
разложим в ряд Фурье:
х2 ~ С0 + Аг sin со/ + Вг cos со/ -f- А2 sin 2 со/ + #2cos 2со/ +
+ ;43sin3co/ + £3cos3co/ + (3-5)
где С0, Аъ Въ А2, В2, Л3, В8, . . . — коэффициенты ряда
Фурье.
Вначале будем полагать, что постоянная составляющая
в колебательном процессе отсутствует, т. е. удовлетворяется
условие
С0~—— f F (a sin \|?) = 0, -ф=со/.
271 о
Это выполняется всегда, когда нелинейная статическая
характеристика является нечетно-симметричной функцией
(рис. 3-2, а, б).
В разложении периодической функции в ряд Фурье (3-5)
отбросим также все высшие гармоники. В этом состоит вторая
приближенность метода. В более точных исследованиях можно
учитывать и высшие гармоники, но при этом усложняются
расчеты.
С учетом указанных допущений (3-5) приближенно можно
записать в виде
х2 == Ах sin со/ + Вг cos со/. (3-6)
60

В (3-6) подставим из (3-4)
sin со/ =
хг
и (после дифференцирования (3-4) по времени: рхх = асо cos со/)
cos со/
Рис. 3-2
В результате имеем
%2
а асо
лг2 —
(3-7)
Соотношение (3-7) линейно связывает входную и выходную
величины нелинейного звена и называется формулой
гармонической линеаризации нелинейностей. Входящие в (3-7)
коэффициенты q (а) и а' (а) называются коэффициентами
гармонической линеаризации и определяются как коэффициенты первой
гармоники ряда Фурье, поделенные на амплитуду переменной
на входе нелинейного звена:
ш
qr (а) -
А.
а
1
2л
па
J* F (a sin г|)) sin г|)аЧ|э,
о
2л
[ F (a sin я|>) cos ypdty, г|) = со/, j
(3-8)
Особенностью гармонической линеаризации в отличие от
обычной линеаризации является то, что входящие в формулу
гармонической линеаризации коэффициенты q (а) и а (а)
являются переменными величинами, зависящими от амплитуды
гармонических колебаний (в общем случае и от частоты) на
входе нелинейности.
61

Полученное линейное соотношение (3-7) для нелинейного
звена объединим с уравнением линейной части (3-1). В
результате получим гармонически линеаризованное уравнение
нелинейной системы для переменной на входе нелинейного звена,
определяющее ее собственное движение,
Ч' (fl)
{(Ш + Я(Р) д(а) + -
со
: 0. (3-9)
Дифференциальному уравнению (3-9) соответствует
характеристическое уравнение
Q (р) + R (р) J ? (а) + р] = 0, (3-10)
где р — переменная характеристического уравнения.
По гармонически линеаризованному уравнению можно
определить периодическое решение в системе и выполнить другие
исследования.
3-2. Определение автоколебаний
в нелинейных системах с помощью критерия Михайлова
Автоколебания в нелинейных системах можно определить
на основании критериев устойчивости линейных систем.
Рассмотрим вначале метод определения автоколебания по
гармонически линеаризованному уравнению нелинейной системы
с помощью критерия устойчивости Михайлова.
В соответствии с характеристическим уравнением (3-10)
гармонически линеаризованной системы аналитическое
выражение для кривой Михайлова запишется в виде
L (/©) = Q (/©) + R (/£) \ Я (а) + й
(3-11)
где О^со^оо—текущая частота вдоль кривой Михайлова.
Отделив в (3-11) вещественную часть от мнимой, имеем
L (/со) = X (а, со, ©) + /Т(а, со, со), (3-12)
причем в выражении X и Y кривой Михайлова, кроме
амплитуды и частоты колебаний на входе нелинейного звена а и со
и текущей частоты со, входят параметры системы (коэффициенты
передачи и постоянные времени звеньев).
Для получения незатухающих колебаний в системе кривая
Михайлова должна проходить через начало координат
(рис. 3-3, а). Причем текущая частота кривой Михайлова в
начале координат будет совпадать с частотой искомого
периодического решения, со = соп, при амплитуде на входе нелинейности
а = ап. Условие прохождения кривой Михайлова через начало
координат дает два уравнения с двумя неизвестными
Х(аи, соп) = 0, Г (ап, соп) = 0, (3-13)
62

из которых й находятся амплитуда ап й чистота соп
периодического решения хх — ansin©ni* для входной величины
нелинейности в зависимости от параметров системы.
Если при заданных параметрах системы ап и соп получаются
в виде вещественных положительных значений, это значит, что
в системе имеется периодическое решение. Если при заданных
параметрах ап и соп не получаются вещественными
положительными, это означает, что при таких величинах параметров
периодического решения в системе нет.
Рис. 3-3
Наличие периодического решения не обязательно
соответствует автоколебаниям. Автоколебания — это устойчивое
периодическое решение или устойчивый предельный цикл. Поэтому
после определения периодического решения необходимо
проверить, является ли оно устойчивым, т. е. сходится ли процесс
в системе от малых и больших значений амплитуды к
периодическому решению или расходится от него.
Устойчивость периодического решения можно определить
следующим образом. В случае периодического решения a = an
кривая Михайлова проходит через начало координат (рис. 3-3, б).
Дадим системе малое отклонение от периодического движения
по амплитуде на величину Да. Тогда кривая Михайлова
отклонится от начала координат в ту или другую сторону. Если в
выражении (3-12) для кривой Михайлова возьмем вместо ап
значение ап + Аа и получим, что деформированная кривая
Михайлова будет соответствовать устойчивой системе (штриховая
кривая 1 на рис. 3-3, б), или значение ап—Аа и получим случай
63

Неустойчивости системы (штриховая кривая 2 на рис. 3-3, б),
это будет означать, что периодическое решение устойчиво и
соответствует автоколебаниям. В противном случае
периодическое решение будет неустойчивым, т. е. в системе имеет место
неустойчивый предельный цикл.
Это можно пояснить также с помощью кривой процесса,
изображенной по времени. Периодическое решение означает
незатухающие колебания с амплитудой ап (рис. 3-3, в). Если
при увеличении амплитуды на величину Да приходим к случаю
устойчивой системы, это означает, что амплитуда ап + Да будет
уменьшаться с течением времени. Если же при уменьшении
амплитуды на величину Да приходим к случаю неустойчивой
системы, это означает, что амплитуда ап—Да будет увеличиваться
с течением времени. Следовательно, при отклонении амплитуды
от периодического решения в ту и другую сторону получаем,
что амплитуда сходится к ее значению в периодическом решении,
т. е. имеем устойчивое периодическое решение, соответствующее
автоколебаниям.
Анализируя все возможные случаи, на основании
указанного геометрического условия Е. П. Попов сформулировал
приближенный аналитический критерий устойчивости
периодических решений. По этому критерию для устойчивости
периодического решения требуется выполнение неравенства
где индекс «п» означает, что в частные производные, взятые от
выражений для X и У кривой Михайлова (3-12), следует
подставить значения а = ап и со = соп того периодического решения,
устойчивость которого исследуется.
3-3. Гармоническая линеаризация однозначных
нечетно-симметричных статических нелинейностей
Пусть имеем нечетно-симметричную однозначную
статическую нелинейность (рис. 3-4, а). Ниже изображено
синусоидальное воздействие на входе нелинейности хг = a sin \|>, \|) = cor.
На выходе нелинейности будем иметь периодическую функцию
х2 — F (a sin \|)) с той же частотой со (рис. 3-4, б).
Для коэффициента q (а) согласно (3-8) имеем
На рис. 3-4, б показаны также функции sin \|) и cos ф.
Очевидно, что вычисление коэффициента q (а) можно выполнить
интегрированием по четверти периода, т. е. для однозначных
нечетно-симметричных статических характеристик
(дХ \п / дУ \п / дХ \п / dY \п
[да ) \д(о) [да / [да )
> О,
(3-14)
1 2?
q (а) = —— J F {a sin sin afa*ip, ф = со/.
о
о
(3-15)
64

Из того же рис. 3-4, б видно, что значение коэффициента
гармонической линеаризации
1 2я
q' (а) = J F (a sin ар) cos tydty
обращается в нуль, так как произведение F (a sin \|)) и cos г|)
изменяет знак в каждой четверти периода.
а)
X2=F(xf)
0
0
л
2л
f
Рис. 3-4
В результате для однозначных нечетно-симметричных
статических нелинейностей формула гармонической линеаризации
приобретает простой вид
x2 = q(a)xv (3-16)
где q (а) вычисляется по формуле (3-15).
Вычислим коэффициент гармонической линеаризации q (а)
для некоторых нелинейностей.
Для релейной статической характеристики с зоной
нечувствительности (рис. 3-5, а) при гармоническом аргументе хх =
= a sin г|?, \|) = со/ периодическая функция на выходе
нелинейного звена х2 = F (a sin \|)) будет иметь вид, изображенный на
рис. 3-5, б.
Вычисляя коэффициент q (а) по формуле (3-15), получим
Я/2 „ „ Л/2
4>1
4c
и, так как
sin яр! =
3 Заказ № 933
65

то имеем
при а < Ь q (а) ~ 0.
Для идеальной релейной характеристики (рис. 3-5, в),
полагая в (3-17) 6=0, получим
q(a)
~ па- '
6) x2~F(asin(j>)
(3-18)
2л
в)
Рис. 3-5
Для статической характеристики с ограничением или
насыщением (рис. 3-6, а) при гармоническом входном воздействии
периодическая функция х2 = F (a sin ф) примет вид,
показанный на рис. 3-6, б.
Выполняя вычисления согласно (3-15), получим
я (а) = ( J ka sin if> sin \|)dif> + J £6 sin \J>da|)
46
о
~~ j sin2 ofcfij? + 4^ j sin i|)a"i|? =
Я/2
66

х2
0 ъ
-4- sin 2tb
4
4kb
cos г|)
Я/2
4>i
6
гр! — sin cos -f- 2 — cos j.
a
x1
^ x2~F(asinf}
2
Рис. 3-6
Учитывая значения sin г)^ = — и cos ifo =
имеем
v
l —
62
<7 (a) = I arcsin
я \
• Ь , Ь /\ 62 \ ,
in U— I/ 1 при a>&.
a a V a? ]
(3-19)
Для значений a < b рассматриваемое звено будет линейным
и, следовательно, q (а) = k.
Возможны статические нелинейности, для которых
входной величиной является скорость изменения переменной. На-
х2
пример, при учете сухого трения в
простейшем случае полагают, что оно постоянно
при малых скоростях и изменяет только
знак с изменением знака скорости (рис. 3-7).
Приведенная характеристика
отличается от идеальной релейной
характеристики, во-первых, тем, что аргументом
является скорость изменения входной
величины рхъ во-вторых, тем, что выходная
величина кроме значений си —с может
принимать любые другие значения: —с<дг2 <с
при рхг = 0 (это изображается в виде
жирной вертикальной линии при рхх = 0, в
отличие от идеальной релейной характеристики).
Если известно, что система не будет иметь остановок, т. е.
рхг = 0 существует мгновенно, то сухое трение учитывают по
характеристике, подобной идеальной релейной, но за
гармоническое входное воздействие нелинейности принимают скорость
рхг = а<о sin со/,
Рис. 3-7
3*
67

выполняя линеаризацию согласно соотношению
*2 = Я (flco) рхг.
При учете значения коэффициента гармонической
линеаризации, как для идеальной релейной характеристики, получим
4с
*2 = (3-20)
После исследования автоматической системы, получив
решение для амплитуды скорости а®, можно перейти к значению
амплитуды самой переменной, учитывая, что а = а©/со, либо
\х2
/
/ 1
у S
ОС'
//
f
0 arctg-q(a)
* V2b
Рис. 3-8
сразу в формуле (3-20) можно заменить на асо и записать
соотношение для нелинейного звена с сухим трением'в виде
4с
х2 ~~= рхг. (3-21)
Аналогично можно выполнить гармоническую
линеаризацию и других однозначных нечетно-симметричных статических
нелинейностей. Для большинства распространенных
нелинейностей имеются в литературе (например, в [5]) формулы для
коэффициентов гармонической линеаризации.
Из рассмотрения гармонической линеаризации
однозначных статических нелинейностей видно, что ее физический смысл
заключается в замене нелинейной характеристики линейной
с переменным коэффициентом наклона, равным коэффициенту
гармонической линеаризации q (а) и зависящим от амплитуды а
на входе нелинейности (рис. 3-8, а). Зависимость коэффициента
гармонической линеаризации q (а) от амплитуды часто
изображают в виде графика. Для релейной характеристики с зоной
нечувствительности такой график приведен на рис. 3-8, б.
Значение qm = при а = У2 b получается из исследования на
nb
максимум выражения (3-17) для коэффициента гармонической
линеаризации.
68

3-4. Определение коэффициентов гармонической линеаризации
для двузначных нечетно-симметричных статических
нелинейностей
Определим коэффициенты гармонической линеаризации для
часто встречающихся двузначных статических нелинейностей.
Для таких характеристик в формуле гармонической
линеаризации
Ч = \Я (а) + р
коэффициенты q (а) ф О и q' (а) ф 0.
^ х2 6> x2=f(asin(
л
2л
fi fz
xz
Рис. 3-9
Рассмотрим релейную характеристику общего вида
(рис. 3-9, а). Такая характеристика может соответствовать
случаю управления двигателем или датчиком моментов с помощью
двух нейтральных электромагнитных реле или с помощью трех-
позиционного поляризованного реле, когда коэффициент
возврата реле значительно меньше единицы.
При изменении входной величины, представляющей собой
ток обмотки реле, по гармоническому закону хг = a sin г|),
г|) = (at выходная величина (напряжение, коммутируемое
контактами реле) будет периодической функцией х2 = F (a sin г[)),
изображенной на рис. 3-9, б. Заметим, что в этом случае изме-
69

нение выходной величины по форме будет одинаковым в
течение каждого полу пер иода. Поэтому вычисление коэффициентов
гармонической линеаризации для двузначных
нечетно-симметричных нелинейностей можно выполнять интегрированием по
формулам (3-8) за полупериод.
Учитывая, что х2< = 0 при 0 <с; г|) ^ и ф2^ф^я, для
первого коэффициента гармонической линеаризации q (а) имеем
2 t2 2с У2
q (а) = J F (a sin ty) sin = j sin if>a4|> =
2c
COS lf>
^3 2c
= — (cos^ — cos^).
Переключение реле происходит при значениях хг — Ъ
и хг — тЬ, где т — коэффициент возврата реле. При этом
аргумент периодической функции имеет значения: ^ - arcsin— ,
а
. тЬ
\р2 = я — arcsin и, следовательно,
а
1 / 1 & . 1 A m2b2
cosfc=-J/ 1- —, cos^=-|/ 1---- .
Подставив значения cos и cos i|)2 в формулу для q (а),
окончательно получим
<7le)= 1/ 1 [.А/ приа>6. (3-22)
ла \ |/ а2 Г а2 '
Для коэффициента гармонической линеаризации q' (а)
имеем
2 ^ 2с Р
qf (а) ~ j F (a sin ij)) cos \j)d\|3 = j cos i|)di|) =
2c . ■
sin ф
*■ 1С
(sin i)^ — sin я|з2).
При учете значений sin ^1 и sin \f2 получим
9ch
q' (a) = — 0 — m) ПРИ a > b- (3"23)
При значениях a < b реле не будет срабатывать на
включение и, следовательно, с = 0, q (а) = 0, я' (а) = 0.
Заметим, что в данном случае (и для всех гистерезисных
характеристик) коэффициент гармонической линеаризации q' (а)
принимает отрицательное значение. Из теории линейных
систем известно, что введение производной в закон регулирования
благоприятно сказывается на динамику процесса регулирования.
Здесь же производная вводится с отрицательным знаком (как бы
70

неправильно) и поэтому гистерезисное запаздывание всегда
вызывает ухудшение качества переходного процесса.
Релейная характеристика с гистерезисной петлей
(рис. 3-9, в) соответствует двухпозиционному поляризованному
реле. Такую характеристику можно рассматривать, как частный
случай характеристики общего вида при коэффициенте возврата
т = — 1. При этом коэффициенты гармонической
линеаризации согласно (3-22) и (3-23) определятся формулами:
q(a)
q' (а)
4с
яа
4сЪ
ла*
а* '
при а>Ь.
(3-24)
3-5. Пример исследования автоколебаний
в нелинейной системе
Исследуем релейную следящую систему местного слежения.
Принципиальная схема системы представлена на рис. 3-10, а.
Система предназначается для передачи угловых перемещений а
от задающей оси 30 к управляемому объекту УО с угловыми
перемещениями р.
му
6)
оъ
9)
1 г-
U1
h
Р
уо
-II
1+тцр
р(^тдр)
^линейная I—,
часть
{^нелинеиное\^\
звено
Рис. 3-10
В качестве датчика рассогласований др служит диск с
контактными полукольцами, разделенными изоляционными
прослойками. Напряжение постоянного тока [/_ подводится к
полукольцам с помощью контактных колец кк l По диску дат-
71

чика рассогласований скользят щетки Щ, жестко связанные
с задающей осью. Напряжение иъ снимаемое щетками через
контактные кольца КК 2 (при наличии рассогласования в
системе), подается на вход магнитного усилителя МУ. Выходное
напряжение и2 магнитного усилителя подается в управляющую
обмотку двухфазного индуктивного двигателя Д. Двигатель
через редуктор Р поворачивает управляемый объект и диск
датчика рассогласований.
При согласованном положении объекта и задающей оси
щетки Щ находятся на изоляционных прослойках диска датчика
рассогласований и система остается неподвижной. При повороте
командной оси в ту или другую сторону щетки переходят на
контактные полукольца. На входе магнитного усилителя
появляется постоянное по величине напряжение соответствующей
полярности, и система приходит в движение. Как видим, датчик
рассогласования выявляет разность углов положения задающей
и командной осей G = а—(3 и преобразует рассогласование 6
в напряжение иг соответственно релейной характеристике,
(рис. 3-10, б). Зона нечувствительности на статической
характеристике датчика рассогласований 2Ь определяется толщиной
изоляционных прослоек между полукольцами диска.
Согласно принципиальной схеме (рис. 3-10, а) изображаем
структурную схему системы (рис. 3-10, в). На структурной схеме
через НЗ обозначено нелинейное звено.
Будем исследовать свободное движение системы. Для
такого исследования удобно всю систему представить свернутой
структурной схемой (рис. 3-10, г), в виде линейной части и
нелинейного звена без учета внешних воздействий.
Передаточная функция линейной части системы с входной
величиной их и выходной 0 согласно структурной схеме
запишется в виде
Ц7Л (р) = Wp , (3,25)
р (1 + 7» (1 + Тдр)
где ky, kA, kp — соответственно коэффициенты передачи
магнитного усилителя, двигателя и редуктора; Ту и Тд —
постоянные времени магнитного усилителя и двигателя.
Уравнение линейной части системы согласно (3-25) будет
(Тур + 1) (7> + 1)рв= — клиъ (3-26)
где kji = kykAkp — коэффициент передачи линейной части
системы.
Для нелинейного звена имеем нелинейную зависимость
между его входной и выходной величинами
их-/49),
определяемую статической характеристикой (рис. 3-10, б).
Выполняя гармоническую линеаризацию нелинейности,
получим
Ul = q(a)Q, (3-27)
72

где коэффициент гармонической линеаризации, согласно ранее
выполненным вычислениям (3-17), будет
4с Va* — Ь
q(a) = при а > Ь, (3-28)
я a2 v
а — амплитуда угла рассогласования 9.
Объединяя (3-26) и (3-27), получим гармонически
линеаризованное уравнение для исследования свободного движения
системы
[(Тур + 1) (7> + 1) р + клд (а)] 9 - 0. (3-29)
Исследуем систему на возможность появления в ней
автоколебаний. Для этого согласно (3-29) запишем
характеристическое уравнение
ТуТАр* + (Ту + Гд) р2 + р + kjlq (а) = 0. (3-30)
Будем определять автоколебания с помощью критерия
устойчивости Михайлова. Заменяя в левой части (3-30) р на /со,
получим аналитическое выражение кривой Михайлова
L (а, /со) = X (а, со) + jY (я, со),
где
X (а, со) = knq (а) - (Ту + 7Д) со2,
У (а, со) = со — ГуГдСоЗ. 1 (3"31)
Потребуем выполнения условия колебательной границы
устойчивости, т. е. потребуем, чтобы кривая Михайлова
проходила через начало координат (X = 0, Y = 0). При этом
текущее значение частоты кривой Михайлова в начале координат
будет совпадать-с частотой искомого периодического решения
со = соп при амплитуде а = ап. В результате из (3-31),
отбрасывая решение для второго уравнения со =■ 0, получим два
уравнения для определения периодических решений:
МК)-Су + Гд)«2=°. )
1-7W>*-*. J
Из второго уравнения (3-32) определим частоту
периодических решений
ЙП=Ж' (3"33)
Заменив в первом уравнении (3-32) соп ее значением из (3-33)
и учитывая значение коэффициента гармонической
линеаризации q (а) (3-28), получим соотношение, связывающее амплитуды
периодических решений с параметрами системы:
kJc_v4-* =Гу + 7д, (3.34)
* а% ТУТЯ
73

Из уравнения (3-34) сложно в явном виде выразить
амплитуды периодических решений через параметры системы. Удобнее
разрешить это уравнение относительно того параметра, влияние
которого на автоколебания исследуется. Представляет интерес
определить, как влияет коэффициент передачи линейной части
системы kn на автоколебания в системе.
Разрешая (3-34) относительно /гл, получим:
4^Д Val-b2
Область
устойчивости
равновесия
Область
а в то колег
баний
wig- /У v*
Рис. 3-11
Из (3-35) видно, что для больших значений амплитуд в
пределе при ап -> оо kn -> оо и для малых значений амплитуд в
пределе при ап->Ь &л -> оо. Это значит, что амплитудам
периодических решений соответствуют две ветви (рис. 3-11) при
некоторых значениях kn. Следовательно, существует значение
&л = &кр> называемое критическим, при котором эти ветви
сходятся. _ *
Для определения /гкр исследуем (3-35) на минимум:
dan
2 и 2
an~b
= 0,
отсюда имеем
или
о£ —2^ = 0,
и, следовательно, значение амплитуды периодического решения
при 1гл = kKp будет
(3-36)
74

Подставив (3-36) в (3-35), получим
2сТуТд
Для определения значений амплитуд при ап > У 2 Ъ следует
в (3-35) пренебречь Ь2 по сравнению с а\. Тогда получим
формулу
ап= 4сГУГ* кл. (3-38)
я(Гу + Гд)
В результате без значительных вычислений приближенно
определяется кривая изменения амплитуд периодических
решений в зависимости от коэффициента передачи линейной
части системы.
Для определения автоколебаний следует полученные
периодические решения исследовать на устойчивость. Выполним
это с помощью приближенного критерия устойчивости
периодических решений Е. П. Попова, т. е. определим, для каких
значений амплитуд выполняется неравенство
, да ) \ да ] [да ) \ да )
Из аналитических выражений для кривой Михайлова (3-31)
/ дУ \п
видно, что Y не зависит от амплитуды а, т. е. = 0. При
\ да ]
этом условие устойчивости упрощается и запишется в виде
' дХ \п/ dY \п.
Из (3-31) имеем
Ь>0.
да I \ dec
да ) Л( da
dY \п п 1
* = 1 — ЗТТ<д2 = 1 — ЗТ 7V —-— = — 2.
да i ~ У *~п ■ " i д
Как видно, для устойчивости периодического решения
требуется выполнение условия
-^)П<0. (3-39)
da /
Зависимость коэффициента гармонической линеаризации q
от амплитуды а для релейной статической характеристики с
зоной нечувствительности в виде графика приведена на рис. 3-8, б.
Условие устойчивости периодического решения (3-39)
выполняется для an>Y2b и не выполняется для b^.an^Y2b.
Следовательно, ветвь больших амплитуд (рис. 3-11) соответствует
75

автоколебаниям (устойчивый предельный цикл), а ветвь малых
амплитуд соответствует неустойчивому периодическому
решению или устойчивости в малом и неустойчивости в большом
(неустойчивый предельный цикл). Это условно показываем
стрелками, сходящимися к верхней ветви и расходящимися от
нижней ветви (рис. 3-11).
Практически всегда найдутся значения амплитуды,
превосходящие нижнюю ветвь, и в системе установятся автоколебания.
Поэтому в целом область при /ел>/гкр называют областью
автоколебаний.
Полученные результаты в области автоколебаний можно
распространить и на область &л<-/гКр. Действительно, при
уменьшении кл до значения /гкр область значений амплитуд
между верхней и нижней ветвями стягивается в точку, и при,
&л — &кр остаются лишь верхняя и нижняя стрелки,
продолжающие друг друга. Это позволяет сделать вывод, что при
£л<^&кр имеем устойчивый, равновесно сходящийся процесс.
Область изменения коэффициента 0^^л^/гКр называют
областью устойчивости равновесия.
3-6. Применение критерия Найквиста
для исследования автоколебаний
Рассмотрим применение критерия устойчивости Найквиста,
или частотный метод, для исследования автоколебаний в
системах со статическими нелинейностями
x2 = F(xlf рхг). (3-40)
Исследование автоколебаний в нелинейной системе в
замкнутом состоянии в этом случае выполняется на основании ее
свойств в разомкнутом виде. Разомкнутая система, как обычно,
представляется состоящей из нелинейного звена и линейной
части (рис. 3-12),
Для линейной части системы имеем уравнение
Q(p)x3=R(p)x2. (3-41)
Замыкание системы соответствует замене
х3 = —х±. (3-42)
Подадим на вход нелинейного звена синусоидальные
колебания
;q = a sin со/. (3-43)
На выходе нелинейного звена в этом случае будем иметь
вынужденные несинусоидальные колебания
x2 = F(asin со/). (3-44)
Если полученную периодическую функцию разложить в ряд
Фурье и сохранить только первую гармонику, это
приближенное представление вынужденных колебаний будет эквивалентно
гармонической линеаризации, рассмотренной ранее. На
основании этого для определения первой гармоники вынужденных
76

колебаний на выходе нелинейного звена можно воспользоваться
частотным аппаратом.
Согласно формуле гармонической линеаризации
/ \ I qf (а)
(3-45)
приближенная передаточная функция для двузначных нечетно-
симметричных статических нелинейностей запишется в виде
WH(p, a, <») = f (fl) + ilW-Pf
(3-46)
а для однозначных — в виде
WH(a) = q(a).
Нелинейное
х2
Линейная
звено
часть
Xj
(3-47)
Рис. 3-12
Комплексный коэффициент передачи нелинейного звена
получится из передаточной функции при р — /со и зависит только
от амплитуды колебаний на его входе:
И7„ (а) = ? (а) + /У (а), WH (a) = ? (а). (3-48)
В случае динамических нелинейностей комплексный
коэффициент передачи будет зависеть не только от амплитуды, но
и от частоты.
Комплексный коэффициент передачи, или частотная
передаточная функция, линейной части системы согласно (3-41)
запишется в виде
R (/©)
W (3"49)
Wn (/со) =
Общая эквивалентная частотная передаточная функция,
или амплитудно-фазовая характеристика всей разомкнутой цепи
системы, будет
W (а, /со) = WH (a) Wn (/со) = [q (а) + \q' (a)) W„ (/со). (3-50)
Незатухающие колебания в замкнутой системе
определяются, согласно частотному критерию устойчивости Найквиста,
прохождением амплитудно-фазовой частотной характеристики
разомкнутой системы через точку (— 1, /0) (рис. 3-13, а). Причем
в точке (— 1, /0) текущая частота амплитудно-фазовой
частотной характеристики будет совпадать с частотой периодического
решения для замкнутой системы со = соп. Тогда согласно (3-50)
можно записать условие для определения периодического
решения
W (а, /со) = — 1
77

или
ГнМ^л (УСО) = -1.
Равенство^ (3-51) можно также переписать в виде
1
Wn (/со
1
WH(a)
0 1r
WH(a)
1
q(a) + jq' (a)
d) - kV
(3-51)
(3-52)
(3-53)
Рис. 3-13
Периодическое решение, соответствующее условию (3-52),
можно определить графически. Для этого надо построить
амплитудно-фазовую характеристику линейной части Wn (j®) и
обратную с обратным знаком амплитудно-фазовую характеристику
нелинейного звена (рис. 3-13, б). Точка пересечения
указанных характеристик и будет определять периодическое
решение. Значение частоты периодического решения со = соп
определяется по амплитудно-фазовой частотной
характеристике линейной части №л (/со), а значение амплитуды — по
характеристике — нелинейного звена. Если указанные ха-
WH (а)
рактеристики не пересекутся, это значит, что при заданных
параметрах периодического решения в системе нет.
Устойчивость периодического решения здесь приближенно
оценивается следующим образом. Для сходимости колебаний
к периодическому решению от больших и малых амплитуд,
согласно критерию Найквиста, требуется, чтобы при
увеличении амплитуды а = ап + Да частотная характеристика всей..
разомкнутой системы W (а, /со) не охватывала точку — 1, /0, а
при уменьшении амплитуды а = ап—Да — охватывала точку
— 1, /со. Перенесем это утверждение на раздельные
характеристики Wn(j(o) и •
№н {а)
78

Согласно условию периодического решения (3-51), при
фиксированном значении характеристики ХРЛ (/со) для
устойчивости периодического решения требуется, чтобы при переходе от
меньших амплитуд к большим WH (а) уменьшалась по модулю.
Для обратной величины это означает, что с ростом
WH (а)
амплитуды модуль ее должен возрастать. Другими словами,
для устойчивости периодического решения требуется, чтобы
при переходе характеристики !— из внутренней области
WH (а)
характеристики Wn (/со) во внешнюю происходило возрастание
амплитуд, как показано на рис 3-13, б стрелкой. Если при
таком переходе будет убывание значений амплитуд, то
периодическое решение неустойчиво.
ГЛАВА ЧЕТВЕРТАЯ
ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ
СИСТЕМ ПРИ УЧЕТЕ ВНЕШНИХ ВОЗДЕЙСТВИЙ
И НЕСИММЕТРИЧНЫХ НЕЛИНЕЙНОСТЯХ
4-1. Определение автоколебаний и ошибок в нелинейных системах
при постоянном внешнем воздействии
До сих пор исследовались симметричные автоколебания как
результат свободного движения системы (т. е. без внешних
воздействий) при симметричных нелинейностях. Для исследования
прохождения внешних воздействий через нелинейную систему
важное практическое значение имеет рассмотрение
несимметричных автоколебаний, т. е. колебаний при наличии постоянной
или медленно изменяющейся составляющей в нелинейном
процессе.
Несимметрия автоколебаний может вызываться различными
причинами: 1) несимметричностью нелинейности как при
наличии, так и при отсутствии внешних воздействий; 2) наличием
постоянного или медленно меняющегося внешнего воздействия
при симметричных нелинейностях; 3) наличием постоянной или
медленно меняющейся скорости внешнего воздействия при
симметричных нелинейностях в астатических системах.
Действительно, если имеется несимметричная статическая
нелинейная характеристика (рис. 4-1, а), то даже при
симметричных колебаниях на входе нелинейности х — a sin ф, ф = со/
возникают несимметричные колебания на выходе нелинейности
F (a sin г|э) (рис. 4-1, б).
Если нелинейность симметрична (рис. 4-2, аУ то при нали^
чии постоянного внешнего воздействия смещается центр
колебаний переменной на входе нелинейности на величину х°, т. е.
79

входная величина нелинейности для незатухающих колебаний
должна определяться в виде
х = х° + a sin со/. (4-1)
Вследствие смещения центра колебаний колебания на
выходе нелинейности F (#° + a sin i|)) становятся
несимметричными по амплитуде и по фазе (рис. 4-2, б).
Пусть задана нелинейная автоматическая система,
динамика которой для входной величины нелинейности при наличии
внешнего воздействия описывается дифференциальным
уравнением
Q(p)x + R(p)F(x) = S(p)f(t). (4-2)
8) kF(asin<p)
F
/ х
0
0
X
С
>>
ж
2п
2я (j^wt
(p = U)t
Рис. 4-1
Положим в простейшем случае что внешнее воздействие
постоянно: I (/) = 1° или 5 (0) £° = М°. Тогда (4-2) запишется
в виде
Q(p)x + R(p)F(x) = M°. (4-3)
Согласно (4-1) решение для входной величины
нелинейности определяется в форме
X — Х° + X*
a sin г|5, ip = со/,
(4-4)
причем имеем три неизвестных л:0, а, со.
С учетом величины смещения х° периодическую функцию
на выходе нелинейности по методу гармонической линеаризации
можно записать в виде
F (х) = F (*° + a sin if) — F0 + + — pj x* + высшие
гармоники.
80

При учете только первой гармоники разложения в ряд
Фурье имеем
F(x) = F (х° + a sin г|>) = F° + -f — **, г[> = со/, (4-5)
где постоянная составляющая и коэффициенты гармонической
линеаризации определятся по формулам:
, 2я
F0 = —- f F (л;0 + a sin i|?) Л|>,
1
яа
2я
| F (л;0 + а sin г|э) sin г|к£ф,
о
2л
| Т7 (а:0 + a sin г|э) cos а|х£ф, if> = со/.
(4-6)
F(x°+asinip)
0
М ! *
я
2п
ф*оиЬ
Рис. 4-2
ф-wt
Из (4-6) видно, что постоянная составляющая и
коэффициенты гармонической линеаризации являются функциями трех
неизвестных: х°, а, со;
Подставив значение х из (4-4) и линеаризованное значение
нелинейной функции F (х) из (4-5) в дифференциальное
уравнение (4-3), получим
Q (р) (х° + х*) + R (р)
F* + [q + ^-p)x*
со
М°. (4-7)
8|

Уравнение (4-7) разобьем на два:
Q (0) х* + R (0) F* = Л4°, (4-8)
Q (р) ** + R (Р) (<7 + 4- х* = 0. (4-9)
Первое алгебраическое уравнение описывает изменение
постоянных или в общем случае медленно изменяющихся
составляющих в системе. Второе дифференциальное уравнение, как
и раньше, описывает быстро изменяющееся колебательное
движение системы относительно постоянной или медленно
изменяющейся составляющей. Причем при разделении уравнения (4-7)
на два сохраняются существенные нелинейные свойства системы,
так как между уравнениями (4-8) и (4-9) остается нелинейная
связь через неизвестные я0, q и а', входящие в F (#°, а, со);
q (*°, а, со), q' (*°, а, со).
Если к уравнению (4-9) применить условие существования
периодических решений, вытекающее из критерия устойчивости
Михайлова, то из него, в свою очередь, получим два уравнения.
В результате будем иметь три алгебраических уравнения с тремя
неизвестными для определения периодического решения
относительно центра колебаний и для определения смещения центра
колебаний по известным параметрам системы:
Q (0) х» + R (0) F° = М°,
X (*<>, аш соп) = 0,
У (х\ ап, соп) = 0.
(4-10)
Условия существования и устойчивости периодических
решений остаются такими же, как и в случае симметричных
колебаний.
Величина х°, получаемая в результате решения уравнений
(4-10), является статической или скоростной ошибкой
соответственно для статической системы и системы с астатизмом первого
порядка. Полученное значение статической ошибки на входе
нелинейности может быть всегда пересчитано в значение ошибки
для любой переменной системы через коэффициенты передачи
линейных звеньев.
В случае наличия несимметричной нелинейности при
отсутствии внешнего воздействия согласно (4-10) при М° = 0
можно записать три уравнения:
Q[(0) x° + R (0) F° ^ 0, ]
Х(х°, а„, соп) = 0, (441)
У (*°, Ап, ©п) = 0, J
из которых также определяются три неизвестных.
82

4-2. Гармоническая линеаризация нелинейностей
при несимметричных колебаниях
Гармоническая линеаризация функции F (х, рх) для
несимметричных колебаний выполняется при условии, что величина
на входе нелинейного звена отыскивается в виде
х = х° + a sin я|), г|) — со/.
Нелинейная функция F (х° + a sin будет в этом случае
периодической с постоянной составляющей F0.
5) ^(х°+а$1пф)
7Z
2п ф-шЬ
ф-шЬ
Рис. 4-3
Выполним гармоническую линеаризацию некоторых
нелинейностей при несимметричных колебаниях.
Рассмотрим релейную характеристику общего вида
(рис. 4-3, а). При гармоническом входном воздействии с
постоянной составляющей получим периодическую функцию на выходе
нелинейности, представленную на рис. 4-3, б.
Определим постоянную составляющую и коэффициенты
гармонической линеаризации при условии а > Ь + \ х°\. Для
постоянной составляющей имеем
* 2я /Я-т-фа 2я—ф4 \
О V фх Я+фз /
= -f- (я — я|)а — ^ — 2я + я|з4 + я + г|)3) =
2я
■№з —*1 + *4—*2>-
2я
83

Соответствующие углы имеют значения:
. Ь — х° , . тЬ — *э
== arcsin , г|)2 = arcsin
. b + x° , . mb + x°
i|)3 = arcsin ! , ij)4 = arcsin —
С учетом значений углов получим
r° = arcsin ■ arcsin \-
2я \ а а
/721) -Л- х® ttlb X® \
+ arcsin ■ arcsin ) при а> b + | х° |. (4-12)
a a J
Находим коэффициент q:
j 2я
q = —— j F (х° + а sin i|)) sin =
яа
rt—*ф3 2я—гр4 \
J sin if>d\|) — j sin )
= (cos ^ + cos o|?2 + cos гр3 + cos г]?4),
яа
что при учете значении углов дает
_ 0
па
Для коэффициента имеем:
2я
j* F (х° + a sin г])) cos ifdij) —
(4-13)
j 2я
с / Л—-фз 2ятг|?4
j" cos tydxp — I cos г|)Лф j =
= (sin г|;2 — sin -{- sin г|)4 — sin г|)3),
яа
что при учете синусов соответствующих углов дает
с [ mb — x^ b — x° ( mb + x° b + х°
Я
па \ а а а

или
(4-14)
Заметим, что значение коэффициента гармонической
линеаризации а' остается таким же, каким оно было для релейной
характеристики общего вида в случае симметричных
колебаний. Это обусловлено тем, что посредством коэффициента q'
при гармонической линеаризации двузначных нелинейностей
учитывается гистерезис или опережение, которые существуют'
независимо от смещения центра колебаний.
а)
x
0
ъ
оь
в)
F
x
0
Рис. 4-4
Релейную характеристику с гистерезисной петлей (рис. 4-4,а)
можно рассматривать как частный случай характеристики
общего вида при т = — 1. В результате из (4-12), (4-13) и (4-14)
получим формулы постоянной составляющей и коэффициентов
гармонической линеаризации:
сп с ( . Ь + х* . b — xo
F° = — arcsin ■ arcsin
с
л \
2с
ла
V
>-(&~;0)2+l/i-(6+/0)8), }
я =
4сЬ
В релейной характеристике с зоной нечувствительности
(рис. 4-4, б) коэффициент возврата следует принять равным
единице. В результате из (4-12), (4-13) и (4-14) при т = 1
получим
гп с ( . Ь + х* . Ь—х»
F° = — arcsin ! arcsin
л \ а а
= 2с
ла
q' = 0.
1/'
(b — *°;
(b + *°)2
(4-16)
85

Для идеальной релейной характеристики (рис. 4-4, в),
положив в (4-16) Ъ = О, имеем
F° = — arcsin —
<? = — Л/
па \
а)
к&"—"
i--Hi_f. ^ = о.
(4-17)
£; в)
Рис. 4-5
Аналогично можно получить формулы постоянной
составляющей и коэффициентов гармонической линеаризации для
несимметричных нелинейных статических характеристик.
Рассмотрим, например, характеристику, представленную на
рис. 4-5, а. Такая характеристика может соответствовать
устройству, содержащему упругие элементы с различной
жесткостью, или вентилю при учете тока в прямом и обратном
направлении.
На рис. 4-5, б представлена периодическая функция
F'(x° + a sin ф), в соответствии с которой и вычислим
постоянную составляющую и коэффициент гармонической
линеаризации q. Для постоянной составляющей согласно (4-6) получим:
"я+ф!
a sin яр) яЧ|) +
. -^1
2я-Ч>1 "1 k о
+ Г *a(*o + asinl>)*|> + ~
F° =
1
2л
86

2я
I Я+Ф1
I 2я-$1
I 2я-ф,
cos г|?
1-Ф,
2л;
I я+Ф.
2я
cos г|)
2я
(я + Shfe) + (я - 2^) + cos ft - cos ah,
k2x*
2я
kid
я
X0
что при учете значения ty1 = arc sin — дает
X
X
х* arcsin — + a j/^l - .
(4-18)
Для коэффициента гармонической линеаризации q согласно
(4-6) имеем:
Г я+ф!
J К (х° + а sin г|)) sin ф^г)? +
<7 =
1
яа
2я—
+ J &2 (#0 + a sin я|)) sin
cos г|)
я-fth
+
+
&х / г|) sin 2г|)
2я—ф,
я V 2
k2 I ^ sin 2г|)
Я+Ф1
-Ф:
k2X*
ла
cos г|)
2я—ф1
+
Я+фх
я V 2
Я+ф!
2^i;C° cos г|)х + А_ (я + 2th)
ла
2я
sin 2фх - cos ^ + А_ (Я - 2^) + А_ sin 2фх.
2я . ла 2я 2я
С учетом значения = arc sin — получим
а
X
X I arcsin — + — I/ 1
(*°)2
(4-19)
Коэффициент = 0, как и в случае симметричных
однозначных характеристик.
Для характеристики (рис. 4-5, в), соответствующей
идеальному вентилю или односторонней реакции упругого элемента,
87

следует в (4-18) и (4-19) положить k2 = 0, kx = k. В результате
получим следующие формулы:
ро —
— х° arc sin У а I/ 1 — /4.2о)
<7 =—-| I arcsin— ' ■ / 1 __ v /
2 я \ а
4-3. Прохождение медленно меняющихся сигналов
в автоколебательных системах
Рассмотрим очень важный для практики случай, когда
внешнее задающее воздействие g (t) или возмущающее воздействие
I (0» приложенное к автоколебательной системе, является
медленно меняющимся. Под медленно меняющимся воздействием
будем понимать такую функцию времени, которая сравнительно
мало изменяется за период автоколебаний системы, т. е. для
которой соблюдается условие
1/(' + Л-/(01«/(0. (4-21)
где Т = 2я/соп, соп — частота автоколебаний.
Указанному условию почти всегда удовлетворяют сигналы
управления, проходящие через автоматическую систему.
Сделанное предположение позволяет величину внешнего
воздействия, например f (/), считать постоянной за период.
Решение для переменной величины на входе нелинейности можно
тоже искать в форме (4-4), т. е.
х = х° ~\- х*, х* = a sin со/.
Здесь а:0, а и со будут не постоянными, а медленно
изменяющимися с изменением внешнего воздействия величинами.
В этом случае, так же как и при приложении постоянного
воздействия, можно написать гармонически линеаризованное
уравнение системы, подобное уравнению (4-7), но отличающееся
от него тем, что постоянные величины теперь становятся
медленно изменяющимися переменными, т. е.
Q (р) (*о + х*) + R (р)
F°+f? + — р\х*
СО
= S(p)f(t). (4-22)
При достаточно медленном изменении f. (/) уравнение (4-22)
может быть разделено на два:
Q(p)x* + R(p)Fo = S(p)f(t), (4-23)
Q (р) x* + R (р) (д + Л1р\х*^о (4-24)
соответственно для медленно меняющейся составляющей и
колебательной составляющей в нелинейном процессе.
При таком разделении уравнений, как и раньше,
сохраняются существенно нелинейные свойства системы. Уравнение
88

(4-23) для медленно меняющихся составляющих теперь является
дифференциальным.
Медленно меняющуюся величину постоянной составляющей
F0 в (4-23) нужно связать со смещением центра колебаний х°.
Эту связь можно найти, воспользовавшись уравнением (4-24)
для колебательной составляющей.
Из уравнения (4-24) после применения условия границы
устойчивости по критерию Михайлова получим два уравнения
для периодических решений:
X (х°, ап, соп) = О, У (х°, ап, соп) = 0.
(4-25)
Эти уравнения позволяют определить амплитуду и частоту
автоколебаний как функции постоянной составляющей х°:
ап = ап(хР)9 соп= С0п(х°)
и, следовательно, найти так
называемую функцию
смещения
Я> = Ф(л;0). (4-26)
Подставив значение
функции смещения в (4-23),
получим уравнение для медленно
меняющейся составляющей х°
Q(p) x» + R (р) ф(дО)«
= S(p)f(t). (4-27)
Рис. 4-6
Функция смещения представляет собой как бы статическую
характеристику нелинейного звена для прохождения медленно
изменяющихся составляющих в автоколебательной системе.
Функция смещения даже для релейных характеристик вблизи
начала координат имеет вид плавной кривой. Этот эффект
называется вибрационным сглаживанием нелинейностей при
помощи автоколебания, а функцию Ф (х°) можно назвать
сглаженной нелинейной статической характеристикой. Так, например,
для идеальной релейной характеристики (рис. 4-4, в) функция
смещения F0 = Ф (х°) имеет вид кривой, изображенной на
рис. 4-6.
В отличие от первоначально заданной нелинейности
функцию смещения для малых отклонений можно линеаризовать
обычным способом (по касательным или секущим). Итак, в
определенном диапазоне можно считать
F° = Ф (*°) = knx°,
(4-28)
где величина kH зависит от параметров системы.
^ После подстановки вместо функции смещения ее
линеаризованного значения kHx° уравнение для медленно изменяющихся
составляющих становится обыкновенным линейным
[Q (p) + R(p)kH]x» = S(p)f(t).
(4-29)
89

Существенно важным обстоятельством является то, что
медленно меняющиеся сигналы проходят через нелинейность
с коэффициентом передачи &н, отличающимся от коэффициента
передачи автоколебаний /q или q + — р\.
4-4. Приближенное определение колебательных переходных
процессов в нелинейных системах
Рассмотрим симметричные относительно оси времени
колебательные переходные процессы (рис. 4-7, а, б) в нелинейной
автоматической системе. Такие процессы в первом приближе-
Рис. 4-7
нии могут описываться затухающей или расходящейся
синусоидой при медленном изменении показателя затухания и частоты,
т. е.
x = a(t)sm^(t)t (4-30)
где текущие значения частоты и угла определяются формулами
dt J0
(4-31)
а текущие значения амплитуды и затухания связываются
зависимостями
da da
— = а£, —
dt a
t
£>dt, a — aQe°
(4-32)
Для линейных систем при со = const и £ = const согласно
(4-31) и (4-32) можем написать:
яр = со/ + яр0, а = а0еУ,
90

что позволяет линейные затухающие и расходящиеся колебания
представить в виде
х = а0е& sin (со/ + яр0). (4-33)
Показатель затухания может характеризовать как быстроту
затухания, так и быстроту расхождения колебаний:
— >0 при £>0,
dt
da_
dt
<0 при*Е<0,
(4-34)
т. е. положительным значениям показателя затухания
соответствуют расходящиеся колебания, а отрицательным — сходящиеся
колебания.
Для нелинейных колебаний по аналогии с (4-33) при учете
4-31) и (4-32) можно записать:
t
№ /< \
х — а0е° sin ( J со dt + яр0 ) . (4-35)
Формулы гармонической линеаризации при рассмотрении
переходных процессов имеют некоторую особенность. В самом
деле, если величина показателя затухания не мала, то,
дифференцируя выражение (4-30) по времени как произведение двух
функций, с учетом (4-31) и (4-32) находим
рх = аса cos яр -f at, sin яр.
Отсюда и из (4-30) имеем
(4-36)
sin Яр =
, рх & р-
cos яр = — — = —
асо
а(о
(4-37)
Поэтому вместо формулы гармонической линеаризации при
учете первой гармоники для незатухающих колебаний
F (х, рх) =
получим
F (х, рх) = i41sin яр + Вг cos яр - А х + 1± Е к х =
а а Гл
(4-38)
91

где коэффициенты гармонической линеаризации при учете (4-30)
и (4-36) определяются формулами
2л
Я = — J F (a sin я]), асо cos \|э + а£ sin ip) sin \|) а*я|),
2я
Я =^"J (а sin г|?, асо cos i|) + at, sin i|>) cos
(4-39)
Здесь в общем случае коэффициенты гармонической
линеаризации зависят от трех неизвестных: а, со, £.
Если рассматривается статическая нечетно-симметричная
нелинейность F (х), то q и ^' сохраняют прежний вид:
2я
^ = —J F (a sin \J?) sin г|? dij?,
2я
q — — J F (a sin i|)) cos i|) a*i|>.
(4-40)
Коэффициенты можно брать в виде, используемом для
определения автоколебаний, учитывая новую форму (4-38)
линеаризации нелинейной функции.
Для нелинейных систем первого класса дифференциальное
уравнение колебательного переходного процесса в свободном
движении будет
Q(p)x + R(p)F(x, рх) = 0, (4-41)
а после гармонической линеаризации примет вид
Q(p)x + R (р) ^ + х = 0. (4-42)
Колебательный процесс в линейной системе, описываемый
решением (4-33), соответствует паре комплексных корней
характеристического уравнения рЬ2 — £ ± /со с фиксированными
значениями £ и со. Аналогично и колебательный процесс в
нелинейной системе, описываемый приближенно решением (4-35),
определяется медленно меняющимися значениями £ (t) и со (/),
которые можно находить из характеристического уравнения,
соответствующего (4-42), гармонически линеаризованной
системы
Q(p) + R (р) (q + ^=^- q' j = 0. (4-43)
Для определения значений £ и со, удовлетворяющих (4-43),
сделаем подстановку р = £ -{- /со. В результате получим
Q а + /со) + R (t + /со) (q + }q') = 0. (4-44)
92

Подстановку р — £ + /со в любой многочлен удобно
выполнять путем разложения его в ряд по степеням /со, например:
Q(C + /©) = Q(C) + f^)/(D+-i-№ (/©)« +
2! \dp* k
л! \dpn)i
где индекс 5 означает, что в выражения производных надо
подставить £ вместо р.
По такой же формуле разлагается в ряд и многочлен
R « +
При малых значениях £ (для медленно затухающих
процессов) удобнее применять разложение по степеням £,
ограничиваясь его первой степенью, а именно:
Q « + /<*>) = (? (/со) + (Щ I )
\dp Jja
Я (С+ /<в) = /?(/©) +
(г) ?
(4-46)
где индекс /со означает подстановку /со вместо р в выражения
для производных.
В комплексном уравнении (4-44) содержится три
неизвестных: £, со и а, причем последняя входит в я и я'. Поэтому
указанное комплексное уравнение позволяет найти две переменные
как функции третьей:
С = £(а), со-со (а), (4-47)
т. е. показатель затухания и частоту как функции амплитуды
затухающего или расходящегося нелинейного процесса.
Когда найдены £ (а) и со (а), можно, пользуясь двумя
дифференциальными уравнениями первого порядка
da Г dyP <л ло\
а/ а/
найти а (0 и г|? (/) для первого приближения искомого решения
нелинейного дифференциального уравнения (4-41) в форме х =
= a sin г|>.
Интегралы уравнения (4-48) при заданных начальных
условиях (а = а0, ф = i|)0 при / = 0) имеют следующий вид:
a t
Со 0
где £ (а) и со (а) — найденные ранее функции (4-47).
Из первого уравнения (4-49) сразу находится а (/), а из
второго (после подстановки значения а), определяется гр (f). В
результате получаем решение в виде
* = a(/)sin\|>(/). (4-50)
93

4-5. Применение диаграмм качества затухания
для определения переходных процессов в нелинейных системах
Операция интегрирования уравнений (4-49) в
приближенных расчетах может и не выполняться. В большинстве случаев
вполне достаточно бывает ограничиться нахождением функций
(4-47) из комплексного алгебраического уравнения (4-44), так
как приближенно процесс может быть оценен величинами £
и со и их отношением £/со, а также характером их изменения в
зависимости от амплитуды колебаний и параметров системы. Это
достигается построением так называемых диаграмм качества
чивости равнове- автоколеда- чивости разно- адтоколеда-
сия ний ' еесия ний
Рис. 4-8
затухания симметричных нелинейных колебаний (рис. 4-8)
представляющих собой семейство характеристик a (k) при £ =
= const и a (k) при со = const, причем k означает какой-либо
выбираемый параметр.
Для линейной системы линии a (k) при £ = const и линии
a (k) при со = const имели бы вид вертикальных прямых, так
как показатель затухания и частота колебательных переходных
процессов в линейной системе не зависят от величины
амплитуды колебаний, а изменяются только с изменением параметров
системы (в данном случае с изменением k).
В нелинейных системах линии диаграммы качества
затухания искривляются или просто имеют наклон в зависимости от
формы нелинейности и структуры системы. Это выражает собой
изменение показателя затухания £ и частоты со в нелинейных
колебательных переходных процессах с изменением амплитуды
колебаний а.
Значение £ = 0 соответствует незатухающим колебаниям,
например, точка С (рис. 4-8) соответствует колебаниям с.
постоянной амплитудой. ап. Поэтому линия £ = 0 на диаграмме
качества в большинстве случаев определяет зависимость
амплитуды автоколебаний от параметра k. По одну сторону
линии £^ Q лежат линии £ = const J> 0, а по другую — линии
94

5= const <J0. Первые соответствуют расходящимся
колебаниям, а вторые — затухающим.
Протеканию переходного процесса во времени
соответствует движение изображающей точки М по вертикали (так как
амплитуда в переходном процессе изменяется, а параметр k
остается постоянным), как это указано на диаграмме
штриховыми линиями и стрелками.
Пусть значение параметра k соответствует точке L (рис. 4-8).
Тогда в переходном процессе изображающая точка из
некоторого положения М0 будет двигаться вниз по штриховой прямой,
проходящей через точку L. Поскольку на всем пути движения
изображающей точки М ее траекторией пересекаются линии
£ = const <J 0, то процесс будет равновесно сходящимся. Такие
процессы возможны для значений параметра kt не
превосходящих значения, соответствующего точке D. Поэтому область
изменения 0 <^ k ^ kD является областью устойчивости
равновесия с затухающим процессом.
В области больших значений параметра k, т. е. при k > kD,
например k = изображающая точка М при больших
значениях амплитуды должна двигаться вниз, так как до линии £ = О
имеем показатель затухания £<0. При малых значениях
амплитуды изображающая точка М должна двигаться вверх, так
как в этом случае имеем показатель затухания £ J> 0. Таким
образом, для приведенной диаграммы при значениях параметра
k >kD имеем область автоколебаний с амплитудами,
определяемыми линией £ = 0, и соответствующими переходными
процессами.
Соответственно движению изображающей точки по
вертикалям на диаграмме £ = const можно определить изменение
затухания, а на диаграмме со = const изменение частоты.
Как видим, построение диаграмм качества дает наглядное
представление о влиянии параметров на ход процесса и
позволяет найти переходный процесс в нелинейной системе или
оценить его качество.
Рассмотрим теперь методику построения диаграмм качества.
Обратимся к уравнению (4-44)
Q «; + /©) + /?№ + /©) (? + Й') = 0.
Выделив в комплексном уравнении вещественную и мнимую
части, как это делалось при определении автоколебаний, и
приравняв их нулю, получим два уравнения с тремя неизвестными,
включающие в себя также параметры системы:
X (а, со, £) = 0, )
(4-51)
У (а, со, £)==0. j
Пусть требуется построить диаграмму качества по
некоторому параметру /г, входящему в коэффициенты уравнений (4-51).
Выразив на основании одного из уравнений величину
со = Ма, £, k) (4-52)
95

и подставив ее в другое уравнение, найдем
k=ft(a, С). (4-53)
Далее, придавая £ постоянные значения, по (4-53) строим
семейство кривых a (k) при £= const. Затем, используя (4-52),
при тех же постоянных значениях £ строятся линии a (k) при
со = const.
ГЛАВА ПЯТАЯ
ПРИМЕНЕНИЕ ПОКАЗАТЕЛЯ КОЛЕБАТЕЛЬНОСТИ
К ИССЛЕДОВАНИЮ НЕЛИНЕЙНЫХ
АВТОМАТИЧЕСКИХ СИСТЕМ
5-1. Применение показателя колебательности в линейных
системах
Показатель колебательности широко применяется для
оценки качества и синтеза корректирующих устройств в
линейных системах. Показатель колебательности может быть
использован и при исследовании нелинейных систем. Рассмотрим
определение показателя колебательности вначале в линейных, а
затем — в нелинейных автоматических системах.
Пусть имеем линейную систему (рис. 5-1, а) с частотной
передаточной функцией в разомкнутом состоянии W (/со),
которую запишем в виде
W (/со) = А (со) e'^W, (5-1)
где А (со) = | W (/со) | и ср (со) — амплитудная и фазовая
частотные характеристики разомкнутой линейной системы.
Для замкнутой системы частотная передаточная функция
будет
ф (/со) = W (/Р)— = м (0)) в/Ф8<®>, (5-2)
1 + W (/со)
где М (со) = |Ф (/со)[ и ф3 (со) — амплитудная и фазовая
частотные характеристики замкнутой линейной системы.
Для амплитудной характеристики замкнутой системы М (со)
характерным является наличие максимума усиления по
амплитуде Mтах = |Ф (7е0) I max при резонансной частоте со = top
(рис 5-1, б). Показателем колебательности линейной системы
называется максимальное значение ординаты Мтах
амплитудной характеристики замкнутой системы при начальной
ординате, равной единице. В дальнейшем индекс max при М будем
опускать, помня, что за показатель колебательности
принимается максимальное из всех значений М амплитудной
характеристики замкнутой системы.
96

Физически показатель колебательности характеризует
резонансные свойства замкнутой системы при подаче на ее вход
гармонических воздействий g — a sin со/, 0 ^со <с: оо. Чем
выше резонансный пик амплитудной характеристики замкнутой
системы или чем больше показатель колебательности, тем
система более склонна к колебаниям в ее свободном и
вынужденном движениях.
В практике проектирования линейных автоматических
систем установлено, что качество переходного процесса связано
со значением показателя колебательности. Приемлемыми
значениями показателя колебательности считаются 1,1 ^ М ^1,7
При этом значения 1,1 ^ М ^ 1,3 соответствуют очень
хорошему, 1,3 ^ М <с: 1,5 — хорошему, а 1,5 ^ М ^ 1,7
—удовлетворительному демпфированию системы. Обеспечение
показателя колебательности М <1,1 требует более сложных
корректирующих средств и ведет к неоправданному усложнению
системы. При пониженных требованиях по запасу устойчивости
иногда можно допускать значения показателя колебательности
1,7 2,5.
Показатель колебательности определяется просто по
известной амплитудной частотной характеристике замкнутой
системы (рис. 5-1, б). Желательно определение показателя
колебательности непосредственно по амплитудно-фазовой частотной
характеристике разомкнутой системы.
Найдем геометрические места на комплексной плоскости
(У, jVf соответствующие значениям М = const. Для этого
отобразим некоторую точку а, соответствующую" М = const
(рис. 5-1, б), на комплексную плоскость сУ, jV (рис. 5-2, а).
Для значения М в соответствии с (5-2) имеем:
у и* + V2
у(\ + и)* + У*'
Возводя в квадрат левую и правую части равенства,
получим
(Л*2 — 1) U2 + (М2 — 1) У2 + 2l7M2 + Л12 = 0.
4 Заказ № 933 97
М
W (/СО)
1 + W (/СО)

Поделив все члены на А12— 1, а затем прибавив и вычтя
М4
, запишем
(Ма— 1)а
Л*4
М4
М2 —1 М4 —1 (Л1Я — 1)а (М2—1)2
Полученное выражение можно представить в виде
/ М2 \2 М2
и+—— +V2=
\ Л1а — 1У (М2— I)2
= 0.
у
и
0
W(ju))
Рис. 5-2
или
где
(U — U0)2 + V2= R2,
U0 = -
М2
М2 — 1
л*
М2 — 1
(5-3)
(5-4)
Следовательно, постоянному значению показателя
колебательности М = const соответствует на комплексной плоскости
U, jV окружность (рис. 5-2, д), определяемая уравнением (5-3),
с абсциссой центра U0 и радиусом R (5-4).
На рис. 5-2, б изображены окружности для различных
значений М = const. На той же плоскости £/, jV нанесена
амплитудно-фазовая частотная характеристика W (/со) разомкнутой
системы. Точкам пересечения характеристики W (/со) с.
окружностями М = const будут соответствовать значения М
амплитудно-частотной характеристики замкнутой системы. Значение
М-той окружности, которой касается амплитудно-фазовая
частотная характеристика W (/со) разомкнутой системы, и будет
показателем колебательности.
98

Следовательно, обеспечение заданного показателя
колебательности М в линейной системе связано с требованием
незахождения амплитудно-фазовой характеристики разомкнутой
системы W (/со) в некоторую запретную зону, ограниченную
окружностью заданного показателя колебательности, например
М4 = const (рис. 5-2, б).
Заметим, что для всех окружностей при 1 ^ М ^ оо
расстояние по оси вещественных до ближайшей к началу координат
точки окружности согласно (5-4)
£/1==|[/0|_Я = _^_ < 1,
а расстояние до наиболее удаленной точки окружности
U2=IUq\+R =-^—> 1.
М — 1
Это говорит о том, что точка с координатами — 1, /0,
используемая для определения устойчивости линейных систем по
критерию Найквиста, всегда находится внутри окружностей
1 ^,оо, При значении М = оо имеем U0 — — 1, R — О,
т. е. окружность вырождается в точку (— 1, /0) и, следовательно,
М = оо соответствует колебательной границе устойчивости.
При значении М = 1 имеем, согласно (5-4), U0 = — оо,
R = оо; при этом Ux = 0,5, U2 = оо. Это значит, что при М = 1
окружность вырождается в прямую, проходящую параллельно
оси мнимых на расстоянии с72 = 0,5.
Величина показателя колебательности может быть
определена и в случае использования логарифмических частотных
характеристик. Для этого следует запретные зоны М = const
для амплитудно-фазовых частотных характеристик на
комплексной плоскости перестроить в запретные зоны для
логарифмической фазовой частотной характеристики разомкнутой системы
на логарифмической плоскости. На окружности М = const
возьмем произвольную точку В и из начала координат проведем
в нее вектор с модулем А (рис. 5-3, а). Угол jx, образованный этим
вектором и отрицательной полуосью вещественных, является
запасом по фазе при заданном показателе колебательности М ~
= const для той системы, у которой частотная характеристика
W (/со) касается окружности в точке В. Расстояние от оси
мнимых до центра окружности М = const обозначим через С.
Величину запаса по фазе и, можно определить по теореме
косинусов из треугольника ОВОг:
R2 = а2 + С2 — 2АС cos jx,
откуда
Л2 + С2 — R*
COS Li = ■ .
2АС
4*
99

_ м2
Подставив в полученное выражение значения С ■
М2 — 1
и R — , получим
М2 — 1
М2 + А2(М2— 1)
и = arc cos ! - _ . (5-5)
2AM2
Рис. 5-3
Максимальное значение запаса по фазе будет при R,
перпендикулярном Л, т. е.
Ус2 — я2 Ум2 — 1 . 1
Umax = arc cos = arc cos = arc sin —
С MM
(5-6)
при
A = M = Vc. (5-7)
V M2—\
По формуле (5-5) при заданном М = const можно
определить значения ц (Л) и, пересчитав А в децибелы по соотношению
L (со) = 20 lg Л, построить запретную зону М = const для
логарифмической фазовой характеристики разомкнутой системы
(рис. 5-3, б). В системе будет обеспечиваться заданный
показатель колебательности, если логарифмическая фазовая
характеристика ф (со) не зайдет в запретную зону, касаясь ее. Верхняя
часть запретной зоны, показанная на рис. 5-3, б штриховой
линией обычно не наносится.
Запретную зону М = const с комплексной плоскости удобно
перестраивать на логарифмическую плоскость геометрически.
Для этого на комплексной плоскости следует из начала
координат провести лучи, например через 10° (рис. 5-3, а),
пересекающие окружность М = const. Соответствующие точкам пересев
чения D и Е первого луча усиления по амплитуде нужно
пересчитать в децибелы. По полученным значениям LD и LЕ следует
100

найти точки на логарифмической амплитудной характеристике.
Проводя через эти точки линии, параллельные оси Z, до
пересечения с линией \i = 10°, получим точки D и Е запретной зоны
для фазовой характеристики ср (со). С помощью следующего
луча, проведенного при \х = 20°, можно определить еще две
точки и т. д.
5-2. Определение показателя колебательности
в нелинейных системах
Пусть имеем нелинейную систему (рис. 5-4), состоящую из
линейной части с передаточной функцией №л (р) и нелинейного
звена со статической нелинейной характеристикой F (х, рх).
Для линейной части согласно ее передаточной функции имеем
частотную передаточную функцию
1Рл </*>>= <5-8>
F(x)
х1
Рис. 5-4
Для нелинейного звена после выполнения гармонической
линеаризации получим эквивалентную передаточную функцию
(комплексный коэффициент передачи)
1Рн(а)=?(а)+/?'(а). (5-9)
Здесь амплитуда колебаний на входе нелинейности берется
в относительных величинах а = а/Ь, где Ъ — характерное
значение х на статической характеристике нелинейного звена.
Эквивалентная передаточная функция с относительной
амплитудой в качестве аргумента называется нормированной.
Частотная передаточная функция для гармонически
линеаризованной замкнутой системы, согласно (5-8) и (5-9), будет
1 +IF л (/со) Wa(a)
ф (/«,,«) = W"<M , (5-10)
г (а) + Wn (/(о)
где z (а) = l/WH (а) — обратная эквивалентная передаточная
функция нелинейного звена.
101

Входящие в (5-10) комплексные величины имеют значения:
Гл(/со)=с7(со) + /Т(со),
1 ?(а)
*(а) =
:r(a) + /V (а) =
q2(a) + q'2(a)
(а)
(а) + ^я (а)
(5-11)
По аналогии с линейными системами за показатель
колебательности для гармонически линеаризованной системы примем
Мтах = |Ф(М а)|тах-
Геометрические места М = const для нелинейной системы
на плоскости (У, jV можно найти по выражению
М =
Vu*+ V2
V{r+U)* + (r'+V)*
(5-12)
так как теперь вместо единицы в частотной передаточной
функции линейной замкнутой системы
W (/со)
Ф (/со) =
1 + W (/со)
в нелинейной системе, согласно (5-10) и (5-11), имеем обратную
эквивалентную передаточную функцию нелинейного звена
z (а) = г (а) +/г' (а).
Проделав преобразования выражения (5-12), подобные
преобразованиям, выполненным в § 5-1 для линейной системы,
получим уравнение
U
гМ2
М2 — 1
2 + (у + "г'М* \2 (г2 + г'2) М2
М2— 1
(Л12 —I)2
где
Vo~-
(U-U0)2 + (V-V0)2 = R\
rM2 __q М2
М2— 1 ~
г'М2
q2 + q'2 М2—\'
= д' М2
М2—\ ~ д2 + д'* М2 — \ 9
М 1
/2
М
M2+l Y q2 + q'2 М2-\
(5-13)
(5-14)
102

Из (S-13) и (5-14) следует, что при различных относительных
амплитудах на входе нелинейного звена постоянному значению
М = const в нелинейной системе соответствует множество
окружностей различных радиусов с центрами, смещенными как
по оси вещественных, так и по оси мнимых. Запретные зоны для
амплитудно-фазовой частотной характеристики линейной
части системы У7Л (/со) теперь образуются касательными
контурами, охватывающими эти окружности (рис. 5-5, а).
В случае однозначных нечетно-симметричных
нелинейностей при q'(a) = 0, г'(а) = 0, V0 = 0 уравнения окружностей
принимают вид
гМ2 \2 г2М2
U Н —— + V2
М2 — 1 I (М2 — I)2
Рис. 5-5
или
(U — U0)2+ V2 = R2, (5-15)
где
гМ2 М2
с70 = ~
М2 — 1 q{M2 — 1) '
. (5-16)
М2 — 1 q(M2 — 1)
Для определения показателя колебательности в
нелинейной системе следует на комплексной плоскости Ut jV построить
запретные зоны М = const и амплитудно-фазовую
характеристику линейной части Wn (/со). За значение показателя
колебательности принимается значение М той запретной зоны,
которой касается характеристика Wn (/со), не заходя в нее (рис. 5-5,а).
Как видим, нелинейные свойства систем отражаются в
расширении и смещении запретных зон М = const по сравнению
103

с линейными системами. Деформации запретных зон происхоч
дят за счет изменения коэффициентов гармонической линеариза^
ции q (а) и q' (а) при изменении относительной амплитуды oft
на входе нелинейного звена. При q' (а) = 0 и q (а) = 1 имее$
линейную систему с запретной зоной в виде одной окружности'
как частный случай нелинейных систем.
Запретные зоны для Wn (/со) с комплексной плоскости
могут быть перестроены в запретные зоны для фазовой
характеристики линейной части срл (со) на логарифмической плоскости
(рис. 5-5, б), как это было показано для линейных систем.
Рис. 5-6
Для нелинейных систем с однозначными
нечетно-симметричными статическими нелинейностями построение запретных
зон М = const на комплексной и логарифмической плоскостях
весьма упрощается, так как максимальный запас по фазе umax
в этом случае не зависит от значения амплитуды а.
Действительно, запас по фазе определяется по теореме косинусов из
треугольника ОБОг для любой из окружностей М = const*
а = var (рис. 5-6, а) и при учете значений
М2 М
С = и R.
q(M2—l)
q(M2— 1)
составит величину
ц = arc cos
M2 + q2A2(M2— 1)
2qAM2
(5-17)
Максимальное значение запаса по фазе будет при R,
перпендикулярном А:
Vc2—R2 M/[qV М2—\
l-*max = arc cos = arc cos —
V M2— 1
= arc cos = arc sin
M M
M2/[q(M2— 1)]
1
(5-18)
104

Как видим, в полученное выражение для ртах не входит
величина q (а) и, следовательно, максимальное значение запаса
по фазе для нелинейной системы с нечетно симметричной
нелинейностью определяется только показателем колебательности М
и совпадает с максимальным значением запаса по фазе линейной
системы, полученной из нелинейной исключением нелинейности.
При построении запретных зон для амплитудно-фазовой
характеристики линейной части системы на комплексной
плоскости в этом случае достаточно построить окружности М =
= const, соответствующие qmax (а) и <7min (а). и соединить их
касательными (рис. 5-6, б). Область ограничения указанными
окружностями и касательными и будет запретной зоной М =
= const для амплитудно-фазовой характеристики линейной
части.
Для динамических нелинейностей, когда коэффициенты
гармоническс^й линеаризации зависят от амплитуды и частоты,
эквивалентная передаточная функция нелинейного звена
WH (а, со) изображается в виде семейства характеристик а =
= const или со = const. Запретные зоны для
амплитудно-фазовой характеристики линейной части образуются в этом случае,
как огибающие для всех областей, соответствующих отдельно
взятым характеристикам.
5-3. Оценка качества процессов
в нелинейных системах по показателю колебательности
Поскольку запретные зоны для определения показателя
колебательности М в нелинейных системах строятся при учете
всех возможных относительных амплитуд а колебаний на входе
нелинейности при всех возможных частотах, то оценка
качества процессов по показателю колебательности является такой
же правомерной, как и в линейных системах. Приближенность
оценки обусловливается приближенностью метода
гармонической линеаризации.
В нелинейных системах возможны в зависимости от
значений параметров системы и вида нелинейности области с
равновесно сходящимися процессами, области процессов, сходящихся
к автоколебаниям, и области расходящихся процессов. При
оценке качества процессов важно прежде всего определить
указанные области. Кроме того, внутри области равновесно
сходящихся процессов желательно оценить качество процессов
по показателю колебательности в зависимости от значений
параметров.
По аналогии с линейными системами можно утверждать,
что обеспечение любого значения показателя колебательности
1 ^ М < оо соответствует устойчивому равновесно
сходящемуся процессу с качеством, определяемым величиной М. Здесь
остаются те же рекомендации к допустимым значениям
показателя колебательности, т. е. 1,1 1,7; иногда 1,1^М^2,5.
Покажем, что при М = оо запретные зоны вырождаются
в линию — z (а), совпадающую с характеристикой - ,
WH (а)
105

используемой для определения автоколебаний с помощью
критерия Найквиста. Для этого, используя уравнение окружностей
(5-13), образующих запретные зоны М= const, будем полагать,
что М -> оо. Тогда для координат центра окружностей и
радиуса получим
U0= lim = —г = ч—„,
Л*-оо V М2 — 1 / q2 + q
VQ = lim j
r'M2
Af2 — 1
Л1-+СО M2— 1
:0.
,2 >
(5-19)
Сравнивая полученные выражения для U0 и V0 с формулой
(5-11) характеристики z (а) = i , видим, что уравнениями
1
М- const
WH (а)
(5-19) как раз определяется величина -—z(а) = ^ ^ в виде
линии на комплексной плоскости.
Для линейных систем значению М = оо соответствовала
точка -— 1, /0, т. е. линия — z (а) в нелинейных системах есть
обобщенный аналог точки — 1, /О линейных систем.
Пересечение указанной линии с
амплитудно-фазовой частотной
характеристикой линейной
части Wn (/со) соответствует
периодическому режиму
в системе (рис. 5-7).
Если же амплитудно-
фазовая частотная
характеристика линейной части
Wn (/со) не охватывает и
не пересекает
характеристику — z (ос), это значит,
что в системе имеет место
равновесно сходящийся
процесс, качество которого
оценивается по запретным
зонам с М — const.
Охват характеристики — z (а) характеристикой Wn (/со)
без пересечения означает неустойчивость нелинейной системы,
т. е. расходимость нелинейного процесса.
В результате ' одним несложным построением можно
оценить появление всех возможных процессов в нелинейной системе
и качество равновесно сходящегося переходного процесса.
Оценим качество процессов в нелинейных системах с
однозначными статическими характеристиками. Вид запретных зон
М = const для амплитудно-фазовых характеристик на
комплексной плоскости или для логарифмических фазовых
характере»
Рис. 5-7
106

рйстйк на логарифмической плоскости связан в этом случае
с диапазоном изменения коэффициента гармонической
линеаризации q (а). Согласно формулам для координат центра и
радиуса окружностей, образующих запретные зоны,
М2 М
U0 = , V0 = 0, R = ,
q(M2 — 1) q(M2-\)
будем иметь различные запретные зоны (рис. 5-8, а, б),
соответствующие диапазону изменения коэффициента гармонической
линеаризации: 1 — когда 0 ^ q ^ qmax> 2 ~ когда qm\n ^
^<7^?тах> 8 — когда qm\n^q^<x>> 4 — когда 0 <с
^ q оо.
Рис. 5-8
Каждому виду запретных зон соответствуют свои
нелинейные однозначные нечетно-симметричные статические
характеристики. Наиболее распространен случай 7, соответствующий,
например, релейной характеристике с зоной
нечувствительности (рис. 1-3, б), характеристике с насыщением (рис. 1-3, в).
Запретной зоне вида 2 соответствует характеристика с
переменным коэффициентом передачи (рис. 1-3, г). Запретная зона вида 3
отвечает характеристике с переменным коэффициентом передачи,
когда значение k2 велико, в пределе k2 -> оо. Запретная зона
вида 4 соответствует идеальному релейному звену (рис. 1-3, а).
Выполним оценку качества процесса в системах с нелиней-
ностями типа /. Полагаем, что в результате структурных
преобразований система приводится к свернутой структурной схеме,
содержащей приведенную линейную часть и приведенную
нелинейность (рис. 5-9, а). Приведение линейной части и
нелинейности заключается в том, что из коэффициента гармонической
линеаризации нелинейности выделяется множитель &н, не
зависящий от амплитуды гармонического сигнала, и передается
в линейную часть. Величина ku чаще берется такой, чтобы
максимальное значение оставшегося приведенного коэффициента
гармонической линеаризации равнялось единице.
Положим, что в качестве нелинейности имеем релейное звено
с характеристикой, обладающей зоной нечувствительности
107

(рис. 5-9, б). Для такой характеристики коэффициент
гармонической линеаризации
Я(<*>)
Ac Vol2 — 1
а —
Представляя коэффициент гармонической линеаризации
в виде
а)
У ^
Приведенная линейная
часть
q (а) = £н<7п (а),
В)
Приведенная нелинейность
Рис. 5-9
%2
О ъ
где
2с
л
Яп (а) =
2 V'a2 — 1
(5-20)
(5-21)
приходим к схеме, изображенной на рис. 5-9, а.
Приведенный коэффициент гармонической линеаризации
теперь изменяется в пределах 0<с:<7п^1> так как максимум
Vol2 — 1
функции F (а) = , входящей в (5-21), равен 0,5 при а =
а2
= V%* Такое представление системы удобно тем, что запретные
зоны образуются окружностями с абсциссой центра и радиусом
М2 М2
Яты(М2-1)
м2
1
М
М
Ят^(М2~\) М2-\
совпадающими с окружностями приведенной линейной системы
(с исключенной приведенной нелинейностью), и касательными
к этим окружностям, проведенными из начала координат
(рис. 5-10). Это упрощает построение и позволяет сравнить
линейный вариант системы с нелинейным.
108

Приведенная характеристика
ос
,2
— zn (а) =
<7п (а)
2 Ка2 — 1
в данном случае будет двузначной.
Из выполненного построения (рис. 5-10) следует, что в
рассматриваемой релейной системе с линейной частью выше
второго порядка при малых значениях коэффициента передачи
&п ^ ^кр имеет место устойчивый, равновесно сходящийся
процесс. Качество процесса легко оценивается по запретной зоне
М = const, касательной
к характеристике Wn (/со).
При* значениях kn > &кр, ^
рактеристики через точ- '
ку — 1, /0 для приведенной рис 5_10
линейной системы означает
границу устойчивости, а для
нелинейной системы — границу, отделяющую область
равновесно сходящихся процессов от области автоколебаний.
Следовательно, область автоколебаний в данной системе
появляется за счет области неустойчивости линейной системы и
значение коэффициента передачи, соответствующее границе
устойчивости, равно критическому значению коэффициента передачи
нелинейной системы, ku = /гкр.
Оценим процессы в нелинейной системе с нелинейным
звеном, имеющим переменный коэффициент передачи (рис. 5-11, а, б).
Приближенно оценку ожидаемых процессов можно выполнить
непосредственно по виду нелинейности, не вычисляя
коэффициентов гармонической линеаризации.
Считаем опять систему состоящей из приведенной линейной
части и приведенной нелинейности (рис. 5-9, а). Для первого
случая (рис-. 5-11, а), когда коэффициент усиления в системе
снижается с возрастанием входной величины нелинейности,
получим примерный вид графика изменения коэффициента
гармонической линеаризации q в зависимости от а (рис. 5-12, а).
с одной частотой со = соп
и двумя значениями
амплитуд а1П и а2П.
Периодические режимы для больших
амплитуд ап >]/^2,
согласно ранее рассмотренному
в § 3-6 условию,
устойчивы, т. е. соответствуют
автоколебаниям.
Периодические режимы при ап^
^ У 2 соответствуют
неустойчивому предельному
циклу. Прохождение
амплитудно-фазовой частотной ха-
109

Йдесь приведение заключается в передаче в линейную часть
коэффициента kt.
Характеристика —г(а) = в этом случае будет
q(a)
однозначной (рис. 5-12, б) и займет на отрицательной полуоси
вещественный отрезок от — 1 до — kjk2 при возрастании ам-
x2 = F(xr)
Рис. 5-11
плитуд а справа налево. Запретные зоны М = const образуются
двумя окружностями и касательными к ним. Меньшая из
окружностей соответствует запретной зоне М = const приведенной
линейной системы, а вторая — определяется абсциссой центра
Рис. 5-12
ц0 = — и радиусом R =
<7min(M2-l) ж""" * <7min(M2-l)
_ k2
Qm'm — ~~— •
К
Если нанести на комплексную плоскость
амплитудно-фазовые частотные характеристики приведенных линейных частей
выше второго порядка (рис. 5-12, б), получим три области
процессов. При малых коэффициентах передачи kn ^ &1Кр это
устойчивые, равновесно сходящиеся процессы с качеством,
определяемым некоторым значением М = const. При значениях коэффи-
110

циента передачи приведенной линейной части &1кр ^ kn^ &2кр
в системе имеют место процессы, сходящиеся к автоколебаниям,
частота и амплитуда которых определяется по точке
пересечения характеристик Wn (/со) и — z (а).
Для больших значений коэффициента передачи
приведенной линейной части kn > 62кр характеристика Wn 0е0)
охватывает характеристику — г (а) и, значит, в системе имеем
расходящиеся нелинейные процессы.
Таким образом, в зависимости от значения коэффициента
передачи здесь имеем три области: область устойчивости
равновесия, область автоколебаний и область неустойчивости, причем
область автоколебаний занимает часть области неустойчивости
приведенной линейной системы.
Рис. 5-13
Оценим процессы в нелинейной системе, когда коэффициент
передачи нелинейного звена возрастает с увеличением входной
величины хг (рис. 5-11, б). Здесь при приведении нелинейности
целесообразно сохранить qm\n = 1, т. е. отнести к линейной
части коэффициент kH = kx. Коэффициент передачи
приведенной линейной части &н&л при малых отклонениях а ^ 1
останется таким же, как и в предыдущем случае.
Приведенный коэффициент гармонической линеаризации
с учетом принятого условия изобразится в виде графика q (а)
(рис. 5-13, а) и будет изменяться в пределах l^q^kjk^
Тогда характеристика —z(a)~- займет отрезок на
Я И
оси вещественных от — kx\k2 до — 1 (рис. 5-13, б). Возрастание
амплитуд вдоль этого отрезка происходит слева направо. Это
значит, что при пересечении характеристик Wn (/со) и — г (а)
получим неустойчивое периодическое решение.
Запретные зоны М = const здесь образуются большой
окружностью, соответствующей приведенной линейной системе,
и малой — соответствующей qn max = k2lh.
Построив амплитудно-фазовые частотные характеристики
для];приведенной линейной части №п'(/со) при различных
коэффициентах передачи kn = &н&л> можно сделать заключение
о процессах в системе.
Ill

Как видим, при малых коэффициентах передачи kn ^ £1Кр
имеем равновесно сходящиеся процессы. При значениях
^1кр^^п^^2кр получим неустойчивые периодические
режимы, т. е. устойчивость в малом и неустойчивость в большом.
Для больших значений коэффициента передачи линейной части
> ^2кр имеем неустойчивость в целом.
Область неустойчивых предельных циклов практически
можно отнести к области неустойчивости, так как всегда
найдутся начальные значения отклонений в системе, выходящие
за предельный цикл. Указанная область, как видно из рис. 5-13,6,
появилась за счет сужения области устойчивости приведенной
линейной системы. Здесь граничный коэффициент линейной
системы &гр = /е2Кр» а практическая, неустойчивость
нелинейной системы начинается при kn = £1Кр-
Рис. 5-14
Рассмотрим систему с идеальным релейным звеном. Для
такого звена имеем коэффициент гармонической линеаризации
4с
д(а) = —, а = а.
да
Коэффициент гармонической линеаризации изменяется в
пределах 0 ^ q ^ со (рис. 5-14, а). Характеристика — z (а) =
= занимает всю полуось вещественных от 0 до — оо
Я (*)
(рис. 5-14, б) при возрастании амплитуд справа налево вдоль
характеристики. Следовательно, при линейной части выше
второго порядка получим режим автоколебаний, определяемый
точкой пересечения характеристик 1ГЛ (/со) и — г (а).
Аналогично выполняется оценка качества процессов и при
наличии в системе двузначных статических нелинейностей, а
также динамических нелинейностей. Правда, несколько
усложняется процесс построения запретных зон М = const.
5-4. Синтез линейных корректирующих устройств
в нелинейных системах
Метод синтеза корректирующих устройств в нелинейных
системах по показателю колебательности М базируется на той
же основе, что и метод синтеза корректирующих устройств в ли-
112

нейных системах. Качество процесса в системе связывается с
выбранной величиной показателя колебательности М = const,
реализуемого в системе.
Если для исходной нелинейной системы построить запретную
зону для выбранного значения М = const и
амплитудно-фазовую частотную характеристику линейной части Wn (/со), то с
помощью линейной коррекции следует так деформировать
характеристику Wn (/со), чтобы ее вывести из запретной
зоны (рис. 5-15, а). Аналогично для логарифмических
характеристик следует деформировать логарифмическую фазовую
характеристику (л. ф. х.) линейной части так, чтобы вывести ее
из запретной зоны М = const (рис. 5-15, б).
Рис. 5-15
Синтез линейных корректирующих устройств выполняется
с помощью логарифмических характеристик и включает в себя
нижеследующие этапы.
1. Построение располагаемой логарифмической
амплитудной характеристики (л. а. х.) приведенной линейной части.
Располагаемая л. а. х. строится по исходной структурной схеме
системы.
2. Построение желаемой л. а. х. приведенной линейной
части системы. Желаемая л. а. х. строится по заданным
требованиям на проектирование и выбранному показателю
колебательности М. Как исходная линейная часть, так и линейная
часть скорректированной системы считаются
минимально-фазовыми (состоящими из устойчивых звеньев). Это обеспечивает
однозначное соответствие друг другу л. а. х. и л. ф. х., и синтез
выполняется только по логарифмическим амплитудным
характеристикам.
3. Определение л. а. х. последовательного
корректирующего устройства. Л. а. х. последовательного корректирующего
звена получается вычитанием из л. а. х. желаемой л. а. х.
располагаемой:
£л. з (<»>) = (со) — Lp(co).
ИЗ

4. Реализация коррекции. Под реализацией коррекции
понимается определение схемы корректирующего устройства
и расчет ее элементов. Если оказывается целесообразным вместо
последовательной коррекции применение параллельного
корректирующего устройства или обратной связи, то выполняется
пересчет последовательного корректирующего устройства по
формулам или таблицам эквивалентного перехода, имеющимся
в литературе [1 ].
5. Проверка результата выполненного синтеза. В проверку
входит построение запретной зоны М = const для л. ф. х.
приведенной линейной части и построение самой л. ф. х.
скорректированной системы. В некоторых случаях при проверке синтеза
строится переходный процесс или выполняется моделирование
скорректированной системы на аналоговых нелинейных
вычислительных машинах.
Рис. 5-16
Наибольшую сложность при синтезе корректирующих
устройств составляет определение желаемой л. а. х. При синтезе
линейных статических систем и систем с астатизмом первого
порядка рекомендуемыми желаемыми л. а. х. являются л. а. х.
типов А, В, D, Е [2] (рис. 5-16). Указанные л. а. х. являются
желаемыми и для линейных частей нелинейных систем.
Рассмотрим наиболее употребительную л. а. х. типа В и
запретную зону М = const для широко распространенных
нелинейностей типа 1 (рис. 5-17), когда коэффициент гармонической
линеаризации изменяется в пределах 0 ^ q ^ <7тах- На
рис. 5-17 также изображена штриховой линией запретная зона
М = const для л. ф. х. приведенной линейной системы.
В линейных системах требуемый запас по фазе
обеспечивался за счет достаточной протяженности h = v3/v2 асимптоты
л. а. х. с наклоном — 20 дБ/дек в окрестности частоты среза сос.
При этом на протяженность асимптоты с наклоном — 40 дБ/дек
hx = Vg/Vj никаких ограничений не накладывалось. Здесь
введены относительные частоты v = со/со0, где со0 — значение
частоты при пересечении оси частот продолжением второй
асимптоты л. а. х.
В нелинейной системе, как видно из рис. 5-17, следует не
только обеспечить достаточную протяженность участка h, но
и наложить ограничение на протяженность участка hx.
Найдем связь между протяженностями участков h и Нх
и показателем колебательности М = const из условия незахож-
114

дения л. ф. х. приведенной линейной части срп (со) в запретную
зону.
Нормированное значение передаточной функции для л. а. х.
будет
W (s) = L±^? f (5.22)
5(1 + Т^)(1 +T3S)
где s = /?/со0 — новое значение оператора; тх = со07\, т2 =
= со0Г2, Тз — ^о^з — относительные постоянные времени.
hf h
Рис. 5-17
Протяженность участка л. а. х. с наклоном — 20 дБ/дек
h = ^ = ^= II (5-23)
протяженность участка л. а. х. с наклоном — 40 дБ/дек
(5-24)
С учетом (5-23) и (5-24) нормированную передаточную
функцию (5-22) запишем в виде
1 -f- hTas
Wn(s)
s(l + hh}x3s) (1 +t3s)
(5-25)
а соответствующая ей нормированная частотная передаточная
функция при s= /V будет
Wn (/v) = -
1 -f jhT9v
/v (1 +jhh1T3v)(l +/t3v)
(5-26)
115

Согласно (5-26) л. ф. х. приведенной линейной части системы
определится соотношением
Фп (to) = —90° — arc tg hh^v + arc tg /ix3v — arc tg t3v, (5-27)
откуда запас по фазе, соответствующий желаемой л. а. х. В,
будет
р =г. фп (со) + 180° = 90° — arc tg ккгх9у +
+ arc tg hr3v — arc tg x3v. (5-28)
При достаточной протяженности участков h и h± желаемой
л. а. х. В приведенной линейной части для частот, близких к
частоте среза, разность
Afx = 90° — arc tg hhii:3v > 0
будет величиной сравнительно малой.
При этом для определения протяженности участка h можно
воспользоваться приближенным соотношением, получаемым из
(5-28) без учета значения Ajlx, т. е.
fx ^ arc tg /ix3v — arc tg t3v. (5-29)
Согласно (5-29) выражение для запаса по фазе можно
записать в виде
. (h— 1)t3v om
[i =.-- arc tg '-^ . (5-30)
1 + h%\
,2
Исследуя последнее выражение на максимум, получим
\im = arc tg k ~1 при vm = —l—:. (5-31)
2 у h т3У h
Это максимальный запас по фазе, обеспечиваемый за счет
протяженности участка h.
Потребный максимальный запас по фазе, определяемый
запретной зоной, согласно (5-18), составляет
V М2 — 1 .1
и = arc cos = arc sin —
mm
или
[im = arc tg 1 (5-32)
У m2 — i
Приравняв тангенсы для \im из (5-31) и (5-32), получим
h — 1 1
2Vh У M2 — \
Откуда
A = *±i, М = A±_Le (5-33)
М-\ h-\
116

Поскольку максимальные имеющийся и потребный
запасы по фазе приравнивались "при частоте v = vm, то участок
л. а. х. с наклоном — 20 дБ/дек следует располагать по
возможности симметрично относительно частоты vm. Деление участка h
пополам относительно частоты vm в логарифмическом масштабе
(рис. 5-17) в обычном масштабе частот означает, что
^l = ysl=Vh.
Для определения протяженности участка hx используем
точную формулу для запаса по фазе (5-28). Потребуем, чтобы
запас по фазе при частоте v^, соответствующей середине участка
hl9 составлял величину \im. Тогда, согласно (5-28), получим
цт = 90° — arc tg hh^vt, + arc tg hx3vb — arc tg x3vb
или
arc tg hhjXavb — arc tg x3vb = (90° — цт) — arc tg x3vb.
Взяв тангенсы разностей углов, соответствующих левой и
правой частям последнего равенства, получим
hWb fa — 1) ^ tg (90° — цт) — x3vb
\ + h\%yb l + Tavfttg(90o-(im)
Подставляя в (5-34) значение
1
ч =
(5-34)
и учитывая, что
h = v3/v2 = т2/т3, ctg um = V М2 — 1,
имеем
hx — 1 _ h Vhx V м2 — 1 — 1
Разрешая последнее равенство относительно h и учитывая
(5-33), окончательно получим
^АЩ^ 2^ + ^+1)/^-^ (5 35)
\ УК I
Полученная формула (5-35) связывает значения протяжен-
ностей участков и и кх с показателем колебательности м для
желаемой л. а. х. приведенной линейной части типа Б,
Аналогично получаются и формулы, связывающие протяженности
117

участков h и hx с показателем колебательности М для других
типовых желаемых л. а. х.: для-л. а. х. типа Л
(ЗА!- 1) —=L=- + vh {hx - 3)
Л Af+ 1 v m*-l .
(з - h) h -—l=? + Vk (щ-1)
У m2 — 1
для л. a. x. типа £>
(3/4 -.1) * + Кfti fa - 3)
ft = M + i_ У m2 — i l.
M-1 (3-^A, J_- + -Kftl(3Ai-l)
У m* — l
(5-37)
для л. a. x. типа £
2vh1 + (h1+l)vm2-l
m — l i лг лг— 1 \
hj 2у m*-\-v ht + Yf]
Во всех приведенных формулах протяженность участка h
выбирается исходя из одного и того же приближенного условия.
Для характеристик Л и В, как было показано при выводе
формулы для л. а. х. В, это условие обеспечивает избыток по фазе
в окрестности частоты среза vc и близкой к ней частоте vm. В
случае характеристик D и Е, когда последняя асимптота имеет
наклон — 60 дБ/дек, возможен и некоторый недостаток в запасе
по фазе в окрестности частоты среза. При выборе
протяженности участка hx обеспечивается нужный запас по фазе (без избытка
и недостатка) при частоте v^.
На рис. 5-18 представлены кривые, построенные по
формулам (5-35), (5-36), (5-37) и (5-38), которые будем называть hy
h1 (М)-кривыми. Используя h, hx (М)-кривые, можно по
заданному показателю колебательности М = const определить
потребные протяженности участков h и hx и, следовательно,
относительные частоты vlf v2, v3 или абсолютные частоты ©х,
со2, со3.
С помощью полученных Л, hx (М)-кривых определение
желаемых л. а. х. линейной части может выполняться без всяких
расчетов. При этом не обязательно выбирать h и h1
соответствующими одному значению М = const. Часто возможны
случаи, когда в интересах простоты корректирующих средств
приходится при выборе протяженности участка h принимать
значение показателя колебательности Мх, а для участка h 1 —
некоторое значение М2 (обычно М2 > Mi). Тогда реализуемый
в системе показатель колебательности будет заключен в
некоторых пределах Мг<С М<С М2. Уточнение реализуемого
значения М легко выполнить построением запретной зоны М = const
118

и логарифмической фазовой характеристики приведенной
линейной части скорректированной системы.
Кроме требований, накладываемых на протяженность
участков Л и Ль необходимо определить подъем желаемой л. а. х.
приведенной линейной части системы, исходя из заданной
точности. Оценка точности нелинейных систем и определение
подъема желаемой л. а. х. связаны с видом статической
нелинейности вблизи нуля.
Рис. 5-18
Если статические характеристики вблизи нуля
аппроксимируются линейным участком (рис. 5-19, а), то нелинейные системы
к концу переходного процесса могут рассматриваться как
линейные. Подъем желаемой л. а. х. в этом случае определяется,
как в линейных системах, по общему коэффициенту передачи
k — &л&2- Причем &ц определяется, как тангенс угла наклона
касательной или секущей нелинейной характеристики вблизи
нуля (рис. 5-19, а). Логарифмическая амплитудная
характеристика приведенной линейной части должна иметь подъем для
пер.вой асимптоты на величину Ln= 20 lg k для статических
систем и такой же подъем при частоте со = 1 для первой
асимптоты в системах с линейной частью, обладающей астатизмом
первого порядка. Здесь для следящих систем можно
пользоваться методом эквивалентного гармонического воздействия при
определении запретной зоны для желаемой л. а. х. (как это
делается при синтезе линейных систем). Нелинейность проявляет
свои особенности только при формировании среднечастотной
части желаемой л. а. х.
Если статические характеристики имеют зону
нечувствительности (рис. 5-19, б) при любом дальнейшем продолжении, то
установившаяся ошибка в основном будет определяться поло-
119

виной зоны нечувствительности. Переходный равновесно
сходящийся процесс может закончиться при любом значении
входной величины нелинейности внутри зоны нечувствительности 26.
В этом случае коэффициент передачи нелинейного звена для
определения подъема желаемой л. а. х. рекомендуется
определять методом статической линеаризации, т. е. взятием
отношения ординат в области, прилегающей к зоне нечувствительности,
к абсциссам нелинейной статической характеристики (рис. 5-19,6).
После получения общего коэффициента передачи k — &л&„
подъем желаемой л. а. х. линейной части определяется по
правилам линейных систем.
Рис. 5-19
5-5. Пример синтеза корректирующего устройства
в нелинейной системе
Выполним синтез корректирующего устройства в следящей
системе со структурной схемой, изображенной на рис. 5-20.
Система состоит из датчика рассогласований с передаточным
коэффициентом kl7 безынерционного усилителя с нелинейной
статической характеристикой с насыщением и коэффициентом
передачи на линейном участке k2> двигателя с передаточным
коэффициентом k3 и постоянной времени Тд и редуктора с
передаточным коэффициентом k4.
Зададимся значениями параметров: kt — 50 В/рад; ks =
— 10 1/с; &4 = 0,01; ТА~ 0,02 с. Ошибка в системе при скорости
®m = 0>2 рад/с без учета момента нагрузки не должна
превышать 0т = 0,002 рад.
Требуется рассчитать линейное корректирующее устройство
и определить коэффициент усиления усилителя k2 при работе
на линейном участке статической характеристики.
Определим потребный коэффициент передачи разомкнутой
системы (добротность по скорости)
£Ю = В2> = _М_=100 1/с.
ет 0,002
120

Запишем передаточную функцию для исходной
разомкнутой системы при работе усилителя на линейном участке
статической характеристики:
W(p)= /л V ч , (5-39)
где /г© — k1k2k3k^.
Для нелинейного звена со статической характеристикой
с насыщением (рис. 5-21, а) гармоническая линеаризация дает
u2 = q (a) uv (5-40)
/ ч 2^2 / • ■ Ь , Ь ^ [ , б2 \ ^ ,
q(a) = —- arcsin 1/ 1 при а>Ь,
п \ а а \ а*
q (а) = k2 при О^а^б.
Датчик
рассогласовании Усилитель Двигатель Реоуктор
Т2
А
(5-41)
Р
Рис. 5-20
Перейдем к относительным амплитудам а = alb и
выполним приведение нелинейности, отнеся коэффициент нелинейного
звена &н = &2 к линейной части системы. В результате из (5-41)
получим значение коэффициента гармонической линеаризации
для приведенной нелинейности:
<7п (а) =
. 1 . V*2-
arc sin 5-
а 1 а2
1
при а > 1,
qn (а) = 1 при 0 ^ а ^ 1.
Примерный график изменения приведенного коэффициентй
гармонической линеаризации в зависимости от относительноа
амплитуды на.входе нелинейности представлен на рис. 5-21, б.
Как видим, передаточная функция (5-39) является
передаточной функцией приведенной линейной части, по которой
строим располагаемую л. а. х. Lp (со) исходной линейной части
(рис. 5-22) при учете значений /г0 = 100 1/с и Гд = 0,02 с. Для
этого через точку со = = 100 1/с проводим линию с
наклоном — 20 дБ/дек. Участок этой линии до частоты со = — =
= = 50 1/с является первой асимптотой L0 (со). Вторую
0,02
асимптоту в соответствии с передаточной функцией (5-39)
проводим с наклоном — 40 дБ/дек.
121

Выбираем тип желаемой л. а. х. ьж (со) приведенной
линейной части. Так как начальная асимптота располагаемой л. а. х.
имеет наклон — 20 дБ/дек, а конечная — наклон — 40 дБ/дек,
то в интересах простоты корректирующего устройства следует
и качестве желаемой взять л. а. х. типа в (— 20, — 40, — 20,
— 40 дБ/дек).
ос
Рис. 5-21
Поскольку задана только максимальная скорость слежения
Qm и не задано максимальное ускорение, это значит, что
слежение происходит с медленным изменением скорости (пря
малых ускорениях). В этом случае не накладывается ограничений
в области низких частот на выбор частоты сох первого излома
ДБ U
Рис. 5-22
желаемой л. а. х. Это дает возможность сразу выбрать
протяженности участков h и кг по Л, нг (М)-кривым.
Зададимся реализуемым в скорректированной системе
показателем колебательности М = 1,5. Согласно (5-7) за счет
участка с наклоном — 20 дБ/дек обеспечивается максимальный
запас по фазе при частоте сот и значении усиления по амплитуде
а м 1,5 ол
У М2 — 1 К 1,5а —1
122

что при пересчете в децибелы дает
Lm = 201g 1,34 = 2,5 дБ.
Проводим линию на уровне Lm = 2,5 дБ (штриховая
линия на рис. 5-22). Участок h желаемой л. а. х. должен делиться
примерно пополам при пересечении этой линии.
Далее, пользуясь Я, кг (М)-кривыми (рис. 5-18), выбираем
подходящий вариант для участков h и hlf с тем чтобы
обеспечить показатель колебательности М ж 1,5. Для обеспечения
заданной точности первая асимптота желаемой л. а. х. должна
совмещаться в низкочастотной области с первой асимптотой
располагаемой л. а. х. В интересах упрощения
корректирующего устройства последняя асимптота желаемой л. а. х. должна
либо совмещаться с последней асимптотой располагаемой л. а. х.
в высокочастотной области, либо проходить параллельно ей.
На рис. 5-22 показан вариант желаемой л. а. х. с участками,
соответствующими, согласно h%
hx (М)-кривым, М ж 1,5, при °1
протяженностях участков 0 1 * t &
со3 50
I
щ 5 с±
„=^ = А = 5 0
1 ©1 1 ' ' Рис. 5-23
Вычитая из желаемой л. а. х. Ьж (со) располагаемую л. а. х.
Lp (со), получим л. а. х. линейного последовательного
корректирующего устройства Ln. з(со). Как видно, в качестве
последовательного корректирующего устройства можно применить
пассивный интегрирующий контур (рис. 5-23) с передаточной
функцией
1РП.8(Р) = Ш^' Tl>T* (5"42)
1 + Тгр
Постоянные времени контура определяются частотами
излома Ь„.3((й) и связываются с величинами сопротивлений R1
и i?2 и емкостью конденсатора С:
Тг = — = (Ri + R2) С, T2 = — = R2C. (5-43)
сох со2
Корректирующее устройство обычно включается между
каскадами усилителя. Если система работает на переменном
токе, то перед корректирующим устройством включается
демодулятор и фильтр, а после корректирующего устройства
ставится модулятор. Поэтому при расчете параметров
корректирующего устройства важно обеспечить согласование его с
выходным сопротивлением цепей перед корректирующим устройством
и входным сопротивлением последующих цепей. Это делается
при расчете усилителя.
123

Для нашего случая имеем
(#i + #а) С = 1 с, R2C = 0,2 с.
Можно задаться величиной емкости конденсатора,
например С = 5 мкФ; тогда из второго соотношения имеем
0 2-10~3
/?a = !L±iiJ = 40 кОм.
5-Ю-6
Из первого условия получим
1 • 10~~3
#i + #2 = ~ = 200 кОм
5-10—6
и, следовательно,
#! = 200 — 40 -= 160 кОм.
Поскольку корректирующее устройство не изменяет
коэффициента передачи системы на низких частотах, то коэффициент
усиления усилителя по напряжению для линейного участка
статической характеристики определится из общего потребного
коэффициента передачи:
ь k<* ЮО on
#2 = = = 20.
kfifa 50-10.0,01
После выполнения синтеза корректирующего устройства
целесообразно выполнить проверку. Для этого построим
логарифмическую фазовую характеристику приведенной линейной
части фп (со) и запретную зону для нее при расчетном показателе
колебательности М — 1,5.
Запишем передаточную функцию приведенной линейной
части скорректированной разомкнутой системы согласно (5-39)
и (5-42):
Wn(p) = *u)(1 + 7>) . (5-44)
р (1 + 7» (1 + 7»
Соответствующая (5-44) частотная передаточная функция
будет
Wn = *«>(1+/7» . (5.45)
/•g)(1+/7>))(1+/7>)
Согласно (5-45) логарифмическая фазовая характеристика
приведенной линейной части определится соотношением
фп (со) = —90° — arc tg Гх(о — arc tg Гдсо + arc tg 72co, (5-46)
что с учетом значений постоянных времени дает
фп (со) = —90° — arc tg со — arc tg 0,02со + arc tg 0,2co. (5-47)
Результаты расчета по (5-47) сведены в таблицу:
0), 1/с 0,5 1 2 5 10 20 50 100 200
Фп, град. .'. -111 -125 -134 -129 —122 -123 —НО -J56 —167
124

По данным таблицы на рис. 5-22 построена характеристика
Фп (со).
Учитывая изменение приведенного коэффициента
гармонической линеаризации для нелинейной статической
характеристики с насыщением 0^^п^1» заключаем, что запретная
зона будет иметь максимальное значение запаса по фазе при всех
частотах со ^ сот и составит согласно (5-18) величину
um = arc sin — = arc sin — = 42°.
M 1,5
Остальная часть запретной зоны при со > сот строится с
помощью окружности М = 1,5 для приведенной линейной системы,
как это было показано в § 5-1.
Из выполненного построения (рис. 5-22) видно, что
потребный запас по фазе \im удовлетворяется точно при частотах
участка hx и удовлетворяется с запасом (как и следовало
ожидать) при частотах участка h. В результате коррекции
обеспечивается качество процесса в системе с М = 1,5 при запасе
устойчивости по фазе Лср ъ 55°, что соответствует хорошему
демпфированию нелинейной системы.
СПИСОК ЛИТЕРАТУРЫ
1. Бесекерский В. А., Попов Е. П. Теория систем
автоматического регулирования. М., «Наука», 1972. 768 с. с ил.
2. Проектирование следящих систем малой мощности. Л.,
Судпромгиз, 1958. 508 с. с ил. Авт.: В. А. Бесекерский, В. П.
Орлов, Л. В. Полонская, С. М. Федоров.
3. Пальтов И. П. Применение показателя колебательности
к расчету нелинейных систем.— В кн.: Методы синтеза
нелинейных систем автоматического управления. М.,
«Машиностроение», 1970, с. 259—311 с ил.
4. Попов Е. П., Пальтов И. П. Приближенные методы
исследования нелинейных автоматических систем. М., Физматгиз,
1960. 792 с. с ил.
5. Попов Е. П. Прикладная теория процессов управления
в нелинейных системах. М., «Наука», 1973. 584 с. с ил.
6. Сборник задач по теории автоматического регулирования.
Под ред. В. А. Бесекерского. М., «Наука», 1969. 558 с. с ил.
7. Тэлер Дж., Пестель М. Анализ и расчет нелинейных
систем автоматического управления. М.—Л., «Энергия», 1964.
448 с. с ил.
8. Хлыпало Е. И. Нелинейные системы автоматического
регулирования. Л. «Энергия», 1967. 452 с. с ил,

ОГЛАВЛЕНИЕ
Предисловие 3
Введение 5
Глава первая. Составление структурных схем и
уравнений нелинейных
автоматических систем 7
1-1. Нелинейности в автоматических системах ... —
1-2. Классификация и структурные преобразования
нелинейных систем 10
1-3. Преобразования нелинейных статических
характеристик 14
1-4. Составление уравнений нелинейных
автоматических систем 18
Глава вторая. Точные методы исследования
нелинейных автоматических систем . . 22
2-1. Исследование нелинейных систем методом
припасовывай и я —
2-2. Графо-аналитический метод исследования
нелинейных систем 27
2-3. Пример на построение переходного процесса в
нелинейной системе графо-аналитическим методом 33
2-4. Исследование нелинейных систем методом
фазовых траекторий 37
2-5. Пример исследования нелинейной системы
методом фазовых траекторий 42
2-6. Применение метода точечного преобразования
для исследования нелинейных систем 45
2-7. Исследование нелинейных процессов методом
изоклин 48
2-8. Теоремы прямого метода Ляпунова для
исследования устойчивости нелинейных систем .... 50
2-9. Частотный метод В. М. Попова для определения
абсолютной устойчивости нелинейных систем . . 56
Глава третья. Основы метода гармонической
линеаризации 59
3-1. Гармоническая линеаризация нелинейностей . . —
3-2. Определение автоколебаний в нелинейных
системах с помощью критерия Михайлова 62
126

3-3. Гармоническая линеаризация однозначных не*
четно-симметричных статических нелинейностей
3-4. Определение коэффициентов гармонической
линеаризации для двузначных
нечетно-симметричных статических нелинейностей
3-5. Пример исследования автоколебаний в
нелинейной системе . .
3-6. Применение критерия Найквиста для
исследования автоколебаний
лава четвертая. Исследование нелинейных
автоматических систем при учете
внешних воздействий и
несимметричных нелинейностях . .
4-1. Определение автоколебаний и ошибок в
нелинейных системах при постоянном внешнем
воздействии
4-2. Гармоническая линеаризация нелинейностей при
несимметричных колебаниях .
4-3. Прохождение медленно меняющихся сигналов в
автоколебательных системах
4-4. Приближенное определение колебательных
переходных процессов в нелинейных системах . . .
4-5. Применение диаграмм качества затухания для
определения переходных процессов в нелинейных
системах
лава пятая. Применение показателя
колебательности к исследованию нелинейных
автоматических систем
5-1. Применение показателя колебательности в
линейных системах
5-2. Определение показателя колебательности в
нелинейных системах
5-3. Оценка качества процессов в нелинейных
системах по показателю колебательности
5-4. Синтез линейных корректирующих устройств в
нелинейных системах
5-5. Пример синтеза корректирующего устройства в
нелинейной системе
писок литературы

Иван Петрович Пальтов
ЕЛИНЕЙНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
АВТОМАТИЧЕСКИХ СИСТЕМ
Редактор Ю. В. Долгополова
Художественный редактор Г. А. Гудков
Технический редактор О. С. Житникова
Корректор Л. П. Горова
Сдано в набор 29/1V 1976 г. Подписано к печати 7/VII 1976 г.
М-27383. Формат 84X108/32. Бумага типографская № 2.
Усл.-печ. л. 6,72. Уч.-изд. л. 7,71. Тираж 9000 экз. Заказ 933. Цена 39 коп
Ленинградское отделение издательства «Энергия».
192041. Марсово поле, 1
Ленинградская типография № 4 Союзполиграфпрома при Государственном
комитете Совета Министров СССР по делам издательств, полиграфии
и книжной торговли. 196126, Ленинград, Ф-126, Социалистическая ул., 14.