Автор: Макарычев Ю.Н. Миндюк Н.Г. Суворова С.Б. Муравин К.С. Монахов В.М.
Теги: математика алгебра
Год: 1981
Текст
ГРАФИК ФУНКЦИИ y=a(x-m)2+n
ТАБЛИЦА КВАДРАТОВ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 10 ДО 99
^ЕДИНИЦЫ датой 0 1 2 3 4 5 6 7 8 9
108 121 Ш 189 196 225 256 289 324 Ж
2 » 441 484 529 576 625 673 729 784 Ш
3 500 961 1С.24 1089 1156 1225 1293 1369 1444 1521
1600 1681 1764 1849 1336 2825 2116 2209 2304 ЙИ *
5 2500 2601 2704 йоэ 2S1S 3025 3136 3243 3364 34®
6 3000 3721 38441 -;;л 4036 4225 4356 4439 4624 4781
7 4030 5041 5184 6329 5476 5625 5770 5329 6084 624
8561 6724 6 BS9 7056 7225 7335 7569 7744 7021
9 8100 3261 8464 8649 8836 9025 8216 9409 9604 9801
УЧЕБНОЕ ПОСОБИЕ ДЛЯ 8-го КЛАССА СРЕДНЕЙ ШКОЛЫ
Допущено Министерством просвещения СССР
Издание 3-е
Под редакцией А. И. МАРКУШЕВИЧА
МОСКВА „П Р О С В Е Щ Е И И Е“
19 8 1
22.14я72
А45
Ю. Н. МАКАРЫЧЕВ, Н. Г. МИНДЮК, В. М. МОНАХОВ, К. С. МУРАВИН, С, Б, СУВОРОВА
60601 — 105
103 (03) — 81
инф. письмо 4306020400
(g) Издательство «Просвещение», 1979 г.
ГЛАВА
КВАДРАТИЧНАЯ ФУНКЦИЯ
§ 1.
КВАДРАТНЫЙ ТРЕХЧЛЕН
1. КВАДРАТНЫЕ УРАВНЕНИЯ (ПОВТОРЕНИЕ)
При решении многих задач мы неоднократно встречались с уравнениями вида ах2 + Ьх + с — 0.
Уравнение вида ах2 -j- Ь* + с ~ О, где Ь и е — некоторые числа., причем а 0, а х — переменная, называется квадратным.
Например, уравнения Зх3 + ох — 1—0, № .— 7х — 0, 5ж2 — 8=0, 4х2 = 0 квадратные. В первом а = 3, Ь = 5, с = —1, во втором а = 1, Ь — —7, с = 0, в третьем а = 5,0=0, с — —g, в четвертом а = 4, Ь = 0, с ~ 0.
Если хотя бы один из коэффициентов Ь или с квадратного уравнения ах2 4~ Ьх + с = 0 равен 0, то такое квадратное уравнение называют неполным, Например, уравнения х2 — 7х = 0, бх2 — 8 = 0 и 4х2 =0 — неполные квадратные уравнения.
Напомним, что наличие корней у квадратного уравнения ах2. -р Ьх + с = 0 и их число зависят от выражения D — Ь2 — 4ас, которое называется дискриминантом квадратного уравнения. В зависимости от знака дискриминанта возможны три случая:
если D > 0, то уравнение имеет два корня;
если D — 0, то уравнение имеет один корень;
если D < 0, то уравнение корней не имеет.
При D 0 корни уравнения ах2 + Ьх -Ь с = 0, где а =£ 0, могут быть найдены по формуле
х== ~Ь j; D-, где D = Ь2— 4ас, (А)
Иногда при решении квадратных уравнений удобно пользоваться формулой корней, записанной в другом виде.
Разделим числитель и знаменатель дроби — на 2:
2а
2а а
«£ .ь,_г *
Внесем множитель Л в выражении -! D под знак корня. 2 2
Так как D Ь1 2 — 4ас, то
Таким образом, формула (А) примет вид:
• - • • ••
(Б)
Формулой, записанной в таком виде, можно пользоваться для решения любого квадратного уравнения, дискриминант которого неотрицателен (очевидно, что если Z) 0, то и — 0).
4 Обычно на практике ее применяют в том случае, когда b — чет-b
ное число, и, значит, — — целое число.
Приведем примеры решения квадратных уравнений с использованием формулы (Б).
Пример 1. Решить уравнение 7х2 — 10х — 8 = 0.
Имеем: ~ = (—5)2 — 7 * (—8) = 81;
х = , х = — -А или х = 2.
Заметим, что использование формулы (А) привело бы к более громоздким вычислениям.
Пример 2. Решить уравнение 4х2 — 4х + 5 = 0.
Имеем: — — (—2)3 — 4 5 = —16.
4
Так как — < 0, то и D <0. Значит, данное квадратное урав-
4
иение корней не имеет.
1. Решите уравнение:
а) 2х2 — 5х — 3 = 0; д) Зх2 — Зх + 1 = 0;
б) Зх2— 8х + 5 = 0; е) х2 + 9х — 22 — 0;
в) 5х2 + 9х + 4 = 0; ж) 7х2 — Их — 6 = 0;
Г) збх3 — 12х + 1 = 0; з) х2 — 12х + 32 = 0.
2. Решите уравнение, воспользовавшись формулой (Б):
а) Зх2 — 10х + 3 = 0; г) х2 + 14х + 33 = 0;
б) х2 — 8х — 84 = 0; д) 5х2 + 26х — 24 = 0;
в) 16х2 + 8х + 1 = 0; е) х2 — 34х + 289 = 0.
3. Решите неполное квадратное уравнение двумя способами— с использованием формулы корней и без нее:
а) 2х2 + 15х = 0; б) 25х2 — 144 - 0.
4. Приведите уравнение к виду ах2 + Ьх + с = 0 и решите его:
а) 3 (х + 4)2 = 10х + 32; в) — Их = И;
б) 31х 4-17 = 15(х +1)2; г)
5. Не решая уравнения, найдите сумму и произведение его
корней (если они существуют):
а) Юх2 — 9х + 2 - 0;
б) х2 + 48х + 11 - 0;
В) 7Х2 _ 56х +20-0;
г) 4х2 + х — 8 — 0;
д) 10х2 — 59х — С;
е) 5х2 — 58-0.
6. Найдите множество корней уравнения:
б)
2. КОРЕНЬ МНОГОЧЛЕНА
В таблице приведены значения многочлена х3 — 2х2 + 5х—10 при некоторых значениях х:
X —3 —2 —1 0 1 2 3 4
— 2х2 + 5х — 10 —70 —36 —18 —10 —6 0 14 42
Из Таблицы видно, что среди взятых значений переменной х есть такое (число 2), которое обращает этот многочлен в нуль. Говорят, что число 2 есть корень многочлена х3 — 2х2 + 5х — 10.
Корнем многочлена с одной переменной называется значение переменной, при котором значение многочлена равно нулю.
Из таблицы мы нашли один корень многочлена х3 — 2х2 + — 5х — 10. Имеет ли этот многочлен другие корни? Чтобы ответить на этот вопрос, нужно решить уравнение х3 — 2х2 — + 5х — 10 - 0.
Разложим многочлен х3 — 2х2 + 5х — 10 на множители: х3 — 2х2 + 5х — 10 —
- х2 (х — 2) + 5 (х — 2) - (х — 2) (х2 + 5).
Уравнение х3 — 2х2 5х — 10 — 0 равносильно уравнению (х — 2) (х2 + 5) — 0. Множитель х2 + 5 положителен при всех
значениях х, поэтому уравнение (х — 2) (х + 5) — 0 име только один корень — число 2. Следовательно, и многочлен _____2х2 + 5х — 10 имеет единственный корень — число 2.
Найдем множество корней многочлена х3 4- 2х2 9х 18»
Для этого решим уравнение х3 + 2х2 — 9х — 18 = 0:
х2 (х + 2) — 9 (х + 2) - 0;
(х + 2) (х2 — 9) - 0;
(х + 2) (х + 3) (х — 3) = 0.
х — —2 или х = —3 или х — 3.
Значит, {—2; —3; 3} — множество корней многочлена х3 + + 2х2 — 9х — 18.
Многочлен х4 + 5х2 + 1 не имеет корней, так как при любом х его значение положительно, и, следовательно, ни при каком х значение этого многочлена не равно нулю.
Иногда приходится решать обратную задачу: находить многочлен, корнями которого служат данные числа.
Пусть, например, нужно найти многочлен, множество корней которого {2; 3; —4}.
Запишем произведение трех множителей: (х — 2) (х — 3) X X (х + 4), где х — переменная. Очевидно, что это произведение обращается в нуль при значениях переменной х, равных 2, 3 и —4, и только при этих значениях х.
Преобразуем произведение (х — 2) (х — 3) (х + 4) в многочлен: \
(х — 2) (х — 3) (х + 4) — х3 — х3 — 14х + 24.
Множество корней многочлена х3 — х2 — 14х 4- 24 есть
{2; 3; —4}.
Можно привести и другие примеры многочленов с переменной х, имеющих то же множество корней. Действительно, если представить в виде многочлена произведение 2 (х — 2) (х — 3) (х 4" 4), то получится многочлен 2х3 — 2х2 — — 28х 4* 48, множество корней которого {2; 3; —4}. Преобразовав в многочлен произведение (х — 2)2 (х —• 3) (х 4* 4) (х2 + 1), мы получим многочлен х6 — — Зх° — 11г1 + 49х3 — 60х3 + 52х — 48 с тем же множеством корней. Вообще существует бесконечное множество многочленов с переменной х, корни которых — числа 2, 3 и —4, и только эти числа.
7. Является ли корнем многочлена х4 — 7х2 4- Зх 4~ 6: а) число 1; б) число J/2; в) число 2?
8. Найдите корни квадратного трехчлена:
а) х2 — 2х — 48; в) 5х2 — х — 22;
б) З#2 + у — 30; г) 4р2 — Ир + 7,
9. Найдите множество корней многочлена:
а) 2х — 3; дУ х3 — 10х2 + 25х;
б) х3 — 4х; jJ у3 4“ 12#2 + 36#;
в) г2 4~ 8; ж) х3 4~ 10х2 — х — 10;
г) #4 — 9; з) 2s — 8s2 — 2г 4- 16.
10. Составьте какой-либо многочлен, зная множество его корней:
а) {2; 3}; в) {0; 7}; д) 0;
б) {—5; 5}; г) {4}; е) {—1; 0; 5}.
Упражнения для повторения
11. Решите неравенство и покажите множество решений на координатной прямой:
а) 5х — 0,7 < Зх + 5,1; в) 2х + 4,2 4х + 7,8;
б) 0,8х + 4,5 > 5 — 1,2х; г) Зх — 2,6 > 5,5х — 3,1.
3. РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЕХЧЛЕНА НА МНОЖИТЕЛИ
Мы уже неоднократно, встречались с примерами разложения на множители многочленов. Решим эту задачу в общем виде для квадратного трехчлена, т. е. для многочлена вида ах2~[~Ъх~г где х — переменная, а а, Ъ и с — числа, причем а #= С.
Возможность разложения на множители квадратного трехчлена ах2 + Ъх + с зависит от того, имеет ли этот трехчлен корни. Наличие корней трехчлена определяется знаком выражения Ъ2 — 4ас, которое называют дискриминантом квадратного трехчлена (по аналогии с квадратным уравнением).
Пусть дискриминант D трехчлена ах2 + Ъх + с положителен. Тогда трехчлен имеет два корня хг и х2, которые являются корнями квадратного уравнения ах2 + Ъх + с — 0. Докажем, что в этом случае квадратный трехчлен ах2 + Ъх + с тождественно равен произведению а (х — хг) (х — х2).
Для доказательства выражение а (х — хг) (х — х2) преобразуем в многочлен:
а (х — Xj) (х — х2) —
= а (х2 — хгх— х2х + ххх2) = а (х2 — (хх + х2)х + Х]Х2).
По теореме Виета
Следовательно,
а (х3 — (хх + х2) х + ххх2) = afx2 + ~x + ~|= пх2 Ъх + с.
\ а а /
Итак, при £)> 0 и а 0 имеет место тождество
ах2 + bx-f-c = а(х— х^(х— х2). (1)
Тождеством (1) можно пользоваться и тогда, когда дискриминант D квадратного трехчлена ах2 + Ъх + с равен нулю, т. е. когда трехчлен имеет единственный корень. В этом случае принято считать, что хх = х2. Тогда
ах2 + Ъх + с = а (х — хх) (х — xj,
т. е. тождество (1) может быть представлено в виде ах2 + Ъх + с = а (х — XJ2.
Если дискриминант квадратного трехчлена отрицателен, т. е. трехчлен не имеет корней, то он не может быть представлен в виде произведения двух многочленов первой степени.
Действительно, если бы в этом случае имело место тождество ах2, + Ьх + с “ ~ (kx + т) (рх + §), где k9 т, р и q_ — какие-либо числа, причем k 0 и р #= О? т то правая часть равенства обращалась бы в нуль, например, при х = — —. Сле-k довательно, при этом значении х обращалась бы в нуль и левая часть, т. е. квадратный трехчлен имел хотя бы один корень. Но это противоречит условию.
Рассмотрим примеры применения тождества (1).
Пример 1. Разложить на множители, если это возможно, квадратный трехчлен:
а) 2х2 — 5х — 3;
б) —25х2 + 10х — 1.
Решение, а) Дискриминант трехчлена, равный (—5)2 — —4 • 2 (—3), положителен. Значит, трехчлен имеет два корня. Найдя по формуле корней квадратного уравнения корни трехчлена — числа 3 и----применим тождество (1):
2
2х2 — 5х — 3 = 2 (х — 3) (х + --\
X 2 /
Полученный результат можно записать иначе: \
2х2 — 5х — 3 - (х — 3) (2х + 1).
б) Вычислим дискриминант трехчлена:
D ю2 — 4 • (—25) • (—1) - 0.
Трехчлен имеет единственный корень, равный —. По тождест-5
ву (1) имеем:
—25х2 + 10х — 1 = — 25 (х — -У.
\ 5/
Полученный результат можно записать в другом виде:
—25х2 + 10х — 1 = (5х — 1) (1 — 5х).
Пример 2.
Сократить дробь
х — 5
Зх2 — 13х — 10 '
Решение. Квадратный трехчлен Зх2 — 13х — 10 (знаменатель дроби) имеет корни, так как его дискриминант положителен. Значит, этот квадратный трехчлен может быть разложен на мно
жители.
2
Корни трехчлена — числа —-- и 5.
Имеем:
(Зх + 2) (х — 5).
Теперь можно сократить данную дробь:
Зх2 — 13х — 10 (Зх -Ь 2) (х — 5) Зх + 2
Пример 3. Решить неравенство х2 — х — 20 < 0.
Решение. Выяснив, что дискриминант трехчлена х2 — х — 20 положителен, найдем корни этого трехчлена: —1 и 5. Разложим трехчлен на множители:
х2 — х — 20 - (х + 4) (х — 5).
Неравенство (х + 4) (х — 5) <0 истинно тогда и только тогда, когда
Множество решений первой системы — числовой промежуток —4; 5[. Множество решений второй системы — пустое множество. Следовательно, множеством решений исходного неравенства является числовой промежуток ]—4; 5[.
Пример 4. Разложить на множители многочлен 4х2 + 9&х + Йд2.
Решение. Данный многочлен можно рассматривать как квадратный
трехчлен относительно переменной х. Выраз
с помощью формулы корней
квадратного уравнения переменную х через Ь. Это может быть сделано, так как дискриминант трехчлена D = (9Ь)2 — 4 • 4 • 5Ь2 = Ь2 неотрицателен.
Имеем:
-9Ь±УЫ —9Ь±.\Ъ\
х _----, г. е. х - ..
5Ь
Отсюда х — — ~~ или х = —&.
4
Применяя тождество (1), полу'
нм
4х2 + 9&х + 5Ь2 = 4x4--------------b (х + Ь).
\ 4 /
Окончательно имеем:
4х2 + 9Ьх + 5Ь2 = (4х + 5&) (х + &).
12. Найдите корни трехчлена и разложите его на множители: а) 2х2 — 5х + 3; в) 2х2 — 5х — 7; д) —у2 + бу—5;
б) бу'2 + 2у — 3; г) х2 — Их + 30; е) — г2—5s +6.
13. Разложите на множители, если возможно, трехчлен:
а) 4х2 — 9х + 5; "г) 16а2 — 24а + 9; ж) Зх2—12х +12;
б) 4d2 — 9Ь + 7; д) х2 — х — 2; з) —48а2—8а +1;
в) —Зу2 + 8у +11; е) у2—7у + 11; и) 4х2+«+0,04.
Представьте в виде произведения двух двучленов много член:
а) 0,1х2 — 10х + 240; б) ~У2 — у — 1; в) О,3х3 + 2,5х — 55.
15. Сократите дробь:
а)
б)
7х2 -|- х — 8 .
7х — 7 ’
5а +10 2а2 + 13а + 18 ’
I/2 — бу — 36#
81 —у2
16. Постройте график функции:
17. Решите неравенство:
а) За2 — 10а — 8 <0;
б) у2 — 26у + 168 < 0;
to) х2 + 6х — 55 > 0;
г) — 2b2 + 9Ъ + 5 > 0.
у
Упражнения для повторения
18. Решите систему неравенств:
в)
г)
19. Постройте график функции у — 0,25х2. Имеет ли построенная кривая ось симметрии? Как называется эта кривая?
20.
Постройте график функции
Рис. 1
21.
ю
х2. Имеет ли гра-
фик ось симметрии? В ка-
ких координатных углах расположен этот график? Укажите наибольшее значение функции.
На рисунке 1 построены графики функций вида у = ах2. Для каждой из кривых укажите соответст-
вующее значение а.
22. Выделите квадрат двучлена из трехчлена:
а) х2 — 2х + 5;
б) 2х2 — 8х + 7.
1
3
§ 2.
ГРАФИК КВАДРАТИЧНОЙ ФУНКЦИИ
4. ГРАФИК
ункции у^а(х — т)2
и
Пусть требуется построить график функции, заданной уравнением
у = ~ х2 — 8х + 35. (1)
Представим это уравнение в другом виде, выделив из трехчлена квадрат двучлена. Получим уравнение
(2)
Выясним, что представляет собой график уравнения (2), а значит, и равносильного ему уравнения (1).
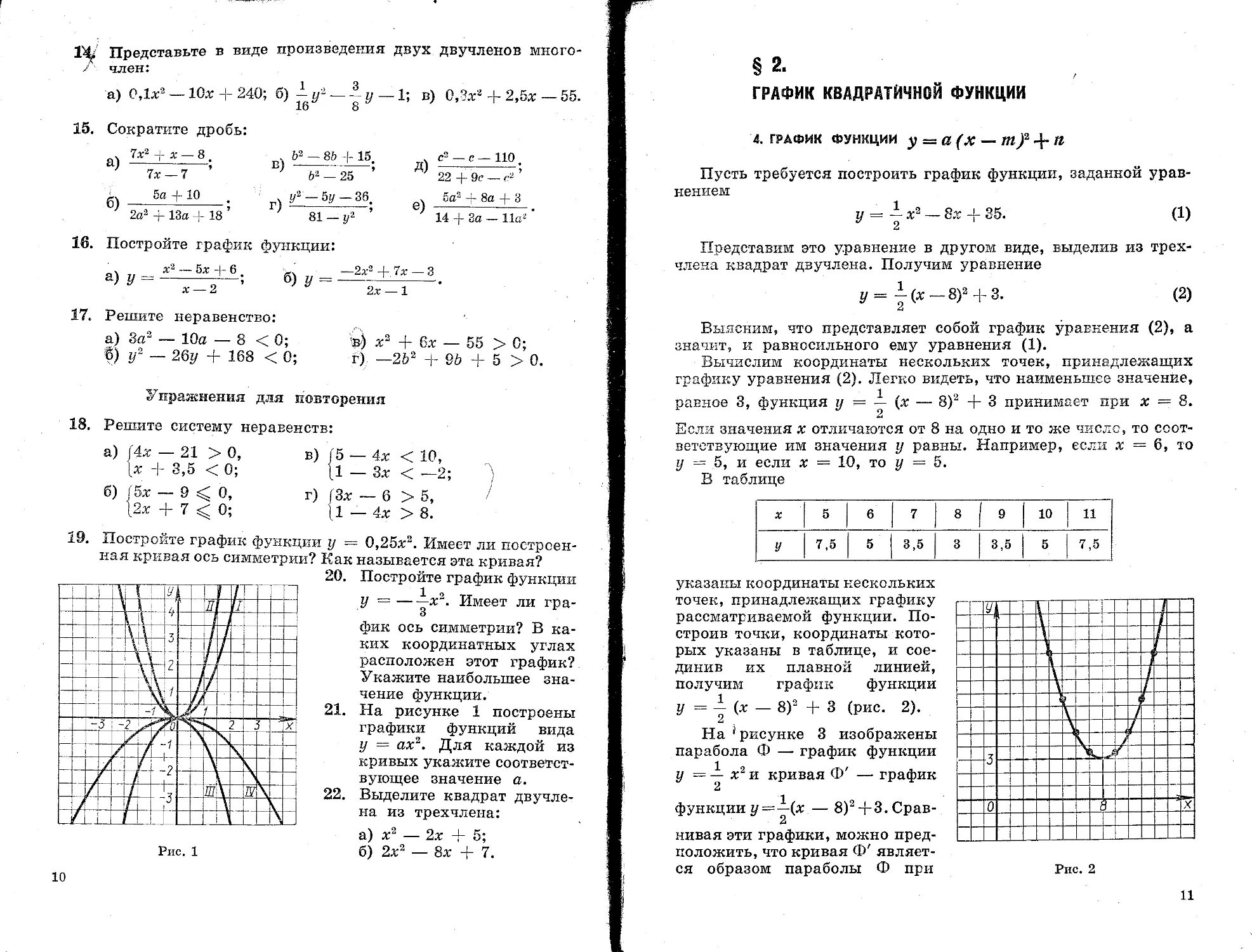
Вычислим координаты нескольких точек, принадлежащих графику уравнения (2). Легко видеть, что наименьшее значение, равное 3, функция у — i (х — 8)2 + 3 принимает при х = 8.
Если значения х отличаются от 8 на одно и то же число, то соответствующие им значения у равны. Например, если х = 6, то у = .5, и если х = 10, то у ~ 5.
В таблице
X 5 6 7 8 ' 9 10 11
У 7,5 5 3,5 3 3,5 5 7,5
указаны координаты нескольких точек, принадлежащих графику рассматриваемой функции. Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции у = — (х — 8)2 + 3 (рис. 2).
На ^рисунке 3 изображены парабола Ф — график функции у = — х2 и кривая Ф' — график 2
функции у = ~-(х — 8)2 + 3. Сравнивая эти графики, можно предположить, что кривая Ф' является образом параболы Ф при
Рис. 4
параллельном переносе, который начало координат (точку 0(0; 0)) отображает на точку О' (8; 3).
Докажем, что это действительно так.
Параллельный перенос ОО' отображает произвольную точку М(х0; г/о) на точку М' (х0 + 8; у0 + 3).
В самом деле, из рисунка 4 видно, что ОМ == Хоег + уое2, О дм' = дм + до' = (хо
8)<?i + (уо + 3)е2, т. е. координаты точки М' равны Хо + 8, уо + 3.
Легко понять, что если точка М (х0; у0) принадлежит пара-боле Ф, то точка М' (х0 + 8; у0 + 3) принадлежит кривой Ф'.
Действительно, если равенство 1 2
У о истинно, то и равенство
Уо + 3 = |((х0 + 8)-8)Ч-3 также истинно.
Значит, какую бы точку параболы Ф мы ни взяли, ее образ принадлежит кривой Ф'.
Верно и обратное: каждая точка параболы Ф является образом одной и только одной точки кривой Ф' при параллельном переносе О'О. Это показывается аналогично.
Следовательно, график уравнения у. = (х — 8)2 + 3, а значит, и равносильного ему уравнения (1) есть парабола, яв-ляющаяся образом параболы у = ~ х2 при параллельном переносе, который начало координат отображает на точку с координатами (8; 3).
Рассуждая аналогично, можно показать, что и вообще гра-фик уравнения у = а(х—т)2-\~п есть образ параболы у = ах2 при параллельном переносе, отображающем начало координат на точку с координатами (ml п).
Мы знаем, что парабола имеет ось симметрии. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Для параболы у = ах2 осью симметрии служит ось у, a вершиной — точка 0(0; 0). При а >0 «ветви» параболы направлены вверх, а при а < 0 — вниз.
Из свойств параллельного переноса вытекает, что графиком функции у — а (х~т)2-Уп является парабола, конгруэнтная параболе у ~ ах2, вершиной которой служит точка с координатами (т', п), а осью симметрии — прямая х — т. При а > О «ветви» параболы направлены вверх, а при а <Г 0 — вниз.
Мы выяснили, что график функции у =? а (х — иг)3 + п есть образ графика функции у — ах2 при параллельном переносе ОО', где О — начало координат, О' — точка с координатами (тп; п). Аналогично показывается, что вообще при указанном параллельном переносе график функции у = f (х — т) + п есть образ графика функции у = f (х).
23.
24.
25.
26.
На рисунке 5 построен график уравнения у = 1,5х2 (парабола Ф) и его образ (парабола Ф') при параллельном переносе ОО', О — начало координат, О' — точка с ко-
ординатами (2; 5). Запишите уравнение параболы Ф'. Запишите уравнение образа графика функции у = 8х2 при параллельном переносе ОО', где О — начало координат, а О' — точка с координатами: а) (9; 4); б) (—2; —16); в) (0;
Какое уравнение имеет образ параболы Ф при параллельном переносе, отображающем точку О (0; 0) на точку О' (—3; 5/, если известно, что парабола Ф является графиком функции: а) у = х2; б) у = —2,5х2?
Найдите координаты точки О', зная, — что при параллельном переносе ОО' (О — начало координат) график функции у график а) б) в)
координат)
--- 5х2 отображается на функции:
; о.
У =
27. Параллельный перенос О(У отображает график функции у = ах2 на график уравнения:
а) у = 3 (х — 2)2 + 10; г) у = (х — 2)2;
б) у = —8 (х — I)2 — 6; д) у = —х2 + 6;
в) у = 1,5х2 — 2; е) у = — (х + 7)2.
Укажите значение коэффициента а в уравнении у = ах2 и
координаты точки О'.
23. Изготовьте шаблон параболы у = 0,5х2. Используя этот шаблон, постройте график уравнения:
а) у = 0,5 (х — I)2 + 2; в) у = 0,5х2 + 4;
б) у = 0,5 (х + 2,5)2 — 3; г) у - 0,5 (х + 4,5)2.
L*
С помощью шаблона параболы у = 2х2 постройте график уравнения:
а) у = —2х2; в) у ~ —2 (х — 4)2 — 6;
б) у = —2 (х + З)2; г) у —2х2 + 8. if
30. Укажите координаты вершины параболы, которая является графиком уравнения:
а) у = 3 (х — 5)2 — 2; в) у — 2х2 — 1;
б) у = —2 (х + I)2 + 3; г) у — (х — 5)2.
Изобразите эту параболу схематически.
31. Представьте уравнение
а) у = х2 — 6х + 1; в) у = х2 + Зх;
б) у = х2 — 4х + 4; г) у = х2 + 4
в виде у = а (х — т)2 + п. Постройте на координатной плоскости вершину и ось симметрии параболы, которая является графиком этого уравнения. Куда направлены «ветви» параболы: вверх или вниз?
Упражнения для повторения
32. а) Найдите множество значений переменной с, при которых уравнение 10х2 + 2бх + с = 0 имеет два корня.
б) Найдите множество значений переменной а, при которых уравнение ах2 + 18х + 3 = 0 не имеет корней.
33. Найдите корни многочлена:
а) 2у3 + бу2 — Зу; б) р* — 16.
5. ГРАФИК ФУНКЦИИ у = ах2 4е Ьх + с
Определение. Функция, которая может быть зада-
на
где а 0, называется
квадратичной.
Выясним, что представляет собой график квадратичной функции. Мы установили, что график функции, заданной уравнением у — а (х — т)2 + п, является образом графика функции у = ах2 при параллельном переносе, отображающем начало координат на точку О' (т; п).
Покажем, что всякую квадратичную функцию можно задать уравнением вида у а (х т}2 ~т п.
Для этого выделим из трехчлена квадрат двучлена:
/ 2 t с \ /9|ОЬ;&2 Ь2 е\
а х2 Н— х----а х^ + 2х —--------—------— —
\ а а / \ 2а 4а2 4а2 а /
/ . ЪЛ2 Ъ2 — 4ае\ / . Ъ \2 &2 — 4ас
х 4---— ------- = а х 4------------.
\ 2а) 4а2 ) ' \ 2а) 4а
у = ах2 + Ьх + с равносильно уравнению
/ , Ь \2 Ь- — 4а?
у ~ а х 4—----------.
\ 2а) 4а
„ Ъ Ъ2 — 4ас
значения выражении —— и------------соответст-
2а 4а
и п. Тогда уравнение (1) примет вид:
Уравнение
(1)
Обозначим
венно через т
у — а (х — т)2 + п. (2)
Итак, мы показали, что всякую квадратичную функцию можно задать уравнением (2). Следовательно, график функции у = ах2 + Ьх с есть парабола, конгруэнтная параболе 2 , Ь .
у — ах2; осью симметрии графика является прямая х =-----;
2а при а > 0 «ветви» параболы направлены вверх, при a <Z 0 — вниз.
Приведем примеры построения графиков функций, заданных формулами вида у — ах2 + Ьх + с.
Пример 1. Построить график функции у = 2х2 + 4х — 1.
Графиком этой функции является парабола. Найдем координаты ее вершины. Для этого можно, выделив из трехчлена квадрат двучлена, представить уравнение у = 2х2 + 4х — 1 в виде у 2 (х + I)2 — 3. Отсюда ясно, что вершина параболы — точка с координатами (—1; —3).
Координаты циссу вычислим
вершины параболы можно найти цначе. Абс-Ь тт
по формуле х = ----. Имеем:
2а
X -- —
уравнение у = 2х2 + 4х — 1, найдем
Подставив х = ординату вершины параболы:
Построив в координатной плоскости вершину параболы—точку с координатами (—1; —3) и зная, что осью симметрии параболы служит прямая х = —1 и что «ветви» параболы направлены вверх, мы можем представить себе общий вид графика функции у = 2х2 + 4х — 1.
Для построения графика найдем координаты нескольких точек, принадлежащих этому графику:
X со 1 —2 0 1
У 5 —1 —1 5
Г </1_ 1
! -
-
1 i
1 Hv*
5
1 i
й г
~1 ; * 1
ГГЙ
♦
пЬ™. 1
Рис. 6
Построив в координатной плоскости точки, координаты которых занесены в таблицу, и соединив их плавной линией, мы получим график функции у = 2х2 + 4х — 1 (рис. 6).
Пример 2. Пусть требу-
ется построить график функ-
Найдем координаты вершины параболы. Абсциссу вычислим по формуле х = — Име-
__1
ем: х = — ----------------= —2. Из
Рис. 7
равенства у — — ~ • (—2)2 — 4
~ (—2) 4-4 найдем, что ордината вершины равна 5.
Построим в координатной плоскости вершину параболы — точку с координатами^ (— 2; б). Зная, что осью симметрии параболы служит прямая х — —2 и что «ветви» параболы направле-
Рис. 8
ны вниз, мы можем представить общий вид графика заданной функции.
Построив несколько точек графика, координаты которых помещены в таблице
X —6 —4 0 ] 2
У 1 4 4 1
и соединив их плавной линией, мы получим график функции у =------х2 — х + 4 (рис. 7).
4
34. Найдите координаты вершины параболы:
в) у = х2 + Зх; г) у = —х2 4 7х.
Куда направлены «ветви» параболы?
35^/ Не выполняя построения, найдите координаты точек пересечения графика функции с осью х и осью у:
а) у = х2 — 5х + 6; г)| у = х2 — 6;
61 у —х2 + 2х + 3; д) у = — 2х2 + 7х;
в) у = х2 — 7х + 13; е) у = Зх2 + 9х.
3Q. Постройте график функции:
г) У = —%? + 6х — 10;
д) у = х2 — 4х;
е) у = —х2 + 5.
87.
39.
40.
Используя график функции Д заданной 1 1
у = —х2 — Зх + 2— (рис. 8), найдите:
2 2
формулой
а) множество значений аргумента, при которых f (х) = 0, f (х) < 0, f (х) > 0;
б) множество значений аргумента, при которых f (х) - 2,5, f (х) - —4;
в) множество значений аргумента, на котором функция f возрастает, убывает; значение аргумента, которому со
ответствует наименьшее значение функции;
г) область значений функции f.
Постройте график функции у = —х2 + 2х + 8. Пользуясь этим графиком, найдите:
а) множество значений аргумента, при которых у = 0;
У < 0; у > 0;
б) множество значений аргумента, на котором функция возрастает, убывает;
в) значение х, при котором функция принимает наиболь
шее значение.
Докажите, что график функции, заданной уравнением у — (х — 2) (х — 4), есть парабола, конгруэнтная параболе у = х3.
Укажите координаты точек пересечения графика функции у = (х — 5) (х + 3) с осью х и с осью у. Постройте график этой функции.
Упражнения для повторения
41. Найдите корни многочлена:
а) 2а5 — 32а; б) у3 + у2 + 9у + 42. Сократите дробь:
ч 4 — х 2х — 1
а) -----------; б) -------------------.
Зх2 — Зх + 60 / 4х2 + 30х —16
6. РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Свойства графика квадратичной функции можно использо-вать при решении неравенств вида ах2 + Ъх + с < 0 и ах2 + + Ъх + с > 0, где а Ф 0. Неравенства такого вида называют неравенствами второй степени с одной переменной. i
Рассмотрим примеры.
Пример 1. Решить неравенство Зх3 + 10х — 8 < 0.
Используем свойства графика функции у = Зх2 + 10х — 8. Этот график представляет собой параболу, «ветви» которой направлены вверх, так как коэффициент при х2 — число * положительное. Чтобы выяснить, как расположена эта пара-бола относительно оси х, вычислим дискриминант трехчлена Зх2 + 10х — 8. Получим: D = 100 + 96 = 196, т. е. D > 0. Значит, трехчлен имеет два корня. Выполнив вычисления, 2
найдем корни трехчлена: —4 и —. Парабола пересекает ось х
в двух точках, абсциссы которых соответственно равны —4 и
Теперь можно показать примерное положение параболы на координатной плоскости (рис. 9). Из рисунка видно, что трехчлен Зх2 + 10х — 8 принимает отрицательные значения, когда—4 <х <~. Следовательно, искомое множество решений ’ неравенства Зх2 + 10х — 8 < 0 есть числовой промежуток
Заметим, что при рассмотренном способе решения неравенства нас не интересовали координаты вершины параболы. Важно было лишь знать, куда направлены «ветви» параболы —
^з
14
вверх или вниз — и каковы абсциссы точек ее пересечения с ОСЬЮ X. •
Пример 2. Решить неравенство 9х2 + ЗОх +25 >0.
«Ветви» параболы, являющейся графиком функции у = 9х2 + ЗОх + 25, направлены вверх (коэффициент при х3 положителен).
Так как дискриминант трехчлена 9х2 + ЗОх + 25 равен 0 (D = 900 — 900 “ 0), то трехчлен имеет единственный корень. Выполнив вычисления, найдем, что корень трехчлена равен 2
—1—. Следовательно, рассматриваемая парабола имеет с осью х
только одну общую точку, абсцисса которой равна —1—. Пара-3
бола у=9х2+30х+25 схематически изображена на рисунке 10.
Из рисунка видно, что неравенство 9х2 + ЗОх + 25 > 0 истин-1 2 но при всех значениях переменной х, кроме —1—
т. е. мно-
жество решении неравенства есть
3
3
Пример 3. Решить неравенство —2х2 + х — 5 >0.
График функции у = —2х2 + х — 5 есть парабола, «ветви» которой направлены вниз.
Дискриминант трехчлена —2х2 + х — 5 — число отрицательное (D =1 — 40 < 0). Значит, парабола не имеет с осью х общих точек.
Схематический график функции у — — 2х2 + х — 5 изображен на рисунке 11. Из рисунка видно, что при всех значениях х значения трехчлена отрицательны. Следовательно, множество решений неравенства —2х2 + х — 5 >0 — пустее множество.
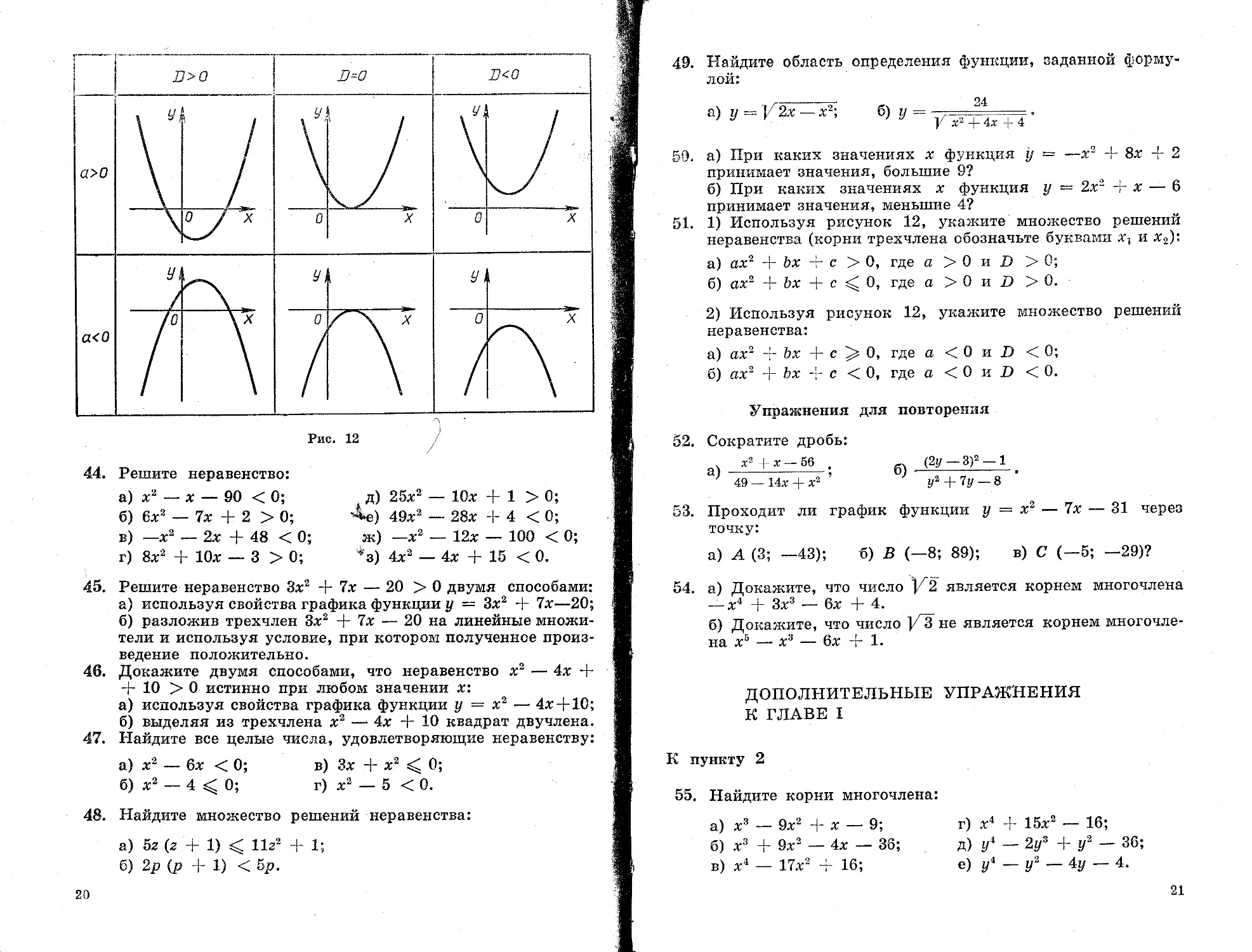
При решении неравенств второй степени мы использовали соображения о расположении графика квадратичной функции относительно оси х. Очевидно, что это расположение определяется двумя условиями: знаком коэффициента а квадратного трехчлена ах2 + Ъх + с и значением дискриминанта J9. Ст знака коэффициента а зависит направление «ветвей» параболы; от знака дискриминанта D — положение параболы относительно оси х (парабола имеет с осью х только две общие точки, только одну общую точку, не имеет общих точек).
Расположение графика функции у — ах2 + Ъх + с, где а =+ 0, относительно оси х показано на рисунке 12.
43. Найдите координаты точек пересечения графика функции у — х2 — Зх — 4 с осью х и покажите примерное положение графика на координатной плоскости. Используя полученный рисунок, решите неравенство:
а) х2 — Зх — 4 < 0; б) х2 — Зх — 4 > 0.
44. Решите неравенство:
а) х2 — х — 90 <0;
б) 6х2 — 7х + 2 > 0;
в) —х2 — 2х + 48 < 0;
г) 8х2 + 10х — 3 > 0;
д) 25х2 — 10х + 1 >0;
<е) 49х2 — 28х + 4 <0;
ж) —х2 — 12х — 100 < 0; %) 4х2 — 4х + 15 <0.
45.
46.
47.
Решите неравенство Зх2 + 7х — 20 >0 двумя способами: а) используя свойства графика функции у = Зх2 + 7х—20; б) разложив трехчлен Зх2 + 7х — 20 на линейные множи-
тели и используя условие, при котором полученное произведение положительно.
Докажите двумя способами, что неравенство х2 — 4х + + 10 >0 истинно при любом значении х:
а) используя свойства графика функции у = х2 — 4х+10; б) выделяя из трехчлена х3 — 4х + 10 квадрат двучлена. Найдите все целые числа, удовлетворяющие неравенству:
а) х2 — 6х < 0;
б) х2 — 4 < 0;
в) Зх + х2 0;
г) х2 — 5 < 0.
48. Найдите множество
решений неравенства:
а) 5з (z + 1) Из2 + 1;
б) 2р (р + 1) < 5р.
49. Найдите область определения функции, заданной формулой:
а) у = ]/2х — х2;
50. а) При каких значениях х функция у = —х2 + 8х + 2 принимает значения, большие 9?
б) При каких значениях х функция у = 2х2 + х — 6 принимает значения, меньшие 4?
51. 1) Используя рисунок 12, укажите множество решений неравенства (корни трехчлена обозначьте буквами хг и х2): а) ах2 + Ьх + с >0, где а > 0 и D >0;
б) ах2 + Ъх + с 0, где а > 0 и D > 0.
2) Используя рисунок 12, укажите множество решений неравенства:
а) ах2 + Ъх + с 0, где а < 0 и D < 0;
б) ах2 + Ъх + с <0, где а < 0 и D < 0.
Упражнения для повторения
52. Сократите дробь:
ч х2 + х — 56
а) ----Z--------;
49 — 14х + х2
(2у - З)2 -1 У2 + 7у-8
53. Проходит ли график функции у = х2 — 7х — 31 через точку:
а) А (3; —43); б) В (—8; 89); в) С (—5; —29)?
54. а) Докажите, что число У2 является корнем многочлена —-х4 + Зх3 — 6х + 4.
б) Докажите, что число | 3 не является корнем многочлена х5 — х3 — 6х + 1.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ I
пункту 2
55. Найдите корни многочлена:
а) х3 — 9х2 + х — 9;
б) х3 + 9х2 — 4х — 36;
в) X4 — 17х2 + 16;
г) х4 + 15х2 — 16;
д) if - 2у* + у2- 36;
е) г/4 — у2 — 4у — 4.
56. Является ли корнем многочлена:
а) х2 — 2 Ох + 80 число 10 — 2 \/ 5;
б) х4 — 6х2 + 1 число ]/2 — 1?
57. Найдите многочлен наименьшей степени, коэффициенты которого — целые числа, зная множество его корней X:
а) X = {5; 7};
б) X - {—3; 0; 3};
58. Найдите многочлен третьей степени, коэффициенты которого — целые числа, зная множество его корней X:
а) X = {0; 2; 5}; в) X = {—3; 3};
б) X = {-1; 4; 6}; г) X = {4}.
59. Напишите какой-либо многочлен четвертой степени, множество корней которого:
а) состоит из 2 элементов; б) пусто.
.
К пункту 3 *
60. Разложите, если возможно, на линейные множители трехчлен: . уу
Q) х2 — 4х — 21; д) а2 + а — 20; и) Зу2—2Ъу—5&2; б) 5х2 + 13х + 8; е) 7Ъ2 — 3b + 1; к) х2—2xz—г2; в) —4х2 + 7х — 3; ж) а2 — ab — 6Ъ2; л) 2c2+cd+4d2; г) 10х2 + Эх — 63; в) х2+ах—30а2; м) х3—12х2+20х.
61. Разложите на множители:
63.
а) а2 (а — 5)3 — 36а + 180;
Сократите дробь: . 5х2 — 13х — 6
й) ----2---О---
х2 — 9
б) 4&5 —
Зе2 — 11с + 19 е
_ ~ 9
(За — 5)2 — 1
7а2 — 9а — 10 ’
Решите уравнение:
4&4 — 81 (&—I)3.
64. Решите неравенство:
' а) х2 — 5х + 6 < 0; в) Зх2 4~ 4х — 7 0;
б) х2 — 7х + 6 > 0; г) —Зх2 — 10х < 3.
65. Найдите область определения функции:
1 • ч Ух-З . м ха+х-б
У “ « 9 -Г/Р Г) У — "7-о---ЧУ— -----------------5 •
У х2 — 144 7 J х2 — 2х — 80 У 9 — хи
К пункту 4
66. Параллельный перенос ОО', где О — начало координат, отображает параболу Ф — график уравнения у — 15х2 — на параболу Ф'. Запишите уравнение параболы Ф', если координаты точки О' равны:
а) (5; 10); б) (-8; И); в) (0; 6); г) (-7; 0).
67. На рисунке 13 построен график функции у — |х| и график его образа при параллельном переносе О (0; 0) -> -> О' (5; 2). Напишите уравнение образа графика функции у = |х|. •
68. Найдите параллельный перенос ОО' (укажите координаты точки О', зная, что О — начало координат), в результате которого:
а) график функции у — | х | отображается на график функции у = |х + 8| — 5; _
б) график функции у — отображается на график функции у = ]/х + 50;
в) график функции у — 4х3 отображается на график функ-
ции у = 4 (х
г) график функции у = —
X отображается на график
69. Постройте график уравнения:
а) у = |х + 3| — 1;
б) у = |х| + 4;
• £1 и
7
г
2 —— '•ячт
Z-
дим
0. 5
г) у = ух + 5. Рис. 13
70. Существует ли параллельный перенос, при котором график уравнения 2х + 5у + 8 = 0 является образом графика уравнения: а) у = —0,4х + 3; б) у = 2х — 5?
71, Существует ли параллельный перенос ОО\ где О — начало координат, при котором график уравнения (1) отображается на график уравнения (2):
а) (1) х + у = 5, (2) х + у 12;
б) (1) у — 2х, (2) у + 2х = 8;
в) (1) у - х2, (2) у - х2 ~ 16х + 67?
72.
Можно ли в результате какого-нибудь параллельного переноса ОО' (О — начало координат) отобразить гиперболу ' у _ На график уравнения: X
73.
74.
75.
Параллельный перенос Т отобразил параболу у — х2 на некоторую параболу Ф, которая проходит через точки А (4; —1) и В (0; 7). Укажите этот параллельный перенос и напишите уравнение параболы Ф.
Постройте график уравнения:
а) у = (х — 4)3 4-2; в) х (у — 2) = 12;
б) у = —х3 — 3; г) (х — 1уу = 12.
Укажите параллельный перенос, при котором график
у ~ (х — 12)2 "1- 5 отображается на график
уравнения
уравнения
У - (х + 8)2 + 7,
К пункту 5
76. Постройте график функции:
а) у = х2 + 2х — 15; г) у = 6х — 2х2;
б) у — 0,5х2 — Зх + 4; д) У (2х — 7) (х + 1);
в) у 4 — 0,5х2; е) у — (2 — х) (х + 6).
77. Не выполняя построения графика, выясните, в каких координатных углах расположена парабола, если: а) у 2х2 — х 4- 3; в) у = х2 + 16х + 3;
б) у = х2 — 2х — 63; г) у = —Зх2 + 2х — 7.
78. Докажите, что график уравнения является параболой: а) х (2у — Зх + 4) + у (Зх — 2у + 1) = (х — 2у) (у—2х)\ б) (2х — Зу)2 — (у — 6х)2 - 8у2 — 5 (х 4- 2)2.
79. При каком значении с график функции у — 2х2 + 7х + с проходит через точку А (—10; 150)?
80. При каком значении Ъ график функции у = х3 + Ъх — 19 проходит через точку D (—11; —30)?
81. Известно, что график функции у = ах2 + Ъх — 48 проходит через точки М (1; 2) и N (2; 10). Найдите значения коэффициентов а и Ъ.
82. Укажите параллельный перенос и значение коэффициента а, при котором график функции у = ах2 отображается на график уравнения:
а) р — 2х2 — 4х + 1;
б) у ~ х3 — 8х + 6;
К пункту 6
83. Решите неравенство:
а) х2 5х + 6 <0;
б) — р2 + 7р — 6 С;
в) Зз2 + 2г + 5 > 0;
84. а) Является ли число 1001 х2 __ 2бх + 944 > 0?
б) Является ли число 2848 101х2 + 8х + 248 < 0?
в) у — 2х — х2:
г) у — — х2 + 7.
г) 4р2 - 36р + 81 < 0;
д) Зх2 > 7 — 4х;
е) -2ц2 - 10и < 41.
решением неравенства
решением неравенства
85. Найдите область определения функции, заданной форму лой:
= ]/зб —х2—4х;
___ /16 — 24х + 9хГ.
х + 2 ’
а) у ~ ]/144 — 9х2;
ж) у
86. Решите систему неравенств:
а) (21х2 + 39х — 6 < 0, /
[ х < 0;
б) Г4х2 + 5х - 6 >0, [ 7х > 0;
в) (х — 3 < 0, [х2 — 144 > 0;
г) (х 7 > О, [х2 + 5х < 0;
д) fx2 — Зх — 4 <0, ]3х - 12 >0;
е) fx2 + 7х И- 10 <0, |х - 1,5 > 0;
ж) Г2х2 + 5х + 20 <0, (4х — 3,6 > 0;
з) / Зх2 - 7х + 128 > О, I 5х — 1,8 < 0.
87.
Найдите область определения выражения:
д) У 7х — 14 —Ух2 — 15х + 56;
е) Ух2 — 6х + 9 — Уб — х;
V 4х2 — 12х — 7
/15 — 19х 4- 6х2
ГЛАВА
УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ
§ з.
УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ
7. УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
Пусть дан многочлен с переменными хну
х2 + Бху2 — 7ху + 8.
Введем понятие степени многочлена с несколькими перемен- ./ кыми. /
За степень многочлена стандартного вида принимается сум- j ма показателей степеней переменных в том из его членов, в кото- j ром эта сумма наибольшая*. j
Например, в данном многочлене одночлен х2 является чле- | ном второй степени (переменная у входит в этот одночлен в нулевой степени), одночлен 5xz/2 имеет сумму показателей степеней переменных, равную трем, значит, это член третьей степени; 4 —7ху — член второй степени, а 8 — член нулевой степени. Следовательно, многочлен х2 + 5ху2 — 7ху + 8 является многочленом третьей степени.
Многочлен х3 — 2х2у2 -j- у4 + 7х2у — Зу3 + вху —8 является многочленом четвертой степени, так как наибольшая сумма показателей степени переменных (во втором и третьем членах) равна 4. z
Рассмотрим уравнение
2х5 + 4x3z/3 — 9x4z/ + уъ — 5х + 27 О
с двумя переменными х и у. Левая часть этого уравнения — многочлен шестой степени, а правая — нуль. Говорят, что это уравнение шестой степени. '
За степень уравнения с несколькими переменными, левая часть которого — многочлен стандартного вида, а правая — нуль, принимается степень этого многочлена.
* Член многочлена, в котором сумма показателей переменных наибольшая,
называют старшим членом многочлена.
Чтобы определить степень уравнения (х3 + у)2 = х6 — 1, преобразуем его так, чтобы левая часть представляла собой многочлен стандартного вида, а правая была равна нулю. Получим уравнение
2х3у + у2 + 1 - О,
равносильное данному. Это уравнение, а значит, и исходное четвертой степени.
В этой главе мы будем рассматривать главным образом уравнения первой и второй степени с двумя переменными.
Как известно, решением уравнения с двумя переменными называется пара значений переменных, обращающая это урав
нение в истинное равенство.
Например, пара чисел (17; 3), в которой на первом месте указано значение переменной х, а на втором — значение переменной у, является решением уравнения х — 2у2 4'1 =0. Действительно, равенство 17 — 2 * З2 + 1 = 0 истинно.
Выбирая произвольно значения у и находя соответствующие
значения х, можно получить сколько угодно других пар, являющихся решениями этого уравнения. Например, взяв значение у, равное 0, получим значение х, равное —1. Пара (—1; 0) — решение уравнения х — 2у2 + 1=0.
Каждое уравнение с двумя переменными х и у определяет некоторое множество пар (х; у) значений переменных, которые
являются решениями этого уравнения, т. е. задает некоторое отношение между значениями переменной х и значениями переменной у. График отношения, заданного уравнением с двумя переменными, или, короче, график уравнения с двумя перемен
ными, есть, как известно, множество точек плоскости, координаты которых служат решениями уравнения.
Мы знаем, что графиком уравнения вида ах + by = с, где а += 0 или Ь =+ 0, служит прямая линия, график уравнения вида у = ах2 + &х + с (а += 0) — парабола, график уравнения вида ху = k (k =+ 0) — гипербола.
На рисунке 14 изображен график уравнения х2 + 9у2 = 81. Кривая такого вида называется эллипсом.
Рис. 15
:Й
1
Покажем теперь, что если точка не принадлежит данной окружности, то ее координаты не удовлетворяют уравнению (1). 'Действительно, пусть точка В (х^ уг) лежит внутри круга (см. рис. 15), тогда
О В | 5 и х? у\ 52.
Если же точка D (х2; z/2) лежит вне круга, то
Итак, равенство х2 4~ у2 — 52 верно тогда и только тогда, когда точка с координатами х и у принадлежит окружности с центром в начале координат и радиусом, равным 5 единицам. Следовательно, окружность, изображенная на рисунке 15, является графиком уравнения х2 + у2 52.
Вообще, окружность с центром в ниноле координат и радиусом, равным г, является графиком уравнения х2 + у2 — г2, где х и у — переменные, г — положительное число.
88. Определите степень уравнения:
а) х2 + у2 — 12 = 0;
: б) 5х —- бу — 1,4 = 0;
в) х3— 5х2г/4+#5—-8^г3 =0;
г) х2—5х3г/+г/4—1 = 0;
д) х — ху == 65;
е) х4 — 8х2#3 + у4 = 16;
ж) Зху = х (у + 1) ™ 5z/;
з) 7х8 —12xy+z/ =7х2 (х6 + 1).
Рассмотрим рисунок 15, на котором изображена окружность | радиуса 5 единиц с центром в начале координат. Попробуем j составить уравнение, графиком которого является эта окруж-1 ность. 1
Пусть точка А (х; у) — произвольная точка данной окруж- 1 ности, не принадлежащая ни одной из осей координат. Тогда! из прямоугольного треугольника ОАА± по теореме Пифагора | имеем: j
89. Является ли решением уравнения х2 — у + 2 — 0 пара значений переменных:
а) х = 1, у = 3;
б) х = 0, у - 0;
в) х = —2, у — 2;
г) х = —1, у = —3?
ЮА12 + IAAI2 - |СМ|2. I
Очевидно, что | OAr |2 = х2, | AAil2 = у2 и | ОА|2 52. Следова- 1 тельно, координаты любой точки окружности, не принадлежа- d щей ни одной из осей координат, удовлетворяют уравнению J х2 + у2 = 52. (1) !
Легко убедиться в том, что координаты каждой из точек пересечения окружности с осями х и у также удовлетворяют уравнению (1). Например, подставив в уравнение (1) координаты точки С (0; —5), получим истинное равенство:
.J
<3
90. Найдите два каких-либо решения уравнения:
а) х — Зг/ — 1; в) х — ху =- 15; д) (х—1) (у—2)=0;
б) 5х + у ™ 2; г) х2 + Зу = 1; * е) (х2 + 1) (у--5) 0.
91. а) Докажите, что уравнение (х + 5)2 + (у — 2)2 —1
не имеет решения.
б) Докажите, что уравнение (х — 7)3 + (у + 4)2 = 0 имеет единственное решение.
92. Постройте график уравнения:
а) 2х — Зу = 6; б) — + ~ = 1; в) х = —4; г) у 2. 2 3
93. Выясните, что представляет собой график уравнения:
а) (х — у) (х + у) ------- 0; б) (х — 3) {у + 1) = 0,
Итак, уравнению (1) удовлетворяют координаты любой тон ки данной окружности.
и постройте этот график.
£ $
94. Постройте график уравнения: а)у = -6-'» б) ху — —12.
X
95. Постройте график уравнения:
а) х2 + у2 = 16; в) х2 + у2 = 6~; д) х2 + у2 = 12;
б) х2 + у2 — 86; г) х2 + у2 = 20; е) х2 + у2 = 0.
96. Напишите уравнение окружности с центром в начале координат и радиусом, равным:
а) 2; б) 4,5; в) /13; г)
97. Принадлежит ли окружности х2 + у2 = 144 точка:
В (7; 9), С (10; 7), D (0; -12), Е (-8; 4]/б)?
98. Напишите уравнение окружности с центром в начале координат, если известно, что она проходит через точку: а)М(5;12); б) 2V(—1; — 3).
Упражнения для повторения
99. Выразите переменную х через переменную у из уравнения:
а) 2х + 8у = 7;
б) Зх —- by = 1;
в) х + ху 10;
г) ху — у2 — 2х = 1с
100. Сократите дробь:
а)
а2 + 7а 4- 6.
(а _ В)2— 16’
б)
4&2 — 7& — 2
81 — (& + 7)2"
101. Решите неравенство:
а) р2 - Юр + 21 < 0;
б) и2 — 8и + 16 > 0;
в) q2 + 6g 4- 13 > 0;
г) —т2 — 2т — 3 > 0.
8. СИСТЕМА УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
Рассмотрим примеры решения системы двух уравнений с двумя переменными, в которых одно уравнение второй степени, а другое — первой.
Решить систему уравнений с двумя переменными — значит найти множество пар значений переменных, которые обращают в истинное равенство каждое уравнение системы.
Другими словами, решить систему уравнений — значит найти пересечение множеств решений уравнений, входящих в эту систему.
Пр и м е р 1. Решить систему уравнений
(х2 + у2 = 100,
I* + У = —2. (1)
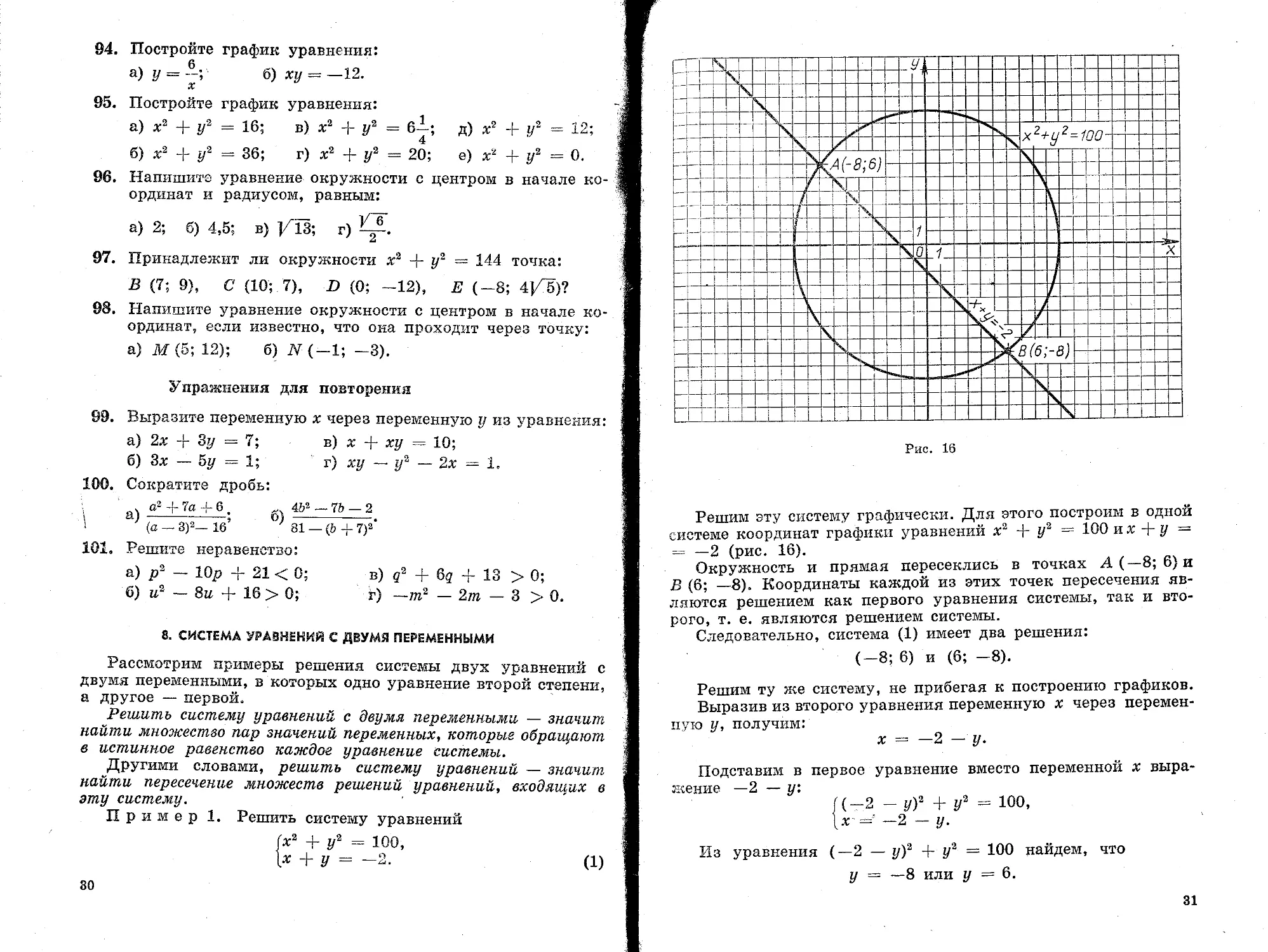
Рис. 16
Решим эту систему графически. Для этого построим в одной системе координат графики уравнений х3 4~ у2 = 100 и х + у = = —2 (рис. 16).
Окружность и прямая пересеклись в точках А ( — 8; 6) и В (6; —8). Координаты каждой из этих точек пересечения являются решением как первого уравнения системы, так и второго, т. е. являются решением системы.
Следовательно, система (1) имеет два решения: (-8; 6) и (6; -8).
Решим ту же систему, не прибегая к построению графиков.
Выразив из второго уравнения переменную х через переменную у, получим:
х — —2 — у.
Подставим в первое уравнение вместо переменной х выражение —2 — у:
Г (—2 - у)2 + у2 - 100,
—2 — у.
Из уравнения (—2 У — У)2 + У2 = ЮО найдем, что = —8 или у = 6.
Поэтому система (1) равносильна предложению
или
Отсюда
7 f х = —8
ИЛИ 1 а
Ответ, {(6; —8);
(-8; 6)}.
Примененный нами способ решения системы уравнений называется способом подстановки. Этим способом можно решить любую систему двух уравнений с двумя переменными, в которой одно уравнение второй степени, а другое — первой.
Пример 2. Решить систему уравнений
(х2 — Зху — 2у2 + 5х — 7у + Ю = 0, [х + 2у = 1.
Для решения этой системы применить графический способ было бы затруднительно, так как мы не знаем, как выглядит график первого уравнения системы. А способом подстановки система решается весьма просто.
Выразив из линейного уравнения х + 2у — 1 переменную х через у и подставив выражение 1 — 2у вместо х в первое уравнение системы, получим систему, равносильную первоначальной:
Г(1 - 2у)2 - 3 (1 - 2у) у ™ 2у2 + 5 (1 - 2у) Чу + 10 - 0, [х = 1 — 2у.
После упрощения первого уравнения система примет вид:
(у* -Зу + 2 = 0, (х = 1 — 2у.
Из квадратного уравнения у2 — Зу + 2 = 0 находим, что у = 1 или у = 2.
Отсюда
Следовательно,
' х = —1 ( X = —
] . или о
\У = 1 {У = 2.
Ответ. {(-1; 1); (-3; 2)}.
Способ подстановки наряду с графическим способом и способом сложения можно использовать также при решении систем линейных уравнений с двумя переменными.
Если система состоит из двух уравнений второй степени, то лишь в частных случаях могут быть указаны простые способы ее решения.
Рассмотрим пример.
Решить систему уравнений f х2 — Зу2 = 22, { ху = 21.
Выразим из второго уравнения системы переменную х через у и подставим полученное выражение в первое уравнение. Получим систему /21 \2 х2 — 3 • — — 22, \ х / 21 у х
Решив первое уравнение, найдем, что х ~ —7 или х = 7. Соответствующие 21 значения у найдем из уравнения у = —. х
Если х — —7, то у — —3, если х = 7, то у ~ 3,
Ответ. {(-7;-3); (7; 3)}.
102.
Решите способом подстановки систему уравнений:
а) Г 5х + 11у = —1, (х = Зу + 5;
б) (х = — 2у — 1, [ 7х — 20z/ = 146;
в) (12х — у = 16, [ 5х + Зу — 75;
г) (7х + бу = 2, [бх — 5у --= 93;
д) f 4х + Зу = 43, [ 5х — 7у = 43;
е) I 8х — 9у — 4, ( —Зх + 4у = 1.
Решите систему уравнений:
а) Гх2 - 2i/2=7, [х = у+2;
б) f х2 — 2ху = 7, [х = Зу +2;
в) (х2—Ьху =10, [х — бу = 1;
г) Г 5ху — у2 = 9, [ 2х — у = 3;
д) Г х2 + у2 = 100, [Зх — 2у =2;
е) Г 2х2— Зу2 = 24, [2х — Зу =0;
ж) Г 4х2—9у2 = 15, [ 2х + Зу = 5;
з) (х2+ху—i/2=ll, [х — 2у 1;
и) f х2+ху— Зу 9, 2у^ — 1.
104. Решите графически систему уравнений:
а) Гх2 + г/2 - 25, б) Гх2 + у2 - 20, в)( х2+у2-Ю0,
(х — у = 5; [ху = —8; у== 1х2_10>
2 Алгебра 8 кл.
33
105.
Найдите множество решений системы трех уравнений:
а)
У = 0, у _ Ю = О,
У2 = 40;
б) г Зх
< X
□
X"
106.
Решите систему уравнений:
107.
г" iW
109.
110.
111.
а) Сумма двух чисел равна 20, а их произведение равно 96. -Найдите эти числа.
б) Разность двух чисел равна 6, а их произведение равно 216. Найдите эти числа.
а) Периметр прямоугольника равен 82 м, а длина его диагонали равна 29 м. Найдите длины сторон этого прямоугольника.
б) Периметр прямоугольного треугольника равен 84 см, а длина его гипотенузы равна 37 см. Найдите площадь этого треугольника.
а) Длина участка прямоугольной формы равна 60 м, а ширина равна 8 м. На сколько метров надо уменьшить длину и на сколько ширину участка, чтобы его площадь уменьшилась вдвое, а периметр уменьшился на 44 м?
б) Периметр прямоугольника равен 80 м. Если одно из его измерений увеличить на 8 м, а другое — на 2 м, то его площадь возрастет в полтора раза.
Какие измерения имеет прямоугольник?
а) Задумано двузначное число. Если к этому числу прибавить удвоенную сумму его цифр, то получится 96. Если же задуманное число умножить на сумму его цифр, то получится 952. Найдите задуманное число.
б) Сумма квадратов цифр задуманного двузначного числа равна 65. Если к задуманному числу прибавить 27, то получится число, которое записывается теми же цифрами, что и задуманное. Какое число задумано?
а) Два велосипедиста выехали одновременно из пунктов А и В, расстояние между которыми 28 км, и встретились через час. С какой скоростью двигался каждый велосипедист, если один прибыл в пункт В на 35 мин позже, чем другой в пункт А?
б) Два поезда выходят одновременно из М и N, расстояние между которыми 45 км, и встречаются через 20 мин. Поезд, вышедший из М, прибывает на станцию 7V на 9 мин раньше, чем другой поезд в М. Какова скорость каждого поезда?
Ц2. а) При совместном действии двух труб бак может быть наполнен за 12 мин. Если сначала полбака наполнить через одну трубу, а затем полбака — через другую, то бак наполнится через 25 мин. За сколько минут каждая труба, действуя одна, могла бы наполнить бак?
б) Один комбайнер может убрать урожай пшеницы с участка на 24 ч быстрее, чем другой. При совместной же работе двух комбайнеров они закончат уборку урожая за 35 ч. Сколько времени понадобится каждому комбайнеру, чтобы одному убрать урожай?
Упражнения для повторения
113. Является ли решением уравнения х2 + Зху + у2 — 41 пара значений переменных х и у: а) (5; 1); б) (1; 5)?
Докажите, что если пара чисел (а; Ь) является решением этого уравнения, то пара чисел (&; а) также является решением этого уравнения. *
114. Является ли решением уравнения х2 + ху + у2 = 29 пара чисел:
а) х = ]<12, у = УЗ; б) х = 3 + У 2, у = 3-]/Т?
115. Найдите два каких-либо решения уравнения:
а) Ух — У у --= 1; б) Ух + у — У у = 1.
116. Не выполняя построения, укажите, в каких координатных углах расположен график уравнения:
в) ху = 6;
г) ху = —12.
§ '*
НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ
9. НЕРАВЕНСТВО С ДВУМЯ ПЕРЕМЕННЫМИ
Неравенство у > —0,5х + 4 содержит две переменные х и у. Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в истинное неравенство.
Чтобы найти какое-либо решение этого неравенства, выберем произвольное значение х, например х = 2, и вычислим соответствующее значение выражения —0,5х + 4. Получим: “-0,5 -2+4—3. Любая пара, в которой значение х равно 2, а значение у больше 3, например (2; 4), (2; 5,2), (2; 100) и т. д., является решением рассматриваемого неравенства.
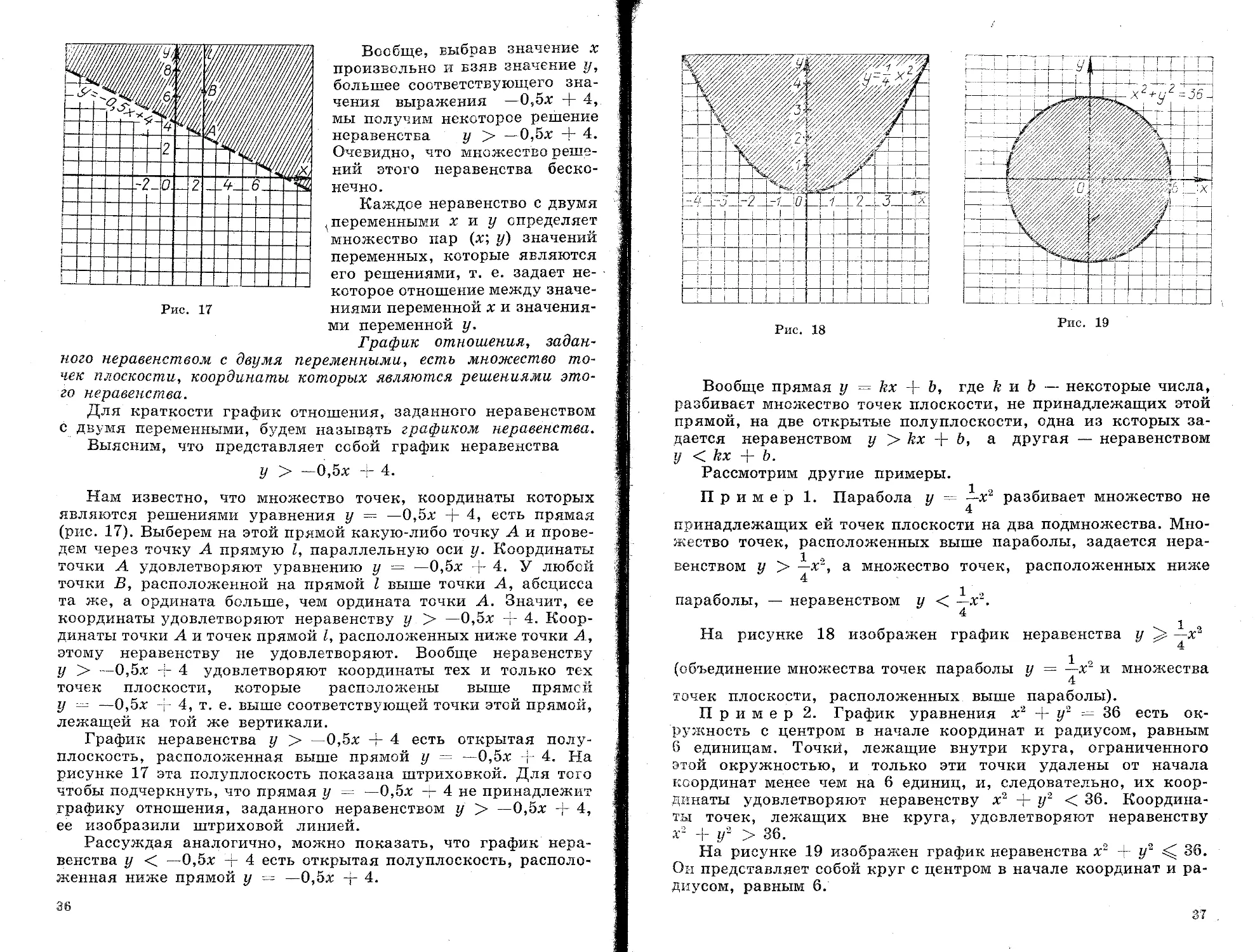
Рис. 17
Вообще, выбрав значение х произвольно и взяв значение у, большее соответствующего значения выражения —0,5х + 4, мы получим некоторое решение неравенства z/ > —0,5х + 4. Очевидно, что множество решений этого неравенства бесконечно.
Каждое неравенство с двумя 5 переменными х и у определяет множество пар (х; у) значений переменных, которые являются его решениями, т. е. задает не- • которое отношение между значениями переменной х и значениями переменной у.
График отношения, задан-
ного неравенством с двумя переменными, есть множество точек плоскости, координаты которых являются решениями этого неравенства.
Для краткости график отношения, заданного неравенством с двумя переменными, будем называть графиком неравенства.
Выясним, что представляет собой график неравенства
у > -0,ох + 4.
Нам известно, что множество точек, координаты которых являются решениями уравнения у -- —0,5х + 4, есть прямая (рис. 17). Выберем на этой прямой какую-либо точку А и проведем через точку А прямую I, параллельную оси у. Координаты точки А удовлетворяют уравнению у = ~0,5х + 4. У любой точки В, расположенной на прямой I выше точки А, абсцисса та же, а ордината больше, чем ордината точки А. Значит, ее координаты удовлетворяют неравенству у > —0,5х 4- 4. Координаты точки А и точек прямой I, расположенных ниже точки А, этому неравенству не удовлетворяют. Вообще неравенству у > —0,5х 4- 4 удовлетворяют координаты тех и только тех точек плоскости, которые расположены выше прямей у —0,5х + 4, т. е. выше соответствующей точки этой прямой, лежащей на той же вертикали.
График неравенства у > — 0,5х -г 4 есть открытая полуплоскость, расположенная выше прямой у = 0,5х + 4. На
рисунке 17 эта полуплоскость показана штриховкой. Для того чтобы подчеркнуть, что прямая у ~ ~~0,5х + 4 не принадлежит графику отношения, заданного неравенством у > —0,5х + 4, ее изобразили штриховой линией.
Рассуждая аналогично, можно показать, что график неравенства у < —0,5х + 4 есть открытая полуплоскость, расположенная ниже прямой у — —0,5х --4.
Рис. 18
Рис. 19
Вообще прямая у - kx + Ь, гДе k и Ъ — некоторые числа, разбивает множество точек плоскости, не принадлежащих этой прямой, на две открытые полуплоскости, одна из которых задается неравенством у > kx + Ь, а другая — неравенством у <Z kx + b.
Рассмотрим другие примеры.
Пример 1. Парабола у = -i-x2 разбивает множество не 4
принадлежащих ей точек плоскости на два подмножества. Множество точек, расположенных выше параболы, задается неравенством > —х2, а множество точек, расположенных ниже 4
параболы, — неравенством у < -х2.
4
На рисунке 18 изображен график неравенства у —х2
1 9
(объединение множества точек параболы у = —-х и множества 4
точек плоскости, расположенных выше параболы).
Пример 2. График уравнения х2 + г/2 — 36 есть окружность с центром в начале координат и радиусом, равным б единицам. Точки, лежащие внутри круга, ограниченного этой окружностью, и только эти точки удалены от начала координат менее чем на 6 единиц, и, следовательно, их координаты удовлетворяют неравенству х2 + z/2 < 36. Координаты точек, лежащих вне круга, удовлетворяют неравенству х2 4~ z/2 > 36.
На рисунке 19 изображен график неравенства х2 — У2 < 36. Он представляет собой круг с центром в начале координат и радиусом, равным 6.
117. Является ли решением неравенства х + Зу + 1 < 0 пара (х; у) значений переменных х и у.
Рис. 20
а) (0; 0); г) (-7,2; 2);
б) (0; —3);
в) (2; -2); ’ з/
118, Найдите три каких-либо решения неравенства:
а) у > Зх — 0,5;
б) у < х2 — 1;
в) у + х — 1 >0;
г) ху < 5.
119. Множество точек F — график неравенства у —х2 + 5. Принадлежит ли множеству F точка:
'А А (0; 2); В (-1; 1); С (10; -96);
z D (20; -100)?
120, Достройте график неравенства:
U) у < 2х + 8;
^б) У — х — 5;
^в) х + у — 2 <0;
чг) 1,2х — у 0.
121. Покажите штриховкой множество точек координатной плоскости, у которых:
а) абсцисса меньше, чем ордината;
б) сумма координат меньше 5.
122. Изобразите на координатной плоскости множество точек с координатами (х; у), для которых:
123. Запишите неравенство, которое задает полуплоскость, показанная штриховкой на рисунке 20.
124. Постройте график неравенства:
125. Принадлежит ли кругу с центром в начале координат и радиусом, равным 3, точка:
А (-1; 1); В (0; 3); С (0,5; 2);
D (-2; 2,5)?
21
Рис.
126. Постройте график неравенства:
а) х2
б) х2
127. Запишите неравенство, график которого изображен на ри сунке 21.
Упражнения для повторения
128. Решите систему уравнений:
а) (Зх + у + 4 = 0, б) f Зх + у = 2, [х2 — у2 = 2; * [х2 — ху = 3,36.
129. Не выполняя построения, найдите координаты точек пересечения:
а) параболы у = х2 — Зх + 3 и прямой 2х — у —1 = 0;
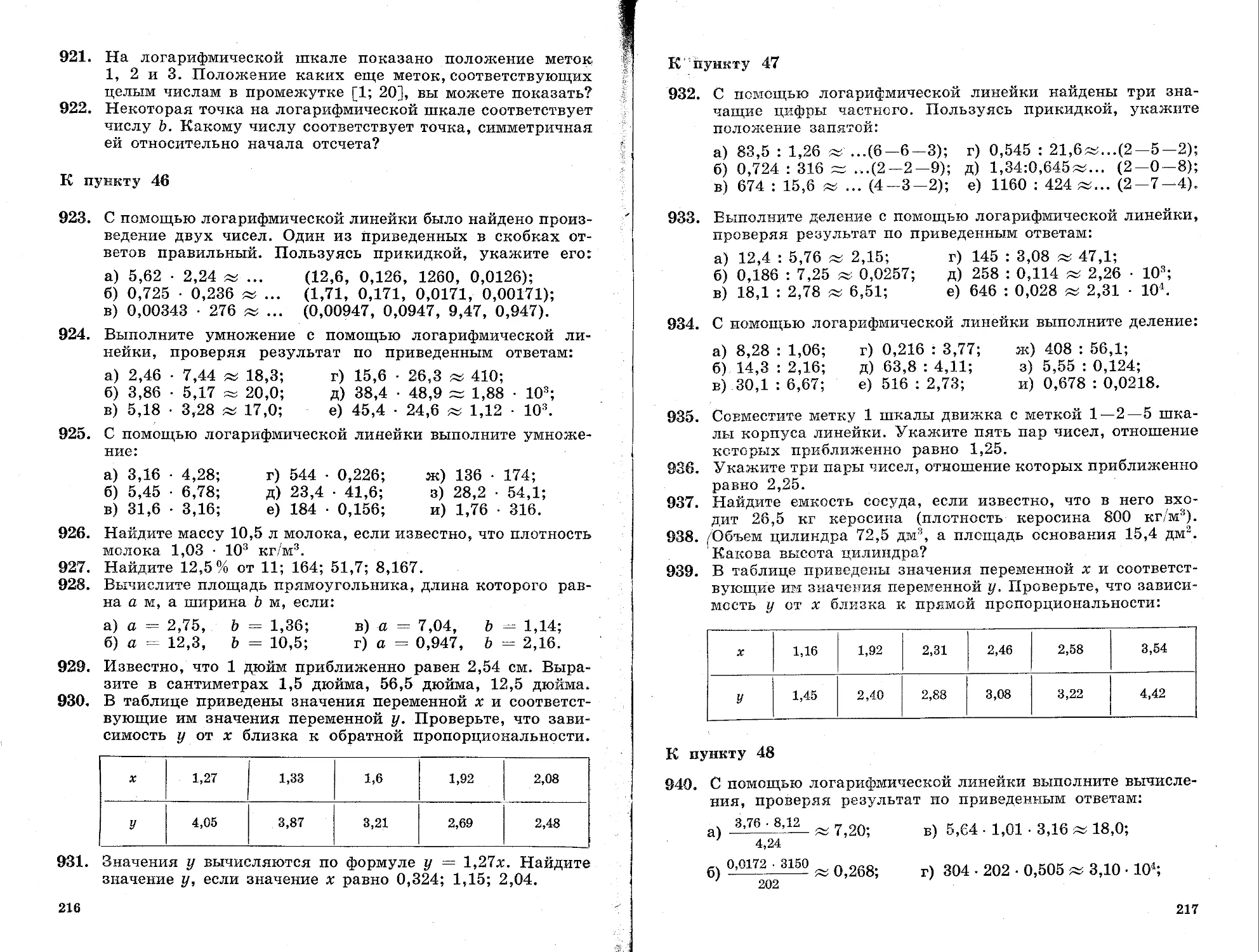
б) параболы у = 2х2 — х + 1 и прямой х = 1,5.
130. Не выполняя построения, выясните, имеют ли общие точки графики уравнений:
а) х2 + у2 = 100 и х + у = 14;
б) х2 + у2 = 64 и х — у — 12.
10. СИСТЕМА НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
Рассмотрим систему неравенств с двумя переменными:
Множество решений этой системы есть пересечение множеств решений входящих в нее неравенств.
Рис. 23
Рис. 24
Выясним, что представляет собой множество точек плоскости, координаты которых являются решениями рассматриваемой системы.
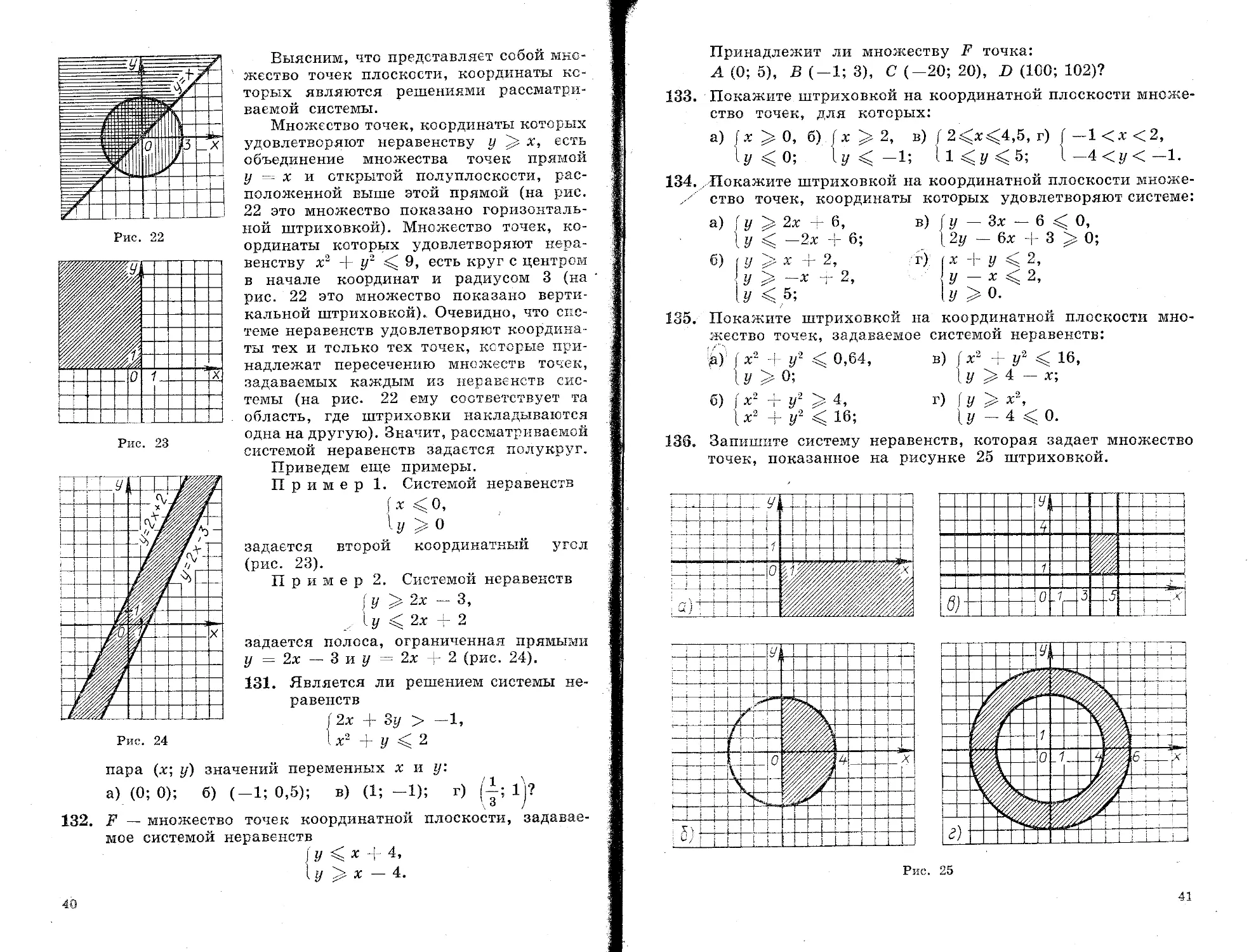
Множество точек, координаты которых удовлетворяют неравенству р х, есть объединение множества точек прямой у х и открытой полуплоскости, расположенной выше этой прямой (на рис. 22 это множество показано горизонтальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству х2 + у2 9, есть круг с центром в начале координат и радиусом 3 (на * рис. 22 это множество показано вертикальной штриховкой). Очевидно, что системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы (на рис. 22 ему соответствует та область, где штриховки накладываются одна на другую). Значит, рассматриваемой системой неравенств задается полукруг.
Приведем еще примеры.
Пример 1. Системой неравенств
(х О, lz/ > О задается второй координатный угол (рис. 23).
Пример 2. Системой неравенств [ у 2х - - 3,
I у 2х + 2
задается полоса, ограниченная прямыми у = 2х — 3 и у 2х + 2 (рис. 24). 131. Является ли решением системы неравенств
f 2х + Зу у> — 1,
I х2 + у 2
пара (х; у) значений переменных х и у:
а) (0; 0); б) (-1; 0,5); в) (1; -1); г) 1)?
132. F — множество точек координатной плоскости, задаваемое системой неравенств
Принадлежит ли множеству F точка:
А (0; 5), В (-1; 3), С (—20; 20), В (100; 102)?
133. Покажите штриховкой на координатной плоскости множе-ство точек, для которых:
а) / х 0, б) Г х 2, в) Г 2^х^4,5, г) Г —1 < х < 2,
1у<0; < —1; 1 1 < У < 5; I— 4<z/<—1.
134. /Покажите штриховкой на координатной плоскости множе-х ство точек, координаты которых удовлетворяют системе:
a) f у 2х + 6, в) (у — Зх — 6 0,
t у < — 2х + 6; [ 2у — 6х + 3 0;
135. Покажите штриховкой на координатной плоскости множество точек, задаваемое системой неравенств:
136. Запишите систему неравенств, которая задает множество точек, показанное на рисунке 25 штриховкой.
Рис.
Упражнения для повторения
137. а) Из некоторого пункта вышли одновременно два пионерских отряда. Один направился на север, а другой — на восток. Спустя 4 ч оказалось, что расстояние между отрядами равно 24 км, причем первый прошел на 4,8 км больше, чем второй. С какой скоростью двигался каждый отряд? б) От вершины прямого угла по его сторонам начинают одновременно двигаться два тела. Через 15 с расстояние между ними стало равно 3 м. С какой скоростью двигалось каждое тело, если известно, что первое прошло за 6 с такое же расстояние, какое второе тело прошло за 8 с?
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К ГЛАВЕ II
К пункту 7
138. Является ли решением уравнения х2 — Зху + у2 — 31 пара: а) (—3; -11); в) (3; -2); д) (2; 3);
б) (3; 11); г) (—2; 3); е) (3 | 2| 2; 3 - 2/2)?
139. Сколько решений имеет уравнение:
а) (х2 - 7) (р2 + 4) = 0; г) (х2 - 9)2 + (г/2-4)2-0;
б) (х - 2у) (х2 + 1) = 0; д) (х - у) (х2 + у2) = 0;
в) (х2 - 9) (г/2 - 4) - 0; е) (х - у)2 + (у - I)2 - 0?
140. Докажите, что уравнение не имеет решений:
а) х2 — 2ху + у2 + 8 — 0; в) х2—10х ; </+100 = 0;
б) х2 + 8х + у2 + 17 — 0; г) х2 — 2ху + 2z/2 + 4г/ + 7 0.
141. Докажите, что уравнение имеет единственное решение: а) х2 + 6х + у2 — 10г/ — —34;
б) 2х2 — бхг/ + 9г/2 — 10х + 25 — 0.
142. Составьте уравнение с двумя переменными, которое:
а) не имеет решений; в) имеет два решения;
б) имеет одно решение; г) имеет три решения.
143. Имеет ли целые решения уравнение:
а) Зх — Зу — 4; в) ху —7,5; д) — + — — —;
X у 6
б) ху 13; г) х —— — 1; е) х2 — у2 — 11?
у2
144. а) Принадлежит ли точка А (5; —4) графику уравнения х3 + 2у2 + 3-0?
б) Принадлежит ли точка В (7; —3) графику уравнения х2 _ 7х^у __ 11х/ + 10х — 19г/ +24-0?
145. Постройте график уравнения:
а) (х — 4) (у — 3) - 0; в) (ху — 6) (х + у) - 0;
б) (х ~ 1) (у — х) = 0; г) х2 — у2 0.
146. Постройте график уравнения:
Ю 1*1 + У = 4; в) Iх| 4- ы = 4; д) \х\ у = 6;
б) х + \у\ = 4; г) |х| + [у| х + у; е) \ху\ = 6.
147. Постройте график уравнения:
а) у ; б) ху = 7,5. X
148. Постройте график уравнения:
а) х2 + у2 = 49; в) х2 / у2 - 42,25;
б) х2 - у2- 48; г) х2 - у2 - - 20,25.
149. Известно, что окружность х2 + у2 = г2 проходит через точку А (а; Ь). Проходит ли эта окружность через точку: В (—а; Ь), С (—а; — Ь), D (а; ~&), Е (Ь; а), К ( — Ъ; а), AL(~b\
150. Известно, что окружность х2 + у2 = г2 проходит через точку А (8; 15). Как расположена по отношению к этой окружности точка: В (7; 16), С (9; 14), D (—1; 12]/ 2)?
К пункту 8
151. Решите графически систему уравнений:
152. Решите способом подстановки систему уравнений:
а) \ 2х — у = 1, в) (ху = 48, д) Гх + ху — у = 7, ')7х -у =9; [х + 2у = 20; [ 2х — г/ = — 1;
б) / х — 4у = 5, г) Г Зх — 2у = 6, е) f 4х — ху + Зу 19,
' [х + 8г/ = — 7; [ху = 120; (х + 2у = —2.
153. Решите систему уравнений:
а)
б) (2х — у =1, [ху — у2 + Зх = —1;
в) Г 2х + У — 11 = 0, д) f 4х2— 9у2 + х— 40у — 19 — 09 I 2х + 5у — у2 — 6 — 0; [ 2х — Зу = 5;
. г)/2х2—Зу2—5х—2i/-26, е) / Зх2 + у2 -г 8х + 13у - 5, 1х — у = 4; 1х — у + 2 = О.
154. При каких значениях г не имеет решений система уравне-НИЙ
155. При каких значениях с имеет решения система уравнений
х2 + if = 100, X + у - - с?
158. Решите систему уравнений:
157. Решите систему уравнений:
a) f (х + у) (х — у) 0, в) / х2 + у2 = 100, \2х — у = 1; {(х — 7у) (х + 7у) = 0;
б) f х2 + у- = 25, г) Г х2 — у2 =- 50,
I (х- - 3) (1/ - 5) = 0; 1 х (у + 1) = 0.
153. Найдите множество решений системы:
а) / х2 + у2 = 40, в) / х2 + у2 = 15, /ху = —12; [ху = 6;
б) / х2 + у2 = 80, г) /х2 + у2 + ху — 9, ху — 24; [ху —24.
ч
159. Имеет ли решения система уравнений
х2 — Зху + у2 + х 4- 2у = 8, < 2х — 5jy —1,
Зу — х = 2 ?
160. Имеют ли общую точку графики уравнений:
х2 4- ху — 2у2 — х 4- у 5 и х
У = 77
161. Решите систему уравнений:
a) f х2 — 4г/2 = 0, в) Г х'2у2 + ху 72,
(х'2 + ху — у2 ~ 20; 6;
б) Г 4х2 — 9у2 = 0, г) f (х 4- у)2 — 2 (х + у) ~ 15,
[х2 — ху — у2 = —1; (х + ху + у = 11.
162. а) Если к числителю обыкновенной дроби прибавить 2, а к знаменателю 3, то значение дроби не изменится.
Если же к числителю прибавить 1, а к знаменателю 6, то значение дроби уменьшится на —. Найдите первоначаль-6 ную дробь.
б) Если к числителю обыкновенной дроби прибавить 1, а к знаменателю 3, то значение дроби будет равно
Если же из числителя вычесть 1, а к знаменателю прибавить 1, то получится дробь, после умножения которой на первоначальную будем иметь —. Найдите первоначальную 5 дробь.
163. а) Длина диагонали прямоугольника 17 дм, а его площадь — 120 дм2. Найдите длины сторон прямоугольника, б) Длина гипотенузы прямоугольного треугольника равна 26 см, а его площадь — 120 см2. Найдите периметр этого треугольника.
164. а) Гипотенуза прямоугольного треугольника равна 13 м. Если каждый катет увеличить на 3 м, то гипотенуза увеличится на 4 м. На сколько квадратных метров увеличится площадь этого прямоугольного треугольника?
б) Гипотенуза одного прямоугольного треугольника равна 29 дм, а другого — 5 дм. Каждый катет первого треугольника больше соответствующего катета второго треугольника на 17 дм. На сколько квадратных дециметров площадь первого треугольника больше площади второго?
165. а) При одновременном действии двух труб бассейн наполняется за 40 ч. Если бы одну треть бассейна наполнила первая труба, а затем остальную часть — вторая труба, то для наполнения бассейна понадобилось бы 78 ч. За сколько времени могла бы наполнить бассейн каждая труба, работая одна?
б) Два комбайна, работая совместно, могут убрать урожай с участка за 20 ч. За сколько часов смог бы убрать урожай каждый комбайн, работая один, если известно, что второй комбайн убрал урожай с одной трети участка на 3 ч скорее, чем первый с его половины?
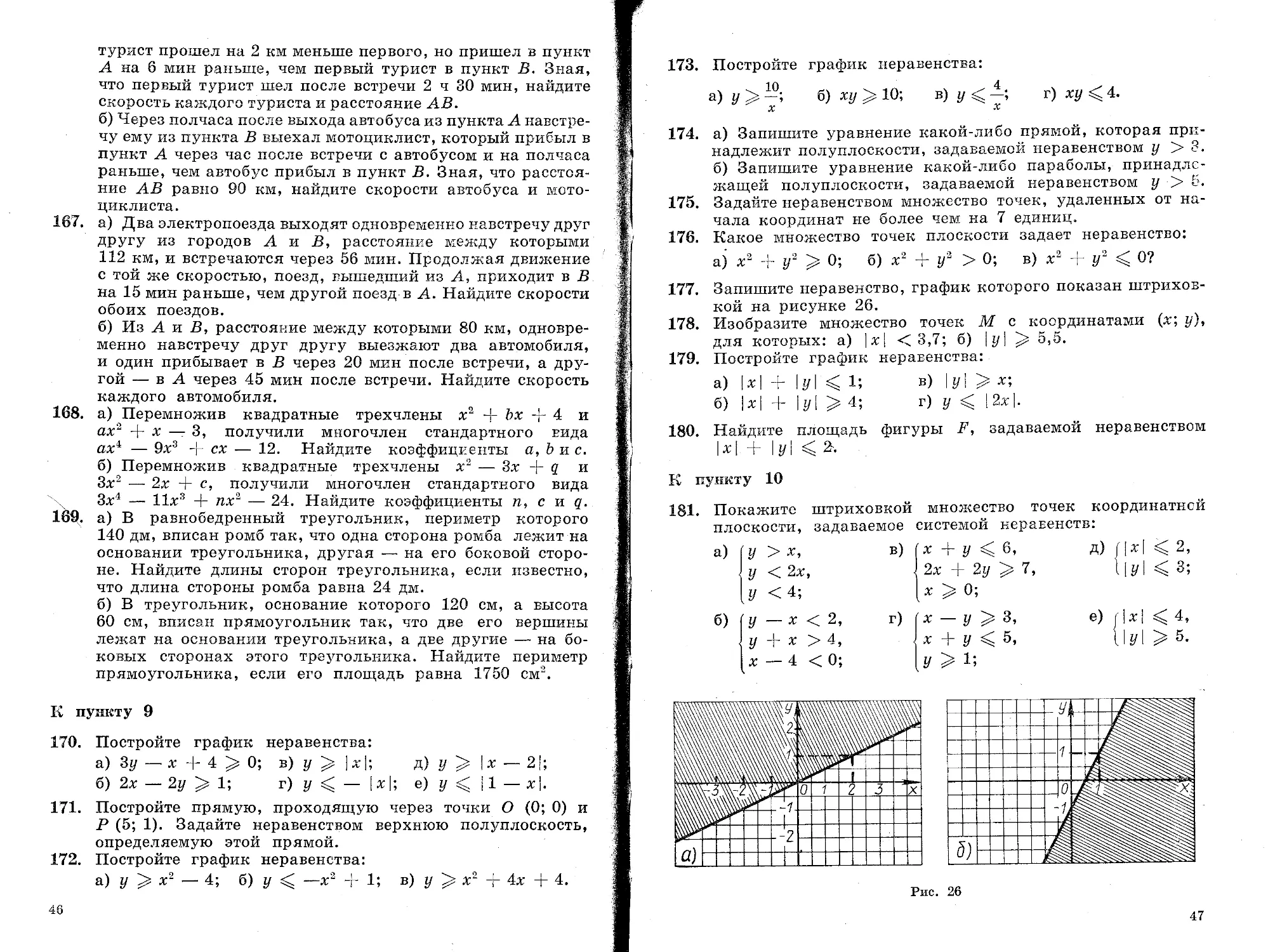
166. а) Через час после выхода туриста из пункта А навстречу ему из пункта В вышел другой турист. До встречи второй
турист прошел на 2 км меньше первого, но пришел в пункт А на 6 мин раньше, чем первый турист в пункт В, Зная, что первый турист шел после встречи 2 ч 30 мин, найдите скорость каждого туриста и расстояние АВ.
б) Через полчаса после выхода автобуса из пункта А навстречу ему из пункта В выехал мотоциклист, который прибыл в пункт А через час после встречи с автобусом и на полчаса раньше, чем автобус прибыл в пункт В. Зная, что расстояние АВ равно 90 км, найдите скорости автобуса и мотоциклиста.
167. а) Два электропоезда выходят одновременно навстречу друг ДРУгу из городов А и В, расстояние между которыми 112 км, и встречаются через 56 мин. Продолжая движение с той же скоростью, поезд, вышедший из А, приходит в В на 15 мин раньше, чем другой поезд в А. Найдите скорости обоих поездов.
б) Из А и В, расстояние между которыми 80 км, одновременно навстречу друг другу выезжают два автомобиля, и один прибывает в В через 20 мин после встречи, а другой — в А через 45 мин после встречи. Найдите скорость каждого автомобиля.
168. а) Перемножив квадратные трехчлены х2 4- Ъх + 4 и ах2 + х — 3, получили многочлен стандартного вида ах4 — 9х3 + сх — 12. Найдите коэффициенты п, Ъ и с. б) Перемножив квадратные трехчлены х2 — Зх + q и Зх2 — 2х + с, получили многочлен стандартного вида X Зх4 — Их3 + пх2 — 24. Найдите коэффициенты п, с и q. 16Q. а) В равнобедренный треугольник, периметр которого 140 дм, вписан ромб так, что одна сторона ромба лежит на основании треугольника, другая — на его боковой стороне. Найдите длины сторон треугольника, если известно, что длина стороны ромба равна 24 дм.
б) В треугольник, основание которого 120 см, а высота 60 см, вписан прямоугольник так, что две его вершины лежат на основании треугольника, а две другие — на боковых сторонах этого треугольника. Найдите периметр прямоугольника, если его площадь равна 1750 см2.
К пункту 9
170. Постройте график неравенства:
а) Зу — х + 4 > 0; в) у > |х|; д) у > |х — 2|;
б) 2х — 2у 1; г) у — [ х е) у [ 1 — х |.
171. Постройте прямую, проходящую через точки О (0; 0) и Р (5; 1). Задайте неравенством верхнюю полуплоскость, определяемую этой прямой.
172. Постройте график неравенства:
а) у х2 — 4; б) у —х2 + 1; в) у х2 + 4х + 4.
173. Постройте график неравенства: ю 4
а) У > б) ху > 10; в) у ;
X X
г) ху 4.
174. а) Запишите уравнение какой-либо прямой, которая принадлежит полуплоскости, задаваемой неравенством у > 3. б) Запишите уравнение какой-либо параболы, принадлежащей полуплоскости, задаваемой неравенством у > 5.
175. Задайте неравенством множество точек, удаленных от начала координат не более чем на 7 единиц.
176. Какое множество точек плоскости задает неравенство:
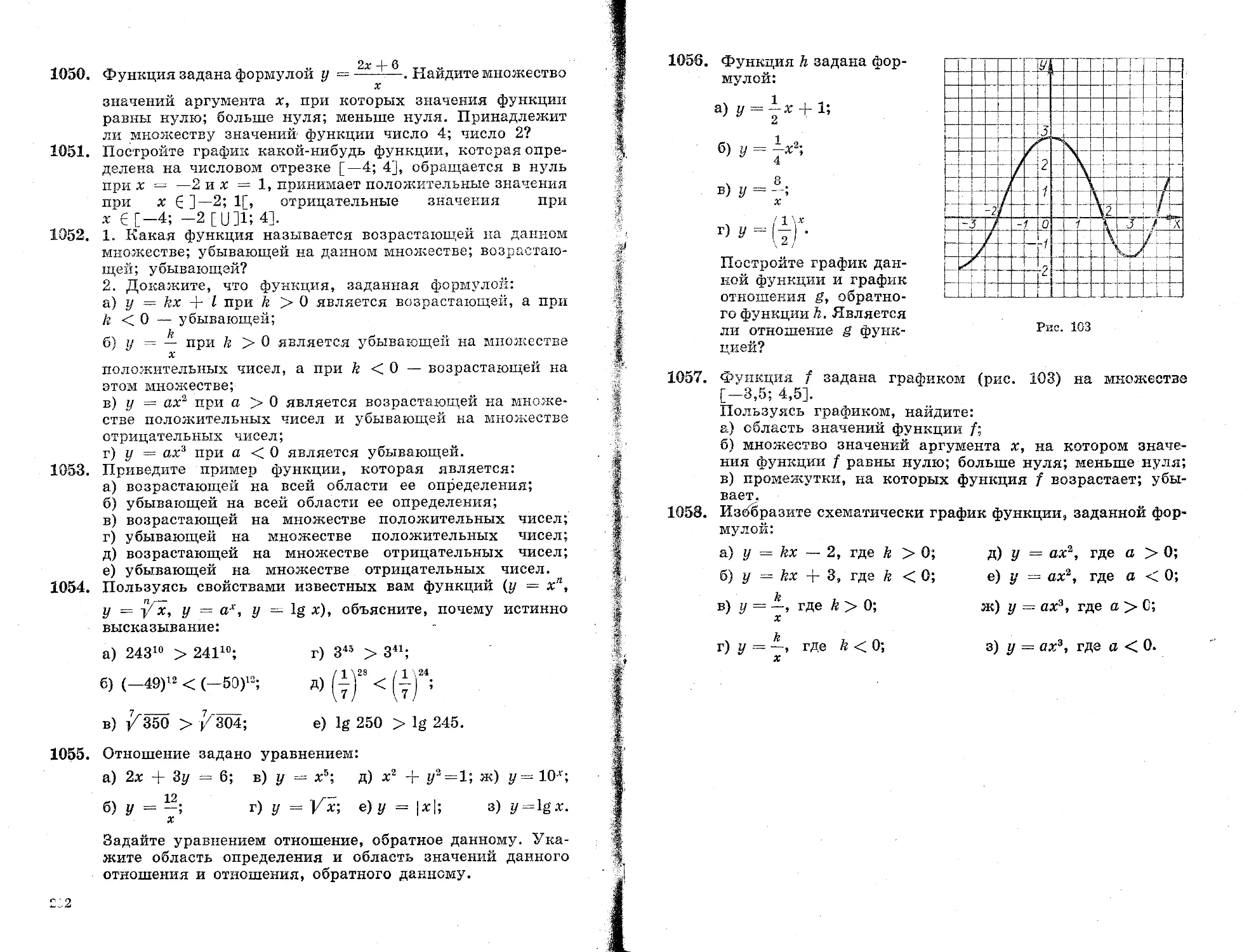
а) х2 + у2 0; б) х2
2 < 0?
177. Запишите неравенство, график которого показан штриховкой на рисунке 26.
178. Изобразите множество точек М с координатами (х; г/), для которых: а) |х| <3,7; б) \у\ 5,5.
179. Постройте график неравенства:
180.
а) | х б) | х
Найдите площадь
фигуры F, задаваемой неравенством
У
К пункту 10
181. Покажите штриховкой множество точек координатной плоскости, задаваемое системой неравенств:
Рис.
1;
26
Рис. 27
182.
Каково множество точек координатной плоскости, задаваемое системой:
183.
184.
185.
Постройте график неравенства:
д) (х + у) (— 4- > 0;
\ X У I
При каких значениях b множество точек стемой неравенств
(У < Зх + 1, [у Зх + &:
задаваемое си-
а) представляет собой полосу;
б) является пустым множеством?
Покажите штриховкой множество точек координатной плоскости, задаваемой системой неравенств:
в) f х2 + у2 100, е) 11X1 < 8;
( х2 + г/2 ^1,44, ж) г у^х2-р 4х + 4, [ху > 0; [у < 4;
гх2 4 г/2^100, з) (у (х — I)2, х2 + у2 > 64, Ь<3,5;
1хг/ < 0;
у х2, и) ( у^(х — 2) (х —3), — х2+ 9; (у 0.
186. Запишите систему неравенств, задающую на плоскости множество точек, показанное штриховкой на рисунке 27.
187. Найдите площадь фигуры F, задаваемой системой неравенств:
1,5.
АРИФМЕТИЧЕСКАЯ
И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
♦
§ 5.
ПОСЛЕДОВАТЕЛЬНОСТИ
11. ПОНЯТИЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Выпишем в порядке возрастания двузначные числа, оканчивающиеся цифрой 5:
15; 25; 35; 45; 55; 65; 75; 85; 95.
Первым записано число 15, вторым — число 25, третьим — число 35, девятым (последним) — число 95. Каждому натуральному числу от 1 до 9 поставлено в соответствие единственное двузначное число, оканчивающееся цифрой 5:
1 15; 2 25; 3 35;
9 95.
Тем самым задана функция, областью определения которой служит множество {1; 2; 3; 9}, а областью значений — мно-
жество {15; 25; 35; ...; 95}. Обозначим эту функцию буквой g, тогда g (1) - 15; g (2) = 25; g (3) - 35; ...; g (9) - 95.
Рассмотрим другой пример. Расположим в порядке убывания правильные дроби с числителем, равным 1:
Мы выписали лишь первые пять таких дробей. Очевидно, что на шестом месте должна стоять дробь —, на седьмом — 7
- 1 1 - 1 дробь —, на тридцатом — дробь , на сотом — дробь —.
8 31 101
Вообще, для любого натурального числа п можно указать соответствующую ему дробь, причем эта дробь будет единственной.
Таким образом, и в данном случае задана функция. Областью определения этой функции служит множество N натуральных чисел, а областью значений — множество правильных дробей с числителем, равным 1. Обозначим рассмотренную функцию
буквой h, тогда Л(1) = —; h(2) = —; й(3)~ —; Л (30) = --; ...
2 3 4 31
...; h (100) = —; ... .
101
Опр еделение, Функция, область определения которой — множество натуральных чисел или множество первых п натуральных чисел, называется последовательностью.
Если последовательность определена на множестве всех натуральных чисел, то такую последовательность называют бес-конечной, а если последовательность определена на множестве первых п натуральных чисел, то ее называют конечной. В первом из приведенных выше примеров мы рассмотрели конечную последовательность, во втором — бесконечную (в записи это показано с помощью многоточия).
Пусть некоторая функция f является последовательностью. Значения функции
/(1); /(2); f (3); ...; f (и); ...,
соответствующие значениям аргумента, равным 1, 2, 3, ... , п, ..., называют первым, вторым, третьим, ...» энным, ... членами последовательности.
Обычно члены последовательности обозначают буквами с индексами. Обозначим первый член последовательности символом (читается: а первое), второй — символом п2 (а второе), третий — символом а3 (а третье), ..., член с номером п — символом а1г (а энное) и т. д.:
f (1) = ар, f (2) = ар, f (3) — ар, ...; / (и) — ар, ... .
В этом обозначении индекс (порядковый номер члена) равен значению аргумента; символом ап обозначено значение функции, соответствующее аргументу п. Саму последовательность будем обозначать так: (а}г).
Например, обозначим рассмотренную выше последовательность, членами которой являются правильные дроби с числителем, равным 1, символом (ап). Тогда
1. 1. 1, 1. 1
£2 1 - , } Йо - , ? fllnn " ’ *
1 2 2 3 3 4 31 00 101
Заметим, что вместо буквы а можно было бы взять какую-либо другую букву.
Числовую последовательность, которая является возрастающей функцией, принято называть возрастающей последовательностью.
Рассмотренная в первом примере последовательность двузначных чисел, оканчивающихся цифрой 5, такова, что большему номеру (большему значению аргумента) соответствует больший член последовательности (большее значение функции). Значит, эта конечная последовательность является возрастающей.
Примером возрастающей последовательности может служить также бесконечная последовательность четных чисел
2; 4; 6; 8; ..., L
в которой каждый член в 2 раза больше своего номера.
Очевидно, что возрастающей является та и только та последовательность, каждый член которой (начиная со второго) больше предыдущего.
Аналогично числовую последовательность, которая является убывающей функцией, принято называть убывающей последовательностью.
Так, например, убывающими являются конечная последовательность —2; —4; —6; —8; —10, а также рассмотренная выше бесконечная последовательность правильных дробей с числителем , равным 1.
Убывающей является та и только та последовательность, каждый член которой (начиная со второго) меньше предыдущего.
Не всякая последовательность является возрастающей или убывающей. Такова, например, конечная последовательность 8; —6; 4; —2; 0, бесконечная последовательность
5; 0; 5; 0; 5; 0; ...,
все члены которой с нечетными номерами равны 5, а с четными — 0, бесконечная последовательность
10; 10; 10; 10; ...,
все члены которой равны 10.
Заметим, что последовательность, все члены которой равны между собой, называют постоянной последовательность^}
Числовую последовательность, как и числовую функцию вообще, можно изображать геометрически с помощью точек координатной плоскости. Так как числовая последовательность— это функция, областью определения которой служит множество N натуральных чисел (или множество первых п натуральных чисел), то ее графиком является множество точек координатной плоскости, абсциссы которых — натуральные числа 1,2, 3, ..., п, ..., а ординаты — соответствующие члены последовательности.
На рисунке 28 изображен график конечной последовательности
—4; —2; 0; 2; 4.
Он состоит из пяти точек, координатами которых служат пары чисел
(1; —4), (2; -2), (3; 0>, (4; 2), (5; 4).
Рис. 28
188. В таблице указаны команды, занявшие первые пять мест в областных соревнованиях по легкой атлетике. Этой таблицей задана конечная последовательность. Назовите первый и последний члены этой последовательности. Какой член по-
189.
190.
следовательности следует за «Вымпелом»? Какой член последовательности предшествует «Востоку»? В таблице дано расписание занятий в VIII классе на один учебный день. Этой таблицей задана конечная последовательность. Каково число членов этой
КЬ места Команда
1 «Вымпел»
2 «Заря»
3 «Зенит»
4 «Восток»
5 «Урожай»
№ урока Учебный предмет
1 Химия
2 Алгебра
3 Литература
4 Литература
5 Черчение
6 Физкультура
последовательности? Есть ли среди членов последовательности одинаковые?
Составьте несколько вариантов расписания из четырех уроков на один учебный день для III класса. Список предметов: физкультура, русский язык, математика, приро-
доведение.
Замечание. В расписание должен быть включен каждый из четырех предметов.
191. Конечная последовательность:
а) 1; 3; 5; 7; 9; в) 1; —1; 1; —1; 1; —1
б) 10; 20; 30; 10; 20; 30;
является функцией с областью определения X и областью значений У. Выпишите множества X и У. Задайте эту же функцию с помощью стрелок и путем перечисления пар.
192. а) Пусть (Ъп) — конечная последовательность, членами которой служат двузначные числа, кратные 13, взятые в порядке возрастания. Укажите Ьг; &7.
б) Пусть (zn) —бесконечная последовательность, все члены которой с нечетными номерами равны —1, а с четными — 0. Найдите 2г; з4; 2100; ?253; k С N; k £ N. 193. Дана конечная последовательность (ап):
а2; а3; «й
а) Какой член последовательности следует за за п4?
б) Какой член последовательности предшествует п2, ц-/?' в) Какой член последовательности не имеет предшествующего?
г) Какой член последовательности не имеет последующего?
194, Дама бесконечная последовательность (с ):
Назовите член последовательности, который: а) следует за с10; с-,; сЛч.,3; сЛ„2;
б) предшествует с50; щ; с/г+7; с^,3.
195. Выпишите члены последовательности (&7), которые расположены между:
а) &20 и д25; б) bk и &Л,+7;
в) &а-2 и &Мз
198. В последовательности п членов. Укажите номер:
а) последнего члена; в) пятого от конца члена;
б) предпоследнего члена; г) &-го от конца члена.
197. Даны последовательности
(аД: 0,1; 0,01; 0,001; 0,0001;
(6J: 0,1; 0,11; 0,111; 0,1111; 0,11111;
(х/г): 1; —2; 3; -4; 5; -6; 7; -8; 9; -10; (yj: 1; 2; 2; 3; 4; 4; 5; 6; 6; 7.
Какие из данных последовательностей являются возрастающими? убывающими?
198. Приведите пример:
а) возрастающей последовательности;
б) убывающей последовательности;
, в) последовательности, не являющейся ни возрастающей, , / ни убывающей.
V 7
199. а) Представьте дробь — в виде бесконечной десятичной 12
дроби. Пусть (хп ) — последовательность, члены которой — десятичные дроби, полученные в результате округления этой бесконечной десятичной дроби до десятых, до сотых, до тысячных и т. д. Найдите х2; х3; х10. Есть ли среди членов последовательности одинаковые? Является ли последовательность (х„) возрастающей или убывающей? f Р-* /
23
б) Представьте дробь — в виде бесконечной десятичной 45
дроби. Пусть (ук) — последовательность, членами которой служат десятичные дроби, полученные в результате округления этой бесконечной десятичной дроби до десятых, до сотых, до тысячных и т. д. Какой член последовательности равен 0,5111111111? Является ли последовательность (уп) возрастающей или убывающей?
г ; ( f i i > J , ... U L
1 r s J j 1 j i h 1 Г 1
ь p i j 4 и 1 L •
! i 1 " I .Б j_ _ ! ! 1 I, J
t. _ 1 [ [ m i г ! 1
L г i f "T Я E J ! ! i •
5 t I J S ! Ё 1 ч J ‘ ! * j -M—I— —— i 1 *•
i 1 б „ Г—— \ • ! - ЛС1 TV: rgntHt :ЛЛЛЯ12 ЪЦ_2_ ! ’ Ф H r f f • J ——"1 I П 1
Г! i H"" i f , i • 1 г ; • " - _ i
Рис. 29
200. Постройте график конечной последовательности:
а) 5; 3; 1; - 1; -3; -5;
б) —1; 3; 0; —2; 4.
201. На рисунке 29 изображены графики последовательностей (а/2), (bj, (сп) и (dj. Какие из этих последовательностей являются возрастающими? убывающими?
Упражнения для повторения •
202. Существует ли прямоугольник с периметром, равным Р см, и площадью, равной S см2, если:
а) Р - 40, S - 84; б) Р = 40, S - 105?
203. а) График уравнения х2 + х + у = 30 проходит через точку, сумма координат которой равна 5. Найдите координаты этой точки.
б) График уравнения х2 + 4у = 20 проходит через точку, ордината которой равна удвоенной абсциссе. Найдите координаты этой точки.
12. СПОСОБЫ ЗАДАНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1. Конечная последовательность может быть задана путем перечисления ее членов в порядке возрастания их номеров. Так задана, например, последовательность (aj:
1; 4; 9; 16; 25; 36; 49; 64; 81; 100. (1)
По существу в этом случае используется табличный способ задания функции. В самом деле, строка (1) представляет собой краткую запись таблицы:
п 1 2 4 5 6 7 8 9 10
а/1 1 4 9 16 25 36 49 64 81 100
2. Последовательность можно задать описанием.
Пусть, например, известно, что членами последовательности (сп) являются взятые в порядке возрастания простые числа, меньшие 20. С помощью этого описания легко найти, что с± — 2; с-2 — 3, — 5, С4 — 7, с-, 11, Cq 13, с. 17, Cg • 19.
Последовательность (с^) конечная; число ее членов равно 8.
С помощью описания можно задать и бесконечную последовательность. Пусть, например, последовательность (dn) такова, что каждый ее член записывается с помощью цифры 2 и число цифр равно номеру члена последовательности.
Это описание позволяет найти любой член последовательности:
п раз
3. Последовательность может быть задана с помощью формулы, которая позволяет найти любой ее член.
Пусть, например, последовательность (Ъп) такова, что для каждого номера п соответствующий член Ъп можно найти по формуле
“ гг — п + 1.
9 ь*
Подставляя в формулу вместо п последовательно натуральные числа 1, 2, 3, 4, ..., получим:
Ьх - I2 — 1 + 1 - 1,
Ъ2 = 22 — 2 + 1 - 3,
Ъ3 З2 — 3 + 1 - 7,
— 42 — 4 + 1 = 13 и т. д.
Формула, выражающая каждый член последовательности через его номер и, называется формулой п-го члена последовательности.
Приведем еще примеры задания последовательности формулой тг-го члена. 4
Формулой ап = ]/ п задается бесконечная последовательность, члены которой — арифметические квадратные корни из натуральных чисел:
/1; у У; ]/3; |/4; ... .
Формулой хп = (—1)^10 задается бесконечная последовательность, все члены которой с нечетными номерами равны —10, а с четными равны 10:
_Ю; Ю; —10; Ю; ... .
204. Выпишите члены последовательности (уД, если известно, что:
а) ее членами служат взятые в порядке возрастания все двузначные числа, в записи которых используются или только цифра 1, или только цифра 2, или обе эти цифры; б) ее членами служат взятые в порядке убывания все правильные дроби со знаменателем 11.
205. Выпишите несколько первых членов последовательности (з7), если известно, что:
а) ее члены — все натуральные числа, кратные 4, взятые в порядке возрастания;
б) ее члены — все натуральные числа, которые при делении на 4 в остатке дают 1, взятые в порядке возрастания;
в) ее члены — все натуральные числа, которые при делении на 4 в остатке дают 2, взятые в порядке возрастания.
206. Найдите пять первых членов последовательности (хД, заданной формулой:
а) хя Зп — 7; г) х„ = ж) х = (—1)» 7;
п
б) Хп = 14 — 2s I; д) хп = 2п~г-, з) хп = 1 + ДЛ
в) хп = -; е) хп = 0,5 • 3й;
207. Последовательность (Ьп) задана формулой &7 = Зп 4- 2. Найдите член последовательности с номером, равным: а) 5; б) 10; в) k; г) k Д 1.
208. Последовательность (ап) задана формулой ап = п“ + 5. Найдите: а) а20; б) п100; в) ak\ г) д) ak.
209. Подберите формулу n-го члена конечной последовательности:
а) 2: 4; 6; 8; 10; r 1_. Д. Д. Д.
б) 1; 3; 5; 7; 9; Д’ 3’ 4’ 5’
в) 3; 6; 9; 12; 15; Д. Д. Д. Д. Д
г) 1; 4; 9; 16; 25; ; 2’ 3’ V 55 6*
210. Последовательность (е,г) задана формулой сп ----- 4п — 1. Найдите номер члена последовательности, равного: а) 91; ё) 399.
211. Последовательность (хп) задана формулой 6 — 4п. Является ли членом этой последовательности число: а) — 102; б) —132; в) 100?
В случае утвердительного ответа укажите номер этого члена.
212. Является ли членом последовательности (Ъп), заданной формулой bn ~ п2, + 2n + 1, число: а) 289; б) 1000?
/ Если является, то каков номер этого члена?
213. Содержится ли среди членов последовательности (а ), где ап = п~ — 17 п, число: а) —30; 6) —72; в) —1С0? Если содержится, то какой номер имеет этот член?
214. Укажите номера членов последовательности (х^), где хч = Зп + 2, для которых верно неравенство:
а) хп 29; б) хп 47; в) хп > 100; г) 80 хп 180.
215. Начиная с какого номера члены последовательности (уп), где — п2, больше: а) 100; б) 1000?
216. а) Начиная с какого номера члены последовательности (а7), заданной формулой ап - тг — п — 6, положительны?
б) Начиная с какого номера члены последовательности (Ьй), заданной формулой Ъп = —п2 + 8и, отрицательны?
Упражнения для повторения
217. Существует ли прямоугольный треугольник, сумма катетов которого равна k дм, а площадь равна S дм2, если:
a) k = 60, S - 500; б) k - 60, S - 400?
13. РЕКУРРЕНТНЫЙ СПОСОБ ЗАДАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ
Пусть известно, что в последовательности каждый член, начиная со второго, равен квадрату предыдущего. Таких последовательностей сколько угодно. Приведем примеры:
2; 4; 16; 256; ...;
5
81’ 656Г
Чтобы задать одну из этих последовательностей, например последовательность 2; 4; 16; 256; ... , достаточно указать первый ее член. Таким образом, эта последовательность задается двумя условиями:
первый член равен 2;
каждый член, начиная со второго, равен квадрату предшествующего.
Если последовательв ость обозначить через (ап), то эти ус- Я ловил запишутся так: Ж
си = 2; a t .= а2
Х ’ /2-г1 П
Рассмотрим последовательность (Ьп), первый член которой равен единице, второй — двум, а каждый член, начиная с треть- || его, равен сумме двух предшествующих членов: S
Зная первые два члена Ъх и &2 последовательности (Ъп) и фор- J мулу Ьп+2 = Ъп + &л+1, можно найти любой член этой последо- у вательности: у
Ъ3 - 1 + 2 - 3; &4 = 2 + 3 - 5; Ъь = 3 + 5 = 8 и т. д. ; Значит, последовательность (Ьп) задана.
Формулу, выражающую любой член последовательности, начиная с некоторого, через предшествующие (один или несколько), называют рекуррентной.
При рекуррентном способе задания последовательности обычно указывают: J
а) первый член последовательности (или несколько первых | членов); |
б) формулу, позволяющую определить любой член последо- | вательности по известным предшествующим членам. Ц
Приведем еще примеры задания последовательности рекур- Ц рентным способом. J
Пример 1. Пусть первый член последовательности (cj Ц равен 12, а каждый следующий, начиная со второго, получает- f ся вычитанием из предыдущего члена числа 5, т. е. сх 12 и || сп+1 = СП — 5- Тогда _ I
с4 = — 5 = —3 и т. д
Пример 2. Первый член последовательности (dn) равен 1, а каждый член, начиная со второго, равен произведению своего номера и предыдущего члена, т. е. di = 1 и dn+1 — dn (п + 1).
Тогда
d2 = • 2 = 1 • 2 = 2,
dg d2 • 3 ~~ 1 2 • 3 6,
di -- d;! 4 -- 1 • 2 • 3 • 4 — 24 и т. д.
В этой последовательности член с номером п равен произведению всех натуральных чисел от 1 до п включительно. В математике произведение 1 • 2 • 3 • ... • п обозначают п\ (читается: эн факториал). Например, 1 2 • 3 • 4 • 5 = 5! Используя это обозначение, можно записать формулу п-го члена последовательности (d/z) таким образом: dn = п\
218. Выпишите несколько первых членов последовательности, если известно, что:
а) первый член равен 4, а каждый член, начиная со второго, получается прибавлением к предыдущему члену числа 12;
б) первый член равен 8, а каждый член, начиная со второго, получается умножением предыдущего на число 3; в) первый член последовательности равен 10, а каждый член, начиная со второго, получается делением предыдущего на число 2;
г) первый член равен 1, го, получается делением комого члена.
219. Найдите первые пять заданной рекуррентным a) = 1, ! । + 1?
б) (i^ =-- 7, 3,
В) а1 - —5, ап^ - 2а^
1 каждый член, начиная со второпредыдущего члена на номер ис-
членов последовательности (аД, способом:
г) аг = 75, ап±г 0Д«/,
д) = —ап\
о
несколько первых членов последовательности
220. Выпишите (сД, если:
221. Выпишите несколько первых членов последовательности (иг) и задайте эту последовательность формулой n-го члена, если:
а) - 10, -=ип^ 10; в) и± — 2, ип+1 = ип + 2;
б) — 10, i+-h — щг • 10; г) щ — 2, -- ' 2.
Упражнения для повторения
222. Решите систему уравнений:
а)
х2 — 2у2 — 14, 2х — Зу = 1;
б) ( Зху ~ 2у2 - 30, I Зх — 2у - 10.
§ 6.
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
14. ОПРЕДЕЛЕНИЕ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
Пусть последовательность («Д такова, что ее первый член равен 5, а каждый следующий, начиная со второго, получается прибавлением к предшествующему члену числа 3.
Вычислим несколько первых членов этой последовательности. Так как щ - 5, то п2 - 5 - 3 - 8, а3 — 8 + 3 .= 11, «4-11+3-14, аь = 14 + 3 - 17.
Определение. Числовая последовательность, каж-
дый член которой, начиная со второго, равен предшествующему
члену, сложенному с
одним и тем же
числом, называется ариф-
метической прогрессией.
Рассмотренная выше последовательность (n/z) — арифметическая прогрессия, так как при любом п £ N а?н1 ап + 3.
Из определения следует, что в арифметической прогрессии (ап) разность между любым членом, начиная со второго, и ему предшествующим равна одному и тому же числу:
Uy (l3 Ct?. ••• an~l ~ = •
Это число называют разностью арифметической прогрессии. Разность арифметической прогрессии принято обозначать буквой d.
Таким образом, арифметическая прогрессия (aj определяется:
1) условием аг — а, где а — некоторое число; 2) рекуррентной формулой ап+1 = ап + d.
Для того чтобы задать некоторую арифметическую прогрессию (nJ, достаточно знать ее первый член и разность d.
Если, например, аг — 1 и d = 1, то мы имеем прогрессию 1; 2; 3; 4; ..., членами которой являются последовательные натуральные числа.
Если а± = 1 и d — 2, то членами соответствующей прогрессии
1; 3; 5; 7; 9; ...
служат положительные нечетные числа, взятые в порядке возрастания.
Если щ — 0 и d = —2, то мы получим прогрессию 0; —2; —4; —6; —8; ...»
члены которой неположительные четные числа, взятые в порядке убывания.
Очевидно, что арифметическая прогрессия, разность которой —положительное число, является возрастающей последовательностью, а арифметическая прогрессия, разность которой — отрицательное число,— убывающей последовательностью. Если разность арифметической прогрессии равна нулю, то все ее члены равны между собой и прогрессия является постоянной последовательностью.
Арифметическая прогрессия обладает свойством: любой член арифметической прогрессии, начиная со второго, является средним арифметическим предшествующего и последующего членов.
Докажем это. Пусть последовательность (ап) — арифметическая прогрессия и — три произвольно выбранные последовательные ее чле-
ны (п 2).
Разность между любым членом арифметической прогрессии и предшествую-
щим ему членом одна и та же, поэтому ап — ^/z-4 ™ Я/г+i — Отсюда
2аЛ ап_1 I
Справедливо и обратное: если некоторая последовательность такова, что любой член ее, начиная со второго, является средним арифметическим предшествующего и последующего членов, то эта последовательность — арифметическая прогрессия.
Действительно, пусть для любых трех последовательных членов ап, (п 2) некоторой последовательности (ап) имеет место соотношение
Тогда <
2а?г — <5/2-1 “Г <5/241> ап ап—1 ” ®Л+1 ^/2»
т. е. разность между любым членом последовательности (ап) и ему предшествующим равна одному и тому же числу. Значит, последовательность (ап) — ариф
метическая прогрессия.
Таким образом, справедлива теорем а: Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый член ее, начиная со второго, есть среднее арифметическое предшествующего и последующего членов.
223. Является ли конечная последовательность арифметической прогрессией:
а) 7; 17; 27; 37; - 1, 1.
б) —17; —7; 7; 17; 27; 4-’ V 4’ 4’
в) 2; 12; 22: 32; е1 ±. ±.
г) 2; 22; 222; ' з ’ 5 ’ 7 ’ 9 '
224. Выпишите первые пять членов арифметической прогрессии (nJ, если: у
a) cii — 10, d — 4; в) = 1,7, d - 0,2;
б) — 29, d = —5; г) = —3-^, d — —.
225. Найдите разность и шестой член арифметической прогрессии, у которой известны первые два ее члена:
а) 70; 100; ...; в) —20; —15; ...;
б) 240; 190; г) Л 1; ... .
226. В записи арифметической прогрессии (&J неизвестны первые два члена. Найдите их:
а) &х; 17; 23; 29; ...; б) 52; —19; —11,5; —4; ... .
227. Пусть (хЛ) — арифметическая прогрессия. Выразите ее разность d через:
а) х10 и хи; б) и xs; в) х20 и х23; г) х12 и х1в.
228. Известны два члена арифметической прогрессии (cj:
а) с6 — 16 и cs — 22. Найдите с7, с5, с10.
б) Сц — 18 и с13 — 8. Найдите с12, с9, с14.
229. Известно, что величины углов некоторого треугольника образуют арифметическую прогрессию. Докажите, что величина одного из углов треугольника равна 60°.
230. Известно, что периметр треугольника равен 24 см. Длины сторон этого треугольника образуют арифметическую прогрессию. Найдите длину средней из них.
Упражнения для повторения
231. Найдите значение выражения:
а) 4а3Ь~5 • 2а~4&4 при а = 6,4 • 103; Ъ — 2,5 • 10-2;
б) (3-1а-1Ь2)2 * 9а3^5 при а = 3,7 • 102; Ь - 1,7 • 10Л
15. ФОРМУЛА П -ГО ЧЛЕНА АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
Зная первый член арифметической прогрессии (а/г) и ее разность, можно с помощью последовательных вычислений найти любой член этой прогрессии.
Например, если а( = 2,3 и d ~ 0,45, то
а2 = 2,75, а3 = 3,2, а4 = 3,65 и т. д.
Пусть нужно найти десятый член арифметической прогрессии, у которой заданы первый член и разность. Эту задачу можно решить, находя последовательно все члены от второго до десятого. Для получения сотого члена нужно проделать еще большую вычислительную работу. Постараемся найти более короткий способ вычисления любого члена арифметической прогрессии.
По определению арифметической прогрессии
(Z 2 — пх d,
а3 -- а2 + d = (ах + d) 4- d - ах -- 2d,
аз + d “ (ai + 2d) + d = + 3d,
+ d = (ах + 3d) - d - ох:- 4d.
Легко сообразить, что а6 = -j- 5d, а10 = 4~ 9d,
а 23 = ах + 22d.
Вообще,
= а1 + d (п — 1). (1)
Приведем примеры использования формулы (1), в которой n-й член арифметической прогрессии выражается через первый член, разность прогрессии d и номер члена п.
Пример 1. Вернемся к задаче, рассмотренной в начале этого пункта. Пусть требуется найти 10-й и 100-й члены арифметической прогрессии (ал), первый член которой 2,3, а разность 0,45. Воспользуемся формулой (1):
а10 - 2,3 + 0,45 (10 — 1) - 6,8 — 0,45 - 6,35; п100 - 2,3 + 0,45 (100 - 1) = 47,3 — 0,45 = 46,85.
Пример 2. Выясним, является ли членом арифметической прогрессии
—10; —5,5; -1; 3,5; ... число 71.
Первый член данной арифметической прогрессии равен —10, а разность 4,5. Число 71 является членом этой прогрессии, если существует такое натуральное значение переменней л, при котором значение выражения —10 + 4,5 (п — 1) равно 71.
Решим уравнение
-10 + 4,5 (п - 1) - 71.
Получим:
4,5 (п - 1) - 81, п - 1 - 13, п - 19.
Выражение —10 + 4,5 (л — 1) принимает значение, равное 71, при п 19, причем 19 — число натуральное. Значит, число 71 — девятнадцатый член данной прогрессии.
Рассмотрим арифметическую прогрессию (аД, заданную условиями 6, d = 4. Найдем л-й член данной арифметической прогрессии:
ап — 6 + 4 (п — 1), т. е. ап - 4п 2.
Мы получили формулу, правая часть которой — двучлен 4л 4- 2, содержащий переменную п (п £ N) в первой степени. Значит, арифметическая прогрессия (ап) является линейной функцией, заданной на множестве N натуральных чисел формулой у = 4х 4~ 2.
График этой арифметической прогрессии представляет собой множество точек с натуральными абсциссами, принадлежащих прямой у = 4х + 2. Это, например, точки (1; 6), (2; 10), (3; 14) и др. (рис. 30).
Вообще, арифметическая прогрессия является линейной функцией, заданной на множестве натуральных чисел.
Для того чтобы доказать это, представим формулу л-го члена арифметической прогрессии ап — ах + d (л — 1) в виде ап dn -г («1 — d).
Мы получили формулу вида ykx-'b, где k d и д од —d - некоторые числа, х пну - ап— переменные, а такой формулой, как известно, задается линейная функция.
232. Пусть (аД—арифметическая прогрессия, первый член которой а разность d. Выразите через и d: а) «3; б) а26; в) а260; г) ат\ д) лт+1;
е) Рис. 30
. аП1 L ? J ! t / ! ' • ? i
/ ! i
Г 1 1 1 i ;
Z i
1 ! i t" ?
•i i j » -J ;
! г <1 — a i •4 !' 1
j 1
^.Х..— С - 1 '2 1 . , „ 1 I
J
в L —
— —
! с $ I г / 5 1
Л 1 ( - i 11 t i 1
• i • r Г T,
I 1 J ! 4 с 3
У
! — < 1 - " * "1 1 i
233. В арифметической прогрессии (с„) с, = 20, d = 3. “f* “Я“ v j-
Найдите:
а) ^5’ б) с101; в) сп.
234. В арифметической прогрессии (ап) известны ее первый член и разность d. Найдите а/г, если:
б) = 5,8, d = —1,5, п = 21;
в) = 25,6, d = —0,4, п = 100;
г) = —1—, d = —, 6 з
п — 61.
члены арифметической прогрес-
235. Найдите 15, 37 и п-й сии:
а) 3; 7; ... ; б) —5; —1; ....
236. В арифметической прогрессии (хп) тридцать членов, х7 = 2,8, d = 0,3. Найдите сумму: а) первого и последнего членов;
б) второго члена и предпоследнего;
в) пятого от начала члена и пятого от конца.
237. Найдите ап если:
а) а1а = 131, d 12; в) а100 = 0, d —3;
^58 = —^50, d = —5; г) а66 12,7, d = 0,2.
238. Найдите разность арифметической прогрессии (&л), если:
а) bt = 2, Ь10 = 92; б) Ъх = —7, &16 — 2.
239.
240.
241.
242.
Найдите первый член и разность арифметической прогрессии (сЛ/), если:
а) с5 = 27, с27 = 60;
б) с47 -- 74, с74 = 47;
а) Между числами 7 и 35 вставьте шесть таких чисел, чтобы они вместе с данными числами образовали арифметическую прогрессию.
б) Между числами 1 и 16 вставьте восемь таких чисел, чтобы они вместе с данными числами образовали арифметическую прогрессию.
а) В арифметической прогрессии ее 31-й член равен 17, а разность 2,5. Найдите 41-й и 47-й члены.
б) В арифметической прогрессии (ап) а7 —100 и
as ~ -—70. Найдите а5 и а15.
Найдите первый член и разность арифметической прогрессии (а^), если:
а) (а± + а7 = 42, в) \а± + аъ = 24,
243.
244.
245.
248.
247.
248.
Напишите формулу n-го члена арифметической прогрессии (хп), в которой =1,7 и d = 0,3, Найдите номер члена, равного: а) 32; б) 46,7. Докажите, что число 62,7 не является членом этой прогрессии.
Узнайте, принадлежит ли арифметической прогрессии 3; 10; ... число: а) 143; б) 551.
В арифметической прогрессии (уп) первый член равен —19,5, а разность равна 1,5. При каких значениях п верно неравенство уп 0? Каковы номера отрицательных членов прогрессии?
а) Найдите первый отрицательный член арифметической прогрессии 5,3; 5,12; ... .
б) Найдите первый положительный член арифметической прогрессии —10,4; —9,65; ... .
Известны первый член и разность арифметической прогрессии (иД: W'l - —53; d ~ 4. Для каких членов после-
довательности верно неравенство:
а) ип 103; б) ип
Последовательность
< 200?
задана формулой
2п -4- 3.
Найдите разность:
а) &2 &i; б) &9; в) Ь^.
Является ли последовательность арифметической прогрессией?
249. Последовательность задана формулой ее n-го члена:
а) у„ = 2п —5; в) уп = 5п + 1;
б) уп = — Зп + 2; г) уп = 10 — 7п.
Докажите, что последовательность (уп) есть арифметическая прогрессия, и найдите ее первый член и разность.
Упражнения для повт орения
Qct^b—1 250. Упростите выражение - : ——
с2 Ъ2
251. Найдите значение выражения:
а)
0,04~2 125* 0.2-1 .
96
252.
253.
Найдите значение и ~ 7, п ~ —1.
Представьте в виде
выражения
при
степени с основанием 2 выражение:
а) 16 • 2";
б) 8 - 2
в) S5 • 4";
г) 163 • 4'г”8;
3 Алгебра 8 кл..
65
16.
ОРМУЛА СУММЫ п ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
Пусть требуется найти сумму первых ста натуральных чисел. Ответ можно получить непосредственным сложением чисел. Однако такой способ решения очень трудоемкий. Попробуем найти нужный результат иначе.
Запишем сумму натуральных чисел от 1 до 100 дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором — в порядке убывания:
1 Я- 2 + 3 -
100 + 99 + 98 -
+ 93 + 99 + 100
+ 3 + 2 -г- 1.
Легко заметить, что сумма пар чисел, расположенных друг
под другом, одна и та же:
1 + 100 - 2 + 99 - 3 +98 - ... ... -98+3-99 + 2 - 100 + 1.
Каждая такая пара чисел в сумме дает 101, число пар равно 100. Поэтому
1+2 + 3 + ...
_ 101 • 100
~ 2
100
101 - 50 - 5050.
Воспользуемся аналогичным приемом для вывода формулы суммы п первых членов арифметической прогрессии.
Обозначим сумму п первых членов арифметической прогрессии (ап) через Sn и выпишем эту сумму дважды, поменяв во втором случае порядок слагаемых на обратный:
*8/2 £1п + + +? 2 4~ ••• + ^3 “Г ^1* (2)
Сложим почленно равенства (1) и (2):
2Sn " (а1 “Ь ап) + (а2 "Ь +z-l) + (#3 +
... + (ай„2 + а3) + (а/г_г + а2) + (ап + aj.
В правой части равенства сумма каждой пары чисел равна ал +<+• Действительно,
: (ах + d) + (ап — d) — аг + afl;
(^2 4" 4“ (*+—1 ~ ^2 + #/г—
НО
следовательно,
Число таких пар равно п. Поэтому
Отсюда
(«1 + ап) • п.
(«1 + ап) • п
(I)
Пример. Найти сумму первых 20 членов арифметической прогрессии (ЬД:
1 5 3,5; ... .
Первый член прогрессии 1, разность 2,5. Найдем 20-й член этой прогрессии:
Ь20 1 < 2,5 • (20 — 1) = 1 + 2,5 * 19 = 48,5.
Теперь можно вычислить искомую сумму:
S20 = Т + 4у\.-..20. = 49,5.10 = 495.
В формуле (I) сумма п первых членов арифметической прогрессии выражена через первый член, n-й член и число суммируемых членов прогрессии. Иногда удобно пользоваться формулой суммы п первых членов, представленной в другом виде.
Заменим в формуле (I) член прогрессии ап выражением av + d (п — 1). Тогда
Итак,
d (п
2
(П)
В формуле (II) сумма п первых членов прогрессии выражена через первый член, разность прогрессии и число членов.
254. Найдите сумму 200 первых членов арифметической прогрессии (сД, если:
а) С] = 10, с200 = 350; б) сх = 6,5, с2М = 7,5.
255. Найдите сумму восьми первых членов арифметической прогрессии (ап), у которой:
а) аг — 100, d = —20; 0 == —13, d 7;
б) —23, d -- 3; аг -- 9, d — —4.
256. Найдите сумму 10 первых членов арифметической прогрессии (аД:
&) 2;5; ...; б) —17; —11; ...; в) —2,6; 0; ...; f) 14,2; 9,6; ... .
257. Докажите, что последовательность (хД есть арифметическая прогрессия, и найдите сумму п первых членов этой прогрессии, если:
а) х„ = 2п — 1: б) х„ — — 12п + 7.
' /4 ' * /*
258. а) В арифметической прогрессии (с^) с7 = 8,6 и с21 = 25,4» Найдите сумму тридцати первых членов этой прогрессии. <0 В арифметической прогрессии (ап) а10 74,9 и п18 ~ 70,1,
Найдите сумму 26 первых членов этой прогрессии.
259. а) Найдите сумму членов арифметической прогрессии с 10-го по 20-й включительно, если первый член равен 7 и разность равна 15.
б) Найдите сумму членов арифметической прогрессии с 11-го по 25-й включительно, если первый член равен 2 и разность равна 8.
260. Найдите сумму:
&) первых 50 натуральных чисел;
б) всех двузначных чисел;
в) всех нечетных чисел, меньших 100;
г) всех двузначных чисел, кратных 5;
д) всех двузначных чисел, некратных 10.
261. а) В арифметической прогрессии (Ьп) Ьг ~ 4,8 и d = 0,4. Сколько последовательных членов этой прогрессии, начиная с первого.; надо сложить, чтобы получить сумму, равную 172?
б) В арифметической прогрессии (Ьп) — 84 и d = —4. Сколько последовательных членов этой прогрессии, начиная с первого, надо сложить, чтобы получить сумму, равную 0?
262. Заполните таблицу, выполнив необходимые вычисления:
№ d п ^/7 8п
1 J ... _ 0 11 0 -
9 -0,6 17 9,5
3 0,5 18 333-
4 140 ' 1050
263. Шары расположены в форме треугольника так, что в первом ряду 1 шар, во втором — 2, в третьем — 3 и т. д. (рис. 31). Во сколько рядов размещены шары, если их число равно 120? Сколько потребуется шаров, чтобы составить треугольник из 30 рядов?
264. На одной стороне угла от вершины отложены десять конгруэнтных отрезков и через их концы (кроме вершины угла) проведены параллельные прямые. Докажите, что длины параллельных отрезков, заключенных между сло-
ев
реками угла, образуют арифметическую прогрессию. Найдите разность этой прогрессии, если известно, что длина наименьшего из параллельных отрезков равна 2 см, а наибольшего равна 47 см. Чему равна сумма длин всех параллельных отрезков, заключенных между сторонами угла?
265. Длины оснований трапеции 26 см и 11 см. Боковая сторона трапеции разделена на 10 конгруэнтных частей, и
Рис. 31
через точки деления проведены прямые, параллельные основаниям. Найдите сумму длин всех параллельных отрезков, заключенных между боковыми сторонами трапеции»
Упражнения для повторения
266. Упростите выражение:
(-8х3г/4)4
267
) (16Л/2)2 • (4х2#4)4 ’
Докажите где п 6 Z
что
(27а3&3)2 > (—За2Ь)3
значение
выражения не зависит от п
а)
б)
16 • 82^"3
43"'^2
1000 • 1252и-2
>4
268. Докажите, что значение выражения есть число рациональное:
§ 7.
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
17. ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Пусть последовательность (Ья) такова, что первый член ее равен 3, а каждый член, начиная со второго, получается умножением предыдущего члена на 2. Тогда
Ъ.2 = 3 • 2 - 6, Ь3 = 6 • 2 - 12, &4 =12-2 = 24, Ы = 24 • 2 = 48, ... . fj? <
Опр е д е л е н и е. Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же, не равное нулю число, называется геометрической прогрессией.
Рассмотренная нами последовательность (Ьп) — геометрическая прогрессия, так как при любом п 1 bnVi = Ъп • 2.
Из определения следует, что в геометрической прогрессии (Ьп) отношение любого ее члена, начиная со второго, к предшествующему равно одному и тому же числу:
&2 : = Ь3 : Ь2 = ... = Ъп : = Ьп+1 : Ъп = ... .
Это число называют знаменателем геометрической прогрессии. Его обычно обозначают буквой q.
Таким образом, геометрическая прогрессия (6J определяется:
1) условием Ьх — Ъ (Ь 0);
2) рекуррентной формулой Ьп+1 = Ъп • q (q ф 0).
Для того чтобы задать геометрическую прогрессию (&J, достаточно знать ее первый член Ъх и знаменатель q. Если, на-пример, Ъх =о, а#^—, то мы имеем геометрическую прогрессию
Условиями = 4, q = —3 задается геометрическая прогрессия 4; —12; 36; —108; ... .
Заметим, что в том случае, когда q < 0, члены прогрессии с нечетными номерами имеют тот же знак, что и первый член, а члены прогрессии с четными номерами имеют знак, противоположный знаку первого члена прогрессии. В этом случае прогрессия не является ни возрастающей, ни убывающей последовательностью.
Если q >0 (q Ф 1), то прогрессия — либо возрастающая последовательность, либо убывающая. Пусть, например, Ьх = = —2, a q = 3. В этом случае геометрическая прогрессия
—2; —6; —18; ...
есть убывающая последовательность.
Если q =-1, то все члены прогрессии равны между собой. В этом случае прогрессия будет постоянной последовательностью.
Геометрическая прогрессия обладает следующим свойством: любой член геометрической прогрессии, начиная со второго, равен среднему пропорциональному предшествующего и последующего членов.
Докажем это. Пусть последовательность (Ьп) — геометрическая прогрессия и b/7-i, Ъп, Ьп+1 — три произвольно выбранных последовательных ее члена (и^2).
Отношение любого члена геометрической прогрессии к предшествующему члену равно одному и тому же числу, поэтому
^/74-1 _
&п—1
Справедливо и обратное: если некоторая последовательность такова, что любой член, начиная со второго, равен среднему
пропорциональному предшествующего и последующего членов, то эта последовательность — геометрическая прогрессия.
Действительно, пусть для любых трех последовательных членов Ъп, 2) некоторой последовательности (Ьп) имеет место соотношение
Значит, отношение любого члена последовательности (b/z) к предшествующему члену равно одному и тому же числу. Последовательность (Ъ/г) — геометрическая прогрессия.
Таким образом, справедлива теорема: числовая последовательность является геометрической прогрессией в том и только в том случае, когда любой ее член, начиная со второго, равен среднему пропорциональному предшествующего и последующего членов,
269. Является ли геометрической прогрессией конечная последовательность:
а) 1000; 100; 10; 1; 0,1; г) —1; 10; —100; 1000; —10 000;
б) 0,1; 0,01; 0,001; 0,0001; д) 1; 1,1; 1,11; 1,111;
в) А; А; А; 2; 8; 16; е) 5'2; 5'1; 5°; 51; б2?
16 8 2
Если является, то чему равен ее знаменатель?
270. Найдите первые пять членов геометрической прогрессии (Ь!г), если:
271. Известны первые два члена геометрической прогрессии. Найдите знаменатель и четвертый член этой прогрессии: ,
а) 3; 15; ...;
б) 15; 3; ...;
в) 6; —12;
г) —20; —10; ...;
д) 2]/ 2; 4;
272. В записи геометрической прогрессии (уп) неизвестны два первых члена. Найдите их:
а) У1, у^ 24; 36; 54; ...; б) z/x; у2; 225; —135; 81; ... .
273. Выразите знаменатель q геометрической прогрессии (хп) через:
а) и х2; б) и х3\ в) хк и .
274. Найдите знаменатель геометрической прогрессии (аЛ), шестой и седьмой ее члены, если:
а) а3 6, а- = 24; в) а3 — —2, аъ — —18;
б) аь = 10, а3 = —10; г) — 24, а3 = 3.
275. Является ли арифметической или геометрической прогрессией последовательность (&„), если:
а) Ял = 5 и ап+1 = 4а„; в) ах =- —8 и ал+1 = + ай;
Xj
б) «л = 5 и all+1 = 4 + а„; г) ах = -8 и ап+1 =-- ^а,г?
£
Если последовательность — арифметическая прогрессия, то укажите ее разность; если геометрическая, то укажите ее знаменатель.
276. Приведите пример геометрической прогрессии (Ьп)3 у которой:
а) Ьг > 0, q > 1;
б) bi > 0, 0 < q < 1;
в) < 0, q >1;
г) bi < 0, 0 < q < 1.
Является ли прогрессия возрастающей последовательностью или убывающей?
Упражнения для повторения
277. Найдите область определения выражения:
б) у 6х —
4
х3 — 16
— |/10- 2х.
18. ФОРМУЛА П -ГО ЧЛЕНА ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Зная первый член Ьл и знаменатель q геометрической прогрессии (6 J, можно путем последовательных вычислений найти второй, третий и вообще любой ее член. Однако при нахождении членов с достаточно большими номерами удобнее пользоваться формулой, которая выражает любой член последовательности (ЬГ) через первый член Ьц знаменатель прогрессии q и номер искомого члена п.
Из определения прогрессии следует, что
Ь.г = • q,
b3 = Ь, • q = (&i q) • q = b± q2,
bt = b3 • q = (&i • a2) • q = • q3,
bb = b 4 q = (bi q3) • q = bt qi и т. д.
Вообще, bn - (1)
' Приведем примеры использования формулы (1).
Пример!. В геометрической прогрессии (Ьп) щ — 0,8 и
1 . ‘
q — —. Найти
* Z
Воспользуемся формулой (1):
1 10 1
&10 ^0,8. 4 .
640’
Пример 2. В геометрической прогрессии (сп) ~ у. Найти п-й член этой прогрессии.
По формуле (1) имеем:
27,
З3
разрежаю-в нем воз-
Пример 3. После каждого движения поршня щего насоса из сосуда удаляется 20% находящегося духа. Определить давление воздуха внутри сосуда после шести движений поршня, если первоначальное давление было равным 750 мм рт. ст.
Так как после каждого движения поршня из сосуда удаляется 20% находящегося в нем воздуха, то в нем остается 80%, 4
или, иначе, —$ имевшегося воздуха.
Для того чтобы узнать давление воздуха в сосуде после
4 очередного движения поршня, достаточно умножить на — чис-
ло, показывающее значение давления воздуха после предыдущего движения поршня. Числа, указывающие последовательно значение первоначального давления воздуха в сосуде, величину давления после одного движения поршня, после двух движений, после трех и т. д., образуют геометрическую прогрессию, первый член которой равен 750, а знаменатель равен -. Числовое
значение давления воздуха после шести движении поршня, выраженное в мм рт. ст., является седьмым членом этой прогрес-/ 4 X 9
сии, значит, оно равно произведению 750 • —) .
\ 5 / ;
Произведя вычисления, получим:
/ 4 750 . 212 750 4096 24576 . АГ7
(ои • — —-------=--------- — — ту (,
\ 5 / 5s 56 125
Итак, после шести движений поршня давление воздуха в сосуде равно 197 мм рт. ст.
278. Пусть (х,.) — геометрическая прогрессия, первый член которой равен х1? а знаменатель q. Выразите через х% и q: а) х.,; б) х21; в) х150; г) хт; д) хш+2; е) xik+i.
279. В гееметрической прогрессии (ип) = 256, q = Найдите: a) б) в) г/10; г) ип.
280.
В геометрической прогрессии (&л) известны ее первый член и знаменатель q. Найдите b , если:
a) b
n
r ---Э
б) = 0,125, q = —2, п = 6; г) Ьх =0,003, ?=/10, п = 7.
281. Задайте геометрическую прогрессию формулой п-го члена, если:
а) &х = 3, Ьп+1 = Ьп • 2; в) Ьг = 25, Ьп+1 = Ъп 5;
б) Ъх = 4, Ьп+1 = Ъп (-3); г) = 12, Ъп+1=Ъп • А .
&
282.
283.
284.
285.
286.
287.
288.
Докажите, что последовательность (сЛ) является геометрической прогрессией, если:
а) сп = 2"; б) сп - 5 • 3"; в) сп = 3 • 2л+1.
Найдите первый член геометрической прогрессии (&Л), если:
a) д8 = 384, с —2; б)
Выразите члены а7, а15 и а40 геометрической прогрессии (ап) через аъ и знаменатель q.
Найдите знаменатель геометрической прогрессии (&Д, если:
а) Ъг — 2, 256; в) Ьб — 25, Ь8 — 9;
б) bt = 5, b9 = 1280; "f) &4 = 2, Ь7 = —54. g
Восьмой член геометрической прогрессии равен 13, а зна- g менатель равен —3. Найдите ее 10-й и 13-й члены. ЛЧ
В геометрической прогрессии (сД съ = 27, с4 = 9. Най- <
дите с8.
Найдите номер п члена геометрической прогрессии (Ьп) если:
4-*'
Ь„ = 162, Ь / £
б)
ьп = 10, Ь{ - 640, q
в) Ьп = -
" 81
289.
Между числами 1 и 16 вставьте такие три числа, чтобы
290.
а)
они вместе с данными числами образовали геометрическую прогрессию.
15
б) Между числами 60 и — вставьте такие пять чисел, 1
16 з
чтобы они вместе с данными числами образовали геометри-ческую прогрессию. :
а) Найдите номер члена геометрической прогрессии 0,1; J 0,3; ..., равного 218,7.
б) Найдите номер члена геометрической прогрессии 1280; 1
640; ..., равного 20. 1
1
291. В какую сумму обратится вклад в 1000 р., положенный в сберкассу на 4 года, из расчета, что вклад ежегодно увеличивается на 2%?
292. Некоторые бактерии, помещенные в питательную среду, делятся пополам каждые полчаса. Сколько бактерий в этом случае получится из одной бактерии через 10 ч?
293. На опытном лесном участке ежегодный прирост древесины составил 10%. Какое количество древесины будет на участке через 6 лет, если первоначальное количество древесины равно 2,0 • 104 м3?
Упражнения для повторения
294. Упростите выражение:
81avz-i\3 / 5 \4
25 / 1,27а3У
295. Разложите на множители
выражение:
а) 4« _ 4«~2. б) 9" — З2""”1.
296. Сократите дробь:
297. Существует ли такое значение х, при котором функция, заданная формулой у = 4х2 — 5х 7, принимает значение, равное: а) 3; б) 6? (При положительном ответе укажите это значение х.)
19. ФОРМУЛА СУММЫ П ПЕРВЫХ ЧЛЕНОВ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Пусть (bj — геометрическая прогрессия. Выпишем п первых членов этой прогрессии:
Ь2; Ь3; Ьп_^ Ьп.
Обозначим сумму этих членов Sn:
Sn = b, + b2 + b3 + ... + Vi + bn. (1)
Если q = 1, то все члены прогрессии равны bx и Sn = nbx. Рассмотрим случай, когда q 1.
Умножим обе части равенства (1) на q:
qSn = + М + bsq + ... + bn_xq + bnq.
Ho bxq = &2> b2q = 6g, b3q = &4, ..., bn^q = bn, поэтому
= &2 + b3 + &4 + ... + bnq. (2)
Вычтем почленно из равенства (2) равенство (1), получим:
QSn — sn= bnq — Sn (q — 1) = bnq — br.
Так как q
1, то
(I)
П р и ые р. Найти сумму десяти первых членов геометрической прогрессии (К):
Первый член прогрессии 1, а знаменатель 2* Найдем 10-й член этой прогрессии:
ъ.. 1 . 910-1 == л?
Теперь воспользуемся формулой (I):
2f 2 - 1 2,0 г = 1()24 j 1023_
Иногда бывает удобно пользоваться формулой суммы п первых членов геометрической прогрессии, представленной в дру-$ $_____________________________________ь.
гои виде» Подставим в формулу Sf, :i-...где g 1? вме-
$ — 1
сто Ьп выражение • qn~l* получим:
-у12 OKI). (И)
q —1
В формуле (II) сумма п первых членов геометрической прогрессии, знаменатель которой не равен 1, выражена через пер
вый член^ знаменатель прогрессии и число суммируемых
членов
293» Найдите сумму пяти первых членов геометрической прогрессии (ли), в которой:
299. Найдите сумму п первых членов геометрической прогрессии (К-h если: •г >•
а) —4, q = 3, п 6; б) Ьг = —32, q п 8.
300. Найдите сумму девяти первых членов геометрической про» глессии: 4-
а) 1; —2; б) 54; 36; ... .
301. Найдите сумму семи первых членов геометрической прогрессии (п/?), если:
302. Найдите сумму первых трех, пяти, п членов геометрической прогрессии (Ъ.?)9 заданной формулой п-го члена: а.) - 1,5 - 4’Ц б) Ь... - 2 • З1’^.
/ И 7 7 7 /л
30'3. Найдите сумму первых десяти, ста, п членов геометрической п р’ о- г р е с с и и:
а) 1; а\ а2; где а — число, отличное от 0 и от 1;
б) 1; с2; с4; .... где с — число, отличное от 0 , от 1 и от —1₽
304. Представьте в виде дроби выражение:
а) 1 х х2 -I- х,; -г х4 -0 х5 -и х° (х^1их^0);
б) 1 — х — х2 — х3 -- х4 — х5 — х4 (х —1 и х СИ-
ЗОЗ. Заполните таблицу, выполнив необходимые вычисления:
t J I F « 1 - 9 1 n 1 ! E n i j ? s
j 1 CQ 1 1 1 j 5 p
! ) 0> • 4 1 i _ _ _ J
•l 1 2 i ! 1458 i 1 7
j
i г i ! о ! -3 ! 121,5 4 I 1 i i
1 i 4 i 1 i_ i 5 2 96 189 i i j
Упражнения пл я повторения
306. Отношение между элементами множества А ~ {12; 20; 21; 221 и элементами множества В — {2; 3; 4} задано описанием:
а) каждом у числу из множества А поставлено в соответствие число из множества В, равное сумме его цифр;
б) каждому числу из множества А поставлено в соответствие число из множества В, являющееся его делителем. Задайте это отношение с помощью стрелок. Является ли рассматриваемое отношение функцией?
307. Графиком функции f служит луч с началом в точке А (3; 5), параллельный оси х и расположенный в первом координатном углу. Постройте этот график. Укажите область определения и область значений функции.
308. Может ли функция у — х2 -0 14х — 15 принимать значение, равное:
а) _1; б) „з; В)
20. тождества (а — b)(a2 + аЬ + Ь1) = а3 — Ь3 |
и (a -j- b)(а3 — а b 4- Ь3) = а3 + Ь3 |
1
Рассмотрим многочлен с двумя переменными а и Ь:
ап~г + ап'2Ь + а‘!~'-Ь2 + аЪп~2 + ty1"1. ' м
h . .д
чС
Легко заметить закономерность, по которой составлены члены этого многочлена: показатели степеней при основании а уменьшаются от п — 1 до 0, а при основании Ъ увеличиваются от 0 до п — 1 (первый член можно рассматривать как произве- Д дение а последний — как произведение а°£/г-1), причем
сумма показателей степеней при переменных в каждом члене многочлена равна п — 1. Число членов этого многочлена равно и.. '
В частном случае при п = 2 многочлен принимает вид а + Ь, при п = 3 он принимает вид а2 + аЬ + 62, при п — 4 он принимает вид а3 + a2b + аЬ2 + Ь3.
Многочлен |
ап~г + ап~2Ъ + ап~3Ь2 + ••• + abn~2 + Ьп~г
J ’
можно рассматривать как сумму первых п членов геометрической прогрессии, в которой первый член равен а'2-1, а знаменатель равен —. Если а=^0, b^Q и а^=Ь, то по формуле суммы < первых п членов геометрической прогрессии будем иметь: |
an~r + ап~2Ь + ап~3Ъ2 + + abn~2 4~ b4"1 ~
Ь Ъп — ап Ж
а а Ь'-— ап .<»
b b - а b — а . ' \
— — 1 -------------
а а
т. е. 'О
с«-1 + ап~2Ь + ап~3Ь3 + ... 4- abn-2 + Ьп-' = -~-ЬП . В
а — ж
Отсюда . -Ж
(а — Ь) (а^1 + ^2Ь + ап~3Ъ2 + ... + abn~* + b^1) = ап— bn. (1) •
При выводе формулы (1) мы предполагали, что а О, b О Ж и а=^Ь. Однако легко проверить, что и при указанных значе- Я ниях переменных это равенство истинно, т. е. формула (1) яв- Я ляется тождеством на множестве всех пар переменных пи Ъ. Я
В частности, при п — 2 и п ~ 3 тождество (1) соответственно Л принимает вид: w
(а — Ь) (а + Ъ) - а2 — Ъ\ (2)... •
(а — Ъ) (а2 4- аЬ + Ь2) = а3 — Ь3. (3) И
Формула (2) нам хорошо знакома. Теперь мы будем выпол- Ж нять преобразования и с использованием формулы (3). в
Пусть, например, требуется разложить на множители двучлен 8х3 — 125г/3. Имеем:
8х3 — 125z/3 = (2х)3 — (5у)3 — = (2х — 5у) (4х2 + Wxy + 25у2).
Заменим в тождестве (3) переменную b на —&, получим:
(а _ (__&)) . (а2 + а(_&) + (_Ь)2) аз _ (_6)3> т. е.
(а + Ъ) (а2 — аЬ Ь2) = а3 + Ь3. (4)
309. Преобразуйте произведение (х — 10) (х2 + 10х + 100) в многочлен стандартного вида двумя способами: а) по правилу умножения многочлена на многочлен;
б) по формуле (а — Ь) (а2 + аЪ + Ъ2) ~ а3 — Ъ\
310. Преобразуйте в многочлен стандартного вида произведение:
а) (х—2) (х2+2х+4); г) (2а + 1) (4а2—2а + 1);
б) (р—5) (р2 + 5р+25); д) (10х~Зу) (100х2 + 30лч/ + 9г/2);
в) (I/+4) (у2—4у + 16); о) (4а + 5Ь) (16а2—20ab+25b2).
311. Используя тождество а3 — Ъ3 = (а — Ъ) (а2 + аЪ + Ъ2) или тождество а3 + Ъ3 = (а + Ь) (а2 — аЬ -г 62), разложите на множители двучлен:
а) х3 — у3;
б) с3 — 8;
в) 27 + х3;
г) 8х3 — 27;
д) 125а3 + 1;
е) п3 — 64m3;
ж) ~у3 — 1000;
и) с3 — 0,001;
к) 0,0С8Ь3 + 125;
л) 0,064 — п3у3;
м)
64х3
312. Докажите, что значение выражения:
а) 3273 + 1733 делится на 500;
б) 7313 — 6113 делится на 120;
в) 47593 — 27793 делится на 1980;
г) 3863 + 2143 делится на 1200.
313. Вычислите наиболее рациональным способом:
314. Сократите дробь:
а)
б)
523
— 67 • 52.
у3 — 1000, у-10 ;
119
18&2+24&+32
27&3 — 64
315. Представьте выражение в виде дроби:
б)
ба3 -4- 12а
а3 + 8 а2
За2
6?/
произведения: д) yQ — 64;
е) 64А6 — nG. произведения
318.
Используя тождество
4 _1_ „2 ’
а) (х — 1) (х5 б) (у - 2) (/ в) (а — 3) (а4
Представьте в виде а) х6 + г/6; в) с6 — 1; б) aG — Ь6; г) nG + 1;
Представьте в виде
двучлена и трехчлена: а) (а б) (У-2)
(1), представьте в виде многочлена: х3 + х2 + х + 1);
6)3
г + 3)3
О? i
9а2
+ 27$ 4- 81),
319.
Сократите дробь: а)
б)
2у — 2
У
Упражнения для повторения
320. Является ли функцией отношение, заданное следующим описанием:
а) каждой точке ломаной АБС (рис. 32) поставлена в соответствие ее абсцисса;
б) каждому действительному числу, принадлежащему промежутку [1; 6J, поставлена в соответствие точка ломаной АВС, для которой это число служит абсциссой (рисунок тот же)?
321. Постройте график функции у = х2 — 2х — 15. На какое множество отображается промежуток [—1; 6j?
322. Докажите, что значение выражения есть число рациональное:
а) (5 -г 2J/6)2 + (5 - 2]/б)2;
б) (К? + 2/10 4- V 7 — 2/10/
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ III
К пунктам 11 и 12
323. Задайте конечную последовательность путем перечисления пар:
а) 1; 2; 0; 1; 2; 0; б) 3; 7; 7; —3; —7.
324, Выпишите члены последовательности трехзначных чисел, сумма цифр которых равна 3, взятых в порядке возрастания.
325. Выпишите члены последовательности:
а) правильных дробей со знаменателем 7, взятых в порядке возрастания;
б) неправильных несократимых дробей с числителем 15, взятых в порядке убывания.
326. Напишите первые пять членов последовательности (с^), заданной формулой и-го члена:
327. Пусть (ап) — последовательность, члены которой — квадраты последовательных натуральных чисел. Найдите а2, <Ч(И , ^+2» &2/?—1*
328. Найдите 5, 8, 50 и 301-й члены последовательности, каждый член которой равен разности между его утроенным номером и единицей. Являются ли числа 20, 179, 1501 членами этой последовательности?
329. Последовательность задана формулой ап — 5п — п2. Найдите номер члена последовательности, равного: а) —36; б) 4; в) 6.
330. Содержится ли среди членов последовательности (6/7), где Ьп ~ бтг2 — и-, число:
а) 5; б) 15; в) 287?
331. Подберите формулу п-го члена конечной последовательности:
а) —6; -3; 0; 3; 6; . J_. J . 1 . _1______L.
6) 1; —2; 3; —4; 5; —6; ; 1. 2’ 2-3’ 3-4’ 4-5’ 5 - б’
1 A. -L. ДА —. \ 1 - 3 3-55*7 7-9
2~’’ ” 3 ’ 4 ’ 5 ’ 6 ’ ~~ 7 ’ 2.4’ 4~б; 6^8’ 8 - 10*
332. Напишите формулу, по которой может быть найден любой член бесконечной последовательности (с/7), если известно, что:
а) все члены этой последовательности с нечетными номерами равны —8, а с четными 8;
б) все члены с нечетными номерами равны 5, а с четными —5.
333. Выпишите несколько первых членов последовательности (ап) и подберите формулу ее n-го члена, если:
а) (а,7) — последовательность всех натуральных чисел, которые кратны 3 и 5;
б) (а.?) — последовательность всех натуральных чисел, которые кратны 6 и 9.
334. Подберите формулу n-го члена последовательности:
а) трехзначных чисел, кратных 37;
б) трехзначных чисел, записываемых с помощью одной цифры, и кратных 37.
335. Подберите формулу n-го члена последовательности:
а) 5; 10; 15; 20; 25; б) 25; 20; 15; 10; 5.
336. Пусть (хп) и (у7) — конечные последовательности, причем
Выпишите последовательность (з/г), если Уп*
и найдите формулу ее n-го члена.
337. Последовательности (ап) и (5Л) заданы формулами ап -- 4и — 1 и b/z — 4к1. Найдите n-й член последовательности (слг), если сп = ап +
338. На рисунке 33 изображены «шахматные доски», перенумерованные в соответствии с числом клеток, содержащихся
339.
в одном ряду.
Сформулируйте правило, по которому каждому натуральному числу п (номеру «доски») ставилось бы в соответствие число ап (число черных клеток этой «доски»). Рассмотрите два случая: a) zz — четное число; б) п — нечетное число.
Число диагоналей выпуклого многоугольника определяет-, . , п (п ~ 3)
ся по формуле ап = ——г\ —число сторон, причем
340.
п 4. Существует ли многоугольник, число диагоналей которого равно 9; 14? У каких многоугольников число диагоналей не превосходит 20?
а) Сколько точек графика последовательности (сл), где сп = 68 — 10п, расположено в верхней полуплоскости? б) Сколько точек графика последовательности (drt), где dn — bn — 47, расположено в нижней полуплоскости?
Рис. 33
341. Пусть (ап) — последовательность, заданная формулой n-го члена. При каких значениях п верно неравенство:
а) ап > -> если = 1---------;
О 72
к. 17 (j
б) ап > 5, если ап — -------?
п
342. Дана последовательность (Ьп), где Ъп “ п + При п
каких значениях п:
а) Ъп > 2; б) Ьп > 5; в) Ъп < 6; г) 3 < Ъп < 20?
343. Последовательность (ал) задана формулой n-го члена. Является ли эта последовательность возрастающей или убывающей:
а) ап =- 10 — п; г) ап = ж) ап (п — 6)2;
п
п + з ч -j,2 ч 1
б) а:г = Т"; Д) ап = 1 + —; 3) ап = 1
2 п
Найдите наибольший ности (уп) (если они
и наименьший существуют),
члены последователь-заданной формулой
п-го члена:
а) Уп = — П2 + 6п + 3; в) уп = —i—;
72 ’— О * 5
б) уп = п2 — 8п -и 1; г) уп = 5” ~12.
345. Напишите несколько первых членов последовательности 3 72 1
(Z?/z), заданной формулой Ъп=-----. Является ли эта
последовательность возрастающей или убывающей? Найдите разность 3 — Ъп п = 1, 2, 3. Покажите, что эта разность положительна при любом н.
346. Выпишите несколько первых членов последовательности
(х^), заданной формулой хп — ™—-. Является ли эта 72
последовательность возрастающей или убывающей? Составьте разность 5 — хп и найдите множество значений п, при которых: *1
а) 5 — хп < --; б) 5 — хп < 0,1; в) 5 — хп < 0,001.
347.
Дана последовательность (хп), заданная формулой хп ~ = 1-. Укажите множество значений и, при которых:
п
a) € Е0; 1];
б) хп с [0,01; 1,01];
в) С [0,001; 0,01];
г) *й£[—0,1; 0,1];
348. Существует ли числовой отрезок, которому принадлежат все члены последовательности:
5 7 2п +1
; 1’ Т •" ; Т”; ” ;
К пункту 13
349. Выпишите несколько первых членов последовательности (сп), заданной рекуррентным способом, и задайте последовательность формулой п-го члена:
а) — 4, сп+1 сп 4, в) <?£ — 2, с/г+1 — с/г -г 1,
350. Последовательность (ап) задана рекуррентным способом. Выпишите шесть первых членов последовательности:
а) “2, =
б) = 5, а„+1 • ап = —5;
в) (Zj ~ 1, — 2, (1п •
г) ~ 1, : г — п.
351. Задайте последовательность рекуррентным способом:
а) 4; 6; 4; 6; 4; 6; 4; 6; б) 1; 3; 5; 1; 3; 5; 1; 3; 5.
К пункту 14
352. Третий член арифметической прогрессии равен 11, пятый равен 19. Найдите первые 10 членов этой прогрессии.
353. В записи конечной арифметической прогрессии (сл):
— неизвестны некоторые члены.
Найдите их.
354. Докажите, что при любых а и b соответственные значения выражений (а -г Ь)\ а'2 + Ъ2 и (а — Ь)2 образуют арифме-
355.
356.
тическую прогрессию.
1 iv.
Докажите, что если числа ------, ---
b + с а с арифметическую прогрессию, то числа образуют арифметическую прогрессию.
образуют
а2, Ь2 и с2 также
Докажите, что никакие три последовательных члена последовательности (ап), заданной формулой п-го члена, не образуют арифметической прогрессии, если:
а) ап = п2; б) ап = У п\
357. Дана арифметическая прогрессия п2; а3; ...; ап; ... . Будет ли арифметической прогрессией последовательность:
а) tip ••• 5 ^2/7—1’ ***’
б) ах +1; а> +1; •••; +1; •••*»
в)
2а2;
• • А 7
.11 1
г) ; ... 9 9
(Zjl а2 ап
Д) 6&19 CZ2, •••> ...?
К пункту 15
358. Найдите 15, 37 и n-й члены арифметической прогрессии:
а) 2; -; ...; б) —0,9; —0,65; ... .
3 6
359.
380.
Докажите, что если (Ъп) — арифметическая прогрессия,
то верно равенство:
а) Ъ3 + Ьп = Ь5 + Ь9; б) Ъп Ч
а) Найдите первый отрицательный
7
прогрессии —; 0,55; ... .
б) Найдите первый положительный о1. q2.
прогрессии -Зд —3 ; ... .
2 9
Ь2 = ь„_.2 + Ь4.
член арифметической
член арифметической
361. Выведите формулу d где d— разность арифме-
т — п
тической прогрессии, ат и ап — ее члены (т п).
362. Докажите справедливость для арифметической прогрессии формулы ап - d a'n^k [п > #).
2
363. Найдите первый член и разность арифметической прогрессии (ал), если:
364. Функция задана формулой у = 0,5х + 4, х С ДГ. Докажите, что эта функция есть арифметическая прогрессия.
365. Докажите, что функция у = kx + b, где k и Ъ — числа, а х С 2V, есть арифметическая прогрессия.
366. Функция задана формулой у = Зх — 2 на множестве всех чисел. Докажите, что если значения переменной х образуют арифметическую прогрессию, первый член которой 19 а разность 1,5, то соответствующие значения переменной у также образуют арифметическую прогрессию.
367. Если функция у = f (х) линейная и значения переменной х образуют арифметическую прогрессию, то и значения переменной у также образуют арифметическую прогрессию. Докажите это.
368. Функция задана формулой у ~ 2х — 4 на множестве всех чисел. Найдите разность арифметической прогрессии, которую образуют значения переменной у, если значения переменной х образуют прогрессию:
а) 3; 6; б) 20; 15; ...; в) —; 1; ...; г) 1; 1-г^; ... • 4
369. Задайте формулой функцию, которая переводит прогрессию 1; 3; 5; 7; ... в прогрессию 2; 4; 6; 8; ... . Задайте формулой функцию, которая переводит вторую прогрессию в первую.
370. Известно, что в арифметической прогрессии (ап) ах = 1 и d > 0. Найдутся ли в этой прогрессии члены, большие, чем: а) 1000; б) 1 000 000?
К пункту 16
371. Найдите сумму десяти первых членов арифметической прогрессии: а) —; —; ... ; б) — ]/8; —]/2; ... .
7 6
372. Выведите формулу суммып первых членов арифметической прогрессии (&J, если: а) ап = 2п 4~ 1; б) — 3—п.
373. В арифметической прогрессии (aj:
а) = —19, d = 2, Sa = 384; найдите п и
б) d п = 37, Sn = 209^ ; найдите и
в) d ~ 2,5, ап = 27, Sn = 157,5; найдите и п;
г) d - 0,2, п =- 21, 8п = 57,75; найдите и ап.
374. Найдите первый член и разность арифметической прогрессии (ап), если — 5,5 и S20 = 130.
375. а) В арифметической прогрессии (Ъп) Ъ7 ~ 16 и — 40. Найдите сумму двадцати первых членов этой прогрессии, б) В арифметической прогрессии (Ъ}1) Ь5~ 16,5 и Ь12 — 6. Сколько последовательных членов этой прогрессии, начиная с первого, надо сложить, чтобы получить сумму, равную 180?
376. а) Сумма 8-го и 15-го членов арифметической прогрессии равна 48. Найдите сумму первых двадцати двух ее членов, б) 9-й член арифметической прогрессии равен 20. Найдите сумму семнадцати первых ее членов.
377. Найдите сумму первых п:
а) натуральных чисел;
б) положительных четных чисел;
в) положительных нечетных чисел;
г) положительных чисел, кратных 5.
378. Найдите сумму:
а) нечетных натуральных чисел, меньших 1000;
б) натуральных чисел, некратных 5 и меньших 200;
в) натуральных чисел, некратных 15 и меньших 120.
379. а) Найдите натуральное число, равное — суммы всех предшествующих ему натуральных чисел.
б) Найдите натуральное число, равное — суммы всех пред-6
шествующих ему натуральных нечетных чисел.
380. Найдите сумму:
а) 1 + 2 + ... + 19 + 20 + 19 + ... + 2 + 1;
б) 1 + 2 + ... + (п — 1) + п + (п — 1) + ... + 2 + 1;
в) 1-3 4- 5 - 7 + ... + 97 — 99;
г) 1 — 2 + 3 — 4 + 5 — ... — 198 + 199 — 200.
381. Упростите выражение:
382. Найдите сумму всех положительных членов арифметической прогрессии:
а) 47; 39; ...; б) 23,2; 21,7; ...; в) 5 -; 5-1; ... . 3 2
383. Найдите сумму всех отрицательных членов последовательности, любой член которой может быть найден по формуле: а) ап = 1,5п — 48; б) ап -- 2,8п — 125.
384, Найдите сумму всех двузначных чисел, являющихся членами последовательности (ап), заданной формулой:
а) ап =’7 + Зтг; б) ап ~ 217 — 4/г.
385. В арифметической прогрессии:
a) S10 ’ 100, S30 = 900; найдите S4();
б) >S1;5 S25 = 150; найдите S30.
386. Известна сумма Sn первых п членов арифметической прогрессии (ап). Найдите:
а) первые четыре члена прогрессии, если Ьп — — п;
4
б) первый член и разность прогрессии, если S}1 = 2n2+3n.
387. Сумма п первых членов некоторой последовательности (Ьп ) вычисляется по формуле Sn = п2 — 2п + 5. Найдите пять первых членов этой последовательности. Является ли последовательность (Ъ!г) арифметической прогрессией?
388. Я вляется ли арифметической прогрессией последовательность (ап), сумма п первых членов которой определяется по формуле:
a) SH = п2 — 2п; в) Sn ~ 7п — 1;
б) S?l - —4лг2 + 11; г) St7 = п2 — п + 3?
389. Катет прямоугольного треугольника разделен на 13 конгруэнтных частей и через точки деления проведены пря
мые, параллельные гипотенузе треугольника. Найдите сумму длин всех параллельных отрезков, заключенных между катетами, если известно, что длины катетов 56 см и 33 см.
390. Найдите первый член и разность арифметической прогрессии, если - 8 и S3 = —3.
К пункту 17
391. В конечной геометрической прогрессии (ап) неизвестны некоторые члены. Найдите их:
а) 162; а3- 72; а5; 32; в) ]Z3; а2- а3; 18]/2; а5; 108]/2;
б) —; а2; а4; а5; —4; г) 1; о2; п3; а/, 49.
3 2
392. Докажите, что при любых а и b (| а I |6 [) соответственные значения выражений (а + &)2, а2 —, Ь2 и (а — Ь)2 образуют геометрическую прогрессию.
393. Докажите, что если числа а, &, с, d образуют геометрическую прогрессию, то истинно равенство
(а — d)2 = (b — с)2 + (с — а)2 + (d — Ъ)2.
394
Пусть (Ь/гг) — геометрическая прогрессия. Будет ли геометрической прогрессией последовательность:
б) Ьр &з, *•*’
В) 1, &2 1? •••> Ьп
> 5
ь3-
2
0
395. Дана конечная геометрическая прогрессия (хп ) со знаменателем q. Выясните, будет ли геометрической прогрессией последовательность, составленная из тех же чисел, но взятых в обратном порядке. В случае утвердительного ответа найдите знаменатель новой прогрессии.
396. Могут ли три последовательных члена геометрической прогрессии составлять арифметическую прогрессию?
К пункту 18
397. В геометрической прогрессии (Ьп) известны ее член и знаменатель q. Найдите Ъ/г, если:
первый.
—]/*6, п 5.
398. Между числами— и 240 вставьте шесть таких чисел, ко--8
торые вместе с данными числами образуют геометрическую прогрессию.
399. Докажите, что числовая последовательность (хл) есть геометрическая прогрессия, если:
а) хп = 4 • ' у j ; в) х„ = 0,1 • 10";
б) хп —Зг/; г) хп = 2Ьп> где b 0.
400. Докажите, что в геометрической прогрессии (ал)
аГ1аг - алк , если р -г г т - п. ЛчЛ / * С* J ъг
401. Если для натуральных чисел и, р и г верно равенство
п , то в геометрической прогрессии (Ь„)
2
’ 5 ^Р ‘ &!" Д0КаЖИТе ЭТО.
402. Если q— знаменатель геометрической прогрессии (с„), то qnr. Докажите это.
сг
403. 1, 20 и 58-й члены арифметической прогрессии образуют геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
404. 1, 2 и 4-й члены геометрической прогрессии образуют арифметическую прогрессию. Найдите знаменатель геометрической прогрессии.
К пункту 19
405. В геометрической прогрессии (Ьд):
a) q = 0,5, Ъп 2, Sn = 254; найдите и и;
б) q = 3, bn = 567, Sn = 847; найдите by и п;
в) q = 2, п = 8, S!t = 765; найдите by и Ь.г;
17
г) bi = 2, bn = —, StJ = 3-; найдите q и п.
8 8
406. а) Сумму п первых членов геометрической прогрессии (уп) можно вычислить по формуле Sn = 2 (5я — 1). Найдите S4, z/i, у у.
б) Сумму п первых членов геометрической прогрессии (уп) можно вычислить по формуле Sn = 3,5 (4п — 1). Найдите у19 g, S5.
407. Докажите, что если сумму п первых членов последовательности (ап ) можно найти по формуле = 3/г — 1, то (ал)— геометрическая прогрессия.
408. Является ли геометрической прогрессией последовательность, сумма первых п членов которой может быть найдена по формуле:
a) Sn - и2 — 1; б) Sn - 2* — 1; в) S4 = 3/г + 1?
409. а) Сумма трех чисел, составляющих арифметическую прогрессию, равна 30. Если из второго члена этой прогрессии вычесть 2, а остальные числа оставить без изменения, то получится геометрическая прогрессия. Найдите эти числа.
б) Сумма трех чисел, составляющих геометрическую прогрессию, равна 93. Если из первого числа вычесть 48, а остальные числа оставить без изменения, то получится арифметическая прогрессия. Найдите эти числа.
410. Найдите сумму Sn первых п членов геометрической прогрессии:
а) 16; 8; 4; где п ™ 6;
где и
9;
, где п
6; г) —100; 10; —1; ... , где п-=6.
411. Сумма первых четырех членов геометрической прогрессии равна 30, а сумма следующих четырех членов равна 480. Найдите сумму первых двенадцати членов.
412. В геометрической прогрессии S3 = 40; S8 ~ 60. Найдите
413. Представьте в виде частного двух двучленов выражение:
- ап, где п £ N, а 1, а 0;
... + х2-7, где п , х Ф —1, х40;х
... 4- хп, где k £ N, п С
X У= 0.
414. Упростите выражение:
415. Сократите дробь:
б)
— 1
55 bi ьз
ь2
6е — 55 54 53 щ 52 „ 5 !
5i3 + 5i2 + 5U + _ + 5 + 1 ’
К пункту 20
416. Преобразуйте в многочлен
*а) (х—4) (х2 + 4х + 16);
>б) 0/ + 10) (г/2—10^/4-100);
стандартного вида:
в) (х—1) (х3+х2+х + 1);
г) (а—Ъ) (а3+а2&+а&2+Ь3).
417. Разложите на множители:
а) с3 — 216; г) 0,008 + у6; ж) (2с + I)3 — 27;
б) k3 + 512; д) х6 + 0,625; з) 8 — (3 — к)3;
в) 0,001 — а3Ь3; е) х12 — у12; и) 8х3 — (5х — З)3.
418. Докажите, что значение выражения:
а) 173 — II3 кратно 6;
б) 613 + 193 кратно 16;
в) 413 -г 193 кратно 60;
г) 793 — 293 не кратно 100;
д) 663 + 343 кратно 400;
е) 543 — 243 кратно 1080;
ж) 2195 — 1085 кратно 37;
з) 347 + 417 кратно 25.
419. Найдите значение выражения:
а)
б)
97 • 83J : (352 — 282);
79 • 41^ : (133,52 — 58,52).
420. Сократите дробь:
. 1 Ц- а 4- а2 4-... 4- а13 + с14
а) ---------------z---------
1 4 а 4 в2 -1- в! + л4
1-у4-у2-- + У18 - У19 + У20
1 — У + У2 — У3 + У4 — И + У6
421. Упростите выражение:
а)
е)
Ур3 - 8 /Г-2’
(/& — /с )2 + /&с*
422. Разложите на множители: a) х3 — 4х2 + 20х — 125; б) 27г/3—Зг/2+2г/—8;
в) (х3 — 27)2 — 81х2 (х—З)2;
г) 9а2Ь2 (а + &)2—(а3 + &3)2.
423.
424.
Докажите, что при любом натуральном значении k значе-
ние выражения
(2k + I)4
4/4 4- 4А
кратно 8.
Решите уравнение:
а) х7 — х = 0;
б) 8yi + у = 0.
ГЛАВА
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ
§ 8.
ФУНКЦИЯ, ОБРАТНАЯ ДАННОЙ
21. ОТНОШЕНИЕ, ОБРАТНОЕ ДАННОМУ
На рисунке 34 отношение р между элементами множества X и элементами множества Y задано с помощью стрелок. Поменяем направление стрелок (рис. 35); получим другое отношение — отношение q между элементами множества Т и элементами множества X.
Говорят, что q есть отношение, обратное отношению р. В свою очередь отношение р является обратным отношению q.
Областью определения отношения р является множество {—3; —2; —1}, а областью значений —множество {2; 3; 4; 5}. Для отношения q, обратного отношению р, областью определения служит множество {2; 3; 4; 5}, а областью значений — множество {—3; —2; —1}. Таким образом, область определения и область значений взаимно-обратных отношений меняются ролями.
Отношение р между элементами множеств X и Y определяется множеством пар:
{(—3; 2); (-2; 3); (-1; 4); ( —1; 5)}.
Поменяв в каждой паре местами ее элементы, получим множество пар, которым задается отношение q, обратное р:
{(2; -3); (3; -2); (4; -1); (5; -1)}.
Рис. 34 Рис. 35
A
В
Рис. 37
Вообще, если отношение определяется некоторым множеством пар, то обратное ему отношение определяется множеством пар, которое получено из первого перестановкой элементов в каждой паре.
Приведем примеры взаимно-обратных отношений.
Пример 1. На рисунке 36 с помощью стрелок показано отношение «меньше» между элементами множеств А = {5; 7; 10} и В = {2; 3; 8; 12}.
Обратное ему отношение (рис. 37) является отношением «больше» между элементами множества В и элементами множества А.
Пример 2. Отношения «быть делителем» и «быть кратным» между натуральными числами — взаимно-обратные отношения.
Действительно, если а и Ъ — некоторые натуральные числа и а — делитель Ъ, то Ъ кратно а, и, наоборот, если b кратно а, то а — делитель Ъ. Например, из того, что «2 — делитель 6», следует, что «6 кратно 2»; из того, что «24 кратно 8», следует, что «8 — делитель 24».
Вернемся к рассмотренным выше взаимно-обратным отношениям р и q.
На рисунке 38, а построен график отношения р, а на рисунке 38, б — график отношения q.
Построим теперь графики отношений р и q в одной и той же системе координат (рис. 39).
Рис. 38
Рис. 39
Рис. 40
Нетрудно заметить, что точки с координатами (—3; 2) и (2; -3), (-1; 4) и (4; -1) и т. д., т. е. точки, у которых абсцисса первой является ординатой второй и ордината первой является абсциссой второй, симметричны относительно прямой у = х. Каждой точке графика отношения р соответствует симметричная относительно прямой у = х точка графика отношения д, и, наоборот, каждой точке графика отношения q соответствует симметричная отно-
сительно прямой у — х точка графика отношения р. Поэтому
графики отношений р и q симметричны относительно прямой
У х- х
Вообще, справедлива следующая теорема:
Графики взаимно-обратных отношений между числами симметричны относительно прямой у = х.
Рассмотрим уравнение
2х — у = 0.
(1)
Этим уравнением задается некоторое отношение между значениями переменной х и значениями переменной у. Обозначим это отношение буквой f.
На рисунке 40 построен график отношения / и график отношения g, ему обратного. Графиком отношения g служит прямая, которая проходит через начало координат и точку с координатами (4; 2). Следовательно, график отношения g может быть за-
1
дан уравнением у = —х или равносильным ему уравнением
2у — х = 0.
(2)
Сопоставив уравнение (1), которым задается отношение /, и уравнение (2), которым задается обратнее ему отношение g, замечаем, что уравнение (2) может быть получено из уравнения (1) заменой х на у и у на х.
Вообще, если некоторое отношение f задано уравнением с двумя переменными хну, то для задания уравнением отношения, обратного /, достаточно в данном уравнении поменять обозначения х на у и у на х.
Заметим, что одним и тем же уравнением с двумя переменными можно задать два взаимно-обратных отношения. Например, уравнением х Ц- 2у ~ 12 может быть задано отношение /, определяемое множеством пар вида (х; у}, каждая из которых это уравнение обращает в истинное равенство. Тем же уравнени
ем можно задать и отношение g, обратное f, определяемое множеством пар вида (у; х), каждая из которых это уравнение обращает в истинное равенство. В этом случае первой переменной в паре считается не х, а у и второй переменной — не у, а х. Однако если соблюдать принятый порядок в обозначении переменных в паре (первой считать х, а второй z/), то для задания отношения g уравнением следует в уравнении х ’ 2у - 12 поменять обозначения х на у и у на х. Тогда получится уравнение у + 2х — 12, которым задается отношение g, обратное /. При этом условии отношение g, так же как и отношение /, определяется множеством пар вида (х; у).
425. Отношение
между числами задано множеством пар:
а) {(1; 20);
(2; 30); (3; 40); (4; 50); (5; 50)};
Изобразите с помощью стрелок данное отношение и отношение, обратное данному.
Какова область определения и область значений данного отношения и отношения, обратного данному?
426. Отношение между числами задано множеством пар:
а) !(|/2; 7); (|/3; 8); (/5; 10); (Кб; 11); (j/7; 12));
б) {(0,3; 1); (Kib; 0); (-2; 1); (К6; 0); (13; 1)};
в) {(1; 12); (2; 6); (3; 4); (4; 3); (6; 2); (12; 1)}.
Задайте множеством пар отношение, обратное данному. Укажите область определения и область значений данного отношения и отношения, обратного данному.
427. Укажите отношение, обратное отношению:
а) «находиться севернее» между городами СССР;
б) «быть старше» между людьми;
в) «быть больше на 2» между числами;
г) «быть меньше в 5 раз» между положительными числами. 428. Отношение между числами задано
с помощью стрелок (рис. 41). Постройте график этого отношения и отношения, ему обратного. Является ли функцией данное отношение; отношение, обратное данному?
429. Известно, что точки А (—8; 1), В (1; 7), С (0; 9) принадлежат графику отношения /. Укажите координаты двух каких-нибудь точек, принадлежащих графику отношения,
обратного /. Рис. 41
430. Графиком отношения / служит отрезок АВ, где А (—3; 2), В (4; 5). Постройте в одной и той же системе координат график отношения f и график обратного ему отношения. Найдите область определения и область значений отношения f и отношения, обратного f,
431. Графиком функции служит расположенная в верхней полуплоскости полуокружность с центром в начале координат, радиус которой равен 3. Постройте график отношения, обратного этой функции, и выясните, является ли V это отношение функцией.
432. Отношение задано уравнением:
’а) х — 5у = 3;
'б) х + Зу = 1; в) х + у = 5;
г) х2 -— z/ - 0;
д) 2x2+5x-y~z/2;
е) ху 10;
ж) хг И- zr — 9;
з) х2 — у~ — 12;
и) х2 — y^ —• 0.
Задайте уравнением отношение, обратное данному. Среди J перечисленных выше отношений укажите те, которые яв-ляются обратными самим себе.
433. Отношение h задано уравнением:
а) X — 2у = 4; б) ~ = 1; в) у = х2; г) (х — 2)2 + у = 0.
Постройте график отношения h и график отношения р, обратного h. Задайте отношение р уравнением.
Упражнения для повторения
434. Сократите дробь:
(& + 4)2 — 1
._ - - ... *
b* 12 5 ’
435. Вычислите:
22. ПОНЯТИЕ
б) 815 • 9“И;
УНКЦИИ, ОБРАТНОЙ ДАННОЙ
На рисунке 42 с помощью стрелок задано отношение р между элементами множеств А и В. Это отношение — функция, так как каждому элементу множества А соответствует не более одного элемента множества В. Отношение h между элементами множеств В и А, обратное р (рис. 43), не является функцией: в множестве В существует элемент (число 2), которому соответствует более одного элемента из множества А (элементы 5 и 6).
Рассмотрим другой пример двух взаимно-обратных отношений.
На рисунках 44 и 45 с помощью стрелок заданы отношение f между элементами множеств X и Y и обратное ему отношение g между элементами множеств Y и Х> Отношение f — функция, отношение g, обратное /, тоже функция.
Приведенные примеры показывают, что отношение, обратное функции, может быть функцией, а может и не быть функцией.
Функция f называется обратимой, если обратное ей отношение — функция.
В этом случае отношение, обратное функции /, называют функцией, обратной /.
Мы рассмотрели примеры функций р и Д заданных с помощью стрелок (рис. 42 и 44). Обратимой оказалась функция в том случае, когда к любому элементу области ее значений было проведено не более одной стрелки, т. е. когда каждое свое значение функция принимала только при
Рис. 42
Рис. 43
одном значении аргумента.
Вообще, функция обратима тогда и только тогда, когда каждое свое значение она принимает лишь при одном зна-
чении аргумента. На рисунках 46 и 47 изображены гра-
я
-t
ики функций g и Л. Функция g обра
тима, так как нет такого значения функции, которое соответствовало бы различным значениям аргумента (любая пря
мая, параллельная оси х, пересекает график не более чем в одной точке).
Функция h необратима, так как существует такое значение функции, например у = 3, которое соответствует трем различным значениям переменной х (прямая у = 3 пересекает график в трех точках).
Нетрудно убедиться, что всякая возрастающая функция обратима.
Действительно, пусть f — возрастающая функция, Ху и х2 — произвольные, неравные друг другу значения аргумента. Тогда Ху > х2 или Ху .< х2. Если xi > х2, то f (хх) > f (х2); если Ху < х2, то f (xj) < </(х2). Таким образом, неравным значе-
Рис. 44
Рис. 45
97
4 Алгебра 8 кл.
Рис. 47
ниям аргумента соответствуют различные значения функции. Значит, функция f каждое свое значение принимает лишь при одном значении аргумента. Следовательно, функция / обратима.
Аналогично можно показать, что всякая убывающая функция обратима.
На рисунках 48 и 49 построены графики функции h и обратной ей функции g. Функция h возрастающая. Обратная ей фуню; ция g также является возрастающей.
Вообще, функция, обратная возрастающей, является возрастающей.
Аналогично функция, обратная убывающей, является убывающей.
Приведем примеры.
Пример 1. Функция f, заданная формулой у = —~2х + 3, убывающая. Поэтому она обратима. Обратная ей функция также убывающая.
Чтобы задать формулой функцию, обратную f, поменяем в уравнении у = — 2х + 3 обозначения х на у и у на х. Получим уравнение х —2у + 3.
5)
Рис. 50
Обычно при задании функции уравнением с переменными х и у переменную у выражают через переменную х.
В данном случае имеем:
2у = —х 4-3, у = —0,5х 4- 1,5.
которой задается функция, обрат-
Мы получили формулу, нал Л
Пример 2. Функция
х € [0; +°°[- Так как g — возрастающая функция, то она обратима, причем обратная ей функция также является возрастающей.
Поменяв в формуле у ~ х2, где х С [0; обозначения х на у и у на х, получим уравнение х г/2, где у £ [0; которым задается функция, обратная g.
Выразим из уравнения х = у2, где у € [0; +оо[, переменную у через х. Так как область значения функции, обратной g, есть множество неотрицательных чисел, т. е. у > 0, то у = ]/х.
у задана формулой у = х2, где
йК
436. Для каждой функции (рис. 50) задайте обратное ей отношение. Является ли функцией отношение, обратное: а) отношению /; б) отношению g; в) отношению Л?
437. Функция f задана множеством пар, причем известно, что среди пар есть такие, у которых вторые элементы одинако-
А
Рис. 51
Рис. 52
438.
439.
440.
441.
вы (например, есть пары (8; 5) и (10; 5)). Достаточно ли этого, чтобы судить, обратима функция / или нет?
Является ли обратимым:
а) отображение окружности на отрезок АВ (рис. 51);
б) отображение отрезка АС на отрезок BD (рис. 52)?
На рисунке 53 заданы графиками различные функции. Вы-
ясните, какие из функций являются обратимыми.
Докажите, что функция, заданная формулой у = 5х, обратима, а функция, заданная формулой у — х2, не является обратимой.
Является ли обратимой функция, заданная формулой:
а) у = 0,5х; б) у = — Зх + 1;
в) у = —2х2; г) у — |х|?
442. Функция задана формулой у = х2, где х С [—1; 2]. Докажите, что эта функция необратима. Выделите из промежутка [—1; 2] подмножество, на котором функция, заданная формулой у — х2, обратима.
443. Задайте формулой функцию, обратную данной:
а) у = 5х;
б) у — —4х;
д) у — 5х —10;
е) у = 0,1х + 1.
Рис. 53
юо
444.
а) Докажите, что функция, обратная прямой пропорциональности у = kx, где й =# О, есть прямая пропорциональ
ность, и найдите коэффициент пропорциональности.
б) Докажите, что функция, обратная обратной пропорцио-
ъ ~
нальности у = —, где й =#= О, есть также обратная про-х
порциональность. Найдите коэффициент обратной про-
445.
порциональности .
Докажите, что
функции, заданные формулами:
взаимно-обратные.
Функция задана формулой:
а) у = 2х;
1
б) у = — -х;
в) у = —, где х > 0;
X
г) у = х2, где х С [0; 2].
Докажите, что стройте в одной
каждая из этих
ункций обратима. По-
и той же системе координат график данной
функции и график обратной ей функции. Покажите, пользуясь графиком, что данная функция и ей обратная являются либо обе возрастающими, либо обе убывающими.
Упражнения для повторения
—• 5х -j- 6 27
х3 — 8 ’ ' 1/2 + 27у + 72 ’
448. Известно, что а > Ъ > 0. Докажите, что:
а) а3— 62 > 0; б) а3 — &3>0; в) —< —; г)а2 + 62>а&. а Ь
§ 9.
КОРЕНЬ п-И СТЕПЕНИ И ЕГО СВОЙСТВА
447. Сократите дробь: h)
23.
УНКЦИЯ
у —•
'А'
Рассмотрим функцию /, заданную формулой у = хк, где п —-натуральное число. Так как выражение хп, где имеет смысл при любых х, то областью определения функции служит
множество действительных чисел.
Мы знаем, что при п — 1 графиком функции f служит прямая (рис. 54), при п = 2 — парабола (рис. 55), при п = 3 — кубическая парабола (рис. 56).
Свойства функций у = х, у = х2 и у ~ х3 нам известны. Выясним свойства функции f и особенности ее графика при любом натуральном п.
1. Если х=0, то хп = 0. Поэтому график функции f проходит через начало координат.
2. а) Если х ^0 и п — нечетное число, то хп при положительном х принимает положительные значения, при отрицательном х — отрицательные значения. Поэтому график функции f при нечетном п расположен в первом и третьем координатных углах.
б) Если х 0 и п — четное число, то хп > 0. Поэтому график функции f при четном п расположен в первом и втором координатных углах.
3. а) Если п — нечетное число (п = 2k — 1, k € N), то противоположным значениям аргумента х = —а и х = а соответствуют противоположные значения функции: f(—a) = (—а)24-1 = == _o2fe-i, f (а) = а24-1, т. е. f (— а) = —f (а).
Следовательно, график функции f при нечетном п имеет центр симметрии, которым служит начало координат.
б) Если п — четное число (п = 2k, k 6 N), то противоположным значениям аргумента х = —а и х = а соответствуют равные значения функции: f (—а) = (—а)24 = а24,/(а)=а24, т. е. f (—а) = f (а). Следовательно, график функции f при четном п имеет ось симметрии, которой служит ось у.
4. а) При нечетном п функция f является возрастающей. б) Пои четном п функция f убывает на множестве отрицательных чисел и возрастает на множестве положительных чисел.
Доказательство, а) Пусть а и & — два произвольных значения аргумента, причем a <Z Ь*
Если 0 < а < 6, то по теореме о почленном умножении истинных числовых
неравенств:
(а <Ь)=Ф (а2 < Ь2) => ... => (а24-1 < Ь24"1), k € N.
Если а < Ъ < 0, то —а > —Ъ > 0. Так как —а и —Ъ — положительные числа, то (—а)24-1 > (—Ь)24-1. Тогда —а24"1 > —Ь24-1 и а24-1 < Ь24"1.
Рис. 54
Рис. 55
Рис. 56
Если а < 0 < &, то а3 "1 < 0 и &2 г 1 > О, т. о. а3 1 1 < б21“-1.
Итак, при любых аи & имеем (а < b) (f (а) < f (&)), т. е. при нечетном п функция / возрастает на множестве всех чисел.
б) Доказательство можно провести аналогично, рассмотрев случаи 0 < а < Ъ и а < b < 0.
5. а) Областью значений функции f при нечетном п служит множество действительных чисел.
б) Областью значений функции f при четном п служит множество неотрицательных чисел.
Эти свойства мы примем без доказательства.
Рассмотренные свойства функции f и особенности ее графика позволяют сделать вывод, что при нечетном и, большем 1, график функции f имеет такой же вид, как и график функции у х3, а при четном п — как график функции у = х2.
На рисунках 57 и 58 построены графики функций у — х4 и у = хг\
449. Функция задана формулой f (х) = X20.
Не выполняя вычислений, сравните:
а) /(2) и f (-2); в) / (-5) ц 0;
б) /(3) и 0; г) /(-7) и /(6).
450. Функция задана формулой
Рис, 58
Не выполняя вычислений, сравните:
a) g (3) и g (—3); в) g (8) и 0;
б) g (—5) и 0; г) g (—9) и g (6).
451.
А
452.
а) Принадлежит ли графику функции у — xw точка: А (2; 1024); В (—2; 1024); С (—3; —79401)?
б) Принадлежит ли графику функции g = х’ точка:
D (2; 128); Е (-2; —128); F (—3; 2187)?
Используя свойства графика функции у = Xе, сравните значения степеней:
а) 56 и 76;
б) 0,36 и 0,2е;
т*
в) 0,8е и 1;
г) (-8)6 и (—9)6;
453.
Используя свойства графика функции у = х7,
значения степеней:
а) 27 и З7;
б) 0,87 и 0,97;
сравните
в) 0,83’ и 1;
г) (—5)’ и (—6)7;
454. Укажите какое-нибудь значение аргумента, при котором значение функции, заданной формулой у = хй, тр,е х € [0; +оо[, больше, чем: а) 2е; б) 106; в) 1012; г) 1018.
455. Укажите какое-нибудь значение аргумента, при котором значение функции, заданной формулой у = х5: а) больше, чем З5; 1010; 1020;
б) меньше, чем —З5; —1О10; —1021.
Упражнения для повторения
456. Упростите выражение:
24. ПОНЯТИЕ КОРНЯ П-И СТЕПЕНИ
Рассмотрим уравнение
хп = а, (1)
где а — некоторое число. Пользуясь свойствами графика функции у = где п — натуральное число, выясним, сколько корней имеет уравнение (1) и каков знак этих корней.
Если п — нечетное число, то прямая у = а и график функции у == хп пересекаются и притом только в одной точке (рис. 59). Поэтому при нечетном п и любом а уравнение (1) имеет единственный корень: при а > 0 этот корень — положительное число, при а = 0 он равен нулю, при а < 0 корень уравнения — отрицательное число.
Если п — четное число, то при а> 0 уравнение (1) имеет два корня, являющихся противоположными числами, прямая у = а и график функции у = хп (рис. 60, а) пересекаются в двух Симмет-
Рис. 59 ричных относительно оси у точках.
Рис. 60
При а ~ 0 уравнение (1) имеет единственный корень, равный нулю (рис. 60, б); при а < 0 уравнение (1) не имеет корней: прямая у = а и график функции у — хп (рис. 60, в) не имеют общих точек.
Корень уравнения хп = а, где п —- натуральное число, называют корнем п-й степени из а.
Определение. Корнем п-й степени из числа а называется такое число, п-я степень которого равна а.
Пусть п — нечетное число.
Рассмотренные случаи решения уравнения (1) показывают, что корень нечетной степени из числа всегда существует и притом только один. Для его обозначения принят знак а (читается: «корень п-й степени из а»). Число п называют показателем корня, число а — подкоренным выражением.
Приведем примеры.
1) Запись у432 означает корень пятой степени из 32. Легко проверить, что )/32 ~ 2, так как 25 ==. 32.
2) Запись У—27 означает корень третьей степени (или ко-з,---------------------------------
рень кубический) из —27. Равенство у —27 = —3 истинно, так как (-3)3 - -27.
7__
3) Запись у 0 означает корень седьмой степени из 0. Так 7Л—
как О7 == 0, то у 0 = 0.
Пусть п — четное число.
При а > 0 существуют два противоположных числа, являющихся корнями п-й степени из а.
Положительный корень п-й степени из а обозначают в этом случае знаком у^а, тогда противоположное ему число запишется
так: —yZal При а = 0 существует единственный корень п-'л степени из ах у^О = 0, так как 0" — 0. При а < 0 корень п-й тт п/~
степени из а не существует. Иначе говоря, выражение у а, где п — четное и а < 0, не имеет смысла.
Приведем примеры.
Запись уг64 означает неотрицательный корень шестой сте-6 у----------
пени из 64. у 64 — 2, так как 2 — неотрицательное число и 26 - 64.
Если п ~ 2, то показатель корня не пишется. Например, вместо пишут ]/10. тг-г п /--
Итак, если п — нечетное число, то выражение у а имеет смысл при любом а; если п — четное число, то выражение уЛп имеет смысл лишь при а 0.
Очевидно, что при всех значениях а, при которых выражение а имеет смысл, истинно равенство (j/а )п = а.
"ПГ х. Л ?-- /
При а 0 выражение у а всегда (как при четном, так и при нечетном п) имеет смысл. Корень n-й степени из неотрицательного числа называют арифметическим корнем п-й степени.
Иными словами, арифметическим корнем п-й степени из неотрицательного числа а называется неотрицательное число, п-я степень которого равна а.
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень той же степени из противо-3/-—__ 3
положного (положительного) числа. Например, у —8 = — у 8; = — /29.
Вообще, если а<0 и то у а ~ — у —а.
Действительно, по определению корня
,2/г—1^—ч 2/г—1 z 2k—1,——Л2/г—1
( у а) = а, ( — у—а) ~—(—а)—а,
Рассмотрим примеры решения уравнения вида хп = а.
Пример 1. Решить уравнение х4 = 7.
Это уравнение имеет два корня, которые являются противоположными числами (см. рис. 60, а). Положительный корень есть положительное число, четвертая степень которого равна 7, 4Л— 4/—
т. е. у 7. Отрицательный корень равен —у 7.
Заметим, что числа —j/7 и у 7 иррациональные. Их приближенные значения с точностью до 0,1 соответственно равны —1,6 и 1,6.
Пример 2. Решить уравнение х3 = 5.
Уравнение имеет единственный корень (см. рис. 59). Этот корень есть положительное число, третья степень которого рав~ 3Л- Зу-
на 5, т. е. у 5. Число у 5 иррациональное. Его приближенное значение (с точностью до 0,1) равно 1,7.
Пример 3. Решить уравнение х5 —50.
Уравнение имеет единственный корень (см. рис. 59). Этот корень есть отрицательное число, пятая степень которого равна —50, т. е. /—50. Выразив ]/—50 через арифметический, получим: у^—50 ~ —]/ 50. Число —50 иррациональное. Его значение приближенно равно —2,2.
457. Докажите, что истинно равенство:
а) ]Ув1 = 3; б) У—0,125 = —0,5;
458. Найдите значение корня:
а) у/1б'; г) j/у, ж) у7 5А; к) У/027;
б) У—32; д) У 1; 3) у__3 3; л) У0,0625;
Г Ь4 г о
в) у" 1; е) у/'—1; и) л/ц?5; м) ]/"—0,00001.
г 64
459. Найдите значение выражения:
S
а) 5/100; г) —4уг27; ж) 12 —6 Уб,125;
б) 0,1 У1000; д) Уб2 + У=8; з) 1 + юДо,ОО81.
в) —2^81; е) Уб25 —У^125;
460. Укажите область определения выражения:
461. Найдите значение степени:
а) (/10)2; в)(У12/ д)(2^3)4; ж) (-У15)6;
б) (Уб)3; г) (У=2)5; е)(-3 /2)3; з) (- Уз)7.
462. Вычислите:
а) У2е; в)2У(=Зр; д) -У253; ж) У125-У(=9р;
б) У 7®; г) 5 Ус=2У3; е) Уз22; з) У32 + У 27^
463. При каких значениях а истинно равенство:
а) У а2 б) у^а3 = а?
464. Решите уравнение:
а) х3 = 4; в) х4 — 10; д) х5 = 6;
б) х3 = —4; г) х4 = —10; е) х6 = 7.
&
Упражнения для повторения .
465.
466.
Постройте график отношения, обратного /, зная, что отношение f задано уравнением у = х2, где х С ] —со; 0].
Решите уравнение:
х 8 14
а)
б)
х3 + Зх — 10*
17
У
= 0.
Мы
25. ФУНКЦИЯ У =
выяснили (см. п. 23), что функция, заданная формулой
-1, где й 6 7V, является возрастающей. Поэтому она обратима.
Чтобы задать уравнением обратную ей функцию, достаточно в уравнении у = х2^”1 поменять обозначения х на у и у на х:
2k—1
Выразив из этого уравнения у через х, получим:
График функции у — Ух (рис. 61) симметричен графику
функции у = х2^”1 относительно прямой у = х.
Рис. 61
Рис. 82
Рис. 63
Функция у = х2/г, где k 6 N, не является обратимой, так как можно указать два значения аргумента, которым соответствуют равные значения функции (любым двум противоположным значениям аргумента, отличным от нуля, соответствует одно и то же значение функции).
Рассмотрим функцию у = х2/г, где х Е [0; + со[. Эта функция является возрастающей. Поэтому она обратима. Обратная ей функция задается уравнением х = где у £ [0; +<х>[. Выразим из этого уравнения у через х. Учитывая, итог/ 0, получим:
2k__
График функции у = у х (рис. 62) симметричен графику функции у = x2k,
где х £ [0; +-оо[, относительно прямой
2k
Л 1j
Функции у— ух м. у = у X, где х£[0; +°°[> как °б-ратные возрастающим функциям, являются возрастающими.
<67. На рисунке 63 построены графики функций у = ]Лх и 4 л-— 3 z-
у = У х; на рисунке 64 — графики функций у = ух и 5/—
У = ух-
Какова область определения и область значений каждой
из этих функций? Докажите, что график каждой из этих функций проходит через начало координат и точку (1; 1).
Пользуясь данными
графиками, сравните:
а) ]5 и у^5; 0,5 и 0,5;
б) ^3 и ^3; у 0J и .
3 — графику функции у = у х точка:
468. а) Принадлежит ли
А (8; 2); В (216; 6); С (27; -3); D (-125; -5)?
. 4/—
б) Принадлежит ли графику функции у = у х точка: Е (81; 3); Г (81; -3); К (-16; -2)?
469. а) Пересекает ли прямая у — 1 000 000 график функции
3/-- 4Л-
у = у х; у = У х?
б) Пересекает ли прямая у = —100 000 график функции
470. Используя свойства функции у — ух, объясните, почему истинно неравенство:
а) 5 > ^3; б) 2^^ЗЖ < 2^=ЗЛ
471. Сравните значения выражений:
а) у^ 2 и у^З; в) —0,2 и ^—0,3; д) у^0,85 и 1;
б) у^З и Vх 5; г) 8 и 1; е) 1/^ и 0,57.
472, Укажите какое-нибудь значение аргумента, при котором:
4—
а) значение функции у — у х больше, чем 2; 3; 10; 10°; '
б) значение функции у — -j/x меньше, чем 1; —10; —106. з,— <
473. Оцените значение выражения у х, если:
а) 1 х <?8; б) —1 х 1; в) —27 х 0.
474. На какое множество функция у = у х отображает промежуток: а) [0; 1]; б) [0; 16]; в) [1; 81[; г) ]256; 625[7 й
475. Решите уравнение:
а) ]/х = 5; б) угх — —0,5; в) у^х = — 2; г) ух = 0. 1
476. Решите уравнение и неравенства:
Упражнения для повторения
477. Докажите, что при положительных значениях переменных истинно неравенство:
а) х4 + у4 х3у Н~ ху3; б) а4 + 1 а3 + а.
26. СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ Я-Й СТЕПЕНИ
Нам известны следующие свойства арифметического квадратного корня:
если а > 0 и b 0, то ]/ ab • ]/&;
Уа
У'ъ'
если а > 0 и Ъ > 0, то
Аналогичными свойствами обладает арифметический
ко-
рень n-й степени и при п > 2.
Теорема 1. Если
Теорема 2. Если
Докажем теорему 1.
Л < Ч. ZX П Г 7 П /
а > 0 и Ъ > 0, то у ab » у а •
а > 0 и & > 0, то
Значение выражения у а • yb
неотрицательно, так как при а 0 и b 0 каждое из выражений имеет смысл и принимает неотрицательное значение. Кроме того, п-я степень
п---П/-Т~
произведения у а • у о равна abx
(j/а • Уъ)п = (j/a )" • Ъ )п --= ab.
Поэтому на основании определения арифметического корня лг-й степени равенство УаЪ — У а -Уб, где а^О и &^0, истинно.
Таким образом, при любом натуральном п корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Рассуждая аналогично, можно доказать второе свойство арифметического корня (теорему 2): при любом натуральном п корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Приведем примеры применения этих теорем.
4,-----
Пример 1. Найти значение выражения у 16 • 81.
4------4 4 г—
По теореме 1 имеем: у 16 • 81 = у 16 • у 81 = 2 • 3 = 6.
Пример 2. Упростить выражение У2 • ]/Т.
Запишем равенство УаЪ = У а * Уъ, где а 0 и Ъ ^>0, иначе: У а • У Ъ = у7 аЬ. Воспользовавшись им, получим:
Пример 3. Найти значение выражения По теореме
tio '27
2 имеем:
1/Л2^ = = * = 11.
V 27 К 27 3,— 3 А3
другие свойства корня n-й степени. Начнем
Рассмотрим с примера. ___
Пусть требуется сравнить значения выражений ]/у 64 и ]Z64:
V(/64 = ]/Т = 2; ^64 = ^2“ = 2.
Мы видим, что значения этих выражений равны, т. е.
ПГ h__ ПЪ_____
то у уа = уа (п, к —
Теорема 3. Если натуральные числа).
Значение выражения yf а неотрицательно. Кроме того,
пк-я степень выражения у у а равна а.
Действительно,
\у у а ) ]/а ) ) - \у а ) ^а.
Следовательно, по определению арифметического корня ра-rt/" k /-- /----- _
венство у у а = у а , где а > 0, истинно.
Теорема 4. Если а > 0, то 'у7amk — (п, k и т —
натуральные числа).
По теореме 3 имеем:
nk
amk = / ат.
Мы доказали, что если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
Это свойство корня иногда называют основным свойством корня (по аналогии с основным свойством дроби).
Приведем пример применения теорем 3 и 4.
Упростить выражение у^2]/~2.
Внесем множитель 2 под знак квадратного корня, получим:
По теореме 3 имеем: V]/23 = ^23. 6 _____________________________ -
Применяя теорему 4, получим: л/ 23 — у"2.
Итак, ^2/2' =/2?
478. Найдите значение выражения: a) /«Г27; г) У625 • 16;
б) /125 • 27; д) 0,001 • 125;
в) У 16 - 81; е) У0,0016 - 81;
479. Вычислите:
а) / 74 • 24; г) У3“ • 0,516; ж) / 54 • 24;
б) /б^¥5; д) у/24^9; з) ^3| • 11.
в) 2е • З13; е) ^75 • 45;
480, Найдите значение а) /20 /б;
б) г ТбО • у1б;
в) /8^3 • /2^27;
г) /2562 /25^8;
произведения:
д) /з^б3 • /з^б2;
е) /т4^!5 • /т2^3;
ж) У 9 + /17 • /9 — /17;
з) V 10-/19- V 10 + /19.
481. Найдите значение корня:
482. Найдите значение дроби:
. /8 -ч /б4 . Уз' . /б
а) -—; б) -—; в) -—; г) —*---.
7 i/'5" 3,— ' 4 ,— ' 5 г---
Г 2 /2 /48 /500000
483. Зная, что буквами обозначены неотрицательные числа,
представьте выражение в виде одночлена:
а) /25а2; б) /8&3; в) /81с4; г) /32х10; д) /8х12.
У
л.
• , 4
484.
485.
дроби:
Представьте выражение в виде
в) j/1.8; е) j/ где Ъ > 0;
ж) т/ где а > 0;
V 6
где b > 0.
Вынесите множитель за знак корня (буквами обозначены неотрицательные числа):
а) /4а; в) /бОх3;
б) /18&; г) У 27^;
д) 16с; ж) 81д6;
е) у^ба4; з) р10с8.
из
486. Внесите множитель под знак корня:
а) 2}/’3; в) 2^5; д) З-р/_1; ж) а у" 2, где а > 0;
б) 3 \/ 2; г) 5 уг2; е) 21/^—; з) Ъ j/'5, где & > 0.
487.
Приведите выражение к виду сцУЪ, где а — рациональное число, Ъ ™ натуральное:
488. Упростите выражение:
8/
г) и У 12;
д) У2
е) У R
489. Вычислите с помощью таблиц квадратных корней:
д) У 5 у 5; ж) У х Ух, где х >0;
а) /18; б) /1,62; в) /з,124; г) /б,25.
490. Упростите выражение:
а) )/б2; в) )/253;
б) 76; г) У363;
491. Сравните числа:
а) у 3 и у^б; в) у'8 и д) у7" 5 и И 2 у 3;
б) У 2 и у"7; г) у^2 и у445; е) уЛ7 и Зу 2.
492. Определите знак разности:
а) ]/2 — ]/ 3; б) /3 — y^4; в) у 4 — у 5; г) У 5 — у 6.
493. Найдите значение выражения:
а) У 7 + /22 • /? — /22;
б) У 1 — 4 /3 • V2 + /3;
Г) У 4 — 2 /2 • /6 4-4/2.
Упражнения для повторения
494. Турист проплыл на байдарке 4 км по течению реки, а затем 3 км против течения, затратив на весь путь столько же времени, сколько ему понадобилось на то, чтобы проплыть
10 км в стоячей воде. Зная, что скорость течения реки равна 3 км/ч, найдите скорость лодки в стоячей воде. 495. Докажите, что последовательность (хп), заданная формулой хп = 8 — Зп, является арифметической прогрессией. Найдите первый член и разность прогрессии.
496. Докажите, что последовательность (уЛ), заданная фор-
сией. Найдите первый член и знаменатель прогрессии.
497. Последовательность (ап) задана формулой ап ~ +за-
является ли членом последовательности число: 6; —6; 5?
§ 10.
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ
27. ФУНКЦИЯ у ах, ГДЕ Х£ Z И ЕЕ СВОЙСТВА
Формула у = ах, где а — некоторое число, отличное от нуля, а х ~ переменная, принимающая целые значения, задает функцию»
Свойства этой функции зависят от того, каким является основание а. Рассмотрим четыре случая: а > 1; 0 < а < 1; а = 1; а < 0.
4
1. Пусть а > 1, например а — _. Тогда функция задается 3
/ 4 формулой у = — . Составим таблицу соответственных зна-у 3 /
чений аргумента и функции, причем значения у выразим в десятичных дробях с двумя знаками после запятой:
X —4 —3 —2 —1 0 1 2 3 4
У 0,32 0,42 0,56 0,75 1,00 1,33 1,78 2,37 3,16
В координатной плоскости отметим точки, координаты которых помещены в таблице. График функции (рис. 65) состоит из отдельных точек, абсциссы которых — целые числа.
2
2. Пусть 0 < а <1, например а = Функция задается
формулой у
Составим
таблицу соответственных зна-
чений аргумента и функции. Зна-
чения у также выразим в десятичных дробях с двумя знаками после запятой:
1 " 3 1 1 to —1 0 1 2 со 4
У 5,06 3,38 2,25 1,50 1,00 0,67 0,44 0,30 0,20
Построим график (рис. 66).
3. Пусть а — 1. Тогда при
Рис. 66
любом целом х значение функции у — Iх равно 1. График функции (рис. 67) состоит из точек, принадлежащих прямой у = 1, имеющих целые абсциссы.
4. Пусть а < 0, например
мулой у — (—2)х, составим таб-
лицу:
Построим график (рис. 68).
Мы рассмотрели примеры функций, заданных формулами вида у = пх, при различных значениях а: а > 1, 0 < а < 1, а — 1 и а < 0. Эти примеры позволяют высказать предположение, что функция, заданная формулой у = пх, где х £ Z:
1) при любом положительном а принимает только положительные значения;
2) при а > 1 она возрастает^ при 0 < а < 1 убывает. Эти свойства функции действительно имеют место.
Докажем первое свойство.
По условию а > 0.
Если х — натуральное число, большее 1, то значение степени ах есть произведение х положительных множителей, каждый из которых равен а. Следовательно, ах > 0.
Если х = 1, то а1 = а. Но а > 0. Значит, ах > 0.
Если х ~ 0, то а0 = 1 и, следовательно, ах>0.
Если х — целое отрица-1 тельное число, то ах —----,
агх где —х — натуральное число. А выше мы доказали, что а~х > 0 (значение степени положительного числа а с натуральным показателем есть положительное число). Поэтому —- > 0, т. е. ах > 0. а~х
Следовательно, при лю-
бом целом х и положитель- Рис. 68
ном а значение степени ах — положительное число.
Докажем второе свойство для случая, когда а> 1, т. е, докажем, что если а > 1 и xt и х2 — любые целые числа, причем х2 > хх, то а4 > а\
С этой целью составим разность а?2 — аХ1 и покажем, что она является положительным числом. Для этого представим разность в виде произведения:
- {/L —ч
_| 4
и
— О-
4 -
1<
“5 4 • -7 X
-4 -2 О. 5 I <
-7
“4^ *
6
п
/
- ' а> й и
г
I I I b-т -
1
— @,xi = xt
1).
^Первый множитель ах^ положителен по свойству 1 (по условию а > 1 и хх С Я).
Второй множитель ах^~~х^ — 1 также положителен. Действительно, так как х2 > хп то х2 — хх > 0, т. е. х2 — х± £ N, По условию а > 1, поэтому ax*~xi > 1 (из того, что а > 1 и n С 2V, следует, что ап > Р, т. е. ап > 1). Значит, _ 1 > 0.
Поэтому произведение ах* — 1) как произведение положительных чисел является положительным числом. Отсюда следует, что а х*— ах* > 0, т. е. ах? >
Аналогично можно показать, что при 0 < а < 1 функция у = где х £ Z, убывающая.
Мы выяснили некоторые свойства функции у = ах при положительном основании а, отличном от 1.
Заметим, что при а =* 1 функция у = ах при любых целых х принимает лишь одно значение, равное 1. Поэтому она не является ни возрастающей, ни убывающей.
При а < 0 функция у == ах кож'? принимать как положительные, так и отрицательные значения и также не является ни возрастающей, ни убывающей, т. е. не обладает ни одним из указанных выше свойств. Это было показано на примере функции у = (—2)\
В дальнейшем (в школьном курсе математики) функция у = ах будет рассматриваться только при положительном основании а.
Постройте график функции, заданной формулой: /1 \*
1) у = 3х, где х £ Z; б) у == — , где х £ Z.
\ з /
Ответьте на вопросы:
1) Является ли возрастающей или убывающей данная функция?
2) Существуют ли значения х, при которых у — 9; 1;
1; —3; 2?
27
3) Принадлежит ли графику функции точка: А
В (—4; 81); С (5; 243)?
4) На основании какого свойства функции у — утверждать, что из равенства х2 € следует, что хх ~ х2?
Решите уравнение:
можно где Xi С Z и
В**
500.
501
9
1;
б) 3х - 81;
Укажите множество целых значений полняется неравенство:
а) 4 < 2х < 16;
б)-?
128;
Докажите, что не
Упражнения Найдите пятый в которой:
= 3 /3? q =
а)
б)
в) 20
100;
х = 0.
х, для которых вы-
16 ' V 2 /
имеет корней уравнение:
для повторения
член геометрической прогрессии (crt),
г) Cj= ]/2, q = у 6.
/з ’
Д) v
4
5
503. Найдите знаменатель геометрической прогрессии (&/2), если:
а) = р Ъв = -51; в) bt = bt = -1;
б) bt = —12, b? = 231; г) &2 = 1, &10 = 1.
16 1О
28. ОПРЕДЕЛЕНИЕ СТЕПЕНИ С ДРОБНЫМ ПОКАЗАТЕЛЕМ
Рассмотрим функцию у — 2\ Выражение 2х имеет смысл лишь при целых значениях переменной х, поэтому область определения функции у = 2х есть множество целых чисел. Кроме того, известно, что при любых целых х и а > 0 выражение ах > 0. Поэтому график функции у — 2х расположен в верхней полуплоскости.
Чтобы построить график этой функции, составим таблицу:
3
О
х
—3
У
4
График функции (рис. 69) состоит из отдельных точек, абсциссы которых — целые числа.
Можно заметить, что построенные точки располагаются по некоторой плавной линии. Проведем эту кривую (рис. 70). Ее можно считать графиком некоторой новой функции Д областью определения которой служит множество всех чисел.
vL
со л *
7
ь -— ******
£
о
-
4 1 > -
*
3
го
. ....
* 0. -1 > _3_ Jr
□ _LJ
Рис. 69
Рис. 76
Значения функции f для целых значений аргумента могут при для
быть найдены по формуле у = 2х. Если бы эта формула нахождении значений функции / оказалась пригодной и дробных значений х, то пришлось бы считать, что
1 3
сте-
L Л
Но выражения 22 , 22 не имеют смысла, так как понятие пени было определено лишь для целого показателя.
Чтобы придать смысл этим выражениям, нужно расширить понятие степени, определив степень с дробным показателем.
При этом будем исходить из двух условий:
1) Основное свойство степени атап — аш+/г, выполняющееся для целых т и п, должно сохраняться и для дробных показателей.
2) Значение степени ах, где а > 0, должно быть положительным числом при любом дробном X.
Приняв эти два условия, постараемся выяснить, какой смысл
следует придать, например, выражению 22.
Исходя из первого условия, мы должны принять, что
1 1 1 / _1\2
22 • 2 2 = 22 2 ~ 21 — 2, т. е. (2 2 / — 2, а исходя из второго —
что
2
0.
Отсюда вытекает, что под выражением 22 следует понимать положительное число, квадрат которого равен 2, т. е. арифметический квадратный корень из двух:
2
Руководствуясь теми же соображениями, т. е. выполнимостью указанных выше двух условий в применении к выражениям _ А
5 4 , должны получить:
2 2 2 2 2
3 к 3 _ к 3 + 3 + 3
___5_ _ _5
10 4 •10 4 • 10
___ _5_5__ _5
-10 4 4 4
2
3
•lo'h
5
4 = 10~5,
2_\3 2
Г = 52 и 5~ > 0.
/ _ А\4
т. е. 10 4
Значит, следует принять, что:
= у б2
5 — "7* 4 г*—_—*
io = Z ю-5.
Рассмотренные примеры показывают целесообразность следующего определения степени с дробным показателем.
О п р е д е л е н и е 1. Если а > 0 и х — произвольное дроб-
ное число, представленное в виде —, где т — целое, а п —пату-п
т
ральное, то ах =s ап = а/\
Определение 2. Если а = 0 и X — дробное положи-
тельное число, то ах = 0.
Согласно принятым определениям имеем:
(0,Т)а =у'"0,7"; 5 • =5“ = У5-'; II}'-3 = ШЙ _ 1/W; 0Т-0.
\з/ \з} У \3j
___L з i
Такие выражения, как 0 5, (—2)8 и (—8)3, не имеют смысла.
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,75 можно представить в виде дроби так:
з
4’
6 9 12
—, —, — и т. д.
8 12 16
Значение степени с дробным показателем не зависит от выбора способа записи числа х в виде дроби; представляя дробное число х в виде отношения целого числа к натуральному разными способами, всегда будем получать один и тот же результат. Покажем это на примере. Пусть а > 0. Тогда
"X 6 3 3 6
8 3/—я У—ч 4 4 8
а = у аь = у аА ~ а и, значит, а =а .
Всякое дробное число можно представить единственным способом в виде р
несократимой дроби —, где р £ Z, g С Ж. Все другие дроби, представляющие
это же число в виде отношения целого числа к натуральному, получаются из . Р
дроби — умножением на одно и то же натуральное число к ее числителя и зна-0.
менателя. Учитывая это, можно легко доказать, что значение степени с дробным показателем не зависит от того, каким образом представлен этот показатель в £
виде отношения целого числа к натуральному, т. е. ад — ад'. Действительно,
Л = = а7
121
4
Замечание. Если а >0 и х—дробное число, 2а-т писанное в виде дроби —, где т С Z, то равенство ап = п
~ у/ат верно по определению степени с дробным показате- • лем. Если а> 0 и х — целое число, представленное дробью —, П т
где и С ДГ, то равенство ап =^/ат также верно, но не на основании определения степени с дробным показателем, а на основании определения арифметического корня. Покажем это на 9
примере: 23 = 23 ™ у/ (23)3 = у/^29.
504. Замените степени с дробными показателями корнями:
3 1 1 111 2
। । -ш* — । ** • 4| и,
а)75;5б) 7;6 3; 10~Ч г) Зх2; (Зх)2; -у5; —у 3;
5
_ 2 __1_ 2 JL А 2
6)2,5 3; (—) 2; О,50'5; д) (аЬ)3; ab~‘, (а + &)3; а3 + &3; V 9 / __________________________________________________
в) а0,5; &1’2; с“0,6; й“1,5; е) ху”1’5; 4(х—у)”1,5; 2х(х+у) 8.
505. Используя таблицы квадратных корней, найдите значение выражения в виде десятичной дроби с двумя знаками после запятой:
1 1 2_ 1 1 _i_
а) 1722 ; б) 2,72; в) О,830Д, г) 32 + 22 ; д) 292 — 62.
506. Замените арифметический корень степенью с дробным показателем:
а) /3; в) у 1432; д) т/С1;
V 1&
б) У0,2; г) у/"733; е) у/ 2“5;
507. Вычислите:
И) ^7 + С;
к) у X2 + У2’
а) 1002;
б) 8Т;
508. Имеет ли
509. Найдите
__L _L
в) 3,61 2; д)06;
1 3
г) 27 3 ; е) 814;
смысл выражение:
к) 0,01~2’5.
2 4
о” 3; О9?
область определения выражения:
1 1 3 _ __ _1_
а)х2; б) (г/— I)3; в)(а + 2)5; г) & 8; д)(с — 5) 3
510. Запишите выражения в виде степеней, показателями которых служат дроби с одинаковыми знаменателями;
1 I 1 1
а) 52 и 7 ’; б) З2, 44 и б1. 1 1 1
511. Оцените значения выражений х2, х 3 и х6 , если:
а) 0 < х < 1; б) 1 < х < 64; в) 64 < х < 1 000 000.
Упражнения для повторения
512. а) Длина одной из сторон прямоугольника на 4 см больше, чем длина другой стороны. Найдите длину диагонали этого прямоугольника, если известно, что его площадь равна 21 см2. (Ответ дайте с точностью до 0,1 см.)
б) В прямоугольном треугольнике один из катетов на 2 см длиннее другого. Найдите длину гипотенузы этого треугольника, если известно, что его площадь равна 84 см2. (Ответ дайте с точностью до 0,1 см.)
29. СВОЙСТВА СТЕПЕНИ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ
Ранее мы установили свойства степени с целым показателем. Если основания степеней положительны, то эти свойства остаются справедливыми и для степеней с любыми рациональными показателями.
Перечислим эти свойства.
При любом положительном а и любых рациональных значенияхр и q
(1)
а,р ; ад ар-^ (2)
(а^==а^. (3)
Кроме того, при а > 0 и & > 0 и рациональном значении р имеют место свойства
(4)
(аЪ)Р == ар • Ър9
(5)
Докажем свойство (1) для р
1
q = —, т. е. докажем, что 5
2 1
Приведем показатели — и — к общему знаменателю.
3 5
2 I 10 3_
Тогда a3a5 = a15a10. 10 3
“—"* I * “ J
Так как a15 = y^a10 и a15 = у a3, то по свойству арифметического корня имеем:
Переходя к степени с дробным показателем, получим:
13
i L3 13
Следовательно, a3 a5 = а15. Но ™ =
2
з
поэтому
Проведем доказательство свойства (1) в общем виде.
Представим показатели р и q в виде дробей с одинаковыми k т , _
знаменателями: р — — и q~-—, где н и т— целые числа, а п п
п — натуральное число. Тогда
k tn k-j-m
apaQ = ап an — -^ай • ===: ak+tn = a n =
= ap+<h
Из свойства (1) следует, что для любого положительного а и любого рационального р
Действительно, ар • а р = а0 = 1. Отсюда а~р
Докажем свойство (3) для р == —, q — т. е. / 7 V 7_ .
= JL ар *
докажем, что
По определению степени с рациональным показателем
Выполняя преобразования, получим:
/ 7 \ 4 7 4
I “ I — • .1
Следовательно, \ан/5 = а11 5. Из свойства (3) следует, что
р /2/--
при всяком рациональном р у ар — ап (а > 0, п€N и п#= 1).
Действительно, по определению степени с дробным показателем и свойству (3) имеем:
Пг- - Р--1-
= (а/)" = а "=а".
Докажем свойство (4) для р = т. е. докажем, что истин-8
но равенство
3 3 3
(а&)8 = а8 Ь8 («>0 и &>0).
По определению степени с дробным показателем и свойству арифметического корня имеем:
1 1 L
(а&)8 = У(ab)3 — у"а3Ь3 ~ у^а3 • у^Ь3 — а8 Ь8 ♦.
513.
Представьте выражение в виде
степени с рациональным
показателем:
0—1д/*0,6
1 1 2 J____5_ /
а) с2 с3; г) а3 а6 а3; ж) (а2
1 1
б) Ь 3 Ъ2; д) у0’8#-5*/7,2; з) (х°’4)~2>5;
Ь2 у3 ; и) (у”0’5)-1.
514. Упростите:
/ 2 \°,6 2 / 1 \ 1 / 1X2
ч I 3 ля 5 . L. 3 • 2 „ 4 I 3,
а) \Х / • х , в) у • \у у ,
/ __5_\°,4 , / 5X1,2 / „ХУ1*5
б) \у 8 у • у0»25; г) \с12/ : \с 3 у
515. Вычислите:
516. Найдите значение выражения:
а) (81 • 16)4 ;
б) (81 16) 4;
/ х 1
В) (0,01 ~ 2;
\ 49/
1
д) 100 000°>2. (0,001)3;
517. Упростите выражение:
__ 2 _ £
a) (125xG) 3; в) (х~2) 2;
__ 1 _ _2_
б) (27х3) 3; г) (64с12) 3";
е) (&~6) 3.
518. Упростите выражение:
j>_ _ 1 I _ 1 J_V / 1
а) а3 • & 6 \а 3 &3 / ; в) (а4 х 3 / 5 • а°’7х°>8;
/ 3 • \3 2 5 / _2_ £\-3,5
б) \с 7 у~°>4/ -с7у°>2; г) p~~vq* \р 7 q/
519. Представьте выражение в виде квадрата (х > 0);
XG
7 л ।
1 I
520. Представьте выражение в виде куба (у > 0):
1 __ 1 __ 2
г/в; г/-2ь у’; г/; г/2 ; г/-1»6; у 3; г/°>а; у 9.
521. Известно, что а — положительное число. Представьте а в виде:
а) квадрата; в) седьмой степени;
б) куба; г) пятнадцатой степени.
L
522. Зная, что З2 1,73, найдите:
а) 3 2 ; б) 3Т; в) 3~Т; г) з“\
1
523. Зная, что 4,312 = а, найдите:
1 1 . jr_ i
а) 4312; б) 431002 ; в) 0,04312 ; г) 0,0004312 .
524. Объем куба равен V. Используя дробные показатели степени, выразите:
а) длину а ребра куба через его объем V;
б) площадь S грани куба через его объем V;
в) поверхность Р куба через его объем V.
525. Зная, что х > 0 и у >0, выразите х через у:
2 __J3_ 4
а) у = х3; в) у = х 2; д) у = эх5;
2
4 ~ 3
б) у = х7; г) у = х“°>75; е) у = --------.
526. Представьте выражение в виде степени с дробным показателем:
ЮЛ— 1Г/—- Ч 7Л— 3- . 10/—
а) ]/ х • У х\ в) у у2 • у у х; д) У уу у2;
б) • ]Za; \г) y^^j/'b; е) У^ х2 угх~~3.
527. Докажите, что при любом а > 0 истинно равенство:
а)
528. Упростите выражение:
529. Укажите множество значений х, при которых истинно равенство:
530. Решите уравнение:
в) х1»5 = 27;
г) х“0’8 = 16;
Упражнения для повторения
531. Решите неравенство:
а) (2,5х + 1) (4х — 3) — 5х (2х + 7) <4;
б) (3 — 4х)2 — (8х — 1) (2х + 9) — 11 >0.
532. Найдите первый член и разность арифметической прогрессии (ал), если:
а) Га4 + ап — 0,2, б) (а2 + а4 — 18, |а9 — а5 = 2,4; ]а3 • а5 — 144.
533. Найдите площадь фигуры, задаваемой на координатной плоскости системой неравенств:
30. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ. СОДЕРЖАЩИХ СТЕПЕНИ С ДРОБНЫМИ ПОКАЗАТЕЛЯМИ
Рассмотрим различные примеры, в которых используются тождественные преобразования выражений, содержащих степени с дробными показателями.
Пример 1. Найти значение выражения
х4 —6/ —12х4 (х 4 —1/ при х = 12,25
Предварительно упростим выражение, т. е. преобразуем его в другое, тождественно равное первоначальному на области его определения, но содержащее меньшее число операций:
х4 _ej — 12х4 (х 4 —1J = х2 — 12х4 + 36 — 12х° + 12х4 =
— х2 +24.
Равенство
1 \2 1 / 1 \ 1
I *—***^* J 1
X4 —в — 12х4 \х 4 — 1 = х2 +24
является тождеством на области определения первоначального выражения, т. е. на множестве положительных значений х.
Подставляя в выражение х2 + 24 данное значение х и учитывая, что 12,25 = 3,52, получим:
(3,52)2 + 24 = 3,5 + 24 = 27,5.
Пример 2. Сократить дробь
з
4
4
25х
х -н ох
Данная дробь определена при х > 0. Разложим на множители числитель и знаменатель дроби и сократим ее:
з 1
4 4
х — 25х
+ / JL
4 I 2
х \х — 25
х — 5/ \х +5
= X
Выражение х4 — 5 тождественно равно первоначальному на множестве положительных значений х, т. е. на области определения исходной дроби.
534. Представьте выражение
е) (2 — у1-5) (2 + г/1’5);
535. Упростите выражение:
в виде суммы:
536. Пользуясь тождеством а2 — Ь2 = (а — Ь) (а + Ь), разложите на множители выражение:
2
а) 3 —х2; г) у5 — 9; ж) х— 2, где х^О;
4
б) у1—5г х д) 25 — р7з) 10— у, где г/>0.
/ _1 \2 !
в) \х3 / — 4; е) а — Ъ2 , где а > 0;
537.
Пользуясь тождеством а3 ± &3 = (а ± Ь) (а2 аЪ + Ь2), представьте выражение в виде произведения:
з
в) р 4~ 1» в
г) q5 —125;
д) 125 — &, где &>0;
з
е) у — 22, где у > 0.
538. Разложите на множители:
1 j_ г 1 г г
а) 24-22; в)а+а2; д) (ab)3 + (ас)3; ж) 153 +203;
1 1 1 1 1 1
6)3—З2; Г)&3—5; е) 62 — 22 , з) (2а)2 — (5а)2;
5 Алгебра 8 кл»
129
i _i_ i i
и) с2 Ц- с4; к) 53 — 54;
12 2 4
л) 125 —25 ; м) 183 —63.
539. Сократите дробь:
в)
540. Найдите значение выражения:
1
2
ч а — 4а ч х 2х 4-16 _ лл ОГ7.
а) —--------—- при а — 81; в) -------------------- при х == 27;
4” . л т ~ т
а + 2а х — 2 х — 4
1 _1_ 1
2 -6 4
х — 9х ч 8 . у — 8у ок
б) —--------— при х = 64; г) —-----------h L___£— при у = 25.
т „ т т ( о т .
х — Зх У +2 у — 4
541. Упростите выражение:
Упражнения для повторения
542. Решите систему неравенств:
а) Г 4 (х — 1) — 2 (х + 1) > О, б) / Зх + 8 — (2х— 5) < О, ( Зх — 1 — 4 (х — 10) <0; [ 2 (6х—4)—3 (х + 1) > 0.
543. а) Найдите сумму всех двузначных чисел, кратных 7.
б) Найдите сумму всех двузначных чисел, некратных 3. 544. а) Турист отправился пешком из города на турбазу. Если бы он проходил в час одним километром больше, то затра-тил бы — того времени, которое ему необходимо теперь;
6
а если бы он проходил в час одним километром меньше, 5
то пробыл бы в дороге на — ч дольше, чем теперь. Найдите 6
расстояние от города до турбазы.
б) Пройдя путь АВ, пешеход рассчитал, что он мог бы прийти в В на 1 ч раньше, если бы проходил в час на 0,8 км больше, и на полтора часа позже, если бы проходил в час на 0,8 км меньше, чем в действительности. Найдите расстояние АВ.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К ГЛАВЕ IV
К пункту 21
545. Отношение между натуральными числами задано уравнением: к) х + у ~ 7; б) 2х + Зу = 36.
Задайте множеством пар данное отношение; отношение, обратное данному.
546. Задайте уравнением с двумя переменными отношение: а) «быть обратным числом» между положительными числами;
б) «быть противоположным числом» между рациональными числами.
Задайте уравнением отношение, обратное данному.
547. Постройте график отношения, заданного предложением «х < z/», где х С {2; 3; 4; 5} и у б {2; 3; 4; 5}, и график обратного ему отношения.
548. Постройте график отношения f и график обратного ему отношения, зная, что отношение / задано уравнением:
а) г/ = ]/х; б) у = 2 | х|; в) у = (х — 2)2; г) у ~х2 — 2х.
549. Постройте график отношения, заданного неравенством у х + 2, где х > 0, и график обратного ему отношения.
550. Докажите, что отношение, заданное уравнением:
а) х2 + У2 = 25; б) ху — 12; в) х + у = 6,
обладает свойством симметричности. Как это отражается
на графике отношения? Что служит графиком отношения
обратного данному?
К пункту 22
551. Точки А (—10; 21) и В (15; 21) принадлежат графику некоторой функции й. Достаточно ли этих данных, чтобы судить, обратима функция h или нет?
552. Точки С (—3; 16) и D (5; 48) принадлежат графику некоторой функции р. Можно ли на основании этих данных сделать вывод, что функция р обратима или необратима?
553. Обратима ли функция, заданная формулой:
а) у = где х > 0; г) у = х2, где х > —5;
X
б) у = где х < 0; д) у = х2 — 2, где х < —1;
X
в) у = х2, где х > 5; е) у = х2 — 2, где х > —1?
554.
Некоторая функция задана формулой у := f (х) на отрезке
[—10; 10], причем известно, что f — возрастающая функ
ция. Будет ли обратимой функция, заданная формулой:
а) у = Л(х), где х С [—5; 5];
б) у = /(х), где X с СО; 5]?
555.
556.
557.
558.
559.
а) Функция q задана с помощью пар: (1; 8), (2; 35), (3; 29), (4; 103). Является ли функция возрастающей; обратимой? б) Функция задана формулой у = (—2)rt, где п Е N. Является ли эта функция возрастающей; убывающей; обратимой?
Известно, что точки А (—8; 1), В (1; 7), С (21; 21) принадлежат графику функции /. Какие из точек D (7; 1), Е (—1; 8), F (1; —8), С (21; 21) принадлежат графику отношения, обратного функции /? О каких точках этого сказать нельзя?
В одной и той же системе координат постройте график
данной ясните, вестно,
функции и график обратного ей отношения. Вы-
является ли это отношение
что данная функция задана формулой:
если из-
а) у = — х; б) у = —х2; в) у = — Xs; г) у = —Ух.
Докажите, где а =^= 0, функцию.
что всякая обратима.
линейная
ункция
Задайте формулой обратную ей
Задайте формулой функцию, обратную данной:
у — ах + &,
К пункту 23
560. Даны функции f (х) = х30 и g (х) = х25. Известно, что f (а) = 50, g (&) — 85. Найдите f (—а) и g (—Ъ).
561. Объясните, почему истинно неравенство:
а)
5Ю0
в) 1,52М
1,6261;
б) 0,87100 < 0,89100;
562. Сравните значения
степеней:
а) 210 и З10;
б) 0,35 и 0,25;
3 \2в1
е) 321 и 87.
в) l,5ia и 1>7i2.
563. Даны функции f (х) = х7 и g (х) = х10.
Не выполняя вычислений, сравните с нулем
а) /(25) —/(12); в) f (0) • f (60); д) g(-9)- g(-17);
б) f (-30)-/(-20); г) g (17)—g (5); e) g(38) g(0).
564. Найдите n, если известно, что график функции у = хп проходит через точку:
а) А (2; 8); б) В (3,5; 12,25); в) С (—3; 81); г) D (—2; —32).
565. Найдется ли такое натуральное значение п, при котором график функции у = хп проходит через точку:
а) А (2;5); б) В (КЗ; 81); в) С (—5; 415); г) D (—7; —343)?
К пункту 24
566. Сколько решений имеет уравнение (k С N):
а) х2й “1; б) х2й ——1; в) х2/г+1 =1; г) х2й+1=—1?
567. Найдите значение выражения:
а) -0,5^1024; г) j/jg • V 5^5 ^-125 (0,1)’;
б) _ A^ZZ2i87; д) т/П; .-1/^; з) у 16^ .-^0Д25Л о г 4 v
в) 1,5^512; е) (0,1) <;; и) у 32 ^ •/1бГ2.
568. Найдите область определения выражения:
569. Решите уравнение:
а) х6 = 12; в) х10 = 0;
б) х9 = 5; г) х11 = —3;
4 у-- 6 >---------
д) Ух+ 1=2; ж)]7х+8=—1;
е)у^х— 2 = 1; з) угх— 7=—2.
К пункту 25
570.
571.
572.
573.
574.
Используя свойства функции у — у х, сравните значения корней:
а) у23 и 27; б) /—5 и /—4; в) —0,1 и у^0,01.
Определите знак разности:
а) у^б — /7; в) j/
б) уп — /10; г) 1 —
Пользуясь графиками функций у = х, у = Ух, у = ух, решите уравнение или неравенство:
а) |х = х; в) |/х < х; д) ух > х;
ч 3/— 3.-
б) у х > х; г) у х = х; е) у х < х.
Постройте график функции:
а) у =— ]Лх; б) у =— ух; в) у = У|х]; г) у = /ГЦ
Оцените значение выражения ух, если:
а) 0 < х < 1; б) 1 < х < 1000; в) 1000 < х < 1010.
К пункту 26
j м 575
576.
577.
Найдите значение выражения:
a) t/*ELJ?Z; в) т/32Е15.
V .125 7 V 16 . 625 7 К 7Ю ’ k
Вынесите множитель за знак корня (буквами обозначены неотрицательные числа):
а) V 16x2i/; б) Ув) у4125а5х3; г) 64д12у7.
Упростите выражение (буквами обозначены положитель ные числа):
81 .
--— ?
6
б) хп/Д;
2 У
578. Определите знак разности:
а) - ^2; 6) /J _ -j/T. в) г) ^7 _ » Г',
579. Расположите в порядке возрастания числа:
а) уЗ; ^6; в) /0,5- ^2;
б) |Л1; у^бТЗб; ^0Д5; г) 5 j/.L; 3 1; 2 у
580. Докажите, что при а > 0 истинно равенство:
581. Является ли равенство тождеством на множестве положив тельных значений х:
а) уг4х2 = V2х; б) 27х3 = у4Зх;
582. Докажите истинность равенства:
583. Представьте выражение в виде дроби с натуральны^ знаменателем:
584.
585.
Оцените значение выражения ]Лх--/~если: а) 0 < х < 1, 1 < у < 8; б) 1 < х < 25, i
Решите уравнение:
10/-~
в) ух -г5 = 0;
< у < 64 ♦
586. Дана геометрическая прогрессия с положительными членами: Ь^, Ъ%\ Ъ3', Ьп*, ... . Является ли геометрической прогрессией последовательность:
К пункту 27
587.
Функция f задана формулой у ~ дите / (0,1), /(0,2), /(0,3).
где 10х £ Z. Пай-
Существует ли значение х, при котором значение функции равно:
588. Покажите, что если переменная х принимает последовательно значения —2, —1, 0, 1, 2, то соответствующие значения выражения 2х составляют геометрическую прогрессию. Найдите знаменатель прогрессии.
589. Докажите, что если переменная х принимает последовательные целые значения из некоторого промежутка, то соответствующие значения выражения 2х образуют геометрическую прогрессию.
590. Докажите, что если последовательность целых чисел /п2, /п3, ... есть арифметическая прогрессия с разностью d, где d С Z, то последовательность 2ms 2m>, 2ms ... является геометрической прогрессией. Найдите ее знаменатель.
К пункту 28
591. Замените степени с дробными показателями корнями:
в) 7а“х»5;
г) —1,2ft-1»2;
Д) aft8;
5
е) (aft)8;
2
ж) (х + у)3;
2 2
3) X 3 + У 3 •
592. Замените выражения степенями с дробными показателями:
а) 2,5 ]/40; в) a ]/а; д) (х + 1)2р^х + 1;
б) —8^2; г) —fty^ft, где ft^O; е) (у — 5)Д/у— 5.
593. Сравните числа: 11 11 11 11 а) 22 и 33; б) 56 и 88; в) 33 и 54; г) 512 и 816.
594. Решите уравнение: 1 1 а) (х — 2)2 = 4; в) (у + 3)3 =- — 1; д) (а — 5)4=0;
Д~ 1 1
б) (х — 2)2 - 42; г) (у + З)"1 - 4; е) (а — 5)° - -4 3 4
595. В одной и той же системе координат постройте графики
1 1
функций у = X 2 , у — X 3 . 1 2_
596. Оцените значение выражения х5 ; х5 , зная, что:
а) - < х < 1; б) 1 < х < 32; в) 32 < х < 1000.
К пункту 29
597. Найдите значение выражения:
1
в) 164;
1
б) (0,81)2 ; г)
1
д) 3433 ;
з
ж) 274 ; и)
2
е) (0,001)3;
з)
2566; к) (0,000001) 3.
598.
Упростите
3 5
ч X 7 X21 а) ——;
X 6
выражение:
а • а0»9
е)
64Ь~3\- з 125а6/
599. Считая значения переменных положительными, упростите выражение, используя степени с дробными показателями:
Г) У*' .
600. Найдите значение выражения:
601. Найдите два каких-либо решения уравнения:
602. Найдите зависимость между
1 1
а) х — t2, б) х = t3, в)
У t 2; у = t6;
переменными х и у, если:
К пункту 30
603. Упростите выражение:
604. Представьте выражение в виде произведения двух множи телей, один из которых равен
L L
а) у2+у~°’е; б) у-1—у-0-4; в) Зу—1; г) у-3 + у2.
605. Пользуясь тождеством
а2 — &2 — (а — Ь) (а + &),
раз
ложите на множители:
а) У9 — 9;
б) а15 —16;
в) 9с0»3—4;
г) 2х3 — 49;
д) ът- 1;
е) У1’5 —У2',
1
ж) 2 2 —0,25;
з) а12 —12, где и > 0;
1 1
и) а264 —49.
606. Пользуясь тождеством а3 ± &3 ~ (а ± Ъ) разложите на множители выражение:
(a2 q= аЪ + Ь2)
а) х + 1000, где х > 0;
б) а0»9 — 8д, где Ъ > 0;
В) 27г/3” — 1;
г) а3>4 + &°Л
607. Разложите на множители:
1 1
ч 2 2
а) х — у 4~ х у ;
1 г
б) и— и2 + v2 — г;
2 1
в) & -4~ 2d -{- 2а -4~ 1;
608.
Выполните подстановку
и упростите выражение:
ху
X2 + У2 '
где х
609. Докажите, что значение выражения не зависит от п:
1
(9«__ 9«-1) 2
а) ----у-
(27я’1 — 19 • 27^-2) 3
610, Решите уравнение;
(16^-1— 16^-2) 4
а) х — 6х2 = 55;
2_ 2.
б) I/3 — 10?/ + 24 — 0;
1 1 3 3
в) Зх2 + 7х 4 + 1 = 0; г) 7у 4 + У8 — 8 = 0.
611. Найдите зависимость между переменными х и у, если:
2
у = (а — 1) , где а
з
2
Упростите выражение: о1,5 +&1’5 4-6*’5
0.5 >0.5
0.5
0.5
а)
а — b
0.5 । .0.5 .
613. Найдите значение выражения
а) при а = 3,75; б) при а = 56,25.
ГЛАВА
- . - - . - - .- • -- ~ -- - ' — .....- ~ . —
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
§ и
СВОЙСТВО ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
31. ФУНКЦИЯ у — 2х
Мы рассмотрели свойства функции, заданной формулой у — 2х на множестве целых чисел (см. п. 27). Теперь, после
введения понятия степени с рациональным показателем, можно
и
рассмотреть функцию, заданную той же формулой, на множе
стве рациональных чисел.
1
Составим таблицу значений функции у ~ 2Л’, с шагом —
4
(каждое последующее значение х будем брать на — больше пре-4
дыдущего).
L
Так как 22 = /2 1,414, то
24 = \22)2 /1414^1,189*.
L _1
Зная значения выражений 22 и 24, найдем значение выра-з_ жения 24:
з х + f 1 1
24 -2 2 4 — 22 • 24 « 1,414- 1,189 — 1,681.
Аналогично можно вычислить значения функции, соответствующие другим значениям х, указанным в таблице. Например:
2 4 =2 4 = 2-1 -24 « 0,5 • 1,681 = 0,8405;
_2+± А
2 2 =2 2 == 2-2 • 22 « 0,25 • 1,414 = 0,3535.
* См.: Б р а д и с В. М. Четырехзначные математические таблицы. М., Просвещение, 1978.
Заполним таблицу, округлив найденные значения выражения 2х до сотых:
Легко заметить, что любому значению переменной х, приведенному в таблице, соответствует положительное значение выражения 2х и что большему значению х соответствует большее значение выражения 2х.
Докажем, что функция, заданная формулой у ~ 2х на множестве рациональных чисел, обладает следующими свойствами:
1) функция принимает только положительные значения;
2) функция является возрастающей.
Доказательство свойства 1. Из определения степени с рациональным показателем следует, что при любом рациональном значении х выражение 2х принимает положительное значение, т. е. любое значение функции есть число положительное.
Доказательство свойства 2. Пусть хх и х2— произвольные рациональные числа, причем х2 > хх. Докажем, что 2*3 > 2\
Как известно, рациональное число можно представить в виде отношения целого числа к натуральному и притом различными способами.
Представим числа хх и х2 в виде дробей с целыми числителями и одинаковыми натуральными знаменателями:
хх = — и х2 где k^Z, т£ Z. п п
По условию х2 > хх, значит, т > k. Отсюда следует, что 2™ > 2й, так как на множестве целых чисел функция у — ах при а > 1 возрастает.
Мы получили, что 2™ > 2й, а так как функция у — jfx на множестве натуральных чисел возрастает, то отсюда следует, что
tn k
т. е. 2" > 2~.
Рис. 71
Рис. 72
Итак, если хх и х2 — рациональные числа и х2 >хп то 2*з > 2^, т. е. функция у =• 2х на множестве рациональных чисел является возрастающей.
Построим в координатной плоскости точки, координаты которых помещены в таблице. Эти точки намечают некоторую линию, расположенную выше оси абсцисс (рис. 71).
Уменьшая шаг таблицы, будем получать точки графика, попадающие на ту же линию и расположенные все более густо. На рисунке 72 построены точки графика функции у. — 2х для значений переменной х, взятых с шагом -i.
Примем без доказательства, что существует возрастающая функция, определенная на множестве действительных чисел и совпадающая с рассмотренной на множестве рациональных чисел. Она задается формулой у = 2х. Область значений этой функции — множество положительных чисел. Графиком ее служит кривая линия, изображенная на рисунке 73.
Это, в частности, означает, что мы уславливаемся считать имеющими смысл такие выражения, как 2|<3 , 2^ и вообще 2^, где ос — иррациональное число. Используя возрастание функ-142
ции у = можно указать границы, выраженные степенями числа 2 с рациональными показателями, в которых заключено значение выражения 2а.
Например, можно указать границы, в которых заключено значение выражения 2^:
так как 1 < |3 <2, то 21 < 2^3 < 22;
так как 1,7 < | 3< 1,8, < 21,8;
то
то z
614.
к как 1,73 < у 3 < 1,74, 73 < 2^3 < 21’74 и т. д. С помощью графика функции у = 2х (см. рис. 73) найдите: а) значение переменной у, соответствующее значению х, равному 0,7;
б) значение переменной х, которому соответствует значение у, равное
615.
616
617
Найдите показатель степени, в которую нужно возвести число 2, чтобы получить число 1; 2; 3; 4; 5; 6; 7; 8. (В необходимых случаях используйте график функции у = 2Л.) Пользуясь графиком функции это возможно, числа 3,5; 0,4; основанием 2.
С помощью графика функции
представьте, если О в виде степени с
решите уравнение:
618.
Сколько решений имеет уравнение 2х
= Ь, где:
9
а) Ъ > 0; б) Ъ < 0?
619. Что больше:
а) 245 или 248; в) 2-°>5 или 2“45; д) 23 или 20Л
б) 23»6 или 2°; г) 2~47 или 2°; е) 27 или 2°>143?
620. При каких значениях х значение выражения 2х: а) равно 1; б) меньше 1; в) больше 1?
621. Каков знак числа х, если:
а) 2х = 6; б) 2х = в) 2х = 0,01; г) 2х = 1000?
622. Пользуясь графиком функции у ~ 2х, укажите границы, в которых заключено:
а) значение выражения 2^\ если 1,4<]^2 < 1,5;
б) значение выражения 2^ , если 1,7 <*|/"5 < 1,8.
623. Укажите несколько значений переменной х, при которых значение выражения 2х:
а) больше 0; 1; 32; 100; 1000; б) меньше 1; -i; 0,002.
64
624. Докажите, что:
а) (х > 7) ==> (2х > 100); б) (х < —3) (2х < 0,2).
4
625. а) Следует ли из неравенства х 5 неравенство:
2х > 50; 2х > 30?
б) Следует ли из неравенства х < —3 неравенство:
2х <10; 2-* < 0,1?
626. Решите уравнение и неравенства:
а) 2х' =» 4,
б) 2х =|, в) 2х = —5,
Упражнения для повторения
627.
X
Л
Упростите выражение:
‘а) (2г’>’5 4- Зх®>25)2 — 4х°>5 (х + 2, ' g1.5 —&М . / д°>5 4-&0’5 _ &°>5
’ ' а°>ъ ~ ‘ I а°>5 а0-5 +Ь0-5
32.
ункция у = ах
И ЕЕ СВОЙСТВА
Многие процессы в природе, такие, как распад радиоактивного вещества, рост численности бактерий, изменение атмосферного давления с изменением высоты над уровнем моря и другие, могут быть описаны с помощью формулы вида у = а*, где а — некоторое число, большее нуля.
Функция, которую можно задать формулой вида у = а*, где а — некоторое положительное число, называется показательной.
В предыдущем пункте мы рассмотрели свойства показательной функции у ~ 2х, заданной на множестве действительных чисел. Аналогичными свойствами обладает любая функция у = аг, где а — некоторое число, большее 1, заданная на множестве действительных чисел*.
* Существование такой функции, так же как и в случае а = 2, мы принимаем без доказательства.
ЙЕ
На рисунке 74 построены графики функций вида у = ах при некоторых значениях а, больших единицы:
свойства
S1
График каждой из этих функций сходен с графиком функции у = 2х.
Сформулируем функции у = ах, при а > 1.
1. Областью функции служит положительных чисел, т. е. функция принимает только положительные значени я,
причем любое положительное
значений множество чисел
число является значением функции. Геометрически это выражается в том, что график функции у — ах при а > 1 расположен выше оси х и любая прямая, параллельная оси х и находящаяся выше ее, пересекает этот график. —
2. Функция является воз-
Рис. 74
ристающей.
Из двух точек графика точка с большей абсциссой расположена выше, чем точка с меньшей абсциссой.
Свойства 1 и 2 примем без доказательства.
3. Если х = 0, то значение функции равно 1; если х > О, то ах >1; если х < 0, то 0 < ах < 1 (это следует из свойств 1 и 2).
График функции у = ах при а > 1 проходит через точку с координатами (0; 1), при х > 0 он расположен выше прямой у = 1, а при х < 0 — ниже этой прямой.
Выясним теперь, какими свойствами обладает функция у = ах при 0 < а < 1.
Для этого докажем сначала, что’график функции у
симметричен относительно оси у графику функции у ~ 2х.
/ 1 _ / I \ л
Так как — == 2 , то уравнение у = | — можно пред
ставить в виде у = 2 х, Легко понять, что если точка A (k\ т)
принадлежит графику функции у = 2х, то симметричная ей относительно оси у точка В (—k; т) принадлежит графику функции у = 2~х. Действительно, если равенство т = 2А истинно, то равенство т ~ 2~<~А) также истинно.
Рис. 76
Рис. 75
Значит, каждой точке графика функции у — 2х соответствует симметричная ей относительно оси у точка графика функции у = 2~х.
Верно и обратное: любая точка графика функции у = 2 х является симметричной относительно оси у некоторой точке
ЛЕ
графика функции у = 2х.
Следовательно, график функции у = 2~х симметричен относительно оси у графику функции у = 2х (рис. 75).
Вообще, графики функций у = их и у = } где а
положительное число, х £ /?, симметричны относительно оси у.
Отсюда ясно, какой вид имеет график функции у = ах при 0 < а <1. График расположен выше оси абсцисс, причем его пересекает любая прямая, параллельная оси х и~ находящаяся выше ее. Из двух точек графика точка с большей абсциссой лежит ниже, чем точка с меньшей абсциссой. График проходит через точку с координатами (0; 1) и расположен ниже прямой у = 1 при х > 0 и выше этой прямой при х < 0.
На рисунке 76 построены графики функций у == их при некоторых значениях а, где 0 < а < 1.
где х С /?, при
Сформулируем свойства функции у О < а < 1.
1. Областью значений функции служит множество положительных чисел, т. е. функция принимает только положительные значения, причем любое положительное число явля
к
ется значением функции.
2. Функция является убывающей.
3. Если х = О, то значение функции равно 1; если х > 0, то О < ах < 1; если х < 0, то ах > 1.
Остановимся теперь на случае, когда а = 1. При а = 1
множество значений
ункции состоит из одного элемента —
числа 1. Графиком функции у = ах при а ~ 1 является прямая, проходящая через точку с координатами (0; 1) и парал
лельная оси х.
Мы рассмотрели некоторые свойства функции у = ах при а > 1, при 0 < а < 1 и при а = 1.
Отметим еще одно важное свойство, которым обладает всякая показательная функция.
Если f (х) = ах, где а > 0, то при любых действительных значениях аргумента хх и х2 истинно равенство
/ (*i) • f (х2)
Действительно, / (xj — aX1 , / (х2) = а*2. Отсюда
628. С помощью графика функции у ~ 3х (см. рис. 74) найдите: i) значение у, соответствующее значению х, равному —1; 0; 0,5; 1; 1,5;
б) при каком х значение у равно 1; 3; 6; 7,1; 0,5;
в) множество решений неравенства: 3* > 5; 3х < 1.
629. Постройте график функции у = 1,5х. Используя его: а) найдите значение выражения: 1,5°>5; 1,52>5; 1,5~0’5; 1,5’^5;
б) найдите показатель степени, в которую надо возвести число 1,5, чтобы получить 1; 2; 3; 4; 5;
в) решите уравнение: 1,5х = 5; 1,5х 7,5.
630. На рисунке 74 построены графики функций вида у — ах для различных значений а, больших 1. Сравните взаимное расположение этих графиков при х > 0 и при х < 0.
631. Известно, что а>&>1. Начертите схематически графики функций у = ах и у = Ъх.
632. Постройте схематически на одном чертеже графики функций у — 2 х и у — 3х. Наметьте примерно, как расположен график функции у 2,7х.
633. Используя график функции у | (см. рис. 75), найдите:
Рис. 77
а) значение у, соответствующее зна-чению х, равному —2; 1,5; 0; 1;
б) показатель степени, в которую 1 г
надо возвести число —, чтобы по-
лучить 4; 3;—; 0,8;
4
в) множество решений уравнения или неравенства:
634. Постройте график функции у~ 0ДЛ. С помощью графика сравните выражения:
0,7“3’2 и ОД"4’7;
635. Каково взаимное
ОД-1’5 и ОД1’5; ОД0’3 и ОД2’3,
расположение графиков функций:
б) у = 0,75" и у = (l|'f ?
\ о /
636.
637.
На рисунке 77 построены графики функций вида у = Для каждой из кривых найдите значение й.
Сравните значения выражений:
а) З1’5 и З1’4;
в) 0Д8~°>7 и 0Д8“0’6;
638.
/ / \ °. /-> ’ ' ‘S / 4 \ / 5 \5
г) /2 3 и у 2 г’; и) - и - ; ' z \ 5 / \ 4 /
д) 0,5^3" и 0,5^; к) 0,02~10 и 5011.
При каком условии из неравенства ак > ап (а > 0) еле-
дует неравенство:
a) k > п; б) А < п?
639. Сравните показатели т и п, если известно, что верно неравенство:
640. Сравните с единицей основание а, если известно, что верно неравенство:
а) а100 > а";
в)
1
641.
б) а0’2 < а3 ; г) а^17 > а4; е) а~°»25> а 1/3 о Сравните с единицей значение выражения:
а) 0,014
д) 0,007°;
ж) 3
642.
б) 0,9910°;
е) 100~°’0i;
Какое заключение можно сделать
о знаке числа х, если:
а) 3х = 0.6; б) (= 10;
\б/
643. Решите уравнение:
в) 10х = 4; г) 0,3х = 0,1?
в) 12 х = 1;
м) 0,2х = ИО.008.
w г) (0,1)х = 1000; з) Iх = 15;
644. Решите неравенство:
Ча) 6х < 68; г) 0,1х > 100;
б) 0,7х >0,49; д) 0,3х > 111; tz
в) 2х <1; е) 11х > у' й; 64
645.
Известно, что если при радиоактивном распаде количе-
ство вещества за сутки уменьшается вдвое, то по истечении х суток от массы Мо останется масса М, вычисляемая / IV М I 1 'х
по формуле М MQ — j . Отсюда — — I .
\ 2 / AZ 0 \ 2 /
Покажите графически, как с изменением х изменяется м" отношение-----.
Используя в случае необходимости построенный график,
ответьте на вопросы:
а) Во сколько раз уменьшится масса радиоактивного вещества по истечении 1,5 суток, 2,5 суток, 3 суток, 4 суток? б) Сколько времени должно пройти, чтобы исходная масса
радиоактивного вещества уменьшилась в 2,5 раза, в 3 раза, в 4 раза?
646. Если железный трос намотан на железный барабан х раз, то за счет трения меньшей силой FQ можно уравновесить большую силу F, причем зависимость между силами F и Fq выражается формулой F — FQ * 3х.
а) Сколько раз намотан трос на барабан, если силой 5 Н удается уравновесить силу 45 Н; 135 Н?
б) Какая сила потребуется, чтобы с помощью троса, обмотанного 3 раза, уравновесить силу 54 Н; 81 Н?
647. Найдите множество корней уравнения:
V) 23х = —; в) 9х = 27; д) 36~х = б/б;
128
б) 0,53х~2= 0,125; г) 25х"1 =125; е) (/7)3л;+1 =49.
648. Найдите множество решений неравенства:
а) 115х > 11е; в) 9V < 27; д) 2 54х < 5/5;
б)
16
81’
г) 16х >0,125;
/ 1 \ 6Х 3
е) 1-М >7/49.
649.
С помощью графиков
выясните, сколько корней имеет
уравнение:
а) 2 х — —х + 3;
б) 3Л = —х2 +4; в) 2V х2.
Упражнения для повторения
650. Сколько решений имеет уравнение:
а) (х + I)2 + у2 = 0; б) х2—10х + 25 + у2 = 0?
651. Решите систему уравнений:
а) /х + 2у + 15 - 0, б) /Зх + у + 5 - 0, |2х2 + у2 - 219; [бх2 + 2ху + у2 = 25.
652. а) Докажите, что прямая х — 2у = 75 не пересекает окружность х3 + у2 — 1089.
б) Докажите, что прямая х + 7у = 50 касается окружности х2 + у2 — 50, и найдите координаты точки касания.
§ 12.
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ С ОСНОВАНИЕМ
10
33. ЦЕЛАЯ И ДРОБНАЯ ЧАСТИ ЧИСЛА
Любое число можно представить в виде суммы двух слагаемых, причем различными способами. Например, число 25,8 можно представить в виде суммы чисел 10 и 15,8, или 20,4 и 5,4, или 25 и 0,8, или—5 и 30,8и т. д. В дальнейшем нам часто придется представлять число в виде суммы таких двух слагаемых, одно из которых является целой частью данного числа, а другое — дробной частью.
Определение 1. Целой частью числа х называется наибольшее целое число, не превосходящее х.
Целую часть числа х обозначают символом [х].
Например:
[25,8] == 25 (целая часть числа 25,8 равна 25);
[0,73] = 0 (целая часть числа 0,73 равна 0);
[—1] = —1 (целая часть числа —1 равна —1);
[—2,47] ~ —3 (целая часть числа —2,47 равна —3).
Очевидно, что если х — целое число, то [х] — х. Если х --нецелое число, то [х] < х; в этом случае число х еаключе-но между двумя последовательными целыми числами:
[х] < х < [х] + 1.
Таким образом, при любом х имеет место неравенство
[х] X < [х] + 1.
На рисунке 78 показано расположение на координатной прямой точек с координатами х и [х] для целого х и нецелого х.
Определение 2. Дробной частью числа х называется разность между числом х и его целой частью.
Таким
Дробную часть числа х обозначают символом {х}. образом,
{х} = X — [х
Например:
{6,4} = 6,4 — [6,4] = 6,4 — 6 = 0,4 (дробная часть
6,4 равна 0,4);
{11} — 11 — [11] = 11 — 11 = 0 (дробная часть числа
числа
11 рав-
на 0); V
{—3,8} — —3,8 — [—3,8] = —3,8 —(—4) = 0,2 (дробная часть числа —3,8 равна 0,2).
Так как [х] х < [х] + 1, то 0 х — [х] < 1, т. е. при любом х истинно неравенство 0 {х} <1. Значит, дробная часть числа — это неотрицательное число, меньшее 1*
По определению дробной части числа {х} = х — [х]. Отсюда х = [х] + {х}, т. е. любое число х можно представить в виде суммы его целой и дробной частей.
Например:
25,8 - 25 + 0,8; —3,7 = —4 + 0,3;
0,12 - О + 0,12; —0,476 - —1 + 0,524.
Формулой у ~ [х] задается функция, областью определения которой является множество действительных чисел. График этой функции изображен на рисунке 79.
Рис. 78
Если 0 х < 1, то у — 0. Если 1 х < 2, то у — 1. Если —1 х < О, то у = —1.
Вообще, если п х < п + 1» где п — целое число, то у = п. Значит, на наледом промежутке вида [п; п + 1[ значение функции равно п.
Формулой у = {х} задается функция, областью определения которой также является множество действительных чисел. График этой функции изображен на рисунке 80.
Рассматриваемую функцию можно задать формулой
—
у = X — [х].
(1)
Если 0 х < 1, то [х] = 0 и формула (1) примет вид у — х, т. е. на промежутке [0; 1[ графиком функции у — {х} служит часть прямой у — х.
Если 1 х < 2, то [х] = 1. В этом случае формула (1) примет вид у — х — 1, т. е. на промежутке [1; 2[ графиком функции у = {х} служит часть прямой у = X — 1.
Если —1 х < 0, то [х] — —1; формула (1) примет вид у = х + 1. Графиком функции у = {х} на промежутке [—1; 0[ служит часть прямой у — х + 1.
Вообще, если п х < п + 1, где п — целое число, то [х] — п и формула (1) примет вид у — х — п. На любом промежутке вида [_п; п + 1[ графиком функции у = {х} служит часть прямой у = х — п.
653. Найдите целую часть числа:
а) 1,8; в) 27; д) —0,4; ж) —35,2;
б) 263,4; г) 0,345; е) —0,97; з) —10,7.
654. Найдите значение выражения:
а) [26,4]; б) [0,33]; в) [-0,54]; г) [—281].
4
1 1 —
—
- / ? — - — МММ Ml — .. .
—' f — — ммм ш
1 1 -1 ( J — чч“ 3
-1— вЛ ! —.
— < )— п -т.
ч
~ * — —
К,
655. Найдите дробную часть числа:
а) 3,6; в) 0,64; д) 6,27; ж) —100,01;
б) 10; г) —0,64; е) —6,27; з) —
656. Найдите значение выражения:
а) {9,18}; б) {45}; в) {0,25}; г) {—134,8}.
657. Найдите И и {х}, если: а) х = 65,4; б) х = —65,4.
658. Представьте в виде суммы целой и дробной частей число:
а) 21,43; в) 14,5; д) —0,068; ж) —5,44;
б) 0,57; г) —14,5; е) —1,05; з) —2-.
23
659. Назовите несколько чисел, целая часть которых равна:
а) 14; б) 1; в) 0; г) —1; д) —5; е) —10.
660. Укажите множество значений переменной х, если известно, что целая часть х равна:
а) 8; б) 1; в) 0; г) —1; д) —17.
661. Покажите на числовой прямой множество значений переменной х, если известно, что:
а) И = 3; б) И = —3.
662. а) Пусть х = 3,7. Найдите: {х}, {х + 4}, {х — 12}.
б) Пусть х = —7,4. Найдите: {х}, {х — 50}, {х + 13}.
в) Сравните значения выражений {х} и {х + п}, где х — любое число, а п\— целое число.
663. Назовите несколько чисел, дробная часть которых равна:
а) 0,9; б) 0,02; в) 0.
Упражнения для повторения
664. Начертите схематически графики функций у = 0,7х и у = 0,4х. С помощью этих графиков решите уравнение 0,7х = 0,4х и неравенства 0,7х > 0,4х; 0,7х < 0,4х.
34. ФУНКЦИЯ у = 10х
В практике вычислений важную роль играет функция у = 10х.
Построим график этой функции на отрезке [0; 1]. Для это-1 го составим таблицу ее значений с шагом —.
8
L
Так как 102 ~ /10 & 3,162, то
1 j j_\_L 1 ( J_Y_L
Ю4 = (102/2 «/ЗД62^ 1,779 и 108-\104/2 ^/1,779^1,333.
Рис. 81
з
Найдем теперь значение выражения 108 .
_3 I 1 1 1
108 = 104 8 = 104 • 10 8 «1,779 • 1,333 « 2,371 и т. д.
Найденные значения выражения 10* занесем в таблицу, округляя их до сотых:
Построим в координатной плоскости точки, координаты которых указаны в таблице, причем по оси абсцисс в качестве единицы масштаба возьмем 10 см, а по оси ординат возьмем 1 см (рис. 81).
Из рисунка видно, что с увеличением значений аргумента х равным приращениям аргумента соответствуют все большие приращения функции, т. е. точки графика располагаются реже. Поэтому для построения более точного графика функции у = 10х на отрезке [0; 1] целесообразно вычислить значения выражения 10* для некоторых промежуточных значений переменной х. Найденные значения выражения 1СИ, округленные до сотых, тоже занесены в таблицу:
X 2 is (0,438) 2 16 (0,563) 11 16 (0,688) 13 16 (0,813) 15 16 (0,938)
10 х 2,74 3,65 4,86 6,49 8,65
Построим в той же системе координат точки, координаты которых указаны во второй таблице, и соединим все построен
ные точки плавной линией.
График
УНКЦИИ у ™ 10х
для
х £ [0; 1] изображен на рисунке 82.
С помощью построенного графика можно находить значения выражения 10х, если 0 х 1. Например, если х ~ 0,37, то 10х 2,3; если х — 0,82, то 10 х 6,6 (см. рис. 82).
Зная значения выражения 10х для х g [0; 1], легко вычислить значение этого выражения для любого х. Поясним это
на примерах.
Пусть нужно найти приближенное значение выражения 102’58. Представим показатель степени 2,58 в виде суммы его целой и дробной частей: 2,58 -- 2 + 0,58.
Тогда
102,58 _ 102+0,58 _ 102 . Ю34
Значение выражения 10°’58 найдем с помощью графика функции у 10х. Получим: 10°>58 ж 3,8. Отсюда 102»58 3,8 • 102.
Рассмотрим еще один пример. Найдем значение выражения Ю-1,73. Для этого представим отрицательный показатель степени —1,73 в виде суммы его целой и дробной частей:
—1,73 - — 2 + 0,27.
Тогда
10-М3 = Ю“2Х°>27 = 10~~2 • 10°>27 1Д • 104
665. С помощью графика функции у = 10х (см. рис₽ §2) найдите:
а) значение выражения 10х, если значение переменной х равно 0,1; 0,25; 0,72; 0,865;
б) значение переменной х, если значение выражения 10х равно 3; 5; 6,2; 9,37.
666. Используя график функции у ~ 10х, найдите значение выражения: а) 10°>2; б) 10°+; в) 10°>47; г) 10°>83; д) 10°+8;\
667. С помощью графика функции у 10х найдите:
а) 104 104 нНА 10~2>s;
б) 10°4 103>58, 10~°4 10”34
668. Найдите значение выражения:
а) 101-’38; б) 1024 в) 10~°4 г) Ю”1*25; д) 1£408-
689. Используя график функции у = 10*, найдите показатель степени, в которую нужно возвести число 10, чтобы получить: а) 1,5; б) 3,7; в) 6,8; г) 8,8,
670. Представьте каждое из данных чисел в виде степени с основанием 10 (используйте, если нужно, график функции у = 10х):
а) 1; 10; 10 000; 0,1; 0,001; в) 3,8; 380; 0,38; 0,038;
б) 7; 70; 0,7; 0,007; г) 5,2; 5200; 0,52; 0,0052.
Упражнения для повторения
671. Представьте в виде степени с основанием 10:
а) 10;
б) уЧОО;
в) 10/10; д) 0,1р10;
г) 0,1/0,1; е) 100р10-3.
672. Решите уравнение:
а) ю1-^ = 1;
б) /100* = 0,1;
в) (0,01)* = 1000;
г) 1О3~2* = 10х2;
д) (0,01)* == У10;
е) 1000* = y/lOO.
673. Найдите множество
решений неравенства:
а) (0,1)*> 10;
б) 10*+1 < 10 000;
в) 10*~2> 0,01;
г) 0,1 < 10* < 10 000;
д) 1 < 10*+1 < 10 000;
е) 0,01 < 100* < /10.
674. Решите уравнение и неравенство:
а) 8*~3 = 16; б) 272’с~1-9; в) 12*<У144; г) 0,4* <15-^.
8
35. ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ у == Ю*
В предыдущем пункте для построения графика функции у — 10х нам пришлось вычислить ряд значений выражения 10х для дробных значений х. Работа эта оказалась довольно трудоемкой. Поэтому мы будем пользоваться готовыми результатами, которые даны в специальной четырехзначной таблице* значений функции у = 10х. Эта таблица содержит значения функции у = 10х для значений переменной х от 0,0000 до 0,9999.
* См.: Б р а дис В. М. Четырехзначные математические таблицы» М., Просвещение, 1978.
Рассмотрим начало этой таблицы:
Таблица XIV
т 0 1 2 3 4 5 6 7 8 9 / 2 3 4 5 6 7 8 9
,00 1000 1002 1005 1007 1009 1012 1014 1016 1019 1021 0 0 1 1 1 £ 2 2 2
,01 1023 1026 1028 1030 1033 1035 1038 1040 1042 1045 0 0 1 1 1 £ 2 2 2
,02 1047 1050 1052 1054 1057 1059 1062 1064 1067 1069 0 0 1 1 1 2 2 2
,03 1072 1074 1076 1079 1081 1084 1086 1089 1091 1094 0 0 1 1 1 2 2 2
,04 1096 1099 1102 1104 1107 1109 1112 1114 1117 1119 0 1 1 1 2 2 2 2
Найдем, например, значение выражения 10°»046, т. е. значение функции у — 10х при х = 0,046. Для этого надо взять строку «0,4» и столбец «6». В их пересечении помещено число 1112. Для того чтобы найти значение выражения 10°’046, заметим, что 10° < 10°>°46 < 101, т. е. 1 < 1О0’046 < 10. Значит, 10°>046 1,112. (Чтобы получить значение функции, мы отде-
лили запятой первую цифру в числе, помещенном в таблице.)
Если бы мы хотели найти значение выражения 10°»0467, то к найденному по таблице числу 1112 нужно было бы прибавить 2 — поправку, помещенную в таблице справа на пересечении строки «0,4» и столбца «7». Таким образом, 1О°’0467 ж 1,114.
С помощью этой же таблицы можно найти значение выражения 10х для любого х. Пусть, например, нужно найти значение выражения 10~2’685. Представим показатель степени —2,685 в виде суммы его целой и дробной частей: —2,685 = —3+0,315. Тогда 10“2>б85 = 10“3+°,315 =2 ю~3 • 10°’315. Значение выражения Ю°,315 находим по таблице: 10°>315 2,065. Отсюда 10“2’085
2,065 • 10-3.
675. Найдите по таблице значение выражения 10+ если значение переменной х равно:
а) 0,18; 0,34; 0,07; 0,94; 0,62; 0,41;
б) 0,8; 0,4; 0,04; 0,1; 0,01; 0,09;
в) 0,264; 0,356; 0,581; 0,299; 0,736; 0,154;
г) 0,216; 0,081; 0,810; 0,001; 0,305; 0,909;
д) 0,3845; 0,1761; 0,9111; 0,8716; 0,5432;
е) 0,0061; 0,0745; 0,6057; 0,1011; 0,2706.
676. Найдите значение выражения:
а) 10°>546, Ю1’546, 10“М54; б) 1О°>028, 1О2>028, 10~°’972.
677. Найдите значение выражения 10х, если значение переменной х равно:
а) 1,2303; в) 3,5914; д) -1,9992; ж) -0,2781;
б) 2,0907; г) 5,0112; е) -3,1254; з) -2,8761.
678. Постройте график функции у = 10х для х g [—1,2; 1,2], составив предварительно таблицу значений выражения
10л с шагом 0,1. (В качестве единицы масштаба по осям возьмите отрезок, равный 1 см.)
679. Пользуясь таблицей квадратных корней и таблицей значений функции у = 10*, найдите приближенное значение выражения: а) Ю1^3; б) 10“в) Ю^10; г) Ю^0’1 .
Упражнения для повторения
680. Последовательность (Ьп) — геометрическая прогрессия, причем Ъх = 10~2’3 и q = 10°>3. Найдите: &10; &7; &i3.
Представьте найденные члены геометрической прогрессии в виде десятичных дробей с двумя знаками после запятой.
681. Найдите значение х, при котором истинно равенство:
/ _ 1V2 2 I _L\6
а) 2х = U~ 3 ) • 83; б) 3х = (э” 3 J • 27°>5.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К ГЛАВЕ V
К пункту 31
682. Сравните значения выражений: 6 7
а) 21 и 28; б) 2^ и 2УТ; в) 2~ и 2-^.
683. Сравните значение выражения с единицей:
а) 2~100; в) 2~"^3; д) ж) 2я;
б) 20»0001; г) 2^; е) 2’~^г; з) 21-я.
684. На какое множество отображается у = 2* числовой промежуток:
графиком функции
а) ]0; +со[; б) ]—оо; 0[; в) ]1; 5[; г) [—1; 1]; д) [0; 1J?
685. При каких значениях х верно равенство:
а) 2х = 32; в) 2х = 0,5; д) 2х = 0,125;
б) 2х = i; г) 2х = 0,25; е) 2х = 128?
686. Укажите множество значений х, при которых верно неравенство:
а) 2х 256; б) 2х < 0,25; в) 2х >—; г) 2х < 2.
687.
Пользуясь графиком функции у = 2*,
выясните, в какам
случае функция получает большее приращение:
а) при изменении х от 0,5 до 1,5 или от 1,5 до 2,5;
б) при изменении х от 0,2 до 0,7 или от 1,2 до 1,7.
К пункту 32
688.
689.
690.
691.
692.
693.
694.
Построите схематически на одном чертеже графики функций у — 1,5х и у = 2х. С помощью графиков решите уравнение 1,5х = 2х и неравенства 1,5х < 2х; 1,5х > 2х.
Найдите множество значений х, при которых обращается в истинное высказывание предложение:
а) 15х - 8х; 15х > 8х; 15х < 8х;
б) 0,9х - 0,8х; 0,9х > 0,8х; 0,9х < 0,8х.
На рисунке 76 построены графики функций вида у = ах для различных значений а, меньших 1. Сравните взаимное расположение этих графиков при х > 0 и при х < 0.
Известно, что 0 < а < b < 1. Начертите схематически графики функций у = ах и у = &х.
Постройте схематически на одном чертеже графики функ-/1\х /1\х
ций у= I — j и г/ — ( — •) . Наметьте примерно, как рас-\ 2 / \ 3 /
положен график функции у — 0,4х.
Постройте схематически графики функций у — ах и у — а при а > 1 и при 0 < а < 1. Сравните взаимное расположение этих графиков.
Сравните значения выражений:
а) 0,04“5 и 256; б)
в) 0,5~и и 2й.
695. Сравните показатели й и ти, если верно неравенство:
в) (/3 -V2)k > (Гз —V2)т;
г) (У7- 1)* < (J/7 - 1)т.
696. Сравните с единицей значение выражения:
а) РЛ б) л-"; в) г) (/з
\ 7 / \ 4 /
697. Какое заключение можно сделать о знаке числа если: а) 5* - 10; б) (0,3)*- 100; в) 7*- 1,003; г) 0,4*-18?
698. Решите графически уравнение:
а) 2х - х + 1; б) (0,3)х - х + 1.
699. С помощью графиков функций г/ — 2х и у — х2 — 2 решите уравнение 2х — х2 — 2.
700. Найдите множество корней уравнения:
а) 3х = -i-; г) 5х = • 1,25 Л
X \5 /
б) 0,4 х =6-; д) 0,2х = 125;
4
701. Найдите множество решений неравенства:
; а) 2х > V23; в) 10х >
/ю
б) 5х < У 25; г) 0,7х >2-;
49
702. Решите уравнение:
а) 25х = —; б) 0,5~2х=0,125;
128
Д) 0,2х < 25;
в)173х=1; г) 0,27х=0,04.
703. Найдите множество корней уравнения:
ж)
216;
= 0,001;
1 \ 5— 2Л'
8 j
28
и)
704.
705.
706.
j) 5х * 2х - 0,001;
Найдите множество
Ш (/7 Г”1. (]/2)-решений неравенства:
Решите уравнение:
а) 81х-1 = 243; б) 362х+3=216; в) 2х2~2х+1=8^ • 23.
Решите уравнение:
а) 2х + 2х+2 = 20; в) 5х + 5х’1 =- 30;
6Х 3х + Зх+1 - 12; г) 4х”1 + 4х + 4х+1 -= 84.
707.
а) Докажите, что любая геометрическая прогрессия является функцией, которая может быть задана на множестве
N натуральных чисел формулой вида у
б) Докажите,
что
ункция, заданная на
сах.
множестве
N
натуральных чисел формулой вида у = сах, является геометрической прогрессией.
К пункту 33
708. Укажите два последовательных целых числа, между кото-2
рыми заключено число: 30,2; 0,49; —у; —10,8.
2
709. Найдите целую и дробную части числа: 105; —7,8; —21у.
710. Представьте число в виде суммы его целой и дробной частей: а) 54,1; б) 12,63; в) —0,97; г) —20,15.
6 Алгебра 8 кл.
161
и
711. Найдите целые части чисел:
а) У2 и —У2; б) /13 и — У13;
712. Вычислите:
в) /47 и —/47.
а) {[17,3]}; б) [{-25,7}]; в) {[15]}; г) [{23}].
713. Найдите несколько таких значений переменной а, при которых верно неравенство:
а) /} < 0,15;
б) {а}
в) {а} 4-0,05 > {а щ 0,05}
714. Решите уравнение:
а) [2,75 + .г] = [2,75];
715. Решите уравнение:
а) [0,21 + х] = [0,21];
б) [г/ - 0,30] = [2,4];
в) Г1,7 + 2] = [—8,2];
5) {2,75 + х} - {2,75}.
г) {0,58 -г х) = 0,58;
д) {у - 0,39} - 0,61;
е) {1,62 4-х} = 0,65.
716. Укажите какое-либо значение переменной х, при котором
неверно равенство:
а) {5,41ц-х} = {5,41} + {х}; б) Г2х] 2 Гхф
717. Верно ли, что дробная часть произведения двух чисел равна произведению дробных частей множителей?
718. Верно ли, что целая часть суммы двух чисел равна сумме ; целых частей слагаемых?
719. Постройте график функции:
а) у = [х] 4- {х}; б) у = [{х}]; в) у = {[х]}.
720. Покажите на координатной плоскости множество точек, для которых: а) Гх] = 0; б) Гг/j ~ 1; в) J[xj = 1, к/ - 2.
721. Постройте график уравнения [xj Гуй
К пунктам 34 и 35
722. Пусть 31,5 — 10а и 0,42 = 103. Представьте в виде степени с основанием 10 выражение:
2
а) 31,5-0,42; б) (31,5)3; в) /М2; г) (31,5)3 • /02.
723. Используя график функции у ~ 10х, найдите значение выражения:
724. С помощью таблицы значений функции у 10х представьте в виде степени с основанием 10 число:
а) 1,594; б) 0,373; в) 51,74; г) 200,1.
ГЛАВА
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
ОРГАНИЗАЦИЯ ВЫЧИСЛЕНИЙ
§ 13.
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
36. понятие ЛОГАРИФМ/
Рассмотрим уравнение
ах = Ь9
где а и Ъ некоторые числа, причем а > 0 и а 1,
При Ъ 0 это уравнение не имеет корней, так как значение показательной функции у = ах положительно при любом х.
При Ъ > 0 уравнение имеет корень, и притом единственный. Действительно, областью значений показательной функции у = ах при а 1 служит множество положительных чисел (следовательно, корень уравнения ах = & существует). Кроме того, каждое свое значение показательная функция принимает только при одном значении аргумента (следовательно* этот корень единственный).
На рисунке 83 показано графическое решение уравнения ах — 6, где а > 1, при различных значениях Ь,
Корень уравнения ах = Ь, где а > 0, а 1, называют логарифмом числа Ъ по основанию а.
Например, корень уравнения 3х = 81, а именно число 4, есть логарифм числа 81 по основанию 3; корень уравнения 10х — 0,001, г. е. число — 3, есть логарифм числа 0,001 по основанию 10.
Определение. Логарифмом числа Ь по основанию а (а > 0, а А- 1) называется показатель степени, в которую надо возвести число а, чтобы получить число Ь.
Для логарифма числа Ъ по основанию а принято обозначение loga Ъ (читается: «логарифм Ь по основанию а»).
По определению логарифма log2 8 — это показатель степени, в которую надо возвести число 2, чтобы получить 8. Легко догадаться, что log2 8 - 3, так как 2:; = 8. Аналогично, 1 1
log3 — = —4, так как З-' --, a log- 1=0, так как 5° = 1,
4 81 81 °
Заметим, что такие выражения, как log3 (—27), log2 0, не имеют смысла, так как уравнения 3х = —27, 2х 0 не имеют корней.
Рис. 83
Вообще, выражение log^ &, где а >0 и а ф 1, имеет смысл лишь при b > 0.
Рассмотрим примеры.
Пример 1. Найти число &, логарифм которого по основанию 2 равен — 5.
По условию log2 Ъ = —5, где Ъ — искомое число. Используя определение логарифма числа, получим:
Ъ = 2“5, т. е. Ъ ~ —.
32
Пример 2. Найти логарифм числа 125 по основанию /5.
Пусть искомый логарифм равен х, тогда (]/5|Л =125.
Для решения полученного уравнения представим каждую его часть в виде степени с основанием 5, тогда
-52 = 53. Отсюда - х = 3, 2
значит, х =6.
725.
Проверьте истинность равенства:
10 ю
б) log6125==3; г) log42=JL; е) logt 81 = — 4.
2 з
726.
Используя знак логарифма,
выразите показатель степени
из равенстз
а) 25 = 32;
б) 3~3= 1;
27
727. а) Найдите нию 2.
б) Найдите
728. Найдите:
в) 121 = 12;
г) 20° = 1;
логарифм числа
огарифм числа 3,
д) 252 = 5;
е) 8 3 = i
2
8, 32, —, 1, 0,5 по основа-
4
1 1
81, —, 1, —по основанию 3.
27 243
a) log24; в) log100,01;
б) iog3г) 1°ё/2-(8)‘’ У
Д) log, 25;
ж) log j 27;
/Г
3) logo,4 6,25.
729. Найдите число b, если:
a) log5 & == 2; в) logj Ъ = —1;
б) loge & = 3; г) logn Ъ = 0;
730. Имеет ли смысл выражение:
а) log5 (—25); в) log12 0;
б) log3 (—7)2; r)log2(—4)3;
д) log10 Ъ = —2;
е) log4 Ь = 1,5.
Д) bg6(—6)~2;
е) — log8 16?
731.
Упражнения для повторения
Постройте график функции /, заданной формулой
У
Задайте уравнением отношение g9 обратное функции Л Укажите область определения и область значений отношения g. Постройте график отношения g.
37. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
В
вычислительной практике широко используются логари
«•
мы чисел по основанию 10 — десятичные логарифмы. Для обо
значения десятичных логарифмов принята специальная запись: вместо log10 &, где Ь — произвольное положительное число, пишут 1g Ъ. Например, вместо log10 1000 пишут 1g 1000, вместо log10 35 пишут 1g 35.
По определению десятичного логарифма 1g Ъ есть показатель степени, в которую надо возвести основание 10, чтобы получить число &. Значит, равенство
10lg* Ь
истинно при любом положительном значении &, т. е. является тождеством на множестве положительных чисел.
Пользуясь этим тождеством, найдем, что
10lglo° = 100; lOW - 0,1; 10lg5 - 5.
732. Используя знак десятичного логарифма, выразите показатель степени из равенства:
£
а) 102 100; в) 10~3 =0,001; д) 102 =/10; __
б) 107 = 10 000 000; г) 10-6 =0,000001; е) 102>5 = 100/10.
733. Докажите, что истинно равенство:
a) 1g 1000 = 3; г) Ig^lO =
3
б) 1g 100 000 = 5; д) 1g /ОД = - -;
в) 1g—— = —4; ё) 1g- — = —1,5;
10 000 100
ж) Igl1090
7 ю
734. Найдите логарифм числа*:
а) 100; г) 0,0001;
б) 1 000 000; д) 10 ~7;
в) 109; е) ]/10; •
з_
ж) У 100; к) 10 8;
з) у 0,1; л) 0,1]/10;
и) р 0,01; м)
1000
735. Решите уравнение:
ж) 1g х • 0;
736. Имеет ли смысл выражение:
a) 1g 0,43; г) lg (—6)~G;
б) lg (- 10); д) 1g (-2,б)45;
в) —lg -1; е) 1g б2,5;
яс) —1g 0,2°/;
з) 1g (2У 3 - 3]/2);
и) 1g (/2 - УЗ)?
737. Пчи каких значениях х имеет смысл выражение:
a) 1g (Зх);
б) 1g
10
в) lg! х I;
г) Ig(lO--j-x);
д) 1g (х — 5);
г__9
е) 1g
о
ж) Ж?/—;
100 — х
3) 1g х3;
л) 1g (9 - х2);
м) 1g (х3 — х)?
738. Найдите значение выражения:
a) 10'g;B г) 10’s3; ж) 102"lga’s;
б) 10igicooM; д) 10's°’3; з) 10,g3~Is2;
в) IO1®0,01; е) 10I+igS; и) 10“Igl;
к) 10-lg 3’8;
л) 102,Ц
4-ig.is м) 10 “
739. Представьте число в виде степени 10:
а) УТООО; б) 7; в) 34; г) 3,2; zi) 0,665.
740. Постройте графики функций:
а) у х и у 10;s *; б) у = %2 и у — 10lgx%
Упражнения для повторения
741. Функция f задала уравнением у=-х2-+-5. Укажите область определения п область значений функции Д Задайте уравнением отношение g? обратное . /. Какова область определения и область значений отношения а? /г . •
* В дальнейшей! лы судезз десятичный логарифм числа называть дога-риф-жолг числа.
742. Докажите, что значение выражения не зависит от значения переменной, принадлежащего области, его определения:
38. ФУНКЦИЯ у = !g X
Функция f, заданная формулой у = 10 ф определена на множестве действительных чисел, областью ее значений служит множество положительных чисел. Эта функция возрастающая, значит, она обратима. Как известно, область. определения и область значений взаимно-обратных функций меняются ролями. Поэтому областью определения функции g, обратной функции /, является множество положительных чисел ]0; + ссф, а областью значений функции g служит множество R действительных чисел.
Чтобы задать функцию g формулой, заменим в равенстве у = 10' переменные х на z/, а у на х и выразим у через х, Получим: х 10у, у = 1g х.
Функция, задаваемая формулой вида у = logc х, называется логарифмической.
Рассматриваемая нами функция является одной из логарифмических функций (а — 10).
На рисунке 84 изображен график логарифмической функции у 1g х; он симметричен графику показательной функции у ЮЛ относительно прямой ух.
Перечислим основные свойства функции у = 1g х, определенной на множестве положительных чисел:
1. Областью значений функции служит множество действительных чисел.
2. Функция возрастает, т, е. большему числу соответствует больший логарифм.
3. При х 1 значение функции равно нулю, т. е. lg 1 = 0.
4. При х > 1 значения функции положительны, а при 0 < х < 1 значения функции отрицательны.
Свойство 2 вытекает из того, что функция, обратная возрастающей, также является возрастающей. Свойство 3 следует из определения логарифма (показатель степени, в которую надо возвести 10, чтобы получить 1, равен нулю). Свойство 4 следует из свойств 2 и 3. Действительно, из того, что функция z/ — 1g х возрастает на всей области ее определения, следует, что если х > 1, то lg х > lg 1, но lg 1 0, значит,
1g х > 0. Аналогично, если х < 1 и х является положительным, числом, то 1g х < lg 1, т. е. 1g х < 0.
. L . // к ►
4
У b
с .. ) i b
-
a
& — • 4. t •
н
1
1 — - ? • (
2
J -
L 3? £ ।
1 • . 9 _
h j
1 J
b 1 t -
1 - / 4 У La X
г । ? i •l •
j
'i 1 ! ~2 -1 0^ • 1 2 ) тн| ur'Tr1 5 4 X
1 to ***
l i i &
i i 1 :
4 1 •
S Я ! ( 1
! a ' 1 f S Ji
f ! i f 2- Г"*' t.
j- | -b"‘
Й --| I 1 jt ... 1
1 i g a 1 *4
i - • J- L 1
a 4 ! 1 J $ ... 1
j 1 i r I 1 L—I
Рис. 84
743.
744.
745.
а) Найдите значение функции у ~ 1g х при х = 1000;
х =- 1; х = 0,001; х = 0,1; х = у 10.
б) При каком значении аргумента значение функции у — 1g х равно —2; —1; 0; 3?
На рисунке 85 построен график функции у = 1g х для х Е [1; 10]. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 2; 3; 4; 5; 7,5;
б) значение аргумента, которому соответствует значение функции, равное —0,2; 0,5; 0,75; 0,9.
Принадлежит ли графику функции у = 1g х точка:
А (100; 2); С (0,001; —3); В (У16; У; D & 166; У?
Z’---iii:3i::“i:44.” ТПТТ~ТТГТ'ТП~"
Ет //Ж- - . 1_ __ zzzzziizizi „ ij - 4-H H- ztztrztz it.:
j-j- -pp r“Tx 1
ГТ *7 * ...... ". Tt ZlTZZ'Z- --"’tt” *i““ “ТГ" TZZ”
__ _ . g ..в «. .... л................. „ - 1 1 - II - 11 F 1 .11
” Is IT IT ТГ г
г _ „ _ _ ™ . _ _ _ _ _> „
— - - ~ - - — - — “ - - - — - -* - -* - “ “pi —Г] ” M— “TT ” --- - -
- ’ " “ * " “ “|j" “ “ * “ “ “ ™ j у ” “““****“ t й 5 ” “ “ ™ “ " Ле*т1 "
if IT | 1 1 ^К1 Т U—Н— «— — - - «. - _л_ - - — t i- - - UR — - 8 - - - - — - - ---1-i- 1 ~ BE -j ~ e •
r X - _ . X _ -pj- - -r | I _
zrzr „ z _ z _ _ _ _ _ __ll ц
4 — - - “ pp J f gpF “ — — • “
J гч Л _ __ „ - _ __ ’ ~
:Л0 z^zz :ziz:z_z
u«;7 : r ~ ~ x::::::: b - - - ------- - -- - ТГ ТЯ* ’
’J ’₽ - *- - — “ - — - — ~—- ~
r ----- — - — — — 1 - - ------- —J— _ - — — — — — — — — — — — 4 F — 1- f f — — — e — — — — Л— — — — -n -ta- M — — — — — - — — — —
_z __ ± ztz : zz — — —
т - — — - — — --- — “ - — — , J « ♦- - — - - — - — — ~. —|— - - —J——r— - -- - - p- ~ - —
j i_ ...
zjieo г - —z " :: z : z zz zz — _ z : z
“i V 5 W | _ _ _ _ -- ,- — »। _ _ — “ —< _
T"’’* T H” ” ~ "" . . oF . .. . . I _ ...
1 rf r I
4 _1_ _ _ _ _ _ _J _ _ JV ri I -r -- ГТ n m
xz: zz - -- z z z +z ± zzz : :z "ft~n 1 f*jft'уtTj.T.TT7Zi"ZZZZ 2ZZZZZZZ’*""'ZZ » ^ZZZ’ZZTZ i"~l~ZZZ *"ZZZZ“*
iz _ - - ZZ’Z_ Z^ ztb5 г " 1 । г* “p --4— - —p -p j“ “ в ! . J
r? TZZSTZ- - X ±__22_222±_ it i
zzzzizzzzzizzzzzzzz—zzzzzzzzzzzi^ ,/ i:i:±22:zzzz:z±z zzzzE
qzzr^zr zt X - - _ - - 4^ U ~ C w /s -i ™ _[ _|_ 1 --••?
\7 X _ ± I- XI .1 II
-i_X-X X— z Xt X—zz zz „ -p — и T 1 — T
±±z±zzz-=zX-:zzxXX + zzzzzz^zz-z-z-z ' x ZT x “T x ^ -- - - - p_ _ _j_ __X~
-i q „Ц M J Л C i _ —_ .. Л. _ . +zzzxXz±z-zxzxxzzxzzzz-x±5Ex±iXixx:ix-
.. .Г ^Z._ Г “T" __ . “ _ 3 “Г -"Г”-". T" “Г ... П-"
-_zp_qz zp qzzpqz zp_! zp___
z||| ХЙфн|ЕЕЕЕЕЕЕ|ЕЕЕЕЕ^| 4Йеее:~ „ _ _ _ X H~L-- 'h'M"- - - - - -
zdH±bzz+z-Xz„.zzzzzz_zzzzzz:zzzzzz^zXzXzzzz|z!z'-~-- ±ееее1ееее|еее?ееееееееееж#еееш#е1ее±ее
^W, zz±z_zXz zzzzEzzzzHzzzzzzzaXzzz+EzXEzzzz -4-^-p i -I I
:tE_znX_j X- X~ 3z„ X- X -X
Zt_^ZIZttZ-.X-X“^ -X- Ti X - 4 X Xt zz zt itr ztzt dx
Х--4ХП T ’ -^X_ XL - x£- 4 X_±t J ^z -ч-4--.~-4- -j-x
X-ffl-HiE Xx=x:=±fii=:::-+r#xtF::r:J pj И Ы
Hzzzzdlz.zz_ zz±__z +- /r-z 4- “ +:zze: zH и- н' - - - -t- - - -и 4”L -t—t- 4— 3 г 1 . 1
__i _ j ' # 1 ' i J 1 11^ T
Л хх -X XM.„4.X- XXX.XXJX X..X--
“L/M rF""T“ -r--”-i---- j *-f*-----R^>^.- - —
; . ? , , x X , X3lX X XX X-X X” "X ' X ” X X X” "'XIEX ~ ’ X -
Ztr X ± x -у . ± it ±_ .._:x r - “ - ---и--*- -
т4‘ ” ” > t- ~tJT Ч- Ч- 4— k * “г-1 x — xi— г г
uttt ii -+-~itt i ±i i ifc ±xt ~~~ iTiiXtt" ' — x ±Е-±т хх---—x —
xpz ztt zt__zj й± jzit x±zt:j±: ztt zt j
XLL-.Zl__X ZZtZ X- TL -XX ±j± zt ^xxzzttxzx -X- ’ " ZZZZtl ~ ."x". —пт"пТ ±TT I ZZ:
H A 4 ~--x ±x sit XXL T1 —ГГТ X x " tI—!хт^ TXT
ьО.З — ±— -ir-/—+X—XXX--X^- -j———L«| u-——L Jj J—
i--t н—f 1—H !—1—!—Н--*--Н u
-) I h j - ~~п4—г—ztix^ + 'LhI h4z”h"#i—нН—4— ziz^f zzxpzxxzizzfxxxixzf^f I4zit4t4ftliii
+HXzzzzzt z_z_z ztzHXX -H# XzhhiXt—X ' ' Tlk J L-U—
zmzzcz.__ztzzix^,x__ ~й zznz > Xzttzzztfc ZT ztzt - x ---Г -4-H ИХ” ” X
ZLJXX-- - - -Ji Zt Xt+ I --it X ZT x^xxxt _±: zt _Z
J ..Lx X-X X-2t -xt x - - X X xtT x ztt I __ ± — H+- x__
lX л HjfL -X ]_ xx z .: X -4- t ’X -4--|-t+- - -X —H”
ДП / --X-X Xt X X zzz xzX--X1Xlx--X22 f I "T 1 S ' T
pu<4 -- _-X 1 —X—X zzz XzXxXX t -J_=| ..... 1 | м I
Г1. ?.. X Xf - XX X zX~- Xl ix ’ d i r | j ] i X
X~ — X__|_z —Hi ' "1— XX--X ± z , т T ii—h—rTTi ~~ ±:_i— -L £ —j |_ - - _ j,J „ _j X _ _ _
Hzztt±zzz±±=zzzzz£z^—+-L-n-X—1XX- J- J 1 1_ j
U Л^..Т.ТГ^г._ ZT _TTI T< -r * . .. ..... Г -* -Г-г- -Г .
f ] -П — — — — . .. n ~ “ »' —*- — —|—I—4 1—I ' - _L ц lj - - — pL 1 ; XL — 4-t-
dn 4 :„i :_„„_fc±„zz zt±z ~~~ттг tH—i X - -ii ;_Zr~-i ----J-ZZ-ZZ- "
дх / ТЕ-- X XX —z - - - ХХ хп у — T x 4 tt "tit ± Zt ZZ X Z'
i i 7. _ J Li | I ] S | -*— —t~t— "j't" - 1- X“ •" —*
H 1 i Xx —1ч X Hr i— —♦— - — — — — . f -X- . l-j .J . -f 1. =zjz + zjz I zzzzpzzzzzzzzp:::x:x+ zzfz i ”: zzz z
Fzzzzzzzz^“ "Я Г—Г 1 гХН+"Ц _2T~’'ZTZ-I‘"^-Z7ZZZZZZT L 44
I r Uf e 4 Ч у ““f-- to — “ • W1 J W R‘ V '"r—7“ “ — * *1
tt 'ziz z_X—z~ “ ±~az"z i !l JH i' ' — -— i -Tf— — “ — — "T" *- — -4- — — j — — - —4— -J— Ill J i IPT в
— — — . -ДЕ — _x_ _ .-L .. 4 > j i j —1.1-1- . j_ . ,i. 1,J _ .... 1... __ । | | j _ _ _ _ | 1 _ j | । . ц ,
к M u ta и "H4" " * ™ «s “ bL XL wtoa (X мнашав X’ -Ц-Lj^^ e . X
И L~ n _l__ X 7 j J. jt LN m r- 1 i-T Jr X Л и» П J \z
H-- (J ---« / L / ’ tj ^н- -и 4- LLLXLI 9 L „ Il n - / -I л j ч -i- ii/ - i *a
Ц- <Xr-r- - -r .... , д _ S/ _ J ГГ, 1 i 1 t ]
X X --X X Х--Г- zrrr.. X ! хТттч „ ^4—_ —p-^-. — j h n
lX, X_ - X rut - itr — i.. l..j TxxX
tt ^_.z±t _ -± znz^zzzz z i±tt ^z±::zn±Li±t±zffi: XJUl __ _x:::i_±_L ML. J± 1.1M1
Рис. 85
746. Найдите область a)y=lg(5x);
определения функции: д) У =lg (8—2х);
-у* 2
В) у = 1g—;
5
г) у = 1g (6х — 3);
и) У =
к) У = л) у = -—,
9—х2’
1g (я2 + 5х)
10
м) у
747. Сравните значения выражений:
г) 1g ~ и 1g 1о 1о
Д) lg/65 и 1g 8;
е) 1g L 120 и 1g 5;
ж) 1g Ь150 и lgyTL2 з) Igy 10 и IgK5,
б) 1g 0,8 и 1g 0,5;
в) 1g 0,7 и lg 1;
748, Оцените значение выражения 1g х, если:
а) 1 < х < 10; в) 100 < х < 10 000;
б) 0,01 < х < 1; г) 0,0001 <х <0,1.
749. Определите знак выражения:
a) 1g5; г) lg
б) 1g 0,75; д) 1g !/_;
в) 1g 1,3; е) lgl,l5;
ж) lg 2~В) * * * 12;
/ 2 \ ~ 23
з) ig (f) ;
\ о /
И) 1g (2-/3);
750. Решите уравнение и неравенства:
a) 1g х = 0; 1g х > 0; lg х < 0;
б) lg х = 1; lg х > 1; lg х < 1.
751. Решите уравнение:
a) lg (2х) =1; г) 1g (2х + 5) = 0;
6)lg| = -2; д) 1g (13-х)= 2;
B)lg(x-4)=3; е) lg (х2+1) = 1;
752. Принадлежит ли число 1 области
к) 1g (5-/10);
л) 1g 70 1g 0,2;
м)
1g 0,37
ж) 1g (х2—26) =1;
з) 1g (676-х2) =2;
и) 1g (х2-120) =0.
значений функции:
а) у = 1g (х2
2х + 12);
б) У = 1g (х2 - 2х + 7)?
753. Решите неравенство:
a) 1g х < 1g 3; г) lg х > lg /2; ж) lg х
754. Найдите множество решений неравенства:
a)lg(5x)<l; г) 1g (—4х) > —2; ж) 1g< —1;
О
б) 1g — > 0; д) 1g (х — 2) >0; з) — 1g (5 — х) > 2;
4
В) — lg^>l; е) lg (1 — 2х) < 2; n)lg-<—3.
3 х
755. Можно ли утверждать, что при любом положительном зна-
чении х истинно неравенство:
a) Igx < lg(х + 1); в) Igx > Ig^-;
б) lgx<lg2x; г) lg х>^;
10
756. С помощью графиков установите, имеет ли уравнение решения, и если имеет, то сколько:
a) 1g х ~ 2 — х; в) 1g х = —2х + 1;
б) 1g х = х — 2; г) 1g х = 2х 3.
Упражнения для повторения
757. Решите уравнение:
758. Упростите выражение:
6а — 18 \ . 5а — 15 а3 + 27 / ' 4а3 + 108 ’
х2 + 4х + 16
2х3 — 128
3 — х
39. ЛОГАРИФМИРОВАНИЕ
Т е о р ем a 1. Логарифм произведения двух любых положительных чисел равен сумме логарифмов множителей:
1g (*1*2) = 1g + lg х2, где > 0 и х2 > 0.
Доказательство. Пусть известны логарифмы чисел хх и х2 (хх > 0, х2 > 0):
1g *1 = У1 и 1g х2 =- у2.
Тогда по определению логарифма
— 10У1 и х2 = 10>2.
Перемножив эти равенства почленно, имеем:
хгх2 = 10У1+ь.
Из полученного равенства следует, что 1g (ххх2) = уi + у2. Но так как yr =- 1g и у2 = 1g х2, то 1g (ххх2) = lg х± + 1g х2. Легко доказать, что установленное свойство справедливо для любого числа положительных множителей.
Например, длй трех множителей х± >0, х2 > 0, х3 > 0
1g (ххх2х3) = 1g - lg (xxx2) + 1g х3
= lg Xi + lg x2 + lg x3.
Т е орема 2. Логарифм степени с положительным основанием равен произведению показателя степени и логарифма ее основания:
1g р* = k 1g р, где р> 0.
Доказательство. Пусть 1g р = у.
Тогда по определению логарифма р = 10у-
Возведем обе части равенства р = 10у в степень 6:
pk - (10у)\ т. е. рк = юЧ
Следовательно, lg pk = ky.
Учитывая, что у = 1g р, имеем:
lg pk -= k lg p.
Приведем примеры:
lg 27 - lg 33 = 3 lg 3;
Igi = lg^ = lg2~5= -5 1g2.
Если некоторое выражение составлено из положительных чисел с помощью операций умножения, деления и возведения в степень, то, используя установленные свойства логарифма произведения и логарифма степени, можно выразить его логарифм через логарифмы входящих в него чисел.
Такое преобразование называют логарифмированием.
Прологарифмируем, например, выражение 100а3&2, где а > О, b > 0.
Применяя теорему о логарифме произведения, имеем: lg (100а3Ь2) = 1g 100 + lg а3 + lg b2.
По теореме о логарифме степени
1g а3 =3 lg a, lg Ъ2 = 2 1g &; значит,
lg (100а362) = 1g 100 + 3 lg а + 2 lg b.
Учитывая, что 1g 100 равен 2, получим:
1g (100а8&2) = 2 + 3 1g а + 2 lg Ъ.
Рассмотрим другой пример.
тт - , 2,5s
Найдем логарифм выражения —-------.
Представим это выражение в виде произведения степеней:
2 5s • i/TQ —
-= 2 56 . 19 3 • 3,2 \
3,25
Логарифмируя, имеем:
_L j
lg(2,56 . 193 . 3,2”5) - 61g 2,5 + — lg 19 — 51g 3,2.
3
759. Истинно ли равенство:
a) lg (ab) = lg a + lg &, где a > 0, b = 1;
6) lg an = n lg а, где a > 0, n = 0?
760. Выразите:
a) lg 15 через lg 3 и lg 5; r) lg 49 через lg 7;
6) lg 77 через lg 7 и lg 11; д) lg 8 через lg 2;
в) lg 60 через lg 2, lg 3 и lg 5; e) lg 28 через lg 2 и lg 7.
761. С помощью графика функции у = 1g х (см. рис. 85) нашли, что 1g 2=^0,30, a 1g 3~0,48. Найдите приближенные значения:
a) 1g 6; в) 1g 0,2; д) 1g 0,06; ж) 1g и) 1g 5.
б) 1g 20; г) 1g 600; е) 1g—; з) 1g 1,5;
6
762. Используя данные предыдущего упражнения, найдите: a) 1g 4; в) 1g 0,16; д) 1g 12; ж) lg 1-i;
б) 1g 32; г) 1g 27; е) 1g 75; з) 1g 1,8.
763. Докажите, что при любых положительных значениях х и у: a) lg — = lg х— 1g у\ б) lg yfxy = ilg x + ilg y.
У n n
764. Докажите, что равенства:
a) lg (x + y) = lg x + lg y, 5) lg — =
У igy
не являются тождествами на множестве пар положитель-V ных значений х и у.
765. Прологарифмируйте выражение (буквами обозначены положительные числа):
а) 5&с;
б) х2у;
\ Я2 ч 1 о--X—
д) —; ж) — х3у 3;
Ь 2
е) 2а2&3; з)
abc
и) 100 (а+Ь);
к) ~(а + &)2-
Выразите логарифм х через чисел а и &, если:
логарифмы положительных
' Г— WwW
а) х=а V Ъ’, в) х = (а&)2;
д) х = (10а&)10;
6) х =
а2Ъ
1000’
г) х — ab2;
е) х = а
767. Представьте выражение в
виде произведения степеней и
прологарифмируйте его:
а2Ъ ч 2&М
в) -7.....
Д)
Vа 2аЬ
bVa JL_±
б) г) 10x3z/ s;
ayb
768. Решите уравнение: а)5х = 3; в) 2 • 3х =
б) 4х =9; г) 7 • 0,5х
0,1Ь
е) ;
11; д) 8х+1 = 0,1;
= 6; е) /-V'1 = 10.
\2/
769. Найдите приближенное значение корня уравнения, используя значения 1g 2 и 1g 3 (1g 2 ~ 0,30 и 1g 3 « 0,48): а) 100* = 3; в) 2* = 10; д) 0,01*= 6;
б) 0,1* = 2; г) 3* = 1000; е) 3* = 2.
770. Выразите переменную у через х, логарифмируя обе части
равенства:
а) х = 2У;
б) х = 2У-1;
в) х = 3 • 5У;
г) х = 5 • Зу+1;
д) х = 2 • 101-у;
1—
е) х = 100 • 3 2 ;
ж) х = 2у • 3 У", з) х = 22у • 5у;
и) х = 10у- 2y+s.
Упражнения для повторения
771г На какой промежуток функция у — 1g х отображает промежуток: а) [1; 10]; б) ]0,01; 100[; в) ]10б; 109[?
772. Укажите два последовательных целых числа, между которыми заключено число:
a) 1g 8; б) 1g 37; в) 1g 0,021; г) 1g 0,0048.
773. а) Разность катетов прямоугольного треугольника равна 5 дм. Если больший катет увеличить на 4 дм, а другой уменьшить на 8 дм, то полученный прямоугольный треугольник будет иметь гипотенузу той же длины, что и первоначальный треугольник. Найдите длины катетов первоначального треугольника.
б) Сумма катетов прямоугольного треугольника равна 79 см. Если один из катетов увеличить на 23 см, а другой уменьшить на 11 см, то новый прямоугольный треугольник будет иметь гипотенузу той же длины, что и данный. Найдите длины катетов данного треугольника.
40. ПОТЕНЦИРОВАНИЕ
Мы научились представлять логарифм выражения, составленного из положительных чисел с помощью операций умножения, деления и возведения в степень, через логарифмы чисел, входя
щих в это выражение.
Часто приходится решать обратную задачу: находить выра-
жение, логарифм которого представлен через логарифмы неко-
торых чисел. Такое преобразование называют потенцированием.
Рассмотрим примеры.
Пример 1. Найти %, если lg х = 1g а + 2 1g &, где а > 0, Ъ > 0.
Из свойства логарифма степени следует, что 2 1g & =_ 1g &2;
значит,
1g а + 2 1g Ь = lg а + 1g
Из свойства логарифма произведения следует, что
lg а + 1g Ь2 1g (а&2);
еле до вате льно,
1g * = 1g («Ь2).
Из равенства логарифмов чисел следует и равенство самих чисел, т. е.
х = ab2.
Пример 2. Найти х, если 1g х = 3 1g 2 — 1g 7,5 + lg 3.
Выполним преобразования, применяя последовательно тождества k lg а = lg ak и lg а + lg Ъ = lg (а&):
Igx = 31g2 —lg7,5 + 11g3 = lg23 + lg7,5-1 + lg3 2
2
I
= lg (23 • 7,5“1 • 32).
Отсюда L
x = 2s 7,5-1 • 32.
I
Учитывая, что 23 = 8, 7,5-1 = — и 32 = 1/3, можно зна-
15
чение х записать в другом виде:
15
774.
Найдите х, если:
a) 1g х = 1g 2,4 + 1g 15;
б) lg х = lg 9,6 — lg 2,4;
в) lg x = 2 lg 12 — lg 18;
r) Igx = lg50 + — lg 4;
2
- lg 125
775. Определите знак выражения:
a) lg 2 + lg 3 + lg 0,16; в) | lg 5 + 1 lg 3 - lg 3,5; И Л
6) lg6 + lg0,7 — — lgl6; r) lg!4 — 0,51g3 — 31g2.
2
776. Истинно ли равенство lg (5 + 6) = lg 5 + lg 6?
Если ложно, то что больше: 1g (5 + 6) или 1g 5 + lg 6? 777. Истинно ли равенство 1g 0,2 + 1g 0,5 = lg 0,7?
778. Сравните значения выражений:
a) 1g 4 + 1g 12 и 2 1g 7; в) 1 + 2 lg 2 и 3 lg 5 — lg 3;
б) lg7 — lg2 и 1; г) 31g 6 — 2 и — lg5.
2 2
779. Найдите число t по его логарифму (буквами а и & обозначены положительные числа):
a) lg/ = 21ga — lg&; д) lg/= —1 — 21ga;
6) IgZ = —Iga + 31g&; e) Igi = Iga —1 —— lg&;
2 2
780a Найдите значение выражения:
781. Выразите х через у:
782. Найдите область определения каждой из двух данных функций и выясните, какая из областей является подмножеством другой:
— 1
а) у = 1g х2 и у = 2 1g х; б) у = 1g У х и у = — 1g х.
и
783. Решите уравнение:
a) lg (2х+10) = 41g2 + lg3; в) lg(x+l)=llgl8-i-lg2;
б) lg (6х-26) =2+4 lg 2; г) lg (5-х)= ilg 27 - 1.
3
784. Существует ли значение переменной х, при котором значение выражения:
a) 1g (х2—х-|70) равно 2; б) lg (х2—Xj-1,1) равно —1?
785. а) Докажите, что если переменная х принимает значения 1; 2; 4; 8; 16, то соответствующая последовательность значений функции у ~ 1g х есть арифметическая прогрессия.
б) Докажите, что если значения переменной х образуют геометрическую прогрессию, все члены которой положительны, а знаменатель прогрессии равен то соответствующие значения функции у — 1g х образуют арифметическую прогрессию. Чему равна разность этой арифметической прогрессии?
Упражнения для повторения
786. Представьте число в виде суммы его целой и дробной частей: а) 12,4; б) —12,4; в) 0,92; г) —0,92.
787. а) Пусть х EZ, Каково значение выражения {%}?
б) Пусть х Z. В каких границах заключено значение выражения {х}?
788. Запишите число в стандартном виде и укажите его порядок: а) 650; б) 13750; в) 0,81; г) 0,00895.
789. Укажите два последовательных целых числа, между которыми заключено число: a) 1g 248; б) 1g 0,03.
790. Найдите значение выражения: a) [1g 26]; б) [1g 0,048].
791. В каких границах заключено значение х, если известно, что: a) [lg х] = 1; б) [1g х] = —2?
§ 14.
ТАБЛИЦЫ ЛОГАРИФМОВ
41. ХАРАКТЕРИСТИКА И МАНТИССА ЛОГАРИФМА
Нам известно, что любое писать в стандартном виде х
Найдем логарифм х:
положительное число х можно за-= а - 1(Р, где 1 < а < 10, п £ Z.
1g % ----- lg (а • 10*) = lg а + 1g 10* = и + 1g а.
Так как 1 а < 10, то 0 1g а <1.
Следовательно, логарифм х представлен в виде суммы целого числа и и неотрицательного слагаемого 1g а, меньшего, чем 1. Значит, п — целая часть lg х, a 1g а — его дробная часть, т. е.
п [lg X], lg а = {1g х}.
Мы установили, что целая часть логарифма числа а • 10*,
где 1 а < 10 и п € Z, равна порядку п этого числа, а дробная часть равна 1g а.
Для целой и дробной частей логарифма приняты специаль-
ные термины: целую часть логарифма называют характеристикой логарифма, а дробную часть — мантиссой.
Рассмотрим числа 4650; 46,5; 0,0465. Они отличаются друг от друга только положением запятой в числе. Представив эти числа в стандартном виде, найдем характеристику и мантиссу логарифма каждого из чисел:
4650 - 4,65 103;
46,5 = 4,65 • 101; 0,0465 - 4,65 • 10"2;
1g 4650 = 3 + 1g 4,65;
lg 46,5 = 1 + lg 4,65;
lg 0,0465 = -2 + lg 4,65.
Мы видим, что логарифмы данных чисел имеют одну и туже мантиссу.
Вообще, если два числа отличаются друг ст друга только положением запятой, то их записи в стандартном виде отличаются только порядком. Значит, логарифмы этих чисел имеют одинаковые мантиссы (дробные части). Другими словами, мантисса логарифма числа не зависит от. положения запятой в этом числе»
Рассмотренное свойство логарифмов имеет важное практическое значение. С его помощью, зная логарифмы чисел из промежутка Г1; Ю[, можно найти логарифм любого положительного ч и ела.
Пусть, например, требуется найти 1g 300. Представив число 300 в стандартном виде, получим:
1g 300 = 1g (3 < 1.02) - 2 + 1g 3.
Следовательно, для нахождения 1g 300 достаточно знать, чему равен 1g 3.
Значение 1g 3 можно найти с помощью графика функции у = 1g х (см. рис. 85). Имеем: lg 3 ж 0,48. Значит, 1g 300 #24 0,48 =- 2,48.
792. Представив данное число в стандартном виде а ° 10Д где 1 а < 10 и п t Z. выразите его логарифм через логарифм а по следующему образцу:
1g 0,024 = 1g (2,4 • IO"2) - lg 2,4 + lg 10~a =>
~ — 2 - H 1 g 2,4.
a) 42,2; в) 2,84; д) 0Д56; ж) 3,00123;
б) 505; г) 320 645; е) 0,0918; з) 0,3123.
793. Найдите характеристику и мантиссу 1g х, если:
a) 1g х = 1,275; в) 1g х —1,45; д) 1g х = —0,515;
б), 1g х - 10,618; г) 1g х - -2,28; е) 1g х - -3,846.
794. Найдите ио графику функции у = 1g х (см. рис. 85) 1g 3,2. Воспользовавшись полученным результатом, вычислите: a) 1g 32; б) 1g 3200; в) 1g 0,32; г) 1g 0,0032.
795. Найдите по графику функции у — 1g х (см. рис. 85) 1g 6,5. Воспользовавшись полученным результатом, вычислите: a) 1g 650; б) 1g 0,65; в) 1g 0,085; г) 1g 65,
796, Используя график функции у = 1g х, найдите:
a) 1g 12; б) 1g 83; в) 1g 0,35; г) 1g 0,024,
Упражнения для повторения
797. Найдите значение выражения:
а~б _ Ъ-^
ab~~2 -г Ъа~2
V- ? г2
при х = —0,12 и у ~ —0,5;
X + у
при а = 0,2 и Ъ ~ ОД
798. а) От двух станций А и В, расстояние между которыми 75 км, отправились одновременно товарный и скорый поезда и встретились через полчаса. Товарный поезд прибыл в В на 25 мин позже, чем скорый в А. Какова скорость каждого поезда?
б) За 70 км до конечной станции поезд опаздывал на 10 мин. Чтобы прийти вовремя в пункт назначения, поезд должен увеличить свою скорость на 10 км/ч. С какой скоростью должен идти поезд последние 70 км по расписанию?
42. ЧЕТЫРЕХЗНАЧНЫЕ ТАБЛИЦЫ ЛОГАРИФМОВ
Для нахождения логарифмов чисел мы пользовались графиком функции у = 1g х, построенным на промежутке [1; 10]. Очевидно, что по графику, даже применяя крупный масштаб, нельзя получить достаточно точных значений логарифмов.
Для практических расчетов используются таблицы логарифмов трехзначные и четырехзначные, а в тех случаях, когда требуется большая точность вычислений. — таблицы с большим числом знаков.
В школьной практике используют «Четырехзначные математические таблицы» В. М. Брадиса.
В этих таблицах приведены мантиссы (дробные части) десятичных логарифмов чисел с точностью др 0,00005. Так как дробная часть логарифма есть число, заключенное между 0 и .1, т. е. число вида 0, то при составлении таблицы в нее записывают только цифры, стоящие после запятой.
Приведем часть четырехзначной таблицы логарифмов:
Табл и ц а XIII
X 0 1 2 3 4 6 7 8 9 i ! 2 3 4 О 6 7 8 9
65 8129 8136 8142 8149 8156!8162 ^8169 8176 8182 8189 1 1 2 3 3 4 5 X •6
66 8195 8202 8209 8215 8222 8228 р235 8241 8248 8254 7 1 2 3 3 4 5 5 6
67 8261 8267 8274 8280 8287 8293 8299 8806 8312 8319 1 2 3 3 4 5 5 6
68 8325 8331 8338,8344 8351 8357 8363 8370 8376 8382 £ 1 2 3 3 4 4 5 6
69 8388 8395 8401' 8407 8414 8420 8426 8432 8439 8445 1 1 2 2 3 4 4 5 3
70 8451 8457 8463 8470 8476 8482 8488 8484 8gG0 8506 1 1 2 2 sl 4 4 5 6
Пользуясь этой таблицей, найдем логарифмы чисел:
1) 675; 2) 67,84; 3) 0,07.
1) 1g 675 - 1g (6,75 • 102) - 2 + lg 6,75.
Найдем мантиссу на пересечении строки с меткой «67» и столбца с меткой «5». Получаем число 8293. Значит, мантисса приближенно равна 0,8293. Отсюда 1g 675 2,8293.
2) 1g 67,84 - 1g (6,784 • 101) « 1 + 0,8315 - 1,8315.
Для отыскания мантиссы мы, прочитав число 8312 на пересечении строки с меткой «67» и столбца с меткой «8», прибавили к этому числу поправку 3 на четвертую цифру. Поправка расположена в правой части таблицы на пересечении той же строки и столбца поправок с меткой «4».
3) 1g 0,07 - lg (7 • 10~2) = —2 +lg 7^-2+0,8451--1,1549.
При отыскании мантиссы логарифма мы использовали свойство {1g 7} - {1g 70} 0,8451.
Для решения обратной задачи (нахождения числа по его логарифму) можно использовать ту же таблицу логарифмов, но удобнее воспользоваться таблицей значений функции у = 10*, с которой мы познакомились ранее.
Пусть, например, 1g х — 3,3192.
По определению логарифма х — 103’3192.
Так как 103>3192 — 10°<3192 • 103, то, найдя по таблице значений функции у — 10* значение выражения 10°>3192, получим
х = 10°>3192 103 2,084 • 103.
7&9. Найдите по четырехзначным таблицам логарифмы чисел:
а) 12; 29; 75; 143; 218; 701; 872; 950; 999; 8;
*б) 0,62; 0,15; 0,4; 0,0125; 0,216; 0,00324;
в) 8,432; 1,681; 3,047; 56,43; 84 440; 68 810; 73 257;
г) 0,1645; 0,08112; 0,3101; 0,04005; 0,32198; 0,26543.
800. Найдите число х, если 1g х равен:
а) 0,1445; 0,1786; 2,3990; 1,4009;
б) 2,4932; 3,7112; 1,8054; 1,29,58;
в) 3,0034; 2,0981; 1,1111; 0,0778;
г) 2,3142; 0,8444; 1,0061; 1,6771;
д) -0,8132; —0,1263; —1,8867; —1,07642;
е) —2,1060; —2,9912; —3,6123; —5,0089.
Упражнения для повторения
801. Найдите значение выражения:
43. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ ЧЕТЫРЕХЗНАЧНЫХ ТАБЛИЦ ЛОГАРИФМОВ
Приведем примеры вычислений, ванием таблиц логарифмов.
Пример 1. Найти значение
Логарифмируя, имеем:
выполняемых с использо-
0,9124* а, если а =---------.
1,583
1g а - 4 1g 0,9124 - 1g 1,583. (1)
Подставив значения логарифмов чисел 0,9124 и 1,583 в равенство (1), получим:
lga&4 • (-0,0398) — 0,1995 = -0,1592 — 0,1995--0,3587.
По таблице значений функции у = 10х найдем а:
а & 10“°>3587 -= 10“г • 10°>6413 4,378 • 10"1.
Ответ, а 0,4378.
П р и м е р 2. Вычислить корень уравнения 1,08х = 648.
Логарифмируя обе части уравнения, имеем:
х 1g 1,08 = 1g 648.
Отсюда
1g 648
х ” ig i,oa*
Мы нашли корень уравнения 1,08х = 648. Вычислим теперь приближенное значение этого корня, найдя по таблице значения соответствующих логарифмов:
1g 648 - 1g (6,48 - 102) - 2 + lg 6,48 2,8116;
lg 1,08 0,0334.
2 8116
Следовательно, x ----------.
0,0334
Выполнив деление, получим:
(В частном сохранены три цифры — столько, сколько значащих цифр имел знаменатель дроби.)
Пример 3. Прирост древесины на лесном участке составляет в среднем 3,5% в год. Какое количество древесины будет на этом участке через 10 лет, если первоначальное количество древесины было оценено в 6,5 • 105 м3?
Очевидно, что количество древесины возрастает за каждый промежуток времени, равный одному году, в 1,035 раза (на 3,5 %).
Обозначим первоначальное количество древесины на участке через Ао, а количество древесины на участке через 1 год, через 2 года и т. д. соответственно через А19 А2 и т. д. Тогда последовательность Ао, А19 А2, ..., А10 — геометрическая прогрессия, состоящая из 11 членов со знаменателем 1,035.
Следовательно, А1о==Ао-1,О3510, т. е. А10 = (6,5-105)-1,03510.
Найдем логарифм А1о:
lg Ao-lg 656+6 + 10 lg 1,035^5,8129 + 10 0,0149^5,9619.
Отсюда А10 105>9619 9,161 • 105.
Учитывая, что в условии содержались данные с двумя значащими цифрами, округляем результат до двух значащих цифр.
Ответ. 9,2 • 105 м3,
862. Вычислите с помощью таблиц логарифмов:
а) 2,41.0,324;
б) 0,084 • 9,12;
Ж)
32 3851
S
8640 ’
г)
103.8 '______•
0,4141 ’
812,8
2-3,3 • 0,5124’
0,9123 • 73 500
803. Яайдите значение выражения:
а) 6,325;
б) 1,73210;
б) 0,385*;
г) 0,242е;
Д) 1,794-3;
е) 0,614~4;
ж) у 1540;
з) у 79200;
и) /6,09046;
к) +,6743;
л) у 0,008462;
м) у7 0,0007116.
804.
Вычислите
с помощью таблиц логарифмов:
а) 0,38513 714,2;
б) 14,54 • /6,1856;
г) 0,08136
Д)
е)
/1,745 .
0,3117 ’
l,G8l_
У/08812
805. Определите с помощью таблиц логарифмов порядок числа:
а) 215; б) З22; в) 7 + г) 1212; д) 0,6 s; е) 0,09"-9.
806. Сравните значения выражений:
а) 226 и З16; б) 431 и З40; в) 621 и 5-s; г) 1213 и 1312е
807, Решите уравнение и вычислите приближенные значения его корней: о
а) .У = 6 000 000; в) х1.2 = 248,6; д) х 3 = 0,236;
б) х5 = 765 000; г) х0»3 = 14,5; е) х_1>25 = 0,08754.
80S. Площадь поверхности шара можно найти по формуле S 4 лД2. Зная, что 1g л 0,4971, найдите значение S, если: а) Л 84,5 м; б) II & 6,35 ? 103 и
809. Воспользовавшись данными предыдущей задачи, найдите радиус шара, если:
a) S ж 86,3 м2; б) S ж 0,4321 км2; в) S;^5,7 * 107 км2.
810.
811.
812.
Объем шара вычисляется по формуле Г =
Пай-
дите объем шара, если: а) 7? ж 2,675 м; б) R « 81,6 м. Воспользовавшись формулой объема шара, найдите радиус шара, если: а) V 736 м3; б) V ж 135 см3.
Найдите приближенные значения корней уравнения:
а) 2* = 5; в) 3,2* = 18; д) 0,12*=4; ж) 0,35*=0,072;
б) 5* = 500; г) 7,6*= 9; е) 0,48* = 24; з) Y-Y' =
813. а) Участок леса содержит 7,2 • 104 м3 древесины. На сколько кубометров увеличится количество древесины через 15 лет, если средний ежегодный прирост древесины 2,8 %? б) Количество древесины на лесном участке оценено приблизительно в 6,8 * 104 иг. Зная, что ежегодный прирост древесины равен 3,0 %, вычислите, какое количество древесины может быть получено с этого участка через 20 лет. Сколько учебников «Алгебра, 8» могло бы быть изготовлено из этой древесины, если на изготовление бумаги идет только около 10 % полученной древесины, плотность древесины 700 кг/м3 и масса одного учебника 0,30 кг?
814. а) В городе 2,40 • 105 жителей. Сколько жителей будет в этом городе через 10 лет, если средний ежегодный прирост населения равен 1,8 %?
б) Население города ежегодно увеличивается на Чему равно р, если известно, что через 10 лет население города удвоится?
Упражнения для повторения
815. Упростите выражение:
816. а) Два автопогрузчика выполнили работу за 20 ч. За сколько часов может выполнить эту работу каждый автопогрузчик, работая один, если известно, что второй может выполнить ее на 9 ч быстрее, чем первый?
б) Два сварщика, работая вместе, могут выполнить задание за 30 ч. За сколько часов сможет выполнить ото задание каждый сварщик, если известно, что первому на выполнение всей работы потребуется времени на 11 ч больше, чем второму?
817. Решите графически уравнение:
а) 2* = х И- 3; б) 2* = 6 — х.
818. Найдите множество решений неравенства:
а) (х + 4) (х 4- 5) — 5 < 7; б) (х + 5) х < 2 (х2 + 2).
§ 15,
ЛОГАРИФМИЧЕСКАЯ ЛИНЕИКА
44. ЛОГАРИФМИЧЕСКАЯ ШКАЛА
В повседневной жизни, в науке и технике постоянно приходится иметь дело с различными шкалами: со шкалой термометра, весов, амперметра, спидометра в автомобиле, с циферблатом часов.
В вычислительной практике широкое применение находит логарифмическая шкала. Ознакомимся с ее устройством.
Пусть на прямой выбраны начальная точка О и положительное направление, например вправо, а некоторый отрезок ОЕ принят за единичный (рис. 86).
Каждому положительному числу а поставим в соответствие некоторую точку М прямой, удовлетворяющую двум условиям:
1) \ОМ\ = 11g а|;
2) если а 1, то точка М расположена правее точки О, если 0 < а < 1, то левее.
Тогда числу 1 будет соответствовать начальная точка, так как lg 1 = 0. Числу 10 будет соответствовать точка £*, т. е. конец единичного отрезка, так как 1g 10 — 1. Числу 2 будет соответствовать точка At расположенная правее точки О на расстоянии, равном 11g 21, приближенно равном 0,30. Числу 3 — точка В, лежащая правее точки О, причем | OB | = 11g 31 w 0,48. Для числа 0,1 соответствующей будет точка С, расположенная левее точки О на расстоянии, равном 1, так как 11g 0,11 = 1.
На рисунке 87 показаны точки О, А, В, С9 Е и числа, которым они соответствуют. Аналогично можно отметить точки, соответствующие и другим положительным числам.
Построенная таким образом шкала называется логарифмической.
Каждому положительному числу соответствует некоторая точка логарифмической шкалы. Каждая точка логарифмической шкалы является образом некоторого положительного числа. Например, точка К9 лежащая правее точки О (рис. 88),
Рис. 86
0____________________________0 А В_______________________Е
Д? Т“ 2 3 10~ '
соответствует некоторому числу &, где b > 1 и [1g &| = |ОЛ*|. Следовательно, логарифмическая шкала задает отображение множества положительных чисел на множество точек прямой.
Рассмотрим важное свойство логарифмической шкалы. Из того, что
1g (10а) = 1g 10 + lg а = 1 + lg а,
следует, что при увеличении числа в 10 раз соответствующая точка логарифмической шкалы перемещается в положительном направлении на единицу. Поэтому отрезок шкалы от 10 до 100 можно получить из отрезка шкалы от 1 до 10 путем параллельного переноса в положительном направлении на единицу. При этом каждая метка а перейдет в метку 10а. Аналогично можно получить отрезок шкалы, соответствующий числам от 100 до 1 000 и т. д. Параллельный перенос в противоположном направлении позволяет получить отрезки логарифмической шкалы от 0,1 до 1, от 0,01 до 0,1 и т. д.
Рассмотренное свойство логарифмической шкалы называется ее периодичностью.
819. Пользуясь таблицей логарифмов, постройте отрезок логарифмической шкалы с метками!, 2, 3, ..., 9, 10, выбрав единичный отрезок равным: а) 100 мм; б) 250 мм.
820. На логарифмической шкале, изображенной на рисунке 89, покажите отрезок, длина которого равна:
a) 1g 2; б) 1g 5; в) 1g 7; г) 1g 3, если за единицу измерения принята длина единичного отрезка шкалы.
821. С помощью логарифмической шкалы (см. рис. 89) покажите, что:
a) 1g 2 + 1g 3 > lg 5; в) lg 7 < lg 2 + lg 5;
6) lg 2 + lg 3 - lg 6; r) lg 10 - lg 2 + lg 5.
822. Одинаковы ли расстояния между метками 2 и 3; 3 и 4; 4 и 5 логарифмической шкалы? Объясните почему.
823. а) На логарифмической шкале показано положение меток 1, 10 и а (рис. 90, а). Покажите положение меток 10а, 0,1а.
g _ 5
7 2 ^3 Ь~ 10
Рис. 88
Рис. 90
б) На логарифмической шкале показано положение меток 1, а и 10а (рис. 90, б). Покажите положение метки 10.
824. На логарифмической шкале нанесены метки 1, 2 и 3 (рис. 91). Пользуясь ими, найдите положение меток 6, 12 и 18.
Упражнения повторения
+
1
Рис. 91
825. Найдите область
ния выражения: а) ]/х* 1 2 3 ~г х — 6;
б) 1g (4х“ + 4х *—
для
определе-
3).
45. ОСНОВНАЯ ШКАЛА ЛОГАРИФМИЧЕСКОЙ ЛИНЕЙКИ
На свойствах логарифмов основано устройство логарифмической линейки — счетного прибора, используемого в практической деятельности инженеров, техников, рабочих.
Логарифмическая линейка (рис. 92) состоит из трех частей:
1) корпуса, в середине которого расположен желобок;
2) движка, скользящего в желобке корпуса;
3) бегунка, на котором нанесена линия — визир*
На корпусе линейки нанесены различные шкалы. Вторая снизу шкала называется основной* Такая же шкала имеется и на движке.
Основная шкала линейки представляет собой отрезок логарифмической шкалы от 1 до 10.
Наибольшее распространение получили линейки, на которых единичный отрезок основной шкалы берется равным 250 мм.
Рис. 92
Каждая метка а на такой линейке удалена от начала отсчета
единиц, т. е. на 250 11g al мм.
На основной шкале такой линейки указаны точки,
соответ-
ствующие целым числам: 1, 2, 3, ..., 10. Намечаемые ими деления называются делениями первого разряда. На шкале указаны также точки, соответствующие десятым долям. Они намечают
деления второго разряда. Наконец, на шкале указаны некоторые из точек, соответствующие сотым долям. Эти точки намечают деления третьего разряда. Цена деления третьего разряда в промежутке от 1 до 2 равна 0,01, в промежутке от 2 до 4 равна 0,02, в промежутке от 4 до 10 равна 0,05.
В силу периодичности логарифмической шкалы мы можем считать, что на линейке представлен ее участок от 10/с до 104% где fe — целое число, например: от 0,1 до 1; от 10 до 100; от 100 до 1000 и г. д, Поэтому одну и ту же точку можно считать соответствующей как числу а, где 1 а 10, так и числу 0,1а, 10а, 100а и т. д., т. е, числу вида а • 10% где k — целее число. Например, считают, что числам 0,432, 0,00432, 432
соответствует на шкале линейки та же точка, что и числу 4,32. При установке числа на линейке для пас важно лишь, что первая значащая цифра. 4, вторая 3, третья 2. Каждое из этих чисел читают так: <4 — 3 — 2» (четыре — три — два). Первой значащей цифре соответствуют деления первого разряда, второй — деления второго разряда, третьей — деления третьего
При установке на линейке чисел, содержащих более трех значащих цифр, их предварительно округляют, оставляя три значащие цифры.
Приведем примеры.
Пример 1. Отметить число 137 (читаем: «один — гри •— семь»).
Устанавливаем визир на точке, удаленной от начальной точки шкалы на одну единицу первого разряда, три единицы второго разряда и семь единиц третьего разряда.
Пример 2. Прочитать число, соответствующее точке, отмеченнохч на линейке визиром бегунка (рис. 93).
r д , 7 Р. д s iQ
|_ II .iiiliwljii. Lilli J-«тяиши 'Iinri№i.-Ti ..... iiinfc»'14.unuiJntnU|Lj ^1 J Т|П1»Ми1Н| ! ||| I I ИНЧ1 !
Рис. 93
Отмеченная точка удалена от начальной точки на две единицы первого разряда, три единицы второго разряда и пять единиц третьего разряда (последнее определяем на глаз). Следовательно, три первые значащие цифры искомого числа: 2—3—5. В промежутке [1; 10] таким числом является число 2,35.
826. Отметьте визиром бегунка на основной шкале числа:
а) 1,64; 2,36; 3,18; 4,45; 6,05; 9,20; 9,55;
б) 123; 17,4; 198; 0,0226; 316; 4280; 8150; 97,5.
827. Определите на глаз, сколько десятых долей отрезка заключено между его началом и вертикальной чертой (рис. 94). Ответ проверьте измерением.
828. Отметьте визиром бегунка на основной шкале числа:
а) 2,63; 3,45; 4,61; 3,89; 6,74; 8,52; 9,58;
б) 816; 24,7; 7,23; 91,8; 3270; 563; 0,737;
в) 57,48; 1619; 0,4647; 3,438; 2,739; 16,16;
г) 31 829; 0,6783; 394,5; 3,007; 51,05; 0,1081.
829. Прочитайте число, которое установлено на основной шка-ле, если визир бегунка совпадает:
а) с меткой 6 на нижней шкале корпуса линейки;
б) с меткой 8 на нижней шкале корпуса линейки.
830. Установите бегунок так, чтобы визир:
а) совпал с одной из меток, обозначенных на основной шкале;
б) не совпал ни с одной из меток, обозначенных на основной шкале.
Прочитайте соответствующее число.
Рис. 94
Упражнения для повторения
831. При каких значениях переменной истинно неравенство: a) 0,2°’27_3jc3 < 1; б) 3*2-6x+7>5 9/3?
46. УМНОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКОЙ ЛИНЕЙКИ
Известно, что сумма логарифмов множителей равна лога-рифму произведения:
lg а + 1g Ъ - lg (ab) (а > О, Ъ > 0).
С помощью двух одинаковых логарифмических шкал, одна из которых нанесена на корпусе линейки, а другая — на движке, можно складывать логарифмы чисел (точнее, мантиссы логарифмов чисел), а значит, и выполнять умножение.
Умножим, например, пользуясь логарифмической линейкой, 2 на 3. Поставим движок так, чтобы метка 1 шкалы движка совпала с меткой 2 шкалы корпуса линейки. Отметим визиром на шкале движка метку 3. На шкале корпуса линейки против нее находится точка, которой соответствует произведение чисел 2 и 3, т. е. число 6.
Нетрудно понять, из чего это следует. Длина отрезка логарифмической шкалы от 1 до 2 равна 1g 2, а от 1 до 3 равна 1g 3 (за единицу измерения принята длина отрезка шкалы от 1 до 10). Значит, длина отрезка шкалы на корпусе линейки от 1 до точки, отмеченной визиром, измеренная в тех же единицах, равна 1g 2 + 1g 3, т. е. 1g (2 - 3) (рис. 95). Следовательно, этой точке соответствует число, равное произведению 2 • 3.
Попытаемся теперь аналогичным образом умножить 2 на 6. Мы не можем прочитать произведение, так как метка 6 на шкале движка выходит за пределы линейки. В силу периодичности логарифмической шкалы ее можно продолжить, повторив имеющийся на линейке отрезок шкалы. Для этого достаточно поставить против метки 2 метку 10 на движке, т. е. совместить с меткой 2 правый конец движка. Тогда точкам нижней шкалы будут соответствовать числа в 10 раз большие, чем те, которые указаны на линейке. Против метки 6 на шкале движка читаем на нижней шкале ответ: 12.
189 с
Вообще, если против метки а на шкале корпуса линейки поставить метку 1 или метку 10 на шкале движка, то против метки b на шкале движка будет находиться метка ab на шкале корпуса.
Так как на движке и на корпусе линейки представлен только отрезок логарифмической шкалы от 1 до 10, то действия над логарифмами чисел мы заменяем действиями над мантиссами их логарифмов. Поэтому в результате мы можем лишь указать значащие цифры произведения. Место запятой в произведении будем определять прикидкой. Чтобы сделать такую прикидку, иногда удобно представлять множители в стандартном виде.
Рассмотрим примеры.
Пример 1. Вычислить произведение 0,346 • 1,27.
Совмещаем метку 1 шкалы движка с меткой 3—4—6 на основной шкале корпуса линейки. Против метки 1—2—7 на шкале движка читаем результат: 4—3—9. Положение запятой в числе находим прикидкой: 0,346 0,3, 1,27 ж 1,3,
0,3 1,3 = 0,39. Очевидно, что искомое произведение приближенно равно 0,439.
Чтобы определить точность результата, выполним умножение в столбик. Получим: 0,346 • 1,27 = 0,43942. Абсолютная погрешность найденного нами приближения равна 0,00042. Значит, в записи 0,439 приближенного значения произведения все цифры верные. Мы получили результат с тремя значащими цифрами.
Вообще, если исходные данные точные или взяты с тремя значащими цифрами, то линейка, как правило, позволяет найти результат с тремя значащими цифрами.
Пример 2. Вычислить произведение 0,0545 • 0,00725.
Совмещаем метку 10 шкалы движка с меткой 5—4—5 на основной шкале корпуса линейки. Против метки 7—2—5 читаем результат: 3—9—5. Чтобы определить положение запятой, представим каждый множитель в стандартном виде. Получим:
(5,45 • 10-2) • (7,25 • 10~3) - (5,45 - 7,25) • 10~6.
Так как 5 • 7 = 35, то произведение в скобках приближенно равно 39,5.
Итак, 0,0545 • 0,00725 39,5 • 10~5 = 3,95 • 10“4.
832.
С помощью логарифмической линейки найдены три зна-
чащие цифры произведения. Запишите ответ:
а) 4,25 -б) 51,6 •
в) 315 • г) 0,05 •
д) 1,85
1,56 ...
2,16 ...
118 ...
4,24 ...
30,8 ж ...
833. Найдите значение произведения 2,58 • 4,25:
а) выполнив умножение с помощью линейки;
б) выполнив умножение в столбик и округлив результат, оставив в нем три значащие цифры.
834. Выполните умножение, проверяя результат по данному ответу:
Выражение Значение выражения Выражение Значение выражения
1 2 3 4 5 1,45 • 2,5 1,96 • 2,4 2,34 . 1,41 5,45 • 2,9 6,85 • 2,7 3,63 4,70 3,30 15,8 18,5 6 7 8 9 10 10,7 -5,2 2,06 • 19,7 9,38 • 4,43 0,822 • 51,8 14,3 • 0,0116 55,6 40,6 41,6 42,6 0,166
835. Выполните умножение и проверьте результат по ответу, содержащемуся среди приведенных ниже:
а) 0,323 • 0,816; в) 442 • 15,3; д) 917 • 6,06;
б) 8,94 • 0,654; г) 71,4 • 3,86; е) 624 - 35,6.
Ответы: 5,56 • 103; 0,264; 2,22 • 104; 5,85; 6,76 - 103; 276.
836. С помощью линейки были выполнены вычисления, два из которых неверны. Найдите ошибки и исправьте их:
а) 13,8 * 1,76 24,3;
б) 0,143 • 69,5 9,94;
в) 102 • 9,56 ^ 97,5;
837. Выполните умножение с
У нейки:
г) 9,68 • 81,3 787;
д) 0,874 • 0,571 0,409;
е) 79,6 • 0,603 & 48,0.
помощью логарифмической ли-
а) 3,16 • 5,28; д) 5,16 • 7,55; и) 0,126 • 305;
б) 7,14 • 6,11; е) 3,32 • 43,2; к) 0,144 • 410;
в) 14,9 • 32,1; ж) 425 • 308; л) 172 • 0,0302;
г) 25,4 • 0,246; з) 144 * 278; м) 0,056 • 185.
838. Пользуясь особой меткой для числа л, найдите с помощью логарифмической линейки длину окружности по ее диаметру, равному: 25,6 мм, 42,2 мм, 63,0 мм, 75,1 мм. Ответ проверьте по таблице VI*.
839. Найдите массу платиновой пластины объемом 16,5 см3 (плотность платины 21,5 г/см3).
840. Одна морская миля приближенно равна 1,85 км. Выразите в километрах расстояние, равное 2,75 морской мили.
841. Площадь основания цилиндра равна 7,25 дм2. Вычислите объем цилиндра, если его высота равна 6,24 дм.
* См.: Б р а д и с В. М. Четырехзначные математические таблицы. М., Просвещение, 1978.
Упражнения для повторения
842. а) Напишите уравнение прямой, которая проходит через начало координат и через точку Е (0,6; —2,7).
б) Напишите уравнение прямой, которая пересекает оси координат в точках К (0; 4) и L (—2,5; 0).
843. На изготовлении определенного вида деталей в цехе работают два станка-автомата. Один из них в час выпускает на 12 деталей больше, чем другой. Сколько времени потребуется каждому станку-автомату для выпуска 360 деталей, если известно, что на выполнение этой работы первый станок затратит времени на 1 ч меньше, чем другой?
47. ДЕЛЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКОЙ
ЛИНЕЙКИ
Известно, что разность логарифмов делимого и делителя равна логарифму частного:
lg а — lg & = 1g- (а > 0, Ъ > 0).
ъ
С помощью двух одинаковых логарифмических шкал линейки можно находить разность логарифмов (точнее, их мантисс), а значит, и выполнять деление чисел.
Разделим, например, пользуясь логарифмической линейкой, 6 на 2. Поставим против метки 6 шкалы корпуса линейки метку 2 шкалы движка. Против метки 1 шкалы движка находится на шкале корпуса линейки точка, которой соответствует частное чисел 6 и 2, т. е. число 3.
Поясним, из чего это следует. Длина отрезка логарифмической шкалы от 1 до 6 равна 1g 6, а от 1 до 2 равна 1g 2 (за единицу измерения принята длина отрезка шкалы от 1 до 10). Значит, длина отрезка шкалы на корпусе линейки от 1 до точки, стоящей против метки 1 шкалы движка, измеренная в тех же единицах, равна 1g 6 — 1g 2, т. е. 1g—. Следовательно, этой 2
точке соответствует число, равное частному 6:2.
Рассмотрим другой пример. Найдем частное 2 : 6. Против метки 2 шкалы корпуса линейки поставим метку 6 шкалы движка. Начало шкалы движка выходит за пределы линейки. Чтобы продолжить шкалу корпуса линейки влево на 1, достаточно заменить метку 1 шкалы движка меткой 10. Против метки 10 шкалы движка находится на шкале корпуса линейки метка 3—3—3. Положение запятой в частном определяем с помощью прикидки (2:6 — 0,3). Искомое частное приближенно равно 0,333.
Вообще, если метку а шкалы корпуса линейки совместить с меткой Ъ шкалы движка, то против метки 1 или метки 10
шкалы движка будет находиться метка ~ шкалы корпуса линейки.
Положение запятой в частном определяется с помощью прикидки. При этом бывает иногда удобно делимое и делитель представить в стандартном виде.
Приведем примеры.
Пример 1. Вычислить частное 8,05 : 2,86.
Совместим метку 8—0—5 шкалы корпуса линейки с меткой 2—8—6 шкалы движка. Против метки 1 шкалы движка читаем на шкале корпуса линейки: 2—8—1. Так как 8 : 3 3, то иско-
мое частное приближенно равно 2,81.
Пример 2. Вычислить частное 0,304 : 540.
Против метки 3—0—4 шкалы корпуса линейки поместим метку 5—4—0 шкалы движка. Читаем метку, расположенную на шкале корпуса линейки против метки 10 шкалы движка: 5—6—3.
Чтобы определить положение запятой, представим делимое и делитель в стандартном виде и выполним преобразования: 0,304 _ 3,04 . 10~1 3,04 1Q_3 540 ~ 5,4 • 102 ~~ 5,4
Так как 3:5 = 0,6, то « 0,563 • 10“3 = 0,006563. 540
844. С помощью линейки найдены три значащие цифры частного. Запишите ответ:
а) 5,35 : 1,16 ... (4—6—1); в) 0,605 : 12,3 ... (4—9—2);
б) 42,3 : 139^... (3—0—4); г) 712 : 33,6^... (2—1—2).
845. Найдите значение частного 2,38 : 1,62 двумя способами: а) с помощью линейки;
б) выполнив деление в столбик и округлив результат, оставив в нем три значащие цифры.
846. При помощи линейки выполните деление, проверяя результат по данным ответам:
Выражение Значение выражения Выражение Значение выражения
1 2,3 : 1,7 1,35 7 132 : 455 0,290
2 3,44 : 2,06 1,67 8 22,7 : 0,545 41,7
3 48,5 : 3,3 14,7 9 9,35 : 61,5 0,152
4 525 : 27,8 18,9 10 114 : 0,164 695
5 0,392 : 0,835 0,469 11 36,19 : 7,05 5,13
6 0,0405: 0,915 0,0443 12 77,5 : 0,965 80,3
193
7 Алгебра 8 кл-
847. Выполните с помощью линейки деление и проверьте результат по ответу, содержащемуся среди приведенных ниже:
а) 5270 : 425; г) 9,1 : 3,33; ж) 1,59 : 1,5;
б) 1,29 : 0,355; д) 0,609 : 0,125; з) 695 : 0,61.
в) 0,805 : 1,36; е) 4,779 : 3,069;
Ответы: 1,14 • 103; 1,06; 12,4; 2,73; 4,87; 1,56;
' 0,592; 3,63.
848. С помощью линейки выполните деление:
а) 13,6 : 2,04; в) 42,6 : 3,18; д) 2,36 : 0,425;
б) 3,45 : 1,26; г) 0,243 : 0,145; е) 0,661 : 2,12.
849. Найдите с помощью линейки произведение и частное чисел:
а) 3,86 и 2,14; в) 31,6 и 42,4;
б) 54,7 и 1,28; г) 425 и 0,167.
850. Найдите длину комнаты, площадь которой равна 25,7 м2, а ширина 4,2 м.
851. Масса металлической детали равна 67,4 г, а ее объем равен 7,55 см3. Найдите плотность металла, из которого, изготовлена деталь.
852. Через сколько секунд тело, начавшее двигаться с ускорением 1,8 м/с2, достигнет скорости 54,5 м/с?
Упражнения для повторения
853. Упростите выражение:
854. Решите графически систему уравнений:
б) (х* + у2 = 10, [ху = —3.
48. СОВМЕСТНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ
ЛОГАРИФМИЧЕСКОЙ ЛИНЕЙКИ
С помощью линейки удобно выполнять несколько последовательных умножений и делений.
Рассмотрим примеры.
Пример 1. Вычислить произведение 1,14 • 3,72 - 4,55.
Умножим 1,14 на 3,72. Отметим визиром точку шкалы корпуса линейки, соответствующую произведению этих чисел, и, не читая результата, умножим на 4,55. Для этого метку 10 194
- 10.
на шкале движка совместим с отмеченной визиром меткой на шкале корпуса линейки. Против метки 4—5—5 шкалы движка читаем ответ: 1—9—3. Так как 1*4*5 — 20, то искомое произведение приближенно равно 19,3.
Пример 2. Найти значение выражения
2,38
Удобно сначала выполнить деление, а затем умножение. Разделим 4,82 на 2,38. Не читая результата, умножим его на 3,76. Так как метка 1 находится против полученного частного, то достаточно прочитать число, которому соответствует на основной шкале корпуса линейки точка, расположенная против метки 3—7—6 шкалы движка. Получаем: 7—6—1.
Сделаем прикидку:
Значение заданного выражения приближенно равно 7,61.
тт о тз 240.0,173
Пример 3. Вычислить -------------.
0,0525
Разделим 240 на 0,0525. Против метки 10 шкалы движка находится на шкале корпуса линейки точка, соответствующая частному. Не читая частного, умножим его на 0,173. Для этого надо прочитать на основной шкале корпуса линейки метку, стоящую против метки 1—7—3 на шкале движка. Не передвигая движок, этого сделать нельзя. Зафиксируем визиром точку, соответствующую частному, и, передвинув движок, совместим с ней метку 1 на шкале движка. Против метки 1—7—3 шкалы движка читаем на основной шкале корпуса линейки ответ: 7—9—1.
Чтобы определить положение запятой, представим числа в стандартном виде и выполним преобразования:
2,4 ’ Ю2 . 1,73 • 10'1
5,25 • 10"2
• 1G3.
Так как
, то частное
приближенно
равно 0,791. Значит, искомое значение выражения приближенно равно 0,791 • 103.
855. Найдите произведение, проверяя результат по данным ответам:
Выражение Значение выражения Выражение - ' — Значение выражения
1 1,36 2,04 3,18 8,82 4 310 • 0,216 • 2,46 165
2 2,16 • 1,34 < 8,05 23,3 5 170 ♦ 210 • 0,0154 5,50 • 102
3 724 . 0,243 * 110 1,94 • 101 6 560 • 0,00163 • 220 201
856.
Вычислите и проверьте результат по ответу, содержащемуся среди приведенных ниже:
ч 2,06 . 160 Д) --------
47,5
ч 13,2 • 815 е) —-------
190
a)
520 • 630
б) ---------
185
1,83
185 • 5,35.
ч 4,35 . 5,15 • 1,74 ж) ---------------—;
170
5,25 • 15,6 . 2,58
3,94 • 12;8
1,77 • 103; 5,82;
857
С помощью линейки найдите неизвестный
а)
член пропорции
ч 1,27 2,66
3,5
4,3
51,6
858. Каков объем комнаты, длина которой 5,45 м, ширина 4,85 м и высота 3,25 м?
859. Размер кирпича 250 х 120 х 65 мм. Каков объем 150 кирпичей?
860. Длины сторон треугольника равны 11,2 см, 15,6 см и 18,4 см. Длина большей стороны подобного ему треугольника равна 58,5 см. Найдите длины двух других его сторон.
861. Площадь большого поршня гидравлической машины 125 см2, малого — 12 см2. С какой силой надо давить на малый поршень, чтобы на большом получить силу 455 Н (трение не учитывать)?
Упражнения для повторения
862. Решите графически и аналитически систему уравнений:
a) fz/ = х2 — 3, б) (у = х2 — 2х + 4,
[у = 2х; [у — 2х = 0.
863. Сократите дробь:
§ 16.
АЛГОРИТМЫ И ЭЛЕМЕНТЫ ПРОГРАММИРОВАНИЯ
Три последних столетия таблицы логарифмов были одним из самых распространенных средств вычислений. Они позволяли выполнять трудоемкие операции умножения и деления многозначных чисел с высокой точностью, что столь необходимо, например, в астрономии.
Со временем характер решаемых задач стремительно усложнялся, все труднее удавалось получить необходимые результаты в условиях ручных вычислений. Явное несовершенство ручных вычислений с использованием таблиц заставило человечество искать новые пути сначала механизации вычислительных работ, а затем решить исключительно важную проблему автоматизации вычислений.
В практике вычислений особенно ответственным стал этап подготовки задачи к решению: разработка эффективного алгоритма решения и удобная форма расположения числовой информации.
49. ПОНЯТИЕ ОБ АЛГОРИТМАХ И СПОСОБАХ ИХ ЗАПИСИ
Алгоритм — это одно из важнейших понятий современной математики. Слово «алгоритм»* означает точное описание некоторого процесса, инструкцию по его выполнению. Фраза «Здесь приведен алгоритм решения такой-то задачи» означает: «Здесь указано, какие действия и в какой последовательности следует выполнить для решения этой задачи».
Рассмотрим несколько примеров алгоритмов.
Пример 1. Пусть требуется по формуле
найти значение у при заданном значении х.
Из формулы (1) видно, какие действия нужно выполнить, чтобы решить поставленную задачу. Однако порядок их выполнения в известной степени произволен: можно вычислить сначала числитель, а затем знаменатель дроби или действовать в обратном порядке — сначала вычислить знаменатель дроби, а затем ее числитель. Такая перестановка действий не влияет на конечный результат.
Формула (1) оставляет некоторую свободу выбора в процессе решения задачи. Поэтому нельзя считать, что этой формулой оп-i ределяется алгоритм решения поставленной задачи, так как понятие алгоритма требует, чтобы были точно определены не только сами действия, но и порядок их выполнения.
Чтобы считать, что формула (1) определяет алгоритм решения нашей задачи, необходимо принять некоторые дополнительные соглашения о порядке выполнения действий, например, условиться, что вычисления всегда производятся (с учетом скобок и старшинства операций) последовательно слева направо, сначала в числителе, а потом в знаменателе. Только при этих условиях формулу (1) можно рассматривать как запись алгоритма решения нашей задачи.
* Термин «алгоритм» происходит от латинского слова, которое является ! записью на латинском языке имени хорезмского математика IX в. Аль-Хорезми.
' 197
i
L
Приведем другую форму описания процесса вычислений по
ормуле (1):
Таблица 1
Описание действия
Умножить х на число 7
Из результата действия 1 вычесть число 4
Умножить х на число 5
К результату действия 3 прибавить число 3
Результат действия 2 разделить на результат действия 4
№
Описание действия
Это так называемая развернутая запись алгоритма. Слово «развернутая» выражает тот факт, что здесь весь процесс вычислений разворачивается в виде последовательно вычисляемых отдельных элементарных шагов.
Алгоритм, представленный в таблице 1, можно записать более лаконично, если ввести обозначения для результатов промежуточных действий.
Обозначим результат первого действия (умножить х на 7) через а. Кратко мы будем это записывать так:
а : = х • 7.
Запись а : = х • 7 читается так: «положим а равным х ' 7» или «присвоим переменной а значение х • 7».
Аналогично результат второго действия обозначим через &, третьего — через с, четвертого — через d. Результат пятого (последнего) действия обозначим буквой у. Получим таблицу 2.
Такую форму записи алгоритма называют табличной.
Если вычисления по формуле (1) нужно произвести для многих значений переменной х, то используют табличную форму записи алгоритма. Так в таблице 3 записаны результаты вы-_____________________________4
числений по формуле у = ------ для двух значений х: 3,26 и
Ч- 3
3,29. В записи частных от деления Ъ на d мы ограничились четырьмя значащими цифрами. Нетрудно видеть, что таблицу 3 можно продолжить вниз для других значений х:
У :
Таблица 3
X а : — х - 7 Ъ : — а — 4 с : — х • 5 d : ~ с - -3 У : = ъ : d
3,26 22,82 18,82 16,3 19,3 • 0,9751
3,29 23,03 19,03 16,45 19,4 0,9789
Заметим, что такую таблицу заполняют обычно не по строкам, а по столбцам: сначала вычисляют для всех значений х соответствующие значения а, затем — значения Ъ и т. д. Такой порядок работы ведет к выполнению однотипных действий, при которых, как показывает опыт, обычно меньше ошибок.
Пример 2. Пусть требуется по формуле у 5/z, где п £ Z, по значению п найти соответствующее значение у.
Воспользуемся определением степени с целым показателем:
если п > 0 и п 1 (т. е. п >1), то 5Л
если п — 1, то Ъп = 5;
если п — 0, то 5п = 1;
если п < 0, то — ---------------------.
5 -5- ... • 5
^_г- - -iMrwr
— п раз
Для того чтобы вычислить значение выражения 5П для конкретного значения п, надо выбрать, какой строкой из указанных выше мы воспользуемся. Сам выбор строки есть одно из действий, которое надо выполнить при вычислении значения выражения 5\ Это действие указывается в явном виде (шаги 1, 2, 3) в развернутом алгоритме вычисления значения выражения 5ft, представленном в таблице 4:
Таблица 4
Описание действия
1
2
3
4
Если л >7, по перейти к действию 4; иначе перейти к действию 2
Если п~1, то перейти к действию 5; иначе перейти к действию 3
Если п =0, то перейти к действию 6; иначе перейти к действию 7
у\=5‘5 • ... -5; перейти к действию 8
п раз
у : = 5; перейти к действию 8
у : = 1; перейти к действию 8
у : ~ 1/(5 • 5 • ... • 5); перейти к действию 8
Конец
Сравнивая алгоритмы, представленные в таблицах 1 и 4, можно заметить их существенное различие. В первом случае действия выполняются в том порядке, в каком они выписаны в таблице. Во втором случае приходится специально указывать действие, к которому следует перейти. Для того чтобы вычислитель мог знать, какой шаг следует считать окончательным, в алгоритме указана операция «конец».
Действие, которое следует выполнить непосредственно за данным действием, принято называть преемником данного действия. Таким образом, алгоритм, представленный в первом
случае, таков, что непосредственно за каждым действием выписан его преемник; во втором случае специально оговорено, какое действие является преемником данного.
Запись алгоритма в таблице 4 может быть несколько упрощена, если принять такое соглашение: не указывать преемника действия в том случае, если он записан непосредственно за данным действием. В этом случае алгоритм вычисления степени по формуле у — 5п запишется так:
Таблица 5
Описание действия
1
2
3
к
4
Если п > 7, то Если n l, то Если п = 0, то
пгреити перейти перейти перейти
действию действию действию действию
6, иначе к действию 7
8
к
5
6
7
у ; = 5; перейти к действию 8 у : = 7; перейти к действию 8 у: = 1/(5 - • ... -5)
л
—п раз
Конец
1Л
С алгоритмами мы встречаемся не только в вычислительных I задачах. I
Пример 3. Человека, незнакомого с правилами улично- g го движения, инструктируют относительно перехода улицы . | с двусторонним движением примерно так, как указано в табли- 'I це 6 (для простоты считаем, что светофор двухцветный — крас- | ный и зеленый). . |
Та блица 6 Й
Nb
Описание действия
1
2
3
4
Если горит красный свет, то
Если горит зеленый свет, то ря на транспорт слева
Если по достижении середины остановись
Если по достижении середины свет, то переходи улицу до конца,
улицу не переходи
улицу переходи до середины, смоги-
улицы зажегся красный свет, то
улицы продолжает гореть зеленый смотря на транспорт справа
Такая инструкция на первый взгляд представляется четкой, и, руководствуясь ею, человек будет правильно вести себя при переходе улицы.
Однако, внимательно прочитав инструкцию в таблице 6, мы без труда обнаружим в ней ряд неточностей. Практически
это не мешает человеку правильно выполнять ее: сам того не сознавая, он мысленно дополняет ее отдельными элементами, которые представляются само собой разумеющимися. Однако буквальное выполнение этой инструкции привело бы к нелепости. В самом деле, если человек, подойдя к месту перехода улицы, увидит красный сигнал светофора, он остановится (действие 1) и ... останется на этом месте навсегда: ничто не предписывает ему посмотреть на светофор еще раз.
Если записать инструкцию по переходу улицы таким образом, чтобы она представляла собой алгоритм в математическом смысле этого слова, то она приобретает такой вид:
Таблица 7
№
Описание действия
1
2
3
4
5
6
7
Посмотреть на светофор; если горит зеленый свет, то перейти к действию 3
Стоять и ждать зеленого света
Переходить улицу до середины, смотря на транспорт слееа
Посмотреть на светофор; если горит зеленый свет, то перейти к действию 6
Стоять и Ждать зеленого света
Переходить улицу до конца, смотря на транспорт справа
Конец
Пример 4. Имеются три урны: белая, черная и полосатая. В полосатой урне находятся белые и черные шары. Надо все черные шары переложить в черную урну, а белые шары — в белую урну. Сортировка производится так: по очереди вынимаются из полосатой урны шары и в зависимости от цвета кладутся или в черную, или в белую урну. Алгоритм сортировки представлен в следующей таблице:
Таблица 8
Описание действия
Взять шар из полосатой урны
Если шар белый, то опустить его в белую урну и перейти к действию 4
Если шар черный, то опустить его в черную урну
Если полосатая урна не пуста, то перейти к действию 1
Конец
Это так называемый циклический алгоритм. В таблице 8 всего пять действий. Однако на самом деле число выполненных по этому алгоритму действий может быть намного больше. Нам удалось так компактно описать алгоритм благодаря тому,
что действия над всеми шарами из полосатой урны одинаковы.
Мы рассмотрели несколько примеров алгоритмов. При этом использовались три формы записи алгоритмов: формульная^
табличная и развернутая. Формульное представление, как и табличное, пригодно только для алгоритмов решения задач одного специального вида — проведения вычислений по заданной формуле. Развернутая форма записи алгоритмов имеет гораздо более широкую область применения: ее можно рассматривать как универсальную.
864. Составьте алгоритм вычисления значения у формуле:
4- Ч б)у==з^4; г) у = (х—1)(х+ 5) —2.
865. Значение выражения 5х2 — 8х 4- 23 можно найти, Поль-зуясь формулами:
у = 5х2 — 8г + 23 и у = х (5х — 8) + 23.
Составьте табличный алгоритм вычисления для каждой из этих формул и выясните, какой из алгоритмов содержит меньшее число шагов.
866. Составьте алгоритмы для различных вычислений значения данного выражения и выражения, полученного в результате упрощения данного:
а) (4х + 1) (2 — Зх) — (3 — 6х) (2х + 5) при х — 2;
4х2 —‘16 — х о
С)-----—----- при х — 3.
1 + 2х 2
867. Продолжите заполнение таблицы 3 для значения х, равного: а) 3,32; б) 3,35.
868. Составьте алгоритм нахождения n-го члена арифметической прогрессии.
869. Составьте алгоритм отыскания значения функции для заданного значения аргумента по графику этой функции.
870. Составьте алгоритм решения уравнения:
а) ах = 25; б) ах = Ь.
871. Составьте алгоритм отыскания квадратного корня с помощью четырехзначных математических таблиц.
872. Составьте алгоритм отыскания логарифма числа с помощью четырехзначных математических таблиц.
873. Алгоритм сортировки шаров, представленный в таблице 8, имеет дефект—он «не работает» в случае, если урна с самого начала пуста. Постройте алгоритм, в котором учитывается случай, если полосатая урна оказывается с самого начала пустой.
Упражнения для повторения
874. Найдите площадь фигуры, задаваемой неравенством: а) х2 + у2 < 6,25; б) х2 + у2 <7.
Ответ дайте с точностью до 0,1.
875. Завод должен изготовить 8000 деталей к определенному сроку. Работая точно по графику, завод выполнил 25 % заказа, а затем стал изготовлять ежедневно по 100 деталей сверх нормы и выполнил задание на 2 дня раньше. Сколько дней понадобилось заводу для выполнения заказа?
876. Бригада рабочих должна была по плану изготовить к некоторому сроку 250 деталей. Изготовляя в день по 6 деталей сверх дневной нормы, бригада уже за 1 день до срока перевыполнила плановое задание на 8%. Сколько дней работала бригада?
50. БЛОК-СХЕМЫ АЛГОРИТМОВ
Развернутая запись алгоритма на практике часто используется в несколько иной, более наглядной форме так называемых блок-схем.
Блок-схема дает наглядное представление о структуре алгоритма. Каждый шаг алгоритма изображается в блок-схеме геометрической фигурой — блоком, внутри которой дается описание соответствующего действия. Последовательность выполнения действий задается стрелками, соединяющими эти блоки.
На рисунке 96 изображена блок-схема рассмотренного ранее алгоритма вычисления значения степени по формуле у — 5п (см. табл. 4 или 5).
В приведенной блок-схеме ромбами выделены блоки, в которых задаются разветвления процесса. Выбор одного из двух преемников в каждом случае производится в зависимости от выполнения условия, записанного внутри ромба: если это условие выполняется, го следует перейти к следующему блоку по стрелке «да»; если же условие не выполняется, то нужно перей-
Рис. 96
Начало
Начало
Рис. 97
Взять шар аз полосатой урны
Шар^ белый
нет
Опустить шар в черную УР*У
Опустить шао в Зелую
УР”У
Рис, 98
нет
Полосата
* урна пуста
ти к следующему блоку по стрелке «нет». Прямоугольниками изображают блоки, в которых записываются результативные действия. От каждого прямоугольника исходит стрелка и притом единственная, так как для каждого результирующего действия всегда существует один и только один преем-. ник. Овалами указаны блоки начала и конца. Эти блоки указывают, с какого действия начинается исполнение алгоритма (вход в алгоритм) и каким оно завершается (выход из алгоритма) .
Взаимное расположение отдельных блоков в блок-схеме, вообще говоря, произвольно; его выбирают так, чтобы блок-схема была наглядной и чтобы легко было провести нужные стрелки. Сравнивая блок-схему на рисунке 96 с таким же алгоритмом в таблице 5, отметим прежде всего, что на блок-схеме все переходы от действия к действию указываются явно; здесь не нужны никакие дополнительные соглашения. С этим связано и появление в блок-схеме действия «Начало», которое введено, собственно говоря, только ради выходящей из него стрелки.
Приведем еще примеры блок-схем алгоритмов.
На рисунке 97 показана блок-схема алгоритма вычисления по формуле у = з (см. табл. 1 или 2). Отсутствие на ней ромбиков свидетельствует о том, что порядок выполнения действий в этом алгоритме является «жестким» — не зависит от значения х.
Каждому шагу таблицы соответствует прямоугольник блок-схемы.
На рисунке 98 изображена блок-схема сортировки шаров. Эта блок-схема не получается непосредственно из таблицы 8, так как некоторые из действий таблицы 8 (а именно действия 2 й 3) сочетают в себе проверку некоторого условия («если шар белый...») с результативной частью («положить в белую урну» или «положить в черную урну»). Такое смешение в блок-схемах не допускается. На рисунке 98 каждое из таких действий таблицы 8 представлено двумя блоками — одним ромбом и одним прямоугольником.
Рассмотрим алгоритм вычисления по формуле
2 + 3 1g х. В него в качестве составных
частей включаются два других алгоритма: алгоритм
отыскания значения выражения 1g х и алгоритм нахождения квадратного корня. Алгоритм, который включается в основной алгоритм, будем называть подчиненным. При построении блок-схемы алгорит-" ма, содержащего подчиненный алгоритм, обычно делают ссылку на подчиненный алгоритм, не расписывая его подробно. На рисунке, изображающем блок-схему алгоритма, название подчиненного алгоритма помещают в многоугольник, имеющий форму флажка. Блок-схема вычисления по формуле у ~ 5 х + 2 + 3 1g х показана на рисунке 99.
Выделение частей общего алгоритма в виде подчиненных алгоритмов очень удобно и на практике широко используется. Работая над сложной задачей, человек никогда не продумывает ее решение сразу во всех деталях. Он выделяет в ней некоторые частные задачи и пишет общую блок-схему, используя в ней эти задачи так, как если бы они были уже решены.
877. Составьте блок-схему алгоритма сортировки шаров, учитывающего случай, что полосатая урна может оказаться пустой с самого начала (см. условие примера 4, п. 49).
878. Алгоритм вычисления по формуле у = | х — 11 + 5 приведен в таблице:
Рис. 99
№ Описание действия
1 Если х < 7, то перейти к действию 3
2 Если х 7, то перейти к действию 4
3 у : =6—х, перейти к действию 5
4 у:=х + 4
5 Конец
Составьте блок-схему этого алгоритма.
879. Значения функции у вычисляются по формулам у = Зх, если х > О,
1 Л
у =----х, если х < 0.
Составьте алгоритм вычисления значения у в развернутой форме, а затем постройте блок-схему этого алгоритма.
880. а) Составьте блок-схему алгоритма вычисления корней уравнения ах. = Ь.
б) Составьте блок-схему алгоритма вычисления решений неравенств ах > 8 и ах < 8.
881. Значение выражения у ~ | х | + | х — 11 вычисляется по следующим формулам: если х < 0, то у = “X + (1 — х) = 1 — 2х;
если 0 х < 1, то у х + (1 — х) = 1;
если х 1, то у = х + (х — 1) = 2х — 1.
Составьте алгоритмы вычисления у сначала в развернутой
форме, а затем представьте его в виде блок-схемы.
Упражнения для повторения
882. Проходит ли через точку пересечения прямых
у — 2х = —8 и Зу 7х — 2:
а) прямая 0,5х — у = 5; б) прямая Зх+0,6у 3,5?
883. Найдите координаты точки пересечения прямых х — у-1 и Зх — 2у = 6.
Чему равно расстояние от точки пересечения этих прямых:
а) до оси х; б) до оси у; в) до начала координат?
51. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ПРОГРАММИРОВАНИИ ДЛЯ ЭВМ
Любые вычисления представляют собой обработку числовой информации. Поскольку в вычислениях, как правило, участвуют многозначные числа, то производить такие расчеты вручную
затруднительно. Поэтому в практических вычислениях стали применять арифмометр, логарифмическую линейку, счеты. В последнее время широкое распространение получили микрокалькуляторы. Небольшие размеры и возможность выполнения большинства элементарных операций сделали их эффективными помощниками человека. Однако перечисленные приборы могут механизировать выполнение только отдельных вычислительных операций. Автоматизировать вычислительный процесс в целом (т. е. обеспечить вычисления по заданному алгоритму без участия человека) они не в состоянии. Производить вычисления без непосредственного участия человека могут только электронные вычислительные машины — ЭВМ.
При ручных вычислениях человек непосредственно руководит вычислительным процессом, или, точнее, управляет им, т. е. неукоснительно следует указаниям алгоритма, осуществляет перенос числовых данных с таблицы на арифмометр, микрокалькулятор или другое вычислительное устройство и обратно, управляет работой этого вычислительного устройства.
Скорость ручных вычислений прежде всего ограничивается физическими возможностями человека (быстротой его реакции, скоростью письма и т. д.). Чтобы добиться существенного ускорения вычислительного процесса, необходимо исключить из него человека, передав его управляющие обязанности автомату. Только в 40-х гг. XX столетия вычислительный процесс удалось автоматизировать. Таким автоматом, принявшим на себя управляющие обязанности человека, явилась ЭВМ.
Решение любой задачи на ЭВМ фактически сводится к переработке информации, которая поступает в машину. Переработка информации в ЭВМ может производиться только в том случае, если четко поставлена задача и точно дан метод ее решения.
Другими словами, решению любой задачи на ЭВМ предшествуют разработка алгоритма ее решения и представление этого алгоритма в форме, в которой он может быть точно воспринят ЭВМ. Алгоритм, написанный в виде, «понимаемом» ЭВМ, принято называть программой, а сам процесс построения «машинного» алгоритма называют программированием.
В настоящее время программы для ЭВМ пишутся на так называемых алгоритмических языках. Рассмотрим один из таких алгоритмических языков программирования — АЛГОЛ-60.
Слово «АЛГОЛ» есть сокращение английского наименования Algoritmic Language — алгоритмический язык; число 60 связано с тем, что официальное описание этого языка, ставшее затем международным стандартом, было опубликовано в 1960 г.
Программа, написанная на алгоритмическом языке, обладает двумя важными свойствами:
а) доступностью для человеческого восприятия (читабельность),
б) практической пригодностью для исполнения на ЭВМ.
Рис. 100
Раскроем эти свойства на примере алгольнои программы для вычисления корней квадратного уравнения.
Запишем сначала алгоритм решения квадратного уравнения ах2 + Ъх + с = 0 в развернутой форме:
и. 1. Вычислить В = Ъ2 — 4ас.
и. 2. Если В < 0, то перейти к п. 4.
п, 3. Вычислить:
(первый корень), (второй корень).
Перейти к п. 5.
п. 4. Уравнение корней не имеет.
п. 5. Конец.
На рисунке 100 показана блок-схема алгоритма вычисления корней уравнения ах2 + Ъх + с 0, где а Ф 0.
Для исполнения на ЭВМ этот же алгоритм приходится записывать в ином виде. Пункт 4 «Уравнение корней не имеет» заменим принудительной выдачей неправдоподобно больших значений корней и х2:
«х1: — 10 000 000 000}
х2: 10 000 000 000».
Увидев такой результат, вычислитель сразу поймет, что квадратное уравнение корней не имеет.
Покажем теперь, как записывается алгоритм вычисления корней квадратного уравнения на языке АЛГОЛ-60:
begin
real a, fe, с, В, xl, х2;
input (а, Ь, с);
В : = b 2 — 4 х а х с;
if В < 0 then goto Ml;
xl (—b + sqrt (Z)))/ (2 х а);
х2 (-—& sqrt (В))/{2 х а);
goto М2;
Ml: xl : - 10 000 000 000;
х2 : - 10 000 000 000;
М2: output (xl, x2);
end
Рассмотрим особенности записи главной части программы:
В : “ b f 2 — 4 х а х if В < 0 then goto Ml;
xl : = (—b + sqrt (D))i{2 x a);
x2 : = (—b — sqrt (D))i{2 X a);
goto М2;
Ml-, xl : = 10 000 000 000;
x2 : = 10 000 000 000;
М2: output {xl, x2);
Строка
D : = b\ 2 — 4 X a x c (1)
J
содержит задание на вычисление дискриминанта. Обратим внимание на чисто языковые особенности ее записи. Во-первых, вместо знака равенства в ней фигурирует уже известный нам символ : —. Таким специальным знаком присваивания подчеркивается следующее: числовое значение выражения в правой части формулы (1) присваивается переменной Z>, стоящей слева.
Второй особенностью формулы является использование знака « j » для обозначения возведения переменной в степень.
Третьей особенностью формулы (1) является употребление знака « х» в качестве знака умножения. Точка как знак умножения в алфавите алгоритмического языка отсутствует, иначе ее легко можно было бы принять за используемую для других целей точку в нижней части строки. В записи операции умножения не разрешается отсутствие знака вообще.
Первой строке программы соответствуют п. 1 в развернутом описании и первый прямоугольник блцк-схемы на рисунке 100.
Преемником, т. е. следующим предложением, к исполнению которого переходит машина, выполнив задание первой строки (если нет никаких других указаний), будет вторая строка программы, а именно
if D < 0 then goto Ml (2)
В этой строке записано разветвление вычислительного процесса. Смысл трех английских слов (if —если, then —то, goto — перейти к) становится ясным, если обратиться к строке п. 2 в развернутой записи алгоритма, где строка п. 2 равнозначна разбираемому предложению (2).
Слова if, then, goto являются основными символами языка АЛГОЛ-60.
Между символами if и then расположено условие D < 0, которое должно быть проверено для конкретного значения переменной D. Если проверка даст положительный результат (ответ «да», см. также ромб на рис. 100), то следует выполнять вторую часть предложения, т. е. то, что написано после символа then. При отрицательном результате проверки (ответ «нет») исполнение этого предложения прекращается и ЭВМ переходит к исполнению следующего предложения программы.
То, что написано после символа then, т. е. конструкция goto Ml, представляет собой самостоятельное предложение, выражающее следующее указание ЭВМ: «перейти к метке М1».
Назначение этого предложения состоит в том, чтобы указать в явном виде преемника. Чтобы указание было понято однозначно, перед предложением-преемником ставится метка (т. е. имя предложения), которая отделяется от него двоеточием. В развернутой форме записи этого же алгоритма метку Ml заменяет номер пункта «п. 4», а на блок-схеме алгоритма — стрелка «Да», выходящая из ромба.
Содержание предложения (2) заключается в следующем: собственно вычисление корней по алгоритму происходит только при неотрицательном значении дискриминанта D. При этом сначала вычисляется первый корень по формуле
xl: = (—& + sqrt (D))/(2 X а) (3)
которой в обычной математической записи соответствует:
Сравнение этих записей достаточно наглядно показывает особенности первой из них. Перечислим их:
1) все символы в алгольной программе пишутся в одну строку, подстрочные и надстрочные индексы не допускаются;
2) в качестве обозначений переменных в программе можно использовать не только буквы, но и совокупности букв и цифр — имена. Каждое имя обязано начинаться с буквы. Конструкция имен в алгольной программе делает недопустимым отсутствие знака при умножении. Так, xl, х2, М2 — это имена, а не выражения вида х X 1, х X 2, М X 2;
3) в качестве знака деления употребляется только косая черта. Двоеточие выполняет другую функцию: оно является признаком метки; «двухэтажная» дробь противоречит общему принципу записи в одну строку, который строго выдерживается в АЛГОЛе;
4) конструкция sqrt (D) означает указание на извлечение квадратного корня из выражения.
После того как результат вычисления по формуле (3) будет записан в память машины (в некоторую ячейку, специально отведенную для xl), т. е. выполнение предложения (3) закончится, ЭВМ переходит к исполнению следующего предложения (так как других указаний не имеется):
х2 := ( —Ъ — sqrt (D))/(2 X а) (4)
Следующая по порядку строка
; goto М2; (5)
представляет собой уже разобранный нами переход к метке, в данном случае к метке М2, Этот переход происходит без проверки какого бы то ни было условия (поэтому он называется «безусловным» в отличие от предыдущего «условного»). Этот
обход хорошо виден на блок-схеме (рис. 100), где он представлен стрелкой.
Разберем теперь следующее по порядку предложение АЛГОЯвной программы:
М1:х1 : - 10 000 000 ООО;
которое означает присваивание переменной xl значения 10 000 000 000 (т. е. запись в соответствующую ячейку памяти неправдоподобно большого числа). С метки Ml начинается та часть программы, которая исполняется в случае отрицательного дискриминанта.
Теперь становится понятной организация обхода двух последующих предложений при неотрицательном дискриминанте, иначе вычисленные значения корней уравнения в ячейках xl и х2 были бы заменены условным числом 10 000 000 000,
Итак, мы продемонстрировали идентичность расчетной части АЛГОЛьной программы другим формам записи того же алгоритма. АЛГОЛьная программа достаточно удобна и проста для чтения: после небольшой тренировки читатель понимает практически все, что написано на АЛГОЛе. Грамотное написание программ на языке АЛГОЛ уже требует от человека твердого знания формальных правил записи предложений (синтаксис языка) и наличия достаточно высокого уровня алгоритмической культуры.
Самое главное свойство разобранной программы заключается в ее практической пригодности для исполнения на ЭВМ.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ VI
К пунктам 36 и 37
884. Найдите:
|3~
a) log)/y4; в) log0>2 25; Д) bg27 —;
б) !og3-i; г) log4(8)-/’2); е) log0j04 (5 у 25)
У •
885. Найдите значение выражения:
a) 10lg6+lg5; г) 10lg8°_~; ж) (/10)Ig25+2;
б) 10,g3~lg3°; д) 100!g7; з) /'/“j'8'' 2;
в) 101-lg2’E; е) 1000lg2°~и) 0,01’8 °’2 2.
886. Представьте число в виде степени 10:
а) 0,00001; в) j/100; д) 50; ж) 0,48;
б) 10 000 000; г) ^0,001; е) 16,5; з) Д
О
К пункту 38
887. Имеет ли смысл выражение:
a) 1g0,01; д) lg(y— у yj; a) lgcos 150°;
б) lg(—2~12); е) 1g ('/б—/15); к) lgsin96°;
В) lg f_ ip7; ж) /lg2,5; л) lg(0,09)-3;
г) lg (/64-2,6); 3)/lg0J5; M) lg(lg55)?
888. Определите знак выражения:
a) lg 5 — lg 3; д) lg 5 — lg 2 /б; и) lg----------, ;
6) lg 9 — 1; e) lg2 11 - lg 11; 5-2/6
в) lg 0,2 + lg 0,3; ж) lg 3 — lg2 3; 7 —/io
r) lg (5 - 2 /6); з) lg 2 • lg 0,2 + lg 1; K> ----з---
889. Между какими последовательными положен 1g х, если:
целыми числами рас-
а) х - 45;
б) х - 267;
в) х 4654; г)’ х = 6,43;
д) х ~ 0,819;
е) х = 0,0626?
890. Найдите область определения функции:
а) у = 1g (100 + х); г) у = 1g (х2+ х); ж)у =—;
1g х — 1g 5
б) у = 1g (х — 10); д) у= 1g (10х — х2); з) у = 1g ~
х —10
891. При каких значениях переменной имеет смысл выражение:
a) /lg (1 — <z);
б) /1g (х —10);
в) /1g х + 5;
г) / 1g (5 — у)2;
д) /2 — lg b;
ж) / (х — 10) 1g х;
и) /Ig(lgx)?
892. Найдите область определения и область значений функции: а) у = 1g (—х); в) у = 1g (х—100); д) у = 1g (х2—16);
6) у = 1g(х + |х|);
е) У = 1g (Ю0 — х2).
893.
894.
Принадлежит ли области значений функции у = 1g (х2 4- 6х 4- 40):
а) число 0; б) число 1; в) число 2; г) число 1,5?
Принадлежит ли области значений
у = lg(15 4-10х—х2):
а) число 0; б) число 1; в) число 2; г) число 1,5?
уцкции
К пункту 39
895. Докажите, что на множестве пар положительных значений х и у выполняется тождество:
a) 1g (ах) — lg (ar/) = lg х — 1g у, где а > 0;
б) lg f—У — lg (—Y = 2 (lg х — 1g у), где а 0.
\а ) \аI
896. Докажите, что равенство 1g (х — у) -1g х — 1g у
не является тождеством на множестве пар положительных значений х и у.
897. Прологарифмируйте выражение (предполагается, что буквами обозначены положительные числа):
а) 2аЬ; в) 2 (а + х);
д)
8
(а + Ь)2
1
б) ЗЬс;
е) lOOafr
__ ж) 100 (ab) 2;
з) (100a&) 2.
898.
Выразите логарифм х через логарифмы положительных чисел a, Ъ и с:
б) х
в) X
899. Зная 1g 2 0,301 и 1g 3 0,477, найдите приближенные
значения корней уравнения:
а) 0,01х = 8; в) 16х = 0,1; д) 9х = 16;
б) 2х = 10; г5 12х = У100; е) 5х = 81.
900. Выразите переменную х через у, логарифмируя обе части равенства:
а) у = 3 • 9Х~Х; б) у = 5 • А; в) у = 21-**.
1QA
901. Найдите сумму п членов последовательности, зная формулу любого ее члена: ап = 1g 2п.
902. Истинно ли высказывание (буквой а обозначено положительное число):
К пункту 40
903. Найдите х, если:
а) Igx =21g2 + lg5;
б) Igx=|lg7-21g3;
в) lgx=lg24—lgl,5—31g 2;
г) Igx = |lg54 + lg5lg 16; 3 о
д) lg x = 3 lg 5 — 1;
e) lgx=2 —lg6|-—lg6.
О
904.
Выполните потенцирование (буквами обозначены положительные числа):
a) Igx = lg2 — Iga — lg5;
6) lgx=21ga— lg2 — — lg&;
2
в) Igx = i(lga — lg&);
r) lgx = —-i(lga —21gb);
О
д) lgx=lg(a +&)+ ylg(a — b)\
e) Igx = —Igb-j-1;
О
ж) Igx = — + + i)*’
2 4
з) Igx = — 2 — lg(a + b) + lg2.
905. Найдите x (буквами обозначены положительные числа), если:
a) lg (lg х) = lg (lg а) + lg b; 6) lg (lg x) = 1 + lg (lg b). 906. Докажите, что если a > 0 и & >0, причем а =^= Ъ, то
907. Укажите множество значений х, на котором истинно равен-
ство:
a) 1g (х2 — 10х) = 1g х + lg (х — 10);
—lg (х2 + 4).
908. Решите уравнение:
a) 1g (х - 13) + 3 1g 2 = 1g (Зх + 1);
б) lg (2х + 2) + 1g (15 - х) = 1 + lg 3;
в) 1g (Зх — 1) + lg (12 — х) = 2.
909. Какие из данных выражений имеют смысл:
a)]/lg0,8; г) ]/21gl,8 —lg3; ж)]/^2Ц-^sin40°;
б) lg/ОЗ; Д) /lg3,2+lgl,5—lg5; 3) ]/Ilg3+lgcos60°?
в) ]/lg0,9+lgl,l; e) ]/lg30- lg 31 —1,5 lg 30;
910. Решите уравнение:
a) xlg-5 = 25; в) x S'27 = 81; д) (100x),g9 = 27;
6) x,g3l; r) (10x)!gl6= 4; e) (0,lx)!g/2 =8.
911. Докажите тождество a1 — blga (a > 0; b > 0) и, пользуясь им, решите уравнение:
а) xlg9 + 9lgx - 6;
б) xIg8 + 8lgx+1 - 4,5;
912. Решите неравенство:
в) „ 35.+250-0;
уЛ Xlg81 _ QlgX — A
а) lg (x-l)+lg (8—x) < 1;
6) lg (x+7)+lg (18-x)<2;
в) lg (г/ + 1)— lg (z/—23) >lg 3;
r) lg (x-2)+lg (27-x) <2.
913. Укажите множество точек (х; у) координатной плоскости» для которых:
a) 1g х + 1g у = 1;
б) 1g х — 1g у = 1;
в) 21g х — 1g у = 1;
г) 1g х + 1g у < 1g 12;
д) lg х — 1g у > —1;
е) 2 lg х — lg z/ > lg 2.
К пункту 43
914. Вычислите значение х с помощью таблиц логарифмов, если:
10 _______ о ___________________
а) х ~ 311 • 25,6; в) х — 34,567; д) х = 574,22;
б) х~3,264 : 0,078; г) х - 1,04100;
У 0,78Э42*
У “6,618 *
е) х =
915.
Вычислите по частям
а)
2,653
0,729
1/1612.
1,284 ’
значение выражения:
б)
29,5а Y3938 .
/85740 2,544 ’
/ 2-
г) 6318 Ц — 0,7633 / 4
916.
Решите уравнение и вычислите приближенные значения корней:
а) хТ = 168; д) 0,84* = 84; и) х1"* = 569;
б) х-7 = 0,876; е) 2isx = 0,01; к) 2х+2х~г+2Х~2 = 7000;
/ в) 3,5* = 53; ж) 5lg* = 166; л) 3*—З*-1—3*~2 =400;
г) 137* = 73,1; з) x,g* = 1000; м) 4* — 2* = 72.
К пунктам 44 и 45
917. Пользуясь таблицей логарифмов, постройте отрезок логарифмической шкалы от 1 до 2 с метками 1,1; 1,2; ...; 1,8; 1,9, выбрав единичный отрезок, равный 250 мм.
918. Каково расстояние между метками:
а) 2 и 3; б) 4 и 7; в) а и 2а; г) а и — ; д) а и а2 логариф-а
мической шкалы?
919. Какому числу соответствует на логарифмической шкале точка А, удаленная вправо от начала отсчета на расстояние, равное:
a) 1g 3 + 1g 15; б) 1g 7,4 - lg 1,4?
920. Зная положение меток 1 и а на логарифмической шкале, 1 2 ч 1
покажите положение меток —, aS, .
а aS
921. На логарифмической шкале показано положение меток |
1, 2 и 3. Положение каких еще меток, соответствующих f
целым числам в промежутке [1; 20], вы можете показать? | 922. Некоторая точка на логарифмической шкале соответствует |
числу Ъ. Какому числу соответствует точка, симметричная t ей относительно начала отсчета? #
К пункту 46
923. С помощью логарифмической линейки было найдено произведение двух чисел. Один из приведенных в скобках ответов правильный. Пользуясь прикидкой, укажите его: а) 5,62 • 2,24 ^ ... (12,6, 0,126, 1260, 0,0126);
б) 0,725 • 0,236 ... (1,71, 0,171, 0,0171, 0,00171);
в) 0,00343 • 276 ... (0,00947, 0,0947, 9,47, 0,947).
924. Выполните умножение с помощью логарифмической линейки, проверяя результат по приведенным ответам:
а) 2,46 ’ 7,44 18,3; г) 15,6 - 26,3 410;
б) 3,86 - 5,17 20,0; д) 38,4 48,9 1,88 • 103;
в) 5,18 • 3,28 17,0; е) 45,4 24,6 1,12 • 103.
925. С помощью логарифмической линейки выполните умножение:
а) 3,16 • 4,28;
б) 5,45 • 6,78;
в) 31,6 • 3,16;
г) 544 • 0,226;
д) 23,4 - 41,6;
е) 184 • 0,156;
ж) 136 • 174;
з) 28,2 • 54,1;
и) 1,76 • 316.
926. Найдите массу 10,5 л молока, если известно, что плотность молока 1,03 • 103 кг/м3.
927. Найдите 12,5% от 11; 164; 51,7; 8,167.
928. Вычислите площадь прямоугольника, длина которого равна а м, а ширина Ъ м, если:
а) а -- 2,75, Ь - 1,36; в) а ~ 7,04, Ъ = 1,14;
б) а -= 12,3, Ь = 10,5; г) а = 0,947, Ъ - 2,16.
929. Известно, что 1 дюйм приближенно равен 2,54 см. Выразите в сантиметрах 1,5 дюйма, 56,5 дюйма, 12,5 дюйма.
930. В таблице приведены значения переменной х и соответствующие им значения переменной у. Проверьте, что зависимость у от х близка к обратной пропорциональности.
X 1,27 1,33 1,6 1,92 2,08
У 4,05 3,87 3,21 2,69 2,48
931. Значения у вычисляются по формуле у — 1,27х. Найдите значение у, если значение х равно 0,324; 1,15; 2,04.
К'"пункту 47
932. С помощью логарифмической линейки найдены три значащие цифры частного. Пользуясь прикидкой, укажите положение запятой:
а) 83,5 : 1,26 ...(6—6—3);
б) 0,724 : 316 ~ ...(2—2—9);
в) 674 : 15,6 ... (4—3—2);
г) 0,545 : 21,6^...(2-5-2);
д) 1,34:0,645^... (2-0-8);
е) 1160 : 424 ж... (2-7-4).
933. Выполните деление с помощью логарифмической линейки, проверяя результат по приведенным ответам:
а) 12,4 : 5,76 2,15;
б) 0,186 : 7,25 0,0257;
в) 18,1 : 2,78 6,51;
г) 145 : 3,08 47,1;
д) 258 : 0,114 2,26 • 103;
е) 646 : 0,028 2,31 • 104.
934. С помощью логарифмической линейки выполните деление:
а) 8,28 : 1,06;
б) 14,3 : 2,16;
в) 30,1 : 6,67;
г) 0,216 : 3,77;
д) 63,8 : 4,11;
е) 516 : 2,73;
ж) 408 : 56,1;
з) 5,55 : 0,124;
и) 0,678 : 0,0218.
935. Совместите метку 1 шкалы движка с меткой 1—2—5 шкалы корпуса линейки. Укажите пять пар чисел, отношение которых приближенно равно 1,25.
936. Укажите три пары чисел, отношение которых приближенно равно 2,25.
937. Найдите емкость сосуда, если известно, что в него входит 26,5 кг керосина (плотность керосина 800 кг/м3).
938. ^Объем цилиндра 72,5 дм3, а площадь основания 15,4 дм2. Какова высота цилиндра?
939. В таблице приведены значения переменной х и соответствующие им значения переменной у, Проверьте, что зависимость у от х близка к прямой пропорциональности:
X 1,16 1,92 2,31 2,46 2,58 3,54
У 1,45 2,40 2,88 3,08 3,22 4,42
К пункту 48
940. С помощью логарифмической линейки выполните вычисления, проверяя результат по приведенным ответам:
а) 3,76'8’- « 7,20; в) 5,64 - 1,01 • 3,16 » 18,0;
4,24
6) 0,0172-‘ 3152 ж 0,268; г) 304 • 202 • 0,505 » 3,10 • 104;
д) ------------
6,64 • 1,14
0,805
0,106 • 3,18
941
Найдите неизвестный
5,14 306
—; б) — =
а)
член
207
415’
пропорции
ч 16,3 2
7,07
4,14
942. Каков объем кислорода, содержащегося в комнате размером 5,45 X 4,85 X 2,65 м, если объем кислорода составляет 21 % объема воздуха?
943. Какова масса платиновой пластины размером 2,45х X 1,65 X 0,45 см (плотность платины 21,5 г/см3)?
944. Длины сторон четырехугольника 15,6 дм, 18,3 дм, 11,4 дм, 16,1 дм. Длина наименьшей стороны подобного ему четырехугольника равна 5,65 дм. Найдите длину каждой из остальных сторон.
ПОВТОРЕНИЕ
вычисления
945. Вычислите:
946. Найдите значение выражения:
(а - ЪУ 2аЪ
при х — 14,4 и у = 3,6;
при а = 4,5 и & — 3,6.
5
947. а) Замените дробь десятичной дробью с двумя знаками после запятой. Укажите абсолютную и относительную погрешность выбранного приближения.
б) Докажите, что число 0,17 является приближенным зна-3
чением дроби — с точностью до 0,01.
948. Найдите значение выражения:
a) при и ж 16,5, v ~ 7,2;
б) .х при х ж 6,3, у 5,8;
ху — у
в) j/"“у— ПРИ а ~ 4’6, Ь ~ 7,8;
г) Уа2+ ab при а ~ 3,5, Ъ ~ 8,6.
949. Найдите 15-й член и сумму первых пятнадцати членов арифметической прогрессии (сл), если сг •= 0,5 и d = 1,8.
950. Найдите 10-й член и сумму первых десяти членов геометрической прогрессии (&^), если = — и q — 2.
64
951. Укажите какое-нибудь число, заключенное между числами:
а) 0,47 и 0,471; в) — и i; 7 3
б) — и —; г) - и 0,273;
\ 7 7 11
I
. г
952. Упростите выражение:
е)
И
24
12
25’
а) (/14—2/35) • 1
/ 7 +/20;
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
в)
5—2/6
5 + 2/6
5 + 2/6, 5 — 2 /6 ’
953. Какие выражения называются тождественно равными на данном множестве? Приведите пример тождественно, равных выражений:
а) на множестве всех чисел;
б) на множестве неотрицательных чисел.
954. Укажите множество, на котором тождественно равны выра- V жения: '
а) а5 • а3 и а8; г) \у\ и —у; ж) 1g %2 и 2 1g х;
955. Докажите, что на множестве действительных чисел имеет место тождество:
а) (а + Ь) (а - Ь) (а2 + /) = а4 - М;
б) (у + 1) (у - I) (/ - у + 1) (у2 + у + 1) = / - 1.
956. Преобразуйте в многочлен стандартного вида:
а) (х — у)2 • (х + у)2; б) (х + у + I)2. *
957. Представьте, если возможно, в виде произведения двух многочленов ненулевой степени:
а) 1,44х2 —0,49/; д) х2 — 7х — 30;
б) 5х2 — 121/; е) у2 + Зу + 4;
в) 8а3 + с3; ж) 7а2 — 5а — 18;
г) х9 - 27; з) / + 12р - 34.
f
9&8.
Упростите выражение и найдите его значение:
а) ab2 + (2а — ЗЬ) (а2 — ЗаЬ + 4&2) — 6&2 (За — 2Ь)
1 7 1
при а--------, Ъ = — ;
2 9
б.) ас2 + (а + 2с) (2а2 — Бас — Зс2) — 2с3 + яс (а -|-
1 1
при а -- — с = — з 6
в) х (2х — З)2 — (х2 — 5х) (4х — 1) при х ~ 2,4;
г) (z/2 + 3) (у + 12) — у (у + 6)2 при у = 0,85.
12с)
959.
Упростите выражение:
з
900. Сократите дробь:
б)
15а2 — 10а5
8&2 — 12аЬ ’
25;с2 — 20хг/, 161/'2 — 20хг/ ’
в)
г)
ах 4- 2х — За — 6
ах — 8а Ц- 2х — 16 ’
2а — 2Ъ + Зах — 35х
2а — 2Ъ 4- ах — Ъх
961. Упростите выражение:
х — 3 6х — 18 \ 5х — 15
. ... _ .__________ I • _________*•
Xs— 3x4-9 х3 4- 27 ) ’ 4х3 4- 108’
4 (х + 3) , х
х2 — Зх Т 9 — х2
г)
х + 3 5
х -j- 6 х — з’
а — 5 . 4 (а + 1) / 9а а + 4 \
6 — За а2 Ц-4а 1а2 — 16 а2 — 4а/’ 45 12 /45 . 25+ 1 , 25~1\
2b — 1 2Ь 4-1 4&2 — 1 3 — 66 4Ь 4- 2/
Зх । 1
х3 — 27 х — 3
\ х3 — Зх2 । Зх + 9
) (х 4- З)2 X2 4- Зх 4- 9 ’
а* 4- 27а
16 — а2
40 — ci^
962. Найдите значение выражения:
2 2 2 2
(I 3 _а 3 л З _к 3
б) ------------р---------- при а — 0,05, b = 0,16.
2 JL JL
ab 3 — Ъа 3 ab 3 + Ьа 3
963. Упростите выражение:
УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
964. Что называется корнем уравнения с одной переменной? Что значит решить уравнение?
965. Является ли корнем уравнения:
а) х* + х2 = 6х число 0, число —3, число —2;
б) (х — 4) (20х — 1) 0 число —4, число 4, число —0,05;
0 _^*2
в) z=r Q число 3, число —3, число 0;
' Х3-3х2
г) ]/~х + 9 х — 3 число 0, число 7;
д) (х2 — 9) ]/х —' 2 0 число 2, число 3, число —3?
966. Следует ли из первого уравнения второе; следует ли из второго уравнения первое:
а) (х2 + 2х) (х2 — 9) = 0, х2 + 2х = 0;
б) (ж + 2) (х~3) = 0, (х 4- 2) (х — 3) = 0?
х2 — 4
967.
Какие уравнения называются равносильными? Докажите, что:
ч /Х2— X
а) ----
\ з
= 0);
б) (х2 + 0,Зх - 0,1) (10х2 + Зх - 1 - 0).
Каково соотношение между множествами решений равно сильных уравнений?
968. Равносильны ли уравнения:
а) (% — 4)2 -1 и |х — 4| = 1;
б) х + 3 - 5 и (х + З)2 - 25?
969. а) Дайте определение линейного уравнения с одной переменной.
б) Каково множество решений уравнения ах = Ь? (Рассмотрите случаи: 1) а 0; 2) а = 0, Ь ф- 0;
3) а = 0, Ъ = 0. Приведите примеры.)
970. Приведите уравнение к виду ах = Ь и решите его:
а) Зх (х — 1) — 17 = х (1 + Зх) + 1;
б) 2х — (х + 2) (х — 2) = 5 — (х — I)2;
ч Зх 1 _2х — 3. ч х —3 2х — 1 4 — х
971. а) Какое уравнение называется квадратным?
б) Приведите примеры полного и неполного квадратного
уравнения.
в) Какова зависимость числа корней квадратного уравнения ах2 + Ьх + с = 0 от знака его дискриминанта?
972. Приведите уравнение к виду ах2 + Ьх + с = 0,
где а + 0, и решите его:
а)
(2х + I)2
25
в)
(2 — х)2 (7 + 2х)2
3 5
(Зх 4- 2)2
11
5)
(6 — х)2 (2х — I)2
--------—--------
8 3
= 7—х.
973., Существует ли значение переменной t, при котором зна-( чение квадратного трехчлена t2 — 2t + 2 равно:
а) 10; б) 0; в) 1; г) 3?
В случае положительного ответа укажите это значение t, 974. При каких значениях переменной t не имеет корней уравнение:
а) 5х2 — 4х — ? = 0;
б) tx2 — 2х + 6 = 0;
в) х2 — tx + 1 = 0;
г) 4х2 + tx + 1 = 0?
975. При каких значениях переменной а уравнение имеет хотя бы один корень:
а) ах2 — 12х + 9 0; в) 18х2 + ах 4- 8 = 0;
б) 5х2 — х г а г 0; г) (а — 1)х3 — 6х — 3 = 0?
976. Решите биквадратное уравнение:
а) 9х4 — 13х2 +4=0; в) х4 — 21х2 —- 100 = 0;
х б) 4х4 + 17х2 + 4=0; г) Зх4 + 2х3 -1=0. \ ,
977. Решите уравнение введением новой переменной:
а) (Зх + 2)2 + 5 (Зх + 2) — 6 = 0;
б) 4 (5 — х2)2 — 9 (5 — х2) 4- 2 = 0.
978. Решите уравнение:
979. Колхозный сад имеет площадь 29,25 га. Найдите периметр сада, если известно, что сад имеет форму прямоугольника, одна сторона которого на 200 м длиннее другой.
980. Два мотоциклиста выезжают одновременно в город из пункта, отстоящего от него на 160 км. Скорость одного из них на 8 км/ч больше скорости другого, поэтому он при-езжает к месту назначения на 40 мин раньше. Найдите скорости мотоциклистов.
981. Моторная лодка прошла 28 км по течению реки и 25 км против течения, затратив на весь путь столько же времени, сколько ей понадобилось бы на прохождение 54 км в стоячей воде. Найдите скорость лодки в стоячей воде, если известно, что скорость течения равна 2 км/ч. . J
982. Катер прошел по течению реки 160 км и столько же против течения, употребив на весь путь 26 ч. Найдите скорость катера в стоячей воде, если скорость течения реки 3 км/ч. j
983. Скорый поезд должен был по расписанию пройти расстоя- j ние MN, равное 300 км, с некоторой средней скоростью. < Однако вначале его скорость была меньше расчетной на 8 км/ч, и поэтому, чтобы прийти в по расписанию, он шел от станции X, отстоящей от М на 180 км, со скоростью, превышающей расчетную на 16 км/ч. Какое время затратил поезд на путь из М в N?
984. От станции в совхоз, расстояние до которого 12 км, выехал трактор, а через полчаса от станции в том же направлении выехал грузовик. Когда грузовик прибыл в совхоз, трактору оставалось ехать до совхоза еще 3 км. Найдите скорости трактора и грузовика, если известно, что скорость грузовика на 20 км больше скорости трактора.
985. Из пункта М в пункт 7V, расстояние до которого 42 км, выехал велосипедист, а через час навстречу ему из N в М со скоростью, превышающей скорость велосипедиста на 48 км/ч, выехал мотоциклист. Найдите скорости велосипедиста и мотоциклиста, зная, что они встретились в 17 км от пункта М.
986. Решите уравнение:
а) 0,12521 = 4х-1; \) ioxt~5x+D =1;
*6) 25х = 0,2х~3; г) 49х2~3х = (-j3-*.
987. Найдите приближенные значения корней уравнения:
а) х4 - 0,00486; в) 3,7* - 1,8;
б) х1»4 - - 127; г) 0,65х - 15.
988. При каких значениях х:
a) 1g (х2 — 5х + 7) равен 0; б) 1g (х2 + 2х + 37) равен 2?
989. Используя графические представления, выясните, имеет ли уравнение корни, и укажите их число:
а) х3 ~~2х + 1; в)-4--- 7х; д) 6х — —Зх + 2;
х
б) ]/~х = 5х — 1; г) 2Х"1 = 2х; е) 1g х = —х.
990. Решите графически уравнение:
а) х3 — 3 — 2х; в) 0,5х2 = 2х;
б) х3 = х + 2; г), х2 — 2х — 8 —.
х
НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
991. Какое из отношений — «меньше», «больше», «равно» — между числами а и Ъ имеет место, если известно, что разность а — b равна:
а) -0,01; б) 3,16; в) 0; г) (—0,1)17?
992. Докажите, что при любом значении переменной истинно неравенство:
аТ(п + З)2 + (а - 5)2 >2 (а2 - 2а);
б) а (а + 1) + За > 4 (а — 0,5).
993.
994.
Докажите, что отношения «меньше» и «больше» между числами обладают следующими свойствами:
а) если а < & и b < с, то а < с;
б) если а < Ъ, то а + с < Ъ + с;
в) если а < Ъ и с — положительное число, то ас < Ъс\
г) если а < & и с — отрицательное число, то ас > &с;
1 . 1
д) если а < b и числа а и Ъ одного знака, то — > — .
а b
Истинно ли высказывание:
б) (—За <—1,8) ===> (а >0,6);
в) (х >6) (х2 > 36);
г) (х > —4) => (х2 >16)?
995. Равносильны ли неравенства:
а) За — 2 > 0 и а
б) 1 — 5а < 0 и а > 0,2?
*
Каково соотношение между множествами решений равно* сильных неравенств?
996. Докажите, что:
а) если а < & и с < d, то а + с < b + d;
б) если а < b и с < d, причем а, &, с и d — положительные числа, то ас < bd>
997. Пусть а и b — длины сторон прямоугольника (в сантиметрах), причем
Оцените периметр и площадь этого прямоугольника.
998. Известно, что
1,21 < х < 1,44, 0,36 < у < 0,49.
' г- V*
Оцените значение выражения: а) }/ х — ]/ у; б) .
Vv
999. Что называется решением неравенства с одной переменной? Является ли решением неравенства х3 — х2 > 1 число —2; число У5?
1000. Что значит решить неравенство с одной переменной? Решите линейное неравенство:
а) —27х
б) 16г/ >
1001. Приведите пример неравенства вида ах < &, множеством решений которого служит:
а) пустое множество; б) множество всех чисел.
1002. Приведите неравенства к виду ах > b или к виду ах < < Ъ и решите его:
а) 0,4 (у - 1) + у > 0,2г/ + 5;
б) 0,2х — 0,6 > 3 (х + 1);
в) 0,2 (Зу + 1) < (0,7г/ - 1) - (ОДу + 4);
г) 7 (х - 0,4) < 2 (2х + 3) - (1,5 - Зх).
1003.
1004.
1005.
1006.
Решите неравенство:
а) 0,8х < —х — в) 1 — 1,5х > -7 ~ Зж;
3 15 2
5х — 3 . 1 ОЕ . 1 ч 4х + 1 19 — х Л
б) < 1,25х + 1; г) —-------------------— х > 0.
4 3 2
Укажите номер члена арифметической прогрессии (хД, начиная с которого все члены этой прогрессии больше 50, если х2 = 0,7 и d — 2,6.
Является ли решением системы неравенств (Зх + 1 > 8, (2 — х < 3
число 6; число У2?
Приведите пример системы двух линейных неравенств с одной переменной, множеством решений которой является пустое множество.
1007. Найдите множество решений системы неравенств:
а) (5х — 2 2х + 1, |2х + 3 <18 — Зх;
б) (4у + 5 > у + 17, 4 [у - 1 > 2у - 3.
1008. Найдите целые решения системы неравенств:
а) Г12х2 — (2х — 3) (6х + 1) > х, ((5х — 1) (5х + 1) — 25х2 > х — 6;
б) Г(6х + I)2 - (2х + 1) (18х - 1) <8, 11 — 0,эх х — 4.
1009.
Решите систему неравенств:
1010. Найдите область определения выражения:
а) ]/12 — 5х + ]/2х — 1; в) ]/х2 +4 +]/12х—17;
б) 1g (2-5x)+lg (5 - 2х); г) lg(12+x2)+lg(l+7x) +lgx.
1011. Решите двойное неравенство:
а) —6 <1 Зх — 2 18; в) 0 < 2 — 5у < 3;
б) —3 < < 7; г) —3 0.
' з 4
1012. Для каких членов арифметической прогрессии (уп)9 в которой z/t —- 15 и d = —1,4, выполняется условие —10 < уп < 0?
1013. а) При каких значениях а значения двучлена 17 —5а принадлежат числовому промежутку [0; 1]?
б) При каких значениях у значения дроби —принадлежат числовому промежутку ]—1; 1[?
1014. Решите неравенство:
а) |х - 5| < 4,1; в) |4,5 - Ь\ < 0,5;
б) |1,1 + у\ > 3,2; г) [3,6 — у\ > 2.
1015. Найдите множество решений неравенства:
а) (17 —2х)(12 —х) > 0;
0,8& -- 7
0,6Ь — 5
1016.
Решите неравенство: а) х2 — 2х — 48 >0;
б) Зх2 — 4х — 15 > 0;
в) х3 — 0,64 < 0;
г) х2 — 3,6х > 0.
1017. При каких значениях х имеет смысл выражение:
а) ]/х2 + Зх + 2;
б) /4Х2 Т2х...+ 9;
в) 1g (х2 — 6х + 5);
г) 1g (х2 - х - 72)?
1018. Найдите множество решений неравенства:
а) Ух < 2; б) Ух 5;
1019. Решите неравенство:
а) 125~6х < J-; 144
б) 0,53-*~8 > 0,25;
в) 13-^2~7 > 169;
1020.
Найдите множество решений
a) 1g (5 — 2х) > 1;
б) 1g (3 - х) < 2;
неравенства:
в) 1g (5х + 8) > —2;
г) lg (1 — 4х) > —1.
УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ.
СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
1021.
1022.
Что называется решением уравнения (или неравенства) с двумя переменивши? Что называется решением системы уравнений (или системы неравенств) с двумя переменными? Что значит решить систему уравнений (или систему неравенств) с двумя переменными?
1) Является ли пара (—2; —1) значений переменных
х и у:
а) решением уравнения 2х2 — у - 9;
б) решением системы уравнений (2х2 ~ у = 9, ]х + ху — 0?
2) Является ли пара (—3; 5) значений переменных х и
а) б)
3)
решением решением Является
уравнений х + у — ху -- 18;
системы уравнений
= 18, 1?
ли пара (3; 0) значений переменных х и
У-
1023.
а) решением неравенства х2 + у б) решением системы неравенств
Постройте график уравнения:
< Ю;
/х2 + у <10, |2х + у > 5,5?
а) 4х2 — Зу = 0;
в) х2 + у2 — 8,5;
б) ху = —4;
г) х2 — 4г/2 = 0.
1024. Какую фигуру задает на координатной плоскости неравенство:
а) х + у < 4;
б) х2 + у2 < 4?
1025. Отношение между натуральными числами задано предложением:
а) х + 2у — 12; б) 4х + у < 8.
Задайте это отношение путем перечисления пар и постройте его график.
1026.
1027.
1028.
1029.
1030,
1031.
1032.
а) В уравнении прямой у kx + 8 подберите значение к так, чтобы эта прямая была параллельна прямой у = Зх — 2.
б) В уравнении прямой у =- 4х + Ъ укажите такое значение Ь, при котором эта прямая пересекает ось у в точке А (0; -6).
В уравнении прямой у = кх + Ъ подберите значения k и Ъ таким образом, чтобы система:
а) (у — kx + &, [у ~ 2,5х — 3
б) (у — кх + Ъ, [у = ~“2,6х + 8
в) (у kx + &, [у = 3,5х — 5
Найдите множество
1033.
не имела решений;
имела бесконечное множество решений;
имела решение х = 4, у ~ 9.
решений системы уравнений:
а) (5х = у + 50,
( —3,4х + 2,бу = 14;
б) (8х — 4у = 9, { 13х + бу —1.
Решите систему уравнений:
& арифметической прогрессии (ап) сумма 6-го и 10-го членов равна 5,9, а разность 12-го и 4-го равна 2. Найдите 25-й член этой прогрессии.
В арифметической прогрессии (Ьп) сумма 5-го и 10-го членов равна —9, а сумма 4-го и 6-го равна 4. Найдите сумму первых десяти членов этой прогрессии.
а) Одним из решений уравнения ах — 5у = 6 служит пара чисел (—6; —6). Найдите множество решений системы
(ах — 5у = 6, [х — 3,5у = 6.
б) Найдите множество решений системы
Г 4х + 9у - 8, (х — ky = 2,
зная, что пара чисел (15; 10) служит решением уравнения Зх — ky = 5.
Найдите расстояние от точки пересечения прямых Зх — у = 5 и 2х + у 10 до оси абсцисс, до оси ординат, до начала координат.
г
1034. Проходит ли через точку пересечения прямых
Зх — у ~ 3 и 5х — Зг/ — 1:
а) прямая 7х —• Зу = 5; б) прямая 12х — 7у ~ 3?
1035. а) При каких значениях а и b парабола у “ ах2 + Ъх + 4 проходит через точки Е (—1; 2) и D (2; 5)?
б) При каких значениях а и с парабола у = ах2 + 4х + с пересекает оси координат в точках А (1; 0) и В (0; 4)? 1036. Покажите на координатной плоскости множество точек, задаваемое системой неравенств:
а)
1037. За 3 футбольных мяча и 15 хоккейных клюшек детская спортшкола заплатила 48 р. После снижения цен на мячи на 20 %, а на клюшки на 10 % за 2 футбольных мяча и 10 хоккейных клюшек заплатили 27 р. 20 к. Сколько стоил футбольный мяч и сколько стоила хоккейная клюшка первоначально?
1038. Две бригады изготовили за месяц 140 деталей. На следующий месяц производительность труда первой бригады возросла на 15 %, а второй — на 20 %, и поэтому они изготовили на 24 детали больше, чем за предыдущий месяц. Сколько деталей изготовила каждая бригада в отдельности за два месяца?
1039. Два пешехода отправились одновременно из пунктов М и N, расстояние между которыми 38 км, навстречу друг другу. Через 4 ч расстояние между ними сократилось до 2 км, а еще через 3 ч первому осталось пройти до пункта N на 7 км меньше, чем второму до М. Какова скорость каждого из пешеходов?
1040. Если к числителю и знаменателю дроби прибавить по 1, - 1
то получится дробь, равная ~, а если из числителя и 3
знаменателя вычесть по 3, то получится дробь, равная —.
5 Найдите исходную дробь.
1041. Из городов А и В, расстояние между которыми 200 км, одновременно выехали автомобиль и автобус и встретились через 2 ч. Автомобиль прибывает в В на 1 ч 40 мин раньше, чем автобус прибывает в А. Найдите скорости автомобиля и автобуса.
1042. Решите графически систему уравнений:
1043.
1044.
1045.
1048.
1047.
1048.
1049.
Решите систему уравнении:
а) Г*2 + У + 8 = ху, [у — 2х — 0;
б) Гх2 + у2 + Зху = 1, [Зг/ 4- х = 0;
в) Г 2х2 + 5х — Зу — —12, \2у — 7х = 8;
г) <у2 — 6х + у = 0, 2х — —у — 1.
Покажите на координатной плоскости множество точек, задаваемое системой неравенств:
а) (у 2х2 + 5х + 2, [у < 5;
б) (у —ж2 —
[у —6;
ю,
г)
ФУНКЦИИ
Какое отношение называется функцией?
Приведите пример отношения, являющегося функцией, и пример отношения, которое не является функцией .
Является ли функцией отношение, заданное графиком: а) на рисунке 101; б) на рисунке 102?
ДвДяется ли функцией отношение, заданное уравнением: а) х2 + у2 = 1; б) х + 2у — 4?
Найдите область определения функции, заданной формулой:
а) у = х2 — + 6;
Укажите область определения и
область значений ной формулой: а) у 2х—3;
б) у = —0,5х;
ч 100
в) у = —;
X
г) у = х2;
д) у = х2 — 4х?
е) у = 1 — х2;
функции, задан-
ж) у = х4;
з) у = х5;
и) у = Vх\
3 — к) у = У х; л) у = 3х; м) у = 1g X.
Рис. 101
4
Рис. 102
2х_6
1050» Функция задана формулой у =---1. Найдите множество
X
значений аргумента х, при которых значения функции равны нулю; больше нуля; меньше нуля. Принадлежит ли множеству значений функции число 4; число 2?
1051. Постройте график какой-нибудь функции, которая определена на числовом отрезке [—4; 4], обращается в нуль при х — —2их ~ 1, принимает положительные значения при х С ] — 2; 1[, отрицательные значения при х 6 [-4; -2 [О; 4].
1052. 1. Какая функция называется возрастающей на данном множестве; убывающей на данном множестве; возрастающей; убывающей?
2. Докажите, что функция, заданная формулой:
а) у ~ kx + I при k > 0 является возрастающей, а при й < 0 — убывающей;
k
б) у — при k > 0 является убывающей на множестве X
положительных чисел, а при k < 0 — возрастающей на этом множестве;
в) у ~ пх2 при а > 0 является возрастающей на множестве положительных чисел и убывающей на множестве отрицательных чисел;
г) у — ах3 при а < 0 является убывающей.
1053. Приведите пример функции, которая является:
а) возрастающей на всей области ее определения;
б) убывающей на всей области ее определения;
в) возрастающей на множестве положительных чисел; г) убывающей на множестве положительных чисел; д) возрастающей на множестве отрицательных чисел; е) убывающей на множестве отрицательных чисел.
1054. Пользуясь свойствами известных вам функций (у = хл, у = jXx, у = ах, у 1g х), объясните, почему истинно высказывание:
а) 24310 > 24110; г) З45 > З41;
/ 1 \28 /1 \24
б) (—49)12 < (-59)12; Д) IП < (у) ;
в) p350 > /304; е) 1g 250 > 1g 245.
1055. Отношение задано уравнением:
а) 2х + Зу = 6; в) у = х6; д) ха + г/2 = 1; ж) у= 10х;
б) у = —; г) у = Vх', е)у = |х|; з) z/=lgx.
X
Задайте уравнением отношение, обратное данному. Укажите область определения и область значений данного отношения и отношения, обратного данному.
1056. Функция h задана формулой:
Постройте график данной функции и график отношения g, обратного функции Л. Является ли отношение g функцией?
Рис. 103
1057. Функция f задана графиком (рис. 103) на множестве с—3,5; 4,5].
Пользуясь графиком, найдите:
а) область значений функции f;
б) множество значений аргумента х, на котором значения функции f равны нулю; больше нуля; меньше нуля; в) промежутки, на которых функция f возрастает; убывает.
1058. Изб^разите схематически график функции, заданной формулой:
а) у ---- kx — 2, где А > 0;
б) у = kx + 3, где k < 0;
в) У = где k> 0; х
г) у = —, где k < 0;
д) У = «X2, где а > 0;
е) у — ах2, где а < 0;
ж) у = ах3, где а > 0;
з) у = ах3, где а < 0.
ТРУДНЫЕ ЗАДАЧИ
1059.
1060.
1061.
1062.
1063.
1064.
1065.
1066.
1067.
1068.
1069.
1070.
Между числами — и — найдите какое-либо число, являю-
щееся квадратом рационального числа. Сколько решений имеет эта задача?
Какая из дробей ближе к единице: правильная или обратная ей неправильная?
При каком условии: []^х; cz [х; у]?
Если четное число оканчивается цифрой, отличной от нуля, то четвертая степень этого числа оканчивается цифрой 6. Докажите это.
Какой цифрой оканчивается число:
а) 21000; б) З1000; в) 71000?
Докажите, что ни при каком натуральном п значение выражения п2 + бтг + 16 не делится на 169.
Дано многозначное число abc ... kxyz. Отделив от него трехзначное число, образованное тремя последними цифрами, получим два числа: abc ... k и xyz. Докажите, что если разность полученных чисел делится на 7 (или на 11, или на 13), то и данное число делится на 7 (или на 11, или на 13).
Докажите, что сумма кубов трех последовательных натуральных чисел делится на 9.
Докажите, что значение выражения п5 — би3 + 4п делится на 120 при любых натуральных п.
Докажите, что если в прямоугольном треугольнике длины сторон — целые числа, то его площадь также выражается целым числом.
Найдите все пары натуральных чисел, удовлетворяющие уравнению: а) х2 — z/2 — 105; б) 2х2 + 5ху — 12z/2 = 28. Найдите хотя бы одну пару натуральных чисел, удовлетворяющую уравнению х2 + У2 = (42 + б2)3.
1071. Найдите множество решений уравнения
х2 + 5z/2 + 4xz/ + 2у + 1 — 0.
1072. Найдите все пары (х; у) целых чисел, которые являются решениями уравнения
1073. Проверьте истинность равенств:
Укажите условие, при котором выполняется подмеченная закономерность. Приведите примеры.
1074. Найдите значение выражения
1_________1_________1
/Г+/2 + /2+/з" /3 4-/4
/99 4-/100
1075. Из первых ста натуральных чисел произвольно взято 51 число. Докажите, что среди взятых чисел наверняка есть два таких числа, из которых одно кратно другому. Указание. Любое натуральное число можно представить в виде 2п • р, где п — целое неотрицательное число, а р — нечетное число.
1076. Имеется 13 монет одного достоинства, среди которых одна фальшивая, отличающаяся массой от остальных. Можно ли/С помощью трех взвешиваний на рычажных весах без гирь обнаружить фальшивую монету?
1077. Расстояние между пунктами А и В 60 км. Из А в В выходит автомобиль, а из В в том же направлении одновременно с первым автомобилем выходит второй. Если скорость первого автомобиля увеличить на 10 км/ч, а второго — на 8 км/ч, то первый автомобиль догонит второй в том же месте, но на час раньше. Какова скорость каждого автомобиля?
1078. Рабочий изготовил 50 деталей, из которых 40 положил в один ящик, а остальные — в другой. Во втором ящике к этому времени уже находилось 30 деталей, причем 10 из них были одного вида, а 20 — другого. Сколько деталей первого вида изготовил рабочий, если известно, что деталь второго вида была в 3 раза дешевле, чем деталь первого вида, и суммарная стоимость всех деталей в первом ящике в 2 раза ниже суммарной стоимости деталей, находящихся во втором ящике?
1079. а) Найдите сумму кубов корней уравнения 2х2 — 5х + + 1-0.
б) Найдите значение выражения — + —, где и Х2 Х1
х2 — корни уравнения 2х2 — 11х + 13 = 0.
235 /
t
/
/
1080. Длины сторон треугольника АВС (в сантиметрах) равны а, b и с. Известно, что а3 = Ь3 + с3.
Является ли угол А острым? прямым? тупым?
1081. Докажите, что при всех положительных значениях а, b и с истинно неравенство 8аЪс (а + Ъ) (Ь + с) (с + а).
1082. Докажите, что если х + у + г -----7, где х 0; у 0;
2^0, ТО Ух + Уу + Уг < 5.
1083. Докажите, что если а + b 1, то истинно неравенство
1084. Докажите, что при любых действительных х и у истинно неравенство:
а) (х - Зг/)2 + 10 (х — 3z/) + 26 > 0;
б) 4ху + 24х — 10у — 5х2 — у2 — 30 <0.
1085. Докажите, что если а, b и с — длины сторон некоторого треугольника, то при любом действительном х истинно неравенство Ь2х2 + (Ь2 + с2 — а2) х + с2 > 0.
1086. Найдите наименьшее целое число п, которое надо прибавить к выражению (а + 2) (а + 5) (а + 8) (а + 11), чтобы полученная сумма была положительной при любых действительных значениях а.
1087. Докажите, что при а > 0 и 6 > 0.
1088. Постройте график функции, заданной формулой:
а) у = | х2 — 4х|;
б) у = х2 — 4 |х|;
в) у |х2 —- 5х + 6|;
г) у = х2 — 5 | х| + 6.
1089. Постройте множество точек плоскости, координаты которых удовлетворяют уравнению:
а) |х| + \у\ = 4; б) |х| — \у\ = 4.
1090. Постройте график отношения, заданного предложением:
а) (Ух + Уу)2 — 2 Уху <5;
б) (х + Уху + у] (х — Уху + у)
9 + ху.
1091. Постройте множество точек плоскости, координаты которых удовлетворяют уравнению:
I X 1 ] ху I
а) х2 + у2 4 х ; б) х2 + У2 “ 4 *у
1092. Решите систему уравнений:
a) fx2
1У
1093. Решите уравнение х2 4
ху + х = 14, ху + У = 28;
1004. Постройте график функции, заданной формулой:
а) У =
(х2 — 5х + 6) (1 — х)
х — 3 ’
б)
ж1 — 13ж- + 36
4 — х2
1095* Покажите множество точек координатной плоскости, задаваемое системой неравенств
|5х + 2г/1 1, |3х — 2у \ 5.
1096.
1097.
1098.
1099.
1100.
1101.
1102.
1103.
1104.
Существует ли равносторонний треугольник, вершины которого на координатной плоскости находятся в точках с целыми координатами?
Найдется ли в арифметической прогрессии 2; 5; 8; ... такой член, который равен квадрату натурального числа? Сколько последовательных натуральных чисел, начиная с 1, надо сложить, чтобы получить трехзначное число, записываемое одинаковыми цифрами?
Найдите сумму всех несократимых дробей вида где
п £ N, 1 п 50.
Имеются две арифметические прогрессии:
(ал): 1; 5; 9; 13; 17; ... и (Ьп): 2; 5; 8; 11; 14; ... .
Докажите, что если выписать подряд все одинаковые члены обеих прогрессий, то полученная последовательность также будет арифметической прогрессией. Чему равна разность этой прогрессии?
Докажите, что если длины сторон прямоугольного треугольника образуют арифметическую прогрессию, то разность этой прогрессии равна радиусу вписанного в этот
треугольник круга.
Могут ли длины сторон прямоугольного треугольника образовывать геометрическую прогрессию? Если могут,
то найдите величины углов этого треугольника.
В арифметической прогрессии
причем т #= п.
Доказать, что Sm+n — 0.
В треугольной таблице помещены последовательные нечет-
ные числа так, что в первой строке находится одно число, во второй — два, в третьей — три и т. д.
13 15 17 19
21 23 25 27 29
Докажите, что сумма чисел в n-й строке таблицы равна п3
1105, Решите уравнение:
а) Р/ 2 + 1/ 3) +UZ 2-]/3 \ -4;
б) (]/ 4 4- ]/'15)’Y -И + 4— У 1§Г = 8;
1106» Постройте график отношения:
а) \У} = {%}',
б) [х -и у] = [ж] + ЕН;
в) EOI-
1107. Функция f, определенная на множестве натуральных чи-сел, задается описанием: f (х) п, если х есть п-значиое число» Например, f (55) 2, f (243) = 3, f (7) 1. До-
кажите, что функцию f можно задать формулой /с(х) = - 1 + Fig xj. Найдите /(94875); / (210); f (2100); f (21000).
1108» Постройте график функции, заданной формулой
где х С [4; 81
1109, Решите уравнение:
1110, Решите уравнение
1111» Постройте гра&ик сЬуняции
Г л а в s 1
пересекает ось
координаты точки пересечения с осью у — (0; 13); ) и (0; —6); д) (0; 0) и (—3,5; 0); е) (0; 0), (—3; 0). -1. 43. а) ]—1; 4[; б) ]—оо; —1 [ (J ] 4; + <»[.
44. а) ]—9; 10[; б)
—8 £ (J ]6;
*
°0 ; д)
9
9
-4[U 1-
]0;
J—оо;
—2^ U ]~~2; оо
50. а) ]1; 7[
б) (х + 1) (5х + 8);
56. а) Да; б) да. в) (х — 1) (3 —> 4х);
60. а) (х — 7) (х 3);
г) (х + 3) (10х — 21); д) (а + 5) (а — 4); е) невозможно; ж) (а + 2Ь) (а—ЗЪУ,
з) (х — 5а) (х + 6а); и) (у
л) невозможно; м) х (х — 10) (х — 2). 61. а) (а—6) (а—5) (а—3) (а— 2) (а -4 1)
5х 4-2
б) (& — 1) (Ь — 3) (2& — 3) (2&2+9&—9). 62. а)-----
Ъ) (Зу — 56); к) (х — z (1 — У2)) (х — г (1+/2)); .
С
5 •
-------. 63. а)
За — 6
64.
б) ] —оо; 1 [ U ]6; +оо[; в)
и 1;+оо ;г)] —оо;—3]U
-7; 7]; б) ]—оо; -12 [ U ]12; + оо[; в) [-6; 7]; г) [0; 10 [ U ]10; +~[;
—8[ U 1—8; 5]; е) ]—3; 3[. 67. у = |х — 5| + 2. 68. а) О' (—8; —5);
О' (0; 50); в) О'
; г) О' (—1; 15). 71. б) Не существует; в) существует,
(8; 3); г) существует, О' (2; 3). 72. а) Можно, О' (5; 3); б) можно, О' (—3; нельзя; г) можно, О' (—2; 1). 73. у = х2 — 6х 7;
перенос ОО', где О (0; 0) и О' (3, —2). 75. ОО', где О (0; О
а = —21, Ъ 71. 83. а)
12. 81.
параллельный
]2; 3[; б) ]1; 6]
/
г) {4,5}; д)
l)]i; +~[;
9
9
12
нет.
б) ]-«>; —7] U [9; + г) [-/З; 1 [ и ]1; /3];
-б] и [7;
е) [—2 - /40;
з) [0; 0,5 [ U ]0,5; 0,8]. 8:
сю;
11Е U111;
оо[;
9
9
б)
з) ]— оо; 0,36[.
87. а) [0; 2]; б) [0; 3]; в)]-оо; 0 [ U ]0; 2] U [3; +°о[; г) ]-оо; 1] U [6; 18 [ U
U 318; +оо[; д) [2; 7] U [8;
з) — оо; О
+ <ю[;
Jit) J ОО *
-0,5] U [3,5; +°°[;
Глава П
г/3 + 1
99. г) х = ——. 101. а) ]3; 7[;
У —2
г) 0. 102.
в) {(3; 20)}; г) {(8; —9)}; д) {(10; 1)}. 103. а)
а) {(2; -1)}; б) {(8; -4,5)};
{(3; 1); (5; 3)}; б) {(-7; -3);
1\) ( / 66 112\1
- ; в) {(10; 1,8)}; г) {(-1,5; -6); (2; 1)}; д) (6; 8); (; е) {(6;4);
о /) ( . \ 13 4 13 / J
(—6; -—4)}; ж)
{(—3; -2); (3; 1)};и) {(3;—5); (5;-8)}. 105. а) 0;
б) 0. 103. а) {(6; 4); (4; 6)}; б) {(10; 4); (—4;
Г/ 1 1\ / 2 20
—10)}; в) 1—; 2— ; 1 ; 1— ; ’ 0 4 20 3 3/1
—21; (6; 15) к 107. а) 8 и 12; б) 18 и 12 или —12 и —18. 108. а) 21 м
и 20 м; б) 210 см2. 109.
а) На 20 м и на 2 м; б) 28 м и 12 м или 24 м и 16 м.
110. а) 68; б) 47. 111. а) 12 км/ч; 16 км/ч; б) 75 км/ч и 60 км/ч. 112. а) За
20 мин и за 30 мин; б) 60 ч и 84 ч. 117. а) Нет; б) да; в) да; г) да; д) нет.
119. Множеству F принадлежат точки A, В, С. 125. Кругу принадлежат точки А, В, С. 128. а) {(—1,5; 0,5)}; б) {(—0,7; 4,1); (1,2; —1,6)}. 129. а) (1; 1), (4; 7); б) (1,5; 4). 130. а) Да; б) нет. 131. а) Да; б) да; в) нет; г) да. 132. Множеству F принадлежат точки В и В. 137. а) 4,8 км/ч; 3,6 км/ч; б) 0,16 м/с; 0,12 м/с. 139. а) Бесконечное множество; г) 4 решения. 151. е) х ~ —4,3; у^—14,3 или х ~ 2,3; у —7,7; з) (3; 1); (—3; —1); (1; 3); (—1; —3). 154. При |г|^з/2. 155. При |с| < 10 /£ 158. а) {(1,5; —2); (10; 15)}; в) {(6; 8); (8; 6)}; г) Я-1; —0; (6; 4)1. 157. а) [М-; —0; (1; 1)1;
(\ 5 5 / ) 0 3. 3 / J
б) {(3; 4); (0; 5)}; в) {(7 V2; /2); (-7 /2; /2); (7 /2; -/2); (-7 V2; —/2)}; г) {(/б+ —1); (—/51;—1)}. 158. а) {(6;—2); (-6; 2); (2;—6); (—2; 6)}; б) {(2/2? 6/2); (—2/2; — б/2); (б/F; 2 /2); (—6/2; —2/2)}. 160. Не имеют. 161. а) {(-4; —2); (4; 2); (-4 /5; 2 /б); (4 /б;-2 /5)}; б) {(-3; -2); (3; 2)}; в) {(3—3/2? 3+3/2); (3 + 3/2? 3 — 3/2); (2; 4); (4; 2)};
г) {(2; 3); (3; 2)}. 162. а) —; б)—. 163. а) 15 дм и 8 дм; б) 60 см. 164. а) На 30 м3; 12 5
б) на 204 дм2. 165. а) За 90 ч и 72 ч или за 104 ч и 65 ч; б) за 36 ч и 45 ч. 166. <а) 4 км/ч, 5 км/ч, 22 км; б) 30 км/ч и 45 км/ч. 167. а) 64 км/ч и 56 км/ч; ' 5
б) 96 км/ч и 64 км/ч. 168. а) а — 2; Ъ = —5; с — 19 или а — ——; Ъ — 8;
4
с — —20. 169. а) 40 дм; 40 дм; 60 дм или 42 дм; 42 дм; 53 дм; б) 190 сл
или 170 см. 180. 8 ед2. 187. а) 16 ед2; б) 3 ед2.
Глава III
192. а) Ьг ~ 13, д4 — 52, 203. а) (5; 0) и (—5; 10);
Ъ7 — 91. 202. а) Существует; б) не существует, б) (—10; —20) и (2; 4). 206. д) = 1, я2 = 2,
— 121,5. 210. а) п = 23; б) п = 100. 211. а) Является, п ~ 27; б) не является;
в) не является. 212. а) Является, п = 16; б) не является. 213. а) Да, п ~ 2 и
п — 15; б) да, п ~ 8 и п ~ 9; в) нет. 214. а) п 9; б) п < 15; в) п 33;
г) 26 ti < 59. 216. а) Начиная с п = 4; б) начиная с п = 9. 217. а) Не су
ществует; б) существует. 222. а) {(8; 5); (—16; —11)}; б) 5у; 3 к 227. в) d =
\ 3 /
-——; г) d = ——228. а) с, = 19, с5 = 13, с10 = 28; б) с,, = 13, 3 4
сд = 28, = 3. 230. 8 см. 231. а) 5,0 • 10“2; б) 2,2 . 103. 234. а) ап = 4;
г) —0,3. 238. a) d -= 10; б) d = 0,6. 239. а) сх - 21, d = 1,5; б) ct = 120, tZ = —1; в) сх — 38, d — —2; г) cL — —2,5, d ~ 0,5. 242. в) а{ — —2, d =* 7; г) аг — —5, d — 3 или ах — 7, d — —3. 244. а) Число 143 — 21-й член прогрессии; б) не принадлежит. 246. а) Число —0,1 (31-й член) является первым отрицательным членом прогрессии; б) число 0,1 (15-й член) является первым поло
жительным членом прогрессии. 247. а) Для всех членов, начиная с 40-го;
б) для всех членов с 1-го по 64-й включительно. 250. 1,5а5. 251. а) 1,25;
б) 63. 253. г) 227“2 * 4; д) 2”; е) 2. 256. а) 155; в) 91. 258. а) 564; б) 1892,8.
259. а) 2387; б) 2070. 260. б) 4905; в) 2500; г) 945; д) 4455. 261. а) 20; б) 43.
262. 1) d = 0,5, Sn = 27,5; 2) at = 19,1; Si7 = 243,1; 3) d — 0,5, n 36;
4) «,= 10, d = 10. 265. 203,5 cm. 266. a) -; 6) 27. 273. 6) q = ]/~*3 или 16x3 r xx
q = — 1/ 5?; в) q — ——, 274. в) q — 3; a6 — —54, a7 = —162 или q —3,
f Я* ъ
a.. = 54, a7 = —162. 277. a) {1,5}; 6)
r) ]_oo; —4 [ U ]— 4; 4 C U 24; 5]. 280. 6)
[0; 4~oo[; B)
r) 3. 283. 6) —3,
1 ~~ °°; 0 [(J
3 3
285. a) 2; 6) 2 или —2; в) или — ; г) —3. 288. а) 5; б) 7; в) 5; г) 4, 5 5
290. а) 8; б) 7. 291. 1082 р. 43 к. 292. 1,05 . 10s 6. 293. 35 тыс. м3.
2х^+2 а
294. а) —-------; б) 296. а) ----------;
у 25 4
34 х7 1
301. а) 205,9; б) 25—. 304. а) -------;
81 х — 1
б) 2 • З^-1. 299. а) —1456; б) —21,25.
) ---. 305. 1) &5 = 1—; S-- = 134—;
х+1 9 9
2) q = 3, S7 — 2186 или q — —3, S7 — 1094; 3) Ь} — —4,5, — 90; 4) bx = 3,
p — q За 1
n = 6. 313. a) 100; 6) 15. 315. a) 6) -------; в) --------;
p2 + pq + q2 a 2 x — 1
317. a) (a -h 5) (a2 + 13a + 43); 6) (y + 1) (y2 - 7y + 19);
в) (x — 1) (x2 + Юх + 37); r) (2x — y) (x2 — xy + y2). 329. a) n = 9;
6) n — 1 и n = 4; в) n ~ 2 и n — 3. 330. б) Нет; в) число 287 — 7-й член последовательности. 340. а) Шесть точек; б) девять точек. 341. а) При и 4;
б) при п 6. 342. б) При п 5; в) при 1 п 5; г) при 3 п 19. 344. а) z/3 = 12 — наибольший член последовательности, наименьшего члена нет; б) — —15 — наименьший член последовательности, наибольшего члена нет; в) у3 — —2 — наименьший член последовательности,
1/1=2 — наибольший член; г) у± =—7 — наименьший член последовательности, наибольшего члена нет. 347. а) При любом п С V; б) при 1 п 100; в) при 100 п 1000; г) при п 10; д) при 1 zz 29; е) при п 21.
« 1 1
360. а) Число —— — 1-й отрицательный член прогрессии; б) число — — 1-й 60 9
положительный член прогрессии. 363. d ~ 3,5; в) — 5, d = —2 или = 3, at = 3, d = 3. 371. б) 25 V2. 373. а)
a) tZj — —7, d — 3; б) — "-8, d =—2; г) аг = —33, d = 15 или
1
zz — 32, ^32 — 43; б) СГ| ,
2 17
а37 — 11—; в) а1 = 4,5, п ~ 10; г) ау -- 0,75, а21 “ 4,75. 374. ==-4—
2
d = “. 375. а) 530;
11
б) нужно сложить 15 или 16 первых членов про
грессии (16-й член равен нулю и на значение суммы не влияет). 376. а) 528; б) 340. 378. а) 250 000; б) 16 000. 379. а) 21; б) 24. 380. в) —50; г) —100. п—п2
381. а) х 2 ; б) х”206. 382. а) 162. 383. а) —744. 384. а) 1605; б) 1210.
385. а) 1600. 389. 455 см. 393. аг = —7, d = 6. 391. а) = 243, а3 = 108,
1
а, _ 48 или aL = —243, а3 = —108, аь = —48; б) а2 “ —— —1,
в) а2 = 3 /2, а3 — 6 У3, а-о = 36 У3;
а4= 7 У7 или а2 = —У 7, а3 = 7, а±~——7 У7.397.
с&2 У 7, а3 7, 12 Уб. 403. 1или2.
г)
404. 1 или ' ~ или .— -----1L2_. 405. а) Ъ{ — 128, п = 7; б) Ъх = 7,
2 2
1 <
п ~ 5; в) Ь] = 3, &8 = 384; г) q ~ , п — 5. 409. а) 4, 10, 16 или 16, 10,4;
2
д.2 «+1 _L J д^+1___ Х&
б) 3, 15, 75 или 75, 15, 3. 412. 70. 413. б) --------------------в) ---------------—.
х + 1 х — 1
1 & — 1
415. в) ------; г) -------------------. 417. и) (3 — Зя) (39я3 — 36х + 9).
х + 1 (b + 1) (&7 — 1) 4
419. а)—; 6) 1. 420. б) и14 — и7 + 1. 422. а) (х — 5) (х2 + х + 25);
9
в) (я — З)4 (я2 + 12я + 9). 424. а)
Глава IV
7 — р х2— 7я + 19
6) 9+Зр + р2* я2—я 4-1
1 1
у = б) у = В)
О 41
а -4-2 1
г) ----, 435. а) 2; б) —;
а —1 9
3 ч 5
у = —; г) у ;
е) у — 10=г — 10.
456. а) о *.f б) ~—|г. 458. а) 2; б) -2; в) 1; г)
2х^ — бху 5а2 2оа 2
У -к 24
1
д) е) —1;
V
ж) 1,5; з) —-1,5; и) 1,5; к) 0,3; л) 0,5; м) —0,1. 459.
а) 50; б) 1; в) —6; г) 12;
д) 0; е) 10; ж) 9;
з) 4.
469. а) [0; 4~оо[; б) Л; в) ]—<*>; 0]; г) [2;
461. а) 10; б) 5; в) 12; г) —2; д) 48; е) —54; ж) 15; з) —3. 462. а) 2; б) 7; в) 6; г) —10; д) —5; е) 2; ж) 2; з) 5. 466. а) {1}; б) {—2}.
473. а) 1 < 3/х < 2; б) —1 < у'Г< 1; в) —3 < 3/х < 0. 474. а) [0; 1];
( 11
б) [0; 2]; в) [1; 3[; г) ]4; 5[. 475. а) {26}; 6) — — ; в) 0; г) {()}. 476. а) {125}; I 8 J
]125; +оо[; ]—оо; 125[; б) {16}; ]16; ~г оо[; [0; 16[. 478. д) 0,5; е) 0,6; ж) 1,5‘»
б) 2Ъ; г) 2х3; д) 2х4. 484. а)
482. б) 3; в) 0,5. 483. а) 5а;
а3
яс) 36 з) с у 10— 486. в) ^40; г) к"2б°! Д) 'V9<> е) V"4; ж) V 2а3; 3>
487. а) —КЗ; б) -^2; в) ^4; г) 33/25; д) 1 j/216; е) 5 |<2. 493. в) /5? 3 2 2
г) к6; д) }^5; е) у 16; ж) угх‘, з) а. 493. а) 3; б) 1; в) 1; г) 2. 494. 5 км/ч.
499. в) {—2}; г) {0}; д) 0; е) 0. 500. а) {2; 3; 4}; в) {5; 6}; г) {0; 1; 2; 3; 4}.
502. a) L®; б) 9/З —11^2; в) 6/З; г) 2 */162. 503. a) q = —1,5; 3 1 2 1 15,_ зг-т-
б) 5^—1—; в) = г) у = у=-. 504. г) 3 ух; У Зх; у у “J/
1 Ч
д) y^ab2; а 52; (а + 5)2; у^а2 + у^Ъ2. 506. и) (7 + а) 4 ; к) (х2 + у2) 6 * 4
507. ж) 16; з) 8; и) —; к) 100 000. 509. б) [1; 4-оо[; д) ]5; +оо[. 9
1 1 1 2^ 1
511. а) 0 < х2 < 1; 0 < х3 < 1; 0<х6<1; б) 1< х2 < 8; 1<х3 <4;
/3
3
1
< 2. 515. а) 1; б)
1
0,577; в) 2; г) 25; д) 9; е) 32. 516. а) 6; б)
6
1
в) 70; г) 15; д) 1; е) 0,12. 518. б) —; в) а; г) у. 523. а) 10а; б) 100а; су
I 2 2 3
в) 0,1а; г) 0,01а. 524. a) а = V3 ; б) 8 == V3 ; в) 6У3 . 525. а) х = у2 ;
7 __ 2_ _ _£
б) х—у 4 ; в) х=у 3 ; г) х=у 3 ; д) х^=
е) х~ (бу) 2 . 526. а) х 6 ; б) а24;
в) У 2I; г) Ь 6 ; д) у 6 ; е) х4
528. а) 1; б) х. 531. а)
532. а) — —3,8; d === 0,6; б) — 2; d =- 3,5. 533. а) 4 кв. ед.; б) 8 кв. ед.
1 1 1 2 3
535. а) 1 + с; б) —2Ъ 4 с4 ; в) х 2 + х3 ; г) 4а°’2х0,2; д) х — у; е) а 2 — Ъ 2 ;
ж) р + о; з) (Ь3 — с3)2. 540. а) 1; б) 5; в) 13; г) 9. 541. а) —!—; б) ----------------------;
у — a J
2
X — Q
1
в) (1 — и)2; г) . 542. а) ]39; +<ю[; б) 0. 543. а) 728; б) 3240.
p—q
544. б) 24 км. 546. а) ху — 1; б) х + у — 0. 559. а) у — х2 — 2х + 3, где
х Е ]—оо; 1]: б) у = х2 — 2х-;~3, где х Е [1! +°°[’» в)
б) 2; в) 3; г) 3,5; д) — 1; е) 50; ж) —0,5; з) 2; и)
Д) ]—оо; — ЗЛ и 33; +°°Г; е) ]—оо; —2 [ U ]—2; +оо[. 576. a) 4xVy,
3Л75 б) ЗЬ в) 5ах а2; г) 4&4у2 у. 577. a) в) ул3&. 583. а) ----.
535. а) {0; 64}; в) 0. 594. а) {18}; б) {2-/2; 2 + ]ЛГ}; в) 0; г) {0}; 1 1
“тг “5“ Зу
д) {5}; е) 0. 598. а) х2 ; в) Ъ2 ; д) —. 600. а) 5; б) 2. 602. а) ху = 1; 2с2
б)
в)
- 1; j (f) ‘ (|)S - «
1; г) р + д; д) 25; е) 1.
г) (2х) 3 = (3i/)2 . 603. а) ху, б) ад;
+ 2/. 612. а) 1; б) 10; в)
2 х + Зу
-----; г) ------; д) 2. 613. а) 1; б) 1,4.
а — 1 х — у
Г л а в а V
620. а) При х = 0; б) при х £ ]—оо; 0[; в) при х £ ]0; +оо[. 626. а) {2}; ]2; +оо[; ]—оо; 2[; б) {—1}; ]—1; +<»[• ]—оо; —1[; в) 0; ]—оо; +°°[, 0* 627. а) 12х; б) а — Ь. 643. а) {6}; б) {—2); в) {0}; г) {—3};д) {—2}; е) {—3);
—2,5[. 647. а)
; в) {1,5};
.<!
г) {2,5}; д)
673. а) ]—оо;
1
— оо:
. 651. а) (7; —11); —10
3
2\) 4
1— .655. г) 0,36; е) 0,73; ж) 0,99; з) —. 656. б) 0; г) 0,2.
ОО
е) ]—1; 0,25[. 674
ф
а) 4—; б)
б) при х = —2,5
— оо;
г)
685. а) При х — 5; б) при х = —6;
681. а) При х——6;
в) при х — —1; г) при х — —2; д) при х — —3; е) при х = 7. 686. а) [8; + оо[;
ос;
б)
в)
]0; +°о[; ]—оо; 0[. 698. а) {0; 1};
б) {-1,5}; в) {0}; г)
з) {2};
689. а) 0; ]0;
б) {0}.
700. а)
701. а)
j 18 I 4 J I
711. а) 1 и —2; б) 3 и —4; в) 6 и —7. 712. а) 0;
714. а) [—0,75; 0,25[; б) множество целых чисел.
б) [2,36; 3,36[;
целых
; в) {1}. 706. а) {2}; б) {1}; в) {2}; г) {2}.
722. а)
в) [-10,7; -9,7[;
чисел; е) множество
10“+3; б) 103“; в) 102
б) 0; в) 0;
целых чисел. 715.
г) множество целых чисел;
чисел вида
10а-(-3(3
_ 15
10
0,03
а) С—0,21; 0,79[;
д) множество где п £ Z.
тг,
имеют смысл.
и) —; л) 9; м)
м) —2—. 735.
737. ж) ]—оо;
ж)
{1}; з) ю 4
736. а), в)
ж), з)
100[; з) при всех х Ф 0. 738. е) 80;
В принадлежат. 746. е) х 2; ж) ]—/2; /2[;
з) ]4; +оо[; И) ]—3; 3[; к) ]—оо; —5[|_)]0; + оо[; л) ]0; 1 [ U ]1; + °о[; м) ]0; 100 [ U ]100; + оо[. 747. ж) 1g ^ТбО > 1g/12; з) 1g |Лд< 1g /^ 748. в) 2 < 1g х < 4; г) —4 < 1g х < —1. 749. а), в), д), е), з), к) положи-
тельно. 751. д) {—87};
е) {—3; 3}; ж) {—6; 6}; з) {—24; 24}; и) {—11; 11}.
752. а) Не принадлежит;
б) принадлежит. 753. a) J0; 3[;
б) ]5; +оо[;
1
в) ]0; 0,1[; д) ]0; 100[; з) ]о; 102 [;
е) ]—49,5; 0,5[; ж) ]—2; —1,5[; з) ( 11
в) — да. 757. а) {2}; б) — — .
762. б) 1,50; е) 1,88; з) 0,26.
и)
10
]4,99; 5[; и)
758. а)
+ °о[. 754. а) 10; 2[;
]3000; +<»[. 755. а), б), 4а —12
----------; б) 6 — 2х. 5
766. д) lg х = 10 (1 + lg а + lg b\,
е)
lg2j
768. а)
в)
1g 11 - 1g 2 lg3
0,24; г) 6,3;
—0,39; e) 0,63. 770. a) у = — ;
21g3
Igx
3)
15 дм и 20
773. a)
778. a) lg 4 + lg 12 < 2 lg 7;
lg х — lg 32
= —----------. 772.
lg20 t
774. e) x — 6;
У = , . ; и> У
lg 4 -j- 1^ 5 дм; б) 16 см и 63 см.
1 + 2 1g 2 < 3 1g 5 — Jg 3; г)
з) X ~
3 lg 6 — 2
1,6.
5
ab 2
——ж)
10
-- ----------- g
t = 100a 3 • &~2; 3) t = 10 2 ab 5.780. e) —
ж) —; з) —• 781. в) x — 2 10';
r) x = 5 • 10-2У.
784. а) Существует; б) не
существует. 791. а) [10; 100[; б) [0,01; 0,1[. 797. а) 0,06; б) 1170. 798. а) 60 и 90 км/ч; б) 60 км/ч. 801. а) 3; б) 10. 802. б) 0,7661; г) 250,7; ж) 0,2020; з) 3,781 • 10~4. 803. а) 10 080; в) 0,02197; д) 0,1732; ж) 11,54; и) 0,3008; л) 0,3850. 804. af40,79; в) 0,7676; д) 3,862. 805. а) 4; б) 10; д) —2; е) 9. 806. б) З40 > 431; в) 523 > 621; г) 1213 > 1312. 807. а) х = 13,48; б) х ж 15,02; г) х ~ 7435; д) х =; 8,723. 808. a) S =: 8,97 . 104 м2; б) S = 5,07 • 108 м2; 809. а) 2,62 м; б) 0,185 км; в) 2,1 • 103 км. 810. а) 80,18 м3; б) 2,28 • 10е м3. 811. a) R ~ 5,60 м; б) R =: 3,18 м. 812. б) 3,861; г) 1,083; е) —-4,329; ж) 2,506; з) 10,09. 813. На 3,7 • 104 м3. 814. а) 2,87 • 105 чел.; б) 7,2%. 815. а) 4xi/. б) 8аЬ. 816. а) 45 ч и 36 ч. 817. а) =; —2,9; х2 =; 2,5; б) х — 2,0; 818. а) [—8; —1]; б) ]—оо; 1] J [4; +оо[. 825. а) ]—оо; — 3] U [2; + <»[; б) ]—оо; —1,5 [ U ]0,5; Н~оо[. 831. а) При х£ [—0,3; 0,3]; б) при xg ]—оо; 1 [ (J и ]5; + ОО[. 836. в) 975; д) 0,499. 837. а) 16,7; б) 43,6; в) 478; г) 6,25; д) 39,0; е) 143; ж) 1,31 • 105; з) 4,00 • 104; и) 38,4; к) 59,0; л) 5,19; м) 10,4. 839. 355 г. 840. 5,09 км. 841. 45,2 дм3. 842. а) у = —4,5х; б) у ?= 1,6х + 4. 843. 5 ч и 6 ч. 848. а) 6,67; б) 2,74; в) 13,4; г) 1,68; д) 5,55; е) 0,312. 849. а) 8,26; 1,80; б) 70,0; 42,7; в) 1,34 • 103; 0,745; г) 71,0; 2,54 • 10®. 850. 6,1 м. 851. 8,93 г/см3. 852. Через 30 с. 853. а) 1; б) —1. 857. а) 0,363; б) 2,12; в) 2,68; г) 8,96. 858. 85,9 м3. 859. 0,293 м3. 860. 35,6 см; 49,6 см.
„ 3 5
861. 43,7 Н. 884. г) 1—; д) —0,5; е) — —.
4 6
ж) 50; и) 250. 886. е) 10!г 13>в. 887. в), г),
885. а) 30; г) 8 V10; д) 49; е) 8;
д), е), в), и) не имеет смысла.
890. a) ] —100; + oo[; в) ]—co; —1 [ [J ]—1;
oo[;. e) ]0; 0,1 [U]0,l; -W.
к) ]—1; 1[. 891. r) J—oo; 4] U [6; +°°[; ж) .0; 1] U [10; +°o[. 892. 6) ]0; +<x>[;-
д) ]—oo; —4 [ (J ]4; +°o[; R', e) ]—10; 10[; J—»; 2[. 893. a), 6) He при-
надлежит; в), г) принадлежит. 894. а), б), г) принадлежит; в) не принадле-1 1
жит. 897. к) 2 — — 1g а ™ ™ 1g 6. 899. в) —0,831; г) 0,618; д) 1,26; е) 2,73. 2 2
Ь И
900.
903.
905.
г)
7,5;
2 — 1g у
,2 4
10 а
б) ложно.
а) х — аь;
п
X —
[ _ _2_^ ( __ _4J Г _______11
909. б), г), ж) имеют смысл. 910. а) {100}; б) {10 3 [; в) {10 ° J; г) {10 2 J;
f -—{ 1 г-1 ( / "Tri { "1
д) (10 2 J; е) {107}. 911. a) (1Q2 I; б) (10 ° J; в) (100; ю'8 ; г) (10J.
912. а) ]1; 3[ U ]6; 8[; б) ]—7; —2[ U ]13; 18[; в) ]23; 35[; г) ]2; 7] U [22; 27[.
914. а) 7,962 • 103; б) 41,85; в) 1,425; г) 50,50; д) 69,08; е) 1,002. 915. а) 34,65;
б) 1,463; в) 230,9; г) 2,441 • 104. 916. а) {2178}; в) {3,169}; д) {—25,4}; е) {2,270 • 10 7}; ж) {2,169 • Ю10}; з) {1,853 • 10"2; 53,93}; и) {45,7; 0,0219}; к) {11,97}; л) {5,99}; м) {3,170}. 925. а) 13,5; б) 37,0; в) 99,9; г) 123; д) 973; е) 28,7; ж) 2,37 10'; з) 1,53 • 10s; и) 553. 926. 10,8 кг. 928. а) 3,74 м3; б) 129 м2; в) 8,03 м2; г) 2,05 м2. 934. а) 7,81; б) 6,62; в) 4,51; г) 0,0573; д) 15,5; е) 189; ж) 7,27; з) 44,8; и) 31,1. 938. 4,71 дм. 941. а) 2,30; б) 614; в) 26,2; г) 9,13. 942. 14,7 м3. 943. 39,1 г. 944. 7,73 дм, 7,97 дм, 9,07 дм.
Повторение
5 5 4
945. г) д) — е) -3-. 9
6 6 7
г) 6,5. 952. а) /2; б) 2 /3; в) 98;
.II. II
959. а) ——; б) ——; в) —2,7р2 ; г) 86 х
а 1
в) 1 — - ; г) —2; д) ; е) 2; ж) 2 6
1 1
з Т.
с — 1 у 4-1 в) -------; г) -------L—. 972.
3 , , 3 3
С +1 У +У
( 26 1
г) <——; 21.973. а) При —2 и
I 35 J
t = 1 — У2 и при t — 1 + У2. 9
1
16. а) 2; б) 948. а) 10; б) 1,4; в) 6,4; 40
г, 20. 058. я) 0, б) -i; .> М.«; г) Г.05.
—240а0’1. 960. в) г) 961. б) бхи; х — 8 х +2
1 1
; з) 10. 962. а) 1; б) 10. 963. б) — а3 Ъ3 ;
fl } f 5 } f 1
I—. 7 I. gj J |. gl. J—|g—. —|
[3 J I 8 j I 7
и /=4; б) не существует; в) при i -1; г) при
1
. а) При t < —0,8; б) при t > —; в) при
—2 < t < 2; г) при —1 < t < 4. 975. а) При а 4; б) при а 0,05;
в) при | а\
977. а)
3
б) -V 3;
5
979. 2,2 км. 980. 40 км/ч и 48 км/ч. 981. 12 км/ч. 932. 13 км/ч. 983. 3 ч 45 мин.
984. 10 км/ч и 30 км/ч. 985. 12 км/ч и 60 км/ч. 986. а)
; б) {1}; в) {2; 3};
. 988. а) При х £ {2; 3}; б) при х £ {—9; 7}. 994. а), б), в) да; г) нет.
14,4; 11,04
895. а) Да; б) да. 997. 14,0 ______ 11
</ V х — У у 0 0,6; б) — 0 г——~ 2. 1000. а) ]-—
7 /г
11,75. 993. а) 0,4
5 +оо[; б) ]0,04;+оо[;
1003. а) ]—оо; —1[; о) ] —оо
1008. а) (0, 1, 2, 3, 4}; б) {—1, 0
+ оо[; в) 0; г) 111; +оо[. 1007. а) [1; 3[; 6)0.
1, 2,3}. 1009. а) ]—29; 3[; б) 0.1010.а) [0,5; 2,4];
б) > В) 1 , '|г ,
г) ]0; +сю[. 1011. а)
; б) ]-2; 5,5[;
в) ]—0,2; 0,4[; г) [3,5; 9,5].
1014. а) [0,9; 9,1]; б) ]—°о;
I I 3R 6; 4- oof
1013. а) При a g [3,2;
1015. а) ]—оо; 8,5[ U ]12;
2Г
1017. а) ]—оо; —2] U [—1; г) 1—оо; — 8 £ U ]9; +°°[.
1018.
а)
3,4]; б)
г) ]—оо; 1,6 [ U
а) ]—оо; —6 [ U
; в) ]-0,8; 0,8[; г) ]—оо; 0 [ U 33,6; + оо[,
оо[; б) 0. 1016.
в) ]27;
г) ]1; 32[. 1019.
в) ]—1,598; +<»[; г)
б)
-/бСШУб; +«>[.
]—оо; 0,225[.
1029. а) {(3; 9)};
б)
— оо;
3— ; В) ]—оо; -3 [ и ]3;
1020.
1023. а)
1032.
1034. а) Проходит;
б) проходит.
1035.
а) ]—оо; — 2,5[; б {(15; 25)}; б) {(0,5;
а) {(—1; —2)};
а) При
У
—1,25)}.
б) {(2; 0)}.
б) при а = —8; с = 4. 1037. Футбольный мяч стоил
хоккейная клюш-
ка 1
р. 60 к. 1038. 172 детали,
132 детали. 1039. 5
км/ч
4 км/ч. 1040.
1041. Скорость автомобиля
60 км/ч, скорость автобуса 40 км/ч.
1043. а) {(4; 8); (—2; —4)}; б)
{(—3; 1); (3; -1)};
в) ((0; 4); (27; 1з|)];
I \ 4 8 / J
Трудные задачи
1060. Неправильная. 1061. Если 0 х 1, у 1 и х < у. 1063. а) Цифрой 6; б) цифрой 1; в) цифрой 1. 1069. а) (53; 52), (19; 16), (13; 8), (11; 4); б) (8; 5). 1071. {(2; —1)}. 1072. (1; 2), (2; 1). 1073. Равенство /И + {«} =
г— Га]
= [а]]/ {а) истинно, если {а} = —~. 1074. 9. 1076. Можно. 1077. 50 км/ч
7 17
и 40 км/ч. 1078. 10 деталей. 1079. а) 11-~; б) 2—. 1086. 210.
8 26
((1; 2); (2; 1)}. 1093.
{—1; 2}. 1096. Нет.
1097. Нет. 1098. 36. 1099. 200. 1105. а) {—2; 2};
1109. а) {0,01; 10}; б) {0,1; 10 000}. 1110. а) {0,01; 20}; б) {0,01; 4}; в) {/10}.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгоритм 197
Блок-схема алгоритма 203
График неравенства 36
Дискриминант квадратного трехчлена 7
Дробная часть числа 151
Запись алгоритма развернутая 198
— — табличная 198
— — формульная 201
Знаменатель геометрической прог-
рессии 70
Квадратный трехчлен 7
Корень многочлена 5
— п-й степени 105
— n-й степени арифметический 106
Логарифм десятичный 165
— числа 163
Логарифмирование 171
Мантисса логарифма 177
Отношение, обратное данному 92
Потенцирование 174
Последовательность 50
— возрастающая 51
— постоянная 51
— убывающая 51
Программирование 207
Прогрессия арифметическая 60
— геометрическая 69
Разность арифметической прогрес сии 60
Рекуррентная формула 58
Рекуррентный способ задания пос ледовательности 58
Степень многочлена 26
— уравнения 26
Функция квадратичная 14
— логарифмическая 167
— обратимая 97
— , обратная данной 97
— показательная 144
Характеристика логарифма 177
Целая часть числа 151
Член последовательности 50
Шкала логарифмическая 184
ОГЛАВЛЕНИЕ
ГЛАВА
ГЛАВА
ГЛАВА
КВАДРАТИЧНАЯ ФУНКЦИЯ
§ 1. Квадратный трехчлен
1. Квадратные уравнения (повторение) .......................
2. Корень многочлена........................................
3. Разложение квадратного трехчлена на множители . . . .
§ 2. График квадратичной функции
4. График функции у — а (х — т)2 + п ...................
5. График функции у — ах2 + Ьх + с .....................
6. Решение неравенств второй степени с одной переменной .
Дополнительные упражнения к главе I......................
УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ
§ 3. Уравнения с двумя переменными и их системы
7. Уравнение с двумя переменными и его график...........
8. Система уравнений с двумя переменными................
§ 4. Неравенства с двумя переменными и их системы
9. Неравенство с двумя переменными ...........
10. Система неравенств с двумя переменными..............
Дополнительные упражнения к главе II.............. . . .
ЕВ АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
§ 5. Последовательности
11. Понятие последовательности ............................
12. Способы задания последовательностей ............ . . .
11
14
18
21
26
30
35
39
42
49
3
5
7
13. Рекуррентный способ задания последовательности ..... .................................
§ 6. Арифметическая прогрессия
14. Определение арифметической прогрессии.................
15. Формула тг-го члена арифметической прогрессии . . . .
16. Формула суммы п первых членов арифметической прогрессии ......................................................
§ 7. Геометрическая прогрессия
17. Определение геометрической прогрессии .................
18. Формула я-го члена геометрической прогрессии...........
19. Формула суммы п первых членов геометрической прогрессии .......................................................
20. Тождества (а — b) (а2 + ab + Ъ2) = а3 — Ь‘3 и (а + b) X
X (а2 — ab + Ъ2) = а3 + Ъ3.............................
Дополнительные упражнения к главе III......................
ГЛАВА
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ
ПОКАЗАТЕЛЕМ
ункцчя, обратная данной
57
59
62
66
69
72
75
78
80
21. Отношение, обратное данному .........................
22. Понятие функции, обратной данной.....................
92
96
§ 9. Корень н-й степени и его свойства
23. Функция у — хп.......................................101
24. Понятие корня тг-й степени...........................104
25. Функция у = у/'х.................................... 108
26. Свойства арифметического корня n-й степени...........111
§ 10. Степень с рациональным показателем
27. Функция у ~ ах, где х£ Z, и ее свойства..............115
28. Определение степени с дробным показателем............119
29. Свойства степени с рациональным показателем..........123
30. Преобразование выражений, содержащих степени с дробными показателями .......................................128
Дополнительные упражнения к главе IV.....................131
I
ГЛАВА
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
§ 11. Свойства показательной функции
31. Функция у — 2х.......................................
32. Функция у — ах и ее свойства.........................
140
144
§ 12. Показательная функция с основанием W
33. Целая и дробная части числа..........................150
34. Функция у ~ 10v ..................................153
35. Таблица значений функции у — 10' . ..................157
Дополнительные упражнения к главе V......................159
ГЛАВА
VI
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ. ОРГАНИЗАЦИЯ ВЫЧИСЛЕНИЙ
§ 11 Логарифмическая функция
36. Понятие логарифма . ............................... 163
37. Десятичные логарифмы ............................. 165
38. Функция у = 1g х.................................. 167
39. Логарифмирование....................................171
40. Потенцирование.................................... 174
§ 14. Таблицы логарифмов
41. Характеристика и мантисса логарифмов................177
42. Четырехзначные таблицы логарифмов ..................179
43. Вычисления с помощью четырехзначных таблиц логарифмов . ...................................................181
§ 15. Логарифмическая линейка
44. Логарифмическая шкала.................................184
45. Основная шкала логарифмической линейки . .............186
46. Умножение чисел с помощью логарифмической линейки . . 189
47. Деление чисел с помощью логарифмической линейки . . . 192
48. Совместное умножение и деление чисел с помощью логарифмической линейки........................................ 194
§ 16. Алгоритмы и элементы программирования
49. Понятие об алгоритмах и способах их записи.......197
50. Блок-схемы алгоритмов . ....................... 203
51. Начальные сведения о программировании для ЭВМ . . . 206
Дополнительные упражнения к главе VI............... 211
ПОВТОРЕНИЕ
Вычисления ................................... . 219
Тождественные преобразования................... 220
Уравнения с одной переменной ............ 222
Неравенства с одной переменной ............... 225
Уравнения и неравенства с двумя переменными. Системы
уравнений и неравенств с двумя переменными ...... 228
Функции . ............. . ................... 231
трудные задачи . ..................................... 234
ответы . ............................................. 239
предметный указатель ............................ . 251
Юрий Николаевич Макарычев, Нора Григорьевна Миндюк, Вадим Макариевич Монахов, Константин Соломонович Муравин, Светлана Борисовна Суворова
АЛГЕБРА
УЧЕБНОЕ ПОСОБИЕ ДЛЯ 8 КЛАССА СРЕДНЕЙ ШКОЛЫ
Редактор Н. Я. Никитина.
Художники Б. Л. Николаев, П. А. Жиличкин.
Художественный редактор Е. Н. Карасик.
Технический редактор Н. А. Баркана.
Корректоры К. А. Иванова, Р. Б. Штутман.
ИВ №. 5584
Сдано в набор 04,07.79. Подписано к печати 21.1 1.79. 60X90V16. Бум. тип. № 1. Гарн. школьная. Печать высокая, Усл. печ. л, 16 4- 0,25 форзац. Уч.-изд. л. 14,12 + +0,34 форзац. Тираж2210000 экз. Заказ 152. Цена 25 коп.
Ордена Трудового Красного Знамени издательство «Просвещение» Государственного комитета РСФСР по делам издательств, полиграфии и книжной торговли. Москва, 3-й проезд Марьиной рощи, 41.
Саратовский ордена Трудового Красного Знамени полиграфический комбинат Рос-главполиграфпрома Государственного комитета РСФСР по делам издательств, полиграфии и книжной торговли, Саратов, ул. Чернышевского, 59.
СВЕДЕНИЯ О ПОЛЬЗОВАНИИ УЧЕБНИКОМ
№ Фамилия и имя ученика Учебный год Состояние в начале года учебнику в конце года
1 к
2 *
3 \ Xi
- / *
5 * я
ТАБЛИЦА ДЕСЯТИЧНЫХ ЛОГАРИФМОВ
00 04 I 08 11 ' 15 18 ! 20 23 126 28
Т йк: . I НН ( IT Н 1к 1г в ; И 1 * i! . j
ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЯ
2х=6-х2
СВОЙСТВА ДЕСЯТИЧНЫХ ЛОГАРИФМОВ
Школьные учебники (((Р
SHEBA.SPB.&U/SHKOLA