Коэффициентные обратные задачи механики.

koefficientnye_obratnye_zadaci_mehaniki_1-27

koefficientnye_obratnye_zadaci_mehaniki_28-54

koefficientnye_obratnye_zadaci_mehaniki_55-81

koefficientnye_obratnye_zadaci_mehaniki_82-108

koefficientnye_obratnye_zadaci_mehaniki_109-135

koefficientnye_obratnye_zadaci_mehaniki_136-162

koefficientnye_obratnye_zadaci_mehaniki_163-189

koefficientnye_obratnye_zadaci_mehaniki_190-216

koefficientnye_obratnye_zadaci_mehaniki_217-243

koefficientnye_obratnye_zadaci_mehaniki_244-270

koefficientnye_obratnye_zadaci_mehaniki_271-272

Автор: Ватульян А.О.

Теги: механика деформируемых тел упругость деформация механика задачи по математике высшая математика прикладная математика

Похожие

Занимательные задачи

Динамические задачи термоупругости

Нестандартные задачи по математике. Задачи с целыми числами.

Веселые задачи

Текст

2019
Коэффициентные
обратные задачи
механики
А.О. Ватульян
1/27

УДК 539.3; 517.95
ББК 22.25; 22.51
В21
Ватульян А.О. Коэффициентные обратные задачи механики.
—
М.: ФИЗМАТЛИТ, 2019. — 272 с. — ISBN 978-5 -9221-1826-2 .
В монографии рассмотрены различные подходы к исследованию обратных
коэффициентных задач, в которых по некоторой дополнительной информации
о решении (смещения, температура, резонансные частоты) определяются ко-
эффициенты дифференциальных операторов, характеристики внутренних де-
фектов (полостей, включений, трещин). Излагаются постановки задач , основы
общих подходов в теории обратных и некорректных задач, особенности реа-
лизации при решении конкретных задачтеории упругости, вязкоупругости,
электроупругости, термоупругости, диагностики предварительного состояния
для стержней, пластин, цилиндров, слоистых структур. Представлены способы
исследования конечномерных обратных задач, схемы построения операторных
уравнений с компактными операторами в итерационных процессах по опреде-
лению функций, приведены результаты вычислительных экспериментов.
Книга адресована научным и инженерно-техническим работникам, студен-
там старших курсов и аспирантам, специализирующимся в области механики,
математического моделирования, прикладной математики, численных методов,
экспериментальной механики.
ISBN 978-5-9221-1826-2
c ФИЗМАТЛИТ, 2019
c А. О. Ватульян, 2019
2/27

ОГЛАВЛЕНИЕ
Предисловие . ...............................................................................
6
Глава 1. Математические модели. Корректные и некорректные
задачи ..................................................................................
7
1.1 . Математические модели в технике и естествознании и их некото-
рые особеннос ти . .................................................................
7
1.2 . Некоторые общие аспекты теории идентификации. Прямая и обрат-
ная задачи . ......................................................................... 11
1.3 . Структурная и параметрическая идентификация. Коэффициентные
обратные задачи . ................................................................. 14
1.4 . Корректные и некорректные задачи. Корректность по Адамару.
Корректность по А. Н . Тихонову (условная корректность) и -кор-
ректность. . ......................................................................... 19
1.4 .1. Корректность по Адамару . ............................................. 19
1.4 .2. Корректность по А. Н. Тихонову (условная корректность)
и -корректность . ......................................................... 27
1.5 . Основные причины и характеристики некорректности . ............... 29
1.6 . Способы преодоления некорректности. Регуляризация . ............... 31
1.6 .1. Метод квазирешений . ................................................... 33
1.6 .2. Метод регуляризации А. Н. Тихонова . ............................. 34
1.6 .3. Метод регуляризации на компактных множествах . ........... 36
1.6 .4. Метод итерационной регуляризации . ............................... 37
1.6 .5. Метод усеченных сингулярных разложений . ..................... 39
1.6 .6. Проекционный метод . ................................................... 41
1.7. Регуляризованные методы вычисления значений неограниченных
операторов. Численное дифференцирование . ............................. 43
1.8 . Построение обратных к вполне непрерывным операторам на приме-
ре уравнения Фредгольма 1-го рода . ....................................... 48
Список литературы к гл. 1 .
.
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
52
Глава 2. Конечномерные ОЗ. Определение постоянных парамет-
ров в краевых задачах (коэффициентов дифференциальных
операторов, параметров дефектов, граничных условий)............ 54
Введение к гл. 2
.
.
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
54
2.1 . Метод Прони . ..................................................................... 57
2.2 . Метод квазилинеаризации . ..................................................... 62
2.3 . Методы решения конечномерных обратных задач на основе гене ти-
ческих алгоритмов . ............................................................... 67
2.4 . Об определении параметров упругих потенциалов . ..................... 73
2.5 . Идентификация полимерных материалов на основе дифференциаль-
ной формы определяющих соотношений . ................................... 80
3/27

4
Оглавление
2.6 . Определение коэффициента температуропроводности . ................. 85
2.7. Конечномерные ОЗ для стержней. Идентификация полости в упру-
гом с тержне при анализе поперечных колебаний . ....................... 89
2.8 . Конечномерные ОЗ для стержней. Определение локализованной
зоны деструкции в упругой балке . ........................................... 97
2.9 . Конечномерные ОЗ для стержней. Идентификация тонкого надреза
при изгибных колебаниях балки . ............................................ . 106
2.10. Конечномерные ОЗ для стержней. Определение параметров дефекта
в балке для модели Ти мошенко . ............................................ . 115
2.11 . Определение параметров упругого закрепления неоднородной балки 121
2.12. Оценка деформативности неоднородной пластины в случае упру-
гого опирания . .................................................................... . 127
2.13. Об определении остаточного упруго-пластического состояния трубы 134
Список литературы к гл. 2 .
.
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
.
.
138
Глава 3. Общие принципы исследования коэффициентных ОЗ
с переменн ыми характеристи ками . Решение ли нейных КОЗ ... . 142
3.1 . Коэффициентные обратные задачи для линейных операторов. Обоб-
щенное соотношение взаимности. Типы коэффициентных обратных
задач, их особенности, первая и вторая постановки . .................. . 142
3.2 . С лабая и вариационная постановки ОЗ . .................................. . 149
3.2 .1 . Слабая постановка ОЗ . ................................................ . 149
3.2 .2. Вариационная постановка ОЗ . ...................................... . 153
3.3 . Решение задач в первой постановке. Коэффициентные ОЗ при изу-
чении продольных и поперечных колебаний упругого стержня (КОЗ
для дифференциальных операторов второго и четвертого порядка) 155
3.3 .1. Задача для уравнения 2-го порядка . .............................. . 156
3.3 .2. Задача для уравнения 4-го порядка . .............................. . 162
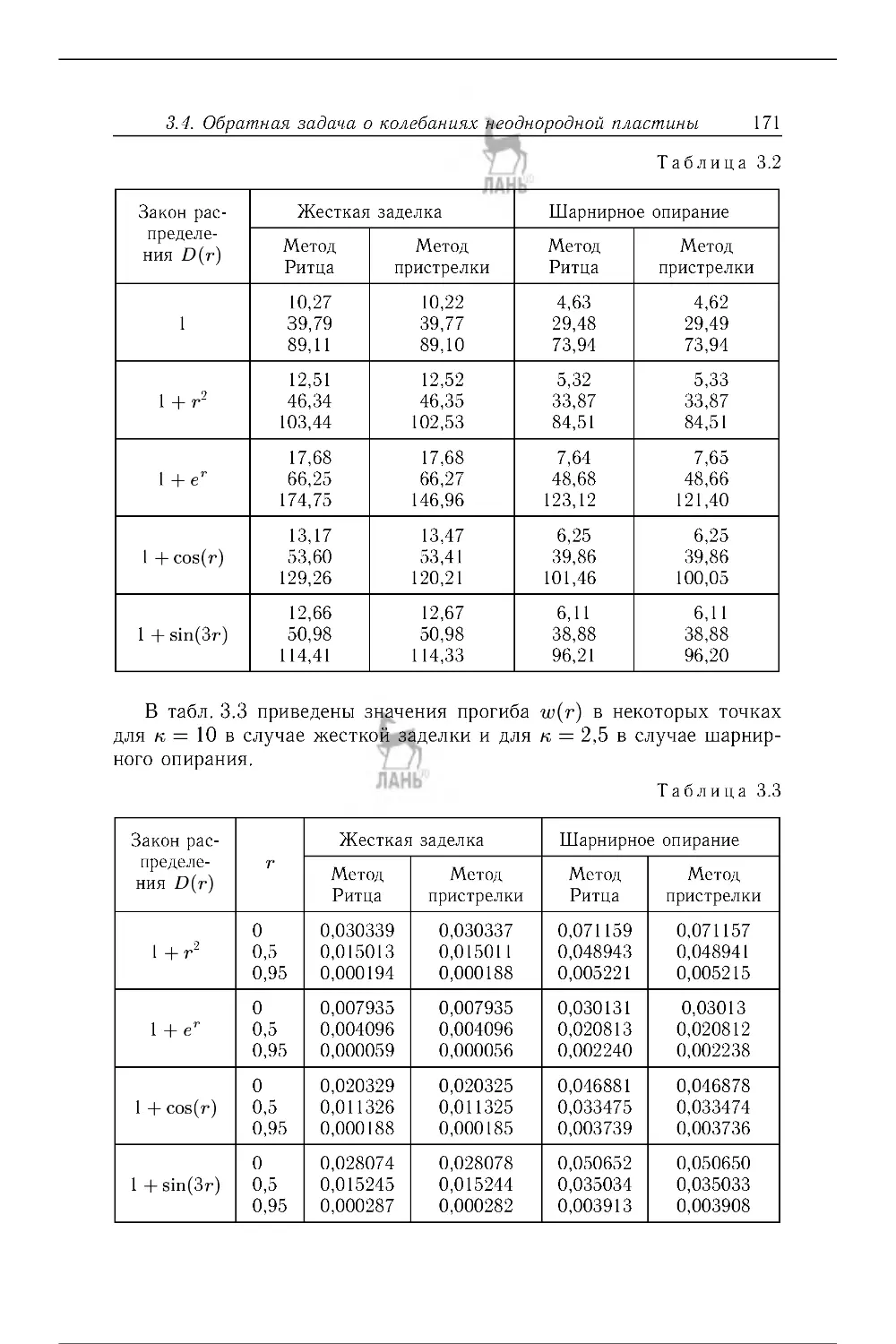
3.4 . Обратная задача о колебаниях неоднородной пластины . ............ . 168
3.4 .1 . Прямая задача . .......................................................... . 168
3.4.2. ОЗ для упругой пластины переменной жесткости . ............ . 172
3.4.3. Результаты вычислительных экспериментов . .................... . 173
3.5 . Коэффициентная ОЗ для уравнения в частных производных в пер-
вой постановке . .................................................................. . 176
3.5 .1 . Прямая задача . .......................................................... . 176
3.5 .2. Обратная задача . ........................................................ . 177
3.5.3. Реконструкция модуля сдвига на основе анализа крутильных
колебаний стержня . .................................................... . 178
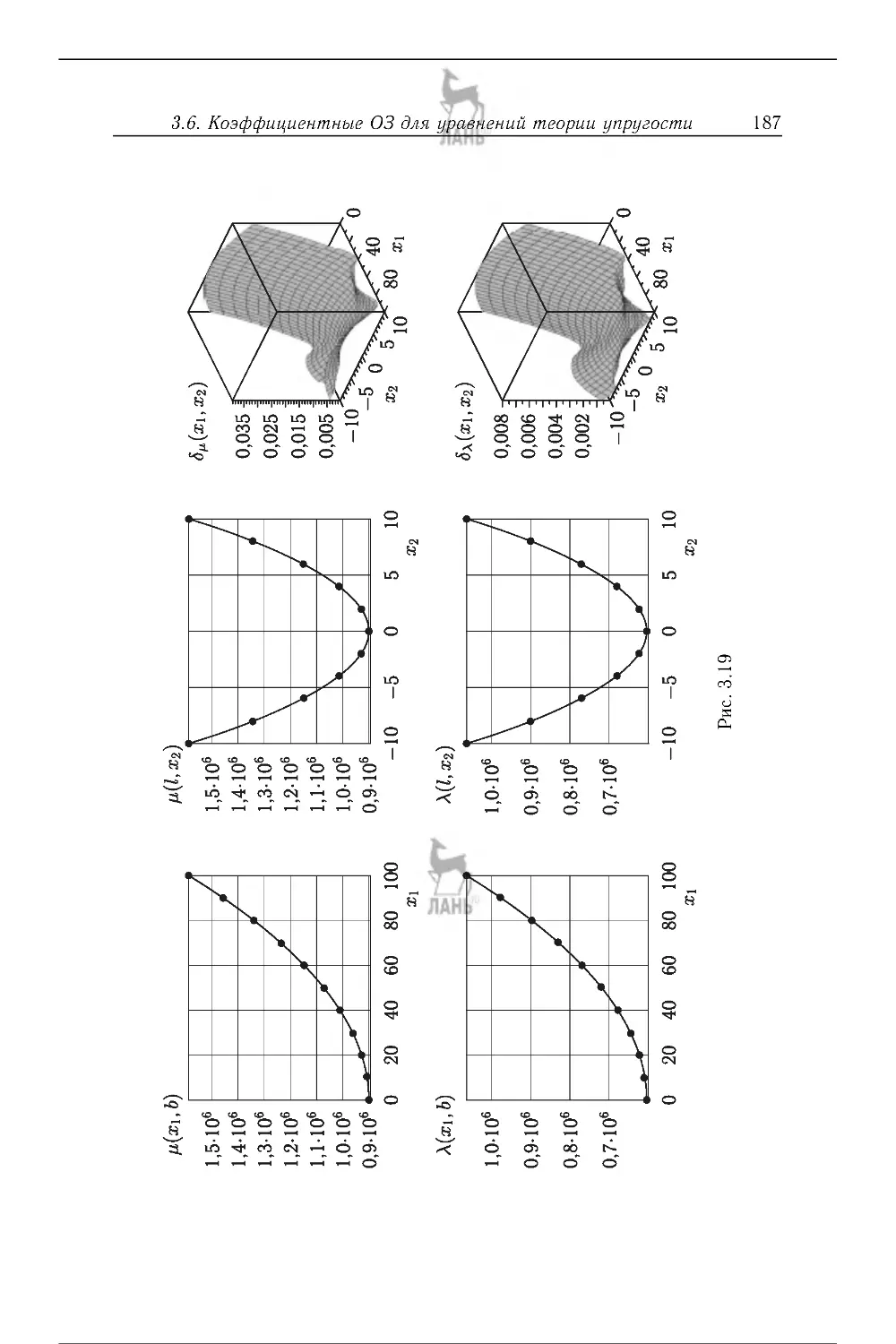
3.6 . Коэффициентные ОЗ для уравнений теории упругости (плоский
случай в первой постановке) . ................................................ . 179
Список литературы к гл. 3 .
.
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
.
.
189
Глава 4. Коэффициентные обратные задачи во второй постановке 192
4.1 . Обратные задачи при исследовании продольных и изгибных коле-
баний неоднородного упругого стержня . .................................. . 192
4.1.1. Исследование обратных задач при продольных колебаниях
стержня . .................................................................. . 193
4.1.2. Исследование обратных задач при изгибных колебаниях
стержня . .................................................................. . 197
4/27

Оглавление
5
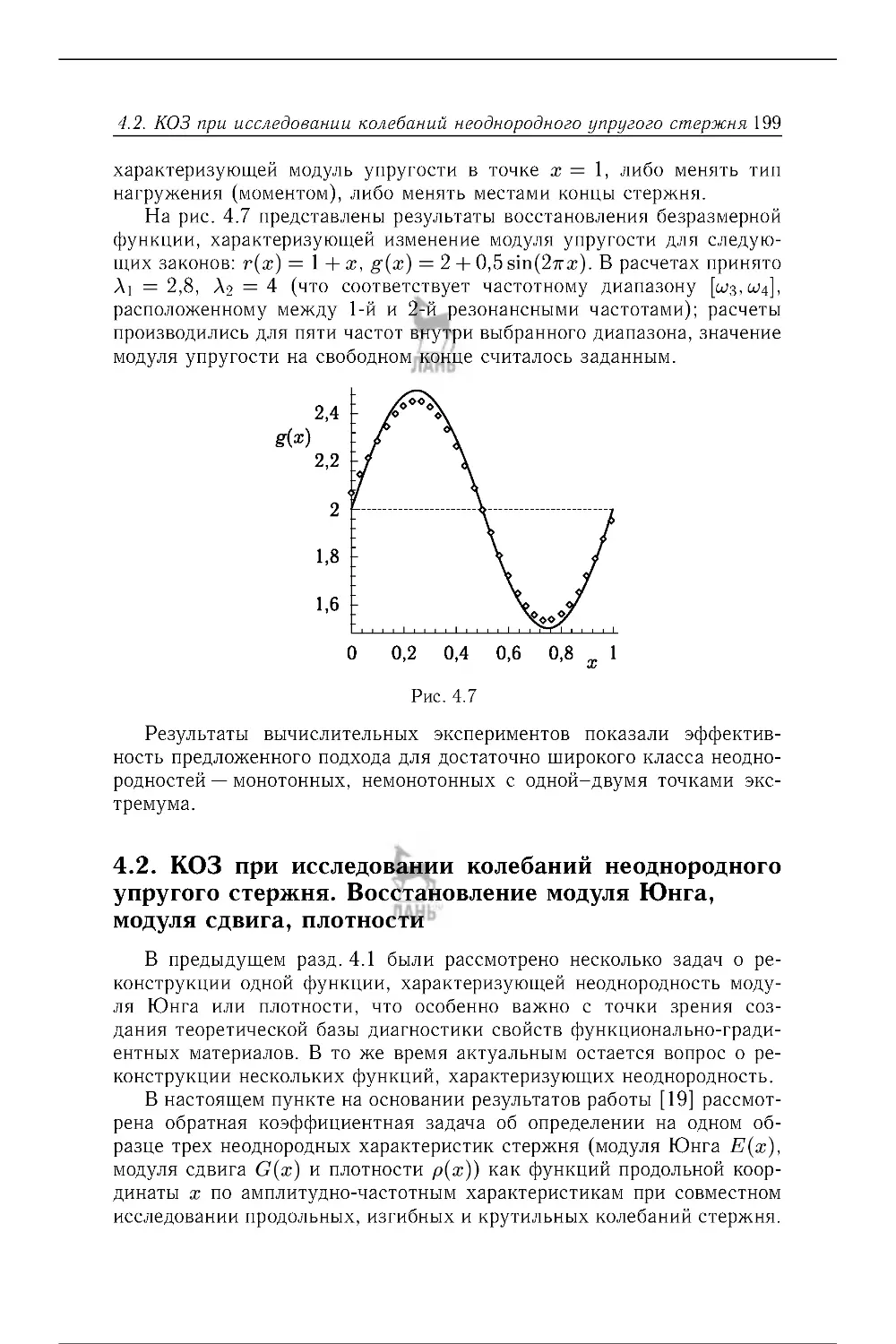
4.2 . КОЗ при исследовании колебаний неоднородного упругого стержня.
Восстановление модуля Юнга, модуля сдвига, плотности . .......... . 199
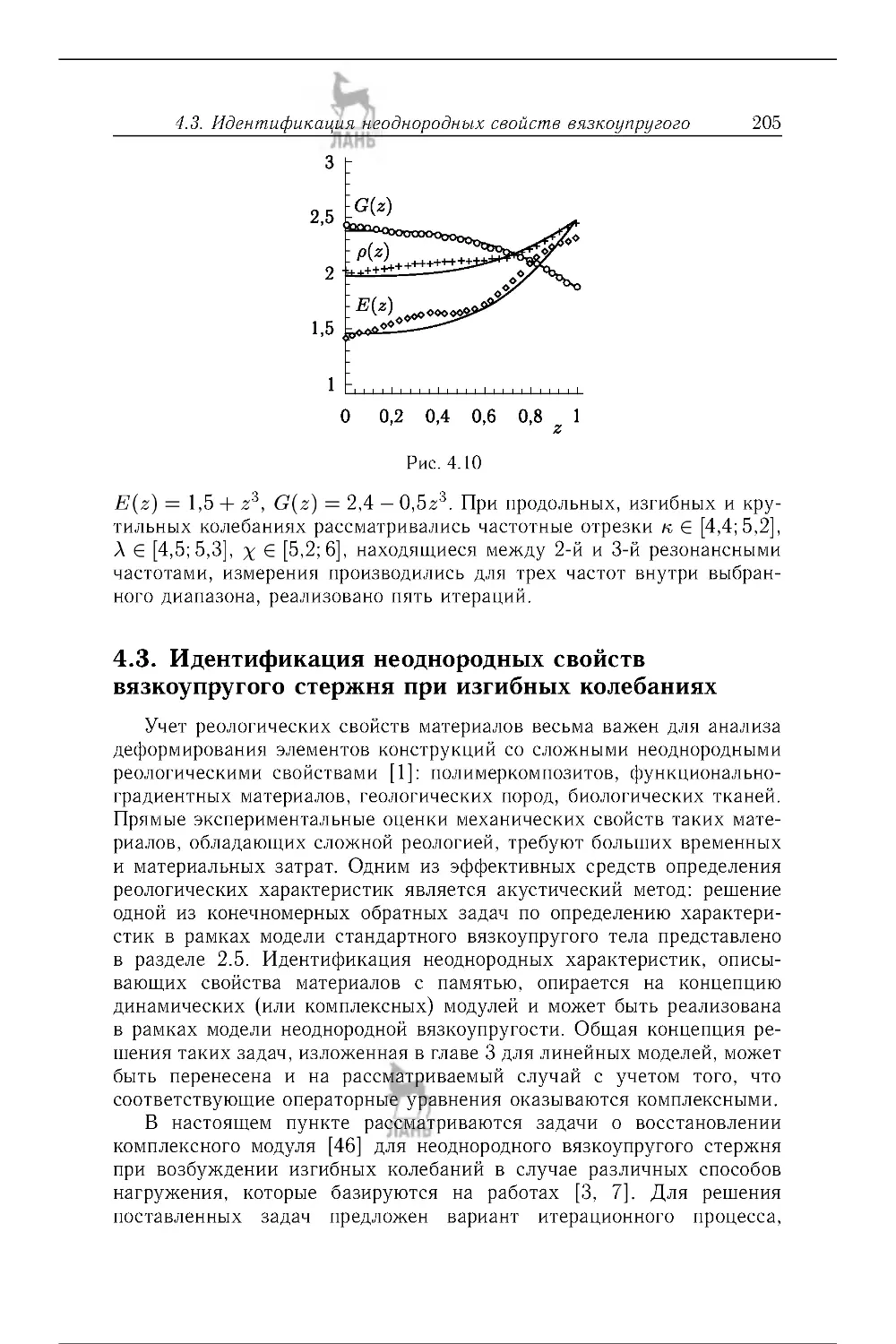
4.3 . Идентификация неоднородных свойств вязкоупругого стержня при
изгибных колебаниях . .......................................................... . 205
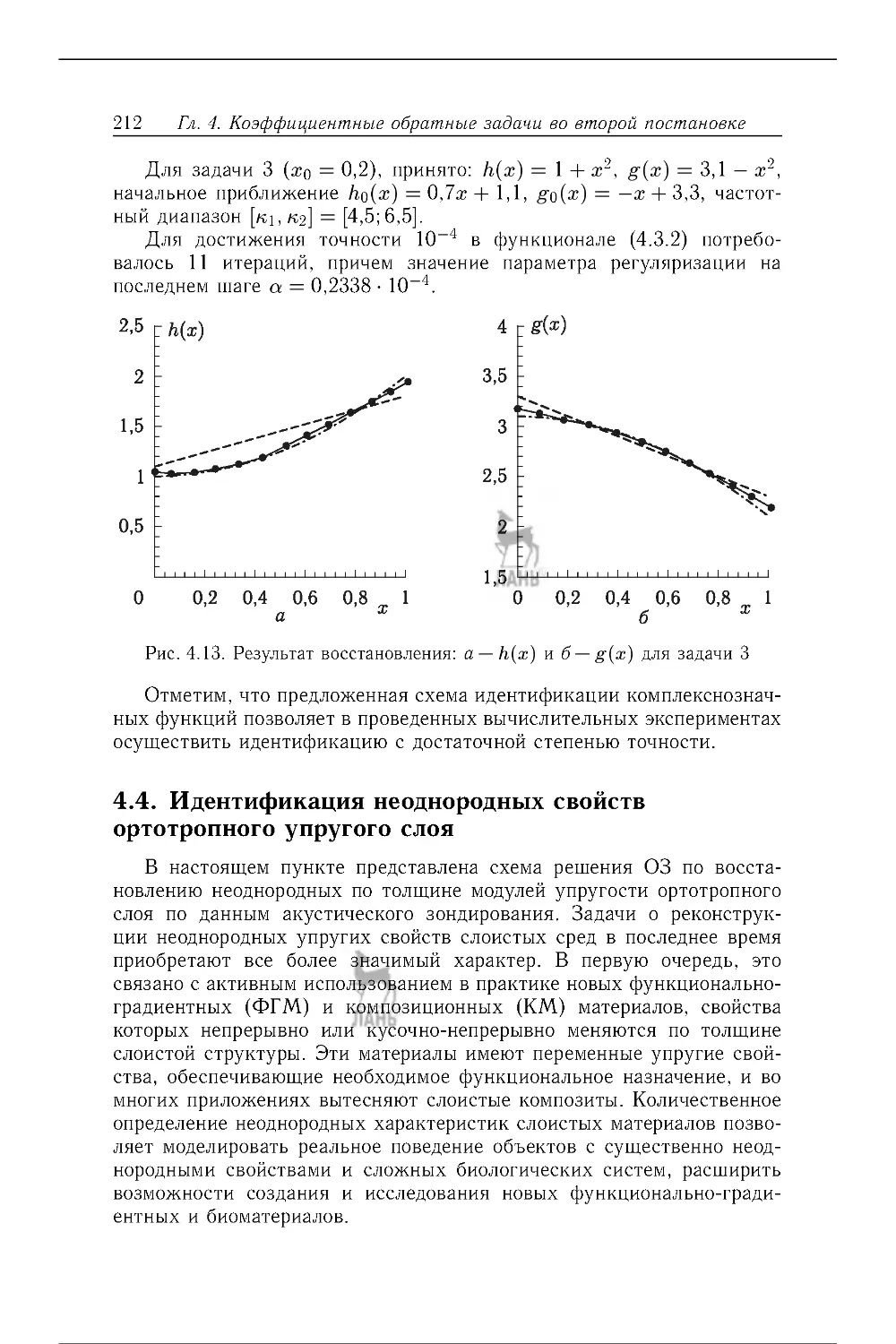
4.4 . Идентификация неоднородных свойств ортотропного упругого слоя 212
4.5 . Обратные задачи термоупругости. Задачи для термоупругого
стержня . ............................................................................ . 221
4.6 . Об идентификации неоднородного предварительного напряженного
состояния в термоупругих телах . ............................................ . 229
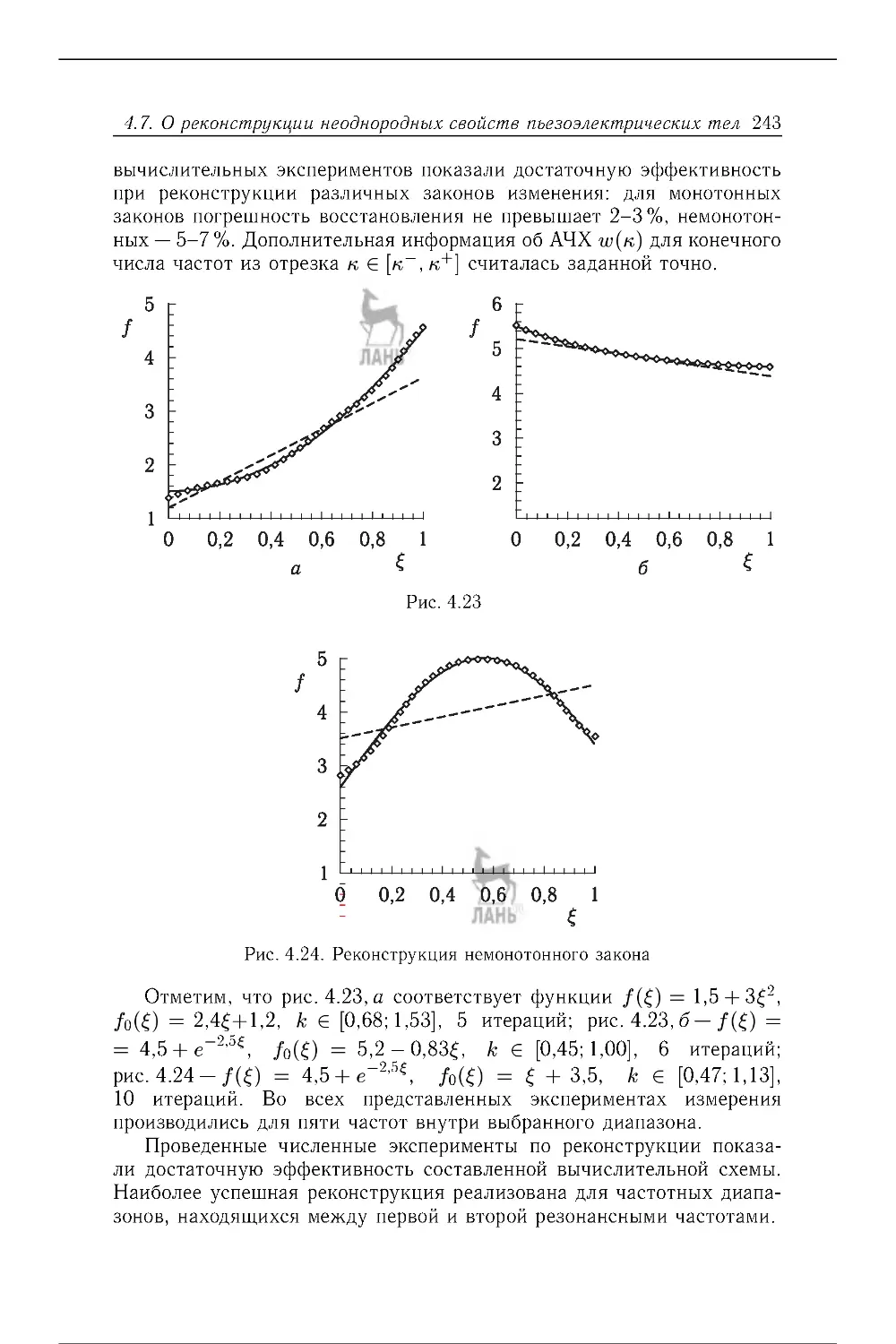
4.7. О реконструкции неоднородных свойств пьезоэлектрических тел . . 237
4.7.1 . Слабая постановка задач о колебаниях неоднородных элек-
троупругих тел . .......................................................... . 238
4.7.2 . Постановка и решение прямой задачи для стержня . .......... . 239
4.7.3. Обратная задача для стержня . ...................................... . 241
4.7.4 . Численные результаты . ................................................ . 242
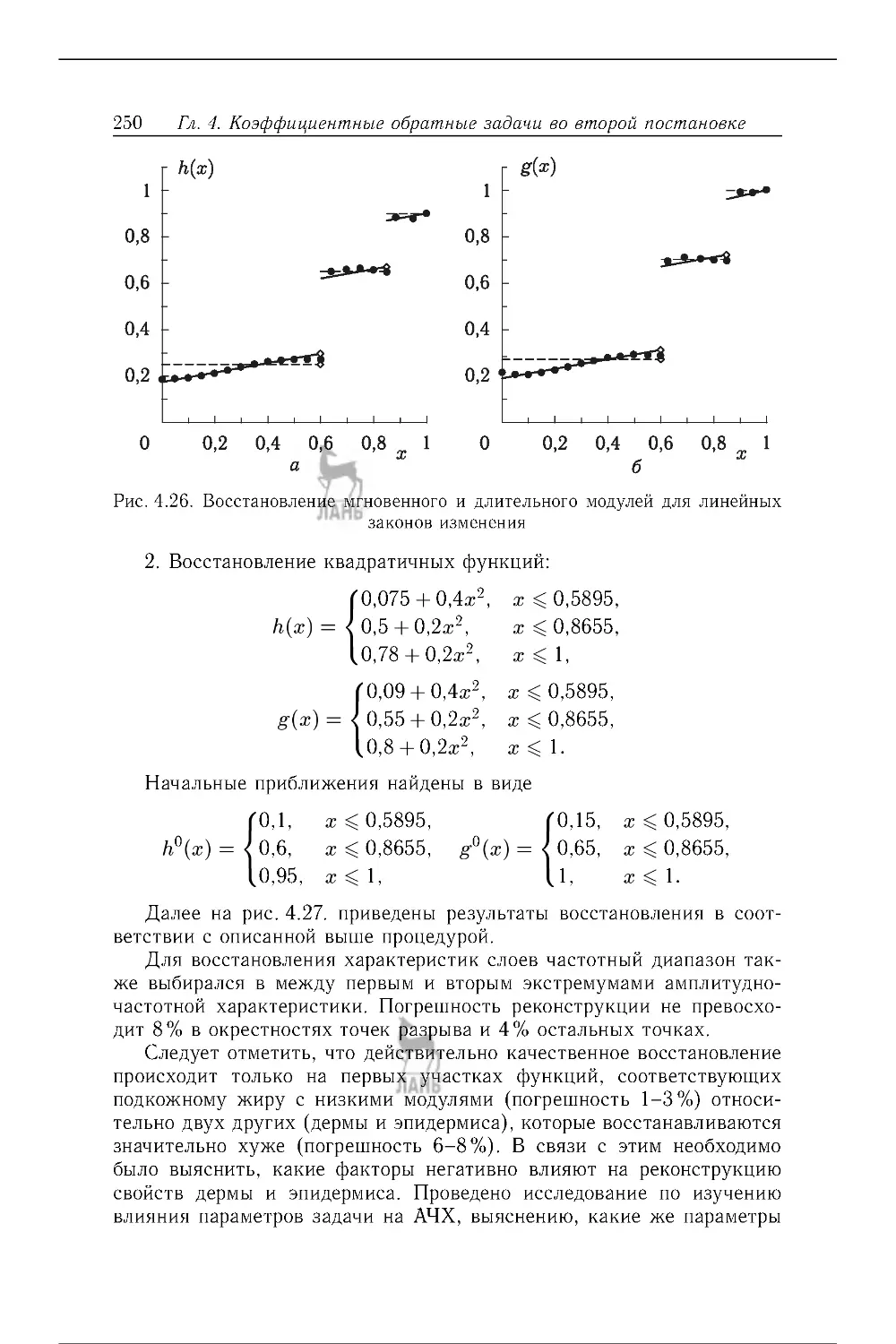
4.8 . Об определении свойств многослойных биологических тканей . .... . 244
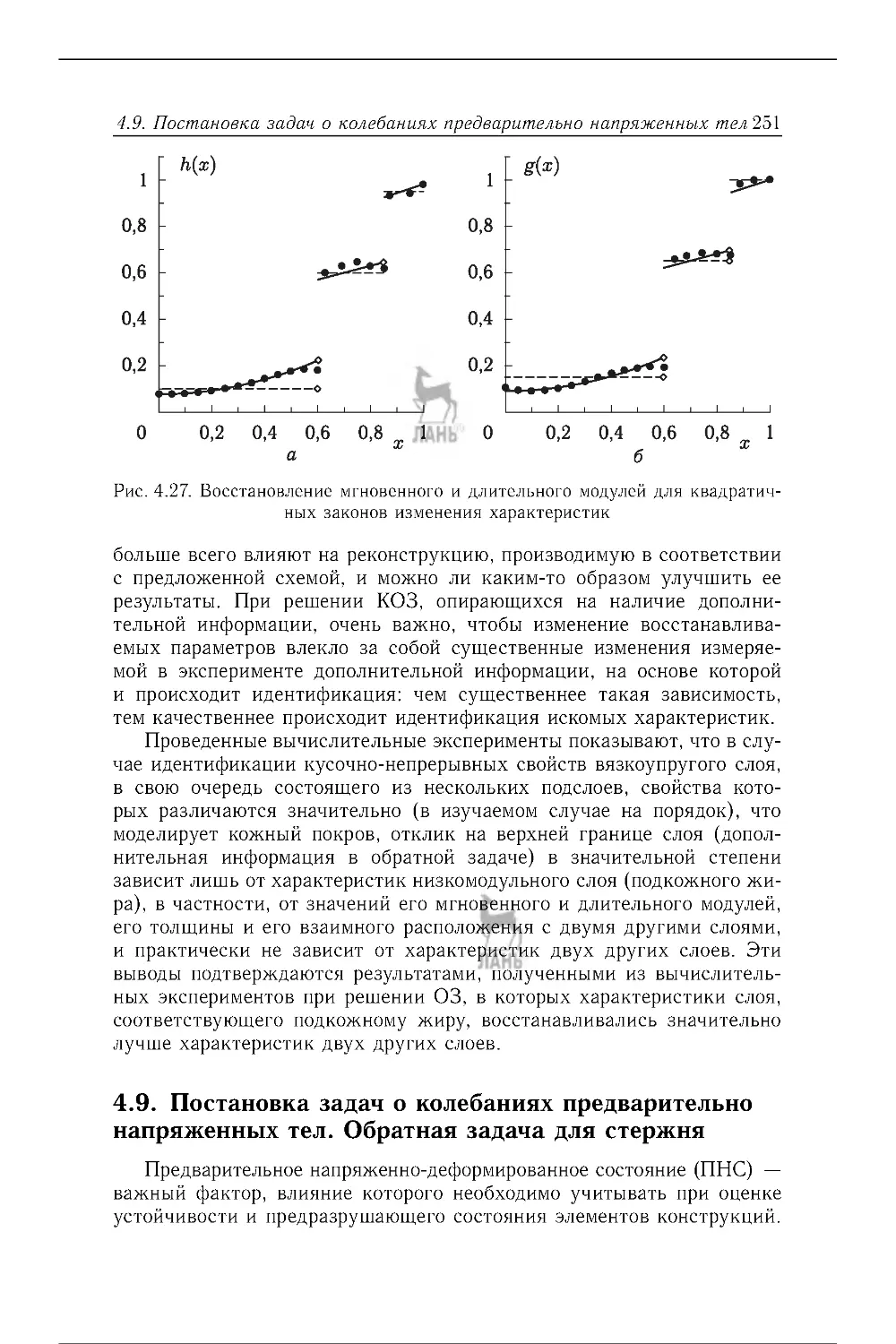
4.9. Постановка задач о колебаниях предварительно напряженных тел.
Обратная задача для с тержня . .............................................. . 251
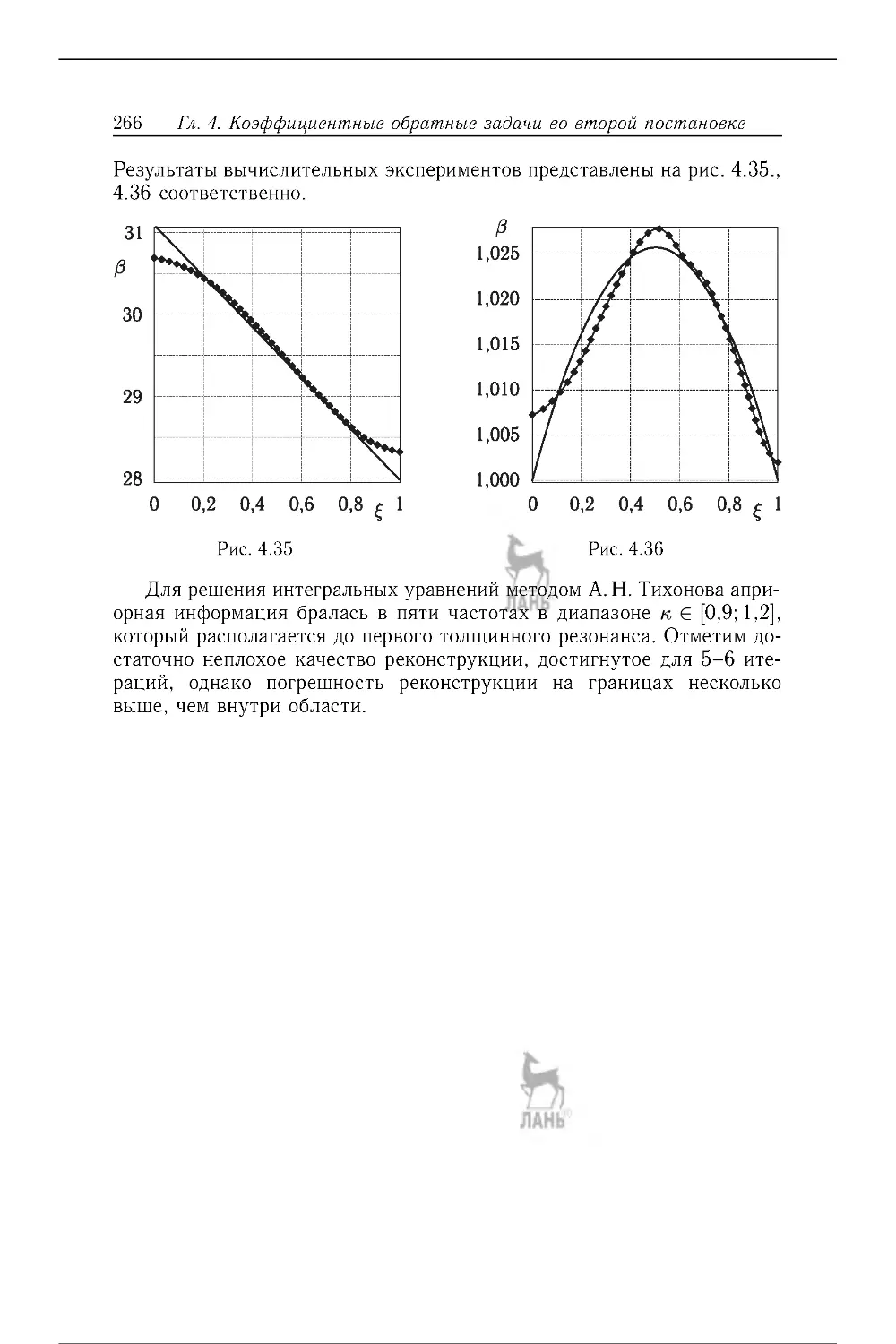
4.10. Об определении предварительного напряженного состояния в трубе 257
4.11 . О КОЗ пороупругости . .......................................................... . 260
4.11.1 . Общая постановка задачи для модели пороупругой среды
260
4.11 .2 . Обобщенное соотношение взаимности . .......................... . 261
4.11.3 . Задача о колебаниях неоднородного пороупругого слоя . .. . 262
4.11.4 . Идентификация свойств неоднородного пороупругого слоя 264
Список литературы к гл. 4 .
.
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
.
.
267
5/27

Предисловие
Коэффициентные обратные задачи — один из важнейших и самых
трудных классов обратных задач, имеющий многочисленные приложе-
ния в различных областях знания.
Обратные задачи стали предметом систематических исследований
относительно недавно. Первые теоретические работы в этом направ-
лении появились в начале ХХ века, были связаны с проблемами гео-
физики и астрономии; эти работы породили новые направления в ма-
тематике. Более интенсивное развитие в этой области, посвященное
различным математическим аспектам, в первую очередь преодолению
некорректности, исследованию устойчивости и единственности реше-
ний обратных задач, началось в 70–80-е годы прошлого века.
К настоящему времени имеется достаточно большое количество
публикаций и монографий, посвященных различным аспектам обрат-
ных и некорректных задач в разных областях знания.
Настоящая монография посвящена различным аспектам решения
обратных задач по определению конечного числа параметров, а также
определению одной или нескольких функций, характеризующих пере-
менные физические свойства (модули упругости, плотность, коэффици-
енты теплопроводности и связанности физических полей). Обсуждены
особенности подходов к решению и формированию итерационных схем
типа Ньютона при решении конкретных обратных задач теории упру-
гости, вязкоупругости, электроупругости, термоупругости и пороупру-
гости. Представлены результаты вычислительных экспериментов для
различных объектов (стержни, балки, цилиндры, слоистые структуры),
обсуждены вопросы задания входной информации и постановки экспе-
римента.
Основой монографии являются работы, опубликованные автором
и его учениками в ряде отечественных и зарубежных журналов. Она со-
здана благодаря многолетней поддержке РФФИ в рамках научных про-
ектов 02-01-01124, 05-01-00734, 10-01-00194,13-01-00196, 16-01-00354.
Автор выражает искреннюю благодарность и признательность сво-
им учителям, академикам РАН Владимиру Андреевичу Бабешко
и Иосифу Израилевичу Воровичу, указавшим путь к новому классу
задач механики.
Автор благодарит своих коллег по научным исследованиям и уче-
ников — И . В. Богачева, О. В . Бочарову, В. В . Дударева, Р. Д . Недина,
С.А. Нестерова, А.В. Осипова, В.О. Юрова и О.В. Явруян за сотруд-
ничество и помощь.
6/27

Глава 1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ.
КОРРЕКТНЫЕ И НЕКОРРЕКТНЫЕ ЗАДАЧИ
1.1 . Математические модели в технике
и естествознании и их некоторые особенности
С давних лет человек пытался проникнуть в суть природных явле-
ний, например: понять причины смены времен года, законы образова-
ния приливных волн; выяснить, почему одни конструкции разрушаются
при небольших нагрузках, а другие служат достаточно долго. Вопросы
прочности при проектировании зданий и сооружений, авиационных
и корабельных конструкций, при конструировании новых приборов
особенно актуальны и на сегодняшний день. В последние годы на
первый план наряду с вопросами прочности стали выходить проблемы
оптимизации конструкций за счет использования не только совер-
шенствования формы, но и за счет использования новых материалов:
композиционных, функционально-градиентных, керамических и т. д .
Попытаемся понять, каким же образом принимаются решения.
Далее любое природное явление или рукотворную конструкцию будем
именовать объектом исследования (далее сокращенно — ОИ). Для того
чтобы понять основные закономерности поведения ОИ, у исследователя
есть два способа получения информации о нем — наблюдение и экс-
перимент. В первом случае наблюдатель лишь фиксирует особенности
изменений (такова, например, Солнечная система), не имея возможно-
сти влиять на них. В случае эксперимента существуют как различные
способы воздействия на ОИ, так и разнообразные способы снятия
информации об изменении в ОИ или отклике. Таким образом, условно
любой ОИ можно представить себе как некоторый черный ящик, у ко-
торого можно установить связь между входом (воздействие) и выходом
(измеряемая информация о компонентах физических полей: смещения,
температура и т. д .) .
Отметим также, что некоторые эксперименты исследователю прак-
тически ничего не стоят, однако есть и такие, которые требуют огром-
ных финансовых затрат (таковы, например, эксперименты в современ-
ной физике элементарных частиц).
Было бы разумно попытаться заменить реальный эксперимент неко-
торым модельным (иногда так и происходит, особенно для уменьшен-
ных моделей кораблей и самолетов). Однако гораздо более дешевым
является способ связать вход и выход ОИ и проанализировать влияние
различных факторов при помощи математического моделирования.
7/27

8 Гл. 1. Математические модели. Корректные и некорректные задачи
Что же такое математическое моделирование? Это замена реально-
го ОИ абстрактным математическим объектом при сохранении основ-
ных черт его поведения. Каждому ОИ можно сопоставить некоторое
множество математических моделей, отличающихся числом учета раз-
личных факторов. Работа не с самим ОИ, а с его моделью дает возмож-
ность относительно быстро и без больших затрат исследовать его свой-
ства и прогнозировать поведение в любых ситуациях и для широкого
спектра воздействий различной природы. Благодаря математической
модели и стремительному развитию современных вычислительных тех-
нологий можно натуральный эксперимент заменить вычислительным,
проводить вычислительные эксперименты, изучать модель, адекватную
ОИ в некотором смысле, подробно и глубоко. Исследователь — созда-
тель модели — всегда стоит перед дилеммой: использовать простейшую
модель описания ОИ или более сложную по числу учитываемых фак-
торов. Достоинство использования простейших моделей (учитывающих
один или небольшое количество факторов) состоит в том, что часто
можно получить аналитическое решение задачи в виде формулы, инте-
грала или ряда, изучить влияние одного или нескольких характерных
параметров ОИ, выявить некоторые качественные свойства и опреде-
лить количественные характеристики его изменения, а на основе явных
решений задачи произвести и оптимизацию. По этому пути развива-
лась наука и техника XIX и XX веков. Ярким примером такой мо-
дели явилось уравнение теплопроводности — дифференциальное урав-
нение в частных производных второго порядка, позволяющее опреде-
лять изменение температуры при различных видах воздействия на ОИ
(моделируемых граничными источниками температур или внутренними
источниками тепла). Для более сложной модели (многофакторной,
например модели термоупругости, термовязкоупругости или термопла-
стичности) часто аналитическое исследование краевой задачи невоз-
можно, ее необходимо анализировать численно; кроме того, в описание
более сложной модели входит достаточно большое количество парамет-
ров или функций, требующих определения. При выборе числа факторов
и размерности модели во внимание принимаются различные соображе-
ния; главное же правило при создании математической модели — адек-
ватность модели изучаемому процессу.
Итак, понятно, что, заменив реальный объект на некоторый матема-
тический, можно работать с ним — проводить вычислительные экспе-
рименты по прогнозированию влияния различных типов воздействия,
например: выяснить для стержневой конструкции, какие наибольшие
нагрузки она может выдержать, не разрушаясь, определить критиче-
ские нагрузки, при которых существуют иные формы равновесия. При
этом главный вопрос — каким образом уточнять модель или строить но-
вую с учетом предшествующего опыта исследования простых моделей.
Таким образом, математическое моделирование — это один из са-
мых простых и дешевых способов дать обоснованные рекомендации
по исследованию какого-либо эффекта, оптимальному конструирова-
8/27

1.1. Математические модели в технике и естествознании
9
нию ОИ или прогнозированию его поведения в будущем при некоторых
типах воздействий.
Отметим, что в настоящее время области математического модели-
рования значительно расширились. Если первые модели касались про-
блем механики, физики, техники, то сейчас с большим успехом мате-
матические модели используются в экономике, экологии, метеорологии
и климатологии, социологии, биологии, горной механике, биомехани-
ке, медицине. Соответственно создаются новые модели, формируются
новые параметры, характеризующие ОИ, совершенствуются старые,
разрабатывается математический аппарат, необходимый для решения
возникающих задач. При этом отметим, что любая модель содержит
некоторые характеристики модели, которые необходимы для расчетов
и прогнозирования. Эта сторона математического моделирования новых
объектов может развиваться на основе наблюдений или экспериментов.
При этом оценка параметров модели основана или на детерминирован-
ном, или статистическом подходе. При первом подходе — детермини-
рованном — определение параметров или функций тесно связано с об-
ращением причинно-следственных связей и приводит к исследованию
задач, именуемых обратными. При решении таких задач необходимо
определить параметры модели, используя дополнительную информа-
цию о решении. Опыт изучения таких задач показал, что они обладают
целым рядом неприятных с математической точки зрения свойств,
среди которых неединственность, отсутствие непрерывной зависимости
от входных данных. Заметим, что задачи такого типа систематически
начали исследоваться совсем недавно, что потребовало изучить осо-
бенности и создать математический аппарат для исследования, а также
специальные вычислительные схемы для их решения.
Отметим, что наиболее часто модели естествознания описывают-
ся при помощи функциональных или дифференциальных уравнений
(часто дифференциальных уравнений в частных производных или ин-
тегро-дифференциальных).
Постановка вопроса о математическом моделировании порождает
следующую последовательность действий, условно состоящую из трех
этапов: модель–алгоритм–программа.
Пусть
—
математическая модель ОИ, где

неко-
торый оператор, ,

—
функциональные пространства.
Для построения математической модели ОИ на основании установ-
ления связи между входом и выходом ОИ необходимо выбрать вид этой
связи или определить структуру оператора , осуществляющего отоб-
ражение входа на выход . Фактически исследователь всегда при со-
ставлении модели решает проблему «черного ящика», на который мож-
но действовать и регистрировать отклик на это воздействие. Например,
если упругий цилиндр растянуть силой и измерить его удлинение
и изменение диаметра, то можно поставить задачу об определении
упругих макрохарактеристик материала: модуля Юнга и коэффициента
Пуассона [20].
9/27

10 Гл. 1 . Математические модели. Корректные и некорректные задачи
Для построенной модели можно решать две задачи.
1. Прямая задача. При заданном операторе ивоздействии(задан-
ном необходимо определить .
2. Обратная задача. В рамках выбранной модели, при заданном
воздействии и решении определить некоторые характеристики опера-
тора .
Отметим, что в реальном моделировании процесс создания модели
как раз начинается с этапа решения обратной задачи. Так, напри-
мер, сформировались знакомые нам физические параметры, такие как
плотность, коэффициент теплопроводности, модуль упругости, а также
были разработаны простые способы их определения.
Прежде чем обсуждать различные аспекты исследования таких
задач, вспомним некоторые математические факты, относящиеся к во-
просам существования и единственности ряда проблем в различных
разделах математики.
Обычно одно из условий в формулировках известных теорем ана-
лиза и алгебры, позволяющих судить о существовании и единствен-
ности решения в некоторой задаче, состоит в проверке выполнения
некоторого равенства 0 . При этом одно из условий существования
и единственности часто формулируется в виде неравенства

0.
Вслучае,когдарешаетсязадачаподобногосортаионаформально
удовлетворяет условиям теоремы (

0), а решение единственно, то
оно весьма сильно зависит от того, насколько близко к нулю.
Рассмотрим несколько простых иллюстративных примеров.
Квадратное уравнение 2

имеет единственное решение при

0. Если возмутить входную информацию при этом значении ,
считая, что 2
Æ ,топриÆ 0 это уравнение не имеет решений,
априÆ 0 имеет два решения, причем, например, при Æ
0,0001
получим 1 ,2
0,01, что на два порядка превышает погрешность
задания Æ .
При этом не только теряется единственность, но и по-
грешность полученных решений значительно превосходит погрешность
входной информации.
При решении линейной алгебраической системы с квадратной мат-
рицей
под понимается определитель системы
.Тогдапри

0 в соответствии с теорией линейных алгебраических систем ли-
бо решение не существует, либо оно неединственно. Разграничение
этих случаев обычно осуществляется в терминах некоторой числовой
характеристики — ранга матрицы в соответствии с теоремой Кроне-
кера–Капелли [13]. Заметим, что нахождение ранга матрицы требует
вычисления нескольких определителей; эта числовая характеристика
матрицы весьма чувствительна к точности входной информации и точ-
ности вычислений и не является непрерывной функцией элементов
матрицы. Таким образом, эта важнейшая числовая функция матрицы
в теории матриц и линейных систем перестает играть свою роль клас-
сического инструмента, в терминах которого формулируются условия
существования и единственности.
10/27

1.2 . Некоторые общие аспекты теории идентификации
11
При формулировке теоремы о неявной функции [28] о нахождении
функции
, удовлетворяющей уравнению ,

0ипроходящей
через точку (0 ,
0
, эту роль играет величина

0,
0
. Если

0, то возможно как несуществование такой функции, так и неедин-
ственность ее определения.
При формулировке условий существования решении задачи Коши
для обыкновенного дифференциального уравнения первого порядка
вида

0,
0

0 вточке1

0,вкачестве
такового параметра можно принять 1
.
Исходя из этих простых примеров можно сформулировать следую-
щий вопрос. При исследовании модельных примеров для малоразмер-
ных ОИ проверить истинность неравенства

0непредставляет
сложности. Однако, если при проверке этого условия используются ли-
бо данные эксперимента, либо результаты приближенных вычислений
и при нахождении получено, например, что 1,2 105
,товоз-
никают трудности с интерпретацией этого условия. Оказывается, что
фактически условия существования и несуществования неразличимы
в рамках некоторой точности. Так, например, если вычисления произ-
водятся с конечной точностью, то часто отличить вырожденные линей-
ные алгебраические системы от плохообусловленных невозможно.
В таких задачах важнейшей априорной информацией является уро-
вень погрешности входных данных — начальных условий, коэффициен-
тов матриц и дифференциальных операторов и т. д . Такие задачи нуж-
даются в более детальном исследовании, которое можно осуществить
исходя из общих методов изучения таких задач, которые именуются
некорректными,икоторыесталиисследоватьсяотносительнонедавно.
Характерным свойством таких задач является утрата непрерывно-
сти поведения их решений при малых изменениях входной информа-
ции. В некотором смысле происходит качественное изменение решений:
образуются своеобразные бифуркации и катастрофический рост [24]
(переводя на язык функций — для таких отображений модуль непре-
рывности весьма высок) погрешности.
Различным аспектам исследования задач об определении парамет-
ров для различных моделей, используемых в механике, по некоторой
дополнительной информации и посвящена эта книга.
1.2 . Некоторые общие аспекты теории
идентификации. Прямая и обратная задачи
Как отмечалось выше, в современном моделировании явлений
и процессов по данным наблюдений есть два подхода, основанных
на детерминированных и стохастических моделях. При этом совокуп-
ность математических средств, применяемых для описания этих клас-
сов моделей, весьма различна. Если для детерминированных моделей
характерно описание динамики ОИ с помощью дифференциальных
11/27

12 Гл. 1 . Математические модели. Корректные и некорректные задачи
уравнений и анализа свойств их решений (аналитического, численного
или асимптотического), то для стохастических моделей чаще всего это
происходит на основе аппарата теории случайных процессов. При этом
различны по своему типу как параметры или функции, необходимые
для описания этих моделей, так и методы идентификации, т.е. средства
для их нахождения. В настоящей книге основное внимание уделено
детерминированным моделям, хотя некоторые подходы могут быть ис-
пользованы для идентификации и стохастических моделей.
Идейное начало идентификации систем (как предмета построения
математических моделей) связано с работами Гаусса и Лежандра, вы-
полненными ими в начале XIX века при исследовании траекторий дви-
жения планет Солнечной системы на основе данных астрономических
наблюдений.
Исследуя задачу об определении траекторий планет по данным
астрономических наблюдений в начале XIX века, Гаусс и Лежандр
почти одновременно пришли к проблеме решения переопределенных
систем линейных алгебраических уравнений

1... ,

,
(1.2 .1)

—
неизвестные коэффициенты разложений,
—известные величи-
ны, определяемые на основе результатов астрономических наблюдений.
Ясно, что такая система совместна крайне редко, особенно когда
результаты наблюдений, т. е . правые части и коэффициенты матрицы
системы, имеют некоторую погрешность. Поэтому ими была изменена
сама постановка задачи и рассматривалась задача о минимизации
функционала невязки

,
(1.2 .2)
что составило основную идею метода наименьших квадратов, который
и на сегодняшний день является одним из самых эффективных средств
обработки результатов эксперимента [1, 9]. Как известно, метод
наименьших квадратов приводит к решению линейной алгебраической
системы с квадратной симметричной положительно определенной мат-
рицей и нахождение решения в этой ситуации происходит достаточно
эффективно.
Таким образом, предложенный метод наименьших квадратов нашел
применение в дальнейшем при исследовании совершенно иных классов
задач (например, в задачах теории приближений и вычислительной
математике), в том числе и для построения математических моделей
управляемых объектов и синтеза законов управления, используемых
в технике (баллистике, автоматике, телемеханике и других областях).
Значительная часть ранних работ по идентификации динамиче-
ских систем была выполнена специалистами в области математической
12/27

1.2 . Некоторые общие аспекты теории идентификации
13
статистикиитеориислучайныхпроцессовидаланачалонаправлению,
именуемому сейчас как статистическое оценивание ОИ (А. Н . Кол-
могоров, Н. Винер). Заметим, что за последние 50–70 лет большая
часть процедур идентификации основывалась на наблюдении реакций
управляемых ОИ (одномерных или многомерных) под воздействием
управляющих воздействий (ступенчатых, импульсных, гармонических).
В этом направлении отметим работу Калмана [11], который заложил
фундамент в технику идентификации таких ОИ. Весьма популярны-
ми в последнее время для анализа стохастических моделей являются
методы SSA (Singular spectrum analysis), которые сочетают элемен-
ты классического анализа временных рядов, многомерной статистики,
теории динамических систем и обработки нестационарных сигналов.
Отметим, что диапазон областей знаний, где методы SSA могут быть
использованы, очень широк: климатология, экология, океанология, гео-
физика, техника, обработка изображений, медицина и др.
Отметим, что наиболее часто детерминированные модели естество-
знания описываются при помощи функциональных или дифференци-
альных уравнений (часто дифференциальных уравнений в частных
производных или интегро-дифференциальных).
При этом заметим, что одному ОИ может быть поставлено в со-
ответствие несколько математических моделей, отличающихся числом
и степенью учета различных факторов и порождающих некоторую
иерархию моделей. В качестве примера в механике приведем модели
изгиба балок: классическая модель Эйлера–Бернулли и более позд-
няя, уточняющая ее, модель Тимошенко. Отметим, что дальнейшее
развитие теории балок связано с развитием теории контактных задач
и с учетом сдвига и обжатия, моделями предварительных напряже-
ний [7]. Гораздо более разветвленной является иерархия в теории
пластин и оболочек, начиная от классической модели Кирхофа–Лява
и заканчивая современными нелинейными теориями типа Кармана.
Для выбранной модели, описывающей ОИ, как отмечено в 1.1,
можно решать две задачи.
1. Прямая задача состоит в том, чтобы при заданном операторе
и воздействии (заданном определить решение . Далеенаоснове
сформированной модели можно составлять алгоритм нахождения на
основе известных или новых вычислительных схем, а на третьем этапе
переходить к этапу программирования и вычислительного эксперимен-
та. Суть такого эксперимента состоит не только в нахождении искомых
функций, но и в оценке влияния различных параметров модели на
решение.
2. Обратная задача состоит в определении структуры и числен-
ных значений параметров модели на основе некоторой дополнительной
информации о решении. Эта информация может позволить определить
параметры модели единственным образом, может оказаться недоста-
точной для единственного определения параметров модели, может при
возмущении входной информации давать довольно сильный разброс
13/27

14 Гл. 1 . Математические модели. Корректные и некорректные задачи
при определении параметров. При этом возможно, что информации
недостаточно в количественном отношении; возможно, недостаточно
точности измерений; возможно, данные экспериментов дублируют друг
друга, что ставит новые задачи перед экспериментаторами как в плане
повышения точности, так и в стратегии измерений.
Отметим, что в реальном моделировании ОИ процесс создания
модели как раз начинается с этапа решения обратной задачи — выдви-
жения гипотез, связывающих вход и выход ОИ, оценок параметров,
соответствия эксперименту. Иногда создание модели связано с опре-
делением некоторых характерных и понятных параметров, таких как
плотность, коэффициент теплопроводности, модуль упругости, а ино-
гда требует решения некоторой математической задачи в рамках уже
выбранной модели, размышлений и требований к эксперименту, его
постановке и точности.
В настоящее время обратные задачи математической физики порож-
дают весьма обширный класс исследований для различный моделей,
включают в себя значительное число математических и вычислитель-
ных проблем, таких как: идентификация систем с шумами, построение
операторных уравнений, связывающих искомые и измеряемые харак-
теристики, исследование единственности и формулировка условий ее
обеспечивающих, создание регуляризованных (устойчивых к зашумле-
нию входной информации) методов построения решений, разработка
эффективных вычислительных схем и проведение вычислительных экс-
периментов.
1.3 . Структурная и параметрическая идентификация.
Коэффициентные обратные задачи
Рассмотрим основные этапы идентификации ОИ. Пусть
—
математическая модель ОИ, где

некоторый оператор,
а,

—
функциональные пространства. Задача определения оператора
(идентификация ОИ), как описано выше, может быть разделена на два
этапа:
1 этап — структурная идентификация,
2 этап — параметрическая идентификация.
На первом этапе структурной идентификации определяется (или
выбирается) структура оператора , которая зависит как от самого ОИ,
так и от целей моделирования. На этапе структурной идентификации
используются фундаментальные законы природы, присущие той или
иной области естественных наук, вариационные принципы, статистиче-
ские закономерности, причем одному и тому же ОИ можно сопоставить
целую иерархию математических моделей. Например, при описании
движения твердого тела (стрелы, ракеты), можно использовать следу-
ющие уровни моделирования и соответствующие характерные опера-
торы, определяющие структуру модели:
14/27

1.3 . Структурная и параметрическая идентификация
15
а) материальная точка, абсолютно твердое тело (модели теоретиче-
ской механики);
б) стержень, балка, пластина (модели сопротивления материалов);
в) трехмерное упругое тело (модели теории упругости);
г) упругое тело с неупругими элементами (модели механики
сплошной среды).
Заметим, что наиболее часто в моделировании используются следу-
ющие основные виды операторов:
—
конечномерный оператор ( —матрица,

—система линей-
ных алгебраических уравнений);
—
дифференциальный оператор (или матричный дифференциальный
оператор);
—
дифференциальный оператор в частных производных (или матрич-
ный дифференциальный оператор в частных производных);
—
более сложные операторы — интегральные, интегро-дифференци-
альные, интегро-функциональные.
На втором этапе параметрической идентификации определяются
числовые параметры или функции, входящие в описание операто-
ра (элементы матриц, коэффициенты дифференциальных операторов
и граничные условия).
Отметим, что с точки зрения соотношения причина–следствие все
задачи математического моделирования можно разбить на два больших
класса: прямые задачи и обратные задачи. Остановимся подробнее на
различияхвэтихдвухклассахзадач.
Для прямых задач известны причины, требуется найти следствия.
В качестве причин в математических моделях, описываемых при помо-
щи наиболее общих дифференциальных операторов в частных произ-
водных, могут фигурировать следующие ниже факторы:
1) начальные условия для модели;
2) коэффициенты дифференциальных операторов, моделирую-
щих ОИ;
3) граничные условия для модели;
4) область, занятая ОИ (геометрия области).
В качестве следствий в математической физике обычно используют-
ся компоненты физических полей (перемещения, напряжения, дефор-
мации, температура, электрический потенциал).
Прямые задачи об отыскании следствий, т. е . расчете компонент
физических полей, составляют суть современной классической ма-
тематической физики, которая формировалась на протяжении более
200 последних лет. Для таких задач детально разработаны аналити-
ческие и численные методы решения, доказаны теоремы существова-
ния и единственности. На сегодняшний день наиболее популярными
численными методами при моделировании в математической физике
являются: метод конечных разностей, методы конечных и граничных
15/27

16 Гл. 1 . Математические модели. Корректные и некорректные задачи
элементов, которым посвящена обширная литература и которые стали
в настоящее время мощным инструментом исследования различных
прикладных задач и прогнозирования динамики ОИ.
Для обратных задач в рамках выбранной модели известны след-
ствия; требуется найти причины и обратить причинно-следственные
связи. В этом суть этапа параметрической идентификации.
В качестве примеров параметрической идентификации рассмотрим
следующие задачи определения параметров модели или функций при
известной структуре оператора.
Пример 1. Рассмотрим уравнение движения материальной точки
под действием силы

(1.3 .1)
Требуется найти ,зная внекоторомнабореточек.Эта
задача относится к обратным задачам динамики точки, различные
аспекты исследования таких задач освещены в [8].
Пример 2. Идентификация сил внутреннего трения в материа-
ле [19]. В качестве модели деформирования с внутренним трением,
пропорциональным скорости, часто используется следующее диффе-
ренциальное уравнение:

2
2

0,
(1.3 .2)
где 2
—
квадрат собственной частоты колебаний системы при отсут-
ствии вязкого сопротивления. Требуется определить параметр ,харак-
теризующий затухание, при наблюдении нескольких циклов колебаний.
Пример 3. Идентификация закона состояния полимерного ма-
териала при одноосном растяжении из опыта на ползучесть, когда

0 (рис. 1.1).
Рис. 1.1
В качестве математической модели, описывающей поведение это-
го ОИ, наиболее часто используется модель стандартного вязкоупру-
гоготела[5,7,19].Приэтомвкачествесоотношения,связывающего
вход и выход, на этапе структурной идентификации используется опе-
раторное уравнение, где в правой и левой частях операторного урав-
16/27

1.3 . Структурная и параметрическая идентификация
17
нения присутствуют линейные дифференциальные операторы первого
порядка:

0
1

(1.3 .3)
В этой модели не известны 3 параметра (один из параметров,
например 1 , можно положить равным 1); их определение на основании
данных эксперимента (по заданному виду напряженного состояния
и измерению деформации как функции времени — эксперимент на пол-
зучесть) составляет суть этапа параметрической идентификации для
модели стандартного вязкоупругого тела.
Пример 4 [7]. Идентификация предварительного напряженного со-
стояния при изгибных колебаниях балки длины .
Требуется опреде-
лить предварительное напряжение 0
11

из следующей задачи:

0
11

2 0,
0

0 0,

0
11

,
,

1, 2
,
(1.3 .4)
где
—модуль Юнга, ,

—
момент инерции и площадь поперечного
сечения балки,
—
частота колебаний.
Пример 5 [6]. Идентификация ростовых коэффициентов в простей-
шей биомеханической модели поверхностного роста фрагмента трубча-
тойкости,занимающейкольцевуюобластьсрадиусами и
.
Требуется определить ростовые функции и

из задачи Коши
для системы дифференциальных уравнений первого порядка

,
(1.3 .5)
0

0,
0

0
при наличии дополнительной информации, в качестве которой могут
выступать значения радиусов, измеренных в дискретном наборе вре-
мен: ,

.
Пример 6 [6]. Определение коэффициентов упругости в гранич-
ных условиях. Отметим, что наиболее подробно различные аспекты
идентификации коэффициентов в граничных условиях освещены в [2].
Требуется определить коэффициенты 1 , 2 ,входящиевграничные
условия в краевой задаче

2 0,
(1.3 .6)
0

0 0,

1 0

2 ,
17/27

18 Гл. 1 . Математические модели. Корректные и некорректные задачи
из условия
,

1, 2

(1.3 .7)
Возможна модификация этой задачи, когда неизвестные коэффи-
циенты упругости в заделке находятся по некоторому набору (обычно
трем) резонансных частот. Подробно вопрос о постановках таких задач
иметодырешенияописанывгл.2
.
Перечень задач параметрической идентификации различных ОИ,
возникающих в различных областях естествознания и техники, можно
было бы перечислять довольно долго.
Отметим, что ОЗ имеют постоянно расширяющиеся области прило-
жения в инженерной практике, среди которых выделим следующие.
1. Определение свойств материалов (механических, теплофизиче-
ских), идентификация полимерных и композитных материалов, пьезо-
керамик, биологических тканей (твердых — костная ткань, мягких —
мышцы, сухожилия, кожа).
2. Задачи сейсморазведки (определение расположения и мощности
залежей полезных ископаемых по отраженным от месторождения зву-
ковым сигналам) [5], прогнозирование землетрясений.
3. Проблемы неразрушающего контроля [9], [13] (определение рас-
положения и конфигурации дефекта по измеренному полю упругих
смещений на поверхности тела или по резонансным частотам).
4. Определение параметров акустической эмиссии и определение
связи основных характеристик эмиссии с характеристиками напряжен-
ного состояния; прогнозирование поведения тела с дефектами.
5. Задачи рентгеновской и акустической томографии [4], [21], [33],
которые находят многочисленные применения в технической и меди-
цинской диагностике ОИ, постоянно совершенствуются, используются
для все более широкого спектра задач.
Заметим, что ОЗ обладают рядом неприятных с точки зрения об-
работки информации свойств. Во-первых, как правило, ОЗ являются
нелинейными (линейными будут ретроспективные задачи и ряд гра-
ничных задач). Во-вторых, возможна неединственность при решении
ОЗ и соответственно возможно восстановление нескольких различных
объектов, отвечающих одной и той же входной информации. В -третьих,
наиболее неприятным свойством ОЗ является их неустойчивость по
отношению к малым изменениям входной информации. Это означа-
ет, что погрешность, присущая всем измерениям, может оказывать
очень сильное влияние на погрешность восстановления ОИ, причем
снижение уровня погрешности за счет совершенствования методики
проведения эксперимента и повышения чувствительности измеритель-
ной аппаратуры не обязательно приводит к более точной реконструк-
ции ОИ. Задачи, обладающие такими свойствами, принято называть
некорректными. Строгое определение некорректной задачи будет при-
ведено в следующем разделе настоящей главы.
18/27

1.4. Корректные и некорректные задачи. Корректность по Адамару 19
Отметим, что в современной научной литературе достаточно мно-
го книг, посвященных различным типам ОЗ, методам их решения,
особенностям применения. При этом отметим монографии и статьи,
посвященные различным аспектам обратных задач [1, 2, 7, 8, 10, 12,
14, 15, 21, 22, 23, 30–34].
1.4 . Корректные и некорректные задачи. Корректность
по Адамару. Корректность по А. Н. Тихонову (условная
корректность) и -корректность.
1.4.1. Корректность по Адамару. Выше был сформулирован ряд
задач, возникающих при математическом моделировании различных
явлений и процессов. При этом все задачи моделирования можно
условно разделить на «хорошие» и «плохие». В 1932-м г. Ж. Адамар
сформулировал понятие хорошо поставленных или «корректных» задач.
Для того чтобы придать смысл этому условному разделению, дадим
несколько определений и введем некоторые понятия.
Рассмотрим операторное уравнение, описывающее поведение неко-
торого ОИ [5], [9]

,
(1.4 .1)
где

—
линейный оператор с непустой областью опреде-
ления, ,

—
функциональные пространства,
—
заданный элемент,

—
искомый элемент. В качестве такового оператора может встречать-
ся либо интегральный, либо дифференциальный оператор, либо любой
другой, обладающий свойством линейности.
Определение 1.1. Задача (1.4 .1) нахождения элемента называет-
ся корректно поставленной по Адамару,если:
1) область значений оператора
совпадает с (решение опера-
торного уравнения (1.4 .1) существует для любой его правой части —
условие разрешимости);
2) равенство 1

2 для некоторых 1, 2

влечет за собой

1 2 , условие единственности;
3) обратный оператор 1 непрерывен на .
Условия 1, 2 этого определения характеризуют математическую опре-
деленность, а условие 3 — физическую детерминированность задачи.
Для корректных задач можно установить соотношение корректно-
сти [9]

,
(1.4 .2)
где —
постоянная. Отметим, что в некоторых монографиях задачи,
для оператора которых выполняется неравенство (1.4 .2), принимаются
корректными по определению. В силу соотношения корректности будет
выполнено условие единственности, т. е .

0
0 , и устойчивости, поскольку из того, что ,следует,что

.
Если дополнительно предположить, что ,

—
банаховы,
19/27

20 Гл. 1 . Математические модели. Корректные и некорректные задачи
область значений
плотнави
—
замкнутый оператор [27], то
можно обосновать и существование решения (1.4.1).
Выполнение условий корректности (1–3) Адамару казалось на-
столько естественным для любой разумной математической задачи, что
в свое время (в 30-е годы прошлого столетия) он высказал мысль
о нефизичности любой некорректной задачи, т. е . такой, для которой
условия (1–3) не выполняются. В то же время Адамар привел пример
некорректнойзадачи,ставшийвпоследствииканоническим—задачу
Коши для уравнения Лапласа. Как выяснилось позже, именно к та-
кой задаче сводятся многие проблемы естествознания и математики.
Так, например, к такой задаче сводится проблема продолжения ана-
литических и гармонических функций, ряд задач теории потенциала,
биофизики, сейсмики и гидродинамики. Эта задача стала своеобразным
эталоном в исследованиях по некорректным задачам; ее изучению
и методам построения устойчивых решений и сегодня посвящают-
ся работы в современных монографиях и математических журналах.
Позднее выяснилось, что свойством корректности не обладают многие
линейные и нелинейные задачи, которые в современной терминологии
называются обратными.
В середине XX века интенсивно начали развиваться методы ре-
шения некорректных (неустойчивых) задач. Отметим, что понятия
«неустойчивость решения по Ляпунову» и «нарушение 3-го условия
корректности по Адамару» (фактически, отсутствие непрерывности
обратного оператора) очень похожи. Если первое понятие относит-
ся к решениям канонической системы дифференциальных уравнений
(операторным уравнениям специального вида), то второе — к общим
операторным уравнениям. Научное направление, посвященное иссле-
дованию некорректных задач, связано с работами крупных совет-
ских математиков: А. Н . Тихонова, Г. И. Марчука, М. М . Лаврентьева,
А. А . Самарского, В. Г. Романова, С. И . Кабанихина и их учеников, —
оказавших значительное влияние на развитие теоретических основ
методологиинекорректныхзадачиопределившихпутиразвитияэтого
раздела математики, тесно смыкающегося с современной вычислитель-
ной математикой, обработкой эксперимента и теорией обратных задач
в целом [3, 10, 14, 15, 18, 22, 23, 25, 26].
Приведем ряд примеров операторных уравнений, корректных по
Адамару.
Пример 1.Пусть —матрица размерности ,

,
обладающая тем свойством, что

0, тогда задача решения ли-
нейной алгебраической системы вида (1.4.1) корректна [13].
Пример 2. Пусть

"
1
0,#,

" 0,#
(1.4 .3)
Нетрудно понять, что при таком выборе функциональных про-
странств задача некорректна, ибо решение находится неединствен-
20/27

1.4. Корректные и некорректные задачи. Корректность по Адамару 21
ным образом, поскольку общее решение дифференциального уравнения
определяется с точностью до произвольной постоянной. Задача стано-
вится корректной, если подчинить решение некоторым данным Коши
и принять, например, что

"
10, # ,
0 0.
Тогда задача
корректна, обратный оператор строится в соответствии с правилом

Ê
0
$$
1

и соотношение корректности принимает вид

Пример 3 [9]. Начально-краевая задача для уравнения теплопро-
водности. Пусть функция ,

"
2,

0, % 0, # иявляется
решением следующей краевой задачи:

,
,

,
(1.4 .4)
,0
,

0,%,
(1.4 .5)
0,
%,

0,#,
(1.4 .6)
где"2
0, # . Положим
,
#
. Определимоператор по
правилу

0, %
Докажем, что для 2
0, % выполняется неравенство

2
,
(1.4 .7)
или

Отметим, что область определения оператора
вэтомприме-
ре задается неявно (как совокупность функций ,допускающих
представление вида
,
#
,г
дефункц
ия есть решение
краевой задачи (1.4.4)–(1.4 .6)). В этом примере будем считать, что

20, % .
Для доказательства оценки корректности в соот-
ветствии с [9] введем функцию

Ê
0
2,
.Покажем,что

0, # Дифференцируя функцию сучетомусло-
вий (1.4 .4)–(1.4 .6), имеем

0
,

0
2

0
Отсюда следует монотонное убывание функции .
Полагая
#
, получаем оценку корректности исходной задачи.
21/27

22 Гл. 1 . Математические модели. Корректные и некорректные задачи
Пример 4. Задача Дирихле для уравнения Лапласа в области

!
2 с гладкой границей & состоит в нахождении функции

"
2 , удовлетворяющей следующей краевой задаче:

(1.4 .8)
Можно показать [16, 28], что задача (1.4 .8) корректна, при этом
достаточно просто устанавливается соотношение корректности (1.4 .2).
Корректные задачи являются предметом исследования в математике
уже давно. Для них доказаны теоремы существования, единственно-
сти, разработаны методы численного исследования. Значительно более
сложной является ситуация, в которой условия корректности не вы-
полняется. Дадим следующее определение.
Определение 1.2. Задача (1.4 .1) называется некорректной,если
для нее нарушается хотя бы одно из условий (1–3) определения 1.1 .
Фактически для некорректных задач либо отсутствует решение
в обычном смысле, либо оно не единственно, либо нет непрерывной
зависимости решения от исходных данных задачи. Возникает вопрос:
с чем же связаны эти качества исследуемых задач. Для того, чтобы
разобраться в этом вопросе, рассмотрим несколько типичных примеров
некорректных задач, возникающих как при решении математических,
так и инженерных задач.
При обработке результатов эксперимента очень часто проблема
идентификации ОИ (особенно на основании метода наименьших квад-
ратов) сводится к решению линейной алгебраической системы, которая
может оказаться как плохообусловленной, так и вырожденной, Напри-
мер, когда измерительные элементы дублируют друг друга (в некото-
рых схемах вибродиагностики).
Начнем рассмотрение примеров с простейшей алгебраической про-
блемы.
Пример 5 [5, 25]. Рассмотрим классический пример, предложенный
А. Н . Тихоновым, о нахождении решения линейной алгебраической си-
стемы следующей структуры:

23
5,

50
(1.4 .9)
Нетрудно видеть, что матрица системы и расширенная матрица
системы имеют ранг, равный 1, поскольку второе уравнение получается
умножением первого на

2 . Таким образом, в соответствии с теоремой
Кронекера–Капелли [13] система совместна и имеет множество реше-
ний, зависящих от одного параметра. При численном исследовании
такой системы возможны следующие особенности. Возьмем, напри-
мер, 100 десятичных знаков в приближении иррациональных чисел
во втором уравнении системы. Будем производить все вычисления
сточностью , характеризующей количество знаков после запятой.
Тогда определитель системы иногда не равен нулю, и можно построить
22/27

1.4. Корректные и некорректные задачи. Корректность по Адамару 23
в соответствии с правилом Крамера единственное решение ,

,
соответствующее сохранению значащих цифр во всех вычислениях.
Оказывается, что построенная таким образом последовательность ре-
шений не имеет предела при увеличении ,хотяисходнаяинформация
становится все точнее и точнее, поскольку используются все более
точные приближения иррациональных чисел рациональными. Это есть
типичная ситуация, характерная при решения некорректных задач. Для
таких задач характерным является неустойчивое нахождение решения
при уменьшении измерительной погрешности.
На рис. 1 .2, 1.3 в соответствии с [6] представлены зависимости
решения системы (1.4 .9) по правилу Крамера от числа :количество
знаков после запятой, отложенное по горизонтальной оси. Как видно
из этих рисунков, при некоторых значениях числа решение не
определено, поскольку главный определитель системы (1.4.9) обраща-
ется в ноль в пределах используемой точности, а при некоторых его
значениях оно находится.
Рис. 1.2
Рис. 1 .3
Примером более общей ситуации может служить линейная алгеб-
раическая система -го порядка. Пусть — квадратная матрица -го
порядка,

.
Как известно из курса линейной алгебры [13],
имеется две возможности.
1. Если определитель матрицы отличен от нуля, то при лю-
бой правой части существует единственное решение вида
1
,
где 1
—обратная к матрице .
2. Если определитель матрицы
равен нулю, система имеет ре-
шениенедлялюбойправойчасти;еслижеоносуществует,тоне
единственно. Таким образом, задача решения линейной алгебраической
системы с вырожденной матрицей является некорректной.
Эта ситуация типична для приложений, когда элементы матрицы
находятся либо из наблюдений, либо определяется в результате неко-
торых приближенных вычислений. Если в процессе расчетов получено,
23/27

24 Гл. 1 . Математические модели. Корректные и некорректные задачи
например, что
1040 , то непонятно, к первому или ко второму
случаю относится эта ситуация; они в принципе неразличимы, и тре-
буется иной подход к решению подобной задачи.
Пример 6. Бесконечномерным аналогом рассмотренной в преды-
дущем примере алгебраической проблемы является задача решения
уравнения Фредгольма первого рода с непрерывным ядром ' ,
(,
к которому сводятся многие некорректные задачи [5, 9, 23, 25, 26].
Пусть

' ,
(((
,

(1.4 .10)
Будем считать для определенности, что ' ,
(,
'

,
(,
'

,
(,

" ,

,
,

"
,
,

"
,

(непрерывные функции
своих аргументов). Покажем, что задача (1.4 .10) является некор-
ректной. Для этого операторного уравнения не выполняется первое
условие корректности, поскольку не у каждого элемента из буде т
существовать прообраз из .
Для этого достаточно взять функцию ,
непрерывную на ,
, но не дифференцируемую. В этом случае инте-
грал в левой части представляет собой непрерывно дифференцируемую
функцию. Для уравнения (1.4 .10) не выполняется и третье условие
корректности в силу полной непрерывности оператора в левой части
и неограниченности обратного 1 к вполне непрерывному [27, 28].
Наконец, заметим, что выполнение второго условия корректности
зависит от конкретного вида ядра (это условие может как выполняться,
так и нарушаться). Рассмотрим 3 характерных примера для уравнений
Фредгольма первого рода с бесконечно дифференцируемыми ядрами,
иллюстрирующих различные ситуации.
Пример 6а. Пусть ядро является вырожденным [27] и имеет вид
' ,
(

(. Введемоператор

( (
(

1
2

( (
(,

((
(
(1.4 .11)
Обратный оператор 1 существует, если правая часть име-
ет тот же самый вид, что и левая, т.е.

1
2

.
Если же возмутить, полагая, например 1

2,топрилюбомсамоммаломÆ обратный оператор 1 не
существует.
Пример 6б. Пусть ядро является вырожденным и имеет вид
' ,
(
)

.
Нетрудно видеть, что для оператора с таким ядром
решение не единственно. Рассмотрим соответствующее однородное
24/27

1.4. Корректные и некорректные задачи. Корректность по Адамару 25
уравнение и будем отыскивать его решение в виде ( 1

0,
тогда

)

(

()

(
0
иможноположить1

()

)

(, т. е . однородное урав-
нение имеет нетривиальное решение и имеет место неединственность.
Пример 6в [9]. Пусть ядро не является вырожденным и имеет
вид ' ,
(
)

.
Для доказательства единственности покажем, что
соответствующее однородное уравнение (с нулевой правой частью)
имеет только нулевое решение

)

(
(
0,

,
,0

(1.4 .12)
Полагая в (1.4.12) 0, получим

(
(
0. Дифференци-
руя равенство (1.4 .12) и полагая
0, получим последователь-
но

(

((
0 1,2, .. . В силу того, что система функций
1,(,...,(

, . . . линейно независима и полна в 2
,
,а( ортого-
нальна этой системе, то ( 0 и, следовательно, единственность
решения имеет место. Таким образом, для разных бесконечно диффе-
ренцируемых ядер могут иметь место совершенно разные ситуации —
отсутствие решений при малом возмущении правой части, единствен-
ность и неединственность.
Рассмотрим вопрос о корректности решения операторного уравне-
ния (1.4.1) в общем случае. Из определения корректной задачи следует,
что задача будет корректной, если на корректно определен обратный
оператор 1
, являющийся непрерывным (ограниченным).
Отметим, в некоторых ситуациях некорректность легко преодо-
леть. Так, например, задачи, некорректные для одной пары про-
странств ,

, могут оказаться корректными для другой. Рассмотрим
простейшие операторные уравнения, содержащие дифференциальные
и интегральные операторы.
Пример 7 [9]. Пусть

0
$ $ ,

" 0,#,

" 0,#
(1.4 .13)
Для определенного таким образом оператора задача (1.4 .1) некор-
ректна. Докажем это, предполагая противное. Пусть задача корректна
(тогда имеет место соотношение корректности .Выберем
25/27

26 Гл. 1 . Математические модели. Корректные и некорректные задачи

" 0,#,

.Тогда

1, а величина

может быть сколь угодно большой при
.
Если выбрать
" 0,#,

"
10,# ив
вестинормуобычным
образом, то можно доказать соотношение корректности и задача ока-
зывается корректной.
Пример 8 [25]. Численное суммирование рядов Фурье, когда ко-
эффициенты известны приближенно в метрике *2
. Пусть1

.Есливместо брать коэффициенты

+
для
1и0

0,получимряд2

.Коэффи-
циенты этих рядов отличаются (в метрике *2

на величину 1

1
1+2

%
2+6, которую выбором
числа можно сделать сколь угодно малой. Вместе с этим разность

2 1

1
1

может быть сколь угодно большой, по-
скольку при
0 последний ряд расходится. Таким образом, если
уклонение суммы ряда брать в метрике " , суммирование ряда Фу-
рье не является устойчивым. Если же расстояние между функциями
оценивать в метрике 2 , то задача суммирования рядов Фурье с при-
ближенно заданными (в метрике *2

коэффициентами будет корректно
поставленной на паре пространств ,
, что легко установить на
основе равенства Парсеваля [27], поскольку

1 2

Упомянем еще некоторые классы задач, приводящие к некоррект-
ным проблемам. Во-первых, это задачи вычисления значений неогра-
ниченных операторов, например, задачи нахождения производных от
функций, заданных таблично или на некоторой сетке, причем узловые
значения находятся при дискретизации некоторой задачи.
Другим важным классом некорректных задач являются задачи на
спектре (например, задача Неймана для уравнения Лапласа [29]). Для
этого класса задач развита теория псевдорешений, причем в эту схему
укладываются методы решения неустойчивых задач (плохо обусловлен-
ных, вырожденных) систем линейных алгебраических уравнений.
Отметимодинважныйвывод.Задача,некорректнаядляоднойпары
пространств, может оказаться корректной для другой пары. В частно-
сти, корректности часто можно достигнуть, сужая область принадлеж-
ности искомого элемента до замкнутого ограниченного множества или
конечномерного, когда искомая функция параметризуется конечным
набором параметров (в инженерной практике наиболее часто использу-
26/27

1.4. Корректные и некорректные задачи. Корректность по Адамару 27
ется аппроксимация неизвестной функции ее отрезком ряда Тейлора,
Фурье, полиномом степени не выше заданной и т. д .) . В иных ситуаци-
ях требуются более глубокое проникновение в причины некорректности
и разработка способов ее преодоления. Об этих аспектах при исследо-
вании некорректных задач и пойдет речь в следующих разделах.
1.4.2. Корректность по А. Н. Тихонову (условная коррект-
ность) и -корректность. В силу того, что при постановке ОЗ правая
часть операторного уравнения известна приближенно, вопросы устой-
чивого построения решения операторного уравнения (1.4.1) приобре-
тают первостепенное значение для практики. При этом главную роль
играют идеи о сужении множества решений из иучетеаприорной
информации. Такая априорная информация о решении часто имеется,
ибо неизвестная характеристика ОИ представляет физическую величи-
ну, для которой характерны некоторые свойства, такие как: а) положи-
тельность, б) ограниченность, в) монотонность, г) выпуклость и т. д .
Учет такой априорной информации позволяет в ряде ситуаций сузить
множес тво до некоторого множества, на котором решение искомой
задачи будет устойчиво. Это обстоятельство привело к развитию по-
нятия корректности по Адамару и формированию понятия корректной
по А. Н . Тихонову или условно-корректной задачи.
Определение 1.3 [25]. Задача (1.4.1) называется условно-коррект-
ной, если выполнены следующие условия:
1) априори известно, что решение задачи существует для неко-
торого класса данных из и принадлежит некоторому заданному
множеству ;
2) решение единственно на множестве ;
3) существует непрерывная зависимость решения уравнения от
правой части при условии, что возмущения не выводят Æ из множества
корректности .
Замечание. В случае если задача (1.4 .1) условно-корректна и
—
компакт, то возможно построение оценок устойчивости при нахожде-
нии обратного оператора.
Однако для многих ОЗ априорная информация либо отсутствует,
либо не позволяет значительно сузить первоначальную область опре-
деления оператора .
Определение 1.4 [4]. Задача (1.4 .1) называется * -корректной,если

0 " 0, такое что
* выполняется нера-
венство

,
(1.4 .14)
где функционал * называется стабилизирующим функционалом
и обладает свойством полунормы [27, 28]. Можно считать "
невозрастающей функцией ,причем

0
"

. Свойство* -кор-
ректности гарантирует единственность и устойчивость решения на
любом множестве вида

Отметим
P owe red by T CP DF (www.tcp df.o rg)
27/27

28 Гл. 1 . Математические модели. Корректные и некорректные задачи
также, что согласно определению 1.4 корректные задачи оказываются
0-корректными, причем " не зависит от .
Приведем некоторые примеры построения оценок * -корректности.
Пример 9 [4]. Пусть ,

—
гильбертовы пространства,

0 , а область значений !

опера-
тора
плотна в ;оператор 1

задан на плотном в
многообразии и тем самым корректно определен сопряженный опера-
тор 1

.Положим* 1

,
*

.Докажем,
что задача нахождения решения операторного уравнения

* -корректна, причем

2
1

(1.4 .15)
и "
1+2 .
В самом деле, если ,

—скалярное произведение
в ,то

2 ,

,
1

22
2

2
Здесь были использованы неравенства Коши–Буняковского и неравен-
ство 2 ,2

,
1

2,где2
,+ 2 . Извлекая квадратный корень
сучетомнеравенства

,
,

0,
приходим к искомой оценке (1.4.15).
Пример 10 [9]. Можно получить оценку * - корректности для одной
из канонических некорректных задач для уравнения теплопроводности
с обращенным временем вида

,
,

0,%0,#,

"
2,
(1.4 .16)
,0
,

0, %,
0,
%,

0,#,
вкоторойпофункции требуется найти функцию
,
#
.
Сформулированная ОЗ некорректна по Адамару, однако для нее
можно получить оценку * -корректности. С этой целью рассмотрим
интеграл
-

0
2 (

2,
(

0,
который в силу уравнения (1.4.16) равен нулю, и преобразуем его,
сделав замену
)

,
,
(1.4 .17)
где (
—
произвольная постоянная. Преобразуя этот интеграл с по-
мощью интегрирования по частям и используя граничное условие,
получим
(
2(#

2 2(#

2
1/27

1.5 . Основные причины и характеристики некорректности
29
Поделив обе части этого неравенства на ( 2 (#

иположив

2 (1
, получаем необходимую оценку

Таким образом, в рассматриваемом случае задача решения уравне-
ния * -корректна, причем " #+2

и растет достаточно
быстро при
0, а *

2
Отметим также, что для такой задачи с успехом применяется метод
квазиобращения, детали реализации которого описаны в [15].
Отметим также следующее обстоятельство. Даже для корректных
задач, для которых выполнено соотношение корректности (1.4 .2), но
константа в этом неравенстве велика, существует значительная потеря
точности при нахождении возмущенного решения. Такая же ситуация
имеет место и для условно-корректных задач. Пусть правая часть опе-
раторного уравнения (1.4 .1) известна с некоторой погрешностью Æ;ему
соответствует решение Æ , задача условно-корректна. Возникает во-
прос, какую минимальную погрешность построения приближенного ре-
шения можно гарантировать и какую минимальную погрешность нор-
мы отклонения

можно обеспечить на множестве
*
.
Несложно показать, что в качестве такой характеристики можно ис-
пользовать меру точности Æ

" Æ , введенную в [5].
В силу свойств функции " этот минимум достигается при некото-
ром значении 0
. Напримердляпримера9,"
2
1 ивявном
виде находится значение 0
2Æ+12
, соответствующее значение
Æ
5

2 +4 Æ 12
.
Из этой оценки понятно, что уменьшение
меры точности может быть достигнуто как за счет уменьшения
(сужения множества поиска), так и за счет Æ (уменьшение погрешности
входной информации). Для примера 10 такие же рассуждения приво-
дят к оценке Æ

12
0

1+ 2

32
0

,однако
0 вэтом
случае определяется из трансцендентного уравнения
0

32
0,

#
+2 Æ ; его анализ позволит определить оптимальные харак-
теристики при постановке ОЗ.
1.5 . Основные причины и характеристики
некорректности
В предыдущем разделе было дано определение корректной и некор-
ректной задач. Из определения корректной задачи следует, что за-
дача решения операторного уравнения типа (1.4 .1) будет корректной,
если на корректно определен обратный оператор 1
,яв
ляющийся
непрерывным (ограниченным). Соответственно в терминах обратного
оператора 1 причин некорректности всего две.
1. Обратный оператор 1 не существует.
2. Обратный оператор 1 существует, но неограничен.
2/27

30 Гл. 1 . Математические модели. Корректные и некорректные задачи
Соответственно возникает вопрос: каким образом можно преодо-
леть некорректность и какой оператор может заменить обратный при
исследовании некорректных задач? Об этом пойдет речь ниже, в п. 1 .6 .
В настоящем пункте выясним, какой точности можно достичь при
решении некорректной задачи в часто используемых пространствах
суммируемых функций, в частности, пространствах Соболева [5, 29].
Для изучения этого вопроса сделаем следующие дополнительные пред-
положения относительно линейного вполне непрерывного оператора
и точного решения .
Пусть:
1 . 0

0
,
,

0;
2 /
0,
0

Всилу1) 1

2 ,нооннеограничен.Этоозначает,что
задача отыскания решения операторного уравнения

является
некорректной для пары пространств 2

, ;приэтом. можно рас-
сматривать как меру некорректности. Фактически требование 2) пред-
ставляет собой условие, накладываемое на степень гладкости точно-
го решения (типичный пример априорной информации), позволяющее
существенно сузить область поиска решения исходного операторного
уравнения.
Пусть известен не сам элемент ,аегоприближениеÆ (напри-
мер, Æ находится из эксперимента с некоторой известной погрешно-
стью), причем Æ Æ Такимобразом,информацияоточном
решении сводится к неравенствам

Æ,

(1.5 .1)
Пусть два элемента 1 , 2 удовлетворяют неравенствам (1.5 .1).
Тогда

2Æ,

2
Введем в рассмотрение меру погрешности

Æ,

Ее можно рассматривать как наибольшую возможную погрешность
восстановления по неточно заданному элементу Æ ,поскольку

2 2Æ,2
Отметим, что асимптотика погрешности при Æ
0 описывается
оценкой, вытекающей из следующей теоремы.
3/27

1.6 . Способы преодоления некорректности. Регуляризация
31
Теорема 1.1 [19]
При выполнении условия 1) существует константа ,
,,
0
такая,
что

Æ,

,
.,
0
Æ

(1.5 .2)
Эта теорема имеет следующую интерпретацию. Если в некоррект-
ной задаче, удовлетворяющей условиям (1, 2) правая часть оператор-
ного уравнения (1.4 .1) задается с погрешностью Æ , то решение можно
найти с точностью 1

Всилутого,что2

1, погрешность решения в этой
ситуации всегда превосходит Æ , т. е . всегда при нахождении решения
некорректной задачи происходит потеря точности. Поэтому можно вве-
сти следующую условную классификацию некорректных задач в зави-
симости от параметра 2 [19].
1Æ
. Сильно некорректные задачи. Эти задачи характеризуются бли-
зостью 2 кнулю.Вэтомслучае,какправило,.

и условие 1)
не выполняется ни при каком конечном . .
2Æ
.
Умеренно некорректные задачи характеризуются промежуточ-
ным значением 2:0 2 1(причем2 неблизконик0,ник1).
3Æ
.
Слабо некорректные задачи: в этом случае 2 близко к 1. Эти
задачи наиболее просты с точки зрения практического построения
решения операторного уравнения (1.4.1).
Отметим, что более глубокая и точная классификация некоррект-
ных задач может быть осуществлена на основе анализа скорости стрем-
ления к нулю сингулярных чисел [27] конкретного вполне непрерывно-
го оператора, в частности на основе исследования их асимптотик при
больших номерах в зависимости от параметров задачи.
Таким образом, можно констатировать, что степень некорректности
зависит не только от оператора ,ноиотгладкоститочногорешения,
т. е . от функционального пространства, в котором оно отыскивается.
При этом любая априорная информация о решении (в частности,
его гладкость, степень изменяемости) может существенно влиять на
степень близости точного и приближенного решений, что необходимо
учитывать при решении конкретных некорректных задач.
1.6 . Способы преодоления
некорректности. Регуляризация
Итак,отметим,чтовсезадачиматематическогомоделирования
можно условно разделить на три категории[4, 9]:
1) корректные;
2) некорректные, но постановка которых может быть изменена с по-
мощью так называемого регуляризующего алгоритма иприведена
к корректной задаче;
3) некорректные, но нерегуляризуемые.
4/27

32 Гл. 1 . Математические модели. Корректные и некорректные задачи
Это разбиение по категориям имеет простую аналогию и очень
напоминает классификацию функций по непрерывности: непрерывные,
имеющие устранимую точку разрыва и разрывные (1-го и 2-го рода).
Перейдем к анализу возможностей построения приближенного реше-
ния операторного уравнения (1.4.1) в случае, когда задача некорректна.
Так, отметим, что в случае если задача (1.4 .1) условно-корректна
и есть априорная информация о решении, что
—компакт, то возмож-
но построение оценок устойчивости нахождения обратного оператора.
Имеет место следующая теорема.
Теор ема 1.2 [25]. Пусть оператор отображает компакт непре-
рывно и взаимно-однозначно на множество . Тогда существует непре-
рывная функция $ ,

0 0, такая что:

1, 2

1 2

Однако, к сожалению, для многих ОЗ априорная информация о ре-
шении либо отсутствует, либо не позволяет значительно сузить перво-
начальную область определения оператора . Для построения прибли-
женных решений некорректных задач в этом случае вводится понятие
регуляризатора.
Определение 1.5 [3]. Оператор ! ,
Æ

называется регу-
ляризирующим для уравнения или регуляризатором, если он
обладает следующими свойствами:
1) Æ1

0!,
Æ
определен для Æ 0, Æ1

и Æ , удовлетворяю-
щих неравенству

Æ,(
,

—
точное решение уравне-
ниясточнойправойчастью ;
2)
0

Æ
0,

Æ
1 такое, что

Æ
0Æ,
где Æ !Æ ,
Æ
Вопросы построения регуляризованных решений составляют суть
теории некорректных задач. Рассмотрим способы построения регуляри-
заторов. Отметим, что (как отмечалось выше) причины некорректности
задачи (1.4 .1) состоят в том, что либо обратный оператор 1 не
существует (не определен на всех элементах пространства ,л
ибо
неограничен. В п. 1.2 описан один из способов преодоления некор-
ректности в том случае, когда обратный оператор не существует —
это метод наименьших квадратов. Рассмотрим идею метода наимень-
ших квадратов в применении к общим операторным уравнениям ви-
да (1.4 .1), когда — вполне непрерывный оператор. Найдем минимум
функционала невязки

.Составимдляэтогофунк-
ционала уравнение Эйлера, для чего найдем выражение для первой
вариации
Æ

,Æ

0
2 Æ,

2Æ,

0,
5/27

1.6 . Способы преодоления некорректности. Регуляризация
33
откуда находим
0или

где
—с
опря-
женный к оператору (в случае линейных алгебраических систем
—матрица,

—
транспонированная матрица ).
Итак, при таком подходе задача нахождения решения операторного
уравнения сводится к проблеме решения операторного уравне-
ния

(в случае алгебраических систем это соотношение
называется системой нормальных уравнений). Если оператор вполне
непрерывен, значит также вполне непрерывен [27, 28], тогда опера-
тор

будет вполне непрерывен и сингулярные числа оператора
стремятся к нулю еще быстрее, чем у оператора .Такимобразом,хотя
метод наименьших квадратов и позволяет строить оператор, заменяю-
щий обратный в случае его отсутствия, для некорректных задач этот
оператор оказывается по-прежнему неограниченным и третье условие
корректности по Адамару не выполняется. Вместе с тем принцип мини-
мизации функционала невязки положен в основу некоторых алгоритмов
регуляризации. Рассмотрим некоторые основные методы регуляризации.
1.6.1. Метод квазирешений. Рассмотрим некорректную зада-
чу (1.4 .1). Предположим, что для точной правой части существу-
ет единственное решение, принадлежащее некоторому компакту .
Однако элемент неизвестен, задано его приближение Æ ивели-
чина погрешности Æ ,такиечто

Æ.Т
ребуется,знаяэту
информацию, построить приближенное решение Æ , которое стреми-
лось бы к точному при Æ
0. Введем в рассмотрение множество

Æ.
В силу некорректности задачи (1.4 .1)
произвольный элемент этого множества нельзя рассматривать в ка-
честве приближенного решения. Поскольку в качестве априорной ин-
формации выступает условие , то естественно сузить Æ до
пересечения с
Æ

Æ
.
Тогда элементы множества
Æ
мож-
но рассматривать в качестве приближенных решений (1.4.1), причем
при Æ
0

0.
Введем в рассмотрение понятие квазирешения. Пусть в (1.4 .1)

непрерывен, а
—компакт в .
Определение 1.6 [9]. Квазирешением уравнения (1.4 .1) называется
элемент , минимизирующий невязку
2

на множест-
ве.
Из определения квазирешения следует, что оно существует для ,
а в силу непрерывности оператора функционал дос тигает на
компакте своей точной нижней грани; в случае, когда ,

совпадает с обычным решением, поскольку
0.
Имеет место следующая теорема.
Теорема 1.3 [9]. Пусть
—
линейный непрерывный оператор,
такой что уравнение

0 имеет только одно решение на
(
—в
ыпуклый компакт в ); тогда для любой функции квази-
решение существует; оно единственно и непрерывно зависит от .
6/27

34 Гл. 1 . Математические модели. Корректные и некорректные задачи
Эта теорема является основой для построения устойчивых мето-
дов решения многих некорректных задач. Часто на основе априорной
информации о решении задачи можно сделать заключение о принад-
лежности его некоторому компакту , а задача отыскания решения
операторного уравнения (1.4 .1) сводится к проблеме отыскания ми-
нимума функционала ]на .
При этом, если известна величина
погрешности правой части, равная Æ , то процесс минимизации можно
закончить сразу, как только найден элемент Æ такой, что выполнено
условие

Æ
1.6.2. Метод регуляризации А. Н . Тихонова. Рассмотрим некор-
ректную задачу (1.4 .1), причем
—
вполне непрерывный оператор.
Из предыдущего пункта следует, что использовать функционал невяз-
ки для построения регуляризованного решения вообще говоря нельзя
и требуется сформировать некоторый другой, более общий функционал
по сравнению с функционалом невязки. Таким функционалом является
введенный А. Н . Тихоновым стабилизирующий функционал

,
,

0
(1.6 .1)
Определение 1.7 . Оператор 1⁄4

называется производной функ-
ционала по Фреше, если

1⁄4

.
,

,
причем

0.
Имеет место следующая теорема.
Теорема 1.4 [25]. Для любого , 0,
задача об отыскании
минимума функционала (1.6 .1) разрешима и имеет единственное реше-
ние ,где —
область определения оператора ;кроме
того, если 0 , то справедливо соотношение корректности

Доказательство представлено в [25], которое базируется на на-
хождении производной функционала 1⁄4

2 ,
и необходимом условии экстремума, откуда получается уравнение Эй-
лера для функционала ,

,
(1.6 .2)
для нахождения элемента, на котором этот экстремум достигается.
Нетрудно доказать и единственность такого элемента.
Остается проверить соотношение корректности. В самом деле,

2
,
7/27

1.6 . Способы преодоления некорректности. Регуляризация
35
а с другой стороны,

2
,
,

Таким образом, из теоремы 1.4 следует способ построения регуля-
ризованного решения для некорректной задачи при любом , 0 .
Отметим, что наиболее важной проблемой при реализации метода
регуляризации А. Н. Тихонова является выбор параметра регуляриза-
ции и его связь с погрешностью входной информации.
Пусть есть точное решение операторного уравнения

Рассмотрим уравнение

Æ
,где

Æ;

—
аппроксимирующий оператор, который может быть и конечномер-
ным,

—
решение, найденное по методу Тихонова, 2
Æ,
3
—вектор
погрешности. Имеет место теорема.
Теор ема 1.5 [25]. Пусть — взаимнооднозначный оператор, точное
решение ;тогда

при 2
0, если , 2
0таким
образом, что

Æ
2

0
Важный вывод из теоремы 1.5 состоит в том, что параметр регуля-
ризации , должен быть согласован с уровнем погрешности 2
.
Для формулировки критерия обобщенной невязки введем меру не-
совместимости: 4 Æ ,

Æ
. Имеет место утверждение.
Теорема 1.6 [25]. Если

Æ,

Æ
,

0при2
0.
Вводим в рассмотрение функцию
5

Æ
,

На основании теоремы имеет место следующий критерий.
1. Если Æ Æ2

Æ
,

2
,тополагаем

0.
2. Если Æ Æ
24Æ,

2
,то:
а) если 5 , имеет корень ,
,товкачестверешенияполага-
ем

;
б) если 5 , 0, то полагаем

,,
0.
В реальных расчетах оказывается, что в достаточно широких пре-
делах изменения параметра регуляризации (различных для различных
типов задач) обратный оператор находится устойчиво.
Пример. Рассмотрим задачу решения следующих алгебраических
систем:
1)

2
3,
24
6,
2) 2
3,
24
6

Æ
Известные средства линейной алгебры (теорема Кронекера–
Капелли) [13] позволяют установить, что первая из этих систем имеет
множество решений (ранг матрицы системы и ранг расширенной
8/27

36 Гл. 1 . Математические модели. Корректные и некорректные задачи
матрицы равны 1), вторая при любых Æ

0 несовместна и решений не
имеет. Построим решение второй системы в соответствии с изложен-
ным выше методом А. Н . Тихонова. Последовательно находим, решая
линейную систему

,-
,25 ,,

152Æ
25
,

304Æ
25

Отметим, что при ,
Æ
0получаем0 3+5,
0 6+5 —так
называемое нормальное решение исходной системы 1, это решение
соответствует минимуму нормы решения функции 2

2 при условии

2
3; фактически это есть решение системы 1 с минимальной
нормой.
Примеры применения метода А. Н . Тихонова к более сложным зада-
чам для построения обратных к вполне непрерывным операторам будут
представлены ниже в разделах гл. 4 . Заметим, что современные методы
решения линейных систем с плохообусловленной матрицей опираются
не только на идеи метода А. Н . Тихонова, но и на идеи использо-
вания пространств А. Н. Крылова, алгоритм Ланцоша [35] и метод
Пэйджа–Саундерса [36].
1.6.3. Метод регуляризации на компактных множествах. Рас -
смотрим операторное уравнение (1.4 .1) в случае некорректной задачи.
Из метода квазирешений 1.6 .1 известно, что, например для процеду-
ры построения квазирешения, необходимо выбирать компактное мно-
жество.
Какой же априорной информацией нужно обладать,
чтобы сузить область определения до компактного множества ?
Для этого необходимо располагать критериями компактности множеств
в различных функциональных пространствах. Приведем один из них,
наиболее часто используемый в приложениях.
Критерий Арцела [25]. Множество " ,

компактно, если
функции из равномерно ограничены и равностепенно непрерывны.
Рассмотрим несколько типичных в практике решения ОЗ способов
выбора компакта .
1.

—
ограниченное множество в !
.
Эта ситуация встречается,
когда исходное операторное уравнение, сформулированное как задача
отыскания решения в некотором функциональном пространстве, мо-
жет быть параметризована конечным числом параметров. Тогда метод
квазирешений в этой ситуации будет аналогом метода наименьших
квадратов.
2. В ряде ОЗ в качестве априорной информации обычно существует
информация о характере решения, такая как: а) положительность,
б) монотонность, в) выпуклость.
Рассмотрим, например, случай, когда c
—
множество ограничен-
ных, монотонно невозрастающих функций:

2 1
,

(1.6 .3)
9/27

1.6 . Способы преодоления некорректности. Регуляризация
37
Имеет место утверждение.
Теорема 1.7 [9, 23].

компактно в 2
,
.
Отметим, что определенные ниже множества также являются ком-
пактами в 2
,
:
̄

—
множество ограниченных, выпуклых вверх функций,

12
2

;
(1.6 .4)
̄

—
множество ограниченных, невозрастающих, выпуклых вверх
функций,

0",

12
2

2
,

2 1
,

(1.6 .5)
Для отыскания квазирешений на компактных множествах обычно
прибегают к процедуре дискретизации, и ее техника имеет свою специ-
фику. Фактически для построения приближенного решения достаточно
научиться строить последовательность
, которая минимизирует функ-
ционал невязки на множестве . О способах дискретизации и свед́е -
нии к конечномерным проблемам речь пойдет в следующих разделах.
Рис. 1 .4
Пример 1. Пусть задача (1.4 .1)
сведена к минимизации функциона-
ла невязки на множестве

20,1.
Простейшая аппроксима-
ция элементов такого подпростран-
ства представляет собой функцию
вида

01
,г
де0 , 1
удовлетворяют условиям 0 0,

10, 0

1 0. Область изме-
нения параметров 0 , 1 представляет
собой компактное множество — внут-
ренность заштрихованного треуголь-
ника, изображенного на рис. 1.4.
Исходя из этой дополнительной информации о принадлежности
решения можно значительно сузить множество поиска решения
задачи и соответственно построить его с меньшими вычислительными
затратами.
1.6.4. Метод итерационной регуляризации.
Пусть зада-
ча (1.4.1) некорректна, такую задачу в соответствии с идеей метода
наименьших квадратов заменим задачей отыскания минимума функ-
ционала
2

, для нахождения которого часто использу-
ются различные итерационные процедуры [1].
Существует несколько способов прямого отыскания минимума
функционала невязки. При этом для некорректных задач характерным
10/27

38 Гл. 1 . Математические модели. Корректные и некорректные задачи
для итерационного процесса является следующее свойство итераций.
Начальные итерации в итерационном процессе достаточно хорошо при-
ближают точное решение, однако (начиная с некоторой итерации) для
них характерно появление немонотонности и итерационный процесс
«рассыпается». Это обусловлено тем обстоятельством, что в случае
незамкнутого образа оператора ! в случае единственности реше-
ния (1.4 .1) не всякая минимизирующая последовательность будет схо-
дящейся, так как обратный оператор 1 неограничен. Возникает про-
блема — на какой итерации исследователю следует остановиться и обо-
рвать итерационный процесс, чтобы избежать его «рассыпания»? Для
выяснения этого обстоятельства рассмотрим основные типы итераци-
онных процессов для квадратичного функционала в соответствии с [1].
Важную роль при построении итерационных алгоритмов играет про-
изводная функционала по Фреше 28 ,котораядлялинейного
оператора
имеет вид 2

Серия итерационных методов обычно строится по следующему пра-
вилу:

1,2,...,
апараметр0 выбирается по-разному, в зависимости от итерационной
схемы.
1. Простая итерация.Вэтомслучаепараметр0
0
;
он выбирается из условия 0 0 2+

2
для обеспечения сходимости
итерационного процесса.
2. Метод минимальных невязок.Здесь0 находится из условия
минимума функционала 1

2
,
0

,
где .
3. Метод наискорейшего спуска
Вэтомметоде0 выбирается из условия минимума функционала
невязки 2
1

2
идает
0

2
Известно, что итерационные методы (1–3) при точных исходных
данных сходятся к нормальному 0 относительно начального прибли-
жения 0 [1], причем решение 0

называется нормальным отно-
сительно 0 , если оно доставляет минимум функционалу

.
Рассмотрим вместо точной задачи (1.4.1) приближенную,

Æ
,

Æ,
причем

—
линейный непрерывный оператор из некоторого
семейства аппроксимирующих операторов, удовлетворяющий условию

3.
В этом случае последовательность приближений ,
11/27

1.6 . Способы преодоления некорректности. Регуляризация
39
построенная в соответствии с одним из итерационных процессов, мо-
жет весьма сильно отличаться от точного решения задачи (1.4.1).
Однако при достаточно малых погрешностях 2 Æ ,
3
первые прибли-
жения в градиентных методах мало отличаются от соответствующих
приближений при точных исходных данных. С ростом номера итераций
приближения могут довольно сильно отличаться от искомых решений,
что характеризует некорректность задачи. Метод итерационной регу-
ляризации состоит в том, чтобы по имеющейся априорной информации
о погрешности входных данных 2 выбрать некоторое приближение,
близкое к точному решению; в частности, для этих методов параметром
регуляризации является номер итерации . Имеет место утверждение.
Теор ема 1.8 [1]. Методы (1–3) порождают регуляризирующее се-
мейство операторов, в котором параметром регуляризации является
номер итерации. При этом регуляризованное приближение сходится
к нормальному относительно начального приближения решению урав-
нения (1.4 .1) при стремлении погрешности в исходных данных к ну-
лю 2
0.
Теорема 1.8 свидетельствует о принципиальном выборе номе-
ра 2 ,прикотором 2 устойчивы к погрешностям исходных
данных, однако не дает конструктивного способа выбора номера итера-
ции. На практике один из возможных способов выбора 2 состоит
в условии согласования с

Æ ,где0
—нормальное
решение (1.4 .1).
Критерий выбора 2 формулируется следующим образом:

,
где
—
некоторый функционал, зависящий от конкретного итера-
ционного метода; например, для метода 2

+2
Замечание. П
рик
о
н
к
ре
т
н
ойреали
з
ац
и
им
о
ж
н
овв
ы
раж
е
н
и
и
для заменить 0 на
.
1.6.5. Метод усеченных сингулярных разложений. Одним из
эффективных методов построения регуляризующего оператора являет-
ся метод усечения сингулярных разложений, тесно связанный с орто-
гональными разложениями, в частности с рядами Фурье.
Определение 1.9. Сингулярным разложением оператора

называется его представление в виде

,
(1.6 .6)
где ,

—
нормированные ортогональные системы в простран-
ствах и

соответственно, а величины называются сингулярными
числами оператора .
12/27

40 Гл. 1 . Математические модели. Корректные и некорректные задачи
Будем считать последовательность {}ограниченной.Тогда
представляет собой непрерывный линейный оператор из в

ссо-
пряженным оператором, который строится по правилу

,
аоператоры

(1.6 .7)
являются самосопряженными в и

соответственно. Спектр опера-
тора

содержит собственные значения 2

, которым соответ-
ствуют собственные элементы и, возможно, собственное значение,
равное нулю, кратность которого может быть как конечной, так и бес-
конечной. То же самое справедливо для оператора с собственными
элементами
.
При этом нетрудно установить, что собственные элементы связаны
соотношениями

(1.6 .8)
Обратно: если ,

—
нормированные системы собственных
элементов операторов

, удовлетворяющие соотношени-
ям (1.6.8), то оператор допускает представление (1.6.6). В частности,
компактные (вполне непрерывные) операторы всегда допускают сингу-
лярное разложение, причем для них
0,6

[27]. Имеет место
следующее утверждение.
Теор ема 1.9 [18]. Если оператор допускает сингулярное разло-
жение (1.6.6), то оператор, заменяющий обратный, строится по правилу

(1.6 .9)
Всилутеоремы1.9оператор неограничен в том и только в том
случае, если
0. В этом случае оператор можно регуляризо-
вать с помощью усеченного сингулярного разложения, если сохранить
конечное число членов ряда в (1.6.9) и отбросить растущие слагаемые

(1.6 .10)
Здесь параметром регуляризации служит число , которое выбирается
исходя из априорной информации о погрешности Æ .
Анализируя структуру сингулярного разложения, можно понять при-
роду некорректности. Пусть Æ аппроксимирует ,т.е
.
Æ

Æ.
13/27

1.6 . Способы преодоления некорректности. Регуляризация
41
Если известно только Æ , то о коэффициентах разложения ! из
теоремы 1.9 можно утверждать лишь то, что

Æ
,
Æ+
Исходя из этой оценки, полагаем, что вклад слагаемых враз-
ложение для малых (практически при Æ) нельзя вы-
числить с приемлемой точностью. Таким образом, зная сингулярные
числа и соответствующие им собственные элементы, можно судить
о том, какие компоненты решения уравнения вида (1.6 .10) вычисля-
ются по приближению элемента Æ , а какие вычислить невозможно
с приемлемой точностью. К сожалению, вычисление или нахождение
асимптотик сингулярных чисел операторов и численное исследование
их зависимостей от параметров некорректной задачи является весьма
сложной проблемой, хотя для некоторых задач можно построить их яв-
ные представления (особенно в случае самосопряженных операторов).
Иногда оказывается возможным численно найти сингулярные числа
оператора, тогда порядок выбора числа становится ясным.
Отметим, что число слагаемых, участвующих в представле-
нии (1.6 .10), определяется из критерия невязки [6]

Æ
Замечание. Нетрудно установить, что процедура минимизации ста-
билизирующего функционала А. Н . Тихонова при наличии сингулярно-
го разложения приводит к решению (1.6 .10) следующего вида:

Æ
, ,
причем параметр регуляризации , 0 должен быть согласован с по-
грешностью входной информации Æ в соответствии с теоремой 1.5
и также может быть выбран из критерия невязки.
1.6.6. Проекционный метод. Отметим, что с практической точ-
ки зрения одним из эффективных способов нахождения регуляризо-
ванного решения и построения приближенных решений операторных
уравнений является проекционный метод [9]. Он базируется на том,
что решение операторного уравнения отыскивается в виде линейной
комбинации некоторой линейно независимой системы функций, име-
нуемых базисными. Таковыми являются методы Бубнова–Галеркина,
Петрова и т. д ., которые обычно применяются при решении оператор-
ных уравнений и краевых задач для дифференциальных уравнений.
При использовании этой идеи для решения операторных уравнений
1-го рода с вполне непрерывными операторами нужно формулировать
достаточно жесткие условия на систему базисных функций, однако
сведение исходной проблемы к некоторой конечномерной проблеме
позволяет эффективно строить решения.
14/27

42 Гл. 1 . Математические модели. Корректные и некорректные задачи
Рассмотрим операторное уравнение (1.4 .1), где
—
линейный
непрерывный оператор

,п
рич
е
м,

—с
епарабельные
гильбертовы пространства [28] и
0.
Будем отыскивать его решение в виде

,
(1.6 .11)
причем 7
—
заданная линейно независимая система в 8 .П
редстав-
ление вида (1.6.11) дает существенную априорную информацию о точ-
ном решении ; размерность представления и коэффициенты этого
разложения требуется определить. Отметим, что если при решении кор-
ректных задач на основе такого подхода с увеличением числа базис-
ных функций, как правило приближается к точному решению, то для
некорректных задач с неточно заданной правой частью Æ это не так.
Рассмотрим способы определения ,е
сли Æ Æ .Опреде-
лим в систему множеств

,
Æ

9Æ

,
9

1
Введем Æ1,Æ
,,
Æ

.
Имеет место теорема, позволяющая осуществить выбор .
Теорема 1.10 [9].

Æ
0 0,такое,чтоÆ для0ÆÆ0
и

£
,Æ

0приÆ
0.
Отметим, что сходимость приближенных решений к точному бу-
дет иметь место лишь при специальном выборе системы 7 . Пусть
дополнительно к требованиям, описанным выше, оператор
вполне
непрерывен. Тогда оператор
—
вполне непрерывный самосопря-
женный оператор, и по теореме Гильберта–Шмидта существует орто-
нормированный базис из собственных элементов 7 оператора
,

, и набор сингулярных чисел :

12
...
Теперь определим множества ,
Æ,т
.е
.
,какэтоуказановыше,
взяв в качестве базисных собственные функции оператора
.Тогда

0 множества ,
Æ
непусты при достаточно большом ииме-
ет место теорема.
Теор ема 1.11 [9]. Если базис из собственных элементов упорядо-
чен по невозрастанию сингулярных чисел, то при Æ
0

£
,Æ

0
Замечание 1. Обычно постоянные в (1.6.11) определяются
из условия минимума квадратичного функционала невязки

2
(практически идентично методу квазирешений), что
15/27

1.7. Регуляризованные методы вычисления значений
43
приводит к решению линейной алгебраической системы

,7,

Æ
, 7,
(1.6 .12)
причем матрица системы есть матрица Грама для системы элемен-
тов 7 , которая невырождена, поскольку

0 в силу линей-
ной независимости 7 .
К сожалению, система собственных функций оператора мо-
жет быть построена не всегда; тогда приходится использовать любую
полную в систему функций, что в значительной степени усложняет
как строгое обоснование этого метода, так и его практическую реа-
лизацию.Врядепримероввпоследующихразделахможноувидеть
сравнительный анализ эффективности различных разложений, а также
числа регуляризации
.
Замечание 2. Из доказательства теоремы 1.10 следует конструк-
тивный способ выбора Æ, при котором выполняются неравен-
ства

Æ
, 7
2

9
2Æ2
,

Æ1

Æ
, 7
2

9
2Æ2

Отметим, что проекционный метод — один из наиболее эффектив-
ных способов алгебраизации некорректных и обратных задач, т. е.
сведению к исследованию конечномерной алгебраической проблемы
и дальнейшему ее анализу.
1.7 . Регуляризованные методы вычисления значений
неограниченных операторов.
Численное дифференцирование
Вычисление значений неограниченных операторов в условиях за-
шумленности исходных данных представляют собой актуальную зада-
чу вычислительной математики и одну из важнейших некорректных
задач. Иногда решение некоторых обратных задач может быть по-
лучено с помощью операции дифференцирования функции, заданной
в некотором дискретном наборе точек.
В настоящем разделе рассмотрим базовую некорректную задачу
численного дифференцирования функции, заданной в наборе точек.
В прикладных исследованиях, где встречается подобного рода пробле-
ма, значения функции задаются с определенной степенью точности, что
является следствием погрешности измерительной техники. Поэтому
стандартные численные методы, основанные на аппроксимации опера-
тора дифференцирования оператором конечных разностей, в этом слу-
чае не применимы, поскольку задача является некорректной и малая
погрешность входной информации может привести к большой погреш-
ности при реализации процедуры численного дифференцирования.
16/27

44 Гл. 1 . Математические модели. Корректные и некорректные задачи
В связи с этим численное дифференцирование требует процедуры
регуляризации, в основе которой лежит учет погрешности задания
функции при выборе шага сетки. Опишем регуляризованную процедуру
численного дифференцирования на основе двух различных подходов,
изложенных в [6, 9, 10].
Первый подход. В основе первого метода лежит традиционная
аппроксимация дифференциального оператора конечноразностным опе-
ратором. Рассмотрим функцию, заданную на отрезке ,

0,
"
1 ,

. Задача состоит в построении ее производной
по функции
Æ " ,

ивеличинепогрешностиÆ ,такойчто

Æ
(1.7.1)
Определим на отрезке ,

сеточную функцию, которая при
выполнении некоторых условий аппроксимирует производную функ-
ции
,
:

,
3

0,
(1.7.2)
Оценим величину погрешности в норме " ,

.
Отметим, что

и
3 0, справедливо неравенство
:

2Æ+3

;,
3

,где; ,
3

3 . Изэтойоценки
получим
:

2Æ

3 ,
(1.7.3)
причем 3 0и3
0,3
0.
Таким образом, функция : будет аппроксимировать производ-
ную функции только в том случае, если параметр метода (шаг сетки 3)
таким образом зависит от точности задания исходной информации Æ ,
что при Æ
0 3Æ 0, Æ+3Æ
0. При этом можно выбирать
3Æ
Æ
(что весьма часто используется при практических реали-
зациях), где ,
9
—
положительные постоянные и 9 1. Важнейший
вывод при нахождении производной функции, заданной таблично, со-
стоит в следующем: шаг сетки должен быть согласован с погрешностью
входных данных, а его простое уменьшение не приведет к успеху при
решении исходной задачи приближенного дифференцирования. Воз-
можны также случаи, что неудачный выбор точек задания функции не
позволит определить значения производной с требуемой точностью.
В прикладных исследованиях часто возникают задачи, в которых
требуется определение значений производной; при этом значение самой
функции может быть вычислено (или измерено) в любой точке с точно-
стью Æ.
В этом случае возможно определение производной с заданной
точностью , если выбрать шаг по правилу 3 Æ Æ ,а9 определять
ниже из неравенства
2Æ

(1.7.4)
17/27

1.7. Регуляризованные методы вычисления значений
45
Например, при 3 0можновыбрать
9

1Æ

(1.7.5)
Рассмотрим алгоритм вычисления производной функции, заданной
приближенно по вышеописанной схеме.
В качестве примера опишем процесс численного дифференцирова-
ния функции

1, в соответствии с [6].
Пусть значения функции в наборе точек задаются с точностью Æ ,
необходимо вычислить значения производной с точностью .
При проведении вычислительного эксперимента зашумление функ-
ции осуществлялось по правилу
Æ
1

< Æ ,где<
—случай-
ная величина с равномерным законом распределения из отрезка 1, 1 .
Задаем 3 Æ Æ ,фиксируем,например 0,5, 9 выбираем со-
гласно условию (1.7.5). Строим по (1.7.2) функцию :

Æ
+3.
Результаты приведены на рис. 1 .5 для Æ 0,001,
0,01, 3
0,201.
Сплошной линией показан график «точной» производной, точками —
значения производной, вычисленные по описанному выше алгоритму.
Рис. 1.5
Рис. 1 .6
По результатам вычислительных экспериментов наблюдается устой-
чивая аппроксимация первой производной с заданной точностью.
Приведем результаты вычисления производной без регуляризации
(рис. 1.6), когда шаг задается 3
0,5 и уменьшается до 3
0,01
(сплошной жирной линией изображен график «точной» производной).
При этом аппроксимация дифференциального оператора ухудшается
(в некорректных задачах ожидаемый эффект от уменьшения шага
вообще не наблюдается в силу отсутствия непрерывной зависимости
от входной информации)
Аналогично осуществляется процедура нахождения производных
более высоких порядков. Приведем формулу и оценку для при-
ближенного определения второй производной от функции, дважды
18/27

46 Гл. 1 . Математические модели. Корректные и некорректные задачи
дифференцируемой на отрезке ,
, заданной с точностью Æ ,

,т
.е
.

Æ.
Рассмотрим сеточную
функцию

2Æ Æ

2
,
3

0,,

(1.7.6)
Можно показать, что

4Æ

23,
(1.7.7)
где 3 0, причем 3
0приÆ
0.
Таким образом, если 3 Æ
0приÆ
0так,чтоÆ+32
Æ
0,
то приÆ
0 стремится равномерно к
на отрезке ,
.
Например при 3 0: полагая 3 Æ Æ ,получимоценку
9

1 Æ
2
4
2

Приведем результаты приближенного вычисления второй произ-
водной (рис. 1.7) для примера, рассмотренного выше:

с регуляризацией (слева) и без регуляризации (справа).
Рис. 1.7
Второй подход. Второй способ численного дифференцирования ос-
новывается на интерполяции функции, заданной таблично с точностью Æ ,
с использованием сплайн-функций. В основе сплайн-интерполяции
лежит следующий принцип. Интервал интерполяции разбивается на
небольшие отрезки, на каждом из которых функция приближается
полиномом небольшой степени, обычно третьей или пятой. Коэффици-
енты полинома подбираются таким образом, чтобы выполнялись опре-
деленные условия (какие именно, зависит от способа интерполяции).
Общие для всех типов сплайнов третьего порядка требования — непре-
рывность функции и, разумеется, прохождение через предписанные ей
точки. Дополнительными требованиями могут быть линейность функ-
ции между узлами, непрерывность высших производных и т. д .
19/27

1.7. Регуляризованные методы вычисления значений
47
Основными достоинствами сплайн-интерполяции являются ее
устойчивость и малая трудоемкость при вычислениях. Системы линей-
ных уравнений, которые требуется решать для построения сплайнов,
хорошо обусловлены, что позволяет получать коэффициенты аппрок-
симирующих полиномов с высокой точностью. В результате даже при
очень больших вычислительная схема не теряет устойчивость.
Фактически применение оператора предварительного сглаживания
исходной информации позволяет преодолеть некорректность постав-
ленной задачи вычисления неограниченного оператора и определить
производные аналитически от предварительно построенной гладкой
сплайн-функции.
Рассмотрим одномерный случай и наиболее употребительную куби-
ческую сплайн-интерполяцию из класса " 2
,
. Нарис.1
.
8приведены
графики функции

, ее первой и второй производных.
Рис. 1.8
Интерполяция осуществлена с использованием кубических сплайнов;
соответствующие результаты изображены точками, точные значения —
сплошными линиями. Точность задания входной информации порядка
Æ
0,01. Значения функции задаются в
15 точках в диапа-
зоне 0, 4 .
20/27

48 Гл. 1 . Математические модели. Корректные и некорректные задачи
Рис. 1.9
Следует отметить, что некорректность задачи проявляется при уве-
личении числа разбиений, например при вычислении второй производ-
ной при
25 (рис. 1.9)
Замечание. Отметим, что задача численного дифференцирования
также может быть решена в рамках идеологии обращения интег-
ральных операторов типа Вольтерра на основе равенства

Ê
0

0 , численное обращение которых возможно с использо-
ванием регуляризованных алгоритмов применительно к интегральным
операторам, например метода А. Н . Тихонова (см. 1 .6 .2).
1.8 . Построение обратных к вполне непрерывным
операторам на примере
уравнения Фредгольма 1-го рода
Как указано выше, одной из наиболее часто встречающихся на
практике некорректных задач является задача решения уравнения
Фредгольма 1-го рода с гладким или непрерывным ядром. Исследуем
регуляризованную процедуру его численного решения на основе метода
А. Н . Тихонова [29], считая для простоты ядро непрерывной функцией:

'
,
(

(
(

,
,
(1.8 .1)
'
,
(

" ,

,
,

2 ,

Пусть вместо известно такое ее приближенное значение Æ ,
что

Æ.
Предположим, что из априорных соображе-
ний известно, что (
—
кусочно-гладкая, тогда выберем в качестве

=
1
2 ,
.
Пусть вместо ' ,
(
известна такая функция ' ,
(,
что

' '

3,тогда

! 1
2 2

3,где
—
интегральный
оператор, соответствующий ядру ',
(.
21/27

1.8. Построение обратных к вполне непрерывным операторам
49
Используя схему построения регуляризирующего алгоритма
А. Н . Тихонова, перейдем от (1.8.1) к минимизации стабилизирующего
функционала ,где

2,
2

1
2
"

,
(

(
(

2( (
2

(
(1.8 .2)
Построим конечномерную аппроксимацию функционала ,ис-
пользуя квадратурные формулы для аппроксимации интегралов. Для
этого вводим равномерные сетки по ипо( с шагами 3 +,
3

+ ;
(

13,

1 3
. Обозначив

(

, #

#
, 6#,
(

#
,используемквадратурнуюфор-
мулу прямоугольников для вычисления интегралов, аппроксимируя
производную разностным отношением

(

Таким образом, конечномерная аппроксимация функционала (1.8 .2)
имеет вид

#
1

1
3

(1.8 .3)
Используя необходимое условие минимума функции переменных

0,
(1.8 .4)
приходим к линейной алгебраической системе с симметричной мат-
рицей

,
(1.8 .5)
где

,",

#
1

#
,

#
1

#
,
(1.8 .6)
"

"
1, "1

1
2

00
1
2

2
2

1
2

...
0
...
...
...
...
...
...
...
...
...
1
2

...
...
...
1
2

1
2

(1.8 .7)
22/27

50 Гл. 1 . Математические модели. Корректные и некорректные задачи
Для решения системы линейных уравнений вида (1.8.5) можно
использовать различные численные методы. При этом следует учиты-
вать, что матрица системы является симметричной и положительно
определенной. Одним из наиболее эффективных методов решения та-
ких систем является метод квадратного корня [25, 26], а также иные
способы решения, основанные на других идеях [35, 36].
В этом методе симметричная положительно определенная матри-
ца представляется в виде произведения верхней и нижней тре-
угольных матриц #

,где# имеет вид
#

1
0
22 ...

2
...
...
...
...
00.
.
.

,
причем элементы матрицы # находятся по формулам

11,

12
>
2,..., ,

;

#
0 >

(1.8 .8)
Таким образом, от системы (1.8.5) приходим к решению системы
#

либо, введя соответствующее обозначение, к решению двух систем
с треугольными матрицами

,
#

(1.8 .9)
Следует заметить, что при выборе параметра регуляризации по
принципу обобщенной невязки приходится неоднократно при различ-
ных , решать системы вида (1.8 .5); при этом правая часть системы
(вектор )иматрица не зависят от , .
Это позволяет строить спе-
циальные экономичные методы многократного решения систем такого
вида. Представим один из вариантов таких схем. Пусть для различ-
ных , 0 необходимо решить систему (1.8.5) или

,
(1.8 .10)
где

—
матрица, транспонированная к

,размерности( ,

,аматрица" определяется согласно (1.8 .7).
23/27

1.8. Построение обратных к вполне непрерывным операторам
51
При помощи метода квадратного корня (формулы (1.8.8)) матри-
цу " представим в виде " ??,где?
—
двухдиагональная матрица.
Сделав замену в (1.8.10)
? (

?
1

), получим

," ?
1

(1.8 .11)
Умножим это уравнение слева на ? 1

,получим

?
1

(1.8 .12)
Представим матрицу ввиде @A !,где@ ,
!

—
ортогональные матрицы, A
—
правая двухдиагональная матрица [29].
Теперь в уравнении (1.8.12) сделаем замену переменных !

(
!1

), в результате получим
!

@A
!

, !
1

или
A

(1.8 .13)
Здесь A A
—
трехдиагональная матрица и матричное уравне-
ние (1.8.13) без труда решается, например методом прогонки или
методом Пэйджа–Саундерса [36]. Исходный неизвестный вектор
?
1
!
1

,
однако часто нет необходимости возвращаться
квектору
,поскольку,например:если3 0, то необходимо лишь
проверить условие

Æ , которое эквивалентно условию

Æ.
Отметим, что представленная вычислительная схема решения ин-
тегрального уравнения Фредгольма 1–го рода с непрерывным ядром
является наиболее часто используемым инструментом при решении
плохо обусловленных или переопределенных систем линейных алгеб-
раических уравнений независимо от их происхождения.
24/27

Список литературы к гл. 1
1. Алифанов О.М ., Артюхин Е.А., Румянцев С.В . Экстремальные методы
решения некорректных задач. М .: Наука, 1988. 288 с.
2. Ахтямов А.М . Теория идентификации краевых условий и ее приложения.
М.: ФИЗМАТЛИТ, 2009. 272 с.
3. Бакушинский А.Б., Гончарский А.В. Некорректные задачи. М .: МГУ,
1989. 200 с.
4. Бухгейм А.Л . Введение в теорию обратных задач. Новосибирск: Наука,
1988. 184 с.
5. Ватульян А.О . Обратные задачи в механике деформируемого твердого
тела. М.: ФИЗМАТЛИТ, 2007. 223 с.
6. Ватульян А.О ., Беляк О.А ., Сухов Д.Ю., Явруян О.В .Обратныеинекор-
ректные задачи. Учебник. Ростов-на-Дону: изд-во ЮФУ, 2011. 231 с.
7. Ватульян А.О ., Дударев В.В., Недин Р.Д . Предварительные напряжения:
моделирование и идентификация. Ростов-на-Дону: изд-во ЮФУ, 2014.
206 с.
8. Галиуллин А.С . Обратные задачи динамики. М .: Наука, 1981. 144 с.
9. Дени сов А.М . Введение в теорию обратных задач. М.: МГУ, 1994. 206 с.
10. Кабан и хи н С .И . Обратные и некорректные задачи. Новосибирск: Сибир-
ское научное издательство. 2009. 458 с.
11. Кал м ан Р .Е . Идентификация систем с шумами // УМН, 1985.
Т. 40: 4 (25-4)
12. Кр ав ч у к А .С . Основы компьютерной томографии. М.: Дрофа, 2001. 240 с.
13. Курош А.Г . Курс высшей алгебры. М .: Наука, 1965. 431 с.
14. Лаврентьев М.М ., Романов В.Г ., Шишатский С .П . Некорректные задачи
математической физики и анализа. М .: Наука, 1980. 286 с.
15. Латтес Р., Лионс Ж.-Л . Метод квазиобращения и его приложения. М.:
Мир, 1970. 336 с.
16. Ми зохата С . Теория уравнений с частными производными. М .: Мир, 1977.
504 с.
17. Мей з Дж. Теория и задачи механики сплошных сред. М .: Мир, 1974. 319 с.
18. Морозов В.А . Регулярные методы решения некорректных задач. М .: Наука,
1987. 240 с.
19. Наттерер Ф. Математические аспекты компьютерной томографии. М .:
Мир, 1990. 280 с.
20. Новацкий В. Теория упругости. М.: Мир, 1975. 872 с.
21. Оль ховой А .Ф . Обратные некорректные задачи. Введение в проблематику.
Таганрог: изд-во ТТИ ЮФУ, 2009. 132 с.
22. Романов В.Г . Обратные задачи математической физики. М .: Наука, 1984.
261 с.
23. Самарский А.А ., Вабищевич П .Н . Численные методы решения обратных
задач математической физики. М .: Едиториал УРСС, 2004. 480 с.
25/27

Список литературы к гл. 1
53
24. Хак ен Г . Си нерге тика. Иерархии неустойчивостей в самоорганизующихс я
системах и устройствах. М .: Мир, 1985. 424 с.
25. Тихонов А.Н ., Арсенин В.Я . Методы решения некорректных задач. М .:
Наука, 1986. 287 с.
26. Тихонов А.Н ., Гончарский А.В., Степанов В.В ., Ягола А .Г . Численные
методы решения некорректных задач. М .: Наука, 1990. 230 с.
27. Треногин В.А . Функциональный анализ. М .: ФИЗМАТЛИТ, 1980. 496 с.
28. Хатсон В ., Пим. Дж. Приложения функционального анализа и теории
операторов. М .: Мир, 1983. 432 с.
29. Хермандер Л . Анализ линейных дифференциальных операторов с частны-
ми производными. Т . 2 . М .: Мир, 1986. 456 с.
30. Юрко В.А . Введение в теорию обратных спектральных задач. М .:
ФИЗМАТЛИТ, 2009. 384 с.
31. Яхно В.Г . Обратные коэффициентные задачи для дифференциальных урав-
нений упругости. Новосибирск: Наука, 1990. 304 с.
32. Ambarzumian V .A . Uber eine Frage Eigengwert theorie // Zeits. f . Phisik.
1929. 53 . P. 690–695.
33. Bui H .D . Inverse Problems in the Mechanic of Materials: An Introduction.
CRC Press, Boca Raton, FL, 1994. 224 p.
34. Isakov V . Inverse problems for PDE. Springer-Verlag, 2005. 284 p.
35. Lanczos C. Iterative solution of large-scale linear systems // J. Soc. Indust.
аnd Appl. Math. 1958. V. 6 . P. 91–109.
36. Paige C.C ., Saunders M.A . An algorithm for sparse linear equations and
Sparse least squares. // Asm trans. Math. Softw. 1982. V. 8. P. 43–71 and
P. 195–209.
26/27

Глава 2
КОНЕЧНОМЕРНЫЕ ОЗ.
ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ПАРАМЕТРОВ
ВКРАЕВЫХЗАДАЧАХ(КОЭФФИЦИЕНТОВ
ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ,
ПАРАМЕТРОВ ДЕФЕКТОВ,
ГРАНИЧНЫХ УСЛОВИЙ)
Введение к гл. 2
Одним из важных классов коэффициентных ОЗ является класс
задач об определении постоянных коэффициентов дифференциальных
операторов по некоторой дополнительной информации о решении. Эта
проблемаможетрешатьсякакврамкахобщихподходов,опирающихся
на теорию обратных коэффициентных задач (об этом речь пойдет в по-
следующих главах), так и в рамках изучения проблемы идентификации
параметров модели. Стратегия исследования общих коэффициент-
ных ОЗ в настоящее время направлена на разработку различных подхо-
дов к изучению нелинейных некорректных проблем, к которым сводят-
ся многие ОЗ. Проблема идентификации модели приводит к некоторой
конечномерной ОЗ, для построения решения которой используются
различные подходы, описываемые в настоящей главе. Отметим, что
в рамках конечномерных обратных задач могут быть изучены многие
обратные задачи, которые и не относятся к классу коэффициентных,
в частности те, где осуществлен этап структурной идентификации или
имеютсяформулы,которыесвязываютпараметрымоделиидополни-
тельную информацию, по которой производится идентификация. Тако-
выми, например, являются задачи об идентификации полостей канони-
ческой формы (сфера, эллипсоид), прямолинейных трещин в упругой
среде по данным акустического зондирования, дефектов в балочных
конструкциях и задачи по идентификации параметров, входящих в гра-
ничные условия.
Отметим, что наиболее изученными являются задачи идентифика-
ции коэффициентов линейных дифференциальных операторов с посто-
янными коэффициентами, которые представляют собой наиболее часто
используемые объекты в математическом моделировании. С помощью
краевых задач или задач Коши для них моделируются различные про-
цессы, например: малые колебания систем материальных точек, дефор-
мирование материалов с реологическими свойствами, деформирование
стержней, пластин.
P owe red by T CP DF (www.tcp df.o rg)
27/27

Введение к гл. 2
55
В частности, к таковым относятся линейные динамические системы,
моделирующие достаточно широкий спектр процессов. Если для ряда
моделей вопрос об определении коэффициентов операторов решается
достаточно просто в силу их ясного физического смысла (плотность,
модуль упругости) и простых экспериментов для их определения, то
для некоторых из них требуется решение обратных задач об их иденти-
фикации на основе некоторой дополнительной информации о решении.
В этом случае, поскольку этап структурной идентификации пройден,
то этап параметрической идентификации сводится к некоторым ко-
нечномерным коэффициентным обратным задачам для обыкновенных
дифференциальных операторов. С точки зрения идентификации линей-
ных динамических систем в этом случае речь идет об определении
передаточной функции [14, 38, 45] линейной динамической системы
в классе рациональных функций. В случае когда идентифицируемая
система линейна, нахождение параметров этой системы по заданному
(измеренному) в конечном числе опорных точек решению может быть
осуществлено на основе двух наиболее распространенных способов.
Один из них приводит к линейной некорректной проблеме, второй —
к нелинейной проблеме.
Первый из них состоит в выполнении дифференциального урав-
нения в опорных точках, что приводит к решению линейной алгеб-
раической системы (возможно, переопределенной) относительно ко-
эффициентов. Отметим, что при реализации этого подхода требуется
знание не только самих решений, но и их производных, что в условиях
неточно заданной входной информации при использовании разностных
аппроксимаций для нахождения производных приводит к большим вы-
числительным погрешностями и, как следствие, к неустойчивой проце-
дуре отыскания коэффициентов. Эта проблема обычно преодолевается
путем использования сплайн-аппроксимаций, позволяющих находить
производные аналитически с небольшой погрешностью.
Второй способ основан на свойстве решений дифференциальных
уравнений с постоянными коэффициентами, которое состоит в том, что
общие решения задач для таких операторов складываются из суммы
функций экспоненциального вида с (вообще говоря) комплексными
показателями, которые и определяют поведение системы. Отметим,
что эти показатели и коэффициенты уравнения связаны характеристи-
ческим уравнением соответствующего дифференциального оператора
и могут быть найдены с помощью метода Прони [68] (см. 2.1) либо
прямой минимизацией некоторого неквадратичного функционала. При
нахождении минимума функционала невязки обычно используются
современные численные методы минимизации функционалов как гра-
диентные, так и не использующие процедуру вычисления производных.
Наиболее популярны среди последних методы глобального случайного
поиска, эволюционные или генетические алгоритмы, основные принци-
пы реализации которых будут изложены ниже в этой главе.
1/27

56
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Отметим также, что важнейший инструмент обработки эксперимен-
тальной информации и соответственно решения ОЗ — это метод наи-
меньших квадратов. В настоящее время имеется большое число моно-
графий, посвященных различным аспектам его применения, например
работы [45, 47, 51]; его использование для решения некорректных
задач тесно связано с методом квазирешений (см. разд. 1.6).
В качестве еще одного замечания к вводной части главы отметим,
что не любая функция подходит в качестве входной информации для
отыскания коэффициентов линейных дифференциальных операторов.
Рассмотрим простой пример постановки задачи об определении по-
стоянных коэффициентов для дифференциального оператора второго
порядка.
Пусть дано обыкновенное дифференциальное уравнение с постоян-
ными коэффициентами

1
2

0,
(2.0 .1)
где 1, 2
—
некоторые постоянные. Таким дифференциальным уравне-
нием, которое широко используется при моделировании различных ли-
нейных систем, описываются различные процессы в механике, физике,
технике, биологии, такие как: колебания материальной точки с одной
степенью свободы в линейно сопротивляющейся среде; ползучесть ли-
нейно вязкоупругих материалов и другие.
Построение решения такого уравнения при заданных значени-
ях 1 , 2 достаточнопростоипредставимовформе

"
1 B1

"
2 B2
,
(2.0 .2)
где B1, B2
—
корни характеристического уравнения, "1 , "2
—произволь-
ные постоянные, определяемые из начальных или граничных условий.
Сформулируем ОЗ для дифференциального уравнения (2.0.1). Пусть
задано его решение
на некотором интервале ,
.Обратная
задача состоит в определении двух параметров 1 , 2 ихарактеризует
конечномерную обратную задачу. Заметим, что для такой простейшей
постановки в первую очередь необходимо дать ответ на два вопроса:
1) существует ли решение такой обратной задачи при любой входной
информации; 2) если существует, то единственно ли оно.
Можно сформулировать следующие (но далеко не исчерпывающие)
ответы на поставленные задачи:
1) не для каждой достаточно гладкой функции
можно решить
эту простейшую коэффициентную обратную задачу и однозначно опре-
делить 1, 2;
2) не любая информация пригодна для идентификации ОИ, т. е.
на
необходимо наложить некоторые дополнительные условия.
Несложно сформулировать условия на входную информацию (функ-
цию
), обеспечивающие нахождение параметров 1 , 2 единствен-
ным образом.
2/27

2.1. Метод Прони
57
Теорема 2.1 [30]. Пусть
—
заданная (измеренная) функция.
Если на отрезке ,

1, 2 такие, что

1
2

0,
(2.0 .3)
тогда ОЗ разрешима и 1 , 2 определяются однозначно.
Отметим, что условие (2.0 .3) относится к таким же типам условий,
как и в сформулированных в разд. 1 .1 примерах. Здесь роль величи-
ны играет разность
1

2
1

2.
Обоснование утверждения теоремы 2.1 основано на выполнении
уравнения (2.0.1) для двух различных значений аргумента 1 , 2 исо-
ставлении линейной алгебраической системы относительно искомых
параметров 1 , 2; условие (2.0 .3) есть условие однозначной разре-
шимости этой системы. Отметим, что функция

B
при
любом B не удовлетворяет этому условию ни на каком отрезке из-
менения и, следовательно, не может быть использована в качестве
входной информации для процедуры параметрической идентификации
уравнения (2.0 .1). К сожалению, условие (2.0 .3) трудно проверяемо на
практике,ибовнеговходятпроизводные
, которые, как правило,
не измеряются, а могут быть найдены лишь численно по известному
решению
.
Процедура их нахождения по
является некор-
ректной и требует регуляризации, которая может быть осуществлена
на основе регуляризованных приемов дифференцирования, изложенных
выше в разд. 1 .7.
Также возникает резонный практически важный вопрос — можно
ли поставить условия, обеспечивающие единственность решения сфор-
мулированной обратной задачи не в терминах величины ,алишь
в терминах измеряемых величин
?
Таким образом, решение даже простейших коэффициентных ОЗ
требует специальных подходов, базирующихся на процедуре регуляри-
зации, не только на этапе решения, но при исследовании единствен-
ности и при формулировке достаточных условий, ее обеспечивающих.
Отметим также, что априорное знание погрешности входной информа-
ции является важнейшей информацией при решении различных клас-
сов ОЗ, которую необходимо учитывать при построении решений.
Ответы на некоторые вопросы, возникающие при исследовании ко-
нечномерных обратных задач, а также методы их решения и будут
представлены в настоящей главе.
2.1 . Метод Прони
Как уже было отмечено во введении к гл. 2, идентификация по-
стоянных коэффициентов дифференциальных операторов по некоторой
информации о решении является одной из весьма распространенных за-
дач математического моделирования. Остановимся подробнее на одном
подходе к анализу задачи об определении коэффициентов линейного
3/27

58
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
дифференциального оператора с исторической точки зрения. Впервые
задача об определении вещественных показателей в представлении
решения в виде линейной комбинации экспоненциальных функций
была рассмотрена достаточно давно, в 1795-м г. в работе [68], которая
иположиланачалоисследованиямвэтойобластиидаланазвание
методу, именуемому сейчас как метод Прони (Гаспар Рише). Анали-
зируя законы расширения газов, он пришел к выводу, что искомые
зависимости могут быть представлены в виде линейной комбинации
экспоненциальных функций с некоторыми неизвестными показателями
и предложил метод определения этих показателей по данным 2 изме-
рений. Этот метод позволил определить функцию, содержащую сла-
гаемых вида " B . Идеяметодасостоитвтом,чтоеслииз-
мерения произведены на некоторой равномерной сетке (скажем, через
равные промежутки времени или равные промежутки по координате),
то возможно упрощение сформулированной обратной задачи и расщеп-
ление обратной задачи на три последовательно решаемые подзадачи.
В дальнейшем этот метод был перенесен на комплексные показатели.
Изложим основные идеи этого метода.
Итак, рассмотрим линейный дифференциальный оператор с посто-
янными коэффициентами

...

(2.1 .1)
Известно, что в случае отсутствия у характеристического многочле-
на оператора (2.1 .1) кратных корней решение однородного уравнения

0представимоввиде

1
"

,
содержащем 2 постоянных " и
B

. Обычно" определяются из
граничных или начальных условий. Если эти данные (соответствую-
щие граничные или начальные условия) известны, то неизвестными
являются лишь показатели B ,которыеинеобходимоопределитьиз
некоторой дополнительной информации о решении, например по дан-
ным

,6
1, 2, . . . , . Еслиинформацииограничныхили
начальных условиях нет или ее трудно верифицировать, то приходится
определять оба набора параметров " и
B

из данных о решении уже
в большем числе точек
,
6
1,2,...,2.П
риэтомнеобхо-
димо решать нелинейную систему уравнений, которая при численной
реализации в условиях зашумленности входной информации может
и не иметь решений. В том случае, когда образуют арифметическую
прогрессию, возможно существенно упростить процедуру реконструк-
ции на основе следующего приема.
Предположим, что 0

1.Введемследующиеперемен-
ные: : " B 0
,
<

.
4/27

2.1. Метод Прони
59
Тогда для решения обратной задачи имеем систему относительно
введенных переменных

1
:

<
1

1,2,3,...,2
(2.1 .2)
В соотношениях (2.1.2) осуществим замену индекса

,
умножим обе части на некоторые параметры и просуммируем от
нулядо.
Получим следующее равенство:

1
:

<
1

1
:

<
1

1,..., 2 (2.1 .3)
Из (2.1.3) следует, что существует некоторая связь между искомы-
ми параметрами. Если

0,
(2.1 .4)
т. е.
<

являются корнями некоторого алгебраического уравнения -й
степени с коэффициентами , то эти коэффициенты находятся из
линейной системы уравнений

1,...,2
(2.1 .5)
Из этих построений вытекает следующая последовательность дей-
ствий при решении исходной задачи определения параметров диффе-
ренциального оператора (2.1 .1).
1. На основе данных задачи формируется и решается систе-
ма (2.1 .5). Поскольку она однородная, то компоненты вектора
находятся с точностью до множителя, для определенности мож-
но принять 0 1.
2. Находятся корни алгебраического уравнения (2.1.4) с коэффици-
ентами,найденныминапервомэтапе;егокорнямиявляются< ,
откуда далее определяются параметры B
1

.
3. Параметры : и соответственно " определяются из решения
системы

1
:

<
1

,
1, 2, . . . , ,cопределителемВан-
дермонда, который обращается в нуль лишь при равных между
собой <
.
Таким образом, эта система однозначно разрешима
(естественно, при наличии дополнительной априорной инфор-
мации о том, что корни характеристического многочлена для
оператора в (2.1.1) различны).
5/27

60
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Пример. В качестве примера использования метода Прони рас-
смотрим весьма часто встречающийся в приложениях случай 2 .
Параметры
находятся из системы (полагаем 0 1
2

3, 4, или

30,

40
(2.1 .6)
Решение (2.1.6) находится по формулам Крамера,

2
21

3,
(2.1 .7)
что совпадает с результатами в задаче идентификации полимерных
материалов [27], где формулы (2.1.7) получены иным, более длинным
путем (см. также далее разд. 2 .5).
Далее решается квадратное уравнение <2

1< 2 0инаходятся
показатели экспонент B
.
По ним уже восстанавливаются коэффици-
енты исходного дифференциального оператора по формулам Виета.
Замечание 1. Опираясь на решения (2.1 .7), нетрудно понять, ка-
ково условие разрешимости задачи в рассматриваемой постановке для
оператора второго порядка, выраженное не через значения заданной
функции и значения ее производной, как это сформулировано в тео-
реме 2.1, а через заданные значения
.
Оно состоит в выполнении
условия

2
21

0
(2.1 .8)
В некотором смысле это условие заменяет условие (2.0 .3), в кото-
ром участвует производная, и может быть использовано при анализе
конкретных задач.
Замечание 2. Несмотря на внешне успешную схему решения сфор-
мулированной обратной коэффициентной задачи, практическая ее реа-
лизация, особенно в условиях зашумления входной информации, редко
позволяет успешно преодолеть некорректность. Погрешность рекон-
струкции нарастает при порядке оператора, начиная со значений 4–5,
особенно, когда корни характеристического многочлена сильно раз-
личаются. В этом случае часть слагаемых в представлении реше-
ния (2.1 .2) может вообще не оказывать влияния на решение в некото-
ром диапазоне изменения параметров в рамках определенной точности
измерений (вычислений); соответственно реконструкция таких экспо-
ненциальных слагаемых не может быть осуществлена с хорошей точ-
ностью. Отметим, что такая проблема присуща задаче идентификации
параметров линейной дифференциальной модели в вязкоупругости из
опыта на ползучесть (см. далее разд. 2 .5).
В то же время для упрощения процедуры идентификации мож-
но использовать один из важнейших принципов самоорганизации
Г. Хакена [53], на основе которого в сложных системах исключается
большая часть переменных и задача сводится к решению ряда задач
меньшей размерности. Отметим, что подобный подход описан в [37]
6/27

2.1. Метод Прони
61
при определении функции релаксации, причем предлагается исполь-
зовать одну экспоненту на каждый порядок величины в эксперимен-
тальных данных. На основе этих рассуждений предложим следующий
прием типа «лесенки» к решению проблемы, сформулированный в нача-
ле настоящего пункта. Пусть решение некоторого дифференциального
уравнения с постоянными коэффициентами имеет вид

1
"

,
(2.1 .9)
где показатели B вещественны и упорядочены следующим образом:
0B1

B
2B3

...B

,
"

0
Пустьизвестнаинформацияорешениивида

,
6
1,2,...,2,
(2.1 .10)
причем будем считать, что 0 1 , 6
1,2,...,2 1,не
обязательно образуют арифметическую прогрессию. Тогда нетрудно
понять, что при больших преобладающим слагаемым в (2.1 .8)
является функция

.
Исходя из дополнительной
информации (2.1 .10) при 6 2 ,2 1 можно оценить показатель
B

2 2 1

2 2 1
и коэффициент "

2 B 2
. Далееобразуемфункцию

.
Относительно нее при больших значе-
ниях также можно установить, что преобладающим слагаемым для

является функция " 1
B
1

(отметим, что знак " 1
неизвестен); и аналогично находим
B
1

2 2

2 3

2 2

2 3
,
"
1

2 2

B
1

2 2

Далее процесс продолжается до тех пор, пока абсолютное значение
сформированной на очередном шаге функции не станет меньше напе-
ред заданной погрешности.
Замечание 3. Требование положительности всех показателей не
является обязательным, в приведенных рассуждениях достаточно выде-
лить преобладающие экспоненциальные решения в некоторой области.
Замечание 4. Условие того, что характеристические показатели
не являются кратными, обычно выполняется для реальных объектов,
моделируемых обыкновенными дифференциальными уравнениями.
7/27

62
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
2.2 . Метод квазилинеаризации
В настоящем разделе обсуждается один из подходов к осуществле-
нию этапа параметрической идентификации при известной структуре
дифференциального оператора, описывающего ОИ в соответствии с ра-
ботами [12, 15]. При этом одним из традиционных способов решения
такой проблемы является построение общего решения и нахождение
параметров с помощью минимизации функционала невязки. Как пока-
зано выше в разд. 2 .1 , даже в случае линейного дифференциального
оператора с постоянными коэффициентами решение такой существенно
нелинейной задачи наталкивается на серьезные вычислительные слож-
ности. В случае когда оператор нелинеен, построение общего решения
далеко не всегда возможно и нельзя предложить простого метода
алгебраизации, как в линейном случае. Точное решение краевой задачи
чаще всего можно построить только численно, возникает вопрос —
можно ли по результатам наблюдения за решением (допустим, что
в некотором наборе точек известно решение некоторой краевой задачи
или задачи Коши для этого дифференциального оператора) эффективно
осуществить этап параметрической идентификации.
Прямые методы отыскания параметров, как, например, рассмот-
ренные ниже в разд. 2 .3 генетические алгоритмы, требуют значитель-
ных вычислительных ресурсов и применяются, когда другие средства
неэффективны. Однако некоторые подобные задачи успешно решаются
с применением метода, в основе которого лежит принцип квазили-
неаризации, который состоит в том, что исходная нелинейная задача
заменяется последовательностью линеаризованных задач Коши, сходя-
щейся к искомому решению. Рассмотрим процедуру применения метода
квазилинеаризации подробнее на некоторых примерах для дифферен-
циального оператора второго порядка.
Этот метод был предложен в работе [12], где имеются многочислен-
ные идеи и приложения к ряду задач другого типа; в настоящем пункте
предложено более подробное описание одного из возможных вариантов
его реализации и конкретные примеры для известных моделей.
Пусть задана задача в форме нелинейного ОДУ второго порядка
(хотя порядок уравнения не имеет решающего значения для реализа-
ции алгоритма) с некоторым параметром B,

,
,
B,
,
(2.2 .1)
с двухточечными граничными условиями 0

0. Обратная за-
дача состоит в определении параметра B по дополнительной информа-
ции о решении. Для построения некоторой аналитической основы для
решения обратной коэффициентной задачи используем метод линейной
аппроксимации правой части дифференциального оператора (2.2 .1);
построим решение краевой задачи как предел последовательности
линейных краевых задач. Будем отыскивать значение параметра B,
8/27

2.2. Метод квазилинеаризации
63
а в качестве второго искомого параметра возьмем значение производ-
ной функции в начальной точке 0
.
В качестве дополнительной информации о решении выступают зна-
чения искомой функции в наборе точек при известном значении
параметра B; в рассматриваемом случае двух параметров для ОДУ
второго порядка необходимо три значения функции. Предположим, что
известны значения ,

0,1,2.
На основе задачи (2.2 .1) строится каноническая система, в кото-
рой искомый параметр B считается функцией, зависящей от времени,
и условие неизменности параметра по времени входит в задачу одним
из уравнений:

,
,
B ,
,
B

0
(2.2 .2)
Следует заметить, что наличие дополнительных неизвестных посто-
янных параметров добавляет соответствующее количество тривиаль-
ных уравнений в каноническую систему, а также соответственно изме-
няет количество одновременно решаемых на каждом шаге линеаризо-
ванных задач, о которых пойдет речь ниже. Далее на основе квазили-
неаризации строим последовательность линейных задач, которые фор-
мируются при линейной аппроксимации функции ,
,
B ,
:

1
,

,
B

,
B
1

0 (2.2 .3)
Для системы (2.2.3) решается задача Коши, причем в качестве
начальных условий на первом шаге алгоритма используется начальное
приближение

0,
B
00

B
0,
(2.2 .4)
которое строится следующим образом: 0
—
известное значение функ-
ции вмомент0 , 0
—
начальное приближение первой произ-
водной, вычисленное на основе разностной аппроксимации 0

10
+
10
.
Далее согласно разностным аппроксимациям
определяются

иB0
—
начальное приближение для параметра B,полученноеиззадачи
Коши для (2.2.1) в точке 0
. Решая задачу Коши (2.2.3), (2.2.4), строим
9/27

64
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
последовательность, обладающую квадратичной сходимостью, в том
числе и находим искомое значение B.
Проиллюстрируем алгоритм метода квазилинеаризации различными
примерами (в том числе и изложенными в [12, 26]).
Пример 1 [12].
Рассмотрим уравнение Ван-дер-Поля, часто встречающееся в при-
ложениях при моделировании автоколебаний, например в кардиологии
и электроэнцефалографии:

B
21

(2.2 .5)
Проведем следующий вычислительный эксперимент. Будем отыски-
вать значения первой производной в начальной точке 0 4ипарамет-
ра B по дополнительной информации о решении в некотором наборе
точек.
Соответствующая уравнению (2.2 .5) каноническая система прини-
мает вид

B
21

,
B

0,
откуда строится линеаризованная система для нахождения соответ-
ствующих последовательностей:

1
,

1,
B
1 0 (2.2 .6)
Предположим, что для точных значений параметров B
9,999824896, 0

0,079186697 имеется информация о значениях
функции: решения в точках 4
1,80843,
6
1,63385,
8
1,40456 С использованием грубого разностного приближения
для первой и второй производных были получены следующие
начальные приближения параметров: B0
9,1249645, 0

4 +2 0,0872900 (табл. 2 .1).
Ниже приведены графики функций иеепроизводной
для различных итераций, а также изображен процесс сходимости по
параметрам. Был использован достаточно жесткий критерий останова
между последовательными итерациями 106
, поскольку в случае
идентификации материальных параметров от точности их определения
будут зависеть результаты дальнейших расчетов на их основе.
Отметим, что существует более сильная зависимость решения
от значения параметра B,чемотпараметра0
.Изрис.2
.
1видно,
10/27

2.2. Метод квазилинеаризации
65
Таблица 2.1
Noитерации

0
1
9,124964519 0,087290000
2
9,849023118 0,054172484
3
9,996368896 0,078399618
4
9,999823148 0,079186191
5
9,999824880
0,079186684
Рис. 2 .1 . Графики функций и

для первых че тырех итераций
что хотя на второй итерации значение 0

сравнительно далеко от
истинного значения, а на основной части интервала наблюдения пове-
дение функции определяется значением параметра B.
Пример 2.
Рассмотрим пример исследования жесткой задачи малой размерно-
сти, имеющей периодическое решение. В качестве такового рассмотрим
уравнения Бонгоффера–Ван-дер-Поля, описывающие ток через клеточ-
ную мембрану [39]:

6
1

6
2 63,
(2.2 .7)
причем известны значения 61 106, 62 3. Требуется определить 63
по следующей информации о решении: 20,2 1,653749451,
20,3 1,628157725, 20,4 1,609505551. При этом приняты:
точное решение 63 0,7, 20,2
0,148945572, начальные прибли-
жения 63

0 0,1, 0
20,2 0,1.
В табл. 2 .2 представлены численные расчеты, демонстрирующие
сходимость метода по параметру, что свидетельствует о достаточно
быстрой сходимости итераций к точному значению.
11/27

66
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Таблица 2.2
Noитерации

0
1
0,1
0,248945572
2
0,631950655
0,153923358
3
0,699359746
0,148938092
4
0,699997876
0,148945950
5
0,699999742
0,148946666
Пример 3.
Рассмотрим уравнения Хиггинса, описывающие простейшую модель
гликолиза и характеризующие релаксационные автоколебания [39]:

,
(2.2 .8)
причем для вычислительного эксперимента выбрано значение , 100.
Требуется восстановить значение параметра 0 по следующей ин-
формации о решении: 2,5 1,881745807, 2,6 3,138590679,
2,7 6,799976140.
При этом приняты: точное решение 0 10, 2,5
1,244246680,
начальные приближения 00 9, 0
2,5 0,1. В рассматриваемой
задаче сходимость по параметру 0

оказалась весьма медленной,
необходимая точность достигнута лишь на 19-й итерации, что отобра-
жено в табл. 2.3.
Таблица 2.3
Noитерации

0
1
8,999999999
1,144246680
2
10,147235930
1,145202160
3
10,001584229
1,184396081
4
9,999974007
1,211173266
5
9,999990613
1,235141890
6
9,999995249
1,239582449
7
9,999997576
1,241872745
...
...
...
19
9,999999924
1,244236166
Кроме того, отметим, что при выборе 00 7 и менее итерационный
процесс для данной задачи сходится к другому решению.
12/27

2.3 . Методы решения конечномерных обратных задач
67
Замечание. Следует отметить, что подобные задачи о восстанов-
лении коэффициентов нелинейных дифференциальных операторов по
информации о решении в наборе точек часто оказываются весьма чув-
ствительными к начальному приближению значений параметров, кото-
роеневсегдаможноопределитьприемлемымобразомспомощьюпри-
веденной процедуры грубого приближения производных на основе раз-
ностного отношения. В этом случае можно рекомендовать использовать
для нахождения начального приближения какой-либо вариант метода
наименьших квадратов или генетический алгоритм [28] (см. разд. 2.3).
2.3 . Методы решения конечномерных обратных задач
на основе генетических алгоритмов
В настоящем разделе рассматриваются методы решения обратных
конечномерных задач на основе генетических алгоритмов. Как было
подчеркнуто ранее, решение обратных конечномерных задач может
быть сведено к задаче минимизации функционала невязки на некото-
ром подпространстве в !
.
Естественно, что для нахождения такого
решения можно использовать методы нахождения минимума функ-
ции многих переменных. При этом необходимо решать либо сложные
нелинейные системы трансцендентных уравнений, либо использовать
итерационные процессы для нахождения минимального значения функ-
ционала невязки, что требует нахождения его градиента. Существует
широкий класс градиентных методов оптимизации, способных опре-
делить направление поиска оптимума в соответствии с информацией
о частных производных функции. Эти методы, именуемые градиентны-
ми, используют на каждом шаге поиска минимума функционала опера-
цию вычисления его градиента, что не всегда приводит к цели. В то же
время возможно использовать некие альтернативные подходы, связан-
ные либо с процедурой глобального случайного поиска [28, 45], либо
с неким промежуточным гибридным вариантом, который позволяет на-
ходить минимум функции многих переменных со сложным рельефом.
Изложим далее основные идеи построения таких алгоритмов поиска,
которыенеиспользуютнахождениеградиента.
Пусть задана некоторая функция, далее именуемая целевой функ-
цией, зависящая от нескольких переменных, и требуется найти такие
значения переменных, при которых значение функции минимально.
Задачи такого рода называются задачами оптимизации ивстречаются
на практике очень часто.
Например, для рассматриваемого класса задач идентификации ОИ
на этапе параметрической идентификации в качестве целевой функции
выступает неквадратичный функционал невязки, минимум которого
требуется определить. Надо отметить, что для этого функционала
линии уровня сильно вытянуты и похожи на извилистые овраги, име-
ются локальные минимумы.
13/27

68
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Известными классическими численными методами поиска решения
многомерной задачи оптимизации являются: методы градиентного и ко-
ординатного спуска, метод оврагов, метод сопряженных градиентов,
метод Гаусса–Ньютона, метод Левенберга–Марквардта, метод глобаль-
ного случайного поиска или простого перебора — Монте-Карло [41].
Такие методы имеют теоретическое обоснование и оценки скорости
сходимости. Однако наряду с достоинствами у них есть также и ряд
недостатков, таких как требование дифференцируемости или непре-
рывности целевой функции, наличие у нее одного экстремума (или его
предварительную локализацию). Отметим, что на сходимость перечис-
ленных методов весьма сильно влияет выбор начального приближения.
Заметим также, что при увеличении числа неизвестных, доставляющих
минимум целевой функции, значительно возрастает объем вычислений.
Альтернативой же классических методов решения многомерных опти-
мизационных задач, где целевая функция, например, имеет сложный
рельеф и не имеет аналитического представления, являются эволюци-
онные алгоритмы, в частности генетические алгоритмы (ГА), получив-
шие широкую популярность в последнее время [15, 28].
ГА (англ. genetic algorithm) — это эвристический алгоритм поиска,
используемый для решения задач оптимизации и моделирования путем
последовательного подбора, комбинирования и вариации искомых пара-
метров с использованием механизмов, напоминающих биологическую
эволюцию. Этот алгоритм является разновидностью эволюционных
вычислений (англ. evolutionary computation). Отличительной особен-
ностью генетического алгоритма является акцент на использование
оператора «скрещивания», который производит операцию рекомбина-
ции решений-кандидатов, роль которой аналогична роли скрещивания
генов в живой природе.
Неоспоримым достоинством ГА является отсутствие ограничений
на целевую функцию, перечисленных выше в классических методах,
кроме тех, которые естественным образом вытекают из постановки
оптимизационной задачи.
В настоящее время ГА получили широкое распространение при
решении многомерных задач оптимизации. Впервые основные принци-
пы ГА сформулированы Холландом [61] в начале 60-х годов. Основны-
ми из них были генетические алгоритмы и классификационные систе-
мы. Целью оптимизации с помощью ГА является лучшее возможное
решение задачи по одному или нескольким критериям. Приведем опи-
сание работы ГА и основные функции, используемые при его работе.
Пусть стоит задача минимизации целевой функции 1 ,...,

,
зависящей от переменных, причем !
!.
Схема работы прос-
того ГА представлена на рис. 2.2. МожновыделитьследующиеэтапыГА:
̄
создание начальной популяции;
̄
вычисление функций приспособленности для особей популяции
(оценивание);
14/27

2.3 . Методы решения конечномерных обратных задач
69
̄
выбор индивидов из текущей популяции (селекция);
̄
скрещивание иили мутация;
̄
вычисление функций приспособленности для всех особей;
̄
формирование нового поколения.
Рис. 2.2
Если выполняются условия останова, то — «конец цикла», иначе —
«начало цикла».
Опишем подробно этапы работы ГА.
1. Создание начальной популяции. На этом этапе случайным обра-
зом генерируется начальная популяция Р(0), состоящая из особей
(векторов) # ,
>
1,...,.
Популяция — совокупность особей, каждая из которых представля-
ет возможное решение поставленной задачи.
Значение элемента для каждой особи # ,
>
1, . . . , ,устанавли-
вается случайно с помощью равномерного распределения на интервале

,
!,где
—
область поиска переменных
—устанавли-
вается пользователем и является важнейшей априорной информацией
при решении обратных задач (см. пример 1 разд. 1 .5 ).
2. Оценка решения. Каждая особь # определяет функцию со-
ответствия # , в качестве которой зачастую принимают целевую
функцию или функцию приспособленности (fitness) .
Далее, происходит отбор лучших особей (векторов) в следующую
популяцию путем селекции. Существует несколько видов селекции,
опишем, например случайную или турнирную селекцию. Такая селек-
ция выполняется по соревновательному принципу, согласно которому
каждый родитель или потомок попарно сравнивается с C противни-
ками.ПриэтомC,
C
1 является параметром ГА, устанавливается
пользователем и обычно принимает значения C 0,05–0,1,где
—
размер популяции. Противники выбираются случайно разным образом,
например, с помощью закона равномерного распределения. Победитель
определяется путем попарного сравнения функций соответствия. Особь
побеждает в соревновании, если ее функция соответствия (по мень-
шей мере) не хуже, чем у ее противника. После этого все особи
15/27

70
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
сортируются по убыванию числа побед. Лучшие особи образуют новую
родительскую популяцию. При одинаковом числе побед преимущество
получает особь с лучшим значением функции соответствия. Совокуп-
ность из особей образует множество родителей, необходимых для
следующего этапа ГА.
3. Формирование нового поколения. На этом этапе происходит гене-
рацияпотомковспомощьюгенетическихоператоров.Отметим,чтодля
решения задач оптимизации необходимо представить каждый объект
в форме, подходящей для использования в генетическом алгоритме. Для
кодирования объекта можно использовать самый простой вариант —
битовое значение этого объекта. Но, к сожалению, такое кодирование
не лишено недостатков. Основной недостаток заключается в том, что
соседние числа отличаются в значениях нескольких битов, так напри-
мер: числа 7 и 8 в битовом представлении различаются в 4-х позициях,
что затрудняет функционирование генетического алгоритма и увели-
чиваетвремя,необходимоедляегосходимости.Длятогочтобыизбе-
жать этой проблемы, лучше использовать кодирование, при котором
соседние числа отличаются меньшим количеством позиций, в идеале —
значением одного бита. Таким кодом является код Грея, который целе-
сообразно использовать в реализации генетического алгоритма.
Как известно, в теории эволюции важную роль играет способ, ко-
торым признаки родителей передаются потомкам. В генетических алго-
ритмах за передачу потомкам признаков родителей отвечает оператор,
который называется скрещиванием (его также называют «кроссовер»
или «кроссинговер»). Действует он следующим образом:
̄
из популяции выбираются две особи, которые будут родителями;
̄
случайным образом определяется точка разрыва компонент вектора
(здесь описан принцип действия так называемого одноточечного
кроссовера;такжеизвестендвухточечный, -точечный, однород-
ный);
̄
потомок определяется как «склеивание» части первого и второго
родителя.
Рассмотрим функционирование этого оператора:
Родите л ь 1 0000000000
Родите л ь 2 1111111111 .
Допустим, разрыв происходит после 3-го бита хромосомы, тогда:
Родител ь 1: 0000000000 » 000 1111111 Пото мок 1
Родител ь 2: 1111111111 » 111 0000000 Пото мок 2 .
Следующий генетический оператор предназначен для того, что-
бы поддерживать разнообразие особей с популяции. Он называется
16/27

2.3 . Методы решения конечномерных обратных задач
71
оператором мутации.Вкаждойстроке,котораяподвергаетсяму-
тации, каждый бит с вероятностью A ,назначаемойпользователем,
изменяется на противоположный. Кроме того, используется еще и так
называемый оператор инверсии, который заключается в том, что хро-
мосома делится на две части и затем они меняются местами. Схемати-
чески это можно представить следующим образом:
000 1111111 » 1111111 000 .
Популяция, полученная после мутации, записывается поверх ста-
рой, и этим цикл одного поколения завершается. Последующие поко-
ления обрабатываются таким же образом: отбор, кроссовер и мутация.
В принципе, для функционирования генетического алгоритма доста-
точно этих генетических операторов, но на практике используют еще
и некоторые дополнительные операторы или модификации этих двух
операторов. Например, кроссовер может быть не одноточечный (как
было описано выше), а многоточечный, когда формируется несколько
точек разрыва (чаще всего две). Кроме того, в некоторых реализациях
алгоритма оператор мутации представляет собой инверсию только од-
ного случайно выбранного бита хромосомы.
После применения генетических операторов происходит оценка по-
томка путем определения значения его функции соответствия, после
чего потомок добавляется в новую популяцию.
4. Критерий останова. В качестве критерия останова могут быть
следующие заданные пользователем события:
а) достижение в ходе эволюции заданного числа поколений A
;
б) достижение заданного уровня качества, когда, например, значение
функций соответствия всех особей в популяции превысило некото-
рое пороговое значение;
в) достижение заданного уровня сходимости, когда особи в популя-
ции настолько подобны, что дальнейшее их улучшение происходит
чрезвычайно медленно.
ГА являются очень перспективными методами при решении многих
обратных задач идентификации коэффициентов дифференциальных
операторов, дефектов, параметризуемых конечным числом параметров,
а также при определении начального приближения в итерационных
процессах среди функций простой структуры: линейных, квадратич-
ных, кусочно-постоянных. При этом необходимо знание области, в ко-
торой находятся искомые параметры (см. п. 1.6.3)
Эффективность ГА сильно зависит от таких деталей, как метод
кодировки решений, о котором упоминалось выше, применяемые ге-
нетические операторы, настройки параметров алгоритма, как частный
критерий успеха. К сожалению, теоретическая обоснованность генети-
ческих алгоритмов оставляет пока желать лучшего. Теоретическая ре-
зультаты, отраженные в литературе, посвященной генетическим алго-
ритмам, на сегодняшний день не дает оснований говорить о выработке
17/27

72
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
каких-либо строгих механизмов для четких предсказаний их поведе-
ния, оптимальной настройке параметров ГА и даже давать какие-либо
гарантии сходимости.
Приведем пример работы типичного ГА на примере поиска миниму-
ма функции Асклея, имеющей достаточно сложный рельеф, представ-
ленной на рис. 2.3, и глобальный минимум в точке 0; 0.
Рис. 2.3
На рис. 2 .4 представлены графики эволюции переменных 1 , 2
в зависимости от числа поколений, отложенных по оси 1.Каквидно,
после 10-го поколения произошла стабилизация решения задачи на-
хождения глобального минимума функции Асклея. Критерием останова
при реализации ГА в рассматриваемом случае было ограничение на
число поколений 50.
Рис. 2.4
Отметим, что генетические алгоритмы стали весьма популярными
при решении самых разных типов конечномерных обратных задач —
коэффициентных, геометрических, смешанных. Основное требование
при использовании ГА — быстрое и достаточно точное решение пря-
мой задачи, поскольку реализация ГА требует обычно от тысячи до
нескольких тысяч обращений к решению прямой задачи.
18/27

2.4. Об определении параметров упругих потенциалов
73
Замечание. Поскольку генетические алгоритмы основаны на неко-
торых эвристических подходах, практически отсутствуют теоретиче-
ские результаты по оценке сходимости и точности, пригодности най-
денного решения. Отметим, что современные математические пакеты
имеют встроенные варианты ГА, однако имеется ряд проблем. Иссле-
дователи отмечают, что если велик размер области поиска решений
и количество идентифицируемых параметров превышает 7–8, эффек-
тивность этого инструмента становится низкой. Требуется как сужение
области поиска, так и разделение большеразмерных проблем на ряд
более простых. Имеется также некоторые аспекты использования ГА,
требующие своего решения, таковыми являются: критерий выхода, на-
значение вероятности мутации, возможное изменение стратегии поиска
на больших итерациях и т. д.
Отметим, что с помощью методов ГА были исследованы задачи об
определении упругих постоянных ортотропного материала [9].
2.4 . Об определении параметров упругих потенциалов
В настоящем разделе описано применение метода квазилинеариза-
ции, описанного в 2.2, для решения обратной задачи идентификации
материальных параметров упругих потенциалов. Алгоритм реализован
для задачи сдвигового кручения полого нелинейно упругого цилиндра.
Вывод уравнений равновесия осуществлен с помощью полуобратного
метода Сен-Венана. Приведены результаты вычислительных экспери-
ментов по идентификации параметров материала Блейтца и Ко и мате-
риала Клоснера–Сегала.
Отметим, что в современной инженерной практике все большее
значение приобретает моделирование деформирования узлов, тел при
помощи конечноэлементных пакетов. В этих пакетах упругое дефор-
мирование материала определяется функцией удельной потенциальной
энергии упругой деформации (потенциалом) = D, зависящей от меры
деформации Коши–Грина [29]. Для моделирования нелинейного по-
ведения материала вводятся модели упругих потенциалов, зависящих
от инвариантов тензора деформаций, и содержащие набор некоторых
параметров. В описанных выше пакетах уже доступны модели матери-
алов, учитывающие пьезоэффект, пористость, различные нелинейные
эффекты при деформации.
Существенной проблемой при решении задач в КЭ-пакетах является
определение (идентификация) параметров, полностью задающих пара-
метры удельной потенциальной энергии при деформации. Их значения
обычно находятся из экспериментов. Задача согласования результатов
эксперимента и теоретических расчетов является очень интересной
и непростой, а важность ее постоянно возрастает в связи с появлением
все большего числа новых материалов и совершенствованием моделей
нелинейных материалов, задающихся с помощью функции удельной
потенциальной энергии. Нахождение параметров, входящих в тот или
19/27

74
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
иной потенциал, приводит к некоторой коэффициентной обратной зада-
че по их определению. Чаще всего такие задачи решаются с помощью
метода наименьших квадратов, что приводит к решению нелинейных
систем трансцендентных уравнений.
Одним из перспективных подходов к решению обратной задачи
идентификации материальных параметров является метод квазили-
неаризации [12]. Он обладает рядом преимуществ, среди которых:
сравнительно низкие вычислительные затраты, линейно зависящие от
размерности задачи, и отсутствие этапа «подстройки» параметров, от-
носящихся исключительно к вычислениям, для решения конкретной
задачи, который необходим, например, в генетических алгоритмах [15].
Из недостатков самый существенный — чувствительность метода к на-
чальному приближению.
В зарубежной литературе одно из самых ранних применений ме-
тода квазилинеаризации, он же обобщенный метод Ньютона–Рафсона,
для идентификации параметров дифференциальных уравнений было
осуществлено в работах [15] и [65]. В работе [15] с помощью этого ме-
тода определялся параметр нелинейной краевой задачи для уравнения
Ван-дер-Поля, в работе [65] решалась задача по определению шести
параметров из краевой задачи для моделирования газового абсорбента.
В последние годы метод квазилинеаризации часто используется
для решения математически сложных задач (сингулярных систем [59],
дифференциальных уравнений в частных производных [67]), а также
проводятся работы по его дальнейшему обобщению [62] и теоретиче-
скому обоснованию [63, 65, 66].
Помимо собственно метода квазилинеаризации, перспективным на-
правлением исследования является комбинирование традиционных де-
терминированных градиентных методов, к которым относится метод
квазилинеаризации, и стохастических методов, например генетических
алгоритмов, основные идеи которых изложены в 2.3 . При таком под-
ходе классический градиентный метод, чувствительный к начальному
приближению, используется для уточнения решения стохастического
метода, который в силу своих особенностей не может обеспечить боль-
шой финальной точности результата, но способен производить поиск
в широком диапазоне изменения параметров. Использованию комбини-
рованных методов и сравнению их со стохастическим и градиентным
подходами посвящена работа [60].
В настоящем исследовании проводилась одновременная идентифи-
кация двух материальных параметров, характеризующих упругий по-
тенциал, по следующему алгоритму. Сначала выводились уравнения
равновесия и решалась прямая задача, для чего использовался полу-
обратный метод Сен-Венана [26, 29]. Краевая задача о деформиро-
вании нелинейно-упругого тела решалась встроенным методом среды
Maple для краевых задач (метод трапеций с интерполяцией Ричард-
сона). Далее формировалась информация, необходимая для постановки
20/27

2.4. Об определении параметров упругих потенциалов
75
и решения обратной задачи, которая затем решалась с помощью метода
квазилинеаризации.
Постановка задачи. Рассмотрим сдвиговое кручение полого
нелинейно-упругого цилиндра (рис. 2 .5). Внутренняя поверхность
его закреплена, внешняя смещается в положительном направлении
координаты 7 на заданный угол, при этом точка недеформированной
Рис. 2 .5
конфигурации переходит в точку .
Положение любой точки деформиро-
ванного цилиндра описывается функ-
циями A E, имеющей смысл нового
радиуса-вектора точки; E,описы-
вающей приращение к координате 7,
иF
—
аппликатой точки. Задача реша-
лась для двух нелинейных потенциа-
лов упругой деформации, причем иден-
тификацияпроводиласьраздельнодля
случаев, когда информация для иден-
тификации материальных параметров
задавалась функциями A E и

E
Для вывода уравнений равновесия прямой задачи был использован
полуобратный метод Сен-Венана [29], в котором использовалось сле-
дующее представление деформирования:

!
A
E,

E ,
F
:
(2.4 .1)
Поведение материала цилиндра задавалось трехпараметрическими
потенциалами Блейтца и Ко [26] (сжимаемый материал),
=

-
1

3
1

, (2.4 .2)
и Клоснера–Сегала (несжимаемый материал),
=

0
-
13

0
-
23

G
-
23
2

(2.4 .3)
Поставим задачу об идентификации параметров ,,
0
материа-
ла (2.4 .2).
На основе соотношений (2.4 .1) и (2.4.2) были получены уравнения
равновесия, которые представляют собой систему двух обыкновенных
дифференциальных уравнений второго порядка, и составлена краевая
задача вида

A
E
A
E ,

E ,
A
E ,

E,
E,
,,
0,

E
HA
E,

E,
A
E,

E ,
E,
,,
0,

A
E
0 E0,AE1

E
1,

E
0 (0,E1

(
1,
(2.4 .4)
21/27

76
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
где в серии расчетов принимались следующие значения параметров:
E
0
0,85, (0
0, E1
1, (1
0,1. Задача была решена для сле-
дующих значений материальных параметров: 4 1, ,
0,5, 0
0
(так называемый «упрощенный» материал Блейтца и Ко). После этого
внутри цилиндра в трех точках (E0 0,88, E
1 0,90, E
2 0,92)
были найдены величины {A E0
,

E
0,
A
E
0,

E
0;
A
E
1,
A
E
2},
необходимые для решения обратной задачи с двумя неизвестными
параметрами. Здесь и далее принимается, что в качестве априорной ин-
формации для идентификации материальных параметров используются
значения функции A E.
Следует отметить, что в случае, когда значения производных не
могут быть получены из имеющихся данных, их можно считать неиз-
вестными параметрами и идентифицировать наряду с искомыми пара-
метрами обратной задачи. Для этого следует соответственно увеличить
количество точек, в которых снимается информация о значении функ-
ции, задающей информацию для идентификации параметров.
Обратная задача состояла в отыскании неизвестных константных
значений материальных параметров ,,
0
для материала Блейтца и Ко
ипараметровG,
0
для материала Клоснера–Сегала. Значения мате-
риальных параметров при проведении вычислительных экспериментов
были взяты из [26]. Подробное описание алгоритма для случая одно-
временной идентификации одного материального параметра и значения
производной в начальной точке представлено выше в разд. 2 .2 . Изло-
жим далее основную идею метода квазилинеаризации в применении
к обсуждаемой задаче кручения цилиндра.
На основе нелинейной задачи (2.4 .4) построена каноническая си-
стема дифференциальных уравнений, состоящая из уравнений первого
порядка, куда неизвестные параметры входят как неизвестные функ-
ции, производные которых равны нулю,

A
1E A2
E,

1E 2
E ,
A
2E 1
A
1E,

1E,
A
2E,

2E,
,E ,
0E,
E,

2E H1
A
1E,

1E,
A
2E,

2E,
,E,
0E,
E,
,
E
0,
0
E
0,
(2.4 .5)
и составляется задача Коши со следующими начальными условиями:

A
1E0

A
E
0,
A
2E0

A
E
0,

1E0

E
0,

2E0

E
0,
,E
0 ,0,
0E
0 00,
(2.4 .6)
причем ,0, 00
—начальное приближение.
Обозначим решение задачи Коши (2.4 .5), (2.4.6) через
A
E ,

E ,

A
E ,

,E ,

0E.
22/27

2.4. Об определении параметров упругих потенциалов
77
Наряду с решением системы (2.4.5), (2.4 .6) на каждом шаге алго-
ритма требуется решение системы, линеаризованной в его окрестности.
Эта система получается из (2.4.5) разложением неизвестных функций
по степеням формального параметра :
A
1E A10 E A11
E ;
A
2E A20
E

A
21E;

1E 10E 11
E ;

2E 20
E

21E;
,E
,
0E ,1
E ;
0E
0
0E 01
E
Собирая коэффициенты при 1 и подставляя вместо A10 E,
A
20E,

10 E,

20E,
,
0E,
0
0E решение нелинейной задачи, приходим
к линеаризованным уравнениям

A
11E A21E,

11 E 21E,
A
21 E 2

A
11E,

11E,
A
21E,

21E,
,
1E,
0
1E,

A
E,

A
E ,

E ,

,E,

0E,
E

21 E H2

A
11 E,

11E,
A
21E,

21E,
,
1E,
0
1E,

A
E,

A
E ,

E ,

,E,

0E,
E

,
,
1E 0,
0
1E 0,
(2.4 .7)
Решение краевой задачи (2.4 .7) определяет коррекцию точного ре-
шения задачи (2.4 .5), (2.4 .6) Будем отыскивать решение задачи (2.4 .7)
ввиде
A
%#
E
A
%#1
E

A
% #2
E ,
(2.4 .8)
где A%#1
E
—
решение системы (2.4.7) с начальными условиями

A
%# 1
E
0 0,
A
% #1
E
0 0,

%#1
E
0 0,

%#1
E
0 0,
,
%# 1
E
0 1,
0
%# 1
E
0 0,
(2.4 .9)
а A%#2
E
—
решение системы (2.4 .7) с начальными условиями

A
%# 2
E
0 0,
A
% #2
E
0 0,

%#2
E
0 0,

%#2
E
0 0,
,
%# 2
E
0 0,
0
%# 2
E
0 1
(2.4 .10)
Решив задачи (2.4.7), (2.4.9) и (2.4 .7), (2.4.10) и подставляя их
решения в (2.4.8), составляем систему линейных алгебраических урав-
нений для определения коэффициентов ,

с использованием инфор-
мации о значениях искомой функции в точках:

A
% #1
E
1 A%#2
E
1 AE1

A
E
1,
A
% #1
E
2 A%#2
E
2 AE2

A
E
2
23/27

78
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Решив ее, находим коррекцию данного шага итерации,
,
1,0

,
0
100

,
и повторяем итерационный процесс. Критерием выхода из итераций
служит малость величины отклонения & функции A E от найденных
в прямой задаче значений A E1
,
A
E
2.
Ниже в табл. 2 .4 представлены результаты расчетов по одновре-
менной идентификации двух материальных параметров для материала
Блейтца и Ко в случае, когда априорная информация для обратной
задачи предоставляется функцией A E . Здесь и далее критерий выхода
(невязка в заданных точках) принимался равным 108 вравномерной
метрике.
Таблица 2.4
No

1 0,8
0
1,27266106 0,19411439 0,12514 103
2 0,47266106 0,19411439 0,32374085 0,06347079 0,33619 103
3 0,14892020 0,13064360 0,29066425 0,05267191 0,12730 103
4 0,14174405 0,07797170 0,16710409 0,03219300 0,34160 104
5 0,30884814 0,04577870 0,07944939 0,01823670 0,51838 105
6 0,38829752 0,02754200 0,03221366 0,00785140 0,63047 106
7 0,42051119 0,01969060 0,00495420 0,00120428 0,79640 107
8 0,42546539 0,01848631 0,00049895 0,00012580 0,18500 108
Истинные значения параметров: ,
0,5, 0
0. Было выбрано
следующее начальное приближение: ,0 0,8, 00 0.
В итоге реализации итерационного процесса были получены следу-
ющие значения параметров: , 0,42546539, 0
0,01848631. Резуль-
таты расчетов для материала Блейтца и Ко в случае, когда априорная
информация для обратной задачи предоставляется функцией, представ-
лены в табл. 2 .5
Истинные значения параметров: , 0,5, 0
0. Начальное прибли-
жение: ,0
0,27, 00
0,01.
Полученные значения параметров: , 0,42514873, 0
0,01856644.
Результаты расчетов для материала Клоснера–Сегала в случае, когда
априорная информация для обратной задачи предоставляется функци-
ей, представлены в табл. 2.6
Истинные значения параметров: G 0,1, 0
0,5. Начальное при-
ближение: G0 0,2, 00 0. Полученные значения параметров: G
0,08320760, 0
0,52774245.
24/27

2.4. Об определении параметров упругих потенциалов
79
Таблица 2.5
No

1 0,27
0,01
1,39247799 0,45024988 0,93811 103
2 1,12247799 0,46024988 1,95671829 0,77121213 0,86099 103
3 0,83424030 0,31096225 0,13470843 0,00888680 0,90034 103
4 0,69953187 0,30207545 0,20701078 0,04721002 0,34869 103
5 0,49252109 0,25486543 0,26564695 0,07256558 0,13019 103
6 0,22687414 0,18229986 0,25965637 0,06749251 0,51618 104
7 0,03278223 0,11480735 0,19422318 0,04786133 0,19407 104
8 0,22700542 0,066946022 0,11791842 0,02874694 0,58873 105
9 0,34492383 0,038199082 0,05934413 0,01452648 0,14456 105
10 0,40426796 0,023672605 0,02001782 0,00490412 0,2888 106
11 0,42428579 0,018768481 0,00086294 0,00020204 0,297 107
12 0,42514873 0,018566436 0,00014104 0,00003535 0,7 1010
Таблица 2.6
No

1 0,2
0
0,094961231 0,58947828 0,18754 104
2 0,10503877 0,58947828 0,031305303 0,05708868 0,76880 105
3 0,07373346 0,53238960 0,009393636 0,00512809 0,10016 105
4 0,08312710 0,52726150 0,000080504 0,00048095 0,51982 107
5 0,08320760 0,52774245 0,000007173 0,00001217 0,11 1010
В табл. 2.7. представлены результаты расчетов для материала
Клоснера–Сегала в случае, когда априорная информация для обратной
задачи предоставляется функцией E.
Истинные значения парамет-
ров: G 0,1, 0
0,5. Начальное приближение: G0 0,2, 00 0,8.
Найденные значения параметров: G 0,09566589, 0
0,48197916.
Таким образом, в качестве заключения к настоящему пункту отметим,
что метод квазилинеаризации позволяет проводить одновременную
идентификацию нескольких параметров дифференциальных уравнений,
в том числе материальных параметров в экспериментах с использовани-
ем математических моделей деформирования нелинейно-упругих мате-
риалов. Главное достоинство этого метода заключается в сравнительно
большой скорости счета и принципиальной возможности увеличивать
количество идентифицируемых параметров без значительного роста
требуемых машинных ресурсов. Недостатком метода является высокая
25/27

80
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Таблица 2.7
No

1 0,2
0,8
0,23378660 0,38024541 0,21993 105
2 0,03378660 0,41975458 0,05795243 0,02334176 0,23083 104
3 0,02416583 0,44309634 0,04967854 0,03003085 0,81904 105
4 0,07384437 0,47312719 0,01989764 0,00791245 0,19653 105
5 0,09374201 0,48103964 0,00192388 0,00093953 0,15728 106
6 0,09566589 0,48197916 0,00002079 0,00003149 0,123 108
чувствительность к начальному приближению; его нахождению следу-
ет уделять больше внимания, возможно основываясь на иных способах
его отыскания.
2.5 . Идентификация полимерных материалов
на основе дифференциальной формы
определяющих соотношений
Проблема определяющих соотношений является одной из основных
проблем в механике деформируемого твердого тела [14, 37]. Определе-
ние констант или функций, входящих в определяющие соотношения,
на основе данных эксперимента есть основная задача эксперименталь-
ной механики. В связи с внедрением в практику новых (композици-
онных) материалов, часто обладающих реологическими свойствами,
проблема оцифровки конкретных материалов на этапе параметрической
идентификации весьма актуальна. В настоящем разделе обсуждаются
некоторые коэффициентные задачи применительно к идентификации
вязкоупругих (полимерных) материалов.
Полимерные материалы являются весьма распространенными кон-
струкционными материалами, область применения которых расширя-
ется с каждым днем. Это происходит как за счет использования из-
вестных полимеров в новых областях человеческой деятельности, так
и за счет создания новых полимерных и композиционных материалов.
В связи с этим весьма актуальными становятся расчеты на прочность
и устойчивость конструкций из таких материалов, что невозможно осу-
ществить без процедуры их идентификации как при изготовлении, так
и в процессе эксплуатации. При этом на современном этапе появилась
возможность производить материалы с наперед заданными свойствами,
что требует достаточно серьезной предварительной проработки мате-
матической модели ОИ и ее оцифровки, т. е . реализации этапа пара-
метрической идентификации при постулировании общего операторно-
го вида определяющих соотношений. Полимерным и композиционным
материалам на основе полимеров свойственно наличие реологических
26/27

2.5. Идентификация полимерных материалов
81
свойств, т. е . существенной является зависимость законов деформиро-
вания от истории нагружения [37, 40]. При этом идентификация для
трехмерных зависимостей может быть осуществлена в рамках модели
линейной изотропной вязкоупругости при помощи двух простейших
экспериментов — опыта на одноосное растяжение и опыта на кручение.
К настоящему времени имеются несколько подходов к моделирова-
нию определяющих соотношений линейной вязкоупругости. Наиболее
популярными являются операторные соотношения, базирующиеся на
двух типах операторов: дифференциальных операторов с постоянными
коэффициентами и интегральных операторах Вольтерра с разностными
ядрами. Отметим, что в ряде моделей эти подходы эквивалентны.
Заметим, что результаты экспериментов свидетельствуют о том, что
полимерным материалам присущи такие свойства, как ползучесть, ре-
лаксация, последействие и сильная зависимость свойств от температу-
ры, причем графической иллюстрацией первых трех свойств являются
кривые, изображенные на рис. 2.6–2 .8
Рис. 2 .6
Рис. 2 .7
Рис. 2 .8
Этап структурной идентификации для полимеров начался еще
в XIX веке, когда были предложены простейшие модели Кельвина–
Фойгта и Максвелла, сыгравшие свою роль в описании реологии этих
материалов, однако не дающие адекватного описания их поведения.
Поиски адекватной и вместе с тем простой модели продолжаются и по
сегодняшний день. Ограничимся рассмотрением одномерной модели.
Опираясь на основные черты механического поведения полимеров,
можносделатьвывод,чтосвязь носит не функциональный,
а операторный характер. В механике деформируемого твердого тела
принято описывать эту связь либо при помощи дифференциальных опе-
раторов с постоянными коэффициентами, либо при помощи интеграль-
ных операторов типа Вольтерра [40], причем долгие годы осуществлял-
ся выбор ядер этих операторов на основании анализа эксперименталь-
ных данных (ядра Абеля, Работнова, Бронского–Слонимского и др.) .
Обоснование выбора конкретной модели, составляющее этап структурной
идентификации, в настоящее время интенсивно обсуждается в научной
P owe red by T CP DF (www.tcp df.o rg)
27/27

82
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
литературе. Вместе с тем простота модели, адекватно учитывающей
основные свойства ОИ, является одним из главных факторов. Будем ис-
пользовать в качестве структурной модель стандартного вязкоупругого
тела (или модель Зинера), которая достаточно адекватно описывает
ползучесть, релаксацию и последействие. Определяющее соотношение
в этом случае имеет вид [14, 37]

/,
(2.5 .1)
где
—
мгновенный модуль, /
—
длительный модуль,
—
время ре-
лаксации, причем / .
Эти параметры (или коэффициенты диффе-
ренциальных операторов) подлежат определению из результатов экс-
перимента, где задается, например ,иизмеряется ,изопыта
на одноосное растяжение в некотором дискретном наборе временных
точек
.
Обратная коэффициентная задача состоит в определении
величин ,
,
/
по . При этом возможны два способа определения
параметров ,
/,
.
Первый опирается на следующий результат.
Теорема 2.2 [14]. Пусть на отрезке 0, # заданы и

и существуют точки 1, 2 , 3 такие, что

0
Тогда ,
/,

определяются однозначно.
Утверждение теоремы доказывается следующим образом. Исходя
из (2.5 .1) и считая, что определяющие соотношения выполняются для
некоторых времен 6 1, 2, 3, получим линейную алгебраическую
систему для определения величин ,
,
/ , определитель которой
в силу условия теоремы отличен от нуля; а значит, эта система имеет
единственное решение.
Заметим, однако, что по заданным и

в некоторые моменты
времени их производные
и

определяются неустойчиво и,
следовательно, для определения
и

необходима регуляри-
зация в соответствии с одним из изложенных выше в гл. 1 способов.
Отметим, что один из наиболее простых методов дифференцирования
функции, заданной поточечно, основан на использовании регуляризо-
ванного метода конечных разностей или сплайн-аппроксимаций, кото-
рые изложены в разд. 1 .7.
Иной способ идентификации состоит в измерении напряжения
(опыт на релаксацию) при постоянной деформации или в измере-
нии деформации (опыт на ползучесть) при постоянном напряже-
нии. В обоих случаях измеряемой функцией является функция вида

B ,причем,
B

0, могут быть как положитель-
ными (релаксация), так и отрицательными (ползучесть). Этап парамет-
рической идентификации состоит в определении фигурирующих выше
трех параметров. Пусть эта функция измерена в моменты времени ,
1/27

2.5. Идентификация полимерных материалов
83
6
1, 2, 3; тогда в стандартном подходе получается нелинейная систе-
ма относительно этих параметров. Введем в рассмотрение величины

1
.
Если измерения происходят через равные проме-
жутки времени,

1 6 1,тонетруднополучить,что
B

1
2
,
после чего параметры и
, входящие линейно в функциональную
зависимость, легко определяются.
Другой способ идентификации основан на применении преобра-
зования Лапласа к (2.5.1). В результате применения преобразования
Лапласа получим
=

,
(2.5 .2)
где =
!

1
" !

#
есть передаточная функция этого динамического
объекта, а

)
'
,

)
'

Очевидно, что = 0
/
1
,=

1
. Непосредственная аппрок-
симация функции + рациональной функцией параметра при-
водит к нелинейной проблеме — решению нелинейной системы алгебра-
ических уравнений. Гораздо более эффективным является общий под-
ход, основанный на сравнении идентифицируемой системы с некоторой
эталонной системой, в качестве каковой обычно выбирается система
с известным временем релаксации 0
.
Рассмотрим подробнее этот
подход.
В НИИМ и ПМ Ростовского госуниверситета (ныне Южного феде-
рального университета) в 90-е годы прошлого столетия была создана
установка АСНИ-полимер, на которой возможно осуществлять следую-
щие эксперименты:
1) режим съема данных ( задано, определяется ;
2) ЛДМ — эксперимент (режим определения параметров линейной
дифференциальной модели);
3) частотный эксперимент (режим определения комплексного мо-
дуля и тангенса потерь, 0
D
>

0, D >
D
>

>D
>,
D
>
—
модуль накопления, D > —модуль потерь, 7
D
+D
).
Подробно о работе этой установки и о методике идентификации
можно узнать из [1].
Вернемся к рассмотрению функционального уравнения (2.5 .2)
Преобразуем = квиду
=

,
0

1
1!$
,
$
"
#
,
,
0,0
$

,
1
1
#

!
#

(2.5 .3)
Тогда
,
0

#$
1
"
,
,
1
1
#

,
0
1
#

1
"

2/27

84
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Далее связь между трансформантами входа и выхода вида

,
0

1
1!$

будем называть ориентированной моделью. При экспериментальной
обработке часто удобнее перейти от ориентированной модели к неори-
ентированной модели, в которой между входными и выходными пара-
метрами предлагается связь вида [14]

,
где :1

:
2

!
1!%1
соответствует фильтру нижних,
а :3

!%
1
1!%1

—
верхних частот.
Вэтомслучае выражаются через ,0 , ,1 , $ инаоборот.Отме-
тим, что постоянные определяются методом наименьших квадратов
из условия минимума функционала невязки

2
и находятся из решения линейной системы с симметричной матрицей
3

,
(2.5 .4)
где

1
:

Из системы (2.5 .4) находятся , а затем определяются ,0 , ,1 , $ ,
что и дает решение ОЗ и позволяет идентифицировать полимерный ма-
териал в рамках выбранной модели. Параметр #1 при этом назначается
произвольно, порой с использованием априорной информации.
Замечание 1. Следует отметить, что в общей теории определяю-
щих соотношений в вязкоупругости можно исходить из соотношений
в трансформантах (2.5.2), причем передаточная функция есть отно-
шение двух полиномов. Некорректность задачи идентификации вязко-
упругих свойств на практике проявляется в том, увеличение степени
полиномов до второй, а числа идентифицируемых параметров с трех до
пяти приводит к сильной неустойчивости процедуры их определения.
Замечание 2. При наличии двух релаксационных механизмов с не
сильно различающимися временами релаксации для уточнения необ-
ходимо расширение модели и увеличение порядка дифференциальных
операторов в определяющих соотношениях (2.5 .1) до второго. Тогда
в опыте на ползучесть или релаксацию этап параметрической иден-
3/27

2.6 . Определение коэффициента температуропроводности
85
тификации (подобно предыдущему) приводит к нахождению уже пяти
параметров, характеризующих семейство функций вида

1 B1

2 B2

При помощи введения параметров

решение
возникающей нелинейной проблемы расщепляется на нахождение па-
раметров B
1

,где<
—
корни квадратного уравнения
<
2<
0,

14
23

,
24
2
3

132
2,
а остальные параметры, входящие линейно, находятся или из решения
линейной системы, или на основе метода наименьших квадратов.
Отметим, что подобная проблема в общей ситуации может быть
решена на основе описанного выше метода Прони, изложенного
в разд. 2.1, дающего те же результаты. Обычно исследователь не знает
о наличии двух или более релаксационных механизмов; выявление
этой особенности деформирования требует не только правильной об-
работки входной информации, но и активное ее формирование путем
изменения во времени характера нагружения, что и было реализовано
всистемеАСНИ-Полимер.
2.6 . Определение коэффициента
температуропроводности
В настоящем пункте изучается одна из простейших обратных ко-
эффициентных задач об определении постоянного коэффициента, вхо-
дящего в уравнение в частных производных — уравнение теплопровод-
ности. При этом используется традиционный подход, позволяющий
построить решение некоторой начально-краевой задачи и на основе
аналитического решения и измерения поля температур в некоторой
точке (или наборе точек) определить искомый коэффициент.
Учет температурных факторов при расчете напряженно-деформи-
рованного состояния твердых тел базируется на модели связанной
термоупругости [14, 15]. В эту модель помимо упругих характеристик
входят и теплофизические величины, которые необходимо определять
из некоторых экспериментов. При этом к уравнениям движения сплош-
ной среды добавляется уравнение притока тепла, которое и служит
для определения поля температур. Наиболее популярной является мо-
дель несвязанной задачи, когда механические поля и поля температур
определяются последовательно: сначала решается уравнение тепло-
проводности и определяется поле температур, а затем на основе его
находятся напряжения. Подробно с постановками ОЗ для уравнений
параболического типа и методах их решения можно познакомиться
в монографиях [34, 35, 50].
4/27

86
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
В качестве примера идентификации рассмотрим простейшую КОЗ
об определении постоянного коэффициента температуропроводности
в соответствии с [14].
Для того чтобы его найти, необходимо воздействовать на ОИ,
осуществить некоторый теплофизический эксперимент и по изменению
температуры определить нужный параметр. Обычно изменение темпе-
ратуры на практике осуществляется путем внесения в эксперименталь-
ную установку нагревательного элемента, который имеет некоторое
контактное сопротивление, а величина его, как правило, неизвестна.
Здесь сталкиваемся с типичной ситуацией, которая возникает при
внесении в ОИ некоторого измерительного устройства, которое само
вносит изменения в отклик ОИ. Поэтому методы подобного типа имеют
достаточно большую погрешность при игнорировании этого фактора.
Значительно более точным зарекомендовал себя метод адиабатного
деформирования, который не требует дополнительных нагревательных
элементов, а изменение поля температуры происходит за счет механи-
ческоговоздействиянаОИисвязанностиполейдеформацийитемпе-
ратуры.
Рассмотрим стержень длины * и толщины ,которыйподвергается
чистому изгибу за счет приложения к его концам изгибающих момен-
тов величины .
В силу связанности полей напряжений, деформаций
и температур и выполнения соотношений Дюамеля–Неймана в термо-
упругости [14] (,
—
коэффициент температурного расширения),

#
B

Æ
#

24#,3B

24 Æ# ,
(2.6 .1)
в образце создается градиент температур, причем в силу того, что
отличная от нуля компонента тензора напряжений 11 линейно зависит
от координаты , в образце в начальный момент времени создается
начальное распределение температур ,0
. ,где.
—некоторый
коэффициент пропорциональности, зависящий от величины изгибаю-
щего момента и изгибной жесткости стержня. Дальнейшее изменение
поля температур происходит в соответствии с уравнение теплопровод-
ности

2
1

,
(2.6 .2)
где
—
искомый коэффициент температуропроводности. В случае теп-
ловой изоляции образца в термокамере граничные условия, имеют вид

2
0
(2.6 .3)
Измеряя граничную температуру +2,
H ,сформулируем
обратную задачу об определении , причем коэффициент температуро-
проводности войдет в выражение для граничной температуры нелиней-
ным образом, что типично для коэффициентных ОЗ.
5/27

2.6 . Определение коэффициента температуропроводности
87
Для формулировки разрешающего соотношения построим решение
прямой задачи методом интегрального преобразования Лапласа. Вве-
дем ,

Ê
0
,
)
'
"
.Тогдаполучим

2
1

,0 или

2
1

.
(2.6 .4)
Решение (2.6.4) строится стандартным образом и имеет вид
,

)
$

!,
B

1;
постоянные
и определяются из (2.6 .3) и имеют вид

2
,

Таким образом, находя трансформанту температуры и обращая
преобразование Лапласа, имеем следующее представление граничной
температуры:

2
,

2&
"#
"#

Введем в рассмотрение число Фурье 0
4

2 и в интеграле произ-
ведем замену переменной :+.Тогда

2
,

4&
" #
"#

(

(
:
(2.6 .5)
Интеграл в (2.6 .5) при 0 00 эффективно вычисляется с помощью
теории вычетов. Для этого находим особые точки подынтегральной
функции. Среди них :
0 есть устранимая особая точка, и счетное
множество полюсов :
04

,4
%
21
2

2
,
0,1,..., рас-
положены в левой полуплоскости. Замыкая контур в левую полуплос-
кость и используя лемму Жордана, по теории вычетов находим

2
,

0
1
2 1
2 04 H
(2.6 .6)
Из представления (2.6 .6) видно, что величина входит в него
под знак экспоненты и для ее определения из данных эксперимен-
та необходимо решать некоторое трансцендентное уравнение, причем
для каждого оно разное. Возникает естественный вопрос — нельзя
ли использовать для описания поля температур и для последующей
процедуры идентификации более простые аналитические зависимости?
Оказывается, что в некоторых областях изменения параметров задачи
6/27

88
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
это сделать можно, что существенно упрощает процедуру решения
коэффициентной ОЗ и не требует решения сложного трансцендентного
уравнения.
Так, например, при 0 (0
—
некоторое положительное значение,
характеризующее максимум граничной температуры) в силу того, что
элементы ряда быстро убывают, можно использовать одночленную
асимптотику решения

2
,

2
'

2
4
и на ее основе обработать результаты эксперимента, измеряя темпера-
туру для двух различных моментов времени 1, 2:

2
,1

2
'

21
,

2
,2

2
'

(2.6 .7)
Из последних двух соотношений находим

2
1

При этом оказывается, что величина . , пропорциональная силово-
му фактору-моменту, не входит в окончательную формулу. Также на
основе этой асимптотики можно далее осуществить статистическую
обработку эксперимента, выбирая несколько пар времен измерения
температуры , определяя по формуле (2.6.7) коэффициент ,азатем
проводя усреднение.
Отметим, что при
0и0
0всеполюса: стягиваются к на-
чалу координат и формула (2.6 .6) становится неэффективной в силу
медленной сходимости ряда в (2.6 .6). Для малых времен 0 это
представление (2.6.6) (а тем более, одночленная асимптотика (2.6.7))
не пригодны для расчета поля температур. В этом случае необходимо
вернуться к интегральному представлению решения. Для асимптоти-
ческого анализа интегрального представления при малых построим
асимптотику подынтегральной функции в (2.6.5) при малых 0 ,учиты-
вая раз ложение
1

(

...

,
атакже,чтопри
11 1
(

1,
1

1
(

(

.Таким
образом, получаем формулу

2
,

1
2

0
1
20
0
1
2

,
(2.6 .8)
которую можно использовать при обработке результатов при малых
(или малых 0.
7/27

2.7. Конечномерные ОЗ для стержней. Идентификация полости
89
Замечание. При малых 0 решение исходной задачи носит характер
погранслоя и может быть найдено проще из решения задачи для полу-
бесконечного стержня.
Также отметим, что рассмотренный простейший пример иденти-
фикации параметра модели является весьма показательным с точки
зрения общей теории идентификации [41]. В этом случае, сокращая
объем экспериментальной информации (в данном случае ограничива-
ясь временами 0

и используя простую асимптотику для описания
поля температур, можно получить более устойчивые результаты при
определении коэффициента температуропроводности, нежели при ис-
пользовании общей формулы для расчета температуры, справедливой
для любых времен.
2.7 . Конечномерные ОЗ для стержней.
Идентификация полости в упругом стержне
при анализе поперечных колебаний
В настоящем пункте рассмотрена задача об установившихся попе-
речных колебаниях цилиндрического стержня, содержащего дефект
в форме полости малого характерного размера в соответствии с [24, 25].
Задачи о колебаниях тел с дефектами различной природы и струк-
туры достаточно давно изучаются в научной литературе, что продик-
товано важностью решений таких задач с точки зрения их влияния на
прочностьконструкций.Отметим,чтонаиболеедетальноисследованы
задачи о колебаниях стержней и пластин с дефектами типа полостей
и трещин. Так, в работах [24, 25, 7] рассматривались прямая и обрат-
ная задачи о поперечных и продольных колебаниях цилиндрического
стержня с дефектом в форме полости малого размера. В [24, 25] реа-
лизован поход к определению местоположения и объема малой полости
произвольной формы на основе асимптотического анализа при иссле-
довании поперечных колебаний, в [4, 7] решена задача об определении
местоположения и объема малой полости произвольной формы на ос-
новании моделирования полости отрицательной массой и исследова-
нии ОЗ по частотному уравнению.
Анализ прямой задачи, в которой наличие полости моделируется
зависимостью геометрических параметров задачи от координат, обыч-
но осуществляется с помощью сведения к интегральному уравнению
Фредгольма 2-го рода с непрерывным ядром [30, 36], которое далее
решается численно методом коллокаций [13, 14]. В настоящем пункте
процедура построения решения осуществлена с помощью разбиения
области, занятой стержнем, на конечное число подобластей с посто-
янными характеристиками и на дальнейшем численно-аналитическом
исследовании. Получены зависимости первых резонансных частот от
характерных параметров полости (центр, объем). Отметим, что подоб-
ные зависимости для продольных колебаний цилиндрического стержня
8/27

90
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
исследованы в публикациях [24, 25], асимптотический анализ смеще-
ния резонансных частот для малых полостей дан в работах [13, 14].
Проведен анализ этих зависимостей и установлены области изменения
частот, когда эти зависимости взаимно однозначны. На основе этой
информации сформулированы обратные задачи о реконструкции поло-
стей малого относительного размера. В линеаризованной постановке
для обратной задачи построено интегральное уравнение относительно
функции, характеризующей форму полости. Интегральный оператор
в соответствующем уравнении имеет гладкое ядро; его обращение
является некорректной задачей и требует применения процедуры регу-
ляризации. В исследовании рассмотрен наиболее важный для практики
случай, когда обратная задача состоит в определении местоположения
и объема полости независимо от конкретной формы ее поверхности.
При этом применен метод регуляризации на компактных (или конечно-
мерных) множествах, когда дефект параметризуется конечным числом
параметров и восстанавливается в классе цилиндрических полостей.
Решение интегрального уравнения сводится к определению двух па-
раметров из функционального уравнения, справедливого в некотором
частотном диапазоне. Асимптотический анализ позволил осуществить
поэтапную процедуру реконструкции и определения этих параметров.
Рассмотрим установившиеся поперечные колебания стержня дли-
ны сполостьюпроизвольнойформы.Будемсчитать,чтоодинконец
стержня,
0, жестко закреплен, а к другому, —

, приложена
периодическая во времени сила A
A
0 >.Наличиеполо-
сти моделируется зависимостью площади имоментаинерции
поперечного сечения от продольной координаты .Размерыполости
будем считать малыми по сравнению с характерным геометрическим
размером поперечного сечения стержня. Требуется определить смеще-
ние незакрепленного торца стержня как функцию частоты колебаний
и первые резонансные частоты.
В предположении малости размеров полости используем уравнение
поперечных колебаний стержня переменного поперечного сечения [52].
В случае установившихся колебаний приходим к следующей краевой
задаче для дифференциального оператора четвертого порядка с пере-
менными коэффициентами:

6
2 0,
0 0,

0 0,

A
0,
(2.7.1)
где 62

2+ ,

—
плотность,
—
частота колебаний,
—модуль
Юнга.
9/27

2.7. Конечномерные ОЗ для стержней. Идентификация полости
91
Такая краевая задача в общем случае изменения коэффициентов
дифференциальногооператоранеможетбытьрешенааналитически,
поэтому для построения решения следует использовать численные ме-
тоды. В работе [13] аналогичная прямая задача сведена к решению
интегрального уравнения Фредгольма 2-го рода. Для локализованного
дефекта примем, что закон изменения площади поперечного сечения
имеет вид

2
,
(2.7.2)
где функция 2 отлична от нуля в интервале ,

0, .Далее
осуществим неравномерное разбиение отрезка 0, на частей сле-
дующим образом, сгущая сетку в окрестности полости:

00,

2
>

1,
>
1,1,

Будем считать, что в > -м
интервале #1 , # функция смеще-
ния # ,афункции и

сохраняют постоянные значения

#
+2 ,

#
+ 2 .Тогдафункции#
удовлетворяют уравнениям 4-го порядка с постоянными коэффициен-
тами

B
4
#

# 1, #,
>
1, ,
(2.7.3)
где B4
#
6
2# +# .Общеерешение>- го уравнения из (2.7.3) имеет вид

"
1#B#B#"2#

B
#

"
3#B#

"
4#B#B#
Постоянные "# находятся из граничных условий и условий сопря-
жения

10 0,

#
,

,
где A0
+
0.
Очевидно, что искомой функцией смещения сво-
бодноготорцастержнябудетфункция
, зависящая от
частоты колебаний. Отметим, что сгущение разбиения в окрестности
полости в значительной степени повышает точность решения прямой
задачи, и с увеличением точность решения возрастает. Предло-
женный алгоритм тестировался на задаче о цилиндрическом стержне
10/27

92
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
радиуса E0
+ 5 без полости. Функция смещения однородного стерж-
ня известна и определяется выражением

0
!

3 1

8
4B2

8
3 B ,
(2.7.4)
где B4
6
2)0

0
,1
*
1
+
,2

*
2
+
,
8
2
1 B*82
B*
8
4 B*;
8
1, 82, 83, 84
—
известные функции Крылова [52]. На всех интер-
валах изменения параметра B,несодержащихрезонансныхчастот,
относительная погрешность приближенного решения не превысила 1 %,
что делает предлагаемый численный алгоритм приемлемым способом
решения задач подобного типа.
Для исследования зависимости первых резонансных частот от па-
раметров полости введем безразмерные величины .# B(
#

,
,
+
и ,гдеB(
#
—параметр B, вычисленный по > - той резонансной частоте,

—
координата центра полости на оси стержня,
—относительный
объем полости. На рис. 2.9–2 .11 представлены зависимости .# , для
первых трех резонансных значений.
Рис. 2.9
Из рис. 2 .9–2 .11 видно, что взаимно однозначное соответствие меж-
ду резонансной частотой и местоположением полости существует толь-
ко для первой резонансной частоты. На рис. 2 .12 представлены графи-
ки отношений I#
.
#

+.
0
#
для первых трех резонансных значений,
причем .0
#
соответствует > - му резонансу однородного стержня, ,
0,5.
Как видно из рис. 2.12, для всех трех резонансов сохраняется взаим-
но однозначное соответствие между резонансной частотой и объемом
полости. Подобные зависимости имеют место для всех значений ,
в интервале 0, 0,6 .
11/27

2.7. Конечномерные ОЗ для стержней. Идентификация полости
93
Рис. 2.10
Рис. 2.11
Следует отметить, что обратные зависимости первой резонансной
частоты от местоположения и объема полости являются однозначными
функциями и могут служить в качестве входной информацией при
определении параметров полости.
В обратной задаче функция смещения свободного торца стерж-
ня считается заданной в некотором диапазоне изменения частоты

1, 2
.
Требуется определить местоположение и объем полости.
12/27

94
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
Рис. 2.12
Рассмотрим краевую задачу (2.7.1). В предположении малости па-
раметров полости применим процедуру линеаризации. Положим

0 1
,

2
,

1
2
92
2

,
(2.7.5)
где
—
формальныймалыйпараметрибудемсчитать,чтофунк-
ция 2, моделирующая наличие полости, удовлетворяет условиям
2
0
0,,
2

20,

1
Подставляя представления (2.7.5) в дифференциальное уравнение
задачи (2.7.1) и приравнивая коэффициенты при одинаковых степе-
нях , будем иметь в соответствии с методом возмущений [13, 43]

0B
4

00;
(2.7.6)

1B
4

12B
4

00
(2.7.7)
Умножим уравнение (2.7.6) на 1 , а уравнение (2.7.7) — на 0 ипро-
интегрируем по отрезку 0, .
Приравнивая интегралы в полученных
выражениях, придем к уравнению
B
4

0
2

2
0

3
,
1

2
,
1

2
,
0

,
1

2
,
0

2 1

3
,
0

0
0
13/27

2.7. Конечномерные ОЗ для стержней. Идентификация полости
95
Удовлетворяя граничным условиям

00 0,

0 0,

0 ,

10 0,

1 0,

1 0
и учитывая, что 0
,

1,
, окончательно получаем
интегральное уравнение Фредгольма 1-го рода относительно функ-
ции 2
B
4

0
2

2
0 0
,
,

1, 2

(2.7.8)
Отметим, что в силу гладкости ядра интегрального уравнения по-
строение решения интегрального уравнения (2.7.8) является некоррект-
ной задачей и требует применения процедуры регуляризации [50, 51].
Поставленную задачу об определении местоположения и объема по-
лости можно решать в классе цилиндрических полостей, образующих
компакт в пространстве 2
0, . Следовательно, к решению интеграль-
ного уравнения (2.7.8) применим метод регуляризации на компактном
множестве, изложенный в разд. 1.6. Положим, что закон изменения
площади поперечного сечения стержня в зависимости от продольной
координаты имеет вид (2.7.2). В случае стержня кругового попереч-
ного сечения 0
%
E
2
0 ифункция2 представляетсяввиде
2
-
-
0

/
3
2
2

,
(2.7.9)
где /
—функция Хевисайда; E ,2
3
—
соответственно радиус и высота
цилиндра. Обозначим E1
E +E
0
2
.
С учетом (2.7.9) уравнение (2.7.8)
примет вид
B
4
E
2
1

2
0 0
,
,

1, 2

(2.7.10)
Подставив в (2.7.10) решение (2.7.4), получим функциональное
уравнение относительно трех параметров полости
E
2
1

2
1!1
,
3,
B

2!12 ,
3,
B

2
2!2
,
3,
B

2
!

0 ,

1, 2
,
(2.7.11)
где введены обозначения
!
1,2
,
3,
B
3

1
2

2B2 B 3

2 B

2B3

B3
,
(2.7.12)
14/27

96
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
!
12 ,
3,
B
1
2

2 B

2B3
2 B

2B3

B3
(2.7.13)
Считая, что параметр 3 мал, к интегралу в уравнении (2.7.10)
применим теорему о среднем. Тогда будем иметь

2
0 23

2
01

3
2

(2.7.14)
С учетом (2.7.14) уравнение (2.7.10) сведется к анализу соотноше-
ния

2
0
!

4
.

1, 2
,
(2.7.15)
где
23+E2
1 — относительный объем полости. Отметим, что ана-
логичный результат получается при разложении выражений (2.7.12),
(2.7.13) в ряды Тейлора по параметру 3 в окрестности нуля.
Такимобразом,задачаореконструкцииполостималогоотноси-
тельного размера свелась к определению двух параметров полости
из функционального уравнения (2.7.15).
На основе предложенного подхода проведена серия вычислительных
экспериментов о реконструкции полостей различного вида. Решение
уравнения (2.7.15) позволяет оценивать объем полости, отыскивая ее
в классе цилиндрических полостей. На рис. 2 .13, 2.14 представлены
результаты реконструкции эллипсоидальных и конических полостей
()
—
относительная погрешность восстановления объема полости).
Рис. 2 .13
Рис. 2.14
Такая процедура позволяет поэтапно восстанавливать местоположе-
ние и относительный объем произвольной полости, зная поле смещений
свободного торца стержня всего на двух частотах. Численные резуль-
таты таких экспериментов сведены в табл. 2.8, 2.9.
15/27

2.8. Конечномерные ОЗ для стержней
97
Таблица 2.8
Параметры полости

0,0002
Форма полости

0,2

0,5

0,9
Цилиндрическая

0,31

0,72

0,03

0,07

0,02

0,01
Эллипсоидальная

0,27

0,72

0,02

0,04

0,05
Коническая

0,14

0,33

0,02

0,03

0,01

0,01
Таблица 2.9
Параметры полости

0,0015
Форма полости

0,2

0,5

0,9
Цилиндрическая

1,21

2,82

0,13

0,29

0,09

0,06
Эллипсоидальная

0,75

1,8

0,08

0,17

0,06

0,04
Коническая

0,6

1,4

0,07

0,14

0,04

0,03
Результаты вычислительных экспериментов показали достаточную
эффективность определения объема и положения полости при изгиб-
ных колебаниях балки.
2.8 . Конечномерные ОЗ для стержней. Определение
локализованной зоны деструкции в упругой балке
В предыдущем разделе была исследована конечномерная ОЗ вос-
становления объема дефекта и его центра по анализу колебаний балки
и изменению резонансных частот.
Гораздо меньше исследованы ОЗ для упругих тел с включением.
Работа [55] посвящена решению задачи идентификации эллипсоидаль-
ной полости или эллипсоидального включения (жесткого или упругого)
в изотропном линейно упругом теле при статическом нагружении.
Для решения задачи использован метод, основанный на использова-
нии функционала взаимности. Предложена конструктивная процедура,
с помощью которой геометрические параметры дефекта выражаются
через значения функционала взаимности. Эти значения могут быть
вычислены, если в статическом испытании на одноосное растяжение
(сжатие) на внешней поверхности тела измеряются перемещения.
16/27

98
Гл. 2 . Конечномерные ОЗ. Определение постоянных параметров
В работах [57, 58] были предложены методы получения верхней
и нижней оценок для объема одиночного дефекта произвольной формы
визотропномлинейноупругомтеле.Приэтомбылрассмотренслучай,
когда дефект представляет собой изотропное линейно упругое включе-
ние. Представленные в [58] оценки записаны через изменение упругой
энергии тела, определяемое наличием дефекта, величина которого мо-
жет быть вычислена по данным о перемещениях и усилиях на внешней
границе тела, полученным в одном произвольном статическом испыта-
нии. Аналогичные оценки для случаев полости и жесткого включения
были получены в работе [64].
В настоящем разделе предложен новый подход к определению пара-
метров включения, которое обладает меньшими, чем материал балки,
модулем Юнга и плотностью, что моделирует зону деструкции в со-
ответствии с [19]. Рассмотрены две ОЗ при анализе изгибных коле-
баний. Первая состоит в определении центра и объема эллипсоидаль-
ного включения, ослабляющего упругий стержень, при известных его
физических характеристиках (модуль Юнга и плотность), а вторая —
в определении физических параметров включения при известной его
геометрии.
Рассмотрим установившиеся колебания жестко закрепленной на
левом конце 0 упругой балки длины с круговым поперечным
сечением радиуса , колебания которой возбуждаются при помощи по-
перечной силы A A >, приложенной в точке . Будем
считать, что в балке имеется включение в виде эллипсоида вращения
с другими (меньшими) физическими характеристиками, причем его ось
совпадает с осью балки.
Уравнение установившихся колебаний с частотой неоднородной
балки для модели Эйлера–Бернулли и соответствующие граничные
условия имеют вид

2 0,
(2.8 .1)

0 0,

A
(2.8 .2)
Здесь введены обозначения
Ê

:
2 ,
!

,где
,
!
—
соответственно жесткость и погонная масса балки;

и
—
переменные модуль Юнга и плотность;
—п
лощадь
поперечного сечения.
Пусть центр эллипсоида расположен в точке и имеет полу-
оси
1и2
.
Тогда уравнение осевого сечения эллипсоида имеет вид

2
1

(
2

2
2
1,
а в формулах (2.8.1), (2.8 .2) следует положить 0
1

1 ,
!

00
1

2 ,где0, 0, 0
—
соответственно жесткость,
17/27

2.8. Конечномерные ОЗ для стержней
99
плотность и площадь поперечного сечения неповрежденной части
балки; 1 , 2
—
положительные функции, отличные от нуля внутри эл-
липсоидальной области.
Вводя безразмерные характеристики ;

.
,*0
.
,0

1
,G
4
/
0)0
0
2
.
4
1
0
, получим, что безразмерные жесткость ; и погонную
массу ! ; можно задать соотношениями

;
"
0
4
4

1
"
0"1
"
0

-
4
2

,
!
;
%
0
2

1
/
0/1
/
0

-
2
2

Здесь переменный радиус E; определяется согласно соотношению
в области включения E; 2 1
2

0
2
.
2

2
1
иравеннулювненего.
В безразмерных переменных уравнение колебаний и граничные условия
примут вид
H
;

;

G
4
3
;
;
0,
(2.8 .3)

1 0,

1
A
0
.
3
1
0
,
(2.8 .4)
где введены следующие функции:
H
;

;

0
Æ,
11
;,

;

0
Æ,
3
;

;

0
Æ,
12
; ,

;

0
Æ,

1; 1

1
2

0
2
Æ
2

2
,

2; 2

1
2

0
2
Æ
2

Здесь1 1
"
1
"
0
,21
/
1
/
0
,

,Æ

1
.
.
Уравнение (2.8.3) имеет переменные коэффициенты, и его решение
может быть построено либо численно, либо на основе асимптотическо-
го анализа в случае малых относительных размеров включения. Преоб-
разуем (2.8 .3) к канонической системе дифференциальных уравнений
1-го порядка:

3
,

3G
4
,

(2.8 .5)
Граничные условия (2.8 .4)запишутся в виде

0 0,
0 0,

1 0,

1
A
0
(2.8 .6)
18/27

100 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Введем в рассмотрение неизвестный вектор J , ,
,

ибу-
дем решать краевую задачу (2.8.1), (2.8 .2) методом пристрелки. Тогда
для системы (2.8 .5) рассмотрим две вспомогательные задачи Коши:

10 0,
10 0,

10 1,

10 0,

20 0,
20 0,

20 0,

20 1
Учитывая, что граничным условиям при ;
0 удовлетворяют оба
решения, введем векторы J1

иJ2

. Согласномето-
ду пристрелки искомое решение задачи (2.8 .1), (2.8.2) может быть
представленоввидеJ

1J1

2J2,где1 и 2
—
неизвестные
параметры. Их значение можно определить при выполнении граничных
условий для функций
и

на правом конце ; 1

1
1
1

2
2
1
A
0,

11
1

22
1 0
Введя определитель системы

1 1

2 1

1 1

21,
по правилу Крамера находим решение, причем равенство 0опре-
деляет резонансные значения задачи, которые находятся методом поло-
винного деления.
На рис. 2.15, а–в представлено сравнение точных резонансных зна-
чений неповрежденной балки и балки с дефектом в зависимости от
координаты центра включения при значениях параметров: Æ
0,05,

0,5, 1
+
0 0,8, 1
+
0 0,6 (такое соотношение модулей упруго-
сти и плотностей характеризует некоторую степень деструкции вклю-
чения). Точками на рисунке изображены резонансные значения балки
с дефектом, а линией — неповрежденной балки для 1-го (а), 2-го (б)
и4-го(в) резонансных значений соответственно. Отметим, что для
первого резонансного значения исследуемая зависимость носит моно-
тонный характер, для второго и четвертого зависимость немонотонна.
Выведем приближенную формулу для вычисления резонансных ча-
стот балки с включением. Составим две краевые задачи, одна из
которых описывает собственные колебания со спектральным парамет-
ром G0 , а вторая — собственные колебания поврежденной балки с па-
раметром G:

0 G4
00 0,

00 0,

010;
(2.8 .7)

1; G4
1

2; 0,

0 0,

1 0,
(2.8 .8)
где G4
0
/
0)0
0
2
0.
4
1
0
иG4
/
0)0
0
2
.
4
1
0
.
19/27

2.8. Конечномерные ОЗ для стержней
101
Рис. 2.15
Отметим, что нетривиальное решение задачи (2.8.7) известно [52],
причем собственная форма неповрежденной балки определяется с точ-
ностью до постоянного множителя и представима в форме

0; G0

G
0G0
;

G
0;

G
0G0

G
0;
G0
;
Проведем следующие преобразования: уравнения (2.8.7) и (2.8 .8)
умножим на и

0 соответственно, проинтегрируем по отрезку [0, 1]
и, вычитая из второго первое, получим равенство
1
0

1;
1⁄41⁄4

00
G
4
1

2; G
4
0

;
0
(2.8 .9)
20/27

102 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Интегрируя первые два слагаемых в подынтегральном выражении
в (2.8 .9) по частям и учитывая граничные условия, найдем приближен-
ную формулу
G
4

G
4
0

4
1Ê
0

2 2,
2
02
1Ê
0

1 2,0
2
2
1Ê
0
,
2
02

(2.8 .10)
Так как 1
;
1 H;,

2; 1

3;
в области включения,
то, учитывая малость отрезка интегрирования и нормируя собственную
форму колебаний условием
1Ê
0

2
0 ; 1, получим упрощенную формулу
G
4

G
4
0 2ÆG
4

2 0

2
0 0

1 0

2
0 0

(2.8 .11)
По этой формуле можно подсчитать поправку к резонансной ча-
стоте, обусловленную наличием включения, зная собственную форму
неповрежденной балки и характеристики включения.
Отметим, что в случае однородного стержня первое резонанс-
ное значение, полученное с помощью метода пристрелки, равно
G
01 1,87510, второе —
G
02 4,69410, третье —
G
03 7,85476, что сов-
падает с известными значениями, приведенными в [52].
В табл. 2 .10 приведены результаты сравнения расчетов по определе-
нию первого безразмерного резонансного значения G1 по приближенной
формуле и путем точного решения краевой задачи методом пристрелки
при 1
+
0 0,8, 1
+
0 0,6 и разных значениях и
Æ.
Таблица 2.10
0
Пристрелка
Формула (2.8.11)
Погрешность, %

0,2; Æ 0,05
0,2
1,87509
1,87508
0,0005
0,5
1,87533
1,87543
0,005
0,8
1,87615
1,87668
0,028

0,2;Æ0,1
0,2
1,87509
1,87506
0,0016
0,5
1,87557
1,87577
0,011
0,8
1,87723
1,87827
0,055
Были проведены расчеты и для других значений параметров, поз-
волившиесделатьвывододостаточновысокойстепениточностипри-
ближенной формулы, что делает возможным использовать ее для про-
цедуры идентификации включения.
21/27

2.8. Конечномерные ОЗ для стержней
103
Перейдем к процедуре восстановления параметров в зоне вклю-
чения. Обратная задача состоит в восстановлении координаты цен-
тра и объема включения по известным значениям трех резонансных
частот при использовании полученной формулы (2.8 .11) для поправ-
ки [13, 14, 20].
Для используемой модели введем обозначение ,#
G
4
#

G
4
0#
,
где G0#
—
резонансное значение для неповрежденной балки; G#
—резо-
нансное значение для балки с локализованным дефектом, которое по-
лучено из решения задачи о поперечных колебаниях неоднородной бал-
ки методом пристрелки. Учитывая также, что 1

0 1

4, 2

22
, на основе формулы (2.8 .11) получаем нелинейную систему
трех уравнений относительно безразмерных геометрических парамет-
ров,,

0:
,
12

G
4
12

0 G01, 0

,
,
22

G
4
22

0G02, 0

0 G02, 0

,
,
32

G
4
32

0G03,0

0 G03, 0

(2.8 .12)
Исключая из системы (2.8.12) характеристику (относительный
объем включения) и разделив первое уравнение на второе, а второе на
третье, получим соотношения

4
142

,
0 01, 0

2
4
1
2

,
0 01, 0

4
242

,
0 02, 0

2
4
1
2

,
0 02, 0

4
242

,
0 02,0

2
4
1
2

,
0 02, 0

4
342

,
0 03,0

2
4
1
2

,
0 03, 0

2
После исключения неизвестной 2 получено трансцендентное урав-
нение вида A 0

0 для определения центра неоднородности.
Отметим, что функция A 0

не является монотонной, что свиде-
тельствует о неединственности решения при восстановлении координа-
ты центра включения по трем первым резонансным частотам. При ре-
шении этой проблемы можно рассмотреть другую тройку резонансных
частот, например первую, вторую и четвертую. На рис. 2 .16 в качестве
примера представлено сравнение графиков функций A123 0

и A124 0

для 0 0,2. Как видно из рис. 2 .16, графики введенных функций пере-
секают ось абсцисс практически в одинаковых точках 0,2, 0,5 и 0,8.
Такоежесвойствонаблюдалосьврасчетахипридругихзначениях
центра; соответственно вопрос о выделении единственного решения
этого трансцендентного уравнения требует самостоятельного исследо-
вания.
22/27

104 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Рис. 2 .16. Сравнение результатов восстановления координаты центра включе-
ния для различных троек резонансных частот
Таблица 2.11

0
"
1 "0

0,8; /1
/
0
0,6;
0,0048;0,8
Полу чен-
ное 0
Получен -
ное
Погреш-
ность ,%
Полу чен -
ное
Погреш-
ность Æ,%
0,1 0,1000
0,739
7,63
0,0043
10,4
0,2 0,1996
0,736
8
0,0043
10,4
0,3 0,2994
0,737
7,88
0,0043
10,4
0,4 0,4012
0,746
6,75
0,0043
10,4
0,5 0,5008
Не восстанавливается
0,6 0,5991
0,743
7,13
0,0043
10,4
0,7 0,7006
0,729
8,83
0,0042
12,5
0,8 0,7997
0,730
8,75
0,0043
10,4
"
1 "0

0,8; /1
/
0
0,6;
0,0094;0,5
0,1 0,1011
0,442
11,6
0,0086
8,3
0,2 0,2039
0,461
7,8
0,0080
14,7
0,3 0,2984
0,442
11,6
0,0084
10,4
0,4 0,4078
0,488
2,4
0,0082
12,5
0,5 0,5006
Не восстанавливается
0,6 0,5939
0,576
15,2
0,0088
6,1
0,7 0,7004
0,402
19,6
0,0083
11,5
0,8 0,8077
0,371
20,2
0,0081
13,6
23/27

2.8. Конечномерные ОЗ для стержней
105
Таблица 2.12

0
"
1 "0

0,9; /1
/
0
0,7;
0,0094;0,5
Получен -
ное "1
"
0
Погрешнос ть
"
1"0,%
Получен -
ное /1
/
0
Погрешнос ть
/
1/0,%
0,1
0,929
3,22
0,691
1,29
0,2
0,929
3,22
0,727
3,86
0,3
0,930
3,33
0,734
4,86
0,4
0,935
3,89
0,736
5,14
0,5
Не восстанавливается
0,6
0,922
2,44
0,732
4,57
0,7
0,945
5
0,733
4,71
0,8
0,944
4,89
0,733
4,71
"
1 "0

0,8; /1
/
0
0,6;
0,0094;0,5
0,1
0,875
7,13
0,599
0,17
0,2
0,857
7,13
0,637
6,17
0,3
0,859
7,34
0,645
7,5
0,4
0,864
8
0,648
8
0,5
Не восстанавливается
0,6
0,852
6,25
0,643
7,17
0,7
0,881
10,13
0,644
7,33
0,8
0,879
8,88
0,644
7,33
Зная координаты центра, можно затем вычислить отношение полу-
осей включения, найдя величину :

4
2
4
1

1
4
2,0

02, 0

2
4
1 ,0

01, 0

1 ,0

02, 0

2 ,0

01, 0

Далее определяется объем включения из (2.8 .12).
В табл. 2 .11 приведены результаты восстановления параметров де-
фекта при некоторых значениях параметров (1
+
0 0,8; 1
+
0 0,6;
0,0048; 0,8) и различных значениях 0
.
Результаты вычислительных экспериментов свидетельствуют о том,
что при расположении включения близко к свободному концу метод,
основанный на приближенной формуле, становится непригодным, осо-
бенно для оценки . Отметим, что при расположении центра включения
24/27

106 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
в центре балки представленная схема позволяет восстановить лишь
координату центра.
Подобно способу, изложенному выше, можно реализовать рекон-
струкцию соотношений модулей упругости и плотностей включения
и неповрежденной части балки на основе формулы (2.8.11)
В табл. 2 .12 приведены результаты восстановления соотношений
модулей упругости и плотностей при различных значениях 0
.
Замечание. Отметим, что в проведенной серии вычислительных
экспериментов не удалось осуществить реконструкцию в случае, когда
центр включения расположен посредине балки. Это связано с тем, что
функция, описывающая третью собственную форму колебаний, имеет
узел, близко расположенный к центру.
2.9 . Конечномерные ОЗ для стержней. Идентификация
тонкого надреза при изгибных колебаниях балки
Задачи о колебаниях тел с дефектами различной природы (полости,
трещины, надрезы) имеют большое значение для оценки их прочности;
при этом диагностика характеристик дефектов по результатам дина-
мического зондирования представляет собой важный этап прогноза.
В предыдущих разделах достаточно подробно описаны методы решения
ОЗ для балок при наличии полостей и включений. В [5, 6] удалось
получить трансцендентные уравнения для координаты центра полости
и далее восстановить ее характерный размер. Кроме того, отметим ряд
работ по анализу колебаний балок c трещинами и надрезами [32, 33],
в которых на основе анализа частотного уравнения определялись три
параметра надреза по трем резонансным частотам.
Отметим, что существует возможность упрощения задачи для тел
простой геометрии и при параметризации дефекта конечным числом
параметров. О типе дефекта и его размерах можно судить по инфор-
мации об изменении первых резонансных частот, а в предположении
о некоторой геометрической форме и малости дефекта по сравнению
с характерными геометрическими размерами тела возможно получе-
ние простых аналитических формул, позволяющих связать измеряемые
и идентифицируемые параметры и облегчающих решение обратной
задачи. Когда геометрия дефекта известна (надрез), в предположении
малости его ширины на основе такого подхода возможно связать изме-
нение резонансных частот и основные параметры дефекта. Процедура
идентификации при этом сводится к решению сложной нелинейной
системы трансцендентных уравнений. Отметим, что процедуру состав-
ления такой системы и ее решения можно упростить путем получения
формул для поправок для первых резонансных частот и собственных
форм колебаний в аналитической форме методами теории возмуще-
ний [20, 43].
25/27

2.9. Конечномерные ОЗ для стержней
107
В настоящем пункте в соответствии с результатами работы [20]
представлены результаты исследования поперечных колебаний кон-
сольно закрепленной балки с тонким надрезом, который смоделиро-
ван как локальное изменение жесткости. Представлены методы ре-
конструкции параметров надреза (ширину, глубину, объем и центр)
по известной информации о резонансных частотах балки с надрезом
или об амплитудно-частотной характеристике. Получены формулы для
решения задачи реконструкции. Проведен ряд вычислительных экспе-
риментов для оценки точности полученных формул.
Рассматриваются установившиеся колебания с частотой упругой
балки длины , ослабленной тонким симметричным двусторонним над-
резом длины 2* сцентромвточке. Будем считать, что балка на конце

0 жестко закреплена, а на конце действует сосредоточенная
сила. Уравнение колебаний неоднородной балки имеет вид [52]
-

2 0,
где
—модуль Юнга, -
—
момент инерции,
—
плотность,
—п
ло-
щадь поперечного сечения. Соответствующие граничные условия име-
ют вид
0

0 0;
-

0;
-

A
Для анализа задачи рассмотрим модель трехэлементной балки, на
каждом участке которой геометрические характеристики постоянны.
Для простоты дальнейших рассуждений считаем, что поперечное сече-
ние балки — прямоугольник шириной ивысотой/ на неповрежден-
ном участке и высотой 3 в ослабленном месте. Считая модуль Юнга
и плотность постоянными по всей длине балки, будем искать решение
задачи на каждом промежутке,

1
/0
2
)
1
"
1

10,

/0
2
)

2
/0
2
)
2
"
2

20,
(2.9 .1)
где

12
/,

3,
-
1-2
#
3
12
,
-

3
12
;

—ш
ирина балки,
—
решение задачи на среднем поврежденном
участке.
26/27

108 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Условия сопряжения и граничные условия для системы (2.9 .1) име-
ют вид

10 0,

1* *,

1* *,
-
11

*
-

*,
-
11

*
-

2 *,

2 *,
-

*
-
22

*,
-

*
-
22

2 0,

"
2

(2.9 .2)
Отметим, что задачу расчета амплитуд колебаний и резонансных
частот можно упростить, сформулировав модифицированные гранич-
ные условия на тонком надрезе и решая задачу для двухэлементной
балки. При этом резонансные характеристики балки с надрезом ме-
няются в зависимости от характеристик надреза и его положения,
что может служить информацией, по которой возможно определение
характеристик надреза.
Задача об идентификации параметров симметричного тонкого над-
реза в балке состоит в нахождении координаты центра надреза иего
объема по известным значениям резонансных частот балки с тонким
надрезом. Обычно эта процедура cводится к исследованию некото-
рого трансцендентного уравнения, однако вычислительные процедуры
при такой реализации являются весьма неустойчивыми. В настоящем
пункте получены аналитические формулы для поправок к резонансным
частотам, на основе которых можно было бы осуществить процедуру
реконструкции дефекта по трем резонансным частотам. Для получе-
ния соотношения, связывающего параметры надреза и резонансные
частоты, рассмотрим обезразмеренное дифференциальное уравнение
для собственной формы неповрежденной балки и уравнение для соб-
ственной формы балки с тонким надрезом (здесь введены безразмерные
характеристики ; +,
6
4
0 2

4+-,

0 +,
*
0 *+):
1

0 6
4
00

0
(2.9 .3)
—
уравнение для собственной формы неповрежденной балки [9], гра-
ничные условия имеют вид 0
0

00 0,
0 1

01 0;
2 H 6
4

0
(2.9 .4)
—
уравнение для собственной формы балки с тонким надрезом, где
соответствующие безразмерные функции имеют вид

0
*0,

#
,

0
*0,
H

0
*0,

3
#
3,

0
*0

(2.9 .5)
P owe red by T CP DF (www.tcp df.o rg)
27/27

2.9. Конечномерные ОЗ для стержней
109
Граничные условия аналогичны и имеют вид 0

0
0,1

1 0.
Домножим уравнение (2.9 .3) на ,
а уравнение (2.9 .4) —
на 0
, затем вычтем из первого соотношения второе и проинтегри-
руем по отрезку 0, 1 .Тогдаполучим
1
0
!

0 ;; H; ; 0
;

6
4
00
;;

6
4
;;
0;
"
;
0 (2.9 .6)
Интегрируя первые два слагаемых в (2.9 .6) по частям, получаем

0 ;; 0
;
;

H;
;

0; H; ;0
;

1
0

1
0
!
1

0 ; ; ;0
;

6
4
;

6
4
0
"
;
0
Учитывая граничные условия, окончательно имеем соотношение
1
0
!
1

0 ; ; ;0
;

6
4
;

6
4
0
"
;
0, (2.9 .7)
откуда получаем точную формулу, связывающую резонансные частоты
и параметры надреза,
6
4

6
4
0

00
Ê

0 0
1 # ,0
2,
2 2

00
Ê

0 0
1
3
#
3
,
0 2, 22
1Ê
0
,
2,
0 22

(2.9 .8)
Упростим эту формулу, исключив неизвестную функцию
в предположении малости ширины надреза. Вводя параметр
1 3+/ ,представим в виде разложения

0 1

1
2
(2.9 .9)
Таким образом, полагая 0

и учитывая условия со-
пряжения в месте надреза (2.9.2), имеем следующее приближенное
соотношение для вторых производных в месте надреза: -1

0
1

30
,где.

#
.
Таким образом, при малых *0 имеем следующую приближенную
формулу:
6
4

6
4
01

2*0

4
0,
2
00

1
3
,
00

2
1Ê
0
,
2
0 22

(2.9 .10)
1/27

110 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Поэтойформулеможноподсчитатьпоправкукрезонанснойчасто-
те, обусловленную наличием тонкого надреза. При этом отметим, что
поправка пропорциональна объему надреза, как это имело место и для
полостей.
На рис. 2.17, а–в представлены значения резонансных частот
в зависимости от расположения координаты центра дефекта при сле-
дующих параметрах надреза: 3+/
0,8, 2*+ 0,01. Точками на
графиках показаны резонансные частоты, полученные из модели трех-
элементной балки, звездочками — резонансные частоты, посчитанные
Рис. 2.17
по формуле (2.9.10), линией, параллельной оси абсцисс, показано
резонансное значение спектрального параметра для неповрежденной
балки. Как видно из рисунков, формула работает достаточно точно, ее
погрешность не превышает 1–2 %.
Отметим, что если первая частота монотонно растет в зависимости
от параметра 0 ,тоаналогичныезависимостидлявторойитретьей
частот существенно немонотонны. Эти зависимости могут служить
2/27

2.9. Конечномерные ОЗ для стержней
111
в качестве исходной информации для решения задачи о реконструкции
параметров надреза.
Результаты вычислительных экспериментов свидетельствуют о до-
статочной точности приближенной формулы (2.9 .10), и она может быть
положена в основу решения первой ОЗ.
Обратная задача 1 состоит в восстановлении центра, ширины и глу-
бины надреза по известным значениям трех резонансных частот при
использовании полученной формулы для поправки частот (2.9.10).
Введем следующие обозначения: 8
2*0

.
—объем дефекта,
E
1
2

3
,

#
1
0

2
060#,
;;,
Æ
#
6
4
#

6
4
0#
,
>
1,...,3
Здесь 60#
—
резонансная частота неповрежденной балки, 6#
—значение
резонансной частоты балки с дефектом, которое получено из задачи
о колебаниях трехэлементной балки. Таким образом, получаем нели-
нейную систему трех уравнений
Æ

6
4
04 EC,
4

2
060 ,

0,
C

060,

02
,

1,2,3
(2.9 .11)
Возможно упрощение этой системы с помощью исключения неко-
торых переменных. Исключая из системы (2.9.11) неизвестную E ,по-
лучим
Æ
141
*

4
01 1
Æ
242
*

4
02 2
5
1
5
2
,
Æ
141
*

4
01 1
Æ
243
*

4
03 3
5
1
5
3

(2.9 .12)
Далее в (2.9 .12) избавимся от неизвестной величины 8 ,разделив
первое уравнение на второе. В итоге получено уравнение
A

0 Æ1

1C2

Æ
22
C
16
4
01 41
C
36
4
03 43
C
1

Æ
11
C
3Æ3

3C1
6
4
01 41
C
26
4
02 42
C
1 0 (2.9 .13)
Найдя из этого трансцендентного уравнения значение 0 ,можно
затем вычислить значение объема, выразив из первого и второго урав-
нений в (2.9.11) величину 8 :
8
Æ
141
5
2Æ2
4
251

4
01 1
5
2
4
02 2
5
1

(2.9 .14)
Далее находится E, затем, решив соответствующее кубическое
уравнение, определяем значение глубины . и ширины *0 надреза:
E

4
01 1
Æ
141
*
5
1
,

3
E,
*
0
*
21

(2.9 .15)
3/27

112 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
В табл. 2 .13 приведены результаты восстановления параметров де-
фекта и значениях 3+/ 0,8, 2*0 0,01 при различных значениях 0:
Таблица 2.13
Результаты восстановления параметров надреза по известным значениям
резонансных частот балки с дефектом

0
Полу чен -
ное 0
Полу чен -
ное #
Погрешнос ть
# ,%
Полу чен-
ное20
Погрешнос ть
2 0,%
0,1
0,1007
0,7113
11,09
0,0052
47,76
0,2
0,1995
0,8109
1,36
0,0107
6,53
0,3 0,3042
0,8597
7,47
0,0168
67,69
0,4
0,4007
0,8373
4,66
0,0136
35,96
0,5 0,4943
—
—
—
—
0,6 0,5991
0,8027
0,34
0,0099
0,31
0,7
0,6970
0,8165
2,06
0,0111
10,81
0,8 0,7983
0,8145
1,80
0,0109
8,93
0,9 0,9001
0,7958
0,52
0,0098
1,50
Заметим,чтовточке0 0,5 удалось восстановить только положе-
ние точки центра надреза. Это происходит в силу того, что некоторые
из собственных форм или их вторые производные в этой точке обра-
щаются в ноль, формулы (2.9 .15) перестают работать
Обратная задача 2 состоит в восстановлении центра, ширины и глу-
бины надреза по трем известным значениям амплитудно-частотной ха-
рактеристики. Аналогично подходу, описанному выше, получим форму-
лу для вычисления амплитудно-частотных характеристик. Рассмотрим
уравнения колебаний неповрежденной балки и балки с тонким надре-
зом при одинаковых значениях безразмерной частоты колебаний 6:
1

0 6
4

0 0
(2.9 .16)
—
уравнение колебаний неповрежденной балки, граничные условия
имеют вид

00 0,

0 1

0;
2 H 6
4

0
(2.9 .17)
—
уравнение колебаний балки с тонким надрезом, граничные условия
имеют вид
0

0 0,

0;
функции H и

аналогичны функциям, описанным в (2.9.5).
4/27

2.9. Конечномерные ОЗ для стержней
113
Рассмотрим амплитудно-частотные характеристики функций 0

и :

06 0

01, 6,

01, 6
(2.9 .18)
Выполним преобразования, аналогичные описанным выше. Домно-
жим уравнение (2.9.16) на , а (2.9.17) — на 0
,в
ычтемиз
первого соотношения второе и, интегрируя по отрезку [0,1], получим
1
0
!

0 ;; H; ; 0
;

6
4

0;; 6
4
;;
0;
"
;
0 (2.9 .19)
Интегрируя первые два слагаемых в (2.9 .19) по частям, получаем

0 ;; 0
;
;

H;
;

0; H; ;0
;

1
0

1
0
!
1

0 ; ; ;0
;

6
4
;

6
4
0
"
;
0
(2.9 .20)
Используя граничные условия и учитывая (2.9.18), получим точную
формулу, связывающую значения амплитудно-частотной характеристи-
ки неповрежденной балки и балки с тонким надрезом:

2
00
6

6
6
4

0 %0

0 %0
1

0;;;

0 %0

3
#
3

0 ; ;; (2.9 .21)
Полагая в (2.9 .21) 0

и
1

30
,прималых*0
имеем следующую приближенную формулу:

066 2*0
1

.6
4

2
06,

0 E0
6,

02
,

01
(2.9 .22)
Для реконструкции параметров надреза рассмотрим систему трех
уравнений, соответствующих различным значениям безразмерной ча-
стоты 6:
Æ

066 86
4

,
4

2
06 ,

0,
C

06,

02
,

1,2,3
(2.9 .23)
Выполняя преобразования, аналогичные преобразованиям, описан-
ным в обратной задаче 1, получим уравнение для нахождения центра
надреза
A

0 Æ1
C
2Æ2
C
16
4
343
C
16
4
141
C
3

Æ
1C3

Æ
3C1
6
4
242
C
16
4
141
C
2 0 (2.9 .24)
5/27

114 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Найдя значение 0 из (2.9.24), далее определим величины 8 и
8
E.
Для этого решим систему линейных алгебраических уравнений, со-
ставленную из первых двух уравнений в (2.9 .23), учитывая найденное
значение 0
.
Наконец, далее получим значения глубины и ширины
надреза в соответствии с (2.9 .15).
Отметим, что для достаточно точного восстановления характери-
стик надреза необходимо определенным образом выбирать значения
безразмерной частоты. На основе ряда вычислительных эксперимен-
тов выяснено, что для получения наиболее точных результатов нуж-
но выбирать значения 6, лежащие в различных промежутках между
резонансными частотами, причем нежелательно выбирать значения 6
меньше спектрального значения, соответствующего первой резонанс-
ной частоте.
В табл. 2 .14 приведены результаты восстановления параметров де-
фекта при значениях
6
13,
6
26,
6
3 10,

#
0,8, 2*0 0,01
для различных значений 0
.
Резюмируя, отметим, что в настоящем пункте предложены два ме-
тода определения характеристик надреза, получены соответствующие
формулы, проведены вычислительные эксперименты, которые проде-
монстрировали достаточную точность данных формул. Результаты вы-
числительных экспериментов показали: хуже всего восстанавливаются
параметры надреза, когда сам надрез находится близко к заделке.
Таблица 2.14
Результаты восстановления параметров надреза по известным значениям
амплитудно-частотной характеристики балки с дефектом

0
Полу чен -
ное 0
Полу чен -
ное #
Погрешнос ть
# ,%
Полу чен-
ное20
Погрешнос ть
2 0,%
0,1
0,1005
0,7879
1,51
0,0089
11,21
0,2
0,2001
0,8113
1,41
0,0107
7,02
0,3 0,2998
0,7549
5,64
0,0066
34,28
0,4
0,4004
0,8092
1,14
0,0104
4,39
0,5 0,5017
0,8093
1,16
0,0105
5,18
0,6 0,5991
0,8086
1,07
0,0102
2,15
0,7
0,6998
0,8015
0,19
0,0103
3,53
0,8 0,8026
0,8055
0,68
0,0101
0,84
0,9 0,9027
0,7919
1,01
0,0096
3,82
6/27

2.10. Конечномерные ОЗ для стержней
115
2.10. Конечномерные ОЗ для стержней. Определение
параметров дефекта в балке для модели Тимошенко
Задачипоидентификациитрещиннаосновеакустическогозон-
дирования — один из важных разделов механики; подробный обзор
истории вопроса содержится в [23]. Для балочных моделей в послед-
ние годы достигнут значительный прогресс в определении параметров
надреза или трещины.
В предыдущем пункте представлено решение ОЗ по определению
надреза в балке для модели Эйлера–Бернулли. В настоящем разделе
обсуждается подобная задача для более сложной модели Тимошенко.
Основная идея, лежащая в основе получения зависимостей, связыва-
ющих резонансные частоты и параметры дефекта, базируется на соот-
ношении, полученном в [14] для тела с полостью. Установлена связь
между резонансными частотами для задачи колебаниях неповрежден-
ного упругого тела 8 и тела с полостью, занимающей объем 80 ,

22
0 80

0
2
06 0

0
Ê

0 *
,
(2.10.1)
где 0
—
некоторая точка внутри полости, причем

00
,
'

0 0

—
соответственно удельные потенциальная и кинетическая
энергия полости; на основе упрощения этой формулы при использо-
вании гипотез изгиба в настоящем пункте предложена процедура по-
этапной идентификации параметров надреза. В [20] на основе исполь-
зования этого подхода получены формулы для поправки резонансных
частот для балки модели Эйлера–Бернулли с тонким симметричным
надрезом, а также предложен метод реконструкции параметров тонкого
надреза с использованием полученных формул и приведены результаты
вычислительных экспериментов по восстановлению параметров дефекта.
В [54] представлено решение задачи идентификации повреждений
в кантилевере, основанное на минимизации специального функционала
невязки между решением (собственные частоты и моды колебаний),
полученным аналитически на базе уравнения модели Тимошенко и рас-
четным путем, в частности, с помощью метода конечных элементов.
В настоящем пункте рассматриваются установившиеся колебания
с частотой упругой балки длины , ослабленной тонким симмет-
ричным двусторонним надрезом длины 2* сцентромвточке.Для
простоты дальнейших рассуждений считаем, что поперечное сечение
балки — прямоугольник шириной ивысотой/ на неповрежденном
участке и высотой 3 в ослабленном месте. Будем считать, что балка на
конце 0 жестко закреплена, а конец свободен. Модуль Юнга
и плотность будем считать постоянными по всей длине балки.
Уравнение колебаний неоднородной балки для модели Эйлера–Бер-
нулли описано в предыдущем пункте; в настоящем для моделирования
будет использована модель Тимошенко.
7/27

116 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Гипотезы для колебаний балки с учетом касательных напряжений
имеют вид [52]

13
1
2

13
I,

13 4 I,

11 3
I
,

33 0,

11 3
I

(2.10.2)
Потенциальная энергия деформации стержня при учете касатель-
ных напряжений:
1
2

3I 2

I
2
?

1
1
2

1- 1
I
21

1
217

1 I1

1
Кинетическая энергия стержня:
'
0
2
2

2
1
2
3

1
0
2
2

1
2

1 -1
I
2

1
Применяя вариационный принцип Гамильтона–Остроградского, по-
лучим

1-1
I

1ÆI

%
0
%
0

1-1
I

1 ÆI 1

1) 1

217

1 I1

%
0

1) 1

217

1 I1

1) 1

217

1 I1

ÆI

2
%
0

11
Æ

-
1I1
ÆI

10
Приравнивая нулю коэффициенты при независимых вариациях, по-
лучим, что уравнения колебаний неоднородной балки модели Тимошен-
ко имеют вид следующей системы:

D
1 1

1 I1

2 1

1 0,

1-1
I

1 6D1

1 1

I
1

2-1
I
1 0
(2.10.3)
8/27

2.10. Конечномерные ОЗ для стержней
117
Корректные граничные условия, соответствующие сдвиговой моде-
ли Тимошенко, для консольного стержня с нагружением сосредоточен-
ной силой на свободном конце имеют вид
0 0, I0 0, -I
0,
6

D
1 1

1 I1

A
Будем рассматривать колебания балки Тимошенко с постоянным
поперечным сечением в виде прямоугольника. Параметр 6 1+ 6
введен С. П. Тимошенко, 6
)

8
2

—
коэффициент, учитыва-
ющий неравномерность распределения касательных напряжений по по-
перечному сечению стержня [52]. Согласно приведенной формуле для
прямоугольного поперечного сечения 6 0,833.
Система уравнений (2.10.3) в безразмерных переменных имеет вид:

Æ
2 I G2

H I

Æ
1Æ2

G
2HI 0,
(2.10.4)
гдевведеныследующиебезразмерныехарактеристикиипараметры:

1
.
,
G
2/0
2
.
2
"
,
Æ
1
)
1.
2

1
,
Æ
2 69
"

Найдем смещения и резонансные частоты для представленной мо-
дели. Аналогично модели Эйлера–Бернулли (изложенной в разд. 2 .9)
построим для модели Тимошенко модель трехэлементной балки, на
каждом участке которой геометрические характеристики постоянны,
где ,
I

—
функции, характеризующие полей смещений в ме-
сте дефекта, 1
,
I
1,

2 ,
I
2 —
функции, характеризующие
поле смещений на неповрежденных участках.
Граничные условия и условия сопряжения на концах тонкого над-
реза для модели Тимошенко имеют вид

10 0,
I
10 0,

1 0

*
0 0

*
0,
I
10

*
0 I0

*
0,

1 I1

0 %0
.

0 %0
,
I
10

*
0 .3

0*0
,

0*0

*
0,
I

0*0

I
20

*
0,
.

0 %0

2 I2

0 %0
,
.
3 I0

*
0 I2

0*0
,

2 I2

10,
I
21 0
(2.10.5)
Отметим, что, несмотря на то, что для определения напряженно-
деформированного состояния модель трехэлементной структуры непри-
годна в силу наличия концентратора, резонансные характеристики опи-
сываются весьма уверенно, что подтверждается сравнением с данными
9/27

118 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
эксперимента, приведенными в [32], причем модель Тимошенко дает
результаты, более близкие к ним.
На рис. 2.18, а–в представлено сравнение точных значений резо-
нансных частот балки с дефектом в зависимости от выбора коор-
динаты центра надреза для моделей Эйлера–Бернулли и Тимошенко,
полученных из модели трехэлементной балки при параметрах надреза
2*0 0,01, 3+/
0,8. Точками на рисунках показаны резонансные
значения балки Эйлера–Бернулли, звездочками — модели Тимошенко.
Как видно из рисунков, графики функций изменения резонансных ча-
стот в зависимости от координаты близки, при этом значения соответ-
ствующих резонансных частот для модели Тимошенко всегда меньше.
Отметим, что если первая частота монотонно растет в зависимости
от параметра 0 ,тоаналогичныезависимостидлявторойитретьей
частоты существенно немонотонны. Эти зависимости могут служить
в качестве исходной информации для решения задачи о реконструкции
параметров надреза.
Для получения соотношения, связывающего параметры надреза
и резонансные частоты, можно действовать различным образом. Мож-
но опираться на общую формулу (2.10.1), а можно получить это соот-
ношение при анализе однородной краевой задачи.
Аналогично модели Эйлера–Бернулли для модели Тимошенко то-
же можно получить соотношение, связывающее резонансные частоты
неповрежденной балки и балки с симметричным тонким надрезом.
На основе общего соотношения Рэлея, учитывая гипотезы модели
Тимошенко в предположении пренебрежения инерцией вращения, не-
сложно получить формулу для резонансной частоты.
Обозначив соответствующие собственные формы колебаний ,
I
для балки с тонким симметричным надрезом, 0
,
I
0
—
собственные формы для неповрежденной балки, упростим эту формулу.
Учитывая, что в месте дефекта выполняются приближенные равенства

0 I0

I+.,
I
0 I +.3
, получим следу-
ющую формулу для поправки к резонансным частотам в балке модели
Тимошенко:
6
4

6
4
080

4
0,
2
00

1:0

2,0

0:0

2
1Ê
0
,
2
0
,
(2.10.6)
где 6
—
спектральный параметр, связанный с резонансной частотой
балки с тонким симметричным надрезом (64
K
2Æ1
,
6
0 —аналогич-
ный спектральный параметр для неповрежденной балки (64
0K2
0Æ1
,
2Æ1
Æ
2 +. . Отметим, что разность резонансных частот также пропор-
циональна безразмерной объемной характеристике 80
.
Сравнительный
анализ формул (2.9 .10) и (2.10.6) свидетельствует о том, что (2.10.6)
переходит в (2.9.10) при I0

0 и что поправки по модели
Тимошенко всегда меньше, чем по модели Эйлера–Бернулли.
10/27

2.10. Конечномерные ОЗ для стержней
119
Р
и
с
.
2
.
1
8
11/27

120 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
На основе построенной формулы (2.10.6) представим метод поэтап-
ного восстановления геометрических характеристик симметричного
тонкого надреза для рассматриваемой модели Тимошенко. Так как фор-
мула (2.10.6) включает в себя четыре неизвестных параметра (0 , 80 ,
1, 2 ), то для их идентификации следует рассматривать набор из че-
тырех резонансных частот, в отличие от метода, описанного выше для
модели Эйлера–Бернулли, где для нахождения трех неизвестных па-
раметров достаточно было знать три резонансных частоты. Параметры
надреза будем искать, решая нелинейную систему четырех уравнений:

Æ
1
*
0
4
1

6
2
012
0601, 0

1 I0
6
01, 0

2 0
6
01, 0

I
0601, 0

,
Æ
2
*
0
4
2

6
2
022
0602 , 0

1 I0
6
02, 0

2 0
6
02, 0

I
0602 , 0

,
Æ
3
*
0
4
3

6
2
032
0603 , 0

1 I0
6
03, 0

2 0
6
03, 0

I
0603 , 0

,
Æ
4
*
0
4
4

6
2
042
0604, 0

1 I0
6
04, 0

2 0
6
04, 0

I
0604, 0

(2.10.7)
Таблица 2.15
Результаты восстановления параметров надреза по известным значениям
четырех резонансн ых частот балки с дефектом для модели Тимошен ко

0
Полу чен -
ное

0
Полу чен -
ное #
Погрешнос ть
# ,%
Полу чен-
ное20
Погрешнос ть
2 0,%
0,1
0,1004
0,792
0,89
0,0094
5,62
0,2
0,2002
0,801
0,16
0,0105
5,02
0,3 0,3002
0,764
4,5
0,0103
3,22
0,4
0,4003
0,808
1,12
0,0103
3,02
0,5 0,5007
0,808
1,16
0,0105
5,14
0,6 0,5996
0,807
0,96
0,0102
2,05
0,7
0,6998
0,801
0,19
0,0103
3,53
0,8 0,8016
0,804
0,54
0,0101
0,84
0,9 0,9017
0,7919
1,01
0,0096
3,82
12/27

2.11. Определение параметров упругого закрепления
121
Выполняя преобразования, аналогичные описанным выше, исклю-
чим поочередно переменные 80 , 1 , 2 и получим трансцендентное
уравнение для нахождения координаты центра надреза. Решая его,
далее находим все остальные параметры.
В табл. 2 .15 приведены результаты восстановления параметров над-
реза в модели Тимошенко для параметров 3+/
0,8, 2*0 0,01 при
различных значениях координаты центра надреза.
Отметим,чтоточностьвосстановленияпараметровнадрезадля
модели Тимошенко выше, чем для модели Эйлера–Бернулли при ана-
логичных параметрах, что обусловлено менее ограничительными гипо-
тезами модели Тимошенко
2.11 . Определение параметров упругого закрепления
неоднородной балки
Как отмечено выше, балочные модели являются одними из наиболее
часто используемых при моделировании различных объектов. Одним
из важных классов задач для таких моделей является определение па-
раметров в граничных условиях в случаях упругого закрепления. При
этом оценка упругости опор конструкции важна как для различных
технических приложений, например трубопроводов, строительных кон-
струкций, так в биомеханике для диагностики элементов биомехани-
ческой системы кость–фиксатор для реальной оценки ее деформатив-
ности. Среди методов, позволяющих оценить характеристики упругих
систем, отметим акустические. Так, в [46] изложены теоретические
основы низкочастотных акустических методов контроля.
Отметим, что задача определения параметров упругих систем по
данным акустического зондирования относится к обратным задачам,
которым присуща некорректность в той или иной форме [14, 38].
Ряд граничных обратных задач по идентификации граничных усло-
вий, возникающих при изучении колебаний балок и трубопроводов
с постоянной жесткостью на упругих опорах, были исследованы в рабо-
тах [2, 3, 8, 56, 57], где определялись коэффициенты упругости, входя-
щие в граничные условия, по некоторому набору резонансных частот.
При этом анализ задач производился для оператора с постоянными ко-
эффициентами, что позволяло составлять частотное уравнение, содер-
жащее искомые параметры, в явном виде и анализировать возникаю-
щие алгебраические проблемы как с точки зрения построения решений,
так и обсуждать важные вопросы единственности. К сожалению, при
анализе колебаний балок переменной жесткости такой подход непри-
меним, нужны иные подходы при исследовании подобного типа задач.
В настоящем пункте изложен иной подход к проблеме идентифика-
ции параметров в граничных условиях в соответствии с [16, 17], где
изучена задача о реконструкции граничных параметров для консольно
закрепленной на одном конце и упруго опертой на другом конце балки
13/27

122 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
с переменной жесткостью, для которой в общем случае неоднородности
невозможно аналитическое построение частотного уравнения.
Рассмотрим собственные колебания упругого стержня длины
с переменной жесткостью. Уравнение колебаний в безразмерных пере-
менных имеет вид [52]

6
4

0,
(2.11.1)
где 64
/0
2
).
4
1
0
,
—безразмерный прогиб, 0, 1
—безразмер-
ная координата,

0 —
жесткость, 0
—
характерная жест-
кость балки, например ее среднее значение, —безразмерная
функция, характеризующая изменение жесткости вдоль оси балки,

—
площадь поперечного сечения балки.
Будем рассматривать свободные колебания консольно закрепленной
на конце 0балки,наконце 1 имеется упругое закрепление,
характеризующееся безразмерными положительными параметрами 01
и02
.
Граничные условия имеют вид [2]

00,

0 0,
1

0
1
1 0,

0
2
1 0
(2.11.2)
В случае постоянной жесткости можно построить в явном виде
частотное уравнение (как это реализовано в [2, 3]) и на его основе
исследовать как влияние параметров 01 и 02 на резонансные значения,
так и строить схемы решения обратной задачи об их восстановлении по
нескольким резонансным значениям. В случае достаточно произволь-
ной переменной жесткости явного представления частотного уравнения
получить нельзя, однако можно разработать схему исследования как
прямой, так и обратной задачи.
Пусть —
положительная ограниченная функция, которая мо-
жет быть непрерывной, а может иметь конечное число разрывов пер-
вого рода. Изучим влияние параметров упругого закрепления на ре-
зонансные характеристики балки. Решение краевой задачи (2.11 .1),
(2.11.2) строится методом пристрелки, для чего сведем дифференци-
альное уравнение 4-го порядка (2.11.1) к канонической системе диф-
ференциальных уравнений первого порядка

1
2,

3
1

3
4,

464

1
(2.11.3)
14/27

2.11. Определение параметров упругого закрепления
123
со следующими граничными условиями:

10 0,

20 0,

3 1

0
1
2
1 0,

4 1

0
2
1
1 0
(2.11.4)
Для системы (2.11 .3) построим решение двух вспомогательных задач
Коши. Для вектор-функции
1

"
сформулируем начальные
условия

1
10 0,

1
20 0,

1
30 0,

1
40 1,
а для вектор-функции
2

"
начальные условия имеют вид

2
10 0,

2
20 0,

2
30 1,

2
40 0
Нетрудно показать, что эти вектор-функции линейно независимы
в силу линейной независимости начальных векторов, и решение исход-
ной краевой задачи (2.11.3), (2.11 .4) можно искать в виде линейной
комбинации

1
2

2 ,причем1 и 2 определяются из решения
линейной алгебраической системы вида

1
31 1

2
31 2

0
1
1
2 11

2
21 2

1
41 1

2
41 2

0
2
1
1 11

2
11 2

0
(2.11.5)
Отметим, что определитель этой системы имеет структуру
0
1, 02, 6

06 1
60
12
6 0
23
6 0
102,
(2.11.6)
где

1
31
2
41

2
31

1
4 1,

1
21
2
41

2
21

1
4 1,

1
11
2
31

2
11

1
31,

1
11
2
2 1

2
11

1
21
Нули уравнения 01 , 02 , 6
0 при фиксированных значениях пара-
метров 01 , 02 определяют резонансные значения для неоднородной
балки.
В большинстве прикладных задач имеется априорная информация
о том, что параметры 01 , 02 или малы, или велики (малые значения
характеризуют ситуацию, когда податливость опоры мала, что близко
к свободному краю; большие значения этих параметров свидетель-
ствуют о наличии опирания, близкого к жесткой заделке). В этих
ситуациях можно использовать регулярные разложения по этим пара-
метрам (или обратных к ним) для нахождения резонансных значений.
Рассмотрим два случая.
15/27

124 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
1. Малые значения 01 , 02
.
Представим резонансные значения при
малых 01 и 02 в виде разложения
6
6
0,1
0
1,2
0
2,
(2.11.7)
где 60
—
корни порождающего уравнения 0
6
0, которое является
частотным уравнением задачи со свободным краем [52]; корни его
могут быть легко найдены (для постоянной жесткости они известны).
Тогда значения коэффициентов в разложении (2.11 .7) легко строятся
по следующим формулам:

,
1

,
,
2

(2.11.8)
2. Большие значения 01 , 02
. Вэтомслучаеимеемследующее
разложение:
6
6
1

2
,
(2.11.9)
где 61
—
корни порождающего уравнения 3
6
0, которое является
частотным уравнением задачи с жестко защемленным краем [52], ко-
торые также могут быть найдены численно (для постоянной жесткости
они известны), а для .1 и .2 имеем формулы

.
1

,
.
2

(2.11 .10)
Рассмотрим частный случай, когда 1, а частотное уравне-
ние (2.11 .6) и все функции, входящие в него, имеют явные представ-
ления

06 65
2
6
6

16 2
6

6 6
22
6

6 6
2,

26 2
6

66
4

2 6
66
4
,

36 2
6
6 6

2,
что позволяет получить простые явные формулы для резонансных
значений, которые в последующем могут быть использованы для про-
цедуры реконструкции. Тогда, опираясь на данные из [52], где приве-
дены значения корней соответствующих трансцендентных уравнений,
из (2.11 .7) получаем формулы
6
01 0,1517 01

0,2874 02

1,8751,
6
02 0,0097 01

0,22095 02

4,6941,
6
03 0,0021 01

0,1271 02

7,8548
(2.11 .11)
16/27

2.11. Определение параметров упругого закрепления
125
В табл. 2 .16 представлено сравнение численного и асимптотическо-
го резонансных значений при малых параметрах, которое свидетель-
ствует о достаточно высокой точности приближенных формул.
Таблица 2.16
Резонансное
значение

2
Численное
значение
Значение, полу-
ченное по (2.11.7)
Погреш-
ность, %

01
0,1 0,2
1,9093
1,9478
2

02
0,1 0,2
4,737
4,7393
0,05

03
0,1 0,2
7,8797
7,8804
0,01

01
0,3 0,02
1,8956
1,9264
1,62

02
0,3 0,02
4,6995
4,7014
0,04

03
0,3 0,02
7,8575
7,858
0,006
В случае больших параметров для первых трех резонансных значе-
ний получаем следующие зависимости:
6
11 102,1627
1

4,7300
1

4,7300,
6
12 485,0865
1

7,8532
1

7,8532,
6
13 1329,3360
1

10,9956
1

10,9956
(2.11 .12)
В табл. 2 .17 представлено сравнение численного и асимптотическо-
го резонансных значений при больших параметрах, которое свидетель-
ствует достаточно высокой точности приближенных формул.
Таблица 2.17
Резонансное
значение

2
Численное
значение
Значение, полу-
ченное по (2.11.9)
Погреш -
ность, %

11
300 250
4,3639
4,3705
0,15

12
300 250
6,4148
6,2048
3,2

11
600 550
4,5455
4,5511
0,12

12
600 550
6,9450
7,0304
1,22
Рассмотрим далее ОЗ о нахождении коэффициентов 01 и 02 по
известным резонансным частотам. Представим 2 варианта реконст-
рукции.
17/27

126 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
1. По асимптотике. Пусть на этапе постановки задачи известно, что
0
1 и 02 малы или велики. Зная 2 резонансных значения, определим
0
1 и 02 из линейной алгебраической системы, опираясь либо на фор-
мулы (2.11 .11), либо на формулы (2.11.12). В табл. 2 .18 представлены
результаты реконструкции параметров упругого закрепления.
Таблица 2.18
Исходные
Заданные
резонансы
Восстановленные
Погреш-
ность, %

2
0,01 0,02
1,8823
4,6986
0,0096 0,0199
4
0,01
0,06 0,02
1,89
4,6991
0,0585 0,02
2,5
0
0,06
0,1
1,9107
4,7162
0,0493 0,0978
18
2
2. В случае промежуточных значений надо следовать общей схеме
реконструкции параметров по двум известным резонансным значениям.
Подставим поочередно известные 2 резонансных значения в (2.11.6)
и получим нелинейную систему алгебраических уравнений вида

061

161
0
12
6
102

361
0
102 0,

062

162
0
12
6
202

362
0
102 0
(2.11 .13)
Нетрудно заметить, что каждое уравнение в (2.11.13) характе-
ризует гиперболу с осями, параллельными осям координат, а реше-
ние (2.11 .13) дает общие точки их пересечения. Находим их путем
сведения задачи к решению квадратного уравнения и получаем два
набора восстановленных 01 и 02
.
Отметим, что один из наборов не
удовлетворяет условиям задачи в силу ограничений (01

0, 02

0).
В табл. 2 .19 представлены некоторые результаты реконструкции иско-
мых параметров.
Таблица 2.19
Исходные
Заданные резонансные
значения
Восстановленные
параметры

2
0,2
0,4
1,9918
4,7758
0,20
0,40
55
2
3,4612
5,3865
55,0
2,0
500
200
4,4985
6,8033
500,0
200,0
1500 100
4,6186
7,4329
1500,0
99,99
18/27

2.12. Оценка деформативности неоднородной пластины
127
Замечание. Отметим, что подобным образом можно осуществить
реконструкцию параметров в граничных условиях при наличии вязко-
упругих связей, моделируемых в рамках модели стандартного вязко-
упругого тела.
2.12 . Оценка деформативности неоднородной
пластины в случае упругого опирания
Задачи о деформировании неоднородных пластин в последние го-
ды все чаще используются при моделировании различных объектов.
Модели биомеханики глаза в последние годы весьма интенсивно ис-
пользовались в практической офтальмологии. Среди важных проблем
биомеханики глаза отметим задачи, связанные с оценкой факторов,
влияющих на внутриглазное давление (ВГД), в частности, на дефор-
мирование решетчатой пластины (РП) и факторов, его определяющих.
Изучение характеристик РП имеет существенное значение в патогенезе
глаукомного повреждения зрительного нерва, поскольку ряд авторов
устанавливает анатомические отличия между РП здорового и больного
глаз [1, 11].
На первых этапах исследования РП моделировалась однородной
изотропной пластиной, где была реализована попытка учета влияния
растягивающих усилий, действующих со стороны склеры, на прогиб
пластины. В современных работах принято моделировать объект неод-
нородной пластиной. Учет неоднородности РП принципиально важен,
поскольку она оказывает существенное влияние на ее деформирование
при повышении ВГД [4]. Это и другие свойства РП и их влияние на
деформирование наиболее полно изучены в работах [1, 11]. Однако сле-
дует отметить, что модели однослойных пластин не позволяют учесть
некоторые экспериментальные данные, например, тот факт, что атро-
фия зрительного нерва при повышении ВГД возникает на «наружном
слое» [10].
Немаловажной задачей является поиск точки перегиба РП [11]. Это
связано с тем, что РП состоит из нескольких листов соединительной
ткани и наиболее сильные деформации претерпевает последний слой.
ПридеформацииРПвозникаетточкаперегиба,характеризующаясме-
ну участков выпуклости и вогнутости, исследование местоположения
которой играет важную роль в практической диагностике глаукомы.
Как отмечалось выше, РП представляет собой задний отдел склеры,
ослабленный множеством отверстий. По различным данным число от-
верстий колеблется около 700, и занимают они примерно 2/3 площади
всей РП. От центра к краю РП становится более разреженной, то есть
эффективный модуль упругости в плоскости изотропии убывает в этом
направлении, и при моделировании переменности модуля упругости
в [1] использован убывающий экспоненциальный закон.
19/27

128 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
На настоящий момент в исследованиях деформирования РП приня-
то моделировать ее как круглую или же близкую к круглой пластину
переменной жесткости с жестко заделанным краем [1]. Вместе с тем
отметим, что непосредственный контакт РП со склерой требует учета
упругого закрепления, что позволит более точно оценивать прогиб
иврамкахтакоймоделиисбольшейточностьювосстанавливатьзна-
чение ВГД.
Моделирование упругого опирания пластины может быть осуществ-
лено различными способами. Так, в работе [21] была рассмотрена
задача о колебаниях неоднородной упруго опертой пластины с двумя
коэффициентами жесткости; в рамках такой модели была решена зада-
ча восстановления этих коэффициентов по известному прогибу или по
двум резонансным частотам. Подходы, развитые в этой работе, могут
оказаться полезными при совершенствовании моделей деформирова-
ния РП.
В настоящем пункте на основании работ [21, 22] рассмотрено
несколько задач о деформировании круглой упругой пластины пере-
менной жесткости с различными граничными условиями, в том числе
упругого опирания. Считается, что пластина по краю имеет упругую
связь, которая характеризуется двумя коэффициентами в граничных
условиях. В осесимметричном случае сформулирована краевая задача
для пластины переменной жесткости при наличии упругого опирания.
Для этого на основе вариационного принципа Лагранжа для пластины
был сформулирован и решен численно на основе метода Ритца ряд
вспомогательных задач, не содержащих искомых коэффициентов; полу-
чено представление прогиба как дробно-рациональной функции, содер-
жащей искомые параметры; построена система нелинейных алгебраи-
ческих уравнений, из которой и находятся коэффициенты жесткости
заделки.
В рамках такой модели также была поставлена и решена задача
о восстановлении трех параметров коэффициентов жесткости и распре-
деленной нагрузки, связанной с ВГД. Проведен ряд вычислительных
экспериментов, показавший хорошую точность реконструкции парамет-
ров. Выяснено, как именно распределение жесткости пластины влияет
на точки ее перегиба.
В рамках исследования также была рассмотрена задача об оценке
влияния коэффициентов жесткости на деформативные характеристики
пластины. Установлено, что неучет упругости заделки ведет к суще-
ственным ошибкам реконструкции в определении амплитуды нагрузки
и ВГД соответственно.
Рассмотрим равновесие РП, которая моделируется круглой упругой
изотропной пластиной радиуса переменной жесткости, на которую
действует распределенная нагрузка 9 . Будем считать, что край пласти-
ны упруго оперт; он моделируется двумя упругими связями на краю.
Безразмерный лагранжиан для такой пластины в случае установив-
20/27

2.12. Оценка деформативности неоднородной пластины
129
шихся колебаний построен в [21], а в рассматриваемом статическом
случае соответствующий функционал Лагранжа имеет вид

1
2
1
0
E

E
2

,
-
-

,
-,
-
-

E
E

1
0
9EE
E
3
1
2

3
2
2

1 2
,
(2.12.1)
где введены безразмерные параметры и переменные по формулам:
E
1
0
E,

0 ;,

=
,
H
1"1

2
1
0,
H
2"2

1
0,
9E
9
0E3
,
E
;
1

Здесь ; —
цилиндрическая жесткость,
;
—функция попе-
речного прогиба пластины, —
радиус пластины, 0 ; ,
3
—толщи-
на пластины, E —
безразмерная жесткость, E —прогиб, "1 , "2
—
коэффициенты жесткости заделки, C
—
коэффициент Пуассона.
Из (2.12.1) путем варьирования функционала и приравнивания
нулю коэффициентов при независимых вариациях можно получить
уравнение равновесия неоднородной пластины

E
1

9E
(2.12.2)
и соответствующие граничные условия

1
!

E
1

H
1

(
1

0
1H1

(
1
0, (2.12.3)

2 ECH0
2H2

(
1

0
2H2

(
1
0
Отметим, что граничные условия содержат два параметра, характе-
ризующие влияние закрепления (в данном случае склеры) на деформи-
рование РП.
Для нахождения прогиба использован метод Ритца. Представим
функцию прогиба в виде линейной комбинации
E

E,
(2.12.4)
где
—
некоторые коэффициенты, 7
—
базисные функции вида
7

E
E
21
,
6
1,2,...,
(2.12.5)
После подстановки (2.12.4) в функционал (2.12.1) и нахождения
его минимального значения построена система линейных алгебраиче-
ских уравнений относительно неизвестных коэффициентов разложе-
ния , решая которую, находим функцию прогиба согласно (2.12.4).
Серия расчетов показала, что достаточно выбрать
8, поскольку
21/27

130 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
дальнейшее увеличение размерности аппроксимации вносит несуще-
ственные поправки. Как отмечено выше, важной задачей в диагностике
глаукомы является нахождения точек, в которых происходит изменение
характера выпуклости пластины, — точек перегиба. Для их нахожде-
ния необходимо выяснить структуру прогиба согласно (2.12.4) и далее
найти точки перегиба. В табл. 2 .20 показано, как точка перегиба E из-
меняется в зависимости от задания закона изменения жесткости E.
Дляпростотывсериирасчетовпринято9 1, коэффициент Пуассона
принимается далее равным 0,4.
Таблица 2.20
Положение точки перегиба в зависимости от закона
изменения жесткости

-
-

1
0,5799
1 0,5-
2
0,6399
'

0,6499
1
-
0,5999
В настоящее время считается, что экспоненциальный убывающий
закон наиболее адекватно описывает реальную жесткость РП — умень-
шение жесткости к краю.
Для того чтобы убедиться в достоверности результатов расчетов
прогиба пластинки, сравним численные значения прогибов для од-
нородной пластины с известным аналитическими результатами [49]
в случае жесткой заделки. В табл. 2.21 представлены сравнительные
результаты определения прогиба.
Таблица 2.21
Сравнение прогибов при жестком закреплении
Точное
решение [49]
Метод Ритца
3
132

104
3
132

5104
3
132

105
-

0
0,015625
0,015681
0,015636
0,015631
-

0,25
0,013733
0,013789
0,013744
0,013738
-

0,5
0,008789
0,008844
0,008799
0,008795
-

0,75
0,002991
0,003043
0,003001
0,002996
-

0,95 0,000149
0,000199
0,000159
0,000153
В табл. 2 .22 приведены прогибы в наборе точек для различных
законов изменения жесткости при условии, что H1
H
2
5104.
22/27

2.12. Оценка деформативности неоднородной пластины
131
Видно, что наибольшие прогибы реализуются при экспоненциальном
распределении жесткости.
Таблица 2.22
Прогибы для различных законов жесткости

1 0,5-
2

0
0,015636
0,021941
0,029942
-

0,25
0,013744
0,019285
0,026318
-

0,5
0,008799
0,012346
0,016847
-

0,75
0,003001
0,004208
0,005739
-

0,95
0,000159
0,000219
0,000294
Если оценивать влияние параметров H1 и H2 на деформативность
пластины, то оказывается, что значительно более выражено влия-
ние H1 ,чемH2
.
Приведем сравнение прогибов в центре однородной пластины
(E 1 ,
вычисленных с помощью метод Ритца, с данными,
имеющимися в литературе [1] для случая жесткой заделки (табл. 2 .23).
Таблица 2.23
Сравнен ие прогибов однородной пластин ы
Параме тры
заделки
Давление

,
мм. рт. ст.
Прогиб,
102
мм
Прогиб [1],
102
мм
Расхожде-
ние, %
3
132

105
15
0,8904
0,86
3,53
3
132

104
15
0,8954
0,86
4,12
3
132

103
15
0,9461
0,86
10,01
3
1103
,
3
2102
15
0,9465
0,86
10,05
3
15

104
,
3
27

104
30
1,7819
1,73
2,99
3
18

103
,
3
22

102
30
1,7937
1,73
3,68
3
19

102
,
3
22

104
30
1,9046
1,73
10,09
3
19

105
,
3
23

104
40
2,3730
2,30
3,17
3
132

103
40
2,5228
2,30
9,69
3
132

105
40
2,3743
2,30
3,23
23/27

132 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Перейдем к следующей конечномерной обратной задаче о рекон-
струкции параметров жесткости. Определим положительные парамет-
ры H1 и H2 по известному прогибу E B ,
6
1,2,..., .Стан-
дартный метод определения параметров состоит в использовании ме-
тода наименьших квадратов. В то же время отметим, что возможен
иной подход к решению этой проблемы, для чего сформулируем три
вспомогательные задачи:
1Æ 0
E9,

0
(1 0,

0
(1 0;
2Æ 1 0,

0
11

(
1
0,

0
21

(
1
1;
3Æ 2 0,

0
22

(
11,

2
(1 0
(2.12.6)
Оператор определен при выводе уравнения равновесия, а 0
1,

0
2 — операторы из краевых условий (2.12.3), не содержащие H1 и H2
.
Прогиб будем искать в виде линейной комбинации описанных выше
вспомогательных задач

0"1

1"2

2
(2.12.7)
В случае установившихся колебаний в [21] установлено, что прогиб
вточкахE# есть дробно-рациональная функция от параметров H1 и H2
вида
E
#

031
3
2

131

232

031
3
21
3
12
3
21
,
где ,

—
известные числовые коэффициенты. В статическом случае
структура прогиба будет иметь аналогичный вид. Таким образом, для
решения задачи об определении параметров достаточно знать прогиб
в двух точках пластины, тогда для определения параметров имеет
место система

1
0H1
H
2
1
1H1

1
2H2

1
30,

2
0H1
H
22
1H1

2
2H2

2
30
(2.12.8)
Каждое из уравнений системы (2.12.8) в пространстве парамет-
ров H1 , H2 задает ветви гипербол с осями, параллельными осям коор-
динат, и такая система, вообще говоря, имеет два решения. Проблема
выбора единственного решения разрешается дополнительным требова-
нием положительности искомых параметров. Вычислительные экспери-
менты показали хорошую степень точности реконструкции параметров,
причем при восстановлении H2 погрешность на порядок выше, чем при
восстановлении H1
. Это объясняется тем, что H2 вносит меньший вклад
в величину прогиба.
В табл. 2 .24 приведены значения коэффициентов из разложе-
ния (2.12.4). для вспомогательных задач (2.12.6).
Сростом коэффициенты убывают, что свидетельствует о кор-
ректности вспомогательных задач и устойчивости вычислительной схе-
мы [42].
24/27

2.12. Оценка деформативности неоднородной пластины
133
Таблица 2.24
Коэффициен ты разложен ия (2.12.4) для решен ий
вспомогательных задач
1Æ
2Æ
3Æ

1 0,0109 0,0110 0 ,0110 0,3111 0,3142 0 ,3143 0,2740 0,2742 0 ,2742

2 0,0035 0,0037 0 ,0037 0,0447 0,0541 0,0549 0,0372 0,0399 0 ,0401

3 0,0010 0,0017 0 ,0018 0,0075 0,0195 0,0223 0,0075 0,0142 0 ,0149

4
0,0008 0 ,001
0,0066 0 ,0111
0,0054 0,0074

5
0,0002 0 ,0006
0,0012 0 ,0051
0,0012 0 ,0037

6
0,0002
0,0017
0,0014

7
0,0001
0,0003
0,0003
В рамках предложенной модели также можно поставить задачу об
определении не только параметров H1 , H2 , но и нагрузки 9 ,моделирую-
щей уровень ВГД. При решении такой задачи необходимо знать прогиб
втрехточкахE :
9
B

,6
1, 2, 3. Тогда на основе представления
прогиба будем иметь систему трех нелинейных уравнений вида
9
1
0H1
H
2
1
1H1

1
2H2

1
3
1
4,
9
2
0H1
H
22
1H1

2
2H2

2
3 2
4,
9
3
0H1
H
23
1H1

3
2H2

3
3 3
4
(2.12.9)
Видно, что выражения в левых частях пропорциональны 9 ,
и (2.12.9) приводится к системе вида (2.12.8) путем деления первого
уравнения на второе, второго — на третье, что позволяет исключить 9 .
Из полученной системы вида (2.12.8) находятся H1 , H2 аналогично
предыдущему пункту, а далее полученные значения подставляются
в одно из уравнений (2.12.9), откуда и находится 9 . Сравне
н
и
е
восстановленных данных с исходными показало достаточную степень
точности реконструкции.
Как отмечалось выше, в большинстве работ РП считается жест-
ко защемленной по краю. Предлагаемая в настоящей работе модель
с упругим опиранием позволяет сформулировать задачу об оценке
ошибки при определении давления, которую влечет за собой неучет
упругости заделки, то есть, если РП считается жестко защемленной
(H1, H2
) . Для моделирования такой ситуации сначала заделка
считается упругой, фиксируются значения H1 , H2 , 9 ,находитсяпро-
гиб E при заданных параметрах. Далее заделка полагалась жесткой
ипонайденномуE восстанавливалось значение 9
. Сравнение изна-
чально заданного 9 и восстановленного 9 и позволяет оценить степень
25/27

134 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
влияния коэффициентов H1 , H2 на определение давления. В табл. 2 .25
приведены погрешности реконструкции давления в различных точках.
Таблица 2.25
Оценка погрешности при восстановлении нагрузки
Заданные
параме тры
Погрешнос ть
восстановления ;
вт.8, %
Погрешность
восстановления ;
вт.2, %
Погрешность
восстановления ;
вт.4
5, %
3
132

105
0,04
0,06
0,26
3
132

5104
0,07
0,12
0,52
3
132

104
0,37
0,62
2,58
3
132

5103
0,74
1,24
5,16
3
132

103
3,71
6,22
25,80
Из табл. 2 .25 видно, что неучет влияния упругости при небольших
значениях параметров H1 , H2 приводит к значительной погрешности
при реконструкции давления. По мере приближения к краю пластины
точек измерения погрешность увеличивается, так как увеличивается
влияние упругости заделки.
2.13. Об определении остаточного
упруго-пластического состояния трубы
Задачи о деформировании твердых тел при наличии предваритель-
ного напряженного состояния (ПНС) имеют практическое применение
во многих областях, в первую очередь, при оценке несущей способ-
ности трубопроводов [44, 48]. Так, изучение влияния ПНС на ди-
намические характеристики в упругом случае и его идентификация
проведены в [18]; в настоящем пункте исследована аналогичная задача
при наличии пластической зоны.
В соответствии с [18] рассмотрим задачу о радиальных колебаниях
трубы с внутренним радиусом E1

0 и внешним радиусом E2

E
1.
Колебания трубы вызываются нормальной нагрузкой, приложенной
к внешней границе трубы, имеющей амплитуду 0 иколеблющуюся
с частотой .
Будем считать, что в трубе имеется поле ПН, которое
возникает в случае разгрузки при наличии пластической деформации.
В дальнейшем будем полагать, что задача осесимметрична, (
E , и среди компонент тензора остаточных напряжений отличны
от нуля только две: 0
(

0
(
E

0,
0
+

0
+
E

0.
Уравнение колебаний имеет вид
%

2 0,
(2.13.1)
26/27

2.13. Об определении остаточного состояния трубы
135
причем [3]
#
(

(

0
(
,
#
(+
0,
#
+

1
-

0
+
,
#
+(
0,

(
B

24 ,

+
B

-
,
(2.13.2)
гдеBи
4
—
постоянные Ламе.
После формирования канонической системы дифференциальных урав-
нений первого порядка и обезразмеривания краевая задача примет вид

;
1

3
1 2
L
;

1
+
2
2

,
L
;

<
2
2

3
122

3
12

;

3
222
2
2

1
3
122
2
2

3
1 2

G
2

,
(2.13.3)
L
;
0 0,L1

(2.13.4)
Здесь введены следующие безразмерные параметры и функции:
E
E
2;,
;

;
0,1 ,
;
0
-
1
-
2
,
E
E
2 ;,
#
(
E
4L
;,

0
(
4H
1;,

0
+
4H
2;,

!
0

2
,
G
2/0
2
-
2
2

В случае наличия пластической зоны в области ;0

;

соот-
ношения, описывающие поля предварительных напряжений в рамках
модели идеальной пластичности, имеют вид [40]
H
1; (

2 2
2

;
2

1
2
2
0
12
2
0

1
1
2
2

H
2;
(

2
2
2

;
2

1
2
2
0
12
2
0

1
1
2
2

,
(2.13.5)
где ;
—
безразмерный радиус зоны пластичности, (

3+ ,

—
предел текучести для исследуемого материала. При
линейном упрочнении аналогичные формулы для компонент предва-
рительных напряжений в пластической области ;0

;

имеют
вид [40]
H
1; ( 23

2
2

3
;
2

;
2

,
H
2; ( 23

2
2

3
;
2

;
2

(2.13.6)
где3 1

+
—
параметр упрочнения,
—модуль Юнга, а
—
модуль упрочнения для исследуемого материала.
Решение прямой задачи об определении значений функций ;,
L
;
из краевой задачи (2.13.3), (2.13.4) при заданных функциях H1
; ,
H
2; реализовано численно на основе метода пристрелки в паке-
те Maple с использованием метода Рунге–Кутта.
P owe red by T CP DF (www.tcp df.o rg)
27/27

136 Гл. 2. Конечномерные ОЗ. Определение постоянных параметров
Задача об отыскании функций H1 и H2 может быть исследована
на основе общих подходов к решению обратных коэффициентных за-
дач [5].
Значение внутреннего давления, при котором в стенках трубы воз-
никает зона пластических деформаций, определяется из трансцендент-
ного уравнения [4]

2
2
0

1
2

1;2

!
2$

,
(2.13.7)
где $
—
значение предела текучести по критерию Мизеса,

—зна-
чение внутреннего давления, при котором возникает область пластич-
ности радиуса ;
.
Отметим, что при малых значениях ; его можно
определять согласно формуле
;

;
0

1
2

12
2
0

,
(2.13.8)
причем ее погрешность для тонкостенной трубы (E1 1002 мм, E2
1020 мм) и давлениях порядка 10 МПа не превосходит 0,5 %.
В табл. 2 .26 для различного уровня внутреннего давления приве-
дены значения ; и первые два резонансных значения параметра G .
Таблица 2.26
!,МПа

2
0,0
0,0
0,8333
1,85088
35,31766
95,0
0,3290 0,8697
1,85087 35,31763
105,25
0,3645 0,9951
1,85085
35,31740
В табл. 2 .27 представлено влияние уровня давления на резонансные
значения для упрочняющегося материала, предварительное напряжен-
ное состояние которого описывается согласно (2.13.6) при 3 0,8.
Таблица 2.27
!,MПа

2
95,0
0,3290 0,8697
1,85274
35,31513
105,25
0,3645 0,9951
1,85298 35,31521
Отметим, что влияние пластического деформирования на резонанс-
ные значения невелико для тонкостенных цилиндров в обоих случаях.
Однако результаты расчетов свидетельствуют о снижении первого
и второго резонансных значений при наличии пластической зоны.
Обратная задача — это восстановление остаточного напряженного
состояния по данным об изменении собственных частот.
1/27

2.13. Об определении остаточного состояния трубы
137
Рассмотрим задачу о восстановлении уровня ПНС по имеющимся
данным об изменении собственных частот колебаний. Сформулиру-
ем однородную краевую задачу для отыскания резонансных значений
и собственных форм, которая имеет вид

H
1 1
+
2

1
2
2

H
1
+
2
2

H
2

G
2

0,
(2.13.9)

H
1 1
+
2

;
0 0,

H
1 1
+
2

1 0
(2.13.10)
На основе метода возмущений получена формула, связывающая
изменение резонансных значений с функциями H1 , H2 ,
G
2G2
0
1Ê

0
3
12 +0

3
2+
2
02

2
1Ê

0
2+
2
02
,
(2.13.11)
где 0
—
собственная форма колебаний для ненапряженного состояния.
Эта формула позволяет оценивать изменение резонансной частоты в за-
висимости от различного вида структуры и уровня ПН.
В табл. 2 .28 приведены точные и восстановленные значения дав-
ления и радиуса зоны пластичности ; , а также соответствующие
им величины резонансных значений. Отметим, что восстановление
происходит с погрешностями, не превышающими 0,3 % и 0,2 % соот-
ветственно.
Таблица 2.28
! ,МПа
2

,МПа
2

2
2
0

89 0,83713 88,75279 0,83592 1,85088 35,31766 0,83333 500
93 0,85797 92,86228 0,85733 1,85087 35,31765 0,83333 500
97 0,88284 97,08996 0,88333 1,85087 35,31760 0,83333 500
101 0,91533 100,95179 0,91503 1,85086 35,31753 0,83333 500
105 0,97871 104,99276 0,97871 1,85085 35,31741 0,83333 500
Таким образом, данные о значениях собственных частот могут
быть использованы для решения обратной задачи идентификации ПНС
в трубе на основе формулы (2.13.11) и в случае наличия пластической
зоны.
2/27

Список литературы к гл. 2
1. Арсеньев Д.Г ., Аранов В.Ю ., Бауэр С.М . идр. Математические модели
и компьютерное моделирование в биоме хан ике . СПб.: Изд-во Полите хн и-
ческого университета, 2004. 516 с.
2. Ахатов И .Ш ., Ахтямов А.М . Определение вида закрепления стержня
по собственным частотам его изгибных колебаний // Прикл. математика
и механика. 2001. Т . 65, вып. 2. C . 290–298.
3. Ахтямов А.М . Теория идентификации краевых условий и ее приложения.
М.: ФИЗМАТЛИТ, 2009. 272 с.
4. Ахтямов А.М ., Аюпова А.Р . О решении задачи диагностирования де-
фектов в виде малой полости в стержне // Журнал Средне волжского
математического общества. 2010. Т . 12, No 3. С . 37–42.
5. Ахтямов А.М, Ильгамов М.А. Модель изгиба балки с надрезом: прямая
и обратная задачи // Прикладная механика и техническая физика. 2013.
Т. 54. No 1. С. 152–162.
6. Ахтямов А.М ., Кар и м о в А.Р . Диагностирование местоположения трещины
в стержне по собственным частотам продольных колебаний // Техническая
акустика. 2010. Т . 10, No 3.
7. Ахтямов А.М ., Сатыев Э.И . Определение местоположения и объема по-
лости в упругом стержне по двум собственным частотам его колебаний //
Дефектоскопия. 2012. No 5. С. 78-83 .
8. Ахтямов А.М ., Сафина Г.Ф . Определение виброзащитного закрепления
трубопровода // Прикладная механика и техническая физика. 2008. No 1.
С. 139–147.
9. Баранов И.В ., Ватульян А.О., Соловьев А.Н . Об одном генетическом
алгоритме и его применении в обратных задачах идентификации упругих
сред // Вычислительные технологии. 2006. No 3. С. 14–25.
10. Бауэр С.М ., Воронкова Е.Б . Модели теории оболочек и пластин в зада-
чах офтальмологии // Вестник СПбГУ. Сер. 1. Т . 1 (59). 2014. Вып. 3.
С. 438–458.
11. Бауэр С.М ., Зимин Б.А., То встик П .Е. Простейшие модели теории оболо-
чек и пластин в офтальмологии. Изд-во СПбГУ, 2000. 92 с.
12. Беллман Р., Ка л аба Р . Квазилинеаризация и нелинейные краевые задачи.
М.: Мир, 1968. 184 с. (Bellman R. , Kalaba R. Quasilinearization and
Nonlinear Boundary Value Problems. New York, Elsevier, 1965.)
13. Бочарова О.В ., Ватульян А.О., Жарков Р.С .Реконструкция малыхполо-
стей в упругих стержнях // Известия вузов. Сев.- Кавк. рег. Естеств. науки.
2006. No 2. С.28–32.
14. Ватульян А.О . Обратные задачи в механике деформируемого твердого
тела. М.: ФИЗМАТЛИТ, 2007. 223 с.
15. Ватульян А.О ., Беляк О.А ., Сухов Д.Ю., Явруян О.В .Обратныеинекор-
ректные задачи. Ростов-на-Дону: Изд-во ЮФУ. 2011. 232 с.
3/27

Список литературы к гл. 2
139
16. Ватульян А.О ., Васильев Л .В . Об определении параметров упругого за-
крепления неоднородной балки // Экологический вестник ЧЭС. 2015. No 3.
С. 14–19.
17. Ватульян А.О., Васильев Л .В . Об определении параметров закрепления
неоднородной балки при наличии затухания // Изв. Сарат. ун-та. Нов.
сер. Сер. Математика. Механика. Информатика. 2016. Т . 16, вып. 4.
С. 449–456.
18. Ватульян А.О., Дударев В.В ., Богачев И.В . Об определен ии предвари-
тельного напряженного состояния в трубе // Доклады РАН. 2014. Т . 456,
No 3. С. 299–301.
19. Ватульян А.О ., Каш т ал ь ян Д .О. Об определении зоны деструкции в упру-
гой балке // Изв вузов. Северо-Кавказский регион. Сер. естеств. науки.
2015. No 4. С. 29–34.
20. Ватульян А.О., Осипов А.В . Об одном подходе при определении параме т-
ров дефекта в балке // Дефектоскопия. 2014. No 11. С. 37–47.
21. Ватульян А.О ., Потетюнко О.А . О колебаниях неоднородной пластины
супругоопертымкраем//Известиявузов.Северо-Кавказскийрегион.
Сер. естеств. науки. 2016. No 2. С. 28–33.
22. Ватульян А.О., Потетюнко О.А. К оценке деформативнос ти реше тчатой
пластинки глаза // Российский журнал биомеханики. 2017. No 1. С . 8 –17.
23. Ватульян А.О ., Соловьев А.Н . Обратные задачи теории трещин в твер-
дых телах // Известия высших учебных заведений. Сев.- Кавк. рег. 2004.
Спецвыпуск «Математика и механика сплошной среды». С . 74 –80.
24. Ватульян А.О ., Солуянов Н .О . Об определении местоположения и размера
полости в упругом стержне // Дефектоскопия. 2005. No 9 . С. 44 –56.
25. Ватульян А.О .,
Солуянов Н .О. Идентификация полости в упругом
стержне при анализе поперечных колебаний // Прикладная механика
и техническая физика. 2008. Т . 49, No 6. С. 1015–1020.
26. Ватульян А.О ., Сухов Д.Ю. Об одном методе определения параметров
упругих потенциалов // Экологический вестник ЧЭС. 2012. No 4. С. 27–32.
27. Ватульян А.О. Явруян О.В . Идентификация композиционных материа-
лов // Механика композиционных материалов и конструкций. 2007. Т . 13,
No 2. С. 174–180.
28. Гладков Л .А., Ку рейчик В.В., Курейчик В.М. Генетические алгоритмы.
2-е изд. М .: ФИЗМАТЛИТ, 2006. 320 c.
29. Грин А., Аткин с Дж. Большие упругие деформации и нелинейная меха-
ника сплошной среды. М .: Мир, 1965. 456 с.
30. Дени сов А.М . Введение в теорию обратных задач. М.: МГУ, 1994. 206 с.
31. Интегральные уравнения. СБМ. Под ред. Забрейко П. П. М.: Наука, 1968.
448 с.
32. Ильгамов М.А ., Хаки мов А .Г . Диагнос тика повреждений консольной бал-
ки с надрезом // Дефектоскопия. 2009. No 6. С. 83–89 .
33. Ильгамов М.А . Диагностика повреждений вертикальной штанги // Труды
института механики УНЦ РАН. Вып. 5. Уфа: Гилем, 2007. С. 201–211.
34. Кабан и хи н С .И . Проекционно-разностные методы определения коэффици-
ентов гиперболических уравнений. Новосибирск.: Наука, 1988. 168 с.
35. Кабан и хи н С .И . Обратные и некорректные задачи. Новосибирск: Сибир-
ское научное издательство, 2009. 458 с.
4/27

140
Список литературы к гл. 2
36. Кр ас н о в М .Л . Интегральные уравнения. М .: Наука, 1975. 305 с.
37. Кристенсен Р. Введение в вязкоупругость. М .: Мир, 1973. 338 с.
38. Лаврентьев М.М ., Романов В.Г ., Шишатский С .П . Некорректные задачи
математической физики и анализа. М .: Наука, 1980. 286 с.
39. Ланда П .С . Нелинейные колебания и волны. М .: Наука. ФИЗМАТЛИТ,
1997. 496 с.
40. Малинин Н.Н . Прикладная теория пластичности и ползучести. М .: Маши-
ностроение, 1975. 117 с.
41. Марпл С.П . Цифровой спектральный анализ и его приложения. М.: Мир.
1990. 547 c.
42. Ми хлин С.Г . Вариационные ме тоды в математической физике . М .: Наука,
1970. 512 с.
43. Найфе А.Х . Методы возмущений. М.: Наука, 1976. 474 с.
44. Никитина Н.Е., Камышев А.В., Казачек С.В. Использование явления аку-
стоупругости при исследовани и напряженного состояни я тех нологическ и х
трубопроводов // Дефектоскопия. 2009. No 12. С. 52–59 .
45. Оль ховой А .Ф . Обратные некорректные задачи. Введение в проблематику.
Таганрог: Изд-во ТТИ ЮФУ, 2009. 132 с.
46. Павлов Б.В. Акустическая диагностика механизмов. М .: Машиностроение,
1971. 224 с.
47. Самарский А.А ., Вабищевич П .Н . Численные методы решения обратных
задач математической физики. М .: Эдиториал УРСС, 2004. 480 с.
48. Рудаченко А.В ., Саруев А.Л . Исследования напряженно-деформирован-
ного состояния трубопровода. Томск: Изд-во ТПУ, 2011. 136 с.
49. Тимошенко С.П ., Войновский-Кригер С. Пластинки и оболочки. М .: Физ-
матгиз, 1963. 635 с.
50. Тихонов А.Н .,
Арсенин В.Я . Методы решения некорректных задач.
М.: Наука, 1986. 287 с.
51. Тихонов А.Н ., Гончарский А.В., Степанов В.В ., Ягола А .Г . Численные
методы решения некорректных задач. М .: Наука, 1990. 230 с.
52. Филиппов А.П . Колебания деформируемых систем. М .: Машиностроение.
1970. 736 с.
53. Хак ен Г . Си нерге тика. Иерархии неустойчивостей в самоорганизующихс я
системах и устройствах. М .: Мир, 1985. 424 с.
54. Шевцов С.Н ., Акопьян В.А., Рожков Е.В. Решение задач идентификации
повреждений в упругом стержне на основе модели балки Тимошенко //
Дефектоскопия. 2011. No 7. С. 65–78
55. Шифрин Е.И . Идентификация эллипсоидального дефекта в упругом теле
по результатам одного испытания на одноосное растяжение (сжатие) //
Изв. РАН. МТТ . 2010. No 3. С . 131–142.
56. Akhtyamov A.M . On the spectrum of an odd-order differential operator //
Mat. Zametki. 2017. V. 101:5. P. 643–646.
57. Akhtyamov A.M ., Mo uftakho v A.V . Identification of boundary conditions
using natural frequencies // Inverse Probl. Sci. Engng. 2004. V. 12, No 4.
P. 393 –408.
58. Alessandrini G., Morass i A., Rosset E. Detecting an inclusion ia an elastic
body by boundary measurements // SIAM J. Math. Anal. 2002. V. 33, No 6.
P. 1247–1268.
5/27

Список литературы к гл. 2
141
59. Ahmad B., Nieto J.J ., Shahzad N. Generalized quasilinearization method for
mixed boundary value problems // Appl. Math. Comput. 2002. V. 133, No 2, 3.
ISSN 0096-3003 . P. 423–429.
60. Chaparro B., Thuillier S., Menezes L., Manach P., Fernandes J.Material
parameters identification: Gradient-based, genetic and hybrid optimization
algorithms // Comput. Materials Science. 2008. V. 44, Iss. 2 . Elsevier B.V.
P. 339 –346.
61. Holland J.H . Adaptation in natural and artificial systems. University of Michi-
gan Press, Ann Arbor, 1975.
62. Lakshmikantham V ., Vat s al a A .S. Generalized quasilinearization for nonlin-
ear problems // Mathematics and Its Applications. V. 440. Springer, 1998.
286 p.
63. Mandelzweig V .B ., Tabakin F . Quasilinearization approach to nonlinear
problems in physics with application to nonlinear ODEs // Computer Physics
Communications. V. 141, Iss. 2. P. 268–281. Elsevier, 2001.
64. Morass i A., Rosset E. Detecting rigid inclusions, or cavities, in an elastic
body // J. Elast. 2003. V. 73, No L-3 . P. 101–126
65. Sylvester R.J ., Meyer. F . Two point boundary problems by quasilineariza-
tion // Journal of the Society for Industrial and Applied Mathematics. Jun.,
1965. V. 13, No 2. P. 586 –602.
66. Stanley Lee E. Quasilinearization, parameter estimation, and distillation col-
umn design // Chemical Engineering Communications. 1974. V. 1, Iss. 5.
P. 249–259.
67. Va s u ndha ra D evi J ., McRae F.A., Drici Z. Generalized quasilinearization for
fractional differential equations // Computers Mathematics with Applications.
2009. V. 59, No 3. Elsevier Ltd, ISSN: 08981221. P. 1057–1062.
68. Prony G.R .B . Essai experemenal et analytique: sur les lois de la dilitabilite de
fluids elastques et sur celles de la force expanslve de la vapeure de l’eau et la
vapeure de l’alkool, a differentes temperatures // J. de L’Ecole Polytechnique.
1795. V. 1. P. 24–76.
6/27

Глава 3
ОБЩИЕ ПРИНЦИПЫ ИССЛЕДОВАНИЯ
КОЭФФИЦИЕНТНЫХ ОЗ
С ПЕРЕМЕННЫМИ ХАРАКТЕРИСТИКАМИ.
РЕШЕНИЕ ЛИНЕЙНЫХ КОЗ
В настоящей главе представлены некоторые общие аспекты иссле-
дования обратных коэффициентных задач для различных моделей, при-
чем основное внимание уделено тому классу КОЗ, когда неизвестными
являются функции одной переменной, входящие в описание диффе-
ренциального оператора (обыкновенного или в частных производных).
Такие задачи уже существенным образом отличаются от конечномер-
ных коэффициентных обратных задач, основные аспекты исследования
которых изложены в гл. 2 . Обсуждены различные типы постановок
таких ОЗ, сформулировано обобщенное соотношение взаимности для
упругих тел, даны слабые и вариационные постановки, изучены некото-
рые вопросы построения решений, предложены эффективные вычисли-
тельные схемы; осуществлено построение решений ряда КОЗ в первой
постановке.
3.1 . Коэффициентные обратные задачи
для линейных операторов. Обобщенное соотношение
взаимности. Типы коэффициентных обратных задач,
их особенности, первая и вторая постановки
Среди основных типов ОЗ два типа (ретроспективные и граничные)
приводят к исследованию линейных проблем [5], а два — геометриче-
ские и коэффициентные — приводят к исследованию существенно нели-
нейных проблем. При этом для геометрических ОЗ существует способ,
основанный на методе граничных интегральных уравнений, позволяю-
щий в аналитическом виде получить нелинейные операторные уравне-
ния, связывающие искомые и измеряемые функции на границе. Этот
класс задач об определении полостей и трещин в рамках избранной
модели исследован достаточно подробно, чему посвящен ряд моногра-
фий и статей [1, 16, 19, 31, 43]. Для таких задач разработаны методы
исследования систем операторных уравнений, созданы итерационные
процедуры решения задач, основанные либо на коротковолновом, либо
на борновском приближении. Кроме того, весьма популярным является
метод, основанный на сужении множества поиска до конечномерного
7/27

3.1. Коэффициентные обратные задачи для линейных операторов 143
при ясной параметризации полостей и трещин конечным числом пара-
метров.
Конечномерные КОЗ и методы их исследования достаточно по-
дробно представлены в гл. 2 . Они могут базироваться как на явном
представлении решений дифференциальных уравнений и выполнении
некоторых дополнительных условий, так и на использовании некоторых
итерационных процедур типа метода квазилинеаризации.
Для коэффициентных обратных задач в случае зависимости иско-
мых параметров-функций от координат операторные уравнения, связы-
вающие заданные и искомые функции, в общем случае неоднородности
в явном виде построены быть не могут. Таким образом, коэффициент-
ные обратные задачи в этом случае, возникающие на этапе формули-
ровки модели, относятся к самому трудному классу обратных задач.
Отметим, что модели математической физики, сложившиеся до-
статочно давно (например, классическая модель теплопроводности),
опиравшиеся на гипотезы однородности и изотропии, позволили с до-
статочной степенью точности описывать различные процессы. Эти мо-
дели требовали определения лишь нескольких параметров на этапе па-
раметрической идентификации, что позволяло строить аналитические
решения для канонических областей, исследовать влияние параметров
задачи, условий нагружения на процесс и делать обоснованные выводы.
Аналогичная ситуация формировалась и при исследовании задач
деформирования твердых тел. Математическая формулировка проблем
деформирования твердых тел на основе простейшего варианта модели
(однородное изотропное тело), в фундамент которой были положены диф-
ференциальные уравнения равновесия Коши и закон Гука [24], позволила
решить целый ряд актуальных научных проблем, придала импульс как
развитию и совершенствованию инженерных расчетов на прочность и ус-
тойчивость, так и созданию теории общих краевых задач для эллиптичес-
ких операторов и их исследованию. Эта модель благодаря определению
двух упругих постоянных — модуля Юнга и коэффициента Пуассона —
на основе простых макроэкспериментов (опыты на растяжение и круче-
ние стержней) стала эффективным средством анализа многих проблем
нетольковмеханикедеформируемоготвердоготела,ноивсмежных
областях (машиностроение, строительство, акустика, геофизика).
При исследовании ряда новых проблем деформирования твердых
тел (механика композитов, геофизика, горная механика, биомеханика)
эта модель оказалась недостаточной для адекватного описания их
поведения, что повлекло за собой отказ либо от гипотезы однородно-
сти, либо от гипотезы изотропии, либо от обеих этих гипотез сразу.
Если теория упругости однородного анизотропного тела на протяжении
XIX и XX веков успешно развивалась и продвинута достаточно далеко
(по крайней мере, в решении многих задач о равновесии тел [21]),
то в теории упругости неоднородного тела (даже изотропного) дости-
жения гораздо скромнее [22, 26, 28]. Это обусловлено тем обстоя-
тельством, что не существует способа построения в аналитическом
8/27

144
Гл. 3. Общие принципы исследования коэффициентных ОЗ
виде общих решений линейных дифференциальных уравнений выше
второго порядка при произвольных законах изменения коэффициентов.
Отметим, что основное внимание при анализе моделей неоднородной
теории упругости уделялось как общим вопросам существования ре-
шений, так и способам построения усредненных моделей в средах
с быстро меняющимися коэффициентами — весьма важным с точки
зрения теории пластин и механики композитов [26].
Заметим, что для анализа равновесия или колебаний однородно-
го анизотропного тела достаточно знать компоненты тензора упругих
постоянных, а для практического использования модели неоднородной
теории упругости в геофизике, дефектоскопии, фундаментостроении,
горной механике, био- и наномеханике необходимо знать в самом про-
стом случае непрерывно-неоднородного изотропного тела три функции
(модули Ламе и плотность среды). При этом физические характери-
стики задаются при помощи функциональных зависимостей, которые
должны быть предварительно определены из некоторых экспериментов
или наблюдений, как правило, связанных с измерением граничных
или внутренних полей смещений или ускорений при возбуждении
колебаний некоторой нагрузкой. Наиболее часто такие зависимости
предполагаются одномерными (особенно при использовании моделей
слоя, полупространства или слоистого полупространства), а наиболее
распространенный способ их определения — анализ отклика исследуе-
мого объекта при возможном варьировании способа нагружения. При
этом задача определения нескольких функций приводит к исследова-
нию довольно сложных нелинейных обратных задач для эллиптиче-
ских и гиперболических операторов, различные аспекты которой стали
предметом исследования относительно недавно [3–12].
Отметим, что довольно часто принимаемый кусочно-постоянный
характер изменения искомых характеристик в ряде ситуаций оправдан,
поскольку это предположение существенно сужает область поиска
и значительно упрощает исследование обратных задач, например
в задачах идентификации слоистых структур [23, 30, 31], однако может
привести к существенному искажению результатов идентификации,
и, как следствие, к ошибкам при прогнозировании ресурса конструкции.
В рамках такого подхода решение исходной некорректной задачи сво-
дится к определению конечного числа параметров в некоторой ограни-
ченной области - мерного пространства поиска. Такой поиск в послед-
ние годы осуществляется на основе метода регуляризации на компакт-
ных множествах, а среди конечномерных вариантов отметим как тра-
диционные градиентные методы нахождения минимумов функционалов
невязки, так и нейросети и генетические алгоритмы, некоторые аспекты
реализации которых для конечномерных задач освещены в гл. 2.
Заметим, что к коэффициентным обратным задачам, в которых
требуется определить коэффициенты дифференциальных операторов по
некоторой дополнительной информации о решении, приводят несколько
различных постановок, что отмечено в обзорной работе [10].
9/27

3.1. Коэффициентные обратные задачи для линейных операторов 145
Во-первых, это собственно коэффициентные обратные задачи
(КОЗ), в которых необходимо найти модули Ламе (или один из них
в рамках модели несжимаемой среды) и плотность как функции коор-
динат (или переменные коэффициенты теплопроводности для класси-
ческой модели теплопроводности). Этот тип задач, порожденный совер-
шенствованием моделей в геофизике, исследовался достаточно давно,
начиная с классической работы Герглотца [44], в которой построено
решение одномерной обратной задачи для шара; это направление
далее развивалось на основе нестационарных постановок и в рамках
этого подхода решен ряд обратных одномерных задач для полупро-
странства [37].
Также отметим работы [39, 40, 41], посвященные ОЗ для моделей
теории упругости. В настоящее время этот класс обратных коэффи-
циентных задач для операторов (как правило, второго порядка) при-
влекает наибольшее внимание исследователей, предлагаются новые по-
становки, итерационные схемы, реализуются экономичные алгоритмы
решения [40, 45–47, 49]. При этом решение проблемы идентификации
для некоторых классов задач опирается на построение точного решения
задачи (например, для обыкновенных линейных дифференциальных
операторов с постоянными коэффициентами) и дальнейшей реализации
этапа параметрической идентификации на основе метода наименьших
квадратов и его модификаций. В последние годы возрос интерес к ко-
эффициентным обратным задачам для связанных полей — моделей тер-
моупругости, электроупругости, пороупругости [30], для которых уже
требуется определять большее число материальных функций.
Во-вторых, это КОЗ, к которым приводятся геометрические обрат-
ные задачи об определении геометрических характеристик малых поло-
стей или включений; задачи такого типа можно трактовать как частный
случай задач первого типа с кусочно-постоянными модулями и плот-
ностью. В рамках классических моделей стержней Эйлера–Бернулли
иТимошенкоипластиниоболочектипаКирхгофа–Ляваспеременной
жесткостью они сводятся к обратным коэффициентным задачам для
операторов с переменными коэффициентами второго или четвертого
порядка [3, 6].
В третьих, это КОЗ об определении структуры существенно неод-
нородного предварительного напряженного состояния [17], который
практически не исследован, хотя в рамках модели акустоупругости [25]
в литературе имеются результаты, на основе которых созданы и успешно
эксплуатируются реальные приборы по измерению уровня однородного
предварительного напряженного состояния в элементах конструкций.
Колебания упругих тел в условиях неоднородного предварительного
напряженного состояния в линеаризованной постановке описываются
краевой задачей для системы дифференциальных уравнений с пере-
менными коэффициентами, которые выражаются через компоненты
тензора предварительных напряжений. Особенность этого типа коэф-
фициентных обратных задач по сравнению с первыми двумя состоит
10/27

146
Гл. 3. Общие принципы исследования коэффициентных ОЗ
в том, что определять необходимо 6 компонент тензора предваритель-
ных напряжений, зависящих от координат (в плоском случае 3 ком-
поненты), которые, во-первых, должны быть подчинены уравнениям
равновесия, а во вторых, для компонент нет дополнительных условий
положительности, которые имеют место для задач первых двух типов.
К сожалению, как показали исследования, проведенные Био, Терстоном
и Мак-Дональдом, распространение волн в напряженном материале
не может быть сведено к анализу волновых процессов в анизотропном
материале с изменившимися модулями упругости. Отметим, что линеа-
ризованные трактовки таких задач имеют достаточно много вариантов
постановок, и это может являться предметом отдельного обсуждения.
В настоящей монографии использован подход Трефтца, далее развитый
А. Н . Гузем [17] и широко представленный при решении конкретных
задач в отечественной и зарубежной литературе [42, 43, 48] (более
подробное обсуждение этого вопроса будет проведено в гл. 4).
Отметим, что КОЗ по восстановлению переменных коэффициентов
дифференциальных операторов по некоторой дополнительной информа-
ции о решении могут быть исследованы в рамках единого подхода [10].
Заметим, что можно рассматривать две кардинально различные по-
становки задачи определения коэффициентов в зависимости от способа
задания дополнительной информации.
Дополнительная информация, по которой строится решение
коэффициентной обратной задачи, может быть самой разнообразной.
В качестве ее может выступать информация о следах решения либо
внутри ОИ, либо на его границе. Естественно, что более приближенной
к практике является вторая постановка, когда измерение производится
с помощью датчиков, измеряющих граничные значения полей, однако
развитие методов измерений позволяет в ряде случаев опираться и на
первую постановку. Кроме того, ее исследование — важный промежу-
точный шаг на пути исследования КОЗ во второй постановке. Так,
например,длямоделейтеорииупругостивпервойпостановкеврамках
установившегося режима колебаний реконструкция искомых характе-
ристик осуществляется по измерению внутренних полей смещений на
некоторой фиксированной частоте колебаний, а во второй — по измере-
нию граничных полей смещений или ускорений в некотором частотном
диапазоне. В первом случае обратная задача линейна, она сводится к за-
даче Коши для дифференциального оператора первого или второго поряд-
ка; во втором случае задача существенно нелинейна. Основная труд-
ностьприизученииКОЗвовторойпостановкесостоитвформулировке
операторных соотношений, связывающих искомые и измеряемые функ-
ции. Переменность коэффициентов дифференциальных операторов не
позволяет построить в явном виде общие представления решений для
соответствующих операторов, как это имеет место для операторов с по-
стоянными коэффициентами. Если коэффициенты дифференциальных
операторов меняются произвольным (непрерывным или разрывным)
образом, то методы решения прямых задач опираются либо на аппарат
11/27

3.1. Коэффициентные обратные задачи для линейных операторов 147
интегральных уравнений Фредгольма второго рода (для стержней
и пластин [2]), численную процедуру обращения соответствующих им
конечномерных операторов, либо на метод пристрелки и, наконец, на
прямое использование конечноразностных или конечноэлементных тех-
нологий. Построение же операторных соотношений в коэффициентных
обратных задачах во второй постановке можно осуществить, лишь фор-
мируя итерационные процессы для отыскания неизвестных функций,
которые основаны либо на обобщении теоремы взаимности, либо на
слабой постановке [10]; при этом на каждом шаге решается стандарт-
ная некорректная задача — обращение интегрального оператора Фред-
гольма первого рода с непрерывным (суммируемым) ядром.
Прежде всего, сформулируем некоторое общее соотношение для
неоднородных упругих тел, которое далее будем именовать обобщен-
ным соотношением взаимности.
Рассмотрим установившиеся колебания с частотой ограниченной
области 8 с границей ?
?

?
,
,а
—
компоненты единичного
вектора внешней нормали к ? .
Уравнения колебаний имеют вид

2# 0,
>
1,2,3,
(3.1 .1)

,%,
(3.1 .2)

(3.1 .3)
Здесь # %
—
компоненты тензора упругих модулей, являющиеся кусоч-
но-непрерывными функциями координат и удовлетворяющие обычным
условиям симметрии и положительной определенности,
—
плотность
среды, ,
&+&

и по повторяющемуся индексу производится сум-
мирование от 1 до 3. Сформулируем задачу определения коэффициен-
тов дифференциального оператора теории упругости по дополнитель-
ной информации

#
,

1, 2

(3.1 .4)
Такая постановка соответствует измерению поля перемещений на
части границы ?, , на которой осуществляется нагружение, в некото-
ром диапазоне частот.
Сформулированная обратная коэффициентная задача является
нелинейной некорректной задачей. Сформулируем кратко обобщенное
соотношение взаимности в соответствии с результатами работ [4, 6].
Теор ема 3.1 . Пусть имеется два решения задачи (3.1 .1)–(3.1.3),
отвечающие различным модулям упругости и различным плотностям:

1
#
,
1
# %
,
1 и

2
#
,
2
#%
,
2
.
Тогда имеет место следующее обоб-
щенное соотношение взаимности:
-

2
# %

1
#%

2
,%

1
#,
8

2
#

1
#

2
-

2
#

1
#
8
0,

1, 2

(3.1 .5)
12/27

148
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Это соотношение является обобщением известной теоремы взаим-
ности (теоремы Бетти в линейной теории упругости) и переходит в нее
при одинаковых механических характеристиках. Его можно трактовать
как нелинейное операторное соотношение, используемое при решении
обратной задачи. На основе соотношения (3.1 .5) легко построить ите-
рационные процессы и сформулировать последовательность линейных
интегральных уравнений Фредгольма 1-го рода с суммируемым ядром
для определения поправок. Осуществим вывод линеаризованных урав-
нений для нахождения поправок. Полагая в соотношении (3.1 .5)

1
#

1
#
,

2
#

1
#

#
,

1
# %

1
#%
,

2
# %

1
#%

#%
,

1
,

и сохраняя в нем линейные по величинам - го приближения слага-
емые, с учетом дополнительного условия (3.1 .4) получим следующее
уравнение относительно поправок

#%
,

[4]:
-

1
,%

1
#,
8

2
-

1
#

1
#
8

1
#

?
0,

1, 2

1,2,...,
(3.1 .6)
Соотношение (3.1 .6) можно трактовать как линейное интегральное
уравнение относительно компонент

и ,еслипредвари-
тельно решена прямая задача о нахождении полей смещений и де-
формаций внутри области 8 и на ее границе ? с характеристиками

1
# %

и 1
.
Линейному операторному соотношению (3.1 .6)
можно дать следующую трактовку. Введем стандартные обозначения
функционалов

,
1

1
2
-

# %

1
,%

1
#,
8
,
'

,
1

1
2

2
-

1
#

1
#
8
,
,

1
#

?
(3.1 .7)
Заметим, что подынтегральные выражения в объемных интегралах
в (3.1 .6) представляют собой по форме аналоги удвоенной удельной
потенциальной энергии деформаций и удельной кинетической энергии,
в которой перемещения и деформации соответствуют 1 -й итерации
(предыдущей), а модули —
- й итерации (последующей). Мерой выхода из
итерационной процедуры является функционал
.
2
Ê
.
1
Ê
*

1
#

2?,
13/27

3.2 . Слабая и вариационная постановки ОЗ
149
и, если его значение становится меньше погрешности входной инфор-
мации, то процесс необходимо остановить.
С учетом введенных обозначений интегральному уравнению (3.1 .6)
можно придать форму
2 '
0
(3.1 .8)
На основе такой трактовки можно формулировать операторные со-
отношения в обратных задачах при реализации итерационных процес-
сов для стержней и пластин, для чего достаточно найти соответству-
ющие выражения для функционалов в (3.1.7); конкретные примеры
построения этих операторных соотношений будут представлены в гл. 4 .
3.2 . Слабая и вариационная постановки ОЗ
3.2.1. Слабая постановка ОЗ. В настоящем пункте излагается
иной подход к исследованию КОЗ для операторов с переменными ко-
эффициентами. Для упругих тел можно пользоваться обобщенным со-
отношением взаимности (3.1.5) и полученным на основе него оператор-
ным соотношением (3.1 .6), представленным в 3.1. При исследовании
коэффициентных обратных задач, состоящих в определении некоторых
функций, характеризующих неоднородность, для общих линейных мо-
делей механики сплошной среды, существенным моментом для их ис-
следования является формулировка слабой постановки, которая весьма
часто используется и для исследования прямых задач. Изложим основ-
ные этапы подхода в соответствии с [10].
Рассмотрим установившиеся колебания ограниченной области 8
с кусочно-гладкой границей ? ? ?, ,а
—
компоненты единич-
ного вектора внешней нормали к ? . Сформулируем постановку коэффи-
циентных обратных задач. Пусть уравнения установившихся колебаний
среды и соответствующие граничные условия имеют вид
,

0,
,

,
(3.2 .1)
где ,
,
,

—
линейные дифференциальные операторы второго
и первого порядков соответственно. Здесь
—вектор полевых пере-
менных, —
вектор-функция коэффициентов с ограниченными компо-
нентами, причем линейность имеет место и по аргументу ;

—спект-
ральный параметр, связанный с частотой колебаний.
Перейдем к слабой постановке, для чего спроектируем опера-
торное уравнение в (3.2.1) на элемент , представляющий собой
вектор-функцию с дифференцируемыми компонентами и удовлетворя-
ющий граничным условиям на ? (далее будем писать, что /0
8
.
Используя теорему Гаусса–Остроградского и учитывая граничные
условия в (3.2.1), приведем соответствующее скалярное произведение
квиду
,
,

,
(3.2 .2)
14/27

150
Гл. 3. Общие принципы исследования коэффициентных ОЗ
где ,
,

есть трилинейная форма (линейная по каждому аргу-
менту) переменных ,
,
,—
линейная форма. Эти формы, напри-
мер для оператора упругости, имеют вид
,
,

-
2# ,
#
, "#%,

8
,

#
#
?,
2# ,
#
, "#%,

"
#%

,%
#,

2# #,
(3.2 .3)
где вектор коэффициентов включает в себя компоненты тензора мо-
дулей упругости и плотность; при этом требуется выполнение обычных
условий ограниченности и положительности упругой энергии и плот-
ности

,
"

"
# %

#
,
где # 0,5#,

,#
;
"

,
—
положительные постоянные.
Аналогичный вид имеет эта форма для оператора вязкоупругости
в рамках концепции комплексных модулей и принципа соответствия,
врамкахкоторого"# %
"
#%
,
; для оператора пороупругости
двухфазной среды эта форма имеет вид
,
,

-
2# ,

#
,#,
8
#
,,

8
,

#
#

08## ?,
2# ,

#
,#,
8
#
,,

,
#,#

2)#) #

@
,
8
#,#

,
#,#

!
,
8
#,#

211

#
#

12#8# # #

22#8# ># # # 8#,
(3.2 .4)
причем вектор коэффициентов включает в себя функции 11 , 12 , 22
и ,,
@,
!,
; они часто выражаются через одну функцию порис-
тости.
Сформулируем задачу определения коэффициентов дифференциаль-
ного оператора из конуса гладких неотрицательных ограниченных
функций D 8 в зависимости от заданной информации о внутренних
полях или их следах на границе.
1. В первой постановке заданным считается поле (смеще-
ний, скоростей, температур, электрического потенциала) внутри тела,
,

0 ,

8
, а под решением обратной задачи понимается
вектор-функция D8 , удовлетворяющая равенству ,
,

для любого /0
8
. В этом случае решение обратной задачи
приводится к проблеме решения либо линейного операторного уравне-
ния с компактным оператором, либо к задаче Коши для уравнения (или
системы уравнений) в частных производных первого порядка [17].
2. Во второй постановке задаются граничные значения полевых
характеристик как функции частоты колебаний. При этом возможно
задание смещений в области носителя нагрузки,
,

,
,

1, 2
,
(3.2 .5)
15/27

3.2 . Слабая и вариационная постановки ОЗ
151
либо вне нее. Под решением обратной задачи в этом случае понимается
пара элементов ,

/
08 D 8 , удовлетворяющая (3.2 .2) для
любого

/
08 .
Нетрудно показать, что два различных решения

1,
1и

2,
2 ОЗ удовлетворяют обобщенному соотношению вза-
имности (3.1 .5) или формуле Грина

2
,
1
,
2

(3.2 .6)
Отметим, что задача во второй постановке является нелинейной
и некорректной проблемой, но билинейность оператора ,

позво-
ляет осуществить значительные упрощения. При этом строится после-
довательность слабых постановок и интегральных уравнений первого
рода с гладкими ядрами, аналогичными построенным в постановке 1,
которые позволяют реализовать итерационную процедуру построения
решения обратной задачи.
Рассмотрим подробнее основные аспекты реализации этих поста-
новок.
Основные аспекты построения решений в ОЗ.
1. Итак, в случае первой постановки из (3.2.2) сразу получается
слабая формулировка для нахождения , а полученное интегральное
уравнение 1-го рода с компактным оператором решается на основе
метода регуляризации А. Н. Тихонова [31]. Отметим также, что воз-
можен подход, основанный на решении задачи Коши для системы
дифференциальных уравнений первого порядка,
,

0 0,
,

(3.2 .7)
Решение задачи (3.2 .7) часто может быть выписано в явном ви-
де через решения дифференциальных уравнений 1-го порядка; ситу-
ация еще больше упрощается, если область 8 представляет собой
цилиндрическое тело или пластину, для описания деформирования
которых можно использовать упрощенные теории. В общей ситуации
теорема Коши–Ковалевской [35] гарантирует единственное решение
задачи (3.2 .7) для гладкого элемента .
2. Отметим, что вторая постановка приводит к анализу некоторой
нелинейной проблемы. Как правило, в этой ситуации решение строит-
ся либо на основе обобщенного бесконечномерного метода Ньютона,
где требуется вычислять производные по Фреше от операторов (этот
подход реализован был ранее в [3, 5]; для простых одномерных задач
проведены и вычислительные эксперименты), либо на основе итераци-
онного процесса. Изложим основные этапы решения обратной задачи
во второй постановке с помощью этих двух подходов.
Первая схема. Пус ть 0
—
начальное приближение для нахождения
искомых коэффициентов, его можно определить в классе ограничен-
ных функций простой структуры (линейных либо кусочно-постоянных,
16/27

152
Гл. 3. Общие принципы исследования коэффициентных ОЗ
в зависимости от наличия или отсутствия априорной информации)
на основе минимизации функционала невязки 0 ,причем

.
2
.
1*,

2?
(3.2 .8)
Тогда 0
—
соответствующее поле, удовлетворяющее слабой постанов-
ке, определится из решения прямой задачи

0
,
0
,

(3.2 .9)
Далее, осуществляя линеаризацию в окрестности (0
,
0
,вычис-
ляя 0

0 и используя (3.2 .2), получим линейное уравнение
для отыскания поправки
Æ
0
,
0
,
0

,
(3.2 .10)
откуда находится элемент 1

Æ
0
. Аналогично, далее задачи
для определения элементов последовательности
,

формиру-
ются следующим образом:

,
(3.2 .11)
а поправка Æ находится из линейного операторного уравнения
с компактным оператором
Æ

,
(3.2 .12)
решение которого описано в случае первой постановки. Итерацион-
ный процесс продолжается до тех пор, пока не будет достигнута
определенная точность при выполнении дополнительного граничного
условия (3.2 .5). Фактически двухэтапная процедура позволяет сразу
формулировать операторные уравнения в обратной задаче, избегая ре-
шения задач первого приближения.
Вторая схема. Второй способ построения решения обратной задачи
основан на следующем подходе. Выбирается начальное приближение
аналогично описанному выше. Далее при 0 строится решение следую-
щейпрямойзадачи,сопряженнойсисходной:

0
,0

0 0,

*
0,

0
(3.2 .13)
Следующее приближение для определения 1 строится с помощью
решения задачи Коши

1
,0

0 0,

1
,
0

*,
,
(3.2 .14)
и далее процесс повторяется с новым начальным приближением для

01 0 до тех пор, пока не достигается определенная точность вы-
полнения дополнительного граничного условия (3.2 .5).
17/27

3.2 . Слабая и вариационная постановки ОЗ
153
3.2.2. Вариационная постановка ОЗ. Отметим, что в ряде задач
математической физики вариационная постановка позволяет как полу-
чать численные решения, так и корректно строить упрощенные поста-
новки для объектов простой геометрии (стержни, пластины). При этом
базовым является формулировка основного тождества. Выше в (3.2 .6)
(или (3.1 .5)) сформулировано соотношение взаимности, которое связы-
вает два различных состояния упругого тела (например, напряжения,
смещения,модулиупругостииплотность)приодинаковыхусловиях
нагружения. Осуществим иной подход к проблеме и сформулируем
основное тождество для модели теории упругости.
Введем понятие возможного поля для рассматриваемого класса
задач. Возможным полем назовем любое непрерывное в 8 поле сме-
щений, поле компонент тензора модулей упругости и плотности из
/
0 8 D8 , которые подчинены уравнениям движения и гранич-
ным условиям.
Теор ема 3.2 . Длявозможногополя # выполняется равенство
-
2# ,
#
, "#%,

#
#
?
0,

1, 2
,
(3.2 .15)
где
2# ,
#
, "#%,

2# # "#%,%
#,

Теорема 3.2 легко доказывается путем умножения уравнений дви-
жения на # и интегрированием по 8 с использованием теоремы
Гаусса–Остроградского. В случае 0 равенство (3.2.15) переходит
в известную теорему Клапейрона [23], однако, поскольку работа внеш-
них сил при наличии дополнительного условия (3.2 .5) известна, то
(3.2 .15) может быть истолковано как некоторое нелинейное оператор-
ное уравнение первого рода, связывающее неизвестные и известные
компоненты полей при произвольных возможных #
.
Это равенство яв-
ляется базовым для формулировки итерационных процессов в обратных
задачах различного типа и применимо не только к коэффициентным,
но и к геометрическим обратным задачам.
Теорема 3.3 . Для возможных полей имеет место следующее вари-
ационное уравнение:
-
2# ,

#
, Æ"#%,
Æ
8

#
Æ
#
?
0,

1, 2

(3.2 .16)
Теорема 3.3 доказывается путем варьирования уравнения (3.2 .15)
по всем переменным, использованием уравнения движения и теоремы
Гаусса–Остроградского. Отметим попутно, что функционал в (3.2 .15)
при #
#
квадратичен относительно полей смещений при фиксиро-
ванных характеристиках среды и линеен относительно модулей упру-
гости и плотности.
18/27

154
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Теор ема 3.4 . Компоненты модулей упругости и плотность могут
быть найдены из следующего итерационного процесса, основанного на
уравнении
-
21
#
,"

# %
,

1
#

?
0,

1, 2

(3.2 .17)
Теорема 3.4 следует из теоремы 3.3; равенство (3.2 .17) совпадает
с приведенным в [4], построенным на основе обобщенной теоремы
взаимности. Это равенство служит базовым операторным уравнением
первого рода с вполне непрерывным оператором, позволяющим опре-
делять поправки к модулям и плотности начиная с некоторого на-
чального приближения, которое обычно ищется на некотором простом
подмножестве функций из D8 (или более широком), например
среди линейных или кусочно-постоянных. Отметим, что одного равен-
ства (3.2.17) недостаточно для определения всех неизвестных функций.
Дополнительные уравнения такого же вида получаются путем измене-
ния места приложения нагрузки и ее структуры.
В случае геометрических обратных задач модули и плотность
кусочно-постоянны, что сужает множество поиска. Так, например, при
наличии в однородном теле включения 81 с известными характеристи-
ками имеем
-

£
21
#
,"
,
# %

1
#

?
0,

1, 2
,
(3.2 .18)
где 8

1+8
1
1
и легко сводится в интегральному уравнению
Фредгольма 1-го рода в рамках предположения о звездности искомой
области[18].
Пример 1. Задача о нахождении закона изменения модуля Юнга
и плотности консольного стержня длины при продольных колебаниях
на основании (3.2 .17) приводит к уравнению

1
,

2 2

1
,

2
A

1
,
,

1, 2

(3.2 .19)
Пример 2. Задача о нахождении характеристик полости малого
характерного размера. Соотношение (3.2.18) позволяет оценить его
объем 81 и координаты центра на основе равенства
20
#
,"
,
#%
8
1
*

0
#

?
0,

1, 2
,
(3.2 .20)
где
0
#
есть поле смещений в теле без полости. Отметим, что ряд
подобных задач исследован в предыдущей главе для балок, когда суже-
ние множества поиска приводит к конечномерной ОЗ (см., например,
пункты 2.7, 2.8).
19/27

3.3 . Решение задач в первой постановке
155
Пример 3. Задача о нахождении закона изменения модуля сдвига
4

в односвязной области ? !2 с гладкой границей *
сводится к краевой задаче (плотность считается известной)
4
,
,

0,
4

0,
*
*

*
,

(3.2 .21)
Введем безразмерные функции и параметры H 4+40 , 6
2

2+40, E
+
0,гдеобозначено40

*
4 ,

*
,

?.
Тогда слабая постановка дает следующее
равенство:
*
H
,
,?6
2
*
E
?
%

*,
(3.2 .22)
опираясь на которое, можно строить итерационный процесс и реше-
ние ОЗ. Вариант такого исследования представлен в [15].
Во второй постановке, считая заданным
%

,
,

1, 2
,
согласно изложенному выше строим итерационный процесс на основе
метода Ньютона, причем интегральное уравнение вида (3.2 .12) имеет
вид
*
H

1
,
,

?
%

1
,

1, 2

(3.2 .23)
Заметим, что ядро в интегральном уравнении Фредгольма 1-го ро-
да (3.2.23) является неотрицательным и непрерывным. При его обра-
щении необходимо использовать регуляризующую процедуру в той или
иной форме.
Замечание. Подход, основанный на слабой постановке, также
с успехом может быть применен и для операторов 4-го порядка, опи-
сывающих колебания пластин и балок переменной жесткости и будет
использован в разделах гл. 4.
Ряд результатов, посвященных решению задач в первой постановке,
изложен в работах [20, 27, 36, 37].
3.3 . Решение задач в первой постановке.
Коэффициентные ОЗ при изучении продольных
и поперечных колебаний упругого стержня
(КОЗ для дифференциальных операторов второго
ичетвертогопорядка)
Как отмечалось выше, в рамках выбранной математической модели
можно сформулировать прямую задачу об определении полей и обрат-
ную: об определении переменных коэффициентов.
20/27

156
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Начнем изучение особенностей этих задач с самых простых — задач
о колебаниях стержней.
Методы определения модулей упругости играют большую роль
в процедуре идентификации объектов в различных областях естество-
знания. Главная проблема при исследовании задач подобного типа —
это формулировка операторной связи между искомыми коэффициента-
ми дифференциальных операторов и известными (измеренными) функ-
циональными зависимостями. А поскольку соответствующие диффе-
ренциальные операторы имеют переменные коэффициенты и построить
явные представления решений не представляется возможным, то един-
ственным эффективным средством анализа прямых задач для неод-
нородных сред являются вычислительные технологии, основанные на
идеологии метода конечных элементов или метода конечных разностей.
Для одномерных задач возможно сведение краевой задачи к интеграль-
ным уравнениям Фредгольма 2-го рода и дальнейший численный анализ.
К сожалению, эти вычислительные технологии не позволяют формули-
ровать искомые операторные отношения в явном виде и их необходимо
формулировать на основе подходов, представленных в предыдущем
разд. 3.2.
Наиболее простыми для исследования являются КОЗ для диффе-
ренциальных операторов второго порядка, которые часто встречаются
при описании продольных и крутильных колебаний стержней пере-
менной жесткости, и четвертого порядка, используемые при описании
изгибных колебаний стержней. При этом, как указано выше в разд. 3 .1 ,
возможныдвепостановкиобратнойзадачипоопределениюзакона
изменения модуля упругости.
Настоящий пункт посвящен исследованию первой постановки ОЗ,
разработке вычислительных схем, основанных на разностных аппрок-
симациях и процедуре сглаживания с помощью сплайн-аппроксимации
и анализу возможностей такого подхода в процедуре идентификации
в различных ситуациях.
3.3.1. Задача для уравнения 2-го порядка. Рассмотрим закреп-
ленный на конце 0 упругий стержень длины ,вкоторомко-
лебания возбуждаются при помощи силы
)
#.
, приложенной
кторцустержня . Будемсчитать,что1
,
,

230,
аупругиймодуль

, плотность ,п
лощадьпопереч-
ного сечения

—
есть произвольные положительные функции
координаты .
Уравнение движения для неоднородного стержня имеет вид [5]

2,
(3.3 .1)
а граничные условия представимы в форме

0,
0,

)
.

(3.3 .2)
21/27

3.3 . Решение задач в первой постановке
157
Замыкают постановку начальные условия, в которых задаются
начальный прогиб и скорость в начальный момент времени. Рас-
сматривая далее задачу об установившихся колебаниях и полагая

)
#.
, после отделения временного множителя получаем
краеваю задачу в виде

2 0,
(3.3 .3)

0 0,

)
.

,
(3.3 .4)
где
—
частота колебаний.
В рамках первой постановки будем считать, что известна дополни-
тельная информация об амплитудно-частотной характеристике торца
стержня следующего вида:

0 ,

0,
(3.3 .5)
В рамках такой постановки можно сформулировать несколько об-
ратных задач. Заметим, что можно обсуждать вопрос о восстановлении
следующих положительных функций: модуля упругости

,
плотности , площади поперечного сечения

. Отме-
тим, что восстановить однозначно все три функции по информа-
ции (3.3.5) невозможно, поэтому рассмотрим три задачи.
ОЗ1. Восстановить неизвестную функцию по информа-
ции (3.3 .5). Будем далее считать (для простоты рассуждений), что
и известны и постоянны.
ОЗ2. Восстановить неизвестную функцию

по информа-
ции (3.3.5) в предположении, что и

известны и постоянны.
ОЗ3. Восстановить неизвестную функцию

по известной
информации (3.3 .5) в предположении, что и

известны и постоянны.
Задачи ОЗ1–ОЗ3 представляют собой коэффициентные обратные
задачи для дифференциального оператора и являются некорректными.
Приведем краевую задачу (3.3.3), (3.3.4) к безразмерному виду,
введя безразмерную координату ;
+ , безразмерные параметры
ифункции
H;
"
2.
"
0
,
E;
/
2.
/
0
,
3;
)
2.
)
0
,
G
2/0
0
2
.
2
"
0
,

0
!

"
0)0
(здесь 0 ,0, 0
—
соответственно характерное значение модуля Юнга,
плотность, площадь поперечного сечения, в частности, их максималь-
ные или средние значения; далее всюду вместо ; будем употреблять ):
H3

G
2E3 0,
(3.3 .6)

0 0,
H
1

0
(3.3 .7)
22/27

158
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Далее в силу линейности задачи о нахождении смещения будем
полагать 0
1. Отметим, что краевая задача (3.3 .6), (3.3 .7) при
H
E
1, 3

имеет точное решение следующего вида:

,
G

, причем при G

1,2,..., эторешение
не существует, что характеризует резонансные значения. При этом
амплитудно-частотная функция G 1, G

G+G
имеет разрывы
второго рода, что соответствует резонансным частотам для однородного
стержня. Подобной структурой обладает решение задачи (3.3.6), (3.3 .7)
для произвольной ограниченной положительной функции H.
Исследуем некоторые свойства решения прямой задачи ,
G
для модели (3.3.6), (3.3 .7) c переменными коэффициентами, считая
3
.
При заданном произвольном законе изменения H
(H может быть гладкой функцией, может иметь конечное число
разрывов первого рода) краевая задача (3.3 .6), (3.3 .7) может быть
исследована лишь численно различными способами. Наиболее часто
ранее это осуществлялось на основе сведения к интегральному урав-
нению Фредгольма второго рода, как это реализовано в [3], на основе
анализа разностной схемы соответствующей дискретной задачи [1];
в последнее время гораздо чаще используется метод пристрелки, не
требующий сведения к интегральному уравнению.
При решении прямой задачи интерес вызывает исследование отоб-
ражения D
,гдеHD,

,
G

,
,
G

0,1 G1, G2
,
для разных областей определения D.
Так, в качестве возможных ва-
риантов областей определения этого отображения могут быть приняты
множества: а) бесконечно дифференцируемых или б) кусочно-постоян-
ных функций. Элементы представляют собой аналитические функ-
ции по второму аргументу в нерезонансной области; в общем случае
это мероморфные функции. Гладкость элементов по переменной
определяется свойствами D: в первом случае это бесконечно дифферен-
цируемые функции, во втором — непрерывные функции с производной,
имеющей конечное число точек разрывов первого рода.
Построим решение краевой задачи (3.3 .6), (3.3.7) в более общей
ситуации, когда плотность переменна и характеризуется безразмерной
функцией E (при 0 1) с помощью разложения в степенной ряд по
степеням B G2
.
Будем искать решение задачи (3.3 .6), (3.3 .7) в виде
ряда
,
B

(3.3 .8)
Тогда, приравнивая операторные коэффициенты при одинаковых
степенях B, получим последовательность краевых задач
H
0
0,

00 0,
H10
1 1,
(3.3 .9)

E
1,

0 0,
H1

1 0,

1,2, .. . (3.3.10)
23/27

3.3 . Решение задач в первой постановке
159
Решая простые краевые задачи (3.3 .9), (3.3 .10), находим следую-
щие рекуррентные соотношения для коэффициентов разложения при
произвольных суммируемых H и
E :

0
2
3
2
,
(3.3 .11)

0
2
3
2
1
/
E2
1
22,

1,2,...
(3.3 .12)
Отметим некоторые вспомогательные свойства коэффициентов раз-
ложений, считая, что H и
E
положительны.
Свойство а: 0.
Свойство б: " 0, 1 и монотонно возрастают, что следует из
положительности функций в подынтегральных выражениях в (3.3.11),
(3.3 .12).
Свойство в: используя рекуррентное соотношение (3.3.12), нетруд-
но показать, что

00,1

0,1

0
2
3
2

1
0
2
3
2

0
и

0,1

0 ,1

0
2
3
2
1
/
E2
1
2
2

1 1

0,1
,
причем

1
1
0
2
3
2
1
/
E22

0E0 ,
E
0
1
0
E;
;
(3.3 .13)
Таким образом, используя признак сходимости Даламбера, нетруд-
но показать, что ряд (3.3.8) сходится при 1
B

1(отметим,что
воднородномслучаеH E 1находим1
1Ê
0
1

;
;
1
2
,откуда
имеем оценку области сходимости B 2; заметим, что при этом точная
оценка области сходимости определяется наименьшим собственным
значением B % 2
+4 .
В силу свойств а, б, в для коэффициентов разложения имеют место
следующие свойства.
Свойство 1.ПриB
1
1 функция ,
B
есть монотонно возрас-
тающая положительная функция по каждому аргументу.
Монотонность ,
B
по следует из того, что 0, а моно-
тонность по аргументу B следует из свойства а.
24/27

160
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Далее легко показать, что ряд (3.3 .8) сходится равномерно в силу
признака Вейерштрасса, и, следовательно, в силу свойства а имеет
местосвойство2.
Свойство 2:

0.
Свойство 3: при B
1
1 функция ,
B
H
,
B
положи-
тельна, монотонно убывает по и монотонно растет по B.
Свойство 3 доказывается на основе представлений (3.3 .8), (3.3 .12)
и отрицательности производной ,
B, следующей из (3.3 .10).
Эти свойства важны при исследовании решений прямой задачи для
малых значений спектрального параметра B.
Исследование задачи при
иных его значениях может быть также построено либо с помощью
разложения в степенные ряды в окрестности некоторого B0 ,либооно
опирается на сведение краевой задачи к интегральному уравнению
Фредгольма второго рода, которое решается численно.
Замечание. Установленные выше свойства могут служить для опи-
сания множества функций, характеризующих АЧХ.
Обратные задачи. Итак, рассмотрим постановку коэффициентной
обратной задачи ОЗ1 в первой постановке для стержня постоянной
плотности с постоянным поперечным сечением, считая, что задана
функция ,
G
0 ,

0, 1, являющаяся решением краевой
задачи

G
2
0 0,

0 0,
H
1

1 1
(3.3 .14)
Поставим задачу о восстановлении функции H (или ее узловых
значений), удовлетворяющей (3.3.14), по известным значениям функ-
ции , заданным в наборе точек на отрезке 0, 1,чтомоделирует
данные измерений. Собственно при известной функции проблема
состоит в решении задачи Коши для дифференциального уравнения
первого порядка и никаких трудностей не вызывает.
Опираясь на установленные свойства, можно показать, что имеет
место следующее утверждение.
Теорема 3.5 . Если G0

G
1,гдеG1
—первое резонансное значение
оператора в (3.3 .14), то решение ОЗ1 существует, единственно и зада-
ется формулой
H

1G2
0
1

;
;

(3.3 .15)
Доказательство основано на интегрировании уравнения в (3.3 .14)
от до 1 с учетом второго граничного условия в (3.3 .14).
В то же время при задании информации в дискретном наборе точек
нахождение производных требует регуляризующей процедуры
в соответствии с описанными выше в разделе 1.7 схемами, поэтому ре-
ально в этой ситуации процедура реконструкции H состоит из двух
25/27

3.3 . Решение задач в первой постановке
161
этапов. На первом этапе функция , з аданная в наборе точек,
аппроксимируется кубическими сплайнами (как описано в разделе 1.8),
что позволит вычислять производные смещения с достаточной точно-
стью. На втором этапе используется операторное соотношение (3.3.15),
связывающее заданную и искомую функцию.
Фактически это и есть решение ОЗ. Дискретизация (3.3 .15) на
равномерной сетке 63,
3
1+ ,
6
0,..., ,

1, позволяет
найти узловые значения искомой функции
H

1G2
0
1

;
;

(3.3 .16)
Заметим, что нахождение искомых узловых значений функции
в соответствии с формулой (3.3.16) возможно, если

0. Это
условие обеспечивается выбором частотного диапазона, в котором это
условие выполняется, а именно: при G0

G
1 достаточно использовать
полученный выше результат о монотонности смещения на всем
отрезке.
Результаты вычислительных экспериментов. Для аналогии с ре-
альными экспериментами функция , используемая как входная
информация для восстановления H , была зашумлена аддитивным
образом с амплитудой Æ .
Зашумление моделировалось с помощью ге-
нератора случайных чисел путем добавления к исходной амплитуде
смещений малой случайной функции (здесь представлены результаты
в соответствии с работой [1]).
Проведены масштабные вычислительные эксперименты по восста-
новлению различных типов функций — монотонных, немонотонных,
разрывных. Отметим достаточную эффективность представленного под-
хода для гладких законов изменения H; для разрывных законов по-
грешность реконструкции значительно выше, причем наибольшее рас-
хождение наблюдается в точках разрыва первого рода.
В случае реконструкции разрывных законов неоднородности прове-
дено усовершенствование представленной схемы, для чего произведена
экстраполяция входных данных в окрестности точек разрыва. Прог-
раммная реализация в этом случае осуществляется на основе предвари-
тельного анализа массива данных с целью выявления подозрительных
на разрыв точек. После этого осуществляется экстраполяция справа
и слева на основе стандартного подхода, что позволило значительно улуч-
шить качество реконструкции.
На рис. 3 .1 представлен результат восстановления разрывной функции
H

1,0
1
3
,
3
4
,
5,
1
3

3
4
,
26/27

162
Гл. 3. Общие принципы исследования коэффициентных ОЗ
при Æ
0,0025 для
20. Здесь сплошной линией показан гра-
фик исходной функции, ромбиками — восстановленной функции H ,
а кружочками — восстановленной функции H с использованием
описанной выше процедуры.
Рис. 3.1
Отметим, что погрешность восстановления разрывной функ-
ции H , изображенной на рис. 3 .1, с применением экстраполяции
позволяет значительно улучшить качество реконструкции разрывных
функций, чего практически невозможно достичь с помощью более
сложной второй постановки, представленной в [3] и в гл. 4 .
ОЗ2. В случае когда определяется плотность при известном модуле
Юнга и постоянным поперечным сечением, соответствующая задача
имеет вид

G
2
0E 0,

00,11
Считая, что в обратной задаче задана функция ,
G
0 ,

0,1,
G
0 G1 , нетрудно аналогично построить решение ОЗ вида
E

2
0

Нетрудно понять, что эта формула дает единственное решение
ОЗ2 всюду, кроме точки 0 , в которой имеется неопределенность
(поскольку в силу уравнения колебаний 0 0 .
Фактически это
означает, что определить плотность неоднородного стержня в месте
заделки невозможно. Чтобы это осуществить, необходимо реализовать
иные граничные условия, например, закрепить конец 1, а воздей-
ствовать на конец 0.
3.3.2. Задача для уравнения 4-го порядка. Проведем анало-
гичное исследование для уравнения 4-го порядка, которое описывает
поперечные колебания неоднородной балки, в соответствии с [14].
P owe red by T CP DF (www.tcp df.o rg)
27/27

3.3 . Решение задач в первой постановке
163
Прямая задача. Рассмотрим установившиеся колебания с часто-
той упругой балки длины переменной жесткости - .Будем
считать, что нагрузка действует в плоскости 11

3 ,итогдаврамках
модели Эйлера–Бернулли смещения выражаются следующим образом
(1
):

1 3

20,

3
Уравнение колебаний балки имеет вид [5]
-

2 0,
(3.3 .17)
где —модуль Юнга, -
Ê

2
3
—
момент инерции,
—
плотность материала,
Ê

—
площадь поперечного сечения.
Будем считать, что балка на конце 0 жестко закреплена, а на конце

действует нагрузка. Рассмотрены два вида нагружения на конце

:
сосредоточенный момент и сосредоточенная сила.
В случае нагрузки сосредоточенным моментом на незакрепленном
конце (задача 1) граничные условия имеют вид
0

0 0,
-

,
-

0
(3.3 .18)
В случае нагружения сосредоточенной силой на конце (задача 2)
граничные условия имеют вид
0

0 0,
-

0,
-

A
(3.3 .19)
Будем далее рассматривать одну из частных причин неоднород-
ности — переменность модуля Юнга при постоянных геометрических
характеристиках. Выполним обезразмеривание задач для данного слу-
чая. Введем безразмерную координату ; +,функциюбезразмерной
жесткости ; -+0
-
0, а также спектральный параметр, связан-
ный с частотой колебаний, 6
4 2

4+0
-
0,где0
—
некоторое
характерное значения модуля Юнга, в частности максимальное (далее
будем обозначать введенную безразмерную координату ; через ) .
Таким образом, уравнение (3.3 .17) примет вид

6
4

0
(3.3 .20)
Граничные условия (3.3 .18) для задачи 1 принимают вид
0

0 0,
1

1 1,

1 0,
(3.3 .21)
а граничные условия (3.3 .19) для задачи 2 имеют вид
0

0 0,
1

1 0,

1 1
(3.3 .22)
1/27

164
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Прямая задача состоит в нахождении из уравнения (3.3 .20) функ-
ции смещения , удовлетворяющей граничным условия (3.3 .21)
или (3.3 .22) при заданном законе изменения функции безразмерной
жесткости для некоторого значения спектрального параметра 6 . Диф-
ференциальный оператор в уравнении (3.3 .20) имеет переменные коэф-
фициенты, поэтому краевые задачи (3.3 .20), (3.3.21) и (3.3 .20)–(3.3 .22)
могутбытьисследованылишьчисленно.
Отметим, что при 0

уравнение (3.3 .20) принимает
вид

6
4

0,
(3.3 .23)
а соответствующие краевые задачи имеют точное аналитическое реше-
ние, которое может быть представлено через функции Крылова [32].
Для дальнейшего изучим некоторые свойства решений краевых
задач. Рассмотрим задачу (3.3 .20), (3.3 .22). Будем искать ее решение
ввидеряда:

0
B

,
(3.3 .24)
где B
6
4, 6 0,601,
6
01 — первая резонансная частота. Найдем
нулевой член ряда в (3.3 .24). Для его определения имеем следующую
краевую задачу:

0
0,
(3.3 .25)

00 0,

01 0,

0 1 1 (3.3 .26)
Интегрируя последовательно и удовлетворяя граничным условиям,
получим решение

2
2
1
1
2
;
(3.3 .27)
Из представления (3.3 .27) следует, что 0

0прилюбом 0 .
Построим рекуррентную последовательность для нахождения

1-го члена ряда через предыдущий. Соответствующее краевая
задача имеет вид

0,
(3.3 .28)

1
0 0,

1
0 0,
1
1
1 0,

1 0
Решение краевой задачи (3.3 .28) представимо в форме

2
1
2

0
2

;

;;2
(3.3 .29)
Принимая во внимание, что 0, а также 0,
из (3.3 .29) находим, что 1

0длявсех, что свидетельствует:
в промежутке до первого резонанса функция смещения всегда моно-
тонно убывает при любом выбранном законе изменения переменной
2/27

3.3 . Решение задач в первой постановке
165
жесткости .
Аналогичное утверждение справедливо для первой
задачи при нагружении сосредоточенным моментом: при любом законе
изменения переменной жесткости функция смещения монотонно
возрастает для любых B, меньших первого резонансного значения.
Обратная задача. Дифференциальное уравнение, описывающее ко-
лебания консольно закрепленной балки с переменным модулем Юнга,
имеет вид (3.3.20), а граничные условия для нагружения сосредо-
точенным моментом на свободном конце имеют вид либо (3.3 .21),
либо (3.3.22).
Пусть известна функция ,
6
при некотором 6 , меньшем первого
резонансного значения (далее будем использовать обозначение .
Заметим, что дифференциальное уравнение (3.3 .20) относительно
функции имеет второй порядок и для ее определения необходимо
задавать два дополнительных условия на границе. Некорректность
обратной задачи в этой постановке состоит в том, что необходимо
находить производные разных порядков от функции, заданной в на-
боре точек. Поэтому на первом этапе аппроксимируем функцию
сплайнами пятой степени, что в соответствии с разд. 1 .7 позволяет
находить необходимые производные с достаточной степенью точности.
На втором этапе построим операторное соотношение, связывающее
функции и

.
Осуществим это построение на примере зада-
чи (3.3 .20), (3.3 .22), для нагружения сосредоточенной силой. Дважды
интегрируя уравнение (3.3.20) от 1 до ,получить,что

;

16
4

;;;
(3.3 .30)
далее, имеем

1
4
1Ê

2,
2
2
,

(3.3 .31)
Для задачи с нагружением сосредоточенным моментом аналогичное
соотношение имеет вид

1
4
1Ê

2,
2
2
,

(3.3 .32)
Равенство (3.3.31) справедливо при всех ,отличныхот1;всилу
граничного условия (3.3.22) знаменатель в правой части (3.3 .31) обра-
щается в нуль. Таким образом, имеет место следующее утвердение.
Теорема 3.6 . Решение ОЗ по определению жесткости при
граничных условиях (3.3 .21) существует, единственно и определяется
формулой (3.3.32) при всех ; решение ОЗ при граничных услови-
ях (3.3 .22) существует, единственно и определяется формулой (3.3 .31)
привсех1.
3/27

166
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Заметим, что дискретизация позволяет найти значения искомой
функции в (3.3.32),

1
,

16
4
1

;
;
;

(3.3 .33)
Для нахождения определенного интеграла
1Ê

;
;
;
была
использована формула трапеций и получены расчетные формулы для
жесткости в наборе точек через узловые значения смещений
Как видно из представления (3.3 .33) и граничных условий (3.3 .21),
(3.3 .22), задача (3.3 .20), (3.3.22) при нагружении сосредоточенной си-
лой на свободном конце является хуже обусловленной, нежели зада-
ча (3.3.20), (3.3 .21) при нагружения сосредоточенным моментом, так
как на конце 1 имеет место неопределенность. Поэтому в этой
точке необходимо либо задавать значение функции ,л
ибоэкс-
траполировать функцию из области 1. Этому факту есть простое
объяснение в рамках рассмотрения задачи Коши. Для задачи с нагру-
жением сосредоточенным моментом граничные условия (3.3.21) дают
два необходимых условия для задачи Коши, а для задачи с сосредо-
точенной силой — только одно, поскольку из условия 1

1 0
в (3.3 .22) и положительности следует 1 0: второе условие
пропадает, а задача Коши становится недоопределенной.
На основе описанного метода проведены эксперименты по рекон-
струкции различных видов неоднородностей: гладкая монотонно воз-
растающая функция, гладкая монотонно убывающая функция, функ-
ция, имеющая на отрезке 0, 1 несколько стационарных точек, кусочно-
разрывная функция.
На рис. 3 .2 –3 .6 представлены результаты восстановления различ-
ных законов изменения функции при различных видах нагруже-
ния. Входная информация о значениях функции внабореточек
получена из решения соответствующих прямых задач об изгибных
колебаниях балок с переменным модулем Юнга. На рис. 3 .2, 3.3 пред-
ставлены результаты восстановления монотонно возрастающей и моно-
тонно убывающей функций для нагружения сосредоточенной силой на
конце. На рис. 3 .4 представлены результаты восстановления монотонно
возрастающей функции при нагружении сосредоточенным моментом.
Как видно из рис. 3.2 –3.4, погрешность восстановления гладких моно-
тонных функций не превышает 1–2 %, что говорит о высокой точности
предложенных методов. На рис. 3.5 представлен результат восстановле-
ния немонотонной функции, имеющей несколько точек экстремума на
отрезке 0, 1 . Как видно из рисунка, в точках экстремума погрешность
увеличивается и составляет 3–4 %, а в остальных промежутках так же,
как и для монотонных функций, наблюдается высокая точность рекон-
струкции. Более высокую точность в окрестностях точек экстремума
можно достичь, увеличив число узлов разбиения.
4/27

3.3 . Решение задач в первой постановке
167
Рис. 3 .2 . Нагружение сосредоточен-
ной силой для монотон но возраста-
ющей функции = 1

2
Рис. 3.3. Нагружение сосредоточен-
ной силой для монотонно убываю-
щейфункции=1

Рис. 3 .4 . Нагружение сосредоточен-
ным моментом для монотонно воз-
растающей функции = 1

3
Рис. 3.5. Нагружение сосредоточен-
ным моментом для немонотонной
функции=1

2
10
Рис. 3 .6 . Решение обратной задачи при нагружении сосредоточенной силой для
кусочно-разрывной функции жесткости =

1,0

13,

>
34,
5, 13
?

34
5/27

168
Гл. 3. Общие принципы исследования коэффициентных ОЗ
В случае разрывных законов неоднородности проведено усовершен-
ствование разработанного метода: входной массив данных исследуется
на предмет точек разрыва (рассматривается изменение первой и второй
производной функции ); в случае обнаружения точек разрыва
в их окрестности учащается сетка разбиения и производится экстра-
поляция функции, что улучшает качество восстановления. На рис. 3.6
приведены результаты восстановления кусочно-разрывной функции.
Результаты реконструкции свидетельствуют о наличии погрешности
в окрестности точек разрыва аналогично представленным на рис. 3 .1 .
3.4 . Обратная задача о колебаниях
неоднородной пластины
Задачи о колебаниях неоднородных пластин имеют многочислен-
ные приложения. При этом одним из важных аспектов моделирования
таких структур является способ определения неоднородных свойств,
в частности, из данных акустических экспериментов. Отметим, что
колебания неоднородной пластины описываются краевой задачей для
уравнения в частных производных 4-го порядка с переменными ко-
эффициентами и ее решение может быть найдено лишь численно.
В наиболее простом варианте осесимметричных колебаний уравнение
колебаний переходит в обыкновенное дифференциальное уравнение,
решение которого может быть получено несколькими численными ме-
тодами. В настоящем разделе опишем два из них: метод Ритца и метод
пристрелки. Если ранее, в предыдущих разделах для этой цели исполь-
зовался метод интегральных уравнений, то для задачи об изгибных
колебаниях пластины такое сведение осуществить не удалось, однако
эффективными оказались прямые методы или основанные на методе
пристрелки.
3.4.1. Прямая задача. Одним из эффективных методов построе-
ния решения является метод Ритца, основанный на нахождении ста-
ционарной точки квадратичного функционала Гамильтона–Остроград-
ского (3.4.1)

1
0
E

E
2

,
-
-

2C
,
-,
-
-

E
E

2
1
0
69EE
E
G
2
1
0

2 EEE (3.4 .1)
Сущность метода заключается в приведении вариационной задачи
к задаче на поиск экстремума функции многих переменных. Такое при-
ведение осуществляется путем отбора из всех возможных допустимых
функций, на которых рассматриваются значения функционала, некото-
рого специального класса функций, линейно зависящих от конечного
6/27

3.4. Обратная задача о колебаниях неоднородной пластины
169
числа неопределенных параметров. Подстановка таких функций в вы-
ражение для функционала превращает его в функцию этих параметров,
экстремум которой может быть найден известными способами.
В соответствии с методом Ритца будем отыскивать решение вариа-
ционной задачи в виде
E

1
"

E ,
(3.4 .2)
где "
—
произвольные постоянные, а 7 E —
координатные функ-
ции, удовлетворяющие геометрическим краевым условиям рассматри-
ваемой задачи; так, в рассматриваемых случаях функции 7E могут
быть выбраны в форме:
1) в случае жесткой заделки
7

E
1

E
22
E
21
,

1,..., ;
(3.4 .3)
2) в случае шарнирного опирания
7

E
1

E
2E2 1
,

1,...,
(3.4 .4)
На множестве функций (3.4 .2) функционал (3.4 .1) становится
функцией независимых переменных " ,

1,2,..., ,

"
1, "2,..., "

, которые могут быть найдены из системы линей-
ных уравнений
)
@
1, @2,...,@

1,...,
(3.4 .5)
Подстановка значений " в (3.4.2) позволяет определить прибли-
женное решение прямой задачи об изгибных колебаниях пластины.
Нарис.3
.
7представленымодыколебанийнеоднороднойупругой
пластинки, полученные методом Ритца для E
1 E2 вслучае
жесткой заделки. Сплошная линия — 1 -я форма на частоте G 12,51;
пунктир — 2 -я форма на частоте G 46,34; точки — 3-я форма на ча-
стоте G 103,44.
Для оценки достоверности результатов расчетов прогиба пластинки
методом Ритца произведено сравнение результатов для однородной
пластинки при G 0 с известными аналитическими формулами [31]
Выражения для прогиба равномерно нагруженной однородной пла-
стинки жесткости E в случае жесткой заделки на краю имеют
вид [32]

;
641
1

E
2

2
,
(3.4 .6)
а в случае шарнирного опирания

;
1-
2

641
55
15

E
2

(3.4 .7)
Относительная погрешность результатов, найденных методом Ритца,
при 1 5составила105
– 106
,апри
10 — порядка 106
– 107
.
7/27

170
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Рис. 3.7
В табл. 3 .1 приведен сравнительный анализ значений прогибов, полу-
ченных методом Ритца при 9+0 1, и значений аналитических реше-
ний (3.4 .6), (3.4.7).
Таблица 3.1
-
Жесткая заделка
Шарнирное опирание
Метод Ритца
Точное
решение
Метод Ритца
Точное
решение
A

5 A10
A

5 A10
0
0,5
0,95
0,015626
0,008789
0,000149
0,015625
0,008789
0,000148
0,015625
0,008789
0,000148
0,072446
0,051404
0,005689
0,072444
0,051403
0,005688
0,072443
0,051403
0,005688
Кроме того, задача была решена методом пристрелки [2] после
приведения уравнения изгиба пластинки к следующему виду:

E
1
1
--

G
2EB9

C
E

1
-
-

1
-
-
2

2E ECE1-
-

2EEE E

(3.4 .8)
В табл. 3.2 проведено сравнение собственных значений для различ-
ных законов распределения цилиндрической жесткости E, рассчи-
танных на основании двух предложенных методов. Точность методов
тестировалась для однородной пластины в случае жесткой заделки, где
собственные значения известны (G1 10,21, G2 39,78, G3 88,90),
и погрешность метода Ритца при 1 7составиламенее1%(врасче-
тах значение коэффициента Пуассона C принято равным 0,1).
8/27

3.4. Обратная задача о колебаниях неоднородной пластины
171
Таблица 3.2
Закон рас-
пределе-
ния1-
Жесткая заделка
Шарнирное опирание
Метод
Ритца
Метод
пристрелки
Метод
Ритца
Метод
пристрелки
1
10,27
З9,79
89,11
10,22
39,77
89,10
4,63
29,48
73,94
4,62
29,49
73,94
1-2
12,51
46,34
103,44
12,52
46,35
102,53
5,32
33,87
84,51
5,33
33,87
84,51
1'
17,68
66,25
174,75
17,68
66,27
146,96
7,64
48,68
123,12
7,65
48,66
121,40
1
-
13,17
53,60
129,26
13,47
53,41
120,21
6,25
39,86
101,46
6,25
39,86
100,05
13-
12,66
50,98
114,41
12,67
50,98
114,33
6,11
38,88
96,21
6,11
38,88
96,20
В табл. 3.3 приведены значения прогиба E внекоторыхточках
для G 10 в случае жесткой заделки и для G 2,5 в случае шарнир-
ного опирания.
Таблица 3.3
Закон рас-
пределе-
ния1-
-
Жесткая заделка
Шарнирное оп ирание
Метод
Ритца
Метод
прис трелки
Метод
Ритца
Метод
прис трелки
1-
2
0
0,5
0,95
0,030339
0,015013
0,000194
0,030337
0,015011
0,000188
0,071159
0,048943
0,005221
0,071157
0,048941
0,005215
1'
0
0,5
0,95
0,007935
0,004096
0,000059
0,007935
0,004096
0,000056
0,030131
0,020813
0,002240
0,03013
0,020812
0,002238
1
-
0
0,5
0,95
0,020329
0,011326
0,000188
0,020325
0,011325
0,000185
0,046881
0,033475
0,003739
0,046878
0,033474
0,003736
13-
0
0,5
0,95
0,028074
0,015245
0,000287
0,028078
0,015244
0,000282
0,050652
0,035034
0,003913
0,050650
0,035033
0,003908
9/27

172
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Анализ данных, приведенных в табл. 3.3, свидетельствует о доста-
точно хорошем совпадении результатов, полученных различными мето-
дами, что позволяет сделать вывод о достоверности и эффективности
предлагаемых вычислительных схем.
3.4.2. ОЗ для упругой пластины переменной жесткости. Сфор-
мулируем задачу об определении функции цилиндрической жесткости
пластины E по известной информации о прогибе пластины — функ-
ции E на некоторой фиксированной частоте G0

G
1, G2
. Этазадача
относится к обратным коэффициентным задачам, причем в такой по-
становке она является линейной.
Длярешенияэтойзадачибылоиспользованодваподхода.Пер-
вый подход заключался в сведении обратной задачи к обыкновенно-
му дифференциальному уравнению первого порядка с переменными
коэффициентами, а второй — в использовании проекционного метода
Галеркина.
Сведем краевую задачу о нахождении E кобыкновенномудиф-
ференциальному уравнению с переменными коэффициентами. Уравне-
ние колебаний имеет вид
EE
E

C
E
E

1
-,
-
-
G
2
EE

6 9E
(3.4 .9)
Проинтегрировав уравнение (3.4.8) в пределах от нуля до 1 и при-
ведя подобные слагаемые, получим

E E
HE,
(3.4 .10)
где обозначено
E
,
-

-,
-
,
- -
-,
-

5,
-
,
HE

Ê
0

2
-,
-

; --
-,
-

5,
-

Отметим, что уравнение (3.4.10) есть обыкновенное дифференци-
альное уравнение первого порядка с переменными коэффициентами.
Его решение в общем случае определяется с точностью до произволь-
ной постоянной. Построим решение (3.4.10), подчиненное дополнитель-
ному граничному условию 1

0:
E

(
0
5
5

(
0
H5

0
0
2
2

1
0
H5

0
0
2
2

1
0
5
5

(3.4 .11)
10/27

3.4. Обратная задача о колебаниях неоднородной пластины
173
Результаты вычислительных экспериментов, проведенных на основе
представления (3.4 .11), показали, что нельзя осуществить восстанов-
ление исходной функции жесткости с приемлемой точностью. Дальней-
ший анализ свойств дифференциального оператора в (3.4.10) показал,
что функции E и
HE
разрывны на отрезке 0, 1 и имеют особые
точки второго рода, определяемые из равенства нулю знаменателя
E
E

C
E
0. Таким образом, для дифференциального уравне-
ния (3.4.10) не выполняются условия теоремы существования решения
(см. также пример 4 в разд. 1 .1)
Второй подход к отысканию решения ОЗ заключается в применении
проекционного метода Галеркина к исходной задаче. Выберем базисные
функции вида I E
E
1
,6
1, ... , ,ипредставимфункцию
жесткости E в виде разложения по этой системе,
E

E
(3.4 .12)
Подставим (3.4.12) в (3.4.8) и введем обозначения для невязки
E
E
2EE E CE2

E
E

EE
E

E
E

G
2E3
E

69E
3
Далее потребуем ортогональности невязки к базисным функци-
ям, т.е.
1
0
EI

EE
E
0,

1,..., ,
и получим систему линейных алгебраических уравнений для нахожде-
ния коэффициентов разложения
1
0

E
2I EE E CE2
I

E
E

E E
E
1
0
G
2E3
E

69E
3I EEE,

1,...,,
(3.4 .13)
решая которую, находим приближенное решение сформулированной ОЗ.
3.4.3. Результаты вычислительных экспериментов. Внастоя-
щем пункте представлены результаты определения функции, характе-
ризующей закон изменения цилиндрической жесткости в зависимости
от радиальной координаты. Расчеты проводились для пластины из
упругого материала при различных законах изменения в виде мо-
нотонных и немонотонных функций, а также различных граничных
условиях. На рисунках сплошной линией показан график исходной
функции, пунктиром — восстановленной.
11/27

174
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Рассмотрим результаты вычислительных экспериментов по иденти-
фикации цилиндрической жесткости пластины E на основе предло-
женной выше проекционной схемы. На рис. 3 .8 в случае шарнирного
Рис. 3 .8
опирания при E
1)( про-
демонстрировано влияние количества
координатных функций на точ-
ность результатов. Пунктиром обо-
значено точное решение, сплошной
линией — приближенное решение при

6, точками — при
15.
Дальнейшие вычислительные экспе-
рименты проводились при следую-
щем наборе параметров: C
0,1;
9
1; 15. Результаты показали,
что для выбранного числа коорди-
натных функций функционал невяз-
ки имеет порядок 103
.
На рис. 3 .9 –3 .12 представлены
результаты идентификации цилиндрической жесткости пластины, из-
меняющейся по различным законам (монотонно возрастающим, моно-
тонно убывающим, немонотонным) для граничных условий жесткой за-
делки; сплошная линия — точное решение, пунктир — восстановленное.
Рис. 3.9. 1
-

1-
2
Рис. 3.10. 1
-

1'
На рис. 3.13–3 .15 при аналогичном наборе параметров изображе-
ны результаты реконструкции цилиндрической жесткости пластины
для монотонно возрастающих, монотонно убывающих и немонотонных
функций в случае шарнирного опирания; сплошной линией изображено
точное решение, пунктиром — восстановленное.
12/27

3.4. Обратная задача о колебаниях неоднородной пластины
175
Рис. 3 .11. 1
-

1
-
Рис. 3.12. 1
-

13-
Рис. 3 .13. 1
-

1'
Рис. 3.14 . 1
-

13-
Рис. 3 .15. 1
-

27-
13/27

176
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Результаты вычислительных экспериментов свидетельствуют о до-
статочно точной процедуре реконструкции на основе проекционного
подхода. Вместе с тем отметим, что результаты, представленные на
рис. 3 .15, свидетельствуют о неудовлетворительной процедуре рекон-
струкции для сильно осциллирующих функций, имеющих более одной
стационарной точки.
3.5 . Коэффициентная ОЗ для уравнения
в частных производных в первой постановке
В настоящем разделе обсуждаются способы решения КОЗ для мо-
делей, описываемых уравнениями с переменными коэффициентами в
частных производных второго порядка. Ранее в гл. 2 было отмечено,
что в первой постановке такие КОЗ являются линейными и основное
внимание необходимо уделить исследованию тех операторных уравне-
ний, которые возникают при этом. Отметим, что различные аспекты
задач в первой постановке обсуждены в работах [13, 20, 46, 49].
В настоящем пункте в соответствии с работой [11] рассмотрена
задача Коши для часто встречающегося в приложениях уравнения
в частных производных второго порядка, описывающего антиплоские
колебания неоднородного упругого тела (при постоянном модуле сдвига
оно переходит в известное уравнение Гельмгольца).
3.5.1. Прямая задача. Рассмотрим установившиеся колебания
плоской области ? с переменным модулем сдвига. Уравнение устано-
вившихся колебаний с частотой имеет вид [11]
4
1⁄4

1⁄4

2 0,
(3.5 .1)
где4 —
переменный модуль сдвига,
—
плотность.
Будем считать, что поперечное сечение стержня ? есть односвяз-
ная область с кусочно-гладкой границей * *1

*
2. Часть границы *1
защемлена, на *2 действует нагрузка. В этом случае краевые условия
имеют вид

%
1
0,
4

%
2

(3.5 .2)
Приведем краевую задачу (3.5.1), (3.5.2) к безразмерному виду, вве-
дя безразмерные параметры и функции и обозначая 40

?:
H

0
,
G
2/0
0
2

0
,

,
,1*
,
(3.5 .3)
H
,
,

G
2 0,
(3.5 .4)

%
100,
H

%
2

0
(3.5 .5)
14/27

3.5. Коэффициентная ОЗ для уравнения в частных производных 177
Краевая задача (3.5 .4), (3.5.5) при известной положительной функ-
ции H1, 2

представляет собой задачу об отыскании 1 , 2
,для
которой несложно установить существование обобщенного решения
при минимальных требованиях относительно гладкости. К сожалению,
решение такой задачи даже в простой области типа прямоугольника
может быть построено лишь численно, на основе либо конечноэлемент-
ного подхода, либо разностных аппроксимаций.
3.5.2. Обратная задача. Рассмотрим задачу, обратную по отно-
шению к сформулированной выше краевой задаче (3.5 .4), (3.5.5). Пос-
тавим задачу об определении функции H 1 , 2

вобласти? по извест-
ной функции 1 , 2
. Тогда в предположениях о некоторой гладкости
(которые будут описаны ниже) имеем следующую задачу Коши для
уравнения в частных производных первого порядка:
H
,1,1 H
,2

G
2 0,
(3.5 .6)
H

%
2

0
Задачитакогопланадостаточнодавноизучалисьвлитературена
основе связи с обыкновенными дифференциальными уравнениями [17].
Далее при исследовании задачи (3.5 .6) будем требовать выполнения
следующих условий:
1

%
2

0;
(3.5 .7)
2) ,1, ,2,
—
непрерывно дифференцируемы в ?;
3) функции
,1,
,2
—
одновременно в ноль не обращаются в ? ,
т. е.

2
1⁄4
1

2
1⁄4
2

0.
Пусть уравнение кривой *2 имеет следующую параметризацию: 1
7
1 (,

272
(,
(

(
1, (2
.
Тогда перепишем граничное условие
длязадачиКошиввиде
H
7
1(,
7
2 (

0 (
(3.5 .8)
Введем понятие характеристической системы [17] в виде

1
,

(3.5 .9)
Пусть 1

—
ее решение. Тогда вдоль характеристик выпол-
няется соотношение
3

H
,1

H
,2

H
,1,1 H,2,2
(3.5 .10)
Утверждение 1. Пусть кривая *2 не касается характеристик. Тогда
задача Коши (3.5.6) однозначно разрешима в некоторой окрестности *2
.
15/27

178
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Доказательство. Проведем из каждой точки 0

*
2 характери-
стику, т. е . решим семейство задач Коши для системы

1
0
E
1 (,

2
0
E
2(,
(

(
1, (2

(3.5 .11)
Обозначим через 1
,
(,

2 ,
(
решение задачи Коши (3.5.11).
В силу (3.5 .10) исходная задача преобразуется к виду
3

G
2 0,
(3.5 .12)
H

0 (
Таким образом, получим, что (3.5.12) представляет собой задачу
Коши для обыкновенного дифференциального уравнения первого по-
рядка. Нетрудно доказать, что H I ,
(
непрерывно дифференциру-
ема. Далее можно выразить координаты ,
(
через 1 , 2 впредполо-
жении, что якобиан

-
1-2

1 , 2
%
2

0,
(3.5 .13)
что выполняется, поскольку *2 не является характеристикой.
Утв ержде ни е 2 . Решение задачи (3.5 .6) единственно.
Доказательство осуществляется аналогично [34]. В предположении
наличия двух решений составим задачу Коши относительно их раз-
ности

#
H
0,
#
H

00,
(3.5 .14)
откуда следует, что #H 0 .
Отметим, что можно осуществить построение решения задачи Ко-
ши (3.5 .6) на основе разностной трактовки, что было реализовано для
различных задач [28]; в случае, когда H зависит от одной координаты,
изучаемаязадачасводитсякрассмотреннойвышевп.3
.
3.1задачедля
стержня.
3.5.3. Реконструкция модуля сдвига на основе анализа кру-
тильных колебаний стержня. Исходя из общей постановки (3.5 .1),
рассмотрим осесимметричную задачу для кольцевой области с пере-
менным модулем сдвига H. Вполярнойсистемекоординат,считаячто
H
H
E , вводим безразмерные параметры и функции (H0
—характер-
ное значение модуля сдвига)
G
2/0
2

2
3
0
,
H
0 H1,
$
0
$
3
0
,
E
;,
;
0;1,
;
0

,
H
;
3
2
3
0
;
16/27

3.6 . Коэффициентные ОЗ для уравнений теории упругости
179
из (3.5 .4) получаем уравнение
H

1
2

G
2

0,
(3.5 .15)
причем граничные условия имеют вид

;
0 0,
H
1
$
0
(3.5 .16)
Решение краевой задачи (3.5.15), (3.5 .16) при заданном законе H ;
может быть построено на основе конечноразностной схемы с исполь-
зованием трехточечного шаблона [28]; таким же образом на основе
разностной аппроксимации решается и обратная задача.
Результаты вычислительных экспериментов отражены в публика-
циях [1, 11]; они показали достаточную эффективность для гладких
законов неоднородности.
3.6 . Коэффициентные ОЗ для уравнений теории
упругости (плоский случай в первой постановке)
Как отмечено в предыдущем пункте, особый интерес для развития
исследований в теории КОЗ представляет исследование простейшей ли-
нейной задачи, в которой известны компоненты поля смещений внутри
области, а требуется определить функции, характеризующие перемен-
ность модулей упругости. Это естественным образом приводит к иссле-
дованию задачи Коши для одного уравнения, рассмотренной в предыду-
щем разделе, или системы уравнений в частных производных первого
порядка, которая рассматривается в настоящем пункте.
Сформулируем КОЗ: по известным в наборе точек области ? ина
ее границе полям смещений # определить модули Ляме, являющиеся
функциями координат. Отметим, что в плоской задаче число неиз-
вестных функций, характеризующих неоднородность упругих свойств,
равно числу уравнений; изучим КОЗ в этом случае.
Планарные колебания области ? описываются следующей краевой
задачей:

# ,

2# 0,
>,

1, 2,

%
1
0,

%
2

#
,
(3.6 .1)
где # BÆ# 4 #,

,#
.
Здесь в постановку задачи входят две положительные функции
B
1, 2

и 41, 2
, характеризующие законы изменения коэффици-
ентов Ламе.
Основное внимание в настоящей работе уделим задаче определения
модулей B1 , 2

и 41, 2

по известным компонентам поля переме-
щений в наборе точек.
17/27

180
Гл. 3. Общие принципы исследования коэффициентных ОЗ
В развернутом виде краевая задача (3.6 .1), (3.6 .2) имеет вид
B

1,1

2,2

,1 4 1 ,2

2,1

,2 4 2 1,1

,1
21 0,
B

1,1 2,2

,2 4 1 ,2

2,1

,1 4 2 2,2

,2 2

20,

%
1
0,
(3.6 .2)
B

1,1 2,2 421,11

1,2 2,12

%
2
A
1,
B

1,1

2,2

4
2 2,2

241,2

2,1

1
%2
A
2
Обратная задача состоит в определении положительных функций
B

1, 2

и 41,2
, удовлетворяющих (3.6 .2) при известных функ-
циях 1

1, 2

и2

1, 2
.
Обезразмерим уравнения и граничные условия в (3.6 .2), вводя без-
размерные параметры и переменные
H

0
,
9

0
,
G
2/0
0
2

0
,
4
0
*
4,

0
*
,
.
/
/
0

Далее будем рассматривать случай, когда
9,
H

?
,
"

?
,

0 0

Тогда краевая задача (3.6 .2) примет вид системы уравнений

119,1 12 H,1 13 H,2 1
,
9,
H
0,

219,2 22
H,1 23
H,2 2
,
9,
H
0;
(3.6 .3)
9
11 H121

H
13 2

%
2
A

1,
9
11 H23

2 H131

%
2
A

2,
(3.6 .4)
где введены следующие обозначения:

11 1,1 2,2

21,

12 21,1 ,

13 1,2 2,1,

22 13,

23 22,2 ,

1.G
21

9
11,1 H 12,1

13,2

2.G
2

2921,2 H 22,1 23,2,
A

4
1
0
Отметим, что задача (3.6 .3), (3.6.4) представляет собой краевую
задачу для системы дифференциальных уравнений в частных произ-
водных первого порядка относительно двух неизвестных функций 9 ,
H.
Для того чтобы сформулировать задачу Коши для этих функций, необ-
ходимо (исходя из (3.6 .4)) определить значения искомых функций на
границе *2
.
Для этого надо, чтобы система (3.6.4) имела положитель-
ные решения; для разрешимости ее необходимо и достаточно, чтобы
выполнялось условие

2
1
2
2

13121

0,
(3.6 .5)
а положительность регулируется ограничениями на нагрузку A
1,A

2.
18/27

3.6 . Коэффициентные ОЗ для уравнений теории упругости
181
Так, например, условие положительности нарушается, когда 2 0,
A

2 0либо1 0, A

1
0, что не дает ограничений на H на границе,
и задача Коши оказывается недоопределенной. Таким образом, на этапе
постановкизадачиужеможновыделитьклассынагрузок,прикоторых
невозможно построить единственное решение обратной задачи.
Если данные задачи таковы, что можно определить положительные
данные Коши для искомых функций, то задача Коши

11 9,1 12H,1 13H,2 1
,
9,
H
0,

219,2 22
H ,1 23
H,22
,
9,
H
0,
9

090,H

0 H0,
(3.6 .6)
является определенной. В этом случае изучим вопрос о ее единственно-
сти. Для этого в (3.6 .6) перейдем к локальной системе координат, свя-
занной с частью границы области ?0

? , где вектор нагрузок A
1,A

2
отличен от нуля. Пусть уравнение границы задано параметрически:

11
(,

22
( ,
(

, ?.
Введем локальную систему коор-
динат (,

соотношениями

11
(

2(,

22
(

1(,
(3.6 .7)
считая, что 1

2
2
1, и перепишем (3.6 .6) во введенной ло-
кальной системе координат. Тогда имеем следующую систему:
11
;

12
;
B

13
3

14
3
B

1 ,
9,
H
0,
21
;

22
;
B

23
3

24
3
B

2 ,
9,
H
0
(3.6 .8)
Разрешив эту систему относительно нормальных производ-
ных &9+& и
& H + & , получим каноническую систему (при условии
11232113

0) вида
;

I
1(,
,
9,
H,
;
B
,
3
B

,
3

I
2(,
,
9,
H,
;
B
,
3
B

,
9

090,H

0H0

(3.6 .9)
В предположении бесконечной дифференцируемости функций 9 ,
H
решение задачи (3.6 .9) строится в виде степенных рядов по координа-
те ; отсюда и вытекает единственность решения.
Этот результат справедлив также для некоторой подобласти ?0

?,
которая получается, если использовать замену переменных (3.6 .7).
Дляоставшихсяподобластей? можно использовать описанную выше
процедуру, поскольку на границе ?0 послепервогоэтапаужебудут
иметься данные Коши. Отметим, что для некоторых типов областей
достаточно однократной процедуры. Таковы, например, прямоугольник,
кольцевой сектор.
19/27

182
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Опишем некоторые аспекты численной реализации. Для проведе-
ния вычислительных экспериментов в рамках поставленной обратной
задачи необходимо располагать входными данными в виде измеренных
в наборе точек области (область ? компонент вектора смещений),
которые могут быть сгенерированы путем решения соответствующей
прямой задачи с заранее заданными законами изменения коэффициен-
тов Ламе, которые на этапе решении обратной задачи подлежат восста-
новлению.
Наиболее эффективными методами решения обратных задач в рам-
ках сформулированной постановки являются различные вариации про-
екционных методов, представленных в п. 1 .6 .6 . Ниже рассмотрим про-
екционный метод, основанный на использовании слабой постановки
исходной краевой задачи (3.6.1). Для ее формулировки введем гладкие
функции C# , удовлетворяющие главным граничным условиям, налагае-
мым на вектор перемещений: C#
%1
0. Умножая уравнения (3.6.1) на
пробные функции C# и интегрируя по области ? ,получим
*

# ,
C
#

2#C#

?
0
Преобразуя интеграл с помощью формулы Грина, получим соотно-
шение
*

# ,
C
#

2#C#

?
*

#
C
#

#
C
#,

2#C#

?,
которое с учетом граничного условия в (3.6 .1) примет вид
%
2

#
C
#
*

#
C
#,

#
C
#

?
0
(3.6 .10)
Отметим, что способ получения слабой постановки показывает,
что для функции # , удовлетворяющей главным граничным условиям,
можно требовать гораздо меньших ограничений на гладкость, чем для
функций сильного решения, что важно при использовании конечноэле-
ментных и проекционных трактовок.
Опишем один из вариантов решения прямой задачи, которая за-
ключается в нахождении функций перемещения 1

1, 2
,

2 1, 2

при заданных коэффициентах Ламе. Представим искомые функции
в виде разложения по некоторым базисным функциям, удовлетворяю-
щих главным граничным условиям. В качестве базиса возьмем набор
бигармонических полиномов. Таким образом,

#
1

#
7
#
,
(3.6 .11)
где
7
11

2,
7
2
2
12,
7
3
3
12,
7
41

3
2,
7
5
4
12,
20/27

3.6 . Коэффициентные ОЗ для уравнений теории упругости
183
7
62
1
3
2,
7
7
3
1
3
2,
7
81

5
2,
7
96
12,
7
10
4
1
3
2,.
.
.
,

#
1

#
7
#
,
(3.6 .12)
то есть
7
1
2
1,
7
21

2
2,
7
33
1,
7
4
2
1
2
2,
7
5
4
1,
7
63
1
2
2,
7
71

4
2,
7
85
1,
7
9
4
1
2
2,
7
10 2
1
4
2,
...
Вкачествепробныхфункцийвыбиралисьтежесамыеэлементы
базиса: C1
7
#
,C2
7
#
.
Подставляя данные представления (3.6.11),
(3.6 .12) в (3.6 .10) и интегрируя по области ? ,получаемсистемули-
нейных алгебраических уравнений относительно неизвестных коэффи-
циентов разложения # ,

#
,>
1, ... , , решение которой дает искомые
коэффициенты разложения функций перемещения.
Перейдем к обсуждению обратной задачи. В качестве дополнитель-
ной информации служат данные о 1

1, 2
,

2 1, 2

внекотором
наборе точек в области ? , полученные в результате решения прямой
задачи, описанной выше. Эта задача является некорректной, в связи
с чем обратная задача решается в два этапа. На первом этапе по за-
данным наборам значений 1

1, 2

и2

1, 2

строится двумерный
интерполяционный многочлен Лагранжа; тем самым преодолевается
некорректность вычисления производной от функций, заданных таб-
лично. На втором этапе используется проекционный метод, описанный
выше; будем искать искомые функции в виде линейной комбинации
B

#
1

#
I
#
,
4

#
1

#
I
#
,
(3.6 .13)
где
I
11,
I
2 1,
I
32
1,
I
4
2
2,
I
5
4
1,
I
6
4
2,...
Как и в случае решения прямой задачи, в качестве пробных функ-
ций выбирались те же самые функции. Используя слабую постанов-
ку, аналогичным образом формируем систему линейных алгебраиче-
ских уравнений относительно неизвестных коэффициентов разложе-
ния # ,

#
,>
1, ... , , решение которой дает искомые коэффициенты
разложений, формирующих реконструкцию неизвестных законов неод-
нородности B 1 , 2

и 41,2
.
Представим результаты вычислительных экспериментов по реше-
нию прямой и обратной задач. Все результаты приведены для пря-
моугольной области ?
0,*
,

спараме
т
рами*
100 cм,

10cм,
7856 кг/см3
.
Будем считать, что граница 1 0защем-
лена, а на границе 1
*
задана касательная нагрузка A2

1%
3кН,
нормальная нагрузка равна нулю, границы 2

свободны от нагру-
жения.
Для оценки точности полученных результатов решения прямой
задачи проведено его сравнение с решением, полученным с помощью
21/27

184
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Р
и
с
.
3
.
1
6
.
С
р
а
в
н
и
т
е
л
ь
н
ы
е
р
е
з
у
л
ь
т
а
т
ы
р
е
ш
е
н
и
й
п
р
я
м
о
й
з
а
д
а
ч
и
п
р
о
е
к
ц
и
о
н
н
ы
м
м
е
т
о
д
о
м
и
М
К
Э
в
с
т
а
т
и
к
е
(
0

.
С
в
е
р
х
у
п
р
е
д
с
т
а
в
л
е
н
ы
р
е
з
у
л
ь
т
а
т
ы
д
л
я

1
,

,
с
н
и
з
у
—
д
л
я

1
,

22/27

3.6 . Коэффициентные ОЗ для уравнений теории упругости
185
Р
и
с
.
3
.
1
7
.
С
р
а
в
н
и
т
е
л
ь
н
ы
е
р
е
з
у
л
ь
т
а
т
ы
р
е
ш
е
н
и
й
п
р
я
м
о
й
з
а
д
а
ч
и
п
р
о
е
к
ц
и
о
н
н
ы
м
м
е
т
о
д
о
м
и
М
К
Э
п
р
и
ч
а
с
т
о
т
е
0

р
а
д
/
с
23/27

186
Гл. 3. Общие принципы исследования коэффициентных ОЗ
Р
и
с
.
3
.
1
8
.
С
р
а
в
н
и
т
е
л
ь
н
ы
е
р
е
з
у
л
ь
т
а
т
ы
р
е
ш
е
н
и
й
п
р
я
м
о
й
з
а
д
а
ч
и
п
р
о
е
к
ц
и
о
н
н
ы
м
м
е
т
о
д
о
м
и
М
К
Э
п
р
и
ч
а
с
т
о
т
е
0

1
1

р
а
д
/
с
24/27

3.6 . Коэффициентные ОЗ для уравнений теории упругости
187
Р
и
с
.
3
.
1
9
25/27

188
Гл. 3. Общие принципы исследования коэффициентных ОЗ
метода конечных элементов. Для оценки точности проанализирована
относительная погрешность Æ#

100% , где #
—
решение за-
дачи проекционным методом,

#
—
методом конечных элементов.
На рис. 3 .16–3 .18 представлены результаты решения прямой задачи
в соответствии с работой [12] для следующих законов изменения:
B

1, 2

B
0H1, 2
,
H
1, 2

0,3

1
2
2

2
2
,
4

1, 2

4
0H1, 2
,
B
0 0,46 106,
4
0 0,69 106 кг/см
2

Графически результаты изменения 1

1, 2
,

2 1, 2

представлены
в двух сечениях области: при 2

ипри1
*.
График относитель-
ной погрешности на всей области S представлен справа на рисунках
в виде поверхности. На графиках сплошной линией показано решение,
полученное методом конечных элементов, пунктиром – решение, полу-
ченное проекционным методом.
Анализ результатов серии численных экспериментов показал, что
относительная погрешность решения прямой задачи предложенным
проекционным способом в сравнении с методом конечных элементов
для прямоугольной области не превосходит 6 % в области при измене-
нии частоты до второго резонанса. Количество базисных функций
варьируется от восьми до пятнадцати; в зависимости от выбора
погрешность может существенно меняться.
Вычислительные эксперименты по реконструкции проводились для
разных законов изменения модулей упругости, включая монотонные
и немонотонные законы; в данной работе представим лишь некоторые
из них. Эксперименты проведены для разных частотных диапазонов до
третьего резонанса. Выявлено, что наиболее благоприятным (с точки
зрения точности реконструкции) частотным диапазоном является пер-
вый, т. е . до первого резонанса. Для оценки точности восстановления
проанализирована относительная погрешность реконструкции Æ2 и
Æ
$
.
На рис. 3.19 приведены результаты по восстановлению неизвестных
B

1, 2

и 41, 2

на частоте 3

2% рад/с (первый частотный
диапазон). На графиках сплошной линией изображено точное решение,
точками — результаты реконструкции; поверхность справа иллюстриру-
ет погрешность идентификации.
Анализируя произведенные вычислительные эксперименты, необхо-
димо отметить, что при восстановлении законов неоднородности из-
менения модулей, являющихся линейной комбинацией базисных функ-
ций, схема работает достаточно эффективно; относительная погреш-
ность не превосходит 0,04 % (без учета зашумления входных данных).
Для иных законов неоднородности погрешность реконструкции дохо-
дит до 9,5 %; уменьшение точности реконструкции особенно суще-
ственно на границах области.
26/27

Список литературы к гл. 3
1. Боброва А.Н ., Ватульян А.О. Об определении закона изменения модуля
Юнга при анализе продольных колебаний стержня // Вестник ДГТУ. 2009.
No 4. С. 613–621.
2. Богачев И.В ., Ватульян А.О ., Явруян О.В . Реконструкция жесткости
неоднородной упругой пластины // Акуст. журнал. 2016. No 3 . С. 369 –374.
3. Бочарова О.В ., Ватульян А.О. О реконструкции плотности и модуля Юнга
для неоднородного стержня // Акустический журнал. 2009. Т . 55, No 3.
С. 281–288.
4. Ватульян А.О . Интегральные уравнения в обратных задачах определения
коэффициентов дифференциальных операторов теории упругости // Докла-
ды РАН. 2005. Т . 405, No 3. С .343–345.
5. Ватульян А.О . Обратные задачи в механике деформируемого твердого
тела. М.: ФИЗМАТЛИТ, 2007. 223 с.
6. Ватульян А.О . Проблемы идентификации неоднородных свойств твердых
тел // Вестник Самарского госуниверситета, естественные науки. 2007.
No 4 (54). С.93 –103.
7. Ватульян А.О . О вариационной постановке обратных коэффициентных
задач для упругих тел // Доклады РАН. 2008. Т . 422, No 2. С .182–184.
8. Ватульян А.О., Дударев В.В . О некоторых проблемах реконструкции неод-
нородного предварительно напряженного состояния в упругих телах // Изв.
Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2009.
Т. 9, вып. 4, ч. 2. С. 25–32.
9. Ватульян А.О . О некоторых пос тановках обратных коэффициентных задач
для линейных операторов // Известия вузов. Сев. кавк. рег. Сер. Естеств.
науки, спецвыпуск «Актуальные проблемы механики». 2009. С . 50–54.
10. Ватульян А.О . К теории обратных задач в линейной механике деформи-
руемого тела // ПММ. 2010. Т . 74, вып. 6. С. 909 –916.
11. Ватульян А.О . Гукасян Л .С . О задаче Коши для уравнен ия в частн ых
производных первого порядка и ее приложениях в теории обратных задач //
Вестник ДГТУ. 2012. No 7 (68). С. 11–20.
12. Ватульян А.О . Гукасян Л .С ., Недин Р.Д .ОзадачеКошивтеориикоэф-
фициентных обратных задач для упругих тел // Владикавказский матема-
тический журнал. 2016. Т . 18, вып. 2. С. 31–40.
13. Ватульян А.О . Гукасян Л .С ., Недин Р.Д .Ободномподходеквосста-
новлению неоднородных свойств упругого основания под распределенной
нагрузкой // Вестник РГУПС. 2016. No 4. С. 130–135.
14. Ватульян А.О ., Бурьян А.Ю ., Осипов А.В . Об идентификации переменной
жесткости при анализе поперечных колебаний балки // Вестник ДГТУ.
2010. Т. 10, No 6. С. 825–833.
15. Горбашова Е.А . Уг л ич П .С . Решение обратной коэффициентной задачи для
двумерной области // Экологический вестник ЧЭС. 2012. No 4. С. 48–55.
P owe red by T CP DF (www.tcp df.o rg)
27/27

190
Список литературы к гл. 3
16. Горюнов А.А., Сасковец А.В . Обратные задачи рассеяния в акустике.
М.: МГУ, 1989. 152 с.
17. Гузь А.Н . Упругие волны в сжимаемых материалах с начальными напря-
жениями и неразрушающий ультразвуковой метод определения двухслой-
ных остаточных напряжений // Прикладная механика. 1994. Т . 30, No 1.
С. 3 –17.
18. Гюнтер Н .М . Интегрирование уравнений первого порядка в частных про-
изводных. М. – Л.: ГИТТЛ, 1934. 181 с.
19. Ко л т он Д ., Кр е с с Р . Методы интегральных уравнений в теории рассеяния.
М.: Мир, 1987. 311 с.
20. Ко зло в П .Л ., Мазья В.Г ., Фомин Л.В. Об одном итерационном методе
решения задачи Коши для эллиптических операторов // Журн. вычисл.
матем. и матем. физ. 1991. No 1. С. 64–74
21. Лехницкий С .Г . Теория упругости анизотропного тела. М.: Наука, 1977.
416 с.
22. Ломакин В.А . Теория упругости неоднородных тел. М .: Изд. МГУ, 1976.
368 с.
23. Лу Л .-Ю ., Жанг Б. -К. Нахождение слоя с малой скоростью сдвиговых волн
релеевской волной с помощью гене тическ их алгоритмов // Акуст. журн.
2006. Т. 52, No 6. С. 811–824.
24. Ляв А. Математическая теория упругости. М .– Л .: 1935. 674 с.
25. Никитина Н .Е . Акустоупругость. Опыт практического применения.
Н. Новгород.: ТАЛАМ, 2005. 208 с.
26. Олейник О.А., Иосифьян Г.А., Шамаев А.С. Математические задачи тео-
рии сильно неоднородных упругих сред. М .: Изд. МГУ, 1990. 312 с.
27. Прейсс А.К. Определение полей напряжений по ограниченной эксперимен-
тальной информации // Машиноведение. 1984. No 2. С. 77 –83.
28. Самарский А.А . Введение в теорию разностных схем. М.: Наука, 1971.
552 с.
29. Санчес-Паленсия Э. Неоднородные среды и теория колебаний. М.: Мир,
1984. 472 с.
30. Сеймов В.Т ., Трофимчук А.Н ., Савицкий О.А . Колебания и волны в слои-
стых средах. Киев: Наукова думка, 1990. 224 с.
31. Сковорода А.Р .,
Агл ям о в С .Р . Определение механических свойств
вязко-упругого слоя на основе импедансных измерений // Матем.
моделирование. 1997. Т . 9, No 8. С. 119–126.
32. Тимошенко С.П ., Войновский-Кригер С. Пластинки и оболочки. М .: Физ-
матгиз, 1963. 635 с.
33. Тихонов А.Н .,
Арсенин В.Я . Методы решения некорректных задач.
М.: Наука, 1986. 287 с.
34. Федорюк М.В . Обыкновение дифференциальные уравнения. М .: Наука,
1985. 448 с.
35. Филиппов А.П . Колебания деформируемых систем. М.: Машиностроение,
1970. 736 с.
36. Фомин А.В ., Прейсс А.К . Определение трехмерного напряженного состо-
яния элемента конструкции по данным измерений на части его поверхно-
сти // Машиноведение. 1982. No 1. С.79–85 .
1/27

Список литературы к гл. 3
191
37. Фомин А.В . Определение напряженного состояния в объеме детали по
известным перемещениям или напряжениям на части ее поверхности //
Машиноведение. 1982. No 4. С. 67–73.
38. Хатсон В. Пим. Дж. Приложения функционального анализа и теории
операторов. М .: Мир, 1983. 432 с.
39. Яхно В.Г . Обратные задачи для дифференциальных уравнений упругости.
Новосибирск :Наука, 1990. 304 с.
40. Bonnet M., Constantinescu A.Inverseproblemsinelasticity//InverseProbl.
2005. No 21. P. 1 –50.
41. Bui H .D . Inverse Problems in the Mechanic of Materials: An Introduction.
CRC Press, Boca Raton, FL. 1994. 224 p.
42. Dudarev V .V ., Nedin R.D., Vatu l yan A .O. Nondestructive identification of
inhomogeneous residual stress state in deformable bodies on the basis of
the acoustic sounding method // Advanced Materials Research V. 996. 2014.
P. 409–414 .
43. Dudarev V .V ., Nedin R.D., Vatulyan A.O . Some aspects of modeling and
identification of inhomogeneous residual stress // Engineering Structures.
2017. V. 151. 201. P. 391–405.
44. Herglotz G. Uber die Elastizitat der Erde bei Boruckshtiqung unter Variablen
Dichte // Zeitschr.fur Math. und Phys. 1905. Bd. 52, No 3. S . 275.
45. Isakov V . Inverse problems for PDE. Springer-Verlag, 2005. 284 p.
46. Khan A.A ., Rouhani B.D. Iterative regularization for elliptic inverse prob-
lems // J. Computers & Mathematics with Applications. 2007. V. 54, No 6.
P. 850 –860 .
47. Jiḿenez R.D., Santos L.C ., Kuhl N .M ., Egana J.C ., Soto R.L.Aninverse
eigenvalue procedure for damage detection in rods // J. Computers & Mathe-
matics with Applications. 2004. V. 47, No 4, 5. P. 643–657.
48. Nedin R.D ., Vat u ly an A .O . Inverse Problem of Non-homogeneous Residual
Stress Identification in Thin Plates // Int. J . Solids Struct. 2013. No 50.
P. 2107–2114.
49. Oberai A.A ., Gokhale N .H ., Feijoo G.R . Solution of inverse problems in
elasticity imaging using the adjoint method // Inverse problems. 2003. No 19.
P. 297–313.
2/27

Глава 4
КОЭФФИЦИЕНТНЫЕ ОБРАТНЫЕ ЗАДАЧИ
ВО ВТОРОЙ ПОСТАНОВКЕ
В настоящей главе основное внимание уделяется одномерным обрат-
ным коэффициентным задачам для стержней, пластин, неоднородных
структур, возникающих при изучении колебаний в слоистых, стержне-
вых или пластинчатых структурах, в том числе и при наличии связан-
ности полей. Решен ряд обратных задач во второй постановке, когда
либо на границе тела заданы амплитудно-частотные характеристики,
либо известны резонансные значения, причем построение решения опи-
рается на регуляризованные итерационные процессы, общая структура
которых описана в гл. 3.
Отметим, что основная трудность при исследовании обратных ко-
эффициентных задач при акустическом зондировании состоит в про-
цедуре построения операторных соотношений, связывающих искомые
и измеряемые (заданные) при анализе колебаний функции. Поскольку
коэффициенты дифференциальных операторов переменны, то в явном
виде построить общие представления решений, как это имеет место
для операторов с постоянными коэффициентами, и использовать эти
решения для анализа обратной задачи не представляется возможным.
В силу нелинейности обратной задачи даже для линейной модели тре-
буется процедура линеаризации и нахождение производной по Фреше
от соответствующего оператора. В силу этого требуются иные подходы,
которые описаны в предыдущей главе. Детализация этих подходов для
конкретных операторов, встречающихся в линейной механике, и вы-
числительные эксперименты по определению неизвестных функций
и составляет основное содержание настоящей главы.
Отметим, что различные аспекты задач, изложенных в настоящей
главе, освещены в публикациях [5, 12, 14, 15, 17, 44, 48, 49, 55].
4.1 . Обратные задачи при исследовании
продольных и изгибных колебаний
неоднородного упругого стержня
Задачи для неоднородных упругих стержней являются базовыми
как для исследования волновых процессов в стержневых структурах,
так и при решении КОЗ во второй постановке о восстановлении пере-
менных характеристик: модуля Юнга, плотности, площади поперечного
сечения. Как упомянуто выше в гл. 3, существуют две постановки
обратных задач и в первой постановке задача линейна и сводится
к задаче Коши для дифференциального уравнения 1-го порядка. Вторая
3/27

4.1. Исследование продольных и изгибных колебаний
193
постановка приводит к существенно нелинейной проблеме. Отметим,
что в [11] эти ОЗ исследованы в том случае, когда физические и гео-
метрические характеристики слабо неоднородны, мало отличаются от
постоянных значений, что требует лишь нахождения одной поправки.
В случае сильно неоднородных структур для построения решения ОЗ
требуется как нахождение начального приближения в простом классе
функций (обычно линейных функций), так и реализация итерационно-
го процесса типа Ньютона.
Особенностям реализации этой общей идеологии исследования ОЗ
для упругих неоднородных стержней и посвящен настоящий пункт.
4.1.1. Исследование обратных задач при продольных колеба-
ниях стержня. Рассмотрим в настоящем пункте задачи о восста-
новлении модуля упругости и плотности в стержне при анализе его
продольных колебаний.
Краевая задача, описывающая продольные колебания консольно
закрепленного стержня постоянного поперечного сечения под действи-
ем силы на конце, после отделения временного множителя имеет
вид (3.3 .3), (3.3 .4)

2 0,
(4.1 .1)
0 0,

A
1
Здесь ,

—
положительные функции, характеризующие законы
изменения модуля упругости и плотности, которые могут быть как
гладкими функциями, так и иметь конечное число разрывов первого
рода, —
площадь поперечного сечения стержня.
Будем считать, что известна дополнительная информация об ампли-
тудно-частотной характеристике торца стержня следующего вида:
,

1, 2

(4.1 .2)
По этой дополнительной информации требуется определить одну из
трех функций ,
,

; вопрос об определении большего ко-
личества переменных характеристик будет обсужден ниже в разд. 4 .2 .
Далее будем считать, что соответствующий отрезок изменения частоты
колебаний не содержит резонансных частот. Таким образом, можно
сформулировать три различные обратные задачи об отдельном опреде-
лении каждой из функций ,
,

при условии, что осталь-
ные две известны. Основное внимание в настоящем разделе уделим ОЗ
об определении механических характеристик ,
. Отметим, что
задачи подобного типа являются существенно нелинейными, поскольку
функция смещения также подлежит определению. На первом этапе
на основе общих операторных уравнений, построенных в разд. 3 .2,
строится итерационный процесс.
4/27

194 Гл. 4. Коэффициентные обратные задачи во второй постановке
Соответствующее операторное уравнение для итераций принимает вид

1
,
0

1
,

A
1 1

1
,
,

1, 2

(4.1 .3)
причем при это соотношение переходит в (3.2.19). Из опе-
раторного уравнения (4.1.3) можно формулировать итерационные про-
цессы как в задаче о нахождении модуля Юнга, так и в задаче о на-
хождении плотности.
Задача об определении модуля упругости. Рассмотрим подробно
задачу об определении модуля упругости . Тогда соответствующее
операторное уравнение (уравнение Фредгольма 1-го рода с непрерыв-
ным ядром) примет вид

1
,
0

A
11

1
,
,

1, 2

(4.1 .4)
Отметим, что первый этап итерационного процесса, как указано вы-
ше, требует знания начального приближения. В настоящем разделе на-
чальное приближение строилось в классе линейных положитель-
ных ограниченных функций вида 0

1.
Из априорной ин-
формации об ограниченности модуля упругости 0
можно получить следующие ограничения на константы 0 и 1:
Рис. 4 .1

,
которые определяют компактное множе-
ство на плоскости изменения параметров

0, 1

и позволяют этап отыскания на-
чального приближения определять тра-
диционными методами, основанными на
минимизации функционала невязки. Зна-
чения постоянных 0 и 1 находились из
условия минимума функционала невяз-
ки на построенном компактном множе-
стве ,изображенномнарис.4
.
1,

.
2
.
1

2
,
(4.1 .5)
где ,

—
функция смещения на свободном конце стержня при
линейном законе изменении модуля 0

1.
5/27

4.1. Исследование продольных и изгибных колебаний
195
На каждом шаге построенного итерационного процесса посредством
решения интегрального уравнения Фредгольма 2-го рода находилось
новое значение смещения ,
, с помощью которого определялись
правая часть интегрального уравнения Фредгольма 1-го рода и его
ядро (отметим, что ядро интегрального оператора в (4.1 .4) строго
положительно). После решения этого уравнения на основе метода регу-
ляризации А. Н . Тихонова вычислялась поправка к модулю упругости,
и с ее учетом реализовался следующий этап итерационного процесса.
Проведена серия вычислительных экспериментов для различных
законов изменения модуля упругости. При этом все вычислительные
эксперименты проводились для безразмерных функций и спектрально-
го параметра, введенных аналогично разд. 3 .3 . Введены безразмерные
параметры и функции
H;
"
2.
"
0
,
E;
/
2.
/
0
,
G
2/0
0
2
.
2
"
0
(здесь 0, 0
—
соответственно характерные значения модуля Юнга,
плотности, в частности их максимальные или средние значения (воз-
можно в качестве таковых использовать и известные априорные гра-
ничные значения ,

)); далее всюду вместо ; будем употреблять .
На рис. 4.2 представлены результаты восстановления безразмерной
функции, характеризующей модуль упругости H 1

2 встержне
постоянного поперечного сечения, со следующим законом изменения
безразмерной плотности: E
1 0,5.
Здесь и далее сплошной
линией показан график исходной функции, квадратиками — восста-
новленной в соответствии с описанным выше итерационным процес-
сом. Прерывистой линией показано начальное приближение, найденное
из условия минимума функционала невязки .
Рис. 4 .2
Рис. 4.3
На рис. 4.3 представлены результаты восстановления безразмерной
функции, характеризующей изменение модуля упругости для следу-
ющих законов: E 1, H
1
% .Всериирасчетовбыло
принято, что G1 2,5, G2 5; это соответствует частотному диапазону,
расположенному между 1-й и 2-й резонансными частотами. Измерения
6/27

196 Гл. 4. Коэффициентные обратные задачи во второй постановке
производились для пяти частот внутри выбранного диапазона, для
восстановления потребовалось 5 итераций.
Был произведен анализ относительной погрешности Æ при восста-
новлении безразмерной функции H 1

1,5 0,72 для E
1 при G1
1,5, G2 3,9, что соответствует частотному диа-
пазону,расположенномумежду1-йи2-йрезонанснымичастотами.
Вычислительный эксперимент состоял в том, что расчеты произво-
дились для двух, трех, пяти частот внутри выбранного диапазона,
для восстановления потребовалось не более 5 итераций. Оказалось,
(рис. 4 .4) что наименьшая погрешность достигается, когда входная
Рис. 4.4
информация задается для пяти частот внутри выбранного диапазона,
т. е. увеличение количества заданной информации положительно ска-
зывается на точности реконструкции. Если же частоты выбирались
вблизи резонансных, то процесс рассыпался на первой же итерации.
Задача об определении плотности. Подобным образом может
быть исследована задача об определении плотности при известном мо-
дуле Юнга. Соответствующее операторное уравнение для нахождения
поправок (интегральное уравнение Фредгольма 1-го рода с непрерыв-
ным ядром) имеет вид

1
,

2 A1

1
1
,
,

1, 2

(4.1 .6)
Схема реализации итерационного процесса для задачи об опреде-
лении плотности такая же, как и в рассмотренной выше задаче об
определении модуля упругости. Вместе с тем отметим одно важное
отличие. Ядро интегрального оператора в (4.1 .6) неотрицательно, но не
является строго положительным в силу того, что 0,
0; соответ-
ственно этим же свойством обладают и все итерации. В силу этого вос-
становление плотности в окрестности точки закрепления с приемлемой
7/27

4.1. Исследование продольных и изгибных колебаний
197
погрешностью осуществить не удается. Это тесно связано с анало-
гичной задачей в первой постановке, которая также обладает подоб-
ным свойством. Есть два пути преодоления этой особенности. Первый
состоит в том, чтобы задавать само значение, второй — в перемене
граничных условий (по сути, концы стержня надо поменять местами).
На рис. 4.5 приведены результаты восстановления немонотонной
функции плотности E 1

0,52 в стержне постоянного попе-
речного сечения, безразмерный модуль упругости которого изменяется
по закону H 3

2.
Квадратиками изображен график восстанов-
ленной функции, когда дополнительная информация о значении E0
на защемленном конце стержня не задана, крестиками показан график
восстановленной функции при известном значении E0.
Видно, что процесс реконструкции в той ситуации, когда инфор-
мация относительно E0 отсутствует, дает достаточно большую по-
грешность и не только в малой окрестности закрепленного торца; зада-
ние E0 коренным образом исправляет ситуацию.
Рис. 4 .5
Рис. 4.6
На рис. 4.6 представлены результаты восстановления безразмер-
ной функции, характеризующей плотность для следующих законов
E
2 1,53
, H
3 0,5.
Безразмерный частотный отрезок
G
1 3, G2 5 был расположен между 1-й и 2-й резонансными часто-
тами. Входная информация задавалась для шести значений спектраль-
ного параметра внутри выбранного диапазона, для восстановления
потребовалось 4 итерации.
4.1.2. Исследование обратных задач при изгибных колебаниях
стержня. Краевая задача, описывающая изгибные колебания кон-
сольно закрепленного стержня постоянного поперечного сечения под
действием силы на конце, после отделения временного множителя
имеет вид (3.3 .17), (3.3.19),

2
,

2 0,

0 0,
,

0 0,
(4.1 .7)
8/27

198 Гл. 4. Коэффициентные обратные задачи во второй постановке

2
,

A
2,
(4.1 .8)

и
—
соответственно площадь и момент инерции поперечного сече-
ния стержня, которые могут быть функциями продольной координаты.
Будем считать, что известна дополнительная информация об
амплитудно-частотной характеристике торца стержня вида
,

3, 4

(4.1 .9)
Можно, как и в задаче о продольных колебаниях стержня, с единых
позиций сформулировать обратную задачу об определении механиче-
ских характеристик ,
. Обратная задача является существенно
нелинейной, поскольку неизвестной является также функция проги-
ба ; решение ОЗ строится на основе итерационного процесса,
причем ключевым моментом является построение операторных соотно-
шений, связывающих известные и искомые функции.
Несложно на основе общего подхода, представленного в гл. 3, по-
строить эти соотношения. В рассматриваемом случае из компонент
вектора перемещений отличны от нуля 3

1 ,1 3
.Тогда
последовательно находя 11

3,11 , 13 33 0 и выражения для
потенциальной и кинетической энергии, получим, что соответствующее
операторное уравнение представимо в форме

2
,
1
,
0

1
,

2
A
22

1
,
,

3, 4

(4.1 .10)
Задача об определении модуля упругости. Рассмотрим на осно-
ве (4.1.10) задачу об определении модуля упругости , когда соот-
ветствующее операторное уравнение (уравнение Фредгольма 1-го рода
с непрерывным ядром) принимает вид

2
,
1
,
0

A
2 2

1
,
,

3, 4

(4.1 .11)
Вэтойзадаче(вотличиеотзадачиовосстановлениимодуля
упругости при продольных колебаниях) ядро интегрального уравнения
Фредгольма первого рода пропорционально ,

2
. Изкраевого
условия задачи (4.1.8) видно, что 1,
0, этим же свойством
обладают все итерации, следовательно, возникают сложности с опре-
делением поправок на конце 1 . Это обстоятельство тесно связано
с решением задач в первой постановке (3.3 .32). Поэтому для решения
поставленной задачи необходимо либо задавать значение функции,
9/27

4.2. КОЗ при исследовании колебаний неоднородного упругого стержня 199
характеризующей модуль упругости в точке 1, либо менять тип
нагружения (моментом), либо менять местами концы стержня.
Нарис.4
.
7представленырезультатывосстановлениябезразмерной
функции, характеризующей изменение модуля упругости для следую-
щих законов: E 1

,
H
2 0,5
2% . В расчетах принято
B
1
2,8, B2
4 (что соответствует частотному диапазону 3 , 4
,
расположенному между 1-й и 2-й резонансными частотами); расчеты
производились для пяти частот внутри выбранного диапазона, значение
модуля упругости на свободном конце считалось заданным.
Рис. 4.7
Результаты вычислительных экспериментов показали эффектив-
ность предложенного подхода для достаточно широкого класса неодно-
родностей — монотонных, немонотонных с одной–двумя точками экс-
тремума.
4.2 . КОЗ при исследовании колебаний неоднородного
упругого стержня. Восстановление модуля Юнга,
модуля сдвига, плотности
В предыдущем разд. 4 .1 были рассмотрено несколько задач о ре-
конструкции одной функции, характеризующей неоднородность моду-
ля Юнга или плотности, что особенно важно с точки зрения соз-
дания теоретической базы диагностики свойств функционально-гради-
ентных материалов. В то же время актуальным остается вопрос о ре-
конструкции нескольких функций, характеризующих неоднородность.
В настоящем пункте на основании результатов работы [19] рассмот-
рена обратная коэффициентная задача об определении на одном об-
разце трех неоднородных характеристик стержня (модуля Юнга ,
модуля сдвига D и плотности ) как функций продольной коор-
динаты по амплитудно-частотным характеристикам при совместном
исследовании продольных, изгибных и крутильных колебаний стержня.
10/27

200 Гл. 4. Коэффициентные обратные задачи во второй постановке
Такаязадачаявляетсяужеболеесложной,чемизученныевпреды-
дущем разделе отдельные задачи: необходимо сформулировать уже
три операторных уравнения, в которые входили бы искомые функции.
Соответственно рассмотрим три задачи для стержня (для простоты
рассмотрения будем считать его поперечное сечение постоянным и кру-
говым).
Вывод операторных уравнений для решения обратных задач осу-
ществим на основе операторного соотношения (3.1 .8), которое мож-
но трактовать как линейное интегральное уравнение относитель-
но ,
D ,
.
При этом нет необходимости анализировать
заново соответствующие краевые задачи, достаточно лишь вычис-
лить удельные потенциальную и кинетические энергии в соответ-
ствиис(3.1
.
7).Приэтомотметим,что8
0, ,где характе-
ризует поперечное сечение стержня.
Будем считать известной (аналогично (3.1 .4)) дополнительную ин-
формацию об амплитудно-частотных характеристиках торца консольно
защемленного стержня следующего вида:
,

1, 2
,
для продольных колебаний;
,

3, 4
,
для изгибных колебаний;
,

5, 6
,
для крутильных колебаний.
Для определения искомых функций предложена следующая схема:
на первом этапе на основе совместного анализа продольных и изгибных
колебаний определены функции, характеризующие законы изменения
модуля Юнга и плотности ;навторомэтапеприизвестной
функции плотности из анализа крутильных колебаний определяется
функция, характеризующая закон изменения модуля сдвига D .
При продольных колебаниях из компонент вектора перемещений
отлична от нуля только одна компонента:

30,
а из компонент тензора напряжений отлична от нуля компонента 11
.
Потенциальная энергия в этом случае имеет вид
1
2
-

#
8
1
2
-

2
11 8
1
2
%
0

2
1
2

2
Кинетическая энергия имеет вид
'

21
2
-

2
#
8
1
2

2
1
2

2
11/27

4.2. КОЗ при исследовании колебаний неоднородного упругого стержня 201
Тогда операторное уравнение, соответствующее (3.1 .8), принимает
вид

1
,
0

1
,

2
A
11

1
,
,

1, 2

(4.2 .1)
При изгибных колебаниях под действием изгибающей силы из
компонент вектора перемещений в рамках модели Эйлера–Бернулли
отличны от нуля следующие компоненты: 3

1, ,

1 3
.
Далее последовательно находим 11

13 33 0ивыраже-
ния для потенциальной и кинетической энергии

1
2
-

#
8
1
2
-

2
11 8
1
2

2
3 2

1
2

2 ,
'
1
2

2
-

2
#
8
1
2

2
1
2

2 ,
где обозначено

2
3
Тогда операторное уравнение, соответствующее (3.1.8), в рассмат-
риваемомслучаепредставимовформе

2
,
1
,
0

1
,

A
2 2

1
,
,

3, 4

(4.2 .2)
Таким образом, имеем на каждой итерации систему интегральных
уравнений Фредгольма 1-го рода (4.2.1), (4.2 .2), из которых можно
определить две характеристики и

с помощью метода
регуляризации А. Н. Тихонова. Таким образом, на первом этапе опре-
деляются две функции ,
.
Для нахождения модуля сдвига используем задачу о крутильных
колебаниях. При крутильных колебаниях стержня круглого поперечно-
го сечения под действием крутящего момента, обозначая угол закру-
чивания , получим, что из компонент вектора перемещений отлич-
ны от нуля следующие компоненты: 3
$
12, 2
$
13
. Тогда
12/27

202 Гл. 4. Коэффициентные обратные задачи во второй постановке
.
12
$
3, .13
$
2, .23
.
11
.
22
.
33
0 и соответственно
выражение для потенциальной энергии имеет вид

1
2
-

#
8
1
2
-
D.
2
12.2
13 8
1
2

0
D
2
22
3 2

1
2

'
D

2 ,
где обозначено

2
22
3 '
В этом случае операторное уравнение для задачи кручения, ха-
рактеризующее закон изменения модуля сдвига D при известной
функции плотности, в рассматриваемом случае представимо в форме

1
,
0

'
D

3
1
,
,

5, 6

(4.2 .3)
Если ввести безразмерные функции и параметры

,
,

: ,
D
D

D:,

'
:,
:

0,1,

0,
,

0 ,
,

'
,
D

0 ,
D ,
G
20
2
.
2
/

,
B
40
2
/

)

.
4
"

,
K
20
2
.
2
/

(4.2 .4)
(отметим, что для сокращения записи у всех функций знак тильды
над ними далее будет опущен), то полученные операторные уравнения
Фредгольма 1-го рода приобретут вид
1
0

1
(,

(

:
:

G
2
1
0

1
:,
G
2 :: : A1

1G
1
1, G,
G

G
1, G2
,
(4.2 .5а)
13/27

4.2. КОЗ при исследовании колебаний неоднородного упругого стержня 203
1
0

2
,
1
(,

(
2

2
:

:
:

B
4
1
0

1
:,
B
2 :: : A2

2B 1
1, B,
B

B
3, B4
,
(4.2.5б)
1
0

1
(,
C
(

'
: D

:
:

3K 1
1, K,
K

K
5, K6

Отметим, что каждый шаг итерационного процесса требует реше-
ния прямой задачи с уточненными характеристиками. Прямые задачи
решались с помощью сведения исходной краевой задачи к интеграль-
ным уравнениям Фредгольма 2-го рода. Так, например, для задачи
о продольных колебаниях интегральное уравнение имеет вид

1
:,
G

G
2
1
0

1
,
G=
,
:

A
3
0
2
)
2"

2
,
=
,
:

,3
0
2
)
2"
2

Для решения интегрального уравнения был использован метод
коллокаций. Интегралы заменялись приближенными значениями по
квадратурным формулам Симпсона. При удовлетворении интеграль-
ного уравнения в наборе точек в соответствии с методом коллокаций
задача была сведена к решению алгебраической системы относительно
узловых неизвестных.
Таким образом, на основании аппарата интегральных уравнений
1-го и 2-го рода строятся итерационные процессы для идентификации
неизвестных функций, которые позволяют осуществить расщепление
исходной обратной задачи на последовательность задач двух типов —
решение прямой задачи с переменными коэффициентами и определение
поправок на основе решения стандартной некорректной задачи — обра-
щения интегрального уравнения Фредгольма 1-го рода с непрерывным
ядром.
Заметим, что, как и при решении ОЗ по определению одной функ-
ции, первый этап итерационного процесса требует знания начального
приближения. Начальные приближения строились в классе линейных
положительных ограниченных функций так же, как описано выше
в разд. 4.1 .
Была проведена серия вычислительных экспериментов в задачах
идентификации переменных механических характеристик стержня при
различных видах неоднородностей. Для проверки работоспособности
14/27

204 Гл. 4. Коэффициентные обратные задачи во второй постановке
предложенных вычислительных схем проведены вычислительные экс-
перименты. На первом этапе рассчитывались смещения торцов стержня
при анализе продольных, изгибных и крутильных колебаний в зависи-
мости от частоты колебаний при выбранных законах неоднородности.
Эти данные затем использовались при решении задач идентификации
неоднородных свойств.
На рис. 4.8 представлены результаты восстановления безразмер-
ной функции, характеризующей изменение модуля Юнга при извест-
ной плотности, для следующих законов: :
1:,
:
2

0,25
3%: .
В серии расчетов было принято G1
2,4, G2 3,6,
что соответствует частотному диапазону, расположенному между 1-ой
и 2-ой резонансными частотами продольных колебаний; измерения про-
изводились для семи частот внутри выбранного диапазона. Результаты
эксперимента показывают, что для восстановления с погрешностью
менее 2 % достаточно семи итераций.
Рис. 4.8
Рис. 4.9
На рис. 4.9 представлены результаты восстановления безразмер-
ных функций, характеризующих законы изменения плотности, моду-
ля Юнга и модуля сдвига для следующих законов: :
2:3
,
:
1:3
, D:
12:3
.
При продольных, изгибных и кру-
тильных колебаниях рассматривались частотные отрезки G 2, 3,
B

2, 3,
K

2; 3,8, находящиеся между 1-й и 2-й резонансными ча-
стотами, измерения производились для трех частот внутри выбранного
диапазона. Для восстановления оказалось достаточно 5-ти итераций.
Отметим, что когда процедура реконструкции производится в ча-
стотном диапазоне, находящемся выше второй резонансной частоты,
погрешность восстановления функций оказывается значительно выше,
что демонстрирует рис. 4 .10.
На рис. 4 .10 представлены результаты восстановления безразмер-
ных функций, характеризующих законы изменения плотности, модуля
Юнга и модуля сдвига для следующих законов: :
2 0,5:3
,
15/27

4.3. Идентификация неоднородных свойств вязкоупругого
205
Рис. 4.10
:
1,5:3
, D:
2,4 0,5:3
.
При продольных, изгибных и кру-
тильных колебаниях рассматривались частотные отрезки G 4,4; 5,2,
B

4,5; 5,3,
K

5,2; 6, находящиеся между 2-й и 3-й резонансными
частотами, измерения производились для трех частот внутри выбран-
ного диапазона, реализовано пять итераций.
4.3 . Идентификация неоднородных свойств
вязкоупругого стержня при изгибных колебаниях
Учет реологических свойств материалов весьма важен для анализа
деформирования элементов конструкций со сложными неоднородными
реологическими свойствами [1]: полимеркомпозитов, функционально-
градиентных материалов, геологических пород, биологических тканей.
Прямые экспериментальные оценки механических свойств таких мате-
риалов, обладающих сложной реологией, требуют больших временных
и материальных затрат. Одним из эффективных средств определения
реологических характеристик является акустический метод: решение
одной из конечномерных обратных задач по определению характери-
стик в рамках модели стандартного вязкоупругого тела представлено
в разделе 2.5. Идентификация неоднородных характеристик, описы-
вающих свойства материалов с памятью, опирается на концепцию
динамических (или комплексных) модулей и может быть реализована
в рамках модели неоднородной вязкоупругости. Общая концепция ре-
шения таких задач, изложенная в главе 3 для линейных моделей, может
быть перенесена и на рассматриваемый случай с учетом того, что
соответствующие операторные уравнения оказываются комплексными.
В настоящем пункте рассматриваются задачи о восстановлении
комплексного модуля [46] для неоднородного вязкоупругого стержня
при возбуждении изгибных колебаний в случае различных способов
нагружения, которые базируются на работах [3, 7]. Для решения
поставленных задач предложен вариант итерационного процесса,
16/27

206 Гл. 4. Коэффициентные обратные задачи во второй постановке
опирающийся на аппарат интегральных уравнений Фредгольма первого
и второго рода.
Уравнение установившихся изгибных колебаний вязкоупругого
стержня длины переменной жесткости в рамках концепции
комплексных модулей в обезразмеренном виде будет иметь вид [3 10]

D ,
>G

2
,
,

G
4
,
G
9,
(4.3 .1)
где D,
>G
&$ 3

1&$
—
неизвестная функция безразмерного
комплексного модуля, зависящая от координаты и безразмерной ча-
стоты колебаний; / 0 H ,
/
/ 03 —
мгновенный
и длительный модули упругости соответственно, которые могут быть
как гладкими положительными функциями, так и иметь конечное
число разрывов первого рода в одних и тех же точках (что мо-
делирует слоистые структуры), G
4
/0
2
)
4
#
0
—безразмерная частота
и$

#
0
/)
4 — безразмерное время релаксации.
В зависимости от способа нагружения рассмотрим 3 задачи.
1. Консольно закрепленная балка, нагруженная на свободном конце
сосредоточенной силой при отсутствии нагрузки (9 0); граничные
условия имеют вид
0,G
0,

0, G
0,
D1, >G 1, G
0,
D 1, >G 1, G
1;
известна дополнительная информация о функции смещения свободного
конца балки в некотором частотном диапазоне G1 , G2
,
1,G

1G
2. Консольно закрепленная балка, нагруженная на свободном конце
сосредоточенным моментом при отсутствии нагрузки (9 0); гранич-
ные условия имеют вид
0,G
0 0,G
0,
D 1, >G 1, G
1,
D 1, >G 1, G
0;
известна дополнительная информация об угле поворота свободного
конца балки в некотором частотном диапазоне G1 , G2
,

1, G

2G
3. Шарнирно опертая балка, нагруженная сосредоточенной силой
9
9
0Æ 0
; граничные условия имеют вид
0,G
0,
1,G
0,

0, G
01,G
0,
17/27

4.3. Идентификация неоднородных свойств вязкоупругого
207
D,
>G
—
не известна на отрезке; известна дополнительная инфор-
мация о функции смещения в точке приложения нагрузки 0

0, 1
в некотором частотном диапазоне G1 , G2
,

0, G

3G
Сформулированные ОЗ, как и в случае упругой балки, являются
нелинейными и при решении требуют построения итерационных про-
цессов на основе метода Ньютона.
Замечание. В сформулированных задачах неизвестными являются
мгновенный и длительный модуль, соответственно H,
3 ;время
релаксации постоянно и известно.
Для построения операторных соотношений в итерационных процес-
сахсформулируемслабуюпостановкузадачи.Пусть ,
G
—г
ладкая
функция; умножим уравнение (4.3 .1) на нее и проинтегрируем резуль-
тат по отрезку 0, 1.
Тогда имеем соотношение
1
0
D ,
>G
,
G
,
G

G
4
1
0
,
G
,
G
9
0 0, G
Осуществляя в левой части последнего равенства интегрирование
по частям, получим базовое равенство
D,
>G
,
G
,
G

1
0D,
>G
,
G
,
G

1
0

1
0
D ,
>G
,
G
,
G

G
4
,
G
,
G
9
0 0, G
(4.3 .2)
Полагая для задач 1 и 2 в (4.3 .2) ,
G
,
G,
0,G

0, G
0 (где черта сверху означает комплексное сопряжение),
получим
D1,>G 1,G 1,GD1,>G 1,G 1,G

1
0
D ,
>G
,
G
1,GG
4
,
G 1, G

0, G
Используяграничныеусловиядлязадачи1иполагая90 0, полу-
чим

1G
1
0
D,
>G
,
G
,
G

G
4
,
G,
G
0;
(4.3 .3)
для задачи 2 аналогично имеем

2G
1
0
D ,
>G
,
G
,
G

G
4
,
G,
G
0
(4.3 .4)
18/27

208 Гл. 4. Коэффициентные обратные задачи во второй постановке
Для задачи 3 ,
G
,
G,
0,G
1,G
0; из уравне-
ния (4.3.2) получим (для простоты далее считаем 90 1)
1
0
D ,
>G
,
G
,
G

G
4
,
G,
G

3 G (4.3 .5)
Итак, далее рассмотрим общее нелинейное операторное уравнение,
связывающее функции D,
>G,
,
G,
1
0
D ,
>G
,
G
,
G

G
4
,
G,
G

G,
G

G
1, G2

(4.3 .6)
Пусть известно некоторое начальное приближение D0
,
>G
реше-
ния уравнения (4.3 .6). Используем метод Ньютона для нахождения
следующего приближения, для чего осуществим процедуру линеариза-
ции. Для получения линейных операторных уравнений с целью опре-
деления поправок представим функции в виде
H ,
>G
H
0,
>G

H
1,
>G,
3 ,
>G
3
0 ,
>G

3
1,
>G ,
D ,
>G
D
0,
>G

D
1,
>G,
,
G

0,G

1, G,
где —
формальный параметр. Подставим эти представления в (4.3 .6)
и соберем слагаемые при одинаковых степенях :
1
0

D
0,
>G
0 ,
G
0 ,
G

G
4

0,
G
0,
G

D
1,
>G

0 ,
G
0 ,
G

1,
G

2,
G

1
2

G,
(4.3 .7)
где

1 ,
G
D
0,
>G
1 ,
G
0 ,
G

G
4

1,
G
0,
G
и

2 ,
G
D
0,
>G
0 ,
G
1 ,
G

G
4

0,
G
1,
G
суть некоторые вспомогательные функции.
Обозначим
1
0

D
0,
>G
0 ,
G
0 ,
G

G
4

0 ,
G
0,
G

0G
Рассмотрим отдельно интегралы, содержащие функции 1
,
G
и2
,
G.
Интегрируя по частям и учитывая граничные условия,
19/27

4.3. Идентификация неоднородных свойств вязкоупругого
209
сохраним главное слагаемое при .
В результате имеем интегральное
уравнение Фредгольма 1-го рода для определения поправки
1
0
D
1,
>G
0 ,
G
0 ,
G

0G,
G

G
1, G2

(4.3 .8)
Если априори известно, что неоднородность локализована на отрез-
ке 1, 2

(задача 3), то уравнение типа (4.3 .8) преобразуется к виду

1
D
1,
>G
0 ,
G
0 ,
G

0G,
G

G
1, G2

(4.3 .9)
Такимобразом,наосновеслабойпостановкизадачисформулиро-
ваны комплекснозначные операторные уравнения Фредгольма 1-го ро-
да (4.3.8), (4.3.9) с вещественными ядрами, из которых возможно
определить функции первого приближения.
Опишем способ решения комплекснозначного интегрального урав-
нения (4.3.8). Разделяя вещественную и мнимую части в выражении
для искомой функции D1
,
> G ,получим
D
1,
>G
!D
1,
>G

>
" D
1,
>G
3
1 $
2

1
1$
2

>
3
1 1
$
2
1$
2

4
H
1:2
G

3
1:1
G

>H
1 31
:
3G,
где введены следующие вещественные функции частоты колебаний:
:
1G
1
1$
2

4,
:
2G
$
2

4
1$
2

4,
:
3G
$
2
1$
2

4
Тогда из комплекснозначного интегрального уравнения (4.3 .8) получим
систему вещественных интегральных уравнений с одинаковыми непре-
рывными ядрами
1
0
H
1:2
G

3
1:1
G
0 ,
G
0 ,
G

0G,
(4.3 .10)
1
0
H
1 31
:
3G0
,
G
0 ,
G

0G
На основе системы интегральных уравнений Фредгольма (4.3.10)
с помощью метода регуляризации А. Н . Тихонова находятся функции
первого приближения.
С помощью представленного подхода может быть построен итераци-
онный процесс уточнения неизвестных функций, когда линеаризации
производится относительно функций следующего приближения.
20/27

210 Гл. 4. Коэффициентные обратные задачи во второй постановке
Для различных типов граничных условий >-й шаг итерационного
процесса описывается следующими операторными уравнениями
1
0
H
#
1:2
G

3
#
1:1
G
#
0 ,
G
#
0 ,
G

! G

#
0 G,
(4.3 .11)
1
0
H
#
13
#
1:3
G
#
0 ,
G
#
0 ,
G
" G

#
0 G,
причем 3
#1
03#
0 3#
1.
Также отметим, что первый этап итерационного процесса, как
и в вещественном случае, требует знания начального приближения.
Начальное приближение D0
,
>G
строилось в классе линейных и экс-
поненциальных комплексных ограниченных функций и представляет
собой конечномерную ОЗ. Искомые коэффициенты находились из усло-
вия минимума функционала невязки на построенном из априорной
информации компактном множестве,

4
2
4
1

0,GG

2
G,
(4.3 .12)
где 0, G
—
функция смещения в заданной точке стержня при неко-
тором законе изменения комплексного модуля. Минимизация функци-
онала осуществлялась на основе генетического алгоритма, описанного
выше в разделе 2.3
На каждом шаге построенного процесса посредством решения ин-
тегрального уравнения Фредгольма 2-го рода находилось новое значе-
ние #
0, с помощью которого вычислялись правая часть интегрального
уравнения Фредгольма 1-го рода и его ядро. Результатом решения
этого уравнения является поправка к неизвестной функции; с ее уче-
том производился следующий этап итерационного процесса. Прове-
дена серия вычислительных экспериментов по восстановлению функ-
ций H,
3
по заданной комплекснозначной амплитудно-частотной
характеристике. В вычислительных экспериментах были рассмотрены
различные типы краевых задач 1–3 и различные классы функций —
полиномиальные, экспоненциальные, кусочно-непрерывные.
Ниже приведены результаты восстановления функций, характери-
зующих законы изменения мгновенного и длительного модулей. Рас-
четы проводились для стержня из вязкоупругого материала в случае
монотонных функций при различных законах изменения характери-
стик в соответствии с [3]. На рис. 4.11 –4 .13 сплошной линией пока-
зан график исходной функции, пунктиром — начального приближения,
точками — восстановленной. Время релаксации считалось известным
и принято равным 0,1.
21/27

4.3. Идентификация неоднородных свойств вязкоупругого
211
Для задачи 1 (3 4

2, H
5 22)начальноеприближе-
ние 30

0,6 4, H0

2,5 4,5.
Рис. 4.11. Результат восстановления: а —

иб— 3

для задачи 1
По рассчитанным амплитудно-частотным характеристикам частот-
ныйдиапазонвыбранследующимобразом:G1 , G2

4, 6.
Для достижения точности 105 при минимизации функциона-
ла (4.3.12) потребовалось 18 итераций. Значение параметра регуляри-
зации на последнем шаге , 0,5983 105
.
Для задачи 2 принято 3 1

22
, H
232
,начальное
приближение 30

0,6 1,1, H0

1,6 2, частотный диапазон
G
1, G2

3; 5,1 . Для достижения точности 104 в функционале (4.3 .2)
потребовалось 20 итераций. Значение параметра регуляризации на по-
следнем шаге , 0,3387 104
.
Рис. 4.12. Результат восстановления: а —

иб— 3

для задачи 2
22/27

212 Гл. 4. Коэффициентные обратные задачи во второй постановке
Для задачи 3 (0 0,2), принято: 3 1

2, H
3,12
,
начальное приближение 30

0,7 1,1, H0

3,3, частот-
ный диапазон G1 , G2

4,5; 6,5 .
Для достижения точности 104 в функционале (4.3.2) потребо-
валось 11 итераций, причем значение параметра регуляризации на
последнем шаге , 0,2338 104
.
Рис. 4.13. Результат восстановления: а —

иб— 3

для задачи 3
Отметим, что предложенная схема идентификации комплекснознач-
ных функций позволяет в проведенных вычислительных экспериментах
осуществить идентификацию с достаточной степенью точности.
4.4 . Идентификация неоднородных свойств
ортотропного упругого слоя
В настоящем пункте представлена схема решения ОЗ по восста-
новлению неоднородных по толщине модулей упругости ортотропного
слоя по данным акустического зондирования. Задачи о реконструк-
ции неоднородных упругих свойств слоистых сред в последнее время
приобретают все более значимый характер. В первую очередь, это
связано с активным использованием в практике новых функционально-
градиентных (ФГМ) и композиционных (КМ) материалов, свойства
которых непрерывно или кусочно-непрерывно меняются по толщине
слоистой структуры. Эти материалы имеют переменные упругие свой-
ства, обеспечивающие необходимое функциональное назначение, и во
многих приложениях вытесняют слоистые композиты. Количественное
определение неоднородных характеристик слоистых материалов позво-
ляет моделировать реальное поведение объектов с существенно неод-
нородными свойствами и сложных биологических систем, расширить
возможности создания и исследования новых функционально-гради-
ентных и биоматериалов.
23/27

4.4. Идентификация неоднородных свойств
213
Поставленная задача уже описывается в рамках модели теории
упругости с помощью краевой задачи для оператора в частных произ-
водных второго порядка с переменными коэффициентами.
Задачи идентификации неоднородных свойств упругих слоистых
структур приводят к малоисследованным математическим проблемам.
Основное внимание исследователей сосредоточено на решении обрат-
ных коэффициентных задач в рамках однородных моделей, характе-
ризующихся конечным набором физических постоянных; причем про-
странство поиска параметров конечномерно, вычислительные схемы
ихидентификациинаосновеанализаоткликанадинамическоевоз-
мущение относительно просты в соответствии с результатами гл. 2;
в большинстве исследований такие задачи решаются путем минимиза-
ции функционалов невязки [1, 54].
В зарубежной литературе на первых этапах исследования таких за-
дач применительно к проблемам идентификации биологических тканей
преимущественно использовалась постановка, где известны (измерены)
физические поля внутри исследуемого объекта [70–72]. В этом случае
задача оказывается линейной, как это описано в гл. 3, и ее исследова-
ние сводится к решению задачи Коши для системы дифференциальных
уравнений первого порядка или к интегральному уравнению Фредголь-
ма первого рода. Если же информация о поле смещений известна лишь
на границе, то обратная задача существенно нелинейна и сводится
к решению нелинейных операторных уравнений, которые содержат
промежуточные переменные — компоненты физических полей. Задачи
в такой постановке могут быть исследованы лишь на основе некоторых
итеративных процедур, основные принципы построения которых опи-
раются на метод линеаризации и слабую постановку.
Для слоистых сред — слоя, полуплоскости, полупространства — пря-
мые и обратные коэффициентные задачи об определении характеристик
среды исследованы в работах [79, 80]. Как правило, работы посвящены
исследованию обратной коэффициентной задачи в рамках изотропной
модели материала, при этом определяются одна или две функции, ха-
рактеризующиенеоднородныесвойстваисследуемыхобластейвклас-
сах либо гладких положительных, либо кусочно-постоянных функций.
Для анизотропных материалов основы методов идентификации для
полуплоскости или полупространства в нестационарной постановке
изложены в монографии В. Г. Яхно [61]. К сожалению, предложенная
методика неприменима к полуограниченным областям типа слоя.
В настоящем пункте в соответствии с работами [36, 37] представле-
но исследование обратной коэффициентной задачи об идентификации
неоднородных свойств ортотропного слоя из анализа данных акустиче-
ского зондирования — полей смещений, измеренных лишь на верхней
границе слоя.
Рассмотрим колебания упругого ортотропного неоднородного по
толщине слоя ?

1, 2

,
,

30,3 вп
лоской(зада-
ча 1) и антиплоской (задача 2) постановках в режиме установившихся
24/27

214 Гл. 4. Коэффициентные обратные задачи во второй постановке
колебаний. Нижняя грань слоя жестко защемлена, на части верхней
границы приложены нагрузки, определяемые вектором )#.
,
—час-
тота колебания. В рамках рассматриваемой постановки после отделе-
ния временного множителя краевые задачи имеют вид

#
0,
>,

1,2,3,
(4.4 .1)

3 0# 0,

3 3#3

#
,

1,
,
0,

1+,

(4.4 .2)
Задача 1 характеризует плоскую деформацию при

1,0,3
,
тогда ненулевыми являются компоненты вектора перемещения 1

11, 3
,

1, 3
; напряжения находятся по формулам

"
11,1

"
3

3,3 ,

13 "55

1,3

3,1
,
6
1, 3
Задача 2 характеризует антиплоскую деформацию,
0, 2 ,0,
ненулевой является компонента вектора перемещения 2

21, 3
;
ненулевые компоненты тензора напряжений находятся в соответствии
сформулами

21 "66

2,1 ,

23 "44

2,3

Здесь 3

—
плотность слоя, "# 3

—компоненты тензора модулей
упругости — произвольные гладкие положительные функции, характе-
ризующие упругие свойства неоднородного слоя.
Замыкают постановки задач условия излучения волн на бесконеч-
ности, при формулировке которых использован принцип предельного
поглощения [38].
Обратная задача состоит в восстановлении функций "# 3

по до-
полнительной информации о полях смещений, измеренных на верхней
границе слоя в режиме частотного зондирования в случае плоских
и антиплоских колебаний,

1,3,

1, ,
*
1,2,3
(4.4 .3)
Отметим, что в случае, когда информация вида (4.4.3) задана на
части границы слоя, задача становится весьма трудной для исследова-
ния, некоторые результаты по решению ОЗ в этом случае представлены
в[35].Внастоящемпунктеограничимсяболеепростымслучаем,когда
дополнительная информация задана на всей границе слоя и появляется
возможность оперировать с осредненными характеристиками. Здесь
достаточно просто строятся операторные уравнения, связывающие ис-
комые и заданные (измеренные) функции, при помощи интегрального
преобразования Фурье. Применим преобразование Фурье к исходным
краевым задачам 1, 2 (4.4.1), (4.4 .2) и введем обозначения для транс-
формант #,,

1, 3, ,)
#
1 1; тогда относительно них
получим следующие ниже краевые задачи.
25/27

4.4. Идентификация неоднородных свойств
215
Задача 1
"
55 1

>,"
55 3

>,"
13 3

2,2
"
11 1 0,
"
33 3

>,"
13 1

>,"
55 1

2,2
"
553 0,

#
0 0,
>
1, 3,
"
55 1
>,"
55 3

1,
"
33 3

>,"
13 1

3
(4.4 .4)
Задача 2
"
44 2

2,2
"
662 0,

20 0,
"
44 2

2
(4.4 .5)
Осуществим процедуру обезразмеривания задач (4.4 .4), (4.4 .5), вве-
дя следующие безразмерные параметры и функции:

3 3,

1 3,

2 3,

33,
6
2 2
3
2+"
55,
"
#
"

55# ,

#
"

55A# ,
>
1,2,3,
(4.4 .6)
где "
55 — характерное значение соответствующего модуля упругости.
Для дальнейшего упрощения задачи учтем, что введенные трансфор-
манты # ,,

3 являются аналитическими функциями параметра , при
малых его значениях и представим их в виде следующих разложений:

0>,1

,
22

... ,

0>,1

,
22

... ,
0>,1

,
2
2 ...,
A

A
0

>,A
1

,
2A
2

... ,

1,2,3
(4.4 .7)
Собирая операторные коэффициенты при одинаковых степенях ,,
после несложных преобразований c учетом дополнительной инфор-
мации (4.4.3) и разложения (4.4 .7) получим разделенные задачи от-
носительно полевых функций и функций, характеризующих упругие
свойства слоя, следующего вида:
,
0

55 0

6
20 0,

00 0,

55 1 0
1
A
0
1,

01, 6

0
1 6,

33 0 62
00,
00 0,

3310
1
A
0
3,
01, 6

0
3 6,

44 0

6
20 0,

00 0,

44 10
1
A
0
2,

01, 6

0
2 6,
(4.4 .8)
26/27

216 Гл. 4. Коэффициентные обратные задачи во второй постановке
,
1

55 1

6
21

13 055 0

33 1 62
155

0 130

10
10 0,

55 1 1
1

551 0
1
A
1
1,

13 10
1

331 1
1
A
1
3,

11, 6

1
1 6,
11, 6

1
3 6,
(4.4 .9)
,
2

55 2

6
22

11 0

13 155 1
0,

33 2 62
255

155 0

13 1

20
20 0,

55 1 2
1

551 1
1
A
2
1,

331 2
1

13 11
1
A
2
3,

21, 6

2
1 6,
21, 6

2
3 6,
(4.4 .10)

44 2

66 0

6
20 0,

20 0,

44 1 2
1
A
2
2,

21, 6

2
2 6
(4.4 .11)
Отметим, что из сформулированных задач возможно поэтапно осу-
ществить реконструкцию некоторых функций, характеризующих упру-
гие свойства слоя. Задачи (4.4 .9)–(4.4 .11) упрощаются в случае, если
воздействие на слой определяется сосредоточенными нагрузками; тогда
все коэффициенты разложения в (4.4.7) равны нулю.
Система (4.4 .8) относительно средних нулевого порядка состоит
из трех однотипных краевых задача, содержащих набор пар функций

55 ,

44,

0 ;

33 ,
0.
Полученные обратные коэф-
фициентные задачи аналогичны обратной коэффициентной задаче об
определении свойств упругого изотропного неоднородного стержня при
продольных колебаниях, представленной выше в раздле 4.1 . Схема
исследования таких задач была ранее обсуждена в работах [18, 36, 37]
и сводится к итерационному процессу, основные этапы которого состо-
ят из следующих шагов, описанных выше.
1. Осуществление линеаризации краевых задач (4.4 .8) в окрест-
ности некоторого начального приближения модулей (способ его отыс-
кания в простых классах функций описан выше в разд. 4 .1). Введем
векторы

55, 44 , 33

и:

0, 0, 0 и будем искать решения
ОЗввидесумм

1
#

Æ
#
,:

#
:
1
#

Æ:
#
,>
1,2,3, где
вторые слагаемые характеризуют поправки на соответствующей итера-
ции. Далее находим функции :
1
#
, соответствующие приближениям
P owe red by T CP DF (www.tcp df.o rg)
27/27

4.4. Идентификация неоднородных свойств
217
восстанавливаемых функций
1
#
, из решения интегральных уравне-
ний Фредгольма второго рода
:
1
#
,
6
1
0
'
1
#
;,
,
6:
1
#
;,
6
;

,
'
1
#
;,
,
6
6
2

/ ,
0

,
;

0,1
(4.4 .12)
2. Определение поправок Æ# из решения соответствующих инте-
гральных уравнений Фредгольма первого рода с гладкими ядрами:
1
0
Æ
#
:
1
1⁄4
#
,
6
2 A##6 :
1
#
1, 6 ,
6

6
1, 62
,
(4.4 .13)

0
1,
0
2,
0
3,
A
A
0
1,A
0
2,A
0
3
Ядра интегральных уравнений в (4.4 .13) представляют собой непре-
рывные на множестве 0, 1 61
,6
2 функции, которые могут быть
определены лишь численно на базе регуляризующих алгоритмов чис-
ленного дифференцирования решений, а построение решений инте-
гральных уравнений (4.4 .13) осуществляется на основе регуляризую-
щего алгоритма А. Н . Тихонова.
Согласно результатам вычислительных экспериментов реконструк-
ция неизвестных функций возможна с погрешностью не более 5 % при
точных входных данных. Таким образом, на данном этапе исследования
удается восстановить три неизвестные функции 55
,

44 ,

33
и соответствующие решения краевых задач (4.4 .8), которые необходи-
мы для дальнейшей процедуры идентификации.
Идентификация функции 13 происходит на следующем этапе.
Рассмотрим первые уравнения систем (4.4.8), (4.4.9). Первое умножим
на 1
,второе—на0
, проинтегрируем по отрезку [0,1] и вычтем
полученные уравнения. С учетом граничных и дополнительных усло-
вий, после несложных преобразований получим интегральное урав-
нений Фредгольма первого рода с непрерывным ядром относительно
функции 13 следующего вида:
1
0

13 0
,
6
0,
6

!
16,
6

6
1, 62
,
(4.4 .14)
!
16 A
0
1
1
1 6A
1
1
0
1 6
1
0

55 0
,
6
0,
6

После восстановления функции 13 из (4.4.14) численно можно
найти значения функций 1
,
6 , 1,
6
из решения системы (4.4 .9), ко-
торые потребуются для дальнейшей реконструкции остальных функций.
1/27

218 Гл. 4. Коэффициентные обратные задачи во второй постановке
На следующем этапе происходит идентификация функции, харак-
теризующей изменение модуля 11
.
Рассматривая первые уравнение
систем (4.4.9) и (4.4.10), проводя аналогичные предыдущему этапу
действия с учетом граничных и дополнительных условий, получаем
интегральное уравнение Фредгольма первого рода с гладким ядром
относительно функции 11
,
1
0

11
2
0,
6
!
26,
6

6
1, 62
,
(4.4 .15)
!
26 A
2
1
0
1 6A
0
1
2
1 6
1
0

13 1
,
6
0,
6

55 1
,
6
0,
6

На последнем этапе происходит идентификация функции, характе-
ризующей изменение модуля 66
.
Рассматривая вторые уравнения
в (4.4.9) и (4.4 .10), после несложных преобразований получаем следу-
ющее интегральное уравнение Фредгольма первого рода с суммируе-
мым ядром:
1
0

66 2
0 ,
6
A
0
2
2
2 6A
2
2
0
2 6,
6

G
1, G2

(4.4 .16)
Таким образом, с помощью решения интегральных уравнений
(4.4 .14)–(4.4.16) можно восстановить последовательно еще три функ-
ции, характеризующие упругие характеристики слоя.
Следует отметить, что из анализа свойств ядер интегральных урав-
нений (4.4.14)–(4.4.16), а именно, в силу обращения их в ноль в точке

0 (согласно граничным условиям) можно сделать вывод о «потере
информации» в этих точках, что повлечет увеличение погрешности вос-
становления соответствующих функций в этой точке на этапе решения
обратной задачи идентификации.
Далее приведем некоторые результаты по численной реализации
обратной коэффициентной задачи.
Следуя предложенной выше схеме, был проведен вычислительный
эксперимент последовательного восстановления неизвестных функций

55 ,

44,

33 ,

66,

11 ,

13 .
В качестве дополнительной
информации были взяты результаты решения прямых задач (4.4 .8),
(4.4 .9) при условии, что известны законы изменения соответствующих
функций # .
Ниже приведены результаты вычислительных экспериментов по ре-
конструкции неизвестных функций для различных законов изменения
(монотонных и немонотонных).
2/27

4.4. Идентификация неоднородных свойств
219
Стоит отметить, что задачи по определению 55
,

33 и

44 ,

66 идентичны, поэтому представлены результаты восстановления
только двух функций: 55
,

33 .
В первых двух вычислительных экспериментах для восстановления

55 и

33 из анализа амплитудно-частотных характеристик ча-
стотный диапазон выбирался между первой и второй резонансными ча-
стотами, которые оказались наиболее информативными с точки зрения
процедуры восстановления. Для дискретизации интегральных урав-
нений Фредгольма 1-го и 2-го рода при реализации итерационного
процесса отрезок 0, 1 разбивался на 15 частей ( 15). При этом для
восстановления 11
,

13 потребовалось измельчить сетку, задавая

100 и 200. На рисунках сплошной линией обозначены графи-
ки точных функций, точками — графики восстановленных функций; на
рисунках, соответствующих реконструкции функций 55

и 33
,
пунктирной линией обозначены графики начальных приближений.
В большей степени сходимость итерационного процесса определяет-
ся удачным выбором начального приближения. В описанных экспери-
ментах начальные приближения отыскивались в классе линейных или
постоянных функций из условия минимума функционалов невязки

:
0

1, 6#,

,6#

(4.4 .17)
Представим результаты вычислительных экспериментов.
В первом модельном примере представлена реконструкция моно-
тонных функций 55

4)
, 33

1)
2
, 11

1,5 )0,5
,

13 3

)
0,5
.
Начальные приближения найдены из условия ми-
нимума функционала (4.4 .16) в виде линейных функций 0
55
1,6 3,
0
33 1,8. Результаты восстановления представле-
ны на рис. 4.14, 4.15
Рис. 4.14. Реконструкция монотонных функций 55 и 33
3/27

220 Гл. 4. Коэффициентные обратные задачи во второй постановке
Рис. 4.15. Реконструкция монотонных функций 13 и 11
Рис. 4 .16. Реконструкция немонотонных функций 55 и 33
Рис. 4.17. Реконструкция немонотонных функций 13 и 11
4/27

4.5 . Обратные задачи термоупругости
221
На рис. 4 .16, 4.17 представлены результаты восстановления немо-
нотонных функций 55

363

62
, 33

263

62
,

11 2

13 4

0,13

.Началь-
ные приближения для первых двух задач найдены в виде 0
55 2,6,

0
33 2,4.
Погрешность восстановления функций 55
,

33 :длямонотон-
ных законов не превосходит 2 %, для немонотонных — 1 %; для функ-
ций 11
,

13 соответственно: для монотонных — 6–9 %, для немо-
нотонных — 12–14 %, что связано с негативным влиянием граничных
условий на ядра интегральных операторов в обратных задачах (сильная
некорректность), а также с накоплением погрешности идентификации
на предыдущем этапе (при восстановлении 11
.
Замечание. Отметим,чтоподобныезадачидляслояврамках
молелей вязкоупругости исследованы в работе [84].
4.5 . Обратные задачи термоупругости.
Задачи для термоупругого стержня
Функционально-градиентные материалы и конструкции из них все
шире внедряются в практику. При том технологии их изготовления
требуют контроля физических свойств как на этапе изготовления,
так и при эксплуатации (для правильной оценки полей температур
и напряжений). При этом для определения исследуемых зависимостей
требуется решать обратные задачи теплопроводности и связанной тер-
моупругости. Отметим, что различные аспекты решения КОЗ термо-
упругости, освещены в работах [76, 78, 79].
В настоящем разделе рассмотрены задачи о восстановлении теп-
лофизических характеристик (коэффициента теплопроводности 6,
удельной объемной теплоемкости , коэффициента теплового рас-
ширения , стержня длины при тепловом нагружении, изложение
осуществляется в соответствии с работами [28–31].
Рассмотрим продольные колебания жестко закрепленного на тор-
це 0 неоднородного термоупругого стержня длины под действием
приложенной к торцу тепловой нагрузки 90
7 :

2,
(4.5 .1)

, <

,
(4.5 .2)

6
D

#
0,

,
(4.5 .3)
0,
<0,
0,
6*
D

*
9
07,

0, (4.5 .4)
<,0
,0

,0 0
(4.5 .5)
5/27

222 Гл. 4. Коэффициентные обратные задачи во второй постановке
Перейдем в (4.5.1)–(4.5 .4) к безразмерным параметрам и перемен-
ным, обозначая
:

.
,
:

0,1,
6:

0
,
:

0
,
:
/
(.
/
0
,
:
"
(.
"
0
,
,:

0
,

1
20

0
,

/
0
"
0
,
$
1

1
,
<
0
;
0.

0
,
=
:,
$
D
D
0
,

0D0
.
,

0D0
"
0
,
Æ

2
0%0
"
0

0
,

/
0
"
0
,
6
0

0 ,
6,

0,
,

0 ,
,

0,
,
,
0

0,
,
Здесь Æ
—
безразмерный параметр связанности,
—отношение харак-
терного времени звуковых колебаний 2 к характерному времени теп-
ловых колебаний 1
.
Тогда начально-краевая задача (4.5.1)–(4.5 .5) примет вид

(

2
+
$
2
1
,
(4.5 .6)

3
:
+
(

,:=

,
(4.5 .7)

(
6:
E
(

:
E
$
1

Æ,::

2
+
($
1
,
(4.5 .8)
0,$1

=
0, $1

0,
6
E
(
,
$
1 7$1
,

3
1,$1

0,
(4.5 .9)
=
: ,0
:,0
+
$
1
: ,0 0
(4.5 .10)
КОЗ для модели (4.5 .6)–(4.5.10) состоит в следующем. По допол-
нительной информации о значении температуры на торце стержня
=

1,$1

$
1,
$
1,
,
(4.5 .11)
определить одну из теплофизических характеристик при известных
остальных.
Для нахождения решения краевой задачи (4.5 .1)–(4.5 .5) в ори-
гиналахнеобходиморешитькраевуюзадачувтрансформантахпо
Лапласу (4.5.6)–(4.5.10) и осуществить обратное преобразование Ла-
пласа. При этом следует учесть, что дифференциальные операторы
в краевой задаче (4.5 .6)–(4.5 .10) являются операторами 2-го порядка
с переменными коэффициентами, поэтому решение краевой задачи
в общем случае изменения коэффициентов может быть построено лишь
численно, например при помощи сведения к системе интегральных
уравнений Фредгольма 2-го рода. Отметим существенную разницу при
анализе ОЗ, когда в (4.5 .11) информация известна на полубесконечном
6/27

4.5 . Обратные задачи термоупругости
223
промежутке времени и когда промежуток времени конечен. В пер-
вом случае возможно обратную задачу анализировать в пространстве
трансформант, во втором случае необходимо осуществлять обратное
преобразование Лапласа. Основное внимание в настоящем пункте об-
ратим на первый случай.
Осуществим сведение краевой задачи в трансформантах (4.5.6)–
(4.5 .10) о колебаниях неоднородного термоупругого стержня при теп-
ловом воздействии к системе интегральных уравнений Фредгольма
2-го рода.
Перейдем от краевой задачи (4.5 .6)–(4.5 .10) к канонической систе-
ме обыкновенных дифференциальных уравнений первого порядка с пе-
ременными коэффициентами относительно трансформант следующего
вида:

E
(
1

(

@:,

1,
(4.5 .12)

F
(

1: Æ,
2
::

= :,

11
Æ,:

: ,

1,
(4.5 .13)

(

22
1: :,

1,
(4.5 .14)

+
(
1
"
(

: ,

1 ,:
= :,

1
(4.5 .15)
Граничные условия преобразуются к виду

0,1

=
0, 1

@1,1

7
1,

3
1, 1

0 (4.5 .16)
Проинтегрируем систему (4.5.12)–(4.5.15) дифференциальных урав-
нений по : на отрезке 0, ::

=
:,

1
3
0
1

@;,
;

"
1,

@: ,

1 1
3
0

;

Æ,
2
;;

=
;,

1Æ
3
0
,;

; ,

1; "2, (4.5 .17)

1
3
0
1
"
2

; ,

1;
3
0
,;

=
;,

1; "3,

3
:,

1
22
1
3
0
;

1; "4

7/27

224 Гл. 4. Коэффициентные обратные задачи во второй постановке
Найдем постоянные интегрирования из граничных условий (4.5.16):
"
1"30,
"
2 71

1
1
0

;

Æ,
2;;
= ;,

1Æ
1
0
,;

1;,
"
4
22
1
1
0
;

1;
Исключив помимо этого из системы (4.5 .17) переменные
@:,

1
и :,

1, приходим к системе интегральных уравнений для определе-
ния функций
=
:,

1и

= :,

1 1
3
0
1

2
1
/

Æ,
2;;
= 2,

12;

1Æ1
3
0
1

2
1
/
,2

2 ,

12; 71

3
0
2

2
,

3
:,

1
2

2
1
1
3
;
/
0
1
"
2

12;

22
1
1
3
;
/
0
,2

=
2,

12; (4.5 .18)
Поменяв порядок интегрирования в двойных интегралах систе-
мы (4.5.18), получим систему интегральных уравнений Фредгольма
2-го рода

= :,

1
1
0
'
1:,
;,

1
= ;,

1;
1
0
'
2:,
;,

1 ;,

1; 1
:,

1,
(4.5 .19)

1
1
0
'
3:,
;,

1
=
;,

1;
1
0
'
4:,
;,

1;,

1;
Здесь ядра '1
:,
;,

1,
'
2:,
;,

1,
'
3:,
;,

1,
'
4:,
;,

1 иправая
часть 1
:,

1 имеют вид
'
1:,
;,

1 1

;

Æ,
2;;

3,
0

,
8/27

4.5 . Обратные задачи термоупругости
225
'
2:,
;,

1 1
Æ,;

3,
0

,
'
3:,
;,

1
2

2
1,;
1

3,
22,
'
4:,
;,

1
22
1
1
"

3,
22,

1:,

1 71

3
0
2

В случае краевой задачи в трансформантах о колебаниях неодно-
родного термоупругого стержня под действием механической нагруз-
ки, применяя в той же последовательности действия, как и в задаче
о тепловом нагружении, придем к системе интегральных уравнений
Фредгольма 2-го рода

=
:,

1
1
0

1:,
;,

2
=
;,

2;
1
0

2:,
;,

2;,

2; ,
(4.5 .20)

: ,

2
1
0

3:,
;,

2
= ;,

2;
1
0

4:,
;,

2;,

2; 2

2
Здесь ядра 1
:,
;,

2:,
;,

3:,
;,

4:,
;,

2 иправая
часть 2

2 имеют вид

1:,
;,

2
!
2

;

Æ,
2;;

3,
0

2:,
;,

2
!
2

Æ,;

3,
0

3:,
;,

2 2
2,;
1

3,
22,

4:,
;,

2 2
2
1
"

3,
22,

B
2
Для решения системы интегральных уравнений (4.5 .19)
или (4.5 .20) будем использовать метод коллокаций, заменяя интегралы
их приближенными значениями по квадратурной формуле трапеций,
для чего введем равномерное разбиение отрезка 0, 1 на отрезков
точками:# :>1(> 1,..., 1),где: 1#
—шаг разбие-
ния. Удовлетворяя, например систему интегральных уравнений (4.5 .19)
в наборе точек в соответствии с методом коллокаций, сведем задачу
9/27

226 Гл. 4. Коэффициентные обратные задачи во второй постановке
к решению линейной алгебраической системы двойной размерности 2
относительно узловых неизвестных:

=
:

1, ,

1,2,

1:,

1, ,

1,2,

,
Здесь через : обозначены узловые точки, через "
—
коэффициенты
квадратурной формулы, через
—
узловые неизвестные.
Для построения операторных соотношений, связывающих искомые
и измеряемые в эксперименте функции, в случае ОЗ связанной термо-
упругости сформулируем слабую постановку прямой задачи для трех-
мерного тела в пространстве трансформант в общем случае. Основные
уравнения термоупругости имеют вид

# ,

#
,
(4.5 .21)

.
#
<,
(4.5 .22)
6
#
<
,

<
0.#
#,
0,
(4.5 .23)
<

0,
6
#
<
,#
*
9,
(4.5 .24)

A
#
,
(4.5 .25)
< ,0

#
,0

#
,0 0
(4.5 .26)
Применим к начально-краевой задаче (4.5 .21) (4.5.26) интеграль-
ное преобразование Лапласа по времени, обозначая соответствующие
трансформанты тильдой.
Для получения слабой постановки задачи введем в рассмотрение
гладкие пробные функции # и

$ , удовлетворяющие главным гранич-
ным условиям #
*
0,
$

0, и воспользуемся методом множите-
лей Лагранжа. Для этого умножим уравнение (4.5.21) на # , уравне-
ние (4.5 .23) — на ,1

$ , сложим полученные выражения и проинтегри-
руем по объему 8 .
Аналогично поступим с граничными условиями:
условие на части ?, умножим на ,2

#
,аначасти? на ,3

$ ,складыва-
ем и интегрируем указанные граничные условия по соответствующим
частям поверхности. В результате получим равенство

,%
8

2
-

#
8

-
.
#

#
0,1

,
1
-
6
#

<
,#
$
,8 ,1
-

<
$
8

,
2# ,2

#
?

,
1,3
6
#

<
,#,
3 9$? 0 (4.5 .27)
10/27

4.5 . Обратные задачи термоупругости
227
Полагая в (4.5.21) ,1
1+#0
,
,
2 1, ,3 1+#0
,получим

,%
8

2
-

#
8

1
!%
0
-
6
#

<
,#

$
,
8

1
%
0
-

<
$
8

-
.
#

<8
*

#
?

1
!%
0
*

9
$
?

В этом случае слабая формулировка выглядит как ,

,
где ,

—
трилинейная форма (линейная по каждому аргументу)
переменных ,

,
;

—
линейная форма, причем эти формы имеют
вид
,

-
2# ,

#
,

$,
"
# %
,.#,
6
#
, ,

8
,

#
?

1
!%
0
*

9
$
?,
(4.5 .28)
2# ,

#
, "#%,
E 3M
"
#%

1
!%
0
6
#

<
,
$
,#

1
%
0

<
$

Реализуя метод линеаризации и сохраняя в соотношении (4.5 .22)
линейные слагаемые, с учетом дополнительной информации #
*

H
#
,
,
<
#

получим
-
Æ"
1
%

1
,%

1
#,
8

2
-
Æ
1

1
#

1
#
8

1
!%
0
-
Æ6
1
#

<
1
,#

<
1
,
8

1
%
0
-
Æ
1

<
1

<
1
8

2
-
Æ.
1
#

1
#,

<
1
8
*

1
?

1
!%
0
*

<
1
?
(4.5 .29)
Соотношение (4.5.29) является интегральным уравнением Фред-
гольма 1-го рода относительно поправок Æ6
1
#
,
Æ
1

,
Æ
1
,
Æ"
1
#%
,
Æ.
1
#

и позволяет находить прибли-
жения коэффициентов, если предварительно решена прямая задача
в трансформантах внутри области V и на ее границе S с тепло-
физическими и упругими характеристиками 6
1
#
,

1
,
"
1
#%
,
.
1
#
.
Итерационный процесс стартует
при выбранном, например методом минимизации функционала невязки,
некотором начальном распределении коэффициентов 6
0
#
,

0
,
"
0
# %
,
.
0
#
.
11/27

228 Гл. 4. Коэффициентные обратные задачи во второй постановке
Одного интегрального уравнения вида (4.5 .29) для реконструкции
всех термомеханических характеристик недостаточно; для нахождения
нескольких характеристик необходимо получить дополнительные инте-
гральные уравнения при изменении вида или области нагружения.
Пример. В качестве примера применения соотношения (4.5 .29)
к решению ОЗ рассмотрим одномерную КОЗ термоупругости для неод-
нородного стержня.
В этом случае уравнение (4.5.29) преобразуется к виду
1
0
Æ
1

2
1
0
Æ
1

1
!%
0
1
0
Æ6
1

D
1

1
%
0
1
0
Æ
1

<
1

2
1
0
Æ.
1

<
1

B
H

;
0G!
!%
0

<
1

1 (4.5 .30)
Так, например, в случае теплового нагружения для нахождения
поправок теплофизических характеристик 6,

,
.
неоднород-
ного стержня из (4.5 .30) получаем интегральное уравнение

1
!%
0
1
0
Æ6
1

D
1

1
%
0
1
0
Æ
1

<
1

2
1
0
Æ.
1

<
1

;
0G!
!%
0

<
1

1 (4.5 .31)
Приведем результаты вычислительных экспериментов по решению
ряда ОЗ термоупругости.
Рассмотрим результаты реконструкции при постановке ОЗ в изоб-
ражениях по Лапласу. На рис. 4 .18 показан пример реконструкции
убывающей функции 6: : при невозмущенных входных дан-
ных и тепловой нагрузке 7$1

/$
1.
Погрешность восстановления
на четвертой итерации не превысила 5 %. Начальное приближение
6
0: 1

0, 4: ,параметрсвязанностиÆ 0, 01.
На рис. 4.19 представлен результат восстановления возрастающей
функции 6: )3 при тепловой нагрузке 7$1

$
1)51 ипараметре
связанности Æ 0, 05, начальное приближение 60
:
0,9 1,8:.П
ри
этом на третьей итерации погрешность восстановления не превыси-
ла 5 %. На рис. 4 .20 показан пример реконструкции немонотонной
функции 6: :2

1 при невозмущенных входных данных и теп-
ловой нагрузке 7$1

Æ$
1;начальноеприближение60
:
10,3:,
12/27

4.6. Об идентификации неоднородного состояния
229
Рис. 4 .18
Рис. 4.19
Рис. 4.20
параметр связанности Æ
0,001. При реконструкции считались из-
вестными значения коэффициента теплопроводности на торцах. Для
достижения заданной точности потребовалось 4 итерации. Максималь-
ная погрешность составила 4 %. Увеличение параметра связанности
до Æ 0,4 практически не изменяла погрешность реконструкции.
4.6 . Об идентификации неоднородного
предварительного напряженного состояния
втермоупругихтелах
Многие элементы различных конструкций находятся в услови-
ях предварительного напряженного состояния (ПНС) и преднагрева.
Такое термонапряженное состояние возникает в результате действия
нагрузок при термоупругом деформировании, в процессе технологиче-
скойобработкиматериалов(литья,прокатки,закалки,сварки,формов-
ки), при жестком соединении разных материалов в контактной зоне,
13/27

230 Гл. 4. Коэффициентные обратные задачи во второй постановке
вследствие неоднородной пластической деформации. Учет предвари-
тельных напряжений позволяет адекватно описывать поведение слож-
ных систем, например трубопроводов, в режиме эксплуатации при
наличии сложного термосилового нагружения.
Отметим, что простейшие модели учета однородного начального
состояния приводят к краевым задачам термоупругости с измененными,
но постоянными коэффициентами. Для строгого описания термомеха-
нических процессов в преднапряженных телах требуется привлечение
определяющих соотношений нелинейных моделей, в частности, теории
термоупругости. Отметим, что для описания многих динамических
процессов подходящей является линеаризованная модель в окрестности
некоторого состояния.
Весьма часто поле предварительных напряжений и преднагрева
существенно неоднородно, особенно в окрестности дефектов типа по-
лостей, трещин, включений. В этом случае влияние начального состо-
яния заключается в зависимости коэффициентов дифференциальных
операторов от координат.
Следует отметить, что преднапряжения в конструкциях могут до-
стигать больших значений, что может привести к разрушению кон-
струкций при нагрузках, значительно меньше допустимых. Поэтому
усовершенствование методов диагностики предварительного напряжен-
ного состояния в термоупругих телах является одной из важнейших
технических проблем. По виду диагностики различают три типа ме-
тодов: разрушающие, полуразрушающие и неразрушающие. В связи
с недостатками разрушающих и полуразрушающих методов, а также
невозможностью их использования при исследовании объектов ответ-
ственного назначения (трубопроводов, оболочек реакторов, элементов
самолетов) развиваются неразрушающие методы, причем среди нераз-
рушающих методов диагностики неоднородного ПНС в последнее вре-
мя получил распространение метод, основанный на решении коэффи-
циентных обратных задач.
В настоящем пункте на основе модели линеаризованной связан-
ноймоделитермоупругости,согласноработе[33],предложенспособ
определения преднапряжений и преднагрева. Для этого получена сла-
баяпостановкапрямойзадачитермоупругостивтрансформантахпо
Лапласу. В качестве примера рассмотрена итерационная процедура
реконструкции начального состояния полого цилиндра.
Сформулируем общую постановку обратной коэффициентной задачи.
Рассмотрим движение преднапряженного термоупругого тела, за-
нимающего объем 8 , ограниченного поверхностью ? и находящего-
ся под действием механических и тепловых нагрузок; массовые си-
лы отсутствуют. Поверхность ? может быть предс тавлена в виде
?
?

?
,
?

?
.
В соответствии с вариантом линеаризованной
модели (аналогично [8, 9]) получим, что начально-краевая задача име-
ет вид

# ,

#
,
(4.6 .1)
14/27

4.6. Об идентификации неоднородного состояния
231

# %

#,
K
0

.
#
<,
(4.6 .2)
6
#
<
, ,#

<
0.#
#,
0,
(4.6 .3)
<

0,
6
#
<
,#
*
9,
(4.6 .4)

A
#
,
(4.6 .5)
< ,0

#
,0

#
,0 0
(4.6 .6)
Здесь K0
#

0
#

.
#
<
0, а предварительные напряжения 0
#
ипредна-
грев <
0 удовлетворяют уравнениям

0
#,
0,
6
#
<
0
,

,#
0
(4.6 .7)
Прямая задача термоупругости заключается в определении функций
смещений # и температуры < из начально-краевой задачи (4.6 .1)–(4.6.6)
при известных термомеханических характеристиках #% ,
,

, 6#,
.
#
ифункциях 0
#
и<0
, характеризующих начальное состояние.
В обратной задаче требуется одновременно определить начальное
состояние, характеризуемое функциями K0
#
и <0 по дополнительной
информации, заданной на границе поверхности:

H
#
,
,

#
1, #2
,
(4.6 .8)
<

(4.6 .9)
Для изучения проблем, которые возникают при решении обратных
задач, естественно начать исследование с некоторых более простых ОЗ,
где неизвестной является только одна функция.
Сформулируем следующие задачи.
Задача 1. Требуется по информации (4.6 .8) или (4.6 .9) восстано-
вить 0
#
из модели (4.6.1)–(4.6 .6) при известных функциях <0 и # % ,
,

, 6#,
.
#
.
Задача 2. Требуется по информации (4.6 .8) или (4.6 .9) восстано-
вить <0 из модели (4.6.1)–(4.6 .6) при известных функциях 0
#
и #%,
,

, 6#,
.
#
.
Для решения поставленных ОЗ необходимо сформулировать опе-
раторные уравнения, для чего получим слабую постановку прямой
задачи термоупругости для преднапряженных тел в пространстве
трансформант по Лапласу. Для этого сначала применим к уравне-
ниям (4.6 .1)–(4.6.3) и граничным условиям (4.6 .4)–(4.6.5) преобра-
зование Лапласа по времени с параметром ;сучетомначальных
условий (4.6 .6) получим

# ,

2# ,
(4.6 .10)

# %

#,
K
0

.
#

<,
(4.6 .11)
6
#

<
, ,#

<
0
.
#

#,
0,
(4.6 .12)
15/27

232 Гл. 4. Коэффициентные обратные задачи во второй постановке

0,
6
#

<
,#
*

9,
(4.6 .13)

A
#

(4.6 .14)
Введем в рассмотрение гладкие пробные функции # и

$
0,удо-
влетворяющие главным граничным условиям задачи в трансформантах

0,
$
0
* 0.
Определение 4.1 . Слабым решением задачи (4.6.10)–(4.6.14) будем
называть компоненты физических полей # ,

< , удовлетворяющие инте-
гральному равенству (4.6.15) при произвольных гладких # и

$
0
,

(4.6 .15)
Здесь
,

#,
8

2
-

#
8

#,
K
0
,

#,
8

1
!
-
6
#

<
,#
$
0,
8

<
$
08
-
.
#

<
#,

<
0#,

$
08
—
трилинейная форма, т. е . форма, линейная по коэффициентам диффе-
ренциальных операторов (
#%
,,

, 6#,
.
#
,<
0,K
0
#
,компонентам
трансформант физических полей (# ,

<
ипробнымфункциям(# ,

$
0);

A
#

#
?

1
!
*

9
$
0?
—
линейная форма от трансформант гладких пробных полей # ,

$
0.
Имеет место утверждение.
Теор ема 4.1 . Из задачи (4.6 .10) (4.6 .14) следует слабая постанов-
ка (4.6 .15).
Для доказательства воспользуемся методом множителей Лагранжа.
Умножим уравнение (4.6 .10) на # , уравнение (4.6 .12) — на ,1

$
0 ипро-
интегрируем по объему 8 .
Аналогично поступим с граничными усло-
виями: условие на части ?, умножим на ,2

#
,аначасти?
—на ,3

$
0
и проинтегрируем их по соответствующим частям поверхности ? (здесь
,
1, ,2
—
произвольные постоянные). Сложив все построенные функ-
ционалы, получим
-

# %

,#8
-

#,
K
0

, #8
-
.
#

<
, #8

,
1
-
6
#

<
, ,

$
08,1

<
$
082
-

#
8

,
1
-
.
#
<
0#,

$
08 ,2
*

A
#

#
?

,
3
*

6
#

<
,#

9
$
0? 0 (4.6 .16)
16/27

4.6. Об идентификации неоднородного состояния
233
Далее, преобразуя первые три слагаемые в равенстве (4.6 .17) и ис-
пользуя теорему Остроградского–Гаусса, получим

#,
8

#,
K
0

#,
8

2
-

#
8

-
.
#

<
#,

<
0,1

$
08 ,1
-
6
#

<
,#
$
0,
8

,
1
-

<
$
08

,
2# ,2

A
#

#
?

,
1,3
6
#

<
,#

,
3 9$0
?
0 (4.6 .17)
Полагая далее в (4.6.17) ,1
1+ ,
,
2 1,,3
1+ ,получим
окончательно

#,
8

#,
K
0

#,
8

2
-

#
8

1
!
-
6
#

<
,#
$
0,
8

<
$
08
-
.
#

<
#,

<
0#,

$
0 8

A
#

#
?

1
!
*

9
$
0? (4.6 .18)
На основе соотношения (4.6 .18) легко можно построить итераци-
онный процесс для решения нелинейной обратной задачи, идеология
которого описана выше в гл. 3 .
Сначала выбирается некоторое начальное приближение коэффици-
ентов 0 , например в классе линейных функций из условия минимума
функционала невязки. Пусть 0
—
соответствующее поле, удовлетворя-
ющее слабой постановке 0 ,

0,
. Тогда последовательность
задач для определения 1 формируется следующим образом в соот-
ветствии с [13, 16]:

1,
,
(4.6 .19)
а поправка Æ1

1 находится из операторного уравнения
1-го рода с компактным оператором:
Æ
1,

(4.6 .20)
Пример. В качестве конкретного примера применения предложен-
ного подхода рассмотрим реконструкцию неоднородного начального
состояния (преднапряжения и преднагрева) для бесконечно длинного
термоупругого цилиндра.
Пусть термоупругий цилиндр находится в условиях плоской де-
формации ((
E,

+
0, 3
) с учетом неоднородного
поля предварительного напряженного состояния и преднагрева. Внут-
ренняя цилиндрическая поверхность радиуса E1

0 теплоизолирована
17/27

234 Гл. 4. Коэффициентные обратные задачи во второй постановке
и свободна от напряжений, а на внешней поверхности радиуса E2

E
1
действует распределенная тепловая или механическая нагрузка. Функ-
ции 0
((
,
0
++
и<0
, определяющие начальное состояние, удовлетворяют
уравнениям равновесия и стационарной теплопроводности

-
0,

-
E6E
D
0
-

0
(4.6 .21)
Начально-краевая задача для случая механического способа воз-
буждения колебаний имеет вид [17]

2,
(4.6 .22)
1
-

-
6EE
D
-

E
D

<
0
.E

1
-

,
(4.6 .23)

((

240
((

.<
0
-

.<,
(4.6 .24)

240
++

.<
0
-

.<,
(4.6 .25)
D
-
E
1,
D
-
E
2,
0,

((
E
1,
0,

((
E
2,

07,
(4.6 .26)
<E,0
E,0

E,0 0
(4.6 .27)
Перейдем в (4.6.22)–(4.6 .27) к безразмерным параметрам и функ-
циям, обозначая
:
-
-
1
-
2-1
,
:
0
-
1
-
2-1
,
(
B

24,

B
,

B
/
,

1
-
2-1

2
-
2-1

,
$

1
,
=
D
B
,
=
0D
0
B
,

-
2-1

(

B
,

0
(

B
,

0
+

B
,
K

0
(

=
0,
Æ
0

1
,

!
0
B

После обезразмеривания начально-краевая задача (4.6.22)–(4.6.27)
примет вид

(
1

K
+
(

4
(

(
0

=
,
(4.6 .28)

+
(

1K::0

C
(

+
(

(
0

(

(
0

2
+
$
2,
(4.6 .29)

0
1
(

(
0

(
:

:
0
E
(

E
$

Æ
0=
0

2
+
($

1
(

(
0
+
$

,
(4.6 .30)
18/27

4.6. Об идентификации неоднородного состояния
235
E
(
0,$
E
(
1,$
0,

(
0,$
0,

(
1,$

7$ ,
(4.6 .31)
= :,0
:,0
+
$
: ,0 0
(4.6 .32)
Решение прямой задачи (4.6 .27)–(4.6 .32) при известной функ-
цииK 0
(

=
0 сведено к решению системы обыкновенных диффе-
ренциальных уравнений 1-го порядка в трансформантах по Лапласу,
которая анализируется на основе метода пристрелки [17–19]. Нахожде-
ние оригиналов осуществлено с помощью процедуры обращении транс-
формант, реализуемой в соответствии с методом Дурбина.
Отметим. что функции, характеризующие начальное состояние,
представлены в виде 0
(
:
2
1H:,
=
022
, : ,где2
—уровень на-
чального напряжения,
—уровень преднагрева, H: и
,:
—з
аконы
неоднородности. Проведено исследование влияния уровня начального
напряжения и преднагрева на граничные физические поля цилиндра.
Анализ влияния уровня начального состояния показал, что это влия-
ние наиболее существенно при 21 0,005 и 22 0,2.
В обратной задаче требуется определить одну из функций 0
(
,=
0
при известной другой по некоторой дополнительной информации
на внешней поверхности цилиндра:
1,$
H$ ,
$

,
,
(4.6 .33)
=
1,$
$,
$

(4.6 .34)
Для идентификации преднагрева цилиндра = 0 при заданном пред-
напряжении 0
(
1 предложен следующий подход. Исходя из второ-
го уравнения (4.6 .21) после обезразмеривания функция преднагрева
ищется в виде = 0
:
"
1"2
:

:
0,гдеконстанты"1 и "2
находятся из условия минимизации функционала невязки на компакте,
построенном при наличии априорной информации об ограниченности
искомой функции. В случае механического нагружения функционал
невязки имеет вид

1
"

1,$
2
$
(4.6 .35)
В случае теплового нагружения функционал невязки имеет вид

= 1,$
2$
(4.6 .36)
Для идентификация преднапряжения 0
(
при известной функ-
ции = 0 сначала находим K0 путем решения обратной задачи на основе
итерационного процесса. Затем последовательно находим 0
(
K
0
=
0 и из соотношения (4.6.31) после обезразмеривания находим

0
+
:

:
0

(

0
(
.
19/27

236 Гл. 4. Коэффициентные обратные задачи во второй постановке
Безразмерная характеристика K восстанавливалась в два этапа.
На первом этапе определялось начальное приближение в классе поло-
жительных ограниченных линейных функций K0
:
6:

.П
риэтом
коэффициенты линейных функций определялись из условия минимума
функционала невязки.
На втором этапе уточнялись законы изменения начального состо-
яния по схеме K : K1
:

ÆK
1
:.
Поправки ÆK1 находи-
лись путем решения интегрального уравнения Фредгольма 1-го рода
с непрерывным ядром
1
0
ÆK
1

+
1
(

+
1

2
(

(
0

1
1,

(4.6 .37)
Для восстановления на конечном временном промежутке к урав-
нению в трансформантах (4.6 .37) применялись теоремы операционного
исчисления, позволившие формулировать операторное уравнение в ори-
гиналах.
При решении уравнения (4.6 .37) был использован метод регуля-
ризации А. Н . Тихонова [57, 58], причем в качестве условий выхода
из итерационного процесса приняты два типа условий: либо по числу
итераций ,либопоневязке .
При проведении вычислительного эксперимента принято, что
7$
/$,
7$
/$,
2
1 0,01, 22 0,5,
0,5, :0 2
Восстанавливались различные типы неоднородностей функции K
в классе степенных и тригонометрических функций. Определены
наиболее информативные временные интервалы для измерения входной
информации. Выяснено, что наиболее информативным с точки зрения
процедуры реконструкции является временной диапазон в ближней
к началу координат зоне. Так, измерение смещения было осуществлено
на интервале ,

0, 1 в 5 точках наблюдения внутри него, а изме-
рение температуры на интервале 0; 0,5 в 4 точках наблюдения внутри
него. При отсутствии зашумления входной информации функции K
цилиндра восстанавливалась с хорошей точностью: погрешность
реконструкции монотонных функций не превышала 6 %, а немонотон-
ных — 12 %. В расчетах полагалось
8,
106
.
На рис. 4.21, 4.22 сплошной линией изображен точный закон, точ-
ками — восстановленный, пунктиром — начальное приближение.
На рис. 4.21 показан пример реконструкции убывающей функции
K:
2 1,5:2
. НачальноеприближениеK0
:
2,1 1,4: ,параметр
связанности Æ0 0,04. Для достижения порогового значения в функци-
онале (4.6.35) потребовалось 4 итерации. Погрешность восстановления
напоследнейитерациинепревысила3%.Нарис.4
.
22показанпример
реконструкции немонотонной функции K
0,5 3%: +2

%+4.
20/27

4.7. О реконструкции неоднородных свойств пьезоэлектрических тел 237
Рис. 4.21
Рис. 4 .22
Начальное приближение K0
:
0,85 0,9: .
Для достижения по-
рогового значения в функционале невязки потребовалось 8 итера-
ций. Погрешность восстановления на последней итерации не превыси-
ла 13%.
4.7 . О реконструкции неоднородных свойств
пьезоэлектрических тел
В настоящем разделе обсуждены некоторые аспекты решения КОЗ
для модели электроупругости. Основу исследования составляет общий
подход к коэффициентным ОЗ, изложенный в гл. 3 для линейных
моделей механики деформируемого твердого тела, а также соответству-
ющий содержанию статьи [8].
Эффективность и точность работы современного оборудования на-
прямую зависит от точности определения констант и переменных,
входящих в определяющие уравнения .В основе работы большинства
диагностических приборов и датчиков лежат принципы, базирующиеся
на явлении пьезоэффекта, который описывается моделью классиче-
ской линейной теории электроупругости [43, 53]. Наиболее распро-
страненными функциональными элементами в подобных устройствах
выступают простейшие изделия (пластины, стержни, цилиндры и т. п .),
изготовленные из пьезокерамики.
Процедура изготовления пьезокерамических компонент с наперед
заданными градиентными свойствами особенно актуальна в последние
годы и является сложным технологическим процессом. Определение
реальных характеристик неоднородного объекта дает возможность дать
оценку о возможности его использования в конкретном устройстве,
оценить возможности его функционального применения при длитель-
ной работе, в том числе и при работе в широком температурном
диапазоне.
21/27

238 Гл. 4. Коэффициентные обратные задачи во второй постановке
В настоящее время задача идентификации свойств неоднородных элек-
троупругих материалов даже для стержневых элементов конструкций
изучена недостаточно [11, 34]. В предыдущих разделах представлены
способы решения КОЗ для моделей в рамках линейной теории
упругости (разд. 4 .1, 4.2), однако постановка и решение КОЗ электро-
упругости имеют свою специфику. Отметим, что существует ряд иссле-
дований, в которых изучался вопрос об определении закона изменения
пьезомодуля от координаты. Так, например, в работах [10, 11, 20–22]
рассмотрен ряд обратных задач для электроупругого стержня с неод-
нородной продольной поляризацией при постоянном модуле упругости.
При этом реконструкция неизвестной функции осуществлена на основе
информации о токе в цепи. Отметим, что переменность коэффициентов
дифференциальных операторов не дает возможности просто сформули-
ровать операторные соотношения, связывающие заданные и искомые
функции; задача реконструкции является существенно нелинейной и для
ее решения требуется построение некоторого итерационного процесса.
Основы построения таких вычислительных схем основаны на слабой
постановке задач электроупругости и на билинейности оператора
электроупругости [10]. В настоящем пункте представлены общие соот-
ношения и решение ОЗ для электроупругого стержня в соответствии
с работой [8].
4.7.1. Слабая постановка задач о колебаниях неоднородных
электроупругих тел. Рассмотрим установившиеся с частотой ко-
лебания электроупругого тела объема 8 с кусочно-гладкой грани-
цей? ??,,
?
?

. Выпишем общие уравнения движения,
определяющие соотношения и смешанные граничные условия [53]:

2# 0,
(4.7.1)

#
"
#%

)
#
7
,,
(4.7.2)

,
0,
(4.7.3)

#
)
#%

%
7
,,
(4.7.4)

0,
7

*
¦
7
0,
(4.7.5)

#
,
(4.7.6)
где #
—
компоненты тензора напряжений, #
—
компоненты поля пе-
ремещения, "# %
—
компоненты тензора упругих постоянных,
—
плотность, )# %
—
компоненты тензора пьезоэлектрических постоянных,
7
—
потенциал электрического поля,

—
электрическая индукция,

%
—
компоненты тензора диэлектрических постоянных, 70
—под-
веденная к телу разность потенциалов,
—
компоненты единичного
вектора внешней нормали к ? ,

#
—
компоненты активной нагрузки,
приложенной к телу. Части поверхности ? и
?

электродированы,
ачасть?
—
неэлектродирована.
Сформулируем слабую постановку задачи. Умножим уравнения дви-
жения на пробные функции I и
#
, удовлетворяющие главным гра-
22/27

4.7. О реконструкции неоднородных свойств пьезоэлектрических тел 239
ничным условиям I
*¦
7
0,
#

0 и используем определяющие
соотношения. Далее проинтегрируем полученные выражения по объе-
му 8 , а результаты сложим. Применяя формулу Гаусса–Остроградского
и используя граничные условия, окончательно получим
-
2# ,
#
, "#%,
)
#
,7,
I,

#
,8

#
,
(4.7.7)
где
2# ,
#
, "#%,
)
#
,7,
I,

#
,
"
# %

,%
#,

)
#
7
,
#,

I
, #,

#
7
,# I,

2# #
—л
инейнаяформапокаждомуизаргументов# ,
#
, "#%,
)
#
,7,
I,

#
,;

#
#
(

7
0(
*

7
0(
—
линейный функционал.
Отметим, что обратную задачу об определении неизвестных пе-
ременных характеристик электроупругого тела можно рассматривать
как задачу об определении коэффициентов (входящих в исходную
краевую задачу) в зависимости от заданной дополнительной и апри-
орной информации (положительность, ограниченность, монотонность
и т. п.). Рассмотрим одну из возможных постановок обратной задачи.
Пусть заданы граничные значения полевых характеристик как функ-
ции частоты колебаний. При этом не накладываются ограничения на
область их задания, например: возможно задание смещений в обла-
сти приложения нагрузки #,

#
,
,

,и
ли
вне нее. Под решением обратной задачи понимается пара элементов
(# и искомые коэффициенты — модули упругости, пьезоэлектрические
постоянные и т. д.), удовлетворяющих равенству (4.7.7) для любых
пробных функций I и
#
.
Отметим, что сформулированная задача
является нелинейной и некорректной, с другой стороны, трилинейность
формы позволяет осуществить значительные упрощения, особенно
для стержневых моделей.
4.7.2. Постановка и решение прямой задачи для стержня.
В рамках представленной выше слабой трактовки задачи электро-
упругости рассмотрим колебания электроупругого стержня длины 2*,
в котором вследствие влияния технологических операций модуль
податливости ( не постоянен, а есть функция продольной координаты.
Выпишем уравнения движения, граничные условия и определяющие соот-
ношения, соответствующие классической теории электроупругости [11]:

2 0,

(

7
,
(4.7.8)

э7,
(4.7.9)
23/27

240 Гл. 4. Коэффициентные обратные задачи во второй постановке
*
,
*
0,
7*
0,
(4.7.10)
где
—
компонента тензора напряжений,
—
плотность,
—частота
колебаний,
—
компонента продольного перемещения вдоль оси стерж-
ня ,

—п
ьезомодуль, 7 —
потенциал электрического поля,
—ком-
понента вектора электрической индукции, э —диэлектрическая посто-
янная. Сформулированные граничные условия (4.7.10) соответствуют
задаче о колебаниях электроупругого стержня, консольно защемлен-
ного на левом конце с закороченными электродами. Продольные коле-
бания вызываются периодической во времени нагрузкой амплитуды ,
действующей на правом конце, величины ,
, э считаются известными
и постоянными.
Поскольку модуль податливости принят зависящем от перемен-
ной , то решение прямой задачи о построении смещения ,как
и в случае упругого стержня, сведем к решению интегрального урав-
нения Фредгольма 2-го рода с непрерывным ядром. Для простоты
вывода этого уравнения и наглядности рассуждения обезразмерим за-
дачу путем введения новой переменной ; 0, 1:

*2;

1 *,
*
и следующих обозначений:
(
(
0 ;,
6
2
0

2
B
0э
,
6
2(0
6
2
024*2
,
где ; —
безразмерная функция, характеризующая закон измене-
ния модуля податливости, 6
2
0 — параметр, характеризующий коэффи-
циент электромеханической связи [53], 6
—спектральный параметр,
прямо пропорциональный частоте колебаний . Изкраевойзадачи
(4.7.8)–(4.7.10) можно исключить все промежуточные переменные и по-
лучить интегральное уравнение относительно смещения следующего
вида:
;
/
0

2
0

6
2K K (
/
0
2(0
(
(

;
1
0
1

6
2K K (
Меняя порядок интегрирования в двойных интегралах, окончатель-
но получим искомое уравнение Фредгольма второго рода относительно
неизвестной функции смещения ;
;
1
0
K' K,
;K

;,
(4.7.11)
где 'K,
;
6
2

6,/
Ê
0

6
2
0 (1

(

—
ядро интегрально-
го оператора, представляющее собой непрерывную функцию, а правая
часть представима в виде ; 2 (0

/
Ê
0
( (.
24/27

4.7. О реконструкции неоднородных свойств пьезоэлектрических тел 241
В силу общности представления функции ; решение уравне-
ния (4.7.11) реализовано численно на основе метода коллокаций с ис-
пользованием квадратурной формулы трапеций. Точность составленной
вычислительной схемы была проверена на примере сравнения с анали-
тическим решением исходной задачи для случая ; 1 . Численный
анализ показал, что для частот, находящихся вдали от околорезо-
нансных областей, относительная погрешность сравниваемых решений
составляет не более 0,05 %.
4.7.3. Обратная задача для стержня. В рамках рассматриваемой
проблемы обратная задача заключается в отыскании закона изменения
модуля податливости ; по некоторой дополнительной информации,
в качестве которой выступают данные об амплитудно-частотной харак-
теристике нагружаемого торца стержня 1, 6
6,
6

6
1, 62
.
Как отмечено выше, одним из наиболее эффективных методов отыс-
кания решения подобных задач является метод построения итерацион-
ного процесса, основанного на процедуре линеаризации.
Слабая постановка задачи может быть легко получена на основе
общего соотношения (4.7.7),
%
%
2,

1, 2, ,
,
,7,
I

,
(4.7.12)
где
2 1

27I
2

1 ,

2 2

э,

1
B
,
э
2
Следует отметить, что форма имеет симметричную структуру
относительно переменных ,
7

, I .Осуществляялинеариза-
цию в (4.7.12), полагая

01,

01, 7
7
071,

1 1011, 2

2021( —
формальныйпараметр),атакже
полагая

0,I
7
0,получим
%
%

10
2

211

070

21 70
2

0*,

(4.7.13)
Используя уравнение (4.7.13), можно построить итерационный про-
цесс для определения поправки неизвестной функции по отношению
к некоторому начальному приближению. Отметим, что из одного
операторного уравнения (4.7.13) невозможно однозначно определить
сразу все неизвестные поправки (1 , 11 , 21 .
При восстановлении
нескольких функций следует составить несколько таких соотношений,
соответствующих различным видам приложенной нагрузки и области
ее приложения; при этом изменятся ядра интегральных операторов
иправыечасти.
25/27

242 Гл. 4. Коэффициентные обратные задачи во второй постановке
Поскольку в рамках представленной проблемы требуется опреде-
лить закон изменения только модуля податливости, а параметры ,
,э
считаются постоянными, то уравнение (4.7.13) примет вид
%
%
(
1
2
0 *,
,

,
(4.7.14)
или, переходя к безразмерным параметрам, имеем
1
0

16
2
062
1
/

0;2(0

2
;
2(0
G

1, G,
G

(4.7.15)
Уравнение (4.7.15) есть интегральное уравнение Фредгольма
1-го рода относительно функции поправки 1
;
закона изменения
модуля податливости ;. При обращении этого оператора необходимо
использовать регуляризующую процедуру. Отметим также, что
проблема выбора частотного диапазона G G
,G

также является
важной задачей с точки зрения организации наиболее эффективной
процедуры реконструкции.
4.7.4. Численные результаты. Отыскание решения обратной за-
дачи по восстановлению закона изменения ; модуля податливости
организовано численно в ходе реализации итерационного процесса.
Следует отметить, что построение итерационного процесса требует
задания начального приближения. В настоящем пункте начальное
приближение 0
;
определялось, как и ранее, из условия минимума
функционала невязки
4

Ê
4
1, G G
2G в классе линейных
функций на некотором компакте, построенном исходя из априорной
информации об ограниченности и положительности восстанавливаемой
функции ;.
Далее на каждом шаге итерационного процесса произ-
водилась поправка к предыдущему приближению, которая находилась
как решение интегрального уравнения(4.7.15). Отметим, что при его
численном решении использован метод регуляризации А. Н. Тихонова
с автоматическим выбором параметра регуляризации [57], а частотный
диапазон выбирался между первой и второй резонансными частотами.
Выход из итерационного процесса осуществлялся либо при достижении
некоторой точности, либо при достижении некоторого числа итераций.
Результаты вычислительных экспериментов показали, что наиболее
точно восстанавливаются монотонные функции; существенно немо-
нотонные зависимости восстанавливаются хуже. На рис. 4.23, 4.24
представлены результаты вычислительных экспериментов по рекон-
струкции различных законов изменения функции ;.
Здесь сплош-
ной линией показан график исходной функции, прерывистой — началь-
ного приближения, точками — восстановленной функции. Результаты
26/27

4.7. О реконструкции неоднородных свойств пьезоэлектрических тел 243
вычислительных экспериментов показали достаточную эффективность
при реконструкции различных законов изменения: для монотонных
законов погрешность восстановления не превышает 2–3 %, немонотон-
ных — 5–7 %. Дополнительная информация об АЧХ G для конечного
числа частот из отрезка G G
,G

считалась заданной точно.
Рис. 4.23
Рис . 4 .24. Реконструкция немонотонного закона
Отметим, что рис. 4.23, а соответствует функции ; 1,5 3 ;2
,

0;
2,4; 1,2, 6 0,68; 1,53, 5 итераций; рис. 4 .23, б —
;
4,5)
2,5 /
,

0;
5,2 0,83; ,
6

0,45; 1,00,
6 итераций;
рис. 4.24—
;
4,5)
2,5 /
,

0;
;

3,5,
6

0,47; 1,13,
10 итераций. Во всех представленных экспериментах измерения
производились для пяти частот внутри выбранного диапазона.
Проведенные численные эксперименты по реконструкции показа-
ли достаточную эффективность составленной вычислительной схемы.
Наиболее успешная реконструкция реализована для частотных диапа-
зонов, находящихся между первой и второй резонансными частотами.
P owe red by T CP DF (www.tcp df.o rg)
27/27

244 Гл. 4. Коэффициентные обратные задачи во второй постановке
4.8 . Об определении свойств многослойных
биологических тканей
Моделирование тканей и органов, проведение ортопедических опе-
раций на основе замещающих искусственных фрагментов, описание
биологических процессов роста и регенерации — все это требует знания
механических характеристик тканей. Биологические ткани в настоя-
щее время исследуются различными способами, причем в связи со
спецификой приложений наибольший интерес представляют методы, не
повреждающие и не разрушающие ткань. Для исследования свойств
биологических тканей в настоящее время применяются акустические
методы анализа и модели, созданные для упругих, вязкоупругих, поро-
упругих материалов, в том числе и неоднородных.
Анализ состояния кожного покрова, который, в отличие от внут-
ренних органов, доступен для непосредственного контакта, является
одним из важнейших методов современной диагностики состояния
здоровья пациента. Изменение вязкоупругих свойств в ряде случаев
может быть связано с патологией внутренних органов человека, на-
пример: на определенной стадии заболевания почек появляется отек
кожи, а степень и динамика его развития свидетельствуют о тяжести
патологии [4, 6]. В таких случаях полезно иметь объективные значения
параметров, характеризующих вязкоупругие свойства, которые врач
в силу своих субъективных ощущений дать не может. Также стоит от-
метить, что большинство методов исследования механических свойств
биологических тканей основано на использовании мертвых образцов,
но, как известно, свойства живых и мертвых биологических тканей
существенно различаются.
В литературе представлен широкий спектр работ, связанных с за-
дачами идентификации характеристик мягких биологических тканей
на основе моделей вязкоупругости. В работе [80] был проведен анализ
экспериментальных данных для определения действительной и мни-
мой части комплексного модуля, соответствующего кожному покрову.
Эксперимент основывался на распространении сдвиговой волны на
поверхности кожи, которая моделировалась как один изотропный вяз-
коупругий слой.
В исследовании [73] приведены результаты использования раз-
личных видов экспериментов для идентификации коэффициентов той
или иной модели. Рассмотрены проблемы идентификации параметров
классических моделей Максвелла, Кельвина, модели стандартного вяз-
коупругого тела. Также произведен эксперимент с отрезком аорты,
свойства которого исследовались при растяжении и кручении.
Для медицины значительный интерес представляют задачи, свя-
занными с проведением пластических операций. Например, в [60, 61]
рассмотрены задачи натяжения кожи при проведении операции по
лифтингу. Приведен анализ наиболее распространенных моделей и сде-
лан вывод о том, что наиболее адекватно поведение реальной кожи
1/27

4.8. Об определении свойств многослойных биологических тканей 245
описывают модель Кельвина и пятипараметрическая модель Бранкова,
однако для моделирования выбрана модель Кельвина ввиду меньшего
количества параметров. Сформулированы условия оптимального натя-
жения кожи и найден оптимальный режим релаксации напряжений.
Эксперименты ставились на растяжение с постоянной скоростью на-
гружения с последующей релаксацией и на ползучесть. Из анализа
результатов экспериментов определены параметры выбранной модели.
В работе [59] на первом этапе кожа моделировалась как несжи-
маемый упругий изотропный материал. Удельная потенциальная энер-
гия деформации на первом этапе исследования задавалась в форме
двухконстантного потенциала Муни. На втором этапе моделирования
использовался вязкоупругий аналог неогуковского тела. Идентифика-
ция сдвиговой характеристики производилась на основе минимизации
специального функционала, построенного с использованием интеграль-
ного оператора Вольтерра для ядра Колтунова.
В исследовании [6] рассмотрена проблема оценки характеристик
эластомеров биологического происхождения на примере кожи человека.
Приведены диаграммы растяжения и релаксации образцов кожи из об-
ласти живота. Представлена разработанная авторами математическая
модель нелинейного вязкоупругого деформирования кожи, основанная
на использовании упругого потенциала и экспоненциального ядра ре-
лаксации, в которой использован потенциал Огдена, обеспечивающий
лучшее совпадение теории и эксперимента. Предложена методика иден-
тификации параметров разработанной модели.
В работе [51] представлена методика идентификации параметров
определяющих соотношений, заключающаяся в сравнении результатов,
полученных по введенной гиперупругой модели с экспериментальными
данными для данной ткани. Представленный подход, основанный на
комбинированных методах «отжига» и Нелдера–Мида, учитывающий
историю нагружения, которая получена из механических испытаний,
позволяет находить параметры модели, при которых расхождение тео-
ретической и экспериментальной кривых минимально. Показано, что
предложенная схема является надежной и эффективной при исследо-
вании сложного механического поведения тканей и учитывает ани-
зотропию свойств, слабую сжимаемость, нелинейный упругий отклик
и геометрическую нелинейность. Представлены аналитические модели
для описания поведения тканей пищевода и периодонта.
Из исследований, выполненных в [56], можно выделить несколько
основных методов исследования кожного покрова: исследование де-
формаций кожи при одноосном и двухосном растяжении, кручении,
методы вдавливания и всасывания, для которых изготовлены приборы,
широко использующиеся на практике, различные акустические методы,
основанные на изучении сдвиговых поверхностных волн. Однако эти
приборы, работающие в определенных диапазонах характеристик, не
всегда подходят для кожи. Изучение современных методов анализа
характеристик кожного покрова показывает, что для их объективной
2/27

246 Гл. 4. Коэффициентные обратные задачи во второй постановке
оценки использование только одного метода малоэффективно и для
более полного изучения свойств кожи необходимо применять совокуп-
ность различных методов.
В настоящем разделе на основе [9] рассмотрена задача о вос-
становлении свойств неоднородного по толщине вязкоупругого слоя
(моделирующего кожный покров), в свою очередь состоящего из трех
слоев, моделирующих подкожный жир, дерму и эпидермис. С помощью
процедуры осреднения двумерную задачу удается свести к более про-
стой одномерной, для которой построена итерационная схема решения,
основанная на методе линеаризации и последовательном решении ин-
тегральных уравнений Фредгольма I и II рода с использованием метода
регуляризации А. Н . Тихонова.
Рассмотрим установившиеся колебания с частотой вязкоупру-
гого [47] изотропного неоднородного по толщине слоя, занимающего
область ?

1, 2

,
,

3 0, 3 в условиях плоской де-
формации. Нижняя грань слоя ?1 жестко защемлена, на части верх-
ней границы ?20 приложены нагрузки, определяемые вектором ,где

0, ,0.
Также предполагается, что вязкоупругий слой в свою
очередь состоит из трех слоев, толщины которых известны. Соответ-
ствующие уравнение и граничные условия после отделения временного
множителя принимают вид
4 ,1 ,1 4,3 ,3 2

*
1
0,
4 ,3
*2

1?20,
0,

1+?20

(4.8 .1)
В рассматриваемой задаче используется модель стандартного вяз-
коупругого тела для неоднородного материала, в соответствии в ко-
торой 43, >
& 0
23

1& 0
—
неизвестная функция комплекс-
ного модуля (аналог модуля сдвига), где 41

3,
4
23

—
мгновенный
и длительный модули соответственно,
—
время релаксации, 3

—
плотность неоднородного слоя. Введенные функции могут иметь конеч-
ное число разрывов первого рода (что моделирует слоистые структуры).
Осредняя введенные в задаче функции по переменной 1 (как это
сделано в задаче, представленной в разд. 4.4) и проводя несложные
преобразования, запишем задачу (4.8.1) в виде
4 ,3 ,3 2

300,
4 ,3
3

,
(4.8 .2)
где

1, 3,)
#
1

1
0

1, 3, 1

3/27

4.8. Об определении свойств многослойных биологических тканей 247
Обратная задача состоит в определении либо функций мгновенного
и длительного модулей, либо плотности с учетом наличия точек раз-
рыва первого рода на основе анализа физических полей на верхней
границе.
Рассмотрим ОЗ о реконструкции функций 41

3,
4
23

и 3, ,
удовлетворяющих (4.8 .2), по дополнительной информации
3,

1, 2

(4.8 .3)
Обезразмеривая параметры и переменные, входящие в рассматри-
ваемую задачу,

3+3,

+3,
G
20

232
+4
23 ихарактери-
стики
E

0,
D ,
>G
&$ 3

1&$
,
H

0
,
3

0
,
$

0
/
0
2,
получим следующие уравнение и граничные условия:
D ,
>G
,
G

G
2E ,
G
0,
0,G
0,
D 1, >G 1, G
1
(4.8 .4)
Дополнительное условие примет вид
1,G
G,
G

G
1, G2

(4.8 .5)
Для произвольных законов изменения H,
3
решение возмож-
но лишь численно с привлечением аппарата численного исследова-
ния интегральных уравнений Фредгольма 1-го и 2-го рода. Подобная
ОЗ возникает при описании продольных колебаний неоднородного по
длине упругого стержня, рассмотренная в разд. 4 .1 . Решение обрат-
ной задачи о реконструкции вязкоупругих характеристик приводит
к нелинейной некорректной проблеме, которая исследована с помощью
построения итерационного процесса. Отметим также, что в настоящем
разделе ОЗ рассмотрена в предположении, что характеристики имеют
точки разрыва первого рода в известных точках, что соответствует
трехслойной структуре кожи.
Итерационный процесс построен с использованием метода линеари-
зации, включающего в себя следующие этапы.
1 этап. Решение прямой задачи для ( 1)-го приближения.
Из интегрального уравнения Фредгольма 2-го рода (4.8 .6) по извест-
ным ( 1) приближениям неизвестных функций 31

и H1

(и соответственно D1
,
> G ) определяется соответствующая функ-
ция 1
,
G,

1
0
'
1
;,

1
;
;

9
1
,
&
,
(4.8 .6)
4/27

248 Гл. 4. Коэффициентные обратные задачи во второй постановке
где
'
1
;,

G
2

/,
0
E2

9
1
,
&
,
;

0,1
Для решения интегрального уравнения (4.8.6) использован метод
коллокаций.
2 этап. Нахождение поправок к восстанавливаемым функциям.
Каждые следующие приближения неизвестных функций 3
3
1

Æ3
и H
H
1

ÆH,гдеÆ3 и
ÆH
—
поправки для длительного и мгновенного модуля, должны удовле-
творять системе интегральных уравнений Фредгольма 1-го рода,
получающейся после отделения действительной и мнимой части:

1
0
ÆH :
2G Æ3:1
G
1
,
G
1
,
G

!
1
3,
G

6,
1
0
ÆH

Æ3 :
3G1
,
G
1
,
G

"
1
3,
G

6
(4.8 .7)
Решение системы интегральных уравнений Фредгольма 1-го ро-
да (4.8 .7) является некорректной задачей и требует использования регу-
ляризационных методов, например, метода регуляризации А. Н . Тихонова.
3 этап. Проверка условия выхода. На втором этапе строятся скор-
ректированные с учетом поправок функции 3 и
H

,которые
дают приближенное решение КОЗ (4.8 .4), (4.8.5) при удовлетворении
условию выхода; в противном случае корректируется ядро интегрально-
го оператора (4.8 .7) для нахождения следующей поправки. В качестве
условия выхода использовано условие

1
1,GG
4
1,42

(4.8 .8)
Отметим, что сформированный итерационный процесс требует зна-
ния начального приближения. В настоящей работе начальное прибли-
жение строилось в классе констант, которые находились для каждого
из составных слоев из условия минимума функционала невязки на
построенном из априорной информации компактном множестве:

4
2
4
1

1,GG

2
G
(4.8 .9)
Минимизация функционала осуществлялась на равномерной сетке
для области 0, 1 G1, G2
.
Далее приведены результаты вычислительных экспериментов по
реконструкции неизвестных безразмерных функций 3,
H
всо-
ответствии с предложенной итерационной схемой. В серии расчетов
плотность выбиралась постоянной ( 1), параметр, характеризующий
5/27

4.8. Об определении свойств многослойных биологических тканей 249
время релаксации, полагался $ 0,1. Толщины слоев эпидермиса, дер-
мы и подкожного жира и их мгновенные и длительные модули прибли-
зительно соответствуют участку кожного покрова в районе предплечья.
Восстанавливаемые параметры предполагались кусочно-непрерывными
функциями на [0,1].
1. Восстановление линейных функций:
3

0,075 0,13 ,

3 0,5895,
0,5 0,13,

3 0,8655,
0,88 0,13,

31,
H

0,09 0,13,

3 0,5895,
0,55 0,13,

3 0,8655,
0,9 0,13,

31
Начальные приближения выбраны из условия (10) в виде
3
0

0,1,

0,5895,
0,55,

0,8655,
0,95,

1,
H
0

0,15,

3 0,5895,
0,7,

3 0,8655,
1,

31
Частотный диапазон выбирался из анализа вещественной и мнимой
частей амплитудно-частотной характеристики (АЧХ) (рис. 4 .25). АЧХ
для восстанавливаемых функций на рисунке обозначена линией, для
начального приближения — крестиками.
Рис. 4 .25. Действительная и мнимая части АЧХ для восстанавливаемой функ-
ции и начального приближения
Для восстановления был выбран отрезок между первым и вторым
экстремумами АЧХ. Далее на рис. 4.26 приведены результаты восста-
новления искомых функций, причем сплошной линией обозначен гра-
фик начального приближения, пунктиром — график точного решения,
точками — результат восстановления.
Погрешность реконструкции не превосходит 6 % в окрестностях
точек разрыва и менее 3 % в остальных точках.
6/27

250 Гл. 4. Коэффициентные обратные задачи во второй постановке
Рис. 4 .26. Восстановление мгновенного и длительного модулей для линейных
законов изменения
2. Восстановление квадратичных функций:
3

0,075 0,42
,

0,5895,
0,5 0,22
,

0,8655,
0,78 0,22
,

1,
H

0,09 0,42
,

0,5895,
0,55 0,22
,

0,8655,
0,8 0,22
,

1
Начальные приближения найдены в виде
3
0

0,1,

0,5895,
0,6,

0,8655,
0,95,

1,
H
0

0,15,

0,5895,
0,65,

0,8655,
1,

1
Далее на рис. 4.27. приведены результаты восстановления в соот-
ветствии с описанной выше процедурой.
Для восстановления характеристик слоев частотный диапазон так-
же выбирался в между первым и вторым экстремумами амплитудно-
частотной характеристики. Погрешность реконструкции не превосхо-
дит 8 % в окрестностях точек разрыва и 4 % остальных точках.
Следует отметить, что действительно качественное восстановление
происходит только на первых участках функций, соответствующих
подкожному жиру с низкими модулями (погрешность 1–3 %) относи-
тельно двух других (дермы и эпидермиса), которые восстанавливаются
значительно хуже (погрешность 6–8 %). В связи с этим необходимо
было выяснить, какие факторы негативно влияют на реконструкцию
свойств дермы и эпидермиса. Проведено исследование по изучению
влияния параметров задачи на АЧХ, выяснению, какие же параметры
7/27

4.9 . Постановка задач о колебаниях предварительно напряженных тел 251
Рис. 4 .27. Восстановление мгновенного и длительного модулей для квадратич-
ных законов изменения характеристик
больше всего влияют на реконструкцию, производимую в соответствии
с предложенной схемой, и можно ли каким-то образом улучшить ее
результаты. При решении КОЗ, опирающихся на наличие дополни-
тельной информации, очень важно, чтобы изменение восстанавлива-
емых параметров влекло за собой существенные изменения измеряе-
мой в эксперименте дополнительной информации, на основе которой
и происходит идентификация: чем существеннее такая зависимость,
тем качественнее происходит идентификация искомых характеристик.
Проведенные вычислительные эксперименты показывают, что в слу-
чае идентификации кусочно-непрерывных свойств вязкоупругого слоя,
в свою очередь состоящего из нескольких подслоев, свойства кото-
рых различаются значительно (в изучаемом случае на порядок), что
моделирует кожный покров, отклик на верхней границе слоя (допол-
нительная информация в обратной задаче) в значительной степени
зависит лишь от характеристик низкомодульного слоя (подкожного жи-
ра), в частности, от значений его мгновенного и длительного модулей,
его толщины и его взаимного расположения с двумя другими слоями,
и практически не зависит от характеристик двух других слоев. Эти
выводы подтверждаются результатами, полученными из вычислитель-
ных экспериментов при решении ОЗ, в которых характеристики слоя,
соответствующего подкожному жиру, восстанавливались значительно
лучше характеристик двух других слоев.
4.9 . Постановка задач о колебаниях предварительно
напряженных тел. Обратная задача для стержня
Предварительное напряженно-деформированное состояние (ПНС) —
важный фактор, влияние которого необходимо учитывать при оценке
устойчивости и предразрушающего состояния элементов конструкций.
8/27

252 Гл. 4. Коэффициентные обратные задачи во второй постановке
В настоящее время имеется немало работ, посвященных моделиро-
ванию влияния ПНС на динамические характеристики упругих тел.
Отметим раннюю работу Трефтца [83], где дана постановка задач
о равновесии упругого тела при наличии ПНС. Далее отметим цикл
работ [39–42], где представлены способы линеаризованных постановок
задач о колебаниях упругих тел в рамках наложения малых дефор-
маций на конечные. Также отметим монографии [45, 46], в которых
на основе решения смешанных динамических задач теории упруго-
сти осуществлена оценка влияния ПН на контактные напряжения,
волновые процессы для слоя, цилиндра при постоянных компонентах
полей ПН. Влияние однородных полей ПН на характеристики бегу-
щих волн и способы реконструкции ПН детально обсуждены в мо-
нографии [52]. Отметим, однородными эти поля можно считать лишь
в первом приближении, а оценка неоднородных полей ПН по данным
акустического зондирования приводит к специальному классу КОЗ.
Основные результаты, полученные в последние годы в области КОЗ
для ПН тел, описаны в монографии [25]. В работе [74] дан обзор
современного состояния проблемы, в работах [23, 24, 27, 69, 70, 77]
представлены различные задачи об идентификации ПН в пластинах,
трубах, дисках.
Представим некоторые общие результаты в теории ПН и приложе-
ния к задачам идентификации.
Рассмотрим упругое тело, занимающее объем 8 ,ограниченноепо-
верхностью ?
?

?
,
, в котором имеется неоднородное предва-
рительное напряженное состояние (первое), характеризующееся ком-
понентами тензора напряжений 0
#
.
Будем считать, что колебания
с частотой вызываются нагрузкой # , приложенной на части ?, ,
ачасть? закреплена. Линеаризованные уравнения колебаний после
отделения временного множителя имеют следующий вид [25, 74]:
#
#,

2# 0,
(4.9 .1)
#
#

,
(4.9 .2)

#
"
# %

,%,
(4.9 .3)

0,
#
#

#
,
(4.9 .4)
где ##
—
компоненты несимметричного тензора Пиолы–Кирхгофа,
определяемого согласно (4.9 .2).
Для более простого построения уравнений движений и граничных
условий в частных случаях сформулируем общую вариационную поста-
новку краевой задачи.
Выберем некоторые гладкие функции Æ# таким образом, чтобы они
удовлетворяли граничному условию на части поверхности ? :
Æ
#

0. Умножим уравнения (4.9 .1) на функции Æ# и проинтегрируем
9/27

4.9 . Постановка задач о колебаниях предварительно напряженных тел 253
по объему 8 .
Используя формулу Гаусса–Остроградского и упрощая,
получим
-
"
#%

Æ
#,
8

#
Æ
#
?

2#Æ#8 0
(4.9 .5)
Нетрудно показать, что правая часть (4.9.5) есть вариация неко-
торого функционала, если ввести следующие обозначения функцио-
налов:
1
2
Ê
-
"
#%

#,
8

Ê
*

#
?
—
потенциальная энергия
тела; ,
1
2
Ê
-

#,
8
—
добавочный функционал, обусловлен-
ный наличием ПН; '
1
2

2
Ê
-

2
#
8
—
кинетическая энергия тела.
Тогда имеем
Æ

0,
(4.9 .6)
что дает обобщение вариационного принципа Остроградского–Гамиль-
тона на случай ПН тел.
В рамках такой трактовки несложно сформулировать краевую за-
дачу, описывающую изгибные колебания колебаниях прямолинейного
упругого изотропного стержня длины под действием силы A спред-
варительным одноосным напряжением 0
11.
Введем следующие обозначения в соответствии с гипотезами стерж-
ней: 1

3 1

—
компонента вектора смещений вдоль оси 1
стержня; 2 0 — компонента вектора смещений вдоль оси 2; 3

1—
компонента вектора смещений вдоль оси 3;
—п
лощадь
поперечного сечения; 8
0;
—
область, занимаемая стержнем;

2
3?
—
осевой момент инерции;
—модуль Юнга. Тогда нену-
левые компоненты тензора ## будут предс тавим ы в виде
#
11 11

1,1

0
11,
#
13 13#31 31 3,1

0
11,
#
33 33

(4.9 .7)
Здесь 11

1,1

3 1
, а функция смещения нейтральной
оси стержня 1

удовлетворяет условию консольного закрепления на
левом конце: 0 0, 0 0.
Упрощая выражения представлений соответствующих функциона-
лов ,
,
, ' ,получим
Æ

2 ,

0
1
2

0
11
20
11
22

2 2

0
11 Æ
0
11Æ

2Æ1

2 Æ

1 A (4.9 .8)
10/27

254 Гл. 4. Коэффициентные обратные задачи во второй постановке
Интегрируя по частям и приравнивая нулю коэффициенты при
одинаковых вариациях, получим

0
11
0
11
2 0,
(4.9 .9)
0 0
0 0,

0
11 0,

0
11
0
11 A
Полученные уточненные граничные условия соответствуют дей-
ствию сосредоточенной поперечной силы на конце консольно закреп-
ленного стержня. Заметим, также что в приведенной постановке пара-
метры системы ,
,

0
11, ,

могут быть заданы как функции
по переменной 1
.
Осуществим сведение краевой задачи (4.9 .9) к интегральному урав-
нениюФредгольмавторогорода.Дляэтоговведемврассмотрение
безразмерные параметры и функции
$

0
11
"
0
,
G
2
1
)
0.
2

0
$,
G
4
2
/
0)0
.
4

0"0

2
,
A
0
.
2

0"0
,
7;

0
11

0
11
,

01
;,

02
;,

03
; ,
;

04
;,
H
1; 1
;
2;,
H
2; 3
;
4;,
где ; + 0;1.
При этом отметим, что безразмерный параметр G1
характеризует величину максимального значения компоненты предва-
рительного напряжения 0
11,аG2
—
частоту колебаний .
Решение поставленной задачи в безразмерном виде сведено к ин-
тегральному уравнению Фредгольма 2-го рода относительно функ-
ции
N,

1
0
'5,
(
((

5,
(4.9 .10)
где 5 5 1A0,
;
H
1;

1$
G
2

'N,
(
1

B
1

G
2
13
272

G
4
25 22 (H2
2

2
Численная реализация определения функции ; (прямая задача)
из (4.9 .10) при заданном виде функции, характеризующей предвари-
тельное напряженное состояние, осуществлена на основе метода кол-
локаций.
1. Для аппроксимации интегрального оператора в уравне-
нии (4.9 .10) использована составная квадратурная формула Симпсона
11/27

4.9 . Постановка задач о колебаниях предварительно напряженных тел 255
с соответствующими коэффициентами ишагом3 *+ 1 ,где

—
нечетное количество узлов. Значения функции
; в выбранных
узлах (#
>

13 находим из решения следующей линейной
алгебраической системы:

(
#

'(
#
,(
(
(
#
,
>
1
2. Вычисление значений искомой функции ; втехжеузлах
(
#
,>
1, ... , 1, осуществлено по квадратурной формуле трапеций,
а для повышения точности на конце стержня — по составной квадра-
турной формуле Симпсона
(

(

(4.9 .11)
Тестирование программы, реализующей представленный подход, по-
казало, что при постоянных параметрах системы для частот колеба-
ний, находящихся ниже второго резонанса, относительная погрешность
приближенного (5.2) решения и аналитического решения [25] в точке
;
1 при 41 узлах не превосходит 0,002 %.
Отметим, что анализ влияния величины однородного предваритель-
ного напряжения на частотные характеристики показал, что это влия-
ние заметно для значений $ 104 ;поэтомупроцедуруреконструкции
следует проводить для частот, не превосходящих первую резонансную
частоту [25], где это влияние наиболее значительно.
Сформулируем обратную задачу об определении функции 0
11 по до-
полнительной информации об амплитудно-частотной характеристике
балки. Для этой задачи аналогично общей ситуации для линейных
операторов можно построить итерационный процесс, на каждом шаге
которого решается интегральное уравнение Фредгольма первого рода

1
1⁄41⁄4

1
1⁄4

1; 2
,
(4.9 .12)
или, переходя к безразмерным параметрам и вводя обозначение 0

1
,имеем
1
0
7

;

$
2; 1
1⁄41⁄4

G
2
13
;

1
1⁄4

;

A
00

1
1 0,
G
2

G
1
2;G
2
2

(4.9 .13)
При вычислительной реализации обратной задачи в качестве ре-
гуляризующей процедуры использован метод А. Н . Тихонова с авто-
матическим выбором параметра регуляризации, а частотный диапазон
12/27

256 Гл. 4. Коэффициентные обратные задачи во второй постановке
выбран до первой резонансной частоты. Начальное приближение опре-
делялось из условия минимума функционала невязки

4
2
2
4
1
2
1,G2

0 G2

2
G
2
в классе линейных функций на некотором компакте, построенном
по данным об условиях ограниченности восстанавливаемой функции.
Отметим некоторую отличительную особенность рассматриваемой за-
дачи по сравнению с аналогичной КОЗ для стержня; в рассматриваемой
задаче отсутствует ограничение положительности искомой функции.
На приведенных ниже рис. 4.28–4.31 представлены результаты вы-
числительных экспериментов по восстановлению безразмерной функ-
ции 7;, характеризующей изменение величины 0
11 ,дляследующих
законов:
1 7; 1

;
2,2

7;
1)/
,
3 7; 1

0,5;2
,4

7;
1

)
0,5 /

В серии расчетов было принято: G1
0,2, G2
0,9; 1,8, что соот-
ветствует частотному диапазону, расположенному до 1-й резонансной
частоты; измерения производились для пяти частот внутри выбранного
Рис. 4.28
Рис. 4 .29
Рис. 4 .30
Рис. 4.31
13/27

4.10. Об определении ПНСв трубе
257
диапазона. Здесь и далее сплошной линией показан график исходной
функции, прерывистой — начального приближения, точками — восста-
новленной функции. Для первого закона произведено 7 итераций, для
второго — 15, для третьего — 4, для четвертого — 11 .
4.10. Об определении предварительного напряженного
состояния в трубе
В настоящем разделе представлено решение ОЗ о реконструкции
ПНС в упругой трубе, изложенное в соответствии с работами [24, 70].
Рассмотрим задачу о радиальных колебаниях трубы в условиях
плоской деформации ((
E,

+
0, 3
)сучетомнеод-
нородного поля предварительного напряженного состояния (ПНС) раз-
личного происхождения. В качестве модели, описывающей напряжен-
ное состояния тела, использована модель Треффтца [25, 83]. При
этом примем следующие допущения: среди компонент тензора ПНС
отличными от нуля являются две (0
((
E

0и0
++
E

0), которые
связаны уравнением равновесия 0
++
E

0
((

0
((
, массовые силы
отсутствуют. Соответствующая краевая задача в кольцевой области
имеет вид
1

13
2

13
2
2

3
;

G
2

0, (4.10.1)

+
2

;
0 0, (4.10.2)
где введены следующие обозначения для безразмерных параметров
и функций:
E
E
2 ;,
;
0E1
+E
2,
6
B +B

24,
;
E+E
2 ;0,1,
G
2 2
E
2
2+B 24,
H;

0
((
+B

24,

E
2+B24
Решение прямой задачи об определении значений функции смещения
;
при известном законе изменения ПНС сведено к решению канони-
ческой системы двух дифференциальных уравнений 1-го порядка, кото-
рая решена численно с помощью метода пристрелки. Анализ решения
этой задачи показал, что влияние уровня ПНС на АЧХ существенно
в окрестности резонансных частот и наиболее значительно для тонких
труб (;0 0,7.
При рассмотрении обратной задачи об определении неоднородного
поля ПНС использован метод акустического зондирования, поскольку
неоднородность свойств исследуемого объекта влияет на его акустиче-
ские характеристики.
1. Определение уровня ПНС для задачи Ляме. С точки зрения
практической значимости отдельно исследована задача об определе-
нии внутреннего давления. На основе постановки (4.10.1), (4.10.2)
14/27

258 Гл. 4. Коэффициентные обратные задачи во второй постановке
рассмотрены две краевых задачи, описывающих свободные колебания
трубы при наличии и в отсутствии неоднородного ПНС.
С помощью ряда преобразований соответствующих краевых задач
получено следующее соотношение для поправки резонансной частоты:
G
2G2
0
1Ê

32
+
0
2

+
2
0

2
1Ê

0
2+
2
02

(4.10.3)
ВслучаекогдафункцияH характеризует напряженное состояние
согласно решению задачи Ляме [25], H;

1;2

;
2
01

,
из (4.10.3) имеем
G
2G2
0
!
0
2
2
0
1
1

1
1

2+
2
0

1
1

+
2
0

2
1Ê

0
2+
2
02

(4.10.4)
В (4.10.3), (4.10.4) 0
;
—
собственная форма колебаний кольца
без ПН.
Отметим,чтополученнаяформуладостаточноточна.Дляанализа
ее точности была проведена серия расчетов собственных частот для
тонкого кольца ;0 0,8. Результаты расчетов показали, что погреш-
ность в определении первой собственной частоты по формуле (4.10.4)
не превосходит 103; для следующих частот она нарастает, не пре-
восходя 0,2 $.
Следует отметить существенное отличие в изменении
значений собственных частот. Для тонких труб с ростом внутреннего
(предварительного) давления значения первой собственной частоты
увеличивается, а значения следующих частот, наоборот, уменьшаются.
По этой формуле, измеряя соответствующее отклонение, например пер-
вой резонансной частоты, легко определяется амплитуда внутреннего
давления.
2. Реконструкция неоднородного ПНС в общем случае. При рас-
смотрении общего случая реконструкции неоднородного осесимметрич-
ного ПНС по данным об АЧХ G 1, G в некотором диапазоне
G

G
1, G2

решение строится с помощью итерационного алгоритма, как
это реализовывалось в более простых задачах для стержней. Началь-
ное приближение выбиралось в классе линейных функций. При этом
коэффициенты линейных функций определялись из условия минимума
функционала невязки
D
2
4
2
4
1

1, G G

2
G
на компакте, построенном по априорной информации об ограниченно-
сти функции
H
. Соотношение, позволяющее вычислять значения
15/27

4.10. Об определении ПНСв трубе
259
функции поправки H1 по отношению к предыдущему на каждом
последующем шаге, получено с помощью метода линеаризации [11, 25]
в виде следующего операторного уравнения:
1
/
0
H
1

;
2

+
2

;

1
/
0
H
1

;

1, G G,
G

G
1, G2
,
(4.10.5)
где ;,
G
—
функция смещения, соответствующая функции H ,по-
лученной на предыдущей итерации. Решение (4.10.5) построено чис-
ленно путем дискретизации интегралов на основе квадратурной фор-
мулы трапеций и разностных формул для производных с последующим
применением метода регуляризации А. Н. Тихонова при обращении со-
ответствующего конечномерного оператора. Проведена серия вычисли-
тельных экспериментов по реконструкции монотонных и немонотонных
законов, показавших достаточную эффективность предложенной схе-
мы. Пример реконструкции приведен на рис. 4.32. Сплошной линией
обозначена искомая функция H; 10%; % 0,4, штриховой
линией — начальное приближение H0
;
10; 9,5, точками — вос-
становленная функция. Относительная погрешность реконструкции не
превосходит7%,частотныйдиапазонвыбранмеждупервойивторой
резонансными частотами, количество итераций равно 20, ;0 0,9.
Рис. 4.32
В рамках другого подхода при рассмотрении предложенной про-
блемы в качестве дополнительной информации считались известными
узловые значения функции ; в конечном наборе точек для заданной
частоты, что соответствует первой постановке задачи согласно терми-
нологии гл. 2. При этом уравнение (4.10.1) может быть рассмотрено
как дифференциальное уравнение первого порядка относительно функ-
ции H; с граничным условием на внешнем радиусе. Его решение
представленоввидеквадратур,ачисленнаяреализацияосуществлена
с помощью конечномерных аппроксимаций. Для вычисления первых
16/27

260 Гл. 4. Коэффициентные обратные задачи во второй постановке
и вторых производных функции смещения использован сплайн пятого
порядка, построенный по заданным узловым значениям. Анализ ре-
зультатов проведенной серии вычислительных экспериментов показал,
что предложенный подход можно успешно применять для реконструк-
ции различных законов изменения ПНС при ;0 0,8. Распределение
относительной погрешности главным образом определяется точностью
вычисления первой и второй производной функции смещения (в кра-
евых точках погрешность обычно наибольшая). Также предложенный
подход существенно зависит от точности входных данных, например,
для успешной реконструкции ПНС с уровнем 103 точность задания
входной информации (узловые значения функции смещения, значения
частоты и параметров 6 и

должна быть задана с точностью до 104
.
4.11 . О КОЗ пороупругости
Моделирование пороупругих сред начало развиваться относительно
недавно, первые работы в этой области принадлежат М. А. Био [64].
Другой популярной моделью для описания деформирования пороупру-
гойсреды,насыщеннойжидкостью,являетсямодель,предложенная
С. Коуином и Дж. Нунзиато [65], в которой авторами была рассмот-
реналинейнаяупругаясредаспустотами,причемобъемнаядоляпор
в соответствующем объеме принимается за кинематически независи-
мую переменную.
Устоявшийся вид модели, а также очень важная связь ее с мо-
делью классической термоупругости представлены в работе С. Коуина
и Д. Чандрасэкхарайя [67]. Отметим также монографии [50, 63, 82],
посвященные различным постановкам и методам решения прямых за-
дач для пористоупругих тел. В рамках этой модели имеется достаточ-
ное количество работ, в которых проведено исследование колебаний
легких конструкций из пористых материалов [63], пластин [68], про-
цессов деформаций костных тканей, а также некоторых мягких тканей:
хрящей, связок, сухожилий [66], методу граничного элемента в задачах
пороупругости [2].
В настоящем разделе в соответствии с работой [26] представлена
модель неоднородной пороупругости, для которой коэффициенты яв-
ляются функциями кооординат, представлены также некторые ОЗ по
определению некоторых коэффициентов по данным частотного зонди-
рования.
4.11.1. Общая постановка задачи для модели пороупругой
среды. Рассмотрим установившиеся колебания ограниченного неод-
нородного пороупругого тела, занимающего объем 8 , ограниченного
поверхностью ? . Колебания вызываются поверхностной нагрузкой, рас-
пределенной на поверхности ?, , и потоками жидкости по поверхно-
сти ?
.
Граница ? жестко защемлена, а на поверхности ?' задано
поровое давление.
17/27

4.11 . О КОЗ пороупругости
261
Для описания движения данной среды в режиме установившихся
колебаний рассмотрим модифицированную модель с учетом высокоча-
стотных слагаемых [50]:

>
G
2
H

00;
(4.11.1)
при этом определяющие соотношения имеют вид

,
&
<

1
G

G
H
,
(4.11.2)
где введены обозначения
%
>

'
> '

21
,

$
/

(4.11.3)
Здесь введены следующие обозначения:
—
обобщенный тензор
напряжений, &
—
объемное расширение жидкой фракции, <
—объ-
емное расширение твердой фракции, "
—тензор модулей упругости,
—тензор модулей Био, '
—
тензор коэффициентов проницаемости
среды, ,

—
плотность среды и плотность жидкости соответственно,

—
частота колебаний среды,
—
вектор смещений среды,
—давле-
ние жидкости в порах, 7 —пористость среды, !
—г
идростатическая
константа,
—
вектор массовых сил в скелете, 0
—
источники давле-
ния в жидкости, две точки между тензорами означают свертку.
Граничные условия имеют вид

?
,
; 9 ',

;

;0,

?
'
,
(4.11.4)
где 9
—
поток жидкости в порах на границе ?
.
Для определения различных коэффициентов системы требуется
знать некоторую дополнительную априорную информацию на границе
тела. Такой информацией могут служить значения амплитуд функций
смещений или давления в некотором диапазоне частот % ,

2.
Одним из этапов при решении обратных задач для определения
коэфициентов дифференциальных уравнений является вывод соответ-
ствующих операторных уравнений, связывающих известные и опреде-
ляемые характеристики. Есть несколько путей для вывода таких урав-
нений, в частности, представленный в предыдущих разделах способ,
основанный на слабой формулировке. В настоящем разделе использу-
ется обобщенное соотношение взаимности [26].
4.11.2. Обобщенное соотношение взаимности. Вобратныхза-
дачах неизвестными являются не только компоненты физических по-
лей — смещений и давления в порах, но и физические характеристи-
ки среды. Для этой ситуации возможна формулировка обобщенного
18/27

262 Гл. 4. Коэффициентные обратные задачи во второй постановке
соотношения взаимности, основанная на общих для линейной меха-
ники принципах, которое возможно получить из основных уравнений.
Для этого рассмотрим два состояния среды, являющихся решениями
основной краевой задачи (4.11 .1)–(4.11 .4). Будем различать эти со-
стояния с помощью верхнего индекса. Тогда система (2.1) для обоих
состояний в компонентах примет вид
"

#
0, (4.11.5)

>
G

2
H

1, 2,
где обозначено

#
#

%
#

Умножим первое уравнение первой системы в (4.11.5) на
2
#
,
а первое уравнение второй системы — на
1
#
,вычтемрезультатыипро-
интегрируем по объему тела 8 .
Аналогично поступим со вторыми
уравнениями системы (4.11.5), домножив их на
1
и
2 соответ-
ственно. Тогда, используя формулу Гаусса–Остроградского, получим
соотношение взаимности для пороупругой среды
*

9
1
#

2
#

9
2
#

1
#

1
&0

3
1

3
2

"
2
# %

"
1
#%

2
,%

1
#,

2
#

1
#

1
#,

2
#,

%
2
##

%
1
##

2
2
#

1
#

'
2
#

'
1
#

1
,

2
,#

G
1 2
H
1

G
2 2
H
2

1
#

2
#

1
#

8
0 (4.11.6)
Эту форму соотношения взаимности можно использовать для по-
строения итерационных процессов и получения соответствующих ин-
тегральных уравнений для определения поправок для искомых коэф-
фициентов.
Для примера далее рассмотрим задачу об установившихся колеба-
ниях пороупругого неоднородного по толщине слоя.
4.11.3. Задача о колебаниях неоднородного пороупругого слоя.
Рассмотрим плоскую деформацию трансверсально-изотропного неод-
нородного пороупругого слоя, занимающего область 1

,
,

3 0, / , под действием системы нагрузок на верхней грани в ре-
жиме установившихся колебаний.
19/27

4.11 . О КОЗ пороупругости
263
Исходя из уравнений (4.11.1) систему уравнений для описания
колебанийможнопредставитьввиде
"
11 1 ,11

"
133,3

"
55 1 ,3

3,1

11
,1

%
112

10,
"
131,1 "33

3,3

"
551,31 3,11

33
,3

%
332

30,
'
11,11 '33

,3,3 > 11

1,133

3,3 >
G
2
H

0
(4.11.7)
Граничные условия задачи:

331, /

11
,

131, /

2 1
,
9
31, /

31
,
(4.11.8)

11 ,0

3 1 ,0
9
31,0 0,

Отметим, что порядки материальных констант (и функций), вхо-
дящих в систему (4.11 .7), весьма сильно (на несколько порядков)
различаются между собой. Введем следующие безразмерные параметры
и функции:

;/,

,
G
2/0
2
#
2
@

33
,
0

;

33
,
.
1;
@
11
@

33
,
.
4;
@
33
@

33
,
.
5;
@
55
@

33
,
.
7;
@
13
@

33
,
C

;
/

/
%

,
4

;
6

33
,
Æ;

33
/
G
2
#
H
6

33
,
2

;

#
6

33
/

(4.11.9)
С учетом введенных обозначений система уравнений (4.11.7) пред-
ставима в виде
.
11,11 .7

3,31 .5

1,3 3,1 ,3 01
A

,1G
2
1

C
11 0,
.
71,1 .4

3,3

.
51,31 3,11

0
3A
,3

G
21

C
33 0,
>GÆA

4
1A,11 43
A
,3

>G2
11,1 23

3,3

0
(4.11 .10)
Применим к (4.11.10) и соответствующим граничным условиям
интегральное преобразование Фурье по переменной ;1
.
Для решения
краевой задачи для преобразованной по Фурье системы использован
метод пристрелки. Решая ее на некоторой сетке изменения параметра
,
1,%,
,
(

и далее обращая интегральное преобразование Фурье,
находим исходные компоненты физических полей.
Особый интерес с точки зрения исследования обратной задачи пред-
ставляет исследование преобразованной по Фурье системы (4.11 .10)
при ,1 0, характеризующей толщинные колебания. В этом случае
20/27

264 Гл. 4. Коэффициентные обратные задачи во второй постановке
система (4.11 .10) сводится к следующей системе обыкновенных диф-
ференциальных уравнений:
.
5 1,3

G
21

C
1 1 0,
.
4

3,3

0
3

G
21

C
3 3 0,
>GÆ

4
3 A,3 ,3 >G23

3,3 0
(4.11 .11)
Изучим более детально краевую задачу для (4.11 .11). Первое урав-
нение относительно 1 отделяется, и далее основное внимание уделим
системе относительно 3 ,

A
со следующими граничными условиями:

A
0 0,

A
1 0,
.
4

3,3
1

(4.11 .12)
Ее решение при известных законах изменения физических характе-
ристик может быть построено при помощи метода пристрелки.
4.11.4. Идентификация свойств неоднородного пороупругого
слоя. Исследование задачи о реконструкции характеристик пороупру-
гого слоя обладает своей спецификой по сравнению с задачей об
упругом слое, описанной в разд. 4 .4 .
Рассмотрим две задачи об определении безразмерного упругого
модуля .4 имодуляБио03 неоднородного пороупругого слоя в режиме
толщинных колебаний. Для описания колебаний среды воспользуемся
системой уравнений (4.11 .11). Пусть известны значения перемещений
среды на верхней границе в некотором диапазоне частот
>GÆ

4
3A
,3

>G2
3 3,3 0,
.
4 3,3

0
3A
,3

G
21

C
3 3 0,

A
,3
0 0,

A
,3
1 0,
.
4

3,3
1

1,G
G,
G

G
%
, G(
(4.11 .13)
При выводе соотношения взаимности (4.11.6) рассматривались два
набора переменных. Проведем линеаризацию задачи в окрестности
некоторого начального состояния для обезразмеренного соотношения
взаимности:

01,
A
1
A
0,
A
2
A
0A1

(4.11 .14)
Для первой задачи примем соответственно, что
.
1
4
.
0
4,
.
2
4
.
0
4.
1
4,
(4.11 .15)
адлявторой
0
1
3
0
0
3,
0
2
3
0
0
30
1
3,
(4.11 .16)
где .0
4и00
3 есть некоторые начальные приближения безразмерных
модулей .4 и 03 ,а0 и A0
—
им отвечающие решения системы,

—
формальный параметр. Подставляя эти разложения в соотношение
21/27

4.11 . О КОЗ пороупругости
265
взаимности и сохраняя главные по слагаемые, получим интегральное
уравнение Фредгольма 1-го рода для определения поправок . 1
4и01
3
искомых коэффициентов дифференциальных уравнений:

0
1, G

1
0
.
1
4 ('1
(,
G
(
0,
G

G
%
, G( , (4.11 .17)

0
1, G

1
0
0
1
3 ('2
(,
G
(
0,
G

G
%
, G( , (4.11 .18)
'
1(,
G

0
1⁄4
(,
G

2
,
'
2(,
G
2A 0
(,
G
0
1⁄4
(,
G
Используя при решении уравнений Фредгольма 1-го рода (4.11.17),
(4.11.18) метод А. Н . Тихонова, получим приближения . 1
4и01
3 ,которые
позволят строить новые приближения и организовать итерационный
процесс. Тем самым решение обратных задач сведено к последователь-
ности решения прямых задач на основе метода пристрелки и решений
интегральных уравнений Фредгольма 1-го рода для определения по-
правок.
Проведена серия вычислительных экспериментов для различных
законов изменения коэффициентов системы дифференциальных урав-
нений. Пусть функция .4 изменяется линейно (.4
1,1 0,1; или
квадратично (.4
1,02 0,1; 0,52
.
Результаты восстановления
представлены на рис. 4 .33., 4.34, где сплошной линией обозначена
точная характеристика, точками — восстановленная:
Рис. 4 .33
Рис. 4 .34
Аналогично проведена серия вычислительных экспериментов для
реконструкции функции 03
. В первом варианте эта функция монотонна
(03 31,1 3,1; , во втором немонотонна (03 31,1 3,1; 0,42
.
22/27

266 Гл. 4. Коэффициентные обратные задачи во второй постановке
Результаты вычислительных экспериментов представлены на рис. 4 .35 .,
4.36 соответственно.
Рис. 4 .35
Рис. 4 .36
Для решения интегральных уравнений методом А. Н . Тихонова апри-
орнаяинформациябраласьвпятичастотахвдиапазонеG 0,9; 1,2,
который располагается до первого толщинного резонанса. Отметим до-
статочно неплохое качество реконструкции, достигнутое для 5–6 ите-
раций, однако погрешность реконструкции на границах несколько
выше, чем внутри области.
23/27

Список литературы к гл. 4
1. Акопьян В.А., Соловьев А.Н ., Шевцов С.Н . Методы и алгоритм определе-
ния полного набора совместимых материальных констант пьезокерамиче-
ских материалов. Ростов на Дону, Изд-во ЮФУ, 2008. 144 с.
2. Аменицкий А.В., Белов А.А., Игумнов Л.А., Карелин И .С .Граничные
интегральные уравнения для решения динамических задач трехмерной
теории пороупругости // Проблемы прочности и пластичности. 2009. No 71.
С. 164–171.
3. Аникина Т .А., Богачев И.В ., Ватульян А.О . Идентификация неодно-
родных характеристи к вязкоупругих стержней при из гибн ых колеба-
ниях // Механика композиционных материалов и конструкций. 2011. No 1.
C. 107–115.
4. Анфиногенов С.Б., Ку ре к М .Ф ., Шилько С.В., Черноус Д.А .Механические
и фрикционные свойства биоэластомеров. Часть 1: Описание релаксацион-
ных зависимостей кожи человека при растяжении // Российский журнал
биомеханики. 2008. Т . 12, No 3. С. 44 –51
5. Бакушинский А.Б., Гончарский А.В . Итеративные методы решения некор-
ректных задач. М.: Наука, 1989. 128 с.
6. Балабанов Е.И . А налитический обзор. Кожа человека, механические свой-
ства, теплопередача // Медицинская техника. Вып. 3 . 2005. С. 15–20.
7. Богачев И.В., Ватульян А.О. Обратные коэффициентные задачи для дис-
сипативных операторов и идентификация свойств вязкоупругих материа-
лов // Владикавказский математический журнал. 2012. No 3. С. 31–44
8. Богачев И.В., Ватульян А.О ., Явруян О.В . Идентификация свойств неод-
нородной электроупругой среды // ПММ. 2012. Т. 76, No 5. С . 860–866 .
9. Богачев И .В ., Ватульян А.О ., Дударев В.В . Об одном методе идентифи-
кации свойств многослойных мягких биологических тканей // Российский
журнал биомеханики. 2013. Т . 17, No 3. С. 37–48.
10. Богачев И.В ., Ватульян А.О ., Дударев В.В. Идентификация характери-
стик функционально-градиентного пьезополимерного стержня // Механика
композиционных материалов и конструкций. 2016. Т . 22, No 2. C. 201–212.
11. Ватульян А.О . Обратные задачи в механике деформируемого твердого
тела. М.: ФИЗМАТЛИТ, 2007. 223 с.
12. Ватульян А.О . Интегральные уравнения в обратных задачах определения
коэффициентов дифференциальных операторов теории упругости // Докла-
ды РАН. 2005. Т. 405, No 3. С. 343–345
13. Ватульян А.О . Проблемы идентификации неоднородных свойств твердых
тел // Вестник Самарского госуниверситета. Естественные науки. 2007.
No 4 (54). С. 93–103
14. Ватульян А.О . О вариационной постановке обратных коэффициентных
задач для упругих тел // Доклады РАН. 2008. Т . 422, No 2. С . 182–184.
24/27

268
Список литературы к гл. 4
15. Ватульян А.О . О вариационном подходе при исследовании обратных коэф-
фициентных задач в теории упругости // Владикавказский математический
журнал. 2009. Т . 11, вып 1. С. 3–8
16. Ватульян А.О . К теории обратных коэффициентных задач в линейной
механике деформируемого тела // ПММ. 2010. No 6. С. 911–918.
17. Ватульян А.О ., Беляк О.А ., Сухов Д.Ю., Явруян О.В .Обратныеинекор-
ректные задачи. Учебник. Ростов-на-Дону: Изд-во ЮФУ, 2011. 231 с.
18. Ватульян А.О ., Бочарова О.В. О реконструкции плотности и модуля Юнга
для неоднородного стержня // Акустический журнал. 2009. Т . 55, No 3.
С. 275–282.
19. Ватульян А.О ., Денина О.В . Об одном способе определения упругих
характеристик для неоднородных тел // ПМТФ. 2012. No . С. 137–147.
20. Ватульян А.О . Домброва О.Б ., Жиров В.Е. Обратные задачи для неодно-
родно поляризованных пьезоэлектрических стержней // ПММ. 2007. No 1.
С. 93–101.
21. Ватульян А.О. Домброва О.Б., Жиров В.Е . К определению неоднородной
поляризации для электроупругого стержня // Известия высших учебных
заведений. Сев. - Кавк. рег. 2002. No 4. С. 7–9.
22. Ватульян А.О . Дударев В.В. О реконструкции неоднородных свойств пье -
зоэлектрических тел // Вычислительная механика сплошных сред. 2012.
No 3. С. 259–264.
23. Ватульян А.О . Дударев В.В., Богачев И.В . Об определен ии предварите ль-
ного напряженного состояния в трубе // Доклады РАН. 2014. Т . 456, No 3.
С. 299–301
24. Ватульян А.О., Дударев В.В., Мнухин Р.М . О влиянии остаточного
упругопластического состояния трубы на динамические характеристики //
Доклады РАН. 2015. Т . 463, No 6. С. 661–663 .
25. Ватульян А.О ., Дударев В.В., Недин Р.Д . Предварительные напряжения:
моделирование и идентификация. Ростов-на-Дону: Изд-во ЮФУ, 2014.
206 с.
26. Ватульян А.О ., Ляпин А.А . Об обратных коэффициентных задачах поро-
упругости // Известия РАН. МТТ . 2013. No 2. C.114 –121.
27. Ватульян А.О ., Недин Р.Д . Сравнительный анализ предварительного со-
стояния в неоднородных балках // Вестник Санкт-Петербургского универ-
ситета. Серия 1. Математика. Механика. Астрономия. 2016. Т . 3, No 1.
С. 110–119.
28. Ватульян А.О ., Нестеров С.А . Об одном способе идентификации термо-
упругих характеристик для неоднородных тел // Инженерно-физический
журнал. 2014. Т . 87, No 1. С. 217–224.
29. Ватульян А.О ., Нестеров С.А. К определен ию неоднородных термомеха-
нических характеристик трубы // Инженерно-физический журнал. 2015.
Т. 88, No 4. С.951–959.
30. Ватульян А.О., Нестеров С.А. Коэффициентные обратные задачи термо-
упругости для функционально-градиентных материалов // Проблемы проч-
ности и пластичности. 2014. Т . 76, No 4. С . 335 –342.
31. Ватульян А.О., Нестеров С.А . Об обратных коэффициентных задачах для
функционально-градиентных материалов // Математический форум. Сер.
Итоги науки. Юг России. Владикавказ, 2015. С. 48–58 .
25/27

Список литературы к гл. 4
269
32. Ватульян А.О ., Нестеров С.А . Об особенностях идентификации неодно-
родных пороупругих характерис тик полого цилиндра // Проблемы прочно-
сти и пластичности. 2016. No 1. С. 22–28.
33. Ватульян А.О., Нестеров С.А . Об особенностях идентификации неод-
нородного предварительного напряженного состояния в термоупругих те-
лах // ПММ. 2017. No 1. С. 103–110.
34. Ватульян А.О ., Соловьев А.Н . Прямые и обратные задачи для одно-
родных и неоднородных упругих и электроупругих тел. Ростов-на-Дону:
Изд-во ЮФУ, 2008. 176 с.
35. Ватульян А.О ., Уг ли ч П .С . Реконс трукци я неоднородных характерис тик
поперечно-неоднородного с лоя при антиплоских колебаниях // ПМТФ.
2014. No 3 . С. 146–153.
36. Ватульян А.О ., Явруян О. В ., Богачев И.В . Идентификация упругих
характеристи к неоднородного по толщи не с лоя // Акустический журнал.
2011. No 6 . С. 723–730.
37. Ватульян А.О ., Явруян О.В., Богачев И .В . Идентификация неоднородных
свойств ортотропного упругого слоя // Акустический журнал. 2013. No 6.
С. 752–758.
38. Ворович И.И ., Бабешко В.А . Динамические смешанные задачи теории
упругости для неклассических областей. М .: Наука, 1979. 320 с.
39. Гузь А.Н ., Махорт Ф.Г ., Гуща О.И ., Лебедев В.К.Основыультразвукового
неразрушающего метода определения напряжений в твердых телах. Киев:
Наук. думка, 1974. 108 с.
40. Гузь А.Н ., Жук А.П ., Махорт Ф.Г . Волны в слое с начальными напряже-
ниями. Киев: Наук. думка, 1976. 104 с.
41. Гузь А.Н ., Махорт Ф.Г ., Гу ща О.И .Введениевакустоупругость. Киев:
Наук. думка, 1977. 162 с.
42. Гузь А.Н . Упругие волны в те лах с начальными напряжениями: В 2-х то-
мах. Киев: Наук. думка, 1986. Т . 1 . Общие вопросы. 374 с. Т. 2. Законо-
мерности распространения. 536 с.
43. Домаркас В.И ., Кажис Р.И . Контрольно-измерительные пьезоэлектриче-
ские преобразователи. Вильнюс: Минтис, 1974. 258 с.
44. Кабан и хи н С .И .Обратныеинекорректныезадачи.Новосибирск:Изд.
ин-та математики, 2009. 458 с.
45. Калинчук В.В ., Белянкова Т .И . Динамические контактные задачи для
предварительно напряженных тел. М .: ФИЗМАТЛИТ, 2002. 240 с.
46. Калинчук В.В ., Белянкова Т .И . Динамические контактные задачи для
предварите льно напряженных электроупругих сред. М .: ФИЗМАТЛИТ,
2006. 272 с.
47. Кристенсен Р. Введение в механику композитов. М .: Мир, 1974. 338 с.
48. Лаврентьев М.М . Теория операторов и некорректные задачи. Новосибирск:
Изд. ин -та математики, 1999. 702 с.
49. Лаврентьев М.М ., Романов В.Г ., Шишатский С .П . Некорректные задачи
математической физики и анализа. М .: Наука, 1980. 286 с.
50. Маслов Л .Б . Математическое моделирование колебаний пороупругих си-
стем. Иваново: ПресСто, 2010. 264 с.
26/27

270
Список литературы к гл. 4
51. Натали А.Н ., Форестиеро А., Кар ни е л ь Э .Л . Идентификация параметров
определяющих соотношений, описывающих механическое поведение мяг-
ких тканей // Российский журнал биомеханики. 2009. Т . 13, No 4. С. 31–41.
52. Никитина Н .Е . Акустоупругость. Опыт практического применения.
Н. Новгород. ТАЛАМ, 2005. 208 с.
53. Партон В.З., Куд рявцев Б.А. Электромагнитоупругость пьезоэлектриче-
ских и электропроводных тел. М .: Наука, 1988. 472 с.
54. Петров Ю.П ., Сизиков В.С . Корректные, некорректные и промежуточные
задачи с приложениями. Учебное пособие для вузов. Политехника, 2003.
261 с.
55. Романов В.Г . Обратные задачи математической физики. М .: Наука, 1984.
261 с.
56. Тимофеев Г.А . Методы аппаратного исследования кожи человека // Кос-
метика и медицина. 2005. No 4. С. 28–38.
57. Тихонов А.Н ., Арсенин В.Я . Методы решения некорректных задач. М .:
Наука, 1979. 288 с.
58. Тихонов А.Н ., Гончарский А.В., Степанов В.В ., Ягола А .Г . Численные
методы решения некорректных задач. М .: Наука, 1990. 230 с.
59. Федоров А.Е ., Ада мов А.А . Моделирование поведения кожи че ловека при
больших деформациях // Российский журнал биомеханики. 2007. Т . 11,
No 1. С. 76–84.
60. Федоров А.Е., Лохов В.А . О применении теории вязкоупругости в эсте-
тической хирургии // Российский журнал биомеханики. 2003. Т . 7, No 4.
С. 32–43
61. Федоров А.Ф ., Самарцев В.А., Ки ри л л о в а Т .А . О механических свойствах
кожи человека // Российский журнал биомеханики. 2006. Т . 10, No 2.
С. 29–42.
62. Яхно В.Г . Обратные коэффициентные задачи для дифференциальных урав-
нений упругости. Новосибирск: Наука, 1990. 304 с.
63. Allard J .-F . Propagation of sound in porous media: Modeling sound absorbing
materials. London: Chapman and Hall, 1993. 284 p.
64. Biot M.A. Theory of propogation of elastic waves in a fluid-saturated porous
solid // J. Acoustic. Soc. Am. 1956. V. 28, No 2. P. 168–178.
65. Cowin S.C ., Nunziato J.W . Linear elastic materials with voids // J. Elast.
1983. V. 13, P. 125–147.
66. Cowin S.C . Bone Poroelasticity // J. Biomech. 1999. V. 32. 3. P. 217–238.
67. Chandrasekharaiah D.S ., Cowin S.C . A complete solution for a unified system
of field equations of thermoelasticity and poroelasticity // Acta Mech. 1993.
V. 99 (1–4). P. 225–233.
68. Cederbaum G. Poroelastic structures. Oxford, Elsevier, 2000. 158 p.
69. Dudarev V .V ., Vat u ly an A.O . On restoring of the pre-stressed state in elastic
bodies // ZAMM Zeitschrift f̈ur Angewandte Mathematik und Mechanik.
2011. V. 91, No 6. P. 485–492.
70. Dudarev V .V ., Mnukhin R.M ., Vatulyan A.O . Vibration of a prestressed tube
in the presence of plastic zone // Journal of Sound and Vibration. 2016. V. 375,
No 4. P. 92–101.
71. Isakov V . Inverse problems for PDE. Springer-Verlag, 2005. 284 p.
P owe red by T CP DF (www.tcp df.o rg)
27/27

Список литературы к гл. 4
271
72. Jadamba B., Khan A.A ., Raciti F . On the inverse problem of identifying
Lamе coefficients in linear elasticity // J. Computers and Mathematics with
Applications. 2008. V. 56 . P. 431–443.
73. Ji L., McLaughlin J.R .RecoveryoftheLaḿe parameter in biological
tissues // Inverse Problems. 2004. V. 20. P. 1–24.
74. Nedin R., Dudarev V .V ., Vat ulyan A . Some aspects of modeling and iden-
tification of inhomogeneous residual stress // Engineering Structures. 2017.
V. 151. P. 391–405.
75. McLaughlin J., Yoon J . -R . Unique identifiability of elastic parameters from
time-dependent interior displacement measurement // Inverse Problems. 2004.
V. 20. P. 25–45.
76. Nedin R., Nesterov S., Vatulyan A. On an inverse problem for inhomogeneous
thermoelastic rod // Int. J . Solids Struct. 2014. V. 51. P. 767–773.
77. Nedin R., Vatu lyan A. Concerning one approach to the reconstruction of
heterogeneous residual stress in plate // ZAMM Zeitschrift f̈ur Angewandte
Mathematik und Mechanik. 2014. V. 94, No 1, 2. P. 142–149.
78. Nedin R., Nesterov S., Vatu lyan A. Identification of thermal conductivity
coefficient and volumetric heat capacity of functionally graded materials //
Int. J. Heat and Mass Transfer. 2016. V. 102. P. 213–218.
79. Nedin R., Nesterov S., Vatu lyan A . On reconstruction of thermalphysic
characteristics of functionally graded hollow cylinder // Applied Mathematical
Modelling. 2016. V. 40, No 4. P. 2711–2719.
80. Pereira J .M ., Mansour J .M ., Davis B.R . The effects of layer properties on
shear disturbance propagation in skin // J. Biomechanical Eng. 1991. V. 113.
P. 30–35 .
81. Romanov V .G ., Weng C .I ., Chen T.C . An inverse problem for a layered elastic
plate // Appl. Math. Comput. 2003. V. 137, No 2, 3. P. 349–369.
82. Schanz M. Wave propogation in viscoelastic and poroelastic continua. Berlin:
Springer, 2001. 170 p.
83. Trefftz E. Zur Theorie der Stabilitat des elastischen Gleichgewichts // ZAMM
Zeitschrift f̈ur Angewandte Mathematik und Mechanik. 1933. V. 12, No 2.
P. 160–165.
84. Vatulyan А.О ., Yavruyan O.V ., Bogachev I.V . Reconstruction of inhomoge-
neous properties of orthotropic viscoelastic layer // Int. J . Solids Struct. 2014.
V. 51. P. 2238–2243.
85. Zhang H., Lin X., Wa ng X ., Zhang Q., Kang Y . Identification of elastic-plastic
mechanical properties for bimetallic sheets by hybrid-inverse approach // Acta
Mechanica Solida Sinica. 2010. V. 23. No 1. P. 29–35 .
1/2

Научное издание
ВАТУЛЬЯН Александр Ованесович
КОЭФФИЦИЕНТНЫЕ ОБРАТНЫЕ ЗАДАЧИ МЕХАНИКИ
Редактор Е.И. Ворошилова
Оригинал-макет: В.В . Затекин
Оформление переплета: А.В. Андросов
Подписано в печать 20.12.2018. Формат 6090/16. Бумага офсетная.
Печать офсетная. Усл. печ. л . 17,0. Уч.-изд. л . 18,7. Тираж 100 экз.
Заказ No
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117342, г. Москва, ул. Бутлерова, д. 17 Б
E-mail: p orsova@fml.ru, sale@fml.ru
Сайт: http://www.fml.ru
Интернет-магазин: http://www.fmllib.ru
Отпечатано с электронных носителей издательства
в АO «Первая Образцовая типография»
Филиал «Чеховски й Печат ный Двор»
142300, Московская область, г. Чехов, ул. Полиграфистов, д. 1
Сайт: www.chpd.ru. E-mail: sales@chpd.ru, тел.: 8 (499) 270-73-59
ISBN 978-5 -9221-1826-2

P owe red by T CP DF (www.tcp df.o rg)
2/2