Висячие мосты больших пролетов - Смирнов В.А.

Автор: Смирнов В.А.
Теги: висячие мосты вантовые мосты строительство строительные конструкции строительное проектирование мосты мостостроение
Год: 1970
Похожие
Строительная наука XIX –XX веков
Неустойчивость в механике. Автомобили, самолеты, висячие мосты
Напряженно армированный железобетон и его практическое применение
Физический фейерверк. Вопросы и ответы по физике
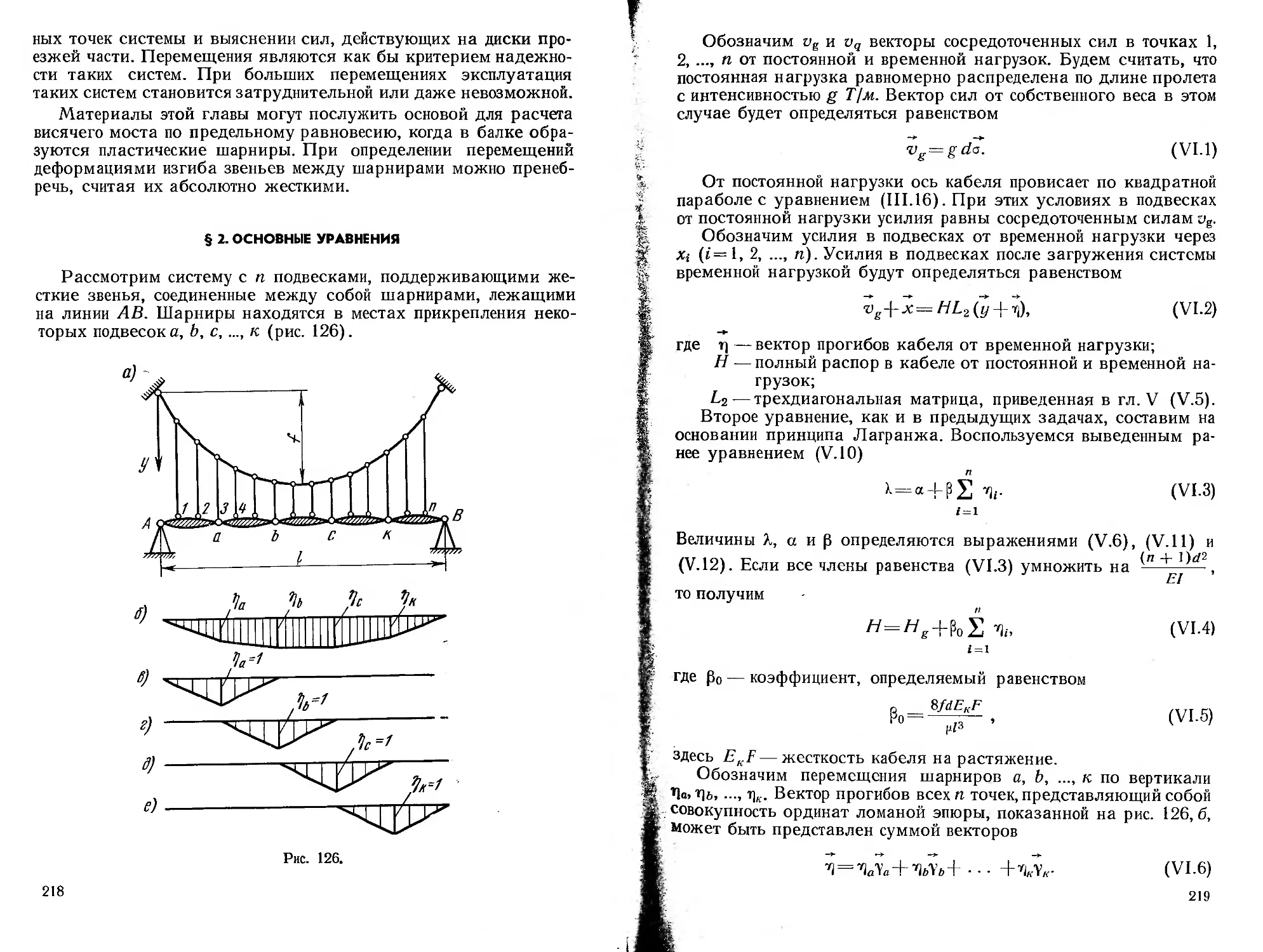
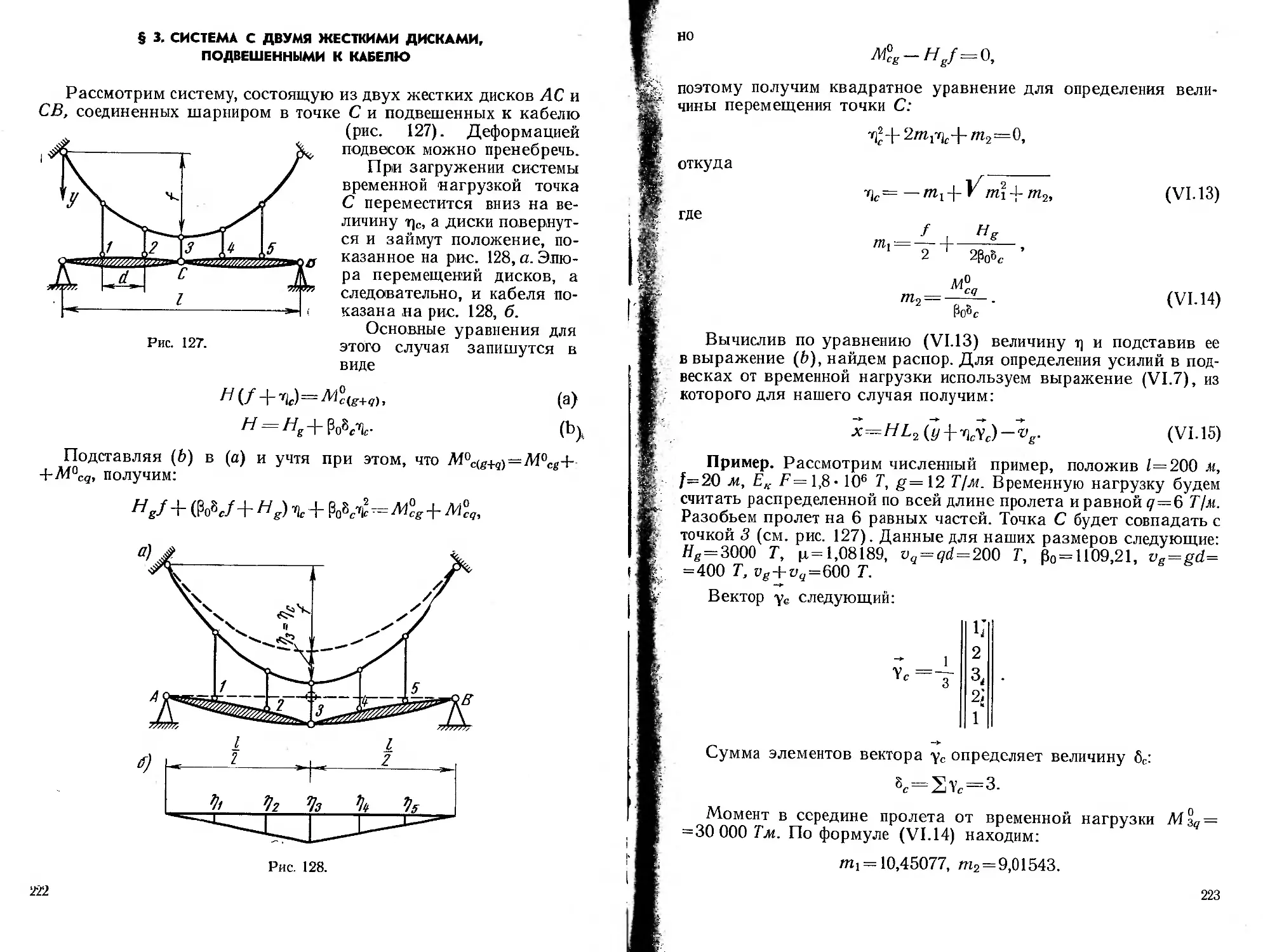
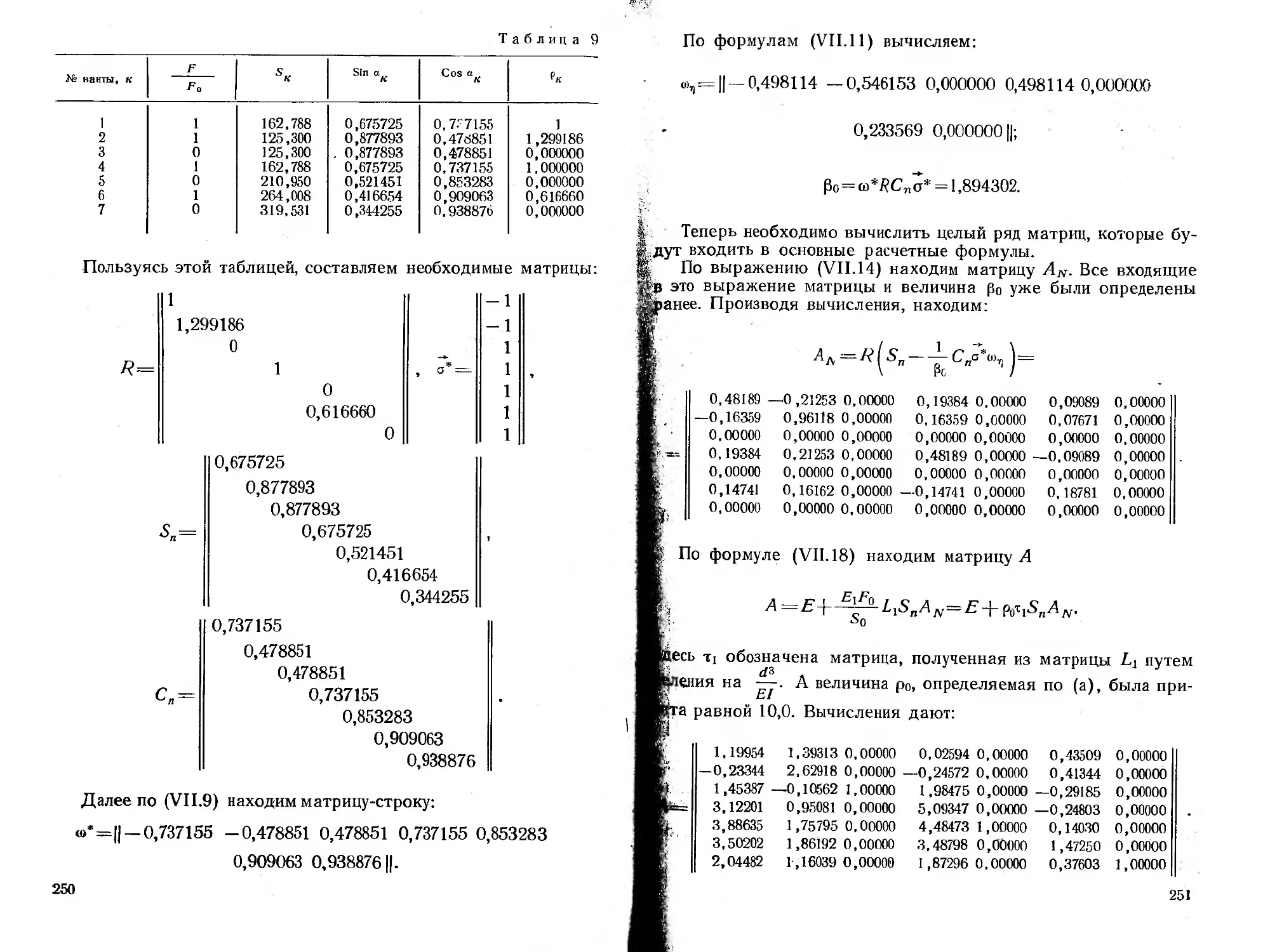
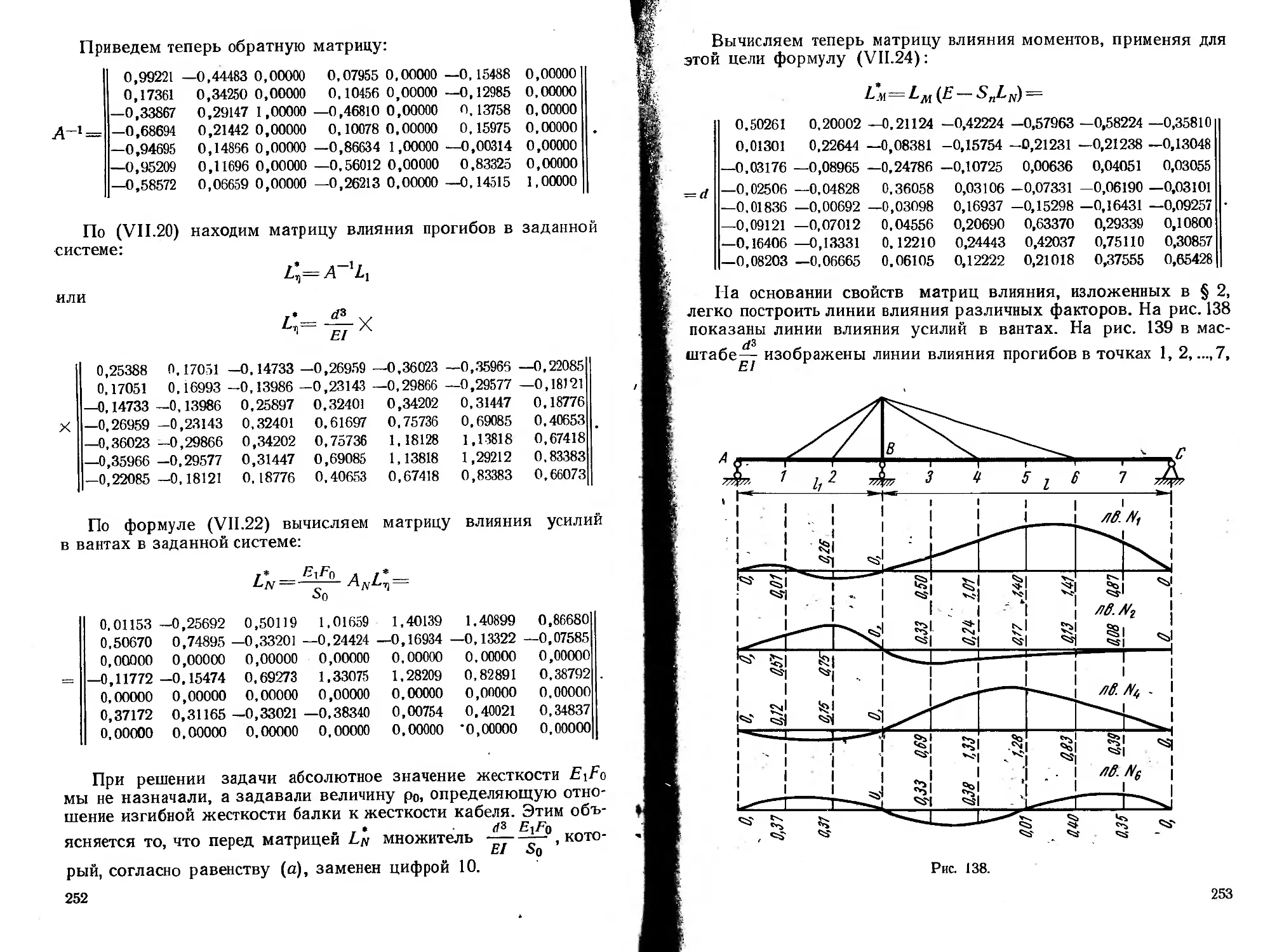
Текст
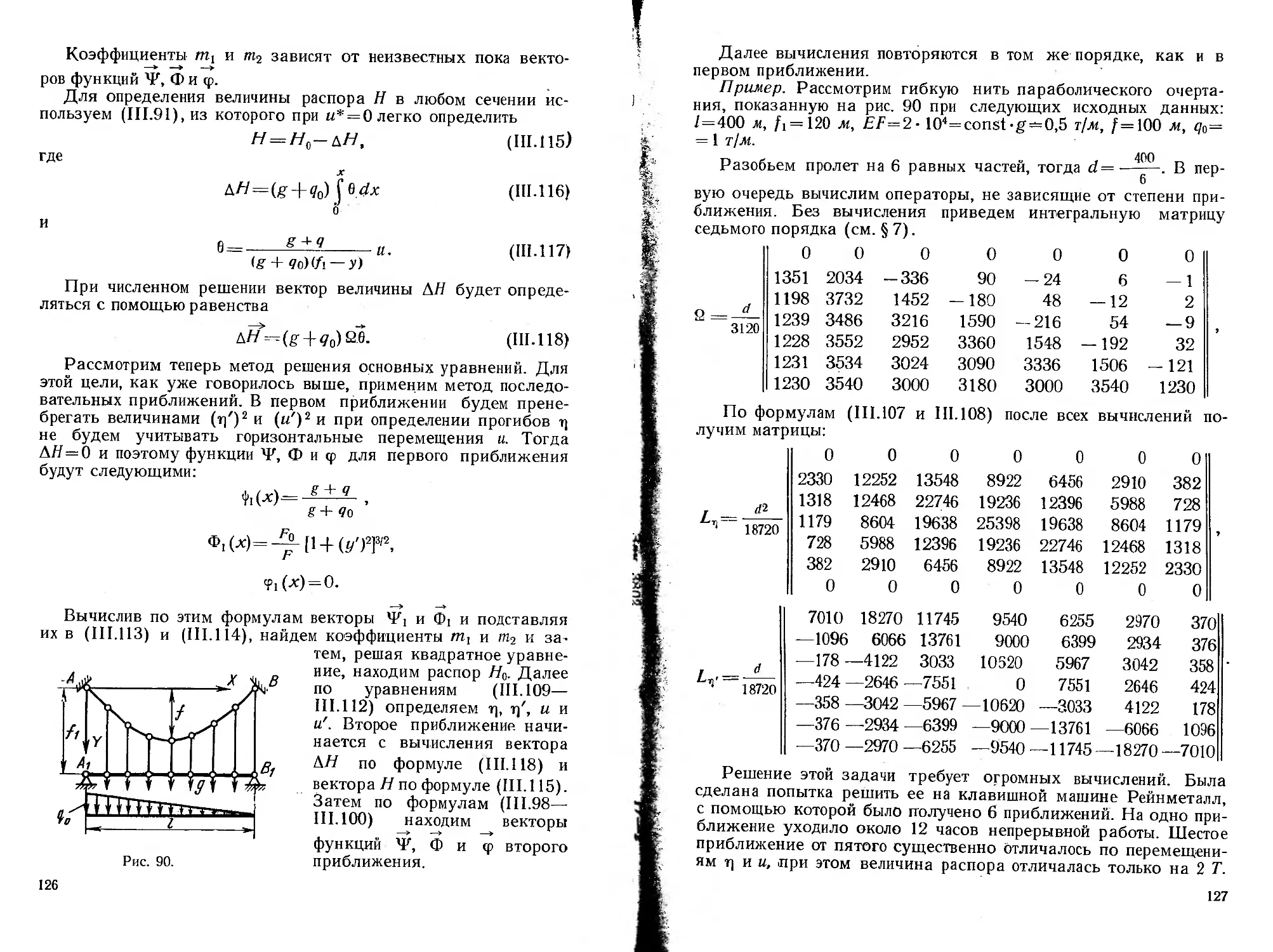
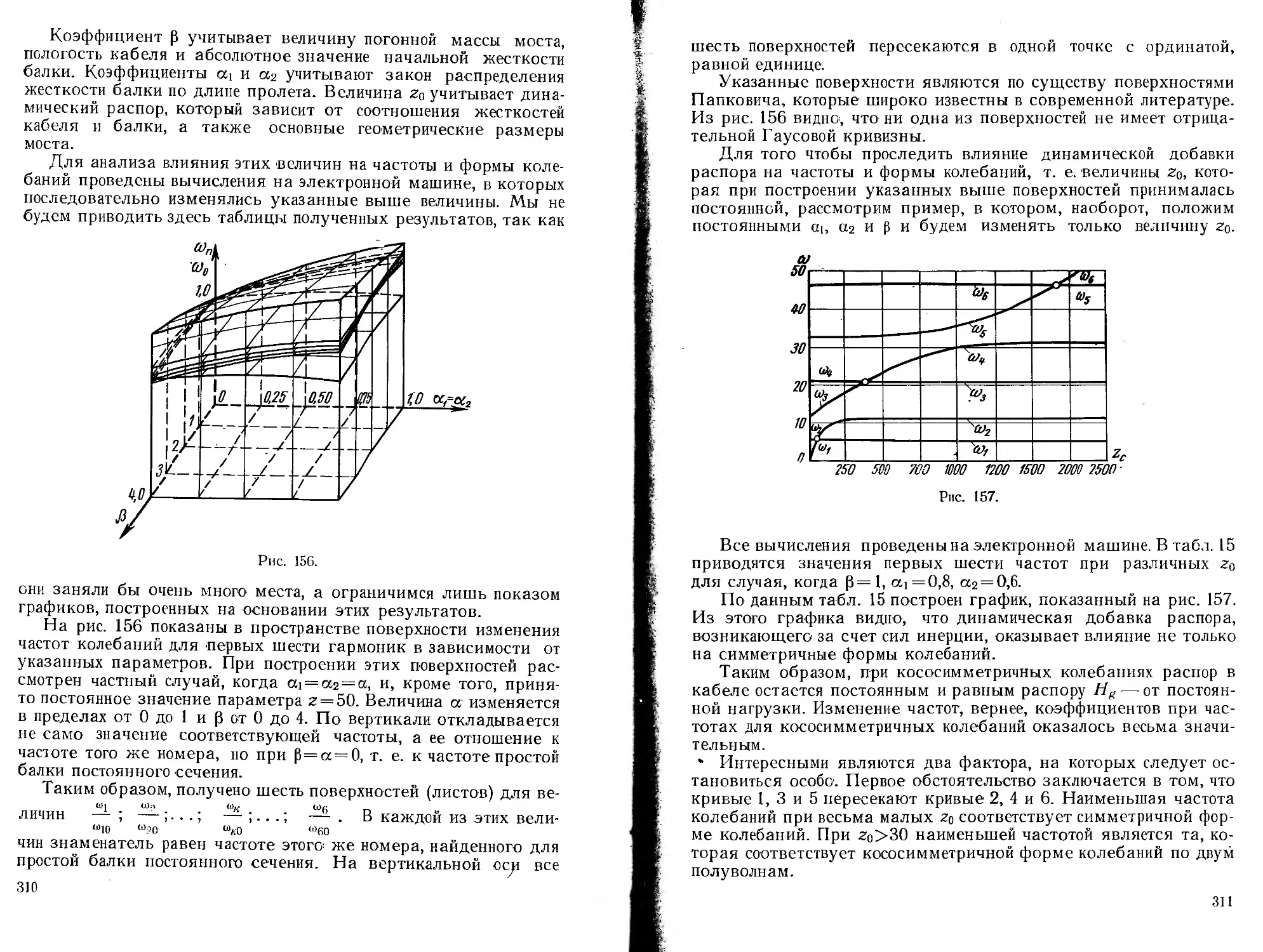
                    a

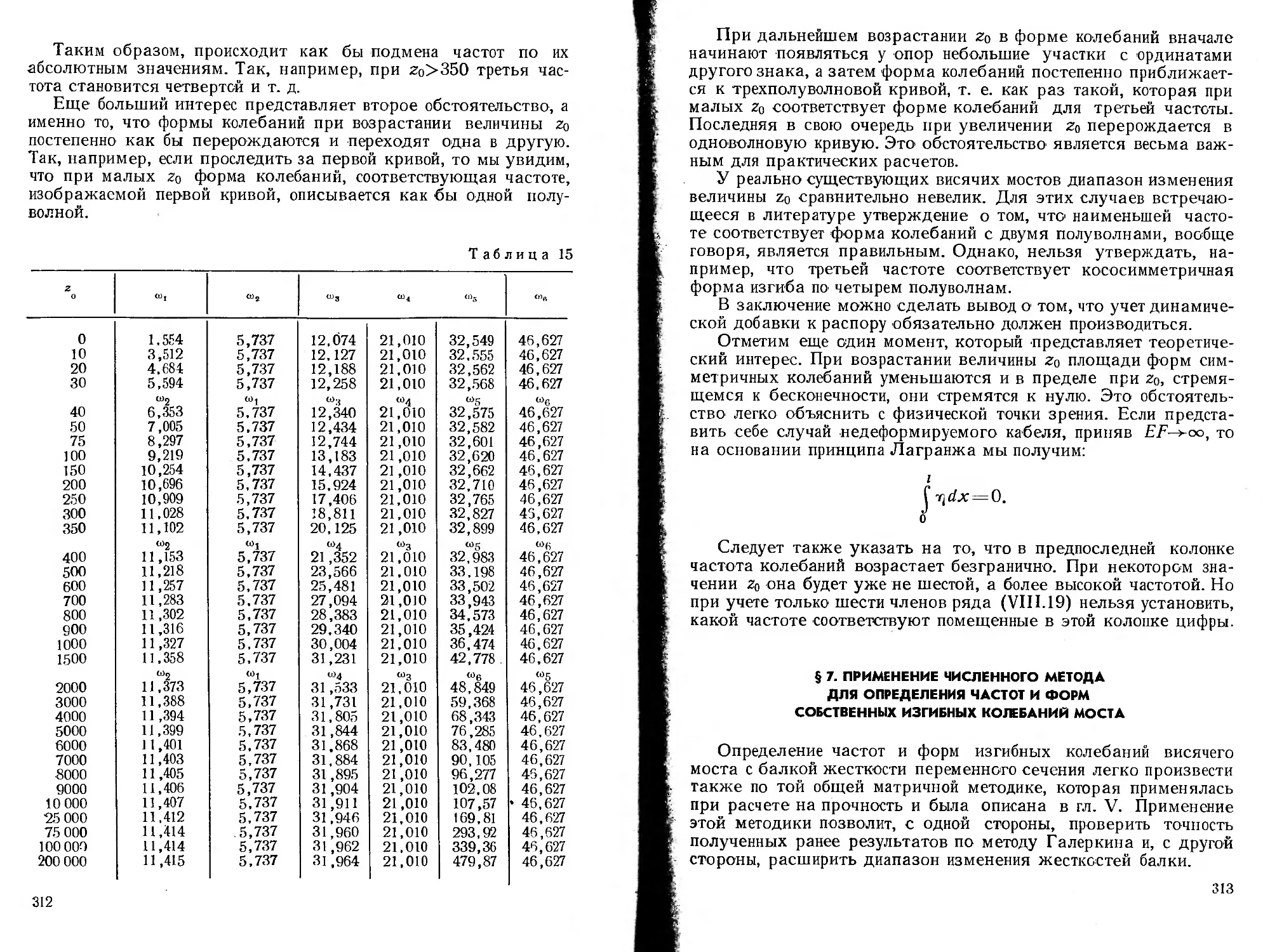
В. А. СМИРНОВ
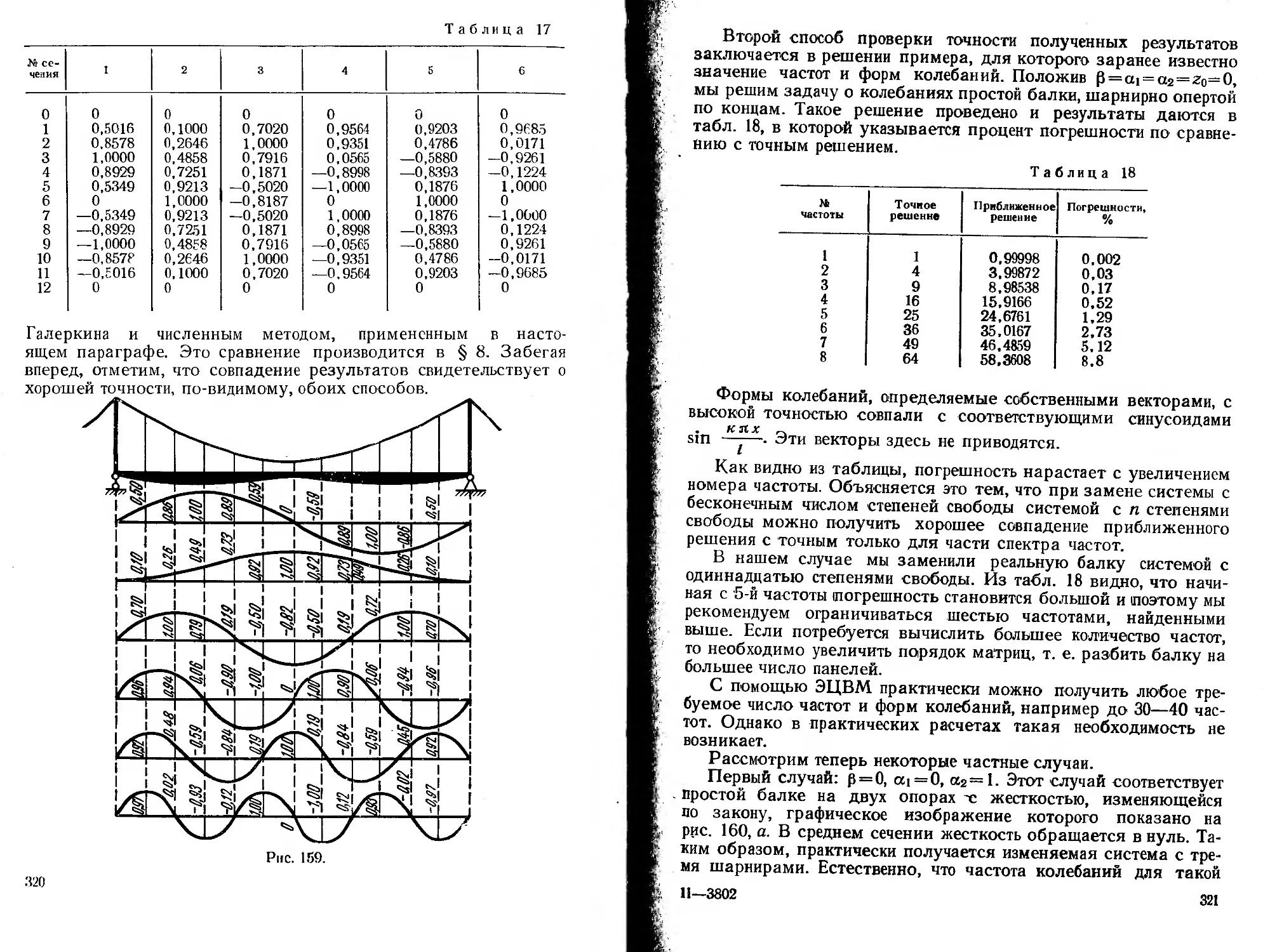
& £ Ч' %
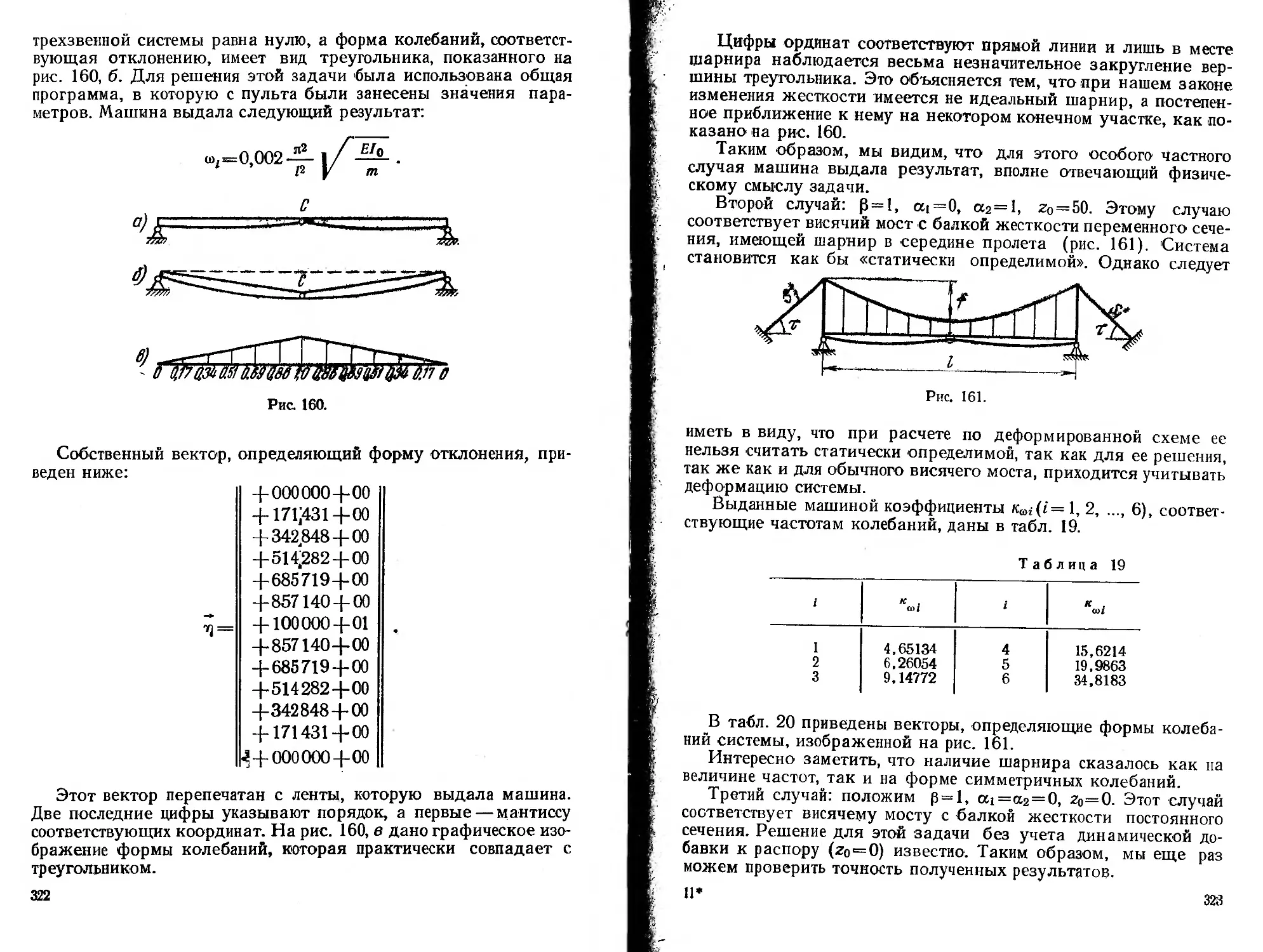
ВИСЯЧИЕ МОСТЫ
БОЛЬШИХ ПРОЛЕТОВ
Допущено Министерством
высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов транспортных
и строительных
высших учебных заведений
Т
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
МОСКВА—1970
3
6С6.5
С50
УДК 624.5
Смирнов В. А. Висячие мосты больших пролетов.
Изд-во «Высшая школа», Г970 г.
С50	В книге кратко изложена история строитель-
ства висячих мостов, приводятся интересные дан-
ные о современных мостах больших пролетов.
Подробно рассматриваются различные типы вися-
чих мостов и их расчетные схемы. Некоторые за-
дачи, рассмотренные в книге, связаны с решением
сложных нелинейных дифференциальных уравне-
ний. Все решения проводятся с применением мат-
ричного исчисления и с использованием ЭЦВМ.
Каждая конкретная задача в книге иллюстрирует-
ся числовым примером.
В пособии много внимания уделено висячим
мостам с многошарнирными балками жесткости,
что представляет особый интерес для научных
работников, занятых исследованиями в этой об-
ласти.
Книга предназначается в качестве учебного
пособия для студентов инженерно-строительных
вузов и факультетов, а также может быть исполь-
зована инженерно-техническими и научными ра-
ботниками.
В книге 173 рис., 38 табл., 196 библ.
С6
125-69
3—18—1
ПРЕДИСЛОВИЕ
О висячих мостах написано большое количество работ как
отечественными, так "и зарубежными авторами. Обзор современ-
ного состояния теории по этому вопросу приводится в гл. I. Из
обзора видно, что в настоящее время расчет висячих мостов, как
правило, проводится с учетом геометрической нелинейности си-
стемы.
Однако было бы неправильно считать, что в этом вопросе все
уже сделано и что нет таких задач, которые нуждаются в даль-
нейших исследованиях. Так, например, в большинстве работ
дается решение для мостов с балкой жесткости постоянного се-
чения, тогда как на практике очень часто сечение балок бывает
переменным.
При определении частот собственных колебаний, как прави-
ло, не учитывается динамическая добавка к распору за счет сил
инерции. Вместе с тем она может оказать существенное влияние
на частоты и формы симметричных колебаний. Таким образом
можно отметить целый ряд задач, требующих дальнейшего изу-
чения.
В настоящей книге излагаются методы расчета висячих мос-
тов с учетом геометрической нелинейности, приспособленные к
использованию современных вычислительных машин.
Работа состоит из восьми глав. В гл. I дается краткая истори-
ческая справка по развитию висячих мостов, приводится описа-
ние крупнейших мостов мира и обзор литературы по современно-
му состоянию теории и развитию методов расчета.
В гл. II приводится классификация основных типов висячих
мостов и дается анализ их расчетных схем.
Гл. III посвящена некоторым специальным вопросам, связан-
ным с расчетом гибкой нити. Эта глава, с одной стороны, являет-
ся подготовительной и используется при изложении вопросов,
изучаемых в последующих главах, и с другой — она содержит но-
вые задачи, как, например, расчет гибкой нити при больших про-
гибах с учетом наклона подвесок. Эта задача связана с решени-
ем сложных нелинейных дифференциальных уравнений, которое
3
проводится с применением матричного исчисления и использо-
ванием вычислительных машин.'
Гл. IV содержит аналитический расчет трехпролетного вися-
чего моста. В ней проводится непосредственное интегрирование
дифференциальных уравнений изгиба балки жесткости, выводят-
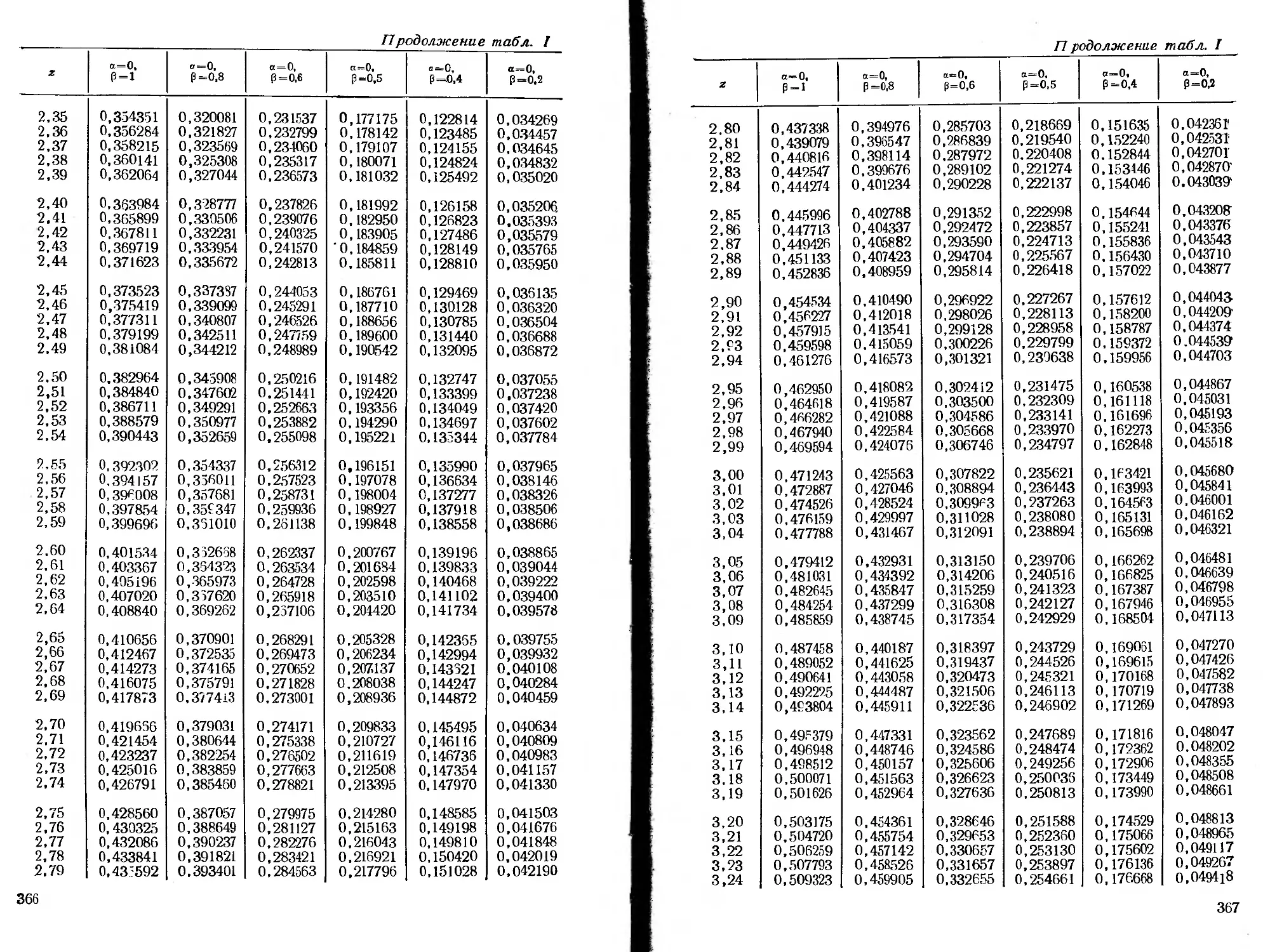
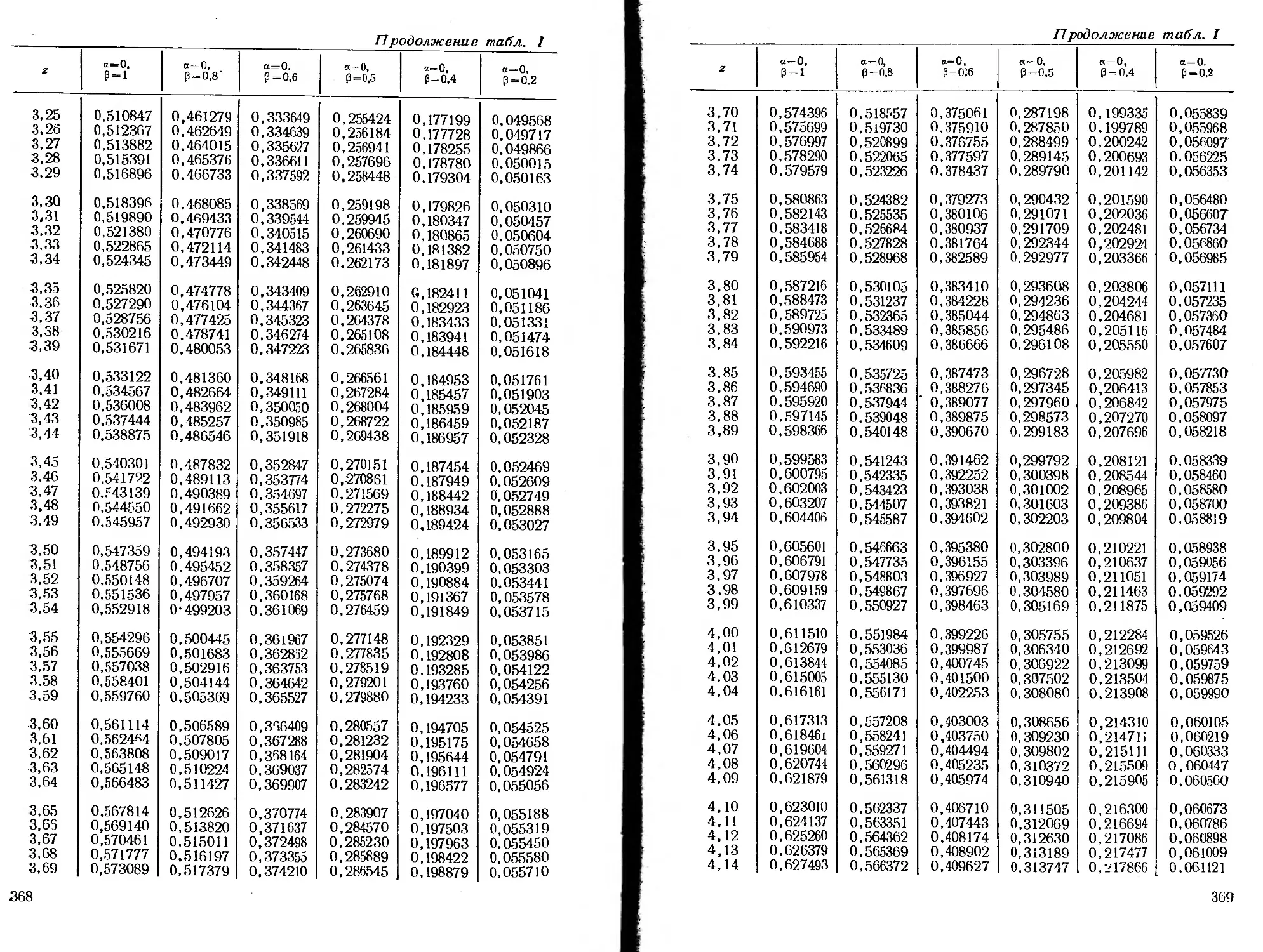
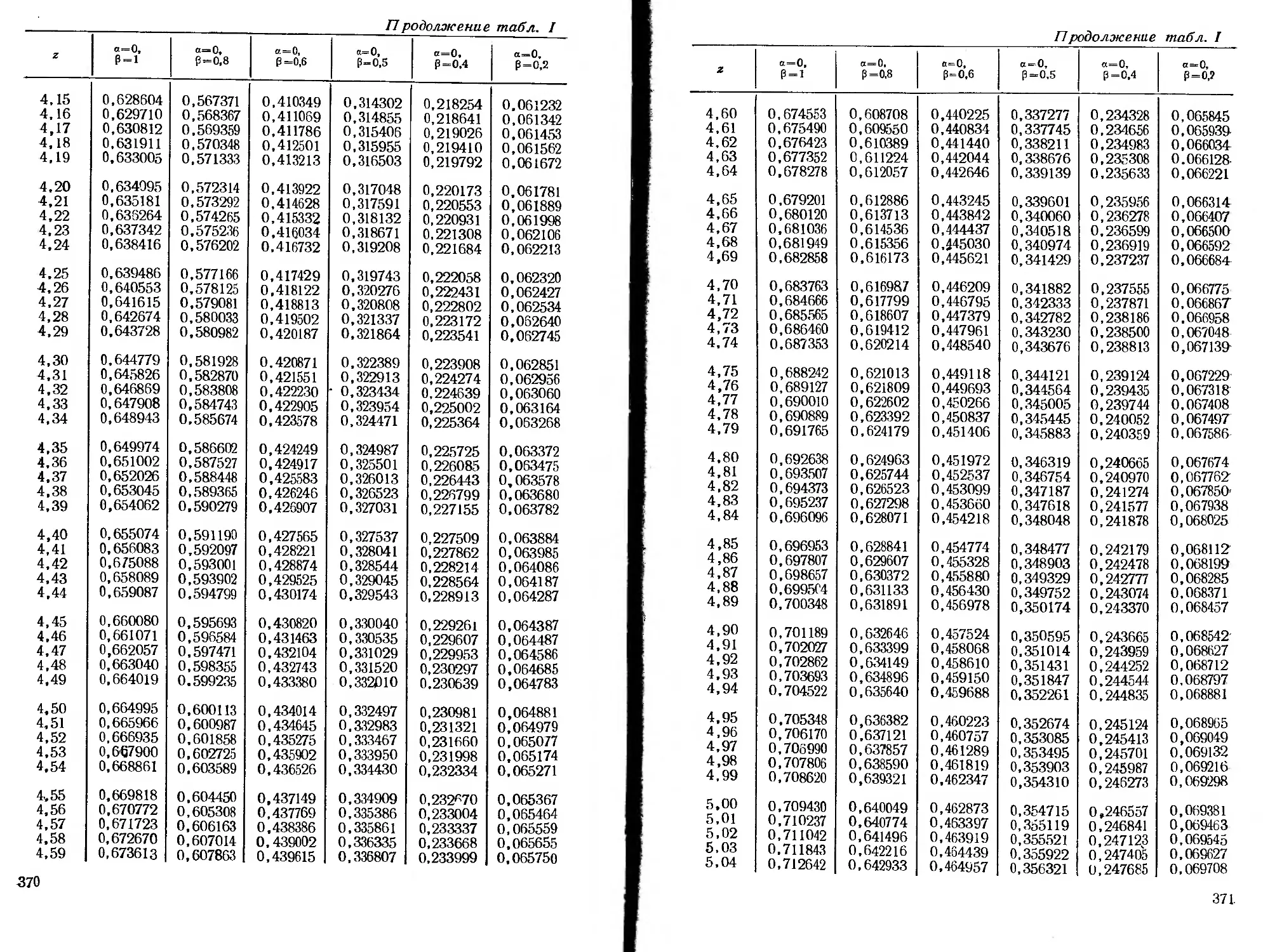
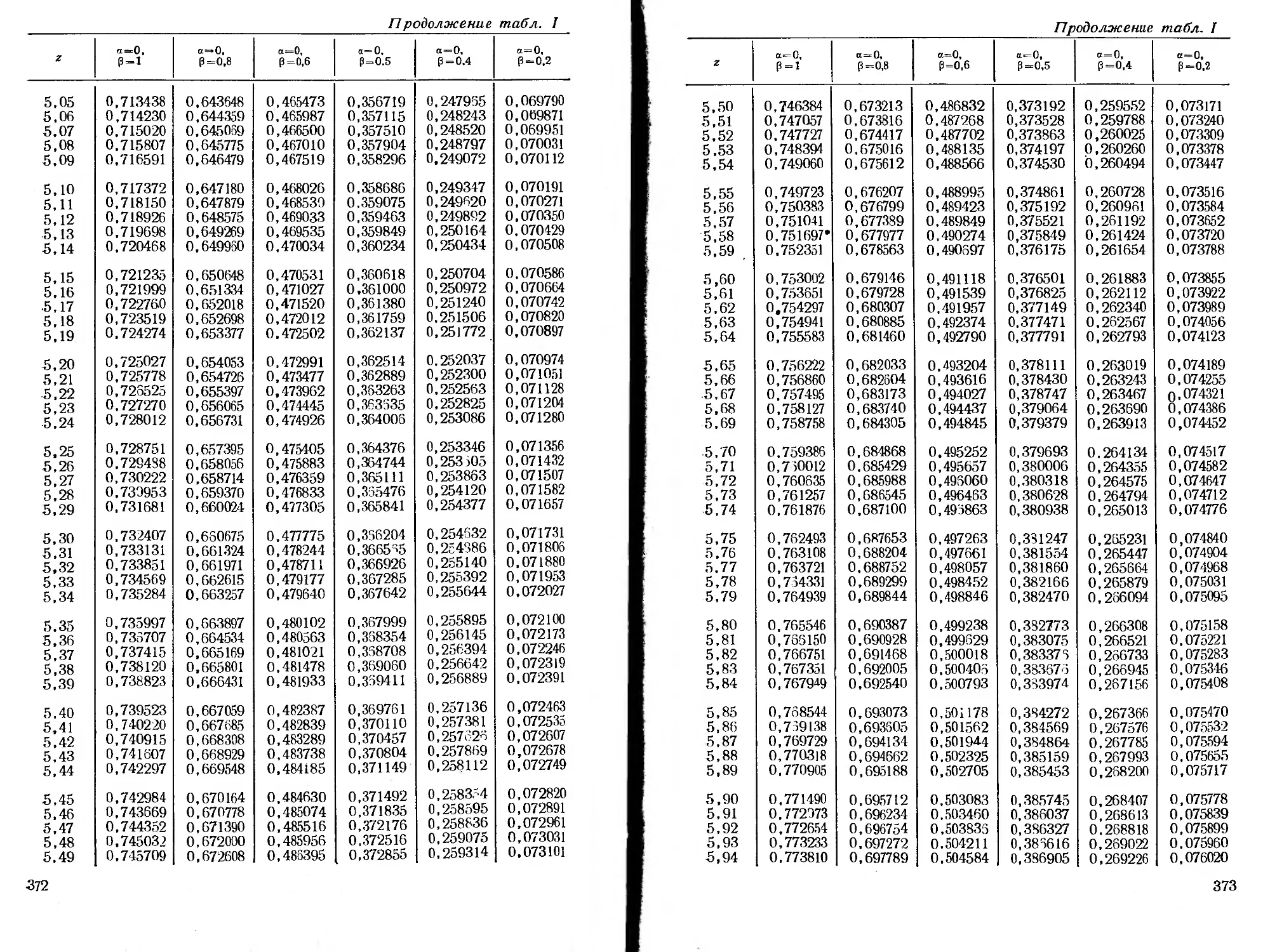
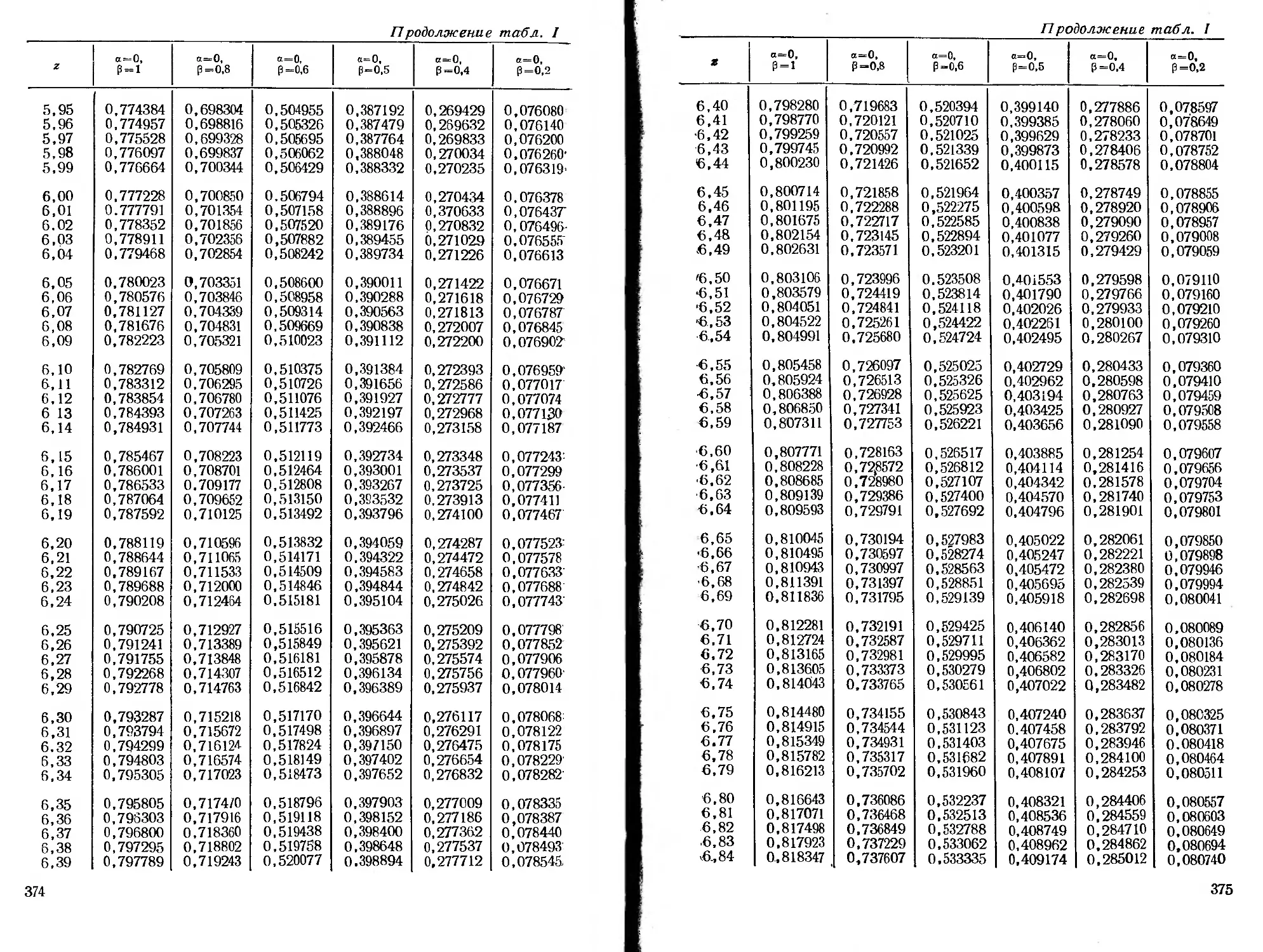
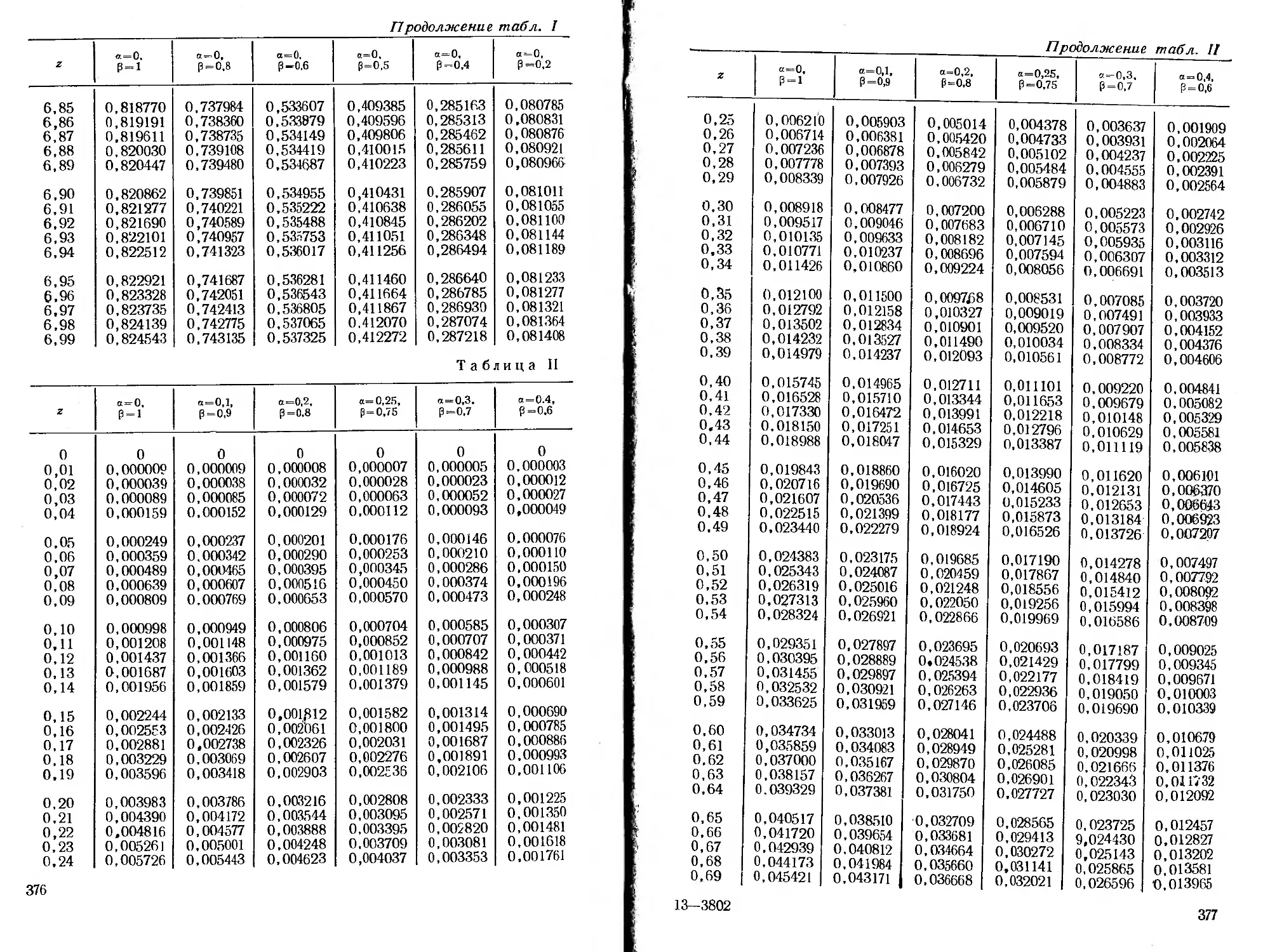
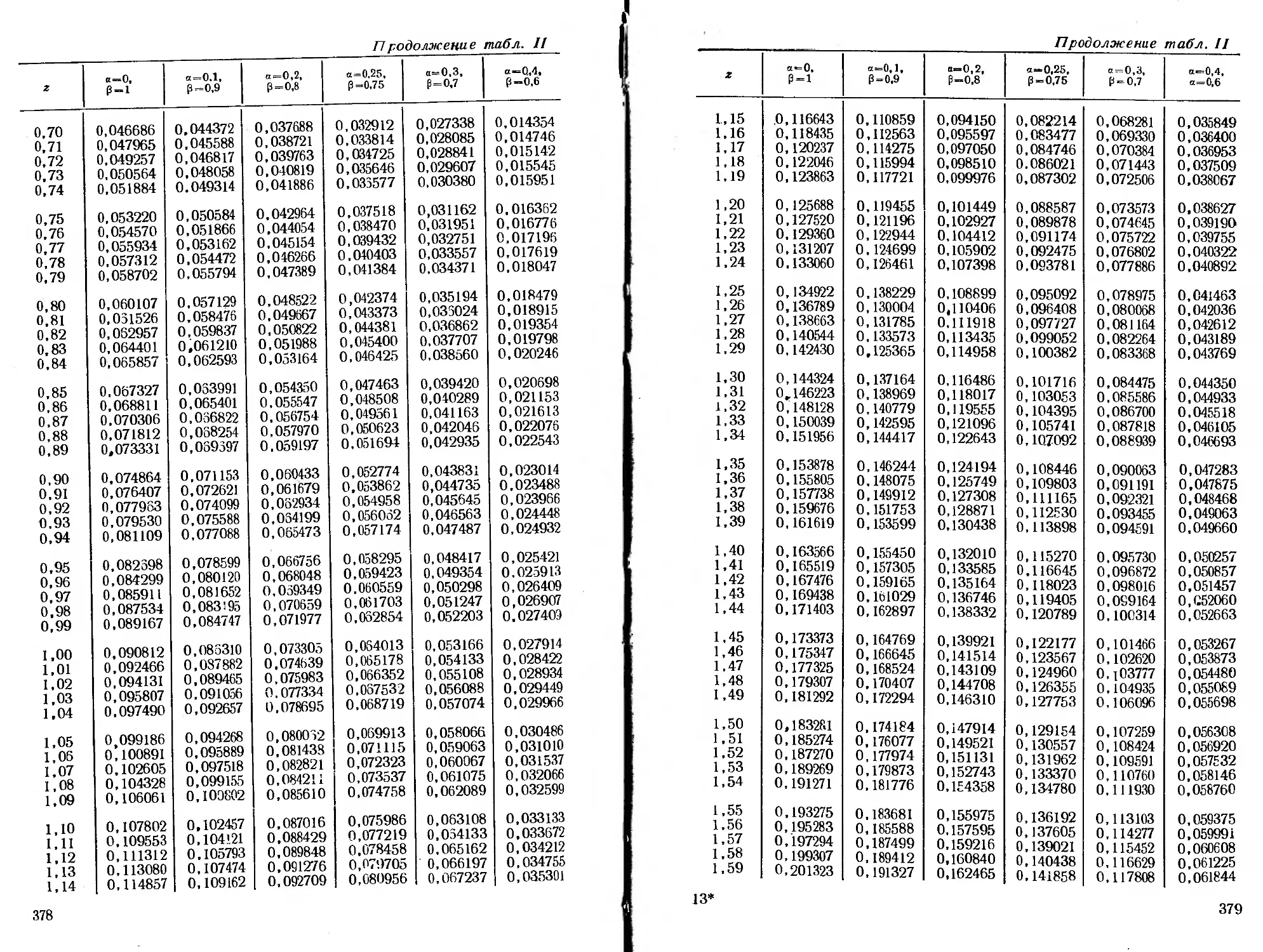
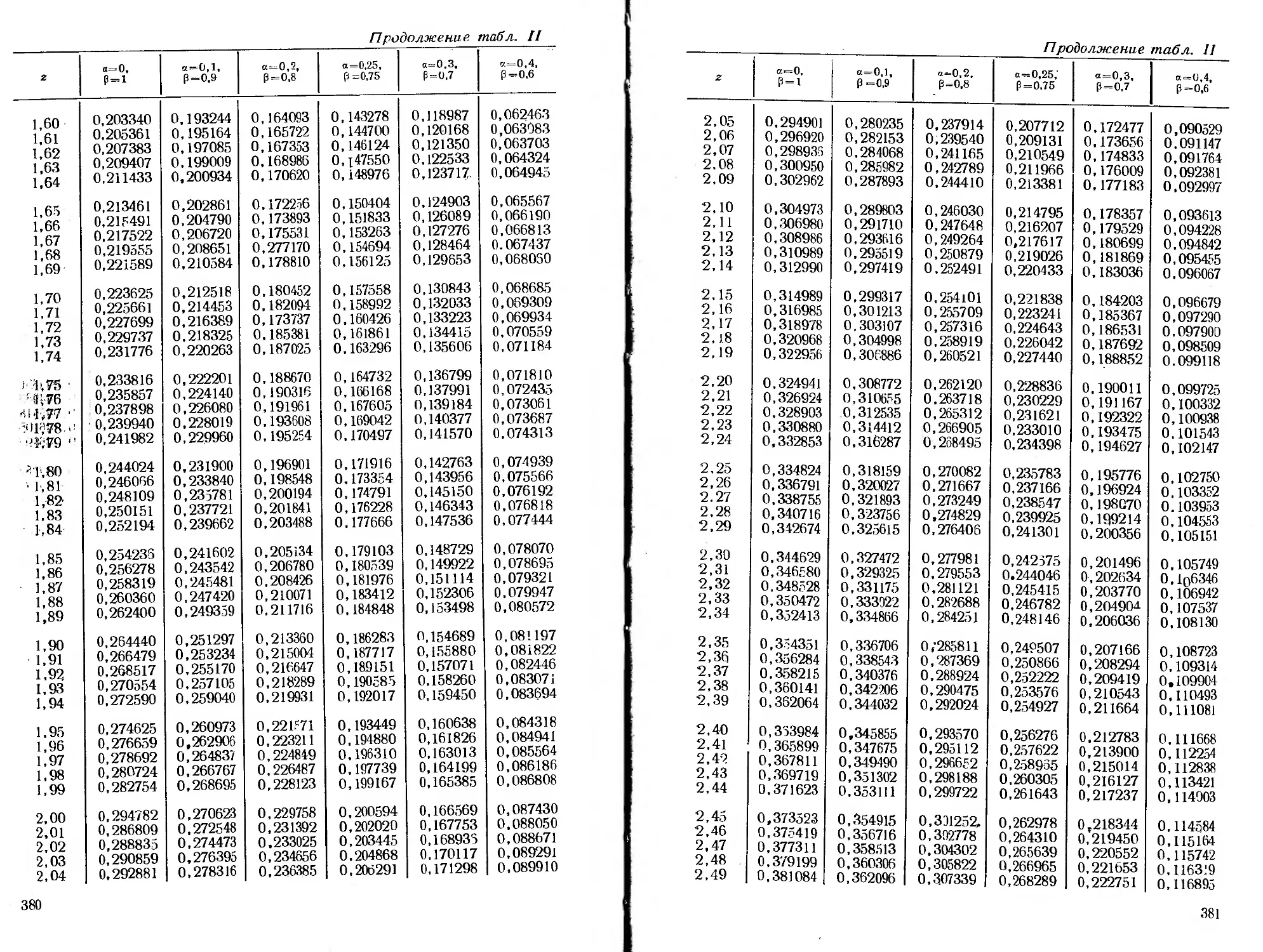
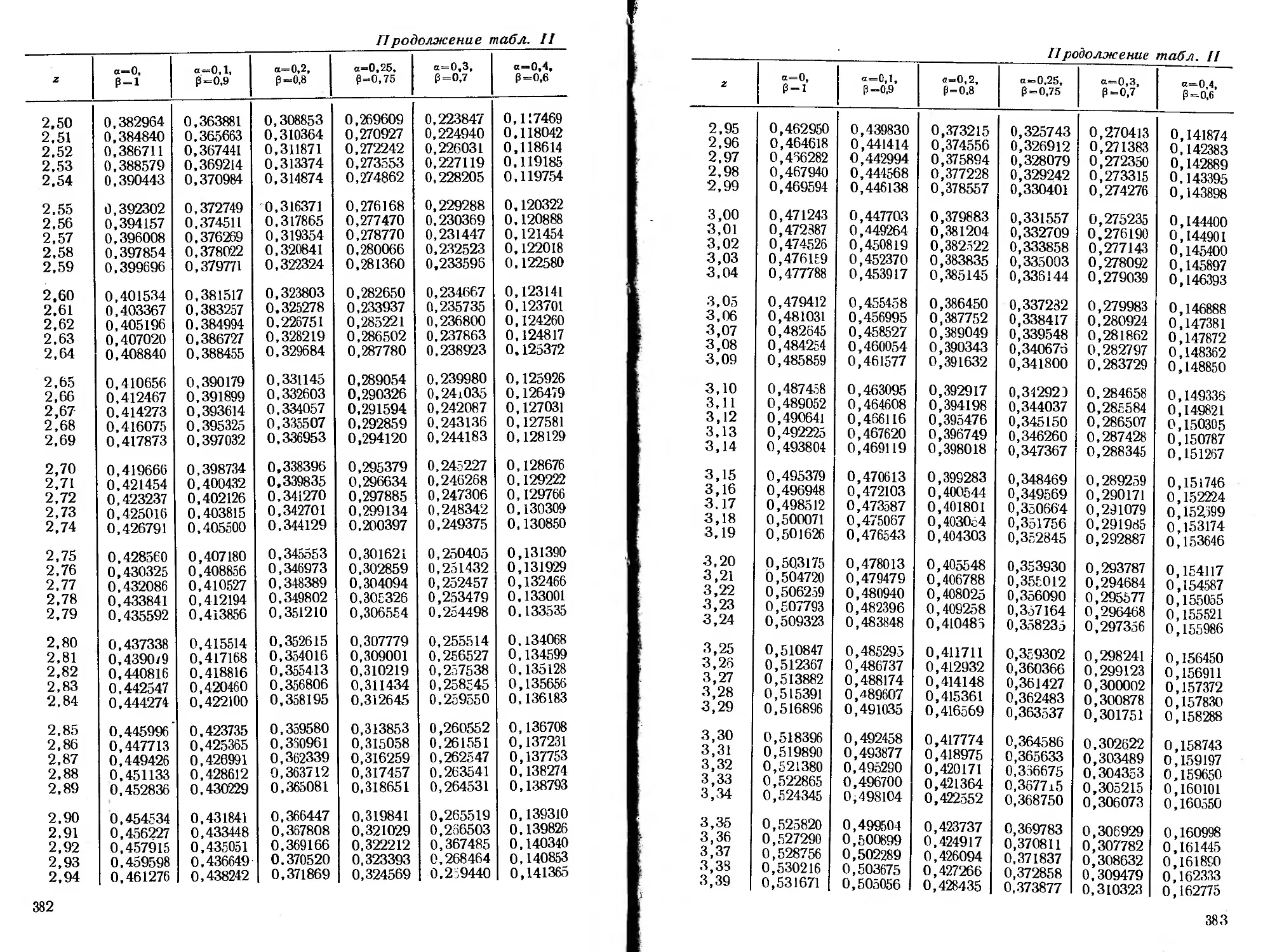
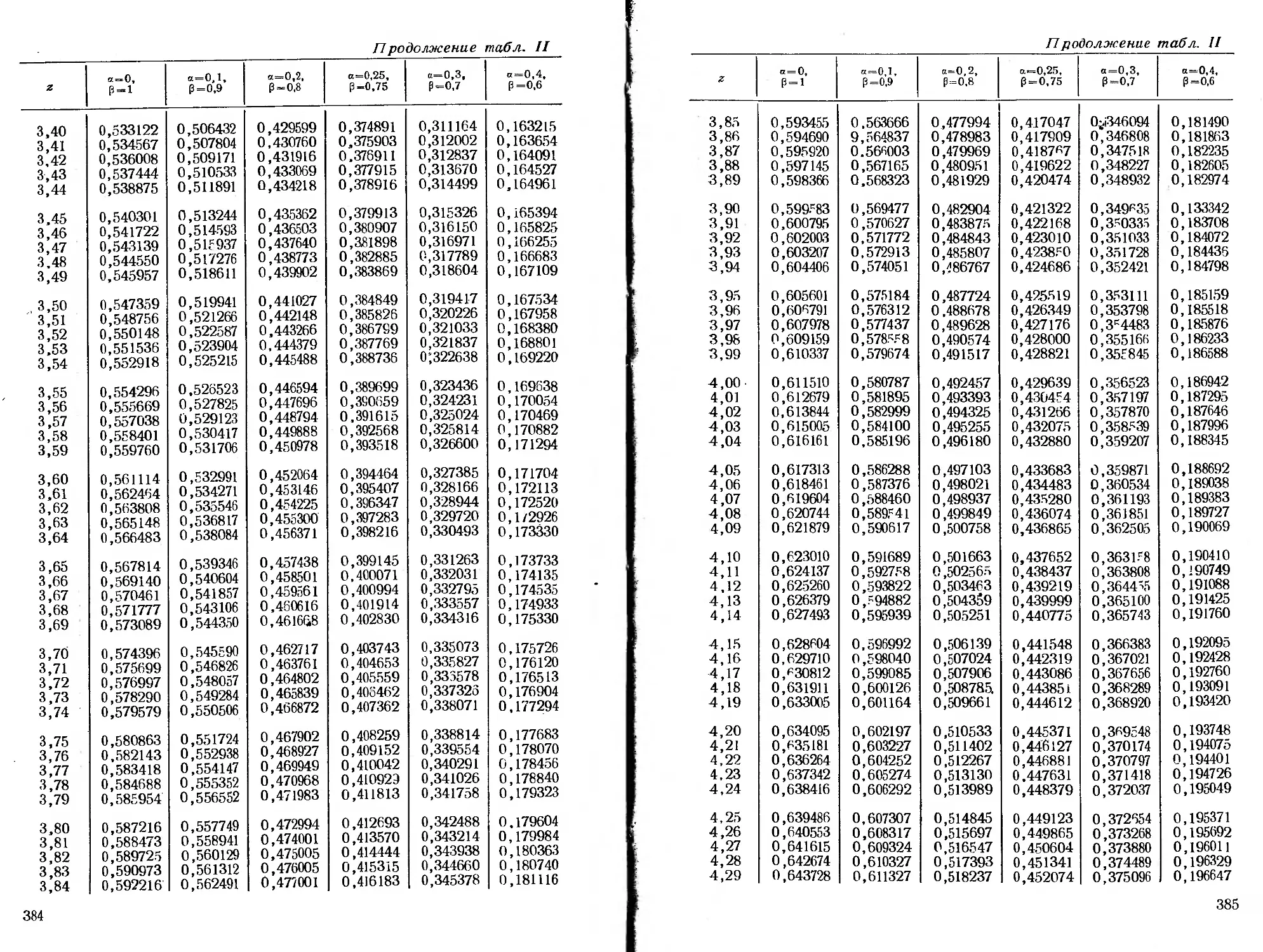
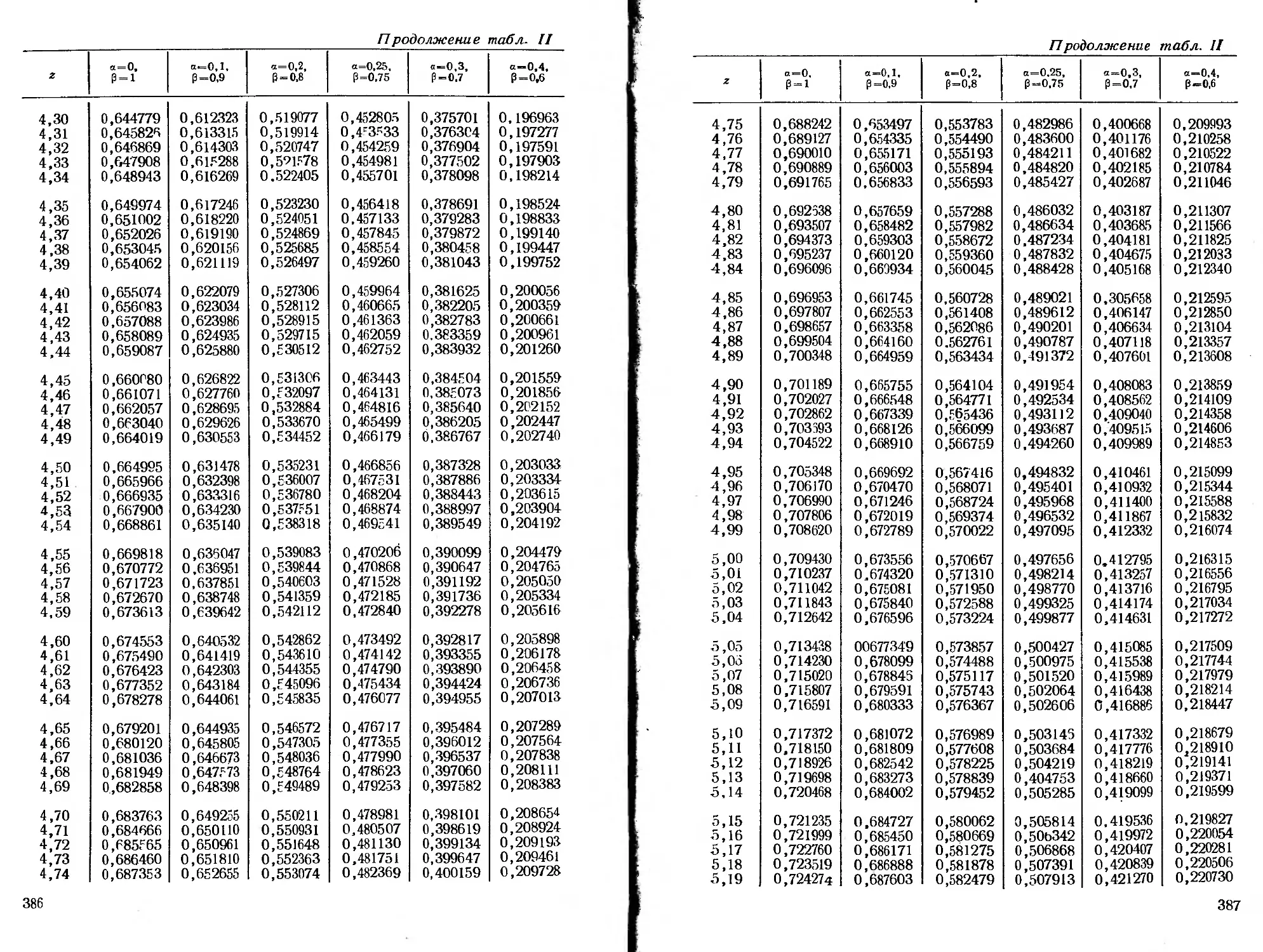
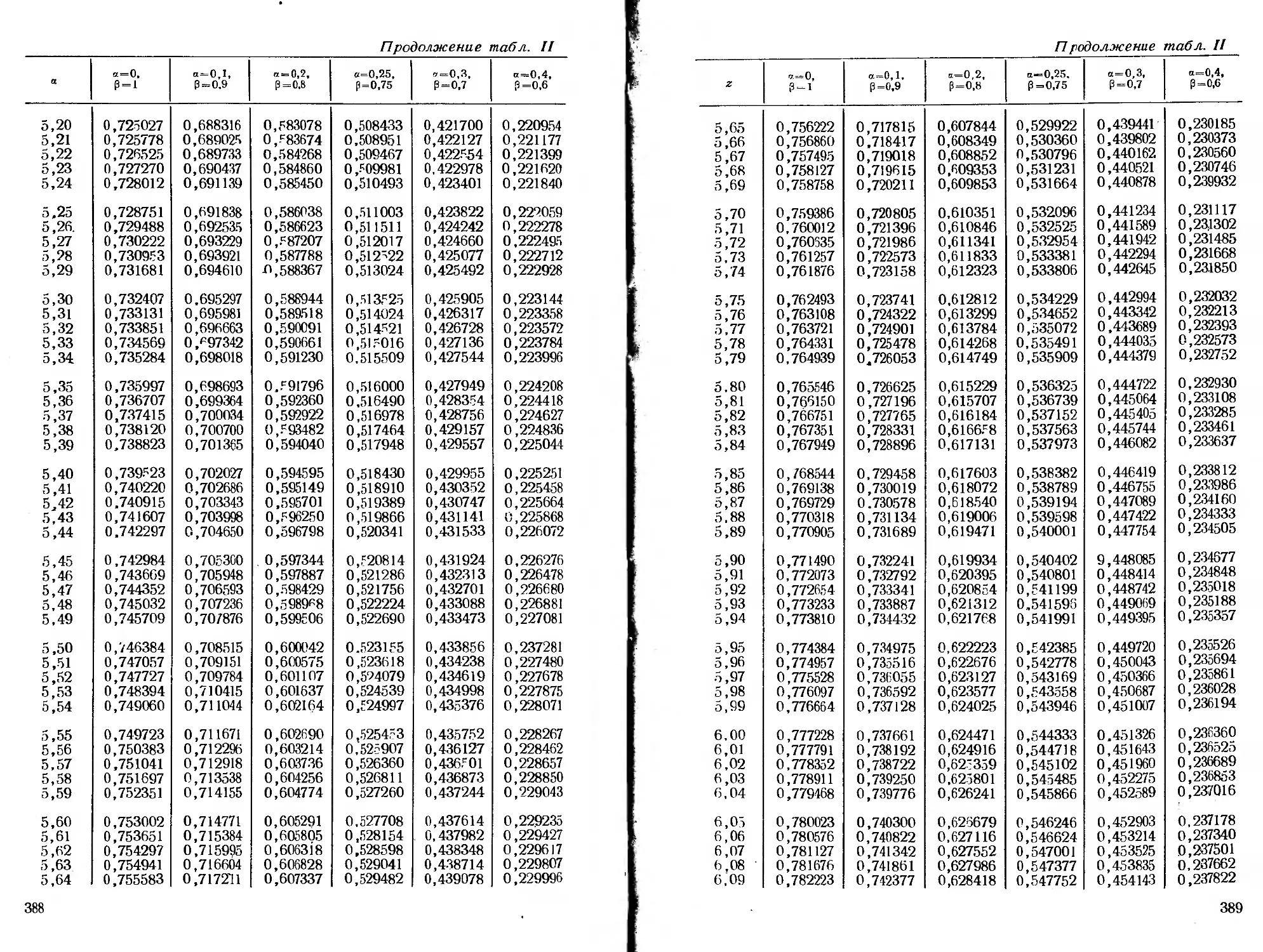
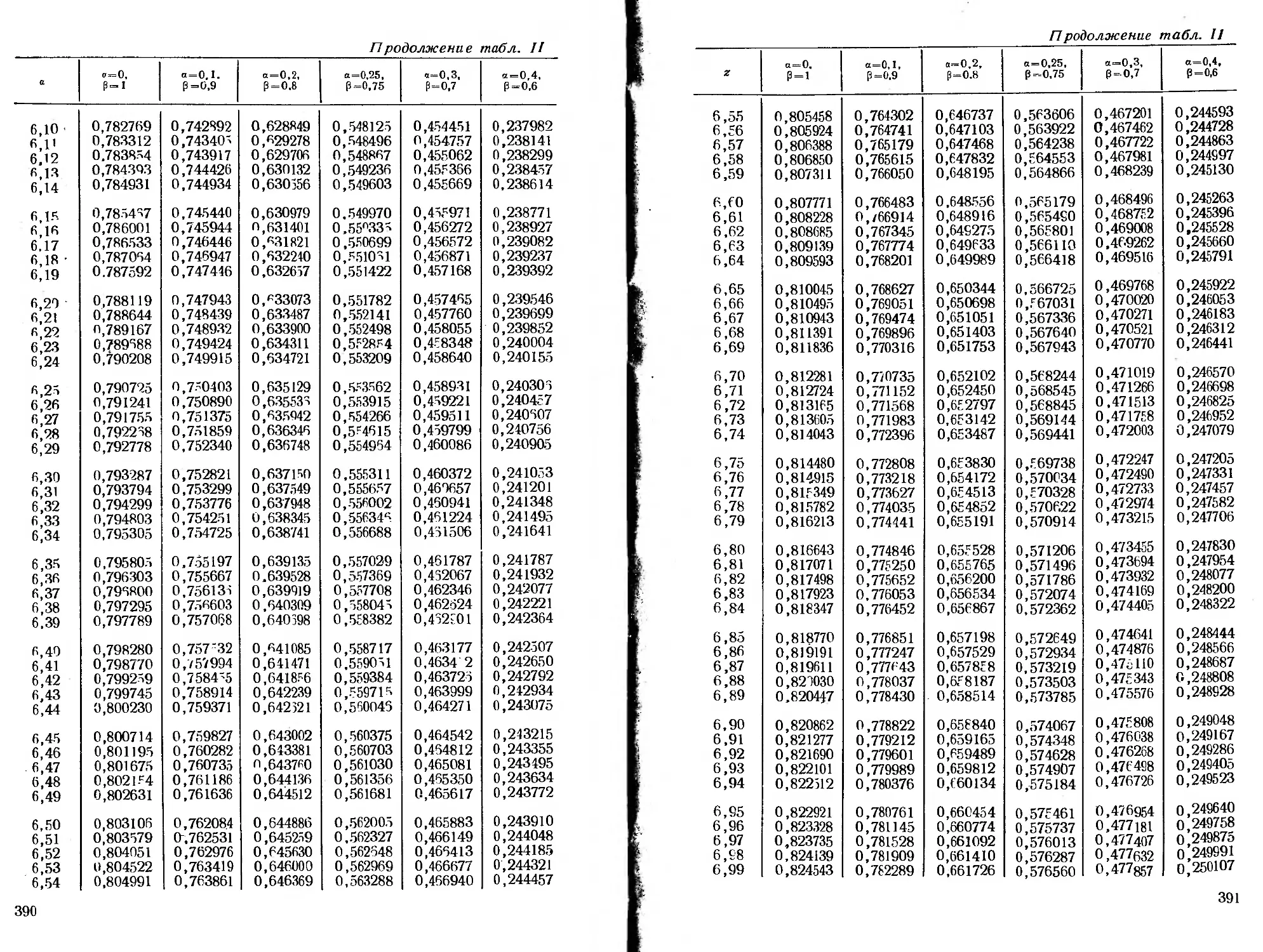
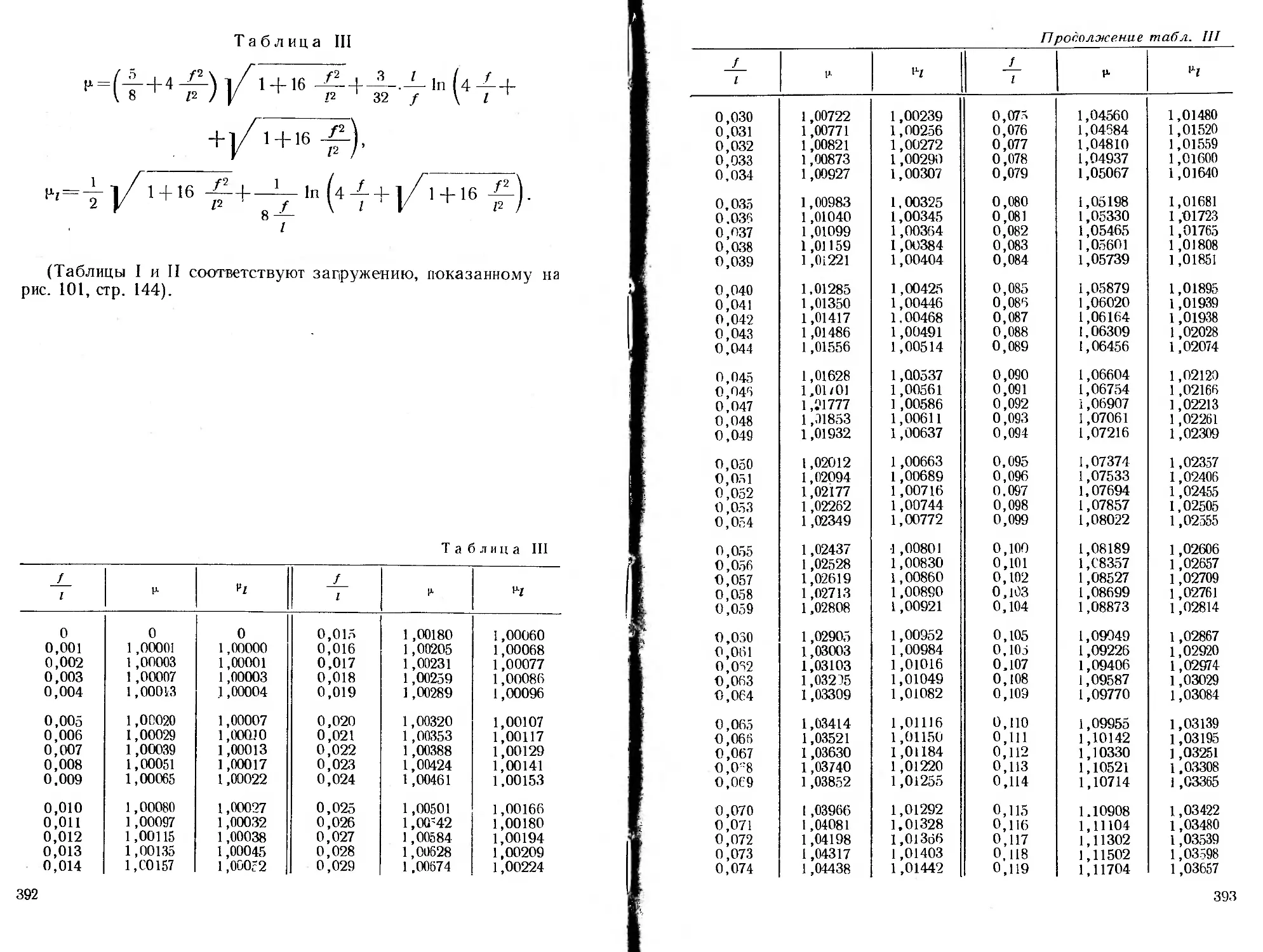
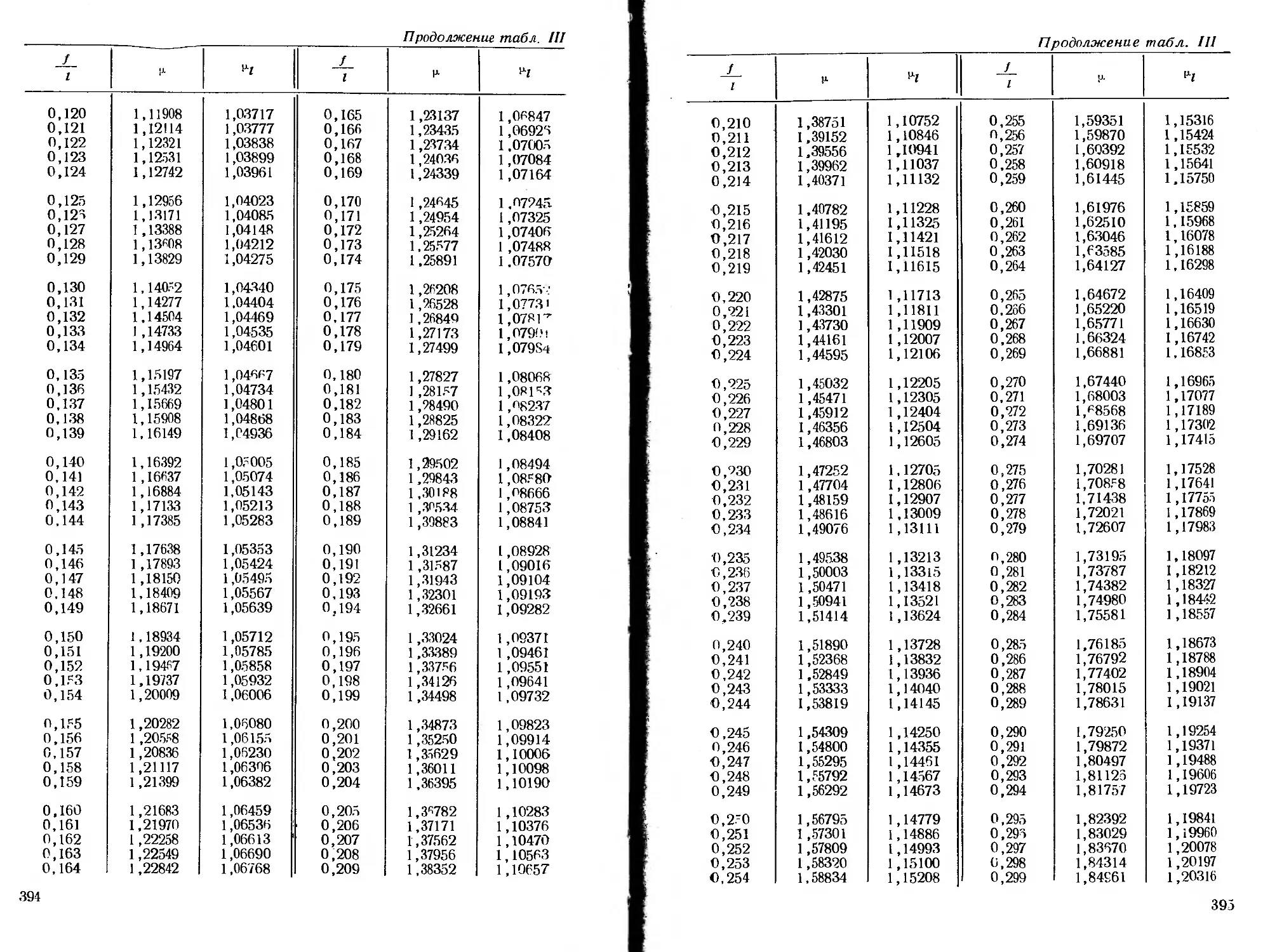
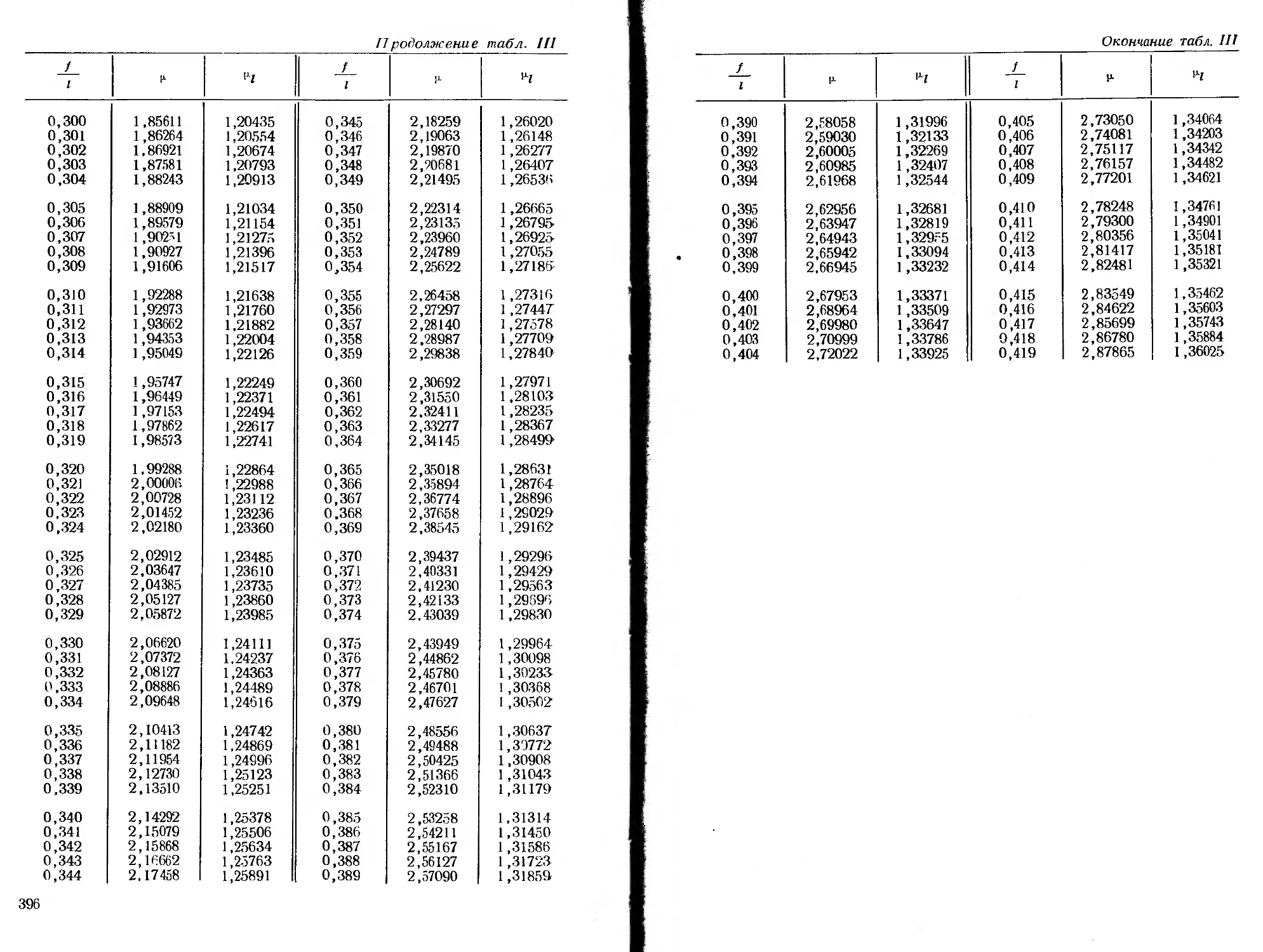
ся специальные функции, для которых в приложении помещены
таблицы.
В гл. V излагаются специальные методы расчета как одно-
пролетных, так и многопролетных мостов с учетом геометриче-
ской нелинейности. Предлагаемый метод имеет широкий диапа-
зон применения и является общим для обширного класса задач.
Так, например, по этому методу без труда учитывается произ-
вольный закон изменения жесткости пролетного строения, подат-
ливость подвесок и некоторые другие вопросы, к числу которых
относятся, например, учет жесткого закрепления кабеля к балке
в середине пролета и т. д.
В гл. VI рассматриваются однопролетные системы с шарнира-
ми в балке жесткости. Они как самостоятельные конструкции не
имеют распространения, однако вопросы, изучаемые в этой гла-
ве, могут представить интерес для исследования работы мостов
в процессе их сборки или после их повреждения, когда в отдель-
ных сечениях балки могут образоваться шарниры. Такая комби-
нированная система может быть также принята в качестве ос-
новной системы при расчете мостов, в особенности при исследо-
вании за пределами упругих деформаций.
Расчету балочно-вантовых мостов посвящена гл. VII. В ней
излагаются два метода. Один обладает большой универсально-
стью и удобен при использовании электронных машин. Второй
метод рекомендуется в случае применения малых средств меха-
низации вычислений, например при использовании клавишных
машин или арифмометра.
Гл. VIII посвящена собственным колебаниям висячих мостов.
В этой главе производится учет изменения распора в кабеле в
процессе колебаний (учет динамической добавки к распору от
сил инерции). Решение этой задачи проводится двумя методами:
в первом — используется вариационный метод Бубнова —
Галёркина, а во втором — матричный метод, построенный по об-
щей методике, разработанной в гл. V. По методу Галёркина
дается решение как для изгибных, так и для крутильных коле-
баний, а второй метод применяется только для изгибных коле-
баний. Хорошее совпадение результатов при определении спект-
ра частот и форм изгибных колебаний позволяет высказать уве-
ренность о высокой точности обоих методов.
В этой главе демонстрируется ряд примеров, в которых рас-
сматриваются мосты с переменной балкой жесткости, произво-
дится анализ влияния различных параметров на частоты и фор-
мы колебаний. Показано, что учет динамической добавки к рас-
4
пору в значительной степени изменяет частоты и формы
симметричных колебаний. В конце главы выводятся приближен-
ные формулы для определения частот изгибных и крутильных ко-
лебаний. В эти формулы входят параметры, учитывающие закон
изменения изгибной и крутильной жесткостей, а также динами-
ческой добавки к распору.
В книге главное внимание уделено расчету висячих мостов.
Данные о конструктивных решениях, приведенные в гл. 1, автор
поместил с целью ознакомления читателя лишь с самыми общими
вопросами, связанными с проектированием и строительством ви-
сячих мостов. Эти данные не претендуют на полноту и не могут
заменить книг, специально посвященных этим вопросам. Вместе
с тем автор считает, что изучающим теорию расчета висячих мос-
тов будет полезно ознакомиться с материалами, изложенными в
этой главе.
В работе широко используются методы линейной алгебры,
которые оказались весьма удобными для решения нелинейных за-
дач. В книге дано значительное количество примеров расчета
висячих мостов, которые могут послужить пособием при реше-
нии аналогичных задач.
Автор пользуется возможностью выразить благодарность
проф.|н. И. Безухову|, проф. К. Г. Протасову и доц. Ю. С. Силь-
ницкому, давшим ценные советы при рецензировании рукописи.

ГЛABA I
КРАТКИЕ СВЕДЕНИЯ
ИЗ ИСТОРИИ РАЗВИТИЯ
ВИСЯЧИХ МОСТОВ
§ 1.	ОБЩИЕ СВЕДЕНИЯ О СТРОИТЕЛЬСТВЕ
висячих мостов
Висячие мосты занимают видное место в истории мостострое-
ния. Они появились на заре развития человеческого общества и
в ранний период имели весьма примитивные конструктивные
формы. Основные несущие элементы—канаты в первых висячих
мостах непосредственно покрывались легким настилом, по кото-
рому происходило движение пешеходов и животных. Такого ти-
па мосты встречались в Южной Америке, Японии, Тибете, на
Кавказе и в других местах. Они были весьма несовершенны, об-
ладали малой грузоподъемностью, плохо сопротивлялись ветро-
вым нагрузкам и сильно раскачивались даже от тяжести одного
человека.
Первый висячий мост, описанный в литературе, конструктив-
ная схема которого близка к современным схемам висячих мос-
тов, был построен в 1741 г. в Англии через реку Тиз. Характер-
ной особенностью этого моста являлось наличие самостоятель-
ной проезжей части, соединенной с цепью подвесками. Этот мост
имел пролет 21 м и служил для прохода горнорабочих.
За истекшие 228 лет с момента открытия указанного выше
моста во всех странах мира было построено большое количество
висячих мостов, конструкция которых постоянно совершенствова-
лась, а пролеты увеличивались.
В первом периоде, продолжавшемся примерно до 1810 г„
строились, как правило, цепные мосты небольших пролетов. Они
обладали значительным собственным весом и сравнительно
небольшой грузоподъемностью. Основным несущим элементом
таких мостов являлась цепь, составленная из колец или отдель-
ных жестких элементов, соединенных между собой болтами
(шарнирами).
7
В начале XIX века уже выявились экономические преимуще-
ства висячих мостов по сравнению с каменными мостами, кото-
рые имели в то время широкое распространение. Так, например,
построенный в 1820 г. в Англии висячий мост через реку Твид
пролетом 110 м стоил примерно в 4 раза дешевле каменного мос-
та такой же длины.
В 1826 г. в Англии был открыт Менейский цепной мост, кото-
рый прослужил около ста лет, имел пролет 177 м при отноше-
нии стрелы к пролету 1/12.
В этот же период был построен еще ряд мостов во Франции,
США и других странах, пролеты которых не превышали 150 м.
Таким образом, Менейский мост по величине пролета являлся
рекордным до 1834 г.
Вторая четверть XIX века ознаменовалась широким примене-
нием кабельных висячих мостов, в которых основной несущий
элемент (цепь) был заменен тросом (проволочным кабелем).
Это привело к значительному прогрессу, так как кабель обладал
более высокой прочностью по сравнению с цепью.
В этот период был построен целый ряд кабельных мостов во
Франции, Англии, Америке и других странах.
Открытый в 1834 г. висячий мост в Швейцарии близ Фрай-
бурга уже имел пролет 265 м и оказался в то время уникальным
по своим размерам. »
Последующий примерно столетний период характерен массо-
вым строительством висячих мостов во многих странах мира.
Конструкции висячих мостов быстро совершенствовались.
Стали применяться высокопрочные материалы, а пролеты мос-
тов постоянно увеличивались и к началу нашего столетия при-
ближались к 500 м. Так, например, в 1883 г. был построен зна-
менитый Бруклинский мост в Нью-Йорке с грандиозным для то-
го времени пролетом — 486 м.
В 1903 г. был сдан в эксплуатацию Вильямсбургский мост в
Нью-Йорке с пролетом 488 м, а в 1924 г. — мост через реку Гуд-
зон (Bear Monntain) с пролетом 497 м, в 1926 г. — мост в Фи-
ладельфии через реку Делавар с пролетом 533 м и, наконец, в
1929 г. — Детройтский мост с пролетом 563 м. Таким образом, с
начала нашего века обозначился этап современного мосто-
строения.
В начале тридцатых годов произошел скачок, характерный
резким увеличеним размеров пролета. Так, например, в 1931 г.
в Нью-Йорке был построен мост через реку Гудзон с пролетом
1067 м, в 1937 г. — в Сан-Франциско открыт знаменитый мост
через залив Золотые Ворота (Golden Gate Bridge) с пролетом
1280 м и, наконец, совсем недавно в 1965 г. закончено строитель-
ство моста в Нью-Йорке (Verrazano—Narrows) с пролетом
1298 м.
8
Подробный перечень построенных висячих мостов в различ-
ных странах мира, начиная с 1741 г., дается в книге Д. Б. Штейн-
мана [165]. В этой книге приводится таблица с указанием раз-
меров и года постройки 243 наиболее значительных висячих
мостов.
Интересные данные приводятся в книге Г. П. Передерия
[26], где дается таблица (стр. 258) наиболее значительных 27 ви-
сячих мостов.
Как у Д. Б. Штейнмана, так и у Г. П. Передерия перечень
заканчивается 1932 г. Более поздние данные содержатся в кни-
ге Н. Shirley — Smith [157], в которой приводятся материалы по
новейшим мостам, в том числе строящимся в настоящее время.
За указанный период строительства висячих мостов можно
отметить мосты «рекордсмены», каждый из которых в свое время
являлся рекордным по величине наибольшего пролета. Список
9
мостов «рекордсменов», составленный автором на основании раз-
личных источников, приведен в табл. 1. По данным этой табли-
цы построен наглядный схематический график роста пролетов
висячих мостов (рис. 1), начиная с 1741 г. и кончая 1965 г.
Таблица 1
№	Дата за- вершения строитель- ства	Место расположения моста	Страна	Тип (цеп- ной или кабельный)	Наиболь- ший пролет, м
1	1741	р. Тисс	Англия	п	21
2	1785	Лаан	Германия	ц	38
3	1807	р. Потомак	США	ц	40
4	1809	Филадельфия	США	ц	47
5	1809	Массачузетс	США	ц	74
6	1816	Филадельфия	США	к	124
7	1819	р. Твид	Англия	и	137
8	1826	Пролив Менэй	Англия	ц	177
9	1834	Фрайбург	Швейцария	к	265
10	1848	Вирджиния	США	к	308
11	1850	Вирджиния	США	к	317
12	1867	р. Огайо	США	к	322
13	1883	Бруклин Нью-Йорк	США	к	486
14	1903	Вильямсбургский	США	к	488
15	1926	р. Делавар	США	к	533
16	1929	Детройт	США	к	563
17	1931	р. Гудзон	США	к	1067
18	1937	Золотые Ворота	США	к	1280
19	1965	Верразано Нерроуз	США	к	1298
В нашей стране висячие мосты не получили такого большого
развития, как в США, Англии, Франции, Японии и других стра-
нах. Во-первых, они появились у нас значительно позже.
Г. П. Передерий считает, что первый висячий мост в России был
построен в 1823 г. в Петербурге в Екатерингофском парке и имел
пролет 15,2 л. Отставание в этой области объясняется многими
причинами, одна из которых заключается в отсутствии сравни-
тельно больших водных преград, которые требовали бы строи-
тельства столь больших пролетов.
В настоящее время проблема строительства висячих мостов
стала привлекать внимание наших наиболее крупных проектных
организаций. Особенно большие работы проводятся в Гипро-
трансмосте под руководством Е. И. Крыльцова, где разрабаты-
ваются новые типы экономичных вантовых и предварительно на-
пряженных висячих систем. Необходимо также отметить боль-
шие исследования, проведенные в Киеве под руководством
В. И. Киреенко, о чем более подробно сказано в следующем па-
раграфе.
10
Рис. 2. Бруклинский мост в Нью-Йорке. Построен
в 1883 г. Средний пролет 486 м
Нет сомнения в том, что в современных условиях в нашей
стране висячие мосты найдут широкое применение в особенности
в связи с появлением искусственных морей, возникающих в
результате строительства крупных гидротехнических сооружений.
§ 2.	КРАТКИЕ СВЕДЕНИЯ О ВИСЯЧИХ МОСТАХ
БОЛЬШИХ ПРОЛЕТОВ
Приведенный в предыдущем параграфе обзор показывает,
что к концу прошлого века в строительстве висячих мостов были
достигнуты большие успехи. В период с 1883 по 1930 гг. пролеты
наиболее выдающихся мостов достигали 500 м и более.
В 30-х годах нашего века прогресс в области мостостроения
достиг небывалого уровня. За короткий период максимальная
длина пролета возросла в два раза и превысила километровый
размер. Для того чтобы составить достаточное представление о
типах наиболее крупных висячих мостов, рассмотрим несколько
примеров.
В 1870 г. в Нью-Йорке по проекту Г. Линденталя было нача-
то строительство Бруклинского висячего моста. Оно продолжа-
лось 13 лет, и сооружение было введено В' эксплуатацию только
в 1883 г. Общий вид этого моста показан на рис. 2. Средний про-
лет его равен 486 м, а боковые — по 287 м. Проезжая часть под-
держивается четырьмя кабелями диаметром 39,4 см каждый.
Кабель состоит из 5282 параллельных проволок диаметром по
3 мм. В плоскости каждого кабеля размещено по 40 наклонных
11
Рис. 3.
Рис. 4. Вид пилона Бруклин-
ского моста со средней пеше-
ходной полосы
вант с обеих сторон пилонов.
Главная балка состоит из 6 про-
дольных решетчатых ферм,
соединенных поперечными бал-
ками. Фермы имеют высоту
5,2 м. Отношение высоты балки
жесткости к пролету 1 :94.
Мост предназначен для желез-
нодорожного и автомобильного
движения. В первый период
эксплуатации моста в крайних
полосах проезжей части осу-
ществлялось автомобильное
движение, в двух соседних —
движение поездов, а в средней
части—пешеходное движение.
Поперечный разрез этого мос-
та показан на рис. 3.
После реконструкции по
мосту проложены четыре колеи
железной дороги. На рис. 4 по-
казана фотография моста, сде-
ланная со средней пешеходной
полосы в непосредственной
близости от пилона. На рисун-
ке хорошо видны наклонные
ванты.
В 1929 г. был построен Амбасадорский мост через реку Дет-
ройт. Мост соединил две соседние страны — Канаду и США.
Строительство продолжалось два года. Средний пролет моста ра-
вен 563 м. Высота стальной решетчатой балки жесткости 6,7 м.
Отношение высоты балки жесткости к пролету 1 : 84. Ширина
проезжей части 14,1 м, тротуаров — 2,4 м. Мост поддерживает-
ся двумя кабелями, состоящими из параллельных проволок.
Диаметр каждого кабеля равен 48,9 см.
12
Рис. 5. Мост Г. Вашингтона через р. Гудзон в Нью-Йорке
с наибольшим пролетом 1067 м.. Построен в 1931 г.
Рис. 6.
I
I
Следующим ш|агом впе-
ред было сооружение моста
Г. Вашингтона ^ерез реку
Гудзон в Ныо-Йорке в
1931 году (рис. 5). Мост
имеет стальные решетчатые
пилоны высотой 181 м. Про-
лет его равен 10б7 м. Попе-
речное сечение моста пока-
зано на рис. 6. Расстояние
между двумя балками жест-
кости равно 32,29 м. Проез-
жая часть поддерживается
четырьмя кабелями диамет-
ром 91,4 см. Кабели этого
моста состоят из 61 пряди.
Каждая прядь изготовлена
из 434 проволок диамет-
ром 4,9 мм. Временное
сопротивление проволоки
15500 кГ/см2, а услов-
ный предел	текучести —-
10500 кГ/см2. Подвески,
между которыми располо-
жены тротуары имеют диа-
метр 78 мм- Каждая попе-
речная балка подвешена че-
тырьмя подвесками. Всего в
одном кабеле содержится
26474 параллельных прово-
лок. Общая длина проволок
в кабеле составляет
171 000 км. Мост был спроек-
тирован двухъярусным. В
1929 г. был сооружен толь-
ко верхний ярус для восьми
полос автомобильного дви-
Рис. 7. Сдвоенный шестипролетный
висячий мост в Сан-Франциско с наи-
большим пролетом 704 м. Построен
в 1936 г.
Рис. 8. Центральная анкерная опора
сдвоенного шестипролетного висячего
моста в Сан-Франциско
жения. В; середине — проезд шириной 12,2 м—предназначен для
грузового транспорта, а по бокам полосы для легковых авто-
мобилей.
В период с 1959 по 1962 гг. был пристроен нижний ярус, что
позволило справиться с возросшим транспортным потоком.
В результате пристройки образовалась ферма жесткости высо-
той 9,14 м.
Проблема перекрытия больших водных преград приводит к
необходимости устройства висячих мостов с большим числом
пролетов. Остроумное решение было найдено при строительстве
так называемого сдвоенного моста «Сан-Франциско—Окленд-
Бэй-Бридж» (рис. 7). Он состоит по существу из двух трехпро-
летных мостов, соединенных на массивной средней опоре. Таким
образом, в целом этот мост имеет шесть пролетов. Длина каж-
дого из главных пролетов 704 м. Высота балок жесткости 9,14 м.
Диаметр кабеля 72,2 см. Основная трудность при строительстве
этого моста состояла в соединении двух мостов на промежуточ-
ной опоре. Иначе говоря, основной проблемой являлось устрой-
ство анкерных закреплений кабелей двух мостов. Решение этой
задачи легко понять из рис. 8. Из него видно как устройство
самой опоры, так и анкерные устройства для кабелей двух
стыкующихся мостов. Теперь будет понятен общий вид моста
(рис. 7), имеющего посредине длины массивную промежу-
точную опору. Массивная средняя опора находится под воз-
действием двух горизонтальных сил — распоров от двух
прилегающих мостов, направленных в разные стороны. При раз-
личных загружениях этих мостов распоры от временной нагруз-
ки различны, поэтому при расчете опоры необходимо было учесть
горизонтальную силу, равную разности распоров и приложен-
ную на уровне примыкания кабелей.
В 1937 г. после четырехлетнего строительства в Сан-Фран-
циско был открыт для движения величайший в мире мост, побив-
ший потому времени все рекорды—мост «Золотые Ворота».
Длина главного пролета этого моста равняется 1280 м (рис. 9).
Он пересекает залив Тихого океана и соединяет город Сан-Фран-
циско с северными предместьями его. Пилоны, несущие нагрузку
в 22 000 т, имеют высоту 227,5 м над водой. Стальная решетча-
тая фэрма жесткости высотой 7,6 м поддерживается двумя ка-
белями из параллельных проволок диаметром 92,7 см.
В 1953 г. после катастрофы с висячим мостом в Такомской
долине (1940 г.), мост «Золотые Ворота» был усилен горизон-
тальными удерживающими кабелями.
В 1940 г. через пролив Бюджет Саунд был построен трехпро-
летный Такомский мост, который, просуществовав всего четыре
месяца, обрушился от колебаний, вызванных действием ветра.
Конструкция этого моста и причины его катастрофы неоднократ-
но описывались в различных журналах и книгах, поэтому на
15
Рис. 9. Висячий мост «Золотые ворота» в Сан-Франциско
с главным пролетом 1287 м. Построен в 1937 г.
Рис. 10. Новый Такомский мост с главным проле-
том 853 м. Построен в 1950 г. на месте обрушив-
шегося в 1940 г. старого Такомского моста

Рис. II. Новый висячий мост в Будапеште, построенный на
старого Елизаветинского моста, разрушенного во время
в 1945 г.
месте
войны
Рис. 12.
Рис. 13
ФУШМШ’АЖЧАЯ
X,
Л/
этих вопросах мы останавливаться не будем. В октябре 1950 г.
было открыто движение по новому Такомскому мосту, построен-
ному на том же месте с использованием старых фундаментов
опор (рис. 10). Длина главного пролета равна 853 м. Новый
мост отличается от старого балкой жесткости, выполненной в
виде стальной решетчатой фермы высотой 10 м. Балка жест-
кости поддерживается двумя кабелями диаметром 50,8 см
каждый.
В 1945 г. нацистская армия разрушила хорошо известный ин-
женерам-строителям Елизаветинский висячий мост в Будапеш-
те. Вскоре на этом месте вновь был построен висячий мост совре-
менного типа по схеме 57 + 290-1-57. Общий вид моста показан на
рис. 11. Ширина моста 27,6 м. Характерной особенностью этого
моста являются качающиеся пилоны, шарнирно прикрепленные
к опорам. Проезжая часть выполнена в виде стальной ортотроп-
ной плиты, на которую непосредственно уложен слой асфальта в
7 см. Стальные листы под асфальтом покрыты антикоррозийным
защитным слоем (оцинковка стальных листов, битумная смаз-
ка и небольшой слой специальной мастики).
Кабель состоит из 61 пряди с поперечным сечением, показан-
ным на рис. 12. Каждая прядь состоит из проволочной сердцеви-
ны и трех рядов фасонной проволоки, плотно прилегающей друг
к другу. Общий вид одной пряди кабеля показан на рис. 13.
Большой научный, интерес представляет собой Танкервиль-
ский мост, построенный в 1959 г. во Франции. Он отличается от
других мостов не только конструктивными особенностями, но и
той глубиной инженерных расчетов, которые были проведены в
процессе его проектирования и строительства. Описание конст-
рукции этого моста и способов производства строительных работ
выделено в отдельный параграф.
Из сооруженных висячих .мостов последнего времени следует
отметить грандиозный мост «Верразано Нерроуз», построенный
в 1965 г. на подходе к Нью-Йоркскому порту (рис. 14). Этот
мост имеет в настоящее время наибольший в мире пролет длиной
1298 м. Мост введен в эксплуатацию осенью 1965 г. Ширина про-
езжей части обеспечивает двенадцатиполосное движение тран-
спорта. Поперечное сечение моста показано на рис. 15. Ширина
моста между осями спаренных кабелей равна 31,4 м. Ширина
проезжей части верхнего яруса 23,8 м. Расстояние между осями
ферм жесткости 30,63 м. В нижнем ярусе каждая из двух раз-
дельных полос проезжих частей имеет ширину 11,3 м. Каждый
из четырех кабелей имеет диаметр 915 мм. Он состоит из 61 пря-
ди, которые в свою очередь состоят из 428 параллельных прово-
лок. Временное сопротивление проволоки равно 15 800 кГ1смА.
Разрывное усилие кабеля около 100 000 т. Вес стальных конст-
рукций 150 000 т. Балка жесткости выполнена в виде стальной
решетчатой фермы высотой 7,3 м. Полная длина моста 4175 м.
18
Рис. 14. Общий вид моста «Верразано-Нерроуз» около Нью-Йорка (по-
строен в 1965 г.). Вес стальных конструкций 150 000 т
Рис. 15.
Продольный уклон проезжей части от середины моста к анкерам
равен 2%.
В 1964 г. в Великобритании через залив Forth построен трех-
пролетный висячий мост под автомобильную дорогу (рис. 16).
Величина главного пролета равна 1006 м. Два крайних пролета
этого моста имеют длину по 408,4 м. Пилоны высотой 154 м с
19
Рис. 16. Трехпролетный висячий мост через Фортский залив в Великобри-
тании под автомобильную дорогу. Главный пролет 1006 м (построен
в 1964 г.)
коробчатым сечением изготовлены из высокопрочной стали. Рас-
стояние между пилонами (по ширине моста) равно 23,5 м. Для
каждого направления движения устроены две полосы автопроез-
да, велодорожка и тротуар. Кабели моста общим диаметром
59,7 см состоят из 37 прядей по 314 проволок в каждой. Всего в
кабеле 11 618 параллельных проволок диаметром 4,8 мм. Шири-
на проезжей части моста 23,7 м, а высота балок жесткости
9,15 м. Вертикальные подвески расположены в местах прикреп-
ления поперечных балок. Неразрезные балки жесткости, связан-
ные между собой поперечными балками, создают необходимую
жесткость пролетного строения.
В сентябре 1966 г. в Англии построен новый висячий мост
через р. Северен (Severen Bridge). Этот мост между берегами
Юго-западной Англии и Южного Уэллса имеет общую длину с
подходами 1800 м. Его центральная часть представляет собой
трехпролетную висячую систему с главным пролетом 988 м и
двумя боковыми пролетами по 305 м. Общий вид моста показан
на рис. 17. Характерной особенностью моста является наличие
наклонных подвесок, как показано на схеме (рис. 18). Наклон-
ные подвески обеспечили повышенную жесткость моста. Попе-
речное сечение моста изображено на рис. 19. Проезжая часть
имеет две полосы для движения автомобилей по 7,3 м и разде-
лительную среднюю полосу около 2,5 м ширины. На консолях
расположены пешеходные и велосипедные дорожки шириной по
3,6 м. Благодаря применению высокопрочных сталей мост имеет
наименьший вес по сравнению с осуществленными мостами та-
кой же длины и при такой же расчетной нагрузке. Пилоны с ко-
20
Рис. 17. Висячий мост в Англии через р. Северен с главным пролетом 988 м
(построен в 1966 г.)
Рис. 18.
1,53
9,90
Ось
кабеля
9,90 г .	,
Раздельные лолЬскО \
о^ашбМЗб 7,31 юо
QJOr  7,31
Автомобильная
дорога
0,60
5,65 Х\
4,56
елосилед
ная дорож-
ка
4,50
6,87
11,43
/,53
Ось
кабеля
Автомобильная
дорога


Оешеход-
HaH^dopani-
4,56
5,87 т
11,43
4,50
Рис. 19.
Рис. 20. Висячий мост через р. Тахо в Лиссабоне с главным пролетом 1012,4 м
(построен в 1966 г.)
Рис. 21.
робчатым сечением изготовлены из высокопрочной стали. Общий
расход стали 17 тыс. т, стоимость моста 28 млн. долларов. Кон-
фигурация балки жесткости обладает хорошей обтекаемостью,
что обеспечивает надежную аэродинамическую устойчивость
моста.
В августе 1966 г. был сдан в эксплуатацию крупнейший в
Европе висячий мост, который пересекает р. Тахо у входа в порт
в Лиссабоне, шириной 2 км (рис. 20). Общая длина моста 3218 м.
Висячая часть моста имеет главный пролет 1012,4 м и два боко-
вых пролета по 482,6 м каждый. Семидесятиметровая высота
подмостового габарита обеспечивает проход в порт самых круп-
ных океанских судов. Отметка верха пилонов относительно уров-
ня воды равна 190 м. В настоящее время мост предназначен для '
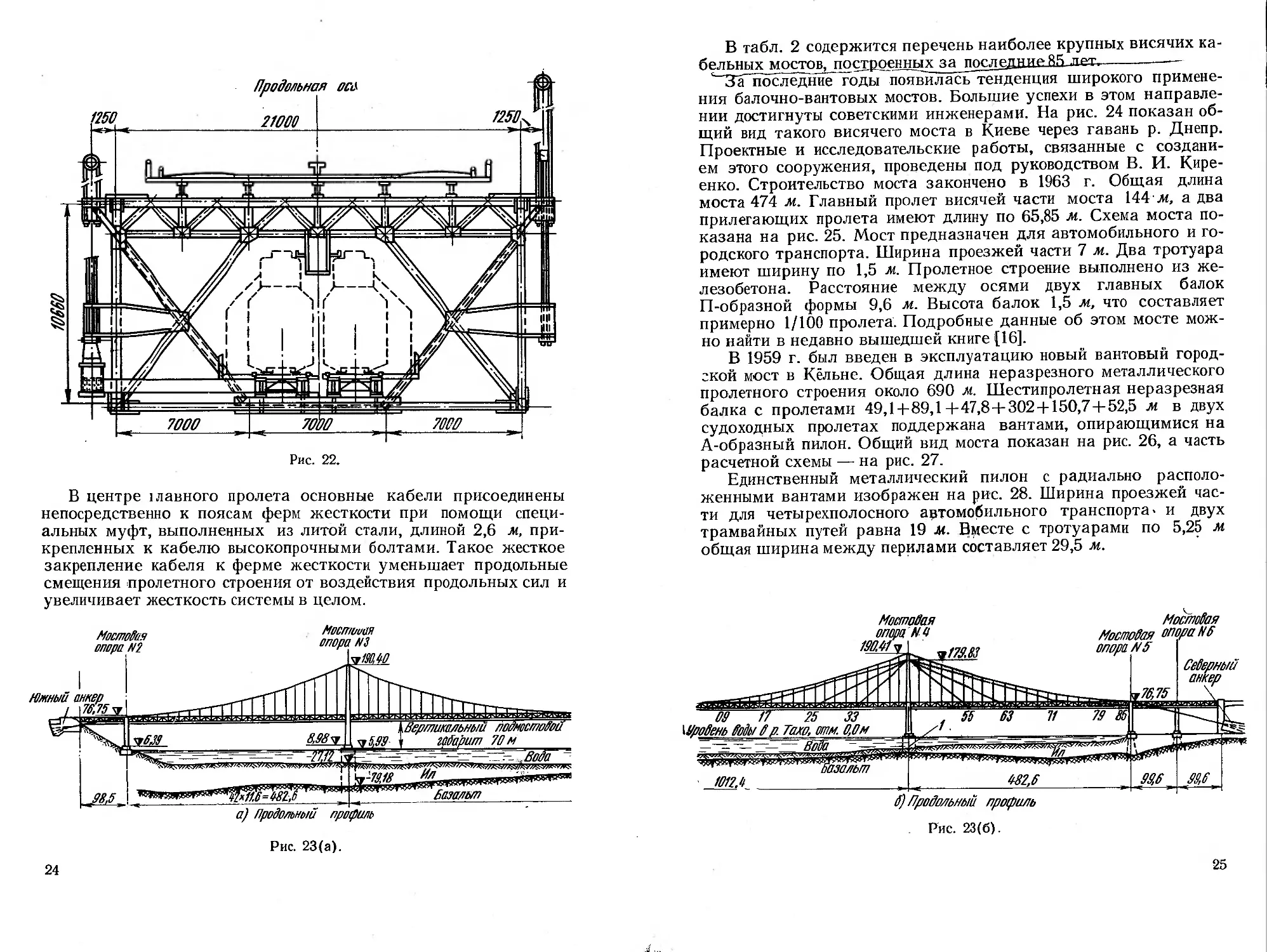
пропуска автотранспорта в верхнем ярусе (рис. 21), проезжая 
часть — четырехполосная. Проектом предусмотрено дальнейшее
сооружение двухколейной железной дороги на нижнем ярусе (
(рис. 22).
На рис. 23 показана общая схема мостового перехода. На
левой части рисунка изображена схема построенного моста, по
которому в настоящее время открыто автомобильное движение.
На правой части показана схема моста в том варианте, в каком
он будет выполнен после завершения 2-й очереди строительства.
На этом рисунке видны ванты и дополнительный кабель. Ванты
и дополнительный кабель увеличивают грузоподъемность моста
и тем самым обеспечивают пропуск железнодорожного транспор-
та по нижнему^ ярусу. Дополнительный кабель состоит из 20 ка-
натов диаметром 75 мм, предварительно свитых из стальной
проволоки. Короткие ванты состоят из 8 предварительно свитых
стальных канатов, каждый диаметром 67 мм. Длинные ванты
состоят из 12 канатов того же диаметра. Фермы пролетного
строения выполнены неразрезными на протяжении 6 пролетов
(главного пролета, двух боковых и трех береговых пролетов).
Общая длина ферм 2275 м. Таким образом этот мост имеет са-
мые длинные в мире неразрезные фермы жесткости. Высота
фермы между осями поясов равна 10,6 м, что составляет 1/95
главного пролета. Ферма жесткости поддерживается двумя глав-
ными кабелями. Диаметр каждого равен 700 мм.
Кабель состоит из 37 прядей по 304 проволоки в каждой, т. е.
всего 11248 оцинкованных проволок диаметром 4 мм. Площадь
поперечного сечения кабеля равна 2190 см2. На изготовление
главных кабелей потребовалось 54 тыс. км проволоки. Стрела
провисания главных кабелей равна 106 м или 1/9,5 главного про-
лета.
Фермы жесткости поддерживаются подвесками из стальных
канатов, расположенных на расстоянии 22,8 м. Каждая подвес-
ка диаметром 57 м выполнена из троса, состоящего из оцинко-
ванной проволоки.
23
Рис. 22.
В центре ыавного пролета основные кабели присоединены
непосредственно к поясам ферм жесткости при помощи специ-
альных муфт, выполненных из литой стали, длиной 2,6 м, при-
крепленных к кабелю высокопрочными болтами. Такое жесткое
закрепление кабеля к ферме жесткости уменьшает продольные
смещения пролетного строения от воздействия продольных сил и
увеличивает жесткость системы в целом.
Рис. 23(a).
24
В табл. 2 содержится перечень наиболее крупных висячих ка-
бельных мостов, построенных за последние 85 лет.------—-
^З^пбследние годы появилась тенденция широкого примене-
ния балочно-вантовых мостов. Большие успехи в этом направле-
нии достигнуты советскими инженерами. На рис. 24 показан об-
щий вид такого висячего моста в Киеве через гавань р. Днепр.
Проектные и исследовательские работы, связанные с создани-
ем этого сооружения, проведены под руководством В. И. Кире-
енко. Строительство моста закончено в 1963 г. Общая длина
моста 474 м. Главный пролет висячей части моста 144 м, а два
прилегающих пролета имеют длину по 65,85 м. Схема моста по-
казана на рис. 25. Мост предназначен для автомобильного и го-
родского транспорта. Ширина проезжей части 7 м. Два тротуара
имеют ширину по 1,5 м. Пролетное строение выполнено из же-
лезобетона. Расстояние между осями двух главных балок
П-образной формы 9,6 м. Высота балок 1,5 м, что составляет
примерно 1/100 пролета. Подробные данные об этом мосте мож-
но найти в недавно вышедшей книге [16].
В 1959 г. был введен в эксплуатацию новый вантовый город-
ской мост в Кёльне. Общая длина неразрезного металлического
пролетного строения около 690 м. Шестипролетная неразрезная
балка с пролетами 49,14-89,1+47,8 + 3024-150,7 + 52,5 м в двух
судоходных пролетах поддержана вантами, опирающимися на
А-образный пилон. Общий вид моста показан на рис. 26, а часть
расчетной схемы — на рис. 27.
Единственный металлический пилон с радиально располо-
женными вантами изображен на рис. 28. Ширина проезжей час-
ти для четырехполосного автомобильного транспорта' и двух
трамвайных путей равна 19 м. Вместе с тротуарами по 5,25 м
общая ширина между перилами составляет 29,5 м.
Мостовая	Мостовая
опора N в	Мостовая опора Nв
Рис. 23(6).
25
Таблица 2
Название моста	Место размещения моста	Дата возведе- ния	Размер глав- ного пролета, м	Ширина меж- ду кабелями, м	Высота балки жесткости, м	Отношение ширины балки жесткости к пролету,м	Отношение высоты балки жесткости к пролету,	Количество кабелей, шг	Диаметр ка- беля, см
‘•Бруклинский	Нью-Йорк	1883	486	25,9	5,18	1:19	1:94	4	39,4
Амбассадорский	Детройт—Мичиган	1929	563	18,1	6,71	1:31	1:84	2	48,9
Г. Вашингтона	Нью-Йорк	1931	1067	32,3	9,14	1:33	1:117	4	91,4
Трансбайский	Сан-Франциско	1936	704	20,1	9,14	1:33	1:85	2	72,7
Золотые Ворота	. Сан-Франциско	1937	1280	27,4	7,62	1:47	1:168	2	92,7
Такомский (старый)	Такома—Вашингтон	1940	853	11,9	2,44	1:72	1:350	2	45,8
Такомский (новый)	Такома—Вашингтон	1950	853	'18,3	10,10	1:47	1:85	2	50,8
Маккинакский	Мичиган	1957	1158	27,0	11,58	1:56	1:100	2	61,6
Танкервильский	Франция	1959	608	16,0	6,0	1:38	1:101	2	60,0
Фортский	Великобритания	1964	1006	23,5	9,15	1:43	1:109	2	59,7
Верразано Нерроуз	Нью-Йорк	1965	1298	51,4	7,31	1:41	1:177	4	91,4
Северенский	Великобритания	1966	988	22,9	3,04	1:43	1:324	2	53,3
Мост через р. Тахо	Лиссабон	1966	1012	23,5	10^66	1:43	1:95	2	70,0
Рис. 26. Городские мосты через р. Рейн в Кёльне. На переднем
плане вантовый мост, построенный в 1959 г.
Рис. 28. Пилон вантового моста через
р. Рейн в Кёльне
Рис. 29. Подходы к Кёльнскому вантовому мосту
Рис. 30. Вантовый мост в Дюссельдорфе с главным пролетом
260 м (построен в 1957 г.)
Ванты выполнены из пучков канатов с временным сопро-
тивлением проволоки 14 000 кГ/см2. Расстояние между осями
двух главных балок 22,3 м. Коробчатое сечение этих балок при-
нято с учетом размещения коммуникаций. Ноги пилона решены в
виде коробчатой стальной конструкции с толщиной стенок от
12 до 30 мм. Высота моста над высшим навигационным уровнем
9,1 м. Подходы к мосту выполнены в нескольких уровнях, как
видно из рис. 29.
В отличие от двух описанных выше мостов применяются
мосты с вантами, расположенными параллельно друг другу.
Примером такого сооружения может служить мост через р. Рейн
в Дюссельдорфе, построенный по проекту проф. Таммса в
1957 г. Общий вид этого моста, представляющего собой трех-
пролетную неразрезную железобетонную балку, поддержанную
системой параллельных вант (система «арфа»), показан на
рис. 30.
Главный пролет равен 260 м, а два боковых пролета — по
# 108 м каждый. Ширина проезжей части моста 15 м. На консолях
расположены два тротуара по 5,8 м. Расстояние между центра-
ми двух продольных балок коробчатого сечения 17,6 м. Высота
с сечения балок 3,12 м, что составляет примерно 1/80 от длины
среднего пролета.
29
':,.Л
&
Верхние и нижние ванты- оперты на пилоне с помощью опор-
ных частей, а средние — жёстко соединены с пилоном. Подроб-
ное описание этого интересного сооружения приводится в книге
В. И. Киреенко [16].
В заключение отметим, что в настоящий краткий обзор
включена лишь небольшая часть осуществленных висячих мос-
тов. Обзор предусматривал ознакомить читателя с висячими мо-
стами лишь в самых общих чертах.
§ 3.	КРАТКОЕ ОПИСАНИЕ ТАНКЕРВИЛЬСКОГО
ВИСЯЧЕГО МОСТА
Танкервил'ьский мост построен во Франции через залив в
устье р. Сены в 1959 г. Он расположен между Гавром и Руаном
и является как бы граничным пунктом, разделяющим Норман-
дию на две части.
Сена в низовьи имеет значительную ширину. Большая длина
моста, огромное водное пространство и особенности рельефа
местности поставили перед инженерами и архитекторами слож-
ную композиционную задачу, которая была успешно решена. Об-
щий вид моста показан на рис. 31.
В строительстве моста принимали участие двенадцать круп-
ных фирм, в которые входили фактически все мостостроительные
организации Франции. Расчеты моста в процессе его проектиро-
вания проводились с использованием самых современных элек-
тронных вычислительных машин. При этом, кроме основного
расчета, проводились расчеты системы для всех промежуточных
состояний, которые могли возникнуть в процессе сборки конст-
рукции.
Параллельно с аналитическим расчетом в большом масштабе
были проведены экспериментальные исследования. Для всех ос-
новных узлов моста изготовлялись модели, которые подверга-
лись испытаниям в лабораториях с использованием современной
измерительной аппаратуры и методов фотоупругости.
Самым опасным врагом современных крупных висячих мос-
тов является ветер. За последнее время особенно большое вни-
мание при проектировании мостов стали уделять аэродинамиче-
ским расчетам. Слишком большим уроком для строителей яви-
лось крушение Такомского моста. Авторы Танкервилнекого мос-
та проявили заботу о повышении сопротивляемости конструкции
ураганному ветру. С этой целью для проведения теоретических
расчетов были привлечены два крупных специалиста в этой об-
ласти: проф. Парижского университета (Сорбонны) И. Рокар и
президент Societe Baundin—Chateauneuf М. Шадансон. Были
проведены тщательные аналитические расчеты по выявлению
аэродинамической устойчивости моста. Расчеты показали, что-
30 •
Рис. 31. Общий вид Танкервильского висячего моста, построенного
во Франции через залив в устье р. Сены в 1959 г. Общая длина
моста 1400 м
мост при любых ветровых воздействиях представляет собой ус-
тойчивую систему. Несмотря на это, были проведены серьезные
экспериментальные проверки устойчивости системы путем про-
дувки модели в аэродинамической трубе. Эти эксперименты сви-
детельствовали о правильности проведенных расчетов.
Аналогичный подход применялся при проверке прочности раз-
личных деталей или частей моста. Каждый раз производился
двойной контроль, основанный, с одной стороны, на точных рас-
четах и, с другой—на тщательных испытаниях. Таким образом,
'при проектировании моста были использованы все достижения
современной науки в области расчетов и экспериментальных ис-
следований строительных конструкций.
Ч, Аналогичный серьезный подход проявлялся к вопросам орга-
•йнизации строительных работ. Большое внимание было уделено
подбору квалифицированных инженерно-технических кадров и
@ рабочих. В особенности это касалось лиц, связанных с выполне-
#Нием монтажных работ. Достаточно сказать, что во время по-
дстройки моста потребовалось около трех с половиной миллионов
Жчасов на акробатические работы опытных верхолазов. Тщатель-
жйой подготовкой всех видов работ можно объяснить то, что за
Jpce время строительства не было ни одного несчастного случая.
I	31
5,1
Рис. 32.
Окончание строительства было осуществлено на 15 дней раньше
намеченного срока, несмотря на небывалые для тех мест небла-
гоприятные метеорологические условия, которые наблюдались в
период строительства в начале 1956 г., и некоторое возрастание
объема работ по возведению фундаментов на левобережной
пойме (из-за того что строители встретились с плохими грун-
тами) .
Таким образом, Танкервильский мост во всех отношениях
являлся интересным объектом. Тщательное изучение проблемы
перехода в сложных условиях, научный подход к вопросам про-
ектирования и организации работ, безукоризненное выполнение
деталей конструкции, а также высокие эстетические достоинст-
ва позволяют отнести этот мост к наиболее замечательным ин-
женерным сооружениям современности. Указанное обстоятель-
ство послужило причиной выбора этого моста в качестве приме-
ра, который помещен в эту книгу.
Танкервильский мост расположен в живописной местности
32
Нормандии. Высокий правый берег Сены состоит из сплошного'
скального массива, а на левом берегу имеется широкая пойма.
Общая схема моста показана на рис. 32, а. Из нее видно, что
Танкервильский мост состоит из двух частей. Первая часть пред-
ставляет собой трехпролетный висячий мост с пролетами:
176+608+ 176 эи, а вторая — эстакаду балочного типа, состоя-
щую из восьми пролетов по 50 м каждый. На стыке двух систем
расположен массивный устой длиной.40,2 м. Общая длина моста
равна Д400,2 м. Балка жесткости моста поддерживается двумя
кабелями, каждый из которых состоит из 56 тросов, соединен-
ных в шестиугольное сечение, имеющее наименьший размер
0,58 м и наибольший (по диагонали) 0,65 м. Поперечное сечение
моста показано на рис. 32, б, на котором показаны основные
размеры.
Судоходный подмостовой габарит обеспечивается высотой
50,85 м и позволяет пропускать суда без каких-либо ограниче-
ний. На протяжении моста проезжая часть имеет уклон 0,3%.
Стрела провисания кабеля в главном пролете равна 67,4 м, что
составляет 1/9 от величины пролета.
Основной отличительной особенностью висячей части этого
моста является жесткое скрепление кабеля с фермой в средине
пролета. На рис. 33 показана упрощенная схема моста с точкой
О, в которой осуществлено это крепление. Исследование, прове-
денное в § 11 гл. V, где излагается метод расчета такой системы,
показывает, что скрепление кабеля с балкой жесткости в значи-
тельной степени увеличивает жесткость всей системы в целом.
За счет указанного скрепления распор в левой и правой частях
кабеля от временной нагрузки, расположенной на половине про-
лета, различен, поэтому на ферму жесткости и в средине моста
Передается значительная горизонтальная сила. Однако она не
вызывает существенной перегрузки фермы, так как последняя
икГеет мощные пояса.
Таким образом схема Танкервильского моста является суще-
ственно новой по сравнению со схемами других висячих мостов
больших пролетов.
Для передачи усилия от кабеля на землю обычно применя-
йся две разновидности анкеровки кабеля. Если в местах необ-
ходимого закрепления кабеля имеются слабые грунты, то соору-
2—3802	33
Рис. 33.
каются массивные устои, в тело которых производится анкеров-
ка кабеля. При наличии скальных пород анкеровка кабеля
производится непосредственно в скалу. В Танкервильском мосте
крепление кабеля на левом берегу осуществлено по первому, а на
правом берегу — по второму способу.
На рис. 34 показан общий вид устоя левого берега, в котором
произведена анкеровка кабеля. Схематическое изображение рас-
положения анкерного устройства дано на рис. 35. На этом же
рисунке показаны генеральные размеры устоя. Данный устой
контрфорсного типа был тщательно обследован французскими
инженерами. Армирование устоя было назначено в соответствии
с законом распределения силовых потоков, передающихся от ка-
беля на устой. Для этой цели был изучен закон распределения
траекторий главных напряжений (рис. 36). Пунктирными линия-
ми изображены траектории сжимающих, а жирными линиями —
растягивающих напряжений. Детальное изучение напряженного
состояния позволило назначить наивыгодное армирование устоя,
обеспечившее его высокую прочность.
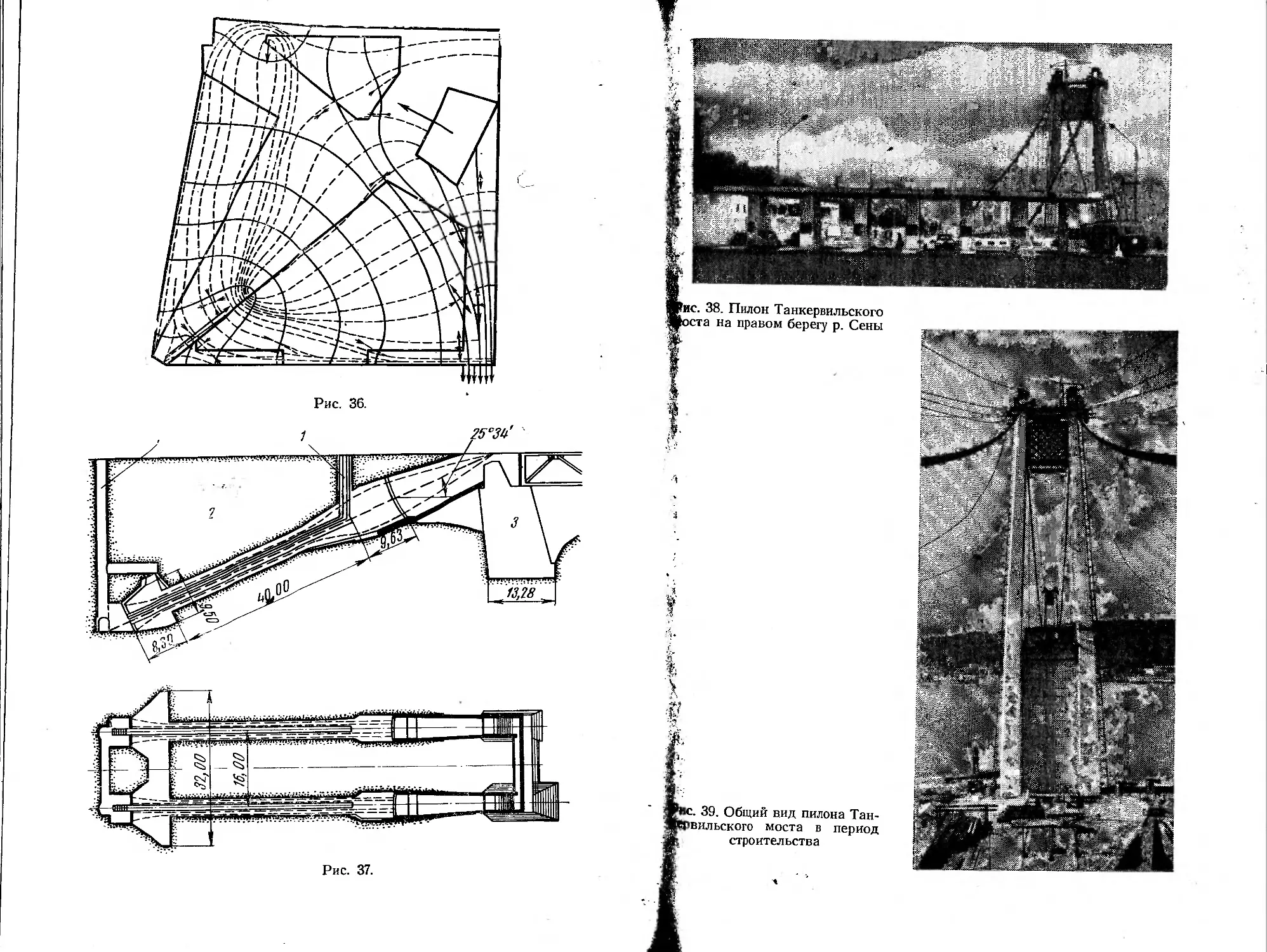
Анкеровка кабеля на правом берегу произведена в тоннеле,
проложенном в скале под углом 25°34' к горизонту (рис. 37).
Сила натяжения кабеля передается на скальные породы. Для
опирания конца фермы жесткости устраивается маленький устой
3, работающий в основном на восприятие вертикального давле-
ния. Два наклонных туннеля, в которых проходят кабели, соеди-
нены с поверхностью земли двумя колодцами 1, которые позво-
ляют производить осмотр и облегчают монтажные работы. Глу-
бина заложения анкера должна рассчитываться на условия
выкалывания скального массива 2, которое может оказаться ве-
роятным при выдергивании кабеля. Закрепление кабеля в скале
приводит к более экономичному решению, чем устройство мас-
сивного устоя, описанного выше. Кроме того, при закреплении
кабеля в скале улучшается внешний вид сооружения, как это
видно из рис. 38, на котором показан правый берег со стороны
примыкающей к мосту эстакады. Отсутствие массивного устоя
придает сооружению вид легкой конструкции.
Железобетонные пилоны моста выполнены в виде плоской
рамы с наклонными стойками переменного сечения (рис. 39).
Высота пилона от уступа фундамента до верха равна 123,4 м.
Расстояние между осями стоек внизу равно 24,7 м, а вверху —
16,00 м. Глубина заложения фундамента с квадратным сечением
12,0X12,0 м под каждой стойкой составляет 18,0 м. В нижней
34
Рис. 34. Общий вид левобережного устоя Тан-
кервильского моста, в котором произведена
анкеровка кабелей
А
1=
Я
Рис. 35.
Рис. 37.
tac. 38. Пилон Танкервильского
юста на правом берегу р. Сены
39. Общий вид пилона Тан-
моста в период
строительства
части стойки соединены сплошной стенкой шириной 18,15 м и
толщиной 0,6 м. Фундаменты с кессонным основанием соединены
вверху плитой, как показано на рис. 40. При расчете фундамен-
тов нога пилона считалась жестко заделанной в тело фундамен-
та. При проектировании было проведено тщательное исследова-
ние напряженного состояния в месте уступа фундамента. С этой
целью был проведен точный расчет для случаев, когда момент
равен 0 и действует только сжимающая сила, а также для слу-
чая действия максимального момента. На рис. 41 слева от верти-
кальной оси показаны изоклины (линии, соединяющие точки с
одинаковыми напряжениями), а справа—траектории главных,
напряжений для первого случая.
При действии максимального момента симметрия в распре-
делении напряжений нарушается. На рис. 42 показаны изоклины,
а на рис. 43 — траектории главных напряжений при действии
максимального момента. На всех трех фигурах, изображающих,
изоклины и траектории главных напряжений, показаны точки А
и В, разграничивающие существенно отличные зоны напряже-
ний, по линии сопряжения этих зон действуют наибольшие каса-
тельные напряжения.
Такой подробный расчет следует считать оправданным, так
как он позволяет установить оптимальную схему армирования
системы, позволяющую предотвратить трещинообразование и
выявить опасные зоны с точки зрения возможного откалывания
тела опоры.
При проектировании Танкервильского моста расчету пилона
уделено большое внимание. Помимо обычного расчета на дейст-
вие вертикальных нагрузок и ветра производился расчет пилона
по деформированной схеме (с учетом продольно-поперечного из-
гиба).
На линии опирания пролетного строения ноги пилона соеди-
нены мощной распоркой. Пролетное строение проходит в среди-
не между колоннами. Общий вид пилона с частью пролетного
строения, кабелями и подвесками показан на рис. 44.
Пролетное строение висячей части моста состоит из двух не-
разрезных трехпролетных ферм с треугольной решеткой. Конст-
рукция ферм чрезвычайно проста. На рис. 45 показан фрагмент
пролетного строения, из которого видны основные конструктив-
ные решения узлов и элементов фермы. В уровне поясов постав-
лены обычные ветровые связи.
Большой интерес представляет собой узел крепления кабеля
к пролетному строению в средине моста. С помощью литого
стального ствола, состоящего из двух половин, кабель зажимает-
ся как бы в обойму. Две половины ствола соединяются болтами
в единое целое с помощью 68 высокопрочных болтов по 45 мм в
диаметре, а затем весь ствол жестко скрепляется с поясом фер-
мы с помощью 192 болтов диаметром 40 мм. Длина этого ствола
38
00'81
Рис. 40.
Рис. 41.
Рис. 42.
- ,7
Рис. 43.
равна 6 м. Силы трения не позволяют кабелю проскальзывать
внутри канала ствола. Общий вид описанного узла показан на
рис. 46.^/^.
Остановимся в общих чертах на производстве строительных
работ при сооружении Танкервильского моста. При сооружении
фундаментов для пилонов Танкервильского моста применялись
кессонные основания. На рис. 47 показаны два квадратных кес-
сонных фундамента в процессе их возведения. На этом рисунке
видны 9 цилиндрических пустот, которые предусмотрены по про-
екту. Схемы фундаментов были показаны на рис. 40.
Большое значение при кессонных работах имеет точность
посадки кессона. Для высоких пилонов малое отклонение опоры
от вертикальной оси приведет к большому отклонению верха пи-
лона. Этим объясняются высокие требования к производству
кессонных работ.
При сооружении пилонов Танкервильского моста пришлось
решать сложную задачу о выправлении одного из пилонов. На
рис. 48 показана схема, объясняющая отклонение пилона в двух
направлениях, а на рис. 49 показан план расположения домкра-
40
Рис. 44. Общий вид пилона
Танкервильского моста в
начале сборки балки жест-
кости
1
i
I
Рис. 45. Момент сборки
пролетного строения
Рис. 46. Общий вид узла крепления кабеля к бал-
ке жесткости
тов и, кроме того, они показаны в разрезе. Всего для выправле-
ния пилона было установлено три группы домкратов: группа
В — 28 домкратов по 300 т, группа С — 8 домкратов по 550 т и
группа Д — 4 домкрата по 500 т. Все домкраты вместе развива-
ли суммарную силу 14 800 т. С помощью указанных домкратов-
удалось выправить пилон и привести его в вертикальное поло-
жение.
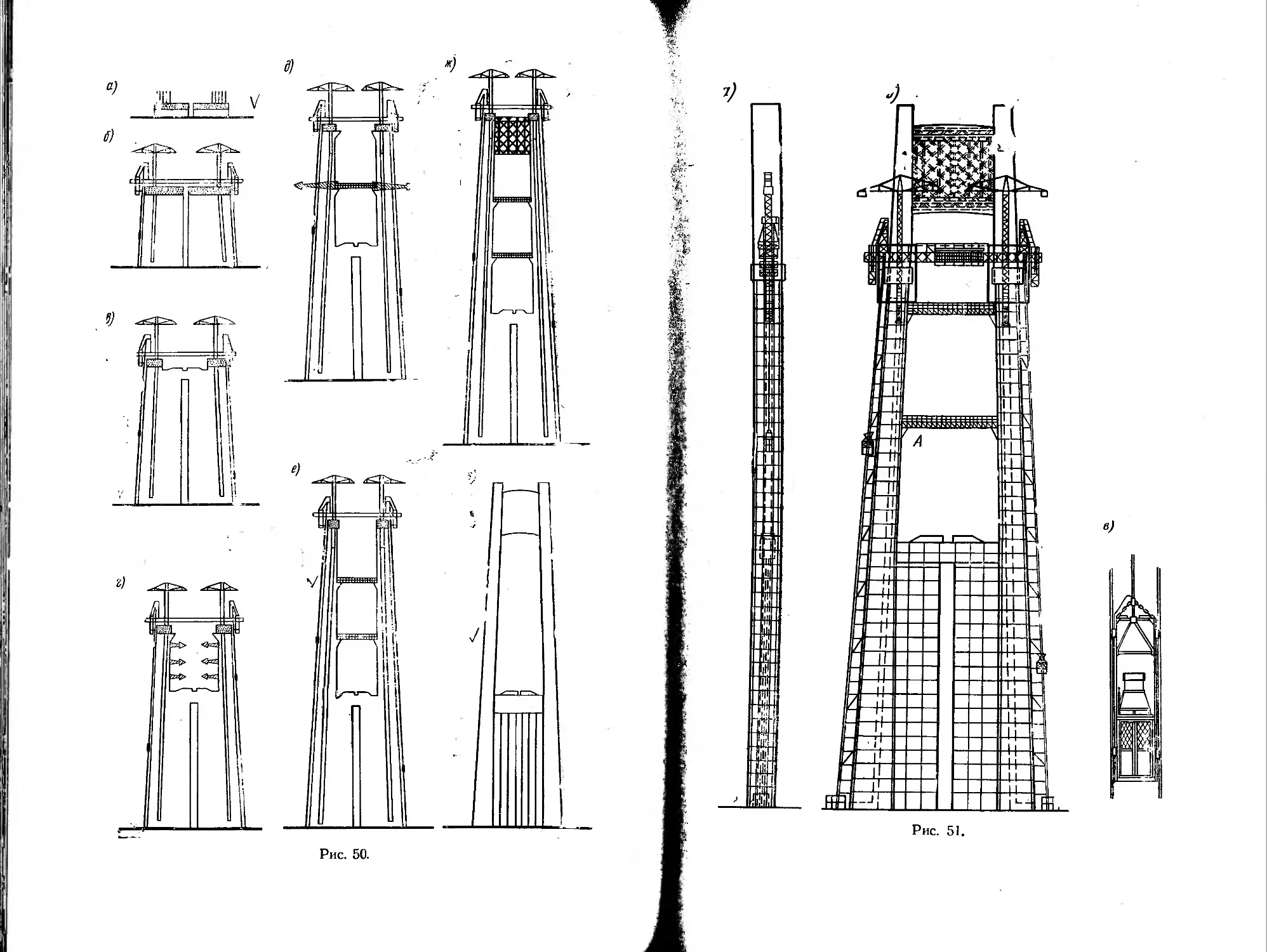
Рассмотрим последовательность работ при строительстве пи-
лона Танкервильского моста. На рис. 50 схематически показаны
стадии сооружения пилона. На схеме а мы видим готовый фун-
дамент с выпущенной арматурой для стоек и стенки пилона. На
схеме в показана стадия, на которой понадобилось впервые ус-
тановить лифты по боковым граням. С помощью этих лифтов по-
давались арматурные каркасы и бетон. Наверху непрерывно ра—
Рис. 47. Кессонные фундаменты в процессе возведения опор
42
«ботали два крана, кото-
рые по мере увеличения
высоты пилона постепен-
но поднимались вверх.
-Стадия в соответствует
-случаю, когда высота опо-
ры превысила уровень
расположения опорных
'частей пролетного строе-
ния. Дальнейшая сборка
каждой колонны пилона
производилась по отдель-
ности. По мере возвыше-
ния колонн их гибкость
возрастает, поэтому появ-
ляется опасность больших
колебаний. С целью устра-
нения этих колебаний де-
Рис. 48.
Дались временные распор-
tu, соединяющие колонны в единую раму. На стадии г стрелками
оказаны направления возможных перемещений при колебаниях.
;В верхней части колонны видны маленькие треугольные консоли
шля первой временной распорки. На стадии д показан выход на
Ягровень второй временной распорки. Стадия е соответствует от-
метке низа постоянной верхней распорки. В последней стадии з
«оказан готовый пилон.
,74.45
Рис. 49.
43
Рис. 50.

Рис. 51.
Рис. 52. Общий вид пилона в период завер-
шения его строительства
На рис. 51 с обеих сторон пилона показаны лифты. Они
поставлены с наружных сторон, как видно на рис. 51, а и 51, б.
Более полное представление о лифтах можно получить из
рис. 51, в. На этом же рисунке можно видеть конструктивное ре-
шение системы передвижных кранов и деталь временной распор-
ки. Фотография пилона в момент последней завершающей ста-
дии работы показана на рис. 52.
Все работы по сооружению пилона (кроме фундамента) про-
изводились в течение 7,5 месяцев. На рис. 53 показан график
производства работ по сооружению пилона. На этом графике
жирной линией показан план выполнения работ, намеченный по
контракту, а пунктирной линией—фактическое выполнение
плана. Сравнение двух кривых свидетельствует о четкости в ор-
ганизации работ.
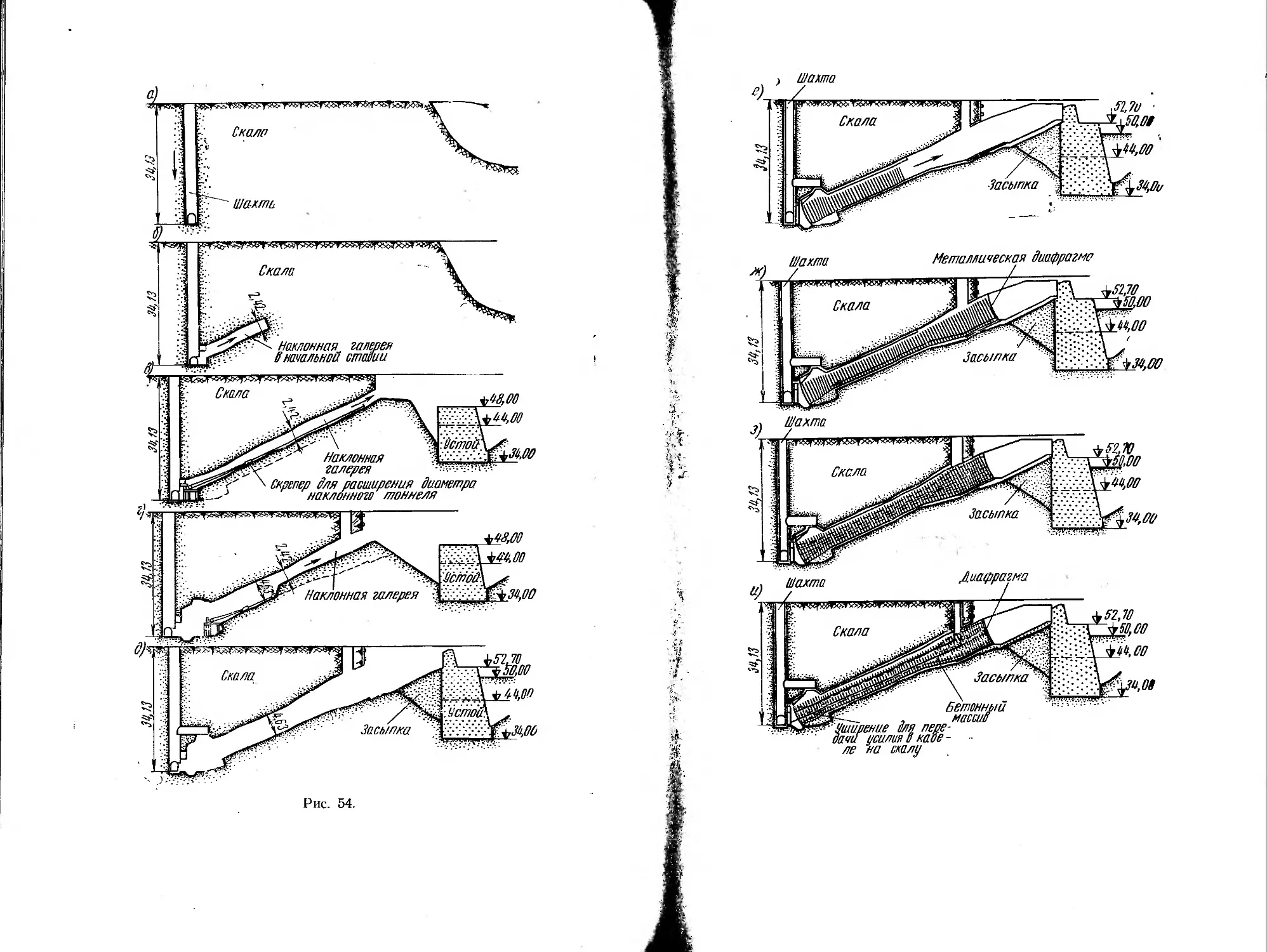
На рис. 54 показаны стадии работ по устройству анкерного
закрепления кабеля в скале. Первая начальная стадия, показан-
ная на схеме а, состоит в проходке вертикальной шахты до наи-
низшей точки на глубину 34,13 м. При рытье шахты применяют-
ся обычные приемы производства работ, оправдавшие себя в тон-
нелестроении.
Вторая стадия, изображенная на схеме б, соответствует
первому периоду проходки наклонного тоннеля. Вначале тоннель
вырабатывается малого диаметра. Удаление породы производит-
ся через вертикальную шахту. На схеме в мы видим работы по
46
Рис. 53.
Рис. 54.
ID а кт о
Метшическая
диафрагма
расширению диаметра
наклонного тоннеля.
Одновременно произво-
дится бетонирование
устоя эстакады. Даль-
нейшее развитие фрон-
та работ показано на
схемах г и д. Этим за-
вершается первый пе-
риод работ.
Во втором периоде,
начиная со схемы е, развертываются работы по устройству анке-
ра. Вначале производится установка частей металлоконструкций
в нижней части тоннеля. Внизу устраивается помещение ввиду
шарового объема ж, где расширяются концы анкерных стержней.
После окончания сборки всех анкерных тяжей, как показано на
схеме з, производится бетонировка тоннеля. На схеме и показан
забетонированный массив. Из этого массива выпущены анкер-
ные тяжи, к которым при монтаже прикрепляются пряди кабеля.
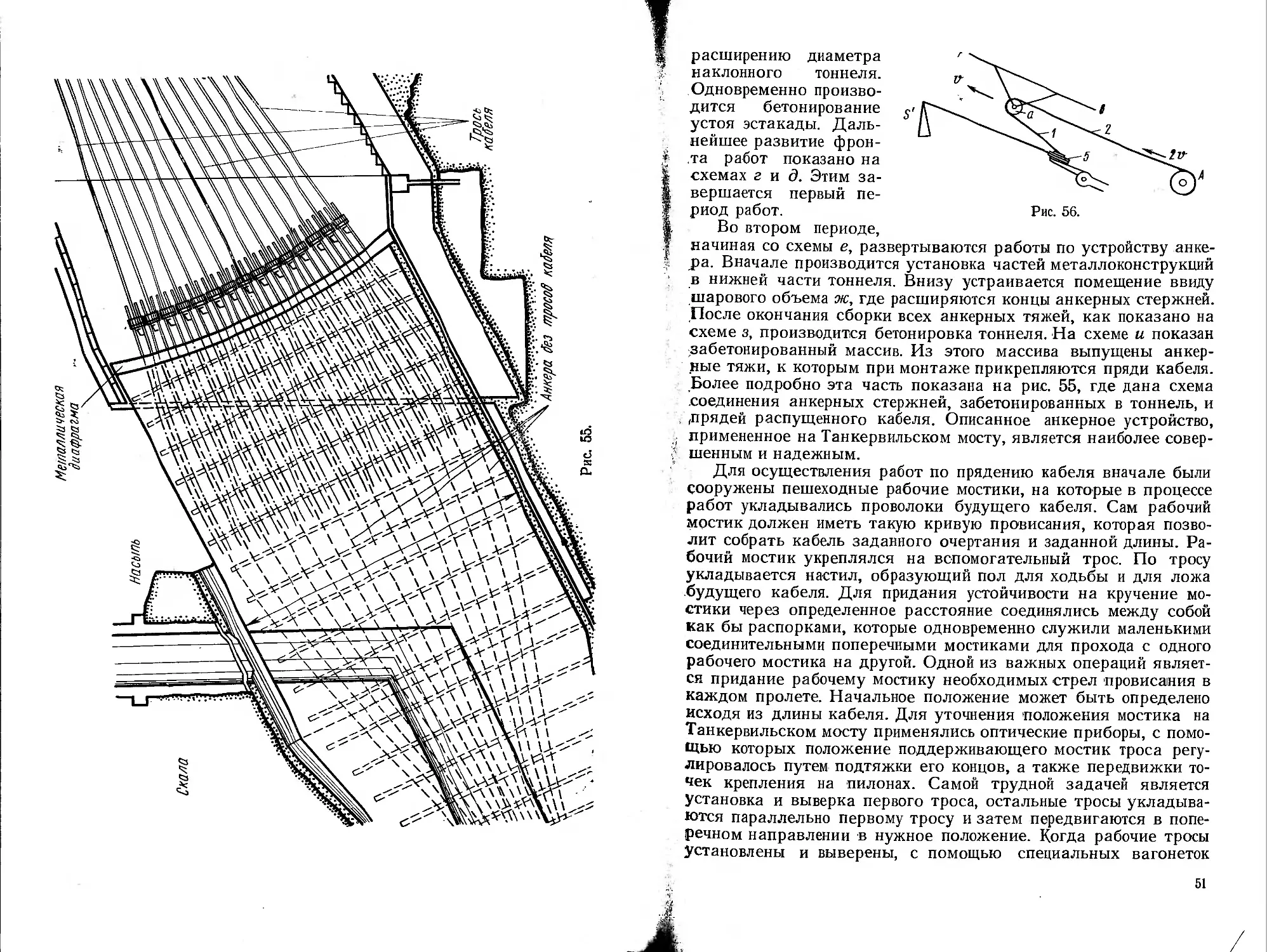
Более подробно эта часть показана на рис. 55, где дана схема
соединения анкерных стержней, забетонированных в тоннель, и
, дрядей распущенного кабеля. Описанное анкерное устройство,
; примененное на Танкервильском мосту, является наиболее совер-
f шенным и надежным.
Для осуществления работ по прядению кабеля вначале были
сооружены пешеходные рабочие мостики, на которые в процессе
работ укладывались проволоки будущего кабеля. Сам рабочий
мостик должен иметь такую кривую провисания, которая позво-
лит собрать кабель заданного очертания и заданной длины. Ра-
бочий мостик укреплялся на вспомогательный трос. По тросу
укладывается настил, образующий пол для ходьбы и для ложа
будущего кабеля. Для придания устойчивости на кручение мо-
стики через определенное расстояние соединялись между собой
как бы распорками, которые одновременно служили маленькими
соединительными поперечными мостиками для прохода с одного
рабочего мостика на другой. Одной из важных операций являет-
ся придание рабочему мостику необходимых стрел провисания в
каждом пролете. Начальное положение может быть определено
исходя из длины кабеля. Для уточнения положения мостика на
Танкервильском мосту применялись оптические приборы, с помо-
щью которых положение поддерживающего мостик троса регу-
лировалось путем подтяжки его концов, а также передвижки то-
чек крепления на пилонах. Самой трудной задачей является
установка и выверка первого троса, остальные тросы укладыва-
ются параллельно первому тросу и затем передвигаются в попе-
речном направлении в нужное положение. Когда рабочие тросы
установлены и выверены, с помощью специальных вагонеток
51
производятся работы по устройству настила. По окончании всех
работ, связанных с устройством рабочих мостиков, завершается
подготовительный период, после чего приступают к сооружению
кабеля.
Для плетения кабеля еще в конце прошлого столетия амери-
канским инженером Реблингом была разработана удачная тех-
нология, которая с небольшими изменениями применяется по
настоящее время. Существо этого метода заключается в следу-
ющем. По тросам, протянутым над рабочим мостиком, параллель-
но настилу на высоте 5—6 м движутся свивочные колеса. Для
перемещения сбивочного колеса к нему прикреплены тянущие
канаты, передвигающие колесо в ту или другую сторону. Таким
образом два свивочных колеса движутся навстречу друг к другу.
Каждое колесо тянет проволоку, которая перекинута через него.
Схема движения колеса с проволокой показана на рис. 56.
Колесо а, прикрепленное к бесконечному движущемуся канату в.
Таких колес на канате два. Когда одно колесо прибудет на
левый устой, второе окажется на правом устое. Колесо а, как
видно из схемы, тянет через реку две линии проволок: 1 и 2.
Ветвь проволоки 1 является неподвижной, а ветвь 2 — подвижной.
Если колесо а движется в сторону, указанную стрелкой, со ско-
ростью v, то проволока сматывается с барабана А со скоростью
2 V. Когда колесо прибудет на устой, то канат в останавливает-
ся. Петля из двух проволок снимается с колеса а и одевается на
башмак анкерного устройства. Такая же операция производится
на противоположном устое. После этого колеса захватывают
следующие ветви проволоки и включается мотор, движущий бес-
конечный канат в. Оба колеса пойдут навстречу друг к другу.
В средине моста они пройдут мимо друг друга (одно на левой,
другое на правой ветви бесконечного каната в) и затем по при-
бытии на устой остановятся. Затем все операции повторяются
вновь.
Скорость движения навивочных колес при постройке каждого
нового моста постепенно возрастает. По мере того как колесо
удаляется от какого-либо сечения кабеля, проволока 1 подтяги-
вается к направляющей проволоке и присоединяется к форми-
рующемуся пучку кабеля. Вторая ветвь выравнивается и присое-
диняется к пучку в момент стоянки колес на устоях.
По описанной выше схеме производилось плетение кабеля
Танкервильского моста.
После окончания укладки проволоки одной пряди произво-
дилось выравнивание всех проволок этой пряди. Окончательная
компоновка каждой пряди обычно проводится ночью. Это де-
лается потому, что температура всех проволок в ночное время по
всей их длине одинаковая. Днем при нагреве пряди солнцем тем-
пература освещенных проволок большая, чем затемненных от
солнца. Пряди, сформированные при солнце, после остывания
52
Рис. 57. Общий вид Танкервильского моста в период сборки
Рис. 58. Расположение крана установ-
ленного на балке жесткости в период
сборки
Рис. 59. Присоединение секции фермы в период
сборки Танкервильского моста
будут иметь неравно-
мерное натяжение про-
волок. Таким образом,
изготовление кабеля
связано с работой в
ночных условиях, что
требует большой ква-
лификации мастеров и
рабочих, а также раз-
работки системы осве-
щения.
Навесная сборка
балки жесткости начи-
нается после того, как
все работы по возведе-
нию кабеля и его за-
креплению на опорах
завершены. При навес-
ной сборке вначале на
специально оборудо-
ванной площадке про-
изводится сборка укру-
пненных элементов.
Эти элементы достав-
ляются к мосту с по-
мощью наплавных
средств и поднимаются
затем в проектное по-
ложение. Сборка обыч-
но начинается от пило-
нов и проводится в обе
стороны — как внутрь
главного пролета, так и
в боковой пролет. В
первую очередь уста-
навливаются секции,
непосредственно опи-
рающиеся на пилон, ко-
торые ставятся на опор-
ные части. Одновре-
менно концы элементов
подвешиваются к ка-
белю. Постепенное на-
ращивание балки жест-
кости производится
симметрично относи-
тельно обоих пилонов.
Рис. 60. Общий вид металлических
листов верхнего пояса с шипами
до момента бетонирования плиты
проезжей части
После того как длины со-
бранных участков увеличатся
на столько, что перемещения
кабеля достигнут ощутимых
величин, начинают подвеши-
вать части балки в средине
пролета. Таким образом про-
исходит постепенная сборка от
средины пролета к пилонам.
Соблюдение симметричного на-
ращивания балок обеспечивает
сравнительно малое формоиз-
менение кабеля. Таким спосо-
бом происходила сборка ферм
жесткости Танкервильского мо-
ста. На рис. 57 показан общий
вид моста в одном из промежу-
точных состояний сборки. Для
подъема с наплавных средств
частей балки жесткости поль-
зуются кранами, установленными на собранных балках жестко-
сти (рис. 58).
На рис. 59 показан момент присоединения одной секции фер-
мы. Из этого рисунка видно, что работа при стыковании узлов
требует большого мастерства, специально обученных сборщиков-
верхолазов.
Балка жесткости в современных мостах работает совместно
с плитой проезжей части, что значительно увеличивает ее жест-
кость. Для осуществления совместной работы плиты с металли-
ческой конструкцией необходимо создать их соединение и устра-
нить возможный сдвиг плиты по металлической конструкции.
С этой целью прибегают к различным средствам. Так, например,
в конструкции Танкервильского моста были приварены к метал-
лическим листам верхнего пояса шипы, которые показаны на
рис. 60. Забетонированная железобетонная плита благодаря
многочисленным шипам соединялась с пролетным строением в
единое целое.
Бетонирование плиты, производилось, начиная от пилонов и
средины моста, с соблюдением строгой симметрии. Работы ве-
лись строго по установленному графику.
Танкервильский висячий мост является интересным инженер-
ным сооружением, при создании которого были использованы
современные достижения науки в области строительства.
§ 4. РАЗВИТИЕ ТЕОРИИ РАСЧЕТА ВИСЯЧИХ МОСТОВ
Первое математическое исследование, посвященное расчету
висячих мостов с учетом влияния собственного веса цепи и про-
езжей части, принадлежит известному французскому инженеру
и ученому, члену Парижской Академии наук, профессору школы
мостов и дорог, знаменитому математику Луи Мари Анри Навье.
Задача о равновесии цепной линии к этому времени была уже
•известна. Изучение кривой равновесия цепи, подвешенной в двух
точках, было проведено еще Эйлером примерно за сто лет до
работ Навье. Навье первый в 1823 г. вывел уравнение кривой,
которую занимает цепь под действием любой сплошной нерав-
номерной нагрузки. Рассмотрев гибкую нить под действием
•собственного веса постоянной нагрузки и частичного загру-
жения временной нагрузкой, Навье определил изменение фор-
мы кривой кабеля и нашел величину опускания полотна
моста.
Учитывая только геометрическое изменение формы цепи (без
учета растяжения кабеля), он вывел формулу для определения
прогиба средины моста под действием нагрузки, приложенной
в средней части пролета, и показал, что при одинаковом отно-
шении стрелы подъема нити к пролету прогиб не зависит от
длины, а зависит только от интенсивности постоянной нагрузки
на погонный метр моста.
Навье рассмотрел ряд вариантов однопролетных висячих
мостов, определил силы, действующие на опоры мостов, и по-
лучил формулу для определения предельного значения пролета
моста исходя из допускаемого напряжения и объемного веса
материала.
В своем исследовании Навье рассматривал примитивные
системы висячих мостов, не имеющих балки жесткости. Под-
робный анализ результатов, полученных Навье для висячих
мостов, можно найти в книге Г. П. Передерия [26].
В последующем чисто практическим путем строители приш-
ли к необходимости применения балки жесткости, подвешенной
к цепи. Однако рассчитывать такие системы они не умели.
Опыты, проведенные П. Барлоу, показали, что сравнительно
легкие балки придают висячим мостам значительную жест-
кость.
Первое аналитическое решение о распределении нагрузки
между цепью и балкой жесткости было проведено Ренкином.
Задаваясь некоторой формой кривой прогиба, Ренкин дал при-
ближенное решение, устанавливающее закон распределения на-
грузки между кабелем и балкой. Основной вывод заключается
в том, что на балку жесткости приходится примерно 4/27 от пол-
ной нагрузки, действующей на мост. Первые исследования Рен-
кина хотя и не отвечали истинной работе висячего моста, одна-
.56
ко сыграли значительную роль в развитии теории расчета этих
мостов.
В 1877 и 1883 гг. Риттер дал более точное решение указанной
задачи, а в 1886 г. М. Леви предложил рассматривать совмест-
ные деформации балки и кабеля и указал вполне научный под-
ход к решению задачи о прочности висячего моста.
В дальнейшем, после работ О. Мора по теории перемеще-
ний, расчет висячих мостов проводился методом сил как стати-
чески неопределимой системы. Нашли широкое применение
общие методы учета подвижной нагрузки с помощью линии
влияния. Однако и такой подход, как выяснилось в последующем,
давал приближенное решение, которое для кабельных мостов в-
настоящее время, как правило, не применяется.
Долгое время расчет висячих мостов проводился по линей-
ной теории. Однако в конце прошлого века появились первые-
работы, в которых предлагалось учитывать изменение очерта-
ния кабеля под действием нагрузки.
Число работ, посвященных этому новому направлению, стало
быстро расти, и в настоящее время все крупные висячие мосты,
рассчитываются с учетом изменения формы кабеля.
В приводимом ниже обзоре мы не будем касаться тех работ,
в которых расчет производится как обычной статически неопре-
делимой системы, так как в настоящее время они потеряли науч-
ную ценность.
Первое новое предложение по учету «деформированной» схе-
мы висячего моста было высказано Мюллером-Бреслау {139] в
1881 г. Более подробно развил эту теорию в 1888 г. Мелан [130].
В 1904 г. эта теория была применена в расчетах Манхаттан-
ского моста Моисеевым, который несколько дополнил труды Ме-
лана.
В 1909 г. Д. Б. Штейнман опубликовал работу, в которой дал
дальнейшее развитие теории Мелана. Эта работа вошла в после-
дующем в монографию [165], которая рассматривается ниже.
Уже в то время Меланом и Штейнманом было показано, что
максимальные изгибающие моменты в балке жесткости при бо-
лее точном расчете по деформированной схеме значительно
меньше, чем найденные по линейной теории с применением ме-
тода сил.
Позднее, в 1928 г., С. П. Тимошенко предложил приближен-
ный метод расчета [182], основанный на применении тригономет-
рических рядов. Он показал, что расчет по деформированной
теории позволяет более точно установить силы взаимодействия
между балкой жесткости и кабелем, которые в старой теории
принимались равномерно распределенными по всей длине моста.
Профессор И. Я. Штаерман в своей работе [60] показал, как
проводить расчет при наличии переменного момента инерции
балки жесткости.
57
В 1929 г. была опубликована монография Д. Б. Штейнмана
[165], в которой для расчета висячих мостов по деформированной
схеме применен энергетический метод. Интересно отметить, что
в этой монографии большая часть отводится старой линейной
теории и лишь небольшая часть посвящена расчету с учетом де-
формативности кабеля. Вместе с тем эта небольшая часть книги
содержит весьма убедительные доказательства необходимости
нового подхода к расчету висячих мостов.
Д. Б. Штейнман показал, что изгибающие моменты, найденные
по новой теории, на 30—40% меньше тех, которые определяются
по обычному методу. Работа Д. Б. Штейнмана оказала большое
влияние на развитие теории висячих мостов. Несколько забегая
вперед, отметим, что Д. Б. Штейнман написал в последующие
годы большое количество работ [162, 163, 164, 165, 166, 167], по-
священных расчету висячих мостов при действии статической и
динамической нагрузок. Особое внимание заслуживают работы
по устойчивости мостов от действия ветра.
Однако вернемся к начальному периоду развития теории,
учитывающей изменение очертания кабеля висячих мостов.
В 1931 г. опубликован русский перевод замечательной книги
Ф. Блейха [1], который провел непосредственное интегрирование
дифференциального уравнения изгиба однопролетной балки
жесткости и получил трансцендентное характеристическое урав-
нение для определения распора в кабеле. Решение этого уравне-
ния с последующим вычислением изгибающих моментов в бал-
ке показывает, что они меньше, чем при расчете по методу
сил.
Аткинсон и Саусвел [65] в 1939 г. для расчета однопролетных
мостов предложили релаксационный метод. Они используют ря-
ды Фурье и делают попытку учесть горизонтальные перемещения
кабеля.
Следует отметить, что в 30-х и 40-х годах опубликовано боль-
шое количество работ, посвященных теории висячих мостов.
Среди них большое место занимают работы по уточнению мето-
дов расчета с учетом изменения формы кабеля [71, 72, 95, 109,
117, 128, 138, 140, 141, 148, 162, 179].
В ряде работ рассматривались отдельные вопросы, например,
связанные с выяснением влияния деформации подвесок на рас-
пределение нагрузки между балкой и кабелем [99], обсуждением
различных условий опорных закреплений и их влияния на рабо-
ту мостов [116], построением методов расчета мостов, имеющих
шарниры в балке жесткости [96] и т. д.
В работе [74] обсуждались вопросы строительства мостов
больших пролетов, а в работе [81] — мосты для особенно больших
нагрузок.
Многих инженеров привлекли вопросы общенаучного харак-
тера, связанные с историей развития висячих мостов [114], с
58
принципиальным обсуждением методов расчета [98, 108] и сов-
ременным состоянием теории и методов конструирования [67].
В 1947 г. вышла книга Кроссвайта [79] — «Уточненная теория
балочных висячих мостов». В своей работе он также применяет
метод релаксации. Все крупные висячие мосты в США проана-
лизированы по этому методу.
В последующие годы появилось большое количество работ, в
которых вновь рассматривались общие вопросы расчета висячих
мостов по деформированной схеме [9—-11, 17, 48, 84—86, 90, 93,
100, 113, 132, 142—145, 153, 159, 174]. В этих работах даются
дальнейшие уточнения методов расчета как однопролетных, так
и многопролетных систем. Так, например, при определении де-
формации балок жесткости все чаще стали применяться общие
методы расчета тонкостенных стержней открытого и закрытого
профиля. По этому вопросу можно рекомендовать книги
[4, 5, 53].
Отметим далее некоторые специфические работы, характер-
ные для последнего периода начиная с 1950 г.
В 1955 г. А. Хайден [112] проводит расчет по деформированно-
му состоянию висячих мостов с трехпролетными неразрезными
балками жесткости. Его метод сводится к замене балки жестко-
сти фиктивной балкой, которая рассчитывается на действие вре-
менной вертикальной нагрузки и давление ветра.
В статье Е. Эгервари [87], опубликованной в этом же году,
применяется матричный метод для определения прогибов балки
жесткости цепных мостов от временной нагрузки, при этом ис-
пользуются ряды Фурье.
Сильверман [158] проводит анализ поперечной жесткости ви-
сячих мостов. Он отмечает, что поперечная жесткость моста
обусловлена отношением жесткости ветровой фермы к жестко-
сти кабеля. Распределение нагрузки между кабелем и фермой
'.-определяется приближенно из условия равенства перемещений
кабеля и фермы в средине пролета.
Практическое решение задач о расчете висячего моста с пе-
ременным по длине пролета моментом инерции при помощи ли-
нии влияния дает И. Зидаровский в работах (175, 176]. Он учи-
тывает изменение жесткости и собственного веса, при этом счи-
тает, что балка жесткости в непосредственной близости от
пилонов не подвешена к кабелю.
В работе Лейнекюгеля [126], опубликованной в 1959 г., приво-
дится расчет висячего моста со статически определимой несущей
конструкцией для очень больших пролетов. Висячая система, к
узлам которой подвешены элементы проезжей части в виде
разрезных алюминиевых балочных ферм длиной 150—100 м, по
его расчетам может достигать длины 300 м.
Заслуживает внимания работа М. Еслингера [84], в которой
изложен приближенный метод расчета на прочность висячих
59
мостов при действии горизонтальных сил, вызванных ветровой
нагрузкой, и крутящих моментов, возникающих вследствие эк-
сцентричного действия временной нагрузки.
В предлагаемом методе деформации кручения вокруг про-
дольной оси и изгиб в горизонтальной плоскости представляют-
ся независимыми друг от друга. Вычисления производятся на
электронной машине. Приведены примеры расчета на кручение
трехпролетного неразрезного симметричного висячего моста об-
щей длиной 2080 м со средним пролетом 1040 м и пример на дей-
ствие горизонтальных сил такого же моста общей длиной 2000 м
•со средним пролетом 1000 м. Построены линии влияния для
опорных реакций М и Q.
В работе [85] того же автора описывается приближенный ме-
тод расчета трехпролетного висячего моста с вертикальными
подвесками и дополнительными наклонными вантами на действие
горизонтальной распределенной нагрузки поперек моста и крутя-
щих моментов.
Разработке практических методов расчета висячих мостов
посвящены также работы С. Асплунда [62, 63, 64]. В работах
этого автора рассматриваются однопролетные и трехпролетные
висячие мосты с разрезной балкой жесткости. Расчет проводит-
ся с учетом изменения формы кабеля. В матричном виде выра-
жается зависимость между изгибающими моментами М, проги-
бами балки W, усилиями в подвесках S и грузами Р, приложен-
ными в конечном числе узлов прикрепления подвесок к балке.
Эти зависимости используются затем для построения линий
влияния и «загружения» последних временной нагрузкой.
Значение распора определяется из условия неизменности рас-
стояния между опорами. В расчете учитывается также измене-
ние температуры. При выводах даны ссылки автора на его курс
Structurae mechanics II Gothenburg 1963 г. В связи с перемен-
ностью Н решение ведется итерационным путем на ЭЦВМ, либо
с помощью таблиц, которые содержат безразмерные коэффициен-
ты влияния (с шагом в 1/16 пролета). Сечение балки постоянно
Jo или усилено (до J=l,25 Jo) на двух участках с каждой сторо-
ны между 1/16 и 5/16 пролета. Даны примеры расчета.
В ряде других работ также рассмотрены методы расчета мос-
тов с неразрезной балкой жесткости [1, 18, 42, 137, 185].
За последнее время начали разрабатываться численные ме-
тоды расчета висячих мостов с применением теории матриц [45,
63, 76, 86, 87]. Эти работы в сильной степени способствовали при-
менению ЭЦВМ [75, 124].
Матричному расчету висячих мостов посвящена статья авто-
ров F. J. Borges, L. С. Silva, Е. R. Arantese [76]. Для гибкого
нерастяжимого кабеля с неподвижными концами, несущего
сплошную равномерную нагрузку интенсивностью р и один про-
извольно расположенный груз Pj в безразмерной форме, уста-
60
навливается нелинейная зависимость вертикального перемеще-
ния произвольной точки Wi и коэффициента увеличения распора
значений Pj. Затем зависимость Wi от Pj линеари-
зуется с оценкой погрешности.
Аналогично исследуется влияние Pj на горизонтальное про-
дольное перемещение средней точки кабеля Wo и влияние гори-
зонтальной продольной силы Ро на прогибы W, а также влияние
поперечной нагрузки на поперечные прогибы.
Указаны приемы, позволяющие дополнительно учесть не
только упругость кабеля, но и податливость опор, неразрывность
трехпролетной системы, изменение температуры. По этой мето-
дике рассчитан строящийся сейчас трехпролетный висячий мост
в Лиссабоне под автодорогу с последующим усилением его под
железную дорогу путем постановки дополнительных наклонных
вант. Расчет выполнен на ЭЦВМ — «Stantes — Zebra». В указан-
ной работе дается описание методики и результаты испытания
модели в 1/500 натуральной величины.
Несколько позднее появились работы по изучению колебаний
висячих мостов. Значительное внимание уделялось собственным
колебаниям (25, 70, 88, 118, 178, 190, 194, 195, 161], аэродинамиче-
ской устойчивости и определению усилий от действия ветра [12,
69, 80, 82, 91, 102—104, 115, 134, 136, 150—152, 155, 164, 183, 184,
186—189, 191—194 и ряд других.
Проблема колебаний висячих мостов особенно привлекла к
себе внимание научных работников после крушения Такомского
моста. Отметим наиболее интересные работы, посвященные этому
вопросу.
В 1948 г. вышла в свет монография И. И. Гольденблата [7],
в которой исследуется устойчивость висячих мостов с балкой
жесткости. При изучении этого вопроса автором сделаны следую-
щие допущения: 1) при изгибно-крутильных колебаниях контур
поперечного сечения балки жесткости не деформируется; 2) под-
вески моста приняты нерастяжимыми; 3) распор принимается
постоянным, т. е. динамическая добавка к распору, возникающая
от сил инерции, не учитывается. В работе И. И. Гольденблата
получены основные уравнения связанных нелинейных колебаний
висячих мостов. Теоретические предпосылки проверены на моде-
ли. В работе отмечена роль ферм жесткости висячих мостов.
В работе В. В. Болотина (2] рассмотрена важная задача ус-
тойчивости колебаний висячих мостов от действия ветра.
В работах С. Scruton [150—152] рассмотрены колебания вися-
чих мостов под ветровой нагрузкой. Исследованы изгибные и
крутильные колебания балки жесткости и соответствующие пе-
ремещения кабеля.
Вопросу динамической устойчивости висячих мостов посвяще-
на работа А. Н. Размадзе [35]. В работе [34] того же автора рас-
61
А
смотрена динамическая устойчивость однопролетных мостов с
балкой жесткости при обратно симметричных колебаниях.
В статье Н. Moppert [134] проводится статический и динами-
ческий расчет висячих мостов при помощи интегральных уравне-
ний. Первый раздел посвящен решению статической задачи. Во
втором разделе приведены интегральные уравнения для изгиб-
ных и крутильных колебаний.
Исследованию динамических характеристик висячих мостов
посвящена работа К- К- Якобсона [61].
J. Emmen [88] рассматривает колебания висячих мостов при
прохождении по ним поездов и при действии ветра. Вычисляется
энергия, сообщаемая мосту быстро движущимся поездом, а так-
же рассматривается динамический эффект, вызванный ветровой
нагрузкой.
Значению аэродинамических проблем при проектировании со-
временных висячих мостов посвящена работа L. Chadenson [77].
Работа японских авторов J. Konishi, J. Jamada [120] посвяще-
на исследованию реакций на землетрясения большепролетного
висячего моста. Для упрощения анализа была принята система
с конечным числом степеней свободы. Предполагается, что воз-
мущения земной коры имеют простую форму, поэтому прини-
мается линейная теория деформации висячего моста.
В работах [121, 122] этих же авторов исследуются колебания
висячего моста с балкой жесткости, вызванные землетрясением.
Система рассматривается как дискретная: балка жесткости и пи-
лоны предполагаются состоящими из элементарных жестких
участков, соединенных в узлах упругими связями, имитирующи-
ми общую жесткость этих элементов. Цепь и подвески приняты
нерастяжимыми, импульсы передаются через опоры. Составлены
дифференциальные уравнения колебаний пилонов и балки жест-
кости с учетом связанности через подвески и цепь. Определены
собственные частоты и формы колебаний, а также колеба-
ния под действием передаваемого через опоры простейшего
импульса.
В работе А. Хираи, М. Ито [107] описываются эксперименталь-
ные исследования ударного действия на висячие железнодорож-
ные мосты. Для оценки динамического эффекта для прогибов и
моментов в большепролетных мостах (500—1400 м) испытано
большое количество моделей, выполненных с учетом законов по-
добия.
Проблемы асейсмичности висячих мостов при продольном
возбуждении колебаний рассмотрены в работе К. Kubo [123].
Экспериментально и теоретически исследуются вертикальные
колебания висячих мостов, вызванные сейсмическими толчками,
направленными вдоль оси моста. Толчки представлены как гори-
зонтальные смещения опор, происходящие по закону синуса. До-
пускается возможность резонанса. Из сопоставления энергий,
62
подведенной и рассеянной, за один цикл колебаний определяется
амплитуда вынужденных изгибных колебаний балки жесткости.
Работа A. Hirai, Т. Okumura, М. Ito, N. Nurita [104] посвяще-
на поперечной устойчивости висячего моста при колебаниях ос-
нования. Ставится проблема исследования динамического пове-
дения висячего моста при сейсмических воздействиях, направ-
ленных перпендикулярно к оси моста. Составлена система диф-
ференциальных уравнений малых поперечных колебаний парабо-
лического кабеля («) и балки жесткости (и), связь между кото-
рыми обусловлена возникающими при отклонении подвесок
горизонтальными составляющими усилий, пропорциональными
(и — и) : h. Длина подвесок h переменна, что приводит к пере-
менным коэффициентам, входящих в систему уравнений. Исходя
из синусоидальной формы отклонений с п полуволнами, на осно-
вании принципа возможных перемещений получается выражение
для собственных частот.
Используя этот результат, авторы далее исследуют вынуж-
денные колебания при заданных движениях опор балки и кабеля
и получают формулу для динамических коэффициентов.
Собственные колебания висячих мостов с наклонными ван-
тами рассмотрены в работе В. Goschy [94]. Применяя метод Рит-
ца, автор определяет частоты и формы колебаний, названные
автором арфообразными и пучкообразными, в зависимости от
•схемы расположения вант. Исследуются изгибные и крутильные
колебания указанной конструкции. Рассмотренная задача связа-
на с динамической устойчивостью мостов такого типа.
Связанные колебания висячего моста изучаются в статье
N. Shiraishi [156]. В этой работе исследуются колебания моста,
состоящего из двух параллельных гибких упруго-растяжимых
кабелей, вертикальных нерастяжимых подвесок и балки с жест-
ким профилем. Движение проезжей части описывается двумя
линейными компонентами Vq, ьу0 и углом закручивания 0. Дви-
жение каждого кабеля— тремя параметрами vi\ Wt, (i=l,2).
Вариационным методом получена система из девяти диффе-
ренциальных уравнений движения, включающих, помимо указан-
ных функций, интенсивности сил взаимодействия кабелей и про-
езжей части. Два дополнительных условия выводятся из допу-
щения нерастяжимости подвесок. Недостатком этой работы
является то, что сопротивление проезжей части скручиванию оп-
ределено по Навье (закон плоских сечений), т. е. без учета депла-
нации сечения. Автор указывает на необходимость последующе-
го уточнения за счет изгибного кручения. Выделяются изгибные
колебания, симметричные относительно продольной плоскости.
Из соответствующей системы трех дифференциальных урав-
нений движения для перемещений со, w и и и одного дополни-
тельного условия нерастяжимости подвесок выведена система
трех обыкновенных дифференциальных уравнений, описывающих
63
форму колебаний и частоту как параметр. Показано, что жесткое
соединение кабеля и балки жесткости в средине пролета приво-
дит к появлению в дифференциальных уравнениях особой точки.
Решения представляются в виде ряда	—.
С развитием теории расчета висячих мостов тесно связано
развитие расчета гибких нитей [14, 15, 36, 43, 51, 57], ферм из тро-
сов [21, 27—29, 32, 56], висячих покрытий [22, 30, 31, 33, 47, 54],
которым в настоящее время уделяется большое внимание.
Среди многочисленных работ по расчету висячих мостов сле-
дует особенно выделить упомянутые ранее работы Л. Б. Штейн-
мана, С. П. Тимошенко [52, 180—182], Ф. Штюсси [168—172],
И. И. Гольденблата [8], В. В. Болотина [2], С. О. Асплунда
[62-64].
Сведения о расчете висячих мостов можно найти также в
монографиях и учебниках [1, 6, 13, 16, 19, 20, 23, 24, 26, 49, 50,
58, 59, 62, 68, 73, 97, 129, 130, 131, 146, 147, 149, 154].
Следует отметить работы, посвященные некоторым специфи-
ческим задачам, как, например, расчету косых висячих мостов
[160], мостов с тяжелым настилом [106], мостов с несовершенно
упругой балкой жесткости [101] и балкой Гербера [173], предва-
рительно напряженным висячим мостам [177], созданию специ-
альных правил (технических условий) [125] и некоторые другие.
Заслуживают внимания интересующихся проектированием и
конструированием висячих мостов работы [55, 66, 78, 89, ПО, 127,
129, 196].
Настоящий обзор не претендует на исчерпывающую полноту.
В него главным образом вошли книги и статьи, посвященные рас-
чету кабельных висячих мостов с учетом геометрической нели-
нейности системы.
ГЛАВА II
ТИПЫ висячих мостов
И ИХ РАСЧЕТНЫЕ СХЕМЫ
§ 1. ОБЩИЕ ЗАМЕЧАНИЯ
В современной практике мостостроения применяются различ-
ные типы висячих мостов. Среди них особое место занимают ка-
бельные мосты, у- которых главными несущими элементами
являются гибкие кабели, изготовленные из высокопрочной про-
волоки и балки жесткости. Мосты такой конструкции обладают
большой грузоподъемностью и позволяют перекрывать очень
большие пролеты. Они успешно применяются для пропуска как
автомобильного, так и железнодорожного транспорта.
За последние годы нашли широкое применение так называе-
мые балочно-вантовые мосты, у которых балочные пролетные
строения работают совместно с вантами. Общие сведения по ука-
занным типам висячих мостов были приведены в гл. I.
В настоящей книге основное внимание уделяется кабельным
мостам, получившим большое распространение в мировой прак-
тике мостостроения. В отдельной главе рассматриваются также
балочно-вантовые мосты, которым в нашей стране уделяется
большое внимание.
§ 2. ОСНОВНЫЕ СХЕМЫ КАБЕЛЬНЫХ МОСТОВ
Основными элементами висячего кабельного моста (рис. 61)
являются:
1)	кабель, состоящий из большого количества высокопрочных
проволочных пучков, объединенных вместе в гибкий элемент,
работающий на растяжение как гибкая нить и обладающий спо-
собностью воспринимать большие вертикальные силы;
2)	балка жесткости, работающая на изгиб. Основное ее на-
значение — создавать всей системе в целом необходимую жест-
кость. Балка придает прогибам моста плавную кривую и тем
самым устраняет резкие перепады в перемещениях отдельных
точек. Термин «балка жесткости» употребляется в обобщенном
3—3802	65
Рис. 61.
смысле. В действительности она представляет собой пролетное
строение, состоящее из главных и поперечных балок, соединен-
ных с проезжим полотном. Во многих случаях роль главных ба-
лок выполняют сквозные фермы с большим числом панелей и с
малой высотой по сравнению с пролетом. Жесткость на изгиб
такого пролетного строения невелика и поэтому без кабеля оно
самостоятельно существовать не может;
3)	подвески, соединяющие кабель с балкой жесткости, обес-
печивают их совместную работу и передают значительную часть
нагрузки на кабель;
4)	пилоны, на которые в верхних точках опираются кабели.
Основное назначение пилонов состоит в передаче нагрузки от
кабеля на фундаменты. Вместе с тем пилоны играют роль пор-
тальных рам, создающих в какой-то степени поперечную жест-
кость висячей системы;
5)	анкерные устройства — неподвижно закрепляющие конце-
вые сечения кабеля.
Довольно часто на практике применяются трехпролстные ви-
сячие мосты. Основными генеральными размерами трехпролетно-
го моста являются: пролеты 1\ и /2, стрелы провисания кабеля
Л и f2, длины оттяжек Si и s2, ширина моста В и высота пило-
нов Н.
Величинами, характеризующими жесткость системы, будут:
жесткость кабеля на растяжение E'F, изгибная жесткость балки
EJ, изгибно-крутильная жесткость балки ЕВЫ и жесткость балки
при чистом кручении GJ^-
На практике встречаются разновидности висячих мостов,
связанные с закреплением кабеля: мосты с кабелем, передаю-
щим усилие на землю, и с кабелем, прикрепленным непосредст-
венно к балке жесткости. Последние условно называются моста-
ми с воспринятым распором. На рис. 61 показан мост первого
типа, а на рис. 62 — второго типа.
Мосты больших пролетов с распором, воспринимаемым бал-
кой, встречаются редко. Объясняется это тем, что при большой
длине балки жесткости в сильной степени сказывается влияние
продольного изгиба. Сечения главных балок увеличиваются, за
счет этого мосты больших пролетов с воспринятым распором с
66

экономической точки зрения
невыгодны, поэтому мы их
рассматривать не будем.
Таким образом .все даль-
нейшие рассуждения будут
относиться к мостам, имею-
щим кабель, закрепленный
в землю. Такие мосты могут
быть однопролетные (рис
63, а), двухпролетные (рис.
63, б), а также трехпро-
летные, показанные на
Рис. 65.	рис. 64.
Трехпролетные мосты мо-
гут иметь различные схемы.
На рис. 64, а показан трехпролетный мост с разрезной балкой
жесткости. Такую схему имеют известные Бруклинский и Ман-
хаттанский мосты. На рис. 64, б показан трехпролетный мост
с неразрезной балкой жесткости, при этом все три пролета
подвешены к кабелю. Этот тип имеет довольно широкое распро-
странение.
В трехпролетных мостах часто подвесным является только
средний пролет, а два крайних пролета не соединяются с кабе-
лем (рис. 64, в). К такому типу относится, например, висячий
мост в Будапеште, показанный на рис. 11.
На рис. 64, г показан трехпролетный мост, у которого кабель
в середине пролета жестко соединен с балкой. Такие мосты об-
ладают повышенной жесткостью и поэтому являются целесооб-
разными. В качестве примера можно указать на Танкервильский
мост во Франции (см. рис. 31), краткое описание которого при-
ведено в § 3 гл. I.
Расчет моста с кабелем, закрепленным в балку в средине про-
лета, сложнее, чем обычного кабельного моста. Усилия в кабеле
в левой и правой половинах моста при несимметричном загруже-
нии различны между собой, что вносит существенное изменение
в методику расчета. Теория расчета таких мостов с числовыми
примерами приводится в § 11 гл. V.
За последнее время стали появляться мосты с наклонными
подвесками (рис. 64, д). Подвески образуют как бы ферму с
треугольной решеткой. Такие мосты обладают более высокой
жесткостью, чем мосты с параллельными подвесками.
При расчете кабельных мостов применяются два основных
метода: первый, приближенный метод, основанный на примене-
нии принципа независимости действия сил,, по существу метод
сил в самой обычной линейной постановке. По этому методу
строятся’Слинии влияния и по ним определяются расчетные уси-
лия. На рис. 65, а показана расчетная схема (основная система)
68
для однопролетного моста, соответствующая этому методу. Сис-
тема рассматривается как однажды статически неопределимая.
Основной особенностью указанного метода является то, что ка-
бель при любой нагрузке, приложенной к балке, в том числе и
несимметричной, испытывает симметричное загружение со сто-
роны подвесок. Следует отметить, что этот метод в настоящее
время применяется редко. Его можно использовать только для
мостов малых пролетов с балкой, обладающей значительной
жесткостью.
Для мостов больших пролетов он не обеспечивает необходи-
мую точность и приводит к утяжелению конструкции. В насто-
ящей книге этот метод рассматриваться не будет.
Второй метод основан на более точных предпосылках. В нем
учитывается изменение очертания кабеля в процессе загружения
моста временной нагрузкой. Закон независимости действия сил
в этом случае применять нельзя, приходится проводить расчет с
учетом геометрической нелинейности системы. Расчет по этому
методу иногда условно называется расчетом «по деформирован-
ной схеме».
За неизвестные при расчете с учетом геометрической нели-
нейности принимаются или перемещения балки по вертикали,
или усилия в подвесках. В первом случае для отыскания проги-
бов составляются дифференциальные уравнения изгиба балки, а
но втором — система совместных уравнений, описывающих де-
формации балки и кабеля.
4
§ 3. О РАЦИОНАЛЬНЫХ СООТНОШЕНИЯХ ОСНОВНЫХ
РАЗМЕРОВ КАБЕЛЬНЫХ МОСТОВ
Г
•Зр Оптимальное проектирование висячих мостов представляет
особой сложную проблему. В настоящее время пока еще отсутст-
вуют объективные научные критерии, позволяющие оценить тот
Йли другой проект и выбрать при сравнении вариантов наилуч-
дций из них. Однако на основании накопленного опыта проектиро-
вания установились наиболее выгодные соотношения генераль-
ных размеров для отдельных типов мостов, которые получили
Jump око е распространение в инженерном проектировании. Так,
^«апример, по данным, собранным и обобщенным Д. Б. Штейн-
^маном [165] для трехпролетных мостов с неразрезной балкой
жесткости, в случае когда подвешенным является только средний
'^цролет (см. рис. 64, в), целесообразно назначить длину крайне-
го пролета равной около 1/4 длины среднего пролета. Для случая
ф&огда все три пролета подвешены к кабелю (см. рис. 64, б), от-
,^ношение длин указанных пролетов обычно принимается око-
Отношение стрелы провисания нити в среднем пролете к дли-
не пролета в большинстве осуществленных мостов больших про-
летов колеблется в пределах от Vs до 1/ю-
Для автодорожных и пешеходных мостов при сравнительно
малой временной нагрузке это отношение несколько меньше.
Оно колеблется в пределах от 7ю до 712.
Для назначения высоты балки жесткости каких-либо строго
установленных рекомендаций не имеется. Отношение высоты
балки к пролету зависит от ряда факторов. Так, например, чем
больше пролет моста, тем меньше это отношение. Для наиболее
крупных осуществленных мостов это отношение колеблется в
пределах от 1/80 до 1/120. Исключение представляют два моста:
Северенский мост, построенный в 1966 г., у которого отношение
высоты балки к пролету составляет 1/324, и старый Такомский
мост с отношением 1/350.
Высота балок жесткости в сильной степени зависит от требо-
ваний, предъявляемых к жесткости моста в целом. Для желез-
нодорожных мостов допускаемый прогиб меньше, а следова-
тельно, требуется повышенная жесткость мостов, что заставляет
делать балку более высокой.
Анализ построенных мостов показывает, что в каждом новом
мосту применяется все более смелое решение в сторону умень-
шения относительной высоты балки жесткости. Применение вы-
сокопрочных сталей позволяет обеспечить прочность балки при
малых размерах ее поперечного сечения. Однако с уменьшением
высоты балки возникает проблема обеспечения жесткости систе-
мы. При малой высоте балки жесткость системы в целом сильно
снижается, что ухудшает эксплуатационные характеристики
сооружения.
Колебания моста при малой жесткости балки приведут к
ограничениям скоростей движения. Однако решающим в этих
случаях является сильное снижение сопротивляемости системы
действию ветровых нагрузок.
Наряду с проблемой минимальной жесткости системы воз-
никает задача создания необходимых аэродинамических харак-
теристик пролетного строения. Необходимо стремиться выбирать
удобообтекаемые формы, при которых завихрения потока ветра
будут минимальными.
Весьма неудачное решение в этом отношении было принято
в старом Такомском мосту, имевшем малое отношение высоты
балки жесткости к пролету (1/350), а также неудачную плохо
обтекаемую форму поперечного сечения.
При назначении генеральных размеров висячего моста мож-
но, в некоторой степени, использовать табл. 2, помещенную в
гл. I, в которой приводятся конкретные данные тринадцати круп-
нейших построенных мостов.
§ 4. ОСОБЕННОСТИ КАБЕЛЬНЫХ ВИСЯЧИХ МОСТОВ
ПО СРАВНЕНИЮ С ДРУГИМИ МОСТАМИ
Висячие мосты по сравнению с другими типами мостов обла-
дают рядом особенностей. В первую очередь необходимо отме-
тить рациональное использование материала в основном несу-
щем элементе — кабеле. Во всех точках поперечного сечения
кабеля (во всех проволоках) напряжение одинаковое. Таким об-
разом, все проволоки работают на полную грузоподъемность.
Так как на кабель падает около 80% всей нагрузки, то можно
считать висячую систему приближающейся к системе наимень-
шего объема.
Так как кабель всегда растянут, то по сравнению с арочным
мостом здесь отсутствуют коэффициенты увеличения площади
сечения, вызванные опасением продольного изгиба. Кроме того,
в кабеле отсутствуют концентраторы напряжений, которые обыч-
но утяжеляют конструкцию.
С экономической точки зрения, как указывает Д. Б. Штейн-
ман {165], висячие мосты под автомобильные дороги становятся
выгодными по сравнению с другими типами мостов, начиная с
пролета примерно 130 м и более, а для железнодорожных мос-
тов — начиная с пролета 480—500 м. Чем больше пролет моста
превышает указанные значения, тем большей становится эконо-
мическая выгода в применении висячего моста по сравнению с
другими типами мостов.
.Естественно, что на указанные цифры необходимо смотреть
как на ориентировочные, так как в реальных условиях проекти-
рования необходимо учитывать местные условия. Так, например,
многопролетные эстакады на суходолах или подходах моста яв-
j ляются самыми выгодными.
Поэтому приведенные цифры верны для случая, когда вслед-
ствие большой высоты опор необходимо применять пролеты
V большой величины.
I. Еще одним огромным преимуществом висячего моста являет-
ся его «живучесть» по отношению к повреждениям балки жестко-
сти. В обычной балочной ферме выход из строя элемента фермы
((например, нижнего пояса) приведет к разрушению моста. Вися-
1«чий же мост можно продолжать эксплуатировать при поврежде-
нии не одного, а ряда элементов балки жесткости.
* Если по каким-либо причинам в балке появился целый ряд
шарниров, то, как показали расчеты, приведенные в гл. VI, полу-
ченная при этом система продолжает обладать достаточно вы-
j.coKoft грузоподъемностью. При повреждении балки жесткости
& можно осуществлять ремонт без перерыва движения.
' К числу достоинств висячих мостов относится также просто-
'*'-та их возведения. Навесная сборка (без подмостей) позволяет
,Л .осуществлять строительство в короткие сроки.
71
Недостатком висячих мостов является их меньшая жесткость
по сравнению с другими типами мостов и повышенная чувстви-
тельность к ветровым нагрузкам.
§ 5. ОСНОВНЫЕ СХЕМЫ БАЛОЧНО-ВАНТОВЫХ МОСТОВ
р.
В настоящем параграфе рассматриваются расчетные схемы
одной из разновидностей вантовых мостов. Имеются в виду ба-
лочно-вантовые мосты, которые за последние годы получили
широкое распространение. На рис. 66 показана схема, в которой
ванты сходятся на- вершине пилона в одну точку, образуя ради-
альный пучок. На этой схеме пилон представляет собой колонну,
заделанную одним концом. На рис. 67, а показан качающийся
пилон, который, вращаясь относительно точки А, может слегка
наклоняться. Так как по концам имеются шарниры, то он всегда
испытывает только центральное сжатие.
Если в схеме, изображенной на рис. 66, ванты в узле А при-
крепляются к подвижной опорной части, поставленной на верши-
не пилона, как это схематически изображено на рис. 67, в, то
пилон будет работать на/сжатие или на внецентренное сжатие,
когда подвижная опорная часть передвинется в какую-либо сто-
рону от оси пилона.
С высокой степенью приближения две схемы, показанные на
рис. 67, а и б, с точки зрения расчета можно считать одинаковы-
ми. В первом случае можно прене-
бречь малым наклоном качающегося
пилона, который будет происходить
при деформации всей системы от
временной нагрузки, а во втором —
наклоном плоскости, по которой бу-
дет перекатываться подвижная опор-
ная часть. Тогда для обоих случаев
сумма проекций усилий в вантах,
сходящихся в узле В, на горизон-
тальную ось равна 0.
Если в схеме, изображенной на
рис. 66, ванты жестко скреплены с
пилоном, то последний, кроме верти-
Рис. 68.
Рис. 69.
калькой силы, будет воспринимать также горизонтальную силу,
а поэтому он будет работать на сжатие с изгибом, что вносит су-
щественные изменения в методику расчета таких мостов. Изло-
жение методов расчета балочно-вантовых мостов приводится в
гл. VII.
На рис. 68 показана схема с параллельными вантами. Расчет-
ная схема таких мостов зависит от способов прикрепления вант.
Так, например, на рис. 69 показан пилон, на котором в точках А,
В и С ванты прикреплены к подвижным
опорным частям.
Наряду с таким случаем возможны и
другие варианты прикрепления вант, на-
пример, во всех трех узлах ванты могут
иметь жесткое скрепление с пилоном. В
каждом отдельном случае будет своя рас-
четная схема и свое количество лишних не-
известных. Однако это не вызовет принци-
пиальных затруднений.
ГЛАВА III
НЕКОТОРЫЕ ВОПРОСЫ
РАСЧЕТА ГИБКОМ НИТИ
§ 1. ОБЩИЕ ЗАМЕЧАНИЯ
В настоящее время по расчету гибких нитей имеется обшир-
ная литература. В отдельных статьях и монографиях решены
многочисленные задачи о равновесии гибких нитей при различ-
ных нагрузках, действии температуры, а также вопросы колеба-
ний нитей или составленных из них различных систем.
В зависимости от целей, которые ставятся в том или ином
исследовании, можно выделить два типа задач по статическому
расчету гибкой нити. Одна из наиболее распространенных задач
состоит в отыскании очертаний нити при действии ее собствен-
ного веса, а также той полезной нагрузки, которую воспринимает
гибкая нить. Эта задача исследована более детально, в ней ос-
новные принципиальные вопросы выяснены с достаточной пол-
нотой.
Вторая задача состоит в определении перемещений отдельных
точек гибкой нити при изменении действующей на нее нагрузки.
Эта задача типична для кабеля висячего моста. При загружении
моста временной нагрузкой усилия в подвесках изменяются и
точки оси кабеля перемещаются как по вертикали, так и по гори-
зонтали. Отыскание указанных перемещений в отдельных слу-
чаях представляет собой весьма сложную задачу, которая тре-
бует разработки специальных методов решения и применения вы-
числительных машин.
К числу таких задач относится, например, задача об опреде-
лении перемещений точек нити, несущей вертикальную нагрузку
при дополнительном одновременном действии на нее вертикаль-
ных и горизонтальных сил. Еще более сложным является расчет
гибкой нити с учетом наклона подвесок. Для больших перемеще-
ний при решении этой задачи приходится иметь дело со сложны-
ми нелинейными дифференциальными уравнениями.
Подобного рода задачи рассматриваются в настоящей главе..
Методика, применяемая для решения указанных задач, исполь-
зуется в дальнейшем при расчете висячих мостов.
74
§ 2. ИЗМЕНЕНИЕ ОЧЕРТАНИЯ ОСИ ГИБКОЙ НИТИ
ПРИ ЗАГРУЖЕНИИ ВЕРТИКАЛЬНОЙ ВРЕМЕННОЙ НАГРУЗКОЙ
Предположим, что гибкая нить переменного сечения загруже-
на постоянной нагрузкой gTfM. В эту нагрузку включается вес
самой нити и вес поддерживаемой ею конструкции, прикреплен-
ной с помощью подвесок. Вес нити мал по сравнению с весом
конструкции. Нагрузку g будем считать равномерно распреде-
ленной по горизонтальной проекции нити. Очертание нити от
нагрузки g будем считать заданным y=f(x). Допустим, что под-
держиваемая конструкция передает нагрузку на нить и не пре-
пятствует свободному перемещению точек гибкой нити.
При загружении системы дополнительной (временной) на-
грузкой q изменяется очертание нити и изменяются нормальные
усилия в ее элементах, что влечет за собой упругое удлинение
нити. Основная задача будет состоять в определении вектора
вертикальных перемещений точек нити
^2
Чп
В этом параграфе рассматриваются пологие нити, для кото-
рых при определении вертикальных перемещений горизонталь-
ными можно пренебречь.
Допустим, что на нить с опорами, расположенными на од-
ном уровне, нагрузка передается только в п узловых точках, рас-
стояния между которыми по горизонтали примем одинаковыми
и равными величине d. Собственный вес нити будем считать
сосредоточенным в узлах. В этом случае между узловыми точ-
ками нить будет очерчена по прямым линиям (рис. 70,а). Сосре-
доточенную силу, приложенную к произвольному узлу, предста-
вим в виде
VK=vgK+VqK,	(а)
где VgK— узловая сила от постоянной нагрузки;
V9K— то же, от временной нагрузки.
На рис. 70, а сплошными линиями показана нить под действи-
ем постоянной нагрузки, а пунктиром — нить после деформации
от временной нагрузки.
j Узловые силы Vi, V2, ..., Vn представляют собой суммарные
| силы, определяемые равенством (а).
Длины участков нити между узлами до деформации соответ-
 ственно обозначены Si, S2, S3....
Усилия в соответствующих элементах нити будем обозначать
к N2, ..., Nn+1. Таким образом, значок у длины участка S и уси-
75
Рис. 70.
лия N будет совпадать с номером узла, расположенного на пра-
вом конце соответствующего участка.
После деформации длины участков соответственно будут
Si+ASb S2 + aS2...
На рис. 70, б показан к-й узел, вырезанный из системы после
деформации. К нему приложены силы NKuN K+i- Длины, примы-
кающие к этому узлу элементов,	SK+i + ASw+i.
Горизонтальные проекции усилий N к и NK+i равны между
собой и равны распору Н.
Между узловыми силами и ординатами узловых точек нити
после деформации существует следующая зависимость:

где
Хр. л  ^Ук ~Г ---------- (У/g—1 +	1) .
d
(Ъ>
(с)
tp ггП—- Gfe+l + т1к+1) — (Ук -Г г1к) .
Ife T/t
d
(d>
Н — распор в гибкой нити от постоянной и временной на-
грузок;
и — углы наклона элементов нити к горизонту слева и
справа от узла к (рис. 70, б).
।
л
76
Подставив выражения (с) и (d) в равенство (Ь), получим
зависимость сил V от ординат у+г]
V к—~~ [~(#к-14"7м-1) + 2й/к+i“kWi)]»	(е)
а.
где т]к— вертикальное перемещение узла к нити.
Написав выражение (е) для п узловых точек, получаем:
Vi =~ [2 (уг + Th)—(У2 + Л
d
^2 ~~ I — (^14_1Jl)’4-2(y2-t'‘42)—(^з + 'Чз)].
а
Vn—~т [ — (Уп—1 4-т]п_1)4-2(г/п-|-т]я)].
d
В матричной форме эта система уравнений запишется в сле-
дующем виде:
V=HL2(y + ^,	(1ПЛ)
где V — вектор суммарных узловых сил от постоянной и вре-
менной нагрузок;
у— вектор начальных ординат узловых точек;
т]— вектор вертикальных перемещений узлов.
Матрица L2 имеет вид
2
(III.2)
Из уравнения (III. 1) получаем
ri = -~L'2У-
(III.3)
В уравнении (III.3) содержатся два неизвестных т) и Н. Сле-
довательно, необходимо составить дополнительное уравнение.
Для этой цели используем принцип Лагранжа, по которому вир-
туальная работа внешних и внутренних сил кабеля от постоян-
ной нагрузки на перемещениях от временной нагрузки равна 0.
77
п
2 v^-u^o,
К=1
(III.4)
тле U — работа внутренних сил Ng (от постоянной нагрузки)
на перемещениях AS (удлинениях элементов нити S
от временной нагрузки);
Л
2 ^gK^K—работа внешних сил (от постоянной нагрузки) на
Л=1
перемещениях т] (от временной нагрузки q).
Работу внутренних сил можно определить следующим об-
разом:
<7=2	<ш-5>
К=1
где
NaKSK
(III.6)
к
ак	’
COS
где EFK—жесткость нити в элементе к (между узлами к и
и к—1);
NgK и — нормальные силы в элементе к от постоянной и
временной нагрузок;
Hg и Нч— составляющие полного распора И от постоянной
и временной нагрузок.
Подставляя выражения (III.6) в равенство (III.5) и обозна-
чая через Fo площадь нити в средине пролета, получаем
U —	d
FFQ jZj FK cos3 <?IC
K= 1
Обозначим
Л+1
---7----= iS-	(И1-7)
FK cos3?K
K=1
При большом числе узлов суммирование в формуле (Ш.7), с
достаточной для практики точностью, можно заменить интегри-
78
рованием. Приняв ось нити за непрерывную кривую и положив
COS <p
находим:
для нити с переменной жесткостью
f dx
.1 cos2 <p ’
0
(III.8)
для нити постоянного сечения
I
C dx
cos3 <p
0
(III.9)
Таким образом,
u=^ll
efq s
(ШЛО)
Учитывая далее, что
q	‘ g
V = Vg + Vq .
(Ш-11)
вместо уравнений (Ш.З) и (III.4) окончательно получаем два
совместных уравнения
(Кг+и,)-»,
у	L
g* *	EFg
К=1
(Ш.12)
Эти уравнения можно представить также в другом, более
удобном виде. Для этого на основании равенства (III.1), поло-
жив в нем т) = 0 и Н=НВ, находим:
Подставляя найденное значение в уравнения (III.12), а также
введя новое обозначение
Hg
(111.13)
Г1
после несложных преобразований получим
(Ш.14)
79
«=1
EF0
(III. 15)
Рассмотрим более подробно частный случай, когда узлы нити
до загружении временной нагрузкой лежат на квадратной пара-
боле с уравнением
—	(III.16)
В этом случае собственный вес g и узловые силы
Vg=Sd
величины постоянные. На основании этого вместо выражения
(III.15) получаем
H-gLs
gdEF0
(III. 17)
Сумму ординат прогибов можно определить с помощью ра-
венства
п
Л-1
где mi — матрица-строка, все элементы которой равны единице,
а ее порядок совпадает с порядком вектора т].
Учитывая равенство (III.14), получаем:
X
нg
q~ (1 ~ ^)т1У-
(III. 18)
Приравняв правые части равенств (III.17) и (III.18) и про-
изведя преобразования, получим квадратное уравнение для опре-
деления величины X:
X2 — \тх-т7== о,	(III. 19)
где
(III. 20а)
Ls .
gdEFQ
80
(III.20)
Величину Ls можно выразить через пролет нити /:
s— р/.
(III .21)
Для нити с постоянным сечением
I	I	3_
р. =— —— = — f [ 1 4- (//Л 2 dx.
I J cos3<p / J 1	• w ' 1
о	0
Величину p для случая, когда опоры нити расположены на
разных уровнях (рис. 71), можно определить приближенно, раз-
ложив в ряд выражение
и +(</')2Г=1+4^'’’+4 <»'>*+• • •
Z	о
Учитывая, что
У = ~-х(1-х)-\-х\^ у0
и сохранив три члена ряда после всех преобразований, получим:
+ 4‘82ь]1«!?о-	(Ш.22)
Если опоры нити расположены на одном уровне (уо = О), то
для р можно получить точную формулу, которая имеет вид
X in 4 —+ 1/ И 16
\ I 1 к	/2
(III.23)
81
Для
Л,
нити с переменным сечением, меняющимся по закону
cos у
I
1 f dx
U. — --- \ --------
I J cos2 <p
0
4-^1
0
или после интегрирования при
параболическом очертании нити
l>=l+44+tf*	(III.24)
о Z2
Полученные формулы позволяют определить перемещения то-
чек деформируемой нити от любой временной нагрузки. Для
этого необходимо по формулам (III.20а) вычислить коэффициен-
ты Ш] и /и2, затем из уравнения (III. 19) определить X, по равен-
ству (III.13) найти полный распор Н и по формуле (III.14) —
вектор перемещений тр
Рассмотрим примеры применения описанной методики.
Пример 1. Нить пролетом / = 200 м нагружена постоянной
нагрузкой £=0,5 Т/м. Стрела провисания f = 20 м. Площадь сече-
ния постоянна по длине и равна Fo = O,01 м2, EFo=O,18333-106 Т.
Нить загружена временной нагрузкой q=\ Т/м, равномерно рас-
пределенной по всей длине пролета. Определить перемещения т],
если первоначальное очертание нити определяется уравнением
(III.16).
Разобьем пролет на шесть равных частей. Длина панели
а=— м. По уравнению (III.16) находим вектор:
11,11111
17,77778
20,00000
17,77778
11,11111
Матрица L2 Для нашего случая имеет вид
-1
2 -1
- 1	2-1
-1	2
82
Обратная матрица L2-1, как известно,
моментов. Для данного случая
равна матрице влияния
5
4
3
2
1
4 3 2 1
8 6 4 2
6 9 6 3
4 6 8 4
2 3 4 5
Матрица-строка coi будет также пятого порядка
^i = ll 1 1 1 1 1||.
Находим произведения матриц:
0^7’ = —1| 15 24 27 24 15||;
6
(0^=77,77778.
Вектор Vq имеет вид
V
(1	6
Следовательно,
«)1£2 'Vq
200
6
105rf _ 1750
1
1
1
По табл. 3, приведенной в приложении, при-у-= 0,1
pi= 1,08189. По формуле (III.21) определяем
£s = p.Z = 216,378 м.
Далее определяем коэффициенты по формулам
III.20):
находим
(III.20а,
015:20№ =
g 8-20
«=-------12*-216'378	= 1,106499,
200
0,5- — -0,18333-106
200
р = — -	-ф 77,77778 = 233,33333.
125	3

83
т} —
Коэффициенты и т?:
77,77778-,.10650
233,33333
= 1,108499 = 0,0047421.
233,33333
m2
Таким образом получаем квадратное уравнение
X2 — 0,328591 л — 0,0047421 = 0,
которое имеет следующие корни:
X, —0,342439,	Х2=-0,013848.
Естественно, что учету подлежит только положительный корень.
По соотношению (III.13) находим полный распор от постоянной
и временной нагрузок:
Н =-----—-----= 365,029 Т.
0,342439
По формуле (III.14) находим перемещения т]
-	0,342439-2002
4 =
125-6-6-6
5
4
3
2
1
4
8
6
4
2
3
6
9
6
3
2
4
6
8
4
2
3
4
5
1
1
1
1
1
— 0,657561
11,11111
17,77778
20,00000
17,77778
11,11111
0,304
0,486
0,546
0,486
0,304
все вычисления сво-
Из рассмотренного примера видно, что
дятся к простым арифметическим действиям. В данном примере
нагрузка была симметричной, однако вычисления нисколько не
усложняются и при любой другой нагрузке. Прежде чем перехо-
дить к более сложному загружению, вернемся к нашему примеру
и рассмотрим один частный случай. Положим EFo = °°- Тогда
а = 0; /п2 = 0,
77,77778 — 0	1
т, = —----------= — ,
1 ООО ооооо	3
233,33333
84
Рис. 72.
3
Суммарный распор Н = -^ = 375 Т.
Если теперь подставить Х= — в формулу (III.14), то получим
3
т) = 0. Полученный результат будет понятен, если рассмотреть
недеформируемую нить под действием суммарной нагрузки
g + <7 = 1,5 Г, для которой
Н =	+ W =: 375 т.
8/
Пример 2. Та же самая нить, что и в примере 1, загружена
временной равномерно распределенной нагрузкой q= 1 Т/м на
половине пролета (рис. 72). Вектор сосредоточенных сил от вре-
менной нагрузки в этом случае имеет вид
200
6
1,0
1,0
0,5
0,0
0,0
Произведение матриц <01Л2-1 останется
ходим:
^L?Vq= А . ~~Н15 24 27 24 15 || X
прежним. Далее на-
1
1
0,5
0
0
1750
85-
Величины р, Ls, Hg, a — останутся прежними, а именно:
♦*=1,08189, 7.^ = 216,378, 77^=125 T, a= 1,10650.
Найдем величину 0:
200
8 = — . -^1 + 77,77778 = 155,55555.
‘	125	6
Коэффициенты и т2 будут:
’77,77778 — 1,10650
тг —
155,55555
0,492887,
1,106499
/По =----—-
155,55555
0,0071132.
Квадратное уравнение для определения X принимает вид
X2-0,492887 X — 0,0071132 = 0,
откуда
>.=0,506920.
Далее находим распор и прогибы:
125
0,506920
246,587 Т,
	5 4 3 2 1		1,0
	4 8 6 4 2		1 0
*	 0,506920-2002	3 6 9 6 3		
Т‘~	125-6-5-6		X	0,5
	2 4 6 8 4		0,0
	1 2 3 4 5		0,0
-0,493080
11,11111
17,77778
20,00000
17,77778
11,11111
2,407
2,499
0,277
-2,007
— 2,099
На рис. 72 показана рассмотренная нить с нагрузкой на по-
лупролете. Жирной линией изображена нить под действием
только постоянной нагрузки, а пунктиром — после загружения
временной нагрузкой.
Пример 3. В третьем примере рассмотрим ту же нить, что и в
предыдущих примерах, но с временной нагрузкой, распределен-
ной по закону треугольника (рис. 73). В этом случае вектор со-
86
.............	., Л ,,,
Рис. 73.
средоточенных сил, заменяющий треугольную нагрузку, подсчи-
тывается элементарно просто:
•200
Вычисляем значение
0,83333
0,66667
0,50000
0,33333
0,16667
0,83333
0,66667
0,50000
0,33333
0,16667
24 27 24 15||Х
= 291,66667.
При тех же значениях ц, Ls, Нё, а находим величину 0:
р =	. 291,66667 4- 77,77778 = 155,55555.
Коэффициенты тг и т2 будут:
= . 77,77778— 1.10650 =
155,55555
1,105499
/По = —---------—
155,55555
0,0071132.
Квадратное уравнение будет таким же, как и в примере 2.
Следовательно, Л=0,506920.
87
Суммарный распор от постоянной и временной нагрузок будет
/7=246,587 Т.
Находим прогибы:
0,506920-2002	5	4	3	2	1	0,83333 4	8	6	4	2	0,66667 3	6	9	6	3 X 0,50000 — 2	4	6	8	4	0,33333 12345	0,16667 11,11111	1,405 17,77778	1,247 20,00000 =	0,277	. 17,77778	-0,755 11,11111	-1,098
'' '	125-6-6-6 -0,493080	
На рис. 73 показана нить до и после деформации. Пунктирная
линия изображает нить после загружении временной нагрузкой.
Интересно отметить, что все коэффициенты и распор оказа-
лись такими же, как и в предыдущем примере. Однако прогибы
резко отличаются друг от друга.
§ 3. УЧЕТ ВЛИЯНИЯ ТЕМПЕРАТУРЫ
ПРИ РАСЧЕТЕ ГИБКОЙ НИТИ
Под действием температуры все элементы нити меняиот свои
размеры, что влечет за собой изменение первоначального» очерта-
ния ее оси. При изменении очертания в свою очередь возникает
изменение натяжения гибкой нити. Ввиду того что задачга о рас-
чете нити является нелинейной, нельзя расчет на температуру
отделить от расчета на действие временной нагрузки.
Целью расчета является определение прогибов и изменения
натяжения нити от одновременного действия нагрузки q и темпе-
ратурного нагрева на tc.
В основу расчета положены те же предпосылки и допущения,
которые были приняты в предыдущем параграфе. Основное урав-
нение для определения прогибов остается таким же, как и при
расчете на действие нагрузки. Оно было выведено в предыдущем
параграфе под номером (III.14). Приведем его без изменения

При составлении второго уравнения, так же как и ранее, бу-
дем исходить из принципа Лагранжа, по которому теперь необ-
88
ходимо приравнять нулю виртуальную работу внешних и внут-
ренних сил от постоянной нагрузки на перемещениях, вызванных
одновременным действием временной нагрузки и температуры.
Это уравнение имеет вид
£	(Ш.25)
«=1
Согласно равенству (III.12)
’Viz	,	,пт
----£F0-----L‘‘	( L26)
Л = 1
По выражению (III.10) получим
Uq = -^-Ls.	(III.27)
С.Г0
Работа внутренних сил на перемещениях от температуры t°
п+1	л+1
и, =	У	—f—	^tS^H^tL,,	(III.28)
Ж = 1	К = 1
где at — коэффициент температурного расширения.
При большом числе делений выражение суммы, с достаточной
для практических расчетов точностью, можно представить в виде
Lt — V —( —ах_=	(П1 29)
cos <ря J cos2 <f>
к=1	О
Значение р,/ совпадает с выражением, найденным в предыду-
щем параграфе (III.24). Таким образом,
ь = 1 + -^-- =g-+tg-v§.	(III.30)
о I1
Учитывая, что Hq = H — Hg, и подставляя выражения (III.26),
(III.27) и (III.28) в равенство (III.25), получим:
Vy	'"'W Ls + H.,tL„
gK	EFn s g 1 1
к=1
Так как и ранее, используем обозначение (III.13) Л = ~g.
Таким образом получим два уравнения
л «г
89

(III.32)
Для случая когда постоянная нагрузка равномерно распреде-
лена по всему пролету, первоначальное очертание нити будет
по квадратной параболе. Для этого, согласно равенства (III.32),
имеем:
gdEFQ
Нк
—
(III.33)
п
Далее заменим в равенстве (Ш.ЗЗ) величину найденным
«=1
ранее значением (III.18). Произведя все преобразования так же
как в предыдущем параграфе, получим квадратное уравнение
/2— mp. — т2 = 0,
где
- а 4-
1
1

—J—«1£2
Hg
Не	&Г>-
—	н=—
gd 1 "	*	8/
(111.34)
(III.35)
Сравнивая формулы (III.20) и (Ш.Зб), заметим, что отЛИЧИе
состоит только в коэффициенте в который входит величина
уг. При / = 0 формулы (III.35) превращаются в (111.20).
Пример. За основу возьмем пример 2 из предыдущего пара-
графа и дополнительно примем, что нить одновременно с прило-
жением временной нагрузки нагревается на 20° С.
По формулам (Ш.ЗО) и (111.29) находим:
Ь = 1+—•— = 1,05333,
3 Г-
Lt =1,05333 • 200== 210,66667 м.
Из примера 2 предыдущего параграфа имеем:
/^=125 Т, а = 1,10650,	0,0071132, «>, у=77,77778,
р = 155,55555.
90
По равенствам (111.35), приняв коэффициент температурного
расширения at=0,000011, находим:
yt=— 0,000011 • 20 • 210,66667 = 0,34760,
*	200
0,5- —
6
тх
77,77778 —1,10650 + 0,3476 0
~	155,55555
=0,495121.
Квадратное уравнение для определения X
X2 — 0,495121X - 0,0071132 = 0
имеет решение
Х=0,509093.
Далее находим распор и прогибы:
125
0,509093
=245,535
-	0.509093-2002
71 =----------------
125-6-6-6
5
4
3
2
1
4
8
6
4
2
-0,490907
11,11111
17,77778
20,00000
17,77778
11,11111
2,465
2,586
0,364
— 1,939
— 2,061
Сравнивая полученные результаты с соответствующими ре-
зультатами примера 2, рассмотренного в предыдущем парагра-
фе, замечаем, что распор уменьшился, а перемещения увеличи-
лись. При остывании нити картина изменится в обратную сторо-
ну: распор увеличится, а перемещения уменьшатся.
§ 4. ГИБКАЯ НИТЬ С ПОДВИЖНОЙ ОПОРОЙ
В дальнейших расчетах мы встретимся с необходимостью
определять усилия и перемещения в гибкой нити, у которой одна
опора может свободно перемещаться по вертикали (рис. 74).
91
Рис. 74.
При действии постоянной рав-
номерно распределенной нагруз-
ки q ось нити провисает по пара-
боле с уравнением
=	(111.36)
Если в основу расчета такой
нити положить предпосылки и до-
пущения, которые были приняты
в предыдущих параграфах, то
выведенные ранее формулы с не-
которыми небольшими измене-
ниями можно применять и для
изменения состоят в следующем:
рассматриваемрго случая. Эти
1)	вместо I необходимо подставлять величину /j;
2)	при разделении пролета на п равных частей сосредоточен-
ная постоянная нагрузка во всех узлах будет равна gd, а в узлеп
на подвижной опоре она будет равна Вследствие этого
Для подсчета суммы, стоящей в скобках, уже нельзя пользо-
ваться матрицей Ш]. Ее необходимо заменить матрицей coi^, у
которой все ординаты равны единице, кроме последней, которая
заменяется величиной 0,5;
3)	матрица 12 будет иметь несколько измененную структуру.
Вместо матрицы (III.2) будем иметь следующую матрицу:
2 -1
-1	2 -1
-1	2 -1
(III.37)
Эта матрица отличается от матрицы (Ш.2) только тем, что
в ней последний элемент последней строки равен не двум, а
единице. Данное отличие резко изменяет обратную матри-
цу L2 .
Для матрицы (III.2) обратная матрица была равна матрице
влияния моментов простой двухопорной балки. Для рассматри-
ваемой матрицы (III.37) обратная матрица будет равна матрице
92
влияния моментов балки, заделанной одним концом. Так, на-
пример, для матрицы шестого порядка матрица £*—1 будет:
	1 1	1 2	1 2	1 2	1 2	1 2	
7.2	= d	1 1	2 2	3 3	3 4	3 4	3 4	(III.38)
	1	2	3	4	5	5	
	1	2	3	4	5	6	
Интересно отметить, что при изменении только одного эле-
мента матрицы £2* (в данном случае последнего элемента по-
следней строки) обратная матрица изменяется очень сильно. Так,
если заменить в матрице (Ш.37) последний элемент с единицы на
два,
	6	5	4	3	2	1
	5	10	8	6	4	2
/У1- —	4	8	12	9	6	3
2	7	3	6	9	12	8	4
	2	4	6	8	10	5
	1	2	3	4	5	6
Рассматриваемая в настоящем параграфе гибкая нить с под-
вижной опорой как бы представляет собой половину симметрич-
ной нити с двумя неподвижными опорами, расположенными на
одном уровне. Это замечание справедливо только в том случае,
когда на симметричную нить действует симметричная нагрузка.
Таким образом, несимметричную нить можно дополнить до сим-
метричной и рассчитывать как обычную нить, рассмотренную в
предыдущих параграфах. Однако такой прием рекомендовать
нельзя прежде всего потому, что он потребует значительно
больше времени, а в тех случаях, когда расчет несимметричной
нити составляет часть в более общей задаче, то такая замена на-
рушит алгоритм и затруднит использование вычислительной
машины.
Пример. Рассмотрим пример
(рис. 75), в котором: /1=100 м,
/1 = 20 м, ££0 = 0,18333- 106 Т. Равно-
мерно распределенная постоянная
нагрузка £ = 0,5 Т/м. Нить загружена
временной равномерной нагрузкой
q= 1,0. Требуется определить проги-
бы и распор.
Рис. 75.
93
Разобьем пролет на три равные части, длина панели будет
100 п	„
. От постоянной нагрузки нить провисает по квадратной
О
параболе с ординатами
11,11111
17,77778
20,00000
Матрица Ь2* и ее обратная матрица:
1 1
2 2
2 3
Матрица-строка wig также третьего порядка, которая в соот- ’
ветствии с замечанием 2 теперь имеет вид
^=11 1 1 0,51|.
।
Находим произведения матриц:	4
с%Д.Г1 = бП|2,5	4	4,51|.	I
^lgy=38,88889.	°
Вектор сосредоточенных сил от временной нагрузки
v,.
3 0,5
Следовательно,
«hX"1 К = — -8,75J = 291,66667J.
е 1	3
Для определения величины р необходимо воспользоваться
табл. 1 (приложение), но при пологости=0,1. Для этого
2/j
случая
Р = 1,08189.
По формуле (III.21) находим:
Ls= 1,08189*100= 108,189 м.
По равенствам (1П.20а, III.20) определяем:
» =^ML=I257-. а=-------------------------о,553249,
8	8/,	100
0,5* — *0,18333.105
94	1
р = -121 - 291,66667 + 38,88889 = 116,66667,
38.88889 — 0,55325
116,66667
0,328591
т,>
__ 0,553249
~ 116,66667
0,0047421.
Квадратное уравнение
X2 —0,32859IX —0,0047421 =0
имеет корень
Распор
X = 0,342439.
125
0,342439
= 365,029 7’.
По формуле (III. 14)
находим перемещения rj:
-*	0,342439-100
X =-------------
125-3
ИЮ
3
0,657561
11,11111
17,77778
20,00000
0,304
0,486
0,546
Полученный результат полностью совпал с тем, который мы
имели в примере 1 § 2. Это обстоятельство легко объяснить тем,
что нить, рассмотренная в примере 1 § 2, а также действующая
нагрузка симметричны. Такую нить можно рассматривать как
систему, состоящую из двух одинаковых половин. Учитывая, что
длина нити /], рассмотренной в настоящем параграфе, в два раза
меньше длины нити I, помещенной в § 2, стрелы провисания нитей
и интенсивность нагрузки в обоих случаях одинаковы, можно за-
ключить, что две'сравниваемые системы идентичны, поэтому про-
гибы в соответствующих точках совпали.
§ 5. ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ВЕРТИКАЛЬНЫХ
И ГОРИЗОНТАЛЬНЫХ НАГРУЗОК
Расчет гибкой нити, подверженной одновременному действию
вертикальной и горизонтальной нагрузок, представляет собой
более сложную задачу по сравнению с обычной задачей равно-
весия нити, загруженной только вертикальной нагрузкой.
95
Рис. 76.
При наличии горизонталь-
ной нагрузки распор в нити из-
меняется по длине пролета, что
сильно усложняет расчет.
Рассмотрим случай загру-
жения гибкой нити (рис. 76)
следующими нагрузками:
1)	постоянной распределен-
ной по горизонтальной проек-
ции нагрузкой g Т{м\
2)	временной вертикаль-
ной нагрузкой qy, распределен-
ной также по горизонтальной
проекции и изменяющейся по
произвольному закону;
3)	временной горизонтальной нагрузкой qx, действующей в
плоскости гибкой нити, распределенной по вертикальной проек-
ции и изменяющейся по произвольному закону.
За исходное состояние нити будем принимать ее очертание
от постоянной нагрузки, при которой она будет иметь пролет I и
стрелу f. Затем прикладываются нагрузки qy и qx, под действием
которых нить займет новое положение.
Задача заключается в определении вертикальных и горизон-
тальных перемещений точек оси нити и возникающих в ней уси-
лий. При решении этой задачи будем учитывать удлинения нити
от указанных временных нагрузок. Жесткость по всей ее длине
примем постоянной и равной EF. Таким образом, задача ре-
шается в общей постановке, при этом легко рассмотреть частные
случаи, полагая равным нулю ту или другую нагрузку. На рис. 76
изображена гибкая нить и эпюры перечисленных выше нагрузок.
Жирной линией показано очертание нити от постоянной нагрузки
g, а пунктиром — искомое положение, которое займет нить после
приложения нагрузок qy и qx.
Предположим, что опорные точки расположены на одном
уровне и постоянная нагрузка равномерно распределена по всему
пролету. В этом случае нить будет очерчена по квадратной пара-
боле с уравнением (III.16) и распор от постоянной нагрузки
Н
g
= gP
8/
Для вывода основных уравнений рассмотрим элемент нити,
вырезанной в произвольном сечении и находящийся в деформи-
рованном состоянии, как показано на рис. 77.
Силы, действующие на этот элемент, кроме Н (х) и Н(х) +
+ dH(x), будут определяться равенствами:
Vy={g + <]y)dx,
96
yx = Qx\dy\,
dx
Q(x)±dQ(x) = (H(x)+dH(x)) P^ + ^-4- ^Ly+^dx].
[ dx	dx2 J
Во втором уравнении величина dy взята по абсолютной вели-
чине. Объясняется это тем, что направление горизонтальной
нагрузки задается в начале расчета и в процессе расчета ее на-
правление не должно изменяться, величина же dy по длине нити
меняет свой знак. Этим объясняется то, что во втором уравнении
вместо dy принята величина | dy |.
Учитывая полученные значения сил, действующих на элемент
нити, и составляя уравнения проекций на вертикальную и гори-
зонтальную оси, получим:
- Н (х) -d-(y-+-^  4- [Н (х) + dH (х)1	4. 12<у+Л> dx} 4-
dx	dx	dx J
+ (g+9y)^=0,
dH (x) + qx\dy\ = Q.
Пренебрегая произведениями dH{x)d^ и dH (x) — ^y + dx,
dx2
после несложных преобразований получим:
Н W -уу+Л W -уг+• -у-+(г + ?У)=°.’  (ш-39)
dx2	dx2 dx dx	
= -qx .	(1Й140)
Подставляя выражение (III.40) в уравнение (III.39), получим
Горизонтальные и вертикальные перемещения связаны между
собой. Они не могут развиваться независимо друг от друга. Для
установления этой зависимости ‘условимся вертикальные переме-
щения т] считать положительными, если они направлены вниз, а
горизонтальные перемещения и принимать положительными,
если они направлены вправо. Обратимся к рис. 78, на котором
изображен элемент в исходном и смещенном состояниях.
Составим выражение разности квадратов длин отрезков а^Ь\
и ab:
(ds -f- Ads)2 — (ds)2= (dx-\- du)2 Д- (dy Д- d-ц)—(dx)2 — (dy)2.
Пренебрегая выражениями (Ads)2, (du)2 и (dr])2, получим:
ds& ds— dxdu-\-dydi\.	(III.42)
Величина Ads представляет собой удлинение элемента ds от
временных нагрузок qy и qx.
Учитывая, что усилие в нити от временных нагрузок можно
определить равенством
N- ,
4	COS <f>
получим:
A ds
H(x)-Hg
-------— ds,
EF cos <p
где <p — угол наклона касательной к оси нити после деформации.
При малых перемещениях его можно принять для пер-
воначальной оси нити.
Подставляя значение Ads в выражение (III.42), получим:
du   dy d-q । 7/ (•* *) Z/g- / dS у
dx	dx dx Ef cos<f> \ dx /
Производя интегрирование по частям и учитывая, что
J dx dx	dx J rfx2
получим *
X	X
dy' i C d2y , . C 7/ (x) Hg Г 1 . / du X213/2
\—dx-
' dx J dx2	J EF [	\ dx /
о	0
- <	(III.43)
------
*-При интегрировании следовало бы добавить произвольную постоян-
ную, но в нашем случае она равна нулю, так как при л=0 а=0.
Таким образом мы получили два уравнения (III.41) и (Ш.43)
для определения перемещений. Однако этих уравнений недоста-
точно для решения задачи, так как, кроме неизвестных т] и и,
необходимо определить также распор //(%), изменяющийся по
длине пролета. Для составления третьего уравнения используем
граничное условие, которое при х=1, и=0 и rj = 0 дает:
Н (x) — Hg
EF
dx^
Tidx=0. (III.44)
Совместное решение уравнений (Ш.41) и (Ш.44) позволит
определить величину распора Н(х) и вертикальные перемещения
т), а уравнение (Ш.43) даст возможность определить горизон-
тальные перемещения и.
Для решения полученных уравнений проведем некоторые пре-
образования. Преобразуем вначале уравнения (Ш.41) и (Ш.44).
Представим распор в произвольном сечении в следующем виде:
Я(л)=Я0 + дЛ/(л),
(III.45)
где Но — распор в начале координат (в нашем случае на левой
опоре). Величина ЛИ (х) находится на основании ра-
венства (111.40) в виде
Д/У (х)= — \ qx
dx [
(III.46)
Подставляя выражение (Ш.45) в равенства (Ш.44) и (Ш.41)
и произведя необходимые преобразования, получим:
=	. Г 1 дх dy \ dy-
dx^
Но
Но + ЬН (х)
.’V
у$9
Обозначим
ЧЭД=-^^- Г 1 +	,	(Ш.47)
/7^ L \ dx / J
Ф(х) =--------[1-----(Ш.48)
7/о + Л7/ (х) [	g + qy dx dx j
Заметим, что
t'[ 1+^Y]3'2(/X=/IX.
J I \dx? ) J
0
Величина p. определяется равенством (III.22) или (Ш.23), а
также по табл. 3 (приложение).
Произведя подстановку и учитывая, что для квадратной па-
раболы
— const =
rfx2
_____
/2	’
получим
4r(x)t/x----i]rfx=O, (III.49)
б	о
4^= _ Лу-----------g + Qy. ф (х).	(III.-50)
dx2 dx2
Применим для решения задачи численное интегрирование с
помощью интегральной матрицы, описанной в книге (38]. Разобь-
ем пролет нити на п равных частей. В соответствии с [38] (см.
стр. 127, уравнение V.22) получим:
= от]0 4- 2aij0 22т;".
Учтя, что т]о=О, получим:
Tj =	4~ S2^'.
(III.51)
Для определения величины tio' используем условие: при х — 1
-т]=0. Выписывая последнюю координату вектора т) и приравни-
вая ее нулю, а такж.е учтя, что последняя координата вектора
Йо равна п, и обозначив последнюю строчку матрицы й2 через ыг,
найдеад:	,	•
too
Следовательно,
------ "г/'.
п
Подставляя это выражение в формулу (III.51), получим
где
Z. = -L.2<Z»0-22.
п
(Ш-52)
(Ш.53)
Запишем уравнение (III.50) в векторной форме
л-£_бФ.
Hg
В этом выражении
nG
Диагональная матрица G имеет вид
f g + Яу \
\ g Л
'	G =	Г + ?у А
1	k g Л
! g + Яу \
\ g /п
а вектор Ф имеет элементы, определяемые по формуле
(III.54)
(Ш.55)
(III.56)
-----------Г 1 :-----— | у I v'l .	(III.57)
Но + ЬН(х)[ g + Яу	J	U ’
Применяя равенство (III.52) и учитывая, что -C-==J£t получим:
I
V=-y+^-~-LG®,	(III.58)
.Вместе с тем с помощью последней строки интегральной матри-
цы 79, которую обозначим со, найдем:
.	i
d.X = <Й7] = (О
о
1 J ’°-' ' ' Ц z г.7	'
Подставив этот интеграл в основное уравнение (III.44) и про-
изведя все преобразования, получим квадратное уравнение для X:
— тп2=0.	(III.59)
Интересующий нас корень этого уравнения
Х =	,	(III-60)
где
"2 А	9
Д р. — и
Д = -^-ш£бФ,
12ыу
v) »
FfEFFy
-Ц=—
I
.(Ш-61)
'Г
ЬН (х)
П W)T/2-
Из этих формул видно, что при определении Л используются
величины, зависящие от искомого значения распора, входящего
в вектор Ф.
Для определения X применим метод последовательных при-
ближений. В первом приближении положим все координаты век-
тора Ф равными единице. Найдя Л .и затем распор /70= вы-
числяем новый вектор Ф, и затем весь процесс повторяется снова
' до тех пор, когда величина А, а также координаты вектора Ф в
двух последних приближениях полностью совпадут. Решение кон-
кретных примеров показало, что приходится делать от 6 до 10
приближений.
После того как найдено значение распора по формуле (III.58),
находится вектор вертикальных перемещений. При определении
вектора и интегралы, входящие в формулу (III.43), будем опре-
делять численным методом. При наших граничных условиях по-
лучаем:
-*	8/ ->ч
м = 2(------
(Ш.62)
где YM=[1+(/)2]3'2-
102
Ч=1,0т/м
Ч'утах ~Ып11м
Пример. Рассмотрим числен-
ный пример для нити, изображен-
ной на рис. 79. Пусть 1 = 160 м,
/ = 20 м. Горизонтальная нагрузка
z/x = 0,09 Т/м равномерно распре-
делена по всей высоте и действует
на обе половины нити. Вертикаль-
ная нагрузка распределена по
закону треугольника. Интенсив-
ность этой нагрузки на правой
опоре принята равной qy—1,2 Т/м,
EF=2-\№ Т, g=\T/M. Разобьем
пролет на 6 равных частей. Инте-
гральная матрица для этого слу-
чая будет (подробное объяснение построения этой матрицы будет
Рис. 79.
дано в § 7):							
	0	0	0	0	0	0	0
	1351	2034	—336	90	-24	6	-1
_	л	1198	3732	1452	— 180	48	-12	2
Q	а 3120	1239	3486	3216	1590	-216	54	-9
	1228	3552	2952	3360	1548	-192	32
	1231	3534	3024	3090	3336	1506	-121
	1230	3540	3000	3180	3000	3540	1230
Опуская все вычисления, приводим матрицу L (III.53)
	0	0	0	0	0	0	0
	2330	12 252	13548	8922	6456	2910	382
и 2	1318	12 468	22746	19 236	12396	5988	728
£ = -^— 3-6240	1179	8604	19638	25 398	19638	8604	1179
	728	5988	12396	19236	22746	12468	1318
	382	2910	6456	8922	13548	12 252	2330
	0	0	0	0	0	0	0
0,97750
0,99555
1,00449
1,00707
1,00927
1,01530
1,02462
Для этой задачи была составлена программа и проведено ре-
шение на электронной машине «Сетунь». Приведем окончатель-
ный результат, который выдала машина:
X =0,624366,
256,260
255,260
254г660
254,460 ,
254,260 *
253,660
252,660
Ф=
103
—►	0,00000 -0,90634 -0,65874		0,00000 0,40529 0,37143
1} =	0,12693	, « =	0,32137
	0,88553		0,39399
	1,05138		0,43417
	0,00000		0,00009
Последняя координата вектора и должна быть равна нулю.
В нашем случае она равна 0,00009. Это говорит о высокой точ-
ности вычислений.
Интересно отметить, что если положить qx = 0, EF—oo, то
распор #0=256 Т. При наличии горизонтальной нагрузки и при
EF= со #0—257,8 Т.
Таким образом, от горизонтальной нагрузки распор почти
поровну передался на обе опоры. Однако нельзя утверждать,
что такое распределение будет во всех случаях загружения.
§ 6. РАСЧЕТ НИТИ, ЗАГРУЖЕННОЙ ВЕРТИКАЛЬНЫМИ
И ГОРИЗОНТАЛЬНЫМИ СОСРЕДОТОЧЕННЫМИ СИЛАМИ
Вернемся к задаче, рассмотренной в предыдущем параграфе,
и заменим в ней распределенные нагрузки сосредоточенными си-
лами. Такая замена приблизит нас к условиям равновесия кабеля
висячего моста и вместе с тем приведет к изменению метода
решения, так как вместо дифференциальных уравнений мы по-
лучим системы алгебраических уравнений.
Предположим, что под действием сосредоточенных сил Vg
нить заняла положение, показанное на рис. 80 жирной .линией.
После дополнительного воздействия на нить сил VQ и W она
перешла в новое положение (показано пунктиром). Наша задача
состоит в том, чтобы определить вертикальные перемещения т] и
горизонтальные перемещения и всех узлов нити.
Расстояние по горизонтали между соседними точками к будем
принимать одинаковыми и равными d. Координаты точек к отме-
ряются от линии, соединяющей
опорные шарниры О и п+1.
Узел к с двумя прилегающими
к нему элементами и <S\+1
переместится в новое положе-
ние (см. рис. 81). Горизонталь-
ные проекции усилий (распо-
ры) в элементах S,. и 5\+i обо-
значим соответственно #. и
/Д+д-
104
Рис. 81.
Приложенные к узлу силы: от постоянной нагрузки от
временной нагрузки VqK и W к, также переместятся вместе с
узлом. Узловые точки получат перемещения ц и и, а длины S —
приращения AS.
Пусть номера у величин S и Н совпадают с номерами пра-
вого узла соответствующей панели. Проекции элементов S, при-
мыкающих к узлу до и после деформации, показаны на рис. 81.
Углы наклона элементов нити после деформации обозначим и
<p\+i. Рассмотрим равновесие узла к в смещенном состоянии.
Приравнивая нулю сумму проекций всех сил на вертикальную
ось, получаем:
VgK + VqK =	— Нк+1 tg <р’+1.
Но так как связь между распорами в соседних панелях опреде-
ляется равенством
HK^ = HK-WK,
то
VgK ' I- VqK = Нк (tg <?'* — tg Тк +1) +	tg +1.
Или иначе
„Г &Ук +
/7 I------------------------------—
[ d + &ик d + AuK+1
~t~ А^к+1
d + Дпл+1
(а)
105
Так как величины Ди малы по сравнению с длиной панели, то
можно воспользоваться приближенным равенством
1	1	1	_ 1 /1 ч
d + Д« d ’ 1 -+• е d 6 ’
где
Подставляя (Ь) в (а) и учтя также, что
ЬУк=Ук~Ук-г A^=7J« — V-р
получим:
VSK+v qK= н А1 — е«) ~ (у к—ук_\ + ^—v-i)+
-№(1 -ек+1) ~ (Ук~ Ук+1+ tJk-^+1)-
или
VgK~WQK= Нк	I ~{yK-A + ^_1) + 2 (Ук~\- Т]х) —
- (Ук+1 + Чс+1)] - е« — I - (Ук-1 + ^-1) + (ук+ ^)1 -
~ел+1	[(//« +^)-(^+1+^+1)1	{--[(^+13к)-
Если теперь индексу к дать значения 1, 2, 3, ..., п, то получим
систему из п уравнений. Записав эту систему в матричной фор-
ме, получим:
^g-VVq = \GH (L2-Gu^-G-GW(C2- G2eZ2n)] (J-H),
или сокращенно
Vg+Vq = (Ghl*2 - GwLl)Су -H)•	(П1.64)
Матрицы, входящие в это уравнение, определяются равенствами
Г2= Z2 -GUL2 -	(III .65)
Лз=Л-С2еЛ^	(Ш.66)
106
где матрица L2 совпадает с матрицей (Ш.2), а остальные матри
цы имеют вид
(III.67)
(III.68)
е
п
е2
(IIL70)
(III.71)
(III.72)
Величины, входящие в матрицы (Ш.69) и (III. 70), в соответ-
ствии с (Ш.63) определяются равенствами
Uk- U-K-1 (к=1, 2................п).	(III.73)
107.
Так как элементы матрицы GH, определяемой равенством
(III.71):
н2=н.-ьнх,
где
д^=04-1Г1 + UZ2H-ЦГк(/с=1,
(III.74)
то эту матрицу можно представить в виде
(III.75)
где
О
Д^
ДЯ2
Подставляя (III.75) в (III.64), получим:
q—(7/iZ<2 1\VL>_ — GWL^) (г/-)*7])-
(III.76)
(III.77)
Решая это уравнение, найдем вертикальные перемещения:
;=(^ + ХЯ/2)-’
(III.78)
где
/? = —GWL%— DwL-i
Hg
(Ш.79)
6 н — Н уЕ —
2,..., «),
Для выяснения зависимости между вертикальными и гори-
зонтальными перемещениями воспользуемся методикой, изло-
женной в предыдущем параграфе. Теперь мы будем рассматри-
вать не бесконечно малый элемент ds, показанный на рис. 78, а
конечный элемент 5^, равный длине звена нити между узлами
к—1 и к. Воспользуемся уравнением (Ш.42), заменив в нем dx,
dy, du и dr[ соответственно на d, by, bu и Дтр
SKbSK = dMiK+ byK^K.	(III.80)
Учтя, что
Д5Л =
EF cos Tk
108
из уравнения (III.80) найдем:
&tlK =
&Ук
d
Нк-Hg
EF cos

но
х	/ <$к \2	9
= tg?K. и = sec2^,
поэтому
Ик~ ик^ = — tg (т]к - Т]к_1) 4
(Нк — Hg) d sec3 <рл.
EF
(III.81)
Здесь — угол наклона элемента S* к горизонту в первичном
ее положении. Уравнение (III.81) справедливо для каждого узла.
Положив к=1, 2, 3, ...» п, будем иметь:
«1= — tg <FPJi 4
ЕЕ
d sec3 <рь
H2 — Hg
«1 = — tg Cf2(7)2 — 7)1)4	gg d sec3 cp2,
EF k

«3 — W2 = " ~ tg ?3 (^3 — %)
EF
d sec3 a>3.
Если во второе уравнение вместо щ подставить его значение
из первого уравнения, а в третье — вместо м2 его значение из вто-
рого и т. д., то получим:
«^-tg'PiTi^Yi,
м2	— Д tg <Р17) 1 — tg <р2Т)2 4- Ъ
= tg Т,7)1 — Д tg %Т)2 — tg <f>3T)3 4- Y3.
Переходя к матричной записи, получаем:
и = — Дпт)4у,
(III.82)
где
tg?i
Д t^cpitg ?2
Д t I Д tg Ср2 tg %
Atg?rMg?2A tg%. . .tg?„
(Ш.83)
109
Здесь
Atg<^=tgcpK — tg<pK+1
2 (Hi — ^sec3^
H^sec^i
i=l
n................
^g-) sec3 ср,-
i=l
(111.84)
Остается теперь преобразовать уравнение (Ш.44). Заменив
интегрирование суммированием по
всем
элементам, получим:
п
Но так как
K=1
-d sec3<t„-
ef
B/d
Р
K = l
НК=НХ-ЬН„
то
d------—— \ ’ sec3 cpi
EF ______
лг=1
_^Sw«sec3<f«
п
Bfd
V
К = 1
J] Ъ= 0.(111.85)
К
К = 1
Входящая в уравнение (Ш.85) величина ДНК определяется
равенством (III.74). Введем обозначения:
л + 1
a = 2sec3?K,
К=1
s=2 4//«sec3’i«’
а=Ц-А_, р. -	,
аН g	al2Hg
тогда из уравнения (III.85) получим:
т]«-
К = 1
(III.86)
(III.87)
Таким образом мы получим три совместных уравнения
(III.78), (Ш.87) и (III.82). Решение этих уравнений вызывает
большие трудности, которые связаны с тем, что матрицы Gle и
G2e, входящие в уравнение для определения прогибов (Ш.78),
зависят от перемещений и, которые, однако, нельзя найти, не зная
величин т). В свою очередь, имеется взаимная сложная связь
между т] и A [(III.78), (II 1.87)]. Полученные уравнения возможно
решить только методом последовательных приближений на ЭВМ.
ПО
В дальнейшем нас будут интересовать главным образом по-
логие нити, для которых полученные уравнения можно сущест-
венно упростить. Для пологих нитей величины е, определяемые
равенством (III.73), весьма малы по сравнению с единицей и
поэтому без ущерба можно положить е=0. Это вносит большие
упрощения. Матрицы Gle и G2e в этом случае будут нулевыми и
вместо (III.65) и (Ш.66) получим:
aUz.2,
L*3=Ln2.
Основное уравнение (Ш.78) теперь будет связано только с
уравнением (III.87), а уравнение (Ш.82) для определения и вы-
деляется в самостоятельное уравнение.
Таким образом, для пологих нитей мы получаем два совмест-
ных уравнения (III.78) и (Ш.87) для определения прогибов и
величины А, через которую находится распор. Эти уравнения
могут быть решены методом последовательных приближений по
той схеме, которая описана ниже в гл. V в § 4 и 6. После того как
найдены т] и А, по уравнению (Ш.82) легко определить горизон-
тальные перемещения и.
Пример. Рассмотрим пример, близкий, к примеру, решенному
в предыдущем параграфе. Сохраняя основные размеры, заменим
ось нити ломаной линией и приложим в ее узлах сосредоточенные
силы, заменяющие распределенные нагрузки. Применим прибли-
женный метод, положив е=0. Величины действующих сил пока-
заны на рис. 82. В табл. 3 приведены геометрические данные,
которые будут использованы в дальнейшем решении. В этой таб-
лице величины <5^ и седаны для элемента, примыкающего к точ-
ке к с левой стороны.
=26,(6)TV^2e,(6)r Vg=2fflr Vs=2e,fG)T
V4r5,(3yrVif1O,(6)rV^16T Уи=2ЦЗ)г
Рис. 82.
Ill
Таблица 3
		SK		secs<p^
0	0	0	0	0
1	11,1111	28,8889	0,416667	1,27141
2	17,7778	27,4874	0,250000	1,09520
3	20,0000	26,7591	0,083333	1,01043
4	17,7778	26,7591	—0,083333	1,01043
5	11,1111	27,4874	—0,250000	1,09520
6	0	28,8889	—0,416667	1,27141
32,0000
37,3333
42,6667
48,0000
53,3333
0,8
0,4
—
0,2
0,4
0,8
О
0,8
—
0,4
0,2
0,4

0,416667
0,166667
0,166667
0,166667
0,166667
0,250000
0,166667
0,166667
0,166667
0,083333
0,166667
0,166667
-0,083333
0,166667
— 0,250900
*
_ 1
2— ~
2 -1
-1	2
— 1
-1
2
-1
- 1
2
-1
2
112
1
-1
1 —1
1 -1
1
По формуле (III.79) находим:
	-0,8	0,8	0	0
	0,8	2	1,2	0
В = — d	0	0,4	— 1	0,6
	0	0	0,2 -	-0,8
Далее находим	0	0	0	0,4
		___ gl'1 8/	= 160	т.
-1
1
О
О
О
0,6
-1,6
По формулам (III.86) находим:
О
0,8
1,2
I,4
1,8
2,6
sec3 ук=6,75408,
К = 1
а= 1

1,008125,
л + 1
£=У, A//sec3tp =8,780304, В = -8/£-£ =11,56708.
ZJ	*	al2He
к = 1	s
Таким образом имеем два уравнения:
^=(fi-X160Z2)-1
32,0
37,3
42,6
48,0
53,3
/ (X) = 1,008125 ф11,56708 jg
К-1
И J
Эти уравнения были решены на электронной машине «Се-
тунь» методом, описанным в § 4 и 6 гл. V.
Приведем окончательные результаты, полученные для данно-
го примера:
Х= 1,602743,
Нг = 256,439 Т.
Вектор распора в звеньях нити будет
256,44
255,64
255,24
255,04
254,64
253,84
Векторы горизонтальных й вертикальных перемещений имеют вид
О
— 0,93977
-0,74135
0,01185
0,76453
0,95627
О
0
0,39321
0,34499
0,28350
0,34744
0,39416
0
Сравнение приведенных результатов с аналогичными резуль-
татами, полученными в предыдущем параграфе, свидетельствует
об их близости. Как и следовало ожидать, перемещение узлов
нити, очерченной по ломаной линии, несколько меньше.
§ 7. ОБ ОДНОМ ВАРИАНТЕ ПОСТРОЕНИЯ
интегральной матрицы*
В задачах строительной механики и многих других чисто ма-
тематических задачах для интерполирования функций можно
применить функции, представляющие собой формы изгиба тонкой
упругой линейки. Рассмотрим систему функций vx(x), v2(x), ко-
торые представляют собой ось изогнутого неразрезного стержня,
закрепленного в п точках при смещении на единицу соответствен-
но 1-й, 2-й и т. д. опоры. На рис. 83 показаны эти функции иг-(х)
(i = 0, 1, 2, 3).
* Интегральная матрица понимается в таком же смысле, как она изло-
жена в § 32 работы [38].
114
Обычно для построе-
ния интегральных матриц
используются "ПОЛИНОМЫ
Лагранжа. Данные кри-
вые, используемые как
координатные функции,
имеют перед полиномами
Лагранжа то преимущест-
во, что они быстро зату-
хают с удалением от мес-
та смещенной точки.
На рис. 84 для срав-
нения показаны две кри-
вые при делении интер-
вала на 6 равных частей,
имеющие единичные зна-
чения ординат в точке 2.
Кривая, отвечающая изги-
бу неразрезного стержня,
имеет затухающий харак-
тер, в то время как соот-
ветствующий полином
Лагранжа, наоборот, не
отличается этой особен-
ностью. Опыт применения
п
функций u(x) = Е yiVi(x), получаемых из условия деформации
4=1
тонкой линейки, как интерполяционных кривых показал, что
точность приближения в этом случае при большом количестве
участков деления довольно высока. Это положение легко понять
' с чисто физической точки зрения. Представим себе, что необхо-
димо провести кривую через заданное количество точек. Изог-
нув тонкую линейку так, чтобы она имела заданные ординаты,
можно добиться сколь угодно большой точности приближения
упругой линии к заданной кривой, если увеличивать число
заданных ординат. Наоборот, при увеличении числа делений
кривая, полученная с помощью полиномов Лагранжа, может
существенно отклониться от заданной кривой в промежуточных
точках, особенно в крайних панелях.
Итак, назначим уравнение аппроксимирующей функции в виде
ряда
п
(П1.88)
/=1
Для построения интегральной матрицы выводить аналитиче-
ское выражение функций Vi(x), вообще говоря, не нужно. Опре-
115
1
Рис. 85.
деление площадей этих функций на отдельных участках легко
произвести н’а основании теоремы о взаимности работ. Рассмот-
рим два состояния неразрезной балки, показанной на рис. 85.
В первом состоянии опора к получила смещение, равное единице.
Ось изогнутой балки представляет собой функцию оЛ. (х). Тре-
буется определить площадь этой кривой на участке di. Зададим
второе состояние в виде балки, загруженной нагрузкой # = 1,
расположенной в пролете di. По теореме взаимности работ имеем:
— Ч‘л1к Ч- A i • 1 = 0.
Так как q= 1, то
Таким образом, площадь функции vK (х) на участке di равна
опорной реакции Ак1 от равномерной нагрузки q= 1 на указанном
участке. Для определения площадей кривой v к(х) достаточно
рассмотреть последовательное загружение пролетов неразрезной
балки на жестких опорах распределенной нагрузкой q=\. Так
как нам потребуется вычислить все площади (*=1, 2, ..., л;
к=1, 2, ..., п), то практически необходимо решить задачу об
определении всех опорных реакций от загружения по очереди
всех пролетов. На первый взгляд эта задача трудоемка. Однако
быстро выясняется рекуррентная зависимость, по которой без
труда находятся все элементы интегральных матриц любого по-
рядка.
Ниже приводятся эти матрицы от третьего до девятого поряд-
ков (при ;г = 2—8):
0 0	0
7 10 -1 ,
6 20	6
Н6
п = 2
			n =	3	0	ООО				
			2 =	d 60	26 23 24	39-6	1 72	27 — 2 66	66	24				
		7Z.=	4	0	0	0	0	0			
		2 =	d	97 86	146 268	— 24	6 104 - 12	-1 2			
			224	89 88	250 256	232	110 208	256	-9 88			
	П-	= 5	0		0	0	0	0	0		
	2	d	362 321 332 329	545 - WOO 934		-90	24	- 389 — 48 869	494	-6 12 54	1 — 2 о		
		836		952		790	904	401		-32		
			330	946		814	814	946		330		
п.—	6	0	0		0	0	0		0	0	
2 =	d 3120	1351 1198 1239 1228 1231 1230	2034 3732 3486 3552 3534 3540	-336 1452 3216 2952 3024 3000		90	—24 -180	48 1590 -216 3360	1548 3090	3336 3180	3000	6 -12 54 — 192 1506 3540		— 1 2 — 9 32 -121 1230	
и—	7 .	0	C		0	0	0	0	С	0	
	d	5042 7591 -1254 4471 13928	5419 4624 13010 12002				336 -90 -672	180 - 5935 -810	24 -48 216	-6 12 -54	1 — 2 9	
Ы4 		11644	4583 13 256 11018 4594 13190 11 282 459113 208 11 210 4592 13 202 11234				12 536 5791 —768 11546 12398 5815 11816 11390 1 2 488 11726 11 726 11 234		192 —32 — 726	1 21 5611 —450 13 202 4592		э
я =	8	0	0		0	ООО		0	0	0	
2 =	d	18817 28330 16686 51980 17257 48554 17104 4Q479		— 4680	1 254 — 336	90 20224 —2508	672	—180 44792 22150 —3024	810 41120 46784 21616 —2880 42104 43094 46256 21754 41840 44084 42560 46412 41912 43814 43568 42650 41888 43904 43232 43904			-24	6	—1 48	—12	2 -216	54	—9 768 —192	32 -2904	726	—121 21664 —2700	450 46568 20950 —1681 41888 49280 17136			
	43456	17145 17134 17137 17136	49226 49292 49274 49280							
117
Рис. 86.
В этих матрицах все элементы
определены в целых числах. Впере-
ди каждой матрицы стоит множи-
тель, вынесенный за скобку. Таким
образом, все элементы даны без
округлений и имеют точные значе-
ния. Легко проверить, что построч-
ная сумма для каждой матрицы со-
ответственно равна 1, 2, 3, ..., п.
Заметим, что при использовании
интегральных матриц, полученных
в настоящем параграфе, для установления связи между функ-
цией и ее производными можно применять только формулы
(II 1.51). Для случая, когда интегральная матрица построена
с помощью полиномов Лагранжа, указанная связь может быть
записана в двух вариантах. Второй вариант приведен, например,
в книге [38] в виде равенства (V.25), которым в нашем случае
пользоваться нельзя.
§ 8. РАСЧЕТ ГИБКОЙ НИТИ С УЧЕТОМ
НАКЛОНА ПОДВЕСОК
Во многих конструкциях несущие гибкие нити загружены
через подвески, горизонтальное перемещение которых на уровне
действия нагрузки резко отличается от горизонтальных переме-
щений гибкой нити. В результате этого подвески наклоняются на
некоторые углы и гибкая нить будет загружаться своеобразной
«следящей» нагрузкой, как показано на рис. 86. Тако£ явление
имеется, например, в висячих мостах и, как правило, в расчетах
мостов не учитывается. Для очень пологих нитей горизонтальные
перемещения обычно не вычисляют, так как они малы по срав-
нению с вертикальными перемещениями. Однако величина угла
наклона подвесок, влияющая на результат расчета, зависит также
от их длины и поэтому для коротких подвесок учет горизонталь-
ных перемещений может дать ощутимые результаты даже для
пологой нити.
В настоящем параграфе рассматривается задача о переме-
щениях гибкой нити, находящейся под действием постоянной
нагрузки и затем дополнительно загруженной временной нагруз-
кой. Предполагается, что при отсутствии временной нагрузки все
подвески находятся в вертикальном положении, а после загру-
жения временной нагрузкой они наклоняются, в результате чего
возникают горизонтальные составляющие силы, которые благо-
приятно действуют на гибкую нить, препятствуя развитию пере-
мещений. Чем короче подвески, тем большее удерживающее
влияние они оказывают на гибкую нить. Предполагается, что
118
полотно АВ не работа-
ет на изгиб (рис. 87).
Такой случай возмо-
жен, например, тогда,
когда на линии АВ
расположена шарнир-
ная цепь из жестких
дисков, удерживающих
нижние точки подвесок
от горизонтальных сме-
щений.
За последнее время
по расчету гибких ви-
сячих конструкций поя-
вилось много работ.
В сборнике статей
под редакцией проф.
И. М. Рабиновича [30]
рассмотрено много ин-
Рис. 87.
тересных задач. Большой интерес представляют работы
канд. техн, наук Г. Э. Райнуса [31—33].
Теперь познакомимся с выводами основных уравнений. На
рис. 87 показана гибкая нить, закрепленная в точках к ко-
торой с помощью подвесок приложена постоянная распределен-
ная нагрузка g. При действии только постоянной нагрузки ось
гибкой нити очерчена по веревочной кривой (на рис. 87 она пока-
зана пунктиром).
Сделаем предположение, что подвески нерастяжимы и непре-
рывно распределены по всей длине АВ. Приложим к подвескам
дополнительную нагрузку q, распределенную по произвольному
закону. Гибкая нить займет новое положение, показанное на ри-
сунке жирной линией.
Выведем дифференциальные уравнения равновесия растяжи-
мой нити. Произвольная точка оси нити к переместится как по
вертикали, так и по горизонтали. Обозначим вертикальные и го-
ризонтальные перемещения точек
оси гибкой нити через г] и и. Вер-
тикальные перемещения точек
шарнирной цепи при нерастяжи-
мых подвесках также будут рав-
ны т], а горизонтальные переме-
щения этих точек обозначим и.
Рассмотрим равновесие бес-
конечно малого элемента нити,
показанного на рис. 88. Проекти-
руя все силы, действующие на
этот элемент, на вертикальную
119
ось получаем:
(g + q)dx-H -(y + + (// + dH) d(f/+T?) 4-dx] = 0.
dx	[ dx d^x J
Пренебрегая произведениями dHdy и dH -2<y + dx, находим:
rfjC2
H	^-=-{g-Yq). (III.89)
cfx2 dx dx dx?
Приравнивая нулю сумму проекций на горизонтальную ось, по-
лучаем:
Относительное смещение концов подвески будет равно разности
горизонтальных перемещений:
и —и*,	(Ь)
при этом
д* = у	(III.90)
о
Нагрузка qx, образующаяся вследствие наклона подвесок,
связана с горизонтальным перемещением и зависимостью
Qx=-^^(g + ^-	(с)
И—У
Из выражений (а) и (с) получаем:
--------^-(£ + 7).	(Ш.91)
dx	Л~У
Произведя подстановку этого выражения в уравнение
(III. 89), будем иметь для т] и и дифференциальное уравнение
н	4т+<«+?)=°- <ш-92>
dx* /1 — у dx	dx*
Перемещения и и т] зависят друг от друга. Для выяснения
этой зависимости рассмотрим произвольный элемент нити ds
(рис. 89).
После деформации нити элемент тп перейдет в новое положе-
ние тщь Перемещение и считаем положительным, если оно
произошло влево. Длина элемента изменится на величину Ads:
Нп ds	Н „ ds
Eds =------9-------—9-------. .	(III .93)
EFcos (у -р d<p)	EFcostp
120
Как и раньше, используем для элемента тп следующее оче-
видное равенство:
(ds)2= (dx)2 -4- (dy)2.	(111.94}
Для элемента /И1П1 соответственно получаем:
(ds-\- Д ds)2=(dx—du)2-{-(dy 4-dr^)2.
Раскрывая скобки и пренебрегая величиной (/ids)2, найдем
(ds)2-f- 2dsД ds = (dx)2— 2dx du-\-(du)2-\-(dy^-\-2dy di\-\-(d-rtf.
Учитывая равенство (III.94), получим:
2dsi ds= — 2dx du-\-2dy d\-\-(du)2Jj-(dri)'2,
откуда
( du \2 2 -^--{-2— • dr‘ | fУ 2 ds HqdS — Q
\ dx / dx dx dx \ dx ) dx dxEF cos <p
Поскольку
2 ds Hgds 2 Нч _ 2 Hq ] । /12
dx dxEF cos <p EF cos3 tp EF ' \ dx / j
то придем к следующему дифференциальному уравнению:
du । 1 / du \2| drl । 1 / dt]
dx 2 \ dx /	dx dx 2 \ dx J
H—Hg
EF
3
2
= 0.
(III.95)
121
Совместное решение в замкнутом виде основных уравнений
(III.92) и (III.95) не представляется возможным, поэтому будем
в дальнейшем применять численный метод их решения.
Предварительно проделаем некоторые упрощения. Будем пре-
небрегать перемещениями и * по сравнению с и. Далее примем
постоянную нагрузку g равномерно распределенной, тогда ось
нити при действии только постоянной нагрузки будет очерчена
по квадратной параболе с уравнением (III. 16). Временную на-
грузку q будем считать непрерывной функцией от х, а ее значе-
ние на левой опоре обозначим через qp.
Горизонтальную составляющую усилия в нити на левой опо-
ре обозначим Но, а в произвольной точке — Н. Соответственно
для площади нити примем обозначения Го и F.
На основе принятых допущений и обозначений преобразуем
уравнения (III.92) и (III.95) к следующему виду:
(III.96)
/	dy
d2^ _ d^y g+ qp g + q Ho I J _ dx
dx^ dx^ Efp	g + qp	H V	f\—У
з
dTj	Hp-Hg	Го	H —		И	/ dy \21	ч	
dx	EFp	F	‘ Hp-			\ dx ]		
du  dy
dx dx
(III.97)
(III .98)
(III.99)
(III. 100)
Условимся в дальнейшем производные по х обозначать штри-
хами.
Интегрируя два раза уравнение (III.96) и учитывая обозна-
чение (III. 98), получаем:
X
i =	\V(x)dx, (Ш.101)
л О •’
о
х х
-ц—^х — у-----ёф(%)dxdx.	(III. 102)
о' о
122
Далее из уравнения (III.97), интегрируя первое слагаемое по
частям и учитывая обозначения (Ш.99) и (III.100), а также то,
что н0=0, найдем:
х н —Н е	г
и= у'-ц — у" \~ydx-------- \ Ф (x}dx-\-1 v(x)dx. (III. 103)
J	EFq J	j
0	0	0
Продифференцировав это равенство один раз, получим:
ч' = у'^-Н-~Не	(Ш.104)
£F0
Для определения величины rjo', входящей в уравнения
(III. 101) и (III. 102), используем граничные условия при x=Z;
т] = 0. По уравнению (III. 102) получаем:
I X
---s j* ф (х) dx dx.
о о
Определив отсюда т)о' и подставив его в равенства (III. 101) и
(II 1.102), получим:
т]= — у +	ty(x)dx dx— ty(x)dx dxj, (III.105)
\ о о	о о’	'
I X	X	\
у- ф (х) dx dx — ф (х) dx j. (Ill. 106)
бо	о /
Для вычисления интегралов, входящих в равенства (Щ.105,
III.106 и III.103), применим численный методе использованием
интегральной матрицы, описанной в § 7. Для этой цели разобьем
интервал 0 — / на п равных частей и будем вычислять значения
всех неизвестных функций только в точках деления. Уравнения
(III.105, III.106, III.103 и III.104) будем в дальнейшем записы-
вать в векторной форме. Введем следующие обозначения:
ъ'=-у' + ^
123
и выразим векторы соответствующих интегралов через эти век-
торы с помощью интегральной матрицы
-------->
X
j ф(х) dx—
о
d
j* <р(х) dx
о
2d
j* ty(x)dx
о
I
j* ' (л) dx
6
J j* (л) dxdx = 22<p,
о 6
z Л
J j ty(x)dx dx~a= ою2ф,
о о
~r\ W dx~	ф(х) dx dx = (|ю2 — Й2)
0 0	0 0
Здесь o)i — последняя строка матрицы Q;
о)2 — последняя строка матрицы Q2;
О
Si
Введем также следующие обозначения для матриц:
£^^2-о2,	,	. (III.107)
=	ot02-C.	4	(Ш.108)
124
Подстановка этих матриц и векторов в формулы (III. 103—
III.106) дает:
Ч = — у 4- -^+-g0- Ад	(III. 109)
Но
(III.ПО)
Hq
->	/	- Но + Н„ ->
л+-гг£®-О,	(in-no
\	EF0	J
-	—	Но —Не-^
и' = у'^--—-®+ч>.	(Ш.112)
Таким образом задача свелась к решению нелинейных урав-
нений (III.109—III.12). Нелинейность видна из формул
(111.98—III. 100). При решении этих уравнений будем применять
метод последовательных приближений. Для определения Но ис-
пользуем граничное условие: при х = 1 и (0 =0. Для этой цели
применяем выражение (III.103). Учитывая, чтотД/) =0, получим:
Но —Н„ г	(•
---------\ Ф (х) dx 4- \ (х) ах.
EFq .)	J
о	о
Переходя к вертикальной форме, находим:
- Hq + Н„
У”^-\--дд—^1ф	=•' 0.
EFo
Подставляя в это выражение вместо т] его значение по
(III.109), получим:
— У" g “А? + ~~ = °‘
Но	EFo
Отсюда получаем квадратное уравнение для определения
Но— 2тх-\-т?=0,
где
_ Hg । EFoit/'^y-F
—z I	--------
2а>1Ф
7/^2 — У	j L» — •
(III. 113)
(III.114)
125
Коэффициенты тх и т2 зависят от неизвестных пока векто-
ров функций Фи
Для определения величины распора Н в любом сечении ис-
пользуем (Ш.91),из которого при и* = 0 легко определить
H =	(III. 115)
где
д/У=(£-Н0)[Ш	(Hi.116)
о
и
е=--------------------------------и.	(in. 117)
(g +	—У)
При численном решении вектор величины Д/У будет опреде-
ляться с помощью равенства
(III.118)
Рассмотрим теперь метод решения основных уравнений. Для
этой цели, как уже говорилось выше, применим метод последо-
вательных приближений. В первом приближении будем прене-
брегать величинами (т/)2 и (и')2 и при определении прогибов ц
не будем учитывать горизонтальные перемещения и. Тогда
Д/У = О и поэтому функции V, Ф и <р для первого приближения
будут следующими:
ф1(Х)=-^±£_ ,
?i (х) = 0.
Вычислив по этим формулам векторы Ti и Ф] и подставляя
их в (III.113) и (III.114), найдем коэффициенты тх и т2 и за-
Рис. 90.
тем, решая квадратное уравне-
ние, находим распор /Уо. Далее
по уравнениям (III. 109—
III. 112) определяем т), т/, и и
и'. Второе приближение начи-
нается с вычисления вектора
Д/У по формуле (III. 118) и
вектора Н по формуле (III. 115).
Затем по формулам (III.98—
III.100) находим векторы
функций W, Ф и ф второго
приближения.
126
Далее вычисления повторяются в том же порядке, как и в
первом приближении.
Пример. Рассмотрим гибкую нить параболического очерта-
ния, показанную на рис. 90 при следующих исходных данных:
/ = 400 м, /1 = 120 м, EF=2- 104=const-g = 0,5 т/лц /=100 м, q0=
= 1 т/м.
Разобьем пролет на 6 равных частей, тогда d=—-—. В пер-
вую очередь вычислим операторы, не зависящие от степени при-
ближения. Без вычисления приведем интегральную матрицу
седьмого порядка (см. § 7).
	0	0	0	0	0	0	0
	1351	2034	-336	90	-24	6	— 1
	1198	3732	1452	-180	48	— 12	2
4190	1239	3486	3216	1590	-216	54	— 9
	1228	3552	2952	3360	1548	— 192	32
	1231	3534	3024	3090	3336	1506	-121
	1230	3540	3000	3180	3000	3540	1230
(III.107 и III.108)
По формулам
лучим матрицы:
после всех вычислений по-
		0	0	0	0	0	0	0	
		2330	12252	13548	8922	6456	2910	382	
	И2	1318	12468	22746	19236	12396	5988	728	
—	1R790	1179	8604	19638	25398	19638	8604	1179	
		728	5988	12396	19236	22746	12468	1318	
		382	2910	6456	8922	13548	12252	2330	
		0	0	0	0	0	0	0	
		7010	18270	11745	9540	6255	2970	370	
		—1096	6066	13761	9000	6399	2934	376	
г ,	d	-178-	-4122	3033	10520	5967	3042	358	
Lrl —	18720	—424	—2646 -	—7551	0	7551	2646	424	
		—358 -	—3042 -	-5967	—10620	—3033	4122	178	
		—376	—2934 -	-6399	—9000	—13761	— 6066	1096	
		—370	—2970 -	-6255	—9540	—11745	—18270	—7010	
Решение этой задачи требует огромных вычислений. Была
сделана попытка решить ее на клавишной машине Рейнметалл,
с помощью которой было получено 6 приближений. На одно при-
ближение уходило около 12 часов непрерывной работы. Шестое
приближение от пятого существенно отличалось по перемещени-
ям т] и и, при этом величина распора отличалась только на 2 Т.
127
По составленной программе машина «Урал 2» за 4,5 мин де-
лала по 52—54 приближения. Начиная примерно с 50-го прибли-
жения распор и перемещения оставались практически неизмен-
ными (совпадалидо восьмого знака).
Программа, составленная для рассматриваемой задачи, поз-
воляла изменять с пульта основные параметры и провести
анализ их влияния на величины распора и перемещений, найден-
ных с учетом наклона подвесок.
Приведем вначале окончательные результаты для перемеще-
ний т] и м, а также распора в элементах цепи (перепечатано с.
ленты, которую выдала машина) для / = 120 м:
4 00 000 000 4- 00
4- 49840 5694-01
4-46244 960+01
417469 214 4-01
— 18563 326+01
-37399 092 4 01
4- оо ооо ооо 4 оо
4-оо 000000400
439324419401
433 534712401
4 26415922 4 01
4 30 366 555 4 01
4 34 600337 4 01
-51965004 — 07
421 201 270 403
4 20 916 262 4 03
420 205682403
4-19 315 754 4 03
418 587 918 403
4 18 090116 403
Распор на левой опоре
Но = 212,013 Т.
Распор на правой опоре составляет 180, 901 Т. Таким образом,
общая горизонтальная сила, образовавшаяся за счет наклона
подвесок и удерживающая нить, равна 31,112 Т. Естественно,
что такая огромная удерживающая сила намного уменьшает
как вертикальные, так и горизонтальные перемещения.
Если провести расчет без учета наклона подвесок, то распор
будет постоянным по длине нити и равным 195,58 Т. Векторы
вертикальных и горизонтальных перемещений для этого случая
составят:
0
7,65300
7,08328
2,25993
— 3,06505
-5,14171
0
0
5,81942
5,29162
4,20500
4,72880
5,14190
0
128
5—3802
На рис. 91 показана рассмотрен-
ная выше система. Пунктирная ли-
ния изображает систему в задан-
ном состоянии, а жирной линией —
в деформированном состоянии пос-
ле приложения временной нагруз-
ки. Высота подвесок очень сильно
влияет на прогибы системы. С уве-
личением разницы fi—f как верти-
кальные, так и горизонтальные пе-
ремещения увеличиваются, а рас-
пор уменьшается.
На рис. 92 показана также си-
стема, но при /4 = 160 л*. Из этого
рис. 92 видно, как увеличились пе-
ремещения и уменьшился распор.
При fi =200 м наблюдается еще
большее увеличение перемещений и
падения распора, что можно видеть на рис. 93.
В пределе, когда подвески имеют бесконечно большую длину,
влияние их наклона сказываться не будет. Выше приводились
данные для этого случая.
На рис. 94 показан график изменения распора при изменении
высоты fi для рассмотренной системы. Все остальные парамет-
ры оставались неизменными.
В заключение отметим, что такое сильное влияние наклона
подвесок на перемещения и распор в гибкой нити наблюдается
при малой пологости. При большой пологости это влияние не
столь существенно.
Таким образом, при расчете висячих мостов с большим про-
висанием кабеля учет наклона подвесок должен проводиться в
„ / 1
обязательном порядке. Для мостов, у которых ——* влия'
ние наклона подвесок необходимо учитывать только в тех случа-
ях, когда по условиям эксплуатации могут быть допущены боль-
шие прогибы. В каждом отдельном случае необходимо этот
вопрос рассматривать отдельно.
§ 9. РАСЧЕТ СИСТЕМЫ, СОСТОЯЩЕЙ
ИЗ ДВУХ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫХ
ГИБКИХ НИТЕЙ
Систему, состоящую из двух предварительно напряженных
гибких нитей, лежащих в одной плоскости и связанных между
собой растянутыми подвесками (рис. 95), назовем двухпоясной
системой. В такой системе можно создать предварительное натя-
130
жение нитей и тем самым обес-
печить довольно высокую жест-
кость всей конструкции и за-
ставить ее работать как стерж-
невую систему.
Расчет двухпоясной пред-
варительно напряженной си-
стемы связан с учетом геомет-
рической нелинейности и поэто-
му представляет определенные
трудности. В настоящем параграфе излагается метод расчета
рассматриваемой системы и устанавливается влияние предвари-
тельного напряжения на деформативность системы.
Предположим, что размеры всех подвесок и очертание обеих
нитей подобраны так, что после предварительного напряжения
обе нити будут иметь параболическое очертание. При этих усло-
виях усилия во всех подвесках будут одинаковыми. Если обе ни-
ти будут очерчены по одной и той же кривой, то распор как в
верхней, так и в нижней нитях будет один и тот же.
Загрузим предварительно напряженную систему временной
нагрузкой, представляющей собой систему вертикальных сосре-
доточенных сил,заданную в виде вектора
Л
Р.2
Пусть сосредоточенные силы приложены в верхних узлах
системы. Расчетная схема представляет собой систему, в которой
разрезаны все подвески, как показано на рис. 96.
Усилия в подвесках от предварительного напряжения обозна-
чим через В процессе загружения системы временной нагруз-
кой усилия в подвесках уменьшатся на величины хг(/=1, 2,...,
п), которые образуют искомый вектор
Распор в верхней нити уве-
личится до Н\, а в нижней —
уменьшится до Н2.
Будем рассматривать' '-''си-
стемы, состоящие из пологих
нитей, для которых горизон-
5*
131
тальными перемещениями будем пренебрегать. Подвески, соеди-
няющие между собой нити, будем считать нерастяжимыми, поэто-
му перемещения т] для нижней и верхней нитей будут одинако-
выми. Условия равновесия нитей можно записать в следующем
виде:
для верхней нити
5 4-Р - х=НхЬ2 Су, + "J),	(Ш. 119)
для нижней нити
5-x = //2Z.2(J2-^),	(III.120)
где г] — вектор перемещений узловых точек;
L2 — матрица, определяемая равенством (III.2).
Пролеты обеих нитей будем считать одинаковыми, поэтому в
обоих уравнениях матрица будет одна и та же.
В уравнениях (III.119 и III. 120) содержатся четыре неиз-
вестные величины: х, Hh Н2, тр Необходимо составить еще два
уравнения. Для этого воспользуемся, как и во всех предыдущих
задачах, принципом Лагранжа. Запишем его для каждой нити в
отдельности. В нашем случае роль постоянной нагрузки в рас-
четной схеме будет играть предварительное натяжение.
Таким образом, приходим к следующим уравнениям:
л + 1		Hi - H]s у		Н1^1	= 0,
1=1	COS '•?/	cos2 <?BEKF i=i	/2		
п+1	H2s	(H2s-H.)d у	8/d		= 0,
L i = l	COS sf”	cos2 ^KEKF	/2		
где His и H2s — величины распоров в верхней и нижней нитях от
предварительного натяжения.
После некоторых преобразований эти уравнения можно за-
писать в следующем виде:
Hi - His	л + 1 v	1	8/1 V-»}
EKF	L i=i	COS3 <pB	/2 2P’ 1=1
H2S-H,	Л + 1	1	
EKF	1=1	COS3 <pn	/2 2j 1=1
или иначе:
п
1=1
13Z
л
^2 = ^25—^2^’
i = l
где
(III Л 22)
*PEKF
1___
COS3 <PB
p2=- *f?E,iF------ .	(IllЛ 23)
/2 V --------
cos3 <рн
Подставляя в уравнение (III. 119) вместо вектора s — х его
значение из уравнения (I11.120) и решая относительно т), по-
лучим:
?= <П,Л24>
/71 “1 ** 2	171 \ 2	17 i । ** 2
Как было выяснено ранее, обратная матрица L~' равна мат-
рице влияния моментов в двухопорной балке L71 =Lm. В свою
очередь, произведение LmP дает вектор балочных моментов от
заданной временной нагрузки:
LmP = M.	(III.125)
Следовательно, вместо уравнения (III.124) получим:
=--------М-------— J, -|------L. (IIIЛ26)
Л1 + Л2 Л1+Л2	Н1+Н2
Далее находим:
п
У =	моУ + 77-^Ъ - моУ2
111 -j- ti^	1^1 i 1^2	+ 112
где coo — матрица-строка, все ординаты которой равны единице,
а порядок ее равен числу подвесок.
Но так как
®о!/ = 2 У1'
i=i
о>0л?=2 м>.
1=1
133
то
п	п	п	п
X =лГТТГ Е Л1‘ - 7ГГ7Г X »' + ~ТГТТГ Е
П j + /79 ihJ	/7] ~г	"1 “Г / /° 1шЛ
1 = 1	1=1	1=1	‘1=1
п
Подставляя значение^Лг в уравнения (III.121 и III.122), по-
4=1
лучим два уравнения с двумя неизвестными:
п	п
н' = н'~ -7ГПГ ₽1 S у'‘ + 7ГПГfl Е /Л' +
/7 J + /7-9	ЛУ1 + /7 2 ЬшА
1=1	/ = 1
п
! 7ГХ7Г₽3ЕЛ'"	(Ш127)
/7 1 + П2
1=1
п	п
Н2=Н7 + ——— р. У уи---------— ро У y2i -
2	25 1 нх + я2 г~ и	Lii
1=1	“	4=1
1
+ н.
п
1=1
(III. 128)
Совместное решение этих уравнений позволяет найти Н\ и
Н2. Отыскание вектора т] по уравнению (III. 126) не составит
особенных трудностей. Так как распоры Нх и Н2 зависят от HSr
т. е. от величины предварительного натяжения, то, следовательно,
и дополнительные прогибы т) также зависят от Hs.
Если Hs принять равным нулю, то мы выключаем из работы
нижнюю нить. Для частного случая, когда обе гибкие нити имеют
одинаковые f и I и, следовательно, H\s=H2s, уравнения (III.126,
II 1.127 и III. 128) примут вид
//1 = ЯЯ
ij —------------М
Н1 + Н2
(III. 129)
Н,-Н2
//1 +
п	п
(III. 130)
1
//1 +
//2=я5
п	п
(III. 131)
134
В дальнейшем эти уравнения будем называть основными
уравнениями. Рассмотрим теперь вопрос решения основных урав-
нений. Для удобства введем следующие обозначения:
— H2=z2
(Ш.132)
°И’	Щ — ^12
.	(ш.133)
Рг 2	Рз	^< = 022
i=l	i=l
Используя эти обозначения, вместо уравнений (III. 130) и
(II 1.131) получим:
^ги+±812,
21	г,
И, = "Л— 62! ~ 822-
21	г2
Складывая эти уравнения и вычитая второе из первого, по-
лучим:
z, = 2/7s-^ (8„ —821)+-L(5к-ад,	(Ш.134)
21	ZX
г2—	- (Оц -*-321)4"  (^12 4~ ^22)"
21	ZX
Далее из уравнения (III.135) найдем величину z2:
__ Cl? + S99)
г1 + (®11 + ®21)
Подставив 22 в уравнение (III.134), получим:
(Ш.135)
(III.136)
(оц — В21)
zx = 2Hs----.
21 + (5ц + 821)
что дает нам кубическое уравнение для определения Zj:
12 — 02гХ
21
(IIIЛ 37)
-где
тч— —(оп-|-821)4-(312 — 322)]	.
^22^11	^21^12
(Ш.138)
135
Для анализа полученных результатов интересно рассмотреть
частный случай, когда 01 = р2 (обе нити имеют одинаковые разме-
ры и жесткости). В этом случае
<>	«Л
JJ - ©21 И 12 “ ^99 •
Коэффициенты шь т2 и т3 будут иметь следующие значения:
/^ = 2^-/^
zn2 =
7713 = 0
(III.139)
Тогда уравнение (III. 137) после сокращения на величину Z\
запишется в следующем виде:
zi-j-mIz1-f-m2=0.	(III.140)
Решая это уравнение, найдем:
Подставляя Zi в уравнение (III. 136), вычислим г2: О' 	 	—	>		
	<>11 +	
Следовательно,		(III.141)
	Hr-H2=	. &11 + Н s	(III.142)
Отсюда находим:	Н^НА		Л 5 2(Вц + Hs)	(III.143)
	= 	.	(III.144)
Рассмотрим теперь такой случай, когда натяжение нижней
нити при загружении верхней нити падает до заданной величины
//2 = ДД тогда по уравнению (III.141) имеем:
//1 = 2Л/5-д7/.
Подставляя это значение в уравнение (III.143), получим квад-
ратное уравнение для определения предварительного натяжения
Hs, обеспечивающее остаточное натяжение А//, которое сохра-
нится после приложения временной нагрузки,
^4- (^п-АЯ)/75-^-|-ВпД//) = 0.	(III.145)
136
Определив из этого уравнения Hs, по уравнениям (III.143) и
(III.144) находим Hi и Hz и затем по уравнению (III.129) проги-
—►	—>
<5ы т). Если после загружения системы нагрузкой Р нижняя нить
полностью потеряет натяжение, то распор в верхней гибкой нити,
•согласно уравнению (III.141), будет равен удвоенному значению
начального натяжения
//1=2/У6..
Следует отметить, чтс чем выше начальное натяжение Hs, тем
меньшими будут прогибы системы от временной нагрузки. По-
добные системы можно
Рис. 97.
рекомендовать для сооружения легких
висячих мостов с гибкой балкой, так
как устройство второго кабеля намно-
го увеличивает жесткость всей систе-
мы в целом.
Можно также применять подобную
систему для устройства легких пере-
крытий кругового очертания в плане
(рис. 97). Расчет такого перекрытия
Рис. 98.
можно производить, разбив систему на отдельные плоские фер-
мы. Такое допущение для пологих нитей вполне возможно. Вре-
менная нагрузка в этом случае будет собираться с площади,
приходящейся на одну двухкабельную ферму. Если нагрузка
равномерно распределена по всему перекрытию, то эпюра на-
грузки, приходящейся на ферму, будет иметь вид треугольни-
ков, как показано на рис. 97, в.
Пример. Рассмотрим пример со следующими данными: /j =
=/2==/=360 м, fi = f2=f=36 м, EKF=\-106 Т, d=60 м. Так как
обе нити одинаковые, то
Р1-?2—Р---
8fEKF
V 1
iti cos3<pz
137
л+1
Величина V----------определяется из геометрических размеров
COS3
системы рис. 98:
п
----L_ = 6,47692; В = 0,34310 • 103.
COS3
1=1
Зададим временную нагрузку в виде треугольника с наиболь-
шей интенсивностью <7тах = 4 Т/м. Вектор узловых сил в этом
случае будет:
200
160
120
80
40
Вектор ординат осей нитей определяется по уравнению пара-
болы (III. 16):
t—> У=		20 32 36 32 20	п ; 2 «=140- 1 = 1				
Далее по уравнению		(III.125) определяем:					
	5	4	3 2 1		200		2200
	4	8	5 4 2		160		3200
М = LmP- —	3	6	9 6 3		120	= 10	3240
m 36	2	4	3 8 4		80		2560
	1	2	3 4 5		40		1400
у М= 126 000 Тм.
/=1
По уравнению (III.133) находим:
, = й21 = р 2 У = 48,0340 • 103,
S22 = г12 = р 2 44 = 43,2306  103.
Зададимся величиной остаточного распора
д/7 = 50 Т.
138
По уравнению (III.145) составляем квадратное уравнение:
•И2 + (48034 - 50) Hs - (21,61530 • 106 -ф 48,034 • 50 • 103) = 0.
Решив это уравнение, получим:
495,42 Т.
Далее по уравнению (III. 143) и (III. 144) находим:
//, = 940,83 Т,
//2=50,01—50 Г,
//, 4//2 = 990,83 Т, Нх — Я2 = 890,83 Т.
В формуле (III. 129) найдем вектор прогибов системы:

4,222
3,526
0,334
-2,933
-3,852
В табл. 4 приведены значения распоров в верхней и нижней
нитях и прогибы в зависимости от величины остаточного распора.
Из приведенной таблицы видно, что чем выше остаточный
распор ЛЯ, т. е. чем больше остаточное натяжение, тем меньше
прогибы системы.
139
Таблица 4
А Н		0	50	500	1000	2000
/71		891,66	940,83	1382,70	1873,85	2856,70
Н2		0	50	500	1000	2000
Hs		446,83	495,42	941,35	1436,93	2428,35
		4,67	4,22	2,31	1,57	1,00
		3,89	3,53	1 ,96	1,40	0,94
	У]	1	0,34	0,33	0.33	0,33	0,32
	1	—3,29	—2,93	—1,43	—0,82	—0,37
		—4,30	—3,85	—1,94	—1,20	—0,65
На рис. 99 представлен график изменения Я], Н2 и rj в зави-
симости от величины А/7. Этот график наглядно показывает
эффективность первоначального натяжения на увеличение жест-
кости системы.
•з
ГЛАВА IV
РАСЧЕТ ВИСЯЧИХ МОСТОВ
ПУТЕМ НЕПОСРЕДСТВЕННОГО
ИНТЕГРИРОВАНИЯ
УРАВНЕНИЙ
§ 1. ОБЩИЕ ЗАМЕЧАНИЯ
л	Применение метода непосредственного интегрирования диф-
ференциальных уравнений изгиба балки жесткости висячего
моста позволяет произвести расчет с учетом геометрической не-
линейности и получить при этом высокую точность. Этот метод
неоднократно применялся различными авторами. Особенное раз-
витие этого метода принадлежит Ф. Блейху [69] и Н. Блейху [68].
В последующем появились работы, в которых указанный метод
доведен до удобной формы (см., например, Хавранек [97]), до-
ступной для проектировщиков.
Вместе с тем следует указать на ограниченность метода,
обусловленную главным образом постоянством сечений балки по
длине пролета. Для случая когда балка жесткости имеет пере-
’ч.' менное сечение и в особенности для многопролетных мостов, ре-
X шение сильно усложняется и уступает численным методам, изло-
женным в последующих главах.
В настоящей главе дается методика расчета для мостов с бал-
кой жесткости постоянного сечения и приводятся примеры.
Расчет по указанной методике можно проводить с применением
клавишных автоматов, однако применение электронных машин
позволяет получить более высокую точность и определять невы-
годное загружение, при котором изгибающий момент в заданном
сечении имеет максимальное значение.
§ 2. ОСНОВНЫЕ УРАВНЕНИЯ
В процессе деформации пролетного строения висячего моста
отдельные точки оси кабеля будут перемещаться как по верти-
кали, так и по горизонтали. Величины горизонтальных перем еще-
141
ний в сильной степени зависят от пологости кабеля. Для случаев
когда	, горизонтальными перемещениями можно пре-
небречь и считать, что все подвески будут перемещаться только
по вертикали.
Предположим, что расстояние между подвесками по сравне-
нию с длиной пролета невелико, поэтому будем считать, что они
сплошь заполняют пространство между балкой и цепью. Примем
гипотезу о нерастяжимости подвесок. На основании сделанных
допущений можно считать, что в каждом сечении вертикальные
перемещения оси кабеля и балки будут одинаковыми. Обозначим
эти перемещения через т], интенсивность временной нагрузки —
q т/м, постоянной — g т/м, распор в кабеле от постоянной нагруз-
ки Hg, а от полной (постоянной и временной нагрузок)—Н.
Рассмотрим вначале систему, изображенную на рис, 100, на
котором пунктиром показана балка, подвешенная к кабелю, очер-
ченному по квадратной параболе, а сплошной линией изображена
та же балка и кабель после деформации от временной нагрузки.
До загружения нагрузкой q балка не прогибается и имеет место
равенство
(а)
Суммарная интенсивная нагрузка в произвольном сечении
балки, которую обозначим qn, после загружения временной на-
грузкой q будет определяться выражением
— н [*/О)-И (*)]"-(£+?)•
Дифференциальное уравнение для прогиба балки в соответ-
ствии с осями координат, показанными на рис. 100, будет:
(х)]" = - qn= Н [у (х) 4- 71(х)]" +(? + g).
142
Для случая £7 = const с учетом равенства (а) получим диф-
ференциальное уравнение прогибов
>llv	. (IV.1)
El	El
где	____
“=1/ 4?'	CV.2)
Если учесть, что
М{х)=-Е1^(х\	(IV .3)
то вместо уравнения (IV. 1) можно записать дифференциальное
уравнение моментов
М"(х)- aW (х) = - (//-Hg) у" (x)-q.	(IV.4)
В уравнение (IV.1), кроме искомой величины ц, входит также
неизвестная величина Н. То же самое можно сказать и в отно-
шении уравнения (IV.4), в которое, кроме М, входит неизвест-
ное Н. Таким образом необходимо составить еще одно дополни-
тельное уравнение.
Так же как и в § 3 гл. III, используем для этой цели принцип
Лагранжа, по которому виртуальная работа внешних и внутрен-
них сил кабеля от постоянной нагрузки на перемещениях от
временной нагрузки (и температуры) равна нулю
azд/ ds^ -ф gy (х) dx — 0.
распространяться на всю длину
dx
COS ср
g=-Hgy"(xY
После всех преобразований получим:
~Р р* Л+ «(Д^+ У"	\ -Ч (х) dx = 0,	(IV.5)
где
Zs=|iZ-]-*S1 sec2T14-52sec2 т2,	(IV.6)
Lt — M + Sec T1 + sec т2-	(IV.7)
_ f f Hqds -I
J COS <P \ fl/^COScp
Здесь интегрирование должно
нити.
Учтя, что
143
Величина р определяется формулой (Ш.22) или для симмет-
ричной нити формулой (III.23). Для определения щ служит фор-
мула (II 1.24).
§ 3. ИНТЕГРИРОВАНИЕ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ДЛЯ ОДНОПРОЛЕТНОГО ВИСЯЧЕГО МОСТА
В настоящем параграфе решается задача об определении
прогибов, углов поворота, моментов и поперечных сил в любом
сечении балки жесткости при частичном загружении моста равно-
мерной нагрузкой, как показано на рис. 101. При таком загруже-
нии для величин тр rf, Л1 и Q необходимо получить уравнения для
трех участков. Если исходить из уравнения (IV.1) и написать три
дифференциальных уравнения для трех участков, то при интег-
рировании возникнет необходимость определить 12 произвольных
постоянных. Для упрощения решения будем пользоваться не
уравнением (IV. 1), а уравнением (IV.4). Будем считать жест-
кость балки EI постоянной, нагрузку от собственного веса рав-
номерной, поэтому примем очертание кабеля по квадратной па-
раболе.
Учтем, что
</'W	•	(b)
/2
Введя обозначение
(IV.8)
после преобразований уравнения (IV.4) запишем его для трех
участков балки:
Mi(x)—a2Mi (х) =	(с)
А
144
Л4п (x) — а2уИц(х) = -^——g — q\ a^x<Lb,	(d)
i_)
/Ицi (x) — а27Иш (x)=——— g;	b < x < I.	(e)
Непосредственное интегрирование уравнений (c, d, е) также
вызывает трудности в связи с необходимостью определения шести
произвольных постоянных, поэтому мы сделаем еще одно упро-

Рис. 102.
щение. Предположим, что функции Alj, Л4ц и 7Ищ графически
изображаются кривыми 0—1, 1—2 и 2—3 (рис. 102). Продлим
кривую Мг от точки 1 до точки 5, а кривую Л4п до точки 4. Рас-
стояние по вертикали между кривыми Мг и 7ИП обозначим AAfj,
а между ТИц и Alni — соответственно АМц. Из рис. 102 видно, что
ординаты функций Л1ц и Мщ можно определить как разность
соответствующих ординат:
A4n(x) = Afi(x) — дЛП (х);	(f)
Alin (х) = 7И! (х) —[дЛ/i (х)4- д7Иц (х)].	(g)
Значения ординат функций AAij и Д7ИП определяются более
просто, чем функции 7ИП и Л1П1.
Вычитая уравнение (d) из уравнения (с), а также уравнение
(е) из уравнения (d), получим дифференциальные уравнения для
функций
ДЛ^! (х) —а2д7И[ (х)=7;	(i)
Д/Иц (х) —-а2д7Ии (х) = ^.	(])
Теперь мы будем интегрировать три уравнения (с), (i) и (j).
Решаем уравнения (с):
(х) = Ло ch ах -4- BQ sh ах— -—.
Ха2
Так как при х=0 Ah = 0, то А = - ~ g ,
/	145
поэтому
АД (х) = ~ g (ch ах — 1) 4-	sh ах.	(к)
Ла2
Интеграл уравнения (i) можно записать в виде следующего
уравнения:
дЛЛ (х)= Aj cha(x — a)4-Bjsha(x— а)----— -
a2
Из условия, что при х=а; Mf = G и AMi'=O, найдем
А = —; ^1 = 0,
а2 1
поэтому
&7Wi (х)= — [ch а (х — а) — 1].	(ш>
д2
Аналогично найдем решение уравнения (j):
дЛ7ц(х)=------------------— [ch a(x — b) — 1].	(n)
a2
Из полученных решений (к), (ш) и (п), согласно равенствам
(f) и (g), найдем уравнения моментов для второго и третьего
участков:
Мц(л)--=—[ch ax— 1 ] -|- Во sh ax—— (cha(x — а)— 1], (u)
Xa2	a2
Л4ш (х) — —~ — [chax — 1]-|- Z?oshax —
Ла2
--—[ch a (х — а) — ch a(x— /?)].	(v)
a2
Остается определить постоянную Во. Для этой цели исполь-
зуем условие 7V1III(Z) =0. Положив в последнем уравнении х=1
и приравняв его нулю, получим:
р  	(1 —~К) g	ch al—1 [ q cha(Z — a) — cha(l-b)
°	Xa2	sh al 1 a2	sh al
Подставляя найденное значение Bq в выражения (к), (и) и
(v), после несложных преобразований получим:
Af i (х)=<//2Ф1 (х)-1 ~~Х gp Ф0(х); 0 <х <С
X
Л4, j (х) = qP Ф jI (х)-gP Фо (х); а < х < b- (IV.9)
Ahn (х)=7/2Фш (х)-----1 Х gP Фо (х); й<х</.
К
146
Значения функций ФДх); Фц(х); Фш(х) и Ф0(х) приведены
ниже равенствами (IV. 13) и (IV.15).
Путем дифференцирования выражений (IV.9) найдем для
поперечных сил:
Qi (х)= ql®*\ (х)--у * £7Фо(х); О^х-^а;
QH (х)= ^/Ф 7,(л) g/Фо (х); а < х < b; (IV.10)
К
Qin (х) = ^/Ф*ц---Ц-^£7Фо(х); &<x<Z.
Для определения прогибов ц необходимо дважды проинте-
грировать выражение моментов
re Af. (х)
т].(х)=\\---------dxdxA-C\ (x)-|-£)i ;
J J El
c AfH (x)
7lI](x)= \\ ———dx dx-\-Cw (x)4-ZS>n;
J J El
Чц1(*)=\5 71411dxdx-\-Cm (х)-|-Дп.
Из условий TJI(O)=T)III (Z)=0; tj, (а)=т]п (a); vJn (fr) = T]I1I (&);
•jjj (a) =щ’п («);	iJu/Z?)можно определить постоянные C iiD.
Опуская все преобразования, приведем окончательный ре-
зультат:
(л-ф1«1 —Ц-Lx
п	к
Х~- PoW — фо(*)]; 0<х<ц;
Г1
7>п(х)=-?-1/?"(Л)—ф" — х
п	к
Х-^-[^о(х) —Ф0(х)];	а<х<6;
/7
7ini(A:) = -“lFiii (х)-Фп1 (X)] Ц^-Х
/7	К
Х^ро(х)-Фои)1; ^<х</.
Г1
147
Углы поворота соответственно составят:
(-у)]--1?* [fo(-*)-°o(x)];
п	К
, (*)=4г [F  ‘W -' I wi —!~^1 F° w -	;
п	К
а^х-'^Ь;	(IV.12)
[^Ш—Ф1п(х)]----Ц^-[Ло(х) — Фо(х)];
/7	К
Входящие в уравнения (IV.9), (IV.10), (IV.11) и (IV.12)
функции при обозначении
(IV.13>
определяются следующими равенствами:
148
§ 4. ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ
ДЛЯ ОПРЕДЕЛЕНИЯ РАСПОРА
Для того чтобы воспользоваться формулами, полученными в
предыдущем параграфе, необходимо предварительно определить
величину г, входящую в выражения функции Ф(х) и Ф*(х), свя-
занную с величиной распора Н соотношением (IV.13). Для этой
цели воспользуемся уравнением (IV.5), которое преобразуем к
более удобному виду. В первую очередь вычислим значение ин-
теграла
lab	I
j* 4i(x)dx~ J	7]п (x) dx-\- J 7]ш (x)dx.
0	0	a	b
149
Пользуясь выражениями (IV.ll), (IV. 13), (IV. 15), (IV.17) и
(IV. 19) находим:
а	а
Tjj (х) dx = U-g2 [Л! (х)- ФI х]- J—-L	X
•'	V /7	к Г1
о	о
I	I
\ r,,„ (x)rfx=\ Ж^,,, (х)-Фш(х)]-Ж^Д X
b	ь
X [/=„ (X) -Ф„ (х)]1 dx=^- Г-Д. (О2 - а?) (l-ьг +
150
b	a
ch z — — ch z—
/	I
z3 sh z
z
sh — 4 sh z
41
l3—b3
6/2
z
*chT
Складывая полученные
интегралы, получим:
где
i
т] (х) dx= ql3
о
'Pi (z)
12//	7
gl3
12//
(IV .20)
ф2
(IV.21)
(IV.22)
1-* g/2
A H
Подставляя (IV.20) в уравнение (IV.5), получим следующее
характеристическое уравнение относительно X:
X 1
(IV.23)
где
1q
— Ф1 (г) 4- ф2 U)
g
(?) — т] 4 azA/ . Lt
- _	,
Г q	1
^2 — Ф1 (г) + ф2 (г-)
(IV ^4)
Необходимо отметить, что уравнение (IV.23) имеет несколько
условный характер. Дело в том, что входящие в это уравнение
коэффициенты А и В сами являются функциями величины рас-
151
пора, так как они зависят от г, а следовательно, и от Н. Возни-
кает также вопрос, почему уравнение (IV.23) приведено не к виду
квадратного уравнения, а к такому своеобразному виду? Объяс-
няется это удобством решения уравнения, что подробно пока-
зано в следующем параграфе.
§ 5. РЕШЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Наиболее сложной задачей в расчете моста является решение
характеристического уравнения (IV.23). Его можно решить
только путем подбора. Левую часть этого уравнения обозначим
через
/(Х)=-у-ф-5-Х.	(IV.25)
Прежде всего выясним, в каких пределах может изменяться
величина к при изменении нагрузки. Согласно (IV.8)
н
Из этого равенства видим, что X может меняться в пределах
1.
В самом деле, только в случае отсутствия нагрузки величина
H = Hg, а во всех остальных случаях H>HS. Еслидавать величи-
не к значения от 0 до 1 и вычис-
лять значения f(X), то примерный
график этой функции будет иметь
вид, показанный на рис. 103 жир-
ной линией. Характерной осо-
бенностью линии f(X) является
то, что на довольно значительном
протяжении она близка к прямой
линии. Это обстоятельство силь-
но облегчает решение задачи.
Из графика видно, что урав-
нение (IV.23) удовлетворится
тогда, когда X примет значение X*.
Если определить значение f(k)
для двух каких-либо величин Xi
и 7,2, отложить ординаты f(Xi) и
f(X2) и соединить их прямой, то
она пересечет ось X в точке, которая будет весьма близка к ис-
тинной нулевой точке кривой f (X).
152
Если вместо функции /(X) взять не выражение (IV.25), а дру-
гое, например, Е(Х) =Л 4-Вл—X2, то функция F (X) будет
иметь вид, показанный пунктиром. Эта кривая не обладает
описанными выше преимуществами, что и послужило причиной,,
заставившей привести характеристическое уравнение к виду
(IV.23).
Близость кривой f(Z) к прямой линии позволяет эффективно
проводить метод последовательных приближений. Запишем урав-
нение (IV.23) в виде
X=-A_j_£.	(IV.26)
Предположим, что мы назначили Х = Хг-, и находим правую
часть равенства (IV.26), тогда для следующего приближения
имеем:
xitl=4+B
или
Х/Ц-дХ/ — — В,
откуда находим:
Д>ч = /(М-	(IV.27)
Из равенства (IV.27) ясна схема проведения последователь-
ных приближений. Задав произвольное значение Хг- по (IV.27),
находим ДХг- и затем Xi+i=Xi + f (Хг-). Процесс приближения про-
должается до тех пор, пока f (X) не будет меньше желаемой ве-
личины.
Описанный здесь метод обеспечивает быстро сходящийся про-
цесс. Он эффективно использовался при решении задачи на элек-
тронной машине. Этот же метод можно применить и при решении
задачи с помощью клавишной машины или арифмометра. Однако
при ручном счете большое значение имеет выбор начального при-
ближения. Для этой цели за начальное значение целесообразно
взять величину Ло, соответствующую обычному решению по ме-
тоду сил. Если линию влияния распора принять за квадратную
параболу и определить наибольшую ординату по приближенной
формуле, а затем по ней найти распор Hq от временной нагруз-
ки, то
Проделав все эти вычисления, получим:
,	(1V.28)
g + кд
153
где
25 V-a? 2	*3—й3ч / is EF ii. \
8 \ /2	3	/3/^'8 ExFp)
Определив к и затем Хо, находим f (Хо) и по (IV.27) AXi, а за-
тем Х1=Хо+ЛМ- Повторяя процесс, находим 'Е2, Х3, ... В процессе
вычислений видно, когда следует закончить процесс приближе-
ний. Необходимо отметить, что значение 7. надо определять с до-
статочно высокой точностью, так как при сравнительно малом
изменении величины X довольно значительно меняются моменты
в балке.
Пример. Пусть: / = 200 м, / = %) м, S] = 35,3 м, -г=45°, Е1 =
= 0,44-108 Тм2, E}F=Q, 183(3) 107 th, £=12 т/м, q = 6 т/м, =
= 3000 т.
Рассмотрим случай, когда нагрузкой q загружен весь пролет.
По формулам (III.22), (IV.6), (IV.24), (IV.13) находим:
р=1-|-8	= 1,08192;
\ I )	5 \ I )
Ls= JJ.Z4-2S1 sec2 т=357,584 м-,
mx = H2Ls =0,585139; m2=-^=- = 10,6667;
1 EF	3,1
zo
1,65145.
По (IV.28),учитывая, что a = 0, b=l, получим
0,712000.
Вычисленные коэффициенты не зависят от к, поэтому опреде-
ляются один раз. Теперь начинаем последовательные прибли-
жения.
Первое приближение:
по формуле (IV. 13) имеем:
z = -^ = 1,95716.
В нашем примере при а = 0 Ь — 1 ф1(г) =ip2(z); пользуясь форму-
лой (IV.22), находим:
12
<!ч (z) =й2 (z) = 1-----------------
7	12 v '	1,957162
1-
th 0,978580
0,978580
=0,276264.
154
По (IV.24) получим:
Л = —
т-2

0,132377;
=0>534289-
в =
(а	\
— + 1
g	I
Теперь по (IV.27) находим:
дХ = °’132377. _|_ 0,534289 — 0,712000=0,008212.
1	0,712000 1
Следовательно,
Второе пр
Х,=Х0-1-д)ч = 0,720212.
и б л и жен ие:
z=-4^-= 1,94597;
th 0,972985
0,972985
=0,273974;
Ф 2(г) = 1----—
1,945972
Л = 0,132038; В = 0,534629;
дХ °-132038	0,534629 - 0,720212 = - 0,002251:
0,720212
К = 0,720212 - 0,002251 = 0,717961.
Решение, полученное на электронной машине, дало
Х=0,718837.
Как видим, л2 отличается от точного значения весьма
тельно.
Ограничиваясь вторым приближением, принимаем
= 0,717961. Найдем теперь момент в середине пролета,
определяем величину ги функции Фц(х); Фо (л):
z=-%-= 1,94901.
незначи-
Х=Х2—
Вначале
При « = 0, Ь = 1 и х= Фц(х) =Ф0(х), поэтому, пользуясь
более простой формулой для Ф0(х) (IV.16), получим:
1---------1----
ch 0,974505
Фп(х) =------—
v '	1,949012
=0,089330.
155.
По (IV.9) вычисляем момент
1 — X
X
ТМ.
Решение, полученное на электронной машине, для этого слу-
чая дало М i =4670 тм.
2
Из полученных результатов видно, что весьма малая погреш-
ность в величине X привела к более значительной погрешности в
величине момента. Это еще раз свидетельствует о необходимости
определять X с высокой точностью.
§ 6. ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОГО МОМЕНТА
В ПРОИЗВОЛЬНОМ СЕЧЕНИИ
ОДНОПРОЛЕТНОГО МОСТА
Наиболее трудной задачей является определение максималь-
ного значения изгибающего момента в произвольном сечении.
Дело в том, что при расчете по нелинейной теории трудно опреде-
лить длину загружения, при которой момент в соответствующем
сечении становится наибольшим. Иначе говоря, требуется опре-
делять такие значения а=а* и b = b*, при которых момент при-
обретает максимальное значение. С математической точки зрения
необходимо дополнительно к основным уравнениям присовоку-
пить еще два уравнения
дМк q
дЬ
Однако функция момента Мк (IV.9) по отношению к а и b
является неявной функцией, так как величины а и b в свою оче-
редь зависят от z и X. Таким образом, воспользоваться равенст-
вами (а) практически невозможно.
Для решения задачи можно использовать два пути. Пер-
вый — можно осуществить только на ЭЦВМ. Для этого также
используется метод последовательных приближений. Положив
вначале а = 0 и Ь = 1, т. е. решив задачу при загружении всего
пролета, мы потом полагаем Ь = 1, а величину а начинаем посте-
пенно увеличивать от нуля, полагая на каждом шаге, что:
ai=ai-i-\-	(Ь)
Для каждого значения (ц полностью решается задача, начи-
ная от определения величины X и кончая определением момента
ЛД.
156
При переходе от аг_1 к щ машина определяет величину AA4K
.Если &М1( положительно, то по формуле (а) определяется новое
значение аг-+1 и все решение повторяется вновь. Вначале величина
Да берется, например, 0,1 I, азатем после первого грубого опре-
деления а0* берется более мелкий шаг, например Ad = 0,01 I.
Отправляясь от а0*, находим более точное значение Ci* и т. д.
Определив а\*, начинаем делать то же самое по отношению к 6,
при этом полагается, что а = а,\*. Оказывается, что затем необхо-
димо повторять процесс решения, но теперь при отыскании но-
вого значения а2* принимаем вместо b не Z, как в первом решении,
а величину Ь\*. Повторяя процесс несколько раз, находим окон-
чательно а* иЬ*. После этого вычисляется 7Итах для интересую-
щей нас точки. Для решения задачи этим методом необходимо
проделать огромные вычисления, что посильно только электрон-
ной машине.
Второй способ решения заключается в том, что величины а*
и Ь* находятся по приближенным формулам, которые выводятся,
исходя из обычной линейной теории, как расстояния до нулевых
точек линии влияния Мк.
Воспользовавшись решением Блейха, приведем готовые фор-
мулы значений а0* и Ьо*, при которых момент в точке к имеет
наибольшее значение:
—5-=1 —-—— ,	(VI.29)
I	3vxA.
b* _ I
~~ 3v(Z-xK) ’
тде
8 EJ'f'l
здесь EI и ЕЕ— жесткость балки на изгиб и жесткость кабеля
на растяжение;
Ls=[il; ц— значение коэффициента, определяемого по
(Ш.22).
Интересно отметить, что применение приближенных формул
“(IV.29) не приводит к большой погрешности в величине Л1тах.
Это легко объяснить, если исходить из линий влияния момента
при расчете по линейной теории. Так, например, при загружении
линии влияния момента в точке к на длине, несколько меньшей
требуемой длины, мы пренебрегаем частью Йлощади линии влия-
ния, которая по сравнению с общей положительной площадью ни-
чтожно мала, поэтому момент Мк при загружении, показанном на
рис. 104, мало отличается от максимального момента. Эти сооб-
ражения подтверждаются вычислениями на ЭЦВМ.
157
Если точка к расположена на небольшом расстоянии от опоры,
то для получения максимального значения момента временная
нагрузка q должна простираться до соответствующей опоры. Так,
например, если точка к близка к правой опоре, то Ь*=1 (или
Рис. 104.
а = 0, если точка к близка к
левой опоре).
Исходя из формулы
(IV.29) можно установить,
на каком предельном рас-
стоянии должна лежать точ-
ка к от той или другой опо-
ры, для которой необходимо
определять только один из
отрезков а* или Ь*. Так, на-
пример, для случая, когда точка к лежит правее середины из
второй формулы (IV.29) при условии, что Ь*=1, находим:
3v (/ хк)
откуда
— =1------(VI.31)
I	Зч
поэтому, если
*
Хк > хк
I I '
Ь л	J,
то мы должны положить — — 1 и определять только отрезок а*.
Пример. Рассмотрим висячий мост с теми же размерами, ко-
торые были приведены в § 4:
а) определение наибольшего момента в середине пролета
-у-=0,5. Решение на электронной машине «Сетунь» дало следу-
ющие результаты:-у-=0,1597, b* = O,8403; Х= 0,744600. Полный
распор 77=4029 т. Максимальный момент Л4тах=4737 тл.
Найдем теперь приближенные значения а0* и Ьо* по форму-
лам (IV.29). По (IV.30) получаем:
____________________1
—	15	0,44-108
+ 8 ’ 0,183333-10’
357,584
202 200
= 0,832542.
Далее по (II 1.29) находим
%
йо
= 1--------=0,199;
I	^хк
— =0,801.
/ 3\хк
158
Как видим, полученные значения очень отличаются от тех,
которые определила электронная машина.
Далее в машину были введены числа =0,199 и
В результате решения получилось:
—=0,801.
/
X = 0,759115;
Н=3952 Т;
1/2=4716 тм.
Момент не очень отличается от максимального. Таким образом,
можно пользоваться приближенными формулами (IV.29) без
серьезных опасений за потерю точности в определении макси-
мальных моментов;
в) определение наибольшего момента в правой четверти про-
лета -у- =0,75. Применяя формулу (IV.31), находим:
— =1 —L^q 59968.
I	3v
Так как хк >хк*, полагаем, что Ь = 1.
Таким образом, необходимо определить только одну величи-
ну а0*. Пользуясь формулой (IV.29), определяем:
ао
I
0,534.
По составленной программе для случая, когда «=0,534 I и
Ь = 1, на электронной машине «Сетунь» было получено:
Afo 75z=52O5 тм.
Интересно отметить, что точное решение этой задачи на ма-
шине привело к следующему результату:
а*
=0,4915 м-
I
(44o.75z)™x = 5255 тм.
Сравнение показывает, что несмотря на ощутимую разность
в отрезках «о* и а* разница в моментах незначительна. Это еще
раз показывает, что для определения длины загружения, т. е.
отрезков а* и Ь*, можно пользоваться приближенными формула-
ми (IV.29).
159
§ 7. ЗАМЕЧАНИЕ О РАБОТЕ БАЛКИ
ЖЕСТКОСТИ ОДНОПРОЛЕТНОГО МОСТА
Применяя электронную машину, легко определить максималь-
ные изгибающие моменты в ряде сечений балки. Для конкретной
задачи на рис. 105 показана такая эпюра для моста с размерами,
приведенными в § 4. Для наглядности показаны не абсолютные,
а относительные значения мо-
—%.	РТ\ ментов, при этом за единицу
д	'л	|\ взят момент в середине проле-
/  _______ 1 I__________X	та. Как видно из рисунка, мак-
I 8 ц 5 6 т 8 9 Ю н 12 симальные изгибающие момен-
ты в четверти пролета больше,
Рис. Ю5.	чем в середине пролета. Это
свидетельствует о том, что бал-
ка постоянного сечения для однопролетного висячего моста
является не вполне рациональной. Закон распределения жест-
костей должен быть определен с учетом закона распределения
максимальных моментов.
Если принять балку переменного сечения с распределением
жесткостей в соответствии с эпюрой, .показанной на рис. 105, то
эпюра значений Mmax изменится и поэтому необходимо менять
закон распределения жесткостей.
Таким образом, можно путем последовательных приближений
прийти к национальной системе. Однако такую задачу нельзя
решить методом, изложенным в настоящей главе, так как все вы-
воды этой главы верны только для балки с постоянной жестко-
стью.
Таким образом, возникает необходимость создания простого
численного метода, позволяющего провести решение как для
моста с балкой постоянного сечения, так и для случая, когда
жесткость балки изменяется по произвольному закону. Этот во-
прос решается в гл. IV.
§ 8. РАСЧЕТ ТРЕХПРОЛЕТНОГО ВИСЯЧЕГО
МОСТА С РАЗРЕЗНОЙ БАЛКОЙ ЖЕСТКОСТИ
Рассмотрим симметричный трехпролетный висячий мост с
разрезной балкой жесткости, как показано на рис. 106. В общем
случае полагаем, что в каждом пролете имеется нагрузка, рас-
положенная на части балки. При расчете такого моста можно
использовать формулы, выведенные в предыдущем параграфе.
Для каждого пролета примем свои оси координат с началом
на левой опоре. Расстояния от левой опоры до произвольного
сечения в первом, втором и третьем пролетах соответственно обо-
значим: Xi, х2 >и х3. Точно так же обозначим «i&i, а2Ь2 и а3Ь3
160
отрезки, определяющие начало и конец загруженного интервала в
каждом пролете. Симметрия моста понимается только в геомет-
рическом смысле. Нагрузка может быть расположена несим-
метрично.
Для всех функций, которые были введены в предыдущем па-
раграфе, будем принимать прежние обозначения, но к каждой
из них будем добавлять по второму индексу, указывающему
номер пролета. Так, например, функция Фг(г) согласно (IV.14)
будет для каждого пролета иметь свое значение, а именно:

(а)

Здесь
Между значениями Zi и z2 существует зависимость
/1
Zj = -i-Z2.
‘2
(IV.32)
Для значений ц, т/, Л1 и Q сохраняются все формулы, которые
были получены в предыдущем параграфе, только для каждого
6-3802	161
пролета должны быть взяты свои значения функций Ф и F. Суще-
ственное отличие будет содержаться в характеристическом урав-
нении. При составлении этого уравнения также будем исходить
из основного равенства (IV.5), однако в нем суммирование де-
формаций должно распространяться на все три пролета. Таким
образом, величины Ls и Lt теперь надо определять по формулам
s — Р-/14“	4 Рз4 4- 1sec2 и 4-^’2sec2 г2
^-/==P'i/i4“ НгА 4 Р-з/з 4'^1 sec хгЬ^2 secT2
(IV.33)
Значения щ, ц2 и ц3 вычисляются по формуле (III.22), а
рп, ц2г и p3t по формуле (IIL24). Вместо третьего слагаемого в
уравнении (IV.5) необходимо взять выражение для трех про-
летов:
It	Ц
С = у\ jpi (х) Jx4- у'2 Tj2 (х) dx уг J tj3 (х) dx =
ООО
8/?
/2
Z2
М2 Л
71) /2
It	It	2 I»
\ 7П(Х)^Х -| Д т;2(х)	А V 7J3(X) dx
J	J	\	/ Ji •>
0	0	0
Используя теперь выражение (IV.20), получим:
С=- -St. —!-ti-f «I .J (2) ф (21) 1 +
/2	12// I /,/2 g	*	1 1 J
4-[—^i2(^)--1^^ii2(^)]4-^[^7i3-ljY*?ii3(2r3)l| •	(b)
L g	Л	J hfi L g	'	JJ
Подстановка в (IV.5) приводит нас к характеристическому
уравнению, которое по форме совпадает с уравнением (IV.23):
Л_1_£_)ч = о.
1	1
Однако, коэффициенты А и В теперь будем определять по фор-
мулам:
А=^-
N
—/П] + atLtLt
~~	N
где
== T?z.2 («2 -|- АгД
7" ^111 ^1)4-Фц2 (^2)4-(—-)-у Фнз (^з).
\ «2 / J1	\ 11 / /2
162
(у-) v-  ~ (г')+— «<**’+(т)т" "7  ” (г’);
\ 12 / л g	g	\b / h g
„ Д-dl;	(1V.34)
1 EF
Необходимо отметить, что мосты с разрезной балкой жестко-
сти встречаются реже, чем с неразрезной балкой жесткости.
§ 9. РАСЧЕТ ТРЕХПРОЛЕТНОГО МОСТА
С НЕРАЗРЕЗНОЙ БАЛКОЙ ЖЕСТКОСТИ
ПОСТОЯННОГО СЕЧЕНИЯ
В настоящем параграфе излагается метод расчета трехпро-
летного висячего моста с неразрезной балкой жесткости постоян-
ного сечения по нелинейной теории. Все допущения, принятые
ранее для однопролетного моста, распространим также на дан-
ную задачу.
На рис. 107, а показан симметричный трехпролетный мост.
Основная система изображена на рис. 107, б. По сравнению с
Рис. 107.
предыдущей задачей мы имеем дополнительно еще два неизвест-
ных: М\ и М2. Для их определения служат условия неразрыв-
ности деформации балки над опорами. На каждом из трех про-
летов приложим временные нагрузки, распределенные на части
пролета, интенсивностью соответственно q\, q2 и q3.
Если мы получим решение для такого загружения, то будет
легко рассмотреть любые частные случаи, которые могут встре-
титься на практике.
В каждом пролете мы' будем иметь три участка, для которых
уравнения прогибов, моментов или поперечных сил будут разные.
6*	165
Условимся, так же как в предыдущем параграфе, сопровождать
каждую из величин т], т/, М и Q двумя индексами. Первый индекс
будет относиться к участку I, II или III одного пролета, а второй
будет обозначать номер пролета. В дополнение к тому, что мы
имеем в 'Предыдущем параграфе, необходимо учесть влияние мо-
ментов Mi и М2 для каждого пролета. Для этой цели необходимо
вернуться к дифференциальным уравнениям однопролетного
моста и учесть, что на концах балки приложены моменты. Если
исходить из уравнения (IV.4), то оно хотя и не изменится, но из-
менятся граничные условия. При х=0 и х~1 теперь мы будем
иметь Л1(0)=Л4леВ; Af(Q=7Wnp. Здесь Л4лев и А4пр моменты, прило-
женные на левой и правой опорах соответствующего пролета.
Если проделать все выкладки, то к выражениям прогибов,
углов поворота, моментов и поперечных сил добавятся слагаемые,
зависящие от /Илев и Л1пр.
В табл. 5 приведены эти дополнительные слагаемые для
отвлеченного пролета.
Таблица 5
164
В этой же таблице в последней строке записаны выражения,
«определяющие изменение площади Асом упругой линии балки,
вызванное моментами Млсв и А1пр. Эти выражения будут исполь-
зованы в дальнейшем при составлении характеристического
уравнения.
Пользуясь табл. 5, легко учесть влияние моментов Alj и М2
для каждого пролета. Так, например, для первого пролета Л1пр =
=Afi, а 7Илев=0. По данным последней колонки таблицы можно
написать дополнительные слагаемые к формулам (IV.9—IV.12),
учитывающим влияние момента Мг. Для среднего пролета
ЛГцр = 7И2, а Л1лев=Д^1. Применяя обе колонки табл. 5, мы получим
два дополнительных слагаемых для величин q, т/, М и Q.
Введем обозначения функций для к-го пролета:
ЪЛхк)=
. (л Х“ \
sh гк (1 — — I
______\______1к /
sh zK

, хк
sh гк~—
_____чс_
sh zK

ZK Ch zK
sh zK
(IV.35)
, XK
zK ch zK ——
----——
sh zK
/(*«)= 1----—
ZK
2
В дальнейшем, для прогибов углов поворота, моментов и по-
перечных сил, определяемых без учета концевых моментов Мх
и М2, будем применять обозначения т]°, (т)0]1, М° и Q0. Для всех
трех участков каждого пролета удобно применять единые обо-
значения (без разделения на участки).
о

П шк(Хк
О 4 хк $ ак
ак $ хц < Ьк
Ьк хк 1К
Таким образом, т]° (xK) представляет собой выражение про-
гиба в любом из участков пролета к, подсчитанного без учета
влияния Мх и М2.
165
Совершенно аналогичные обозначения будут и для других
факторов (моментов, поперечных сил, углов поворота). Для опре-
деления величин т>°, [П0]', М° и Q0 необходимо соответственно
применять формулы (IV.ll), (IV.12), (IV.9) и (IV.10), приведен-
ные в § 3.
Пользуясь новыми обозначениями, мы можем теперь записать
выражения интересующих нас факторов для неразрезного моста
в упрощенной форме. Применяя табл. 5 и обозначения (IV.35),
будем иметь следующие формулы:
а) для прогибов в трех пролетах
rh(xi) = т,°(Х1) + ~1 [77--------<?21 (Х1)1 »
Н 11	J
^2	= Ъ°2 М +	[ 1 — "7^----Т12 (хг)1 +
п [	/2	J
+	(IV.36>
П L *2
т1з (хз) ~	(Хз) Ч ~ГГ 1	— ^13 (ХзЯ ’
77 L *з	J
б) для углов поворота в трех пролетах
’ll (*i)= к Д|)Г+[1 - (-*1)1 /7/1		; (IV.37)
Ъ (хг)=1112х21,+	Г7Д9	Г712	
(хз)Г	+-^ie.8U3)-n	
в) для моментов в трех пролетах
Мх (xj = М\(xj 4- TMj<p21 (xj
ТИ2 (х2)	М°2 (х2) -4-	(х2) ТИ2<р22 (х2)
7И3 (х3) .= Л1з(х3)	М/Р13 (х3)
г) для поперечных сил в трех пролетах
Qi (xi)=Qi (xi) Ч~ -^1^21 (xi)
Q? (хг) — Р2 (-^г) Ч- ^1^12 (хг) 4"-^2®22 (хг)
Q3 (Хз) ~Рт(-Уз) Ч"'^2®13 (хз)
(IV.38)
(IV.39)
166
Составим уравнения для определения моментов и М2. Для
этой цели используем условия равенства углов поворота под
промежуточными опорами
(zi) = 7i2(°);
т12 (^2) — т13 (°)-
Используя формулы (IV.37), получим:
М (ОГ+-£- [1 -«21 Ю]=К(°)Г+~ Р>2 (0) -11+
iil\
+ -^Ч1-М<>)1;
К (01'+Iе, г (4) -11 + ~ 11 - ою (О1 =
/742	47^2
=K(0)l' + -^ie„(0)-i|.
nl-л
Произведя преобразования и сократив все члены на величину
----, получим систему двух уравнений с двумя неизвестными:
Н12
8ц(^)^14-812(г)ЛТ2 + д1р(г)=0, |
М*) ^1+МгУИ2 + д2р(г)==0, )	1
где
8„(г)=Л[1-е2,(/,)]-|-[1-01г(О));
ч
812 (г) = «21 (г) = - [ 1 - еи (0))=[ в12 (У - 1 ];
8^ (г) = [1 - 022 (01 + ^-11 - е.з (0)];
«3
Д1р(^)=///2{[^(/1)Г-ЬО2(0)П;
Дгр (z)=Hl2 {|т)2 (/2)Г — Из (0)']}.
Подставляя значения функций 0 и [т)0]', получим следующие
выражения для коэффициентов канонических уравнений (IV.40):
8 (2)= АГ 1----------ctl£.i. 1 _i_ 1 —z2_ch г?
Z) L sh 24 J	sh г2
812 (г)= «2, (z)=	----1
sh z2
(IV.41)
«22 (Z)= 1
g2chz2 । Z2
Sh z2 Z3
z3 ch z3
shz3 .
1
167
^2 — fl2
___ 1 ^2 4~ fl2
2 1ч )
ch z2
Z2 sh z2
г	2ч -i
1 - X g/j 1	2
X 2	z->
~2	-
(IV .42)
1	^2 -J- ^2
2	/2
a2 62
ch z2 •— — ch z2 —
b<2 — a2______________Z 2___________Z2
/2	^2 sh z^
^2p(z) —
/ a3 \
ch z3 1 —	— ch z3
______\ z3 /____________
z3sh z3
(IV.43)
Теперь осталось получить характеристическое уравнение. Для
этой цели необходимо повторить выводы, приведенные в § 4.
Также будем исходить из уравнения (IV.5). Для определения
величины С (см. формулу (Ь) § 8) необходимо дополнительно
учесть влияние моментов Mi и М2. Представим эту величину в.
виде двух слагаемых:
С=С04"С1,
где Со — определяется равенством (а), приведенным в § 8;
Ci — будет зависеть только от моментов ЛЦ и М2.
Если учесть, что дополнительная площадь линии прогибов от
опорных моментов определяется выражениями, приведенными в
168
последней строке табл. 1, а также использовать обозначение
(IV.35), то можно получить следующее выражение:
или иначе
8/i
>1
f„ \	8/2 (A4j + jU2) Z2 _	4
X	~ '	^T, X \z2) —
/2
'2
2Н
Z2 12/У
8/з
/2
fa
/1*2
/2/1
~—3  х(z3),
2Н d
6Л4]
gfy
+Гx(z2)+~ xte3)]	•
L	/2/3 J gl% j
Если теперь подставить C0+Ci в уравнение (IV.5) и повто-
рить выводы, приведенные в § 8, то окончательно получим харак-
теристическое уравнение (IV.23):
А
X
Здесь по-прежнему
А=-^-
N
 т7К] — тх -|- atktLt
тх
N
HgLs
EF
I6/2
3/2
к\ =
(IV.44).
Разница будет только в величине к2- Теперь для этого коэф-
фициента получим формулу:
*2 = (-7)	^12 +
Л h / hg	g
+ (-7-? 7^- Ф13 (гз) -I-V {[77-Х(21)+х (^2)1	+
\ /2 ) fag	gi[ IL /2/1	J
+ [ X + 77 X fell .	(I V.45)
L	fa'fa	J J


, = W2
169
§ 10. ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ
ДЛЯ ТРЕХПРОЛЕТНОГО МОСТА
Расчет трехпролетного моста состоит из двух частей: 1) реше-
ние характеристического уравнения; 2) определение моментов
поперечных сил и прогибов.
Первая и наиболее сложная часть состоит в определении
величины X, при которой удовлетворяется характеристическое
уравнение (IV.23). Решение, так же как и для однопролетного
моста, проводится путем последовательных приближений.
Задаем Х = Хь Определив по (IV.41, IV.42, IV.43) коэффици-
енты 6ц (г), 612(2), 622(2), Aip(z) и A2p(z), решаем систему кано-
нических уравнений и находим Af> и Л12. Далее по (IV.44) с уче-
том (IV.45) находим А и В. После этого по (IV.27) определяем
АХ] и затем новое значение Х2 = Х1+АХ]. Процесс повторяется до
тех пор, пока АХ не будет меньше заранее заданной величины,
предусмотренной желаемой точностью.
Найдя X, решаем вторую часть задачи, которая сводится по
существу к вычислениям по известным формулам. Применение
электронной машины позволяет решать задачу по отысканию
максимальных моментов и соответствующих им способов загру-
жения моста.
ГЛАВА V
ЧИСЛЕННЫЙ МЕТОД
РАСЧЕТА ВИСЯЧИХ МОСТОВ
§ 1. ОБЩИЕ ЗАМЕЧАНИЯ
В главе IV был изложен аналитический расчет висячих хвостов
с учетом геометрической нелинейности. Из содержания этой
главы видно, что непосредственное интегрирование дифференци-
альных уравнений приводит к весьма громоздким выводам и
поэтому затрудняет расчет.
Применение геометрических рядов, предложенное С. П. Тимо-
шенко [181], также содержит значительное количество вычисле-
ний, в особенности при действии прерывистых нагрузок.
Энергетический метод, разработанный Д. Б. Штейнманом
[162], позволил ее автору решить большое количество различных
задач, однако этот метод не удобен для механизации вычисли-
тельных работ.
В настоящее время возникла необходимость в развитии чис-
ленных методов, которые позволили бы широко использовать
современную вычислительную технику. В этом отношении заслу-
живают внимание работы Ф. Штюсси [168], в которых в основном
применяются численные приемы, позволяющие решать разнооб-
разные задачи. Идеи Ф. Штюсси получили дальнейшее развитие.
В связи с этим следует отметить работы Е. Эгервари [86, 87],
который предложил простую методику расчета висячих мостов
численным методом.
В настоящей главе излагается практически удобный числен-
ный метод, который в свою очередь является дальнейшим раз-
витием метода Е. Эгервари. Этот метод пригоден для расчета как
однопролетных, так и многопролетных висячих мостов при дей-
ствии любой, в том .числе и прерывистой нагрузки.
В главе указываются приемы расчета с применением настоль-
ных клавишных машин. Однако основным, по мнению автора,
является полностью механизированный расчет с помощью ЭЦВМ.
171
Использование матричного исчисления позволило в большой
степени сократить выводы, сделать их «наглядными» и вместе
с тем удобными для составления алгоритмов и программирования
для современных вычислительных машин.
§ 2. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ
Рассмотрим вначале однопролетный висячий мост с балкой,
жесткость которой меняется по произвольному закону. В даль-
нейшем будет показано, что предлагаемый метод может быть
легко распространен на случай неразрезных многопролетных ви-
сячих мостов. Основные размеры и обозначения показаны на
рис. 108.
Рис. 108.
Сделаем следующие допущения:
1.	Постоянная нагрузка g Т 1м равномерно распределена по
длине пролета. Учитывая, что вес несущей балки составляет не-
большую долю от общего веса пролетного строения моста, ука-
занное допущение может быть принято, как для балок жесткости
постоянного, так и переменного сечений.
2.	Ось кабеля очерчена по квадратной параболе и поэтому
при условии замоноличивания балок, после того как ее части
подвешены к кабелю, изгибающие моменты в балке от постоян-
ной нагрузки равны нулю.
3.	Будем рассматривать случаи, когда кабель можно отнести
к пологим гибким нитям и поэтому горизонтальными перемеще-
ниями точек оси кабеля пренебрегаем.
4.	Подвески будем считать нерастяжимыми. Учет растяжи-
мости подвесок, как будет показано в дальнейшем, не внесет
никаких дополнительных трудностей в решение задачи. В данном
случае это допущение принято исключительно из соображений
простоты и наглядности выводов основных уравнений.
172
Распор и усилия в подвесках от постоянной нагрузки
. g& .
g 8/ ’
(V.I)

(V.2)
где d — расстояние между подвесками.
В процессе загружения моста временной нагрузкой усилия в
подвесках изменяются. Обозначим дополнительные усилия в под-
весках от временной нагрузки через хк(к — 1, 2, ..., и).
Рис. 109.
На рис. 109 показана расчетная схема, которая получена из
заданной системы путем одновременного разрезания всех под-
весок. В этом случае балка и кабель могут рассматриваться как
отдельные системы, у которых, однако, должны быть совместные
деформации.
При загружении балки временной нагрузкой на нее будут
действовать следующие силы, которые будем считать сосредото-
ченными в узлах: силы, действующие вниз — от собственного
веса vg и от временной нагрузки vq; силы, приложенные кверху
в виде натяжения подвесок vg и х. Таким образом, суммарные
силы, приложенные к балке, следующие:
'V^'Vg—x.	(а)
На кабель будут действовать силы от собственного веса vg и
от временной нагрузки х. Они направлены в одну сторону и по-
этому суммарные силы, приложенные к кабелю вниз, будут:
.	(Ь)
Обозначим прогибы балки жесткости в точках прикрепления
подвесок через тр Тогда вектор этих перемещений будет сле-
дующий:

^2
Чп
173
Вектор прогибов балки можно определить с помощью следу-
ющего равенства:
(V.3)
где Lx — матрица влияния прогибов, которую можно построить
любым из известных способов.
Между усилиями в подвесках и ординатами оси кабеля после
деформации существует следующая зависимость;
+ Л = н (fc ?«)»
где Н—полный распор от постоянной и временной нагрузок;
ср* и ср"—углы наклона элементов кабеля слева и справа от
соответствующей подвески в деформированном со-
стоянии.
Из рис. НО видно:
Рис. 110.
поэтому
, I V ti ( Ук Ук—\ Ук^\—Ук. \
—7-----------~d---J +
+	—Vu) (*=>• 2..... «)•
Выражение в первой скобке представляет собой разность
тангенсов углов наклона <рко элементов цепи в узле к до загруже-
ния временной нагрузкой. Обозначим вектор этих величин
Atg<pKo.
174
Переходя к векторной записи, получим:
(^4-х) =//Д tgcp0-b//A2T6
(V.4)
где
ssa
Д tg ср0 =
A tg <рю
A tg <р20
A tg ?я0
-1
2
- 1
2	-1
-1 2
(V.5)
Для кабеля, ось которого до деформации очерчена по квад-
Л	А 4.	$fd
ратной параболе, величина Atg(pA.o постоянная и равна - .
следующем
Поэтому вектор Д tg д>0 может быть представлен в
виде:
8fd
Atgcpo^-j^-o,
где
Определив из (V.4) вектор х и подставив его
(V.3), получим
(Е + НL	7} = L, Д vt
Как будет видно из дальнейших выводов, удобно
дующее обозначение:
/7ц2
Л =-------------- .
(п 4- 1) EI
в формулу
(b)
ввести сле-
(V.6)
Разрешив уравнение (Ь) относительно т], получим:
^(f + ur1 (гГ-Гу^,
(V.7)
175
L,~ rf
2
— 1
а =
1
1
1
1

где
Д=.<”+1)£/ ££
rf2
72*=л1(^4-^)
(V.8)
-%	8/£/	, -*
и —-------------LjO
(n + l)d3
Уравнение (V.7) недостаточно для решения задачи, так как
в пего, кроме искомого вектора прогибов балки т], входит еще
неизвестный параметр X.
Необходимо составить одно дополнительное уравнение дефор-
мации оси кабеля. Для этой цели воспользуемся так же как и
при расчете гибкой нити, описанным в гл. III принципом Лаг-
ранжа (работа внешних и внутренних сил для кабеля от постоян-
ной нагрузки на перемещениях от временной нагрузки равна
нулю). Для нашего случая с учетом двух оттяжек кабеля So
(рис. 108) получим:
.^=0. (V.9)
е I cos г cos iEF cos2 <pK EF I
к=1	x	«=1	/
Величины Sqht показаны на рис. 108.
S —длина элемента кабеля между точками к и к-1.
Подставляя в это выражение вместо vg его значение (V.2),
после сокращения на Hg и замены Hq=H—Hg получим:
Н~Не	Sfd
—~ (is+2S„ sec^)=— £	(с)
«=1
где EF — жесткость кабеля на растяжение;
Ls — приведенная длина, о которой подробно рассказыва-
лось в.Гл. Ш((Ш.7) и (III.21)].
(d)
Уравнение (с) с учетом обозначений (d) и формулы (V.6)
после всех преобразований может быть приведено к виду
п
Х=а4-р V
«=1
где
а=------------ ;
(л -f 1) Е1
____________8/££__________
/	2S0
' (л + J )4 EI / (л 4- —-— sec2 т
(V.11)
(V.12)
176
Совместное решение уравнений (V.7) и (V.10), которые в
дальнейшем будем называть основными уравнениями, дает воз-
можность определить вектор ц и параметр X, после чего по урав-
нению (V.4) легко определить усилия в подвесках и затем все
остальные усилия, необходимые для расчета моста.
Полученные уравнения нельзя решить в замкнутом виде, так
как они являются нелинейными по отношению к искомой величи-
не X, что характерно для расчета висячего моста по деформиро-
ванной схеме. Методы решения этих уравнений специально об-
суждаются в § 4 и 6.
§ 3.	ВЫЧИСЛЕНИЕ МАТРИЦЫ А
Для того чтобы составить матрицу А, входящую в основное
уравнение (V.7), необходимо вначале построить матрицу пере-
мещений £ь Для этой цели можно применить различные методы.
Один из наиболее удобных численных методов изложен в книге
коллектива авторов [38]. По этому методу матрица Li опреде-
ляется произведением трех матриц:
(V.13)
где Lm— матрица влияния моментов в простой балке;
— матрица упругих грузов;
[}т—матрица влияния моментов в фиктивной балке.
Формула (V.13) справедлива как для балки постоянного, так
и переменного сечений. Учет перемен-
ности сечения производится матрицей
упругих грузов.	£ / f J 4 у s
Рассмотрим более подробно случай . X J L Г**
однопролетного моста с балкой посто- 4^---- ----------ч
янного сечения. Задача заключается
'В'том, чтобы выразить вектор прогибов	Рис. 111.
т) от сил Рк (к= 1, 2, ..., п) приложен-
ных к балке, показанной на рис. 111. Для рассматриваемого
случая имеет место равенство
L — L* —	1 I
т т (п + 1)2
где 1п представляет собой матрицу, каждая строка которой со-
стоит из ординат линий влияния моментов в точках 1, 2, ..., п,
I	I
взятых в масштабе ------ .
(п+ О2
177
Так, например, для балки,
разбитой на шесть частей (п = 5),
получаем:
5
4
2
1
4 3 2 1
8 6 4 2
6 9 6 3
4 6 8 4
2 3 4 5
Матрица упругих грузов будет:
р  d
(а)
где Bi для случая п = 5 будет:
4 1
1 4 1
1 4 1
1 4
(Ъ)
Произведение двух матриц Bi
цию от матрицы 1п (см. (38]):
и 1п представляет собой функ-
в\!п= (bKK + 2^к) In - biK (п + 1) Е.
В этом выражении Ькк^4 (диагональный элемент), a biK = 1 —
побочный элемент матрицы Ви Е — единичная матрица.
Следовательно,
BJ^ei^^n+DE.
Естественно, что
Iп = п — (л+1) /„,
поэтому
(VJ4)
Учитывая, что матрица L2 (V.5) также является модулирован-
ной якобиевой матрицей с элементами 2 и — 1, найдем:
/A=-7([2+2(-l)]/„-(-D(<»-|-l)£)=-24-LF.
cl	’ а
На основании равенств (V.8) и (V.14) устанавливаем:
4 = /„
(V.15)
6
178
По этой формуле легко составить матрицу А для любого чис-
ла делений балки. Так, например, для случая п = 5:
4
3
2
4 3
7 6
6 8
4 6
2 3
2 1
4 2
6 3
7 4
4 4
(V.16)
Аналогично можно построить матрицу А для балки перемен-
ного сечения.
§ 4. РЕШЕНИЕ ОСНОВНЫХ УРАВНЕНИЙ
ПРИ ИСПОЛЬЗОВАНИИ НАСТОЛЬНЫХ КЛАВИШНЫХ МАШИН
Наиболее трудоемкую задачу представляет решение основных
уравнений (V.7) и (V.10), полученных в § 2:
п
К=1
Основная задача заключается в определении параметра X,
через который определяется распор Н. Легко заметить, что ре-
шение задачи в замкнутом виде невозможно, так как уравнение
(V.7) по отношению к X является нелинейным.
Кажущийся на первый взгляд заманчивым метод последова-
тельных приближений применить непосредственно к уравнениям
(V.7) и (V.10) нельзя, так как процесс итерации является в дан-
ном случае плохо сходящимся. Единственная возможность со-
стоит в разложении матрицы (Е + ХА)_| в степенной ряд. Однако
для сходимости ряда необходимо (вначале провести специальные
преобразования. Для выяснения смысла намечаемых преобразо-
ваний приведем сначала элементарный пример. Предположим,
что необходимо вычислить с помощью ряда функцию
f(x) = —= 1 - х-ф х2 — л3-!------
При |х|>1 этот ряд является расходящимся. Пусть, напри-
мер, требуется найти разложение функции f(x) в окрестности
точки х=х0. Произведем замену х = Хо+Ах,
тогда
/(»)=-- 1 —=/ .
1 + Xq + Дх	1 + Е
179
где	t
Ar
e =-----.
1 +-vo
Искомое разложение будет иметь вид
/(х)=/(х0)(1-б + ^-Н-|-...).
Полученный ряд является сходящимся при
Н<1.
Проведем аналогичное преобразование с матричной функцией
/W=(£'+^)-1.
Положим, что
Х=Х0-|-ДХ.	(V.17>
Найдем сначала матрицу
(^+ХА)=С0(Е+дХА*),
где
Со=(£+М);	(V.18)
Д' —С^'А.	(V.19)
Далее находим обратную матрицу:
(Е + ХА)-1 =- (£ + ДХА
Подставляя это выражение в основные уравнения, получим
новую систему:
(F-b ДХА)-1 (V ~ ДХ?*),	(V.20)
ДХ=«Ч₽2 I,.	(V.21)
Л = 1
где
= Г = СГ' (tf->.„/);	(V.22)
=	(V.23)
Следовательно
(Е+ДХА *)-1 - Е -ДХА * + ДХ2А *2 -...
Следует отметить, что величину Хо всегда можно задать до-
статочно близкой к искомой величине. Так, например, определив
распор Н из условия, что вся нагрузка передается на кабель
(балка жесткости не способна работать на изгиб), можно вычис-
лить приближенное значение Хо-
180
Для решения уравнений (V.20) и (V.21) можно эффективно
воспользоваться быстро сходящимся рядом
^=(£- ДЫ*+ Д Х2Д*2-----) Й** - дХ^* *).
Далее введем матрицу-строку:
4=111 1 1...1Ц.
Произведение юоЛ Дает сумму значений т), следовательно,
« -
2	~ Wo1J = (“° ~ д>а01 + ДХ2(Ь2 + • - ) С7!** — ^У**\
К = 1
где
(i)1=:(o0^*; w2—о13 = <о2Д*.	(V.24)
Подстановка в формулу (V.21) даст:
дX=а* + ₽ (<оо - ДXwj + дХ20>2 4-...) Й** — ДХу**).
После преобразований получим уравнение для определения АХ:
с0 — ДXcjЛХ2с2... =0,
(V.25>
где
с0=а*4-₽«>оН**
C2-P(<o2TJ**4-w1y**)
^3=P(0)37i**4-w2/*)
(V.26)
После решения уравнения (V.25) по формуле (V.17) находит-
ся величина X, затем по уравнению (V.7) — вектор прогибов т]
и, далее, по (V.6) — распор И. Изгибающие моменты в сечении
балки можно определить равенством
Перед этим величина х находится из уравнения (V.4).
§ 5. ПРИМЕР РАСЧЕТА ОДНОПРОЛЕТНОГО МОСТА
Рассмотрим численный пример расчета моста равномерно за-
груженного по всему пролету имеющего следующие размеры:
/=200 м; / = 20м; So=35,3 м; т=45°; F=0,l м2; Е = 2,2-107 Т/м2;
Ек=~ ;g=12 Т/м; q=6 Т/м; 7=2,0 м*; р,= 1,08189.
1 tz
181
где	t
Ar
e =-----.
1 +-vo
Искомое разложение будет иметь вид
Полученный ряд является сходящимся при
Н<1.
Проведем аналогичное преобразование с матричной функцией
Положим, что
Х=Х0_|_ДХ.	(V.17>
Найдем сначала матрицу
(^+ХЛ)=СО(Е+ДХА*),
где
с0=(£+М);	(V.18)
Д' —С^'А.	(V.19)
Далее находим обратную матрицу:
(Е + ХА)-1 =- (£ + ДХА
Подставляя это выражение в основные уравнения, получим
новую систему:
(£-Ь ДХА)-1 (V - ДХ?*),	(V.20)
ДХ=«Ч₽2 I,.	(V.21)
Л = 1
где
=	Г = СГ' (tf->.„?);	(V.22)
=	(V.23)
Следовательно
(Е+ДХА *)-1 - Е - АХА * + АХ2А *2 -...
Следует отметить, что величину Хо всегда можно задать до-
статочно близкой к искомой величине. Так, например, определив
распор Н из условия, что вся нагрузка передается на кабель
(балка жесткости не способна работать на изгиб), можно вычис-
лить приближенное значение Хо-
180
Для решения уравнений (V.20) и (V.21) можно эффективно
воспользоваться быстро сходящимся рядом
Ч=(£- ДХД*ф- д ХМ*2------) (V* - ДХ?*).
Далее введем матрицу-строку:
«0=111 1 1...1Ц.
Произведение юот) Дает сумму значений т), следовательно,
« -
2	=“о1! = (°’о —	+ АХ2<о2 + • - ) (V* — &У**),
К = 1
где
о)1;=(о0Д*; w2=<u124*; i»3 —<о2Д*.	(V.24)
Подстановка в формулу (V.21) даст:
ДX=а* + ₽ (<оо- дХо)! + дХ20>2 4 . . .) (V — AXj**).
После преобразований получим уравнение для определения АХ:
cQ — ДXfjАХ2с2-J- ... =0,
где
с0—а* 4
Г1 = 1 4 Р (“i1!** 4“ шоУ**)
с2-Р(ю212**4ш1/*)
<?3 = P(°Vi**4-w2/*)
(V.25>
(V.26)
После решения уравнения (V.25) по формуле (V.17) находит-
ся величина X, затем по уравнению (V.7) — вектор прогибов т]
и, далее, по (V.6) — распор Н. Изгибающие моменты в сечении
балки можно определить равенством
Перед этим величина х находится из уравнения (V.4).
§ 5.	ПРИМЕР РАСЧЕТА ОДНОПРОЛЕТНОГО МОСТА
Рассмотрим численный пример расчета моста равномерно за-
груженного по всему пролету имеющего следующие размеры:
/=200 м; f = 20 м; So=35,3 м; т=45°; F=0,l м2; Е = 2,2-107 Т/м2;
Ек=~ ;^=12 Т/м; q=6 Т/м; 7=2,0 jw4; р,= 1,08189.
1 tz
181
По этим данным находим:
£7=44-10е Тм\ EKF = 1,83333-1()6 Т.
Разобьем балку жесткости на шесть равных частей:
,	200
а = —
6
В этом случае все матрицы будут пятого порядка (п = 5).
Матрица А для п = 5 дана равенством (V.16). По (V.6) находим:
6£/
(V.27)
Далее по формулам (V. 11) и (V.12) находим:
а = _3^£_ = ] 26263.10-2
4/£/
fEKF
(2S
и + —— sec2 т
I
— =0,28772-10-2.
Е/
Применяя формулу (V.14), найдем матрицу:
		25	38	39	31	17
		38	64	69	56	31
Z1=	rf3	39	69	81	69	39
	18£/	31	56	69	64	38
		17	31	39	38	25
По (V.8) определяем векторы
т]* и у*, учтя при этом,
что
^=12flf; vq = 6d:

102
23.76
1
1,72
1,98
1,72
1
104
45
1 1 '
1,72
Л, 98
Л,72
| 1
182
После подстановки найденных значений в основные уравне-
ния (V.7) и (V.10) получим:
4
4
3
2
1
4 3 2 1
7 6 4 2
6 8 6 3
4 6 7 4
2 3 4 4
4,20875
7,23906
8,33333
7,23906
4,20875
222,(2)
382,(2)
440,0
382,(2)
222,(2)
(V.28)
1 = 0,0126263 + 0,0028772 j?	(V.29)
К=1
Из этих уравнений видно, что величина X лежит в пределах
0,0126 <Х< 0,0189.
В самом деле, если предположить, что прогиб в середине про-
лета отсутствует, то из уравнения (V.28) получим:
Х	0,0189,
1	440
а из (V.29) при 2т) = 0 Х2 = 0,0126.
Зададим Хо=0,0175. Тогда из (V.18) получаем:
	1,0700	0,0700	0,0525	0,0350	0,0175	
	0,0700	1,1225	0,1050	0,0700	0,0350	
	0,0525	0,1050	1,1400	0,1050	0,0525	•
	0,0350	0,0700	0,1050	1,1225	0,0700	
	0,0175	0,0350	0,0525	0,0700	1,0700	
Обратная матрица:
	0,94074 - 0,05361 -0,03588 - 0,02198 - 0,01043 — 0,05361	0,90486 - 0,07560 — 0,04631 —0,02198
сг'=	-0,03588 —0,07559	0,89442 —0,07559 —0,03588 —,0,02198 — 0,04631 -0,07560	0,90486 — 0,05361 — 0,01043 —0,02198 -0,03588 —0,05361	0,94074
183
Далее находим:
	3,38646 3,06359	3,06358 5,43676	2,05030 4,31971	1,25613 2,64650	0,59621 1,25613	
	2,05030	4,31971	5,43676	4,31971	2,05030	
	1,25613	2,64650	4,31971	5,43676	3,06358	
	0,59621	1,25613	2,05030	3,06358	3,38646	
	0,31986		0,23326
	0,55017		0,40030
	0,63333	==	0,46032
	0,55017		0,40030
	0,31986		0,23326
J**=Co1i/* = lO2
1,62056
2,78099
3,19806
2,78099
1,62056
а* = а - Хо - — 0,0048737.
По выражению (V.24) находим значения матриц-строк со:
-о=Н 1 1 1 1.111-
^=<0^*= || 10,35286 16,72268 18,77299 16,72268 10,35268||,
«2=®^*= ||151,959	260,989	300,184	260,989	151,9591(.
Коэффициенты характеристического уравнения будут:
с0=a* -f-	=0,0000965,
q = 1 + ₽ (ад* *+-о?*) =4,53026,
с2 = р (ад**+-1?*) = 54.S9214.
Подстановка дает:
54,89214дХ2-4,53026дХ 4-0,0000965=0.
Наименьший корень этого уравнения
ДХ= 0,0000213.
Таким образом,
Х=Х0 4-дХ =--0,0175213.
484
Практически можно взять с округлением
-0,0175.
По формуле (V.7) находим:
0,233
0,400
0,460
0,400
0,233
Наибольший прогиб составляет — I.
Е	435
Из формулы (V.27) имеем:
/7=Л^£1=4158 т.
d?
По уравнению (V.4) находим:
562,66
576,75
569,34
576,75
562,66
Суммарная узловая нагрузка, действующая на балку,
(^-х)= (^4- vj -
Вектор изгибающих моментов в сечениях
37,34
32,25
30,63
32,25
37,34
балки жесткости
~M = Lm (Za—x) = —
т\ q !	36
509,43		2830
794,82		4416
886J1	—	4926
794,82		4416
509,43		2830
Тм.
При расчете этой же системы по методу сил максимальный
изгибающий момент составляет 5600 Тм. Расхождение—11%.
При увеличении временной нагрузки, процент расхождения бы-
стро нарастает. Процент погрешности в некоторой степени связан
185
с максимальным прогибом системы. Так при—, Разни-
ца для данного примера достигает 50%.
В данном примере пролет делится на шесть частей. При уве-
личении числа делений изгибающий момент Л4тах и максималь-
ный прогиб несколько уменьшаются. Аналогичная картина полу-
чается и при расчете по методу сил. Однако разница между
результатами расчетов по деформированной схеме и по методу
сил при любом числе подвесок остается неизменной.
Отметим, что наличие балки переменного сечения ни в какой
степени не усложняет расчета. Различие будет в составлении
матрицы L}, которая также определяется по формуле (V.13), но
в ней матрица упругих грузов изменяется.
§ 6.	О РЕШЕНИИ ОСНОВНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ЭЦВМ
Из примера, приведенного в предыдущем параграфе, видно,
что основная трудность в расчете моста по деформированной
схеме состоит в решении основных уравнений. При высоком по-
рядке матрицы описанный в § 4 метод становится трудоемким
и поэтому требует применения более мощных вычислительных
средств.
При использовании электронных вычислительных машин изло-
женный ранее метод применять не целесообразно, так как более
простой алгоритм, хотя и более трудоемкий, легче программи-
руется, более экономно расходует оперативную память машины
и поэтому заслуживает большого внимания.
Запишем вновь основные уравнения (V.7) и (V.10):
И
71к-
К=1
Второе уравнение перепишем в виде
п
/Й=-Н«+₽2ч,.	(V.30)
«=1
Теперь решим систему уравнений (V.7) и (V.30) методом
последовательных приближений. Задавая величину
kz+1=A.-}-Ak, (/=1, 2,..., п)
и подставляя каждое из этих значений в уравнение (V.7), полу-
чим векторы прогибов и соответственно суммы Етр После подста-
186
новки этой суммы и соответствующего значения X в уравнение
(V.30) получим ряд значений функций fi(X); [2 (к).
Необходимо отыскать такое значение X*, при котором функции
f(Z) обращаются в ноль. На рис. 112 показано примерное изобра-
жение этой функции. По программе, которую автор составил для
машины «Урал 2» значение X* отыскивает сама машина. Подоб-
ным путем можно вычислить значение %* с любой, наперед задан-
ной точностью. Признаком, по которо-
му машина заканчивает процесс итера-
ции, служит величина е, заложенная
в программе, с которой производится
сравнение функции f(X). Задачу по
отысканию X* машина заканчивает
тогда, когда будет в первый раз выпол-
нено неравенство
Рис. 112.
/(**)<*•
Такой метод был неоднократно применен при решении задач,
приведенных в настоящей работе, в том числе рассмотренной
в следующем параграфе.
§ 7.	РАСЧЕТ ТРЕХПРОЛЕТНОГО МОСТА
С НЕРАЗРЕЗНОЙ БАЛКОЙ ЖЕСТКОСТИ
Расчет трехпролетного моста по деформированной схеме пред-
ставляет собой сложную задачу, которая усугубляется необхо-
димостью рассмотрения большого количества загружений. При-
менение электронной машины позволяет преодолеть эти труд-
ности.
Методика расчета и основные уравнения для трехпролетного
моста мало чем отличаются от таковых для однопролетного мо-
ста, однако имеются свои особенности, которые требуют специ-
альных пояснений.
Расчетная схема и основная система для трехпролетного
моста такие же, как и для однопролетного (рис. 113).
Исходное уравнение для определения прогибов совпадает с
выражением (V.3):
(V.31)
Также не меняется и уравнение (V.4):
Д tg^о-|-ЯЛ271,
(V.32>
187
здесь
Atg%=
Д tg ?10
д tg <р20
Atg?„o
(V.33)
где A tgq)0 — разность тангенсов углов наклона элементов кабе-
ля в начальном состоянии до приложения времен-
ной нагрузки.
Рис. 113.
Необходимо иметь ввиду, что нумерация точек должна начи-
наться с первого пролета и идти подряд до конца третьего про-
лета. Ввиду того, что в разных пролетах размеры Inf могут быть
различными, замена вектора (V.33) через единичный вектор о,
как это было сделано ранее, будет уже неправомерной.
Рис. 114.
Матрица L2 должна быть построена для всего моста в целом.
Она будет представлять собой квазидиагональную матрицу сле-
дующего вида:
Z2—
^-2,2
(V.34)
^2,3
Каждая из матриц £2.ь £2,2, £2,3 строится для своего пролета.
188
Для симметричного трехпролетного моста с отношением про-
летов /2=2 /1 при нумерации точек, как показано на рис. 114, мат-
рица £2 будет иметь следующий вид:
2 -1
-1	2 -1
— 1	2-1
— 1	2
Определив из равенства (V.31) вектор х, подставив его в
уравнение (V.32), и разрешив относительно т), получим для век-
тора прогибов следующее уравнение:
+ ХА )-1 • (7)* - \у *),	(V.35)
где
\=НН
А =—£х£2
^* = £i(^ + ^)
/ = V Л1А %
h
(V.36)
Величина h представляет собой некоторый числовой коэффи-
циент, который выбирается исходя из удобства расчета. Дело в
том, что при составлении матриц L\ и Ъ2, а следовательно, и мат-
рицы А некоторые числовые значения, как, например, длина
панели, жесткость и т. д., могут быть вынесены за скобку. Все
это в совокупности и составит множитель А. Такой прием оказы-
вается удобным при использовании ЭЦВМ, так как при хранении
величины h в какой-либо ячейке можно с пульта изменить те или
другие параметры.
Перейдем теперь к составлению уравнения деформации кабе-
ля. Так же как и ранее, используем для этого принцип Лагранжа,
приравнивая нулю работу внешних и внутренних сил кабеля от
постоянной нагрузки на перемещениях от временной нагрузки.
В отличие от полученного ранее выражения (г) теперь полу-
чим:
189
(t„+l,2+z,3)=(и,/,+|x2/2
EKE	EKE
i Р'зАз)—
_ 8/1^1 V । 8/^2 V	, B/3rf3 УЧ
(2Z,)2 Zj ГТ /2	Zj (2/3)2 U
/1	12	ig
(V.37)
Входящие в это выражение коэффиценты ць ц2 и щ опреде-
ляются по формуле (III.23), но для каждого из них должны учи-
тываться свои значения I и f.
Индексы, стоящие под знаком S в равенстве (V.37), показы-
вают, что суммирование прогибов производится в пределах ука-
занного пролета.
Из уравнения (V.37) находим:
Н = Н -|------------------Г V т] +
(ЛН1 + ^Р-2 +/зМз)	(2Zi)2 jtaJ
+-^S ’I •	(V38)
2 Z2	Zs
Умножая
чение (V.36)
все члены этого равенства на h и учитывая обозна-
(Х = /г/7), получим второе расчетное уравнение:
где a=hHg\
х= а 4- ₽1	*1+₽2 2 + Рз 2
Zi	Z2	/3
_ h EkF	8/иЛ
Д1Л + Р-2^2 + НзАз	(2/1)2
__д£«7	8fad?
Д1Л 4- Р2^2 +|азЛ-5	/2
__	ЕКЕ 8/grf3
Д1Л + Р-2^2 + Ц.зЛз	(2/з)2
(V.39)
(V.40)
Уравнения (V.35) и (V.39) являются основными уравнениями,
из которых необходимо определять величину X и вектор q.
Теперь вычислим матрицу перемещений L], которая должна
быть подсчитана для неразрезной трехпролетной балки. Естест-
венно, что этот процесс должен быть максимально механизиро-
ван. Наиболее удобным является методика, разработанная
Б. Я. Лащениковым [38], которую мы и примем. По этой методике
матрица перемещений определяется матричным равенством
Lx = {L^BL^-(LP)'BLX (L'x BLX)~XLXBL^. (V.41)
Формула (V.41), хотя и является довольно слбжной, но в нее
входят всего только три матрицы Lx, В, L°, которые вводятся в
190
память машины. Приведенная выше формула Б. Я. Лащеникова
получена на основании общего решения статически неопредели-
мой системы. Входящие в равенство (V.41) матрицы имеют зна-
чения:
В — матрица упругих грузов для основной системы;
L0 — матрица влияния моментов для основной системы;
Lx — матрица, столбцы которой состоят из изгибающих
моментов, возникающих в основной системе от
единичных неизвестных;
(L°Y и L/— матрицы, транспонированные по отношению к L0
и Lx.
Найдем матрицу Ц для случая, когда средний пролет в сим-
метричной трехпролетной балке в два раза больше крайних про-
летов. Разобьем балку на 12 участков, так как показано на
рис. 114. Для этого случая матрицы, входящие в формулы (V.41),
определяют равенствами:
О О
5 4
1 2
О О
В^-^—
6EF
41
141
141
141
141
141
141
141
14
О
О
О
1
2
3
4
5
6
4
2
191
ггавляя эти матрицы в формулу (V.41), после всех вы-
й получим матрицу перемещений
5-72£/
960
768
-520
—704
-648
—448
-200
80
64
768	—520	—704	—648	-448	-200	80	64
852	—650	-880	—810	—560	-250	100	80
—650	1375	2072	1971	1384	623	—250	—200
—880	2072	3904	4104	3008	1384	—560	—448
—810	1971	4104	5103	4104	1971	—810	—648
—560	1384	3008	4104	3904	2072	-880	—704
—250	623	1384	1971	2072	1375	—650	—520
100	—250	-560	—810	—880	-650	852	768
80	—200	-448	—648	—704	-520	768	960
«ер. Рассмотрим численный пример трехпролетного моста
>езной балкой жесткости, показанного на рис. 115. Поло-
= 2 /1=500 м, f=50 м, EI = 80- 106 Тм, EKF=6- 106 7,
/м. Нагрузка q варьируется. По табл. 4 (приложение)
: р= 1,08189.
Рис. 115.
«энные представляют собой исходный материал, вместе
IM в машину вводились матрицы Lx и Т2, приведенные
ица Lm вычислялась машиной по соответствующей про-
Программа занимает около 600 ячеек. В ней широко
ются стандартные матричные подпрограммы матричной
Ниже показано, как выглядят результаты, выдаваемые
: на печать при каждом загружении. Так, например, при
ши среднего пролета нагрузкой <у = 0,5 g получены сде-
ланные (этот пример служил контрольным примером
раммы):
/(Х)= — 23203938 - 0,7;
Х= +29882 904+00;
//=+89 229873+04.
Далее приводятся три вектора—прогибов, изгибающих мо-
ментов и суммарной нагрузки на балку:
-12 348 221 + 01
-12 074481+01
+ 11 905866 + 01
+ 19 526021 + 01
+ 22128 482+ 01
+ 19 526 021+01
+ 11 905 866 + 01
-12 074 481+01
-12 348 221 + 01
— 17613 382 + 05
— 16789466+05
+32045235 + 04
+ 51368 423 + 04
+ 58847997 + 04
+ 60596 734 + 04
+ 58 847 997+04
4-51368 423+04
+ 32 045235 + 04
-16 789466 + 05
-17613382+05
<7
-22 124759 + 03
-23004087 + 03
+ 14378 758 + 02
+65 441 622 + 01
+45 298114+01
-4-65 441 622 + 01
+ 14 378 757 + 02
— 23 004087 + 03
— 22 124 759 + 03
В программе предусмотрены поиски величины интенсивности на-
грузки (при каком-либо определенном загружении), при которой
максимальный прогиб будет равен допускаемой величине, напри-
1 ,
мер — I.
к 200
При этой нагрузке вычисляются и выдаются на печать
те же три вектора. Так, например, при загружении среднего про-
лета и при допускаемом прогибе 2,50 м машина выдала на пе-
чать следующие данные:
= 2,5000041 м,
а искомая величина интенсивности нагрузки
<7 = 0,57171 g.
Остальные данные (перепечатанные с ленты) выглядят так:
/(Х)=—47779395 - 07;
+31116 269 +00;
Н= +95912 681 + 04.
7—3802
193
-138607644-01
-13 5638214-01
4-13434309 4-01
4-22 053 9894-01
4-25 000 0414-01
4-22 0539894-01
4-13 434 309 4-01
-13 563 8214-01
— 13 860 7644-01
v— х=
-24765 0744-03
-25 758 3094-03
4-17 241 770 4-02
4-76 643 786-j-01
4-52 2844744-01
4-76 643 7864-01
4-17 241 7704-02
— 25 758 3094-03
— 24 765 0744-03
-19 749 2734-05
-18 860985 + 05
4-34925 611+04
4-57859 220 + 04
4-66590 985 + 04
+-68 603 207 + 04
4-66590 986 + 04
4-57859 219 + 04
4-34925 611+04
— 18 860 985 + 05
— 19749 273+05т
С помощью зычислитсльной машины легко исследовать влия-
ние различных факторов на изменение усилий и деформаций в
висячей системе. Так, например, на рис. 116 показан график из-
менения распора, наибольшего изгибающего момента и макси-
мального прогиба при загружении среднего пролета нагрузкой
/у = 0,5 g в зависимости от жесткости балки.
Рис. 116.
194
Аналогичный график показан на рис. 117 при том же загру-
жении в зависимости от изменения жесткости кабеля.
Как уже указывалось ранее, при расчете висячих мостов по
деформированной схеме закон независимости действия сил не
соблюдается, поэтому нельзя пользоваться линиями влияния,
полученными по методу сил. Это в сильной степени затрудняет
Рис. 117.
учет подвижной нагрузки. При изменении характера загружения
весь расчет приходится производить заново. Таким образом,
объем работ при расчете по деформированной схеме намного
больше, чем при обычном расчете по линейной теории.
Рис. 118.
Программа, составленная для рассмотренного примера, позво-
лила изменять характер загружения и проводить расчет при мно-
гократных комбинациях нагрузки. На рис. 118 показана схема
загружений, для которых проведены расчеты трехпролетного
моста.
Приводить все числовые данные, полученные для указанных
загружений, не целесообразно, так как от этого сильно возраста-
ет объем настоящей работы. Ограничимся лишь приведением
7*
195
двух графиков. На рис; 119 показан график изменения опорных
моментов Ма и Мь, а также момента в середине пролета в зави-
симости от загружения. На рис. 120 изображен график прогиба
в середине второго пролета при тех же загружениях.
Рис. 119.
Рис. 1ZU.
§ 8. СРАВНЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА
ТРЕХПРОЛЕТНОГО МОСТА
ПО ДВУМ МЕТОДАМ
При расчете трехпролстного висячего моста с неразрезной
балкой жесткости как трижды статически неопределимой си-
стемы Ф. Блейх [1] получил формулы для ординат линии влияния
распора.
При движении единичного груза в пределах среднего пролета
эта формула приводилась в § 8 гл. IV. Пользуясь формулами
этого параграфа, для нашего случая находим:
m,= /K,+4Z±=9_/
2(21, + 31,)	16
г=2/, й+24'|+/41+84')=2/Ф+84'1 
\	\	12 )	\	12 )
Значение распора при единичном грузе в среднем пролете,
расположенном на расстоянии от опоры:
- 2бз -ь 6) -	(£ - $2)
f~[ = 3_________________-_______—
17	4 (от')2 El L,
30' 12	. 3/2 EKFl\
27
(^-263 + 6)-—(S-$2)
=------------------32--------.	(а)
139 f
--- *	I | 1 “T" О 9 I _ _
. 320 l2 fl2\ l2)EKF
196
Загрузив средний пролет равномерной нагрузкой q, найдем
распор от временной нагрузки. Для, этой цели произведем инте-
грирование выражения (а) в пределах среднего пролета, поло-
жив q = 0,5g. Выполнив интегрирование, (получим
19
, ,	320 'ql
— • — +— 1 + 8— ---------
320 I fl \ Р J EKF
19	/2
____________ а —
_____________139-/_________
1920 /	/2	\	Е1
1 +----- 1 + 8 — -----
139/2	/2	/	EKF
Подставив в эту формулу наши размеры: /2 = 500 м = 2 l\f =
,= 50 м, q=5 Т/м, Е F=6- 106 Т и сохранив EI в общем виде,
после всех преобразований получим окончательно:
Я —	3417.266
q~ 1 + 0,009453-10-8 EI
Давая значения изгибной жесткости:
£7 = 0,1-108, 0,2-108, 0,3-108,..., 1,0-108,
получим значения распора от временной нагрузки, которые при-
ведены в табл. 6. Там же приведены значения полного распора
Н= ННq, при этом учтено, что распор от постоянной нагрузки
—=6250 Т.
g 8/
В этой же таблице приведен распор Н*, полученный с по-
мощью электронной машины при расчете по деформированной
схеме. В третьем столбце указано расхождение между двумя
распорами в процентах:
Таблица 6
EI 108		н	н*	Л/7, %
0.1	3383,62	9633.62	8789,68	9.7
0,2	3350,62	9300,62	8843,29	8,6
0.3	3318,26	9568,26	8880,56	7,7
0,4	3286,52	9536,52	8903,49	7,1
0.5	3255,39	9505,39	8916,82	6,6
0.6	3224,83	9474,83	8923,39	6.1
0,7	3194,85	9444,85	8925,03	5,8
0,8	3165,42	9415,42	8922,99	5,5
0,9	3136,52	9386,52	8918,12	5.3
1,0	3108,15	9358,15	8911,08	5,0
197
Проведем теперь сравнение изгибающих моментов, найденных
двумя способами. Найдем вначале момент по линейной теории.
Для этого используем формулу

(б)
Г7	1/0
где	Мц2 =----момент в середине пролетает еди-
8
ничного распора;
М°ц2=—= 78 1257м—момент в середине пролета нераз-
16
резной балки от нагрузки q.
Учитывая значения распора по табл. 6 и значения моментов
по формуле (б), найдены моменты Mt/2 и приведены в табл. 7.
В этой же таблице приведены моменты, полученные с помощью
электронной машины «Урал 2», при расчете по деформированной
схеме. В третьей колонке дается процент расхождения моментов,
найденных двумя способами.
Таблица 7
EI 10®	W 1! 2	м* ift	дм. %
0,1	4108,3	1079,1	73,7 )
0,2	4830,2	1928,1	60,1 1 В
0,3	5538,1	2687,1	51,5 J
0,4	6232,3	3402,5	45,4 х
0,5	6913,3	4091,7	40,8
0,6	7581,8	4762,1	37,2
0,7	8237,7	5417,4	34,2	А
0,8	8881.4	6059,7	31,8
0,9	9513,6	6690,1	29,7
1,0	10134,6	7309,6	27,9
Произведем теперь сравнение опорного момента, для которого
78 125;
поэтому
М,„ = -78125+ —Н,.
О
Найденные по этой формуле моменты приведены в табл. 8,
в которой даны также моменты при расчете по деформированной
схеме, полученные с помощью машины.
198
Таблица 8
10»		7И* оп	EI 10’	^оп	оп
0,1	1703.9	2048,9	0.6	1257,3	3677,0
0,2	1611,1	3037,1	0,7	1173,0	3475,7
0,3	1520,1	3541,9	0,8	1090,2	3204,5
0.4	1430,8	3707.6	0,9	1009,0	2880,9
0,5	1343.3	3783,3	1.0	929,2	2517,5
Из табл. 6 видно, что величина распора при изменении жест-
кости балки изменяется незначительно — от 5 до 10%, в то время
как изгибающие моменты как в середине пролета, так и на опоре
(табл. 7 и 8) меняются очень сильно.
Так, например, момент в середине пролета при расчете по
нелинейной теории уменьшается по сравнению с моментом при
обычном расчете на 28—74%. Чем меньше жесткость балки, тем
значительнее уменьшается изгибающий момент. Физически это
положение легко объясняется. При исчезающе малых прогибах
балки оба метода расчета дадут совпадающие результаты. При
весьма гибкой балке, наоборот, перераспределения усилий в под-
весках при расчете по нелинейной теории будут весьма значи-
тельными. Кабель будет воспринимать на себя большую нагрузку
и при стремлении жесткости балки к нулю моменты в ней падают
до нуля.
Необходимо, однако, отметить, что в реальных мостах проги-
бы ограничиваются допускаемыми по техническим условиям
величинами, поэтому эффект снижения максимальных моментов
при расчете по нелинейной теории также ограничен.
Для приведенных в табл. 7 значений моментов можно выде-
лить ту область, отмеченную буквой А, для которой максималь-
ные прогибы не выходят за пределы возможных допускаемых
величин. Так, например, если допустимый прогиб ограничить ве-
личиной^/, то наибольший процент снижения максимального
момента в середине пролета ограничивается величиной 45%.
Опорный момент при расчете по нелинейной теории оказы-
вается большим, чем при обычном расчете. Но так как он по
абсолютной величине для реальных систем не является макси-
мальным, то он не является лимитирующим. Интересно отме-
тить, что он при расчетах по обоим методам оказался положи-
тельным. Объясняется это тем, что в крайних пролетах появля-
ются значительные усилия в подвесках, которые направлены
вверх.
Естественно, что приведенный анализ относится только к рас-
смотренному примеру и не является общим для висячих мостов.
199
Достаточно изменить соотношение пролетов или сделать балку
переменного сечения, как изменится и картина перераспределе-
ния моментов. Поэтому задача о рациональном назначении раз-
меров висячих мостов чрезвычайно сложна. Однако автор не
ставил перед собой эту задачу.
§ 9. ЗАМЕЧАНИЕ О РАСЧЕТЕ МНОГОПРОЛЕТНЫХ
МОСТОВ С НЕРАЗРЕЗНОЙ БАЛКОЙ ЖЕСТКОСТИ
Многопролетные висячие мосты с неразрезной балкой жестко-
сти применяются очень редко. Объясняется это тем, что они очень
чувствительны к осадке опор и могут применяться только при
наличии скальных оснований.
В настоящем параграфе мы не будем проводить детального
расчета таких систем, а ограничимся только приведением основ-
ных расчетных формул. Они принципиально ничем не отличаются
от полученных ранее для трехпролетных мостов.
Основной задачей является решение двух совместных урав-
нений:
+	(V.42)
т
+	(V.43)
1=1	/,
Последнее уравнение написано по аналогии с уравнением
(V.39) с той только разницей, что здесь суммирование выра-
жений
т
Pf S
i=i
распространяется не на три, а на все пролеты.
Значение р определяется для каждого пролета в отдельности
по формуле
о  EkF	&fjdl
т	.2
2 Mi
1 = 1
Для крайних пролетов вместо Ц необходимо брать 2 Zi или
2 1п- Величина а по-прежнему будет
a. = h.H g,
где h — постоянный множитель, выбираемый из удобства
расчета;
Hg — распор от постоянной нагрузки.
200
Система уравнений (V.42) и (V.43) по-прежпему является
нелинейной и решается по методу, описанному в § 6.
Матрица А и входящие в нее матрицы L\ и Ь2 имеют такую
(же структуру, как для трехпролетного моста, но в матрицах L] и
£2 число квазиматриц будет не три, а т (т — число пролетов).
Для многопролетного моста все матрицы будут высокого по-
рядка, поэтому расчет можно провести только с применением
электронной машины.
§ 10. РАСЧЕТ ВИСЯЧЕГО МОСТА
С УЧЕТОМ НАКЛОНА ПОДВЕСОК
В процессе деформации висячего моста точки прикрепления
подвесок к кабелю перемещаются как по вертикали, так и по го-
ризонтали. За счет горизонтальных перемещений подвески
наклоняются и поэтому на кабель, кроме вертикальных сил, пере-
даются также и горизонтальные. Эти
силы всегда направлены в сторону,
противоположную горизонтальным -пе-
ремещениям, и поэтому они играют
роль удерживающих сил, делающих
рею систему более жесткой.
Из обзора, приведенного в гл. I
,(§ 3), видно, что в абсолютном боль-
шинстве работ, посвященных расчету
висячих мостов, учет наклона подвесок
не производился. Объясняется это дву-
доя причинами: во-первых, в мостах с
пологим кабелем или в случаях, когда
цодвески имеют значительные длины,
учет наклона подвесок дает малый эффект; во-вторых, такой
учет весьма сильно усложняет расчет. Это можно видеть из
гл. III (§ 5, 6 и 8) настоящей работы, где производится расчет
(гйбкой нити при действии вертикальных и горизонтальных сил,
а также при учете наклона подвесок. Из указанных расчетов
•можно видеть, насколько эта задача сложнее, чем задача рас-
чета нити в обычной постановке.
В дальнейшем можно будет убедиться, что учет наклона под-
весок, как правило, можно производить в том случае, когда в
средней части моста подвески имеют небольшие длины (влияние
(Наклона подвесок ощутимо) .
Н'а рис. 121 показан узел к и наклонившаяся подвеска, пере-
дающая на кабель силы vK и wK.
Условимся перемещения ик, а также горизонтальные силы
считать положительными, если они направлены вправо. При
201
таком правиле знаков связь между силами vK u.wK будет опре-
деляться равенством
'WK
hK
(V.44)
Так же как и раньше, в качестве основной примем систему,
в которой все подвески разрезаны сечением I—I, как показано на
рис. 122. Ввиду малости углов наклона подвесок вертикальные
составляющие v можно считать равными самим усилиям в под-
весках.
Связь между перемещениями и усилиями, передающимися на
кабель при действии вертикальных и горизонтальных сил, была
установлена ранее в гл. III (§ 6).
Обозначим, как и раньше, усилия в подвесках от постоянной
нагрузки vg, а изменения этих усилий от действия временной на-
грузки— х. В соответствии с формулой (III.77) получим:
(у+ч).	(а)
Все входящие в это уравнение матрицы были приведены ра-
нее в гл. III (§ 6). Прогибы балки жесткости (V.3) определяются
выражением
^==£1(^—Д	(Ь)
Вектор vq определяет систему приложенных к балке сосредо-
точенных сил от временной нагрузки.
Определив из равенства (а) вектор х и подставив его в урав-
нение (Ь), после всех преобразований получим:
(£1 + //1А1Г2-иЛ1В)	у, (V.45)
где

(V.46)
202
Введем такие же обозначения, как и в § 2 настоящей главы:
л= <п + 1>ет L L.
dP
I
Кроме этого, обозначим:
L^y^Z*.
Величина X, в отличие от (V.6), теперь будет:
(л 4-1)^7
(V.47)
(V.48)
(V.49)
Подстановка в уравнение (V.45) и определение из него век-
тора дает:
;= (Е 4- С+ХА)-1 Й* - Z* - Ху*).	(V.50)
Это уравнение сходно с уравнением (V.7). Если положить
С = 0 и Z* = 0, то оно совпадает с уравнением (V.7).
Для составления второго уравнения воспользуемся результа-
тами, полученными в гл. II (§ 6) для гибкой нити. Будем исходить
из уравнения (III.85). Если дополнительно учесть деформации
оттяжек между пилонами и анкерами, то это уравнение при-
мет вид
(л+1	X
d sec3 <р 4- 2S0 sec2 т I —
/с=1	/
л+1
A//*sec3<?—(v-51)
Л'=1
где
дяк=о+да14-'^24-----(V.52)
Как и в гл. III (§ 2), примем:
i
Sd sec3 ср — ——— =
J COS3 <Р
о
203
Величина g определяется по (III.23) или по табл. 1 (прило-
жение). Далее в соответствии с обозначением (V.49) найдем:
Н1==л .(” + 9-£-/.
Д2
После подстановки в уравнение (V.51) двух приведенных ве-
личин и решения этого уравнения относительно Л. будем иметь:
п
К=1
(V.53)
где
J2
а =-------------
(и + 1) EI
п
Д-- *=-1-------------
?	{Л/ + 2S0 sec2 z
8fEKF______________
I	2S0 o \
I p. + — - sec2 т I
(V.54)
(V.55)
Сравнивая выражения аире аналогичными выражениями
(V.11) и (V.12), замечаем, что учет наклона подвесок не оказал
влияния на величину р.
Если горизонтальные силы, передающиеся на кабель за счет
наклона подвесок, не учитывать, т. е. положить ЛДК —0 (к=1,
2, ..., п), то выражения (V.54) и (V.11) совпадут.
Для определения горизонтальных перемещений и восполь-
зуемся выводами, приведенными в гл. III (§ 6). Таким образом,
и=—Аи^у.	(V.56)
Матрица Аи и вектор у определяются равенствами (III.83) и
(II 1.84), приведенными в гл. III (§ 6).
Таким образом, решение задачи сводится к совместному ре-
шению трех уравнений (V.50), (V.53) и (V.56). Для висячих
мостов с пологим кабелем можно величины 8 (III.73) принять
равными нулю. Тогда мы получим некоторые упрощения. Однако
и в этом случае все три уравнения продолжают оставаться сов-
местными. Задача должна решаться методом последовательных
приближений. В первом приближении примем горизонтальные
перемещения равными нулю. И в этом случае необходимо про-
водить решение методом последовательных приближений, как
указано в § 6 настоящей главы.
Определив вектор и первого приближения, вычисляем матри-
цы Gw и Dw. Затем весь расчет повторяем заново. Поступая
204
также и во всех последующих приближениях, продолжаем про-
цесс до тех пор, пока векторы ц и и двух последних приближений
будут одинаковые. По мере уменьшения размера ho (см. рис. 122)
влияние наклона подвесок будет увеличиваться.
Для того чтобы определить предельный случай, можно поло-
жить Ао=0. Этот случай соответствует жесткому скреплению ка-
беля с балкой в середине пролета. Однако этот предельный слу-
чай удобнее решать в предположении наличия двух кабелей
(левого и правого), поддерживающих балку. Решение этой
задачи дается в следующем параграфе.
§ 11. РАСЧЕТ МОСТА С КАБЕЛЕМ, ЖЕСТКО
ПРИКРЕПЛЕННЫМ К БАЛКЕ
В СЕРЕДИНЕ ПРОЛЕТА
В последнее время в висячих мостах стали применяться такие
системы, в которых кабель жестко соединен с балкой в середине
пролета. Основная идея, породившая эту конструкцию, состоит
в увеличении жесткости системы при несимметричном загруже-
нии временной нагрузкой. Расчет таких систем усложняется в
связи с тем, что появляется еще одно лишнее неизвестное — го-
ризонтальное усилие, передающееся с кабеля на балку жест-
кости.
В указанной конструкции по существу имеется два самостоя-
тельных кабеля, к которым подвешена балка. Основные расчет-
ные уравнения, естественно, усложняются. Однако применение
ЭЦВМ позволяет преодолеть трудности, связанные с расчетом,
и получить решение при различных загружениях моста временной
нагрузкой.
Для вывода основных уравнений в § 4 (гл. III) предваритель-
но была рассмотрена гибкая нить, у которой один конец имеет
подвижную опору в вертикальном направлении.
Рассмотрим однопролетный мост с балкой постоянного се-
чения. При решении системы с балкой переменного сечения не
возникает никаких затруднений. Различие будет состоять только
в построении матрицы упругих грузов. Методика расчета и все
основные допущения остаются прежними. Величины перемещений
и усилий, относящиеся к левой и правой частям, будем обозначать
одинаковыми буквами и снабжать их индексами «л» и «п».
Между усилиями в подвесках и ординатами оси кабеля после
Деформации существует следующая зависимость:
Для левой половины
(^+г,)=Н’«(»+Л	(V.57)
205
для правой половины
(v„+?)=т; (у+Ъ,	(v.58)
где Нл и Нл — величины распоров в левой и правой частях
кабеля;
т]л и т]п — прогибы в левой и правой частях балки от за-
гружения системы временной нагрузкой.
Введем обозначения:
нл + яп
2
=Н;

2
откуда найдем:
Ил = Н-\- д//|
нп=н-^н]'
(V.59)
Подставив значения (V.59) в уравнения (V.57) и
лучим:
для левой половины
(^4-хл)=//^(;+?)+дж (й-тп,
для правой половины
(V.58), по-
(V.60)
(V.61)
(^4-rn)=//L2n(r/+f)-й/+П
В этих уравнениях матрицы L* и Л2 имеют следующий вид:
2 -1
— 1	2 —1
-1	2—1
-1 1
1 -1
— 1	2 -1
1	-12-1
— 1	2-1
— 1	2
Объединив уравнения (V.60) и (V.61), запишем их в виде
одного уравнения. Сняв индексы, получим:
+x)=HL, (J+4- д/Ш2 Су +}).	(V.62)
206
Здесь матрицы £2 и AL2 имеют следующий вид:
Л£2
л ।
I
2 ।
(V.63)
Из выражения (V.63) видно, что матрицы £2 и I" наклады-
ваются друг на друга так, что у них суммарным является один
элемент. Легко заметить, что матрица L2 будет совпадать с обыч-
ной матрицей £2, применявшейся в предыдущих параграфах.
Матрица А£2 является новой матрицей. Она, как нетрудно заме-
тить, будет обладать косой симметрией. Средний ее элемент будет
равняться нулю.
Решая уравнение (V.62) относительно х, получим:
—х = — Я£2 (^ + ^1) — Д д£2 (г/ 4- т]).	(V .64)
Прогибы балки жесткости, как и ранее, определяются урав-
нением
71 = Л(^ — Д	(V.65)
Подставляя уравнение (V.64) в уравнение (V.65), получим:
Ч = Л [('Vg+v^ — HL^ (t/4-Ti)—д//д£2(*/-Н)]-
После некоторых преобразований уравнение примет вид
Ц = L!(vg-f-vq) —HL(уЦ-tj) —	(y4-tj). (V.66)
Как видно из дальнейших выводов, удобно ввести следующие
обозначения:
л— hn —h----
2
2
a^—l^
h 1
 .
Д A = — д£2
(V.67)
(V.68)
207
^*=^1(^4^)
=	— Tjn-l
Ду*г = лНу*
(V.69)
Подставляя в выражения (V.66) обозначения (V.67), (V.68),
(V.69) и решая полученное равенство относительно т), получим:
^(^Ч-лДН-ЗДД)-’	(V.70)
Одного уравнения (V.70) для решения задачи недостаточно,
так как в него, кроме искомого вектора прогибов rj, входят еще
неизвестные параметры X и 6. Поэтому необходимо составить два
дополнительных уравнения деформаций кабеля. Для этого, как
и ранее, воспользуемся принципом Лагранжа. Теперь придется
этот принцип использовать для каждой половины кабеля в от-
дельности. Приравнивая работу внешних и внутренних сил кабеля
от постоянной нагрузки на перемещениях от временной нагрузки
нулю, получим:
для левой половины
ip
1 С
COS
cos ю
dx
(V.71)
для правой половины
COS <Р
ЕКР J
о
(V.72)



Но так как
Нлч=Ня-Нё
и
11п 1-1' U
Иq — tl II
TO
’	V (V
s I	2 I EKF j cos3 ю
4=1	/	о
208
и
_Hg(Hn-Hg) / dx
EKF	cos3 <p
Z/2
На основании § 2 (гл. Ill) получаем:
i
C dx
Ц2
C	dx	C	dx	I
\ --------= \ -----------= p. —
J	cos3	J	cos3 <p	2
0	Z/2
где p,—-имеет прежнее значение (III.23).
Учтя, что
получим два уравнения:
НЛ = Н^2
8fdEKF
ls[j.
п
(V.73)
//п=
8fdEKF
(V-74).
Складывая эти уравнения, а затем вычитая уравнение (V.74)
из уравнения (V.73), получим два уравнения:
п
H"4-Hn=2kfg4-2 8/(/ЕкР^-
1 = 1
п
(V.75)
8fdEKF
/3[Л
Учитывая обозначения (V.67), получим:
а-- v
Z = l
(V.76)
(V.77)
/=1
йгде
а = hH g,
\8hfdEKF
/зр.
209
Совместное решение уравнений (V.70), (V.76) и (V.77), кото-
рые будем называть основными, дает возможность определить ц,
л, 6, после чего по уравнению (V.62) найти усилия в подвесках
и все остальные величины, необходимые для расчета висячего
моста. Из уравнений (V.70), (V.76) и (V.77) видно, что задача
является, как и в случаях рассмотренных ранее, весьма трудо-
емкой. Решение ее «вручную» не представляется возможным. Она
решалась на электронной машине «Урал 2».
Программа была составлена так, что можно было с пульта
менять характер загружения, интенсивность нагрузки и другие
данные по размерам и жесткости системы. Каждый раз на печать
выдавались четыре столбца данных: первый столбец содержал —
X, б, е, Н, /\Н, //л, Нп. Здесь величина е характеризует точность
решения уравнений.
Остальные три столбца содержали векторы прогибов, момен-
тов и суммарной нагрузки на балку.
В качестве примера ниже приводится результат расчета на
машине «Урал 2» (перепечатан с ленты) при загружении поло-
вины пролета ^ременной нагрузкой 7 = 0,5 g.
Предположим: / = 200 м, [=20 м, £7 = 44* 106 Т/м2, EKF =
।	200
= 1,83333- 106 Т, d=— м.
6
тэ	- 1	.	,	6Д2
В дальнейшем выбрано h = —	.
Для сравнения справа помещены аналогичные результаты для
той же системы, но при отсутствии жесткого закрепления сред-
него узла.
Х= 4-54336 8794-00;
8=4-21 791 232 - 01;
в =—72 250259-08;
Н= 4- 35 862 3414-04;
дН= 4-143822144-03;
Нл = 4-37 300 5624-04;
Нп = 4- 34 424 119 + 04;
л= +54340886 + 00;
8=+00 000 000 + 00;
е= —24490873 —07;
/7—+35864985 + 04;
дН = 4-00000000 + 00;
Нл= 4-35864985 4-04;
Я" =+35 864985-|-04;
+ 16 833091 + 00
+ 25 1 31 969 + 00
+ 22 861 709 + 00
+ 14 613 301+00
+ 63136 137-01
+ 18 104 073 + 00
4-26 403464+00
+ 22 866 614 + 00
+ 13358 807 + 00
+ 50594175-01
210
+ 38968 217 + 04
+ 46900018+04
+ 24554 444+04J
-30769 954+ 03,
-11028 059 + 04
+ 93109 246 + 02
+ 90832127+02
+ 15857 594+02
— 59041 216 + 02
— 56937 189+02
+ 45007148 + 04
+ 52 930576 + 04
+ 24 499201+04
-90575266+03
-16 981054 + 04
+ 11 125 086 + 03
+ 10 906 501 + 03
+ 15 375 757 + 02
— 76 899 600+ 02
— 74713 745 + 02
Q
Из приведенных данных видно, что система с жестко закреп-
ленным кабелем в середине пролета обладает большей жестко-
стью по сравнению с обычной системой. Правда, уменьшение про-
гибов оказалось не столь зна-
чительным, но зато изгиба- а) ____________
югцие моменты уменьшились
СИЛЬНО.	1-----1---1----
Рассмотренный случай яв-
ляется как бы предельной	___
оценкой влияния наклона под-	------
весок при расчете висячих мос-
тов. Жесткое закрепление ка- f ,	।	,	,
беля в середине пролета рав-
несильно случаю, при котором
высота средней подвески стре-	Рис. 123.
мится к нулю.
На рис. 123 показаны эпюры прогибов и моментов в двух рас-
смотренных системах. Сплошной линией показаны значения для
моста с закрепленным кабелем, а пунктирной линией — для обыч-
ного моста.
Анализ данных показывает, что система с закрепленным ка-
белем является более совершенной и ее можно рекомендовать для
широкого применения.
§ 12. УЧЕТ ВЛИЯНИЯ ПЕРЕМЕННОГО
СЕЧЕНИЯ БАЛКИ ЖЕСТКОСТИ
Выше неоднократно упоминалось о том, что переменность
сечения балки жесткости не вносит существенных изменений в
технику расчета висячего моста по предлагаемой методике. Если
применять метод непосредственного интегрирования дифферен-
 Циальных уравнений, то трудности в интегрировании будут зави-
211
сеть от закона изменения Момента инерции. Во многих случаях
они будут непреодолимо велики. Применение численного метода,
как будет видно из дальнейшего изложения, позволяет без ка-
ких-либо ограничений практически решить любую задачу не
только на прочность, но и на колебание моста.
Для случая когда балка имеет переменное сечение, весь алго-
ритм и основные уравнения остаются неизменными. Изменяется
только одна матрица Д, в которую входит матрица упругих гру-
зов Bw.
L\ = LmB wLm.	(а}
Наиболее просто задача решается для случая, когда, момент
инерции балки изменяется скачкообразно. При большом числе
панелей любой закон изменения жесткости может быть апрокси-
мирован кусочно-непрерывной функцией, которую мы и рассмот-
рим в первую очередь.
Применяя известную формулу для упругого груза
W.=~ (24+4-1)+(24+4+1).	(Ь>
6£ZK	6£/к+1
легко построить матрицу упругих грузов. В общем виде она мо-
жет быть записана так:
а11а12
а21а22а23
а32а33а34	. .
а43а44а45
» _ d
w 6EI0
ал(л—1) ап
Элементы этой матрицы определяются равенствами
®л(к-1) ~Рк»
аЛК=2(рк+р,<+1);
Хк(к+1) ~Рк+1’
где
Подставляя эту матрицу в формулу (а), находим матрицу L<
и затем проводим весь расчет по стандартной методике.
212
.Для иллюстрации приведенных рассуждений рассмотрим чис-
ленный пример. На рис. 124 показана расчетная схема, из кото-
рой видно, что в четвертях пролета жесткость балки увеличена.
Пусть /=200 м, f=2Q м, EI=44- 106 Тм2, EKF= 1,8333- 106 Т,
£=12 Т/м, q = 6 Т/м.
Разобьем балку на шесть частей: d= —, So = 35,3 м, т=45°,
6
А = 0,75.
/
Рис. 124.
Точно такой же пример рассмотрен в § 4, но балка жесткости
там была постоянного сечения. Поэтому интересно сравнить ре-
зультаты решения.
По (с) находим матрицу упругих грузов:
3,50 0,75
0,75 3,50 1,00
1,00 4,00 1,00
1,00 3,50 0,75
0,75 3,50
Коэффициенты аир будут такие же,
примере, приведенном в § 4,
как и в упомянутом
а = 1,262663;
0 = 0,28772.
Матрицы влияния моментов будут:
L —С— —
L'm—— g
5
4
3
2
1
4 3 2 1
8 6 4 2
6 9 6 3
4 6 8 4
2 3 4 5
D ___
W~ 6f/0
213
Находим матрицу Li = L7nBwLm*.
L^-f-
б3ЕГ0
266,0	409,0	427,5	338,0	184,0
409,0	698,0	765,0	616,0	338,0
427,5	765,0	909,0	765,0	427,5
338,0	616,0	765,0	698,0	409,0
184,0	338,0	427,5	409,0	266,0
Векторы т]* и у* остаются прежними.
Полученные данные были введены в машину и получено пол-
ное решение задачи. Ниже приводятся результаты решения и па-
раллельно (справа) — аналогичные результаты из § 4.
Параметры:
7=0,017447, Х =0,0175213,
//=4145 Т,	// = 4158 Т.
Прогибы:	Моменты:
—»	0,225 0,390	—►	0,233 0,400	—>.	3013 4695	—>	2830 4416	
	0,454		0,460	, Л4 =	5219	, м=	4926	-
	0,390		0,400		4695		4416	
	0,225		0,233		3013		2830	
Как и следовало ожидать, для системы с усиленной жесткостью
прогибы слегка уменьшились, а изгибающие моменты возросли.
Ввиду того что изменения в жесткости балки были небольшие,
то и конечные результаты изменились мало.
При более значительных перераспределениях жесткостей бал-
ки по длине пролета изменения в результатах расчета будут
весьма ощутимы. Таким образом, при расчете реальных мостов
переменность момента инерции балки должна учитываться обя-
зательно.
Если момент инерции балки изменяется плавно по какому-
либо закону, то необходимо соответствующим образом построить
матрицу упругих грузов. В настоящее время этот вопрос хорошо
разработан. Можно рекомендовать в этом случае книгу [38].
§ 13. УЧЕТ РАСТЯЖЕНИЯ ПОДВЕСОК
ПРИ РАСЧЕТЕ ВИСЯЧЕГО МОСТА
В § 2, где выводились основные уравнения для расчета вися-
чих мостов по нелинейной теории
214
»1=(Е'+хд)-,й«->5-),
п
х =	7j,.,	(а)
1=1
| было сделано допущение о нерастяжимости подвесок. Это допу-
I' щение позволило приравнять прогибы балки вертикальным пере-
- мещениям кабеля. Если учесть растяжение подвесок, то прогибы
балки будут больше перемещений кабеля на величины удлине-
% ния подвесок. Возникает вопрос, как изменятся уравнения (а)
% при учете этих удлинений? Для того чтобы ответить на этот во-
Д' прос, необходимо вновь проследить выводы основных уравнений.
Ц. Обозначим длины подвесок Si, S2, .... Sn- Площадь сечения
Ж подвесок будем считать одинаковой и равной Fn.
Ь, Усилия в подвесках от временной нагрузки Xi, х2, хп вызовут
Ж удлинения подвесок
f	Д5, = -^-(<=1, 2,..., я).
Ж	п
ж В векторной форме получим:
В	&S=Gsx,	(b)
У где G3—диагональная матрица.
€	I si
Если перемещения точек кабеля по вертикали обозначим т],
то прогибы балки будут q +As. Вместо равенства (V.3) получим:
|	TJ-hZj=Ll(^—х).
Учитывая равенство (Ь), получим:
I	—Zjx,	(с)
&где
fc.	Li=Li~{-Gs.	(d)
£  Равенство (V.4) остается без изменения. Из него находим
Г	x=—vg-]~FfMg^0^-HL^y.
215
Подставляя это выражение в формулу (с), после несложных пре-
образований получим:
(е)
где
- 1 * 1 -> • <f>
/=4-£1tgTo=4-A1r/
h	h
Таким образом, уравнение (е) полностью совпало с уравне-
нием (а). Второе основное уравнение из (а) остаётся также не-
изменным. Разница состоит только в определении величин ц и у*,
для которых при учете удлинения подвесок надо пользоваться
формулами (f) настоящего параграфа.
Отметим, что в реальных мостах удлинение подвесок настоль-
ко невелико по сравнению с прогибами балок, что им можно пре-
небречь.
ГЛАВА VI
РАСЧЕТ ВИСЯЧЕГО МОСТА
ПРИ НАЛИЧИИ ШАРНИРОВ
В БАЛКЕ ЖЕСТКОСТИ
§ 1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
; В настоящей главе рассматриваются висячие системы, состо-
I ящие из отдельных балок или жестких дисков, соединенных
Р между собой шарнирами и подвешенных к кабелю. Одна из таких
| систем показана на рис. 125. Подобного рода системы могут быть
| статически определимыми _
(система с балкой, содер-
| • жащей один шарнир) и из-
Ц меняемыми (система, пока-
к . занная на рис. 125).
№ Изменяемые системы при
к. большом весе проезжей ча-
к ,сти и сравнительно неболь-
£ шой временной нагрузке
К; могут довольно хорошо ра-
№ -ботать даже при наличии
№ подвижной нагрузки.
К Расчет подобного типа
Евисячих систем должен про-
К изводиться только по деформированной схеме, т. е. с учетом из-
•вменения очертания оси кабеля, а также его удлинений в процес-
загружения системы временной нагрузкой.
Вй Следует различать два случая расчета таких систем: в первом
МЕслучае учитываются деформации изгиба звеньев шарнирной цепи,
Кг во втором эти звенья считаются абсолютно жесткими. Первый
И.тип может быть рассмотрен как частный случай систем, подроб-
Куо изученных в предыдущих параграфах, поэтому мы их не будем
^рассматривать. Второй случай определяет особый тип систем, ме-
^Ьодика расчета которых содержит специфические особенности,
расчетам этих систем и посвящена настоящая глава.
|К,' Основная задача состоит в определении перемещений отдель-
217
ных точек системы и выяснении сил, действующих на диски про-
езжей части. Перемещения являются как бы критерием надежно-
сти таких систем. При больших перемещениях эксплуатация
таких систем становится затруднительной или даже невозможной.
Материалы этой главы могут послужить основой для расчета
висячего моста по предельному равновесию, когда в балке обра-
зуются пластические шарниры. При определении перемещений
деформациями изгиба звеньев между шарнирами можно пренеб-
речь, считая их абсолютно жесткими.
§ 2. ОСНОВНЫЕ УРАВНЕНИЯ
Рассмотрим систему с п подвесками, поддерживающими же-
сткие звенья, соединенные между собой шарнирами, лежащими
на линии АВ. Шарниры находятся в местах прикрепления неко-
торых подвесок а, Ь, с, ..., к (рис. 126).
Рис. 126.
218
Обозначим vg и vq векторы сосредоточенных сил в точках 1,
2, п от постоянной и временной нагрузок. Будем считать, что
постоянная нагрузка равномерно распределена по длине пролета
с интенсивностью g Т/м. Вектор сил от собственного веса в этом
случае будет определяться равенством
vg = gda.
(VI.1)
От постоянной нагрузки ось кабеля провисает по квадратной
параболе с уравнением (III.16). При этих условиях в подвесках
от постоянной нагрузки усилия равны сосредоточенным силам vg.
Обозначим усилия в подвесках от временной нагрузки через
Xi (i = 1, 2, ..., п). Усилия в подвесках после загружения системы
временной нагрузкой будут определяться равенством
J-vJ,	(VI.2)
где т] —вектор прогибов кабеля от временной нагрузки;
Н — полный распор в кабеле от постоянной и временной на-
грузок;
L2—трехдиагональная матрица, приведенная в гл. V (V.5).
Второе уравнение, как и в предыдущих задачах, составим на
основании принципа Лагранжа. Воспользуемся выведенным ра-
нее уравнением (V.10)
п
>.=«+₽ s	(VI.3)
Величины X, а и 0 определяются выражениями (V.6), (V.11) и
(V.12). Если все члены равенства (VI.3) умножить на	,
то получим
+ Ль	(VI.4)
/=1
где 0о — коэффициент, определяемый равенством
о %fdEKF
Ро =—,	(VI.5)
[Л/3
здесь EKF — жесткость кабеля на растяжение.
Обозначим перемещения шарниров а, Ь, к по вертикали
Ла, т]ь, •••, т)«- Вектор прогибов всех и точек, представляющий собой
совокупность ординат ломаной эпюры, показанной на рис. 126,6,
Может быть представлен суммой векторов
Л = ЛЛа+ЛйЪ +  • • 4-ЛЛ-	(VI.6)
219
Векторы уа, уь, ук составляются из ординат, взятых из
треугольных эпюр, изображенных на рис. 126, в, г и т. д. при
Па= 1, Т]6= 1, Лк = 1.
Подставляя выражение (VI.6) в уравнение (VI.2) и (VI.4),
получим:
®г+-'=//£2(!/ + п,Т<,+'»|Л+ •  • +ЧЛ’«).	(VI.7)
И=Н„+₽„ (8Л+8Л + ... + 8Л),	(VI.8)
где 6а, бь, ..., б,.— суммы ординат векторов	(* = 1, 2, ..., п).
Нетрудно заметить, что двух уравнений (VI.7) и (VI.8) недо-
статочно для решения задачи, так как число неизвестных х, Н,
i]a, ць, •> Лл' превышает число уравнений. Для составления допол-
нительных уравнений используем условие равенства нулю момен-
тов в шарнирах, соединяющих диски проезжей части.
Суммарные силы, действующие на цепь АВ, определяются век-
тором vq — х, поэтому вектор моментов в простой балке опреде-
ляется преобразованием
Л1=£т(^-Д	(VI.9)
где Lm — матрица влияния моментов для двухопорной балки.
Для того чтобы из вектора М выделить какой-либо один мо-
мент, достаточно помножить этот вектор на матрицу строку:
<», = ||0 0...1 ... О ... 0||.
В этой строке единица расположена в том месте, которому
соответствует номер точки I. Для точек а, Ь, ..., к соответственно
будем иметь матрицы ыа, &ь, ык.
Помножая выражение (VI.9) на указанные матрицы и при-
равнивая их нулю, получим систему дополнительных уравнений
®Лп(^-*)=о
(VI.10)
Подставим в этих уравнениях вместо х его значение, которое
найдем из уравнения (VI.7). Вначале проведем преобразование
220
только для первого уравнения системы (VI. 10). После подста-
новки:
MaLm {^g + ®?) - НwaLmL± (У +	+ ЧьУь Н----+ ЧЛК) = О-
Матрицы Lm и L2 являются обратными друг к другу, поэтому
их произведение дает единичную матрицу:
LmL^E.
Далее заметим, что
но
и}а^(К+Ч>~ -Мя(я+<7),
где Mafg+q) — момент в точке а, подсчитанный как в простой бал-
ке от постоянной и временной нагрузок.
Таким образом:
+ =	(VI-П)
Кроме того,
(оаТ« = 1,	=0, шаус = 0.
Учитывая сказанное, вместо первого уравнения получим сле-
дующее равенство (момент в шарнире равен нулю):
н («/а + 71й)-у'и°(я+9) = 0-
Такие же равенства получим и для других точек. Таким обра-
зом, для комбинированной системы, имеющей к шарниров будем
иметь к уравнений. Они вместе с уравнениями (VI.8) дадут раз-
решающую систему уравнений для комбинированной системы:
н	M^(k+q)
Н (УьЛ-'Чь)—Mb(g-\q)	(VI 12)
Н =	+ Ро (8Й^О + ъьЧь Н---h SA)-
Нетрудно увидеть (подставив выражение VI.8 в уравнения
VI.12), что полученная система уравнений относительно искомых
перемещений -qfl, т]Ь, т]л. является нелинейной. Решение ее в общем
виде весьма затруднительно, поэтому удобнее рассматривать
отдельные конкретные виды комбинированных систем.
221
§ 3. СИСТЕМА С ДВУМЯ ЖЕСТКИМИ ДИСКАМИ,
ПОДВЕШЕННЫМИ К КАБЕЛЮ
Рассмотрим систему, состоящую из двух жестких дисков АС и
СВ, соединенных шарниром в точке С и подвешенных к кабелю
(рис. 127). Деформацией
подвесок можно пренебречь.
При загружении системы
временной нагрузкой точка
С переместится вниз на ве-
личину т]с, а диски повернут-
ся и займут положение, по-
казанное на рис. 128, а. Эпю-
ра перемещений дисков, а
следовательно, и кабеля по-
казана на рис. 128, б.
Основные уравнения для
этого случая запишутся в
виде
+	—^c{g+q),	(а)
(Ь^
Подставляя (6) в (а) и учтя при этом, что М°с(й+(2)=7И%+
4-Л1°Сд, получим:
Hgf 4" (₽08с/ + Hg) Г1с + ₽O8cTk ~ ^cg 4- 7И GCq,
Рис. 128.
222
но
<-///=О,
|£; поэтому получим квадратное уравнение для определения вели-
чины перемещения точки С:
К	7^+2mfQc4-m2=0,
к откуда 
Ж;	ric~ —	ml-}-т2,	(VI.13)
где
В	f , Hs
К	1	2 1 2МС
&	М°
Г	<VL14)
& Вычислив по уравнению (VI.13) величину т] и подставив ее
Е в выражение (6), найдем распор. Для определения усилий в под-
К весках от временной нагрузки используем выражение (VI.7), из
К; которого для нашего случая получим:
К	^=^2(^4-^сТс)-^-	(VI.15)
F; Пример. Рассмотрим численный пример, положив /=200 м,
 f=2Q м, Ек F=l,8- 106 Т, g=l2 Т/м. Временную нагрузку будем
IP: считать распределенной по всей длине пролета и равной 7=6 Т/м.
Е ’ Разобьем пролет на 6 равных частей. Точка С будет совпадать с
К’ точкой 3 (см. рис. 127). Данные для наших размеров следующие:
Е f/g=3000 Т, р= 1,08189, og = ?d=200 Т, ро = 11О9,21, vg=gd=
Е =400 Т, vg+vq=GW Т.
К. Вектор уе следующий:
Il
2
3.
21
1
Сумма элементов вектора ус определяет величину бс:
sc-2yc=3-
Момент в середине пролета от временной нагрузки Л4з9 =
=30 000 Тм. По формуле (VI.14) находим:
mi = 10,45077, m2 = 9,01543.
223
По равенству (VI. 13) определяем прогиб в точке С:
т|с—0,42278 м.
По формуле (&) находим распор:
// = 4406,855 Т.
По формуле (VI.15)
временной нагрузки:
находим вектор усилий в подвесках от
4406,855 с
---------6
200
2 -1
-1	2-1
— 1	2
-1
-1
2
-1
	0,(3) 0,(6)			400 400		187,58 187,58	
4- 0,42278	1,о		—	400	—	224,84	
	0,(6)			400		187,58	
	0,(3)			400		187,58	
Найдем теперь суммарную нагрузку, действующую на балку:
	200 200		187,58 187,58		12,42 12,42
—> —►	200	—	224,84	=	- 24,84
	200 200		187,58 187,58		12,42 12,42
Найдем изгибающие моменты в балках АС и СВ. Для этой
цели рассмотрим систему двух балок, как одну двухопорную бал-
ку. Такой прием одновременно позволит проверить точность
вычислений, так как в результате всех расчетов изгибающий мо-
мент в точке 3 должен равняться нулю:
	5 4 3 2 1		12,42		414
	4 8 6 4 2		12,42		414
ли®	3 6 9 6 3		- 24,84	-	0
36	2 4 6 8 4		12,42		414
	1 2 3 4 5		12,42		414
Из полученного вектора видно, что Л43 = 0.
Необходимо иметь в виду, что в процессе расчета приходится
встречаться с вычислением близких чисел, поэтому при опреде-
224
лении коэффициентов и решении квадратного уравнения вычисле-
ния необходимо производить с высокой точностью.
Рассмотрим теперь ту же задачу, но при другом загружении.
Пусть загружена правая половина пролета нагрузкой той же
интенсивности. Момёнт в середине пролета будет в два раза
меньше:	'*•
М°£ = 15000 Тм. По формуле (VI.14) получим:
mi= 10,45077, «2=4,50772.
По уравнению (VI. 13) находим прогиб:
т]с=0,21348.
Распор Н равен:
Н =3710,382 Т.
Вектор усилий от временной ’йагруз'Ки (VI.15):
3710,382 „
----------о
200
2
-1
Суммарная нагрузка, действующая на балку:
	0		94,72		— 94,72’
	0		94,72		— 94,72
	юо	—	110,56	%		-10,56
	200		94,72		105,28
	200		94,72-		105,28
Изгибающие моменты в балках АС и СВ					
	5^ 4 3 2 1		-94,72		-3157
Й 200	4 8 6 4 2		— 94,72		-3157
36	3 6 9 6 3	•	—10,56	=	0
	2 4 6 8 4		105,28		3515
f	1 2 3 4 5		105,28		3515
так как и следовало ожидать, М3			<о.		
8—3802
225
§ 4. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
На рис. 129 показана система, состоящая из трех жестких
дисков, соединенных шарнирно в точках С и D и подвешенных
к кабелю. Данная система является изменяемой системой с одной
степенью свободы. Такая система может воспринимать нагрузку
I)
г)
Рис. 129.
только в том случае, когда все элементы кабеля и подвесок испы-
тывают растяжение. Вопрос о том, можно ли применять подоб-
ного рода системы в качестве висячих мостов, решается на осно-
вании изучения деформативности системы.
Рассмотрим общий случай действия сил на диски AC, CD и
DB. Собственный вес системы принимается равномерно распре-
деленным. Эпюра перемещений т] показана на рис. 129, б, на
рис. 129, в, г —эпюры, определяемые векторами ус и уь- Основные
уравнения (VI. 12) и (VL8) можно записать в следующем виде:
Н (Ус т1с) —	(а)
Н (^£>_ЬТ1£>)=='^о<5г+9)’	О3)
(с)
226
и
Разделив левые
друга, получим:
правые части уравнений (а) и
(Ь) друг на
У С	__ ^C(g+q)
«о + ^D Л’°О(УМ)
откуда находим:
(VL16)
где

а0 — ктУс — Уй' а1 — Кт
Л4°	 •
__MD(g+q)
Кт	0
Л!С(£+<7)
Подставив в (с) вместо т]л (VI. 16), получим:
=
(VI. 17)
(VI.18)
где

^1— ?о(^С 4~ ^£>al) I
Подставив теперь в уравнение (а) вместо Н его
формулы (VI. 18), получим:
(^0 — ^1^с) {УС "Ь ^с) ~ C(g+q),
отсюда находим:
(VI.19)
значение из
7)2,=2m ^ — /«2= О,
(Ф
где
mi 2
М?
плане, как
А
2^ ’
Ж	т = C(g+q) Ьр&с
Е	2 Ьх
Дальнейшее решение проводится в таком же
и для предыдущей задачи.
Ж Пример. Рассмотрим систему, изображенную на рис. 129.
Ж. Размеры I, f, d и жесткость кабеля, величины постоянной и вре-
д|; Ценной нагрузок возьмем те же, что и в предыдущем параграфе.
Ж  По рис. 129, в, г находим:
(VL20)
- 1
Yc==T
1
2
1
О
О
О
о
1
2
1
1
227
По этим векторам получим:
8С = 2, Zd = 2.
Координаты оси кабеля над шарнирами С и D:
Ус~Уо~^7^77778
Рассмотрим разные случаи загружения:
1.	Загружен весь пролет временной нагрузкой q=6 Т/м,
vg = 400а, т>9=200а, ^4-47 = 600<з.
Моменты в точках С и D, как и в простой балке, от постоян-
ной и временной нагрузок:
^^+^ = 7^^ = 80000 Тм, Н=Ш Т.
По уравнению (VI.17) находим: Km=l, Яо=О, tzi = l.
Следовательно, tjc=iid-
По уравнению (VI. 19) находим:
60=ЗООО, Ьг =4436,84.
Находим коэффициенты квадратного уравнения:
mi =9,22697, Ш2 = 6,01028.
Решение квадратного уравнения дает:	•' 
Лс = т]т>=0,32014 м.
По формуле (с) находим:
/7 = 4420,410 Т.
а
Найдем вначале следующие величины:
	11,11111		1		0		11,27118
	17,77778	, 0,32014	2	. 0,32014	0		18,09792
у + Ч =	20,00000	"1 2	1	_|	!	 ‘	2	1	=	20,32014
	17,77778		0		2		18,09792
	11,11111		0		1		11,27118
Далее получаем:
4420,410 _
---------6
200
2 - 1
— 1	2-1
-1	2 —1
-1	2 -1
-1	2
228
11,27118		400		189,39
18,09792		400		210,61
20,32014	—	400	—	189,39
18,09792		400		210,61
11,27118		400		189,39
Суммарная нагрузка, действующая на балку:
10,61
— 10,61
10,61
-10,61
10,61
Изгибающие моменты в балках AC, CD и DB
	5 4 3 2 1		10,61		177
XI 200	4 8 6 4 2		— 10,61		0
Л1 =— 36	3 6 9 6 3	•	10,61	=	177
	2 4 6 8 4		-10,61		0
	1 2 3 4 5		10,61		177
2.	Загружен участок DB равномерной нагрузкой q= 6 Т/м.
Вектор сил от временной нагрузки и суммарные узловые силы:
О
О
О
100
200
400
400
400
500
600

Изгибающие моменты в точках С и D от суммарных сил, как
в простой балке.
Mc(q+g}=57777,78 Тм, M°D{g+Q) = 62222,22 Тм.
По формулам (VI. 17), (VI. 19) и (VI.20) находим коэффи-
циенты:
Кт =1,07692; а0= 1,36747; ах = 1,07692; Ьо= 6033,623;
&1 = 4607,481; тх =9,54365; т2= -10,74050.
После решения квадратного уравнения получаем:
т)с=-0,58035 м.
229
По формуле (VI. 16,) определяем:
1)0= 0,74248 м.
По формуле (VI. 18) находим распор:
/7=3359,676 Т.
Далее находим:

11,11111
17,77778
20,00000
17,77778
11,11111
0,58035
2
3359,676
•6
200
1
2
1
О
О
0,74248
2
-1
2
— 1
-1
2
-1
о
о
1
2
1
-1
2
10,82093
17,19743
20,08106
18,52026
11,48235
2
- 1
2
— 1
10,82098		400		47,96
17,19743		400		-47,96
20,08106	—	400	=	47,96
18,52026		400		152,04
11,48235		400		47,96
Суммарная нагрузка на балку
	0		47,96		— 47,96
	0		— 47,96		47,96
Ч,— х =	0	—	47,96		— 47,96
	100		152,04		-52,04
	200		47,96		152,04
Изгибающие моменты:
	5 4 3 2 1		-47,96		-799
->	9Л0	4 8 6 4 2		47,96		0
м=~	3 6 9 6 3	•	-47,96	=	-799
ои	2 4 6 8 4		— 52,04		0
	1 2 3 4 5		152,04		2534
230
3.	Загружен участок СВ равномерной нагрузкой 7=6 Т]м.
Вектор сил от временной нагрузки и суммарные силы:
	0 100		400  500
V = Q	200		600
	200		600
	200		600
Изгибающие моменты такие же, как в простой балке:
Л4^ =71И 1,11 Тм, M°D = 75555,56 Тм.
По уравнениям (VI. 17), (VI. 19) и (VI.20) находим коэффи-
циенты:
кт= 1,06250; л0= 1,Ш1; «1= 1,06250; Ьо = 5464,909;	4575,491;
=9,48608; m2 = — 5,69181.
Решение квадратного уравнения дает:
Пс=—0,30491 м.
По уравнению (VI.16) находим:
т)о=0,78714 м.
По уравнению (VI. 18) находим распор:
/7=4069,796 Т.
Далее находим:
	11,11111 17,77778	0,30491	1 2	. 0,78714	0 0		10,95865 17,47287	
	20,00000 17,77778 11,11111	2	1 0 0	1	2	1 2 1	—	20,24112 18,56492 11,50468	э
4069,796
200
2 -1
-1	2 -1
— 1	2
-1
10,95865		400		142,64
17,47287		400		57,36
20,24112	—	400		142,64
18,56492		400		257,36
11,50468		400		142,64
231
Суммарная нагрузка на балку:
	0		142,64		-142,64	«»
	100		57,36		42,64	
^<7 — ^ =	200	—	142,64	=	57,36	
*1	200		257,36		- 57,36	
	200		142,64		57,36	
Изгибающие моменты:
	5	4 3	2
Г* 200	4	8 6	4
Л/ =— 36	3	6 9	6
	2	4 6	8
	1	2 3	4
1
2
3
4
5
—142,64		— 2377
42,64		0
57,36	=	,956
— 57,36		0
57,36		95б[
Интересно отметить, что когда загружен весь пролет, при рас-
чете по недеформированной схеме моменты во всех сечениях ба-
лок равны нулю. Таким образом, мосты с балкой, имеющей шар-
ниры, необходимо рассчитывать ^только по деформированной
схеме.
ГЛАВА VII
*рас4ет
БАЛОЧНО-ВАНТОВЫХ
МОСТОВ
X
1 д,
§ 1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ - Z
В обзорной главе мы встречались ,с понятием «балочно-ван-
товые» мосты. В отличие от висячих кабельных мостов в них бал-
ка жесткости поддерживается в ряде точек с помощью прямоли-
нейных вант. На рис. 24, 28 и 30 показано несколько таких мостов.
Ванты.-поддсрживающие балку жесткости, прикрепляются к пи-
лону в всрхнсйего.точке (рис. 27), или в различных точках~по
высоте пилона (рис. 30).
Расчет таких мостов существенно отличается от расчета
кабельныхумостов^ рассмотренных в предыдущих главах. Основ-
ная особенность учета геометрической нелинейности в кабельных
мостах, которая возникла вследствие постоянного формоиз-
менения кабеля, В вантовых мостах с балкой жесткости от-
сутствует.
Прямолинейные ванты в мостах, рассматриваемых в настоя-
щей главе, хотя и изменяют свой наклон в процессе деформации
системы, одиако это изменение не настолько значительно, чтобы
оно привело к необходимости проводить расчетов нелинейной по-
становке.
Вместе с тем в расчетах балочно-вантовых мостов имеется
другая особенность/Дело в том, что ванты представляют собой
по существу односторонние связи, которые способны работать
^только на растяжение и не могут воспринимать сжимающих" сил.
Тем не менее при расчете системьтомы смотрим наванТыкакна
обычные стержни.j Такая постановка вопроса возможна потому,
чтопод действием собственного веса ванта работает на растяже-
ние так, что суммарное усилие от постоянной и временной нагру-
зок будет положительным.
Если при какой-либо нагрузке в одной из вант суммарное уси-
лие окажется сжимающим (хотя этот случай мало вероятен), то
проведенный расчет теряет силу и его необходимо повторить,
мысленно исключив данную ванту из системы.
233
Естественно, что при таких условиях расчет должен быть мак-
симально «механизирован» с тем, чтобы оказалось возможным
без особого труда проводить повторные расчеты. Метод в обыч-
ной постановке для решения поставленной задачи оказывается
недостаточно удобным.
Целью настоящей главы является изложение численного ме-
тода, позволяющего применять вычислительные машины и в рав-_
ной степени пользоваться средствами малой механизации вычис- -
лений. С этой целью весь расчет проводится в матричной форме.
Применение теории матриц позволяет стандартизировать ив
значительной степени упростить расчет.
§ 2. КРАТКИЕ СВЕДЕНИЯ О МАТРИЦАХ ВЛИЯНИЯ
Предположим, что на заданную систему, например балку,
ферму, арку и т. д., действует группа сил, определяемых вектором
Эти силы приложены в фиксированных точках 1, 2, ..., п, на-
пример в узлах фермы, или в точках соединения продольных и
поперечных балок и направлены вниз. Поставим задачу: опреде-
лить величины какого-либо интересующего нас фактора в ука-
занных точках, например прогиба угла поворота, изгибающего
момента и т. д. от заданной группы сил. '
Эту задачу легко решить с помощью так называемых матриц
влияния, которые осуществляют линейные преобразования:
r^LTlP
M^=LMP
(а)
Рассмотрим более подробно последнее равенство, записав
его в развернутом виде:
234
Предположим, что первый груз равен единице (Р=1), а все
остальные равны нулю, тогда равенство
(а) примет вид
откуда получаем:
Таким образом, при действии груза Р=1, приложенного в точ-
ке 1, изгибающие моменты в точках 1, 2, ..., п равны элементном
первого' столбца матрицы LM. Следовательно, первый столбец
матрицы влияния моментов состоит из ординат эпюры моментов
jxt-хиды, равной единице, приложенной в первой точке. Если
теперь мы будемграссматривать движущийся груз Р=1 и после-
довательно будем ставить его в точки 1, 2, п, то придем к вы-
воду, что элементы первой строки состоят из ординат линии влия-
ния момента в точке 1.
Все сказанное относится также к любому столбцу и любой
строке матрицы Таким образом, столбец к состоит из ординат
эпюры моментов от Р=1, приложенной в точке к, а строка с но-
мером i состоит из ординат линии влияния момента в точке i.
Аналогичными свойствами обладают и другие .матрицы влияния:
прогибов L^, углов поворота Лф, нормальных сил LN и любого
другого фактора.	—
При расчете мостов в линейной постановке, т. е. в тех случаях,
когда можно пользоваться законом независим ости, действия сил,
иначе говоря, можно пользоваться линиями влияния, применение
матриц влияния приводит к весьма существенному упрощению и
облегчению всех вычислений.
Таким образом, одной из главных задач является составление
этих матриц и получения для этого необходимых формул. Приме-
нение матриц позволяет ’^большим эффектом использовать вы-
числительные машины для расчета мостов7~{Тассматриваемых в
настоящей главе.
§ 3. ОПРЕДЕЛЕНИЕ УСИЛИИ В ВАНТАХ
Рассмотрим двухпролетную балку, поддержанную вантами,
исходящими из вершины качающегося пилона, расположенного
6 \	235
[ '
на средней опоре (рис. 130). В процессе деформации при нагруз-
ке, расположенной в правом пролете, верхняя точка качающего-
ся пилона переместится вправо на величину Uq. Примем допу-
щение о том, что точки прикрепления вант к балке перемещаются
только по вертикали. Иначе говоря, мы будем пренебрегать сме-
йщениями этих точек по горизонтали за счет искривления оси
/
Найдем удлинение произвольной ван^ы ок, которая после
деформации система перешла в положение о'к'.	t
До деформации между длиной этой ванты и ее проекциями
существует равенство	д
w	S2K=h2+a2.	' м /
4 •
После деформации соответственно получим:	ч
Д*^/с)2=(^Ч“71к)2+ (ак~ «о)2-	J)
Раскрыв в этом равенстве скобки и вычтя из него предыдущее
равенство, после пренебрежения квадратами перемещений т]2 и
«о и величиной AS2 по сравнению с величинами, содержащими
первые степени указанных величин, получаем следующее равен-
ство:	
SK^K=h^-aKii^
откуда находим:
Ок	ОЛ-
Учитывая, что
h
--------------------------— sin ак,
ак
—= COS ак,
SK
получаем:
—T^sin w0cos ак,	(а)
236
где ак—угол наклона ванты SK до деформации системы от вре-
менной нагрузки.	} ) .>
Значения тригонометрических величин для новых углов нак-
лона а* можно определить равенствами
sin а*
SK -г ДЗЛ
bS.. \ .
—— | SIH «...
с I к
/
COSCXk =
ак иа
SK + &SK
ItQ
ак
bSK
Sk
(Ь)
COS ак
1
I
7
h
Из выражений (&) видно, что существенное отличие в старых
и новых углах будет иметь место только при больших перемеще-
ниях, что в реальных мостах не встречается, поэтому изменением
углов наклона вант в дальнейшем будем прене'брегать.
Пользуясь законом Гука, из равенства (а) найдем усилие в
ванте второго пролета после деформации от временной нагрузки:
EXFK
к <?
(VinaK-M0cosaJ.
(С)
Усилие в вантах первого пролета
Si
fasin az + «0cosaj.
(d)
Для совокупности усилий во всех вантах можно записать
единое векторное равенство. Однако прежде чем это делать, мы
условимся относительно обозначений и некоторых общих положе-
ний. Прежде всего обозначим вектор:
<3
-1
— 1
1
1
1
р	So77*
Рк	SKF0
(VIM)
(VII.2)
В векторе о* число отрицательных единиц соответствует числу
точек в левом пролете. В формуле (VI 1.2) величины Fo и So
представляют собой площадь и длину какой-либо из вант, вы.-
бранной за образец. Разобьем балку на ряд частей с узловыми
точками делёнйяГГ, 2, ..., п. Ради стандартизации вычислений
условимся считать, что ванты поддерживают /все без цсключения
узлы точки, намеченные как в правом, так и в левом пролетах.
Если в действительности ванты в ряде точек отсутствуют, то до-
статочно положить площадь сечения отсутствующей ванты, рав-
ной нулю, и тогда автоматически будет учитываться истинное
количество вант.
Теперь вместо двух равенств (с) и (d) запишем одно равен-
ство в векторной форме
•Эо
(VII.3)
где
sinaj
sin а2
Р„
(VII .4)
(VII.5)
sin ал
cos
' cos а2
(VII.6)
cosan
Вектор о*, входящий в уравнение (VII.3), служит для объеди-
нения двух равенств (с) и
втором слагаемом. Иначе
(d), которые отличаются знаками во
говоря, этот вектор изменяет знаки
второго слагаемого для тех координат, которые относятся к
вантам первого пролета.
Матрица R учитывает разные длины и сечения вант. Ее эле-
менты определяются по формуле (VII.2). Диагональные матрицы
Sn и Сп состоят из синусов и косинусов углов наклона вант к
горизонту или углов наклона хорд ^соединяющих узловые точки
балки с вершиной пидЬна, где сходятся ванты.
238	< ''	'	‘ ч Г. '
При составлении уравнения (VII.3) производится .разбивка
балки на ряд панелей, при этом узловые точки намечаются обя-
зательно в точках примыкания вант к балке, а также в ряде про-
межуточных точек. Предполагается, что временная нагрузка
будет приниматься в виде сосредоточенных сил, приложенных в
узловых’точках. ГТсгтгому—чем больше намечено узловых точек,
тем точнее можно учесть ту или другую временную нагрузку.
На рис. 131 показана двухпролетная система с семью узло-
выми точками. Ванты примыкают в точках 1, 2, 4 и 6. Матрица /?
и вектор о * для этой задачи будут выглядеть следующим об-
разом :	"= ———
-1
-1
1
1
1
1
1
В матрицах Sn и Сп можно значения sin а и cos а для точек 3,
5 и 7 не вычислять, а поставить на места соответствующих диаго-
нальных элементов нули или любые другие числа. Однако в том
случае, когда вычисления проводятся на ЭЦВМ по определенной
программе, то проще их вычислить, не внося изменений в про-
грамму.
§ 4. УЧЕТ ВЛИЯНИЯ СПОСОБОВ
ПРИКРЕПЛЕНИЯ ВАНТ НА ПИЛОНЕ
Полученное в предыдущем параграфе уравнение (VII.3) спра-
ведливо для случая, когда все ванты сходятся на пилоне в одну
точку. При этом рассматривался случай, когда ванты прикреп-
ленье на вершине качающегося пилона (см. рис. 131), что рав-
" носильно условной задаче, когда они прикреплены жестко к
балансиру подвижной опоры, поставленной на верху массивного
пилота, как, например, показано на рис. 132.
239
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
<	1
Однако наряду с указанными случаями возможно многоярус^	|
ное расположение вант, как это показано на рис. 133. Для этих
случаев уравнением- (VII.3) пользоваться уже нельзя. Вместо
одного уравнения (VII.3) мы должны составлять столько уравне-
ний, сколько имеется точек объединения вант на пилоне. Так,	,
например, для двухъярусного расположения вант, изображенного
на рис. 133, а, необходимо составлять не одно, а два векторных
уравнения.
Обозначим перемещения по горизонтали точек I и II
(рис. 133, б) через Ui и и2.
а' I	6) I Предположим, что как из точ-
*	ки А так и из точки II выходят
z'	\ пучки вант во все узловые точ-
х&х. ки балки. Для каждого яруса
	|	вант можно составить свои мат-
'	’““ГТ”""” рИЦЫ /?1, Т?2, ’Sin» Ojn И >$2n> C2n.
A	•	Тогда вместо одного урав-
нения (VII.3) получим два
Рис. 133.	уравнения:
я>км-«,с,й
V2=^/?2[S^- «АЙ
^0
(VII.7)
По первому уравнению будут определяться усилия в вантах
верхнего яруса, а по второму — в вантах нижнего яруса. Число
уравнений типа (VII.7) в общем случае будет равно числу ярусов
в расположении вант.
§ 5. ПРЕОБРАЗОВАНИЕ ФОРМУЛ
ДЛЯ ОПРЕДЕЛЕНИЯ УСИЛИЙ В ВАНТАХ
Для того чтобы было удобно пользоваться формулами
(VII.3) и (VII.7), необходимо определить входящие в эти фор-
мулы величины горизонтальных перемещений,^ Эта задача в
значительной степени зависит от устройства закреплений вант
на пилоне.	* 1
В основу мы положим случаГй,1 изображенный на рис. 132,
когда ванты жестко соединены /с верхним подвижным баланси-
ром. В этом случае равнодействующая усилий во всех вантах
всегда будет направлена вертикально. При наличии качающего-
ся пилона указанная равнодействующая будет направлена по
оси наклонившегося пилона. Однако при малых перемещениях
«о и больших высотах пилонов наклоном равнодействующей
240
%
можно пренебречь и так_^ке, как и в первом случае, принимать
ее за вертикальную соду.	//	•'
Таким образом,/для двух рассмотренных случаев получим
один общий критерий, кото рыц 'поможет определить величину
перемещения щ. ,По этому критерию необходимо приравнять/
нулю горизонтальную проекцию равнодействующей усилий в
вантах. Некоторым исключением является случай, показанный
на рис. 133, а. Качающийся пилон в этом случае работает на
из.гиб, поэтому для установления зависимости между перемеще-
ниями узловых точек / и 1I необходимо зацирятг у| Пгжнии рви
новесия, а также определять/его де-
формации при изгибе. Этот случаи
ЗаслуживаеГсПёЦиалБногд изучения, ~
поэтому в настоящей главе мы егсг'
рассматривать не будем.	/	\	
Ита/к, рассмотрим случай, изоб- ^Nk 1 ' n „ J \
/раженный на рис. 134. Пусть в ле-	WWM
|вую сторону действуют силы Ni(i=
= 1, 2, ..., к), а в правую — силы	Рис. 134.	*~
iMj(j=K+ 1> —> п)- Из условия равен-
|$гва нулю суммы проекций всех сил на горизонтальную ось
^получим уравнение
— А4 cosctj — TV2cosa2 — .. . —VKcosaK-]-7VK+iX
X COS aK+14-...+?Vncos a„ = 0.
Это уравнение можно записать в векторной форме
со*У=0,
(VII.8)
где со* — матрица-строка, имеющая вид	-
со* = II — cos щ-cos ct2 —cos алсоз cu-н... cos aj|. (VI 1.9)
ектор V представляет собой столбец, составленный из усилий
вантах.
Для случая двухъярусного расположения вант, как показано
а рис. 133, б, будем иметь два уравнения:
«^=0,
«2^2 = 0.
Л 4-»
атрицы-строки он* и со2* определяются по (VII.9) для каждо-
। яруса в отдельности.
^Подставим в уравнение (VII.8) вместо вектора -N его значе-
<е, определяемое. равенством (VII.3), после сокращения на
241
г -	£)Л)
общий множитель ------- получим:
So	. .
co*MSnn — н0С„о*]=0.	(VI1.10)
Введем обозначения:
w*7?Sn = o>11; ]
(VII.11)
(о*7?С„о* = ₽о, ’
при которых получим:
(ОтД] — «о₽о=0.	(VII.12)
Решая это уравнение относительно «о, получим:
1
«о = ~ "М-
РО
Подставляя найденное значение в уравнение усилий в вантах,
окончательно найдем:
•Зо
где матрица
(VII.14)
\ РО
§ 6. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ
Для вывода основных уравнений представим себе основную
систему в виде балки, отделенной от системы вант, как показа-
но на рис. 135.
Рис. 135.
На балку будут действовать внешние силы Рх, Р2,..., Рп и
усилия в вантах, возникшие от временной нагрузки. Усилия в
вантах от постоянной нагрузки будем считать заранее задан-
ными. Очевидно, ..чтоэти_.усилиящ_ какой -то степени можно
регулировать по-нашему^ желанию, например' путём создания
предварительнщона.тжженияДВ данном'параграф'е'мы’поставим
242
задачу: определить прогибы, усилия в вантах и изгибающие мо-
менты в балке от временной нагрузки.
Усилия, передающиеся с вант на балку, разложим- на две
составляющие. Влиянием продольных составляющих на величи-
ну прогибов в системе будем пренебрегать.
Вертикальные составляющее усилий в вантах будут:
Vi = A/i sin at,
1	У] = У2 sin a2.
Вектор этих сил, направленных вверх, будет определяться ра-
венством
>	V=SnN,	(VII.15)
, где матрица Sn является диагональной с элементами, состоя-
h щими из синусов углов наклона вант. Эта матрица уже приво-
Г дилась ранее (VII.5).
Обозначая через вектор Р систему сил от временной нагруз-
х ки, получим суммарные силы, действующие в узловых точках
Р- балки:
(	P—V=P — SnN.	х (VII.16)
Подставляя вместо// его значение по (VII.12), получим:
S	P-V = P-^SnA~r,	(VIU7)
Обозначим матрицы влияния моментов и прогибов в нераз-
вк резной балке соответственно LM и L\. Вопрос о построении этих
матриц будет рассмотрен в следующем параграфе.
ЕГ Пользуясь этими матрицами, можно записать:
fc.	M = LM(P-V),	(а)
Б''	_ _
в	(b)
Подставляя в равенство (Ь) значение (VII. 17), получаем:
I	Лт)=£]Р,	(с)
I где матрица
fc	A = E + -^-LrS„AK.	(VII.18)
в
к Решая уравнение (с) окончательно, находим:
J	(VII.19)
В, , где
Ь	2^ = А-,£1.	(VII.20)
243
Матрица L^* есть матрица влияния прогибов в заданной си-
стеме. Все матрицы, относящиеся к заданной системе, будем
обозначать с применением верхнего индекса в виде звездочки.
Подставляя (VI 1.19) в формулу (VII. 13), найдем вектор уси-
лий в вантах:
N = L^~P,	(VII.21)
где
Cn = -^S-AnL’v	(VII.22)
Далее найдем вектор суммарных сил. По (VII.Гб) с учетом
(VII.21) имеем:
P-V = (E-SnL*N)P.	(d>
Теперь легко определить значение изгибающих моментов в
заданной системе. Для этого подставим значение нагрузки (d)
в формулу (а). Окончательно получаем:
(VII.23)
где
Lm=Lm(E-S„L*n).	(VII.24)
Здесь необходимо различать две матрицы L*M и LM. Первая
представляет собой матрицу влияния моментов в заданной си-
стеме (т. е. в системе с вантами), а вторая — матрицу влияния
моментов в неразрезной балке.
Матрица влияния моментов Е^ содержит совокупность ли-
ний влияния моментов во всех точках к (лг = 1, 2,..., 7) для за-
данной системы, а матрица LM— то же, но для неразрезной
балки.
На основании выведенных формул легко устанавливается по-
рядок расчета системы. Он сводится к вычислению последова-
тельности матриц, что без каких-либо затруднений выполняется
даже без применения ЭЦВМ. Лишь одна операция вызывает
трудности — отыскание обратной матрицы А.
Конечной целью является отыскание матриц, отмеченных
звездочкой. Именно эти матрицы, позволяющие построить все
необходимые линии влияния, содержат в себе необходимый и
достаточный материал для полного расчета системы на проч-
ность.
§ 7. СОСТАВЛЕНИЕ МАТРИЦ Lm И Ц
ДЛЯ НЕРАЗРЕЗНОЙ БАЛКИ
Для составления матриц LM и £] для неразрезной балки бу-
дем применять формулы, полученные Б. Я. Лащениковым и
приведенные в книге [38].
244
i,' По Б. Я. Лащеникову, эти матрицы определяются с помощью
L следующих формул:
|.	£, = (£«)' BLK
в, В этих формулах:
Г Lm— матрица влияния моментов в основной системе;
к В — матрица податливости (упругих грузов);
Ь Lx — матрица, состоящая из ординат единичных эпюр мо-
£	ментов от лишних неизвестных в основной системе.
с Все матрицы, отмеченные штрихом, являются транспониро-
К ванными по отношению к тем же матрицам. Таким образом, в
К формулы (VII.25) входят всего только три матрицы, что яв-
Д ляется большим преимуществом указанных формул. Разумеется,
Д что окончательный результат не зависит от того, как выбрана
Д основная система. Для неразрезной балки удобно выбирать в
Д качестве основной системы простые балки, приняв за лишние
К неизвестные опорные моменты.
Д* Для выяснения техники решения рассмотрим конкретный при-
Дз-мер. Возьмем двухпролет|ую неразрезную балку, у которой nep-
s'. вый пролет в два раза меньше второго пролета (рис. 136).
(VII.25)
Рис. 136.
^Разобьем длину балки на девять равных панелей. В первом
нпролете будет 3, а во втором — 6 панелей.
Р Матрицы, входящие в формулу (VII.25), будут иметь следу-
|ющий вид:
0 0:0	0	0	0	0
5	4	3.2.1
4	8	6	4	2
3	6	9	6	3
2	4	6	8	4
1	2	3	4	5
245
(а)
В^-—-
6 El
4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4
2
4
6
5
4
3
2
1
Заметим, что матрица L°m прямоугольная порядка 8X7, матри-
ца Lx прямоугольная порядка 8X1, а матрица В квадратная
8-го порядка.
Естественно, что все вычисления необходимо производить с
помощью электронной машины. Однако в данном примере срав-
. ’ нительно нетрудно провести вычисления на обычном арифмо-
/"-метре. Для выяснения всех деталей проведем подробные вычис-
ления обычным способом.
В первую очередь найдем произведение трех матриц LXBLX,
которое, как нетрудно видеть, обратится в число.
I-х BLX
d
&EI
2
4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4
1
3d
El '
Обратная матрица соответственно будет число:
За
246
Найдем теперь произведение матрицы податливости В на
'	V	г О
матрицу влияния моментов в основной системе
f
36Е/	18 12 12 18	0
	2 4	5	4	3	2	1
	0	24	24	18	12	6 24	42	36	24	12 18	36	48	36	18 12	24	36	42	24 6	12	18	24	24
Составим далее произведение Lx на В1?м
[/проведено сокращение всех чисел на 6).
(после вычислений
16 20 55 80 81 64 35
Lx
36EI
Теперь составим произведение трех матриц
		2		
		4		
Ю,- »		6		
| LX(LX BLX)~'L BL0M=—^~ К	18-36		5 4	•|| 16 20 55 80 81	64 351| =
Ко-		3		
		2		
		1		
Гс’-	32	40 ПО		160 162 128 70	
ВТ.'	64	80 220		320 324 256 140	
	96 120 330		480 486 384 210	
К' _ d	80 100 275		400 405 320 175	
Г	18-36	64	80 220		320 324 256 140	(О/
К?	48	60 165		240 243 192 105	
	32	40 ПО		160 162 128	70	
кх -	16	20	55	80	81	64 35	
^вменяя первую из формул (VII.25), т. е. вычитая матрицу
) из матрицы (а), получим матрицу влияния моментов в не-
зрезной балке
247
	400 152	176 352	•7-110 —160 —220 —320		—162 —324	—1'28 —256	—70 —140		
	—96	-120	—330 -	-480	—486	—384	-210		
Z — d . М 18-36	—80 —64	—100 —80	265 212.	32 544	-81 324	—104 176	—67 76	•	(с)
	—48	-60	159	408	729	456	219		
	-32	-40	106	272	486	736	362		
	— 16	-20	53	136	243	368	505		
Обратим внимание на			то,что	матрица влияния			моментов		яв-
ляется прямоугольной порядка 8x7. Дополнительной строкой
является третья строка, которая определяет собой момент над
средней опорой. Все остальные строчки соответствуют сечениям
1,2,.-,7-
Отметим также известный факт о том, что'элементы строк
данной матрицы определяют собой ординаты линий влияния
моментов в соответствующих точках. Так, например, первая
строчка определяет ординаты линии влияния моментов в точ-
ке 1, вторая — в точке 2 и т. д. Ординаты линии влияния момента
в опорном сечении даны третьей строкой. Таким образом, по эле-
ментам данной матрицы можно построить линии влияния во всех
пронумерованных сечениях, а также в сечении над промежуточ-
ной опорой.
Теперь найдем матрицу влияния прогибов Lj. Пользуясь вто-
рым из равенств (VII.25), находим произведение трех поимено-
ванные там матриц. Вычисления привели нас к следующему
результату:	1472	1192	-880	—1280	—1296	—1024	—560	
	1192	1328	-1100	—1600	—1620	—1280	—700	
✓/3	—880	—1100	2375	3808	3969	3176	1747	
Ц = —		: 1	18-63£/	—1280	—1600	3808	7424	8424	6976	3896	• (d)
	—1296	— 1620	3969	8424	10 935	9720	5589	
	—1024	—1280	3176	6976	9720	9728	5968	
	—560	—700	1747	3896	5589	5968	4175	
Матрица	обладает аналогичными				свойствами,		как и мат-	
риц'а LM. Строчки матрицы L\ содержат ординаты линии влия-
ния прогибов в точках 1, 2, ..., 7. Эта матрица уже является
квадратной 7X7.
Интересно отметить, что здесь, так же как и при расчете вся-
кой статически неопределимой системы, можно проводить про-
верки правильности решения задачи. Так, например, в качестве
деформационной проверки- мы должны составить выражение
(см'. [38] формула VII. 13)	сд
LXBLM—O.	(е)
248
11 10 8
Для применения этой проверки находим:
||4
12Е/ 11
Составляя произведение
LXBLM
6 4 2||.
тождественный ноль:
ООО 0||.
система с конкретными размерами показа-
§ 8. ПРИМЕР РАСЧЕТА МОСТА С ПУЧКОМ ВАНТ,
ПРИКРЕПЛЕННЫМ К ПОДВИЖНОЙ
ОПОРНОЙ ЧАСТИ НА ВЕРХУ ПИЛОНА
(е), получаем
II о о О о
12-18-36Е/ 1
Таким образрм проверка сошлась.
3d=180
Рис. 137.
Приведем теперь пример расчета моста в виде балки подкреп-
ленной вантами. Эта
на на рис. 137.

Жесткость балки по всей длине постоянна и равна EI. Жест-
окость вант одинакова и равна fiFo- Длина панели d=60 м. Вы-
сота пилона h = 110 м. Все ванты прикреплены к балансиру
'Подвижной опорной части, установленной на вершине пилона.
Шролеты моста соответственно равны 180 и 360 м.
Положим, что
(а)

p0=-.^F°tf3 =10,0.
E/So .
Как было сказано ранее, мы предполагаем, что количество
вант равно количеству выбранных узловых точек на балке. Вы-
явление истинного количества вант производится автоматически
^матрицей R. Такой подход удобен при расчете на ЭЦВМ. Доста-
’точно изменить й1кой-либо элемент матрицы /?, как получается
новая схема с новым количеством вант.
В табл. 9 приведены геометрические размеры* системы, по ко-
торым в последующем строятся интересующие нас матрицы.
В Первой и в последней колонке в графах бтсуТствующих
•-Вант поставлены нули; этим самым автоматически будет учтено
*П) число вант, которое указано на рис. 137.
249
Таблица 9
№ ванты, к	F л0	SK	Sin о- К	Cos а К	
1	1	162,788	0,675725	0,7-'7155	1
2	1	125,300	0,877893	0.476851	1,299186
3	0	125,300	. 0,877893	0,478851	0,000000
4	1	162,788	0,675725	0.737155	1, оооооо
5	0	210,950	0,521451	0,853283	0,000000
6	1	264,008	0,416654	0,909063	0,616660
7	0	319,531	0,344255	0,938876	0,000000
Пользуясь этой таблицей, составляем необходимые матрицы:
1
1,299186
О
О
0,616660
0,675725
0,877893
0,877893
0,675725
0,521451
0,416654
0,344255
0,737155
0,478851
0,478851
0,737155
0,853283
0,909063
0,938876
Далее по (VII.9) находим матрицу-строку:
<»*=|| — 0,737155 - 0,478851 0,478851 0,737155 0,853283
0,909063 0,9388761|.
250
По формулам (VII.11) вычисляем:
«>ч = II — 0,498114 — 0,546153 0,000000 0,498114 0,000000
0,233569 0,0000001|;
ро=ю*/?Сэта* = 1,894302.
Теперь необходимо вычислить целый ряд матриц, которые бу-
дут входить в основные расчетные формулы.
? По выражению (VII. 14) находим матрицу Л^у. Все входящие
Йр это выражение матрицы и величина р0 уже
ираиее. Производя вычисления, находим:
были определены
Sn
1 *
— СпО <ОТ.
Рс
0,48189 —0 ,21253 0,00000	0,19384 0,00000	0,09089	0,00000
—0,16359	0,96118 0,00000	0,16359 0,00000	0,07671	0,00000
0,00000	0,00000 0,00000	0,00000 0,00000	0,00000	0,00000
0,19384	0,212530,00000	0,48189 0,00000	—0,09089	0,00000
0.00000	0,00000 0,00000	0,00000 0,00000	0,00000	0,00000
0,14741	0,161620,00000	—0,14741 0,00000	0.18781	0,00000
0,00000	0,00000 0,00000	0,00000 0,00000	0,00000	0,00000
I По формуле (VII. 18) находим матрицу Л
^-L,SnAN=E+W^„AN.
^0
;есь -п обозначена матрица, полученная из матрицы Lx путем
43	*
ления на А величина р0, определяемая по (а), была при-
та равной 10,0. Вычисления дают:
1,19954	1,39313 0,00000	0,02594 0,00000	0,43509	0,00000
-0,23344	2,62918 0,00000	—0,24572 0,00000	0,41344	0,00000
1,45387	—0,10562 1,00000	1,98475 0,00000	—0,29185	0,00000
3,12201	0,95081 0,00000	5,09347 0,00000	—0,24803	0,00000
3,88635	1,75795 0,00000	4,48473 1,00000	0,14030	0,00000
3,50202	1,86192 0,00000	3,48798 0,00000	1 ,47250	0,00000
2,04482	1,16039 0,00000	1,87296 0,00000	0,37603	1,00000
25!
Приведем теперь обратную матрицу:
	0,99221	—0,44483 0,00000	0,07955 0,00000	—0,15488	0,00000	
	0,17361	0,34250 0,00000	0,10456 0,00000	—0,12985	0,00000	
	—0,33867	0,29147 1,00000	—0,46810 0,00000	0,13758	0.00000	
	—0,68694	0,21442 0,00000	0,10078 0.00000	0,15975	0,00000	ж
	—0,94695	0,14866 0,00000	—0,86634 1,00000	—0,00314	0,00000	
	—0,95209	0,11696 0,00000	—0,56012 0,00000	0.83325	0,00000	
	—0,58572	0,06659 0,00000	—0,26213 0,00000	—0,14515	1,00000	
По (VI 1.20)
системе:
находим матрицу влияния прогибов в
заданной

или
4 EI Х
0,25388 0,17051 -0,14733 -0,26959	—0,36023	—0,35966	—0,22085
0,17051	0,16993 -0.13986 -0,23143	—0,29866	—0,29577	—0,18121
—0,14733 —0,13986 0,25897 0,32401	0,34202	0,31447	0,18776
—0,26959 -0,23143 0,32401 0,61697	0,75736	0.69085	0,40653
—0,36023 -0,29866 0,34202 0.75736	1.18128	1,13818	0,67418
—0,35966 -0,29577 0,31447 0,69085	1,13818	1,29212	0.83383
—0,22085 —0.18121	0,18776 0,40653	0,67418	0,83383	0,66073
По формуле (VII.22) вычисляем матрицу
в вантах в заданной системе:
влияния усилий
Z* __ £lF0 д Г*_
i-N—	„	--
«->0
0,01153 —0,25692 0,50119	1,01659	1,40139	1.40899	0,86680
0,50670 0,74895 —0,33201 —0,24424	—0,16934	—0,13322	—0,07585
0,00000 0,00000 0,00000	0,00000	0, ооооо	0,00000	0,00000
-0,11772 -0,15474 0,69273	1,33075	1,28209	0,82891	0,38792
0,00000 0,00000 0,00000 0,00000	0,00000	0,00000	0,00000
0,37172 0,31165 —0,33021 —0,38340	0,00754	0,40021	0,34837
0,00000 0,00000 0.00000 0,00000	0,00000	‘0,00000	0.00000
При решении задачи абсолютное
значение жесткости E\Fc
мы не назначали, а задавали величину р0, определяющую отно-
шение изгибной жесткости балки к жесткости кабеля. Этим объ-
„ j •	rf3 Е\Fq
ясняется то, что перед матрицей LN множитель —— —— , кото-
EI Sq
рый, согласно равенству (а), заменен цифрой 10.
252
Вычисляем теперь матрицу влияния моментов, применяя для
этой цели формулу (VII.24):
Lm — SnLN) —
0.50261	0,20002	—0,21124 -0,42224 -0,57963 —0,58224 —0,35810
0,01301	0,22644	—0,08381 -0,15754 -0,21231 —0,21238 —0,13048
—0,03176	—0,08965	—0,24786 -0,10725 0,00636 0,04051 0,03055
—0,02506	—0,04828	0,36058 0,03106 -0,07331 —0,06190 —0,03101
—0,01836	—0,00692	—0,03098 0,16937 -0,15298 —0,16431 —0,09257
—0,09121	—0,07012	0,04556 0,20690 0,63370 0,29339 0,10800
—0,16406	—0,13331	0,12210 0,24443 0,42037 0,75110 0,30857
—0,08203	—0,06665	0.06105 0,12222 0,21018 0,37555 0,65428
На основании свойств матриц влияния, изложенных в § 2,
легко построить линии влияния различных факторов. На рис. 138
показаны линии влияния усилий в вантах. На рис. 139 в мас-
d3
штабе— изображены линии влияния прогибов в точках 1, 2,...,7,
Рис. 138.
253
Рис. 139.
Рис. 140.
а на рис. 140 в масштабе d представлены линии влияния изги-
бающих моментов. При построении указанных линий влияния
были использованы строчки соответствующих матриц влияния.
На рис. 140 пунктиром показаны линии влияния для системы
без вант.
§ 9. РАСЧЕТ МОСТА ПРИ НАЛИЧИИ
ОПОРНОЙ ВАНТЫ
Опорной вантой будем называть ванту, прикрепленную
к опорному сечению, расположенному над одной из крайних
опор. На рис. 141 показана опорная ванта ао, присоединенная
к сечению над левой опорой. В отдельных случаях (когда усилие
в опорной ванте большое) ванту целесообразно заанкерить
в устой.
Рис. 141.
Опорная ванта сильно уменьшает горизонтальное перемеще-
ние «о, точки прикрепления ванты на пилоне и поэтому- сущест-
венно изменяет работу всей системы в целом.
Расчет моста при наличии опорной ванты по сравнению с рас-
смотренной ранее системой отличается только тем, что величина
Ро в формуле (VII.11) заменяется величиной р*.
Для определения величины р* рассмотрим вновь равновесие
подвижного балансира. Вместо формулы (VII.8), полученной из
условия равенства нулю суммы проекций усилий в вантах на го-
ризонтальную ось, теперь мы будем иметь следующее равенство:
—Afacosa0 + (o*/V=0,	(VII.26)
где Na — усилие в опорной ванте;
aa — угол наклона опорной ванты к горизонтали.
В соответствии с формулой (d) § 3, учитывая, что прогиб на
опоре равен нулю (т]а=0), получим:
^e = ^-«ocosaex
256
Подставив это значение в формулу (VI 1.26) и заменив N его
значением из формулы (VI 1.3), после сокращения на -1 — по-
•$о
лучим:
— «ОРа COS2 (1а + U>*R (*$пЦ — Н0СпО*) = О,
где
(VII.27)
Таким образом, вместо равенства (VII.11) находим:
Мо(ро+ДЗ)=О,	(VII.28)
здесь G?n и 00 имеют прежние значения, определяемые по фор-
муле (VII.10), а величина Др равна:
Др = росо52аа.	(VI 1.29)
Предположим
ро+Ар = р*,	(VII.30)
тогда выражение (V 11.28) будет отличаться от выражения
(VII.11) только тем, что вместо Ро в него войдет величина р*.
Все последующие расчетные формулы будут те же, что и
в системе, рассмотренной в предыдущих параграфах.
Усилие в опорной ванте легко определить из равенства
(VII.26):
Ve = ----1---oAV.
cos аа
Если мы захотим построить линию влияния усилия /Va, то
необходимо вместо N подставить его выражение из формулы
(VII.21):
N = -—-—	(VII.31)
COS аа
Матрица в правой части выражения (VII.31) представляет
собой матрицу-строку, элементы которой и будут ординатами
линии влияния усилия в опорной ванте.
ч Рассмотрим пример расчета системы, изображенной на
рис. 141. Эта система отличается от той, которая была рассмот-
рена в § 8 только наличием дополнительной опорной ванты оа.
Пример 1. Назначим площадь сечения опорной ванты такую
же, как и всех остальных Fa=Fo. По формулам (VII.27) и
(VII.29) находим:
а
= о,77169?
210.Р50
9—38С2
257
Др=ра cos2 о.а = 0,561861,
следовательно,
₽* = ₽о+Д₽ = 1,894302+ 0,561861= 2,456163.
По-прежнему назначаем
ро= 10,00.
Матрицы R, Sn, Сп, со* и ып остаются прежними. Они приведены
в § 8. Все остальные матрицы изменяются. Мы не будем приво-
дить все матрицы, а ограничимся только окончательными ре-
зультатами. Кроме этого, во всех элементах матриц влияния мы
сохраним только по три знака после запятой. Подсчет приводи-
мых ниже матриц был осуществлен с высокой точностью на
ЭЦВМ. Однако в окончательном результате можно округлить
полученные величины без ущерба потери точности при их даль-
нейшем использовании. Приводим три матричных равенства.
Уравнение для определения прогибов имеет вид
или иначе
tj—L^P,
		0,150	0,084	—0,056	—0,096	—0,125
1?		0,084	0,099	—0,064	—0,088	—0,104
1з		—0,056	—0,064	0,178	0,171	0,136
14	rf3	—0,096	—0,088	0,171	0,327	0,366
15		—0,125	—0,104	0,136	0,366	0,653
16		—0,125	—0,101	0,108	0,299	0,609
17		—0,076	—0,062	0,061	0,166	0,349
—0,125	—0,076		Pl
—0,101	—0,062		Pl
0,108	0,061		р3
0,299	0,166		Рд
0,609	0,349		р5
0,762	0,508		Рв
0,509	0.461		Р7
Усилия в вантах определяются по уравнению
N = L*nP,
258
или
М		0,418	0,079	0,144	0,339	0,486
М		0,461	0,711	—0,292	—0,168	—0,066
м	—	—0,055	—0,103	0,638	1,227	1,141
м.		0.130	0,112	—0,118	0,019	0,551
		Pi Р2
0,492	0,304		Р3
-0,030 -0,012	X	Р<
0,688	0,301		Р5
0,944	0,683		Рб Р7
Изтнбаюшие моменты в балке
Л1 = LmP1
		0,334	0,061	—0,063	—0,142	—0,201
м2		—0,049	0,176	-0,030	—0,055	—0,074
4'ол		—0,027	-0,086	—0,252	—0,116	—0,005
Л43		—0,016	—0,040	0,352	0,015	—0,095
;И4	= d	—0,004	0,005	—0,043	0,146	—0,185
		—0,030	—0,020	—0,008	0,106	0,497
		—0,056	—0,044	0,028	0,065	0,178
М7		—0,028	—0,022	0,014	0,033	0,089
—0,203	-0,125		Pl
—0.074	—0,045		Рч
0,029	0,024		Р3
—0,083	-0,044		Р4
—0,196	-0,112	X	р5
0,156	0,024		Рб
0,509	0,160		р7
0,254	0,580		
Приведенными выше формулами можно пользоваться непо-
средственно при произвольной нагрузке, заданной вектором Р.
В этом случае необходимо только помножить соответствующую
матрицу на указанный вектор сил Р. Вместе с тем по элементам
этих матриц легко построить линии влияния.
Линии влияния прогибов в масштабе — показаны на
рис. 142. Для изгибающих моментов линии влияния в масшта-
бе d приводятся на рис. 143. Сравнивая линии влияния для тех
же факторов, полученных для системы без опорной ванты (см.
рис. 139 и 140), видим, что опорная ванта значительно снизила
9*
259
Рис. 142.
i'.'
•Г»
Рис. 143.
прогибы и изгибающие моменты. На основании этого возникает
мысль о том, что опорная ванта должна иметь более мощное се-
чение, чем остальные ванты. Тогда ее влияние окажется еще бо-
лее существенным. Это можно проследить из приведенного ниже
примера.
Пример 2. Положим, что диаметр опорной ванты в два раза
больше диаметра остальных вант. Проследим влияние повышен-
ной жесткости ванты на работу системы. Все размеры и схемы
остаются такими же, как и в предыдущем примере. Для рас-
сматриваемого случая
= jSo^=162J88 22 = 3 О8б7е0_
а SaF0 210,950
Величина Ар также в четыре раза больше, чем в примере 1
Ар= ра cos2 аа = 2,24744.
По-прежнему р0= 10,00.
Приведем окончательные результаты в таком же виде, как
и в примере 1.
а) для прогибов:
т1=	Е/		0,113 0,0'4 -0,023 - 0,054	0,073	-0,037	- -0,023 —0,037 0,150 -0,035 —0,037 0,118 _0,043 —0,036 0,063 -0.042 —0,033 0,035 -0,025 —0,020 0,016	-0.035 - -0,037 - 0,118 0,225 0,228 0,161 0,081	-0,042 - -0,036 - 0,063 0,228 0,466 0,422 0,234	-0,042 -0,033 0,035 0,161 0,422 0,576 0,394	—0,025 —0,020 0,016 0,081 0,234 0,394 0,390	Р;
б)	для		усилий в вантах:					
	N--		0,562	0,198	0,018 0,445	0,698	—0,278 —0,033	—0,085	0,618 0,045	0,042	—0,043	0,100 —0,141 1,190 0,161	0. 163 -0,030 1,092 0,743	0,169 0,006 0,638 1,136	0,105 0,010 0,271 0,801	Р\
в)	ДЛЯ		изгибающих моментов:					
			0,275	0,012 -0,011 - -0.070	0,158 -0,011 - -0,025 —0,084 —0,254 -	-0,043 - -0,019 - -0,118 -	-0,068 - -0,025 - -0,009	-0,070 -0,025 0,025	—0,043 —0,015 0,021	
М =	-(1		-',012 —0,038 0,349 0,001	0,009	—0,048 -0,009 —0,002 —0,027 -0,018 —0,013 —0,006 ...0,009 —0,006 —0,003	0,010 - 0,138 - 0,070 0,002 0,001	-0,102 - -0,196 - 0,448 0,093 0,046	-0,091 -0,207 0,108 0,423 0,212	—0,049 —0,119 —0,006 0,107 0,554	—> р.
262
Сравнивая эти уравнения с аналогичными уравнениями в при-
мере 1, можно видеть весьма существенную разницу. Прогибы и
моменты в целом уменьшились.
Для того чтобы оценить, какова возможность уменьшения
прогибов и моментов в балке при увеличении диаметра опорной
ванты, достаточно рассмотреть предельный случай, когда жест-
кость опорной ванты обращается в бесконечность
В этом случае необходимо положить р* = оо.
Приведем результаты, соответствующие случаю
Остальные размеры сохраним прежние (ро=Ю).
а)	прогибы:
(Др = оо).
	0,094	0,038	—0,007	—0,003	0,000	0,001	0,001	
	0,038	0,061	—0,024	—0,011	—0,001	0,002	0,002	
Д3	—0,007	-0,024	0,136	0,090	0,026	-0,002	—0,007	—>
•У1 = 	 4 Е1	—9,003	—0,011	0.090	0,173	0,158	0,091	0,038	Р;
	—9,000	—0,001	0,02'1	0,158	0,371	0,327	0,176	
	0,001	0,002	—0,002	0,091	0,327	0,480	0,335	
	0,001	0,002	—0,007	0,038	0,176	0,335	0,354	
б)	усилия в вантах:
	0,635 0,259 —0,046 —0,022 —0,002 0,004	0,004			
Л т	0,437 0,691 —0,270 —0,127 —0,011	0,025	0,021		—>	
JV =	—0,022 —0,075 0,609 1,171	1,066	0,613	0,255		Р;	
	0,002 0,006 —0,005 0,233 0,841	1,234	0,861			
				
в) изгибающие моменты:				
		0,245 —0,013 0,015 0,001 0,001 -0.001 —0,001		
		—0,081	0,148 —0,001 —0,000 —0,000 0,000 0,000		
		—0,024 —0,083 —0,255 —0,120 -0,011	0,023 0,020		
M = d		—0,011 —0,036 0,348 0,007 -0,106 -0,095 -0,051		/л
		0,003 0,011—0,050 0,134 -0,201 -0,213 —0,’122		
		0,002	0,007 —0,036 0,052 0,424 0,083 —0,021		
		0,001	0,003 —0,023 —0,030 0,049 0,379 0,080		
		0,000	0,002 - 0,011-0,015 0,025 0,190 0,540		
Таким образом, мы видим, что при р* = оо уменьшились про-
гибы и моменты. Для того чтобы уяснить смысл полученного ре-
зультата, предположим вначале, что все ванты нерастяжимы.
263
Тогда при наличии опорной ванты наша система превращается
в неразрезную балку. В рассмотренном выше предельном случае
мы только опорную ванту считаем нерастяжимой, поэтому сис-
тема превратилась как бы в балку на упругих опорах.
Приведенные примеры показывают, что рассмотренные в на-
стоящей главе арфообразные мосты обладают рядом интересных
свойств. Необходимо отметить два обстоятельства:
1) наличие опорной ванты значительно улучшает работу сис-
темы и облегчает ее конструкцию. Опорную ванту следует де-
лать значительно более мощной по сравнению с другими;
2) особенную сложность представляет собой создание опти-
мальных размеров системы. По-видимому, этот специальный во-
прос заслуживает отдельного рассмотрения.
§ 10. РАСЧЕТ МОСТА С ВАНТАМИ,
ЖЕСТКО ЗАКРЕПЛЕННЫМИ НА ПИЛОНЕ
В предыдущих параграфах рассматривался расчет вантового
моста с балкой жесткости при одной конструктивной особенно-
сти: пучок вант скреплялся с подвижной опорной частью, распо-
ложенной на вершине пилона. Таким образом верх пилона вос-
принимал только вертикальное давление от вант. Горизонталь-
ная сила на верх пилона не передавалась.
В практике строительства встречаются мосты, в которых пу-
чок вант жестко соединен с пилонами. В этом случае пилон бу-
дет воспринимать не только вертикальную, но также и горизон-
тальную силу Д/7, которая возникает за счет горизонтальных со-
ставляющих усилий в вантах.
Все основные уравнения, полученные в предыдущих пара-
графах, остаются справедливыми и для задачи, рассматривае-
мой в настоящем параграфе. Однако в некоторые из них необхо-
димо внести изменения. Вместо уравнения (VII.8) теперь следу-
ет написать
Ю*У=АЯ.	(VII.32)
Напомним, что смысл уравнения (VII.8) состоял в отсутст-
вии общей горизонтальной составляющей в подвижной опоре.
При жестком прикреплении пучка вант к вершине пилона сумма
горизонтальных составляющих усилий в вантах будет равна си-
ле АД.
Для установления правила знаков рассмотрим равновесие
узла В, к которому крепятся ванты (рис. 144, а). При выводе
уравнения (VII.9) силы, приложенные к точке прикрепления
вант, считались положительными, если они направлены вправо.
Уравнению (VII.32) соответствует случай, когда сила АД на
264
узел В со стороны пилона действует влево, г. е. так, как показа-
но на рис. 144, б. К пилону эту силу необходимо приложить в
правую сторону.
Величина силы \Н зависит от жесткости пилона. Если обо-
значить перемещение точки В от силы, равной единице, через
бп (рис. 144, в), то перемещение точки прикрепления пучка
вант «о будет определяться равенством
Uo—61
Рис. 144.
откуда находим:
.	ДН = — щ
&и
Таким образом, вместо равенства (VII.8) получим новое ра-
венство
=	(VII.34)
вп
На основании выражения (VII.34) вместо (VII. 10) теперь по-
лучим:	9
~	=-^- .	(VII.35)
*0	Оц
Заметим, что при получении равенства (VII. 10) было прове-
дено сокращение на величину —i-L-. Такое сокращение теперь
'S’o	—»
проводить нельзя, так как выражение m*N в нашем случае не
равно пулю. Запишем (VII.35) в виде
•  <vu-36)
Л]Го6п
В дальнейших выводах разница будет только в величине f>0,
которая теперь в отличие от выражения (VII.11) определяется
равенством
Й=,.,*А>СХ + —(VII.37)
265
Последнее выражение удобно записать в следующей форме:
р;=₽о + Др,	(VII.38>
где Ро — величина, определяемая по выражению
Ро = (о*ЯСпо*,	(VI 1.39 >
а
=-~- •	(VII.40>
£i^b°n
Так же как и р0, величина Др является безразмерной, что
легко проверяется по равенств}7 (VII.40). В самом деле, величи-
на fi/^o измеряется в единицах силы (например, Т), 6ц — пере-
мещение от единичной силы, a Eifofin — перемещение от конеч-
ной силы, которое измеряется в единицах длины, т. е. как вели-
чина So. Таким образом, Др — безразмерная величина.
Все остальные формулы, полученные ранее, будут справедли-
вы для нашего случая. Порядок расчета моста с вантами, жест-
ко закрепленными к вершине пилона, ничем не будет отличать-
ся от того, который был разработан в предыдущих параграфах
для случая прикрепления вант к подвижной опоре, расположен-
ной на вершине пилона. Сравнивая формулы (VII.30) и (VII.38),
видим, что расчет моста с вантами, жестко прикрепленными на
вершине пилона, аналогичен расчету, проведенному в § 9 для
случая, когда имеется опорная ванта.
Остается выяснить методику определения величины бц —пе-
ремещения верха пилона от силы, равной единице. Отдельно
стоящий пилон можно рассматривать как стержень, заделанный
одним концом. На рис. 145, а показан пилон, а на рис. 145, б —
его расчетная схема.
При вычислении величины бц необходимо учитывать то, что
пилон имеет переменную по высоте жесткость. Без особых за-
труднений вычисление 6ц можно провести как по формуле Мора,
так и графо-аналитическим методом. В первом случае формулу
Мора удобно представить в виде
1	Tf2	1
р	ЛК	р —*—
= \---dx — \ ЛМ4, dx,
11	J	EI	У
о	о
где М\ — ордината эпюры от силы, равной единице, в произ-
вольном сечении пилона;
Mi* — ордината в произвольном сечении эпюры .
ЕI
На рис. 146 показаны три эпюры: первая определяет закон
изменения^ жесткости EI по высоте пилона; вторая эпюра — мо-
ментов М\ от единичной силы приложения вверху пилона,
266
а третья эпюра получена из двух первых путем деления каждой
ординаты эпюры М\ на соответствующую ординату эпюры
жесткостей. Между узловыми точками, в которых найдены орди-
наты Mi*, эпюру можно провести по прямым линиям. Таким об-
разом, эпюру очерчивает ломаная линия.
Применяя правило Верещагина, легко найти величину бц.
Рис. 145.	Рис. 146.
§11. ПРИМЕР РАСЧЕТА МОСТА С ЖЕСТКИМ
ПРИКРЕПЛЕНИЕМ ПУЧКА ВАНТ
К ВЕРХУ ПИЛОНА
Рассмотрим пример расчета моста с вантами, закрепленны-
ми на верху пилона. Возьмем систему, рассмотренную в § 10
(см. рис. 137), но теперь будем считать, что ванты жестко при-
креплены к вершине пилона. Все размеры системы сохраним
такими же, как в примере, проведенном в § 8 настоящей главы.
По-прежнему принимаем р0= 10,0. Табл. 9, а также матрицы /?,
Sn, Сп и величина р0 остаются такими же, как в § 8. Если пилон
имеет весьма малую изгибную жесткость, когда перемещение ве-
лико, то Др будет мало. В пределе для случая, когда пилон не
способен сопротивляться изгибу, но может воспринимать про-
дольную силу (качающийся пилон), Др стремится к нулю. В этом
случае решение совпадает с тем, которое было получено в § 8.
При абсолютно жестком пилоне теоретически бц->0, а Др—>оо.
Таким образом, в принципе Др может колебаться в весьма
широких пределах.
Проведем расчет для разных значений величины Ар. Назна-
чим Др=3, 10, 100. Напомним, что основная задача состоит
в отыскании матриц влияния, по которым определяются проги-
бы, нормальные усилия в вантах и изгибающие моменты в бал-
267
ке жесткости от группы сил Р2, Рп,
ром А
N = L*n~P ••
Л1 = ГЛ1Р
определяемых векто-
(VII.41)
Кроме этого, необходимо определить матрицу-строку Ь\ц
для определения горизонтального усилия ДЯ, передающегося на
вершину пилона,
АН=1АнР.
Приведем также характерные матрицы, получаемые в про-
цессе промежуточных вычислений Адг, А и А-1.
Вначале подробно проследим расчет для первого случая, а для
двух других ограничимся приведением окончательного резуль-
тата.
Итак, пусть
Др = 3; р0= 10,0,
тогда	'
р* = р0 + Др = 1,894302 + 3 = 4,894302.
Далее с помощью ЭЦВМ вычисляем ряд матриц, которые будут
входить в основные расчетные формулы. По выражению (VII. 13)
находим матрицу А^. Пропуская промежуточные выкладки, по-
лучим:
А^у —7? / Sn — —— С „о «>Л=
\. Ро /
+ 0,60070 —0,08226	+ 0,00000	+0,07502	+ 0,00000	+0,03518	+ 0,00000
—0,06332 +1,07113	+ 0,00000	+0,06332	+0.00000	+ 0,02969	+ 0,00000
+ 0,00000 +0,00000 + 0,00000 +0,000!,О +0,00000 +0,00000 +0,00000
+0,07502 + 0,08226	+ 0,00000	+ 0,60070	+ 0,00000	—0,03518	+ 0,00000 •
+0,00000 + 0,00000	+0,00000	+0,00000	4-0,00000	+0,00000	+ 0,00000
+0,05705 + 0,06256	+0,00000	—0,05705	+0,00000	+ 0,23018	+ 0,00000
+0,00000 + 0,00000 + 0,00000 +0,00000 + 0,00000 +0,00000 + 0,00000
По формуле (VII. 18) находим матрицу А. Как и в § 8,
А = Е +	L,5„АЛ = Е + р„т,5„ЛЛ. =
+ 2,13686
+ 7,67716
+0,07076
+ 0,28694
+ 0.57125
Г 0,61830
+0,38831
+2,42084
+ 3,72688
—1,77730
-2,15769
—1,87686
— 1,29991
—0,65587
+0,00000
+0,00000
+ 1,00000
+0,00000
+0,00000
+0,00000
+ 0,00000
—0,91137 + 0,00000 —0,00443 + 0,00000
—1,24687 + 0,00000 —0,05601 +0,00000
+3,50939 + 0,00000 +0,42306 +0,00000
+7,92854 + 0,00000 +1,08136 + 0,00000
+7.79983 +1,00000 +1,69477 + 0,00000
+6,37169 +0,00000 +2,82469 +0,00000
+3,52947 +0,00000 +1,15277 +1,00000
268
Обратная матрица:
4-0,60914 —0,38883 -j-0,00000 + 0,02065 + 0 00000 —0,01465 + 0,00000
—0,14317 + 0,38881 +0,00000 + 0,05586 + 0,00000 —0,01390 +0,00000
-0,00219 + 0,24228 +1,00000 —0,41637 + 0,00000 + 0,01442 +0,00000
-0,04887 +0,12114 +0,00000 +Q.19888 +0,00000 —0,07381 -rO.OOOOO
-0,08469 + 0,02261 +0,00000 —0,73378 +1,00000 —0,31876 +0,00000
—0,08898 —0,00922 +0,00000 —0,42742 +0,00000 + 0,51733 +0,00000
—0,05537 —0,01094 + 0,00000 —0,18059 +0,00000 —0,33927 +1,00000
По (VIL20) находим матрицу влияния прогибов в заданной
системе:
L^i = A~1L1,
или
+0,10847 +0,05027 —0,01961 —0,02740 —0,03294 —0,03205 —0,01954
+ 0,05027 + 0,07050 —0,03424 —0,03115 —0,02800 —0,02485 —0,01474
* rt3 —0,01961 —0,03424 + 0,14678 + 0,11128 +0,05454 + 0,02671 +0,01094
Li=— -0,02740 —0,03115 + 0,11128 + 0,21355 + 0,21219 + 0,14515 +0,07122 .
EI -0,03294 —0,02800 + 0,05454 + 0,21219 + 0,44456 + 0,40074 +0,22105
-0,03205 —0,02485 + 0,02671 +0,14515 + 0,40074 + 0,55395 + 0,38026
—0,01954 —0,01474 + 0,01094 + 0,07122 +0,22105 +0,38026 + 0,38202
По формуле (VII.22) вычисляем матрицу влияния усилий
в вантах: (ро=1О)
/* — E'F° л г*
ln—~—
•-’о
40,57843 +0,21187 +0,00325 +0,07232 + 0,12533 +0,13168 +0,08195
+0,44292 +0,69620 -0,27598 -0,13799 -0,02575 +0,01050 + 0,01246
+0,00000 +0,00000 +0,00000 +0,00000 + 0,00000 +0,00000 +0,00000
= -0,03057 -0,08266 +0,61618 +1,18558 +1,08591 ф0,63254 +0,26726 .
+0,00000 +0,00000 +0,00000 +0,00000 +0,00000 +0,00000 +0,00000
+0,03519 +0,03336 -0,03462 + 0,17715 +0,76505 +1,15845 +0,81428
. +0,00000 + 0,00000 +0,00000 +0,00000 +0,00000 +0,00000 +0,00000
Матрицу влияния моментов получим по (VII.24). Вычисления
привели нас к следующему результату:
(Е —
+0,26820 +0,00618 -0,00534 —0,03179 —0,05199 —0,05408 —0,03357
—0,07274 +0,15553 -0,00849 -0,01471 —0,01930 —0,01918 —0,01177
-0,02485 —0,08393 -0,25393 —0,11877 —0,00921 +0,02494 +0,02098
—0,01182 —0,03734 +0,34896 +0,00901 —0,10311 —0,09173 —0,04934
+0,00120 + 0,00926 -0,04816 +0,13678 —0,19701 —0,20839 —0,11965
-0,00643 —0,00000 -0,02891 +0,06568 +0,44286 +0,10237 —0,00938
-0,01406 —0,00927 -0,00966 -0,00542 +0,08273 +0,41313 +0,10090
—0,00703 -0,00463 -0,00483 - 0,00271 +0,04137 +0,20657 + 0,55045
269
Рис. 147.
J
й
На рис. 147 по найденной матрице влияния моментов постро-
ены линии влияния моментов, для чего использованы соответст-
вующие строчки матрицы L*M. Они изображены в масштабе d.
Для расчета пилона необходимо знать величину горизонталь-
ной силы, передающейся от вант. На основании равенства
(VII.32) определяем, что
Учтя равенство (VII.21),
окончательно находим:
где матрица-строка
т* * г *
Ln.
(VI1.42)
(VII.43)
Элементы этой матрицы-строки означают собой ординаты линии
влияния силы Л/7. Вычисления дают:
||_0,62902 - 0,52017 + 0,55251 +1,04775
+ 1,41590 +1,41729 + 0,870871|.
Линия влияния горизонтального усилия АД показана на
рис. 148. Все ординаты показаны в масштабе ° . Для случая
•So
Др= 10,0 и р0= 10,0 приведем окончательное значение матриц вли-
яния:
+0,09862 + 0,04212 —0,01095 —0,01098 —0,01075 —0,00984 —0,00589
+0,04212 + 0,06376 —0,02708 —0,01757 —0,00965 —0,00648 —0,00345
-0,01095 -0,02708 + 0,13918 4-0,09686 +0,03505 4-0,00720 —0,00105
-0,01098 —0,01757 +0,09686 +0,18620 + 0,17523 + 0,10815 + 0,04848
-0,01075 -0,00965 +0,03505 +0,17523 + 0,39461 +0,35074 + 0,19033
-0,00984 -0,00648 4-0,00720 + 0,10815 +0,35074 +0,50390 + 0,34951
-0,00589 -0,00345 -0.00105 + 0,04848 +0,19033 + 0,34951 +0,36313
271
4-0,61686 J-0,24366	— 0,03051 4 0,00830	4-0,03882	4-0,04508	+0.0287311
4-0,43859 + 0,69263	— 0,27218 - 0,13079	—0,01602	4-0,02024	4-n,01845
+ 0,00000 4-0,00000 4-0,00000 + 0,00000 + 0,00000 + 0,00000 +0,00000
—0,02466 —0,07778	+ 0,61099 +1,17573	+1,07251	+0.61922	+0,25907 .
+0,60000 +0,00000	+ 0,00000	+ 0,00000	+ 0,00000	+ 0,00000	+ 0,00000
+ 0,01238 4 0,01449	— 0.01458	+ 0,21515	+ 0,81641	+1,20986	+0,84587
+ 0,00000 +0,00000	+ 0,00600	+ 0,00000	+ 0,00000	+0,00000	+o,ooooo|
Ьм—d X
+0,25231 —0,00696 + 0,00862 - 0,00532 —0,01622 —0,01827 -0,01157
—0,07855 + 0,15072 — 0,00339 —0,00503 —0,00621 —0,00608 -0,00372
—0,02438 —0,08354 —0,2'434 —0,11955 —0,01026 +0,02388 + 0,02033
—0,01098 — 0,03660 + 0,34817 + 0,00751 —0,10513 —0,09375 -0,05058
+0,00253 +0,01035 —0,04933 +0,13457 —0,20000 —0,21138 -0,12149 >
—0,00068 + 0,00475 —0,03396 + 0.05611 +0,42992 + 0,08942 -0,01733
—0,00389 — 0,00086 —0,01859 —0,02236 +«,05984 +0,39022 +0,08682
—0,00195 —0,00043 — 0,00930 —0,01118 + 0,02992 +0,19511 +0,54341
LbH=
= ||—0,67167 —0,55544 +0,58997 +1, 1<879
+ 1,51190 +1,51338 +0.92991Ц,
Приведем также эти матрицы для случая Др= 100,0; р0= 10,0:
*
71 “ £7
+ 0,09445	+0,03867 —0,00729	—0.00103	—0,00133	—0,00044	—0,00012
+ 0,03867	+0,05091 —0,02405	—0,01183	—0,00189	+0,00129	+0,00132
—0,00729	—0,02405 + 0,13596	+ 0,09076	+0,02581	—0.00105	—0,00612
—0.00403	—0,01183 +0,09076	-i 0,17463	+0,159S0	+0,09250	+0,03887
—0,00136	— 0,00189 + 0,02681	+0,15960	+0.37348	+0,32959	+0,17734
—0,00044	+ 0,00129 —0,00105 +0,09250		+0,32950	+0,48274	+0,33650
—0,00012	+ 0,00132 —0,00612	+0,03887	+0,17734 +0,33650		+0,35513
					
+0,63312	+ 0.25710 —0,04479	—0,01877	+0,00222	+0,00845	+0.00623
+ 0,43676	+0,69111 —0,270'8	—0,12774	—0,01190	+0,02437	+0,02098
+0,00000	+0,00000 + 0,09000	+ 0,09900	+0,00000	+0,00000 +0,00000	
—0,02216	—0,07571 +0,60879	+ 1,17157	+1,05599	+0,61359 +0,25561	
+0,00000	+ 0.00000 -t 0,00000	+0,09000	+0,00000	1-0,00000 +0,00000	
+ 0,00273	+ 0,00351 —0.09310	+0,23123	+0,83813	+1,23161	+0,85923
+ 0,00000	+ 0,00000 +0,09009	+ 0,09000	+0,00900	+0,00000 +0,00000	
272
Ljvi=d X
+0,24559 —0,01252 + 0,01452 +0,00588 —0,00109 —0,00313 —0,00226
—0,08101 +0,14859 —0,00123 —0,00093 —0,00067 -0,00054 —0,00031
-0,02418 —0,08338 —0,25451 —0,11988 —0,01071 +0,02343 +0.02005
—0.01055 —0,03628 4-0,34783 +0,00388 0,10599 -0,09460 —0,05111
+0,00309 + 0,01082 —0,04982 + 0,13354 —0,20126 —0,21264 —0,12227
+0,09175 + 0,00575 —0,03509 +0,05208 +0.42445 +0,08394 —0,02070
+0,00041 +0,00270 —0,02237 —0,02952 + 0,05016 + 0,38053 + 0,08087
+0,00020 + 0,00135 —0,01118 —0,01476 +0,02508 + 0,19026 +0,54043
11-0,68971 —0,57036 +0,60582 +1,14884 +1,55250 +1,55402 +0.95489Ц.
Так же как и для первого случая (Ар = 3), по приведенным
матрицам легко построить линии влияния прогибов, усилий в ван-
тах, изгибающих моментов и величину горизонтальной силы, пе-
редающейся на вершину пилона. Мы не даем изображение этих
линий влияния. Однако по элементам матриц £*, L*N и L*M
можно судить о влиянии жесткости пилона на указанные сило-
вые факторы.
Величины прогибов в различных сечениях балки с увеличе-
нием жесткости пилона (с увеличением Ар) уменьшаются, а уси-
лия в вантах увеличиваются. Также увеличивается сила А//, что
видно по элементам матрицы строки L\H.
Более сложная картина наблюдается с изменением изгиба-
ющих моментов в сечениях балки. В целом их величина с увели-
чением Ар уменьшается. Так, например, при загружении право-
го пролета равномерной нагрузкой q необходимо положить, что
0
О
q d
qd
qd
qd
qd
Осуществляя перемножение матриц влияния на вектор Р, со-
гласно равенствам (VII.41) получим численное значение проги-
бов и моментов в различных сечениях балки. Эти величины при-
водятся к виду
Л4 = KMqd2.
Значения величины и км приводятся в табл. 10.
273
Таблица 10
№ сечений	Прогибы			Моменты		
	Д?=3	ДЗ=10	Д? = 100	Д,3 = 3	А,3 = 10	АЗ-100
1	-0,131	—0,048	-0,013	-0,177	—0,043	0,014
2	—0,133	—0.064	-0,03’5	—0,073	-0,024	—0,037
а	0	0	0	—0,336	—0,340	—0,342
3	0,350	0,277	0,245	0,114	0,106	0,103
4	0,753	0,615	0.556	—0,436	—0,448	— 0,452
5	1,333	1,146	1 ,067	0,572	0,524	0,504
6	1,507	1,319	1,240	0,582	0,496	0,460
7	1,065	0,950	0,902	0,790	0,748	0,730
Из таблицы видно, что с увеличением жесткости пилона про-
гибы во всех сечениях балки уменьшаются. Уменьшаются также
положительные моменты, а отрицательные моменты незначи-
тельно увеличиваются. Вместе с тем можно отметить, что при
значительном увеличении жесткости пилона изменение величин q
и М не очень велико, поэтому нет необходимости устройства
очень мощных пилонов.
§ 12. РАСЧЕТ ВАНТОВОГО МОСТА С ПРИМЕНЕНИЕМ
КЛАВИШНЫХ МАШИН ИЛИ АРИФМОМЕТРА
Метод расчета вантового моста с балкой жесткости, изло-
женный в предыдущих параграфах, обладает универсальностью
и позволяет так составить программы для решения на ЭЦВМ,
чтобы по ним можно было обследовать большое количество ва-
риантов, меняя с пульта машины основные параметры системы,
а также количество вант.
Однако, если расчетчик не имеет возможности использовать
ЭЦВМ и проводит расчет с применением клавишных машин или
арифмометра, то для сокращения вычислений и наглядности ре-
шения приходится жертвовать универсальностью решения и по
возможности прибегать к привычным методам, изучавшимся в
основном курсе строительной механики.
В настоящем параграфе рассматривается применение мето-
да сил для расчета системы с качающимся пилоном, которая
рассматривалась в § 9. Рассмотрим этот метод на примере рас-
чета вантового моста, изображенного на рис. 141.
Основная система по методу сил и эпюры от единичных значе-
ний неизвестных показаны на рис. 149, а. Прежде чем приступить
к расчету, необходимо сделать оговорку, касающуюся работы
вант.
В процессе расчета мы будем смотреть на ванты как на обыч-
ные стержни, способные работать как на растяжение, так и на
274
Рис. 149.
сжатие. Такой подход будет оправдан при том условии, что окон-
чательные расчетные усилия с учетом как временной, так и по-
стоянной нагрузок будут только растягивающими. Короче гово-
ря, необходимо учесть все оговорки, которые были сделаны ранее
на стр. 233.
Применение метода сил в обычной его трактовке, даже при
использовании малых средств механизации, иногда встречает
затруднения. Они состоят в том, что коэф-
__ Х5 фициенты канонических уравнений (6?Л.) мо-
, * Ц рГ Г гут иметь различную размерность. Если,
* например, неизвестное хх является силой, а
%%—моментом, то коэффициенты бц и 622
формально имеют разную размерность, что
иногда затрудняет расчет. Поэтому мы усло-
Рис. 150. вимся вместо опорного момента в сечении
над средней опорой принимать в качестве
неизвестного силу Х5 (рис. 150), которая создает момент в сече-
нии, равный х5- С. Для удобства, которое выяснится позднее,
назначим C=d. Вот почему на рис. 149, а спорный момент_на
основной системе показан равным x$-d. В этом случае эпюра М5,
соответствующая случаю х5=1, построена не от единичного
момента, а от момента, численно равного величине d.
Из единичных эпюр, изображенных на рис. 149, б, видно, что
размерность ординат всех эпюр одна и та же. Это позволит в
дальнейшем сохранить размер d в буквенном виде до конца
решения.
При вычислении перемещений б7\ необходимо учитывать два
интеграла формулы Мора:
MjMK
El
ММ,
——— ds.
EF
Первый интеграл учитывает деформацию изгиба балки, а вто-
рой— продольные деформации вант. Для определения изгибных
деформаций балки построены эпюры М, а для определения де-
формаций вант потребуется вычислить усилия в опорной ванте
от единичных значений неизвестных. Из рассмотрения равнове-
сия верхнего узла «&» находим:
7У1==._ cos gL . ^=cosa3 .
COS aa	' COS aa
fry	COS a9 # jTT COS Я]
1V 2 —---------\ * * 4 —	)
COS _	cos
TV5 = 0.
Длины вант и площади их сечений будем соответственно обо-
значать: Sa, Si, 52, ... и Fa, Fx, F2.... Модуль упругости вант в
отличие от модуля упругости балки Е будем обозначать Ев-
276
Применяя обычные правила вычисления интегралов Мора,
находим:
4rf3si”2a . Sa cos2a, 	.
9Е/ EBFa cos2aa
4d3 sin2 a? । Sa cos2 a? , S?
9Е/ EBFa cos2 aa EBFo
^33
39 d3 sin2 a3
Sa cos2 a3
844
EBFa COS2 aa
3?d3 sin2 a4 . Sa cos2g4
9EI	EBFa COS2 “a
9E1
$4	.
£b^4

R 3^3
855 =---- ,
El
?>I2— 821 —
18E1
7z/3sina1sinaQ j So cos Я] COS aQ
EBFa COS2 aa
Sn COS a, COS a3
O31 =---------------~ i
EBFa cos2 aa
g __ __ Sa COS a, COS a4
41	COS2 aa
~	4J3sinni
15=	;
Ь 9Е/
J.___ Sa cos ao COS a3
О9о-Oop -- -
EBFaco^aa
Sa cos a-; cos a4
o24 = o42 ---------------;
EBFa COS2 aa
s s 5d3sinao
625--O52 —	~
9E1
j. «.	28J3 sin aasin a4
'*34 — 'J43
9 El
Sa COS a3 COS a4
£B/-a COS2 aa
^35 — ^53
20d3 sina3
9E1
16rf3 sina4
845	854	9E1
Условимся в дальнейшем, как и в § 6, считать:
277
EiF0 — жесткость ванты, которая принята в качестве основной;
So — длина этой же ванты.
О =. FflS°
F0Sa
Fк$о
F0SK
(VII.44)
Рк = 1,2,3,4
а также
rf3£BF0
P°~ EIS0
A₽ = P„COS2 aa
(VII.45)
На основании найденных перемещений и принятых обозначе-
ний матрицу перемещений А можно представить в виде
А
EI
Ar
1
Ро
f— Л+Я-1}
(VII.46)
где матрицы ЛЬЛ2 будут иметь следующий вид:
	8 sin2 aj	7 sin a4 sin a, 0	0	8 sin	
1	7 sin a4 sin a2 8 sin2 a2	0	0	10 sin a2	
Д1=- 18	0	0	64sin2a3 56 sina3 sin ot4 40sina3	
	0	0	56 sin a3 sin a4 64 sin2 a4 32 sin a4	
	8sina4	lOsin a2 40sina3	32sina4 54	
(VII.47)
COS2 «1
cos аг cosa2
—cos «j cosa3
cos a4 cosa4
0
cos a, cos a2 —cos 04 cos a3 —cosa1cosa4 0
cos2a2 —cosa2cosa3 — cosa2cosa4 0
— cosa2cosa3 cos2a3	cos 03 cos a4 0
— cosa2cosa4	cosa3cosa4	cos2a4 0
0	0	0	0
(VII.48)
Диагональная матрица R приведена в § 3, однако в уравнение
входит обратная матрица R~l, которая дополняется нулем. Она
будет иметь вид
1
Pi
I
Р2
1
Рз
I
(VII.49)
О
278
Для построения линий влияния лишних неизвестных будем
исходить из системы канонических уравнений, которая в матрич-
ной форме запишется так:
ДхЧ-ДрР = 0,	(VII-50)
где А — матрица перемещений, определяемая равенством
(VII.46);
х — вектор лишних неизвестных;
Др—матрица перемещений от грузов, равных единице в
точках 1, 2, ..., 7. Строчки этой матрицы состоят из
ординат линий влияния перемещений по направлению
неизвестных х2, х$ в основной системе.
Для определения коэффициентов матрицы Др на рис. 149, в
изображены эпюры моментов от силы Р=1, поставленной после-
довательно в точки 1, 2,..., 7.
По эпюре Mi и грузовым эпюрам последовательно находим:
4^з	7</з
Д1(РЗ) = Д1(Р4) =- Д1(Р5) = Д1(Р6) — Д1(Р>7) — 0.
Таким образом, первая строка матрицы Др будет иметь вид:
^L±_Looooo
EI 9
Аналогичным образом по М2 и всем грузовым эпюрам моментов
найдем вторую строку и т. д.
В целом матрица Др имеет следующий вид:
16sinaj 14 sin a, 0	0	0	0	0
14sina2 16sina2 0	0	000
X 0	0 76sina3 128sina3 138sin a3 112 sina3 62sina3
0	0 62sina4 112sina4 138 sin a4 128 sina4 76 sina4
16	20	55	80	81	64	35
(VII.51)
Решая уравнение (VII.50), получим вектор неизвестных:
х— —А~1ЬрР,
или иначе
х -- Гх />,
279
где матрица влияния лишних неизвестных
Lx= —Д-'кр.
(VII.52)
Эта матрица будет иметь 5 строк и 7 столбцов. Каждая
строчка матрицы L* содержит ординаты линий влияния соот-
ветствующего лишнего неизвестного.
Для построения линии влияния каких-либо других величин,
например, изгибающего момента или прогиба, используем соот-
ветствующие зависимости, известные из курса строительной
механики:
S = ^о4~^\-*1Ч-,$'2-’£:2 4_,$'зл:’з	4''^5Л'5-	(VII.оЗ)
Таким образом, линия влияния фактора S будет состоять из
шести линий влияния этого фактора: линии влияния So в основ-
ной системе и пяти линий влияния лишних неизвестных х. Вели-
чины Si, S2, ..., S5 являются числовыми множителями и пред-
ставляют собой значение фактора S от единичных значений
лишних неизвестных = 1 (лг = 1, 2, ..., 5).
Если нам необходимо построить линии влияния сразу для
л величин Si, S2, ..., Sn, то вместо равенства (VI 1.53) необходи-
мо воспользоваться матричной записью, тогда вместо алгебраи-
ческого равенства (V1I.53) получим следующее матричное
равенство:

(VII.54)
где Ls — прямоугольная матрица с семью столбцами и п стро-
ками. Число столбцов этой матрицы равно числу то-
чек, в которых последовательно ставится груз Р = 1
(в данном случае семь точек), а число строк равно
числу величин S (Sb S2, .... S„);
Т 0	г *
Ls — такая же матрица, как и Ls, но построенная для
основной системы (в нашем случае для двух простых
балок);
т *
Ед.— матрица влияния лишних неизвестных, определяе-
мая равенством (VII.52).
Так, например, пусть требуется построить линии влияния
моментов в восьми точках: 1, 2, а, 3, 4, 5, 6, 7. Точка а принад-
лежит сечению над промежуточной опорой а. Матрица влияния
для указанных моментов будет определяться равенством
Lm = L°m^ ML*,	(VII.55)
Г О	V
где матрица LM состоит из ординат линии влияния моментов в
восьми точках для основной системы. Так как основная система
состоит из двух простых балок, то для них ординаты линий вли-
280
яния моментов вычисляются весьма просто. Эта матрица поряд-
ка 7X8 приведена в настоящей главе равенством (а) в § 7.
Матрица М имеет порядок 5X8, ее столбцы состоят из ординат
эпюр моментов от лишних неизвестных, равных этим эпюрам без труда находим:					единице. По	
	2 . — sin а, 3	1	1 . .— sin а.-> 3"	2	0	0	1 T	
	1 . — sin а, 3	1	2 . — sin а9 3	2	0	0	2 3	
	0	0	0	и	0	1	
	0	0	2 .	1 — sin	— 3	3	sin ot4	5 6	
М = — d	0	0	4 .	2 		 Sin Oto 		 3	3 3	sin a4	2 3	. (VII.56)
	0	0	sin ot3	sin a4	1 2	
	0	0	2	.	4 — Sin a, — 3	3	sin a4	1 T	
	0	0	I .	2 — sin a, -— 3	3 3	sin a4	1 Т	
Для построения матрицы влияния прогибов можно приме-
нить два различных метода. Первый метод заключается в при-
менении того же приема, который был применен для изгибаю-
щих моментов. По аналогии с равенством (VII.54) можно за-
писать:
+ HL\,	(VII.57)
где —матрица влияния прогибов для основной системы;
Н—матрица прогибов от единичных значений неизвест-
ных. Каждый столбец этой матрицы состоит из проги-
бов в семи точках от Xi=l. Для построения матрицы
L° необходимо определять прогибы в основной си-
стеме от единичных сил. Каждая строка такой мат-
рицы состоит из ординат линий влияния прогибов со-
ответственной точки. Составление этих матриц
требует трудоемких вычислений.
Второй метод несколько проще. Применяя графо-аналитиче-
ский метод, можно определить прогибы как фиктивные моменты
в фиктивной балке от фиктивной нагрузки (или упругих грузов).
Последняя представляет собой эпюру моментов в заданной си-
стеме. Этот метод в матричной форме сводится к перемножению
28'1
трех матриц. В самом деле г ^реход от изгибающих моментов к
упругим грузам осуществляется с помощью матрицы упругих
грузов
W = BwM.	(VII.58)
В свою очередь от упругих грузов к фиктивным моментам
переходим с помощью матрицы моментов
^=L°MW.	(VII.59)
Подставляя значение W по равенству (VII.58) в равенство
(VII.59), получаем:
4 = L*MBWM.	(VII. 60)
Если это равенство применить не для векторов, а для матриц
влияния, то вместо равенства (VII.60) получим:
L\ = L^BwL\u	(VII.61)
где Lm — матрица влияния моментов в фиктивной системе, ко
торая состоит из двух простых шарнирно опертых
балок, иначе говоря она берется для основной систе-
мы. Мы уже встречались с этой матрицей в предыду-
щем примере;
Bw— матрица упругих грузов. Эта матрица приведена в § 3
гл. V [см. равенства (а) и (Ь)].
Мы будем применять в дальнейшем второй метод. При исполь-
зовании равенства (VII.61) необходимо предварительно выяснить
некоторые особенности вычислений. Будем определять прогибы
в точках 1, 2, ..., 7 при фиксировании единичного груза в этих же
точках. Матрица Ет. будет квадратной матрицей седьмого по-
рядка. При вычислении упругих грузов необходимо, однако,
учесть изгибающие моменты не только в указанных выше семи
точках, но также момент в опорном сечении а. С этой целью мы
будем использовать прямоугольную матрицу Lm порядка
7x8. Таким образом, формальное применение равенства
(VI 1.58) невозможно.
Для простоты решений задачи мы условимся вначале опреде-
лять матрицы упругих грузов не для семи, а для восьми точек.
L*w=BwLm,	(VII.62)
где Bw — квадратная матрица упругих грузов восьмого порядка.
282
D __
4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4 1
1 4
(VIL63)
Таким образом L*w, найденная по равенству (VI1.62), будет
иметь семь столбцов и восемь строк. Третья строка этой матри-
цы определяет величину упругого груза для опорной точки а.
Так как фиктивная система состоит из двух простых балок с
шарниром на опоре а, то опорный упругий груз не будет вызы-
вать фиктивных моментов и его можно не учитывать. С этой
целью мы вычеркнем третью строку из матрицы L'w и, сплотив
ее по вертикали, получим новую матрицу Лщ, которая будет
квадратной седьмого порядка.
Матрица для фиктивной системы состоит из двух прямо-
угольных матриц, полученных для левого и правого пролетов.
	 ‘-М ф —		/0(л) ДМ ф	,0(п) ф		•		
В левом пролете две точки 1 и			2, поэтому для левого пролета				
		d	2 1				
ф —		= Т	1 2	•			
Для правого пролета		5	4 3	2	1		
		4	8 6	4	2		
ф —	d р.	3	6 9	6	3		
	о	2	4 6	8	4		
		1	2 3	4	5		
Таким образом, в отличие		от	т 0	и ьм, определяемой равенством				
(а) § 7, получим.:							
	4	2 0 0		О'	0	0	
	2	4 (	3 0	0	0	0	
	0	0 5 4		3	2	1	
/0	ч ЬМф = — п	0	0 4 8		6	4	2	(VII.64)
и	0	0 3 6		9	6	3	
	0	0 2 4		6	8	4	
	0	0 1	2	3	4	5	
283
Перемножая теперь две матрицы, найдем матрицу влияния
прогибов:
, * _ ,0	, **
—Lm фЬ ц/,
(VII.65)
где Ьмф находится равенством (VII.64), a L*w определяется
описанным выше способом.
Практическое применение равенства (VII.65) легко уяснить из
приводимого ниже примера.
Пример. Рассмотрим систему, рассчитанную ранее в § 9 и
показанную на рис. 141. Это позволит произвести сравнение ре-
зультатов, полученных по двум различным методам, и даст воз-
можность читателю выбрать один из них, который для него
окажется наиболее удобным.
Все размеры системы возьмем такими же, как в примере, при-
веденным в § 9. В табл. И приведены выборочные данные для
решения нашей задачи, которые взяты из табл. 9.
Таблица 11
№ неизвестного	Длина ванты	sin а	COS Ct	р
1	162,788	0,675725	0,735155	1
2	125,300	0,877893	0,478851	1,299186
3	162,788	0,675725	0,737155	1
4	264,608	0,416654	0,909063	0.616660
вычислены
Согласно приведенным в этой таблице данным
элементы матриц Ах; Д2; R~1', Ар; А; Л”1; Lm и М.

0,20294
0,23059
0,00000
0.00000
0,30032
0,23069
0,34253
0,00000
0,00000
0,48772
0,00000
0.00000
1,62348
0,87591
1,50161
0,00000
0,00000
0,87591
0,61725
0,74072
0,30032
0,48772
1,50162
0,74072
3,00000
Согласно равенства (VII.48) находим матрицу:
	0,54340 0,35299	0,35299 0,22930	-0,54340 -0,35299	—0,67012 —0,43531	0,00000 0,00000
л2=	—0,54340	—0,35299	0,54340	0,67012	0,00000
	—0,67012 0.000ОО	—0,43531 0,00000	0,67012 0,00000	0,82640 0,00000	0,00000 0,00000
284
По (VII. 49) легко находим

1
0,76971
1
1,62164
0
0,30032
0,34141
0,00000
0,000(49
0,44444
0,26278
0,39018
0,00009
0,09000
0,55556
0,00000
0,00000
1,42653
0,71757
1,52778
0,00090
0,00090
2,40258
1,29623
2,22222
0,00000
0,00000
2,59028
1,59717
2,25000
0,00000
0,00000
2,10226
1,48144
1,77778
0,00000
0,00000
1,16375
0,87960
0,97222
Для дальнейших вычислений необходимо
ро; А₽. Как и в примере 1 § 9, назначим:
задать величину
др =0,561861, Ро=1О,О.
В этом случае матрица А, вычисленная на основании матриц Ai
и А2 по формуле (VII.46), определяется равенством
/УЗ	0,39955 0,29352	0,29352 0,45031	—0,09671 —0,06282	—0,11927 —0,07748	0.30032 0,48772	
А=—	—0,09671	-0,06282	1.18202	0,99518	1,50161	
Е1	—0,11927 0,30032	-0,07748 0,48772	0,99518 1,50161	0,92649 0,74072	0,74972 3,00000	
Обратная матрица:
	4,86456	-2,85484	0,01793	0,49051	—0,15294
Л-1	EI	—2,85484	5,10068	0,87542	—0,12024	-0,95193
А -=		0,01793	0,87542	2,06665	—1,49778	—0,80874
d?	0,49051	-0,12024	—1,49778	2,69811	0.05396
	—0,15294	-0,95193	—0,80874	0,05396	0,89488
По формуле (V 11.52) находим матрицу влияния лишних не-
известных:
	0,41831	0,07945	0,14389
	0,46093	0,71110	—0,29181
z:=	—0,05518	—0,10302	0,63780
	0,13024	0,11196	0,11810
	0,02680	0.08555	0,25221
0,33902 0,48574 0,49245 0,30362
—0,16800 -0,06531 —0,03009 — 0,01248
1,22658	1,14132	0,68800	0,30134
0,01882 0,55110 0,94429 0,68269
0,11552 0,00481 —0,02933 —0,02358
Каждая строчка этой матрицы содержит ординаты линий
влияния лишних неизвестных в точках 1, 2, 3, ..., 7.
285
Для составления матрицы влияния моментов L*M приведем
матрицы Lm и М. Согласно равенства (а) § 7 имеем:
	4	2	0	0	0	0	0
	2	4	0	0	0	0	0
	0	0	0	0	0	0	0
/0	d Lm ~ —	0	0	5	4	3	2	1
6	0	0	4	8	6	4	2
	0	0	3	6	9	6	3
	0	0	2	4	6	8	4
	0	0	1	2	3	4	5
Во избежание недоразумений отметим еще раз, что приведен-
ная матрица L°m и матрица £«ф, данная равенством (VII.64),
отличается друг от друга. В матрице (VI 1.64) не восемь, а семь
строк. Объясняется это тем, что при определении прогибов нет
необходимости определять фиктивный момент над опорой, так-
как прогиб над опорой равен нулю.
По формуле (VI 1.56) при значениях синусов, приведенных
в табл. 11, получаем:
M = d
0,45048
0,22524
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,29263
0,58526
0,00000
0,00000
0.00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,45048
0,90097
0,67573
0,45048
0,22524
0,00000
0,00000
0,00000
0,13889
0,27777
0,41665
0,55554
0.27777
0,33333
0,66667
1,00000
0,83333
0,66667
0,50000
0,33333
0,16667
Далее по формуле (VII.55) вычисляем матрицу влияния мо-
ментов в заданной системе:
Дм-
0,33441	0,06093	—0,06350	—0,14207	-0,20102	-0,20326	—0,12523
—0,01852	0,17556	—0,02977	—0,05505	-0,07381	-0,07375	—0,04530
—0,02080 —0,08555	—0,25221	-0,11552	-0,00481	0,02933 0,02368
—0,01556 —0,04043	0,35225	0,01526	-0,09467	—0,08329 —0,04415
— а —0,00433	0,00469	—0,04331	0,14598	-0,18458	-0,19594 —0,11200	'
-0,03038 —0,01981	—0,00788	0,10557	0,49676	0,15632	0,02378
—0,05643 —0,04430	0,02755	0,06515	0,17810	0,50858	0,15955
—0,02821 —0,02215	0,01378	0,03257	0,08905	0,25429	0/ 7978
Для вычисления матрицы влияния прогибов L*, вначале
найдем матрицы Lw и £ »-. По формуле (VII.62) с учетом ра-
венства (VII.63) находим:
286
Lw
a
e:
0,21485	0,05989	—0,04729	—0,10389	—0,14532	—0,14780 —0,09104
0,01892	0,11294	—0,07245	—0,07963	—0,08351	—0,07815 -0,04712
—0.02855	—0,03451	—0,11439	—0,08364	—0,03129	—0,00662 0,00088
—0.01556	—0,04043	0,18558	0,01525	—0,09458	-0,08329 -0,04416
—0,01054	—0.00691	0,02852	0,11745	—0,05604	—0,11845 —0,07806
—0,03038	—0,01981	—0,00788	0,10557	0,33009	0,15632 0,02378
—0.04738	—0,03653	0,01935	0,06545	0,21637	0,40749 0,20696
—0,02821	—0,02215	0,01378	0,03257	0,08905	0,25429 0,41311
Путем вычеркивания третьей строки получаем:
d
EI
0,21485 0,01892	0,06988 —0,04729 —0,10389 —0,14632 —0,14780 —0,09104 0,11294 —0,07246 —0,07953 —0,08351 —0,07815 —0,04712
—0,01556	—0,04043	0,18558	0,01525	0,09468 —0,08329 -0,04416
—0,01054	—0,00691	0,02852	0,11746 —0,05604 —0,11845 —0,07806
—0,03038	—0,01980 —0,00788	0,10557	0,33009 0,15632 0,02378
—0,04738	—0,03653	0,01935	0,06646	0,21637 0.40749 0,20696
—0,02821	—0,02215	0,01378	0,03257	0,08905 0,25429 0,41311
Теперь по формуле (VII.61) находим:
r * d3
0.14954 0,08423	0,08423 —0,05568 —0,09580 —0,12538 —0,12458 -0,07640	
	0,09858 —0,06407 —0,08772 —0,10445 -	-0,10137 —0,05176
—0,05568 -	-0,06407	0,17848	0,17138	0,13575	0,10799 0,06089
—0,09580 -	-0,08772	0,17137	0,32751	0,35618	0,29928 0,16593
—0,12538 -	-0,10445	0,13574	0,36518	0.65265	0,60902 0,34904
—0,12458 -	-0,10137	0,10799	0,29928	0,60903	0.76244 0,50837
—0,07640 -	-0,06176	0,06088	0,16593	0,34904	0,50837 0,46074
Остается	теперь сравнить результаты двух	решений одной и
той же задачи. Матрицы LM и АТ|, приведенные в данном пара-
графе, полностью совпадают с аналогичными матрицами приме-
ра 1 в § 9. Четыре строки матрицы Lx в данном параграфе и оп-
ределяющие усилия в вантах полностью совпадают с ненулевыми
строчками матрицы Луу, полученной в § 9. Полное совпадение
результатов свидетельствует о высокой точности обоих методов.
Необходимо только отметить, что нумерация усилий в вантах не
совпадает. В данном примере номера усилий совпадают с номе-
рами лишних неизвестных, а в § 9 эти номера совпадают с номе-
рами точек, к которым прикреплены ванты.
ГЛАВА VIII
СОБСТВЕННЫЕ КОЛЕБАНИЯ
ВИСЯЧИХ МОСТОВ
§ 1. ОБЩИЕ ЗАМЕЧАНИЯ
Проблема собственных колебаний висячих мостов, как было
сказано в первой главе, решена сравнительно недавно. Однако
решение в основном проводилось для мостов с балкой жесткости
постоянного сечения. Кроме того, в большинстве работ даются
приближенные решения, в которых, как правило, не учиты-
вается динамическая добавка к распору, возникающая от сил
инерции.
Для случая когда балка жесткости имеет переменное сечение
и учитывается динамический распор, нахождение частот и форм
колебаний представляет собой сложную задачу, связанную с ин-
тегрированием сложных дифференциальных уравнений с пере-
менными коэффициентами.
Подобные задачи не решаются в замкнутом виде, поэтому
приходится применять вариационные методы и применять при
этом вычислительные машины.
При изучении собственных колебаний висячего моста, так же
как и при расчете на прочность, будем предполагать, что от дей-
ствия постоянной нагрузки изгибающие моменты в балке жестко-
сти равны нулю. Такое условие, как уже выяснялось ранее, может
быть обеспечено при навесной сборке, когда замыкание подве-
шенных к кабелю звеньев балки жесткости производится после
того, как все работы по сборке пролетного строения полностью
закончены.
Несмотря на то, что балка жесткости будет иметь переменное
сечение, мы будем предполагать, что масса 1 м длины пролетно-
го строения моста постоянна по всей длине.
Такое допущение не является противоречивым. Дело в том,
что погонная масса складывается из массы всего пролетного
строения, в которую входят массы: проезжей части, настила, пе-
рил, покрытия проезжего полотна и т. д. Масса самой балки
жесткости, хотя и является переменной, ее доля составляет незна-
чительную часть от общей массы моста.
288
В расчетах на прочность мы считали, что задача относитель-
но продольной оси моста является симметричной, т. е. нагрузка
в поперечном направлении расположена симметрично. Это поз-
волило один кабель и одну несущую балку рассматривать как от-
дельную плоскую систему. В связи с этим все геометрические
размеры — моменты инерции балки, площадь кабеля, а также
силовые величины — распор, изгибающие моменты, постоянную
и временную нагрузки — следует определять для половины
моста.
При изучении колебаний мы имеем дело с пространственной
задачей (например, при крутильных колебаниях), поэтому сле-
дует особо оговорить обозначения, принятые в настоящей главе.
Будем обозначать:
g — интенсивность постоянной нагрузки, прихо-
дящейся на один кабель (т. е. для половины
поперечного сечения моста);
Hg—распор от постоянной нагрузки в одном
кабеле;
EI (х) — жесткость одной несущей балки в произволь-
ном сечении;
EIw(x) и GId(x)— секториальная жесткость и жесткость чисто-
го кручения, подсчитанные для всего попе-
речного сечения (включая обе балки жест-
кости) ;
А/7Т)(/) —дополнительный распор от инерционных сил
при изгибных колебаниях, возникающий в
одном кабеле;
— то же, в одном кабеле при крутильных коле-
баниях;
т—масса одного погонного метра половины
моста, т. е. масса, приходящаяся на один
кабель (на 1 м длины всего моста масса со-
ставит 2 т).
В настоящей главе для решения поставленной задачи при-
меняются два метода: вариационный метод Бубнова — Галер-
кина и численный метод, который применялся в предыдущих
главах.
Это позволило, с одной стороны, установить двойной контроль
получаемых результатов и, с другой — расширить класс решае-
мых задач. Обнаружилось, что каждый метод имеет свои пре-
имущества и свои недостатки. Поэтому в тех случаях, когда один
из методов вызывал затруднения, другой — оказывался более
удобным.
Все вычисления проводятся в матричной форме, что позволи-
ло широко использовать вычислительные машины.
10—3802
289
§ 2. ВЫВОД ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
Рассмотрим однопролетный висячий мост с балкой жестко-
сти переменного сечения, обладающий двумя осями симметрии,
продольной осью и поперечной, проходящей через середину мос-
та (рис. 151).
Рис. ibl.
При колебаниях моста произвольное поперечное сечение пере-
мещается по вертикали на величину т](х, /), по горизонтали —
на величину и(х, t) и поворачивается на угол 0(х, t), как пока-
зано на рис. 152.
Таким образом, пролетное строение испытывает изгибные ко-
лебания в двух плоскостях и крутильные колебания вокруг про-
дольной оси моста.
В большинстве случаев горизонтальными перемещениями и
можно пренебречь, так как они значительно меньше вертикаль-
ных перемещений. Масса кабеля в десятки раз меньше массы
пролетного строения, поэтому инерцию кабеля учитывать не бу-
дем, а его массу присоединим к массе моста. Удлинениями под-
весок, как и ранее, пренебрегаем.
При сделанных допущениях собственные изгибные и крутиль-
ные колебания можно рассматривать, как показано на рис. 153.
При изгибных колебаниях суммарное усилие в подвесках, пе-
редающееся на балку с одного кабеля (рис. 153, а), найдется из
условия равновесия элемента кабеля:
290
Раскрыв скобки и учтя собственный вес g, а также связь
е дх2
~ё,
найдем дополнительные усилия, действующие на балку:

д-т^ (х, t) I
~дх* J ‘
(VIII.1)
Присоединив к этому выражению силу инерции —	^х-
а также силу упругости —
нение изгибных колебаний:
02т] (х, /) 1
дх~ I ’
получим урав-
<?X2 [	Йх2 J 8 dx?	’ [ Px2 ‘ C>x2 J '
-Tm-^(x’-° ^0.	(VIII.2)
При крутильных колебаниях (рис. 153, б) усилия, передаю-
щиеся с каждого кабеля де (/), образуют пару:
те(/) = 6^е(/).
Величину 7в (0 можно определить по формуле (VIII.1), под-
ставив в нее вместо A//n(Z) величину	вместо прогиба
Ч(*, /) величину —0(х, /). Таким образом:
°V '	2 <Эх2 '	[ дх^ * 2 <Эх2 J
Следовательно,
т. (/)= -"'1 .	+ ЬЩ, (/) pt+ ± .	'> 1.
°	2 dx'i	U [ ^2	2 dx2 J
Момент от сил инерции:
о 9 Э2в (х, t)
— 2/zzp2-------—-
dfi
(a)
(b)
где р — полярный радиус инерции всего сечения пролетного
строения;
2m — масса одного погонного метра моста.
10*
291
Производную момента как для тонкостенного стержня с пере-
менной жесткостью можно представить выражением
М-= -g_[£/„(х)gfe 'О-------*-[о/Длг)	(С)
дх дх [	дх'л J дх [	дх J
где Е1а — секториальная жесткость всего поперечного сечения;
Gid — жесткость при свободном кручении того же сечения.
Складывая (а), (Ь) и (с), получим дифференциальное урав-
нение крутильных колебаний:
д [г. г	^(х, t) ] д	. dfifx, 01	HgbW(x, t}
77 Г “( } "1^'J" 77 L d ( } j
- ДЯ0 (/) b Г4- 2mp2 ^2e(x’-° - = 0. (VIII.3)
k ’ I dx2 1 2 cW ] '	Й2
В уравнениях изгибных колебаний (VIIL2) и крутильных ко-
лебаний (VIII.3) входят неизвестные величины динамических до-
бавок к распору Д/7г](0 и Д/7е(/), возникающие за счет сил
инерции.
Найдем вначале	используя для этого принцип Лаг-
ранжа, по которому работа внешних и внутренних сил для кабе-
ля от постоянной нагрузки на перемещениях от временной на-
грузки (в данном случае от сил инерции) равна нулю:
1	1 Н
\	t)dx-\---—
J	J	COS Ч
о	о
(f)dx Hg Щ (Q
cos у EF cos <р	cost cost
^1=0.
EF
Учтя, что
ё 8f ’
и обозначая, как ранее (III.21),
i
г dx ,
\  : =W,
J COS3<P
о
получим
i
(/) = а\ J TQ (х, /) dx,
о
(VIII-4)
где
^т]—
/3(р- +
8fEF
2S*
----sec2 t
I
(VIII.5)
292
Коэффициент ц определяется по формуле (111.23), а величи-
на Si* показана иа рис. 151.
Аналогичным образом найдем динамическую добавку к рас-
пору при крутильных колебаниях. Используя формулу (VIII.4),
ь
подставив в нее вместо ц(х, t) величину — 0(х, t), получим:
z
Д/7е (/)=кв j* 6(л, i)dx,
о
(VIII.6)
где
AbfEF
К9 =-----------——
/	2S*
Z3 (p. 4---- sec2 т
(VIII.7)
Подставляя значения Af/n(0 и AZ?e(/) в уравнения (VIII.2) и
(VIII.3), получим уравнения колебаний висячего моста:
— If7	Z)] Н ^(х’ ° -к trdx f\dx-F
dxi[ { ) дх^ ]	дх2	дх2 yi(x,t)dx+
0
I
' ^^2r}(x’ t) dh(x, t) f . л, „	/, тттточ
Тт - ,.2	— к-ч 2	\ Ч t) dx=Q). (VIII.8)
с-	Is-X’	»j
0
Elm(x)
d3e (x, t)
dx^
020 (x, t)--b j V e (x /) 2mp2 d2e(x’ f) _
dx2 ) ' ’ ’	1 Г Э/2
0
Z?2k6
~dF~
020 (X, Z) }
----------- \ 6 (*,
0X2 J V
0
Z) dx=0.
(VIII.9)
Последнее слагаемое в каждом из этих уравнений представ-
ляет собой нелинейный член, что затрудняет решение задачи.
Однако указанные слагаемые при изучении малых колебаний
можно отбросить как величины второго порядка малости. Таким
образом, мы приходим к следующим уравнениям:
[EI (х)	_ Hs	-2»-	(х, t) dx 4-
0X2 I V 0x2	0X2	’ 0X2 J
0
+ /П'^2 Л =0’	.(VIII.1O)
293
д
дх
EIW (х)---(х- °]
<3x3 J
д
дх
CId(x)^JY
дх
Hg№
2
дЩх, t)---ЬК9^-У [б(х t)dx^2mp2	(VIII. 11)
дх2	dxi J v	*	dfi
о
Обозначим соп — частоту собственных изгибных
сое — то же, крутильных колебаний.
Положим:
TQ (X, /) = 7j • sin (o>Tj/ -L v)
6 (х, f) = 6 sin -j- v)
колебаний
(VIII. 12)
где г] и 0 являются функциями только абсциссы х.
Подставив выражения (VIII.12) в уравнения (VIII.10) и
(VIII.11), сократив все члены первого уравнения на sin(cor/+v)
и второго на sin(toe^+v), а также для сокращения записи
приняв:
£/(х)=£7;	GId(x)=GId,
получим обыкновенные дифференциальные уравнения:
-HUei
dx'2 \ dx2 / Ё dx2
i\//.r	-----mw2-n— 0;
71 dx>
(VIII.13)
rf f r? j d3G \ d / r df) \ b dg
----- I	' I I d I Z
dx V dx3 ) dx\ dx / .	2
X _^L _ яе	0.
dx^	dx2
(VIII.14)
Величины А// теперь уже не зависят от времени и имеют вид:
— j" -qdx]
о
i
j* Odx.
о
(VIII-15)
(VIII.16)
Точное решение уравнений (VIII.13) и (VIII.14) вызывает
большие трудности. Наиболее удобными оказались два метода:
вариационный метод Бубнова — Галеркина, который применяет-
ся в § 3, и численный метод, изложенный в § 7.
При изучении изгибных колебаний применяются оба метода,
что позволило иметь двойной контроль и обследовать точность
обоих методов. При изучении крутильных колебаний применяется
только метод Галеркина, который оказался удобным и достаточ-
но точным.
294
§ 3. ПРИМЕНЕНИЕ МЕТОДА ГАЛЕРКИНА
К ОПРЕДЕЛЕНИЮ СОБСТВЕННЫХ ЧАСТОТ
И ФОРМ ИЗГИБНЫХ КОЛЕБАНИЙ

Применим метод Галеркина для решения дифференциального
уравнения изгибных колебаний висячего моста с балкой жестко-
сти переменного сечения и с учетом динамической добавки к рас-
пору. возникающей за счет сил инерции (VIII.13):
J2
d^
djfi

dx^ ч ‘
Иначе это уравнение можно записать так:
EI	+	^=0.
dx* dxdx'A \ dx- 8) djfi	dx? 4
(VIII.17)
Произведем замену переменной, положив лх =<р:
dK...   лл'
dxK	1К
dK
(к=1, 2, 3, 4,..
d<fK v	’ z’
и условившись производные по новой переменной ср обозначать
штрихами, после преобразования уравнения (VIII.17) и сокра-
л4
щения всех его членов на ——— получим:
Eh^ 4- 2£/\ш4- (—
к	л2
Д/^/2
Я2
У------7—7i = o-
Л4
(VIII.18)
В соответствии с методом Бубнова — Галеркина зададим:
= 2 а«8‘ПА:?-	(VIII.19)
лг=1
Подставляя это выражение в формулу (VIII. 15), найдем зна-
чение динамической добавки к распору, которая возникает за
£чет сил инерции:
с ,къ VI г
д/7^ = Д'Т( \t\dx =---\л ак \
О	к = 1	о
295
При нечетных и четных значениях	к величина	интеграла раз-
лнчна:		
7С		
sin тсртАр—— (лг=1, J	к 0	3, 5, .. .),	
1С		(VIII.20)
sin/cpd<p=O (/<—2,	4, 6,.. .).	
0		
Поэтому окончательно находим:
«=1,3,5
Переменную жесткость балки можно представить в следующем
виде:
EI = EIO(1 -J-aiSin<p4-a2sin3cp).	(VIII.21)
Влияние коэффициентов cti и сс2 на закон изменения жестко-
сти легко представить из рис. 154. Варьируя значениями постоян-
ных «1 и а2, можно с достаточно большой точностью апроксими-
ровать тот или иной закон изменения жесткости балки.
Рис. 154.
Учтя, что •
п
т/ v= 2 к4ак sin ну
Л = 1
п
11 = — £	ак cos /ср
№=1
П
— — У, № а,£ sin /ср
«=1
(VIII.
296
и подставляя значения (VII.19, VI1.21, VII.22) в дифференциаль-
ное уравнение (VIII. 18), учтя также при этом, что у" ^с—=
уч у
=— —, после сокращения всех членов на EIq вместо нуля полу-
312
чим некоторую величину:
п
£ Cf) — (1 “Fai s’n ? т а2 sin 3?) У акк4 sin лчр— 2 (ах cos <р ф-
ЛГ = 1
п
фЗа2 cos 3<р) У аккг cos лхр ф-(04 sin ср ф- 9а2 sin Зсрф р) X
к = 1
п	р п	п
a^sinwcp-l-— £	-----У a^sin/op. (VIII.23)
_	2	/с X
к—1	«=1,3,5	«=1
Здесь
(VIIL24)
л2£70
32//з/<
Рч =---------—
' ЗРЕ/0
1	та>^14
X	Л4Е/0
Для определения постоянных ак(к=\, 2, 3, ..., п), согласно
методу Галеркина, будем иметь следующую систему линейных
уравнений:
г.
J £ (<р) sin <pofcp = O
о
У г (<р) sin 2<р jep = О
6
(VIII.25)
У s(cp) sin ncpcfcp = O
о
Система уравнений (VIII.25) после всех выкладок даст нам си-
стему п однородных канонических уравнений по отношению к по-
стоянным ак:
297
Гllal~hrI2a2~^~'  --h rinan— 0
rl\a\ + r22a2 -t"  -Ь Г2nan— 0
(VIII.26)
Гп1а14~Гл2а2+ ' rnnan ----0
Для определения частот колебаний необходимо приравнять
нулю определитель системы (VII 1.26).
Если в величине е(<р) все значения а, кроме а к,положить
равными нулю, а значение ак принять равным единице и полу-
ченное при этом значение е(<р) обозначить ЕЛ(<р), то коэффициен-
ты гKi можно определить по формуле
rKi = j ч (?) sin /с? Jcp,
6
(VIII.27)
где
ек (<р) = (1 -J- ос 1 sin tp ф я2 si*13?) л4 sin др —
— 2 (ot] COS ср -ф За2 COS Зр) Л3 COS Др 4-
-ф(й1 sin а-ф9а2 sin Зр-фР)л2 sin дер-—sin дер фр —— . (VIII.28)
X	‘2 к
В последнем слагаемом
д=1, 2, 3...
Легко заметить, что при вычислении интеграла (VIII.27) мы
встретимся с двумя различными случаями: случай i^=K и слу-
чай i = к. В силу ортогональности функций sin мр и sin Дф при 1фк
имеем:
sin др-sin zp Jp - 0.	(VIII.29)
о
Во втором случае при 1=к
к	к
sin дер • sin /<р Jcp= sin2 др Jp= -5-.
о	о
(VIII.30)
Это замечание касается только трех слагаемых, входящих
в формулу (VIII.28) для ък (<р), а именно, слагаемых, содержа-
щих величины р, —, а также слагаемого д4 sin д<р, которое воз-
X
никает при раскрытии первой скобки.
Вычислив значения rf i при /#=д, мы легко построим матрицу
значений этих коэффициентов, а затем к диагональным элемен-
там этой матрицы добавим три, указанных выше, слагаемых,
298
найденных при 1=к. Таким способом будет получена полная ма-
трица коэффициентов гкь входящих в систему канонических
уравнений (VIII.26).
Итак, найдем вначале гЛ/, положив 1=£к:
'Х=--“1(«4+*лг)
o'
sin © - sin хер • sin z‘<p dy -p
ф- a2 (zc^4” 9№) \ sin 3© sin /<© • sin itp dy — 2at№ \ cos © - cos ку • sin z© X
о	0
X dy— 6a0№ \
d
cos Зср-cos лхр-sin z© dy -j-pT|A riK
(VIII.31)
Необходимо отметить, что значения интегралов, входящих в
это выражение, разные при разных i и к. Так, например, послед-
нее слагаемое справедливо только при нечетном к, а при чет-
ном к оно отпадает. Это условие вытекает из равенства
(VIII.20).
Вычисления показывают, что для случая, когда к+i—-число
нечетное, все четыре интеграла, входящие в (VIII.31), равны
нулю, а в том случае, когда к + i— четное число, эти интегралы
имеют следующие значения:
«1 =	Г sin ср • sin zeep • sin iy dy =	-			, (VHI.32) J	i — (к — z)2	1 — (к + z)2 0
S2~ 0	l sin 3© - sin ку • sin z© zZ© =	-			, (VIII-33) J	‘	9- (K —Z)2	9-(*+02	4
53 =	( cos © • cos zz© • sin z© dy = —	*.+ 1_ z vill.34) J	1—(ЯГ —Z)2	l-(K-H)2 0
7U 0	cos 3cp-coswep-sin i©-t/© = —-— 		—K~ 1— . (VIII.35) 9 — (к — z)2	9 - (к 4 z)2	4
Найдем теперь выражение
= sinzcpz/cp
о
(Л = 1, 3, 5,...).
299
Учитывая, что
к
о
sin /ср d<? = — (/=1, 3,5,...),
о
sin/ср dcp = О (/ = 2, 4, 6,...),
о
получим:
(« = 1, 3, 5,...;
’ ix
к— 1, 3, 5,...),
(VIII.36)
«=2, 4, 6,...).
Таким образом, Дггк при четных / и к равно нулю.
Значения интегралов (VIII.32—VIII.36) могут быть вычисле-
ны заранее для разных i и к. Ниже приводятся матрицы Si, S2,
S3, S4 и — для случая, когда числа / и к последовательно
изменяются от 1 до 6. Эти матрицы не зависят от параметров
задачи и поэтому вычисляются один раз.
S1 =
-1-1,333333 + 0,000000 —0,266667 + 0,000000 —0,038095 + 0,000000
+0,000000 +1,066667 + 0,000000 —0,304762 + 0,000000 —0,050793
—0,266667 + 0,000000 +1,028570 + 0,000000 —0,317460 + 0,000000
+0,000000 —0,304762 + 0,000000 +1,015870 +0,000000 —0,323232
—0,038095 4-0,000000 —0,317460 + 0,000000 +1,010100
+0,000000 —0,050793 + 0,000000
—0,323232 + 0,000000
+0,000000
+ 1,006990
(VIII.37)
-0,266667 + 0,000000 +1,028570 + 0,000000 —0,317460 + 0,000000
+0,000000 + 0,761905 + 0,000000 + 0,755555 +0,000000 —0,374026
4-1,028570 +0,000000 + 0,444444 + 0,000000 + 0,654545 + 0,000000
+0,000000 +0,755555 +0,000000 + 0,387879 + 0,000000 + 0,632967
—0,317460 +0,000000 +0,654545 + 0,000000 + 0,366300 + 0,000000
+0,000000 —0,374026 + 0,000000 + 0,632967 4-0,000000 + 0,355556
(VIII.38)
з
+0,666667 4-0,000000 + 0,933333 + 0,000000 + 0,438095
+0,000000 4-0,266667 4-0,000000 +0,838095 + 0,000000
—0,400000 + 0,000000 4-0,171429 +0,00X00 + 0,793651
+0,000000 -0,495238 +0,000000 + 0,126984 + 0,000000
—0,095238 4 0,000000 —0,539683 + 0,000000 + 0,101010
+0,000000 -0,139683 + 0,000000 —0,565657 + 0,000000
4-0,000000
+0,393651
+0,000000
+0,767677
+0,000000
+0,083916
(VIII .39)
300
-0,400000 + 0,000000 + 0,171429 +0,000000 +0,793651 +0,000000
+ 0,000000 + 0,571429 + 0,000000 —0,177778 +0,000000 +0,716883
+0,971429 + 0,000000 + 0,222222 +0,000000 —0,254545 +0,000000
+0,000000 + 0,622222 + 0,000000 + 0,145455 +0,000000 —0,290110
-0,349206 + 0,000000 + 0,545455 +0,000000 +0,109890 +0,000000
+ 0,000000 —0,425974 + 0,000000 + 0,509890 +0,000000 +0,088888
(VIII .40)
Определив по равенствам (VIIL36) величины составим
матрицу Л/?:
	1	0 1/3	0 1/5	0	
	0	0 0	0 0	0	
	1/3 0 1/9	0 1/15 0	
	0	0 0	0 0	0	(VIII.41)
	1/5 0 1/15 0 1/25 0	
	0	0 0	0 0	0	
Теперь найдем добавочные слагаемые к диагональным эле-		
ментам. Для этого, как было сказано, положим / = к и найдем
коэффициенты при 0, —, а также слагаемое, соответствующее
Л
первому члену, содержащемуся в выражении (VIII.27), которое
равно выражению /с4 sin кер dy.
о
Учтя равенство (VIII.30), получим:
\к=-~- + ^2~
1 л
X 2 ‘
Таким образом, имеем:
rKi=ai (л4 + к2) + а2 (к4 + 9№) $2 2ai«3s3 —
— 6а2/Л4 — p^rKh	(VIII .42)
v (“4 + Р*2 —+ а1 (,<4	51 + а2<*4 +	52 ~
1 = к 2 \	Л J
— 2aj№s3 — 6a2K3s4 Ыкк,	(VIII .43)
где
^rKK = LrKl при к—1.
В дальнейшем целесообразно ввести новое обозначение: пусть
301
Учитывая формулу (VIII.24) найдем:
Zo =-------'^EkF—--------- ‘	(VIII.44)
л6 4- - — sec2 т j EIо
При этом обозначении последний член, входящий в выраже-
ния г К1 и г кк, будет записан в виде
— z^Ki.
С)	V nt
Составим теперь матрицу С коэффициентов г, входящих в
систему уравнений (VIII.26). Для этой цели используем выра-
жения (VIII.42) и (V1II.43) с учетом нового обозначения
(VIII.44):
1
х
c=-|(g1+₽G2
-ф a] (G3S! — G4S3) -ф
Е

(VIII.45)
Матрицы 51,2,3,4 уже были приведены, диагональные матри-
цы имеют элементы:
{G5U=k4 + 9№;
{G2U=№; (G4U = 2v3; {G6U = 6.A	(VI1I.46)
V-fG^-G^);	(VIII.47)
Л
£г = — (С5Х,-6Д).	(VIII.48)
Л
Для определения частот необходимо определитель матри-
цы С приравнять нулю. После сокращения на—— представим
его в виде:
R-—E =0,
А
(VIII.49)
где
/? = /?,+A/?.	(VIII.50)
Уравнением (VIII.49) пользоваться неудобно, так как наи-
большему корню этого уравнения соответствует наибольшая
частота колебаний. Целесообразно это уравнение представить
в другом виде. Определив вначале обратную матрицу
А =/?-’,	(VIII.51)
302
вместо выражения (VIII.49) запишем:
|Л—7.ZT| =0.
(VIII.52)
Таким образом, задача свелась к решению характеристиче-
ского уравнения (VIII.52). Для решения этого уравнения мы
будем применять в дальнейшем стандартные программы, со-
ставленные для машины «Сетунь» и «Урал-2».
Заметим, что все матрицы О2, В\, В2 и AR могут быть вы-
числены заранее, так как они не зависят от параметров систе-
мы. Приведем эти матрицы для случая, когда in к изменяются
от 1 до 6. В этом случае все матрицы будут шестого порядка.
Вычисления дают:
81
256
625
1296
1
4
9
16
25
36
Матрицы В[ и В2, так же как и Sb S2, S3, S4, вычислялись на
машине «Сетунь». Вычисления привели к результатам:
г-1-0,848827
+ 0,000000
(-1,527890
1— +0,000000
—0,606305
I -I- 0,000000
+0,000000 —1,527890
+ 10,86500 + 0,000000
+0,000000 + 53,03950
—12,41710 +0,000000
+0,000000 —45,47290
—4,656420 4-0,000000
+•0,000000 —0,606305 +0,000000
—12,41710 +0,000000 —4,656420
+ 0,000000 —45,47290 4-0,000000
4-165,5620 +0,000000 —118,5270
+0,000000 + 401,9070 + 0,600000
—118,5270 4-0,000000 +830,8290
—0,169765 + 0,000000 + 5,893280
+0,006 ОС 0 +7,760700 + 0,0000^0
+5,893280 + 0,000000 + 22,91830
+0,000000 + 28,97330 +-0,000000
—5,052530 +О.СООССО +93,75680
+0,000000 -34,28820 +’0,000000
+ 0,000000 —5,052554 + 0,000000
+28,97330 4-0,000000 —34,28820
+0,000000 + 93,75680 + 0,000000
+63,21440 +0,000000 +232,1050
+0,000000 4-145,7460 +0,000000
+232,1050 4-0,000000 4-293,3550
В
Z?2 =
Дальнейшее решение задачи возможно лишь при учете кон-
кретных данных той или другой задачи. Частоты и формы коле-
303
баний будут зависеть от величины 0, учитывающей значение
распора Ле, пролета /, жесткости балки Е10, величин сц и а2, ха-
рактеризующих закон изменения жесткости по длине балки
EI(x) =f(x), и величины г0, зависящей от отношения жестко-
стей кабеля и балки. Коэффициент z0 характеризует собой ди-
намический распор, возникающий в процессе колебаний.
Анализ параметров существующих висячих мостов показыва-
ет, что величина 0 изменяется в диапазоне от 0,1 до 3, а величина
cti и аг — в пределах от 0 до 2. Величина Zo может меняться в
широких пределах.
§ 4. ПРИМЕР ПРИМЕНЕНИЯ МЕТОДА ГАЛЕРКИНА
Для определения частот и форм колебаний висячих мостов
была составлена программа, по которой весь расчет механизи-
рован от начала и до конца. Значения параметров 0, он, аг и Zq
могут меняться с пульта по желанию расчетчика.
Прежде чем проводить общий анализ этой задачи, приведем
один пример. Положим: 0=1, ai = 0,8, а2=0,6, г0=5О.
Машина выдает сразу окончательный результат в виде частот
и форм колебаний. Однако представляют интерес некоторые про-
межуточные результаты, которые легко получить, остановив ма-
шину в нужном месте программы и выдав на печать необходимые
данные.
Приведем некоторые данные для рассматриваемого примера.
Так, например, матрицы R и А будут иметь вид
+52,57720 +0,000000 +18,98030
+0,000000 +33,34840 +0,000000
+ 18,98030 +0,000000 +151,7380
+0,000000 +7,450270 +0,000000
+6,483440 +0,000000 +23,20910
+0,000000 —24,29810 +0,000000
+0,000000 +6,483430 + 0,000000
+7,450270 + 0,000000 —24,29810
+0,000000 +23,20910 +0,000000
+442,3780 + 0,000000 +44,44110
+0,000000 +1060,970 +0,000000
+44,44110 +0,000000 +2172,680
А = 10“4
+ 199,239 +0,000000 —24,8188
+0,00000 +303,641 +0,00000
—24,8188 +0,000000 +69,2161
+0,00000 —5,46608 + 0,00060
—0,67461 +0,00000 —1,36248
+0,00000 + 3,50758 + 0,00000
+ 0,000000 —0,67461
—5,46608 +0,00000
+ 0,000000 —1,36248
+22,7498 +0.00000
+0,00000 +9,45949
—0,52647 +0,00000
4-0,000000
+3,50758
+0,00000
-0,52647
+0,00000
+4,65262
Согласно последней из формул (V1II.24)
представим в следующем виде:
частоту колебаний
1

Л2
/2
£/о
т
304
Обозначив
1
V *
получим
(VIII.53)
Ниже приводится вектор л+, выданный электронной машиной:
5,73739
7,00455
->	12,4343
К<°~ 21,0096 '
32,5820
46,6271
Таким образом, первые шесть частот колебаний составят:
21,010л2 , Г ElQ
«>4 =----------1/	------
/2 у т
32,582л2 , / £/0
-- --------- I /
/2	|/ т
_ 46.627л2 Г Е10
6 Г- |/ т
Согласно выражению (VIII.19) формы колебаний будут оп-
ределяться функцией
лх ।	. 2лх ,	,	. блх
= sin —— а2 sin—------ф •• • -ф а6sin—-— .
Значения коэффициентов	2, 3, ..., 6) для каждой час-
тоты будут свои. Они представляют собой координаты собствен-
ных векторов матрицы А, также вычисляемые машиной. Эти век-
торы в свою очередь образуют матрицу а, которая для рассмат-
риваемого примера имеет вид
-1-0,000000 +1,000000 +0,184311
+1+00000 +0,000000 + о, оооооо
+ 0,000000 -0,184368 +1,000000
—0,019471 +0,000000 + 0,000000
+0,000 00 —0,002179 —0,026926
+0,011760 + 0,000000 + 0,000000
+ 0,000000 +0,006910 +0.000000
+ 0,019767 + 0,000000 —0,011265
+ 0,000000 + 0,025657 + 0,000000
+ 1,000000 + 0,060000 —0,025619
+0,000000 +1,000600 + 0,000000
—0,025393 +0,000000 +1,000000
Каждый столбец этой матрицы дает значения коэффициентов
для соответствующей частоты. Первая, четвертая и шестая фор-
305
мы являются кососимметричными. Этим объясняется то, что
коэффициенты а\, а3 и а5 равны нулю. Для симметричных форм
(вторая, третья и пятая) коэффициенты «2, «4 и равны нулю.
Приведем два уравнения двух (первой и второй) форм коле-
баний, которые составляются на основании первого и второго
столбцов матрицы а:
= sin — — 0,019471 sin4-0,011760 sin ;
I	I	I
В программе предусмотрено вычисление ординат всех шести
форм колебаний. Для рассматриваемого примера ординаты ука-
занных форм приводятся в табл. 12.
306
Таблица 12
1	2	3	4	5	6
+000000-30	+000000 -30	+000090—30	+ 000000—30	+ 000000—30	+000003-30
+494897+ 00	+ 126347 + 00	+728801 + 00	+ 850616+00	4 985856+00	+ 101655+01
+849163+00	+ 314543+00	+ 107869 + 01	+ 883144+00	+529112 + 00	+124309-01
+ 988240 тОО	+ 578279 + 00	+856474 + 00	+451594—01	—684078 + 00	—101127+01
+ 882888+00	+ 867912+00	+ 182937+00	-848907+00	— 860041 + 00	—319424—01
+ 528623-) 00	+ 109573+ 01	—536045 + 00	—881535 + 00	+247352 + 00	+ 972181+00
+ 7510:3-07	4 118219+01	+842615+00	-151255- 06	+ 981253+ 00	+2122р4—06
-528623 + 00	+ 109573+01	-536045+00	+ 881535+00	+247352+-00	-972181+00
-882888+00	+867912+00	+ 182937+00	+848907+00	—8₽0041 у 00	+ 319421-01
—988240 + 00	+ 578279 + 00	+856474 + 00	-451592- 01	—684078 + 00	+ 101127+01
-849163+00	+31+43 + 00	+ 107869+01	—883144+ 00	+529112+00	—124308-01
-494897+00	+ 126347+00	+728802 + 00	—850616+00	+ 985856 + 00	-101655+01
-149453-06	+292450-07	+223826- 06	—138827—06	+222863 -06	-443493-06
, По данным этой таблицы изображены формы колебаний, по-
казанные на рис. 155.
Электронная машина позволяет вести расчет с весьма высо-
кой точностью, которая в методе Галеркина зависит от числа
удерживаемых членов в ряде (VIII.19). Анализ этого вопроса
производится в следующих параграфах.
§ 5. АНАЛИЗ ТОЧНОСТИ МЕТОДА ГАЛЕРКИНА
Точность метода Галеркина легко проверить, изменяя число
членов ряда (VIII.19) в выражении прогибов:
п
£ a^sin/ctp.
К=1
С помощью электронной машины не составляет труда решить
эту задачу, последовательно применяя в выражении г] постепен-
но увеличивающееся число слагаемых. В табл. 13 приводятся
значения частот колебаний для рассмотренного выше примера
(р — 1, 01 = 0,8, о2 = 0,6, Zq= 50).
Таблица 13
Число членов, удерживаемых в ряде (VIII.19)
1	о	3	4	5	6
		5,77481	5,77481	5,76305	5,76305	5.73739
7,25102	7,25102	7,00488	7,00488	7,00455	7.00455
—-	—	12,4598	12,4598	12,4343	12.4343
—	—	—	21,0361	21,0361	21,0096
.—-	——	-—	—	32,5820	32,58'0
		—	—	—	46,6271
307
Примечание: все члены таблицы умножить на_ _|
Z2
(VII.19) будет бо-
ограничиваясь од-
частоту, а вторую,
частоте соответст-
двум полуволнам.
EIq
т
Из табл. 13 видно, что для рассмотренного1 частного примера
частоты колебаний при увеличении числа членов в ряде (VIII.19)
изменяются незначительно. Однако расчеты показывают, что та-
кое заключение нельзя распространить на все случаи, которые
могут встретиться в висячих мостах.
Оказывается, что при увеличении коэффициента z0 падение
точности с уменьшением числа членов в ряде
лее значительным. Интересно отметить, что,
ним членом ряда, мы определяем не первую
При заданном значении 2о = 5О наименьшей
вует кососимметричная форма колебаний по
Колебания по одной полуволне происходят, для данного приме-
ра, при второй частоте.
В § 6 показано, что при очень маленьких значениях величины
20 первой частоте могут соответствовать колебания по однознач-
ной симметричной кривой. Такие случаи в реальных мостах
могут встретиться крайне редко. Из табл. 13 видно, что изменение
значений той или иной частоты происходит при изменении числа
членов ряда (VIII. 19) на два. Объясняется это тем, что каждый
член ряда (VIII.19) оказывает влияние либо только на симмет-
ричную, либо на кососимметричную формы изгиба. Так, напри-
мер, добавив в ряд (VI И. 19) член a?sin , мы
прямосимметричной формы изгиба, а следовательно, и не изме-
ним частоты, соответствующие прямосимметричным формам ко-
лебаний.
Проследим теперь, как меняются формы колебаний в зави-
симости от числа членов ряда (VIII.19). Проделаем это только
для первой и второй частот. Ординаты форм колебаний приведе-
ны в табл. 14.
Из табл. 10 видно, что формы колебаний при увеличении чис-
ла членов в разложении кривой изгиба (VIII.19) постепенно
не изменим
уточняются.
Для обеих, приведенных в табл. 14, форм лишь первое при-
ближение является грубым, а дальнейшее уточнение незначитель-
но. Интересно отметить, что для частот с более высоким номером
(например, для пятой или шестой частоты) уточнение форм ко-
лебаний является более значительным, в то время как значение
частоты практически не изменяется. В этой таблице указывается,
сколько членов ряда (VIII.19) принято в расчете при вычислении
цифр соответствующей колонки.
.308
Таблица 14
№ сечения	Первая форма колебаний			Вторая форма колебаний		
	2 3	4	5	6	7	1	2	3	4	5	6
0	0	0	0	0	0	0
1	0.50000	0,48423	0,50078	0,25882	0,10811	0,10687
2	0,86603	0,85026	0,85926	0.50000	0,26596	0,26607
3	1, ооооо	1,00000	1,00000	0,70711	0,48646	0,48916
4	0,86603	0,88179	0,89339	0,86603	0,73091	0,73415
5	0,50000	0.51577	0,53491	0,96593	0,92554	0,92686
6	0	0	0	1,00000	1,00000	1,00000
7	—0,50000	—0,51577	—0,53491	0,96593	0,92554	0,92686
8	—0,86603	—0,88179	—0,89339	0,86603	0,73091	0,73415
9	—1,00000	,00000	—1,00000	0,70711	0,48646	0,48916
10	—0,86603	—0,88179	-0,85926	0,50000	0,26596	0,26607
11	-0,50000	—0,48423	-0,50078	0,25882	0,10811	0,10687
12	0	0	0	0	0	0
§ 6. ЗАВИСИМОСТЬ ЧАСТОТ И ФОРМ
ИЗГИБНЫХ КОЛЕБАНИЙ ОТ СООТНОШЕНИЯ
ОСНОВНЫХ РАЗМЕРОВ И ЖЕСТКОСТЕЙ МОСТА
Частоты и формы изгибных колебаний висячего моста в зна-
чительной степени зависят от геометрических размеров закона
изменения жесткостей балки, а также от соотношения жесткостей
кабеля и 'балки. Для анализа этого вопроса рассмотрим случай,
когда момент инерции балки изменяется по закону (VIII.21).
В таком случае, частоты колебаний будут функциями следу-
ющих основных величин *:
Н gl~ gH
Р л-2£/0	8/л2£/0 ’
2 [(1^2-2) El0-V2EIl/2 + 2Elll4]
Я1—----------------—-------------
(2 -Ь1/ 2 ) £/0
( /2 - 2) Е10 - V 2 EIll2 + 2£/z/4
а2=	----------------------------•
zo —
(2+1Л2)£/0
512/2££~______
2S*	\
л6 I [J. 4- —— sec2! I EIq
* Эти формулы легко получить из выражения (VIII. 21) и условия, что
, I	I	Рг гг
при х~— и х = — жесткость равна Е1 и Е1 .
4	2
309
Коэффициент р учитывает величину погонной массы моста,
пологость кабеля и абсолютное значение начальной жесткости
балки. Коэффициенты а\ и «2 учитывают закон распределения
жесткости балки по длине пролета. Величина Zo учитывает дина-
мический распор, который зависит от соотношения жесткостей
кабеля и балки, а также основные геометрические размеры
моста.
Для анализа влияния этих величин на частоты и формы коле-
баний проведены вычисления на электронной машине, в которых
последовательно изменялись указанные выше величины. Мы не
будем приводить здесь таблицы полученных результатов, так как
Рис. 156.
они заняли бы очень много места, а ограничимся лишь показом
графиков, построенных на основании этих результатов.
На рис. 156 показаны в пространстве поверхности изменения
частот колебаний для первых шести гармоник в зависимости от
указанных параметров. При построении этих поверхностей рас-
смотрен частный случай, когда ai = cc2 = a, и, кроме того, приня-
то постоянное значение параметра z = 50. Величина ос изменяется
в пределах от 0 до 1 и р от 0 до 4. По вертикали откладывается
не само значение соответствующей частоты, а ее отношение к
частоте того же номера, но при |3 = сс = 0, т. е. к частоте простой
балки постоянного сечения.
Таким образом, получено шесть поверхностей (листов) для ве-
(»1	<о.?	и>к	СО6
личин	—	;	—	. -;	— ;...;	—	. В каждой из этих вели-
Ы]0	<о?0	ыл.о	<о60
чин знаменатель равен частоте этого же номера, найденного для
простой балки постоянного сечения. На вертикальной о ср все
310
шесть поверхностей пересекаются в одной точке с ординатой,
равной единице.
Указанные поверхности являются по существу поверхностями
Папковича, которые широко известны в современной литературе.
Из рис. 156 видно, что ни одна из поверхностей не имеет отрица-
тельной Гаусовой кривизны.
Для того чтобы проследить влияние динамической добавки
распора на частоты и формы колебаний, т. е. величины Zo, кото-
рая при построении указанных выше поверхностей принималась
постоянной, рассмотрим пример, в котором, наоборот, положим
постоянными «1, «2 и р и будем изменять только величину Zq.
Все вычисления проведены на электронной машине. В табл. 15
приводятся значения первых шести частот при различных z0
для случая, когда (3=1, cxi = 0,8, а2 = 0,6.
По данным табл. 15 построен график, показанный на рис. 157.
Из этого графика видно, что динамическая добавка распора,
возникающего за счет сил инерции, оказывает влияние не только
на симметричные формы колебаний.
Таким образом, при кососимметричных колебаниях распор в
кабеле остается постоянным и равным распору Hg-—от постоян-
ной нагрузки. Изменение частот, вернее, коэффициентов при час-
тотах для кососимметричных колебаний оказалось весьма значи-
тельным.
• Интересными являются два фактора, на которых следует ос-
тановиться особо'. Первое обстоятельство заключается в том, что
кривые 1, 3 и 5 пересекают кривые 2, 4 и 6. Наименьшая частота
колебаний при весьма малых 2о соответствует симметричной фор-
ме колебаний. При z0>30 наименьшей частотой является та, ко-
торая соответствует кососимметричной форме колебаний по двум
полуволнам.
311
Таким образом, происходит как бы подмена частот по их
абсолютным значениям. Так, например, при го>35О третья час-
тота становится четвертей и т. д.
Еще больший интерес представляет второе обстоятельство, а
именно то, что формы колебаний при возрастании величины Zo
постепенно как бы перерождаются и переходят одна в другую.
Так, например, если проследить за первой кривой, то мы увидим,
что при малых zo форма колебаний, соответствующая частоте,
изображаемой первой кривой, описывается как бы одной полу-
волной.
Таблица 15
Z о			“s	<u4	“s	
0	1,554	5,737	12,074	21,010	32,549	46,627
10	3,512	5,737	12,127	21,010	32.555	46,627
20	4,684	5,737	12,188	21,010	32,562	46,627
30	5,594	5,737	12,258	21,010	32,568	46,627
	а>2	''1	CO3	CO4	(05	w6
40	6,353	5,737	12,340	21,010	32,575	46,627
50	7,005	5,737	12,434	21,010	32,582	46,627
75	8,297	5,737	12,744	21,010	32,601	46,627
100	9,219	5,737	13,183	21,010	32,620	46,627
150	10,254	5,737	14,437	21,010	32,662	46,627
200	10,696	5,737	15.924	21,010	32,710	46,627
250	10,909	5,737	17,406	21,010	32,765	46,627
300	11,028	5,737	18,811	21,010	32,827	46,627
350	11,102	5,737	20,125	21,010	32,899	46,627
	<О2	“1	<04	co3	“5	“6
400	11,153	5,737	21,352	21,010	32,983	46,627
500	11,218	5,737	23,566	21,010	33,198	46,627
600	11,257	5,737	25,481	21,010	33,502	46,627
700	11,283	5.737	27,094	21,010	33,943	46,627
800	11,302	5,737	28,383	21,010	34,573	46,627
900	11,316	5,737	29.340	21,010	35,424	46,627
1000	11,327	5.737	30,004	21,010	36,474	46,627
1500	11,358	5,737	31,231	21,010	42,778.	46,627
	<о2		<’>4	“3	"6	w5
2000	11,373	5,737	31 ,533	21,010	48,849	46,627
3000	11,388	5,737	31,731	21,010	59,368	46,627
4000	11,394	5,737	31,805	21,010	68,343	46,627
5000	11,399	5,737	31,844	21,010	76,285	46,627
6000	11,401	5.737	31.868	21,010	83,480	46,627
7000	11,403	5,737	31,884	21,010	90,105	46,627
8000	11,405	5,737	31,895	21,010	96,277	45,627
9000	11,406	5,737	31,904	21,010	102,08	46,627
10 000	11,407	5.737	31,911	21,010	107,57	• 46,627
25 000	11,412	5,737	31,946	21,010	169,81	46,627
75 000	11,414	.5,737	31,960	21,010	293,92	46,627
100 009	11,414	5,737	31,962	21,010	339,36	46,627
200 000	11,415	5,737	31,964	21,010	479,87	46,627
312
При дальнейшем возрастании zq в форме колебаний вначале
начинают появляться у опор небольшие участки с ординатами
другого знака, а затем форма колебаний постепенно приближает-
ся к трехполуволновой кривой, т. е. как раз такой, которая при
малых Zq соответствует форме колебаний для третьей частоты.
Последняя в свою очередь при увеличении го перерождается в
одноволновую кривую. Это обстоятельство1 является весьма важ-
ным для практических расчетов.
У реально существующих висячих мостов диапазон изменения
величины zo сравнительно невелик. Для этих случаев встречаю-
щееся в литературе утверждение о том, что наименьшей часто-
те соответствует форма колебаний с двумя полуволнами, вообще
говоря, является правильным. Однако, нельзя утверждать, на-
пример, что третьей частоте соответствует кососимметричная
форма изгиба по четырем полуволнам.
В заключение можно сделать вывод о том, что учет динамиче-
ской добавки к распору обязательно должен производиться.
Отметим еще один момент, который представляет теоретиче-
ский интерес. При возрастании величины Zq площади форм сим-
метричных колебаний уменьшаются и в пределе при zq, стремя-
щемся к бесконечности, они стремятся к нулю. Это обстоятель-
ство легко объяснить с физической точки зрения. Если предста-
вить себе случай недеформируемого кабеля, приняв ЕД—>-оо, то
на основании принципа Лагранжа мы получим:
i
J =
о
Следует также указать на то, что в предпоследней колонке
частота колебаний возрастает безгранично. При некотором зна-
чении г0 она будет уже не шестой, а более высокой частотой. Но
при учете только шести членов ряда (VIII. 19) нельзя установить,
какой частоте соответствуют помещенные в этой колонке цифры.
§ 7. ПРИМЕНЕНИЕ ЧИСЛЕННОГО МЕТОДА
ДЛЯ ОПРЕДЕЛЕНИЯ ЧАСТОТ И ФОРМ
СОБСТВЕННЫХ ИЗГИБНЫХ КОЛЕБАНИЙ МОСТА
Определение частот и форм изгибных колебаний висячего
моста с балкой жесткости переменного сечения легко произвести
также по той общей матричной методике, которая применялась
при расчете на прочность и была описана в гл. V. Применение
этой методики позволит, с одной стороны, проверить точность
полученных ранее результатов по методу Галеркина и, с другой
стороны, расширить диапазон изменения жесткостей балки.
313
Подсчеты показали, что применяемый в настоящем парагра-
фе метод пригоден для любого закона изменения жесткости.
В предельном случае, когда в ряде сечений жесткость балки об-
ращается в ноль, мы автоматически получим частоты и формы
колебаний для комбинированных систем.
Будем исходить из общих уравнений, полученных в гл. V (см.
уравнения V.7 и V.10). Перепишем эти уравнения, внеся неболь-
шие изменения в обозначения:
+	Of-X*?);	(VIII.54)
(VIII.55)
где ц — вектор прогибов балки жесткости в точках 1, 2, ...;
л* — параметр, зависящий от распора:
Х* =-----.	(VIII.56)
(« + 1)£/0
Матрица А, а также величины -q* и у* даны формулами (V.8)
гл. V.
Приведем здесь значения постоянных ос* и р*. В соответствии
с формулами (V.11) и (V.12) получаем:
(п + 1) EIq
8fEF
(п+ 1)*Е/0
(а)
где EIq — жесткость балки на левой опоре;
(/г+1) —число панелей.
По сравнению с формулами (V.7) и (V.10) величины X, а и р
снабжены здесь звездочками. Объясняется это тем, что при изу-
чении колебаний этими же буквами были обозначены характери-
стические числа в вековом уравнении и параметры жесткости
балки. Таким образом, в дальнейшем будут фигурировать X и X*;
а и а*; р и р*, которые обозначают различные величины.
Приступим теперь к выводу уравнений свободных колебаний.
Для случая свободных колебаний вместо временной нагрузки q
теперь мы должны учесть силы инерции
(х, t)
q =. — щ----—------ ,
учтя, что
и
7](Х, /) = 7jSin(0/
(Pfi(x, t)	о 	,
-----!------— — — (О"Г1 Sin Он
,1 ’
314
получим для амплитуд (sin со/ = 1):
7=ты2т].
Заменим распределенную инерционную нагрузку системой
сосредоточенных сил. На рис. 158 показана часть балки и распре-
деленная на этом участке инерционная нагрузка. Для определе-
ния сосредоточенной силы в узле
к необходимо произвести пере-
множение эпюр нагрузки q и тре-
угольной эпюры vK, представля-
ющей собой линию влияния дав-
ления на узел к при узловой пе-
редаче нагрузки. Если предполо-
жить, что на протяжении каждых
двух панелей кривая нагрузки q
очерчена по квадратной парабо-
ле, то вектор инерционных сил
можно определить с помощью
матричного равенства
Рис. 158.
(VIII.57)
где матрица как показано в книге [37], имеет вид
Для вывода уравнений малых колебаний предварительно пе-
репишем уравнение (VIII. 54) в виде
Произведя подстановку вместо X* выражения (VI 11.56) и
вместо т]* и у* их значения (V.8), получим:
z=i
4 =
—» L-_ Д у
(n+l)d3	(п+1)ДЗ	1
1= 1
(VIII.59)
315
Так как рассматриваются малые колебания, то произведени-
Л
ем 5т]Лг] как величиной малой по сравнению с другими членами
Z = 1
можно пренебречь.
п
Для определения суммы Sr], входящей в правую часть равен-
/=1
ства (VIII.59), используем очевидное равенство
п
i = l
где о*—матрица-строка, все элементы которой равны единице:
»* = || 1 1 1 ... 1 1||.
Кроме того, заметим, что
(Viii.60)
1 g (л-Ь l)rf3
В самом деле, учитывая значение а*, а также
то, что
‘	8/’
получим:
(л-|- l)rf3
gl2
d(n+ 1)2
=gd—,vg= const.
Но так как vgLiG=L]Vg, то равенство (VIII.60) доказано. Учиты-
вая изложенное, вместо равенства (VI 11.59) получим:
(£4-a A)^ — L,va------т].
v 1	19 (л + ljrf3
Подставляя вместо vq его значение по равенству (VIII.57),
а также заметив, что произведение ои* представляет собой квад-
ратную матрицу: 1	1	1 1	1	1 аз* — Ва = ............. 1	1	1	(VIII.61)
получим:
(£ + «• А) ^=^£,5,-») -Д.Д.4
(п + 1) ds
Подставляя в это выражение вместо матрицы А
(V.8):
ее значение
А= (n + 1)g/° А|£г<
J2
316
получим:
/Е ^(п+1)£/0 L I^_р J*8/£Z0 . цВа _ю2тцд\ *= о.
\ ' J2	(n + 1) d3	)
Помножив все члены, стоящие в скобках, на L } и заменив
а* и 0* по равенству (а), получим:
-I
_________MfiEF_________
I 2S1
(n + 1 )5 d3 I p. +- —-— sec2 t
Ba~ <S>2mBx \ Tj —0.
Далее учтя, что
^1 — LmB WG Lm,
1* — Г •	/ -1 — /
получим:
________MpEF_________
/ 2Sj
(п + I)5 d3 I н + —— sec2 г
Ba — М2тВ{ \ 7] — (),
(VIH.62)
Так же, как в § 3, обозначим:
ОТсо2/4
X л4£70 ’
г	HS12
Р=--------- ,
‘	л2/£/0
ty^EF_______
2S*	\
>л + —— sec2 т I EIq
(VIII.63)
(VIII.64)
(VIII.65)
z0 =

и, кроме того, перейдем к безразмерным матрицам L2; Bw\ В\.
Эти матрицы отличаются от соответствующих матриц £2; Bw\ Bi
1 5d rd
тем, что у них отсутствуют множители —; -- ; — .
d SEIq R
Подставляя в уравнение (VIII.62) и сокращая все члены на
5rtdEI0
множитель -------- , получим:
L2(k2G гВ^Ь2+№1Е + ?0Ь2Ва)-(VIII.66)
317
где
Пусть
6 / г у ,
5 nd /
?л2
20 (п + 1)
(VIII.67)
где
/?! = Г2 (/г&-ВДГ2 рад.
Обозначим:
C = R~lBx,
тогда вместо выражения (VII 1.66) получим:
(VIII.68)
(С-Х£)т;^0.
Ненулевому значению ц соответствует равенство нулю опре-
делителя
|С-к£|=0.	(VIII.69)
Следует отметить, что величина z0 так же, как и при решении
по методу Галеркина, учитывает влияние динамической добавки
к распору, которая возникает от сил инерции. В отличие от ре-
шения по методу Галеркина эта величина входит во все элементы
матрицы
kR=zQk2Ba.
Однако величина 20, так же как и раньше, оказывает влияние
только на те частоты, которым соответствуют прямосимметрич-
ные формы колебаний. Это обстоятельство легко объяснить. Все
элементы матрицы АТ? равны друг другу и поэтому произведение
этой матрицы на кососимметричный вектор равно нулю. Поэтому
RT]кс ~ (Bl + А/?) Т]лс = Т?Щ КС-
Следовательно, характеристические числа, соответствующие
кососимметричным векторам для матриц В и Bi, одинаковые.
Напомним, что матрица G~l, входящая в Bi, имеет вид
Eli
Е/о
Е19
ER
Е1п
Е10
318
Таким образом, задача свелась к решению векового уравне-
ния (VIII.69), т. е. к определению собственных значений X и соб-
ственных векторов. По характеристическим числам X легко опре-
деляются частоты колебаний:
(VIIL70)
По рассмотренной выше методике была составлена програм-
ма для машины «Сетунь», которая позволила решить множество
задач при самых различных исходных данных.
Для иллюстрации метода вначале рассмотрим пример, кото-
рый был решен по методу Галеркина. Возьмем такой же закон
изменения жесткости балки. Разобьем балку на 12 равных ча-
стей. Примем, как и раньше, р= 1, «1 = 0,8, «2=0,6, zo=5O. Эти
данные вводились в машину как исходный материал. Все коэф-
фициенты и матрицы вычислялись машиной. Программа постро-
ена так, что она позволяет выдать на печать любые промежуточ-
ные числовые материалы, например выдавались матрицы А и R.
Однако приводить здесь эти матрицы мы не будем, так как они
имеют одиннадцатый порядок и займут слишком много места.
Ограничимся приведением окончательного результата. Обо-
значим:
Л2
0)^---I
Найденные машиной коэффициенты Kwi для рассматриваемо-
го примера приводятся в табл. 16 (даются для первых шести
частот).
Таблица 16
1	k оэ	i	К со
1	5,7362	4	20,7827
2	6,9901	5	31,9451
3	12,3393	6	45,1177
В табл. 17 приводятся значения координат собственных векто-
ров, определяющих формы колебаний.
Координаты собственных векторов, приведенные в табл. 17,
округлены до четвертого знака после запятой. По данным
табл. 17 построены кривые шести первых форм колебаний моста,
которые показаны на рис. 159. Естественно, возникает вопрос о
точности полученных результатов. Этот вопрос можно разрешить
двумя путями: во-первых, можно сравнить результаты, получен-
ные для одного и того же примера двумя методами — методом
319
Таблица 17
№ се- чения	1	2	3	4	5	6
0	0	0	0	0	0	0
1	0,5016	0,1000	0,7020	0,9564	0,9203	0,9685
2	0.8578	0,2646	1,0000	0,9351	0,4786	0,0171
3	1,0000	0.4858	0,7916	0,0565	—0,5880	-0,9261
4	0,8929	0,7251	0,1871	—0,8998	—0,8393	-0,1224
5	0,5349	0,9213	-0,5020	—1,0000	0,1876	1,0000
6	0	1,0000	-0,8187	0	1,0000	0
7	—0,5349	0,9213	—0,5020	1,0000	0,1876	-1.0000
8	—0,8929	0,7251	0,1871	0,8998	—0,8393	0,1224
9	—1,0000	0,4858	0,7916	—0,0565	—0,5880	0,9261
10	—0,8578	0,2646	1,0000	—0,9351	0,4786	—0,0171
11	—0,5016	0,1000	0,7020	—0,9564	0.9203	-0,9685
12	0	0	0	0	0	0
Галеркина и численным методом, примененным в насто-
ящем параграфе. Это сравнение производится в § 8. Забегая
вперед, отметим, что совпадение результатов свидетельствует о
хорошей точности, по-видимому, обоих способов.
Рис. 159.
320
Второй способ проверки точности полученных результатов
заключается в решении примера, для которого заранее известно
значение частот и форм колебаний. Положив 0 = ai = a2=zo=O,
мы решим задачу о колебаниях простой балки, шарнирно опертой
по концам. Такое решение проведено и результаты даются в
табл. 18, в которой указывается процент погрешности по сравне-
нию с точным решением.
Таблица 18
№ частоты	Точное решение	Приближенное решение	Погрешности, %
1	1	0,99998	0,002
2	4	3,99872	0,03
3	9	8,98538	0,17
4	16	15,9166	0,52
5	25	24,6761	1,29
6	36	35.0167	2.73
7	49	46,4859	5,12
8	64	58,3608	8.8
Формы колебаний, определяемые собственными векторами, с
высокой точностью совпали с соответствующими синусоидами
. клх „
sin —-—. Эти векторы здесь не приводятся.
Как видно из таблицы, погрешность нарастает с увеличением
номера частоты. Объясняется это тем, что при замене системы с
бесконечным числом степеней свободы системой с п степенями
свободы можно получить хорошее совпадение приближенного
решения с точным только для части спектра частот.
В нашем случае мы заменили реальную балку системой с
одиннадцатью степенями свободы. Из табл. 18 видно, что начи-
ная с 5-й частоты погрешность становится большой и поэтому мы
рекомендуем ограничиваться шестью частотами, найденными
выше. Если потребуется вычислить большее количество частот,
то необходимо увеличить порядок матриц, т. е. разбить балку на
большее число панелей.
С помощью ЭЦВМ практически можно получить любое тре-
буемое число частот и форм колебаний, например до 30—40 час-
тот. Однако в практических расчетах такая необходимость не
возникает.
Рассмотрим теперь некоторые частные случаи.
Первый случай: 0 = 0, ai=0, a2=l. Этот случай соответствует
простой балке на двух опорах х жесткостью, изменяющейся
по закону, графическое изображение которого показано на
рис. 160, а. В среднем сечении жесткость обращается в нуль. Та-
ким образом, практически получается изменяемая система с тре-
мя шарнирами. Естественно, что частота колебаний для такой
11—3802
321
трехзвенной системы равна нулю, а форма колебаний, соответст-
вующая отклонению, имеет вид треугольника, показанного на
рис. 160, б. Для решения этой задачи была использована общая
программа, в которую с пульта были занесены значения пара-
метров. Машина выдала следующий результат:
«,=0,002 —
1	' р
С
Рис. 160.
Собственный вектор, определяющий форму отклонения, при-
веден ниже:
4-000000-1-00
4-i7i;43i 4-оо
4-3428484-00
4-514,2824-00
4-6857194-00
4-8571404-00
4-1000004-01
4-8571404-00
4-6857194-00
4-5142824-00
4-3428484-00
4-1714314-00
^4-0000004-00
Этот вектор перепечатан с ленты, которую выдала машина.
Две последние цифры указывают порядок, а первые — мантиссу
соответствующих координат. На рис. 160, в дано графическое изо-
бражение формы колебаний, которая практически совпадает с
треугольником.
322
Цифры ординат соответствуют прямой линии и лишь в месте
щарнира наблюдается весьма незначительное закругление вер-
шины треугольника. Это объясняется тем, что при нашем законе
изменения жесткости имеется не идеальный шарнир, а постепен-
ное приближение к нему на некотором конечном участке, как по-
казано на рис. 160.
Таким образом, мы видим, что для этого особого частного
случая машина выдала результат, вполне отвечающий физиче-
скому смыслу задачи.
Второй случай: р = 1, ai=0, «2=1, zo=50. Этому случаю
соответствует висячий мост с балкой жесткости переменного сече-
ния, имеющей шарнир в середине пролета (рис. 161). Система
становится как бы «статически определимой». Однако следует
иметь в виду, что при расчете по деформированной схеме ее
нельзя считать статически определимой, так как для ее решения,
так же как и для обычного висячего моста, приходится учитывать
деформацию системы.
Выданные машиной коэффициенты кШг(г=1, 2, ..., 6), соответ-
ствующие частотам колебаний, даны в табл. 19.
Таблица 19
i	к г ан	i	К J (1)1
1	4,65134	4	15,6214
2	6,26054	5	19,9863
3	9.14772	6	34,8183
В табл. 20 приведены векторы, определяющие формы колеба-
ний системы, изображенной на рис. 161.
Интересно заметить, что наличие шарнира сказалось как на
величине частот, так и на форме симметричных колебаний.
Третий случай: положим 0 = 1, ai=a2 = 0, z0=O. Этот случай
соответствует висячему мосту с балкой жесткости постоянного
сечения. Решение для этой задачи без учета динамической до-
бавки к распору (zo=O) известно. Таким образом, мы еще раз
можем проверить точность полученных результатов.
11*	323
Таблица • *
№ сече- ния	Номер формы колебаний					
	1	2	3	4	5	о
0	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000
1	+0,42713	+0,03323	+0,53800	+0.63717	+0,52585	+0.9689b
2	+0,76922	-0,00447	+0,90511	+0.77483	+0.54735	+0,40394
3	+0,97788	-0.13179	+ 1,00000	+0,33721	+0.07403	—0,76751
4	+ 1,00000	-0,35363	+0,74364	—0,46401	-0,52226	—0.70792
5	+0,73389	-0,67069	+0.05890	—1,00000	—0,46566	+ 1,00000
6	0	-1,00000	—0,87979	0	+1,00000	0
7	—0,73389	-0,67069	+0,05890	+ 1.00000	—0,46566	—1,00000
8	— 1,00000	-0,35363	+0,74364	+0.46401	—0,52226	+0,70792
9	—0,97788	-0,13179	+ 1,00000	—0,33721	+0,07403	+0,76751
10	—0,76922	-0,00447	+0,90511	—0.77483	+0,54735	—0.40394
И	—0,42713	+0,03323	+0,53800	—0,63717	+0,52585	—0,96896
12	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000
В табл. 21 приводятся величины к^. Приведенный пример
надо рассматривать как условный, так как в нем не учитывалось
влияния сил на распор. Следует, однако, отметить, что учет дина-
мической добавки к распору начали проводить сравнительно не-
давно. В старых расчетах это влияние не учитывалось.
Таблица 21
№ частоты	к . СОГ		Погрешность, %	Примечание
	точное реше- ние	приближенное решение		
1	4,4721	4,4709	0.03	= (1+0 X
2	9.4868	9,4723	0,15	
3	16,4924	16,4091	0,51	х V1 + (1 +о2
4	25,4951	25.1713	1,27	
5	36.4966	35,5134	2,69	
6	49,4975	46,9837	5,06	
§ 8. СРАВНЕНИЕ РЕЗУЛЬТАТОВ, ПОЛУЧЕННЫХ
ПО МЕТОДУ ГАЛЕРКИНА И ЧИСЛЕННОМУ МЕТОДУ
В двух предыдущих параграфах изложены два различных ме-
тода определения частот и форм колебаний висячего моста с
балкой жесткости переменного сечения: метод Галеркина и чис-
ленный метод, которым мы пользовались на протяжении всей
работы.
В обоих указанных параграфах был рассмотрен один и тот же
численный пример, когда жесткость балки изменяется по закону
324

i.
Е/(х)=Е70 +«, sin -^4-<z2 sin
Коэффициент, учитывающий значение распора в обоих случа-
г?т 1<пЛ’ 22 пРиведены коэффициенты Kwi, входящие в формулу
\
t и когда ai = 0,8; a2=0,6, zo = 5O.
Г : ;
|t *ях был принят равным единице (0=1).
лгт?т со\Л’ 22 пРиведены коэффициенты Kwi, входящие в формулу
В’ (уШ.оЗ) для определения пяти первых частот изгибных коле-
В'баний.
			Таблица 22			
". ’ 1к‘-г	№	Значения				
	частоты	ПО	I	по численно-		Примечание	
		Галеркину |	му методу			
г? ‘ -	1	5,7374	5.7362			
						
	2	7,0046	6,9901	= к.	Л^	/ — X 1 /	Е/о
к#	3	12,4343	12.3394		/2 у	
	4	21,0096	20,7828			
	5	32,5820	31,9451			
Г’	6	46,6271	45,1180			
					Таблица 23	
	Первая форма		Вторая форма		Третья форма	
Е’с.	по Галеркину	по численно- му методу	ПО Галеркину	по численно- му методу	ПО Галеркину	по численно- му методу
г 1 К*"	0,0000 +0,5008	0,0000 +0,5015	0,0000 +0,1069	0.0000 +0,1000	0,0000 +0,6756	0,0000 +0,7020
И?»	“|“0,8593	+0,8578	+0,2661	+0,2646	+1,0000	4-1,0000
1 ч .	+1,0000 +0,8934 +0,5349	+ 1,0000 +0,8929 +0,5349	+0,4892 +0,7342 +0,9269	+0,4858 +0,7251 +0,9213	+0,7940 +0,1696 —0,4969	+0,7916 +0,1871 —0 5020
К ь '•	0,0000	0,0000	+1,0000	+ 1,0000	—0,7812	—0 8187
	—0,5349	—0,5349	+0.9269	+0,9213	—0,4969	—0,5020
	—0,8934 —1,0000 —0,8593 —0.5008 0,0000	—0,8у 2У	+0,7342	+0,7251	+0,1696	+0,1871
		—1,0000	+0.4892	+0,4858	+0,7940	4-0,7916
		—0.8578	+0.2661	+0,2646	+1,0000	+ 1,0000
г.с 		—0,5016 0,0000	+0,1069 0,0000	+0,1000 0,0000	+0,6756 0,0000	4-0,7020 0,0000
	Четвертая форма		Пятая форма		Шестая форма	
	0,0000	0,0000	0.0000	0,0000	0,0000	0 0000
	+0,9648	+0,9564	+ 1.0047	+0,9203	+1,0456	+0,9684
	+ 1,0018 +0.0614	+0,9351 +0,0565	+0,5302 —0,6971	+0,4787 —0,5880	+0,0128 —1,0402	4-0,0171 —0,9261
	—0,9630	—0,8998	-0,8765	—0,8393	—0,0329	—0,1224
	—1,0000	—1,0000	+0,2521	+0,1876	+1,0000	+1,0000
	0,0000	0,0000	+1,0000	+ 1,0000	0,0000	0,0000
	-J-1 « 0000	+1,0000	+0,2521	+0,1876	—1,0000	—ijoooo
	+0,9630 —0,0614	+0,8998 —0,0565	-0.8765 -0.6971	—0,8393 —0,5880	+0,0329 +1,0402	+0,1224 +0.9261
г Ь.-	—1,0018 —0,9648 0,0000	—0,9351	+0.5302	+0,4787	—0,0128	—0.0171
		—0,9564	+ 1.0047	+0,9203	—1,0456	—0,9684
tv		0,0000	0.0000	0,0000	0,0000	0,0000
	1*—3802					325
Из этой таблицы видно, что значения частот, полученные по
обоим методам, весьма близки друг к другу. Наибольшая разни-
ца в значении пятой частоты составляет всего 2,7%.
В табл. 23 даны координаты векторов, определяющих форму
колебаний. Для удобства сравнения векторы приведены к одно-
му масштабу, чтобы координаты, принятые за единицу, распола-
гались в одних и тех же местах.
Из этой таблицы видно, формы колебаний, найденные по
двум методам, совпадают очень хорошо. Естественно, возникает
вопрос, какой из методов является более точным и более удоб-
ным? Оказывается, что на этот вопрос нельзя дать однозначный
ответ. Метод Галеркина для тех случаев, когда жесткость балки
изменяется плавно и разница максимальной и минимальной жест-
костей невелика, оказался несколько точнее и удобнее в приме-
нении.
Однако для тех случаев, когда жесткость изменяется весьма
значительно, более удобным и более точным оказывается второй
метод. Этим определяется выбор метода, которым следует поль-
зоваться на практике.
§ 9. КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВИСЯЧЕГО МОСТА
Дифференциальное уравнение крутильных колебаний висяче-
го моста в общем виде было получено в § 2 (VIII.14).
d	dW\ d (rt db\	tf2e
dx \ dx?> j dx \ dx /	2 dx~
Иначе это уравнение можно представить в виде
Д30
J40
U)
dx
d2e b&H0	- 2/пр2ш1б=0.
dx2
dx2
(VIII.71)
„3
dx^ \
77g&2
2
В этом уравнении величина 0 представляет собой амплитуду
угла закручивания в произвольном сечении и является функцией
только абсциссы х.
Перейдем к безразмерной переменной, положив
ЛХ
Учтя, что
dQ	dO	d<p	dK0	nK	dKf)
	—	.—L- и 	=	.	 ,
dx-----------------------------------dy-dx	dxK-lK-dyK
326
и обозначив производные по <р штрихами, вместо уравнения
(VIII.71) получим:
^-EIaQiV	— [GZd + ^i]6z'-
/4	* /4	/2 [	2 J
—^Нфу"-----^Gl'dW-0.	(7111.72?
Для решения этого уравнения применим метод Бубнова —
Галеркина, для чего положим
6=2	..(№1, 2, 3,..., п).	(VIII.73)
Прежде всего, найдем значение динамической добавки к рас-
пору, которая возникает при колебаниях за счет сил инерции.
Для этого воспользуемся формулой (VIII.16):
I	л	те	»
д//в = «0 \Qdx=-^- ка ак	‘ •
О	к=1	о
но так как
?	,2 1«=1, 3, 5,...),
I Sin = - 
j	v=2, 4, 6,...),
дЯв=-^-/о V	(VIII.74)
л	к
№1,3,5,...
Для аналитического выражения переменных жесткостей
Е1а и GId так же, как это было принято при изгибных колебани-
ях (§ 8), положим:
Е1ш~Е1и>0 (1 4~ai sin<p-|~a2 sin3<?) 1
}• (VIII .75)
GId=GIdo (1+Tisin<p-|-Y2sin3?) J
Эти формулы обеспечивают симметричный относительно
средины моста, закон распределения жесткостей. Варьируя зна-
чениями ai, «2 и у1, у2, можно с достаточной точностью апрокси-
мировать почти любой закон изменения жесткости. В этих фор-
мулах Е1и>0 и GIda— величины жесткостей в начальном сече-
нии (на левой опоре).
П**	327
Для сокращения записи введем обозначения:
/1 (ф) = 1 + «1 sin ф -}- а2 sin Зф |
/2(<р) = 1+yi sin ф + угзш 3<р J
Разделив все члены уравнения (VIII.72) на -
значив:
1
Л
Z2G/d
г .	а0
• ID-
Я2£Л
О>0
п HRbW
2л2£/(1)о
__ 32*/73К0
Ре~ л5£/ю
О>0
ТИр2<о|/4
л4Е/ш
<D0
(VIII.76)
— и обо-
п
(VIII.77)
Г
I
а также учтя, что
ц —------—
У	«2
получим:
/1 (?) elv +/; (?)- клад+и е’+
Z	К
« = 1,3,5,...
1
-6=0.
х
(VIII.78)
Учтя, что
п
6'=как cos лг<р (а)
«=1
0yz= — 2 №aKsin (b)
«=1
6'" = — S COS ЛГф (с)
«=1
6IV=J] tt4aKsin/c<p (d)
K = 1
а также то, что
/i (?)=aicos ?+3«2 cos 3<р,
(VIII .79)
/2 (?)=Yi cos <р4- Зу2 cos 3<р,
328
7 и подставив (VIII.74), (VIII.76), (VIIL79) в уравнение (VIII.78),
получим выражение дифференциального оператора (функции
*• «ошибки») з
п
Ч<Р)=(1-Н1 sin -J- а2 sin Зср) У, к^ак sin ку —
к-1
п
— (o^cos <p-f-’3a2cos Зср)	к3ак cos кер -|-
к=1
п
(гш 4 sin <Р гшу2 sin Зср -j- р) £ к2ак sin «ср—
«=1
п
— (r«>Yi cos <p-f- 3ra!y2cos Зср) У как cos «<р —
К=1
_tS fl«sinwf+-r S	(V1II.80)
к=1	«=1,3,5,...
Следуя методу Галеркина, необходимо приравнять
стему интегралов:
нулю СИ-
к
j е (ср) sin<pc?cp=O
о
тс
j е (ср) sin 2ср cfcp=o
о
7Г
J е (ср) sin «ср of ср = О
о
После выполнения интегрирования получим
нений
гuai 4 r 12а2 + • • • 4~ гinan — О
г21й1 ~hr22a2-j-	* А~г2пап — О
f	г2па2-]------\-Гппап==1^
(VIII.81)
систему урав-
(VIII.82)
Для того чтобы эта система имела ненулевое решение, необ-
ходимо приравнять нулю ее определитель.
Займемся теперь вычислением коэффициентов гк{. Для этой
4 цели используем методику, изложенную в § 3. Положив ак = 1, а
329
все другие коэффициенты а равными нулю и обозначив функцию
е(ф) при данных условиях через ък (<р), получим:,
rKi = pK(<p)sinz<p й,
6
где
ек (ср) = (1 -J-ct] sin rp -J- аз sin Зср) л;4 sin к®—
— (aj cos <р ф- За2 cos Зср) к3 cos ку ф-
ф-(г®4"г<»Т1 sintp-L-rcoYgSin Зср ф-Р) № sin/сер —
Ре i
— (гшУ1 cos <р 4* Згшу2 cos Зср) к cos ку ф- —-sin к у
(«=1, 3, 5,...).
Так же как и в § 3, вычислим вначале rKi при 1=Ьк. Так как
sin/ccp и sin/ср при являются взаимно ортогональными, то
тс
J sin Kcp-sin/<pfiftp=O,
о
поэтому
тс
при к 4=i rKi~(a.^ 4-гшУ1«2) J sin ср sin к<р sin Ар d<pф
о
TU
ф- (а2/Ф ф- г(,у2к2) j* sin 3<р • sin к р • sin Ар da —
о
ТС
— (арс3 ф- J cos<р cos д-ср• sin icp d<p —
о
— (За2к3ф- 3ro,Y2^) J cos Зср cos к<р sin /<р дГср ф- реД rllc.	(VIII.83)
о
Значения интегралов, входящих в эту формулу, были вычис-
лены в § 3 и приведены в выражениях: VIII.32—VI 11.36. Сохра-
няя для них прежние обозначения, после подстановки их в выра-
жение (VIII.83) получим:
Гк1 = «1 ('<4 — K3S3) 4- «2 («% — Зк354) 4-
ф- ГшУ1 (*2S 1 — KS3) 4- ГшУг («Ч—3VS4) 4-РоДгкг.	(VIII.84)
Для вычисления диагональных элементов, так же как и в § 3,
необходимо в формуле (VIII.84) положить i—к и, кроме того, до-
330
давить к полученному значению слагаемые, которые исчезли за
счет ортогональности синусов. Дополнительные слагаемые будут:
Здесь &гкк определяется по (VIII.36) при i=K, а величина р*
<£• по формуле
P,=₽+'S^-	(VHI.85)
®0	»
£ Таким образом,	
| гкк~ (к4+Г*2—у)+«1 ('<4—А)+а2 («4 s2—3№s4) 4-
f	+^,Yi(№si — к$3)-|-Га>Т2(№£2—Зл^+роДГдаг (VIII.86)
Далее целесообразно ввести новое обозначение

Учитывая формулы (VIII.7) и (VIII.77), найдем:
Z0 = fA\ --------46 7	.	(VIII.87)
(	\ «/ /	2S;	\
h + —sin27£/“o
Теперь составим матрицу из коэффициентов г, входящих в
уравнения (VIII.82). Для этой цели необходимо использовать
формулы (VIII.85) и (VIII.86). Эта матрица будет иметь вид
—/Gj -|-Р*О2 —— f'j -|-ai Д1 + а2^2~|~ г “Yi^3 + r <¥2^4 ~Ь тт ^оДг •
Z \	Л, J	z
'Помножив все матрицы на — и приравнивая определитель ну-
'ЛЮ, получим:
Г	|т?--г£‘1 = °-	(VIII.88)
I л
4 Здесь /? определяется равенством
гДе
,	/?1 = 01 + Р*С2+-^-а1^14--^-а2Д2-|—~	гюу2В4,
л	л	л	л
A/?=Z0Ar.
^Матрица Дг имеет элементы — (i, к=1, 3, 5,...). Для матрицы
£	331
AR было приведено готовое выражение. Так, например, для слу-
чая, когда все матрицы будут шестого		порядка, матрица AR	
будет:	10 1/3	0 0	0	0	0 1/3	0	1/9	0 0	0	0	0	1/5 0 0	0 1/15 0 0	0	•
%	1/5 0 1/15 0 0 0 0	0	1/25 0 0	0	
Матрицы, входящие в Rb определяются равенствами:
R1=a:451—k3S3
В 2—k*S2 — 3№S4
B3=kzS1—kS3
B^iczS7—3kS^
Элементы1 диагональных матриц Gi и С2 будут:
lG2}KX=^2
(VIII.89)
(VIII.90)
Для случая, когда все матрицы будут шестого порядка, мож-
но воспользоваться готовыми матрицами S, приведенными в §3.
Уравнение (VIII.87) представим в виде
где
|Л— Zf|=O,
Д-R-1.
(VIII.91)
(VI 11.92)
Таким образом задача свелась к определению соответствен-
ных значений и собственных векторов матрицы А, определяе-
мой равенством (VIII.92).
Матрицы Bf, В2\ В3; В± не зависят от исходных параметров
и поэтому могут быть вычислены заранее. Так, например, для
случая шестого порядка эти матрицы, вычисленные на машине
«Сетунь», приводятся ниже:
+0,66667
+о, ооооб
—10,8000
+0,00000
—11,9048
+0,00000
+0,00000
+ 14,9333
+ 0,00000
—46,3238
+ 0,00000
-35,6571
—1,20000
+0,00000
+78,6857
+0,00000
—130,952
+ 0,00000
+ 0,00000
- 11,5810
+ 0,00000
+251,937
+0,00000
—296,727
—0,47619 +0,00000
+0,00000 -3,36190
—47,1429 + 0,00000
+0,00000 -131,879
+618,687 +0,00000
+0,00000 +1286,94
332
	+0,93333	+0,00000	+0,51429	+0,00000	-2,69841	+0,00000
	+0,00000	—1,52381	+0,00000	+15.6444	+0,00000	—23,1896
=	+4,62857	+0,00000	+ 18,0000	+0,00000	4-73,6364	+0,00000
		+0,00000	+62,5778	+0,00000	+71,3697	+0,00000	+217,741
	—67,4603	+0,00000	+204,545	+0,00000	+ 187,729	+0,00000
	+0,00000	—208,706	+0,00000	+489,917	+0,00000	+403,200
	+0,66667	+0,00000	—1,20000	+0,00000	-0,47619	+ 0,00000
	+ 0,00000	4-3,73333	+0,00000	—2,89524	+0,00000	—0,99084
D 		—1.20000	+ 0,00000	+ 8,74286	+0,00000	-5,23810	+0,00000
—	+0,00000	—2,89524	+0,00000	+15,7460	+0,00000	—8,24242
	—0,47619	+0,00000	—5,23810	+0,00000	+24,7475	+0,00000
	+0,00000	—0,99048	+0,00000	—8,24242	+0,00000	+35,7483
	+ 0,93333	+0,00000	+0,51429	+0,00000	-2,69841	+0,00000
	+0,00000	—0,38095	+0,00000	+3,91111	+0,00000	—5,79740
о 		+0,51429	+0.00000	+2,00000	+0,00000	+8,18192	+0,00000
	+ 0,00000	+3,91111	+0,00000	+4,46061	+0,00000	+13,6088
	—2,69841	+0,00000	+8,18182	+0,00000	+7.50916	+0,00000
	+0,00000	—5,79740	+0,00000	+13,6088	+0,00000	+ 11,2000
Матрицы Я и А будут зависеть от конкретных параметров.
Так, например, для случая, когда P* = l, ai —0,8, аг=0,6,
/юу1=0,2, гиу2=0,1, z0=5O в процессе расчета на машине были
выданы на печать матрицы К и А. Эти матрицы могут служить
проверочным эталоном при ручном счете, поэтому мы их при-
водим ниже:
+52,8403
+0,00000
+ 12,8142
+0,00000
—22,0634
+0,00000
+ 0,00000
+27,4745
+0,00000
+0,19078
+0,00000
—98,3753
+ 16,1319
+0,00000
+ 143,746
+0,00000
+14,6244
+0,00000
+0,00000
—0,04204
+0,00000
+429,860
+0,00000
+35,8293
+8,49434
+0,00000
+7,30463
+0,00000
+ 1042,43
+0,00000
+0,00000
—11,3708
+0,00000
+15,8224
+0,00000
+2146,71
Д = 10~4
+ 193,895 +0,00000 —21,6146 + 0,00000 —1,42851 +0,00000
+0,00000 +371,014 +0,00000 -0,12760 +0,00000 +1,96614
+ 17,5057 + 0,00000 +71,5683 + 0,00000 —0,35885 +0,00000
+0,00000 —0,79096 +0,00000 +23,2777 + 0,00000 —0,17576
+4,34946 +0,00000 —1,46151 +0,00000 +9,56774 +0,00000
+0,00000 +17,0145 + 0,00000 -0,39435 +0,00000 +4,75112
Характеристические числа матрицы A (VIII.92) и ее собст-
венные векторы позволяют определить частоты и формы кру-
тильных колебаний. Если обозначить:

1
333
где Xt- — характеристические числа матрицы А, то для частот
получим выражение 
»<=«-,	(VIII.93)
Формы колебаний можно найти по уравнению (VIII.77), при
этом коэффициенты а представляют собой координаты собст-
венных векторов матрицы А. Программа, составленная для оп-
ределения частот и форм крутильных колебаний, работает по
такому же принципу, как и программа для изгибных колебаний.
£ помощью этой программы было решено большое количество
задач. Приведем лишь некоторые результаты. Прежде всего при-
ведем частоты и векторы, определяющие формы крутильных ко-
лебаний, для случая, когда Р* = 1, ai=0,8, 02=0,6, гюу1=0,2,
ЛоУ2=0,1, zo=5O. Коэффициенты к«ч, входящие в формулу для
частот (VII.93), даны в табл. 24.
Таблица 24
i	Л > W/	i	k .
1	5,19100	4	20,7252
2	7,12685	5	32,2856
3	12,0775	6	46,3429
В табл. 25 приведены ординаты форм крутильных колебаний
для первых шести частот.
Таблица 25
Ординаты форм крутильных колебаний для шести частот
1	2	3	4	5	6
0	0	0	0	0	0
0,54446	0,18347	0,74005	0,84543	0,97402	1,00530
0,86404	0,37239	1,08012	0,86645	0,51261	0,00333
0,95356	0,59109	0,83748	0,02132	—0,69511	—1,00536
0,86802	0,84497	0,15968	-0,86561	—0,85848	—0,01262
0,54844	1,07105	—0,54379	-0,88662	0,26141	0,98934
0	1,16408	—0,83976	0	1,00047	0
—0,54844	1,07105	—0,54379	0,88662	0,26141	—0,98934
—0,86802	0,84497	0,15968	0,86561	—0,85848	0,01262
—0,95356	0,59109	0,83748	-0,02132	—0,69511	1,00536
—0,86404	0,37239	1,08012	-0,86645	0,51261	—0,00333
—0,54446	0,18347	0,74005	-0,84543	0,97402	—1,00530
0	0	0	0	0	0
-По данным этой таблицы построены формы крутильных ко-
лебаний, изображенные на рис. 162.
334
На рис. 163 показан общий вид однопролетного моста при
колебаниях по первой форме, соответствующей первой частоте.
На оснований многочисленных решений, полученных с по-
мощью вычислительной машины, исследовался вопрос влияния
Рис. 163.
различных параметров на частоты и формы крутильных колеба-
ний, были получены данные, приведение которых очень перегру-
зило бы главу. Поэтому мы ограничимся тем, что поместим в за-
ключение рис. 164, на котором показаны в пространстве поверх-
ности изменения частот крутильных колебаний для первых шести
гармоник. При рассмотрении этих поверхностей рассмотрен слу-
чай, когда ai = a2=a, ryi = 0,2, гуг=О,1, z0=5O. Величина а изме-
нилась в пределах от 0 до 1, а параметр £* в пределах от О до 4.
Так же как и для изгибных колебаний, здесь по вертикаль-
ной оси откладывалось не само значение частоты крутильных
колебаний, а ее отношение к частоте того же номера, подсчи-
Рис. 164.
тайного для простой балки постоянного сечения. Таким обра-
„	CD-I (Dq
зом, получено шесть поверхностей для величин —; — ; ...;
“О “20
— . На вертикальной оси все шесть поверхностей пересекаются
в точке с ординатой, равной единице.
§ 10. СОБСТВЕННЫЕ КОЛЕБАНИЯ МОСТА
ПРИ НАЛИЧИИ ШАРНИРОВ В БАЛКЕ
ЖЕСТКОСТИ
В гл. VI мы рассматривали расчет мостов, имеющих шарни-
ры в балке жесткости на прочность. При этом деформациями
изгиба звеньев балки мы пренебрегли. При действии статиче-
ских нагрузок такое допущение можно было считать оправдан-
ным, так как сама по себе такая система может применяться в
висячих мостах только при значительной постоянной нагрузке и
при сравнительно малой временной нагрузке.
При изучении колебаний такой системы картина резко изме-
няется, так как инерционные силы при большой массе пролет-
ного строения могут оказать ощутимое влияние на деформацию
звеньев этой системы, и поэтому возникает необходимость про-
336
изводить более точный расчет. Задачу о колебаниях подобных
систем в такой постановке оказалось возможным решить, без
особенно больших трудностей, численным .методом, изложенным
в §7.
Рассмотрим, наприм-ер, систему, изображенную на рис. 165.
Эту систему можно рассматривать как частный случай системы
висячего моста с балкой переменного сечения. Достаточно толь-
ко подобрать такой закон изменения жесткости балки, чтобы
момент инерции в точках а и b обращался в нуль. Так, напри-
Рис. 165.
мер, если в принятом законе изменения жесткости (VIII.20)
положить ai=0, 02=1, опустить единицу и брать sm—-— по
абсолютной величине, мы получим систему, изображенную на
рис. 165. При этом элементы Аа, ab и ЬВ будут иметь перемен-
ную жесткость, изменяющуюся по синусоидальному закону.
Можно жесткость балки задавать и другим путем. Имея в
виду, что переменность момента инерции балки учитывается в
расчете диагональной матрицей жесткостей
Е1^о
Е1*о
можно изменять элементы матрицы по своему усмотрению.
Для случая когда жесткость балки постоянца по длине про-
лета, матрица G-1 обратится в единичную матрицу Е. Если те-
перь вместо одного или нескольких элементов этой матрицы по-
ставить нуль, то расчет будет соответствовать системе с балкой
постоянного сечения при наличии одного или нескольких шар-
ниров, в том числе и той, которая показана на рис. 165, но звенья
балки будут иметь постоянную жесткость по длине.
Таким образом, алгоритм, разработанный в § 7 и применен-
ный там для расчета висячего моста с балкой жесткости пере-
33
менного сечения, остается неизменным. Изменения должны быть
внесены только в матрицу G-1. Естественно, что составленная
единая программа для ЭЦВМ может быть использована много-
кратно для расчета целого ряда различных комбинированных
систем.
Ниже приводятся результаты расчета для различных случаев,
отличающихся друг от друга количеством шарниров в балке-
жесткости комбинированных систем.
А. СИСТЕМА С ОДНИМ ШАРНИРОМ И БАЛКОЙ
ПОСТОЯННОГО СЕЧЕНИЯ
Матрица жесткости для этой системы имеет следующий вид:
Все остальные матрицы будут такими же, как в § 7. В табл. 26’
приведены частоты колебаний для этой системы.
Таблица 26
№ частоты	Значение частоты	№ частоты	Значение частоты	Примечание
1	4,4709	7	35,5134	Числа, помещенные в
2	5,7875	8	35,7991	таблице, умножить на.
3	8,3730	9	58,8595	
4	16,4092	10	63,3807	/ pi 	1 /	/Ч)о
5	20,0051	И	79,5289	J/ т
6	26,2352	—	—	
В табл. 27 приводятся координаты первых шести векторов-,
определяющих формы колебаний системы.
Всего в этом расчете получено одиннадцать векторов, опре-
деляющих одиннадцать форм колебаний, однако мы все их при-
водить не будем.
338
Таблица 27
1	2	3	4	5	6
0	0	0	0	0	0
0,49997	0,08363	0,59041	0,99994	1,00000	0,40412
0,86602	0,14091	0,94438	1,00000	0,46432	—0,59058
1,00000	—0,00178	1,00000	0,00002	-0,44027	—0,22545
0,86603	—0,28972	0,69978	—0,99998	—0,87172	0,32839
0,50001	—0,66047	0,22273	—1,00000	0,35468	0,54106
0,00000	—1,00000	—0,38624	0,00000	0,33681	—1,00000
—0,50001	—0,66047	0,22273	1,00000	0,35468	0,54106
—0,86603	—0,28972	0,69978	0,99998	—0,87172	0.32839
—1,00000	—0,00178	1,00000	—0,00002	-0,44027	—0,22545
—0,86602	0,14091	0,94438	—1,00000	—0,46432	—0,59058
—0,49997	0,08363	0,59041	—0,99994	-1,00000	0,40412
0	0	0	0	0	0
На рис. 166 изображены первые шесть форм колебаний си-
стемы с одним шарниром в балке жесткости, а также показана
сама упругая система.
Рис. 166.
339
Б. СИСТЕМЫ С ДВУМЯ И БОЛЬШИМ ЧИСЛОМ ШАРНИРОВ
Если в матрице жесткостей несколько элементов положить
равными нулю, то мы получим комбинированную систему, у
которой балка жесткости имеет несколько шарниров. По единой
программе последовательно были проведены расчеты для систе-
мы с двумя, тремя, пятью и одиннадцатью шарнирами. Для всех
этих случаев были найдены по одиннадцати частот и столько же
векторов, определяющих формы колебаний.
В табл. 28 приведены частоты для указанных систем. В верху
каждой колонки стоит цифра, указывающая на число шарниров
в балке жесткости. На рис. 167, 168, 169 и 170 показаны сами си-
стемы и изображены формы колебаний, соответствующие при-
веденным в табл. 28 частотам. Расчет приведен для 01 = 02 = О,
₽*= 1,2о = 50.
Таблица 28
№ частоты	Число шарниров в балке			
	2	3	5	1]
1	2,2410	2,1342	2,0459	1,9997
2	6,6922	3,4782	3,3012	3,1948
3	10,0695 	5,2964	4,3351	3,9896
4	12,1600	10,9861	4,6056	4,1955
5	17,0697	14,9195	5,8469	5,4267
6	33,7553	16,4092	12,2852	5,9175
7	35,5133	25,0202	15,6805	6,4317
8	46,6098	35,3158	28,8812	7,6395
9	59,5894	58,8591	35,5134	8,3892
10	72,6148	63,0564	43,4186	8,8899
11	78,8180	66,9278	56,6541	17,0584
Все числа таблицы необходимо умножить на —1/ —•
/2 у т
Из этой таблицы видно, какое сильное ослабляющее влияние
оказывают шарниры в балке жесткости. Все одиннадцать частот
с увеличением числа шарниров в балке уменьшаются по своей
величине. В значительной степени меняются и формы колебаний,
как это можно увидеть из рис. 167—170.
Из приведенных в этом параграфе расчетов видно, что ком-
бинированные системы с двумя и большим числом шарниров в
балке не обладают достаточной жесткостью. Изучение собствен-
ных колебаний подтверждает высказанное ранее суждение о
том, что такие конструкции можно применять только с малой
временной нагрузкой, составляющей небольшую долю от собст-
-венного веса системы. Такие системы не могут иметь широкого
Рис. 167.
I
2,1m
3,0181
5,2.964
10,9861
14,9195
25,3158
63,0566
fr~2,l3
tf2=3,08
fr =5,30
fr=10,99
^5=16,92
fr =16,41
\fr =25,02
25,0202
^8 '35,32
58,6591
(f>s-58,86
fro ~63,06
fr, =66,93
4sl
16,0092
Рис. 168.
^3,30
PtT^8*
ft =12,28
^7=7^
^35,51
% =28f88


<«1
!§i
^1
[£T= Const
! &



l^-i VI ^'1 Vl


Рис. 169.
Рис. 170.
применения на практике, поэтому мы не будем проводить более
подробных расчетов комбинированных систем.
Материалы, приведенные в двух параграфах, которым уде-
лялось внимание как комбинированным системам, не следует
рассматривать как рекомендации к их применению. Эти пара-
графы надо оценивать как подсобный материал, который может
быть полезным в дальнейших исследованиях. Например, если
будет поставлена проблема расчета висячих мостов по разру-
шающим нагрузкам, то полученные результаты могут быть ис-
пользованы с точки зрения кинематики таких конструкций.
§ 11. ПРИБЛИЖЕННЫЕ ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ
ЧАСТОТ КОЛЕБАНИЙ ВИСЯЧИХ МОСТОВ
В настоящем параграфе рассматривается приближенный спо-
соб определения частот изгибных и крутильных колебаний вися-
чих мостов с балкой жесткости переменного сечения. Закон из-
менения жесткостей принимается в соответствии с формулами
(VI1I.20), (VIII.73), которые мы вновь приведем в этом пара-
графе:
El=EIq(\ sin ср-j-а2sin Зср),	(VIII.20)
Е1Ш — Е1Шо (1 -f-«i sin <р-фа2 sin %) ]
G/d=G/j0(l+'Y’isin<p4-T2sin3?) J* (VIII.73)
Приближенность решения состоит в том, что вместо матри-
цы 7? принимается некоторая приближенная матрица. Как для
изгибных, так и для крутильных колебаний в первом приближе-
нии отбрасываются все побочные элементы матрицы и, таким
образом, матрица R превращается в диагональную матрицу.
Учитывая, что частоты колебаний связаны с характеристиче-
скими числами матрицы A = R~' соотношениями
мы можем не определять обратной матрицы 7?-1, а исходить в
этом простом случае непосредственно из характеристических
чисел матрицы R. Но так как характеристические числа в этом
случае будут равны диагональным элементам RICK, то
Рассмотрим сначала изгибные колебания. Учитывая формулы
(VIII.46—VIII.50), получим:
J 2—3802
345
9
*«,=о4 + ₽«s 1- — «, К*4 + К2) s, - 2к®53] +
Л
о
-«2[(«49№)s2-6/<3S4)]4
л
*0
к2
(Ь)
В этой формуле последнее слагаемое берется при к=1, 3, 5,
7,а при четном к — отбрасывается.
Найдем значения величин RKK. Положив в формулах
4VIII.31—VIII.34) i = K, получим:
S j = 1---1--= —;
1—4«2	4№—1
__ 1______3	4/с2
2~ 3	9 —4№ ~ 3(4к2 —9) ’
S 3 = 0---—;
1 — 4к2	4к2 — 1 ’
54 = 0----'2/;- =---— .
9— Art	4№—9
Подстановка дает:	'
4 10 2 1	8к6	।	1
Р = кл 4-	+ а1---------к “2--------F zo —
кк ГГ Т I Л(4/С2_1)	Зл(4№ —9) 1 ° rt
к=1, 2,3, 4. 5....	«=1, 3,’5,7,...
По равенству (а) находим:
для нечетных к
ю =^-1/ Ш/МВк24- — (— 4--____________
к /2 у /и [	‘ ‘ л И/<2-1	3(4«2 —9) у] ‘ K-i
(к=1, з, 5, 7);	(VIII.94)
для четных
(о — — 1 Г	М I В/г2 I 8/<6 gl	। а2 \1
к &У	т [	+ л	I 4«2—1	‘	3(4/<2 —9)/]
(/< = 2, 4, 6, 8).	(VIIL95)
Здесь
В—	(VIII.96)
Р	Л2£/О	’
( 2 \в	8f*EF
— I	)	/	*	\
\ л)	/	2SX	\
1р. 4-——sec2^ I Е10
величины, входящие в эти формулы, такие же, как -в § 7.
346
При использовании формул (VIП.94) й (VI 11.95) следует
иметь в виду, что индекс у величины и может не соответствовать
номеру частоты в спектре частот, расположенных в порядке их.
возрастания. Так, например, если определить частоты при к= 1
и при к=2, то может оказаться, что при к = 2 частота меньше, чем
при к=1.
Аналогичная картина может получиться при определении
третьей и четвертой, затем пятой и шестой частот. Объясняется?
это тем, что в формулу (VIII.94) входит величина z0, котораяг
не содержится в формуле (VIII.95).
Если проделать аналогичные выкладки для крутильных ко-
лебаний, то получим:

Г 2№—]
ai-----
I 4№—1
2№ — 9
3(4№ —9)
 4к4 Г Г<Л1 2№— 1	.	2№ —9 ] . z0
‘ л [ «2	4/<2 —1	№	3(4Л2 —9) J ' «2 ’
Формулы первого приближения для крутильных колебаний
будут иметь следующий вид:
<’)«=0>ок
2л-2-1
Д № ) 4/С2-1 • '
(№1, 3, 5, 7,...),
2№—9 1  zp
3(4№—9)] '
(VIII.97)
где
2№— 1
4«2_ 1
(№2, 4, 6, 8,...),
—9 1
3(4№ —9)]
(VIII.98)
<’\=(Во«

№л2
“Ок——
, lGfd
I_____
Г Л2£/
IDq
Hgb№
ш0
т
*0=
4№f1EF
2s*
sec2 т I EI
/ шо
а остальные обозначения даны раньше.
Так же как и при изгибных колебаниях, нумерация частот
в формулах (VIII.97 и VIII.98) может не соответствовать номе-
рам в спектре частот, расположенных в порядке их возрастания.
Для того чтобы установить, какую точность дают формулы
первого приближения, сравним результаты, получаемые по при-
12*	347
СлЭ
rfx ОО	- .						 Таблица 29										
Zo	1		2		3			4		5		6	
	г	<2>	Г	ф	г	Ф	ZO	Г	ф	Г	Ф	г	Ф
0	1,554	1,605	5,737	5,775	12,074	12,091	0	21,010	21,033	32,549	32,542	46,627	46,612
10	3,512	3,546	5,737	5,775	12,127	12,137	10	21,010	21,033	32.555	32,548	46.627	46,612
20	4,684	4,752	5,737	5,775	12,188	12,182	20	21,010	21,033	32,562	32,554	46,627	46,612
30	5,594	5,708	5,737	5,775	12,258	12,228	30	21,010	21,033	32,568	32,560	45,627	46,612
40	6,353	6,525	5,737	5,775	12,340	12,273	40	21,010	21,033	32,575	32,566	46,627	46,612
50	7,005	7,251	5,737	5,775	12,434	12,318	50	21,010	21,033	32,582	32,573	46,627	46,612
75	8,297	8,808	5,737	5,775	12,744	12,430	75	21,010	21,033	32,601	32,588	46,627	45,612
100	9,219	10,128	5,737	5,775	13,183	12,542	100	21,010	21,033	32,620	32,603	46.627	46,612
150	10,254	12,352	5,737	5,775	14,437	12,761	150	21,010	21,033	32,662	32,634	46,627	46,612
200	10,696	12,977	5,737	5,775	15,924	14,233	200	21,010	21,033	32,710	32,664	46,627	46,612
250	10,909	13,189	5,737	5,775	17,406	15,893	250	21,010	21,033	32,765	32,695	46,627	46,612
300	11,028	13,398	5,737	5,775	18,811	17,395	300	21,010	21,033	32,827	32,726	46,627	46,612
3.50	11,102	13,604	5,737	5,775	20,125	18,777	350	21,010	21,033	32,899	32,756	45,627	46,612
400	11,153	13,807	5,737	5,775	21,352	20,064	400	21,010	21,033	32,983	32,787	46,627	46,612
50o	11,218	14,204	5,737	5,775	23,566	22,418	500	21,010	21,0,33	33,198	32,848	46,627	46,612
600	11,257	14,589	5,737	5,775	25,481	24,547	600	21,010	21,033	33,502	32,909	46,627	46,612
700	11,283	14,965	5,737	5,775	27,094	26,506	700	21,010	21,033	33,943	32,969	46,627	46,612
г0		1		2		3			4		Продолм 5	пение табл. 99 б	
	Г	Ф	Г	Ф	Г	ф	zo	г	Ф	Г	ф	г	ф
	800	Н.302	15,332	5,737	5,775	28,383	28,330
	900	11,316	15,690	5,737	5,775	29,340	30,043
	1000	11,327	16,040	5,737	5,775	30,004	31,664
	1500	11,358	17,688	5.737	5,775	31,231	33,451
	2000	11,373	19,194	5,737	5,775	31,533	33,749
	3000	11,388	21,898	5,737	5,775	31,731	34,336
	4000	11,394	24,303	5,737	5,775	31,805	34,914
	5000	11,399	26,490	5,737	5,775	31,844	35,482
	6000	11,401	28,511	5,737	5,775	31,868	35,041
	7000	11,40,3	30,397	5,737	5,775	31,884	36,592
	8000	11,405	32,172	5,737	5,775	31,895	37,135
	9000	11,406	33,855	5,737	5,775	31,904	37,669
	10 000	11,407	35,458	5,737	5,775	31,911	38,197
	25 000	11,412	45,376	5,737	5,775	31,946	54,074
	75 000	11.414	63,710	5,737	5.775	31,960	92,084
	100 000	11,414	71,127	5,737	5,775	31,962	106,100
	200 000	11,415	95,179	5,737	5,775	31,964	149,561
<м							
4^ СО							
800	21,010	21.033	34,573	33,030	46,627	46,612
900	21,010	21,033	35,424	33,090	46,627	46,612
1 000	21,010	21,033	36,474	33,151	46,627	46,612
1500	21,010	21,033	42,778	38.763	46,627	46,612
2 000	21,010	21,033	48,849	44,750	46,627	46,612
3 000	21,010	21.033	59,368	54,796	46,627	46,612
4 000	21,010	21,033	68,343	63,266	46,627	46,612
5 000	21,010	21,033	76,285	70,729	46,627	46,612
6 000	21,010	21,033	83,840	77,476	46,627	46,612
7 000	21,010	21,033	90,105	83,681	46,627	46,612
8 000	21,010	21,033	96,277	89,457	46,627	46,612
9 090	21,010	21,033	102,08	94,882	46,627	46,612
10 000	21,010	21,034	107,57	100,01	46,627	46,612
25 000	21,010	21,033	169,81	158,12	46,627	46,612
75 000	21,010	21,033	293,92	273,87	46,627	46,612
100 000	21,010	21,033	339,36	316,23	46,627	46,612
200 000	21,010	21,033	479,87	447,22	46,627	46,612
ближенным формулам и по методу Галеркина, найденные для
случая, когда матрица R была шестого порядка. Приведем это
сравнение для изгибных колебаний, для этого приведена табл. 29
для первых шести частот.
Колонки, обозначенные буквой Г, содержат цифры, найден-
ные по методу Галеркина, а буквой Ф—по формулам (VIII.94—
VIII.95). Из сравнения цифр видно, что для частот, соответству-
ющих кососимметричным формам колебаний (колонки 2, 4 и 6),
приближенные формулы дают исключительно 'высокую точность.
Иначе обстоит дело с частотами для симметричных колеба-
ний. Здесь сказывается влияние величины z0, учитывающей вли-
яние сил инерции на распор. При z0> ЮО погрешность в опре-
делении второй частоты становится значительной и поэтому при-
ближенной формулой (VIII.94) пользоваться нельзя.
Цифры, сведенные в табл. 29, даны для частного случая, ко-
гда ₽=1, ai = 0,8, 02=0,6, 2о=50. Однако можно отметить, что
при других данных картина в общем остается той же.
Для малых значений z0, правда встречающихся в реальных
мостах довольно редко, можно уточнить формулы первого при-
ближения. Так как это уточнение потребуется провести только
для второй (или первой) частоты, то провести его довольно лег-
ко. Взяв вместо матрицы R матрицу третьего порядка и прирав-
няв нулю определитель
получим:
где
Rn
о
—X о
$22 —
О
‘чз
О
$зз~
=0,
(VIII.99)
д _+ Дз.з
Д1—2
Д _#11--Дзз
2-- п
(VII 1.100)
Дз — $к
Воспользовавшись равенствами (а) и (Ь) и положив в них
к=1 и «=3, найдем величины Дп и /?33 и по выражениям
(VIII.100)—значения Д1 и Д2. Для определения Д3 необходимо
использовать формулы (VIII.36) и (VIII.83).
Если проделать все указанные вычисления, то получим:
для изгибных колебаний
Д1 — 41Т 5 р "г 26,94 0С14“ 10,87 ос 2 Т 0,56 Zq~,
350
A2 =—40 — 4 р — 26,10cti — 11,54 аг4-0,44 Zo;
Аз=—1,53 ai4-5,89 a24-O,33zo,
для крутильных колебаний
Ai =41+50* +25,26ai +6,03a2 +3,ООу1Гш +0,93у2гы +O,56zo;
А2=40 — 4 р* —24,83 щ — 5,43 a2 —2,57 Yirw — 0,34у2гш4-
+0,44 z0;
A3 = -—0,76 czi + 0,33 a2 — 0,76 yi^c>4-0,33 ytfю + 0,33 Zq.
Формула (VIIL99) дает для первой (второй) частоты значи-
тельно более точные результаты. Она пригодна практически при
любых z0.
Таким образом, формулами второго приближения являются
совокупности формул:
а)	для изгибных колебаний (VIII.99), (VIII.94) и (VIII.95);
б)	для крутильных колебаний (VIII.99), (VIII.97) и (VIII.96).
При пользовании этими формулами следует исключить ин-
декс к = 1 в формулах (VIII.94) и (VIII.97).
Применение приближенных формул как первого, так и вто-
рого приближений в сильной степени облегчает решени-е задачи
о собственных колебаниях висячих однопролетных мостов.
§/Г2. СОБСТВЕННЫЕ КОЛЕБАНИЯ
'у уъ А Л ОЧНО-ВАНТОВЫХ МОСТОВ
Для определения частот колебаний балочно-вантовых мо-
стов практически очень трудно использовать дифференциальные
уравнения изгиба балки. Дело в том, что балка, подкрепленная
вантами, представляет собой комбинированную систему. При-
ложенные к балке усилия от вант в отдельных точках разбивают
систему на ряд участков, поэтому мы должны иметь дело с
системой дифференциальных уравнений. Непосредственное ис-
пользование этой системы уравнений приведет к весьма слож-
ным выкладкам, которые провести очень трудно.
Иначе обстоит дело с применением численного метода. Для
этой цели мы воспользуемся решением, которое было получено
в гл. VII при изучении прочности балочно-вантовых мостов.
/ В § 6 гл. VII мы получили следующее основное уравнение
/(VII.19):	f'	+	- t >	f
= £*р.	( |	(а)
j В этом уравнении:
т] — вектор прогибов для точек 1, 2,..., п балки;
351
Р — вектор сил, приложенных в этих точках;.
L*—матрица влияния прогибов, построенная для заданной
системы и определяемая равенством (VI 1.20):
Ц=А-’£,.
Если учесть значение матрицы А согласно- равенству
(VII.18), то для матрицы L* получим следующее выражение:
+	(Ь>
\	^0	/
Матрица Li, определяемая по (VII.25), может быть представ-
лена в виде матрицы, имеющей безразмерные элементы, но с
множителем, стоящим перед этой безразмерной матрицей. Так,,
например, для двухпролетной неразрезной балки, показанной на
рис. 136, она представлена равенством (d) в § 7 гл. VII. Желая
сохранить множитель — в буквенном обозначении, представим
EI
матрицу Li в виде равенства
т d3 -f-	. .
А-—Л-	(С)
Черточка вверху у матрицы будет показывать, что она получена
из матрицы Li путем отбрасывания множителя . Подставляя
Е/
в равенство (Ь) вместо Li ее значение по (с), получим:
(VIII.101)
£/
Этим выражением мы и будем в дальнейшем пользоваться.
Отметим, что все входящие сюда матрицы определены в гл. VII.
Так, например, матрица Sn определяется равенством (VII.5),
матрица AN— равенством (VII.14). Величина d представляет
собой длину панели (см. рис. 141).
Итак, матрица L * для конкретного примера может быть
легко получена по формуле (VIII.101). Если теперь в равенстве
(а) -вектор внешних сил Р заменить вектором сосредоточенных
сил инерции Vj, то мы получим уравнение колебаний моста.
Для определения вектора Vj воспользуемся методикой, изло-
женной в § 7 настоящей главы, где дается формула для опреде-
ления сил инерции, сосредоточенных в 'узлах 1, 2,..., п (см.
VI 11.57),
Vj = /n(o2BiT].	(d)
352
Входящая сюда матрица В{ определяется формулой
(VIII.58). Подставляя в равенство (а) вместо вектора Р вектор
инерционных сил (d), мы получим следующее уравнение:
^=пМ\Вм-	(VIII. 102)
Теперь целесообразно перейти от матрицы L* к безразмерной
матрице L* , точно так же заменить матрицу Вх безразмерной
матрицей В\. Для этой цели произведем замену:
. » у*
в 1=^-въ
.6
тогда на основании равенства (VIII.102) получим:
/пы2</4 5	—
Здесь
АЧ = (Е	1Ll,
(VIII. 103)
1
0,1
0,1
1 0,1
0,1	1 0,1
0,1 1
Из уравнения (VIII.103) находим:
где
(С —Z£)n = O,
С=4-Дв,;
х=_Д'_.
(е)
(VIII. 104)
(VIII.105)
Равенство (е) возможно^ в двух случаях:
1) вектор перемещений тождественно равен нулю;
2) определитель системы (е) равен нулю.
Естественно, что первый случай, при котором колебания от-
сутствуют, нас не интересует, поэтому приравниваем нулю опре-
делитель:
|С—ZE|=0.	(VIII.106)
Из уравнения (VIII.106) необходимо определить характери-
стические числа Хь Л2;...;ЛП и векторы, определяющие формы
колебаний.
353
По найденным характеристическим числам в соответствии с
равенством (VIII.105) легко вычисляются частоты колебаний
моста:
где
Kj
(VIII.107)
EI
т
(VIIIЛ 08)
Приведем примеры определения частот и форм колебаний
арфообразного моста.
Пример 1. Рассмотрим систему, показанную на рис. 137, для
которой в § 8 гл. VII был проведен расчет на прочность. Все
размеры принимаем такими же, которые были приняты в ука-
занном § 8. Получение матрицы С, а также вычисление ее ха-
рактеристических чисел произведено на ЭЦВМ. Приведем ко-
нечный результат. Матрица L* для данного случая дана на
стр. 252. Матрица С получилась путем помножения на мат-
рицу В] и на коэффициент Б/6. Вычисления привели к резуль-
тату:
	0,22580 0,15625 —0,13443	0,15097 0,14416 —0,10725	—0,13103 —0,12167 0,23115	—0,26695 —0,22940 0,32009	—0,35263 -0,34814		-0,21401 -0,17566 0,18267	
					—0,29282 0,33823	-0,28646 0,30621		
С =	—0,24394	—0,18832	0,30214	0,60426	0,74012	0,67270	0,39635	•
	—0,32508	—0,25040	0,32324	0,75807	1,14237	1,10310	0,65667	
	—0,32437	—0,25024	0,29499	0,69676	1,11373	1,24110	0,80254	
	—0,19914	—0,15377	0,17524	0,41060	0,66518	0,80610	0,62009	
Характеристические числа этой матрицы даны в первой стро-
ке табл. 30. Во второй строке этой же таблицы приведены зна-
чения Кг, входящие в формулу для определения частот коле-
баний.
Таблица 30
	1	2	3	4	5	6	7
Ki	3,52735 19,17	0,34198 61,56	0,14979 93,02	0,11045 108,3	0,03624 189,1	0,02536 226,1	0,01773 270,3
Координаты семи собственных векторов даны в табл. 31. По
этим координатам построены формы колебаний, показанные на
рис. 171. Необходимо учесть, что в табл. 29 приведены переме-
щения при соответствующей форме колебаний только для точек,
пронумерованных от 1 до 7 и лежащих в пролетах. Опорные
точки в таблице пропущены, так как в этих точках перемещения
равны нулю.
354
Рис. 171.
Таблица 31
	Координаты собственных векторов						
	1	2	3	4	5	6	7
1	—0,32513	0,46304	1,00000	0,62173	0,18282	0,72023	—0,10710
2	-0,26995	0,43191	0,70900	0,25167	—0,26605	— 1,00000	0,04570
3	0,31026	—0,85819	—0,19808	1,00000	0,91630	—0,07036	0,64196
4	0,63562	—0,97128	0,24509	0,37764	—0,84241	—0,00376	-0,99064
5	0,95574	—0,25191	0,67954	—0,68955	—0,18047	0,09339	1,00000
6	1,00000	0,74095	0,33078	—0,11856	1,00000	—0,14222	-0,82285
7	0,64097	1,00000	—0,50274	0,75830	—0,86535	0,09425	0,46166
Пример 2. Рассмотрим теперь систему с опорной вантой (см.
рис. 141) при тех же размерах и при услов-ии, что сечения всех
вант, включая опорную ванту, одинаковые. Величина Др =
=0,561861 (см. пример 1 в § 9 гл. VII). р0=Ю. Матрица для
этого случая приведена на стр. 258. Матрица С, подсчитанная
по формуле (VIII. 104), имеет вид
	0,13164	0,07801 —0,04737
с =	0,07841 —0,05174 —0,08715	0,08383 —0,05249 —0,04316	0,15767 —0,06680	0,16279
	—0,11319 —0,11227 —0,06881	—0,08618	0,13493 —0,08586	0,10648 —0,05276	0,05942
-0,09492 —0,12285 —0,12063 -0,07405
.0,08714 —0,10280 -0,09832 -0,05991
0,16899 0,13639 0,10637 0,05973
0,31771	0,35737	0,29374	0,16321
0,37084 0,62513 0,59099 0,34161
0,30915	0,59599	0,72848	0,48718
0,17243	0,34705	0,49112	0,42631
Характеристические числа и коэффициенты к приведены в-
табл. 32, а координаты соответствующих собственных векторов,
определяющих формы колебаний, приведены в табл. 33.
Таблица 32
	I	2	3	4	5	6	7
*1	1,82158 26,67	0,31809 63,83	0,14207 95,51	0,10980 108,7	0,03623 189\2	0.02535 226,1	0,01765 271,0
На рис. 172 показаны формы колебаний и рядом с формами
выписаны соответствующие им частоты колебаний.
Сравнивая рис. 172 с рис. 171, мы видим, что частоты коле-
баний для системы, имеющей опорную ванту, возросли. Вместе
с тем для высших гармоник частоты мало отличаются друг от
друга. Объясняется это тем, что при высших гармониках коле-
баний ванты моста почти не работают и поэтому мало влияют на
соответствующие частоты.
В заключение рассмотрим случай, когда опорная ванта имеет
356
Рис. 172.
Таблица 33
Ьй	Координаты		собственны!	векторов:	Др =0,561861, р0 = 10		
о							
2	1	2	3	4	5	6	7
1	—0,21083	—0,36569	1,00000	0,72656	0,18906	—0,71458	-0,10118
2	—0,17618	—0,35981	0,72233	0,31887	—0,26431	1,00000	0,05897
3	0,22709	0,84515	—0,32481	1,00000	0,91337	0,06782	0,64234
4	0,52817	1,00000	0,14748	0,38557	—0.84194	0,00494	—0,99887
5	0,90709	0,38013	0,65798	—0,68893	0,18275	—0,09724	1,00000
6	1,00000	—0.60943	0,04012	—0,12231	1,00000	0,14478	—0,82486
7	0,66962	—0,91864	—0,51809	0,75853	—0,86577	—0,09639	0,46070
диаметр в два раза больший, чем остальные. Площадь опорной
ванты будет в четыре раза больше, чем у остальных вант. Ко-
роче говоря, рассмотрим систему, которая была изучена в § 9
гл. VII (стр. 262). Для нее Др=2,24744, ро=10. Матрица L
дана на стр. 262, матрица С следующая:
	0,09845	0,05229 —0,01787 — 0,03428 —0,04184 —0,04043 —0,02470					
	0,05096	0,06256	—0,02810	—0,03699	—0,03581	-0,03200 -	-0,01911
	—0,02259 —0,02057	0,13176	0,11572	0,06524	0,03592	0,01639
	—0,03i87 —0,02396	0,11366	0,21669	0,22244	0,16014	0.08102
	—0,03849 —0,02828	0,06854	0,23433	0,44279	0,41045	0,23055
	—0,03749 —0,02791	0,04003	0,17250	0,41347	0,54777	0,37600
	—0,02287 —0,01715	0,01858	0,08847	0,23490	0,38008	0.35800
Характеристические числа			X и к даны в табл. 34, а			собстве
ные векторы приведены в табл. 35.
Таблица 34
1	1	2	3	4	5	6	7
К[	1,24690 32,24	0,29213 66,61	0,13172 99,20	0,10819 109,5	0,03521 189,2	0,02533 226,2 Та	0,01755 271,8 блица 35
№ точек	Частоты колебаний Др = 2,24744, р0 = 10						
	1	2	3	4	5	6	7
1 2 3 4 5 6 7	—0..09973 —0,08464 0,13901 0,41493 0,85198 1,00000 0,70113	—0,22652 -0,25483 0,80286 1,00000 0,50479 —0,45634 —0,82378	1,00000 0,75301 -0.58313 0,00047 0,70936 0,05589 —0,62444	1,00000 0,49448 0,99351 0,40244 —0,68803 -0,13223 0,75721	0. 19824 —0,26176 0.90906 —0,84124 -0,18610 1,00000 —0,86638	—0,70663 1,00000 0,06422 0,00663 —0,10266 0,14838 -0,09940	0,09162 -0,07694 -0,63609 1,00000 -0,98950 0,81907 -0,45454
358
и
На рис. 173 изображены формы колебаний. Сравнение
Р'Ис. 173 с рис. 172 показывает, что форма колебаний одной и
той же системы, но при разных жесткостях опорных вант отли-
чаются друг от друга. Заметно отличаются первые частоты ко-
лебаний. Величины старших частот близки друг к другу.
359
ПРИЛОЖЕНИЕ
ТАБЛИЦЫ I И II ДЛЯ ФУНКЦИЙ ifc И ф2
ф,=3 (р2 - а2) — 2 (р3 — а3)-— [р - а - -sll-z(0'5 -«l-shz^S—g)
z2 L	, z
zch--
2
при а = 0 P=l;
Ф1=^.
Для малых £•<; 1
if i = [0,25 (p2—а2) —0,25 (p4—а4).+0,1 (₽5—а5) ]z2—[0,025 (p2—а2) —
—0,0208333(p4—a4)+0,00833333(p6—a6)—0,00238G95(P7—a7)]z4+
+[0,00252976 (p2—a2) -0,00208333 (p4—a4) + 0,000694444 (p6—
— a6)—0,000148810(p8—a8) +0,0000330688(p9—a9)]z6—
—[0,000256283 (p2—a2) —0,000210813 (p4-a4) + 0,0000694444 (p6—
— a6) —0,0000124008 (p8—a8) + 0,00000165344 (p10—a10) —
—0,000000300625(pn—au)]z8 ...
Таблица I
z	*CD Я “1	<7=0, (3 = 0,8	•CD Я II И Op CD	a-0, (3=0,5	o’© II II в со.	та я II И о Я ъ
0	0	0	0	0	0	0
0,01	0,000009	0,000009	0,000006	0,000004	0,090003	0,000000
0,02	0,000039	0,000036	0,000026	0,000019	0,000013	0,000003
0,03	0,000089	0,000081	0,000058	0,000044	0,000031	0,000008
0.04	0,000159	0,000144	О.ОООЮ4	0,000079	0,000055	0.000015
0.05	0,000249	0,000225	0,000163	0,000124	0,000086	0,000024
0,05	0,000359	0,000325	0,000235	0,000179	0,000124	0,000034
0,07	0,000489	0,000442	0,000320	0,000244	0,000169	0,000047
0,08	0,000639	0,000577	0,000418	0,000319	0,000221	0,000051
0,09	0,000809	0,000731	0,000529	0,000404	0,000280	0,000077
360
Продолжение табл. I
Z	а = 0, ₽ = 1	СО о О II II е со. !	л=0, Р-0,6	XD Я II II р.° СЛ	TD Р I' 1 Р-°	CS о о II II к со.
0,10	0,000998	0,000902	0,000653	0,000499	0,000345	0,000096
0,11	0,001208	0,001092	0,000790	0,000604	0,000418	0,000116
0,12	0,001437	0,001299	0,000940	0,000718	0,000497	0,000138
0,13	0,001687	0,001524	0,001102	0,000843	0.000584	0.000162
0,14	0,001956	0,001767	0,001278	0,000978	0.000677	0,000188
0,15	0,002244	0,002028	0,001467	0,001122	0,000777	0,000216
0,16	0,002553	0.002307	0,001669	0,001276	0,000884	0,000245
0.17	0,002881	0,002604	0,001883	0,001440	0,000997	0,000277
0,18	0,003229	0,002918	0,002111	0,001614	0.001118	0,000311
0,19	0,003596	0,003250	0,002351	0,001798	0,001245	0,000346
0,20	0,003983	0,003500	0,002604	0.001991	0,001379	0,000383
0,21	0,004390	0,003967	0,002870	0,002195	0,001520	0,000422
0.22	0,004816	0,004352	0,003148	0,002408	0,001667	0,000463
0,23	0,005251	0.004754	0,003439	0,002630	0,001821	0,000506
0,24	0.005726	0,005175	0,003743	0,002863	0.001982	0,000551
0,25	0,006210	0,005612	0,004060	0,003105	0,002150	0,000598
0,26	0,006714	0,005067	0,004389	0,003357	0,002324	0,000646
0,27	0.007236	0,005539	0,004730	0,003618	0,002505	0,000697
0,28	0,007778	0,007029	0,005085	0,003889	0,002693	0,000749
0,29	0,008339	0,007535	0,005451	0,004169	0,002887	0,000803
0,30	0,008918	0,008059	0,005830	0,004459	0,003088	0,000859
0,31	0,009517	0.008600	0,006222	0,004758	0,003295	0,000916
0,32	0,010135	0,009158	0,006625	0,005067	0,003509	0,000976
0,33	0,010771	0,009733	0,007041	0,005385	0,003729	0,001037
0.34	0,011426	0,010325	0.007470	0,005713	0,003956	0.001100
0,35	0,012100	0,010934	0,007910	0,006050	0,004189	0,001165
0,36	0,012792	0,011560	0,008362	0,006396	0,004429	0,001232
0,37	0,013502	0,012202	0,008827	0,006751	0,004675	0,001300
0,38	0,014232	0.012861	0,009304	0,007116	0,004927	0,001370
0,39	0,014979	0,013536	0,009792	0,007489	0,005186	0,001442
0,40	0,015745	0,014228	0,010293	0,007872	0,005451	0,001516
0,41	0.016528	0,014936	0,010805	0,0082-4	0,005723	0.001592
0,42	0,017330	0,015661	0,011329	0,008665	0,006000	0,001669
0.43	0,018150	0,016401	0,011865	0,009075	0,006284	0,001748
0.44	0,018988	0,017158	0,012413	0,009494	0,006574	0,001829
0.45	0,019843	0,017931	0,012972	0,009921	0,00'^870	0,001911
0.46	0,020716	0,018720	0,013543	0,010358	0,007173	0,001995
0.47	0,021607	0,019525	0,014125	0,010803	0,007481	0,002081
0.48	0,022515	0,020346	0,014719	0,011257	0,007795	0,002169
0,49	0,023440	0,021182	0,015324	0,011720	0,008116	0,002258
0,50	0,024383	0,022034	0,015940	0.012191	0,008442	0.002349
0,51	0,025343	0,022901	0,016567	0,012671	0,008775	0,002441
0,52	0,026319	0,023784	0,017206	0,013159	0,009113	0,002535
0,53	0,027313	0,024682	О,0178Г>6	0,013556	0,009457	0,002631
0,54	0,028324	0,025595	0,018516	0,014162	0,009807	0,002728
361
Продолжение табл. I
Z	а = О, ₽-1	ОО о <= II II а ах	а=0, ₽ = 0.6	а=0, 6=0,5	а=0, ₽ = 0,4	а=0, ₽=0.2
0.55	0,029351	0,026523	0,019188	0,014675	0,010163	0,002827
0,56	0,030395	0,027467	0,019870	0,015197	0,010524	0,002928
0,57	0,031455	0,028425	0,020563	0,015727	0,010892	0,003030
0,58	0,032532	0,029398	0,021267	0,016266	0.011264	0,003134
0,59	0,033525	0,030385	0,021982	0,016812	0,011643	0,003239
0,60	0,034734	0,031388	0,022707	0,017367	0,012027	0,003346
0.61	0,035859	0,032404	0,023442	0,017929	0,012417	0,003455
0,62	0,037000	0,033435	0,024188	0,018500	0,012812	0,003564
0,63	0,038157	0,034481	0,024944	0,019078	0,013212	0.003576-
0,64	0,039329	0,035540	0,025711	0.019664	0,013618	0,003789
0,65	0,040517	0,036613	0,026487	0,020258	0,014030	0,003903
0,66	0,041720	0,037701	0,027274	0,020860	0,014446	0,004019
0,67	0,042939	0,038802	0,028070	0,021469	0,014868	0,004137
0,68	0,014173	0,039916	0,028877	0,022086	0,015295	0,004256
0,69	0,045421	0,041045	0,029693	0,022710	0,015728	0,004376
0,70	0,р46686	0,042187	0,030519	0,023342	0,016165	0,004498-
0,71	0,047965	0,043342	0,031355	0,023982	0,016608	0,004621
0,72	0,049257	0,044509	0,032198	0,024628	0,017056	0,004745
0,73	0,050564	0,045690	0,033054	0,025281	0,017508	0.004871
0,74	0.051884	0,046885	0,033917	0,025942	0,017965	0.004999-
0,75	0,053220	0,048091	0,034791	0,026610	0,018428	0,005127
0,76	0,0545/0	0.049311	0,035672	0,027284	0,018896	0,005257
0,77	0,055934	0,050545	0,036566	0,027967	0,019369	0,005390
0,78	0,057312	0,051789	0,037465	0,028655	0,019845	0,005522
0,79	0,058702	0,053046	0,038375	0,029351	0,020327	0,005656
0,80	0,060107	0,054315	0,039293	0,030053	0,020813	0,005792
0,81	0,061526	0,055597	0,040221	0,030763	0,021305	0,005929
0,82	0,062957	0,056890	0,041156	0,031479	0,021801	0,006067
0,83	0,064401	0,058194	0,042099	0.032200	0,022301	0.006206
0,84	0,065857	0,059511	0,043051	0,032928	0,022805	0,006346
0,85	0,067327	0,060838	0,044012	0,033663	0,023314	0,006488
0,86	0,058811	0,062179	0,044982	0,034405	0,023828	0,006631
0,87	0,070305	0,063529	0,045958	0,035152	0,024345	0.006774
0,88	0,071812	0,054891	0,046944	0,035906	0,024867	0,006920
0,89	0,073331	0,066264	0,047937	0,036666	0,025394	0,007057
0,90	0,074864	0,067648	0,048939	0,037432	0,025925	0,007215
0,91	0,076407	0,069043	0,049948	0,038203	0,026459	0,007363
0,92	0,077963	0,070449	0,050965	0,038982	0,026998	0,007514
0,93	0,079530	0,071865	0,051989	0,039765	0,027541	0,007665
0,94	0,081109	0,073291	0,053020	0,040554	0,028088	0,007817
0,95	0,082698	0,074727	0,054059	0.041349	0,028638	0,007970'
0,96	0,084299	0,076174	0,055106	0,042149	0,029193	0,008125-
0,97	0,085911	0,077630	0,056160	0,042955	0,029751	0,008281
0,98	0,087534	0,079096	0,057220	0,043767	0,030313	0.008437
0,99	0,089167	0,080572	0,058288	0,044583	0,039879	0,008594
362
Продолжение табл. I
Z	0=0, ₽=1	а=0, Р=0,8	а=0, ₽=0.6	а=0, ₽=0,5	а=0, Р=0,4	а = 0, ₽=0,2
1,00	0,090812	0,082058	0,059363	0,045406	0,031448	0,008753
'1,01	0,092466	0,083552	0,060444	0,046233	0,032021	0,008913
1,02	0,094131	0,085057	0,061533	0,047066	0,032598	0,009074
1,03	0,095807	0,086571	0,062628	0,047903	0,033178	0,009235
.1,04	0,097490	0,088093	0,063728	0,048745	0,033762	0,009397
1,05	0,099186	0,089624	0,034836	0,049593	0,034349	0,009561
1,06	0,100891	0,091164	0,065950	0,050445	0,034949	0,009726
1,07	0,102605	0,092713	0,067071	0,051302	0,035533	0,009891
1,08	0,104328	0,094269	0,068197	0,052164	0,036130	0,010058
1,09	0,106061	0,095835	0.059330	0,053030	0,036731	0,010225
1,10	0,107802	0.097409	0,070468	0,053901	0,037334	0,010393
1,11	0,109553	0,098991	0,071612	0,054776	0,037940	0,010562
1,12	0.111312	0,100580	0.072762	0,055656	0,038549	0,010731
1,13	0.113Q80	0,102178	0,073918	0,056540	0,039162	0,010902
1,14	0,114857	0,103784	0,075079	0,057428	0.039778	0,011074
1,15	0,116643	0,105396	0,076245	0,058321	0,040396	0,011246
1,16	0,118435	0,107016	0,077417	0,059217	0,041017	0,011419
1,17	0,120237	0,108644	0,078595	0,060118	0,041641	0,011593
1.18	0,122046	0.110278	0.079777	0,061023	0,042268	0,011767
а, 19	0,123863	0,111920	0,080965	0,061931	0,042898	0,011943
1,20	0,125688	0,113569	0,082158	0,062844	0,043530	0,012119
1,21	0,127520	0,115224	0,083355	0,063760	0,044165	0,012296
1,22	0,129360	0,116886	0,084557	0,064680	0,044802	0,012474
1,23	0,131207	0,118554	0,085764	0,065603	0.045441	0,012652
1,24	0,133050	0,120229	0,086976	0,066530	0,046084	0,012831
1,25	0,134922	0,121911	0,088192	0,067460	0,046729	0,013911
1,26	0,135789	0,123598	0,089413	0,068394	0,047376	0,013191
1,27	0,138663	0,125290	0,090637	0,069331	0,048025	0,013372
1,28	0,149544	0,126989	0,091866	0,070272	0,048676	0,013554
1,29	0,142439	0,128694	0,093099	0,071215	0,049339	0,013736
1.30	0,144324	0,130405	0,094337	0,072161	0,049986	0,013919
1,31	0,146223	0,132120	0,095578	0,073111	0,050644	0,014102
1,32	0,148128	0,133841	0,096823	0,074063	0,051304	0,014286
1,33	0,150039	0,135568	0,098072	0,075019	0,051966	0,014471
1,34	0,151956	0,137299	0,099324	0,075977	0,052631	0,014656
1,35	0,153878	0,139035	0,100581	0,076939	0,053297	0,014842
1,35	0,155805	0,140777	0,101840	0,077902	0,053964	0,015028
1,37	0,157738	0,142523	0,103103	0,078869	0,054634	0,015214
1,38	0,159676	02144274	0.104370	0,079838	0,055306	0,015402
1,39	0,161619	0,146029	0,105639	0,080809	0.055979	0,015590
1,49	0,163566	0,147788	0,106912	0,081783	0,056654	0,015778
1.41	0,165519	0,149552	0,108188	0,082759	0.057330	0,015966
1,42	0,167476	0,151320	0,109467	0,083738	0,058009	0,016156
1,43	0,169438	0,153092	0,110749	0,084718	0,058688	0,016345
1,44	0,171403	0,154868	0,112033	0,085701	0.059369	0,016535
363
Продолжение табл. I
Z	с = 0, ₽=1	а=0, ₽=О,8	IIII В ео-	а=0, ₽=0,5	а=0, ₽ = 0,4	и==0, ₽ = 0,2
1,45	0,173373	0,156647	0,113321	0,086686	0,060052	0,016725
1,46	0,175347	0,158431	0,114611	0,087673	0,060736	0,016916
1,47	0,177325	0,160217	0,115903	0,088662	0.061422	0,017107
1,48	0,179307	0,162007	0,117198	0,089653	0,062109	0,017299
1,49	0,181292	0,163801	0,118495	0,090646	0,062797	0,017491
1,50	0,183281	0,165598	0,119795	0,091640	0,063486	0,017683
1,51	0,185274	0,167397	0,121097	0,092636	0,064176	0,017876
1,52	0,187270	0,169200	0,122401	0,093634	0,064868	0.018069
1.53	0,189269	0,171006	0,123707	0,094634	0,065561	0,018262
1,54	0,191271	0,172814	0,125015	0,095635	0.066255	0,018456
1,55	0,193275	0,174625	0,126325	0,096637	0,066949	0,018650
1,56	0,195283	0,176439	0,127637	0,097641	0,067645	0,018844
1,57	0,197294	0,178255	0,128951	0,098646	0,068342	0,019038
1,58	0,199307	0,180073	0,130266	0,099653	0,069040	0,019233
1,59	0,201323	0,181894	0,131583	0,100661	0,069739	0,019428
1,60	0,203340	0,183717	0,132902	0,101670	0,070438	0,019623
1,61	0,20г 351	0,185541	0,134222	0,102680	0,071138	0,019819
1,62	0,207383	0,187368	0,135543	0,103591	0,071839	0,020014
1,63	0,209407	0,189197	0,136866	0,104704	0,072541	0,020210
1,64	0,211433	0,191027	0,138190	0,105717	0,073243	0,020406
1,65	0,213461	0,192859	0,139515	0,106731	0,073946	0,020603
1,66	0,215491	0,194692	0,140841	0,107746	0,074650	0,020799
1,67	0,217522	0.196527	0,142168	0,108761	0,075354	0,020995
1,68	0,219555	0,198363	0,143496	0,109778	0,076059	0.021192
1,69	0,221589	0,200200	0,144825	0,110795	0,076764	0,021389
1,70	0,223625	0,202038	0,146155	0,111812	0,077469	0,021586
1.71	0,225661	0,203877	0,147485	0,112831	0,078175	0,021783
1.72	0,227699	0,205718	0,148816	0,113849	0,078882	0,021980
1.73	0,229737	0,207559	0,150148	0,114869	0,079588	0,022178
1,74	0,231776	0,209401	0,151481	0,115888	0,080295	0,022375
1,75	0.233816	0,211243	0,152813	0,116908	0,081003	0,022573
1,76	0,235857	0,213086	0,154146	0,117928	0.0817Ю	0,022770
1,77	0,237898	0,214930	0,155480	0,118949	0,082418	0,022968
1,78	0,239940	0,216774	0,156814	0,119970	0,083126	0,023166
1,79	0,241982	0,218618	0,158148	0,120991	0,083834	0,023363
1,80	0,244024	0,220462	0,159482	0,122012	0,084542	0,023561
1,81	0,246066	0,222307	0,160816	0,123033	0,085250	0,023759
1,82	0,248109	0,224152	0,162151	0,124055	0,085958	0,02.3957
1,83	0,250151	0,225966	0,163485	0,125076	0,086666	0,024155
1,84	0,252194	0,227841	0,164819	0,126097	0,087374	0,024353
1,85	0,254236	0,229685	0,166153	0,127118	0,088082	0,024550
1,86	0,256278	0,231529	0,167487	0,128139	0,088790	0,024748
1,87	0,258319	0.233372	0,168820	0,129159	0,089498	0,024946
1,88	0.260360	0,235216	0,170153	0,130180	0,090206	0,025144
1.89	0,262400	0,237058	0,171486	0,131200	0,090913	0.025342
•364
Пюооолжение. табл. I
Z	<х=0.	а=0, (3=0,8	т=0, ₽=0,6	TD Я II 1 рР СП	а=0, (3=0,4	сч do II II е ах
1,90	0,264440	0.238900	0.172819	0,132220	0,091621	0,025539
1,91	0,266479	0,240741	0.174151	0,133239	0,092328	0,025737
1,92	0,268517	0,242582	0.175482	0.134258	0,093035	0,025934
1,93	0,270554	0,244422	0,176813	0,135277	0,093741	0,026132
1,94	0,272590	0,246261	0,178143	0,136295	0,094447	0,026329
1,95	0,274625	0,248098	0,179472	0,137313	0,095153	0,026527
к 96	0.276659	0,249935	0,180801	0,138330	0,095859	0,026724
1,97	0,278692	0,251771	0,182128	0,139346	0,096563	0,026921
1,98	0,280724	0,25.3605	0,183455	0,140362	0,097268	0,027118
1,99	0,282754	0,255439	0,184781	0,141377	0,097972	0,027315
2,00	0,284782	0,257270	0,186106	0,142391	0,098676	0,027512
2,01	0,286809	0,259101	0,187430	0.143405	0,099379	0,027708
2,02	0.288835	0.260930	0,188753	0,144418	0.100082	0,027905
2,03	0,290859	0,262757	0,190075	0,145429	0,100784	0,028101
2,04	0,292881	0.264583	0,191396	0,146440	0,101485	0,028297
2,05	0,294901	0,266408	0,192715	0,147451	0,102186	0,028493
2,06	0,296920	0,268230	0,194033	0,148460	0.Ю2886	0,028689
2,07	0,298936	0,270051	0,195350	0,149468	0,103586	0,028885
2,08	0,300950	0,271870	0,196666	0,150475	0,104284	0,029080'
2,09	0.302962	0,273586	0,197980	0,151481	0,104982	0,029276
2,10	0,304973	0,27,5501	0,199293	0,152486	0,105680	0.029471
2,11	0,306980	0,277314	0,200604	0,153490	0,106376	0,029666
2,12	0,308986	0,279125	0,201914	0,154493	0,107072	0,029860
2,13	0,310989	0,280934	0,20322.2	0,155495	0,107767	0,030055
2,14	0,312990	0.282741	0,204529	0,156495	0,108461	0,030249
2,15	0,314989	0,284545	0,205834	0,157494	0,109154	0,030443
2,1,6	0,316985	0,286347	0,207138	0,158492	0 109847	0,030637
2,17	0,318978	0.288147	0,208439	0,159489	0,110539	0,030831
2,18	0,320968	0,289944	0,209739	0,160484	0,111229	0,031024
2,19	0,322956	0,291739	0,211037	0,161478	0,111919	0,031217
2,20	0,324941	0,293531	0,212334	0,162471	0,112608	0.031410
2,21	0,326924	0.295321	0,213628	0,163462	0,113296	0,031603
2,22	0,328903	0,297108	0,214921	0,164452	0,113982	0,031795
2,23	0,330880	0,298892	0,216211	0,165440	0.114668	0,031987
2,24	0,332853	0,300674	0,217500	0.166427	0,115353	0,032170
2,25	0,334824	0,302453	0,218787	0,167412	0,116037	0,032370
2,26	0,336791	0,304229	0,220071	0,168396	0,116720	0.032561
2,27	0,338755	0,306002	0,221354	0,169378	0,117401	0,032752
2,28	0,340716	0,307773	0,222635	0-170358	0,118082	0,032943
2,29	0,342674	0,309540	0,223913	0,171337	0,118761	0,033133
2,30	0,344629	0,311305	0,225189	0,172314	0,119440	0,033323
2,31	0,346580	0,313066	0,226463	0,173290	0,120117	0,03.3513
2,32	0,348528	0,314825	0,227735	0,174264	0,120793	0,033703
2,33	0,350472	0,316580	0,229004	0,175236	0,121468	0,033892
2,34	0,352413	0,358332	0,230272	0,176207	0,122141	0,034081
365.
Продолжение табл. I
Z	а=0, ₽ = 1	а = О, ₽=О,8	а = 0, 6=0,6	1Л О о* II И в 0Q.	«=о, ₽=0,4	а=0, ₽=0,2
2,35	0,354351	0,320081	0,231537	0,177175	0,122814	0,034269
2,36	0,356284	0,321827	0,232799	0,178142	0,123485	0,034457
2,37	0,358215	0,323569	0,234060	0,179107	0,124155	0,034645
2,38	0,360141	0,325308	0,235317	0,180071	0,124824	0,034832
2,39	0,362064	0,327044	0,236573	0,181032	0,125492	0,035020
2,40	0,363984	0,328777	0,237826	0,181992	0,126158	0,035206,
2,41	0,365899	0,330506	0,239076	0,182950	0,126823	0.035393
2,42	0,367811	0,332231	0,240325	0,183905	0,127486	0,035579
2,43	0,369719	0,333954	0,241570	"0,184859	0,128149	0,035765
2,44	0,371623	0,335672	0,242813	0,185811	0,128810	0,035950
2,45	0,373523	0,337387	0,244053	0,186761	0,129469	0,035135
2,46	0,375419	0,339099	0.245291	0,187710	0,130128	0,036320
2,47	0,377311	0,340807	0,246526	0,188656	0,130785	0,036504
2,48	0,379199	0,342511	0,247759	0,189600	0,131440	0,036688
2,49	0.381084	0,344212	0,248989	0,190542	0,132095	0,036872
2,50	0,382964	0,345908	0,250216	0,191482	0,132747	0,037055
2,51	0,384840	0,347602	0.251441	0,192420	0,133399	0.037238
2,52	0,386711	0,349291	0.252663	0,193356	0,134049	0,037420
2,53	0,388579	0,350977	0.253882	0,194290	0,134697	0,037602
2,54	0,390443	0,352659	0.255098	0,195221	0,135344	0,037784
2,55	0,392302	0,354337	0.256312	0.196151	0,135990	0,037965
2,56	0,394157	0,356011	0,257523	0,197078	0,136634	0,038146
2,57	0,396008	0,357681	0,258731	0,198004	0,137277	0,038326
2,58	0,397854	0,359347	0,259936	0,198927	0,137918	0,038506
2,59	0,399696	0,351010	0,251138	0,199848	0,138558	0,038686
2,60	0,401534	0,352658	0,262337	0,200767	0,139196	0,038865
2,61	0,403367	0,354323	0,263534	0,201684	0,139833	0,039044
2,62	0,405196	0,-365973	0,264728	0,202598	0,140468	0,039222
2,63	0,407020	0,357620	0,265918	0,203510	0,141102	0,039400
2,64	0,408840	0,369262	0,257106	0,204420	0,141734	0,039578
2,65	0,410656	0,370901	0,268291	0.205328	0,142355	0.039755
2,66	0,412467	0,372535	0,269473	0,206234	0,142994	0,039932
2,67	0,414273	0,374165	0,270652	0,207137	0,143521	0.040108
2,68	0,416075	0,375791	0,271828	0,208038	0,144247	0,040284
2,69	0,417873	0,377413	0.273001	0,208936	0,144872	0.040459
2,70	0,419656	0,379031	0,274171	0,209833	0,145495	0.040634
2,71	0,421454	0,380644	0,275338	0,210727	0,146116	0,040809
2,72	0,423237	0,382254	0,276502	0,211619	0,146736	0,040983
2,73	0,425016	0,383859	0,277663	0,212508	0,147354	0,041157
2,74	0,426791	0,385460	0,278821	0.213395	0,147970	0,041330
2,75	0,428560	0,387057	0,279975	0,214280	0,148585	0,041503
2,76	0,430325	0,388649	0,281127	0,215163	0,149198	0,041676
2,77	0,432086	0,390237	0,282276	0,216043	0,149810	0,041848
2,78	0,433841	0,391821	0,283421	0,216921	0,150420	0.042019
2,79	0,435592	0,393401	0,284563	0,217796	0,151028	0,042190
366
П родолжение тпабл. I
Z	<х-=0, ₽ = 1	00 IIII в ох	«=о, ₽=0,6	©© IIII в ох	а=0, ₽=0,4	а=0, (3=0,2
2,80	0,437338	0,394976	0,285703	0,218669	0,151635	0,042361'
2,81	0,439079	0,396547	0,286839	0,219540	0,152240	0,042531
2,82	0,440816	0,398114	0,287972	0.220408	0.152844	0,042701
2,83	0,442547	0,399676	0,289102	0,221274	0,153446	0,042870’
2,84	0,444274	0,401234	0,290228	0,222137	0,154046	0.043039
2,85	0,445996	0,402788	0,291352	0,222998	0,154644	0,043208
2,86	0,447713	0,404337	0.292472	0,223857	0,155241	0,043376
2,87	0,449426	0,405882	0,293590	0,224713	0,155836	0,043543
2,88	0,451133	0,407423	0,294704	0,225567	0,156430	0,043710
2,89	0,452836	0,408959	0,295814	0,226418	0,157022	0,043877
2,90	0,454534	0,410490	0,296922	0,227267	0,157612	0,04404»
2,91	0,456227	0,412018	0,298026	0,228113	0,158200	0,044209'
2,92	0,457915	0,413541	0,299128	0,228958	0,158787	0,044374
2,93	0,459598	0,415059	0.300226	0,229799	0,159372	0.044539
2,94	0,461276	0,416573	0,301321	0,239638	0,159956	0,044703
2,95	0,462950	0,418082	0,302412	0,231475	0,160538	0,044867
2,96	0,464618	0,419587	0,303500	0,232309	0,161118	0,045031
2,97	0,466282	0,421088	0,304586	0,233141	0,161696	0,045193
2,98	0,467940	0,422584	0.305668	0,233970	0,162273	0,045356
2,99	0,469594	0,424076	0,306746	0,234797	0,162848	0,045518
3,00	0,471243	0,425563	0,307822	0,235621	0,163421	0,045680
3,01	0,472887	0,427046	0,308894	0,236443	0,163993	0,045841
3,02	0,474526	0,428524	О.ЗО99ЯЗ	0,237263	0,164563	0,046001
3,03	0,476159	0,429997	0.31Ю28	0,238080	0,165131	0,046162
3,04	0,477788	0,431467	0,312091	0,238894	0,165698	0,046321
3,05	0.479412	0,432931	0,313150	0,239706	0,166262	0,046481
3,06	0,481031	0,434392	0,314206	0,240516	0,166825	0,046639
3,07	0,482645	0,435847	0,315259	0,241323	0,167387	0,046798
3,08	0,484254	0,437299	0,316308	0,242127	0,167946	0,046955
3,09	0,485859	0,438745	0,317354	0,242929	0.168504	0,047113
3,10	0,487458	0,440187	0,318397	0,243729	0,169061	0,047270
3,11	0,489052	0,441625	0,319437	0,244526	0,169615	0,047426
3,12	0,490641	0,443058	0,320473	0,245321	0,170168	0,047582
3,13	0,492225	0,444487	0,321506	0,246113	0,170719	0,047738
3,14	0,493804	0,445911	0,322536	0,246902	0,171269	0,047893
3,15	0,495379	0,447331	0,323562	0,247689	0,171816	0,048047
3,16	0,496948	0,448746	0,324586	0,248474	0,172362	0.048202
3,17	0,498512	0,450157	0,325606	0,249256	0,172906	0,048355
3,18	0,500071	0,451563	0,326623	0,250036	0,173449	0,048508
3,19	0,501626	0,452964	0,327636	0,250813	0,173990	0,048661
3,20	0,503175	0,454361	0,328646	0,251588	0,174529	0,048813
3,21	0,504720	0,455754	0,329653	0,252360	0,175066	0,048965
3,22	0,506259	0,457142	0,330657	0,253130	0,175602	0,049117
3,23	0,507793	0,458526	0,331657	0,253897	0,176136	0,049267
3,24	0,509323	0,459905	0,332655	0,254661	0,176.668	0,049418
367
Продолжени е табл. I
Z	а = 0, ₽ = 1	а=О, ₽ = 0,8	та я II II рр	та я U сп	а=0, ₽ = 0,4	а = 0, ₽=0.2
3,25	0,510847	0,461279	0,333649	0,255424	0,177199	0,049568
3,26	0,512367	0,462649	0,334639	0,256184	0,177728	0,049717
3,27	0,513882	0,464015	0,335627	0,256941	0,178255	0,049866
3,28	0,515391	0,465376	0,336611	0,257696	0,178780	0,050015
3,29	0,516896	0,466733	0,337592	0,258448	0.179304	0,050163
3,30	0,518396	0,468085	0,338569	0,259198	0,179826	0,050310
3,31	0,519890	0,469433	0,339544	0,259945	0,180347	0,050457
3,32	0,521380	0,470776	0,340515	0,260690	0,180865	0.050604
3,33	0,522865	0,472114	0,341483	0,261433	0,181382	0,050750
3,34	0,524345	0,473449	0,342448	0,262173	0,181897 .	0,050896
3,35	0,525820	0,474778	0,343409	0,262910	0,182411	0,051041
3,36	0,527290	0,476104	0,344367	0,263645	0,182923	0,051186
3.37	0,528756	0,477425	0,345323	0,264378	0,183433	0,051331
3,38	0,530216	0,478741	0,346274	0,265108	0,183941	0,051474
3,39	0,531671	0,480053	0,347223	0,265836	0,184448	0,051618
3,40	0,533122	0,481360	0.348168	0,266561	0,184953	0,051761
3,41	0,534567	0,482664	0,349111	0,267284	0,185457	0,051903
3,42	0,536008	0,483962	0,350050	0,268004	0,185959	0.052045
3,43	0,537444	0,485257	0,350985	0,268722	0,186459	0.052187
3,44	0,538875	0,486546	0,351918	0,269438	0,186957	0,052328
3,45	0,540301	0,487832	0,352847	0,270151	0,187454	0,052469
3,46	0,541722	0,489113	0,353774	0.270861	0,187949	0,052609
3,47	0,543139	0,490389	0,354697	0,271569	0,188442	0,052749
3,48	0,544550	0,491662	0,355617	0,272275	0,188934	0,052888
3,49	0,545957	0,492930	0,356533	0,272979	0,189424	0,053027
3,50	0,547359	0,494193	0,357447	0,273680	0,189912	0,053165
3,51	0,548756	0,495452	0,358357	0,274378	0,190399	0,053303
3,52	0,550148	0,496707	0,359264	0,275074	0,190884	0,053441
3,53	0,551536	0,497957	0,360168	0,275768	0,191367	0,053578
3,54	0,552918	0*499203	0,361069	0,276459	0,191849	0,053715
3,55	0,554296	0,500445	0,361967	0,277148	0,192329	0,053851
3,56	0,555669	0,501683	0,362852	0,277835	0,192808	0,053986
3,57	0,557038	0,502916	0,363753	0,278519	0.193285	0,054122
3.58	0,558401	0,504144	0,364642	0,279201	0.193760	0,054256
3,59	0,559760	0,505369	0,365527	0,279880	0.194233	0.054391
3,60	0,561114	0,506589	0,366409	0,280557	0,194705	0,054525
3,61	0,5624^4	0,507805	0,367288	0,281232	0,195175	0,054658
3,62	0,563808	0,509017	0,368164	0,281904	0.195644	0,054791
3,63	0,565148	0,510224	0.369037	0,282574	0,196111	0,054924
3,64	0,566483	0,511427	0,369907	0,283242	0,196577	0,055056
3,65	0,567814	0,512626	0,370774	0,283907	0,197040	0,055188
3,65	0,569140	0,513820	0,371637	0,284570	0,197503	0.055319
3,67	0,570461	0,515011	0,372498	0,285230	0,197963	0.055450
3,68	0,571777	0,516197	0,373355	0,285889	0.198422	0,055580
3,69	0,573089	0,517379	0,374210	0,286545	0,198879	0,055710
368
Продолжение табл. I
Z	та й	° II в СО.	о о II И В ОО.	«=о, ₽=0,5	«=о, (3 = 0,4	та й II 1 О? 'го
3,70	0,574396	0,518557	0,375061	0,287198	0,199335	0,055839
3,71	0,575699	0,519730	0,375910	0,287850	0.199789	0,055968
3,72	0,576997	0,520899	0,376755	0,288499	0,200242	0,056097
3,73	0,578290	0,522065	0,377597	0,289145	0,200693	0.056225
3,74	0.579579	0,523226	0,378437	0.289790	0,201142	0,056353
3,75	0,580863	0,524382	0,379273	0,290432	0,201590	0,056480
3,76	0,582143	0.525535	0,380106	0,291071	0,202036	0,056607
3,77	0,583418	0,526684	0,380937	0,291709	0,202481	0,056734
3,78	0,584688	0,527828	0,381764	0,292344	0,202924	0,056860
3,79	0,585954	0,528968	0,382589	0.292977	0,203366	0,056985
3,80	0,587216	0,530105	0,383410	0,293608	0,203806	0,057111
3,81	0,588473	0,531237	0,384228	0,294236	0,204244	0,057235
3,82	0,589725	0,532365	0,385044	0,294863	0,204681	0,057360
3,83	0,590973	0,533489	0,385856	0,295486	0,205116	0,057484
3,84	0,592216	0,534609	0,386666	0.296108	0,205550	0,057607
3,85	0,593455	0,535725	0,387473	0,296728	0,205982	0,057730
3,86	0,594690	0.536836	0,388276	0,297345	0,206413	0.057853
3,87	0,595920	0,537944	‘ 0,389077	0,297960	0,206842	0,057975
3,88	0,597145	0,539048	0,389875	0,298573	0,207270	0,058097
3,89	0,598366	0,540148	0,390670	0,299183	0,207696	0,058218
3,90	0,599583	0,541243	0,391462	0,299792	0,208121	0,058339
3,91	0,600795	0,542335	0,392252	0,300398	0,208544	0,058460
3,92	0,602003	0,543423	0,393038	0,301002	0,208965	0,058580
3,93	0,603207	0,544507	0,393821	0,301603	0,209386	0,058700
3,94	0,604406	0,545587	0,394602	0,302203	0,209804	0,058819
3,95	0,605601	0,546663	0,395380	0,302800	0,210221	0,058938
3,96	0,606791	0,547735	0,396155	0,303396	0,210637	0,059056
3,97	0,607978	0,548803	0,396927	0,303989	0,211051	0,059174
3,98	0,609159	0,549867	0,397696	0,304580	0,211463	0,059292
3,99	0,610337	0,550927	0,398463	0,305169	0,211875	0,059409
4,00	0,611510	0,551984	0,399226	0,305755	0,212284	0,059526
4,01	0,612679	0,553036	0,399987	0,306340	0,212692	0,059643
4,02	0,613844	0,554085	0,400745	0,306922	0,213099	0,059759
4,03	0,615005	0,555130	0,401500	0,307502	0,213504	0,059875
4,04	0.616161	0,556171	0,402253	0,308080	0,213908	0,059990
4,05	0,617313	0,557208	0,403003	0,308656	0,214310	0,060105
4,06	0,618461	0,558241	0,403750	0,309230	0,214711	0,060219
4,07	0,619604	0,559271	0,404494	0,309802	0,215111	0,060333
4,08	0,620744	0,560296	0,405235	0,310372	0,215509	0,060447
4,09	0,621879	0,561318	0,405974	0,310940	0,215905	0,060560
4,10	0,623010	0,562337	0,406710	0,311505	0,216300	0,060673
4,11	0,624137	0,563351	0,407443	0,312069	0,216694	0,060786
4,12	0,625260	0,564362	0,408174	0,312630	0,217086	0,060898
4,13	0,626379	0,565369	0,408902	0,313189	0,217477	0,061009
4,14	0,627493	0,566372	0,409627	0,313747	0,217866	0,061121
369
П родолжение табл. I
Z	а=0, ₽=1	•CD R II У О© i °0	а = 0, р=0,6	а=0, ₽=0,5	а=0. ₽=0.4	а=0, ₽=0,2
4,15	0,628604	0,567371	0,410349	0,314302	0,218254	0.061232
4,16	0,629710	0,568367	0,411069	0,314855	0,218641	0,061342
4,17	0,630812	0.569359	0,411786	0,315406	0,219026	0.061453
4,18	0,631911	0,570348	0,412501	0,315955	0,219410	0.061562
4,19	0,633005	0,571333	0,413213	0,316503	0,219792	0,061672
4,20	0,634095	0,572314	0,413922	0,317048	0,220173	0.061781
4,21	0,635181	0,573292	0,414628	0,317591	0,220553	0.061889
4,22	0,636264	0,574265	0,415332	0,318132	0,220931	0,061998
4,23	0,637342	0,5752.36	0.416034	0,318671	0,221308	0,062106
4,24	0,638416	0,576202	0.416732	0,319208	0,221684	0,062213
4,25	0,639486	0,577166	0,417429	0,319743	0,222058	0.062320
4,26	0,640553	0,578125	0,418122	0,320276	0,222431	0,062427
4,27	0,641615	0,579081	0,418813	0,320808	0,222802	0.062534
4,28	0,642674	0,580033	0,419502	0,321337	0,223172	0,062640
4,29	0,643728	0,580982	0,420187	0,321864	0,223541	0,062745
4,30	0,644779	0,581928	0.420871	0.322389	0,223908	0.062851
4,31	0,645826	0,582870	0,421551	0,322913	0,224274	0.062956
4,32	0,646869	0,583808	0,422230	 0,323434	0,224639	0,063060
4,33	0,647908	0,584743	0,422905	0.323954	0,225002	0,063164
4,34	0,648943	0,585674	0,423578	0,324471	0,225364	0,063268
4,35	0,649974	0,586602	0,424249	0,324987	0,225725	0,063372
4,36	0,651002	0,587527	0,424917	0,325501	0.226085	0,063475
4,37	0,652026	0.588448	0,425583	0,326013	0,226443	0,063578
4,38	0,653045	0,589365	0,426246	0.326523	0,226799	0,063680
4,39	0,654062	0,590279	0,426907	0,327031	0,227155	0,063782
4,40	0,655074	0,591190	0,427565	0,327537	0,227509	0.063884
4,41	0,656083	0,592097	0,428221	0,328041	0,227862	0.063985
4,42	0,675088	0,593001	0,428874	0,328544	0,228214	0,064086
4,43	0,658089	0,593902	0,429525	0,329045	0,228564	0,064187
4,44	0,659087	0.594799	0,430174	0,329543	0,228913	0,064287
4,45	0,660080	0,595693	0,430820	0,330040	0,229261	0.064387
4,46	0,661071	0,596584	0,431463	0,330535	0,229607	0.064487
4,47	0,662057	0,597471	0,432104	0.331029	0,229953	0,064586
4,48	0,663040	0,598355	0,432743	0,331520	0,230297	0,064685
4,49	0,664019	0.599235	0,433380	0,332010	0.230639	0,064783
4,50	0,664995	0,600113	0,434014	0,332497	0,230981	0,064881
4,51	0,665966	0,600987	0,434645	0,332983	0,231321	0,064979
4,52	0,666935	0,601858	0,435275	0,333467	0,231660	0,065077
4,53	0,667900	0,602725	0,435902	0,333950	0,231998	0,065174
4,54	0,668861	0,603589	0,436526	0,334430	0,232334	0,065271
4.55	0,669818	0.604450	0,437149	0,334909	0,232р70	0.065367
4,56	0,670772	0,605308	0,437769	0,335386	0,233004	0,065464
4,57	0,671723	0.606163	0,438386	0.335861	0,233337	0,065559
4,58	0,672670	0.607014	0,439002	0,336335	0,233668	0,065655
4,59	0,673613	0,607863	0,439615	0,336807	0,233999	0,065750
370
Продолжение табл. I
Z	й в СО.	та Я IIII Ор 00	II II в со.	а=0, ₽=0,5	та я 11 рр	а=0, ₽=0,?
4,60	0,674553	0,608708	0,440225	0,337277	0,234328	0,065845
4,61	0,675490	0,609550	0,440834	0,337745	0,234656	0,065939
4,62	0,676423	0,610389	0,441440	0,338211	0,234983	0,066034
4,63	0,677352	0,611224	0,442044	0,338676	0,235308	0.066128
4,64	0,678278	0,612057	0,442646	0,339139	0,235633	0,066221
4,65	0,679201	0,612886	0,443245	0,339601	0,235956	0,066314
4,66	0,680120	0,613713	0,443842	0,340060	0,236278	0,066407
4,67	0,681036	0,614536	0,444437	0,340518	0,236599	0,066500
4,68	0,681949	0.615356	0,445030	0,340974	0,236919	0,066592
4,69	0,682858	0,616173	0,445621	0,341429	0,237237	0,066684
4,70	0,683763	0,616987	0,446209	0,341882	0,237555	0,066775
4,71	0,684666	0,617799	0,446795	0,342333	0,237871	0,066867
4,72	0,685565	0,618607	0,447379	0,342782	0,238186	0,066958
4,73	0,686460	0,619412	0,447961	0,343230	0,238500	0,067048
4.74	0,687353	0,620214	0,448540	0,343676	0,238813	0,067139
4,75	0,688242	0,621013	0,449118	0,344121	0,239124	0,067229
4,76	0,689127	0,621809	0,449693	0,344564	0,239435	0,067318
4,77	0,690010	0,622602	0,450266	0,345005	0,239744	0,067408
4,78	0,690889	0,623392	0,450837	0,345445	0,240052	0,067497
4,79	0,691765	0,624179	0,451406	0,345883	0,240359	0,067586
4,80	0,692638	0,624963	0,451972	0,346319	0,240665	0,067674
4,81	0,693507	0,625744	0,452537	0,346754	0,240970	0,067762
4,82	0,694373	0,626523	0,453099	0,347187	0,241274	0,067850’
4,83	0,695237	0,627298	0,453660	0,347618	0,241577	0,067938
4,84	0,696096	0,628071	0,454218	0,348048	0,241878	0,068025
4,85	0,696953	0,628841	0,454774	0,348477	0,242179	0,068112
4,86	0,697807	0,629607	0,455328	0,348903	0,242478	0,068199
4,87	0,698657	0,630372	0,455880	0,349329	0,242777	0,068285
4,88	0,699504	0,631133	0,456430	0,349752	0,243074	0,068371
4,89	0,700348	0,631891	0,456978	0,350174	0,243370	0,068457
4,90	0,701189	0,632646	0,457524	0,350595	0,243665	0,068542
4,91	0,702027	0,633399	0,458068	0,351014	0,243959	0,068627
4,92	0,702862	0,634149	0,458610	0,351431	0,244252	0,068712
4,93	0,703693	0,634896	0,459150	0,351847	0,244544	0.068797
4,94	0,704522	0,635640	0,459688	0,352261	0,244835	0,068881
4,95	0,705348	0,636382	0,460223	0,352674	0,245124	0,068965
4,96	0,706170	0,637121	0,460757	0,353085	0,245413	0,069049
4,97	0,706990	0,637857	0,461289	0,353495	0,245701	0,069132
4,98	0,707806	0,638590	0,461819	0,353903	0,245987	0,069216
4,99	0,708620	0,639321	0,462347	0,354310	0,246273	0,069298
5,00	0,709430	0,640049	0,462873	0,354715	0,246557	0,069381
5,01	0,710237	0,640774	0,463397	0,355119	0,246841	0,069463
5,02	0,711042	0,641496	0,463919	0,355521	0,247123	0,069545
5.03	0,711843	0,642216	0,464439	0,355922	0,247405	0,069627
5,04	0,712642	0,642933	0,464957	0,356321	0,247685	0,069708
371.
Продолжение табл. I
Z	OF4 II И в со.	а=0, ₽=0,8	to ©<= В II в ах	tD я II II ©о СП	©о II Л В СО-	СМ О о II II в ах
5,05	0,713438	0,643648	0,465473	0,356719	0,247965	0,069790
5,06	0,714230	0,644359	0,465987	0,357115	0,248243	0,069871
5.07	0,715020	0.645069	0,466500	0,357510	0,248520	0,069951
5,08	0,715807	0,645775	0,467010	0,357904	0,248797	0,070031
5.09	0,716591	0,646479	0,467519	0,358296	0,249072	0,070112
5.10	0,717372	0,647180	0,468026	0,358686	0,249347	0,070191
5.11	0,718150	0.647879	0,468530	0,359075	0.249620	0,070271
5,12	0,718926	0,648575	0,469033	0.359463	0,249892	0,070350
5,13	0,719698	0,649269	0,469535	0,359849	0,250164	0.070429
5,14	0,720468	0,649960	0,470034	0,360234	0,250434	0,070508
5,15	0,721235	0,650648	0,470531	0,360618	0,250704	0,070586
5,16	0,721999	0.651334	0,471027	0,361000	0,250972	0.070664
5,17	0,722760	0.652018	0,471520	0,361380	0,251240	0,070742
5,18	0,723519	0,652698	0,472012	0,361759	0,251506	0,070820
5,19	0,724274	0,653377	0.472502	0,362137	0,251772	0,070897
5,20	0,725027	0.654053	0.472991	0,362514	0,252037	0,070974
5,21	0,725778	0,654726	0.473477	0,362889	0,252300	0,071051
5,22	0,726525	0,655397	0,473962	0,363263	0,252563	0,071128
5,23	0,727270	0,656065	0,474445	0,363535	0.252825	0,071204
5,24	0,728012	0,656731	0,474926	0.364006	0,253086	0.071280
5,25	0,728751	0,657395	0,475405	0,364376	0,253346	0,071356
5,26	0,729488	0,658056	0,475883	0,364744	0,253505	0,071432
5,27	0,730222	0,658714	0,476359	0,365111	0,253863	0,071507
5,28	0.73Э953	0,659370	0,476833	0,355476	0,254120	0,071582
5,29	0,731681	0,660024	0,477305	0.365841	0,254377	0,071657
5,30	0,732407	0.660675	0,477775	0.356204	0,254632	0,071731
5,31	0,733131	0,661324	0,478244	0,366565	0,254886	0,071806
5,32	0.733851	0,661971	0,478711	0,366926	0,255140	0,071880
5,33	0,734569	0,662615	0,479177	0,367285	0,255392	0,071953
5,34	0,735284	0,663257	0,479640	0,367642	0,255644	0,072027
5,35	0,735997	0,663897	0,480102	0.367999	0,255895	0,072100
5,36	0,736707	0,664534	0,480563	0,368354	0,256145	0,072173
5,37	0,737415	0,665169	0,481021	0,358708	0,256394	0,072246
5,38	0,738120	0,665801	0.481478	0,369060	0,256642	0,072319
5,39	0,738823	0,666431	0,481933	0,359411	0,256889	0,072391
5.40	0,739523	0,667059	0,482387	0,369761	0,257136	0,072463
5,41	0,740220	0,667685	0.482839	0,370110	0,257381	0,072535
5'42	0,740915	0,668308	0,483289	0,370457	0,257626	0,072607
5,43	0,741607	0,668929	0,483738	0,370804	0,257869	0,072678
5,44	0,742297	0,669548	0,484185	0,371149	0,258112	0,072749
5,45	0,742984	0,670164	0,484630	0,371492	0,258354	0,072820
5,46	0,743669	0,670778	0,485074	0,371835	0,258595	0,072891
5,47	0,744352	0,671390	0,485516	0,372176	0,258836	0,072961
5,48	0,745032	0,672000	0.485956	0,372516	0,259075	0,073031
5,49	0,745709	0,672608	0,486395	0,372855	0,259314	0,073101
372
Продолжение табл. I
Z	О’-* и и а со.	ОО О о II11 в со-	а=0. ₽=0,6	ю О О IIII а ах	а=0, ₽=0,4	TD Я f 1 РР КЗ
5,50	0,746384	0,673213	0,486832	0,373192	0,259552	0,073171
5,51	0.747057	0,673816	0,487268	0,373528	0,259788	0,073240
5,52	0.747727	0,674417	0,487702	0,373863	0,260025	0.073309
5,53	0,748394	0.675016	0,488135	0,374197	0,260260	0,073378
5,54	0.749060	0,675612	0,488566	0.374530	0,260494	0,073447
5,55	0,749723	0,676207	0,488995	0.374861	0,260728	0.073516
5,56	0,750383	0,676799	0,489423	0,375192	0,260961	0,073584
5,57	0,751041	0,677389	0.489849	0,375521	0,261192	0,073652
5,58	0.751697*	0,677977	0,490274	0,375849	0,261424	0.073720
5,59	0.752351	0,678563	0,490697	0,376175	0,261654	0,073788
5,60	0,753002	0,679146	0,491118	0,376501	0,261883	0,073855
5,61	0,753651	0,679728	0,491539	0,376825	0,262112	0,073922
5,62	0.754297	0,680307	0,491957	0,377149	0,262340	0,073989
5,63	0,754941	0,680885	0,492374	0,377471	0,262567	0,074056
5,64	0,755583	0,681460	0,492790	0,377791	0,262793	0,074123
5,65	0,756222	0,682033	0,493204	0,378111	0.263019	0,074189
5,66	0,756860	0,682604	0,493616	0,378430	0.263243	0.074255
5,67	0,757495	0,683173	0,494027	0,378747	0,263467	0,074321
5,68	0,758127	0,683740	0,494437	0,379064	0.263690	0,074386
5,69	0,758758	0,684305	0,494845	0,379379	0,263913	0,074452
5,70	0,759386	0,684868	0,495252	0,379693	0.264134	0,074517
5,71	0,710012	0,685429	0,495657	0,380006	0,264355	0.074582
5,72	0,760635	0,685988	0,496060	0,380318	0.264575	0.074647
5,73	0,761257	0,686545	0,496463	0.380628	0,264794	0,074712
5,74	0,761876	0,687100	0,495863	0,380938	0.265013	0,074776
5,75	0,762493	0,687653	0,497263	0.331247	0,265231	0,074840
5,76	0,763108	0,688204	0,497661	0,381554	0,265447	0.074904
5,77	0,763721	0,688752	0,498057	0,381860	0,265664	0,074968
5,78	0,734331	0,689299	0,498452	0,382166	0,265879	0.075031
5,79	0,764939	0,689844	0,498846	0,382470	0,266094	0,075095
5,80	0,765546	0,690387	0,499238	0,382773	0,266308	0,075158
5,81	0,766150	0,690928	0,499529	0,383075	0,266521	0,075221
5,82	0,766751	0,691468	0,500018	0,383375	0,266733	0,075283
5,83	0,767351	0,692005	0,500406	0,383576	0,266945	0,075346
5,84	0,767949	0,692540	0,500793	0,333974	0,267156	0,075408
5,85	0,768544	0,693073	0,501178	0,384272	0.267366	0,075470
5,86	0,759138	0,693505	0,501562	0,384569	0,267576	0.075532
5,87	0,769729	0,694134	0.501944	0,384864	0,267785	0,075594
5,88	0,770318	0,694662	0,502325	0,385159	0,267993	0,075655
5,89	0,770905	0,695188	0,502705	0,385453	0,258200	0,075717
5,90	0,771490	0,695712	0,503083	0,385745	0,268407	0,075778
5,91	0,772073	0,696234	0,503460	0,386037	0,268613	0,075839
5,92	0,772654	0,696754	0,503835	0,386327	0.268818	0,075899
5,93	0,773233	0,697272	0,504211	0,385616	0,269022	0.075960
5,94	0,773810	0,697789	0,504584	0,386905	0,269226	0,076020
373
Продолжение табл. I
Z	а=0, ₽ = 1	ОО О о IIII в ах	оо II II в ах	а=0, ₽=0,5	та я II И рр	О1 ©о II II в ах
5,95	0,774384	0,698304	0,504955	0,387192	0,269429	0,076080
5,96	0,774957	0,698816	0,505326	0,387479	0.269632	0,076140
5,97	0,775528	0,699328	0.505695	0,387764	0,269833	0,076200
5,98	0,776097	0,699837	0,506062	0,388048	0,270034	0,076260’
5,99	0,776664	0,700344	0,506429	0,388332	0.270235	0,076319-
6,00	0,777228	0,700850	0.506794	0,388614	0,270434	0.076378
6,01	0.777791	0,701354	0,507158	0,388896	0,370633	0,076437'
6.02	0,778352	0,701856	0,507520	0,389176	0,270832	0,076496-
6,03	0,778911	0,702356	0,507882	0,389455	0,271029	0,076555'
6,04	0,779468	0,702854	0,508242	0,389734	0,271226	0,076613
6,05	0,780023	0,703351	0,508600	0,390011	0,271422	0,076671
6,06	0,780576	0,703846	0,508958	0,390288	0,271618	0,076729
6,07	0,781127	0,704339	0,509314	0.390563	0,271813	0,076787
6,08	0,781676	0,704831	0,509669	0,390838	0,272007	0,076845
6,09	0,782223	0,705321	0,510023	0,391112	0,272200	0,076902
6,10	0,782769	0,705809	0,510375	0,391384	0,272393	0,076959'
6,11	0,783312	0,706295	0,510726	0,391656	0,272586	0,077017
6,12	0,783854	0,706780	0,511076	0,391927	0,272777	0,077074
6 13	0,784393	0,707263	0,511425	0,392197	0,272968	0,077130
6,14	0,784931	0,707744	0,511773	0,392466	0,273158	0,077187
6,15	0,785467	0,708223	0,512119	0,392734	0,273348	0,077243:
6,16	0,786001	0,708701	0,512464	0,393001	0,273537	0,077299
6,17	0,786533	0.709177	0,512808	0,393267	0,273725	0,077356
6,18	0,787064	0,709652	0,513150	0,393532	0.273913	0,077411
6,19	0,787592	0,710125	0,513492	0,393796	0,274100	0,077467
6,20	0,788119	0,710596	0,513832	0,394059	0,274287	0,077523:
6,21	0,788644	0,711065	0,514171	0,394322	0,274472	0,077578
6,22	0,789167	0.711533	0,514509	0,394583	0,274658	0,077633'
6,23	0,789688	0,712000	0,514846	0,394844	0,274842	0,077688
6,24	0,790208	0,712464	0,515181	0,395104	0,275026	0,077743
6,25	0,790725	0,712927	0,515516	0,395363	0,275209	0,077798
6,26	0,791241	0,713389	0,515849	0,395621	0,275392	0,077852
6,27	0,791755	0,713848	0,516181	0,395878	0,275574	0,077906
6,28	0.792268	0,714307	0,516512	0,396134	0,275756	0,077960
6,29	0,792778	0,714763	0,516842	0,396389	0,275937	0,078014
6.30	0,793287	0,715218	0,517170	0,396644	0,276117	0,078068
6,31	0,793794	0,715672	0,517498	0,396897	0,276291	0,078122
6.32	0,794299	0,716124	0,517824	0,397150	0,276475	0,078175
6,33	0,794803	0,716574	0,518149	0,397402	0,276654	0,078229'
6,34	0,795305	0,717023	0,518473	0,397652	0,276832	0,078282
6,35	0,795805	0,7174/0	0,518796	0,397903	0,277009	0,078335
6,36	0,795303	0,717916	0,519118	0,398152	0.277186	0,078387
6,37	0,796800	0,718360	0,519438	0,398400	0,277362	0,078440
6,38	0,797295	0,718802	0,519758	0,398648	0,277537	0,078493
6,39	0,797789	0,719243	0,520077	0.398894	0,277712	0,078545
374
Продолжение табл. I
г	а=0, ₽ = 1	QO О о IIII в ш.	<х=0, ₽=0,6	о=0, ₽=0,5	а = 0, ₽=0,4	а = 0, (3=0,2
6,40	0,798280	0,719683	0,520394	0,399140	0,277886	0,078597
6,41	0,798770	0,720121	0,520710	0,399385	0,278060	0,078649
6,42	0,799259	0,720557	0.521025	0,399629	0,278233	0,078701
6,43	0,799745	0,720992	0,521339	0,399873	0,278406	0,078752
*6,44	0,800230	0,721426	0,521652	0,400115	0,278578	0,078804
6,45	0,800714	0,721858	0,521964	0,400357	0,278749	0,078855
6,46	0,801195	0,722288	0,522275	0,400598	0,278920	0,078906
6,47	0,801675	0,722717	0,522585	0,400838	0,279090	0,078957
6,48	0,802154	0,723145	0,522894	0,401077	0,279260	0,079008
6,49	0,802631	0,723571	0,523201	0,401315	0,279429	0,079059
'6,50	0,803106	0,723996	0.523508	0,401553	0,279598	0,079110
6,51	0,803579	0,724419	0,523814	0,401790	0,279766	0,079160
6,52	0,804051	0,724841	0,524118	0,402026	0,279933	0,079210
6,53	0,804522	0,725261	0,524422	0,402261	0,280100	0,079260
6,54	0,804991	0,725680	0,524724	0,402495	0,280267	0,079310
6,55	0,805458	0,726097	0,525025	0,402729	0,280433	0,079360
6,56	0,805924	0,726513	0,525326	0,402962	0,280598	0,079410
6,57	0,806388	0.726928	0,525625	0,403194	0,280763	0,079459
6,58	0,806850	0,727341	0,525923	0,403425	0,280927	0,079508
6,59	0,807311	0,727753	0,526221	0,403656	0,281090	0,079558
6,60	0,807771	0,728163	0,526517	0,403885	0,281254	0,079607
6,61	0.808228	0,72,8572	0,526812	0,404114	0,281416	0,079656
6,62	0,808685	0,728980	0,527107	0,404342	0,281578	0,079704
6,63	0,809139	0,729386	0,527400	0,404570	0,281740	0,079753
6,64	0,809593	0,729791	0,527692	0,404796	0,281901	0,079801
6,65	0,810045	0,730194	0,527983	0,405022	0,282061	0,079850
6,66	0,810495	0,730597	0,528274	0,405247	0,282221	0,'079898
6,67	0,810943	0,730997	0,528563	0,405472	0,282380	0,079946
6,68	0,811391	0,731397	0,528851	0,405695	0,282539	0,079994
6,69	0,811836	0,731795	0,529139	0,405918	0,282698	0,080041
6,70	0,812281	0,732191	0,529425	0,406140	0,282856	0,080089
6,71	0,812724	0.732587	0,529711	0,406362	0,283013	0,080136
6,72	0,813165	0,732981	0,529995	0,406582	0,283170	0,080184
6,73	0,813605	0,733373	0,530279	0,406802	0,283326	0,080231
6,74	0,814043	0.733765	0,530561	0,407022	0,283482	0,080278
6,75	0,814480	0,734155	0,530843	0,407240	0,283637	0,080325
6,76	0,814915	0,734544	0,531123	0.407458	0,283792	0,080371
6.77	0,815349	0,734931	0,531403	0,407675	0,283946	0.080418
6,78	0,815782	0,735317	0,531682	0,407891	0,284100	0,080464
6,79	0,816213	0,735702	0,531960	0,408107	0,284253	0,080511
6,80	0,816643	0,736086	0,532237	0,408321	0,284406	0,080557
6,81	0,817071	0,736468	0,532513	0,408536	0,284559	0,080603
6,82	0,817498	0,736849	0,532788	0,408749	0,284710	0,080649
6,83	0,817923	0,737229	0,533062	0.408962	0,284862	0,080694
6., 84	0,818347	0,737607	0,533335	0,409174	0,285012	О', 080740
375
Продолжение табл. I
						04 о О* IIII в со.						Продолжение		табл. II
Z	а=0, ₽=.!	и=0, 0 = 0,8	а=0, 0=0.6	а=0. 0=0.5	а=0, р=0,4				а = 0.	а=0,1.	а=0,2,	а=0,25,	«=0,3,	а=0,4,
									₽=1	0=0,9	0=0,8	₽=0,75	6 = 0,7	6 = 0,6
														
6 85	0,818770	0,737984	0,533607	0,409385	0,285163	0,080785		0,25	0,00621’0	0,005903				
6,86 6 87	0,819191	0,738360	0,533879	0,409596	0,285313	0.080831					0,005014	0,004378	0,003637	0,001909
	0.819611	0,738735	0,534149	0,409806	0,285462	0,080876		0,26	0,006714	0,006381	0,005420	0,004733	0,003931	0,002064
6,88	0 820030	0,739108	0,534419	0,410015	0,285611	0,080921		0,27	0.007236	0,006878	0.005842	0,005102	0,004237	0,002225
6,89	0,820447	0,739480	0,534687	0,410223	0,285759	0,080966		0,28	0,00/ / /8	0,007393	0,006279	0,005484	0,004555	0,002391
						0,081011		0,29	0,008339	0,007926	0.006732	0,005879	0,004883	0,002564
6 90	0,820862	0,739851	0,534955	0,410431	0,285907			0,30	0,008918					
6 91	0^821277	0,740221	0,535222	0,410638	0,286055	0,081055				0,008477	0,007200	0,006288	0,005223	0,002742
6,92	0,821690	0,740589	0,535488	0,410845	0,286202	0,081100		0,31	0,009517	0,009046	0,007683	0,006710	0,005573	0,002926
6,93	0,822101	0,740957	0,535753	0,411051	0,286348	0,081144		0,32	0,010135	0,009633	0,008182	0,007145	0,005935	0,003116
6,94	0,822512	0,741323	0,536017	0,411256	0,286494	0,081189		0.33	0,010771	0,010237	0,008696	0,007594	0,006307	0,003312
					0,286640	0,081233		0,34	0,011426	0,010860	0,009224	0,008056	0,006691	0,003513
6 95	0,822921	0,741687	0,536281	0,411460				0,35	0,012100					
6.96	0,823328	0,742051	0,536543	0,411664	0,286785	0,081277	i			0,011500	0,0097/58	0,008531	0,007085	0,003720
6,97	0,823735	0,742413	0,536805	0,411867	0,286930	0,081321		0,36	0,012792	0,012158	0,010327	0,009019	0,007491	0,003933
6,98	0,824139	0,742775	0,537065	0,412070	0,287074	0,081364	j	0,37	0,013502	0,012834	0,010901	0,009520	0,007907	0,004152
6,99	О;824543	0,743135	0,537325	0,412272	0,287218	0,081408		0,38	0,014232	0,013527	0,011490	0,010034	0,008334	0,004376
								0,39	0,014979	0,014237	0,012093	0,010561	0,008772	0,004606
					Таблица 11									
							-	1		0,40	0,015745	0,014965	0.012711 0,013344	0,011101 0,011653	0,009220 0,009679	0.004841 0,005082
		а=0,1, р - 0,9	а=0,2, 0=0,8	а— 0,25,	а=0,3.	а=0.4,	i	0,41	0,016528	0,015710				
Z	В —1			0 = 0,75	0=0,7	0=0.6		0,42	0,017330	0,016472	0,013991	0,012218	0,010148	0.005329
								0.43	0.018150	0,017251	0,014653	0,012796	0,010629	0,005581
				Q	о	0		0,44	0,018988	0,018047	0,015329	0,013387	0,011119	0,005838
0 0,01 0 02	0 0,000009	0 0,000009	0,000008	0,000007	0,000005	0,000003		0,45	0,019843	0,018860	0,016020	0,013990	0,011620	0,006101
	0,000039	0,000038	0,000032	0,000028	0.000023	0,000012		0,46	0,020716	0,019690	0,016725	0,014605	0,012131	0,006370
0,03 0,04	0,000089	0,000085	0,000072	0,000063	0,000052	0,000027		0,47	0,021607	0,020536	0,017443	0,015233	0,012653	0,006643
	0,000159	0,000152	0,000129	0,000112	0,000093	0,000049		0,48	0,022515	0,021399	0,018177	0,015873	0,013184	0,006923
					0,000146	O.OOOO76		0,49	0.023440	0,022279	0,018924	0,016526	0,013726	0,007207
0 05	0,000249	0,000237	0,000201	0,000176										
0 06	0,000359	0.000342	0,000290	0,000253	0,000210	0,000110		0,50	0,024383	0,023175	0,019685	0,017190	0,014278	0,007497
0 07	0,000489	0,000465	0,000395	0,000345	0,000286	0,000150		0,51	0,025343	0,024087	0,020459	0,017867	0,014840	0,007792
0 08	0,000639	0,000607	0,000516	0,000450	0.000374	0,000196		0,52	0,026319	0,025016	0,021248	0,018556	0,015412	0,008092
0,09	0,000809	0.000769	0,000653	0,000570	0,000473	0,000248		0,53	0,027313	0,025960	0.022050	0,019256	0,015994	0,008398
					0,000585	0,000307		0,54	0,028324	0,026921	0,022866	0,019969	0,016586	0,008709
0 10	0,000998	0,000949	0,000806	0,000704										
о’11	0,001208	0,001148	0,000975	0,000852	0,000707	0,000371		0,55	0,029351	0,027897	0,023695	0,020693	0,017187	0,009025
0,12	0,001437	0,001366	0,001160	0,001013	0,000842	0,000442		0,56	0,030395	0,028889	0.024538	0,021429	0,017799	0,009345
0,13	0,001687	0,001603	0,001362	0,001189	0,000988	0,000518		0,57	0,031455	0,029897	0.025394	0,022177	0,018419	0,009671
0,14	0,001956	0,001859	0,001579	0,001379	0,001145	0,000601		0,58	0,032532	0,030921	0,026263	0,022936	0,019050	0,010003
					0,001314	0,000690		0,59	0,033625	0,031959	0,027146	0,023706	0,019690	0,010339
0 15	0,002244	0,002133	0,001,812 0,002061	0,001582										
0,16	0,002553	0,002426		0,001800	0,001495	0,000785		0,60	0,034734	0,033013	0,028041	0,024488	0,020339	0,010679
0,17	0,002881	0,002738	0,002326	0,002031	0,001687	0,000886		0,61	0,035859	0,034083	0,028949	0,025281	0,020998	0,011025
0,18	0,003229	0,003069	0,002607	0,002276	0,001891	0,000993	.		0.62	0,037000	0,035167	0,029870	0,026085	0.021666	0,011376
0.19	0,003596	0,003418	0,002903	0,002536	0,002106	0,001106	(		0,63	0,038157	0,036267	0,030804	0,026901	0,022343	0,011732
				0,002808	0,002333	0.001225		0,64	0.039329	0,037381	0,031750	0,027727	0,023030	0,012092
0 20	0,003983	0,003786	0,003216											
0,21	0,004390	0,004172	0,003544	0,003095	0,002571	0,001350		0,65	0,040517	0,038510	0,032709	0,028565	0,023725	0,012457
0,22	0,004816	0,004577	0,003888	0,003395	0,00/820	0,001481 0,001618 0,001761	г	0,66	0,041720	0,039654	0,033681	0,029413	9,024430	0,012827
0,23	0,005261	0,005001	0,004248	0,003709	0,003081			0,67	0,042939	0,040812	0,034664	0,030272	()’025143	6,013202
0,24	0,005726	0,005443	0,004623	0,004037	0,003353			0,68	0,044173	0,041984	0,035660	0,031141	0,'025865	0*013581
								0,69	0,045421	0,043171	0,036668	0,032021	0,026596	0,013965
13—3802
377
376
Продолжение табл. II
Продолжение табл. II
Z	а=0, ₽ = 1	а = 0.1, ₽=0,9	а = 0,2, ₽=О,8	а=о,25, ₽=0,75	а—0,3, ₽ = 0,7	а = 0,4, ₽=0,6
0 70	0,046686	0,044372	0,037688	0,032912	0,027338	0,014354
071	0,047965	0,045588	0,038721	0,033814	0,028085	0,014746
о’72	0,049257	0,046817	0,039763	0,034725	0,028841	0,015142
073	0,050564	0,048058	0.040819	0,035646	0,029607	0,015545
0*74	0,051884	0.049314	0,041886	0,033577	0,030380	0,015951
0 75	0,053220	0,050584	0,042964	0,037518	0,031162	0,016362
0 76	0,054570	0,051866	0,044054	0,038470	0,031951	0,016776
0 77	0,055934	0,053162	0,045154	0,039432	0,032751	0,017196
0 78	0,057312	0,054472	0,046266	0,040403	0,033557	0,017619
0,79	0,058702	0,055794	0,047389	0,041384	0,034371	0,018047
0 80	0,060107	0,057129	0,048522	0,042374	0,035194	0,018479
0 81	0,051526	0,058476	0,049667	0,043373	0,035024	0,018915
0 82	0,052957	0,059837	0,050822	0,044381	0,036862	0,019354
0 83	0,064401	0,061210	0,051988	0,045400	0,037707	0,019798
О'84	0,065857	0,062593	0,053164	0,046425	0,038560	0,020246
0 85	0 067327	0.053991	0,054350	0,047463	0,039420	0,020698
0 86	0,068811	0,065401	0,055547	0,048508	0,040289	0,021153
0 87	0,070306	0,056822	0,056754	0,049561	0.041163	0,021613
0 88	0,071812	0,058254	0,057970	0,050623	0,042046	0,022076
0^89	0,073331	0,059597	0,059197	0.051694	0,042935	0,022543
0 90	0,074864	0,071153	0,060433	0,052774	0,043831	0,023014
0*91	0 076407	0,072621	0,061679	0,053862	0,044735	0,023488
0 92	0 0779S3	0,074099	0,062934	0,054958	0,045645	0,023966
093	0,079530	0,075588	0.054199	0,056052	0,046563	0,024448
0’94	0,081109	0,077088	0,065473	0,057174	0,047487	0,024932
П 9Б	0 082598	0,078599	0,066756	0,058295	0,048417	0,025421
	0 084^99	0,080120	0,068048	0,059423	0,049354	0,025913
VZ f Л Q7	0 085911	0,081652	0,059349	0,060559	0,050298	0,026409
Л QR	0.087534	0,083195	0,070659	0,061703	0,051247	0,026907
0,99	0,089167	0,084747	0,071977	0,052854	0,052203	0.027409
1 ЛЛ	0 090812	0,085310	0,073305	0,054013	0,053166	0,027914
1 Л1	0 092466	0,087882	0,074639	0,065178	0,054133	0,028422
1 Л9	0 094131	0,089465	0,075983	0.066352	0,055108	0,028934
1 02	0 095807	0,091056	0,077334	0,057532	0,056088	0,029449
1,04	0,097490	0,092657	0,078695	0,068719	0.057074	0,029966
1 ОБ	0 099186	0,094268	0,080032	0,069913	0,058066	0,030486
1 OR	О*100891	0,095889	0,081438	0,071115	0,059063	0,031010
1 07	0*102605	0,097518	0,082821	0,072323	0,060067	0,031537
1 08	0 104328	0,099155	0,084211	0,073537	0,061075	0,032066
1,09	0,106061	0,109802	0,085610	0,074758	0,062089	0,032599
1 10	0,107802	0,102457	0,087016	0,075986	0,063108	0.033133
1 11	0,109553	0,104’21	0,088429	0,077219	0,054133	0,033672
1 12	0,111312	0,105793	0,089848	0,078458	0,065162	0,034212
1 13	0,113080	0,107474	0,091276	0,079705	0,066197	0,034755
1,14	0,114857	0,109162	0,092709	0,080956	0,067237	0,1)35301
Z	TD Я ip	TD Я ОО	а-0,2, ₽=0,8	а»0,25, ₽ = 0,75	с=0,3, ₽ = 0,7	а =>0,4, а=0,6
1,15	0,116643	0,110859	0,094150	0,082214	0,068281	0,035849
1,16	0,118435	0,112563	0,095597	0,083477	0,069330	0,036400
1,17	0,120237	0,114275	0,097050	0,084746	0,070384	0,036953
1,18	0,122046	0,115994	0,098510	0.086021	0,071443	0,037509
1,19	0,123863	0,117721	0,099976	0,087302	0,072506	0,038067
1,20	0,125688	0,119455	0,101449	0,088587	0.073573	0,038627
1,21	0,127520	0,121196	0,102927	0,089878	0,074645	0,039190
1,22	0,129360	0.122944	0,104412	0,091174	0,075722	0,039755
1,23	0,131207	0,124699	0,105902	0,092475	0,076802	0,040322
1,24	0.133060	0,126461	0,107398	0,093781	0,077886	0,040892
1,25	0,134922	0,138229	0,108899	0,095092	0,078975	0,041463
1,26	0,136789	0,130004	0,110406	0,096408	0,080068	0,042036
1 '2?	0,138663	0,131785	0,111918	0,097727	0,081164	0,042612
1,28	0,140544	0,133573	0,113435	0,099052	0,082264	0,043189
1,29	0,142430	0,125365	0,114958	0,100382	0,083368	0,043769
1,30	0,144324	0,137164	0,116486	0,101716	0,084475	0,044350
1,31	0„146223	0,138969	0,118017	0,103053	0,085586	0,044933
1,32	0,148128	0,140779	0,119555	0,104395	0,086700	0,045518
1,33	0,150039	0,142595	0,121096	0.105741	0,087818	0,046105
1,34	0,151956	0,144417	0,122643	0,107092	0,088939	0,046693
1,35	0,153878	0,146244	0,124194	0,108446	0,090063	0,047283
1,3b	0,155806	0,148075	0,125749	0,109803	0,091191	0,047875
1,37 1,38	0,157738 0,159676	0,149912 0,151753	0,127308 0,128871	0,111165 0,112530	0,092321 0,093455	0,048468 0,049063
1,39	0,161619	0,153599	0,130438	0,113898	0,094591	0,049660
1,40	0,163566	0,155450	0,132010	0,115270	0,095730	0,050257
1,41	0,165519	0,157305	0,133585	0.116645	0,096872	0,050857
1,42 1,43 1,44	0,167476	0,159165	0,135164	0,118023	0,098016	0,051457
	0,169438	0,161029	0,136746	0,119405	0,099164	0,052060
	0,171403	0,162897	0,138332	0,120789	0,100314	0,052663
1,45 1,46 1,47 1,48 1,49	0,173373 0,175347 0,177325 0,179307 0,181292	0,164769 0,166645 0,168524 0,170407 0,172294	0,139921 0,141514 0,143109 0,144708 0,146310	0,122177 0,123567 0,124960 0,126355 0,127753	0,101466 0,102620 0,103777 0.104935 0,106096	0,053267 0,053873 0,054480 0,055089 0,055698
1,50 1,51 1,52 1,53 1,54	0,183281 0,185274 0,187270 0,189269 0,191271	0,174184 0,176077 0,177974 0,179873 0,181776	0,147914 0,149521 0,151131 0,152743 0,154358	0,129154 0,130557 0,131962 0,133370 0,134780	0,107259 0,108424 0,109591 0,110760 0,111930	0,056308 0,056920 0,057532 0,058146 0,058760
1,55 1,56 1,57 1,58 1,59	0,193275 0,195283 0,197294 0,199307 0,201323	0,183681 0,185588 0,187499 0,189412 0,191327	0,155975 0,157595 0,159216 0,160840 0,162465	0,136192 0,137605 0,139021 0,140438 0,141858	0,113103 0,114277 0,115452 0,116629 0,117808	0,059375 0,059991 0,060608 0,061225 0,061844
13*
379
378
Продолжение табл. II
Z	а=0, ₽ = 1	а—0,1, ₽=0,9	а=0,2, ₽=0,8	а=0,25, р =0,75	а=0,3, ₽=О,7	«=0,4, Р=0.6	Z	а=0, ₽ = 1	а=0,1, ₽ =0,9	«“0,2. ₽=0,8	I ipc я=0,25,‘ ₽=0,75	ммжение «—0,3, ₽=О,7	таол. ц а=О,4, ₽ = 0,6
1,60 1,61 1,62 1,63 1,64	0,203340 0,205361 0,207383 0,209407 0,211433	0,193244 0,195164 0,197085 0,199009 0,200934	0,164093 0,165722 0,167353 0,168986 0,170620	0,143278 0,144700 0,146124 О,;47550 0,148976	0,118987 0,120168 0,121350 0,122533 0,123717.	0,062463 0,063983 0,063703 0,064324 0,064945	2,05 2,06 2,07 2,08 2.09	0,294901 0,296920 0,298936 0,300950 0,302962	0,280235 0,282153 0,284068 0,285982 0,287893	0,237914 0,239540 0,241165 0,242789 0,244410	0,207712 0,209131 0,210549 0,211966 0,213381	0.172477 0,173656 0,174833 0,176009 0,177183	0,090529 0,091147 0,091764 0,092381 0.092997
1,65 1,66 1,67 1,68 1,69	0,213461 0,215491 0.217522 0,219555 0,221589	0,202861 0,204790 0,206720 0,208651 0,210584	0,172256 0,173893 0,175531 0,277170 0,178810	0,150404 0,151833 0,153263 0,154694 0,156125	0,124903 0,126089 0,127276 0,128464 0,129653	0,065567 0,066190 0,066813 0.067437 0,068050	2,10 2,11 2,12 2,13 2,14	0,304973 0,306980 0,308986 0,310989 0,312990	0,289803 0,291710 0,293616 0,295519 0,297419	0,246030 0,247648 0,249264 0,250879 0,252491	0,214795 0,216207 0,217617 0,219026 0,220433	0,178357 0,179529 0,180699 0,181869 0,183036	0,093613 0,094228 0,094842 0,095455 0,096067
1,70 1,71 1,72 1,73 1,74	0,223625 0,225661 0,227699 0,229737 0.231776	0,212518 0,214453 0,216389 0,218325 0,220263	0,180452 0,182094 0,173737 0,185381 0,187025	0,157558 0,158992 0,160426 0,161861 0,163296	0,130843 0,132033 0,133223 0,134415 0,135606	0,068685 0,069309 0,069934 0.070559 0,071184	2,15 2,16 1	2,17 2.18 2,19	0,314989 0,316985 0,318978 0,320968 0,322956	0,299317 0,301213 0,303107 0,304998 0,306886	0,254101 0,255709 0,257316 0,258919 0,260521	0,221838 0,223241 0,224643 0,226042 0,227440	0,184203 0,185367 0,186531 0,187692 0,188852	0,096679 0,097290 0,097900 0,098509 0,099118
) 711,75  ’1;76 <i4>77 ’ ч¥,*79 "	0,233816 0,235857 0,237898 0,239940 0,241982	0,222201 0,224140 0,226080 0,228019 0,229960	0,188670 0,190316 0,191961 0,193608 0,195254	0,164732 0,166168 0,167605 0,169042 0,170497	0,136799 0,137991 0,139184 0,140377 0,141570	0,071810 0,072435 0,073061 0,073687 0,074313	2,20 2,21 2,22 2,23 2,24	0,324941 0,326924 0,328903 0,330880 0,332853	0,308772 0,310655 0,312535 0,314412 0,316287	0,262120 0.263718 0,265312 0,266905 0,268495	0,228836 0,230229 0,231621 0,233010 0,234398	0,190011 0,191167 0,192322 0,193475 0,194627	0,099725 0,100332 0,100938 0,101543 0,102147
<1,80  1,81 1,82 1,83 1,84	0,244024 0,246066 0,248109 0,250151 0,252194	0,231900 0,233840 0,235781 0.237721 0,239662	0,196901 0,198548 0,200194 0,201841 0,203488	0,171916 0,173354 0,174791 0.176228 0,177666	0,142763 0,143956 0,145150 0,146343 0,147536	0,074939 0,075566 0,076192 0,076818 0,077444	2,25 2,26 2.27 2,28 2,29	0,334824 0,336791 0,338755 0,340716 0,342674	0,318159 0,320027 0,321893 0,323756 0,325615	0,270082 0,271667 0,273249 0.274829 0,276406	0,235783 0,237166 0,238547 0,239925 0,241301	0,195776 0,196924 0,198070 0,199214 0.200356	0,102750 0,103352 0.103953 0,104553 0,105151
1,85 1,86 1,87 1,88 1,89	0,254236 0,256278 0,258319 0,260360 0,262400	0,241602 0,243542 0,245481 0,247420 0,249359	0,205134 0,206780 0,208426 0,210071 0,211716	0,179103 0,180539 0,181976 0,183412 0.184848	0,148729 0,149922 0,151114 0,152306 0,153498	0,078070 0,078695 0,079321 0,079947 0,080572	2,30 2,31 2,32 2,33 2,34	0,344629 0,346580 0,348528 0,350472 0,352413	0,327472 0,329325 0,331175 0,333922 0,334866	0,277981 0,279553 0,281121 0,282688 0,284251	0,242575 0.244046 0,245415 0,246782 0,248146	0,201496 0,202634 0,203770 0,204904 0,206036	0,105749 0,106346 0,106942 0,107537 0,108130
1,90 1,91 1,92 1,93 1,94	0,264440 0,266479 0,268517 0,270554 0,272590	0,251297 0,253234 0,255170 0.257105 0,259040	0,213360 0,215004 0,216647 0,218289 0,219931	0,186283 0,187717 0,189151 0,190585 0,192017	0,154689 0,155880 0,157071 0,158260 0,159450	0,081197 0,081822 0,082446 0,083071 0,083694	2,35 2,36 2,37 2,38 2,39	0,354351 0,356284 0,358215 0.360141 0,362064	0,336706 0,338543 0,340376 0,342206 0,344032	0,’285811 0,287369 0.288924 0,290475 0.292024	0,249507 0,250866 0,252222 0,253576 0,254927	0,207166 0,208294 0,209419 0,210543 0,211664	0,108723 0.109314 0,109904 0,110493 0,111081
1,95 1,96 1,97 1,98 1,99	0,274625 0,276659 0,278692 0,280724 0,282754	0,260973 0,262906 0,264837 0,266767 0,268695	0,221571 0,223211 0,224849 0,226487 0,228123	0,193449 0,194880 0,196310 0,197739 0,199167	0,160638 0,161826 0,163013 0,164199 0,165385	0,084318 0,084941 0,085564 0,086186 0,086808	2,40 2,41 2,42 2,43 2,44	0,353984 0,365899 0,367811 0,369719 0,371623	0,345855 0,347675 0,349490 0,351302 0,353111	0,293570 0,295112 0,296652 0,298188 0,299722	0,256276 0,257622 0,258965 0,260305 0,261643	0,212783 0,213900 0,215014 0,216127 0,217237	0,111668 0,112254 0,112838 0,113421 0,114003
2,00 2,01 2,02 2,03 2,04	0,294782 0,286809 0,288835 0,290859 0,292881	0,270623 0,272548 0,274473 0,276395 0,278316	0,229758 0,231392 0,233025 0,234656 0,236385	0,200594 0,202020 0,203445 0.204868 0,206291	0,166569 0,167753 0,168935 0,170117 0,171298	0,087430 0,088050 0,088671 0,089291 1 0.089910	2,45 2,46 2,47 2,48 2,49	0,373523 0,375419 0,377311 0.379199 0,381084	0,354915 0,356716 0,358513 0,360306 0,362096	0,ЗЭ1252. 0,302778 0,304302 0,305822 0,307339	0,262978 0,264310 0,265639 0,266965 0,268289	0.218344 0,219450 0,220552 0,221653 0,222751	0,114584 0,115164 0,115742 0.116319 0,116895
380								-					381
П родолжение табл. II
Z	71 а со.	«=0,1, ₽=0,9	а=0,2, ₽=0,8	а=0,25, ₽=0,75	СО* ©О II II в ах	«=0,4, ₽=0,6
2,50	0,382964	0,363881	0,308853	0,269609	0,223847	0,117469
2,51	0,384840	0.365663	0,310364	0,270927	0,224940	0,118042
2,52	0,386711	0,367441	0,311871	0,272242	0,226031	0,118614
2,53	0,388579	0,369214	0,313374	0,273553	0,227119	0,119185
2,54	0,390443	0,370984	0,314874	0,274862	0,228205	0,119754
2,55	0,392302	0,372749	0,316371	0,276168	0,229288	0,120322
2,56	0,394157	0,374511	0,317865	0,277470	0,230369	0,120888
2,57	0,396008	0,376269	0,319354	0,278770	0,231447	0,121454
2,58	0,397854	0,378022	0,320841	0,280066	0,232523	0,122018
2,59	0,399696	0,379771	0,322324	0,281360	0,233595	0,122580
2,60	0,401534	0,381517	0,323803	0,282650	0,234667	0,123141
2,61	0,403367	0,383257	0.325278	0,233937	0,235735	0,123701
2,62	0,405196	0,384994	0,226751	0,285221	0,236800	0,124260
2,63	0,407020	0,386727	0,328219	0,286502	0,237863	0,124817
2,64	0,408840	0,388455	0,329684	0,287780	0.238923	0,125372
2,65	0,410656	0,390179	0,331145	0,289054	0,239980	0,125926
2,66	0,412467	0,391899	0.332603	0,290326	0,241035	0,126479
2,67	0,414273	0,393614	0,334057	0,291594	0,242087	0,127031
2^68	0.416075	0.395325	0,335507	0,292859	0,243136	0,127581
2,69	0,417873	0,397032	0,336953	0,294120	0,244183	0,128129
2,70	0,419666	0,398734	0,338396	0,295379	0,245227	0,128676
2,71	0,421454	0,400432	0,339835	0,296634	0,246268	0,129222
2,72	0,423237	0,402126	0.341270	0,297885	0,247306	0,129766
2,73	0,425016	0,403815	0,342701	0,299134	0,248342	0,130309
2,74	0,426791	0.405500	0,344129	0,200397	0,249375	0,130850
2,75	0,428560	0,407180	0,345553	0,301621	0,250405	0,131390
2,76	0,430325	0,408856	0,346973	0,302859	0,251432	0,131929
2,77	0,432086	0,410527	0,348389	0,304094	0,252457	0,132466
2,78	0,433841	0,412194	0,349802	0,305326	0,253479	0,133001
2,79	0,435592	0,413856	0,351210	0,306554	0,254498	0,133535
2,80	0,437338	0,415514	0,352615	0,307779	0,255514	0,134068
2,81	0,4390/9	0.417168	0,354016	0,309001	0,256527	0,134599
2,82	0,440816	0,418816	0,355413	0,310219	0,257538	0,135128
2,83	0,442547	0,420460	0,356806	0,311434	0,258545	0,135656
2,84	0,444274	0,422100	0,358195	0,312645	0,259550	0,136183
2,85	0,445996’	0,423735	0,359580	0,313853	0,260552	0,136708
2,86	0,447713	0,425365	0,350961	0,315058	0,261551	0,137231
2,87	0,449426	0,426991	0,362339	0,316259	0,262547	0,137753
2,88	0,451133	0,428612	0,363712	0,317457	0,263541	0,138274
2,89	0,452836	0,430229	0,365081	0,318651	0,264531	0,138793
2,90	0,454534	0,431841	0,366447	0,319841	0,265519	0,139310
2,91	0,456227	0,433448	0,367808	0,321029	0,266503	0,139826
2,92	0,457915	0,435051	0,369166	0,322212	0,367485	0,140340
2,93	0,459598	0,436649	0.370520	0,323393	0,268464	0,140853
2,94	0,461276	0,438242	0,371869	0,324569	0,259440	0,141365
к			 IIродолжение табл. II							
		а = 0,	а=0,1.	о=0,2,	« = 0,25,	«=0,3,	o'о II и в ах
		₽ = 1	₽=0,9	₽ = 0,8	₽ = 0,75	₽=0,7	
	2,95	0,462950	0,439830	0,373215	0,325743	0,270413	0.141874
	2,96	0,464618	0,441414	0,374556	0,326912	0,271383	0,142383
	2,97	0,456282	0,442994	0,375894	0,328079	0,272350	0.142889
	2,98	0,467940	0,444568	0,377228	0,329242	0,273315	0,143395
	2,99	0,469594	0,446138	0,378557	0,330401	0,274276	0,143898
	3,00	0,471243	0,447703	0,379883	0,331557	0,275235	0,144400
	3,01	0,472887	0,449264	0,381204	0,332709	0,276190	0,144901 0 145400
	3,02	0,474526	0,450819	0,382522	0,333858	0,277143	
	3,03	0,476159	0,452370	0,383835	0,335003	0,278092	0,145897 0,146393
	3,04	0,477788	0,453917	0,385145	0,336144	0,279039	
	3,05	0,479412	0,455458	0,386450	0,337282	0,279983	0 146888
	3,06	0,481031	0,456995	0,387752	0,338417	0,280924	0,147381 0,147872 0 148362
	3,0/	0,482645	0,458527	0,389049	0,339548	0,281862	
	3,08	0,484254	0,460054	0,390343	0,340676	0,282797	
	3,09	0,485859	0,461577	0,391632	0,341800	0,283729	0,148850
	3,10	0,487458	0,463095	0,392917	0,342921	0,284658	0,149336
	3,11	0,489052	0,464608	0,394198	0,344037	0,285584	0,149821 0 150305
	3,12	0,490641	0,466116	0,395476	0,345150	0,286507	
	3,13	0,492225	0,467620	0,396749	0,346260	0,287428	0 150787
	3,14	0,493804	0,469119	0,398018	0,347367	0,288345	0,151267
	3,15	0,495379	0,470613	0,399283	0,348469	0,289259	0,151746 0,152224 0,152.599 0,153174 0,153646
	3,16	0,496948	0,472103	0,400544	0,349569	0,290171	
	3,17	0,498512	0,473587	0,401801	0,350664	0,291079	
	3,18	0,500071	0,475067	0,403054	0,351756	0,291985	
	3,19	0,501626	0,476543	0,404303	0,352845	0,292887	
	3,20	0,503175	0,478013	0,405548	0,353930	0,293787	0,154117 0 154587
	3,21	0,504720	0,479479	0,406788	0,355012	0,294684	
	3,22	0,506259	0,480940	0,408025	0,356090	0,295577	0,155055 0,155521 0,155986
	3,23	0,507793	0,482396	0,409258	0,357164	0,296468	
	3,24	0,509323	0,483848	0,410485	0,358235	0,297356	
	3,25	0,510847	0,485295	0,411711	0,359302	0,298241	0,156450 0,156911 0,157372 0,157830 0,158288
	3,26	0,512367	0,486737	0,412932	0,360366	О'299123	
	3,27	0,513882	0,488174	0,414148	0,361427	0,300002	
	3,28	0,515391	0,489607	0,415361	0,362483	О'300878	
	3,29	0,516896	0,491035	0,416569	0,363537	0,301751	
	3,30	0,518396	0,492458	0,417774	0,364586	0,302622	0,158743 0,159197 0 159650
	3,31	0,519890	0,493877	0,418975	0,365633	0,303489 0,304353	
	3,32	0,521380	0,495290	0,420171	0,356675		
	3,33	0,522865	0,496700	0,421364	0,367715	0,305215	0 160101
	3,34	0,524345	0,498104	0,422552	0,368750	0,306073	0,160550
	3,35 3,36 3,37	0,525820 0,527290 0,528756	0,499504 0,500899 0,502289	0,423737 0,424917 0,426094	0,369783 0,370811 0,371837	0,306929 0,307782 0,308632 0,309479	0,160998 0,161445 0 1618с0
	3,38	0,530216	0,503675	0,427266	0,372858		0 162333
1	3,39	0,531671	0,505056	0,428435	0,373877	0,310323	О", 162775
382
383
Продолжение табл. II
Продолжение табл. II
Z	1=0, Р = 1	а=О,1, ₽=0,9	а=0,2, (3 — 0,8	04 о” о II II а ох	а—0,3, ₽=0,7	а ==0,4, (3=0,6
3,40	0,533122	0,506432	0,429599	0,374891	0,311164	0,163215
3,41	0,534567	0,507804	0,430760	0,375903	0,312002	0,163654
3*42	0,536008	0,509171	0,431916	0.376911	0,312837	0,164091
3,43	0,537444	0,510533	0,433069	0,377915	0,313670	0,164527
3,44	0,538875	0,511891	0,434218	0,378916	0,314499	0.164961
3 45	0,540301	0,513244	0,435362	0,379913	0,315326	0,165394
3 46	0,541722	0,514593	0,436503	0,380907	0,316150	0,165825
347	0,543139	0,515937	0,437640	0,331898	0,316971	0,166255
3 48	0,544550	0,517276	0,438773	0,382885	0,317789	0,166683
3,49	0,545957	0,518611	0,439902	0,383869	0,318604	0,167109
3 50	0,547359	0,519941	0,441027	0,384849	0,319417	0,167534
3 51	0*548756	0,521266	0,442148	0,385826	0,320226	0,167958
3’52	0*550148	0,522587	0,443266	0,386799	0,321033	0,168380
3,53	0,551536	0,523904	0,444379	0,387769	0,321837	0,168801
3,54	0,552918	0,525215	0,445488	0,388736	0,322638	0,169220
3 55	0,554296	0,526523	0,446594	0,389699	0,323436	0,169638
3,56	0,555669	0,527825	0,447696	0,390659	0,324231	0,170054
3,57	0,557038	0,529123	0,448794	0,391615	0,325024	0,170469
3,58	0,558401	0,530417	0,449888	0,392568	0,325814	0,170882
3,59	0,559760	0,531706	0,450978	0,393518	0,326600	0,171294
3,60	0,561114	0,532.991	0,452064	0,394464	0,327385	0,171704
3,61	0,562464	0,534271	0,453146	0,395407	0,328166	0,172113
3,62	0,563808	0,535546	0,454225	0,396347	0,328944	0,172520
3*63	0,565148	0,536817	0,455300	0,397283	0,329720	0,1/2926
3*64	0,566483	0,538084	0,456371	0,398216	0,330493	0,173330
3,65	0,567814	0,539346	0,457438	0,399145	0,331263	0,173733
3 66	0 569140	0,540604	0,458501	0,400071	0,332031	0,174135
3,67	0,570461	0,541857	0,459561	0,400994	0,332795	0,174535
3*68	0,571777	0,543106	0,460616	0,401914	0,333557	0,174933
3,69	0*573089	0,544350	0,461668	0,402830	0,334316	0,175330
3,70	0,574396	0,545590	0,462717	0,403743	0,335073	0,175726
3,71	0,575699	0,546826	0,463761	0,404653	0,335827	0,176120
3,72	0,576997	0,548057	0,464802	0,405559	0,333578	0,176513
3*73	0,578290	0,549284	0,465839	0,406462	0,337326	0,176904
3,74	0,579579	0,550506	0,466872	0,407362	0,338071	0,177294
3,75	0,580863	0,551724	0,467902	0,408259	0,338814	0,177683
3 76	0,582143	0,552938	0,468927	0,409152	0,339554	0,178070
3,77	0*583418	0,554147	0,469949	0,410042	0,340291	0,178456
3,78	0*584688	0,555352	0,470968	0,410929	0,341026	0,178840
3,79	0,585954	0,556552	0,471983	0,411813	0,341758	0,179323
3,80	0,587216	0,557749	0,472994	0,412693	0,342488	0.179604
3,81	0,588473	0,558941	0,474001	0,413570	0,343214	0,179984
3,82	0,589725	0,560129	0,475005	0,414444	0,343938	0,180363
3*83	0,590973	0*561312	0,476005	0,415315	0,344660	0,180740
3,84	0,592216	0,562491	0,477001	0,416183	0,345378	0,181116
Z	TD Я О Л р	ТС Я	<1=0,2, ₽=0,8	а=0,25, (3 = 0,75	а = 0,3, ₽=0,7	а — 0,4, ₽=0,6
3,85	0,593455	0,563666	0,477994	0,417047	0^346094	0,181490
3,86	0,594690	9,564837	0,478983	0,417909	0,346808	0,181863
3,87	0,595920	0,566003	0,479969	0,4187^7	0,347518	0,182235
3,88	0,597145	0,567165	0,480951	0,419622	0,348227	0,182605
3,89	0,598366	0.568323	0,481929	0,420474	0,348932	0,182974
3,90	0,599583	0,569477	0,482904	0,421322	0,349/35	0,133342
3,91	0,600795	0,570627	0,483875	0,422168	0,350335	0,183708
3,92	0,602003	0,571772	0,484843	0,423010	0,351033	0,184072
3,93	0,603207	0,572913	0,485807	0,423850	0,351728	0,184435
3,94	0,604406	0,574051	0,486767	0,424686	0,352421	0,184798
3,95	0,605601	0,575184	0,487724	0,425519	0,353111	0,185159
3,96	0,606791	0,576312	0.488678	0,426349	0,353798	0,185518
3,97	0,607978	0,577437	0,489628	0,427176	0,3'4483	0,185876
3,98	0,609159	0,578558	0,490574	0,428000	0,355166	0,186233
3,99	0,610337	0,579674	0,491517	0,428821	0,355845	0,186588
4,00	0,611510	0,580787	0,492457	0,429639	0,356523	0,186942
4,01	0,612679	0,581895	0,493393	0,430454	0,357197	0,187295
4,02	0,613844	0,582999	0,494325	0,431266	0,357870	0,187646
4,03	0,615005	0,584100	0,495255	0,432075	0,358539	0,187996
4,04	0,616161	0,585196	0,496180	0,432880	0,359207	0,188345
4,05	0,617313	0,586288	0,497103	0,433683	0,359871	0,188692
4,06	0,618461	0,587376	0,498021	0,434483	0,360534	0,189038
4,07	0,619604	0,588460	0,498937	0,435280	0,361193	0,189383
4,08	0,620744	0,589541	0,499849	0,436074	0,361851	0,189727
4,09	0,621879	0,590617	0,500758	0,436865	0,362505	0,190069
4,10	0,623010	0,591689	0,501663	0,437652	0,363158	0,190410
4,11	0,624137	0,592758	0,502565	0,438437	0,363808	0,190749
4,12	0,625260	0,593822	0,503463	0,439219	0,3644/	0,191088
4,13	0,626379	0/94882	0,504359	0,439999	0,365100	0,191425
4,14	0,627493	0,595939	0,505251	0,440775	0,365743	0,191760
4,15	0,628604	0,596992	0,506139	0,441548	0,366383	0,192095
4,16	0,629710	0,598040	0,507024	0,442319	0,367021	0,192428
4,17	0 /30812	0,599085	0,507906	0,443086	0,367656	0,192760
4,18	0,631911	0,600126	0,508785.	0,44385i	0,368289	0,193091
4,19	0,633005	0,601164	0,509661	0,444612	0,368920	0,193420
4,20	0,634095	0,602197	0,510533	0,445371	0,369548	0,193748
4,21	0,635181	0,603227	0,511402	0,446127	0,370174	0,194075
4,22	0,636264	0,604252	0,512267	0,446881	0,370797	0,194401
4,23	0,637342	0,605274	0,513130	0.447631	0,371418	0,194726
4,24	0,638416	0,606292	0,513989	0,448379	0,372037	0,195049
4,25	0,639486	0,607307	0,514845	0,449123	0,372654	0,195371
4,26	0,640553	0,608317	0,515697	0,449865	0,373268	0,195692
4,27	0,641615	0,609324	0,516547	0,450604	0,373880	0,196011
4,28	0,642674	0,610327	0,517393	0,451341	0,374489	0,196329
4,29	0,643728	0,611327	0,518237	0,452074	0,375096	0,196647
385
384
Продолжение табл. II
Z	TD Р 1°	а = О,1, ₽=0,9	ТлЗ й и II ©р со ю	а=0,25, ₽=0,75	®=о,з, ₽ = 0.7	а=0,4, ₽=0,6
4,30	0,644779	0,612323	0,519077	0,452805	0,375701	0,196963
4,31	0,645826	0,613315	0,519914	0,4'3? 33	0,376304	0,197277
4,32	0,646869	0,614303	0,520747	0,454259	0,376904	0,197591
4,33	0,647908	0,615288	0,591578	0,454981	0,377502	0,197903
4,34	0,648943	0,616269	0.522405	0,455701	0,378098	0,198214
4,35	0,649974	0,617246	0,523230	0,456418	0,378691	0,198524
4'36	0,651002	0,618220	0,524051	0,457133	0,379283	0,198833
4,37	0,652026	0,619190	0,524869	0,457845	0,379872	0,199140
4,38	0,653045	0,620156	0,525685	0,458554	0,380458	0,199447
4,39	0,654062	0,621119	0,526497	0,459260	0,381043	0,199752
4,40	0,655074	0,622079	0,527306	0,459964	0,381625	0,200056
4,41	0,656083	0,623034	0,528112	0,460665	0,382205	0,200359
4,42	0,657088	0,623986	0,528915	0,461363	0,382783	0,200661
4,43	0,658089	0,624935	0,529715	0,462059	0,383359	0,200961
4,44	0,659087	0,625880	0,530512	0,462752	0,383932	0,201260
4,45	0,660080	0,626822	0,531306	0,463443	0,384504	0,201559
4,46	0,661071	0,627760	0,532097	0,464131	0,385073	0,201856
4,47	0,662057	0,628695	0,532884	0,464816	0,385640	0,202152
4,48	0,663040	0,629626	0,533670	0,465499	0,386205	0,202447
4,49	0,664019	0,630553	0,534452	0,466179	0,386767	0,202740
4,50	0,664995	0,631478	0,535231	0,466856	0,387328	0,203033
4,51	0,665966	0,632398	0,536007	0,467531	0,387886	0,203334
4,52	0,666935	0,633316	0,536780	0,468204	0,388443	0,203615
4,53	0,667900	0,634230	0,537551	0,468874	0,388997	0,203904
4,54	0,668861	0,635140	0,538318	0,469541	0,389549	0,204192
4,55	0,669818	0,635047	0,539083	0,470206	0,390099	0,204479
4,56	0,670772	0,636951	0,539844	0,470868	0,390647	0,204765
4,57	0,671723	0,637851	0,540603	0,471528	0,391192	0,205050
4,58	0,672670	0,638748	0,541359	0,472185	0,391736	0,205334
4,59	0,673613	0,639642	0,542112	0,472840	0,392278	0,205616
4,60	0,674553	0,640532	0,542862	0,473492	0,392817	0,205898
4,61	0,675490	0,641419	0,543610	0,474142	0,393355	0,206178
4,62	0,676423	0,642303	0,544355	0,474790	0,393890	0,206458
4,63	0,677352	0,643184	0,545096	0,475434	0,394424	0,206736
4,64	0,678278	0,644061	0,545835	0,476077	0,394955	0,207013
4,65	0,679201	0,644935	0,546572	0,476717	0,395484	0,207289
4,66	0,680120	0,645805	0,547305	0,477355	0,396012	0,207564
4,67	0,681036	0,646673	0,548036	0,477990	0,396537	0,207838
4,68	0,681949	0,647573	0,548764	0,478623	0,397060	0,208111
4,69	0,682858	0,648398	0,549489	0,479253	0,397582	0,208383
4,70	0,683763	0,649255	0,550211	0,478981	0,398101	0,208654
4,71	0,684666	0,650110	0,550931	0,480507	0,398619	0,208924
4,72	0,685565	0,650961	0,551648	0,481130	0,399134	0,209193
4,73	0,686460	0,651810	0,552363	0,481751	0,399647	0,209461
4,74	0,687353	0,652655	0,553074	0,482369	0,400159	0,209728
386
Продолжение табл. II
Z	а=0, (3 = 1	а =0,1. (3=0,9	а=0,2, ₽=0,8	а=0.25, (3=0,75	а—0,3, Р-0,7	ТО Я и II ©Р СЛ 4*-
4,75	0,688242	0,653497	0,553783	0,482986	0,400668	0,209993
4,76	0,689127	0,654335	0,554490	0,483600	0,401176	0,210258
4,77	0,690010	0,655171	0,555193	0,484211	0,401682	0,210522
4,78	0,690889	0,656003	0,555894	0,484820	0,402185	0,210784
4,79	0,691765	0.656833	0,556593	0,485427	0,402687	0,211046
4,80	0,692538	0,657659	0,557288	0,486032	0,403187	0,211307
4,81	0,693507	0,658482	0,557982	0,486634	0,403685	0,211566
4,82	0,694373	0,659303	0,558672	0,487234	0,404181	0,211825
4,83	0,695237	0,660120	0,559360	0,487832	0,404675	0,212033
4,84	0,696096	0,669934	0,560045	0,488428	0,405168	0,212340
4,85	0,696953	0,661745	0,560728	0,489021	0,305658	0,212595
4,86	0,697807	0,662553	0,561408	0,489612	0,406147	0,212850
4,87	0,698657	0,663358	0,562086	0,490201	0,406634	0,213104
4,88	0,699504	0,664160	0.562761	0,490787	0,407118	0,213357
4,89	0,700348	0,664959	0,563434	0,491372	0,407601	0,213608
4,90	0,701189	0,665755	0,564104	0,491954	0,408083	0,213859
4,91	0,702027	0,666548	0,564771	0,492534	0,408562	0,214109
4,92	0,702862	0,667339	0,565436	0,493112	0,409040	0,214358
4,93	0,703593	0,668126	0,566099	0,493687	0,409515	0,214606
4,94	0,704522	0,668910	0,566759	0,494260	0,409989	0,214853
4,95	0,705348	0,669692	0,567416	0,494832	0,410461	0,215099
4,96	0,706170	0,670470	0,568071	0,495401	0,410932	0,215344
4,97	0,706990	0,671246	0,568724	0,495968	0,411400	0,215588
4,98	0,707806	0,672019	0,569374	0,496532	0,411867	0,215832
4,99	0,708620	0,672789	0,570022	0,497095	0,412332	0,216074
5,00	0,709430	0,673556	0,570667	0,497656	0.412795	0,216315
5,01	0,710237	0,674320	0,571310	0,498214	0,413257	0,216556
5,02	0,711042	0,675081	0,571950	0,498770	0,413716	0,216795
5,03	0,711843	0,675840	0,572588	0,499325	0,414174	0,217034
5,04	0,712642	0,676596	0,573224	0,499877	0,414631	0,217272
5,05	0,71343.8	00677349	0,573857	0,500427	0,415085	0,217509
5,06	0,714230	0,678099	0,574488	0,500975	0,415538	0,217744
5,07	0,715020	0,678845	0,575117	0,501520	0,415989	0,217979
5,08	0,715807	0,679591	0,575743	0,502064	0,416438	0,218214
5,09	0,716591	0,680333	0,576367	0,502606	0,416886	0,218447
5,10	0,717372	0,681072	0,576989	0,503145	0,417332	0,218679
5,11	0,718150	0,681809	0,577608	0,503684	0,417776	0,218910
5,12	0,718926	0,682542	0,578225	0,504219	0,418219	0,219141
5,13	0,719698	0,683273	0,578839	0,404753	0,418660	0,219371
5,14	0,720468	0,684002	0,579452	0,505285	0,419099	0,219599
5,15	0,721235	0,684727	0,580062	0,505814	0.419536	0,219827
5,16	0,721999	0,685450	0,580669	0,50b342	0,419972	0,220054
5,17	0,722760	0,686171	0,581275	0,506868	0,420407	0,220281
5,18	0,723519	0,686888	0,581878	0,507391	0,420839	0,220506
5,19	0,724274	0,687603	0,582479	0,507913	0,421270	0,220730
387
Продолжение табл. II
Продолжение табл. II
а	а си.	о'о II II В СП.	см оо о© II II в 02-	а=0,25, ₽=0,75	’=0,3, ₽=0,7	а=0,4,	1 (3=0,6	£	z	3=1	6 СП.	’=0,2, (3=0,8	см г* О© II 0 а СП.	00 Is* сГо II II а сп.	а=0,4, (3=0,6
5,20	0,725027	0,688316	0,583078	0,508433	0,421700	0,220954	г	5,65	0,756222	0,717815	0,607844	0,529922	0,439441	0,230185
5,21	0,725778	0,689025	0/83674	0,508951	0,422127	0,221177	5,66	О;756860	0.718417	0,608349	0,530360	0,439802	0,230373
5,22	0,726525	0,689733	0,584268	0,509467	0,422554	0,221399	5,67	0,757495	0,719018	0,608852	0,530796	0,440162.	0,230560
5,23	0,727270	0,690437	0,584860	0, ?09981	0,422978	0,221620	5,68	0'758127	0,719615	0,609353	0,531231	0,440521	0,230746
5,24	0,728012	0,691139	0,585450	0,510493	0,423401	0,221840	5,69	0,758758	0,720211	0,609853	0,531664	0,440878	0,239932
5,25	0,728751	0,691838	0,586038	0,511003	0,423822	0,222059	5,70	0,759386	0,720805	0,610351	0,532096	0,441234	0,231117
5,26.	0,729488	0,692535	0,586623	0,511511	0,424242	0,222278	5,71	0,760012	0,721396	0,610846	0,532525	0,441589	0,231302
5,27	0,730222	0,693229	0,587207	0,512017	0,424660	0,222495	5,72	0,760535	0,721986	0,611341	0,532954	0,441942	0,231485
5,28	0,730953	0,693921	0,587788	0,512-22	0,425077	0,222712	5,73	0,761257	0,722573	0,611833	0,533381	0,442294	0,231668
5,29	0,731681	0,694610	Л.588367	0,513024	0,425492	0,222928	5,74	0,761876	0,723158	0,612323	0,533806	0,442645	0,231850
5,30	0,732407	0,695297	0,588944	0,513525	0,425905	0,223144	5,75	0,762493	0,723741	0,612812	0,534229	0,442994	0,232032
5,31	0,733131	0,695981	0,589518	0,514024	0,426317	0,223358	,	5,76	0,763108	0,724322	0,613299	0,534652	0,443342	0,232213
5,32	0,733851	0,696663	0,590091	0,514-21	0,426728	0,223572	5,77	0,763721	0,724901	0,613784	0,535072	0,443689	0,232393
5,33	0,734569	0 /97342	0,590661	0,515016	0,427136	0,223784	Г	5,78	0,764331	0,725478	0,614268	0,535491	0,444035	0,232573
5,34	0,735284	0,698018	0,591230	0,515509	0,427544	0,223996	5,79	0,764939	0.726053	0,614749	0,535909	0,444379	0,232752
5,35	0,735997	0,698693	0.591796	0,516000	0,427949	0,224208	5.80	0,765546	0,726625	0,615229	0,536325	0,444722	0,232930
5,36	0,736707	0,699364	0,592360	0,516490	0,428354	0,224418	5,81	0,766150	0 ,727196	0,615707	0,536739	0,445064	0,233108
5,37	0,737415	0,700034	0,592922	0,516978	0,428756	0,224627	5,82	0,766751	0,727765	0,616184	0,537152	0,445405	0 ,233285
5,38	0,738120	0,700700	0,593482	0,517464	0,429157	0,224836	5,83	0,767351	0'728331	0,616658	0,537563	0,445744	0,233461
5,39	0,738823	0,701365	0,594040	0,517948	0,429557	0,225044	5,84	0,767949	0,728896	0,617131	0,537973	0,446082	0,233637
5,40	0,739523	0,702027	0,594595	0,518430	0,429955	0,225251	5,85	0,768544	0,729458	0,617603	0,538382	0,446419	0,233812
5,41	0,740220	0,702686	0,595149	0,518910	0,430352	0,225458	5,86	0,769138	0,730019	0,618072	0,538789	0,446755	0,233986
5,42	0.740915	0,703343	0,595701	0,519389	0,430747	0,225664	5,87	0,769729	0.730578	0,618540	0,539194	0,447089	0,234160
5,43	0,741607	0,703998	0,596250	0,519866	0,431141	0,225868	5,88	0,770318	0,731134	0,619006	0,539598	0,447422	0,234333
5,44	0.742297	0,704650	0,596798	0,520341	0,431533	0,226072	5,89	0,770905	0,731689	0,619471	0,540001	0,447754	0,234505
5,45	0,742984	0,705300	0,597344	0,520814	0,431924	0,226276	5,90	0,771490	0,732241	0,619934	0,540402	9,448085	0,234677
5,46	0,743669	0,705948	0,597887	0,521286	0,432313	0,226478	5,91	0,772073	0,732792	0,620395	0,540801	0,448414	0,234848
5,47	0,744352	0,706593	0,598429	0,521756	0,432701	0,226680	5,92	0,772654	0,733341	0,620854	0,541199	0,448742	0,235018
5,48	0,745032	0,707236	0,5989^8	0,522224	0,433088	0,226881	5,93	0,773233	0,733887	0,621312	0,541596	0,449069	0,235188
5,49	0,745709	0,707876	0,599506	0,522690	0,433473	0,227081	5,94	0,773810	0,734432	0,621768	0,541991	0,449395	0,235357
5,50	0,746384	0,708515	0,600042	0.523155	0,433856	0,237281	 5,95	0,774384	0,734975	0,622223	0,542385	0,449720	0,235526
5,51	0,747057	0,709151	0,600575	0,523618	0,434238	0,227480	5,96	0,774957	0,735516	0,622676	0,542778	0,450043	0,235694
5,52	0,747727	0,709784	0,601107	0,594079	0,434619	0,227678	5,97	0,775528	0,736055	0,623127	0,543169	0,450366	0,235861
5,53	0,748394	0,710415	0,601637	0,524539	0,434998	0,227875	5,98	0,776097	0,736592	0,623577	0,543558	0,450687	0,236028
5,54	0,749060	0,711044	0,602164	0,524997	0,435376	0,228071	5,99	0,776664	0,737128	0,624025	0,543946	0,451007	0,236194
5,55	0,749723	0,711671	0,602690	0,525453	0,435752	0,228267	6,00	0,777228	0,737661	0,624471	0,544333	0.451326	0,236360
5,56	0,750383	0,712296	0,603214	0,525907	0,436127	0,228462	6,01	0,777791	0,738192	0,624916	0,544718	0,451643	0,236525
5,57	0,751041	0,712918	0,603736	0,526360	0,436501	0,228657	6,02	0,778352	0,738722	0,62'359	0,545102	0,451960	0,236689
5,58	0,751697	0,713538	0,604256	0,526811	0,436873	0,228850	6,03	0,778911	0,739250	0.625801	0,545485	0,452275	0,236853
5,59	0,752351	0,714155	0,604774	0,527260	0,437244	0,229043	6,04	0,779468	0,739776	0,626241	0,545866	0,452589	0,237016
5,60	0,753002	0,714771	0,605291	0,527708	0,437614	0,229235	6,05	0,780023	0,740300	0,626679	0,546246	0,452903	0,237178
5,61	0,753651	0,715384	0,605805	0,528154	0,437982	0,229427	6,06	0,780576	0,740822	0,627116	0,546624	0,453214	0,237340
5,62	0,754297	0,715995	0,6063i8	0,528598	0,438348	0,229617	6,07	0,781127	0,741342	0,627552	0,547001	0,453525	0,237501
5,63	0,754941	0,716604	0,606828	0,529041	0,438714	0,229807	6,08	0,781676	0,741861	0,627986	0,547377	0,453835	0,237662
5,64	0,755583	0,717211	0,607337	0,529482	0,439078	0,229996	6,09	0,782223	0,742377	0,628418	0,547752	0,454143	0,237822
388
389
Продолжение табл. II
а	0 = 0, ₽=i	а = 0,1. ₽ =0,9	то я II II •°.° ОО N3	а=0,25, ₽=0,75	’=0,3, ₽=0,7	у’to О О II II е tn.
6,10 '	0,782769	0,742892	0,628849	0,548125	0,454451	0,237982
6,1’	0,783312	0,743405	0,629278	0,548496	0,454.757	0,238141
6,12	0.783854	0,743917	0,629706	0,548867	0,455062	0,238299
0,13	0,784393	0,744426	0,630132	0,549236	0,455366	0,238457
6,14	0,784931	0,744934	0,630556	0,549603	0,455669	0,238614
6 15	0,785467	0,745440	0,630979	0.549970	0,455971	0,238771
6 16	0,786001	0,745944	0,631401	0.55л335	0,456272	0,238927
6,17	0,786533	0,746446	0,631821	0,550699	0,456572	0,239082
6,18 •	0,787054	0,746947	0,632240	0,551061	0,456871	0,239237
6,19	0.787592	0,747446	0,632657	0,551422	0,457168	0,239392
6,29	0,788119	0,747943	0,Р33073	0,551782	0,457465	0,239546
6^21	0,788644	0,748439	0,633487	0,552141	0,457760	0,239699
6 22	0,789167	0,748932	0,633900	0,552498	0,458055	0,239852
6,23	0,789588	0,749424	0,634311	0,552854	0,458348	0,240004
6,24	0,790208	0,749915	0,634721	0,553209	0,458640	0,240155
6,25	0,790725	0,750403	0,635129	0,553562	0,4589-31	0,240305
6,26	0,791241	0,750890	0,635533	0,553915	0,459221	0,240457
6,27	0,791755	0,751375	0,635942	0,554266	0,459511	0,240507
6,28	0,792258	0,751859	0,636346	0,554615	0,459799	0,240756
6:29	0,792778	0,752340	0,636748	0,554964	0,460086	0,240905
6,30	0,793287	0,752821	0,637130	0,555311	0,460372	0,241053
6,31	0,793794	0,753299	0,637549	0,555657	0,469657	0,241201
6’,32	0,794299	0,753776	0,637948	0,556002	0,460941	0,241348
6,33	0,794803	0,754251	0,638345	0,556346	0,461224	0,241495
б;з4	0,795305	0,754725	0,638741	0,556688	0,451506	0,241641
6,35	0,795805	0,755197	0,639135	0,557029	0,461787	0,241787
6,36	0,796303	0,755667	0.639528	0,557369	0,452067	0,241932
6,37	0,795800	0,756133	0,639919	0,557708	0,462346	0,242077
6,38	0,797295	0,756603	0,640309	0,558045	0,462624	0,242221
6,39	0,797789	0,757068	0,640598	0,558382	0,452^01	0,242364
6,40	0,798280	0,757'32	0,641085	0,558717	0,463177	0,242507
6,41	0,798770	0,757994	0,641471	0.559051	0,4634 2	0,242650
6',42	0,799259	0,7584'5	0,641836	0,559384	0,463725	0,242792
6,43	0,799745	0,758914	0,642239	0,559715	0,463999	0,242934
6,44	0,800230	0,759371	0,642521	0,560045	0,464271	0,243075
6,45	0,800714	0,759827	0,643002	0,560375	0,464542	0,243215
6,46	0,801195	0,760282	0,643381	0,560703	0,464812	0,243355
6,47	0,801675	0,760735	п,6437R0	0,561030	0,465081	0,243495
6,48	0,802154	0,761186	0,644136	0,561356	0,465350	0,243634
6,49	0,802631	0,761636	0,644512	0,561681	0,465617	0,243772
6,50	0,803106	0,762084	0,644886	0,562005	0,465883	0,243910
6,51	0,803579	0,762531	0,645259	0,562327	0,466149	0,244048
6,52	0,804051	0,762976	0,645630	0,562548	0,465413	0,244185
6,53	0,804522	0,763419	0,646000	0,562969	0,466677	0,244321
6,54	0,804991	0,763861	0,646369	0,563288	0,466940	0,244457
390
Продолжение табл. II
Z	а=0. ₽ = 1	а=0,1, ₽=0,9	я=0,2, ₽=0.8	а = 0,25, ₽—0,75	а=043, р-0,7	а=0,4, ₽=0,6
6,55	0,805458	0,764302	0,646737	0,563606	0,467201	0,244593
6,56	0,805924	0,764741	0,647103	0,563922	0,467462	0,244728
6,57	0,806388	0,765179	0,647468	0,564238	0,467722	0,244863
6,58	0^806850	0,765615	0,647832	0,564553	0,467981	0,244997
6,59	0,807311	0,766050	0,648195	0,564866	0,468239	0,245130
6,60	0,807771	0,766483	0,648556	0,565179	0,468496	0,245263
6,61	0,808228	0,/66914	0,648916	0,565490	0,468752	0,245396
6,62	0,808685	0,767345	0,649275	0,565801	0,469008	0,245528
6,63	0,809139	0,767774	0,649633	0,566110	0,46-9262	0,245660
6,64	0,809593	0,768201	0,649989	0,566418	0,469516	0,245791
6,65	0,810045	0,768627	0,650344	0,566725	0,469768	0,245922
6,66	0,810495	0,769051	0,650698	0,567031	0,470020	0,246053
6,67	0,810943	0,769474	0,651051	0,567336	0,470271	0,246183
6,68 6,69	0,811391 0,811836	0,769896 0,770316	0,651403 0,651753	0,567640 0,567943	0,470521 0,470770	0,246312 0,246441
6,70	0,812281	0,770735	0,652102	0,568244	0,471019	0,246570
6,71	0,812724	0,771152	0,652450	0,568545	0,471266	0,246698
6,72	0,813165	0,771568	0,652797	0,568845	0.471513	0,246825
6,73	0,813605	0,771983	0,653142	0,569144	0,471758	0,246952
6,74	0,814043	0,772396	0,653487	0,569441	0,472003	0,247079
6,75	0,814480	0,772808	0,653830	0,569738	0,472247	0,247205
6,76	0,814915	0,773218	0,654172	0,570034	0,472490	0,247331
6,77	0,815349	0,773627	0,654513	0,570328	0,472733	0,247457
6,78	0,815782	0,774035	0,654852	0,5706.22	0,472974	0,247582
6,79	0,816213	0,774441	0,655191	0,570914	0,473215	0,247706
6,80	0,816643	0,774846	0,655528	0,571206	0,473455	0,247830
6,81	0,817071	0,775250	0,655765	0,571496	0,473694	0,247954
6,82	0,817498	0,'775652	0,656200	0,571786	0,473932	0,248077
6,83	0,817923	0.776053	0,656534	0,572074	0,474169	0,248200
6,84	0,818347	0,776452	0,656867	0,572362	0,474405	0,248322
6,85	0,818770	0,776851	0,657198	0,572649	0,474641	0,248444
6,86	0,819191	0,777247	0,657529	0,572934	0,474876	0,248566
6,87	0,819611	0,777643	0,657858	0,573219	0,475110	0,248687
6,88	0,821030	0,778037	0,658187	0,573503	0,475343	0,248808
6,89	0,820447	0,778430	0,658514	0,573785	0,475576	0,248928
6,90	0,820862	0,778822	0,658840	0,574067	0,475808	0,249048
6,91	0,821277	0,779212	0,659165	0,574348	0,476038	0,249167
6,92	0,821690	0,779601	0,659489	0,574628	0.476268	0,249286
6,93	0,822101	0,779989	0,659812	0,574907	0,476498	0,249405
6,94	0,822512	0,780376	0,660134	0,575184	0,476726	0,249523
6,95	0,822921	0,780761	0,660454	0,575461	0,476954	0,249640
6,96	0,823328	0,781145	0,660774	0,575737	0,477181	0,249758
6,97	0,823735	0,781528	0,661092	0^576013	0,477407	0,249875
6,98	0,824139	0,781909	0,661410	0,576287	0,477632	0,249991
6,99	0,824543	0,782289	0,661726	0,576560	0,477857	0,250107
391
Таблица III
I
(Таблицы I и II соответствуют загружению, показанному на
рис. 101, стр. 144).
Таблица III
f 1	р-	*1	f 1	р	v-l
0	0	0	0,015	1 ,00180	1,00060
0,001	1,00001	1,00000	0,016	1,00205	1,00068
0,002	1,00003	1,00001	0,017	1,00231	1,00077
0,003	1 ,00007	1,00003	0,018	1,00259	1,00086
0,004	1,00013	1,00004	0,019	1,00289	1,00096
0,005	1,00020	1,00007	0,020	1,00320	1,00107
0,006	1,00029	1,000,10	0,021	1,00353	1,00117
0,007	1,00039	1,00013	0,022	1,00388	1,00129
0,008	1,00051	1,00017	0,023	1,00424	1,00141
0,009	1,00065	1,00022	0,024	1,00461	1,00153
0,010	1,00080	1,00027	0,025	1,00501	1,00166
0,011	1,00097	1,00032	0,026	1,00'42	1,00180
0,012	1,00115	1,00038	0,027	1,00584	1,00194
0,013	1,00135	1,00045	0,028	1,00628	1,00209
0,014	1,СО 157	1,00052	0,029	1,00674	1,00224
392
nt				яосолжение табл. Ill	
f I	p	v-l	f i	P-	
0,030	1,00722	1,00239	0,075	1,04560	1,01480
0,031	1,00771	1,00256	0,076	1,04584	1,01520
0,032	1,00821	1,00272	0,077	1,04810	1,01559
0,033	1,00873	1,00290	0,078	1,04937	1,01600
0,034	1,00927	1,00307	0,079	1,05067	1,01640
0,035	1,00983	1.00325	0,080	1,05198	1,01681
0.036	1,01040	1,00345	0,081	1,05330	1,01723
0,037	1,01099	1,00364	0,082	1,05465	1,01765
0,038	1,01159	1,00384	0,083	1,05601	1,01808
0,039	l,0i221	1,00404	0,084	1,05739	1,01851
0,040	1,01285	1,00425	0,085	1,05879	1,01895
0,041	1,01350	1,00446	0,086	1,06020	1,01939
0,042	1,01417	1.00468	0,087	1,06164	1,01938
0,043	1,01486	1,00491	0,088	1,06309	1,02028
0,044	1,01556	1,00514	0,089	1,06456	1,02074
0,045	1,01628	1,00537	0,090	1,06604	1,02120
0,046	1,01/01	1,00561	0,091	1,06754	1,02166
0,047	1,?1777	1,00586	0,092	1,06907	1,02213
0,048	1,41853	1,00611	0,093	1,07061	1,02261
0,049	1,01932	1,00637	0,094	1,07216	1,02309
0,050	1,02012	1,00663	0,095	1,07374	1,02357
0,051	1,02094	1,00689	0,096	1,07533	1,02406
0,052	1,02177	1,00716	0,097	1,07694	1,02455
0,053	1,02262	1,00744	0,098	1,07857	1,02505
0,054	1,02349	1,00772	0,099	1,08022	1,02555
0,055	1,02437	•1,00801	0,100	1,08189	1,02606
0,056	1,02528	1,00830	0,101	1,08357	1,02657
0,057	1,02619	1,00860	0,102	1,08527	1,02709
0,058	1,02713	1,00890	0,103	1,08699	1,02761
0,059	1,02808	1,00921	0,104	1,08873	1,02814
0,050	1,02905	1,00952	0,105	1,09049	1,02867
0,061	1,03003	1,00984	0,105	1,09226	1,02920
0,052	1,03103	1,01016	0,107	1,09406	1,02974
0,063	1,03245	1,01049	0,108	1,09587	1,03029
0,064	1,03309	1,01082	0,109	1,09770	1,03084
0,065	1,03414	1,01116	0,110	1,09955	1,03139
0,066	1,03521	1,01150	0,111	1,10142	1,03195
0,067	1,03630	1,01184	0,112	1,10330	] ,03251
0,0'8	1,03740	1,01220	0,113	1,10521	1,03308
0,069	1,03852	1,01255	0,114	1,10714	1 ,03365
0,070	1,03966	1,01292	0,115	1.10908	1,03422
0,071	1,04081	1.01328	0,116	1,11104	1,03480
0,072	1,04198	1,01366	0,117	1,11302	1,03539
0,073	1,04317	1,01403	0,118	1,11502	1,03598
0,074	1,04438	1,01442	0,119	1,11704	1,03657
393
Продолжение табл. III
/ 1	JJ.	v-l	/ 1	р-	o-Z
0,120	1,11908	1,03717	0,165	1,23137	1,06847
0,121	1,12114	1,03777	0,166	1,23435	1,06925
0,122	1,12321	1,03838	0,167	1,23734	1.07005
0,123	1,12531	1,03899	0,168	1,24036	1,07084
0,124	1,12742	1,03961	0,169	1,24339	1,07164
0,125	1,12956	1,04023	0,170	1 ,24645	1,97245
0,123	1,13171	1,04085	0,171	1,24954	1,07325
0,127	1 ,13388	1,04148	0,172	1,25264	1,07406
0,128	1,13508	1,04212	0,173	1,25577	1 ,07488
0,129	1,13829	1,04275	0,174	1,25891	1,0757(1
0,130	1,14052	1,04340	0,175	1,26208	1,0765/
0,131	1,14277	1,04404	0,176	1,26528	1,07731
0,132	1.14504	1,04469	0,177	1,26849	1,0781^
0,133	1 ,14733	1,04535	0,178	1,27173	1,079'4
0,134	1,14964	1,04601	0,179	1,27499	1,0798ч
0,135	1,15197	1,04667	0,180	1,27827	1,08068
0,136	1,15432	1,04734	0,181	1 ,28157	1,0816,8
0,137	1,15669	1,04801	0,182	1,28490	1,98237
0,138	1,15908	1,04868	0,183	1,28825	1,08322
0,139	1,16149	1,04936	0,184	1,29162	1.08408
0,140	1,16392	1,05005	0,185	1,29502	1,08494
0,141	1,16637	1,05074	0,186	1.29843	1,08580
0,142	1,16884	1,05143	0,187	1 ,30188	1,08666
0,143	1,17133	1,05213	0,188	1 ,30534	1,08753
0,144	1,17385	1,05283	0,189	1,39883	1,08841
0,145	1,17638	1,05353	0,190	1,31234	1,08928
0,146	1,17893	1,05424	0,191	1,31587	1,09016
0,147	1,18150	1,05495	0,192	1,31943	1,09104
0,148	1,18409	1,05567	0,193	1,32301	1,09193
0,149	1,18671	1,05639	0,194	1,32661	1,09282
0,150	1,18934	1,05712	0,195	1 ,33024	1,09371
0,151	1,19200	1,05785	0,196	1,33389	1,09461
0,152	1,19467	1,05858	0,197	1,33756	1,09551
0,153	1,19737	1,05932	0,198	1,34126	1,09641
0,154	1,20009	1,06006	0,199	1 ,34498	1,09732
0,155	1,20282	1,06080	0,200	1,34873	1,09823
0,156	1 ,20558	1,06155	0,201	1,35250	1,09914
0,157	1,20836	1,06230	0,202	1,35629	1,10006
0,158	1,21117	1,06306	0,203	1,36011	1,10098
0,159	1,21399	1,06382	0,204	1,36395	1,10190
0,160	1,21683	1,06459	0,205	1,36782	1,10283
0,161	1,21970	1,06536	0,206	1,37171	1,10376
0,162	1,22258	1,06613	0,207	1,37562	1,10470
0,163	1,22549	1,06690	0,208	1,37956	1,10563
0,164	1,22842	1,06768	0,209	1,38352	1,10657
394
Продолжение табл. III
/ Z	р	v-l	/ Z	р-	
0,210	1,38751	1,10752	0,255	1,59351	1,15316
0,211	1,39152	1,10846	0,256	1,59870	1,15424
0,212	1,39556	1,10941	0,257	1,60392	1,15532
0,213	1,39962	1,11037	0,258	1,60918	1,15641
0,214	1,40371	1,11132	0,259	1,61445	1,15750
0,215	1,40782	1,11228	0,260	1,61976	1,15859
0,216	1,41195	1,11325	0,261	1,62510	1,15968
0,217	1,41612	1,11421	0,262	1,63046	1,16078
0,218	1,42030	1,11518	0,263	1,63585	1,16188
0,219	1,42451	1,11615	0,264	1,64127	1,16298
0,220	1,42875	1,11713	0,265	1,64672	1,16409
0,221	1,43301	1,11811	0,266	1,65220	1,16519
0,222	1,43730	1,11909	0,267	1,65771	1,16630
0,223	1,44161	1,12007	0,268	1,66324	1,16742
0,224	1,44595	1,12106	0,269	1,66881	1,16853
0,225	1,45032	1,12205	0,270	1,67440	1,16965
0,226	1,45471	1,12305	0,271	1,68003	1,17077
0,227	1,45912	1,12404	0,272	1/8568	1,17189
0,228	1,46356	1,12504	0,273	1,69136	1,17302
0,229	1,46803	1,12605	0,274	1,69707	1,17415
0,230	1,47252	1,12705	0,275	1,70281	1,17528
0,231	1,47704	1,12806	0,276	1,70858	1,17641
0,232	1,48159	1,12907	0,277	1,71438	1,17755
0,233	1,48616	1,13009	0,278	1,72021	1,17869
0,234	1,49076	1,13111	0,279	1,72607	1,17983
0,235	1,49538	1,13213	0,280	1,73195	1,18097
0,236	1,50003	1,13315	0,281	1,73787	1,18212
0,237	1,50471	1,13418	0,282	1,74382	1,18327
0,238	1,50941	1,13521	0,283	1,74980	1,18442
0,239	1,51414	1,13624	0,284	1,75581	1,18557
0,240	1,51890	1,13728	0,285	1,76185	1,18673
0,241	1,52368	1,13832	0,286	1,76792	1,18788
0,242	1,52849	1,13936	0,287	1,77402	1,18904
0,243	1,53333	1,14040	0,288	1,78015	1,19021
0,244	1,53819	1,14145	0,289	1,78631	1,19137
0,245	1,54309	1,14250	0,290	1,79250	1,19254
0,246	1,54800	1,14355	0,291	1,79872	1,19371
0,247	1,55295	1,14461	0,292	1,80497	1,19488
0,248	1,55792	1,14567	0,293	1,81125	1,19606
0,249	1,56292	1,14673	0,294	1,81757	1,19723
0,2'0	1,56795	1,14779	0,295	1,82392	1,19841
0,251	1 ,57301	1,14886	0,296	1,83029	1,19960
0,252	1,57809	1,14993	0,297	1,83670	1,20078
0,253	1,58320	1,15100	G.298	1,84314	1,20197
0,254	1,58834	1,15208	0,299	1,84961	1,20316
395
П родолжение табл. Ill
/ 1	Р-		/ i	н	v-l
0,300	1,85611	1,20435	0,345	2,18259	1,26020
0,301	1 ,86264	1,20554	0,346	2,19063	1,26148
0,302	1,86921	1,20674	0,347	2,19870	1,26277
0,303	1,87581	1,20793	0,348	2,90681	1,26407
0,304	1,88243	1,20913	0,349	2,21495	1,26536
0,305	1,88909	1,21034	0,350	2,22314	1,26665
0,306	1,89579	1,21154	0,351	2,23135	1,26795
0,307	1 ,9024	1,21275	0,352	2,23960	1,26925
0,308	1,90927	1,21396	0,353	2,24789	1,27055
0,309	1,91606	1,21517	0,354	2,25622	1,27186
0,310	1,92288	1,21638	0,355	2,26458	1,27316
0,311	1,92973	1,21760	0,356	2,27297	1,27447
0,312	1,93662	1,21882	0,357	2,28140	1,27578
0,313	1,94353	1,22004	0,358	2,28987	1,27709
0,314	1,95049	1,22126	0,359	2,29838	1,27840
0,315	1 ,95747	1,22249	0,360	2,30692	1,27971
0,316	1,96449	1,22371	0,361	2,31550	1,28103
0,317	1,97153	1,22494	0,362	2.32411	1,28235
0,318	1,97862	1,22617	0,363	2,33277	1,28367
0,319	1,98573	1,22741	0,364	2,34145	1,28499
0,320	1.99288	1,22864	0,365	2,35018	1,28631
0,321	2,00006.	1,22988	0,366	2,35894	1,28764
0,322	2,00728	1,23112	0,367	2,36774	1,28896
0,323	2,01452	1,23236	0.368	2,37658	1,29029
0,324	2,02180	1,23360	0,369	2,38545	1,29162
0,325	2,02912	1,23485	0,370	2,39437	1 ,2929(5
0,326	2,03647	1,23610	0,371	2,40331	1,29429
0,327	2,04385	1,23735	0,372	2,41230	1,29563
0,328	2,05127	1,23860	0,373	2,42133	1,29696
0,329	2,05872	1,23985	0,374	2,43039	1,29830
0,330	2,06620	1,24111	0,375	2,43949	1,29964
0,331	2,07372	1,24237	0,376	2,44862	1,30098
0,332	2,08127	1,24363	0,377	2,45780	1,30235
0,333	2,08886	1,24489	0,378	2,46701	1,30368
0,334	2,09648	1,24616	0,379	2,47627	1,30502
0,335	2,10413	1,24742	0,380	2,48556	1,30637
0,336	2,11182	1,24869	0,381	2,49488	1,39772
0,337	2,11954	1,24996	0,382	2,50425	1,30908
0,338	2,12730	1,25123	0,383	2,51366	1,31043
0,339	2,13510	1,25251	0,384	2,52310	1,31179
0,340	2,14292	1,25378	0,385	2,53258	1,31314
0,341	2,15079	1,25506	0,386	2,54211	1,31450
0,342	2,15868	1,25634	0,387	2,55167	1,31586
0,343	2,16662	1,25763	0,388	2,56127	1,31723
0,344	2,17458	1,25891	0,389	2,57090	1,31859
396
Окончание табл. Ill
f 1	р	^Z	/ 1	р-	и-z
0,390	2,58058	1,31996	0,405	2,73050	1,34064
0,391	2,59030	1,32133	0,406	2,74081	1,34203
0,392	2,60005	1,32269	0,407	2,75117	1,34342
0,393	2,60985	1,32407	0,408	2,76157	1,34482
0,394	2,61968	1,32544	0,409	2,77201	1 ,34621
0,395	2,62956	1,32681	0,410	2,78248	1,34761
0,396	2,63947	1,32819	0,411	2,79300	1,34901
0,397	2,64943	1,32955	0,412	2,80356	1,35041
0,398	2,65942	1,33094	0,413	2,81417	1,35181
0,399	2,66945	1,33232	0,414	2,82481	1 ,35321
0,400	2,67953	1,33371	0,415	2,83549	1,35462
0,401	2,68964	1,33509	0,416	2,84622	1,35603
0,402	2,69980	1,33647	0,417	2,85699	1,35743
0,403	2,70999	1,33786	0,418	2,86780	1,35884
0,404	2,72022	1,33925	0,419	2,87865	1,36025
ЛИТЕРАТУРА
1.	Блей х Ф. Теория и расчет железных мостов. Огиз. Гострансиздат,
М„ 1931.
2.	Болотин В. В. Динамическая устойчивость упругих систем. Госу-
дарственное изд-во технико-теоретической литературы, М., 1956.
3.	Болотин В. В., Гольденблат И. Й., Смирнов А. Ф. Совре-
менные проблемы строительной механики. Госстройиздат, М.» 1964.
4.	Власов В. 3. Тонкостенные упругие стержни. Стройиздат, М., 1940.
5.	Власов В. 3. Строительная механика тонкостенных пространствен-
ных систем. Стройиздат, М., 1949.
6.	Г'ибшм а н Е. Е. Металлические мосты. М., 1937.
7.	Гольденблат И. И. Динамическая устойчивость сооружений
Стройиздат, М„ 1948.
8.	Гольденблат И. И. Современные проблемы устойчивости и коле-
баний инженерных конструкций. Стройиздат, М., 1947.
9.	Гольденблат И. И., С и з о в А. М. Справочник по расчету строи-
тельных конструкций на устойчивость и колебания. Госстройиздат, М„ 1952.
10.	Д у р о в И. С. К вопросу определения усилий в балках жесткости ви-
сячих систем. Тр. Новочеркасского политехнического ин-та, 1955.
11.	Дуров И. С. Деформационный расчет висячих мостов по линиям
влияния. Тр. Новочеркасского политехнического ин-та, 1958.
12.	Золотов П. В. Распределение поперечного давления ветра между
кабелем и проезжей частью висячей системы. Известия Высших учебных заве-
дений. Ж- «Строительство и архитектура», 1959, № 6.
13.	Ильясевич С. А. Металлические мосты. Росвоениздат, М„ 1940.
14.	К а чур ин В. К. Гибкие нити с малыми стрелками. Государственное
изд во технико-теоретической литературы, М., 1956.
15.	Качурин В. К. Теория висячих систем. Госстройиздат, М., 1962.
16.	Киреенко В. И. Вантовые мосты. Изд-во «Будивельник», Киев,
1967.
17.	Кирсанов Н. М. Расчет однопролетных висячих мостов с учетом
прогибов. Сб. трудов Московского строительного ин-та, 1956, № 10.
18.	Кирсанов Н. М. Расчет неразрезных висячих мостов с учетом про-
гибов. Сб- трудов Воронежского инженерно-строительного ин-та, 1958, № 4.
19.	Крыльцов Е. И. Проектирование вантовых мостов. Справочник ин-
женера-дорожника. Под ред. проф. Н. М. Митропольского. М„ 1931.
20.	Крыльцов Е. И., Попов О. А. Железобетонные мосты за рубе-
жом. Научно-техническое изд-во автотранспорта и шоссейных дорог РСФСР,
М„ 1963.
21.	Кузнецов Э. Н. Статический расчет двухпоясных вантовых систем.
Ж- «Строительная механика и расчет сооружений», 1962, № 5.
22.	М ац е л и н ски й Р. Н. Статический расчет гибких висячих конструк-
ций. Стройиздат, М., 1950.
23.	Мельников Н. П. Развитие металлических конструкций. Госстрой-
издат, М., 1965.
398
24.	Муханов К- К- Металлические конструкции. Госстройиздат, М.,
1963.
25.	Нел а сов А. Б. Вертикальные колебания висячих мостов. Сб. трудов
МИСИ, М., 1937.
26.	Передерий Г. П. Курс мостов. Ч. II. НКПС Госжелдориздат,
М. — Л., 1933.
27.	Протасов К- Г. Новые вантовые фермы. Всесоюзное изд. полиграф,
объединение. МПС, М., 1963.
28.	Рабинович И. М. К теории вантовых ферм. Сб. трудов ин-та ин-
женерных исследований, М., 1924.
29.	Р а б и н о в и ч И. М. Вантовые фермы в мостостроении. Сб. трудов
ин-та инженерных исследований. Трансжелдориздат, М., 1930.
30.	Висячие покрытия. Под редакцией» Рабиновича И. М. М., Госстрой-
издат, 1962.
31.	Рай нус Г. Э. Принципы расчета висячих покрытий с несущей конст-
рукцией из гибкой нити. (Висячие покрытия.) Госстройиздат, М., 1962.
32.	Р а й н у с Г. Э. Статический расчет ферм из тросов. ДНТП Л., 1962.
33.	Р а й н у с Г. Э. Висячие покрытия типа пространственных мембран.
(Армоцементные конструкции в строительстве.) Госстройиздат, М., 1963.
34.	Размадзе А. Н. Некоторые вопросы динамической и аэродинамиче-
ской устойчивости висячих мостов. Тр. Грузинского политехнического ин-та,
1957, № 9.
35.	Размадзе А. Н. Вопросы динамической устойчивости висячих си-
стем. Тр. Грузинского политехнического ин-та, 1961, № 3.
36.	Р ж а н и ц и н А. Р. Статика и динамика пологой упругой нити. (Ви-
сячие покрытия). Тр. совета по исследованию и внедрению висячих покрытий.
Госстройиздат, М., 1962.
37.	Смирнов А. Ф. Устойчивость и колебания сооружений. Трансжел-
дориздат, М„ 1958.
38.	Смирнов А. Ф., Александров В. А., Лащеников Б. Я-,
Шапошников Н. Н. Расчет сооружений с применением вычислительных
машин. Госстройиздат, М., 1964.
39.	Смирнов В. А. Расчет трехпролетной балки переменного сечения.
Ж- «Транспорт», 1963, № 7.
40.	С м и р н о в В. А. Расчет трехпролетного висячего моста по деформи-
рованной схеме. «Строительная механика», вып. 174. Тр. Моск, ордёй'а Ле-
нина и ордена Трудового Красного Знамени ин-та инженеров ж. д, транспорта,
М., 1963.
41.	Смирнов В. А. Расчет висячих комбинированных систем по дефор-
мированной схеме. Тр. Моск, ордена Ленина и ордена Трудового Красного
Знамени ин-та инженеров ж. д. транспорта. «Вопросы прикладной механики»,
вып. 193, М., 1964.
42.	Смирнов В. А. Численный метод расчета висячего моста с учетом
геометрической нелинейности. Исследование по теории сооружений. Сб. статей,
вып. XIII. Госстройиздат, М., 1964.
46.	Смирнов В. А. Расчет гибкой нити при одновременном действии
вертикальной и горизонтальной нагрузок. Исследования по теории сооруже-
ний. Сб. статей, вып. XIV, Госстройиздат, М., 1965.
47.	Соботка 3. Висячие покрытия. Госстройиздат, М., 1964.
48.	С т е п к и н С. К- К расчету висячих цепных мостов с балкой жестко-
сти с учетом деформации. Сб. трудов ЛИНДТ, вып. 142. Трансжелдориздат,
М., 1950.
49.	С т р е л е ц к и й Н. С. Курс мостов. Ч. II. Госстройиздат, М., 1931.
50.	С т р е л ецк и й Н. С. Курс металлических конструкций. Ч. III. Гос-
стройиздат, М„ 1944.
51.	Тартаковский Г. А. Новая система сооружений трубопроводов в
виде провисающих нитей. Изд-во МКХ РСФСР, М., 1961.
52.	Тимошенко С. П. История науки о сопротивлении материалов. Го-
сударственное изд-во технико-теоретической литературы, М., 1957.
399
53.	Уманский А. А. Расчет тонкостенных стержней. Справочник маши-
ностроителя. Т. 3, гл. 7. Машгиз, М., 1951.
54.	Фрей О. Висячие покрытия. Госстройиздат, М., 1960.
55.	Хэммонд Р. Аварии зданий и сооружений. Госстройиздат, М., 1960.
56.	Цаплин С. А. Многоцепные висячие фермы. Гострансиздат.'М., 1931.
57.	Ц а и л и н С. А. Теория расчета гибких нитей. Всесоюзная строитель-
ная выставка. М., 1937.
58.	Цаплин С. А. Висячие мосты. Гострансиздат, М., 1937.
59.	Цаплин С. А. Висячие мосты. Дориздат, М., 1949.
60.	Ш т а е р м а н И. Я. О точном расчете цепных мостов с балкой жестко-
сти. Изд-во научно-исследовательской кафедры инженерно-строительных наук,
Киев, 1928.
61.	Якобсон К- К. Некоторые динамические характеристики висячих
мостов. Тр. Новосибирского института желзнодорожного транспорта, Вып. 12.
М., 1955.
62.	A s р 1 u n d S. О. On the Deflection Theory of Suspension Bridges.
Ingeniorvetetenskapsakademiens Handlingar N 184. Stockholm, 1943.
63.	Asplund S. O. Column — beams and Suspension Bridges analyzed by
«Green’s matrix». Chalmers tekn. hogskol handl. N 204, 1958.
64.	Asplund S. O. Practical calculation of Suspension Bridges. Chalmers
tekn. hogskol handl. N 273, 1963.
65.	Atkinson and Southwell. On the Problem of Stiffened Suspen-
sion Bridges and its Treatment by Relaxation Methods. Proc. J. С. E. 1939.
66.	В a rd re R. Neubau der Luitpold-—Hangebriicke fiber die Donnau in
Passau. Stahlban Bd. 21. S. 9, 25, 56. 1952.
67.	Beer H. Eine Betrachtung zum heutigen Stand der Teorie und Gestal-
tung von Hangebrucken. Osterr. Bauzeitschrift. Bd. 1, 1946.
68.	В 1 e i c h H. H. Die Berechnung verankerter Hangebriicken. Wien:
Springer. 1935.
69.	Bleich. F. Dynamic Instability of Truss — stiffened Suspension Bridges
auter Wind Action. Proceedings of the American Society of Civil Engineers.
Bd. 74, 1948.
70.	Bleich, Me Cullough, Rosecrans, Wincent. The mathema-
tical theory of vibrations in Suspension Bridge. Dept, ef Commerce, 1950.
71.	В lick W. Formanderungen und statische Funktionen bei versteiften
Hangebrucken. VDJ. Bd. 76, 1932.
72.	BlickW. Erhohung der Wirtschaftlichkeit von versteiften Hangebrucken
durch Beriicksichtigung der Formanderungen. VDJ. Bd. 77. S. 921, 1080, 1933.
73.	В о h п у С. M. Hangebriicken. Berlin, 1934.
74.	Bohn у F. Hangebriicken fiber mehrere Offnungen. Bautechnik. Bd. 15.
1937.
75.	Borges. J. Computer Analysis of Structures. 11 Conference of Elechro-
nik Computation Amarican Sociehy of Civil Engineers, Pittsbury. September, 1960.
76.	В о r g e r F. J., S i 1 v a lima C., A r a n t e s E. R. Matrix analysis of
Suspension bridges. Bull. Reunion internat. labs essais et rech. mater et
constr. N 19, 1963.
77.	Chadenson L. La importancia de les problemas aerodinamiccs en la
concepcion de les grandes puentes colgantes. C. J. C. N 84. 1958.
78.	Cichocki. F. Eine neue Hangebriickeniorm. Stahlban. Bd. 20. 1951.
79.	С г о s t h w a i t e. The corrected theory of the stiffened Suspension
bridge. Proc. J. С. E. 1947.
80.	Deutschmann H. Schwingungen von Hangebrucken unter windlast.
Bautechnik. Bd. 31. 1954.
81.	Dischinger F. Hangebriicken.fiir schwerste Verkehrslasten. Bauinge-
nieur. Bd. 24, S. 65, 107, 1949.
82.	D i sch i и g er F. Der EinfluB der Torsionssteifigkeit der aussteifenden
Trager auf die Stabilitat der Hangebriicken. Bauingenieur. Bd. 25. S. 166, 246.
1950.
400
83.	D i s c h i n g e r F. Torsionsteifigkeit der Hangebriicken. Der Bauinge-
nieur. Mai — Juli, 1950.
84.	Eb linger M. Antisymetrische Belastuny von Hangebriicken. Elektron.
Datenverarb. N 4. 1963.
85.	Eslinger M. Charger antisymetriques des ponts suspendus. Ann.
ponts et shaussees. N 5, 1963.
86.	Eger vary E. Afuggohidak altulanos elemelettenek megalapozasa es
felepitese matrixczamitas segitsegevel. Maguar tud. akad. Mat. Kutato int. Kozl.
N 1—2, 1957.
87.	Eg e r v a ry E. On the application of the matrix theory of the calculating
of Chainbridges. Actu. techn. Acad.-sei. hung. N 1—2, 1955.
88.	Emmen J. Enkele algemen beschouwingen over hangbruggen berustend
op nienul inzichten betreffende de benegingen der bruggen vevoorzaakt
spoorwegverkeer en wind. Ingenieur (utrecht). N 23, 1955.
89.	Endo Tokuyasi. Расположение главной балки и проезжей части
сварного подвесного моста с ездой по верху. Нихон дайгаку кэнкюсё ихо.
J. Res. Inst. Techn. Nihon Univ. N 18, 1958.
90.	Enneper P. Beitrag zur Berechnung echter Hangebriicken. Stahlbau.
Bd. 23. S. 134, 159. 1954.
91	Erzen C. Z. Lateral bending of Suspension Bridges. Proc. Amer. Soc.
Civil Engrs. N 663, 1955.
92.	Farquharson F. B. Aerodynamic stability of Suspension Bridges.
I 1949—1950. II 1950. Ill—1952. V. 1954. Bull. Univ. Wash. Engng. Experim.
Stat.
93.	Go d m a n R. F. Design of large Span Syspension Bridges. J. and Trans.
Soc. Engrs N 4, 1961.
94.	Go sc h у В. Eigenschwingungen der schragseilbrucken. Actu. techn.
Acad, scient. hung. N 1—2, 1961.
95.	H a r t m a n n F. In sich verankerte Hangebriicken mit waagerecht
festgehaltenem Gurtscheitel. Stahlbau. Bd. 13, 1940.
96.	Ha wr a nek. A. Hangebrucken mim einem Zweigelenkrabmen—Ver-
steifungstrager. Stahlbau. Bd. 7. S 134, 145, 1934. Bd. 8 1935.
97.	H a w r a ne k A. — Steinhardt. Theorie und Berechnung der Stahlbriicken.
Springer Verlag. Berlin 1958.
98.	Her twig A. Beitrag zum Hangebriickenproblem. Stahlbau. Bd. N 13,
1940.
99.	Hertwig A. EinfluB der nachgiebigen Hangestangen auf die Be-
rechnung der Hangebriinge. Stahlbau N 14, 1941.
100.	H i b a Z. Beitrag zur theorie der Verankerten Hangebriicken mit einem
Mittelgelenk im Versteifungstrager. Stahlbau. Nil, 1957.
101.	Hiba Z. Viseci mostovi sa gredom za ukrucenj'e nepotpune fleksibil-
nesti. Teknika N 3, 1958.
102.	Hiba Z. Winddruk auf Hangekriicken mit schrag lie genden Tragka-
beln. Stahlbau N 4, 1959.
103.	Hirai A. Aerodynamische Stabilitat von Hangebriicken unter Windbe-
lastung. Bauingenieur. Bd. N 31, S. 402, 1956.
104.	H i r a i A., Okumura T.,Jo M., N u r i t a N. Lateral stability of
a Suspension Bridge subjected to foundation-motion. Proc. 2 nd. World conf.
Earthquake Ingng. Tokyo-Kyoto, vol. 2, 1960.
105.	Hirai A. Oscillations of Suspension Bridge due to aerodynamic
disturbing forces. Proc, sth Japan Nat. Congr. Appl. Meeh. Tokyo, 1956.
106.	Хираи А. Ито, M. Висячий мост без подкреплений с тяжелыми на-
стилами. Trans. Japan Soc. Civil Engrs. N 64, 1959.
107.	Хираи А. Ито M. Экспериментальные исследования ударных дей-
ствий для висячих железнодорожных мостов. Сото сикэнсё немпо.
Annual Rept. Engng. Res. Inst. Fac. Engng. Univ. N I, Tokyo, 1962.
108.	Hoening K. Die rechnerische Behandlung der versteiften Hange-
briicken. Bautechnik. Bd. 18, 1940.
401
109.	Hoening К- Beitrage zur Berechnung der versteiften Hange-
briicke min Hilfe unmittelbarer Integration. Bauingenieur. Bd. 24. S. 292, 379,
1949.
110.	Hom berg H. Die neue Autobahnbriicke fiber den Rhein in Roden-
kirchen beiKoln. Stahlbau. Bd. 24. S. 153, 177, 1955.
111.	Hoyden A. Experimentelle Untersuchung der aerodynamischen Stabi-
litat von Hangebrficken. Bauingenieur. Bd. 28, 1953.
112.	Hoyden A. Naherungsberechnung von erdverankerten Hangebrficken
under Berficksichtigung des veranderlichen Tragheitsmomentes des Versteifung-
stragers. V. D. J. Forschungshelt N 452. Dusseldorf 1955.
113.	Ива см Маса аки. Линии влияния подвесных мостов. Когаку кэн-
кю. Civil Engng. Mag, N 10, 1961.
114.	J a k k u 1 a A. A. A. History of Suspension Bridges in Bibliographical -
Form. The Bulletin of the Agricultural and Mechanical College of Texas. 1941.
115.	Karman. Aerodynamic stability of Suspension Bridges. E. N. R. 1940.
116.	Klop pel K„ Lie К- H. Hangebrficken mit besonderen Stfitzbedin-
gungen des Versteifungstragers. Stahlbau. Bd. 13, 1940; Bd. 14, 1946.
117.	К lop pel. K-, Lie К- H. Berechnung von Hangebrficken nach der
Theorie 11. Ordnung unter Berficksichtigung der Nachgiebigkeit der Hanger.
Stahlbau. Bd. 14. 1941.
118.	К lop pel K, Lie К. H. Die lotrechten Eigenschwingungen der
Hangebrucken. Bauingehieur Bd. 23. 1942.
119.	Кови си Ити p о. Испытание на вибрацию висячих мостов. Кёто дай-
гаку когаку кэнкюсё ихо. Bull. Engng. Res. Inst. Kyoto Univ. 1959.
120.	Kenishi Ichiro, JamadaJoshikazu. Fundamental studies on
earthquake response of a long span suspension bridge. Mem. Fac. Engng.
Kyoto Univ. N 3, 1960.
121.	Konishi Ichiro, JamadaJoshikazu. Earthquake responses of
a long span Suspension Bridge. Proc. 2nd World Conf. Earthquake Engng
Tokyo — Kyoto Vol. 2, 1960.
122.	Konishi Ichiro, Jamada Joshikazu, Takaoka No-
buyoshi. Studies on earthquake response of a long span Suspension Bridge.
Proc. 10. th Japan Nat. Cong. Appl. Meeh. 1960.
123.	К ub о К. Aseismicity of Suspension Bridges forced to vibrate longitudi-
nally. Proc. 2nd World Conf. Earthquake Engng. Tokyo — Kyoto. Vol 2. 1960.
124.	Kuntz, Avery, Burkes. Analysis of the Suspension Bridges on
electronic digital compyters. Conf, on electronic comp. The committee on
electronic comp, structural biv. Kansas City 1958 (1959).
125.	Leinekugel le Cocq. G. Conditions nouvelles a imposer aux
ponts suspendus. Genie civil. N 14. 1956.
126.	Leinekugel le Cocq. G. Systeme de pont suspendu a foger isasta-
tique pour tres grandes portees. Genie civil. N 17 1959.
127.	Leonhardt F. Die Autobahnbriicke fiber den Rein bei Koln —
Roden — kirchen. Bautechnik. Bd. 27 S. 225, 246, 289, 351. 1950; Bd. 28. S. 169,
237, 283, 310, 1951.
128.	L i e К- H. Praktische Berechnung von Hangebrficken nach der Theorie II.
Orgnung. Stahlbau. Bd. 14. S. 65, 78. 1941.
129.	Melan J. Konstruktion der Hangebrficken. Handbuch der Ingenieur —
Wissenschaften, 4. Aufl., VI Bd. Leipzig, 1925.
130.	Melan J. Handbuch der Ingenieurwissenschaften. Leipzig, 1888...
131.	Melan J. Theorie der eisernen Bogenbrficken und der Hangebrucken,
1906.
132.	Miklofsky H. A. Bending interaction in Suspension Bridges. Proc.
Amer. Soc. Civil Engrs. N 652. 1955.
133.	M oi s s e i f f. Transactions A. S. С. E. Vol 55. 1905.
134.	Moppert H. Englische Untersuchungen uber die aerodynamische Sta-
bilitat von Hangebrucken mit besonderer Berficksichtigung der Severn — Brucke.
Stahlbau. Bd. 21, 1952.
402
135.	Moppert H. Statische und Dinamische Berechnung erdverankerter
Hangebrficken mit hilfe von Greenschen Funktionen und Integralgleichungen.
Veroffentlichungen des Deutschen Stahlbau — Verbandes H. G. Koln, 1955.
136.	Mfillenhoff A. Der Entwurt von Brucken mit Rucksicht aut den
Winddruch. Bautechnik. Bd 26. S. 57, 188, 282, 348, 380. 1949. Bd. 27. S. 164, 308,
1950.
137.	Muller K- A. Das Verfahren von H. Neukirch zur Berechnung der
Hangebrficke be duchlaufendem Versteifungsbalken. Bauingenieur. Bd. 23, 1942.
138.	M fi 11 e r K- A. Die Berechnung echter Hangebrficken mittels Rekursion
der Momente. Stahlbau. Bd. 16. S. 81, 92, 1943.
139.	Mui ler—Breslau. Zeit. d. Arch.— Ing. ver. Z. Hannover, 1881.
140.	Neukirch H. Berechnung der Hangebrficke bei Berficksichtigung der
Verformung des Kabels. Inqenienr — Archiv, Bd. 7, 1936.
141.	Neukirch H. Ahgenaherte Berechnung der Hangebrficke unter Be-
rficksichtigung ihrer Verfornung. Stahlbau. Bd. 9. 1936.
142.	Окамура Тока о, К а тао к а Кэй. Элементарный метод расчета
висячих мостов. Engineering N 2, 1964.
143.	Окамура Така о. Расчет висячего моста по методу Кани. Добо-
ку Гидзюцу. N 12. 1959.
144.	Peery D. J. An influence line analysis for Suspension Bridges. Proc.
Amer. Sos. Civil Engrs. N 558, 1954; N701, 1955.
145.	P о c k i tt T. J. The application of elastic catenarg functions to the ana-
lysis of suspended cable structures. Struct. Engr. N 5, 1963.
146.	Pugsley A. The Theory of Suspension Bridges. London. Edward
Arnold Ltd. VII, 1957.
147.	Rankin W. J. M. Applied mechanics, Vol 14. p. 370. 1895.
148.	Schaechterle K-, Leonhardt F. Hangebrficken. Bautechnic.
Bd. 18. S. 377, 1940. Bd. 19, S. 73, 125, 1941.
149.	S c h 1 e ich e r F. Taschenbuch ffir Bauingenieure. Band 1. Springer.
Berlin 1955.
150.	Scruton C. An Experimental Investigation of the Aerodinamic Sta-
bility of Suspension Bridges with Special Reference to the Proposed Severn Brid-
ge. Proceedings of the Institution of civil Engineers, Part I. Vol 1. 1952.
151.	Scruton C. Eine Untersuchung fiber die Schwingungen von Hange-
brucken infolge Wind Vorbericht ffir deni 4. Kongres der Internationalen Ve-
reinigung ffir Briickenbau und Hochbau. Cambridge und London, 1952.
152.	Scruton C. Schwingungen von Hangebrficken unter Windtast.
Bautechnik (Berlin) N 12, 1954.
153.	S e 1 b e rg A. Hangebrficken kliner und mittlerer Spannweite. Stachlbau.
Bd. 23, 1954.
154.	S el berg A. Design of Suspension Bridges. Trondhein. 1946.
155.	Selberg A. Berechnung des Verhaltens von Hangebrficken unter
Windbelasting. Stahlbau. Bd. 14. 1941.
156.	Shiraishi Naruhito. On the coupled free vibrations of a Suspen-
sion Bridge. Mem. Fac. Engng. Kyoto. Univ. N 2, 1963.
157.	Shirley H. — Smith. The world’s Great Bridges. London, 1964.
158.	S i 1 v e rm a n I. K. The Lateral rigidity of Suspension Bridges.
J. Engng. Meeh. Div. Proc. Amer. Sic. Civil Engrs. N 3, 1957.
159.	Си ма да Ицуро, К а вад а Тадаки. Теория расчетов при про-
ектировании висячих мостов и применение ее на практике. Добоку Гидзюцу.
N 4, 5. 1959.
160.	Симидзу Эйса к у, К ом ура Сатоси. Проектирование и рас-
чет косого висячего моста в Кацусэ. Доро. N 228, 1960.
161.	So ch ting F. Selbsterregte Schwingungen von Brucken. Bauinge-
nieur. Bd. 23, S. 136, 1942.
162.	Steinman D. B. A. Generalized Deflection Theory for Suspension
Bridges. Proceedings of the American Society of Civil Engineers. Bd. 60, 1934.
403
163.	Steinman D. В. Rigidity on Aerodinamic Stability of Suspension
Bridges. Transaktions of the American Sosiety of Civil Engineers. Bd. 110.
1945.
164.	Steinman D. B. Aerodinamic Theory of Bridge Oscillations. Procee-
dings of the American Sosiety of Civil Engineers. Bd. 75, 1949.
165.	Steinman D. B. A practical treatise Suspension Bridges. New-
York, London, 1929.
166.	Steinman D. B. Le probleme aerodynamique des ponts suspenses.
L’Ossature metallique 1954.
167.	Steinman D. B. The aerodynamic stability of the Machinac Bridge.
Road’S and Engng. Constr. N 12, 1955.
168.	Stiissi F. Zur Berechnung verankerter Hangebriicken. Abhandlungen
der Internationalen Vereinigung fiir Briickenbau und Hochbau. Bd. 4. S. 531.
Zurich 1936.
169.	Stiissi F. Zur Allgemeinen Formanderungstheorie der verankerten
Hangebriicken. Schweiz. Bauzeitung. Bd. 117. S. 1, 18. 1941.
170.	S t ii s s i. F. Ausgewalte Kapitel aus der Theorie des Briickenbaues, in
Schleicher. Taschenbuch fiir Bauingenieure. 2 Aufl. 1 Bd. S. 905. Berlin (Gottin-
gen) Heidelberg: Springer, 1955.
171.	Stiissi F. Entwurt und Berehnung von Stahlbauten. Springer —
Verlag. Berlin, 1958.
172.	Stiissi F. und Amstutz E. Verbesserte Formanderungstheorie ve-
rankerter Hangebrucken im Stabbogen. Schweiz. Bauzeitung. Bd. 116, N 1.
173.	Судзуки Тосно. Подвесной мост с вспомогательной балкой же-
сткости Гербера. Добоку Гидзюцу N 4, 5, 1962.
174.	SzidarovszkyJ. Corrected deflection theory of Suspension Rridges.
J. Struct. Div. Proc. Amer. Soc. civil Engrs. N 11, 1960.
175.	SzidarovszkyJ. A practical solution for stiffened Suspension Brid-
ges of variable inertia moment and its application to influence-line analysus. Acta
Techn. Acad. Scient. N 3—4, 1958.
176.	Szidarovszky K- Prodcing influence lines of Suspension Bridges
with variable flexural rigidity by successive aproximation. Acta techn. Acad.
Scient. hung. N 1—2. 1962.
177.	Тана д а Кэндзо, КавадаТадсеки, КавабатаХидзо.
Расчеты висячего моста с предварительно напряженными вспомогательными
конструкциями. Добоку Гидзюцу. N 12, 1961.
178.	Татэ Дзюнъити, Тан К эй. О вертикальной вибрации подвес-
ного моста Добоку Гидзюцу. N 10. 1961.
179.	Theimer О. F. Beitrag zur Theorie der Seitensteifigkeit weitgespan-
nter Hangebrucken. Bauingenieur. Bd. 22. 1941.
180.	T i m о s h e n k о S., Way S. Suspension Bridges with a Continueus Stif-
fening Truss. Abhandlungen der Internationalen vereinigung fiir Briickenbau
und Hochbau. Bd. 2 S. 452. Zflrich, 1934.
181.	Timoshenko S. The Stiffness of Suspension Bridges. Trans.
A. S. С. E. Vol 94. 1930.
182.	Timoshenko S. Zeitschrift fiir angewandte Mathematik und Mecha-
nik. Bd. 8. H. 1. 1928.
183.	Tomas H. A. Wind aseillations of Suspension Bridges. E. N. R.
1941.
184.	Topaloff B. Stationarer Winddriick auf Hangebriicken. Stahlbau. Bd.
23. 1954.
185.	Tschauner J. Berechnung der Hangebriicke mit durchgehendem
Versteifungstrager der andem Pylonenpfeilern nicht abgestiitzt ist. Bauingenieur.
Bd. 22. S. 283. 1941.
186.	Vincent G. S. Aerodynamic stability of Suspension Bridges. Bull.
Univ. Wash. Engng. Experim. Stat. N 116. 1954.
187.	Vincent G. S. Aerodynamic characteristics of a Suspension Bridge.
Analysis based on tests of a section midel. Public. Roads. N 8. 1955.
404
188.	Vlasov V. Z. Theory of spase vibration of thinwalled bars and shells
as well as aerodynamic stability of Suspension Bridges. Act. IX Congr. Internat.
Meehan. Appl. v. 7 Bruxells Univ. 1957.
189.	W a 11 к i ng F. W. Hangebrucken unter statischem Wind. Bauingenieur.
Bd. 25, 1950.
190.	Waling F. W. Praktische Berechnung der Eigenfrequenzen von
Hangebriicken. Bauingenieur. Bd. 25. S. 208, 254. 1950.
191.	Waltking F. W. Aerodynamische Theorie Briikenschwingungen.
Bauingeniur. Bd. 26, 1951.
192.	Waltking F. W. Steinmans aerodynamische theorie in der Fachdis-
hussion. Bauingenieur. Bd. 26. 1951.
193.	Waltking F. W. Windkrafte, schwingungen aerodynamische stabi-
litat, in: Die neue Koln-Miilheimer Brucke. S. 46. Koln 1951.
194.	Wa Itking F. W. Schwingungsdampfung in Hangebriicken. Bauinge-
nieur. Bd. 28. 1953.
195.	Waltking F. W. Schwingungen in der Bautechnik in Schleicher:
Taschenbuch fiir Bauingenieur. 2 Aufi. 1 Bd. 1048 Berlin (Gottingen).
Heidelberg: Springer, 1955.
196.	Журнал посвящен висячему мосту Танкервиль. (Pont-Ronie <>е
Tancarville. N 157, 1961).
ОГЛАВЛЕНИЕ
Стр.
Предисловие................................................... 3
Глава I
КРАТКИЕ СВЕДЕНИЯ ИЗ ИСТОРИИ РАЗВИТИЯ висячих мостов
§	1.	Общие сведения о	строительстве висячих мостов................ 7
§	2.	Краткие сведения	о висячих мостах больших пролетов...........11
§	3.	Краткое описание	Танкервильского висячего моста..............30
§	4.	Развитие теории расчета висячих мостов.56
Глава II
ТИПЫ ВИСЯЧИХ МОСТОВ И ИХ РАСЧЕТНЫЕ СХЕМЫ
§ 1.	Общие замечания.........................................65
§ 2.	Основные схемы кабельных мостов ........................65
§ 3.	О рациональных соотношениях основных размеров кабельных
мостов...........................................................69
§	4.	Особенности	кабельных	висячих	мостов	по сравнению с другими
мостами........................................................71
§	5.	Основные	схемы	балочно-вантовых	мостов.72
Глава III
НЕКОТОРЫЕ ВОПРОСЫ РАСЧЕТА ГИБКОЙ НИТИ
§ 1.	Общие замечания.........................................74
§ 2.	Изменение очертания оси гибкой нити при загружении вертикаль-
ной временной нагрузкой.......................................75-
§ 3.	Учет влияния температуры при расчете гибкой нити........88
§ 4.	Гибкая нить с подвижной опорой..........................91
§ 5.	Одновременное действие вертикальных и горизонтальных нагрузок 95
§ 6.	Расчет нити, загруженной вертикальными и горизонтальными со-
средоточенными силами......................................... 104
§ 7.	Об одном варианте построения интегральной матрицы.......114
§ 8.	Расчет гибкой нити с учетом наклона подвесок............118-
§ 9.	Расчет системы, состоящей из двух предварительно напряженных
гибких нитей ................................................. 130-
Глава IV
РАСЧЕТ ВИСЯЧИХ МОСТОВ ПУТЕМ
НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ УРАВНЕНИЙ
§ 1.	Общие замечания......................................... 141
§ 2.	Основные уравнения....................................... 1411
406
Стр.
§ 3.	Интегрирование дифференциальных уравнений для однопролетно-
го висячего моста............................................... 144
§ 4.	Характеристическое уравнение для определения распора ....	149
§ 5. Решение характеристического уравнения...........................................................................................152
§ 6. Определение максимального момента в произвольном сечении од-
нопролетного моста......................................... 155
§ 7.	Замечание о работе балки жесткости однопролетного моста . . . 160
§ 8.	Расчет трехпролетного висячего моста с разрезной балкой же-
сткости ........................................................ 160
§ 9.	Расчет трехпролетного моста с неразрезной балкой жесткости по-
стоянного сечения............................................... 163
§ 10.	Порядок решения задачи	для трехпролетного моста................................................................................ 170
Глава V
численный метод расчета висячих мостов
§	1.	Общие замечания...............................................................................................................171
§	2.	Вывод основных уравнений......................................................................................................172
§	3.	Вычисление матрицы А..........................................................................................................177
§ 4.	Решение основных уравнений при использовании настольных кла-
вишных машин.....................................................179
§	5.	Пример расчета однопролетного	моста......................................................................................181
§	6.	О решении основных уравнений	с	помощью ЭЦВМ...................................................................................186
§	7.	Расчет трехпролетного моста с	неразрезной	балкой жесткости . . 187
§ 8.	Сравнение результатов расчета трехпролетного моста по двум
методам..........................................................193
§ 9.	Замечание о расчете многопролетных мостов с неразрезной балкой
жесткости........................................................200
§	10.	Расчет висячего моста с учетом	наклона подвесок...............201
§ 11.	Расчет моста с кабелем, жестко прикрепленным к балке в середи-
не пролета...................................................... 205
§	12.	Учет влияния переменного сечения балки жесткости................................211
§	13.	Учет растяжения подвесок при	расчете висячего моста.........214
Глава VI
РАСЧЕТ ВИСЯЧЕГО МОСТА ПРИ НАЛИЧИИ ШАРНИРОВ
В БАЛКЕ ЖЕСТКОСТИ
§	1.	Предварительные замечания...............................................................................217
§	2.	Основные уравнения...............................................................................218
§	3.	Система с двумя жесткими дисками, подвешенными к кабелю . . 222
§	4.	Система с одной степенью свободы.226
Глава VII
РАСЧЕТ БАЛОЧНО-ВАНТОВЫХ МОСТОВ
§ 1.	Предварительные замечания.......................*	. . . . 233
§ 2.	Краткие сведения о матрицах влияния . ........................................................................................234
§ 3.	Определение усилий в вантах...................................................................................................235
§ 4.	Учет влияния способов прикрепления вант на пилоне...............................................................................239
§ 5.	Преобразование формул для определения усилий в вантах .... 240
§ 6.	Вывод основных уравнений......................................................................................................2-2
§ 7.	Составление матриц Lm и Ц для неразрезной балки...............................................................................244
§ 8.	Пример расчета моста с пучком вант, прикрепленным к подвиж-
ной опорной части наверху пилона ............................... 249
§ 9.	Расчет моста при наличии опорной ванты........................................................................................256
§ 10.	Расчет моста с вантами, жестко закрепленными на пилоне .... 264
407
Стр.
§ 11. Пример расчета моста с жестким прикреплением пучка вант к
верху пилона.................................................267
§ 12.	Расчет вантового моста с применением клавишных машин или
арифмометра........................................................274
Глава VIII
СОБСТВЕННЫЕ КОЛЕБАНИЯ ВИСЯЧИХ МОСТОВ
§ 1.	Общие замечания............................................288
§ 2.	Вывод дифференциальных уравнений . . .  ...................290
§ 3.	Применение метода Галеркина к определению собственных частот
и форм изгибных колебаний........................................295
§ 4.	Пример применения метода Галеркина........................ 304
§ 5.	Анализ точности метода Галеркина.........................  307
§ 6.	Зависимость частот и форм изгибных колебаний от соотношения
основных размеров и жесткостей моста.............................309
§ 7.	Применение численного метода для определения частот и форм
собственных изгибных колебаний	моста........................313
§ 8.	Сравнение результатов, полученных по методу Галеркина и чис-
ленному методу...................................................324
§ 9.	Крутильные колебания висячего	моста........................326
§ 10.	Собственные колебания моста при наличии шарниров в балке
жесткости........................................................336
§11.	Приближенные формулы для определения частот колебаний вися-
чих мостов.......................................................345
§ 12.	Собственные колебания балочно-вантовых мостов..............351
Приложение.......................................................360
Литература...................................................... 398
Владимир Анатольевич Смирнов
ВИСЯЧИЕ МОСТЫ БОЛЬШИХ ПРОЛЕТОВ
Редактор Ж. А. Беспалько
Худож. редактор С. Г. А б е л и н
Ретушь Г. М. Зеленина
Графика В. Н. Литвишко
Техн, редактор С. П. Передерий
Корректор В. А. Орлова
Т—14029 Сдано в набор 18/IV 1969 г. Подп. к печати 9/ХП 1969 г.
Формат бОхЭО’/ю	Объем 25,5 печ. л.	Уч.-изд. л. 22,02
Изд. № СТР—91	Тираж 5000 экз.	Цена 97 коп.
Тематический план издательства «Высшая школа» (вузы и техникумы) на 1969 год.
Позиция № 125.
Москва. К-51, Неглиниая ул., 29/14,
Издательство «Высшая школа»
Московская типография № 8 Главполиграфпрома
Комитета по печати при Совете Министров СССР,
Хохловский пер.. 7. Зак. 3802.