Текст
' J» и ' т. Пи .— ir»'
4 Й
ТЕОРИЯ
ЭЛЕКТРОМАГНЕТИЗМА
М.С.РАБИНОВИЧА
В.М.ХАРИТОНОВА
^гр^б.С.М.РЫТОВА/
r
V
J-
•j^.
ОГИЗ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 48 ЛЕНИНГРАД
АННОТАЦИЯ
Книга содержит полное и систематическое
изложение современной макроскопической теории
электричества. Главное внимание уделено быстро-
переменным электромагнитным полям, в особенности —
теории излучения и распространения радиоволн.
Книга является настольным руководством для
научного работника и инженера, соприкасающихся в
своей работе с вопросами электромагнетизма.
/
Редактор В. А. Угаров. ' Техн. редактор С. Н. Ахламо*.
<. . , , .—— . -—
Подписано к печати 10/ХИ947 г. 23,75 печ. л. 53,64 уч.-изд. л. 63 530 тип. зн. в печ. л. А09Й20.-
Тираж 8 000 экз. Цена книги 32 руб. Переплёт 2 руб. Заказ № 593*
4-я типография им. Евг. Соколовой треста сПолиграфкнига» ОГИЗа
при Совете Министров СССР. Ленинград, Измайловский пр., 29.
■г
ОГЛАВЛЕНИЕ
От редактора 9
Предисловие И
ГЛАВА I
УРАВНЕНИЯ ПОЛЯ
Уравнения Максвелла 15
1.1. Векторы поля 15
1.2. Заряды и токи 16
1.3. Дивергенция векторов поля 19
1.4. Интегральная форма уравнений поля 20
Макроскопические свойства материи 22
1.5. Абсолютные проницаемости е и [л 22
1.6. Электрическая и магнитная поляризации 24
1.7. Проводящая среда 26
Единицы и размерности 28
1.8. MKS-система или система Джорджи 28
Электромагнитные потенциалы 33
1.9. Векторный и скалярный потенциалы 33
1.10. Однородная проводящая среда 36
1.11. Вектор Герца или поляризационный потенциал 37
1.12. Комплексные векторы поля и потенциалы 40
Граничные условия 42
1.13. Разрывы непрерывности векторов поля 42
Координатные системы 45
1.14. Основные и взаимные координатные векторы 45
1.15. Дифференциальные операторы 50
1.16. Ортогональные системы 53
1.17. Уравнения поля в обобщённых ортогональных координатах .... 55
1.18. Свойства некоторых простейших систем 55
^Тензоры поля 62
1.19. Ортогональные преобразования и их инварианты 62
1.20. Элементы тензорного анализа 66
1.21. Пространственно-временная симметрия уравнений поля 70
1.22. Преобразование Лоренца 74
1.23. Преобразование векторов поля к движущейся системе координат . 77
v ГЛАВА II
СИЛЫ И ЭНЕРГИЯ
Напряжения и деформации в упругой среде 82
2.1. Тензор упругих напряжений 82,
2.2. Анализ деформаций 86
2.3. Упругая энергия и соотношение между напряжениями и
деформациями . .- 90
Электромагнитные силы» действующие на заряды и токи 93
2.4. Определение векторов Е и В ., 93
2.5. Тензор электромагнитных напряжений в свободном пространстве . 94
2.6. Импульс электромагнитного поля 99
1
*
■'' 4 ■ '' ОГЛАВЛЕНИЕ . " . ч , - /^
. ' " * . • i .'■■'' •> ■
Электростатическая энергия ,_ ICO
2.7. Электростатическая энергия как функция плотности зарядов ... 1СО ,
2.8. Электростатическая энергия как функций напряжённости поля . . 103
2.9. Теорема векторного поля 106
2.10. Энергия диэлектрического тела в электростатическом поле .... 107 .:
2.11. Теорема Томсона 109
2.12. Теорема Ирншоу ПО
2.13. Теорема об энергии незаряженного проводника 111' ■-
Магннтостатическая энергия 112 .■
2.14. Магнитная энергия стационарных токов 112 .
2.15. Магнитная энергия как функция напряжённости поля 11?
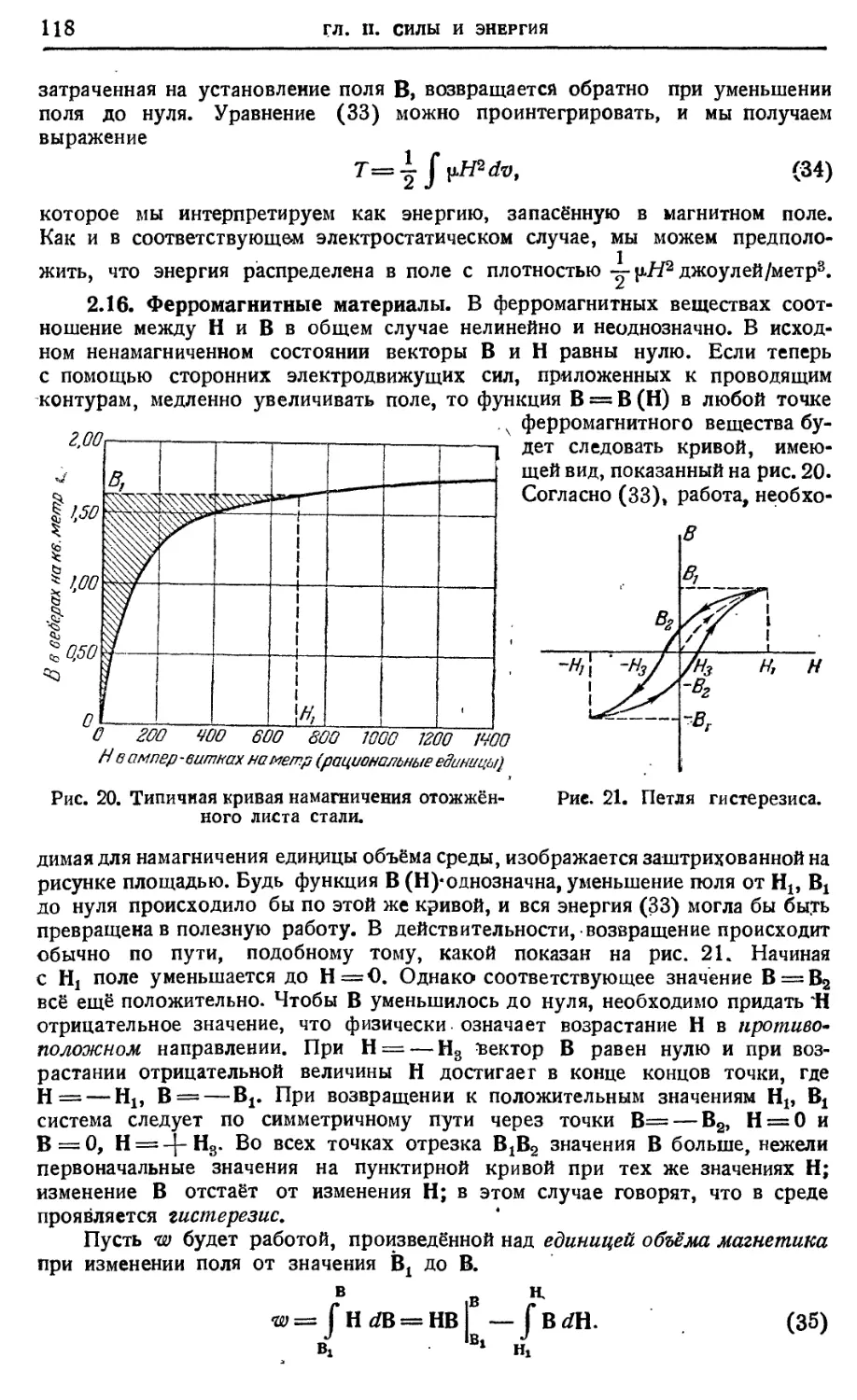
2.16. Ферромагнитные материалы 118 \.
. 2.17. Энергия магнитного тела в магнитостатическом поле 11$ -*
2.18. Потенциальная энергия постоянных магнитов 121 ,
Лоток энергии 123 •
2.19 Теорема Пойнтинга 123
2.20. Комплексный вектор Пойнтинга 126 -.-
Силы, действующие на диэлектрик в электростатическом поле 128
2.21. Объёмные силы в жидких средах 128 ~
2.22. Объёмные силы в твёрдых телах 130"
2.23. Тензор напряжений 136
2.24. Поверхности разрыва 137 .
2.25. Электрострикция 139
2.26. Силы, действующие на тело, погружённое в жидкость 140
• Силы в статическом магнитном поле • . . 142 ,
2.27. Неферромагнитные вещества 142 ^
2.28. Ферромагнитные вещества 144
Силы в электромагнитном поле ». . . 145
2.29. Силы, действующие на тело, погружённое в.жидкость ...... 145
ГЛАВА III
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
с -' ■'■
Общие свойства электростатического поля 148 ь,
3.1. . Уравнения"для поля и потенциала • - . 148 ;;
3.2. Граничные условия 151
Определение, поля по заданному .распределению зарядов -. 152 ',
3.3 Теорема Грина * 152
3.4. Интегрирование уравнения Пуассона 153
3.5. Поведение в бесконечности 155
3.6. Кулоново поле • .. 15Q ,
3.7. Сходимость интегралов 157
Разложение потенциала по сферическим функциям 158 ,■
3.8. Аксиальные распределения зарядов 158
3.9. Диполь . 160'
ЗЛО. Осевые мультиполи 162
3.11. Произвольные распределения зарядов 163^
3.12. Общая теория мультиполей 164
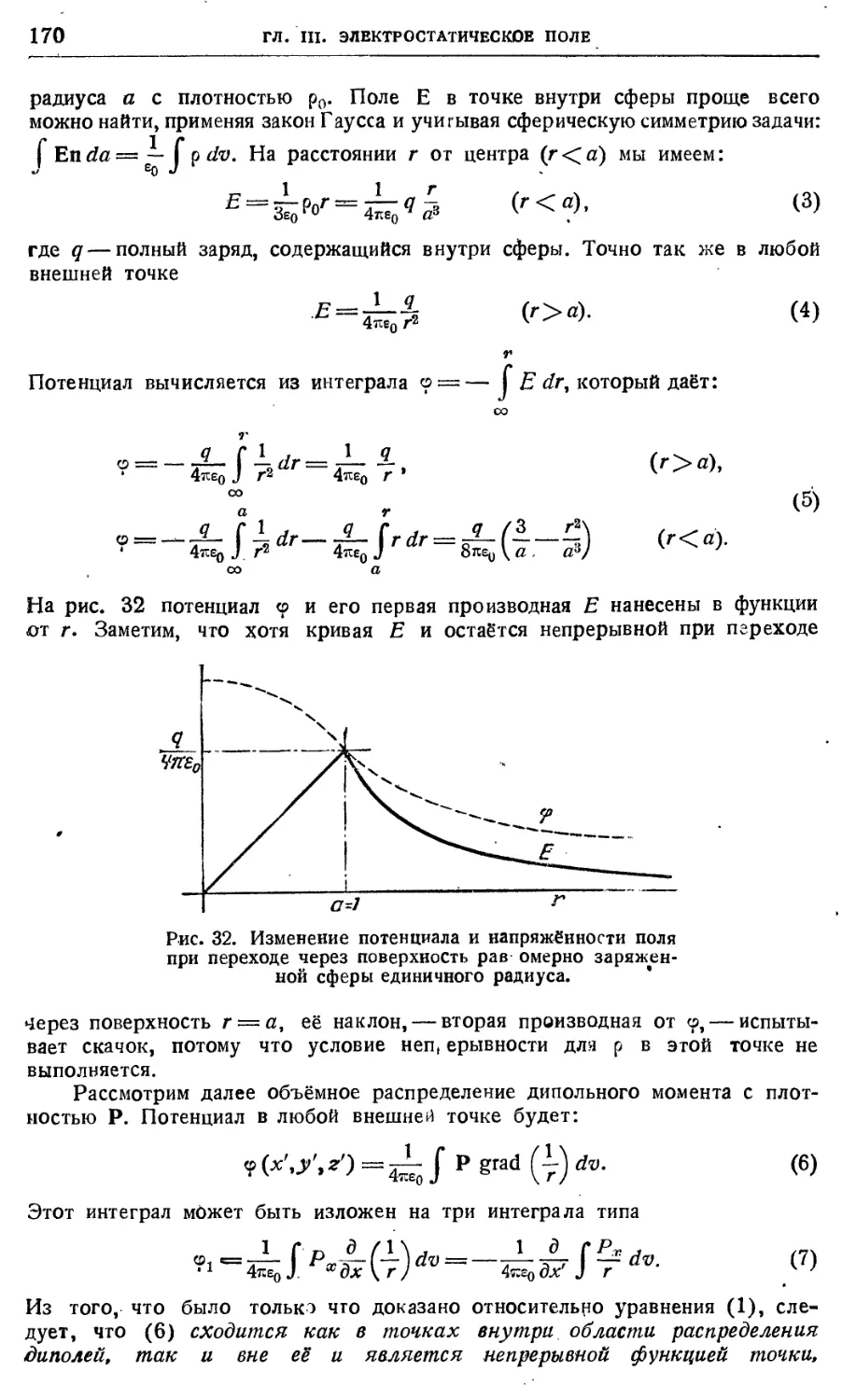
Диэлектрическая поляризация 167
3.13. Интерпретация векторов Р н П 167ч
Разрывы непрерывности интегралов, встречающихся в теории
потенциала , • 169
3.14. Объёмное распределение зарядов и дипольного момента . .' ... . 160 ''
3.15. Простой заряженный слой .171
3.16. Двойной заряженный слой 172
3.17. Интерпретация теоремы Грина 175 ;
3.18. Метод изображений . . . .> . 176
ОГЛАВЛЕНИЕ V/ 5
№Ш
роевые задачи 177
3.19; Формулировка электростатических задач • 177
3.201 Однозначность решений 178
3.21. Решение уравнения Лапласа 179
ft Задача о шаре 183
к^; 3.22. Проводящий шар в поле точечного заряда 183
3.23. Диэлектрический шар в поле точечного заряда,. ., 185
а
fe; - 3^4. Шар в параллельном поле 186
^Задача об эллипсоиде 188
t .,, 3.25. Свободные заряды на проводящем эллипсоиде 188
|р|^' 3.26. Проводящий эллипсоид в параллельном поле ". . 190
j^S£Л 3.27. Диэлектрический эллипсоид в параллельном поле 191
|f^#-i 3.28. Определение Е и D с помощью полостей 194
"'*% 3.29. Вращающие моменты, действующие на эллипсоид . 195
Щ^- Задачи. . . . , 197
§?:.' глава iv
Ш:. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
ЩОбщие свойства магнитостатического поля 204
W'£\:- 4:1. Уравнения поля и векторный потенциал 204
\j*,$^\ 4.2. Скалярный потенциал 205
|*wf 4.3. Исследование Пуассона 206
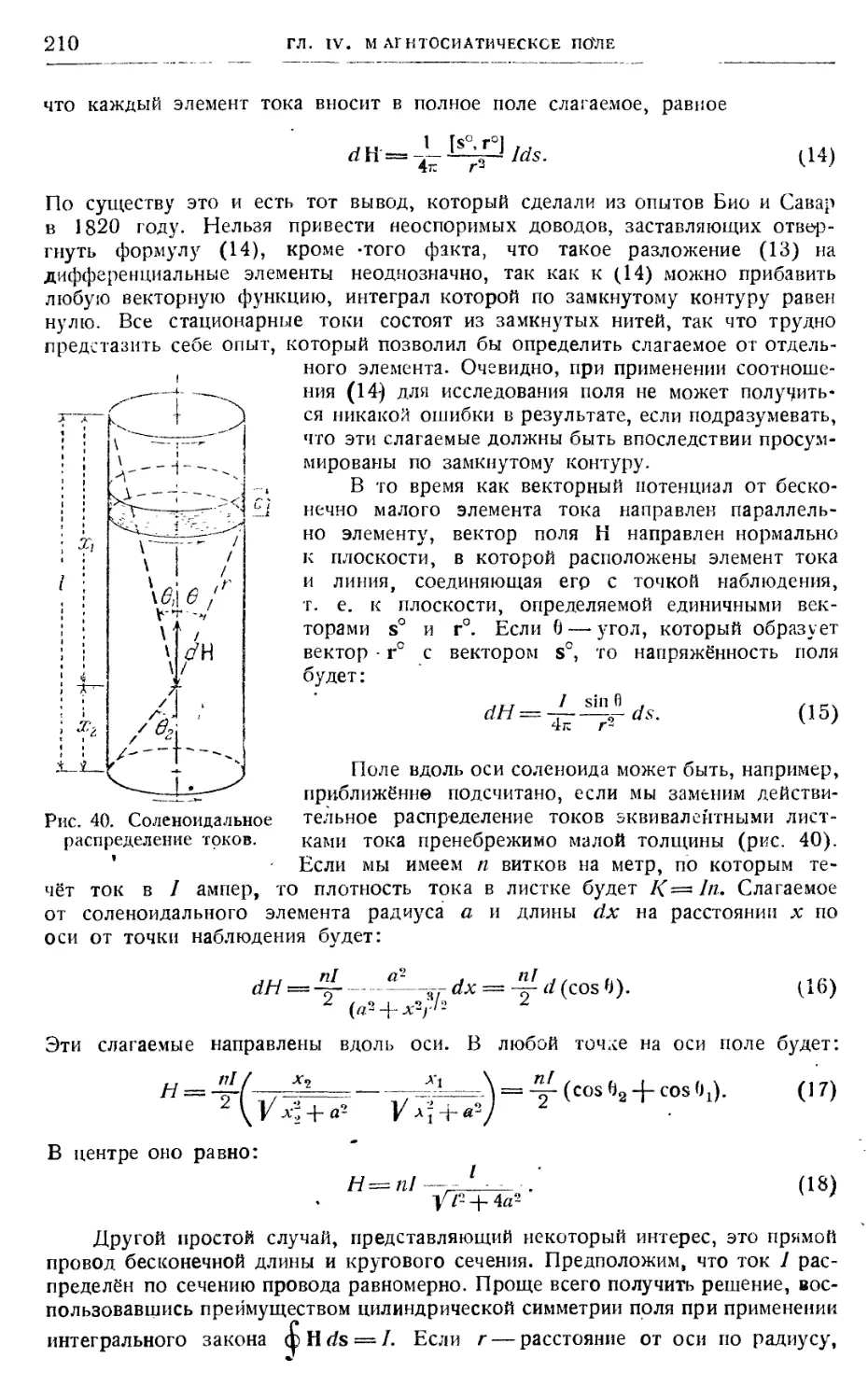
^фйСчёт поля данного распределения токов 208
Щ5д^; 4:4' Закон Био и Савара 208
I'lfffc 4»5. Разложение векторного потенциала 211
гр.£аШ:. ;4Д. Магнитный диполь 213
:-,Ла
gc^%54i7. Магнитные листки . / 214
р Отступление по поводу единиц и размерностей . 215
Щ 4Л. Основные системы 215
Щ:\ 4.9.. Закон Кулона для магнитных зарядов . . . ' 217
^ Магнитная поляризация 218
Щк'^ 4.10. Эквивалентное распределение токов . 218
ЩУ 4.Ц. Поле намагниченного стержня и шара 219
I Разрывы непрерывности векторов АиВ 220
|/ 4.12. Поверхностное распределение токов . . 220
||у ( 4.13. Поверхностное распределение магнитного момента 222
! Интегрирование уравнения rot rot A = p. J 224
Щ$У"_ 4.14. Векторный аналог теоремы Грина 224
|U' 4.15. Применение к векторному потенциалу 225
^Краевые задачи С 228
|^ 4.16. Формулировка задачи магнитостатики • 228
Щ- 4.17. Однозначность решения А ...... . 230
;& Задача об эллипсоиде 230
Й- ''"' 4.18. Поле однородно намагниченного'эллипсоида 230^
4.19. Эллипсоид ns магнетика в параллельном поле 231
> Цилиндр, в-параллельном поле 231
*'■' 4.20. Подсчёт поля 231
4»21. Силы, действующие йа цилиндр 234
Задачи 235
ГЛАВА V
>; ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
у- г
/Распространение плоских волн 240
£} 5.1. Уравнения одномерного поля 240
|; * 5.2. Плоские волны, гармонические во времени 243
!'' 5.3. Плоские волны, гармонические в пространстве 248
ж- ■
6 -• ОГЛАВЛЕНИЕ
5.4. Поляризация 248*
5.5. Поток энергии л250
5.6. Импеданс • . . . 251
Общие решения одномерного волнового уравнения 253
5.7. Элементы гармонического анализа (теорема Фурье) . . . . • . . 253
5.8. Общее решение одномерного волнового уравнения в непоглощаю-
щей среде ,. 260
5.9. Поглощающая среда; заданное распределение во времени .... 264
5.10. Поглощающая среда; заданное распределение в пространстве . . 268
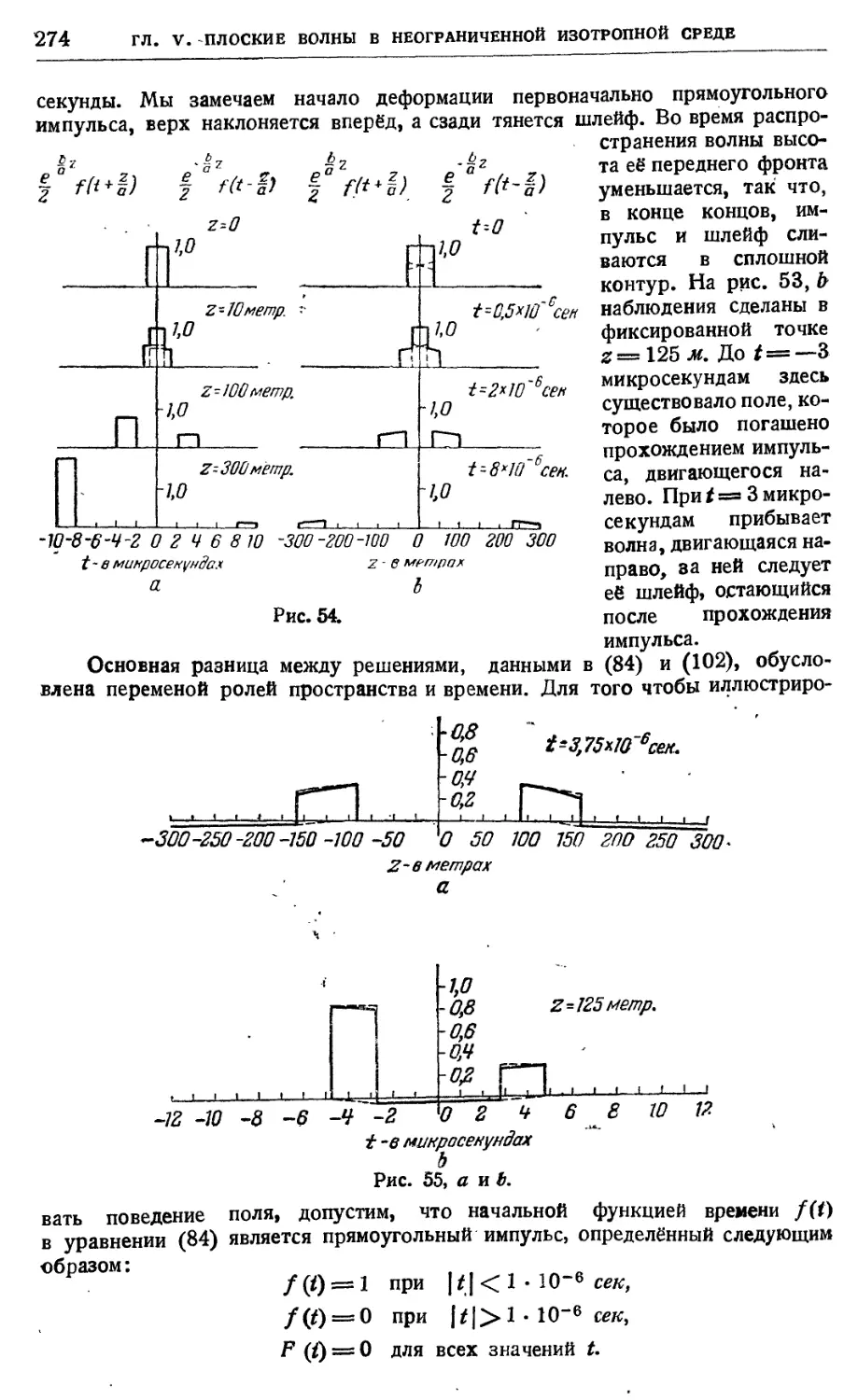
5.11. Дискуссия численного примера \ . . 2t0
5.12. Элементарная теория преобразования Лапласа 275
5.13. Применение преобразования Лапласа к уравнениям Максвелла . . 283
Дисперсия . . . 285
5.14. Дисперсия в диэлектриках ..." 285" .
5.15. Дисперсия в металлах 289
5.16. Распространение в ионизованной атмосфере (ионосфере) 290
Скорости распространения 293
5.1.7. Групповая скорость 293
5.18. Волновой фронт и скорость сигнала 296
Задачи 301
• ГЛАВА VI
ЦИЛИНДРИЧЕСКИЕ ВОЛНЫ
Уравнения цилиндрического поля 309
6.1. Представление посредством векторов Герца 309
6.2. Скалярный и векторный потенциалы . . 311
6.3. Импедансы гармонических цилиндрических полей 313
Волновые функции кругового цилиндра . -. . . 314..
6.4. Элементарные волны 314
6.5. Свойства функций Zp(p) 315
6.6. Поле круговых цилиндрических волновых функций ......... 317
Интегральные представления волновых функций 319
6.7. Построение из плоских волн 319
6.8. Интегральные представления функций Zn(p) 321
6.9. Интегралы Фурье-Бесселя 325 .
6.10. Представление плоской волны 327
Теорема сложения для круговых цилиндрических волн 328
6.11 * • 328 '
Волновые функции эллиптического цилиндра 330
6.12. Элементарные волны . .' 330
6.13. Интегральные представления 334
6.14. Разложение плоских и круговых волн 338
Задачи • 340
/ ГЛАВА VII
СФЕРИЧЕСКИЕ ВОЛНЫ *
Векторное волновое уравнение 345..
7.1. Фундаментальная система решений 345
7.2. Применение к цилиндрическим координатам 348
Скалярное волновое уравнение в сферических координатах 352
7.3. Элементарные сферические волны 352
7.4. Свойства радиальных функций 356
7.5. Теорема сложения для полиномов Лежандра . 358
7.6. Разложение плоской волны 359
7.7. Интегральные представления 360
7.8. Интеграл Фурье-Бесселя 362
7.9. Разложение цилиндрической волновой функции 363
7.10. Теорема сложения для функции z${kR) 364
ОГЛАВЛЕНИЕ - 7
Векторное волновое уравнение в сферических координатах 365 >
7.11. Сферические векторные волновые функции 365
7.12. Интегральные представления 367
7.13. Ортогональность 368
7.14. Разложение плоской векторной волны 369
Г Задачи 371
ГЛАВА VIII
ИЗЛУЧЕНИЕ
Неоднородное скалярное волновое уравнение 374
. 8.1. Метод интегрирования Кирхгофа '. 374
8.2. Запаздывающие потенциалы ; 378
8.3. Запаздывающий вектор Герца 379
Разложение на мультиполи 380
8.4. Определение моментов 380
8.6. Электрический диполь 383
8.6. Магнитный диполь 386
Теория.излучения систем линейных антенн 387
8.7. Поле излучения одиночного линейного осциллятора 387
8.8. Излучение от бегущих волн 392
8.9. Гашение противоположных фаз 393
8.10. Направленные устройства 395
8.11. Точный расчёт поля линейного осциллятора • . 400
8.12. Определение сопротивления излучения по методу вычисления э. д. с. 403
Принцип Гюйгенса-Кирхгофа 405
8.13. Скалярная волновая функция 405
8.14. Непосредственное интегрирование уравнений поля . . . . • ... 409
8.15. Разрывы поверхностного распределения 412
Четырёхмерная формулировка задачи об излучении 415
Ь.16. Интегрирование волнового уравнения 415
8.17. Поле движущегося точечного заряда 417
Задачи 420>
ГЛАВА IX
КРАЕВЫЕ ЗАДАЧИ
Общие теоремы 426
9.1. Граничные условия u 426
9.2. Единственность решения 429
9.3. Электродинамическое подобие 430
Отражение и преломление на плоской поверхности 432
9.4. Законы Снелля 432
9.5. Формулы Френеля 433
9.6. Диэлектрические среды 435
9.7. Полное отражение 438
9.8. Преломление в проводящей среде 441
9.9. Отражение от проводящей поверхности 444
Плоские слои 449
9.10. Коэффициент отражения и коэффициент прозрачности ...... 449
■ 9.11. Применение к диэлектрическим средам .... • 451
9.12. Поглощающие слои 452
Поверхностные волны 453
9.13. Комплексный угол падения 453
9.14. Скин-эффект 457
Распространение вдоль круглого цилиндра 460
9.15. Собственные виды волн 460
9.16. Проводник, помещённый в диэлектрик 463
9.17. Дальнейшее рассмотрение основной волны 467
9.18. Волны в полых трубах 471
'f %■* * j vsu^s» ^j*, ч T ^ *>',. г' ".' ..«-. '*> :~- ■-■' '' i:.r>'- :-, ";-V.". <£"'* -. .••■.• ~\**«
_b.
"-1 '' 1"
Коаксиальные линии ♦ 47&
9.19. Постоянная распространения 478 /
9.2Q, Бесконечная проводимость ».....'.... J80
9.21. Конечная проводимость t 483
-Колебания сферы - 486-
9.22. Собственные колебания " 486
9.23. Колебания проводящей сферы 48§
9.24. Колебания в сферической полости, . . . .. \ . . 490
Дифракция плоской волны на сфере *.....• 493
9.25. Разложение дифрагированного поля ' . :'■ 493
9.26. Полное излучение '. 497
J 9.27. Предельные случаи 499*.
Влияние земли на распространение радиоволн 501
9.28. Решение Зоммерфельда 501
9.29. Решение Вейля : 506 }
9.30. Решение Ван дер Поля 510-
9.31. Приближённые выражения интегралов '. *5П >
Задачи , •„ . <5>Щ г
♦
Приложение I 526
A. Числовые значения основных констант 526
B. Размерности электромагнитных величин . . • . ; 527 -/
C. Таблицы перехода 527
Приложение II 529
Формулы векторного анализа 52$
Приложение III .. 530,-
Проводимости различных материалов , 530
Относительные диэлектрические постоянные диэлектриков 531 „ „
Приложение IV ...... 532" '\
Присоединённые функции Лежандра ' 532 Л
Именной указатель . . * . f 533.. :,
Предметный указатель ' 535*
ОТ РЕДАКТОРА
В своём предисловии автор сам с полной ясностью разъясняет задачу,,
которую он себе ставил. «Теория электромагнетизма» Дж. А. Стрэттона,
конечно, не является учебником. Эта книга непригодна для первого
ознакомления с теорией электромагнитного поля и не предназначена для этого.
Уравнения Максвелла выступают здесь не как результат длительного
восхождения от частного к общему, от эмпирических законов к теории, а как мощный
рабочий инструмент. Они появляются поэтому не на предпоследней странице:
(после чего следует обычно вывод формул Френеля и этим дело
заканчивается), а на самых первых. Вся книга учит затем с ними работать. В этом
^заключается всё её значение и интерес. С этой целью в ней собраны в
большом количестве и необходимые вспомогательные средства (элементы тензх>р-
Hpto анализа и теории упругости, сведения по специальным функциям,
гармоническому анализу, преобразованию Лапласа и т. п.).
Потребность в такого рода дедуктивном и обстоятельном изложении
Зисто макроскопической теории поля назрела уже давно, и в этом отношении
перевод книги Стрэттона отвечает на запросы, возникшие у многих. Для.
каждого, кто так или иначе соприкасается в своей научной или инженерной
работе с вопросами электромагнетизма, эта книга будет настольной. И не
только в силу своей полноты и систематичности, но и в силу своей
направленности в сторону наиболее актуальных современных задач, связанных
главным образом с быстропеременными полями.
Конечно, книга небезупречна. Я не буду касаться отдельных замеченных
неточностей или мелких ошибок, которые либо снабжены примечаниями,
либо просто исправлены. Основных недостатков можно указать два.
Во-первых, полное незнание автором советской научной литературы и, во-вторых,.
|о, что в некоторых вопросах книга уже успела устареть. Сказанное отно-
vCHtcfl в особенности к теории антенн и к распространению
электромагнитных волн над земной поверхностью. Советская теоретическая мысль заняла.
здесь ведущие позиции, но автору неизвестно, повидимому, даже то, что уже
было сделано у нас ,ко времени выхода его книги A941 г.). Основные из.
сделанных мною примечаний имеют в виду исправление именно этих
недостатков. Я не выходил, однако, за гределы того материала, который
содержится в книге. Так, например, я не сослался на прекрасные работы-
• Г. А. Гринберга о применении интегральных уравнений в
электростатике, поскольку метод интегральных уравнений в книге Стрэттона вообще
незатрагивается.
В заключение сделаю несколько замечаний^ касающихся терминологии,,
обозначений и единиц. В некоторых отношениях изложение Стрэттона.
стремится быть ультрасовременным. Все дифференциальные операции он
записывает только с помощью оператора Гамильтона (набла), а векторное
умножение обозначает косым крестом. Это приводит, конечно, к большому
единообразию, но, на мой взгляд, к ещё большему однообразию. В пере-
10 СОРЕДАКТОРА
воде сохранены принятые у нас и для большинства привычные обозначения
grad, div, rot и квадратные скобки Для векторного произведения. - <
Термин «проницаемость» в применении не только к е, ио и.-к jjl, вероятно,
не вызовет никаких недоразумений, несмотря на привычку, называть е
диэлектрической постоянной даже тогда, когда она зависит .<от координат.
Я рискнул также отказаться от укоренившихся у нас анахронизмов,
расходящихся с тем, что принято во всех языках мира. Мне кажется, что пора
говорить просто о полном отражении (total reflection) и двойном
преломлении (double'refraction) вместо полного внутреннего отражения и двойного
лучепреломления. Всякое отражение является «внутренним» (т. е.
возвращением - волны в ту среду, из которой падает первичная волна), а в теории
двойного преломления речь идёт в первую очередь не о лучах (вектор Пойн-
тинга), а о волновой нормали.
В несколько особом положении находится вопрос о единицах. В нашей
теоретической литературе широко принята абсолютная гауссова система
электромагнитных единиц. Сторонников этой системы Стрэттон объявляет
консерваторами («тори»). Сам он последовательно придерживается системы *
MKS (система Джорджи), в которой вакуум наделяется проницаемостями
е = 8, 854 • Ю-12 фарад/метр и jjl —4тс • 10~7 генри/метр. Нельзя отказать
в убедительности аргументам автора в пользу этой системы, оперирующей
<. практическими единицами (кулон, вольт, ампер, ом и т. д.). Её
применение подчёркивает направленность всего изложения в сторону приложений
и именно поэтому я не счёл возможным ломать большую часть текста,
переделывая всё на абсолютные гауссовы единицы. Подобная переделка хотя
и придала бы многим формулам более привычный вид, но в корне разошлась
•бы с замыслом автора и нарушила стиль книги.
Перевод выполнен В. Харитоновым (I—IV, VIII—IX главы) и М.
Рабиновичем (V—VII главы).
С. М: Рытое
ПРЕДИСЛОВИЕ
Образец, каким около 70 лет тому назад явился максвелловский
«Трактат по электричеству и магнетизму» оказывал неизменно до наших дней
преобладающее влияние почти на каждый последующий английский или
американский учебник. «Трактат» был написан с намерением дать связное
изложение всей совокупности известных электрических и магнитных явлений с
единой фарадеевской.точки зрения. Таким образом «Трактат» содержал немного
или, вернее, совсем не содержал упоминаний о гипотезах, выдвинутых
ранее на континенте Риманом, Вебером, Кирхгофом, Гельмгольцем и другими.
Отнюдь не является очевидным, что полное забвение этих более старых
теорий было благоприятным для последующего развития физики. В той мере,
в какой замыслом «Трактата» было распространение идей Фарадея, цель
несомненно была достигнута, но изложение собственного вклада автора оказалось
менее успешным. Сплошь и рядом теории и учения, принадлежащие самому
Максвеллу — концепция токов смещения, тождество света и
электромагнитных колебаний — изложены там едва ли более полно и, возможно даже, менее
привлекательно по форме, чем в первоначальных статьях. Весь первый
том и ббльшая часть второго отведены стационарному состоянию.
Фактически из всей 1000 страниц только десяток посвящен общим уравнениям
электромагнитного поля, восемнадцать — распространению плоских волн и
электромагнитной теории света, и ещё страниц двадцать — магнитооптике. С тех дней
английских и американских авторов почти в той же степени привлекали
математическая законченность теории потенциала и практическая ценность
теории электрических цепей. Только оригинальный и одинокий гений Хивисайда
преуспел в преодолении этого течения.
За дальнейшими исследованиями, касающимися основного содержания
уравнений Максвелла, необходимо вновь вернуться на континент. Работы
Герца, Пуанкаре, Лоренца, Абрагама и Зоммерфельда, совместно с их
сотрудниками и последователями, привели к более глубокому пониманию
физических явлений и к грандиозному промышленному развитию.
В этой книге делается попытка дать изложение теории переменного
электромагнитного поля и теории распространения волн, более соответствующее
предъявляемым ныне требованиям. Некоторое внимание уделено стационарному
состоянию, но лишь с целью введения основных понятий при простых
условиях и всегда с учётом дальнейшего приложения их в общем случае.
Читатель должен владеть основными знаниями по электричеству и магнетизму,
12 , . r V ПРЕДИСЛОВИЕ _ . "*•'
которые могут быть почерпнуты из элементарных руководств, основанных
, на экспериментальных законах Кулона, Ампера и Фарадея,ч и из
последующих'переходных курсов, в которых рассматриваются-, более, общие свойства
электрических цепей, термоионные и электронные устройства элементы
электромагнитных машин и которые заканчиваются формулировкой уравнений
Максвелла. Данная книга начинается с этого пункта. В первой главе уста-,
навливаются общие уравнения, которым подчинены поля и потенциалы. В ней
приведён обзор теории единиц, справочный материал по системам *
криволинейных координат и элементы тензорного анализа; она заканчивается фор-О
мулировкой уравнений поля в пространственно-временном континууме.
Вторая глава также является общей по своему характеру, и многое из неё может
быть при первом чтении опущено. Здесь читатель найдёт обсуждение основ- .<
ных свойств поля, которые могут быть выведены безотносительно к какой-
либо конкретной координатной системе. Анализ размерностей уравнений
Максвелла приводит к основным определениям векторов Е и В, а исследование"
энергетических соотношений даёт выражения для механических сил, действуюв~
щих на элементы заряда, тока и нейтральной материи. Таким путём
устанавливается прямая связь между наблюдаемыми силами и векторами, которые-
используются для описания структуры поля.
В-III и IV главах рассматриваются стационарные поля, как частные случаи*
уравнений переменного поля. Вопрос о распространении волн впервые под*
нимается в V главе, которая посвящена однородным плоским волнам. Методам ',.
гармонического анализа уделено особое внимание и несколько более детально
рассмотрена проблема дисперсии. Главы VI и VII рассматривают распростри- ,
нение цилиндрической и. сферической волн в неограниченном пространстве.
Там -же имеется необходимое количество вспомогательного материала по
бесселевым и сферическим функциям и даны векторные решения волнового
уравнения. Соотношение между полем и его источниками, общая теория '
излучения и основные черты теории дифракции Кирхгофа-Гюйгенса рассмо-
-трены в главе VIII.
Наконед, в главе IX мы исследуем влияние плоской, цилиндрической
и сферической поверхностей на распространение электромагнитных полей*4
Фактически эта глава иллюстрирует приложение развитой ранее общей теории ?
к вопросам, имеющим практический интерес. Читатель найдёт здесь наиболее-
важные законы физической оптики, основы теории распространения волн вдоль
цилиндрических проводников, рассмотрение колебаний внутри полостей и очерк
теории распространения войн вдоль земной поверхности.
К сожалению, численные решения специальных задач не могли быть даны
чаще и более детально. Недостаток места в книге, охватывающей столь
обширную область, сделал это невыполнимым. Основная цель книги —
основательнее изложение электромагнитной теории; примеры были выбраны поэтому
лишь для иллюстрации основных теоретических положений. Мы не
пытались исчерпывающим образом рассмотреть антенные устройства, характери-'
стики передающих линий и аналогичные вопросы, важные для инженеров. Автор- -
надеется, что настоящая книга обеспечит основные знания, необходимые для <
ПРЕДИСЛОВИЕ 13,
критической оценки оригинальных статей по специальным вопросам и
удовлетворит нужды тех, кто неохотно принимает инженерные формулы без
,. Знания их происхождения и границ их применимости.
За каждой главой, за исключением двух первых, следует, некоторое
■;. количество задач. Только применение теории к конкретным примерам является
! удовлетворительным путём для её изучения. Задачи были выбраны с учётом
[ этого, обстоятельства, но вместе с тем они охватывают многие вопросы,
/которые пришлось исключить из основного текста. Это в особенности
относится к последним главам. В большинстве случаев приведены ответы или
^соответствующие ссылки.
^ , Эта книга касается исключительно макроскопических явлений. Весьма
, соблазнительно распространить рассмотрение на ту плодотворную область,
;■ которую Френкель назвал «кпазимикроскопическим состоянием», заняться мно-
Ягими прекрасными результатами классической электронной теории материи.
^■Однако в свете современного развития каждый, кто попытался бы осуще-
; ствить подобную программу, был бы вскоре остановлен сомнениями. Хотя
^многие законы классической электродинамики непосредственно приложимы
; к субмикроскопической области, но мы не имеем исходного пункта для отбора.
..Автор твёрдо убеждён в том, что переход должен осуществляться от
квантовой электродинамики к классической теории, а не в обратном направлении.
< В какой бы форме ни были окончательно приняты уравнения квантовой
I электродинамики, их статистическое усреднение по большому числу атомов
j должно приводить к уравнениям Максвелла.
* Мы пользуемся исключительно системой единиц MKS (метр-килограмм-
секунда). Среди многих физиков до сих пор ещё сохранилось убеждение,
что эта система навязывается им агрессивной группой инженеров. Возможно,
/что это так, хотя первым, кому пришла идея использовать эту систему,
. был сам Максвелл. Во всяком случае, система MKS вполне хороша, легко
..усваивается и позволяет избежать бесконечной путаницы в практических
приложениях. В настоящий момент, повидимому, нет сомнения в том, что
© ближайшем будущем она сделается общепринятой. На странице 217
предлагается помощь тем консерваторам (tones) среди нас, которые
придерживаются гауссовой системы.
»: , В противоположность позиции, занятой в отношении системы MKS,
у автора отсутствуют сколько-нибудь серьёзные доводы в пользу
рациональных единиц. Рациональные единицы применяются потому, что за исходный
пункт взяты уравнения Максвелла, а не закон Кулона, а исходный пункт нам
-кажется разумным сделать настолько простым, насколько это возможно.
/ *В результате этого выбора все уравнения, касающиеся энергии и
распространения волн, свободны от фактора 4тг. Соотношения же указанного рода прак-
, тически более важны, нежели те, которые выражают потенциалы и векторы
«Оля через их источники.
Ещё одним пунктом, вызывающим некоторые возражения, является упо-
. требление временного фактора в виде e-itot вместо е+ш. Это было сделано
/ «Отому, что временный фактор всегда исключается, а для волны, распростра-
14 ПРЕДИСЛОВИЕ
няющейся в положительном направлении, несколько удобно удерживать- ,
положительный экспонент e+ikR. Чтобы привести какую-либо формулу
к виду, принятому инженерами, достаточно всюду заменить — i на -|- *•
Для материала своей книги автор использовал'.очень много источников
и многим обязан своим коллегам как по физическому^ *гак и по
электротехническому отделению Массачузетского Технологического института. Особую
благодарность автор выражает профессору М. Ф. Гарднеру, чьи советы
в отношении практического вида теории преобразования Лапласа явились
неоценимыми, и д-ру С. Сильверу. который с большим вниманием прочёл часть
рукописи. В заключение автор пользуется "случаем выразить свою сердечную
благодарность Катрин Н. Стрэттон за неизменную поддержку во время
подготовки рукописи и неутомимую помощь при корректуре.
Джулиус Адаме Стрэттон
Кембридж, Массачузетс
Январь, 1941.
ГЛАВА 1
УРАВНЕНИЯ ПОЛЯ
Всё необъятное количество экспериментальных фактов, накопившихся
в течение прошлого века, приводит нас к твёрдой уверенности в том, чта
макроскопические электромагнитные явления описываются уравнениями
Максвелла. К серьёзным доводам в пользу этого взгляда могут быть
отнесены кулоново определение закона сил взаимодействия между зарядами,
исследования Ампера по взаимодействию элементов тока и наблюдения
Фарадея над переменными полями. Для начинающих обычно рекомендуется
N исторический подход, поскольку он является самым простым и доставляет
»; наиболее быстрое удовлетворение.' В этой книге мы предполагаем, однако,.
' что читатель уже закончил подобного рода предварительное ознакомление,
' и что он уже обладает знанием экспериментальных фактов и их
теоретической интерпретации. Согласно точке зрения, принятой в этой книге,
электромагнитная теория есть теория уравнений Максвелла. В соответствии
с этим, мы с самого начала постулируем эти уравнения и в дальнейшем
изложении выводим из них структуру и свойства поля, наряду с его связью
. с источниками. Один единичный эксперимент не доказывает теорию;
действительная проверка наших исходных предположений осуществляется в
постоянном и неизменном согласии выводов с наблюдениями.
В первой главе мы займёмся не очень увлекательным делом формулиро-
• вания основных уравнений и приготовлениями для наших исследований.
УРАВНЕНИЯ МАКСВЕЛЛА
1. 1. Векторы поля. Под электромагнитным полем мы будет понимать
совокупность четырёх векторов Е и В, D и Н. Эти векторы
предполагаются конечными во .всём поле и во всех обыкновенных точках
непрерывными функциями положения и времени, обладающими непрерывными
производными. Разрывы непрерывности векторов поля или их производных
могут встречаться на поверхностях, отмечающих резкое изменение
физических свойств среды. В соответствии с традиционной^ терминологией, Е и Н
называются напряжённостями соответственно электрическогр и магнитного
полей, D называется электрической, а В — магнитной индукцией. В
конечном счёте, векторы поля должны определяться посредством таких
экспериментов, которые позволяют их измерить. До того, как подобного рода
. эксперименты будут указаны, нет никаких оснований считать один из
векторов поля более основным, нежели другой; поэтому слово напряжённость мы
будем применять для обозначения любого из четырёх векторов поля в
какой-либо точке пространства и в какой-либо момент времени;
Источниками электромагнитного поля являются электрические заряды:
и токи. Поскольку нас интересуют только макроскопические эффекты,
постольку можно принять, что распределения токов и зарядов являются»
a 6 — : * ГЛ/ Ь УРАВНЕНИЯ ПОЛЯ
непрерывными, а не дискретными, и определяются как функции точки ,
-и времени посредством плотности заряда р и вектора плотности тока J.
Мы постулируем, что в любой обыкновенной (не особой) точке
пространства векторы поля подчинены уравнениям Максвелла:"
rotE + ^«0, A)
rotH—§ = J. B)
Под обыкновенной точкой мы будем подразумевать такую точку, в
окрестности которой физические свойства среды непрерывны. Выше было отме-'
чено, что переход векторов поля и их производных через поверхности/
ограничивающие материальные тела, может быть разрывным; такого рода
^поверхности должны быть поэтому исключены из рассмотрения до тех пор,
лока мы не будем в состоянии исследовать характер подобных разрывов.
1. 2. Заряды и токи. Хотя корпускулярная природа электричества твёрдо
установлена, размеры элементарного кванта заряда слишком малы, чтоНу
в макроскопической теории надо было учитывать эти элементарные заряды
как существующие раздельно. Граница, отделяющая область явлений боль*
шого масштаба от микроскопических, очевидно, условна. Для уверенности
в правильности макроскопического подхода рассматриваемый макроскопй**,
ческий элемент объёма должен содержать громадное число атомов; однако
само по себе это условие не является достаточным критерием, поскольку
многие кристаллы, включая металлы, часто обнаруживают микроскопически
«зернистую» или «мозаичную» структуру; подобные случаи будут
исключены из нашего рассмотрения. По всей вероятности, мы не допустим ошибки/
если предположим, что одна десятая миллиметра есть наименьший
допустимый предел для элемента длины. Однако имеется много экспериментов, — ,
как, например, рассеяние света частицами диаметром на более Ю-3 мм,— v.
которые показывают, что макроскопическая теория может быть продол*"
жена и за "указанный предел. Тем не менее, мы уже вторгаемся 8Д€Сь
* область, принадлежащую квантовой теории, которая и должна в
конечном счёте определить законность наших положений в микроскопической
области.
Предположим, что заряд, 'содержащийся в элементе объёма Дг>, есть
Ад. Плотность заряда в какой-либо точке внутри Ai> будет определяться J
* соотношением:
A<7 = pA'Z/. . C)
Таким образом, под плотностью заряда в некоторой точке мы
подразумеваем средний* заряд на единицу объёма в окрестности этой точки. В"строгом,
смысле, соотношение C) не определяет непрерывной функции положения,
поскольку Ью не может стремиться к нулю неограниченно. Тем не менее, .
мы примем, что р может быть представлено функцией координат и времени*,
которая в обыкновенных точках непрерывна и обладает непрерывными про**,
мзводными. Значение полного заряда, получаемое интегрированием этой
функции по макроскопическому объёму, в крайнем случае будет отличаться
о г ^истинной величины содержащегося в нём заряда .на микроскопическую
величину.
Всякое упорядоченное движение зарядов образует ток. Распределение
токрв характеризуется векторным полем, которое определяет в каждой
точке не только величину тока, но и его направление. Как и при изучении
движения жидкости, удобно представлять себе линии тока, т. е. линии,
проведённые через распределение тока и касательные в каждой точке к на-
УРАВНЕНИЯ МАКСВЕЛЛА [1.2] 17
^травлению тока. Рассмотрим поверхность, ортогональную к системе линий
Ттока. Плотность тока в какой-либо точке этой поверхности определится
Тогда как вектор J, направленный вдоль линии тока, прозгодящей через эту
точку, и равный по величине заряду, который проходит через единичную
площадку в окрестности этой точки за единицу времени. С другой стороны,
ток / сквозь любую поверхность 5 равен заряду, проходящему через эту
поверхность в единицу времени. Если п единичный вектор нормали
^4£ элементу Ал поверхности 5, то мы имеем:
р::. * A/ = JnAa. D)
Поскольку Да — макроскопический элемент площади, то уравнение D) не
определяет плотность тока как непрерывную функцию положения
математически строго; но опять-таки мы можем представить распределение тока
подобной функцией без допущения заметной ошибки. Полный ток через
поверхность 6" будет тогда:
/ = j Jn da. /c\
s -
Так как электрический заряд может быть как положительным, так
а отрицательным, то необходимо условиться, какой ток считать
положительным. Если поток через элемент площади состоит из положительных
зарядов, вектор скорости которых образует с положительным
направлением нормали п угол, меньший 90°, то говорят, что ток положителен. Если
угол больше 90°, то ток отрицателен. Аналогично, если угол меньше 90°,
/ но заряды отрицательны, то ток через элемент отрицателен. В случае
металлических проводников носителями электрического заряда являются
отрицательные электроны, и поэтому направление вектора плотности тока
противоположно направлению движения электронов.
Предположим теперь, что поверхность 5 в уравнении E) замкнутая.
В дальнейшем мы будем считать, как это обычно принято, что
положительная нормаль к замкнутой поверхности направлена наружу. Из
определения тока, как потока заряда через поверхность, следует, что
поверхностный интеграл нормальной компоненты J по поверхности 5 должен быть
мерой убыли заряда из области, расположенной внутри поверхности S.
У-нас нет экспериментальных фактов, указывающих на возможность
возникновения или исчезновения зарядов в макроскопических количествах при
обычных условиях. Мы можем поэтому написать:
&Jnda =—'-^Jpdv ' F)
s v
(где V—объём, охватываемый поверхностью 6), в качестве уравнения,
выражающего закон сохранения заряда. Поток зарядов через какую-либо
поверхность может возникнуть двумя путями. Либо поверхность 6" может быть
фиксирована в пространстве, а плотность р может быть некоторой
функцией времени, равно как и координат, либо же плотность заряда
постоянна во времени, тогда как поверхность 5 движется каким-либо
определённым образом. В последнем случае правый интеграл в уравнении
F) является функцией времени благодаря тому, что меняются со временем
пределы интегрирования. Если, однако, поверхность фиксирована и интеграл
d
сходится, то мы можем ввести -з- как частную производную под знак
интеграла:
Jn da — — f ^ dv. G)
v
§
Теория эпектфомагыешзма.
18 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Нам представится много случаев для применения теоремы векторного
анализа о дивергенции 1). Пусть А (х> у, z\ будет какая-либо векторная'
функция точки, непрерывная вместе со своими первыми производными во
всём объёме V и на граничной поверхности S. Поверхность 5 регулярна,
а в остальном произвольна2). Тогда можно показать, что
ф An da = J div A d%). (8)
/
Существенно то, что это соотношение может быть с удобством
использовано как определение дивергенции. Для того чтобы получить значение
div А в точке Р внутри объёма V, мы допустим, что поверхность 5
сжимается около точки Р."Когда объём V станет достаточно малым, интеграл
в правой части может быть заменён на VdivA, и мы получим:
div А = lim т. <Ь An da. (од
s-*> v $ КЩ
Таким образом дивергенция вектора в какой-либо точке интерпретируется
как интеграл его нормальной компоненты по бесконечно-малой поверхности,
охватывающей эту точку, делённый на ограниченный этой поверхностью
объём. Поток вектора через замкнутую поверхность является мерой силы
источников, находящихся внутри этой поверхности; следовательно,
дивергенция определяет силу источников в данной точке. Поскольку
поверхность 5 сжимается около точки Р, значение А в любой 'точке поверхности
5 может быть выражено аналитически через значения А и его производных
в Р, что делает возможным вычисление интеграла в уравнении (9). В
случае прямоугольных координат это вычисление приводит к следующему
выражению:
divA = ^E + ^-r-^. A0)
дх ' ду ' dz • х /
. Применяя эту теорему к уравнению G), преобразуем поверхностный
лнТеграл в объёмный:
/(div J +1)* = 0. A1)
У
Подинтегральное выражение в A1) является непрерывной функцией
координат и, следовательно, должна существовать достаточно м,алая область,
в пределах которой оно не меняет знака. Так как интеграл A1) исчезает
для произвольного объёма V, то подинтегральное выражение должно
обращаться в нуль тождественно. Дифференциальное уравнение
.. ' divj + | = 0 A2)
1) Теорем'а Гаусса. Прим. ред.
2) Регулярный элемент дуги представляется в параметрической форме
уравнениями х = х(/), y=y(t), z = z(t), причем в интервале а<£<6 х, у, z есть
непрерывные однозначные функции t с непрерывными производными всех порядков,
если только не установлены иные ограничения. Регулярная кривая составляется
из конечного числа подобных дуг, соединённых конец к концу, но так, что кривая
сама себя ц| пересекает. Таким образом регулярная кривая не имеет двойных точек
и является кусочно дифференцируемой. Элемент регулярной поверхности есть
участок поверхности, проекция которого на выбранную соответствующим образом
плоскость является внутренней областью замкнутой регулярной кривой. Отсюда
следует, что он сам себя не пересекает. См. Kellogg, Foundations of Potential
Theory, стр. 97, Springer, 1929.
УРАВНЕНИЯ МАКСВЕЛЛА [1-3] Г*>
т
ь% выражает закон сохранения заряда в окрестности какой-либо точки. По-
•: аналогии с подобным соотношением в гидродинамике, уравнение A2) часто-
щ называют уравнением непрерывности.
'{& Если .в каждой точке определённого объёма плотность заряда посто-
^/янна во времени, то ток, входящий в объём через ограничивающую его
1.4 поверхность, должен быть всё время равен току, выходящему наружу. Для.
i. ограничивающей объём поверхности мы имеем тогда:
§
а для любой точки внутри:
Jn da = 0, A3)
divj = 0. A4>
; Движение, характеризуемое векторными или скалярными величинами, не зави-
(; сйщими от времени, называется постоянным или стационарным. Таким обра-
^; зом, стационарное течение электричества определяется вектором J, который
* в каждой точке области постоянен по величине и направлению. Из того,
г. что дивергенция такого распределения тока всюду равна нулю, следует, что
\ в стационарном состоянии все линии или нити тока замкнуты сами на себя.
I, Поле вектора J является соленоидальным.
1.3. Дивергенция векторов поля. Два дальнейших условия, которым
р удовлетворяют векторы В и D, можно вывести непосредственно из уравнений
^Максвелла, заметив, что дивергенция ротора любого вектора тождественна
., равна нулю. Взяв дивергенцию уравнения A), мы получаем:
? „ div^ = ~divB*=0. * A5)
Перестановка операторов div и -, • допустима потому, что, по
предположению» в обыкновенной точке поля вектор В непрерывен со всеми своими
производными. Из A5) следует, что в любой точке поля дивергенция
В постоянна. Если поле когда-либо в прошлом отсутствовало, то эта по-
; стоянная должна быть равна нулю, и так как разумно предположить, что
.первоначальное возникновение поля произошло не бесконечно давно, то мк
j заключаем, что
div В = О, A6>
откуда следует, что поле вектора В соленойдальне
Подобным же образом дивергенция уравнения B) приводит к уравнению^
divJ-f-^divD = 0, A7)
или, в силу A2),
JL(divD—р) = 0. A8)
. Опять-таки, если мы допустим, что в какой-либо период времени в прошлом,
-или в будущем поле может исчезать, то необходимо
divD = p. A9}
> Следовательно, заряды, распределённые с плотностью р, являются
источниками вектора D.
|/ Уравнения с дивергенциями A6) и A9) часто включаются в систему
^уравнений Максвелла. Необходимо отметить, однако, что если принять зако»
^охранения заряда, то эти соотношения не являются независимыми.
№•*
2*
20 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
1.4. Интегральная форма уравнений поля. Свойства
электромагнитного поля, которые были охарактеризованы дифференциальными уравнениями
A), B), A6) и A9), могут быть также выражены эквивалентной системой
интегральных соотношений. Для получения этой эквивалентной системы мы
применим вторую основную теорему векторного анализа.
Согласно теореме Стокса, циркуляция вектора, взятая по любому
замкнутому контуру, может быть преобразована в интеграл по поверхности,
опирающейся на этот контур. Контур С должен быть либо регулярным,
либо разложимым на конечное число регулярных дуг; с другой стороны,
предполагается, что произвольная поверхность S, опирающаяся на контур С,
является двусторонней и может быть разбита на конечное число регулярных
элементов. Положительная сторона поверхности 5 сопоставлена с
положительным направлением обхода по контуру С путём обычного условия: для
наблюдателя, движущегося по контуру С в положительном направлении,
положительная сторона поверхности 5 должна находиться с левой стороны.
Тогда, если А (а:, у, z) — векторная функция точки, непрерывная вместе
со своими производными во всех точках 5 и С, то можно показать, что
f
A ds = J* rotA n da, B0)
# s
где ds — элемент длины вдоль С, а п — единичный вектор нормали к
положительной стороне элемента площади da. Это преобразование можно
рассматривать так же, как уравнение, определяющее ротйр. Для определения
значения rotA в точке Р на поверхности 5 мы предположим, что контур С
стягивается около точки Р, пока опирающаяся на него поверхность 5 не
сведётся к бесконечно малому элементу плоскости, нормаль к которой
определяется направлением п. Интеграл с правой стороны равен rotAnS
плюс бесконечно малые более высокого порядка; следовательно, проекция
вектора rot А на направление нормали будет
rotAn= lim ±r&Ads. B1)
Ротор ■ вектора в какой-либо точке интерпретируется, таким образом, как
циркуляция вектора по охватывающему эту точку бесконечно малому
контуру на "поверхности, отнесённая к единице выделяемой контуром площади.
Так как вектор А, по предположению, является аналитическим в окрестности
точки Р; то его значение в любой точке на С может быть выражено через
значения А и его производных в точке Р, так что вычисление интеграла
в B1) по бесконечно малому контуру может быть действительно проведено.
В частности, если элемент 5 ориентирован параллельно координатной
плоскости y,z, то для А:-компоненты ротора получается
дА~ • dAv , п.
(«rtAX. gi gi. B2)
Поступая подобным же образом с у и z компонентами, мы получаем:
/ЪАВ дАу\ /дАх дАг\ / дАу дАх\
i J k
JL A JL
дх ду dz
Ac Ay Az
B3)
УРАВНЕНИЯ МАКСВЕЛЛА [1.4]
21
ли
Проинтегрируем теперь нормальную компоненту вектора -п по произвольной
регулярной поверхности $, опирающейся на контур С. Из A) и B0)
следует, что
& Е ds -f J -^j n da = 0. B4)
О 8
Если контур С фиксирован, то оператор ^- можно вынести из-под знака
интеграла:
B5)
ф Е ds = — jr Г Bn da.
с s
По определению, величина
Ф = f Bn da
s
B6>
является магнитным потоком, или, точнее, потоком вектора В через
поверхность 5. Согласно уравнению B5), циркуляция вектора Е по любой замкну-
, той регулярной кривой равна скорости уменьшения во времени магнитного
потока через любую поверхность, опирающуюся на эту кривую. Соотно-
• шение между направлением обхода контура и положительной нормалью
к поверхности, опирающейся на этот контур, иллюстрирует рис. 1.
Положительное направление обхода контура С выбирается
. произвольно, и поток Ф получается тогда
положительным или отрицательным, в зависимости от
направления линий вектора В по отношению
к нормали. Скорость изменения Ф в свою
очередь положительна или отрицательна, в
зависимости от того, уменьшается или увеличивается
п
/
Рис. 1. Связь между
положительным направлением
нормали п к площадке и
направлением обхода
контура С, ограничивающего
эту площадку.
положительный поток.
Напомним, что применение теоремы Стокса
к уравнению A) 3akqHHO только в том случае,
если вектор Е и его производные непрерывны во
всех точках поверхности 5 и контура С.
Поскольку разрывы непрерывности обоих векторов
Е и В встречаются при переходе через
поверхности, отмечающие резкие изменения физических свойств среды, то может
возникнуть вопрос о том, в какой к.ере уравнение B5) выражает общий закон
электромагнитного поля. Предположим, например, что контур охватывает замкнутый
сердечник трансформатора, или проходит через него. Для того чтобы обойти
эту трудность, можно представить себе, что на поверхности любого
помещённого в поле материального тела физические свойства меняются хотя
и очень быстро, но непрерывно, в тонком поверхностном слое, от значений
с г.нутренней стороны граничной поверхности, до значений с внешней её
стороны. Таким путём мы исключаем из поля все разрывы непрерывности,
' и уравнение B5) может б^ть применено к любому замкнутому контуру.
Опыты Фарадея показали, что соотношение B5) выполняется независимо
/от причины изменения потока. Частная производная предполагает переменную
, плотность потока, пронизывающего фиксированный контур. Однако полный
> поток мо&£т меняться также благодаря деформации контура. Для того чтобы
, это учесть, закон Фарадея обычно пишут в форме:
г F Е ds = — ■—• j Bn da. B7)
с s
22 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Можно показать, что уравнение B7) действительно является следствием
дифференциальных уравнений поля, однако доказательство должно быть
основано на электродинамике движущихся тел, которой мы коснёмся в
разделе 1.22. ■ ' ^
Таким же точно путём уравнение B) может быть заменено интегральным
соотношением:
& Hds = /+-~ jDnrffl, ' B8)
V • 8
где /—полный ток, охватываемый контуром, как определено уравнением E).
В стационарном состоянии интеграл справа равен нулю, и ток проводимости /
через любую регулярную поверхность равен циркуляции вектора Н по
контуру, на который она опирается. Если, однако, поле переменно, то с
вектором -Г7- связано точно такое же поле Н, какое было бы вызвано токами,
распределёнными с плотностью
"Этой величине Максвелл дал название «тока смещения»—термин,-которым
мы будем пользоваться от случая к случаю; пока мы не возьмём на себя
ответственности за какую-либо конкретную интерпретацию вектора D.
Два оставшихся уравнения поля A6) и A9) могут быть выражены
в эквивалентной интегральной форме с помощью теоремы о дивергенции.
Мы получаем соотношение -ф,
Bn da = 0, C0)
§
означающее, что полный поток вектора В через любую замкнутую
регулярную поверхность равен нулю, и соотношение
Dn da
fpdv = q, C1)
что означает то, что поток вектора D через замкнутую поверхность равен
полному заряду q, содержащемуся внутри неё. Кружок на знаке интеграла
испол.ьзуется для того, чтобы подчеркнуть, что контур или поверхность
замкнуты.
МАКРОСКОПИЧЕСКИЕ СВОЙСТВА МАТЕРИИ
1.5. "Абсолютные проницаемости е и.{а. Единственное предположение,
которое было до сих пор сделано, состоит в том, что электромагнитное
поле может быть охарактеризовано четырьмя векторами Е, В, D и Н,
которые в обыкновенных точках удовлетворяют уравнениям Максвелла, и что
распределение токов, порождающее это поле, обеспечивает сохранение заряда.
Ме^^ду пятью векторами Е, В, D, Н и J имеются только два независимых
соотношения (уравнения A) и B) предыдущего раздела) и поэтому мы
должны наложить дальнейший условия, если хотим сделать систему
полной.
Начнём с предположения, что в любой данной точке поля, как в
свободном пространстве, так и внутри материи, вектор D может быть
представлен как функция Е, а вектор Н как функция В:
D = D(E), H = H(B). A)
МАКРОСКОПИЧЕСКИЕ СВОЙСТВА МАТЕРИИ [1.Ц . 23
Характер этих функциональных соотношений должен определяться
исключительно физическими свойствами среды в непосредственной окрестности
рассматриваемой точки. Наиболее часты следующие простые случаи. v
1. В свободном пространстве D отличается от Е только постоянным
множителем, как и Н от В. Следуя традиции, мы будем писать:
D = s0E, Н = —В. B)
Числовые значения и размерности констант s0 и <j.0 будут зависеть от
принятой системы единиц. Лишь в одной из многих, совершенно произвольных
систем, D в свободном пространстве сводится к Е, а Н к В.
2. Если физические свойства тела в окрестности любой внутренней
точки одинаковы по всем направлениям, то говорят, что тело изотропно.
В каждой точке изотропной среды D параллельно Е, а Н параллельно В.
Более того, почти во всех разрешимых задачах электромагнитной теории
соотношения между векторами являются линейными. Для случая изотропной
среды, принимая линейные зависимости, мы положим поэтому
D = eE, Н = -В. C>
Множители е и {а называются абсолютными диэлектрической и магнитной
проницаемостями среды. Безразмерные отношения
. *»=~ D)
Е
не зависят от выбора единиц и их мы будем называть относительными
диэлектрической и магнитной проницаемостями *). Свойства однородной среды
постоянны от точкц к точке, и в этом случае принято называть v.e
диэлектрической постоянной, а у.т проницаемостью. Однако в общем случае,
диэлектрическую и магнитную проницаемости надо рассматривать как
скалярные функции точки, которые и характеризуют электромагнитные свойства
материи.
3. Свойства анизотропной среды различны по разным направлениям
в дгнной точке. В этом случае векторы D и Е, Н и В параллельны только
вдоль определённых выделенных осей. Если можно предполагать, что
соотношения всё ещё линейны, как это бывает в большинстве случаев, то мы
можем выразить каждую прямоугольную компоненту D в виде линейной
.функции трёх компонент Е:
D<c = hl^x ~Г S12E«/ ~Г е13Ег>
Vy = е21Егс ~Г е22Ег/ ~Т~ е23Ег»
D2 = е31Еж ~Ь е32Е# + еЗЗЕг;] ^
E)
коэффициенты eik этого линейного преобразования являются компонентами
симметричного тензора. Аналогичное соотношение может быть установлено
и между векторами Н и В, но случаи подобной линейной анизотропии редки
в задачах, которые могут быть названы макроскопическими по существу.
1) Автор пользуется терминами inductive capacities для е и {л. и specific inductive
•capacities для %е и %от. Первые названы при переводе абсолютными
проницаемостями, а вторые — относительными. Отклонение от обычной терминологии допущено
только в отношении %е, котору ю у нас принято называть диэлектрической постоян-
«ой яаже при наличии зависимости от координат. Прим. ред.
24
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Нигде различие между микроскопической и макроскопической точками
зрения не проявляется острее, чем в интерпретации параметров s и ja или
их тензорных эквивалентов. Микроскопическая теория должна вывести
физические свойства материи из её атомной структуры. Она должна давать
возможность вычислять, не только среднее поле, превалирующее внутри тела,
но также и его локальные значения в окрестности отдельных атомов. Она
должна сказать нам, как будет деформироваться атом под влиянием этого
местного поля, и как совокупный эффект этих атомных деформаций может
быть в целом представлен с помощью таклх параметров, как е и \i.
С этой точки зрения мы занимаемся только ойисанием. Наше знание
материи является, если воспользоваться громким словом, чисто
феноменологическим. Каждое вещество характеризуется в отношении
электромагнитных свойств с помощью минимального числа параметров. Зависимость
параметров е и [а от таких физических переменных, как плотность, температура
и частота, устанавливается экспериментально. Данные, получаемые из
подобных измерений, проливают свет на характер внутренней структуры материи,,
но эта внутренняя структура нас здесь не интересует.
1.6. Электрическая и магнитная поляризации. Для описания
электромагнитного состояния элемента материи оказывается удобным ввести два
дополнительных вектора. Мы определим векторы «электрической и магнитной
поляризации посредством уравнений:
P = D —s0E, M--1-B — Н. . F)
Таким образом, векторы поляризации связаны только с материей и исчезают
в случае пустого пространства. С помощью #1их соотношений мы теперь
исключим векторы Dh Низ уравнений поля. В результате получаем систему:
дВ
dt
дЕ (, ,' дР
rotE+^-0, 1
rotB-soFo-^. = ^0(j + ^ + rotM), \ G>
div В = 0; -div Е = X (р — div P), I
которую мы можем интерпретировать следующим образом: присутствие
е электромагнитном' поле твёрдых материальных тел может быть
полностью учтено с помощью эквивалентного распределения зарядов с
плотностью— div.P и эквивалентного распределения токов с плотностью
— _L-rotM
*dt l roim*
В изотропной среде векторы поляризации параллельны соответствующим
векторам поля и, за исключением ферромагнитных тел, пропорциональны им.
Электрическая и, магнитная восприимчивости уе и ут определяются
соотношениями:
, Р = Хее0Е; М = ХтоН. . (8)
Рассуждая логически, магнитную поляризацию М следовало бы положить
пропорциональной В. Однако традиция связывает М с Н и, чтобы избежать
путаницы в вопросе, не имеющем большого значения, мы присоединяемся
к этой условности. Восприимчивости уе и ущ, определенные соотношениями
(8), представляют собой безразмерные отношения, числовые значения
которых не зависят от употребляемой системы единиц. В своё время будет
показано, что Е и В являются силовыми векторами, и в этом смысле основными^
Щг, МАКРОСКОПИЧЕСКИЕ СВОЙСТВА МАТЕРИИ "[1.6] 25-
; >D и Н — производные векторы, связанные с состоянием материи. Вектор
^поляризации Р имеет размерность D, но не Е, в то время как Ми Н имеют
одну и ту же размерность. Из C), F) и (8) непосредственно слецует, чта
восприимчивости связаны с диэлектрической и магнитной проницаемостями
, следующими уравнениями:
У.е==1*е 1» К.т== xw * • ("/'
В анизотропной среде восприимчивости выражаются компонентами тензора.
Частью нашей задачи в последующих главах будет установление
экспериментов, с помощью которых можно точно измерить восприимчивость
'- среды. Подобные измерения показывают, что электрическая восприимчивость
всегда положительна. В газах она порядка 0,0006 (воздух), но в жидкостях
" может достигать значений порядка 80 (вода). На внутреннее различие в
природе векторов Р и М указывает тот факт, что магнитная восприимчивость %т
J' может быть как положительна, так и отрицательна. Вещества,
характеризующиеся положительною восприимчивостью, называются парамагнитными,
I в то время как вещества, магнитная восприимчивость которых отрицательна* •
называются диамагнитными. Металлы ферромагнитной группы, включая
железо, кобальт, никель и их сплавы, составляют особый класс веществ
1 с очень большой положительной восприимчивостью, численное значение
которой может быть порядка многих тысяч. Ввиду нелинейности
соотношения между М и Н, свойственной этим материалам, восприимчивость ут
должна быть теперь интерпретирована как тангенс угла наклона касатель-
■t ной к кривой М — Н в точке, соответствующей данному значению Н. Чтобы
включить и такие случаи, определение восприимчивости обобщается
следующим образом: '
дМ nm
Восприимчивости всех неферромагнитных материалов, как парамагнитных,
так и диамагнитных, настолько малы, что ими можно пренебрегать в
большинстве практических случаев. *
Поскольку до сих пор предполагалось, что существует функциональная
связь между векторами Р или М и приложенным полем, постольку их сле-
, довало бы называть индуцированными поляризациями. Однако при
определённых условиях с ферромагнитным| телом может быть связано поле и
в отсутствие какого-либо внешнего возбуждения. В этих случаях говорят,
что тело находится в состоянии постоянного намагничения. Мы будем при-
. держиваться нашего первоначального предположения, что поле как внутри,
так и вне магнита полностью определяется векторами В и Н. Но теперь
во внутренних точках эти векторы разнятся на заданный вектор М0,
который может быть назван плотностью намагничения,, и который не связан
никакой функциональной зависимостью с Н. Наоборот, намагничение М0,
должно быть интерпретировано как источник поля. Если внешнее поле
накладывается на поле постоянного магнита, интенсивность намагничения
должна будет увеличиться благодаря индуцированной поляризации М. В
любой внутренней точке мы будем иметь, следовательно:
B = ft)<H + M + M0). (П)
Об индуцированной поляризации мы можем пока сказать лишь то, что она
является функцией результирующего поля Н в той же точке. Соотношение
между результирующим полем внутри тела и интенсивностью приложенного
поля, возбуждаемого внешними источниками, зависит не только от
намагничения Щ, но также и от формы тела. Нам представится случай для более
тщательного изучения этого вопроса в главе IV.
26 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
1.7. Проводящая среда. Теперь необходимо добавить к уравнениям
Максвелла третье и последнее эмпирическое соотношение — соотношение
между плотностью тока и полем. Мы предположим, что в любой точке
жидкости или твёрдого тела плотность тока является функцией поля Е:
J = J(E). ^ A2)
Распределение токов в ионизированной газообразной среде может зависеть
и от интенсивности магнитного поля. Но так как электромагнитные явления
в газовом разряде определяются множеством других факторов, не учтённых
в настоящей теории, то подобные случаи мы исключим из дальнейшего
рассмотрения *).
В высшей степени широком диапазоне условий как в случае твёрдых
тел, так и в случае слабо ионизированных растворов, соотношение A2)
оказывается линейным:
J = aE. A3)
Множитель а называется проводимостью среды. Разграничение между
хорошими и плохими проводниками — или изоляторами — относительно и
произвольно. Все вещества в некоторой степени обладают проводимостью, но
область наблюдаемых значений а необычайно велика. Проводимость меди,
например, в Ю1 раз больше, чем проводимость такого «хорошего»
проводника, как морская вода, и в 1019 раз больше, чем обыкновенного стекла.
В приложении III можно найти таблицу проводимостей наиболее .типичных
материалов.
Уравнение A3) является просто законом^ма. Представим себе,
например, стационарное распределение тока во всём объёме, какой-либо
проводящей среды. В силу соленоидального характера потока, это распределение
может быть представлено замкнутыми линиями тока. Если анЬ—две точки
на какой-либо определённой линии тока и ds— элемент её длины, то мы
.имеем:
ь ^ л
J Eds = j* "J #s. A4)
a a
Пучок смежных линий тока, проходящих через замкнутую кривую,
составляет нить, или трубку тока. Так как поток соленоидален, то сила тока /
чере.з любое поперечное сечение нити тока одна и та же. Пусть 5 будет
площадь поперечного сечения нити тока, проведённого нормально к
направлению лотока. Площадь 5 не должна быть обязательно бесконечно малой,
но предполагается, что она настолько мала, что плотность тока всюду на
ней постоянна. Тогда 'SJds = Ids и
ъ ь
f E ds = у Г -L ds. A5)
а а
Множитель
R-j-^ds A6)
а
равен сопротивлению нити между точками а и Ь. Сопротивление вытянутого
однородного проводника постоянного поперечного сечения 5 и длины /
х) Хотя и справедливо, что распределение токов в жиакости или твёрдом
теле может быть изменено наложением магнитного поля, но величина этого эффекта,
так называемого эффекта Холла, настолько мала, что им можно пренебречь без
„допущения заметной ошибки.
m
сбудет:
МАКРОСКОПИЧЕСКИЕ СВОЙСТВА МАТЕРИИ [1.7] 27
«=Н- <17>
«формула, которая строго справедлива только в случае стационарных
токов.
В области с проводимостью, не равной нулю, не может быть постоян-
■■ «ого распределения свободных зарядов. Эта чрезвычайно важная теорема
легко может быть доказана, если среда однородна и такова, что
соотношения между D и Е и J и Е линейны. По уравнению непрерывности:
divJ + ^ = divcE-f-|==0. A8)
О другой стороны, в однородной среде
1
\
divE = -^p, A9)
Е
что, совместно с A8), даёт
-| + 4р = °- ' B0)
Е
Юткуда, плотность заряда в момент времени t будет:
i .. р=р0е е . Bi)
тде константа интеграции р0 равна плотности заряда в момент t = 0. Заряд,
^распределённый первоначально по всему проводнику, в каждой точке
убывает со временем экспоненциально, причём по закону, совершенно не
зависящему от приложенного поля. Если первоначально плотность зарядов была
.равна нулю, то она будет оставаться равной нулю и в будущем.
Промежуток времени
*=~, B2)
необходимый для того, чтобы заряд в какой-либо точке уменьшился до \\е
от" своей первоначальной величины, называется временем релаксации. Во всех,
даже плохих, проводниках т необычайно мало. Так, в морской воде время
релаксации порядка 2 . 10~10 сек.; даже в таком плохом проводнике, как
- дестиллированная вода, оно не более чем 10-6 сек. В лучших изоляторах,
, как, например, плавленный кварц, оно может, тем не менее, принимать
значения, превосходящие 106 сек. — иллюстрация необычайно широкого
диапазона возможных значений параметра о.
Предположим, что в момент t = 0 заряд сконцентрирован внутри не-
«больйюй сферической области, находящейся где-либо внутри проводящего
тела. Во всякой другой точке проводника плотность заряда равна нулю.
Заряд внутри сферы начинает теперь экспоненциально исчезать, но, согласно
<21), нигде внутри проводника заряд появиться вновь не может. Куда же он
' девается? Поскольку заряд сохраняется, уменьшение заряда внутри
сферической поверхности должно сопровождаться потоком электричества наружу,
или током. Заряд не может накапливаться ни в одной внутренней точке;
[ следовательно, поток должен быть соленоидальным. Заряд будет задержи-
? ваться, однако, на наружной поверхности проводника и здесь-то мы и най-
i „дбм тот заряд, который исчез из центральной сферы. Этот поверхностный
|%аряд появляется в точности в тот момент, когда внутренний заряд начинает
|;;.«(счезать, поскольку полный заряд является постоянным.
»//
28
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
ЕДИНИЦЫ И РАЗМЕРНОСТИ
1.8. MKS-система или система Джорджи. До сих пор
электромагнитное поле являлось у нас всего лишь совокупностью векторов,
подчиняющихся постулированной системе дифференциальных уравнений. Для тога
чтобы следовать дальше, мы должны установить физические размерности
этих векторов и условиться относительно единиц, которыми они измеряются.
В обычном смысле «абсолютная» система единиц есть такая система,
в которой любая величина может быть измерена или выражена через три
основные величины — массу, длину и время. Но в электромагнитной теории
имеется существенный произвол в отношении размерностей, который вносят
множители 30 и ja0, связывающие соответственно D с Ей Н сВ в пустом
пространстве. Пока ещё не придумано опыта, с помощью которого можно
было бы присвоить размерность либо е0, либо [а0, как неким независимым
физическим сущностям. С другой стороны, из уравнений поля непосред-^
ственно следует, чго величина
должна иметь размерность скорости и любой вйгоор s0 и $0 должен-
подчиняться' этому ограничению. Величина этой скорости не может быть
подсчитана a priori, но может быть определена с помощью подходящего опыта.
Значение, полученное по методу Роза и Дорсей в Бюро стандартов и
исправленное Кэртисом *) в 929 г., составляет:
с = —*_ = 2,99790 -10» м\сек B>
Ve0t*0
или, для всех практических целей:
с = 3- 108 м!сек. C)
В течение всей ранней истории электромагнитной теории во всех
научных исследованиях пользовались абсолютной электромагнитной системой
единиц. В этой системе сантиметр принимался за единицу длины, грамм
за "единицу массы, секунда за единицу времени, а в качестве четвёртой
единицы избирался множитель \iQ, произвольно принимавшийся равным
единица и считавшийся безразмерным. Размерность s0 ^однозначно определяется
тогда из соотношения A) и можно показать, что единицы и размерности
всякой другой величины, вводимой в теорию, могут быть выражены через
сантиметры, граммы, секунды и [ад. К несчастью, эта абсолютная система
оказалась не в состоянии удовлетворить нуждам практики. Единицы
сопротивления и электродвижущей силы были, например, слишком малы. Для»
устранения этого дефекта была принята практическая система единиц.
Каждая единица практической системы имеет размерность соответствующей
электромагнитной единицы и отличается от неё по величине на степень
десяти, которая, по крайней мере в случае напряжения и сопротивления,
совершенно произвольна. Практические единицы имеют большое
преимущество благодаря их удобной величине и поэтому они теперь повсеместно
используются для технических измерений и вычислений. Поскольку они
определены как произвольные кратные абсолютных единиц, они не
составляют абсолютной Системы. В настоящее время величины массы, длины и
l) Rosa and Dorsey, A New Determination of the Ratio of the Electrostatic Unit of
Electricity, Bur. Standarts, Bull. 3, 433 A907). Curtis, Bur. Standarts. J. Research. 3,.
€3 A929).
ЕДИНИЦЫ И РАЗМЕРНОСТИ [1-8] 29
|-иремени являются фундаментальными исключительно потому, что физически
& >нашли удобным возвести их в этот ранг. То обстоятельство, что должны
;5 существовать и другие фундаментальные величины, очевидно из того факта,
'что все электромагнитные единицы не могут быть выражены только через
;'■ эти три. Ограничение применения термина «абсолютная» только к системам,
основанным на массе, длине и времени, является поэтому совершенно
необоснованным; от подобной системы можно требовать только того, чтобы
- она была внутренне последовательна, и чтобы любая величина определялась
; через минимальное количество основных независимых единиц. Антипатия
физиков прошлого к практической системе электрических единиц
основывалась не на какой-нибудь твёрдой уверенности в святости массы, длины и
времени, а скорее на отсутствии внутренней последовательности в этой
системе.
К счастью, было найдено наиболее удовлетворительное решение этой
, трудности. В 1901 г. Джорджи *), разрабатывая идею, первоначально
высказанную ещё Максвеллом, обратил внимание на тот факт, что практическая
система может быть превращена в абсолютную путём соответствующего
выбора основных единиц. Действительно, необходимо только выбрать за
единицу длины интернациональный метр, за единицу массы килограмм, за
единицу времени секунду, а за четвёртую единицу — любую электрическую
величину, принадлежащую к практической системе, как, например, кулон,
ампер или ом. Тогда из уравнений поля можно вывести единицу и
размерность любой электромагнитной величины, выраженную через эти четыре
основные единицы. Более того, производные величины будут относиться
друг к другу точно так же, как и в практической системе, и могут быть
поэтому выражены через практические единицы. В частности, было найдено,
что параметр [а0 должен иметь значение 4тг • 10~7, а значение е0 может, быть
подсчитано тогда из уравнения A). Наоборот, с таким же успехом можно
принять это значение ja0 за четвёртую основную единицу, и затем вывести
весь ряд практических единиц из уравнений поля.
На пленарной сессии Международной электротехнической комиссии
{М. Э. К.) в июне 1935 г. единогласно была принята система MKS,
предложенная Джорджи. Один вопрос необходимо, однако, ещё разрешить.
По поводу четвёртой основной единицы никакого официального соглашения
пока^не достигнуто. Сам Джорджи рекомендовал ввести в качестве основной
величины ом, стандарт которого установлен как сопротивление
определённого столба ртути при определённых условиях давления и
температуры. Если ja0 = 4tt. Ю-7 выбрано в качестве четвёртой единицы и
принято безразмерным, то все производные величины могут быть выражены
только через массу, длину и время, причём размерность каждой из них будет
тождественна с размерностью соответствующей величины в абсолютной
электромагнитной системе и системы будут различаться только численными
значениями единиц. Это предположение приводит, однако, к дробным показателям
в выражениях размерности многих величин, в прямом соответствии с нашим
произволом в выборе массы, длины и времени в качестве единственных
основных единиц. В абсолютной электромагнитной системе размерность
заряда, например, есть грамм1/а • сантиметре, — иррациональность, которая
едва ли может иметь физический смысл. Эти дробные показатели совер-
!) Gio-rgi, Unita Razionali Ш Elettromagnetismo, Atti delV A. E. I. A901).
Исторический обзор развития практической системы, включающий отчёт о мероприятиях,
предпринятых в 1935 г. на совещании Международной электротехнической
комиссии и обширную библиографию, дан Кеннелли, J. Inst. Elec. Engrs. 78.
235—245 A936). См. также Glazebrook, The MKS System of Electrical Units.
J. Inst. Elec. Engrs. 78, 245—247.
30 ' ГЛ. I. УРАВНЕНИЯ ПОЛЯ
шенно исключаются, если мы выберем в качестве четвёртой единицы кулон;
по этой причине, в разное время заряд выдвигался в качестве основной
величины, совершенно независимо от вопроса о численном значении этой
величины *). В этой книге мы. будем придерживаться исключительно системы
метр — килограмм — секунда — кулон. Если в будущем М. Э. К. изберёт в
качестве основной другую электрическую величину, то это никак не повлияет
на величину наших единиц или на форму уравнений 2).
'Чтобы показать, что предложенные единицы образуют внутренне
последовательную систему, рассмотрим нижеследующие ,примеры. Единица тока
в системе MKS — абсолютный ампер, а единица сопротивления — абсолютный
ом. Эти величины таковы, что работа, расходуемая каждую секунду током
силою в 1 ампер, проходящим по сопротивлению в 1 ом, будет 1 джоуль
(абсолютный). Если R — сопротивление участка проводника, по которому
проходит постоянный ток силою в / ампер, то работа, рассеиваемая в виде
тепла, в t секунд будет:
W==PRt джоулей. , D>i
Возникающее тепло может быть измерено с помощью калориметра, и таким*,
образом можно определить^ количество элект{2Цческой энергии,
приходящееся на-единицу количества тепла. Желательно, чтобы джоуль, определённый
уравнением D), был идентичен с джоулем, определённым как единица
механической работы, т. е. чтобы и в электрическом, и в механическом
случае имело место соотношение:
1 джоуль = 0,2389 грамм-калорий (средних). E)
Теперь, на основании уравнения непрерывности F) (стр. 18) мы определим-
ампер как силу тока, который переносит через какую-либо поверхность
1 кулон в 1 секунду. Тогда ом будет производной единицей, величина и
размерность которой определяются уравнением D):
, , ватт , . килограмм метр2 ,лЛ
1 ом == 1 s- = 1 V— ^— , F>
ампер2 кулон2 секунда v
так как 1 ватт равен 1 джоуль/сек. Удельное ■ сопротивление среды
определяется как сопротивление, измеренное между параллельными гранями
единичного куба. Обратная величина ,есть прговодимость. Размерность с следует
из уравнения A7), стр. 27:.
*ч , 1 г кулон2 секунда /vV
1 единица проводимости = = 1 — г. G>
к ом метр килограмм метр3 ч '
В Соединённых Штатах обратный ом. обычно называется «мо», но название,
официально принятое М.Э.К. для обратного ома—сименс. Таким образом,,
единицей приводимости является 1 сименс/метр.
t Вольт будет определяться просто как ватт/ампер, или
- ватт , килограмм метр2 ,оч
1 вольт = 1 = 1 £ %- . (8)
ампер кулон секунда2 v '
!) См. дискуссию у Wallot, Elektrotechnische Zeitschrift, № 44—46 A922);.
а также: Sc^mmerf eld, Ueber die ElektromagnetischenEInheiten, 157—165и Zeemar*
Verhandelingen, Martirius Nijhoff, The Hague, 1935; Physik. Z. 36, 814—820 A935).
2) Пока не было принято никаких постановлений по вопросу о рационалнзиро-
вании единиц и, повмдимому, мнения разделяются поровну за и против. Если
основывать теорию на уравнениях Максвелла, то определённо представляется выгодным
опустить множитель 4я, который стоит перед плотностями заряда и тока в нерацио»
нализированной системе. В этой книге мы будем пользоваться рациональной систе~
мой единиц.*;
ЕДИНИЦЫ И РАЗМЕРНОСТИ IK8] 3U
■I. ^
f-VTaK как единица плотности тока 1 ампер/метр2, то из соотношения
J-i J = oE мы получаем:
, ^ «? 1 • ватт , вольт , килограмм метр ,ЛЧ
1 единица Е = 1 = 1 = 1 ~. (9)
ампер метр метр кулон секунда 2 J
Следовательно, энергия, выделяемая в единице объёма током плотности J
будет JE ватт/метр3. Мы видим,! далее, что произведение заряда на
напряжённость электрического поля Е имеет размерность силы. Поместим заряд
чв 1 .кулон в электрическое поле напряжённостью 1 вольт/метр. Тогда
. ч, , вольт 1 джоуль , килограмм метр /1ПЧ
*;;:,, ; 1 кулон X * = ^—=! =г—- • A0)
^ , ■. - J 'N метр метр секунда2 v
гЖГШдиница силы в системе MKS называется ньютоном и эквивалентна 1 джоу-
||^адЬ/метр или 10б дин.
Поток вектора В будет измеряться в веберах
Ф== f Вп da вебер, A1)
s
а напряжённость поля В или плотность потока может быть выражена,
следовательно, в веберах на квадратный метр. Согласно B5), стр. 21
I
Е*=-§- <12>
Линейный интеграл Г Eds измеряется в вольтах и называется, обычно, элек-
а
тродвижущей силой (сокращённо э.д. с.) между точками а и Ь, хотя его
значение в случае нестационарных полей зависит от пути интегрирования.
Э. д. с, индуцированная в замкнутом контуре С, равна, следовательно,
скорости уменьшения потока, пронизывающего этот контур, так что между
соответствующими единицами имеет место соотношение:
! вольт ==1_^бер__
секунда v y
или
1 вебер *= 1 moyhb = 1 килогРамм метР2 . A4)
* ампер кулон секунда ч '
Существенно отметить, что произведение тока на магнитный поток есть
энергия. Заметим также, что произведение В на скорость имеет размерность
вольт/метр и является, следовательно, величиной того же рода, что и Е:
1 единица В = 1 ^Щ= 1 *илограмм , A5)
метр3 кулон секунда * '
1 единица I Bj. \v\= 1 ^Ц X 1 ■■ М6Тр =1 ^£11 = 1 единица Е. A6)
1111 метр2 секунда метр х
Выведенные выше единицы образуют абсолютную систему в том смысле,
что любая из них выражается через четыре основные величины — массу,
длину, время и заряд. То, что эта система идентична с совокупностью
практических единиц, может быть выяснено заменой:
1 килограмм = 103 граммов; 1 метр в^= 102 сантиметров;
10
1 кулон = -^ абс. кулона. A7)
32 „ ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Легко видеть, что численные множители, которые тогда появятся в каждом
соотношении, будут теми же, которые выражают соотношение между
практическими и абсолютными электромагнитными единицами. Например, из F):
, , килограмм метр2 103 грамм 104 сантиметр2 „л0 -. ,-оч
1ом=1 ^ -= л,л * ъ — = 108абс. ом A8)
кулон2секунда 1С2абс. кулон2секунда v '
и, опять-таки из (8):
1 вольт = 1 килограмм метр2 _ 10» грамм 10* сантиметр2 = 1р8 вольт
кулон секунда Ю-1 абс. кулон секунда2 * v 7
Наш ряд единиц должен быть завершён определением единиц и
размерностей векторов D и Н. Так как D = еЕ, Н = — В, то необходимо и
достаточно, чтобы е0 и \ь0 были определены так, чтобы удовлетворялось
уравнение B) и чтобы достигалось необходимое соотношение между
практическими и абсолютными единицами. Мы будем обозначать массу, длину,
время и заряд буквами М, L, 7 и Q, соответственно, и используем знак [А]
для обозначения «размерности А». Тогда из уравнения C1), стр. 22
f
Dn da = q кулонов B0)
и, следовательно: ~
кяюнО
метр2 L? v '
г„ 1 _ Г D __ кулон _ Q2 Т^ г22ч
1*° ~~ L *е-В J ~ вольт метр ML* ' к }
Фарада, производная единица ёмкости, определяется как ёмкость
проводника, потенциал которого повышается на 1 вольт при сообщении ему заряда
в 1 кулрн. Она равна, другими словами, 1 кулон/вольт. Параметр е0 в
системе MKS имеет размерность, и может быть измерен в фарадах на метр.
ъ
. По аналогии с э. д. с, линейный интеграл Г Н ds, взятый вдоль опре-
а
делённого пути, обычно называется магнитодвижущей силой (сокращённо
м.д.с). В случае стационарного магнитного поля:
4
hds = I ампер, B3)
о
где /—»6к, определяемый потоком зарядов через любую поверхность,
опирающуюся на замкнутый контур С. Если поле переменно, то / должно
включать и ток смещения, как в B8), стр. 22. Согласно B3),
магнитодвижущая сила имеет размерность тока. На практике, однако, ток часто
проходит по виткам катушки или обмотки, которые охватываются контуром С.
Если имеем п таких витков, несущих ток /, то полный ток, пронизывающий
контур С, будет и nl ампер-витков, через которые обычно и выражают
магнитодвижущую силу, хотя в отношении размерности п является просто
числом.
[м. д. с] = ампер-витки, B4)
ампер-витки . Q ю§\
мегр LT
Отсюда видно, что размерность D и размерность Н, делённая на скорость,
совпадают. Для параметра \ь0 находим:
Ы = Г * 1 = вольт секунда = Ж B6)
L %т,Н\ ампер метр С?2 4
откуда
[HI = Z77^ Tf '
ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ [1.9] 33
, » ^штшттшшш —■ —■■» . ,, ,■.■ ■m.i.. .■ш..,...., .., , ■ -.-■■м,. ■ ■■ —■.. i.i i ■■ —>■ ■■ ■ ■ ■■ ■ ■ ■■.■!■■■ i —,..,.— .■
* *
Как и в случае е0, удобно выражать [а0 посредством производной единицы,
в данном случае генри, определяемом как 1 вольт секунда/ампер (генри — это
такая индуктивность, при которой изменение тока со скоростью в 1
ампер/секунду индуцирует э.д.с. в 1 вольт). Параметр {а0 может, следовательно,
измеряться в генри на метр.
Из B2) и B6) следует теперь, что
= -у2 B7)
Г—1
и что наша система согласуется, таким образом, в отношении размерностей
с уравнением B). Поскольку известно, что в рациональной абсолютной
CGSM-системе {а0 численно равно 4те, постольку уравнение B6)
устанавливает также и значение (а0 в системе MKS:
. грамм сантиметр . 10~3 килограмм Ю-2 метр /ПОч
uh = 4т: • -£—з 5—^ = 4те • ^ $ — B8)
' ° абс. кулон2 11И кулон2 v '
или
4т: . килограмм метр _ i0-6 i^Pil, B9)
ги кулон2 метр v '
Соответствующее значение е0 определяется тогда из
с =—4^ = 2,998 • Ю8-^^- B)
Уч-Ро секунда v '
и мы получаем:
з0 = 8,854 . 10-" Кул° СеКуНДа1 = 8,854 . 10"» -^-Д. C0)
и ' килограмм метр2 метр v
Часто бывает полезно знать обратные числовые значения этих множителей:
— =0,7958. 106 2^L; _L = 0,1129. 10" /^Р-, C1)
Ро генри £0 фарада ' v '
а также величины
лГ^- =376,6 ом; лГ^- =2,655- 10~8 сименс, C2)
часто встречающиеся при исследовании распространения волн.
В приложении I можно найти сводку единиц и размерностей
электромагнитных величин, выраженных через массу, длину, время и заряд.
ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ
1.9. Векторный и скалярный потенциалы. Исследование
электромагнитного поля часто упрощается введением вспомогательных функций,
называемых потенциалами. В каждой обыкновенной точке пространства векторы
поля удовлетворяют системе уравнений
rotE + ~f- = 0, (I) divB = 0, (III)
rotH — 4r = J> (П) divD = p. (IV)
Согласно (III), вектор В соленоидален. Следовательно, его можно
представить как ротор другого вектора А0:
, B = rotA0. A)
Я Зак. SQ3. Тропттет awmmnwamio-moxra
34 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Однако А0 определяется уравнением.A) неоднозначно, поскольку В равен
также ротору вектора А:
В = rot A, B)
где
А = А0 — grad«J>, C)
а 4* — произвольная скалярная функция точки.
Если теперь в (I) заменить В через A) или B), то мы получим
соответственно:
«*(Е+^Н; '°'(е+1г)=°. <*>
Таким образом поля векторов Е-\--^~- и Е-\-~-кт- являются безвихревыми
и равны градиентам двух скалярных функций о и <ро:
? Е = — grad<p0- df, E) х
Е = —grade? А. F)
Очевидно, функции <? и у0 удовлетворяют соотношению
?==?о + -^-- G)
Функции А являются векторными потенциалами, а <р являются
скалярными потенциалами поля. А0 и <р0 составляют лишь одну пару
потенциалов, из которых поле может быть получено посредством A) и E). По C)
и G) может быть построено бесконечное количество потенциалов,
определяющих то же самое поле.
Предположим, что среда однородна, изотропна, и что е и |i не зависят
от напряжённости поля: i \
D = eE, B = fAH. (8)
Переходя к потенциалам, имеем:
D = — e(grad<p + 4£), H = ^rotA, (9)
что, после подстановки в (II) и (IV), даёт:.
rotrotA-f{iegrad-^- + {ie-^-={iJ, A0)
A<p-t-div^7- = — — p. A1)
Все частные решения A0) и A1), удовлетворяющие одним и тем же
граничным * условиям, дают одно и то же электромагнитное поле. Они
различаются между собой произвольной функцией ty. Наложим теперь на А и 'о
дополнительное условие:
divA-f ^s|f-=0, A2)
Для выполнения которого необходимо только, чтобы $ удовлетворяло
уравнению:
Щ- ^S^ivAo-f^, A3)
Cv^' ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ |1-9] 35
g^eafc—.т- , , , , „ и ■ ■
' тде <р0 и А0 — какие-либо частные решения уравнений A0) и A1). Потен-
?• Цйалы <р и А теперь однозначно определены и являются решениями
уравнений:
г. ■
к rot rot А — graddivA-j-fie--^-=jxJ, A4>
% Д9_И^ = _1Р. A5)
:J- Уравнение A4) приводится к тому же виду, что и A5), с помощью вектор-
" ного тождества:
> rotrotA = graddivA —ДА. A6)
]г Последний член в A6) есть оператор Лапласа, действующий на
прямоугольные компоненты А. *
Окончательно A4) приобретает вид:
; ' ДА— ^е -^ = — fij. A7)
'/. Распространение оператора А на криволинейные системы будет рассмотрено
:■ в разделе 1.16, стр. 53 и 54.
;,. Соотношения B) и F) для векторов В и Е ни в коем случае не
& являются общими. К ним может быть прибавлено любое частное решение
V, однородных уравнений: '
f- rot Е +-^-= 0, (la) divB = 0, (Ilia)
{.:■ rotH —-~- = 0, (На) divD = 0. (IVa)
У'. ■■ *
Из, симметрии этой системы сразу же видно, что она может быть тожде-
v ственно. удовлетворена, если положить
Ь, D = -rotA*, H = — grad<p* —-Щ-, A8)
t откуда мы получаем:
Г E=-4-rotA*' B«-ii(gnidT*+-^-). A9}
Новые потенциалы подчиняются следующим условиям:
ДА* — иг-^-=0
А?*—^-^1 = 0, } B0>
divA* + ye-^-=0, ,
Общее решение неоднородной системы (I—IV) будет, следовательно
(ТА;
dt
riA*
В = rot A — ^~ ^grad<p*, B1>
dA 1
E = — grade? — ■—■—-rot A*, B2)
i при условии,. что p. и e постоянны.
|; Функции <p* и А* являются потенциалами источников, которые нахо-
§-дятся вне рассматриваемой области. Обычно <р* и А* полагаются равными
я*
36
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
нулю, а потенциалы всех зарядов как удалённых, так и находящихся в
рассматриваемой области, представляются с помощью ср и А.
В каждой точке, где заряд и плотность тока равны нулю, возможным
полем б/дет поле, определяемое потенциалами oQ = О и А0 = 0. В этом случае
функция ^ представляет собою любое решение однородного уравнения
(см. 13):
^-^^■ = 0. B3)
Поскольку в этой Же точке скалярный потенциал о удовлетворяет тому же
уравнению, 6 мож§т быть выбрано так, чтобы <р исчезло. В этом случае,
поле может быть найдено с помощью одного лишь векторного потенциала:
B = rotA, E = —^, . B4)
^-^-^- = 0, divA = 0. B5)
Что касается единиц и размерностей этих новых величин, то отметим
прежде всего, что Е измеряется в вольтах/метр и, следовательно, скалярный
потенциал о должен измеряться в вольтах. Если q заряд, измеренный
в кулонах, то, следовательно, qy представляет собой'энергию, выраженную
в джоулях. Из соотношения В = rot А ясно, что векторный потенциал А
может выражаться в веберах/метр, но с равным успехом в вольт-секундах/метр
или джоулях/ампер. Следовательно, произведение тока на векторный
потенциал представляет собой энергию. Для размерности А* находим, что она
равна кулону/метр, в то время как <р измеряется в ампер-витках.
1.10. Однородная проводящая среда. Ввиду малости времени
релаксации можно предположить, что внутри проводника плотность свободных зарядов
всегда равна нулю. Уравнения поля для однородной изотропной среды
сводятся тогда к системе: *
rotE + ~ = 0, (lb) divB_=0, (Illb)
. rotH — ^ — oE =0, (lib) divD = 0. (IVb)
Мы вольны- теперь выражать через векторный потенциал либо В, либо D.
В первом случае мы имеем:
i дА
B = rotA, E = -grade — -£. B6)
Если векторный и скалярный потенциалы подчинены соотношению
} divA + l«§+№ = 0, B7)
то возможное электромагнитное поле может быть построено из любой пары
решений уравнений:
л? —1"^|—1"^ = 0. B9)
Как. и в Предшествующем параграфе, мы замечаем, что векторы поля
инвариантны .по отношению к замене потенциалов при соблюдении условий
? = ?о+у,, A=A0-gradu, C0)
ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ [1.11J 37
где с0, А0—потенциалы возможного поля, а ^ — произвольная скалярная
функция. Для того чтобы А и о удовлетворяли B7), необходимо только,
чтобы, ф подчинялось дополнительному условию:
A^_jJ/e__,_fAa_^===divA0 4-Н-е-^+н.ов0. C1)
К частному решению уравнения C1) мы можем добавить любое решение
,рднородного уравнения
A^~\is~ — iia~=0. C2)
Часто бывает удобно выбрать ф таким образом, чтобы скалярный потенциал
равнялся нулю. Поле внутри проводника будет определяться тогда только
вектором А:
B-rotA, E=-j£, C3)
ЛА-^^-^^ = 0; divA = °- C4>
Поле может также быть выражено и через потенциалы о* и А!::
D = — rot A*, H= — gradcp*~^—~A*. C5)
Если с* и А* удовлетворяют B8) и B9), то они необходимо связаны
соотношением:
divA* + iie^g = 0. C6)
{ Доле, определённое уравнениями C5), инвариантно ко всем преобразованиям,
потенциалов типа
?* = ?о -f Ц~ + f П А* = Acj—grad Г , C7)
где, как и ранее, с0 и Ао являются потенциалами любого возможного
электромагнитного поля. Для выполнения соотношения C6) необходимо только
выбрать ф* так, чтобы удовлетворить соотношению
Л'' V-s~dW ~~^"дГ = divAo + as-^. C8>
Наконец, соответствующим выбором Л* скалярный потенциал с* может
быть сделан равным нулю:
D = —rot A*, Н = — ^_1а®, C9)
• ДА'-^^—^^^О. divA* = 0. D0)
1.11. Вектор Герца или поляризационный потенциал. Мы видели,
что интегрирование уравнений Максвелла может быть сведено к нахождению
векторного и скалярного потенциалов, которые в однородной среде
удовлетворяют одному и тому же дифференциальному уравнению. Герц показал1),
что при обычных условиях имеется возможность определить
электромагнитное поле с помощью- только одной векторной функции.
*) Hertz. Ann. Physik, 36, 1 A888). Общее решение дано Righi. Bologna Mem..
E), 9, 1 A901) и Л Nuovo Cimento, E) 2, 2 A901).
38 ГЛ; I. УРАВНЕНИЯ ПОЛЯ
Ограничимся здесь областью изотропной среды, внутри которой нет
ни токов проводимости, ни свободных зарядов. Уравнения поля сводятся
тогда к однородной системе (la) — (IVa). По причиням, которые станут
сейчас ясными, мы предположим, что векторный потенциал А
пропорционален производной по времени от вектора П:
A = ps^5. D1)
Следовательно, ч
В = уего^; Е = —grado —це-р-, D2)
и когда это выражение для Е мы в свою очередь внесём в (На), то
найдём, что:
-|(rotrotII + gradc? + v* |5) = 0. D3)
Напомним, что в точках, где нет зарядов, скаляр мая функция о должна
лишь удовлетворять уравнению B3), а в остальном является совершенно
произвольной. В данном случае мы выберем её так:
о = —-divBE. ' D4)
Интегрируя D3) по времени, мы получаем:
rot rot П—graddiv П. + ^е^- = const. D5)
Значение константы не влияет на определение ноля и мы можем поэтому
положить её равной нулю. Уравнение (IVa) тоже удовлетворено, так как
дивергенция ротора тождественно равна нулю. Следовательно, мы можем
утверждать, что любое решение векторного уравнения
rotrot П—graddivll-f ii£|^ = 0 D6)
определяет некоторое электромагнитное поле посредством выражений'.
. B = fierot~; E = graddivll — це ■—. D7)
Условие B3), которому должно удовлетворять <р> выполняется в силу D6).
Уравнение D6) может быть переписано в виде:
ДП-^ = 0 D8)
при условии, что оператор Л предполагается действующим на прямоугольные
компоненты П.
Так как в пространстве, свободном от зарядов, вектор D соленоидален,
как и В, то может быть построено другое решение вида:
A*s={ie~r, 9*== — divH*. D9)
D = -г це rot -зр Н == grad div И — це -^-, E0)
где П*—любое из решений D6) или D8).
Из полученных результатов мы заключаем, что в области, в которой е
и ^ постоянны, а р и J равны нулю, электромагнигное поле может быть
w
ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ [1.11] 8&
разложено на два составляющих поля — одно, выводимое из вектора П и
другое из вектора И*. Источники этих полей находятся вне рассматриваемой
■области. Для того чтобы установить физический смысл векторов Герца,
необходимо теперь связать эти векторы с их источниками; иными словами,
• мы должны найти неоднородные уравнения, из которых может быть, выведено
уравнение D8).
Выразим вектор D через Е и электрическую поляризацию Р. Согласно
«F), стр. 24, D = e0E-{-P. Следовательно, вместо (Па) и (IVa) мы должны
теперь написать:
rot H-e0-^ = ^, divE=--i-divP. E1)
Легко убедиться, что эти два уравнения, так же как и Aа) и (Ша) попреж-
нему удовлетворяются тождественно выражениями D7), при. том только
условии, что е заменено на е0 и что теперь является любым решением
уравнения
ДП-^0^=—IP. E2)
Источником вектора И и электромагнитного поля, получаемого из него,
[является распределение электрической поляризации Р. В дальнейшем мы
дадим интерпретацию вектора Р как электрического дипольного момента
«единицы объёма среды. Поскольку П связано с распределением электри-
; ческих диполей, то часто говорят, что определяемое им частичное поле есть поле
, электрического типа, а сам вектор И может быть назван электрическим
•'". поляризационным потенциалом.
Таким же точно путём можно показать, что поле, связанное с И*,
создаётся распределением магнитной поляризации. Согласно F), стр. 24, вектор В
связан с Н соотношением В = \ь0 (Н -\~ М), которое, будучи подставлено
ш Aа) (Ша), даёт:
rotE-\-^ = -Hd§; divH = -divM. E3)
"Эти уравнения, так же как и (Па) и (IVa), удовлетворятся тождественно
выражениями E0), если мы заменим ^ на р-0 и потребуем, чтобы П* было
решением уравнения
ДП -^е^-^-М. E4)
Мы покажем позднее, что поляризация М может быть интерпретирована как
шютность распределения магнитного момента. Таким образом, можно
представить себе, что частичное поле, определяемое из П*, создаётся магнитными ди-
, полями и может быть названо полем магнитного типа.
Электрическая поляризация Р может индуцироваться в диэлектрике
этолем Е, но может также определяться совершенно иными факторами.
В практических приложениях теории интересуются обычно только
независимой от поля частью Р0, которая, как будет показано, представляет собой
.электрический момент дипольных осцилляторов, возбуждаемых внешними
источниками энергии. То же справедливо и в отношении магнитной
поляризации. Чтобы отразить это положение, мы будем писать уравнение F),
'-стр. 24, в изменённом виде:
D = £E-j-P0, H = ^B-M0, E5)
40 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
где Р0 и М0 заданы независимо от Е и Н, и где индуцированная
поляризация среды снова включена в параметры е и jx. Следовательно,
электромагнитное поле, вызванное заданным распределением Р0 и М0, определяется
выражениями
E = graddivII - це ll-nrot *£, E6)
Ц= е rot -^-|- §rad div "■ "^-W* (*
где П и Н* являются решениями уравнений:
Д11 — us-^-= —М0 •
E8)
В силу второго из уравнений E8) и тождества A6), мы можем написать
E7) также в виде:
Н = s rot -£ + rot rot И* — М0. E9)
Так как В = rot А, то из последнего соотношения с^чёвидно,, что векторный
потенциал А может быть получен из векторов Герца следующим образом:
А = jj.e -щ 4~ !J- rot П' — grad Ь , F0)
где ф — произвольная скалярная функция. Соответствующий потенциал ©будет
««-divll+jj;, Fi)
причём 4» подчинено только тому условию, что оно удовлетворяет уравнению
Дф-^ = о- F2>
Обобщение этих уравнений на однородную проводящую среду может
быть сделано без труда. Читатель может убедиться прямой подстановкой, что
системе (I —IV) в. среде, свободной от заданных поляризаций Р0 и М0,
•удовлетворяют выражения
Е с= rot rot 1Г—у rot ~, (,Щ
1 Н == rot (е ~ + Л) + rot rot П\ • F4)
. ' rot rot П-grad div 1Г -f Y*7£ + ¥" й? = °. I
6t 6t \ F5)
roHtflT-grad div П* + ^+^ = 0. j
1.12. Комплексные векторы поля и потенциалы. Зильберштейн,
Бейтман и другие показали, что уравнения, которым удовлетворяют векторы
поля 'и потенциалы, могут быть приведены к весьма компактной форме путём
пс строения комплексного вектора, действительная и мнимая части которого
составляются из векторов, определяющих магнитное и электрическое поля1).
!) Silberstein. Ann. Phys. 22, 24, 19071 Также Phil. Mag F), 23, 790 A912).
В at em an, Electrical and Optical Wave Motion, гл. I, Cambridge University Press.
ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ [U2] 41
^: « и ■ i ■ ■ i —
'$* •'
" Операция эта не им*еет наглядного физического истолкования, но часто
Р упрощает исследование.
I- ^ Рассмотрим опять однородную изотропную среду, в которой D = гЕ,
р В —jj-Н. Если мы определим теперь комплексный вектор поля Q как
'i. Q==B + /l/eji-E, F6>
\\те уравнения Максвелла (I) — (IV) приведутся к виду:
V' rotQ + /l/"iii^ = jjJ, divQ = /j/~-^p. F7)
ь Векторная операция rot Q может быть исключена из F7), если взять
[ ротор от обеих частей. С помощью тождества A6) мы получаем уравнение
'', grad -div Q — AQ -j- /]Лу rot ~ = ji rot J, F8).
''■ которое, после подстановки значений ротора и дивергенции Q из уравне-
■ ний (€7), приводится к виду:
AQ ~ e^ W ~ ~~ * ^rot J "~l ^8^ dt ~~ 1~^ ьгаC Р)- F9)"
Если разделить в последнем уравнении действительную и мнимую части,
то мы получим уравнения, которым удовлетворяют векторы Ей Н порознь:
AH-eag^-rotJ, G0)
ДЕ — е?д£==У,дГ~ 7^radP- G1)
Далее, определим Q через комплексные скалярный и векторный
' потенциалы L и Ф уравнением
Q = rot L — iV^V- jf — 1У*Р §'rad ф> G2)
где L и Ф подчинены условию
div-L +eii^ = 0. G3)
Легко убедиться, что G2) является интегралом F7) при условии, что
комплексные потенциалы удовлетворяют уравнениям:
&L — ^ = -vJ, G4>
ДФ_ч1^ = _±р. G5)
Если напирать действительные и мнимые части этих потенциалов в виде:
L = A — i]/~£-А*, Ф = ср — 1\/~т<?* Gб)
и подставить в G2), то после разделения действительной и мнимой частей
мы вновь получим общие уравнения для векторов поля, определённых
уравнениями B1) и B2).
Если в рассматриваемой области свободные заряды и токи всюду равны
нулю, то уравнения F7) принимают вид: > i
rotQ + fj/^iP^O, divQ = 0. (J7)
42
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Электромагнитное поле может быть выражено теперь через единый
комплексный вектор Герца Г:
Q = цг rot ~ -f- /W8 rot Wt Г,
dt
где Г — любое из решений уравнения
ДГ — гр.
\
М, наконец, если, определить Г как
г=П-
"д2Г
дР
0.
,/|1Г.
G8)
G9)
(80)
то после подстановки в G8) и разделения мнимой и действительной частей,
мы снова получим в точности выражения D7) и E0) для электрического
и магнитного векторов поля.
Если среда является проводящей, то уравнения поля перестают быть
-симметричными и описанный метод оказывается непригодным. Трудность
может быть преодолена в случае поля, изменяющегося гармонически. Время
входит в этом случае явно, как множитель вида е-т * После
дифференцирования по времени, система (I) — (IV) может сделана симметричной введением
комплексной диэлектрической проницаемости е' = edzi— .
ГРАНИЧНЫЕ УСЛОВИЯ
1.13. Разрывы непрерывности векторов поля. Уравнения поля были
постулированы только для обыкновенных точек пространства, т. е. для
точек, в окрестности которых физические свойства среды меняются
непрерывно. Но при переходе Через поверхность, отделяющую какое-либо тело
тпп среду от другого,* происходят резкие изменения параметров е, ja, о.
В макроскопическом масштабе подобные изменения могут обычно
рассматриваться как разрывы немрерывно-
П — ~ ~ сти и, следовательно, можно
ожидать, что и сами векторы поля
испытывают здесь
соответствующие скачки.
Предположим сначала, что
Грфц/чная поверхность 5, отделяющая среду
поверхностьв A) от среды B), заменена очень
тонким переходным слоем, внутри
"Ряс. 2а. К граничным условиям для нормаль- которого параметры е, ja, о ме-
ных компонент. . няются очень быстро, но непре-
*• рывно от их значений около S
в среде A) до их значений около 5 в среде B). Внутри этого слоя,
как и 'в средах A) и B), векторы поля и их первые производные
являются непрерывными ограниченными функциями точки и времени. Построим
теперь перпендикулярно слою маленький цилиндр, как показано на рис. 2а.
Образующие цилиндра нормальны' к поверхности 5, а его основания лежат
. на поверхностях, слоя, так что они отстоят друг от друга как раз на толщину •
«слоя А/. Обратимся сначала к полю вектора В, для которого мы имеем
§
Bn da = 0.
A)
;* ГРАНИЧНЫЕ УСЛОВИЯ 11.13] * 43
g где интегрирование распространено на боковую поверхность и основания
| цилиндра. Если основание цилиндра, площадь которого Да, сделано доста-
| 1чно малым, то можно считать, что В имеет постоянное значение на каждом
г- из оснований. Пренебрегая бесконечно малыми более высокого порядка, мы
f можем приближённо записать соотношение A) в виде:
$ (Вп1-|-Вп2)Да-|-доля боковой поверхности = 0. B)
г. Часть поверхностного интеграла, соответствующая боковой поверх-
? «ости прямо пропорциональна толщине слоя Д/. Пусть теперь переходный
I; слой сжимается в поверхность 5. В пределе, при Д/-> 0 основания цилиндра.
£ расположатся как раз по обе стороны 5, а часть, связанная с боковой по-
; / верхностью, станет исчезающе малой. Обозначим значение В в точке на 5 в
Ь среде A) через Bj, а соответствующее значение В в той же точке поверх-
, 'ности 5, но на другой её стороне, в среде B), через В2. Кроме того, положи-
1-- тельную нормаль к поверхности 5 мы обозначим единичным вектором п,
*•• проведённым от A) к B). В соответствии с этим условием, среда A) нахо-
' дится с отрицательной стороны поверхности 5, а среда B) — с положитель-
/ ной, и Щ = —п. Следовательно, при Д/->0, Да->■(),
U (Ba— B^i^O; C)
л следовательно, при переходе через какую-либо поверхность разрыва непре-
,, рывностй • cgjedbiy нормальная компонента вектора В остаётся
непрерывной. Уравнение C) является прямым следствием условия divB = 0
и иногда называется поверхностной дивергенцией.
С вектором D можно поступить подобным же образом, но в этом
случае поверхностный интеграл нормальной компоненты по замкнутой
поверхности равен полному заряду, содержащемуся внутри неё:
ф Dn da = q. D)
Этот заряд распределён в поверхностном слое с плотностью р. При сближе-
' яии оснований цилиндра полный заряд q остаётся неизменным, поскольку
он сохраняется:
q = р Д/ Да. E)
В пределе, при Д/ -> О объёмная плотность р становится бесконечной. В этом
случае произведение рД/ удобно заменить поверхностной плотностью (а,
определённой как заряд единицы площади.
Изменение нормальной компоненты век- »/2) Ег,/12,ог
тора D при переходе через какую-либо * т
поверхность 5 даётся теперь выражением. " А
Наличие на поверхности S зарядов вы A) £/f/2Jtor
зывает скачок нормальной компоненты
вектора D; величина её скачка равна Рис 2Ь. К граничным условиям для
поверхностной плотности заряда, изме- тангенциальных компонент.
ренной в кулонах на квадратный метр.
Обращаясь теперь к поведению тангенциальных компонент, мы заменим
цилиндр рисунка 2а прямоугольным путём, проведённым как показано на
рисунке 2Ь. Стороны прямоугольника длиной As лежат по обе стороны
переходного слоя, а длина отрезков, проходящих сквозь слой, равна его
толщине Д/. Этот прямоугольник образует контур С0, вдоль которого
(j) Erfs-f f^n0da = 0, G)
Со S0
44 v гл. i. уравнения поля
где S0 — площадь прямоугольника, а п0 — её положительная нормаль»
Положительное направление этой нормали определяется, как на рисунке 1,
стр. 21, направлением обхода контура С0. Пусть хх и х2 будут, как показана
на рисунке BЬ), единичные векторы в направлении обхода контура, вдоль
нижней и верхней его частей. Пренебрегая бесконечно малыми высшего
порядка, можно аппроксимировать соотношение G) выражением:
(EXj -f- Ex2) As -J- доля концевых отрезков = — ^-- n0 As А/. (8)
По мере того, как слой сжимается в поверхность 5, доля, вносимааконцевыми
отрезками и пропорциональная А/, становится исчезающе малой. Если п
опять будет обозначать положительную нормаль к поверхности S,
проведённую от среды A) к среде B), то единичный касательный вектор х можно
определить соотношением:
х=[п0, п]. (9>
Так как
[n0, n]E = n0[n, E], A0)
то в пределе, при А/ -» 0, As -» 0 мы имеем
п0 {[о; Е2 - EJ + Hm (^ А/)} = 0. A1)
Ориентация прямоугольника, а следовательно, и п0, ' совершенно
произвольна, откуда следует, что скобка в A1) должна равняться нулю, т. е.
[п, Е2 — EJ = -lim(§^/). A2)
Векторы поля и их производные, по предположению, ограничены;
следовательно, правая часть в A2) обращается в нуль вместе с А/:
[п, Е2— Е^О. A3)
При переходе через поверхность разрыва тангенциальная компонента
вектора Е остаётся непрерывной.
Поведение вектора Н .на границе можно вывести сразу же из A2)
и уравнения поля
<J)Hds— [^ n0da = fjn0da. ' C14S
'-'О 1>0 '-0
»
Мы имеем, таким образом:
[n, H2~H1] = lim(^ + j)A/. A5)
Первый член справа в A5) при Д/-> 04.исчезает, потому что D и её
производные ' ограничены. Если" плотность тока J конечна, то второй член тоже
исчезает. Может случиться, однако, что по мере того, как стороны
прямоугольника сближаются, ток / = Jn0AsA/ сквозь прямоугольник сжимается
в бесконечно тонкий слой на поверхности 5.*Такой поверхностный ток удобно
представлять поверхностной плотностью К, определённой как предел
произведение J А/ при Д/->0 и J—>со. Тогда
[n,H2—HjJ^K. A6)
Если проводимости соприкасающихся сред конечны, то поверхностный ток
невозможен, поскольку Е ограничено и, следовательно, произведение с£Д/
исчезает вместе с А/. В этом случае, который и является обычным
[п, Н2 — HJ —0(при конечной проводимости). A7)
КООРДИНАТНЫЕ СИСТЕМЫ [1.14] ' - 45
Нередко, однако, бывает необходимо положить проводимость тела
бесконечной с целью упрощения анализа его поля. В этом случае граничное
условие следует применять в виде A6), а не A7).
Суммируя вышеизложенное, мы можем теперь пополнить уравнения поля
четырьмя условиями, определяющими изменение векторов поля при переходе
из одной среды в другую через разделяющую их поверхность разрыва
непрерывности:
n(B2 —B^O, [n.Hg —HJ^K, J g
[n.Ea —EJ = 0, n{D8 —D,) = «. J
Из них сразу же следуют условия для изменения нормальных компонент Е и Н:
п(н*-йн')=0 п(Е*-1Е0=?- <19>
Аналогично, тангенциальные компоненты D и В должны удовлетворять
,условиям
[n.D.-bD^O; [n,B8 —^B^jieK. B0)
КООРДИНАТНЫЕ СИСТЕМЫ
1.14. Основные и взаимные координатные векторы. Одно из
принципиальных преимуществ векторного исчисления заключается в том, что
уравнения, определяющие свойства, общие всем электромагнитным полям, могут
быть формулированы безотносительно к какой-либо конкретной системе
координат. Однако для того, чтобы установить характерные черты, которые
отличают данное поле от других возможных полей, приходится, к несчастью,
разлагать каждое векторное уравнение в подходящей системе координат
■ на эквивалентную систему скалярных уравнений.
Пусть в заданной области
■ u1=f1(x,y, z), u2=f2(x,v,z), и*=/9(х,у,г) A)
являются тремя независимыми, непрерывными, однозначными функциями
прямоугольных координат х, у, z. Эти уравнения могут быть разрешены
, относительно х, у, z и дают тогда
х=о1(и1,и9,иъ), y = <p2(u1t и2, и8), г = ч9(и1,и*,иъ) B)
три функции, которые тоже независимы, непрерывны и при определённых
.^ограничениях однозначны. В общем случае функции' <р*> равно как и fit
"■ непрерывно дифференцируемы, но в некоторых отдельных точках это
свойство может и нарушаться. Поэтому в дальнейшем, при применении
общих формул следует соблюдать осторожность.
Посредством уравнения A) с каждой точкой Р(х, у, г) в
рассматриваемой области связаны три значения и1, и2, и3; обратно (в пределах, зависящих
от границ области), каждой тройке и1, и2, иъ соответствует определённая
точка. Функции к1, и2, иэ называются обобщёнными, или криволинейными
координатами. Через каждую точку Р проходят три поверхности:
и1 = const., и2 = const., и3 = const., C)
называемые координатными поверхностями. На каждой координатной
поверхности одна из координат постоянна, а две другие меняются. Поверхность
обозначается координатой, которая остаётся постоянной. Две поверхности
пересекаются по кривой, называемой координатной кривой, вдоль которой
две координаты постоянны, а "одна меняется. Координатная кривая
обозначается меняющейся координатой.
46 , ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Пусть г обозначает вектор, проведённый из произвольного начала отсчёта
к переменной точке Р (а:, у, z). Эта точка, а следовательно, и определяющий
её положение вектор г, могут рассматриваться как функции криволинейных
координат и1, и*, и3:
х = х(и\ и2, и3). D)
Бесконечно малое изменение вектора г, обусловленное малыми
перемещениями вдоль координатных кривых, выражается в виде:
dx = |^ du1 + |^ du2 4- Ц± dus. E>
Если теперь переместиться на единицу длины вдоль кривой и1, то измене*
ние г будет направлено по касательной к этой кривой и равно -g-^. Векторы
дг дг дг ,~\
^■~Ш* Ва~<Р' Л*~Ш к>
называются координатными векторами, связанными с точкой Р. Они
составляют базисную систему отсчёта для всех других векторов, связанных
с этой точкой:
dx = аг du1 -J- a2 du2 -{- а3 dub. G)
Следует подчеркнуть, что координатные векторы не 'обязательно имеют,
единичную длину и что их размерности зависят от характера криволинейных
координат.
Три базисных вектора а1э а2, а3 определяет параллелепипед, объём
которого равен
V = a1 [а* а3] = а2 [а3, aj = a3 [alf aa]. (8>
Тройка векторов, определённых соотношениями.
а =-р'[а2, а3], а =-у [а3, а2], а = ^ [а1э а2], (У>
перпендикулярна соответственно к плоскостям, определяемым парами"(а2, а3),
(а3, aj), (alf a2). Образуя всевозможные скалярные произведения типа а^а^
легко убедиться, что они удовлетворяют условию:
а'а, = 8^ (Ю>
где. 8^-—обычно используемый символ, равный единице при i=j и нулк>
при i^pj. Координатные векторы могут быть выражены через систему
векторов а1, а2, а3 с помощью идентичных по форме соотношений:
а, =£[ая, *3];а2=^[а3,аЧ; а3 = ^[а1,а2]. A1)
О t двух совокупностях некомпланарных векторов, связанных
соотношениями (8)-^-A1), говорят, что они образуют взаимные системы. Три
вектора а1, а2, а3 называются взаимными 'координатными векторами и могут
служить базисной системой наравне с координатными векторами.
Есяи в качестве базисной системы используются взаимные
координатные* векторы, то дифференциал dx нацишется в виде:
dx = a}dult ~f- a2 du2 -j- a3 dus. A2)
Дифференциалы duv du21 du3 являются, очевидно, компонентами dx в
направлениях, определяемых новыми базисными векторами. Величины . и1г и2, %
'являются функциями координат и1, и2, и3, но дифференциалы dult du2, duz
КООРДИНАТНЫЕ» СИСТЕМЫ [1.14]
47
&■" •
| he являются обязательно полными. Наоборот, они связаны с дифференциалами
jf координат системой линейных уравнений, которые в общем случае неинте-
Р" грируемы. Таким образом, приравнивая G) и A2), мы получаем
У 3 3
;' dx = 2 а^и* — 2 BJdtij. A3)»
* = i
i=i
:* Путём скалярного умножения A3) по очереди на а* и на а^, мы находим
V благодаря A0):
3 3
du.i = 2 л^и*; ^=2^^- (Н>
4=1
j'=i
? Принято записывать скалярные произведения основных и взаимных векторов.
с помощью символов:
gij— aiaj— Sji*
gij = a*E? == gj*.
A5)
A6)
: Тогда компоненты dx в главной и взаимной
;•' базисных системах будут связаны соотноше-
V ниями:
]л 3 3
У duj^^gjiduK du< = 2 gVty. A7)
»=i
3=1
■ .Данный вектор F а точке Я «ожег быть 5^ЙЕ£в£2£
: разложен на компоненты как по отношению
■-•■■, к основной базисной системе а1э е2, е3, так и по отношению к взаимной*
системе а1, е2, е3:
;-■ • зз
L F = 2 /% = 2 Ла/.
= i
з = 1
A8)'
, Очевидно, компоненты F в основной системе связаны с его компонентами
'■', во взаимной системе соотношениями:
Л=2^Д /*=2£%
* = 1 а = 1
A9)
/ а ввиду ортогональности базисных векторов е^ по отношению к векторам
взаимной тройки е% выражаемой уравнениями A0), мы можем написать
также:
/* = Ftf, fj=*FRj. B0>
: Отсюда следует, что A8) эквивалентно
F = 2 (Fe*)e,- = 2 (Fa.) еЛ
4 = 1
3 = 1
B1)
Величины /* называются контравариантными компонентами вектора F,..
в то время, как /г- называются ковариантными компонентами F. Маленькая
буква для обозначения этих компонент была использована для того, чтобы
не путать их с компонентами Flf F2, FB вектора F по отношению к
базисной системе векторов, совпадающих с е4, но имеющих единичную длину.
Выше было отмечено, что длина и размерность координатных векторов,
зависят от характера криволинейных координат. Соответствующая система
единичных векторов, которые, так же как и координатные векторы ait каса-
■48
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
тельны к кривым иг, определяется соотношениями
и следовательно,
где
V^ii - YE,*1' k~ Y^ *2' k~TS
Pi = VYuf-
a3»
B2)
B3)
B4)
Величины Fi имеют ту же размерность, что и сам вектор F.
Вектор dv представляет собой бесконечно малое смещение из точки
Р(иг,и^, Ф) в соседнюю точку с координатами ^-j-du1; u2-\-du2, uB-{~du3.
Величину этого смещения (она является элементом длины) мы обозначим
через ds. Тогда:
3 3 3 3
ds2 = dr dr == 2 2 а^а^- duldu) =22 a*a*d«*rf«/, B5)
или в обозначениях A5) и A6)
4 = 1,7 = 1
3 3
ds2= 2 gijdtfduJ = 2 g^dUfdiij
i, 2=1 i, j=l
B6)
gij и g*J входят здесь как коэффициенты двух дифференциальных
квадратичных форм, выражающих длину линейного элемента в пространстве
обобщённых координат и*', или в пространстве
взаимных им коордийат щ. Обычно их называют
метрическими коэффициентами.
Относительно просто получить теперь
выражения для элементов дуги,
поверхности и объёма в криволинейной
системе координат. Пусть dst будет
бесконечно малое смещение в точке Р(их, и2, к3)
вдоль кривой и1:
dst = ах du1, dst = | dst | = Vgn dul- B7)
Рис. 4. Элемент площади на
поверхности и1.
Аналогично, для- элементов длины вдоль
кривых и2 и иъ имеем:
*а = Vg2~2 <*, ds9 = VH^u\ B8)
Рассмотрим далее бесконечно малый параллелограмм на поверхности
и1, ограниченный Пересечением кривых и2 и ifi, как показано на рис. 4.
По величине площадь такого элемента равна
а,
' dax = | [ds2, ds,] | = [ [а2, а8] | du4u* = ]/[а2, а3] [a2, a8] rf«a da8. B9)
Согласно 'Хорошо известному векторному тождеству *)
[а, Ь] [с, d] ~ (ас) (bd) —(ad) (be),' C0)
"где a, b, с и d — любые четыре вектора, получаем:
[а21 а3] [а2, а3] = (а2а2) (а3а3) — (а2а3) (а3а2) = g.2Lgm — gh- C1)
*) Так -называемое тождество Лапласа. Прим. ред.
КООРДИНАТНЫЕ СИСТЕМЫ [U4]
49
Для площади элемента на поверхности и1 мы имеем, следовательно,
dat = Vg22g33 — g% dtt-du
и аналогично для элементов на поверхностях и2 и и3:
da2 = Vgwgu —gltdu8 du,
dab = Vgu ^22 — g% du1 du*.
C2)
C3)
,Наконец, элемент объёма, ограниченный координатными поверхностями,
напишется как
dv = dsx [ds2, d$s] = SLt [a2, a3] duldu%dtfi. C4)
Если теперь мы положим в B1) F = [а2, а3], то получим:
[а2,а3] =(ах [а2,а3])а1-}-(а2 [а2,а3])а2-На3 [а2, а3])а3 C5)
или, заменяя а* их значениями из (8) и (9):.
а! [а2, а3] = {а**а^ {([а2, а3] [а2, а3])а1 + ([а3,а1] [а2, а3])а2 +
+ ([а!,а2] [а2,а8])аэ}. C6)
Величины в скобках могут быть разложены с помощью C0) и члены могут
% быть сгруппированы так:
(aj [а2, а3]J = а^ {(а2а2) (а3а8) — (а2а3) (а3а2)} -f
+ а^а {(а^з) (ааа,)—(a2aj) (a3a3)} +
+ aja3 {(a2aj) (a3a2) — (а2а2) (a3aj)}. C7)
Наконец, скалярные произведения в C7) заменяются соответствующими g{j
и мы получаем выражение для элемента объёма:
dv^VJduiduZdu?, C8)
е котором:
£ =
Six gvz ёп
£Г21 §22 £23
£1 £"з2 £зЗ
C9)
Соответствующие выражения для элементов длины, площади и объёма
во взаимной базисной системе могут быть получены заменой gi3- на g^, но
в последующем они нам не понадобятся.
Очевидно, коэффициенты g^ достаточны для полной характеристики
геометрических свойств пространства по отношению к какой-либо
криволинейной системе координат; поэтому для нас важно знать, как эти
коэффициенты могут быть найдены. Для единообразия мы будем обозначать
прямоугольные координаты х, у, z точки Р соответственно буквами а:1, л:2, л^. *
Тогда:
ds2 = (dx1J + (dx2f + (dx*f. D0)
В этой, самой простой из всех систем, метрические коэффициенты равны:
A при /=у
Q при /:£./. .
D1)
4 Зак. £93. Теория электромагнетизма.
50 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Из ортогональности координатных плоскостей и из определения (9) очевидно,
что основные и взаимные координатные векторы здесь совпадают, имеют
единичную длину и являются базисными векторами. Обычно их обозначают
буквами i, j, k.
Предположим теперь, что прямоугольные координаты функционально,
связаны с криволинейными координатами уравнениями, подобными
уравнениям B):
х1 = х1 (в1, и2, и*), х2 = х2 (и1, и2, и?), х* = х3 (и1, а\ я3). ' D2)
Дифференциалы прямоугольных координат являются линейными функциями
дифференциалрв обобщённых координат, как это видно в результате
дифференцирования уравнений D2):
dxl = 7БЯ dul + S d + Х5 du*>
ди1 ' ди* ' дФ
dx2 = з-т- du1 4- 5—; du2 4- -^-s du^,
да1 ' ди^ ' ди3 '
dx3 = з1! du1 4- -f-; du2 4- з-^j ^и3.
дм1 ' d«2 ' ди*
D3)
Согласно B6) и D0)
^=2 2 £*АЛй* = S (^J, ' D4)
откуда, после возведения в квадрат дифференциалов в D3) и приравнивания
коэффициентов при одинаковых членах, мы поручаем:
&Ч ди* диз"""" дм* диз ' ди^диз ' ^ '
1.15. Дифференциальные операторы. Градиентом скалярной
функции о (и1, и2, и3) называется вектор, определяемый по величине и
направлению быстротой наибольшего изменения о по отношению к координатам.
Изменение о при смещении dr будет, следовательно:
з
rf? = grad о dr « ^ 'g_ А*'. D6)
V «=*
rfaf являются контравариантными компонентами вектора смещения dr и
поэтому, согласно B0),
du1 — a?dr. D7)
Эти значения 'du1, будучи подставлены в D6), приводят к равенству
з
;grad9-2a^)^ = °, D8>
и, поскольку смещение dr произвольно, мы находим для градиента
скалярной функции в любой системе криволинейных координат:
з
grad? =2 a*|t. D9)
В этом выражении базисная система образуется взаимными координатными
векторами, но они могут быть заменены основными координатными векто-
КООРДИНАТНЫЕ СИСТЕМЫ [1.15] 51
рами посредством преобразования
E0)
Дивергенцию Еекторной функции F (и1, и2, и3) в точке Р проще всего
вывести из её ^определений в уравнении (9), стр. 18, как предела
поверхностного интеграла нормальной компоненты вектора F по замкнутой
поверхности на единицу заключённого внутри неё объёма. Рассмотрим те две
грани элемента объёма, изображённого на рис. 5, которые лежат на
поверхностях и2. Левой грани соответствует значение и9, а правой u2-\~du*.
Площадь грани на поверхности и2 определяется выражением [ара8] du1 du\
где порядок векторов такой, что нормаль направлена наружу, т. е. влево.
Общая доля} вносимая этими двумя гранями в значение потока,
направленного наружу, будет поэтому
F [a3, aj dul du? \ u*+dv? + F [a1} a3] du1 da3 j M?,
E1)
где индексы при вертикальных прямых означают, что соответствующие
выражения должны быть взяты соответственно при u2-\-du? и при и2. При
достаточно малых значениях du2 E1) может быть
аппроксимировано линейным членом ряда
Тейлора:
■^{Г^ъииЧиЪи*}, E2)
где [а1} %] заменено на—[а3, aj. С помощью
B1), B0) и C7) мы получаем далее:
F [a3, aj = F • а2 (а2 [а8, л{[) = Л/?; E3)
таким образом доля этих двух граней в
поверхностном интеграле будет:
jL(f*Vg) ditduW.
diP
E4)
Рис. 5. Элемент объёма в
криволинейной системе ко-
. ординат.
Аналогичные слагаемые даются и двумя
остальными парами граней. Поскольку интеграл должен
быть отнесён к единице объёма, мы делим его на
dv = Yl? du1 du2 du9 и переходим к пределу
при du1 -* 0;*/и2->0; с?а3-»0, благодаря чему действительно исчезают все
члены ряда Тэйлора, кроме линейных. Дивергенция вектора F в
криволинейной системе координат равна, следовательно,
8
div F = -4= V. Л, (fiVF\. E5)
Таким же способом мы найдем и ротор вектора F, подсчитывая
линейный интеграл от F по бесконечно малому замкнутому пути. Согласно
уравнению B1), стр. 20, компонента ротора в направлении, определяемом
единичной нормалью п, есть
1
(rotF)n = lim ~i)Fds.
с-
E6)
Возьмём линейный интеграл F по контуру прямоугольного элемента
площади, расположенного на поверхности и1, как показано на рис. 6. Стороны
4*
52
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
прямоугольника равны a2du? и a$du?. Направление обхода должно быть
таково, чтобы положительная нормаль совпадала с положительным
направлением кривой и1. Слагаемые от сторон,
параллельных кривым и3, будут
F а8^и310+аи>—F a^da* J uh
а от низа и верха, параллельных кривым и2, мы
получаем:
— F a2da21 и*+аи* -j- F SL2du9-1 из.
иг-нравеы, Аппроксимируя эти'разности линейными членами
ряда Тэйлора, мы получаем для линейного интеграла
значение:
E7)
Рис. 6. К вычислению дта величина должна быть теперь разделена на пло-
ротора в криволинейных , X—-
координатах. щадь прямоугольника, т. е. на у [а2,а3] [a2,a3]d«2 du?;
что касается единичной нормали п, то, как мы
отмечали, взаимный вектор а1, но не основной вектор а1э всегда нормален
.к поверхности и1.
Вектор нормали должен быть единичным, следовательно:
п
Уа*а»
E8)
E9)
F0)
F1)
Эти значения, будучи подставлены в E6), дают
(Г0,Р) У^Г= У1%. а!) 1» «d ( Я» <Р ^ ~ ТО У Ц •
Согласно (9) и C7),
[а2, а3] = (aj [a2, a3]) a1 = Via1,
благодаря чему^Э) приводится к виду:
(rot F) а' = J= | да (F %) - ± (F %)} .
Две остальные компоненты rotF получаются из F1) перестановкой
индексов. Таким образом, согласно B1):
8
rot f=S ^rot F a^a*- F2^
Вспоминая, что Fa4 является ковариантной компонентой /f, мы получаем из
F1) для ротора вектора в системе обобщённых координат выражение
Рассмотрим, наконец, операцию Д<?, под которой мы должны понимать
divgrad<p- Нам необходимо только положить в E5) F = grad9- Контра-
вариантные компоненты градиента будут:
3=1 3 = 1
F4)
КООРДИНАТНЫЕ СИСТЕМЫ 11.16] 53-
Следовательно,
divgrad? = A? = -l=£ j &(*>Уё£)- F5)
Ы6. Ортогональные системы. Единственное ограничение, которое было
пока наложено на базисные векторы, это требование их некомпланарности.
Однако в большинстве случаев оказывается, что в приложениях с успехом
могут быть использованы только ортогональные системы, для которых
выведенные выше формулы существенно упрощаются. Косоугольные системы также
могут иметь большое практическое значение, но, к несчастью, они приводят^
к дифференциальным уравнениям в частных производных, которых
современный анализ разрешить не может.
Координатные векторы аь а2> а3 ортогональной системы по
определению взаимно перпендикулярны, откуда следует, что а* параллелен а$ и обра-
тен ему по величине:
at«i eii
Далее,
aja2 == а2а3 = а3а! == 0, F7)
откуда gy — O при i-ф]. Обычно в- случае ортогональных систем принято
вводить сокращённые обозначения 1):
h = Vgu> К = УИь h^Vlhs, F8)
^ = - = 1. F9)
gu ht
Величины h( могут быть подсчитаны по формуле
хотя обычно их значения очевидны из геометрии системы. Элементарна»
ячейка, ограниченная координатными поверхностями, является теперь
параллелепипедом, рёбра которого равны
ds1 = /4 du1, ds2 = h2 du2, ds3 = h3 du?f G1)
а объём
dv = hx /z2 /z3 du1 du2 du\ G2)
Все недиагональные члены в детерминанте g исчезают и поэтому
V~g=KhJib. G3)
Различие между контравариантными и ковариантными компонентами
вектора по отношению к основной или взаимной базисной системе
существенно для понимания инвариантных свойств дифференциальных операторов^
и скалярных и векторных произведений. Однако в фиксированной системе-
отсчёта это различие в большинстве случаев можно игнорировать. В этом,
случае удобно выражать вектор F через его компоненты или проекции Flt..
F2, F3 B ортогональной базисной системе единичных векторов ib i2, i3.
Согласно B2) и F6), имеем:
а,- = ЗД, а* = ^1г. G4>
!) Эти величины называют коэффициентами Ламэ. Прим. ред.
54
ГЛ; I. УРАВНЕНИЯ ПОЛЯ
Контравариантные и ковариантные компоненты F, выраженные через
компоненты Fit будут
'Ч
Кроме того,
^/'lii+^i.-r/Vs. G6)
i.ik = hjk. G7)
Градиент, дивергенция, ротор и лапласиан в ортогональной
криволинейной системе координат могут быть написаны непосредственно на основании
результатов предыдущего раздела.
j, Из D9) мы имеем для градиента:
grad?^ *i,.
G8)
3=1
Согласно E5), дивергенция вектора F будет:
divF=ds[s-'(*AF') +»(W*) +ei(A.V,)] • G9>
По уравнению F3), для ротора F имеем:
rotF=7ik[e|(ABFs)-^№F2)]i.+ ^ х
+тк [т (V.) - т «л)] к + h\R [& (*л) - ± (*,#=■,)] i, (so)
Можно заметить, что (80) представляет собой'разложение детерминанта:
h^ h2\2 /*3i3
rotF
1
ъ.хнгнг
du1
du*
du*
(81)
h\F\ № hsFs
Наконец, лапласиан инвариантного скаляра о будет:
v~^2ft3la«4 fcj d«y ' ди*\ h2 диУ~Т~диЗ\ h3 дФ)\' ^£>
Под инвариантным скаляром подразумевается величина, подобная
температуре или энергии, которая инвариантна при вращении координатной
системы. Числа, которыми^измеряются компоненты F,- вектора F тоже являются
скалярами, но* при преобразовании базисных векторов они
трансформируются и не являются поэтому инвариантными скалярами.
При исследовании поля мы часто встречаем операцию
rot rot F = grad div F — AF.
(83)
До сих пор мы не 'придали никакого смысла AF. В прямоугольной
декартовой системе координат л;1, х2, хъ ясно, что этот оператор эквивалентен
d*F*
d^Fi
2d * dt*1J ' д (л:2J ' д (л?J [
(84)
КООРДИНАТНЫЕ СИСТЕМЫ [1.18]
55
т. е. лапласиану, действующему на прямоугольные компоненты F. В
обобщённых координатах rot rot F представляется детерминантом.
rot rot F
1 .
hzh3 1
_d_
1 .
д
du2
ък [ш < V5".) ~ Шг (w] ^ [ш WJ ~ Ш < w]
1 .
ft,fc, 'в
a_
/^,[ai(V.)-^(AiFi)]
(85)
Вектор AF можно получить, вычитая (85) из развёрнутого выражения для
graddivF. Полученный результат будет отличаться от того, который
получается при непосредственном применении оператора Лапласа к
криволинейным компонентам F.
1.17. Уравнения поля в обобщённых ортогональных координатах.
Во всякой ортогональной системе криволинейных координат,
характеризующейся коэффициентами hlt h* A8, уравнения Максвелла могут быть
разложены в систему восьми дифференциальных уравнений в частных
производных для скалярных компонент векторов поля:
4[я.(*А>-»М+^-°-|
1
h3h±
1
hxh2
gp(V^)-ap(Vyj
+
дВ2
dt
0. \
(I)
1
1
hihz
А(^)-я4г(^з)
d«8V"l7 dul
3 (ВД ^
ак1
дм-
(W
= J2. }
dt
dD2
dt
Яг <Wi) + ^1 <MA) + 2P < MA) = 0.
^г (Wi) + aJ2 (¥A)+^ (MA) = We p.
(П)
(III)
(IV)
Разрешить в общем виде уравнения этой системы так, чтобы разделить
компоненты векторов поля и получить уравнения, которым удовлетворяла бы
каждая из компонент в отдельности, не представляется возможным. В каждой
конкретной задаче необхбдимо максимально использовать выгоды и особые
возможности, предоставляемые различными координатными системами.
1.18. Свойства некоторых простейших систем. Как было показано,
ортогональная координатная система полностью характеризуется тремя
метрическими коэффициентами hv h2, A8. Эти параметры будут теперь
определены для некоторых элементарных систем; в некоторых случаях, для удобства
ссылок будут приведены и дифференциальные операторы.
56
ГЛ I. УРАВНЕНИЯ ПОЛЯ
6
1. Цилиндрические координаты. Пусть Р' будет проекцией точки
Р(х, у, г) на ^-плоскость, и г, 0 будут полярными координатами точки
Р' на этой плоскости (рис. 7). Переменные
* «i = r, и2 = 0, u* = z (86)
называются круговыми цилиндрическими координатами. Они связаны с
прямоугольными координатами уравнениями:
л; = г cos 0, у~г sin О, г = 2". (87)
Координатными поверхностями являются коаксиальные круговые цилиндры*
'х'
Рис. 7. Круговые
цилиндрические координаты.
Рис. 8. Сферические коорди-
» i наты.
пересекаемые ортогонально плоскостями 0 = const, и ^ = const. Бесконечно
малый элемент длины равен
ds2 = dr* -J- rW -f- ^2, (88)
откуда ясно, что метрические коэффициенты равны:
/г1==1, /f2 = r, /г3=Ь (89)
Если Л —какая-либо скалярная, a F — векторная- функция координат, то
находим: ' ~
\
dfrF-J^ + lg+g
з.
>
\ (Щ
2. Сферические координаты. Переменные:
й1==г, «2 = &, «8 = 9, (91)
связанные с прямоугольными координатами преобразованием
* д: = г sin & cos <р, у = г sin • Ь sin ©, 2r=rcos0, (92)
называются сферическими координатами точки Р. Координатные поверхности
re==const.—концентрические сферы, пересекаемые меридиональными
плоскостями tp'= const, и семейством конусов Ъ = const. Единичные векторы
hs h* h проводятся в направлении возрастания г, Ь и о так, что
составляют правую базисную систему, как показано на рис. 8. Линейный элемент
КООРДИНАТНЫЕ СИСТЕМЫ П.1*1
ЪТ
равен
dt? = dr2 + г2 d№ -J- г2 sin9 & du*,
откуда для метрических коэффициентов получаем:
(93>-
(94>.
/г2 ===== 1, h2 = ri /z3=rsin0.
Эти значения приводят к следующим выражениям:
divF==^№i) + _^_^ (sin8F2) + __L_^;
v r*drV dr) i" r'sin» d»^sin d&J"*" r*sin2 & d<p2 *
3. Эллиптические координаты. Пусть координаты двух фиксированных
точек Pt и Р2, расположенных на оси дг, будут х = с и х-= — с и пусть
гх и г2 будут расстояния переменной точки Р в г-плоскости от Рх и Р2.
Тогда переменные
и1 = ^ к2 = 4j, «3 = ^ (96)
определённые уравнениями
П + г2 „ rt—r2
Г
Y]:
(97>.
2с ' ■' 2с
называются эллиптическими координатами. Из этих соотношений видно, что
&>1; — 1<т)<1. (98>
Координатная поверхность £ = const, есть цилиндр эллиптического сечения,.,
фокусы которого суть Pj и Р2. Большая и малая полуоси эллипса ^ даются
формулами:
a = d, Ь = сУР—1 . (99)
а эксцентриситет равен
A00)
А 5
Поверхности tj = const, представляют собой семейство конфокальных
гиперболических цилиндров, состоящих из двух полостей каждый, как показана
на рис. 9. Уравнения этих двух конфокальных систем будут
х*
f
„2 Xй
■ г* _ .
откуда мы получаем формулы преобразования:
с\
х~сЬ\, y = cY(& —1)A—rf) r z = z.
A01)
A02)
Переменная i\ соответствует косинусу угла, измеряемого от оси лг, и
следовательно, единичные векторы i±, i2, i3 правой базисной системы
направлены так, как показано на рис. 9, где вектор i3 перпендикулярен к
плоскости чертежа и направлен от читателя.
i
-58 -- ГЛ> I. УРАВНЕНИЯ ПОЛЯ
Метрические коэффициенты подсчитываются из A02) и G0), откуда
СУ 1-rf'
_^/ИЗ
h^cy
е2—1
h*
Лд=1.
A03)
4. Параболические координаты. Если г, Ь — полярные координаты
точки на г-плоскости, то можно определить два семейства взаимно
ортогональных парабол уравнениями:
&
;г- _ &
$ = Уг sin -ъ, ii = yrcos -s- •
A04)
Поверхности £= const, и v\ — const, представляют собой пересекающиеся
параболические цилиндры,
образующие которых параллельны оси г,
как показано на рис. 10. Параметры
Ч)-Зтт/2
и1 = £, и2 = ij.
яа
A05)
называются параболическими
координатами. Заменяя в A04) г и &
прямоугольными координатами,
находим: %
A06)
откуда для преобразования от
параболических координат к
прямоугольным имеем:
1)~TL ?■
х-
1
0чв—Р), у=-Ьь
Рис. 9. Эллиптические цилиндрические
координаты. Неопределённость в знаке
устранена тем, что полажено £ = ch и и
Y] = COS V. •
A07)
Единичные векторы \t и i2
направлены как показано на рис. 10,
причём i3 нормален к плоскости чертежа и направлен от читателя.
Подсчёт метрических коэффициентов из A07) согласно G0) даёт
*i = ^ —УР + Ч8. ^з=1-
A08)
5. Биполярные координаты. Пусть Рх и Р2 — две фиксированные точки
на какой-либо .г-плоскости с координатами (а, 0), (— я, 0) соответственно.
Уравнение ■ .
(* — «cth62 + V2 = «2csch2^ A09)
с параметром £ описывает два семейства окружностей с центрами, лежащими
на оси х. Эти два семейства симметричны относительно оси у, как показано
иа рис. 11. Точка Pt {a, 0) соответствует £ = -|-со, в то время как её
изображение Р2 (—а, 0) достигается при £== — оо. Линия, даваемая уравнением
A09) при £ = 0, совпадает с осью у. Ортогональное семейство также
представляет из себя семейство окружностей, центры которых лежат на оси у
и которые все проходят через фиксированные точки Pt и Я2. Они
определяются уравнением:
* ' x2-j-(y—a ctg y]J — a2 cosec2 kj, (НО)
КООРДИНАТНЫЕ СИСТЕМЫ 11.18]
59
в котором изменение параметра ч\ ограничено пределами 0<Cif)^2iT. Для
того чтобы координаты точки Р в заданном квадранте были однозначными,
каждая окружность этого
семейства разделяется точками Рх и
Р2 на два сегмента. Значения
меньше 7с, приписываются дугам,
лежащим выше оси х, в то время
как нижние дуги обозначаются
значениями yj, равными те плюс
значение tj, соответствующее
верхнему сегменту той же окруж-
иости.
Переменные
$=5
Ь
?v
УН
п-о
и1
г, «2=7!, «»=* (in) ^
«азываются биполярными
координатами. Из A09) и (ПО)
преобразование к-прямоугольным
координатам получается в виде:
ash% )
У
ch£ — cosy] *
«sinij
ch£ — cos y] '
tf
4-
\ 012)
Z'-~5
---4
(\Jk
7J=-4 у
$r
\&
_Д^-;
bo
X
——-lAl'?
У$-г
>4v
•q-S
Рис. 10. Параболические координаты.
Единичные векторы ij и i2 направлены в сторону возрастания ^ и ч\, как
ш.казано на рис. 11, в то время как i3 направлен от читателя вдоль оси z.
Подсчёт метрических коэф-
l/tj-.TlfG
фициентов даёт:
А«
а
d ch £ — cos y]
h*
1A13)
1.
6. Сфероидальные
координаты. Эллиптические
координаты были образованы
трансляцией системы конфокальных
эллипсов вдоль оси z.
Сфероидальные координаты
получаются вращением тех же
эллипсов вокруг оси симметрии.
При этом необходимо
различать два случая в зависимости
от того, происходит ли
вращение вокруг большой или
вокруг малой оси. На рис. 9
большая ось ориентирована
вдоль оси х прямоугольной системы координат. При вращении рисунка
вокруг этой оси образуется система вытянутых сфероидов, ортогональными
поверхностями которых является система двуполостных гиперболоидов.
Если о измеряет угол поворота от оси у в л;-плоскости, а г — расстояние
точки по перпендикуляру от оси х, то
Рис.* 11. Биполярные координаты.
.y—^coso, z = r sin ©.
A14)
60 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Переменные
u1 = Z, u? = % и3 — <?, A15)
определённые уравнениями (97) и A14), называются вытянутыми
сфероидальными координатами. В качестве уравнений двух конфокальных систем
мы имеем вместо A01):
v2 pa v2 »»2
gr-f gnzT^2' ^~тг^вс9» A16>
откуда получаем
Х = С%Ч[Ъ Д> = С ]/"((? 1)A Y]2)C0SO, ]
> A17)
z = cV(F—l)(l~rl2)smo, )
5>1, —1<ч<1, 0<в<2«. A18)
Подсчёт метрических коэффициентов даёт
.hi=cVh=V' h*-cV~b^$> *8=cV(p—i)(i—4е). (П9>.
Если эллипсы рис. 9 вращаются вокруг оси д>, то сфероиды получаются
сплюснутые и фокальные точки Рх и Р2 описывают круг в плоскости у = 0.
Пусть г, <?, у будут цилиндрические координаты "относительно оси у:
2 —г cos о, Ar = rsin<p. A20)-
Если под Pj и Р2 мы будем подразумевать «то^рь точки, в которых фокаль- •
ное кольцо радиуса с пересекает плоскость o = const., то переменные £ и ^,
будут попрежнему определяться уравнением (97), но в качестве уравнений
координатных поверхностей мы будем, иметь:
откуда выводим преобразование от сплюснутых сфероидальных координат
«1 = 6, в»«Ч| в» = в A22>
к прямоугольным координатам:
* = cfrq sin ©, jj = с У(Ф— 1) A — 42), z = cb\co$®. A23)
Поверхности £ = const. — сплюснутые- сфероиды, в то время как
ортогональное семейство *] —const, представляет собой однополастные гиперболоиды-
. Метрические коэффициенты будут
*i='l/~pzi£» u2=/|5~?> h = ^- (i24>
Практическую ценность сфероидальных координат можно понять и&
того, что при приближении эксцентриситета к единице, вытянутые
сфероиды становятся стержнеобразными, а сплюснутые сфероиды
вырождаются в плоские эллиптические диски. В пределе, при фокальном расстоя- '
н«и 2с и эксцентриситете, стремящемся к нулю, сфероидальные координаты
совпадают со сферическими, причём £-»/", а ч\ -> cos 0.
7. Параболоидальные координаты. Другая система координат с
симметрией вращения мож^т быть получена вращением парабол рис. 10 вокруг
их осей симметрии. Переменные
• К1 =aes \% В2 = Y], И3 — <p, A25)
КООРДИНАТНЫЕ СИСТЕМЫ П.18]
61
определённые соотношениями:
1
X = fr] cos 9, J = Sy] sin <p, гг = -2-(^2—yj2),
A26)
«азываются параболоидальными координатами. Поверхности £ = const.,
iq = const, являются параболоидами вращения вокруг оси симметрии, за
«которую в данном случае была взята ось г. Плоскость у = 0 пересекается
с этими поверхностями по кривым:
*2 = 2£2(|--г), *» = Jif (£+*),
A27)
которые, очевидно, являются параболами с фокусами, расположенными
& начале координат и с параметрами £2 и yj2. Метрические коэффициенты равны
8. Эллипсоидальные координаты. Уравнение
м-
V-2 V2 . 9й
A28)
A29)
является уравнением эллипсоида с главными полуосями a, b и с.
Тогда
л;2
«2+£
.У
1~ 6*4-5 ~*~
z>-
+ g i c2-H
X2
+
У
62 _j_ v]
+
4-
у
+
c2 + rj
= 1
= 1
= 1
(-
C2>1Q>-
£2>c>
&2),
-a2)
A30)
являются соответственно уравнениями эллипсоида, однополостного
гиперболоида и двуполостного гиперболоида, которые конфокальны с эллипсоидом
A29). Через каждую точку пространства будет проходить только одна
поверхность каждого рода и каждой точке будет соответствовать только
одна система значений I, yj, С.
Переменные
и1
г, «я
%
и*
A31)
называются эллипсоидальными координатами. Поверхности yj = const. — одно-
полостные гиперболоиды, а \ = const. — двуполостные. Преобразование
к прямоугольным координатам получается разрешением A30) относительно
х, у, г, что даёт:
-- - - ' +л«)(С + л*)ТА \
г — -4- Г(ё + *а)(ч+Д*)(С + А«I*
~~L (*2 — я2) (с2 — a2) ' J '
_+. [(б + УХч + ^ХС + У)!^ ^
— L (с2 — *2) (a2 — *2) J '
-4- Г F + ^H
— L («2-
(у]4-с2)(С + с2)
с2) (б2 —с2)
■]*. J
A32)
Взаимная ортогональность этих трёх семейств поверхностей может быть
установлена подсчётом коэффициентов g4j из A32) при помощи D5). Они
равны нулю при Ьф.}', для диагональных членов находим:
If (е-чХб-С) T/t )
2 L(S + a2)E + 62)(^ + c2) J »
If (ч-О(ч-б) ГА .
2LD + «2)D + 62)^ + c2)J '
1 f (c-енс-ч) т/»
2 L(^ + «2)(^ + &2)(C + c2)J • J
A33)
62 ГЛ. I, УРАВНЕНИЯ ПОЛЯ
Удобно ввести сокращённое обозначение:
Ka = V(s+<P)(s + P){s + c*) (* = *, ч, С). A34)
Для лапласиана от скаляра <|> мы получаем тогда:
м=A-,)(£Д)(,_С) [ (ч-о *| (* g) +<с-э*,£(*,$+
ТЕНЗОРЫ ПОЛЯ
1.19. Ортогональные преобразования и их инварианты. В теории
относительности ставится задача такой формулировки законов физики
и, в частности, уравнений электромагнитного поля, чтобы они были
инвариантны по отношению к преобразованиям системы отсчёта. Хотя в этой
книге нам не представится случай рассматривать основы теории
относительности, тем не менее, иногда оказывается выгодным пользоваться
симметричной четырёхмерной системой обозначений, введенной Минковским и Зом-
мерфельдом, и преобразованием Лоренца, по отношению, к которому
уравнения поля инвариантны. Для определения величин*, остающихся
инвариантными при преобразовании от одной системы криволинейных координат
к другой, существенно различие между ковариантными и контравариант-
ными компонентами векторов и между основяоЬ и взаимной координатными
базисными системами. Однако для наших целей достаточно будет
ограничиться системой прямоугольных декартовых координат, в которых, как мы
видели, ковариантные и контравариантные компонентны совпадают1).
Пусть ij, 12, i3 три ортогональных, единичных базисных вектора,
определяющих прямоугольную координатную систему X, начало которой
находится в фиксированной точке О, и пусть г — вектор, определяющий
положение какой-либо точки Р по отношению к О:
г == ATji! -f- x2i2-j-x3i3. A)
Так как
то координаты Р в системе» X будут
*fc = rifc. C>
Предположим теперь, что i^, \'г, \'3 являются базисными векторами второй
прямоугольной системы X', начало которой совпадает с О и которая,
следовательно, отличается от X только поворотом координатных осей.
Так как
г = <ii4-*& + *&, D)
то координаты точки Р по отношению к системе X будут:
х1. = и;=xtf. -}- х,ц\г. + *8i8i;f E>
т. е. каждая координата Р в системе X' является линейной функцией её
координат в системе X, причём коэффициенты
' , */& = *>'& F>
1) Этот раздел основан главным образом на следующих работах: Minkowski.
Ann. Physik. 47, 927 A915); Sommeifeld, Ann. Physik. 32, 749 A910) и 33, 649 A910);
Mie, Ann. Physik..37, 511 A912); Паули, Теория относительности, Гостехизда^
1947^г.
тензоры поля [Lis]
билинейной формы являются, очевидно, направляющими косинусами
координатных осей X' по отношению к осям X. Следовательно, вращение
прямоугольной системы координат влечёт за собой изменение координат точки,,
которое может быть представлено линейным преобразованием:
^=2V* С/=1.2,3). G)
Коэффициенты а^к подчинены определённому условию, которое является
следствием того факта, что расстояние от точки О до точки Р, иначе
говоря, абсолютная величина г не зависит от направления координатных
осей:
S ЪГ= ± ЦJ. (8)
з=1 з-1
Но:
iцJ = s(sа&*)(i«****)=ii*#**s(****)» <9>
i = l д = 1 * = l u = 1 » = lk = l /=1
откуда следует, что
4i f *» ПРИ ' = &> Mn,
j = i [ 0, при izpk.
Уравнения A0) выражают соотношения, которым должны удовлетворять
косинусы углов между координатными осями для того, чтобы последние были
ортогональными, и они известны поэтому как условия ортогональности.
Преобразование G) при условии выполнения A0) называется ортогональным
преобразованием. Можно показать, что прямым следствием A0) является
равенство единице квадрата детерминанта | а^к \ и, следовательно, \ ajlc \ = ztl.
Любая система коэффициентов а$ъ удовлетворяющих A0), определяет
некоторое ортогональное преобразование в том смысле, что соотношение (8)
выполняется. Геометрически преобразование (8) представляет вращение
только тогда, когда детерминант | а$к \ = -J- 1. Ортогональное преобразование
с детерминантом, равным—1, соответствует отражению с последующим
вращением. .
Поскольку детерминант ортогонального преобразования не равен нулю,
хк могут быть выражены как линейные функции х'.. Проще всего, получить
• эти соотношения, написав, как и в E):
или
**= iw4 (*=*. 2, з>> <12>
откуда, совместно с (8), следует, что
з
2 ааащ — ^ifr A3)-
3=1
& Пусть А—произвольный приложенный (т. е. с закреплённым началом) Еектор •
а=2лА=2-4^- A4>
<4 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Компоненты А', этого вектора по отношению к системе X' даются
выражениями:
так что прямоугольные компоненты фиксированного вектора преобразуются
при вращении координатной системы как координаты точки. Хотя каждый
вектор имеет в общем случае три скалярные компоненты, отсюда не
следует, что любые три скалярные величины составляют компоненты вектора.
Для того чтобы три скаляра Аи А2, А3 могли быть интерпретированы
.как компоненты вектора, необходимо, чтобы они преобразовывались как
координаты точки.
Среди скалярных величин мы должны различать вариантные скаляры
и инварианты. Величины, подобные температуре, давлению, работе и т. п.,
не зависящие от ориентации координатной системы, называются
инвариантами. С другой стороны, координаты точки и компоненты вектора обладают
■численной величиной, которая меняется при преобразовании координатной
системы. Такие величины мы назовём вариантными скалярами. Известно, что
•скалярное произведение АВ двух векторов А и В я§ляется скаляром.
Спрашивается, что это за скаляр? В силу A2) и A3) мы имеем:
ав= 2 аа~ s (S V4)(£ ъЛ)=± *&• <16)
^Скалярное произведение двух векторов является инвариантом
ортогонального преобразования координатной системы.
Пусть о является инвариантом; рассмотрим совокупность трёх величин:
В силу A2)
«
и, следовательно:
dxi
ч--Зг-2&&-2<а <19>
&Xi ^dxk <Ц
* к=\ н * к = 1
Величины Bt преобразуются как компоненты вектора, и,
следовательно, градиент _ о
*™"Ь-Ц&,ь • <2°>
к = 1
подсчитанный в точке Р, является приложенным в этой точке
вектором.
Пусть Лг- будет прямоугольной компонентой вектора А и пусть
i
дх.
Тогда, по A8) и A5):
я« = -т£г- B1)
ТЕНЗОРЫ ПОЛЯ [1.19] 65
Откуда, согласно A0), следует, что
дА., 3
i = l 7.=1 j = l » = 1 3=1
Дивергенция вектора есть инвариант ортогонального преобразования
координатной системы.
Наконец, из того, что градиент инвариантного скаляра есть вектср,
а дивергенция вектора является инвариантом, следует, что лапласиан
з
A? = divgrad<?=Vi!i B4)
< = г дх*
является инвариантом при ортогональном преобразовании.
Трансформационные свойства векторов могут быть распространены и
на многообразия с числом измерений большим трёх. Пусть хи х2, xs, хА
будут прямоугольными координатами точки Р относительно координатной
системы X в четырёхмерном континууме. Положение точки Р по отношению
к заданному началу отсчёта О определяется вектором
г = 2 *А. iA=V B5)
3 = 1
Линейное преобразование
4
*;=2>,7Л, (/=1,2,3,4) B6)
называется ортогональным, если его коэффициенты удовлетворяют условию:
4
2вл=8й- К27)
3 = 1
Специальным свойством ортогонального преобразования является
инвариантность суммы квадратов координат:
2(^J = 2(*'J. B8)
3=1 3=1 J
Легко показать, что квадрат детерминанта, образованного из а^,
положителен и равен единице; следовательно, сам детерминант может быть
равен z±z 1. Однако, если B6) включает тождественное преобразование
*; = *,- (/ = 1,2,3,4), B9)
то детерминант должен быть, очевидно, положительным. Впредь мы
ограничимся подгруппой ортогональных преобразований, которые характеризуются
удовлетворением соотношений B7) и условием
«*Н + 1. (зо)
Тогда геометрически это преобразование соответствует вращению
координатных осей.
Мы определим теперь четыре-вектор как любую совокупность четырёх
вариантных скаляров Л4 (i=l, 2, 3, 4), преобразующихся при вращении
системы координат как координаты точки:
■^SV4» \=Ъа*А'г [C1)
k=l 3=1
5 Зак. 593. Теоржа Бгшзхрвмагвехиммь
66 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Тогда легко, как и выше, показать, что скалярное произведение двух* четыре-
векторов и четырёхмерная дивергенция четыре-вектора являются
инвариантами по отношению к вращению координатной системы:
ав=2лА=2л?;> C2)
к -1 э = 1
Далее, производные скаляра
В* = 1ъ (/=1,-2, 3, 4) C4),
преобразуются как компоненты четыре-вектора и, следовательно,
четырёхмерный лапласиан от инвариантного скаляра: ■]
4 4
□.?_2т&-2т*-. (85) ;
i = l г j=l 3
тоже инвариантен по отношению к ортогональному преобразованию. ;
1.20. Элементы тензорного анализа. Хотя большинство физических J
величин может быть классифицировано на скаляры, если они характеризуются \
только численным значением, и на векторы, если они характеризуются вели- J
чиной и направлением, существуют некоторые величины, которые не могут ."',
ёыть представлены должным образом ни посредством скаляров, ни посред- I
ством векторов. Смещение центра тяжести металлического стержня, напри- ]
мер, может быть охарактеризовано вектором; однако стержень можно также 1
растягивать вдоль оси, прилагая напряжения к двум его концам, без того, 1
чтобы центр вообще смещался. Величина, которая должна быть использована j
для того чтобы представить подобное растяжение, должна, таким образом, \
определять два направления. Неадэкватность векторного представления стано- i
вится ещё более очевидной, если попытаться описать объёмную деформацию, ;
принимая во внимание и боковое сжатие стержня. В этом разделе мы кос- I
нёмся тензорного исчисления только в простейшем виде, в каком оно является
подходящим аппаратом для рассмотрения подобных задач.
Пусть в трёхмерном континууме каждая прямоугольная компонента
вектора В являэтся линейной функцией компонент вектора А:
£?! = 7цА1 -}- T12A2-f- 7\3Л3,
В2 = Г21Л, + 7^А2 + 7'23Л3, C6)
Вя^ТмА1 + ТюА2-\-ТааА2.
Для того чтобы эта связь компонент В с компонентами А в системе X
сохранялась и при повороте системы координат, необходимо, чтобы
коэффициенты Tjk преобразовывались специальным образом. Следовательно,
Tjk являются вариантными скалярами. Тензор — точнее говоря, тензор
второго ранга, — мы определим теперь как линейное преобразование компонент
вектора А в компоненты вектора В, которое инвариантно по отношению
к поворотам координатной системы. Девять коэффициентов Tjk линейного
преобразования называются компонентами тензора.
Для того чтобы установить способ, по которому должны
преобразовываться компоненты тензога, напишем сначала C6) в сокращённой форме:
Bj=^TjkAk. \ C7)
ТЕНЗОРЫ ПОЛЯ [1.201 67
, Если C7) инвариантно по отношению к преобразованию
3 3 j.
*} = 2«/л, 2^я/*:==8гй> C8).
к -l э = \
то 7jk должны преобразовываться в Т'и так, чтобы имело место
Bi=^r'uAi 0'= 1,2,3). C9)
1 = 1
Умножим C7) на a{j и просуммируем по индексу у:
з зз
2 OijBj =2 2 a-ij Tjk Ak. D0)
j = i з - 1 к = -i
Но
^=2^Л л*=2«*и; D1>
и> следовательно, D0) запишется в виде
1 = 1-j = l fc = l Z=l
Итак, компоненты тензора второго ранга должны преобразовываться по закону:
П* = 2 2 ai3amTiu С ^=1,2,3) D3)'
и обратно, любая совокупность девяти величин, которые преобразуются
согЛадно D3), составляет тензор.
'Аналогичным путём можно показать, что обратное преобразование будет:
* -с
Если порядок индексов во всех компонентах тензора может быть
изменён без того, чтобо1 изменился сам тензор, так что 7)ъ~Тщ, то говорят,
что тензор симметричен. Тензор называется антисимметричным, если
^перестановка индексов в каждой из компонент меняет в результате знак тензора.
Диагональные члены антисимметричного тензора очевидно исчезают, в то
время как для недиагональных членов T3-jc = — Тщ. Из D3) ясно, что если
Tjk ~ Tkf т0 и гй = Ти- Точно так же из Tj}, = — Tkj следует, что и
Т'и = — Т'и. Таким образом, симметричный или антисимметричный характер
тензора инвариантен по отношению к вращению координатной системы.
Сумма или разность двух тензоров строится из суммы или разности
соответствующих им компонент. Если 2R—сумма тензоров 2S и 2Т, 1) то
компоненты 2R, по определению, равны:
V==«SJ*+ Ti* (/» *== 1» 2, 3). •'" D5)
Ввиду линейного характера преобразования D3), величины Rjk
преобразуются так же, как S3-k и Т3-к и, следовательно, составляют компоненты
тензора 2R. Из этого правила следует, что любой несимметричный тензор
1) Тензор, второго ранга будет отмечаться верхним индексом, как написано
в тексте.
5*
68
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
может быть представлен в виде суммы симметричного и антисимметричного
тензоров. Полагая, что 2R — данный асимметричный тензор,- мы строим
симметричный тензор 2S с компонентами
Sjk^^iRft + R^Sv D6>
и антисимметричный тензор 2Т с компонентами
Tjk = у {Rjjc — Rkj) — — Tkj. D7)
Тогда, согласно D5), сумма так построенных 2S и 2Т равна 2R.
В трёхмерном многообразии антисимметричный тензор сводится к трём
независимым компонентам и в это'м смысле напоминает вектор.
Преобразование C6) сводится, например, в этом случае к такому:
В,= 0 — Т21А2 -f Г]3Л3,
Щ= ПЛ+ 0 —^з2^з, D8)
В9=*—Т19А1+Т9ЛА2+ 0.
Но В; являются компонентами вектора:
В=1ТА1,- D 9
где вектор Т имеет компоненты
Напомним теперь, что в векторном анализе принято различать полярные
векторы, используемые, например, для представления перемещений и
механических сил, от аксиальных векторов, с которыми связаны направления
вращений. Геометрически полярный вектор представляется" отрезком или линией,
в то время как полярный вектор соответствует площади. В результате
векторного перемножения двух полярных векторов мы получаем типичный
аксиальный вектор, и из предыдущего мы должны заключить, что
аксиальный вектор в действительности является антисимметричным тензором и что
его компоненты должны по существу обозначаться двумя индексами, а не
одним. Таким образом, для компонент Т= [АВ] мы напишем:
Tjk = А£к — AjJBj = — Тщ (У, h = 1, 2, 3). E1)
При повороте системы координат компоненты А и В преобразуются согласно
i=i * ъ=1
Подставив эти значения в E1), находим:
*Р* ~ \Щ=22 v* № ~ ЛК) E3>
l = 1 г ~ 1
соотношение, которое совпадает с D4) и показывает, что компоненты
«векторного произведения» двух векторов преобразуются как
компоненты тензора. Существенная разница в свойствах полярных и аксиальных
векторов (с помощью которых представляются такие величины, как угловые,
скорости, моменты и т. п.) теперь ясна: аксиальные векторы являются
векторами только по способу их построения, но не по закону их'преобр'азо-
• вания, Существзнно добавить, что антисимметричный тензор может быть
представлен аксиальным или псевдо-вектором только в трёхмерном
пространстве, и то только в прямоугольных компонентах.
ТЕНЗОРЫ ПОЛЯ [1.20.] 69
Поскольку векторное произведение двух векторов является фактически
антисимметричным тензором, можно предвидеть, что то же справедливо и
дА-
в отношении ротора вектора. То, что величина -=—-, где Л$ — компонента
OXjc
вектора А, является компонентой тензора, видно сразу же из уравнения Г22):
дА'- vN V4 дА*
в t if = i й- = 1 ft
дАк dAj
Компоненты rot A:
T»-TJf—w—г« </•* = ». *. а) <55)
преобразуются, следовательно, как компоненты антисимметричного тензора.
Дивергенция тензора определяется как следующая операция:
з
(div2T),.= 24v==^ (/=1*2*3)- E€>
Легко показать, что величины В- преобразуются как компоненты вектора.
Имеем:
1?-1в»^ = 12'*в«в*-£ E7)
* fc = 1 « й- = 1 з! = 1
или, суммируя по индексу / и применяя условие ортогональности:
з -,^ з / з .,„, \ з
3 = 1 'fc = l л j = :
z = i * i=i *& = i K i=i
Дивергенция тензора второго ранга является вектором, или тензором
первого ранга. Дивергенция вектора есть инвариантный скаляр или тензор
нулевого ранга. Это — примеры процесса, известного в тензорном анализе
как свёртывание или сокращение индексов.
Как и в случае векторов, понятие тензора может быть распространено
и на многообразие четырёх измерений. Любая совокупность 16 величин,
преобразующихся по закону
П*= 2 2 Wm hb V> / = 1, 2, 3, 4) E9)
или ему обратному:
hn = 22 Vi*£« (У, Л - 1, 2, 3, 4) F0)
г=11=1
называется тензором второго ранга в четырёхмерном многообразии. Как и
в трёхмерной случае, говорят, что тензор симметричен, если 7)^— 7^-,
и антисимметричен, если Т3-ь = —• Тщ, причём 7^ = 0. Из определения ясно,
что антисимметричный четыре-тензор имеет только шесть независимых
компонент. Развёртывая E9), заменяя Тщ на — Тз1с и затем перегруппировывая
члены, мы получаем формулу для преобразования антисимметричного тензора
в виде соотношения:
т'ц= 21 2 <*«*» ~ ew ri*в 2 2
^ (Л>У). F1)
.70 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Любые шесть величин, которые преобразуются по этому закону, составляют
антисимметричный четыре-тензор или, как его часто называют, шести-вещпор.
В трёхмерном пространстве векторное произведение представляется
Геометрически в виде площади параллелограма, стороны которого
определяются двумя векторами, проведёнными из общего начала. Компонентами
этого произведения являются тогда проекции площади на три координатные
плоскости. По аналогии векторное произведение в четыре-пространстве
определяется как «площадь» параллелограма, образованного двумя четыре-
векторами А и В, проведёнными из общего начала. Компонентами такого
обобщённого произведения будут проекции этого параллелограма на шесть
координатных плоскостей, площади которых равны:
Tjl{ = AjBk — A1iBj^= - Tkj (/,'*= 1, 2, 3, 4). F2)
Векторное произведение двух четыре-векторов является,
следовательно,-антисимметричным, четыре-тензором или шести-вектором.
Если опять А является четыре-вектором, то можно показать, как и в E4),
что величины
Т*-щ-ъ;г-Тч С/. * -1. а. в. 4) F3)
преобразуются как компоненты антисимметричного тензора. Величины Tjk
могут быть интерпретированы как,компоненты ротора четыре-вектора.
Как и fi случае трёх измерений, дивергенция четыре-тензора
определяется соотношением:
4 дТ
(div *Г), = ^ -£ U == 1, 2, 3, 4), F4)
т. е. является совокупностью величин, образующих, очевидно, четыре-вектор.
!1.21. Пространственно-временная симметрия уравнений поля. Если
в уравнения электромагнитного поля ввести в качестве независимых
переменных четыре длины:
х1 = х, х2=у, x2==z, Xi = ict, F5)
где с — скорость света в пустом пространстве, то сразу становится
очевидной замечательная симметрия этих уравнений. Записанные в
прямоугольных координатах уравнения
rotH —-~ = J (II), divD = p (IV)
предстарляются системой:
F6)
0 , дН3 дНг .с dD1==J
' дхъ дх5 дх± *'
dxt dx2~t~ u lc dx4~-JZ'
. dDx . . dD2 , . dD3 , _
Будем рассматривать правые члены уравнений этой системы как компоненты
плотности «четыре-тока»:
i
Jt—Jx, J2 = Jyi Jz=Jz, Л = ^Р. F7)
ТЕНЗОРЫ ПОЛЯ [1.21]
71
и введём в левые части систему зависимых переменных, определённых
соотношениями:
ои = о
G21 = — На
G31 = Н2
G41 = icD1
G12 = Щ
G22 = 0
Оая = —/fj
G42 = f'cD2
G13= — H2
^23 = Я1
G33 = 0
G43 = /cDs
G14 = — icDt
G24 = — icD2
Gu=—icDs
G44 = 0.
> F8)
Тогда в системе отсчёта ^уравнения (II) и (IV) сведутся к уравнениям
4
OUn'T,
(/=1,2,3,4). F9)
fc=i
Только шесть величин из Gjfe независимы, и сходство системы этих величин
с компонентами антисимметричного четыре-тензора совершенно очевидно.
Так как дивергенция четыре-тензора является четыре-вектором, то из F9)
следует, что если Ojk составляют тензор, то Л- являются компонентами
четыре-вектора. Обратно, если мы сможем показать, что J действительно
является четыре-вектором, то мы можем сделать заключение о тензорном
характере 2G. До сих пор, однако, мы не привели доказательств в
подтверждение подобного предположения. В предшествующих разделах было
показано, что векторные или тензорные свойства системы скалярных величин
определяются способом их преобразования при переходе от одной системы
отсчёта к другой. Очевидно, ортогональному преобразованию координат хк
соответствует одновременное изменение как пространственных координат
л:, у, z, так и времени /, и только обратившись к опыту, мы сможем
сказать, какого преобразования векторов поля можно ожидать при подобных
обстоятельствах. В разделе 1.22 мы приведём кратко экспериментальные
факты, которые приводят к заключению, что Jk действительно являются
компонентами четыре-вектора, a Gjjc — компонентами тензора поля. Временно
мы будем рассматривать F9) и выводы, которые последуют ниже, просто
как сжатую и симметричную запись уравнений поля в фиксированной
системе координат.
Два однородных уравнения
rotE
дВ
61
= 0 (I), div'kB = 0 (III)
представляются системой:
0 +
дЕо
дх*
дЕ3
—£?+ °
dx-i
dff2
дВ1
dxt
дЕ* , .. dBi
дх3 ' дх±
о, ]
dEt
дВ*
дх»
дхо.
о,
0.
дЕА
дВч dBs
дВ3
дх»
дх±
0
G0)
72
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
После деления первых трёх уравнений на ic, система антисимметричных
компонент определится следующим образом:
Fn = 0
F21 = -B3
F31 = В2
F12 == В3
^22 = 0
F —
Bi
F13 = — B2
F2b = BX
^зз = 0
'24 == 7 ^2
F F
'34 — ,. CS
Г A1 jtl
41
Г ЛО jto ' J!) = bO i АЛ U
42
43
44
G1)
Все уравнения G0) содержатся тогда в системе:
dF.
ч
дхь
+
dF*,
ы
дх/.
dXi
0.
G2)
где z, у, £— любые три числа из четырёх чисел 1, 2, 3, 4.
Системы F8) и G1) согласованы в том , смысле, что в каждой из них
действительные компоненты связаны с магнитным полем, в то время как
мнимые компоненты связаны с электрическим полем. Чтобы отметить это
расчленение, удобно представить систему компонент символами
2F = (В, — 4 Е), 2G = (Н, - icD).
G3)
Но уравнения поля могут быть с равным успехом выражены и через
«дуальную» систему
2F
* = (- {- Е, В), 2G* = ( — М),Н),
G4)
или
Fu = 0
^21 = Y^3
^31 = — Т
F41 = — В±
Е2
* | _
F2.z = 0
^32 =—El
fI^ — b.,
з?* I ts ■
* /
F23^ — TE1
/=i = o
^Гз = ~^з
i4
Fu
Fit
Fu
B*
G5)
и соответствующую систему для компонент 2G*. После подстановки этих
значений в (I) и (III), и (II) и (IV), соответственно, мы получаем:
4
0 (/ = 1.2,3,4),
V д/>
д3/ ,
<3xfc '
^J, дхк
к = 1
h {i,j, К /=1, 2, 3, 4).
G6)
G7)
Разными авторами было указано, что последнее представление, является
искусственным, так как G4) содержит в себе утверждение, что вектор Е —
аксиальный, а В — полярный, te то время как известно, что в
действительности верно обратное. Представление
dFM dF**
'—£-=° С-/. A==1. 2,3,4), G2)
dF--
дхь
дхл
dGjk
= !■ (j =1,2
ТВНЗОРЫ ПОЛЯ [1.21 J 7$
следует в этом смысле рассматривать как «естественную» форму уравнений
поля. К ним мы добавим ещё уравнение непрерывности
divJ + ^7 = °. (V>
dt
которое в четырёхмерных обозначениях примет вид:
ЪШ=°- <78>
Если выразить компоненты Fjk через компоненты «четыре-потенциала» Ф
посредством
дфь <5Ф,-
то можно легко убедиться, что уравнение G2) удовлетворяется при этом
тождественно. В трёхмерном пространстве векторы Е и В выводятся из
векторного и скалярного потенциалов с помощью соотношений
Е = —grade? — — , B = rotA, (80)
dt
или в компонентах
i д '/ i \ dAj дАк dAj
где индексы i, j, k следует брать в циклическом порядке. Очевидно, все
эти уравнения будут .заключаться в системе G9), если мы определим
компоненты четыре-потенциала соотношениями
Ф1 = АХ, Ф2 = ^, ФЛ = А„ Ф4 = 4?' <82>
Как и в трёх измерениях, четырёх-потенциал полезен только в том
случае, если мы можем определить из него поле 2G(H, —icD) наряду с полем
2F (В, ЕJ. Поэтому на Ф нужно наложить некоторое дополнительное
условие, чтобы F9) удовлетворялось, как и G2). Необходимо,
следовательно, чтобы компоненты Ojk были функционально связаны с Fjk. Мы
Ограничимся здесь обычным случаем однородной изотропной среды и
предположим, что соотношения линейны. Для того чтобы сохранить симметрию
обозначений, удобно писать фактор пропорциональности, который
характеризует среду в виде x,fc> так что
°Л< = ЪкГЛ'- (83>
Из F8) и G1) ясно, что *)
Yfe=— при у", k=l, 2, 3; -fyfc = sc2 при у" или k, равном 4. (84)
*) Соотношение (83) можно сохранить и для анизотропной в электрическом
или магнитном отношении среды при условии, что коорцинатные оси совпадают
с главными осями анизотропии. В случае наличия электрической и магнитной
анизотропии одновременно для этого необходимо, чтобы главные оси электрической ани-
ввтропии совпадали с главными осями магнитной анизотропии. [В общем случае
произвольной анизотропии связь между тензорами 20 и 2F должна быть установлена
с помощью тензора у четвёртого ранга. См. L. I. Mandelstamm und lg. Та mm,
Math. Annalen 95, 154, 1925. Прим. ред.]
74
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Фактически эти коэффициенты являются компонентами симметричного
тензора и, имея в виду последующие применения, мы придадим диагональным
членам значения:
Ъз -IT С/ = 1, 2, 3), Т44.= ртМ. (85)
Уравнение F9) можно теперь заменить следующим:
\^^~ = Jj G = 1,2,3,4). (86)
V4 dFft
Подставив сюда G9), находим, что (86) удовлетворяется при условии, чтэ
Ф является решением уравнения
4
2 -£з ^^=~^' ° ^г'2,3> 4)' (87)
k = l k
удовлетворяющим условию
S^fe^)==0 (/=1,2,3,4). (88)
Последнее соотношение, очевидно, эквивалентно
divA + {xe-^- = 0, (89)
а (87) заключает в себе два уравнения:
ДЛ —p-igii ^Ь 0'= 1, 2, 3) 1
л * i } (90)
г д& в r j
В свободном пространстве ^0=-^, Tjfc— — ДЛЯ всех значений индексов.
Уравнения (87) и (88) приобретают тогда простой вид:
Sf*i~^ i}4t- = ° (/=1.2,3,4). (91)
1.22. Преобразование Лоренца. Физическое значение полученных
результатов гораздо более важно, чем их чисто формальное изящество. Ряд
опытов, наиболее решающим из которых было знаменитое исследование Майкелъ-
сона и Морлея *), привёл к установлению двух фундаментальных постулатов,
весьма вероятных, если не абсолютно достоверных. Согласно первому из них,
называемому постулатом относительности, путём физических
экспериментов, проведённых в системе отсчёта X, невозможно обнаружить равномерное
поступательное движение по отношению к другой системе отсчёта X'. То,
что земля движется по орбите вокруг солнца, мы знаем из наблюдений над
удалёнными звёздами. Но если бы земля была окутана облаками, то никакие
наблюдения на её поверхности не смогли бы обнаружить равномерное
поступательное перемещение в пространстве. Течение естественных явлений не
должно поэтому меняться, если система координат, по отношению к которой
!) Michelson and Morley, Am. J. ScL, 3, 34, 1£87.
ТЕНЗОРЫ ПОЛЯ Ц.22] 75
производится отсчёт, движется без ускорения; Bqe системы отсчёта,
движущиеся равномерно и прямолинейно друг относительно друга, эквивалентны.
В том виде, в каком он нам сейчас понадобится, мы сформулируем этот
принцип относительности следующим образом: Законы физики,
надлежащим образом сформулированные, инвариантны по отношению к переходу
от одной системы координат к другой, движущейся прямолинейно с
постоянной скоростью относительно первой. Прямым следствием этого
постулата является то, что компоненты всех векторов или тензоров, входящих
в уравнения, должны преобразовываться одним и тем же способом, или
ковариантно. Существование подобного принципа, ограниченного
равномерным перемещением, было установлено для классической механики Ньютоном,
но его обобщением на электродинамику мы обязаны Эйнштейну.
Второй постулат Эйнштейна более примечателен:скорость
распространения электромагнитного возмущения в свободном пространстве является
универсальной константой с, не зависящей от движения источника. Это
предположение является, очевидно, прямо противоположным нашему опыту
в отношении механических и акустических волн в материальной среде, о
которых известно, что измеряемая их скорость зависит от относительного
движения наблюдателя и источника. Было сделано много попыток объяснения
экспериментальных фактов без обращения к такому радикальному
предположению, из которых наибольшее значение имела электродинамика Ритца1).
Результаты всех этих исканий показывают, что хотя постоянство скорости
света и не обязательно для объяснения отрицательных результатов опытов
Майкельсона-Морлея, но лишь один этот постулат совместим и с этими
опытами, и с другими оптическими явлениями 2).
Предположим например, что источник света расположен в начале отсчёта О
системы координат X (х, у, z). В момент t—Q эгог источник испускает
сферическую волну. Наблюдатель, расположенный в точке л:, у, z системы
координат X, впервые отметит прохождение волны в момент t, и уравнение
точки на поверхности волнового фронта будет, следовательно,
Х2_|_3;2_|_<г2_с2_^==0> (92)
Наблюдатель может, однако, измерять положение и время и по отношению
к другой системе отсчёта X' (л:'," у', z'), движущейся с постоянной
скоростью относительно О. Для простоты положим, что начало О' совпадает
с О в момент t — 0. Согласно второму постулату, световая волна
распространяется в X' с той же самой скоростью, что и в1, так что уравнение
волнового фронта в X' будет:
*'2-f/2-f-*'2— с2/'2 = 0. (93)
Под t' мы должны подразумевать время, измеренное наблюдателем в системе
X' с помощью инструментов, расположенных в этой системе. В этом,
следовательно, содержится ключ к преобразованию, которое связывает
координаты ху у, z, t наблюдения или события в X, с координатами х', у\ z , t'
того же самого события в X': оно должно быть линейным и должно
оставлять инвариантным квадратичную форму (92). Линейность следует из
требования, чтобы равномернее прямолинейное движение частицы в X оставалось
линейным и в А"'.
Пусть:
хх = х, х2 —у, х3 = z, x4 = ict (94)
!) Ritz, Ann. Chim. Phys., 13, 145, 1908.
2) Обзор этих исследований можно найти в книге Паули, loc. cit.
76
ГЛ. I. УРАВНЕНИЯ ПОЛЯ'
будут компонентами вектора R в четырёхмерном многообразии Х(х1У х2, хв, х±)г
#2 _ Xl _|_ Хг _|_ Хз _[_ Х4_
(95)
Постулат постоянства скорости с будет удовлетворён группой
преобразований, которая оставляет инвариантной длину этого вектора. Но в разделе Г. 19
было показано, что (95) инвариантно по отношению к группе вращений
в четырёхмерном пространстве, и мы можем заключить поэтому, что
преобразования, которые позволяют перейти от координат события в X к
координатам того же события в Х\ имеют вид:
причём
хз — 2j азкХ]с
4
V
2j ajiajk = °ik
3 = 1
(/=1,2, 3,4),
(/, &=1, 2, 3, 4)
B6)
B7)
и детерминант \а3-к\ равен единице.
Мы должны теперь найти эти коэффициенты. Вычисление упростится,
если мы предположим, что поворот испытывают только оси х3 и х±. Общность
результата от этого отнюдь не страдает. Мы полагаем поэтому х1 = х1У
x-z = х2 и пишем следующую матрицу коэффициентов:
х[
х%
9
Xs
x't
■*1
1
0
0
0
■*«
0
1
0
0
Хз
0
0
язз
о4з
*i
0
0
«34
й44
(96)
Условия ортогональности- сводятся к равенствам:
' - <4+а23=1, a|4-|_flJ4=l, e33«84H-«43a44 = 0. (97)
Если мы положим ат^=<х, а34 = /а|3, то из (97) найдём, что a43 = zp/a[3,
а у 1—p^ = ztl. Только верхний знак удовлетворяет требованию равенства
детерминанта коэффициентов положительной единице, а это в свою очередь
является необходимым условием для того, чтобы группа содержала
тождественное .преобразование. Выражая коэффициенты только через параметр {3,
получаем:
1 /р
я33 — аи —
а
а для самого преобразования получаем:
xi== -^i >
34 "
а
43
ТЛ— р '
(98)
Л*2 — А2>
X'
уг
(*з + Ф**)» x'i ~~
Yi-F
(дг4 ipxs).
(99)
' X,
ТЕНЗОРЫ ПОЛЯ [1.23J 77
Возвращаясь к исходному пространственно-временному многообразию,
полунаем, что это преобразование эквивалентно такому:
х' = х, у' = у,
г' = г * г (г — $ct), t'= r l (t—Lz): A00)
Параметр {3 можно определить, рассматривая координаты х', у', z'
фиксированной точки в X'. По отношению к X координаты этой точки будут х, у, z.
Поскольку dz' = 0, постольку
£ = « = fc p_i. A01)
Таким образом, поворот, определяемый (96) и (97), эквивалентен
перемещению системы Хг вдоль оси z с постоянной скоростью v относительно не-
штрихованной системы X.
Преобразование
х' = х, v'=y,
г' = -=Л= (z — vt), tf = -7=L=r (t — ~ z), A02)
получаемое из A00) подстановкой значения {3, или ему обратное:
х — хг, у—у'
г== _ 1 (г' + Рр, t = -~L= (f + ^rz1) A03)
было названо именем Лоренца, который первый показал1), что уравнения
Максвелла инвариантны по отношению к замене переменных, определяемой
соотношениями A02), и не инвариантны по отношению к «галилееву
преобразованию» :
z' = z — vt, t' = t. A04)
Все известные электромагнитные явления могут быть объяснены, если
пространственные и временная координаты события в движущейся системе
координат X' связаны с координатами того же события в произвольной
фиксированной системе X лоренцовым преобразованием. В пределе, при v <§^ с,
A02) принимает вид галилеева преобразования классической механики A04),
которое может быть интерпретировано как применение принципа
относительности к миру, в котором электромагнитные возмущения распространяются
с бесконечной скоростью.
1.23. Преобразование векторов поля к движущейся системе
координат. Мы не будем говорить подробно о многочисленных следствиях лорен-
цова преобразования — сокращении Фицджеральда-Лоренца, новом понятии
одновременности, изменении кажущейся массы, верхнем пределе с, который
г) Это утверждение не вполне точно. Первым, кто действительно показал
(формальную) инвариантность уравнений поля при преобразовании A02) и назвал это
преобразование лоренцовым, был А. Пуанкаре. Сам Лоренц, написав A02), не смог
добиться полного сохранения вида уравнений, так как не ввёл соответствующего
этому преобразованию закона сложения скоростей. Конечно, ни Лоренц ни Пуанкаре
не придавали преобразованию A02) того прямого физического смысла, который оно
приобрело лишь у Эйнштейна, благодаря признанию относительности понятия
одновременности удалённых событий. См. например, сборник «Принцип относительности
Лоренц, Пуанкаре, Эйнштейн, Минковский» в серии «классики естествознания», ОНТИ,
1935. Прим. ред.
78
ГЛ. I. УРАВНЕНИЯ ПОЛЯ
накладывается на скорость движения материи,—всё это относится по
существу к теории относительности. Однако приложение принципов этой
теории к уравнениям электромагнитного поля существенно для понимания
четырёхмерной их формулировки, данной в разделе 1.21.
Преобразование Лоренца было выведено из постулата о постоянстве
скорости света и было показано, что оно эквивалентно повороту в пространстве
xlt х2, х3, x±=ict. Согласно постулату относительности, соответствующим
образом формулированные физические законы должны иметь один и тот же
вид во всех системах, движущихся друг относительно друга равномерно и
прямЪлинейно; в противном случае, очевидно, было бы возможно обнаружить
такое движение. В разделах 1.19 и 1.20 было показано, что ротор, дивер-^
генция и лапласиан вектора или тензора инвариантны по отношению к
повороту координатной системы. Следовательно, для уверенности в том, что
уравнения инвариантны по отношению к лоренцову преобразованию,
достаточно предположить, что четыре-ток J и четыре-потенциал Ф действительно
преобразуются как векторы, а величины 2F, 2G — как тензоры. Другими
словами, мы обосновываем векторный и тензорный характер этих
четырёхмерных величин непосредственно двумя указанными постулатами.
Четыре-ток J удовлетворяет уравнению
При повороте координатной системы компоненты J преобразуются так:
4
J J'= 2 ajkJk, A05)
или, если подставить значения д-л из (98):
f— J f = J
J^~vh¥^-^ p'= vfbf (p-£7*)' ' A06)
A07)
-^r=f2 VT-p-
а обратное преобразование будет:
J _ г' J =J'
Впредь мы будем предполагать, что система отсчёта X' жёстко связана
с телом, движущимся с постоянной скоростью г> по отношению к системе X.
Последняя обычно будет предполагаться покоящейся по отношению к земле.
Если скорость v намного меньше скорости света, то уравнения A07)
приближённо таковы:
Jg = f2 + vp', р = р'. A08)
Наблюдатель на движущемся теле измерит плотность заряда р' и плотность
тока /г, в то время .как его коллега, покоящийся в системе X, найдёт, что
ток /г увеличен на конвекционный ток vp'.
Подобным же образом соотношения между электрическими и магнитными
векторами, определяющими заданное поле в неподвижной и движущейся
ТЕНЗОРЫ ПОЛЯ [1.23J
79
системах, получаются непосредственно из правила F1) для преобразования
компонент антисимметричного тензора. После подстановки соответствующих
значений для коэффициентов а3-к, получаем для компонент 2F:
Г12 — <%11#22^ 12 :
12
F
12»
)
Fu = «ii«43/7i3+ anatiFu =
F23 = «22^33^23 ~T" ^22^34^24 ==
/*24 == й22°'43^23 ~T~ й22й44^24 ==
1
Vi-P
1
l
/г
■£3
1
F34 = (Я33Я44 a34a43) ^34 = *84>
(^13"t"ZP^14)>
(/=3+1№Д
(^24 ZV*W»
A09)
и отсюда:
В
1
х-
B'=yT
1
P.2
P
yi-P2
1
(Ex — vBv),
7{Ey-\-vBx),
B2 = B
г*
A10)
Ограничение направления скорости вдоль оси z может быть снято, если
написать v в виде вектора, выражающего скорость перемещения X'
(движущегося тела) в любом направлении по отношению к неподвижной системе X.
Поскольку в (ПО) ориентация оси z была произвольна, мы имеем в общем
случае:
#11»
En = En,
1
У 1 — §2
(В-?ЬЕ])±- £i = 7=^E+[v,B}b
(Ш>
где знак Ц отмечает компоненты, параллельные направлению перемещения, а
8нак_]_—перпендикулярные. Опуская члены с-у, что допустимо во всех
случаях, когда тело движется со скоростью v<^3 • IQ8 метров/секунду, мы
получаем приближённые формулы:
Ви=В
II»
£ц =Еп,
A12)
В± = ВЪ E±*=EL+[vtB]L. j
Следствия этих результатов поистине поразительны: электрическое и
магнитное поля Е и В не имеют независимого существования как
самостоятельные величины. Основным образованием является тензор поля 2F—(В, EJ;
разложение поля на электрическую и магнитную компоненты целиком
связано с относительным движением наблюдателя. Если мы покоимся
относительно постоянных магнитов или относительно стационарных токов, то мы
измеряем чисто магнитное поле В. Наблюдатель же, движущийся вместе
с телом или системой X', заметит приблизительно такое же магнитное поле»
но кроме того ещё и электрическое поле с напряжённостью Е' = [v BJ.
80 ГЛ. I. УРАВНЕНИЯ ПОЛЯ
Обратно: движущееся тело может нести какой-либо определённый заряд.
Для наблюдателя, находящегося на этом теле и движущегося вместе с
зарядом, поле является чисто электростатическим, в то время как его
неподвижный коллега обнаружит наряду с электрическим ещё и магнитное поле,
совершенно законно отождествляя движущийся заряд с током.
Подобным же образом из тензора 2Gs=(H,—icD) получаются
преобразования векторов Н и D от неподвижной к движущейся системе:
Н и =Нп, Dii =D|i,
«i-yf-irai-rv.Dib Di=7rJ=r(D+ >,н])±.J (Ш)
Инвариантность уравнений Максвелла по отношению к равномерному
перемещению сводится к следующему: если векторные функции Е, В, Н, D
определяют электромагнитное поле в системе X, то уравнения:
rot'E' + ^- = 0, div'B' = 0, )
д?
rot'H' |t-=J', div'D' = p'
удовлетворяются в системе Х\ которая движется с постоянной скоростью v
по отношению к X; операторы rot' и div' обозначают дифференцирование
по переменным х\ у\ г'. Наблюдатель, покоящийся в X', будет
интерпретировать векторы Е', В', D', Н' как напряжённости электромагнитного поля,
удовлетворяющие уравнениям Максвелла. Ясно, что соотношения D с Е и Н
с В не являются одинаковыми в обеих системах. Макроскопические
параметры е, jj., а также должны подвергаться преобразованию, которое может
быть приписано действительному изменению структуры материи при,
движении. Практически интересуются в большей мере механическими и
электродвижущими силами^ измеряемыми в неподвижной системе X, коте-
рые действуют на движущуюся материю, нежели преобразованными
яапряжённостями поля Е', В', Н\ D'. Нахождение этих сил и
дифференциальных уравнений, которым они удовлетворяют в рамках теории относитель-'
ности, было завершено Минковским в его исследованиях по электродинамике
движущихся тел.
Векторный характер четыре-потенциала демонстрируется уравнением G9),
которое выражает тензор поля 2F как ротор Ф. При преобразовании Лоренца
получаем:
4
Ф^Ц^Ф* (/==1,2,3,4), A15)
или, переходя к скалярному и векторному потенциалам:
А-х &х* Ау •"?/>
А' \ ( А V \ , 1 , „ ч (П6)
Как и в случае Еекторов поля, разложение на векторный и скалярный
потенциалы в трёхмерном пространстве определяется относительным движением
наблюдателя.
В заключение можно отметить, что поворот координатной системы оставляет
инвариантным скалярное произведение любых двух векторов. Лоренцово
преобразование мы вывели фактически из требования инвариантности величины
RR = /?2 = A;2-j-3/2-f г2— сЧ\ A17)
ТЕНЗОРЫ ПОЛЯ [1-23] 81
Поскольку было показано, что плотность тока J и потенциал Ф являются
четыре-векторами, постольку величины
ф2==л^+4+4-^, I 018>
с I
ФЛ = AJX + AyJy + AJz— W )
являются инвариантными скалярами в пространственно-временном континууме.
Более того, имеются и другие инвариангные скаляры, имеющие
фундаментальное значение для общей теории электромагнитного поля. Из формулы
преобразования E9) читатель может установить, что если 2S и 2Т— два
тензора второго ранга, то суммы
4 4 4 4
2 2 $jkTjk = инвариант, 2 2 5^7^ = инвариант A19)
j = l k=l j=lк=1
инвариантны по отношению к повороту координатных осей. Эги величины
могут быть интерпретированы как скалярные произведения двух тензоров^
Образуем сначала скалярное произведение 2F на самого себя. Согласно G1)
и A19), находим:
2 2 /\Jfc=2(#2 — \e*) = инвариант. A20)
j = 1 к = 1 v- c '
Теперь построим скалярное произведение 2F на дуальный тензор 2F*,
определённый по G5):
4 4,
2 2 РА = - 4 f BE = инвариант. A21)
j=lk=l c
Из тензора 2G и ему дуального 2G* можно построить инварианты:
4 4
2 2 G% = 2 (Я2 — с2/J) = инвариант, A22)
4 4
2 2 GjkG}k = — 4tc HD = инвариант. A23)
Следуя тому же пути, получаем:
4 4 4 4
2 2 FihGjk =-2 2 Р]кО]к = 2 (ВН — ED) = инвариант, A24)
4 4 4 4
2 2 ^О^ =22 ^^7с = - 2/ (с BD + 7"ЕН) = инвариант. A25)
J = lfe=l j = lfc = l \ с . /
Инвариантность этих величин в конфигурационном пространстве очевидна;
они отличаются от других трёхмерных скалярных произведений тем, что
сохраняют одно и то же значение во всякой системе, движущейся с
постоянной относительной скоростью.
б Зак. 593. Теория электромагнетизма.
ГЛАВА II
СИЛЫ И ЭНЕРГИЯ
Чтобы использовать математические построения, развитые на предыдущих
страницах, для истолкования экспериментов, осуществляемых в лаборатории,
мы должны рассчитать силы, действующие на элемент заряда или тока, или
на нейтральное материальное тело, находящееся в поле. В этой главе будег
показано, как при соответствующем определении -векторов Е и В эти силы
могут быть выведены непосредственно из уравнений Максвелла. При этих
исследованиях мы должны будем принять во внимание упругие свойства
материальной среды. Небольшое отступление в область анализа упругих
напряжений и деформаций даст нам соответствующую базу для рассмотрения
объёмных и поверхностных сил, вызываемых электрическими или магнитными
полями.
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГОЙ СРЕДЕ
2.Ь Тензор упругих напряжений. Предположим, что данное твёрдое
лли жидкое тело находится в состоянии статического равновесия под
действием . определённой системы внешних сил.
Внутри этого тела мы выделим некоторый
объём V с помощью замкнутой
поверхности Sy как показано на рис. 12.
Поскольку предположено, что тело
находится в равновесии во всех своих
частях, равнодействующая F сил,
действующих на вещество внутри S, должна
равняться нулю. Эта равнодействующая
слагается из объёмных сил, подобных силе
тяжести, и из поверхностных сил,
действующих со стороны элементов материи,
расположенных с внешней стороны границы
выделенного объёма, на смежные элементы
внутри него. Поэтому мы предположим, что
силы в объёме V распределены с
плотностью f на единицу объёма, в то время
как силы, действующие со стороны материи
вне 5 на единицу площади Sf будут выражаться вектором t Очевидно,
компонентами t являются нормальные давления или натяжения и
тангенциальные или скалывающие напряжения. Условие равновесия относительно
поступательных перемещений выражается уравнением:
У
Рис. 12. Ограниченная ьоверх-
ностью 5 область V упругой
среды, в которой имеются
напряжения.
J I dv -f- ф t da
v s
0.
A)
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГОЙ СРЕДЕ [2.1] 83
■M^WII III—!■■ Ч IIII4IIIII ■ ■■ ■ «I ЩИ. ■!■ I .^^т.^^т**щт*Ш^*^^^*Ш~Ш*ЩШт1^т*ШЯШШ—Ш1шт-т~~»тш~'^—~тЯт~——> I" — I IMM—■—■—■——■■—■■■
Для обеспечения равновесия в отношении вращения необходимо также, чтобы
результирующий вращающий момент был равен нулю, т. е.:
J [r, i)dv+§[r, t]tfa = 0, B)
V S
где г — радиус-вектор, проведённый из произвольного начала отсчёта О
к элементу объёма или поверхности.
Переход от интегральных соотношений A) и B) к дифференциальной
или локальной системе, выражающей те же самые условия в
непосредственной окрестности произвольной точки Р (х, у, г), может быть совершён
способом, которым мы пользовались в первой главе: поверхность S сжимается
около точки Р, и компоненты t разлагаются в ряд Тэйлора. Мы получаем
при этом возможность вычислить поверхностный интеграл и получить после
перехода к пределу условия равновесия, выраженные через производные t
в точке Р. Однако применяя теоремы, имеющиеся в нашем распоряжении,
мы можем избежать этого. Пусть п будет единичным вектором внешней
нормали к элементу поверхности S. Тогда имеются три вектора X, Y, Z,
которые удовлетворяют уравнениям:
*ж=гХп, ty = Yn, tz = Zn. C)
Хп является, очевидно, ;е-ой компонентой силы, действующей по
направлению во вне на единичный элемент поверхности, ориентация которой
определяется нормалью п. Развёрнутая форма скалярных произведений:
*х = Xa/ix + ХуПу -f- Xenzl
*г = Zxna _f Zytlv + ZjHn
D)
может рассматриваться так же, как линейное преобразование компонент
п в компоненты t; компоненты пя, пу1 пг являются направляющими
косинусами п по отношению к координатным осям. Равновесие .^-компонент сил,
действующих на вещество, находящееся внутри S, выразится теперь
соотношением:
ffxdvJr§Xnda=:0, E)
V S
которое, по теореме о дивергенции и ввиду произвольности объёма V",
эквивалентно тому, что во всех точках внутри .S соблюдается условие:
/я + (ИуХ = 0. F)
Для у' и -^-компонент имеем аналогично:
/„ + divY«0, /e-fdivZ = 0. G)
Равновесие относительно вращения, выраженное соотношением B),
накладывает дальнейшие условия на девять компонент трёх векторов X, Y, Z.
Например, дг-компонента этого уравнения есть:
j{yfz—2f»)'dv + f(yte — zty)da = 0. (8)
V 8
Подстановка значений tn и ty, определённых по C), приводят к уравнению:
fWa—*/„)rf*-f/Ов — zY)nda = 0, (9)
V S
б*
$4 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
которое опять-таки, согласно теореме о дивергенции и произвольности объёма V,
эквивалентно:
Уfx~ zfy +div (VZ~zY) = 0. (Ю)
Но
div OZ) = у djv Z -f Z gradj; =j/ div Z -j- Z„, A1)
и уравнение A0) приводится к виду:
y(f,+ dtoZ) — z(fv + divY) + Zv—Y, = 0 A2)
или, учитывая G):
Zy=Yz. A3)
Подобным же способом можно из _у- и ^--компонент уравнения B) вывести
соотношения симметрии:
Xy—Yx, XZ = ZX. A4)
Девять компонент Хх, Ху, ... Z2, представляющие собою силы,
действующие на единичный элемент поверхности, называются напряжениями.
Диагональные элементы Хх, Yy, Zz действуют в направлении, нормальном
к поверхности элемента, и являются, следовательно, давлениями или
натяжениями. Остальные шесть компонент являются тангенциальными
напряжениями, действующими в плоскости элемента. Эти девять величин являются
компонентами симметричного тензора, как это очевидно из D) и из того,
что t и п являются полярными векторами (ср. раздел 1.20). Для сокращения
обозначений мы будем в дальнейшем писать компоненты тензора напряжений
в виде 7)а-, где:
хх =
— Mi» Ху = Т12
*х — ^ 21> * * *
Zz~ /33.
A5)
Итак, для того чтобы жидкая или твёрдая среда, подвергающаяся
действию напряжений, находилась в равновесии, необходимо чтобы в каждой точке
f -}- div2 T = 0, 7> = Tkj. A6)
Представим себе в такой среде бесконечно малый плоский элемент
поверхности, содержащий точку (х, у, z). Напряжения, действующие на этот
элемент поверхности, будут в общем случае как нормальными, так и
тангенциальными. Однако имеются три различных направления, в которых
напряжения являются чисто нормальными. Если результирующая сила t,
действующая на единицу площади плоского элемента, направлена по положительной
нормали п, то мы можем положить
* t = An, A7)
где л — неизвестная скалярная функция координат х, у, г элемента. Наложив
это условие на уравнения D), мы получим однородную систему:
А«. = 27>я* (/=1*2,3). A8)
й=1
Для того чтобы эти однородные уравнения были совместны, необходимо,
чтобы детерминант системы равнялся нулю. Отсюда следует, что скалярная
функция К может быть определена из уравнения:
= 0, A9)
Тй-
т*
7-si
~К М2 Т^з
722 Л 7^3
7з2 Тш — \
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГОЙ СРЕДЕ [2.11 85>
конечно, при условии, что компоненты тензора напряжений Tjk по отношению
к какой-либо произвольной системе координат известны. Вековое уравнение
A9) имеет три корня: Х0, Кь и Хс, определяющие через уравнения A8) три
ориентации элемента поверхности, которые мы обозначим соответственно
через п<а;, п(ь), п<с). Если корни (.19) различны, то направления,
определённые единичными векторами п(о), п(ь), п(с) и называемые главными осями
напряжений, взаимно перпендикулярны. Рассмотрим, например, п<о) и п(ь).
Согласно A8): 3
1 *,'а)
кащ
2j Т^щ ,
к=Х
rf=2rf-
B0)
Умножая первое из этих уравнений на щ ], второе на ttf1, вычитая второе
из первого и суммируя по индексу у, получаем:
Ai- 4J «Г*?' =ii ТМпР„Г- Wnf\ BD
j=»l 3 = 1 fe = l
Правая сумма равна нулю, откуда
(.К— Хь) п(«> п&> = 0. B2)
Если ХафХъ, то, как мы и утверждали, вектор п(о) ортогонален к п(ь).
Физический смысл главных осей можно уяснить себе и иначе. В точке
Р среды, подвергнутой напряжениям, симметричный тензор 2Т связывает
с единичным вектором п результирующую силу t, действующую на
единичный элемент поверхности, нормальный к п. Пусть начало прямоугольной
системы координат расположено в точке Р. Масштаб длины в этой новой
системе координат произволен, и мы можем положить, что компоненты
нормали п, проведённой из точки Р, равны &, ч\, С Скалярное произведение t и
п, которое мы обозначим через Ф, квадратично относительно &, ч\, С:
ФF, ij, 0 = ^1=7^4- ад>+ ТврН-2Г]2^ + 2ЗД+2Г310!. B3)
Поверхность Ф = const, называется поверхностью или квадрикой
напряжений. Поворотом координатных осей B3) может быть приведено к сумме
только квадратичных членов, и
главные оси напряжений п(а), п(ь), п(с),
очевидно, совпадают с главными осями
квадрики. Можно заметить, что:
1
t = 2" grad ф-
B4)
Это свойство позволяет найти
напряжения, действующие на какой-либо
поверхностный элемент в точке Р,
путём графического построения.
Предположим, что напряжения таковы, что
квадрика является эллипсоидом, и
проведём вокруг Р поверхность Ф=1.
Радиус-вектор из точки Р к любой
точке Р' этой поверхности есть п.
Согласно B4), результирующая сила,
действующая в точке Р на элемент с нормалью п, направлена вдоль grad Ф,
т. е. нормально к поверхности Ф = 1 в точке Р'. Величина t, согласно B3),
обратна величине проекции NP', показанной на рис. 13. Вдоль главных
осей а, Ь, с нормаль к поверхности Ф = 1 совпадает с вектором п, и
Рис. 13. Графическое определение
напряжений, действующих на элемент
площади в точке Р, с помощью
квадрики напряжений.
86 ' гл. и. силы и энергия
напряжение, действующее на элемент в точке Р, является чисто нормальным.
Если эти главные напряжения известны, то можно построить квадрику
напряжений и графически определить напряжения, действующие на любой
произвольно ориентированный элемент.
2.2. Анализ деформаций. Если поверхностные и объёмные силы
приложены к абсолютно твёрдому телу, то возникающее в результате движение
может быть описано как перемещение тела в целом и вращение вокруг его
центра масс. Если, однако, тело деформируемо, то отдельные его части
испытывают также относительные смещения, которые возрастают до тех пор, пока
возникающие в процессе деформации внутренние силы не восстановят
равновесия. Изменения относительного расположения частей тела под действием
напряжений называются деформациями.
Пусть в сплошной среде положение точки Р по отношению к
произвольному фиксированному началу отсчёта определяется в отсутствие
напряжений радиусом-вектором г. Под влиянием приложенных сил среда
испытывает деформацию, в процессе которой вещество, локализованное первоначально
в точке Р, перемещается в точку Р' с радиусом-вектором г' = г
-j-s.'Смещение s, соответствующее данной деформации, зависит от координат исходной
точки Р; мы предположим, что s — непрерывная функция г. Рассмотрим
теперь какую-либо соседнюю точку Pv положение которой определяется
радиусом-вектором rv Исходное положение точки Рх по отношению к Р
определяется вектором 8г:
Ьг = гх— г. B5)
Смещение Pt при деформации равно sx и является функцией rv
Относительное смещение двух соседних точе^к Р и Р1У возникающее при
деформации, будет, следовательно:
88 = 8! — s = s(r-f8r) — s(r). B6)
Поскольку функция s(r-j-8r) непрерывна, она может быть разложена в ряд
Тэйлора; для точек достаточно малой области вблизи Р мы можем удержать
только линейные члены
8s = (8rgrad)s B7)
или в компонентах
з
8^ = Е1|8Л:* (/-1,2,3). B8)
к = 1
«
(Для удобства суммирования, вместо х, у, г, опять написаны индексы 1, 2, 3.)
Девять производных dSjjdxk являются компонентами тензора ^ср.
уравнение E4), раздел 1.20), который в общем случаз является асимметричным.
Однако по способу, данному в уравнениях D6) и D7), стр. 68, он может
быть разложен на симметричную часть
а*-ЦШ+Щ) </,* = !, 2, 3) B9)
и часть антисимметричную
»*-4(|£—а£) </•*-»• * *>■ Ю
Компоненты антисимметричной части тензора тождественны, очевидно, с
компонентами аксиального вектора Ь, определённого соотношениями:
b = yrots, C1)
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГОЙ СРЕДЕ 12.21 8?
Относительное смещение 8s также может быть разложено на часть 8s',
связанную с симметричным тензором а^с, и на часть 8s", связанную с антисимме -
тричным тензором bjk. Тогда, согласно B8) и C0),'
8s" = [b, 8r] = i [rot s, 8r]. C3)
Физически C3) означает, что вещество, содержащееся внутри бесконечно
малого объёма около Р, испытывает поворот как абсолютно твёрдое тело.
Вращение происходит около мгновенной оси, проходящей через точку Р
в направлении rot s, с угловой скоростью, равной у | rot s j. Это локальное
вращение обусловливается напряжениями, ротор которых отличен от нуля.
В то время, как локальный поворот C3) сохраняет относительное
расположение точек в непосредственной окрестности точки Р, симметричный
тензор B9) определяет местную деформацию — растяжение и изгибание.
Прежде всего нас интересует вопрос, имеется ли такой вектор 8г,
проведённый из точки Р, направление которого после деформации не изменяется;
иначе говоря, имеются ли такие точки Рх (рис. 14), которые в процессе
деформации движутся вдоль линии,
определяемой вектором 8г?
Необходимым условием этого будет:
, 8s'=-X8r, C4)
где X — неизвестная скалярная
функция координат точки Р, или
з
Л 8л;. = 2 а& Ьхк (j = 1,2, 3). C5)
Параметр X находится из условия,
что детерминант этой однородной
системы должен быть равен нулю.
Как и в аналогичном случае тензора
напряжений, разобранном в
предыдущем параграфе, легко показать, что три корня определяют три главных
направления, которые в общем случае взаимно ортогональны. Вдоль этих
главных осей деформации и только вдоль них деформация является чистым
растяжением. Характер деформации вдоль какой-либо другой оси может
быть иллюстрирован с помощью квадрики деформаций, подобной B3).
Пусть точка Р', рис. 14, имеет координаты Ъи &2, ^з по отношению к Р.
Построим поверхность:
з s
W = 8r8s' = 22 ajkblk = const. C6)
Если все прямые, проведённые из Р, растягиваются, или все сжимаются, то
поверхность деформаций будет эллипсоидом; если часть прямых сжимается,
а часть растягивается, то поверхность будет гиперболоидом. Относительное
смещение точки Pt по отношению к Р даётся выражением:
8s'=y^adW- C7)
Радиус-вектор, проведённый из точки Р в точку Pt на поверхности ч7=»1?
есть 8г. На рис. 15 предположено, что поверхность деформаций являете»
эллипсоидом. Направление относительного смещения 8s', вызванного дефор*
[8r-grad)$
Рис. 14. Векторное изображение
деформации сплошной среды.
88
-ГЛ. II. СИЛЫ И ЭНЕРГИЯ
манией, совпадает с направлением нормали, проведённой в точке Р,, а
величина смещения обратна длине проекции NPt радиуса-вектора 8г на нормаль.
Очевидно, векторы 8s' и 8г параллельны только вдоль главных осей
эллипсоида. Эти оси представляют собой-
&s'=jffrad4:
также направления максимального и
минимального сжатия или
растяжения.
Интересная физическая
интерпретация может быть дана
компонентам тензора а^. Если
относительное положение точек Р и Ръ
до деформации определялось
вектором 8г, то после деформации их
относительное положение будет
определяться вектором 8r' = 8r+8s'„ „
где штрих у 8s' указывяет на то,,
что локальное вращение
исключено. Предположим теперь, что 8г
направлен по д^-оси, так что 8лга= 8л:3 = 0. Тогда 8г' будет вектором с
компонентами:
Рис. 15. Графическое определение
деформации в точке Р с помощью квадрики
деформаций.
^x[ = (l~{-all)bxv ox'2=a2lQxl, ox'3 = a3luxv C8>
Абсолютная величина расстояния между Р и Р, после деформации равна:
I or' | = y-(T+^)«"-f a\t -f- a^ 8*lf C9>
а относительное изменение длины составит:
| or' | — bxt
bxi
= a
и
что получается разложением C9) в ряд и отбрасыванием всех членов порядка
выше первого. Аналогичные выражения мргут быть получены и для
деформаций линейных элементов, расположенных первоначально вдоль х2 и д:3-осей,
откуда мы заключаем, что диагональные компоненты ajj — dSjjdXj
представляют собой растяжения линейных элементов, которые в недефор-
мированном состоянии были параллельны координатным осям.
Пусть опять 8а будет линейным элементом, который в недеформирован-
ном состоянии параллелен д^-оси, а 8Ь — линейным элементом, первоначальна
параллельным д;2-оси. Локальная деформация преобразует вектор 8а=118д:1,
в элемент:
8a' = i1(l-}-eii)^1 + i2«2i^i + i3%i^t, D1>
в то время как 8b = i2 8д:2 преобразуется в
6b' = i1a128>:a4-i2(l + a22>8A:2-bia%a8^2' D2>
В первоначальном состоянии 8а и 8Ь взаимно ортогональны, но после
деформации они образуют угол, который несколько отличается от it/2 и который
мы обозначим через 4jj 012, так что
8а'8Ь' = 18а' 11 8b' | cos (|-
Но
*»)*
D3>
cos \^ — e13J=sin е12 ^ е12.
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГОЙ СРЕДЕ 12.21
$&
и, следовательно,
612 = «12 С1 4" «ll) + «21 A + «22> + «31 «32,
или, если пренебречь членами порядка выше первого,
И
12
dSi
«12+«21— ThZ^WZr-
ds2
дх% ' dxi
D5>
D6>
Таким образом, в общем случае, коэффициенты а^к с }ф-к равны половине"
косинуса угла, образуемого после деформации двумя линейными элементамиг.
которые до деформации были направлены вдоль двух ортогональных
координатных осей.
Сообразно этому, принято писать компоненты тензора деформации^
в несколько ином виде. Коэффициенты, определяемые соотношениями:
Cll~~ dxt* 1*~dx2-dxi
'21 >
ds*
ds»
— e - -
еМ—~дТъ> ^ — dxl^dx^*™'
dsri
еы-~дх<' esi~-^--h^r — e
d?3 . dst
dxi • dxs
13'
D7>
называются компонентами деформации; компоненты относительного
смещения двух любых точек Р и Plt вызванного локальной деформацией, будут,,
следовательно:
К = еп ЬхЛ 1 е12 Ч Н- тс1зЧ,
Ч = 2" *21 8ЛГ1 ~Ь *:>2 8*2 4" 2" *23 8*3>
Ч = У еп Ч +. " ез2 Ч + езз 8л:з •
D8>
Если начало произвольной координатной системы xv xa, х3 поместить в точке
Р и затем повернуть координатные оси до совпадения их с главными осями
эллипсоида деформации, связанного с данной точкой, то все недиагональные
компоненты деформации обратятся в нуль. Будем измерять расстояния вдоль
главных осей деформации координатами ии и2, %. Тогда компоненты любой;
локальной деформации по отношению кР будут:
OS.
щ
ei4» Ч.^Ч» Ч3=«зЧ>
где
е -^
е0 =
ds.
ди3
D9>
E0>
и где Ъии 8м2, 6«3— компоненты 8г по отношению к главным осям.
Коэффициенты еи <?2> ез называются главными деформациями или главными
удлинениями.
С деформацией бесконечно малой области связано изменение её объёма.
Если оа, 8Ь, 8с — три вектора, определяющие параллелепипед,, то его объём
даётся выражением
bat Ъа% 8a3
8К=[8а,8Ь]8с =
8&! 862 8^3
^ ^ 51 -
ОС у 0С2 ОС3
E1>
'90 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
8К' = [8а\ 8Ь'], 8с' =
hx1bx2cx3. E3)'
Не уменьшая общности, мы можем выбрать в качестве исходного элемента
прямоугольный параллелепипед, стороны которого параллельны координатным
•осям:
8а = 1,8*!, 8Ь = 128лг2, 8c = i38x3. E2)
Деформация изменяет эти векторы согласно D1) и D2), откуда для объёма
после деформации находим:
1 -f «11 «21 «31
й12 1 Ч~ «22 «32
«13 «23 1 ~\~ «33
Разлагая детерминант в ряд и пренебрегая всеми членами порядка выше
гпервого, получаем для относительного изменения объёма:
——=au4-«22 + «33 = dlvs E4)
— величина, называемая коэффициентом объёмного расширения.
Таким образом, вкратце проведённый анализ показал, что в наиболее
общем случае смещение частиц в окрестности какой-либо точки может быть
разложено на перемещение и на локальное вращение этой окрестности, как
целого, и на деформацию этой окрестности, характеризуемую компонентами
.деформации е^к и сопровождающуюся изменением объёма. Компонента
вращения в полной деформации может быть вызвана только вращающими
напряжениями, т. е. силами, ротор которых не равен тождественно' нулю.
2.3. Упругая энергия и соотношение между напряжениями и
деформациями. Под действием внешних сил частицы, составляющие сжимаемую
жидкость или твёрдое тело, испытывают относительные смещения. Эти
смещения, в свою очередь, вызывают внутренние силы, которые, в случае
статического равновесия, очевидно, компенсируют приложенные напряжения.
Работа, совершённая приложенными объёмными и поверхностными силами
при смещении каждой точки среды на 8s, равна:
bW= ff 8srft> + <£ tbsda. E5)
«Согласно уравнению C):
18s = bsx Xn -f bsy Yn -f bsz Zn E6)
м; следовательно:
§tbsda = fdiv(Xbsx + Y8sy-f Zbsz)dv. E7)
Далее
div (X bsx) = 8se div X -+- X grad 8^; E8)
ш так как, согласно F), fa=s— [divX, то E5) сведётся к выражению:
8 W = J (X grad bsx + Y grad 8s„ -f Z grad bse) dv. E9)
;Ho слагаемые подинтегрального выражения могут быть записаны в виде:
X grad Ьвх = Тп9$*) + Та 8 (-^-) + Г18 8(-|f) и т. д., . F0)
«что, в обозначениях D7), даёт следующее выражение:
^33 8б33 4" ^12 8е12 + ^23 8е23 "+"
+ TnbeK)dv F1)
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГОЙ СРЕДЕ 12.31 91
"■ ' ■ —— ™ ■'I'»»" «I'W ■!■ Il.ll—1.11 !»■■-■■■— —.■■■..И.Н — -»■■-. 1^1—■!■■ „11 1 — !■■!—— ■■■-. 1 HI! ■■ I — ■ — ■ ■ —
для работы, произведенной приложенными силами против сил упругости
« процессе бесконечно малого изменения деформации. Если предположить, что
это изменение происходит настолько медленно, что изменениями
кинетической энергии можно пренебречь, и что во время этого процесса не
сообщается и не отнимается тепло, то 8W должно быть равно увеличению
потенциальной энергии U, содержащейся в упруго деформированной среде. Если
^обозначить упругую энергию, заключенную в единице объёма, через и, то
W=W= f budv. F2)
Плотность энергии и в какой-либо точке должна зависеть от локального
состояния напряжения и, следовательно, можно положить, что
и = и (е1и ет ..., е33), F3)
«ли
8У= Дтёг 8г»+•£ 8е*>+ ik8йзз+ ~%к 8е'г+
Компоненты деформации е^к совершенно произвольны. Отсюда следует, что
компоненты приложенных сил (которые в состоянии статического
равновесия равны и противоположны вызванным ими упругим напряжениям) могут
€ыть получены из скалярной потенциальной функции:
Существование упругого потенциала, которое было здесь показано для случая
квази-стационарных адиабатических деформаций, может быть показано также
и для изотермических процессов.
Пока деформации не слишком велики, компоненты упругих напряжений
могут быть выражены в виде линейных функций компонент деформации:
7*11 — СПеП 4" С12е22 4~ С13е33 4" С14е12 4" С1Бб23 4" С16еЗЬ
Т12 = CAlen -f- £42*22 4" С43е33 4- CUe12 + С4б*23 4" С46*31>
F6)
Коэффициенты стп называются упругими константами среды. Упругий
потенциал и является в этом случае однородной квадратичной функцией
компонент деформации. Существование скалярной функции и(е^),
удовлетворяющей уравнениям F5) и F6), накладывает на упругие константы
условия:
стп = спт (п, т=1, 2,..., 6), F7)
благодаря чему число параметров, необходимых для определения
соотношения между напряжениями и деформациями в анизотропной среде, уменьшается
с 36 до 21. Всякое дальнейшее уменьшение этого числа связано с
использованием симметрии в структуре среды. Если, в частности, среда упруго
изотропна, то квадратичная форма и должна быть инвариантна по отношению
к ортогональному преобразованию системы координат, и число независимых
констант сводится тогда к двум. Упругий потенциал принимает вид:
» = Т Xt(«n 4- Ч% -f ej + \{e\x + £ -f e|3 + \ 4 +\e\% + \ «y, F8)
92 гл. п. силы и энергяи
7-12
^23
7-м
=
=
*2
Л
Л
^12>
^28»
eZV
откуда, согласно F5):
Ти = Л, (еп -f- ^2 + езз) + 2 h еи>
Т<& — К (*ц + в22 -f ^ЗЗ) 4" 2^2 *22» ^23 = Х2 ^23> } F9)
^33 = *1 (е11 + ^22 4 ^Зз) 4" 2А2 %3>
Условия статического равновесия выражаются уравнением:
f-^div2T = 0. A6)
Подставляя компоненты F9) в развёрнутое выражение для дивергенции
л выражая компоненты деформации е^ через деформацию s, мы получаем
f _|_ (X! + h) Srad div s + X2 As == 0 ' G0)
в качестве уравнения, определяющего деформацию изотропного тела, на
которое действуют объёмные силы f. Постоянные интегрирования должны быть-
выражены через величины, дающие либо смещения точек на граничной
поверхности, либо распределение напряжений на ней.
Параметры Xt и Х2 являются положительными величинами. Л2 называется»
модулем сдвига, поскольку через Л2 выражаются деформации, вызываемые
тангенциальными или скалывающими напряжениями. В Xt нельзя вложить.
какой-либо простой физический смысл; однако Xt может быть выражено-
через более известные константы Е и о, где модуль Юнга Е есть
отношение простого продольного натяжения к вызываемому им относительному
удлинению, а коэффициент Пуассона о является отношением поперечного
сжатия стержня к его продольному удлинению под действием натяжения.
Именно:
Х1= A+а,A_2а) ' A2==2(i+0)- G1>
В идеальной жидкости напряжения сдвига существовать не могут, и
следовательно, Х2 = 0. Напряжение, действующее на какой-либо элемент замкнутой
поверхности внутри такой жидкости, является, следовательно, обычным
давлением:
7п = Т<22 — 7зз = — р, Тп = 723 = Тьх = 0, G2)
где отрицательный знак показывает, что напряжение направлено внутрь.
Компоненты деформации еп, е^, £33 все равны между собой и
р=— M*n4:*aa4-f8S^=s— Xidivs> G3>
в то время, как уравнение равновесия принимает вид:
f — grab* p=0. G4)
Пусть V0 будет первоначальный объём элемента жидкости, Vx — его объём
при давлении рх и V2 — его объём при давлении jt?2. Из определения E4)
коэффициента объёмного расширения divs мы имеем:
и для достаточно малых изменений:
ft-ft—V55^- G6>
Для бесконечно малого изменения давления получаем:
„р =_*,!£=, Я, £., G7)
где - — плотность жидкости. Величина, обратная Xlt называется в этом
случае сжимаемостью. ,
ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯДЫ И ТОКИ [2.4\ 93
ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯДЫ И ТОКИ
2.4. Определение векторов Е и В. Электромагнитное поле определяется,
согласно нашей первоначальной гипотезе, четырьмя векторами Е, В, D и Н,
удовлетворяющими уравнениям Максвелла. Физическая природа этих
векторов должна быть установлена через опыты, посредством которых они могут
•быть измерены. Легко показать, что рЕ и [J, В] является величинами,
размерность которых совпадает с размерностью плотности силы. Согласно
разделу 1.8, имеем:
кулон v вольт килограмм
[рЕ] =
метр1
метр секунда2 • метр2'
гп on ампер вебер килограмм
[[J, В]]= .,отп, Хтдд^то„г.„от,
A)
метр"' 'N метр2 секунда2-метр2" v '
Мы можем поэтому определить векторы Е и В как силы, действующие
со стороны поля на единичный элемент соответственно заряда и тока.
Точнее, если мы предположим, что заряд распределён по объёму V с
макроскопически непрерывной плотностью р, то Е определяется так, что
полная механическая сила, действующая на заряд,
равна:
Fe=$9Edv C)
v
и распределена с объёмной плотностью
fe = pE. D)
Если V достаточно мало, то поле внутри этой
области в какой-либо момент можно считать
однородным, и в пределе:
Fe = E f $dv = qE (F->0).
Рис. 16. Направление силы, дей-
E) ствующей на элемент тока
/ ds в магнитном поле В.
Точно так же магнитный вектор В связывается с силой, действующей на
единичный объёмный элемент тока, с помощью уравнения
fm=[J, В], F)
что даёт:
Fw= j[J, B]dv G)
v
в качестве полной силы, действующей на ток, распределённый по объёму V.
Если ток идёт по линейному проводнику достаточно малого поперечного
сечения, то В можно считать однородным, а линии тока параллельными
элементу длины ds. Сила, действующая на линейный элемент тока, будет
тогда: *
dFm=I[ds, В]. (8)
В то время как сила, действующая со стороны электрического поля на
элемент заряда, направлена вдоль вектора Е, сила, действующая на элемент
тока в магнитном поле, нормальна к плоскости, определяемой элементом
ds и вектором В.
Произвольность в нашем определении векторов Е и В неизбежна.
Взаимные силы; с которыми заряды действуют на заряды или токи на токи,
могут быть измерены, но сами векторы поля «не являются независимыми
величинами,- доступными прямому наблюдению. Определения Е и В, данные
94 ГЛ. II, СИЛЫ И ЭНЕРГИЯ
уравнениями C) и G), были подсказаны исключительно соображениями
размерности и совместимости с уравнениями Максвелла. В дальнейшем мы должны
будем показать, что свойства полей векторов Е#и В, определённых подобным;
образом и удовлетворяющих этим уравнениям, полностью согласуются с опытом.
Зная силы, вызываемые зарядами и токами, можно определить работу,
необходимую для создания поля; из энергетических соотношений, в свою
очередь, можно вывести силы, действующие на элемент нейтральной материи.
2.5. Тензор электромагнитных напряжений в свободном пространстве..
Предположим, что некоторая ограниченная область пространства содержит
распределённые заряды и токи, но свободна от всякого нейтрального диэлек-»-
трического или магнитного вещества. Поле вызывается частично зарядами
и токами, находящимися в рассматриваемой области, частично же источниками»,
лежащими вне её. В каждой внутренней точке:
rotE-b^~ = 0, (I) divB = 0, (III)
rot В - ^Щ- = tvl, (II) div E = ± p. (IV)
Умножим (I) векторно на e0E, a (II) на В. После сложения и
перегруппировки членов, получаем:
e0 [rot Е, Е] + ~ [rot В, В] = [J, В] -f «о ^ [Е, В]. (9>
В прямоугольнрй системе координат первый член без множителя s0 можно
представить детерминантом:
i j k
[rotE, EI=
дЕ
г
ду
Е
X
)Ev.
dz '
дЕ дЕ
X Z .
dz ax *
F
,У
V а»
дх- ду
Ez
A0>
.^-компонента этого вектора равна
irot Е, Е] I - В. ^ +Ej>lf +E^—E^-EV^—E^ =
• -я{А—h £*)+-§;& Е»)+ЫЕ'Е*)-Е*д1чЕ- A1>
Так как величины
5<?=г0(й—Ij?), 8{й = нЕхЕу, S{U = 4EXEZ A2)
преобразуются как компоненты тензора, (уравнение D3), стр. 67), то-
первые три члена в правой части соотношения A1) образуют дг-компоненту
дивергенции тензора 2S<e). Остальные компоненты получаются из у- и z-коч-
понент e0[rotE, E]. Таким образом, мы приходим к тождеству:
e0[rotE,E]=div2S(^ —e0EdivE; A3)
компоненты aS<e) приведены в таблице I (стр. 95).
Преобразование [rot В, В] проводится аналогично и даёт:
— [rot В, В] « div2S(m) i-B div В. A4>
Компоненты 2S(w) представлены в таблице II (стр. 95).
ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯДЫ И ТОКИ 1Щ 95* ,
Таблица I. Компоненты 5$ тензора 2S(e) в свободном
пространстве
IX
1
О
3
1
ЦСуСх
^qEz^-x
2
EQCXCy
в Е2 — -^ Я2
ЗоАг^у
3
г0^х^г
В0СуСг
е0са 2
Таблица II. Компоненты S^ тензора 2S(W,) в свободном
пространстве
X
1
2
3
1
[А0 Ж 2jX0
— ВуВх
го
BzBrj,
2
-ib****
£*"»
3
Ho
■ Ву&г
-LbI-±b*
Ho * 2^
После подстановки в (9) вместо первых двух членов A3) и A4) и с
учётом (III) и (IV), мы получаем следующее тождество:
div «S = Ер + [J, В] + % Ж [Е, В],
где компоненты тензора 2S равны:
и где:
*«-S Sve
3 = 1 к = 1
A5>
A6>
A7>
С помощью уравнения (.15) силы, действующие на элементы заряда и тока
в любой точке пространства, не содержащего материи, могут быть выражены1
только через векторы Е и В.
Проинтегрируем это тождество по объёму V. Интеграл от дивергенции
:'. тензора по объёму V равен интегралу вектора по поверхности, ограничив
* • вающей этот объём. Чтобы доказать эту тензорную аналогию- векторной тео-
х ремы о дивергенции, положим, что п — единичный вектор нормали в точке на
граничной поверхности и будем рассматривать Sn как лг-компоненту вектор.
%/ - ,
"96 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
у- и г-компоненты которого равны нулю. Компонента этого вектора в
направлении нормали п будет Snnx, откуда, по теореме о дивергенции:
fsnnxJa = f6-±±dv. A8)
•Очевидно также, что:
A9)
* J* Snnyda = J ^»- dv,
j S13neda = J* -^f- dv.
После сложения этих трёх тождеств, мы получаем:
, J (Snnx -f Snny -f Slsnz) da= f (^ + Щ*. + Ц&) dv, B0)
Подинтегральное выражение в правой части является лг-компонентой div 2S
и, следовательно,
tx = Sunx -J- 51влу -f 518ия B1)
есть компонента вектора t, который, согласно B0), и должен быть
проинтегрирован по поверхности, ограничивающей объём V. Лоступая подобным
образом и для других компонент, получаем общую теорему:
j t da = f div 2S dv, B2)
где компоненты t равны:
з
^=XV** (/ = 1,2,3), B3)
или, в сокращённых обозначениях:
t = 23n. B4)
Применение к уравнению A5) теоремы о дивергенции B2) даёт:
§*Snda = Fe + Fm-{Te0~f[E, B]dv, B5)
где Fe и ¥т представляют собой, как и в уравнениях C) и G),
результирующие силы, действующие соответственно на заряды и токи,
находящиеся внутри V.
Сначала рассмотрим стационарное распределение зарядов и токов. В этом
случае поля не зависят от времени, и третий член в правой части уравнения
B5) равен нулю. Уравнение B5) теперь показывает, что сила, действующая
со стороны поля на стационарные заряды и токи, может быть представлена
в виде интеграла вектора по какой-либо регулярной замкнутой поверхности,
охватывающей эти заряды и токи. Оно не утверждает, что объёмные силы
Fe и Fm находятся в равновесии с силами 2Sn, распределёнными по
поверхности. Равновесие должно устанавливаться благодаря механическим силам
какого-либо другого рода, и мы вскоре действительно покажем, что
распределение зарядов не можег поддерживаться в статическом равновесии
действием одних только электрических сил. Конкретнее, представим себе
статическое распределение заряда, разделённое на две части произвольной
замкнутой поверхностью £. Силы, действующие со стороны внешних зарядов,
на заряды, находящиеся внутри £, должны каким-то образом передаваться
через эту поверхность. Результирующая сила, действующая на внутренние
s0 [Ex ~2 J ^O^af^y
so^y^x so \py ~2 )
%EZEX B0^e^y
-k
B(fix^z
&QpyEz
ч(Е1—-2"£3) — л
ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯДЫ И ТОКИ [2.5J 97
заряды, может быть, согласно B5), подсчитана в предположении, что через
элемент площади da передаётся сила 2S(e)n da и что компоненты && являются,
следовательно, действующими напряжениями в электростатическом поле.
С каждой точкой поля связана квадрика напряжений, с помощью которой
могут быть определены нормальные и тангенциальные компоненты напряжений,
действующих на элемент с нормалью п. Чтобы найти главные оси этой
«вадрики по отношению к направлению поля, мы применим способ,' описанный
в разделе 2.1. Введённый там вековой детерминант A9) примет в данном
случае вид:
= 0. B6)
Развёртывая этот детерминант и учитывая, что
Ех \ Еу ~Т~ Ех == Е ,
получим, что уравнение B6) эквивалентно уравнению
8А3 + 4Е*к2 — 2£4А — £6 = 0. B7)
Следовательно, корни B6) будут:
Л=82°-£2, Аь-Ав-—;»£» B8)
откуда видно, что квадрика напряжений имеет осевую симметрию.
Пусть п(а) будет единичным вектором, определяющим направление главной
оси, соответствующей значению ка. Согласно A8), стр. 84, компоненты п(а)
по отношению к произвольной системе отсчёта должны удовлетворять
уравнениям:
(Е% — £*) n{aJ + ЕхЕуПу™ + ВД«(? = 0, ]
EyEj$-\-{E\-E*)«(? + Eytzn{? »0, } B9>
E^J^^E^f-i-iEl — E*)ti{? =0. ,
Из теории линейных однородных уравнений известно, что отношение
него) (а) (о)
известных пх, я/, п\' равно отношению миноров детерминанта системы,
«а основании чего легко получить из B9), что
Пх -My 'fig === t-x 't-'y • E'z* (.""/
Главная ось квадрики электрических напряжений в какой-либо точке
поля направлена вдоль вектора Е в этой точке. Напряжение, передаваемое
через элемент поверхности, нормаль к которому ориентирована по этому
направлению, является простым натяжением
№=4г'Е2^а)- C1)
Напряжения через элемент, в плоскости которого находится вектор Е, т. е.
элемент, нормаль к которому перпендикулярна к силовым линиям, тоже
7 Зак. 593. Теория электромагнетизма.
У8 гл. и. силы и энергия
нормальны, но отрицательны, что соответствует давлениям:
t(b) = _^ EW\ tW = — -J ^n^.
C2)
Предположим, наконец, что нормаль к элементу поверхности,
находящемуся в поле, ориентирована в произвольном направлении, определяемом
вектором п. Пусть ось z координатной системы, находящейся в
рассматриваемой точке, проведена параллельно Е, а ось д: возьмём перпендикулярной
к плоскости, проходящей через Е и п. Пусть угол между п и Е будет Ь.
Тогда:
Ех = Еу = 0, |Е| = Е2,
пх = 0, ny = sinb, ne = cos6,
откуда, согласно B3), компоненты напряжений равны:
4 = 0, L
-|-£2sin6, 4 = -|£2cos6.
C3)
Абсолютная величина напряжений, передаваемых через какой-либо
находящийся в поле элемент поверхности, независимо от его ориентации будет,
следовательно:
C4)
£о
jt| = f-£2.
Кроме того, вектор t лежит в плоскости векторов Е и. п и направлен так»
что вектор Е делит пополам угол между п и t, как показано на рис. 17.
В свете этих представлений легко понять попытки Фарадея и Максвелла
свести проблему электрического и магнитного полей к силам, действующим
в упругой непрерывной среде. Концепция
распространения сил от одной точки среды к другой
без участия промежуточной среды казалась обоим
совершенно несостоятельной и, за отсутствием
чего-либо более осязаемого, всепроникающий
«эфир» и был t в конечном счёте постулирован
для выполнения этой роли. Затем компонентам
напряжений поля была даже в пустом
пространстве приписана физическая реальность и
делались отважные попытки приписать эфиру
свойства, аналогичные деформации упругой среды.
Рис. 17. Соотношение между Эти попытки не принесли успеха. Дальнейшие
натяжением 1, действующим .исследования показали, что электромагнитные
на элемент поверхности в явления МОгут быть описаны без применения
электростатическом поле, и „ -. J „ .Г
напряжённостью поля Е. какой-либо выделенной системы отсчета, и что \
нет оснований для предположения, что силы
могут распространяться только путём непосредственного соприкосновения
соседних элементов материи или эфира. С современной точки зрения
представление электростатического поля через компоненты напряжения S $
не имеет существенного физического значения. Всё, что можно и необходимо
сказать, это то, что взаимные силы, действующие между элементами заряда,
могут быть правильно подсчитаны в предположении, что в поле существует
фиктивное состояние напряжений, как это описано выше.
Поскольку тензоры 2S(m) и 2S(e) имеют одинаковый вид, всё, что
говорилось в предыдущих параграфах, приложимо полностью и к полю,
создаваемому стационарным распределением токов. Силы, действующие со стороны
внешних источников на токи, заключённые внутри произвольной замкнутой
ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯДЫ И ТОКИ [2.6] 99»
поверхности, могут быть получены интегрированием по этой поверхности*
напряжений, абсолютная величина которых равна
lt|—£», 185>
и направление которых по отношению к ориентации элемента поверхности,
и направлению поля В такое же, как и на рис. 17.
Если в уравнение B3) подставить компоненты Sjk из таблиц I и II, та
становится очевидным, что напряжения, передаваемые через элемент
поверхности с положительной нормалью п, могут быть записаны векторно в виде г
t(e) = 2S(e)n = е0 (En) Е — -|- Е2 п, C6>
t(«) ^ 2S(m)n = -1 (ВП) В — ~ £2П. C7>
/ [АО /[А0
Следовательно, для любого объёма, ограниченного замкнутой регулярной
поверхностью £, для случая стационарного распределения зарядов и токов;
мы имеем:
f f e0(En)E— ^^n \ da = J* ?Edv, C8>
i v
/{1L(Bn)B-5LB«»i}&-J[J.B]<to. ^39>
2. 6. Импульс электромагнитного поля. В постоянном поле
равнодействующая сил, передаваемых через замкнутую поверхность £,
ограничивающую область, не содержащую ни зарядов ни токов, равна нулю. Если,.
однако, поле переменно, то из уравнения B5) ясно, что это уже не так.
Как же тогда должны мы интерпретировать действие силы на элемент объёма
пустого пространства? Поскольку размерность e0E = D есть QL-2, а
размерность B=jx0H есть MQ-1!-1, постольку величина
g = e0[E,B] = ^ JE,H] D0)
имеет, очевидно, размерность количества движения {или импульса) на:
единицу объёма. Q исчезает из выражения для размерности произведения [D, 8J,
и поэтому указанное заключение не является следствием применения какой-
либо особой системы единиц.
Тождество
[ *Sn da =>±fgdv D1>
i v
может быть интерпретировано в том смысле, что с электромагнитным полем
связан импульс, распределённый с плотностью g. Полный импульс поля,
находящегося внутри V, будет
G= \ gdv кгм/сек, D2>
v
и D1) является теперь утверждением того, что силы, передающиеся через
поверхность 2, связаны с увеличением импульса поля внутри £. Вектбр 2Sn
измеряет поток импульса, направленный внутрь через поверхность £,
приходящийся на единицу площади поверхности, в то время как величина— Sjk
7*
100 гл. и. силы и энергия
может быть интерпретирована как импульс, который переносится в единицу
времени в направлении j через единичный элемент поверхности, нормаль
к которому направлена вдоль оси k.
Прямым следствием этой гипотезы является заключение, что третий
закон Ньютона и закон сохранения импульса строго справедливы только
при учёте импульса электромагнитного поля, наряду с импульсом материи,
которая это поле вызывает. Предположим, что внутри замкнутой
поверхности 2 распределены заряды с плотностью р, и что движение этих зарядов
может быть описано током плотности J. Силы, действующие на заряженную
материю, находящуюся внутри 2, будут тогда равны
Fe + F„ = J (рЕ + U, В]) dv = ± G мех, D3)
где GMex — полный импульс движущихся, весомых зарядов. Поэтому закон
сохранения импульса для системы, состоящей из зарядов и поля, находящихся
внутри ограниченной области, выражается, согласно уравнению B5), в виде:''
й с
—J7 (Омех-у" Оэлектромаг) z=z I ЬП da. D4)
Если поверхность 2 увеличивать до тех пор, пока она не будет заключать
в себе всё поле, то правая часть уравнения D4) исчезнет, и мы получим
в этом случае:
Омех ~\~ Оэлектромаг =: CQnst. D5)
Таким образом оказывается, что с электромагнитным полем должно быть
связано свойство инерции, сходное с инерционными свойствами весомой
материи.
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ
2.7. Электростатическая энергия как функция плотности зарядов.
Конечный заряд, сконцентрированный в столь малой области, что её
протяжённостью можно пренебречь по сравнению с другими макроскопическими
размерами, называется точечным зарядом. Сила, действующая на подобный
точечный заряд q в поле стационарно распределённых зарядов, равна qE,
а работа, совершаемая при перемещении заряда q из точки г = г1 в другую
точку г = г2, будет:
г,
W^qJEds. A)
Так как ротор Е равен нулю в каждой точке электростатического поля,
вектор Е равен отрицательному градиенту скалярного потенциала о, и мы
имеем: ^
Е ds = — grab* о ds = — do, B)
где do — изменение потенциала вдоль элемента ds пути интегрирования.
Отсюда следует, очевидно, что работа, производимая при перемещении
заряда q из rt в г2, не зависит от выбора пути и является функцией только
начального и конечного значений потенциала о:
г»
W=— q j do==q{o(r1) — <?(r2)}. C)
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2*7] 10Г
В частности, работа, произведённая при перемещении* заряда по замкнутому
пути, равна нулю. Говорят, что силовое поле консервативно, если работа,
производимая при перемещении системы частиц из одного положение
в другое, зависит только от начальной и конечной конфигураций и не
зависит от последовательности бесконечно малых изменений, с помощью-
которых получается конечное перемещение. Консервативный характер
электростатического поля устанавливается уравнением C) или, точнее,
условием rot Е = 0. При этом перемещения и изменения в электростатическом
поле следует представлять себе настолько медленными, что они эквивалентны^
последовательности стационарных состояний. В термодинамике про подобные
процессы говорят, что они обратимы.
В главе III будет показано, что если все источники электростатического
поля расположены на конечном расстоянии от' какой-либо произвольной,
точки, то потенциалы и напряжённости поля в достаточно удалённых точках-
становятся исчезающе малыми. Работа, которую совершит заряд q при
перемещении из начальной точки г=г1, в точку г2 = ос, будет равна,
следовательно,
W=qo(r). D>
Сам скалярный потенциал, очевидно, может быть интерпретирован как
работа, совершаемая против сил поля единичным зарядом, при перемещении^
его из бесконечности в точку г, или как работа, отдаваемая системой при
удалении единичного элемента заряда в бесконечность:
(х, у, z)
До некоторой степени произвольно мы будем применять термин энергия
электростатической системы для обозначения работы, произведённой над
системой при перемещении элементов её зарядов из бесконечности в заданное
распределение посредсгвом последовательности обратимых ступеней. Мы,
предполагаем, что температура всех диэлектриков или магнетиков,
находящихся в поле, поддерживается постоянной1).
Энергия точечного заряда q2 в поле одиночного точечного источника qx есть..
U=<l2*2l> F>
где 92i — потенциал от заряда q1 в точке, в которой находится заряд q2.
Далее, поскольку работа, затраченная на внесение заряда д% из
бесконечности в заданную точку в поле заряда qv должна быть возвращена, если
заряд q1 удаляется в бесконечность, постольку
^=^1С?12- G)"
Взаимная энергия двух зарядов может быть, следовательно, выражена,
симметричным соотношением
Если в поле q± вводится сначала q2, а затем q3, то энергия будет
что, в силу взаимности между парами зарядов, эквивалентно выражению:
1 * 1 г1
U = y &12 + ?1з) Яг + 2" 0?Я1 + ?2з) + у (?si + ?») ?в- A0>
*) В действительности энергия, о которой мы здесь говорим, является в
термодинамическом смысле свободной энергией.
102 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Но индукции мы можем заключить, что энергия замкнутой системы из п
точечных зарядов равна:
п п п
4 = 1 3=1 * = 1
еде 9» — потенциал в точке нахождения git создаваемый остальными п—1
зарядами системы.
Заметим, что A1) справедливо лишь для случая полной или замкнутой
системы. Если напротив, п зарядов расположены во внешнем поле с
потенциалом <р0, то появляется член, не содержащий множителя -к-. В этом случае
п п
Рассмотрим теперь область пространства V, в которой находятся
закреплённые проводники и диэлектрики. Внутри диэлектриков заряды
распределены с объёмной плотностью р, в то время как на поверхности этих
диэлектриков и на проводниках может находиться тонкий слой зарядов
с поверхностной плотностью ш. Пусть потенциал, создаваемый в точке (лг, у, z)
внутри области V данным распределением зарядов и возможными
источниками, расположенными вне" V, будет <э. Работа, необходимая для увеличения
заряда в точке (х, у, z) на бесконечно малую величину 8<7, будет ? Ьд,
а увеличение энергии, которое произойдёт вследствие увеличения объёмной
плотности зарядов на величину 8р и поверхностной плотности на величину 8а>,
•будет
W1= f «8рЛ>4- (o&ada. A3)
Второй интеграл должен быть распространён по всем поверхностям,
находящимся внутри V, на которых имеются заряды. С другой стороны, увеличение
элемента заряда на величину 8# в точке (х,у, z) увеличит потенциал во
всех точках как внутри, так и вне V на величину 8<э, в результате чего
энергия зарядов, уже находившихся внутри V, возрастёт на
8£/2= J"p89<to+ f mboda. A4)
Работа Ю1У произведённая над системой при увеличении плотности зарядов,
равна потенциальной энергии 8£/2, накопленной полем, при условий, что
система замкнута, т. е. при условии, что область интегрирования V настолько
велика, что включает всё заряды, создающие поле. В этом случае:
W = 8^ = W2, )
W=y J* (? 8Р+Р 8<?)dv + Y f &8co~f~ ш8с?)da" J
что после интегрирования даёт:
U=~2 J?prff+^ (owda A6)
в качестве выражения- для электростатической энергии системы зарядов
относительно нулевого состояния р = ш = 0 *).
х) Сходимость этих интегралов будет показана в главе III.
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ 12.81 ЮЗ
2.8. Электростатическая энергия как функция напряжённости поля.
Представим себе на время, что все проводники удалены из поля и что все
поверхности разрыва на границах диэлектриков заменены тонкими, но
непрерывными переходными слоями. Заряды распределены по всему
диэлектрику с плотностью р, но мы предположим, что это распределение
ограничено конечной областью; тогда потенциалы и напряжённости поля
в бесконечности равны нулю. Области, не содержащие материи,
рассматриваются, конечно, как диэлектрики с единичной относительной диэлектрической
постоянной. Работа, необходимая для увеличения плотности* заряда в любой
точке поля на величину 8р, равна
W=f<?tydv, A7)
где ср—потенциал, создаваемый первоначальным распределением р. Приращение
плотности заряда связано с изменением вектора D соотношением:
8р = 8 (div D) = div (8D). A8)
Кроме того:
ср div (8D) = div (ср 8D) — 8D grad 9 = div (ср 8D) -j- E 8D A9)-
м, следовательно, уравнение A7) эквивалентно:
8£/= Г Е8D dv\- f div (ср 8D) dv,
что, после применения теоремы с дивергенции, даёт:
W= f E№dv-±- (Kcp8Dntfa, B1)
где S — замкнутая поверхность, ограничивающая объём V. Область , V не
обязятельно должна включать в себя все заряды, создающие поле, но, если
мы допустим, что поверхность S бесконечно увеличивается, как сфера
с центром в произвольной точке, то доля, вносимая поверхностным
интегралом, исчезнет, ибо, как в дальнейшем будет показано, на достаточно
больших расстояниях от источника ср убывает как 1/r, a D как 1/г2. Поверхность
увеличивается с возрастанием радиуса как г2, и, следовательно, поверхностный
интеграл убывает как 1/г. Прирост энергии, запасённой в электростатическом
поле, определяется из интеграла
8£/=J*E8D^, B2)
распространённого на всё пространство.
На практике заряды лишь в редких случаях распределены по объёму
диэлектрика, а обычно располагаются тонким слоем по поверхности
проводников с поверхностной плотностью ю. Эти проводники можно
рассматривать как электроды конденсаторов, и прирост энергии поля может быть
результатом работы, совершённой, например, электродвижущими силами
батарей в процессе образования зарядов на электродах. Предположим, что
имеется п проводников, поверхности которых мы будем обозначать через Siy
помещённых в бесконечный диэлектрик. Одну из этих поверхностей,
например Sn, будем предполагать замкнутой и охватывающей все остальные, как
показано на рис. 18. Чтобы быть уверенным в непрерывности потенциала
и поля, необходимых для применения теоремы о дивергенции, мы снова
можем заменить поверхности с резким изменением свойств диэлектрика
B0)
104
гл. и. силы и энергия*
тонкими переходными слоями, нисколько не уменьшая этим общности
результатов. Работа, необходимая для увеличения плотности заряда на
поверхности Si на величину 8w, равна
п
Ъи= Л. I ср 8шda^
B3-)
4 = 1 iS.
Сумма п таких .поверхностных интегралов может быть представлена в
вид-водного поверхностного интеграла «путем проведения двусторонних
соединительных поверхностей, от внутренних проводников к Sm как показано на
рис. 18. Интегрирование начинается с точки Р на Sm производится далее-
по одной стороне соединительной поверхности до Q, затем по St и потом*
мы возращаемся в Р по другой стороне соединительной поверхности. На
двусторонней поверхности PQ зарядов нет, и поэтому она ничего в
интеграл не вносит. Таким образом, пространство внутри поверхности $п сводится-
к простой односвязной области *),
ограниченной единой поверхностью
п.
■2*
и
*• = 1
NJ— I срош da.
s
B4>
Рис 18. Проводники, i омещённые
в диэлектрик и ограниченные
поверхностями Si, Sit . . .
В разделе 1.13 было показано, что н&
любой поверхности разрыва нормальные и
тангенциальные компоненты векторов D и Е.
удовлетворяют условиям:
n (D2 — D2) = еъ [П, Еа — Et] = 0. B5>
Положительная нормаль к поверхностям- Sf
направлена в диэлектрик, и поскольку п.
в параграфе 1.13 проводилось из среды A)
в среду B), индекс A) обозначает теперь-
внутреннюю область проводника, в то время как B) относится к диэлектрику.
В главе III нам представится случай подробней рассмотреть
электростатические свойства проводника, теперь же нам нужно только учесть тот
элементарный факт, что в любой внутренней точке проводника поле равно нулю.
Если бы это было не так, свободные заряды в проводнике начали бы
двигаться, в противоположность нашему предположению о статическом
состоянии. Следовательно, внутри проводника и на его поверхности мы имеем,
область постоянного потенциала. Плотность заряда во внутренних точках
равна нулю (уравнение B1), стр. 27), и каков бы заряд проводника ни был,
этот заряд распределён по его поверхности таким образом, что поле внутри*
проводника равно нулю. Поскольку E1=D1 = 0, постольку
nD.>
О)
[п,Е2] = 0;
в точке, лежащей снаружи непосредственно у поверхности проводника^
тангенциальная компонента вектора Е равна нулю, а нормальная компонент*,
вектора D равна плотности поверхностных зарядов.
х) Смотри раздел 4.2, стр. 205.
V
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2.8] 105»
f
Внося в B4) первое из этих соотношений и опуская индекс, мы
получаем:
Ш= [csoDnrfa. B7>
s
Для того чтобы выразить этот результат в виде интеграла по объёму
диэлектрика, ограниченного поверхностями Siy мы опять применим теорему
о дивергенции, но, поскольку нормаль п в B7) направлена внутрь
диэлектрика, должен быть взят знак минус:
bU = — Jdiv (cpSD)fifo = f E 8D dv — f с? div (8D) dv. B8>
Если плотность зарядов в диэлектрике, равна нулю или постоянна, то
div(8D) = 0, и как и в B2) мы получаем, что работа, затрачиваемая
батареями на увеличение зарядов на электродах на величину 8ю, равна
Ш== JEbDdv, B9>
где интеграл распространяется на всё пространство, занятое полем, и что
эта работа накапливается в поле в виде электростатической энергии.
Поскольку энергия oif оказывается запасённой в поле, подобно тому»
как потенциальная энергия растянутой пружины запасена некоторым образом
внутри неё, постольку представляется не лишённым основания предположить,.
что электростатическая энергия распределена в поле с плотностью
Ьи = E6D джоулей /метр3. C0)
Трудно подтвердить или опровергнуть подобную гипотезу. Преобразование
поверхностного интеграла в объёмный, очевидно, неоднозначно, так как
к <р 8D в B7) можно прибавить любой вектор, интеграл от нормальной
компоненты которого по поверхности 5 равен нулю. Более того, может быть
задан вопрос о том, имеет ли термин «плотность энергии» вообще какой-либо
физический смысл. Ведь энергия является функцией конфигурации системы
в целом. Несколько причудливым образом против локализации энергии
возразили Мезон и Вивер *), заявив, что спрашивать об этой локализации имеет
не,больше смысла, чем утверждать, что красота картины особым образом-
распределена по холсту. Будучи остроумной, подобная аналогия представляется
всё же не вполне обоснованной. Энергия неоднородно деформированной'
упругой среды безусловно сконцентрирована главным образом в областях
наибольшей деформации, и плотность упругой энергии имеет в этом случае
вполне определённый физический смысл. Соглашаясь с тем, что аналогия
между электростатическим и упругим полем не является полной, и что мы
можем быть уверены только в правильности выражения B9), в котором
производится интегрирование по всему полю, мы тем не менее можем сделать,
правдоподобное предположение о том, что энергия локализована в областях
поля с большей напряжённостью, как это и предписывает выражение C0).
Для того чтобы найти полное количество запасённой в поле энергии,,
надо проинтегрировать приращение № от начального состояния D = 0 до
конечного значения D:
D
U= f JEcDdv. C1)
vo
х) Mason and Weaver, The Electromagnetic Field, стр. 266, University of
Chicago Press, 1929.
106 , \ гл. и. силы и энергия
В случае, если среда изотропна и описывается линейными соотношениями -
<между D и Е, так что е в соотношении D = еЕ может быть функцией точки,
«о не Е, мы имеем:
ESD = -^-8E2
-и, следовательно,
U=~f eE4v. C2)
v
2.9. Теорема векторного поля. Пусть Р и Q будут две векторные
•функции точки, которые во всём пространстве удовлетворяют условиям:
rotP = 0; divQ = 0, C3)
я также непрерывны и обладают непрерывными производными всюду,
за исключением замкнутой регулярной поверхности S,. Тангенциальная
компонента Р и нормальная компонента Q предполагаются непрерывными при
переходе через поверхность Slt для нормальной же компоненты Р и
тангенциальной компоненты Q допускаются произвольные разрывы. Условия,
.имеющие место на поверхности St, будут, следовательно:
[п,Р+ — Р_]=0, n(Qf — Q_) = 0. C4)
Единичный вектор нормали п проведён наружу от поверхности St и векторы
в непосредственном соседстве с наружной стороной поверхности обозначены
индексом «-{-», в то время как расположенные непосредственно у
поверхности изнутри — индексом « — ». Наконец, предполагается, что источники
полей Р и Q расположены на конечном расстоянии от произвольного начала
отсчёта и что Р и Q стремятся в бесконечности к нулю так, что
limrP = 0, HmVQ = 0. C5)
Г->со r->co
При этих предположениях можно показать, что интеграл по всему
пространству от скалярного произведения потенциального вектора Р и солено-
идалъного вектора Q равен нулю, при условии, что Р и Q и их производные
непрерывны всюду, за исключением конечного числа регулярных
замкнутых поверхностей, на которых разрывы непрерывности удовлетворяют
условиям C4).
Поскольку rot Р =5= 0, мы можем написать, что Р = — grad cp и,
следовательно,
PQ = _ div(<?Q) -f- о div Q. C6)
Объём, ограниченный поверхностью Slf мы обозначим через Vlt а объём
вне этой поверхности — через V2, так что всё пространство, занятое полями
Р и Q, будет Vj -}- V2. Последний член в C6) равен нулю и, следовательно:
JpQ dv = —J*di v (<?Q) dv — J*div (<?Q) dv. C7)
Применяя к этому выражению теорему о дивергенции, мы принимаем
во внимание, что Vj ограничен поверхностью Su и что V2 ограничен внутри
поверхностью Su а снаружи — поверхностью S, которая удаляется в
бесконечность. Ввиду того, что поведение. Р и Q в бесконечности определено
соотношениями C5), интеграл от oQn no .S равен нулю. Положительная
шормаль к замкнутой поверхности по условию направлена наружу от
замкнутого объёма; поэтому, в силу C4), два интеграла от cpQn no St имеют про-
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2.10] Ю7
\ . : ■
тивоположные знаки при одинаковой абсолютной величине, и уравне-
«ение C7). переходит в следующее:
$PQdv = — f ®Q+n da-{- j\?Q_nda = 0, C8)
Vx+V, Sx St
как это и утверждалось. Распространение этой теоремы на конечное число
замкнутых поверхностей разрыва не представляет затруднений.
2.10. Энергия диэлектрического тела в электростатическом поле.
Теорема предыдущего раздела может быть применена для решения
следующей задачи. Предположим, что в диэлектрической среде создано поле Ev
Для упрощения мы предположим, что среда изотропна и линейна и
характеризуется, следовательно, диэлектрической проницаемостью е1} которая
постоянна или, в крайнем случае, является скалярной функцией точки. Пусть
теперь непроводящее тело с диэлектрической проницаемостью е2 внесено
в поле Ер в то время как источники поля Ег поддерживаются строго
неизменными. Мы хотим знать энергию инородного диэлектрического тела,
связанную с пребыванием его в поле.
Первоначальная энергия Uu представляющая собою полную работу,
необходимую для установления первоначального поля, получается
вычислением интеграла
f/1 = jjE1D1rf©1 C9)
взятого по всему пространству. После внесения тела изменившееся поле
в какой-либо точке будет Е и таким образом, разность Е2 = Е — Ej пред-
. ставляет собой поле, появившееся в результате поляризации тела. Объём,
занятый инородным телом, мы обозначим через Vv а объём остальной среды —
через V2. Энергия поля в этом новом состоянии будет:
U2 = -~ [ EDdv, D0)
Ух + ГЛ
и разность
«7=^ — ^ = 1 J* (ED —EA)^ D1)
должна представлять собой энергию тела во внешнем поле Elt и,
соответственно, работу, производимую при внесении тела в поле. Уравнение D1)
эквивалентно уравнению:
U = -2- j E{D~Dt)dv + ± f (E — E^D.dv. D2)
Fi+Fa Гх+Тш
Ротор Е везде равен нулю; дивергенция D—Dx также всюду равна нулю,
ибо первоначальное распределение зарядов задано. На поверхности,
отделяющей среду е2 от среды е1} условия
[И,Е+ — Е-] = 0, n{(D-D1) + ~(D — ^)_} = 0 D3)
выполнены, если только на этой поверхности нет зарядов. Тогда, по теореме
раздела 2.9, первый интеграл в D2) равен нулю, и мы получаем:
£/ = lf(E — EJD, Af4~J"(E — EODjrft». D4)
108
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
/
J* E1{D — D1)dv = fE1(D — D1)dv-^-fE1(D — Dl)dv = 0, D6>
vx+vt ух rt
откуда:
\ f Ex (D —D,) dv = -i- j E, (D —D,) A>. D7>
Подставляя D7) в D4), мы получаем выражение для энергии
диэлектрического тела, погружённого в диэлектрическую среду, в виде интеграла,
распространённого не по всему пространству, а только по объёму этого
тела:
U = у f (EaD, — EiDg) dv D8),
у\
или, поскольку внутри Vj: D1=e1E1, D==e2E,
U = ~ J (EDX — EjD) dv = у J(Sl — e2) EEX di>. D9>
Ух Ух
В этом случае, когда внешняя среда является свободным
пространством, проницаемость st сводится к е0. Тогда, поскольку результирующее
поле в теле связано с его поляризацией, согласно разделу 1.6,
соотношениями
D = е0Е + Р = е2Е, Р = (е2 — е0)Е, E0)
можно написать U в виде
,£/=_! [рЕ^. E1>
Ух
Плотность потенциальной энергии диэлектрического тела в свободном
пространстве в заданном внешнем поле Е1 равна Т^^ч-
Вариирование потенциальной энергии U, данной выражениями D9) или
E1), по отношению к малым перемещениям, даёт нам механические силы»,
действующие на поляризованный диэлектрик. Из уравнения D9) видно, что-
при е2>е1 энергия отрицательна и уменьшается с уменьшением е„
увеличением е2 или увеличением напряжённости поля Et. Мы можем ожидать поэтому,,
что если ^2^гъ т0 тело будет втягиваться в области с большей
напряжённостью поля или с меньшей проницаемостью вх. С другой стороны, если
ei > sa» чт0 возможно в случае твёрдого тела, погружённого в жидкость
с большой проницаемостью, силы, действующие на тело, будут стремиться,
вытолкнуть тело из поля.
Прямым следствием D9) является теорема о том, что всякое
увеличение проницаемости диэлектрика приводит к уменьшению полной энергии-
поля. Предположим опять, что Ei-1-поле заданной системы зарядов,,
находящихся в диэлектрической среде с проницаемостью е == е (х, у, z). Если»
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2.111 Ю9
© каждой точке е увеличится на бесконечно малую величину 8$, то
соответствующее изменение электростатической энергии будет, согласно D9),
.равно
W=— — jbeE^dv, E2)
-так как произведение 8е EEj отличается от 8е Е2 на бесконечно малые второго
.-порядка.
Но энергия электростатического поля полностью определена
распределением зарядов р и ш и диэлектрической проницаемостью е (х, у, z).
Уравнение E2) выражает изменение энергии в результате малого изменения
• чв свойствах диэлектрика, во время которого заряды поддерживаются
постоянными:
U=—£-Г JE^dsdv (заряды неизменны). E3)
о
С другой стороны, вариация
W = f? 8p dv -f Г» ооо da = f E 8D dv E4)
звыражает приращение энергии в результате малого изменения плотности
зарядов, во время которого свойства диэлектрика поддерживаются
постоянными.
2.11. Теорема Томсона. Заряды, находящиеся на системе заданных
проводников, погружённых в диэлектрик, распределятся по поверхности
этих проводников таким образом, что энергия получившегося в
результате электростатического поля будет минимальной.
При доказательстве этой и последующих теорем мы ограничимся
случаем изотропного диэлектрика с линейной связью между векторами D и Е.
Предположим, что имеется п проводников, ограниченных поверхностями
£{ (/= 1, 2, —, п), причём каждый из проводников несёт заряд qt. Разрывы
в свойствах диэлектрика могут быть без уменьшения общности теоремы
заменены тонкими переходными слоями, и поэтому мы будем предполагать
диэлектрическую проницаемость среды е непрерывной, а в остальных
отношениях произвольной функцией точки. Мы будем предполагать также
наличие заряда, распределённого по объёму диэлектрика, хотя подобные
условия встречаются на практике редко.
В каждой точке диэлектрика поле находящихся в равновесии зарядов
должно удовлетворять условиям:
divD = p, rotE = 0, Е =— grade? E5)
ша поверхности Sj каждого проводника:
с?г- = const., (unda^q^ E6)
з в бесконечности потенциал должен исчезать как \\г 1).
Предположим, что ?', Е', D'—какое-либо другое возможное
электростатическое поле; оно удовлетворяет условиям E5), но не обязательно E6),
*i где-либо, если не всюду, отлично от с?, Е, D. Так как объёмное
распределение р и полный заряд на каждом из проводников заданы,, то мы имеем:
div(D' — D) = 0, J(D' — D)nda = 0. E7)
i) Смотри раздел 3.5, стр. 155.
110 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Если U и U' — электростатические энергии этих двух полей, то их
разность
U' — U = ^ j E' D' dv — ~ JE D dv, E8>
или, поскольку D' = eE',
U' — U = \г/.(Е' — Е) (D' — D)fifo + JE(D'~-D)dv. E9)
Второй член правой части равен нулю, так как, положив Е = Р, D' — D—Q,
мы убеждаемся, что условия теоремы, доказанной в разделе 2.9,
соблюдены. Таким образом, остаётся:
U' — U = у Js (E' — Е)9 dv, F0),
что является существенно положительной величиной. Теорема таким образом,
доказана, ибо если в какой-либо области пространства Е' отличается от Е,
то получающаяся в результате энергия U' будет больше, чем U. Условие
электростатического равновесия характеризуется, таким образом,
минимальным значением электростатической энергии, и мы можем поэтому заключить,
что для определения равновесия энергия U играет в электростатике ту
же роль, что потенциальная энергия в механике;
2.12. Теорема Ирншоу. Заряженные тела, находящиеся в
электростатическом поле, не могут удерживаться в состоянии устойчивого
равновесия под действием одних только электрических сил.
Мы предположим, что первичное поле создаётся системой зарядов
ц1 (/=1, 2, ..., и), находящихся на п заданных проводниках, ограниченных
поверхностями S& Эти проводники погружены в диэлектрик,
диэлектрическая проницаемость е которого может быть непрерывной функцией точки,,
но в котором отсутствуют объёмно распределённые заряды. Мы замечаем
прежде всего, что ни сам потенциал, ни какая-либо из его частных
производных не могут иметь ни максимума, ни минимума ни; в одной из точек,
внутри диэлектрика, поскольку для абсолютного максимума ср необходимо,
чтобы все три частных производных д-о/дх2у d2<pfdy2, d2<?/dz2 были в
рассматриваемой точке отрицательны, что несовместимо с уравнением Лапласа
^+5^ + 53 = °- (ь1>
Точно так же для существования абсолютного минимума необходимо,
чтобы все эти три производные были положительны, что опять-таки
несовместимо с F1). Те же соображения применимы и к производным от
потенциала.
Предположим теперь, что заряд <7о находится на проводящей
поверхности S0. Предположим на время, что распределение зарядов на всех
проводниках фиксировано, и внесём поверхность S0 в поле остальных п зарядов.
Если ш0 — поверхностная плотность зарядов на SQi то энергия этого
проводника будет:
£/0=2-JVo0da, ( F2>
So
где <р — потенциал первоначального поля. Пусть лг, у, z будут координаты
какой-либо точки, фиксированной на S0, a &, tj, С — координаты
произвольной точки на этой поверхности. Потенциал в точках поверхности SQi
обусловленный другими я-зарядами, может быть представлен в виде ряда Тэй-
ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ 12.13) НЕ
■ .. , , 1 .'•■ '
ч
лора через значение потенциала и его производных в точке х, у, z,
9^^^-?{xty,z)^{l~x} + d^{rl-y)i-pz{C~-z)^..., F3>-
а следовательно, и энергия также может быть определена через значение
потенциала и его производных в этой точке. Но так как о не может иметь,
минимума в точке xt у, z, то всегда можно сместить проводник S0 таким
образом, чтобы энергия U0 уменьшилась. Если после такого смещения
заряды, которые до сих пор предполагались «замороженными» на
поверхностях S0, Sit освободить, то эти поверхности снова сделаются
эквипотенциальными и, по теореме Томсона, энергия поля ещё более уменьшится. Таким
образом, в электростатическом поле не существует минимума энергии
UQ(x, у, z\ и, соответственно, проводник S0 нигде не может находиться
в состоянии статического равновесия.
2.13. Теорема об энергии незаряженного проводника. Введение
незаряженного проводника в поле заданной системы зарядов уменьшает-
полную энергию поля.
Пусть проводники будут такие же, как и в предыдущей теореме, но
поверхность S0 будет теперь незаряженной. Пусть Е, D—векторы,
характеризующие поле до внесения S0, a E', D' — после внесения. Изменение
энергии будет:
U— U'=^-JEDdv—^JE'D'dv. F4),
у
Объёмный интеграл должен быть распространён по всему пространству, но
так как внутри поверхностей S0, Si поле отсутствует, эти области в
интеграл ничего не вносят. Пусть V — объём поля, внешний по отношению
к «-проводникам Si до внесения 50>. a V0 — объём, ограниченный S0. Тогда-
Vt = V— Vp F5),
представляет собой объём области, занятой полем после внесения S0, и
уравнение F4) может быть'записано в виде:
U—If = ~ J* ED dv — y/e'D' dv = у J ED dv -f -*- [(ED — ED') dv =
V Vt V0 Vt
= ^JEDdv-\-l2-f(E—E')(D — D')dv-\- fE'(D — D')dv. F6>
Можно показать, что последний интеграл справа равен нулю, так как
E'(D— D') = —grade?'(D — D') = —div{©' (D —D')} + ?'div(D —D')
и div(D — D') = 0. По теореме о дивергенции
п
f E'(D — D') dv = J div {<p'(D'— D)} dv = ^ <?/ J(D' — D)n da, ф7у
Vx Tx i=l Si
i
где <p£—потенциалы проводящих поверхностей S^ Полный заряд на каждой'
из поверхностей задан, так что
j D'n da = J*Dn da = qi% F8>
Л12 гл. и. силы и энергия
и следовательно,
f(D — D)n da = 0. F9)
Разность между начальной и конечной энергиями будет поэтому:
U— U'^^\sE?dv-\-^$s{E — E'fdv, G0)
а это существенно положительная величина.
МАГНИТОСТАТИЧЕСКАЯ ЭНЕРГИЯ
2.14. Магнитная энергия стационарных токов. Рассмотрим
стационарное распределение токов, ограниченное конечной областью пространства.
Зти токи могут протекать в проводящей среде, или же представлять собой
движение зарядов в свободном пространстве.
Уравнение непрерывности сводится к условию
div J = 0, в силу чего мы можем представить себе,
что распределение токов разложено на линии
тока, замыкающиеся сами на себя. Трубка или нить
тока, может быть построена из линий тока,
проходящих через бесконечно малый элемент
Рис. 19. Иллюстрация смеще- площади. Трубка ограничена линиями, прохо-
ния нити тока. дящими через точки контура этого элемента
площади. Поток в каждой точке поверхности
трубки является чисто тангенциальным — ток из трубки не выходит и,
соответственно, через любое поперечное сечение трубки за данный промежуток
времени проходит один и тот же заряд.
Подсчитаем прежде всего потенциальную энергию одиночной
изолированной нити тока в поле В заданных внешних источников. Пусть ток,
несомый нитью, будет /, и пусть он проходит первоначально по контуру,
обозначенному на рис. 19 через Сг. Сила, действующая со стороны поля на
линейный элемент нити, равна
f = /[A,B]. A)
Предположим теперь, что нить Сх перемещена и деформирована таким
образом, что каждый элемент ds сместился на бесконечно малую величину
8г, перейдя в элемент контура С2. Смещение 8г предполагается
непрерывной функцией положения на Clt а в остальном произвольно. Работа,
совершённая силой A) при смещении элемента ds, будет:
f8r = /[ds, B]8r = /B[8r, ds]. B)
Пусть St—любая регулярная поверхность, опирающаяся на контур Cv
Другая поверхность S2 пусть опирается на контур С2, проходит через точки
.контура С\ и далее совпадает с поверхностью $v Поверхность
<S3 = «S2 — *^i C)
«будет, следовательно, полосой или лентой ширины or, ограниченной
кривыми Сх и С2. Если da3— элемент S3, то мы имеем, очевидно:
[Ьт, ds] =n3tfa3, • D)
где п3 — положительная единичная нормаль к поверхности £8.
Положительные стороны St и S2 определяются обычным условием, что положительная
МАГНИТОСТАТИЧЕСКАЯ ЭНЕРГИЯ P.14J
ИЗ
сторона должна находиться с левой стороны от наблюдателя, движущегося
по контуру в направлении тока. Магнитные потоки, пронизывающие
контуры Сг и С2, будут:
Фг = J" Вщ йаъ Ф2 = J Bn2 йОъ, E)
отсюда полное изменение магнитного потока в результате перемещения
контура равно:
8Ф = ф2 _ ф1 = J Bn3 daB. F)
С другой стороны, полная работа, совершённая механическими силами,
может быть получена интегрированием выражения B) по замкнутому контуру
Cv откуда в силу D) получаем:
№=& !8г = /8Ф. G)
Если теперь предположить, что во время виртуального перемещения 8г
внешние источники и ток / поддерживаются неизменными, то работа,
совершённая механическими силами, компенсируется уменьшением
потенциальной энергии U:
8£/= —81Р= —/8Ф, (8)
или
£/=-/Ф = — / fBnrfa, (9)
8
где S представляет собой любую поверхность, опирающуюся на нить тока.
Обратно, механические силы и вращающие моменты, действующие на нить
тока в магнитостатическом поле, могут быть получены вариированием
функции U при неизменном токе / и неизменной силе источников поля.
Если 8г является действительным, а не виртуальным перемещением, то
необходимо затратить работу для поддержания тока постоянным. Изменение
магнитного потока на 8Ф индуцирует электродвижущую силу:
К-ГЕ*=-$, A0)
С
где 8*— время, затрачиваемое на перемещение. Эта индуцированная
электродвижущая сила должна быть сбалансирована равной и противоположно
направленной сторонней электродвижущей силой V. Работа, произведённая
в контуре сторонней э. д. с. за время 8£, будет:
1/78* =+/8Ф. (И)
Работа, производимая поперечными механическими силами при малом
перемещении линейного контура, полностью компенсируется энергией,
затрачиваемой продольными электродвижущими силами, необходимыми
для поддержания тока неизменным. Полная работа, произведённая над
контуром, равна нулю.
Предположим теперь, что источником поля В является другая нить тока.
Таким образом, мы представим себе сейчас распределение токов, состоящее
из двух изолированных замкнутых нитей 1г и /2. Поля, создаваемые этими
соками, будут соответственно В± и В2. Потенциальная энергия контура /а
8 Зав. 593. Теория электромагнетизма.
114
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
во внешнем поле Bj равна:
^2i = — /а/в^йЦэ, A2)
St
где 5а — любая поверхность, опирающаяся на нить тока /2. Точно так же
потенциальная энергия контура 1 в поле тока /2 равна
Ul2 = — I1JB2n1dal. A3)
Si
U12 и U%\ являются скалярными функциями точки и конфигурации
контуров; их производные дают силы и вращающие моменты, действующие со
стороны одной нити на другую. Из равенства действия и противодействия
следует, что
и12 = и21 = и, A4)
а значит и взаимная потенциальная энергия может быть выражена в виде:
tf=-1/^-1/^2, A5)
где Ф1 — магнитный поток, пронизывающий контур /t.
Взаимная энергия U, которая обращается в нуль при бесконечном
удалении нитей друг от друга, не равна полной работе, которая должна быть
совершена при сближении нитей из бесконечности до данного
взаиморасположения, и поэтому не представляет собой полной энергии системы.
Действительно предположим, что контур 2 испытывает малое перемещение под
действием сил со стороны 1, в результате чего потенциальная энергия
уменьшается на величину — 8/7. Для того, чтобы поддерживать ток /2 во время
смещения неизменным, в контуре 2 должно быть совершено равное
количество работы bW с тем, чтобы компенсировать действие индуцированных
э. д. с. До сих пор полное изменение энергии было равно нулю. Но теперь
мы должны учесть, что в результате смещения /2 меняется поток,
пронизывающий контур /„ вследствие чего индуцируется э. д. с. V^,
противоположная току /j. Если ток 1Х должен поддерживаться неизменным, то к
контуру 1 необходимо приложить стороннее напряжение Vlt компенсирующее Vx и
производящее в единицу времени работу /jV^. Индуцированная э. д. с.
зависит, однако, только от относительного движения 1 и 2. Работа,
производимая электродвижущими силами, индуцированными в контуре 1 при
перемещении контура 2, должна равняться работе, которая была бы
произведена, если бы контур 2 был неподвижен, а контуру 1 было сообщено I,
авное и противоположное перемещение. Работа, совершённая . в контуре
р будет, следовательно, bW. В результате, если механическим силам,
действующим на обе нити тока, дана возможность совершать работу, то
хотя и получается уменьшение взаимной потенциальной энергии на
величину— 8/7, но это уменьшение перекрывается работой 28V7, которая должна
быть совершена, над системой для того, чтобы поддерживать токи 1Х и /а
неизменными. Если полную магнитную энергию системы мы обозначим через
Т, то изменение Т, связанное с относительным перемещением 'при неизмен*
ных токах, будет:
или, согласно A5),
8r = 28y7-f8i/ = 8= — №, A6)
у—т№-+т№ О?)
МАГНИТОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2.U]
115
В общем случае, если система состоит из п отдельных нитей тока, магнитная
энергия будет:
те
7-4 2 7<** (i8>
где Ф{ — магнитный поток, пронизывающий контур /, обусловленный
остальными п — 1 контурами.
Уравнение A8) даёт выражение работы, необходимой для перемещения
п замкнутых нитей тока из исходного положения в бесконечности в
некоторое заданное положение в конечной области пространства. Поперечное
сечение любой из нитей тока очень мало, но не исчезающе мало, и нить
тока в том смысле, в каком мы пользовались этим понятием выше, не
является особой линией. Каждая нить или трубка тока может быть разделена
на пучок более тонких нитей, каждая из которых несёт долю
первоначального тока. В пределе, при исчезающе малом поперечном сечении, ток,
несомый нитью, бесконечно мал, как бесконечно мала и энергия, необходимая
Для его установления. Соответственно, полная энергия данного
распределения токов равна просто взаимной энергии бесконечно тонких нитей тока,
на которые это распределение токов может быть разложено.
Практически, однако, распределение токов в проводящей среде не
может быть установлено посредством математически простого приёма
собирания нитей из бесконечности и, хотя A8) является правильным для
выражения магнитной энергии п замкнутых контуров в среде, в которой
соотношение между Н и В линейно, но отсюда ещё не следует, что оно верно и в общем
случае. Вместо непрерывного распределения рассмотрим теперь п линейных
контуров, помещённых в магнитную среду. Пусть сопротивление i-ro
контура будет Rb а мгновенный ток, который он несёт, равен Jt. К каждому
контуру пусть теперь будет приложена сторонняя э. д. с. Vrv создаваемая
химическим или механическим путём. Эти сторонние э. д. с. вызывают
изменение токов и соответствующее изменение магнитных потоков,
пронизывающих каждый из'контуров. Если V{ — э. д. с, индуцированная изменением
Ф$, то соотношение между током и полной э. д. с. в контуре в каждый
момент будет:
vj+^^ад, A9)
Иф.
или, поскольку Vi — -т~,
^=ед+^. B0)
Мощность, затрачиваемая приложенной э. д. с. Vi, будет Vji и
соответственно работа, совершённая в /-ом контуре за время 8/, равна
Из этой работы количество, равное R$$t рассеивается в виде тепла, в то
время как количество, равное 1<ЬФ< накапливается в виде магнитной энергии1).
Изменение магнитной энергии п нитей вследствие приращения магнитного
патока будет, следовательно:
8Г= 2/<8Ф„ B2)
*=i
*) Часть энергии /<&Ф$ может, однако, совсем исчезнуть благодаря явлению
гистерезиса. См. раздел 2.16.
8*
116
ГЛ. П. СИЛЫ И ЭНЕРГИЯ
и полная энергия, затрачиваемая на систему при медленном возрастании
токов от нуля до их конечных значений, за вычетом рассеивающихся в виде
тепла омических потерь в проводниках, будет:
Г= ^ J /,8Ф„ B3)
где Ф^0 — магнитный поток, пронизывающий /-ый контур в начальный момент,
когда все токи равны нулю. Первоначальный поток был бы равен нулю,
если бы отсутствовало остаточное намагничение среды, окружающей контуры.
Выражение B3) может быть интерпретировано как энергия, запасённая
в магнитном поле, только в том случае, если соотношение между /f и Фг-
однозначно (отсутствие гистерезиса); B3) сводится к A8) только тогда,
когда соотношение между Н и В и, соответственно, между /f и Ф$ линейно,
так что /г8Фг- sb Ф^.
Не представляет труда распространить выражение B3) от конечного
числа нитей тока на непрерывное распределение токов. В пространстве,
в котором распределены токи, выберем произвольную элементарную площадку
do. Линии тока, проходящие через точки do, образуют трубку тока,
которая, в силу стационарного характера распределения, замыкается сама на себя.
Если J — плотность тока, то скалярное произведение Jn do — dl постоянно
для каждого сечения трубки. Пусть В' будет магнитным полем в любой
точке внутри трубки, создаваемым всеми нитями тока, лежащими вне её.
Приращение энергии тока dl, связанное с бесконечно малым увеличением
поля внешних нитей тока, будет
b(dT) = dI№' = dlf№'nda, B4)
где интеграл должен быть распространён по любой поверхности,
опирающейся на контур нити тока dl. Если А' — векторный потенциал поля В', то
В' = rot А', и B4) может быть преобразовано по теореме Стокса в линейный
интеграл вдоль контура нити:
8 (d Т) = Jn do & 8А' ds. B5)
Полный векторный потенциал А на какой-либо линии внутри трубки d
равен А' плюс слагаемое, связанное с самим током dI = 3ndo. Но по мере
того, как площадь поперечного сечения do -*■ 0, это слагаемое стремится
к нулю, так что в пределе А' может быть заменено через А. Более того,
поскольку вектор плотности тока J, единичный вектор п, нормальный к do,
и элемент длины вдоль трубки • ds параллельны друг другу внутри трубки
бесконечно малого сечения, постольку вместо B5) можно написать:
Z(dT) = &) ibkdods. B6)
Произведение dods = dv представляет собой объём участка трубки
бесконечно малой длины. Полное приращение энергии при заданном
распределении токов получится суммированием слагаемых от всех трубок, на которые
это распределение было разложено, а это суммирование эквивалентно,
очевидно, интегралу от произведения J 8А по всему объёму, занятому токами
8Г= jjbAdv. B7)
МАГНИТОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2.15] 117
Таким образом, работа, необходимая для установления непрерывного
распределения токов посредством приложенных электродвижущих сил, равна
в общем случае
А
Т= Jj ibkdv. B8)
Ао
Если соотношение между током и создаваемым им векторным потенциалом
линейно, то это выражение принимает вид:
-И"
dv. . B9)
2.15. Магнитная энергия как функция напряжённости поля. Мы будем
предполагать, что разрывы непрерывности в магнитных свойствах среды,
находящейся в поле, могут быть заменены слоями с быстрым но непрерывным
изменением этих свойств. Поле может частично вызываться токами,
частично— постоянными магнитами или остаточным намагничением среды; во
всяком случае, все источники поля находятся на конечном расстоянии от
какого-либо произвольного начала отсчёта. В главе IV будет показано, что
при этих условиях векторы А и В исчезают в бесконечности как г-1 и д—2.
Плотность тока J в любой точке связана с вектором Н в той же точке
соотношением
J = rotH. C0)
Далее, согласно хорошо известному тождеству,
J 8А = 8А rot Н = div [Н, 8А] -f Н rot 8А == div [Н, 8А] -f Н 8В. C1)
После подстановки C1) в B8) и применения теоремы о дивергенции, мы
получаем:
Т== ffndBdv-\-ff[H, dA]nda, C2)
V В0 S А„
где V—любой объём, ограниченный поверхностью S, охватывающей все
источники поля. Если поверхность 5 неограниченно увеличивать, то второй
интеграл в C2) исчезнет, поскольку подинтегральное выражение убывает
как г~3, в то время как S растёт только как г2. Следовательно, работа,
совершённая сторонними э. д. с. (которые создаются, например, батареями
или генераторами), при увеличении магнитного поля от начального значения
В0 до конечного значения В, может быть выражена в виде интеграла
в
Т= jdvjUdB, C3)
Во
распространённого по всему пространству. Необходимо подчеркнуть, что
интеграл C3) представляет собой энергию, связанную с установлением
данного распределения токов в присутствии магнетиков, и не включает
внутреннюю энергию постоянных магнитов или взаимную энергию систем
постоянных магнитов.
Магнитные свойства всех материалов, за исключением ферромагнитной
группы, мало отличаются от магнитных свойств свободного пространства;
соотношение между В и Н линейно в широких пределах изменения
напряжённости поля; множитель ja в соотношении В =s= jxH почти равен {л0, а
заметное остаточное намагничение отсутствует. При этих условиях работа,
118
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
затраченная на установление поля В, возвращается обратно при уменьшении
поля до нуля. Уравнение C3) можно проинтегрировать, и мы получаем
выражение
T=±JvH*dv, C4)
которое мы интерпретируем как энергию, запасённую в магнитном поле.
Как и в соответствующем электростатическом случае, мы можем
предположить, что энергия распределена в поле с плотностью — рН* джоулей/метр3.
2.16. Ферромагнитные материалы. В ферромагнитных веществах
соотношение между Н и В в общем случае нелинейно и неоднозначно. В
исходном ненамагниченном состоянии векторы В и Н равны нулю. Если теперь
с помощью сторонних электродвижущих сил, приложенных к проводящим
контурам, медленно увеличивать поле, то функция В —В(Н) в любой точке
ферромагнитного вещества
будет следовать кривой,
имеющей вид, показанный на рис. 20.
Согласно C3), работа, необхо-
2.00
Ь,50
%
two
I
ZQ50
«а
О
в,
mm
^тт
^§Ж
w§§^
Щу-
§ш
s®?*
и
(
О 200 ЧОО 600 800 1000 1200 №0
И в ампер-витках на метр (рациональные единицы)
Рис. 20. Типичная кривая намагничения
отожжённого листа стали.
Рие. 21. Петля гистерезиса.
димая для намагничения единицы объёма среды, изображается заштрихованной на
рисунке площадью. Будь функция В (Н)«однозначна, уменьшение поля от Н1} Bt
до нуля происходило бы по этой же кривой, и вся энергия C3) могла бы быть
превращена в полезную работу. В действительности, возвращение происходит
обычно по пути, подобному тому, какой показан на рис. 21. Начиная
с Н, поле уменьшается до Н=0. Однако" соответствующее значение В = В2
всё ещё положительно. Чтобы В уменьшилось до нуля, необходимо придать *Н
отрицательное значение, что физически означает возрастание Н в
противоположном направлении. При Н = — Н3 твектор В равен нулю и при
возрастании отрицательной величины Н достигает в конце концов точки, где
Н= — Н1} В = — Bj. При возвращении к положительным значениям Н1} Bt
система следует по симметричному пути через точки В= — В2, Н = 0 и
В = 0, Н = -|~Нз- Во всех точках отрезка BjB2 значения В больше, нежели
первоначальные значения на пунктирной кривой при тех же значениях Н;
изменение В отстаёт от изменения Н; в этом случае говорят, что в среде
проявляется гистерезис.
Пусть w будет работой, произведённой над единицей объёма магнетика
при изменении поля от значения Bt до В.
в в н.
<ze>=fHrfB = HB — Гв<Ш. C5)
в.
МАГНИТОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2-171 119
Если изменение поля пройдёт полный цикл, следуя по гистерезисной петле
от Bj через В2, ;—Вь —В2 и возвращаясь к В1э то полная работа,
произведённая над единицей объёма, будет равна
w
■§
BdH
C6)
— величина, представляемая, очевидно, площадью, находящейся внутри
гистерезисной петли, показанной на рис. 21. Полная работа за один цикл во
всём поле будет:
Q = — fdv&BdH. C7)
Q является потерей на гистерезис — частью энергии поля, необратимо
рассеявшейся в виде тепла.
2.17. Энергия магнитного тела в магнитостатическом поле.
Предположим, что в магнитной среде с помощью заданных источников создана
поле Bj. Мы примем, что соотношение между Вг и Ht линейно и что среда
изотропна. Тогда Bt = [^Hj, где jxx является
самое большее скалярной функцией точки; ^
есть константа в случае однородной среды.
Энергия поля выражается интегралом
7\ = -j J* ВД dv,
C8)
В*//,Н
Рис. 22. Область V1 занята
магнитным телом, помещённым
в однородную изотропную
среду Vj.
распространённым по всему пространству.
Уменьшим теперь интенсивность источников до
нуля, и внесём в подходящую полость,
сделанную в первой среде, тело, которое мы
предположим ненамагниченным; магнитные свойства
этого тела произвольны. Как и в разделе 2.10,
объём, занятый внесённым телом, мы обозначим
через Vj (рис. 22), а остальную область вне тела — через Va. Если внешние
источники являются токами, то работа, которая должна быть совершена,
чтобы восстановить их первоначальную величину, равна:
в в
Г2 = J dv j H dB = ~ J* HB dv -j- J dv J* H dB. C9)
В этом выражении конечное поле В отличается в каждой точке от поля Вг
на величину В2 = В—В1} что является следствием магнитной поляризации
вещества, находящегося в Vt. Увеличение энергии, необходимое для
восстановления первоначальной силы тока, равно
в
Т=Т2— 7,1=-jJ(HB — Hfijdv-^ $dv(f HdB —^B,). D0)
v,
Vi
Мы предположили, что в области V2, внешней по отношению к телу,
соотношение между В и Н линейно:
B1 = jx1H1, В = ^11 в Vr
Поэтому первый интеграл в выражении D0) эквивалентен:
D1)
D2)
va
12@ ГЛ. И. СИЛЫ И ЭНЕРГИЯ
По условию, первоначальное и конечное распределение токов в источниках
одинаково, так что и в Vx и в V2 условия
divCB + BO^O, rot(H —H!)==0 D3)
удовлетворены, тв о время как на поверхности, ограничивающей Vu мы
имеем, согласно A8), стр. 45:
п {(В + В1)+-(В+В1)_} =0, \
[п {(Н-Н0+ — (H-HjUJ^O. J
Таким образом, мы можем применить теорему раздела 2.9, что даёт
-1/(Н~Н1)(В + В1)^ =
= i/ (H-H1)(B + B1)^ + 1 j (Н-Н,) (B+BJdv^O D5)
или
2
i-/(H —H1)(B + B1)^=-yJ(H-Hi)(B + Bi)^' D6)
v,
Дополнительная работа, необходимая для установления тех же токов в
присутствии тела, может быть, таким образом, выражена через интеграл,
распространённый по объёму, занятому телом. Подставляя D6) в D0), получаем:.
в
-Г= ~ j (HjB — HB! — НВ + 2 j HrfBW D7)
Vt 0
Если явлением гистерезиса можно пренебречь (Н—однозначная
функция В), то величина Т может быть интерпретирована как энергия тела
в магнитном поле какой-либо системы постоянных источников, и вариация
Т при виртуальном перемещении тела определяет действующие на него
механические силы. Если, кроме того, магнитные свойства вещества внутри
Vx могут быть охарактеризованы магнитной проницаемостью [i^, так что
В = jx2H, то D7) сводится тогда к
Г~ у J <H*B- НВ1> dv=sali I**- Ъ) HHi dv. D&)
vt « vt
Так как предполагалось, что первоначально тело не имело остаточного
намагничения, то соответственно векторы В и Н внутри Vl связаны с
индуцированным намагничением М, согласно разделу 1.6, соотношением
, В = МН + М), D9)
и, поскольку В = р2Н, это даёт:
М = (-^ — 0н = (- Х-)ъ. E0)
Следовательно, если полость Vt первоначально не содержала магнетика,
то мы можем положить jxj == jxq и написать D8) в виде:
'=IJ*MBlfito , E1)
МАГНИТОСТАТИЧЕСКАЯ ЭНЕРГИЯ [2.18] 121
— выражение, которое соответствует соотношению E1), стр. 108, для
электростатического случая во всём, за исключением знака. Однако это
различие является фундаментальным. В то время как в электростатическом
случае работа, совершённая внешними источниками при виртуальном
перемещении, сопровождается уменьшением потенциальной энергии U,
механические силы, действующие на намагниченное Ало, должны, как мы скоро
увидим, определяться из увеличения Tt так что Т в этом смысле ведёт себя
как кинетическая, а не потенциальная энергия.
Из соотношения D8) может быть выведен полезный аналог уравнению-
E2), стр. 109, для магнитостатического поля. Предположим опять, что Bt
есть поле заданных источников — безразлично токов или постоянных
магнитов,— и что в каждой точке пространства магнитная проницаемость
{1 = }А (л;, yt г) является непрерывной функцией точки. Если магнитная
проницаемость изменится теперь на бесконечно малую величину 8ji, то-
соответствующее изменение магнитной энергии будет:
tT=±ftyH*do; E2)
и, следовательно, магнитная энергия некоторого распределения вещества-
в заданном поле будет равна:
T==Yfd'vI1H2dv' G^Po*»)» E3>
V-0
при условии, что первоначально вещество было ненамагничено, и что \ь не
зависит от Н. Для парамагнитных материалов f* > р0»у»» > 1» но в случае
диамагнитного вещества f*.<fj^, и магнитная энергия первоначального поля
при внесении диамагнитных тел уменьшается.
2.18. Потенциальная энергия постоянных магнитов. Исследование
энергии материальных тел в магнитом поле становится намного труднее, если
эти тела первоначально намагничены. В этом случае даже в отсутствие
внешних источников имеется остаточное магнитное поле, которое связано
с магнитами и которое мы будем обозначать через В0, Н0. Соотношение
между В0 и Н0 может быть попрежнему выражено в виде:
B0 = f*o(H0-f-M0), E4)
но М0 — интенсивность намагничения — теперь совершенно не зависит от
Н0, определяясь исключительно предыдущей историей образца. Если теперь
налагается внешнее поле, то индуцируется дополнительная составляющая
намагничения, которую, как и ранее, мы обозначим через М. Это
индуцированное намагничение М зависит прежде всего от полного поля Н внутри
магнита (и исчезает, когда Н сводится к Н0), но также и от состояния
магнита и от его постоянного или остаточного намагничения М0.
В = f*0 { Н + М (Н, М0) + М0). E5)
Полное поле Н во внутренних точках определяется кроме того формой магнита,
равно, как и интенсивностью и распределением внешних источников.
Мы ограничимся выводом простого, но часто используемого
выражения для потенциальной энергии системы постоянных магнитов. Доказательство
основывается на предположениях, которые на практике приблизительно
выполняются, а именно, что намагничение М0 строго постоянно и что
намагничением М, возникающим в каком-либо магните под действием внешнего
122
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
поля других магнитов, можно пренебречь по сравнению с М0. Поле во всех
точках внутри и вне намагниченного тела, занимающего объём Vu в точности
такое же, какое было бы создано стационарным распределением токов по
объёму Vt с плотностью
J = rotM0, E6)
совместно с поверхностными токами, распределёнными по поверхности St
ограничивающей объём Vlt с плотностью *)
К = [М0, п], E7)
где п — единичный вектор нормали к поверхности S. Прямым следствием
анализа, проведённого в разделе 2.14, и, в частности, уравнения (9),
является то, что потенциальная энергия магнита Vt в поле других постоянных
магнитов или постоянных токов равна
£/= — JjAtffl— fKAda, E8)
Vi S
или, в силу E6) и E7),
U = — J rot M0 A dv — J[M0,n] A da. E9)
Vi S
Лз лее
ArotM0 = div[M0,A] + MrotA, F0)
[Mo, A] n = [n, M0] A = — [M0, n] A, F1)
так что, применяя теорему о дивергенции и полагая В = rot А, получаем
из E9):
U= — (*M0Bfifo. F2)
vi
В уравнении F2) можно рассматривать dm = M.0dv, как магнитный
момент элемента dv магнита. Его потенциальная энергия в результирующем поле
В равна dU= —В dm. Результирующее поле В состоит из первоначального
поля Bj всех внешних источников и поля В2, обусловленного всеми другими
элементами самого магнита Vv Следовательно, работа, необходимая для того,
чтобы собрать вместе первоначально намагниченные элементы магнита, в
отсутствие внешнего поля должна быть равна
U2= — fM0B2dv. F3)
Эти элементы должны удерживаться вместе силами немагнитного характера.
Работа же, необходимая для перенесения магнита, как жёсткого целого, из
бесконечности в некоторую точку во внешнем поле Вь будет:
Ul=^JM0B1dvi * F4)
VI
а силы, действующие со стороны внешних источников на единицу объёма
магнита, будут:
f^+gradCMoB,). F5)
*■) См. разделы 1.6 и 4.10.
ПОТОК ЭНЕРГИИ 12.191
123
Различие между F4) и E1) объясняется тем, что F4) является только
потенциальной энергией намагниченного тела во внешнем поле, в то время
как E1) включает и работу, связанную с увеличением намагничения от нуля
до М, и основывается на предположении, что существует линейное соотношение
между Вх и Hj и, соответственно, между Вх и М.
ПОТОК ЭНЕРГИИ
2.19. Теорема Пойнтинга. В предшествующих параграфах настоящей
главы было показано, что работа, совершаемая при осуществлении малых
вариаций в величине или распределении зарядов и токов в источниках поля,
может быть выражена через интегралы от векторов поля, распространённые
по всему пространству. Вид этих интегралов наводит на предположение -(но
отнюдь he доказывает его), что электрическая и магнитная энергии
распределены в поле с объёмными плотностями соответственно
D В
и== JEdD, w = JndB. A)
.0 О
Вывод этих соотношений основывался на предположении обратимости
процессов; предполагалось, что возникновение поля происходит настолько
медленно, что оно может быть представлено последовательностью равновесных
состояний. Сейчас мы установим, остаются ли эти выражения для плотности
энергии справедливыми и в том случае, когда поля меняются с произвольной
скоростью. Очевидно далее, что если наша гипотеза о распределении энергии
по' всему полю вообще справедлива, то изменение напряжённости поля и
плотности энергии должно быть связано с потоком энергии от источника,
или по направлению к нему.
Соотношение между скоростью изменения энергии, запасённой в поле,
и потоком энергии может быть выведено как общий интеграл уравнений поля:
rot Е+ -^Г =°> С) divB = 0, (III)
rotH — 4£ = J, (II) divD = p. (IV)
Заметим, что EJ имеет размерность мощности на единицу объёма (ватты
на 1 куб. метр); это подсказывает нам скалярное умножение (II) на Е:
ErotH — E^=EJ. B)
Для того чтобы каждый член в (I) мог иметь размерность мощности на
единицу объёма, необходимо умножить (I) на Н:
HrotE + H^=0. C)
Вычитая B) из C) и применяя тождество
div[E,H] = H rot E —ErotH, D)
мы получаем:
div[E,H] + EJ=— Е®_ н^. E)
Наконец, интегрируя E) по объёму V, ограниченному замкнутой
поверхностью St получаем:
&[Е, Н] п da4- f Eidv = — [ (е — + н —V<>- F)
124 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Этот результат впервые был выведен Пойнтингом в 1884 г., и
независимо в том же году Хевисайдом. Обычная интерпретация этого соотношения
следующая: мы предполагаем, что формальные выражения для плотностей энергии,
запасённой в поле, таковы же, как и при стационарном режиме. Тогда правая
часть в соотношении F) представляет уменьшение электрической и магнитной
энергии, содержащейся в данном объёме. Уменьшение этой энергии должно
быть обусловлено членами левой части уравнения F). Пусть о будет
проводимостью среды, а Е' — напряжённостью сторонних электродвижущих сил^
таких, какие возникают, скажем, в областях химической активности, например,
внутри батарей. Тогда:
J==o(E + E'),E==^~E', G)
и отсюда:
JEJdv= jL Pdv — Je'J dv. (8)
v v c ,v
Первый член в правой части (8) представляет собою мощность,
рассеиваемую в виде джоулева тепла — превращение необратимое. Второй член выражает
мощность, затрачиваемую потоком зарядов против сторонних сил;
отрицательный знак показывает, что эти сторонние силы совершают работу над
системой, частью компенсируя джоулевы потери и стремясь увеличить
энергию, заключённую в поле. Если, наконец, все материальные тела в поле
абсолютно тверды, так что исключён возможный переход электромагнитной
энергии в упругую энергию деформации среды, то баланс энергии должен
поддерживаться потоком энергии через поверхность, ограничивающую объём
V. Этот смысл, согласно Пойнтингу, и придаётся поверхностному интегралу
в соотношении F). Уменьшение электромагнитной энергии, содержащейся
в поле в объёме V, частично объясняется потерями на джоулево тепло,
лишь отчасти скомпенсированное энергией, даваемой сторонними силами;
остающаяся часть вытекает через граничную поверхность S, представляя
собою потери, определяемые в джоулях в секунду или ваттах интегралом
JSn da = j [E, H] n da. (9)
s s
Вектор Пойнтинга S, определяемый соотношением
S = [E, HI ватт/метр2, (ДО)
может быть интерпретирован как плотность потока энергии в какой-либо
точке поля, т. е. как количество энергии, пересекающее за одну секунду
единичную площадку, нормаль к которой ориентирована по направлению
вектора [Е, Н].
Молчаливо было предположено, что в среде отсутствует явление
гистерезиса. Если соотношение между В и Н неоднозначно, то количество энергии,,
равнре Q (уравнение C7), стр. 119), рассеивается в среде за каждый полный
цикл вдоль гистерезисной петли. Если поле меняется со временем
гармонически с частотой v, то мы будем иметь v циклов/cw, и соответственно,
потери на гистерезис составят vQ джоулей /сек.
В отсутствие ферромагнитных веществ, соотношение между В и Н обычно
линейно, и если среда в то же время ещё и изотропна, то теорема Пойнтинга
в дифференциальной форме принимает вид:
div[E,Hj+ I J» + ^(!-£2+^tf3) = E'J. (М>
ПОТОК ЭНЕРГИИ 12-19] 125
В качестве общего интеграла уравнений поля теорема Пойнтинга
обоснована безупречно. Её физическая интерпретация, однако, может быть
подвергнута некоторой критике. Мы уже отмечали, что из того, что объёмный
интеграл представляет полную энергию поля, нельзя, строго говоря, делать
заключений об её распределении.. Энергия электростатического поля была
выражена сначала в виде суммы двух объёмных интегралов. Один из них
по теореме о дивергенции был преобразован в поверхностный интеграл,
который исчезал при расширении поверхности за пределы поля. Обратно,
к выражению и = — ED, которые мы условились принимать за плотность
электростатической энергии, можно прибавить дивергенцию любой векторной
функции, должным образом исчезающей на бесконечности, не изменив этим
полной величины энергии. Подобная же неопределённость возникает и в случае
статических магнитных полей.
Можно поставить также вопрос о том, насколько уместно принимать,
что Е^тиН^- выражают скорость изменения плотности энергии в случае
быстрых изменений в той же мере, что и при квазистатических процессах.
Хотя подобное предположение и представляется правдоподобным, мы должны
отметить всё же, что преобразование функции, выражающей энергию через
векторы поля, к выражению энергии через плотности зарядов и токов
приводит к трудностям в отношении поверхностных интегралов. Пусть
-/("£+»?)* («о
будет скоростью, с которой внешние силы производят работу над системой.
Вводя потенциалы
дА
Е=—grades — £, В = rot A A3)
к применяя тождества
grad^f = div(?f5)-4(divD)> Hrot^ = div[^,H]-^rotH, A4)
мы получаем:
dW
dt
-№'£)*-/(,£+[«■£]>*'. <15>
где S — поверхность, охватывающая всё электромагнитное поле. В
стационарном и квазистационарном случаях можно показать, что потенциалы убывают
с расстоянием как г-1, а поля как г-2, и следовательно, интеграл по сфере
бесконечного радиуса равен нулю. Однако в дальнейшем будет показано, что
векторы полей от переменных источников убывают только как г-1, и
в этом случае последний член в A5) не может быть устранён просто
путём распространения интеграла на бесконечно удалённую поверхность.
С другой стороны, мы знаем, что поля и потенциалы распространяются с
конечной скоростью. Если, следовательно, поле впервые возникло не
бесконечно давно, то можно представить себе такую поверхность, элементы которой
настолько удалены, что поле их ещё не достигло. Векторы поля на этой
поверхности тогда строго равны нулю и, следовательно, при этих условиях
^-/(»4Н-'£)* ' «•>
126
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Наконец, следует признать, что если даже полный поток энергии через;
замкнутую поверхность и может быть представлен точно выражением (9),,
то мы не можем отсюда с определённостью заключить, что плотность потока
энергии в точке равна S = [E,H]; к последней величине можно прибавить
любой вектор, интеграл от которого по замкнутой поверхности равен нулю,,
отчего величина полного потока не изменится.
Классическая интерпретация теоремы Пойнтинга в значительной мере
покоится на гипотезе. Время от времени предлагались различные взаимно-
исключающие формы теоремы *), но ни одна из них не имеет большей
правдоподобности или большей простоты, чтобы её можно было
рекомендовать. Не лишено значения и то, что ни одна другая трактовка до сих пор
не дала ничего ценного для теории. С другой стороны, предположение
о распределении энергии в поле с определённой плотностью и о пбтоке
энергии с интенсивностью S = [Е, Н] оказалось необычайно плодотворным.
Всякая теория является не абсолютной истиной, а внутренне согласованной
аналитической формулировкой соотношений, которым подчиняется
определённая совокупность явлений природы. При таком подходе всё говорит за
то, чтобы придерживаться точки зрения Пойнтинга-Хевисайда, пока
столкновение с новыми экспериментальными фактами не потребует её пересмотра.
2.20. Комплексный вектор Пойнтинга. Если мы теперь допустим, чта
h == и -\- w представляет собою плотность электромагнитной энергии в какой-
либо момент, a Q = — J2 — E'J мощность, затрачиваемую в единице
объёма благодаря термохимическим процессам, то теорема Пойнтинга для
полей, свободных от явлений гистерезиса, может быть написана в виде
div[S + §-+Q = 0. A7).
В стационарном поле h не зависит от времени, так что A7) принимает вид:
divS + Q = 0. A8)
Величина Q может быть положительной или отрицательной, в зависимости
от того, превышает ли работа сторонних электродвижущих сил-Е' энергию,
расходуемую на тепло, или нет. Соответственно, направление потока
энергии из элемента объёма или в него зависит от того, ведёт ли себя этот
элемент объёма как источник энергии, или как её сток.
Источники и их поля* в большинстве практических приложений
электромагнитной теории являются периодическими функциями времени. Среднее
значение плотности энергии h постоянно, и dhjdt = dhjdt = 0, где черта
показывает, что берётся среднее значение, получаемое усреднением за период.
Следовательно, в случае периодических полей:
divS-{-Q = 0 или f Snfifo-f- [~Qdv = Q. A9)
8 V
Если в объёме V источников нет, то энергия, рассеивающаяся в объёме V
в виде тепла, равна среднему значению потока, втекающего внутрь через
поверхность S.
^Macdonald, Electric Waves, Cambridge University Press, 1902; Livens, The
Theory of Electricity, Cambridge University Press, стр. 238 и далее, 1926; Mason and
Weaver, The Electromagnetic Field, University of Chicago Press, стр. 204 и далее,
1929.
ПОТОК ЭНЕРГИИ [2.20J 127
Преимущества комплексных величин для рассмотрения периодических
процессов достаточно хорошо известны, чтобы была надобность в
подробном их изложении. Необходимо, однако, напомнить читателю, что следует
соблюдать некоторые предосторожности при составлении произведений и
квадратов. Во всём последующем изложении мы будем обычно представлять
гармоническое изменение во времени в виде комплексной функции
координат, умноженной на ег~ыг. Таким образом, если А— рассматриваемая
величина, то мы пишем:
А = А0е~ ш = (а + *Р) е~ ш = (а-ИР) (cos <*t —i sino>0, B0)
где аир — действительные функции координат х, у, г. Величина, комплексно
сопряжённая с А, получается заменой / =* У — 1 на —/, и обозначается
знаком ***
Л* = (а — /0) «*««*. B1)
Хотя при аналитических операциях и удобно пользоваться комплексной
записью, но величины, имеющие физический смысл, должны в конечном счёте
представляться действительными функциями. Если А удовлетворяет
линейному уравнению с действительными коэффициентами, то и действительная и
мнимая части А являются решениями этого же уравнения, и каждая из них
в конце вычислений может быть выбрана, как представляющая некоторое
физическое состояние. Однако в случае квадратов и произведений мы
сначала должны взять действительные части сомножителей, а затем перемножить,
поскольку произведение действительных частей двух комплексных величин
не равно действительной части их произведения. Действительную часть А
мы будем обозначать через Re (А), а мнимую часть — через 1т (А).
Re (Л) = a cos <ot + Р sin <ot = V«2 Н~ Р2 sin (<at -f ?),
Im (A) = P cos <at— a sin <at = j/а2 -\~ p2cos (mt-\~ 9),
<p = arctgj.
B2)
Квадрат абсолютной величины А получается умножением на комплексно
сопряжённую величину:
ЛЛ* = а2 + Р2- B3)
Действительная часть А даётся также выражением:
А -Х- А*
/?е(Л) = ^-±^-. B4)>
Произведение действительных частей двух комплексных величин Ах и Л2
равно, следовательно:
Re (At) Re (a2) = ^{Ax-\-A^ (a2 + A% =
= \ ОМ з +а1а1+АХА\ + A 24). B5)
Среднее по времени значение периодической функции определяется
соотношением:
A=±JAdt, B6)
о
где х— период. Если А—простая гармоническая функция времени, то
среднее значение её, конечно, равно нулю. Среднее значение функций, подобных.
128
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
cosatf и sinorf, также равно нулю и поэтому мы получаем из B5)
следующий результат:
Re(^)Re(^2) = \ (аха1 + А,А^) = ± (ад + ptp2), B7)
:ИЛИ
Re (Лх) Re (л2) = 1 Re^MD- B8)
В соответствии с предшествующими формулами, среднее значение потока
энергии в гармоническом электромагнитном поле равно:
S = [Re (E), Re (H)] = ^ Re ([E, Н*]), B9)
т. е. действительной части комплексного вектора -^ [Е, Н*]. Свойства этого,
так называемого комплексного вектора Пойнтинга очень интересны. Мы
будем обозначать его через
S+=1[E, H*]. C0)
Предположим, что среда определяется константами е, ц, о и что в величины,
характеризующие поле, время входит только в виде множителя e~itot. Тогда
уравнения Максвелла для областей, свободных от сторонних электродвижут
щих Сил Е', будут:
rot Е = kdjxH, rot H = (о — /сое) Е. C1)
Уравнение, комплексно сопряжённое второму из них, есть
rotH* = (o + /<oe)E*. C2)
Комбинируя его с первым из уравнений-C1), как это было сделано в
разделе 2.19, получаем:
div S+ = — 1 оЕЕ* + i<» (j HH* — у ЕЕ*), C3)
чили, в силу B8) и B3),
divS+ = — Q-\-i2<a(w — и). C4)*
Дивергенция действительной части S+ определяет количество энергии,
рассеиваемой в виде тепла в единице объёма за каждую секунду, в то время
как дивергенция мнимой части в 2<о раз превышает разность средних
значений плотности магнитной и электрической энергии. Для любой области
поля, ограниченной поверхностью 5, мы имеем:.
Re Г S+n da = полной энергии, рассеиваемой в виде тепла, C5)
Im j S+n da = 2ш X разность средних значений магнитной и элек-
s
трической энергий. C6)
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
2.21. Объёмные силы в жидких средах. Рассмотрим
электростатическое поле зарядов, которые расположены на поверхностях проводников,
погружённых, в изотропный диэлектрик. Чтобы упростить анализ, мы
предположим на время, что во всём поле нигде, кроме поверхностей проводни-
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 12.21J 129
■' ■ ... -■■.,. 1н.::. ... ..,...- ,. ..... ■ . ,.., ■. .. ....... . ■ т
жов, диэлектрическая среда разрывов не имеет. Кроме того, мы
предположим, что D = eE, где е—непрерывная функция точки. Полная
электростатическая энергия поля будет, следовательно:
£/ = iJ*e£%fo, A)
еде интеграл распространён по всему пространству.
Положение любой точки диэлектрика по отношению к фиксированному
•началу отсчёта определяется вектором г. Сместим теперь каждую точку
диэлектрика на произвольную бесконечно малую величину s(r).
Предполагается, однако, что проводники остаются неизменными, и смещение частиц
диэлектрика, находящихся около поверхности проводников, по
необходимости тангенциально. В результате смещения или деформации, параметр е
изменится, и соответствующее изменение электростатической энергии будет
равно:
' 8£/ = — -fbeE^dv. B)
В то же время произойдёт и небольшое перераспределение зарядов на
поверхности проводников. Первоначально заряды на поверхности
находились, в состоянии статического равновесия, и первоначальная энергия A),
в соответствии с теоремой Томсона (разд. 2.11), являлась минимальной по
отношению к бесконечно малому изменению распределения зарядов.
Следовательно, изменение энергии, связанное с перераспределением зарядов,
является бесконечно малой величиной второго порядка, которой можно
пренебречь по сравнению с B).
Рассмотрим диэлектрик, первоначально находившийся в объёме dvt.
Поскольку смещение сопровождается деформацией, объём этого элемента
после деформирования, согласно уравнению E4), стр. 148, будет:
dv2 = A -j- div s) dvv ? C)
Масса элемента сохраняется, и поэтому для плотности, обозначаемой через т,
мы будем иметь:
x1d©1 = т2 A -f- div s) dvv D)
или, для бесконечно малого смещения:
8т = т2 — tj = — т div s. E)
Диэлектрическая проницаемость е является функцией точки в
диэлектрике и зависит также от плотности г. Элемент, который после смещения
оказывается в заданной точке г, до смещения находился в точке г — s, и
часть 8е, связанная с неоднородностью диэлектрика, будет, следовательно,
— sgrade. Если мы предположим, что е зависит только от г и т, то
полное изменение е. будет:
8е = — s grad e -f- -^~ 8т = — s grad e — т ~ div s; F)
изменение электростатической энергии, вызванное деформацией, будет:
8£/=ij7£2grades-f £2 т-|j-div s) fcfo; G)
«о
£»tAdivl==div(£»x^e) — sgrad (№-£), (8)
и, следовательно:
W=j[l^gTads~lgr^(Eh^)}sdv-^j^6iv^z^s)dv. (9)'
9 Зак. 593. Теория влектромагнетизма.
130 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Эти объёмные интегралы должны быть распространены на всё поле.
Поверхности проводников, внутри которых поле равно нулю, будем
обозначать через Sv 52, . • • , .Sn. Поверхность S0 проведём так, чтобы она
содержала в себе все проводники и все части диэлектрика, в которых поле имеет
сколько-нибудь заметную величину. Внутри области, ограниченной извне
д"
поверхностью S0, а изнутри поверхностями Su S2r — ,Sn, функция E^x—s.
непрерывна. Следовательно, ко второму интегралу в (9) может быть
применена теорема о дивергенции, что даёт:
п
/Tdiv(B*t£»)*'-2J£*t£,,,<fa- (l0>
На поверхности S0 вектор Е равен нулю; на поверхностях же жёстких
проводников Su ... , Sn мы приняли, что нормальная компонента s
отсутствует. Следовательно, интеграл A0) равен нулю.
Если пренебречь гравитационными силами, то можно считать, что
единственными объёмными силами будут силы f, действующие со стороны поля
на элементы диэлектрика. Работа, совершённая этими силами в единице
объёма при деформации равна fs, и следовательно, в соответствии с
законом сохранения энергии:
fisdv = —fl^EZgTade—±gmd(E*T~y\sdv. A1)
Так как смещение s произвольно, мы получаем:
f = -1 £»grad e -1- \ grad (&x Ji) . A2)
При наличии также и зарядов, распределённых по диэлектрику, к величине
силы надо добавить член рЕ.
Последний член в A2) связан с деформацией диэлектрика.
Предположение, что е может быть выражено в виде функции только точки и
плотности, допустимо для жидкостей и га.зов, но не обязательно справедливо
в случае твёрдых тел. Весьма хорошим приближением, выражающим
соотношение между абсолютной диэлектрической проницаемостью xj (е = хе0) и
плотностью для газов, жидкостей и даже некоторых твёрдых тел, служит
закон Клаузиуса-Моссоти:
•*.— 1 ~ ч * ЗОс
ф58^ или х— 1яя,-ПГоГ» ^13>
где С— константа, определяющаяся природой диэлектрика. Простой подсчёт
приводит к выражению:
^ = lf(y— 1} (* + 2)' A4>
и силы, действующие со стороны поля на единичный объём жидкости или
газа, будут, следовательно:
l = —^£»gradx-f |grad{^(x—1)(х + 2)}. A5)
2.22. Объёмные силы в твёрдых телах. Объёмные силы A2),
действующие на диэлектрик в электростатическом поле, были выведены в
предположении, что изменение диэлектрической проницаемости е при бесконечно малой
деформации может быть рассчитано, если известны неоднородность диэлек-
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ [2.22]4 131
трика и изменение плотности, связанное с деформацией. Однако, в твёрдых
телах могут быть деформации, не сопровождающиеся изменением объёма;
строгая теория должна, следовательно, выражать изменения е через
компоненты деформации. Поскольку предполагается, что диэлектрик находится
в состоянии статического равновесия, механические силы, действующие
со стороны поля, должны уравновешиваться силами упругости,, возникшими
во время деформации. Наша задача состоит в том, чтобы найти эти силы
и найти деформацию, которая получается в конечном счёте в результате
наложения поля. Мы ограничим наше рассмотрение средой, у которой
электрические и упругие свойства в ненапряжённом состоянии изотропны.
Так как изменение е зависит от компонент деформации, то трудно
предположить, что твёрдое тело останется изотропным в электрическом отношении
и после возникновения деформации. Первая наша задача — установить
выражение для электростатической энергии анизотропного диэлектрика.
В разделе 2.8 было показано, что плотность электростатической
энергии в диэлектрике равна:
D
u==JEdD A6)
о
независимо от соотношения между D и Е. Мы предположим теперь, что
в анизотропной среде компоненты D являются линейными функциями
компонент Е:
А:=2е;А (/'=1, 2, 3). A7)
Поскольку величины Ек и Ц^ преобразуются как компоненты векторов, ясно,
что величины е^ являются компонентами тензора второго ранга.
Соответствующим поворотом координатных осей этот тензор может быть приведён
к главным осям, определяемым единичными векторами а, Ь, с, так что:
Da = eaEa, Оъ = ЧЕь, De = seEc. A8)
Тогда
Е dD = eaEadEa -f Ч^ъа^ъ + se^edEe = D dE, A9)
и плотность энергии в анизотропной среде с линейным соотношением между
D и Е будет, следовательно:
tt = lED = lSS epEjEjt (ejk = ekj). B0)
Мы должны далее подсчитать изменение энергии, получающееся в
результате вариирования параметров е^к при неизменных зарядах. Если мы
пересмотрим доказательства раздела 2.10, то увидим, что они полностью могут
быть применены и в этом случае. Чтобы избежать путаницы в индексах, мы
заменим индекс «1» параграфа 2.10 для обозначения начальных условий
штрихом. Таким образом, диэлектрик в поле первоначально характеризовался
коэффициентами е' В области V1 эти значения перешли в e.J{. Полное
изменение энергии поля, согласно уравнению D9), стр. 108, будет:
£/ = - J(ED' — E'D)dv,. B1)
Ух
9*
132 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
или, в силу A7):
+(ei2- я да+адо+(««- «а да+^)+
+ K~<i)(*i3 + *VS)}*'- С22)
Если вариации ejfc бесконечно малы, то это выражение переходит в такое:
W = — \ J* (beL1El + 8s22^I + 8езз£з + 28s12£t£2 +
+ 28е23Е2£3 + 2UBlEQEl) dv. B3)
Теперь параметры ejfc должны быть связаны с компонентами деформации.
Для достаточно малых деформаций мы можем положить:
з з
«ъ=2 2 «йч, <£--££• <24>
Коэффициенты а|^, число которых равно 81, являются компонентами тензора
четвёртого ранга. В силу соотношений e?fc = e^-, elm = emh мы имеем:
< = ^ = <Г B5)
Тогда из 81—9 = 72 недиагональных членов только 36 независимы, и
полное число независимых коэффициентов сводится к 36 -f- 9 =45. Для
доведения системы коэффициентов до ещё меньшего числа, необходимо
воспользоваться условиями симметрии, и мы введём теперь ограничение, согласно
которому среда первоначально изотропна *), хотя и не обязательно однородна.
Вариация плотности энергии, вызванная малой деформацией будет:
8» = -1-2 2 2 2 "&Wv B6>
j —■ X ft — X I — л. rtk — X
Коэффициенты а^ имеют в каждой точке определённые значения,
характеризующие диэлектрик, но меняются от точки к точке, если среда
неоднородна. Далее, поскольку мы предполагаем, что первоначально диэлектрик
был изотропен, уравнение B6) должно быть инвариантно по отношению
к перемене направления любой из координатных осей. Так например,
перемена направления оси Xj меняет знак Ej и е^к (кф/), но оставляет все
остальные сомножители неизменными. Следовательно, для того чтобы Ьи
не изменялось при перемене направления осей или при замене одной оси
на другую, необходимо чтобы некоторые коэффициенты исчезали.
Действительно, очевидно, все коэффициенты, за исключением трёх типов, равны
нулю; именно отличны от нуля
<*§ = ?!' *& = «■' а$ = аъ (/=£*>• B7)
Таким образом уравнение B6) принимает вид:
S« = — у {ах (fijku -\-Elte,2 + Е&ея) + а, \{е\ + £j) Ьеп + (Й + Й) **■ +
9 + (El + Й)М + 4«з (EJSJbea + ад8*и -f £e3tai)J. B8)
x) Анизотропный случай был рассмотрен Pockels'oM, Encyklopadie der mathe-
matischen Wissenschaften, т. V, ч. II, Teubner, 1906.
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ [2.22] 133
- i ■ 1 , .
Но Ьи должно быть инвариантно также и по отношению к повороту
координатных осей, а это приводит к дополнительным соотношениям между
параметрами аъ а2, а3. Эти соотношения легко найти, если переписать
^28) в виде:
1 3
Ьи = — т {(аг — а2 — 4я3) 2 ФеМ + Ч^ 2 8е# +
+ 4% (Е?8в11 + Й8вИ + fife* + ^А* 11 + ВД^ + ^l^Sl) J' B9>
3
где Е" =*Е{-\-E-i-f-Ез- Сумма 2л ejp согласно уравнению E4), стр. 90,
3 = 1
представляет собой коэффициент объёмного расширения — величину, не за-
• висящую от системы координат. Поэтому средний член в B9) инвариантен
по отношению к повороту системы отсчёта. То же справедливо и по
отношению к последнему члену, так как при замене деформаций ejfc
коэффициентами 2аjk из раздела 2.2 этот последний член превращается в
инвариантную квадратичную форму, сходную по виду с квадрикой деформаций,
уравнение, C6), стр. 87. Таким образом, при вращении координатной
системы меняется только первый член, и поэтому необходимо, чтобы *)
1
Ч— «2~4fl8=°» Я3 = -(<*! — Я2)- C0)
Вариация плотности электростатической энергии, вызванная локальной или
чистой деформацией изотропного диэлектрика, равна окончательно:
ои8 = — -g { (ax£i + а*Ё\ + ЯгЕI) Ьеп -\- (а^\ -J- axE22 -f- ДаЙ) Se22 -+-
-f (а2Е\ + а^ -+- axEt) 8е33 + (% — я2) (ВД8е12 -+- Е2£38е2з + Е*ЕМд}. C1)
Индекс 5 добавлен для того, чтобы подчеркнуть, что это только та
часть полной вариации, которая вызвана чистой деформацией. Напомним,
что наиболее сбщая деформация упругой среды состоит из перемещения,
локального вращения, определённого уравнением ^33), стр. 87, и локальной
деформации, определённой уравнением B9), стр. 86, которую только мы
и учли в уравнении C1). В анизотропном диэлектрике локальный поворот
влечёт за собой изменение компонент тензора ejk и вследствие этого на
каждый объёмный элемент диэлектрика действуют вращающие моменты 2).
В рассматриваемой здесь первоначально изотропной среде, эти вариаций
(вследствие поворота) отсутствуют. Вариация в плотности электростатической
энергии вследствие бесконечно малого перемещения 8s неоднородного
диэлектрика была подсчитана нами в разделе 2.21:
4=4E2grade8s' C2)
где е — диэлектрическая проницаемость в недефоркированном изотропном
состоянии.
г) Операция сведения констант электрострикции к двум, которую мы здесь
провели, тождественна с операцией сведения констант упругости с^ раздел 2.3,
к двум параметрам Xt и Х3. Смотри, например, Love, Treatise on the Mathematical
Theory of Elasticity, гл. VI, 4-е изд. Cambridge Press, 1927. (А. Л я в, Математическая
теория упругости М. — Л., ОНТИ, гл. VI, 1935.) Определение этих констант для
различных классов анизотропных кристаллов было проведено Фохтом: V о i g t,
[Compendium der theoretischen Physik, т. 1, стр. 143—144, Leipzig, 1895. Его результаты
приведены у Love, loc. cit,
2) P о с k e 1 s, loc. cit, стр. 353.
134 гл. и. силы и энергия
Деформация диэлектрика влечёт за собой наряду с изменением
электростатической энергии также и изменение упругой энергии. Согласно
уравнению F8), стр. 91:
Ьие = (Xj div s -j- 2X2en) Ьеп -f- (Xt div s -J- 2X2eP2) 8e22 +
-(- (Xj div s 4- 2X^33) 8*33 -f- X2 {e12be12 -f e288e23 + esi8e3i )• C3)
Работа, совершённая механическими силами, действующими на
диэлектрик в объёме Vx и на поверхности Slt ограничивающей объём Vv во время
бесконечно малого смещения 8s, должна равняться уменьшению всей энергии,
могущей превращаться в работу, т. е. упругой плюс электростатической. Мы
пишем поэтому для баланса энергии:
f ibsdv-\-j tbs da = ~Ъ§ (ие-{-us + ut)dv.
C4)
Полную объёмную силу f, действующую на диэлектрик, удобно разбить
совершенно произвольно на две компоненты f и f", где
f' = — у£2 grade
C5)
— доля, обусловленная неоднородностью диэлектрика; i" — сила, связанная
с чистой деформацией. Последняя должна удовлетворять соотношению:
J* f'8s dv -\-j t"8s da = — 8 J (ue + us) dv.
C6)
Разложение объёмных и поверхностных сил на силы, связанные с
перемещением, и силы, связанные с деформацией, таково, что
J* i'dv -f J t'da = О, [ f"dv -f Г t"da = 0.
C7)
В этом случае, согласно разделу 2.3, правая часть уравнения C6) может
быть преобразована к виду:
8 W" = f ( Tiben + T&bea +" ^338^33 -f 7i'28e13 r|- T^be2S + T3M1) dv. ( 38)
Вариации компонент деформации произвольны и, следовательно, приравнивая
коэффициенты соответствующих членов из C1) и C3), мы получаем:
Тп = - (Хх div s + 2А2еи) + \ («i^J + «2^! + а24),
Г2'2 = — (К div s + 2X3622) + y (^1 + ai^2 + Я2Й),
7ю — — {h a*v s -f- 2X2%$) + 2" (^ + °*& + ^Х
7l2 == Х2е12 -j 2 4^1^2»
^23 == ^2^23 = cj— E2E2,
W + ^=^Е&.
C9)
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В, ЭЛЕКРОСТАТИЧЕСКОМ ПОЛЕ 12.22] 135
Эти величины являются компонентами тензора напряжений, отрицательная
дивергенция которого даёт нам равнодействующую объёмную силу,
связанную с деформацией. Если объёмные силы исключительно электрического
происхождения, как это будет в случае пренебрежения гравитационными
эффектами, то дивергенция упругих напряжений исчезает, и мы получаем
для ^-компоненты силы:
f"x = — y jfr («i£i + аА -Ь «2^1) — -2 Qj {(«i — а*) Е±Е2 } —
-ТаГз1^1"-^1^1' D0)
и аналогичные выражения для/2 и /3. К этим выражениям необходимо
приубавить компоненты f из C5) и тогда мы получим полную объёмную силу,
действующую на изотропный диэлектрик в электростатическом поле.
Параметры ах и а2 для данного вещества должны в общем случае
определяться из измерений. Физически ах выражает приращение е,
соответствующее удлинению параллельно линиям напряжённости поля, в то время как %
определяет приращение для деформаций под прямым углом к этим линиям.
Если диэлектрик, содержащийся в объёме Vlt однороден^ не содержит
зарядов, то градиент е равен нулю, и вектор Е удовлетворяет уравнениям
divE = 0, rotE = 0. В этом случае V ~ О, и равнодействующая сила f" = f
сводится к
f = — l^ + ^gradE2.. D1)
В жидкостях или газах все деформации сдвига ejh равны нулю и,
следовательно, по уравнениям B4) и B7), а3 = (^ = 0% ах~а% = а. Кроме того,
в этом случае в диэлектрических свойствах не должно быть
преимущественных направлений и соответственно е^-& = 0 при j^pk, еи = е^ = е33 = е.
Вместо B4) мы можем написать:
Обозначая коэффициент объёмного расширения через ^• = 6ll-\~e^i-\-e9&>
мы получаем:
«=-&;-£• Н=а8Д- <43>
Но, согласно E),
■зз
дг дг д% дг
D4)
и, соответственно, полная сила, действующая со стороны
электростатического поля на единицу объёма жидкого или газообразного диэлектрика,
будет:
f = — у Е2 grad е +1 grad (&с -~), D5)
что и было выведено непосредственно в разделе 2.21.
Вывод объёмных сил из энергетических соображений, как это изложено
в предшествующих параграфах, был впервые предложен, повидимому, Корт-
вегомх) и развит Гельмгольцем 2) и другими. Полное изложение теории:
х) К о г l e w e g, Wied. Ann. 9, 1880.
*) Helmhottz, Wied. Ann. 13, 385, 1881.
136 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
со ссылками на предшествующую литературу дано у Поккельса *). Этот
метод подвергся критике со стороны Лармора 2) и Ливенса 3), которые
предложили другие выражения для сил. Эта критика не представляется, однако,,
достаточно обоснованной. Возражения против специальной формы интеграла
энергии, использованного Гельмгольцом, устраняются при применении более
строгих методов. Ливенс предпринял обобщение этого метода на. среду,
у которой соотношение: между D и Е нелинейно, стремясь показать, что
этот метод ведёт к абсурдным результатам. При этом он пропустил
существенный член, связанный с деформацией. С другой стороны, выражение
для объёмной силы, предложенное Ливенсом, может быть очень просто
выведено как в электрическом, так и в магнитном случае, исходя из
предположения, что поляризованное вещество эквивалентно области, по которой
распределены заряды с плотностью р' = — div P и токи с плотностью
дР
f — -jrr- -\~ rot M (ср. разд. 1.6). Силы могут быть тогда подсчитаны точно-
так же, как и в разделе 2.5. Этот путь был бы вполне удовлетворительным,
если бы среда была абсолютно твёрдой. Согласно теории Ливенса, ми
должны сначала подсчитать силы, действующие со стороны поля на
поляризованное вещество, а затем ввести эти силы в уравнения теории упругости
для определения деформаций. Деформации, однако, влияют на поляризацию,
и обе части задачи не могут в общем случае рассматриваться подобным'
способом порознь. При некоторых условиях, в частности, для жидкостей
и газов, обе теории приводят к одинаковым результатам, но в большинстве
случаев их результаты различны. Нам представляется, что оснований для.
сомнения в принципиальной правильности энергетического метода Кортвега
и Гельмгольца очень мало.
2.23. Тензор напряжений. Мы опять предположим, что S1~ замкнутая
поверхность, проведённая в изотропном диэлектрике, находящемся под
действием электрических напряжений. Свойства диэлектрика предполагаются
непрерывными во всех внутренних то'чках *и при переходе через эту
поверхность; другими словами, эта поверхность не является поверхностью
.разрыва, ограничивающей диэлектрическое тело. Полная С1Ш, действующая на
вещество и заряд внутри ,SU равна:
F = f (рЕ — \ Е* grad e -J- r) dv. D6>
Ух
Мы хотим показать теперь, что сила F' может быть представлена в виде
интеграла по поверхности Sv Для этого необходимо только представить
подинтегральное выражение в виде дивергенции тензора. Член i" уже написав
в таком виде в уравнении D0) и в дальнейших преобразованиях не нуждается.
В первом члене мы заменим р на div D и воспользуемся тождеством
£2grade = grad(e£2) — 2(Dgrad)E, D7>
которое справедливо, только при rotE = 0. Тогда получаем без
затруднений, что компоненты вектора рЕ — уЕ2grade равны:
Р5-Т* TSJ= S -Щ С5°»>-Т 7^<ED> <48>
1) Pock els, Arch. Math. Phys. B) 12, 57—59. 1893 и Encyklopadie der mathe-
matischen Wisse nschaften, т. V, часть II, стр. 350—392, 1906.
2) L a r m о r, Phih Trans., A. 190, 280, 1897.
3) Livens, Phil. Mag., 32, 162, 1916, и в его книге «The Theory of Electricity»,,
стр. 93, Cambridge University Press, 1926.
^
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В, ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ [2.Z4] 137*
и подинтегральное выражение в D6) может быть представлено как
дивергенция тензора 2S,
рЕ — 1 £2 grad е + Г = div 2S, D9>-
компоненты которого S3-k ьыписаны ниже:
*->12 == е^1^2 ~1 О ^12 == *^21»
С — rF F 1 **2-"^ р Р — С J ^50)'
°i3 — ес1£::зп § 1сз — °3i»
J
В результате применения теоремы о дивергенции (см. уравнения B2)v
и B3), стр. 96) оказывается, что сила F, действующая на заряды и
вещество внутри Sv эквивалентна интегралу по поверхности St от поверхностной
силы с плотностью:
t = (e + ^^)E(En)-i+A2^n, E1)-
где п, как обычно, единичный вектор внешней нормали к элементу
поверхности Sv Для сохранения равновесия необходимо, чтобы среда, находящаяся7*
вне поверхности Slt действовала бы на частицы, составляющие поверхность
St с равными и противоположными силами.
Компоненты тензора E0) и поверхностные силы t отличаются от
соответствующих выражений, выведенных для свободного пространства в разделе 2.5,
тем, что е0 заменено на е, а деформации учтены с помощью
коэффициентов ах и а2> чт0 привело к появлению дополнительных чденов, которые
могут быть весьма существенны. В любой точке на поверхности Sx вектор t
лежит в плоскости векторов Е и п, но теперь вектор Е уже не делит угол
между п и t пополам, как это было в случае, изображённом на рис. 17г
стр. 98.
2.24. Поверхности разрыва. В предшествующем анализе
предполагалось, что разрывы непрерывности в свойствах среды, как например на
поверхностях, ограничивающих диэлектрические тела, могут быть заменены
слоями с быстрым, но непрерывным переходом. По мере того, как
переходный слой становится исчезающе тонким, возникает разрыв непрерывности <
и градиент е принимает бесконечное значение, но объём слоя также
стремится к нулю, * и мы должны найти предел плотности объёмной силы f,
чтобы определить полную силу, действующую на получающуюся в
результате поверхность разрыва.
На рис. 23 заштрихованная площадь изображает сечение переходного
слоя между диэлектрическими средами A) и B). Силы, действующие со
стороны поля на вещество и заряды, находящиеся в этом слое, могут быть •
найдены интегрированием E1) по двум поверхностям, ограничивающим слой.
Два параметра, которыми характеризуется изотропный диэлектрик, мы будем
обозначать через
«^e-f^LZfL, pei±^. E2*
138
ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Сила, действующая на единицу поверхности в направлении от среды A) к
среде B), по мере приближения толщины слоя к нулю становится равной
t^jaECEn^-HaECEn)}! — {р£%}2—{р^,
E3)
где индексы показывают, что значения величины берутся для той или
другой из сторон поверхности 5. Следует отметить, что п, = — п2.
В литературе было опубликовано очень немного надёжных измерений
констант а1 и а2 для твёрдых тел. Натяжение t может быть, однако,
подсчитано для случая соприкосновения двух жидкостей, к которым применим
закон Клаузиуса-Моссоти. Согласно уравнениям D3) и A4),
дг
а,
а*
дъ
Таким образом, для жидкостей:
a = е, р =
= -А(х_ 1)(х + 2).
■3j-(x» —2х —2).
E4)
E5)
На поверхности соприкосновения тангенциальная компонента Е непрерывна,
Еп = ЕР2', в отсутствие поверхностных зарядов мы имеем также etEnl = ^2Еп2.
Поле Е в E3) может быть, следовательно, выражено через его напряжённость
в; любой из сред. Значения а и р из E5), подставленные в E3), приводят
к выражению:
* = t ("^ ^ "f" 4х"*2 ~~ 6*lX* ~~ Зх' + 2Xl + 2) Е"х +
+ [*2 (*а — 2) — х, (хх — 2)] еЦ щ
E6)
ДиэлектринA) v%A Диэлектрик B)
Напряжение, действующее со стороны поля на поверхность раздела двух
жидких сред, нормально к этой поверхности и направлено из среды A)
в среду B), что является,* конечно,
необходимым следствием того факта, что в жидко.-
сти не может быть напряжений сдвига.
Если средой B) является воздух, то k2
может быть приближённо положено равным
единице. Уравнение E6) принимает тогда
вид:
t-^PU-UH, E7)
Натяжение максимально, когда Е нормально
к поверхности и направлено в сторону
убывания диэлектрической проницаемости (ср.
стр. 108). Однако если Е лежит в
плоскости поверхности раздела, так что Еп1 = 0,
то натяжение становится отрицательным,
представляя собой давление, действующее на диэлектрик, находящийся в поле.
Другим интересным случаем, является тот, когда среда A) — проводник.
Тогда Ej = 0, Еп = 0 и E3) сводится к
t = (a-^P)££n=:e-^^n, ' E8)
еде все величины равны их значениям непосредственно снаружи у поверхности
металла в диэлектрике A). Если этот диэлектрик является жидкостью, то
Рис. 2о. Сечение переходного
слоя, разделяющего две
диэлектрические среды.
, 1 / , де\ ,,2 1 д , ч „2
E9)
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ [2.25] 139
Эти выражения справедливы независимо от того, заряжен ли проводник или
нет, поскольку Еп связано с поверхностной плотностью зарядов
соотношением гЕп = со. Однако уравнения E8) и E9) не выражают
равнодействующей силы, приходящейся на единицу поверхности, так как они в некоторой
степени компенсируются напряжениями или давлениями, возникающими
в диэлектрике под действием поля. Этими силами мы сейчас и займёмся.
Подобное внутреннее давление можно игнорировать только в том случае,
если среда A) является свободным пространством или же газом с
диэлектрической проницаемостью, очень близкой к единице. Тогда мы имеем
-z-r = 0, и E9) переходит в
t = -g-e0Ejn = -^a>EnIl, v F°)
где со — заряд единицы поверхности.
2.25. Электрострикция. Упругая деформация диэлектрика под влиянием
сил, действующих на него в электростатическом поле, называется электро-
стрикцией. Смещение s любой внутренней точки изотропного вещества
должно удовлетворять уравнению G0), стр. 92.
f-K^ + *2)graddivs-f*2As = °, Fl)
где объёмные силы f = f' -j- f" даютея теперь в общем случае уравнениями
C5) и D0). Если нужно, то к ним можно добавить силы Ер для учёта
объёмных зарядов и гравитационные силы xg. Мы должны найти решение
уравнения F1) в подходящей системе координат. Это решение должно
удовлетворять краевым условиям на границе диэлектрика. На этой границе должны
быть заданы либо приложенные напряжения, либо смещения. Если граничная
поверхность является свободной, то на неё будут действовать только
напряжения со стороны поля, из которых можно будет определить и граничные
значения s.
В твёрдых тепах этот эффект мал и легко может быть замаскирован
деформациями, возникающими от посторонних причин. Силы притяжения
между металлическими электродами, находящимися в соприкосновении с
диэлектриком, могут вызвать внутри диэлектрика деформации, ничего общего не
имеющие с электрострикцией. Экспериментальные данные по этому вопросу
немногочисленны и часто противоречивы. Теория электрострикции в
цилиндрическом конденсаторе была, однако, развита довольно подробно. Метод,
описанный выше, был применён Адамсом *) и его результаты были позднее
приведены Кембелом 2) в соответствие с более ранней работой Сакердота 3).
Обширный перечень ссылок дан Кэди4).
Электрострикцич жидкостей более доступна для расчёта, поскольку
модуль сдвига Х2 равен нулю, а Кг обратно пропорционально сжимаемости.
Согласно G3), стр. 92, давление в жидкости связано с объёмным
расширением соотношением р = — Xt div s. Это выражение вместе с объёмными
силами f из уравнения D5), после подстановки в F1), приводит к связи
-iЕ2grad е + ~grad(ЕЧ Ji) — gradp = 0 F2)
между давлением и напряжённостью поля в какой-либо точке. Для того чтобы
проинтегрировать это выражение, необходимо задать зависимость давления
х) Adams, Phil Mag. F) 22, 889, 1911.
8) Kemble, Phys. Rev. B) 7, 614, 1916.
3) Sac er dote, Jour, physique C) 8, 457, 1899; 10, 196, 1901.
4) С a d y, International Critical Tables, т. VI, стр. 207, 1929.
140 гл. п. силы и энергия
и диэлектрической проницаемости от плотности т. Для химически
однородной жидкости или газа мы можем положить, что p=p(x)t е = е(х) и что-
зависимость от точки включается в независимую переменную т. Тогда:
grad (& £ т) = т grad (z* ■£) + £» £ grad х,
grad г = ~ grad т, F3>
и, таким образом, F2) сведётся к
т grad (e2 -£) = - grad p. F4>
Определим скалярную функцию давления Р(р) так, что
р
Pa
где pQ—давление в той точке жидкости, где Е = 0. Если ds— элемент длины
вдоль пути, соединяющего две точки, в которых давления равны
соответственно р и р0, то gra.dPds = dP и F4) удовлетворяется соотношением
Т*=^*Г- ' С36*
В жидкостях cfp = X1— (уравнение G7), стр. 92)
или
Р—Рп
X = Т0 <? *1 . F7);
Параметр Xlf обратный сжимаемости, является весьма большой величиной и,
таким образом, г ^ т0. Следовательно, для жидкостей
Р—Ро=ЕЧ-^у F8>
или, если применить закон Клаузиуса-Моссоти:
p—pQ =-%&{*—\)(i + 2). F9>
RT
Для газов F7) следует заменить соотношением Р==х~Т/Гу гл-е R —га_
зовая постоянная, Т—абсолютная температура, и М—молекулярный вес1)»
2.26. Силы, действующие на тело, погружённое в жидкость.
Результаты нашего исследования могут быть с пользой подытожены рассмотрением
следующей задачи: на рис. 24 диэлектрик или проводник показан
погружённым в жидкость. Мы хотим получить выражение для результирующей силы^
действующей на тело в целом после приложения электростатического поля.
Проведём поверхность Su охватывающую тело и расположенную в жидкости
непосредственно у границы 5 твёрдого тела. На каждый объёмный элемент
твёрдого дела действует сила с плотностью:
f = PE — l£9grade4-f", G0>
х) Abraham, Becker and Dоuga 11, The Classical Theory of Electricity and
Magnetism, стр. 98, Blackie, 1932. [Абрагам-Беккер, Тегрия электричества, 2-е из2и
Л. — М., ГОНТИ, 1939, стр. 94—95.J
Жидкость
СИЛЫ, ДЕЙСТВУЮЩИЕ НА' ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ [2.26J HI
i " i ■ i i i 1 —.——.ШШЛт
где f" даётся выражением D0), а на каждый элемент поверхности, на
которой имеется разрыв непрерывности, действует натяжение, даваемое
выражением E3). Вместо того, чтобы подсчитывать объёмный интеграл от f и интеграл
по граничной поверхности 5 от t, нам необходимо лишь подсчитать интеграл
ют t из уравнения E1) по поверхности Sx. Так как Sx проведена в жидкости,
то ^ = «2 = — х -j- , и E1) сводится к
t-eE(En)-|fi»n + l^.£«n, G1)
где п — единичный вектор нормали, направленной из твёрдого тела в жидкость,
а е и т имеют значения, соответствующие жидкости. Интеграл от этого
натяжения по поверхности 6Х даёт силы, действующие непосредственно со
стороны поля на объём и поверхность тела. Но поле, как мы только что
видели, вызывает также давление F8) и в жидкости, которое в каждой
точке Si действует по нормали внутрь, т. е. по направлению к твёрдому
телу. Равнодействующая сила на
единицу поверхности 54 равна G1)
за вычетом F8), и полная сила,
испытываемая телом в поле —
сила, которая должна быть ском-
ренсирована посторонними
связями, — равна:
F = Л еЕ (En) —~ Eb^da.G2)
Таким образом, для того чтобы
получить результирующую силу,
действующую на тело в целом, Рис- 24- Твёрдое тело, помещённое в жидкий
нам нет надобности знать кон- диэлектрик,
станты ах и а2 ни для твёрдого
тела, ни для жидкости, так как силы, с которыми связаны эти константы,
локально компенсируются другими напряжениями. Кроме того, поскольку
жидкость находится в равновесии несущественно, что S1 лежит в
непосредственном соседстве с поверхностью тела S. Полная сила, действующая на
жидкость, находящуюся между поверхностью St и произвольной
охватывающей поверхностью 52> равна нулю и, следовательно:
J I eE(En) — ^Е*й )da = J* { еЕ(Еп)— ~ЕЧ ]da, G3)
если мы сохраним условие, что п направлена наружу из охватываемого
объёма. Поверхность £2 может быть, следовательно, выбрана любым
способом,, облегчающим интегрирование, при том лишь условии, что она не
пересекает и не охватывает никакого другого тела.
Если твёрдое тело является проводником, то поле Е нормально его
поверхности. Полная сила, действующая на изолированный проводник, будет
поэтому:
• F = ~- $ eE*nda = ~j aEda, G4)
Si S,
где о) — плотность зарядов на поверхности 5. Последнее верно, конечно,
только для поверхности Su непосредственно прилегающей к проводнику.
142 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Ясно теперь, что силы, действующие на твёрдое тело, окружённое
вплотную другим твёрдым телом, могут быть подсчитаны только в том
случае, если указан характер контакта на их общей поверхности. Задача
усложняется ещё и тем обстоятельством, что упругие напряжения на границе
раздела должны уравновешивать не только нормальные давления, но и
напряжения сдвига.
СИЛЫ В СТАТИЧЕСКОМ МАГНИТНОМ ПОЛЕ
2.27. Неферромагнитные вещества. Исследование, проведённое в
разделе 2.22, может быть непосредственно применено к статическому
магнитному полю во всех случаях, когда соотношение между В и Н имеет вид:
з
By- ^* G=1,2,3), A>
где компоненты ,^к тензора магнитной проницаемости могут быть функциями
точки, но не зависят от напряжённости поля. Изменение магнитной энергии
изотропного тела в результате варьирования параметра и. даётся выражением
E2) раздела 2.17:
ZT = ^j^H2dv, B>
а обобщением этого выражения для случая анизотропного тела, занимающего
объём Vlt будет:
+ 28{Al2tf1/V+28f*23tf2tf3 +2bHlHtfi1)dv. C) ,
Эти вариации могут быть выражены через компоненты деформаций, если мы
примем, что соотношение между компонентами тензора магнитной
проницаемости и компонентами тензора деформации линейно:
Если мы предположим далее, что в недефоржированном состоянии среда изо-
тропна, то коэффициенты Ь\т сведутся к двум:
так что вариация магнитной энергии, связанная с чистой деформацией, будет:
+ {bi — b2) {HXH2 Ье12 -г H2H3 Ъе23 + ИъНг Ьеъх)} dv. F>
Уравнение F) формально отличается от уравнения C1), стр. 133,
только знаком. Электростатическая энергия U представляет собой работу,
совершаемую при создании поля против сил, действующих между
элементами зарядов. С другой стороны, магнитная Энергия Т представляет собой
работу, совершаемую против взаимных сил, действующих между элементами.
' , ■ t
' *СИЛЫ В СТАТИЧЕСКОМ МАГНИТНОМ ПОЛЕ ]2.27] 14&-
■ i > -- - ■
токов, плюс работа, совершаемая против индуцированных электродвижущих
сил. Работа, необходимая для совершения малого смещения или деформации
тела в магнитном поле, частично тратится против механических сил,
действующих на тело, частично расходуется в источниках тока для
поддержания токов постоянными *). После вычитания работы, совершённой против
индуцированных электродвижущих сил, из полной магнитной энергии, остаётся
потенциальная энергия взаимных механических сил, которая, как мы нашли
в разделе 2.14, равна и противоположна Т:
8С/ = _8Г. G>
Силы, действующие со стороны поля на тела, находящиеся в объёме Vlt
могут быть подсчитаны из соотношения F), взятого с обратным знаком.
Полностью аналогично случаю электростатического поля мы находим,
что объёмная сила, действующая со стороны поля на среду, которая в неде-
формированном состоянии изотропна, магнитная проницаемость которой не
зависит от напряжённости поля и которая свободна от остаточного
магнетизма, но в которой могут течь токи плотности J, равна:
. . з
' *-1
4" *Г (»!«•)• (8)
2 дх3
Если среда однородна и в ней нет токов, то соотношение (8) сводится
к следующему:
f=—~(bli-d2)gradfP. (9)
В газах или жидкостях bt = b2 —— х~ , и (8) может быть написано
в виде:
f=.x[J, H]-l^grad^ + lgrad(^T.^). ч (Ю)
Как и в случае электростатического поля, объёмные силы, компоненты
которых даны уравнением (8), могут быть представлены в виде дивергенции
тензора 2S:
f = div2S, A1)
компоненты которого будут
A2>
Следовательно, силы, действующие со стороны магнитного поля на вещество,
находящееся внутри замкнутой поверхности 5lt- будут точно такими же, как
если бы мы приложили к поверхности Sx поверхностные силы с плотностью-
1 = ^-|--^^)н(Нп)-Ц-^п. A3)
г) Если источниками ярляются постоянные магниты, то это замечание
неприменимо, но тогда энергия поля не даётся выражением 3r=-s- Г ВН do.
144 ГЛ. II. СИЛЫ И ЭНЕРГИЯ
Подобным же образом силы, действующие на единицу площади поверхности
^разрыва, могут быть получены подсчётом сил A3) по каждой из сторон
^поверхности. В результате получим для магнитного поля выражение,
аналогичное E3). Особо важен случай магнитного тела, погружённого в
жидкость, магнитная проницаемость которой с достаточной степенью
приближения не зависит от плотности и равна |л.0 — значению для свободного
пространства. Пусть область A) представляет тело, а область B) — жидкость
.{рис. 23). Тогда силы, действующие на единицу площади граничной
поверхности, будут:
t=JH-p ^1+^ч^щ 1ц+£/йВ1 + 2цАн-1ц111. (U)
где константы Ьъ #2 относятся к магнитному телу, а Щ следует измерять
-внутри тела непосредственно у поверхности.
В отношении параметров Ьг и Ь% известно не очень много, хотя имеются
указания на то, что они могут быть весьма велики. Они должны быть,
конечно, известны, если нужно рассчитать упругую деформацию тела.
Ж счастью, в большинстве практических задач мы интересуемся только
полной силой, действующей на тело как целое. Силы, возникающие благодаря
деформациям, локально компенсируются вызванными ими упругими
напряжениями, и соответствующие члены, включающие Ьх и Ь%, выпадают. Как
и в случае электростатического поля, результирующая сила, действующая
со стороны статического магнитного поля на неферромагнитное тело,
погруженное в какую-либо жидкость, получается вычислением интеграла
F = jL Н (Нп) — £ #%} da . A5)
s,
-по какой-либо поверхности, охватывающей тело.
2.28. Ферромагнитные вещества. Предшествующие формулы применимы
к ферромагнитным веществам в достаточно слабых полях. Если, однако,
магнитная проницаемость заметно зависит от напряжённости поля, то энергия
магнитного тела не выражается более уравнениями B) или C), и вместо
них мы должны воспользоваться интегралом, полученным в разделе 2.17:
в
Т=±-${П1В — HBj — HB 4-2 fhujtydv. A6)
Vi О
Исследование объёмных и поверхностных сил для этого случая было
проведено Поккельсом 1), который разобрал также вкратце и вопрос о
магнитострикции. Явление магнитострикции определяется, однако, не только простой
упругой деформацией, но и рядом других важных факторов. Образец железа,
например, в целом являющийся изотропным, под микроскопом обнаруживает
мелкозернистую структуру. Свойства каждого зерна или микрокристалла,
строго анизотропны. Тот же порядок величины, что и эти зёрна, имеют
группы или области атомов, каждая из которых ведёт себя как постоянный
магнит. Группы эти необязательно должны отождествляться с микрокристал-
. лами. В ненамагниченном состоянии ориентация намагничения жаждой из этих
магнитных областей случайна, и полный магнитный момент равен нулю.
-Слабые внешние поля лишь слегка смещают эти маленькие магнитики из их
первоначального положения равновесия. В результате мы получаем небольшой
индуцированный магнитный момент, и поведение железного образца при
этих условиях совершенно аналогично поведению поляризующегося диэлек-
г) Pockels, loc. cit. стр. 369.
СИЛЫ В ЭТЕКТРОМАГНИТНОМ ПОЛЕ [2.29] 145
трика в электрическом поле. Однако по мере увеличения напряжённости
тюля области намагничения начинают внезапно перескакивать в новые
положения равновесия вдоль приложенного поля, с соответствующим изменением
упругих свойств образца. Удлинение в слабых полях может смениться
сокращением, когда поле увеличивается, прямо противоположно тому, что
предсказывает теория магнитострикции при применении её к строго
изотропным телам. В этом вопросе мы встречаемся, таким образом, с задачей,
в которой макроскопическое поведение вещества не может рассматриваться
отдельно от его микроскопического строения.
СИЛЫ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
2.29. Силы, действующие на тело, погружённое в жидкость. Выражения
W = — ~fE4adv, 8Г=у|я28а^ A)
для энергии тела в стационарном электрическом или магнитном поле были
обоснованы в разделах 2.10 и 2.17 безвихревым характером векторов Е
и Н — Hj, а также соответствующим поведением этих векторов в бесконеч-
«ости. В переменном поле эти условия не выполняются, и поэтому
соотношения A) нельзя применить для вывода сил, действующих на тело или на
элемент тела, не пересмотрев весь вывод. В лучшем случае, наш анализ
будет содержать некоторые гипотетические элементы, поскольку наше пред-
положение, что величины Е-зт и Н -^т- представляют собой скорости
изменения плотностей энергии в электромагнитном поле, является в конце
концов лишь правдоподобной интерпретацией теоремы Пойнтинга.
В разделе 2.5 было показано,- что полная сила, передаваемая
электромагнитным полем через замкнутую поверхность £ в свободном пространстве,
выражается интегралом:
F = J {% (En) E + ^ (Вп) В — у (s0£2 +1 В») n| da. B>
х
Для стационарных полей мы могли показать затем, что если поверхность £
проведена полностью в жидкости, где не могут существовать
напряжения сдвига, то полная сила даётся тем же выражением B), если только
заменить е0 и ja0 на соответствующие их значения в жидкости:
F = Иг (En) Е 4- \i (Нп) Н—j (e^+H-tf2) nl da. C>
i
Эта' сила является результирующей сил, действующих на заряды, токи
и вещество, находящиеся внутри поверхности £■ Вещество внутри
поверхности £ не обязательно должно быть жидкостью и в нём могут встречаться
поверхности разрыва непрерывности физических свойств. Однако соотношения
между Е и D и между В и Н предполагаются линейными.
Далее, поскольку B) справедливо в динамическом случае в той же мере,
как и в статическом, то имеются все основания предположить, что C) можно
применить и к переменным полям. Нетрудно привести доводы в пользу
подобного предположения, в особенности заимствованные из теории
относительности. Однако правая часть уравнения C) должна быть теперь
интерпретирована в смысле раздела 2.6 не как сила, действующая со стороны
поля на вещество, находящееся внутри поверхности, а как поток импульса
Ю Зак, 593, Теория электромагнетизма.
146 гл. ii. силы и энергия
через поверхность 2 в единицу времени, направленный внутрь. Обозначим
полный механический импульс вещества, находящегося в £, включая весомые
заряды, через GMex, а импульс электромагнитного поля через Ge. Тогда:
^(GMex + Ge) = Jje (En) E + у. (Hn) H — ~ (e£2-f tx//2) nJ dum
2
Поверхностный интеграл в D) может быть преобразован в объёмный.
Имеем прежде всего
-j J е ЕЧ da = 1 J grad (e£2) ^ E)
2 F
и далее:
у grad (гЕ2) = 1Е2 grad e -f (Dgrad) E + [D, rot EJ; F)
(Dgrad) E = А (ед +JJL (Z^E) + A (дЕ) - E div D; G)
J {~ (ДА) + ~ (АД*) + ^ (DA) } ^ == J (Dn) Ex da, (8)
что, очевидно, сокращается с .^-компонентой вектора е(Еп)Е в C). Поступая
подобным же образом и с магнитными членами и используя соотношения
rotE = — ™, rotH=^-j-J, divD = p,
мы приходим к уравнению:
JL
dt
(GMex + Ge) = J {pE + [J, B] —I £2grad e-'1H* grad p. +
+ -^ [D, Bj} A>. (9)'
Приращение механического "Импульса является результатом действия сил
со стороны поля на заряды и нейтральную, материю:
F—|jO„. ' (Ю)
Если, следовательно, мы сможем разделить правую сторону (9) на две части,
которые можно будет отождествить соответственно с GMex и Ge, то мы
сможем определить и силы. Как произвести подобного рода разделение,
ни в какой степени не очевидно; предлагались разные гипотезы1). Согласно
теореме Пойнтинга, поток энергии даже внутри весомого вещества
определяется вектором
S = [Е, Н] джоулей/сел; • метр2. AЦ
Абрагам и Лауэ приняли за плотность электромагнитного импульса
ge = u-0e0S = -д S кг\сек • метр2. A2)
1) Паули, Теория относительности, Гостехиздат, 1947.
СИЛЫ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ [2.29] 147
Согласно этой гипотезе, равнодействующая сил, действующих на заряды,
токи и поляризованное вещество, находящиеся внутри поверхности £, равна:
F= J(pE + [J,Bl — lE2grade~lH2gradH, + -^=^^)^, A3)
v
или:
F= J|e(En)E + ^(Hn)H — L(eE*+V.H*)n}da~-±~f[E,ll]dv. A4)
x v
Практически, точный вид выражения для электромагнитного импульса
не имеет большого значения, поскольку множитель 1/с2 делает его слишком
малым, для того чтобы он мог бы быть легко обнаружен.
На основании A3) иногда утверждают, что сила, действующая со стороны
электромагнитного поля на единицу объёма изотропного вещества, равна
f = PEJr[J,B]-i^grade_^№grad^ + ^2Zll^. A5)
Подобное заключение, очевидно, неверно, поскольку A5) не включает в себя
силы, связанные с деформацией. Как отмечено выше было, эти стрикцион-
ные силы частично компенсируются упругими напряжениями и не входят
в интегралы A3) или A4) для результирующей силы, необходимой для
поддержания в равновесии всего тела, как целого.
10*
*
ГЛАВА III
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
От основных уравнений и общих теорем мы переходим в следующих
главах к изучению структуры и свойств конкретных полей. Простейшими
из них являются поля, связанные со стационарным распределением зарядов.
Нужно сказать, что из всех разделов нашего предмета свойства
электростатического поля получили наиболее полную и исчерпывающую трактовку.
В этой главе мы рассмотрим только важнейшие из этих свойств и тех
методов, которые были разработаны для их исследования.
ОБЩИЕ СВОЙСТВА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
3.1- Уравнения для поля и потенциала. Уравнения, которым
удовлетворяет поле стационарно распределённых зарядов, получаются
непосредственно из уравнений Максвелла, если все производные по времени положить
равными нулю. Для всех обыкновенных точек электростатического поля мы
имеем, следовательно:
rotE = 0, (I)
div D = p. (II)
Согласно (I), линейный интеграл от напряжённости поля Е по любому
замкнутому пути {циркуляция Е) равен нулю и, следовательно, поле
консервативно.
Консервативный характер поля является необходимым и достаточным
условием для существования скалярного потенциала, градиенту которого
равен вектор Е:
Е = —grade. A)
Знак здесь совершенно произволен; минvc был выбран для того, чтобы
направление Е соответствовало общепринятому условию, согласно которому вектор Е
напраблен от положительного заряда к отрицательному. Уравнение A) не
определяет потенциала однозначно, поскольку к о можно прибавить любую
постоянную 9о) не нарушив условия
rotgrad(?4-?0) — °- B)
В главе II было показано, что скалярный потенциал электростатического
поля может быть интерпретирован как работа, необходимая для перемещения
единичного положительного заряда из бесконечности в точку поля (лг, у, г):
(ж, у, z)
o(x,y,z)= — jEdr. C)
со
Мы покажем ниже, что поле системы зарядов, заключённой в конечной
области пространства, исчезает в бесконечности. Условие, что о исчезает
ОБЩИЕ СВОЙСТВА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ 13.1] 149
в бесконечности, определяет-, таким образом, постоянную <ро> которая до
этого являлась совершенно произвольной.
Поверхности, на которых <р постоянно, называются эквипотенциальными
поверхностями. В любой точке эквипотенциальной поверхности
напряжённость поля Е нормальна к этой поверхности. Пусть
о(х, у, z) = const. D)
будет эквипотенциальной поверхностью; образуем первый дифференциал:
Дифференциалы dx, dyt dz являются компонентами Еектора смещения. dxy
вдоль которого мы хотим определить изменение ср, и так как fifcp = 0, то
этот вектор должен лежать на поверхности ср = const. С другой стороны,
dv дф д'-о
частные производные -р, -к1, -г1 определяют изменение ср соответственно
вдоль х-, у- и г-осей и, как было показано, являются компонентами другого
вектора, а именно, градиента:
dcp представляет собой, таким образом, скалярное произведение этих двух
векторов и, поскольку это произведение равно йулю, эти векторы
ортогональны. Исключение составляют те точки, в которых все три частные
производные одновременно обращаются в нуль. Напряжённость поля в этом
случае равна нулю, и точки эти являются точками равновесия.
Ортогональные траектории эквипотенциальных поверхностей образуют
семейство линий, которые в каждой точке поля касательны к вектору Е.
Они называются силовыми линиями. Часто бывает удобно представлять поле
заданной системы зарядов графически, вычерчивая проекции этих линий
на какую-нибудь плоскость, проходящую через поле. Пусть ds представляет
собой малое смещение вдоль силовой линии:
ds = idx'-{- j dy' -f k dz\ G).
где штрихи введены для того, чтобы избежать путаницы с текущими
координатами (х, у, г) на эквипотенциальной поверхности. Так как, по
определению, силовая линия в каждой точке касательна к вектору напряжённости
поля, прямоугольные компоненты f/s и Е(х',у\г') должны быть
пропорциональны'между собой:
Ex=\dx, Ey = \dy', Ez = \dz . (8>
Дифференциальные уравнения силовых линий будут, следовательно:
dxr dyr dz' ,q\
Ex (*', у, z') Ey (x', У, z') Ez (x't y, zr)"
'Соотношения между компонентами векторов D и Е в большинстве
случаев линейны. Если среда вместе с тем и изотропна, то можно положить:
D = eE= —egrad<p, U°>
откуда, согласно (II), ср должно удовлетворять соотношению:
div (e grad ср) = е Дер 4- grad e grad ср = — р. A1)
150
ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
В случае однородной среды <в должно быть решением уравнения Пуассона:
Д? = —1р. • A2)
В точках поля, в которых нег зарядов, A2) сводится к уравнению Лапласа:
Дс? = 0. A3)
Основная задача электростатики состоит в определении скалярной
функции ср (дг, у, г), удовлетворяющей в каждой точке пространства уравнению
Пуассона, а на заданных поверхностях — необходимым граничным условиям.
Иногда рассматривается значительно более простая обратная задача: задан
потенциал, как определённая функция координат, найденная из
эксперимента; требуется найти систему зарядов, которая создаёт такой
потенциал. Плотность необходимого непрерывного распределения тотчас же
получается выполнением дифференцирования, указываемого уравнением A2). Однако
в общем случае будут иметься дополнительно точечные заряды, присутствие
и свойства которых не выявляются уравнением Пуассона. В таких точках
потенциал становится бесконечным; обратно, мы можем ожидать нахождения
точечных зарядов или систем точечных зарядов в особых точках
потенциальной функции. Характер подобных систем или, как их называют, мультипо-
лей, будет предметом дальнейших разделов, но простой пример может
послужить иллюстрацией этого положения.
Пусть потенциал даётся функцией
1 е~аГ /-1/1Ч
©=- , A4)
где г — расстояние по радиусу от начала координат до точки наблюдения,
а а — константа. В силу сферической симметрии этой функций, уравнение
Пуассона, написанное в сферических координатах, принимает вид:
а-2 дг\ дг) г Р' *10'
выполнив дифференцирование, находим для плотности необходимого
непрерывного распределения заряда:
а'- е-аг
4тс г
A6)
Заряд, содержащийся внутри сферы радиуса г, получается интегрированием
р по объёму этой сферы, т. е.
г
fodv = e~ar(ar -[- 1) — 1. A7)
о
Если радиус становится бесконечным, то полный непрерывно
распределённый заряд будет
j p dv—
1. A8)
Но это не весь заряд, необходимый для создания потенциала A4). При г=0
потенциал становится бесконечным, и мы должны искать точечный заряд,
расположенный в этой особой точке. Для того чтобы выявить его, нам нужно
лишь применить (II) в интегральной форме. Если q — точечный заряд, заряд,
ОВЩИВ СВвйетВА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ [3-2] 151
расположенный в начале координат, то
[ Dn da ==[q -f U dv, A9)
s v
где поверхностный интеграл распространён на поверхность S,
ограничивающую объём V. Имеем:
fDrda=(ar-L l)e~ar, B1)
«, следовательно,
Я ■-= + Ь B2)
Таким образом, потенциал, определённый функцией A4), вызывается
единичным положительным зарядом, расположенным в начале координат, и равным
ему отрицательным зарядом, распределённым вокруг него с плотностью р.
Система в целом является нейтральной.
3.2. Граничные условия. Поведение векторов поля при переходе
через поверхность разрыва непрерывности в среде было разобрано в разделе 1.13,
и результаты этого раздела непосредственно приложимы к случаю
электростатического поля. Предположим, что две среды соприкасаются по
поверхности 5 и что единичная нормаль п проведена от среды A) к среде B),
так что среда A) расположена с отрицательной стороны S, а среда B) —
<: положительной. Тогда
[п,Е2 — Ejl=0; n(D2—D^^co, B3)
где со — плотность поверхностных зарядов, расположенных на S.
Для дальнейшего удобно ввести единичный вектор t, касательный к
поверхности S. Производные д&[дп и dyjdt представляют соответственно изме-
«ения ср в нормальном и тангенциальном направлении. Граничные условия B3)
могут быть выражены через потенциал с помощью соотношений
^-^1=0, ч&1—.(£1—■ B4)
dtj2 ~ Vat Л - и' е2 \Тпк ~~ l W,
Из консервативности поля следует также, что и сам потенциал должен быть
непрерывен при переходе через поверхность S, так как работа, требуемая
для переноса малого заряда из бесконечности в любую из двух соседних
точек, расположенных на противоположных сторонах S, должна быть одинакова.
Отсюда
?1=?2- B5)
Два условия
Ъ = Ъ 4$),-..®),™ <ЭД
являются независимыми.
Проводники играют в электростатике особую роль. Для целей чисто
макроскопической теории достаточно рассматривать проводник как замкнутую
область, внутри которой заряды могут свободно перемещаться. Если
проводником является металл или электролит, то поток зарядов прямо
пропорционален напряжённости Е электрического поля: J = о Е. Заряды могут
свободно перемещаться по поверхности проводника, но покидать её могут
только под влиянием очень сильных внешних попей, или при* высоких
температурах (термоэмиссия). Если заряды на проводнике находятся в состоянии
152
ГЛ„ III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
электростатического равновесия и все токи прекратились, то очевидно, что-
в каждой внутренней точке проводника, находящегося в
электростатическом поле, результирующая напряжённость поля Е равна нулю, и в
каждой точке на его поверхности тангенциальная компонента Е также равна
нулю. Отсюда электростатический потенциал э внутри проводника
постоянен, и поверхность каждого из проводников является
эквипотенциальной. Предположим, что незаряженный проводник внесён в заданное
внешнее поле Е0. В первый момент возникнут временные токи. Согласно
разд. 1.7, заряд не может накапливаться во внутренних точках проводника,
но произойдёт такое перераспределение зарядов по поверхности, чтобы
поверхностная плотность со удовлетворяла условию:
fco da = 0. B7)
Поверхностное распределение зарядов вызывает индуцированное, или
вторичное, поле с напряжённостью Ех. Равновесие достигается при таком
распределении, при котором в каждой внутренней точке проводника
Ео-ЬЕ1=°- B8>
Равным образом, если заряд q помещён на изолированном проводнике, то он
распределится по поверхности проводника с поверхностной плотностью cos
подчинённой условию B8), а также соотношению
Гсо da = q. . B9)
s
Внутреннюю область проводника, находящегося в состоянии
электростатического равновесия, мы будем обозначать индексом A), а внешний
диэлектрик индексом B). Тогда на поверхности 5:
Е1 =» D, = 0, [п, Е2] = 0, nD2 = со, C0>
или через потенциал:
о = const., е2^ = —со. C1)
Если может быть найдено решение уравнения Лапласа, которое сохраняет
постоянное значение на поверхности заданных проводников, то
поверхностная плотность зарядов может быть определена подсчётом нормальных
производных от потенциала.
ОПРЕДЕЛЕНИЕ ПОЛЯ ПО ЗАДАННОМУ РАСПРЕДЕЛЕНИЮ ЗАРЯДОВ
3.3. Теорема Грина Пусть V будет замкнутая область пространства,
ограниченная регулярной поверхностью S, и пусть о и ty— две скалярные
функции точки, которые непрерывны внутри V и на поверхности S вместе
со своими первыми и вторыми производными х). Тогда' применение теоремы
о дивергенции к вектору <];grade? даёт:
Г div ( й grad <?)dv = Г (& grade?) nda. A)
v s
Развёртывая дивергенцию по формуле
div ( ty grad с?) = grad 6 grad о -j- ty Дс? B)
1) Это условие сильнее, чем необходимо. Вторая производная функции <\> не
обязательно непрерывна.
ОПРЕДЕЛЕНИЕ ПОЛЯ ПО ЗАДАННОМУ РАСПРЕДЕЛЕНИЮ ЗАРЯДОВ [3.4] 153
и замечая, что
grad<pn=^, C>
где ду/дп — производная по направлению положительной нормали, мы
получаем соотношение, известное под названием первого тождества Грина:
Г grad ty grad о dv -\- Г^ Дер dv = Г ^^ da. D)
v v s
Если, в частности, мы положим ty = ? и возьмём в качестве о решение
уравнения Лапласа, то уравнение D) перейдёт в следующее:
J(grad oV dv = Jcp Ц- da. E)
v s
Поменяем местами функции © и 6, т. е. применим теорему о
дивергенции к вектору ср grad ^:
(gradо • gradtydv-\- | ?A^cfo = lo—^da. F)
Вычитая F) из D), получаем соотношение- между объёмным и поверхностным
интегралами:
f (,L Дс?-? Д«» ^ = J (б ^ — ? Ц) <*«, G)
к' s
известное под названием второго тождества Грина или часто также под
названием теоремы Грина.
3.4. Интегрирование уравнения Пуассона. С помощью теоремы Грина
потенциал в заданной точке (х',у',г') внутри объёма V может быть выражен
через объёмный интеграл по объёму. V
и поверхностный интеграл по
поверхности S. Предположим, что заряд
распределён с объёмной плотностью р(х,у,г).
Мы будем считать функцию р(х,у,<г) —
ограниченной; в остальном она есть
произвольная функция точки. Проведём произ- Уг
вольную регулярную поверхность S,
охватывающую объём V (рис. 25). Совсем не
обязательно, чтобы 5 заключала в себе
все заряды или хотя бы даже часть их.
Пусть О — произвольное начало координат, рис. 25. Применение теоремы Гри-
ах—х', y=y', z — z'—заданная точка на- на к области V, ограниченной
блюдения, находящаяся внутри V. Потен- с внешней стороны поверхностью
циал в этой точке, вызываемый всем рас- s> а с внутретне^й стороны сфе-
пределением зарядов, будет <?(х',у\ г').
В качестве функции ф мы возьмём центрально симметричное решение
уравнения Лапласа:
44*0', г; *',/,*>-у > (8)
Где г — расстояние от переменной точки (x,y,z), находящейся внутри
объёма V, до заданной точки (*', у', г'):
Однако этга функция не удовлетворяет необходимым условиям непрерывности
при г = 0. Чтобы исключить особенность из рассматриваемой области, мы
154 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
проведём небольшую сферу радиуса гх с центром в точке (х',у',г). После
этого объём К будет ограничен извне поверхностью S, а изнутри — сферой Sx.
Внутри V как о, так и ty удовлетворяют теперь требованиям теоремы Грина
и кроме того Дф = 0. Таким образом, G) сводится к равенству:
Я>=Л^-^ШЬ ™
где поверхностный интеграл должен быть распространён по обеим
поверхностям 6" и Sv На сфере Sx положительная нормаль направлена по радиусу
к центру (х\у',г), ибо это направление является внешним по отношению
к объёму V. Следовательно, на поверхности Sx
*L = -E2. \-д-(Ц\ =-L A1)
дп дг> ldn\r)}r=ri rl ■ U1'
Так как гх постоянно, то слагаемое, вносимое в правую часть
соотношения A0) сферой, будет:
( -r^ da —> —о I о da.
Если через <р и до/дг обозначать средние значения о и dofdr на Slt то это
слагаемое будет равно
гх I дг г2
что в пределе при г^О сводится к — 4т:<р(х',у',г'). После подстановки
этого значения в выражение A0), мы получаем для потенциала в любой
внутренней точке (х',у\г')
V В
В случае однородной среды мы можем ввести плотность зарядов р с помощью
' ■ А 1
соотношения Дсз = р:
н*,м=-Ь!*-,*>+ы[т%-*НЩ<1а- A3)
V 8
Если объём V, ограниченный поверхностью S, зарядов не содержит, то
выражение A3) примет вид:
?(*',/„')=У[!!Ь?!.A)Ь (">
в
Очевидно, поверхностные интегралы в A3) и A4) выражают долю, вносимую
в потенциал в точке (*', у', в') всеми зарядами, расположенными вне S.
Если значения о и его производных по нормали на поверхности S известны,
то потенциал в любой внутренней точке может быть определён
интегрированием. Уравнение A4) может быть интерпретировано, следовательно, как
решение уравнения Лапласа для области V, удовлетворяющее заданным
условиям на границе. Интеграл
?(*'./. *'>=4^f TdV A5>
V
ОПРЕДЕЛЕНИЕ ПОЛЯ ПО ЗАДАННОМУ РАСПРЕДЕЛЕНИЮ ЗАРЯДОВ 15.5] 155
является частным решением уравнения Пуассона для точки (х, у', г'). Общее
решение получится прибавлением интеграла A4) однородного уравнения
Лср = 0. Если вне поверхности 5 зарядов нет, то поверхностный интеграл
должен равняться нулю.
3.5. Поведение в бесконечности. Предположим, что все элементы
некоторого распределения зарядов расположены на конечном расстоянии- от
какой-либо произвольной точки О. Представим себе, что это распределение
зарядов ограничено внутренней областью поверхности Sx, которая содержит
также и точку О. Расстояния г, гх и R показаны на рис. 26. Имеем:
г = (Я2 -f r\ — 2rxR cos b)*.
A6)
Потенциал в любой точке P(x't у', z')i расположенной вне поверхности Sv
будет, следовательно:
?&,?.*—( ^Afl^-^. A7)
Ft i^ + rl —2rtRcos Ь)"
По мере удаления Р в бесконечность, члены г\ и 2rPcos6 становятся
пренебрежимо малыми по сравнению с R2 и в пределе, при R -> оо, мы
получаем:
lim в = -—= Г р dv = -: %,
A8)
где q — полный заряд системы. Говорят, что потенциальная функция
регулярна на бесконечности, если при R-+co произведение Ry остаётся
ограниченным. ■ Вектор напряжённости ^
поля Е*=—grade? на больших ^"" *""■"
расстояниях направлен по радиусу
ют точки О, и функция /?2|Е|
также остаётся ограниченной.
Все реальные системы
зарядов расположены в областях
конечных размеров и,
следовательно, их поля регулярны на
бесконечности. Часто, однако, решение
.задачи упрощается в
предположении, что внешнее поле
однородно. Такое поле не исчезает
в бесконечности и может вызываться только источниками, расположенными
на бесконечном расстоянии от начала отсчёта.
Существенно отметить, что поверхность S делит всё пространство на
две области — внутреннюю Vt и внешнюю V2, и если функции о и ф
регулярны на бесконечности, то теорема Грина применима не только к Vv но
и к внешней области V2. Действительно, теорема может быть применена
к замкнутой области, ограниченной изнутри поверхностью S, а извне —
другой поверхностью S2. Если S.2 удаляется в бесконечность, и величины ^~-
и <?-**~ исчезают как l/r3, то интеграл по поверхности S% стремится к нулю.
Следовательно:
Рис. 26. Иллюстрация к разделу 3.5.
Г (-1» Дер — о Д']>) dv == Г ($
дп
дп
Ada,
A9)
156 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
■ГцГ.,/
ъ
xfyjz-
но теперь положительная нормаль в точках на 5 направлена из К0,
т. е. внутрь Vv Предположим, например, что система зарядов полностью
ограничена областью Vv заключённой внутри поверхности S. Потенциал
в любой точке (х', у', г') области
V2 вне поверхности 5 может быть
вычислен из A7) или же, по
известным о и d's>jdn на поверхности S,
из A4), см. рис. 27.
3.6. Кулоново поле. Согласно
A8), потенциал заряда на
расстояниях, очень больших по сравнению
с размерами самого- заряда,
приближается к значению
Рис.27. Применение теогемы Грина к
области \/~2> внешней по отношению к
замкнутой поверхности S.
^'./.«O-^-f. B0)
Если заряд q расположен в точке {х, у, z), то расстояние от q до точки
наблюдения (л;', у', z') равно
г = У(х'— xf -f (У —у)* + {г' — zf. B1)
Пусть г° представляет собой единичный вектор, направленный от источника,
т. е. от (х, у, г) к (х', у', г'). Тогда:
orad'(l) = -grad (!) = --! г«,
B2)
где штрих при операторе градиента обозначает дифференцирование по
переменным точки наблюдения (л;', у', z'). Напряжённость поля в этой точке
будет:
Е(х', У, г') = — grad'<p =
4 тел2
B31
Поле точечного заряда обратно пропорционально квадрату расстояния
и направлено по радиусу от заряда q, если заряд положителен. Это
есть закон, который был установлен экспериментально Кулоном и Кавен-
дишем и который обычно берётся за отправную точку в теории
электростатики. Выражение «точечный заряд» используется здесь в смысле заряда*
размерами которого можно пренебречь по сравнению с г. Математически
можно представить себе, что размеры q становятся исчезающе малыми, в то
время как плотность р возрастает так, что q остаётся постоянным. В
пределе возникает особая точка, и выражение B3) имеет смысл во всех точках,
кроме г = 0. Нет никаких оснований полагать, что подобные особенности-
действительно существуют в природе, но на достаточно больших
расстояниях удобно представлять поле таким, какое могло бы быть вызвано
системой точечных зарядов в математическом смысле. В последующих разделах
нам представится возможность развить это представление дальше.
Потенциал в точке (*', у', г') получается интегрированием слагаемых
от каждого из элементов заряда dq = p dv по всему пространству:
do {x', У, z') = J^- i%^> dv, B4)
dE= — — P (x, y, z) grad' (y) dv = -^ p (x9 y, z) grad (~ ) dv. B5)
Напряжённость поля, создаваемого всем зарядом, распределённым в
однородной изотропной среде, будет, следовательно:
Е (х\ У, г') == ■—■ f p (х, у, z) grad (у) dv.
B6)
ОПРЕДЕЛЕНИЕ ПОЛЯ ПО ЗАДАННОМУ РАСПРЕДЕЛЕНИЮ ЗАРЯДОВ [3-7] \157
3-7. Сходимость интегралов. Доказательство сходимости интегралов
для потенциала и напряжённости поля содержится в самом методе, которым
они были выведены. Мы опишем, однако, другой способ, который может
послужить примером подобного рода доказательств. Поскольку элемент
интегрирования в точке (л;, у, г) мэжет совпасть с (л;', у', г') и при этом под-
интегральное выражение обращается в этой точке в бесконечность, то совсем
«е очевидно, что интеграл действительно имеет смысл. Мы покажем, что
хотя несобственный интеграл подобного типа и не может быть определён
•обычным образом как предел суммы, но при соответствующем определении
он может быть сделан абсолютно сходящимся.
Пусть точка Q(x', у', z), в которой мы хотим определить поле,
окружена замкнутой поверхностью S произвольной формы, разделяющей всю
область V, занятую зарядом, на две части — часть Vu представляющую
объём внутри S, и часть V?, внешнюю по отношению к 6\ По области V2
интеграл в уравнении B6) ограничен, и, следовательно, заряд,
расположенный вне поверхности S, вносит в значение напряжённости поля в точке Q
конечную величину, а именно, слагаемое Е3:
Е2 (х\ У, zf= -L С р (х, у, г) grad (I) do. B7)
Обозначим напряжённость, создаваемую зарядами, расположенными внутри S,
через Ej. Для того чтобы напряжённость поля Е == Ех -f- E2 имела в точке Q
определённое значение, необходимо, чтобы в пределе, при стягивании
поверхности 5 около точки Q, поле Ех было бы равно нулю. Небольшое рассуждение
покажет нам, что так оно и получается в действительности, хотя
знаменатель подинтегрального выражения обратно пропорционален квадрату
расстояния и стремится к нулю, элемент заряда в числителе пропорционален
объёму V'j, который уменьшается пропорционально кубу линейных размеров.
Мы молчаливо предположили при этом, что плотность заряда р в каждой
точке объёма V конечна. Существует, следовательно, такое число т, что
\?\<т и
ницы следует далее, что
|р grad A)|<£ B8)
и
j J p grad A) <й/ <m [4г- B9)
Поверхность S, ограничивающая объём Vl7 может иметь произвольную форму,
и поэтому, чтобы избежать неудобств, связанных с оценкой интеграла по
этой области, мы проведём сферу радиуса а с центром в Q, охватывающую
область Vv Поскольку элемент объёма интегрирования положителен,
интеграл, распространённый по объёму Vlt будет меньше, или, в крайнем случае,
равен интегралу по объёму охватывающей сферы:
dv /4
р тп
<~ во всех точках V. Из существования этой верхней гра-
г
Jdv
Т5"
,3««. C°)
Ух
который, очевидно, стремится к нулю вместе с а. Таким образом,
напряжённость в точке Q от зарядов, расположенных внутри поверхности S,
становится исчезающе малой по мере того, как поверхность S сжимается
около точки Q, и, следовательно, интеграл B6), в случае зарядов,
распределённых по объёму, сходится как для внешних точек, так и для внутренних.
158
ГЛ. lit. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Интеграл, выражающий потенциал
, / > /, 1 Г lp (x, v, z) ,
C1)
тоже является несобственным интегралом, если точка наблюдения берётся
в области распределения заряда, но, поскольку знаменатель подинтегрального
выражения исчезает лишь как первая степень г, вышеприведённое
доказательство заведомо справедливо и для данного случая. Если р—ограниченная
интегрируемая функция положения, то C1) является непрерывной функцией
координат х'у у, г\ имеет непрерывные первые производные и всюду
удовлетворяет условию Е =—grad'cp. Можно показать, кроме того, что
если р и все производные р порядка ниже п непрерывны, то потенциал <р
имеет непрерывные производные всех порядков, ниже чем п-\- 1 х).
РАЗЛОЖЕНИЕ ПОТЕНЦИАЛА ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ
3.8. Аксиальные распределения зарядов. Предположим сначала, что
элемент заряда q находится в точке z = С на щрл z прямоугольной системы
координат с началом в точке О. Мы хотим получить выражение для
потенциала от заряда q в точке Р через координаты точки Р по отношению
к началу отсчёта О. Прямоугольные координаты Р будут х, у, zy но так как
поле симметрично относительно оси z, то
достаточно определить положение точки Р посредством
двух полярных координат г и 0 (рис. 28).
-Расстояние от q до Р обозначим г2, и потенциал
в точке Р будет, следовательно:
о (г, 0)=/- -
' v ' J 4 те Го
A)
Рис. 28. Иллюстрация к
разделу 3.8.
поскольку мы предполагаем, что среда однородна
и изотропна.
B)
г2=(Н +
2rCcos6J,
Необходимо рассмотреть два случая. Первый и, возможно, менее общий,
когда точка Р расположена внутри сферы, проведённой из О как из центра
и проходящей через точку С Тогда г < С, и мы можем написать:
Скобка может быть разложена по биному, если
C>
2 -у cos 6
<1.
Если кроме того
2 -у cos 0
<1, то получающийся ряд сходите»
абсолютно и, следовательно, члены могут быть сгруппированы произвольно,
и любые степени могут быть вынесены за скобки. Группируя члены ряда
по восходящим степеням г/С, мы получаем:
т,-Ц1+г«**ЧтК
V3 2fi 1
2COS2(i-2
К"'}'
D)
*) Смотри, например, Kellogg, Foundations of Potential Theory, гл. VI, Springer,
1929 или Phillips, Vector Analysis, стр. 122 и ел., Wiley, 1933.
РАЗЛОЖВНИЕ ПОТЕНЦИАЛА ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ [3.8] 159
что можно записать сокращённо так:
E)
71 — 0
Коэффициенты при г/С являются полиномами относительно cos 0 и известны
под названием полиномов Лежандра:
P0(cos6) = l,
Рх (cos 6) = cos 6,
Р2 (COS 6) = у C COS2 6 -
Ръ (cos 0) = у E cos3 6 -
*
-1) ==1C cos 26+1),
- 3 cos 6) = 1 E cos 36 + 3 cos 6).
F)
Абсолютная величина коэффициентов Рп никогда не превосходит единицы
и, следовательно, ряд сходится абсолютно при условии, что г<|С|.
Второй случай тот, когда Р лежит вне сферы радиуса С, так что г>С-
Соответствующее разложение получается переменой местами г и С в C) и E)
±-i{ 1+(i;_s I*.,}-*, G)
•^ = 7г2/,-1см°)(т)" О')-
(8)
и=0
Последний результат может быть получен несколько иным путём.
Рассмотрим величину, обратную расстоянию от точки г=С до Р, как
функцию С и разложим её в ряд Тэйлора около точки С = 0.
1
/(r)==JL==(r2_|_r2_2rCcosG) *,
В прямоугольных координатах г2 равно:
Следовательно,
'2 = {*2+.у2 + и-ч>2р,
±(±Л = -±(±
\дп/(щ __ .я г д»лщ __, , п у/со)
L ac« Jr=0 ' L*dzn Jr=0"~l ' <^
и так как /@) == 1/г, мы имеем:
/(С) = 1 = 1
dz
7J+-..C"
(— \)п дп (\
я!
дгп \ г
,п '
+ ...
(9)
A0)
A1)
A2)
A3)
A4)
Потенциал от заряда q в точке Р вне сферы может быть записан в любом
из видов:
со со
q у гиЛЛсозв)^ q у г„ (- \)п дп (\
4 таг 2л "* rn+i 4та Zj '"
п = 0 11 = 0
ее
п\ dz?
A5),
160 ГЛ. Ш. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
откуда очевидно, что
Pn(cosb) (—1)" дч /1
^и+1 п\ dzw V г
A6)
Предположим, наконец, что заряд распределён непрерывно на длине /
оси z с плотностью р = р(С). Потенциал на достаточно больших расстояниях
-от начала координат будет:
оо со Z
?('. fo=£ ?»=-i S .Г р(^)^^^#^ (^>о. A7)
И=0 И = 0 0
Первый член этого ряда
7
?0 = J- ±.f pQ«r, = ^_! , A8)
*и 4^£ r./iV/ 4тс г '
0
где <7 — теперь полный заряд отрезка, является очевидно кулоновым
потенциалом точечного заряда q, расположенного в начале координат. Од гако
теперь мыслим такой случай, когда плотность может принимать
отрицательные значения наряду с положительными, так что полный заряд
Я
= /р(С)Л A9)
может оказаться равным нулю. Главный член, к которому стремится
потенциал при г~^$>1, будет тогда:
в1в^1_^1Е^) fpCOCd!:^/-^. B0)
4Т.Е Г2 ." 4Я£ И
о
Величина •
р = |р(£КяГ, B1)
о
называется дипольным моментом данного распределения зарядов. В общем
случае мы напишем:
и определим
о =-_!_ р^Ысо53 B2)
7
p('*v = Jp(C)CwC B3)
как осевой мулътиполъ п-го порядка.
3.9. Диполь. Для того чтобы потенциал линейно распределённого заряда
мог быть представлен диполем, необходимо, чтобы полный заряд системы был
равен нулю (т. е. система в целом была бы нейтральна) и чтобы расстояние
до точки наблюдения было велико по сравнению с длиной отрезка, на
котором распределён заряд. М'-л видели, что потенциал ©0 таков, какой был бы
создан математически точечным зарядом, расположенным в начале координат.
При г= 0 потенциал ©0 имеет особую точку, поскольку истинный точечный заряд
подразумевает бесконечную плотность. Поставим теперь вопрос — можно ли
сконструировать такое распределение точечных зарядов, которое создавало бы
липольный потенциал cpt?
РАЗЛОЖЕНИЕ ПОТЕНЦИАЛА ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ 13.9]
161
Расположим точечный заряд -J- ^ в точке г = 1 на оси z и равный ему
отрицательный заряд —q в начале координат. Согласно уравнению (8),
потенциал в удалённой точке будет:
_1_\ ql_ cos 6
о =
Ч-(У
4тсе
Л COS О . ^ ,-..
■— —j—f- члены более высокого порядка. B4)
4тсе \/-2
Произведение p~ql является, очевидно, дипольным моментом данного
расположения. Предположим теперь, что / -* 0, но что q в то же время
возрастает по величине таким образом, что произведение р Остаётся постоянным.
Тогда в пределе получится точка с диполъной особенностью, потенциал
которой всюду, кроме начала координат, будет:
р cos 6 р д
4ие л2 4тс
о
±A)
dz \rj-
B5)
Таким образом с точкой связывается некоторое направление. Фактически
дипольный момент является вектором р, направленным в данном случае
вдоль оси г. Пусть единичный вектор, направленный вдоль г от диполя по
направлению к точке наблюдения, будет опять г°. Потенциал равен тогда г)
pro
.
B7)
Рис. 29. Силовые линии в
меридиональной плоскости, проходящей через ось
диполя р.
—Я-Рвичф- B6)
Поле диполя цилиндрически
симметрично относительно его оси.
Следовательно, в любой меридиональной
плоскости радиальная и поперечная
компоненты напряжённости поля будут:
р df 1 р cos 6
F 1_ ду_ 1 psin 6
Lb ~' г дЬ~ 4те ~W~'
Потенциальную энергию диполя во внешнем поле легче всего определить
из потенциальной энергии двух его точечных зарядов. Пусть заряд ~\-q
расположен в точке а внешнего поля, потенциал которого о (х, у, z),
а заряд —q в точке Ь, удалённой от точки а на расстояние 1.
Потенциальная энергия системы будет тогда:
U=qy(a)—qo(b), B8)
«ли при b -> a
U=qdo = ql grad о = — рЕ = — рЕcos 0, B9)
где 6 — угол между диполем и внешним полем Е.
Силы, действующие на диполь со стороны внешнего поля, равны
отрицательному градиенту от U при фиксированной ориентации:
F = grad (рЕ) 8=const»
C0)
С другой стороны, при изменении ориентации диполя в данной точке,
потенциальная энергия также меняется. Вращающий момент, действующий на
1) В B6) г = Y х*-\-у*-\-z2 и Srad (Ifr) означает дифференцирование в точке
наблюдения. Если диполь расположен в точке (лг, v, z) и потенциал измеряется в точке
(*', у, г'), то мы будем иметь > (*', y'f z') = — — р grad' (—J = + -—■ р grad (—j;
см. уравнение B2), стр. 156.
И Зав. §М, Теория электромагнетизма.
162 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
диполь во внешнем поле, будет:
Т = — 4^=~ pEsmb, C1)
или в векторной форме:
Т=[р,Е]. C2)
ЗЛО. Осевые мультиполи. Вернёмся снова к уравнению A7) для
потенциала линейно распределённого заряда. Это разложение справедливо для
всех точек пространства, расположенных вне сферы, диаметр которой равен
длине заряженного отрезка. Первый член ряда <р0 — это просто потенциал,
который создавался бы точечным зарядом q, расположенным в центре сферы.
Второй член cpj представляет собой потенциал диполя р, расположенного
в том же центре. Мы покажем, что остальные члены оп также могут быть
интерпретированы как потенциалы от особых точек более высокого порядка,
соответствующих зарядам, собранным в центре сферы.
Диполь, момент которого мы обозначим теперь через р№, был
образован отрицательным зарядом —qt помещённым в начале координат, и
положительным зарядом -{- q, помещённым в точке г = /0 на оси z. Затем они
совмещались, так что pW=pl0 оставалось постоянным. Потенциал
полученной в результате особой точки был равен:
ф =- —
I ^ д
p»Ur)- <33>
Особую точку следующего более высокого порядка можно получить, помещая
диполь с отрицательным моментом —р^1} в центре и другой диполь, с
равным положительным моментом -f-pA)» на небольшом расстоянии lt от него.
Мы ограничимся сейчас специальным случаем, когда оси обоих диполей,
равно как и смещение llt направлены вдоль оси г. Потенциал, получающийся
в результате этой конфигурации зарядов, равен:
?J=?l + 'l(iF-) +••■-?!> C4>
или, в силу A2):
'2 4кг
1 т. &
рA''^(тН •■•• <35>
Осевой квадруполъный момент определяется как произведение:
р& =2(рО>/1) = 2D/^). C6)
Математически квадруполь получается при /0-»0, /j->0 и q\-> oo, причём
так, что произведение C6) остаётся конечным и отличным от нуля.
Потенциал подобного рода конфигурации будет тогда точно равен
.«.=,-!_ £^-*.('Г) ' C7)
•2 Аъг 2! dz* \r) V '
во всех точках, кроме г = 0.
По индукции можно построить особые точки заряда или мультиполи
ещё более высокого порядка. В каждом случае мультиполь порядка п — 1
с отрицательным моментом —pin-i) располагается в центре, а равный
положительный мультиполь p(n-D на расстоянии \п от него» В общем случае,
с которьм мы будем иметь дело ниже, смещение произвольно по
направлению. Если же, как в данном частном случае, все эти величины совпадают
ло направлению, то мультиполь называется осевым. Потенциал приближённа
разложение потЕййиАйлйо Сферическим функциям l&ui
163
даётся первым членом разложения Тэйлора^ который, согласно A2), может
быть записан в виде:
ф>
(_l)n p(n-l) ln_t
п
дп
dzH
4те (л —1)!
«-польный момент определяется как предел произведения
C8)
,(п)
«р(и_1L-
C9)
при /п-»0 и /7fo-1) -> со, причём p^-^l^ остаётся конечным.. Потенциал
точечного заряда «-го порядка будет тогда:
со,
/7(И> (— \)п дт
п
4тсе n\ 6zn \r)
(я = 0, 1, ...).
D0)
Pte&z)
Потенциал заряда, произвольно распределённого вдоль отрезка конечной
длинЫу вне сферы, диаметр которой совпадает с этим отрезком,
тождественен с потенциалом системы мульти-
полей, расположенных в центре сферы.
Моменты этих мульгиполей могут быть
определены из распределения зарядов на отрезке
по уравнению B3).
3.11. Произвольные распределения
зарядов. Мы рассмотрим теперь заряды,
распределённые совершенно произвольным
образом в некоторой конечной области
однородного изотропного диэлектрика или на
поверхности проводников, помещённых в такой
диэлектрик. Пусть- область, содержащая
заряды, лежит внутри сферы конечного
радиуса R, проведённой вокруг начала
координатной системы О. Мы хотим выразить потенциал данного распределения
зарядов в точке Р вне сферы через координаты точки Р по отношению к О.
Прямоугольные координаты точки Р будут х, у, г, а её полярные
координаты— г, 6, ty, где
X = г sin 0 cos 4>,
у г= г sin 6 sin &, .г = г cos 6. D1)
Подсчитаем прежде всего потенциал в точке Р от элемента заряда dq=p dv,
расположенного в переменной точке Q(\,%С).Если г2 (рис. 30) е:ть
расстояние от dq до точки Р, то слагаемое от этого элемента будет:
Рис. 30. Иллюстрация к
разделу 3.11.
d* = ±-!l
dq
4 те г2 4те У (л: — kf + (у — v]J + (z ~ СJ
D2)
Знаменатель этого выражения мэжег быть разложэн в окрестности начала
координат по степеням £, ч\, С, точно так же, как и в уравнении A4),
в результате чего получим:
+И*'£G)+*£®+*£®+.
11*
164 ГЛ. Ш. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Этот ряд сходится при условии, что r1 = Yi2-{-fi2-\~^2<CR, r>R. Теперь
мы проинтегрируем D3) по. всему заряду, т. е. по координатам £, ij, £,
причём г = У х2-\-у2-\-z2 ПРИ этом интегрировании остаётся постоянным.
х
Мы рпять запишем <р в виде суммы частичных потенциалов «ри: ? = 2 ?i
«—О
Тогда первый член разложения будет:
1 Р@)
^ = Т^-Г, D4)
где
P{0) = q = $?($,% Qdv D5)
есть полный заряд. На достаточно больших по сравнению с R расстояниях
потенциал произвольного распределения зарядов может быть приближённо
представлен кулоновым потенциалом точечного заряда, расположенного
в центре.
Второй член, который является главным, когда полный заряд равен
нулю, будет:
?.=-4^P(I,grad(y)' <46>
где р(!) — вектор дипольного момента, прямоугольные компоненты которого
равны:
P^=j?^dv, pf = $wdv, pf = $9tdv. D7)
Потенциал произвольного распределения зарядов, алгебраическая сумма
которых равна нулю, может быть на больших расстояниях приближённо
представлен потенциалом диполя, компоненты которого
определяются соотношениями D7).
Подобным же образом частичный потенциал <р2 обусловливается квадру-
полем, компоненты которого будут:
' /S=J>^> Pfy=$rfdv, p% = f9r*dv, }
г г с \ D8)
В то время как дипольный момент — вектор, величины, определённые в D8), .
составляют компоненты тензора второго ранга. Мультипольные моменты
более высоких порядков, определённые из соответствующих членов
разложения D3), являются тензорами более высокого ранга.
3.12. Общая теория мультиполей. Пусть \г будет вектором,
проведённым из начала координат О в точку Q(£, % i); направляющие косинусы
его по отношению к координатным осям х, у, z обозначим соответственно
at, Cy, yf. Пусть потенциал, создаваемый в точке Р (х, у, z) особой точкой
— р^ любого порядка, расположенной в начале координат, будет равен
-л—fAxi У, z)- Если теперь на другом конце вектора \ расположить осо-
4 tee
бую точку того же порядка и такой же величины, но противоположного
знака, то потенциал такой пары мультипольных точек в точке Р будет равен:
Br-{Mx—aili> у—№> *—V<)—/<(*.>. *) Ь D9)
РАЗЛОЖЕНИЕ ПОТЕНЦИАЛА ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ 13.12]
16S
откуда можно видеть, что изменение потенциала в точке (лг, у, z), вывзанное
смещением источника из начала координат в точку Q, координаты которой
равны £ = а^, ?] = C^, С = тА» тождественно с тем изменением, которое
получится при равном и противоположном смещении точки Р в точку
(лг—£, у— ч\, z— (,), при котором источник остаётся неподвижным в начале
координат. Разлагая D9) в ряд Тэйлора, мы получаем:
4- члены более высокого порядка относительно /г. E0)
Выражение в скобках является, очевидно, производной от fi по направлению
вектора 14-.
#<_„ Vt
а
dfi
dfi
1~^~^7+^-дГ-
dz
E1)
dli "* дх ' г* ду
Мультипольный момент i-J-1-го порядка определяется опять-таки через
момент г-го порядка, как предел произведения
р('+1) = (/+1)р»/< (г==0, 1, ...), E2)
при /г->0 и р(Ъ-+со при условии, что их произведение остаётся конечным.
Потенциал в любой точке (х, у, z), вызываемый мультиполем с моментом
/?(*+*), расположенным в начале
координат, булет тогда равен:
?<+i
1 р(*+*> dfi
4 те (*" НЬ1) dli
(/ = 0,1,...). E3)
Одиночный точечный заряд можно
рассматривать как особенность
нулевого порядка с «моментом»
/?(°) = #:
?о = 4ir Р@) (у) ' /о = (}) • E4) Квадруполь.
+
И
Рис. 31Ь.
Октуполь.
Потенциал диполя, ориентированного в произвольном направлении,
определяемом вектором 10, будет, соответственно:
Ф1
4 те
10-).
dt.
ёШ-
E5)
Квадруполь -получается смещением диполя параллел^нэ его оси в
направлении, определяемом вектором 11# Для потенциала квадруполя ti3 E3) и E5)
находим:
I р^ _д*
Фо
£__
4та 2!
JL(Tj
E6)
Таким путём, по индукции, для потенциала произвольного мультиполя
«-го порядка получаем:
дп
?п-
(—1)п р(п) _
4 та п\ ~dlQdli.. .dlt
'п (г)"
E7)
Построение квадруполя и октуполя показано на рисунках 31а и 31Ь.
Результат я-кратного применения оператора
d
«««Т^+Р
d . д
ду
E8).
166 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
1
и функции — = {x2-\-y2-\-z2) 2 должен иметь вид
1 ,.л К,
СЭ™ -
или
г»—ыг«*^, E9)
где Уп — функция косинусов углов ^ между г и п осями 1{ и
направляющих косинусов och $it ti углов меж.пу векторами 1^ и коор/инатными осями.
Но углы |лг- связаны со сферическими координатами 6, 4* точки Р уравнением
cos ^ = (о^- cos 4* -f- p< sin 40 sin 0 -J~ ^ cos 6, F0)
которое можег быть получено подсчётом расстояния QP = г2 (рис. 30)^;
с одной стороны через г^—/г-, r и углы ^, а с другой стороны — через их
проекции на координатные сси. Таким образом Yn является функцией углов
О и 4*, т. е. положения точки на поверхности единичной сферы. Для диполь-
пого члена мы имеем:
= lk ^7* (ao*+. PoV + То*)- F1)
После замены прямоугольных координат сфэричесхими, согласно
уравнению D1), это выражение принимагт вид:
^^^^K^^^+Posin^sine-bToCOse},-: [F2)
?1 = ~^- { («0 cos ^ + po sin 4») Pi (cos 6) + ToP°t (cos 6) }, : F3)
где Рп (cos 6) — присоединённые функции Лежандра, определяемые
соотношением
JAM
PS (cos 6) = sin- 6 ~щгп Pn(cos 6). . F4)
Между четырьмя константами рA\ а0, Ро и То существует одно соотношение,
а именно ао + ро + То=1» и остаётся, следовательно, три произвольных
параметра, которые и определяют'величину и направление диполя.
Поступая подобным же образом и для квадрупольного члена, мы
получаем:
Н- у [(PoTi + PiTo) sin * 4-4 ^o«i + Tiao) cos *] 4 sin;26 +
+ [t (eoPi + aiPo) ^n 24» + \ K«i + Ш cos 2ф] 3 sin* 6.} , F5)
или, пользуясь функциями F4):
%ii = _L^1 {a^rf (cos 6) + (ajcos 4» 4- b21 sin ф) P} (соз 6) +
-|- (a22 cos 2ty + b92 sin 24»)P2 (cos 6) ] . F6)
Между шестью направляющими косинусами существуют два соотношения
вида aJ + p5-J-f5 = l, и, следовательно, вместе с произвольным моментом
pi2) мы имеем пять произвольных констант для определения величины и
Ориентации квадруполя.
ДИЭЛЕКТРИЧЕСКАЯ ПОЛЯРИЗАЦИЯ I3.13J 167
Решения уравнения. Лапласа называются гармоническими функциями.
Поскольку ко'ординаты г, 6, $ произвольны, каждый член оп в разложении
to должен сам по себе удовлетворять уравнению Лапласа и, следовательно,
являться гармонической функцией. Обобщая, мы заключаем, что
гармоническая функция oni представляющая потенциал мультиполя «-го порядка, является
однородным полиномом п-й степени от лс, у, г. После перехода к
сферическим координатам г, 6, ^ функция оп может быть записана в виде E9),
где Гга@, ^) будет теперь определяться соотношением:
та и
Уп Ф, 40 = 2 Упш в 4») = 2 («Wcos Щ + bnms\n Щ) Р? (cos 6). F7)
т -0 т = 0
Гармоническая функция п-го порядка содержит 2/г—j— 1 произвольных
постоянных, достаточных для определения величины момента и направления осей
соответствующего мультиполя. Если заряды распределены произвольным
образом внутри сферы конечного радиуса, то потенциал во всех точках вне
сферы должен быть гармонической функцией и, кроме того, должен быть
регулярным в бесконечности. Этим условиям удовлетворяет выражение:
со
Если распределение зарядов известно, то компоненты мультипольных
моментов вычисляются так, как было показано в разд. 3.11; если распределение
зарядов неизвестно, но задано внешнее поле, то эти константы, как мы
вскоре увидим, получаются из граничных условий.
ДИЭЛЕКТРИЧЕСКАЯ ПОЛЯРИЗАЦИЯ 1
3.13. Интерпретация векторов Р и П. Хотя двух векторов Е и D и
достаточно для полного описания электростатического поля в любой среде,
представляется, однако, удобным ввести третий вектор Р, определённый
в разделе 1.6 как разность этих двух векторов:
P = D — e7£ A)
В свободном пространстве вектор Р исчезает и поэтому он совершенно
определённо связан с состоянием диэлектрика. Уравнение, выражающее
дивергенцию D, переходит в такое:
divE=^-(p — divPJ, B)
откуда' мы заключаем, что влияние диэлектрика на поле может быть
подсчитано путём введения эквивалентного распределения зарядов с объёмной
плотностью:
р' = —divP. C)
В каждой точке внутри диэлектрика потенциал удовлетворяет
видоизменённому уравнению Пуассона:
Д?==_Ьр + р'). D)
Справедливость уравнения D) не зависит более от изотропности и
однородности среды. Если, однако, имеются поверхности разрыва непрерывности
как, например, границы диэлектрика, то вектор D подчинён условию:
n(D2 — Di) = *t . E)
и(Е2-Е1) = 1ш-.1п(Р2-Р1) = 1(ш-г-ш'). F)
168 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Первичными источниками электростатического поля являются «истинные»
заряды, объёмная и поверхностная плотности которых равны соответственно
р и ш. Влияние присутствия твёрдых диэлектрических тел на потенциал
может быть полностью учтено путём введения индуцированных или
«связанных» зарядов, распределённых с объёмной плотностью р', а на каждой из
поверхностей разрыва непрерывности среды с поверхностной плотностью:
c/ = -n(P2 — Pt), G)
где единичный вектор п проведён от среды (/) к среде B). Если (/) —
диэлектрик, а B)— свободное пространство, то индуцированные
поверхностные заряды равны просто oo'snPj, где п — внешняя нормаль. В случае
перехода от диэлектрика B) к проводнику (/), несущему свободные
поверхностные заряды ш, результирующий поверхностный заряд будет ш — пР2,
поскольку вектор Pj в проводнике равен нулю.
Потенциал в любой заданной точке внутри или вне диэлектрика может
быть выражен в виде:
/„> г к 1 Гр —divP , , 1 fw + nCPj —P2) . ,оч
Поверхностный интеграл должен быть распространён по всем поверхностям
разрыва. Едва ли нужно указывать, что анализ этот в большинстве случаев,
является чисто формальным, так как для того, чтобы определить Р, обычно
необходимо вычислить сначала потенциал.
Физический смысл вектора Р становится ясным, если мы преобразуем
(8) с помощью тождества:
^ = div(£)-Pgrad(I). (9)
Диэлектрик можно разбить на отдельные объёмы Vit ограниченные
поверхностями разрыва непрерывности St. Для каждого такого объёма
П Si
Суммируя эти интегралы по всем частичным объёмам Vi и помня, что пг-
направлено из Vit т. е. внутрь соседних объёмов Vn, мы найдём, что (8)
приводится, к виду:
Третий интеграл представляет собой, очевидно, потенциал, обусловленный
непрерывно распределённым дипольным моментом и поэтому Р должно быть
интерпретировано как диполъный момент единицы объёма или
поляризация диэлектрика. Согласно A1), диэлектрическое тело, помещённое в
данное поле внешних источников, создаёт такое индуцированное вторичное
поле, какое давало бы непрерывное распределение диполей с моментом Р
на единицу объёма.
Это практически всё, что можно сказать о векторе поляризации в чиста
макроскопической теории. Макроскопически заряженный проводник ведёт
себя так, как будто заряд распределён по нему с непрерывной плотностью,,
хотя мы и знаем, что фактически заряд состоит из отдельных заряженных
электронов. Точно так же нейтральная материя под действием внешнего-
поля ведёт себя так, как будто диполи распределены с плотностью,
являющейся непрерывной функцией точки. Теперь мы знаем, что нейтральные
атомы и молекулы в действительности состоят из равного числа положи-
РАЗРЫВЫ НЕПРЕРЫВНОСТИ ИНТЕГРАЛОВ [3.14] 169
тельных и отрицательных элементарных зарядов. Микроскопическая
электродинамика должна показать, как можно подсчитать электрические моменты
каждого атома или, по крайней мере, их наиболее вероятные значения. Тогда
соответствующим процессом усреднения по элементам макроскопического
объёма мы сможем определить поляризацию единицы объёма из моментов
отдельных атомов и осуществить переход от микроскопических величин
к макроскопическим.
Нужно сказать теперь несколько слов относительно физического смысла,
вектора Герца П, введённого в более общей связи в разделе 1.11.
Предположим, что плотность свободных зарядов р в диэлектрике равна нулю.
Если потенциал ю выражен через дивергенцию вектора П:
<р= —divll, A2>.
то уравнение Пуассона принимает вид div Г АН —| PJ = 0, и это условие
будет, конечно, удовлетворено, если
ДЦ = — 1р. A3)
Следовательно, вектор П может быть найден через поляризацию путём-
вычисления интеграла
Щ*'.У.Л=5й/£1*г^*'- A4)
Поэтому вектор П называют иногда поляризационным потенциалом.
РАЗРЫВЫ НЕПРЕРЫВНОСТИ ИНТЕГРАЛОВ, ВСТРЕЧАЮЩИХСЯ В ТЕОРИИ
ПОТЕНЦИАЛА
3.14. Объёмное распределение зарядов и дипольного момента.
Согласно предыдущему, проводник представляет собой просто область, где поле
равно нулю, ограниченную поверхностью, на которой расположен слой
зарядов с поверхностной плотностью ш, в то время как твёрдый диэлектрик
может быть представлен либо в виде эквивалентного распределения зарядов
с объёмной плотностью р' = — div P, ограниченного поверхностным слоем
зарядов с плотностью ш', либо как область непрерывного распределения
диполей с моментом Р на единицу объёма. Граничные условия, которые
ранее были выведены из уравнений поля, должны, очевидно, вытекать
непосредственно и из аналитических свойств интегралов, выражающих потенциал
и его производные через объёмные и поверхностные плотности зарядов и
дипольных моментов.
В разделе 3.7 было установлено, что несобственные интегралы
Е (*', /, г') = JL J p (х> у, г) grad (I) dv B)
сходятся и являются непрерывными функциями х', у', z't если плотность
зарядов р — ограниченная и кусочно непрерывная функция, т. е. если объём,
занимаемый зарядами, может быть разбит на конечное число объёмов,
в каждом из которых р конечно и непрерывно. Таким образом, с каждой
стороны поверхности, отмечающей разрывное изменение р, величны <р и Е должны
иметь одни и те же значения, хотя производные от Е в общем случае
разрывны. Рассмотрим, например, заряд, равномерно распределённый по сфере
170 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
радиуса а с плотностью р0. Поле Е в точке внутри сферы проще всего
можно найти, применяя закон Гаусса и учитывая сферическую симметрию задачи:
J En da = — I p dv. На расстоянии г от центра (г<а) мы имеем:
F— l ! Г
(r<a),
C)
где q— полный заряд, содержащийся внутри сферы. Точно так же в любой
внешней точке
р_ 1 Я.
4тсе0 г2
(г>а).
D)
Потенциал вычисляется из интеграла 9 = — I Е dr, который даёт:
со
г
o — — -2—\—dr=-.— ■£- (г>а),
4та0 J Г2 4та0 Г * \ ^ />
со
(S)
На рис. 32 потенциал <о и его первая производная Е нанесены в функции
от г. Заметим, что хотя кривая Е и остаётся непрерывной при переходе
Я
ЧПЕ0
ч .
4J
/ i
1 С=7 Г
Рис. 32. Изменение потенциала и напряжённости поля
при переходе через поверхность рае омерно
заряженной сферы единичного радиуса. "
^ерез поверхность г = а, её наклон, — вторая производная от с?, —
испытывает скачок, потому что условие неп, ерывности для р в этой точке не
выполняется.
Рассмотрим далее объёмное распределение дипольного момента с
плотностью Р. Потенциал в любой внешней точке будет:
^'•^^/Pgrad (!)"*.
Этот интеграл может быть изложен на три интеграла типа
?i
1 CPxf(±)dv==- 1 *Г£а,.
4tie0 J х дх \ г) 4га0 дх J r
F)
G)
Из того, что было только что доказано относительно уравнения A),
следует, что F) сходится как в точках внутри области распределения
диполей, так и вне её и является непрерывной функцией точки,
РАЗРЫВЫ НЕПРЕРЫВНОСТИ^ ИНТЕГРАЛОВ [3.15] 171
t i. -- - ■■— i .i . - .»■ ■■ - ■■-*--"——,..,..— — —... , ■«.".,■..— i.i .1.,^.- 4, '.;.. - —... . ■■ .,,, ,— ,.--■., ,■-,..., ■-
если только Р(х, у, г) ограничено и кусочно непрерывно. Поскольку
диэлектрик эквивалентен области с распределённым дипольным моментом,
постольку мы имеем здесь доказательство непрерывности потенциала при
переходе через поверхность диэлектрика, не прибегающее к закону
сохранения энергии.
При. переходе через поверхность разрыва Р нормальная производная от
F), а следовательно, и нормальная компонента Е испытывают скачок.
Проще всего величину скачка можно найти, заменив объёмное распределение
дипольного момента эквивалентным объёмным и поверхностным
распределением зарядов, определённым в разделе 3.13. Вектор Е меняется
непрерывно при переходе в область с объёмно распределённым зарядом, но мы
сейчас покажем, что при переходе через слой поверхностных зарядов
нормальная компонента испытывает скачок.
3.15. Простой заряженный слой. Пусть заряды распределены по
поверхности 5 с плотностью ш, которую мы будем считать ограниченной и кусочно
непрерывной функцией точки на поверхности 5. Потенциал в любой
точке, не лежащей на поверхности S, равен:
^./.О-^/^М.*, (8)
S
где г проведён, как обычно, от элемента заряда со (х, у, г) к точке
наблюдения. Если точка (х\ у', z') лежит на поверхности S, то интеграл (8)
становится несобственным, и необходимо удостовериться в его конечности
и непрерывности. Проведём вокруг точки (х', у', г') на поверхности 5
окружность радиуса а. Если радиус а достаточно мал, то получающийся
таким образом круглый диск можно считать плоским. В точке (л;', у', г'),
потенциал от поверхностных зарядов, расположенных вне диска, является
ограниченной и непрерывной функцией точки в окрестности точки (л/, у' г').
Обозначим эту часть потенциала через <?2. Остаётся часть 9i от зарядов,
расположенных на самом диске. Поскольку поверхностная плотность со
ограничена, мы можем поступить так же, как и в разделе 3.7. Существует число
11^ Ш
т, такое, что во всех точках диска | со [ < т, —
_ т
<— и, следовательно:
и
1 I 1 I Г «> , ^ т С \ , та /гА
st о
где St означает, что поверхностный интеграл распространяется на
поверхность диска. Полный потенциал в любой точке на поверхности диска будет,
следовательно:
С?=<?1 + ?2> A0)
где и cjjj, и <р2, как было показано, ограничены, а ?2 также и непрерывен.
Но 9Г стремится к нулю вместе с стремлением к нулю площади диска и,
таккак можно сделать потенциал с? сколь угодно мало отличающимся от
непрерывной функции, то он сам, следовательно, является непрерывной функцией. То,
что мы специализировали форму диска, приняв её круглой, не накладывает
каких-либо ограничений на общность доказательства, поскольку окружность
можно считать описанной вокруг диска произвольной формы. Потенциал
-от поверхностно распределённых зарядов является ограниченной и
непрерывной функцией точки во всех точках как вне поверхности^ так и на
ней. Таким образом, функция, определённая уравнением (8), при переходе
через заряженную поверхность остаётся непрерывной.
172 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Интеграл, выражающий напряжённость поля:
Е (*', У, z') = — J со (х, j, z) grad G) da,
(И)
является непрерывной функцией с непрерывными производными всех порядков
во всех точках, не лежащих на заряженной поверхности, и испытывает
скачок при переходе точки (л;', у\ г') через поверхность S. Природа
разрыва может быть определена непосредственно из (III), но мы ограничимся
здесь лишь простым приёмом, использованным нами в разделе 1.13 и
основанным на свойстве дивергенции и ротора Е. Скачок
вектора Е при переходе через слой 5 определяете»
соотношением:
Е+ — E_=f-om, A2)
где п — единичный вектор нормали, проведённый
наружу от положительной стороны поверхности. Если
под ш мы будем понимать сумму истинных и
связанных зарядов ш — n(Pj_—Р_), то A2)
эквивалентно:
(е0Е+ + Р+) п — (е0Е_ + Р_) п =
= (D+ — D_)n =
со. A3)
Рис. 33. Элемент
площади da, на которой
опирается положительный
телесный угол с вершиной Это соотношение определяет в то же время и ска-
в точке P-L и отрицатель- ЧОк Е при переходе через поверхность разрыва
ный телесный угол с вер- в расПредеЛении диполей.
шиной в точке Р2. v *Г.М „ „ „ „
3.16. Двойной заряженный слои. Часто
случается, что потенциал данного распределения заря-
'дов совпадает с потенциалом, который мог бы создать слой .диполей,
распределённых по поверхности. Мы представляем себе такое поверхностно.е
распределение дилолей в виде положительного заряда, распределённого
с плотностью-]-» по положительной стороне регулярной поверхности 6",
и тождественного с ним распределения, зарядов противоположного знака по
отрицательной стороне этой поверхности. В результате получается двойной
слой зарядов, разделённых бесконечно малым расстоянием 1. Дипольный
момент единицы площади, или поверхностная плотность х,% есть вектор,
направленный по положительной нормали 5 и равный пределу: ».
т = пНт (со/) при /
О, со
оо.
(Н)
Дипольный момент, соответствующий элементу площади da двойного слоя,
будет х da, а потенциал этого элемента в точке (л/, у', z'), не лежащей
на поверхности S, равен:
, 1т cos 6 . 1 . /1\.
A5)
cos 6
Но —^ ^а как раз равно телесному углу dQ, под которым элемент da виден
из точки наблюдения (л;', у\ z'). Этот угол положителен, если
радиус-вектор, проведённый из точки (л;', у\ Zr) к элементу da, образует с
положительной нормалью п острый угол. .Таким образом, на рис. 33 элемент da
виден из точки Pt под положительным углом, а из точки Р2 — под отри»
х) Смотри Kellogg, loc. cit; Phillips, loc. cit., гл. VI.
РАЗРЫВЫ НЕПРЕРЫВНОСТИ ИНТЕГРАЛОВ [3.16] 173
нательным. Потенциал отвсех зарядов, распределённых по поверхности,
может быть записан в виде:
9 W. У. *0 -ss-J ч (*, У. *) grad(i) da = --АJ t Д», A6)
где 2 — телесный угол, под которым видна поверхность 5 из точки
(х\ У, z'). To, что второй интеграл должен иметь отрицательный знак,
ясно из того, что dQ положительно, если слой виден с отрицательной
стороны, где потенциал отрицателен.
Потенциал ю имеет различные значения на противоположных сторонах
двойного слоя. Предположим сначала, что поверхность 5 замкнута, и что
заряды распределены с постоянной плотностью, так что х может быть
вынесено за знак интеграла. Положительный заряд расположен на наружной
стороне S, так что х имеет то же направление, что и положительная
нормаль. Существует известная теорема о телесном угле, которую можно
применить к нашему случаю. Она гласит: «если 5 является замкнутой
поверхностью в трёхмерной области, то полный телесный угол, под которым
поверхность 5 видна из точки Р, равен нулю, если точка Р расположена
вне области, ограниченной этой поверхностью, и равен 4т:, если точка Р
лежит внутри этой области» *). Потенциал в любой точке внутри 5 будет
поэтому равен ©_ = х, а в любой точке вне 5 потенциал о+ = 0. Скачок
потенциала при переходе с одной стороны двойного слоя, на другую равен,
таким образом,
Ео
Убедимся теперь в том, что A7) определяет скачок о при переходе через
двойной слой и в том случае, когда поверхность 5 не замкнута.
Действительно, поверхность 5 может быть сделана замкнутой прибавлением
произвольной поверхности Sr. В любой точке вне и внутри этой замкнутой
поверхности потенциал может быть разложен на две части — долю <р от
зарядов, расположенных на S, и долю с/ от зарядов на S'. Внутри
замкнутой поверхности результирующий потенциал опять-таки равен х, а вне её—
Ео
нулю. Таким образом, при переходе через поверхность 5 потенциал ©-f-cp'
меняется скачком на величину—х; но о' от слоя 5', очевидно, непрерывен
при переходе через 5 и, следовательно, весь скачок обусловлен скачком <р,
как это и выражено уравнением A7).
Остаётся показать, что A7) справедливо и тогда, когда х является
функцией точки на поверхности S. Проведём около произвольной точки Р
на поверхности 5 окружность радиуса а. Пусть а будет настолько мало,
что на площади круга радиуса а можно считать х постоянным, равным х0.
Потенциал о в окрестности точки Р снова может быть разложен на две
части — долю ©' от бесконечно малого диска и дрлю о" от дипольного слоя,
лежащего вне окружности. <р" непрерывно в точке Р. С другой стороны, ©'
испытывает при переходе через диск скачок, равный — х0. Полный
потенциал © = ©'-р ср" Должен, следовательно, иметь скачок той же величины,
и при переходе к пределу при а-+0 мы получаем, что A7) сохраняет
*) Об аналитических свойствах телесных углов смотри у Phillips, loc. cit.
стр. 112.
174
ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
силу и для переменного распределения, если для х мы будем брать его
значение в точке перехода через поверхность S.
Эти результаты означают ещё и то, что работа, необходимая для
перемещения единичного положительного заряда по замкнутому пути,
пересекающему один раз поверхность, по которой распределены диполи с
постоянной плотностью т0, равна :±: — т0, где знак зависит от направления движе-
ния. При наличии подобного двойного слоя потенциал оказывается
многозначной функцией; к значению потенциала в точке (л^, у\ г') можно
прибавить — mi, где т — любое положительное 1и л и отрицательное целое
число. Для того чтобы получить различные значения о, достаточно вернуться
в исходную точку после пересечения поверхности S. Всё это представляется
противоречащим консервативному характеру электростатического поля.
В действительности, математический двойной слой является особой
поверхностью, точного подобия которой в природе не существует. Мы покажем
4 ниже с помощью теоремы Грина, что потенциал внутри замкнутой области,
ограниченной поверхностью 5 от зарядов, расположенных вне этой
поверхности, точно такой же, какой мог бы быть создан некоторым распределением
диполей на поверхности 5. Этот эквивалентный дипольный слой не даёт,
однако, правильного значения © вне поверхности 5.
Применение интеграла ф En da= — q к небольшому прямому цилиндру,
основания которого расположены на разных сторонах двойного слоя, по
способу, использованному в разделе 1.13, тотчас же обнаруживает отсутствие
разрыва у нормальной компоненты вектора
поля Е при переходе через слой, так как
полный заряд в цилиндре равен нулю:
(Е+ — Е-)п = 0. A8)
Рис. 34. Скачок тангенциальной ком- 0днак0 линейный интеграл Е по замк-
поненты вектора Е при переходе че- нутому пути не обязательно равен ну-
рез двойной слой. лю; соответственно, мы можем предви-»
деть наличие " скачка у тангенциальной
составляющей. Пусть обход контура начинается в точке /, рис. 3*4,
где дипольная плотность равна х. Скачок потенциала между точсами I
и 2, согласно A7), равен ©i—ва = —.-с. (Следует обратить внимание на
£о
то, что напряжённость поля Е определяется производной потенциала, а не
разностью потенциалов по обе стороны от поверхности разрыва.
Нормальная же производная непрерывна.) Если Al — длина пути вдоль поверхности,
то плотность диполей в 3 будет T-j-gradx Д1, и разность потенциалов
между точками 4 и 3 равна:
Но величина (©2 — cpi) -f (©3—©2) -|- (©4 _ <р3) _|_ (^ _ <р4) тождественно равна
нулю, и, следовательно:
—-•= + (% — <?2)"f -^Cc + gradxAljlf (?1 —e4) = 0. A9)
Вводя сокращённые обозначения ©4 — ©1== д© <р3 — ©aS=sA©_, получаем
A9) в виде:
Д<Р+ Дср_ 1
frt*;' РАЗРЫВЫ НЕПРЕРЫВНОСТИ ИНТЕГРАЛОВ Р.17] 17&
^*:^< , : —, ^ .
п:*': где t—единичный вектор, касательный к поверхности 5. Предел — До/ДГ
при Д/ -* 0 равен компоненте Е в направлении t, так что, в силу
непрерывности нормальной компоненты Е, скачок вектора поля определяется
соотношением:
Е+ —Е-=—-gradx. B1)-
Понятно, что glad x обозначает здесь градиент х на поверхности, и является
поэтому вектором, касательным к 5. Доказательство проводится в
предположении, что х и первые производные от х на поверхности 5 непрерывны.
3.17. Интерпретация теоремы Грина*, В разделе 3.4 было показано,
что потенциал в любой внутренней точке области V, ограниченной
замкнутой регулярной поверхностью S, может быть представлен в виде:
v s s
На основании предыдущего параграфа мы приходим к следующему
истолкованию этого результата. Объёмней интеграл предствляет собой, разумеется,,
потенциал от зарядов, находящихся внутри поверхности S, а поверхностные
интегралы учитывают все заряды вне её. Однако первый из
поверхностных интегралов эквивалентен также потенциалу простого слоя зарядов,,
распределённых по поверхности 5 с плотностью
•=•&. ад-
а второй может быть, очевидно, истолкован, как потенциал двойного слоя
на поверхности 5 с плотностью
т = еср. B4),
Заряды, лежащие вне поверхности S, могут быть заменены
эквивалентными простым и двойным слоями, плотность которых определяется по*
B3) и B4), без какого-либо изменения потенциала во внутренних точках.
Однако вне поверхности 5 потенциал от этих слоев ни в какой степени не
соответствует потенциалу от истинного распределения зарядов. Очень важно
отметить, в противоположность этому, что эти эквивалентные поверхностные
i слои, которые дают правильные значения потенциала во всех внутренних
точках 5, как раз такие, какие необходимы для того, чтобы свести,
к нулю как потенциал, так и поле Е во всех внешних точках. Прежде-
всего мы видим, что простой слой вызывает скачок нормальной производной-
'о,- равный
©--(©♦-Т-- <25>'
Нормальная производная в уравнении B3) должна быть подсчитана на
внутренней, отрицательной стороне поверхности 5', поскольку только она одна;
принадлежит к рассматриваемой области V. Заменяя (cb/d«)_ её значением
из B3), мы получаем, что (дср/д«)+ = 0. Далее, скачок потенциала,
вызываемый двойным слоем, определяется соотношением A7), которое вместе с B4)
и показывает, что и о+ = 0. То, что © и его производные исчезают всюду вне
Ы поверхности S, легко показать, применяя B2) к области 1/2, внешней по
|; отношению к поверхности 5. Поскольку в V2 зарялов. теперь нет, то Д© = 0.
Ijh В бесконечности потенциал регуляре н и, следовательно, потенциал в области
g?;; V% определяется только значениями ©+ и (^©/дл)+ на поверхности .S. Но*
последние, как только что было показано, равны нулю. Функция © (л:', у', 2?),,,
176 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
определяемая уравнением B2), непрерывна и имеет непрерывные
производные. Следовательно, напряжённость поля Е вне поверхности 5 также
равна нулю.
Из предыдущего рассмотрения ясно, что всегда можно любую часть
электростатического поля окружить некоторой поверхностью, обратив
снаружи поле и потенциал в нуль и учитывая влияние внешних зарядов на
поле внутри поверхности посредством соответствующих распределений на
ней простого и двойного слоев. Поучительно рассмотреть эти результаты
с точки зрения напряжённости поля Е. Простой слой даёт необходимый
скачок нормальной компоненты Еп* оставляя неизменным поведение
тангенциальной составляющей. С другой стороны, двойной- слой никак не влияет
на поведение нормальной компоненты, но может быть подобран так, чтобы
обеспечить необходимую величину скачка
для Et или, согласно B1):
fXry'zr
Р 1 flfx
'*+
О, B6)
b-ci-cJ
Рис.#35. Применение теоремы
Грина к методу изображений.
где /—какое-либо направление, касательное
к поверхности 5. Если, в частности,
поверхность 5 является эквипотенциальной, то
[п, Е] = 0, и надобность в дипольном
распределении отпадает; поле внутри
поверхности 5 от зарядов, расположенных вне её,
может тогда рассматриваться. как поле про-
стого слоя с плотностью зарядов <о=е .,—,
расположенного на эквипотенциальной
поверхности.
3.18. Метод изображений. Эти
принципы находят себе важное применение в
методе изображений. Эквипотенциальные
поверхности пары равных точечных зарядов,
одного положительного и * другого
отрицательного, в однородном диэлектрике с
диэлектрической проницаемостью & образуют,
семейство замкнутых поверхностей вращения вокруг прямой, соединяющей эти
заряды. Пусть 5 представляет собой какую-либо эквипотенциальную
поверхность, окружающую заряд—q (рис. 35). Эта поверхность разделяет, таким
образом, всё пространство на две области и, ввиду регулярности потенциала на
бесконечности, теорема Грина применима к ним обеим, причём поверхность
5 будет ограниченной в каждом случае, т. е. каждая из областей может быть
сочтена за «внутреннюю» по отношению к S- Если, следовательно, заряд—q
удалить, то поле в области, где находится заряд -j- q, останется неизменным,
если по поверхности 5 распределить заряд с плотностью со, определяемой
соотношением B3). Обратно, если заряд -\-q расположен по отношению
к проводящей сфере как показано на рисунке, то на поверхности 5
индуцируются такие поверхностные заряды ш, что она сделается эквипотенциальной.
Изменение, которое этот индуцированный заряд вносит в поле .вне
проводника S, проще всего определить теперь, заменив поверхностное
распределение эквивалентным точечным зарядом — q. Говорят, что заряд — q является
изображением заряда Ц-q по отношению к данной поверхности. В случае,
«ели эквипотенциальной поверхностью является плоскость х' =0, проходящая
посередине между зарядами, расчёт особенно прост. Потенциал в какой-либо
КРАЕВЫЕг ЗАДАЧИ P.19J,. 177
точке (л;', у', z') справа от х' = 0 будет:
о (*', У, г') = /- { —г L — - l \. B7)
Нормальная производная при хг = 0 должна быть взята в направлении
отрицательной оси хг, так как область справа от х' = 0 должна
рассматриваться как внутренняя по отношению к этой эквипотенциальной поверхности:
(- *) —4 в"' ■ B8)
\ дх' )х'=й 2кг 3. \ /
отсюда, согласно B3), поверхностная плотность заряда будет:
— ~5ГЗ- ' B9>
где r2 = a2-j-/2 + *'2 О-
КРАЕВЫЕ ЗАДАЧИ
3.19. Формулировка электростатических задач. Анализ, проведённый
в предыдущих разделах, позволяет вычислить потенциал в любой точке
электрического поля, если распределение зарядов и поляризации полностью
заданы. На практике, однако, задача редко бывает столь проста. Обычно
заданы лишь определённые внешние источники, или приложенное внешнее
поле, а поляризация диэлектриков и распределение поверхностных зарядов
на проводниках должны быть определены из них так, чтобы удовлетворять
граничным условиям на поверхностях разрыва.
Среди электростатических задач этого типа можно различать два класса:
однородные краевые задачи и неоднородные задачи. Для иллюстрации первого
класса задач рассмотрим уединённый проводник, помещённый в диэлектрик.
Проводнику сообщён некоторый заряд, и мы хотим знать, как он
распределится по поверхности проводника, и каков будет потенциал проводника по
отношению к земле или бесконечности. Во всех точках вне проводника
потенциал должен удовлетворять уравнению Лапласа. В бесконечности он
должен исчезать (регулярность), а на поверхности проводника должен
принимать постоянное значение. Мы покажем, что эти условия достаточны для
однозначного определения <о. Плотность поверхностных зарядов может быть
тогда определена из нормальной производной от <р» с тем условием, что
I <о da по всей поверхности проводника должен равняться его полному
заряду.
Неоднородная задача имеет место в случае диэлектрика или проводящего
тела, внесённых в заданное поле внешних источников. Заряд,
индуцированный при этом на поверхности проводника, должен сам собою
распределиться так, чтобы результирующий потенциал был постоянен на этой
поверхности. Интеграл \<ada райен теперь нулю. Равным образом в диэлектрике
возникнет индуцированная поляризация, поле которой сложится с первичным
полем и даст в результате поле,, удовлетворяющее граничным условиям.
Выпишем условия, которые должны удовлетворяться в любой краевой
задаче. Чтобы упростить дело, мы предположим далее, что диэлектрик
*) По поводу метода электрических изображений см. J e a n s, Mathematical Theory
of Electricity and Magnetism, 5-е изд., гл. VIII, Cambridge University Press; или
'Mas ой and Weaver, The Electromagnetic Field, стр. 109 и дал., University of Chicago
Press, 1929.
}2 3as. 598. Теория елеетромагнетиама,
178
ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
является изотропным и однородным, за исключением конечного числа
поверхностей разрыва.
A) Дер == 0 во всех точках, не лежащих на граничной поверхности
и не занятых внешними источниками.
B) Потенциал ср непрерывен всюду, включая границы диэлектриков
и проводников, кроме поверхностей с двойными слоями.
C) Потенциал со конечен всюду, за исключением точек
местонахождения точечных зарядов^ введённых в задачу в качестве первичных
внешних источников.
^ пдя) —е* (dn) ~ ® пРи пеРех°де через поверхность, разделяющую
ёва диэлектрика.
E) е -р = — ш на границе между проводником и диэлектриком.
F) На поверхности проводника либо
(а) <р равен заданной постоянной ю4-, либо же
(б) <р равен неизвестной постоянной, но
J
s
*таа===-ъ-
G) Потенциал о регулярен на бесконечности, при условии, что все
источники поля находятся на конечном расстоянии от начала отсчёта.
В D) предполагается, что на поверхности между диэлектриками зарядов
нет; это и бывает в большинстве случаев. Нормаль направлена из среды 1
в среду 2, а в случае E) — от проводника в диэлектрик.
Задача электростатики состоит в том, чтобы среди всех возможных
решений уравнения Лапласа найти такое частное решение, которое удовле-
творяет перечисленным выше условиям на поверхностях заданных проводников
и диэлектриков.
3.20. Однозначность решения. Пусть © будет гармонической функцией
(т. е. решением уравнения Лапласа), имеющей непрерывные первую и вторую
производные в области V и на ограничивающей её поверхности 5. Согласно
первому тождеству Грина [уравнение E), стр. 153], <р удовлетворяет
соотношению:
J(grad9J^==j\p^. A)
V S
Предположим теперь, что на поверхности 5 потенциал со = 0. Тогда
I (grad oJdv = 0. Но подинтегральное выражение — величина существенно
F
положительная и, следовательно, grad со должно равняться нулю во всей
области V.
Пусть теперь epi и о2 будут две функции, гармонические в замкнутой!
•бласти V, ц пусть
9 = ?! — <р2. B)
Тогда, если <ог и ср2 на граничной поверхности 5 равны, то их разность
тождественно равна нулю во всей области V. Гармоническая функция,
Фбладающая непрерывными производными первого и второго порядка &
замкнутой регулярной области V, однозначно определяется своими
значениями на границе S этой области.
Рассмотрим теперь систему проводников^ помещённых в однородный
.диэлектрик; потенциалы проводников заданы. Покажем, что в> этом случае
КРАЕВЫЕ ЗАДАЧИ [3.21]
179
потенциал в любой точке пространства определён однозначно.
Соображения, высказанные в предыдущем параграфе, могут быть применены теперь
к области V, которая ограничена с внутренней стороны поверхностями
проводников, а с внешней стороны — сферой очень большого радиуса R.
Предположим, что имеются два решения cpj и ©2, удовлетворяющие
заданным граничным условиям. Тогда на поверхностях проводников ср = <рг — о2 — 0.
Поскольку предположено, что ?i и ср2 являются решениями задачи, обе эти
функции должны удовлетворять условиям раздела 3.19; следовательно,
разность этих двух функций является гармонической функцией, значение
которой на поверхности проводников равно нулю, а поведение на бесконечности
регулярно. Поверхностный интеграл в правой части A) должед быть
распространён как по внутренней, так и по внешней границе области.
На внутренней границе «э = 0, и интеграл исчезает. На внешней сфере
л0 Ди „ л 1 dtp ■
^i = -r— . По мере увеличения R потенциал с? стремится к нулю как "р * *щ
1 дф - 1
как -^2 • Подинтегральное выражение ср *J убывает, следовательно, как « ,
в то время как площадь растёт только как #2. Поэтому в пределе при
/?->оо поверхностный интеграл по внешней границе равен нулю. Отсюда
следует, что объёмный интеграл в A), взятый по всему пространству вне
проводников, равен нулю, и мы заключаем, как и выше, что если две функ-*
ции cpt и ср2 совпадают на границах, то они совпадают всюду, т. е.
существует только одна потенциальная функция, которая принимает за данные-
значения на поверхностях данной системы проводников.
Если ^ на замкнутой граничной поверхности 5 равно нулю, то правая^
часть уравнения A) также равна нулю. Отсюда опять-таки следует, что*
gradcp^O во всей области V и, значит, потенциал <р всюду постоянен,.
хотя и не обязательно равен нулю, так как условие -Л = 0 не означает,
что ср на поверхности 5 обращается в нуль. Отсюда, аналогично
предыдущему, можно заключить, что если нормальные производные -^ и -Д-двух
решений совпадают на границах, то сами решения могут отличаться только
на константу. Иными словами, значение нормальной производной на
границах области определяет потенциал однозначно с точностью до
аддитивной постоянной. Но нормальная производная в свою очередь
пропорциональна поверхностной плотности заряда и, следовательно, данной системе
зарядов на проводниках соответствует только одно решение.
При наличии в электрическом поле диэлектриков, требование
непрерывности первых производных со и самого потенциала со уже более не
выполняется, и мы не можем применить соотношение A) непосредственно.
Однако область вне проводников может быть разбита на частичные объёмы Vt,
ограниченные поверхностями Sit внутри которых диэлектрики однородны.
Тогда соотношение A) приложимо к каждому из этих объёмов в отдельности.
При переходе через какую-либо из поверхностей St потенциал непрерывен,
а его нормальные производные с одной стороны St определяются через
нормальные производные на другой стороне. Легко видеть, что также
и в этом, более общем случае, задача электростатики полностью
определена, если заданы значения зарядов или потенциалов на проводниках
системы.
3.21. Решение уравнения Лапласа. Очевидно, основной вопрос при
решении задач электростатики заключается в отыскании решения уравнения
Лапласа в такой форме, которая позволила бы удовлетворить граничным
условиям путём соответствующего подбора произвольных постоянных. Иногда с этой
им
180 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
целью могут быть применены некоторые специальные приёмы, как например
метод электрических изображений. Но если не считать теории интегральных
уравнений, то имеется лишь один приём, являющийся как общим, так и
практически пригодным,—это метод, известный под названием «разделения
переменных». Предположим, что уравнение поверхности 5, ограничивающей
проводящее или диэлектрическое тело, есть:
Мх,у,г) = С. C)
Введём теперь, как в разделе 1.14, систему ортогональных криволинейных
координат и1, к2, к3, такую, чтобы одна из координатных поверхностей,
например и1 = С, совпадала бы с заданной границей C). Если в этой
координатной системе мы сможем найти гармоническую функцию ^(и1, «2, к3),
то, очевидно, нормальная производная в любой точке границы будет
пропорциональна производной от © по координате и1, а производные по и2
и к3 будут тангенциальными.
Согласно (82), стр. 54, уравнение Лапласа в криволинейных
координатах есть:
з _
У д ( Yg ду\
0, Vg=hxhh- D)
Предголожим, что метрические множители ht удовлетворяют условию
^ = М,Д(Ц1)/2(Ц2)/з("в)> E)
где каждая из функций /*(м*) зависит только от переменной и*, а
множитель М$ не содержит и\ но может зависеть от двух других координат.
Мы предположим далее, что ?* также может быть выражена в виде
произведения трёх функций, каждая из которых зависит только от одной из
переменных:
? = F1(«i)/72(«2)^()- F)
Тогда D) можно записать в виде:
Если, наконец, Mt является рациональной функцией, то уравнение G)
может быть разложено на три обыкновенных дифференциальных уравнения.
.Лучше всего продемонстрировать этот метод на примерах.
1. Цилиндрические координаты. Согласно 1, стр. 56, имеем:
л Г- Yl __r T^ — l j£k—r (X)
откуда
fi=*r, /2=/3=1, /^ = ^3=1, M2 = -i. " (9)
.Ургвн-ение G) напишется в виде:
Первые два члена A0) не содержат zt последний член не зависит от г и <р.
Изменение z не должно влиять на первые два члена и, следовательно, по-
КРАЕВЫЕ ЗАДАЧИ [3.211
181
следний член должен быть равен постоянной, чтобы A0) удовлетворялось
тождественно для любого значения г:
1№ -Cv A1)
F3dz*
Произвольная постоянная С, называемая постоянной разделения, взята
с отрицательным знаком исключительно из удобства, а частные производные
заменены на полные, потому что Fs зависит только от г.
Заменяя третий член в A0) на —Сх и умножая на г2, мы получаем:
L д (г dFA-u l d*F* -r*c <^9\
р:тЛг -л7;-г>:-Ж2—r Ч- С12)
г д (
ТхТгК
drj ' f2 аез
Очевидно, что второй член в A2) равен константе; откуда получаем два
обыкновенных дифференциальных уравнения:
^4-сл-о, A3)
Уравнения для F2 и Fs удовлетворяются экспоненциальными функциями
действительного или мнимого аргумента, в зависимости от знака,
приписываемого постоянным разделения; Ft есть функция Бесселя. В том довольно *
обычном случае, когда потенциал о не зависит от гу константа Сх равна нулю,
и вместо A4) мы получаем:
'i('$)-<V A5)
2. Сферические координаты. Согласно 2, стр. 56 мы имеем:
y7=/^in6, 12=/*sinef J-[f = sine, ^jf=-~, (К)
h\ Щ hs sin 6
откуда
/, = * /2 == sin 6, /3=1,
M1 = lt Afe = ^, Ms= r2s.n26 . A7)
Уравнение G) принимает вид:
Id/ 2dF;A , 1 д f . fl dF2\ ■ 1 а2/гз _ n /1Яч
/V*drX~dF)~T i*sin6F2 d6^sin ° 06/"Г ^sin26F3 d^ ~~ ' ^*'
где в данном случае азимутальный угол обозначен через ty вместо обычного <р.
Разделение переменных приводит к трём обыкновенным дифференциальным;
уравнениям:
rf*F3
3-т-С2Г3=0. A9c)
Из трёх этих уравнений несколько сложно только уравнение Лежандра A9b).
3> Эллиптические координаты. Согласно 3, стр. 57, мы имеем:
Vg YP^T Yg_ /1^? VI^ с«F»—ч»)- . B0)
182 ГЛ. Ш. ЭЛЕКТРОСТАТИЧЕСКОЕ ffOjffi
—" —-■■■-— -- ,■ _,.*.,... „,... — —«■ -*■— ■■— —. ■ — „ .^—»,,»„>■■ -ииГи ГШАИЛ^ши... ,.,.i. ' .„i,*-
что даёт:
*i~n=?- m»~jt=t' ^-^-^7-V)- ' B1)
Уравнение Лапласа для эллиптического цилиндра будет:
+ ^^^=0. B2)
/=8 ^
откуда, после разделения переменных, получаем
1 «i'fis
Fi-Ш —С" B3а>
^^UVW^^-^C^C^ C81»
Fj и F2 являются функциями Мать'ё, но существенно упрощаются при
Cj = 0, что имеет место в том случае, когда потенциал <р вдоль оси цилиндра
постоянен.
4. Сфероидальные координаты. Согласно б, стр. 59, мы имеем:
/, = £■—1, /2=1-^2, /з = 1, )
ж_ с м £_ с<Р-ч») > B5)
Уравнение Лапласа имеет вид:
1 д \т udFx\ 1 a J dF2\ P-tf ^LQ0 Г26\
Л Ж F ~1} -аё} + ъ Ц \A ~ *> щ) + 7ё=щ=^ Ж ° B6)
и разделяется на три обыкновенных уравнения:
k^w=-c» <27а>
кж¥-1)д-ш\-^~с*' B7Ь)
вд^-^^т-т^?—с«- B7с)
Уравнения B7Ь) и B7с), очевидно, одинаковы, и удовлетворяются
присоединёнными функциями Лежандра.
Критерии разделимости уравнения Лапласа, сформулированные нами
на стр. 180, не являются наиболее общими из известных, но они
охватывают все обычно используемые координатные системы. Более общие
системы координатных поверхностей, допускающих разделение переменных,
примером которых могут служить тороидальные поверхности, образуемые
вращением системы биполярных координат, были исследованы Бохером1).
!) B6cher, Ueberdie Reihenentwickelungen derPotentialtheorie,Dissertation, 1894.
ЗАДАЧА О ШАРЙ [3.22J
183
Обсуждение свойств различных функций, удовлетворяющих
приведённым выше уравнениям, и методов определения произвольных постоянных
увело бы нас слишком далеко в сторону. В дальнейшем на протяжении
этой книги мы будем постоянно встречаться со случаями использования
функций Бесселя и Лежандра. Мы отсылаем читателя к классическим
работам Гобсона *) и Ватсона2), а также Уиттекера и Ватсона3). Подробный
разбор применения методов решения краевых задач к вопросам
электростатики можно найти у Джинса4) и у Смита6).
~~"~~-~-^.
52v
НЛ
Гг
^
S
,'Г
*№)
ЗАДАЧА О ШАРЕ
3.22. Проводящий шар в поле точечного заряда. Рассмотрим
проводящий шар радиуса rlt центр которого совмещён с началом координатной
системы. Шар помещён в однородный
изотропный диэлектрик с диэлектрическЬй
проницаемостью е2. В точке z = С > гх оси z
расположен точечный заряд q (рис. 36). Мы хотим
«айти потенциал и распределение зарядов на
шаре.
Пусть <j>o будет потенциал от источника q,
а »! — потенциал от индуцированных зарядов,
распределённых на шаре. Результирующий
потенциал чв любой точке вне шара будет
ip = (p0-|-cp1. Индуцированный потенциал cpt
должен быть однозначным, — условие,
которое выполняется только в том случае, если
постоянная разделения С2 (уравнение A9с),
стр. 181) является квадратом целого числа:
С2 = /я2, т == О, :±: 1, z*z 2,... Точно так
же, единственное решение уравнения A9Ь), которое конечно и однозначно
на всей сфере, является присоединённой функцией Лежандра P™(cos6),
что ограничивает Сг значениями Сх =.п(п-\-1), « = 0, 1,2... При этих
условиях уравнению A9а) удовлетворяют как rnt так и г"". Условие
однозначности потенциала будет удовлетворено функцией:
Рис. 36. Шар в поле
точечного заряда, расположенного
в точке г = С.
со п
?1=2 2 {аппГп + *£-)& (cos 6) **»+
A)
я = 0 т=й
где апт, Ьпт — произвольные константы. Но потенциал ot должен быть
регулярен и на бесконечности, что заставляет нас положить апт = 0. Кроме
того, первичный потенциал <р0 симметричен относительно оси z, и поэтому
в данном случае т = 0. Таким образом, потенциал индуцированных зарядов
выражается рядом:
00
?i = S^Tr^(cos6). B)
я=0
!) Hob son, Spherical and Ellipsoidal Harmonics, Cambridge University Press,
1931.
8) Watson, Treatise on the Theory of Bessel Functions, Cambridge University
Press, 1922.
3) W h i 11 a k e r and W a t s о n, Modern Analysis, Cambridge University Press,
1927; E. Т. Уиттекер и Г. И. Вате он, Курс современного анализа, Л. — М., ГТТИ,
1933.
4) J e a n s, loc. cit.
Б) S my the, Static and Dynamic Electrisity, Mc Graw-Hill, 1939.
184
ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Разложение первичного потенциала <c>q в сферических координатах было*
приведено в разделе 3.8. При г<С:
и результирующий потенциал на поверхности г —/убудет следовательно:
со
<? е.. •>=2 {з4 ШТ.+4s}р» (cos е>=*• <*>
Но ©в постоянен, а так. как D) должно быть справедлиро на шаре для всех
значений 6, то коэффициенты при Pw(cos6). должны^ ;бьп?ь равны нулю для
всех /г, ббльших нуля, коэффициенты Ьп определятся,, следовательно, из
системы соотношений:
В любой точке вне шара
со 2и-4-1
Чтобы определить плотность зарядов, мы вычисляем нормальную
производную на поверхности шара:
00 jrt—1
откуда плотность индуцированных, зарядов будет:
со л_1
«в=0
Полный заряд на поверхности шара равен:
it 2it .
<7t = § far] sin bdbd^ (9)
о о
Хорошо известным Свойством функций Лежандра является их
ортогональность: ' !
J Pn (cos 8) Pm (cos 0) sin 6 db = 0, rv ф т. A0)
о
Мы можем взять т = 0, P0(cos6)—1, и получим, что интеграл от Pn(cos0)
от 0 до it при п > О равен нулю. Следовательно:
откуда для потенциала шара получаем:
ср =>,U4-_Ll ■- A2)
™ 4та2 Г! T4iE5 С- ., v 7
где ^— избыточный заряд, который был предварительно сообщён
изолированному шару. Если Шар заземлён, то <рв можно положить равным нулю.
■ £ШШ- '$"« ШАрв$Щ ■-'■ \Ш
Интересно заметить, что потенциал ©j of' икдуцировйнных на шар&
зарядов в любой точке вне шара такой же, как и от заряда 4тсе2 #0 = qlit
диполя с моментом 4т:г2^1 = — q-„ и т. д., расположенных в начале
координат и ориентированных вдоль оси z (раздел 3.8); Имеется, однако, и другая
простая интерпретация. Точку г = С (рис. 36), где (&'=*==/*], называют
взаимной с точкой z по отношению к поверхности шара. Величина, обратная
расстоянию от этой взаимной точки до точки наблюдения, согласно
уравнению (8), стр. 159, будет: >
со • со 2п
2 п=0 п—0
Следовательно, полный потенциал F) может быть записан в виде:
2 ■ ч
Вне шара потенциал <р равен потенциалу заряда qt расположенного в точке г = С».
плюс потенциал его изображения q'== — q j~ * расположённого во взаимной-
точке z = С', плюс потенциал заряда qt (который равен нулю, если шар не заря-*
жен), расположенного в центре, и потенциалу заряда q-1- в центре шара,
благодаря которому потенциал шара принимает требуемое значение во внешнем
поле. '
3.23. Диэлектрический шар в поле точечного заряда. Потенциал
в любой точке вне шара, проводимость которого равна нулю, а
диэлектрическая проницаемость равна.elt будет:
оо
Обозначение <р+ будет применяться для обозначения потенциала или поля вне
или на положительной стороне замкнутой поверхности. Разложение <р4
по обратным степеням г внутри шара не пригодно, так как потенциал
должен быть * всюду конечен. Мы должны обратиться, следовательно,
к другому решению уравнения Лапласа, которое получается из A), если
положить равными нулю все коэффициенты Ьпт. В любой внутренней точке
полный потенциал будет:
оо
?~^Sa№/""p"(cosG) (r<r\)- (i6>
п = 0
ю- включает в себя как слагаемое от заряда q, так и слагаемое от
индуцированной поляризации, поскольку особая точка, связанная с этим точечным
зарядом, расположена вне области, для которой определено A6). Вблизи
поверхности имеем /-<|С|, так что ср0 может быть разложено как и в C).
Непосредственно с внешней стороны сферы:
*+~2{^*(г)" + тМ/,"<ео»,>- A7>
П я■ О
При переходе через поверхность:
9+ =<?-, H^j? = *i%r (r^=/-i). A8>
186 ГЛ. Ш. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
.., _» , , , ■ , , ■ ■ ■ ■ ■ -
Из этих граничных условий мы можем получить выражения для коэффициентов
разложений:
д 2п +1 \
Сп — 4яС»+1" пгх + (п + 1) е2 '
. __ q r\ ч — ч п
A9)
'Потенциал в любой точке вне шара будет:
00 2г?4-1
+ 1 ? , g Ч — ЧХ} п ^Ч Я»(cos6) .2m
' ~ 4пе2 Гг"^ 4*4 пг1-\-(п-\-1)ц, Cn+l /^+1 ' K '
п = о
тогда как во внутренних точках
со
? =т- 7; 1 / . tv—ягхт^и(cos 6). B1)
Существенно отметить, что области с бесконечно большой
диэлектрической проницаемостью ведут себя подобно незаряженным проводникам.-
По мере того как &г становится очень большим, первый член ряда B0),
• соответствующий п = 0, равен нулю, так что в пределе получается
соотношение F) для случая qx = 0.
3.24. Шар в параллельном поле.. По мере того как точечный источник q
удаляется от центра, поле в окрестности шара становится однородным
и параллельным. Мы рассмотрим теперь случай шара, помещённого в диэлектрик
с диэлектрической проницаемостью е^ в однородном параллельном внешнем
поле Е0, направленном вдоль положительной оси z. Первоначальный потенциал
..равен тогда
с3о = _£,02г = — E0r cos Ь=—^/-Pi (cos 6). B2)
•Следует заметить, что <р0 уже не регулярен на бесконечности, поскольку
сам источник, бесконечно удалён. Потенциал вне шара, вызванный
индуцированными поверхностными зарядами или поляризацией, будет попрежнему:
оо
9tSK?^. B3)
п = 0
Если шдр является проводящим, то результирующий потенциал на его
поверхности и внутри него должен. быть постоянен и равен <pg. Таким
«образом,
оо
Ъ = — *Wi (cos 6) + V Ъп ^Р-. B4)
71=0 Г1
•<р8 не зависит от 6, откуда следует, что
bQ = ri<?s* b^ = r\EQl bn = 0 при /г>1} B5)
?+ = -£0rcos&4-M^ + ?/f. B6)
„-Плотность заряда и полный заряд равны соответственно:
' co = 3e2£0cos6-f^, ^=41сгЛвв. B7)
«Потенциал индуцированных поверхностных зарядов равен, следовательно,
«потенциалу диполя с моментом р = 4т:е2£,0/-^ т. е. с моментом, пропоциональ-
ЗАДАЧА О ШАРЕ 13.241.
187
иым объёму шара. Если шар заряжен, то к этому потенциалу добавляется
потенциал от заряда qv
Если шар является диэлектрическим с диэлектрической проницаемостью elf
то потенциал во внутренних точках имеет вид A6). Для того чтобы
удовлетворить граничным условиям A8), коэффициенты должны быть теперь равны:
а0 — Ь0 — 0, «!— с._]_9„- ^о» *i 774^O7 ri^o> '
Ч + ^Ч
ап==^п==^ ПРИ «>!•
Результирующий потенциал будет тогда:
<?" = A— E0r cos 6.
Внутри шара поле параллельно и однородно:
Е
J
B8)
B9)
__ d<p
3e«> p
1 + 2н °
C0)
Диэлектрическая постоянная сферы xt может быть как больше х2, так
и меньше. Таким образом, поле внутри сферической полости в однородном
диэлектрике с диэлектрической константой у.2 равно:
£ -+2*« ^0>^о-
C1)
Далее мы замечаем, что индуцированное поле вне шара равно полю
диполя, ориентированного вдоль оси z и имеющего момент:
Р-ЬЪ^Фо- С32)
«Очевидно, сферическая полость также ведёт себя как диполь. Этот эффект
4. <Р
Рис. 37а. Проводящая сфера
в параллельном поле.
Окружающая среда — воздух.
Рис. 37Ь. Сфера из
диэлектрика в параллельном поле.
Окружающая среда —
воздух.
легко может быть понят^ если мы вспомним, что на стенках полости
•находятся связанные заряды с плотностью ю' = — пР2, где Р2—поляризация
внешней среды.
В случае диэлектрического шара в воздухе ц, = е0. Поляризация шара
•будет тогда:
Pi = Ч (*i - 1) Б" = 3 ^=1 е0Е0, C3)
л его дипольный момент:
п^±тггЗр —4гг3^^еЕп <34>
188 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Энергия такого поляризованного шара во внешнем поле будет:
Ц = — ~ / Р^о dv = - 2«г;-^=1- в0Е1 = - 1 рЕ0. C5)
v
Поляризация диэлектрика изменяет поле внутри шара. Это изменение
удобно выражать непосредственно через Pt: Коэффициент деполяризации
L определяется соотношением:
Е~ = Е0 — LPt. C6)
Из C0) и соотношения Pt = e0 (xj — 1) Е~ можно подсчитать, что для шара
параллельном поле
L = 4~ У*п . C7)
В случае шара, находящегося в воздухе, х2 = 1 и L"= о— •
Зе0
ЗАДАЧА ОБ ЭЛЛИПСОИДЕ
3.25. Свободные заряды на проводящем эллипсоиде. В
эллипсоидальных координатах в силу соотношений A3^), стр. 62, уравнение Лапласа
имеет вид:
<4-C)*£M)+ff-9*,£(*,&)+
Свойства эллипсоидальных гармонических функций, удовлетворяющих этому
уравнению, были подробно изучены; мы построим здесь лишь некоторые
простейшие из них, которых будет достаточно для задач, с которыми нам
придётся встретиться.
Рассмотрим прежде всего проводящий эллипсоид, помещённый в
однородный диэлектрик с диэлектрической проницаемостью е2. Главные полуоси
эллипсоида пусть будут я, Ь, с и пусть q — полный заряд эллипсоида.
Первоначально мы предположим, что внешнее поле отсутствует. Мы хотим
определить потенциал и распределение зарядов на проводящей поверхности^
Чтобы решить эту задачу, необходимо найти потенциальную функцию,
удовлетворяющую уравнению A), регулярную на бесконечности и
постоянную на поверхности данного эллипсоида. Пусть £ будет параметром семейства
эллипсоидов, конфокальных с заданным эллипсоидом £ = 0, полуоси которого
определяются величинами а, Ь, с. Переменные tj и С являются параметрами
конфокальных гиперболоидов и служат для определения положения
точки на любом из эллипсоидов S = const. Следовательно, на поверхности
1 = 0 потенциал <р должен быть независимым от yj и С. Если мы сможем
найти функцию только от S, удовлетворяющую уравнению A) и ведущую
себя на бесконечности должным образом, то её можно будет подобрать
так, чтобы она правильно выражала потенциал в любой точке вне
эллипсоида I = 0.
Итак, предположим, что ю = о>@« Уравнение Лапласа примет вид:
ЗАДАЧА ОВ ЭЛЛИПСОИДЕ \3.2Ц
189
что в результате интегрирования даёт:
оо
9@-^11, C)
где Cj — произвольная константа. Верхний предел выбран бесконечным для
того, чтобы обеспечить соответствующее поведение <р на бесконечности.
Когда S становится весьма большим, /?£ приближается к I'1 и
* = -7f F-+со). D)
С другой стороны, уравнение эллипсоида может быть написано в виде:
l + f 1 + j l+-f-
Если г2 = х% -{-у2 -f-г'2—расстояние от начала координат до какой-либо
точки на эллипсоиде £, то очевидно, что по мере того, как £ становится
очень большим, £ -» г2 и, следовательно, на больших расстояниях от начала
? = ^7-- F)
Следовательно, решение C) в бесконечности регулярно. Соотношение F)
позволяет нам кроме того тотчас же определить значение константы Cv
Действительно, выше было показано, что каково бы ни было распределение
для удалённых точек, главный член разложения представляет собой потенциал
точечного заряда, расположенного в начале координат и равного полному
распределённому заряду, в данном случае q. Следовательно, С1=з-т~-, и
потенциал в любой точке будет:
оо
Эквипотенциальные поверхности—эллипсоиды £ = const. Уравнение G)
является эллиптическим интегралом, значения которого табулированы *).
Чтобы получить нормальную производную, мы должны вспомнить, что
расстояние вдоль криволинейной координаты и1 измеряется не величиной du1,
a htdux (раздел 1.16). В эллипсоидальных координатах:
h - 1 УЕ—ч>Е-с> (%\
Н^-2 *-Щ ' (8)
д<$> 1 dy q 1_
О)
dn AtdS 4тсе2 VC5 — -ч)E—С)
Плстность заряда на поверхности £ = 0 будет:
—4£L-*?i- A0)
Если теперь в трёх уравнениях A32), стр. 61, определяющих х, у> г
^через I, yj, С, мы положим 1 = 0, то без труда убедимся, что
!) См. например, J a h n ke~Emde, Tables of Functions, 2 изд.» Teubner, 1933.
190 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Следовательно, плотность заряда на поверхности эллипсоида в прямоугольных
координатах будет:
q 1
ш
АщЬс
V а4 ' б4 • с4
A2)
Интересны несколько частных случаев. Если две оси одинаковы, то тело
превращается в сфероид и выражение G) может быть проинтегрировано
в элементарных функциях. Например, если а = Ь> с, то мы имеем
сплюснутый сфероид и
со
<р=_£_ Г d\ д —Jl srrtgl/^^ A3)
I
При с = 0 сфероид вырождается в плоский диск. С другой стороны, если
я>& = с, то мы имеем вытянутый сфероид и для потенциала получаем:
<? = •—;—ч In r "^ ^ ' —. A4)
8те2 У а2— б2 У%-\-Ф— У а2 — ft2 v
Эксцентриситет вытянутого сфероида равен е—1/ 1—(—) . По мере того
как е-> 1, сфероид вырождается в тонкий длинный стержень.
3.26. Проводящий эллипсоид в параллельном поле. Мы предположим
сначала, что постоянное параллельное поле EQ направлено вдоль оси х, т. е.
вдоль главной оси эллипсоида. Потенциал этого поля равен:
©,
?о— £0* ^о\ (&2__а2)(С2_а2) ; . С1»;
где значение х в эллипсоидальных координатах подставлено из уравнения A32),
стр. 61. Ясно, чго этот первичный потенциал является решением уравнения
Лапласа и имеет вид произведения" трёх функций:
Однако на бесконечности он не регулярен.
Если мы хотим удовлетворить граничным условиям, то потенциал
индуцированных зарядов «J должен на каждой из поверхностей I = const, меняться
таким же точно образом, как и <?0. От у0 он отличается регулярным
поведением на бесконечности. Мы предположим поэтому, что vt является функцией
вида
Vi^C&WFMFsW, A7)
где
Для того чтобы найти уравнение, которому удовлетворяет функция G(£),
мы должны только подставить A7) и A8) в A), в результате чего получим:
*;£-(*-£)-№+>•-* <19>
Уравнение A9) — обыкновенное уравнение второго порядка, имеющее
два независимых решения. Одно из них, как мы уже знаем, будет Fx = У-|-вР,
ЗАДАЧА ОБ ЭЛЛИПСОИДЕ 13.27] 19Х:
Известна теорема *), которая гласит, что если одно решение линейного-
дифференциального уравнения второго порядка известно, то второе
независимое решение может быть определено из него посредством квадратур.
Если ух — решение уравнения
то независимое решение у2 будет:
У2 = ^1 §—dx. B1)
*®=w$=h*** <22>
Gi(e)==FiJw' B3>
В нашем случае:
откуда
Пределы интегрирования произвольны, но легко показать, что Gx (£) убывает"
в бесконечности должным образом, если верхний предел выбран бесконечным.
Потенциал индуцированных зарядов будет, следовательно:
ъ-*»^ е+ччдг B4)
Наконец, константа С2 определяется из условия, что на эллипсоиде
£ = 0 потенциал постоянен и равен нулю:
о
В любой внешней точке потенциал будет:
со = соп 1
со
1 Г &\
°1 ? <% J(Z + a2)Ri
h
J (c + «2)/?e Г ^26)'
5 + a2) /?£
Интеграл, с которым мы встретились в B6), называется эллиптическим
интегралом второго рода 2).
В случае поля, параллельного одной из малых осей, необходимо только-
заменить выше параметр а2 на Ь2 или с2. Таким путём потенциал вокруг
проводящего эллипсоида, ориентированного произвольным образом
относительно однородного параллельного поля Е0, может быть определён
разложением поля Е0 на три компоненты, параллельные главным осям эллипсоида,
и сложением трёх получающихся в результате решений типа B6).
3.27. Диэлектрический эллипсоид в параллельном поле. Теперь не*
представит труда подсчитать то изменение, которое вносит в однородное-
*) Смотри, например: I n с е, Ordinary Differential Equations, стр. 122, Longmans,.
1927. Также Степанов, Курс дифференциальных уравнений, Гостехиздат, 1945,.
стр. 183. Прим. ред.
2) Смотри, например, Е. Т. Уиттекер и Г. Н. Ватсон, Курс современного
анализа. Л. — М., ГТТИ, 1933, т. II, стр. '366 и след.
192 ГЛ. lib ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
^параллельное поле диэлектрический эллипсоид. Предположим, что
диэлектрическая проницаемость эллипсоида равна еь и что он помещён в однородную
среду с диэлектрической проницаемостью е2. Поле Е0 направлено произвольно
по отношению к системе отсчёта и имеет компоненты вдоль осей эллипсоида,
равные E0Xi Е^у E0z.
Рассмотрим прежде всего компоненту £0ir. Вне эллипсоида
результирующий потенциал должен представляться в общем виде теми же функциями,
что и в предыдущем примере, и отличаться только значением константы С2.
Следовательно, в этой области
оо
?+=?о + ?1+^^П(т^^ B7)
Под знаком интеграла переменная % заменена на s для того, чтобы не путать
её с нижним пределом.
Внутренняя область эллипсоида соответствует значениям — с2-^£<^0,
если а^Ь^с. В этой области «""должен меняться с изменением tq и £,
•как это определяется функцией -/^(^/^(С), и» поскольку уравнение A9)
имеет только два независимых решения, зависимость от £, чтобы удовлетворить
уравнению Лапласа, должна представляться либо функцией Ft (£), либо <3, (£).
Но функция G1(^) обращается в бесконечность при £ = — са, в то время
как F^) конечна во всех точках внутри поверхности £ = 0. Таким образом,
потенциал внутри этой области должен иметь вид:
i~=*CbFi{l)FAuFb<®, B8)
где С3 — некоторая постоянная1).
Константы Са и С3 должны быть подобраны так, чтобы удовлетворить
граничным условиям:
ф+ = о~*~, е.
KrL-ttrL- ^
Первое из них даёт:
а второе:
c.-c.+^/frt«;: C0)
в
4^-^=^-С3. C1)
Поскольку е>0 := — Е0хх, мы находим, что потенциал во внутренних течках
эллипсоида равен:
со
— — Е^х . __ г ds
l + '%£'to~~**)Al •
i-fis + ^R.' C2)
*а напряжённость поля;
** =—аг12 • C3)-
1 + -2iT(ei~e2Ml
!) Выбор F\ (£) вместо G% E) в тех случаях, когда поле не параллельно ©си г,
диктуется требованием конечности внутри эллипсоида напряжённости ноля, а не
потенциала <?. Прим. ред.
ЗАДАЧА ОБ ЭЛЛИПСОИДЕ 13.27]
193
Компоненты вдоль двух других осей находятся точно таким же способом.
Полный потенциал приложенного поля равен
% = — Е0х* Е0уУ E0z?>
и результирующий потенциал во внутренних точках эллипсоида
C4)
? = —
£0х*
. , abc , ч .
+
ЕруУ
2б2
t . abc . . .
+
2е2
+
Eos*
1 + -2Г(Ч— ч)Аъ
C5)
где константы А2 и Л3 определяются выражениями:
оо
ds * г ds
со
А
5 + &2)/?8
, Л3 = J
(S-H2)/?S•
C6)
Остальные компоненты изменённого поля равны:
Еу —
_Еру
л , abc . . . '
1 +-^~(Ч—Ч)А2
'(SZ
, , abc , ч .
C7)
Мы приходим к выводу, имеющему большое практическое значение:
если приложенное поле первоначально однородно и параллельно, то
результирующее поле внутри эллипсоида также однородно и параллельно,
независимо от ориентации осей эллипсоида. Однако Е" вектор в общем
случае не параллелен вектору Е0, так как константы Al9 A2f AB равны
между собой только в случаях вырождения.
Вне эллипсоида результирующий потенциал, связанный с первичной
компонентой £0а;, даётся соотношением B7)
abc ti — ea
со
= <?0
!
ds
Ч J (s + a^Rs
1 +
abc ej — e2
J
C8)
ds
e2 J{S + a?)Rs
с Соответствующими потенциалами для полей Е0у и £s. Если в C8) мы
положим е1-> оо, то найдём, что ср+ сведётся к B6). Потенциал вне тела
с бесконечной диэлектрической проницаемостью точно такой же, как и
вне заземлённого проводника той же формы.
Индуцированная поляризация Рг внутри эллипсоида стремится уменьшить
приложенное поле. Коэффициенты деполяризации Lu Z,2» ^з определяются
соотношениями
Ex'==lEox ^l^la» Щ, ~Е0у ^Р\уу ^г—^Ог ^3°1г- W°)
Полагая Р1 = (е1 — е0)Е*" и вводя компоненты Е~ из C3) и C7), получаем:
**—£2=л?4» С/- 1,2,3).
2еа Ч — 1
D0)
Чаще всего средой вне эллипсоида является свободное пространство, ха=1.
13 Зак, 593. Теория электромагнетизма.
194 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
В этом случае коэффициенты деполяризации зависят только от формы
эллипсоида:
/ — аЬс л
^3— 2е0 3
(/=1,2,3).
Поляризация может „быть тогда определена из простой формулы:
Рт =
Li +
1
D1)
D2)
ч—ч
и соответствующих выражений для Ру и Pz.
3.28. Определение Б и D с помощью полостей. Поле внутри
эллипсоидальной полости даётся уравнениями C3) и C7) при г^ = е0. Два случая
представляют значительный интерес: дискообразная полость, плоскость
которой нормальна к направлению приложенного поля, и иглообразная полость,
параллельная полю.
Рассмотрим сначала случай внешнего поля, направленного вдоль оси г.
Тогда, по мере того, как с становится очень малым, эллипсоид
вырождается в диск, изображённый на рис. 38,а. Мы не уменьшим общности, если
положим, что диск круглый, т. е. а = Ь\ в этом случае эллиптический
интеграл А3 сведётся к более элементарной функции:
*=/■
ds]
(s + a*)(s + c*)
(а2
с2)а
(
У а? —с*
arctg
У а2 — &
)• D3)
Предел произведения а?сА3 при с -> О равен 2. Поле внутри полости чисто
поперечное, и так как х1=я1, равно:
Е =х2Е0 = —D0.
D4)
JT
С точностью до постоянного множителя е0, напряжённость поля Е~ внутри
дискообразной полости равна вектору D0
первоначального поля в диэлектрике.
На рисунке 38,£ поле направлено
вдоль главной оси вытянутого
сфероида а >£ = с;
ds
а- „* .V v.- > Ь
Рис. 38. Иллюстрация к
определению векторов Е и D с помощью
полостей. Стрелки показывают
направление приложенного поля.
0 (s + &)(s + a*J
D5)
где е
-/1-5-
эксцентриситет. При
е -> 1 сфероид вырождается в длинную,
иглообразную полость, ji произведение ab2Ax стремится к нулю. В каждой
точке внутри полости Е = Ео: напряжённость поля Е~ точно такая же,
какая первоначально была в диэлектрике. 1
Такого рода определение векторов Е и D с помощью полостей в весомой
среде было предложено лордом Кельвином. Очевидно, прямые измерения Е
или D путём определения сил или вращающих моментов, действующих на
Малое пробное тело, в твёрдом диэлектрике невыполнимы, а если сделать
- , ч
ЗАДАЧА ОБ ЭЛЛИПСОИДЕ [3.29] 195^
, - ■ ->-'■, Г - ■■ ■- , ■ I ■ ■ ■■
»
полость, то поле внутри неё будет зависеть от её формы. Наш ■ подсчёт
показывает, однако, что напряжённость электрического поля в диэлектрике
совпадает с напряжённостью, измеренной в иглообразной полости,
показанной на рис. 38,#, в то время как поле, измеряемое в плоской щели рис. 38,а,
отличается от D в диэлектрике только на постоянный множитель.
3.29. Вращающие моменты, действующие на эллипсоид.
Напряжённость электростатического поля может быть измерена наблюдением
вращающего момента, действующего на малое пробное тело изЕестной формы и
известной диэлектрической проницаемости, подвешенное в поле на нити.
Обратно, если напряжённость поля известна, то подобный эксперимент
может быть использован для определения диэлектрической проницаемости
или восприимчивости образца диэлектрического вещества. В общем случае,
поле и поляризация внутри образца неоднородны, и точные вычисления
трудны или невозможны. С другой стороны, преимущества для этой цели
■ пробного тела эллипсоидальной формы очевидны. Поляризация всего образца
одинакова, и действующий вращающий момент зависит только от ббгёма
и диэлектрической пронипаемости его.
Согласно уравнению D9), стр. 108, энергия диэлектрического тела во
внешнем поле равна:
U=e-^=pJE-E0dvt D6)
у,
где, как и выше, Е~ обозначает результирукщее поле внутри тела, а Е0—
первоначальное поле. Если тело имеет эллипсоидальную форму и поле Eq
однородно, то, согласно C3) и C7), имеем:
Е-Р Соа? | fog ,
4
и так как объём эллипсоида равен -~ ъа1су то
1+а_Н^-^уз
и = ~ъаЬс (е2—Н)Е"Eq- D8)
Эта энергия зависит не только от напряжённости первоначального поля, но
и от ориентации главных с сей по отношению к полю. Пусть вектор Ь<а
представляет ссбой виртуальный поворот эллипсоида вокруг его центра,
а х—результирующий вращающий момент, действующий со стороны поля.
Как Т, так и 8ю являются аксиальными векторами (стр. 68), и компоненты
bwXt 8<о , 8<оя представляют собой углы поворота соответственно относительно
осей х, у и г. Работа, совершённая при таком повороте, равна:
8W = Т 8ео = Тх 8о>, + Т9 Ъку + Тг 8о>я. D9)
Эта работа должна компенсироваться уменьшением потенциальной энергии U.
В силу однородности и квадратичности D7) мы м"ожем написать:
Ш= §- vatc(e2 — e,)8(E-Eo).= ^ъаЬс(Ч-"Ч)Ъ-Ш0. E0)
Оси отсчёта были взяты ссвпадакщкми с главными осями эллипсоида.
Относительно этой системы, фиксированней в теле, изменение Е0,
соответствующее виртуальному повороту 8w, будет:
8Е0 = 1Е0, 8w], E1)
IS*
196 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
откуда для баланса энергии получаем:
bU= ~ ъаЬс (е2 — h) Е" 1Ео» 8о)] =
о
E2)
Так как компоненты виртуального поворота произвольны, то вращающий
момент, действующий со стороны поля, равен, следовательно:
Т = -д. vabc (e, — е2) [Е~, Е0].
Компоненты этого вращающего момента:
E3)
Ъ
Ty = ^*{abc)* bz^LEoeE0aX
Xj A+^^^;2)(^^^л3) }
X
I A+е|£^лз)A+^ ^л>)
Тг = |тг (а',СJ (i^-4* 5* X
Ло —Л1
Xj A+-* *=*.*) (i+$*p.*)
!.
E4)
J
Для исследования устойчивости эллипсоида мы должны выяснить
относительную величину констант Аи А2 и Л3. Прежде всего, из их
определения C2) и C6) ясно, что все они положительны при любых значениях
а, Ьу с. Легко показать, кроме того, что порядок их относительных величин
обратен порядку величин этих трёх параметров. Таким образом, если я>#>с,
то Л1<Л2<Л3. Далее находим, что сумма эгих трёх интегралов может быть
приведена к более простому интегралу, который, если ввести новую
переменную M=/?g, даёт:
A1 + At + At = 4.
abc
(/=1,2,13),
ZLAjX) (/=1, 2, 3).
E5)
E6)
E7)
Поскольку все три константы' положительны, отсюда следует, что
о<д;<4-
^ ■> ^ abc
1 _L a^C. -*1 —
1"Т" ^
Таким образом, знаменатели, в E4) положительны и при е1>еа, и при г^г^
и направление. компонент вращающего момента не зависит от
соотношения величин е1 и е2- Если приложенное поле параллельно какой-либо из
трёх главных осей эллипсоида, то все эти компоненты равны нулю, так что
эти три направления являются положениями равновесия.
Устойчивость равновесия зависит от направления вращающего момента,
а последнее, как мы видели, зависит только от знака А$-~Аъ который,
в свою очередь, определяется относительной величиной осей a, b и с. Так,
ЗАДАЧИ , . 197
например, Аь-— А2 положительно, если Ь^>с, и отрицательно, если с>£.
Компоненты вращающего момента таковы,'что стремятся повернуть больщую
ось в направлении поля кратчайшим путём. Эллипсоиду большая ось
которого направлена вдоль приложенного поля, находится в состоянии
устойчивого равновесия; положения равновесия вдоль малых осей неустойчивы.
ЗАДАЧИ
1. Координаты £, к), С получаются из прямоугольных координат преобразованием:
£+»]=/(х + iy), С = 2,
где /—какая-либо аналитическая функция комплексного переменного x-\-iy. Пока»
зать следующие свойства этого преобразования:
a. Дифференциал линейного элемента равен:
ds* = Л2 (d& + drf) -f di\
где h = 1/ \f\, a /' обозначает производную по переменному x-\-iy.
b. Система £, t\, £ ортогональна.
c. Преобразование конформно, так что любая бесконечно малая фигура в
плоскости ху преобразуется в геометричесьи подобную бесконечно малую фигуру на
плоскости £y].
Показать, что в этих координатах лапласиан скалярной функции ср принимает вид:
и найти выражения для дивергенции и ротора вектора.
2. Как и в задаче 1, рассмотреть координаты, определяемые следующими
преобразованиями:
5 + Ы = 1п(л:_4-/у), A)
■* + (У — а ch E + nj)t B)
* + <y«(€ + *n)V C)
е -Н ivj = (л: + /уJ. ' D>
,. , . , *х 4- iy -f a
1 ' {л + iy — а у '
x + iy = iactgj ^2 . F)
3. Система кольцевых или тороидальных координат X, ja, <Ь определяется
соотношениями:
sin р.
chX-f- cos p.
где
jtsarCOS^, у =■ Г Sink, 2 = '
shX
ch X -f- cos {J.*
Показать, что поверхности ф — const, являются меридиональными плоскостями,
проходящими через ось г, поверхности Х= const. — торами, меридиональные сечения
которых — круги:
x* + z* — 2лгсШХ+1=0,
а поверхности jx = const. — сферы, меридиональные сечения которых — круги:
AT* + 22 + 22tglJ—kl=0.
Показать, что система ортогональна, за исключением некоторых особых точек, и найти
эти точки. Найти выражение для дифференциала линейного элемента, и показать, что:
shU ( д f t>4\jiJL(r £L\ ' JL <?М
д?= -7sr~\ax~V ЖПдА др)~г sh*x wf
Разделяются ли переменные в уравнении Лапласа в этих координатах?
4. Пусть F{x, у, z)»=X представляет семейство поверхностей, и пусть F имеет
непрерывные частные производные первого и второго порядков. Показать,что необ-
■ Л
198 ГЛ. Ш. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
ходимым и достаточным условием для того, чтобы эти поверхности моглл быть
эквипотенциальными, является
"% (gradFJ=jr(X)'
где /(X) — функция только ).. Показать, что если это условие выполнено, то
потенциал имеет вид:
l-dje-SfWdk + Cb
где сх и с2 — константы.
5. Показать, что ф = F{г -\- ix cos и -\-iy sin а) является решением уравнения
Лапласа:
в трёх измерениях для всех значений параметра и и для любой аналитической
функции F. Показать далее, чго любая линэйная комбинация из 2я-{- 1 независимых
частных рзшений может быть выражена в виде интеграла
+«
Ф = }(* + '■* cos и + iy sin и)п fn (и) du>
где fn(u)—рациональная функция от е*и, и, наконец, что любое решение уравнения
Лапласа, аналитическое в некоторой сферической области, может быть выражено
в виде интеграла
1С
ф = I f(z,-\- ix cos и -f- iy sin и, и) du.
(См. Е. Т. Уиттекер и Г. Н. «$Затсон, Курс созременного анализа, гл. XVIII.)
6. Заряд распределён вдоль бесконечной прямой линии с постоянной плотностью
q кулонов/метр. Показать, что напряжённость поля в любой точке, расстояние
которой от этой линии равно г, будет: г
г 2пе г '
и чго это поле является отрицательным градиентом потенциальной функции:
гда г0— произвольная константа, представляющая собою радиус цилиндра, на
котором ср = 0. *
Исходя из этих результатов, показать, что если заряд распределён в двумерном
пространстве с плогнэсгью <о (л:, у), то потенциал в любой точке плоскости ху будет
9lx',y') = ^f«>b!jrda,
где r= Y{x'—t*)a + (y—У)\ и что <?(х,у) удовлетворяет уравнению
Показать далее, что эта потенциальная функция в общем случае нерегулярна в
бесконечности, и чго если полный заряд равен нулю, т. е. Г<лйа = 0, то при- г-» с»
произведение г<р ограничено.
7. Заряд распределён в двумерном пространстве по площади конечных размеров
с плотностью <о (х9 у). Дать выражение потенциала в точке х', у', расположенной
вне этой площади в- виде ряда по степеням г — расстояния от произвольного начала
отсчёта до фиксированной точки х', у'. Показать, что последовательные члены
являются потенциалами ряда двумерных диполей.
ЗАДАЧИ « 199
8. Пусть С—какой-либо замкнутый контур в плоскости ху, ограничивающий
площадь S, и пусть <р — двумерная скалярная потенциальная функция. Показать
с помощью теоремы Грина, что
2я«(#',у') = I lnrA'fdfl— ((\nr-~- — (pr-lnrjds,
s с
где и = <р (х\ У),*если ж', у' — внутренняя точка, и и = 0, если ж', у' —, внешняя точка.
В этой формуле
А*=ш+ш> r=V(x'-xJ+(y'-y)*
' дл:3 ~ ду
и п — внешняя нормаль к контуру С.
9. В двумерном пространстве проведена окружность радиуса я. Положение на
окружности определяется углом 6'. Потенциал на круге является заданной функцией
<р(а, б').-Показать, что в любой точке с полярными координатами г, 6, лежащей вне
окружности, потенциал будет::
»(г.•> = ^J«fcJO r,+a347rcosF-e0 «.
Этот интеграл был получен Пуассоном.
10. Бесконечная прямая линия с плотностью заряда q кулонов на единицу длины
идёт параллельно проводящему цилиндру. Показать, что индуцированное поле
совпадает с полем соответствующим образом расположенного изображения. Найти
распределение заряда на цилиндре.
11. Радиусы двух бесконечно длинных проводящих цилиндров кругового
сечения равны соответственно а и Ъ, а расстояние между их осями' есть с, причём
с>л + 6. Внешняя среда — жидкость с диэлектрической проницаемостью е. Разность
потенциалов между цилиндрами V вольт. Получить выражения для плотности
зарядов и для механической силы, действующей на единицу длины одного цилиндра со
стороны другого. Решить задачу, введя в уравнение Лапласа биполярные координаты
и снова применяя метод изображений.
12. Бесконечный диэлектрический цилиндр помещён в параллельное однородное
поле F0, перпендикулярное к его оси. Подсчитать индуцированный на единице длины
дипольный момент и коэффициент деполяризации L (стр. 188).
13. Два точечных заряда помещены в бесконечную однородную диэлектрическую
жидкость. Показать, что кулонопы силы, действующие со стороны одного заряда
на другой, могут бы ть найдены вычислением интеграла
UF-JjleECEn)-;-£-£* п} «fa
(уравнение G2), стр. 141) по любой бесконечной плоскости, пересекающей прямую,
соединяющую эти два заряда.
14. Два жидких диэлектрика с диэлектрическими проницаемостями в± и е2
соприкасаются вдоль бесконечной плоскости. Два заряда дг и q2 расположены по
разные стороны от этой поверхности на расстоянии а от неё, причём соединяющая их
прямая перпендикулярна этой плоскости. Рассчитать силы, действующие на заряды
Ч\. и #2. учитывая, что они ке равны между собой.
15. Проводящий шар радиуса г± с зарядом Q расположен в поле точечного
заряда q того же знака. Пусть #<€.<?• Начертить график силы, действующей со
стороны шара на заряд q в функции расстояния от центра шара, и найти точку,
в которой направление силы меняется на обратное.
16. Заряд q расположен внутри проводящей полой сферы радиуса Ь, в точке,
расстояние которой от центра полости равно а, причём а<^Ь. Рассчитать потенциал
сферы, плотность зарядов на внутренней её поверхности и силу, действующую на
заряд q. Предполагается, что сфера изолирована и не заряжена.
17. Найти распределение зарядов, двумерное поле которого в любой точке
плоскости ху имеет потенциал
2*ео
( .arctg -±£. -f arctg ^-—)
200 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
18. Показать, что электростатический потенциал <р однозначно определяется
значениями <р или ду/дп на поверхности проводников, помещённых в изотропный н&-
однородный диэлектрик.
19. Система из л проводящих тел помещена в изотропную, но необязательно
однородную диэлектрическую среду. Показать, что если при сообщении этим
проводникам зарядов qlt q2,..., qn их потенциалы будут <pi. <Рг»..., <р»> а при сообщении
зарядов q\, q'2 qn соответственно <ft, <р21 • • •. <РЛ> т0
п п
<«1* * i=l
20. Найти в кулонах величину заряда, который необходимо сообщить
металлической сфере радиуса а метров, чтобы повысить её потенциал по отношению к бес*
конечности на один вольт.
21. Бесконечная плоскость делит пространство на две части: одну, занят}ю
диэлектриком с диэлектрической проницаемостью е, и другую — воздухом. Заряд q
расположен со стороны воздуха на расстоянии а от плоскости. Получить
выражение для потенциала во всех точках в воздухе и в диэлектрике и показать, что
потенциал в каждой из частей пространства может быть представлен с помощью
соответствующих изображений. г
Какова плотность а/ индуцированных или связанных зарядов на поверхности
диэлектрика?
Рассчитать силу, действующую на заряд q, и работу, совершаемую при
удалении заряда в бесконечность.
22. Радиусы двух металлических сфер равны соответственно а и Ь, а расстояние
между их центрами с, причём с >*?+*• При помещении заряда qa на первую из
них, потенциал её принимает определённое значение сра. Потенциал второй сферы уъ
посредством её заземления поддерживается равным нулю. Получить выражения для
зарядов qa и qb и найти их распределения на сферах путём построения
последовательности изображений во взаимных точках сфер (стр. 185).
Метод этот принадлежит лорду Кельвину. Смотри дискуссию у F. Noether в Rie-
mann — Weber, Differential und Integralgleicriungen der Physik, т. II, стр. 281, 1927.
23. Две бесконечные параллельные проводящие поверхности совпадают с
плоскостями х •= 0 и х ■■ а. Поверхности 1эти заземлены. Заряд q расположен на оси х
вточке.* = с, причём 0 < с< а. Показать, что плотность индуцированных на
плоскости х «= 0 зарядов будет*
о
2па-\-с
r2\2j
п= -со {{Bпа— с)»-f- г2} 2 {Bпа + сJ + г*}
где г—расстояние от начала координат до точки у, z на этой плоскости. Какова
плотность зарядов на плоскости х = о? Показать, что полный заряд на двух
плоскостях равен — q. (Келлог.)
24. Доказать, что поверхностная плотность заряда в любой точке заряженного
эллипсоидального проводника пропорциональна расстоянию от центра эллипсоида
до плоскости, касающейся поверхности эллипсоида в этой точке.
25.- Уравнение A4), стр. 190, даёт потенциал вытянутого заряженного сфероида.
Показать, что по мере того, как длина -»оо, а эксцентриситет -*-1, эта функция
стремится к логарифмической потенциальной функции двумерного пространства.
Применить теорему к задаче 24 и найти величину заряда на единицу длины.
26. Заряд распределён с постоянной плотностью внутри эллипсоидальной
полости, ограниченной двумя подобными эллипсоидальными поверхностями с главными
осями а, Ь,с и а[\ + -§•)» *A + 'о")' ^V1"^"?) " Показать» чт0 поле равно нулю во
всех внутренних точках, и найти выражение для потенциала во внешних точках.
27. Большая ось проводящего вытянутого сфероида равна 20 см, а его
эксцентриситет есть е. Сфероид подвешен в воздухе и несёт полный заряд q кулонов.
Максимальная напряжённость поля у поверхности сфероида ни в одной точке не\
должна превышать 3 X К-6 вольт/метр. Дать график зависимости наибольшей
величины заряда, который может быть помещён на сфероиде при выполнении этого
условия, от эксцентриситета.
28. Действие1 громоотвгдов было изучено Лармором (Proc. Roy. Soc. A, 90, 312,
1914) на следующей задаче. Полусфероидальный стержень возвышается над плоской
проводящей поверхностью. Потенциал <р0 заряженного облака над ним постоянен
в окрестности стержня. Найти потенциальную функцию <р, постоянную на поверхно-
ЗАДАЧИ 201
сти сфероида и на плоскости. Нарисовать график отношения градиента потенциал»
на конце стержня к напряжённости приложенного поля в зависимости от
эксцентриситета стержня. Предполагается, что длина стержня (большая полуось) фиксирована,
и равна одному метру. Рассмотреть влияние поперечных размеров стержня на поле
как функцию эксцентриситета.
29. Очень тонкий круглый металлический диск радиуса а несёт заряд д.
Показать, что плотность заряда на единицу площади равна.
Q 1
где г—расстояние по радиусу от центра диска.
Подсчитать напряжённость поля на .поверхности диска в вольтах на метр на
кулон в зависимости от отношения г/а и начертить соответствующий график.
Предполагается, что диск находится в воздухе.
30. Сфероидальное диэлектрическое тело подвешено в однородном
электростатическом поле. Большая ось сфероида вдвое длиннее его малой оси, а
диэлектрическая проницаемость равна 4. Внешняя среда — воздух. При какой ориентации
приложенного поля по отношению к осям вращающий момент максимален?
Подсчитать величину этого наибольшего вращающего момента на единицу объема материала
и на вольт напряжённости приложенного поля.
31. В изотропной, но необязательно однородной среде поддерживается
стационарное распределение токов. Показать, что в общем случае в среде появится
объёмное распределение зарядов с плотностью:
р = (с gradе—е grad с) gradср,
где сие — соответственно проводимость и диэлектрическая проницаемость среды.
32. Две однородные изотропные среды, характеризующиеся константами elt at
и е2, <т2, соприкасаются по поверхности S. Поверхность 5 пересекают стационарные
токи из одной среды в другую. Если cpj и ср2—углы между линиями токаи нормалью
к поверхности в точке пересечения, то показать, что каждая линия тока
преломляется по закону
ff2Ctgcp2 = a1ctgcp1.
Показать также, что на поверхности 5 появится заряд с поверхностной плотностью
33. Во многих практических задачах, касающихся распределения токов, можно
положить, что система идеально проводящих электродов помещена в плохо
проводящую среду, которая либо однородна, либо имеет разрывы только на определённых
заданных поверхностях. Потенциалы электродов поддерживаются постоянными и
либо эти потенциалы, либо токи на электродах заданы. Показать, что распределение
токов однозначно определяется потенциальной функцией, удовлетворяющей
следующим условиям:
(а) Д? = 0 во всех обыкновенных точках среды;
(Ь)ср = ср^ — константа для /-го электрода; •■
(c) на поверхностях разрыва непрерывности среды условия перехода
определяются соотношениями:
(d) регулярности в бесконечности
(e) условие (Ь) может быть заменено следующим:
где с — проводимость среды непосредственно у поверхности электрода, граничная
поверхность которого есть Si, и где Ц — полный ток, стекающий с электрода.
34. Система электродов помещена в проводящую среду. Потенциалыcpj,<р2»...,?„.
на электродах поддерживаются неизменными, a /j, /8,. ..,£»—"токи, стекающие
с электродов. Показать, что полное джоулево тепло, выделяющееся в среде, равно:
»
02 ГЛ. III. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
i ь , , ——
35. Доказать, что в системе стационарных токов, поддерживаемых
электродвижущими силами, токи распределяются таким образом, что выделяющееся тепло будет
наименьшим для действительного распределения по сравнению со всеми другими,
совпадающими с действительным в области, где действуют электродвижущие силы,
и соленоидальными во всём остальном пространстве. Среда предполагается
изотропной, и соотношение между напряжённостью поля и плотностью тока линейным.
36. Электрод в виде круглого диска радиуса а соприкасается с бесконечным
полупространством с проводимостью с (например, поверхность земли).
Расстояние до всех других электродов велико по сравнению с радиусом а. Показать, что
распределение токов определяется условиями:
(a) Д-f = 0 внутри проводящего полупространства;
(b) ду/дп = 0 на всей границе, за исключением места соприкосновения с диском;
(c) — = — . в месте соприкосновения с диском, где г — рас-
дл 2noaVd» — r*
стояние по радиусу от центра диска.
37. Стационарный ток течёт по тонкому изогнутому листу постоянной толщины.
Предполагается, что лист настолько тонок, что распределение токов по существу
двумерное. Если £ и т) — криволинейные координаты на поверхности листа, то
геометрические свойства поверхности определяются выражением для элемента дуги:
d& = gnd& + 2gudZ]d4 -f gndrt*,
где свойства gik были определены в разделе 1.14. Скалярный потенциал,
определяющий распределение токов, удовлетворяет уравнению Лапласа
№ "" дер дер дер дер
д£
Vgugn — A дП Vgngtt — gh
Определить сопряжённую функцию ф из соотношения
дер ; дер дер дер
di> = т— ■ ■- с ~\ у ' —— <Щ
Vgugw—^2 " V<
gllg2S — g12
»
и показать, что ф удовлетворяет том/же уравнению, что и ср. Функции ери ф являются
потенциальной и токовой функциями на поверхности, а функция Ф = срЦ— £ф
называется комплексной потенциальной функцией на той же поверхности. Выберем теперь
£ и г] так, чтобы £ = £ -f- щ само было такой функцией. Показать, что в этом случае <f
удовлетворяет простому уравнению
и что ер и ф-^связаньГсоотношение'м'
ду _ дф дер д'Ь
тогда как линейный элемент -сводится к ds2 = gtl(dp + дГтJ). Таким образом,
комплексные функции на поверхности являются аналитическими функциями друг от
друга, и преобразование £ jf- iy\ = x -+-iy отображает конформно поверхность листка
на комплексную 2-плоскость. Если конформное отображение поверхности на
плоскость известно, то задача нахождения распределения токов сводится к решению
уравнения Лапласа в прямоугольных координатах. Обратно, если распределение
токов на изогнутой поверхности может быть определено экспериментально, то те!и
самым мы найдем конформное отображение поверхности на плоскость. (Кирхгоф.)
38. Используя задачу 37, показать, что
ft
г в аеЧ tg -^
, ЗАДАЧИ ^03
является конформной стереографической проекцией сферы радиуса а на комплексную
плоскость, где z = x-\*iy и р — экваториальный угол или долгота, а 6 — широта на
-сфере. Показать далее, что
Ф = ср + Щ =fBaei? tg A) =f(z)
•будет комплексной потен циальной функцией на сфере, где /— любая аналитическая
функция z.
39. Постоянный ток / втекает на проводящую полую сферу радиуса а с
поверхностной проводимостью о в некоторой точке на поверхности и покидает поверхность
в диаметрально противоположной точке. Найти потенциал в любой точке и уравне-
ние линий тока.
40. Цилиндрический конденсатор образован двумя концентрическими металли-
. ческими трубками. Пространство между трубками заполнено твёрд ум диэлектриком
с диэлектрической проницаемостью е, но этот диэлектрик непосредственно С трубками
не соприкасается, а отделён от ник тонкими слоями непроводящей жидкости с
диэлектрической проницаемостью е'. Концы металлических трубок находятся настолько
далеко за концами твёрдого диэлектрика, что полем рассеяния можно пренебречь.
Между металлическими электродами поддерживается постоянная разность
потенциалов. Получить выражение для относительного удлинения диэлектрика. (К е m b I e,
Phys. Rev. % 614, 1916.)
ГЛАВА IV
МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
Методы, развитые для исследования электростатического поля, широка
применимы и к магнитостатическому полю. Любое магнитостатическое поле
может быть заменено тождественным по структуре электростатическим полем*
создаваемым соответствующим распределением диполей и фиктивных двойных
слоев. Однако эта эквивалентность чисто формальная. В магнитостатике нет
величины, соответствующей свободному заряду, и особые поверхности,
возникающие при введении двойных электрических слоев, б действительности не
существуют. Двойной слой приводит фактически к многозначности
потенциала и соответственно к неконсервативности поля. Каковы бы ни были
аналитические преимущества электростатической аналогии, необходимо помнить,
что физическая структура поля, создаваемого стационарным распределением
токов, принципиально отличается от строения поля любой конфигурации
электрических зарядов.
ОБЩИЕ СВОЙСТВА МАГНИТОСТАТИЧЕСКОГО ПОЛЯ
4.1. Уравнения поля и векторный потенциал. Уравнения, которым
должны удовлетворять магнитные векторы стационарного поля, получаются
из уравнений Максвелла, если в них положить производные по времени
равными нулю:
rotH = J (I), divB = 0. (II)
К ним надо добавить уравнение непрерывности, которое в этом случае имеет
вид:
divj = 0. (Ill)
В стационарном поле распределение токов соленоидально; все линии тока
либо замыкаются сами на себя, либо начинаются и кончаются в
бесконечности. Из (II) следует также, что линии вектора В — линии магнитного
потока, как их обычно называют,—также замыкаются сами на себя.
Предположим, что плотность потока поля, создаваемого нитью тока /и есть Bt. Все
линии этого поля пронизывают контур Iv Часть потока Bj может, однако,
лронизывать и вторую нить тока /2. Понятие «связи через поток», часто-
используемое при практическом исследовании электромагнитных вопросов,
основано на соленоидальных. свойствах тока и магнитного потока в
стационарном состоянии. Распространение этого понятия на медленно меняющиеся
поля (квазистационарное состояние) законно лишь до тех пор, пока dpjdt
остаётся исчезающе малым по сравнению с divj.
Применяя теорему Стокса к уравнению (I), мы получаем эквивалентное
интегральное уравнение /
(Ia) J*Hrfs = Jjnrfa = /,
С S
ОБЩИЕ СВОЙСТВА MAfHHfОСТАТИЧЕСКОГО ПОЛЯ 14.2] 205
где 5—любая поверхность, опирающаяся на контур С, а I — полный ток,
пронизывающий эту поверхность. Линейный интеграл от Н по замкнутому
контуру равен охватываемому этим контуром току; это означает, что
магнитное поле неконсервативно.
Любое соленоидальное поле может быть представлено с помощью
векторного потенциала. Как и в разделе 1.&, уравнение (II) тождественно
удовлетворяется, если мы положим:
В = rot А. A)
Вектор А нужно теперь выбрать так, чтобы удовлетворить уравнению (I), и,
» следовательно, должно быть дано соотношениз Н = Н (В) между магнитными
векторами. Если среда неферромагнитная, то это соотношение линейно; если,
кроме того, среда однородна и изотропна, то мы можем положить В = j*. • It
v и придём тогда к следующему уравнению для векторного потенциала:
rot ret А =я jjJ. B)
В разделе 1.9 было показано, что к вектору А можно прибавить гра- ч
диент произвольной скалярной функции 4*> не изменяя соотношения A).
Соответствующим выбором <|* дивергенцию А всегда можно сделать равной
нулю. Векторный потенциал однозначно определяется уравнением B) и
условием
divA = 0. C)
В прямоугольных координатах уравнение B) сводится тогда к такому:
AA=-yJ, K D)
которое надо понимать в том смысле, что оператор Лапласа действует на
каждую из прямоугольных компонент А.
4.2. Скалярный потенциал. Существование потенциальной функции,
связанной с электростатическим полем, является прямым следствием
безвихревого характера поля, вектора Е. Если распределение зарядов в виде .
двойных слоев исключено, то ротор Е всюду равен нулю; отсюда мы можем
выразить Е как отрицательный градиент скаляра <р. Кроме того, поскольку
циркуляция вектора Е равна нулю по любому замкнутому пути в
рассматриваемой области, потенциал будет однозначной функцией координат.
Область пространства, ограниченная определёнными граничными
поверхностями, называется связной, если можно пройти из одной точки области
в любую другую бесконечным числом путей, каждый из которых полностью
расположен в рассматриваемой области. Любые два пути, которые могут
быть совмещены непрерывной деформацией, не выводящей за пределы
области, называются взаимно совместимыми. Любая замкнутая кривая или
поверхность называется приводимой, если непрерывной деформацией, не
выводящей за пределы области, она может быть стянута в точку. Два взаимно
совместимых пути вместе образуют приводимый контур. Если, наконец, область'
такова, что все пути, соединяющие любые две точки, взаимно совместимы,
или такова, что все замкнутые контуры, проведённые внутри неё, приводимы,
то она называется односвязной. Электростатическое поле объёмно
распределённых зарядов образует односвязную область пространства, внутри которой
любой замкнутый путь является приводимым.
Геометрические свойства магнитного поля стационарного распределения
. токов совершенно противоположны геометрическим свойствам
электростатического поля. Обозначим область, занятую токами, через Vlt а область,
206
ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
в которой J — 0, обозначим через V2. На рис. 39 изображено плоское
сечение поля; заштрихованные участки изображают, например, поперечные
сечения проводников, по которым протекают токи. В области Vx ротор Н не
равен нулю и, соответственно, скалярного потенциала не существует. В области
Vg имеем:
rotH = 0, E)
и, следовательно, в этой области Н может быть выражено в виде
отрицательного градиента скалярной функции <р* (л:, у, г)
Н = — grad<p*. F>
Линейный интеграл от Н по какому-либо контуру, соединяющему две точки
Р и Q и расположенному целиком в области V2, будет:
Q Q
j Uds = -~ J grad <p* ds = <p'* (Р) - © *(Q).
G>
/зкй**^^
Рис. 39. Иллюстрация к понятию
двусвязной области.
Однако не все пути, по которым можно из точки Р притти в точку Q,.
являются взаимно совместимыми/ Замкнутая кривая, состоящая из двух
отрезков, подобных PEQ и QFP непривойи-
ма, так как при стягивании в точку она.
неизбежно должна пересечь область Vx.
Таким образом, область V2, занятая
магнитным полем. и внешняя по
отношению^ областям, в которых распределены
токи, является многосвязной. Скалярный
потенциал <р*—многозначная функция
положения, поскольку к её значению в
любой точке Р можно прибавить в
результате и полных обходов вокруг тока /
член nl. Область V2 может быть, однако,
превращена в односвязную, а потенциал —
в однозначную функцию, введением сечений или перегородок,
предотвращающих образование таких замкнутых контуров, которые охватывали бы токи.
Эти воображаемые перегородки, конечно, могут быть проведены
бесконечным числом способов. Но если ток состоит из пучка нитей, образующих
одну замкнутую петлю, то проще всего представлять себе перегородку в виде
поверхности, затягивающей эту петлю. Линия MN на рис. 39 изображает след
подобной поверхности. В таком «разгороженном» пространстве линейный
интеграл от Н по любому замкнутому пути равен нулю, поскольку барьер
исключает контуры, охватывающие токи. Соответственно, потенциальная
функция <р* является "однозначной. В точках, лежащих по разные стороны от
барьера, но бесконечно близко к нему, значения <р* отличаются на /. Таким!
образом, мы имеем скачок потенциальной функции, равный
ф ?;-?!=л (8>
где индексы-j-и — относятся к положительной и отрицательной сторонам
поверхности. Согласно разделу 3.16, скачок <р* при переходе через барьер
эквивалентен скачку при переходе через поверхностный дипольный слой
с постоянным моментом I на единицу площади. Только в том случае, когда,
все токи равны нулю и источниками поля являются постоянные магниты,
потенциал становится однозначной функцией положения.
4.3. Исследование Пуассона. В любой точке, в которой плотность
токов равна нулю, в частности во внутренних точках постоянных магнитовv
ОБЩИЕ СВОЙСТВА МАГНИТОСТАТИЧЕСКОГО ПОЛЯ [4.3] 207
'"'! С '" —' ■
мы имеем:
B = -{x0grad(p*-f {x0(M + M0). (9>
Поскольку дивергенция вектора В равна нулю, скалярный, потенциал
удовлетворяет уравнению Пуассона
Д9* = _1_р* р*= —div(M + M0). A0)
Величина р* является магнитным аналогом плотности «связанных зарядов», и
в старой литературе её часто называли смагнитным флюидом» Пуассона *).
При переходе через какую-либо поверхность разрыва в среде
магнитные векторы, согласно разделу 1.13, удовлетворяют условиям
п(В2 — 80 = 0, [п, Н2 — Н,]=0. A1)
Эквивалентные условия, налагающиеся на скалярный потенциал, будут,
следовательно:
(£н*).~-■ т-т=°- <12>
@* = п{(М4-М0I-(М+М0J}. A3>.
Внутри любой замкнутой области, в которой содержатся постоянные
магниты и поляризующееся вещество, но плотность тока в проводимости
J равна нулю, магнитостатическая задача математически эквивалентна
электростатической.
Вычисление потенциала о* по плотностям р* и о* было описано в
предыдущей главе. Мы имеем:
• <?* (*', У, ^) = ~ / Р* (х, у, z) A-dv -f ~ j со* (х, у, z) -L da. A4>
где, как обычно, r=Y(x'— Х)*-{~(У—УР~\-(*?— ■гJ- Для Т0Г0 чтобы
вычислить интеграл, мы должны знать как постоянное намагничение М0, так
и индуцированное намагничение М; однако индуцированное намагничение
само является функцией напряжённости поля, а значит и функцией <?*. Однако
если постоянно намагниченные тела расположены не слишком близко друг
к другу, то индуцированным намагничением можно обычно пренебречь по
сравнению с М0. Затем делаются некоторые предположения относительно Щ
и постоянное или первичное' поле источников подсчитывается с помощью
A4). В окружающих поляризующихся телах, например мягком железе, это
первичное поле индуцирует намагничение М. Расчёт индуцированного или
вторичного поля представляет собой краевую задачу, которую мы
рассмотрим позже.
Подсчитаем теперь магнитный моМент намагниченного образца
вещества. По аналогии с электростатикой (раздел 3.11) этот момент выражается-
интегралом
т= Jr,p* ($, т), С)Л>+ Jiyo* (£, 7i, Qda, A5y
v s
где г1 = Ц-\-}'ц-\-Ыш (рис'. 30, стр. 163) является вектором, проведённым
из начала координат к элементу «магнитного заряда», а 5—поверхность,
ограничивающая тело, объём которого есть V. Заменяя р* и ш* их
значениями согласно A0) и A3) и выполняя затем преобразование посредством-,
тождества
\ div М = div (Щ) — M'grad %,
*) В оригинале — ideal magnetic matter. Прим. ред.
'208 ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
применяемого к каждой из компонент г1} мы найдём, что A5) принимает вид:
m = J*(M + M0)rfo. A6
v
Магнитный момент тела равен объёмному интегралу от его намагничения.
Наконец, если уравнение A4) преобразовать по формуле (9), стр. 168,
заменив р* и ю* из A0) и A3), то для потенциала ю* мы получим:
9* (*', у', г') = i- J(M + М0) grad (|) dv. A7)
v
Если размеры намагниченного тела достаточно малы по сравнению с
расстоянием до наблюдателя в точке (х\ у', г'), то изменением grad Г—J в объёме
V можно пренебречь, и мы получаем выражение для скалярного потенциала
•магнитного диполя
<?*(*', У\ *0 = ^ragrad(^) = -^mgrad'(-L). A8)
РАСЧЁТ ПОЛЯ ДАННОГО РАСПРЕДЕЛЕНИЯ ТОКОВ
4.4. Закон Био и Савара. Выше было показано, что в однородной
изотропной среде с постоянной магнитной проницаемостью jj. векторный
потенциал удовлетворяет системе уравнений
ДА,^ — yjjt divA = 0 (/=1,2, 3), A)
где А^-—прямоугольная компонента вектора А, но ограничение
прямоугольными координатами не должно обязательно распространяться на скалярный
оператор А. Рассматривая А^- и Jj как вариантные скаляры, мы можем
непосредственно применить к уравнению A) теорию интегрирования уравнения
Пуассона, развитую в разделе 3.4. Если область распределения токов может
быть ограничена сферой конечного радиуса, то каждая компонента
векторного потенциала может быть выражена в виде интеграла
А,- (*', V', г') = JL J J3. (х, Ч г) ±-dv (j = 1, 2, 3), B)
распространённого по всему пространству. Эти компоненты можно теперь
соединить в вектор
А (*', У, г') = -£ j J (х, у, г) i- dv, C)
где г = Y(x'—xf ~\- (у' —yf -|- (г' — гJ. Кроме того, из раздела 3.7
следует, что если J — ограниченная и интегрируемая функция, то А —
непрерывная функция координат (х\ у', z'\, имеющая нецрерывные первые
производные в каждой точке как внутри распределения токов, так и вне его.
Если J и все производные порядка ниже п конечны и непрерывны, то
векторная функция А имеет непрерывные производные всех порядков ниже п-\-1.
Векторный потенциал, определённый выражением C), удовлетворяет
условию div А = 0 только тогда-, когда распределение токов пространственно
ограничено. Интеграл регулярен и, следовательно, допускает
дифференцирование под знаком интеграла:
. div'A = £ J J (х, у, z) grad' (±-)dv =
= - £ j J (xt у, г) grad (-1) dv. D)
J grad (I) = div у — у div J = div у , E)
РАСЧЕТ ПОЛЯ ДАННОГО РАСПРЕДЕЛЕНИЯ ТОКОВ ^ 209
в силу условия divj = 0. Следовательно:
div'A = — Л- fdiv — dv = — Л (~da = 0, F)
S
ибо все линии тока замыкаются сами на себя в конечной области пространства,
и поверхность 5 может быть выбрана так, чтобы нормальная компонента
тока на ней отсутствовала.
Обратим' внимание на то, что слагаемое dk векторного потенциала
параллельно элементу тока J dv. Уравнение C) может быть упрощено в
случае токов в линейных проводниках, т. е. в проводниках, поперечные сечения
которых da настолько малы по сравнению с расстоянием гу что вектор
плотности тока на этом сечении можно считать постоянным и направленным вдоль
проводника:
J dv = J dads = / ds, G)
?ле— / полный ток, протекающий по проводнику, a ds — элемент длины
проводника. Поскольку стационарный ток / должен быть постоянен во всём
контуре, выражение C) принимает вид:
А (*',У, *') = -£[ j-^-ds, (8)
с
где интеграл должен быть распространён по всему контуру С.
Поле может быть получено непосредственно из C) подсчётом ротора А
в точке (x',y',z'). В силу сходимости интеграла и непрерывности его первой
производной, дифференциальный Оператор может быть введён под знак
интеграла:
Н (*',y\z') = ±f rot-1 J (xf z) \ dv. (9)
Разложение подинтегрального выражения в соответствии с элементарными
правилами даёт:
rot' *<?>У_Л = 1 rot' J (х,у, г) + [grad' 1, J {xyy, г) J . / A0)
Но плотность тока является функцией текущих координат xyyyz, в то время
как дифференцирование производится по координатам х',у', z'\ соответственно
первый член в правой части равен нулю, и для вектора поля получаем:
Если г° — единичный вектор, направленный от элемента тока к точке
наблюдения, то уравнение A1) эквивалентно уравнению
H(x\y',z')=±f&gl-dv, A2)
которое для линейного контура принимает вид:
К(*',/,г') = -^ p-^pds, A3)
с
где s° — единичный вектор, направленный вдоль элемента тока /. Закон,
выраженный соотношением A3), часто формулируется в виде утверждения,
14 Зак. 593, Теория электромагнетизма.
210
ГЛ. IV. М ЛГЫТОСИАТИЧЕСКСЕ ПОЛЕ
что каждый элемент тока вносит в полное поле слагаемое, равное
dti
1 [s°, r°]
7 гз
Ids.
A4)
По существу это и есть тот вывод, который сделали из опытов Био и Савар
в 1820 году. Нельзя привести неоспоримых доводов, заставляющих
отвергнуть формулу A4), кроме -того факта, что такое разложение A3) на
дифференциальные элементы неоднозначно, так как к A4) можно прибавить
любую векторную функцию, интеграл которой по замкнутому контуру равен
нулю. Все стационарные токи состоят из замкнутых нитей, так что трудно
лредстазить себе опыт, который позволил бы определить слагаемое от
отдельного элемента. Очевидно, при применении
соотношения A4) для исследования поля не может
получиться никакой ошибки в результате, если подразумевать,
что эти слагаемые должны быть впоследствии
просуммированы по замкнутому контуру.
В то время как векторный потенциал от беско-
J нечно малого элемента тока направлен
параллельно элементу, вектор поля Н направлен нормально
к плоскости, в которой расположены элемент тока
и линия, соединяющая его с точкой наблюдения,
т. е. к плоскости, определяемой единичными
векторами s
вектор - г0
будет:
и
с
г°. Если 6—-угол, который образует
вектором s°, то напряжённость поля
dH =
1 sin О
4л: ~2
ds.
A5)
i_±_r
Рис. 40. Соленоидальное
распределение токов.
Поле вдоль оси соленоида может быть, например,
приближение подсчитано, если мы заменим
действительное распределение токов эквивалентными
листками тока пренебрежимо малой толщины (рис. 40).
' Если мы имеем п витков на метр, по которым
течёт ток в / ампер, то плотность тока в листке будет К= In. Слагаемое
от соленоидального элемента радиуса а и длины dx на расстоянии х по
оси от точки наблюдения будет:
dti = -х vr- dx = ~ d (cos H).
(a- + x~yi-
nJ
2
A6)
Эти слагаемые направлены вдоль оси. В любой точ.се на оси поле будет:
и __ til f х2 д-1 ^
п!
= -^-(cosQ2-j-cos01).
В центре оно равно:
Н=п1
У Г- + 4а2
A7)
A8)
Другой простой случай, представляющий некоторый интерес, это прямой
провод бесконечной длины и кругового сечения. Предположим, что ток /
распределён по сечению провода равномерно. Проще всего получить решение,
воспользовавшись преимуществом цилиндрической симметрии поля при применении
интегрального закона ф Н ds = I. Если г — расстояние от оси по радиусу,
РАСЧЕТ ПОЛЯ, ДАННОГО РАСПРЕДЕЛЕНИЯ ТОКОВ [4.5] 211
а а — радиус провода, то очевидно
2тсгН = 1, H = h> ^>й)- A9>
Поле вне провода, не зависящее от его радиуса, может быть получено
также и из закона Био и Савара. Если, однако, мы попытаемся подсчитать
векторный потенциал с помощью соотношения (8), то увидим^ что интеграл
расходится, так как в рассматриваемом случае распределение токов не
ограничивается областью конечной протяжённости. В действительности векторный
потенциал будет:
Л, = Ле = 0,Ля==^-1п1 (/•><*), ,B0)
что можно проверить, подсчитав ротор в цилиндрических координатах
(стр. 56). При г—»■ оо эта функция становится бесконечной.
4.5. Разложение векторного потенциала. Следуя примеру раздела 3.11
для случая скалярного потенциала, мы найдём разложение векторного
потенциала стационарного распределения токов по координатам точки
относительно заданного начала отсчёта. Чтобы обеспечить регулярность
на бесконечности, • мы предположим, что вся область распределения
токов может быть окружена сферой конечного радиуса R, с центром
в начале координат. Мы будем рассматривать здесь только точки наблюдения
вне этой сферы. Распределение токов может быть совершенно произвольным,
но необходимо предположить, что магнитная проницаемость ja всюду одинакова
и постоянна. Практически мы исключаем тем самым только ферромагнитные
вещества, допуская проводники любой другой природы и формы, помещённые
в диэлектрик любого вида.
Обозначения в основном будут те же, какие были приняты в разделе
З.Н и показаны на рис. 30. Для удобства суммирования мы будем
обозначать координаты точки Р через xv x9, лг3, а координаты элемента тока через
£i> ^2» ^3* Расстояние от начала О до точки Р равно г = Yx\ + х\ ~Ь ХЬ &
от элемента J (£lf £2, £8) dv до Р:
Ч
В точке Р векторный потенциал равен, следовательно:
v
где интеграл распространён по всему объёму V, ограниченному сферой'
радиуса R. Если гй — вектор, компоненты которого ^-, то разложение 1//"э-
в ряд Тэйлора около точки О даёт:
Соответственно, векторный потенциал может быть представлен в виде
разложения:
А (х£) = £ А<») = £ 1J J Ь) dv - £ j (rlgrad -I)j (£,) dv +
+ |r/{r1grad(r1gradi)}j(e)^-... B3>
n-0
14*
212 ГЛ. IV. МЛГНИТОСТАТИЧЕСКОЕ ПОЛЕ
Заметим, что J и гх являются функциями £/, по которым должно
производиться интегрирование; функция — зависит только от х/ и оператор
grad действует только на эти координаты.
В силу своего стационарного характера, распределение токов может
быть разложено на нити, причём see они замыкаются сами на себя в
пределах области V. Выделим одну из этих нитей. Предположим, что dax—
бесконечно малое сечение этой нити, а ток, протекающий по этому линейному
контуру, пусть'будет / = |J| dav Положение точки на контуре определяется
вектором rlt проведённым из начала координат (рис. 41), а элемент длины
вдоль контура в направлении тока будет dtx. Тогда для каждой нити или
трубки:
С
где С—замкнутая нить тока (если V содержит только часть токов, то А(°)
не обязательно равно нулю).
Таким образом, главным членом разложения будет второй, который мы
преобразуем следующим образом:
(rx grad i-) dvx = у [[r1} drx\ grad 1] -f-| d {(rx grad yj r,|. B5)
Полный дифференциал при интегрировании по замкнутой нити исчезает, а
член -х- [rx, drx] = n da является вектором площади бесконечно малого
треугольника, заштрихованного на рис. 41.
Следовательно :
A«='-g//[nrfe,gradl].
B6)
Величина
га =/[ п da = ~ j[Tl, flfrj, B7)
Рис. 41. Замкнутая нить тока, обра- по определению, есть магнитный дипольный
зующая контур С. момент замкнутого тока. Поскольку
поверхностный интеграл может быть распространён
,на любую регулярную поверхность, опирающуюся на контур, постольку
магнитный момент зависит только от силы тока и формы контура.
Дипольный потенциал всего распределения получается суммированием по
«сем нитям тока. По определению, магнитный дипольный момент объёмного
распределения токов по отношению к началу отсчёта О есть:
m=Y J[r1(J]
dv.
B8)
v
Намагничением, области с током точно также может быть определено, как
магнитный момент единицы объёма:
.. dm 1 , t1
M==d*==2"Iri'J1-
B9)
Очевидно, намагничение по отношению к данному началу отсчёта будет
получаться всякий раз, когда плотность тока имеет компоненту,
перпендикулярную к вектору rv т. е. когда заряды обладают вращательным движением
вокруг тбчки О как центра. Если р — заряд единицы объёма, a v — скорость,
РАСЧЕТ ПОЛЯ ДАННОГО РАСПРЕДЕЛЕНИЯ ТОКОВ [4,6] 213;
так что J=pv, то намагничение М будет:
М = i-[r„ pv], C0)
что тождественно с плотностью момента количества движения, если р
интерпретировать как плотность массы.
Остающиеся члены разложения B3) представляют собой векторные
потенциалы магнитных мультиполей высшего порядка. Таким образом, мы
дали два различных определения магнитного момента: через эквивалентные
магнитные заряды Пуассона — в полном соответствии с электростатическим
случаем (раздел 4.3), и через распределение токов. Теперь мы должны
показать тождественность двух этих точек зрения.
4.6. Магнитный диполь. Согласно разделу 4.3, намагниченный кусок
вещества имеет дипольный момент, определяемый соотношением A5), стр. 207,
скалярный потенциал которого на достаточно большом расстоянии даётся
формулой A8) того же раздела. Наша первая задача состсит в том, чтобы
определить эквивалентный векторный потенциал, векторную функцию, ротор
которой даёт то же поле, что и градиент скалярной функции <р*. Снова
будем считать (х\ у', г') точкой наблюдения и помещать диполь в (х, y,z).
Тогда:
П(х',у',г')= — grad'9* =~ grad' (га grad'l). C1).
и, следовательно:
rot' А =£ grad' (m grad'l). C2)
Чтобы раскрыть правую часть C2), мы учтём, что га — постоянный вектор,."
или в крайнем случае функция (x,y>z), тогда как rot' и grad' действуют лишь
на координаты (х', у', г'). Кроме того,
rot' grad' A) = 0, div'grad'(y)=0. C3)
Можно без труда убедиться в том,^что
grad' (mgrad' ~) = -rot' [ш, grad' ij, C4)
откуда
rot' A =; —5Г 'of [m, grad' 1]. C5>
Следовательно:
A + Ь [га' 2гаа' т] = grad7«/, *')> C6)
где /—произвольная скалярная функция. Дивергенция правой части должна
быть равна нулю, и следовательно / может быть любым решением уравнения
Лапласа. Однако / ничего ье добавляет к полю Н, и мы вправе положить
её равной нулю. Векторный потенциал магнитного диполя будет поэтому
A(V,y.O--£lJ«5g»a'4]-£[".8i^, .1(87)
Уравнение C7) совпадает с выражением для векторного потенциала,
который мы связали в предыдущем разделе с дипольным моментом тока. На.
достаточно больших расстояниях поле любого источника — намагниченного
вещества, или стационарного тока — сводится к полю магнитного диполя-
214 ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
Это представляет собой не более, чем новое выражение того обстоятельства,
что намагниченная область полностью эквивалентна распределению токов
с плотностью J' = rot M и даёт нам математическое подтверждение ампе-
ровской интерпретации магнетизма с помощью бесконечно малых круговых
токов.
4.7. Магнитные листки. Пока что мы показали, что потенциал любого
замкнутого линейного тока может быть разложен в ряд мультипольных
потенциалов. Стягивая замкнутый контур тока около некоторой точки
(л:, у, г) до бесконечно малых размеров, мы можем представить этот
потенциал всюду, за исключением самой этой особой точки, одним лишь ди-
польным членом. Магнитный момент
получающегося в результате элементарного линейного тока
равен:
dm = /n da, C8)
где п—положительная нормаль ' к бесконечно
малой плоской площадке da. Элементарный
момент зависит от величины тока и от охватываемой
контуром площади, но не от формы контура.
Любой линейный ток произвольного
размера и формы может быть разложен на систему
элементарных токов. Пусть S (рис. 42) будет
какой-либо регулярной поверхностью,
опирающейся на замкнутый контур С; построим сетку из
пересекающихся линий, оканчивающихся на
контуре С. Представим себе теперь, что по
контуру каждой элементарной площадки протекает
ток /, равный по величине току, протекаю- г
щему по. контуру С, и направленный в ту же
сторону. Магнитное поле от подобной, сети токов всюду совпадает с
магнитным -полем тока / в простом контуре „С, так Как токи, текущие по
общим границам соприкасающихся элементов поверхности, всюду взаимно
компенсируются, за исключением внешнего контура. По мере увеличения
густоты подразделения, поле каждой ячейки всё более приближается к полю
диполя, ось которого направлена по положительной нормали. Очевидно,
в пределе поле сетки и, соответственно, поле тока / в контуре С будет
•совпадать с полем диполей, распределённых по поверхности S, т. е. с полем
двойного слоя на поверхности S. Плотность или мбмент единицы площади
эквивалентного поверхностного распределения постоянна и равна:
Рис. 42. Разложение тока /,
циркулирующего по
контуру С, на элементарные
токи.
dm т
х = -=- = /п.
da
C9)
Таким образом, всякий линейный замкнутый ток действует как
намагниченный листок. Скалярный потенциал такого листка был определён в
разделе 3.16 в связи с двойными слоями зарядов:
<?* (*', у', *') ~ -^ J <<ю =—т,
D0)
сдеЙ— телесный угол, под которым поверхность 5 видна из точки (х'у у'у г').
Кроме того, как было показано, потенциал двойного слоя многозначен.
Скачок ©* при перехбде через поверхность 5, согласно A7), стр. 173, равен
* * г
со, — о = т = /,
D1)
ОТСТУПЛЕНИЕ ПО ПОВОДУ ЕДИНИЦ И РАЗМЕРНОСТЕЙ 14.8] v 215
ш соответствии с тем, что линейный интеграл от Н по какому-либо
замкнутому контуру, пересекающему поверхность 5 один раз, есть
(£ Hrfs = — &do*=*I. D2)
Поверхность S, несущая двойной слой или магнитный листок, совершенно
произвольна и, очевидно, математически эквивалентна «перегородке»,
посредством которой магнитное поле в разделе 4.2 превращалось в односвязную
область.
ОТСТУПЛЕНИЕ ПО ПОВОДУ ЕДИНИЦ И РАЗМЕРНОСТЕЙ
4.8. Основные системы. В разделе 1:8 анализ размерностей
электромагнитных величин был основан непосредственно на уравнениях Максвелла,
и выбор системы единиц MKJS оправдывался тем, что она является
одновременно и «абсолютной» и практической системой. Исторически развитие
различных систем шло иным путём. До тех пор, пока электростатические и маг-
«итостатические явления рассматривались как совершенно независимые друг
от друга, было естественно, что для измерения электрических и магнитных
величин должны были существовать две независимые абсолютные системы.
Открытие Фарадеем закона индукции и последовавшее много позднее
доказательство того, что токи представляют собой не что иное, как
движущиеся заряды, установило связь между этими двумя группами явлений
м наложило определённые условия на выбор некоторых констант, которые
до этого были произвольны.
Выбор единиц и их размерностей для электростатических величин
обычно основывался на законе Кулона: сила, действующая между двумя
зарядами, прямо пропорциональна произведению их величин и обратно
пропорциональна квадрату расстояния между ними:
"Так как наличие вещества не влияет на размерность заряда, то мы будем
далее предполагать, что все силы измеряются в свободном пространстве.
В системе «рациональных» единиц коэффициент пропорциональности k^
выбран равным 1/4тсе0; в «нерациональных» системах множитель 4~ опущен.
Константа эта совершенно произвольна и не обязательно безразмерна, так
что размерность заряда может быть выражена только через е0. Из A) мы
получаем:
1 JL 1 _i
[д]=е02ЖЧ2Г , B)
Из уравнения непрерывности ясно, что размерность тока равна размерности
заряда, делённого на время:
[/] = e0^M"La Т-2. C)
Вывести из этих соотношений размерности всех остальных чисто
электрических величин не представляет труда.
Более естественным образом свойства магнитного вещества могут быть
описаны с помощью магнитного момента га, а не с помощью фиктивных
-«магнитных зарядов». Вращающий момент,. испытываемый магнитом' или
витком тока с моментом га2, помещёнными в поле В, создаваемое источником
с моментом ш1э равен:
Т=[ш2,В], D>
V
216 ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
а вектор В выражается через магнитный момент источника тг посредством
C1), стр. 213. Из этих двух соотношений мы легко можем вывести, чтс*
размерность магнитного момента есть:
_Jl. J- L
[m]==ti-0 2M*L2T-1. E>
Соотношение E) выведено непосредственно из выражения для взаимных
вращающих моментов двух магнитных диполей, являющегося по существу
магнитным аналогом закону Кулона. Однако, это не единственный
экспериментальный закон, в который входит магнитный момент. То, что магнитный
момент га небольшого витка или катушки с током / пропорционален току
и площади витка, также известно, как опытный факт. Коэффициент
пропорциональности, который мы будем обозначать через 1/?, подобно е0,
и [а0 произволен по величине и размерности, так что размерность m должна
также выражаться уравнением
i. J- L -2
[ra] = «v-1[/]L2 = 7-l£o2M2L2T • 16)
Связь магнитного момента с током и тока с электрическим зарядом
накладывает, таким образом, условие на произвольные константы е0, {х0 и ^.
Каков бы ии был выбор этих трёх коэффициентов, их размерности должны
быть таковы, чтобы соотношения E) и F) были совместны. Приравнивая
E) и F), получаем, что
■< -L--c. <7>
Vwv
г
Величина характеристической скорости с должна быть определена из опыта.
В главе I она фигурировала как скорость распространения полей и
потенциалов в свободном пространстве; теперь она встретилась нам в качестве
отношения электрических и магнитных единиц. Для того чтобы определить
величину ,с, не обращаясь к непосредственным измерениям скорости, выбирают
такую величину, которая может быть подсчитана в одной системе единиц,
а измерена в другой. Сравнительно просто, например, подсчитать ёмкость,
конденсатора, исходя из его геометрической формы, а электростатическая ёмкость
любого другого конденсатора может быть измерена с помрщью этого
первичного эталона и ёмкостного моста. С другой стороны, баллистический
гальванометр измеряет заряд на обкладках конденсатора благодаря магнитным
действиям, которые производит ток при разряде конденсатора через
гальванометр. Можно показать, что отношение полученных таким образом двух
значений ёмкости есть
- §*=7Zr = c2> <8>
где Се-г-расчётное электростатическое значение ёмкости, а Ст — значение,
измеренное в электромагнитных единицах. Принятое для с значение равна
примерно 3 • 108 метров)сек.
Разнообразные системы размерностей, которые в то или иное время,
применялись в литературе по электромагнитной теории, получались в
результате того, что двум из трех констант е0, ^0 и Т приписывались
произвольные значения, а значение третьей определялось тогда из соотношения
G). Мы дадим краткий обзор наиболее важных из этих систем.
1. Электростатическая система. Если е0 = 1, f = 1, то все величины
и электрические, и магнитные выражаются в электростатических единицах.
Из соотношения G) мы получаем для |t0 значение
jx0== 1/9- ТО0 (сек/смJ. (9)
ОТСТУПЛЕНИЕ ПО .ДОВОДУ ЕДИНИЦ И РАЗМЕРНОСТЕЙ [4.9] 217
Единицы CGS в этой системе основываются на определении заряда из закона
Кулона: два единичных точечных заряда, расположенных на расстоянии
1 см друг от друга, взаимодействуют с силой в 1 дину.
2. Электромагнитная система получится в том случае, если мы положим:
Н.0= 1, <y=1, е0= 1/9.10-20 (cetcjcM)*. A0)
Отношение значений заряда, измеренного в этих двух системах, равно:
где де— величина заряда, измеренного в электростатических единицах, а дт<—
величина того же самого заряда, измеренного в электромагнитных единицах.
3. Система MKS, подробно описанная в разделе 1.8, является по
существу электромагнитной системой, в которой единицы массы и длины
подобраны таким образом, чтобы единицы электрических и магнитных величин
были пригодны для практических измерений. В том виде, в каком эта система
принята в настоящей книге, кулон введён в качестве независимой единицы,
что приводит к значениям:
{а0 = 4ir-Ю-7 генри/метр, 7=1,
е0 = 8,854-10-12 фарад/метр. A2)
В другом варианте системы MKS полагают:
jj.0 = 4^- Ю-7/ -у= 1» е0=8,854-10-12 (сек/метр)*, A3)
что в отношении размерностей тождественно с электромагнитной системой.
4. Гауссова система до последнего времени применялась в научной
литературе наиболее широко. Она представляет собой смесь из
электростатической и электромагнитной систем, которая получается, если положить:
ео=1» Po=h Ч = с- (I4)
Коэффициенты е0 и [а0 из всех уравнений выпадают, электрические величины
выражаются в электростатических единицах, а магнитные—в
электромагнитных. Однако преимущества всего этого сомнительны. Вспомнить, в каком
месте надо написать коэффициент с, входящий в электромагнитные
уравнения, написанные в гауссовой системе, не проще, чем с самого начала
сохранять коэффициенты е0 и \ь0. Система MKS столь же «абсолютна»
и «научна», как и Гауссова, и едва ли для многих единицы системы CGS
более предпочтительны, чем вольты, омы и амперы. В общем, нам кажется,
что чем скорее излюбленная ранее система будет оставлена, тем скорее
придёт конец совершенно излишнему поводу для путаницы.
Любое уравнение, содержащееся в этой книге, может быть переписано
в гауссовой системе единиц заменой е0 и jx0 на */с» a J и р — соответственно
на J/c и р/с.
4.9. Закон Кулона для магнитных зарядов. В старой литературе
магнитная система единиц, обычно основывалась на законе сил, действующих
между магнитными «полюсами». «Заряд», или сила полюса д* определялась
так, чтобы произведение д* на длину диполя / равнялось моменту диполя
т. Согласно E), размерность д* равна тогда:
_Л JL 1 _,
[0*]=^ 2M2L2T 9 A5)
в то время как для закона сил* соответствующего закону Кулона, мы получаем:
4п г* '
A6>
/ -1 " .-
;218 гл. iv. магнитостатическое. поле
Это выражение отличается от обычно принятого тем, что ^0 находится
is числителе, а не в знаменателе х). В основе этого странного результата
лежит то обстоятельство, что выводимая из уравнений Максвелла сила,
действующая на элемент тока (раздел 2.4), равна [J, В], а не [J, HJ.
Соответственно вращающий момент, действующий на диполь, равен [га, В], а сила,
действующая на магнитный «заряд», будет F = ^*B.
Для того чтобы A6) в точности «соответствовало электростатической
модели, принято обычно писать ja в знаменателе, и определять вектор Н
с помощью соотношения F = g*H. Однако этот способ, пока ja0 считается
отвлечённым числом, приводит к неувязкам в размерностях в уравнениях
ноля и в его пользу можно сказать немного. Сходство в природе
векторов Б и В и векторов D и Н было осознано более поздними авторами.
МАГНИТНАЯ ПОЛЯРИЗАЦИЯ
4.10. Эквивалентное распределение токов. Эквивалентность
намагниченного тела и соответствующим образом распределённых токов уже
неоднократно отмечалась выше. Посмотрим теперь, как подобное распределение
может быть найдено в общем виде для тела объёма V, ограниченного
поверхностью S.
Мы предположим, что величина намагничения, или поляризация М,
содержит и постоянное намагничение М0, если таковое имеется. Согласно
^37), стр. 213, векторный потенциал в любой точке вне тела равен:
А « у', г') = J£ J* [м (*, у, г), grad 1] dv. A)
v
В силу векторного тождества
Г™ а П fotM * М /оч
^М, grad yJ = — rot— B)
и основной формулы о преобразовании объёмного интеграла от ротора
вектора в поверхностный интеграл от тангенциальной компоненты этого
вектора:
Jrot-£,ft, = p^U, C)
• V S
.мы находим, что правую часть соотношения A) можно разложить на две
части:
А (У, У, О - £ / *¥- *+ ■£ / -^ da. D)
V S -
Таким образом, векторный потенциал, связанный с намагниченным телом,,
будет точно таким же, как и векторный потенциал объёмных и
поверхностных токов, плотности которых равны соответственно:
J' = rotM, K' = [M, п]. E)
Справедливость этого результата как для внутренних точек, так и для
внешних легко может быть доказана. Поверхностный интеграл сходится,
очевидно, во всех точках, не лежащих на поверхности S, а объёмный
интеграл может быть разложен на три скалярных компоненты, каждая из
которых эквивалентна скалярному потенциалу соответствующим образом
распределённых зарядов.
J) Sommerfeld, Ueber die elektromagnetischen Einheiten, стр. 161, Zeeman,
Verhandelingen, Martinus Nijhoff, The Hague, 1935.
МАГНИТНАЯ ПОЛЯРИЗАЦИЯ 14.1 Ц 219
к-'.' •■." , . .
f; Напомним, что магнитная поляризация была введена первоначально
Ж разделе 1.6 как разность векторов В и Н:
М = —В —Н. F)
На поверхности разрыва между двумя магнитными средами векторы поля
удовлетворяют граничным условиям раздела 1.13, а именно:
п(В2 — В1) = 0, [п-На —HJ--.K, G)
_ которых в случае конечной проводимости плотность поверхностных токов.
Зравна нулю. В соответствии с F), эти условия эквивалентны таким:
п(В2—В1) = 0, [п,В2 — BJ = !х0 (К + К'), (8)
оде
K'^lMi — M2, п]. (9)
4.11. Поле намагниченного стержня и шара. В качестве примера мы
.рассмотрим стальной стержень или цилиндр кругового сечения, равномерно
намагниченный вдоль оси. Длина цилиндра пусть будет /, радиус сечения я,
*а намагничение М0. Так как мы предполагаем, что намагничение однородно
т, следовательно, М0 постоянно, объёмная плотность эквивалентных токов
J' равна нулю. Плотность токов на поверхности цилиндра есть К' = [Mq, n].
Таким образом, намагниченный стержень эквивалентен соленоиду тех же
размеров. Векторный потенциал и поле в любой внутренней или внешней
точке могут быть теперь подсчитаны из разложений в ряд, выведенных
в разделе 4.5. Значение В вдоль оси уже было подсчитано в разделе 4.4.
3 частности, мы нашли, что в центре:
B = ti,0Mo . _ . A0)
Наше предположение о постоянстве намагничения для реальных
магнитов довольно сомнительно, особенно вблизи концов. Если, однако, длина
щилиндра либо очень велика, либо очень мала по сравнению с радиусом,
такое приближение оказывается обычно хорошим. Так, например, если 0>а,
так что магнит имеет иглообразную форму, то поле в центре будет:
В=={г0М0. (И)
«В случае l<^ja магнит вырождается в диск, и поле будет:
В = 0. A2)
Если цилиндр сделан не из стали, а из мягкого железа и помещён во
внешнее поле Н0, то постоянное намагничение М0 яолжно быть заменено
индуцированным намагничением М и A0) должно быть интерпретировано,
как индуцированное поле Ъг. В центре длинной иглы в параллельном полеН0
результирующее поле будет:
B^Bo + Bt-Bo+jioM. h = 4-B-M = IV' A3)
таким образом, поле Н внутри иглы точно такое же, какое имело место
первоначально. В случае диска:
В = В0, Н = Н6 —М. A4)
; Очевидно, предположение об однородном намагничении цилиндра из
мягкого железа со срезанными под прямым углом торцами является прямым
.нарушением граничных условий для векторов В и Н. С другой стороны,
220
ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
индуцированное намагничение сферы или эллипсоида в параллельном внешнем
поле должно быть однородным, поскольку магнитная задача совершенна
аналогична электростатической, рассмотренной в разделах 3.24 и 3.27.
Индуцированное или вторичное поле Ъ1 может быть теперь приписано
поверхностным токам, которые циркулируют по зонам, концентричным оси
намагничения, но плотность которых, очевидно, меняется с широтой. Если
6 — угол между внешней нормалью и намагничением М, то
AT'=|[M,n]| = yWsin6. A5)
По закону Био и Савара компонента ВГв направлении М равна:
dBZ = ■&■£■sin2ЫЬ=^- sin3ЫЬ. A6)
После интегрирования это даёт для результирующего поля в центре
выражение
В~ = ^Г / sin3 Ш = 4 ^0 М, A7)
о
в то время как для полного поля получается:
В-= В0-Ь ВГ = Ко (Н0 +1 М),
н~=н0—^-м.
A8)
Важным следствием этого результата является значение поля в центре1
сферической полости, вырезанной внутри жёстко и однородно
намагниченной среды. Поверхностное распределение токов будет точно таким же, но
так как нормаль направлена теперь внутрь сферы, токи будут циркулировать
в противоположном направлении. Индуцированное поле в центре будет
— Y^o М0| а полное поле будет:
2
В =В0— f f%M& = y<o(Ho-f -g-Mo),
A9)
где Н0 и В0 — первоначальные значения полей в среде. Очевидно, эти поля
не удовлетворяют обычным граничным условиям для нормальных и
тангенциальных компонент, и осуществимы только в том случае, если полость
сделана после того, как вещество получило жёсткое намагничение.
РАЗРЫВЫ НЕПРЕРЫВНОСТИ ВЕКТОРОВ А и В
4.12. Поверхностное распределение токов. Из раздела 3.1^4
непосредственно следует, что векторы А и В являются всюду непрерывными
функциями точки при условии, чт© токи распределены объёмно и что их
плотность является всюду ограниченной и кусочно непрерывной. Если*
однако, мы допускаем бесконечную проводимость тела, или хотим
представить намагниченное состояние тела в виде эквивалентного распределения
токов, то становится необходимым учитывать также и поверхностные tokhv
на которых вектор В испытывает разрыв непрерывности. Представим себе
ток конечной объёмной плотности J, заключённой в слое толщины t.
Предположим теперь, что толщина слоя уменьшается, но так что полная сила
РАЗРЫВЫ НЕПРЕРЫВНОСТИ ВЕКТОРОВ А И В [4.12] 221
тока, проходящего через поперечное сечение слоя, остаётся неизменной.
При t -> 0 объёмная плотность необходимо стремиться к бесконечности.
Поверхностная плотность тока определяется как предел произведения:
K = Hm£J при £->0, J->oo. . A)
Поскольку значение J становится бесконечным, такое распределение образует
«особую поверхность.
' Мы будем предполагать, что К—ограниченная, кусочно непрерывная
•функция точки на регулярной поверхности 5. Векторный потенциал в лю-
йай точке (x',y',z), не лежащей на поверхности S, равен:
А(^У,^) = §/1^^^, B)
8
^де г, как обычно, отсчитывается от элемента К (л:, у, г) до фиксированной
точки (х',у', г'). Каждая из прямоугольных компонент 'А представляет собой
интеграл, совпадающий по форме с интегралом, дающим электростатический
потенциал поверхностно распределённых зарядов. В параграфе 3.15 было
показано, что подобные интегралы являются ограниченными непрерывными
функциями координат (x',y',z') во всех точках пространства, включая и
точки, лежащие на поверхности 5. И нормальная и тангенциальная
компоненты векторного потенциала шменяются непрерывно при переходе через
одиночный слой поверхностных токов.
Обращаясь теперь к вектору В, мы получаем, согласно уравнению A1),
стр. 209, что в точках, не лежащих на поверхности Sy
В (*',/, г') = £ j [К(х, у, г), grad ±1 da. C)
s
Разложив К на его прямоугольные компоненты:
K^Mk+jAi + kff,
ты видим, что соотношение C) эквивалентно
В (*', У, г) = g- {[i, J* К* grad ± da] + [j, J* K^grad A da] +
s s
+ [k,jK.gradi&]}. D)
s
Мнтеграл вида:
E (*', у, z') = A- j (o (*, y, z) grad 1 da E)
с точностью до размерного множителя е0 может быть интерпретирован, как
поле, вызываемое поверхностными зарядами, распределёнными по поверхности 5
с плотностью (о. В разделе 3.15 было показано, что при переходе точки
{#', У, z') через поверхность 5 этот интеграл испытывает скачок, равный:
Е+ — Е_ = ш п, F)
•где ш — значение поверхностной плотности в точке перехода. Применяя
этот результат к соотношению D), мы сразу же получаем, что
В+ —B_=ti.0[K,n]. G)
Лри переходе через слой поверхностных токов нормальная компонента
вектора В остаётся непрерывной'.
п(В+— 6^ = 0. (8)
222 ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
Тангенциальная компонента вектора В испытывает скачок, определяемый
соотношением '"
[п,В+—B_]=ii.0[n[K, п]]. (9)
С помощью известного тождества правая часть этого соотношения может
быть преобразована к виду:
[п, [К, п]] =Кй2 — п(пК). (Ю)
Но так как вектор К лежит на поверхности 5 и, следовательно,
ортогонален к единичной нормали п, соотношение (9) сводится к такому:
[n,B+ — BJ=t*0K. (И)
Смысл этого результата станет более ясным, если мы сравним его
с граничными условиями, выведенными непосредственно из уравнений
Максвелла в разделе 1.13. Согласно разделу 4.10, намагниченная среда
эквивалентна токам, распределённым по пространству с объёмной плотностью
J' = rotM; разрывы же непрерывности в намагничении должны учитываться
слоями поверхностных токов с плотностью К' = In, M+ — М_]. Скачок
вектора поля при переходе через подобную поверхность равен:
[п, В+ —В.] = {.0{К+[п,М+—М.]} A2)
или, поскольку — В — М = Н,
[п, Н+— Н_]=К. A3)
Непрерывность нормальной компоненты вектора В при переходе через
границу раздела обеспечивается соотношением (8).
4.13. Поверхностное распределение магнитного момента.
Эквивалентность линейного контура тока и поверхности, несущей распределённые
на ней магнитные диполи, была показана в разделе 4.7. Мы рассмотрим
несколько детальнее разрывы непрерывности, которые испытывают поле и
потенциал в окрестности подобных особых поверхностей, не ограничиваясь
случаем нормального направления намагничения. Пусть вектор М
представляет теперь плотность поверхностного намагничения — магнитный момент
единицы площади поверхности 5. Направление М по отношению к
положительной нормали п произвольно.
В любой точке, не лежащей на поверхности S, векторный потенциал
такого распределения, согласно уравнению C7), стр. 213, равен:
А (*', У, *')=•■£/ U (х, у, z), grad 1] da. A4)
s
Нам достаточно только заметить внешнее сходство этого выражения с
соотношением C), чтобы заключить, что при переходе через поверхность, по
которой распределён магнитный момент, векторный потенциал испытывает
скачок. Величина скачка равна:
А+ — А_ = {а0 [М, п]. A5)*
Нормальная компонента вектора А непрерывна:
п(А+ —А_)=0, A6)
а тангенциальная компонента непрерывна только в том случае, если-
намагничение нормально к поверхности. В противном случае:
[п,А+ — А_] = ^0М — Уо(пМ)п. A7>
РАЗРЫВЫ НЕПРЕРЫВНОСТИ ВЕКТОРОВ А И В 223
Для того чтобы исследовать разрывы вектора В при переходе через
поверхностный слой магнитного момента, целесообразно воспользоваться
выражением вида C1), стр. 213, которое мы в данном случае запишем так:
В(х\ У, г') = - -*£- grad' J M (л-, >>, г) grad-da. A8)
s
Поверхностная поляризация М может быть разложена на нормальную и
тангенциальную компоненты посредством тождества:
M = (nM)n-f [n, M], п], A9)
так что вместо A8) мы получим:
В (х, уу г) =
= — и- ^rad' Г (п, М) n grad l da — -^-grad' f [ [n, Mj, nl grad -l- da. B0)
S S
Из сравнения с соотношением A6), стр. 173, ясно, что первый интеграл
может быть интерпретирован как скалярный потенциал двойного слоя с
моментом т = (Мп) п, тогда как отрицательный градиент от этого потенциала
в точке (х , у\ z') даёт напряжённость поля. В разделе 3.16 было показано,
что по обе стороны от такого слоя нормальная компонента напряжённости
поля при приближении к нему стремится к одному и тому же пределу,
а тангенциальная компонента при переходе через слой испытывает скачок,
выражаемый уравнением B1), стр. 175, и равный в данном случае
Я,+ —Д,_ = —р0^(Мп). B1)
Таким образом, компонента вектора В вдоль любого касательного к
поверхности направления испытывает при переходе через слой поверхностно
распределенного магнитного момента скачок, величина которого
пропорциональна степени изменения нормальной компоненты поляризации в этом
самом направлении.
Обращаясь теперь к слагаемому, даваемому, вторым интегралом в B0),
мы приведём его к более привычному виду путём некоторых преобразований
лодннтетрального выражения. Легко убедиться в справедливости тождества:
[Щ, М], n] gradi = [n, M] [n, grad.1-]. - B2)
Разложим далее [n, M] на его скалярные компоненты:
[n, MJ = i/i+ j/2-f кЛ-
Мы имеем тогда:
f [п, MJ, п] grad у = i [n, fx grai ~ J -f j [\i, /a grad -~J -f- к \п, /3 grad J.-J =
= 1 [n, grad £] + J [n, grad ^]-f-k[n, grad Ц ] —
-i[n,«]-j[n, £^Д]-к[п,^]. B3)
Если / (x, yt z)— функция, непрерывная на поверхности 5 и на
ограничивающем её контуре С вместе со своими первыми и вторыми производными, то
J" [n, grad/| da = (fds. B4)
224 гл. iv. мАгнитостАтичр.ское поле
Отсюда следует, что если тангенциальные компоненты М удовлетворяют на
поверхности 5 поставленным условиям, то три поверхностных интеграла,
подинтегральные выражения которых имеют вид i n, grad — , могут быть.
преобразованы в интегралы по любому замкнутому контуру, лежащему на
поверхности 6', так что:
i f Гп, grad 4] da + j f [n, grad Al da-\- k [ [n, grad ^-1 da =
-J('T+J'v + kT)*=JJbrL*- <25>
С О
Оставшиеся три члена подинтегрального выражения могут быть
преобразованы с помощью соотношении
,[n,J^A]_j[„,£^u]_k[„,««!lA]
= "- ! И. g«d /,] + Ij, grad /a] + [k, grad /,)} = - £12!!»-ЛУ.. B6>
Таким образом, второй член правой части соотношения B0) преобразован
нами в сумму контурного и поверхностного интегралов:
-—grad' J[[n,M],n]grad|^
= _i£gnd' fl«fJ ds+ *» grad' j HS^Lda. B7>
Контурный интеграл является непрерывной и непрерывно дифференцируемой
функцией точек, лежащих на поверхности 5 внутри контура. С другой
стороны, -последний член соотношения B7) может быть интерпретирован как
напряжённость поля в точке (х, у', г) о г зарядов, распределённых по
поверхности с плотностью:
— nrot [п, Щ.
Мы должны, следовательно, заключить, что тангенциальная компонента
поверхностного намагничения приводит к скачку нормальной компоненты
вектора В на поверхности 5, равному по величине:
£„+—-£„_ = —1*0 nrot [п,М]. B8У
Дифференцирование ограничено направлениями, касательными к поверхности.
Следовательно, вектор grad (Мп") касателен к поверхности, в то время как
вектор rot [пМ] нормален к ней. Скачок непрерывности, испытываемый
еекторо и В, при переходе через поверхность с распределённым по ней
магнитным моментом может быть выражен в виде единой формулы:
В_и — В_ = — и, [ grad (пМ) + rot [n, M] }. B9)
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ rot rot А = у. J
4.14. Векторный аналог теоремы Грина. Классический способ
нахождения векторного потенциала основывается на разложении его на
прямоугольные компоненты. В предположении div A= 0 можно показать, что каждая
из компонент удовлетворяет уравнению Пуассона, и для решения задачи
могут быть применены методы, развитые при рассмотрении
электростатического потенциала.
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ TOtrot A = {A J H-lo] 225
возможность непосредственного интегрирования уравнения rot rot A = jaJ
путём применения ряда векторных тождеств, совершенно аналогичных
тождествам Гри ia для скалярных функций, повидимому, осталась незамеченной.
Пусть У — замкнутая область пространства, ограниченная регулярное
поверхностью S; пусть Р и Q — две векторные функции точки, непрерывные в
области У и ьа поверхности 5 вместе со своими первыми и вторыми
производными. Если теперь применить теорему о дивергенции к вектору [Р, rotQ],
то получим:
f div[P,i\>tQ|rf<0 = [ [P, rotQ] nda. A)
У S
Развёртывая подннтегральное выражение объёмного интеграла, мы получаем
векторный аналог первого тождества Грина (стр. 153):
Г (rot P rot Q — Р rot rot Q) dv = J* [P, rot Q] n da. B)
V 's
Аналог второго тождества Грина получается переменой местами Р и Q
и вычитанием из B). В результате имеем:
Г (Q rot rot Р — Р rot rot Q)dv = [ {[Р, rot Q] — [Q, rot P]j n da. C)
v s
4.15. Применение к векторному потенциалу. Мы предположим, что
объёмнал плотность тока J{x,y, z) является ограниченной, а в остальных
отношениях произвольной функцией точки. Регулярная поверхность S,
ограничивающая область I-7, не обязательно должна полностью охватывать все
источники поля или какую-либо часть их. Как и в разделе 3.4, мы выберем
точку О в качестве произвольного начала отсчёта, а через х = х', у=у',
z = z будем обозначать координаты точки внутри объёма V.
Пусть Р является теперь векторным потенциалом А, который подчинён
условиям:
rot rot A = JJ-J, div A = 0, D)
где \i — магнитная проницаемость среды, которая предполагается
однородной и изотропной. Q можно выбрать двумя способами. Напомним, что
в скалярном случае функция Грина й удовлетворяла уравнению Лапласа
Дй = 0 и могла быть интерпретирована как потенциал в точке {x',y',z')
от заряда 4us, расположенного в точке (х, у, г). Точно так же векторная
функция Грина Q может быть выбрана так, чтобы представлять в точке
(x',y',z) вектор! ий потенциал от тока с плотностью 4тг/«х,
расположенного в точке (х, у, z) и ориентированного произвольно, вдоль направления,
определяемого единичным вектором а:
Q (x,y, z; x\y\ z') = ~, г = У(*' — х)* + (у' — J"* + (?'~~W- E)
Однако дивергенция этой функции не равна нулю, и, следовательно, E) не
удовлетворяет условию rot rot Q = 0. С другой стороны было показано, что
векторный потенциал некоторого распределения магнитных моментов всюду
удовлетворяет уравнению rot rot A = 0, так что для теперешней нашей
задачи подходящей функцией Грина будет также:
grad --,а
-rot-?-. F)
Очевидно, F) можно интерпретировать как векторный потенциал диполя
с моментом — а.
15 Зак. 593. Теория электромагнетизма.
226 ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
Для интегрирования уравнения D) можно применить кяк E), так и F),
но необходимые преобразования оказываются более простыми в случае
применения E), несмотря на то, что дивергенция E) не равна нулю.
Действительно, мы имеем в случае E):
rot Q = grad —, а , rotrot Q — grad ( a grad —J, {7)
P rot rot Q = A grad fa grad ~\ = div [fa grad -i ) a} . (8)
При всех этих преобразованиях, а также и при последующих, мы должны иметь
в виду, что а — постоянный вектор. Левая часть тождества C) может бить
теперь записана в виде:
f (*- J - div •[ (a grad 1) А } ) dv =
v
= а Г - - dv — а Г (A, n) grad — da. (9}
v s
Переходя к преобразованию поверхностных интегралов, имеем:
[Р, rot Q] n= [A [grad 1 , а ]] п =, a [grad A [A, n]"|, A0>
[Q, rot Р]п ==[-*-, rot A]n = a-^f A1)
где вместо rot А написано' В. Тождество C) принимает вид:
.ц J" ^ dv = f (An) grad I da -f f [grad ± [A, nl] da -f f ljl~] da. A2)
V S S " R
Справедливость этого соотношения установлена только для тех
областей, в которых обе функции Р и Q являются непрерывными и обладают
непрерывными первыми и вторыми ироизводными. Однако Q имеет
особенность в точке г = О и эта точка должна быть, следовательно, исключена.
Опишем вокруг точки (л;', у', г') небольшую сферу радиуса гх. Область V
ограничена теперь поверхностью сферы St и ограничивающей её извне
1 г°
поверхностью. S, как показано на рис. 25, стр. 153. Поскольку grad — = -.,,.
поверхностный интеграл по St может быть написан в виде:
Л f r°(An) rfa + -L f [r° [A, n]] Л+ 7- f [n, B] da.
Подинтегральное выражение среднего члена преобразуется так:
[г°[А, п]].= (г°п)А —(A n)r°+[A[r°, n]] A3)
и, поскольку на поверхности сферы г° п = 1, а [г°, п] = 0 интеграл по пояерх-
ности St сводится к выражению:
—-- Г A da-\- — Г [п, В] da.
Если через А и [п, В] мы обозначим средние значения векторов А и [п, В}
на поверхности сферы, то интегралы эти будут иметь значение
А . 2 , 1П. В] . 2
л
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ K)trot A = |i.J[4.1SJ 227
которые в пределе, при гх -* 0, сведутся к 4т:А(х', у',21). Внося этот
результат в A2) и переставив члены, мы найдём, значение векторного
потенциала в любой данной точке, выраженное через объёмный интеграл и через
поверхностные интегралы по внешней граничной поверхности, попрежлему
обозначаемой через 5:
,,,,,. и. rS(x.y,z) , 1 С [п, В] ,
v s
~kS [[n' A1 §rad 71 da ~ ~k / (n> A)grad 7 do- A4>
s s
Доказательство того, что дивергенция A4) в течке (х, у', г") равна
нулю, мы предоставляем читателю. Очевидно, поверхностные интегралы
представляют собой слагаемые векторного потенциала от всех источников,
внешних по отношению к поверхности 5. Во всех точках внутри области У
вектор А (х\ у'у -г'), определённый соотношением A4), является непрерывным
и имеет непрерывные производные всех порядков. Из вида поверхностных
интегралов следует, однако, что при переходе через поверхность 5 вектор А
и его производные будут испытывать разрьш непрерывности. Действительно,
мы покажем, что вне поверхности 5 вектор А всюду равен нулю.
Первый из поверхностных интегралов в A4) может быть
интерпретирован как векторный потенциал поверхностных токов:
К = —1[п, В_], A5)
Iх
где индекс «_» у В обозначает, что значение В берётся непосредственно
внутри у поверхности 5. В разделе 4.12 было показано, что слой
поверхностных токов не влияет на векторный потенциал, но вызывает скачок
вектора В, равный
[п, В,— В_]={аК. A6)
После замены К его значением из A5) получаем, очевидно, что
непосредственно снаружи у поверхности 5
[п, В,.]=0. A7)
Аналогично, второй поверхностный интеграл эквивалентен векторному
потенциалу поверхностной магнитной поляризации с плотностью:
М==~[А_, п]. A8)
Нормальная компонента А остаётся непрерывной при переходе через
подобный слой, в то время как тангенциальная компонента скачком обращается
в нуль, как это видно после подстановки A8) в A7), стр. 222.
[n, A+— A_]=- [n, A_]-4-(n[n, А_]]п, A9)
откуда
[п, А,]=0. B0)
Математическое значение последнего члена в соотношении A4) совершенно
ясно, но представить себе распределение токов или магнитных моментов
требуемого типа трудно. Интегралы подобного вида мы связыЕали с
напряжённостью поля поверхностных зарядов, распределённых с плотностью А_п
15*
228
ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
и дающих скачок нормальной составляющей, определяемый соотношением:
п(Аг —А_) = пА_, B'1>
вследствие чего мы заключаем, что:
пАь==0. B2)
Пока что мы показали, что на положительной стороне поверхности S
тангенциальная и нормальная компоненты вектора А и тангенциальная
компонента вектора В всюду равны нулю. Отсюда тотчас же следует, однако,
что и нормальная компонента вектора В должна быть равна нулю на
положительной стороне поверхности S, поскольку в нормальную компоненту
ротора А входят частные производные от компонент вектора А только по
направлениям, касательным к поверхности. Далее нам нужно лишь применить
само соотношение A4) к области, внешней по отношению к поверхности 5,
чтобы доказать, что А, а значит и В, равны нулю всюду. Вне области V токи
и магнитная поляризация отсутствуют, так ка.с их действие представлено
соответствующими поверхностными интегралами. Следовательно, поскольку
in, B+], [п, А+] и п А+ все равны нулю, из A4) следует, что А(х',у', г)
должен равняться нулю во всех точках вне области V.
Если вместо E) мы возьмём в качестве функции Грина Q = grad —, а ,
L г J
то легко показать, что:
В(*\ /,*') = £ f k grad}]*^ —~J in, В] grad-i] da —
1 * 8
— ~/(nB)gradl/to. B3)
s ^
Это представляет собой распространение закона Био и Савара на область
конечной протяжённости, ограниченную поверхностью 5. Доли, вносимые
в поле токами и магнетиками, расположенными вне поверхности S,
учитываются двумя поверхностнымл интегралами.
КРАЕВЫЕ ЗАДАЧИ
4.16. Формулировка задачи магнитостатики. Пусть однородное
изотропное тело вносится в постоянное поле неподвижных заданных токов или
постоянных магнитов. Наша задача состоит в том, чтобы найти получающееся
в результате полное поле как внутри тела, так и вне его. В том случае,
кэгда плотность тока во всех точках внутри тела равна нулю, вторичное
поле, появляющееся от индуцированного намагничения, может быть всюду
представлено однозначным потенциалом о*, так что методы, развитые при
решении задач электростатики, могут быть полностью применены и в этом
случае. Схема решения может быть записана следующим образом.
Пусть скалярный потенциал первичного поля равен о*. Если источниками
первичного поля являются токи, то потенциал о* неоднозначен; однако эго
никак не позлияет на определение индуцированного поля о*.
Результирующий полный потенциал будет ©*==©*-{--©*. Магнитную проницаемость тела
мы будем обозначать через у^, а магнитную проницаемость однородной
среды, в которую оно помещено,—через <j.2. Тогда функция ср* должна быть
построена таким образом, чтобы выполнялись условия:
1) До* = 0 ео всех точках, не расположенных на границе тела;
2) о* конечна и непрерывна всюду, включая и границу;
КРАЕВЫЕ ЗАДАЧИ [4.16] 229
3) При переходе через границу нормальные производные от полного
потенциала <?* удовлетворяют условию
-(за-*®).-».
где индексы « -f-» и « — » означают, что производные долоюны быть
подсчитаны соответственно для внешней а внутренней поверхностей границы.
Индуцированный потенциал ?* подчинён условию:
где /— известная функция точки на границе, удовлетворяющая условию::
4) jVfita = 0.
5) В бесконечности ср* должна стремиться к нулю по меньшей мере
как 1/г2 с тем, чтобы г2ср* оставалось конечным при г—>сс, поскольку
свободных магнитных зарядов нет и <?* должна исчезать, следовательно,.
как потенциал диполя или мультиполя высшего порядка.
В том случае, когда по телу протекают токи, внутреннее поле не может
быть представлено скалярным потенциалом и краевая задача должна решаться
с помощью векторного потенциала. Подобный случай имеет место, например,
когда железный провод, по которому протекает ток, вносится во внешнее
магнитное поле. В стационарном случае магнитное поле не влияет на
распределение тока. Нахождение последнего фактически является
электростатической задачей. Пусть векторный потенциал первичных источников будет А0;
а потенциал индуцированного и постоянного намагничения тела и токов,
которые могут по нему протекать, мы будем обозначать через А^
Функция А1 подчинена следующим условиям:
1) rot rot Ax = u-j J во всех точках внутри тела, в которых плотность
тока равна J.
2) rot rot Aj = 0 во всех других точках, не лежащих на границе S\
3) div Aj = 0 во всех точках, не лежащих на границе S;
4) At конечен и непрерывен всюду и меняется при переходе через
граничную поверхность непрерывно (разделы 4.10 и 4.12).
5) При переходе через границу нормальные производные от потенциала
А1} равно как и производные от полного потенциала А, удовлетворяют
условию:
(жг-(ж1=^1м,-м.,„]>
где п — внешняя нормаль, М_—поляризация тела, а М;. — поляризация
среды, причём обе берутся непосредственно у границы раздела.
Поскольку М+ и М_ определяются по крайней мере частично самим
полем, это соотношение обычно не помогает в определении А-,. Вместо^
него применяют обычное граничное условие для тангенциальных компонент
полного поля:
6) [п, Н+ - Н_J = [п, В+ - ^ В_] = 0,
которое даёт соотношение между производными от А е данной
конкретной системе координат;
7) При г -> со произведение г А1 остаётся конечным.
230 ГЛ. IV. МАГНИТ0СТАТИЧЕСКОЕ П@ЛЕ
4.17. Однозначность решения. Доказательство того, что только одна
функция ?* удовлетворяет условиям, перечисленным выше, было дано в
разделе 3.20. Соответствующая теорема об однозначности для векторного
потенциала может быть выведена из тождества B), стр. 225. Положим Р = Q = А
и предположим сначала, что в области Vv ограниченной поверхностью S,
плотность токов равна нулю. Тогда rot rot A = 0 и
(* (rot AJ dv = — f A [n rot A] da. A)
V S
Из того, что подинтегральное выражение слева существенно положительно,
следует, что если вектор А равен нулю на поверхности 5, то вектор В = rot A
равен нулю всюду в области VT,. Следовательно, А либо постоянен, либо
в крайнем случае равен градиенту от некоторого скаляра ty. Однако поскольку
А на поверхности 5 равен нулю, нормальная производная -^ на поверхности .S
также равна нулю, а этих условий, как было показано в разделе 3.20,
достаточно для того, чтобы функция <!> имела постоянное значение во всей области Vv
Следовательно, если А равен нулю на какой-либо замкнутой поверхности,
то он равен нулю также и во всех точках внутренней области этой
поверхности. Отсюда ясно также, что векторная функция А определяется в области Vx
однозначно своими значениями на границе 5 этой области, ибо, если мы
имеем какие-либо двд вектора А1 и А2, удовлетворяющие заданным условиям
на границе, то разность их должна быть равна нулю не только на
поверхности S, но и во всей области Vv
То, что в области Vt rot А = 0 и А — grad ty, можно установить также
и из того обстоятельства, что на поверхности 6' равен нулю rot А или
тангенциальный вектор [n, rot А]. Однако в этом случае не обязательно
следует, что и А равен нулю всюду: если две функции rotAj—Bj и rotA2 = B2
совпадают на поверхности 5, то В1 и В.? совпадают во всех внутренних
точках, .а At и А2 могут различаться самое большое на градиент от скалярной
функции.
В случае наличия в области -Vx токов, потенциал А разлагается на часть А',
вызываемую, этими токами, и на часть А", зависящую от внешних источников.
Вектор А' однозначно определяется распределением токов, в то время как
значения А"или ротора А" во всех внутренних точках определяются через
их значения на поверхности 5.
Поскольку векторный потенциал регулярен на бесконечности,
доказательство непосредственно применимо и к области 172, внешней по отношению
к поверхности 5. В любой области вектор В однозначно определяется
значениями тангенциальной составляющей [п, В] на границе этой
области.
ЗАДАЧА ОБ ЭЛЛИПСОИДЕ
4.18. Поле однородно намагниченного эллипсоида. Пусть имеется
постоянно и однородно намагниченный эллипсоид с главными полуосями а, Ь и с.
Направление намагничения может быть произвольным, но так как мы всегда
можем разложить вектор намагничения на три компоненты, параллельные
главным осям, то нам достаточно будет рассмотреть только тот случай,
когда намагничение М0 постоянно и параллельно оси а.
Ввиду однородности намагничения р* =— divM0 = 0 во всех точках
внутри эллипсоида. Следовательно, потенциал нашего магнита обусловлен
«прверхностными зарядами», имеющими плотность ш*==пМ0. В качестве
ЦИЛИНДР В ПАРАЛЛЕЛЬНОМ ПОЛЕ [4.20]
231
внешней среды мы берём свободное пространство. Задача полностью
эквивалентна задаче о поляризованном диэлектрическом эллипсоиде, рассмотренной
в разделе 3.27. Из уравнений B7), C2) и D2) потенциал vv создаваемый
поляризацией РХУ может быть выражен через Рх и параметры эллипсоида.
Вычёркивая коэффициент е0 и заменяя Рх на М0х, мы получаем для
скалярного магнитного потенциала в точках внутри эллипсоида:
со
* аЪс . ,, г ds /1ч
Во внешних точках
о
-t^*J (*+«»,/?,• B)
с
Поле внутри эллипсоида будет:
ч
т *
О? /2 Л,-
^=--df-=—V'Mw C)
Таким образом, если намагничение эллипсоида параллельно главной оси, то
поле Н внутри эллипсоида однородно и параллельно той же оси, но по
направлению противоположно намагничению.
4.19. Эллипсоид из магнетика в параллельном поле. Пусть эллипсоид
из однородного изотропного вещества вносится в заданное однородное
параллельное поле Н0. Пусть остаточное намагничение в эллипсоиде отсутствует
и пусть далее можно предположить, что в достаточно слабых полях
магнитная проницаемость ^ эллипсоида, равно как и магнитная проницаемость [х2
среды, постоянны.
Обращаясь к разделу 4.16, мы замечаем, что условия, которым должен
удовлетворять <?*, в точности те же, что и условия для о, если только s
заменить на jx. Следовательно, выражение для поля мы можем
заимствовать из электростатической задачи. Полный магнитный потенциал во
внутренних точках эллипсоида будет, следовательно:
Н«гх Hn„v Инг
'0г.Л ijjsilv i 0;
■; D)
' ~~ , > abc . ч . -, "be , . . abc , „ .
1 + oTT ^ ~~ ™ Al J T о— LH — iH) A 1 + к— fa — ;a2) AA
tpf вне эллипсоида мы получим из выражения C8), стр. 193, заменив е на [х
и прибавив слагаемые, индуцируемые Н0у и Н0г.
Вращающий момент, действующий со стороны поля на эллипсоид, также
может быть определён непосредственно из уравнения E4), стр. 196, после
аналогичной замены. Результаты эти имеют фундаментальное значение.
Существуют экспериментальные методы для очень точного определения малых
вращающих моментов. Магнитное поле в центре длинного соленоида весьма
близко к параллельному и однородному и его напряжённость можно
вычислить, зная токи; таким образом можно с большой точностью определять
магнитную проницаемость или восприимчивость различных образцов.
ЦИЛИНДР В ПАРАЛЛЕЛЬНОМ ПОЛЕ
4.20. Подсчёт поля. В качестве примера применения векторного
потенциала рассмотрим следующую простую задачу. Цилиндр или провод круглого
сечения с магнитной проницаемостью \ht помещён в среду с магнитной
проницаемостью ^.3. Пусть провод будет бесконечно длинным, радиус его пусть
232
ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
будет а; по проводу протекает тох /. Внешнее поле В0 направлено
перпендикулярно к оси провода и всюду параллельно и однородно. Прежде всего
определим полное поле в точках внутри и вне цилиндра.
Ось х системы отсчёта мы выберем параллельно вектору В0, а ось г
совместим с осью цилиндра и направим по направлению тока (рис. 43).
Надо найти векторный потенциал, удовлетворяющий следующим условиям:
rot rot A = 0 {г > а),
rot rot А = jj-!J (/-<«).
Плотность тока имеет только ^-компоненту:
J.
х
Л=°.
л =
{г<а).
A)
Bi
C)
Векторный потенциал может быть разложен на две части: потенциал А0
внешнего заданного поля и вторичный потенциал А1} вызываемый частично
током /,-а частично индуцированным
намагничением проводника. Очевидно, В0
можно получить из векторного
потенциала, направленного вдоль оси г. Если
i8 — единичный вектор в направлении оси
Нп
г, то
A0^isBoy-^LsBors\:\lL
D)
Рис. 43. Цилиндр в однородном маг
нитостатическом поле.
Более того, так как намагничение может
быть представлено эквивалентными
объёмными и поверхностными токами,
векторный потенциал Aj также направлен
вдоль той же оси: вектор индуцированного намагничения лежит,
очевидно, в плоскости, перпендикулярной к оси г, а эквивалентные токи
J' =*=rotMj и К'=[п, М2 — MJ (раздел 4.10) направлены, следовательно,
вдоль оси цилиндра. Так как векторный потенциал всегда параллелен токам,
то А1Х' — А1у — 0. Теперь легко разложить B) на компоненты. Из
соотношения (85), стр.. 55, мы имеем:
J. JL
г дг
ЗА
дг
+
1 д*А
г* dG2
:V,
Со)
где индекс z опущен.
Прежде всего должно быть найдено общее решение однородного
уравнения, которое мы получим, положив правую часть E) равной нулю.
Разделение переменных в подобном уравнении было рассмотрено в разделе
3.21 и так как векторный потенциал является однозначной функцией 0, то
мы сразу же можем написать:
А' — 2 (ап C0S W'J -\-*>n Sin П^) гП 4" 2 {Са C0S /2'J "J- dn C0S /fJ) r'
u=J
==-0
F)
Кроме того, векторный потенциал должен быть конечен во всех точках
пространства и, следовательно, внутри цилиндра коэффициенты сп и dn равны
нулю.
Общее решение уравнения E) получается обычным способом путём
прибавления к F) какого-либо частного решения E). Поскольку rV
зависит только от г, мы можем предположить, чго это частное решение А"
ЦИЛИНДР В ПАРАЛЛЕЛЬНОМ ПОЛЕ.[4,20]
233
ке зависит от 6:
-^ [г -гг А" ) = — \i,rJ = —
а — ) = U>,rJ = —^ Г,
dr J ' ! т.<?2 '
G)
А" = -^(±). (8)
Следовательно, во внутренних точках полный векторный потенциал будет
со
А- = — {{ (i)*+ ^ (a. cos пЧ-}-ba sin nb)r^. (9>
п = О
Так как векторный потенциал индуцированного намагничения регулярен
на бесконечности, мы положим в F) вне проводника ап — Ьп — 0. К этому
выражению мы должны прибавить векторный потенциал тока /, равный, как
мы показали (уравнение B0), стр. 211), -^ In —, и, наконец, должны
прибавить само внешнее поле D). Результирующий векторный потенциал,
в любой точке вне цилиндра равен поэтому:
со
Л+ = B0r sin f» -f >;- In 1 + 2j (cn cos nH -T dn sin n0) /F"''• A0)
n = 0
Коэффициенты разложения в ряд определяются из того условия, что
векторный потенциал и тангенциальные компоненты Н должны быть
непрерывны на границе г = а. Из выражения для ротора в цилиндрических
координатах (стр. 56), мы имеем:
3» = —-»^, (П>
Q — 1 дА~
°г— г дц i
О/'
так что граничные условия, налагаемые на векторный потенциал, будут:
А~=А'- —^1 = -1-дА~ (г = а)
A2)
В результате приравнивания коэффициентов при подобных членах (9) и A0)
мы получаем:
ил.
£0, rfj ==
;j.t — [а2 „о
а2£п,
I
A3)
все же другие коэффициенты равны нулю. Таким образом:
Л,=ё/,п7-^ + (г+ЙТ^Mо8тО (r>a);
С помощью соотношений A1) можно подсчитать и поле
Р-1 — М-2 °
> A4)
Я+:
1 +
Яь
~ 2 кг
Н~~ =
. ,, , #0 cos О
I __ \HllVl 5-_) н0sin 0,
(/•>«), •
\4 4 f-2
■—, Br, cos H
V-i 4 !*2
(/-<«)
HV =
2тш2 [x-i -f u-2
Z?0 sin 0).
A5)
A6)
234
ГЛ. IV. МАГНИТОСГАТИЧЕСК0Е ПОЛЕ
Характер поля внутри цилиндра становится более ясным, если перейти
к прямоугольным координатам:
Их = Hr cos 6 — Нн sin О, \
Ну = нгsin ° + ^cos ,3 ■ /
>
я* =
2Я0
Iх! + .а2 2"Я:
^
Ну =?
2ъа1
х.
A7)
A8)
Намагничение цилиндра даётся выражением
М =
М-1 — М-0 ц _
;аг — и.0
в„
У-1 'Г iu2 !-"-o
i_i ! у
;ло
A9)
2/
p.0 2^o2 "'
I
Очевидно, намагничение, индуцированное приложенным полем В0, направлено
в положительную сторону оси х. На него накладывается намагничение,
индуцированное током /. -
4.21. Силы, действующие на цилиндр. Если среда, в которой
находится провод, является жидкостью или немагнитным твёрдым телом, то сила,
действующая на единицу длины провода, может быть подсчитана с помощью
Уравнения A5), стр. 144. Будучи разложено на прямоугольные компоненты,
оно даёт: ё
)
/v-JY2Da.
4- Н"cos birdti,
* J
B0)
F,
j \h {НуНг — Y И* sin 6 ]r dH-
Из A5)и A7) можно подсчитать прямоугольные компоненты поля вне цилиндра:
/£=//«>-И
,и, — :-1, а*
: - Н0 cos 20 — -=-
^i + ;J-2 f2 ° 2яг
sin Ь,
HI
til
;а« а-
^-~#osin20-f о—cos 6.
B1)
//2 равно сумме квадратов этих двух компонент:
н> = /й + 2 £i=JiL ( «_ Jяз cos 20 + ^^ЛУ^-У/й 4-
P-1-l-H-i \г
\p-*tav_x\m. sinu+ f„. B2)
Подставляя B1) и B2) в B0) и вычисляя интегралы, мы получаем
полную силу, действующую со стороны поля на провод и на ток, который
течёт по нему:
Fx = 0, Fv = \^0[. B3)
Таким образом, индуцированный магнитный момент провода ничего не
прибавляет к полной силе, что является результатом однородности приложен-
ЗАДАЧИ
235
ного поля. Если это поле создаётся током, протекающим по находящемуся
поблизости проводнику, то распределение индуцированного намагничения
уже не будет симметричным и сила будет действовать на цилиндр даже
в отсутствие тока /.
ЗАДАЧИ
1. Бесконечно длинный прямой проводник ограничен извне круглым цилиндром
радиуса а, а изнутри круглым цилиндром радиуса Ь. Расстояние между центрами
цилиндров равно "с, причём «>6 + с. Внутренний цилиндр полый. По проводнику
протекает постоянный ток I, равномерно распределённый по поперечному сечению.
Показать, что поле внутри цилиндрической полости равно:
Я= С±—
2те («* — &2)
и направлено перпендикулярно к диаметру, соединяющему центры цилиндров.
2. По двум прямым, бесконечным параллельным проводам, протекают в
противоположных направлениях постоянные токи I. Проводимость проводов с конечна. Радиус
каждого из проводов равен а. растояние между центрами — Ь.
a) Пользуясь биполярной системой координат, найти выражение для
электростатического потенциала и для продольной и поперечной компонент напряжённости
электрического поля внутри и вне проводника;
b) Найти выражения для соответствующих компонент напряжённости
магнитного поля;
c) Рассмотреть поток энергии в этом поле.
3. Круглый виток проволоки радиуса а, по которому течёт постоянный ток I,
лежит в плоскости ху так, что его центр совпадает с началом координат. Точка
пространства задаётся цилиндрическими координатами г, ср, г, где х = г cos ?, у ~ rsin ср
показать, что векторный потенциал в любой точке поля будет:
■ 2п J (a? + r24-z* — 2arcosa)/* %k \r ) \ 2 J
о
где № = Ааг\ {(а 4- гJ 4-22}1, а К и Е — полные эллиптические интегралы первого
и второго рода.
i
Показать, что при (г2 4-г2J >« это выражение сводится к уравнению C7),
стр. 213, для векторного потенциала магнитного диполя.
4. Из выражения для векторного потенциала кругового витка, полученного в
задаче 3, показать, что компоненты напряжённости магнитного поля будут:
нг = [х1
2т г { (д 4-г)з-f-*а }
а/ 1
к +
(а-
а2 -\- г2
(а — rf
— у2 — _j2
rf -\- г2
-l-z
+ 22
4
4
h,= *L 1 -Ы
2т. {(fl 4- rf + z* }/2 I
5. Поле двух коаксиальных катушек Гельмгольца, радиусы которых равны а и рас
стояние между центрами которых также равно а, приблизительно однородно вблизи
оси посередине между ними. Предположим, что каждая из катушек имеет п витков, что
поперечное сечение катушки мало по сравнению с а, и что по обеим катушкам
течёт один и тот же ток. Воспользовавшись результатами задачи 4, написать
выражения для продольной и радиальной компонент вектора Н в точках, лежащих на оси
и в любой точке плоскости, нормальной к оси и расположенной посередине между
катушками. Какова напряжённость поля в средней точке оси? Найти разложение
продольной компоненты Иг в ряд по степеням zja, справедливое на оси в
окрестности средней точки, и соответствующие разложения для Иг и Нг по степеням г/а,
справедливые на перпендикулярной плоскости, проходящей через среднюю точку оси.
6. По линейным контурам С\ и С% протекают постоянные токи соответственно
/i и /2. Показать, что магнитная энергия системы равна
& "с,
236
ГЛ. IV. МАГНИТОСТАТИЧЕСКОЕ ПОЛЕ
где rfsj и ds2 — векторные элементы длины вдоль контуров, а г12 — расстояние между
этими элементами. Магнитную проницаемость р- считать постоянной.
Коэффициент взаимной индукции определяется соотношением
Т I Г Т f ^ - X.JL d^ dS;
= i§§
'12
2и = и. V«*{(|--a)k-4e /.
7. Показать, что коэффициент взаимной индукции двух круговых коаксиальных
витков в среде с постоянной магнитной проницаемостью равен
где а и Ь — радиусы витков, с — расстояние между центрами, К и Е — полные
эллиптические интегралы первого и второго рода, a k определяется соотношением:
/•is = V-a I In — 2 ),
Показать, что если расстояние между центрами с мало по сравнению с радиусами
а и Ь, и радиусы эти одного порядка, то формула сводится к такой:
~d
где '
d= У {а — &J + с2.
8. Коэффициент самоиндукции Ln контура, по которому протекает постоянный
ток /j, определяется соотношением
где T-i—магнитная энергия контура. Следовательно, Ln может быть вычислен с
помощью любого из выражений:
:и = 7г/ Mdo = -l fpfFdv
при условии, что В является* линейной функцией Н, В первом случае объёмный
интеграл распространяется на область, занятую токами, а во втором случае — на всё
пространство. Та часть Lu, которая связана с энергией поля внутри проводника,.
называется внутренней самоиндукцией Ln.
Показать, что внутренняя самоиндукция длинного прямого проводника с
постоянной магнитной проницаемостью \^ равна:
zli = g£ генри/метр.
9. Показать, что самоиндукция кругового витка радиуса R и радиуса
поперечного сечения г равна.
A=/?|!A2(ln^-2)-f 1^},
где p-i — магнитная проницаемость провода, а ,а2 — магнитная проницаемость
окружающей среды; и и ,а2 предполагаются постоянными.
10. Тороидальная катушка навита равномерно однослойной обмоткой из п
витков на поверхность, образованную вращением круга радиуса г метров вокруг
оси, расположенной на расстоянии R метров от центра круга. Показать, что
самоиндукция катушки равна:
L = \xn-(R~ УН2— г2) генри.
11. Круговой виток проволоки помещен в плоскости, параллельной плоской
поверхности полубесконечной среды с постоянной магнитной проницаемостью. Найти
увеличение самоиндукции витка, вызванное наличием магнетика.
Показать, что если плоскость витка совпадает с поверхностью магнетика, то
увеличение самоинд>^ции витка определяется коэффициентом, не зависящим от
его формы.
ЪЗАДАЧИ
2£7
12. Найти выражение для изменения самоиндукции кругового витка проволоки,
вызванного наличием другого кругового витка коаксиального с первым.
13. Бесконечно длинный полый цилиндр с постоянной магнитной
проницаемостью [Aj помещён в заданное однородное магнитное поле, направленное
перпендикулярно к образующей цилиндра. Потенциал этого первичного поля равен
<р* = — H0r cos 6, где гиб — цилиндрические координаты в плоскости,
перпендикулярной оси цилиндра, которая служит началом отсчёта. Поперечное сечение цилиндра
ограничено двумя окружностями: наружной радиуса а и внутренней радиуса Ь.
Магнитная проницаемость внешней и внутренней среды постоянна и равна \и,_.
Показать, что потенциал в любой точке внутри полости равен k
( '-D)' 1
** = - р - I ' > И, г cos 0 (r<ft).
( Vh-i — \h) \a) J
14. Полая сфера с наружным радиусом а и внутренним радиусом Ъ, с
постоянной магнитной проницаемостью p-j помещена в заданное однородное магнитное
голе Ир. Внешняя и внутренняя среды имеют постоянную магнитную
проницаемость |л2. Показать, что поле внутри полости однородно и даётся выражением
Н= < 1
f 1_ (ь^
а
[ 2(^—1x2J и у
#о (r<b).
Рассмотреть относительную эффективность магнитного экранирования с помощью
полой сферы и полого цилиндра.
15. Магнитное поле, наблюдаемое у земной поверхности, может быть вызвано
либо токами или магнетиками, расположенными внутри земли, либо же токами,
циркулирующими на её поверхности. Измерения показывают, чго поле внешних
источников составляет не более нескольких процентов полного поля. Показать, как
путём измерения горизонтальной и вертикальной компонент напряжённости
магнитного поля на земной поверхности млжно отличить поле внешних источников от
поля источников, находящихся внутри земли.
16. Предположим, что магнитное поле земли вызывается стационарными токами
или намагниченным веществом, расположенным внутри земли. Скалярный потенциал
ко внешних точках может быть тогда представлен в виде разложения по
сферическим функциям. Показать, что коэффициенты при первых четырёх функциях
могут быть определены измерением компонент напряжённости магнитного поля
в восьми точках на поверхности земли.
17. Обмотка из тонкой проволоки должна быть намотана на сфероидальную
поверхность так, чтобы поле катушки было таким же, как и поле сфероида,
однородно намагниченного вдоль большой оси. Как должна быть распределена обмотка
по поверхности сфероида?
18. Заряды равномерно распределены по поверхности медного шара радиуса а.
Шар вращается вокруг своего диаметра с постоянной угловой скоростью.
Подсчитать векторный потенциал и магнитное поле в точках внутри и вне шара.
19. Твёрдый незаряженный проводящий шар вращается с постоянной угловой
скоростью со в однородном магнитном поле В так, что ось вращения совпадает
с направлением поля. Найти плотность объёмных и поверхностных зарядов и
электростатический потенциал в точках внутри и вне шара. Предполагается, что
магнитным полем вращающихся зарядов можно пренебречь.
20. Поляризация Р неподвижного изотропного диэлектрика в электростатическом
поле Е выражается формулой
Р = (е —^Е.
Если каждый элемент диэлектрика перемещается в магнитном поле со скоростью_v,
то поляризация с точностью до членов первого порядка относительно \/с = у'о.'-о
будет:
P = (s-*o)(E + [v,B]).
Диэлектрический цилиндр радиуса а вращается вокруг своей оси с постоянной
'угловой скоростью oj в однородном статическом магнитном поле. Поле параллельно
оси цилиндра. Найти поляризацию цилиндра, связанные заряды, появляющиеся hi
его поверхности, и электростатический потенциал внутри и вне цилиндра.
238
ГЛ. IV. МАГНИТОСТАТЙЧЕСКОЕ ЛОХЕ
I
21. Диэлектрическая сфера радиуса а вращается в однородном статическом
магнитном поле с постоянной угловой скоростью <а вокруг оси, параллельной
направлению поля. Пользуясь выражением для поляризации, данном в задаче 20„
найти плотность связанных объёмных и поверхностных зарядов и потенциал внутрч
и вне сферы.
22. Показать, что сила взаимодействия между двумя линейными элементами
токов rfSj и d$2 равна:
где г° — единичный вектор, направленный вдоль линии г, соединяющей rfsj и ds2
от элемента d$t к элементу rfs2.
23. Длинный прямой провод, по которому проте! ает постоянный ток, помещен
в полубесконечную массу железа с магнитной проницаемостью р. на расстоянии d
от плоской поверхности. Провод отделён от железа изолирующим слоем
пренебрежимо малой толщины. Найти выражения для поля внутри и вне железа.
24. Длинный прямой провод, по которому протекает постоянный ток, расположен
в воздушном зазоре между двумя параллельными железными стенками с
бесконечной проницаемостью. Предполагается, что провод
параллелен стенкам и имеет бесконечно малое поперечное
сечение. Найти напряжённость поля в любой точке
£ в воздушном зазоре. Начертить график зависимости силы,
действующей нз единицу длины проводника с током
Воздух I в один ампер, в функции расстояния от одной из стенок.
А * 25. Длинный прямой проводник с бесконечно малым
t T~~Th | поперечным сечением помещён в бесконечно глубокую
/,44/^/&/У/У///'/У/'//'/? Щель с параллельными стенками, прорезанную в массе
jf*^s/?W//////y///////. железа с бесконечной проницаемостью. Пусть ширина
елезс . щ^ли ^ а положение проводника определяется
параметрами s и h, как показано на рисунке. I-ассчитать
напряжённость поля в точках внутри щели и силу, действующую на единицу
длины проводника с током в один ампер. (См. Н a g u e, Electromagnetic Problems
in Electrical Engineering, и binder, /. Am. Inst. Elec. Engrs., 46, 614, 1927.)
26. Бесконечный эллиптический цилиндр из мягкого железа, форма поверхности
которого определяется уравнением
Рх2 + сРу* = ФЪ\
помещён в заданное однородное магнитное поле, направленное перпендикулярно
к образующей цилиндра. Найти выражения для скалярного магнитного потенциала во
внутренних и внешних точках и подсчитать силу и вращающий момент,
действующие на единицу длины цилиндра. Рассмотреть случай эксцентриситета, равного
единице, когда цилиндр вырождается в тонкую пластинку.
27. Частица с массой т и зарядом q влетает в поле магнитного диполя.
a) Написать дифференциальные уравнения движения частицы в сферической
системе координат, начало которой совпадает с центром диполя.
b) Показать, что компонента момента количества движения в направлении
оси липоля остаётся постоянной.
c) Рассмотреть траекторию для того случая, когда частица первоначально
влетает в экваториальной плоскости.
28. Небольшой магнитный стержень помещён вблизи плоской поверхности
очень большой массы мягкого железа с магнитной проницаемостью ц. Даны
расстояние от магнита до плоскости и угол между осью магнита и перпендикуляром
к плоскости. Рассматривая только дипольный момент магнита, найти силу и
вращающий момент, действующие на магнит благодаря индуцированному намагничению
железа.
29. Два небольших магнитных стержня, дипольные моменты которых равны
соответственно тг и ш2, лежат на идеально гладком столе. Расстояние между
центрами магнитов велико по сравнению с их длиной. 8г и $2— углы между осями
диполей и линией, соединяющей их центры.
a) Рассчитать силу, действующую на диполь пь со стогоны ш^ и вращающий
момент, действующий на диполь ш2 относительно вертикальной оси, проходящей
через его центр.
b) Рассчитать силу, действ) ющую на диполь тг со стороны т2, и вращающий
момент, действующий .на диполь гг^ ошосительно вертикальной оси, проходящей
через его центр. »
c) Найти полный угловой момент системы относительно точки, лежащей в
плоскости стола. Является ли он постоянным?
ЗАДАЧИ 239
30. Показать, что сила, действующая между небольшими стержневыми
магнитами, обратно пропорциональна четвёртой степени расстояния между ними,
независимо от их ориентации в пространстве.
31. Статическое магнитное поле создаётся некоторым распределением
намагниченного вещества. Нигде нет никаких токов. Показать, что распространённый по
всему полю интеграл
-\ (BHdv = 0.
32. Показать, что если J(x,y, z)— плотность тока в какой-либо точке области V,
ограниченной замкнутой поверхностью S, то магнитное поле в любой внутренней
точке (x',y',zr) будет:
В (х/у, z') = £ [ Г J, grad -1 \dv - ~ J {[ [п, В] gradЦ ~f (п В) grad Ц da;
где г=У(х'—Х)*-\-{у'—\)%-\-{z' — zf, и что для внешних точек
поверхностный интеграл равен нулю.
. 33. Определить поле магнитного квадруполя, воспользовавшись разложением
векторного потенциала, данным на стр. 211, уравнение B3). Дать геометрическую
интерпретацию квадрупольного момента с помощью бесконечно малых линейных
токсв.
ГЛАВА V
ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Каждое решение уравнений Максвелла, конечное, непрерывное и
однозначное bj всех точках однородной и изотропной области, представляет
возможное электромагнитное поле. Не считая стационарных полей,
исследованных в предыдущих главах, самыми простыми решениями уравнений
поля являются решения, зависящие от времени и одной пространственной
координаты. Факторы, характеризующие распространение этих
элементарных одномерных полей, определяют в значительной мере и
распространение тех сложных полей, которые встречаются в, практических задачах.
Мы будем изучать свойства плоских волн в безграничном изотропном
пространстве, не интересуясь пока теми распределениями токов и зарядов,
которые необходимы для возникновения плоских волн.
РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН
5.1. Уравнения одномерного поля. Булем пока предполагать, что
среда однородна, изотропна и безгранична. Предположим, кроме того, что
соотношения
D = sE, 8--;xH, J = aE A)
линейны, так что среда в отношении её электромагнитных свойств может
быть охарактеризована тремя константами: е, ^ и з. Если проводимость
отлична от нуля, то любое начальное распределение свободных "зарядов
r среде должно самопроизвольно исчезать (раздел 1.7). В последующем р
будет полагаться равным нулю как в диэлектриках, так и в проводниках.
Тогда уравнения Максвелла, которым удовлетворяют векторы поля, буду г:
rot E -f !^7 *= °» 0) divH = 0, (Ш)
rctH —s^ —oE = 0, (li) divE = 0. (IV)
Мы ищем теперь решения этой системы, которые зависят от времени и от
расстояния, отсчитываемого лишь вдоль одной пространственной оси. Это
выделенное направление не обязательно должно совпадать с координатной
осью системы отсчёта. Предположим поэтому, что поле является функцией
координаты С, измеренной вдоль линии, направление, которой определено
единичным вектором п. Прямоугольные компоненты этого единичного
вектора «ж, пу, пг являются, очевидно, направляющими косинусами новой
координатной оси С. В нашем предположении подразумевается, что в каждый
момент времени векторы Е и К постоянны по направлению и величине на
плоскостях, нормальных к п. Эти плоскости определяются уравнением
гп = const., B)
I ч
РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН [5.1]
241
где г — радиус-вектор, проведённый из начала координат к любой чточке
плоскости, как показано на рис. 44.
Так как поля зависят лишь от
с и * ' Xf \ ^^
е=е(с,о. н = н(с,о. (з;
-АОЗ&ЯЕЯаЮЮЛ
то частные производные по
прямоугольным координатам могут быть
выражены в виде:
а__ а
dx~n*di'
д _ д
д_
дг
П*дХ,
D)
Рис. 44. Однородная плоская волна,
распространяющаяся в направлении
вектора п.
Из этих выражений мы построим оператор grad и получим таким образом
упрощённые выражения для rot и div:
grad=|i-+ji + kK« (i^ + j^-f кяг)|; = п|г,
ду
dz
dl
ас
rotE = [n,^] = ^[n,E],
divE=n^=~(nE).
ас ~~ac
В силу этих соотношений уравнения поля принимают следующий вид:
dt
E)
F)
G)
дЕ
dt
ОЕ:
= 0, (I)
0, (II)
n-^ = 0, (III)
ac
(IV)
Теперь решаем совместно эту систему: дифференцируя сначала уравнение
(I) по С, а затем умножая его векторно на п и дифференцируя уравнение
(II) по t, мы получаем:
г г a2Eii / &е\ . ч а2Е а2Е
Г дЩ1
= -*Чп,а7ас]'
Г д*Н1 д*Е . дЕ /оч
[п'-дШ\==£Ш+адТ- <8>
Исключая члены с Н, находим, что вектор Е удовлетворяет уравнению:
а2Е дт_
ас2 ^ а^
аЕ п
1*0 -^гт- = 0.
а*
(9)
Исключение Е, проводимое аналогичным путём, приводит к такому же
уравнению для Н:
дЩ дЩ дН п /|т
ас2
а*а
а*
Так как п п, -^~\ тождественно равно нулю, то, как следует из (I),
дП л „_ _ ,тттч „ _„_.
п-^г = 0. Совместно с (III) это даёт:
Таким образом мы заключаем, что изменение С-компоненты вектора Н, свя-
16 Зак. 593. Теория электромагнетизма.
242 ГЛ. V. ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
занное с изменением С или t, несовместимо с предположением о постоянсгве
поля вдоль плоскостей, нормальных к оси С в каждый момент времени.
Уравнение A1) допускает лишь статические поля в направлении С, но так
как здесь мы интересуемся переменными полями, то мы положим Нс=0.
Таким же образом из (II) следует:
п (е-^- + °Е) = 0, A2)
что, совместно с (IV), приводит к равенству:
П ("f-^ + f E^+~-^c) = n(rfE + f Erf ) = 0. A3)
Компонента Е, нормальная к семейству плоскостей, удовлетворяет поэтому
уравнению
TT + f^O. A4)
которое после интегрирования даёт:
£< = £„,*-"К • A5>
где £ос—продольная компонента Е в момент £ = 0, а т = ——время
релаксации, определённое на стр. 27. Если проводимость конечна, то
продольная компонента Е экспоненциально затухает: статическое электрическое поле
не может поддерживаться внутри проводника. Согласно A5), возможна
компонента Е^ в идеальной диэлектрической среде, но тогда этот частный
интеграл не содержит времени.
Уравнения A1) и A3) Доказывают поперечность поля. В любом
электромагнитном поле, имеющем вид C), векторы Е и Н лежат в плоскостях*
нормальных к координатной оси С.
Введём вторую систему прямоугольных координат £, ?), С, у которой
начало координат совпадает с началом фиксированной системы х,у, z, а ось С
ориентирована в направлении, определяемом п. В этой новой системе
вектор Е имеет компоненты Е^ E-^v. E^ = 0. Обе компоненты Е$ и Ег>
удовлетворяют уравнению (9), которое решается разделением переменных. *
Пусть
A=/i(C)/2@, A6)
тогда
/i ~W~~h~M~T-J- dt — "> V*
где — k2—постоянная разделения. Общее решение уравнения для ft имеет
вид:
/t (С) = Ае*к + Be-™, A8)
где А и В—комплексные постоянные. Для /2 мы возьмём частное решение:
f2(t) = Ce-P*. A9>
Тогда р должно удовлетворить характеристическому уравнению:
Таким образом р и постоянная k2 связаны определённым соотношением. Значение
одной из них может быть задано; но тогда другая будет уже определена.
Из A8) и A9) может быть построено частное решение следующего вида:
££ = Ец&к-р* + Е#е-™>-р*; B1)
РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН [5.2]
24^
так же как и для другой прямоугольной компоненты:
£ч = Ене*Ьъ-р*-\-Е2г>е-*к-Р*.
B2)
Четыре комплексные постоянные Ец, Е%, Е^, Егп являются комплексными
векторными амплитудами, лежащими в плоскости £, г\. Комбинируя B1) и
B2), получим:
Е = Е1еЖ-з>*Л-Е2е-^~рК B3)
Это векторное решение уравнения (9) в свою очередь подставляется
в уравнения поля для того, чтобы получить соответствующий магнитный
вектор Н. Так как Н должно иметь
ту же функциональную зависимость от
С и t, то мы можем написать:
Н = Н^к-р*-\-Ще-ж-Р* B4)
и затем определить постоянные Нь Н2
через Ej и Е2.
Дифференцируя B3), имеем:
Ш- = ik Е^ж-р* — ik Е2е-ж-р\
дН „ B5)
Эти производные, подставленные в (I),
приводят к соотношению:
{[ikn, EJ —p^Hj) eiJ£-pt—
— ([ikn, E2] -f ррН2)е-*к-р* = 0.
B6)
Рис. 45. Относительное расположение
электрического и магнитного векторов
в волнах, распространяющихся в
положительном и отрицательном
направлениях.
Коэффициенты при экспонентах должны каждый в отдельности равняться
нулю и, следовательно,
H^i^EJ, Н2 =
или в прямоугольных компонентах:
ik
р&
[п, Е2],
B7)
Я1£=-
ik
PV-
'ltj»
Hli> =
ik
hb
я2£ =
ik
PP
'2t)>
Я
2т)
ik c
■ tint.
p\x *
B8)
Так как E[n, E] = 0, то, следовательно, ЕН = 0. В поле вида C)
электрический и магнитный векторы ортогональны к. направлению п и друг к
другу. Взаимное расположение этих векторов иллюстрирует рис. 45.
5.2. Плоские волны, гармонические во времени. В зависимости от
выбора р и k имеется два подлежащих рассмотрению случая; их удобно
рассмотреть раздельно.
Допустим сначала, что поле является гармоническим во времени и что
поэтому р чисто мнимое. Постоянная разделения определяется тогда из B0):
р = /w, k2 = [Аеш2 -j- /{Aoto. B9)
В проводящей среде k2t а значит и само k -^- комплексно. Знак корня мы
будем выбирать таким образом, чтобы мнимая часть k всегда была
положительна. Положим
k = a -j- /p. C0)
16*
244 ГЛ. V. ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Амплитуды Efo..., £2y] тоже комплексны и мы запишем их теперь
в виде:
Е& = at Ф\ Е& = а^\ 3 .
где новые постоянные alt...tb2t б^...,^ действительны. В силу этих
определений для ^-компоненты вектора Е — мы имеем:
Ek = a1e-^+i i^-urf+w _}_ д^+рс-* («с+««*-&). C2)
Так как C2) есть решение линейного уравнения с действительными
коэффициентами, то его действительная и мнимая части также должны быть
решениями. Действительная часть C2) равна:
Ef. = аге-К cos (Ы — <£ — 6t) -f а2е№ cos (arf + «С—62). C3)
Фазовые углы 6t и 62 произвольны и, следовательно, выбор мнимой части
уравнения C2) не может привести к решению независимому от C3).
Тем же способом из B2) получается ^-компонента Е:
Ещ = bte-K cos (arf— aC —«J»i)+ VPc cos (w*-f aC — <J>2). C4)
Компоненты соответствующего магнитного поля получаются из B8).
Мы имеем теперь:
«.^о+а^л^+Ел, T=arctgi. (з5)
Комплексная ^-компонента Н равна:
Нг = Я1£е-Рг-+* <<*-«*> 4- H$efc-*l*+*u. C6)
Подставив соответствующие значения //^ и //2£, мы получим для
действительной части
#Е = —ftt^ + ^e-^cosfo* —аС—4*1 —?) +
(Л, (О
+*a^?±5eWcos(erf+eu —ФЯ —Т). C7>
Аналогично для -^-компоненты :
// =a ^°8 + Р- е-Р* cos (w* — ос£ — 6, — ч)
flsV531^cosH+aC-62-T). . C8)
Очевидно, эти решения соответствуют плоским волнам,
распространяющимся в положительном и отрицательном направлениях вдоль оси С
Рассмотрим сначала наиболее простой случай, когда среда является непроводящей
и все амплитуды за исключением ах равны нулю. Тогда о, а следовательно,
и {3 равны нулю, и поле описывается уравнениями:
Е^с^ cos (at — осС — 60, C9)
Н. — -^-ал cos(wt— aC—6i).
Это поле периодично в пространстве и во времени. Частота равна w/27u = v,
а период по времени равен — ь= Г. Пространственный период называется
длиной волны и определяется соотношением
a = ^L; X = —. D0)
РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН [5.2] 245
Аргумент периодической функции <p1=otf — а£ — 8Х называется фазой,
а угол 6ls который определяется из начальных условий, называется фазовым
углом, В каждый момент векторы Е и Н постоянны в плоскостях С = const.
Выберем теперь плоскость, на которой в момент t = О фаза имеет
некоторое заданное значение, и займёмся вопросом, как эта плоскость должна
перемещаться вдоль оси С для того, чтобы её фаза не изменялась с
течением времени. Так как на любой такой плоскости фаза постоянна, то мы
имеем:
^=0)^—аС—6Х = const., do1=(adt — <xdX — 0. D1)
В поле, описываемом уравнениями C9), поверхностью постоянной фазы
является плоскость, перемещающаяся в направлении положительной оси С
с постоянной скоростью
v называется фазовой скоростью волны. Она представляет собой всего
лишь скорость распространения фазы или состояния и не обязательно
совпадает со скоростью, с которой распространяется энергия волны или
сигнал. В сущности v может превышать критическую скорость с, ни
в малейшей степени не нарушая постулата относительности.
В непроводящей среде
а = (в|/>е> р ==-= 1 , D3)
где с — скорость света в свободном пространстве, а хе, хт — относительные
диэлектрическая и магнитная проницаемости. В оптике отношение п= — == —
V а»
называется показателем преломления. Так как во всех материалах, кроме
ферромагнитных, хт очень близко к единице, то показатель преломления
равен корню квадратному из хе. Этот результат впервые был получен
Максвеллом и послужил основой для его утверждения, что свет —
электромагнитное явление. Максвеллу были известны значительные отклонения от
ожидаемых значений п. Эти отклонения были объяснены позже, тогда, когда
было обнаружено, что диэлектрическая проницаемость при высоких частотах
не обязательно имеет значения, полученные из измерений в статических «ли
квазистатических условиях. Функциональная зависимость п от частоты
приводит к соответствующей зависимости для фазовой скорости, т. е. к
явлениям, известным под названием дисперсии.
При данной частоте длина волны определяется свойствами среды:
*-■?.-£. («)
где Х0 — длина волны в свободном пространстве при той же частоте. Во
всех неионизованных средах п > 1 и, следовательно, в веществе фазовая
скорость уменьшается, а длина волны укорачивается.
Обращаясь опять к выражениям C9), мы видим, что соотношение
между магнитным и электрическим векторами таково, что векторное
произведение [Е, Н] направлено в сторону распространения волны. Магнитный
вектор распространяется в том же направлении и с той же скоростью,- что
и электрический вектор и в непроводящей среде они находятся точно
в фазе, а их амплитуды отличаются множителем
Л- = j/"y = 2,654-10-з j/~^L (o = 0). D5)
246 ГЛ. V. ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Если в уравнениях C3) — C8) положить равными нулю все амплитуды,
кроме а2, то получится другое частное решение, которое в непроводящей
среде принимает вид:
Е% = а2 cos {<at -f- <x£ — 62),
//4 = ea|/"yCos(arfH-eC— 62). D6)
Это поле отличается от предыдущего лишь направлением своего
распространения. Фаза равна ср2 = со/ —[— otC, — 62 и поверхность постоянной фазы
распространяется в направлении отрицательной оси С, со скоростью v = .
Два частных решения с амплитудами Ьх и &2 представляют вторую пару
волн, распространяющихся в положительном и отрицательном направлениях.
Обе эти волны имеют электрический вектор, параллельный оси ч\.
Не будем теперь ограничиваться идеальной диэлектрической средой
и исследуем явления, возникающие вследствие конечной проводимости..
Тогда магнитный и электрический векторы экспоненциально уменьшаются
в направлении распространения. Волны, распространяющиеся в отрицательном
«аправлении, умножаются на е+$\ н0 так как С уменьшается в этом
направлении, то это также приводит к ослаблению. Проводимость среды вызывает
не только затухание волн, но влияет и на их скорость. Константы а и р
могут быть вычислены из значений ^, е и о. Возводя C0) в квадрат и
приравнивая действительную и мнимую части соответственно действительному
ш мнимому членам в B9), получаем:
ae — pa^jW», ap = i~-. D7)
Решая эти уравнения совместно, находим:
— fcC/H^ + Q]*. D8)
Р—[£(/+КГ^)]4- <49>
Неопределённость в выборе знака, которая возникает при извлечении
первого корня, устраняется требованием действительности а и р.
Плоскости постоянной фазы распространяются со скоростью
„^[^(jA+^ + l] \ E0)
которая увеличивается с частотой, если постоянные xe, v.m и о от частоты
не зависят.
Уменьшение амплитуды на поверхности постоянной фазы определяется
коэффициентом затухания C, который также увеличивается с увеличением
частоты. Комплексный коэффициент k мы будем называть постоянной
распространения', его действительная часть может быть названа фазовой
константой, хотя этот термин применяется также к углам б и i|.
Влияние частоты и проводимости на распространение плоских волн
проще всего выявляется при рассмотрении двух предельных случаев* Из
формул D8) и D9) непосредственно видно, что поведение коэффициентов a
и р существенно зависит от величины „ 2 . Полная плотность тока в любой
точке среды есть
J = оЕ ~\- е -J??- = (a — дое)Е. E1)
- РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН [5.2] 247
Отсюда видно, что -г- равно отношению плотностей тока проводимости
к току смещения.
Случай I. —гт<0Р-- Ток смещения значительно сильнее тока
проводимости. Это может иметь место либо в недостаточно проводящей среде,
либо в относительно хорошем проводнике (таком, как морская вода), если в нём
распространяются волны очень высокой частоты. Разложение D8) и D9)
© ряд по ~yy дает:
a = «Vl*e^l-f-g-^-f-... J, E2)
Р = т/>==188>3°/~-^
E3)
Заметим, что в этом приближении коэффициент затухания не зависит от
, частоты. В подобных средах, по мере увеличения частоты, затухание
асимптотически приближается к максимальному значению E3).
о2
Случай II. -тт^" *• Т°к проводимости значительно превышает ток
-смещения. Это всегда имеет место в металлах, в которых о порядка
107 1/ом-метр. О диэлектрической проницаемости металлов известно немного,
но нет никаких оснований принимать её значения большими. Так как
величина е, вероятно, порядка Ю-11, то ток смещения не может равняться току
проводимости при частотах, меньших 1011, лежащих в области атомных
явлений, к которым, очевидно, настоящее рассмотрение неприменимо. Для а
и р мы получаем приближённую формулу
« = Р = ]/~^- - 1,98710-s y^— E4)
Увеличение частоты, магнитной проницаемости или проводимости одинаковым
образом способствует увеличению затухания. Фазовая скорость увеличивается
также при возрастании частоты, но уменьшается с увеличением о или km.
Таким образом, в сложной периодической волне гармоники высшего порядка
всё время убегают вперёд относительно низших гармоник.
Амплитуды электрического и магнитного векторов плоской волны
связаны соотношением:
141 = -*^ |Е|, E5)
1™ = /i('+^)"'. E6)
Для плохо проводящей среды разложение E6) даёт:
J^l±i2^ 2,654- 10-st/~5l(i -f0,807.102°-^—V E7)
тогда как в хороших проводниках:
^S?s/Z= 355,8 гАХ (-£»!). E8)
fXCO Г ЦШ V ЧЪт \E2{08 -^ ) Ч У
В идеальном диэлектрике электрический и магнитный векторы
колеблются в фазе; если же среда проводит, то магнитный вектор отстаёт
248 ГЛ. V. ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
на угол тс> причём:
159>
Если -2~2-^>1, то это огношение обращается в единицу, т. е. магнитный
вектор плоской волны, проникающей в металл, отстаёт от электрического»
вектора на угол 45°.
5.3. Плоские волны, гармонические в пространстве. Предположение,
что р в уравнении B0) чисто мнимое, приводит к комплексным значениям к
и к электромагнитным полям, которые являются простыми гармоническими
функциями времени. Поле, которое в любой данной точке на оси С, является
известной периодической функцией t, может быть разложено с помощью
теоремы Фурье на гармонические компоненты, распространяющиеся вдоль оси С,
так как это только что было описано. Изменение во времени в любой
другой фиксированной точке может быть тогда найдено посредством
суммирования этих компонент в исследуемой точке. Вместо изменения поля с
течением времени t в некоторой точке С может быть задано распределение поляг
в зависимости от С при определённом значении t и задача заключаете»
в том, чтобы определить поле в любой последующий момент. Теорема Фурье
может быть тогда применена относительно переменной С
Пусть постоянная разделения k2 действительна. Тогда р — комплексна»
величина, выражающаяся формулой:
-г-y , то электрический вектор,,
определённый в B3), примет вид:
E = Eje 2e -4-Е2е 2е . F1>
а2 №
Если -д-2< — > то величина iq чисто мнимая и поле представляет собой
плоскую волну, распространяющуюся вдоль оси С с фазовой скоростью
*=§=±|. F2>
Амплитуда колебаний в любой точке экспоненциально уменьшается
с ростом t; скорость убывания определяется временем релаксации х== —.
Если o2/4s2 > k2/\ie, то величина iq действительна и нет никакого
распространения в указанном выше смысле. Поле периодично по С, но монотонно-
затухает со временем. Начальная форма волны совершенно не смещаете»
вдоль пространственной оси: волновое явление вырождается в диффузию.
5.4. Поляризация. Так как волны, распространяющиеся вправо или
влево, отличаются лишь знаком скорости, мы ограничимся теперь волной,,
распространяющейся в положительном направлении (направо). Кроме того,,
эффект затухания из-за конечной проводимости однородной изотропной
среды, описываемый экспоненциальным множителем, общим для всех
компонент поля, не играет роли в поляризации и не будет нами учитываться-
РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН [5.41
249'
Предположим далее, что амплитуды и фазовые константы прямоугольных
компонент Е уже определены и исследуем геометрическое место-
| Е | = у Ё{ -J- Ё\ в плоскости С = const.
Чтобы определить эго геометрическое место,
нужно исключить из уравнений
£,£ = acos(c?+6), £; = 6 cos (<?-И), £, = 0 F3)
переменную, составляющую фазы у = аХ, — Ы. Для
этой цели перепишем F3) в виде:
-EL = cos ('© -f 6).
Щ- = cos (© -f 6) cos 8 — sin (<р -f 6) sin 8, F4)
Рис. 46. Эллипс поляри-
где 8 = ф — 6. Возведением в квадрат можно исклю- зашш.
чить периодический множитель cos(<p + 6) и тогда
получается, что прямоугольные компоненты должны удовлетворять
соотношению
*Ь П
т-*И"»*+т-«°*-
Дискриминант этой квадратичной формы отрицателен:
cos^o
аЧ*
4 =-^-sin28<0,
fl*№
am
F5)
F6)
и поэтому геометрическое место конца вектора с компонентами Z?e, En
является эллипсом на плоскости (£, 7j).
В этом случае говорят,
Лравое вращение Левое вращение-
Рис. 47. Круговая поляризация
Окружности изображают
траекторию конца вектора Е. Волна
распространяется нормально к
рисунку по направлению к
читателю.
что в<злна эллиптически поляризована.
Точки касания эллипса с описанным
прямоугольником определяются из F5) и равны
(±а, zt^cosS) и (ztacosS, zt.b). В
общем случае главные оси эллипса не
совпадают с координатными осями £, ч\, но их
можно совместить'поворотом координатной
системы около оси С на угол 6,
определённый из соотношения
tg2b
2ab
а?
№
cos 8.
F7)
Если амплитуды прямоугольных
компонент равны, а фазы отличаются на чт/2,
умноженное на нечётное число, то эллипс вырождается в окружность:
тк
E( + Ei = a* (a = ft, 8 = ^-, m = =tl,
■)•
F8)
В. этом случае говорят, что волна поляризована по кругу. Различают два
случая в соответствии с положительным или отрицательным направлением
вращения электрического вектора вокруг оси С. О0ычно принято называть
правополяризованным лучом тот, в котором Е вращается по часовой стрелке,
если наблюдать против направления распространения, глядя на источник.
Наиболее важным из всех частных случаев является тот, при котором
эллипс вырождается в прямую линию. Он осуществляется при Ъ = -±1ГШ7
где т — любое целое число. Геометрическое место Е в плоскости (£, •/])
превращается в прямую линию, составляющую с осью £ угол Ь? определяемый-
.250 ГЛ. V. ПЛОСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
из соотношения: * •
tg*>=|W(-ir~. " F9)
Такая волна линейно поляризована. Магнитный вектор плоской волны
нормален к электрическому вектору и поэтому Н колеблется вдоль линии,
с тангенсом угла наклона (— 1)т -г-. Обычно поляризацию определяют по Е
и считают линию F9) направлением линейной поляризации. Однако в оптике
по традиции определяют ориентацию векторов по «плоскости поляризации»,
являющейся' плоскостью, нормальной к Е, содержащей Н и направление
распространения..
б.б. Поток энергии. В электромагнитном поле скорость, с
которой энергия протекает через поверхность, определяется вектором Пойн-
тинга S = [Е, HJ, введённым в разделе 2.19. Так как, согласно B7),
ik
H = zt— [n, E] (знак зависит от направления распространения), то, очевидно,
*%оток энергии нормален к плоскостям постоянной фазы и параллелен
направлению распространения.
Вычисление мгновенных значений потока энергии нужно производить,
оперируя с действительными частями комплексных волновых функций.
С другой стороны, усреднённые значения потока энергии могут быть быстро
определены при помощи комплексного вектора S+ = -^-[E, H*J, как это было
показано в разделе 2.20. Для простоты рассмотрим плоскую волну, линейно
поляризованную вдоль оси х и распространяющуюся в направлении
положительных г. Тогда
Ех = ае- z+a«z-<»t+b)t \
т * т/'а2_4_В2 . .. . 1Й . . \ G0)
" (J-C0 ' j
■м комплексный вектор потока энергии равен:
S+ = i£^ = aaJ^tE*-*-<T. G1)
У
Его действительная часть представляет, в среднем, энергию, проходящую
в секунду через единицу площади плоскости х, у.
Sz = -г—*-—-1-Х- е -2Р *cos y. G2)
Коэффициент cosy, появившийся из-за смещения фаз между Ей Н, может
быть выражен через аир:
tgf^l соП= у±—, G3)
5 —£--** <74>
Согласно теореме Пойнтинга, дивергенция от вектора усреднённого потока
энергии даёт энергию, -' превращающуюся в тепло в единице объёма за
секунду. В данном случае
div S = ■%- = —^- аЧ-W* = —1- аЧ~^\ G5)
что, в свою очередь, очевидно, равно проводимости, умноженной на среднее
.квадратичное значение электрического вектора поля Е.
РАСПРОСТРАНЕНИЕ? ПЛОСКИХ ВОЛН [5.6] 251
6.6. Импеданс. В мире, в котором внешне всё так несхоже,
утешительно обнаруживать иной раз единство и заманчиво размышлять о его
значении. Неискушённому человеку представляется, что система
колеблющихся грузов, подвешенных на пружинной сетке, имеет мало общего с
колебаниями токов в системе, состоящей из катушек и конденсаторов. Но эта
^электрическая цепь может быть сконструирована так, что её поведение и
колебания некоторой механической системы будут выражаться одной и той
же системой дифференциальных уравнений. Между ними имеется взаимно
-однозначное соответствие. Току соответствует скорость, напряжение — силе,
а масса и упругие свойства пружины изображаются самоиндукцией и ёмкостью
конденсатора. Если осмелиться думать о таких вещах, то представляется,
что «абсолютная реальность» — это свойство инерции, а масса и
самоиндукция являются лишь его представлениями или названиями.
' Каков бы ни был философский смысл эквивалентности механических,
электрических и химических явлений, физик успешно использовал её для
облегчения своих исследований-Техника анализа электрических цепей,
развитая за последние тридцать лет, была с успехом применена к механическим
-системам, исследование которых не так давно представлялось весьма
трудным. Механические задачи самого сложного характера представляются
электрическими аналогами, которые могут быть легко исследованы в
лаборатории. Не только методы, но и понятия из области электрических цепей
распространились в другие разделы физики. Конечно, самым важным из них
•является понятие импеданса, связывающего напряжение и ток по амплитуде
я фазе. Это понятие применяется в механике для выражения соотношения
между силой и скоростью, в гидродинамике, и особенно в акустике — для
измерения отношения давления к потоку.
Распространение понятия импеданса на электромагнитные поля, в общем,
яе ново, но недавно это понятие было вновь пересмотрено и развито в очень
интересной статье Щелкунова1). Импеданс для данной среды и волн дан-
«ого типа тесно связан с потоком энергии, но для того, чтобы уяснить его
сложную природу, лучше всего начать с аналогии, именно, с одномерной
передаточной линией, как это и делает Щелкунов.
Пусть z—длина, измеряемая вдоль электрической передающей линии
«пусть V = У0е~ш, / = /0е-^*—соответственно, напряжение между
проводами и ток в линии в какой-то точке г. Величины V0 и /0 являются
функциями только от z. R—сопротивление единицы Длины линии, a L —
индуктивность, отнесённая к единице длины линии. Утечка между проводами
в каждой точке описывается проводимостью G и шунтирующей ёмкостью С.
Импеданс Z и шунтовой адмитанс Y запишутся поэтому так:
Z==R—mL, Y=G — i(oC. . G6)
Напряжение и ток удовлетворяют соотношениям2):
% = -Zl, % — YV. G7)
Эти уравнения имеют два независимых решения, представляющих волны,
которые распространяются в положительном и отрицательном направлениях:
/1 = Л1^г-^, V1=Z0I1, G8)
I2 = A2e-ite-i«*, V2 = — Z0U,
^Schelkunoff, Bell. System Tech. J., 17, 17, January, 1938.
8) Смотри, например, Gu ill em in, Communitation Networks, том И, гл. II,
Wiley, 1935,
252 гл. V. ПЛОСКИЕ волны в неограниченной изотропной среде
где
k = iYYz, Zo = l/"^ . G9>
k — постоянная распространения, Zq — характеристический импеданс
линии 1).
Рассмотрим теперь плоскую электромагнитную волну,
распространяющуюся в направлении, определяемом единичным вектором п. Расстояние
в этом направлении мы опять будем измерять координатой С и предположим,
что время входит лишь в виде множителя е-«»**. В то время, как напряжение
и ток являются скалярными величинами, Е и Н, конечно, векторы. Для того
чтобы установить постоянное правило для определения знака, уравнения поля
будут написаны таким образом, чтобы связать вектор Е с вектором [Н, п]^
который параллелен Е и направлен в ту же сторону. Имеем:
^^-=ш^.[Н, п], ~[W, n]=/((os-l-/a)E. (80)
По аналогии с G7):
Z = — /со[л., Y=—i(cos-]-/o). (81)
Постоянная распространения k равна
^ = iyrZ = "|/"co2sji-f/C0J1O, " (82).
как и в B9), стр.- 243, в то время как внутренний импеданс среды для-
плоских волн определяется Щелкуновым как величина
г,= л/'^ = -/' -^^ = --^=ге-ч. (83>
В свободном пространстве этот импеданс принимает вид:
Zq = ]/^ = 376,6 ома. (84)
Так как мы приняли, что п направлена в сторону распространения, различение
положительного и отрицательного направлений становится ненужным и
соотношения между электромагнитными векторами принимают вид:
[п, EJ = ZqH, Е = Zq [Н, п] . (85)
Между внутренним импедансом и комплексным вектором Пойнтинга
имеется тесная связь:
S+ = 1 [Е. Н*, = i [е М] =, A^ (86>
И, следовательно,
1 Е^
-^0 ~ IS+ I * ^^^^'
1) Наши формулы отличаются знаком при мнимой компоненте от обычно при-
^ водимых в литературе по электротехнике, так как мы употребляем е-^* вместо
е^*. Очевидно, выбор знака совершенно произволен. Хотя в электротехнике удобнее
использовать е*'***, в волновой теории мы всё-таки будем чаще интересоваться
пространственным множителем, чем временным. Распространение выводов на
криволинейные кбординаты, которое будет дано в следующей главе, оправдывает выбор е-»»**..
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ [5.71 253
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ
Мы рассматривали в этой главе некоторые частные решения уравнений
.«10ЛЯ, которые были функциями от одной пространственной координаты и
ют времени. Благодаря линейности уравнений, их общее решение может быть
получено суммированием частных решений, умноженных на произвольные
постоянные. Поскольку мы имеем в своём распоряжении бесконечный ряд
\констант, постольку должна существовать возможность строить решения,
удовлетворяющие любым заданным начальным условиям. Мы покажем,
например, что вектор поля может быть задан в определённый момент t = /д, как
функция от С и тем самым поле однозначно определяется для всех после-
,дующих моментов времени, или же вектор поля может быть задан как
функция времени в какой-то одной плоскости С = Со и тогда поле
определится во всех других точках пространства и времени. Методы, которыми
мы располагаем для исследования общих интегралов дифференциальных
уравнений в частных производных второго порядка, распадаются, в
основном, на два класса: методы Фурье и Коши и методы Римана и Вольтерра.
В последние годы методы Римана и Вольтерра сделались наиболее общим
подходом к теории дифференциальных уравнений в частных производных;
щх применение к теории распространения волн развито в ряде блестящих
!ИССледований Адамаром i). Хотя метод характеристик, впервые предложенный
Риманом, даёт более глубокое проникновение в суть задачи, но пока он
:менее приспособлен для целей практического решения, чем методы гармо-
«ического анализа, которые будут занимать наше внимание в этой части главы.
6.7. Элементы гармонического анализа (теорема Фурье). Для удобства
■читателя, знакомого до некоторой степени с предметом, элементарные
сведения, касающиеся ряда Фурье и интеграла Фурье, мы изложим здесь без
доказательства. ' «
Рассмотрим тригонометрический ряд
-~ -}- («1 cos д; -j- ^1 sin а:) -|- ... -f (а^ cos пх -\- Ьп sin пх) -\- ... A)
<с известными коэффициентами а„ и Ь^ i% предположим, что ряд равномерно
сходится в области 0^а:<! 2'зг. В таком случае ряд A) равномерно
сходится для всех значений х и изображает периодическую функцию f(x)
с периодом 2тт:
/(л:-Ь27г)=/(л:). B)
Коэффициенты ряда могут быть выражены через f{x). В силу
предположения о равномерной сходимости ряд A) может быть умножен либо на
•созидг, либо на sin па: и почленно проинтегрирован. В области 0<^а:<^2тт
тригонометрические функции ортогональны, т. е.
2ii: 2ic
Г COS пх COS тх dx = О, Г sin пх sin тх dx = Q {тф п), ■, C)
о о
2к
Г COS пх sin тх dX = 0.
i)Hadamard, Legons sur la propagation des ondes; A. Hermann, Paris,
3903; Lectures on Cauchy's Problem, Yale University Press, 1923.
254 гл. V. ПЛОСКИЕ волны в неограниченной изотропной среде
Так как
271 2ic
ТО
i cos^nxdx:^ I sin^ mxdx :=-к, D>
0 6
an = — \ f{x) cos nxdxy
°2. (m==0, 1, 2, ...).} E>
^и = — Г f{x) sin nxdx. I
0 J
Предположим обратное, т. е. предположим, что дана функция fix).
Тогда чисто формальным путём можно сопоставить функции f{x) «ряд
Фурье»:
оо
/(■^) = -у-+ 2^ {р-п COS пх-\- Ьп sin пх), ^^г
коэффициенты которого определяются из E). Однако правая часть F) будет
сходиться к f{x) в области 0^л:^2тт, только в том случае, если /(л;)
удовлетворяет некоторым условиям. Вопрос о сходимости рядов Фурье,
взятый в целом, является весьма тонким; даже непрерывность f {х)
недостаточна для обеспечения сходимости. К счастью, оказывается, что при
определённых условиях ряд всё же может быть просуммирован и точно
представляет функцию внутри определённого интервала ^). Нахождение наименее-
жёстких условий, которые должны быть наложены на функцию для того,,
чтобы она могла быть разложена в сходящийся или суммируемый
тригонометрический ряд, по-^ебовали бы длинного и сложного изложения. Так как
мы интересуемся лищь функциями, встречающимися в физических
исследованиях, мы можем удовлетвориться некоторыми достаточными (но отнюдь
не необходимыми) условиями. Мы потребуем только, чтобы в интервале
0<^а:<^2тт функция и её первая производная были кусочно непрерывны.
Про функцию f{x) говорят,- чтб она кусочно непрерывна в данном
интервале, если она непрерывна во всём этом интервале за исключением
конечного числа точек. Если Xq такая точка, то функция стремится к
конечному значению/(atq+O), если подходить к Xq справа, и к значению /(aTq — 0),.
если подходить слева. В точках разрыва в качестве значения функции берут
среднее арифметическое
/(•Уо + 0)+/(.Уо —0)
2
Разложение Фурье особенно хорошо приспособлено для представления
функций, которые не могут быть вырая^ены в замкнутой аналитической форме,
и которые состоят из ветвей или кусков аналитических кривых, не
обязательно соединяющихся на концах друг с другом. В виду допущенных нами
разрывов функции или её производной, то обстоятельство, что два ряда Фурье
представляют в некотором частичном интервале одну и ту Ае функцию,
вообще говоря, ещё не означает, что эти ряды представляют одну и ту же
функцию вне этого частичного интервала. Это и есть то существенное, что
отличает функцию от её представления. Разложение в тригонометрический
ряд, записанный в правой части уравнения F), эквивалентно кусочно непре-
1) Е. Т. У и ттекер и Г. Н. Ват сон, Курс современного анализа, Л. — М.^
ГТТИ, 1933, глава 9.
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ 15.7] 255.
^^*-*— ■ : : :—
/рывной функции f{x) в области 0<^ х<^2t. Вне этой области значения,.
: йринимаемые рядом, повторяются периодически по л: с периодом 2тт, в то
время как функция /(х) может вести себя произвольным образом. Только
в том случае, если f{x) удовлетворяет дополнительному условию B), она
будет совпадать с её Фурье-представлением во всей области— оо <х< -f" °°-
Если внутри некоторой области ряд Фурье функции f{x) равномерно
сходится, то он может быть почленно проинтегрирован и полученный таким
'Путём ряд равен в каждой точке интегралу от f{x) взятому в тех же
пределах. Для того чтобы ряд Фурье можно было почленно дифференцировать
i; полученный ряд приравнять -—• ещё недостаточно равномерной сходимости.
Если, кроме того, /(х) имеет разрыв в некоторой точке внутри интервала,
то её ряд Фурье не сходится равномерно внутри всего интервала и,
следовательно, разложения Фурье для интеграла и производной f{x) требуют
, особого внимания ^).
Обычно бывает удобно заменять ряд F) эквивалентным комплексным
рядом с экспоненциальными членами следующего вида:
4- оо
/(л:) = 2 с^е*'»^. G)
w = —с»
Коэффициенты определяются из соотношения
сп = -^ //(«) е-^гшda (« = 0,± 1, ±2,...). (8)
о
Так как
е^^^^ = cos пх-\-i s\w пх, (9)
то ясно, что комплексные коэффициенты Сп выражаются через
действительные коэффициенты а-п и Ьп уравнениями:
A0>
При помощи подходящей замены переменных разложение Фзфье G)
может быть видоизменено так, чтобы изображать функцию в области
—/<;л:<; -{-/:
оо гпк гПк
/(x)=2 с»^"""^. ^»»=-9Г f/(«)« ^"^«- A1)
П =; —оо ■** J
Это растяжение основного интервала или периода от 2тт до 2/ наталкивает
на мысль о возможности такого перехода к пределу, когда основной
интервал становится бесконечным и этим достигается представление Фурье
непериодической функции для всех действительных значений х, лежащих между
—оо и -|~°^- ^" предположим, уто во всей области —оо<х<+°о»
f{x) и её первая производная кусочно непрерывны, что в точках разрыва
значение функции определяется как среднее арифметическое от значени*^
2Сп — С1п 10 п
2cq = UQ
2cn = a_n-\-ib_n
(« > 0), 1
(« = 0),
in < 0). 1
1) Эти вопросы подробно разобраны в книге Саг si aw Introduction to the
Theory of Fourier's Series and Integrals, гл. VIII, Macmillan, 1921.
256 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
-J-O0
■ справа и слева и что, кроме того, интеграл | f{x)dx абсолютно сходится
—оо
или, другими словами, интеграл I |/(л;I<^л: существует. Пусть-^ = Ди.
—со
Тогда A1) может быть записано в виде:
со +1
/(х) = ^ 2 Ди |/(о[)е*'^Д«(^-«Ш. A2)
п = — оо —I
оо
'■-С другой стороны определённый интеграл Г ср(")'^^ определяется как пре-
—оо
дел суммы при Ди->0:
+О0
JO0
<p(tt)^tt = lim V ^{n^u)tiu. A3)
Am-» о «JTrv,
_оо - п = —со
Если / стремится к бесконечности, то Ди стремится к нулю и мы можем не
без основания ожидать, что предел A2) есть
оо оо
/ (л;) = — Г^и Г/(а) е*« ^<^ -«^ da. A4)
—с» —со
Это И есть теорема об интеграле Фурье, согласно которой произвольная
функция, удовлетворяющая лишь условиям кусочной непрерывности и суще-
оо
ствования интеграла i \f(x)\dXy может быть выражена через двойной инте-
—со
трал ^). Следует заметить, что результат получен чисто формальным переходом
,к пределу, что делает существование такого представления вероятным, но
не доказывает его. Строгое доказательство выходит за пределы этих вводных
замечаний.
Если f{x) действительна, то мнимая часть интеграла Фурье должна
равняться нулю и, следовательно, A4) принимает вид:
со -J-CO
f(x) = — \ du Г/(а) COS И (л: — а) <ia. A5)
о —со
Так как
cos и{х — а) = cos их cos иа -\- sin их sin иа, A6)^
то интеграл Фурье для действительной чётной функции /(—д:)=/(х),
очевидно, равен:
оо оо
/ (jfc) ^= — 1 COS их I / (а) cos иа da йщ A7)
о о
1) Читатель может иметь в виду, как общий справочник по данному вопросу
книгу Е. Т и ч м а р ш, Введение в теорию интегралов Фурье, ГТТИ, 1947.
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ P-'^l
257
а^для действительной нечётной функции /(— х)==—f{x)
<Г> ОО
/(х) = — I sin их I /(а) sin ua^da du.
A8)
. Из этих формул мы видим, что интеграл Фурье некоторой функции
может быть интерпретирован, как её разложение по гармоническим компонентам
частоты и/2тг в непрерывном спектре частот, лежащих между нулём и беско-
': «ечностью. Например, в A8) можно рассматривать функцию
g{u)f=il/ — I /(а) sin иа da
A9)
как амплитуду или спектральную плотность f(x) в интервале частот от
и до u-f-du. Тогда
со
f(x) = У — gin) sin их du.
B0)
Соотношение между f(x) и g (и) взаимно. Про g(u) говорят, что она
является представлением Фурье f(x), а f(x) представлением Фурье g(u).
В более общем случае зфзвнения A4) спектральную плотность для
функции f(x) можно записать в виде:
со
>(«) = -^ jf(x)e't^^:dx, B1)
—00
откуда для f(x) получится! обратное
выражение:
00
f(x) = ~= j g(u)e^^^du. B2)
УШ'
I
Рис, 48. Ступенчатая
функция.
Обширные таблицы преобразований Фурье были опубликованы Кэмбеллом
и Фостером 1).
Применение интеграла Фурье может быть проиллюстрировано несколь-
, кими примерами, имеющими практический интерес. Рассмотрим сначала
разрывную ступенчатую функцию, определенную следующим образом:
/(д:)=1, при |х|</,
/(x)=-i, при 1х| = /, B3)
/(д:) = 0, при |л:|>0.
Так как функция чётная и действительная, то можно применить A7).
[Представление Фурье есть
8 / ч ,/" 2 Г , ,/* 2 sinK/5
[g.(ti)=y —J cosuxdx=y -^ -^p..
B4)
1) Campbell and Foster, Fourier Integrals for Practical Applications, Bell Tele -
phone System Tech. Pub., Monograph B-684, 1931. Ранее опубликована в Bell Syst
Tech. J., Oktober, 1928, стр. 639—707.
17 Зак. 593, Теория электромагнетизма.
258 гл. V. ПЛОСКИЕ ЙОЛНЫ в НЕРГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
г интеграл Фурье
со оо
чс/ч --/Г,х , 2Г sin и/COS их , .оегч
f{x) = y ~ g (и) COS их du = '-:^ du. B5)
о о
Возьмём далее в качестве /(х) «кривую ошибок»:
/(х) = е~^". B6)
Для того чтобы найти её' представление Фурье, мы должны вычислить
интеграл
со
__ gSx»
^ (и) = |/ — е 2 COS их dXj B7)
о
который равен, очевидно, действительной части комплексного интеграла
^(„) = |AJ-J» ' "''■ B8)
После дополнения показателя до квадрата, B8) можно записать так:
^ (и) = |/-i-е 2о« е 2 V а^) dx =
о
Ае~2аТ е 2 ^р. B9)
Путь интегрирования идёт по мнимой оси от -— iuja^ к О, а затем вдоль
действительной оси от О до оо. Мнимая часть интеграла получится лишь на
т
интервале 5-^р<0, атак как мы интересуемся только действительной
а
частью, то нижний предел можно положить равным нулю. В результате
имеем определённый интеграл с хорошо известным значением:
\е '.d^=L/S., C0)
О
а значит представлением фун^сции- е ^ является
g{u)=-^e 2«*. C1)
Тогда /(л;), как представление Фурье функции g{u), имеет вид:
/""9" Г е 2«* - —
/(Х) = у — I COS ихdu^e 2 C2)
В частном случае а=1, уравнение C2) становится однородным интеграль-
ж*
ным уравнением, которому удовлетворяет функция е ^ . Пара функций.
v:c
ОБЩИЕ РЕШЕНИЯ рШбМ]«РН0ГО ВОЛНОВОГО УРАВНЕНИЯ [5.7]
259
определёнйых посредством C1). и C2), обладает ещё другим свойством,
более важным для нас в данный момент. Изменим немного C1), чтобы
получить функцию
5 {х,а) =
sen
2а*
У27С
а
C3)
Площадь, расположенная между этой кривой и осью х, равна единице при
всех значениях параметра а:
Г 5(а, x)dx== 1,
C4)
как это непосредственно следует из C0)
меньше и меньше. Тогда в окрестности
уменьшае1ся, в то время как высота его
няется неизменной, как это показано на рис.
сжимается к прямой а; = 0, на которой
Таким образом получилась особая
функция —дельта-функция ^),
ограничивающая единичную площадь в ближайшей
окрестности точки д; = 0.
Дельта-функция, исчезающая всюду, кроме точки
x = Xq, где она обращается в бесконеч- :
ность, изображается следуюишм образом:
—(х — х^*
. Пусть теперь а становится всё
х = 0 ширина пика кривой всё
растёт так, что площадь сохра-
49. В пределе при а -> О кривая
она обращается в бесконечность.
5о(х —Xo) = lim -^
2о*
а
/одч Рис. 49. Импульсная или дельта-
^ ' функция S (х, а) для а = 1 и а = 0,2
Всякая произволь.ная функция F (S), подчиняющаяся обычным условиям
непрерывности, может быть выражена в виде бесконечного интеграла
с»
F{1) = j Soil —х) Fix) dx.
C6)
Из C2) очевидно, что Фурье-представлением дельта-функции Sq{x)
является прямая линия, расположенная на расстоянии 1/2тс от
горизонтальной оси.
В качестве последней иллюстрации теоремы об интеграле, Фурье
рассмотрим гармонический йолновой цуг, ограниченный во времени. Такой цуг
возникает при включении и выключении рубильника, связывающего
электрическую цепь с генератором переменного тока; такой цуг представляет собой
излучение света атомами, во время перехода их на другой энергетический
уровень. Пусть
/@ = 0, при \t\>-f,
Т \ C7)
f(t)=cosoiQt, при |^|<~..
1) В оригинале — «impulse function», т. е. «импульсная функция». В переводе
применён принятый в русской литературе термин «дельта-функция», введённый
Дираком. Следует отметить, что представление дельта-функции как предела гауссовой
функции ошибок, конечно, является совершенно специальным. Существенны лишь
нормировка к 1 и возникновение особенности в одной точке. Укажем, например.
на lim
а
c->o«(a2.-f-x2)
Прим. ред.
260
гл. v.. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Для ТОГО чтобы облегчить интегрирование, мы положим, что. f{t) равна
Т
действительной части e^'^o^ в области U|<-9~, и используем уравнения B1)
и B2):
+^
g (ш) = —^ Г е!^{'^о-^) t dt= лГ—
т
sin
(Шо-ш)Г
0H-
(О
C8)
Но интеграл Фурье для f{t) соответствует действительной части B2), т. е.:
+«
/@ = ^/
+°° z\n ^""""""^ ^
0)fl Ш
COS 0)^ <ia) =
— оо
4J[
со . (юу-ю)^
sin
tOfl.
to
+
sin
(Шо+«в)Т
ojo+to
]
cosa)^<ia).
C9)
Уравнение C9) можно интерпретировать, как спектральное разложение
функции, которая представляет собой синусоиду частоты шд в течение конечного
интервала Т. Амплитуда
возмущения в окрестности. какой-либо
частоты О) даётся функцией
Л(о)) =
1
sin
(шо — to) г
"К
D0)
СОг
■to
Амплитуда обращается в нуль
в точках
27СИ
О)
Шг
Рис. 50. Амплитудная функция
^ IsinOoo-^)^^
тс tOQ to
(« = ±1,:±:2, ...), D1)
как это показано на рис. 50,
и имеет максимальное значение
при (й = т^. Если
продолжительность волнового цуга Т
увеличивается, то амплитудная
функция сжимается в горизонтальном направлении, пока в пределе, при
Т-* сх), всё возмущение не стягивается к одной линии спектра а) = @о.
Простые гармонические колебания, которые так часто используются нами,
представляют собою математическую идеализацию; колебания реальных
механических или электрических систем имеют конечную длительность и
соответствующие вблны периодичны лишь приближённо. Мы обнаружим скоро,
что при наличии диспергирующей среды весь характер распространения
может зависеть, от продолжительности волнового цзпга.
6.8. Общее решение одномерного волнового уравнения в непогло-
щающей среде. Для того чтобы в дальнейшем облегчить себе пользование
интегралом Фурье, полезно остановиться на элементарной задаче нахождения
общего решения волнового уравнения в непроводящей среде. Пусть tb есть
х- или з'-компонента любого из электромагнитных векторов. Тогда <Ь удо-
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ [5.8]
261
влетворяет уравнению
а2ф
1 дЧ
г>2==.
dz^ v^ dfl ' fxe
D2)
Согласно разделу 5.2, частное решение уравнения D2) представляется
функцией
D3)
i — г
^ = (Ае « -]-Ве ^ )е
-1ы
Коэффициенты А п В произвольны и могут, зависеть от частоты ш; можно
сказать, что мы сопоставляем каждой гармонической компоненте
соответствующую амплитуду, которая может быть записана как Л(а)) и Б (со). Общее
решение уравнения D2) можно получить теперь сз^мированием по о. ,В том
случае, когда <j^ — периодическая функция, суммирование происходит по
дискретному ряду частот. В общем случае волновая функция апериодична
в пространстве и во времени, и поэтому её частотный спектр непрерывен:
^{z, t)= \ {А{(а)е* ^^-\-В{*й)е « ^]е-^^^*с1ш. D4)
-с»
Предположим, что в плоскости z = 0 значения функции <j^ и её
производной по направлению распространения волн — известные функции времени:
«о.^)=/@. DIU,=^@.
D5)
Задача состоит в том, чтобы найти коэффициенты Л (со) и В{<а)у
удовлетворяющие этим двум условиям, и таким образом показать, что задание
функции и её производной в некоторой точке пространства (или времени)
достаточно для определения ^(z^ t) всюду.
Если мы допустим пока, что интеграл в правой части D4) равномерно
сходится, то мы можем дифференцировать под знаком интеграла по
параметру Z и получим:
— i—г.
Положив z = 0 в D4) и D6), получим:
со
f(t)=^j [А (<о) 4- в (ш)] е- i^t da>,
—со
со
F{t) ^^ f О) [Л (ш) — в (<o)J е-^^^Чш.
D6)
D7)
Из сравнения с B1) и B2) очевидно, что коэффициенты при множителе
g-iuit 2 подинтегральных выражениях D7) являются представлениями Фурье
функций fit) и F(t):
00
— со
сх>
I^(A-B) = ^j F(f)^-tat.
D8)
262
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Разрешая совместно эти два соотношения относительно А и В и заменяя *)
переменную интегрирования t через а, мы получаем:
— со
со
^ ("*> = bS^ (<^)+ -^ F(a)l .-«^а;
D9)
что, после подстановки в D4), даёт:
со со ^ UJ
1 г Г ^ ^ . . i^ («Ч 1) ', гш (о — — z—t)
• со —со
со со
iv
4п
frfo) f ^(е* «^ —е «^)е«'«(«-«)^а. E0)
•со —со
Первый из этих двойных интегралов является разложением Фурье функции,
которая, если учесть A4), может быть сразу написана. Во втором интеграле
изменим порядок интегрирования:
со со
+ ^ JF{a)da J sin ^^.^-(а-.)^. (gl)
— со —со
Мнимая часть последнего интеграла равна нулю, так как
— sin — sin <о (а — t)
есть нечётная функция ш. Поэтому
со со
8Ш —^wla-<) — == I sin—COS О) (a t) — =
V Ш J V ^ ^ to
CO CO
CO
= /[si„c.{. + ^-<)-sina,(a-^-^)l!^. E2)
0
Путём незначительного изменения условий, которые определяют ступенчатую
функцию B3), легко показать, что каждый из двух последних интегралов
представляет функцию с простым разрывом. Действительно:
f |-, при /7>0,
г s\x\px ^у.__ , о, при р = о,
-|-, при р<0.
E3)
1) Переменные о и р, фигурирующие на нескольких следующих страницах,
очевидно никак не связаны с действительной и мнимой частями числа k — a-\- i% опре-
дедёвного на стр. 243.
ОВЩИЕ РЕШЕНИЯ ОДНОМВРвОГО В0;Ш0В0Г0 УРАВНЕНИЯ «[^8} 239
Следовательно, E2) обращается в нуль всякий раз, когда аргументы
Z Z '^
a-f- — — t и а 1 имеют одинаковый знак. Изменения знака происхо-
Z Z
дят при ct. = t и a = t-\ . Поэтому интеграл E2) отличен от нуля
Z 1 Z
лишь Б интервале ^ <а<^Н , в котором он равен .тс. Общее
решений D2) выражено теперь через заданные начальные условия:
Z
t—
V
Определим функщ1Ю Л(Р) следующим соотношением:
Р
/г(р)==—-у jF(a)rfa. <55)
§=A'(P) = -^F(P). E6)
Тогда
rfp
Вместо E4) можно написать:
^(,,t)=^f{t-^)+{f{t + l) + \h{t-^)-\h[t + ^). E7)
Когда г = 0, то 4* (О, О переходит, очевидно, ^ f{t)y а T^j _ —в —Л' или
F(^). Можно убедиться также путём дифференцирования и подстановки,
что D2) удовлетворяется любой функцией, имеющей аргумент вида
t ±— . Замена переменной ^в/(Она^ означает смещение или
распространение направо вдоль оси г со скоростью.«» без искажения функции.
Начальное возмущение разделяется, таким образом, на две волны; одна движется
направо, другая — налево. На эти две волны накладываются Л-волны,
выбранные таким образом, что при г = О они взаимно уничтожаются, а
производная от ^ принимает заданное значение F(t).
Задания двух функций f(t) и F(t) в плоскости г=0 достаточно для
того, чтобы полностью определить электромагнитное поле. Предположим,
например, что электрический вектор плоской волны поляризован вдоль
оси X. Тогда уравнения Максвелла имеют вид:
^ + ,^ = 0, ^+е^ = 0. E8)
Пусть Eg, изображается функцией <Ь(-г, ^) в .виде E4) или E7).
Дифференцируя затем по / и по z, мы найдём с помощью E8) выражения для
_jt И -^«^; в свою очередь из них несложно вывести выражение для Ну
«.=т/|[^('-т)-/('+т)+Ч'-^)+Ч'+т)]-
E9)
264
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Эти ПОЛЯ, 'очевидно, таковы, что на плоскости z = 0
0
Поэтому электромагнитное поле определено, если на плоскости z = 0 заданы
как независимые функции времени любые две из величин F0),
содержащих как /(О» так и F{t). Таким образом могут быть заданы либо
электрическое поле и*его нормальная производная, либо электрические и магнитные
поля без наложения ограничений на их производные.
5.9. Поглощающая среда; заданное распределение во времени. Мы
перейдём теперь к более трудней задаче определения электромагнитного^
поля в проводящей среде, которое обращается на плоскости г = const.
в заданные функции времени. Мы опять допускаем, что <^ есть какая-нибудь
прямоугольная компонента электромагнитного вектора, удовлетворяющая
уравнению
дЧ дЧ д<Ь
dz^
а/2
di
F1>
Для дальнейшего удобно ввести две новые константы:
а =
1
у^г
ь=
2е '
k == j/^{i,saJ -j- /fioo) — -^ У^ш^ -j- 2bm.
F2)
Заметим, что в поглощающей среде а отличается от фазовой скорости у=с1п.
гармонической компоненты. В этих обозначениях^ волновое уравнение
принимает вид:
'-| + 2.#-.^^з = 0.
dfi
dt
dz^
F3)
Частные решения F3), гармонические во времени, были исследованы в
разделе 5.2; они имеют вид:
^ = (Ае^^ 4~ Ве-^^^) е-^*^*.
F4)
Допуская, что коэффициенты А и В равно как и комплексная величина к-
являются функциями частоты, мы составим общее решение, просуммировав
гармонические компоненты:
^(z, t)= f [А (ш) е^^^ -|" В (ш) е-^Щ е-**^* do).
F5)
Предположим вновь, что на плоскости -г = const, волновая функция и-
её нормальная производная — заданные функции времени. Для удобства
поместим начало системы отсчёта в этой плоскости, так что константа равназ
нулю.
но. t)^ fit). (i)^_„=^@.
F6>
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ [5.91
265»
в физических задачах характер функции ^ (z, t) обычно таков, что интеграл F5>
/СХОДИТСЯ равномерно. Допустив такую сходимость, можно дифференцировать-
интеграл по параметру z ^).
^= f ik [А (со) е^^^ — В (ш) е-»лг] ^-гш*^/^j
— оо
На плоскости z = 0 F5) и F7) принимают вид
)
F7>
f{t)= J [А (ш) -f В {ш)]е -i^t doi] I
—оо
оо
F (/) = f ik [А (со) — В (со)] e-*^^« rfto.
F8>
Коэффициенты при е-'^^^* опять могут рассматриваться как представление
Фурье соответственно /(^) и F(t).
со
Л+в=1 J/(a)e*^-«rfa,
-ОО
А — В=^^ jF(a)e»"^«rfa.
— со
Разрешая относительно А и В, находим:
оо
— оо
оо
F9>
—оо
G0>
Если подставить эти значения в F5), то после изменения порядка интегри--
рования получим выражение
оо оо
«J»(г-, ^) = 2^ Г^«/(«) ( coskze^^^^-*)dш-{-
оо оо
-i-~^jdaF{a) J ■'^"^^^g^"> («-Q ffo>. G1>
До сих пор вычисления формально не отличались от вычислений для случая^
непоглощающей среды. Однако теперь мы сталкиваемся с трудностью из-за
того, что k комплексно, и мы должны будем отвлечься на время для того,
sin kz
чтобы рассмотреть представление функции —-— при помощи определённого-
интеграла. Основой этого представления является fИнтeгpaл Гегенбауера \.
1) Смотри, например, С а г s I а w, Introduction to^ the Theory of Fourier's Series»
and Integrals, главы IV и VI, Macmillan, 1921.
2) W a t s о n, A. Treatise on the Theory ol Bessel Functions, стр. 379, Cambridge
University Press, 1922. Уравнение G2) является^^частным случаем уравнения F9>„.
стр. 362, выведенного в разделе 7.7 этой книги.-
1266
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
«который в рассматриваемом простейшем случае имеет вид
sin и 1
и ~~ 2
J Jq {и sin <р sin 6) е*« «os ? cos е gjn е db.
G2)
Jq (и sin 9 sin 6) обозначает функций Бесселя нулевого пврядка от
аргумента и sin Ф sin 6.
Сделаем подстановку:
tt = i;/(p + A)(pH-jx).
где Л и {1 — действительные или комплексные постоянные.
ucoso = vlp-[—~ ), usin^ = i-^(K —.{л), cos 6 = — ,
sin0= -lAl —4» sin8^6=—^.
Тогда G2) принимает вид
G^
G4)
^J^iILX^iMli±}^^U JoC^ G5)
—»
.Заметим, что функция в левой части уравнения G5) является представле-
/иием Фурье функции ^(Р), определённой следующим образом ^):
§-(р) = 0 при 1р|>^,
gm = }/'^Jo(}=pV¥'^e^'-^* при IP Кг..
Наконец, дадим параметрам в этой формуле значения:
iMcKOMoe соотношение будет тогда:
G6)
. ^ asin— yto2_L-2*to/
+■
У<02-^2*<0/
= у / -^0 D V^'^^ — «^P^ ) ^^^"""^^ ^Р- (^^)
2
После этого небольшого отступления вернёмся снова к уравнению G1).
Во второй интеграл правой части, который для удобства может быть
обозначен через ^^ мы подставим G7), а затем изменим порядок
интегрирования:
а оо оо
^^2 == -|/ '^Р ^"'{^ j"^^!"?(«'Р)^*"^("^^-*^ ^«] , G8)
Z
а
—оо —с»
где
«(«, P) = F(«)УoDV^^-«'^^)
G9)
1) Campbell and Foster, loc. cit. No. 872.2.
Общие решений O^CfMBi^H&ro волнового уравнения {5.9] 267
ЛвойноЙ интеграл внутри скобок является раа^Ожением Фурье функции
^{t—р, Р); следовательно,
о
'}'2=|-J^(^—Р)Л(-|У^'-«Т)«-^Р^Р. (80)
а
ИЛИ после замены переменных:
t+-
^ а
^2 = 1 / F^)Jo{^Vz^-aHt-?f)e-b(t-^)d^. (81)
а
Для ТОГО чтобы вычислить первый интеграл правбй части уравнения G1),
который мы обозначим через ^^у нам нужно только заменить Р(а) в ^2 "^
/(а) и произвести частное дифференцирование по г. Так как пределы
интегрирования в (81) являются функциями Z, то это дифференцирование должно
быть произведено по формуле
j f{x,z)dx=j
± j f{x,z)dx== j%dx^f{x„z)^-^~fix,, ^)^, (82)
откуда
Ъ b
z z
a
-V^e-bt J fфeЬ^|-J^{LYг^^a^it-^f)d^, (83)
t-1
a
Волновая функцияt которая в поглощающей среде в плоскости г = О
обращается в f{t)y а её нормальная производная в F(f), определена всюду
выражением:
ь ь
— Z Z
Нг, 0 = ^/(<+j) + ^/(<-^) +
О
~\-±e-bt j .f^)eb^p^(lY^2_aHt-pf)dp-{-
a
t + L
a
Из (84) очевидно, что характер распространения существенно изменяется
при наличии даже небольшой проводимости. При г = О интеграл равен нулю
из-за равенства пределов интегрирования. Затем начальное возмущение /(^)
268 гл. V, ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
распадается на две волны с амплитудами, равными половине начальной, как
л в непоглощающей среде. Эти отдельные волны распространяются направо
и налево со скоростью а, во всех случаях не зависящей от частоты, а также
и от проводимости. Кроме того, как это можно было предвидеть, они
экспоненциально затухают в направлении распространения. Заметим, что в
случае гармоничной волны коэффициент затухания в пределе при a^je^oi^ -^со-
приближается к значению
|. = |-/'|= 188.36 .|/"|, (85>
которое совпадает с E3) на стр. 247. Начальная функция уже не
распространяется без изменения формы, так как члены с интегралами представляют
добавки, остающиеся отличными от нуля в течение бесконечного времени
в точках, уже пройденных волновым фронтом. Волна тащит теперь
в своём кильватере остаток или шлейфу экспоненциально убывающий со
временем.
Характер этих добавок будет разъяснён численным примером, который
мы рассмотрим в разделе 5.11.
5.10. Поглощающая среда; заданное распределение в пространстве.
Начальные условия часто задаются другим способом. Предположим, что
в момент г = О поле ^ ^ ^го производная по времени -^f заданы как
функции пространственной координаты z:
Ч(г,0)=-^(г), (-^\^^ = 0{z). (86)
Гармонический анализ в пространстве применяется чаще, чем во времени, и
общее решение может быть составлено из частных решений,
рассмотренных в разделе 5.3:
-■^t
<1; = е 2е (ЛегЗ«_|.5е-гд«)егЛг^ (87)
где
q=^^-^^^=Y аЧ^-ЬК (88)
Константы а тл b определены так же, как и в разделе 5.9, но k теперь —
действительная переменная. Для того чтобы исключить общий
экспоненциальный множитель, удобно положить:
^^u{z,t)e-bt^ ^ = (^^-^bu)e-bt, (89)
Общее решение составляется в предположении, что амплитуды А и В
зависят от ky путём суммирования по всем положительным и отрицательным
значениям k:
со
и B-, t)= f [А {Ще^о* J^B{k)e-»з*] е^^ dk. (90)
— °° *
Для производной имеем:
оо
^ = г iq \А (kyut — B (k) е-Щ ^kz dk. (91)
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ {5.10]
2G9
(92)
Дальнейшие шаги в основном те же, что и в предыдущем параграфе.
При ^ = 0
г оо
—оо
оо
G{z) = ^ [Iq \А{К)—В {Щ\—Ь \А {k)\B{K)\} e^^^dk,
—со
я коэффициенты легко определяются по теореме о преобразовании Фурье
оо
A{k) = ^^^ [G —i^)^(«)-'^'G(a)l e-^^-da,
—оо
оо
(93)
Подстановка этих формул в (90) приводит после простых преобразований
а< выражению
со оо
и {z,t) = 2;^ f dag (а) f cos qt e'^ (^-<
)dk
00 uu
—00 —00
00 00
+ i^Jc?aG(a) Ji^M£e£fc@-«)^;fe. (94)
Ha основании G5) функция ^^- ^
/^
sin a г 1/ ^2
«2
«1/ ^^-|'
может быть выражена
определённым интегралом. Придадим параметрам в G5) значения
v^=at, q =— k. X = — , u, = ,
что даёт
Sin«^ Vfe2—*2/e2 1
a у k^—b^l
^-=2^/лA1^'Р^^^^)-'^^^Р
(95)
—at
Обозначим три члена на правой части (94) соответственно через и^, U2, %
Тогда
at
00 00
агде
«в = 4 J ^Р [21^ i^^i «(а,Р).^'^(-«-.р)^«] ,
—at —00 !—00
<р (а, р) = G (а) УоD- Ур2 —«2^2) •
(96)
(97)
27(У гл. V, ПЛОСКИЕ волны в неограниченной изотропной среде
По теореме Фурье двойной интеграл внутри скобок представляет
разложение <p{z—Р, Р) и, следовательно,
at
"8 "= 2^ / ^^^— Р>'^о(а У^^ — аЧ^) ^Р, (98)
—at
или, после замены переменных:
г+at ^
"8 = ^/ 0(?)JoUV(^—?r-a4^)dp. (99)
г—о^
Подобным же образом получаем:
«2 = ^ / ^(P)Л(TV(^-P)^-«^^^>P, (ЮО)
z~at
откуда ttj получается дифференцированием по t:
1 , . .X . 1
и
1 = у^С^ + аО-Ьз-^С-г-—«О +
z+at
+ Га S Sm§-M-^V(z-b)^- а2^) dp. A01)
z—at
Волновая функция, которая в проводящей среде обращается в момент'
t = OBg(z) и которая имеет производную по времени в этот же моменту
равную О {г), определена в любой момент времени выражением
^{z,t) = e-bt^^gi^z-\-at)-\-^g{z — at)^-
z+at
-{-Та J [^^(P)+G(P)jyo DV'7^'=^P?^=^^^)^P +
z—at
z+at
+ Й / ^(P) TtJo{^V(.'-^Y-a4^y^]- A02)
Z—at
По своим основным свойствам это решение не отличается существенно от
решения, выведенного в предположениях, сделанных в разделе 5.9.
Начальное поле, распределённое вдоль оси г, разделяется на две волны,
распространяющиеся соответственно направо и налево. Если проводимость отлична
от нуля, то после прохождения волнового фронта получается остаток или
шлейф, и поле спадает экспоненциально со временем.
5.11. Дискуссия численного примера. Физический смысл полученных
результатов может быть проще всего разъяснён на частном примере. Пресная
вода — удобная среда для такого рассмотрения, так как при радиочастотах
она занимает среднее место между хорошим проводником и хорошим
диэлектриком. Возьмём следующие константы:
Тогда находим:
л = ~--108 ;и/сел:, & = 1,4-Ю^ 1/сел:, ~==4,2-Ю-^ l/jit.
ОБЩИЕ РЕШЕНИЯ ОДЙОМЙРНО^б ЙОЛНОВОГО УРАВНЕНИЯ {5.111
271
Обычно легче представить себе распределение и распространение вдоль
нространственной оси, чем во времени; по этой причине мы рассмотрим
сначала решение A02). Предположим, что при ^ = 0 поле равно нулю всюду,
за исключением области — 25<2-<25, где его амплитуда равна единицей
^B-)=1 при |2|<25,
g(z) = 0 при |г|>25,
G {z) = О ДЛЯ всех значений г.
На рис. 51, а -^ g(z-\-at)~[-g(z — at\ изображено как функция z для
различных значений t, а ка рис. 51, b то же выражение изображено как:
функция t для различных значений z. Эти два рисунка изображают рас-
g=(z-*-at).
П
g=fz-af)
g={z+at)
10
t-OMS^W'^ceK
Jf
t=375"When.
-IQ
n
W
t=-8.25*W'^ceK.
nl.O
r
П
I I 1 I L__J I 1 I I Л I i I ' 'I l_
g=(?.-at)
Z--0
Z -15 метр
Z -125 метр
-l.O
n
Z-275 метр
1.0
_l L
. П.
~300 -zoo -wo 0 100 zoo 300 -10-8-6-4-2 0 2 Ч 6 8 10
2-е метрах i -в мимросемундах
a h
Рис. 51.
пространение начального возмущения во времени и в пространстве в среде-
с проводимостью, равной нулю. Функция /(г — at) равна нулю либо при
либо при
z<iat—25 или
t<~-(z—25) или
2'>а^4-25,
^>~(г—25).
Аналогично волна, распространяющаяся налево, gB:-\-at) равна нулю во
всех точках, в которых
или
z<—at —25
1
или
г> — й^-|-25,
^< — — B5 4-2-) или t> — B5~z).
а
На рис. 52, а и 52, ^ те же самые функции умножаются на затухающий
множитель е~^>*. Мы ничего не, говорили о происхождении рассматриваемога
поля, но предполагали, что оно было вызвано некоторое время тому назад
системой соответствующим образом расположенных источников, от которых
поле распространялось и затухало так, что при ^ = О его распределение
соответствовало верхнему рисунку 52, а. В данном примере очевидно, что волна
12.72
гл. V. ПЛОСКИЕ волны Б НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
возникла в виде двух импульсов в некоторый момент t<i—10-10-^сел:;
ЮДИН из них возник в отдалённой точке на положительной оси z и двигался
налево, другой — в некоторой точке на отрицательной оси и двигался
■направо. В окрестности t = 0, z = 0 они встречаются, проходят друг через
друга, соответственно складываясь, а затем продолжают своё движение.
Их последовательные продвижения показаны при ^ = 0,45, ^ = 3,75 и ^ = 8,25
микросекундам. Картина, имеющая место в определённой точке простран-
<ства, иллюстрирована серией чертежей на рис. 52, Ь. Рассмотрим, на-
fipHMep, г = 275 м. Фронт волны, распространяющейся налево, достигает
-6t
2 fffz+at)
е
2
■bt
,-bt
g(z-at) |, g(z*ai)
t--0
dt
_o.
J I I , .1..
10
±^0.Ч5т'^СЕК.
t=3.75xW'fce/i.
-10.
jri
t'-8.25xm'^ceH.
[\
ID
л 1 1 L
n
10
•bf
g(z-ot)
2 = 0
С
■ f5 метр.
z -125 метр.
10
n
w
7.-275 метр.
I--, t L
300 -200-WD_ 0 WO 200 300 'Ю'8-6-Ч-2 0 2 Ч 6 8 W
Рис. 52.
Z-e метрах
a
t-e минросвнундах
b
этой точки при t = —9 микросекунд и продвигается далее к меньшим
значениям Z. Требуется интервал в 1,5 микросекунды для того, чтобы волна прошла
рассматриваемую точку. Всё это время она экспоненциально уменьшается.
.От t = —7,5 до / = -}-7,5 микросекунды всё спокойно, затем приходит
фронт волны, распространяющейся направо, с сильно уменьшенной
амплитудой, так как амплитуда волны прошла уже через своё единичное
значение в начале координат и волна продолжает распространение в сторону
•положительных точек наблюдений.
Эта простая история поля должна быть видоизменена, если мы
примем во внимание добавки от интегральных членов в уравнении A02).
В большинстве случаев оценка этих членов требует численного или
механического интегрирования, но, благодаря простому виду функции g{z)
в данном примере, интегрирование может быть проведено аналитически для
достаточно малых значений г и t. Из теории функций Бесселя мы заим-
.^твуем следующие соотношения:
/о(^) = 1
х^
л^
22
2242 24^62
"!•••»
dJo(x)
dx
X
= — Ji(x), J^{x) = -^
дгз
.v6
28.21 ~ 25213!
!&«■"-
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ [5.11]
273
ЙЙодстановка соответствующих значений х даёт:
I +й(-1У1(^'-р)'-'''^'---->
Исследование сходимости этих рядов показывает, что в данном прихмере
/ мы не делаем большой ошибки, если ограничимся двумя членами
разложения, при условии, что г не достигает 300 м. Функции Бесселя приближённо
выразятся поэтому так:
Эти функции нужно умножить теперь на g(J^) и проинтегрировать по
р. Относительно пределов интегрирования заметим следующее. Предположим,
-I L-f--
-200 450 -100 -50
W
0.8
-0,6
-0,4
t--375^W'^cef<.
0^/
Остаток
li::
J с_
О 50 то 150 200
к
Z - в метрах
а
J.0
0,8
-0,6
-0,2
J L
Z = I25'^emp.
„J i_
п.
.,(, I. I i i
0 2
-c - e микросенундса
Рис. 53.
8 10
что t положительно. Если z — о^>25 или z-\-at<i — 25, то ргзультирую-
щее поле ^{z^f) равно нулю. Если — at-\-2Ъ <^ z <С at — 25, то части поля,
описываемые g{z-\~at) и g{z—at), равны нулю, но интегралы не
исчезают, вне зависимости от того, как велико t. Остаточное поле
задерживается в области, пройденной ранее волновым импульсом. Если z-\-at'^2%
и Z — at <i—25, то пределы интегрирования могут быть положены
равными±25, так как вне этих значений g{^) равно нулю. Поэтому такие
пределы годны для всей области между импульсами—at'\-2b<iz<iat — ^Ъ.
Результаты интегрирования изображены на рис. 53, «, и 53, Ь.
Эффективное поле ^ (z, t) изображено сплошной толстой линией; частичные поля,
описываемые различными членами в A02), показаны пунктиром. Рис. 53, л
изображает распределение поля вдоль оси z в момент t = 3,75 микро-
18 ^лк, S93 Теория влевтрокагнетизма.
274
гл. V. -ПЛОСКИЕ волны В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
секунды. Мы замечаем начало деформации первоначально прямоугольного
импульса, верх наклоняется вперёд, а сзади тянется шлейф. Во время
распространения волны
высота её переднего фронта
уменьшается, так что,
в конце концов, им-
f^ffi-§) f"^(t-§J f\(t*l) l''fft~§)
п
E
п
-I I L
10
z-.O
10
г-Юметр. -■
hO
-О.
Z-WO метр.
xnJ
Ho
Z-300 метр.
-I I U
-1 I 1 L-
hO
t--o
w
ho
i=2>^W'^ceh
пульс и шлейф
сливаются в сплошной
. контур. На рис. 53, Ь
t=D,5xW'%efi наблюдения сделаны в
фиксированной точке
z==\2b м. Ло t = —3
микросекундам здесь
существовало поле,
которое было погашено
прохождением
импульса, двигающегося
налево. При ^ = 3
микросекундам прибывает
волна, двигающаяся
направо, за ней следует
её шлейф, остающийся
после прохождения
импульса.
Основная разница между решениями, данными в (84) и A02),
обусловлена переменой ролей пространства и времени. Для того чтобы иллюстриро-
t'-S^Uf^ceH.
\hO
J—)—I i.rrrrt
10-8-6-4-Z 0 2 Ч 6 810 -300-200-WO 0 WO 200 300
t-Bминросекундсх z - в мргпра>^
a b
Рис. 54.
1 \ f ' I' ' 11 ' •' '
^300-250-200-150 -100 -50
t^3,75m~^cm.
0,0
Yo,4
0,2
J—I—' I' ■ I 11 I ( I i_
V 50 100 150 200 250 300^
Z-виетрах
a
П
'III 1 L
-J=r=;
-IZ '10 -5 -5 -^ -2
0,8 Z=125 метр.
-0,6
-0.Ч
-0,2 rn
.1. '. II -i,J' ■ I—I I—I—'—\—I
6 8 10 IP.
^0 г Ч
f -в мииросенундах
Ь
Рис. 55, а vib.
вать поведение поля, допустим, что начальной функцией времени f{i)
в уравнении (84) является прямоугольный импульс, определённый следующим
образом: , , ^ ^ „
/ (О = 1 при I (I < 1 • 10-6 сек,
/@ = 0 при |^|>1 • 10-6 сел:,
F @ = 0 для всех значений t.
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ 15.12] 275
»>*- ■' '■ ' ' ~« • у^ ■ — — ' ' "^
ь _ ь
— Z — я
Функции —9~"/( ^Н ) ^ —9—f\^ J изображены при различных
значениях гг и ^ на рис. 54, а и 54, Ъ. В силу определения / (Р) ясно, что
третий член в правой части (84) ничего не даёт, если t— — > 1 или
^+^<—1. Если 1—J< t<^— 1, то функции/(/+f) и/(^—^)
равны нулю, но интеграл отличен от нуля. В этом интервале, лежащем на
оси i между импульсами, пределы интегрирования будут ± 1. На рис. 55, а
и 55, Ъ показана обусловленная, шлейфом волны деформация импульса
(вначале прямоугольного) в определённой точке пространства и времени.
При изучении этих рисунков следует всё время помнить предположение
о двух предсуществующих волнах, приходящих от источников,
расположенных в бесконечности, так что интерференция этих волн даёт правильное
распределение при /==0 или при г=0. Отдельная волна с нулевой
амплитудой для всех значений ^ и г, меньших нуля, может быть вызвана лишь
источником в начале координат, являющимся особенностью поля, — задача,
которую мы ещё не рассматривали.
5.12. Элементарная теория преобразования Лапласа. Преобразование
Лапласа является одним из самых старых и наиболее важных методов
решения линейных дифференциальных уравнений. Если в уравнении
^ + р(г)^+?(^)™=0 A03)
произвести преобразование искомой функции w.
(z) = j uit)e'^tdi, A04)
w
TO-BO многих случаях оказывается, что u(t) удовлетворяет более простому
дифференциальному уравнению, чем A03). Фактически и (/) часто оказывается
элементарной функцией, в то время как wiz)^ вообще говоря, не может
быть непосредственно выражена через элементарные трансцендентные
функции*). Если коэффициенты р(г) и g(js) являются функциями независимой
переменной г, то необходимо соответствующим образом выбрать, пзпгь
интегрирования в комплексной плоскости, для того чтобы A04) было решением
A03); независимые решения отличаются тогда выбором пути интегрирования.
Результатом является представление частных решений в виде контурных
интегралов. Если же коэффициенты р и q постоянны, то уравнение не имеет
никаких других особенностей, кроме существенной особенности в
бесконечности, и путь интегрирования может быть выбран вдоль действительной оси.
Тогда решения выражаются через интегралы в бесконечных пределах, тесно
связанные, если не эквивалентные, интегралам Фурье.
В последние годы физики и инженеры с растущим интересом стали
рассматривать применение преобразования Лапласа к линейным уравнениям
с постоянными коэффициентами; повидимому, последовательные и точные
рецепты такого решения быстро заменяют квазиэмпирические методы
операторного исчисления Хевисайда. Хотя методы Лапласа и не приводят к
результатам, которые не могли бы быть получены непосредственным применением
интеграла Фурье, однако, с точки зрения удобства они обладают некото-
1) In се, Ordinary Differential Equations, главы VIII и XVIII, Longman»,
London, 1927.
276 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ Среде
рыми несомненными преимуществами. В частности, они хорошо
приспособлены к оперированию с функциями, которые не обращаются в нуль в -|- оо
и, следовательно, не удовлетворяют условию абсолютной сходимости; кроме
того, они прямым и простым способом приводят к решению уравнения,
выраженному через его начальные условия. Однако, с другой стороны,
методы Лапласа могут быть применены лишь к задачам, в которых
функции для всех отрицательных значений независимой переменной могут
быть положены равными нулю; короче говоря, интеграл Лапласа
применим к задачам, в которых важно будущее, а прошедшее не представляет
интереса.
Мы подойдём к теории преобразования Лапласа с точки зрения интеграла
Фурье и лишь наметим доказательства наиболее важных теорем. Рассмотрим
функцию ДО» которая равна нулю для всех отрицательных значений t.
Тогда, если не считать множителя 1//^211, представлением Фурье f{t) будет
•фз^кция
F (со) = г / (О е - ^tdt, A05)
о
со
^ри том условии, что интеграл 1 \f{t)\dt существует. Если/(if) должным
о
образом не стремится к нулю на бесконечности, то интеграл не сходится,
но при некоторых обстоятельствах аб.солютная сходимость может быть
восстановлена путём введения множителя е"'(*. Тогда представление Фурье для
e-'i*f(t) будет:
со
F (Y + ш) = j f(t)e- (Y+*''*> tdt, A06)
0
Если существует действительное число if> такое, что
т
lim [\e-i*f{t)\dt<: со, A07)
то говорят, что f{t) является преобразуемой функцией.
Нижняя граница Yo всех y, которые удовлетворяют A07), называется
абсциссой абсолютной сходимости. Предположим, например, что /(/)== е^>*
при ^>'0 и /(/)== О при ^<0. Тогда f(f) — преобразуемая функция
в смысле A06) и Y>^=To- С другой стороны, f{t) = e^ не является
преобразуемой функцией, так как для неё не существует действительного
числа if> приводящего к сходимости A06).
Обратное преобразобание следует из свойства обратимости
преобразований Фурье [уравнения B1) и B2)]
со
/ (О е - г< = ^ г F (y + /со) е"'* ^ш, A08)
где Y > То- Функция, которую определяет интеграл с правой стороны, равна
f(t) e-t^ только для положительных значений t и равна нулю при ^<0.
Для того чтобы явно выразить это обстоятельство, . мы введём единичную
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ [5.12]
27Z
ступенчатую функцию u(f), равную нулю при ^<0 и равную единице при
^>0. Тогда обратное преобразование может быть записано так:
/{t)u (О = ^ J ^ ("^ + ""^ ^ ^''^^^* ^^•
A09)
Если Ча^^у ТО после выполнения интегрирования, указанного в A06)
или A09), можно перейти к пределу ^-^-О и таким образом определить
-представление Фурье для функций, которые другим способом не могут быть
проинтегрированы. Такой приём в наших расчётах не является существенным,
и преобразование Лапласа содержит этот множитель, обеспечивающий
сходимость, неявно. Введём комплексную переменную s = '{-\-m. Тогда
преобразование Лапласа, которое в дальнейшем будет обозначаться через оператор
L [/(^J, будет:
L\f{t)\==^^ f{t)e-'^dt==F{s),
ReE)>Y,
at
(ПО)
Плоскость t
где ReE) — обычное сокращение для слов «действительная часть 5», а Та
определяется каждый раз из свойств функции fify. Обратное
преобразование представляется интегралом, взятым вдоль прямой в комплексной
плоскости S'.
V + г о©
L-^{F{s)\==^.^F{s)etsds^f{t)a{t\ A11)
Y— г оо
где т>То- Преобразование Лапласа может быть интерпретировано как
отображение точек положительной действительной оси t на ту часть
комплексной плоскости 5, которая лежит справа от абсциссы Yo-
Область /(О и её отображение F{s\ показаны на рис. 56.
Из линейности
операторов следует, что если
= ^2E), ТО
^[Л@±/2@] =
= /="iE)=b:F2D-A12)
Если, кроме того, а —
какой-либо параметр, не
зависящий от / и 5, то
L\af{{)\ = aL\f{t)\ =
= aF{s).' A13)
Применение преобразования Лапласа "к решению дифференциальных
уравнений основывается на теореме о преобразовании производной.
Предположим, что f{t) и её производная ^>/@ — преобразуемые функции в смысле
A07) и что f{t) непрерывна при t = 0.
Тогда, интегрируя по частям, получаем:
О
Область fft)
Рис: 56. Преобразование Лапласа отображает
положительную часть действительной оси i на
заштрихованную часть плоскости.
со оо
dt
dt\
278 гл. V. ПЛОСКИЕ волны в неограниченной изотропной среде
следовательно, если L [f (t)] = F {s), то
i^[^] = sF(s)-f@). A14)
Эта теорема важна потому, что она вводит начальное значение /@)
функции f(f). Повторное интегрирование по частям приведёт нас к теореме
о преобразовании второй производной, которое содержит не только
начальное значение/@), но также начальное значение производной {-^)
Таким образом, преобразование зависимого переменного в дифференциальном
уравнении второго порядка выражается через его начальные значения. Эти
результаты не имеют никакой аналогии в теории преобразований Фурье.
Faltung-теорема, или теорема «умножения», является одним из применений
хорошо известного свойства интеграла Фзфье ^). Предположим опять, что
L\fi(t)]==F^(s),Llf2(f)] = F^is); пусть мы хотим определить
преобразование Лапласа для произведения функций fi^tyf^it)- Имеем:
со со » Yi + € оо
о о Y«—*°° -
Yt + * со со
= ^ J ^oFg(а) J Л (О е-(«-»)*^^; A16)
ff — ico о
отсюда вытекает первая теорема
Yj + « ОО \
L [Л (ОЛ т = ^- J ^t (^ - °) ^2 (-) do, .
Ys — € со » ^ '
Т2>То2. ReE —'з)>То1-
Чаще используется вторая Faltung-теорема об обратном преобразовании
произведения функций. Мы хотим определить функцию, преобразование
Лапласа которой даёт произведение F^ {s) Fq (s).
Y + 4oo
^-4/="! E)/= EI = -4 I F,is)F^is)e^tds =
Y —4 CO
Y+ «oo CO CO f +i CO
•V ~ i oo 0 0 '{ — ica
CX)
= ^ и{х)/,{Ь-1)иЦ—1)йи A18)
0
Так как единичная ступенчатая функция равна нулю для
отрицательных значений аргумента, то верхний предел t может быть положен
1) См. например, ВбсЬпег, Vorlesungen fiber Fouriersche Integrate и Wiener,
The Fourier Integral, стр. 45, Cambridge University Press, 1933.
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ 15.12] 279
равным t и, следовательно,
t
L-1 \F,{s)F^is^\^ jf,{t-^x)f^{x)dz, A19)
или t °
I [ J/i (^—^)Л(^)d-^ =^1 (^)^2 E). A20)
о
Геометрически произведение /^1E)^2E) представляет собой.
Преобразование площади, образованной следующим образом: функщ1я Д (г) сначала
переводится на отрицательную полуплоскость путём замены г на—-с, а затем
передвигается направо на величину t. Вслед за этим ордината /j {t — г)
умножается на f^{x)dx и площадь интегрируется от О до ^.
Ряд операций, применённых нами ранее при обсуждении свойств
интеграла Фурье, может быть отнесён к операциям смещения. Пусть
а—параметр, не зависящий от 5 и ^. Тогда,
со
L[ef'*f{f)]^^f{t)e-i^'a)t(it==F{s — a). A21)
о
Уравнение A21), очевидно, справедливо как для положительных, так и для
отрицательных значений а. Рассмотрим далее преобразование f{t—а):
оо
L{f{t — a)\ =jf(t—a)e-^dt=^e-^sjf{x)e-^dt. A22)
о —о
Но мы постулировали, что f(t) равна нулю для всех отрицательных
Значений аргумента, и, следовательно, нижний предел а может быть заменён
нулём. Как следствие мы получаем:
L[/(^—«)]"== e-«sFE), а>0,/@ = 0 при /<0. A23)
Аналогично мы можем написать:
Llfit-{-a)]=e<^Fis)i а>0,/@ = 0 при /<д. A24)
Следует, однако, из осторожности отметить, что последний результат
применим лишь к функциям, которые по определению равны нулю при ^ < д.
Замена t на t — а или t-\-a означает смещение /(/) на расстояние а
соответственно направо или налево.
В добавление к предыдущим основным теоремам имеется некоторое
количество элементарных, но полезных соотношений, которые могут быть
выведены непосредственно из (ПО). Следующие формулы выписаны для
справок; их доказательство представляется читателю:
Ю]
L[tfit)] = -^.^, ■ A26)
aF(as), A25)
in
ds
L[^fit)'j=^JFio)da, ^ A27)
s
dF{s,a)
00
4^^]
ia • A28)
/@) = lim sF(s), A29)
8->CO
lim/@ = lim sF (s). A30)
280 гл. V, ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДВ
Вычисление контурных интегралов, встречающихся при обратных пре^
образованиях, легче всего производится с помощью теории вычетов.
Функции /@> с которыми приходится иметь дело, являются аналитическими ,
функциями комплексного переменного /, за исключением конечного числа
полюсов. Напомним, что в окрестности полюса, скажем / = д, функция
может быть разложена в ряд вида
т=ф^ + (Дт;^. + • • • +fe^+9 @. D31)
где <р(/) — функция, аналитическая в точке д и в её окрестности и поэтому
содержит только положительные степени {t — д). Говорят, что особенность
является полюсом т-го порядка, если т — конечное целое число. Если же
необходимо бесконечное число отрицательных степеней для представления
/(^), (т. е. т бесконечно), то говорят, что особенность является
существенной. Если функцию /(/) проинтегрировд1Ть в плоскости t по любому
замкнутому контуру С, который окружает полюс а, но не содержит другой
особенности, то можно показать, что- в разложении A31) обратятся в нуль
все члены, за исключением члена с коэффициентом Ъ_^. В результате получим
j f{t)dt = 2'Kib_i. A32)
с
Коэффициент b_i называется вычетом в этом полюсе. В том случае, когда
контур окружает несколько полюсов, значение интеграла равняется 271/,
умноженному на сумму вычетов. В,частности, если/(^) — функция, анали^
тическая во всей области, ограниченной контуром С, то интеграл равен нулю.
Эти результаты являются следствием основных теорем теории функций
комплексного переменного." Если f(t)—аналитическая внутри и на контуре С,
т. е. /(t) может быть разложена в ряд лишь по положительным степеням,
то значение f(t) в любой внутренней точке а может быть выражено так:
/(«) = 2-5j'?^i*- A33)
О
Это — известная теорема Коши.
Если функция f{t) обращается должным образом в нуль на бесконечности,
то контур интегрирования, который является [Как в A11)] бесконечной
прямой, может быть замкнут окружностью бесконечного радиуса, и таким
образом задача сводится к теоремам предыдущего параграфа. Ограничения,
которым подчинено применение теории вычетов к вычислению интегралов
в бесконечных пределах, выражаются так называемой леммой Жордана,
гласящей:
Если Q(z)-*0 равномерно относительно arg-г, когда (^l-^cx) в области
0<;arg2r^TT, и если Q(z) аналитическая при |2-|>С (С—постоянная)
и O^nrgz^it, то
lim (e^i''Q(z)dz = 0,
Р -^и» г
где Г — полуокружность радиуса р, лежащая над действительной осью и с
центром в начале координат ^).
1) Е. Т. У и т т е к е р и Г. Н. В а т с о н, 1ос. cit, стр. 154. В главах V и VI этой
книги читатель найдёт вей, что является существенным для применения теори»
фушщий к решению физических задач.
ОБЩИЕ РЕШЕНИЯ ОДНОМ:ЕРНОГО волнового УРАВНЕНИЯ 15.12] 281
-■ II I .1.1.. ■! .1-—..»-—. —,--.■■...-_ •■ .III 1...Ч,— I.., -., -.,-_|_....._. I , I ■■ , ,. , I
Как уже было упомянуто, эта лемма применяется к вычислению
интегралов, распространённых вдоль .действительной оси от —оо до -|-со, но
она может быть видоизменена с тем, чтобы включит^ и интегрирование
вдоль мнимой оси; при подходящих заменах переменной окружность может
быть перемещена из верхней полуплоскости в нижнюю или из правой
полуплоскости в левую.
Если Q (z) имеет полюсы внутри замкнутого контура на расстоянии |г | <С С
от начала координат, то значение интеграла отлично от нуля и равно сумме
вычетов.
Отношение этих теорем к теории преобразования Лапласа может быть
иллюстрировано с помощью двух элементарных примеров. Сначала рассмотрим
ступенчатую функцию
/@ = 0 при ^<0, )
} A34)
f(t) = 1 при ^ > 0. J
Заметим попутно, что A34) не входит в круг функций, к которым применима
со *
теорема Фурье^так как интеграл J |/(/) | dt расходится. Преобразование Лапласа
о
для A34) имеет вид:
со
о
Мы проверим этот результат, применив обратное преобразование A11):
f — ico
F{s) имеет полюс первого порядка при s = 0. Абсцисса абсолютной
сходимости равна нулю, а значит, необходимо Re E) > 0. Интегрирование должно
быть распространено вдоль любой прямой, параллельной мнимой оси и
находящейся от неё направ©. Подинтегральное выражение A36) удовлетворяет
условиям леммы Жордана, и путь интегрирования может быть замкнут
бесконечной окружностью. Если ^> О, то путь интегрирования может быть
деформирован налево так, что ReE)-> — оо. Замкнутый контур от y — ^'^■
до '^-j-i со далее до —оо-|-гсо затем до —со — / оо и обратно
до Y—^°° содержит полюс в 5 = 0. Вычет равен единице, и следовательно,
по A32) правая часть A36) для ^>0 тоже равна единице. Так как F{s)
определена только в правой полуплоскости, то может возникнуть вопрос,
насколько допустимо распространение интегрирования на левую полуплоскость.
Следует тщательно различать функцию и её представление в ограниченной
области, l/s является представлением F (s) при ReE)>0, но ввиду
возможных .разрывов F{s) эти две функции не обязательно всюду совпадают при
Re E)<0. Вдоль линии y — * о^» тН~*<^ ^^ интегрируем функцию 1/^;
для интегрирования мы можем использовать любое из её аналитических
свойств. Мы пользуемся аналитическим продолжением на левую
полуплоскость функции 1/5, а не F{s).
Если ^<0, то обращение в нуль подинтегрального выражения может
быть обеспечено деформацией контура направо. Внутри замкнутого контура.
от '{-^ioo до Y-|~^°° далее до co-\-ioo, затем до оо—/со и обратно
:282
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Мы убедились, что единичная ступенчатая функция может быть
аналитически выражена следующим образом:
Y+ioo
"(«=2^/т^'*> t>°-
A37)
Y — ico
Представляет интерес применить к этому результату теорему смещения A23),
положив й = —
V
'-Н^-^)]=' "*^(*)=т» ''•
^или
Y+€oo
\ V/ 2ni J s
A38)
A39)
Y —4 CO
Из предыдущего изложения очевидно, что A39) обращается в нуль
при t <0 и равно единице при t >0. На рис. 57, й и 57,^ величина
« (t j изображена как функция / и z соответственно.
afi-z/v) uft-2/u}
f=z/v t
u(t-z/v)=0, t<z/v,
U(t-Z/V)--t, t>Z/V
о
Рис. 57.
z'^vt z
u[t-z/v)rO, z>vt,
U(t-Z/V)--I, 2<Vf
b
в качестве второго примера представим себе, что при / = 0 мгновенно
возникает гармоническая волна, йродолжающаяся потом неограниченное время:
f(t) = 0 при /<0,
f(t)^e-'^^t при t>0
■}
со
L[f{m==j^-''''-''dt=j~^, ReE)>0.
A40)
A41)
Как ив предыдущем случае, мы можем проверить A41), применив обратное
яреобразование
Y +4 со
L-1 [-4-1=0^ Г ^ds, ш>0. A42)
Если ^>0, то контур опять деформируется налево. Окружённый полюс
находится в точке 5== — т\ применив теорему Коши, мы увидим, что A42)
действительно равно е-»"^^ С другой стороны, если /<0, то контур дефор-
ОБЩИЕ РЕШЕНИЯ ОДНОМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ 15.13] 283
мируется направо и интеграл обращается в нуль, В общем случае
^v+p^K*-|0_^^^ jo при .-Л<0.
''""J^ ' + '- \ -Н'-т) пщ t-^>0.
5.13. Применение преобразования Лапласа к уравнениям Максвелла.
Пусть Ex=^f{z^t\ Hy==g(z,t) являются компонентами плоского
электромагнитного поля. Предположим, что/Bг, О и ^(г:,^) преобразуемы в смысле A07)
и обращаются в нуль для всех отрицательных значений t\ они связаны, кроме
того, друг с другом уравнениями поля
Если рассматривать z как параметр, то преобразование Лапласа этой
системы относительно t будет:
-^^^-^^,sG(z, s)-v^g iz, 0) = О, 1
.^^^Ц,,sF(z,s) + aF(z,s)-гf{z,0)r=0. j
После исключения G{z,s) получим для Fiz,s) обыкновенное неоднородное
уравнение, в которое s^ входит лишь как параметр:
g_ (;..s= + ^.)F = i. [Jl^l^^-^^sm, 0). A46)
Так как производная от giz,t) по z в момент времени ^ = 0 может быть
выражена через f{z,0), а Г-^) из A44), то последнее уравнение
эквивалентно такому:
^_(j,s5'^-j-p,o5)r=- (ei.s + vo)f{z, 0) ~ JXS A)^^^; A47)
f(z,0) означает, строго говоря, предел/(г:,/) при ^—♦0. Функции
Л(^) = Ит/(г,0, Uiz) ==^Пт^ф^ A48)
представляют начальное состояние поля и предполагаются известными.
Обозначив /^^ = {хз5^-|-{XOS, получим окончательно:
Общее решение A49) является суммой решения однородного уравнения
^'^ .h^F=0, A50)
dz^
содержащего две произвольные постоянные, и частного решения уравнения A49).
Можно легко убедиться, что уравнению A49) действительно удовлетворяет
функция
F{s, г)=Лей^+ Be-^^^-{-^^j e-J^^Z (z,s)dz~ ^ j е^Z{z,s) dz, A51)
в которой h есть тот корень |/Л^ который положителен, когда А^
действительно и положительно. Константы А и В выбираются так, чтобы удовле-
284 гл. V. ПЛОСКИЕ волны в неограниченной изотропной среде
творить граничным условиям в точках z^=Zi и 2- = -г-д. После того как
Avi В рассчитаны через 5-, обратное преобразование вернёт нас от A51)-
к решению /(г*, t) уравнения A44), удовлетворяющему как начальным, так
и граничным условиям.
Для иллюстрации рассмотрим сначала элементарный случай, когда поле
в начальный момент ^=0 везде равно нулю. Тогда Z=0, и мы имеем дела
лишь с решением однородного уравнения. Предположим, что в £• == О имеется
источник, включающийся в момент /=0 и излучающий волны в
положительном направлении z, интенсивность которых в начале координат равна
/(О, t)=f^if). Таким образом, в этом примере второе граничное условие
ъ z = Zi^ заменено требованием, чтобы поле распространялось вдоль оси z
направо. Преобразование граничных условий изображается так:
/='@,5)=/='8E)-i[/s@l- A52)
Так как волна распространяется направо, то константу А следует поло-
жить равной нулю, с?то ясно при о = 0,
смещения на стр. 279
F{z,s)^
f{^,t>
•
z
= Fj (s) «" °^ '=
<^-^)•
так как тогда
h =
=4/«(^-^)i
(^>0, z>0\
a
И
no теореме
A53)
' A54)
Если проводимость не равна нулю, то решение является более трудным.
В этом случае мы напишем' h^^^iis YХ^^Л^-^у ~ °) —J^ ^ применим
интеграл ^) ^
со _ - (V~Z S + - I/ -^ 5 1 V~^'+Z»
После подстановки У fi^-{-z^= at, он приводится к виду
i-^ == а je-^tjQ {^Vz^ — аЧ^) е-'* dt, A56)
Z
а
где а=—р=-,&=—, как они определены на стр. 264. После дифферен-
цирования получим окончательно:
со
д , fb
е~^' = е "^5 ^ ^~aje-bf^^jQ(^Yz^—a4^)e-^fdt, A57)
я
а
или
gmhz^g а^е ^a_aLlf(z,t)], A58)
1) Е. Т. У и т т е к е р и Г. Н. В а т с о и, гл» XVII, стр. 2(М.
ДИСПЕРСИЯ [5.14] 285
л'де 9 (-г"» t) — функция, определяемая соотношениями
оB-, 0 = ■
О при 0<^<^,
'-''§-г^о{^У^^Щ при t>^.
A59)
Располагая этим преобразованием, мы можем написать:
Р^г, s)==F,(s)e-^^'^ = L[f^it)\e " е "—«/.[ДСО] ^ [?!• A60)
К этому выражению мы применим теорему смещения и Faltung-теорему,
стр. 278, вместе с обратным преобразованием неоднородного уравнения
_b.t
/(г, 0=^ "'л(^-~)-«//з(^-'=)^-'^|л(|1^^^-"^'^')^^ A61)
Z
а
или, после замены переменной интегрирования:
а
J{z,t)^e
^y(^t—^y,e-btf fnO>'^^,Jo{^V^'-^4t-^)')d:^- A62)
Читатель может убедиться, что эта функция удовлетворяет волновому
уравнению в поглощающей среде и изображает волну, распространяющуюся
в положительном, направлении и обращающуюся в точке г = О в Д (О Д-^я
всех значений i>0.
ДИСПЕРСИЯ
6.14. Дисперсия в диэлектриках. Импульс или «сигнал» любой задйн-
«ой формы может быть образован суперпозицией гармонических волновых
цугов бесконечной длины и продолжительности. Скорости, с которыми
распространяются поверхности постоянной фазы этих составляющих волн,
зависят, как это было показано, от параметров s, }а и о. В частности, если
среда непроводящая, а величины s и jt не зависят от частоты
приложенного поля, то фазовая скорость оказывается постоянной и сигнал рас-
йространяется без искажения. С другой стороны, наличие проводимости
нриводит к зависимости фазовой скорости, равно как и коэффициента
затухания, от частоты. Следовательно, гармонические составляющие сигнала
смещаются по фазе относительно друг друга в направлении
распространения, и сигнал прибывает в некоторую отдалённую точку в изменённом и
возможно даже неузнаваемом виде. Срэду, в которой фазовая скорость зависит
от частоты, называют диспергирующей.
При достаточно высоких частотах вещество может обнаруживать
дисперсионные свойства даже тогда, когда проводимостью о, обусловленной
свободными зарядами, можно полностью пренебречь. В диэлектриках фазовая
скорость связана с показателем преломления п соотношением г» = —, где
п == У^у-е У-т- При частотах, меньших 10^ ииклов/сек, диэлектрические
проницаемости большинства материалов в основном не зависят от частоты, но'
эта зависимость становится совершенно явной в области, которая зачастую
начинается при ультравысоких радиочастотах и простирается в инфракрасную
'Область и ниже. Именно поэтому показатель преломления воды, равный
286 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
при частотах, меньших 10^, примерно 9, испытывает колебания в облает»
частот около 10*° циклов/сел; и, в конце концов, падает до значения 1,32
в инфракрасной области. За исключением растворов или кристаллов
ферромагнитных солей, дисперсия непроводников может быть полностью
приписана зависимости v.^ от частоты.
Все современные теории дисперсии учитывают молекулярное строение
вещества и рассматривают молекулы как динамические системы, обладающие
собственными нормальными частотами, которые возбуждаются приходящим
полем. Простая механическая модель, которая привела к удивительно удачной
дисперсионной формуле, была предложена Максвеллом и независимо Зель-
мейером. Дальнейший успех в этой области связан с именем Лоренца,
который развил теорию вещества, состоящего из собрания большого числа
молекулярных осцилляторов; Лоренц смог, по крайней мере качественно,
объяснить большое число электрических и оптических явлений. Однако,
согласно Лоренцу, эти молекулярные системы подчиняются законам
классической механики; в настоящее время известно, что они подчиняются законам
квантовой механики. Вслед за быстрыми успехами наших знаний о структуре
атомов и молекул был проведён пересмотр теории дисперсии, которая в
настоящее время может рассматриваться как весьма удовлетворительная.
Как классическая, так и квантовая теории дисперсии рассчитывают
смещение заряда от центра масс атомной системы в зависимости от частоты
и интенсивности возмущающего поля. После усреднения по всем атомам,^
содержащимся внутри соответствующим образом выбранного элемента объёма,
получают выражение дл5Г поляризации среды, т. е, для дипоЛьногф момента
единицы объёма. Классический результат весьма близок по виду к квантов©-
механической формуле и приводит в большинстве случаев к правильному
выражению для показателя преломления в зависимости от частоты. Поэтому
мы ограничим наше рассмотрение случаем, когда электрическая
поляризация в окрестности резон|1НСной частоты может быть приближённо выражена
действительной частью следующего выражения *):
а^ ■
Р=-2 • 2 ^~ Ф' A)
Под интенсивностью электрического поля мы понимаем теперь
действительную часть комплексного вектора
Е = Еое-*''^*. B)
Константа a^ прямо пропорциональна числу осцилляторов с собственной
частотой (Oq в единице объёма. Константа шд связана с этой собственной
частотой равенством
0H = О)? — io «^ C)
так, что при достаточно малой плотности среды Шд—j-coq. константа g
учитывает диссипативные силы, имеющие характер трения и обусловленные
столкновениями молекул. Константы Шд и g^ которые характеризуют молекулы
рассматриваемой среды, могут быть определены из экспериментальных'
данных. .
1) Вывод этой формулы смотри у Лоренца, Теория электронов, или в любом
учебнике по физической оптике, какими являются, например, книги М, Берн».
Оптика (Харьков — Киев ГНТИ, 1937}, F О г s t е г I i п g, Lehrbuch der Optik, Hlrzel, 1928.
К. Шефер, Теоретическая физика, т. III, ч, 2, стр. 315,
ДИСПЕРСИЯ- 45.14] 287
При достаточно малых частотах поля поляризация Р приближается,
согласно A), к постоянному значению
а2
Р = ^^^оЕ, D>
и, так как относительная диэлектрическая постоянная связана с поляризацией
соотношением '
р = (х —1)еоЕ, E).
то можно выразить v. через молекулярные константы
, «^
^=1+^' F)
Но если частота поля увеличивается, то пренебрежение двумя другим» ^
членами в знаменателе становится недопустимым. В этом случае, по
аналогии, мы определим комплексную относительную диэлектрическую
проницаемость vl с помощью какого-либо из уравнений
р = (х'—l)soE, D = it'soE. GХ
Отсюда и из A) мы получаем:
у! = \-\-~=2 1—г-г. (8)
С этим комплексным параметром уравнения Максвелла для среды с
магнитной проницаемостью jiq будут:
го*Е + н.о^ = 0; rotH —sox'^=:0. (9)
Из них следует, что прямоугольные компоненты векторов [поля
удовлетворяют волновому уравнению
Решение A0) в виде плоской волны описывается функцией
Tj* = Tj*Qe«^«-«'**, (И)
где
^ = ^>^7=a4-ip, A2>
так что
Волна распространяется со скоростью 'z> = —=—, но а и показатель пре-
ломлейия п являются теперь явными функциями частоты, которые можно
получить, подставив (8) в A3).
В газах и парах плотность поляризованных молекул так невелика, что
х' очень мзло отличается от единицы. Поэтому мала и константа а^^ так
что Шд 0ТЛ1.чается от собственной частоты Шд на пренебрежимо малую
величину и корень из vf может быть вычислен с сохранением лишь двух членов
биномиального разложения. Таким образом,
w 2 to*—0J — i^g . ,
288
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Когда приложенная частота о) достаточно низка, можно пренебречь в
знаменателе последними двумя членами, так что
а2 .
ас
ш
П
1-Ь
2ш^
A5)
В этом случае показатель преломления, а следовательно, и фазовая скорость
не з(ависят от частоты; дисперсия отсутствует.
Если приложенная частота ю сравнима с резонансной частотой %, но
не приближается к ней слишком близко, то член, выражающий затухание,
можно ещё не учитывать: jooq — (a^\^^<og и
ас - , 1 а^
= n=il-\
О) -i Wn О)"
A6)
Коэффициент поглощения равен нулю и среда прозрачна, но показатель
преломления и фазовая скорость являются функциями частоты. Если оо < Шд, то п
будет больше единицы и увеличение оо приведёт к увеличению п и
уменьшению V. Если со > ooq, то Показатель преломления меньше единицы, но
увеличение 00 опять имеет своим результатом увеличение
численного значения п.
В этом случае дисперсия называется
нормальной.
Пусть, наконец, ю приближается к
резонансной частоте оод. После разделения A4) на
действительную и мнимую части, получаем:
ас а2 о.2_<,2 \
п = —=1-} , I
^ g
2с
со
\ A7)
Р =
Рис. 58. Кривые дисперсии
и абсорбции в окрестности
резонансной части.
(ш^_ш2J_{_(й2^2
На рис. 58 изображены показатель преломления и
коэффициент поглощения ^с/оо для газа как функции
частоты. Коэффициент поглощения имеет острый
максимум при Шд, так что в этой области > среда непрозрачна для волн.
Когда О) возрастает от значений, лежащих^ниже ooq, коэффициент
преломления достигает максимума при ooj, а затем быстро спадает до значения,
меньшего единицы при 002, после чего он опять увеличивается с ростом оо,
приближаясь, в конце концов, к единице. Если (как это имеет место в области ooj Шд)
увеличение частоты приводит к уменьшению показателя
преломления и увеличению фазовой скорости, то дисперсию называют
аномальной. Согласно этому определению, дисперсия, получающаяся из-за
проводимости среды и рассмотренная в предыдущих разделах этой главы, является
аномальной. Почти всегда можно утверждать, что «аномальный» ход является
более обычным, чем «нормальный».
В жидкостях и твёрдых телах наши результаты должны быть в
некоторой степени видоизменены, так как уже нельзя предполагать, что среда
имеет малую плотность, но сильного влияния на общий ход дисперсионной
кривой это не оказывает. Кроме того, наше рассмотрение было ограничено
поведением констант распространения в окрестности одной резонансной
частоты. В действительности молекула является сложной динамической
системой и обладает бесконечным ряд )М собственных частот, каждая из
которых участвует во взаимодействии молекулы с падающим полем. Классическая
ДИСПЕ*»СИЯ 15.15Г • 289
теория не может определить значения этих частот. Соответствующей под-
гонкрй констант к экспериментальным данным можно установить
эмпирическую дисперсионную формулу, для которой (8) является типичным членом и
которая удовлетворяет экспериментальным данным в широкой области частот.
6.15. Дисперсия в металлах. Удивительно точную теорию оптических
свойств металлов можно получить из следующей, довольно грубой, модели.
Представим себе» что закреплённые положительные ионы проводника
образуют область постоянного электростатического потенциала. Внутри этой
области облако (или «газ») свободно двигающихся электронов достигло
статического равновесия, так что средняя сила, действующая на какой-
нибудь электрон проводимости, равна нулю, и, помимо обычных флуктуации,
полный заряд внутри любого элемента объёма также равен нулю.
Наложение внешнего поля Е вызывает общий дрейф свободных электронов в напра-
. влении поля. Движению препятствуют постоянно повторяющиеся соударения
в узлах решётки, занятых тяжёлыми ионами; получающаяся при этом
передача количества движения от дрейфующих электронов к ионам решётки
' вызывает, с одной стороны, тепловые колебания ионов, с другой, —
замедление движения электронов. Вопрос о точном характере локальных
(микроскопических) сил, действующих на электрон проводимости, является довольно
тонким, но в той мере, в какой можно пренебрегать влиянием связанных
электронов кристаллической решётки, оказывается оправданным
предположение, что величина действующегб поля равна макроскопическому полю Е,
господствующему внутри проводника.
Пусть г будет смещением из начального положения свободного заряда
е с массой т. На заряд действует внешняя сила еЕ, а движению его пре-
dt ^
пятствует сила—^^S ~тт •> пропорциональная скорости. Эта сила эмпирически
описывает диссипативное действие соударений. Поэтому уравнение для
усреднённого движения заряда е имеет вид
^^■\-^S%=-e^^e-i^'\ A8)
его частное решение имеет вид
Еоб-'"^*. A9)
Если в единице объёма имеется N свободных электронов, то плотность
. тока равна:
■' = '^^# = ^Е. B0)
Таким образом, по аналогии со стационарной проводимостью, определяемой
из соотношения J.^=^, мы вводим комплексную проводимость о', равную
8 силу B0):
е^
N~
о' = ~^. B1)
Постоянные распространения и затухания плоской волны могут быть
получены теперь обычным способом из соотношения k^==\t.e<i}'^-}-io'it.(i).
Известно, что резонансные частоты связанных электронов металлических
атомов лежат далеко в фиолетовой или ультрафиолетовой области, так что
для видимого красного света, для инфракрасного и, конечно, для радиочастот
диэлектрическую проницаемость металла можно с уверенностью положить
' 19 Зак. 593. Хеория влешфошагнетизма,.
2«P = 4:^::rf^- B3)
290 гл. V. ПЛОСКИЕ волны В НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
равной Sq. Кроме того, если проводник сцелан из неферромагнитного
материала, то и {1 приближённо равно {Aq, поэтому
*^ = (« + W = ^(l+-^)- B2)
Подставляя о' из B1) и отделяя действительную и мнимую части, получаем:
^ с^\ men to- + g-2/'
При достаточно малых частотах^инерциальная сила fn-^ в уравнении
A8) пренебрежимо мала по сравнению с силой трения т^— . В этой
области проводимость о', определённая по B1), сводится к действительной
и постоянной величине
^■ = ^, B4)
mg . ^ '
которая должна быть, идентична со стационарной проводимостью о. В ряде
фундаментальных исследований Хагеном и Рубенсом ^) было показано, что
значения проводимости, измеренные при стационарных условиях, могут быть
использованы без заметной ошибки вплоть до инфракрасной области. Однако
при длинах волн короче, чем приблизительно 25-10-* см, проводимость
обнаруживает резкую зависимость от частоты, и наблюдаемая дисперсия
может быть грубо рассчитана из соотношений B3).
Итоги изложенных исследц)ваний и их содержание показывают, что
дисперсионные формулы, • выражающие зависимость s, ji и о от частоты,
допускают расширение классической теории электромагнетизма далеко за те
пределы, которые были произвольно установлены в первой главе.
5.16. Распространение в ионизованной атмосфере (ионосфере).
Недавние исследования распространения радиоволн в ионизованных верхних
слоях атмосферы привели к некоторым весьма интересным проблемам.
В разреженном газе средняя длина свободного пробега электрона
чрезвычайно велика и, следовательно, коэффициент затухания пренебрежимо мал.
'Таким образом кажущаяся проводимость^ оказывается чисто мнимой:
о =1 , B5)
откуда
П^ = %^1 ^; р = 0. B6)
Электромагнитная волна распространяется в электронном газе без затухания
и с фазовой скоростью, большей чем скорость света в свободном
пространстве. При частотах, меньших некоторого критического значения,
определённого выражением
0H = -^ , B7)
показатель преломления становится мнимым, и можно показать, что от
границы такой среды волна будет полностью отражаться.
1) Ann. Physik, 11, 873, 1903. См. главу IX, стр. 447.
ДИСПЕРСИЯ 15.16}
291
в действительности задача о распространении в ионосфере осложнена
наличием магнитного поля земли. Предположим, что плоская волна
распространяется в направлении положительной оси z прямоугольной системы
координат. Для примера мы допустим, что в единице объёма пустого
пространства находится лишь N частиц с зарядом е и массой т. Имеется также
статическое магнитное поле, которое можно разложить на компоненту,
параллельную направлению распространения, и поперечную компоненту. Лишь
продольная компонента, величину которой мы будем обозначать Я^,
приводит к эффектам первого порядка.
"^^равнения движения частицы таковы:
х=-££,+^^«(>.Яо-;я,),
3;=
z=^
■,п'^У + -
■■^(-",
т
1
{zH^~xHq),
B8)
Отношение силы, с которой действует на заряд магнитный вектор
распространяющейся волны, к силе, обусловленной электрическим вектором, равно
отношению скорости заряда к скорости света. Поэтому в B8) можно
пренебречь членами, содержащими Яд, и Ну, так что уравнения движения
сводятся к более простой системе
"z =0.
т
eixoHo
I
т
'V,
B9)
Движение частицы происходит целиком в плоскости ху, векторы
падающей волны также параллельны этой плоскости, поэтому удобно
воспользоваться комплексными величинами. Положим:
C0)
Тогда уравнения движения выражаются посредством одного комплексного
уравнения
е
т
т
Уравнения же поля принимают вид
дЕ . дН _
п дН , . дЕ .,, •
C1)
C2)
где вместо плотности тока введено произведение заряда единицы объёма
на среднюю скорость.
Решение должно быть найдено для этой системы трёх совместных
уравнений. Попробуем положить:
Be ±Hh3-^iot)
Я:
Се ±* (hz~ii>t)^
C3)
292
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Это — гармонические волны, распространяющиеся в положительном
направлении с волновым числом h. В то время как в отсутствие поля Hq знак
в экспонентах не играет никакой роли, в данном примере его
выбор позволит, как мы сейчас увидим, определить два различных решения.
Действительно, подсгавив C3) в C1) и C2), получаем:
-i.^+i-
т
О,
М-J-г {1-0 0N = О, j
sq 00 Л --j- ШВ 4- Л/is 00 С= 0. J
C4)
Чтобы эта сисгема однородных уравнений для амплитуд А, В, С имела
нетривиальное решение, необходимо, чтобы её детерминант обращался в нуль:
е
т
h
So»
О
г>оа)
ih
ОО''
^Ро^о
to
т
О
Л/еоо
= 0.
Г35)
Развёртывание этого детерминанта приводит к уравнению для постоянной
распространения h
7Vg2
2—gl^O^Qta
00
C6)
т
(О
Фазовая скорость f = -т- и, следовательно, C6) есть квадрат показателя
'^ - , •
преломления /г. ' . »
Таким образом, получается, что электронный газ, на который наложено
стационарное магнитное поле, действует подобно анизотропному двояко
преломляющему кристаллу, в котором существуют два вида бегущих волн
с двумя различными скоростями. Кроме того, мы видим, что при подходящем
выборе 00 показатель преломления среды по отношению к одной из этих
волн становится бесконечным:
«1=х_=1 ^«-—. C7)
00'
е\У'йЩ^
т
Аналогично, при другой частоте показатель преломления
2
«4-
t
1
meo
00'
'+
e|j-o^o
to
C8)
m
обращается в нуль. Замечательные оптические свойства слоя Кеннели-Хи-
висайда могут быть в значительной степени описаны этими формулами.
Линейно поляризованная волна, входящая в такую среду, разлагается на право- и
левополяризованные по кругу компоненты, одна из которых распространяется
СКОРОСТИ РАСПРОСТРАНЕНИЯ 15.17] 293
СО скоростью V+J а другая — со скоростью г>_. Так как отражение от слоя
определяется показателем преломления, то поляризация волны,
возвращающейся на землю, сильно изменяется, и часто эта волна содержит сильнзлю
поляризованную по кругу компоненту, которая способствует явлению
фединга ^).
СКОРОСТИ РАСПРОСТРАНЕНИЯ
6.17. Групповая скорость. Понятие фазовой скорости применимо только
к полям, которые периодичны в пространстве и, следовательно, представляют
волну, бесконечно продолжающуюся во времени 2). Если состояние среды
описывается функцией ^{z,t), где
^iz,t) = Ae^(^^-'^0^ A)
то поверхности постоянной фазы определяются равенством
kz — ш/ = const., B)
и эти поверхности распространяются со скоростью
с другой стороны, волновой цуг конечной длины не может быть представлен
простой гармонической функцией A), и фазовая скорость теряет свой точный
смысл. Тогда довольно небрежно говорят о «скорости света» или о
«скорости волнового фронта». Необходимость точного определения понятия
волновой скорости стала очевидной некоторое время тому назад, в связи
с некоторыми экспериментами, являющимися основными для теории
относительности; в настоящее время этот вопрос имеет важное отношение
к вопросу о связи с помощью коротких волн, распространяющихся вдоль
проводников. Так как электромагнитное поле никогда не может быть точно
локализовано ни в пространстве, ни во времени, то в каждом определении
скорости должен содержаться существенный произвол. Наклон и высота
волнового фронта изменяются во время его распространения, а понятие
«центра тяжести» становится неопределённым, если импульс расплывается.
Пожалуй, для читателя представляет ббльшую практическую ценность знать,
чего некоторые общеупотребительные термины не означают^ чем
приписывать им слишком точный физический смысл.
После понятия фазовой скорости следующим по важности является
понятие групповой скорости. Рассмотрим суперпозицию двух гармонических
волн, которые немного отличаются по частоте и волновому числу:
^ . 4'i = cos(^2r —оо/), ^^ = cos [{k-{-bk) Z —((О-{'boi)t]. D)
Их сумма
'}' = '}'i + '}'2 = 2cos-il2r8A;-^8a)Jcos[(^ + |Jr-(a) + ^)^] E)
является хорошо известным выражением явления «биений». Поле изменяется
1) Более полный расчёт распространения волн в ионизованной среде и
библиографию можно найти в статье Mimno, Rev. mod. Phys. 9, 1—43, 1937. См. также
Ergebnisse der exakten, Naturwissenschaften, Vol. 17, Springer, 1938.
(Имеется русский перевод; Мимно. Физика ионосферы, Связьиздат. 1940.
Кроме того, см. А. И. Щукин, Физические основы распространения радиоволн
в ионосфере, Связьиздат, 1940. Прим. ред.
2) Говоря о поле, периодическом в пространстве, автор имеет здесь в виду
синусоидальную (монохроматич-! кую) ьолну. Прим. ред.
294
гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
С частотой, немного отличающейся от ш, в то время как его амплитуда
1
Л = 2 cos •- i^zbk—Ьш)
F)
медленно изменяется между суммой амплитуд слагаемых волн и нулём.
В результате усиливающей и ослабляющей интерференции распределение
поля как вдоль временной, так и вдоль пространственной осей имеет вид
ряда периодически повторяющихся «биений» или «групп», подобных тем,
что изображены на рис. 59. Поверхность постоянной амплитуды группы А
определяется уравнением
zbk—^8@ = const., G)
из которого следует, что сама группа распространяется со скоростью
0@
И =
bk'
(8)
Групповая скорость определяется отношением разности частот к разности
волновых чисел. Если среда недиспергирующая, то 8/г = —-Зш, и
следовательно, групповая скорость
совпадает с фазовой скоростью v.
В диспергирующей среде их
значения различны.
В только что приведённом
примере суперпозиция двух гар-
Рис. 59. Биения. монических волн привела к пе-
^ риодической последовательности
групп. Одна единственная группа или импульс лк1бой желаемой формы
может быть составлена, согласно теории интеграла Фурье, подбором
амплитуд составляющих гармонических волн в виде подходящей функции частоты
или волнового числа и. интегрированием:
^{z,t)^-^ A{k)e'(^^-^^f)dk. (9)
-00
Понятие групповой скорости применимо лишь к таким представлениям
Фурье, которые ограничены узкой полосой спектра. Если величина
амплитудной функции А{k) пренебрежимо мала вне области kQ — bk^k^kQ-\-bk^
то мы можем заменить С9) интегралом
6= J Aik)e^f'^-^')dk, A0)
kg ok
который изображает функцию, называемую обычно «волновым пакетом».
Мы будем предполагать, что k действительно и что (о — известная функция k.
Внутри достаточно малого интервала 28А функция ш (k) будет лишь
немного отличаться от её значения при А = ^о и поэтому может быть пргд-
ставлена двумя первыми членами ряда Тейлора
co(A) = co(^o)-f(^)^^ (k — ko)+... A1)
Условие, что членами высшего порядка в этом разложении можно пренебречь,
накладывает необходимые ограничения на 8А. Имеем:
кг — (at = koZ ■
■О),
^ + (k-k^[,-(^^)^j]+... A2)
{
СКОРОСТИ РАСПРОСТРАНЕНИЯ 15.17} ,, 295
Волновой пакет может -быть изображён теперь функцией
tj; = ^О^'ХМ-'^оО , A3)
где «Ьо — средняя амплитуда, определённая равенством
4-0= Г Л(^J ^ ^^f'Jk^kJdk. A4)
kci—bk
Эта амплитуда постоянна вдоль поверхностей
Отсюда очевидно, что волновой пакет распространяется с групповой
скоростью
-(Ml. ('«>
в случае недиспергирующей среды и совпадает с фазовой скоростью v,
но в общем случае и является функцией волнового числа Aq,
Из соотношений k = —, (a = kv мы можем вывести несколько эквива-
лентных выражений для групповой скорости, которые иногда оказываются
более удобными, чем A6):
d , } t-dv •. dv rfv 1 .^ _,
Чт) Ы
Из самого способа определения групповой скорости очевидно, что это
понятие является вполне точным лишь в случае волнового пакета, составленного
из элементарных волн, лежащих внутри бесконечно узкой области спектра.
Если интервал bk увеличивается, то разброс в фазовой скорости
гармонических компонент в диспергирующей среде становится более заметным;
пакет быстро деформируется, и групповая скорость как скорость пакета
в целом теряет свой физический смысл. Заметим, что сосредоточение поля
в малом участке пространства не только не означает соответствующего
сосредоточения частот или длин волн спектра, а наоборот. Рассмотрим,
например, гармонический волновой цуг конечной длины
/@)=О, при |2г1>4, 1
[ \ A8)
f{z) = zo%kQZ при Ul<^. ]
Амплитуда.возмущения в окрестности произвольного волнового числа k даётся
формулой D0) на стр. 260
вид этой функции изображён на рис. 50. С увеличением L интервал волновых
чисел 8й, внутри которого A{k) имеет заметную величину, уменьшается.
С другой стороны, импульс, образованный при резком включении и
выключении генератора, размазан по спектру и не может быть даже приближённо
представлен в виде (Ю). Такой широкий спектральный состав является
обычной неприятностью для всякого работника лаборатории, который должен
защищать чувствительную электроаппаратуру от атмосферных разрядов или
от импульсов, возникающих при включении и выключении мощных машин.
' f
Й96 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕИНЬй ИЗОТРОПНОЙ СРЕДЕ ^
5.18. Волновой фронт и скорость сигнала. Бели дисперсия в среде
нормальна и "не слишком сильна, то импульс или волновой пакет может
пройти большое расстояние, заметно не расплываясь. Поскольку считается,
что энергия локализована в области, занятой полем, то скорость
распространения энергии должна, очевидно, по крайней мере приближённо,
равняться групповой скорости. При нормальной дисперсии увеличение длины
волны обусловливает увеличение фазовой скорости и, следовательно,
согласно A7), групповая скорость при этом всегда меньше фазовой. Если же,
наоборот, дисперсия аномальна, как это имеет место в проводящей среде,
то производная -^ отрицательна, и групповая скорость больше фазовой
скорости. И действительно, нет недостатка в примерах, показывающих, что
и может превышать скорость света с. Так как одно время вообще считали,
что групповая скорость обязательно эквивалентна скорости распространения
энергии, то в первые годы после публикации Эйнштейном специальной
теории относительности примеры такого рода предлагались как явно
противоречащие постулату о невозможности распространения сигнала со скоростью,,
большей с. Ответ на эти возражения и разъяснение всей проблемы были
даны в 1914 г. в прекрасном исследовании, проведённом Зоммерфельдом и
Бриллюэном^), чтение которого сохраняет интерес и поныне.
Зоммерфельд рассмотрел специальную задачу о сигнале, который
приходит в точку 0 = 0 или возникает в ней в момент времени / = О, а затем
продолжается бесконечнб долго в виде гармонического колебания с
частотой О). Сигнал распространяется\ направо, в диспергирующей среде, и мы
хотим узнать время, необходимое, для прохождения заданно1^о расстояния^.
Мы видели, что интеграл .Фурье для неограниченного волнового цуга не
сходится, хотя эта трудность, и может быть обойдена деформацией пути
интегрирования в комплексной области переменной ш. С другой стороны,
преобразование Лапласа было введено именно с. целью исследования таких
функций, и, действительно, можно п(жазать простой заменой переменной,,
что комплексный интеграл Фурье, применённый Зоммерфельдом, в точности.-
равен представлению исследуемой функции, определённому в уравнении A4Э) '
раздела 5.12. Соответственное видоизменение оригинального исследования
облегчит наше рассмотрение.
В точке 0 = 0 сигнал описывается функцией
1 ^"^^°° е^ fO при ^<0,
/(«'0 = -2^- J -7^^^ И,-.* при ,>о. B^>
Y-*oo ^
Представление этого поля в любой точке z среды получится продолжением.
B0) в виде решения волнового уравнения, которое согласно A0), стр. 287,
имеет вид
^_^i!/_o ' r2iv
i
уравнению B1) удовлетворяют элементарные функции вида
1) S о m m е г f е 1 d, Ann. Phys. 44,77—202,1914; В г i 11 о u i n, ibid., 203—240.
Полное и более современное изложение этой работы было опубликовано Бриллюэном.
в докладах Congres International (TElectricite, том II, 1"^^ Sec. Paris, 1932.
скорости РАСПРОСТРАНЕНИЯ [5.J8J 297
ИЗ которых МЫ И образуем сигнал
f(''') = 4u J % + ,-. "^^ T>0. B2).
В недиспергирующей среде х' — константа и B2) совпадает с A43), .
стр. 283. Если, однако, среда диспергирующая, то у.' является функцией s.
Мы предположим, что дисперсия может быть описана формулой (8) на
стр. 287, и, заменив — i(a на s, получим
V ^ s^ + sg + i^'o
B3)
Для того чтобы включить в наше рассмотрение проводники, нужно лишь
положить ооо = 0. Следовательно, волновая функция, которая при ^>0'
переходит в гармонические колебания в точке 2- = О, будет
Y+гоо s[«-p{8)-J-]
/<^'0=2S? J ^-7+ы "*> •r>0- B4).
Y—г'оо
При ^->-±гоо функция Р(^)->'1. Если теперь x = t <0, то контур
может быть замкнут, согласно лемме Жордана, стр. 280, правой
полуокружностью бесконечного радиуса. Такой контур не содержит особенностей под-
интегрального выражения и, следовательно, f{Zyt)=-0. Таким образом мы
убедились в том^ что в точке z среды поле равно нулю, до тех пор пока
^<-— И, следовательно, в том что скорость волнового фронта не может
С/
превышать константы с.
Если x==t > О, то контур может быть замкнут лишь слева.
Охватываемые при этом особенности суть полюс ^ = — т и точки ветвления р.
Эти последние находятся в точках, где. р=0 и р=:оо. Если ^{s) записать .
в виде
i-
-2 . ,2
Р(^)=1/ —г-—-=2—» B5) ■
то легко видеть, что
р = оо при s= — j^=tyJ/4(oS—^2,
р = 0 при s = ~-^g±^y^(^l^a^) — g\ B6)
Расположение этих особенностей на комплексной плоскости s показано на
рис. 60а, где
2 ^~ 2
B7).
Если мы обойдём точки ветвления в плоскости s, то мы вернёмся к
начальному значению р, но с противоположным знаком. Этой трудности избегают
введением «разрезов» или барьеров вдоль какой-нибудь линии, соединяющей^
:298
ГЛ, V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
.а
+
I Т*
I I к
с,\Ь
А
Cif
/
л
'2(.\У^ ^-^,
III
У;"
S-плосносгпъ
tCi)
Сп
ж Ъj^b vi линии, соединяющей а^ и ^_. На такой «разрезанной»
плоскости, которая в теоретико-функциональном смысле представляет собой один
лист римановой поверхности ^(s\ функция .р(^) однозначна, так как ввиду
^_^ ^ запрещения переходить
барьер любой контур
должен окружать
чётное число точек
ветвления. Путь
интегрирования в B4), кото-,
рый идёт по прямой
от Y — гсзо до '{^iooy
2l затем замыкается
слева бесконечной
полуокружностью, может
быть теперь
деформирован любым способом
в «разрезанной»
плоскости, без изменения значения интеграла, при единственном условии, что
т процессе деформации контур не пересекает полюса в точке ^= —т или
какого-нибудь из двух барьеров. В частности, путь интегрирования может
быть сжат до контура, изображённого на рисунке 60b. Величины
интегралов, взятых в прямом и обратном направлении вдоль прямых линий,
соединяющих Со с Cj и Со с Cg, взаимно сокращаются, и B4) сводится к
трём интегралам, взятым вдоль замкнутых контуров Сд, С^ и Сд.
Первый из этих трёх интегралов
-9/2 ,
Г"
■
S-r
-ш
i
noct
V
,
! Д
Рис. 60. Пути интегрирования в s-плоскости.
•^o<^'^^ = i'J
. {t-m ^)
s~\-m
ds.
B8)
•может быть сразу же вычислен п© теореме Кошн
'Согласно B5),
Р(-гш) =
tO^ -j-^ iiug tOQ «2
to2_J- Hug Oq
n-\-ih^
B9)
C0)
•И, следовательно,
/оBг, 0 = e'
"^ ^ e
4^'-"')
C1)
Другие два интеграла, описывающие петли во[С|)уг барьеров, не могут быть
вычислены каким-либо столь же простым способом и будут обозначаться
.далее через
/12(^,0=2^- J '—Тлгт:г-^^' C2)
8-\-Ы
Таким образом, результирующее волновое движение в любой точке
.среды может быть представлено в виде суммы двух членов
/(^,0=/o(^,0+/is(^.0.
C3)
СКОРОСТИ РАСПРОСТРАНЕНИЯ [5.18] 299
физически ЭТИ две компоненты могут быть интерпретированы как
вынужденные И свободные колебания зарядов, из которых состоит среда.
Вынужденные колебания, определяемые f^i^. О» не затухают во времени и имеют
ту же самую частоту, что и приходящий волновой цуг. Свободные
колебания /laC-s", t) в результате тормозящей силы, действующей на колеблющиеся
ионы, затухают во времени, и их частота определяется упругими силами
связи. Процесс распространения в среде можно обрисооать следующим об-
разом. До момента t = ~ всё находится в покое. Даже, если фазовая
скорость V больше с, никакая волна не достигает точки г, раньше чем через
время t=—. При ^ = — интеграл fi^(^,t) принимает первоначально
значение, отличное от нуля, показывая, что ионы начали колебаться. Если мы'
под термином «фронт волны» понимаем самое первое прибытие возмущения,,
то скорость волнового, фронта всегда равна с вне зависимости от среды.
Можно показать, однако, что в это первое мгновение ^ = — вынужденный
член /оB^, О, описывающий установившееся состояние, как раз погашает
член /j2 (-^j ^)> изображающий процесс
установления,, так что^ процесс начи- ^4\f\J\p\J\p^f\.f)JXf\-j ■'*
нается всегда с нулевой амплитуды. ^ v v л/ v v \j f
Затем стационарное состояние
постепенно вырисовывается по мере того,
как переходный процесс замирает,
точно таким же образом, как при
внезапном включении переменной
электродвижущей силы в электрическую сеть
возникает переходное возмущение, ко- 2/^
торое, в конце концов, заменяется
гармоническими колебаниями. • Рис. 61. Определение фазы в стацио-
Прибытие волнового фронта и «^Р"°^ состоянии,
роль скорости v в определении фазы
изображены на рис. 61, который, однако, относится лишь к стационарному
члену. Ось — проведена нормально к оси t. Тогда линия, проведённая под
углом в 45°, определяет скорость волнового фронта, так как она проходит
через точку z в момент —. Линия, тангенс наклона которой eCTbtgO = —-,
определяет время t = ~ прибытия в точку г волны, имеющей скорость v.
В действительности фазовая скорость не имеет ничего общего с
распространением; она определяет только фазу, да и то, строго говоря, лишь в
случае бесконечного волнового цуга. Фаза вынужденных колебаний измеряется
от точки пересечения с пунктирной линией при ^ = — , а фаза волнового
фронта t = — подбирается соответственно. Если г>>с, то &<45°. Фаза
стационарного состояния опять определяется пересечением с линией — в точке
/=— , но сам фронт волны прибывает позже. Переход от исчезающе
малых амплитуд у волнового фронта к относительно большим значениям
сигнала был тщательно исследован Бриллюэном. Это исследование является
гораздо более тонким, и мы вынуждены ограничиться здесь теми выводами,
которые могут быть получены после вычисления C2). Согласно Бриллюэну,
«Игнал — это цуг колебаний, начинающихся в некоторый момент. В про-
300 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
цессе своего распространения сигнал деформируется. Основной части сигна*
л а предшествует первый предвестник, который во всех средах
распространяется со скоростью с. Этот первый предвестник прибывает с нулевой
амплитудой, а затем его частота и амплитуда медленно растут, как показана
на рис, 62а. Затем амплитуда уменьшается, а период приближается к соб-^
ственному периоду электронов. Теперь начинается новая фаза возмущения^
которая может быть названа вторым предвестником, распространяющимся
со скоростью ■ _*"° - с. Эта скорость получается в предположении, чта
в комплексном показателе переломления р(—ш) в уравнениях C0) и C2)
рассматриваемая частота <л мала по сравнению с атомной резонансной часто-
«^iovVi/Vn»- . '^\,^'\J^
z/c Л/<^о+а^„
mk
Сигнал
Рис. 62а. Характер изменения Рис. 62Ь. Иллюстрация прибы-
амплитуды первого предвест- тий первого и второго пред-
ника. вестников и сигнала.
той. ooq. Период второго пр.едвестника сначала очень велик, а затем
уменьшается, в то время как амплитуда растёт и потом падает примерно так же^
как и у первого предвестника.
Прибытие основной или главной части возмущения ознаменовывается!
внезапным ростом амплитуды. Эта главная часть распространяется со
скоростью -ш, которую Бриллюэн назвал скоростью сигнала. Ясное и простое
выражение для w не может быть дано и её определение включает
некоторый произвол, связанный с методом вычисления интеграла C2). Её
физический смысл совершенно ясен. На рис. 62Ь показаны два предвестника и
окончательный внезапный рост до установившегося состояния.
В применении к этой третьей и последней части возмущения термин-
«сигнал» означает ту часть волны, которая способна.приводить в действие
измерительные приборы. Действительно, при этом предположении измерени»
должны показать, что скорость распространения приблизительно равна w.
Следует, однако, отметить, что по мере роста чувствительности приёмника
скорость, полученная в результате измерения, также будет увеличиваться,
пока в пределе, при бесконечной чувствительности, мы не зарегиструем
прибытие фронта первого предвестника, который всегда распространяется со
скоростью с. По крайней мере качественно мы можем представить себе среду
в виде области пространства, густо усеянной электронами. Бесконечно малое
количество энергии проходит сквозь незаполненное пространство, как сквозь
сито, распространяясь, конечно, со скоростью с. Каждый последующий слой
зарядов приводится в колебание первичной волной и излучает энергию как
назад, так и вперёд. Из-за инерции зарядов эти вторичные колебания
отстают по фазе от первичной волны, и такое постоянное отставание в
процессе прохождения через последовательные слои приводит к уменьщению
скорости главной части возмущения.
Определённая выше скорость фронта волны таким образом
всегда равняется константе с. Фазовая скорость v связана лишь с
установившимся состоянием и может быть как больше, так и меньше с. Груп-
ЗАДАЧИ
301
повая скорость и отличается от фазовой скорости только в диспер-
тирующих средах. Если дисперсия нормальна, то групповая скорость
меньше 1}; она больше фазовой
скорости, если дисперсия
аномальна. В окрестности полосы
Поглощения и может стать
бесконечной , и даже отрицательной.
Скорость сигнала w совпадает
«с групповой скоростью в области
нормальной дисперсии, но
заметно отличается от неё всякий
раз, когда и ведёт себя
аномально. Скорость сигнала всегда
меньше с, но в окрестности
полосы поглощения довольно
трудно дать ей определение, не
являющееся до некоторой
степени произвольным. На рис, 63
отношения скоростей, характеризующих распространение волнового цуга
к скорости с, изображены в окрестности полосы поглощения.
с/и и-еруптВ. скорость
C/v v-сразовая скорость
C/tu Zu-cf(opocmb сигнала
Рис. 63. Поведение групповой, фазовой
скоростей и скорости сигнала в окрестности ре*
зонансной частоты.
ЗАДАЧИ
1. Пусть Eq — амплитуда электрического вектора в вольтах на метр, а S — сред-
«ий поток энергии в ваттах на кв. метр для плоской волны, распространяющейся
в пустоте. Показать, что
' 5=1,327.10-з.£2 ватт/метрз.
S вольт/метр.
2. Пусть Eq — амплитуда (в вольтах на метр) электрического вектора плоской
волны, распространяющейся в пустоте. Показать, что амплитуды магнитных
векторов //(, и Bq связаны численно с Eq соотношениями
Hq = 2,654 • 10-3 £q ампервитков/метр = -^-10-* эрстед,
Бо = 4 • 10-8 Eq -^^ = 4- • 10-* f о гаусс,
" Метр2 3 "
где эрстед — нерационализованная единица в электрома гнитной системе CGS.
Показать, что если Eq выражено в электростатической системе, то
Hq — Eq эрстед, Bq — Eq гаусс.
Показать, что если заряд д движется со скоростью v в поле плоской электромагнит
ной волны, то отношение сил, вызываемых магнитной и электрической компонен-
V
тами, имеет порядок — .
С
3.'Теорию однородных плоских волн, развитую в гл. V, можно распространить на
неоднородные волны. Если 4* — любая прямоугольная компонента электромагнитного
шектора, то за общее определение плоской волны можно принять выражение ^
ф = d'o^^'P» ? = ~*"^ -f ^^^'^
в котором фо — комплексная амплитуда, а ср — комплексная фаза. Коэффициент
распространения к является теперь комплексным вектором, который можно записать
а виде
к = ki + /к2 = ащ + фп2,
тдеП1 и щ — единичные векторы. Показать, что о — действительная фазовая константа,
что поверхности постоянной действительной фазы представляют собой плоскости,
ябрмальные оси ni, а поверхности постоянной амплитуды — плоскости, нормальные
302 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
I
оси «2 И ЧТО р — коэффициент, являющийся мерой затухания в направлении наиболее
быстрого изменения амплитуды. Истинная фазовая скорость v направлена по щ-
Показать, что оператор grad можно заменить на ik и что уравнения поля имеют
вид
[кЕ] — toB = О, кВ = О,
[кН] + toD = — /J, kD = 0.
Показать также, что для изотропной среды
k'^ = ky — ^2"Ь 2/kik2 == «V^ -\- ft"^*-'^.
Полагая kik2 = k^k^ cos 0, найти выражения для k^ и k^ через \х, в, с а угол &.
4. Продолжая задачу 3, предположим, что электрический вектор линейно
поляризован. Показать, что Е перпендикулярно к ki и к^, а Н лежит в плоскости этих двух
векторов. Каково геометрическое место концов магнитного вектора Н? Показать^
что если, наоборот, Н линейно поляризован, то Н перпендикулярен к к^ и к2, а Е
лежит в плоскости (ki, кг). Эти неоднородные плоские волны тесио связаны с так
называемыми «Н-волиами» и «Е-волнами» (раздел 9. 18).
5. Теорию плоских волн можно распространить на однородные анизотропные
диэлектрики. Пусть а = 0, ix=ixq, а свойства диэлектрика характеризуются тензоронб.
с компонентами е^-;;.. Выбирая главные оси в качестве осей координат, получим
Dj == BokjEj и = 1. 2, 3).
Уравнения поля для Е и D имеют вид
[к [кЕ] 1 + to2;j.oD = 0, kD = 0.
Пусть к = kn, где п — единичный действительный вектор, составляющие которого
по главным осям равны л^, щ, По.
у, ш с
пусть v= — iiVj — -y:=:r; Vj — главныв скорости. Показать, что компоненты Е
удовлетворяют однородной системе
и написать уравнения, определяющие фазовую скорость в произвольном
направлении, задаваемом вектором п. Показать, что это уравнение имеет три
действительных корня, один из которых бесконечен и должен быть отброшен. Поэтому
распространение в навравлении п может происходить двумя различными способамне
с фазовыми скоростями я/ иг/'. Соответственно имеется два типа линейных
колебаний по определённым направлениям, характеризуемых векторами Е', D' и Е'', D".
Показать, что эти векторы связаны следующим образом:
D'E''= D'<E' = D'D" = О,
E'E'' 9^ О,
En :?е 0.
6. Показать, что в однородном анизотропном диэлектрике фазовая скорость
удовлетворяет соотношению Френеля
У
v^ — г;2
где fij — направляющие косинусы волновой нормали п по отношению к главным
осям, а Vj—фазовые скорости в направлениях главных осей (см. задачу 5). Показать,
также, чю
где Yj — направляющие косинусы вектора D по отношению к главным осям.
7. Показать, что если в задаче 6 v^^V'^v-i,., то имеются два направления, в
которых V имеет единственное значение. Найти эти направления в функции Vi, v^, v^.
и показать, что в обоих случаях скорость равна г>2- Определяемые таким образом»
ЗАДАЧИ ЗОЯ;-
направления являются оптическими осями среды, которая в этом случае называется
двуосной. Каковы необходимые условия для того, чтобы была только одна
оптическая ось?
е. Показать, что для плоской волны в анизотропном диэлектрике
S = [Е,Н] = -^^ [ п£2 - (пЕ) Е \,
где V — фазовая скорость, определённая в задаче 5.
Векторная скорость распространения энергии и в направлении 5 определяется^
уравнением
Скорость U связана с фазовой скоростью v соотношением
i г; = nu.
Показать, что
ft = -lED + -iixoH2,
откуда следует, что поток энергии равен общей плотности энергии, умноженной на
скорость U, где
Е2п —(пЕ)Е
11 = i L— ч;
£2_(nE)S ^'
или по величине
£2
(^;--
9. Показать, исходя из результатов задачи 8, что величина скорости и
распространения энергии в плоской волне может быть найдена в функции.постоянных.
v-i, г/з» ^3 из уравнения
= 1.
2 1~(Ъ\'
j=i \и J
где Ij — направляющие косинусы вектора «.
Показать также, что в общем случае имеется два конечных значения и,
соответствующие каждому направлению. В каких направлениях оба эти корня совпадают?
Какова связь этих особых осей с оптическими осями?
10. Непроводящая среда бесконечной протяжённости изотропна, но её относи-
£
тельная диэлектрическая постоянная у. = — является функцией точки. Пдказать, что
вектор электрического поля удовлетворяет уравнению
ДЕ 4- fe2E = — grad ( Е — grad е^,
где fe2 =. to'ejj, и время входит только через множитель
ехр (— ivit).
Предположим теперь, что пространственное изменение е щ протяжении длины
волны мало, так что |grady.|X< 1. Показать, что членом в правой части можно
тогда пренебречь и что распространение волны приближённо определяется уравнением
Ad- + Щ = О,
где ф—прямоугольная компонента Е или Н, а k — медленно меняющаяся функция
точки. Пусть далее ф==6оег?, где фаза u)=—to/-f/fegS, feo = —. а 5 — функция--
точки. Показать, что фазовая функция 5 определяется уравнением
(grad 5J+ 7lr^5-x.
где
<^-:^)-(i;+(iT+(i;
304 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
Заметьте, что S, вообще говоря, комплексно, хотя % и действительно, и что амплитуда
волны также является медленно меняющейся функцией времени.
И. Переход от волновой оптики к геометрической можно обосновать
результатами задачи 10. Показать, что когда волновое число k становится очень большим,
viro фазовая функция определяется уравнением первого порядка второй степени
(gradS)= = Q"=x.
а амплитуда удовлетворяет уравнению
grad In фо grad 5 = —2" ^^•
Так как теперь 5 действительно, то фронт волны представляется семейством
5 = const., а волновые нормали или лучи определяются в каждой точке
выражением grad 5. Функция 5 называется «эйконалом» и тождественна с
«характеристической функцией» Гамильтона. Пусть вектор п равен показателю преломления У~^,
умноженному на единичный вектор в направлении волновой нормали. Тогда
gi ad 5 = п, п grad In фо = о" ^^^ ""
Заметьте, что эти соотношения имеют место лишь в тех областях, где изменение %
на протяжении одной длины волны мало. Поэтому они нарушаются вблизи острых
краёв или тел, размеры которых поря;уса длины волны. В этих случаях следует
применять полное волновое урабнение. [Sommerfeld und Яипее, Ann. Phys.
35,290A911).]
Пусть dr — элемент длины в направлении луча. Тогда
/"
■dr.
S — функция координат Хо,уо, zo фиксировадной начальной точки и координат х,у, z
конечной точки, достигнутой лучом. Из всех возможных путей между этими двумя
точками луч идёт в действительности по тому пути, на котором 5 минимально, или
о5 = 5 f п dr = 0.
(ато. Уо, Ze>
Это — принцип Ферма. Ееля возмущение начинается при Xq, уо, Zq в момент ^о и
приходит в точку X, у, Z ъ момент t, то
5(д^о, Уо, zdi x,y,z)^t— to,
и путь луча таков, что время прихода луча минимально^).
12. Плоские волны возбуждены в неоднородной среде,- диэлектрическая прони-
даемость которой меняется в направлении распространения. Примем это направление
за ось г и предположим, что поле не зависит от х и у. Тогда волновое уравнение
■примет вид
0 + ^?^(^L' = о.
где ^0 = t"^eoP■o» ^ время входит только в множитель
ехр (— Ш).
1) Изложенный (и обычный) способ перехода к приближению геометрической
оптики основывается на замене векторных уравнений электромагнитного поля скаляр-
. яым уравнением для какой-либо компоненты (см. задачу 10). Тем самым в приближе-
: НИИ геометрической оптики остаётся в стороне всё, что касается поляризации. Между
тем можно последовательно провести переход к случаю больших k, отправляясь
непосредственно от уравнений Максвелла, и получить в результате закон изменения
вдоль луча не только величины амплитуды, но и поляризации — см. С. М. Рытов,
Доклады Акад. Наук СССР, 18, 263, 1938.
В отношении принципа Ферма следует отметить, что он отнюдь не всегда
сводится на требование минимума S. Условие экстремума (bS = 0) не предрешает
того, что 5 = Sjaiw и можно указать случаи, когда действительному лучу отвечает
«5 == .Smax- Прим. ред.
ЗАДАЧИ
305
Предположим, что % -> г.^ при z -> —схэ и * ->• у^ при г -> со, где y.t и %^ — постоян-
яые. Можно построить четыре частных решения, которые acHMnT0tH4ecKH ведут себя
следующим образом:
ф1 -> ехр {ik^"^t^z) при
^2 -^ ехр (— ik^ V^\Z) при
z-^
со,
Z Ч>- ОО,
фз -^ ехр (iko 'V'Hz) при г -^ 4- со,
ф4 -> ехр (— /^оТ^ ■^2^^) при z-^-\-co.
Таким образом ф^ и фз переходят в плоские волны, бегущие в положительном
направлении, а фз и ф4 — в волны в отрицательном направлении. Из этих решений
только два являются линейно независимыми,! и следовательно, должна существовать
аналитическая связь вида
Фз = йхф) + «зфг. Ф4 = Щ\ + Щч.'
Математически эта связь представляет собой аналитическое продолжение фз из
одной области в другую, а физически коэффициент отражение даётся отношением
«2
а\
Пусть
y.» = %i| +
[(%2-Xi)(e!;+l) + V-3]^'
(^:+l)8
еде С
s
7.3 — постоянная, а s — дополнительный параметр. Заменив z новой
независимой переменной и = ехр (С), показать, что волновое уравнение приводится
м. гийергеометрической форме. Выразить ф^ ... ф^ как гипергеометрические функции
и вычислить коэффициенты aj, «2» ^i« ^2 и коэффициент отражения. Форма ■х,(г)
такова, что она допускает очень широкий выбор вида переходных слоев [Epstein,
Proc. Nat. Acad. Sci. 16, 627 A930I1).
13. Умноженный на 10 десятичный логарифм отношения начального потока
энергии к конечному намеряет затухание плоской волны в децибелах. Показать, что
для плоской волны в однородной изотропной среде потеря мощности = 8,686 р
децибел/метр, где р — коэффициент затухания, определённый равенством D9),
«тр. 246.
14. Построить график зависимости затухания плоской волны в децибелах на
метр от частоты в интервале от О до 10^ циклов/сел: для сред, константы которых
лриведены в таблице
Среда
Морская вода . . . . ,
Влажная почва ....
Проводимость
1/ом • метр
4
10-3
10-3
е
81
81
10
4
Воспользуйтесь для чертежа полулогарифмической бумагой или же
откладывайте по абсциссе логарифм частоты.
1) Эта задача и работа Эпштейна, на которой она основывается, связана
^ вопросом о распространении радиоволн в ионосфере. Если отвлечься от поглощения
и земного магнитного поля, то вопрос сводится к распространению в среде с перемен^
ным показателем преломления,
такого рода, но принимающие
в работе С. М. Р ы т о в а и Ф.
волн от ' слоя с отрицательной
.Прим. ред.
Некоторые библиографические ссйяки на работы
другой вид функции %(гг), читатель может найти
С. Ю д к е в и ч а. Об отражении электромагнитных
диэлектрической постоянной, ЖЭТФ, 10, 887, 1940.
20 Эак. 593. ^-еорзхя влектфонагнетивна.
306 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
15. функция f{x) определена следующим образом:
/(х) = е-р«', х>0. р>0.
Показать, что
со
... 2 г В cos ил: .
/(л:) = — I -—-.——du
О
16. Получить интегральное представление Фурье для функции /(О»
определённой так:
f{t)z=z(i при ^<0,
/(/) = e-b*costo/ при f^O,
Построить график амплитуд гармонических компонент в функции частоты
(спектральная плотность) и исследовать связь между шириной пика и логарифмическим
декрементом.
17. Импульсы в линиях передачи, вызываемые грозовыми разрядами, часта
воспроизводятся в электротехнике с помощью импульсных генераторов, дающих
направленный в одну сторону импульс напряжения вида
= КоуГ^-^^-Р^ *_e-t«+P) л.
где аир — постоянные, определяемые параметрами цепи. Эти функции представляют *
собой импульс, или всплеск, резко по!аьиыающийся до гребня, а затем спадающий
более медленно в виде длинного шлейфа. Форму волны можно охарактеризовать
двумя константами /j и t^, tjit t^ — время, необходимое для достижения гребня,
а ^2 — интервал времени от нулевого напряжения до точки на шлейфе, в которой
напряжение равно половине напряжения на гребне. Стандартный набор импульсов
характеризуется постоянными
a) ^1 = 0.5. 4=^5.
b) /1=1.0, ^2=10.
c) ^1 = 1,5. 4 = 40
микросекунд.
По этим величинам можно найти значения констант аир. Произвести спектральный
анализ формы волны и определить частоты, при которых спектральная плотность
максимальна, для этих трёх стандартных случаев.
18. сТелеграфное уравнение»
имеет начальные условия
Показать, что
u^fix), -j^=g{x) при / = С.
at
« = 4l-^(^ + «^)+^^-«0} + ^//(-^4-P)y^/o[*}/^^''-(-|JjrfP +
•at
at
+i/«('+»'»['/"-AI "?•
— at
где
/у {x) = — Г со8(л: cos X) dk.
3ie решение было получено независимо Хивисайдом и Пуанкаре.
19. Электромагнитный импульс распространяется в однородной изотропной
среде с постоянными е, fx, а в направлении положительной оси г. В момент / = 0
ЗАДАЧИ 3G7
форма импульса задана выражением
а»
1 е '-''
A(^)=^lira /(г./)=-^—Г-.
где 8—параметр. Найти выражение для импульса f{z, t) в любой последующий
момент.
20. Там, где можно пренебречь током смещения по сравнению с током
проводимости [—>l), поле приближённо удовлетворяет уравнениям
rotE + iJ.^ = 0, rotH = J.
Показать, что в том же приближении
Е = -гт. Н = — rot А,
at (л
ЙА
ДА —{Аа~ = 0. divA = 0
и что плотность тока удовлетворяет уравнениям
AJ_fAa-^ = 0, divJ = 0.
at
Какие граничные условия налагаются на вектор плотности тока? Этим уравнениям
подчиняется распределение тока в металлических проводниках при всех
радиочастотах или более низких частотах.
21. Уравнение, полученное в задаче 20 для распределения тока в
металлическом проводнике, совпадает с уравнением теплопроводности. Рассмотреть одномерный
случай прямоугольной компоненты J, распространяющейся по оси z:
dV dJ
Показать, что
^=4/^//w^" " ""
— оо
является решением, обращающимся при t = Q в f{z) и непрерывным вместе со своими
производными для всех значений z при t^O.
22. В задаче 21 найдено, что уравнению
^ Лг2 dt
удовлетворяет функция
. . +00 («—г)»
—,оо
Показать, исходя из теории преобразований Фурье, что 6 можно переписать в виде
л = —00 О
Очевидно, уравнению удовлетворяет также функция
+СО 2я
.J; = — V Г ^ »' (г-о) n-7mtf (а) da.
П~-~оаО
Сравнить эти решения и из теоремы единственности доказать тождество
-f-t» +00 (г—«+2«я)"
L ^ -у -t 1а '
SJ4v«
П=.—со П = —00
Это соотношение было применено Эвальдом к теории распространения воли
S кристаллах.
308 гл. V. ПЛОСКИЕ волны в НЕОГРАНИЧЕННОЙ ИЗОТРОПНОЙ СРЕДЕ
-ш^
^' ' 23. Показать, что если радиоволны распространяются в электронной атмосфере
в поле земного магнетизма, то следует ожидать резонансных явлений вблизи длины
во^ны около 212 м. В этой области действительно наблюдалось заметное
избирательное поглощение. Положить е=1,60-10-*в кулон/электрон, /п = 9-10-31 лг/электрон
и напряжённость магнитного поля земли Во = 0,5 • 10-* вебер/метр^.
24. Радиоволна распространяется в ионизированной атмосфере. Найти и
проанализировать зависимость групповой скорости от частоты, определяя постоянную
распространения из выражения C6), стр. 292. Концентрация электронов в
определённых областях ионосферы предполагается порядка Ю^^ электронов/метрз.
25. Плоская линейно поляризованная волна входит в электронную атмосферу
с плотностью 10^2 электрон/метр. В направлении распространения наложено
статическое магнитное поле напряжённости Bq = 0,5 • 10-* вебер/метрЗ. Получить
выражение для изменения состояния поляризации на длине волны в направлении
распространения.
26. Радиоволна распространяется в ионизированной: атмосфере при наличии
данного магнитного поля. Найти постоянную распространения для случая, когда
статическое поле перпендикулярно к направлению распространения.
27. В качестве простой модели атома можно принять неподвижный
положительный заряд, с которым квазиупругой силой связан отрицательный заряд е массы т.
Если пренебречь силами трения, то уравнением движения этой системы будет
mr-f/r = 0,
где г — радиус-вектор зарядам, а /—постоянная связи..Пусть теперь наложено
магнитное поле. Показать, что имеются, две различные частоты колебаний и что
соответствующие движения представляют собой круговые движения в
противоположных направлениях в плоскости, перпендикулярной к направлению наложенного
поля. Какова частота вращения? Это рассмотрение является элементарной теорией
эффекта Зеемана.
28. Если частица движется со скоростью v в магнитном поле В, то На единицу
заряца действует сила Е' = [v. В]. Вызванная движением электродвижущая сила
в гамкнутом контуре есть
V' = & E'ds = f rot [v. В] n da.
В любой фиксированной точке пространства скорость изк;енения В со временем
есть -^. Если под Е понимать суммарную силу, действующую на единицу заряда
движущегося тела, то
до
rotE= —■^+rotlvB].
Показать, что правая часть равна с обратным знаком полной производной
dB дЪ , , .. _
-^ = .-a--f(vgrad)B.
так что лля движущейся среды закон Фарадея имеет вид
rotE = —^^-.
Скорость перемещения предполагается малой по сравнению со скоростью света.
ГЛАВА VI
ЦИЛИНДРИЧЕСКИЕ ВОЛНЫ
Вообще говоря, электромагнитное поле не может быть получено из одной
скалярной функции, зависящей от точки и времени; вследствие этого анализ
электромагнитных полей по самому их существу сложнее, чем изучение
тепловых потоков или передачи ввуковых колебаний, В трёхмерном
скалярном волновом уравнении переменные разделяются в 11 различных системах
координат ^), но полные решения векторного волнового уравнения в форме,
непосредственно применимой к решению краевых задач, известны в
настоящее время лишь для определённых разделяющихся систем цилиндрических
координат и для сферических координат. Как будет показано, в таких
системах электромагнитное поле может быть разложено на две составляющие поля,
каждое из которых получается из
одной скалярной функции,
удовлетворяющей волновому уравнению.
УРАВНЕНИЯ ЦИЛИНДРИЧЕСКОГО
ПОЛЯ
6.1. Представление
посредством векторов Герца.
Предположим, что одна система координатных
поверхностей образована семейством
цилиндров, образующие которых
параллельны оси г. Пока это
специально не оговорено, эти
цилиндрические поверхности не
предполагаются обязательно круговыми или
даже замкнутыми. По отношению к
каждой поверхности семейства
единичные векторы ij, \с£, ц
расположены, как показано на рис. 64.
Таким образом, вектор ij нормален к цилиндру, ig касается его и направлен
вдоль его образующих, а ig касается его поверхности и перпендикулярен
к ij и ig. Положение по отношению к осям координат, определяемым этими
тремя единичными векторами, характеризуется координатами и^ а^, г-, а
бесконечно малый элемент длины равен
О У
Рис. 64. Взаимное расположение единичных
векторов на цилиндрической поверхности..
Образующие параллельны оси г.
ds = i^h^du^ + ig V"" + h^2-
A)
Определим теперь компоненты электромагнитного поля, связянного с
вектором Герца П, направленным по оси z, так что П1 = П2 = 0, И^фО.
1) Е i S е п h а г t, Annals of Math. 35, 284, 1934.
310 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
в этой главе мы будем считать среду не только изотропной и однородной,
но и безграничной. Тогда по F3) и F4), стр. 40, электрические и
. магнитные векторы поля определяются выражениями
E(i) = rotrotn, H(i)=('s-^4-°)rotn; B)
так как П^ и Ilg равны нулю, то по (81) и (85), стр. 54—55, легко найти
компоненты Е^^) и Н^^):
T^^) — J ^Ш^ рB)_ 1 дт, ]
^^ ~" hi дгди^ ' '^ ~ h^ dzdu^ ' I
^^ ~ hih^ldu^\hi du\)~^ ди^\кг дф)\' J
Таким образом мы получили из скалярной функции П^ = ^
электромагнитное поле, характеризующееся отсутствием осевой или продольной
компоненты магнитного вектора. Ввиду того, 4jro П является Электрическим
поляризационным потенциалом, это поле • можно назвать полем электрического
типа (стр. 39), но в настоящее время представляется более подходящим
термин поперечно магнитное поле^ недавно предложенный Щелкуновым ^).
Так как П^ является прямоугольной компонентой, то она должна
удовлетворять скалярному волновому уравнению
или по (82), стр. 54:
Элементарные гармонические решения этого уравнения имеют вид
^^/(и\ tt^)e*•^'^"-^^"^ G)
где /(«Ч и^) является решением|уравнения
Тф^ 'Ш \Jh Ш) "^ Th/h-diT^ [ji^ ЫГу ~Ь (^^ — h^)f= 0. (8)
Точно таким же образом можно вывести частный вид поля из второго
вектора Герца П*
.ЕB) = —>;^rotn*, HB) = rotrotn*; (9)
если П* направлен по оси z, тЬ составляющие эхих векторов равны
р^^) ' ^ р'^} ' '^^^ py^i п f^n\
1 d'^n! ,,, 1 d^n!
(И)
"^ ~ hih^ld^Khi du>^"^~^ da^^h^ дФ^У .
Скалярная функция П^ является решением уравнения E), а полученное из
1) Schelkunoff, Transmission Theory of Plane Electromagnetic Waves, Proc.
Inst. Radio Engrs. 25, 1457—1492, November. 1937.
УРАВНЕНИЯ ЦИЛИНДРИЧЕСКОГО ПОЛЯ [6.2]
311
«её поле магнитного типа или «поперечное электрическое поле:»
характеризуется отсутствием продольной составляющей Е.
Электромагнитное поле, получаемое наложением частных видов полей,
получаемых из П^ и П^, является настолько общим, что оно может
удовлетворить заданным граничным условиям на любой цилиндрической поверхности
с образующими, параллельными оси г, т. е. на любой координатной
поверхности «1 = const, или w^ = const, или на плоскости z = const. Однако выбор
этих семейств ортогональных поверхностей практически ограничен теми
координатными системами, в которых переменные в уравнении (8) разделяются.
6.2. Скалярный и векторный потенциалы. Поперечные электрическое
и магнитное поля, определённые в предыдущем параграфе, обладают
интересными свойствами, которые выявляются при рассмотрении скалярного
и векторного потенциалов. Рассмотрим сначала поперечное магнитное
поле, в котором //^*^ = 0;
£(!)= —grad© — ^, B(^) = rotA,
<Р = —divH, A = }i.(e-^+o)lI.
В данном случае 6 = П^, откуда
О:
dz *
дФ
A = l^^-TT-r\^°'^y Ai = A2 = 0.
A2)
A3)
A4)
Компоненты E^') имеют поэтому вид
£?>==
1 аср
^?
дЧ дЧ
Е^
A)
3 ' "
р,о
dt '
1
d<f
я компоненты В^^)
^"'=i
дА
да
,2 »
в?^.
г дА
hi ди^
М*'=о,
A5)
A6)
где вместо А^ написано А без индекса.
Заметим, что в плоскости 2" = const, вектор Е^^) безвихревой;
следовательно, в этой поперецной плоскости линейный интеграл от E^^J между
любыми двумя точками а и ^ не зависит от соеди- ^
няющего их пути. Действительно, элемент длины
в плоскости Z = const, имеет вид
ds =^ iih^du} -j~ i^^du^
м, следовательно.
J
Е«)Л =
= -/(^''"' + t''"'') = ^^"^-?(*^- ('^)
/.'
Рис. 65. Кривая аЬ
изображает сечение
цилиндрической поверхнасти
плоскостью ху, в которой
лежат также векторы п и ВЧ
Разность потенциалов или напряжение
между любыми двумя точками поперечной
плоскости имеет определённое значение в каждый момент^ независимо от
частоты или вида цилиндрических координат.
Далее, можно заметить, что скалярная функция А играет роль функции
тока для вектора В^*). Пусть кривая, соединяющая точки а и b на. рис. 65,
представляет соббй след цилиндрической поверхности, пересекающей пло-
312 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
скость г = const. Вычислим поток вектора В^*> через лентообразный элементг
поверхности, ограниченный кривой аЬ и имеющий ширину, равную единице
в направлении оси г. Если п — единичный вектор нормали к этой
поверхности, а ig — единичный вектор, направленный по оси гг, то
(В^п) da = ВA> Из, ds] = ц [rfs, B(i>I, A8>
где ds означает элемент длины вдоль кривой. Раскрывая A8), получаем
В^^'п da=hBfdu}- — hsB^du^ = — dA, A9>
откуда
ъ
j В^^^'п da = A {a) —A {b). B0)
a
Магнитный поток через любую единичную по ширине полоску
цилиндрической поверхности^ проходящую через две точки в плоскости г: = const.,,
не зависит от формы полоски.
Если выразить составляющие Е^^) и В^^^ через скалярную функцию ^у
то легко показать, что . .
ё?В?Л-Е'М'==0, B1)
и, следовательно, проекция вектора Е^^) на плоскость г: == const, всюду
перпендикулярна вектору В^^>. В' поперечной плоскости семейства кривых
9 = const, (эквипотенциальные. линии) и А = const, (линии «toKa»
вектора В^^)) совпадают. Из A4) и G)'ясно, что при гармоническом изменении
во времени эквипотенциальными являются линии
/(aS «2) = const., B2)
где /(tt^ и^) удовлетворяет уравнению (8).
Поперечное электрическое поле "обладает подобными же свойствами, н(>
роли электрических и магнитных векторов меняются. Согласно C5), стр. 37:
D^2)=--rotA*, HB)=»—grad<p*——- —^Л* B3>
cp*=_divn*, А*==Н'е^« B4>
Полагая ^|; = 11г, IIi==n2 = 0,* получ^1М
dii .* д<1> .* .* _.
?*==—•|j, Az^V-e^, Л = Л2 = 0; B5)
Компоненты векторов поля будут поэтому:
1 ал* ^B) 1 дА*
B7 >
Проекция Н^-) на поперечную плоскость является безвихревой, и
следовательно, криволинейный интеграл, представляющий магнитодвижущую силу
между двумя точками в этой плоскости, не зависит от пути интегрирования:
Г Ht^)rfs = 9* («) — ?* Ф). B8>
УРАВНЕНИЯ Цилиндрического ПОЛЯ 6.31 313S
Подобным же образом поток вектора D^^^ через полоску единичной ширины,,
изображённую на рис. 65, зависит только от конечных точек
ъ ъ
ГD(^)nc?a = JйrЛ* = Л*(&) —Л*(а). B9>
а а
Проекция Н^^) на плоскость г: = const, всюду перпендикулярна к вектору Df^^.
Отсюда следует, что семейства кривых о* = const, и А* = const, совпадают.
Поле D^^), Н^^^ является в этом смысле сопряжённым полю Е^^), В^^).
6.3. Импедансы гармонических цилиндрических полей. Предположим,,
что время входит лишь в гармонический мнои^итель е-^*»*. Тогда потенциалы,
и компоненты напряжённостей поперечного магнитного поля имеют вид
ср = -р ih^, А = — / (}1.есо -j- /|хо) ^^ C0)
/4*)=__i^ i|i^ 4*-^=.i^i|i ///^=0, 'C2)
где /г^ = }i.eш-|-/}JLoш. Верхний знак относится к волнам, распространяющимся1
в положительном направлении по оси z, нижний — к волнам,
распространяющимся в отрицательном направлении.
Совокупность импедансов, относящихся к напряжённостям поля, может
быть определена теперь на основе раздела 5.6. Величина импеданса зависит,,
очевидно, от направления, в котором он измеряется. По определению
Согласно стр. 252, внутренний импеданс однородной изотропной среды;
для плоских волн есть
^0 = /'
—Ь-=^^ C4).
так что C3) можно представить в виде
4'^ = ±4^0- C5>
Аналогично, импедансы в направлениях поперечных осей можно
определить соотношениями
4'^ = -ZM\ E?,==Z^M''. C6)
Знак компонент электрического и магнитного векторов определяется,
очевидно, положительным направлением вектора Пойнтинга. Так как И^^^
равно нулю, то компонента тока, представляемая членами E^^tf^^ и l^^t^^
отсутствует, и соответствующие импедансы бесконечны. Подставляя
соответствующие выражения для компонент поля в C6), получаем
Определение соответствующих импедансов для гармонических компонент
поперечного электрического поля не нуждается в дальнейших разъяснениях.
314 гл. VI, ЦИЛИНДРИЧЕСКИЕ волны
Потенциалы и векторы поля в этом случае имеют вид
ср* = zp Щ, Л* = — /[i-eco'i^, C8)
^^^' = '>"^^. ^'—^^Ш' ^^^' = «. C9)
^' = ±^й- "^' = ±f i- Hf^(k^-k^y^. D0)
Из этих соотношений вычислены импедансы:
yC2) ik дФ у у2) ik ди^ у D3)
Отсюда получается любопытный ряд соотношений
4^L^) _ 4^2) _ ^^1)^2) _ ^2,; • D4)
ВОЛНОВЫЕ ФУНКЦИИ КРУГОВОГО ЦИЛИНДРА
6.4. Элементарные волны. Простейшим случаем разделяющихся пере-
;менных является тот, когда семейство и^ == const, представляет собой
совокупность коаксиальных круговых цилиндров. Тогда, согласно 1, стр. 56,
к1 = г, «2 = 6, /fi=l, /г2 = г, A)
и уравнение (8) раздела 6..1 принимает "вид
где переменные легко разделяются, если п{)едставить /(г, б) как
произведение
^=/lW/2F), C)
В котором Д (г) И/2 (б) — произсольные решения обыкновенных дифферен-
щмгяьных уравнений
#+/'%= 0. E)
Параметр /?, так же как и Л, является постоянной разделения; его выбор
диктуется физическим требованием однозначности поля в фиксированной
точке пространства. Если неоднородности и разрывы непрерывности среды
исключены, как это и предположено в настоящей главэ, то поле должно ,
быть периодическим по б и значения р ограничены целыми числами п = О,
ztl, i±:2, ... С другой стороны, если поле представляется частными
решениями уравнений ^4) и E) в секторе пространства, ограниченном
плоскостями 6 = 6^ и 6=6g, то параметр /; должен принимать, вообще говоря,
нецелые значения.
ВОЛНОВЫЕ ФУНКЦИИ КРУГОВОГО ЦИЛИНДРА F.51 315
Уравнение D), которому удовлетворяет радиальная функция /^ (г), есть
уравнение Бесселя. Его решения можно было бы назвать бесселевыми
функциями, но так как это название применяется обычно лишь к тому
частному решению Ур (|/^Л^ — h^r), которое конечно на оси г = 0, то мы
будем называть произвольное частное решение уравнения D) круговой
цилиндрической функцией и будем обозначать её через /^ = Zp {]/^k^—h^r).
Аргументом функции является l/^k'^—Л^г, а р называется её порядком. Таким образом
частные решения волнового уравнения E), стр. 310, периодические по/ и в,
могут быть построены из элементарных волн вида
Постоянная распространения h, вообще говоря, комплексна: следовательно,
поле не обязательно периодично вдоль оси г. Явное выражение для h
в функции частоты о и констант среды можно получить, лишь задавая
поведение ^ на цилиндрической поверхности г = const, или в плоскости 2" = const.
6.6. Свойства функций Zp(p). Предполагая знакомство читателя с
теорией уравнения Бесселя, полезно всё же дать для справок обзор важнейших
свойств решений этого уравнения.
Если в уравнении D) заменить независимую переменную на р = Y^^—^^'■»
то мы получим, что Zp{p) удовлетворяет уравнению
которое характеризуется регулярной особенностью при р = 0 и
существенной особенностью при p=co. Бесселевой функцией ^ (р) или
цилиндрической функцией первого рода называется частное решение G), конечное при
р = 0. Оно может быть, таким образом, разложено в ряд по возрастающим
степеням р, а так как в плоскости комплексного переменного р нет других
особенностей, кроме точек р = 0 и р = оо, то этот ряд сходится, очевидно,
для всех конечных значений аргумента. Для любого р, действительного или
комплексного, и для действительн1,1х или комплексных р имеет место
разложение
со
Если заменить в G) р на —/?, то уравнение остаётся неизменным;
следовательно, при нецелых р второе фундаментальное решение можно получить
из (8), заменяя р на —р. Но если р==п является целым числом, то Jp(p)
становится однозначной функцией точки. Гамма-функция Т{п-^т~\-1)
заменяется факториалом (n-f-wt)!, так что
'^(Р)==Е„,\„;^)|Ш (« = 0,1.2....). (9)
Функция У-п(р) У^^ ^^^ является независимой от (9), а связана с ней
соотношением
i-«(p) = (-l)"^(p). A0)
так что для нахождения второго решения следует прибегнуть к какому-либо
зшому методу.
Функция Бесселя второго рода определяется соотношением
316 " гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
Это решение уравнения G) является независимым от Jp(p) для всех
значений р, но правая часть принимает неопределённый вид О/О при целых /?..
Однако значение её можно подсчитать обычным способом, дифференцируя;
числитель и знаменатель по /7 и переходя затем к пределу при /?->«.
Получающееся разложение довольно сложно ^); мы приведём лишь первый член,,
годный в окрестности начала отсчёта:
Л^о(Р)=^-^1п|, N„(p)c^ ~^'^' A)" («=1.2.---), A2>
где 7=1,78107 и | р | <С^ t. Характерным свойством функций второго рода,
является наличие особенности в начале координат. Ввиду того что они
обращаются в бесконечность при р = О, они не могут быть применены длж
представления полей, которые по своему физическому смыслу конечны
в окрестности р = 0.
Дальнейшие сведения о характере функций Jp (р) и Л^^ (р) даёт изучение;
их поведения при очень больших значениях^. Разложения в окрестности
начала координат сходятся для всех конечных значений р; Ур(р) и Л^(р)'
являются всюду аналитическими функциями /? и р, кроме точек р = О и.
р=схэ. Однако для очень больших р ряды сходятся на'столько медленно,
что становятся бесполезными для практических вычислений, и здесь
пользуются поэтому представлениями этих же функций в виде рядов по
обратным степеням р. Действительно, можно показать, что уравнение Бессел»
формально удовлетвсгряется разложениями
Jpi9)= -]f Тр [^„(P)C0S9—Q^p)sin9], A3)
A^^P)=V^~[^i6(p)sin? + Q^(p)cos9], A4>
p Го->-1 Dp'-l)Dp^-9)' ,
^p^9)—^ ■ 2! (8p)s ' г
О rn^-i£izil Dp^-l)Dp^-9)DjP^-25) , ' '
Qp^} 8^ ■ зущз—: +•••' (i6>
где фазовый угол о даётся выражением
f=9-{p\+{)l. an
Оказывается, однако, что эти ряды расходятся для всех значений р и»,
следовательно, не имеют в точности аналитических свойств тех функций^
которые они должны были бы представлять. С другой стороны, при
больших р первые члены быстро уменьшаются по величине, и в этом смысле
ряды являются «полусходящимися». Можно показать, что если прервать
разложения вблизи члена, где последующие члены начинают расти, или,
перед этим членом, то разложения дают приближённое значение функции,
причём можно оценить получающуюся ошибку. Чем больше р, тем ближе
значение суммы нескольких первых членов к истинному значению функции.
Поэтому такие представления называются асимптотическими.
1) См. Wats on,. А Treatise on the Theory of Bessel Functions, гл. Ill, Cambridge-
University Press, 1922, и Janke —Emde, Tables of Functions, стр. 198, Teiibner, 1933^
ВОЛНОВЫЕ ФУНКЦИИ КРУГОВОГО ЦИЛИНДРА [6.61 317
Отметим, что при достаточно больших р
; V(P)^l/"f cos(p-i£±lr) A8)
__ jpl>>i, Ip1»'IpI.
iV^(p)c^|/"lsin(p-^£±i^). A9)
"Ha очень больших расстояниях от начала координат цилиндрические функции
первого и второго рода относятся друг к другу как косинус и синус,
«о затухают с ростом р благодаря множителю l/l/ip". Эти функции удобны
для представления стоячах цилиндрических волн.
По аналогии с показательными функциями можно построить линейную
комбинацию решений Jp(p) и Nj^(p), дающую функции, связанные с бегу'
щами волнами. Бесселевы функции третьего рода, или, как их чаще
называют, функции Ганкеля определяются соотношениями
H^i\9) = Jp(9)-\-iN^i9\ B0)
f^49)=M9) — i^p(9)- B1)
Из предыдущих формул легко найти, что для рчень больших р
H?(9)^}/'Je'^'~^^'\ B2)
7'2).
1р1»1, \9\:>\р1
2p + Ti
/ / * "Р -Г^ \
H;'if)^/le-'('—^'>. :B3)
К разложениям самих функций в ряд мы добавим для справок
некоторые наиболее важные рекуррентные формулы:
^р-1 ~Т~ ^р+1 ^^ "У ^р' ^24)
-^ = -^Z,_,-lz,,, B5)
-^1Р^^ЛрI = Р^^р-1' B?)
-^IpPZ^p)l=-p-^Zp^i- B7)
6.6. Поле круговых цилиндрических волновых функций. Внутри
однородной изотропной области любое электромагнитное поле может быть пред-
<:тавлено линейной комбинацией элементарных волновых функций
^пш == е^Чп (/^2ir^'V)e ± ^'^^-*-*, B8)
^^^^ = ein^li^ {yWZTi^r) е± ibz-ш^ B9)
Для конечных областей, включающих ось г = 0, применимы лишь функции
{28); на больших расстояниях от источника должны применяться функции
<29), так как они асимптотически переходят, согласно B2), в радиально
расходящуюся волну. Каждая элементарная волна определяется тройкой
параметров п, й, Л. При ^ = 0 поле симметрично вокруг оси; при h=s.Q
распространение происходит лишь в радиальном направлении, и поле является
строго двумерным. Можно сказать, что функции вида B8) и B9)
представляют неоднородные плоские волны. Плоскости постоянной фазы
распространяются вдоль оси Z со скоростью, V = ш/а, где а — действительная
318
гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
часть й, но амплитуды в этих плоскостях являются функциями г и Ь. Таки&
волны могут создаваться лишь источниками, находящимися на конечных
расстояниях от начала координат или же в средах с разрывами непрерывности.
Плоские волны, изученные в предыдущей главе, однородны в строгом смысле
слова, так как плоскости постоянной фазы являются также плоскостями
постоянной амплитуды. Они могут существовать лишь в бесконечных
однородных средах при бесконечно удалённых источниках возбуждения.
Из формул, выведенных в разделе 6.3, можно выразить импедансы и
компоненты векторов поля через волновую функцию ^:
7^1) _
Ы
U У/г2
/fe2
h^}r
yd) _ _H m^h
Z^z ' ' to •
/fe2
C0)
Er — — ^''^ ^ '
ap
c-d) _4_ ih дФ
;A)
Er = {k^
tB^ = 0.
/Z2L-, C1>
C2)
Подобным же образом, для поперечного электрического поля
dZni?)
а)[х
Vh^-k^^ Z,,(P)
Hr^ = ±iih
k^ — h^ г '
4^) = ±^;:. C3>
Ef' = 0, ■ C4>
Я?^ = (A;2 —/z2N. C5)
Если заданы начальные условия на некот1эрой плоскости или
цилиндрической поверхности, то решение образуется суперпозицией элементарных
волновых функций. Для фиксированных значений ш (или k) и /г для
результирующего поля получаются в цилиндрических координатах следующие
выражения:
Е^ = ih
1
а.
д<Ь.
О0
\
п
П ^г
~ ^ пЬп'^п^
п-
-оо
do
П = —00
оо
п
п = —со
^й = —7" 24 "^«'К —':-^"> 2л ^'^'Т?
п= ~<х>
оо
АЗ 1
\т
п = —со
C6>
« = — со JJ. = — 00
оо со
дг
Н,=
П — —оо
п= —оо
оо
H,={k^~h^) 2 К'^п,
п = —00
C7>
где «„ и Ьп—коэффициенты, определяемые из начальных условий.
Направление распространения положительно или отрицательно в зависимости от знака h^
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ ВОЛНОВЫХ ФУНКЦИЙ [6.71
319^
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ ВОЛНОВЫХ ФУНКЦИИ
6.7. Построение из плоских волн. Если С измеряет расстояние вдоль
произвольной оси, направление которой по отношению к фиксированной
системе отсчёта (л;, у, z) определяется единичным вектором п, то, согласно
разделам 5.1—5.6, простейший тип плоской волны можно представить
функцией
В которой постоянные Л и ш могут быть и
действительны и комплексны. Пусть
R—радиус-вектор, проведённый из начала координат в точку
наблюдения, прямоугольные координаты
которой лг, у^ Z. Тогда фаза волновой функции
в данный момент времени измеряется величиной
Е: = пН=я^-}-й^,_У-}-я^. B)
, Направляющие косинусы п^, Пу, п^ вектора п
удобнее выразить через полярные углы аир,
показанные на рис. 66:
Пд, = sin а cos р, Пу = sin а sin р, п^ = cos а, C)
Рис 66. Фаза элементарной;
плоской волны измеряется
вдоль оси С, направление
которой определяется
единичным вектором п. Точка
наблюдения имеет радиус-
вектор R.
откуда
ф = е^^ С^з ^'° " ^^^ Р+2/ sin а sin р+г cos a)-iiot^ /4")
Меняя параметры аир, можно придать оси
распространения любое направление. Каждому
направлению распространения сопоставляется амплитуда
^(а, Р), зависящая только от углов а и р. Так как уравнения поля в
рассматриваемом случае линейны, решение можно построить путём
суперпозиции плоских волн одной и той же частоты, но с различными направлениями
распространения и с соответствующими амплитудами ^):
6 {х,у, Z, t) = e-i^^t { da { d^gia, p) e*^' i^^^^ «'^'^^ ?+2/ ^m asinp+'. cos «j_ E^
Если углы действительны, то а изменяется в пределах от О до тг, а р от
О до 2т:. Такое решение с математической точки зрения отнюдь не является
самым общим, так как E) удовлетворяет волновому уравнению как при
действительных, так и при комплексных значениях параметров а и р, и
мы скоро обнаружим, что комплексные углы действительно должны быть
включены в рассмотрение, если мы хотим представить таким интегралом
любое поле.
При действительном ш волновая функция, определяемая равенством E),
является гармонической во времени. Для представления поля, которое на
определённой координатной поверхности изменяется со временем более
сложным образом, необходимо просуммировать или проинтегрировать E) по
параметру ш. Определим векторную постоянную распространения как
к = ^п, прямоугольные компоненты которой равны ,
k^ = k sin а cos р, k2 = k sin а sin р, k.^ = k cos a.
F).
^) Общая теория этаких решений волнового уравнения изложена в книге
Е. Т. Уиттекер и Г. Н. Ватсон, Курс соврел1енного анализа, Л. — М., ГТТИ,..
ШЗ, гл; XVIII.
•320 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
так что элементарная плоская волновая функция может быть записана в виде
^_,gikR-»:to#^ G)
Внося G) в волновое уравнение
мы находим, что компоненты к должны удовлетворять единственному
соотношению
kl-\- k-j-}- ks=^ {ASOD^ -j- /{JLOO) = k^, (9)
a в остальном совершенно произвольны. Таким образом, из параметров k^,
^2> ^3» '^ можно выбрать произвольно любые три параметра, после чего
'Четвёртый определится равенством (9). ^^
Предположим, что на плоскости z = 0 функция ^ задана:
^^^ix.y, 0,t)=f(^x,y;t).
Искомое решение будет
6 (х, у, 2, t) =
оо оо оо
—оо —оо —оо
S
где ki, k^ и (О—действительные переменные, ^а k^ — комплексная величина,
определяемая соотношением
к^=^-иа\г-[-1^ш—k{—k^i. A1)
Амплитудная функция g{k^^ ^2> ^) такова, что
со оо оо *
fipc,y,t) = {£fi J J ]g{k,,k^,,^)eHKv^^i'*y-^t)dk,dk^d^. A2)
— оо —оо -S-oo
Если /(л:, у, t) и её первые производные кусочно непрерывны и абсолютно
интегрируемы, то g{k^^ k^, ш) является представлением Фурье функции
J{x,y^ t) и равна
оо оо оо
3
§(A;i, А;2, ш) = A)т J J j f(x, у, t)e-i И'^^+^'^у^*) dx dy dt A3)
—oo —oo —oo
При 3 = 0 каждая гармоническая компонента распространяется вдоль оси z
х:о скоростью "О = (»/;feg, но так как к^^=у ш'''{Ае — k\ — k^ не является
линейной комбинацией ш, ki и ftg, то начальное возмущение /(л:, у^ О» очевидно,
не будет распространяться без искажения формы даже в отсутствие дисси-
пативного члена. Точнее говоря, общего решения уравнения (8) вида
../ЫуУ,^ ) не существует.1
ИНТЕГРАЛЬНЫЙ П^едСГАЕкЛ^НЙЙ бОЛНОёыХ ФУНКЦИЙ [6.8] '3^1
Равным образом можно было бы задать функцик) ^ (х, у, z, t) во
всём пространстве в начальный момент времени tt=0. Пусть, например,
*^(х,у, Z, 0) = f(x, у, z). Поле представляется в виде тройного интеграла
оо оо со
—ся —с» —оо
% котором k^y k^ k^—действительные переменные, а ш — комплексна^'
величина, определяемая из (9):
m=:^b-±LiYo^{iA-{-^i-\-k^—b^, A5)
где а==1/|Л{Ае, b =^о\Чг (см. стр. 264). Амплитудная или весовая функция
^(^1, ^2. ^з) такова, что
оо оо оо-
/ (X, у, Z) = (~р j j j g{k„ Й2, k^) ei (*i»+A^+A-,.) dk, dk^ dk^. A6)
-c» —oo —00
Если /(jc, _y, z) обладает необходимыми аналитическими свойствами,
^о представление Фурье существует и имеет вид
_ оо оо оо
3
^(^1,А;2,А;з)==(~)з-J J ^f{x,y,z)e-^0^-^-^J<^y^i^^-)dxdydz. A7)
-оо —с» —-оо
Мы рассматривали в предыдущих разделах только положительные или
расходящиеся волны, а начальные условия налагались только на самую
функцию ^. Если определённые условия налагаются как на функцию <|<, так
« на её проиаводную^ по одному из четырёх аргументов, необходимо
включить в рассмотрение и положительные и отрицательные волны в
<:оответствии с методами, описанными для одномерного случая в разделах
,5.8, 5.9 и 5.10.
6.8. Интегральные представления функций Z„(p). В произвольной
системе цилиндрических координат а^ и^, z волновому уравнению F),
»стр. 310, удовлетворяет ■ функция
^iL = /(ai, u'^)]eihz-^t^ A8)
где h и о»—действительные или комплексные постоянные. В обозначениях
предыдущего параграфа А =-^3 = Л cos а, а так как ^ == |Л{Аеш*-}-'Р-^о»» то
угол а, образованный направлением составляющих плоских волн с осью z,
также постоянен. Другими словами, элементарная цилиндрическая волна A8)
может быть разложена на однородные плоские волны, направления
которых образуют круговой конус вокруг оси z, но угол раствора конуса
в общем случае комплексный:
fiu\ и^) = ( g(^) е^^ *>'" « («""^ ^+У **" ^) </р, A9)
где хну следует выразить через цилиндрические координаты и^ и м^.
В системе координат кругового цилиндра мы имеем x=,rcqsb,
y = rsmb, откуда .,. ,
iccos р-h 3^ sin purees F ^^р). B0)
21 -Зак. Иа. Т«ортя влеврромагнетизма.
322 гл» VI. ЦИЛИНДРИЧЕСКИЕ волны
в обозначениях предыдущего параграфа мы получаем далее
krsina = rYk^~fi^=p, B1)
так что
/(г, 6) = j gi^)e^P «=«« (fi-P) dp. B2)
Заменим теперь в B2) переменную интегрирования |3 на 9 = ? — ^ ^
заметим, что так как переменные в уравнении для /(г, 6) разделяются, то
^(cp-f-6) можно представить как произведение двух функций, каждая из
которых зависит лишь от одной переменно^:
^(Р)=^(? 4-6) = ^! (9)^2F); B3)
следовательно,
/(Л 6) =/1 (ОЛ @) = g2F) г ^1 (?) ^'^ -^"^ "^ ^?. B4)
Угловая функция g2{b) должна быть, очевидно, некоторой линейной
комбинацией показательных функций е*Р^ и e-fi'^, а амплитудный или весовой
множитель ^j (ср), должен быть выбран так, чтобы радиальная функция/^ (г)
удовлетворяла уравнению D), стр. 314, которое при аргументе р имеет вид
Подставим в B5) интеграл
* /i(p) = /^i(?)^^P"^'Pcf?. B6)
Дифференцируя под знаком ин/еграла, получим
^ = Г / cos w ^1 (и) е*Р"' "Р й?9. f^^ = — f c°s^ '■? ^1 (?) ^^'^ ''''^ "^ ^?J B^)
следовательно, согласно B5),
Г (р2 sin^ 6 -4- /р cos 9—/2) ^^ (<р) е*> «^«'^ -f йГсг = 0. B8)
Это уравнение мы преобразуем далее интегрированием по частям.
Уравнение B8), очевидно, эквивалентно такому:
[gi (?) "-^2 h Я^^1 (?) ^'^ ^""^ J d? == 0. B9)
Е^ли Р и Q — две функции от ср, то
что ь применении.к B9) даёт
Первый из этих двух интегралов может быть обращен в нуль, если
выбрать контур интегрирования Так, чтобы выражение под знаком
производной имело одно и то )ке значение в начальной и конечной точках; второй
интеграл обращается в нуль, если подинтегральное выражение равно нулю.
ИНТЕГРАЛЬНЫЕ ИРЕДСТАбЛ^ВИЯ волновых ФУНКЦИЙ 16.81 32;^
СлеАобательно, B6) является решением урабнения Бессиля, если gi^o) удо-
йле-ГёЬря'ет ура Биению
'^'f + P^^l-O, ' ' : C2)
а путь интегрирования таков, что
Уравнению C2), очевидно, удовлетворяет функция e^Pf, Однако, как мы
увидим, для того, чтобы /j (р) была тождественна с цилиндрической
функцией Zja(p>, определённой в ^разделе 6.5, следует добавить постоянный мно-
_ . л
1 —гр —
житель — е 2. Таким образом, полагая
. 1 ipU—^)
C4)
мы получим интегральное представление цилиндрических функций по Зоммер-
фе^ьду 1):
' Zp (Р) = -^-^^— J е^ ^Р '"'^ * +-^*^ йГс?, C5)
с
где контур С таков, что
(р sin о ~\~ р) е* (Р *^os <?+/"?> I = О* C6)
Различие между р^^зными. частными решениями Jj,(p), Л^(р), ^j,(p)
сведено теперь к различию в контурах интегрирования в плоскости комплекс^
ного переменного о* Рассмотрим сначала самый элементарный случай, когда
/7 = п является целым числом. Тогда очевидно, что если интегрирование
производится по действительной оси с? от —ir до -|-7г или по любому
другому отрезку длины 2-^, то условие C6) выполняется, и определённый
интеграл
Jfi (Р) = -^ J ^^^ """^ '^"^*"* ^'-Р ^37>
являете^ решением уравнения Бесселя. В том, что функция, определённая
рабёвством C7), действительно тождественна с частным решением (9), стр. 315^
Можно убедиться, разлагая е*Р «°^ ^ в ряд в окрестности точки р = О и инте-^
грйруя этот ряд почленно.
В общем случае, когда р не является целым числом, или же для
получений Другого нёз!авйсимого решения, для' того чтобы C6) обращалось в нуль
в койечных точках, перееденной о следует приписать комплексные значения..
Пусть ю i= Y-j-гтг]. Тогда
гр coi^o -|- ipo :^ р sin 7 sh 7) — pvj 4~ Ф cos 7 ch yj -]- ip-^^ C8)
Если p комплексно^ то мы положим р = а-\-1Ь^ где а—существенно поло-
>кйтельная величине Тогда подходящим выбором т и iQ «ожно сделать
действительную часть C8) бесконечно большой Отрицательной величиной^ а при
этШ ехр (/р cos а> -\- ipo) ^-» 0. Это условие выполняется, например^ если поло-
1) Stimmeffeld, Math. Ann. 47, 335, 1896.
S24
гл. VI. ЦИЛИНДРИЧЕСКИЕ ВОЛНЫ
жить t}-*.-|-oo, а для f принять значения —-^/2 или -f-311/2; но эта
показательная функция обращается в нуль также и при iq -> —г оо, если только
If = -{-«/2. Для того чтобы C5) представляло решение уравнения Бесселя,
необходимо лишь, чтобы контур С соединял любые две из этих точек.
Зоммерфельд выбрал в качестве пары фундаментальных решений два
«нтеграла
/йЧр)=
•ipl
к
J
g*P COS 9+грв ^^
C9)
—+4O0
COS «p + ijB?
rf«.
D0)
-y—*CX)
Контур Cj, no которому берётся интеграл C9), начинается в y] = оо, ^ = —it/2,
пересекает действительную и мнимую оси при <э = О и заканчивается при
'»)=—оо, Y=f|-«/2. Контур Сд, по
которому берётся интеграл D0),
начинается в конечной точке контура Cj,
пересекает действительную ось при
•^ = 7: и заканчивается в '») = оо,
1[' = 3it/2. Оба контура показаны на
рис. 67. Точка пересечения с
действительной осью, конечно, несущественна
для определения ^унющй. Контуры
можно деформировать произвольным
обрдзом, лишь бы только они
начинались в бескойечно удалённой
центральной точке одной заштрихованной
области и заканчивались в
соответствующей точке другой
заштрихованной области.
Преимущества проведения Cj и
Сз через точки -у = О и т = 'с
действительной оси становятся очевидными
при вычислении интегралов C9) и D0)
для очень больших значений р. Если действительная часть р очень велика,
то множитель ехр (/р cos а>) становится исчезающе малым во всех точках
заштрихованных областей на рис. 67, кроме ближайшей окрестности точек
тг] = О, Y == О» — '^» ~ 27Г, ... В этих точках действительная часть /р cps <р,
согласно C8), равна нулю, как бы ни было велико р; следовательно, если
Ci и Сд проведены, как показано на рис. 67, то полная величина контурного
$1нтеграла определяется значением интеграла, взятого лишь в окрестности
начала координат и точки ^)=0, "{ = 7:. Из заштрихованной области, в
которой значения подинтегральной функции исчезающе малы, контур С^ проходит
через крутой «перевал» или «седлообразную точку», где подинтегральная
функция велика, а затем переходит на другую заштрихованную плоскость,
где функция резко убывает, и значение интеграла по этой области опять
пренебрежимо мало. Контур Cg имеет подобную же седлообразную точку
при t) = 0, -{ = т:. Чтобы свести интегрирование к возможно более корот-
Рис. 67. Контуры интегрирования для
цилиндрических функций.
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛШ1ИЯ бОЛИОВЫК ФУНКЦИЙ 1в.9] 325>
кому отрезку контура, нужно приближаться к перевалу по линии с наиболее-
крутым' подъёмом, а спускаться с «вершины» в «долину:» по линии с
наиболее крутым спуском. В данном случае это означает, что контуры Cj и Сд.
должны пересекать ось под углом в 45°* Дебай *) использовал поведение
интегралов C9) и D0) в окрестности седлообразных точек для вычисления,
асимптотических разложений функций щ^{р) и Н^\р). При р, очень
больших по сравнению с единицей и с порядком р, получаются соотношения
B2) и B3), стр. 317, что показывает тождественность интегралов C9) и D0)
с функциями Ганкеля, определёнными в разделе 6.5. Дебай рассмотрела
также случай, когда р больше аргумента р; его результаты были
улучшены и расширены позднейшими исследованиями.
Представление /р(р) при нецелом р в виде контурного интеграла
следует непосредственно из соотношения
^1,(р)=у[4'Чр)+4'ЧрI, D1>
откуда
п
Jp (Р) = ^^ [ «*Р «^"^?+*i"p drp. D2Х
а
3
Контур Cg, показанный на рис, 67, представляет собой допустимую
деформацию контура Ci-j-Cg.
6.9. Интегралы Фурье-Бесселя. Мы показали, как выводятся из
скалярной функции ^ в цилиндрических координатах два основных типа
электромагнитного поля. Если цилиндрические координаты являются круговыми,
то 4» получается, в общем случае, суперпозицией элементарных волн типа
частных решений B8) и B9), стр. 317. Наша задача заключается теперь,
в следующем: заданы значения ^(г, 6, 2-, t) в момент /=0 в плоскости z=0'^
требуется найти if для всех других значений z и t.
Предположим, что при t = z = 0 функция 4»=/(г, 6). Будем считать.
/ (г, Ь) ограниченной и однозначной функцией переменных, кусочно
непрерывной вместе со своими первыми производными. Тогда /(г, 6) должна быть
периодической по 6 и может быть разложена в ряд Фурье, коэффициенты,
которого являются функциями только от г:
2я
/{г,Ц^^ f„{r)einb, fnir)==±ffir,b)e-inbdb. D3>
п = —-оо
Если /(г, 6) стремится к нулю при г-^ со так, что обеспечивается сходи-
со
мость интегралов Г|/п ('")! V^'"^'"» то каждый коэффициент/„ (/•) может быть.
о
представлен видоизменённым интегралом Фурье 2).
Рассмотрим функцию f{x,y) двух переменных, допускающую
интегральное представление Фурье
~оо —со
*) Debye, Math. Ann. 67, 535, 1909, см. также Watson, loc. cit., стр. 235'
и след.
?) Интеграл Фурье-Бесселя выводится более строгими методами в гл. XlV мнигик
W а t S о п'а, Bessel Functions.
326 гл. VI. ЦИЛИНДРИЧЕСКИ* волны
■ ) 111
Совершим теперь преобразование к полярном координатам как в коорди.-
натном пространстве, так и в ^-пространстре:
X r=rcos8, J/ = г sin 6, I
ki = kcos^, ^2=^sinp, J ■
так что в обозначениях предыдущих параграфов >. ^=/г sin а = ]//г*-* — h^.
Тогда kiX-\-k2y=krcos{^ — 6), и D4) как объёмный интеграл в А-про*
странстве принимает вид:
2IE
f{r, б) = ^ J А dk J d^ g{k, 8) e«»-«°« (Р-в). ^ D6)
0 0
Легко раскрыть физический смысл этого ггредставлрния. Функция
ехр [ikr cos (^ — 6) — Ш] представляет србой плоскую волну с постоянной
распространения X, бегущую в направлении, перпендикулярном к оси\г и
составляющем угол р с осью х. Каждая плоская волна зпиножена на
амплитудный множитель g{k, Р); затем волны просуммированы вначале по [3
от О до 211, а затем по постоянной распространения или пространственной
частоте к.
Представление Фурье функции /{х^у) имеет вид
оо оо
^(^1. -^2) = ^ J J f{^> П) е-' ^^'■''''^ dUr,, D7)
—оо —оо
что при переходе к полярным 1^оордйнатам i == р cos jx, y) = р sin ji. даёт
со 2к •
g{K Р) = -^ / Р^Р / ^Н-/(Р, V) е-''^ ^'^ ^^-i^>. D8)
о о ■
Наконец, допустим, что f{r,b)=f^{r)e^^. Тогда
оо ' 2iE
g{K Р) = ^ |рйГр/„(р) J^e-f?'=-(P-i-)+^E.^ D9)
о о
что после замены переменной о = ^' — Р—тс даст
. ff(X.P) = /"(^ + '")//„(p)J„(^prfp=?„W/"^'+-^"^ E0)
О
Подобным же образом D6) принимает вид:
оо 2л / 3 \
fir, e)=/.(r)^.. = i J ЛЛг„(Х)/^рЛ"°"'-^'+*"('+^ E1)
о о,
или, если положить ^=.р — 9:
оз.
/„ (г) e"»s = е'«9 J g^ (I) j^ Q,r) к dk, E2)
ИНТЕГРАЛЬНЙЕ ПРЕДСТАВЛЕНИЯ ВОЛНОВЫХ ФУНКЦИЙ [6.10] 3^7
Таким образом мы получаем пару представлений Фурье-Бесселя:
оо
fn in = jgn (^) Jn (Л'^ Л dk, E3)
о
оо
gn (^) = J/« (Р) Jn (^9) Р ^Р- E4)
о
Функция
со
со _
.^^е^ш 2 e*»9j ^,Дл)У„(лг)е±*^'«*->'2л^/л E5)
Я»=—со
является решением волнового уравнения в круговых цилиндрических
координатах, которое при t = О переходит в /(г, 6) на плоскости г ~ 0. Но это,
очевидно, не самое общее решение, удовлетворяющее этим условиям, так
как в нашем распоряжении остаются ещё два параметра ш и ^, на которых
наложено только одно условие А^ = {^.еш^-|-гз{хш. При действительных ш
можно суперпозицией гармонических волновых функций типа E5)
представить произвольный закон изменения 4* во времени в плоскости z = 0. Если
рассматривать как положительные, так и отрицательные волны, то можно
задать при z=0 значения как 6, так и -j-. Рассмотрение подобных задач
было дано в главе V.
6.10. Представление плоской волны. Теорема Фурье-Бесселя даёт очень
простой способ представления элементарной плоской волны через
цилиндрические волновые функции. Пусть волна с постоянной распространения k
бежит в направлении, определяемом единичным вектором п, сферические
полярные углы которого относительно фиксированной системы отсчёта равны
« и р, как показано на рис. 66, стр. 319. Тогда
ф ;^:; gik sin о£ (аз cos ^+у sin ^) , ^гкг cos а-гш# E6)
« наша задача сводится к представлению функции
f(x v) = ^*^ ^'" " ^* ^^^ ^"^^ ^'" Р^ = 6'^^ ^'° " ^^^ (?"•') E7^
а виде ряда
оо
f(r,b)= 2 fn(r)ein\ E8)
n=—со
Согласно D3), мы имеем
/^ (^r) = ~^j е»*»-^i" «^ 003 {?-6) -гпь а^^ E9)
о
Заменой р — 6 на о это переходит в
/п (г) = е'' (^ "" ^) 4 (kr sin а), F0)
и мы получаем полезное разложение
оо
«соз(?-9)==, 2 r4(^rsina)e*«(?-9). F1)
,гкг siti
Некоторые другие хорошо известные ряды являются прямыми следствиями
Зтого разложения. Так, если мы положим р = Аг sin а, а 6—р = <р — -к-» то
328 гл. VI.. ЦИЛИНДРИЧ]ЕСКИЕ ВОЛНЬГ
соотношение F1) примет вид
со
gipsinrf^ 2 J„(p)e*'*^ F2>
п*=—со
что после разделения на действительную й мнимую части даёт
аз
COS (р Sin 9)= 2 Лг(Р)С08П9,
п = —со
со I
• sin(psinc))= 2 i«(p)sin«cp' j
«= —со J
ТЕОРЕМА СЛОЖЕНИЯ ДЛЯ КРУГОВЫХ ЦИЛИНДРИЧЕСКИХ ВОЛН
' 6.11. Из формул предыдущего раздела можно вывести ряд важных
соотношений, относящихся к переносу оси распространения параллельно самой
себе. На рис. 68 О и О^ означают
начала координат двух прямоугольных систем
- отсчёта. Плоскость чертежа совпадает
'^/ '' \~ ^ с плоскостью ху обеих систем, а оси Xi^
-^~ —^ ^^^ ^^^ проходящие через Oj, параллельны
'Ъ) ' ' ' соответственным осям х, у^ г. Функции
Л»(^1)е*"^Ь умноженная на exp(rt:f/i2'i—ш^)^^
О ' "^' представляет элементарную цилиндрическую-
Рис. 68. Перенос системы отсчёта, волну, отнесённую к оси z^. Мы хотим
выразить эту цилиндрическую волну в виде
суммы цилиндрических волновых функций, отнесённых к параллельной ос»
2г, проходящей через О.
Напишем сначала
1 г г>''1 cos с + т (и + в, )
—к
Из чертежа ясно, что 6^ = 6 -р 'т' ^
Tj cos *Ь = Ti cos Fj — 6) = г — Гд cos F — бд),
rj sin 6 =
riC0sFi — 6) = г—rocosF — вд), I
Tj sin Fi — 6) = Го sin F — Oo). J
B>
Кроме того, в силу периодичности подйнтегрального выражения, A)
эквивалентно
Из B) следует, что
г^ cos (9 — '!') = '■ cos © — Гд cos (9 -4- 0 ■>_ 9q), D)»
откуда
I f Arcosffi—гХгоС08{ф+в—8в)-!-г«1ср+в—-)
Согласно F1), стр. 327,
' ^^.'^'^ • CO
гтк
in "—oo
ТЕОРЕМА СЛОЖЕНИЯ^ для КРУГОВЫХ; ЦИЛИНДРИЧ]@СКИХ ВОЛН [6.11] 329^
В силу равномерной сходимости можно изменить порядок суммированияк
и интегрирования:
— ТС
оо
т =—со
Щвв оо
При замене 6j на б-J-'l' это выражение принимает вид
се
т = —00
Аналогичное разложение для волновой функции Н1Р (\г^) е^^^ можно получить-
из интеграла
//f (Хг,) .*"* = i J Л^ "'^^ ^'^-*^+'^* (^- ?) ^9,
(9)
где Ci — контур, изображённый на рис. 67, стр. 324, со сдвигом на величину <^'
вдоль действительной оси, обеспечивающим обращение показательной
функции в нуль в конечных точках. Заменяя экспонент по B), находим, что
При I г 1 > \г^ COS F — 6q) I можно, действуя совершенно аналогично^,
притти к выражению
При Го==0 оба центра совпадают; Jm(P) = 0 для всех значений /и, кроме-
нуля, а Уо @) = 1 • ^^ол «J* равен нулю, и правая и левая части равенства A1),,
очевидно, тождественны. В справедливости разложения можно убедиться
также при очень больших г и г^, так как в этом случае функции Ганкеля
можно заменить их асимптотическим представлением B2), стр. 317. Угол 6-
равен приблизительно нулю, и г^с^г — TqCos (8 — бд). Амплитудный
множитель "|/^2/т:г1 можно без заметной ошибки заменить на У 2/т:г, но член,-
ГоС08F — бд) в фазе следует оставить. Тогда A1) принимает вид
т = —оо
а правая часть A2) в свою очередь является, согласно F1), стр. 327,
точным разложением плоской волны, стоящей в левой части. В самом деле,
при неограниченно возрастающем г^ расходящаяся цилиндрическая волновая:^
функция, определяемая (И), должна асимптотически переходить в плоскую^
волну.
При |г|<|ГоС08F — 6о)| разложение (И) не сходится и заменяется,
разложением
ЯП^О^*"^- 2 H'SQ^o)Jn+mi^r)^^^'\ A3>.
т = —со
330 гл. VI, ЦИЛИНДРИЧЕСКИЕ волны
которое конечно при 7- = О, В этой точке Jn+mi^^) равна нулю, кроме
т = — п. Кроме того; 4- = - + ^о — ^ «» так как И%(р) = е'^'Н^^(р),. то,
очевидно, правая и левая части равенства A3) тождественны. В другом
предельном случае очень больших Гд мы полагаем г^==г^ — г cos F—9q)
м с помощью асимптотических представлений функций Ганкеля находим, что
A3) стремится к
т — —со
Т. е. К плоской волне, распространяющейся от О^ к О вдоль линии,
соединяющей эти два центра.
ВОЛНОВЫЕ ФУНКЦИИ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
6.12. Элементарные волны. Круговые цилиндрические функции являются,
по существу, вырожденной формой эллиптических волновых функций,
получаемой при приравнивании эксцентриситета.цилиндров нулю. В
эллиптических координатах исследование поля и свойств функций должно неизб(ежно
оказаться сложнее, чем в круговых координатах, но зато и результаты
значительно более интересны.
Согласно 3, стр. 57, полагаем
ttl=e, tt2 = t],- $>1, —1<YJ<1, A)
'^i = ^0/"IEt . ^2 = ^о1Лгз|- B)
Внося это в (8), стр. 310, находим, что f{l, у\) должно удовлетворять
уравнению
-\-cl(k^-h^)(^—t)f^O. C)
Это уравнение в свою очередь легко разделяется, если положить/=/1 Qi)f2{y^*
что даёт:
^l-'^'>^+'^^ + ^^-^o(*^-'^^)'l'JA = 0, E)
где b — произвольная постоянная разделения. Таким образом, Д ($) и/gC^j)
удовлетворяют одному и тому же дифференциальному уравнению.
Уравнения D) и E) являются частными случаями соответствующего уравнения
Матьё 1)
■ {\—z^)'w" — '2{a-\-\)zw'-\-{b~c''Z^)w=^Q, F)
которые получаются, если положить параметр а = ^. Эти уравнения
характеризуются нерегулярной особенностью в бесконечности и регулярными
особенностями при z=-±i\. При ^"^1 D) переходит в уравнение Бесселя.
Существенного упрощения D) и E) можно достичь заменой
независимых переменных. Пусть
^ = chtt, 'Г) = со81', G)
^) Е. Т. У и т т е к е р и Г. Н. В а т с о н, 1ос. cit., главы X. и XIX; I п с е. Ordinary
Differential Equations, глава XX, Longmans, 1927.
I-'
ВОЛНОВЫЕ ФУНКЦИИ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА 16.151 . 331
так что преобразование к прямоугольным координатам выражается
уравнениями'
д/ = Cq chtt cos V, У =^0 s^" sin v. (8)
Тогда вместо D) и E) получаем
^^(cll^ch^u-b)A = 0, (9)
^ + (.b-clk^cos^v)U^ = Q, A0)
где, как и в предыдущих разделах 'h=yk^ — h^. Расстояние между
фокусами на оси л: (рис. 9) равно 2Cq, а эксцентриситет конфокальных эллипсов
e = ljchu. Переход к случаю круговых координат получается в пределе при
€q->0. и tt->oo. Тогда Ср ch «-> Cq sh-tt-> г, а v является, очевидно, углом
между радиусом г и осью х. По этой причине мы будем называть /^ (и)
радиальной, функцией, а f^(p)—угловой функцией. При « = О
эксцентриситет равен единице, и эллипс вырождается в отрезок прямой длины 2Cq,
соединяющей фокусы на оси л:.
Уравнения Матьё (9) и A0) изучались многими авторами. Рассмотрим
сначала угловую, функцию /2('о). Решения уравнения (Ю) имеются, конечно,
при любом значении постоянной разделения Ь. Но электромагнитное поле
является однозначной функцией точки и поэтому, если свойства среды
однородны по отношению к переменной v, то f^iv) необходимо должна быть
периодической функцией угла v. Но уравнение A0) допускает периодические
решения только лля определённых, характеристических значений параметра Ь.
Эти характеристические значения образуют счётную последовательность
Ь^, 1?2, , Ьт, • • . Их определение довольно сложно, так что мы ограничимся
ссылкой на таблицы *) и перейдём непосредственно к определению функций,
удовлетворяющих (9) и A0), когда b совпадает с характеристическим зна-
-чением ^^.
Уравнение A0) допускает для собственных значений b как чётные, так
и нечётные периодические решения. Обозначим счётную последовательность
характеристических значений, дающих чётные решения, через Ь^^;
соответствующие характеристические функции можно представить в виде рядов по
косинусам:
Setn(co\ cosv)=^^ D^cosnv (w = 1, 2, 3...), (И)
n
где суммирование со штрихом производится по чётным я, если т четно,
и по нечётным я, если т нечётно. Рекуррентную формулу, связывающую
коэффициенты D^.(c^\)^ можно найти, подставляя A1) в A0). Таким образом
все коэффициенты ряда выражаются через один начальный коэффициент,
^) Очень ясное изложение теории функций Матьё дано у Уиттекера и Ватсона,
1ос. Ш., гл. XIX; дальнейшие детали с подробными ссылками на литературу
опубликованы Стрёттом в монографии «Функции Ляме, Матьё и родствевные им в физике,
и технике», Харьков — Киев, ГНТЙ Украины, 1935. Таблицы функций Матьё н
характеристических значений опубликованы Гольдштейном, Trans. Cambridge Phil. Soc. 23,
303—336, 1927. Функции Se^n и So^, определённые в тексте, отличаются от функций
сет и scjn этих авторов лишь коэффициентом пропорциональности. В то время как
' Гольдштеин выбирает свои коэффициенты так, чтобы нормирующий множитель был
равен >Гт1, мы сочли более удобным нормировать функции так, чзгобы чётная
функция и производная от нечётной функции обращались в единицу в полюсе v= 0.
См. Stratton, Proc. Nat. Acad. Sci. U. S. 21, 51—56, 316—321, 1935 и Morse,
ibid., стр. 56—62. ПодробшЛе таблицы коэффициентов разложения D^
характеристических значений Ь^ ц нормирующих множителей рассчитаны Морзе и вскоре
Л^йдут в свет.
332 ' гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
который остаётся произвольным. Удобно так выбрать этот начальный
коэффициент, чтобы сама функция имела единичное значение при г» = 0, что
соответствует 7)= cos г» =1. Для этого мы наложим на £^ условие
Нечётные периодические решения уравнения A0) соответствуют второй
последовательности характеристических значений, которую мы обозначим ^^>.
Эти функции можно представить в виде рядов по синусам
So^ <^о^' cos г>) = 2' fl^ sin nv, A3^
я
на коэффициенты которых (F^VqX) мы наложим условие 2 "^ == 1- Следова-
тельно единичное значение при v==0 будет иметь производная от So^ (CqA., cos v)x
[■^^^*»^^оЛ, cost>)j _ =1. (И>
Характеристические функции S^^ и So^ образуют полную систему
ортогональных функций. Пусть bfi и Me)—два характеристических значения,
а Se^ и Se^-—соответствующие им функции. Они удовлетворяют уравнениям
^^(bf~cll4os^v)Se, = 0, A5>
^^-i-(bf—cl\^cos'^v)Sej=^0. A6)
Умножим A5) на Se^-, A6) на Se,- и вычтем одно из другого:
^(s^J-|rS<^'-S''*irS'^ + (*r'-*f)S<^*S..= 0. A7>
Интегрируя A7) от О до 2т: и з'^читывая периодичность функций,
получаем, что
J( о, fzb 1.
Ъе^{с^к, cosv)Se^{cQ\, zosv)dv=\ . ' A8>
о 1М , г=;.
Нормирующие множители Л/^ можно подсчитать по разложениям функций,
в ряды.
Диалогично можно вывести, что
Г SOi(CoA, cosi;)S^ (с^А, zosv)dv = \ ' ^ A9>
и
. . I Se{ (Cq\, COS v) Soj (сqX, cosv)dv = 0^ B0)-
0
причём последнее соотношение верно как при i = j, так и при iфJ.
1^[аждому ха|)актеристическому значению Ь^ соответствует одно и только^
одно периодическое решение S<?»,. Но для этого же числа bi^ должно суше-^
ствовать другое независимое решение уравнения A0). Так как второе
решение является непериодическим, оно несущественно для физических задач^
по крайней мере пока среда однородна' по отношению к углу v. Если^
ВОЛНОВЫЕ ФУНКЦИИ ЭЛЛИПТ№(ЧЕСКОГО ЦИЛИНДРА F.12] 33$
однако, свойства среды испытывают разрывы непрерывности на поверхностях
гг = const., то граничные условия могут потребовать^ применения функций
второго рода.
Обратимся теперь к радиальным функциям. Можно без особого труда
«оказать, что уравнение (9) удовлетворяется рядом функций Бесселя,
коэффициенты которого отличаются лишь множителем от коэффициентов рядов
A1) и A3). Таким образом, если параметр b принимает одно из
характеристических значений ^»«\ то соответствующая радиальная функция будет
ReL (СоК О = |/"-J S ^•'"~"/)«Л (Coll), B1)
где S = ch и, /»*-»» = ехр i (т — п) w-1- Так как все решения уравнения
Бесселя удовлетворяют рекуррентным соотношениям B4) и B5), стр. 317, то
•чётные радиальные функции второго рода определяются через функции
Бесселя второго рода соотношением
Я^(соК S) = lAjS'''"*"'*^«А/«(^о^^)- B2)
Сходимость подобных рядов функций доказать нелегко, но в данном случае
она, повидимому, удовлетворительна. Большим преимуществом этих
представлений является то, что они сразу приводят нас к асимптотическим
выражениям для очень больших значений CqXS. Согласно A8) и A9), стр. 317,
Яе1 (соК 1)- у== cos (^0^^-- ^^ ^), B3)
CqKI -> со.
Яе1 (ГоХ, S) ~ -^ sin (соП — ^^---^ Л B4)
По аналогии с функциями Ганкеля, образуем линейные комбинации
Re^ (V. ^) -= ReL 4- ^R4» -= -l/^^ Y ^~ ""D^f^^^ {соЩ, B5)
Rei» {CoK I) = Rei, — iRel = j/"-^S' ^"^""/^n^f (соЩ, B6)
n
асимптотическое представление которых имеет вид
2т + 1
Ч4.(ЧК 5)=-^,/("'^-^'1 B7)
У Сок
_,(,«_2«±i.)
Cq'/Л —*■ оо.
ReUicoKD^-r-re-'^""'' * ^ . B8)
Функция Re^ удовлетворяет тому же уравнению, что и угловая
функция Se^; обе они нигде не имеют особенностей, кроме бесконечно удалённой
точки. Следовательно, они должны быть пропорциональны друг другу:
Se,„ (соК S) = УЪ &Яе1 (соК 1), B9)
— V in-m..JL (при чётных т),
I 2 VI' о!?
I >, nl*^-•'^—. (при нечётных т).
334 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
Слейа cos?) заменён на ^. Следовательно, при и i= О, -Е^=^1 мы имЬём
ReL (^0^. 1) = -7L -1:, l—Rel (гоА, ch и)] = 0. .. C0)
V> ^: Ida J„^o
■' Соответствующие соо1ношенйя Моййо получите и для нечётных
радиальных функций. Определим ' . •
Roi, (гоХ, 1) = Vl^ i/"! 2''"-"«^:ГЛ(^оаО, C1>
п
RoL (^о>^, ^) - ^^1~^ }/'^ S'^""пРТгЫп(roXt), C2)
п
RoL (^оА, S) -= Roi, 4- i Ro.«. Roi» (^o>^, S) = RoL — i RoL- C3)
Асимптотические выражения для нечётных функций тождественны с
асимптотическими выражениями для соответствующих чётных функций. Наконец,.
^So^ {с^\ I) == |/^ Й> Roi, (соА, \), C4)
tin I
4 ул' с
—5-5 7, Я——f'*-"* (при Чётных /Я),
^;«»
V —ц'""."* (при нечётных w).
при tt = о, Е == 1 имеем
Roi,(coA, 1) = 0, \^Яо1г(соК chu)] =-l^'i-. C5>
Теперь, имея в своём распоряжении эти функции, мы в состоянии
написать элементарную волновую функцию для эллиптического цилиндра^ Чётная
и нечётная волновые функции, коне«/ные всюду и, в частности, вдоль оси^
соединяющей фокусы, образуются из радиальных функций первого рода
.'^ет= Sem(f^oX, cost;) ReJre(CoA, 5N" А-«-)»г-4о>#^ ^^g)
•^L = So^ (CoK cos V) Roln (coK ^) e""' ^'^^^'-''^*, C7)
Если известно, что на больших расстойниях от оси цилиндров поле
распространяется радиально вовне, то элементарные волновые функции образуются
из радиальных функций третьего рода
?еш = Se„j (CqA, cos v) Re^ (cqI, ?) e , C8)
7o»» = So,„ (СоЛ, COS г;) Ro,M (соЛ, ч)е . . C9)
Компоненты электрического и магнитного векторов находятся по
правилам, изложенным в разделе 6.3.
6.13. Интегральные представления. Согласно A9), стр. 321, в любой
системе цилиндрических координат
/ (и1, м^) = f g{p) е^^ ^''1« (* "^^^ ^+2^ ^*" Р) rfp. D0)
Если заменить прямоугольные координаты эллиптическими с помощью пре- ■
образования л'= Ср ch м cos-г/, y==CQshus\nv, то D0) можно переписать
в виде
/(u,v)= jg{^)e^^Pd^, . D1>
ВОЛНОВЫЕ ФУНКЦИИ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА 16.13) 335
« '
где, как й pjanee, \ = \/1^-—h^ = k sin й-, и где
p(u,v,P) = xcos^-^ysih^ = CQ{chucosvcos^-\-sh usin'o^in^'SJ D2)
Функция f(u, v) должна удовлетворять уравнению
li-^-iF+^?^^(ch^и-cos2t;)/=0, D3)
но, так как f=fi{u)f2{p), то она должна, очевидно, удовлетворять также
и уравнению
да + (^5^^^сЬ2и-^)/=0. D4)
которое получается умножением (9), cip. 331, на/2('п). Дифференцируя D1)
по щ получаем
следовательно, для того чтобы D1) удовлетворяло D4), необходимо, чтобы
Величина р является функцией § и и, причём легко убедиться, что
д2р д'^р
D8)
au2 а.б2 •
Следовательно, D6) эквивалентно уравнению
J^(P) [^ + (^ —^?^'cos^р) е^р\ d? == 0. D9)
Наконец, согласно C0), стр. 322,
Следовательно, D1) является решением D4), если g{P) удовлетворяет
уравнению
^-\-(b~cll^cos^P)g==0, E1)
а путь интегрирования выбран так, что
•о'-^- ^''^ж! =0. E2)
Заметим, что уравнение для амплитуды gi^) тождественно с уравнением
для угловой функции f^iv) и лишь несущественным образом отличается от
уравнения для Д (и), из которого мы исходили. Это свойство является
общим для представлений Фурье всех решений уравнений, относящихся
к группе, определённой равенством F), стр. 330.
Полученные результаты верны при любых значениях постоянной
разделения h„^. Но если ограничиться чётной и нечётной последовательностями
характеристических значений Ьт и Ь^у то удобно в качестве g(ff) взять,
периодические решения уравнения E1), обозначенные через Se^ (CqX, cos р),
SojniCok, cosp). Так как р{и, v, р) также периодично по р с периодом 2тт, то,^
очевидно, E2) будет удовлетворено, если за путь интегрирования взять любойи
-^Зб гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
_а_
«отрезок действительной оси длиной 2т:. Тогда интегральное представление
J{Uy 1»), верное для ft, принадлежащих последовательности ft^', имеет вид
/Й'(«, -г;) - J Se^C^o)., cosp)e^^'^«' ^' ^U^. E3)
о
Отсюда можно сразу же найти интегральное представление для fiiu),
•полагая v = 0.
/2(«) = JSe^(CoA, cosP)/««^«»^«-^Prfp. E4)
о
Остаётся найти связь частного решения, определяемого E4), с ранее
известными функциями. Вводя разложение Se^ в ряд по косинусам и полагая
для сокращения CQXchu = p, получаем
2ic
/12 («) = S'd:? Г /^ ^■''^ P'cos «р jp = 27:2 '^•;?/„ (о). E5)
"о '^
Заметим далее, что «»=«(—1)"/-», и вспомним, что суммирование
производится по чётным п при чётных т и только по нечётным — при нечётном т.
Поэтому (—!)» = ( —1)»», и, в силу определения B1), стр. 333,
Rei» (с^К S) = ^ / Se^ (Cf,K cos р) e^*^'^ •^"^^ rf^, ( 56)
о
где s==ich«. Кроме того, Se^ (CqX, cos р) пропорциональна Rei»(rQX, cos Р),
<где i заменено через cosp, так что по B9), стр. 333, функция Reit(CoX, $)
удовлетворяет интегральному уравнению
Rei,(CoXJ) = i-'»-f-J Rel{c^KcosP)e''<>'^''''^d^. E7)
о
Можно получить и другое представление Re«j, разлагая в ряд подинте-
..гральное выражение в E7). Имеем
Яе1 (с^К S) - /ё^ ]/"-^ 2' /-"ОГ / Jn (^0^ cos Р) ^'^ ''' ^rfp. E8)
« о
.Но ' •
к
У„ (CqI cos Р) == ~ fcos П9 е'''"' '°^ ^ '*" "d^, E9)
о
^ откуда
2я 2я
J /„(CoXcosP)e''^'*'°^^rfp = i-'^J cos«c?yot^o^(<-[-cos<?)]^?. F0)
о о
Вспоминая ещё раз, что (—!)» = (—1)"»^ получаем
_ 2я
ReJ„(CoA, с) = /ЙЧ-1Г>/"|- f^l^o4^ + cos(p)]Se^(CoX, cos9)rf<?. F1)-
а
ВОЛНОВЫЕ ФУНКЦИИ^ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА [6.131 337
Интегральные представления радиальных функций третьего и четвёртого
рода можно получить, выбрав другие контуры интегрирования. Для
упрощения положим ch м = S, •г' = О, cos ^ = t. Тогда различные радиальные
функции представляются интегралами вида
/S (S) = J Se^ (с^К t) е**^^" A - ^)'" "^ dt, F2)
с
где контур С таков, что обеспечено обращение в нуль так называемого
«билинейного конкомитанта» E2), который здесь имеет вид
(l-^')'[V^Se„(.„M)-Ase„(.oM)>-t=«- («3)
Когда t становится очень большим, асимптотическое представление Se^ будет
Se^(с^К t) -&] |/^ cos(^c^lt— ^^il ^) ; F4)
следовательно, обращение F3) в нуль в бесконечности обеспечивается
множителем explcQX(^—1)/. Поэтому, если действительная часть CqK(^—1)
больше нуля, то начало или конец контура могут быть взяты при / = ioo,
а за другой предел можно взять-j-1 или—1. В результате получим
Яе1 (с^К S) = /-*" |/"-| J Se^ (гоХ, t) е''^^* A — ^^) "^ dt, F5)
ioo
ReJ,(CoX, S) = t-'"|/| ^Se^{c^Kt)e''^^*{\--t^)~'^dU F6)
—1
при условии, что действительная часть [cQ^iJi—1)]>0. Возвращаясь к
комплексной ^-плоскости, находим, что F5) эквивалентно равенству
--ioo
Re?. (гоХ, S) = /-'" |/~| J Se^ (CoX, cos .8) e**^'^ °°^ ^ rf^; F7)
0
соответствующий интеграл имеет место и для Ret» (CqX, ^).
С помощью F7) можно вывести ряд других интегралов типа F1).,Так,
вместо E8) можно написать
— '—i со
ReL(coX,S) = UY2^2;^-~"^« f Л.(Го^со8р)е'^'^'^*^°'Р^Р =
--ioo
= Й^|/~|2'(—lf^« f ^?cos«<pJ rfpe*''o^«+-^^)'=°*P. F8)
о О
Но, согласно C9), стр. 324, при р = 0 имеем
-— —i оо i оо
2 2
-+»оо
338 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
если действительная часть р > Oj следовательно,
Яе1 (с^К S) = &^ (- 1Г }/~|- J ^?* К^ (^ + cos <?)] Se^ (СоХ, cos 9) ^?, G0)
о
если действительная часть IcqK(^—1)]>0. Комбинация F1) и G0) даёт
2ic
Я^1г(соК е) = ЙЧ—1Г}/"| /л^оМ(^ + со8<?)]&е^(ГоА, coscp)^?. G1)
о
Для нахождения интегральных представлений нечётных функций
исходным является соотношение
2п 2ic
J ^ic„X£ cos P g. jj ^p ^^5 p ^P _ _^ J ^«CoX? CCS P ^^^ ^^ ^^^ ^^2)
0 0
которое получается интегрированием по частям. Доказательство соотношений
, 2ic
Rol (СоК ^) = :^ ^'~"* У^^^ / So^ (^0^» cos Р) е*'^^ ^"« ^ sin ^ ^^ =
= -f^ /5-""* V^^^=^ / Roi (го^, COS P) e''<^ "« P sin p rfp =
0
2«
= CoVS^ (-1)"* |A| yF=T J л [^0^ (^+COS 9I X
0
XSo^(^o^,cos(p)-pp^rf?, G3)
■ 2«
Ro^« (гоХ, S) = ГоХ/2Ч~1Г|/^/Р-^ //^f^ [^0^ (S+ COS ?)] X
0
X^o^ic^K cosy)^_^'"J^^t/y G4)
предоставляется читателю.
6.14. Разложение плоских и круговых волн. Периодические функции
Se„t (г^А, cos v) и ЗОда (CqX, cos г)) образуют полную ортогональную систему
функций. , Следовательно, если /(«, <&)—периодическая по v функция
с периодом 2тг, кусочно непрерывная по аргументу v вместе со своей первой
производной dfj-dvt то она может быть разложена в ряд
со 00
/(«, ^) = S fm^ (и) Se^ (СоХ, cos ^) + S /2^ (и) So^ (с,Х, cos t»), G5)
коэффициенты которого определяются равенствами
■^^("^^Т^/-^^"' ^)Se^(CoX, cos^)rfv,
'"о I
G6)
Это разложение можно применить для представления плоской водны
с константой распространения ^, бегущей в направлении, определяемом-
ВОЛНОВЫЕ ФУНКЦИИ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА [6.141 33$^
единичным вектором п, образующим с фиксированной системой отсчёта
полярные углы а и р, как показано на рис. 66, стр. 319. Имеем
ф -_, gift sin о£ (а? cos P+f/ sin Р) . ^Тсг ccs «—iwf ^ G7V
Выражая X VI у через и и г' и полагая А = ^ sin а, получим
/(м, «у, р)==е*>р, ps=Co(chwccst;cosp4"Sh«sint»sinp). G8)
Так как выражение G8) совершенно симметрично относительно ф и р,
разложение G5) можно записать в виде
со
е*>р = 2 ««г («) Se^ {cqK cos р) Se^ (соА, cos г;) -f
«1 = 0
оо
+ S *m (и) So^ ccqX, cos P) So^(coA, cos v\ G9)
ra = 0
где коэффициенты a^{u) и b^(u) зависят юлько от и. В силу G6) имеем
2ic
«m («) A^S^Se^ (соА, соs р) = J S е^ (cqA, cos г;) e«p rft;. (80)
0
Так как коэффициенты a^(u) не зависят от значения р, то можно положить
P = 0,Se^(coA, 1)= 1, p = coch Mcost;. Тогда, согласно E6),
^т (и) = '""^^ ReJ, М» ch и). (81)
Аналогично найдём
*«г («) A/£^So^ (соА, COS Р) = J So^ (соХ, cos г;) е^>р dv. (82)
о
Продифференцируем теперь это последнее равенство по р, а затем положим
Р = 0. Тогда, в силу A4), коэффициент ^>^ (и) окажется равным
К («) = -rfer ^°« (^оХ, Ch а). ( 83)
Таким образом, полное разложение для плоской волны произвольного
направления имеет вид
оо
е^Р ^ /8^2 Н-;^Яе1{соК ch и) Se^ (соА, cos г;) Se^ (соХ, cos p)-f
+ j^ Яощ (соА, ch и) So^ (соК cos г;) So^ (cqA, cos P)l. (84)
Последний результат позволяет нам сразу написать интегральное
представление для тех элементарных эллиптических волновых функций, которые
остаются конечными вдоль оси. Для этого нужно только умножить (84) на
Se„, (i^oA, cos р) и проинтегрировать по периоду. Тогда из ортогональности
функций следует, что
211
1—4»
Rei» {соК ch и) Se^ (соК cos г;)= '-^ J Se^ (cqA, cos ^N^p d^; (85)
0
и аналогично для нечётных функций
Roi» (соА, ch и) So^ {соК cos г;) = -^ f So„ {СоК cos р) е*>^Р dp. (86)
У 8" У
340 гл, VI. ЦИЛИНДРИЧЕСКИЕ волны
с помощью F7) можно также показать, что элементарные функции
эллиптических волн, бегущих от оси наружу, представляются контурным интегралом
Re^ (со^, ch и) S8,„(coX, cos г;) == i-^Y \ j^^mi^oK cos Р) е±^^р dp. (^^^
о
Верхний знак в показательной функции берётся при—тт/2 < г; < •зг/2,
отрицательный знак — при тг/2<'г'<Зтг/2. Подобное же равенство можно вывести
для нечётных функций.
Из раздела 6.8 легко усмотреть, что чётная круговая волновая функция
cos «9 У„(А.г), остающаяся конечной на оси, может быть представлена интегралом
2тг/'^ cos nbJ„ (Аг) = f cos пре^^Р d§, (88 )
где р = A:cosp4->'sin p = rcos(P — 8). Умножая на £);Г и суммируя по чётным
«ли нечётным п, получаем равенство
Rein (с А, ch и) Se^(c л^ cos v) = у-^^' ir^-^Dn cos nbJ^ {\r\
(89)
n
которое выражает эллиптическую функцию в виде разложения по круговым
волновым функциям. Подобное же выражение можно найти для нечётных
функций.
Теорема сложения для круговых и эллиптических волн, отнесённых
к двум параллельным осям, выведена Морзе ^).
ЗАДАЧИ
1. Показать, что уравнению
удовлетворяет волновая функция вида
ф = Се* ^^ + ^) cos {h^x -\) cos {h,,y — цу^^^-^"^*, ^J ^ й| + й| = k\
Пусть ф = Т1г, Па. = П^ = 0 будут компонентами вектора Герца, ориентированного
в направлении распространения. Показать, что это приводит к поперечному
магнитному полю, электрические компоненты которого равны
,£^ = — ihji^ сё (^1 + ^*> sin (h^x — 8i) cos (h^y — UJ e^^^ - *"^*,
Ey^— ih^hsCe*^^^ + ^*lcos{Н^х — Ь,)sin (h^y — Ь^У^^''"*"^*,
E^ = (A;a - hi) Ce* <^^ + ^*) cos (h^ x — 5i) cos {h^ - Sg) e^'' " *""*
a импедансы
E k^ — f^l
Найти составляющие соответствующего поперечного электрического поля, полагая
л — тг * тг* = тг* = 0
1) Morse, loc. cit.
ЗАДАЧИ 341
Множитель e^ ^^- "^ ^ введён для того, чтобы включить как бегущие, так и
стоячие волны. Так, при \=^ico поле ведёт себя, как .е*'**®.
2. Двумерное волновое уравнение в недиссипативнсй среде имеет рид
дх^"^ду'^ Ф Ы ~
Показать, что
at 2я at "Ы
dfj J уаЧ^—г"^ J J Va^i^—r*
0 0' 00*^
где
x' — x=rcosb, у—j;=rsine,
и
дй)
'^ — gix.y), jf = G(x,y) при / = 0.
Это—формула Пу.ассона-Парсеваля. Заметьте, что в мсмент f волновая функция (J>
определяется начальными значениями ^ и О во всех точках на окружности и внутри
круга радиуса af. Таким образом, даже в недиссипативных средах возмущение
остаётся после прохождения фрснта волны. Это свойство характерно для волнового
движения в пространствах с чётным числом измерений.
3. Показать, что волновое уравнение
имеет частное решение вида
218
«р = — \ F (z-\-ir C0SO, t— — sin о j da.
о
которое переходит в ^ = F{z,() на оси г=0, где F—произвольная функция.
Показать, что другим решением этого уравнения является
со
ф= ( F(z — rs\\a,t~Lcb.a\da. (Bateman)
—00
4. Частным случаем решения, полученного в 3-й задаче, является симметричная
двухмерная волновая функция
* = 2^/^('-^'''°)''-
представляющая волну, распространяющуюся от однородного линейного источника
силы F{f) вдоль оси Z,
Показать, что если^/' {t) = О при ^^О, то
с
0. = ^ Г
• 2п J
—со
и равна нулю всюду, пока /<[/Ус.
Показать, что если источник действует только в течение конечного времени т,
так что F(f) = 0 для всех f, за исключением интервала 0<;|/<;|т;, то волна оставляет
остаток или «шлейф», форл а которого при t [^т определяется выражением
_j-f(P).p.
2ll У с 2^—/-2
о
( Ламб. Гидромеханика. Гостехиздат 1947 г.)
5. Показать, что уравнению
342 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
удовлетворяет
= J
sin Л (S + о) d$
г4о V'^^~i^--^o)^-iy-yof
где
г'^ = х^+у\ г^о = х1+у1. (Bateman)
6. Показать, что уравнению
удовлетворяет функция
~ »" лч
^де /-2J—д:2_|_j;2^ а /и F—произвольные функции. Каким ограничениям подчинено
это решение?
Получить таким способом частное решение
1 ~\г -^
ф =— е (x-r-iy) ^ . (Bateman)
7. Уравнение
приводится подстановкой
ф = е~^*м {х,у, О
к виду
Начальные условия таковы:
«=-§'(^.3'). -^1"^<^(^'У) при< = 0.
Пусть г—радиус сферы, описан1ной вокруг точки наблюдения, а о, р, у
—направляющие косинусы г по отношению к осям х, у, Z. Показать, что
к (J^, J'. О = 2^ ^ J J tg{x-\- ata.y + аЩ CQS{ibtf) dQ. +
+ ^ Г Г / G (a: + a/a, J/ -!- at^) cos (/&/^) ^S (Boussinesq)
является решением, где S — телесной угол, опирающийся на элемент поверхности
сферы.
8. Показать,'что
к
Ур(р) = ,,., гг COS (р COS ср) sin2/'!j) dcp
2^r(i)r(p+i)a' ^
является интегральным представлением функции Еесселя первого рода, верным для
всех значений порядка р, если только Re(p)>- — -^ .
9. Вывести интегральные предсТгавления
^о<
оо
2
ijB) = — — Г COS B ch о) da. Im г^»®
о
для функции Бесселя второго рода нулевого порядка и
п
Hf (Z) = f^+ 1 Г е-'' «^ь « ch pa da, Im 2<в.
ЗАдачи . 343
10. Показать, что видоизменённому уравнению Бесселя
удовлетворяет функция
со
«1 = 0
где
Ip (z) = е ^ J^ (iz) при — 3^<arg 2<-J .
Наиболее употребительное независимое решение определяется соотношением
Полная совокупность рекуррентных соотношений для этих функций приведена у Ват-
сона, Bessel Functions, стр. 79.
11. Доказать следующие интегральные представления видоизменённых функций
Бес селя:
ch (z cos о) sin ^Ра da =
+1 1
Р--7:
-1
1С
1 / z\P г ± ^ cos« . -
= i (±Y I e Sin ^Pada.
4''+2 J
0
Предполагается, что
Re(p + -|)>0 и larg^K^.
12. Показать, что для очень больших значений аргументов асимптотическое
поведение видоизменённых функций Бесселя даётся выражениями
оо — г + из 4-г) "* °°
/ (Z) с^ ^^ V (—^Г(/^> ^) , ^ V ^Р' ""^
€cли—|■<arg2<2- к,
«1 = 0
где
т!Г1/? — т-{-—-]
Оставляя лишь первый член, получаем
344 гл. VI. ЦИЛИНДРИЧЕСКИЕ волны
13. Доказать, что если R=s Yr'^-\-z^ — расстсяние между двумя точками, то
обратное расстояние ь ожно г редставить в виде
1 = -|/«о^Р^^о(И^Р.
О
где Ксфг)—видоизменённая функция Бесселя, определенная в задаче 10.
14. В качестве частного случая задачи 4 показать, что уравнению
LAfrM Li!l_n
г дг \ дг) са ла ~"
удовлетворяет функция
^{r,t)^K9(ikr)ei^t,
где k = <iyfc, а /Гц —видоизмеяённая функция Бзссзля, определезная в зада le 1Э^
Это решение играет в распространении двухмерных волн такую же рэль, какую
в трёх измерениях играет функция e^^^/R.
15. Показать, что уравнению
1 д / д<Ь\ . 1 дЧ , ,,,
удовлетворяет функция
оо J ^ !L
^^(И + 2 2^ " '^У^ (X,-)cos^e,
т = 1 п
имеющая период 2ип по 6 и поэтому многозначная относительяо обхода вокруг
оси. Показать, что это решение можно пред:тавить интегралом
Ф = 1 r__i:i_>-xr COS (в-«) ^„
по надлежащим образом выбранному контуру Се комплекснэй пюскости о. Эта
решение всюду KOneqHj и неп^ерывю- В бесконечности ф ведбт себя, как плоская
йолна, если | 6|<:;;я, и обращается в нуль (функция регулярна), если 6 лежит между
какой-либо парой предельных значений
к < е <уЗп, Зп <|е <:.5ii,... — Зп]< 6 <—11,
которые определяют 2-й 3-й...я-й листы римановой поверхносги. Такая многэл нет-
ная волновая функция применена Зоммерфеяьдом в задачах дифракции.
16. Вывести ы явном виде выражения дла радиального и тангенциального^
импедансов эллиптических цилиндрических электромагнитных волн.
17. Показать, чтэ интеграл
оо
о .
является цилиндрической волмовой функцией, равной e^^^/R, R* = r'^-{-z^ прв
/(?i) = l.
,=/
ГЛАВА VII
СФЕРИЧЕСКИЕ ВОЛНЫ
В предыдущей главе было показано, как аналитические трудности^
связанные с рассмотрением векторного дифференциального уравнения в
криволинейных координатах, могут быть преодолены в цилиндрической системе
координат разложением поля на два частичных, каждое из которых может
быть получено из ^скалярной функции, удовлетворяющей волновому
уравнению. К счастью, этот приём применим также и в сферических координатах^
к которым мы сейчас обратимся. Особые преимущества цилиндрических и
сферических координат являются следствием простоты их геометрических
свойств. Более глубокое представление о сущности стоящей перед нам»
задачи и о трудностях, которые появляются при переходе к криволинейным
координатам в общем случае, мы получим предварительно коротко изучив
векторное волновое уравнение.!^
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ
7.1. Фундаментальная система решений. В пределах замкнутой
области, из которой удалены все источники и которая заполнена однородной
изотропной средой, все векторы, характеризующие электромагнитное поле,
именно векторы поля Е, В, D и Н, векторный потенциал и вектор Герца,
удовлетворяют одному и тому же дифференциальному уравнению. Если через
С обозначить какой-либо из этих векторов, то это уравнение имеет вид:
В силу линейности этого волнового уравнения поле, произвольно меняющееся
во времени, может быть построено из гармонических решений, и мы не
уменьшим общности, если положим, что вектор С содержит время только
в виде множителя е-**"*. Под оператором А, действующим на вектор, мы
должны понимать AC = gTaddivC — rot rot С; поэтому вместо A) мы пишем
graddivC —rotrotC + A;2C = 0, B>
где, как обычно, k^ = ejxco^ -f- io]m.
Векторное уравнение B) всегда может быть заменено соответствующей
системой трёх скалярных уравнений, но разрешить эту систему относительно
какой-либо из компонент С в большинстве случаев оказывается практически
невозможным [см. (85), стр. 55]. Лишь в том случае, когда мы
разлагаем С на три прямоугольные компоненты, мы получаем три независимых
уравнения
AQ + k^Cj = 0, О' = лг, У. г) CV
где оператор А может быть представлен уже как в прямоугольных, так и
в криволинейных координатах. До сих пор определению независимых век-^
346 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
lb
торных решений уравнения B) было уделено очень мало внимания, но
недавно такая попытка была предпринята Ганзеном i) в ряде интересных
работ, посвященных исследованию излучения антенн.
Пусть скалярная волновая функция <^ является решением уравнения
^^-^Щ = 0^ D)
■ц пусть а будет каким-либо постоянным единичным вектором. Мы строим
теперь три следующих независимых векторных решения уравнения B):
L = grad4>, M = rot(a»}>), N=~rotM. E)
Если С в уравнении B) положить равным L, М или N, то уравнение B)
будет удовлетворено тождественно при условии, что ^ удовлетворяет
уравнению D). Ясно, что, поскольку а — постоянный вектор, мы можем написать
,М в виде
М = [L, а] = -|- rot N. F)
Для одной и той же производящей функции ^ вектор М перпендикулярен
к вектору L, т. е.
LM = 0. G)
Векторные функции L, М и N обладают некоторыми замечательными
свойствами, следующими непосредственно из их определения. Вектор L без-
' вихревой и
rotL==0, divL = A^ = —^2<Ь, (8)
векторы М и N соленоида льны:
divM = 0, divN = 0. (9)
Частные решения уравнения D), конечные, непрерывные и однозначные
в данной области, образуют дискретную систему. Обозначим временно какое-
либо из этих решений через «{>„. С каждой из характеристических функций
^п связано три векторных решения уравнения B) L„, М„ и N„, ни одна
пара из которых не коллинеарна. Можно предположить, что произвольная
волновая функция может быть представлена в виде комбинации
характеристических векторных функций; коэффициенты разложения могут быть определены,
поскольку L„, М„ и N„ обладают свойствами ортогональности, которые мы
в дальнейшем докажем. Если заданная функция чисто соленоидальная, то она
может быть представлена в виде комбинации только М^ и N„. Если же
дивергенция данной векторной функции нулю не равна, то в разложении
должны присутствовать и функции L„.
Векторы М и N, очевидно, пригодны для представления полей Е и Н,
так как каждый из них пропорционален ротору другого. Таким образом,
если время входит только в виде множителя е—^^* и если плотность
свободных зарядов всюду равна нулю, то для однородной изотропной среды с
проводимостью о мы имеем
Допустим теперь, что мы можем разложить векторный потенциал по
характеристическим векторным функциям в виде
А = -^2<^п^п + *Л4-^nLn), (И)
п
Е = ^ rotH, H=r^rotE. - A0)
1) Hansen. Phys. Rev. 47, 139—143, January 1935; Physics 7, 460 — 465,
December, 1936; J. Applied Phys. 8, 284 — 286, Aprils 1937.
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ {7.11 347
где коэффициенты а„, &„ и с„ должны быть найдены из
распределения токов.
Согласно (8), A0) и соотношению p,H=rotA мы получаем для
векторов поля
Е = -^ %a„fA„ + ^«N„). Н == - А. ^ (a^N„ + ^М„). A2)
п п
Скалярный потенциал о не играет роли в вычислениях, но, очевидно, может
быть определён непосредственно из A1), так как согласно B7), стр. 36,
divA=-^k^o; и, следовательно, из (8)
? = —21^«Ф«- A3)
U)
п
Таким образом, grad <э =—-^c^Ln, и соотношение
п
E = -grad<?—^.
очевидно, снова приводит к формуле A2). Наконец, если мы напомним, что
при данных условиях электромагнитное поле может быть выражено через два
вектора Герца с помощью уравнений
E==rotrotn-f ia)[j,rotn*, H = £-rotn-f-rotrotn*, A4)
то отсюда становится сразу же ясным, что
П = —у5!1ад„а, П* = —v;j^^a„»}>„a, A5)
п п
где а — постоянный вектор.
Прежде чем применить эти результаты к цилиндрической и сферической
системам координат, мы рассмотрим элементарный пример волн в
прямоугольных координатах. Плоская волна, волновой вектор которой равен
к = ^п, может быть представлена в виде
^^gikR-iw^^ A6)
где R—радиус-вектор, проведённый из фиксированного начала отсчёта. Так
как kR = k^ -j- куу -j- k^, то легко видеть, что
L = i^K М ==/<]>[к, а], N = l<!^[[k,al,k]. A7)
В этом частном случае LM = MN = NL = 0; все три вектора взаимно
перпендикулярны и L — чисто продольная волна. Пусть а и р — полярные
углы, определяющие направление вектора к, как это показано на рис. 66,
стр. 319; общее решение уравнения B) может быть получено
интегрированием этих функций для плоской волны по всем возможным направлениям.
Если g-(a, р) — скалярная амплитуда (весовой множитель), то в какой-либо
координатной системе мы можем написать для L при выполнении условий
сходимости
L =/е-**"* J й?а pPg (а, Р)к(а, ^^)e^^^ A8)
и аналогично для М и N
М = гб^^*"* J da J й?р g{a, Р) [к, а] е*»*», A9)
N=-|^e-«'"« Jcfa Jrfp^(a, р) [[к, а], к] e^^R. B0)
348
гл. Vn. СФЕРИЧЕСКИЕ ВОЛНЫ
7.2. применение к цилиндрическим координатам О- Скалярные харак>
теристические функции волнового уравнения в цилиндрических координатах
были приведены в уравнении F), стр. 315. Применение функций
комплексного угла ехр (гпб) связано с некоторыми неудобствами, и, оказывается, проще
пользоваться двумя действительными функциями созпб и sinn6, которые мы
будем обозначать просто как чётные и нечётные. Цилиндрические волновые
функции, построенные из бесселевых функций первого рода и, следовательно,
конечные на оси, будут обозначаться через ^„\ а волновые функции,
образованные из //„(Хг) и /%^ (Хг)—соответственно через ^„^ и t|)^^. Таким
образом
^% = cos иб J„ (Хг) е^л^ - i^^t,
1.A) _.-„ J.C г ,ч_ч -rfb,— rf.„* I (^Ь
Гопх = sin иб У„ (Хг) е^^^ ~ <">«,
,1^^'^х = cos пЬ /yj? (Хг) e!^J^^ - **"«,
ii.<;„>x = sin пЬ Н^!^ (Хг) е*'»^ - **"«,
B2)
где, как обычно, Х = |/^2—/^^ = ^sina. Функции первого рода выражаются,
определёнными интегралами вида
2я
;-п л
Лпх = ^ J •^*'^'' """^ ^^ - ^> cos пр fiJp е^^^ -*''"<,
о
2я
B3)
а представления для функций других родов отличаются только выбором пути
интегрирования.
Из B3) мы построим теперь интегральное представление для векторных
волновых функций. Так
A)'
A)
Ve^x = grad ^'^^
^А , . 1 д& . аЙ^)
гепХ.
B4)
Дифференцируя B3) по г, б и г и замечая, что ^ sin а cos (^ — б),
^ sin а sin (Р—б)-и ^cosa являются компонентами р'ектора к относительна
ссей, определяемых единичными векторами i^, ig, ig, так что
k=ii^sin a[cos(P—б)-j-1*2^ sin а sin (Р—6)-f ig^fecosa, B5)
мы получаем для чётной функции выражение
A)^
215
Ц^^ = ~ j ке^^ cos (р-в) cos п^ d^e^T^^-i^\
о
B6)
которое икеет тот же вид, что и A8). Соответствующее выражение для
нечётной функции получается заменой под интегралом cos «р на sin пр. При?
применении этих характеристических функций для разложения по ним
произвольной векторной волны представляется удобным исключить множитель
1) Результаты этого парагргфа следует сравнить с уравнениями C6) и C7) на
стр. 318 — 319.
ВЕКТОРНОЕ ВОЛНОВОЙ УРАВНЕНИВ 17.2] ^ 349
«хр(гйг — ioit), поэтому определим векторные аналоги скалярной
функции f(r, 6) (глава VI) соотношениями
L—— 1 pihz—ivii АЛ — «и oihz—iiot Л
— П piJiz-iiat I ^ '
Из B6) имеем
■ »ii=='^/b*'^^'-'^"MP-«)^'.>M?. B8)
2lE
Таким же способом мы получим интегральные представления и для
других независимых решений. Если в качестве постоянного вектора а мы
.возьмём единичный вектор ig, направленный вдоль оси г, то найдём:
• МЦ' = [grad С !з1 = ~^-^h ~^-$- к, B9)
откуда нетрудно получить, что
. 2гс
о О
И так как го1М„ = Ш„, то мы имеем
2lE
"?ы =|г J(^^*3-/^k).*^-cos(p-e,iCos^p^p^ ^31)
о о
Исходя из этих интегралов, можно легко получить и прямоугольные
компоненты волновых функций. Фигурирующая , в подинтегральном выражении
векторная функция угла разлагается на свои прямоугольные компоненты,
которые могут быть затем объединены с cos «р или с sin п^. Получающиеся
в результате скалярные интегралы могут быть вычислены путём сравнения
их с B3).
- Для того чтобы произвольную функцию от г и 6 можно было
разложить по функциям le^^y ^впх ** "е„х' ^^'^ ДОЛЖНЫ показать, что эти функции
0 0 о
ортогональны. Пусть i^, Iq и ig будут единичными базисными векторами
круговой цилиндрической системы координат (рис. 7, стр. 56), а Z^Q^r) —
цилиндрическая бесселева функция любого рода. Тогда, согласно E), мы
получаем
Кх = Тг^п (И '°п '^б »1 =^ Т ^« (^'■> со" '^^ ^2 + ^^^n i:^r) "^^ пЬ is, C2)
т
sin „ , д „ ,\ ^ cos
«пХ
Т Zn i}^r) 2^ nQ i, - §-^Z„ ilr) l^ nb k, • C3)
ih д ^ /^ ^ cos o. ihn „ ,. » sin q. i ^^ t /i ч cos £>. /ол\
"««X ==-kd-r^^ (^'■> sin '^^ »i =^ -^ ^- (^'■> COS '^^ »2 + -^ ^n i^r) ^^ nb I3. C4)
0
Из этих выражений сразу же видно, что интеграл по б от О до 2тг от
скалярного произведения любых двух из этих функций равен нулю, если
только индексы п у этих функций различны. Далее:
J Wonx db= j le„^le„,v ^6 = 0, если пфп'. C5)
350 гл. vn. СФЕРИЧЕСКИЕ волны .
Будем подразумевать под 1 функци19 1, у которой знак при ih изменён
на обратный ^). Тогда нормирующий множитель может быть найден и»
интеграла
j4xX„x.^e = (l-f8)^r^Z„(^r)^Z„(Vr)-f
. о
о о
4- - Z„ (Хг) Z„ (XV) + hh'Z^ (Хг) 2„ (XV)] , C6)
где 8=: О при пфЬ, и 8=1 при «==0. Первые два члена правой части
можно объединить с помощью рекуррентных соотношений B4) и B5),
стр. 317, что даёт
/кх\х/^б = A4-8Oг { ^'[Z«_i(Xr)Z„_i(Xr) +
+ Z„+i(Xr)Z„+i(XV)]+M'Z„(Xr)Z„(XV) { , C7)
Те же рекуррентные соотношения приводят также к следующим интегралам:
О о о <>
2>с
гае^«"епх/ ^6 = A+ 8) ^ ^ [Z„.i (Хг) Z„_i (XV) +
+ 2„+i(Xr)Z„^.i(XV)l, C9)
2>с 2>с
О О о в
2я
J Ve«x' ^6 = A + 8)^{ ^ [Z„_i (Хг) Z„_, (XV) +
о о о ^
+ -^«4.i(H^„+ia>)l + a^T^«(Xr)Z„(XV)}. D1)
Кроме того,
2я 2я 2я
J 'епХ»"е^. ^9 = / те„,Пе„,, db = J Je^x "о^, ^6 = 0. D2)
qOo qOO q о e
и, воспользовавшись ещё раз тем же рекуррентным соотношением, мы
получаем
2>с 2л
J *е«Х»"««Х/ ^б = / »"епхП««Х/ ^^ = «. D3)
О О е О о е
Осталась только одна комбинация, которая, к сожалению, приводит к
некоторой трудности:
2>с
J Кх^е^х' ^6 =' A + 8)-I I ^X'2Z„ (Хг) Z„ (XV)-
-^[2„-i(Xr)Z„.,(XV) + Z^+i(Xr)Z„^.i(XV)] |, D4)
о о
^) Эта функция не обязательно является комплексно сопряжённой, поскольку
\ н h могут быть комплексными.
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ [7^1 35 Г'
'■111 . . .. ь „ д
Т. е. получается величина, неравная нулю тождественно. Таким образом;,
ввиду D4), система векторов 1е^^, Ше^ и Пе^^ не является полностью орто-
« о о о
тональной по отношению к б. Во многих случаях это не существенно, ибо,
если дивергенция векторной функции равна нулю, как это и имеет место
для векторов электромагнитного поля в отсутствие свободных зарядов, тО'
она может быть разложена только по т^^ и Пе„^. Но полное разложение
о о
векторного потенциала требует включения и функций Ц^^ ^).
о
Для случая функций первого рода Ганзен применил теорему Фурье-Бес--
селя с тем, чтобы получить полную ортогональность и упростить
выражения для нормирующих множителей. После очевидной замены переменных-
мы получаем из E3) и E4), стр. 327,
оо оо
f (X) ==\^rdr J V dX'f (X') J„ (XV) J„ (Xr). D5)/
0 0
Заменяем в C7), C9), D1) и D4) Z„(Xr) на Jni^) и применяем
соотношение D5). Вместо /(X') мы будем иметь X', h' ==Ук^ — Х'^, й'Х' и т. д.
Необходимо заметить при этом, что справедливость теоремы Фурье-Весселя^"
оо
была доказана только для того случая, когда интеграл Г |/(Х)||ЛХ cfX.
о
существует; в данном случае это условие не выполняется. Ухищрения,,,
которыми пользуются для того, чтобы обеспечить сходимость, связаны*
с математическими трудностями, которые выходят за пределы этой книги^
С некоторыми оговорками мы можем ввести экспоненциальный множитель^
обеспечивающий сходимость, как мы делали это в теории преобразования
Лапласа на стр. 276. Будем, следовательно, под 1^^) подразумевать предел^
о
к которому стремится 1W g—is|x ^рц $-*-0. Тогда
о
оо оо
lim Г г rfr f X' а' { Х'е-1« "^' } У„ (XV) J„ (Хг) = К D6>*
В соответствии с этим выражения для нормирующих множителей примут вид
со оо 2я
о о о о о
оо оо Зп
J J J mW Jm<4, ^' d^'r dr db = {\+ b) ^\^ D8>
0 0 0 о о
* со оо 2ic
/ J / <A ^' ^'^^'d^ = A + S) ^X^, D9>
0 0 0 о о
^) Полнота системы векторных функций не была нами доказана, но её можно,
предполагать, исходя из полноты системы функций '^е^-^.
о
352 гл. VII. СФЕРИЧЕСКИЕ волны
, тогда как для неприятного выражения D4) мы получим ^)
оо со 2гс
о о о о о
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ
7.3. Элементарные сферические волны. Поскольку произвольно
изменяющееся во времени поле может быть представлено по теореме Фурье
в виде суммы гармонических составляющих, мы не уменьшим общности
результатов, если будем в дальнейшем полагать, что
C^==fiR,b,o)e-i-'K A)
В однородной изотропной среде функция /(/?, б, ср) должна удовлетворять
уравнению
А/+^У=0, B)
которое, согласно (95), стр. 57, имеет в сферических координатах вид
Переменные в этом уравнении разделяются, так что, положив
/=Л(«)Л(в)Л(?).
«4^ + 2«§|+(А^К^-ЛЛ = 0, D)
-^+?Уз = 0. F)
Параметры р и д, являющиеся постоянными разделения, определяются
из физического требования однозначности поля в любой данной точке
пространства, /з (ср) должна быть, очевидно, периодической функцией ср с периодом,
равным 211, и область возможных значений д ограничивается, следовательно,
целыми числами /и= О, г±:1, ±2,,.. Чтобы определить параметр р, мы
покажем сначала, что решение /з тождественно с присоединёнными функциями
Лежандра. После подстановки т) = cos б уравнение E) принимает вид
Это уравнение имеет регулярные особенности только в точках iq = — 1,
fl = ~\~l и 7)=схэ. Его решениями будут, следовательно,
гипергеометрические функции. Далее, при /и = О G) сводится к уравнению Лежандра,
которое имеет два независимых решения. Каждое из этих решений может быть
разложено в ряд по возрастающим степеням iq в окрестности y] = 0. Однако
в общем случае эти ряды при iq= + 1 не сходятся. Но если взять
р^=п(^п-\-1), где « = 0,1,2,..., то один из рядов оборвётся после конеч-
«ого числа членов и будет иметь конечное значение в полюсах. Эти решения
мы получим
1) Следует заметить, что предел, к которому .стремится интеграл D6) при 5 -» О,
не обязательно равен значению интеграла при 5 = 0, так как последнее требует
«епрерывности функции, определяемой этим интегралом, в окрестности точки 5 = 0.
Этот момент и лежит в основе всей теории преобразования Лапласа. См., например,
у С а г S1 а W, Introduction to the Theory of Fourier's Series and Integrals, 2-е изд.,
<:тр. 293, Macmiilan, 1921.
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕР^!ЧЕСКИХ КООРДИНАТАХ [7.3]
353
в виде полиномов, удовлетворяющие уравнению
{l-ff)
^'^^ + '^(''+1)^ = ^'
(8)
называются полиномами Лежандра и обозначаются через Pn{fi)- Если
продифференцировать (8) /п раз по % то получится
., оч d^w п f 114 dw
где w = d^vfctrf^. Сделав, наконец, последнюю замену зависимой перемен-
т
ной 'ау = A—г^^) 2 /2G)), мы получим уравнение G) в виде
Решениями уравнения A0), конечными в полюсах iQ = rt:l и, следовательно,
периодичными относительно 6, будут присоединённые полиномы Лежандра
dri
A0)
(П)
Для каждой пары целых чисел существует ещё одно независимое решение
Qli i^i), которое обращается в бесконечность при irj = dz 1 и которое,
следовательно, непригодно, для представления физических полей в пределах всей сферы.
Данное в A1) определение присоединённых полиномов Лежандра имеет
смысл только для положительных целочисленных пит. Функции с
отрицательными индексами довольно просто связаны с функциями с
положительными индексами, но мы не приводим их, так как они нам не понадобятся.
Для того чтобы избежать какой-либо путаницы в этом вопросе, мы возьмём
в качестве частных решений F) действительные функции cos wcp, sin то
и ограничим значения W и п целыми положительными числами или нулём.
Из A1) ясно, что при т^п полином P^(v]) равен нулю, так как Р„ (-rj) есть
полином п-й степени. Действительно, мы имеем
т
A — У]2J ^n+m(vj2__l)n
РпХ^)
2^»л!
A2)
Функции Лежандра являются наиболее известным примером
гипергеометрических функций, свойства которых были изучены настолько подробно,
что едва ли представляется возможным в пределах имеющегося в нашем
распоряжении места дать сколько-нибудь исчерпывающее изложение
многочисленных интегральных представлений этих функций или их разложений
в ряды. Мы выпишем только необходимые рекуррентные соотношения:
(„_;„-^1)Р«^^_Bп4-1)'/)Рп+(« + '«)^п-1=^0,
рОТ
if:
-,m —1
'п+х=>'ПРп-{-Кп^т)УГ^^РТг
|/rZ-^p^ + i = 2/n^P^ —(й4-/и)(п —/и-|-1)У'Г=^/>^
— I
VT^^p^=^{pZX\-p'^±\).
т
VT
^n=lyi[in-m-{-l)in^m)P^-' + P';i+'-]Jr
-hmVl-fi^P^.
A3)
23 Зак. 593. Теория эпектромагнетизма.
354
гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
К НИМ МОЖНО добавить дифференциальные соотношения:
I»»
dp'
A-7J)
diq
{n+m)PT-i — niiPn,
^-=_,лг:г^^-^=4{(«-'"+1)(''+'»)^'Г'-яГ")
dy]
A4)
Заметим мимоходом, что этим же соотношениям удовлетворяют и функции
второго рода Q^.
Функции cos то Рп (cos б) и sin пкр Р^ (cos 8) периодичны на поверхности
единичной сферы, и число )гзловых линий определяется индексами тип.
Так при /n=sO поле от экваториального з^ла ц> не зависит; если при
этом п также равно нулю, то
функция на всей поверхности
сферы постоянна. При л = 1 имеется
одна узловая линия, проходящая
по экватору б = 1с/2, вдоль ко-'
торой функция равна нулю. При
п = 2 узловых линий две; они
проходят по параллелям,
соответствующим приблизительно б = 55°
и б = 125*^. Таким образом,
сфера делится при этом на три зо-
Рис. 69. Развёрнутая поверхность сферы, на ко- ""' Функция положительна в по-
торой показаны узлы функции sin ScpPHcos 6). лярных зонах и отрицательна
Заштрихованные области соответствуют её от- в экваториальной зоне. Продолжая
рицательным значениям. .-. тем же. путём дальше, мы
получим, очевидно, что число узловых
линий равно п, а число зон, в пределах каждой из которых функция
сохраняет свой знак, равно п-\-1. В пределах каждой из зон функция сохраняет
свой положительный или отрицательный бнйк. Поэтому, функции Я„ (cos б)
часто называются зональными гармоническими функциями. Если теперь т
480°
180 9
т
ОТЛИЧНО ОТ нуля, ТО благодаря- множителю A — f^)'^ функция обращается
в нуль в полюсах, а число узловых линий, параллельных экватору, равно
п — т (см. приложение IV). Кроме того, функция обращается в нуль и вдоль
меридианов, определяемых корнями cos/na> и sin/no). Очевидно, имеется т
меридиональных узловых линий, пересекающих широтные узловые линии под
прямым углом, и, таким образом, поверхность сферы разделена на
прямоугольные области или клетки, в пределах каждой из которых функция
попеременно либо положительна, либо отрицательна. Функции zosm^Pn {zosb) и
sin /иа> Р^ (cos б) часто называют поэтому тессералъными гармоническими
функциями п-й степени т-то порядка. Очевидно, имеется 2п-\-\ тессе-
ральных гармоник п-й степени. Подобное разделение поверхности сферы
.на положительные и отрицательные области показано графически для функции
sin Зф ^5 (cos б) на рис. 69.
Если тессеральные гармонические функции з^ножить на систему
произвольных постоянных и просуммировать, то мы получим
поверхностную сферическую гармоническую функцию п-й степени, с которой
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ Б СФЕРИЧЕСКИХ КООРДИНАТАХ [7.31 355
МЫ уже имели дело в главе III:
Уп F, ?) == 2 («пш cos m-f -|- Ьпт sin /пер) Pt (cos б).
A5>
Тессеральные гармонические функции образуют полную систему функций^
ортогональных на поверхности сферы ^). Интегрированием A2) по частям
легко показать, что
+1
+1
dy]
J Pi (v)) Pf (^) rfv) = 0, J р:г (-/)) T^rH ifr^2 = 0
—1 —1
при n-zfzl или при тф1. соответственно и что
2 (П + /И)!
A6).
/{/^"(^)Р^^ =
—1
+1
^ [РпЫУ
rfv]
2w-t-l (л —m)!'
1 (л + т)!
—1
m (Л — т)\
A7)
Из этих соотношений следует фундаментальная теорема о разложении
произвольной функции в ряд по сферическим гармоническим функциям: Пусть
^(8,9) будет произвольной функцией на поверхности сферы, непрерывной
вместе со всеми своими первыми и вторыми производными. Тогда ^(б,а>)
может быть представлена в виде абсолютно сходящегося ряда
поверхностных гармонических функций
со
^(e.?)=2Ko^«(cose)H-
п = 0
п
-Ь2 («nmCOsmcp-|-&«»»sin/n<p)Pn (cosG)], A8)
7П =1
коэффициенты которого определяются соотношениями
а
2л+ 1
2>с 1С
по
4те
f J ^ F, ?) Яп (cos б) sin е db rfcp,
о о
«»w 2Г~ (л + m)!
2>с 1С
/ J ^ F. ?) Рп (COS б) cos /иср Sin ЫЬ d%
о о
2к 1С
*«ш = ^ Й-г-5; / / ^ F. ?) ^п (cos б) Sin то sin е ^е d^.
о о
A9)
В случае функции, зависящей только от 6, условия сходимости разложения
по полиномам Лежандра совпадают с условиями сходимости ряда Фурье.
В указанном случае достаточно, чтобы функция ^F) и её первая
производная были кусочно непрерывны в интервале О <] б <^ 2тт. С другой стороны»
теория сходимости разложения A8) по сферическим поверхностным гармо-
1) Доказательство этого утверждения и следующей далее теоремы о
разложении можно найти V Р. Куранта и Д. Гильберта, Методы математической
физики, М.—Л., ГТТИ, 1933, гл. VII, § 5. За дальнейшими подробностями следует
обратиться к Hobson, Theory of Spherical and Ellipsoidal Harmonics, Cambridge
University Press, 1931.
■^56 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
никам представляет значительно большие трудности, и распространение тес
ремы о разложении на разрывные функции выходит за пределы этого обзора.
Нам осталось только установить характер радиальных функций fi(R),
_ 1_
удовлетворяющих уравнению D). Если мы напишем Д в виде Д = (kR) ^ v {R),
то легко показать, что v{R) удовлетворяет уравнению
Следовательно, согласно разделу 6.5, v{R) — цилиндрические функции
полуцелого порядка
Характеристические или элементарные волновые функции, конечные и
однозначные во всех точках на поверхности сферы, будут, следовательно,
^е = -TFUF ^п-'^ ^^> ^" <^'^' ^> s°n "''^- B2)
тп \ kR n-rj- s»n
Как и в случае цилиндрических волн, в области, включающей начало
координат, мы берём в качестве Z i {'iR) бесселевы функции первого рода, а
там, где поле представляет собой бегущую волну, — функции третьего рода.
7.4. Свойства радиальных функций. В разное время для радиальных функ-
1
ций {kR) ^Z 1 {kR) применялись различные обозначения, но ни одно из
" + -^
них не получило всеобщего распространения*). Мы будем придерживаться
обозначений, которые были недавно предложены Морзе 2) и которые
представляются нам более или менее логически обоснованными. В соответствии
с этим мы определим сферические бесселевы функции соотношениями
2? M+i-^'^"' •'^^^'^ V 2p-„4-i^
B3)
Разложение этих функций в ряд около точки р =^0 может быть
получено непосредственно из (8) и A1), стр. 315. Если вспомнить, что V{z-\- 1) =
= 2'Г(г'), rf-p-j = '|/'it и воспользоваться формулой удвоения, согласно ко-
,торой
"То для 7„(р) получим
со
/ {о\ = 2попУ {-\)-^{п + т)\ о^ 25)
JnKV) — '^9 Za m!Bn-i-2m-t-l)! Р ' ^^^^
fM=0
1) См. Watson, Bessel Functions, стр. 55, Cambridge University Press, 1931.
2) M о r s e. Vibration and Sound, стр. 246, Me Graw-Hill. 1936.
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ [7.4] 357
откуда очевидно, что /„ (р) является цеЛрй функцией. Точно так же и»
соотношения N i (р) = (—1)'»--У j (р) для функции второго рода
мы получаем
со
^пК^)— 2V^-i^ m!i (n-m+l) Р ' ^"-^^
т — О
Обратимся теперь к представлениям в случае, когда р — очень большое
число. На стр. 316 разложение по убывающим степеням р было дано для
функций произвольного порядка р. Подобные ряды формально удовлетворяют
уравнению Бесселя, но являются лишь полусходящимися. Однако, как мы
можем заметить, при р = п-\--^ ряды Р i (р) и Q i (р) обрываются^
J 2
так что вопрос о сходимости вообще отпадает. Соответственно - с этим,,
выражения A3) и A4), стр. 316, будут аналитическими представлениями.
J 1 (р) и N 1 (р). Очевидно, кроме того, что эти функции полу-
целого порядка могут быть представлены в виде конечного числа членов^.
Из B3) и из уравнений A3) и A7), стр. 316, мы получаем, что
;„ (Р) = j { Я^ ^_, (Р) cos (р - ii±i .) - Q^ ^ ^ (р) Sin (р - iii-.) }. B7>.
«п (р) = у [я^ ^ L (р) ^^Чр ~ ^"") + ^п+4-^^^''^К''~" ~t-^)]' <^2^>
где
% + :1.^Р) —1 W^^ 1 2*^4!^* •••' ^^^У
^п+ \-^> 2Тй^ ^ЛГ? 1- ' • • C0>
Для функций третьего и четвёртого рода эти выражения дают
hl\^) = ир1е^9 {Р , (Р) 4-i-Q„ , 1 (Р) },
т+1
h'i'(Р)=~-^-''{Р,,^ (р)-^'^ . 1 (р)}• I
C1>
Эти ряды сходятся весьма быстро, так что при больших р достаточно
точные значения дают уже одни только первые члены. Таким образом, при;
р —>-схэ
;„ (р) ^ - cos ^р — ^?Ц— 7г), п„ (р) ^ - sin ^р — .^ф- тг),
л;?)(р)^ l(_/)n+Vp, h^^\p)^-in+ie~^
C2>,
Рекуррентные соотношения, которым удовлетворяют сферические бес-
селевы функции, получаются непосредственно из уравнений B4) — B7),
стр.317:'
■2'и-1 ~Г ^«4-1 ^= 1 ^п> C3).
-;^2-„(p) = 2^^^il«^n-i~(«-flJ-„+i}, C4>
^ { Г-^'^п (Р) } = P'^+^^n-l, -Jf { r^'Zn (Р) } = -Р-'^^ПЧ-!- C5>
358
гл. VII. СФЕРИЧЕСКИЕ волны
Определив таким образом радиальные функции, мы можем, наконец,
написать общее решение уравнений C) в виде суммы элементарных
сферических волновых функций. В том случае, когда f(R, 6, <р) должна быть
конечна в начале координат, мы имеем
/(^)(/?,e,cp)=2/n(^ko/^n(
п
« = 0
:cos 6) + 2 (Лпж COS то -{-
m = 1
-\-b„^smmo)P^icosb)\,
C6)
в то время как поле, у которого поверхности равной фазы перемещаются
наружу, выражается функцией /®(/?, 6, о), получаемой из C6) заменой
Jni^R) на п^ {кН). Сферически симметричные решения получаются в том
случае, когда все коэффициенты, за исключением uqq, равны нулю. С
точностью до произвольного множителя мы получаем, следовательно, что
A) sin kR
/о —
kR
-B) COS kR
fl
?)
kR
e^
J<R
/0
D)
kR
-iJiR
C7)
7.5. Теорема сложения для полиномов Лежандра. Если ^F, <р) —
какая-либо функция, удовлетворяющая условиям теоремы о разложении A8),
то её значение в полюсе 8 = 0 должно быть равно
2>с 1С
[^(е,?)]б=о = 2'''^о=^^B«+1)//^а?)я„(со5еMше^ейГ'^,C8)
«=0 п=0 0 0
-Ml
потому что Р;Д1)=1, Р„A) = 0. Возьмём, в частности, в качестве
функции g(b,(f>) какую-либо позерхностную гармоническую функцию п-й
степени У„F, 9)t выражение которой даётся
формулой A5). Тогда, в силу соотношений
ортогональности, сумма C8) сведётся только
к одному члену, и в результате мы получим
следующую формулу:
2к к
. j / Уп(<^. '■P)/'„(cos 0) Sin е rfO do
о о
4зх
ф^у{Уп(<Ь 9)]ь^0' C9)
Рис. 70. К теореме сложения.
С помощью этой формулы мы получим
выражения для преобразовакия зональных
гармонических функций при переходе к новой
системе отсчёта. Пусть Р на рис. 70 будет
точкой на сфере, координаты которой в
данной ортогональной системе отсчёта будут 6 и «р. Координаты другой точки Q
пусть будут а и р, а угол между осями QP и 0Q равен- ^. Зональные
гармонические функции в точке Р по отношению к новой полярной оси 0Q
будут иметь вид P^(coSy). и наша задача состоит в том, чтобы выразить
Pnico^i) через координаты б, ср и ее, р.
На единичной сфере cos^ равен, очевидно, проекции линии ОР
на ось 0Q. Если х, у^ г — координаты точки Р, а х', у\ г\ — ко-
Ы-fIfi ■ ■-■■!
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ [7.^ 359
1 "
Ординаты точки Q, то
cos Y == хх' -{-уу' + гг' = sin 6 sin а cos (9 —■ Р) + cos б cos ее, D0)
Предположим, что искомое разложение для Р^(с08^) имеет вид
и
Рп (cos т) = -f Рп(cos 6) -}- 2 (с„, COS mcp + d^ sin /«(?) P,? (cos 8); D1)
OT = 1
умножим обе части на Р^ (cos б) cos то и проинтегрируем по всей
единичной сфере. Воспользовавшись ещё раз соотношениями ортогональности, мы
получим
J J Р izos ч)РТ, (COS Ь) COS то sin bdb do = ^^-^±^с„,. D2)
0 0
Но, согласно C9),
Г Г ^и (cos "О Рп (cos б) COS то sin 6 йб cfc =
о о
= 2^ ^^" (^°' ^^ ^°' '^'^^т=о = slTfT Р» (cos а) cos /«р, D3)
так как при ^=0 имеем 6= а, о = р. Следовательно,
Аналогично
^- = 2-(Ьг^^"(^°'^>'^"''^Р- . (^^>
Искомое разложение или формула сложения будет, следовательно,
Рп (cos fi = Рп (cos ос) Рп (cos б) -f-
п
m = 1
На основании этого результата мы можем дать иное выражение для
теоремы, сформулированной на стр. 355, а именно: если g{^,o) и её
производные обладают необходимыми свойствами непрерывности на поверхности
.сферы, то ряд Лапласа A8) для этой функции будет иметь вид
g{%^)='lYn{M), D7)
или, в силу A9) и D6),
и = 0
2ic г:
^F, ?)=^S(^'' + ^> J /^^"' ^)Pn{zos4)sma\dad^. D8)
n=0 О О
7.6. Разложение плоской волны. Теперь можно сравнительно просто
получить разложение плоской волны, распространяющейся в произвольном
направлении, на элементарные сферические волны относительно какого-либо
заданного центра. Направление распространения и длина волны определяются
в плоской волне .волновым вектором к, прямоугольные компоненты которого
равны
^^^ =^sinacosp, kg = ^ sin а sin р, ^3 = ^ cos ее. D9
360 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
Координаты произвольной точки наблюдения будут
л: = /?sin6 cos9, y==Rsinbsin% z = Rcosb. E0)
Фаза ВОЛНЫ определяется тогда выражением
kR = ^/? [sin ос sin 6cos(cp — р)-}- cos а cos б] =Ai?cosY. E1)
Функция /^^^ (/?, б, ф) = ехр {ikR cos ^) непрерывна и имеет непрерывные
производные всюду, включая и начало координат R = 0. Она может быть,
следовательно, разложена -по формуле C6), стр. 358. Рассмотрим прежде
всего ось, направление которой совпадает с направлением распространения
волны. В силу симметрии волны относительно этой оси, мы можем написать,
что
с»
gikRcosf^ 2 anUikR) Рп {cos-i), E2)
и = 0
Коэффициенты могут быть определены обычным способом, путём
умножения обеих частей равенства на Р„ (cos -у) sin т и интегрирования по т от О
до 71. Тогда, учитывая A7), получаем
1С
anjn {kR) = ?^^ J ei^R^'^^'-i Р„ (cos -у) sin -уйГт. E3)
о
Для того чтобы избавиться в этом соотнскиении от зависимости от R^
продифференцируем обе части по р = kR и положим затем р = 0. Так как,
согласно B5),
Гrf"in(P) 1 _ Пп\)^ . ....
L а^г Jp.=o"Bn-hl)!' ^^^>
■к
о
Интеграл справа легко берётся, и мы получаем, что а^ = Bп -j- 1) /», т. е.
со
^гкВ cos f == 2 i'^ Bп -f 1 );n (kR) Pn (COS 7). E6)
и = 0 ,
' i.
Если ось z координатной системы не совпадает с направлением
распространения волны, то.мы можем воспользоваться теоремой сложения D6),
для того чтобы записать E6) относительно произвольной системы
координатных осей. Мы получим тогда
то
со
gik Е COS т ^ 2 in Brt -\- \)j^ (kR) I P„ (cos Of) Pn (cos 6)
n = 0
n
+ 2 S -(^ТЙГ^"^'°'°'^^"^'°' e)cosm(9-p)}: E7)
7.7. Интегральные представления. Мы нашли, что в определённых
случаях оказывается удобным представлять волновую функцию в виде суммы
плоских волн с соответствующими весами или амплитудными множителями.
Направление распространения каждой из таких плоских компонент
определяется углами аир. Интегрирование должно быть распространено по
всем возможным направлениям в пространстве и может- в некоторых
случаях включать и мнимые значения а или р. Как и в разделе 6.7, мы
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ в' СФЕРИЧЕСКИХ КООРДИНАТАХ [7.7] 361
^' ■ ■ II II. ■ —М^-.Ч . ■■,.,- I ,-■.■■„■„ i III |..,|».| II .11 .11- .III „I ,
хотим найти представления вта.
f (X, у, Z) = (da fd^ g (a, p) e*'''(a'9in«cosp+2/sin«einP+2cosa) ^53^
или, если x = Rsinbcos cp, у = Rsin б sin cp^ z = cos 6,
f(R. 6, ?) = jdajd^gia, P) e*v.J2cosT^ E9y
где a и p — углы, показанные на рис» 66 и 70. В случае цилиндрической
волны постоянная частота и постоянная длина волны вдоль оси z приводят
к постоянному значению а, так что направления плоских волн,
представляющих цилиндрическую функцию /(а^, и^), образуют круговой конус.
Поскольку у сферических волн подобное преимущественное направление
отсутствует, интегрирование должно производиться и по а, и по р.
Интегральное представление элементарной сферической волновой
функции может быть получено непосредственно из разложения E7). Если обе
части этого уравнения умножить на Рп (cos а) cos т^, или на Р^ (cos а) sin mp,.
то благодаря соотношениям ортогональности A9) мы получим в результате
in ikR) Рп (COS б) ^°! тер = -^ г се*^-=£со8т р^ (cos а) ''?^ /ир sin а da rfp. F0)
^111 fxTw J J dill
и 0
После умножения обеих частей на произвольные постоянные а^щ и Ь^^ и
суммирования по т результат этот может быть записан также в виде
2r r
inikR) F„(e, cp) = l^ J Je^'^BcosT Y„{oi, p)sinadocrfp. F1)
0 0
Из этих общих формул можно получить много полезных выражений для<
различных специальных случаев. Так, например, положив m = О, 8=0, мы
получим представление для сферической бесселевой функции JnO^R)
к
;•„ {kR) = ^ J e«'^^*^°s«P„ (cos а) sin а da, F2)
или
+1
-1
Легко показать, что интеграл
Jn {kR) = V J ^'''^' ^" ^'^^ '^'^- ^^^>
z„ikR) = i-nj e^J^^-^P„ifl)d'n F4)
с
действительно удовлетворяет уравнению D), стр» 352, при условии, чта-
пзп'ь интегрирования С выбран таким образом, что билинейное выражение
A —^^) (^ - №Рп) е^^-^ 1^ = О F5)
исчезает на пределах интегрирования. Вместо y] = ±: 1 мы можем
выбрать такие значения, при которых исчезает экспоненциальный
множитель. Так, если k действительно^ то в качестве верхнего предела мы
362 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
можем взять ri=-ico и получить следующие представления:
1 )
h^n\kR) = i-"^ J ^^'^ Рп {ч\) d-n.
ico
ioo
h^^ (kR) ==;/-" J ei^^-^ P„ (Yj) d-q.
—1
F6)
Если из-за проводимости среды k комплексно, то мы можем взять тот из
«орней k^^ мнимая часть которого положительна, и предел y] = /oo заменить
на 7) = со.
Из F0) и E4) мы можем получить представления и для функций
Р„ (cos 6), положив о и R равными нулю:
РГ(со8 е) = ~^j^^ j j cos^-iPn (COS a) COS m^ sin a dad^. F7)
0 0
Выполнить интегрирование по a с помощью имеющихся в нашем
распоряжении формул затруднительно; можно, однако, показать иным путём, что
выражение F7) приводится к такому:
р^ (COS б) == ^"^^^^ i"^ j (cos е-I-'i sin e cos P)'^cos m^ d^. F8)
0 ■
Заметим, наконец, что воспользовавшись для бесселевой функции
интегральным представлением C7), стр. 323, можно привести правую часть F0)
к однократному интегралу. При © = О
Jn(kR)P%(cosb)==
== '-^ J е«*^ *^°« «*^о« в j^ (^kRsin е sin а) Рп (cos а) sin а da. F9)
о
7.8. Интеграл Фурье-Бесселя. Предположим, что /(л;, у, г) —
произвольная кусочно непрерывная функция с кусочно непрерывными первыми
производными и что интеграл от абсолютной величины этой функции,
распространённый по всему пространству существует. Тогда .для этой функции
существует интеграл Фурье -
Z оа со со •
fix, у, Z) = (J^J j j jg(k,, k^ k^) ^(^^1^ + ^>y + адdk, dk^ dk^, G0)
—OO CO OQ
a функция, преобразованная по Фурье относительно /, будет
3 оо CXS со
^(^1, ^2,^з) = (-^)^ J J ^f(,x,y,z)e-^^^^^^ + ^*y + ^^'')dxdydz. ill)
-оо CO CXS
Мы Преобразуем теперь эти интегралы к сферическим координатам,
предполагая молчаливо, что тройной интеграл по бесконечному кубу может
быть заменён интегралом по сфере бесконечного радиуса. Следуя тому же
пути, что и в разделе 6.9, и замечая, что k^x-\-k^-^k^^kRcos-^i,- мы
СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ 17.91 ЗбЗ
ai<viy4aeM
3 оо к 2к
ПЯ, 8, 9) = (^) 'J f J^(a. ^,k)e-i'^^'^<^-'k^sinadkdad^, G2)
(К о о
3 оо в 27С
g{a\ р, ^)=(-^) ^ J f j f(^> ^' о) e-i^^^'^^iR'^ sin bdRdb do. G3)
0 0 0
Предположим теперь, что /(/?, 6, w) =/„ (/^) К„(б, cp). Ha функцию
Уп (^)> в остальных отношениях произвольную, мы наложим условие
кусочной непрерывности вместе с её первой производной и потребуем существо-
оо
вания интеграла j\fn{R)\dR. Тогда
о
3 оо ге an
^(ос, ^^k) = (j^y J RMRfniR)j (* F(Q,9)e-^^^<^<'«ifsin6rf6rfc?. G4)
о о
Это выражение, в силу соотношения F1) и того, что 7„(—kR) =
= (—iyjn(kR), переходит в следующее:
g
— "^
(ос, р, k) = (- 1)-F„(a, P)l/ ^ jfn (R)Jn(kR)R^dR, G5)
или g(a, p, k)={— 1)*^ J'n(°'> P)§"n(^)- Внося это значение для
преобразованной функции обратно в G2) и снова меняя порядок интегрирования, мы
находим
— °°
fn(R)yni^4>)=^y ^j gnik)Jn(kR)k4kr„(b,o), G6)
о
откуда получается ещё одна симметричная пара взаимно преобразующихся
функций
/ °°
о
оо
g(k)=}/^^jf(R)U(kR) R4R. G8)
о
Индекс п здесь опущен; поскольку он не имеет более какого-либо
специального смысла. В частном случае и = 0 уравнения G7) и G8) сводятся
к обычному интегралу Фурье A8), стр. 257. Если выбранное значение
R совпадает с точкой разрыва непрерывности функции /(/?), то мы напишем
оо оо
4/ ^^йrA; J/(p);„(^p);„(^p'^dp = l[/(/? + 0)+/(/?-0)l. G9)
о о
7.9. Разложение цилиндрической волновой функции. При подсчёте
излучения заданного распределения переменных токов иногда бывает
необходимо выразить цилиндрическую волновую функцию в сферических
координатах. Интегральное представление для волновой функции, конеч-
364 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
ной на ОСИ, будет
COS - - '■-*"
sin
■°^ ms>J^ Ckr) е^^' = V^ Г е^^ ««^ №-?) +*^^^ ^°^ wS й?8. (80)
in ' "^^ ^ 271 J sin ^^ ' vv^"/
о
Далее
kR = Arcos(p — 9)Ч"'^'2' = ^^{ sin а sin 6 cos (© — ^)-|-cqsa cos 6 }, (81>
a на стр. 360, формула E7), мы имеем разложение функции ехр (fkR) по
соответствующим сферическим волновым функциям. Интегрируя по р, мы
получаем
"^^^m^J^ Ckr) е^^^ =
sin ' т\ /
со
= V i.-B« + l)|^^^°;m'^P^(cosa)Pr(cos6);,(A;/?). (82)
и = 0
Так как при т^п полиномы Р^ равны нулю, то первые /и членов в (82) —
нули, и можно написать разложение в виде
J^ (Ar) e'^^ =
= 2 ^'Мг» Н- 2^ + 1) („ j^m)l ^"+" ^^"' "> ^^+ ^ ^'°' ^^-^''^^^'^ ^^-^>- ^^^>
л!
г« ( z« ч-ZW-+- 1);—г
Если ОС = тг/2, то Л = О, X = yfe, и
■
О, если я нечётное,
'^n+wiO)— S : 1—^—-—,—'- ^—, если п четное. К°^г
2n+m-i(^^y,(±^,n-iy.
В результате мы получаем разложение цилиндрической бесселевой функции*
в ряд по сферическим бесселевым функциям
со
-^2^1-^rn-i 2/+2m /!(/+m-l)! Р-21+ш (cos b)j^.,^(kr). (85)-
г;=о
7.10. Теорема сложения для функции Zo(kR). Пусть P(Ro, ^, ®) будет
точкой наблюдения, а QiRu^u?i) — источником сферической волны.
Координаты Rq, 6, <р и /?j, 6j, ©1 берутся относительно фиксированной системы
координат, начало которой находится в точке О. Расстояние от Q до Р-
равно
R = V^Rli-Rl — 2RoR,cos^^
где cos "Y = cos 6 cos 6j -j- sin 6 sin 6^ cos (<p —©j). Наша задача состоит в том,
чтобы выразить сферическую волну, распространяющуюся из точки Q, в виде
суммы сферических волн, источник которых расположен в точке О. Решение
этой задачи в общем виде требует длительных вычислений, а её
практическое значение не настолько велико, чтобы оправдать затрату времени и
места. Однако в теории излучения мы будем иметь пример применения*
одного специального случая этой теоремы, а именно случай преобразованиям
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В. СФЕРИЧЕСКИХ КООРДИНАТАХ [7.11] 365
ВОЛНЫ, сферически симметричной относительно источника Q. Для этого
случая без особого труда можно получить следующие разложения:
со
Jo (f^R^ = '-^ = ^Bп + 1)Р„ (COS т);п ikRo)u ikR.X (86)
n = 0
С об
о ^'^^^ ikR
,A),
2 Bл -Ь 1) ^п (COS 4)jn ikRo) Ий' {kR,) (/?о< /?i),
":' (87)
2 Bи +1) Р„ (cos т);„ (A;/?i) Л^^^ (А;/^о) (^?о > ^?i)-
l и = о
Их доказательство предоставляется читателю.
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ
7.11. Сферические векторные волновые функции. Как и в случае
цилиндрических координат, можно получить решения векторного
волнового уравнения в сферических координатах непосредственно из
характеристических функций соответствующего скалярного уравнения. Следуя
обозначениям предыдущего раздела, мы положим «{'е =/е -е—**"*, где 4 —
характеристическое решение
Согласно разделу 7.1, одйо из решений векторного волнового уравнения
grad div С — rot rot С -j- ^^С = О B)
может быть получено, если просто взять градиент от A). Мы
определяем L как grad 4* и отщепляем временной множитель, полагая L = Ie~*'"*.
Тогда,. согласно (95), стр. 57,
\тп =4п^п т)Рп {COS 6) 1'^ mcpii + ^г, (kR) -^ Р^ (COS 6)'^^ moi,zt
~ТШГЬ ^» (^^> ^" (^«^ ^> с1" '"^^з, C)
где i^, 12 и ig—единичные векторы, изображённые для сферической системы
координат на рис. 8, стр. 56.
Для того чтобы получить независимые решения М и N, мы должны
в соответствии с разделом 7.1 ввести постоянный вектор а. Подобная
операция в данном случае, конечно, допустима, но полученные таким образом
функции М и N не будут на всей поверхности сферы ни нормальны, ни
чисто тангенциальны. Вместо а мы воспользуемся радиальным вектором i^;
тогда векторная функция [L, ij будет тангенциальна на всей поверхности сферы.
Нэ i^ — не постоянный вектор, и мы не можем, следовательно, утверждать
а priori, что получим таким образом независимое решение. Мы покажем, однако,
что тангенциальное решение М действительно может быть построено с
помощью радиального вектора i^. К сожалению, этот путь неприменим для более
общих координатных систем.
Попробуем построить решение уравнения B) в виде вектора
M = rot(ii«(/?L.)==[L,iJ«(/?),
366 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
- _
где u{R) — неизвестная скалярная функция R. Тогда, если AJ^y М^ и Ж^
представляют собой /?-, 6-, <р- компоненты вектора М, то
Дивергенция М равна нулю, и уравнение rot rot М — к^Ш = 0 мы разложим
теперь на /?-, 6- и ^-компоненты по формулам (85), стр. 55. /^-компонента,
тождественно равна нулю при любом выборе и (R). Условия. для 6- ш
<р-компонент будут выполнены, если и (R) будет удовлетворять уравнению
al-c»'!') + ^4гг -ш ['•"«-к («*) ] +
+^inl^W+*M=o- E>
(Особое преимущество сферической системы координат по сравнению с более
общими системами состоит в том, что это условие одинаково для обеих
тангенциальных компонент.) Следовательно, если мы возьмём и (R) = /?, то
соотношение E) сведётся к требуемому уравнению
^^-]~кЦ = 0. F>
ч
Таким образом, в сферических координатах уравнение B) удовлетворяется-
функцией
М = rot (R 4-) = [L, R] = ;^ гЫ N, G)
компоненты которой равны
Компоненты третьего решения легко могут быть найдены из соотношения
A5N = rotM:
^^^— дй^ -Ь'гА^ф, ^^—kR dRdQ ' ^Q — kRsiriQdRd^' ^^^
Так как 4* должно удовлетворять уравнению D), стр. 352, то радиальная.'
компонента приводится к более простому виду ^) . .
м,=.ищ^^: - СО)
Для того чтобы получить развёрнутые выражения дли векторных волновых
функций М и N, нам необходимо только произвести
дифференцирование A) в соответствии с формулами (8) и (9). Временной множитель мы
1) Первое полное исследование электромагнитной задачи о сфеое было
проведено Ми ГМ i е), Ann. Physik 25, 377, 1908, и Дебаем(ВеЬуе), Ann. Physik, 30,.
57, 1909. Оба автора пользовались парой потенциальных функций, которые приводят
непосредственно к нашим векторам М и N. Связь между этими решениями и
радиальным вектором Герца была указана Зоммерфельдом в книге Франк-Мизес^
Интегральные и дифференциальные уравнения математической физики, ОНТИ, 1937^
стр. 892.
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ 17.121 367
отщепляем; написав М = m е-*"»*, N = пе-*"*', и получаем
%„ = "Т-' ^» (*«>""" ("^ *> sin «^'i +
-*«3;лщ1'?^»(*«м^(-=°^<!^'«<рЬ- A2>
7.12. Интегральные представления. Волновые функции 1, m и п
могут быть представлены в виде интегралов от плоских векторных волн,,
подобных интегралам A8)—B0), стр. 347. Согласно соотношению F0),.
стр. 361, для функций первого рода, которые конечны в начале координат,
мы имеем
/0) =^^\\ е'"'^'''' 'P^icos a)?Vpsinarfarfp. A3>
о 0 0
Прежде всего дифференцированием под знаком интеграла мы найдём выра-
df I df 1 df ,,
жения для компонент градиента, а именно -ш i -р "Ш ^ р • в ~г • *^з
рис. 70, стр. 358, видно, что если вектор к (а,Р) направлен вдоль линии 0Q,.
а RF,cp) — вдоль линии ОР, то
kii z=kcos'{ = k [sin а sin 6 cos (cp — P)-j-cosacos 6],
kig = k [sin a cos 6 cos (o—P) — cos a sin 6],
kig = — k sin a sin (cp — p),
A4)
где единичные координатные векторы сферической системы координат
берутся, конечно, в точке наблюдения Р. Тогда без дальнейших вычислений^
ясно, что
'"L = l?// k(a,P)/"'->P:(cosa) ^°^ m?slnadad?. ^'^
О О О
Соответствующие представления для т^** и пО) мы получим, заметив, что
iR, к] = /ji?{ sinasin(cp — p)i2-|-[sina cos 6 cos (ф —Р)—cos а sin 6] ig},
[[к, RI, к] = k^R {sin^Yii — cos -y [sin a cos 6 cos (cp — p)—cos a sine] ig-f ; A6>
+ cos Y sin a sin (9—P) is},,
и дифференцируя согласно (8) и (9), в виде:
< =1?// [k.Rl^''^'"^^^(cosa)^^°^^mPsinarfadp, A7>
о*"" о о
2я к
1-п
°г„=1^ / /1 !№• «1Ч+2*1 ^'"^ "■' X
о О
COS
XP^icosayT^m^slnadad^. A8>
368 гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
Лля того чтобы получить интегральные представления функций третьего
и четвёртого рода, надо заменить интегрирование по а от О до тг
интегрированием по соответствующему контуру в комплексной области, как это было
описано на стр. 361—362.
С помощью этих интегральных представлений без труда можно
вычислить прямоугольные компоненты векторов I, m и п, хотя получающиеся
в результате выражения довольно длинны и громоздки. Подинтегральные
векторные выражения разлагаются на прямоугольные компоненты, после чего
мы получаем их в виде выражений, содержащих явно а, р, 6, о. Так,
например, ^а,= Л sin а cos р. Затем с помощью рекуррентных соотношений для
сферических гармоник эти множители исключаются, и интегралы приводятся
к виду, в котором они могут j6biTb вычислены с помощью A3).
7.13. Ортогональность. Очевидно, скалярное произведение любого
нечётного вектора на любой чётный вектор или на любой вектор с иным
индексом т будет ортогонально; необходимо рассмотреть, следовательно,
только такие произведения, которые не исчезают при интегрировании по со
от О до 27Г. Так
о о'"'* о
ДрШ pip'"* 9 \ 1
+{-ж ^г+ ^PnP^yk^n('"^:>''"(kR)], A9)
тде 8 = 0 при те>о и 8 = 1 при т ==0. Для того чтобы преобразовать
A9), мы Ьоспользуемся формулой
о
[ о, при п Ф п',
= { 2 (пНгтI ,. , 14 , B0)
I о—гт- т-^—(; п(п-\~\) при п=^п'.
\ 2п-\-\ {п—т)\ ^ ' ^ ^
*
Следовательно, при интегрировании A9) по 6 при пфп' мы получаем нуль,
а при п = п'
2к к
f ( L L sinbdbdo= ^
о х> о о ^
ч
Это выражение можно преобразовать к окончательному виду, воспользо-
•вавшись реккурентными соотношениями C3) и C4), стр. 357; тогда нор-
зйирующий множитель мы получим в виде
Я le™. h^ Slum d?=(i +8) (-5sw гаг "" f«'^»-' <*^)''+
+(п + 1)[г„^.1 (№))«). B2)
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ [7.14] 369
Те же формулы непосредственно приводят к интегралам:
2ic к
/Я»»-w^'" *'«''<?=('+«>2;гЬ |^»(«+1I^»(*«Ж B3)
о ji о о
2ic 1С
ЯПе Пе Sin bdbd(?=
О О о О
+ «K+i(A;i?)l2), B4)
в то время как все остальные произведения, в которых индексы п различны,
дают нуль.
Рассматривая произведения векторов различного типа, мы получаем,
во-первых,
2к
О
откуда
к 2ic
/ J »е«„П1,^п. Sin 6^6^9 = 0 B6)
0 0^
независимо от значений п и п'. Аналогично *
к 2п
Г/п1е«„зПо.„, Sin 6^6^ = 0. B7)
о о <> в
Как и в цилиндрической системе координат, ортогональность получается
неполной из-за произведения Ig^^ ^тп' ' интеграл от которого по всей сфере
при п =
1С 2ic
J J *«*""
0 0
п' не
"бтп
0
равен
нулю;
sin bdb do =
о
в
о
этом
случае
= ^^ +^> Bп+1)^ |n-m)i! ^("+ 1)fe{[^n-iX^^)P- [^n+i (fe/^)]^}- B8)
Для того чтобы получить полную ортогональность, мы можем, как и в
разделе 7.2, считать k' переменным параметром и интегрировать по k' и по R;
однако в большинстве случаев подобная операция оказывается излишней.
7.14* Разложение плоской векторной волны. При рассмотрении
дифракции плоской волны с заданной поляризацией на сферическом
препятствии мы должны сначала разложить падающую плоскую векторную волну
по сферическим волновым функциям 1^^^, ш^^^, Og^^
о о о '
Рассмотрим векторную функцию
f B') = ае*^ = ае**^<'°^'', B9)
г^ а — амплитудный вектор, ориентированный произвольно по отношению
к прямоугольной системе отсчёта. Разложим вектор а по трём единичным
24 Зак. Б93. Теория влевтромагнеткзма.
370 Гл. vii. СФЕРИЧЕСКИЕ волны
векторам, направленным соответственно вдоль осей л:, д> и г. Тогда
За; = sin 6 cos ср i^ 4~ cos 6 cos ср ig—sincpig; 1
aj^ = sie6sincpii-}-cos6sincpi2-}-cos<pi8; > C0),
a^ = cos 6 i^—sin 6 ig, )
где ii, ig, is — попрежнему единичные векторы, показанные для сферической
системы координат на рис. 8, стр. 56. Дивергенция векторных функций
йде ехр (ikz) и Ej, ехр (Ikz) равна нулю и, следовательно, они могут быть
разложены только по характеристическим функциям шип. При Rz=ssO поле
конечно, и нам нужны будут поэтому функции первого рода. Очевидно,
далее, что зависимость от <р вида C0) ограничивает нас значением т=\\
если мы рассмотрим после этого свойства чётности и нечётности у A1) и A2),
то установим, что разложение должно иметь вид
00
^jUR^b _ ^ (^^^w j^ ^^^w ^^ ^31)
n = 0
Для определения коэффициентов разложения мы применяем соотношения
ортогональности предыдущего раздела
1С 2R
J J a«m??„ е^^^ '"'^ ^ sin 6 db dcp=27t/» п{п +1) l/„ (kR)]^, C2)
о о
откуда, согласно B3),
<= ■^uirr)-"- <^^>
Аналогично
/ J a^niiL е*^^'''' sin bdbd^== . -
о о
=:~27:/»+ii^g±f |(«+l)L/„_i(^/?)l2 4-«[/„+i(A/?)l2}, C4)
что даёт, в силу B4),
Следовательно,
со
а^еш _ 2 in ^2^Д1-^ 1т^}п]-т%]. C6)
п = о '
Тем же путём для плоской волны, поляризованной в направлении оси^,
мы получаем '
со
Так как дивергенция от продольной волновой функции а^ ехр (ikz) не равна
нулю, то её разложение должно содержать и функции 1. Фактически
оказывается необходимой система только этих функций, и можно без труда
получить, что
1» = 0
ЗАДАЧИ , 371-
ЗАДАЧИ -
Ь Показать, что сферические бесселевы функции удовлетворяют соотношениям
+00 f О при mz^iii
J in (Р) Jm (Р) <?Р =
[ Y-2^"P«" = ^'
если п и m—целые числа, причём п ^О и т>>0. Относительно применения этих
интегралов к разложениям в ряды по бесселевым функциям с;м. Watson, Besset
Functions, стр. 533.
2. Показать, что цилиндрические бесселевы функции удовлетворяют соотйо^
шениям
и с помощью этих формул показать, что сферические бесселевы функции могут быть
записаны в виде
w.)>(-.,«p.)«,-^.(fi^)=-(-i ^п^).
3. Показать, что если /?2 —j^3_|_j^2_2j^q;?jCOsy,. то
+1
И
+1
COS kR ,, ,
-^^d{cosTf) = ^
1
sin URq cosfei?! D ^ D
cos*/?o sinfei?i D -^ D
—*ГБ л5 • '^O -^ '^l*
Л/?0 kRy
4. Показать, что в вытянутых сфероидальных координатах, определённых на
стр. 60, уравнение
Аф + /fe2 ф _ о
принимает вид
Показать, что если положить Ф ='I'l (^) Фа (>]) Фз (9)t то предыдущее уравнение
распадается на следующие три;
где m и С — постоянные разделения. Показать далее, что система волновых функций
для сплюснутой системы сфероидальных координат может быть построена из
от т
Ф«гп = а»-1)' A-4^)' Sei,„(c.Y])Re^„(c,6C"'f,
тле «радиальная функция» Re и «угловая функция» Se — обе удовлетворяют уравнению
, A — «2) у» _ 2 (т + 1) гу' -\-{Ъ — cV) у = О,
в котором m — целое-число или нуль, 6 = б"—от, а сЬ=Ы = 2яй/Х.
24*
372
гл. VII. СФЕРИЧЕСКИЕ ВОЛНЫ
5. Если волновые функции предыдущей задачи применить к полному сфероиду,
то нужно ПОЛОЖИТЬ mssO, 1, 2, ... и найти такую постоянную разделения Ь, при
дсоторйй поле в полюсах y] = :±: 1 бстёвалось бы койечйым. Тогда мы получим систему
дискретных значений в виде
*п = « (« +1) +/п(^). « = О, 1, 2, ...
Показать, что функции Se и Re могут быть представлены в^виде рядов
_т
S^lm ^'' ^) = ^^s TTi^)> Tf (z) = A - 2^) 2 Я«^^ (Д
8
где Р^л.гп — присоединённая функция Лежандра, а штрих над знаком суммы
показывает, что при п чётном надо суммировать по чбтным значениям s, а ripn п нечётном —
по нечётным значениям s:
8
тле js+m(c''') — сферическая бесселева функция. Независимое решение получается
заменой jfs+m(<^^) на л^+и» (<?«). Показать, что коэффициенты удовлетворяют
следующей рекуррентной формуле:
(s + 2m + 2)is + 2m+l) sjs-l) ' ,
Bff + 2OT-f 5)B5 + 2m + 3) ^+' "^ B5 + 2/я — 1) B* + 2m — 3) "«"^^
Дать с помощью этого соотношения способ определения характеристических
значений 6„.
6. Доказать, что сфероидальные функции, определенные в задаче 5,
удовлетворяют соотношениям
5е1^ = 1П2гЧ+Ш1пЯе1„
Se 1,„ (с, Z) = Х„ J eic^t A _ fi)m sej^ (с, t) dt,
— 1
где X„ — любое число из дискретного ряда характеристических значении.
7. Написать уравнение Дф -}- й^ф =^ О в системе сплюснутых сфероидальных
«соординат и записать решения через функции Se и Re, определенные в задаче 5.
8. Система координат $, y], ср, обладающая симметрией вращения, определяется
^квадратичной формой ^
где г — расстояние по перпендикуляру от оси вращения. Если поле обладает той же
симметрией, что и рассматриваемая система координат, то его компоненты от ср не
зависят. Показать, что уравнения
rotE —i<ofxH = 0, rotH + (/o>e —ff)E = 0
распадаются иа две независимые группы
1 d
rh^ dri
(гЕ^) — №{л Яе = О,
jj^ -^ (гЕ^) -Ь bi>. Я^ = О, ,
(I)
(П)
ЗАДАЧИ " 37^
Показать, что уравнениям (II) удовлетворяет потенциал Q, причём
д (h^ dQ
ae \rh
Аналогичным образом может быть проинтегрирована и система (I). (Абрагам.)
9. Метод задачи 8 применить к нахождению электромагнитного поля,
обладающего симметрией вращения, в системе вытянутых сфероидальных координат.
Показать, что если электрические колебания направлены вдоль меридианов, то Q
удовлетворяет уравнению
которое распадается на следующие:
где Q~Qi F) Qi (y])- Заметьте, что оба эти уравнения являются частными случаямш
уравнения
A — «2) у^/_ 2 (а + 1) zy + F — с2г2) j; = О
при а = — 1. Показать, что поле определяется формулами
i tofj. Qi dQi
Ec=s
•^ d«*2 УF2—l)F2_^2) dfi '
— Q2 dQi
d2^2 уA_^2)(ег_^2) d6 •
я.=-
10. в этой главе были рассмотрены два вида электромагнитных волн:
поперечные электрические, для которых £^ ^ О, и поперечные магнитные, для которых ^jg = 0.
Получить выражения для радиального волнового импеданса, подобно тому как это
было сделано ранее в случае цилиндрических волн.
11. Доказать справедливость разложений (86) и (87) раздела 7.10 и показать,,
что при GjL = я и ^1 -» сю уравнение (87) асимптотически переходит в разложение для.
плоской волны.
12. С помощью метода, упомянутого в конце раздела 7.12, получить выражения»
мая прямоугольных компонент векторных сферических волноьых функций 1, ш и п..
ГЛАВА vm
ИЗЛУЧЕНИЕ
На протяжении трёх последних глав мы изучали распространение
электромагнитных волн, не касаясь того, как они получены. Мы рассмотрим теперь
источники этих волн и основную задачу теории излучения, состоящую
в определении напряжённости и структуры поля, создаваемого заданным
распределением зарядов и токов.
НЕОДНОРОДНОЕ СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ
8.1. Метод интегрирования Кирхгофа. Математически задача
нахождения соотношения между полем и его источником сводится к интегрированию
неоднородного дифференш1ального^ уравнения. Пусть 4» представляет собой
скалярный потенциал или любую прямоугольную компоненту какого-либо
вектора поля, и пусть g{Xy _у, г, t) буДет* функцией, определяющей
плотность источников. Мы предположим, что в области V, где находятся
источники, среда однородна и изотропна и что её проводимость равна нулю.
Наличие проводимости приводит к значительным аналитическим ,трудностям,
которых можно, однако, избежать в бол^.шинстве практических приложений
теории. Влияние проводящих тел, находящихся в соседстве с
осциллирующими источниками, будет рассмотрено в главе IX как краевая задача. При
1указанных. ограничениях скалярная функция ^ удовлетворяет уравнению
^^ — :^гШ^'=-ё{х,У. г\ A)
где <[) = -7= фазовая скорость.
yefx
Разработанный Кирхгофом/способ интегрирования этого уравнения
представляет собой развитие метода, применённого в разделе 3.3 для
интегрирования уравнения Пуассона. Пусть V— замкнутая область, ограниченная*
регулярной поверхностью 5, а ср и ^—две любые скалярные функции, непрерывные
е этой области и на поверхности 5 вместе со своими первыми и вторыми
производными. Тогда, согласно G), стр. 153
J(9A1>-4'A<?)rf^;=/(<?^-<}'^)rfa, B)
V S
где ^ обозначает дифференцирование в направлении положительной, т. е.
внешней нормали. Пусть (л:', у\ г') — фиксированная точка наблюдения внутри
области Vt а
г = у (У _ хУ + {у'.^уТ + (г' - гу C)
—' расстояние от переменной точки (д:, у^ г), находящейся внутри области V
или на поверхности S до фиксированной точки наблюдения. В качестве 9'
Рг '^':'\
НВОДНОРОДНОВ. СКАЛЯРНОЕ ВОПИОВОП УРАВНЕНИЕ . 31
МЫ возьмём сферически симметричное решение
однородного уравнения
где/U-j""") — произвольная аналитическая функция аргумента t-j--^.
Аналогично задаче, относящейся к статическому полю, ср имеет
особенность в точке г=0; эта точка должна быть исключена из области V путём
проведения небольшой сферы S^ радиуса г^ с центром.в (л:', у\ г'). Область V
ограничена теперь снаружи поверхностью S и изнутри Sj. Далее, если ^ мы "^
обозначим левую часть B) через / и используем A) и E), то получим
/=-/,,..+1/(,^-Ф|1>.. F)
V V
или, поскольку
/=_/,^..+ J,^f(/^_*^).,. G)'
V V
После интегрирования по времени от — оо до -|- оо это даёт
+ 00 +00
— со —со
Теперь задача состоит в таком выборе функции /U-J-—) .чтобыпослед-
НИИ член в (8) исчезал. Для этого мы положим t' = ~H в качестве/(^-j-^')
возьмём импульсную функцию^% определённую соотношением C5)на стр. 249,
I»
(t+tfy
nt + f)=y^'—^='SoU + n. (9)
причём
+ 00
jfit-\-t')d(t-\-t') = l. A0)
•00
Для того чтобы избежать каких-либо вопросов, связанных с непрерывностью
функции / и её производных, мы будем считать 8 очень малым, но
переходить к пределу 8 = 0 пока не будем. Определенная таким образом
функция SQ(t-\-t') всюду равна нулю, за исключением весьма малого интервала
в окрестности момента t = — t'. Если иметь это в виду, то очевидно, что
для произвольной функции времени F(t)
+ 00
F(-0= / S,(tJrf)F(£)dt; A1)
— 00
если 8 ->• О, то -яг равно нулю для всех значений t, лежащих вне
окрестности i=—/<.
1) Т. е. в пределе 8->• О — дельта-функцию. Прим. ред.
t
376 гл. VIII. ИЗЛУЧЕНИЕ
Следовательно, поскольку (р и •—■ на пределах t = — оо и t = oo^)
равны нулю для всех конечных значений г, последний член в выражении (8)
также должен равняться нулю, и мы получаем
= — j^g(x,y,z,—i')dv. A2)
■CO V —00
V
Приравнивая это правой части B), получаем
+ 00
lL,d.+ fdtf{,^-^^)da +
-f- ОО
■со S
-f- оо
• со Л'1
с д д
На поверхности S^ имеем -г- = — -^, так что
St
j^dals,{t+^)j{^l^^da.m
Переходя к пределу при г^ -► О, мы получим
/(^1|-^ж)^«;=-^^*^о(^)^(л:'.У, г\ t)) A5)
откуда, согласно (II),
+ 0О
/ dt ^[^^~^^)da = -A^Hx', у\ z\Q). -A6)
— coSi
Подстановка этого значения в A3) даёт
4» (л:', у', z\ 0) = ^ / ]:gix, у, г, -1') dv +
S -co
Для того чтобы преобразовать эти интегралы к более простому виду,
заметим, что
^) Очевидно, пределы могут быть выбраны теперь так, чтобы охватывать лишь
г
бесконечно малый интервал, содержащий момент /== .
НЕОДНОРОДНОЕ СКАЛЯРНОЕ ВОЛНОВОЕ 5ТАВНЕНИЕ [вЛ] 377
и ЧТО
Интегрирование по частям даёт:
00 CO
И, Применив A1), мы получаем
Согласно B1), значение <]* в точке л:', у\ г в момент ^ = 0 получаете»
суммирование слагаемых от^ отдельных элементов, причём фаза каждого
из слагаемых отстаёт на'величину ^' = —. Однако ограничение точки
наблюдения моментом времени, равным нулю, совершенно произвольно, так что
формула Кирхгофа может быть написана в виде
где знак
\g\=g{^.y,z,t^^ B3)
означает функцию с запаздывающей фазой.
Объёмный интеграл в B2) является частным решением неоднороднога
волнового уравнения, представляющим собой физически ту часть ^ {х\ у', z\ /),
которая вызывается всеми источниками, расположенными в области V..
К это|Ау частному решению надо добавить общее решение однородного
уравнения E), выраженное в виде поверхностного интеграла по поверхности S
и учитывающее все источники, расположенные за пределами этой
поверхности. В том случае, когда значения <^ и производных <{* на поверхности S
известны, поле во всех внутренних точках определено полностью, однако
задавать эти значения произвольно столь же недопустимо, как и в
статическом случае. Ниже нам представится повод рассмотреть этот вопрос
подробнее в связи с принципом Гюйгенса.
Поведение функции »]» на бесконечности не столь уж очевидно, поскольку
г входит теперь явно в f^J через запаздывающую временную переменную
t . Распространение поля происходит, однако, с конечной скоростью^
и следовательно, если все источники расположены на конечном расстоянии
от некоторого заданного начала отсчёта и если они существуют в течение
конечного промежутка времени, то мы можем положить, что поверхность S
вынесена дальше первого волноврго фронта. Она лежит тогда целиком в той
области, до которой возмущение к моменту / ещё не дошло и в которой ^
378 гл. Vni. ИЗЛУЧЕНИЕ
« все производные от <|» равны нулю. В этом случае
^(х\ У\ г\t)==-^f^g [х,y,z,t^^)dv, B4)'
V
^где V является теперь полным объёмом, занятым источниками поля.
Без сомнения, читатель заметил, что выбор функции/и-|—j с плюсом
•совершенно произволен, поскольку однородное уравнение E) допускает также
и решение—/и —\. Эта функция приводит, очевидно, к опережению
во времени и означает, что величина ^ может быть наблюдаема раньше того
момента, когда она будет возбуждена источниками. Привычная связь
причины и следствия оказывается в этом случае обёрнутой, и это второе
решение могло бы быть поэтому отброшено как логически невозможное. Однако
лрименение принципа «логической» причинности в случаях, подобных
данному, является весьма шатким обоснованием, и мы поступим лучше, если
ограничимся запаздывающим действием единственно потому, что только это
решение согласуется с современными физическими данными.
8.2. Запаздывающие потенциалы. Применив B4) к скалярному потен^
диалу и к прямоугольным компонентам вектбр'ного потенциала, мы получаем
следующие формулы:
^ (^'» ^> = 4^ / 7-Р Ц Г)^^. B5)
V
k{x\t) = -^\^):S{x,ndv, B6)
»
которые позволяют вычислить поле при заданном распределении зарядов
и токов. В этих формулах х' представляет собой тройку коорД1у1ат х\у\ z',
SLX — тройку х,у, г, в то время как запаздывающее время обозначено через
.t* = t . Соотношения эти должны, однако, удовлетворять ещё одному
условию. Мы пока показали лишь то, что B5) и B6) являются решениями
неоднородного волнового уравнения. Для того чтобы они представляли
потенциалы электромагнитного поля, необходимо, чтобы они удовлетворяли
соотношению
div'A+ti.e-^- = 0. B7)
Штрих при операторе div обозначает, что дифференцирование производится
по координатам точки наблюдения х\ у', г'.
Мы покажем, что B5) и B6) удовлетворяют этому условию, если
плотности токов и зарядов удовлетворяют уравнению непрерывности. Так как
• для фиксированной точки пространства ^- = -^, то мы имеем
V
div'A=i^Jdiv'ii:^rft; = -|^/Г Jgrad' (l)-fldiv'jlrft;. B9)
V F.
Применяя оператор grad к любой степени г, мы можем написать, что gradr» =
= —grad'r». Переменные У входят в S{x^t*) только через t* = t— —
НЕОДНОРОДНОЕ СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ [8.3] 379
И, следовательно,
div' J= §, grad' ^* = -1 ^ grad' г = 1 -^ grad г. C0)
С другой стороны,
divJ = —l.|^gradr + (divJ),,^^„„^,, C1)
так что
div'J = (divJ),,^,^„^;^divJ. C2)
Уравнение B9) может быть теперь написано в виде
aiVA = —^jdw{^)dv+-^fl:(mi),.,^dv. . C3)
По теореме о дивергенции
Jdiv(i-)rft>=Ji-nrfa = 0, C4)
v s
так как замкнутая поверхность 5, ограничивающая объём V, может быть
взята настолько большой, что J на поверхности S всюду равно нулю.
Комбинируя B8) и C3), мы получаем
l<liv'A+.:^=i/l((divJV_^,+ |i,}rf». C5)
у <"
что должно равняться нулю, ибо сохранение заряда требует, чтобы
«'lv%.„„, + |£r=0 ■ C6)
В любой точке, местное время в которой равно t*.
8.3. Запаздывающий вектор Герца. В силу C6) достаточно задать
распределение в пространстве и времени одних только токов. Плотность
зарядов может быть тогда вычислена и потенциалы определятся вычислением
интегралов B5) и B6). В большинстве случаев выгодно, однако, получать
поле из единой функции, характеризующей источники, с помощью вектора
Герца.
Будем выражать плотности токов и зарядов с помощью одного
вектора Р, определенного соотношениями
J = ~.. р = —divP. C7)
Уравнение непрерывности удовлетворяется тогда тождественно, а уравнения
поля принимают вид
rotE-|-ii.^ = 0, (I) divH = 0, ДШ)
rot Н — е ^ = :^, (П) div Е = — i dIv P. (IV)
Как было показано в разделе l.ll,' этим уравнениям удовлетворяют выражения
. E^graddlvn^H-s-^, H = erot-^, C8)
где вектор П является каким-либо решением уравнения
rotrotII^graddivII4-H'e-^ = 7"'*' (^^)
380
гл. VIII. ИЗЛУЧЕНИЕ
Прямоугольные компоненты П удовлетворяют, следовательно,
неоднородному волновому уравнению
АЩ- {AS
dm,
а/2
1
е J
(у = 1, 2, 3).
D0>
Едва ли нужно говорить о том, что вектор Р, определённый
соотношениями C7), не совпадает с вектором диэлектрической поляризации,
определённым ранее в разделе 1.6. Вектор Р данного раздела измеряет
поляризацию или момент единицы объбма распределения свободных зарядов и
поэтому не равен D — е^Е.
Для облегчения последующих вычислений мы несколько изменим
обозначения. Точка наблюдения, расстояние которой от данного начала отсчёта О
равно R, будет обозначаться прямоугольными
координатами л:,, ATg, лгд (рис. 71), а элемент
тока; расположенный на расстоянии R^ от
начала отсчёта, — координатами (^i, ^2, Sg). Таким
образом, расстояние от этого элемента тока
до точки наблюдения равно
Рис. 71. Элемент тока
расположен в точке 6i, Sjt Sa. а Xt, х^,
Xs — фиксированная точка
наблюдения.
5/.
D1)
Поскольку в общем случае устанавливающееся
или установившееся переменное поле может
быть разложено на гармонические составляющие, нам достаточно
рассмотреть только эти гармонические компоненты. Пусть
D2)
D3)
Так Kajc в данном случае Л == <о |Л}Ае = —, то, применив B4) к D0), мы
получаем основную формулу
П(л:, 0 =
■i*ot
4яе
JP.(E)V
■dv.
D4)
РАЗЛОЖЕНИЕ НА МУЛЬТИПОЛИ -
8.4. Определение моментов. Для того чтобы вычислить интеграл для
запаздывающего вектора Герца, часто бывает необходимо прибегнуть к
какому-либо разложению в ряд. Характер этого разложения определяется
частотой токов и геометрическими свойствами их распределения. В этом
разделе мы рассмотрим распространение теории мультиполей, развитой в
разделах 3.8—3.12 и 4.4—4.7 для электростатических и магнитЬстатических
полей, на случай переменных полей.
Согласно (87), стр. 365, при /?>/?i подинтегральное выражение
соотношения D4) предыдущего раздела может быть разложено в ряд
—= /ife S <2й-|-1) Р„ {cos t)/„(*/?i) f&i^)
A)
и = в
РАЗЛОЖЕНИЕ Hii МУЛЬТЙПОЛ и 18.4] 3$1
' ;—zz.^—.-zz^
След6вател4.йо, если R больше, чем радиус сферы, содержащей все
источники, ТО
од
предположим теперь, что РоB) выражено в виде функций от /?i, 7, ?,
где 9—экваториальный угол относительно оси, проведённой из точки О
через точку наблюдения. Тогда вектор PqC^i, т» ?) может быть разложен
на скалярные компоненты, а каждая компонента разложена в ряд по
сферическим гармоническим функциям, как это было сделано в формуле C6)^
стр. 358. В силу ортогональности функций. Р„ (cos f) интеграл спр^к
сведётся к коэффициенту разложения, умноженному на IJnikRi)]^- Успех этого
способа зависит от вида распределения токов и от тех трудностей, с
которыми будет связан подсчёт коэффициентов разложения.
Если длина волны переменного поля во много раз больше, чем
наибольшие размеры области, занимаемой токами, то ряд B) может быть представлен
в виде электрических и магнитных мультиполей, расположенных в начале
координат. Мы предположим, что для всех значений R^ в пределах области V
kR, = ^^h C)
где X — длина волны в данной среде, определяемой значениями е и }а.
Следовательно, функция Jni.kR{) может быть заменена первым членом её
разложения в ряд. Согл'асно B5), стр. 356,
Полное поле будет состоять из суммы частичных полей
со
П(л:, 0=2 П(»)(л:, t), E)
п = о
причём
^^""^^""'^^^^-^ W ^'^^'^-'^*f&\k^)hom>n(cOS•i)dv. F)
Так как Pq(cos y) = 1 и ho\kR)=—Тр^^^^г то для первого члена
мы сразу же получаем
и =4^Р'"-Н—• P« = /P.E)''«. G)
Пусть ^ будет любой скалярной функцией точки. По теореме о дивергенции
/ div (A>Ро) dv=j 'l^Poii da (8)
F 6'
И, следовательно,
J* Pq grad (}> dt> = — f (}> div Pq rft> + J t{>Pj)n da. (9)
V V S
Если 5 охватывает все источники данного распределения, то на
поверхности 5 произведение РдП равно нулю, и поверхностный интеграл исчезает.
382 гл. Vni. ИЗЛУЧЕНИЕ
Возьмём теперь в ^качестве ^ прямоугольную компоненту 5< радиуса-вектора^.
Rj. Тогда
fp,jdv = — fljdivPodv; A0>
V V
соответственно,
p(i) = JPodt;=jRiPorfi;. A1>
V V
Частичное поле П^^ возбуждается переменным електрическим диполем,,
дипольный момент р^*) которого определяется в точности так же» как
и в случае электрического поля {уравнение D7), стр. 164).
Так как Pj (cos i) — cos y, Л?^ {Ш) ==—"^ (^ + "щУ^^^у ^o второй
член уравнения F) мы получим в виде
n<» = -:i-(:^+w)«"^~'""/PoE)«iCosvd^.. A2)
V
Для интерпретации этого интеграла мы прежде всего разложим подинте-
гральное выражение
Po/?icos Y = (Ril^) ^ = 2V {[^^1' ^0] R] + Ро (RiR) + Ri (RPo) }• A3)
Магнитный]рипольный момент был определён соотношением B8), стр. 212,
как
m(i)=-iJ[Ri,jQ]dt;. A4)
V'
Так как R от переменных интегрирования I не зависит, то мы имеем,
следовательно,
4r / [iRi- Ро] R] ^^ = 7^ [m^^), R]. A5)
Электрические квадрупольные моменты некоторого распределения
зарядов были определены на стр. 164 соотношением D8) как компоненты
тензора
Pij = J Щн ^"^ = — / Щ diiv Ро dv. A6)
V V
Полагая в (9) t{> = 5^5j-, мы получаем
Рц = 1 ^iPoi + ^Л) ^^ = Pai- A7)
V
кроме того,
3 3
RiR = ^S^iE» PoR = ^2:Po.-^. A8)
j = i ^ 3 = 1 -^
Следовательно,
3
^ J [/^oi (RiR) + ^i (PoR)l ^^ = T S ^J d-^oi + Si^a,) ^^ ==
s
— 1 V« ^^ 1 B) ,10v
-^m.
РАЗЛОЖЕНИЕ НА МУЛЬТИПОЛИ 18.5]
38^
Величины р^р являются компонентами вектора
pB) = 2pgrad/?,
B0>
где 2р —тензор с компонентами p^j [ср. с уравнениями B3) и B4), стр. 1961.
Частичное поле П(*) представляет собой Часть поля^ обусловленную
магнитным диполем и электрическим квадруполем
Сравнение B1) с G) показывает, что два эти поля отличаются прежде всего
коэффициентом V^j^e, т. е. приблизительно, в 3 • 10^ раз, и следовательно,
моменты тО) и р^2> должны быть очень велики по сравнению с рС^), для
того чтобы ПС*) имело заметную величину. С другой стороны, необходимо
напомнить, что электрический момент токов зависит не только от
геометрических свойств их распределения, но и от их частоты [уравнение D3),
стр. 380]. Если рB> выразить через токи, а не через заряды, то мы увиДим,.
что величина IIW от частоты не зависит, в то время как величина ПСО>
с увеличением частоты убывает как —.
Остальные члены ряда ПИ дают ту часть поля, которая
вызывается электрическими и магнитными мультиполями высших порядков. Они
должны выражаться через соответствующие тензоры, но трудность подсчёта*
быстро возрастает с увеличением
порядка. Величина последующих членов
меняется в общем как ^—j . В тех случаях,
когда ряд сходится настолько медленно, что
необходимо учитывать члены более высокого
порядка, для расчёта излучения приходится
обычно применять какой-либо иной метод.
8.6. Электрический диполь.
Предположим, что заряды распределены так, что
существенен только электрический диполь-
ный момент.' Это имеет место, например,
в случае переменного тока в
прямолинейном отрезке проводника, длина которого
очень мала по сравнению с длиной волны.
Ориентируем систему координат так^ чтобы
положительная ось г совпадала с
направлением дипольного момента р(*). Вектор рС*) может быть разложен на
его компоненты в сферической системе координат, как показано на рис 72:
рA) = p(i)cos Oil —p(^>sin Oig, B2>
где ij, 12, ig — единичные .векторы сферической системы координат,
указанные на рис. 8, стр. 56. Согласно G), вектор Герца П(^) параллелен р^*>
и может быть разложен аналогичным образом. Векторы поля могу* быть
подсчитаны затем с помощью формул C8), стр. 379, которые в елучае
гармонического временного множителя принимают вид
E = graddivn-fA2n, Н= —/toe rot П. B3>
Дифференциальные операторы, выраженные в сферических координатах
соотношениями (95), стр. 57, применяются к вектору
n@) = /7@)cos(Hi —Я@)81п012. B4>
Рис. 72. Компоненты поля
электрического диполя.
'384 гл. VIII. ИЗЛУЧЕНИЕ
Если Ro^gradi?—единичный вектор, направленный от диполя к наблюда-
телю, и t* = i—~, то
-^[Ro[Ro, pC^)ll}, B5)
H@) = _ge~*u>f»(^_|)lp(i), /?^,. B6)
Из этих выражений легко установить основные особенности строения поля
диполя. Мы замечаем прежде всего, что электрический вектор лежит в
меридиональной плоскости, проходящей через ось диполя, а магнитный вектор
перпендикулярен к этой плоскости. Магнитные силовые линии являются
концентрическими окружностями, проведёнными вокруг диполя. При частоте,
равной нулю, в формуле B5) исчезают все члены, кроме первого,
при ^, который, согласно форм(уле B7), стр. 161, совпадает с полем
электростатического диполя. Далее, если мы заменим р(^) согласно формуле
^3) на стр. 380 на линейный элемент тока — /ds, то первый член в B6),
очевидно, можно будет интерпретировать как распространение закона Био
и Савара [A4), стр. 310] на переменные поля. Отдельные члены в B5)
и B6) расположены в порядке обратных степеней R, и отношение
р
последовательных членов равно kR или 21: у • ^ непосредственном соседстве
с источником преобладают «статические» и «индукционные» поля,
убывающие как ш и -52, в то время как на расстояниях, для которых R '^ Я,
или kR'^ 1, необходимо принимать в расчёт только поле «излучения»
H@)^g[Ro, P^^)i4:^. J
B7)
Ha расстояниях от источника, больших по сравнению с длиной волны,
поле становится поперечным относительно направления распространения.
Если мы положим, что R—*co, но в то же время pW возрастает так, что
напряжённость поля остаётся неизменной, то в пределе мы получим плоские
волны, рассмотренные в главе V.
Свойство поперечности волнового движения на больших расстояниях
является общим для всех электромагнитных источников колебаний, но не
следует упускать из виду, что в непосредственной близости от источника
имеется и продольная компонента вдоль направления распространения.
Так, например, поле излучения электрического диполя равно нулю в
направлении его оси, но при достаточно малых значениях R имеется
заметная продольная компонента £"@) вида
^'=wG-F«)lP'"l'-'"°''- B8)
Именно эта компонента, а не поле излучения, определяет распределение
токов в вертикальной антенне, расположенной над землёй.
Для подсчёта потока энергии в поле используем комплексный вектор
Пойнтинга, введённый в разделб 2.20. Если S—среднее значение энергии.
РАЗЛОЖЕНИЕ HA МУЛЬТИПОЛИ[8.53 385
Проходящей в секунду через единичную площадку в напр1авлении
положительной нормали, то
S = Re(S+), S+=i-[E, Н'*]. B9)
Для того чтобы подсчитать комплексный вектор Пойнтинга, мы прежде
всего напишем в компонентах формулы B5) и B6)
Е'^ = Ш-^-§)'^^^\Р''Пе-^-*\
^'^'^J-a.-lL-^sm^lpWle-^^
щ /ш/ 1 ik^
^L=-t^(^-'l)^'"'"""l^-"'-
C0)
Из этих выражений мы образуем
S+ = ^EbHlii—^EEHli^ • C1)
и получим
16
к{-^ь-^У^^^овЬ\ра)\%ц. C2)
Теперь надо проинтегрировать нормальную компоненту S+ по поверхности
сферы радиуса R:
0 0
Согласно B9), стр. 128, действительная часть C3) даёт с]реднее значение
потока энергии, вытекающего через сферическую поверхность,
охватывающую колеблющийся диполь. Поскольку действительная часть не зависит
от радиуса сферы, поток этот должен быть одинаковым для всех
концентрических сфер; мы получили таким образом, что система теряет энергию
£ прстюянной мощностью, равной
ШО) =. ~ i^yi^ I рA) |2 ватт. C4)
Величина W определяет радиационные потери диполя, В разложении
электромагнитного поля излучение дают только те члены, которые исчезают
в бесконечности, как -^. В данном случае имеется, конечно, мгновенный
поток энергии, св$гзанный с другими членами B5) и B6), но в среднем
за период этот поток равен нулю. Члены с -^ и -gg связаны с энергией,
распределённой в поле, которая периодически то вытекает из источника,
то возвращается к нему обратно, но не утрачивается системой.
В свободном пространстве jaq = 41:10-'^, V^i^o^o = "о" Ю-^ и,
следовательно,
ШО) = -1 10-15@* I рA) |2 = 173 • 10-16 v41 рA) |2 ватт, C5)
где V—частота. Излучение очень быстро растёт с увеличением частоты и
уменьшением длины волны.
ОС Яате КОЗ. TflriTJiia: впектоомагнетизма.
386 гл. VIII. ИЗЛУЧЕНИЕ
8.6. Магнитный диполь. Распределение токов может быть таково, что
существенную роль играет только дипольный магнитный момент т(^).
При достаточно малых частотах именно это будет иметь место в случае
проводника в виде замкнутой петли. Тогда
п<"=i /?[">«. ад (-i+М'~""'- «зв>
Подсчитанные по B3) компоненты векторов поля будут
4' = |/"H^- + W)sin»lm(b|.-
„— iwt* \
(S7>
Структура этого поля совпадает со, структурой поля электрического диполя^
но векторы Е и Н поменялись местами. Вектор Н(^) лежит теперь в мери-
дианальной плоскости, проходящей через диполь, и имеет как радиальную,
так и поперечную компоненты. Линии вектора EW являются
концентрическими окружностями, проведёнными вокруг оси диполя. При k = 0 формулы
C7) переходят в выражения, выведенные в разделе 4.5 для статического
поля постоянного магнитного диполя.
Для подсчёта излучения мы снова, как и в C1), образуем комплексный
вектор Пойнтинга и интегрируем по поверхности сферы радиуса R его
нормальную компоненту. В результат войдут из C7) только члены, содержащие
1
"о, И мы получим
1^A) = ^ |/~^ [l.m(i) |2 ватт. C8)
В свободном пространстве т/ ^t= 376,6 ома,^и в этом случае
Wi^) = 10 k^ m(i) Р ватт. C9)
Рассмотрим для примера переменный ток в одиночном витке радиуса R^ м.
Пусть максимальное значение тока будет /q, а длина волны очень велика
по сравнению с R^. Фаза тока во всех точках витка будет по существу
одна и та же, из чего, согласно D3), стр. 380, и A1), стр. 382, следует,
что электрическим дипольным моментом можно пренебречь. Магнитный
момент I тС^)]= "^RiIq- Следовательно, излучаемая мощность равна
'.^=1601^6 ЗУ/о.' D0)
Сопротивлений излучения dt определяется как такое эквивалентное омическое
сопротивление, в котором рассеивается та же мощность. Так как
максимальная амплитуда тока равна /q, то
w=~mJl D1)
и, следовательно, в рассматриваемом примере
9?= 3207гб^^У = 3.075 .IQb^^iJoMoe. дD2)
Результат этот ограничен прежде всего ^тем условием, что второй член
в разложении j\ (kRj) должен быть исчезающе малым по сравнению
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН 18.7] 387
С первым; имеем
л(ад.)=^A-^+-..). («)
и следовательно, j\ (kRj) может быть аппроксимировано первым членом,
если kRi < 1. Фактически оказывается общим правилом, что эти функции
могут быть представлены их первыми членами до тех пор, пока их аргумент
не превышает их порядка. Если, например, Х= lOR^, то сопротивление
излучения равно около 30 омов. 01 очень быстро возрастает при уменьшении Л,
но при этом начинают играть роль и электрические дипольные и квадру-
польные моменты. С другой стороны, очевидно, что при увеличении длины
волны излучение становится вскоре исчезающе малым. Токи, длина волны
которых велика по сравнению с наибольшими размерами системы
проводников, по которым они протекают, не дают сколько-нибудь заметного излу^
чения и называются квазистационарными.
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН
8.7. Поле излучения одиночного линейного осциллятора. Точное
определение распределения токов в проводнике является краевой задачей:
требуется найти такое установившееся решение волнового уравнения,
соответствующее данным э.д. с, которое удовлетворяло бы условию
конечности во внутренних точках проводника и условию непрерывности
тангенциальной компоненты напряжённости поля при переходе через его поверхность.
Для цилиндрического проводника конечной длины эта задача полностью ещ&
не решена, но неплохое представление о том, что здесь происходит, может
быть получено при изучении проводящего вытянутого сфероида,
эксцентриситет которого мало отличается от единицы. Подробное исследование
впервые было проведено Абрагамом ^); в последнее время целый ряд работ
также был посвящен этому вопросу 2). Все эти работы подтверждают то, что
естественно было ожидать с самого начала: распределение тока вдоль
изолированного прямого проводника в основном является гармоническим, а отношение
длины антенны к длине волны, пока размеры поперечного сечения антенны
весьма малы по сравнению с её длиной, равно полуцелому числу.
Значительно ббльшим источником ошибки, нежели конечность диаметра
проводника, является затухание вследствие излучения. При протекании тока от точки
1) Abraham, Ann. Physik 66, 435, 1898.
2) В настоящее время решение краевой задачи о вынужденных колебаниях
тонкого проводника конечной длины настолько продвинуто, что уже нельзя согласиться
с высказанным выше противоположным утверждением автора. Основными здесь
явились работы Галлена и работы советских авторов. В работе Галлена (Е. Hallen,
Nova Acta Uppsala 11, 1, 1938) последовательно используется малость радиуса
провода а по сравнению с его длиной /, что позволяет привести задачу к
интегральному уравнению, содержащему малый параметр 1/1п(//а). Численная обработка
результатов Галлена была сделана Кингом и Блэком (R.King а. Blake, Proc. J. R. E. 30,
335, 1942). Независимо М. A. Леонтовичем и М. Л. Левиным (ЖТФ 14, 481, 1944),
благодаря использованию того же малого параметра, задача была приведена к инте-
гро-дифференцкопальному уравнению для полного тока в антенне, которюе можно
рассматривать как «телеграфное уравнение однопроводной линии». В работе М. Л. Левина
(ДАН 54, 599, 1946) получено далее интегральное представление входного реактанса
антенны, аналогичное соответствующему представлению сопротивления излучения.
Таким образом, расчёт реактанса сведён к квадратурам, причбм вычисление может
быть проведено для самых различных профилей (тонкого) провода, в отличие
от расчётов, предполагающих специализированный профиль (например, вытянутый
сфероид—Page а. Adams, Phys. Rev. 53.819, 1938; Stratton a. Chu, J. Applied Phys. 12,
230, 1941; конус — Schelkiinoff, Proc. I. R. E. 29, 493, 1941). Кроме того, указанное
интегральное представление реактанса позволяет обобщить теорию на случаи
антенны в волноводе, объёмном резонаторе и т. п. Прим. ред.
OR*
388
гл. VIII. ИЗЛУЧЕНИЕ
подвода питания к концам антенны энергия рассеивается и в виде тепла
и в виде излучения. Следовательно, предположение о постоянстве амплитуды
в пучностях тока вдоль провода не соответствует действительности. На стоячую
волну тока в антенне накладывается затухающая бегущая волна, восполняющая
потери энергии. Влияние подобного изменения распределения тока в антенне
на характер излучения может быть очень заметным.
На распределение токов в антенне влияет также близость земли или
каких-либо других предметов. Современное направление развития ведёт
к системам линейных антенн, подвешенных на некотором расстоянии над
землёй,' а в этом случае влиянием земли на распределение токов можно
обычно пренебречь, С другой стороны, если в качестве" антенны используется
стальная башенная конструкция, то ёмкость её по отношению к земле может
существенно повлиять на распределение токов.
В этом разделе мы рассмотрим радиационные свойства линейных антенн,
изолированных в свободном пространстве. Каким образом излучение
отражается и преломляется затем землёй, будет рассмотрено в следующей главе.
Мы предположим, что измерение 'ТОКов произведено в ряде точек вдоль
каждого из проводников и что измеренное таким
образом распределение токов может быть
представлено с помощью одной или нескольких стоячих или
бегущих синусоидальных волн.
Рассмотрим сначала одиночный прямолинейный
проводник длины /, как показано на рис. 73. Ток
в любой точке на расстоянии S от середины
проводника пусть будет 1=иA) ехр(—icut); тогда, согласно
D4), стр. 380, вектор Герца для такого
распределения равен
+f
Рис. 73. Одиночный
линейный осциллятор.
n(x,t) =
47LW£f|
-i4>i
fua)^dl.
A)
где d^—элемент длины вдоль проводника. Поле излучения элемента d^
по формуле B7), стр. 384, будет
dEu =
dH^ =
icujxg sin О
aikr—ivat
47Г г
m sin 0
Aizc r
ii{^)dl.
е^^г-1Ыц^^^1^
B)
так что, интегрируя по всем элементам вдоль проводника, мы получаем
Ее = |/"^ Я, = - ^>--' / ~ ^^-и {I) d\\ C)
Если f^U то можно рассматривать
sin О
как медленно меняющуюся
функцию от ^. Это значит, что радиусы-векторы, проведённые от различ-
. sin 6
ных элементов тока к точке наблюдения, почти параллельны и —-— может
быть заменён на
sin О
R
и вынесен из-под знака интеграла. Это приближение
тем более точно, чем больше /?, а так как через все концентрические сферы
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН [8.71 389
С центром в точке О проходит одно и то же ^излучение, то мы можем брать /^
сколь угодно большим. Фазу, однако, необходимо рассматривать с большей
точностью. Из рисунка ясно, что время, необходимое волне, испущенной
элементом в точке ^ для того, чтобы достигнуть удалённой точки, меньше
соответствующего времени для волны, испущенной элементом в точке О, на
величину i . Соответственно фазы этих волн отличаются на величину
k^ cos 6, поскольку k = -~ , Таким образом при R-^oo напряжённости поля
стремятся к пределу
-ь!
Я8==|/~^^Я^ = —i^^e*''^-^-'^--« J e-»«cosO^^(^) ai. D)
Синусоидальное распределение токов даётся функцией
u{l) = lQsm{kl'—a\ E)
а условие равенства нулю токов на концах проводника при S=_t:--
выполняется при
« (О = ^0 sin tnTz\j +2")» ^ = Т ■ ^^^
Целое число т равно числу полуволн, укладывающихся на длине /, а /q —
амплитуда тока в пучности. Интеграл D) легко вычисляется и даёт
/ / ixn I сов е ——— COS е ^ 1 tleR—tu^t , ^
Численный коэффициент равен
1|/"^? = 59,92 ^60, (8)
следовательно,
(f^"^- fi^
cos \-к- cos 0 1 ^гкВ—icit
£q = — г60/о— ,— о при т нечётном (9)
cose)
60/п—^-4-й—-—75— При т чётном. A0)
sm {-J5- cos о ) ^iuR—i^ot
Излучение зависит только от типа возбуждённых колебаний, но не от длины
излучателя. Лоле излучения одиночного линейного осциллятора такое же^
как и поле диполя^ расположенного в его центре, но с амплитудой,
умноженной на фазовый множитель F{b),
Интенсивность излучения в каком-либо данном направлении опять-таки
выражается через комплексный вектор Пойнтинга, направленный по радиусу
и равный по величине
5+ = |£вя;, )
30
/2 COS^f-^C0S8j
f°2.;' sin^e (m^l. 3.5. ...),} (U)
^,_30l^:^^H ,,„_2 4 6 )
•^ 27г/?2 sin'9 (т — г,%ь,...).
390
гл. VIII. ИЗЛУЧЕНИЕ
Из расположения нулей и максимумов этих функций можно получить
вполне отчётливое представление о диаграмме излучения. При т нечётном
нули 5+ получаются при
cos 6=—, —, ...,-, A2)
в то время как максимумы находятся из соотношения
пт
^- tg 6 sin 6 = ctg (^ cos 6 j
Аналогично, при т чётном нули получаются при
cos 6 = 0,
т ^ т '
т
A3)
A4)
■ tg 6 sin 6 == tg Г~ cos 6 j
A5)
/77= /
a максимумы соответствуют углам, удовлетворяющим соотношению
^2
Диаграммы излучения для первых четырёх типов колебаний показаны
на рис. 74. В каждом случае пунктирной кривой показано распределение
тока вдоль
излучателя, которое в
различных участках
осциллятора либо
совпадает по фазе, либо
различается на 180°.
Интерференционное
взаимодействие подобных
участков тока
приводит к разделению
диаграммы на
отдельные лепестки, число
которых равно числу
т участков. Между
лепестками
располагаются узлы поля
излучения.
Интенсивность
излучения имеет
наибольшую величину в
направлении осей
лепестков,
расположенных . ближе всего
к излучателю, и при
т-^ со излучение
направлено полностью
вдоль провода.
Энергия может
распространяться вдоль
бесконечного
проводника, но в этом
случае отсутствует
направленный в
сторону радиальный
поток энергии. В дальнейшем мы увидим, что наличие внутри проводника
потерь на джоулево тепло приводит к появлению компенсирующего потока
энергии, направленного в проводник.
/77= J
Рис. 74. Диаграммы излучения линейного осциллятора,
возбуждаемого в различных тонах: m = 1, 2, 3, 4.
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН [8.7]
391
Полученные нами теоретические диаграммы на практике видоизменяются
из-за затухания, вызываемого потерями на джоулево тепло и на излучение.
Вследствие этого амплитуды последовательных пучностей тока уменьшаются
по мере удаления вдоль антенны от точки подвода питания. Лепестки
диаграммы излучения, лежащие в экваториальной плоскости 6 == -к- или около
«её, усиливаются за.счёт сужения наружных лепестков. Этот эффект
становится более резко выраженным во мере увеличения сопротивления материала
антенны, что иллюстрирует рис. 75. Кривые были получены Бергманом i)
из измерений, проведённых над линейными осцилляторами, в которых
возбуждались колебания порядка m = Z, в бронзовой и стальной проволоке
разных диаметров. Отношение амплитуды тока в центральной пучности
к амплитудам в крайних пучностях было
порядка 1,4:1. Расчёт излучения при
таком распределении амплитуд привёл к
результатам, хорошо согласующимся с
наблюдёнными значениями.
Излучаемая мощность получается
интегрированием S+ по поверхности сферы
очень большого радиуса R с центром
S точке 0. При т нечётном имеем
1^= jj S-^R^ sin 6 й?о db =
о о
-30/jj
cos-(^-
cos^
-- Бронза, Зиаметр ^,0 мм
-Столь, диаметр ^4,0мм
- Сталь, диаметр 0,5мм
sin 6
db. A6)
Рис. 75. Влияние сопротивления
антенны на излучение по измерениям
Бергмана.
Для вычисления этого интеграла мы заменим переменную 6 на к
с пределами изменения от-}-1 до —1. Тогда ввиду того, что
\ — tCi 2\1+M^1 —мУ'
A6) преобразуется к виду
+1
W
= 15/„^J
—1
1 -j- cos rmzu
du.
cos 6
A7)
A8)
V
Пвложив далее \-\-u = —— , получим
/ИТГ
2пт
W
^=15У2/
1 — COS V
V
dv
A9)
или
где Y='1,7811, а С\х — интегральный косинус
С1лг = — )—^;—й?г>,
X
B0)
B1)
значения которого приведены в таблицах функций Янке и Эмде.
Точно такой же результат получается и при нечётном т. В обоих
случаях сопротивление излучения равно:
9? = 30Aп2итт —Ci2m7r) (от= 1, 2, 3, ...) B2)
г) Bergmann, Ann. Physik 82, 504, 1927.
392
гл. VIIl. ИЗЛУЧЕНИЕ
ИЛИ, поскольку
1п2тг7 = 2,41^1,
Ог = 72,454-301пт —30Ci2TCOT омов.
B3)
Если m > 2, то членом с Ci 2'кт можно пренебречь. Соотношение между
сопротивлением излучения и порядком возбуждения показано графически на
рис. 76. Выражение B3) справедливо только в случае резонанса, когда
2//Х = от является целым числом. Для промежуточных значений длин волн
сопротивление излучения следует
кривой, колеблющейся между
резонансными значениями, нанесёнными на
рис. 76. Точная форма этой кривой
зависит от способа возбуждения ^).
8.8. Излучение от бегущих волн^».
Распределение токов, рассмотренное
в предыдущем параграфе, образует
стоячую волну, узлы которой
расположены на концах провода.
Соответствующим устройством концов
осциллятора часть отражённой волны или
всю её можно погасить, в результате
чего токи будут распространяться по
проводнику в виде бегущей волны.
Подобный случай мы имеем, напри-
Мер, в передаточной линии, где для
обеспечения наиболее эффективной
передачи энергии принимают все меры,
чтобы избежать стоячей волны.
Для расчёта потерь на излучение
одиночной антенной конечной длины *),
в которой отсутствует отражённая компонента тока, предположим, что
распределение тока даётся функцией
tt(S) = /o^*fc5. B4)
Если, как и в предыдущем случае, антенна питается в центральной точке, т€>
напряжённость поля излучения будет
£в = |/"[^Я,= -^J^^/^!}^e^JrE-ш J ,iJ. ii-cosща^^ ^25)
//5Z7
•^l 720
I
^ WO
I
^ 80
I
^ 60
^o 20
0
—
—
—
—
-—
j
j
"I
v
„_H
_. —
/ г 3 Ч 5 6 7 8 9 Ю и 12
т=-у , поря дон возбуждения
Рис. 76. Сопротивление излучения
линейной антенны при резонансе.
2*
ЧТО после интегрирования даёт
£"9 = — /бО/о sin 6
sin |^2-(l —cos e)j ^^;,2г_
ivat
1 — cose
Поток излучаемой энергии определяется функцией
R
B6)
, 30/2 Sin2 е Sin2 г к- A — COS 6I ,
•^ — 2^e"iP— 2я A--cos 6J /?2
B7)
1) См., например, интересную статью L а b и s, Hochfrequenztechn. u. Elektreak.
41. 17, 1933.
^) Задача с двумя параллельными линиями — прямой и обратной — была
впервые вравильио рассмотрена МаппеЬаск'ом, J. Am. Inst. Elec. Engrs. 42, 95,1923.
mm-
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН [8.9]
39е-.
Излучаемая мощность равна, следовательно.
W
= ЗОЙ J
isin2 6sin2r^'(l—cose)!
A—COS 6J
sin 6 db.
Для того чтобы выполнить интегрирование, мы полагаем
к = 1 — cos 6, rftt = siii0flf6,
в результате чего B8) приводится к виду
W
= ЪОГо J
B — и) 8Ш2 -J-
и
da.
B9)
Опуская элементарные промежуточные вычисления, мы получаем для W
выражение
47l/\
C0)
а для сопротивления излучения
. 47L/
„, sm -г-
9? = 84,9-}-б01пу+бО- ^
4п1
X
— 60Ci
47L/
C1)
I
ч^
SL_
Мы видим, что для одинаковой длины волны и для одной и той же антенны
сопротивления излучения для бегущей волны больше, чем для стоячей.
8,9. Гашение
противоположных фаз.
Направленные свойства од-
нопроводной антенны
могут быть усилены
путём гашения одной из
противоположных фаз
тока. В антенне типа Мар-
кони-Франклина такое
гашение осуществляется
путём включения вдоль
линии соответствующих
индуктивных нагрузок на
расстоянии полуволны
друг от друга. Каждый
из участков с
противоположной фазой настолько
сокращается по длине,
что излучением от него
можно пренебречь, в
результате чего такая
антенна оказывается
эквивалентной системе
синфазных полуволновых изяз^ателей, расположенных вдоль одной
прямой, вплотную друг к другу. Схематически это показано на рис. 77.
Слагаемое поля излучения от колебаний в каком-либо из отрезков
приходит в удалённую точку с упреждением по фазе на ^czzzcadjc по срав-
/!^
Чг:
ij
pa
а
Рис. 77. а — антенны Маркони-Франклина; Ь —
идеализированное распределение токов.
94
гл. VI I. ИЗЛУЧЕНИЕ
«ению с соседним нижним отрезком. Результирующее поле будет,
следовательно.
£п = — 60iL
cos( jr- COS e) .._ . . ^
sin<
C2)
m=0
где n— число пучностей тока. Величина be~^"^^ является вектором на ком-,
плексной плоскости, повёрнутым на угол—т^ по отношению к действитель-
иой оси. Таким образом, суммирование в формуле C2) может быть
осуществлено простым геометрическим построением. На рис.. 78 начерчена
соответствующая векторная диаграмма, на которой сумма представляется очевидно
хордой правильного многоугольника. В
соответствии с обозначениями на рисунке мы имеем
г> = 2а sin 1 , ^ =;2asin ^ ,
Ь sin -~
где 7 ,= ъ— составляет с действительной
о^-
1
1
^ /
\
/
/
/
/
\\
sin
§
Рис. 78. Вычисление ряда
п
2 Ье-^Щ.
я»=о
oi^\^ ОСЬЮ угол а ==—(я—O-f" • Так как в нашем
' случае ^ = 1, то мы получим
^е-^ш^= %.е ' ^2 . C3)
т=0
sin-
'Вместо р мы пишем ш^/с = тг cos G, поскольку d = -^ cosb, и получаем
, f^ cos 6 ) sin f~ cos 6 ) ^iJ^R--*"># -i{n-i)Y <=°^^
cos I
Eft = 60i/n
sin 6
sin (-K cos 6
C4)
Поток энергии равен
5+=
Щ
i-K
COS f н- COS 6 j sin [ у cos 6 j
sin 6 sin (-rr cos 6 j
C5)
« полная излучаемая мощность
W
cos^f^cose) sin^f^cose)
==304 f _A2 ), _Sl Lb.
0 sin 6 sin2 ("^ cos 6 j
C6)
Этот интеграл был вычислен Бонч-Бруевичем ^), который получил
'ПК (и —1)г: {п—2)к (п—3)к
1Г=(—1)'^-130/,
9 Г"" ^
45 + 85 — 125 ~j-
0 о
4 (я
-^>f]'
C7)
1) В о п t S с h-B г U е W i t S с h, Лл/7. Р/гу^/У^; 81, 437,1926.
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН 18.10]
оУО
^ тк
5 = I du=-^ (In 2m7rY — Ci 2/W7r).
C8)
Сопротивление излучения равно, следовательно,
(ПК (п — 1)г: ■ (п — 2)п
S— 45 + 85
0 0 о
)
C9)
л
600
500
400
^300
200
100
О
U
1
/ г 3 ч 5
п
а
На^рис. 79,а показана концентрация излучённой энергии в экваториальной
плоскости для случая трёх пучностей тока; рис. 79, ^>, на котором нанесены
значения сопротивления излучения,
показывает значительное увеличение излучаемой
мощности, достигаемое в результате гашения
одной из противоположных
интерферирующих фаз.
8.10. Направленные устройства. Одно-
проводная антенна является направленной
только в том смысле, что излучение
концентрируется в круговом конусе, осью
которого является антенна. Система
расположенных вдоль прямой полуволновых
излучателей, возбуждаемых в одной и той же
фазе, ограничивает излучение тонкой
круглой дископодобной областью, вроде
показанной на рис. 79,а. Если мы хотим
получить преимущественное направление также и
в самой экваториальной плоскости или
какой либо иной вид осевой асимметрии, то
однопроводный излучатель должен быть
заменён группой или устройством из
полуволновых антенн, которые соответствующим
образом расположены в пространстве и
в которых возбуждаются колебания с
соответствующими фазами. На практике обычно
выдерживаются одикаковые расстояния между
центрами излучателей, так что устройство
образует пространственную решётку. Между задачами о распространении
рентгеновских лучей в кристаллографии и конструированием
коротковолновых ' антенных систем действительно существует некоторая аналогия.
Из дифракционных пятен на рентгенограммах физики стремятся сделать
заключения о расположении атомных диполей, вызывающих дифракцию, и
определить таким образом строение кристалла. Радиоинженер должен
выбрать пространственную решётку и фазу токов в диполях таким образом,
чтобы получить заданную диаграмму излучения. В обоих случаях
распределение излучения характеризуется фазовым множителем, или коэффициентом
формы, зависящим от полярных углов 6 и Ф, и методы, развитые для
анализа строения кристаллов, в значительной мере могут быть применены и
к проектированию антенн.
Для того чтобы упростить задачу, мы предположим, что все излучатели
устройства параллельны друг другу. Антенны возбуждаются в центральных
течках с помощью фидеров, которые могут быть сконструированы так,
чтобы излучаемая ими энергия была пренебрежимо мала. Кроме того, фазо-
Рис. 79, а — диаграмма излучения
антенны, распределение токов
в которой показано пунктиром;
b—сопротивление излучения п
полуволновых отрезков,
колебания в которых происходят син-
фазно.
396
гл. VIII. ИЗЛУЧЕНИЕ
вая скорость распространения вдоль этих фидеров может быть сделана как
меньше, так и больше с; в соответствии с этим, фазовые соотношения
между различными элементами
устройства могут быть заданы
практически совершенно произвольно *).
Фазовый множитель одиночной
полуволновой антенны мы будем
обозначать через FqI
cos
FoW-
(J cose)
sin 6
D0)
Шо,
l\ Центры осцилляторов регулярно pac-
|i' положены в виде пространственной
1. решётки, которая определяется
тремя базисными векторами а^, a2t ад,
как показано на рис. 80.
Положение /-Г0 осциллятора в решётке
определяется вектором
Рис. 80. Система полуволновых вибраторов,
расположенных в виде пространственной
решётки, определяемой базисными
векторами ai, 32, ад.
г,=Ла1+;2а2-ЬЛаз. (^О
где _/j, j^, Уз—три целых числа, не
исключая и нуля. Фаза у-го
осциллятора по отношению к осциллятору, расположенному в начале рещётки,
пусть будет ^f
Pi=Л «1 +к «2+h «3- D2)
Таким образом, а^ — сдвиг фазы любого осциллятора по отношению к
ближайшему его соседу на оси,' определяемой базисным вектором aj, и т. д.
Поле излучения у-го осциллятора будет, следовательно,
Ej = — /601,j F, F) -^ ^-^ '— , D3)
где Rq — единичный вектор в направлении радиуса-вектора R. Напряжённость
результирующего поля получается суммированием*по всей системе:
£ = — / 60 Fo-^-^ 2d 'of ~ ^ ^^'^ ""^ +^^')• D4)
R
Соответствующим подбором амплитуд, расположения осцилляторов в
пространстве и фаз их колебаний в выражении D4) можно добиться почти
любой требуемой формы диаграммы излучения. Мы рассмотрим только
наиболее обычное устройство, в котором амплитуды всех токов ошнаковы,
а базисные векторы aj^ag, &q определяют прямоугольную решётку, стороны
которой параллельны координатным осям х^ у и z. В каждом ряду,
параллельном оси л:, имеется «j излучателей; в ряду, параллельном оси у их п^,
а в столбце, параллельном оси г^ их число, равно «g, так что решётка
целиком заполнена излучателями. Имеем
RpFy- =j\ Cj sin 6 cos <o-\-J2 «2 sin e sin ?Н~Л^з cos б, D5^
«
^) В техническом отношении эта задача разбирается у многих современных
авторов. Можно обратиться к Carter, Hans ell and Lindenbiand, Proc. Inst.
Radio. Engrs. 19, 1773, 1931; W i 1 m о 11 e and McP e t r i e, /. Insi. Elec. F.ng. (Londom
€6, 949, 1928; Hund, Phenomena in High-frequency Systems, McGraw-HiH,
1936; Hoi Ira an, Physik und Technik der ultrakurzen Wellen, f. II, Springer, 1936.
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН [8.10]
397
где а^у «2, «3—расстояния между осцилляторами вдоль х^ у п z осей
соответственно. Напряжённость в любой точке поля излучения будет
£ = —гбО/о^оЛ/а/з
„iJcR — iwf
D6)
где комплексные фазовые множители Д равны
у — Т] е — ij'i (fcoi sin е cos ip + «i) ^
"s
Уд = 'У\ e~ *Js'{^«s sin e sin ip + Kg)
/з'== 2 e ~ *-^3 ^^'^^ ^°* 6 + «з).
Если мы положим
Yi = ^«1 sin 6 cos cp -]- «J, ^г = ^й;2 sin 6 sin о -f- «2»
•lf3=^%cos6-fa3,
TO, согласно C3), можно записать D7) в виде
® sin - ,' ■
D7)
D8)
-^Js Ts
,-€(Ио-1)
Те
sm
Ts
D9)
E=1,2,3) («,>1).
Из выражения для плотности энергии фазовые множители исключаются; мы
получаем
-где
30 /^
sin
«sYs
sm
Ts
E=1. 2,3).
E0)
E1)
Все формулы излучения, выведенные выше, являются частными случаями
этого выражения. Например, однопроводная антенна, описанная в разделе 8.7
ш возбуждаемая в каком-либо высшем порядке, представляет собой линейное
•распределение полуволновых осцилляторов при а1 = а2 = 0> fl;3 = ^/2, а^^тс.
В этом случае
/^1
^2=1,
sin ^ (COS 6 + 1)
COS f-й- COS 6)
E2)
что непосредственно приводит к выражению (И), стр. 389. Если,,как в
разделе 8.9, колебания во всех осцилляторах, расположенных вдоль одной
прямой линии, происходят в одной и той же фазе, то мы должны положить
.Л1 = а2 = 0, «3 = -^, ctQ=p^ и получим тогда выражение C5).
Рассмотрим теперь систему вертикальных полуволновых осцилляторов,
расположенных вдоль горизонтальной оси х. Мы предположим, что все
эти осцилляторы возбуждаются в одной и той же фазе и находятся на рас-
398
гл. VIII. ИЗЛУЧЕНИЕ
стоянии полуволны друг от друга. Следовательно, cLi=-2'> ^2 =
«3 = 0»
а*
О и
27г7?2
cos
{-^ COS в j sin [-\- sin в cos ср j
sin (-^ sin 6 cos 9 j
sin 6
E3)
— выражение^ зависящее теперь от экваториального угла ср. Нули
получаются под теми углами, для которых величина «j 1г/2 sin 6 cos о имеет
какое-либо из значений тг, 21:,... Для экваториальной плоскости 6=1г/2 и,
следовательно, узлы на диаграмме излучения определяются соотношениями
COS со = it —, =ti — ,.
или
COS сэ = rt: —
2_
«1
+ ±
Wv—1
E4>
в зависимости от того, четно п^ или нечётно. Главные максимумы
получаются при о ==7:12. Таким образом, это устройство даёт боковое излучение
энергии. Дополнительные
максимумы определяются
условием dFi/d<s = О,
которое в данном случае
приводит к соотношению
«J tg (~ sin 6 cos о j =
a
Рис. 8], a—два полуволновых синфазных вибратора,
расстояние между которыми равно полуволне;
диаграмма излучения в экваториальной плоскости;
b — четыре пол^волновых синфазных вибратора,
расположенных на расстоянии полуволны друг от друга;
диаграмма излучения в экваториальной плоскости.
sin 6 cos ср]. E5)
При 6 = ср i= 7с/2 имеем
FqF^= «j, так что
интенсивность излучения
в направлении главного
максимума в и| раз
больше максимальной цнтен-
сивности излучения
одиночного осциллятора. С
другой стороны, каждый
из осцилляторов получает
только Ijn^ часть всей
мощности, отдаваемой
источником (в
предположении, что она
распределяется поровну) и,
следовательно, выигрыш в
интенсивности
излучения в данном избранном
направлении получается в п^ раз, где щ — число осцилляторов.
Соседние нули, расположенные по обе стороны от главного максимума,
определяются соотношением cos,<p = =t:2/Wi. Следовательно, чем больше и^,
тем ^же луч. Луч, очевидно, ограничен областью, определяемой углами ср^
и <р2, для которых cos<Pjj — cos<Pi=4/nj, расположенными по обе стороны
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН [8.101
399^
7Г
от <р= -^ . Диаграммы излучения в экваториальной плоскости для устройств,,
СОСТОЯЩИХ из двзос и четырёх излучателей, приведены на рис. 81,а и 81,Ь.
В заключение мы применим соотношение E0) к двум антеГниам,
расположенным на расстоянии четверти волны друг от друга и несуш.им токи,
сдвинутые по фазе на 90°. Полагая а^ = Х/4, а2 = аз = 0, а^ = — тг/г,
получаем
^ 120 7g
cos;
(J cos»)
SIH'
cosf-^,(sln& cos <p-
^)).
E6h
Диаграмма излучения в экваториальной плоскости показана на рис. 82.
Энергия излучается в виде широкого пучка в положительном направлении
оси X. Излучение в обратном направлении
снижено до весьма малой величины. Во
многих практических установках задняя
антенна не связана непосредственно с
источником колебаний. Возбуждение её
происходит благодаря индуктивной связи
с расположенным впереди осциллятором,
так что её действие подобно действию
рефлектора. Однако в этом случае
расстояние не равно точно Х/4 и, кроме того,
необходима некоторая подстройка
рефлектора по длине.
Иглообразный пространственный луч
может быть получен комбинированием
описанных выше простых антенных
устройств. Концентрация излучения в
меридиональной плоскости осуществляется
с помощью горизонтального ряда
вертикальных осцилляторов. Удлинение этих [вертикальных излучателей рядом
полуволновых осцилляторов, возбуждаемых в той же фазе, приводит к кон-
Рис. 82. Два полуволновых
вибратора, расположенных на расстоянии
в четверть ьолны, колебания в
которых происходят со сдвигом фазы на
90°; диаграмма излучения в
экваториальной плоскости.
в=7Г/2
Рис. 83. Горизонтальный ряд
вертикальных полуволновых вибраторов,
позади которых расположен ряд ре^
флекторов; диаграмма излучения в
экваториальной плоскости,
иллюстрирующая сосредоточение энергии в на^
правленном вперёд пучке в зависимости
от числа вибраторов. (Гольман.)
^ = 7т/г
Рис. 84. Вертикальная система
полуволновых вибраторов; позади
расположены рефлекторы;
диаграмма излучения в
меридиональной плоскости. (Гольман.):
центрации излучения в экваториальной плоскости. Наконец, позади такого^
двумерного устройства, на расстоянии примерно Х/4, располагается
соответствующая система рефлекторов. На рис. 83 начерчены диаграммы излучения?
400
гл. VIII. ИЗЛУЧЕНИЕ
В экваториальной плоскости 6 = •jr/2 для горизонтального ряда вертикальных
осцилляторов, позади которых расположены соответствующие рефлекторы,
при различном п^ — числе осцилляторов в ряду, а на рис. 84 — для
меридиональной плоскости Ф = '7г/2 вертикальной системы осцилляторов. В обоих
случаях эффективность увеличения п совершенно очевидна. Естественно, что
наибольшее улучшение получается при малых я, когда добавление ещё одйого
осциллятора даёт весьма заметный эффект. Относительный выигрыш с
увеличением числа осцилляторов падает, и, наконец, мы достигаем такого момента,
■когда дальнейшее увеличение числа элементов устройства становится
экономически неоправданным.
8. И. Точный расчёт поля линейного осциллятора. Метод Пойнтинга,
который мы применяли до сих пор для расчёта сопротивления излучения,
целиком основан на определении потока энергии на больших расстояниях
от центра излучающей системы. Но если энергия всё время теряется, то она
должна всё время доставляться источником. Следовательно, над токами
в антенне всё время должна производиться работа, для чего необходима
компонента э. д. с, параллельная проводу на его поверхности и сдвинутая
по фазе на 180° по отношению к антенным токам. Знание фазовых соотношений
между токами и э. д. с. вдоль проводника должно привести к тому же
значению сопротивления излучения, что и ранее. Фактически оно может дать
нам больше, ибо это сопротивление является лишь действительной частью
комплексного радиационного импеданса, который, конечно, должен быть
известен, если мы хотим рассматривать излучатель как элемент цепи тока.
Очевидно, результаты предыдущих параграфов не могут быть
использованы при этом втором методе, поскольку они справедливы только для
больших расстояний от источника.
Существенно, однако, что мы имеем точное выражение
для поля в непосредственной близости к
каждому из проводников. Доказательства того, что
, . точное выражение в конечном виде действи-
•л'-г' ' тельно может быть найдено, были даны Брил-
люэном ^), Писталькорсом ^) и Бехманом з) и
явились чрезвычайно важным вкладом в
теорию антенн.
Мы снова рассмотрим одиночный
прямолинейный проводник, совпадающий с отрезком
1_и^
f не. 85. Координаты линейного „„*:„„
.вибратора, рассматриваемого|.в оси г, но центр проводника теперь не обяза-
разделе 8.11. ^ тельно должен совпадать с началом коорди-
' нат. Какая-либо точка проводника опре'деляется
её координатой ^, а длина проводника / = ^2—^i» ^^^^^ показано на рис. 85.
Распределение токов синусоидально, но, если учитывать нагрузки на концах,
яе обязательно равно нулю в этих точках. Подобные нагрузки могут быть
осуществлены использованием ёмкостного эффекта металлических пластин,
заземлением через сосредоточенную самоиндукцию или сопротивление, или
с помощью какого-либо из многочисленных других устройств. Ток, таким
•образом, снова равен
/'= /о sin (k^ — а) е- ^*, E7)
а вектор Герца для такого распределения будет
е. -к
Й. (^> О = 1^ ^-*"^* J sin {k^ - а) ^ dt E8)
?i
1) В г i 11 о u i n, Radioelectricite, Апрель 1922.
2) Pi stalker s, Proc. Inst. Radio. Engrs. 17, 562, 1929.
3) Be eh man, ibid., 19, 461, 1471, 1931.
?--ч>;'
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН (8.11] 401
I '^- ' ■ ^ , ., , , I
I
Это выражение можно написать также в виде
с с
Цилиндрические координаты произвольной точки поля будут р, о, г,
расстояние от какого-либо элемента тока до этой точки равно
г = /р2 + (г —е)^
Положим теперь
ui=r-\-l — Zjdu^'—dt F0)
Тогда
Ji!fpirfE=>*J^d„. F1)
«t
где ttj = /-i-|-^i—2-, U2 = г^-\-^ — 2, a /"i и /-g — расстояния от концов
проводника до томки наблюдения. Аналогично, если
1>с=/- — $ + г, dv= ^rfS, F2)
то
f:^!^ai=-e-^j^av, ' F3)
где i:>j = /-J — ^1 -{- -s", '^2 = ''2 — ^-\-^- Вектор Герца будет, следовательно.
Интегралы с экспонентами простыми преобразованиями могут быть
приведены к виду, для которого имеются табулированные значения. Мы
замечаем прежде всего, что
«{j оо оо
ji|:id«=j^d«-/i^rf«. F5)
щ щ щ
Согласно определению интегрального косинуса и интегрального синуса,
оо щ
Q ku^ = — Г ~—— du. Si Attj = Г iHLJ? ddif F6)
«1 о
и ввиду того, что Si оо =^«/2, имеем
giku
со
f-^du= —а ku^ — i Si ku^-{-^ F7)
yiku
Ш1И
Г .£!fl rftt =;Ci;Att I -f i Si им I. F8)
Таблицы этих функций можно найти у Янке и Эмде.
26 Эак, 593. Теория «яектфоиагнетизма.
402
гл. VIII. ИЗЛУЧЕНИЕ
Для подсчёта поля мы применяем формулы
E = graddivII + ^^n, Н==~ш8Го1П,
которые в цилиндрических координатах имеют вид
k П2, Лр— ^р^^ , Е^
О,
аш
G0)
ф-^^"^'^-
Так как Мц Мд и т. д. в F4) зависят как от г, так и от р, то нужна
дифференцировать и пределы интегралов. Например,
и щ dz щ dz '
dz
,iks.
dz
г ^гки
) и
Аналогично
«1
eiJi (r,+e,)
гч
К
Г71)
oiks.
giku
dp
''a
da
eik(rt+^t)
eik (rt+^i)
Г2 — B: — ?2)
'•2
пх
ri-{z-^i)
G2>
После выполнения дифференцирования и приведения подобных членов ми
получаем для компонент напряжёйности поля
^« = fc^ 1^^-—-cos(^?2—а)— ^_-cos(^ei —а) +
■ + -aJ (-7Г) ^^" (^^2 - «) - li (-77-) '^" (^^1 - «) J' ^ ^ ^>
л« =
Ще
— ivut
'" 47гевш V р Гг
|l(£ziM..^cos(^?,-a)_
IP '•2 V 2 ^
5__у __ cos (^^1 — «) + у -^ [(^ ~ У -;г-1 Sin (^^9 — а)—
-7ai-r'~^^>rj'^"^^^^-"°')}
Яф = -«4^ [^-у- cos (й?2 — «) р- cos (й^1 — а) +
G4>
^ Р ь^2 5ш(^^2 —«)-~--^-—-^^—_-.sm(A;Si— аI. Gо>
В случае изолированного провода со свободными концами токи в
точках ^=^1, ^ = ^2 равны нулю. Тогда /j = ar/w//, где т — снова число
полуволн, укладывающихся вдоль провода. Так как
sin \--j^ — а j =^sin \—j^ ~ aj =. О,
TO мы можем положить a = •^^-= irw f 1 ^j. Формулы для напряжён-
ностей поля примут тогда сравнительно простые выражения:
г pikr. pikr. 1
£,=-30iv-^-* [(- \Y~ -^J.
P 0 L^ ^ P '•s P /-i J *
и — i_<). />-tof _ j r \\m pikrt pikrx\
G6)
ТЕОРИЯ ИЗЛУЧЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АНТЕНН I8.12J 403
8.12. Определение сопротивления излучения по методу вычисления
э. д. с. Выражения для поля, выведенные в предыдущем параграфе, являются
точными и справедливы для всех точек пространства, в том числе и в
непосредственной окрестности токов. Особенности, которые получаются в
концевых точках проводника при /■j = 0, /-2 = 0, появляются вследствие
предположения о линейном распределении токов. Практически, в результате
конечности сечения провода, мы можем быть уверены в конечности
значений напряжённости поля, хотя вблизи этих точек следует ожидать
относительно больших напряжённостей. Во всех других точках проводника
соотношение между фазами тока и' параллельной ему компоненты Е может быть
определено из G3) или из G6), а следовательно, может быть подсчитана и
работа против сил реакции поля, необходимая дхля поддержания токов
в антенне.
В разделе 2.19 было показано, что для действительных векторов Е,
Н и J и при токах, распределённых в свободном пространстве, дивергенция
вектора Пойнтинга удовлетворяет соотношению
divS = —EJ—|-(-^Я2+^|Я2). G7)
Если поле является периодическим, то среднее за период изменение
распределённой в поле энергии равно нулю, так что
div S = div S = —- EJ. G8)
Если теперь вместо действительных векторов мы будем оперировать
комплексными напряжённостями поля и токами, то, согласно разделу 2.20,
получим
S = ~Re[E, H*l = ReS+, |
1 \ G9)
ReEReJ =-iRe(EJ*), j
где знак* обозначает сопряжённые величины. Полная средняя мощность,
излучаемая системой токов, будет, следовательно,
1^.= JSn^a = —yRe Г EJ*tfx;. (80)
s V
Энергия излучения может быть подсчитана либо путём интегрирования
нормальной компоненты вектора Пойнтинга по какой-либо замкнутой
поверхности, охватывающей все источники, либо путём интегрирования
мощности, расходуемой в единице объёма^ по всему объёму^ в котором
оаспределены токи.
Предположим теперь, что в пустом пространстве имеется и линейных
проводников, по которым текут токи. Не теряя общности, мы можем
предположить, что проводники системы параллельны друг другу и оси г. Пусть
комплексная величина Ij есть ток в /-м проводнике, z — компонента
электрического поля, вызванного i-u током в у-м проводнике, будет E^j.
Тогда, согласно (80), полное излучение системы будет
WH - ^ I^e S S f ^iM-. (81)
где интегралы должны быть распространены вдоль каждого из проводников.
Это выражение даёт нам мощность, с которой индуцированные э. д. с. про-
56*
404
гл. VIII. ИЗЛУЧЕНИЕ
изводят работу над токами системы,. Напишем 1^ и Е^^ в виде
Eji = JoiUjie-^-K
(82)
где амплитуды /q,- и /q^ в общем случае комплексны, а функция Uji опреде
'03
ляется соотношением G3). Тогда
W
где
п п
2"R^ 21j ^hi^Ol^ji I
J=:li = l
^23
(83)
(84)
Величины Z^j являются коэффициентами связи^ или, в некотором смысле,
переходными импедансами. Действительная часть коэффициента Z^
представляет собой сопротивление излучения /-го проводника при удалении всех
остальных цроводников.
Очень изящный метод для расчёта излучения был предложен Бехманом *).
Если, как в (82), распределение токов синусоидально, то можно написать
—kv:
Напряжённость поля Ejf удовлетворяет соотношению
d4li
km,.
Кроме того,
(85)
(86)
(87)
и следовательно.
1 г = 1
f an,- \
'"^3
(88)
Из F4) и F8) мы имеем
n.=^c^i«'<'^i-">i(Ci*«+'Si*«)i:!!+
4i
g—i(/i^j-—о)
{Cxkv^iSikv)
2г\
(89)
где в данном случае к = г,.^-[-^f — ^^, г> = /-^^—Sf-f^^-. Координата li
относится к точке антенны, ток в которой равен /^, в то время как ij
представляет точку >го проводника. Индексы 1 и 2 обозначают, как и прежде,
координаты соответственно верхнего- и нижнего концов антенны. Для
нахождения излучения системы линейных проводников никакого
дальнейшего интегрирования не требует£я. Поскольку амплитуды токов Jq{ и /qj
входят в (88) в виде множителей, мы можем найти интегральнбе
выражение для импеданса Zj^.
^) Bechmann, lac. cit., стр. 1471.
ПРИНЦИП ГЮЙГЕНСА-КИРХГОФА (8.131 _ 405
в случае ненагруженной антенны ток /^ на концах ^,j. и ^ равен нулю.
Тогда k^ij — а^ = 0, k^Qj—ау = т,тс, и мы получаем
п п
^ = 4 ^^ 2 2^41 (- 1РП,($2,0 - П, {^,j)}. (90)
трудность возникает при применении этой формулы к колинеарным
проводникам. Рассмотрим, например, как и в разделе 8.7, излучение одиночного
линейного осциллятора. Этот случай является пределом двух параллельных
проводников, расстояние между которыми стремится к нулю. Есди мы
примем, что концы двух проводников совпадают, то
при ^^- = ^1: «if = 0 + ^1 — ^1 = О, «2г = ^+^2 — ^1 = 2/,
г»1^ = о —$1 + ^1 = 0, t>2f=/—е2 + ^1==0,
и при ^j = ^2- «1г=/+^1—?2=0, tt2«=0-f ^2 —$2 = 0,
^1г==^—^1 + ^2==2/, г;2,- = 0 —$2+^2 = 0.
Согласно (89),
h=2l
ы = 0
Но Д; = _=:_, 2^
>тГ V г "^ 60, и, следовательно, согласно (90),
W^—lbilCi^ ^
Этот результат, очевидно, ошибочен, поскольку Ci О обращается в
бесконечность. Трудности этой можно избежать, если сначала рассчитать
излучение двух параллельных проводников, разделённых малым, но конечным
расстоянием р. При переходе к пределу р = 0 бесконечные члены выпадают i),
и мы получаем, как и в разделе 8.7, что
Wr=. 157оAп 2тщ — С\ 2тт:). (91)
ПРИНЦИП ГЮЙГЕНСА-КИРХГОФА
8.13. Скалярная волновая функция. Пусть V—любая область внутри
однородной изотропной среды, ограниченная замкнутой регулярной
поверхностью S, а «l* (х, з'» «2^) — какое-либо непрерывное и обладающее
непрерывными первыми производными в объёме V и на границе 5 решение уравнения
д.], _j_ Д;2^ == 0. ( 1 )
Тогда из теоремы Грина, уравнение G), стр. 153, непосрдственно следует,
что значение ^ в любой внутренней точке х', v', гг' может быть выражено
через интеграл по поверхности 5 от <}; и нормальной производной ^:
S
где, как всегда.
1) Подробности даны у Бехмана, 1ос. cU., стр. 1477.
Г-а/
406
гл. VIII. ИЗЛУЧЕНИЕ
расстояние от переменной точки на поверхности 5 до фиксированной
внутренней точки х\ у', г'. Соотношение B) является фактически частным
случаем уравнения B2), стр. 377, который имеет место тогда, когда все
источники поля расположены вне поверхности 5, а временной множитель е-^*
исключён.
Функция, определённая соотношением B), является непрерывной и имеет
непрерывные производные во всех внутренних точках объёма К, но терпит
разрыв при переходе точки л:', у\ £ через поверхность S. В разделе 3.15
было показано, что функция
S
непрерывна при переходе через поверхность 5. Следовательно, разрыв
непрерывности функции B) тождественен с разрывом, рассмотренным в разделе
3.17 в связи со статическим потенциалом.. Если У, у', У — любая точка,
безразлично внутри или вне поверхности S, то функция, определённая
интегралом
S
E)
во всех внутренних точках тождественна с решением ^, значения которого
были заданы на поверхности S, а во всех внешних точках равна нулю *).
Так же, как и в статическом
случае, значения ^ и производных ^
во всех внутренних точках
однозначно определены значениями на
поверхности S только ^ (задача Дирихле) иди
только V- (задача Неймана), Следо-
аф
вательно, значения «^ и, ~-
одновременно не могут быть заданй на
поверхности произвольно, если мы хотим,
чтобы во внутренних точках к и 4»
^ ^ совпадали. Функция к, определённая
Рис.86. Поверхность Sy может быть соотношением E), удовлетворяет урав-
замкнута в бесконечности. I нению A) и является регулярной во
всех внутренних точках объёма V при
всяком выборе ^ и ^ на поверхности S, но значения, принимаемые и и
•^ на поверхности S, в общем случае будут отличаться от заданных ^ и -^.
|. Все элементы поверхности S, бесконечно удалённые как от источника,
так и от точки наблюдения, ничего не вносят в значение интеграла B).
На рис. 86 все элементы источника расположены в пределах конечного
расстояния Ri от заданного начала отсчёта Q. Поверхность 5 представляется
в виде бесконечной поверхности S^, замыкаемой сферической поверхностью 5^
очень большого радиуса г с центром в точке Р. Точка наблюдения Р^х', у\ г')
лежит внутри поверхности S, в то время как все элементы источника распо-
') Аналитические свойства волнор.ой функции Кирхгофа разобраны лодробно
у Poincare, Theorie matheraatique de la lumiere, т. И, гл. VII. См. также весьма
полезную книгу Pockels'a: Ober die partielle Different algleichung Дм-|-Л^ц __'o^
Teubner, 1891 и Hadamard, Lectures ort Cauchy's Problem, Yale Umversity Press,
1923.
ПРИНЦИП ГЮЙГЕНСА-КИРХГОФА [8.13| 407
ложены вне её. Если R — расстояние от точки Q до элемента площади — ^2
очень велико по сравнению с наибольшим значением R^, то, согласно (87),
<:тр. 365, и C2), стр. 357,
^ikBt • « ikR ~
Zi (-0П2« + l)PacosTi);«(^/?i) =
==^~^2j^n(Ti./?i). F)
°2 йазйо^ ° ^ _ Q
откуда
gikR AJiR ^
»=0
^ikR^ gibr
n=:0
СО
^йЙо, ^о), G)
'Ь = -\- = -V-/(To, Yi, /?о, ^i)- (8)
На поверхности y',S2
■ an— =а7 -- = (.'^-7)(-г] ^(^0' т^» ^0,/?i),
.Ы (—)=('l-7)(-V)/( ^0. ъ Ro, Ril (9)
111
откуда следует, что члены с —, —j- ^ — в развернутом подинтегральном
выражении в B) взаимно сокращаются, а остающиеся члены имеют порядок
-^, л^З и, следовательно, ничего не вносят в интеграл по поверхности
4S21 если г -^ со.
Предположим теперь, что поверхность 5 представляет собой
непрозрачный экран, отделяющий источник от наблюдателя. В силу только что
доказанной теоремы можно считать, что бесконечно протяжённая незамкнутая
поверхность замыкается в бесконечности. Если в поверхности Si проделать
небольшое отверстие, то поле в некоторой степени будет проникать и
а область, в которой расположен наблюдатель. Задача состоит в том, чтобы
определить интенсивность и распределение этого дифрагированного поля.
Очевидно, если известны значения ^ и ■^ в отверстии Sj и на стороне экрана,
обращенной к наблюдателю, то дифрагированное поле можно было бы
определить подсчётом интеграла B). Эги значения нам неизвестны, но для
того, чтобы получить приближённое решение, предположим, вслед за
Кирхгофом, что
a) На внутренней стороне экрана
b) На поверхности 5j щели или отверстия поле тождественно с полем
еевозмущённой падающей волны.
Почти все расчёты дифракции от щелей или решёток, произведённые
со времён Кирхгофа, были основаны на этих предположениях ^). Легко ука-
1) О классической теории дифракции см., например, М. П л а н к. Введение в
теоретическую физику, ч. 4 (Опгик.!), М. — Л. 1934 или Б о р н. Оптика, 1934. Для того чтобы
получить более ясное представлеше о физической сущности явления, кроме описан-
мого ниже метод;| Кирхгофа, читателю следует также познакомиться с работой
Rubinowicz'a Ann. Physik 53, '257, 1917, а также Kottler, ibid. 70, 405, 1923.
Уже после написани! этого и последующих параграфов рассмотрение этого
вопроса было лано в книге The Mathematical Theorv of Huygens' Principle, Baker and
С ops on, Oxford, 1939.
408 ^ гл. VIII. ИЗЛУЧЕНИЕ
зать основные аналитические ошибки, допускаемые при этом. Прежде
всего предположение о равенстве нулю «|^ и -^ на внутренней поверхности
экрана означает разрыв непрерывности ^ на контуре Cj, ограничивающем
отверстие Si, в то время как теорема Грина справедлива только для
функций, непрерывных всюду на полной замкнутой поверхности S. Эта трудность
не может быть устранена простым приёмом замены контура, на котором
имеет место разрыв, узкой областью с быстрым, но непрерывным
изменением рассматриваемой функции. Если '^ и ^ равны нулю на каком-либо
конечном участке поверхности S, то они равны нулю во всех точках
пространства, охватываемого этой поверхностью ^). Во-вторых,
электромагнитное поле не может быть в общем случае представлено с помощью одной
только скалярной волновой функции. Оно характеризуется системой
скалярных функций, представляющих собой прямоугольные компоненты
электрического и магнитного векторов. Каждая из этих скалярных функций
удовлетворяет уравнению A) и её значение в какой-либо внутренней точке х\ у', г
выражается с помощью соотношения B) через значения на границе 5. Однако
эти компоненты должны удовлетворять не только волновому уравнению A),
но должны быть также и решениями максвелловских уравнений поля.
Реальная задача состоит не .в интегрировании волнового уравнения, скалярного-
, или векторного, а в одновременном интегрировании системы векторных
уравнений первого порядка, связывающих вектора Е и Н.
Несмотря на эти возражения, классическая теория Кирхгофа приводит
к удовлетворительному решению многих • дифракционных задач физической
оптики. Успех этот обязан прежде всего тому факту, что в оптических
задачах отношение длины волны к наибольшему размеру отверстия мало.
Вследствие этого дифрагированное излучение отбрасывается, главным
образом, вперёд, в направлении падающего луча, и предположение о равенстве
нулю поля на затенённой стороне экрана приблизительно выполняется.
Кроме того, при измерениях обычно интересуются интенсивностью, а не
поляризацией. По мере увеличения длины волны дифракционная картина
расширяется. Вычисление ^ из соотношения B) приводит тогда к наличию
интенсивности непосредственно позади экрана, которая никоим образом не равна
нулю, в противоположность нашему исходному предложению. Разные авторы
предполагали, что эти нулевые значения могут рассматриваться как первый
член в ряде последовательных приближений,' и значения ^ w j^ на
поверхности S, полученные из первого приближения, должны быть взяты в качестве
граничных условий для второго. Доказательства сходимости такого расчёта,
однако, нет, а трудности интегрирования делают этот способ практически
непригодным.
Новейшие достижения в технике генерирования ультракоротких
радиоволн стимулировали интерес к ряду задач, имевших ранее очень небольшое
практическое значение. Естественным следствием этой тенденции к
использованию коротких волн явилось применение методов физической оптики
к расчёту интенсивности и распределения электромагнитного излучения из.
полых труб, рупоров или малых отверстий в полых резонаторах. Но в
радиотехнике длина волны обычно того же порядка, что и размеры" отверстия;
поляризация дифрагированного излучения легко наблюдается. Трудно
ожидать поэтому, что и при т^ких условиях можно полагаться на формулу
Кирхгофа B).
1) Прямое следствие теоремы Грина. См. Pocjkels, loc. ciU стр. 212,
ПРИНЦИП ГЮЙГЕНСА-КИРХГОФА [8.Щ 409
8.14. Непосредственное интегрирование уравнений поля О- Задача,-^
состоящая в том, чтобы выразить векторы Е и Н во внутренних точках
какого-либо объёма через их значения на поверхности, ограничивающей этот
объём, рассматривалась многими авторами ^). Требуемый результат может быть
получен просто и непосредственно, если к уравнениям поля применить
векторный аналог теоремы Грина. В разделе 4.14 было показано, что если Р
и Q — любые две векторные функщ1и положения, удовлетворяющие
соответствующим условиям непрерывности, то
JCQrotrotP —ProtrotQ)rf'0= J {[ProtQ] —[QrotPJjn^a, A0)
V s
где S, как обычно, регулярная поверхность, ограничивающая объём V.
Предположим, что векторы поля содержат время только в виде
множителя ехр (— Ш), и напишем уравнения поля в виде
rotE —гсо[хН = —J*, (I) divH= —р*, (Ш) -
rot Н-|-/ш£ Е = J, (II) divE=-^p. (IV)
Среда предполагается однородной, изотропной и непроводящей. Величины:
J* и р* являются фиктивными плотностями «магнитных токов» и «магнитных
зарядов», которые, согласно всему, что мы знаем, не имеют реального
физического существования. Вскоре, однако, у нас встретятся случаи, когда мы
будем предполагать существование произвольных разрывов непрерывности обоих
векторов Е и Н, разрывов, которые в действительности физически
невозможны, но которые вызывались бы поверхностно распределёнными
магнитными токами и зарядами, если бы они существовали. Токи и заряды обоих
типов подчинены уравнениям непрерывности
divJ —шр = 0, divJ*—шр* = 0. (V)
Векторы Е и Н удовлетворяют уравнениям
rotrotE —й2Е = г(й[А^ —divJ*, (И)
rotrotH —A!2H = i@£j*4-divJ, ' A2)
где й^ = <й^ SIX.
Положим в A0) Р=Е, Q = oa, где а — единичный вектор произволь-
ного направления, а о = ——. Расстояние г, измеряемое, от элемента х, у, г
до точки наблюдения х', у', z\ определяется C). Мы имеем тождественно
rot Q = [grad <р, а], rot rot Q = а k-o -\- grad (а grad 9), 1
i rotrotP = A;^E-f mjxj —rotJ*. J ^^'^^
Следуя способу раздела 4.15, легко показать, что вектор а является
общим множителем для всех членов соотношения A0) и, так как а
^) Разделы 8.14 и 8.15 написаны совместно с д-ром L. J. С h и.
2) Love, Phil. Trans. (А) 197, 19Э1: L arm о г. Lond. Math. Soc. Proc. 1, 1, 1903,
Ignatowsky, Ann. Phvs. 23, 875. 1907; и 25, 99. 1908. To nolo, Annall di Mat. 3.
17. 1910; Macdonald,>roc. lowcf.Afo//?. Soc. 10, 91, 1911 и Phil. Trans. (A) 2i2;
295, 1912. Tedone, Link Rendi E) 1. 286, 1917; Коttier, Avn. Phys 71, 457, 1923.
Schelkunoff, Bell. System Techn.J. 15, 92,1936; Baker and Copson, loc.cit., гл. III.
410 гл. VIII, ИЗЛУЧЕНИЕ
произволен, то, следовательно,
j (/ш{А J ср—rot J*cp + — р grad 9) dv =
г
=J {i^\>-[n, HI 9 -Ь [[п, El grad о] + (пЕ) grad о — [п, J*] 9} da. A4)
' Тождество
J rot J* (sdv= j [n, J*]^9 rfa 4- J [J*, grad 9] dv A5)
V S ■- V
позволяет привести это соотношение к виду
J {/(ujx J9 — [J*, grad 9l 4- -- p grad o]dv=^
V
= J{/a)[x[n,Hl-L[[n, E]grad9]-f (nE)grad9}fifa. A6)
s
-Исключение особенности в точке /-=0 было описано в разделе 4.15. Сфера
радиуса /"i описывается вокруг точки л:', у\ z\ нормаль к сфере направлена
из объёма V и, следовательно, по радиусу к центру. Имеем
grad9=(-^—гй)-^Го, A7)
так как на этой сфере n=rQ, Площадь сферы уменьшается с радиусом как
4'jr/-^, и так как
[[n,Eln] + (n,E)n = E, A8)
то слагаемое от интеграла по поверхности сферы в правой части A5)
сводится к 4'7гЕ(л;', у', г'). Значение Е в любой внутренней точке V будет,
следовательно,
Е(л;', у',г') =^ J {^^^^9— Р*, grad 9I -[-- pgrad 9} dv —
V
—J;^J{iu)H-[n,Hl9+l[n,Elgrad9]-f (nE)grad9}rf«. A9)
Очевидно, перемена местами векторов Е и Н приведёт к соответствующему
выражению^ для Н:
Н(л:', у', 2r')=:i:J|beJ*9+[J,grad9]+-^p*grad9.}£?t» +
+ 1 J [шг [n, El 9 — l[n, HI grad 9] — (nH) grad 9} da. B0)
s
Последнее соотношение является обобщением уравнения B3), стр. 228, на
случай динамического поля.
Если все токи и заряды могут быть окружены сферой конечного радиуса,
то поле регулярно на бесконечности, и любая сторона поверхности S может
быть выбрана в качестве «внутренней>^.
s» ПРИНЦИП ГЮЙГЕНСА-К|^РХГОФА 13.14] 411
в предыдущих разделах этой главы мы рассматривали расчёт полей
заданного распределения зарядов с помощью векторного и скалярного
потенциалов и с помощью вектора Герца. Теперь мы показали, что векторы Е и Н
могут быть подсчитаны и непосредственно, без введения потенциалов.
Поверхностные интегралы в A9) и в B0) выражают поля, вызываемые источниками,
расположенными вне поверхности 5. Если S удаляется в бесконечность, то
жожно считать, что эти поля исчезают. Огбрасывая магнитные заряды и токи,
мы получаем следующие важные формулы:
B1)
Поскольку распределение токов предполагается известным, плотность
зарядов может быть определена из уравнения непрерывности.
В разделе 9.2 будет показано, что электромагнитное поле внутри
ограниченной области полностью определяется заданием тангенциальных
компонент векторов Е и Н на ограничивающей поверхности и начальным
распределением поля по объёму области. Отсюда следует, что если значения [п, Е]
и [п, Н] в A9) и B0) заданы, то выбор пЕ и пН не может быть сделан
произвольно. Этот выбор должен быть совместим с условиями, которые
наложены на векторные пэля, удовлетворяющие уравнениям Максвелла. Такие
же ограничения в выборе <Ь и ^ были подчёркнуты в разделе 8.13.
Зависимость нормальной компоненты Е от тангенциальной компоненты Н
эквивалентна зависимости р от J.
Предположим временно, что распределение зарядов и токов в A9)
ограничено тонким слоем на поверхности S. Пусть по мере уменьшения
толщины слоя плотности возрастают, так что в пределе мы, как обычно,
объёмную плотность заменим поверхностной. Если внутри области V и на
её границе 5 зарядов и токов нет, то поле во внутренних точках будет
E(.v', У, 2-') = —1/{гш:Мп,Н1ср-[-[[п, Elgrad<?l-f (nE)grad<?}rffl. B2)
s
Отсюда ясно, что поле это точно такое же, какое вызывалось бы
электрическими токами, распределёнными по поверхности 5 с поверхностной
плотностью К, магнитными токами, распределёнными с поверхностью К* и
поверхностными электрическими зарядами плотности % где
К!=—[п,Н1, К* = [п, Е], t| = —snE. B3)
Значения Е и Н в B3) являются значениями непосредственно у поверхности
€ внутренней её стороны.
Функция Е(л:', у\ z^), определённая формулой B2), разрывна при
переходе через S. Можно показать, как это было сделано выше, что разрыв,
gikr
связанный с 9 = » таков же, как и в случае стационарного поля, когда
t^''= — . Тогда, согласно разделу 3.15, скачок интеграла*
Ез (л:', у, 2-') = ^ J •», grad <? da B4)
s
412
гл. VIII. ИЗЛУЧЕНИЕ
*ч^
При переходе через поверхность 5 равен nAEg = — , где ДЕд — разность зна-^
чений Eg с внешней и внутренней стороны поверхности. Следовательно,
третий член в B2) не влияет на величину скачка тангенциальной компоненты^,
а величину нормальной компоненты Е сводит к нулю. Точно так же скачок
Е^х', У, ■2^')'=:^ J [К*, gradcpl da,
1
471
Г" S
B5)
согласно разделу 4.13, определяется соотношением [п, ДЕ21=К*, так что
второй член в B2) сводит к нулю тангенциальную компоненту вектора Е,
не оказывая влияния на нормальную. Первый член в B2) непрерывен при
переходе через поверхность S, но имеет разрывную производную. Ротор Е
в точке х', у, z' равен
rof Е (д;',У, У) = —i|^ J [[п, Н] grad <?] da.
B6)
Рис. 87. С — контур на замкнутой
поверхности S, разделяющий её
на две 4acTii Sj и S2.
Это выражение типа B5), Вектор Е и тангенциальная компонента его
ротора на положительной стюроне поверхности S равны нулю:
следовательно, вектор Е равей нулю во всех
внешних точках. Те же рассуждения применимы
и к вектору Н.
8.15. Разрывы поверхностного
распределения. Результаты предыдущего раздела
справедливы только в том случае, если
векторы Е и Н непрерывны и имеют
непрерывные «первые производные во всех точках
поверхности 5. Следовательно, их нельзя
применить непосредственно к задаче о
дифракции на щели. Для того чтобы
распространить выражение B2) и на
подобные случаи, рассмотрим замкнутую поверхность 5 (не исключается и
случай поверхности, замкнутой в бесконечности), разделённую на две зоны
Sj и ^2 контуром С, расположенным на поверхности S, как показано на
рис. 87. Векторы Е и Н и их первые производные непрерывны на 6\; то
же самое справедливо 'и относительно S^. Однако тангенциальные к
поверхности 5 компоненты Е и Н могут теперь испытывать разрыв непрерывности
при переходе через контур из одной зоны в другую. Для того чтобы
совместить возможность подобных разрывов с уравнениями поля, необходимо
сделать дальнейшие предположения о наличии линейного распределения
зарядов и токов вдоль контура С. Это линейное распределение источников
определённым образом изменяет поле, и только при учёте этого изменения
получающиеся в результате выражения для Е и Н удовлетворяют уравнениям
Максвелла.
Метод нахождения распределения зарядов и токов на контуре, сов-
. местимого с требованиями задачи, был предложен Котлером *). Выше
было показано, что поле во внутренних точках тождественно с нолем,
создаваемым поверхностными зарядами и токами, определёнными соотношениями
B3). Скачок тангенциальных компонент Е и Н при переходе на поверхности S
из зоны 5j в 30HJF Sa предполагает, следовательно, скачкообразное
изменение поверхностной плотности тока. Обрыв линий тока, согласно уравнению
непрерывности, в свою очередь связан с накоплением на контуре С заряда.
1) К о 111 е г, Ann. Physik 71, 457, 1923.
? : ПРИНЦИП" ГЮЙГЕНСА-КИРХГОФА 18.15] 4l3
'Пусть ds будет элемент длины вдоль контура С, положительное
направление которого определяется положительной нормалью п (рис. 87). Пусть flj ,
•€удет единичным вектором, нормальным к п и элементу контура ds'n
направленным в сторону зоны 1. Линейные плотности электрических и
магнитных зарядов мы будем обозначать через о и о*. Уравнения (V)
применительно к поверхностным зарядам примут вид
Hi (Ki — К2) -= «too, Щ (Ki — К) = /0H* B7)
«, следовательно, согласно B3),
/cDci = ni(In,H2]—[п, HJ) = (H2~Hi)[ni, п],
/ша*=П1([П, Ell—[П, Eg])
= (Щ~Щ)[щ,п], \
= —(E2-Ei)[ni, п]. J.
B8)
Вектор {Hj, п] имеет то же направление, что и ds. Если ^2 представляет
собой непрозрачный экран, на поверхности которого Е2 == Нд = О, то поле
в любой точке на затенённой стороне равно
E(y,y,^')=-^-l-|gradcp(H,rfs)-
— i /1 ''"^f^-I"' "il"? + [[п. Ell grad cp] 4. (nEi) grad о | da, B9)
что, как можно показать, тождественно с
47:Е (х\ у\ г') = - j^^ gr^^ f (H^s) +
с
+ |cp[E„dsl-/(E.|j-o^)da. C0)
О Si
Для магнитного поля получим
47гН (л;'. y',z')^~-j grad cp (E^rfs) +
с
-т- f \ i^^ In. El] <? — [in, HJ grad 0] — (nHi)grad o\da =
ZWjJL J
С с Si
Остаётся показать, что дивергенции полей, выражаемых этими
интегралами, действительно равны нулю и что поля эти удовлетворяют
уравнениям (I) и (II) ^).
1) Формулы B9)—C1) определяют Е и Н внутри поверхности через значения
на 5 как тангенциальных, так и нормальных компонент векторов поля. Задание
-стольких составляющих на 5 является, вообще говоря, излишним, поскольку, как
это следует из теоремы единственности (раздел 9.2), поле внутри S однозначно
определяется заданием либо Ef, либо Н( (так называемые первая и вторая граничные
задачи электродинамики). Соответствующие формулы, определяющие поле, могут
быть получены применением леммы Лоренца, играющей роль векторной теоремы
Грина, и должным образом подобранного вспомогательного поля, играющего роль
'•функции Грина. В общем случае негармонических процессов аналогичные результаты
могут быть получены при псмощи «обобщенной леммы Лоренца» (см. Я. Н. Фель д,
-:ЖЭТФ 13, ПО, 1943 и 14, 330, 1944; ДАН 41, 294, 1943 и 48, 181, 1945). Следует
-отметить также, что формулы типа B9) — C1) легко получаются из леммы Лоренца,
если в качестве вспомогательных полей ввести поле электрического (для на-
„;хождения Е) и магнитного (для нахождения Н) диполя в свободном простран-
--етве. Прим. ред.
414 гл. VIII. ИЗЛУЧЕНИЕ
Рассмотрим сначала дивергенцию B9) в точке х', у', z':
div'Е (*', у. г') =-тгг ilr I ^^ (И'''») +
с
-f-1-J {/Ш11. [п, HJ grad о-f (nEi) А? } ^й; = —-|^-^ § cpHi^fs- ■'
J (п, E{)oda-^^^ [n, HJ grad<prfa, C2)>
47L
St Sj
если учесть, что при применении к функции о и её производным grad' =»
= — grad. Далее,
Г [п, Н] grad ^da = J cprotH nrfa — J cpHcfs. C3>
s so'
Линейный интеграл, получающийся в результате этого преобразования, равен
нулю, если поверхность S замкнута; если же она ке замкнута, то он как
раз скомпенсирует контурный интеграл в C2). Обратно, только наличие в
выражении B9) контурного интеграла приводит к тому, что дивергенция
равна нулю, и к тому у что на больших расстояниях от отверстия S^ волны
поперечны. Из (П) и из со07НОшения-;—= — ш\к немедленно следует, что
div'E{x',y',z') = 0.,, C4>
Такое же доказательство справедливо и для Н (л:', у', г').
Покажем, наконец, что B9) и C1) удовлетворяют (I) и (II):
rot' Н (х\ /, ^') = _ i-J {[п, HJ А9 -f
s-
-^^1 - St
+ k^o [П, Hi] — /ше [ [n, EJ grad o] } da,
поскольку ротор градиента тождественно равен нулю. Далее,
J [п, HJ A^da = — I* { n [gradgrad «= HJ } grad (oda =^
St
J (n, rot Hi) grad (oda— Г [n, grad (H^ grad o)] da =
St St
= — Ф grad о (Hids) — /ше f (nEi) grad ссйГа, C6)
с Si .
где оператор gradgrad^ действует только на grad 9. Последним интегралом
учитывается тот факт, что уравнения поля, по предположению,
удовлетворяются на S^. Таким образом,
rot' Н (д;', У, г')=^-^§ grad о (H^ds) -f
и
-Г -^ / {'«^Н- [п. Hi] 9 + [[п. EJ grad oj + (nEi) grad о} й?й ==
= —/шеЕ(л:',У,-гг'). C7)
Удовлетворение уравнению (I) устанавливается таким же способом i).
1) Эти формулы были применены L. J. С h и и автором к расчёту дифракции
от прямоугольной щели й идеально проводящем экране. Полученные результаты
относительно удовлетворительны, если сравнивать их с результатами Mors е und
Rubinstein, Phys. Rev. 54, 895, 1938, которые решали задачу с двумерной щелью
совершенно строго введением гиперболических цилиндрических координат; Phys. Re'»^
56, 99, 1939. См. также решение подобных задач у Щелкунов а, ibid., стр. 308.
■;■^
ЧЕТЫРЕХМЕРНАЯ ФОРМУЛИРОВКУ^ ЗАДАЧИ ОБ ИЗЛУЧЕНИИ 18.161 41Б-
ЧЕТЫРЁХМЕРНАЯ ФОРМУЛИРОВКА ЗАДАЧИ ОБ ИЗЛУЧЕНИИ
8.16. Интегрирование волнового уравнения. В разделе 1.21 было пока»
зано, как с помощью тензоров уравнения поля могут быть записаны в
чрезвычайно сжатой форме. Если ввести мнимое расстояние х^ = ict в качестве
координаты в некотором четырёхмерном многообразии, то действительно-
уравнения переменного поля будут формально тождественны с уравнениями-
для статического состойния, и методы, которые были применены для
интегрирования уравнения Пуассона, могут быть непосредственно
распространены и на этот более общий случай. Четырёхмерное представление теории
более абстрактно, нежели методы, описанные ранее в этой главе, и поэтому
не применяется в практических задачах расчёта излучения антенн. Но,
помимо своего формального изящества, четырёхмерная трактовка приводит
иногда к весьма важным результатам наиболее прямым путём. Сказанное
относится в особенности к довольно трудной задаче определения поля
отдельного произвольно движущегося заряда.
Мы ограничимся рассмотрением зарядов и токов в свободном
пространстве. Как и в соотношениях (82), стр. 73, векторный и скалярный
потенциалы могут быть представлены в виде четыре-вектора, прямоугольные
компоненты которого равны
Аналогично плотности токов и зарядов могут быть представлены в виде
четыре-вектора с компонентами
/j = Хр, /д ^= Jy* J8 ^^^ *'S> J^ = ^^P• B)'
Четыре-потенциал удовлетворяет соотношению
Согласно обозначению C5), стр. 66, □ — символический четыре-вектор,
компоненты которого равны -^—. Следовательно, уравнения C) могут быть
сокращённо записаны в виде
П2Ф = —f^oJ, ПФ = 0. D>
ilycTb V—область четырёхмерного пространства, ограниченная
трёхмерной «поверхностью» .S, а п — единичная внешняя нормаль к 6'. Тогда
в четырёхмерном пространстве, так же как и в трёх измерениях,
( ОФ dv = jФпс1а. E)
V S
Если и и W — две скалярные функции от четырёх координат х^, х^, Xq, х^,,.
непрерывные в объёме V к ■ на. поверхности 6' вместе со своими первыми
и вторыми производными, то
( n(uOw)dv= f u{\Jwn)da, F>>
V
/(Пи'П^)^^ + / ua^wdv=j а~- da. G>
16 гл. Vni. ИЗЛУЧЕНИЕ "'!
Мы получаем таким образом, четырёхмерный аналог теоремы Грина
j(wCi^u—un^'^)dv= f(w^^ — u^ya. (8)
V S -
г
Пусть Xj будет координатой фиксированной точки наблюдения, нахо"
Дящейся внутри поверхности .S, а Хл—координатой переменной точки
внутри области V или на поверхности 5. Расстояние от х^ до х^ равно
/?=|/5(х;-х/. (9)
Непосредственным дифференцированием можно убедиться, что уравнению
U^w==Q A0)
удовлетворяет функция
w = -^ A1)
во всех точках, за исключением особой точки /? = 0, которая исключается,
как обычно, сферой Si радиуса R^. Если отождествить и с какой-либо
компонентой четыре-потенциала Ф^, то получим
На поверхности Si мы имеем
Для определения площади сферич-еской гиперповерхности 5^ введём
полярные координаты
Xi = Rcos^i, Xq =/?sin &i cos 6^2» I /144
X^ =/? sin Oj sin Og cos o, л:^ =/? sin {^i sin Og sin 9, |
которые удовлетворяют соотношению
xl-{-xl + xl~\-xl==RK A5)
-Метрические коэффициенты h^ подсчитываются так же, как и по формуле G0),
стр. 53, и оказываются равными
hi=l, h^ = R, /?3 = /^sm0i, /?4 = /?sin&iSinV A6)
Элемент объёма будет
d-o = hih^^h^ dRdbi d^^ d^ = R^ sin^O^ sin Og dR d^^ d%^do, A7)
SL площадь поверхности гиперсферы равна, следовательно,
те Jt2i:
R^ J J J•sш^ »i sin&s^f»! d^^do = 27fiR^ . A8)
000
Таким образом
при Ri -T> 0,
ЧЕТЫРЕХМЕРНАЯ ФОРМУЛИРОВКА ЗАДАЧИ ОБ ИЗЛУЧЕНИИ [б.Щ 41Т
|Г Заменяя П^Ф_;- на — ^qJj и соединяя компоненты Ф^ в четыре-вектор, мы
Г- йолучаем дЛя Ф в точке х' выражение
:?, V S
к
f. Для того чтобы найти векторы поля, мы должны вычислить компоненты
К тензора ^F в точке х'. Согласно G9), £тр. 73,
Г ^^_^^ (/,^^ = 1,2,3,4). B1)
^ Предположим временно, что все источники расположены в пределах объёма V.
Тогда интеграл по поверхности 5 в формуле B0) ничего не прибавляет
к значению Ф, и в этом случае ^
V 3 « V
где [J, Rljfc = /j/?fc—JkRj и где R—радиус-вектор, проведённый из точки х
в точку л:'.
Векторное произведение [J, R] является шести вектором или
антисимметричным тензором, компоненты которого определяются соотношениями F2),
стр. 70. В сокращённом виде
V
8.17. Поле движущегося точечного заряхка. Пусть отдельный заряд q
движется в свободном пространстве с произвольной скоростью v.
Предполагается, что расстояние от заряда до наблюдателя таково, что заряд
можно считать геометрической точкой. Движение заряда по траектории
определяется заданием его координат как функции от t:
Xi=fi(t), x^==f^(f), л:з==/з@. x^=fi(t) = icL B4)
Необходимо отметить, что здесь t является не временем^наблюдателя, а
собственным временем движущегося заряда. Тогда
+ 00
J j fjjdx^ dx^dx^=^[q -^^Я-аТ (/'=1' 2' 3, 4) B5)
— 00
и, согласно B0),
+00
^J-'Ulf "-шУ"*- B6)
—00
Начало отсчёта на оси времени мы можем менять совершенно произвольно,
не теряя в общности. Удобно принять, что в момент наблюдения время
наблюдателя f ^= 0. Тогда лг/ = О и
/?^=/•2-{-4. B7)
где г—расстояние в трёхмерном конфигурационном пространстве от заряда
до точки наблюдения. Полюсы подинтегрального выражения в B6) расположены
в точках
х^ = — ir, х^ = -\- 1г. B8)
'- 27 Зав. 593. Теория эяектрокагнехнзка.
418
гл. VIII. ИЗЛУЧЕНИЕ
По условиям задачи координаты траектории определены для действительных
значений t, которые меньше чем ^' и, следовательно, в данном случае меньше
нуля. Таким образом функции fj(t) определены только для значений х^ на
отрицательной части мнимой оси. Однако мы предположим, что fjO) —
аналитические ф)шкции от х^ = let и могут быть аналитически продолжены на
всю комплексную плоскость х^. Поскольку единственными особенностями B6)
являются полюсы B8), то по лемме Жордана, стр. 280, конт)ф
интегрирования может быть деформирован из действительной оси в небольшой круг
около полюса х^^==- — /г, проведённый в показанном на рис. 88 направлении,
и тогда интеграл может быть вычислен методом
ioo вычетов, стр. 280. Разложение R^ в ряд^ около
ir даёт
\ х^ = ir
-ОО
в
+в<^
Хи = - ir
dx,
B9>
dR-i
3
^4S(-^—^•)'"^
3 = 1
-too
Рис. 88. Контур
интегрирования сводится к небольшой отсюда
окружности, проведённой во- .pg.
круг полюса ^4 SS —ir. {-—• )
\dx^J^_Q
2/
=^уг + 2л:,;
C0>
2г
с
vr —2гг = 2/г(-^—1), C1>
где v^—компонента скорости заряда в направлении радиуса-вектора г^
проведённого от заряда к наблюдателю.
Интеграл B6) принимает теперь вид
ф. =
3 4те2
-1 с^^
1
dt x^+ir
r-dx,.
If *
C2)
Обход контура совершается по часовой стрелке и, следовательно, согласно
Поэтому
q dfj
*dfi
теореме Коши, интеграл в C2) равен — 2то-^
лч f*0
ф. = —
э 4я
(■-тО
dt
C3)
или, в виде векторного и скалярного потенциалов,
qv 1
4те
i^-Г)'
?
47:so
(^-тО
C4>
Это формулы Льенара-Вихерта. Значения г и v заряда q надо брать для
момента времени, предшествующего моменту наблюдения на величину —.
Вместо того чтобы дифференцировать эти выражения, более прямым
путём для получения векторов поля является применение того же способа
прямо* к выражению B3). Это было сделано Зоммерфельдом ^), который
и получил формулы, вывод которых прежними способами связан с большими
1) Франк иМизес, Уравнения.математической физики. ОНТИ, 1937, стр.831,
Р. Беккер, Теория электричества. ГТТИ, 1941, стр. 66—67, и Френкель,.
Электродинамика, т. I, гл. VI.'
ЧЕТЫРЕХМЕРНАЯ ФОРМУЛИРОВКА ЗАДАЧИ ОБ ИЗЛУЧЕНИИ (8.17]
419
усложнениями. Выражения для поля удобно разложить на две части: полец
связанное со скоростью, в котором нет членов, содержащих ускорение v,
и поле, связанное с ускорением, которое исчезает при v, стремящемся к нулю..
Для поля, связанного со скоростью, мы получаем
где
Y =
vr©
C5>
C6)
а Го — единичный вектор в направлении г от заряда к наблюдателю для
момента времени t' . Эти формулы могут быть получены также примене-
С
нием преобразования Лоренца A03), стр. 77, к полю статического заряда
с учётом того, что A03) относится к времени наблюдателя.
Поле, связанное с ускорением, равно
_1_
^'.(ro-^)(roV.)-v}, j
C7)
Прежде всего следует отметить, что оба поля, как связанное со скоростью,
так и связанное с ускорением, удовлетворяют условию
" = /1^«-0'
Е1.
C8)
Магнитный вектор всегда перпендикулярен к радиусу-вектору,
проведённому из эффективного положения заряда^ под которым подразумевается
то положение, которое он занимал в момент/' . Электрический вектор
С
поля, связанного со скоростью, не поперечен, но для поля, связанного
с ускорением.
Е = l/"g [Н. Го1, Его«НГо = 0.
C9)
_2 >
В то время как поле,^
Поле, связанное со скоростью, убывает, как
1
связанное с ускорением, только как —. Таким образом, на больших
расстояниях поле, связанное с ускорением, превалирует; это поле является
чисто поперечным и только оно одно обусловливает излучение.
В том случае, когда скорость заряда очень мала по сравнению со
скоростью света, уравнения C7) для поля на больших расстояниях переходят
в следующие приближённые выражения:
Е^-Л-4[Го[Го, V]],
47CS0 ГС-
D0)
напоминающие уравнения B7), стр. 384, для поля излучения диполя.
Результаты этого раздела оснсваны на предположении, что движение
и траектория заряда известны, аналогично тому, как ранее предполагалось.
27*
420 гл. Vni. ИЗЛУЧЕНИЕ
■что распределение токов может быть задано. Однако в обоих случаях мы
допускаем нестрогость, предполагая, что вопрос о движении заряда или о
распределении токов можно рассматривать независимо от вопроса об
излучении. Предположим, например, что заряд движется в Заданном магнитном
поле. Если пренебречь излучением, то механическая сила, действующая на
, заряд, будет равна q [v. В], и из этого выражения для силы мы можем
методами классической механики определять движение заряда. (Если скорости
велики, то необходимо сделать также поправку на релятивистское изменение
массы.) Но результатом действия этой силы является ускорение заряда в
поперечном направлении и, следовательно, возникновение потери энергии
вследствие излучения. Рассеяние энергии вследствие излучения не может быть
объяснено действием силы q [v. В]. Необходимо включить дополнительную
силу—реакцию излучения^ которая грубо может быть уподоблена трению.
Реакция излучения в свою очередь оказывает влияние на вид траектории,
-откуда ясно, что точное решение, может быть получено только введением
полной действующей силы с самого начала, что представляет собой задачу,
намного более трудную. К счастью, в большинстве случаев реакщ1я
излучения чрезвычайно мала, так что, даже полностью пренебрегая ею, мы всё же
лолучаем удовлетворительное приближённое решение для движения.
ЗАДАЧИ
1. Показать, что эффективная напряжённость йоля на больших расстояниях
*от полуволнового линейного осциллятора даётся формулой
£■ _ —^ i_——'_ вольт метр,
тяе W — излучаемая мощность в ваттах,/? — расстояние от осциллятора в метрах
и Ь—угол между радиусом-вектором R и осью осциллятора.
Показать, что эффективная напряжённость поля на больших расстояних от
электрического диполя равна
Е = 6,7 g- У W вольт/метр
три. условии, что длина волны весьма велика по сразнению с длиной диполя.
2. Пусть <L является решением уравнения
шепрерывным вместе со своими первыми и вторыми производными внутри замкну*
того контура С на плоскости х, у, включая и сам контур, и пусть
с
еде г= У(х' — д:J -f (у' —j/)8, п обозначает внешнюю нормаль к контуру С,
а Н^^ (kr) — функция Ганкеля. Показать, что если фиксированная точка х', у' лежит
вне контура С, то м = О, в то время как и = «J' Д^" точки внутри контура С.
Теорема справедлива также и для того случая, когда функция Н^Р заменена
на N(kr). Эта теорема является двумерным аналогом формулы Гельмгольца E),
стр. 406, и выведена Вебером, Math. Ann. 1, 1—36, 1869.
3. Рассмотреть аналог формулы Кирхгофа для двух измерений. Доказательство,
основанное на формуле Вебера, задача 2, было дано V о 11 е г г а. Acta Math. 18,161,1894.
(Очень интересная работа, касающаяся распространения волн в двумерном
пространстве, была недавно сделана М. R i е s z'om. См. также Baker and С о р s о п, Huygens*
Principle, Cambridge University Press, стр. 54,1939.)
ЗАДАЧИ i^2l
4. Пусть j(f,y' — какая-либо фиксированная точка внутри плоской двумерно^г;
области, ограниченной замкнутой кривой С, и пусть ф—решение уравнения
непрерывное и обладающее непрерывкыми первыми производными на контуре С
и охватываемой им площади S. Показать, что
2^^{X', J'') = /{^ ^0iikr)-^-^^Ко(Ikr)Us+~^j-n(x,y)Ко(ikr)da,
с s
где r^ = (x'—л:)^4-(у'—У)\ & Ко (ikr)—изменённая функция Бесселя, разобранная
в задаче 10, глава Vl; п—внешняя нормаль к контуру С.
5. Пусть распределение токов в объёме V задано функцией i(x)e-^*, где л:
поставлено вместо трёх координат х, у, г. Показать, что напряжённость
электрического поля, вызванного этими токами, может быть представлена интегралом
to—hat f { \ pikr
V
где х' заменяет три координаты точки наблюдения, fe = <ol/"[xe и •
г2 = (д:'—д:J + (У — jJ 4-B'—2J.
6. Применяя георему задачи 5 к идеальному проводнику, мы получаем
Е ix', t) = i| I \ (K, grad) grad+Л8К > ^ da,
4ite<o J \ ) ^
S
где К—плотность поверхностных токов в точкед:,^', z на поверхности проводника 5^
Пусть теперь S будет поверхностью линейного проводника. Предположим, что
кривизна провода непрерывна и что его поперечное сечение всюду мало по сравнению^
с радиусом кривизны и по сравнению с длиной волны. Показать, что поле такого»
линейного гроводника даётся выражением
^(^'.0 = 4;^,^—'grad'{/_ +^-—ds\-^-±^I—ds,
где grad' применяется в точке наблюдения, а интеграл распространён по контуру С
проводника между точками s^ и Sj-
7. Применить формулу задачи 6 с тем, чтобы получить выражение для пол»
линейного осциллятора, и сравнить это выражение с результатами раздела 8.11.
8. В том случае, когда линейный контур задачи 6 замкнут, ^1=^2 и
проинтегрированный член равен нулю. На поверхности проводника тангенциальная
компонента Е равна приближённо
ie-iwt р/дЧ , ,„Ле**»*
Е,^
с
§(?^+*")^'*=''-
откуда следует, что ток / должен иметь вид
I
где /—длина контура, а т — целее число. Показать, что поле такого замкнутого
летлесбразнсго осциллятора даётся выражением
Е(--'*0 = ^/'^|] ^-^"'"^'Х-
Я1 = 1
X \grad'ф ds+iktnф ' ''s J
422 гл. Vin. ИЗЛУЧЕНИЕ
Это выражение является в пределе точным, при исчезающе малом поперечном
сечении проводника, и верно приближенно, если поперечное сечение мало по
сравнению с длиной волны и радиусом кривизны в каждой ¥очке контура. Применение
этой формулы к вибраторам Герца, какие применялись в ранние дни беспроволочной
телеграфии, разобрано в 1902 г. в очерке М а с d о п а 1 d'a на премию Adams'a,
озаглавленном Electrical Waves.
9. По полубесконечному линейному проводнику, совпадающему с отрицатель-
0)
ной частью координатной оси z, проходит ток частоты -^. Найти выражения для
компонент напряжённости электрического и магнитного полей и подсчитать
полную величину энергии, протекающей через плоскость, перпендикулярную к
проводнику.
10. Подсчитать сопротивление излучения линейного полуволнового осциллятора
методом э. д. с, описанным в разделе 8.12.
11. Изолированная линейная полуволновая антенна излучает 50 кет при длине
волны в 15 м. Вычертить графики значений параллельной и нормальной компонент
напряжённости электрического поля вдоль антенны, принимая гармоническое
распределение тока и диаметр проводника 6 мм.
12. Нечётная и чётная функции
р{о) = sin (g COS 0) ^^^^ ^ cos (а cos ^)
sin О ' sin О
очень часто встречаются в теории линейных осцилляторов. Положив yj = cos О,
показать, что эти функции являются решениями уравнения
(i_^2)/../_2viF'+|cc4i-^'';-Y—^>/='=о.
Полагая F= У^1—r^G, показать, что G удовлетворяет присоединённому уравнению
Матьё F), стр. 330.
A — Y]2) и>* — 2 (я + 1) YjttJ'-f (& — cV) к» = О
для того частного случая, когда я = 1, Ь = а'- — 1, с = а.
Следует обратить внимание на то, что хотя F(o) и Fifi) являются
периодическими функциями от О для всех значений а, в полюсах они остаются конечными
только для некоторых характеристических значений. Для чётных функций эти зна-
1е\ 2т 4-1
чения принадлежат к дискретному ряду о^'==—к^—К для нечетных функций они
образуют ряд a^^=m7i;, где т — целое число.
Доказать ортогональность этих функций, выражаемую соотношениями
1 - +1
J ^=S H?(l --П^) d^=f /=Й>/-Г A - vi^) d>j = О (тф п),
— 1 —1
— 1
у тфп.
где индексы внизу определяют заачения а; показать также, что функции эти
нормированы. Рассмотреть связь между этими функциями и полем излучения линейной
антенны при произвольном распределении тока.
13. Источник электромагнитного поля расположен в точке Pi. Другой источник,
действующий с той же частотой, расположен в точке Р^. Промежуточная среда
изотропна, но не обязательно однородна. Все соотношения между векторами поля
линейны, и время входит в виде гармонического множителя. Пусть векторы поля,
связанного с источником Pj, будут Eiи Hi, а поля, связанного с историком ра. Ег
и Hj. Показать, что всюду, где эти векторы конечны и непрерывны, они
удовлетворяют симметричному соотношению
div([Ei, Hi]-[E2, Н2]) = 0.
ЗАДАЧИ 423
Этот результат был получен Лоренцом и был развит в целую систему теорем
взаимности, имеющих фундаментальное значение для радиосвязи.
14. На стр. 383 было показано, что вектор Герца электрического квадруполя
равен
3
Pf = SР^з дГ» Pi3= f ЩРо dv,
3=1 ^ г
где Po(Si, ^2» ^з)—плотность заряда. Пусть р^, /?&, р^ будут сферическими
компонентами вектора рB). Показать, что поле излучеиня квадруполя в области, для которой
Ai?>l, даётся выражениями
Еь
-|/"^//,, E^^-j/'^m,
^»^-8тГ^^—^-' ^ч>^ ^Р^ R •
тогда как радиальна*. компонента исчезает, как ■^. Показать, что среднее значение
интенсивности излучения равно
''i2 = wl^^(^»+^9^-
15. Показать, что компоненты р» и р^ вектора рB) предыдущей задачи связаны*
с компонентами p{j тензора квадруполя соотношениями
р& = — sin 20 (pii cos2? +Р22 sin2 9 —pss +P12 sin 2<p) + cos 20 (pig cos f + p^ sin cp),
p^ = — sin 0 sin 29 (P22 —Pu) +P12 sin ^cos2«p +P23cos 0 cos <p —pgj cos 0 sin 0.
Если поворотом системы координат привести её оси в совпадение с главными
«сями тензора квадруполя, то тогда р12=Р2з=Рз1 = 0. и предыдущие соотношения
принимают вид
р» = sin 20 (Qi — Q2 cos 2ср), р^ = 2 sin О sin 2'f Q^,
.где
Pi = J (Pll +P2S — 2р8з), , Q2 = ^ (P22 —Pll)-
Показать теперь, что полная величина квадрупольного излучения равна
Если средой, сгружающей квадруполь, является воздух, то fxsss-^ и—"l/— =60
«, следовательно.
424 гл. VIII. ИЗЛУЧЕНИЕ
16. Заряды —е помещены на противоположных концах отрезка, вращающегося
с постоянной угловой скоростью вокруг перпендикулярной к нему оси, проходящей
через его центр. Заряд -^2е находился в центре. Дипольный момент всей системы
равен, таким образом, нулю. Рассчитать компоненты квадрупольного момента и найти
полное излучение (Van VIeck;.
17. Два заданных диполя расположены в одной плоскости. Их оси параллельны
друг другу, но моменты направлены в противоположные стороны. Диполи вращаются
с постоянной угловой скоростью вокруг оси, параллельной им и расположенной
посредине между ними. Рассчитать компоненты квадрупольного момента и найти
полное излучение (Van Vleck).
18. Положительный и отрицательный заряды, связанные вместе квазиупругими
силами, образуют гармонический осциллятор. Показать, что потери на излучение
могут быть учтены введением сил трения, которые, однако, пропорциональны
скорости изменения ускорения, а не скорости изменения смещения.
19. Положительный точечный заряд колеблется с очень малой амплитудой около
фиксированного отрицательного заряда той же величины. Показать что формулы
для поля колеблющегося диполя могут быть получены непосредственно из уравнений
C5) и C7), стр. 419, которые относятся к ускоренно движущемуся точечному
заряду.
ГЛАВА IX
КРАЕВЫЕ ЗАДАЧИ
Можно считать, что читатель теперь знаком с принципами,
определяющими возникновение электромагнитных волн, и с тем, как эти волны
распространяются в неограниченном однородном изотропном пространстве.
Неограниченное пространство является, конечно, чистой абстракцией.
Фактически наиболее интересные физические явления вызываются именно
поверхностями разрыва непрерывности среды или быстрого изменения её физических.
свойств.
Такого рода краевые задачи бывают, грубо говоря, трбх типов.
Предположим, что волна, распространяющаяся в одной среде, падает-
на поверхность разрыва непрерывности, являющуюся границей другой среды.
В первом случае линеййые размеры поверхности очень велики по сравнению
с длиной волны. Часть падающей энергии отражается от поверхности,,
а остальная часть проходит во вторую среду. Направление распространения?
в общем случае меняется; подобное изменение направления проходящих-
лучей называется преломлением.
Законы отражения и преломления электромагнитных волн на
бесконечных поверхностях сравнительно просты. Если,: однако, одно или оба„
измерения поверхности разрыва имеют размеры порядка длины волны, — это
второй случай краевой задачи, — то трудности математического анализа,
значительно возрастают. Возмущение первоначального поля при этих
условиях называется дифракцией. В обоих случаях вторичное поле
индуцированных зарядов возбуждается первичными волнами от независимого'^
источника.
Оба вида задач являются неоднородными краевыми задачами, как они,
были впервые определены для статического поля на стр. 177.
Третий из указанных выше случаев представляет собой однородную задачу.
Проводящее тело находится в диэлектрической среде. Заряды смещены из
положения равновесия и затем освобождены. Возникающие колебания зарядов
сопровождаются колебаниями в окружающем поле. В каждом случае это-
поле может быть представлено в виде суперпозиции характеристических
волновых функций^ вид которых определяется формой тела, а относительные,
их амплитуды — начальными условиями. С каждой характеристической
функцией связано характеристическое число, определяющее частоту данного
частичного колебания. Колебания затухают частью из-за конечной проводимости
тела, частью же в результате рассеяния энергии в виде излучения.
Проводник и диэлектрик можно, однако, поменять местами по отношению к
разделяющей их границе. В этом случае электромагнитные колебания будут
происходить внутри полости, заполненной диэлектриком и ограниченной
проводящими стенками. Если проводимость стенок бесконечна, то как тепловые, так.
и радиационные потери отсутствуют, и колебания всех частот будут
незатухающими.
426 гл. IX. КРАЕВЫЕ ЗАДАЧИ
ОБЩИЕ ТЕОРЕМЫ
9.1. Граничные условия. В разделе 1.13 было дано соответствующее
доказательство условий, которым удовлетворяют нормальные и
тангенциальные компоненты векторов поля на границе. В главах III и IV была
установлена связь между этими граничными условиями и разрывными свойствами
некоторых интегралов для стационарного режима; на основании разделов
е. 13 и 8.14 тот же способ может быть распространён и на переменные поля.
Предпосылая разбору задач этот анализ, мы уделим большее внимание
тому важному случаю, когда проводимость одной из двух сред стремится
к бесконечности.
Из1'.?;нения тангенциальной компонентчы вектора Е и нормальной
компоненты в^тора D при переходе через поверхность соприкосновения двух
сред выражаются соотношениями
In„E2—Ei] = 0, n(D2 —Di) = 8. A)
где, как мы условились ранее, п — единичная нормаль, направленная из
среды A) в среду B), а 8 — плотность поверхностных зарядов (вместо ю,
чтобы избежать путаницы с cu=2'jrv). В тех случаях, когда проводимость
какой-либо из сред или обеих сред конечна и не равна нулю, поток
зарядов через границу или к границе должен удовлетворять также уравнению
непрерывности
n(J,-J,)==—|. B)
Предположим теперь, что время входит только в виде обычного множителя
ехр( — Ш) и что, за исключением границы, обе среды однородны и изотропны.
Тогда A) и B) дают
^2^2п—Oi^m^ftuS. J
Посмотрим прежде всего, при каких условиях плотность поверхностных
зарядов может быть равна нулю. Если 8 =0, то детерминант C) должен
обращаться в нуль и, следовательно,
Если ^ак это обычно и бывает) 8 не равно нулю, то оно может быть
исключено из соотношений C), и мы получаем в качестве условия для
нормальной компоненты вектора Е
2 2 * \
}^1^2^2« —}^2^1^1«=0- E)
Если проводимость одной из сред бесконечна, то выражение E) становится
неопределённым, но из C)
£,„ = iff^zi^ 8, ^2^^'"^"'^^ F)
и в пределе при о^ ->■ со
^1«->0, Е^^^^К .y,„==a,^,„->fi:zp8. G)
Кроме того, из уравнений поля имеем
El ==„ I- , rot Hi, Hi =-Д- rot R, (8)
И, таким образом, если, по предположению, напряжённости поля ограничены,
то как Ej, так и Hj стремятся при о^ -> оо к нулю во всех внутренних
ОБЩИЕ ТЕОРЕМЫ [9.1] 427
точках среды A). Тангенщ1альная компонента Е при переходе через границу
непрерывна, и следовательно, в случае среды с бесконечной проводимостью
[п, Eal - [п, EJ =0. (9)
Рассмотрим теперь поведение магнитного поля на границе. В общем случае
п(В2—Bi)=0, [п, На-НЛ-К, A6)
где плотность поверхностных токов К равна нулю во всех случаях, когда
проводимость среды у границы не равна бесконечности. Только что было
показано, что если а^ становится бесконечным, то Н^ исчезает и,
следовательно, в этом случае
пВ2 = 0, [п, Hal-K. A1)
Дальнейшие полезные граничные условия для магнитного поля в случае
идеальной проводимости могут быть выведены следующим образом *). Пусть
граничная поверхность S определяется уравнением
С =/i (л:, J, 2-) = const. A2)
и совпадает с координатной поверхностью ортогональной системы
криволинейных координат 5, TQ, С (см. раздел 1.16). Если о^ -> со, то
тангенциальная компонента Eg и пропорциональная ей тангенциальная компонента rot Hq
стремятся к нулю. Следовательно, согласно (80), стр. 54,
За нормальную координату принята С. Так как о^ бесконечна, Н^ равно
нулю; следовательно, поскольку коэффициенты при единичных векторах
должны обращаться в нуль независимо друг от друга, мы получаем,
непосредственно у поверхности снаружи проводника:
-^(Л,Я,) = 0, -|^(Л,Я,) = 0. A4)
Величины h^H^ и h^H^ являются ковариантными компонентами (см. стр. 54)
вектора Hg вдоль поверхности S. Условие на границе будет, следовательно,
таково: нормальные производные 'от ковариантных компонент вектора
магнитного поля, касательного к границе, стремятся к нулю по мере
того, как проводимость с одной стороны границы становится бесконечной.
Под именем «граничных условий» мы будем рассматривать также и
поведение поля на бесконечности. В этом отношении переменное поле явно
отличается от статического. Если в случае стационарного состояния все
источники расположены на конечном расстоянии от начала отсчёта, то
напряжённости поля стремятся к нулю на бесконечности так, что lim R^E и
lim R^ остаются конечными при R-^co, где R — расстояние от начала.
Скалярный потенциал удовлетворяет уравнению Д^ = О и lim R(p при R -^ со
конечен. Любая функция о, регулярная на бесконечности и
удовлетворяющая уравнению Лапласа во всех точках пространства (источников нет),
необходимо равна нулю. С другой стороны, если переменные источники
расположены на конечном расстоянии от начала, то напряжённости поля исчезают
на бесконечности так, что при R-* со остаются конечными lim /?Е и
lim RW. Скалярный потенциал и прямоугольные компоненты векторного
потенциала, а также напряжённостей поля — все удовлетворяют уравнению
A^-f/fe2^ = 0, A5)
во всех точках, в которых плотность источников равна нулю. Кроме того,
^) Автор обязан Е^ Н. S ш i t h 'у за приводимое ниже доказательство.
428 гл. IX. КРАЕВЫЕ ЗАДАЧИ
существуют функции 4^, удовлетворяющие уравнению A5) во всём
пространстве и равные нулю на бесконечности, которые не рабны нулю всюду.
Решение уравнения Лапласа однозначно определяется источниками
потенциала и условием регулярности потенциала на бесконечности. Этих
двух условий недостаточно для однозначного определения волновой функции
4», поскольку уравнение A5) допускает возможность как сходящихся^ так
и расходящихся волн. Этот вопрос был исследован Зоммерфельдом *)
в связи с функцией Грина уравнения A5) в бесконечном пространстве.
К условиям, аналогичным условиям статической задачи, должно быть
добавлено так называемое сусловие излучения».
Задача формулируется так. Плотность g {х, у, г) распределения
источников задана; пусть все эти источники расположены в пределах области
конечных размеров. Тогда 4^ определено однозначно, если:
a'f^eo всех точках внутри замкнутой поверхности 5 (которая, в случае
необходимости, может быть разложена на ряд изолированных замкнутых
поверхностей) «^ удовлетворяет уравнению
^^J^kЦ=.-g^ A6)
b) на поверхности 5 фзгнкция «^ удовлетворяет однородным граничньш
условиям типа at^-}-р-^-^-=0, где а и р — постоянные числа или заданные
функции точки;
c) 4* исчезает на бесконечности таким образом, что lim/?<]/ остаётся
ограниченным при /? -> со; это условие мы снова назовём условием
регулярности на бесконечности;
d) ^ удовлетворяет условию излучения
которое означает, что на больших расстояниях от источника поле
представляет собой расходящуюся бегущую волну. Молчаливо было
предположено, что время входит только в виде множителя ехр (— itaf).
Смысл условия A7) может быть выяснен применением теоремы Грина
к уравнению A6) в области, ограниченной изнутри 'поверхностью S^
а извне S^. Тогда, как и в разделах 8.1 и 8.13,
V S
So
Первые два члена справа представляют бегущую волну, исходящую от
источника. Третий же член выражает сумму всех волн, бегущих внутрь от
элементов поверхности 5о, и должен, следовательнб, исчезать при удалении 5^
в бесконечность. Если обозначить этот третий член через U, то мы имеем
Вь S,
где dQ — элемент телесного угла. Второй интеграл в A9) должен быть
распространён по конечной области 47с и при /?->оо исчезает, если ^
регулярна на бесконечности^ как это предположено выше в пункте с)»
1) Sommerfeld, Jahresber. deut. math. Ver. 21,326, 1912.
ОБЩИЕ ТЕОРЕМЫ 19.21 429
Для того чтобы и исчезало, достаточно, чтобы
д-«(:^-'**!!)=о- B°)
Если на больших расстояниях поверхность Sq заменить сферой радиуса /?,
то условие B0) совпадёт с A7)i).
9.2. Единственность решения. Пусть V будет областью пространства,
ограниченной изнутри поверхностью S, а извне — поверхностью Sq.
Поверхность 5 может быть разложена в случае необходимости на совокупность
отдельных замкнутых поверхностей Si, как это изображено на рис. 18, стр. 104.
Тогда область V будет многосвязной (стр. 205), и поверхности Si будут
представлять собой границы различных помещённых в поле инородных тел.
Мы предположим на время, что свойства среды в V изотропны, хотя
параметры (А, е и с могут быть произвольными функциями точки. Пусть
теперь Ej, Н^ и Е^, Й^ будут двумя решениями уравнений поля, которые
8 момент / = 0 совпадают во всех точках V. Мы хотим найти минимальное
число условий, которые должны быть наложены на компоненты векторов
поля на границах S и Sq для того, чтобы эти два решения оставались
тождественными и во все последующие моменты времени ^>0.
В силу линейности уравнений поля (ферромагнитные вещества мы из
рассмотрения исключаем) разностное поле Е = Eg — Е^ и Н = Нд — Н^ также
будет решением. Не уменьшая общности, мы можем положить, что все
источники поля расположены целиком вне области V, поскольку в
предыдущей главе было показано, что если заряды и токи заданы; то поле
определено однозначно. Или же, если внутри области V источники имеются, то
иадо считать, что в обоих случаях их распределение и мощность
электродвижущих сил одинаковы. Тогда для разностного поля в области V теорема
Пойнтинга, стр. 123, даёт
jJ(~E^ + ^H^)dv-j-j^Pdv = -j[E,H]nda. B1)
V V S+So
Для того чтобы член в правой части исчезал, достаточно, чтобы либо
тангенциальные компоненты Ei и Eg, либо тангенциальные компоненты Н^ и Hg
совпадали для всех значений ^>0, ибо тогда либо [п, Е]=0, либо
Jn, HI = О и [Е, HI не имеет на границе нормальной компоненты. В этом
случае мы имеем
miii^'+i"')''^—f^J"'^- B2)
V V
Правая часть всегда меньше нуля или равна нулю. Интеграл слева,
выражающий энергию, существенно положителен или равен нулю и исчезает
е момент ^==0. Следовательно, соотношению B2) можно удовлетворить
только значениями Е=Ез — £^ = 0, Н = Н2—Hi = 0 для всех ^>0; это
и требовалось доказать. Электромагнитное поле в пределах ограниченной
области V однозначно определяется для всех моментов времени f^O на-
чалъными значениями электрического и магнитного векторов внутри
области V и значениями тангенциальной составляющей электрического
{или магнитного) вектора на границе этой области для моментов
времени f^O.
При удалении Sq в бесконечность область V становится неограниченной
с внешней стороны. Для того чтобы обеспечить равенство нулю интеграла
1) Другое доказательство дано в разделе 8.13, стр. 406.
430 гл. IX. КРАЕВЫЕ ЗАДАЧИ
от вектора Пойнтинга по бесконечно удалённой поверхности, необходимо»
только предположить, что среда обладает некоторой проводимостью, хотя
бы очень малой. Если с момента возникновения поля прошёл конечный про-
меж)ггок времени, то этой трудности мы можем избежать также
предположением, что Sq лежит вне той области, которую поле, распространяющееся^
с конечной скоростью с, займёт к моменту t. Только что доказанная
теорема не учитывает полностью эту конечность скорости распространения
электромагнитного поля. Мы установили, что значения Е и Н в объёме V
в момент t однозначно определяются тангенциальными граничными условиям»
и начальными значениями во всей области V. Физически очевидно, однако,
что это больше, чем йам необходимо. Поле распространяется с конечной
скоростью, и следовательно, необходимо принимать во внимание только те
элементы V, расстояние которых от точки наблюдения <^ (^ ^— ^о) ^*
Классическое доказательство однозначности, данное выше, было в этом смысле
разЦ;зто Рубиновичем^).
*||еорема применима и к анизотропным телам. В этом случае
электрическая и магнитная энергия выражаются в виде дефинитных положительных
форм (см. стр. 131), т. е. положительных или равных нулю при всех
значениях переменных. В остальном доказательство остаётся без изменений.
Одна сторона теоремы, на первый взгляд, может показаться странной.
Мы видели выше, что поле определяется значениями на границе либо [п, Е],
либо [п, Н], в то время как в задачах, которые мы вскоре рассмотрим,
окажется необходимым применить оба граничных условия
[п.Ез —Ei] = 0, [п. На—Hi] = b, B3)
где Eg и Ej представляют собой значения напряжённости поля по обе
стороны границы. Причина кажущегося противоречия заключается, конечно,
в том, что [п, Е] и [п, Н] относятся к тангенциальным компонентам
результирующего поля по одну сторону поверхности. Обычно они неизвестны,
и цель краевой задачи в том и состоит, чтобы найти их. Уравнения B3)
определяют просто изменение векторов поля при переходе через поверхность
разрыва и оба вместе позволяют нам аналитически продолжать данное
первоначальное поле из одной области в другую. После того как мы определили
таким образом полное поле, мы можем утверждать по теореме об
однозначности, что иных возможных решений не существует. Если, однако, с одной
стороны границы мы имеем среду с бесконечной проводимостью, то
значение тангенциальной составляющей полного поля нам известно, так как
в этом случае [п, Е] == О, и для решения задачи достаточно одного
граничного условия.
9.3. Электродинамическое подобие. Ещё со времён Ньютона принцип
подобия и теория моделей оказывали большое влияние на развитие
прикладной механики. Это справедливо, в частности, в отношении проектирования
судов и самолётов, которое в значительной степени направлялось данными,
получаемыми из опытов с небольшими моделями в гидродинамических
каналах и в аэродинамических трубах. Условия опыта выражаются обычно
через некоторые безразмерные величины, как, например, число Рейнольдса.
Таким путём результаты единичного опыта над данной моделью могут быть
применены к серии объектов подобной формы и отличающихся только
по размерам, при условии, что вязкость жидкости и скорость потока
изменены так, чтобы число Рейнольдса осталось неизменным.
Аналогичные принципы оказываются полезными и при конструировании
электромагнитных аппаратов. Мы напишем прежде всего уравнения поля
i)Rubinowicz, Physik. Z, 27, 707, 1926.
ОБЩИЕ ТЕОРЕМЫ [9.3] 431
в безразмерном Ьиде. В однородном изотропном проводнике
rotE+}A^=0, rotH — el^ —оЕ = 0. B4>
Пусть теперь
8 = 8оУе, {|, = }1^у^, c = OoS, B5)
длина = /oZ,, время = ^дГ,
где £■, //, yg, у^, 5, L и Т—безразмерные числа, которыми измеряются
переменные поля в системе, в которой единичными величинами являю1ся е,
Л, Sq, }Aq, /(), Cq и ^0- Числа эти удовлетворяют уравнениям
rot £-f «^«1^ = 0. I
rot^ —рУе^—Y5£=0, I
где
«= —^- P=-Xb ^=°o^oi B7)
— безразмерные постоянные. Исключая общий множитель е/Л, получаем
{Ао^о (') "^ const., }AqOq ^ = const. B8)
Из первого из этих равенств следует, что произведение {Aq^o Должно иметь
размерность, обратную квадрату скорости. Это обстоятельство является,,
без сомнения, самым существенным в подходе к проблеме единиц и
размерностей i).
Для того чтобы две краевые электромагнитные задачи были подобными,
необходимо и достаточно, чтобы коэффициенты ау^, ру^ и 7° были в обеих
задачах одинаковы. Возьмём, например, в качестве ^д период т поля, а в
качестве /д — какую-либо длину, характеризующую одно из ряда тел,
отличающихся друг от друга только размерами. Так /д может быть радиусом системы
концентрических сфер или главной осью системы эллипсоидов. Условия
подобия требуют, чтобы два характеристических параметра С^ и С^
^V-^C„ ^а^^С^ B9>
-D)
6.ЫЛИ инвариантны при преобразовании масштаба. Предположим, что
характеристическая длина /д уменьшается вдвое. Тогда обе величины С^ и С^
останутся неизменными, если магнитная проницаемость в каждой точке поля
учетверится. С практической точки зрения это средство не является удобным,
но это — единственный njrrb, с помощью которого можно воспроизвести
состояние, подобное исходному, изменением только одного параметра. Если
оставить }А и е такими, какими они были, то неизменности С^ можно
достигнуть также уменьшением вдвое периода или удвоением частоты, но одно
лишь это изменение не сохранит значения Cg. Для того чтобы вдвое меньшая
модель в точности воспроизводила условия, имеющие место при нормальных
размерах, необходимо также, чтобы проводимость в каждой точке удвоилась.
Этот принцип может быть иллюстрирован ссылкой на обычный
высокочастотный радиогенератор, поддерживающий стоячие электромагнитные
1) См. разделы 1.8, 4.8 и 4.9.
432
ГЛ^ IX. КРАЕВЫЕ ЗАДАЧИ
волны В резонирующей полости с металлическими стенками. Частота
колебания существенно определяется размерами полости, в то время как потери
зависят преимущественно от проводимости стенок. Если размеры уменьшаются
вдвое, то частота примерно удвоится; если проводимость стенок останется
при этом неизменной, то вполне возможно, что получившееся в результате
'Относительное увеличение потерь перейдёт через критическое значение, так
-что колебания в приборе половинной величины не возникнзгг.
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ
9.4. Законы Снелля. Пусть две однородные изотропные среды безграг
нично продолжаются от разделяющей их плоскости S. Единичный вектор п,
«ор]^лльный к плоскости 5, направлен из области (е^, jaj, Cj) в область
(sg, %, С2). Пусть О будет фиксированным началом отсчёта, который для
удобства мы расположим на плоскости S. Тогда, если г — радиус-вектор,
^проведённый из точки О и определяющий положение какой-либо точки области
A) или B), то плоскость
СредаB) ■- /"^ Среда СП , 5 определится уравнением
11Г = 0. A)
Пусть плоская волна,
распространяющаяся в среде
B), падает на S. В
соответствии с B7), стр. 243,
Н.
0)JJ'2
[По, Е«1, B)
Рис. 89. Отражение и преломление на плоской
поверхности 5.
где Ед — комплексная
амплитуда падающей
волны, а По — единичный
вектор, который определяет
направление её распространения i), как показано на рис. 89. Плоскость,
определяемая парой векторов п и п^, называется плоскостью падения.
Продолжение первичного поля в среду A) определяется граничными
условиями на S. Для того чтобы удовлетворить граничным условиям, мы
должны предположить наличие в среде B) отражённого или вторичного
тюля. Физически ясно, что первичное поле вызывает колебательное
движение свободных и связанных зарядов около плоскости 5, которые в свою
очередь излучают вторичное поле обратно в среду B), равно, как и вперёд,
в среду A). Мы попробуем предположить, что и отражённая
ная волны являются плоскими, и напишем
и преломлён-
Е^ = El е*''! "!■'-*"'*;
Н,
н»
<0{Л2
[П2,Е^],
C)
1) Очевидно, пока мы рассматриваем данную задачу, было бы более логичным,
с точки зрения обозначений, считать падающую волну распространяющейся из среды
A) в среду B). Вскоре, однако, плоскость 5 будет заменена замкнутой поверхностью 5,
охватывающей всё тело. Как мы условились раньше, нормаль п должна быть
направлена наружу из замкнутого объёма, из среды A) в среду B). Сделанный выше
выбор По облегчит сравнение формул настоящего раздела с формулами дальнейших
япраграфов.
jSKJiV'ii
ОТРАЖЕНИЕ и ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ [9.51 433
^де единичные векторы Hj и Пд определяют направление распространения
прошедшей и отражённой волн соответственно, а Е^ и Е2 — комплексные
амплитуды; все эти векторы пока ещё не определены. По предположению,
El, Eg и Eq не зависят от координат, и следовательно, для того чтобы тан-
геящ1альные составляющие векторов результирующего поля были непрерывны
при переходе через поверхность S, необходимо, чтобы экспоненщ1альные
множители в B) и C) тождественно совпадали бы на плоскости пг = 0.
Но
г = (пг)п—[п, [п, ГЦ. D)
Следовательно, в любой точке граничной плоскости г, = — [п, [п, г]].
Поэтому
*2«0 In, [П, г] 1 = ^2«2 [П» In/ГП, I
^2«0 !«' [П, Г]] = ^tfli [П, [П, Г]1, J ^ ^
«ли, поскольку По [п, [п, гЦ = [Пд, п] [п, rj^ то
([По,п] —[Па, п])[п,г] = 0.
([По,п] —[Па, п])[п,г] = 0, 1
(k^ [По, п] — ^1 [Щу п]) [п, г] = 0. 1
F)
Из этих двух соотношений следует, что векторы п, По, п^ и Пд компланарны.
Плоскости равной фазы как прошедшей, так и отражённой волн
нормальны к плоскости падения. Из первого соотношения F) следует
также, что
sin вд = sin (тг — во) = sin Оо, G)
откуда угол падения во равен углу отражения вд. Из второго
соотношения F) получаем
Уравнения G) и (8) выражают законы Снелля для отражения и
преломления.
9.5. Формулы Френеля. Мы используем теперь граничные условия для
определения соотношения между амплитудами Ео, Е^ и Eg. Во всех точках
плоскости S имеем
{п, Eo-h Е2З = [п, EJ [п, Но + Hal = fn, HJ. (9)
В силу B) и C), второе из этих двух уравнений может быть записано
через электрические векторы •
[П1 (По, Ео] + [П2, ЕаН ^ = [п, [nj, ЕJ] А. (Ю)
[- г"!
Раскрывая скобки, мы получим члены вида
[п, [По, Ео]] = (пЕо)По—(пПоШо- (П)
Направление первичного вектора Ео совершенно произвольно, но он всегда
может быть разложен на составляющую, нормальную к плоскости падения
и, следовательно, касательную к 5, и на составляющую, лежащую в
плоскости падения (см. раздел 5.4, стр. 248). Исследование значительно
упрощается при раздельном рассмотрении этих двух компонент падающей волны.
Случай I. Ео нормально к плоскости падения.
Тогда
пЕо = ПоЕо = 0.
■ Поскольку среды изотропны, индуцированные электрические векторы про-
Ш'едшей и отражённой волн должны быть параллельны Ео и, следовательно,
^g Зак. 593. Хео^ия влектфоиагветвзка.
434
гл. IX. КРАЕВЫЕ ЗАДАЧИ
тоже нормальны к плоскости падения, так что пЕ^ = пЕа = 0. Из рис. 89
получаем
пПо = cos (тс — 6q) = — cos вд,
cos (тг — 6i) = — cos 6j,
nni
A2)
nn2=C0S 62.
Умножая первое из уравнений (9)^векторно на п и используя A1) и A2)^
мы находим,' что амплитуды должны удовлетворять соотношениям
Ео -р Ег — El,
cos 8q Eq COS 02 E2 = "Л COS 61 Ej.
A3)
Отнс%1тельное направление электрического и магнитного векторов для этого
случая показано на рис. 90. Разрешая A3) относительно Е^ и Е2 череа
амплитуду первичного поля Ед, получаем
Е = ^-1^2 (cos 62 + cos 6о>
^ [Х1^2СО8 02 + Н'2^1СО8 Oj О
F __ J^lk^ COS бр — lUjki COS 6i
^ [Xj /52 COS 62 + [X2 ^1 COS 61 0-
(при пЕо = 0),
A4)
Эти соотношения не так просты, как это кажется с первого взгляда, так
как если одна из сред [A)или B)] является проводящей, то 8^ будет ком-
/ ^,?>М2'^2
Рис. 90. Падающая волна поляризована нормально
к плоскости падения.
плексным; 6^ может быть комплексным даже в том случае,, если обе
среды являются диэлектриками. Согласно G) и (8)
cos82 = cos8q, AiCosei=y^f—A|sin28Q- • A5>
Углы отражения и преломления могут быть исключены из A4), и мы
получим эти соотношения в другом виде:
2 [XI ^2 cos 60 _,
Ei =
{X 1^2 cos бо + [Х2 Y^t — *2 si"'' ^0
,х,^2 COS ео-н Vki^kl^nH, ^"Р" "^« = ^^'
-* -Ер-
[Xi*2 COS %-{-у-2У k\ — *2 Si"^ ^0
A,6)
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ [9.6]
435
Комплексные значения коэффициентов при Eg означают, что сами амплитуды
El и Eg комплексны и что прошедшая и отражённая волны отличаются по
фазе от падающей волны.
Случай П. Ео лежит в плоскости падения. В этом случае нормальны
к плоскости падения и параллельны 5 магнитные векторы
nHo = nHi = nH2.
Из B) и C) мы имеем
Ео = -^ {Щ> Но], Ej =
О) у,-»
7^[П1, HJ, ,
Eg = — -^ [П2> H2I,
\
J
A7)
что, после подстановки в (9), даёт следующие условия на границе:
созвдНр — со8в2Н2= -^ COS e^Hj,
Ho-hH2 = Hi.
К
A8)
Относительное расположение электрического и магнитного векторов для этого
случая показано на рис. 91. Решение соотношений A8) даёт
Hi
[X2^1 (cos 62+COS бо)
Н,
Н2 =
fX2^1 COS 62 + ^*2 С OS 61
_ Ml COS бе-{.ife, COS 61 „ <"P" n"o =0). f
A9)
u
[X^^l COS Go + [Ai^2 COS 61 0'
или no исключении 6^ и вд с помощью A5):
Hi =
2[X2^I COS Cfl
[X2^2cOSfo-l-{Xi^2>^^5-
[X2^1 COS 60 — JJ^ft, V k\-
-klsm^Q
-ti^sin^Q
Hr
(при пНо=0),
^ [X2^J с OS 60 + pi^2 y^J—yfe^sinSOo °"
B0>
Если падение нормальное, то 6о = 0, и эти два случая ничем не
отличаются друг от друга, а выражения для амплитуд прошедшей и отражённой
волн сводятся тогда к та- ^.
ким:
2 Ma-l-p-a^i °',
B1)
Соотношения A4) и
A9) были выведены впервые
в несколько менее общем
виде Френелем в 1823 г. из
динамических свойств
гипотетического упругого эфира.
9.6. Диэлектрические
среды. Мы - рассмотрим
сначала случай, когда обе
проводимости Oj и Og равны нулю, т. е. обе среды идеально прозрачны.
Магнитные проницаемости исчезающе мало отличаются от jj.©, и закон
Рис. 91. Падающая волна поляризована параллельно
плоскости падения.
28*
436 ' гл. IX. КРАЕВЫЕ ЗАДАЧИ
Снелля может быть записан в виде
sin 61 sin 61 , /~ еч V^ /ооч
-у -г---^=«12, B2)
sin бо sin 62 г ei г/2
где v^ и V2 — фазовые скорости, а п^^ — относительный показатель
преломления для этих двух сред. Если ei>e2, то ni2<.l, и каждому углу падения
% соответствует действительный угол преломления В^. Если, однако, ej<e2,
как, например, в случае волны, выходящей из жидкого или твёрдого
диэлектрика в воздзос, то тогда Bj действительно только для тех "значений 6q, для
которых rti2sineQ<;i. При Я12 5швд>1 возникает явление полного отра-
лсения; мы исключим на время этот случай и рассмотрим формулы Френеля
для действительных углов от О до tz/2.
При Е, нормальном к плоскости падения, мы получаем из A4)
_ 2 cos бо sjn Sj
^ "" "^йГ(бГ+~ео)'^о („Ео = 0),
^ _ sin F1—Со) g
B3)
B4)
^^2 Sin F1 +ft))
а для компонент Е, лежащих в плоскости падения, получаем из A9)
, Р ] 2 cosPpsinet , Р
l^i'^^il - sin(Ро +61) cos (Со-61) 1"о, tol
tarp _fi^ (пНо = 0),
1"^-Е<.1= lie;+ 6.) ["O'Eol-
Поскольку коэффициенты при Ер в B3) и B4) действительны, отражённая
и преломлённая волны либо совпадают по фазе с падающей волной, либо
сдвинуты на 180°. Очевидно, фаза прошедшей волны в обоих случаях
совпадает с фазой падающей. Фаза отражённой волны зависит, однако, от
относительной величины в^ и в^. Так, если е^ > е^, то в^ < вр и Eg в B3)
имеет направление, противоположное Eq, т. е. отличается по фазе на. 180 .
При тех же условиях tg(eQ — 6^) положителен, но знаменатель tgi^o-\-^i)
становится отрицательным при ^qA- ^i^-^ ,и фаза соответственно скачком
меняется.
Средний поток энергии даётся действительной частью комплексного
вектора Пойнтинга. В оптике эта величина обычно называется «интенсивностью»
света, но этот термин является двусмысленным, так как он применяется также
и к амплитуде поля *). В данном случае
S; l[E„H;i = jSiEo[no,Eo]l = -»^£5no, ]
. _ \ B5)
Первичная энергия, падающая за секунду^на единицу поверхности границы
между диэлектриками,'равна не вектору S^, а лишь нормальной компоненте
этого вектора, т. е. п8^=з— * ^ Щ cos бр. Аналогично количество энергии,
уходящей с единицы площади границы благодаря отражению и преломлению,
равно _
n\=tR Е\ cos бо, nS,= -- 'Ц- El cos 6^. B6)
1) Последнее замечание не касается русской терминологии. По-английски
интенсивность света — intensity of light, а напряжённость поля — field intensity. Прим. ред.
^^^ ОТРАЖЕНИЕ И ПРЕЛ^0МЛ1гНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ 19.6] 437
'#..
Согласно закону сохранения энергии, нормальная компонента потока энергии
при переходе через.границу должна быть непрерывна:
или
n(Si+S,)=nS„ B7)
Y^2^l COS вд = Yh eI cos 61 +1/^2 eI cos 6q. B8)
Легко установить, что формулы Френеля B3) и B4) удовле.творяют этому
условию. Коэффициенты отражения и прохождения определяются
отношениями
P^^J^Sr £з »р__ nSt __ ■ш/~Ч cos 6i ^1 /29)
Если Eq нормально к плоскости падения, то эти коэффициенты равны
р _._sin2Fi—бр) ^ _sin2eojin2ei. ,^^.
^-L — sin2 (Oj + 60)' -^ ~ sin2 (el + бо) ' ^ -^
если же Eq лежит в плоскости падения, то
/? == tg2(eo-6i) _ sin26osin26i
^" tg2(eo + ei)' ^11—sin2(eo+ei)cos2(eo-ei)- ^^'^
Если падение нормальное, то 60 = 61 = 0, и из B1) и B2) следует, что
(Уч-\-УчГ («12+1Я'
C2)
Коэффициент отражения равен нулю только в одном случае. При
бд -j- ^1 -> 4^/2 имеем tg (бд -|- ^i) -> со и тогда /?||->- 0. Отражённый и
преломлённый лучи при этом нормальны друг к другу (Hjiig =: 0) и sin 6^ = sin (^ — бо)==
, ==cos6q. Из B2) следует, что
t§6o=l/ = «2i. C3)
Угол, удовлетворяющий условию C3), известен под названием угла полной
поляризации или угла Брюстера. Как мы видели, волна, падающая на плоскую
поверхность, может быть разложена на две составляющие — одну^
поляризованную нормально, и другую, поляризованную параллельно плоскости
падения. Коэффициенты отражения для этих двух типов компонент различны,
и следовательно, поляризация отражённой волны зависит от угла падения.
В частности, есЛи падение происходит под углом Брюстера, то отражённая
волна полностью поляризована в направлении, нормальном плоскости падения.
В оптике иногда используют это явление для получения поляризованного
света из естественного, хотя практически этот метод менее эффективен, чем
методы, основанные на применении двоякопреломляющих призм.
Оптические показатели преломления по отношению к воздуху обычно
порядка П21=1А; при радиочастотах они могут быть во много раз больше,
с чем связано, и соответствующее увеличение угла полной поляризации.
В случае воды, например, «21 увеличивается примерно от 1,33 до 9 при
: радиочастотах, а угол полной поляризации — от 53° до 84*^,6, что уже
1-\ близко к скользящему падению. Нерегулярность радиопередач над водными
^■^'.
438
ГЛ, IX. КРАЕВЫЕ ЗАДАЧИ
пространствами в некоторых случаях может быть, без сомнения, приписана
этому явлению. Заметим также, что при угле полной поляризации Ц
равняется единице и что это единственный случай, когда вся энергия первичной
волны может войти во вторую среду без потерь на отражение на границе,
9.7. Полное отражение. Мы вернёмся теперь к случаю, исключённому
н^ми в разделе 9.6; пусть волна переходит из среды B) в среду A),
показатель преломления которой меньше, чем показатель преломления среды B).
Формулы раздела 9.6 справедливы при.
любом относительном значении е^ и eg, но
если Ьд таково, что
rii^sin Во =у ^ sin Во > 1,
i'peaai /;
"'''■' j^-,Q''-'''^''^^^'^'^y^yyvy///77: z то ИМ МОЖНО удовлетворить только
комплексными значениями б^. Физически ком-
Рис. 92. Полное отражение от поверх- "лексный угол преломления означает ска-
лости, совпадающей с плоскостью yz. чок фазы и появление затухающего
множителя.
Итак, предположим, что sin6i>l. Косинус тогда будет чисто мнимым:
cos 6j = —y=^B^s\vr- 6q — Ej = ш^2 V^sih^ 6q—lu^-
ye,
C4)
Корень имеет два значения, выбор между которыми определяется условием,
чтобы поле нигде не становилось бесконечным. Для того чтобы немного
упростить дело, предположим, что отражающая поверхность S совпадает с
плоскостью x=0, как показано на рис. 92. Все точки среды A) соответствуют
отрицательным значениям х. Фаза прошедшей волны будет, следовательно,
^^п^г = со |/Sj^Xj ( — Xcos^х-\- zsin 6^)
где предположено, что jx^
'будет
Ь 1
где
= ш V^SajJ-a ( — гл: ]/ sin^ Oq — «li -|- 2" sin 6^), C5)
jx, = jxq, a напряжённость поля прошедшей волны
(х<0).
а = ш|/'е.^{Х2 sin бр, ш|/ё^ —
^2
р J = o)"|/e2jx2 l^sin^ Oq — n%x
2n ]
w !
1
j
C6)
C7)
CO,
Поле, определённое соотношением C6), экспоненциально затухает при х-^
чем и оправдывается выбор положительного знака в C4).
Амплитуды отражённого и прошедшего поля определятся далее из
формул Френеля после исключения 6j. Из A4) мы получаем
2 cos %
)
'^■^ cos Ofl + i ysins бо — «ii ^-^'
cos 00 + i y"sin2 % — л 11 j
a из A9) и C) для случая поляризации в плоскости падения
2«2i cos 6о
C8)
' ^' 2"^ .nf,cos0. + //sin8 8o-«|i ° ^' i
\
C9)
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ [9.7] 439
■ 1
Поскольку коэффициенты при Ео комплексны, фазы прошедшей и отражённой
волн, очевидно,- уже не совпадают у поверхности с фазой падающей волны.
Коэффициент отражения, согласно B9), равен R == E^EIJEq, и из C8) и C9)
сразу же следует, что
^± = ^11=1, 7^±==Г,| = 0. D0)
Интенсивность потока энергии в отражённой волне в точности равна
интенсивности падающей волны; таким образом, поток энергии в среду с меньшим
показателем преломления в среднем равен нулю. Однако напряжённость
поля в среде A) вовсе не равна нулю. В действительности мгновенная .
нормальная компонента потока энергии через поверхность существует, но среднее
её значение по времени равно нулю; среднее же значение потока энергии
в среде A), параллельного её поверхности (т.е. в направлении оси г), нулю
не равно. Эта последняя компонента не затухает в направлении
распространения, но очень быстро спадает по мере увеличения расстояния от
поверхности S благодаря множителю ехр f^^x. Поверхностями постоянной фазы
в прошедшей волне являются плоскости 2" = const., которые нормальны к
поверхностям постоянной амплитуды х = const. Ясно, что Е^[[ и Н^:| имеют
составляющие вдоль оси г, т. е. вдоль направления распространения в среде
A). В случае полного отражения возбуждение в среде A) представляет
собой непоперечную волну {которая может быть поперечно-электрической
или поперечно-магнитной, стр. 310—311), локализованную в
непосредственной близости поверхности раздела.
Проведённый выше анализ не даёт нам ключа к тому, как энергия
первоначально вошла в среду A), так как он основан на предположениях о.
стационарности процесса и о бесконечной протяжённости, разделяющей
диэлектрики поверхности и волновых фронтов. Фактически, падающая волна
ограничена как во времени, так и в пространстве. Полное отражение светового
луча с конечным сечением было разобрано Пихтом ^), который показал, что
средний поток энергии в направлении, нормальном к границе, в этом случае
строго нулю не равен. Всякое изменение, влекущее за собой колебание потока
энергии в прошедшей волне, нарушает полноту отражения.
Рисунки, показывающие расположение магнитных силовых линий и линий
потока энергии при полном отражении, были опубликованы Эйхенвальдом ^),
Шефером ^) и Гроссом ^),
Рассмотрим, наконец, относительные сдвиги фазы отражённых волн.
Напишем C8) и C9) в виде
E^ll = e-mE^^, \ D1)
Тогда, поскольку
е-*8±[=:[е-«81!|=1.
TTW-'-''^ tg_ = - D2^
1) Picht, Ann. Physik 3, 433, 1929; см. также Noeth e г, ibid. 11, 141, 1931.
2) A. Эйхенвальд, О движении энергии при полном ьнутреннем отражении.
Изв. имп. МОСК. инж. уч., ч. 2, вып. 2,1Р08. Прим. ред.
3) См. Шефер, Теоретическая физика, т. 1И, ч. 2, Оптика, §68, Прим. ред.
4) S с h а е f е г and Gross, Untersuchungen fiber die Totalreflexion, Ann. Physik.
32, 648. 1910.
440 гл. IX. КРАЕВЫЕ ЗАДАЧИ
iii-
. «II
_)/sin2eo—n^i
COS Pj)
)/sin2eo-n|i
мы имеем '
1
'I
\ D3)
I
Предположим, что падающая волна линейно поляризована в направлении,
которое не является ни нормальным, ни касательным к плоскости падения.
Мы разложим её поэтому на соответствующие компоненты и найдём тогда,
что получающаяся в результате отражения волна образуется в результате
сложения двух гармонических колебаний, происходящих под прямым углом
друг к другу со сдвигом фаз на
8 = 8„_8j^. D4)
Отражённая волна эллиптически поляризована^ так как, согласно D3),
относительный сдвиг фаз в общем»случае не равен нулю:
Ч ,а SX
tg"_tgi ccse^J/sin^eo-n^'i ^,-.
tp-.! ^ £_ = . ,, . D5)
Оба скачка фазы Ь^ и 8jj исчезают при падении под углом полной
поляризации «60= arcsin «21, а их разность равна нулю также и при скользящем
падении, Ь^ = — . Между этими пределами относительный сдвиг фаз 8
достигает максимума; соответствующий угол может быть получен
дифференцированием D5) по 6о и приравниванием производной нулю. Максимум
получается при
sin^eo = —-V, D6)
что, в результате подстановки в D5), даёт
\g^=l:zA, D7)
Эго свойство отражённых волн, имеющих место при полном отражении,
было использовано Френелем для получения света, поляризованного по кругу.
Для этого прежде всего необходимо, чтобы падающая волна была плоско
поляризована под углом в 45° к нормали плоскости падения. При этом
амплитуды f'gj^ и Е^\\ равны по величине. Относительный показатель
преломления Wgi и угол падения в^, должны быть затем подобраны так, чтобы
Ь = ~ или tg -|- = 1. Согласно D7), это условие может быть выполнено
только при 1 — n^i>2«3i, т. е. n2i<0,414 или /Zia>2,41. Минимальное
требуемое значение показателя преломления оказывается больше, чем
у какого-либо обычного прозрачного вещества в области видимого спектра.
Для того чтобы обойти эту трудность, Френель заставил луч света испытать
полное отражение дважды внутри стеклянного параллелепипеда,
обладающего соответствующим углом. С другой стороны, в области радиочастот
показатель преломления может принимать очень большие значения. Так,
например, в случае поверхности, образованной водой и воздухом, «i2=9'
/г^д = 0,11. Условие lgy= 1 удовлетворяется при этом либо при угле
ЖГ:
»■<*■•.
ОТРАЖЕНИЕ^ И ПРЕЛОМЛЕНИЕ НА ЦЛОСКОЙ ПОВЕРХНОСТИ !9.81 44В
во=б°,5, либо при 6() = 44°,6. Последняя цифра была подтверждена
измерениями с длиной волны в 250 сМ *).
9.8. Преломление в проводящей среде. При наличии проводимости
в той или другой из обеих сред явления отражения и преломления сильно
изменяются. Формально закон Снелля и формулы Френеля попрежнему
справедливы, но, как и в слу<!ае полного отражения, комплексное значение
угла 6i приводит к совершенно иной физической интерпретации.
Предположим, что среда B) попрежнему является идеальным
диэлектриком, в то время как преломляющая среда A) будет проводящей.
Постоянные распространения определяются соотношениями
. } D8>
где a^ и Pj. выражаются через Sj, [Xj и o^ формулами D8) и D9), стр. 246,
По закону Снелля мы имеем
_^ ^;„ ft 02.
что удобно записать в виде
sin Ь, = ^ sin % = -^ (a2~^'Pi) sin Во, D9)
«и «1 + Pi
sin e^ = (а — ib) sin вд. E0)?
Комплексный косинус будет тогда
cos 61 = /1 — (^^2 _ г»''^ — 2аЫ) sin2 q^ = ре*т. E1)
Абсолютная величина р и фаза ^ получаются путём возведения E1) в
квадрат и приравнивания действительной и мнимой частей обеих сторон
р2 cos 2^ = р2Х2 cos2 Y — 1) = 1 — @:2 — г>2) sin^ бо, \
p2sin2'y = 2p2sinxcos'v = 2a:^'sin2eo. J ^^^^
Фаза^ преломлённой волны, как и в C5) и на рис. 92,, равна
^jti^r = (ttj -|- £^i) ( —д: cos 61 -}- 2 sin в^) =—д:р (аj cos ^ — ^i sin y) —
-j-/xp(pi cos'^-\-a^sin'^)-\- z{aai-\-b^{) sin e^j-|-/г(a:,3j—ha^)sin bg, E3)
Из D9) и E0) легко усмотреть, что (аа^ -\- Ь^^) sin 60 = «2 sifi вд и
(a^j — b(Xj)=Q. Внутри проводящей среды прошедшая волна выражается,
следовательно, так:
Е^ = Е^еР^+^ {-qx+otz sin %—ы) (д.<^ 0) E4)
где
/7 = р (Pi cos Y -f «1 sin y), I ^55^
^ = p(aiCos'v—Pisin-v). J
Заметим, что поверхностями равной амплитуды являются плоскости
рх= const, а поверхностями равной фазы плоскости qx-\-oi^ sin ^qZ = const,
и что в общем случае эти два семейства плоскостей не совпадают.
В среде A) поле представляет собой систему неоднородных плоских волн,
как и в случае полного отражения. Плоскости равной амплитуды параллельны
отражающей поверхности S\ направление же распространения определяется
нормалью к поверхностям постоянной фазы. Угол ^ между этой волновой
^) Bergmanп, Die Erzeugung zirkular polarislerter elektrischer Wellen durcb
einmalige Totalreflexion, Physik. Z. 33, 582, 1932.
442
гл. IX. КРАЕВЫЕ ЗАДАЧИ
нормалью и нормалью к плоскости границы (в данном случае —
отрицательной осью х) есть действительный угол преломления, определяемый из
соотношения
— A:cos<J'-]-^sin<J' = const. E6)
или
' ,1
cosw
81Пф:
I
J
ag sin %
E7)
Vq^ + ai
sin" e„
Соотношение между плоскостями равной амплитуды и поверхностями равной
фазы показано на рис. 93.
Изменённый закон Снелля для действительных углов выражается
соотношениями E7) или
''(9о) = -4^^ = 4->'°»^"'% + «'- E8)
8ШФ
«а
Величина «(Oq) представляет собой действительный показатель преломления
и зависит от угла падения, в чём видно явное отличие от закона
преломления для непоглощающей сре-
Плоскость постоянной
амплитуды
и постоянной фазы
\
Среда B)
ды. Фазовая скорость,
определяемая как скорость
распространения плоскостей
равной фазы, будет
t'l (9о) =
Среда {/}_
Плоскость
постоянной фазы
W///y>////A{//////////,'///, Z
Плоскость
постоянной ампщтуды
Волновая
нормаль
Рис. 93. Преломление на плоской поверхности
проводящей среды.
п (Оо)
Не только эта скорость
зависит от угла падения, но,
как и в случае полного
отражения, имеется также
составляющая напряжённости
в направлении распрос^гра-
нения. Поле внутри
проводника не является строг*
поперечным.
Подсчёт р, д и п через константы среды и угол' падения представляет"
собой элементарную, но скучную задачу. Из E2) и E5), совместно с опре-
.делением а и Ь, заключённым в D9), мы получаем следующие соотношения:
Р^ (%) = Y { - «I -f К- + < siп^ 6^ + ^
• + /4«^R + («1 - Р! - «I sin'^ ЬоГ},
+ У^<^ш+(«;—R - «1 sin2 %г~},
• + V^<^^ + («1 — PJ — <^l Sin2 0^)9) .
F0)
m*-i: '-.
ОТРАЖЕНИЕ и ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ [9.8] 443
Из ЭТОЙ вспомогательной системы соотношений, известной под названием
уравнений Кеттелера, легко вывести, что
F1)
Общий характер зависимости /г@о) от угла падения и от постоянных «^
и Pi, выраженной соотношениями F0), был подтверждён измерениями,
проведёнными в видимой части спектра *). Однако никакой прямой связи между
наблюдёнными значениями «j и pj при оптических частотах и статическими
или квазистатическими значениями параметров е, [х, о не существует.
В действительности «^ и ^^ при оптических частотах могут принимать такие
значения, которые при радиочастотах возможны только для сильно
ионизированных сред. Так, например, Ши нашёл, что для меди ffi/a2 = 0,48 —
значение, меньшее единицы, а ^^/«2=2,61 вместо весьма большого значения,
которого можно было бы ожидать для такого хорошего проводника. В
данном случае фазовая скорость в металле больше,' чем скорость света.
Аномальное поведение этих параметров при оптических частотах приводит
к весьма интересным явлениям в области оптики металлов, которые, однако,
лежат за пределами, которыми мы ограничили излагаемую здесь теорию ^).
Хотя экспериментальные данные, которые могли бы подтвердить
уравнения F0) при радиочастотах, повидимому, отсутствуют, имеются все
основания, чтобы считать их точными. Мы рассмотрим только тот случай,
когда токи проводимости в среде во много раз больше, чем токи смещения.
Пусть TQ = o/(os. Тогда наше предположение заключается в том, что iq^^^l.
Напомним, что при этом условии (стр. 247)
Из F0) получаем
■»2
«..SpiSj/"-^. F2)
P^=^(sin^e„ + |/"-J^ + sin'eo), F3)
НО так как мы предположили, что iq^ гораздо больше, чем максимальное
значение sin^6Q, то мы получаем приближённые формулы
откуда /г->оо при о->оа или со-^0. В то же время
^i"* = V^^^"'«o. F5)
И 4* "^ о* По мере увеличения проводимости или уменьшения, частоты
плоскости постоянной фазы становятся параллельными плоскостям
равной амплитуды, и распространение в проводнике происходит нормально
его поверхности.
г) Shea, Wied. Ann. 47, 271, 1892; WiIsеу.Р/гу^. Rev. 8, 391, 1916.
') Прекраснее изложение вопросов отражения и преломления в оптике дано
у Кб nig'а в Handbuch der Physik в главе, посвященной электромагнитной теории
света, т. XX, стр. 197—253, Springer, 1928.
444 * гл. IX. КРАЕВЫЕ ЗАДАЧИ
В случае меди о^=:5,82'10 см-^ метр-^ та^с что ^ чрезвычайно
незначительно отличается от нуля. Каков бы ни был угол падения, прошедшая?
волна распространяется в направлении нормали. Величина
V-
tujjijaj
F6>
определяет глубину проникновения. Она является характерной для всех,
явлений при скин-эффекте и даёт расстояние от поверхности проводника
до той точки, в которой амплитуда электрического вектора равна 1/е =
= 0,3679 от его величины на поТверхности. Отставание по фазе на этом
расстоянии равно 180°. Поскольку 8 определяет эффективность материала
для целей экранирования, представляет интерес поря цок её величины.
Таблица, приведённая ниже, даёт значения 8 для меди при различных частотах..
Они получены из приближённой формулы 8 = 6,6 • |/v см:
V
колебаний в секунду
60
103
106
0
см
0,85
0,21
0,007
Глубина проникновения уменьшается с увеличением магнитной проницаемости^,
но этот эффект обычно перекрывается плохой проводимостью большинства
материалов с большой магнитной проницаемостью.
Угол <^ может быть почти равен нулю и для веществ со значительно-
меньшей проводимостью,, чем металлы. В случае морской воды
о^=:Зомам-^ метр-^, ei=:81eQ,
откуда находим
- ^c^J^Z.ios, п = Щ-10^ Ь = Щ^ метров. F7>
при V = 106 получаем п = 164, 4'<0'', 35 и 8 = 29 ел. Приближение это»
при v = 10s ещё справедливо, так как в этом случае
irji.= 45;^l; при этой частоте «=16,4, «1^ < 3°,5, 8 = 2,9 см. «,
9.9. Отражение от проводящей поверхности. Мы рассмотрим теперь
фазу и амплитуду волны, отражённой от плоской поверхности, разделяющей
диэлектрик и проводник. По закону Снелля
^ k^cosb^ = \/^ki—kls'm^%y F8>
и из F0) и F1) следует, что
4
Из этих соотношений легко вывести, что
^1 COS 0^ = 1/^2+^е"^, G0>
где
. tgl-=e, cos^= ,-1__.,. sin.l= , Р . G1>
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ [9.9] 445
Подставляя G0) в формулу Френеля A4) для отражённой компоненты
электрического вектора, поляризованной нормально к плоскости падения,
шолучаем
[xtoa CCS бс + (X2 У9^+/?2 e =^
Лля того чтобы получить амплитуду и фазу, надо привести дробь к виду
E2i = pj.e-*sj-Eoi, G3)
т в результате вычисления мы найдём, что
2 _ ff^ig -- P'ia2 cos РоJ + [Х^ р9
"^ ({Xj9 + [xioa cos есJ + [j| /?2 '
2p.j[Jka2/? cos Pfl
tgs± =
[x|a|cos^Po —[x|(9^ + /;2)-
G4)
Таким же путём мы найдём и компоненту, поляризованную в другом
'направлении, хотя подсчёт в этом случае более длинен. Согласно B0),
Фторая формула Френеля будет
Т
Н21 = ; ^ Ho_L. G5)
2
[Х2 COS ^0 (а\ — р| + 2aipj/) + И^г Уgf^ _|- ;?2 g ^
Длинную процедуру приведения этого комплексного выражения к
тригонометрическому виду можно обойти и получить результат сразу же. Вводя
сокращение
[Пз, E2ii]=piie-*sii[no, Ео||], G6)
щаходим
2 __ {м-а (°i — Pi) cos Pq — [хха^дг}"^- + {2[i^_aih cos ^o - P-iQ-^P)^
" {^-2 («1 — Pi) cos Po + [iia^qY + B[X2aipi cos Po ^ [xiagp)^ '
tg8||=-^
2ИР'2«2/' ^9^ +P-— °1 Sin2 Pfl) COS f'e
^«2(9''+/'') —M'i'ei + Pi)-cos2Po
Есди проводник немагнитный, так что jx^ = Цд, то выражение для
амплитуды р|| переходит в форму, выведенную Пфейфером i) в его работах по
-оптике:
2 ^ (^-a2COs6oP+/>^ ^gf-aoSinPotgPb)^+P^ .„8^
f"" (9 4-a2COsPoJ+/72 • (9 + a2SmPotgPoi2+/,2 • V ^«J
Как и в случае полного отражения, две компоненты падающего
излучения, поляризованные в различных направлениях, отражаются по разным
законам. Следовательно, линейно поляризованная волна, направление
поляризации которой не совпадает ни с плоскостью падения, ни с нормалью
к ней, будет после отражения поляризована эллиптически. Характер
поляризации определяется отношением
h.e^H-W =ре*8. G9)
I) Pieiffer, Diss. Giessen, 1912, KOnig, lac. cit., стр. 242; см. также Wilsey,
ioc. cit, стр. 393.
446
гл. IX. КРАЕВЫЕ ЗАДАЧИ
Выражения для р и 8 приводятся к сравнительно простому виду только
в слзгчае немагнитных веществ. Если jxj ==: jxg, то, проделав трудоёмкий
подсчёт, найдём
(9 + a2sineotgeoJ+p2 »
2а^ sin бо tg е©
tef8 =
4sin2eotg2eo—(g' + p2)
I
(80)
Коэффициент отражения мы опять определим как. отношение потока
энергии падающей волны к потоку энергии отражённой волны. Таким
образом
(81)
2 9
В случае нормального падения R^ = r^=r и
2d2
R =
(P^ai —1^102)-+ ^-2^1
Степень поляризации обычно измеряется отношением
(82)
(83)
'21' ' i^-gi
где g^==Eo\ilEo± — отношение интенсивностей в падающей волне.
Благодаря тому что величины q и р являются функциями как параметров
среды, так и угла падения [уравнения F0)], сложность, казалось бы,
простейшей задачи об отражении плоской волны от плоской поглощающей
поверхности оказывается поистине удивительной. Формулы сллшком сложны,
чтобы понять их содержание с первого взгляда, и характер явления
отражения выясняется только из рассмотрения некоторых предельных случаев.
Для теории электричества одним из наиболее важных из них является
2 4
Случай I. 73i = ——2-^^^' Тогда, как было показано на стр. 443, '
и
«1
2
0-
=1/"^
2~
<84)
(l + ^^eose,f+l
tgS
X
ИОг
'1
2 cos %
(85)
Так как Н-х/р^г = f^i/f^o = ^mi — относительная магнитная проницаемость
проводника, ae2/eQ = Xgj — относительная диэлектрическая проницаемость
диэлектрика, мы можем написать
х-
(86)
где V —частота. Далее для всех металлических проводников {л^аа/и-а»! <С U
и (85) приводится к виду
Р^^ ^ 1 — 2jc cos %у tghj^^—2x cos %.
(87)
ОТРАЖЕНИЕ и ПРЕЛОМЛЕНИЕ НА ПЛОСКОЙ ПОВЕРХНОСТИ 19.9]
447
Это приближение получено применением к (85) формулы бинома и
справедливо до тех пор, пока можно пренебречь квадратом Hi«2/f*2*i "^ сравнению
с первой степенью. Аналогично, если поляризация параллельна плоскости
йадения,
2 ^ 2cos^6o—2л:со5Ро + ^^ )
Р" ~ 2 cos2 Сс + 2л: cos е^, + а:^ ' |
. ^ 2xcoseo
t£fO„= ^t_2cos2eo.
(88)
*D
J
Член с л'2»удержан потому, что при некоторых значениях 6q
числитель р^) становится очень малым. Этот критический угол является, очевидно,
аналогом угла Брюстера, рассмотренного выше. Минимальное значение
р^1 соответствует углу падения, удовлетворяющему соотношению 1/2 cos % = х.
Следовательно, если минимум выражен достаточно остро, то значение
отношения [Xj/aj может быть определено непосредственно из наблюдения
отражательных свойств вещества.
Из полученных результатов ясно, что коэффициент отражения дл»
металлов практически не зависит от угла падения и очень мало отличаете»
вт единицы даже для наиболее высоких радиочастот. Так, для границы
воздух—медь x^i = l, х^2=1, а^ = 5,82-10'^ см
-1
метр
-1
так чтб
д; = 2,77 • lO-^j/v. В случае железа проводимость примерно в десять раз
меньше, а магнитная проницаемость i) может быть порядка 10^, однако,
X попрежнему мало, даже для длин волн в несколько сантиметров. Формула
/?== 1—4,22 . 10-* -i/!^mi2^ ,
(89)
к которой приводятся (87) и (88) при нормальном падении, была проверена
для инфракрасной области спектра Хагеном и Рубенсом 2).
Результаты их измерений приведены в следующей таблице для Л = 12 jju
и Х = 25,5 {Jt, где 1 [а=10-* см.
1МеТаЛ.л
Си .
А1 . ,
Ли . ,
Pt. . .
Ni . ,
Sn .
Hg .
l — R, % при X = 12[x
Измеренное
1,15
1,6
2Л
3,5
4,1
Вычисленное
1.3 ,
1,4
1.6
3,5
3,6
1 — /?, % при '^ = 25,5 [X
Измеренное
1,13
1,17
1,97
1,56
2,82
3,20
3,27
7,66
Вычисленное
1,15
1,27
1,60
1,3»
2.96
3,16
3,23
7,55
Теоретические значения, с которыми сравниваются результаты измерений,,
подсчитаны на основании электростатических значений проводимости. При.
длинах волн меньше 12 [х отклонения становятся более заметными, а при волнах
оптической длины всякое соответствие пропадает. Поведение этих цифр-
1) При ультравысоких частотах магнитная проницаемость может быть намного^
меньше. Ср. с измерениями, сделанными Qlathart, Phys. Rev. 55, 833, 1939.
') Hagen and Rubers, Ann. Physik 11, 873, 1903,
^^448
гл. IX. КРАЕВЫЕ ЗАДАЧИ
/В высшей степени многозначительно. Они показывают, что пока мы имеем
дело только с металлами, макроскопическая электромагнитная теория
справедлива для всех волн, длина которых больше чем примерно 10-^ см,
т. е. частота меньше примерно 3 • 10^^ колебаний в секунду.
Отражение радиоволн от поверхности моря или земли приводит к резуль-
"татам иного порядка. Рассмотрим сначала случай поверхности воздух — море,
для которойх^1 = Хе2= 1;°1==Зом-1метр-1и^с= l,22-10-*lA^ Поскольку
приближения (87) и (88) справедливы только при х<^\, мы ограничены
-теперь частотами, меньшими 10^ колебаний в секунду. Возьмём, например,
.широковещательную частоту в 600 Кц, Х = 500 м. Тогда д:*= 0,094. На
рис. 94 нанесены в функции от угла
падения значения коэффициентов отражения
/?_L и Щ для волны, поляризованной
нормально и параллельно к плоскости
падения. Мы видим, что /?jL >/?|| и что при
86°,2 Щ достигает своего минимума.
Следовательно, если электрический вектор
падающей волны линейно поляризован
в направлении, не совпадающем ни с
плоскостью падения, ни с нормалью к ней,
то волна, отражённая от поверхности
моря, будет эллиптически поляризована.
Кроме того, если антенна передатчика
направлена вертикально, то волна будет
поляризована в плоскости падения;
следовательно, если она встретит морскую
поверхность под скользящим углом, то она
гложет почти полностью поглотиться.
Если теперь частота увеличена или
же волна падает на поверхность пресной
воды или землю, проводимость которых
-обычно порядка 10-* и меньше, то приближения (87) и (88) уже
непригодны; однако характер явления отражения изменится не очень сильно.
-Мы должны рассмотреть таким образом
I€0
.90
.80
70
:| 60
% 50
I 40
/?а
Л',,
30
20
10
О
О W 2030 40 50 60 70 80 90
Oq, в градусах \
лРис. 94. Коэффициенты отражения
йплоской радиоволны от поверхности
моря.
Случай П. 1ГI =
2 2
СО Sj
<С1. Согласно E2) и E3), стр. 247
ч~-,Уу'ех^ ^1=^^^'^"!;^
(90)
Шсли частота достаточно велика, то «j^pj, и уравнения F0),
приведённые выше, примут вид
ра^О, ^2^af—а^зш^бо. (91)
Шоэтому
» •
Р1= Т
(т-е! — ■x-es sin« %^ ^ -j- У"%^ cos б^
^ %el COS Оо — У^ег^^е!—y-eSSin^y^
р II = ' -^— Y .
Xel COS бо •\- У'А^ (%gi — %е2 Sin^ бо) ^
(92)
^»i
ПЛОСКИЕ слои [9.10]
449
в этом приближении входят только, диэлектрические свойства среды, и
формулы (92) тождественны с результатами, полученными в разделе 9.6.
Следующий порядок внесёт малые поправки в Р^ ^).
Возьмём, например, поверхность пресной воды: Xg2=l, v-ei = ^^i
2 • 10-* СМ-* метр-^
4,45-10-4
Ъ= ;:— »
Тогда
а,
l,88.10-'?v, Pi ^4,18-10-3.
Приближение (92) справедливо, таким образом, при v > Ю^. Для почвы
и горных пород константы меняются в очень широких пределах, но как
типичный случай мы можем взять v.^^ = 6,
о, = 10-^ Тогда
3-10*
щ =
«1—5,1 • 10-^v,
Pi ^7,7-10
_4
так что опять-таки (92) справедливо при
v> 10^. При частотах, больших 10^
колебаний в секунду, пресная вода, сухая
земля и горные породы ведут себя,
с точки зрения их отражлт£Льных
свойств, как диэлектрики. Прошедшая
волна, конечно, быстро затухает из-за
коэффициента Pj. Зависимость
коэффициентов отражения для этих двух случаев
от угла падения показана на рис. 95.
Подобные кривые были экспериментально
подтверждены Пфаненбергом^).
Хотя в случае металлов формулы и
15 30 45 во 75 SO
0„, в градусах
Рис. 95. Коэффициенты отражения
плоских радиоволн от поверхности
земли и от поверхности пресной
воды при частотах, больших чем один
мегацикл в секунду.
справедливы для частот, заходящих
в инфракрасную область, это не имеет места в случае диэлектриков и плохо
проводящих веществ. При длине волны порядка нескольких сантиметров
большинство диэлектриков обнаруживает заметное увеличение поглощения
по причинам иного рода, чем электрическая проводимость. Так, при длине
волны в 2,8 см значение р для дистиллированной воды, подсчитанное исходя
из электрической проводимости о=2- 10-* ом-^ метр-i, равно 4,2- \Q-^,
в то время как измерения^) дают 494 (система MKS, расстояние в метрах!).
Этот пример является крайним случаем, соответствующим дипольному
резонансу молекул воды, но, очевидно, при подобных обстоятельствах
приближение (95) несправедливо. Общие формулы могут быть применены всегда
даже в области оптического спекгра, при том условии, что взятые значения
констант а и Р измерены при соответствующей частоте.
ПЛОСКИЕ СЛОИ
9.10. Коэффициент отражения и коэффициент прозрачности. Мы
рассмотрим только случай нормального падения, имеющий значительный
практический интерес. Три произвольные однородные среды,
характеризующиеся константами распространения k^, k^, k^, разделены плоскостями, как
1) Обзор различных поиближённых формул, применяемых в оптике, дан
у к о н и г а, 1ос. cit, стр. 246.
2) Р f а п п е п b е г g, Z. Physik 37, 758, 1926.
3) В а z, Physik. Z. 40, 394, 1939.
29^ Звк. 5S3. Теория электромагнетизма.
450
гл. IX. КРАЕВЫЕ ЗАДАЧИ
показано на рис. 96. Мы можем рассматривать только абсолютные величины
векторов и поэтому для падающей и отражённой волн в среде A) напишем
£,•=^£o^^'^•t^-*^"^ Hi
сор.
i"-!
F.
k.
p — p p-Utz-iiot W -^ _ J!L. p
F-l
A)
B>
Поле внутри слоя B) должно быть выражено как через полом^ительную^
так и через отрицательную волны
д
т
со|д,2
(£+е*М__я
26 ) е у
тогда как прошедшая волна будет
cojxg
D)
Удобно воспользоваться здесь понятием внутреннего импеданса, введённым
в разделе 5.6, стр. 251. Для плоской волны в изотропной однородной среде
Я,
СО'Л;
-+- ZH- Z- = ■^•'-
Отношение импедансов мы обозначим через
V-sh
Er,Hr
(f<3}
Eo^t
E)
F)
ZjjiZj^j=lf ZijZjj^==Zij^. G)
Выражая граничные условия через
отношения импедансов, мы приходим к
четырём соотношениям между пятью
амплитудами :
Яо -j- ^1 = ^ -\- ^»
^0 — ^1 = ^la (^а — ^2"),
Решая эти уравнения относительно амплитуд отражённой и прошедшей волн»
находим
z^d
Рис. 96. Отражение и прохождение
плоской волны через плоский слой.
(8)
Е = (^ -Zn) A +^2з) + A + Zi,) A -ZaO е^^^*<^
i?« =
^ )
A +^15)A + ^2з) + A-Z,2) A -Zs,) ^^*^*^ °' ^
I
J
4е
— ikadt
(9)
Введём обозначения для комплексных отношений
1
4Jc
Zfc--Zj
1 -j- Z^ Zjt + Z_,-
fci-
A0)
Физический смысл этих отношений станет очевидным, если мы заметИ'м, что
^jTi
A1)
A2)
ПЛОСКИЕ СЛОИ [9.111
451
Величина /?_,й является коэффициентом отражения от плоской поверхности,
разделяющей две полубесконечные среды при нормальном пацении,
[уравнение (82), стр. 446]; величина /-^-^ представляет собой комплексное отношение
амплитуд отражённой и падающей волн. Коэффициент отражения от границы
равен нулю, если внутренние импедансы соприкасающихся сред равны.
С помощью величин г^^ соотношения (9) преобразуются к виду
1
4е*' (^'»—^з) Л
A +-2i3) A + Z23) 1 + /•]2^23^
2%кф
A3)
Коэффициент отражения и коэффициент прозрачности слоя равны квадратам
абсолютных величин этих отношений. Написав
7 ^ЗЛ^^.Л^11.^.^ I
."•л-г '^.i + ^i
Чг
»#
A4)
to-й — ^^i^^-- ^"fe^-^" ~ ^-i^^^
[-1(«? + Й)-'^|(«1 + Й) '
A5)
мы замечаем, что Y^fc = — Tfcj> а 8^fc = ^~^fc^ Вводя эти фазовые.углы в A3)
и умножая затем каждое из этих отношений на сопряжённое ему, мы
получаем
R =
2 ^ /?12 + 2 У"/?12/?2i е - "^^^^ COS @23 — 5i2 Ч- 2a2rf) + ^23g ~ ^^'"^
l+2//?j2^^e~^^^'^COSl8i2 + S23 + 2М) + /?12^2.^~''^''^ *
i^2i^3(«;+Pt)(a2 + P2)
"" ((P^Qi + (ЧОз)" + (l-^Pi + l^.lp2)'J 10^302 + i^2aj)^ + ((^зР2 i- ^-263)^1
' l+2|^^?23^~'^*^COS(Si2+ S23 + 2a2d) + /?l2/?23^~'^'* *
Уравнение A7) может быть преобразовано к виду
A6)
X
A7)
' Р-З
«f+Pf
X
I-»-! «iQj + Р1Р3
[A - /?.2) (I — /?2J) " 4 У;?,2/?2:? sin 0,2 Sin б^з] e -^<P« - Рз) ^
X
1 + 2 y/?.2'?23 ^~'P*^ COS (812 + S23 + ?«2rf) + /?12/?23^ ~'^*'^
применением формул
l/"/?,:fc sin 8.ft =
2i-«'j-t^A: (ojfcPj- -zi^a^A.
■Jk ^jk ^^^„. -1:: ^^.a;tJ + Ыз- + 1фсГ- '
1 p = 4;XJ[X;fc(aja;;.+ Pjfa)
A8)
A9)
B0)
9.11. Применение к диэлектрическим средам. Явления интерференции,
выражаемые формулами A6) и A8), часто применялись для определения
оптических констант веществ в инфракрасной и электрической областях
29*
452
гл. IX. КРАЕВЫЕ ЗАДАЧИ
спектра с таким же успехом, как и в видимой области *)• Д-"я того чтобы
физически уяснить поведение коэффициента отражения при изменении толщины
слоя, мы рассмотрим простой случай тонкого диэлектрического слоя,
разделяющего два полубесконечных диэлектрика, как показано на рис. 96.
Диэлектрические проницаемости трёх сред равны е^, eg, eg, ^j^z=^^z=^^ = 0
8. ~ " ~
и, следовательно, 6^2 = 823 = 0- Тогда
R =
B1)
B2)
(I + /•12Г2зJ — 4Г12Г23 sin- Ogrf '
Причём а^=2т:11^, где Л2—длина волны в слое. Если величина е^ лежит
между Bj и eg, то произведение r^^r^Q положительно и R — осциллирующая
функция d. Mинимaл^нoe значение R
имеет место при d == Х2/4, и равно
нулю, если /■]2 = '*23' ^' ^- ^ '^^^ С^У"
чае, когда eg является геометрическим
средним между е^ и eg i^2=^V ЧЧ^-
При этих условиях от поверхности
ничего не отражается, и вся энергия
прохошт из среды A) в ере ту B).
Введение слоя толщиной в четверть
волны с соответствующей
диэлектрической проницаемостью играет
ту же роль, что и подбор импеданса
в месте соединения двух
передаточных элекпърических линий. На рис. 97
нанесены кривые, показывающие
влияние диэлектрического слоя на
поверхности раздела воздуха и воды.
Этот принцип был недавно
применён для производства оптически
«невидимого» стекла. В ре.ультате покрытия плёнкой с соответствующим
показателем преломления отражение света от поверхности стекла
уменьшается почти до нуля. ^
9.12. Поглощающие слои. Если среда по обе стороны слоя одна и та же,
то уравнения A6) и A8) принимают вид
/^^g [A _ g-2M)!? 4- 4g~^^»'^sin^ ggrfl
A - /?а2^-^И2 + AR^^e-'^^ s\v? (^12 + «2^) '
A - R^e- ^Р'^^Я + 4/?j2^ -^P»** sin2 (Bi2 + «2^)'
Дальнейшего упрощения мы достигнем, положив
Рис- 97. Koэфtи■лиeнты отражения от
плоских диэлектрических слоев в
зависимости от их толщины и
диэлектрической проницаемости.
R
B3)
>12
Y^"^12'
B5)
1) См., например, у Drude, Lehrbuch der Optik, гл. ll, 1900. П. Друде,
Оптика, М.—Л,. ОНТИ, 1935. В инфракрасной области этот метод гримеиялся Черни
и его студентами: С z е г л у, Z Physik 65, 600, 1930; Barnes und С z е г п у, Phys.
R'^v. 38. 338, 1931; С а г t w г i g h t and С z е г n у, Z. Physik 85, 269, 1933; W о 11 e r s-
dorf, ibid. Недавно тот же метод был применён к ультракоротким радиоволнам.
См.. например, В а z, Phys. Z. 40,394, 1939 и VП sie t unu^oih, Hochfreq. und
ШеШгоак. 51, 156, U38, которые распространили формулу для коэффициента
отражения на случай произвольного угла падения.
ПОВЕРХНОСТНЫЕ ВОЛНЫ [9.131
453
что после подстановки в B3) и B4) даёт
sin2 а^ -4- sh? р2^
R
sin-'' (ajd + 812) -f sh2 (^,d + 5,2) '
(sinnig + sh^^i^)pP*'^
sin2 (agd + S12) + sh2 (p2d + 512) *
B6)
B7)
Коэффициенты отражения и прозрачности снова являются осциллирующими
функциями толщины слоя rf, но амплитуда колебаний уже не остаётся
постоянной. На рис. 98 представлена зависимость Rot d для тонкого слоя роды в
воздухе при длине ролны 9,35 см (воздух по обе стороны слоя\ Выше мы
заметили, Mto коэффициент затухания для воды в этой области значительно больше,
чем даёт учёт одной только электрической проводимости. Наблюдённые зназе-
ния составляют «2 = 595 метров^^ Р2 = '^^>6 мегра"^ Внутри слоя длина
волны Д2= «о^о/°^2= 1>05 см, и
минимумы получаются на
расстояниях примерно в полволны, В общем,
чем меньше коэффициент затухания,
тем точнее совпадают минимумы
с точками, расположенными друг от
друга на расстоянии в полволны.
Для промышленных изоляторов а^
по меньшей мере в 10^ раз
превышает р2> так что Хд, а следовательно
и «2» могут быть определены
непосредственно из наблюдённых
колебание коэффициента отражения.
Численная величина минимумов
определяется потерями в слое, и кривая,
подобная начерченной на рис. 98,
даёт один из наилучших способов
определения ^2 "Р" сверхвысоких
частотах.
О 0,2 0,4 0,6 OjB 1,0 1,2 1,4 1,6 18 2fi Z^
d, в санти/^етрш
Рис. 98. Коэффициент отражения от
плоского слоя воды толщины d ем при
Хо = 9,35 см\ «2 = 5,95 см-\ р2 = 0»456 ем~^.
В случае металлического слоя затухание настолько велико и коэффициент
отражения настолько близок к единице, что даже для тончайших листко»
прозрачностью можно пренебречь. Например, коэффициент прозрачности
медного листка толщиной в 1 }х (Ю"* см) при частоте 10^ колебаний в секунду
меньше 10"^. Эгот подсчёт даёт, однако, совершенно ошибочное представление
об эффективности экранирования, поскольку он относится только к
бесконечной плоскэй поверхности. При отражении от поверхности, радиус кривизны
которой мал по сравнению с длиной волны, потери на отражение отнюдь
не являются всегда большими^). Единственный общий критерий, имеющий
значение в эгом случае, это — вгличина коэффициента затухания ^2 или
обратная ему величина — глубина скин-слоя, определённая на стр. 444.
ПОВЕРХНОСТНЫЕ ВОЛНЫ
9.13. Комплексный угол падения. Возмомшости, предоставляемы?
формулами Френеля, далеко не исчерпаны тем, чго было рассмотрено в
предыдущих разделах, так как мы ограничивались только действительными углам^г
падения. Формулы эти представляют собой формальное решение задачи с
определёнными краевыми условиями, аналитически справедливое для комплексных
1) Для цилиндрических экранов это обстоятельство хорошо показал
Щелкунов, Bell System Techn. J. 13, 532, 1934.
Ч
454
Гл. iX. KPAEBbtE ЗАДАЧИ
углов В той же мере, как и для действительных. Комплексные углы
преломления уже встречались нам в связи с явлениями полного отражения и
отражения от проводящих поверхностей. Получающиеся здесь плоские волны
оказались неоднородными: плоскости равной амплитуды не совпадали с
плоскостями равной фазы. Есть все основания ожидать поэтому, что комплексный
угол падения будет связан с неоднородной первичной волной. Мы не будем
рассматривать здесь, как подоб«ые волны получаются, но напомним, что
й разделах 6.8 и 7.7 было показано, что в наиболее общем случае
цилиндрические и сферические волны могут быть представлены в виде суперпозиции
плоских волн, направляющие косинусы которых принимают как
действительные, так и комплексные значения:
При действительном угле падения первичная волна в общем случае даёт
.начало волне, отражённой от поверхности разрыва. Только в случае плоской
волны, поляризованной в
Плосиоать "^ ПЛОСКОСТИ падения и
падающей на границу
раздела двух
полубесконечных диэлектриков под
углом Брюстера (стр.437),
мы имеем исключение из
этого правила. Если одна
из сред является
проводящей, то отражённая
волна получается всегда.
Если, однако, допустить
комплексный' угол
падения, то коэффициент,
отражения может оказаться
равным нулю при любых
свойствах
соприкасающихся сред.
постоянной фазы
\
\ Плосиость
^ постоянной фазъ/
:*-Волновай
нодмоль
Рис. 99. Преломление плоскостей равной фазы,
характерное для поверхностной волны.
Мы рассмотрим несколько подробнее тот случай, когда электрический
вектор параллелен плоскости падения. Пусть, как и в формуле A5), сгр. 451,
г\\ представляет отношение магнитных векторов падающей и отражённой волн.
Тогда формула Френеля A9), стр. 435, даёт
cos бр — ^12 COS 6^
''11 ~~ cos"eoT~^i2 COS Oi'
где
A)
'12
[Hf^'2
[Hh '
^21 —
4
'12
B)
как было принято на стр. 450. Для того чтобы отражённая волна
отсутствовала, числитель в A) должен обратиться в Нуль. Это условие, совместно
с законом Снелля, приводит к двум соотношениям
cos е^ ==^21 COS 00, sin Oi = ^ Zi2 sin fjo.
C)
которые определяют углы падения и преломления. Исключая 6^,, получаем
• Oft 1 —Zl2
1-{Щ'Л.'
cos^ Gq = Zlt
kMJ
D)
Для упрощения мы предположим, что поверхность соприкосновения
двух сред совпадает с плоскостью д: = 0. Ось х нормальна к этой поверх-
'ЙОВЕР'ХНОСТНЫЁ ВОЛНЫ 19.13] 4^5
ности и направлена из среды A) в среду B), как показано на рис. 99.
Плоскость падения параллельна плоскости xz\ следоватеяьно, магнитное поле
име€г только компоненту Ну. Электрический вектор лежит в плоскости
падения и имеет в общем случае обе составляющие Erg. и Е^. Поле является,
таким образом, поперечно-магнитным'^'). Поскольку магнитный вектор ка-
сателен к поверхности разрыва, при переходе из одной среды в другую он
остаётся непрерывным, следовательно, согласно разделу 9.4.
E)
где С — произвольная постоянная.
Положим далее:
h=k^s,\nbQ = k^s\nb^, F)
и определим действительную и мнимую части коэффициента, стоящего в
показателе E), следующим образом:
ik^ cos 61 = -f / К" ^1 — ^^ = — Pi -Ь ^Яv
G)
Знаки при радикалах выбраны так, чтобы при бесконечных значениях ± х
поле исчезало. Тогда в обозначениях G) получим
Я^^СТз (^>0),
Hy^os, (^<о), ^^
где
¥2 = ехр[ —рзл^ — р-г--]-/( —^2-^-!-«<?) —ш^]. j
Рассмотрим прежде всего характер падающей волны. Плоскости постоянной
фазы определяются уравнением
— ^2'^-|-а^ = const., A0)
в то время как плоскости равной амплитуды удовлетворяют уравнению
— Рдл: — ^2- = const. (И)
Плоскости равной фазы и равной амплитуды не совпадают.
Действительный угол падения ^^ есть угол между нормалью к плоскости постоянной фазы
и положительной осью х. Он удовлетворяет соотношению
ATCos^-j-^-sin^^: const., A2)
•откуда
cos^o = ,-7-i=:, s\n^^=-~^==. A3)
Ка-^Т^' ^" |Ла-
^-f9f
Плоскости постоянной фазы распространяются в направлении их положигель-
яой нормали с фазовой скоростью
ш
'^2-.^-—-. , A4)
|/"в^+й
1) См. раздел 6.1, стр. 309 и след.
456
гл. IX. КРАЕВЫЕ ЗАДАЧИ
которая меньше, чем нормальная скорость однородной плоской волны в
бесконечной среде с теми же свойств;^ми. С другой стороны, скорость данной
точки на фазовой плоскости, параллельная оси z, может быть больше, чем
скорость в свободном пространстве. Причина этого я:на из рис. 100. Длина
волны Ag определяется расстоянием между дв^мя плоскостями с одной и той
же фазой, измеренным по нормали
ч-=
2г.
j/"a2 +
я1
A5)
Расстояния между теми же двумя плоскостями, измеренные вдоль осей х
и Zt равны соответственно
Xj 271: J • Xg 2?!:
sin A*0 С'
^2^— С08фо"~92' ^^'
A6)
Точка на фазовой плоскости должна проходить эти расстояния за один
период, так что кажущиеся скорости равны
ш
'"^^~~~1г'
-^аз^
ш
A7)
а знйчения этих величин лежат между v^ и
бесконечностью. Нормаль к плоскостям равной
амплитуды сб, азует с осью х угол ^'^,
удовлетворяющий соотношению
— xcos^l^o-r-S"sin <^о= const., A8)
Рис. ICO. Компонента фазе- откудг
вой скорости, параллельная л В
оси Z, может быть больше tg «1о = • A9)
скорости света. ^-
Плоскости равной амплитуды, =которые в случае
большой проводимости почти перпендикулярны к плоскостям постоянной
фазы, на рис. 99 не показаны.
Обращаясь теперь к прошедшей волне в области д:< О, мы видим из (9)^
что плоскости равной фазы и плоскости равной а.шлитуды олределяются
соответст:!енно выражениями
и
■qiX-\- а2г = const.
Pi^ — р2г= const.
B0)
B1)
и нормали к ним образуют с отрицательной осью х углы ^^^ и «J»!,
определяемые соотношениями
Р
tg^l^i--^, tg^, = ^^
Фазовая скорость равна
v^ =
ш
j/"a^ +
9l
B2)
B3)
Компоненты электрического вектора проще всего подсчитать из
уравнения поля
E = 9^rotH, B4)
Ш'^
р
ПОВЕРХНОСТНЫЕ ВОЛНЫ 19.14]
457
которое в прямоугольных компонентах даёт
Е^==:
/о>,а дН,
'X
k^ dz
k^ дх
B5>
Из (8) и (9) следует, что
2
К
{х>Щ
B6>
(д:<0) ^
I
J
B7>
Физически поле, описываемое уравненмями (8), B6) и B7), связано-
с током, текущим в направлении оси z^ распределение которого вдоль оси у
однородно. Подобное поле является магнитно-поперечным, а продольная,
составляющая электрического поля зависит от потерь в каждой ,из сред,
так как произведение EJHy представляет собой нормальную составляющую'
потока энергии к границе раздела. С другой стороны, поперечная
компонента Eg, приводит к потоку энергии, параллельному границе. Всю задачу
в целом можно сраянить с предельным случаем тока, текущего вдоль
проводника, радиус которого становится бесконечным. Рассмотрение другой
составляющей падающей волны, соответствующей условию г^==0, приводит
к волнам поперечно-электрическим и может быть интерпретировано как пре-^
дельный случай задачи о распространении вдоль соленоида бесконечно
большого радиуса. В этом случае ток перпендикулярен к элементам
цилиндрической поверхности.
9.14. Скин-эффект. Если обе среды являются идеальными
диэлектриками, то угол 6q в случае /■||=0 дейстрител^н и соответствует углу
полной поляризации Брюстера. Значительно больший практический интерес
представляет тот случай, когда среда A) является проьодником, а среда B)'
диэлектриком. Тогда мы можем положить |Zi2p<C^l« Согласно D) и F),
h^ = kl
\-Zt
1
B8>
-2 ^ Z*
m)
13
Выражение это мОжно разложить по степеням Z^g'
h = kc
1
B9)
В рассматриваемом приближении мы сохраним в этом, разложении только
квадратичные члены. Поскольку, по предположению, проводимость среды B>
равна нулю, мы можем написать
2,!
1'\
е2;-»2«
2
[t-xH ^—Щх
1^2 ^IJ^I*"^ + fdip-jO)
где, как и раньше, T,j = aJsj(o. Тогда
|^2e, 1
2 '
^1
Л —^2(
1
1 £2^-1 1
%:-ч fix
2 ei:J-2 1 + "Пх 2eia2 I + у\^
)■
C0)
C1>
458 гл. ,IX. КРАЕВЫЕ ЗАДАЧИ
-Заметим, что а — действительная часть этого выражения — меньше k^ и,
следовательно, скорость точки на плоскости постоянной фазы в направлении оси z
•больше скорости свободной волны в диэлектрике. Мы видели выше, что
это только кажущаяся скорость и что действительная фазовая скорость
меньше скорости, определяемой коэффициентом k^.
Сделаем теперь дальнейшее предположение, что tf^'^ 1 и что,
следовательно, величиной l/if]2 можно пренебречь по сравнению с l/tj^. В этом
приближении ,
.^.Vi,r,, Р-^/|. C2)
Таким образом, скорость в направлении оси z в основном характеризует
фазовую скорость в среде, а коэффициент затухания стремится к нулю
с увеличением проводимости.
В том же приближении
«,2
eoUt «..
eil^2 1 + ^ii
что, согласно G), дабт
Аналогично
q^-p^^^B^^^£^. C4)
k\ — h^ с^ 0J (sjjxi — sgu-a) + ioJf^iOi, C5)
9i^Pi^.]A^. C6)
Из полученных результатов мы прежде всего замечаем, что
92 Р f Pies"^
_^2|i^ C7)
откуда согласно A3) и A9) следует, что 'в падающей волне плоскости
равной амплитуды нормальны к плоскостям постоянной фазы. При а^ -> схо
tg «1^0 "^ ^ и % -> тг/д. По мере увеличения проводимости плоскости
постоянной фазы в диэлектрике становятся почти нормальными к поверхности
проводника.
Соответствующие соотношения для проводника определяются из B2):
tg^.^_|/^J!!^, tg^,l^i/^.. 'C8)
при Oj -> сЪ оба угла (J^j и ^!^^ стремятся' к нулю. Плоскости равной
амплитуды и плоскости постюянной фазы в проводнике почти параллельны егш
поверхности. В то же время длина волны становится очень малой, так как
Xi = ^ —2ir |Л—-. C9)
Напомним, что для металлов а^ имеет порядок Ю"* ом-^метр-Ч
Отклонениями 4*0 от it/2 и ^^ от нуля можно поэтому полностью пренебречь,
£
и длина волны в металле составит по порядку величины v ^ л«. Даже над
поверхностью морской воды при частоте в 1 мегацикл/сел: угош наклона
плоскостей постоянной фазы всего лишь порядка 10". Наклон радиоволн
вперёд при распространении над поверхностью сухой земли может быть
ПОВЕРХНОСТНЫЕ ВОЛНЫ [9.14]
459
■более значительным. Соотношение между плоскостями постоянной фазы и
ПЛОСКОСТЯМИ равной амплитуды в этом случае подобно тому, какое
изображено на рис. 101. Необходимо помнить, однако, что условие ffl^^ 1
здесь уже не обязательно выполняется.
Подставляя приближённые соотношения C2), C4) и C6) в B6), мы
получаем для'компонент поля выражения
-х
-/"?
ОТ
2»
-Я}-
'*УЧ1^^ ^~^Т Q\^
к
ix > 0), D0)
CWi (X < 0).
D1)
Диэлситрин
Заметим, что тангенциальная компонента Е^ на границе л: = О непрерывна
i.
•и в (|Ai(o/a^) 2 раз больше тангенциальной компоненты магнитного поля.
При Oj -> оо продольное
электрическое поле исчезает.
i^^H Нормальная и
тангенциальная компоненты Е
различаются по фазе на 45° (более
точный расчёт показывает, что
в случае плохих проводников
угол меньше 45°).
Следовательно, конец
результирующего электрического вектора
описывает в каждой точке
эллипс. В точке диэлектрика
непосредственно над поверхностью проводника эллипс этот вписывается в
прямоугольник со сторонами 2о;2 = 2 ([Xg/sg)*''^ 2^2= 2([Xi(o/a^)V2, ^2<С[^2' ^^^
показано на рис. 102, а.
Поскольку величина z роли не
играет, координаты эллипса
равны
^Я!= «2^05@^, ]
ЧровоЯнан
Рис. 101. Сплошные линии — поверхности
равной фазы; пунктирные — говерхности постоянной
амплитуды.
£'^=^oCos( @^
^ + ^)-
\ D2)
-Zb^-
а
1Рис. 102. а — геометрическое место точек,
описываемых концом электрического вектора в
какой-либо точке диэлектрика; Ъ —
геометрическое место точек, описываемых концом
электрического вектора в какой-либо течке
проводника.
Электрический вектор в
диэлектрике вращается против
часовой стрелки. В остальных
точках диэлектрика эллипс по
форме такой же, но имеет
меньшие размеры в
соответствии с затуханием.
В проводнике эллипс,
описываемый концом
электрического вектора, вписывается
сторонами 2aj = 2(o(e2jJ'2y^'/<3i, 2^1 = 2 ([^.^(о/а)*/».
в прямоугольник 60
i»! !^ «1 (см. рис. л 02, ^). Координаты эллипса равны
Е^==а cos (<at-\-~j, E^ = b^cos(^t-]- ~У
D3)
Здесь Е^ отстаёт от Е^ и, соответственно, электрический вектор в
проводнике вращается .по часовой стрелке.
460
гл. IX. КРАЕВЫЕ ЗАДАЧИ
Глубина проникновения поля в проводник определяется фактором
затухания pi't обратная ему величина — в точности равна величине 8, которая
была определена на стр. 444. Плотность тока в направлении оси z будет
J^==a^Eg, а полный ток, проходящий через бесконечную полосу в проводнике,
параллельную плоскости ху и равную по ширине 1 м, будет •
1 о
/ = Oj Г Г Ej^dxdy = Се-Р^+* '«^-tu*)^
D4>
о —схэ
С другой стороны, ток через подобную полосу глубины d равен
M=I{\--e-Pr^+iuxd^. D5)
Так как для хороших проводников р^ очень велико, ток почти
полностью.ограничивается тонким поверхностным слоем (skin-кожа). Следует^
однако, отметить, что фаза нитей тока с глубиной меняется. Явление скин-
эффекта может быть выражено и с помощью понятия внутренней
самоиндукции !)•
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА
9.16. Собственные виды волн. Бесконечно длинный круглый цилиндр
радиуса а помещён в неограниченную однородную среду с постоянной
распространения ^2» ^ ''^ время как постоянная распространения внутри
цилиндра равна k^. На проводимость цилиндра и среды никаких ограничений
пока не налагается. Компоненты по^я в круговых цилитрических
координатах были выведены в разделе 6.6. Поле в центре должно быть конечш,
и следовательно, волновые функции внутри проводника должны быть
построены из бесселевых функций первого рода. Вне цилиндра требуемое
поведение на бесконечности обеспечивают фх'нкции Ганкеля Н}:\
Согласно C6) и C7), стр. 318—319, для внутренних точек проводника
(г < а) мы имеем
оо
4= S [r/n(Kr)a'„~tr^ J.(Kr-)bi]F„
n= —оо
n = —оо L 1
оо
^* = У] \Jn iKr) an\ Fn,
1^\Ы
^;(V)^';JF..
«= —oo
A>
K-
Hi
Hi=
n = —00 L ' »■ J^
n I
n = —00 L' ^ ^ i J
oo
У i/n(V)^/=-«.
ns
rf>
B)
« = —00
^) Cm. изложение этого вопроса Зоммерфельлом в книге Франк-Мизес^
Дифференциальные и интегральные уравнения математической физики, 1937, стр. 911
и далее.
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА {9.15]
461
Во всех внешних точках (г > а)
El =
El
2 If НГ (hr) < - !^" Hf a,r) к] F„,
п = —00 L 8 • з'' J
со
со
2 ln^n\hr)al]F.,,
C)
Я^
«= — с»
со
П = —00
00
б— ^
« = — 00
/л
/^и.
[Л203А2 А-г
D)
E)
и = —00
в этих соотношениях
Fn = exp (itib -j- гЛ,г — Ш), )
a штрихи при цилиндрических функциях обозначают дифференцирование по
^pryMeHty Хг.
Коэффициенты разложения и постоянная распространения h остаются
пока неопределёнными. Однако на границе г = а тангенциальные компоненты
напряжённости поля должны быть непрерывны, и это условие приводит
к определённым соотношениям между коэффициентами разложения. Из
непрерывности тангенциальных компонент Е мы получаем
F)
а из непрерывности тангенциальных компонент Н:
/AjJ / ,- nh А ikt, /i\'
JAjOJH
U^
nh
/A),
'^.
где
w
G>
(8)
Соотношения F) и G) образуют систему однородных линейных
уравнений, которым удовлетворяют четыре коэффициента а*^, Ь^^, а^, Ь^. Система
допускает нетривиальное решение только в том случае, если детерминант её
равен кулю. Постоянная распространения h определяется из условия
равенства нулю детерминанта системы F) и G). Раскрывая этот
детерминант, мы приходим к трансцендентному уравнению
г l2 г/
kXiu) klH^^yiv)
Р-хиЛ» (и)
(9)
462 гл. IX. КРАЕВЫЕ ЗАДАЧИ
V-
корни которого дают возможные значения постоянной распространения и
определяют таким образом характеристические или собственные волны,
могущие распространяться вдоль цилиндра. Корни эти дискретны и
образуют двумерное бесконечное многообразие. Функции Бесселя трансцендентны,
и для каждого значения п имеется бесчисленное множество корней, каждый
из которых может быть обозначен индексом т. Каждый корень уравн^ия
(9) может быть поэтому записан в виде к^т-
Общего метода для нахождения корней уравнений (9) указать нельзя,
но, к счастью для практических задач, связанных с распространением волн
вдоль металлических проводников, можно допустить приближения,
значительно упрощающие решение. Из уравнения F) мы замечаем, что при
конечной проводимости для удовлетворения граничным условиям всегда
необходима суперпозиция волн электрического и магнитного типов,
за исключением симметричного случая и = 0. Поле не является поперечным
ни по отношению к электрическому вектору, ни по отношению к
магнитному. Если, однако, проводимость одной из сред бесконечна, то граничные
условия могут быть удовлетворены либо поперечно-магнитным, либо
поперечно-электрическим полем. В этом случае задача полностью определена
либо условиями
Яб = 0, Е^ = 0 (г=а), A0)
либо условиями
^(гЯв) = 0, ^Я, = 0 (/--=«), (И)
которые получаются из выражений A4), стр. 427, если тангенциальная
компонента Н не равна нулю. В случае идеально проводящего цилиндра, noMejtueH-
ного в диэлектрик, виды собственных поперечно-магнитных и поперечно-
электрических волн определяются соответственно корнями уравнений
Амплитуды а^ и Ь^ теперь совершенно независимы и определяются
исключительно способом возбуждения. В обратном случае диэлектрического
цилиндра, окружённого идеальным проводником, виды поперечно-магнитных
и поперечно-электрических волн определяются соответственно корнями
уравнений
:!i^^o, ^=0. A3)
4 (и) ^(«)
Практически проводимость металла хотя и не бесконечна, но столь велика,
что внутри него цилиндрические функции могут быть заменены их
асимптотическими представлениями. Тогда оказывается, что в каждом из возможных
видов волн превалирует либо поперечно-магнитный тип, либо поперечно-
электрический." Небольшая компонента противоположного типа, «портящая»
поперечность, может рассматриваться как малый поправочный член,
учитывающий конечность проводимости.
Если возбуждается только симметричный вид л = 0, то поле не зависит
от 6, и коэффициенты uq и Ьд независимы друг от друга при любой
проводимости. Из F) ясно, что в этом случае поперечно-магнитная волна
удовлетворяет на границе соотношениям
Jo(u)ab = m\v)c^,
'МФ'о='~:ЩН^)а1, (И>
I
PACllPOCГРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА [9.161 463
В ТО Время как для поперечно-электрической волны
Допустимые виды поперечно-магнитных волн определяются, следовательно,
корнями Лдда трансцендентного уравнения
^Jjjv^^^f^ A6)
1; а виды поперечно-электрических волн получаются из уравнения
f !^f Л («) [х.^?(^) ,,7>
\ 9.16. Проводник, помещённый в диэлектрик. Мы рассмотрим только
t случай волн, в которых преобладает поперечно-магнитный тип, что соотвег-
\- ствует практически важной за паче об осевом токе в длинном прямом проводе ^).
; Прежде всего мы рассмотрим аксиально-симметричное решение и == 0.
S Затем мы покажем, что асимметричные виды волн, если и возбуждаются»
:' то немедленно затухают, так что никакого влияния на распространение тока
. вдоль сплошного проводника они не оказывают.
Предположим сначала, что проводимость цилиндра бесконечно велика.
Согласно A2), постоянная распространения определяется тогда из уравнения
^ t^ = 0. A8)
Если V очень мало, то Я<^)('о) может быть аппроксимировано выражением
„,,,, . 21, -iv dH^oi^} 2i .,QV
Я<')('г;) c=i—In ^, —-^ cii—, AУ>
где Y= 1,781. Эти выражения получаются в результате оценки интеграла C9),
стр. 324, в окрестности начала координат. Функция Ганкеля, конечно, много-
' значна, но мы берём, как и в случае логарифма, только её главное значение.
Это главное значение проще всего может быть определено асимптотическим
' выражением
l^)(v)c^}/'
^^2i
2^
4
B0)
которое справедливо при v'^X, p <^v. Если положить v = \v\e^<f, то
главные значения Ж') (-г;) будут лежать в пределах ^ <се< у.
Главное значение или ветвь Я(') (v) обращается в нуль во всех бесконечно
удалённых точках положительной мнимой полуплоскости. Это имеет место
только для корней главной ветви, которая нас и интересует; можно
показать далее, что в пределах .своих главных ветвей //(^) (г>) и /У(|) (©)•
1) В случае поперечно-электрических волн линии тОка представляют собой
концентрические окружности с центрами на оси проводника. Это решение может быть,,
таким образом, применено при исследовании распространения вдоль идеального
соленоида. См. Sommerfeld, Ann. Physik 15, 673, 19С4. В случае сплошного провод-
.ника поперечно-электрические волны быстро затухают.
464 ГЛ, IX. КРАЕВЫЕ ЗАДАЧИ
*сорней не имеют ^). Следовательно, отношение
имеет только одно решение г» = О, а значит h = ^g- ^^-^^ проводимрсть
цилиндра бесконечна, то скорость распространения поля вдоль оси
цилиндра определяется исключительно свойствами окружаюш^ей среды. Если
это пустое пространство, то волны распространяются вдоль цилиндра со
скоростью света и без затухания.
Если проводимость цилиндра хотя и не бесконечна, но, как у металлов,
•очень велика, то h отличается от k^. Однако существует по крайней мере
■один вид воли, для которого эта газ шца очень мала, так что v = aYk\—Л^
является малой величиной. Приближение B1) попрежнему справедливо для
правой части A6)» Что касается левой части, то мы видим, что |^ill:^^2>
поскольку ^д:^|/г|, ac^k^a'^X. Функции Бесселя J^ (м) и J^ (и) могут
•быть заменены, следовательно, их асимптотическими представлениями.
Мнимая часть и положительна. Следует помнить, что ^]=ai4-«Pi и что
«j^^Pj при очень больших Oj. Тогда, в силу A8), стр. 317:
Уравнение A6) принимает теперь вид
г;21п^ = /^1 ^, B3)
«"де правая часть от h не зависит.
Это уравнение для h может быть легко разрешено посредством
последовательных приближений. Метод, предложенный Зоммерфельдом ^), состоит
в следзтощем: пусть
Тогда B3) принимает вид
\\n\^f\. B4)
Величина f\ является известной, и мы хотим определить t
Логарифм от $ является по отношению к \ медленно меняющейся
функцией. Следовательно, если мы нашли п-е приближение, то п-\-\
приближение можно получить из
e„,ilne„ = 'r,, B5)
яли
1п-^
In
In-^-
In-^.— B6)
«
Можно показать сходимость этого выражения как для комплексных, так и
.для действительных значений tj. Корни уравнения B4), лежащие вблизи
1) Зоммерфельд. В книге Франк-Мизес, 1ос. cit., стр. 869 — 870.
') Gottinger Nachr., 1899. см. Франк-Мизес, lac. cit., стр. 926.
•
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА 19.16] 465
!
^ = 1 или вне главной ветви логарифма, из рассмотрения исключаются.
Оказывается, что In I является отрицательным числом порядка — 20; принимая
это значение в качестве In $q, можно ускорить сходимость полученного
выражения. Из B4) в соответствующем приближ^ии получаем
Y] —A -I--0 1,75 • 10-18а vjA'-i'"^'''^'' 4 B7)
где V—частота, а а выражено в метрах.
Для иллюстрации изложенного мы приведём следующий численный
пример, заимствованный у Зоммерфельда О- Медный провод диаметром 2 мм
окружён воздухом. Частота колебаний равна Ю^ герц. Тогда из B7) имеем
tj=—A+0 7,25- 10-"^.
Полагая 1п£в= —20 в качестве первого приближения, получаем
l, = {l-\-i) 3,6.10-«
In ^1 = — 16,8 + /^ ■= — A6,8 — 0,78 /) .
Аналогичн®
1п^2 = —A6,7 —0,83/),
Sg очень мало отличается от ^^ " на нём мы можем остановиться. Малость $
оправдывает первоначально принятые приближённые выражения для функций
Бесселя и Ганке ля. Возвращаясь к выражениям B4), мы находим -у, а
следовательно, и постоянную распространения h для й = 1 мм:
Л = ^2 {1+F,0 + 6.40 • 10-6} = а-|-/р.
Фазощая скорость распространения вдоль провода равна
К= сA—6,0- Ю-б),
в то время как расстояние, на котором амплитуда волны затухает до 1/е
от своей первоначальной величины, составляет г=770м. Хотя полученная
скорость распространения отличается от скорости в свободном пространстве
на незначительную величину, но затухание для столь высокой частоты и для
данного диаметра провода, с точки зрения применения для линий связи,
относительно велико.
Если радиус а очень мал, то величина w^ak^ может также оказаться
малой, несмотря на большую проводимость. Для иллюстрации этого Зоммер-
фельд разобрал случай платиновой проволоки, проводимость которой равна */g
проводимости меди, а радиус a = 2\i = 2- 10-^ метра и v=3- 10^ циклов
в сек. Для и получаем и^{1 -\- iH,19, и, следовательно, бес(?елевы функции
Jq (и) и Jj (и) не могут быть заменены их асимптотическими выражениями.
В рассматриваемом случае значение и настолько мало, что мы можем
приближённо положить Jq(u) == 1, Jj (к) = --- и после этого поступать в
соответствии с приведённым выше методом. Тогда мы получим
/г ^0,08 +0,061/.
1) См. Франк-Мизес, /ос. sU., стр. 926.
30 Зак. 593. Теория электромагнетизма.
466 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Фазовая скорость оказывается равной только 76% от скорости в пустом
пространстве, а затухание настолько большим, что амплитуда уменьшается
в i/g раз на расстоянии г == 16 см.
До сих пор мы рассматривали только один корень уравнения A6),
корень, который в случае большой проводимости даёт /г^^^ и приводит
к волне, которую мы назовём основной волной. Имеются, однако, и другие
корни, для которых v = aY kl — h^ очень велико. С помощью
асимптотических выражений B2), стр. 317, для функций Ганке ля мы можем теперь
аппроксимировать A6) уравнением
^^ — /'"^-J Hi.. B8)
М kl и Ji (м) ^ ^
Если левая часть B8) очень велика, то корни его в первом приближении
даются уравнением J^(u)==0. Но корни /Дм) лежат на действительной
оси и-плоскости. Следовательно, мнимая часть k^ должна равняться мнимой
части k^. Это означает, что в случае металлических проводников коэффициент
затухания р в к = а-\-ф будет порядка 2 • 10-^ V^vajXi^, и, следовательно,
дополнительные волны, соответствующие другим корням уравнения (l6),
немедленно затухают.
Корни уравнения A7), которые дают аксиально симметричные виды
поперечно-электрических волн, могут быть исследованы тем же способом.
Однако, поскольку не суш.ествует «магнитной проводимости», здесь нет
и основной волны, характеризующейся малым затуханием. Все аксиально-
симметричные поперечно-электрические волны в сплошном проводнике
затухают слишком быстро, чтобы их можно было заметить.
Мы видели, что в асимметричном случае поле является линейной
комбинацией поперечно-магнитных и поперечно-электрических видов волн.
Существование основной волны предполагает, что /г—^2i> '^<^^- Так как теперь
п отлично от нуля, то получаются чрезвычайно большие значения правой части
условия (9), которое может быть выполнено только при почти бесконечной
проводимости Oj. Оказывается, что даже при проводимости меди мнимая часть
постоянной распространения h всё ещё очень велика^ и затухание таково, что
исключает возможность существования асимметричных волн на сколько-нибудь
заметном расстоянии от источника.
Результаты нашего анализа могут быть подытожены следующим образом.
Имеется бесконечное количество видов волн, могущих распространяться вдоль
сплошного проводящего цилиндра. Амплитудами этих волн являются
коэффициенты а„ и Ьп, значения которых определяются первичным возбуждением,
т. е. свойствами источника. Однако из всех этих видов волн только один
основной вид, соответствующий симметричной поперечно-магнитной волне,
обладает сравнительно малым затуханием. Все остальные виды волн затухают
в пределах одного-двух сантиметров от источника даже для столь малых
частот, как 60 циклов в сек^). В следующем разделе мы увидим, что поле
основной волны стремится внутри проводника сконцентрироваться в тонком слое
у его поверхности. При высоких частотах середина проводника почти
свободна от поля и тока, чему соответствует незначительный переход энергии
в тепло. С другой стороны, поле и распределение тока в цилиндре,
соответствующие дополнительным волнам, почти однородны. Скин-эффект является
в этом случае как бы «внешним», а переход энергии в тепло соответственно
значительным. По мере уменьшения проводимости цилиндра затухание основ-
1) Стандартная частота, принятая для переменного тока в США. Прим. ред.
ЕНа
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА [9.17] 467
НОЙ волны возрастает, в то время как затухание дополнительных волн
уменьшается, пока, наконец, в пределе, в случае идеального диэлектрического
цилиндра, основная волна не исчезает совсем, а дополнительные волны не
начинают распространяться без затухания.
9. 17. Дальнейшее рассмотрение основной волны. Мы видели, что в слу^
чае сплошного проводящего цилиндра имеет существенное значение только
основная волна. Следующая наша задача состоит в том, чтобы привести
полученные результаты к виду, наиболее удобному для численного
рассмотрения. Прежде всего мы выразим коэффициенты а^ и а^ через полный ток
проводимости в, цилиндре, так как обычно он является наиболее легко
измеримой величиной. Вектор плотности тока в любой точке внутри цилиндра
параллелен его оси и равен /g=Oj£^; полный ток будет, следовательно,
а 2к а
1= j j J^rdr db = 2rMoOi f Jq {\r) r dr е»лг-г>> , B9)
0 0 0
Согласно B6), стр. 317,
a
J г ""a
0 Ч 0 4
C0)
и таким образом
27i:aaj
Аналогично, согласно A4),
/=^рй^Л(>ча)е''л^""*"'* - C1)
Амплитуда полного тока определяется из выражения
1 = 1^е^ьг-ыг^ C2)
и следовательно,
< = ^ ^^^, , . C3)
al = '-^f;^, . C4)
Продольный и поперечный импедансы были определены на стр. 313 соот"
ношениями
Ej. = Z^Hf), £g = — Z^H^. C5)
Следовательно, из уравнения C0), стр. 318, или непосредственно из
уравнений A) — D) раздела 9.15 мы получаем
Заметим мимоходом, что, согласно A6),
Z*==Z« при г=а. C8)
Непрерывность тангенциальных компонент векторов Е и Н ко: границе
обеспечивается равенством радиальных импедансов при г = а.
Поверхностный импеданс Zg определяется как отношение продольной
э. д. с, измеренной на поверхности проводника, к полному току:
Eg = ZJ при г = а, C9)
30*
468 гл. IX. КРАЕВЫЕ ЗАДАЧИ
откуда, согласно A) и C3),
Z^ = _1l_:^^. D0)
Наконец, подставляя выражения для а* и а!| в B) и D), мы получаем
т=-^
27ta<o(jijai Ji (XjO!)'
Из ЭТИХ соотношений и соответствующих формул для импедансов можно
определить компоненты поля в любой точке.
Для всех металлических проводников справедливо соотношение о^/е^ш^^Ь
Поэтому во всех практических случаях можно принять, что
Ui|:>A^ —Л, Л, —i%i. .. D2)
Для продольных импедансов получаем таким образом
Zla^ — ^!:L^^, 2|^тЛ5. ' D3)
Вне цилиндра продольный импеданс стремится к внутреннему импедансу
окружающего диэлектрика. Внутри цилиндра он чисто мнимый; следовательно,
средний поток энергии вдоль оси внутри цилиндра равен нулю.
Действительно,
Si=- ^Ке(йнГ) == -^ ЩЧ\Щ?) -О- • D4)
Перенос энергии вдоль цилиндра происходит исключительно во внешнем
диэлектрике. Энергия внутри цилиндра колеблется вдоль оси и восполняет
потери 1 а джоулево тепло.
Поперечный импеданс во внутренних точках приводится к виду
yi^nf'
Если г = l/coiXjOj -> со, то, как и ранее в B2), отношение /о(^1'')/Л (^i^) ~*—^>
что даёт в пределе
у- in
^^■ш/'Л^е *", D6)
т. е. точно то же выражение, которое мы получили в формуле D0) на
стр. 459 для случая волны, распространяющейся вдоль бесконечной
плоскости. Заключение, которое можно сделать из полученного результата,
имеет большое практическое значение. Если под г мы будем подразумевать
радиус кривизны некоторой хорошо проводящей поверхности, то вполне
правдоподобным является предположение, что при г I/cojajOj ^^ 1 можно
приближённо принять
/
гп
*^1 ^~Т
,^ е *Я2, D7)
где fg и Яд — компоненты векторов поля, Касательные к поверхности
и ортогональные друг к другу. В том же приближении можно принять, что
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА |9.17)
469
напряжённость магнитного поля на поверхности металлического проводника
НИЧТОЖНО мало отличается от напряжённости в той же точке при
бесконечной проводимости. Следовательно, задача, связанная с металлическими
проводниками, может быть в первом
приближении решена в предпо- S
ложении идеальной проводимости.
Приближённое значение для со-
ответствующей величины
тангенциальной компоненты вектора Е
находится затем из D7), после 3
чего можно определить потери д
в системе, подсчитав поток энер- р
гии, направленный в проводник,
и полагая, что эта энергия
полностью переходит в тепло. При- /
мер подобного вычисления будет \ *
дан ниже ^). р
На рис. 103 нанесены
величина и фазовый угол отношения
я
2
U}
г
¥ V
■
i
!
'
ki
^
6 8
X
W
12
фб'
D8)
Рис. 103. График функции
h{x^fi)
в функции от д: = г |Ла)}х^о^. Значения взяты из таблицы Янке и Эмде 2).
Мы видим, что даже при д: = 3 отклонение от асимптотического значения—i
очень мало. В системе MKS
/(ojxioi = 2,81 • 10-3 /vxi^oi,
•l/~^^=2,81.10-8l/"-^!b«».
D9>
и проводимость металлов порядка 10' ом-^ метр-*. Радиус провода должен
быть выражен также в метрах. Следозательно, при не слишком большом
радиусе и при малых частотах х может быть намного меньше единицы.
Рассмотрим, например, случай медного провода №12 с радиусом г == 1,026 мм.
Тогда л: = 0,022 |Л^ При v = 60 циклов в сек «с = 0,17. При v=10S герц
л: =6,9, и из кривых рис. 103 видно, что для этой и для всех более
высоких частот поле вблизи поверхности провода почти такое же, как и вблизи
бесконечной плоскости.
С помощью B1) выражение C7) для внешнего радиального импеданса
приводит к виду
^'—/?^'"-^+-(^0-|)^'»:^
E0>
1) Изложенные здесь соображения были развиты в работах советских . авторов
ещё в 1940 г.; см. СМ. Р ы т о в, К расчёту поглощения электромагнитных волк
в трубах, ЖЭТФ 10, 176, 1940 и Расчёт скин-эффекта" методом возмущений, ЖЭТФ
10, 1Ь0, 1940, Как указал М. А. Л е о н т о в и ч, из этой последней работы вполне
строго следует условие D ) для тангенциальных компонент Е и Н на не слишком
искривлённой поверхности хорошего проводника. В дальнейшем это условие
Леонтовича было применено в ряде работ (см. Я. Л. Альперт, ЖТФ 10, 1358,
1940; С. М. Рыто в, ДАН 51, 107, 1946, а также примечание редактора на стр. 502»
п. 4). Прим. ред.
2) Tables of Fanctions, 2-е изд. cтp.^316—317, 1933. ,
470
гл. IX. КРАЕВЫЕ ЗАДАЧИ
Магнитное поле внутри проводника даётся приближенным выражением
HI
^^^ /l(ay wfxiaiO '
E1)
в то время как вне проводника при не слишком большом г
/
27СГ-
E2)
Можно представить себе структуру поля более наглядно, заметив, что
l^i|<C|4|' И||»Кг|' И' соответственно, |f^|<C|£j| и|£«|:>|Я||.
Внутри цилиндра линии вектора Е идут почти параллельно его оси,
отставая от волн; вне проводника
они выходят почти радиально,
с очень небольшим наклоном
вперёд. Заряды на поверхности
проводника распространяются
подобно волне в направлении
его оси. Таким образом мы
имеем попеременно пучности-
положительных и
отрицательных зарядов, движущиеся
вместе с полем. Линии вектора Е
выходят из пучностей
положительных зарядов и
кончаются в соседних пучностях
отрицательных з.арядов. Небольшая часть линий начинается или кончается
в бесконечности. Примерная картина поля показана на рис. 104.
Распределение тока внутри цилиндра даётся величиной
Диэлентри.н
Псавоанан
Рис. 104. Структура поля вблизи поверхности,
разделяющей проводник и диэлектрик.
V:
Jo (kia)
Je {^D yr) '
E3)
которая представляет собой отношение плотности тока в какой-либо
внутренней точке г к плотности т'ока на поверхности проводника. Здесь, как
и раньше, х = ^V^M^^ ^ Xq — аУ^^^о^. Если д:<С1. то U может быть
подсчитано с помощью представления бесселевых функций в виде степенных
рядов. При AT^^l можно использовать асимптотические выражения. Таблицы
значений этого отношения даны у Янке и Эмде и приведены также во
многих справочниках и учебниках по электротехнике. На рис. 105 показано
отношение плотностей тока в функции от радиуса для различных значений
параметра Xq. При достаточно больших значениях Xq п х асимптотическое
выражение для U будет
D-1) (о-г)
а —
,Ai
E4)
где 8 = ■1Л2/@{х^о^ — глубина проникновения, определенная выше, на стр. 444.
Абсолютная величина отношения плотностей тока будет, следовательно,
и\^/^е
а— г
E5)
Плотность тока экспоненциально уменьшается от поверхности внутрь про-
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА 19.18]
471
w\
водника совершенно так же в данном приближении, как и поле вблизи
бесконечного плоского проводника. Если а^Ь, то на оси цилиндра токов
практически нет; если а<8, то один слой
токов налагается на другой. Для проводник
кта с поперечным сечением любой формы
мы можем считать, что распределены»
токов и поле вблизи его поверхности
лишь незначительно отличаются от
токов и поля вблизи поверхности бесконечной
плоскости, при условии, что радиус
кривизны сечения во много раз больше
глубины проникновения.
В заключение мы выведем
классическое выражение для сопротивления цилиндра
переменному току. Согласно C9),
поверхностный импеданс Zg равен отношению
продольной компоненты напряжённости
электрического поля в точке на поверхности
проводника к полному току. Для единицы
длины линии мы имеем уравнение
Я, = /?/ + L ^^ - (/? — /coL) /, E6)
W
0,8
0.6
0,4
0,2
О
ЗСс
-~o
-~U
1 i
Хо=2 1 i 1 t J
!
Xq
--3
Xo^5
.
Xo
:^b
■^^
—i—"^^
1
L X
i
\^
i
I
1
„-jQ -
/^ i /
0 0,2
0.Ч 0,6 0,8
a
W
Рис. 105. Распределение тока
в круговом цилиндре
и =
X = г
MxYi)
где R — активное сопротивление переменному току, а L
индукция единицы длины. Таким образом
Z^ = R~mL
2itaCTi Jj (Xiu )
внутренняя само-
E7)
и, следовательно,
R — ЫЬ
щ 7о (л-рУТГ) ^ -J-
2 //(л'оУГ)
E8)
где опять Xq^= aY^'^г^и ^ Ro=l['r:a^'^i—сопротивление единицы длины
постоянному току. Величину и фазу отношения бесселевых функций можно
взять непосредственно из рис. 103. Если л:о<^1, то мы получаем
R — mL
или
/?(,— ~Г12\.2У' Rq — 2\2 ) '
E9)
F0)
Если, как это имеет место при сильно выраженном скин-эффекте, х^^\
то асимптотическое разложение выражения E8) приводит к формуле Релея
R — ш1 1 — i л"о 1
A - О
а
F 1)
/?о 2 V2" 2
9,18. Волны в полых трубах. Общая теория, развитая в разделе 9.15,
получила интересное приложение к распространению волн вдоль
диэлектрических цилиндров, ограниченных извне средой с иной диэлектрической
проницаемостью или же покрытых металлической оболочкой. Распространение
электромагнитных волн по трубам впервые было подробно рассмотрено
Релеем^), теория же распространения вдоль диэлектрического провода была
рассмотрена на несколько лет позже Гондросом и Дебаем^) и подтверждена
1) R ау lei g h. Phil. Mag. 43, 125, 1897.
2) H о n d r о s and D e b у e, Aim. Physik 32, 465, 1910.
472 гл. IX. КРАЕВЫЕ ЗАДАЧИ
экспериментально Шривером*), До недавнего времени эти работы не имели
большого практического значения из-за трудностей генерирования колебаний
достаточно высокой частоты. Прогресс в развитии коротковолновых
генераторов полностью устранил эту трудность, и возможности подобного
способа направленной передачи волн были в 1936 г. независимо исследованы
сотрудниками лаборатории Белла2) и Барроу^). С тех пор появились
Многочисленные исследойания по этому вопросу.
При очень высоких частотах потери становятся заметными даже в лучших
промышленных диэлектриках; поэтому вполне очевидны преимущества таких
направляющих волны устройств, в которых диэлектрические опоры полностью
устранены из поля. Этого можно достигнуть, направив волны по полому
цилиндру с хорошо проводящими стенками. Другим преимуществом подобных'
устройств является отсутствие полей рассеяния вне металлического цилиндра.
При тех крайне высоких частотах, применение которых оказывается
необходимым, даже очень тонкие по-,!рытия ведут себя как идеальный экран. Мы
можем считать поэтому, что полость цилиндра является идеальным
диэлектриком, который окружён бесконечной проводящей средой. Возможные
собственные виды волн даются в общем случае формулой (9). Если
проводимость внешнего цилиндра конечна, то всегда будет иметь место некоторая
связь между поперечно-магнитными и поперечно-электрическими видами волн,
за исключением аксиально-симметричного случая- Однако практически
проводимость металлов настолько велика, что этим эффектом можно пренебречь
и рассматривать каждый вид волн как принадлежащий к какому-либо одному
из этих типов. Волна, которая является по преимуществу
поперечно-магнитной, обычно называется теперь £-волной (имеется продольная компонента
вектора Е), а волна, по преимуществу поперечно-электрическая, называется
//-волной (имеется продольная компонента вектора Н).
Прежде всего мы рассмотрим случай без рассеяния энергии, при котором,
следовательно, проводимость внешней среды бесконечна. Возможные виды Е-
и //-волн даются корнями уравнения A3), и мы сразу же видим
фундаментальное отличие от рассмотренного ранее случая сплошного металлического
цилиндра. Выше мы отмечали, что на главных ветвях функций Ганкеля t^^ip)
и tt]!{v) нулей нет и что поэтому их отношение равно нулю только при
■о = 0. В результате мы получали основную волну, для которой hc^k^.
В случае конечной проводимости проводника дополнительные волны, которые
могли быть возбуждены, тут же исчезли вследствие, большого их затухания.
Теперь же положение как раз обратное. Для действительных значений п
функции Jniu) и /п{и) имеют бесконечный ряд нулей на действительной оси,
причём можно показать, что нули Jn(") " Лг+1(м) чередуются (разделяют
друг друга)*). Следовательно, /„(«) и /«(м) не могут равняться нулю
одновременно, и виды £'-волн определяются уравнением
/„(«) = О, F2)
тогда как виды Я-волн даются корнями уравнения
J^(tt)=0, F3)
1) Zahn, Ann. Physik, 49, 907 1916; Schriever, Ann. Physik, 63, 645, 1920.
2) S 0 u t h w 0 r t h, Bell System Tech. J. 15, 284, 1936; С a r s о n, M e a d and
Schelkunoff, ibid., p. 310.
3) Barrow, Proc. Inst.. Radio Engrs. 24, 1928. 1936.
4) Wats on. Theory of Bessel Functions, гл. XV, Cambridge University Press, 1922.
P. O. Кузьмин, Бесселевы функции. ОНТИ, 1935, гл. Ш § 7. Прим. ред.)
/■
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА [9.181 47S
где и = \а = а'Х/'Щ—Л^. Далее, и = 0 не является корнем Jq(м) = 0. Это
значение и удовлетворяет 7„ (м) = О при «> О, но в этом случае исчезает
само поле, как это видно из уравнений A), стр. 4Q0. Следовательно, в полых
трубах основной волны нет. Для того,чтобы подобные проводники были
практически пригодны для целей связи, необходимо показать, что затухание
тех видов волн, которые допускаются соотношениями F2) и F3) и
соответствуют дополнительным волнам предыдущего случая, относительно невелико.
Для каждого числа п уравнение F2) имеет бесчисленное количество
корней, которые мы будем обозначать через м„^. Постоянная
распространения hnmt соответствующая данному виду £-волны, будет, следовательно,
hnm=]/~k!-[^J- F4)
Если k^ действительно и больше чем Unml^^ то /г„^ также действительно,.
и волна распространяется без затухания. Ъс л и k^ < ^^-, то A„^ — чисто
мнимое, и затухание настолько велико, что данный вид волны сразу гасится.
В этом смысле труба ведёт себя как высоко селективный волновой фильтр.
Граница пропускания соответствует критической частоте v„^. Для диэлекг
трика k^ = aY^x H-iJ следовательно
v„^=-r^r=. F5>
Это же соотношение может быть выражено и через длину критической
волны А„^:
Km = -;;— . F6).
^^пт
где под А„да подразумевается длина волны при частоте v„^, распространяющейся,
в неограниченной среде k^. Если частота меньше v„^ или же длина
свободной волны больше Х^т^ то соответствующий вид волны гасится. Первые
несколько корней F2) равны
«01 = 2,405, «02=5,520, «03= 8,654, |
«11 = 3,832, «^2= 7,016. , > F7>
Наибольшая свободная длина критической волны соответствует виду «qi
и равна
Ло1= 2,61а. F8)
Этот предел, грубо говоря, равен диаметру трубы, так что волноводы в виде
полых труб могут быть практически использованы только в-,сантиметровом
диапазоне волн.
Возможные виды поперечно-электрических или //-волн определяются тем
же путём. Обозначая корни F3) через [«„„»,.мы получаем
I „ „ /
«01=3,832, «02 = 7,016, ..., 1
/ / \ F9)
«11=1,84, «12 = 5,33, ... j
Формулы для постоянной распространения и для критической частоты
тождественны с F4) и F5). Оказывается, что из всех возможных видов //-волн
//ji имеет наибольшую критическую длину свободной волны; однака
на практике это преимущество перекрывается тем обстоятельством, что»
474
гл. IX. КРАЕВЫЕ ЗАДАЧИ
.она испытывает также и более сильное затухание, чем какие-либо другие
виды волн.
Характер распространения вблизи критической частоты можно выяснить
с помощью графиков фазовой и групповой скоростей. Напишем постоянную
,распространения какого-либо допустимого вида волн следующим образом:
0,v»
3,0
2,5
2,0
/Д
W
0,5
0
—"■"""'jiS'e-at^^j^^^^^
(
i
i
i
1
1
—4- —
hnш=K^^-(^■^У^ G0)
Фазовая скорость будет тогда
•v.
со
Va
пт
h.
пт
i/"^-C-^'"T
G1)
где 'Г>1 = l/V^ej[Xj—фазовая скорость в
неограниченной изотроцной среде с постоянной
распространения ^j, а групповая скорость,
согласно A7), стр. 295 будет
V.
пт
= -ah" -«/l-C^T • <^'>
rfco
О Q.2 0,4 0,6 0,8 Ifi 1^
Фазовая и групповая скорости связаны
соотношением
' пт
V
^ nw^nm, "^l*
G3)
Зависимость фазовой и групповой скоростей
Рис. 106. Фазовая и групповая око- от частоты распространяющихся волн пока-
рости в полой трубе, v=\IY4Vai зана на рис. 106. Мы видим, что фазовая
скорость в трубе всегда больше, нежели
в такой же безграничной среде. Она растёт с уменьшением частоты и
вблизи критической частоты стремится к бесконечности. Групповая скорость
падает с уменьшением частоГы и при v^v^^ равна нулю. Мы имеем, таким
образом, нормальную дисперсию, которая вблизи критической частоты v„,„
становится очень большой.
Компоненты поля внутри трубы могут быть выписаны непосредственно
из уравнений A) и B), стр. 460—461. В силу G0) и F5) мы имеем
Для всякого вида волн типа Е поле будет
и
пт
а
G4)
^г-'^пш\[[^- 1 ^п(-f «п» )eos «6
Еа =±ia
cos
sin
«6 \ е
'Кт^-^'"*
G5)
^2 ^пт,п\ ^ ^^'пт ]
COS
sin
«6
ej nv
a
jj^u..,.)
COS
rl ^nm '"^nm ^ /sill
«6
' H-l ^nm ^"
JKn^-^^^*
G6)
\sin
)■
COS
nb
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА 19.181
475
Для всякого вида волн типа Н мы получим
/Ту = =1- 10пт 1 / 7 7— -'и I — "и
COS г,
пт I • ""
Sin
—~г—Jn I — Unm 1 „„„ f^"
/W-*-*^ ^77)
Sin
COS
«e
H. = :±zib
i/.(^«L)'°>e }
'И
■•^г —Рпт^п ("^ ^K«t
sm
COS
йб
/"«.«''-«'-^ G8)
Произвольные амплитуды йпт и bnm определяются условиями возбу-
:ждения. Существуют теоремы, аналогичные теоремам о разложениях Фурье,
согласно которым функцию /(rja) можно разложить по бесселевым функ-
'циям. Предположим, что f(^t)—произвольная функция, определённая в интер-
1 j_
вале O^^^l и такая, что существует интеграл | \t^f{t)\dt. Обозначим
о
1
-F—f—^ f ^f СО Jn itttnm) dt G9)
a
пт,
Пусть x = rja—какая-либо точка интервала (aTj лгд), где 0<a;j<.V2<1,
причём полная вариация функции f(t) в интервале (aTj aTq) ограничена.
Тогда ряд Фурье-Бесселя
2 ^пт-^п (Xt^mn) = j[f (^ -Г 0) + /(Х — 0)]
(80)
т=1
будет сходиться и сумма его будет равна правой части (80) ^). Из
возбуждённых видов волн распространяться будут только те, у которых
постоянные распространения hn,n действительны.
Заметим мимоходом, что при критической частоте v = v„„j поток
энергии имеет место только в поперечной плоскости; поток, параллельный оси
цилиндра, отсутствует. Продольный импеданс для £-волн равен
^^=t=/'-(^T/"e7
И стремится к нулю при v
Для,//-волн имеем
ПТП'
Z =
1
■ш/ J (^пт
(81)
(82)
^ )
Подсчитаем теперь полный поток энергии в направлении оси трубы»
Среднее по времени значение этого потока равно
о О
») Watson, loc. clL, гл. XVIII.
476 гл. IX. КРАЕВЫЕ ЗАДАЧИ
где
5, = ^Re (Е,И1 — Е,И1). (84>
Для £-волн
После интегрирования множители sin^/гб и соз^пв дают коэффициент ir.
Пусть г = ах. Тогда, в силу рекуррентных формул B4) и B5), стр. 317,
и условия У„^ (Чпт) = О мы получаем
/ {[•^» а«»»)]'+{^'ы^""- )j\""--
= Y J [4-1 (хи„^) 4- 4+1 (^«nm)] xdx= y4+i (tt«w) (86>
0
И, следовательно.
W. = I I«,» P«^/^ |Al - (^)' (;^) 4+. («,„). (87>
Для //-волн аналогично
Пользуясь теми же рекуррентными формулами и соотношением У (м^,^)=Оу
получаем после интегрирования для полного потока энергии
W,
=т1*».»|^«^^/-(%У@['-(^)>»(«^»)- т
Остаётся вопрос о рассеянии энергии. Если проводимость стенок конечна^
то постоянные распространения h„^ имеют небольшую мнимую часть,
которая обусловливает затухание поля по мере его перемещения вдоль оси трубы.
Эти комплексные постоянные распространения должны быть определены,
теперь из уравнения (9). Вычисление до некоторой степени упрощается те»
обстоятельством, что, благодаря большой проводимости внешнего
металлического цилиндра, функции Ганкеля могут быть заменены их
асимптотическими представлениями. Корни уравнения (9) будут поэтому лишь на
небольшую величину отличаться от значений, получаемых из F2) и F3) для
случая бесконечной проводимости. Их без труда можно определить, разлагая,
функции Jn {и) и /„ (w) вблизи точек и^т и u„tH в ряды.
Однако более поучительным будет подсчёт затухания с помощью
приближённого метода, описанного на стр. 469. Если проводимость
бесконечна, то тангенциальные компоненты Е^ и fe #равны нулю при г==а;
в случае металлического цилиндра глубина скин-слоя 8 будет, очевидно»
РАСПРОСТРАНЕНИЕ ВДОЛЬ КРУГЛОГО ЦИЛИНДРА (9.181
477
намного меньше радиуса а. Тогда при г^а с большой точностью можно
принять
(В
"Г
(90)
Таким образом мы можем подсчитать радиальный поток энергии,
направленный в металл; поскольку этот поток идёт за счёт потока внутри трубы,
мы тем самым можем найти и затухание. Напишем постоянную распростра-
з{ения в виде
"■пт ^^^ ^пт "Т ^Vnm' \"^ )
Средний радиальный поток энергии на единицу длины трубы на поверхноста
цилиндра равен
2я
W,
у= I Sj.adb,
TAt
Для £-волы
Sr = ~4^{E,H,~EJtil).
«^,=-|-U„«J^-j^|/"ij(-^T4+t(...)^
-2р,
ит*
SL ДЛЯ поперечно-электрических или //-волн
(92)
(93)
(94)
W„
Л{ипш)е-^^пш'. (95)
В том же приближении поток энергии вдоль оси попрежнему даётся
выражениями (87) и (89), если их умножить на затухающий коэффициент
8 виде ехр (— 2Pjj^2r) или ехр( — 2^пт^)- Энергия, рассеивающаяся на
единицы длины, равна
dW^
dz
-2p«mV^.= ^r
Следовательно, коэффициент затухания для ^-волн будет
Р«- 2 ^^- а У
Si для //-волн
pL^-y
/•-(%J
(—у
(96)
(97)
(%)
+
(^8)
Результаты эти справедливы только в том случае, когда v больше
критической частоты.
Если а или V стремятся к бесконечности, то коэффициент затухания
для £-волн^ стремится к пределу Pq:
^«Ч/
Hl^2
(99)
478
гл. IX. КРАЕВЫЕ ЗАДАЧИ
который растёт обычным образом как квадратный корень из частоты. На
рис. 107 нанесены отношения- коэффищ1ентов затухания ^„ml^Q и ^nm/Po
в функции от Vqi/v для двух первых видов Е и //-волн. Vqi — критическая
частота основной волны Eq^. Вблизи критических частот затухание растёт
очень быстро. Наиболее интересным является поведение кривой
коэффициента затухания волны Hq^, который уменьшается с увеличением частоты
и при V -> со стремится к нулю. Даль-
нейшее исследование показывает, однако,
что подобное аномальное поведение не
является общим для всех полых труб, а
присуще лишь определённым
симметричным поперечным сечениям, как, например,
круг или квадрат. Стабильность первых
тонов по отношению к малым изменениям
поперечного сечения была рассмотрена
Бриллюэном ^) и Чу 2) в связи с
распространением волн в полых трубах
эллиптического и прямоугольного поперечного
сечения.
КОАКСИАЛЬНЫЕ ЛИНИИ
9. 19. Постоянная распространеняя.
Наиболее серьёзным недостатком полых
О 02 0^ 0,6 0,8 10 12 волноводов является отсутствие основного
Уо1 вида колебаний и соответствующее огра-
"v" ничение длины волны, которая должна
Рис. 107. Отношение коэффициентов быть порядка диаметра трубы или мень-
затухания Ё-волн и//-волн; Vqi — кри- ше. Эту трудность можно преодолеть
тическая частота для волны £oi. введением осевого проводника. В этом
случае основной вид колебания существует
и делает возможным распространение волн всех частот в промежутке между
двумя концентрическими цилиндрами. Для коаксиальных линий сохраняется
основное достоинство полого волновода, заключающееся в том, что поле
ограничено только внутренней его областью и тем самым исключено
взаимодействие с внешними высокочастотными контурами. С другой стороны,
потери подобного устройства выше из-за скин-эффекта в центральном
проводнике и несовершенной изоляции в тех местах, где он закреплён.
На практике толщина внешнего цилиндра, конечно, не бесконечна. При
низких частотах глубина проникновения поля может превышать толщину, и поле
в этом случае будет проникать во внешнее пространство. Задача устранения
«перекрёстных помех» между телефонными кабелями и помех,
индуцированных в линиях связи экранированными силовыми кабелями, является весьма
серьёзной. Мы не даём здесь, однако, исчерпывающего рассмотрения
подобных проблем, поскольку нашей целью является лишь иллюстрация
применений электромагнитной теории. Коаксиальные линии играют в настоящее время
важную роль в радио и телефонной связи при частотах выше 100 кц1сек\ в
этом разделе рассмотрение и будет ограничено частотами такого порядка.
Мы предполагаем, таким образом, что глубина скин-слоя во много раа
меньше толщины внешнего проводящего цилиндра, которую мы можем
1) BriUouin, Electrical Communication^ 16, 359, 1938.
2) Ghu, /. Applied Phys. 9, 583,1938.См. также Ghu and Barrow, Proc. Inst
Radio Engrs. 26, 1520, 1938.
fi
КОАКСИАЛЬНЫЕ ЛИНИИ [9.19]
479
поэтому принять бесконечной. На рис. 108 проводящие концентричные
цилиндры A) и C) разделены диэлектриком B), которому, однако, можно
в случае надобности приписать небольшую проводимость. Внутренний и
внешний радиусы равны соответственно а^ и а^. Нам нужно рассмотреть
только симметричные поперечно-магнитные виды волн (Е-волны). Аси1имет-
ричные виды хотя и могут быть возбуждены, но если длина их волны будет
того же порядка, что и разность а^ — а-^^ то их постоянная расирострене-
ния будет чисто мнимой и они тотчас же будут затухать. Компоненты поля
можно взять непосредственно из формул C6)" и C7), стр. 318, положив
«==0. Пусть / будет полный ток в центральном проводнике, а 1^ — его-
амплитуда
Тогда, точно так же, как и в разделе 9.17, для
центрального проводника, при г<С,а^, мы имеем
rf^ = -
ik\l
Л ('^lO
Г2)
Продольный и радиальный импедансы определяются
соотношениями
Е^ = ^г^е, -Eg = — ZJri^. C)
Для области A), как и в разделе 9.17, мы имеем
7A) ^V'-ih- у ^у-Фх Joih'')
ft! '
D)
Рис. 108. Поперечное
сечение коаксиальной
линии.
ikj Jj (л^ г)
Для того чтобы построить решение, соответствующее промежуточной'
области B), которое можно было бы согласовать с условиями как на
внутренней, так и на внешней границе, необходимо использовать две
независимые функции Бесселя. Какие именно — безразлично, так как
каждое решение может быть представлено в виде линейной комбинации двух
любых независимых решений. Если радиусы а^ и Oq очень велики, то об-
ластьB) фактически ограничена двумя параллельньщи плоскими
поверхностями. При этих условиях для построения решения мы, конечно, должны
были бы применить простые гармонические функции — косинус и синус. На^
помним теперь (стр. 317), что если аргумент р становится очень большим, го>
Ур«^о(р)~*У ^^°^\Р 4)' ^ ^° время как функция второго рода?
WNq (р) -> у — sin f р — ~j. Следовательно, для области й^ < г^ <
а(
мы должны написать
ihl
1)[Х2Л2
{AJ, {■k^r)-{-BN, {\^г)\ е^ь^-ш^
E)
где А и В — пока неопределённые коэффициенты. Компоненты вектора Е(^>
получаются затем из формул C) и из соотношений
,B) @[Х2^
zr'=
а >
_B)___ Ш[Х^Х2 AJq (Xgr) -f- B^lQ (Xgr)
Ш1 AJ^{\r) + BN^CK^r)
m
Bo внешнем цилиндре требуемое поведение поля на бесконечности
'Получится, если мы возьмём,, как и в разделе 9.15 функции Ганкеля..
480
гл. IX. КРАЕВЫЕ ЗАДАЧИ
Таким образом, при г"^ а^
Zf =
^•^M'^(V)
17)
(8)
•^8 V'
Коэффициенты Аф и С определяются из граничных условий. Как при
r==aj, так и при г = а2 должны быть непрерывны z — компоненты
вектора Ей 6—компоненты вектора Н. Эти два условия равносильны
требованию непрерывности радиальных импедансов. Следовательно,
Z^? = zf при r = fl!i, \
при г = flig j
Z?
7C)
(9)
или
^1^
kl AJ^Ck.,ai)-{-BNi(k^a^)
f^34^0^(V2) f^2^2 ^*^0(V2) + ^^^0(M2)
Ч Wf4V2) *1 ^JJXafl.j + ^ATilXaa^)
^ЛО)
Эти два однородных относительно А и В уравнения дают нам лишь их
•отношение, но не независимые значения. Из A0) следует
А
В
M)(^2«l)
[XjXj*2 ^(^l^l)
i^ihK Jiih^i)
Niil^i)
Jq (Ml)
Ji (^2^1)
Л'о(>^2^2) , ^j Ы1)/1 Г ^1 ^^'2«S)
1^Л^з^1 (^3^2)
Jo (M2) —72 тйттт;—г ''^ ^''2*^2)
(П)
Корнями детерминанта этих уравнений будут характеристические значения
Арда(т==1, 2, 3,...), которые и определяют допустимые симметричные
виды волн.
9. 20. Бесконечная проводимость. Выражение (И) настолько сложно,
что для определения корней приходится прибегать к приближённым
методам. Рассмотрим сначала относительно простой случай, когда внешний и
внутренний цилиндры йвляются идеально проводящими. Напомним, что
,Xi = k] — Ль а Хз = kl—h^. Мнимая ч^сть h должна оставаться конечной, так
как в противном случае распространения волны вообще^ не будет.
Следовательно, когда проводимость стремится к бесконечности, Х^-^ k^, Хд-^^з,
в то же время абсолютные значения k^ и k^ стремятся к бесконечности и
-(И) принимает вид
А ^ ЛГоГХг^!) ^ А^оСХгДг) /^2)
В Л (Ml) JoC^vf^z)
Если Xg очень мало, то yo(^2^i)^^^(^^2)^=^li ^^^ функций же Nq
мы воспользуемся приближёнными выражениями A2), стр. 316. Тогда ста-
.(Новится очевидным, что главный корень A2) соответствует п = 0 или
/г = ^^2. A3)
КОАКСИАЛЬНЫЕ ЛИНИИ 19.20] 481
Таким образом, в этом случае имеется основная волна, постоянная
распространения которой совпадает с постоянной распространения в той
среде, которая ограничена двумя бесконечно проводящими цилиндрами.
Кроме того, имеются также и дополнительные волны. Если Лд очень
велико, то справедливы асимптотические представления A8) и A9), стр. 317,
и уравнение A2) принимает вид
sinXoC^r^ — а^)с::=:0. A4)
Корни этого уравнения равны
K,.^/kl-{,^f («=•!, 2,3,...). A5)
Если ^2 действительно и больше, чем —--^-—, то /г^^^^ действительно, и
соответствующая волна распространяется без затухания. Но если k^ меньше
. , то /года является чисто мнимым, и затухание настолько велико, нто
волны сразу же гасятся. Все эти результаты могут быть сопоставимы
с результатами, полученными для полых труб в разделе 9.18. Критические
«частоты получаются равными
2г. («2 — «l) у ^^[>'2
а критические длины волн равны
^=» = ^^2^- A7)
В практических линиях связи расстояние uq—а^ обычно не больше
нескольких сантиметров, и дополнительные волны совершенно исключены. Те же
рассуждения применимы и к асимметричным видам волн, так что далее мы
займёмся только основной волной.
2
При Хо^-^-О имеем М (Х^О-*- т~,- "> следовательно, ввиду A2)
первым членом в E) можно пренебречь. Таким образом, для достаточно
•малых значений Хд магнитное поле между проводниками будет:
Я{2)^ i_ ^ ег7.-,2-г«>«, A8)
Большая часть тока проводимости течёт по поверхности внешнего и
внутреннего цилиндров. Если промежуточный диэлектрик обладает некоторой
проводимостью, то будет также и поперечная составляющая тока от одного
цилиндра к другому, в результате чего получится уменьшение амплитуды
тока вдоль линии. Продольный ток, текущий по внутреннему цилиндру,
может быть найден непосредственно из закона Ампера. Он равен 2'rMiHf'\
где /уР взято при г = а^. Следовательно,
В=!!^1^, A9)
где / —амплитуда тока проводимости вдоль внутреннего проводника. Таким
образом
Z?' = "f?, Z<') = 0, •' B1)
31 Зак 593. Теория впектромагнетпзма.
482
гл. IX. КРАЕВЫЕ ЗАДАЧИ
Поперечное напряжение в какой-либо точке линии по определению
равно
B3)
aj
отисшение же поперечного напряжения к току в бесконечной линии
называется её характеристическим импедансом Z^.
^с = 2;>°.,.
B
А ■•»
где Zo=a)U2/j^2 — внутренний импеданс среды с постоянной
распространения ^2, определённый формулой (83), стр. 252.
Рассмотрим линию с распределёнными параметрами, схематически npei-
ставленную на рис. 109. L—последовательная самоиндукция, R — после-
С^
\g 4=
-¥Tir6"\wvv
Рис. 109. Схема передаточной линии с
распределёнными параметрами.
довательное сопротивление, С—параллельная ёмкость, G — утечка; все
величины взяты на единицу длины линии и предполагаются равномерно
распределёнными. Легко показать, что уравнения, которым подчинены
распределения тока и поперечного напряжения вдоль линии, будут
UZ
dl
L% ~-Rf = — (^R — mL)I,
di
GV== — {G — mC) V.
B5)
B6)
Величина Z=R — шЬ — последовательный импеданс, a F= G — /coC—шунто-
В0Й адмитанс линии. Разрешая совместно B5) и B6), мы получим так
называемое «уравнение телеграфистов»:
ач/
LC
dV
iLG-{-RC)^—RGV=0,
dt
или
'^^--y-
B7)
B8>
и идентичное уравнение для тока. Постоянная распространения равна
i y^YZ, а характеристический импеданс, как и в разделе 5.6, равен Y-^l^ •
Если мы продифференцируем теперь B6) по z^ то получим
dz
2п
B9)
В рассматриваемом нами случае последовательное сопротивление равно нулю;
отсюда получается, что последовательная индуктивность на единицу длины
коаксиальной линии равна ^
L = ^ In —^ генри]метр.
C0)
КОАКСИАЛЬНЫЕ ЛИНИИ [9.2П 483'
Постоянная распространения равна k^^, откуда находим, что шунтовой
адмитанс равен
Y =-. ■— (Со — шгсЛ. (о1)
Утечка и параллельная ёмкость равны, следовательно,
G==-^^^0M-^ Aiemp-^, С = ~-^--фарад, метр-^. C2)
In — In -^
Отсюда видно, что L и С удовлетворяют соотношению
LC = SgJJ-g. C3)
9.21. Конечная проводимость. Практически цилиндрические проводники
изготовляются из металла, проводимость которого хотя и не бесконечна,
но очень велика. Распределение поля между коаксиальными цилиндрами
с большой точностью такое же, как и в случае идеальных проводников, но,
для того чтобы учесть дополнительное затухание, постоянная
распространения должна быть несколько изменена. Для упрощения задачи мы
предположим, что внутренний и внешний цилиндры сделаны, как это обычно и
бывает, из одного и того же материала. Тогда
Так как Лд, хотя теперь и не равно нулю, но всё ещё очень мало,
приближение A2), стр. 317, справедливо:
Т= 1,781.
Применительно к A1) мы имеем
t.2 о 1.2
[ C5)
мЧ^\
^|NAh^^д^-~%^f^l-, C6)
2 .2
\],{:к^а,)с=,-^л/'±1-а,. C7)
Хотя мы и допустили возможность наличия некоторой проводимости у
промежуточного диэлектрика k^, но при оценке порядков величин ею можно
пренебречь. Тогда, полагая k^c^ixi/c, мы получаем для меди
|>^^-10-"v''^- • C8)
Памятуя, что а^ и а^ измеряются в метрах и, следовательно, также являются
малыми величинами, мы видим, что знаменатели детерминантного уравнения
A1) могут быть заменены единицей и поэтому^
_- А iL ^_ 1 п -2- -L iL i/"IK± Jo 0-i^i) _
.._,„_^+jL|/-:ei^l!!^, C9)
48 4
гл. IX. КРАЕВЫЕ ЗАДАЧИ
откуда мы получаем
«_ ■'•2 г /и
In ■—? '^
«1
1^
D0)
D1)
О 9
Но Х2 = ^а — ^^ и, следовательно, окончательно
P-i
«1
1 /сСпТ^Т) 1^^'(х.У/)
Приближённое значение отношения /4/S может быть теперь из C9)
подставлено в E) для определения магнитного поля в какой-либо то^ке
диэлектрика. Мы получаем
ik^,
В
7Г ШрзЛ^
Г 2;л2
yihs—iMt
D3)
Логарифмический член как явно малый был отброшен. Проводимость
диэлектрика Og мы предполагаем очень малой, если только она вовсе не равна
нулю. Второй член в D3) возрастает, следовательно, в основном
пропорционально частоте в степени три вторых. Простой подсчёт показывает, что,
как и в C8), этим вторым членом можно пренебречь по сравнению с первым
даже для частот поряака 10^^ циклов jcefc, если только а^ не очень мало
или г не очень велико. Постоянная В определяется из условия, что на
поверхности внутреннего проводника 2iza^H^^'^ =/, так что с большой
точностью
^' --2^'
D4)
как и в предыдущем случае идеального проводника. Физически это
означает, что токами проводимости и токами смещения в диэлектрике можно
пренебречь по сравнению с токами проводимости в центральном проводнике.
Радиальное электрическое поле будет
рB) 4^'Mh „^2)
а поперечное напряжение равно
(О'Ля
A—ДА;)
271 г
D5)
@(Х2
а->
2.*,('-^*)'''ir^-
D6)
Для характеристического импеданса это даёт
ОЗ'Лч
^«=ii|(i-^*)'"^-
«1
D7)
Последовательный импеданс и шунтовой адмитанс получаются
непосредственно из соотношений
Z \
h' = —YZ, Zl^~, I
^C f
D8)
КОАКСИАЛЬНЫЕ ЛИНИИ [9.21} 485
Приближённое выражение для шунтового адмитанса, дающее практически
вполне достаточную точность, равно
1r:kt 1 Отт:
у^,__±_2_ ==_£!!_ (аз— шзз), D9)
т. е. точно тому же выражению, что и в случае идеальных проводников.
С другой стороны, для последовательного импеданса мы получаем
Z —— ^|^2„A—А^J1п-|1 = /? —ЬЛ. E0)
С технической точки зрения поведение линий полностью определено теперь
уравнениями B5) и B6).
Если, как это обычно бывает, Xi"^!, то цилиндрические функции
можно заменить их асимптотическими значениями
A^aVZi^ / ^о'Ч.у,ут)_ , .
Тогда
ДА = _.й+|.1/-7Гс1,, M_L_. E2>
«1
Этот поправочный член настолько мал, что (А^J можно отбросить.
Последовательное сопротивление и индуктивность будут тогда
у'4^ г cj \ai~^ омметр >
, 2п |_ «1 ' у 471 (J-a F v^i \ «t ■ aJ\ метр
J
Для проводников из меди а^ = 5,8-10^ , и мы получаем
/?-o,4i6.io-V^f~4--)-^ , ^
' * \а^ * a^^J метр '
E3)
E4>
метр
Затухание определяется из постоянной распространения
/г = ^2 A — А^) = а + ^'р.
При очень больших частотах потери в диэлектрических перегородках очень
быстро возрастают, но при частотах меньше мега-цикла утечкой правильно
сконструированной линии можно обычно пренебречь. Если мы положим, что
A'2 = <o|/£2u.2, то выражение для коэффициента затухания примет вид
ах
В инженерной практике принято выражать затухание через логарифм
отношения мощностей. Десятикратный десятичный логарифм отношения
выходящей мощности к входящей даёт нам затухание в децибелах.
Поскольку отношение мощностей равно ехр (— 2^z), то затухание на
единицу длины линии в децибелах будет
^аь = - 20 р Ig S = - 8,686 р ^~^f. E6)
486
гл. IX. КРАЕВЫЕ ЗАДАЧИ
КОЛЕБАНИЯ СФЕРЫ
9.22. Собственные колебания. Рассмотренные выше задачи с плоскостью
и цилиндром осались бесконечных поверхностей, которые служили в
качестве направляющих для бегущих волн. Сфера даёт нам пример тела,
ограниченного замкнутой поверхностью, внутри которой может существовать'
система стоячих волн.
Мы будем предполагать, что сфера радиуса а, характеризующаяся
в отношении электрических ..свойств постоянной Aj, помещена в
неограниченную однородную среду k^. Поле мы будем выражать через сферические
волновые функции, рассмотренные в разделах 7.11—7.14. Согласно
уравнению A2), стр. 347,
•2-7Г7(«Л + г^Л,). A)
E = ~^iaJA,,
h N ^
н =
Да)(А
Индекс п стоит здесь вместо всех индексов, которых в данном случае
имеется три. Функции могут быть нечётными или чётными, и индексы т и п
определяют число узлов относительно сферических углов о и 0. Напомним,
что радиальная компонента любой функции Ме^^^ равна нулю. Следовательно,
о
если возбуждены только члены с Ь^у а все а^ равны нулю, то
электрический вектор поля имеет радиа1ьную компоненту, магнитный же вектор
всегда перпендикулярен к радиусу-ве-ктору. На поверхности сферы должны
выть поэтому распределены электрические заряды. Колебания, амплитуды
которых выражаются только через коэффициенты Ъ^^ являются
колебаниями электрического типа. Раньше мы их называли также поперечно-
магнитными ила Е-волнами. Если, наоборот, возбуждены только
коэффициенты а^, то поле будет такое, какое создали бы переменные магнитные
заряды, расположенные на поверхности сферы, и называется полем
магнитного типа. Эти колебания можно также назвать
поперечно-электрическими или Н-волнами.
Рассмотрим сначала колебание магнитного типа
t == \"етп^етп ~т" ^onin"^omnf ^ 1
Коэффициенты А^ пока что произвольны, а частота ш вскоре определится
из граничных условий. Функции М и N. должны быть выбраны так,
о о
чтобы поле было конечно в центре и регулярно на бесконечности.
Согласно A1) и A2), стр. 367, при R<^a мы имеем
I
JLh =
1
sin
дК
-гш*
дК
Jnik,R)e-i"^t,
. nin-^-l) уг Jl^ . ^ t D\ p~ic:,t
\
mn
C)
H'g
Hi = —
H^ =
lO^J.^
R-
1
1
dK* 1
""^l^ik.RJnik.R)]'e-^^^\
I
R
dY^ 1
гш{Л1 sine df R
[k,R]n{k,R)\'e-i-K
D)
КОЛЕБАНИЯ СФЕРЫ [9.22] 487
где Vinn — тессеральная сферическая функция
Yinn = (Almn COS mcp -}- Almn siH /и?) P'^- (cos 0), E)
a штрихи в D) означают дифференцирование по аргументу k^R,
Внешнее поле в области R'^a получается заменой в C) и D) к4„
«а Yf
тп-
(8)
Ymn = {Almn COS Itl'O -{- Almn sin 1Щ) P^' (COS 6), F)
k^ и iXj на ^2 и !^ ^^ Jni^J^) иа ^«4^2-^)-
Ha поверхности сферы непрерывность тангенциальных компонент
приводит к соэтношениям
Lo_^,, /:,-/.„• ^^_^^^
которые приводятся к условиям
-Г^ешп [^lajn iK^)]' = -Г ^emn [^2^^^ (•^20]' f
И к паре таких же условий для нечётных коэффициентов A.lmn и Almn*
Положим
p = j^2^> J^J = Л/■'г2, k^a = IVp. (9)
Условия (8) выполняются только для дискретного ряда
характеристических значений p,^g, являющихся корнями трансцендентного уравнения
\N?Jn{No)]' ^ [р4'^(р)Г
Поскольку допустимые значения р образуют дискретный ряд, постольку
мы имеем соответствующий ряд собственных частот или собственных
колебаний. Согласно (9),
Ы = {Щ18Н^-2 -f i^^nsV'2'^2) О'^', A1)
следовательно, собственные частоты магнитных колебаний будут
2 FT
—^ д 1-^у-. A2)
Как и во всякой задаче о характеристических значениях, амплитуды
допустимых видов колебаний определяются начальным распределением поля.
Предположим, что в момент ^=0 радиальная компонента Н* является
заданной функцией вида /i @,?)/2('%). Прежде всего мы замечаем, что
собственные частоты co„g не зависят от распределения по углу <р. Как и в A8),
стр. 355, коэффициенты А^ однозначно определены функцией/F, о). Ряд
о
со
и= 1
с»
где Yn=2j^ Ymn будет тогда зависеть требуемым образом от в и сз при ^=0.
Мы можем построить бесконечное число таких рядов—по одному для каждого
«орня 5 уравнения A0); каждый из этих рядов можно умножить на свой
488
гл. IX. КРАЕВЫЕ ЗАДАЧИ
коэффициент А1 и произвести суммирование по s:
оо со
Hh-=-J\yAi^^-^^''^^ A4>
S = о W = 1
где Ад должны быть определены так, чтобы в момент ^=0 A4) переходило
в f^iR)- Представление произвольной функции в виде ряда Фурье-Бесселя
рассматривается у Ватсона^); теория может быть применена и к сферическим
бесселевым функциям JnifiiR)- Заметим, наконец, что можно до
суммирования умножить каждое частное решение на k^R и затем продифференцировать.
по этому аргументу. Коэффициенты А1^^ менять не нужно, ко суммирование
о
по 5 надо видоизменить таким образом, чтобы удовлетворить условиям,
наложенным на Н^ или на Hi. Таким путём находится поле, которое
удовлетворяет условиям, заданным внутри сферы для момента ^ = 0. Множитель
ехр (—f%sO определяет поведение этого поля во все последующие моменты
времени, а в силу теоремы раздела 9.2 об однозначности решения псле
•пределено также и для всех внешних точек. Колебания электрического типа
совершенно не зависят от магнитных, но поля и собственные частоты^опреде-
ляются совершенно так же. В этом случае вместо B) мы имеем
И поле в какой-либо внутренней точке /? < а будет
\ дУ^ \ I
,/^Ь = о, j
ш\>.х sin6 ()(]^ J n \ \ ^ J 1 '^ A/;
Амплитуды внешних и внутренних полей связаны граничнымиУусловиями
которые приводят к трансцендентному уравнению
определяющему характеристические значения р,^^. Собственные частоты ш^^
получаются затем из A2).
1) Watson, loc. ciL, глава XVIII.
КОЛЕБАНИЯ СФЕРЫ [9.23]
489
9.23. Колебания проводящей сферы. Мы предположим, что
проводящая сфера помещена в идеальный диэлектрик ^). Рассмотрим сначала
предельный случай Oj->oo. Два детерминантных уравнение A0) и A9)
принимают тогда вид
ЛпЧр) = 0, И^'Чр)]' = 0; B0)
корни этих уравнений являются характеристическими значениями для
магнитных и электрических видов колебаний соответственно. Каждая функция,
hn\p) может быть, однако, представлена в виде умноженного на экспонент
полинома (раздел 7.4, стр. 356). Рассматриваемые корни являются корнями;
этих полиномов, и, следовательно, число их для любой из функций
конечного порядка п конечно. Рассмотрим, например, первое электрическое
колебание, для которого «=1. Согласно C1), стр. 357,
M^P) = -j^^<H-^,
Iph^ip)]' = -
.е»-р(р2_^/р__1>1^
B1)
B2),
и искомые корни являются корнями уравнения p^-j-w—1=0, т. е.
Pjj = 0,86 — / 0,5, Pi2 = — 0>86—/ 0,5, Так как с^ = 0, то собственные
частоты получатся из
<о,
lis
= -^У^2,
а
и следовательно, для наинизшего электрического колебания
g-iwt :== Q
0.5 «OiSS
1
B3).
B4).
Амплитуда уменьшается до доли -^ от своей первоначальной величины за
время, необходимое для прохождения волной расстояния, равного диаметру
сферы. Длина волны во внешней среде равна X = ^^j^ й = 7,3а. Поскольку
проводимость бесконечна, затухание должно быть приписано полностью
потере.энергии на излучение. Потеря эта происходит очень быстро даже в
случае 'иаинизшего колебания; в только что рассмотренном примере амплитуда
уменьшается до доли — от своей первоначальной величины за время, равное;
0,27 полного периода.
— hx {
— г?2 1
Магнитные колебания
~1
—1,50 4-4 0,?6
— 1,50 — i 0,86
-2,26
— 1,87+ /1,75
-1,87-/1,75
Электрические
колебания
-^ 0.5Э + / 0.86
— 0,50 — / 0,86
— 1,60
— 0,70 +П,81
— 0,70 —П,81
— 2,17 +/0.87
— 2,17-/0,87
— 0,РЗ + г2.77
-0.83-/2,77
В таблице приведены несколько первых характеристических значений
для случая бесконечно проводящей сферы. Минимальный коэффициент
затухания соответствует низшему электрическому колебанию.
1) D е b у е, Ann. Physik 30, 57, 1909.
490 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Если мы имеем металлическую сферу, то проводимость конечна, но N
всё же очень велико. Мы можем ожидать поэтому, что корни A0) и A9)
окажутся близки к корням B0). Если |Л/р|^:^1, то асимптотическим пред-
сгавлением A0) будет
л+1 p-i [р^1Р(р)]'
Пусть отклонение от какого-либо корня р^^ уравнения ^,г,"('^')=^ О равно Ар^^.
Разлагая правую часть B5) в ряд Тэйлора около точки р^р,^^ и сохраняя
только линейные члены, мы получаем
, У± I
'ns~ _. .., .-n + i) . B6)
Др
Это выражение даёт нам те погтравки, кото}>ые необходимо внести в
собственные частоты магнитных колебаний. Аналогично, для электрических
колебаний мы заменяем A9) на
Л/ — • 2 '^''" -xi /;'1'(Р)
~*S(^?--^^)---~^- B7)
Пусть p,jg — корень уравнения [р^^/|(р)]'= О, а Ap^g — отклонение, вызванное
конечной проводимостью. Имеем
[рС(р)]' = lp/z;J4p)]: .,^^Др„,4- ... B8)
Из уравнения D), стр. 352,
Р [Р^п^(Р)Г + [Р^-п(п-{-1)] /4:) (р) = о, B9)
откуда
2
^Pns ^ -^ -^ ——г: к i^Pns - ^ ^)' C0)
Таким образом, поскольку тангенс очень большого комплексного числа
равен -^i, для основного электрического колебания мы получаем
- ф, =.-0.50 ±,-0.86A--!^^). C1)
в случае металлической сферы
(J.J 1 — / A)£г>
(j-sTV V dj
C2)
Напомним, наконец, что при рассмотрении собственных видов волн,
распространяющихся вдоль цилиндра, основная волна соответствовала
следующим условиям: Х^а очень велико внутри цилиндра, а к^а почти равно нулю
вне его. Было показано также существование системы дополнительных волн,
для которт>^ к^а было,' однако, малым. Подобное же положение вещей
получается и в случае сферы. Как показал Дебай, система корней A0) и A9)
такова, что Л/'р остаётся конечным, даже если N очень велико. Если
проводимость сферы конечна, то, как и в случае дополнительных цилиндрических
волн, затухание колебаний очень велико.
9.24. Колебания в сферической полости. Насколько можно в
настоящее время предвидеть, сверхвысокочастотные радиоконтуры сведутся, повид'и-
мому, к трубчатым волноводам и полым резонаторам. Последние являются
КОЛЕБАНИЯ СФЕРЫ [9.24]
491
электромагнитными аналогами резонаторов Гельмгольца, применяемых в
акустике. Подобные системы не излучают; мы можем, следовательно, приписать
определённые значения их электрической и магнитной энергии и,
соответственно, ^определённые эффективные индуктивность, ёмкость и
сопротивление, которые будут зависеть только от конфигурации. Затухание возникает
в результате проникновения поля в металлические стенки на расстояние,
равное примерно глубине скин-слоя,
Характед колебаний в резонаторе может быть иллюстрирован на
примере сферической полости. Предположим, что внутри сферы—идеальный
диэлектрик, так что ^^ = со|/е^{А^, в то время как внешняя область обладает
бесконечной проводимостью. Тогда N=^0, и характеристические значения
для магнитных и электрических видов колебаний определятся соответственно
из соотношений
Jn (^1«) == О, [^1« jn ik-id)]' = 0.
C3)
Пусть
•ней равны
и
ns
будут корни уравнения jn{k^a) = 0. Первые из этих кор-
«11 = 4,50, «12 = 7,64,
и
21
5,8,
C4)
Поскольку ^iB = <o |/ei»j,i и:, характеристические частоты для магнитных
колебаний даются соотношением
'«s
и
пч
'iTia у Sjjj,!
C5)
Формально это соотношение тождественно с уравнением F5), стр. 473, для
характеристических частот полой трубы. Длина свободной волны, т. е, длина
волны той же частоты в
безграничной среде, равна
2г.а
и,
IS
C6)
Наибольшая допустимая длина
волны для магнитных
колебаний равна Xji = 2^^/4,5= 1,4а.
В этом случае векторы поля имеют
только компоненты Е^, Hf^ и /ig
и потоки зарядов направлены
параллельно линиям широты.
Распределение электрических и
магнитных силовых линий в
меридиональной плоскости показано
на рис. 110.
Корни второго из
уравнений C3) мы будем обозначать че-
Рис. 110. Поле в меридиональной плоскости
сферического резонатора для наинизшего
магнитного вида колебаний.
pes и
/?§'
а характеристические
частоты электрических колебаний—через v'^. Формулы C5) и C6) остаются
справедливыми и при наличии штрихов, а для длины свободной волны основ-
иого электрического колебания подсчёт даёт
Х'^^ = 2тга/2,75 = 2,28а.
Это — наинизший из всех возможных видов колебаний как электрических, так
и магнитных. Аксиально-симметричный случай соответствует переменному
492
гл. IX. КРАЕВЫЕ ЗАДАЧИ
потоку зарядов вдоль меридианов, от одного полюса к другому; магнитные
силовые линии направлены вдоль широтных параллелей. Силовые линии в
меридиональной плоскости показаны на рис. 111. Для какой-либо внутренней
точки сферы из A6) и A7) при т = 0, я=1 мы имеем
Ев
2Аа
.,75;?--"АB.75f).-■""',
Н, = i)/i А sin Од B,75|) е
— гш,.^
C7)
/?\ -гш t
где шц== 2,75/А!|/е^[х,.
Плотность поверхностных токов К в любой точке на стенке полости
равна К = [п, Н], где п — единичный вектор, направленный по радиусу
внутрь, а значение Н берётся на поверхности со стороны полости. Поскольку
имеется только компонента Н , вектор
поверхностной плотности тока направлен вдоль
меридианов. Полный ток, пересекающий
экватор за секунду, равен
J=2r.aK=- 2r.ail/'^Aj\ B,75) е~'"''''*. C8>
Эквивалентные индуктивность и
сопротивление осциллирующей системы могут быть
определены через этот полный ток ^). Средняя-
магнитная энергия внутри полости равна
а и
= ^М2 J J [л B,75 -| J R^ sin3 О dO dR =
о о
а
^ Т '^-^'1 L-^'i (^'^^ Щ ^^'^^' ^^^^'
Рис. 111. Поле в
меридиональной плоскости сферического
резонатора для наинизшего
электрического вида
колебаний.
Интеграл можно без труда вычислить, применяя общие формулы для
интегрирования цилиндрических бесселевых функций, или же непосредственно,,
замечая, что
J\ (k,R) = - ^^- (cos k,R r~ ^ sin k,R).
Мы находим, что
D0).
откуда
fjl (х) хЧх == у [jl {X) -Уо ('^)Уо {х%
Г^^^е^Л^йЗ. 0,054.
D1)
D2)
1) Hansen, J. Applied Phys. 9, 654,1938.
ДИФРАКЦИЯ плоской волны НА СФЕРЕ [9.25] 493
Индуктивность L мы определяем далее по формуле
7 = 1-L72 = 1l//^ D3)
Если для тока в D3) мы совершенно произвольно возьмём ток,
пересекающий экватор, то, согласно C8), D2) и D3), эквивалентная индуктивность
■будет
Z, == 0,077 [j-jfl генри. D4)
До сих пор мы предполагали, что проводимость стенок бесконечна, так что
компонента fg при R = a равнялась нулю и затухание отсутствовало. Если
стенки маталлические, то пангенциальная компонента Е на их поверхности
может быть получена из приближённого соотношения D7), стр. 468. При R = a
Е ^ -/^^ЯоГ ^c^lA У ^^il^'i^ Sin 6Л B,75) е ' "^^ . D5)
Таким образом, теперь появляется направленный в металл радиальный
поток знергии, средняя плотность которого равна
5i2 = Re5iT = 2yf~|/ -r|~-"sin20y?B,75). D6)
Потеря энергии за единицу времени получается интегрированием D6) по
ловерхности сферы
1к г. -
lF=a2jJ:Sijsin6«fe^9 = |^'^t-AB,75), D7)
о о
где o = i/ -; глубина скин-слоя, определённая на стр. 444. Эквива-
лентное последовательное со1ротив ление Ш. определяется соотношением
1^=9?72 = Ш//*, D8)
откуда
Для характеристики эффективности конгура часто применяется
параметр Q^), определяемый как отношение индуктивного сопротивления к
последовательному омическому сопротлв гению. Для основной частоты колебаний
в полой сфере Q равно
Q = lii^ = 0,725 ii^-^^. E0)
ДИиРАКЦИЯ плоской волны НА СФЕРЕ.
9.25. Разложение дифрагированного поля. Периодическая волна,
падающая на материальное тело, вызывает, независимо от природы этого
тела, вынужденные колебания свободных и связанных зарядов, синхронные
с колебаниями приложенного поля. Эти вынужденные колебания зарядов
создают в свою очередь вторичное поле внутри и вне тела. Вектор резуль-
') Q называется добротностью контура. Прим. ред.
494 гл. IX. КРАЕВЫЕ ЗАДАЧИ
тирующего ПОЛЯ в какой-либо точке является, следовательно, суммой
векторов первичного и вторичного полей. В обшем случае эти вынужденные
колебания не удовлетворяют условиям, существующим в момент
возникновения первичного поля. Для того чтобы удовлетворить граничным условиям
во все моменты времени, необходимо добавить член, выражающий процесс
Зттаковления и состоящий из собственных колебаний, взятых с
соответствующими амплитудами. Однако эти колебания очень быстро затухают из-за
поглощения и потерь на излучение и остаются лишь стационарные
синхронные члены.
Простейшей и в то же время имеющей большой практический интерес
задачей этого типа является задача о плоской волне, падающей на сферу.
Как и в предыдущем разделе, мы предположим, что сфера радиуса а с
постоянной распространения k^ находится в безграничной однородной среде
с постоянной распространения k^. Плоская волна, электрический вектор
которой линейно поляризован в направлении оси х, распространяется в по-
ложительном направлении оси z. Разложение первичного поля на векторные-
сферические волновые функции было дано в формуле C6), стр, 370
Е, = 2.,E,eii^^^-i-t = E^e-i-^Y^ ^'"iT^^l) («^^. - ш^Л,
и
!
A>
"^ — ^У р-зо^^о^ "~ (xgo. ^ 2J^ л (п + 1) '^ "'" ' "'''^ '
11—1
где ^Q—амплитуда, а
«,f^) _+- 1 ,• /г, п\ пг / пч cos . , ^и г>\ ^Р^,{со^Щ sin . ,„.
^lyn^^'^;^JnihR)Pn{^osb)^^^ou^—j,,{k.R) j^ cos? »S' B;
„A) n{n-\-l) , /r riN m / u\ sin . ,
^'\n = lZr J^b (k^R) Pk (COS 0) cos?»i +
1 , dP}, (cos 0) cin
+ -ff^ [ko^Jn ik,R)Y ^'^0 Z 9 h ^
~ fe,r/sin6 t^2^-^'- {k^R)]' P'n (COS 6) ""Z 9 is. C)
Штрихи означают дифференцирование по аргументу k^R.
Вторичное индуцированное поле должно быть составлено из двух
частей — одной, относящейся к точкам внутри сферы, и другой, обладающей
требуемой регулярностью на бесконечности], для точек вне сферы. По
аналогии с задачей о плоской границе, рассмотренной в разделах 9.4—9.9,,
мы будем называть эти две части прошедшей и отражённой волнами, хотя,
строго говоря, эти термины применимы лишь тогда, когда длина волны
намного меньше радиуса сферы. Запишем отражённую и прошедшую волны
в виде
Е =- £ e-i^^t V/'* 2п + 1 /Г C) ,г{щ V
П
п = 1
^2 в .-i,n*\^.-^ 2п-\-1
*" ши,
;j,2 0^ Zj n (л -f 1) \^"^eln Л- ШпПот)-,
н». = —
wp.2 "
11 = 1
D)
ДИФРАКЦИЯ плоской ВОЛНЬК НА СФЕРЕ [9.2i>l
4 95.
при R ^ а (отражённая волна) и
Е, = Er,e-i^^t У/" Д^^"".-. i^i^oin ~ ibWeli),
'О" ^^ /z(rt-j-l)
П = 1
> E)'
при R<ia (прошедшая волна). Функции т'^е^^ и п^^^^^ получаются из B)
о о
и C) заменой j'nik^R) на hn (k^R). В E) вместо /^2 следует писать к[.
Граничные условия при R = а
[ii,(E, + E,)] = [ii,E,], 1
[i„(H, + H,)]===[i„H,] I ^ ^
приводят к двум парам неоднородных уравнений для коэффициентов
разложения
4Уп (^9) — 4й^ (р) == А (Р). !
G)
(8)
(9)
bn [щ]п imY—^bn \9k: (p)i'=л^ [рУп (p)]', j
где попрежнему
Решая эту систему относительно коэффициентов отражённого поля, получаем
/ — _ Р-- jn (Щ Ып (р)]' — Р-?^ (р) [%/n (^о)]'
'^dn (Л^Р) [рЛ:,^> (р)]' - v^<,h\l^ (р) [7VR/n (Л^Р)]' '
С!"П, —
jT ^ MJn (Р) [Л^рУп (Л^Р)]^ - •^'^N^n (Л^Р) [р/п (Р)Г
f^i^i'^ (Р) l7VR/n (Л^Р)]' - [^2Л^2;;»(Л^Р) [рЛ^^^ (Р)]'
A0)
(И)
Если проводимость или проницаемость сферы велики по сравнению
с их значениями в окружающей среде и в то же время радиуса не слишком
мал, то |Л^р|^Э>1 и A0) и A1) можно значительно упростить, воспол1»зо-
вавшись асимптотическими выражениями
Уп(Л^р)^^рС08(л^р~'^+^
в этом случае
bVpynW)]'——sin(A^p
2 ^)'
2
UnC^-
}ni?)
bn^=^
[рУгДр)]'
A2)
A3)
/С(Р)' ^"~ К?(Р)]'
Поскольку hil^ (р) ==Уи (р) -|- in^ (р), коэффициенты эти могут быть также
представлены в виде
ttn г:^ ie*b sin y^, ^и ^^ ic ^'' sin Y^.
где
tgT« =
Уи (р)
xgY
[pjn(p)V
(И)
A5)
'" «n(P)' '^'n lpn„(p)]'-
Резюмируем. Мы нашли, что первичная волна возбуждает определённые
колебания в сфере. Эти колебания не являются собственными колебаниями,.
496
гл. IX. КРАЕВЫЕ ЗАДАЧИ
Первый вид
Второй вид
рассмотренными в разделе 9.22, так как все они синхронны с приложенным
полем. Эти частные колебания и связанные с ними поля могут быть, однако,
разделены на электрический и
магнитный типы на тех же самых
основаниях, которые были указаны в
разделе 9.22. Коэффициенты й„
представляют собой амплитуды колебаний
магнитного типа, а Ьп —
электрического. Если частота приложенных
колебаний о приближается к какой-
либо характеристической частоте ш^^
свободных колебаний, то возникает
явление резонанса. В разделе 9.22
было показано, что
характеристические частоты магнитных колебаний
удовлетворяют приведённому там
соотношению A0). Но это как раз то
З^словие, пр« котором внаменатель
в выражении A0) для а^
обращается в нуль. Подобным же образом
собственные частоты колебаний
электрического типа удовлетворяют
соотношению A9) раздела 9.22,
которое является в то же время
условием обращения в нуль знаменателя
в выражении для ^^. Заметим,
однако, что <o^jg всегда комплексны,
в то время как частота о
приложенного поля действительна.
Следовательно, знаменатели dn и Ь^п
могут быть сведены к их минимальным
значениям, но не могут быть
сделаны равными нулю, так что
катастрофа— появление бесконечных
амплитуд—благополучно избегнута.
На рис. 112 показаны
электрические и магнитные силовые линии
для первых четырех частичных
колебаний электрического типа.
Рисунки заимствованы из оригинальной
работы Ми 1).
Падающая волна линейно
поляризована так, что её электрический
вектор параллелен оси х. На очень
больших расстояниях от сферы ра-
Третий вид
Четвертый вид
Рис. 112. Силов е линии, соответствующие
первым четырём колебаниям
электрического типа. Слева — электрические силовые
линии, справа — магнитные.
диальная компонента вторичного поля исчезает, как 1//?^, в то время как
тангенциальные компоненты £^8 и Е^ убывают, как \\R. В этой волновой зоне
поле поперечно к направлению раслространения. Кроме того, компоненты
£,-9 и Е^^ перпендикулярны друг к другу и в общем случае сдвинуты по
фазе. Вторичное поле, излучаемое сферой, эллиптически поляризовачо.
Два направления являются исключительными. При o = Q £'^^==0, а при
1) Mie, Ann. Physik, 25, 377, 1908.
i; ДИФРАКЦИЯ плоской волны НА СФЕРЕ [9.26] 497
1э = -я- £у9 = 0. Следовательно, при наблюдении вдоль оси х или оси у
втори»^ное излучение линейно поляризовано. Обратно, если первичная волна
не поляризована, как это имеет место в случае естественного света, то
вторичное поле имеет частичную поляризацию, зависящую от направления
наблюдения. Это явление было изучено в связи с рассеянием света взвесями
коллоидных частиц. Наиболее полное численное исследование задачи, по
крайней мере для области видимого спектра, было проведено Блюмером i).
9.26. Полное излучение. Полное поле в любой точке вне сферы
является суммой первичного и вторичного полей
Е == Ef-|~ Еу, Н = Н;-|-Ну. A6)
Радиальная компонента полного комплексного вектора Пойнтинга равна
st=~iE,H;--E^H*,) A7)
и, в силу A6), может быть разложена на три группы членов
•5ij = 2" (^feM?"—Ei^Hifi) ~\- {E^^Hr^—Е^^Нгь) +
+ " {^гв^гц, -f- ^гь ^f<р — Ei^Hrb — E^Hib). A8)
Опишем вокруг сферы, вызывающей дифракцию, концентрическую
сферическую поверхность радиуса R. Интеграл по этой сфере от действительной
части вектора Sr равен потоку энергии через поверхность сферы. Для
упрощения мы предположим, что внешняя среда B) — идеальный диэлектрик,
так что ^2 = ^1^£2Н'2' Если сфера, вызывающая дифракцию, также
непроводящая, то поток энергии через любую поверхность, охватывающую сферу,
должен быть равен нулю. Если же внутри сферы происходит переход
электрической энергии в тепло, то поток энергии должен быть направлен внутрь
и равен количеству поглощённой энергии. Поглощающуюся в сфере энергию
мы будем обозначать через W^i
Wa = ~Re jj stR^sinbdodb. A9)
о о
Первый член в правой части выражения A8) даёт поток энергии в
падающей волне. Если Og = О, то интеграл от этого члена по замкнутой
поверхности равен нулю. Второй член даёт, очевидно, направленный наружу поток
вторичной или рассеянной от сферы энергии; полная величина рассеянной
энергии равна
1С 27!;
W; = 1 Re jj {Е,,Н% —E,^HU) R^ sin bdbdo. B0)
0 0 .
Для сохранения энергетического баланса интеграл от третьего члена в A8)
должен быть равен сумме поглощённой и рассеянной энергии
ГС 2ic
• ==-^RejfiE,,H%-\~E,,H-^--Ei^H;b--E,^Mib)R^smmdo. B1)
о о
Wf равно, следовательно, полной энергии, извлечённой из первичной волны
и затраченной в виде тепла и рассеянного излучения.
1) Biumer, Z.Physik 32, 119, 1925; 38. 304, 1926; 38, 920, 1926; 39, 195, 1926.
32 Зав. 593. Теория эпек-громагнетизма.
498 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Для того чтобы подсчитать Wg и Wp мы возьмём R очень большим
и воспользуемся асимптотическими разложениями
y„(p)-ilcos(p—^тг), /г«(р)^1( —/)n+VP. B2)
После подстановки B2) в B) и C), мы можем подсчитать интеграл с
помощью уравнения B0), стр. 368:
/tf^+ii^^>»)^-«''«
[ О, еслипфт,
= ■? 2 (л + 1)! , , ,. . B3>
I 2МП (^Ijr " ('^ + 1)'^'^^^ '^ ='"
и соотношения
л"/Pi, dPl pI dPl,s
I I-^ ^ + -Л -Ж-) sinQ йГ Q = 0. B4)
J Vsin G d6 ' sin 6 d6 / \ /
0
Для энергии, рассеянной в виде излучения, ыы найдём
>я=^1|-]/-2B'^+1И!«.':Р+1*»а B5)
а для суммы поглощённой и рассеянной энергий
|\Г,= ^-^|/ ^^Re2B«+1)(«; + ^';). B6)
Средний поток энергии в падающей волне через единицу площади равен
Поперечное сечение рассеяния определяется как отношение полной энергии,
рассеянной за секунду, к плотности потока энергии падающей волны:
со
Qs = p ^i:2n-\-\)i}alf-\-\blf)метров'^. B8>
2 п = 1
Аналогично мы можем определить поперечное сечение Q^:
со
Q, = ||-Re У Bя + 1) К 4- ^«) метров^. B9)
Если проводимость или проницаемость сферы настолько велики, что
iVpl^^l, то в выражения для поперечных сечений можно ввести
приближения A4) и A5), и эти выражения примут вид
^« = 7^ S (^'' + ^^ <^'^"''^" + '^"' ''-^' • ^^^>
k
со
^ и = 1
^* = li-^^2i''B''-b ^П^''^ sm7n-l-^"''"sinY;). C1)
г
в случае непоглощающей сферы -у^ и -уя действительны Jh, очевидно, тогда
Qs = —Q*.
ДИФРАКЦИЯ ПЛОСКОЙ волны НА СФЕРЕ 19.27] 499
9.27. предельные случаи. Хотя предшествующие формулы и кажутся,
на первый взгляд, очень простыми, вычисление коэффициентов является
обычно довольно трудоёмкой задачей. В двух предельных случаях
рассмотрение упрощается. Если p=|/5ia|^l, то функции У„ (р) и h^^p могут быть
заменены их асимптотическими значениями. Величина р представляет собой
с точностью до множителя 2тс отношение радиуса сферы к длине-волны;
таким образом, это тот случай, когда радиус сферы намного больше длины
волны. Результаты, получаемые только что указанным методом, должны
приближаться к тем, которые были получены в разделах 8.13—8.15, исходя
из принципа Гюйгенса-Кирхгофа. Другой предельный случай получается при
длине волны, намного большей радиуса сферы, так что | р | <^ 1 и
радиальные функции могут быть заменены одним-двумя первыми членами их
разложения по степеням р.
Случай I. р;^1. Подставляя асимптотические выражения A2) и B2)
в A0) и A1), мы получаем для коэффициентов выражения
bl^^in+ie-i9^hS£l£Myji:]^:lI^^ ^ C3)
где
я+1
о '^>
y=Np~-!^'K. C4)
То, что верно в этом примере, справедливо и в общем случае: коэффициенты
разложения являются осциллирующими функциями от р и от порядка п.
Небольшие изменения р или п могут привести к значительным колебаниям значений
коэффициентов. Абсолютная величина коэффициентов разложения колеблется
между нулем и единицей.
Если заменить в C2) « на п-\-1, то нетрудно усмотреть, что «и+г ;=^'^п-
Амплитуда колебаний электрического типа п-го порядка примерно сов-
падает с амплитудой колебаний магнитного типа на единицу высшего
порядка.
Асимптотические выражения, применённые при выводе C2) и
C3),,справедливы только до тех пор, пока порядок п во много раз меньше значений
аргументов j р | и | Л/р |. Асимптотические формулы для бесселевых функций,
справедливые для всех порядков, были найдены Дебае1й, который показал
также, что число членов разложения, которое надо удерживать, как раз равно
численной величине 1р|^). Различные приёмы суммирования коэффициентов
были рассмотрены Иобстом^).
Случай II. р<^1. Возьмём из раздела 7.4, стр. 356, разложения
радиальных функций по степеням р или Np
1) D e b У e, loc. cit.
2) J ob St, Ann. Physik lb, 863, 1925; 78. 158, 1925.
32*
500 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Коэффициенты также разлагаюгся по степеням р:
г 2^"п! (/г + IV- Р^'^+^ у
X j ^-2— 1^1 Bn + 2)B/2 + 3) Р f ' ^^'^
Z'" —^ Bл)!Bл+1)! н(/г+1) + {Х2УУ2л^
Х||х, —jXgAT^ B;,+2)B/7 + 3) Р ?• (^^>
Если I р I настолько мало, что можно пренебречь всеми степенями выше пятой,
то достаточно рассмотреть только первые четыре коэффициента:
^ 15 Зи + 2(Л2Л/2 Р •
Если, кроме того, jx^ = i-ig, то эти выражения принимают вид
^r-i(iV2-l)pS,
1 3 Va^2_|_2 Р 10 Л^2 + 2 Ру'
А»^ ,—' . ' rfi
2— 152Л^ + ЗР*
Правило, согласно которому амплитуда колебаний магнитного типа я-|-1-го
порядка такова же, как и амплитуда колебаний электрического типа «-го
порядка, остаётся справедливым до тех пор, пока проводимость конечна.
Если отношение радиуса сферы к длине волны настолько мало, что
можно пренебречь р^ по сравнению с р^, то можно ограничиться только
колебаниями электрического типа первого порядка. Этот случай был впервые
рассмотрен лордом Ре леем. Амплитуда колебаний в этом случае равна
Ьг 2''i!^!=loS D1)
Если подставить это значение в выражения B), C) и D) и сравнить
полученный результат с выражением C0) на стр. 385, то мы увидим, что поле
основного колебания совпадает с полем электрического диполя,
ориентированного вдоль оси X и обладающего диполъным моментом
/^=47rs2-^^^y-aS£o. D2)
Сравнение с формулой* C2), стр. 192, показывает, что это выражение
тождественно с результатом, полученным в электростатическом случае. Таким
образом, амплитуда рассеянного или дифрагированного малой сферой
излучения на больших расстояниях от сферы увеличивается пропорционально
квадрату частоты, а энергия — пропорционально четвёртой степени. Это и
есть знаменитый релеевский закон рассеяния, применённый его автором для
D0)
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН [9.128] 501
объяснения синевы неба. Если наблюдатель смотрит не непосредственно на
солнце, то "в его глаз попадает лишь свет, рассеянный частицами пыли или
молекулами атмосферы. Так как длина волны видимого света намного больше
радиуса подобных субмикроскопических частиц, закон .четвёртой степени
справедлив, и коротковолновая часть солнечного света рассеивается сильнее,
нежели более близкая к красному концу спектра. Если смотреть
непосредственно на солнце, то наблюдается противоположный эффект, ибо если синие
лучи рассеиваются сильнее красных, то они будут представлены в прямом
свете относительно слабее, и преобладать будет уже красный цвет. Этот
эффект особенно про вляется- тогда, когда солнце находится вблизи горизонта
и лучи его проходят через слои воздуха, насыщенные частицами пыли ^).
Таким же путём можно объяснить различные оттенки туманов и дымов;
хорошо известно, что цвета коллоидных суспензий металлических частиц
в жидкостях или газах часто совершенно отличны от истинного цвета самого
металла. Однако по мере увеличения радиуса частиц, члены высшего порядка
начинают играть всё большую роль. Сильно селективный характер релеев-
ского рассеяния исчезает, и предсказать диаграмму направленности
рассеянного излучения становится возможно только в результате сложных
расчётов. Члены высшего порядка могут быть интерпретированы как излучение
электрических и магнитных мультиполей ^). Экспериментальная проверка
теории для радиоволн была выполнена Шефером З).
Дифракция плоской волны на эллипсоидальном теле может быть
рассмотрена тем же способом, как и на сфере, но аналитические свойства
волновых функций в этом случае значительно сложнее. Приближённое
решение было дано Гансом*) и более строго Герцфельдом^). Наиболее полными
до настоящего времени являются исследования Мёглиха^). Однако ни
в одном случае численные расчёты не были проведены настолько полно,
^тобы дать результаты, применимые в специальных задачах, многочисленные
же практические приложения теории делают дальнейшую работу в этом
направлении весьма желательной.
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН
9.28. Решение Зоммерфельда. В 1909 г. было опубликовано
классическое исследование Арнольда Зоммерфельда о влиянии бесконечной
проводящей плоскости на излучение осциллирующего диполя"^). С тех пор на
эту тему появилось чрезвычайно большое количество работ. Без
преувеличения можно сказать, что ни одна другая сторона вопроса о распространении
1) Автор становится здесь на первоначальную точку зрения Релея, согласно
которой рассеяние в атмосфере и голубой цвет неба объясняются запылённостью
воздуха, т. е. дифракцией на взвешенных частицах (эффект Тиндаля). Однако уже
со времён классических работ Мандельштама (Ann. Physik 23, 626, 1907) и
Смолуховского (Ann. Physik 25, 205, 1908) известно, что причиной рассеяния
в атмосфере является прежде всего оптическая неоднородность воздуха,
обусловленная флуктуациями его плотности. Тиндалевское рассеяние на взвешенных частицах
происходит лишь в нижних слоях и играет подчинённую роль. Изложение автора
представляется поэтому несколько странным. Прим. ред.
2) G а п S and Н а р р е I, Ann. Physik, 29, 277, 1909.
8) S с h а е f е г and W i i m se п, Z. Physik, 24, 345, 1924.
4) Gans, Ann. Physik, 37, 881, 1912; 47, 270, 1915, 61, 465, 1920.
5) Herzfeld, Wiener Ber. 120, 1587. 1911.
6) M б g 11 с h. Ann. Physik, 83, 609, 1927.
') S о mm erf e id, Ann. Physik 28, 665, 1909; Jahrbueh d. drahtl Tele graphic 4,
157, 1911. Эти ранние статьи содержат ошибку в знаке, которая была поправлена
ъ Ann. Physik Ъ\, 1135, 1926. Тоже и у Riemann — Weber, /ос. d/.; стр. 542.
Однако некоторые следствия этой ошибки оказались незамеченными.
502
гл. IX. КРАЕВЫЕ ЗАДАЧИ
радиоволн не привлекала такого внимания *). Дать исчерпывающе^е изложение
теории в пределах этой главы невозможно, но представляется небесполезным
посмотреть, как ставится задача. Как и во всех дифракционных задачах, за
исключением разве простейших из
Воздух :'к^=а)^/с^
'P/////////////^/////MV///////////////////,
Земля: к/^ О! %/1, + ia,fi, w
Рис. 113. Вертикальный электрический диполь,
расположенный на поверхности плоской земли
с конечной проводимостью.
(г,(р.^)
них, основные трудности
возникают в связи с необходимостью
перехода от формального
решения к такому его виду, который
позволял бы проводить численные
расчёты.
В первой задаче,
разобранной Зоммерфельдом,
рассматривался вертикальный диполь,
расположенный на поверхности
плоской земли, обладающей конечной
проводимостью. Ось диполя
совпадает с осью Z прямоугольной
системы координат, а плоскость 2г = 0 представляет поверхность земли. Все
точки, для которых 2^<0, лежат внутри земли, постоянная распространения
которой равна k^. Постоянная распространения воздуха в области г>0
равна ^2==<»/с. Точка наблюдения определяется цилиндрическими
координатами г, ср, г и её расстояние от начала координат равно (рис. ИЗ)
/? = |/г2-|-г«.
A)
1) Основные из этих работ можно разбить на следующие группы: 1) исследова-
йця, в которых выводятся в замкнутой форме строгие выражения для поля над
поверхностью земли — плоской (Sommerfeld, loc. cit.\ Wеу 1, Ann. Physik 60,
481, 1919; Van der Pol, Physica 2. 843, 1935; B. A. Фок, гл. XXIII в книге
Ф. Франк и Р. Мизес, Дифференциальные и интегральные уравнения
математической физики, ОНТИ, 1937) или сферической (Watson, см. Б.
А.Введенский, Основы теории распространения радиоволн, 1934; В.А.Фок, Дифракция
радиоволн вокруг земной поверхности, изд. АН СССР, 1946). Земля предполагается
однородной. Эти строгие выражения, однако, столь громоздки или непрозрачны, что
из них непосредственно можно извлечь лишь очень немного следствий для
сравнения с опытом. 2) Исследования, в которых указанного рода строгие решения
преобразуются или приспосабливаются к частным задачам, в результате чего становится
возможным анализ структуры поля, сравнение с экспериментом и т. п. (Для плоской
земли — цитируемые далее автором работы Ниссена, Ван дер Поля, Бэрро-
уза, Уайза, Раиса, Нортона, Рольфа, Стретта, а также работы
П. А. Р я 3 и н а, см. Сборник статей «Новейшие исследования распространения радио-,
волн» под ред. Л. И. Мандельштама и Н. Д.*Папалекси, Гостехиздат, 1946.
Для сферической земли—Б. А. Введенский, Ван дер Поль и особенно
В. А. Фок, loc. cit.) 3) Исследования, в которых вместо отыскания точных решений
с последующим выводом приближённых формул, для практически особенно важного
случая больших значений [k^jl^ (См. далее) преобразуются путём отбрасывания
малых членов исходные дифференциальные уравнения и граничные условия,
после чего решение получается весьма просто (для плоской земли — М. А. Леон-
то в и ч. Изв. АН СССР, серия физ., 8, 1. 1944; для сферической земли — М. А. Л е о н-
тович и В. А. Фок, ЖЭТФ 16, 1946). 4) Исследования, в которых рассматриваются
проблемы, вообще не поддающиеся строгому решению, например, распространение
над электрически неоднородной поверхностью земли (в частности, явления
береговой рефракции), распространение над неровной поверхностью. Здесь оказалось
продуктивным применение приближённого метода, указанного в п. 3. (Г. А.
Гринберг, Е. Л. Ф е й н б е р г, см. статьи во II сборнике «Новейшие исследования
распространения рациоволн». Изд. АН СССР, 1948). 5) Исследования
распространения в плоскопараллельном слое между двумя средами. Случай идеально
проводящих сред см. R. Weiri ch, Ann. Physik 85, 5, 1928; общее решение и дискуссия ряда
частных случаев — П. А. Рязцн ц Л. М. Бреховских, Изв. АН СССР, серия
физ., 10, 285, 1946. Прим. ред.
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН 9.28] 503
Поле обладает цилиндрической симметрией относительно оси г, а вблизи
начала координат должно обращаться в бесконечность, как поле диполя.
Напомним, что поле диполя [см. G), стр. 381] может быть выражено
с. помощью направленного по оси вектора Герца, который при /?->0
обращается в бесконечность, как IjR. Поэтому г'-компоненту вектора Герца
для результирующего поля мы напишем в виде суммы двух частей
? \ B)
noAr.z):==j^ei^*^-\~F^{k^;r,z) (г-> 0). ]
Первый член учитывает особенность в начале координат. Дипольный момент
совершенно произвольно выбран так, чтобы коэффициент при этом члене
был равен единице, а обычный временной множитель в виде ехр (— Ш)
опущен. Функции Fj и Fg» конечные всюду, включая точку ^? = О,
удовлетворяют волновому уравнению и условию излучения на бесконечности i). Они
дают слагаемые, связанные с дифрагированной волной, и должны быть
подобраны таким образом, чтобы выполнялись граничные условия на плоскости г= 0.
Векторы поля получаются из вектора Герца с помощью соотношений
E = graddivП + ^^П, Н = -^го1П, C)
которые для тангенциальных компонент дают
^»-—drdz' "f iwix дг ' ^^
Для земли можно положить jj-^ = {Xg == Н-о- ^ любой точке плоскости г- = О
функции B) должны удовлетворять условиям
-^ = ^. *?^-^^ (-0). E,
Эти условия справедливы для всех значений г и, следовательно, могут быть
. проинтегрированы по г. И функции и их производные при г -♦ со стремятся
к нулю, так что постоянная интегрирования должна быть равна нулю. Таким
образом, граничные условия принимают вид|
^ = ^-, kln^^klu, (. = 0). F)
1) Как отметил В. А. Ф о к (Ф р а и к и М и з е с, гл. XXIII), это неверно. Желаа
выделить из Щ и Па члены, содержащие особенность при /? = О, следует писать
Hi (г, г) = -^—}-?1 (^i; ^ ^). I
fii-jr к^
П2 {г, г) = -о- <?2 i.k^\ г, Z).
'^l ~Г «2
Только при таком выборе коэффициентов у первых членов функции cpi и ^рз будут
всюду ограничены, так как выделенные члены, имеющие особенность в R = 0, сами
удовлетворяют приводимым ниже граничным условиям F). В формулах B) это не
имеет места, но дальнейшие выкладки приводят автора к правильной окончательной
„ gikz В
формуле B1). Как видно из этой формулы, при j^il^/^g-» со имеем Щ-)- 2—^^— и,
gikiR
следовательно, Fi->- —5— . Прим. ред.
504 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Для того робы найти функции F^ и F^^ удовлетворяющие этим
условиям, мы должны разложить «первичное возбуждение» е^^^Щ и «вторичное
возбуждение» F по цилиндрическим волновым функциям. В разделе 6.6
было показано, что любое электромагнитное поле в однородной изотропной
среде может быть представлено в виде суперпозиции элементарных
цилиндрических волн типа
6 (г, <р, z) = е«и9У„ (Yk^ — /?2 г) е^^^. G>
В нашем случае поле обладает осевой симметрией и, следовательно, /г = 0.
В качестве параметра разложения мы возьмём X'^ = k^ — h^ вместо h и
каждую волновую функцию умножим на амплитуду /(X), зависящую от X.
Параметр X может принимать любое комплексное значение. Знак корня
ih = ~Y^^ — k^ должен быть выбран таким, чтобы при z->±.oo поле
исчезало. Мы сделаем этот выбор, считая, что действительная часть
X^—k^ всегда положительна. Тогда условиям в начале координат и в
бесконечности удовлетворяет разрывный вектор Герца, радиальная и
азимутальная компоненты которого равны нулю, а г'-компонента равна
Щ =_L eihR-\- J/j (X) Jq (Xr>e+^^'^^^*^rfX (г < 0),
о
оэ
[ (8>
П2= ~ 5^'^»^ + /л (X) Уо (Хг).е-^^'-'-.''Ш (г > 0).
Следующий шаг состоит в том, ' чтобы представить таким же образом
и известное нам первичное возбуждение. Для этого мы используем теорему
Фурье-Бесселя, формула E3), стр. 327. Если при г-> с» функция /(г)
стремится к нулю таким образом, что интеграл от /(г)|/Т абсолютно сходится, то
со схз
/(г)=: fxrfX/рф/(р)Уо(Хр)Уо(Хг).. (9)
6 о
в качестве функции /(г) возьмём сначала е**»*/г.
ос схз
~ = j\dXJQ {Xr)j Op/^pJq (Хр). A0)
о о
Интегрирование по р можно выполнить, если • бесселеву функцию Jq (Хр)
заменить её интегральным представлением C7), стр. 323:
схз -ft СХЗ -ft
— я О —П
Мы предположили здесь, что мнимая часть k положительна, так что при
верхнем пределе подинтегральное выражение обращается в нуль. В реальных
условиях ^2 действительно, но в целях упрощения интеграции мы можем
приписать атмосфере очень малую проводимость, которую после вычисления
интеграла можно будет положить равной нулю. Последний интеграл
эквивалентен интегралу по замкнутому контуру. Пусть
u = ei^i du = iud^. A2)
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН |9.2&1
505
Тогда
, +к
2гЛ J А; -f X cos р я J 2Лм + X A + «2^ tiX J (м — Mj) (м — М2) '
где интегрирование производится в комплексной м-плоскости по единичной
окружности с центром в начале координат и где и^ и и^ — корни уравнения
о , 2ku , 1 ^
„2_1—_ 4-1=0.
A4)
Произведение корней равно единице, и, следовательно, и^^ лежит внутри
круга, а «2 — снаружи. Согласно теореме Коши, формула A33), стр. 280,.
7tX J (и — Ml) (и — щ) яХ («1 — Mg) J м — М]
2/
X(Mi —«2) УХ'^ —^2 ■
Следовательно,
уха —;fe2
A5)
A6)
Это выражение даёт нам первичное возбуждение e'^^'^jR во всех точках
плоскости £■ = 0 в виде суммы элементарных цилиндрических волн,
амплитуды которых выражаются функцией к(к^ — k^)~^l*. Выражение для любых
других точек следует непосредственно из G)
R
1
/
Jo(Xr)e^^^-''i''^
y-k^-kl
Idl
'iJlmR
=p
Je(lr)e-^''~^-''
XrfX
(^ < 0),
(^ > 0).
A7)
0 |A^^
Для вектора Герца результирующего поля мы имеем
схз
Hi = J [j/==^ +/1 (^)l ^(Ar).^^^=^^^a (z < 0).
CX3
r)e-^^^'-V«rfX (г>0).
A8)
Функции /i (X) и /2(A) должны быть теперь определены из граничных
условий F). Некоторые трудности связаны с первым из этих условий, так
как, если мы продифференцируем A7) под знаком интеграла по г- и затем
положим г равным нулю, то интегралы разойдутся. Зоммерфельд указал,
однако, НТО
[dz [ R )\z^o~ldR\ R ) R \z=o
A9)
50б гл. IX. КРАЕВЫЕ ЗАДАЧИ
Следовательно, в этом случае в A8) первичное возбуждение можно
отбросить. Простое вычисление даёт нам тогда следующий результат:
y}:'-ki [kiy-K^-ki + kiyx^-ki
\
kiyi^-kl-kiyi^-~kl\ \
^( -у-^2^:ц\kiy}j:^^+kiy}F^j'j
Подставляя эти выражения в A8), мы получаем окончательно
схз
Hi = 2^1 J i^ e'^'^^^i'^XdX (г<0),
о
со
U^ = 2kif ^^e-'^^'^^^^'^dX {2 > 0),
B0)
о
B1)
где
N = кЦ/'х^ -~ki + kiyx^ — kl B2)
Формально решение получено в виде интегралов в бесконечных пределах,
выражающих вектор Герца результирующего поля во всех точках как над,
так и под поверхностью 1).
9.29. Решение Вейля. Зоммерфельдом было с самого начала указано,
что его решение может быть интерпретировано как система плоских волн,
падающих на поверхность земли под различными углами и отражаемых и
преломляемых ею. Эта точка зрения была развита позднее Вейлем 2). Основой
его решения является интегральное представление функции щ {kR),
полученное в разделе 7.7. Согласно F6), стр. 362,
JkR *
tf4^^)H-^-- f^^^'^^rf^- B3)
<(
Как и на рис. 70, стр. 358, волновая нормаль каждой из элементарных
волн образует угол а с осью z и угол j3 с осью х. Точка наблюдения. Р
задаётся сферическими координатами {R, 6, о), а угол между
радиусом-вектором R и вол1^овой нормалью к равен т- Таким образом
(kR) == ^/^ cos Y и
Y] = cos Y == sin 8 sin a cos (<? — j3) -b cos 6 cos a, |
R cos Y = л: sin a cos p -J-J' sin a sin ^ -j- ■^^ cos a. j
1) Заметим, что при 1 ^^ | > ^| (очень длинные волны или очень большая
проводимость земли) Пз становится исчезающе малым по сравнению с Ht. причём
Щ?5^2—^. Если же kl== kl (обе среды — воздух), то Щ^^^^ПгРг^—^. Таким
образом, только при {k^f^kl поле над поверхностью вдвое больше того, которое
данный диполь создавал бы в воздухе. /7/?мж. ред.
2) W еу 1, Ann. Physik 60, 481, 1919.
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН [9.29]
507
Переходя в B3) от переменной интегрирования iq к т> мы получаем
я . 1С .
i_^= J e«^s<=o«TsinY^T = -^ J f ^■'^^*=°^TfsinYu?T^^, B5)
0 0 0
где <L — экваториальный угол системы полярных координат, ось которой
совпадает с радиусом-вектором R. Но sin'^d'^d'b является элементом
площади на единичной сфере с центром в начале координат, а значение
интеграла инвариантно относительно поворота координатных осей. Следовательно,
JkR
2я 2
— г оо
R
"" ^ ]* J ^*^^ ''"^ ^ ^^" ^ ^^ ^^•
B6)
воздух ^
Огпран<еинAЯ
волна
Это и есть представление сферической волновой функции через плоские
волны. Зоммерфельдовские соотношения A7) получаются из B6)
интегрированием по р. Вейль указал^ однако, что, доступая подобным образом, мы
теряем возможность
произвольного поворота системы
координат в положение,
наиболее облегчающее
интегрирование. Для последнего
более удобной является ось,
системы координат,
направленная вдоль
радиуса-вектора R, а не вдоль
нормальной к поверхности земли
оси Z.
Предположим, что
диполь расположен на
расстоянии 2^0 от поверхности
земли. В любой точке, для которой 2г>0, результирующее поле Пг может
быть выражено в виде суммы прямого или первичного поля По и
отражённого поля Па- В области Q^z^Zq между диполем и поверхностью земли
пербичное излучение даётся выражением
<77777777777777Т7777.
Земля к J
777777777777777
Преломленная
волна
Рис. 114. Излучение диполя может быть
представлено суперпозицией плоских волн, отражаемых и
преломляемых поверхностью земли.
eih^R
2ic "
— г со
Д — . =; JLZL I I g<fcsla;smagCosPj-f-ysina,siiiPi-f-(so —s)cos«g]^Q B7)
тде
dQ,^ = sin agdag^Pg. B8)
Для этой области «g представляет угол между волновой нормалью и
отрицательным направлением оси z^ как показано на рис. 114. Он является
в то же время углом, под которым элементарная первичная плоская волна
падает на поверхность земли.
Таким же образом можно построить из плоских волн и потенциал
Герца П^ для отражённого поля. Каждая из элементарных волн пучка будет
иметь вид
f gilt {^ sin «г cos Pj-f-y sin o^ sin ?a + {so+z) cos «,]_
Аналогично, преломлённое или прошедшее поле в области ^<0 может быть
построено из элементарных волн
f gil;%Zo cos Kg ^ki {X sin «i cos Pi-f-2/ sin «i sin Pi — г cos otj)^
508 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Оставшиеся пока неопределёнными функции /^ и /^ являются соответственно
коэффициентами отражения и преломления. Для упрощения обозначений
положим
кдГ = ^2 (^ si" ^2 cos Р2 "Ьз^ sin аз sin (За), |
j^r = ^j (д: sin а^ cos Pi -{"^'sinai sin p^). J
Тогда BO всех точках области О^г'-^гд результирующее поле будет
B9)
2« Т-*~
П2 = -4-^ f f (/^e«^-s2cas«s_^g-«gscos«s-^gfkgr+«vo cosog ^Q^. C0)
0 0
Bo всех точках, для которых г-^^О,
„ -^— * со
2тс 2
П1 = -^ Г Г f^e^^lr-iklSCOsal+iJ{^ZoCoso^^(lQ^^ (-31)
О О
Граничные условия при г = 0 дают
f^ = -^. *P, = Api^. C2)
Налагая эти условия на C0) и C1), мы получаем прежде всего, что
ki sin а^ = ^2 si" «2, Pi = ^2- B2)
Элементарные волны образуют круговой конус вокруг оси z, а угли
отражения а преломления удовлетворяют закону Снелля (8), стр. 433.
Дальнейшее вычисление даёт для коэффициентов отражения и преломления
_ feiCOSag —fe^COSCi __ ^21 COS °2 — V^-^21 — ^ + COS^ Cg
Jr~ /feiCOsa2 + ^2COsai " ^2^cos as + j/'zli - 1 + cos^ a~,'
2;feiCOsa2 1 2Z2iCOsa2
^*~Ш ^1
COS «2 + /^2 COS ai zl^ ^2 s аз + j/z^ - 1 + cos^ a^ '
C4)
где ^21 = V^k^lv-i^i- Силовые линии магнитного поля являются окружностями,
центры которых лежат на оси г. Меридиональные плоскости на, рис. 114
являются в то же время и плоскостями падения, отсюда, очевидно, что
магнитный вектор каждой из элементарных волн перпендикулярен к
плоскости падения, а электрический вектор параллелен этой плоскости, хотя
и не перпендикулярен к направлению распространения. Если мы обратимся
к формулам A9), стр. 435, то увидим, что с точностью до коэффициента
при /^ функции fy и ff. совпадают с френелевыма коэффициентами
отражения и преломления для плоской волны.
При z'^Zq выражение C0) должно быть видоизменено так, чтобы на
бесконечности оно должным образом обращалось в нуль. Измеряя теперь а
от положительно направленной оси Zy мы пишем
2тс 2
Il2=~ f f (;'^e»7-«8oCOS«j_|_^-«fr»SoCOscj')gik,r+f7i-aCOS«i^Qg C5^
О О
'' " ' - , •>
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТ^>АНЕНИВ РАДИОВОЛН [9.29] 509
■' V'. / ' ' '
7- Если, наконец, Zq == О, то это выражение принимает вид
— * ОО
2л 2
Пз = —% ft {«2) е^^'^ ^'' ^^" ^* """^ ^"^ -Р"^ +^ ''"^ "*' sin a^da^d[:iQ, C6)
^ о о
тогда как под поверхностью мы имеем в этом случае
тс
и^ = -^ f j ft (аз) е^'^'*'" ^i^ «*«°«l^P - ^^) - ^^'^ - ^^ «i^" "* sin agdagrfpa- C7)
о о
Теперь легко произвести переход к решению Зоммерфельда. Согласно
соотношению (80), стр. 364, мы имеем
2я:
Jq (Хг) е^^^ = -^ J ^^^'* ''"^ ^'^ ~ ^^+*'''' ^Р- C8)
о
Пусть
X = ^2sina2' Л=^2 ^os аз = г l/X^ — ^2. C9)
' ТС
При а2 = 0 имеем л = 0, а при а = ~ / оо имеем Х = со. В силу этих
соотношений C6) преобразуется в виду
- - ~г оо ^
ik^ С
П2 = -^- J /,(a2)yo(Vsina2M**«^<=°^«^sina2fira2 =
*^ о
схз
о
выражение C7) та же подстановка преобразует к виду
СО
Hi = Щ [ -^-^^ e'tV^^^^^zX^х, D1)
о'
где N — функция, определённая по' B2). Таким образом, решение
Вейля формально тождественно с решением Зоммерфельда для частного
случая 2'q = 0.
В общем случае, когда г^ф.^^ мы должны заменить /^ в C5) на
Л = (-|)'Л-1. D2)
После этого C5) может быть разложено на три части, которые, в силу
B7) и D0), приводятся к виду
схз
П2=-^--~ + 2Д.1 J -^.-1^^'-^И(^+^о)ЯйХ, D3)
510
гл. IX. КРАЕВЫЕ ЗАДАЧИ
где R^ и /?2—расстояния, указанные на рис. 115. Это выражение
справедливо при всех значениях г'>0. Результирующее поле в точке
наблюдения состоит, следовательно, из слагаемого, непосредственно от
вертикального диполя, расположенного в точке z=-]-Zq, слагаемого от его
изображения в точке г= — ^-q и дополнительного члена, который учитывает влияние
конечной проводимости земли^). При
Воздух
7777777777777777777?7,
(r,(p,z)
k^-^oo последний член в D3) имеет
пределом
Земля
А~ ~'Zfj
lim 2/г2
Рис. 115. Изображение диполя^располо-
жено в земле, в точке г ="— Zq.
и, в силу уравнения A7),
п,
Ri
Ri
D4>
D5>
Тождественные результаты были получены и Ниссеном ^), применившим
метод Гюйгенса-Кирхгофа, рассмотренный в разделе 8.13. Поверхностные
интегралы должны быть распространены по поверхности земли и по малым
сферам, исключающим особенности, имеющиеся в источнике и в точке
наблюдения.
9.30. Решение Ван дер Поля. Интересное и практически важное
преобразование выражений Вейля-Зоммерфельда было найдено Ван дер Полем ^).
Отправляясь от интеграла для отражённого поля
со
п.
J
_ г klVl'-4-kl Vl'-kl j^(ir)e -1^^^=^(^ +
So)
kiYx^__ki+ki V>^^~ki
y-^^ - k
XdK
D6)
получаемого из 'A8) и B0), Ван дер Поль показал, что полное поле —
первичное и отражённое— в любой точке над поверхностью земли может
быть представлено в виде объёмного интеграла, распространённого по
некоторой области действительного пространства. Последовательные этапы
доказательства опираются на свойства бесселевых функций, рассмотренные на
предшествующих страницах этой книги. Подробности мы здесь опустим. Длш
всех значений г'>0 Ван дер Поль получает выражение
П.
е
.щв^
R2
R-y
+
Rx
Ж
vj
Р
dv.
D7)
Элемент объёма есть dv = р dp dC,d§^ а пределы интегрирования О^р^оо^
1) Очевидно, такая трактовка неправильна, так как второй член имеет фазу
обратную фазе волны от изображения диполя, третий же член при ki-> оо не
исчезает. Впрочем, это непосредственно видно из D4) и D5). Прим. ред,
2) Niessen, Ann. Phys. 18, 893, 1933.
3) V а п der Р о 1, Physica 2, 843,1935.
влияний ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН [9.31 ]
511
О <! С <; СО,. О <^ Р <; 27:. Расстояние р = ]/р2 -\- С^, а величина R^
представляет собой «комплексное расстояние», определяе!мое соотношением
/
^^ = 1/ p2-{-2prcosp + ^' + U + -^o
{
D8)
^'С ^^,2/
Предполагается, что k^ действительно, а знак у корня выбран;,так, чтобы
действительная часть в D8) была положительной. Область интегрирования
может быть интерпретирована как полупространство под геометрическим
изображением источника; она представлена заштрихованной частью рис. 116.
Переменные р. С, j3—цилиндрические координаты, начало которых взято>
в точке z==—Zq^ в которой расположено изображение источника. Ось С
направлена вниз.
Если проводимость земли велика, то постоянная распространения k^
имеет большую мнимую часть. Соответственно, волна —stf"!" ) оыстро
затухает и её роль в интеграле заметна только при малых р. Иными
словами, вторичные волны посылаются
к наблюдателю только той частью
нижней среды {земли), которая
расположена в непосредственной
близости к геометрическому изо-
бражению источника, но ниже его.
В пределе при бесконечной
проводимости, область, в которой
находятся источники, фактически дающие
вторичное излучение, сжимается
в точку, совпадающую с самим
геометрическим изображением.
Аналогичное, но несколько
более простое решение дано Ван дер
Полем и для случая магнитного
диполя; метод может быть
распространён и на горизонтальные диполи. Ввиду того, что любой источник
электромагнитного излучения может быть представлен в виде некоторого распределения
электрических и магнитных диполей, применимость этих расчётов ко многим
другим задачам физической оптики и электромагнитной теории очевидна.
Можно упомянуть, например, довольно сложные явления, связанные с
полным отражением, которое мы рассмотрели только в идеализированном
случае бесконечной плоской волны.
9.31. Приближённые выражения интегралов. Легко показать, что
интегральные представления поля или,- точнее говоря, вектора Герца этого
поля, к которым приводят все различные способы подхода к задаче об
отражении от плоской поверхности, тождественны между собой. Значительно
более трудной является задача, привлекавшая внимание многих
исследователей и состоящая в том, чтобы привести эти интегралы к практическим
формулам для напряжённости поля. Метод Зоммерфельда основывался на
деформировании пути интегрирования в комплексной плоскости X. Функция
IjN, определённая соотношением B2), имеет точки ветвления при
Л = ± /г^ и при X = zt ^2 ^ полюс при
Рис. 116. В решении Ван дер Поля областью
интегрирования является полупространство,
расположенное ниже плоскости г = —Zq.
k^ki
Vk\+ki
D9)
512 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Соответствующая' риманова поверхность имеет четыре листка; только на
одном из них выполняются условия в бесконечности, необходимые для
сходимости интеграла. Согласно Зоммерфельду, путь интегрирования на этом
листке может быть разложен на три части: первая часть — петля, идущая из
бесконечности вокруг точки ветвления X==-|-^i, вторая часть — подобная же
петля вокруг точки ветвления X = -{- ^2 и третья часть — небольшая
окружность вокруг полюса в точке X = Iq. Обозначим слагаемые
интегрирования по петлям вокруг точек ветвления через Qj и Qg' ^ вычет при
интегрировании по окружности — вокруг полюса Р; таким образом, 112 =
= Qi + Q2~l~^' Члены Qj и Qg были разложены Зоммерфельдом по
обратным степеням расстояния от диполя, причём главные члены этих рядов
пропорциональны соответственно e^^^^jR и e^^*^/R. Поэтому Qj и Q2 были
интерпретированы как «пространственные волны». С другой стороны, для Р
Зоммерфельд получил функцию вида
р L giXor-V X„*-fr,=» z (г > 0),
Yr
р ^ _i_ e*V+TV-Ai*^ (^ <;0),
I
E0)
которая была интерпретирована им как «поверхностная волна».
Исторически эти поверхностные волны имеют значительный интерес.
Направляющее действие плоской поверхности раздела диэлектрика и
хорошего проводника на распространение плоской волны, повидимому, было
впервые исследовано Коном *) и вскоре затем Уллером 2), Ценнек ^) указал
на связь этих исследований с вопросом о распространении радиоволн и
показал, что уравнения поля допускают решение, которое может быть
интерпретировано как поверхностная волна, направляемая плоской поверхностью
раздела двух любых сред. Это решение тождественно с поверхностной волной,
полученной нами иным путём в разделе 9.13. Ценнеку были совершенно
ясны ограничения, которым подчинялись его результаты. Он показал, что
волна, фронт которой имеет некоторый наклон вперёд и которая следует
вдоль плоской поверхности земли, затухая, как в горизонтальном, так К в вертиг
кальном направлении, совместима с уравнениями Максвелла и что подобными
волнами объясняется множество явлений, наблюдаемых при распространении
радиоволн. С другой стороны, до сих пор не доказано, что радиоантенна
действительно возбуждает волны подобного типа. Зоммерфельдовская работа
1909 г. была написана с тем, чтобы завершить доказательство этого, и член
Р в уравнении E0) он интерпретировал как поверхностную волну (в
цилиндрических координатах).
Впервые сомнения в правильности зоммерфельдовского расчленения
решения были высказаны Вейлем в его работе 1919 г. Применяя к интегралу C6)
«метод перевала» (стр. 324—325), Вейль получил представление
дифрагированного поля в виде асимптотического ряда. При \k^\'lk2'^l решение Вейля
также приводится к виду, в котором оно может быть интерпретировано как
суперпозиция пространственной и поверхностной волн. Но
поверхностная волна Вейля нетождественна с поверхностной волной Зоммерфельда и
Ценнека.
Расхождение между двумя видами решения было в последние годы
*1Сследовано более внимательно, но едва ли можно сказать, что задача пол-
1) Cohn, Das elektromagnetische Feld, Leipzig, 1900.
2) Uiier, Rostock Diss., 1903.
3) Zen neck, Ann. Physik 23. 846, 1907.
ВЛИЯНИЕ ЗЕМЛИ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН 19.31] 51S
ностью разрешена i). Бёрроуз ^) указал на то, что в числовом отношении
формулы для распространения, полученные на осирвании решения Зоммер-
фельда, отличаются от соответствующих формул Вейля как раз членом Р,
дающим поверхностную волну, и произвёл тщательные измерения, которые
подтвердили результаты Вейля. Расхождение велико только в том случае, когда
токи смещения в почве сравнимы с токами проводимости. Асимптотические
разложения были даны Уайзом ^) и Райсом ^), которые показали, что если
учесть все члены в разложениях Q^, Qg и Я в решении Зоммерфельда, то
член Р сокращается. Наконец, Нортон ^) обратил внимание на ошибку в знаке,
которая имелась в работе Зоммерфельда 1909 г. В работе 1926 г. эта ошибка
устранена, но приведённые в ней числовые результаты являются точными
лишь при большой проводимости земли.
, С точки зрения практики мы можем в итоге сказать следующее. Если
токи смещения сравнимы с токами проводимости, как это имеет место в
случае ультракоротких волн, то на решение Зоммерфельда и основанные на
нём диаграммы Рольфа ^) полагаться нельзя. Формулы Ван дер Поля, Нис-
сена, Бэрроуза и Нортона '^) являются в большей своей части развитием
результатов Вейля. Напряжённости поля, подсчитанные по этим формулам,
согласуются друг с другом и, повидимому, находятся в хорошем согласии с
опытом. То же справедливо и в отношении результатов, полученных Стрё-
том ^), который применил для получения асимптотического решения другой
метод.
1) В свете последних работ советских авторов (экспериментальные—см. сборник
«Новейшие исследования распространения радиоволн», изд. АН СССР, 1945;
теоретические—В. А. Фок, глава XXIII в книге Франк иМизес, Дифференциальные и
интегральные уравнения математической физики, ОНТИ, 1937; П. А. Р я з и н,
сборник «Новейшие исследования . . .») положение полностью разъяснилось.
Ценнек в 1907 г. показал, что поверхностная волна, экспоненциально
убывающая с расстояниями и движущаяся с фазовой скоростью, зависящей от свойств
земли, является решением уравнений Максвелла, удовлетворяющим граничным
условиям. Наглядность этой простой картины оказала влияние на все дальнейшие
исследования и даже побудила авторов, шедших по верному пути, искать в своих формулах
эту поверхностную волну. Однако решение Ценнека не отвечало физической задаче,
так как прежде всего оно ничего не говорило о способе возбуждения указанной
поверхностной волны и, соответственно, не содержало особенности в месте
расположения диполя. Л. И. Мандельштам и Н. Д. Папалекси с сотрудниками доказали
экспериментально, что реальные излучатели никакой ценнековской волны не дают. Они
показали, что скорость распространения с увеличением расстояния от излучателя
перестаёт зависеть от свойств почвы и стремится к значению скорости в воздухе,
что никакого экспоненциального убывания поля нет.
В. А. Фок повторил (совершенно строгий по идее) вывод Зоммерфельда и
показал, что в ходе вычислений Зоммерфельд допустил ошибку, устранение которой даёт
результат, совпадающий с формулой Вейля и не совпадающий с зоммерфельдовской
формулой 1909 г. (противоположное замечание в книге Франка и Мизеса на стр. 954
после формулы G5) сохранилось после внесённого Фоком исправления выкладок по
яедоразумению). Разбиение поля на поверхностные и пространственные волны
типа E0) совершенно ошибочно и не отвечает реальным фактам. Наконец, Рязин путём
разложения точного решения в ряды, вычислил поле и получил целый ряд его
характеристик, которые полностью совпали с упомянутыми выще экспериментальными
результатами.
С другой стороны, приводимые далее формулы F4) и F5) правильны, но
содержащееся в них разбиение на поверхностные и пространственные волны имеет
совершенно иной характер, чем у Ценнека. В частности, отдельно взятая «поверхностная
волна» F5) не удовлетворяет граничным условиям D). Прим. ред.
2) Burrows, Nature, Aug. 15,1936; Pro с. Inst. Radio Engrs. 25, 219, 1937.
3) Wise, Bell System Tech. J. 16, 35, 1937.
, *) Rice, Bell System. Tech. J. 16. 101, 1937.
») Norton, Nature 135, 954. June 8.1935; Proc. Inst. Radio Engrs. 2Ъ, 1192, 1937.
6) Rolf, Proc. Inst. Radio Engrs. 18, 391,1930.
7) Norton, Proc. Inst. Radio Engrs. 24, 1367, 1936; 25, 1203, 1937.
8) Strutt, Ann. Physik 1, 721, 1929; 4, 1, 1930; 9, 67, 1931.
33 Зак. 593. Теория епектромагнетизма.
514 гл. IX. КРАЕВЫЕ ЗАДАЧИ
Для ТОГО чтобы дать некоторое представление о характере формул,^
применяющихся для практических расчётов, мы приведём вкратце результаты,,
полученные Нортоном для вертикального электрического диполя. Вектор
Герца результирующего поля в любой точке над поверхностью земли равен
где V—интеграл в бесконечных пределах, соответствующий третьему члену
формулы D3). Приближённая формула, предложенная для V, такова:
V^=[(l—/?,)/=•+1-f/?J-^, E2>
где
Z^j COS 61 — l/^Z|i — sin2 61
R^ = ~ ' E3>
zliCosei + j/^z^j-sin2e,
/?„ — френелевский коэффициент отражения для плоской волны, падающей
под углом Oj. Кажущийся источник расположен в данном случае под
поверхностью земли на расстоянии 2:5 (см. рис. 115). Функция F выражается так:
F = [ 1 4- / Ут^ e-^erfc (— i Y'^)]. E5)
где
со Yw
erf С (— i Yw) = -4= { e-^*dx==~{ e^* dx, E6>
уте J т/те J
-iVw . *■«' •
J/z|i—sinseij A—^r)
E7)
Pi = f^^ (^'1 - sin2 8,) = ре^ъ. E8)
Так как
TO мы можем написать также, что
»
>>=^' t[-^+'(> -;^^'"''в.)] ^j^. F0).
где Л — длина волны в свободном пространстве. У Нортона дано подробное
численное исследование функции F.
Для того чтобы окончательная формула давала напряжённость поля от
элемента тока, вектор Герца умножается на соответствующий амплитудный
фактор. Согласно D4), стр. 380, вектор Герца для'линейного элемента
тока Idz равен
I е
dJl=-^'--Idz. F,1)
4«oj£ R ^ ^
Умножая E1) на iIdzJAi:(aB^ и применяя C), Нортон получает следующее
ВЛИЯНИЕ ЗВМЛЙ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН [9.311 515
выражение для «--компоненты напряжённости электрического поля в вольтах
на метр:
dE, = ^^ Idz[sin2 \^^K sin^8, ^-^
^iJi^Bx
-J- члены высшего порядка по отношению к -^ 1. F2)
Члены с \\IU. и 1//^2 относятся к «статическому» и «индукционному» полям,
и ими можно пренебречь на расстояниях порядка десятка длин волн от
источника. Угол вд определяется соотношением
cos 82 = i=^. F3)
Аналогичное выражение может быть получено и для компоненты dB^y
которая, совместно с F2), определяет наклон или поляризацию поля.
В частном случае, когда элемент тока расположен на поверхности земли
или оченц близко от неё, 2-0 = 0 и i?j = i?2 = ^> 81 = 82 = 8. Полная
напряжённость ^поля в любой точке, для которой R'^>\, может быть теперь
выражена в виде некоторой суммы двух компонент:
йЖпространств = — ^ Idz 8ш 8 A + R^) —„— Зе, F4)
4. /^^A-^.)^V
/(ОМ- gi^iR
"^поверхности ^= л 1UZ\\ R^) г q /\
X [а.+а,^ (l +^yz|,-si„^e] , F5)
где ag — единичный вектор, касательный к меридиану, проходящему через
точку наблюдения в направлении увеличения угла 8 и, следовательно,
перпендикулярному к радиусу-вектору R, тогда как а^ и а^ — единичные векторы
цилиндрической системы координат, параллельные z- и г-направлениям. Если
проводимость земли стремится к бесконечности, то R^-> 1. Компонента F5)
тогда исчезает, и полное поле F4) сводится в каждой точке к полю диполя
и его изображения. В случае конечной проводимости /?^ -» — 1 при 8 -»7г/2.
Вблизи поверхности земли теперь исчезает компонента F4), и полное поле
выражается одним только членом (t'5). Поскольку поле распадается на две
такие части, мы должны согласиться с Нортоном, что термины
«пространственная» и «поверхностная» волны полностью оправданы, хотя
поверхностная волна F5) и не совпадает с поверхностной волной, предсказанной
Ценнеком и Зоммерфельдом. Уравнение F5) представляет собой выражение
для «вемной волны», которой объясняется в главной своей части
длинноволновая радиосвязь, в то время как F4) соответствует излучению под
большими углами к поверхности земли, которое отражается от ионосферы и
даёт сильные сигналы на больших расстояниях.
Распространение формального решения от случая плоской земли на
случай сферической не представляет серьёзных затруднений. Поле диполя или
элемента тока может быть выражено с помощью сферических волновых
функций методами, подобными рассмотренным в главе VIII. Однако, поскольку
радиус земли гораздо больше длины волны, получающиеся ряды сходятся
очень плохо, и трудности сведения формального решения к практически
применимым формулам становятся действительно грандиозными. В последнее
S3*
516 гл. IX. КРАЕВЫЕ ЗАДАЧИ
время был достигнут значительный прогресс в преодолении этих чирто
аналитических трудностей; детальное рассмотрение дифракции поля диполя на
бесконечно проводящей сфере для всех значений отношения радиуса сферы
к длине волны было дано Ван дер Полем и Бреммером ^).
ЗАДАЧИ
1. Нормально падающая плоская волна, отражённая от плоской поверхности,
выражается формулой
где г — коэффициент отражения, равный отношению амплитуды отражёаной волны
к амплитуде падающей. Полагая
л- = — e-2Y,
показать, что
6 = 2Me-Tsin {kz — /у).
Заметьте, что сдвиг фаз падающей и отражённой волн при -г = О равен удвоенной
мнимой части у. а отношение амплитуды (безотносительно к фазе) равно е~^^^^'^\
2. Плоские волны отражаются от плоской границы, разделяющей два диэлектрика.
Пусть первичная волна падает из средыA) и преломляется в среду B);
относительный показатель преломления л= y^TTi^ Пусть г—отношение амплитуд
электрического вектора отражённой волны и электрического вектора падающей волны.
Показать, что при Е, перпендикулярном к плоскости падения,
_ п cos Gq — Y\ — n2sin2 0o
-L n cos % 4- У1 — rfl sin2 %
a при E, параллельном к плоскости падения,
cos Bq — п У1 — rf- sin2 ё^
г и =
COS Во + п yi — и2 sin2 Во
где 6о — угол падения.
3. Плоская волна отражается от плоской поверхности раздела двух диэлектриков,
диэлектрические проницаемости которых отличаются на очень малую величину.
Применяя обозначения предыдущей задачи и полагая п=1-\-Ь.п, показать, что
г.с^г» и оба приближённо равны ' •
1 — УТ^^ШП^Ь^ 9 — Уср2_ 0,657-Ю-^Дп
f СУ :- -■■■ —^—-■ — г>у JL- *.—^ ■ . .
1 4- /i—2Awtg2e7 ср 4- У^Р2 — 0,657. Ю-4Дп'
7U %
где «р = -?[• — 6о и во второй формуле выражено в градусах.
Применить этот результат к отражению радиоволн от границы между
различными воздушными массами в тропосфере. Начертить г в функции от <^, полагая
Дп = rt 10-4^ При каких условиях может наступить полное отражение?
4. Нормально падающая плоская волна отражается от поверхности земли. Начертить
величину скачка фазы при отражении от поверхности в функции проводимости для
волн длиной в 10 и 500. ж, полагая диэлектрическую проницаемость земли равной 9,
а проводимость — от 10-2 до 10-^ обратных омов на метр (в зависимости от
влажности).
i)Van der Pol иВгеттег, Phil. Mag. 24, 141, 825, 1937; 25, 817, 1938.
Проблема дифракции вокруг земли в настоящее время решена полностью благодаря
работам В. А. Фока, (Дифракция радиоволн вокруг земли, изд. АН СССР, 1946).
Формально правильное разложение в ряд по сферическим функциям, которое само
по себе получается весьма просто, здесь бесполезно, так как число членов ряда,
которые необходимо учесть при вычислениях, имеет порядок удвоенного числа длин
волн, укладывающихся на окружности земли. Фок преобразовал это решение и свёл
его к квадратурам, дав как асимптотические выражения для крайних случаев, так и
табулированные функции для промежуточных случаев. Прим. ред.
ЗАДАЧИ 517
5. Воспользовавшись развитой в разделе 9.7 теорией полного отражения,
вычислить для предыдущего случая средние по времени потоки энергии параллельно
и нормально к поверхности отражения в oiSenx средах.
6. Волна радиоальтиметра в 20 см падает нормально на ледяное поле,
образовавшееся на поверхности солёной воды. Вычислить примерную толщину льда, при
которой коэффициент отражения будет минимальным. Каково это минимальное значение
коэффициента отражения? Проводимость льда предполагается пренебрежимо малой.
7. Пусть на плоской границе раздела двух диэлектриков мы имеем
поверхностные волны типа, описанного в разделе 9.13. Рассмотреть поле этих волн и свойства
потока энергии. Показать, что угол падения, необходимый для возникновения
подобных волн, совпадает в этом случае с углом Брюстера.
8. Вопрос о влиянии переменного переходного слоя на отражение волн, идущих
из одной среды в другую, имеет большое значение, и приближённые решения
могут привести к ошибочным заключениям. Истинный характер этого явления был
выяснен благодаря исследованиям Валлота (W а 11 о t, Ann. PhysikGO, 734, 1919) i).
Предположим, что среды A), B) и C) отделены друг от друга плоскими
поверхностями раздела -г = О и z = d, как это показано на рис. 96, стр. 450. Проводимость
всех трёх сред равна нулю. Диэлектрик в областях A) и C) однороден, и
диэлектрические проницаемости равны соответственно ei и ез. Диэлектрическая
проницаемость среды B) зависит от г по закону
H^Hi^ + ^^r'f
где константа а связана с толщиной слоя d соотношением
1
ad
Ш--
или
Линейно поляризованная волка проходит из среды A) в среду B) нормально
к поверхности раздела. Пусть
Вводя новую перемену w, определяемую соотношением
2
W — Wq— I l/"e dz,
■ О *'
показать, что уравнения поля будут иметь вид
dE ш|х dH . _/■-„
dw |/7 dw '
Е +~ Ё + ay^ixE = о, Н—~ Н + а>^Н = о,
где точки обозначают дифференцирование по w. Для принятого нами закона
изменения в^ мы имеем
9 тА" ^+2 те+2
'" = ^гТ2)-(' + ''") ' =A + '^-) ^
или
, 2п
Полагая
/г + 1 2 о — 1
1) Валлот, повидимому, не знал о классической работе Релея, в которой гораздо
более простым путём, чем в данной задаче (т. е. у Валлота), ещё в 1880 г. были
совершенно строго получены те же результаты. См. Rayleigh, Proc. Lond. Math.
Soc 11 51, 1880 или Sci. Pap. т. I, 460 A889). Прим. ред.
518 гл. IX. КРАЕВЫЕ ЗАДАЧИ
получить уравнения поля в виде
2р — 1 .
1—2/?' .
и показать, что в переходном слое
Определить из граничных условий константы Л и В и получить выражения для
отношений амплитуд отражённой и прошедшей волн к амплигуде падающей волны.
Показать, что отражение имеет заметную величину только в том случае, когда
толщина переходного слоя порядка длины волны, и что в пределе для бесконечно
тонкого слоя мы получаем классическое выражение для коэффициента отражения.
Обратить внимание на то, что эта теория применима также к распространению тока
и напряжения вдоль передаточной линии с переменными параметрами.
9. Плоская бесконечная плита толщины 2а помещена в диэлектрик.
Постоянные распространения внутри плиты и во внешней среде равны соответственно ki
и ^2* Показать, что вдоль плиты могут распространяться как
поперечно-электрические, так и поперечно-магнитные волны. Показать, что в случае
поперечно-магнитных волн с вектором Н, параллельным плите, постоянная распространения Л,
определяющая фазовую скорость и затухание допустимых волн в направлении их
распространения, определяется корнями уравнения
XhaYlfi.
/г2
ft2
Задача эта решается быстрее всего посредством волновых функций задачи 1 главы VI
и путём приравнивания нормальных волновых импедансов на каждой из
поверхностей. ,
10. Определить давление, «оказываемое плоской электромагнитной волной
падающей на плоскую поверхность, в зависимости от угла падения и вида
поляризации.
11. Плоская волна падает под углом 6 на бесконечную плоскопараллельную
плиту толщины d. е, (л, о — электрические постоянные плиты, по обе стороны от
которой находится свободное пространство. Вычислить давление, оказываемое
волной на плиту. (D е b у е, Ann. Physik 30, 67, 1909; L е b е d е w, Ann, Physik 6, 433,
1901; Nichols и Hull, Ann. Physik 12, 225, 1903).
12. Вертикальный электрический диполь расположен в среде A), постоянная
распространения которой равна k^, в точке с координатами а: = 20, г = 0. Среда B)
имеет вид бесконечной плоскопараллельной плиты с постоянной распространения
k^ граничные поверхности которбй имеют координаты z = a<^ZQ и z == 0.
Полупространство z<^ заполнено веществом с бесконечной проводимостью. Полагая,
ехр (ikR) ^
что первичное поле имеет вид —~—- , показать, что вектор Герца вторичного
(отражённого) поля в первой среде равен
Пв^орич. = //^0(И^-^^^-^-^^^'-^^°-^^> у^
л
k\ [/"х^ — Izl + кЦ/'-к^ — kl th Г[/"Х2 — А!| а^
где г—расстояние по горизонтали от источника до точки наблюдения (Van der Pol
und Bremmer, Phil. Mag. 24, 825, 1937).
ЗАДАЧИ 51 f
13. В большинстве практических случаев, даже при очень высоких
радиочастотах, поле и распределение тока в металлическом проводнике могут быть с
достаточной точностью найдены из уравнений
Е =1 г(оА, В = rot А, * J = /шоА,
ДА + /«{^оА = 0, div А = О
•{см. задачу 20, гл. V). Здесь полностью пренебрегается влияние внешнего поля на
•постоянную распространения волн внутри проводника и считается, что время
входит в виде множителя ехр (—/«/); J и А должны быть всюду конечны, а на
поверхности, разделяющей проводник и диэлектрик, нормальная компонента
J должна быть равна нулю.
14; С помощью этих уравнений найти распределение продольных токов по
поперечному сечению очень длинного прямого круглого провода. Получить
выражение для продольной компоненты напряжённости поля Е в виде
!сде / — полный ток, /? и L^—сопротивление и вяу/и/7екняя самоиндукция,
рассчитанные на единицу длины.
15. Переменное магнитное поле направлено перпендикулярно к длинному,
проводящему цилиндру радиуса Ь. В рассматриваемой области поле однородно, а длина
волны намного больше а. Рассчитать мощность, рассеиваемую в единице длины
«проводника индуцированными в нём токами Фуко. (См. Френкель.
Электродинамика, т. II).
16. Тонкий бесконечный плоский проводящий лист помещён в однородное
переменное магнитное поле. Частота поля настолько мала, что толщина «скин-слоя»
намного больше толщины листа. Найти выражение для векторного потенциала
индуцированных в листе токов Фуко и рассеиваемую на единицу площади мощность.
17. Следуя общей теории, развитой в разделе 6.2, расомотреть
распространение волн вдоль идеального цилиндрического проводника. Показать, что в
ортогональной системе цилиндрических координат м^, м^ z, в предположении Eg = ffg = 0
•остальные компоненты поля могут быть получены из двух скалярных функций
9 и ф по формулам
Е =_1 il Е = — 1 ^
_1__^ 1^ ^
h2 ди"' ^~ hidu^'
лричём эти потенциальная и токовая функции удовлетворяют уравнениям
dz^ dt ~" • y^. dz ^ di~"'
ди> Ui диЧ "^ дФ \h^ диУ ~ '
r- 1
где jj, и e относятся к внешнему диэлектрику.
Пусть д—заряд на единицу длины, / — ток в каком-либо проводнике,
а С — замкнутый контур, охватывающий только этот проводник и лежащи|[ в
плоскости Z = const. Показать, что
J дп [J- J дп у гл
ип у ■ "
G
еде дифференцирование производится по внешней нормали.
Теория эта применима к любому числу параллельных проводников
произвольного, но постоянного поперечного сечения, при з'^словии, что сумма зарядов
<q в любой перпендикулярной плоскости равна нулю. В противном случае функции
520 гл. IX. КРАЕВЫЕ ЗАДАЧИ
«риф нерегулярны (логарифмически) на бесконечности. В случае двух
параллельных проводников а к b мы имеем да= —Яъ- Ёмкость и индуктивность на
единицу длины определяются выражениями
С=—^^— L— '^^-"^^
такими же, как и для статического режима. Показать, что в системе единиц MKS
и что ток и заряд удовлетворяют соотношениям
с dz~^ di~ ' dz~^ dt ~ '
dz-^ di^ ' dz"^ ^ dfi
18. Теория распространения электромагнитного поля вдоль параллельных
цилиндрических проводников, рассмотренная в задаче 17, была распространена Абрагамом
на случай конечной проводимости. Данное им приближённое решение достаточна
точно и вполне применимо в большинстве практически важных случаев.
а) Предполагается, что волны поперечно-магнитные. Мы видели в разделе 9.15,
что во всех случаях, когда поле не обладает аксиальной симметрией, это, строго
говоря, неверно; однако допускаемая при этом ошибка в, общем очень мала.
Предполагается далее, что поле гармоническое. Взяв для скалярного потенциала
выражение
dz
ср=--^=/(«1. П2)е*>-*^"*
показать, что в любой точке проводника или диэлектрика компоненты поля могут
быть получены из соотношений
Hi = :z £2. H2 = -—\Ei, Hz = 0,
Вычислить ^-компоненту комплексного вектора Пойнтинга S+ и проинтегрировать
её по всей х, ^'-плоскости, перпендикулярной к проводнику. Пусть величина этого
интеграла равна 1Г+. Показать, что
2т 2y
W+ = —■— X магнитная энергия диэлектрика 4--г-^Х магнитная энергия проводника
^— =джоулеву теплу-1-2г(о (электрическая энергия —магнитная энергия),
где индекс е отмечает величины, относящиеся к внешней среде, а индекс i —
величины, относящиеся к проводнику, а все остальные величины рассчитаны на единицу
длины проводника. Сделаем теперь cлeдyющr^e предположения:
b) В диэлектрике продольная компонента yf^s очень мала по сравнению с
поперечным полем и, следовательно, для внешней среды значения компонент Е\^, Е^, Hi, Н^
совпадают с теми, которые получаются для случая идеального проводника. Кроме
того, значения ёмкости С и внешней индуктивности L^ остаются неизменными,
причём, как и в задаче 17, >е^ = 1е^' Электрической энергией диэлектрика,
приходящейся на продольное поле, можно пренебречь.
c) В металле можно пренебречь поперечной компонентой электрического поля
по сравнению с продольной и электрической энергией по сравнению с магнитной.
Рассмотрим пару проводников, по которым текут равные токи
противоположного напрйвления. Пусть R будет удвоенным сопротивлением переменному току
единицы длины проводника, Li — внутренняя индуктивность единицы длины обоих
проводников. Обе эти величины являются функциями частоты и зависят как от
расстояния между проводниками, так и от размеров их поперечных сечений. Прибли-
ЗАДАЧИ 52 i
жённо они могут быть получены методом, указанным в задаче 13. Учитывая, чтО'
рассматриваемые энергии являются средними по времени, показать, что
dW+ 1 „,«. , . / YY* ,\ 1 , r«, гЪ
^2
Вторым членом в W+ можно пренебречь, и тогда для постоянной распространения
мы получаем
19. Согласно задаче 18, для волн, распространяющихся вдоль пары параллельных
цилиндрических проводников, мы имеем для постоянной распространения
выражение
Полагая у = « + /р и L = Ц-\- L^, где L — полная индуктивность единицы длимые.
показать, что
ЕСЛИ (^f)'«;i.TO
20. Система Лехера состоит из двух длинных проводов круглого сечения,
натянутых параллельно друг другу. Пусть радиус каждого из проводов равен Ь, а
расстояние между их центрами 2а. Показать, что ёмкость и внутренняя
самоиндукция равны соответственно
С= —■ фарад! метр,
■п(''+-^;'-*')
Ig = — 1п(—■—-7 1 генри/метр.
Если а'^^Ь, то влиянием одного из проводников на.распределение тока в другом
можно пренебречь, и сопротивление и внутренняя самоиндукция на единицу длины
проводника приближённо даются формулами, приведёнными в конце раздела 9.17,
Для того чтобы получить представление о порядке величин, предположим, что
проволоки медные радиуса 2 мм, а расстояние между ними 10 см. Вычислить С, L^ Ц
и R для частот IQS, Ю^ и 10^ циклов в сек. и определить затухание в децибелах на
метр. Рассмотреть зависимость различных параметров от расстояния между
проводниками и от их радиуса..
21. Если в предыдущих задачах мы учтём утечку через диэлектрик, то для
распространения токов вдоль пары параллельных проводников общим уравнением
будет уравнение B7), стр. 482:
62/ ^2/ dl
522
гл. IX. КРАЕВЫЕ ЗАДАЧИ
-Это уравнение было подробно изучено впервые лордом Кельвином в связи с
подводными кабелями. С помощью преобразований Фурье или Лапласа, рассмотренных
в главе V, найти общее решение, выраженное через начальные условия, налагаемые
яа токи и напряжение. Показать, что при соответствующем выборе параметров
скорость распространения волн и их затухание могу г быть сделаны не зависящими от
частоты, так что сигналы будут распространяться без искажения.
22. Возможность прокладки трансатлантического кабеля была впервые доказана
лордом Кельвином в его теоретической работе, опубликованной в 1885 г. В
рассматриваемом случае можно пренебречь самоиндукцией и утечкой по сравнению с
сопротивлением провода; потенциал по отношению к земле удовлетворяет уравнению
^^ dt ~ дг^ •
По Кельвину, время, необходимое для того, чтобы данный потенциал возник на
расстоянии 2-от начала, пропорционально произведению CR на квадрат • расстояния.
Получить этот результат.
23. Задача, состоящая в избавлении от перекрёстных помех («cross talk») между
двумя телефонными линиями с помощью цилиндрических экранов, имеет большое
техническое значение. Для того чтобы привести задачу к такому виду, в которое! и
она может быть удовлетворительно разрешена, предполагают обычно, что изменением
поля вдоль линии можно пренебречь, тах что поле является двумерным. Это
предположение справедливо до тех пор, пока длина волны намного больше расстояния
между проводниками и между проводником и экраном. Показать прежде всего, что
при этих предположениях уравнения поля распадаются на две группы:
/(OJJ. 1 дН^
Ж'
Еь =
Ж 1?
и^ }
1 г ё дЕг
56
]=
ш\).Н^
A)
Hv
Яе
1
Я
дЬ '
/@|i дг '
(II)
Помехи от полей первого типа обычно называются «электростатическими»
перекрёстными помехами, а связанные с полями второго типа — «электромагнитными». Эти
термины совершенно неудачны и могут привести к путанице, но они укоренились
в технической литературе.
Вторая группа уравнений представляет собой поле одной или нескольких нитей
переменного тока. Показать, что поле, связанное с одиночной нитью /, равно
iki
Нь=^~ Я?> {Щ е-ш, £. = - Т- ^?^ (И е
(О р./
-i^sЛ
И что его радиальный импеданс равен
Е, _ mv.t^^\kr)
Соленоидальные или вихревые линии тока создают поля первого типа, но точно
такие же поля могут быть созданы и двумя заряженными нитями с зарядами
противоположного знака, откуда и происходит название «электростатическая» помеха.
24. Передаточная линия состоит нз двух проводников радиуса Ь, расстояние
между центрами которых равно 2а. Индуктивность и ёмкость единицы длины
известны из результатов задачи 20. В отношении внешнего поля система эквивалентна
паре нитей тока силы / и противоположных знаков и паре заряженных нитей с
зарядом q на единицу длины и противоположных знаков. Рассмотреть задачу в
биполярных координатах и показать, что положение этих нитей не совпадает с центрами
проводников, но что влиянием этого отклонения на поле можно пренебречь, за
исключением, быть может, непосредственной окрестности Самих проводников. Пусть
ЗАДАЧИ . 523
^иния, проходящая посредине между проводниками, совпадает с осью г цилиндриче-
'Ской смстемы координат. На расстояниях от этой оси, намного меньших длины волны,
лоле под^иня(|тся уравнениям задачи 23.
Показать, что в точках, для которых расстояние г от центральной оси "^^а,
лтоле пары токов равно
Е^ = -^аШ^^^ikr) cosGe-i^t,
Яе = -^ — [//J*> (kr)— krh^^^{kr)\ cosee-«<
Найти поле соответствующей пары заряженных нитей.
25. Расширить результаты задачи 24 с помощью формулы (П) раздела 6.11 и
«оказать, что любая пара эксцентричных нитей может быть заменена системой
линейных источников, расположенных на центральной оси и испускающих цилиндрические
волны разных порядков.
26. Передаточная линия, описанная в задаче 24, окружена коаксиальным
медным экраном с внутренним радиусом с и толщины о. Полагая с'^>а, найти
выражения для поля, проникающего через экран. Рассмотреть зависимость этого поля от
«го частоты и от размеров системы как для электрического, так и для маг-нитного
типов волн. (По поводу этой и предыдущих задач см. дискуссию и библиографию у
Щелку нова, Schelkunoff, Bell System Tech. Joarn. 13, 532, 1934.)
27. Полая труба прямоугольного сечения ограничена толстыми металлическими
стенками. Внутренние размеры х = а, у = Ь. Считая сначала стенки идеально
проводящими, найти выражения для допустимых видов волн поперечно-электрического
поля (Я-волны) и для соответствующих поперечно-магнитных видов волн (f-волны).
Компоненты поля могут быть написаны непосредственно из результатов задачи 1
главы VI. Если тангенциальная компонента Е должна на границе исчезать, то поле
должно быть периодично в направлении х- и у-оссп. Следовательно, h^ = тк/а^
h^ = пте/6. Соответственно с этим различные порядки Е-волн обозначаются через
Е^ те, ^ различные порядки Я-волн — через //„ „.
Найти выражения для фазовой и групповой скоростей и для длины волны
в трубе, для критической частоты и для критической длины волны. Нарисовать
силовые линии электрического и магнитного полей нескольких первых порядков для
Е- и //-волн. Поле Н^^ имеет простейшую структуру, наинизшую критическую
частоту и наименьшее затухание в случае труб с конечной проводимостью. По этой
(Причине этот вид волн чаще всего и используется на практике.
Полагая, что стенки металлические и имеют конечную проводимость, вывести
приближённое выражение для затухания волн Н^^ъ децибелах на метр. Показать,
что имеются оптимальные значения отношения afb и частоты, при которых затуха-
яие минимально.
28. Найти наинизшую собственную частоту для электромагнитных колебаний
в полости, которая имеет форму прямого кругового цилиндра радиуса а и длины /.
Металлические стенки обладают проводимостью о. Вычислить эквивалентные
индуктивность, сопротивление и добротность Q для этого собственного колебания. При
решении придерживаться пути, изложенного в разделе 9.24.
29. Рассмотреть распространение поперечно-электрических и
поперечно-магнитных волн по полой трубе эллиптического сечения.
30. Ось бесконечно длинного кругового цилиндра совпадает с осью z
координатной системы. Постоянная распространения для цилиндра равна ^j, а для внешней
среды ^2- На цилиндр в направлении оси х падает плоская волна. Найти выраж^ие
для дифрагированного поля и для поперечного сечения рассеяния. Получить
приближённые формулы для случая а/Х<1. Рассмотреть два случая:
a) Электрический вектор падающей волны параллелен г-осй.
b) Магнитный вектор падающей волны параллелен г-оси.
Теория была экспериментально подтверждена Шефером (Schaefer, Ann. Physik,
31, 455, 1910; Zeit Physik 13. 166, 1923).
31. Плоская линейно поляризованная волна рассеивается сферическим телом
радиуса а. Постоянная распространения для вещества сферы Л^, а для внешней среды,
которая предполагается непроводящей, k^r Пусть R — радиус-вектор, проведённый из
центра сферы к точке наблюдения. Плоскость, проходящая через вектор R и ось
распространения, называется плоскостью наблюдения. Плоскость, проходящая через
направление поляризации падающей волны и ось распространения, называется пло'
скостью колебаний. Пусть ср — угол между плоскостью наблюдения и плоскостью
524
гл. IX. КРАЕВЫЕ ЗАДАЧИ
колебаний, а 6 — угол между R и осью распространения. Показать, что при "К^а,
где X — длина падающей волны во внешней среде, интенсивность релеевского
рассеянного излучения даётся формулой *
So
B7tL
«6
Х4;?2
kl-
«2
kl -f 2Щ
(cos^ e cos^:? + sin2 cp),
где S — среднее значение интенсивности рассеянного излучения, а So — среднее
значение интенсивности падающей волны. Рассмотреть поляризацию рассеянного
излучения.
32. Линейно поляризованный свет рассеивается очень малыми непроводящими
частицами. Показать, что в направлении, параллельном электрическому вектору
падающей волны, интенсивность рассеянного света меняется обратно пропорционально
восьмой степени длины волны. Голубой цвет рассеянного в этом направлении
поляризованного белого света кажется более чистым, чем при наблюдении по другим
направлениям. Это явление называется «голубым светом Тиндаля».
33. Рассмотреть затухание радиоволн сверхвысоких частот, вызываемое
рассеянием на дожде и тумане, воспользовавшись следующими данными, взятыми из книги
Гемфриса «Физика воздуха» (Humphreys, Physics of the Air):
Радиус капель 1 Число капель
в метрах [ на метрз
5-10-6
2- iO-4
5.10-*
10-3
107
4000
500
450
Выразить спадание интенсивности в децибелах на километр.
34. Вычислить силу, действующую на диэлектрическую сферу при падении на неё
плоской линейно поляризованной волны, считая, что длина волны очень велика по
сравнению с радиусом сферы (D е b у е, Ann. Physik 80, 57, 1909).
35. На идеально проводящую сферу падает плоская линейно поляризованная
электромагнитная волна. Найти полную силу, действующую на сферу, считая, чта
радиус сферы очень мал по сравнению с длиной падающей волны (D е b у е, Ann.
Physik 30, 57, 1909).
Оценить изменение результата для случая медной сферы.
36. Сферическая полость радиуса 17,5 см, подобная описанной в разделе 9.24,
ограничена толстыми медными стенками. Найти частоту и логарифмический
декремент затухания для наинизшего из возможных видов колебаний. Сделать то же самое
для сферы вдвое меньшего радиуса.
37. На расстоянии b от центра сферы радиуса а, так что й<С.Ь, помещён
переменный электрический диполь, ориентированный по радиусу. Постоянная
распространения для сферы равна k^, а для внешней среды k^. Показать, что вектор
Герца, удовлетворяющий граничным условиям и ведущий себя в месте нахождения
диполя как e^^'*^fik2R, при г>я равен
JhR
Jn (^2«) ,
И = /^ + И B" + » ''« ^OЙГ'*«» т А«) (V) Рп (cos 6).
п = о
Л^^ (М)
а при /■<^ а
П = -rl-y B« + 1) A + ^п) -М—^ MP (^2&) in ikxr) Рп (COS 6),
где
/?.
В
с1х
In {xjn {х)]
п
+
1
[у dy
'п [yjn (У)]
[j -i 'n и;>м)] ^_,^- [} ^ .п W. W1
y='kia
l=T<ia
И где R — расстояние от диполя до наблюдателя, г—расстояние от центра сферы
до наблюдателя, а 6 — полярный угол, откладываемый от оси диполя. Вектор Герца
направлен по радиусу.
ЗАДАЧИ 525
38. Ось бесконечного идеально проводящего прямого кругового конуса совпадает
<: отрицательной осью z координатной системы. Вершина конуса совпадает с
началом координат, а угол между его образующей и положительным направлением оси
^ равен 6 = Bq. Внешняя среда — диэлектрик. Исследовать собственные виды волн,
могущие распространяться по конусу (М а с d о п а 1 d. Electric WBves, Cambridge
University Press, 1902).
39. Рассмотреть излучение с открытого конца полубесконечного прямого
провода, по которому течёт переменный ток, полагая в результате задачи 38 %-^ я.
Сравнить с задачей 9 главы VIII.
40. В задаче 9 главы VII было найдено выражение для поля, обладающего
симметрией вращения в сфероидальных координатах. Применить эти выражения к
идеально проводящему вытянутому сфероиду, эксцентриситет которого очень мало
отличается от единицы. Рассчитать частоты основных собственных колебаний и
написать приближённые выражения, достаточные для подсчёта затухания вследствие
излучения (Abraham, Mat. Ann., 52, 81, 1899).
41. По круговому проволочному витку радиуса 15 м протекает переменный
ток частоты 60 циклов в секунду и силой в 10 ампер. Виток лежит на плоской
поверхности земли, для которой е/ео = 4, с = 10—* If ом метр.
a) Найти напряжённость электрического поля в вольтах на метр в точке на
поверхности земли, расстояние которой от центра витка равно л
b) Каково эффективное сопротивление витка? Потерями в проводнике
пренебречь и считать, что все потери обусловлены конечной проводимостью земли.
(Примечание. При столь малых частотах виток эквивалентен вертикальному
магнитному диполю. Поле может быть подсчитано методами, изложенными в
разделах 9.28—9.31, а потери могут быть подсчитаны из среднего вертикального потока
энергии на поверхности земли.)
42. Рассмотрим систему проводников и диэлектриков, характеризуемых
параметрами е, (Л, о. Среда предполагается изотропной, но не обязательно однородной.
Поверхности скачкообразного изменения параметров могут быть заменены слоями
быстрого перехода от одних значений к другим. В этом случае мы имеем два вида
действующих сил: силы Fi, обусловленные поляризацией диэлектрика, и силы Рг,
вызываемые токами проводимости. Таким образом,
D = e(E + Fi). J = o (E-f F2).
El и р2—непрерывные функции точки. Силы эти возникают в течение
бесконечно короткого интервала времени Д^, кончающегося к моменту /=0, после чего
•остаются постоянными. Пусть
t
A = ^dt^iv[F,§ + fJ)
О F
€удет работой, произзодимой над системой действующими на неё силами за период
ют начального момента и до момента t, и пусть
t
W= f dt f dvF^J
0 V
— полное количество тепла при окончательной мощности, соответствующей
конечному значению плотности тока J. Если U и Г—электрическая и магнитная энергии
поля в конечном состоянии, то показать, что
Л= lF-f2(£/—Г).
Эта теорема была впервые высказана Хийвисайдом в его «Electrical Papers», т. II,
стр. 412 и доказана Лоренцом, Ргос. Nat Acad. ScL 8, 333, 1922. Аналогичная
теорема для электрических цепей приведена у Пирса, Electric OscilIa«ons, стр. 40, 1-е
мзд., 1920.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ I
А. Числовые значения основных констант
Диэлектрическая проницаемость свободного пространства е^:
Sq = 8,854 • 10-12 с^ ~ . 10-э фарад J метр.
Магнитная проницаемость свободного пространства Aq:
ti,Q==4T:. 10-"^== 1,257 • 10-^ генриjметр,
с = -Гг=- = 2,998 . Ю^г^З • 10^ MempoBfcefc.
l/so= 1,129 • 10" метров1фарад.
l/[j.o = 7,958 • 10^ MempoBJzeHpu.
1/^f^= 376,7 ома.
i- -j/To = 59,95 r^ 60 омам.
j/"-" = 2,654 . 10-^^o {IfoM).
Постоянная распространения k = a-\- /p,
^2 = ejx(B2 -^ i («jAa = в[хш2 A -f" ^'i^)»
'/] = -^ 1,796. 1010—r^ 1,8- 1010—,
где о—проводимость в обратных омах на метр, v — частота и
у.^—относительная диэлектрическая проницаемость s/sq. Если iq^^I, то
a^j3£=;l,987 • 10-3l/vo:t^::^2 • lO-^j/vox^,'
^ = ос -}- /j3 с=; |/itojAo,
где у.^ — относительная магнитная проницаемость u/jxq. Если 1Г]<С!1» то
1
а = ш1/5A + 1-'Г|2-}-...),
?—2
■/"Т = 188'За /^ .
ПРИЛОЖЕНИЕ I
527
В. Размерности электромагнитных величин
Размерности помещённых в нижеследующей таблице величин выражены
через массу Ж, длину L, время Г и заряд Q. В системе MKS Джорджи,
которой мы только и пользовались в этой книге, масса измеряется в
килограммах, длина в метрах, время в секундах и заряд в кулонах.
Величина
Символ
Размерность
Наименование единицы
в системе MKS
Сила
Энергия
Мощность
Заряд
Ток
Плотность заряда ......
Плотность тока
Сопротивление
Проводимость
Электрический потенциал , . .
Напряжённость электрического
поля
Ёмкость
Диэлектрическое смещение . .
Диэлектрическая
проницаемость
Электрический дипольный
момент
Магнитный поток
Плотность потока
Магнитодвижущая сила . .. .
Напряжённость магнитного
поля
Индуктивность
Магнитная проницаемость . .
Магнитный дипольный момент
I
р
J
R
а
?
Е
С
D
Ф
В
м. д.
Н
m
ML'^T-'^Q-^
LQ
T-^Q
MLQ-^
Ньютон
Джоуль
Ватт
Кулон
Ампер
Кулон/куб. метр
Ампер/кв. метр
Ом
Обратные омы • метр
Вольт
Вольт/метр
Фарада
Кулон/кв. метр
Фарад/метр
Кулон • метр
Вебер
Вебер/кв. метр
Ампер-витки'
Ампер-витки/метр
Генри
Генри/метр
Ампер • кв. метр
С. Таблицы перехода
Умножьте значение величин,
перечисленных ниже и
выраженных в MKS
Ампер/метр^
Вольт
на
10-1
10-5
10-1
10-7
10-9
10»
107
10-11
105
10»
108
108
104
для того чтобы получить
значение этих величин в
электромагнитной системе CGS
Ток /
Плотность тока J
Заряд д
Плотность заряда с
Ёмкость С
Индуктивность L
Энергия (эрг) W
Проводимость а
Сила (дина) F
Сопротивление R
Потенциал ср
Магнитный поток (Максвелл) Ф
Плотность потока (Гаусс) В
528
ПРИЛОЖЕНИЕ I
Умножьте значение величин,
перечисленных ниже и
выраженных в MKS
Ом
Вебер/метр2
на
3.109
З-Юб
8-109
3-1рз
9.1011
i/g. 10-11
107
9-109
105
1/9.10-11
1/3-10-2
V3-10-2
V3-io-«
для того чтобы получить
значение этих величин в
электростатической системе CGS
Ток /
Плотность тока J
Заряд q
Плотность заряда р
Емкость С
Индуктивность L
Энергия (эрг) W
Проводимость а
Сила (дина) F
Сопротивление R
Потенциал ср
Магнитный поток Ф
Плотность потока Б
Величины, данные в предыдущих таблицах, не рационализированы.
Единицы MKS, применённые в этой книге, рационализированы.
Электромагнитная и электростатическая системы C)GS обычно не рационализируются.
Множители перехода для трёх наиболее важных величин, подвергнутых
рационализации, табулированы ниже.
Умножьте рационализированную
величину
Ампер-витки
Единица MKS для диэлектриче-
на
47С10-1
4к10-з
47:10-6
для того чтобы получить нераЦио-
нализированную единицу в
электромагнитной системе CGS
Магнитодвижущая сила (джиль-
берт)
Напряжённость магнитного поля Н
(эрстед)
Диэлектрическое смещение D
Умножьте рационализированную
величину
, Единица MKS для диэлектриче-
на
12;:-109
127:-107
127г. 103
для того чтобы получить нерацио-
нализированную единицу в
электростатической системе CGS
Магнитодвижущая сила
Напряжённость магнитного поля И
Диэлектрическое смещение D
Если единицы CGS являются также и рациональными, то множитель 4тс
должен быть опущен.
CN
^ ' ПРИЛОЖЕНИЕ II 529
ПРИЛОЖЕНИЕ li
j Формулы векторного ана^лиза
; Латинские буквы обозначают векторы. Скалярные функции обозначаются
греческими буквами.
(a[bcj) = (b[ca])==(c[ab]). A)
[a[bc]J = (ac}b —(ab)c. B)
[а b] [с dj = (а [b [с d]J) = a(b d) с — (be) d) =
= (ac)(bd) —(ad)(bc). C)
[[abj[cd]] = ([ab]d)c —([ab]c)d. D)
grad (<p -f- tj>) = grad о -\- grad <|>. E)
grad (<ptL) = о grad ^-^-'^grado. F>
div(a + b) = diva + divb. G)
rot (a -\- b) = rot a -|- rot b. (8>
div oa = a grad 9 -j- 9 div a. (9)
rot oa == [ grad <p a] + <p rot a. ' A0)
grad (a b) =p (a grad) b -}- (b grad) a -j- [a rot b] -f- f b rot a]. A1)
div[ab]=-(brota)—(arotb). A2)
rot [ab] =a divb — bdiva-j-(bgrcid)a — (a grad) b. A3)
rot rot a = grad div a — grad a. A4)
rot grad 9 = 0. A5)
div rot a = 0. A6)
Если r = ix•-]-}y-{-kz является радиусом-вектором, проведённым из
начала координат в точку (аг, у, г); то
divr = 3, rotr==0. A7)
В нижеследующих формулах V является о^^ъёмом, ограниченным
замкнутой поверхностью 5. Единичный вектор п нормален к S и направлен всегда
наружу.
igiRd<pdv= 1 onda, A8)
, V S
f dWadv = f (an)da, A9)
f rotadv = j [n a] da. B0)
Пусть теперь 6"—незамкнутая поверхность, ограниченная контуром С.
Тогда
S с
24 8ак. 593. Теория эдектромагнетивмв.
f[ngrad9]^« = J ?й^8, B1)
.S с
г rot а nda = 1 ads. B2)
530
ПРИЛОЖЕНИЕ m
ПРИЛОЖЕНИЕ III
Проводимости различных материалов
Металлы и сплавы
Материал
Проводимость 9
в 1/ом • метр при 20° С
Алюминий, промышленный, холоднотянутый
Вольфрам
Железо 99, 98% чистое
Золото, чистое, тянутое
Константан, 60"/о Си, 40% Ni
Магний
Манганин, 84% Си, 12% Мп 4% №....
Медь, отожн<ённая
Медь, холоднотянутая
Монель-металл _
Нейзильбер, 18% Ni . .
Никель
Нихром
Олово ...
Ртуть
Свинец
Серебро 99,98о/о чистое
Сталь
Сталь марганцевая . . .
Цинк, следы Fe . . . .
3,54.
1,81
1,0..
4,10.
0,20-
2,17.
0,23.
107
107
107
107
107
10?
5,8005.107
5,fi5-10P
107
107
107
107
-107
0,24
0,30
1.28.
0,10-
0,869
0,1044 • 107
0,48.107
6,139-10'
0.5—1,0-107
0,14-107
1,74-107
Диэлектрики
Материал
Приблизительная
проводимость в 1/ом • метр
при 20° С >
Бакелит (средние пределы). . .
Глиптоль
Дерево парафинированное .
Кварц кристаллический Ц оси .
» » J_K оси
Кварц плавленный
Мрамор
Парафин
Резина твёрдая
Сера
Слюда
Смола
Стекло обычное
Фарфор
Фибра твёрдая
Целлулоид .... •
Церезин
Шеллак
Шифер
Вода дестиллированная 18° С .
Нефть
Спирт метиловый
Спирт этиловый 15° С
10-8_10-1в
10-м
10-8—10-11
10-12
3 10-1S
<2-10-17
10- 7—10-9
10-1*—10-16
10-М—10-1»
10-15
10-"—1015
2-10-15
10-12
3 • 10-13
5-10-9
10-8
<2-10-17
10-м
10-6
2 -10--*
10-м
7.1.10-4
3,3-10-4
ПРЙЙдЙМйЕ III
531
Проводимости геологических материалов изменяются настолько сильно
от одного места к другому, что могут быть даны только их приближённые
значения. Следующие цифры указывают на порядок величин.
Морская вода от 3 до 5 ом-^ метр-*. Пробы, взятые в Атлантическом
океане вдали от побережья Массачузетса и Нью-Джерси, имели проводимость,
равную 4,3 ом-^ метр-*.
Пресная вода 10-^ ом-* метр-*. Проводимость маленьких озёр с
пресной водой может быть в 5 или 10 раз больше.
Влажная земля — от 10-2 др ю-з ом-* метр-*.
Сухая земля — от 10-* до 10-*^ ом-* метр-*.
Относительные диэлектрические постоянные диэлектриков
Значения величин, приведённые ниже, приблизительно не зависят от
частоты, пока частота меньше одного мегацикла в секунду. Если нет других
указаний, то предполагается, что давление равно атмосферному, а
температура 20° С.
Газы
Водород О' С 1.000264
Водяной пар 145° С 1,00705
Воздух 0^ С 1.00359
40 атмосфер 1.0218
80 атмосфер 1,0439
Жидкости
Ацетон О** С
Бензол,.
Вода дестиллированиая
Воздух 191° С
• . 26.6
. . 2.29
. . 81,1
1,43
Глицерин 15^ С 56,2
Масла
Касторовое 4,67
Льняное . 3,35
Нефть 2.13
Спирты
Амиловый 16.0
Метиловый 31,2
Этиловый 25,8
Твёрдые тела
Алмаз 16,50
Асфальт 2,68
Бумага (для изоляции в
кабелях) 2,0-2.5
Гутап^рча 3.3—4.9
Дерево
красный бук J_ к волокнам 3,6—7.7
красный бук II волокнам . 2,5—4,8
д>б ± к воло нам .... 3,6—6,8
дуб II волокнам 2,5-~4.2
Кварц
J_ к оси
II оси
Мрамор
Парафин
Резина
Сера
аморфная 3,98
литая чистая (свежая) . . 4,22
Слюда 5,6—6,0
Стекло
флинт, плотность 4.5 ., . 9.90
флинт, плотность л87 . . . 6,61
свинцовое, нлотн. 3,0—3,5 . 5,4—8,0
Фарфор 5,7
Шеллак 3,1
Шифер 6,6—7.4
4,69
5.06
8.3
2,1
2.3-4.0
Данные, приведённые в этом приложении, взяты в основном из
«Smithsonian Physical Tables» и из «Handbook of Chemistry and Physics*. В этих
источниках можно найти данные для других материалов и для
температурных коэффициентов.
34*
532 Приложение iv
ПРИЛОЖЕНИЕ IV
Присоединённые функции Лежандра
Pj {2) "- г =-^ cos 0.
1
1\ (г) :^- 2- C^^~ 1) ^^ Т ('"^ cos 29 + П.
- 3
Р1(г)=г{1~г^)- z^ 1 sin 20.
Pi (г):-: 3 A — г^) :=! A —cos 20).
Pg (г) = 2- {^г^ — Зг) =r 1- E cos ЗО + 3 cos б).
^U^) --- 1A—г^)"-'Eг'3—l) = i (sin О 4-5 sin 30).
Pg (г) = 15 A — г2) г -- ^| (cos 0 — cos 30).
РИг) =- 15 A — г2)"'* =r= 1^C sin 0 — sin 36).
Pi {г) = ^ C5г* -- ЗОг^-f 3) = i C5 cos 40 -f 20 cos 20 -f- 9).
P\ (г) -- -| A — z^-Y'-^ i7z^ — 3z) ^ j-^ B sin 20 + 7 sin 40).
P4 (^) -- ^ A — г^) Gг2~ 1) =:- II C + 4 cos 20 — 7 cos 40).
P!(^) = 105 A — z"yf^2 ^ ~ B sin 20 —sin 40).
о
Pt (г) -=: 105 A - z^-r- -= %' C - 4 cos 20 -f cos 40).
ИМЕННОЙ УКАЗАТЕЛЬ
Абрагам, y\brah.ain 140, 373, 387, 418
Адамар, Hadamar 263, 406
Адаме, Adams 139, 387
Барнес, Barnes 452
Барроу, Barrow 478
Без, Baz 449, 452
Беккер и Копсон, Baker and Copson
407, 409
Беккер, Becker 140, 419
Бергманп, Bergmann 391, 441
Бетмап, Batemann 400, 341, 342
Бехман, Bechman 400, 404, 405
Блэк, Blake 387
Блюмер, Blumer 497
Бонч-Бруевич, Bontsch-Bruewitsch 394
Борн, Born 286, 407
Бохер, B:6cher 182
Бохнер, Bochner 278
Бреммер, Brenimer 516, 518
Бреховских 502
Бриллуен, Brillouin 296. 400, 476
Буссинеск, Boussinesq 342
Бэрроуз, Burrows 513
Валлот, Wallot 30, 517
Ван дер Поль, Wan der Pol 502, 510
Ван Флек, Van Vleck 423, 424
Ватсон, W-atson 183, 265, 316, 325
В'веденский 502
Вейль, Weyl 502, 506
Внльмот, Wilmot 396
Вильмсен, Wilnisen 501
Вильсей. VVilsev 443, 445
Винер, Winer 278
Вихерт, Wiechert 418
Вольтерра, Volterra 420
Вольтерсдорф, Wioltersdorf 452
Гаген, Hagen 290, 447
Гагу, Hague 238
Галлен, Hallen 387
Ганс, Hans 501
Гаппель, Happel 501
Гельмгольц, flelmgoltz 133
Герц, Hertz 37
Герцфельд, Herzfeld 501
Гобсон, Hobson 183, 335
Гольдштейн, Goldstein 331
Глазбрук, Glazebrook 29
Глатхарт, Glathart 447
Говдр'Ос, Hondros 471
Гринберг 502
Гроос, Gross 439
Гюллемии. Guillemiii 251
Гуль, Hull 518
Гунд, Hund 396
Дебай, Debye 325, 366. 471, 489, 524
Джине, Jeans 1177, 183
Джорджи. Giorgi 29
Дореей, Dorsey 28
Друде, Drude 452
Дулалл, Dougall 140
Зельмейер, Sellmeyer 321
Зильберштейн, Silberstein 40
Зоммерфельд, Sommerfeld 30, 61, 218.
296, 323, 428, 501
Зоммерфельд и Рунге, Sommerfeld und
Runge 304, 463
Игнатовский. Ignatowsky 409
Ине, Inee 191, 275, 330
Иобст, lobst 499
Кавендлш, Cavendish 156
Карслоу, Carlslaw 255, 265, 352
Кареон, Carson 472
Картер. Carter 396
Картрййт. Cartwright 452
' Келлог, Kellogg 18. 158, 172, 173
Кельвин, Kelvin 194, 200, 521
Кеннели. Kenneli 29
Кениг, Konig 443, 449
Кембл, Kemble 139. 203
Кон, Cohn 512
Кортвег, Kortweg 135
Котлер, Kottler ^^407, 409, 112
Кэмпл, Campbell 257, 266
Кэртис, Curtis 28
Лабуе, Labus 393
Ламб, Lamb 342
Лармор, Larmor 136, 200, 409
Левин, 387
Ленард, Lenard 418
Леонтович 387, 502
Линденблад, Lindenblad 396
Линдер, binder 238
Ливене, Livens 126, 136
Лоренц, Lorentz 77, 286
Ляв, Love 133, 409
Макдональд, Macdonald 126, 409
Мак Петри, Me Petrie 396
Мандельштамм, Mandelstamm 73, 501
Маинебек, Manneback 393
534
ИМЕННОЙ УКАЗАТЕЛЬ
Майкельсон, Michelson 74
МезЪя и Вивер, Mason and Weaver 105,
126, 177
Ми, Mie 62, 366, 496
Мид. Mead 472
Мимно, Mimno 393
Минковский, Minkowski 62
Моглих, M6gHch 501
Морзе, Morse 330, 340, 356. 414
Морлей, Moriey 74
Никольс, Nichols 518
Ниссен, Niessen 510
Нортон, Norton 513
Нотер, Noether 200
Паж, Page 387
Паули, Pauii 62. 146
Пирс,'Pierce 525
Писталькорс, Pistalkors 400
Пихт, Picht 439
Планк, Planck 407
Покельс, Pockeis 132, 133, 136. 406, 408
Пуанкаре, Poincare 77, 306. 406
Пуассон. Poisson 206
Пфанненберг, Pfannenberg 449
Пфейфер, Pfeifer 445
Пфистер, Pfister 452
Райе, Rice 513
Релей, Rayleigh 471. 517
Риги, Righi 37
Ритц, Ritz 75
Роза. Rosa 28
Рольф, Rolf 513
Рот, Roth 452
Рубенс, Rubens 290. 447
Рубинович, Rubinowicz 407, 430
Рубинштейн, Rubinstein 414
Рытов 304, 305. 469
Рязин 502
Сакердот, Sacerdote 139
Смит, Smythe 183
Смолуховский, Smoluchowski 501
Соутворт, Southwort 472
Степанов 191
Стретт, Strutt 513
Стреттон. Stratton 331. 387
Тамм, Tamm 73
Тедон. Tedone 409
Тичмарш, Tichmarch 256
Тоноло, Tonolo 409
Уайз, Wise 513
Уллер, иИег 512
Фейнберг 502
Фельд 413
Филипс, Phillips 158, 172
Фок, Fock 502, 517
Форстерлинг, Forsterling 286
Фостер, Foster 257, 266
Фохт, Voight 133
Френкель 419
Хивисайд, Heaviside 306
Цан. Zahn 472
Ценнек, Zennek 512
Черни, Czerny 452
Чу, Chu 387, 414, 478
Шефер, Schaefer 286, 431
Ши, Shea 443
Щелкунов, Schelkunoff 231, ilO, 387,
409. 414, 453. 472
Щукин, 293
Эйзенхарт, Eisenhart 309
Эйнштейн. Einstein 77
Эйхенвальд 439
Эпштейн, Epstein 305
Юдкевич 305
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адмитанс коаксиальной линии 482, 485
Алгебра комплексных чисел 126—128
Антенна вертикальная 501—516
—; геризонтальная. над землёй 511
— направленная 395—400
— линейная 387—392. 400—402, 420
Антенны изображение 511
Бесселя уравнение 181
— функции 315—317
изменённые 343—344
сферические, представления
интегральные 361
Био-Савара закон 210, 228
Брюстера угол 437, 447, 454, 457
Вебер, единица потока 31
Вектор аксиальный 68, 72
— единичный 47, 53
•~ поляризации 24
— полярный 68, 72
Вектор Герца 87—40, 169
, связь с векторной волновой
функцией 347
для произвольного источника 379
для цилиндрического поля 309—
311
■ для сферического поля 366
Векторы взаимные 46, 62
— координатные 46, 62
— поля комплексные 40, 42
Взаимоиндукция 236
Виток Гельмгольца 235
Волна плоская, неоднородная 301, 318.
450
— поверхностная 212—215
— поперечная 242
Волны дополнительные 466
в коаксиальных линиях 481
— основные в коаксиальных линиях 486
в полых трубах 466
в цилиндрических проводниках 472
Восприимчивость электрическая и
магнитная 24
, измерение 231
Вращающий момент, действующий на
диполь 161, 218
на эллипсоид 195—197
Галилеевы преобразования 77
Ганкеля функции 317
Гармоники зональные 354
— тессеральные 354, 486
— эллилсоидальные 180
Гельмгольца резонатор 491
Генри 33
Герца вектор 37—40, 169
для. произвольного источника 379
для цилиндрического поля 309—
311
для сферического поля 366
, связь с векторной волновой
функцией 347
Гистерезис 115, 118, 119, 124
Глубина проникновения 444, 471
Градиент в криволинейных координатах
50. 54
Гюйгенса принцип 377, 405—414, 498,
510
Децибелл 305, 485
Дивергенция 18
— в криволинейных координатах 51, 54
— , инвариантность 65, 66
— тензора 69, 70
Диполь магнитный 212, 511
i осциллирующий 382, 386—387
— электрический 160—161, 164, 166
осциллирующий 382, 383—386
Дирихле задача 406
Дисперсия аномальная 288
— в диэлектриках 285—289
— в металлах 289—290
— нормальная 288
Дифракция поля диполя на сфере 515
— плоской волны на сфере 493—501
на эллипсоиде 500
— , теория Кирхгофа-Гюйгенса 405—414
Диффузия 248, 307
Добротность контура 493
Е-волны 302, 486
— в коаксиальных линиях 479
— в полых трубах 471—478
Единицы 28—33, 215—217, 431
— Гауссовы 217
—, MKS 29—33, 217
— практические 28, 32
— рационализованные 215
-- электромагнитные 28, 217
— электростатические 217
Жордана лемма 289, 279, 418
Задача Дирихле 406
— Неймана 406
536
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Закон Био-Савара 210, 228
— индукции Фарадея 21. 308
— Клаузиуса-Масотти 130. 138. 140
— Кулона 256, 260. 164, 215. 217—218
— Ома 26
Законы Снеля 433, 441, 508
для проводящей среды 442
Заряд, сохранение 17
— , плотность 16—17. 43. 411
— магнитный 206—208, 217. 409
— поверхностный, связь с поляризацией
168
— точечный 100, 150
— — движущийся 417, 410
Зснухание, приблизительный подсчёт 468,
469
— вдоль коаксиальной линии 485
— в полых трубах 476—477
Излучение антенных устройств 395—400
— бегущих волн 392
— квадруполя 383, 423
— линейной антенны 389. 392
— магнитного диполя '386—387
— сферы 497—499
— электрического диполя 384—385
Импеданс внутренний сфеоы 252
— коаксиальной линии 479—480, 482
— плоской волны 251—252, 450
— поверхностный 467
— характеристический 252, 482
— — коаксиальной линии 484—485
— цилиндрического проводника 647 и
далее
Импеденса подбор, связь с граничными
условиями 450, 452. 468
Импульс, сохранение 100
— электромагнитный 99—100, 145—146
Инвариантность п пространстве и
времени 81
— лапласиана 65, 66
— уравнений Максвелла 80
Индукция длинного прямого провода 471
— коаксиальной линии 482, 485
Инерция электромагнитного поля 100
Интеграл Фурье 256
Ионосфера 290
Исчисление операторное 275
Квадрика деформаций 87
— напряжений 85
Квадруполь 162, 164. 166, 382—383. 423
Колебания полости 491—493
Компоненты ковариантные 47, 53, 62
— контравариантные 47, 53, 62
Координаты биполярные 58
— криволинейные 45
— параболические 58
— параболоидные 60
— сфероидальные 59. 182
— тороидальные 137
— цилиндрические 56—58, 180—181
— эллипсоидальные 61
Коэфициент деполяризации 188, 193
— затухания 246
— " объёмного расшмрення 90, 92
Коэфициент отражения 437, 446, 447, 19,
508, 514
, плоского слоя 451—453
— поглощения 288
— прохождения 437
— Пуассона 92
— распространения для коаксиальной
линии 481, 484, 485
для круглого цилиндра 462, 464
для полого цилиндра 473—474
Коэфициенты Ламэ 53
— метрические 48
Кривая регулярная 18
Лсшласа преобразование 275—283
— уравнение 150, 154
— — решение в ортогональных
координатах 179—183
— — решение через определённый
интеграл 197—198
Лапласиан в криволинейных координатах
52, 54
— инвариантность 65, 66
Лежандра полиномы 159
— уравнение 181
Лежандра функции 35'3—356
присоединённые 166, 532
Лемма Жордана 289, 297. 418
Линия коаксиальная 478—486
— силовая 149
— тока 16
Листок магнитный 207
Лоренца преобразование 77. 78, 80, 419
Магнит постоянный 121
Магнитострикция 145
Международная электротехническая
комиссия 29
Метод перевала 324—325
Модуль сдвига 92
— Юнга 92
Момент магнитный 207
Мультиполи 150, 162—167, 213, 301,
380—383
Намагничение 25, 207, 212, 213—214
Г1апряжение 84
— поперечное 482
Ньютон, единица силы 31
Октуполь 165
Определение Е и Д полостное 194-
Оптика металлов 443
— геометрическая 304
Оси деформации главные 87, 89
— напряжения главные 85
— оптические 302
Отображение конформное 197, 202
Отражение диэлектриками 436
— земной поверхностью 508
— полное 438—441, 511
— проводниками 444
ПадещТе скользящее 448
Плоскость наблюдения 623
- падения 432
195
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
537
Плотность спектральная 257 *
— тока 17
поверхностная 44, 219, 221—222,
41 i, 426—427
— электрического заряда 16—17
поверхностная 43, 411
— электрической энергии 105, 123
—' магнитной энергии 117, 123
Поверхность регулярная 18
Подобие электродинамическое 430—432
Показатель преломления 245, 285—288,
292, 436
Поле излучения элемента тока 388—389
— индукций 515
— консервативное 101
— магнитного типа 39, 311,462, 48G, 49й
— магнитное поперечное 310, 439, 455,
457. 462—463. 472. 486
— соленоида 210—211
— стационарное 204
— электрического типа 39, 310, 462, 486,
496
— электрическое поперечное 311, 439,
462—463, 472, 486
Полиномы Лежандра 159
Полость сферическая 187
— эллипсоидальная 194—195
Поляризация диэлектрика, движущегося
в магнитном поле 238
— круговая 249, 440
— линейная 249
■Н магнитная 24, 218—220
— электрическая 24, 167—169
— 'эллиптическая 249, 440. 445, 448, 496
Помехи перекрёстные 478, 521—522
Поперечное сечение рассеяния 498
Поперечность 414, 419
Постоянная распространения А' 244, 246
— фазовая а 246
Постулаты теории относительности 74—
75
Потенциал запаздывающий 378—379
— поляризации 36, 169
— векторный 33—37, 205
— распределения токоз 211—213, 227
^— намагниченного тела 218
— запаздывающий 378—379
— комплексный 40—42
— поляризации 39, 169
— магнитостатического поля 205—208
— упругий 91
— электростатический 148
в двух измерениях 198—199
Поток магнитный 21
— энергии в плоской волне 250
Пойнтинга вектор 124
комплексный 126—-128
— теорема 123—128, 408
Представления интегральные
сферических бесселевых функций 361
' функций Бесселя 323, 325, 342
Ганкеля 323, 342
эллиптических волновых функций
334—342
Преломление в проводниках 441—444
— в диэлектриках 436
Преломление излучения диполя в земле
508—510
Преломления показатель 245, 285—288,
292
Преобразование Лапласа 275—283
— Лоренца 77—78, 80, 419
Преобразования ортогональные 63, 65
Принцип Гюйгенса 377, 405—414, 498,
510
Проводимость 26
— комплексная 289
Проводники 104, 151—152, 289
Произведение тензоров 81
Проницаемость диэлектрическая 22—21
комплексная 42, 2о7
— магнитная 23
— — при высоких частотах 447
Пуассона коэфйциеит 92
Пуассона-Парсеваля формула 341
Пуассона уравнение 150, 153—155,- 208
Размерности 431
Разрыв непрерывности А 222
В 222, 224
Е 172, 175, 176
— — поверхностного распределения
412—414
потенциала 173. 175
Распределение тока, связь с
электростатическим потенциалом 201—202
Распространение вдоль бесконечной
плоской поверхности 454—460
— вдоль коаксиальной линии 478—485
— вдоль цилиндрического проводника
463—471, 519—522
— в ионизированной среде 290—293
— в однородном диэлектрике 244—246,
260—264
— в однородном проводнике 247—248,
264—274, 283—285.
— в полых трубах 471—478
— радиоволн над плоской землёй 501—
515
1 над сферической землей 515
Распространения константа к 244, 246
Рассеяние на сфере 497—499, 500, 52i
Реакция излучения 420
Резонатор Гельмгольца 491
Релаксации время 27
Решение Кирхгофа для волнового
уравнения 376—377
Ротор в криволинейных координатах 51,
52, 54
— , как антисимметричный тензор 69
— , определение 20
~ четыре-вектора 69, 78
Самоиндукция 236—237
Свёртывание тензора 69
Связное пространство 205, 215
Сжимаемость 92
Силы, действующие между элементами
тока 238
на диполь 161
на распределение зарядов 93, 99
на распределение токов 93, 99
538
ПРЙДМЕТНЫЙ УКАЗАТЕЛЬ
Силы, действующие на тело, взвешенное
в жидкости 140—142, 144, 146
— — на цилиндр в магнитном поле 234
на элемент жидкости 130, 135
на элемент поверхности 135—139,
144
на элемент твёрдого тела 134—
135, 142—144
Скаляры, вариантные и инвариантные 64,
66
Скин-эффект в цилиндрических
проводниках 466
— на плоской поверхности 457—460
Скорость групповая 293—296, 3Q0
в полых трубах 474
— сигнала 299—301
— фазовая 245, 246, 298—301
ббльшая, чем с 455—456
в дисдергирующей среде 288
в ионизированной среде 290, 292
в полом цилиндре 474
i в проводящей среде 442
— фронта волны 297—301
Слои двойные, распределение 172—176
Слой Кеннели-Хивисайда 292
Снеля законы 433, 441, 500
для проводящей среды 442
Сопротивление излучения бегущей волны
393
линейной антенны 392
магнитного диполя 386
Состояние квазистационарное 204, 387
Среда анизотропная 27, 73. 302
— диамагнитная 25
— парамагнитная 25
— ферромагнитная 25, 118. 144
Стокса теорема 20
Сфера в электростатическом поле 183—
188
— , свободные колебания 486—493
Сходимость интегралов, определяющих
потенциал 157—158, 170-^171, 186,
187
Тензор 66, 69
— антисимметричный и симметричный 67
— натяжения, электромагнитный 94—95,
137, 143
— , свёртывание 69
Тензоров произведение 81
Теорема Грина 152—153, 175—176, 374,
405
в векторной форме 225, 409
в четырёх измерениях 416
— взаимности 422
— Иреншоу ПО—111
— Коши 289
— Пойнтинга 123—128, 408
— сложения для круговых
цилиндрических волн 328—330
~ для полиномов Лежапдра 359
-— для сферических функций Бесселя
364—365
— для эллиптических волн 340
— Стокса 20
— Томсона 109, 129
Теория квантовая 16
— Киргофа дифракционная 405—414
— макроскопическая, её границы 1б, 390
494
Ток конвекционный 17. 78 ,
— магнитный 409
— смещения 22
Томсона теорема 109, 129
Трубы полые, прямоугольные 471—478,
623
Угол Брюстера 437, 447 454, 457
— падения, комплексный 453 _
-- полной поляризации 437
-- телесный 173
Условие излучения 428—429
Уравнение Бесселя 181
— Лапласа 150, 154
-. , решение в ортогональных
координатах 179—183
, решение через определённкй
интеграл 197—198
— Лежандра 181
— Матьё 182, 330—332
— непрерывности 19
в четырёх измерениях 73
— Пуассона 150, 153—155, 208
— телеграфное 306, 482
— Френеля 433-,435, 436, 441, 453—455,
516
Условия граничные 42—45
' однородные 482
Фаза плоской волны 245
Фазовая константа а 246 •
Faltung-теорема 278—279, 285
Фарада 32
Фарадея закон индукции 21, 308
Формула Пуассона-Парсеваля 341
Формулировка электростатической зад!-
чи 177—178
Френеля уравнение 433—435, 436, 441,
453—455, 516
Функции Бесселя 315—'S17
— волновые векторные 346, 347
сферические 365—369
цилиндрические 348—352
— Ганкеля 317
— гармонические 167, 315—318
— Лежандра 353—356
присоединённые 166. 532
Функция импульсная 259. 375
— кусочно-непрерывная 254
— Матьё 331—334
—' ошибок 258, 514
— ступенчатая 257, 281
Фурье-Бесселя интеграл 325—327
для сферических функций 363
Фурье — Бесселя ряд 575
Фурье интеграл 256—260
Фурье представление 504
Фурье ряд 253—255
Характеристические значения 331
для сферы 487, 489—492
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
538
Характеристический импеданс 252, 482
коаксиальной линии 484—485
Н-волны 302, 313
-— в полых трубах 472—478
Холл-эффект 26
Четыре-вектор 65
Четыре-потенциал 73, 78, 81, 415—417
Четыре-тензор 69
Четыре-ток 70, 78, 81, 415
Шести-вектор 70
Эйконал 98
Электрострикцйя 139—140
Эллиисоид в магнитостатическом поле
23Ь
Эллипсоид в электростатическом юле
188—197
— намагниченный 230
Энергии поток 123—128
в плоской волне 250—251
Энергия магнитная в сферической
волости 492
~ магнитостатическая 112—125
анизотропной среды 142
— , скорость распространения 303
— упругая. 90
— электростатическая 100—112
анизотропной среды 131
Эфир 98
Юнга модуль 92
ОГИЗ при Совете Министров СССР
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
„ГОСТЕХИЗДАТ"
Москва, Орликов пер., 3
ИМЕЮТСЯ В ПРОДАЖЕ НОВЫЕ КНИГИ
Баранов С. С. Поляроидные полярископы в исследовании
напряжений. Стр. 132. Цена 4 руб.
Волькеиштейи Ф. Ф. Электропроводность полупроводников.
Стр. 352, Цена 14 р. 25 к.
Мезон. Монография, составленная коллективом сотрудников Физического
Института им. П. Н .Лебедева Академии Наук СССР под ред. И. Е. Тамма.
Стр. 272. Цена 11 р.
Паули В. О б щ и е принципы волновой механики. Перевод с нем.
под ред. К. В. Никольского. Стр. 332. Цена 14 р. 50 к.
Паули В. Теория относительности. Перевод с нем. В. Л. Гинзбурга
и Л. М. Левина. Стр. 300. Цена 11 руб.
Шаронов В. В. Измерение и расчёт видимости далёких
предметов. Стр. 284. Цена 12 р.
Книги продаются в книжных магазинах КОГИЗа и других
книготорговых организациях.
Книги высылаются также наложенным платежом без задатка.
Заказы шлите по адресу: Москва, центр, Куйбышевский проезд,
дом № 8. МОГИЗ. -Книга-почтой".
Опечатки
о.
ь
и
Строка
Напечатано
Должно быть
•в
189
193
250
288
312
312
325
371
ф-ла G)
ф-ла C8)
ф-лаG1)
подпись
к рис.58
ф-лаB6)
ф-ла B7)
ф-лаD2)
12 сн.
/
1 +
аЬс е|—Gj
1+-
abc Ej—eg
CO
if ds
J(«4-««)/?,
0
3
части
дА*
ди
fl3
д
РГ
e
($2-1)
00
/
Тип.
Г
в6с ej—eg
~.Г
1-}- Е^
/ds
Авт.
00
■^ 2 е. J(«-bG2)
S2 J(«+«2)/?«,
0 )
5+
частоты
dA*
au2
Тип.
Ред.
Тип.
-{Aff
д^
6t
n
Ред.
(E-.)t
Заказ 593. Стрэттон. яТеория электромагнетизма*.