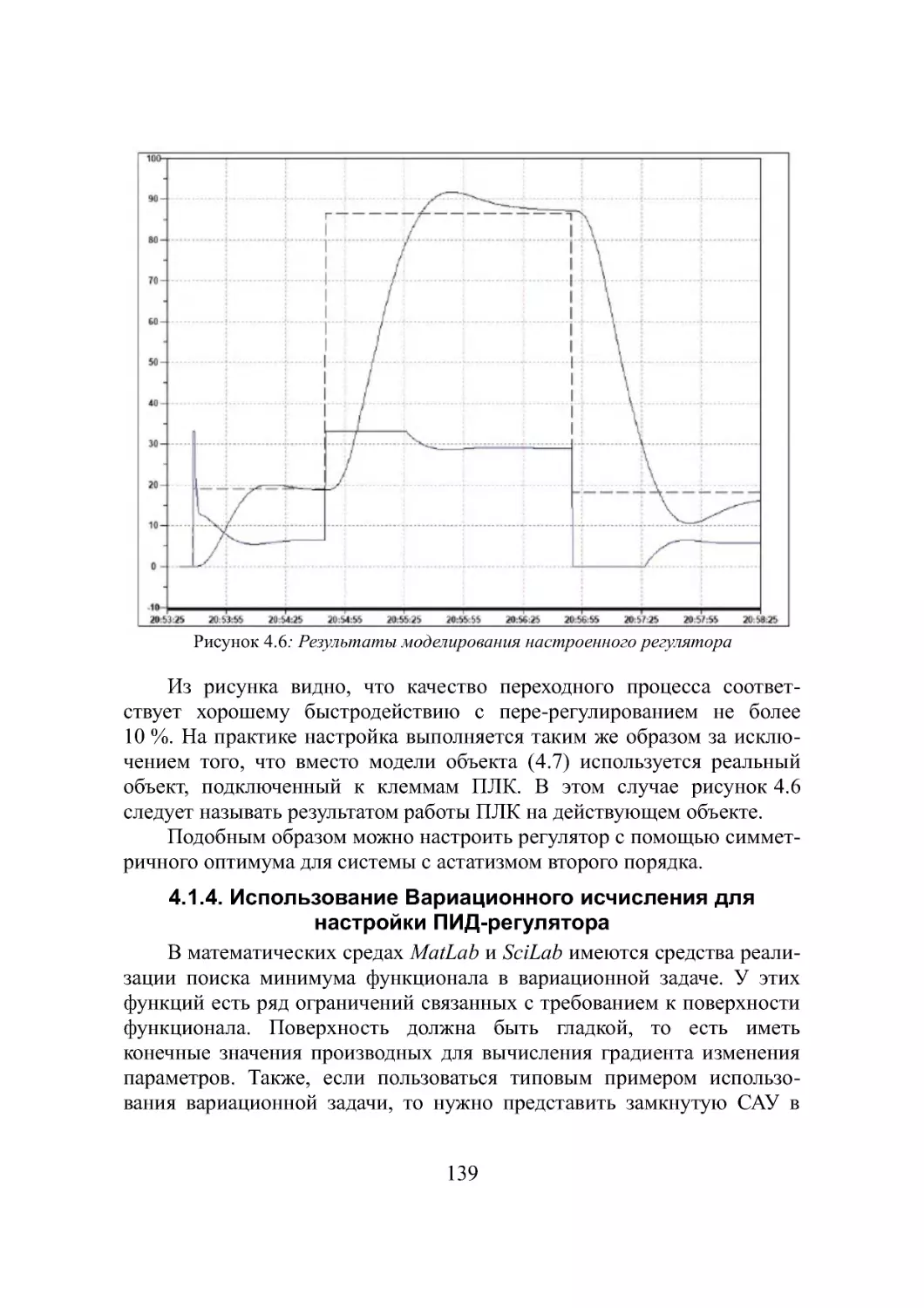
Автор: Шилин А.А.
Теги: управление предприятиями, организация производства, торговли и транспорта электроэнергетика электротехника учебное пособие теория автоматического управления издательство томского политехнического университета цифровая схемотехника управляющие системы
ISBN: 0-00000-000-0
Год: 2022
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
А.А. Шилин, В.Г. Букреев, Н.А.Воронина
СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Рекомендовано в качестве учебного пособия
Редакционно-издательским советом
Томского политехнического университета
Издательство
Томского политехнического университета
2022
1
УДК 65-83(076.5)
ББК 31.291я73
ШЗЗ
Шилин А.А.
ШЗЗ Системы автоматического управления: учебное пособие /
А.А. Шилин, В.Г. Букреев, Н.А.Воронина; Томский политехниче-
ский университет. - Томск : Изд-во Томского политехнического
университета, 2022. - 267 с.
ISBN 0-00000-000-0
В учебном пособии рассматриваются вопросы аппаратной организации
основных узлов цифровой схемотехники, необходимые для успешного
освоения микропроцессорной техники и её использования в управляющих
системах.
Предназначено для студентов, обучающихся по направлению 13.03.02
«Электроэнергетика и электротехника».
УДК 65-83(076.5)
ББК 31.291я73
Рецензенты
Доктор технических наук, профессор,
директор НИИ промышленной электроники ТУ СУР
Г.Я. Михальченко
Доктор технических наук, профессор,
профессор кафедры КСУП, ТУ СУР
А.А. Светлаков
ISBN 0-00000-000-0
© ФГАОУ ВО НИ ТПУ, 2022
© Шилин А.А., 2022
© Оформление. Издательство Томского
политехнического университета, 2022
2
Оглавление
Введение.....................................................6
1. Принципы построения современных систем управления.........7
1.1. Современные SCADA системы.............................7
Вопросы к разделу.......................................15
1.2. Программируемый логической контроллер................15
Вопросы к разделу.......................................31
1.3. Стандарт МЭК(1ЕС)-61131-3............................31
1.3.1. CoDeSys проект...................................32
1.3.2. Structured Text..................................37
1.3.3. Язык функциональных блоков FBD и CFC.............44
1.3.4. Релейные диаграммы LD............................47
1.3.5. Диаграммы последовательностей SFC................52
Вопросы к разделу.......................................58
2. Дискретные системы автоматического управления............60
2.1. Теоретические основы дискретных систем...............62
Вопросы к разделу.......................................73
2.2. Реализация основных динамических элементов...........73
2.2.1. Инерционное звено................................73
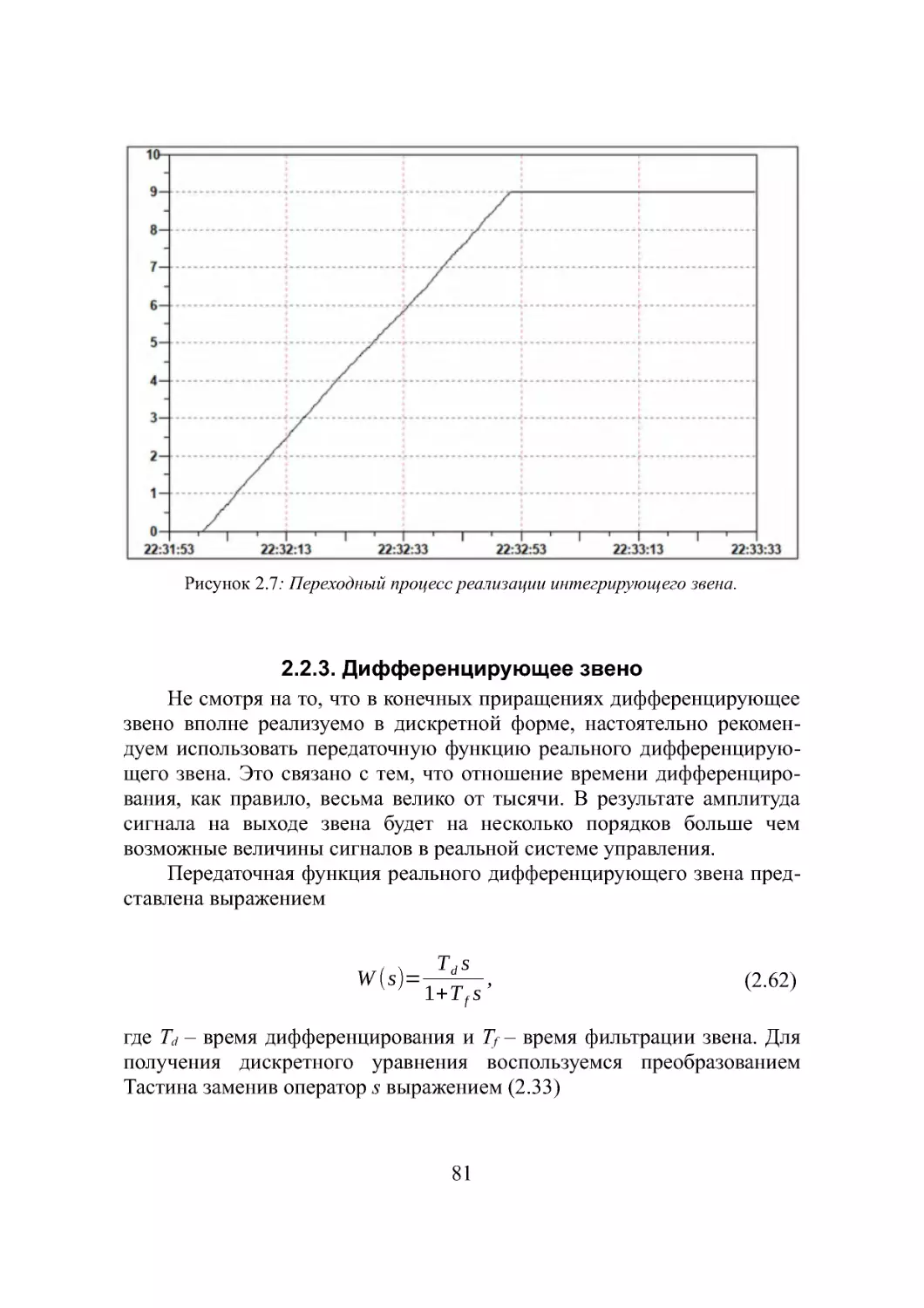
2.2.2. Реализация интегрирующего звена..................78
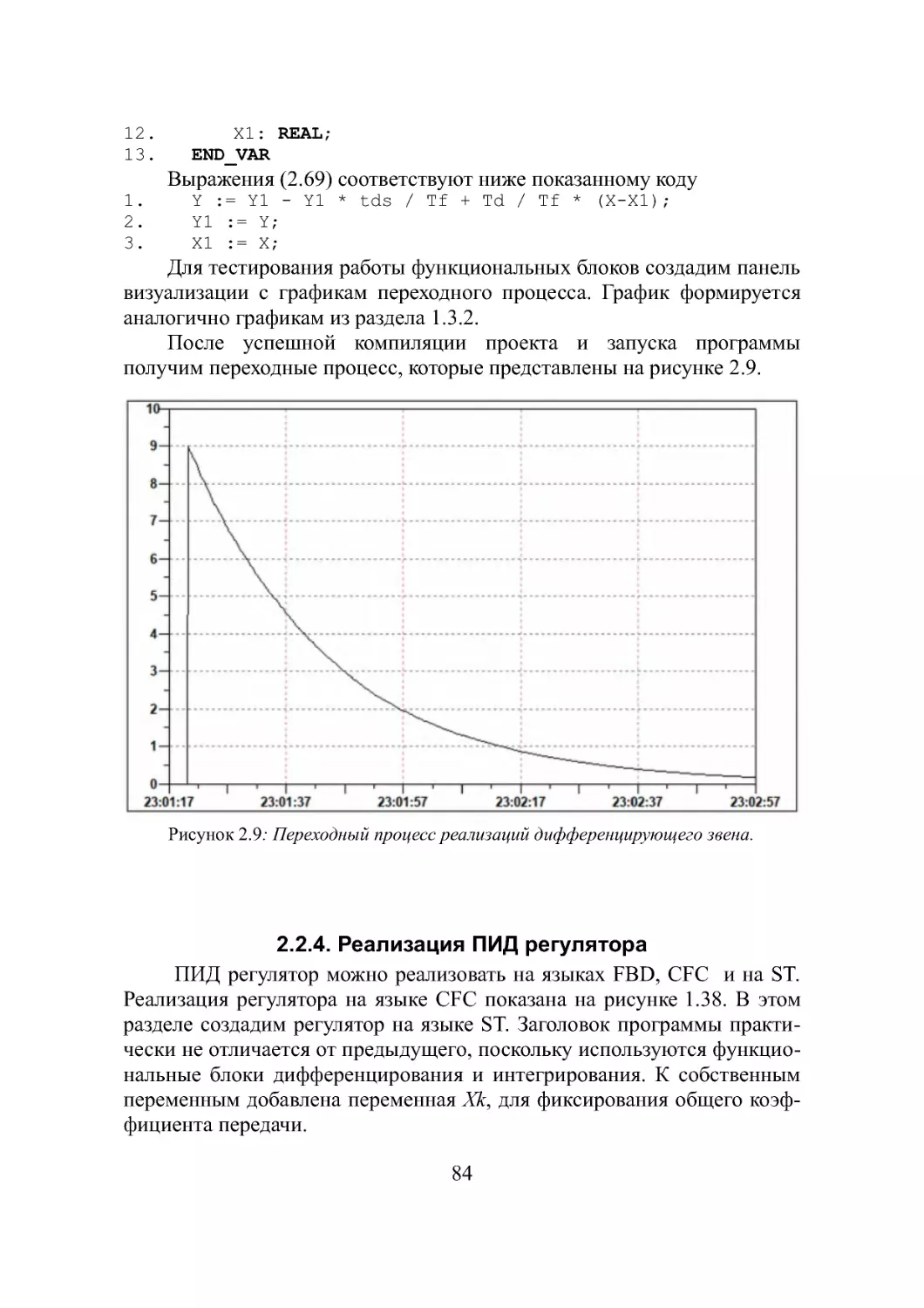
2.2.3. Дифференцирующее звено...........................81
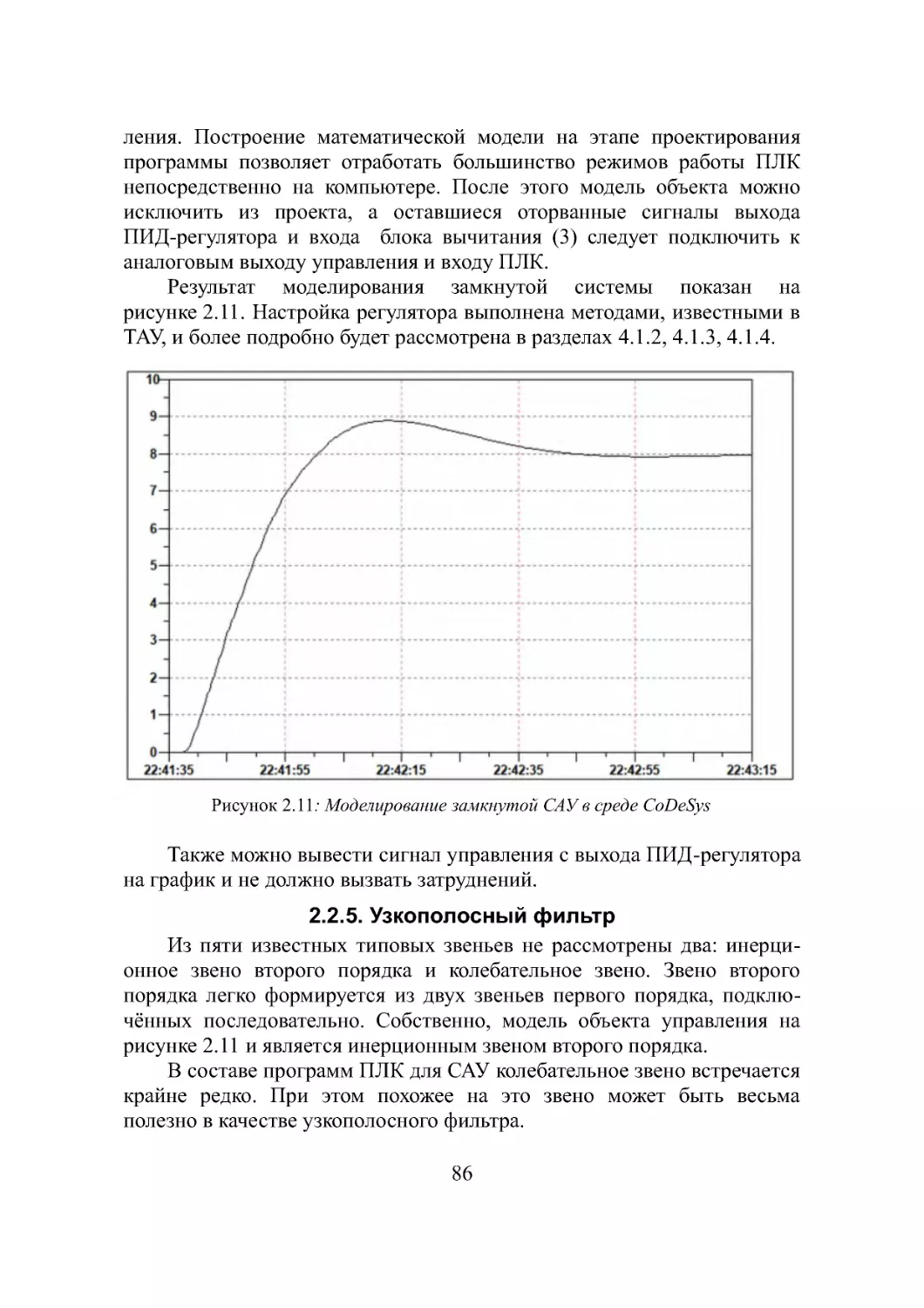
2.2.4. Реализация ПИД регулятора........................84
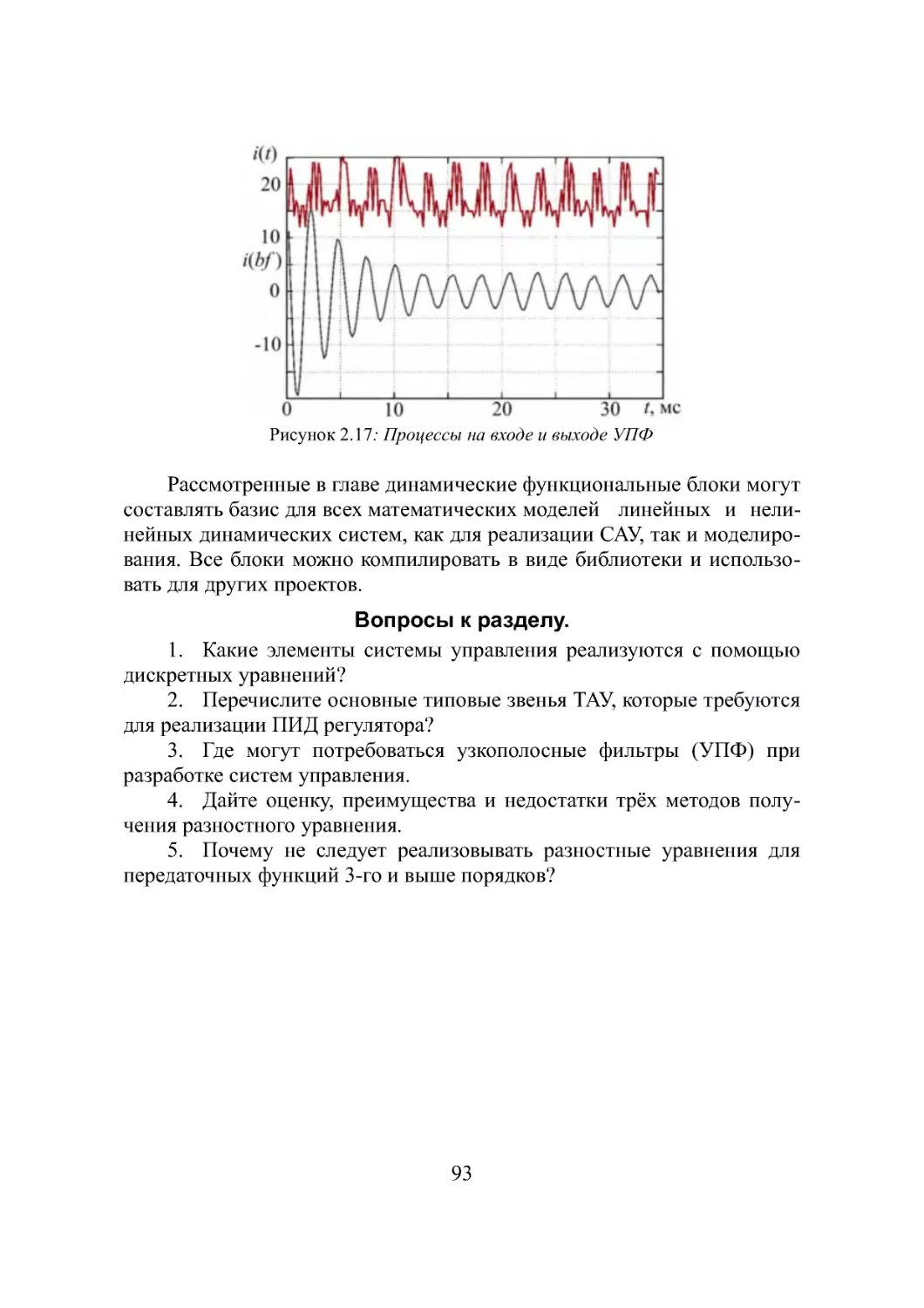
2.2.5. Узкополосный фильтр..............................86
Вопросы к разделу.......................................93
3. Нелинейные системы.......................................94
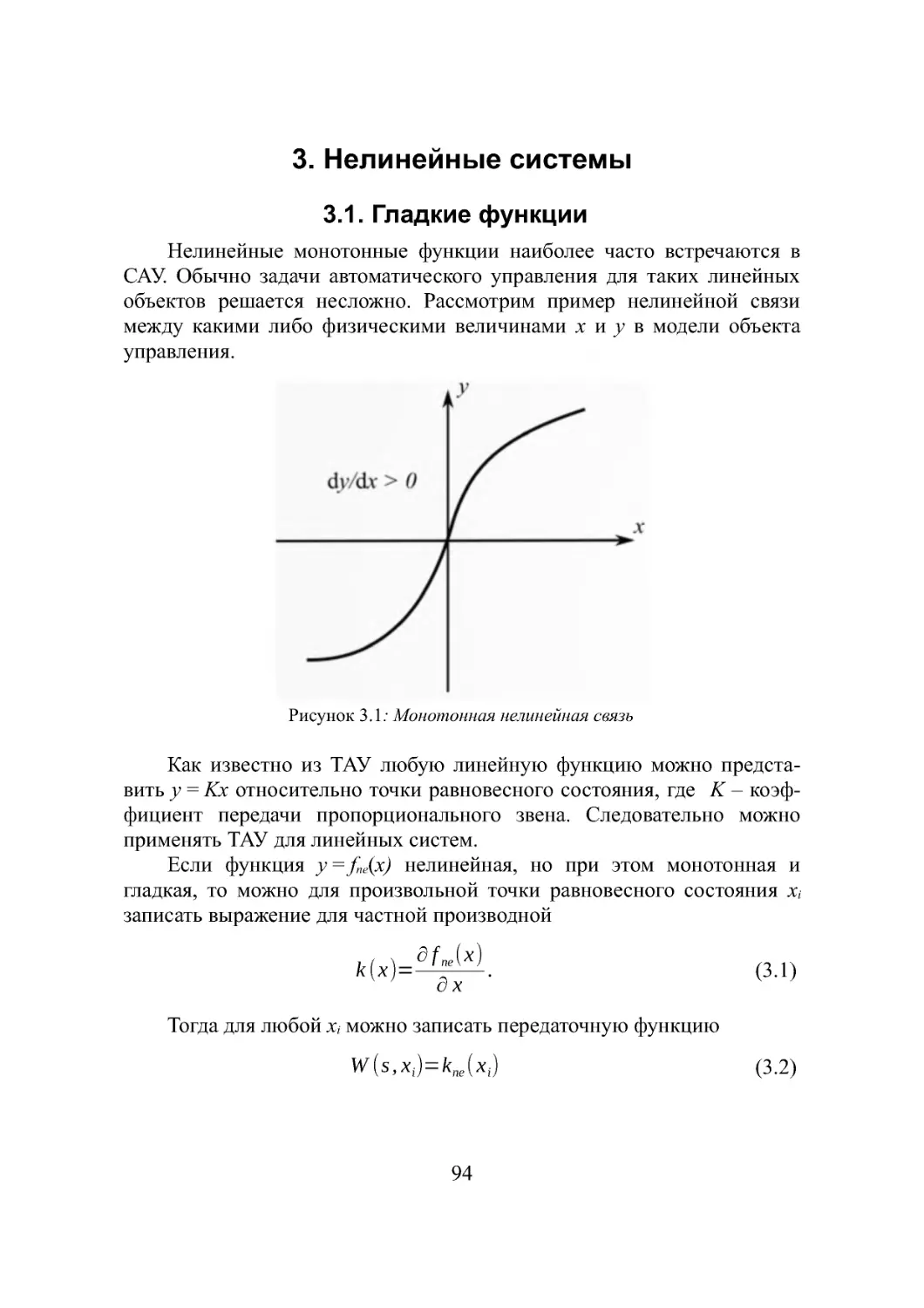
3.1. Гладкие функции......................................94
3.2. Кусочно-линейные функции.............................97
3.2.1. Функции с ограничением по выходу.................97
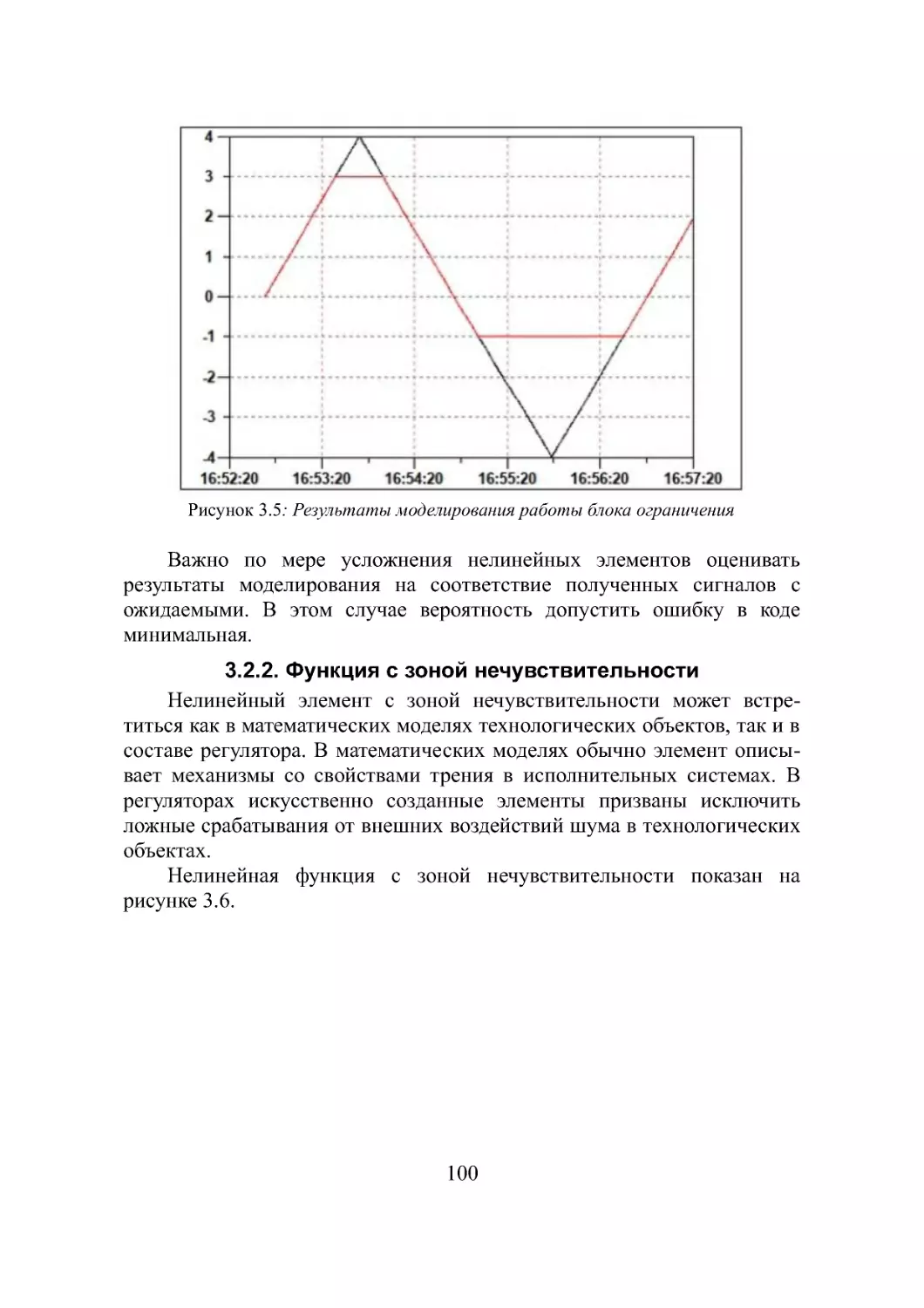
3.2.2. Функция с зоной нечувствительности..............100
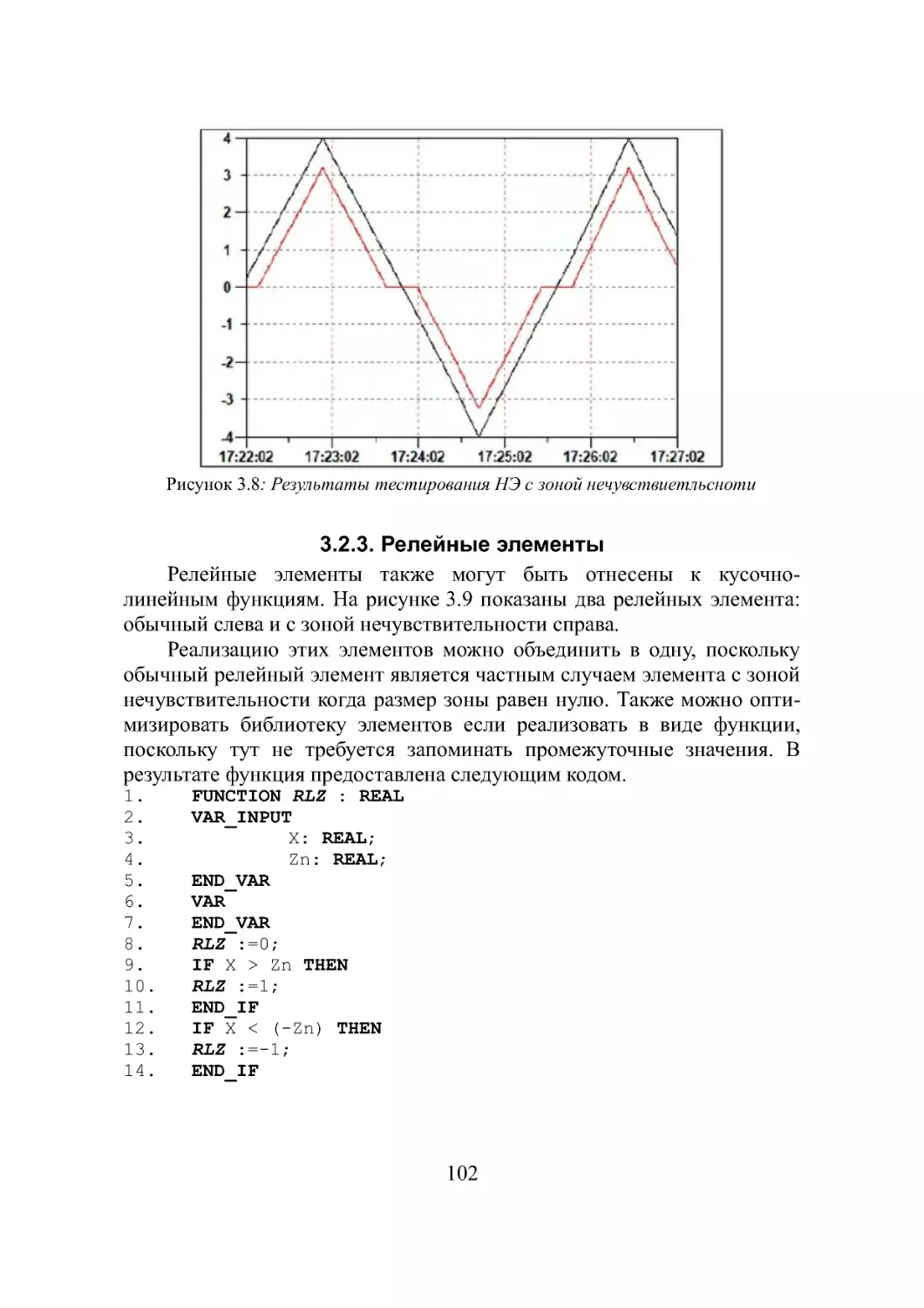
3.2.3. Релейные элементы...............................102
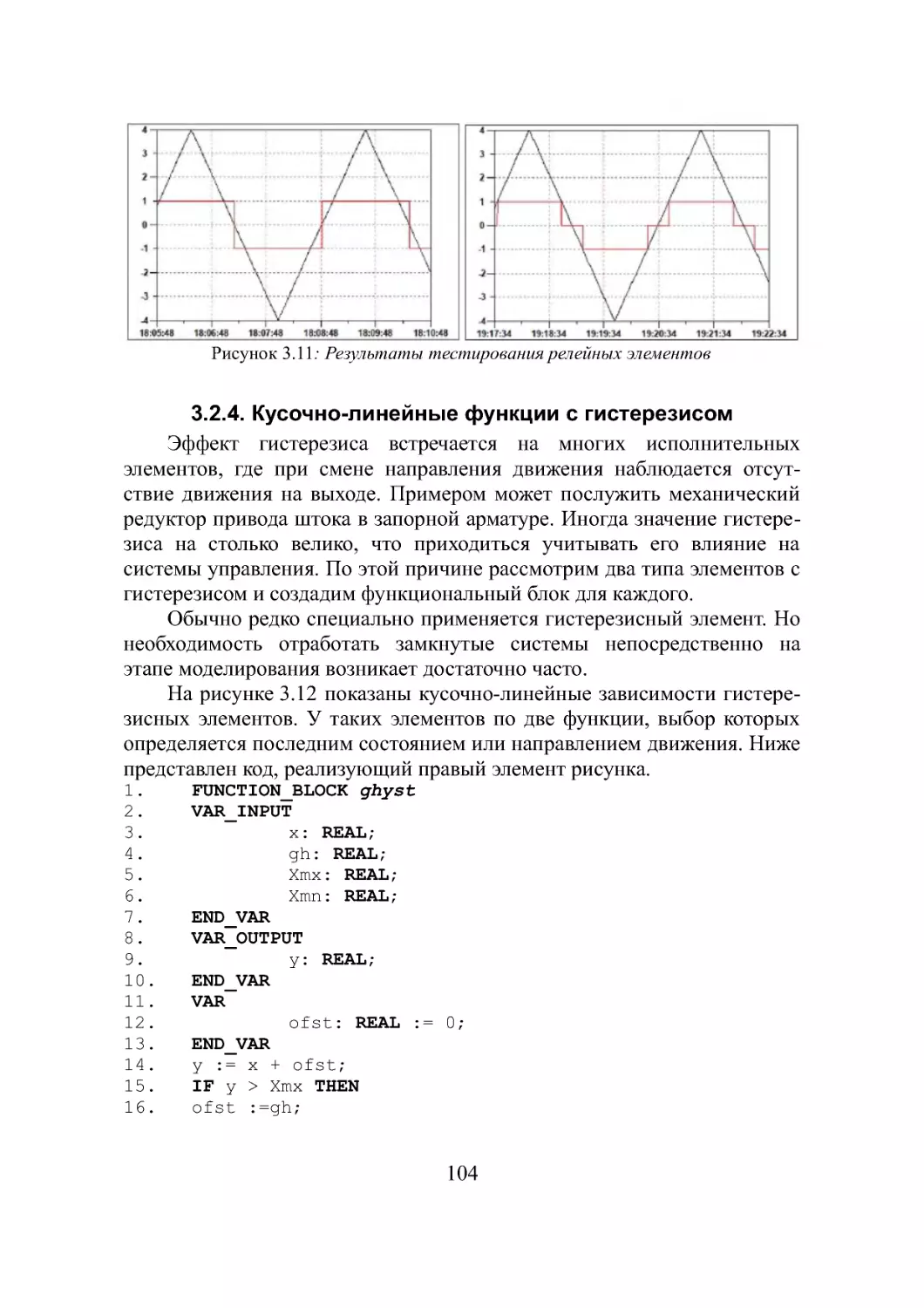
3.2.4. Кусочно-линейные функции с гистерезисом.........104
Вопросы к разделу......................................106
3.3. Устойчивость нелинейных систем......................107
3.3.1. Линеаризация....................................107
3.3.2. Функция Ляпунова................................108
3.3.3. Гармоническая линеаризация.......................ПО
Вопросы к разделу......................................117
3.4. Реализация ШИМ......................................118
3.4.1. Программная реализация ШИМ......................118
3
3.4.2. Аппаратная реализация ШИМ........................121
3.4.3. Использование релейных элементов для реализации
непериодических ШИМ.....................................123
Вопросы к разделу.......................................129
4. Современные САУ..........................................130
4.1. Оптимальные системы управления.......................130
4.1.1. Классификация....................................130
4.1.2. Модальное управление.............................131
4.1.3. Практическая реализация модульного оптимума на ПЛК....133
4.1.4. Использование Вариационного исчисления для настройки
ПИД-регулятора..........................................139
Вопросы к разделу.......................................146
4.2. Автоподстройка в САУ.................................146
4.3. Адаптивные САУ.......................................155
4.3.1. Адаптивная САУ с эталонной моделью с сигнальной
адаптацией..............................................157
4.3.2. Адаптивная САУ с эталонной моделью с параметрической
адаптацией..............................................159
4.3.3. Идентификация модели объекта управления..........160
Вопросы к разделу.......................................164
4.4. Теория нечётких множеств.............................165
Вопросы к разделу.......................................175
5. Моделирование и управление электромеханических объектов...176
5.1. Модель ЭО в пространстве переменных состояний........176
5.2. Модели взаимосвязанных ЭО в пространстве состояний...181
5.3. Линеаризация нелинейных моделей ЭО...................193
5.4. Модели ЭО с упругими механическими связями...........198
5.5. Нормальная и каноническая формы векторно-матричных
уравнений.................................................203
5.6. Моделирование непрерывных ЭО с использованием переходной
матрицы состояния.........................................206
5.7. Способы определения переходной матрицы состояния
электромеханических объектов..............................216
5.8. Цифровое моделирование непрерывных процессов в ЭО на
основе метода Эйлера......................................219
5.9. Примеры вычисления переходной матрицы и моделей переходных
процессов в ЭО............................................221
Вопросы к разделу.......................................229
6. Средства согласования модулей расширения ПЛК.............230
6.1. ModBus протокол обмена...............................230
4
Вопросы к разделу.......................................241
6.2. Аппаратный интерфейс CAN.............................241
Вопросы к разделу.......................................246
6.3. ОРС серевер..........................................246
Вопросы к разделу.......................................256
Заключение..................................................257
Список условных обозначений и сокращений....................258
Глоссарий...................................................258
Список литературы...........................................259
Приложения..................................................266
1. Первое приложение......................................266
2. Второе приложение......................................266
5
Введение
Современные программируемый логические контроллеры (ПЛК)
имеют широкие возможности для реализации очень сложных систем
автоматического управления (САУ). Такие системы включают в себя не
только контроллеры, но и программные средства диспетчеризации,
удалённого наблюдения и взаимодействия человека с оборудованием
через устройства отображения информации в удобном виде.
Программные средства уже давно приобрели свои правила и стан-
дарты построения сложных систем автоматического управления.
Обычно эти программные средства представлены так называемой
SCADA системой, разработанной зарубежными и отечественными
производителями программного обеспечения.
Среда проектирования сложны систем автоматического и автомати-
зированного управления технологическими процессами весьма сложна
и требует обучения методам проектирования. По этой причине произво-
дители ПО SCAD А систем уделяют много усилий для организации
обучающих семинаров, учебных пособий и руководств пользователя.
Все это доступно в большей мере на бесплатной основе в интернет
ресурсах производителя. Можно сказать, что собранный материал доста-
точный, чтобы освоить методы и подходы построения проекта.
Отдельно рассматриваются подходы к программированию контрол-
леров различными методами, включающими в себя программирования с
помощью функциональных схем систем управления и текстовых
программ. Также можно найти исчерпывающую информацию о
программировании контроллеров в системах автоматического управ-
ления.
Основная сложность заключается в том, что в инженерной практике
направления систем автоматического и автоматизированного управления
рассматривается именно в ключе использования ПЛК и SCADA систем
и мало затрагиваются темы теории автоматического управления (ТАУ).
Учебных дисциплинах предмет САУ содержит в большей мере мате-
риалы ТАУ практически не рассматривая методы реализации полу-
ченных решений в ПЛК.
Данное учебное пособие рассматриваются элементы проектиро-
вания САУ на ПЛК, где требуется знание решений ТАУ чтобы приме-
нить из в задачах программирования и построения сложных SCADA
систем. Предполагается, что обучающийся уже имеет базовые знания
линейной ТАУ
6
1. Принципы построения современных систем
управления
1.1. Современные SCADA системы.
Современные автоматизированные системы управления технологи-
ческими процессами (АСУ ТП) и техническим оборудованием формиро-
вались совместно с технологами и программистами. На этапе создания
системы управления технологи нуждались в работе программистов. В
свою очередь, программистам так же в течение всего процесса проекти-
рования и разработки требовалась постоянная помощь технологов.
Попытки уменьшить издержки в длительных общениях двух разных
специалистов привели к созданию программного обеспечения, которое в
позволяет большей мере выполнять работу технологами, включая
элементы программирования. Данное программное обеспечение
призвано дать обширный инструментарий технологам для создания
технологической системы, о которой мало что известно программистам.
В процессе создания стало понятно, что большинство задач можно
унифицировать, формализовать, классифицировать и реализовать на
языке, понятном технологу. В результате родился набор инструментов
для технолога:
• перенос различных элементов управления (поворотные или
ползунковые регуляторы, кнопки, рубильники) на экран
обслуживающего персонала;
• возможность формировать мнемосхемы или экранные формы для
отображения переменных состояния процесса в виде: полосковых или
цифровых индикаторов, стрелочных индикаторов, согласно
ассоциативного представления о процессе для технолога,
обслуживающего персонала или ответственных работников;
• для изучения и анализа нештатных ситуаций имеется инструмент
для формирования архивов поведения переменных состояния процесса
и аварий, событий во времени. Такие элемента специалисты называют
трендами;
• адаптивный для технолога язык реализации алгоритмов
управления, логических и математических вычислений;
• формирование документации к алгоритмам программа, а так же
самого технологического процесса;
• средства обеспечения детерминизма поведения системы,
включающие в себя ядро или монитор реального времени. Он
7
обеспечивает предсказуемое и допустимое время отработки и
отображения события;
• внушительный набор драйверов для оборудованию нижнего
уровня АСУ ТП;
• сетевые инструменты обмена переменными состояния ТП;
• средства исключающие несанкционированный доступ к
параметрам АСУ ТП;
• графические редакторы для создания многооконного человеко-
машинного интерфейса - Human Machine Interface (HMI) и другие
отображающие функции;
• возможность импорта из баз изображений, а также создание
собственных библиотек элементов мнемосхем, рисунков, алгоритмов,
динамических объектов и т. п.
Это далеко не полный список инструментов и с развитием будет
непременно пополняться. Но уже на этом этапе пользователи технологи
и технические специалисты могут выбирать необходимые инструменты
и формировать свою систему управления без участия программистов.
Исторически так сложилось, что этого рода программное обеспечение
называется SCADA системой. На английском - Supervisor Control And
Data Acquisition, на русском - контроль или управление с широкими
средствами наблюдения и сбора данных.
В данном пособии рассматриваются лишь некоторые инструменты,
которые позволяют реализовать на уровне подготовленного инженера
основные решения, известные в рамках дисциплины ТАУ
На рисунке 1.1 показана структурная схема системы управления с
автономным SCADA-приложением установленном на персональном
компьютере. Компьютер может выполнять роль
• автоматического рабочего места (АРМ),
• монитора реального времени (МРВ).
Эти две роли имеют принципиальное отличие. АРМ предполагает
присутствие обслуживающего персонала в течение технологического
процесса. МРВ является устройством для отображения технологиче-
ского процесса и автоматического принятия решений реализованного на
ПК и не предполагающего постоянного присутствия персонала.
8
АРМ оператора (МРВ, мрв», До«мРв«,
GSMMP&», OPCMPB.)
Технологический процесс (ПЛК. Счетчики)
Рисунок 1.1.- Система управления с автономной SCADA.
К персональному компьютеру непосредственно или через сетевое
оборудование подключены исполнительные и измерительные устрой-
ства и программируемые логические контроллеры (ПЛК). Для обеспе-
чения подключения устройств на физическом уровне в ПК обычно уста-
навливается дополнительное оборудование с последовательными RS232
и RS485 портами.
На программном уровне все гораздо сложней, поскольку суще-
ствует очень большое количество типов оборудования у которых
имеется RS232 и RS485 интерфейс на физическом уровне, где протокол
обмена данными может быть каким угодно согласно стратегии произво-
дителя. Поэтому поставщики SCADA систем стараются обеспечить
связь с большинством типов устройств. Так например, компания Adastra
в своей реализации SCADA TraceMode обеспечивает подключение
более чем 2500 устройств различного типа, включая стандартные обще-
принятые протоколы, такие как ModBus.
В составе подключаемых устройств могут быть ПЛК которые
можно программировать на удобных для технологов и инженеров
языках. Состав этих языков стал стандартом для многих устройств,
АРМ, МРВ и др. Поэтому все SCADA системы содержат в себе реали-
зацию этого стандарта. Международное название стандарта
IEC 6-1131/3, в России стандарт назван МЭК 6-1131/3.
9
В автономной SCADA решения, представленными программами в
стандарте МЭК 6-1131/3 могут выполнятся не только на базе АРМ или
МРВ, но и на базе ПЛ К, если в нем имеется поддержка стандарта.
Следует отметить, что далеко не все периферийные ПЛК поддерживают
стандарт и программируются другими средствами и языками.
Автономные системы относятся к простейшим реализациям
SCADA и, как правило, сконцентрированы на одной технологической
площадке. Если измерительное и исполнительное оборудование распре-
делено по большой территории и требует диспетчеризации и управления
с единого центра, то такую SCADA обеспечивают средствами удалён-
ного доступа.
На рисунке 1.2 показана структурная схема с телеуправлением.
Технологический процесс (ПЛК, Счетчики}
Рисунок 1.2.- SCADA: телемеханическая архитектура
Слово телемеханика предполагает исполнительное устройство,
котором можно управлять на расстоянии, однако к технической литера-
туре часто это слово используют более широко. В результате, когда
говорят об оборудовании телемеханики, предполагается удалённый
доступ, как к исполнительному, так и к измерительному оборудованию.
Основным отличием телемеханической структуры является
наличие оборудования удалённого доступа к приборам с помощью
средств Ethernet, GPRS, GSM, ZigBee, WiFi [x] и др. технологий.
10
Простейшим примером телемеханической архитектуры может
послужить система диспетчеризации оборудования жилищно-комму-
нального хозяйства. Как правило, оборудование расположено в подвалах
жилых домов с ограниченным физическим доступом и включает в себя
электросчётчики, теплосчётчики, счётчики расхода воды и контроллеры
управления потреблением, повышающими давление насосными стан-
циями, аварийной защитой и др..
Кроме контроля потребления в такой системе можно формализо-
вать ряд задач, которые на уровне АРМ могут выполнятся автомати-
чески или в автоматизированном режиме. Примером задач, поддаю-
щимся автоматизации могут быть: автоматическое закрытие запорной
арматуры при нештатном расходе воды в следствие порывов в трубопро-
водах, выявление воровства электричества потребителями на основании
показаний индивидуальных счётчиков и данных с основного счётчика.
К более сложным системам можно отнести клиент-серверная струк-
тура, показанная на рисунке 1.3.
ПЛК, е т.ч. и с
Micro TRACE MODE
Технологический процесс (ПЛК, Счегчикм)
Рисунок 1.3: Клиент-серверная система на базе SCADA.
11
Принципиальным отличием является наличие ПК-сервера. Этот
компьютер может выполнять также роль АРМ или МРВ, но основной
его задачей является сосредоточение всего ядра SCADA системы в
единой базе данных. Поскольку сервер может не иметь дисплея и других
средств взаимодействия с человеком, также предполагается несколько
АРМ или МРВ на базе отдельных ПК, которые связанны с сервером по
Ethernet сети.
Есть объекты управления, которые имеет один из статусов: страте-
гический важный, взрывоопасный объект. Или другими словами,
объекты, для которых остановка или поломка системы управления
критически опасна. В таких система управления используется промыш-
ленная Ethernet сеть, которая включает в себя многоуровневое резерви-
рование каналов связи, специализированные сетевые коммутаторы и
многое другое. Однако с точки зрения пользователя такой сети: програм-
миста, технолога, технического специалиста, нет особых отличий от
обычной Ethernet или Internet сети, кроме высокой надёжности.
Как уже отмечалось, количество АРМ и МРВ может быть доста-
точно большим и все они могут отличаться друг от друга конфигура-
цией. В частности конфигурация зависит от специалиста на АРМ.
Именно под его задачи настраивается HMI панель с различными
правами доступа к данным и управлению. Современные SCADA позво-
ляют создавать АРМ не только для технических специалистов, но и для
поставщиков материала для производства, контролирующих эффектив-
ность труда, бухгалтерии и начальства. Грамотная организация всех
АРМ позволяет повышать эффективность труда каждого специалиста
включая учёт рабочего времени и результаты работы, поддающиеся
измерению.
Ещё более сложные SCADA могут иметь несколько серверов со
своими базами данных, где определённая часть данных дублируется на
всех серверах. Они обычно называются распределенными системами
управления (РСУ). Такая структура, представленная на рисунке 1.4,
позволяет выделить локальные задачи в рамках технического объекта,
обособленного цеха или сооружения, где глобальные задачи выполня-
ются на серверах с обеспечением обмена данных между ними.
12
ПК с перекрестным рччрряироеамием |М₽в. мев». До.*лее». GSMMPfr*.
Рисунок 1.4: Распределенная система управления (РСУ) на базе SCADA
Распределенные системы управления оправдано использовать в
качестве единой системы управления достаточно крупного завода с
несколькими производственными цехами, зданиями и сооружениями.
Более развитые системы позволяют давать информацию заказчику
о процессе и этапах производства продукции. Для этого в состав
проекта включают поддержку WEB-технологии передачи данных заказ-
чику. На данный момент поставщики наиболее популярных SCADA
(TraceMode, Мастер SCADA, возможно и другие) предоставляют
готовый конфигурируемый WEB-сервер, позволяющий передавать необ-
ходимую информацию внешним наблюдателям. Технология передачи и
отображения данных на браузерах пользователей мало отличается от
графических сетевых игр. Со стороны пользователя ПО SCADA техно-
логия построения удалённого МРВ практически не отличается обычного
МРВ.
На рисунке 1.5 показан обще принятый способ подключения
SCADA в международную сеть Internet. В целя информационной
безопасности компьютер-сервер кроме того, что включает в себя ПО
SCADA, также имеет две или более сетевые карты с интерфейсами
Ethernet. Одна из них предназначена для связи с внешним миром, а в
рамках ядра операционной системы имеется маршрутизатор, обеспечи-
вающий только необходимые типы подключения от внешней сети.
Настройкой маршрутизаторов занимаются администраторы сети и,
обычно, технические специалисты не участвуют в этой части проектной
работы.
13
Рисунок 1.5: WEB-система на базе SCADA.
Дальнейшим развитием WEB в SCADA стали облачные техно-
логии, которые предоставляются многими сетевыми компаниями, в том
числе и производителями ПО SCADA. На рисунке 1.6 показана
Облачные системы на базе SCADA.
Рисунок 1.6: Облачная-система на базе SCADA.
Основным отличием от WEB-системы является наличие сервера с
базой данных во внешней Intemet-сети. Основной сервер, который
сосредотачивает у себя всю информацию о технологическом процессе,
14
имеет программные средства для публикации данных выбранных для
внешнего доступа.
При создании облачной системы также формируется
WEB-поддержка для устройств с интернет браузерами. Разработчики
могут предоставить приложения для мобильных устройств, обеспечива-
ющих передачу и отображение данных на устройстве. Мобильные
приложения, в отличие от МРВ на базе браузера, могут иметь фоновые
службы, отслеживающие нештатные ситуации или другие события на
облачном сервере. Примером фоновых событий на мобильном устрой-
стве может послужить сервис WhatsApp, который способен издавать
звуки даже, если устройство находится в кармане в спящем режиме.
Также можно позволить, показывать поверх всех окон свежие сооб-
щения.
В рамках большой SCADA на различных платформах (АРМ, МРВ,
ПЛК и, просто, технологический контроллер-регулятор технологиче-
ского процесса) выполняются различные задачи управления, которые
формализовал технолог. Как правило, большинство таких задач доста-
точно статичны и мало связанны с быстрой динамикой объекта управ-
ления. Однако среди этих задач есть весьма сложные, которые связанны
с управлением динамическими системами. Подобного рода задачи
требуют специальных технических знаний и специализации. По этой
причине отдельным направлением проектирования САУ является разра-
ботка алгоритмов управления замкнутыми системами, построенными на
базе теории автоматического управления. Большинство таких задач
реализуются на программируемых логических контроллерах. Следу-
ющий раздел им посвящён.
Вопросы к разделу.
1. Опишите структуру современных SCADA систем управления.
2. Перечислите основные задачи SCADA систем.
3. Какие устройства SCADA систем программируются в стандарте
МЭК 6-1131/3.
4. В чем отличия локальных и распределенных систем?
5. В чем отличие серверных и облачных систем?
6. Можно ли использовать мобильные устройства в SCADA в
качестве чего?
1.2. Программируемый логической контроллер
ПЛК - достаточно широкое понятие, включающая в себя контрол-
леры с дисплеями, клавиатурами, носителями информации и т. д.. По
15
этой причине АРМ, МРВ и просто персональные компьютеры также
можно назвать программируемыми логическими контроллерами. С
точки зрения структурной схемы также есть много общего с ПК. Однако
существует принципиальное отличие ПЛК от обычного ПК особенно
для управления динамическими системами. Это отличие связанно с тем,
что существует жёсткое требование ко времени и периодичности вычис-
ления алгоритма управления, особенно для динамических систем. Это
отличие обеспечивается специальными операционными системами
реального времени.
Операционная система реального времени, построена так, чтобы
гарантировалось своевременное выполнение алгоритма управления при
любой планируемой загрузки процесса. В отличии от ПЛК в АРМ и
МРВ установлена операционная система Windows, где без особых
настроек строгая и заданная периодичность отработки задач не гаранти-
руется.
В этом разделе будем рассматривать различные ПЛК, где использу-
ется ОС реального времени. На рисунке 1.7 показана типичная струк-
тура ПЛК.
Программируемый логический контроллер (ПЛК)
+10...+30В
DC/DC-
преобразователь
Защитные функции
Промышленный Etherret.
RS-485, CAN
Коммуникационные
интерфейсы
Процессор
Беспроводные
протоколы
Аналоговые выходы
Дискретные входы
Дискретные выходы
Аналоговые входы
Специальные
входы/выходы
Рисунок 1.7: Структурная схема ПЛК
Электропитание для большинства типов ПЛК обеспечивается
внешним источником в диапазоне от 10 до 30 В. Это позволяет доста-
точно свободно выбирать типовые источники питания из популярного
ряда выходных напряжений (12, 20, 24, 36 В). Как правило, популяр-
ность и большое количество серийно выпускаемых источников обеспе-
чивает им небольшую стоимость. Следует отметить, что некоторые
производители включают источник питания в конструкцию ПЛК. Так
16
например в компании ОВЕН предлагают ПЛК с переменным напряже-
нием питания в диапазоне (-120-270 В).
Интерфейсы. В отличие от ПК в ПЛК реализовано несколько
коммуникационных интерфейсов. Кроме общепринятого Ethernet канала
имеются несколько RS485 портов для связи с дополнительным оборудо-
ванием или с верхним уровнем SCADA системы. Также могут встре-
чаться интерфейсы стандартов CAN, SPI, I2C для подключения модулей
расширения подобно шине PCI в персональном компьютере.
Беспроводные физические протоколы типа WiFi, ZigBee, bluetooth
также могут применятся в ПЛК. Однако такой вид связи с верхним
уровнем используется для узлов автоматики и диспетчеризации, где
требования к надёжности не столь высоки как у систем, работающих в
реальном времени.
Важным атрибутом ПЛК является реализация защитных функций
на аппаратном уровне. Для понимания необходимости таких функций
можно представить ситуацию, когда персональный компьютер «зави-
сает» - не реагирует на сигналы с клавиатуры и мыши, при этом на
экране картина не меняется. В этом случае пользователь, несколько
подождав, нажимает кнопку «Reset» перезапуская ПК. В свою очередь
ПЛК не является АРМ или МРВ, может не иметь клавиатуры, мыши и
даже дисплея. В таком случае ситуация с зависанием «программы» в
ПЛК становится катастрофической и не приемлемой. Для решения этой
проблемы практический во всех ПЛК, даже самых дешёвых есть физи-
чески реализованное устройство - сторожевой таймер (WatchDog).
Принцип работы устройства заключается в следующем. Сторо-
жевой устройство отсчитывает время до перезапуска процессора. Если
ничего для предотвращения этого не произойдёт, то WatchDog непре-
менно перезагрузит ПЛК. В свою очередь в каждой жизненно важной
программе, есть часть кода, оповещающего операционную систему, что
код выполняется корректно. Если важных подпрограмм несколько, то
организуется дополнительная программа арбитр, следящая за работо-
способностью всех задач. Программа арбитр восстанавливает
WatchDog-счётчик, оттягивая время перезагрузки ПЛК. Достаточно
некорректной работы одной из важных задач, включая
арбитр-программу чтобы ПЛК перезагрузился на аппаратном уровне.
WatchDog - не единственная защитная функция ПЛК, реализо-
ванная аппаратно. Есть некоторые функции напрямую связанные с
системой прерываний процессора.
Есть элементы, без которых процессор нельзя назвать ПЛК. Это
средства связи в измерительным и исполнительным оборудованием
17
системы автоматического управления. На рисунке 1.8 показаны неко-
торые элементы автоматики, подключаемые к ПЛК.
Рисунок 1.8: Дискретные входа и выхода ПЛК
Командные кнопки, датчики физических величин, тумблеры и
дополнительные контакты пускателей позволяют воздействовать на
ПЛК и выполняемые программы с помощью дискретных входов. Для
этого в ПЛК имеется схема согласования входного сигнала от датчика с
контактом процессора. Схемы согласования могут иметь или не иметь
гальваническую развязку. На рисунке 1.9 показана одна из реализаций
гальванической развязки.
Рисунок 1.9: Схема согласования дискретного входа с гальванической развязкой
Роль гальванической развязки сложно переоценить, так как в
системах управления силовыми агрегатами возникают электромаг-
нитные помехи на столько сильные, что способны вывести из строя
процессор. К примеру, в станках с числовым программным управлением
(ЧПУ) сигналы о состоянии концевых выключателей поступают по
проводам, расположенными рядом с силовыми линиями. В результате
есть вероятность ложного срабатывания сигнала, что для станков с ЧПУ
18
очень критично. По этой причине всегда используется гальваническая
развязка, даже если общие провода процессора и датчика объеденины.
Очень важно принять правильное решение при выборе ПЛК внима-
тельно читая характеристики дискретных входов для объектов с элек-
тромагнитными помехами.
Дискретные входя могут отличаться по способу передачи сигнала:
• Напряжение с заданной амплитудой (есть напряжение / нет
напряжения).
• «Сухой» контакт (замкнут / разомкнут).
• Открытый коллектор (OK), open collector (ОС), открытый сток
(ОС), open drain (OD). Выходной транзистор датчика (открыт / закрыт).
Обычно производители ПЛК стараются организовать универ-
сальный вход и обеспечить все перечисленные способы подключения. В
руководствах пользователя обычно достаточно подробно описаны и
приведены схемы подключения всех возможных способов [].
Дискретные выходы имеют такие же способы передачи сигнала как
и входы. Важным отличием, кроме того, что это выходы, являются
наличие силовых характеристик выхода. На рисунке 1.10 показана схема
согласования мощной нагрузки с выходом процессора ПЛК.
Рисунок 1.10: Схема согласования дискретного выхода с гальванической развязкой
Мощность нагрузки определяет напряжение и ток, который может
длительное время выдержать симистор. Промышленностью выпус-
каются симисторы, позволяющие коммутировать токи выше 100 ампер.
В этом случае часть схемы, выделенная цветом реализуется за преде-
лами ПЛК и управляется открытым коллектором. Для универсальности,
часто в ПЛК качестве выхода реализованы именно открытые коллек-
тора или стоки. Узкоспециализированные ПЛК могу содержать в себе
гальванически развязанные симисторные схемы или небольшие (с током
коммутации до 10 А) электромагнитные реле.
19
Аналоговые входы и выходы с гальванической развязкой встреча-
ются достаточно редко, поскольку само значение аналогового сигнала
очень критично к помехам. Обычно сигнальные аналоговые линии
прокладывают по специальным экранированным каналам. На
рисунке 1.11 показаны унифицированные методы подключения анало-
говых сигналов. К унифицированным аналоговым сигналам относятся:
1. Напряжение, обычно в диапазоне (0-10 В). С помощью этого
способа можно измерять разные физические величины используя схемы
преобразования значения физической величины в напряжение.
Основным недостатком такого подключения является значительная
чувствительность к электромагнитным помехам. Поэтому такая схема
подключения используется при хорошем экранировании линий подклю-
чения с малыми расстояниями до 2 метров.
2. Для уменьшения электромагнитных помех сигнал в ПЛК можно
передавать с помощью генератора тока. Такие схемы хорошо зарекомен-
довали себя в САУ, поэтому этот стандарт более распространён.
Принято два диапазона передачи сигнала (0-5 мА) и (4 - 20 мА), где
обеспечена линейная зависимость физической величины передаваемому
току. Минимальному значению физической величины соответствует
минимальное значение тока, максимальному - максимальное значение
тока. Датчики тока могу быть активными или пассивными. Активные
датчики требуют отдельного подключения источника питания.
3. Пассивные датчики, также используют источник питания, но
при этом имеют всего два контакта, а источник питания подключен
последовательно с датчиком. В результате датчик передает сигнал в виде
потребляемого тока. Поскольку для питания схемы измерения требуется
какой то минимальный ток, то принят стандарт передачи сигнала в
диапазоне (4 - 20 мА), где оставлено 4 мА для питания схемы изме-
рения. Данный способ передачи аналоговых сигналов наиболее попу-
лярен в САУ Практически для всех известных физических величин,
которые можно измерить, существует промышленно выпускаемый
датчик с выходом (4-20 мА).
Иллюстрация схем подключения рассмотренных типов датчиков
показана на рисунке 1.11.
20
Если кратко отметить отличие привычного все персонального
компьютера от ПЛК, то первым делом следует отметить наличие у ПЛК
контактов со схемами согласования процессора и дискретных или
аналоговых входов или выходов. Именно это отличие позволяет создать
на базе ПЛК простейшую САУ. Простейшая схема использования ПЛК
показана на рисунке 1.12. Такого типа задачи встречаются очень часто
для регулирования температуры в помещении, инкубаторе, хранилище и
т.д..
Transminer
PLC
20rnA
4-;
PWM
I
RID
Tempe ratu re
Sensor
HEATER
Solid State Relay Drive
(SSR)
Рисунок 1.12.- Простейшая схема использования ПЛК
Как видно из рисунка в качестве входа применяется датчик темпе-
ратуры со стандартной схемой включения (4-20мА). В качестве выхода
релейный элемент подающий напряжение питания на элемент нагрева
или электродвигатель компрессора. Задача САУ заключается в изме-
21
рении температуры объекта, сравнения с заданной и принятие решения
на увеличение или уменьшение воздействия на объект.
На этапе программирования контроллера решаются несколько
подзадач. Опишем только самый необходимый набор подзадач для
минимальной реализации САУ.
Со стороны ПЛК каждому аналоговому входу создана переменная,
где хранится результат измерения. На примере обозначения gAi2 можно
полагать, что переменная глобальная и видна для любой подпрограммы,
относится к аналоговым сигналам и вероятно это второй аналоговый
вход. Конечно в процессе проектирования предполагать и на это
опираться не всегда корректно. Разработчику САУ следует внимательно
прочитать руководство пользователя к ПЛК. Кроме перечисленного, из
руководства необходимо узнать к какому типу чисел и диапазону
значений принадлежит переменная gAi2. В случае если ПЛК имеет
АЦП с разрядностью 10 бит, диапазон gAi2 будет соответствовать
значениям [0 ... (210-1)] или [0 ... 1023] целым числам.
Чтобы превратить целое число в значение физической величины
следует найти в руководстве пользователя датчика инструкцию пере-
счета показания АЦП в значение физической величины. Обычно произ-
водители датчиков обеспечивают линейную характеристику, где указано
соответствие для минимального (4мА) и максимального (20мА)
значения тока минимальному и максимальному значению физической
величины. К примеру, датчик измеряет температуру от Tmin = -50°С до
Tmin = 100°С. Не сложно составить систему простых уравнений и найти
линейную функцию пересчёта значения АЦП gAi в gTc:
gTc(gAi)=a0+a1gAi, (1.1)
коэффициенты ао, ai - можно вычислить из системы уравнений
_ 4mA
min °0 О1'20тА тах’ (1.2)
max ~ °0 + а 1 ‘ N max ’
где Nmax - максимальное значение АЦП. Если это значение равно 1023,
то несложно посчитать коэффициенты (1.1) решив систему урав-
нений (1.2). В результате получим выражения
22
(Tmax-Tmin) 20 mA
Q =-----7------------V,
NmaJ20 mA-4 mA)
(1.3)
^0 Tmax ^1 Nmax ’
Конечно, знающие характеристики большинства ПЛК могут утвер-
ждать, что выражение (1.3) не обязательно получать и реализовывать в
программе, так как на этапе конфигурации ПЛК достаточно ввести
характеристики датчика и получить готовую переменную со значением
физической величины. Действительно, процедура получения
функции (1.1) на столько стандартная и часто встречающаяся, что в
большинстве ПЛК реализована, но всегда будут существовать недорогие
контроллеры, где эту задачу нужно реализовать самостоятельно.
Важно отметить, что для корректного вычисления переменные
gTc, ао, ai - должны быть числами вещественными с плавающей или, в
крайнем случае, с фиксированной, точкой.
Далее полагая, что переменная для измеренной физической
величины имеется, следует сравнить ее с заданной и решить: включать
или выключать исполнительное устройство. В ТАУ реализация этой
процедуры связанно с понятием отрицательной обратной связью. Если
целевая величина меньше, то следует нагревать объект. Если она больше
то следует остужать объект. Отрицательную обратную связь нужно
обеспечить решением включать исполнительное устройство или выклю-
чать. Это решение выглядит просто
и=
//(gToTsJ 0,
if(gTc<TSet) 1,
(1-4)
где значение не равное 0 считается активным и предполагается вклю-
чение исполнительного устройства.
На этом этапе, можно протестировать интуицию программиста,
поскольку для двух типов исполнительного устройства:
1. нагревательный элемент, который повышает температуру при
включении;
2. двигатель компрессора холодильника, который понижает темпе-
ратуру при включении.
В одном случае обеспечивается отрицательная обратная связь в
другом положительная.
Кроме анализа типа обратной связи есть множество проблем,
которые возникают в процессе создания САУ с обратной связью. К ним
23
относятся проблемы устойчивости и оптимального управления, которые
решаются в рамках дисциплины ТАУ линейных систем. Поскольку
исполнительное устройство имеет дискретный вход, то САУ содержит в
себе как минимум один нелинейный релейный компонент
Выражение (1.4), даже при обеспечении отрицательной обратной
связи, может быть неработоспособно, поскольку канал АЦП подвержен
помехам и частое изменение значение gTc в области Tset приведёт к
частым переключениям исполнительного устройства, что губительно
для электродвигателя. Для решения подобных задач разработчик должен
уметь использовать релейные элементы с зоной нечувствительности или
гистерезисом. Данные компоненты рассматриваются в (OPS) параграфе.
ПЛК в отличие от персонального компьютера может иметь множе-
ство интерфейсов передачи данных, выведенных на внешние разъемы.
Изучать работу с таких интерфейсов лучше изучать на конкретных
примерах и задачах один из примеров рассматривается в (OPS) пара-
графе. Методы подключения Ethernet интерфейса ПЛК мало отличаются
от методов организации корпоративной сети предприятия со средствами
защиты с помощью так называемых «брэндмауэров». В рамках отдель-
ного предприятия может существовать отдельная Ethernet сеть для
контроллеров, также отделенная от корпоративной брэндмауэром.
Подобная трехслойная сеть показана на рисунке 1.13. Как уже отмеча-
лось, разделением сети занимаются отдельные специалисты админи-
страторы сети. Более подробную информацию по конфигурации Ethernet
сети и средств защиты можно взять из учебных пособий [... ].
24
Рисунок 1.13: Схема взаимодействия ПЛК со SCADA
Внешний вид ПЛК значительно отличается от персонального
компьютера, и даже различными типами ПЛК. На рисунке 1.14 показано
изображение ПЛК у которого в штатном режиме работы не преду-
смотрен дисплей и клавиатура. Такие ПЛК работают автономно и
связанны с верхним уровнем одним из доступных последовательных
интерфейсов (Ethernet, Rs485, ... ). Тем не менее, в них имеется
SVGA-разъем для подключения к монитору и клавиатуре, обычно для
настройки и конфигурации. Данного типа ПЛК имеют параллельный
коммуникационный интерфейс (parallel communication interface - PCI)
для модулей расширения.
Рисунок 1.14.- ПЛК с модулями расширения на PCI шине
25
PCI представлен в виде шины, куда можно подключить различные
модули расширения для обеспечения необходимого количества
дискретных и аналоговых входов и выходов. Более подробное описание
модулей расширения выходит за рамки учебного пособия, поэтому
отметим, что модули расширения могут иметь типичные характери-
стики:
• количество выходов и их нагрузочные характеристики,
• количество входов,
• наличие или отсутствие гальванической развязки,
• время опроса - дискретизация,
• типы входных и выходных схем (0-5 мА, 4-20 мА, 0-10 В,
открытый коллектор, сухой контакт и т.д.)
Для более простых задач, не требующих высокого быстродействия
вполне уместны недорогие контроллеры размером в кусок мыла, как
показано на рисунке 1.156. Такие контроллеры обычно представлены
процессором с операционной системой реального времени и несколь-
кими интерфейсами типа RS485 через которые подключены модули
расширения (рисунок 1.15а). Номенклатура таких модулей расширения
не уступает другим, борее дорогим ПЛК.
а) б)
Рисунок 1.15: Модуль расширения на базе последовательного порта
Программирование этих контроллеров требует знания языка Си и
структуры операционной системы реального времени. Тем не менее,
освоить программирование таких устройств не сложно. Для этих целей
существует популярная в мире среда разработки Arduino, где принцип
программирования взят в большей мере именно у этих ПЛК. Также
обучение программированию на языке Си не входит в рамки данного
пособия, но важно отметить, что Arduino-средой разработки пользуются
школьники, любители и без особого образования легко осваивают
программирование.
26
Производители ПЛК отдавая себе отчет в том, что если они не
предоставят удобный и понятный технологам инструмент для програм-
мирования, то им придётся вникать во все технологические процессы,
где планируется использование контроллера. Одним из успешных
решений разработчиков стала среда программирования на функцио-
нальных блоках, напоминающая среду моделирования Simulink MatLab
или X-Cos SciLab, поскольку грамотный современный специалист
достаточно хорошо владеет этими средствами.
Существуют ПЛК для которых производитель разработал графиче-
скую среду программирования для создания достаточно сложных САУ.
На рисунке 1.16 показан один из самых популярных в России недорогих
контроллеров, программируемых с помощью функциональных блоков.
Среда программирования представляется бесплатно производителем.
Рисунок 1.16: ПЛК с нестандартным индикатором
Также есть ПЛК, которые можно программировать с помощью
встроенной системы. Обычно такие контроллеры нацелены на
несложные задачи реализации релейной логики.
Рисунок 1.17: ПЛК с встроенной средой программирования
Иногда такие ПЛК называют программируемыми реле. Основным
недостатком таких контроллеров является зависимость от производи-
27
теля в выборе контроллера, поскольку проект разработан в их среде
программирования и достаточно сложно переносится на другие
контроллеры. Решением такой проблемы стал принятый стандарт
программирования ПЛК техническими специалистами и технологами.
Таким стандартом стал МЭК(1ЕС)-61131-3 включающий в себя пять
языков программирования и единый подход к программированию.
Наибольший вклад в доступность и свободу выбора внесла среда
программирования CoDeSys. Эта среда является единой для более чем
500 типов контроллеров выпускаемых производителями всего мира. В
результате, освоив среду и разработав проект, пользователь может
выбрать несколько типов контроллеров, удовлетворяющих текущей
задаче и, после отладки проекта, внедрить своё решение в любой из этих
контроллеров.
На рисунке 1.18 показаны ПЛК, поддерживаемые средой програм-
мирования CoDeSys для двух ее популярных версий (2.3 и 3.5).
Рисунок 1.18: ПЛК с поддержкой CoDeSys без индикации
Слева контроллер имеет небольшой набор входов и выходов, позво-
ляющий решить достаточно широкий спектр задач САУ. Справа ПЛК
имеет только интерфейсы связи с модулями расширения, при этом
содержит в себе полноценный WEB-сервер, позволяющий организовать
простейшие МРВ и АРМ на базе обычного интернет браузера на ПК или
мобильном устройстве.
Среда CoDeSys на прямую не поддерживает средства индикации
ПЛК, однако производители нашли решения включив в библиотеку
необходимый функционал для поддержки индикации и кнопок. На
рисунке 1.19 показан ПЛК с поддержкой индикатора с кнопками,
программируемый в среде CoDeSys.
28
Рисунок 1.19: ПЛК с поддержкой CoDeSys и с индикацией
В данном пособии рассматривается среда CoDeSys для ознаком-
ления, поскольку является наиболее простым и эффективным способом
освоить программирование контроллеров.
Обычно контроллеры с поддержкой CoDeSys имеют стоимость от
средних до максимальных значений. По этой причине в этом разделе
представлены ПЛК почти в десять раз дешевле вышеупомянутых, но без
поддержки CoDeSys.
На рисунке 1.20 представлен контроллер с 14 гальванически развя-
занными входами и 10 выходами 4 из которых могут коммутировать
переменный ток. Кроме дискретных входов и выходов имеется 4 анало-
говых входа.
Рисунок 1.20.’ Не дорогой ПЛК с нестандартной средой программирования
29
Это достаточно внушительный арсенал для создания достаточно
сложных САУ, при этом производитель предоставляет среду разработки
на функциональных блоках. Набор функциональных блоков весьма
органичен и производитель не несёт ответственность за программное
обеспечение. Учитывая эти недостатки успешно использовать такие
контроллеры может только грамотный специалист в области САУ и
программирования.
На рисунке 1.21 показан ещё более дешёвый контроллер в бескор-
пусном варианте устанавливаемый на специальные клипсы сопряжения
с DIN-рейкой. К сведению, DIN-рейка самое популярное средство креп-
ление электротехнических устройств и контроллеров в шкафах автома-
тизации.
Рисунок 1.21: Бескорпусные ПЛК
В пользу приобретения навыков программирования на языке Си на
рисунке 1.22 показан совсем дешёвый контроллер.
максим
Рисунок 1.22: Минимальная комплектация ПЛК
30
Его стоимость сопоставима со стоимостью килограмма мяса говя-
дины на рынке. При этом на нем можно делать достаточно интересные
задачи САУ, включая локальные системы, поскольку контроллер
содержит индикатор и несколько кнопок для минимальной конфигу-
рации и настройки на объекте.
Обучение программированию такого рода контроллеров следует
посвятить отдельное учебное пособие, поэтому все остальные примеры
будут рассматриваться в рамках стандарта Стандарт МЭК(1ЕС)-61131-3.
Вопросы к разделу.
1. Программируемый логический контроллер. Структура и
основные функциональные элементы. Характеристики.
2. Аналоговые входные и выходные цепи. Характеристики и
принятые стандарты.
3. Дискретные входные и выходные цепи. Характеристики и
принятые стандарты.
4. Что такое гальваническая развязка? Какие схемы реализации
существуют?
5. Физические и программные протоколы связи с верхним
уровнем.
1.3. Стандарт МЭК(1ЕС)-61131-3
Программирование контроллеров часто вызывает страх и неуверен-
ность технических специалистов, поскольку полагают, что это совсем
другие незнакомые специализация и научное направление. Тем не
менее, не умаляя опыт профессиональных программистов, важно
принять, что необходимые начальные знания о программировании
весьма просты и доступны. Тут важно знать несколько принципов и
логических конструкций выраженных лингвистическим способом. И
английский не обязательно знать, можно ограничится 60 словами,
которые используются в программировании.
Если рассмотреть пример из жизни, когда папа восьмилетнему
сыну говорит «Зайди в кухню, открой холодильник. Если там есть сыр,
то принеси сыр, иначе возьми сало». Кто то сомневается, что это
неподъемная задача для мальчика? Тогда почему сомневаетесь в своих
способностях к программированию?
Список языков программирования, которые прижились у техно-
логов и технических специалистов составляет стандарт с названием
МЭК(1ЕС)-61131-3. Этот список приведём в конце раздела, вместе со
структурой проекта. При этом для изучения методов программирования
31
будем использовать особый порядок рассмотрения языков, который по
мнению авторов более оптимальный для освоения.
1.3.1. CoDeSys проект
Для осваивания методов программирования следует установить
программу CoDeSys 2.3 [], которая распространяется совершенно
бесплатно. И даже если нет опыта программирования, важно начать
делать самые простые задачи, именно до изучения стандартов языка.
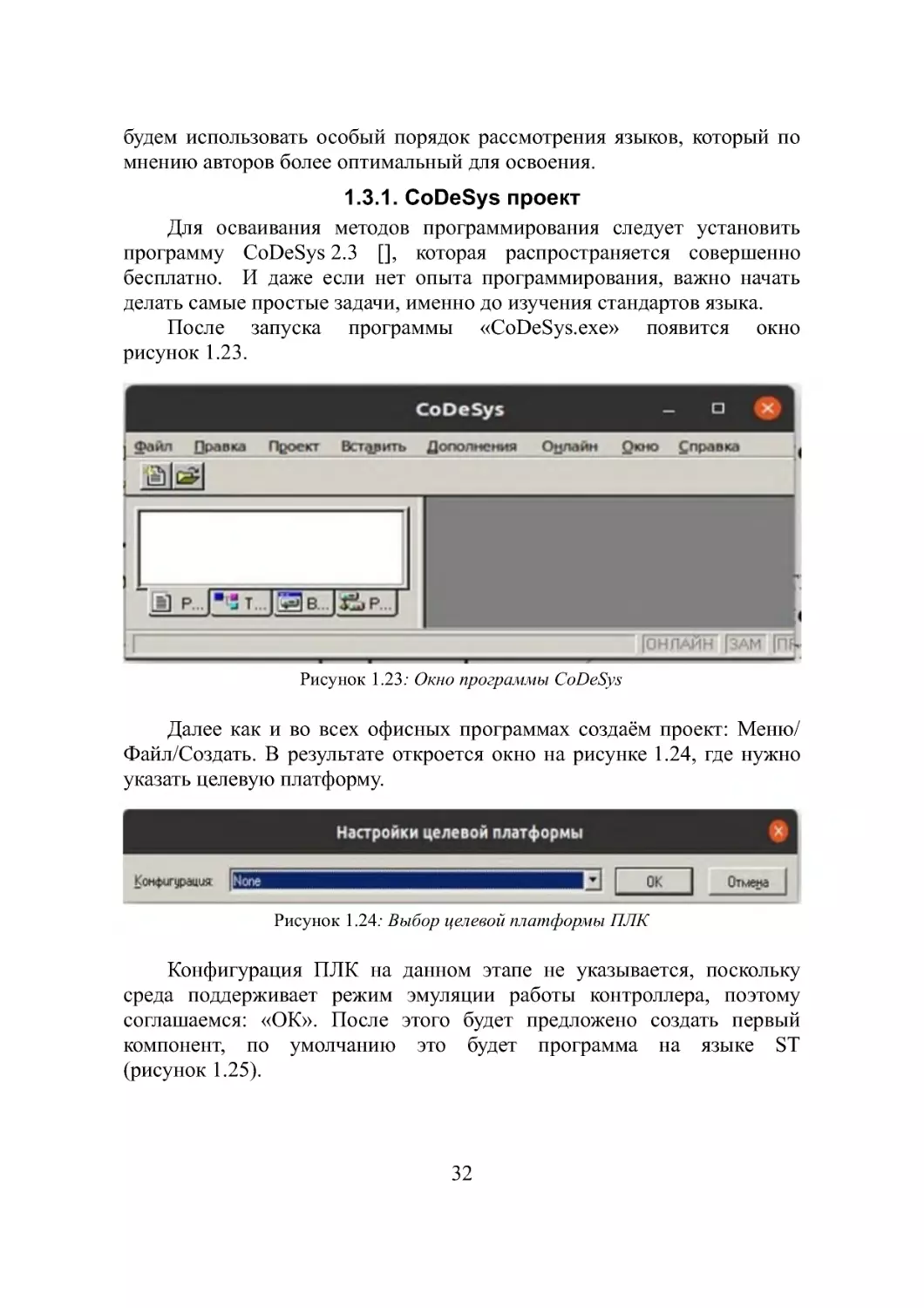
После запуска программы «CoDeSys.exe» появится окно
рисунок 1.23.
Рисунок 1.23: Окно программы CoDeSys
Далее как и во всех офисных программах создаём проект: Меню/
Файл/Создать. В результате откроется окно на рисунке 1.24, где нужно
указать целевую платформу.
Рисунок 1.24.- Выбор целевой платформы ПЛК
Конфигурация ПЛК на данном этапе не указывается, поскольку
среда поддерживает режим эмуляции работы контроллера, поэтому
соглашаемся: «ОК». После этого будет предложено создать первый
компонент, по умолчанию это будет программа на языке ST
(рисунок 1.25).
32
Рисунок 1.25: Окно создания нового компонента
В качестве первой инструкции создадим обычный нарастающий
счётчик: «Y=Y+1;», как показано на рисунке 1.26.
Рисунок 1.26.’ Первая инструкция
Как только курсор перейдёт на 2-ю строку, появится окно на
рисунке 1.27, где нужно будет указать класс переменной из списка:
VAR, VAR INPUT, VAR OUTPUT, VAR IN OUT, VAR GLOBAL.
Тип переменой выберем INT и укажем начальное значение.
33
Объявление переменной
Рисунок 1.21: Введение новой переменной
Комментарий
ок |
Отмена
Г CONSTANT
Г gETAIN
Г PERSISTENT
Результат добавления переменной показан на рисунке 1.28.
Сохраним проект: «Меню/Файл/Сохранить». На этом этапе можно и
нужно компилировать проект клавишей «F11», чтобы убедится в отсут-
ствии ошибок и предупреждений, то также можно увидеть на
рисунке 1.28.
Рисунок 1.28: Откомпилированный проект
Эту процедуру следует делать всегда после изменений в проекте,
даже после незначительных правок. Тогда достаточно просто искать
допущенные ошибки, когда свежи в памяти последние шаги, которые
34
привели к ошибке компилирования. Если этого не делать, то нужно
будет исправлять множество ошибок в окнах, которые были корректиро-
ваны достаточно давно и уже не помнится: что именно. Чтобы
программа выполнялась, её нужно запланировать. Для этого выберем
обозреватель ресурсов: последняя вкладка внизу слева на рисунке 1.29.
М [ПРОСМОТР
Рисунок 1.29.’ Добавление задачи
Задача добавляется через правую кнопку мыши выбором «Конфи-
гурация задачи/Добавить задачу». У задачи есть несколько свойств
кроме имени. На этом этапе важно указать, что задача выполняется
циклически с периодом времени 100 мс.
Далее следует указать вызов программы в рамках этой задачи.
Указатель мыши наводим на значок задачи, правая кнопка, выбираем
«Добавить вызов программы». Кнопка «...» позволяет открыть диало-
говое окно выбора программ, где можно указать нами созданную
программу как показано на рисунке 1.30. Не забываем сохранять и
компилировать проект после каждого минимального изменения
клавишей «F11».
35
Рисунок 1.30: Добавление вызова программы
Осталось убедиться в работоспособности проекта. В режиме
эмуляции последовательно выполняем простые шаги:
• выберем обозреватель программ POU: первая вкладка внизу слева
на рисунке 1.29;
• выберем программу PLCPROG, так чтобы переменные и код
программы был виден на экране;
• подключаемся к виртуальному ПЛК: «Онлайн/Подключение» или
быстро с клавиатуры «Alt+F8»;
• запускаем ПЛК: «Онлайн/Старт» или быстро с клавиатуры «F5»;
• наблюдаем работу ПЛК, выраженную увеличением значения Y
10 раз в секунду, как показано на рисунке 1.31;
CoDeSys - First.pro - [PLC_PRC (PRC-ST)] — OX
Файл Правка Проект Вставить Дополнения Онлайн Окно
£ правка _______________________________________________—JfllXl
дН1и| х |ча|е|ч>1«|
Рисунок 1.31: Имитация работы ПЛК
Дальнейшее рассмотрение методов программирования предпола-
гает, что проект создан и проверен согласно этой инструкции.
36
1.3.2. Structured Text
Structured Text (ST) - один из самых удобных для изучения языков.
Недостатки ST перед другими языками весьма полезны для понимания
работы контроллера. ST - Паскаль подобный язык, поэтому знакомым с
языком Паскаль будет достаточно просто освоить. Ещё одно важное
свойство языка ST опишем в виде утверждения:
Все задачи, которые выполняются в рамках стандарта
МЭК(1ЕС)-61131-3 можно выполнить исключительно только на языке
ST. Или другими словами: знания этого языка достаточно, чтобы решать
все задачи программирования ПЛК.
Не смотря на то, что программа на этом языке может быть очень
сложной, она всегда разделена на подзадачи. В свою очередь подзадача
также делится на более мелкие функции и подпрограммы, до тех пор
пока локализованная задача не станет совсем простой и понятной. По
этой причине осваивая основные логические конструкции будем
рассматривать простейшие задачи.
Рассмотрим одну из таких. Задача поддержания уровня в воды в
бункере в заданном диапазоне с помощью двигателя помпы. Уровень
воды обычно измеряется датчиком давления, подключенный ко входу
4-20 мА. Как уже отмечалось на стр. 23 измеренное значение может
быть пересчитано в значение физической величины (например в санти-
метры) и сохранено в памяти. Соответствующая ячейка памяти на этапе
программирования имеет уникальное название gLevel. Управляющее
воздействие имеет два состояния: включено выключено хранится в
именованной ячейке памяти gbOut. Предполагается, двигатель помпы
включён когда gbOut = 1, при этом вода поступает и уровень gLevel
растёт. Двигатель выключен когда gbOut = 0.
Положим нужно словами объяснить человеку когда включать и
выключать помпу. Объяснить можно по разному, а можно придержи-
ваться определённого стиля или логической конструкции предложения:
если уровень высок, то выключи помпу. Если уровень низок, то включи
помпу, иначе нечего не предпринимай. Программный код мало отлича-
ется от того, что говорится в предложении.
1. IF (gLevel > 165) THEN
2. gbOut := 0; (* выключаем помпу *)
3. ELSE
4. ; (* ничего не предпринимаем *)
5. END_IF
6. IF (gLevel < 145) THEN
7. gbOut := 1; (* включаем помпу *)
37
8.
END IF
Чтобы компилятор программы для ПЛК понимал код, важно при
описании решения пользоваться конструкциями, принятыми в языке. В
данном случае конструкция представлена простыми английскими
словами выделенными жирным шрифтом. Кроме слов есть конструкции
символов, к примеру (* любой поясняющий текст - комментарий *).
Конструкцию для комментариев можно использовать для пояснения
кода, вся эта область игнорируется компилятором и служит для
подсказок к чтению кода.
Очень важно уметь читать код с позиции ПЛК и мысленно
пытаться его выполнить: в первой строке сравниваем уровень с верхней
меткой 165 см. Если он больше ее, то бункер наполнился, следовательно
выключаем помпу. Также в 6-й строке проверяем на нижнюю границу
145 см. Если уровень ниже её, то включаем помпу.
Важное замечание когда gZeve/=150. Если не выполнились оба
условия (gLevel > 165) и (gLevel < 145), то переменная gbOut не поменя-
ется и будет хранить последнее решение, предыдущее значение. Это
возможно, поскольку для этой переменной выделена память в ПЛК.
На этом этапе можно утверждать, что задача решена. Далее
усложним задачу: нужно управлять несколькими (8 баков) такими
конструкциями, причём в каждой конструкции свой уровень который
нужно поддерживать. Теперь у нас есть несколько значений уровней
(gLevell, gLevel2, ... gLevel8) и соответствующие им значения для
управление помпой (gbOut 1, gbOut2, gbOut8). Задача решается просто:
аккуратно пишем 64 строки кода по 8 для каждого решения.
А можно обобщить решение в виде подпрограммы или функции. В
языке ST, как и в Паскаль между подпрограммой и функцией есть суще-
ственное отличие. В начале создадим подпрограмму.
1. FUNCTION_BLOCK CtrlPomp
2 . VAR_INPUT
3. iLevel: WORD;
4. iLmax: WORD;
5. iLmin: WORD;
6. END_VAR
7 . VAR_OUTPUT
8. bOut: BOOL;
9. END_VAR
10. IF (iLevel > iLmax) THEN
11. bOut := FALSE; (* выключаем помпу *)
12. ELSE
38
13. (* ничего не предпринимаем *)
14. END_IF
15. IF (iLevel < iLmin) THEN
16. bOut := TRUE; (* включаем помпу *)
17. END_IF
С 1-ой no 9 строки представлена область переменных, которыми
оперирует функция. С 10-ой строки код функции. Теперь можно приме-
нить одну и туже функцию для всех каналов управления.
1. PROGRAM AllCtrlPomp
2 . VAR
3. fCtrlPomp: CtrlPomp;
4. END_VAR
5. fCtrlPomp(iLevel:=gLevell, iLmax:= 165, iLmin: = 145);
6. gOutl := CtrlPomp.bOut;
7 . 8 . fCtrlPomp(iLevel:=gLevel2, gOut2 := CtrlPomp.bOut; iLmax:= 155, iLmin: = 135);
9. 10 . fCtrlPomp(iLevel:=gLevel3, gOut3 := CtrlPomp.bOut; iLmax:= 145, iLmin: = 125);
11. 12 . fCtrlPomp(iLevel:=gLevel4, gOut4 := CtrlPomp.bOut; iLmax:= 135, iLmin: = 115);
13. 14 . fCtrlPomp(iLevel:=gLevel5, gOut5 := CtrlPomp.bOut; iLmax:= 125, iLmin: = Ю5) ;
15. 16. fCtrlPomp(iLevel:=gLevel6, gOut6 := CtrlPomp.bOut; iLmax:= 115, iLmin: = 95) ;
17 . 18 . fCtrlPomp(iLevel:=gLevel7, gOut7 := CtrlPomp.bOut; iLmax:= 105, iLmin: = 85) ;
19. 20 . fCtrlPomp(iLevel:=gLevel8, gOut8 := CtrlPomp.bOut; iLmax:= 95, iLmin:= 75) ;
Если собрать программу в ПЛК и запустить выполнение, то можно
обнаружить, что программа работает не так как планировалось. Чтобы
наглядно убедится нужно освоить метод построения графиков на панели
визуализации. Для этого нужно выбрать предпоследнюю вкладку внизу
слева (рисунок 1.30). Добавить объект визуализации правой кнопкой. Из
имеющихся элементов выбрать значок тренда и создать его на области
индикации. В появившемся элементе визуализации двойным кликом
откроем параметры настройки и настроим оси. Горизонтальная ось
задаёт метки времени, как показано на рисунке 1.32. Метки времени
должны быть меньше длительности всего тренда в 5-10 раз, иначе сетка
графика будет слишком пёстрой.
39
Горизонтальная ось
Деления пиалы
Г> -вщнщ
Шкало IТ Й1 DsChis
Попгтки--
Шрифт
CZE
Шкала
П гцгегъность IГ #1 mOsOrns
Осндэл-я: |r#1Cte0™
£спдеп-я F#5s3mi
Дискретность Панс/ъ управления
1Т#200т» Г рклсчене
Рисунок 1.32.- Горизонтальная ось
Вертикальная ось задаёт диапазон и сетку по амплитуде, как пока-
зано на рисунке 1.33
Рисунок 1.33: Вертикальная ось
40
Для обеспечения отрисовки графиков нужно указать, какие пере-
менные и какой линией будут отображаться. Нажав кнопку «Выбор
переменной» получим диалоговое окно на рисунке 1.34.
Рисунок 1.34.- Выбор переменных для построения графиков
Результаты изменения уровней на рисунке 1.35 не соответствуют
заданным и ведут себя не предсказуемо.
Рисунок 1.35: Результат работы проекта
Это связанно с тем, что функции не способны хранить предыдущее
значение bOut для каждого канала, поскольку переменная общая для
всех каналов. Это одна из самых распространённых ошибок при
программировании на языке ST.
41
Имеется существенное различие между функциональным блоком и
функцией. Функция в памяти представлена только программой и не
хранит значения переменных от вызова к вызову Даже если в функции
объявлены переменные в области: VAR (список переменных)
END VAR, эти переменные временные существуют только во время
выполнения функции. Поэтому их нельзя использовать для сохранения
предыдущих результатов.
Функциональный блок - это функция вместе с выделенными для
неё переменными, которые существуют в течение всего времени работы
ПЛК. Следовательно в этих переменных можно хранить предыдущие
решения. Однако если функциональный блок использовать повторно в
другом месте программы, то переменные блока будут использоваться
также повторно. Так в 3-ей строке кода CtrlPomp - ссылка на описание
функционального блока, a fCtrlPomp - непосредственно экземпляр
функционального блока, который кроме кода программы из CtrlPomp
имеет собственные переменные. Так, чтобы для каждого канала управ-
ления были свои переменные нужно создать экземпляр блока для
каждого канала. Например:
fCtrlPompl: CtrlPomp; fCtrlPomp2: CtrlPomp; ... fCtrlPomp8: CtrlPomp.
Язык позволяет описать одно-типные экземпляры в виде массива
используя конструкцию
fCtrlPompAr: ARRAY[1..8] OF CtrlPomp. Теперь переменная
fCtrlPompAr содержит восемь экземпляров функциональных блоков.
1. PROGRAM AllCtrlPomp
2 . VAR
3. fCtrlPompAr: ARRAY[1..8] OF CtrlPomp;
4. gLevelAr: ARRAY[1..8] OF WORD;
5. gLmaxAr: ARRAY[1..8] OF WORD :=
6. 165, 155, 145, 135, 125, 115, 105, 95 ;
7. gLminAr: ARRAY[1..8] OF WORD :=
8. 145, 135, 125, 115, 105, 95, 85, 75;
9. gOutAr: ARRAY[1..8] OF BOOL;
10. 1: INT;
11. END_VAR
12. FOR i:=l TO 8 BY 1 DO
13. fCtrlPompAr[1] (iLevel:=gLevelAr[1],
14. iLmax:= gLmaxAr[i], iLmin:= gLminAr[i] );
15. gOutAr[i] := fCtrlPompAr[i].bOut;
16. END_FOR
42
Работа этой программы показана на рисунке 1.36, из которого
видно, что все уровни изменяются в рамках своих заданных корридоров
и не влияют друг на друга.
Рисунок 1.36: Результат работы проекта
Это обеспечивается тем, что на 13-ой строке вызывается не просто
функция, но она выполняется в рамках тех данных, которые прикреп-
лены в функциональному блоку. Чтобы избежать такой достаточно
неочевидной ошибки не следует вызывать экземпляр блока более одного
раза.
Конечно, в рамках небольшого раздела сложно рассмотреть для
каждого инструмента языка хотя бы по одному примеру. Поэтому далее
рассмотрим только основные возможности и конструкции синтаксиса
языка. Многие из которых в качестве примера будут использоваться в
дальнейшем изложении.
При создании программы на языке ST можно использовать:
• операции сравнения (<, >, =, != ....) результатом которой является
булева величина (true, false);
• основные математические операции сложения, вычитания
умножения, деления, ...;
• логические операции с битами целых чисел;
• основные типы переменных - знаковые и без-знаковые целые
числа различной длины (1,2, 4, 8 байт), а также числа с плавающей
точкой;
• элементы объектно-ориентированного программирования,
включая сложные структуры;
43
•функции и функциональные блоки в функциональных блоках и
программах с достаточно большой глубиной вложения.
Основные элементы языка приведены в приложении 1. Однако для
более детального изучения всех возможностей следует использовать
руководства и справочные пособия языка. Даже для программистов
профессионалов чтение упомянутых документов является нормальной
практикой, поэтому не следует пытаться охватить весь стандарт языка,
чтобы начать программировать.
Чтобы начать программировать достаточно освоить следующие
понятия:
• переменной, она может быть целым или вещественным числом
хранящимися в оперативной памяти и должно иметь имя;
• доступности переменных, которые могут быть глобальными или
локальными в рамках функционального блока или программы;
• уникальности имени переменной в зоне видимости, чтобы не
было путаницы;
• операции с переменными, которые включают математические и
логические операции, а также операции присваивания, копирования,
перемещения и т. д.;
• программы, подпрограммы, функции;
• функционального блока, в экземпляр которого входит набор
переменных, которые хранят результаты вычислений от вызова к вызову
блока.
• Основных конструкций-опраторов языка, таких как
1. IF () THEN () ELSE () END_IF;
2. FOR () ТО () BY () END_FOR;
3. WHILE () DO () END_WHILE;
4. REPIT () UNTIL () END_REPIT.
В стандарте языка есть ещё несколько приятых конструкций и ключевых
слов, которые можно найти в приложении 1.
Как любой другой язык программирования, ST лучше изучать на
конкретных примерах, которые будут рассмотрены в
разделах 2.2, Ошибка: источник перекрёстной ссылки не найден, 3.4.
1.3.3. Язык функциональных блоков FBD и CFC
Рассмотрим реализацию функционального блока на странице 38.
Строки от 1-ой до 9-ой представляют заголовок функционального блока
вместе с входными, выходными и внутренними переменными. Этот
функциональный блок можно представить в графическом виде, как
показано на рисунке 1.1.
44
fCtrtPomp
CtrlPomp
-i Level bOut —
- iLmax
-iLmin
Рисунок 1.37: Графическое представление функционального блока
Изображение блока логично и однозначно соответствует полям
входных и выходных переменных. Внутренние переменные на рисунке
не отображаются, но существуют в рамках экземпляра. Следует разли-
чать название блока и экземпляра блока. Название блока (на рисунке -
CtrlPomp) в программе может встречаться несколько раз, когда блок
вызывается. Название экземпляра блока (на рисунке - fCtrlPomp),
связанно с внутренними переменными и должно быть уникально в
рамках программы и использоваться один раз (помним про типичную
ошибку при программировании ПЛК из раздела 1.3.2).
Далее, имея весь необходимый набор функциональных блоков и
функций, которые можно представить в графическом виде, можно
построить функциональную схему системы или модели объекта в
привычном для инженеров виде. Такая методика построения в большей
мере совместима с математическими моделями в среде Simulink и X-
Cos, а также с функциональными схемами, принятыми в ТАУ
Стандарт МЭК построен так, что можно использовать функцио-
нальные блоки, построенные на языке ST в схемах FBD и CFC, а также
FBD и CFC блоки в ST. Придерживаясь такого принципа можно
построить ПИД-регулятор на языке CFC, как показано на рисунке 1.38.
Рисунок 1.38: Реализация ПИД-регулятора на языке CFC
45
Функциональная схема содержит два динамических блока интегри-
рования (intg) и дифференцирования (diff). Для реализации этих блоков
можно использовать язык ST, где подобно рисунку 1.37 определены
входные и выходные переменные. Эти переменные отображаются на
графической версии блока. Для интегратора: х, Т, ymax, ymin - на входе
и у - на выходе. Поскольку это блоки, то для них выделяется опера-
тивная память в экземпляре для интегратора - переменная zl, для
дифференциатора - dl.
На рисунке явно видно отличие функционального блока и функции.
Функции (MUL, ADD) не предполагают хранения переменных в памяти,
поэтому не имеют экземпляра. Кроме знакомых из среды Simulink
линий связи между входами и выходами блоков и функций. На схеме
есть, так называемые порты, имена которые связанны с переменными в
памяти. Эти переменные обязательно должны быть представлены где-то
в структурах:
VAR, VARJNPUT, VAR_OUTPUT, VAR_IN_OUT, VARGLOBAL.
Заголовок FBD и CFC полностью совместим с языком ST, пред-
ставлен кодом:
1. FUNCTION_BLOCK PID
2. VAR_INPUT
3. X: REAL;
4. Кр: REAL;
5. Ti: REAL;
6. Td: REAL;
7. Tf: REAL;
8. Ymx: REAL;
9. Ymn: REAL;
10. END_VAR
11. VAR_OUTPUT
12. Y: REAL;
13. END_VAR
14. VAR
15. 11: intg;
16. dl: diff;
17. END_VAR .
He трудно представить графическое изображение блока ПИД-регу-
лятора для схем, где его можно использовать. Для того чтобы увидеть
разницу между FBD и CFC, построим функциональную схему на языке
FBD, как показано на рисунке 1.39. Как видно из рисунка входные
порты ПИД-регулятора полностью соответствуют строкам 3-9, как по
содержанию так и по порядку. Выходной порт один строка - 12.
Внутренние переменные в строках 15-16 не показаны на графическом
изображении.
46
Рисунок 1.39: Использование ПИД-регулятора на языке FBD
На рисунках 1.38 и 1.39 имеются компоненты, у которых одина-
ковое название экземпляра — z 1. В разделе 1.3.2 не рекомендовалось так
делать, поскольку будет использоваться одно и тоже место в памяти. В
данном случае такой ошибки не произойдёт, поскольку экземпляр zl на
рисунке 1.38 принадлежит экземпляру регулятора PID1 на схеме 1.39.
Относительно головной схемы 1.39 свой экземпляр имеет имя й, а
внутренний из ПИД-регулятора имеет имя PIDl.il. Это разные имена и
их переменные имеют свои собственные места в памяти.
Не смотря на то, что FBD и CFC сильно похожи, есть суще-
ственные различия:
• расположение блоков определяет FBD редактор самостоятельно, в
CFC блоки можно располагать произвольно;
• в FBD отсутствует возможность проводить линии как в CFC;
• порядок вычисления функции блоков в FBD строго и однозначно
определяется расположением блоков, в CFC пользователь
самостоятельно определяет порядок указывая порядковый номер.
Выбор языка остаётся за автором проекта.
1.3.4. Релейные диаграммы LD
Построение релейных схем защиты, резервирования уже давно
стало самостоятельным направлением инженерной деятельности. Ещё
до появления доступных вычислительных машин существовали
проекты автоматических систем управления сложными коммутацион-
ными аппаратами запуска оборудования по строим технологическим
47
сценариям. Естественно в учебных заведениях до сих пор присутствуют
дисциплины, где студенты обучаются приёмам реализации различных
подходов к построению конечных автоматов с применением электромаг-
нитных реле. Если это не целое научное направление, то уж точно
целый мир интересных решений созданных исключительно на электро-
магнитных реле с набором контактных групп. Все эти решения хранятся
в технической документации устаревшего оборудования и представляют
особый интерес как готовые проверенные решения. Из этого можно
выделить две весомые причины создания особого языка программиро-
вания построенного в виде релейных диаграмм:
1. Существует большое количество грамотных инженеров созда-
ющих автоматические системы с помощью релейных схем и стиль их
логического мышления опирается исключительно на решения в виде
релейных схем. Такие дисциплины, как релейная защита и автоматика
присутствуют в рабочих программах учебных заведений.
2. В проектных организациях достаточно сложно принимаются
новые техничские и программные решения, при этом отдаётся предпо-
чтение готовым решениям, которые нужно использовать в новом обору-
довании с ПЛК вместо реле.
Создавать наработанную на реле автоматику в ПЛК достаточно
просто, если использовать несколько простых приёмов.
Первый приём позволяет установить соответствие элементов
релейной схемы в стандарте ЕСКД с стандартом, принятым в языке LD,
которое показано в таблице 1.1.
Таблица 1.1.
Соответствие элементов
LD ЕСКД Описание
Нормально разомкнутый контакт
— Нормально замкнутый контакт
-(>- —| |— Обмотка реле
48
Рассмотрим простейший пример автомата управления двигателем
бетономешалки, где в качестве исполнительного элемента будет пуска-
тель двигателя. В качестве входных сигналов кнопки «старт» и «стоп».
При кратковременном нажатии кнопки «старт» пускатель должен вклю-
читься и сохранить своё состояние. При кратковременном нажатии
кнопки «стоп» пускатель должен выключиться и сохранить своё состо-
яние. Задача достаточно стандартная и соответствует схеме на
рисунке 1.40 в стандарте ЕСКД.
Рисунок 1.40.’ Схема в стандарте ЕСКД
Для реализации этой схемы нужно создать проект с программой на
языке LD. Графически программа представлена на рисунке 1.41. В ней
присутствуют все элементы схемы (рисунок 1.40), а именно логическая
цепочка 1 и 3. Также присутствует ещё 2-я цепочка, которая фиксирует
инверсное состояние выхода в переменной nOut.
Следует придерживаться правила: все имена на ZD-схеме должны
быть объявлены как переменные.
В качестве глобальных переменных будем использовать входные
сигналы состояния кнопок и выходной сигнал на пускатель.
1. VAR_GLOBAL
2. bStop: BOOL; (* кнопка старт *)
3. bStart: BOOL; (* кнопка стоп *)
4. gOut: BOOL; (* выходной сигнал на пускатель *)
5. END_VAR
Собственные переменные программы объявлены в заголовке
программы.
1 . VAR
2 . KI: BOOL; (* состояние реле *)
49
3. nOut: BOOL; (* инверсия состояния реле *)
4. END_VAR
В результате компиляция проекта должна пройти успешно.
Рисунок 1.41.- Схема в редакторе LD
Для тестирования проекта воспользуемся панелью визуализации,
которую можно создать выбрав третью вкладку снизу окна программы.
Выше над ней правой кнопкой на тексте «Визуализация» создадим
новый объект. Фрагмент окна программы представлен на рисунке 1.42.
Элементы визуализации должны быть связанны с переменными
проекта. В частности:
• Кнопка старт должна быть связана с переменной bStart в её
свойствах: «Ввод/Переменная_кнопка/.Ь81агЬ>. Указать название кнопки
можно в свойствах: «Текст/строка/Start».
• Кнопка стоп должна быть связана с переменной bStop в её
свойствах: «Ввод/Переменная_кнопка/.Ь81ор». Указать название кнопки
моно в свойствах: «Текст/строка/Stop».
• Состояние пускателя обеспечивается отображением рисунка,
привязанного к переменной в свойствах рисунка:
«Переменные/Невидимость/.gOut» для отображения выключенного
состояния. Аналогично «Переменные/Невидимость/PLCPRG.nOut» для
отображения включённого состояния.
• На схеме визуализации видно три изображения лампы. Реально их
там 4-е лампы, две большие расположены в одном и том же месте. Это
50
позволяет получить эффект переключающейся лампы, а не исчезающей,
как показано ниже на отдельных изображениях.
Рисунок 1.42: Схема визуализации
Вызов диалоговых окон с параметрами элементов визуализации и
описание каждого параметра приведено в руководстве эксплуатации
программы, а также в руководствах на русском языке [].
После компиляции подключитесь к ПЛК и запустите программу,
откройте окно визуализации. Коротко нажимайте на кнопки старта и
стопа в различных комбинациях и убедитесь в работоспособности
проекта.
Кроме элементов, указанных в таблице 1.1 имеются дополни-
тельные элементы ZD-диаграмм, которые можно увидеть руководстве
пользователя. Прежде чем использовать каждый элемент, следует внима-
тельно почитать принцип его работы. Там можно найти таймеры, реали-
зующие работы, так называемых реле задержки, и многое другое.
В качестве самостоятельной работы можно попытаться решить
задачу резервирования работы двигателей двух насосов. На выходе
контроллера: два сигнала включения двигателей, два сигнала текущего
состояния аварии двигателя.
На входе:
1. Сигнал отсутствия давления в трубопроводе, при котором вклю-
чать двигатели запрещено.
51
2. Два сигнала аварии от каждого двигателя.
Требуется включать один из двигателей на заданное время (2 часа),
после чего поменять работающий двигатель. При аварии одного насоса
следует включать рабочий и на выход подать соответствующий сигнал
аварии. При аварии обоих, не включать двигатели, выдать сигналы
аварии. Такая задача возникает очень часто в проектной деятельности и
в технологических установках, которую грамотный инженер должен
решать легко.
1.3.5. Диаграммы последовательностей SFC
Этот метод программирования в виде диаграмм лучше изучать от
простых задач, поскольку руководствах [] в основном приводятся
элементы и возможности языка. Возможности языка на столько
обширны, что изучение может привести к полному непониманию -
зачем это все нужно. В качестве примера задачи рассмотрим технологи-
ческий процесс сушки пиломатериала, который включает в себя
несколько этапов. Каждый этап начинается и заканчивается определён-
ными условиями. Рассмотрим эти этапы:
1. Инициализация процесса. Даже, если на этом этапе ничего не
делается, он все равно присутствует. У него нет входных условий,
поскольку он первый. Выходное условие обычно связанно с состоянием
тумблера, включение которого начинает технологический процесс.
2. Этап прогрева камеры сушки начинается условием от предыду-
щего этапа, как и все последующие. На этом этапе целью является
заданная температура (7% =50 °C) и влажность (рс =95 %) в камере.
Условием окончания этапа является достижение обоих целей или
истечение времени более заданного tset = 24 ч.
3. Этап сушки при влажности в камере (рс=84%) и температуре
(Tset= 45 °C). Условием окончания является достижение влажности мате-
риала (pw =35%) или истечение времени tset = 96 ч.
4. Этап сушки при влажности в камере (рс =65%) и температуре
(Tset= 50 °C). Условием окончания является достижение влажности мате-
риала (pw =25%) или истечение времени tset = 96 ч.
5. Этап сушки при влажности в камере (рс =30%) и температуре
(Tset= 65 °C). Условием окончания является достижение влажности мате-
риала (pw =6%) или истечение времени tset = 96 ч.
6. Этап пропаривания материала при влажности в камере
(рс =95%) и температуре (7% = 85 °C). Условием окончания является
истечение времени tset = 6 ч.
52
7. Этап постепенного остывания материала от 85 °C до 25 °C за
12 часов. Условием окончания является истечение времени tset = 12 ч.
Предполагается, что замкнутые контура поддержки температуры и
влажности в камере реализованы, к примеру на языке FBD. Задающие
параметры ( рс, ри , Tser) формируются программой на языке SFC.
Создаем проект согласно разделу 1.3.1, только вместо программ из
раздела выбираем в качестве основной программы FBD. Также дополни-
тельную создадим программу на языке SFC. Как показано на
рисунке 1.43.
_jPOU
Ь [б] PLC_PRG (PRG)
Steps (PRG)
Рисунок 1.43: Структура POU
Для того, чтобы интерактивные диалоги ввода новых переменных
не беспокоили можно объявить все глобальные переменные в начале.
1. VAR_GLOBAL
2. gTime: DT; (* Системное время в расширенном
формате *)
3. gITime: DWORD; (* Системное время в формате Unix
Time ★)
4. bStart: BOOL; (^Состояние входа от кнопки старт*)
5. Team: REAL; (* Аналоговый вход: Температура в
камере *)
6. Tset: REAL; (* Параметр: заданная температура в
камере*)
7. Рс: REAL; (* Аналоговый вход: Относительная
влажность воздуха в камере*)
8. Pcset: REAL; (* Параметр: Заданная отн. влажность
воздуха в камере*)
9. Pw: REAL; (* Аналоговый вход: Относительная
влажность древесины*)
10. Pwset: REAL; (* Параметр: Заданная отн. влажность
древесины*)
11. END_VAR
Описание использования этих переменных будем рассматривать по мере
формования проекта.
Основная программа на функциональных блоках представлена на
рисунке 1.44. На первой линии используется системный блок из библио-
теки «Standart.lib», которую нужно добавить к проекту в дереве
«Ресурсы/Менеджер библиотек». Системный блок RTC формирует пере-
менную gTime с информацией о текущей дате и времени.
53
Ч» PLC.PRG (PRG-FBD)
^IPJxJ
0001 PROGRAM PLC.PRG
0002 VAR
0003 RTC: RTC;
0004END.VAR
nnnd
Рисунок 1.44: FBD-программа на функциональных блоках
На второй линии текущая дата и время преобразуется, в так называ-
емое число Unix Time gITime, которое представляет собой 32-битное
число - количество секунд от времени 00:00:00 и даты 1 января 1970
года относительно Лондонского времени. На третей линии запускается
программа Steps на языке SFS.
Программа на языке SFS показана на рисунке 1.45 и состоит из
семи шагов (1 - 7) в соответствии с техническим заданием. Первый шаг
всегда стандартный инициирующий, в котором выполняется простая
процедура присваивания влажности древесины начального значения:
Pw = 60.
Каждый имеет состояние активное или ожидающее. Шаг имеет три
подпрограммы, которые выполняются, если он активен, по следующим
событиям:
1. Когда условие на входе шага выполняется первым и один раз
выполняется входное действие. Если это действие прописано, то на
изображении шага отображен квадрат с литерой «Е».
54
2. Затем при каждом вызове SFS программы выполняется
основное действие, до тех пор пока выходное условие состоится.
3. Когда выходное условие выполнится, то один раз выполняется
выходное действие. Если это действие прописано, то на изображении
шага отображен квадрат с литерой «X». После выполнения выходного
действия отрабатываются события следующего блока.
Init
Рисунок 1.45: Программа на языке SFS
В начале при запуске программы и при условии, что флаг
bStart =false, будет выполнятся основное действие блока Init, до тех пор
пока его выходное условие не состоялось. Как только условие состоится
bStart =true, эстафета перейдет к следующему шагу Step2.
Выполнится входное действие шага Step2.
1. bEndOfStep := FALSE;
2. Tset := 50;
3. Pcset := 95;
4. TimeMx := 24;
5. gStartTime := gITime;
Действие может быть создано на любом из стандарта языке. Как
видно из кода, это язык ST. На первой строке сбрасывается флаг выход-
ного условия, чтобы программа выполнялась до признака окончания
55
данного шага. В 2-3 строках устанавливаются параметры работы камеры
согласно требований в 2. В пятой строке фиксируется время начала
работы шага, поскольку время работы ограничено параметром
TimeMx.
Основное действие содержит следующий код.
1. IF (Team >Tset) AND (Pc>Pcset) THEN
2. bEndOfStep := TRUE;
3. END_IF
4. gtTimeOfStep := gITime - gStartTime;
5. IF (gtTimeOfStep > TimeMx) THEN
6. bEndOfStep := TRUE;
7. END_IF
В подпрограмме проверяется условие окончания шага. Выход возможен
по двум условиям: достигнуты температура и влажность до заданных
значений (1-3 строки) или время истекло (4-7 строки). В переменной
gtTimeOfStep фиксируется время работы на текущем шаге.
Остальные блоки также имеют код подпрограммы для входного
действия, где устанавливаются целевые параметры согласно шагов 3-7 и
фиксируется время старта. Основное действие формируется из условий
выхода из шагов 3-7.
В 7 шаге есть код, который обеспечивает постепенное остывание
уменьшением заданной температуры.
1. gtTimeOfStep := gITime - gStartTime;
2. IF (gtTimeOfStep > TimeMx) THEN
3. bEndOfStep := TRUE;
4. END_IF
5. Tset := 85 - (85-25) * gtTimeOfStep / TimeMx;
Для тестирования добавим HMI-панель визуализации как показано
на рисунке 1.46.
Кнопка старт настраивается следующими параметрами:
• «Категория/Текст» - «Start»;
• «Категория/Ввод» - «bStart»;
• остальные поля - по умолчанию.
Серые квадраты на примере Tset настраивается следующими
параметрами:
• «Категория/Текст» - «Tset %s»;
• «Категория/Переменные/Вывод текста» - «Tset»;
• остальные поля - по умолчанию.
Белые квадраты ввода значений настраиваются также как и серые.
Отличия на примере Team представлено параметрами:
• «Ввод/Ввод в переменную 'Вывод текста'» - текст от 0 до 100.
56
^igjxj
Рисунок 1.46: HMI-панель визуализации
После компиляции в режиме работы можно наблюдать основные
переменные на HMI-панели. Для тестирования следует изменять
значения работы камеры (Team, Рс, Pw) проверяя условия и значения
каждого шага.
По отношению к этому способу описания работы ПЛК следует
указать, что есть еще возможность построения альтернативной и парал-
лельной ветвей.
Альтернативная ветвь добавляется перед условием шага, которая
может включать свои шаги и условия. По виду альтернативная ветвь
похожа на параллельную. Отличие заключается в том, что у каждой
ветви есть свое условие выхода. И первая ветвь, которая заканчивает
свое действие, завершает все альтернативные ей ветви. Другими
словами можно описать работу альтернативных ветвей представив их
учениками, которым дается задача: «Ученикам нужно слепить одну
Чебурашку. Лепят все. Как первый слепил, остальные останавливаются
и уже не стараются успеть. Одна Чебурашка уже есть.»
Параллельная ветвь имеет общее условие входа и выхода. Поэтому
начинают работать параллельно и одновременно, одновременно и закан-
чивают. Если объяснять на Чебурашках, то задание примерно так описы-
57
вается: «Ученикам нужно лепить много Чебурашек. Лепят все сразу как
начался урок. Урок закончился - прекращаем лепить.»
Для того чтобы более качественно изучить любой язык програм-
мирования важно научиться решать простые задачи и подробно тестиро-
вать все возможные состояния режимы. Поэтому настоятельно предла-
гаем все рассмотренные задачи реализовать в виде простых проектов и
протестировать работы. Такой подход более эффективен в обучении
САУ.
Практически любую задачу можно выполнить на языке ST, однако
стиль мышления технологов обычно не совпадает со стилем мышления
программистов. Поэтому с точки зрения восприятия и понимания
графические языки могут быть удобней, наглядней и понятней.
Не рассмотренным в пособии остался язык инструкций IL. Этот
язык имеет простейший набор инструкций, соответствующий набору
команд микропроцессора Intel-структуры. Поэтому и само програм-
мирование очень похоже на программирование на языке ассемблера.
Применять такой язык могут подготовленные программисты, но не
будут, если можно обойтись языком ST. Оправданное использование
этого языка может быть в том случае, когда нужно экономить очень
скромные ресурсы ПЛК. На данный момент, даже самые дешевые и
простые микропроцессоры имеют внушительные вычислительные
ресурсы и оперативную память, что бы не программировать на IL.
Если все же есть желание освоить этот язык, то рекомендуется
изучить не большой набор инструкций ассемблера или IL, и значи-
тельный набор:
• приемов программирования с использованием стека,
• методов распределения памяти,
• флагов состояния микропроцессора и его арифметического
логического устройства,
• методов перемножения и деление чисел с фиксированной точкой и
с плавающей,
• условных переходов и т. д.
Вопросы к разделу.
1. Какие языки входят в стандарт МЭК(1ЕС)-61131-3?
2. Какое программное обеспечение используется для создания
программ в стандарте МЭК(1ЕС)-61131-3? Укажите их преимущества.
3. Опишите структуру проекта в стандарте МЭК(1ЕС)-61131.
4. Какие типы переменных используются в стандарте МЭК.
5. В чем отличие функции от функционального блока?
58
6. Каким образом и когда выполняются подпрограммы?
7. В чем отличие глобальной переменной от локальной?
59
2. Дискретные системы автоматического
управления
Обычно основой для изучения систем автоматического управления
(САУ) является теория автоматического управления (ТАУ) линейными
непрерывными объектами. Понятие линейные и непрерывные системы
непосредственно связаны с математическим описанием работы объекта
и устройства управления. Другими словами в ТАУ для описания,
анализа и синтеза используются линейные алгебраические или диффе-
ренциальные уравнения. Таким образом, под непрерывной системой
будем понимать объект или устройство управления, которое представ-
лено дифференциальным уравнением.
Как известно из теории автоматического управления, линейные
дифференциальные уравнения могут быть представлены в виде переда-
точных функций, которые весьма удобно использовать в системах в виде
функциональных схем. Такой подход используется при моделировании
САУ в математическом пакете Simulink MatLab или X-cos SciLab.
Результатом синтеза САУ, как правило, является функциональная схема
полученная с помощью математических средств ТАУ
В различной литературе понятия САУ и ТАУ часто смешиваются и
можно увидеть в большей мере совпадающий материал. По этой
причине в даном пособии будем придерживаться понятий, которые
позволят разделять смысл учебных дисциплин САУ и ТАУ
ТАУ - представляет собой теоретическое основы управления, пред-
ставленные в виде математического изложения, доказательств, свойств,
приёмов, правил и т. д.
САУ - содержит информацию, позволяющую физически реализо-
вать устройство управления в промышленности, где используются
результаты синтеза из ТАУ
В конце прошлого века САУ реализовывались в большей мере как
непрерывные системы на операционных усилителях (ОУ), с помощью
которых можно было реализовать алгебраические и дифференциальные
уравнения. Однако уже тогда стремительно развивались цифровые
системы управления.
В качестве примера, позволяющего понять различия между непре-
рывной системой и дискретной рассмотрим простейшую задачу.
Положим вам дали поручение следить за уровнем воды в 200 литровой
бочке, которая наполняется стабильным потоком 10 литров в минуту из
60
водопровода. К примеру, необходимо отправить сообщение о дости-
жении уровня наполнения 70 %, а при 95 % выключить поток воды.
Если вы, как чрезмерно ответственный сотрудник, будете посто-
янно (непрерывно) смотреть за уровнем и в своё время выполните два
поручения, ты вы представляете собой непрерывную систему. Если вы
умный и изобретательный сотрудник, который чувствует динамику, то
представив процесс в виде дифференциального уравнения
dh _ у
dt S
(2-1)
где h - уровень воды в бочке, v - скорость потока воды, S - площадь
поверхности бочки. Далее оценив примерно размеры стандартной бочки
вычислите площадь S = 0.2 м2, высоту бочки Н = L0 м. Полагая, что
напор воды 0,01 м3/мин, можно вычислить скорость повышения уровня
0.05 м/мин. Весьма разумно вместо того, чтобы 20 минут непрестанно
не смотреть за процессом, можно спланировать ежеминутный подход к
бочке, а остальное время использовать для других задач. Также и высоту
можно оценивать с определённой точностью, к примеру 1.0 см. В этом
случае решение принимается не постоянно, в заданные моменты
времени. Таким образом, можно оптимизировать нагрузку наблюдателя
за уровнем выбирая промежутки времени и точность оценки высоты.
Принятие решения через конечные (не бесконечно малые) проме-
жутки времени отличают дискретную систему от непрерывной. В
данном случае перевод непрерывной системы управления в дискретную
оправдан и желателен, поскольку позволяет освободить ресурсы наблю-
дателя.
Придерживаясь дискретной системы управления наблюдатель
может контролировать уровень в нескольких бочках, периодически
бегая между ними. Очевидно, что дискретное представление решения
задач управления позволяет, так называемую многозадачность одного
исполнителя.
С другой стороны микропроцессорное устройство в принципе
является дискретным на том простом основании, что выполняет одну
самую простейшую операцию за конечное время. Пусть даже очень
короткое, но все же конечное время. Любая, даже самая простая подпро-
грамма, выполняющая некоторую команду содержит приличное количе-
ство простейших операций и занимает ещё большее время. Очевидно,
что высокое быстродействие процессора позволяет выполнять «одновре-
менно» несколько задач даже используя одно вычислительное ядро.
61
Разделение времени и ресурсов процессора в программировании
называют многозадачностью, которые строятся на специально разрабо-
танных операционных системах. Не вдаваясь в подробности работы
многозадачной операционной системы [], важно отметить, что каждой
задаче выделяется отрезок времени работы процессора в циклической
очереди задач. Так работают программы для воспроизведения звука,
выполняя подпрограмму 44 тысячи раз в секунду. Наверное многие
знают, что стандартные цифровые проигрыватели звука работают в
рамках дискретной системы с частотой дискретизации именно 44 кГц.
В силу того, что производительность микропроцессоров стреми-
тельно растёт, то реализации систем автоматического управления на
цифровых устройствах практически вытеснили устройства на операци-
онных усилителях. Соответственно способность грамотно пользоваться
оборудованием на микропроцессорах для создания систем управления
весьма ценится у работодателя.
Основным средством для реализации современных систем управ-
ления является программируемый логический контроллер (ПЛК).
Отечественная и зарубежная промышленность предлагает очень
широкий набор ПЛК для различных целей в производстве и народном
хозяйстве. Для оптимального выбора в рамках проектной деятельности
важно хорошо ориентироваться в характеристиках и грамотно класси-
фицировать промышленные ПЛК. А для проектирования САУ используя
средства ТАУ важно знать теорию дискретных систем управления,
которая уже давно сформировалось как отдельное научное направление.
Более подробно изучить теорию дискретных систем можно используя
пособия [ops] и научные работы [ops], В рамках данного пособия будут
рассмотрен необходимый минимум теории дискретных систем, позволя-
ющий использовать её в прикладных задачах программирования ПЛК.
2.1. Теоретические основы дискретных систем
На этом этапе рассмотрим дискретный сигнал по времени, полагая
что по амплитуде сигнал задаётся с достаточной точностью. Введём
понятие дельта функции - это функция, имеющая единичное значение
только в заданный момент времени, в остальное время функция равна
нулю. Математически может быть представлена в виде
(2.2)
62
где /о - время относительно которого строится функция. Используя эту
функцию можно описать последовательность значений плавной
функции в виде суммы произведений амплитуд непрерывной функции
на, соответствующие моменту времени, дельту-функции.
На рисунке 2.1 показан непрерывный сигнал, набор
дельта-функций (2.2) и дискретный сигнал, представленный данными
функциями.
Рисунок 2А: Дискретный сигнал, представленный последовательностью дельта
функций
В результате, значение в любой момент времени для дискретного
сигнала можно представить в виде функции
xd(t)= x(t)S(t0-n At),
п
(2-3)
где х( t) - исходный непрерывный сигнал. Для дискретного сигнала
применим преобразование Лапласа
е s£dt,
(2.4)
где вместо непрерывной функции используем дискретную (2.3). Тогда
выражение (2.4) будет выглядеть
63
X(s)=J0 2L n At)e stdt}.
n
(2-5)
Поскольку операции интегрирования и суммирования обладают свой-
ством коммутативности, их можно в выражении (2.5) поменять местами
2ф) = Е Jo |^(f)S(t-nAt)e“s£dt|, (2.6)
п
а произведение непрерывной функции и дельта-функции обозначим
x(t)6(t—nAt)=x(n) (2.7)
назовем отчетом функции х( t) на шаге п.
В силу того, что в (2.6) подынтегральное выражение для каждого
отчета существует только в одно мгновение существования отчета (2.7),
можно (2.6) записать с учетом (2.7) в следующем виде
v ( \ Х^ ( ( \ -snAt\
= )• (2.8)
п
Выражение (2.8) является преобразованием Лапласа для дискрет-
ного сигнала. Как известно из ТАУ - умножение оригинала на функцию
est во временной области соответствует смещению на функции на
значение t. Если это смещение обозначить символом z, преобразование
можно записать как зависимость от z
Xd(z)=^ (x(n)z"n),где z=esAt (2.9)
п
Выражение (2.9) будем называть дискретным преобразованием или
Z-преобразованием. В дальнейших рассуждениях не следует забывать,
что оператор z непосредственно связан оператором s, который физи-
чески измеряется как частота. Также важно заострить внимание, что
выражение (2.8) может дать представление о спектральных свойствах
дискретного сигнала, так как используя замену s = j со получим
дискретное преобразование Фурье
V ( \ Х^ I ( \ -усопДО
^(ra)(s=,)LW'i)e )• (2.10)
64
Как известно [], преобразование Фурье для дискретного сигнала
представляет собой периодический частотный спектр. В этом не сложно
убедится записав выражение (2.10) в виде
. I 2*кп.
-J ПЛ£
е
(2.И)
п
где к - любое целое число. Тогда можно записать выражение (2.11)
разделив на две части экспоненту,
\ X ’ I ( \ -/con At
Х[ы)=2^ х(п)е
— / 2 * к я п
е
= lVke(±l,±2...)/
(2-12)
где вторая равняется единице на основании формулы Эйлера [].
Из вышеупомянутых рассуждений важно знать, что выражение
(2.8) периодично вдоль мнимой оси и ширина периодичных спектров
обратно пропорциональна времени дискретизации и равна (2 л) / At.
Не теряя общности можно рассуждать о дискретном преобразо-
вании передаточной функции какого либо линейного динамического
элемента системы управления, поскольку это есть дискретное преоб-
разование переходного процесса динамического звена. Касательно пере-
даточных функций рассмотрим, как в дискретном преобразовании смот-
рятся нули и полюса передаточной функции. Для это выражение (2.8)
представим для всей комплексной плоскости оператора s в виде
(s=0+jco)
л (a,cd) — /, ),
n
(2.13)
разделив его на вещественную и комплексную часть
it-t \ X 1 ( / \ -апЛ1 -jconAt\
Al0,(D)=2jlX'-n)e е )•
п
(2-14)
Подобно (2.11) выражение (2.14) периодично по комплексной оси,
по вещественной оси при условии уменьшения времени дискретизации
до бесконечно малого значения количество нулей и полюсов, также их
расположение будут совпадать с нулями и полюсами передаточной
функции в форме Лапласа. А при конечном времени дискретизации эти
полюса будут периодично отражаться по мнимой оси. В графическом
65
виде нули и полюса показаны
дискретной функции.
на
рисунке 2.2 для непрерывной и
Xis)
Jtt)
О
X
*------
X
о
Рисунок 2.2: Нули и полюса непрерывной и дискретной функции
Как видно, у дискретной функции большое количество полюсов и
нулей, причем информация вне основного спектра повторяется и,
собственно, лишняя. Если построить эти же нули и полюса в плоскости
оператора z, который на основании (2.9) также имеет вещественную и
комплексную часть, то расположение нулей и полюсов измениться а их
количество будет совпадать с непрерывной функцией как показано на
рисунке 2.3.
Если вспомнить о критерии устойчивости замкнутой системы по
расположению полюсов ее передаточной функции, рассматривая
принцип перемещения полюсов в плоскость z, можно сформулировать
критерий устойчивости для передаточной дискретной функции.
Замкнутая система будет устойчива, если все его полюса расположены
на расстоянии менее единицы от начала координат.
66
Рисунок 2.3: Нули и полюса дискретной функции в пространстве z
Возможно возник вопрос, с какой целью заостряется внимание о
количестве нулей и полюсов в дискретной функции? Основная цель всех
рассуждений это передаточная функция в дискретной форме, поскольку
именно она легко поддается программированию в ПЛК. Если положить,
что передаточная функция строится на основании дискретного преоб-
разования переходного процесса типового динамического звена, то в
выражении
Y(z)=H(z)X(z)
(2-15)
H(z) — передаточная функция равна E(z), если X(z) = l. Размерность
множества параметров такой передаточной функции равна количеству
выбранных отчётов, число которых весьма произвольная величина и
достаточно большая. Очевидно такое большое количество параметров
передаточной функции явно не оптимально.
В этой связи, если опираться на то, что передаточная функция в
комплексном пространстве z имеет совпадающее количество нулей и
полюсов с Лапласовой передаточной функцией W(s) в пространстве s,
уместно равенство
67
H(z)=H(e~st)
М-1
П(z-iU
т=0
М-1
X bnz~
т=0
(2-16)
В выражении (2.16) на основании, что передаточная функция имеет
М нулей и N полюсов, то зная их корни в комплексной плоскости можно
полином числителя и знаменателя записать в виде произведения
разности оператора z и корня полиномов знаменателя и числителя
Раскрыв скобки представить в виде полиномов вполне определённого
порядка.
Для дальнейшего рассуждения потребуются три свойства Z-преоб-
разования.
Сумма сигналов. Изображение дискретной функции (2.9) суммы
двух сигналов х и у равна сумме изображений
g(n) = x(n)+y (и) <=>G(z)=X(z)+Y (z). (2.17)
Доказательство: Применим к (2.17) Z-преобразование (2.9)
Gd(z) = S |x(n)+y(n)|z“n=^x(n)z“n+^ y(n)z~n,
п п п (2.18)
X(z) Y(z)
где на основании коммутативного свойства сумм по одинаковому
индексу п можно разделить на две отдельные суммы получить сумму
изображений (2.18).
Задержка сигнала на т шагов, эквивалентна умножению изобра-
жения сигнала на z'm
( А —/71 Т7" ( \
х[п— m)<^>z X[z).
Действительно, если использовать (2.9), то получим
V ( \ X1 ( \ —п X1 ( \ ~п ~т v ( \ ~т
xd[z)=2^X^n~m)z =Lx\n)z Z —X[Z)Z ,
n n
(2-19)
(2.20)
где оператор z из свойств преобразования Лапласа имеет смысл
смещения по времени на время дискретизации. Смещение на ш шагов
назад соответствует множителю z’”' к изображению.
68
Свёртка сигналов. Свойство лучше запомнить так: произведение
изображений двух дискретных функций соответствует изображению
свёртке этих функций. Понятие свёртка введена в курсе высшей матема-
тики [], поэтому просто запишем её свойство выражением
N-1
G(z)=S
п=0
z п <=>G(z)=X (z)-y(z).
(2.21)
Доказательство. Выражение (2.21) можно записать в виде
N-1 N-1
G(z)— Е x(m)‘E y(n~m)'z
(2.22)
и ко второму множителю применить свойство задержки сигнала, а
множитель zm использовать с первой суммой тогда
N-1 N-1
^(z)~ Е x(m)-z~n- y(n)-z~n=X(z)-Y(z).
m=0 n=0
(2.23)
Покажем, что H(z) - является передаточной функцией. Полагая, что
передаточная функция может быть записана двумя способами: в виде
отношения изображения выхода к изображению входа и в виде (2.16),
составим уравнение
ДГ-1 М-1
h(z)=tH=^---------— (2-24)
к=0 п = 0
Из уравнение (2.24) составим следующее
М-1 М-1 N-1 N-1
Е yWz~k'H amz~n=T. xWz”k‘E bnz~n> (2.25)
k = 0 m=0 k=0 n=0
произведение двух изображений перепишем в виде изображения
свёртки
69
М-1 /м-1
Е Е ату(к-т)
к=0 \т=0 /
N-1
z-‘=Z
к=0
(2.26)
Если N и М неравны, то можно выбрать из них максимальное, полагая
что несуществующие коэффициенты равны нулю. В этом случае в (2.26)
и сами свёртки функций равны тогда имеет место выражение
N-l N-1
Е апУ(к-п)=Е ъпх(к-п),
п = 0 п=0
(2.27)
которое будем называть разностным уравнением. В этом уравнении есть
значение выхода у( к ) на А;-том шаге, текущие и прошлые значения
входа и выхода у( к -I) и х(к -I), через которые можно выразить
текущее значение выхода
(2.28)
Выражение (2.28) легко поддаётся программированию и его можно
использовать для создания функциональных блоков динамических
звеньев. Если коэффициента нормировать относительно «о, то (2.28)
можно записать в матричной форме
eW 0 -01 — ап ьо Ь1 ь2 Ьп eW
y(fc-i) 1 0 0 0 0 0 0 y(k-l)
у(/с-п) 0 0 0 0 0 0 0 y(k-n)
х(к) — 0 0 0 0 0 0 0 x(k) (2.29)
х(к-1) 0 0 0 1 0 0 0 х (к—1)
х(к-2) 0 0 0 0 1 0 0 х(к—2)
х(к—п) 0 0 0 0 0 0 0 х (к—п)
Подобно дифференциальному уравнению в форме Коши, вектор пере-
менных состояния включает в себя текущие и прошлые значения водов
и выходов. В матричном произведении (2.29) входной величиной
является х(к), все остальные составляющие вычисляются из матричного
70
произведения. Выходное значение у(к) вычисляется на основании
разностного уравнения (2.28), а после прошлые значения переменных
состояния вычисляются из текущих согласно выражений
у(к-п)=у(к-п+1),у(к-2)=у(к-1),у(к-1)=у(к),
х(к—п)=х(к—п+1),х(к—2)=х(к—1),х(к — 1)=х(к).
Квадратная матрица включает в себя параметры динамического блока
ине включает переменные состояния, потому соответствует опреде-
лению передаточной функций.
Осталось найти значения
an,bnVne(0...(N-l)),
соответствующие исходной передаточной функции динамического
объекта в Лапласовой форме. Пересчёт нулей и полюсов из выражения
(2.16) достаточно сложный с множеством рутинной работы, где нужно
быть предельно внимательным на всех этапах вычислений.
Более простым методом получения коэффициентов разностного
уравнения является билинейное преобразование или преобразование
Тастина []. Из выражения (2.9) распишем оператор z в виде
sAt/2
____ sAt___ sAt/2 sAt/2____ &
z—e — e e — . .
-sAt/2
e
(2.30)
Числитель и знаменатель разложим в ряд Тейлора []
п
п=0
п!
(2.31)
используя два члена ряда
l+sAt/2
------—.
1—sAt/2
(2.32)
Приняв за равенство (2.32) выразим оператор Лапласа получим выра-
жение для билинейного преобразования Тастина
/ л
z—1
At (z+1
At) 1+z-1
(2.33)
71
Если подставить в передаточную функцию W(s) вместо оператора s
выражение (2.33), то можно получить передаточную функцию H(z) для
выражения (2.15) в виде полинома с отрицательными степенями относи-
тельно оператора z
b0+b1z 1+b2z 2...bnz
. “I . “2
a0+a1z +a2z ...anz
(2-34)
Из уравнения (2.34) можно выразить Y
y_J^(b0X+b1X z-1+b2X z~2 ...bnX z~n+
-a1Yz~1-a2Yz~2...-anYz~n i
(2-35)
Из дискретной форма перейдём во временную
1 box (k)+b1x(k — l)+b2x(k—2)...bnx(k—n)+'
ао( -а1у(к-1)-а2у(к-2)..-апу(к-п) t
(2-36)
получив выражение разностного уравнения (2.28).
Разностное уравнение также можно получить непосредственно из
дифференциального уравнения на примере второго порядка
d2y , , dx
JF=b”x+b1^
dy
a‘dt ’
(2-37)
где все дифференциалы заменяем на отношение приращений к времени
дискретизации дискретного сигнала
dy = у(к)-у(к-1)
dt At
у(к)-у(к-1) у(к-1)-у(к-2)
d2y= At At (2.38)
dt2 At
y(k)-2y(k-l)+y(/<-2)
At2
72
Подставив (2.38) в (2.37) можно выразить у(к) и получить разностное
уравнение (2.28). Практическое применение обоих методов рассмотрим
в следующем разделе.
Вопросы к разделу.
1. Дискретное преобразование, что это?
2. Свойства дискретного преобразования.
3. Передаточная функция Z - преобразования, её свойства.
4. Нули и полюса передаточной функции дискретного преобразо-
вания.
5. Разностное уравнение, что это?
6. Опишите метод получения разностного уравнения из переда-
точной функции Лапласа
7. Опишите метод получения разностного уравнения из диффе-
ренциального уравнения.
2.2. Реализация основных динамических элементов
В этом разделе рассмотрим три динамических звена первого
порядка, из которых можно создавать схемы различных решений в
области управления и моделирования. В частности рассмотрим проце-
дуру создания ПИД-регулятора на основе этих звеньев.
2.2.1. Инерционное звено
Как известно из курса ТАУ передаточная функция инерционного
звена представлена выражением
W^=iW~s’ <239>
где К - коэффициент передачи и Т - время инерции. Для получения
дискретного уравнения воспользуемся преобразованием Тастина
заменив оператор s выражением (2.33)
X К
Vv I z) —----------.
х ! 2Т (l-z"1) ’ (2.40)
(1+z х)
Выражение (2.40) преобразуем в двухэтажную дробь
73
(2.41)
Сгруппируем полиномы числителя и знаменателя по оператору z
Y(z)_ Ktd+Ktdz 1
V( гЛ ~ Нт . * \ \ -1 •
(2.42)
Из (2.42) запишем равенство
( ЧТ . * \ \ Нт ± \ v \ -1
(2.43)
которое нормируем относительно У( z )
-1 2Vtd
d
(2.44)
а1
ь,
bi
Согласно свойствам дискретного преобразования переменные
состояния во временной области будут представлены выражениями
y=y(t),yi=y(t-td)^=^(t)^i=x(f-fd)-
(2.45)
В результате разностное уравнение инерционного звена, полученное с
помощью преобразования Тастина примет вид
(2Т—td) Ktd
У^ОхЛ+Ьо^+Ь^^где qi=(2r + rj’bo=bi=(2r+rj- (2-46)
Второй способ формируется из дифференциального уравнения,
полученного из передаточной функции (2.39)
dt Т
Дифференциал представим как приращение функции за конечный,
не бесконечно малый промежуток, времени равный времени дискрети-
зации. Из уравнения
, -----=---------------- (2.48)
fd 1
74
выразим текущее значение выхода у( t) и получим разностное урав-
нение
( d -rr td
У[Ч=У1-У1—+К-х.
(2.49)
В классическом виде разностное выражение примет вид
td
1У1+Ьох,где аг= 1-^ ,Ь0=К^
(2-50)
Для проверки работы блока создадим проект с двумя функциональ-
ными блоками, реализующими выражения (2.46) и (2.49) и основной
программой на языке CFC показанный на рисунке 2.4. Далее опишем
только отличия от стартового проекта из раздела 1.3.1.
Рисунок 2.4.- Инерционные блоке на языке CFC
Функциональный блок инерционного звена, реализованного с
помощью билинейного преобразования представлен следующим кодом.
1. FUNCTION_BLOCK Inertt
2. VAR_INPUT
3. X: REAL;
4. К: REAL;
5. T: REAL;
6. END_VAR
7. VAR_OUTPUT
8. Y: REAL;
9. END_VAR
10. VAR
11. Yl: REAL;
12. XI: REAL;
13. al: REAL;
75
14. b: REAL;
15. END_VAR
Выражения (2.46) соответствуют ниже показанному коду
1. al:=(2*T - tds) / (2*Т + tds);
2. b := К * tds / (2*T + tds);
3. Y := al * Yl + b * (X + XI);
4. Yl := Y;
5. XI := X;
Функциональный блок инерционного звена, реализованного с
помощью замены производной отношением приращения функции пред-
ставлен следующим кодом.
1. FUNCTION_BLOCK Inertd
2 . VAR_INPUT
3. X: REAL;
4. К: REAL;
5. T: REAL;
6. END_VAR
7. VAR_OUTPUT
8. Y: REAL;
9. END_VAR
10. VAR
11. Yl: REAL;
12. END_VAR
Выражения (2.49) соответствуют ниже показанному коду.
1. Y := Y1 + (К * X - Yl) * tds / Т;
2. Yl := Y;
В заголовках каждой подпрограммы объявлены все необходимые
переменные кроме одной с названием tds. Эта переменная соответствует
времени дискретизации динамического звена и должно быть равно
периоду времени выполнения программы объявлена как глобальная
вместе с переменными выходов программы на CFC.
1. VAR_GLOBAL
2. tds: REAL :=0.1;
3. gYl: REAL;
4. gY2: REAL;
5. END_VAR
Для тестирования работы функциональных блоков создадим панель
визуализации с графикам переходных процессов с обоих блоков. График
формируется аналогично графикам из раздела 1.3.2.
После успешной компиляции проекта и запуска программы
получим переходные процесс, которые представлены на рисунке 2.5.
76
Рисунок 2.5: Переходные процессы двух реализаций инерционного звена.
На рисунке показаны два переходных процесса, однако в силу их
полного совпадения наблюдаем только один. По этой причине практи-
чески нет разницы, какой подход использовать. Но можно заметить, что
реализация разностного уравнения на основе дифференциального урав-
нения проще и менее требовательна к ресурсам ПЛК.
Эквивалентную программу (рисунок 2.4) на языке можно написать
на языке ST.
1. PROGRAM PrgSt
2 . VAR
3. Inrtt: Inertd;
4. Inrtd: Inertt;
5. END VAR
6.
7. Inrtd(X:=1,К:=9,T:=20);
8. gYl:=Inrtd.Y;
9. Inrtt(X:=1,К:=9,T:=20);
10. gY2:=Inrtt.Y;
В этом случае также в заголовке программы создаются экземпляры
блоков, которые запускаются в коде программы. Результат работы функ-
ционального блока фиксируется в отдельной строке.
77
2.2.2. Реализация интегрирующего звена
Реализация интегрирующего звена выполняется по той же мето-
дике, что и в предыдущем подразделе для его передаточной функции.
Существенным отличием этого звена является отсутствие статической
связи входа и выхода, поэтому практически всегда звено имеет ограни-
чение на диапазон возможных значений выхода.
Для передаточной функции
W(s)=-^, (2.51)
Т s
где Т - время интегрирования. Для получения дискретного уравнения
воспользуемся преобразованием Тастина заменив оператор s выраже-
нием (2.33)
W(z)=______-____.
2Т (1—z"1) ’ (2.52)
С (1+z х)
Выражение (2.52) преобразуем в двухэтажную дробь
Сгруппируем полиномы числителя и знаменателя по оператору z
y(z)=
X(z) 2T—2Tz-1"
Из (2.54) запишем равенство
2TY(z)-2TY(z)z~1 = tdX(z)+tdX(z)z~1,
которое нормируем относительно У( z )
(2-54)
(2-55)
У У1 X хг
Ьо Ъх
(2-56)
Согласно свойствам дискретного преобразования переменные
состояния во временной области будут представлены выраже-
ниями (2.45). В результате разностное уравнение интегрирующего звена,
полученное с помощью преобразования Тастина примет вид
78
у=у1+60х+61х1,где b^b^^-. (2.57)
Также получим разностное уравнение из дифференциального урав-
нения, на основе передаточной функции (2.51)
dy-А
dt Т'
(2-58)
Дифференциал представим как приращение функции за конечный,
не бесконечно малый промежуток, времени равный времени дискрети-
зации. Из уравнения
(2.59)
выразим текущее значение выхода у( t) и получим разностное урав-
нение
У[Ч=У1+-х.
(2.60)
В классическом виде разностное выражение примет вид
у(г) = а1У1+Ьох,где 0. = !,^=
£1
Т'
(2-61)
d
т
Для проверки работы блока создадим проект с двумя функциональ-
ными блоками, реализующими выражения (2.46) и (2.49) и основной
программой на языке CFC показанный на рисунке 2.6. Далее опишем
только отличия от стартового проекта из раздела 1.3.1.
Рисунок 2.6: Интегрирующий блок на языке CFC
79
Функциональный блок инерционного звена, реализованного с
помощью билинейного преобразования представлен следующим кодом.
1. FUNCTION_BLOCK Intgr
2. VAR_INPUT
3.
4 .
5.
6.
7 .
8 .
9.
10
11
12
X: REAL;
T: REAL;
Ymax: REAL;
Ymax: REAL;
END_VAR
VAR_OUTPUT
Y: REAL;
END_VAR
VAR
Yl: REAL;
13. END_VAR
Выражение (2.60) соответствуют первой строке ниже показанного
кода.
14. Y := Yl + X * tds / Т;
15. IF Y > Ymax THEN
16. Y := Ymax;
17. END_IF
18. IF Y < Ymin THEN
19. Y := Ymin;
2 0. END_IF
21. Yl := Y;
Строки 15-20 ограничивают выходной сигнал в рамках значений
( Ymin, Ymax). Последняя строка формирует прошлое значение выхода
для следующего шага.
Тестирование выполняется также, как и в предыдущем подразделе,
за исключением содержания основной программы (рисунок 2.6). Пере-
ходный процесс представлен на рисунке 2.7, из которого можно увидеть
ограничение выходного сигнала сверху.
80
Рисунок 2.7: Переходный процесс реализации интегрирующего звена.
2.2.3. Дифференцирующее звено
Не смотря на то, что в конечных приращениях дифференцирующее
звено вполне реализуемо в дискретной форме, настоятельно рекомен-
дуем использовать передаточную функцию реального дифференцирую-
щего звена. Это связано с тем, что отношение времени дифференциро-
вания, как правило, весьма велико от тысячи. В результате амплитуда
сигнала на выходе звена будет на несколько порядков больше чем
возможные величины сигналов в реальной системе управления.
Передаточная функция реального дифференцирующего звена пред-
ставлена выражением
W(s)=
1+Tfs’
(2.62)
где Td - время дифференцирования и 7} - время фильтрации звена. Для
получения дискретного уравнения воспользуемся преобразованием
Тастина заменив оператор s выражением (2.33)
81
(2.63)
Выражение (2.63) преобразуем в двухэтажную дробь
(2-64)
Сгруппируем полиномы числителя и знаменателя по оператору z
Y(z)_ 2T.-2T.z~1
Т\~ (’-.Г . . \
(2-65)
Из (2.65) запишем равенство
М т \ TZ I \ /пт- . \ v \ -1
(2.66)
которое нормируем относительно У( z )
-1_ d
d
а
У1
b,
Ь1
(2-67)
Согласно свойствам дискретного преобразования переменные
состояния во временной области будут представлены выражениями
(2.68)
В результате разностное уравнение реального дифференциорующего
звена, полученное с помощью преобразования Тастина примет вид
(27\—t.) 2Т.
у=а1у1+Ьох-Ь1х1,гр,е ^1= (2Т +t j ;Ь0=Ьг= +f (2.69)
Второй способ формируется из дифференциального уравнения,
полученного из передаточной функции (2.62)
_^±dx____у_
dt Tf dt Tf'
82
Дифференциал представим как приращение функции за конечный,
не бесконечно малый промежуток, времени равный времени дискрети-
зации. Из уравнения
— y(t-t d)
[ f
(2.71)
выразим текущее значение выхода у( t) и получим разностное урав-
нение
/ \ h Та/ \
У{Ч = У1-У1Т+—{х-Х1)-
(2.72)
В классическом виде разностное выражение примет вид
/ \ I Td
y{t)=a1y1+box-b1x1,rp,e а}= 1- — ,b(.=b} =—.
\ Т1 т
(2.73)
Для проверки работы блока создадим проект с двумя функциональ-
ными блоками, реализующими выражению (2.72) и основной
программой на языке CFC показанный на рисунке 2.8. Далее опишем
только отличия от стартового проекта из раздела 1.3.1.
Рисунок 2.8: Инерционные блоке на языке CFC
Функциональный блок инерционного звена, реализованного с
помощью выражения (2.72) представлен следующим кодом.
1. FUNCTION_BLOCK Rdiff
2. VAR_INPUT
3. X: REAL;
4. Td: REAL;
5. Tf: REAL;
6. END_VAR
7. VAR_OUTPUT
8. Y: REAL;
9. END_VAR
10. VAR
11. Yl: REAL;
83
12. XI: REAL;
13. END_VAR
Выражения (2.69) соответствуют ниже показанному коду
1. Y := Y1 - Yl * tds / Tf + Td / Tf * (X-Xl);
2. Yl := Y;
3. XI := X;
Для тестирования работы функциональных блоков создадим панель
визуализации с графикам переходного процесса. График формируется
аналогично графикам из раздела 1.3.2.
После успешной компиляции проекта и запуска программы
получим переходные процесс, которые представлены на рисунке 2.9.
Рисунок 2.9: Переходный процесс реализаций дифференцирующего звена.
2.2.4. Реализация ПИД регулятора
ПИД регулятор можно реализовать на языках FBD, CFC и на ST.
Реализация регулятора на языке CFC показана на рисунке 1.38. В этом
разделе создадим регулятор на языке ST. Заголовок программы практи-
чески не отличается от предыдущего, поскольку используются функцио-
нальные блоки дифференцирования и интегрирования. К собственным
переменным добавлена переменная Хк, для фиксирования общего коэф-
фициента передачи.
84
1. FUNCTION_BLOCK PidST
2. VAR_INPUT
3. X: REAL;
4. Kp: REAL;
5. Ti: REAL;
6. Td: REAL;
7. Tf: REAL;
8. Ymx: REAL;
9. Ymn: REAL;
10. END_VAR
11. VAR_OUTPUT
12. Y: REAL;
13. END_VAR
14. VAR
15. 11: Intgr;
16. dl: Rdiff;
17. Xk: REAL;
18. END VAR
19.
20. Xk:= X *Kp;
21. il(X:= Xk, T:=Ti, Ymax:=Ymx, Ymin:=Ymn);
22. dl(X:=Xk, Td:=Td, Tf:=Tf);
23. Y:= Xk + 11.Y + dl.Y;
24. IF (Y>Ymx) THEN
25. Y:= Ymx;
2 6. END_IF
27. IF (Y<Ymn) THEN
28. Y:= Ymn;
2 9. END_IF
На этом этапе можно собрать замкнутую систему управления
используя рассмотренные динамические звенья и ПИД-регулятор. Такая
система показана на рисунке 2.10.
Рисунок 2.10: Замкнутая система на языке CFC
Таким образом в среде CoDeSys можно моделировать САУ в
реальном времени используя математическую модель объекта управ-
85
ления. Построение математической модели на этапе проектирования
программы позволяет отработать большинство режимов работы ПЛК
непосредственно на компьютере. После этого модель объекта можно
исключить из проекта, а оставшиеся оторванные сигналы выхода
ПИД-регулятора и входа блока вычитания (3) следует подключить к
аналоговым выходу управления и входу ПЛК.
Результат моделирования замкнутой системы показан на
рисунке 2.11. Настройка регулятора выполнена методами, известными в
ТАУ, и более подробно будет рассмотрена в разделах 4.1.2, 4.1.3, 4.1.4.
Рисунок 2.И: Моделирование замкнутой САУ в среде CoDeSys
Также можно вывести сигнал управления с выхода ПИД-регулятора
на график и не должно вызвать затруднений.
2.2.5. Узкополосный фильтр
Из пяти известных типовых звеньев не рассмотрены два: инерци-
онное звено второго порядка и колебательное звено. Звено второго
порядка легко формируется из двух звеньев первого порядка, подклю-
чённых последовательно. Собственно, модель объекта управления на
рисунке 2.11 и является инерционным звеном второго порядка.
В составе программ ПЛК для САУ колебательное звено встречается
крайне редко. При этом похожее на это звено может быть весьма
полезно в качестве узкополосного фильтра.
86
Чтобы увидеть ситуацию, где узкополосный фильтр может потребо-
ваться рассмотрим структурную схему камеры сушки пиломатериала на
рисунке 2.12.
Рисунок 2.12.- Камера сушки пиломатериала
На рисунке обозначения:
• 1,2 показывают поток воздуха против и по часовой стрелке;
• 3 -пиломатериал;
• 4 - датчики температуры, устанавливаются по обе стороны;
• 5 - перегородка обеспечивающая поток воздуха через
пиломатериал;
• 6 - заслонки вместе с приводами;
• 7 - реверсивный электропривод вентилятора;
• 8 - потоко-направляющие конструкции;
• 9 - нагреватель воздуха;
Очевидно на значениях температур как-то отражается работа
приводов заслонок и вентилятора. На рисунке 2.13 переходные
87
процессы с датчиков температур, на которых видно воздействие
приводов заслонок в системах вентиляции. При это видны фрагменты,
где температуры не проседают в следствии не открытия заслонок по
разным причинам.
Может возникнуть ситуация, когда от ПЛК сигналы на открытие
заслонок поступали, но заслонки не открывались из-за ряда нештатных
ситуаций. В частности в системах сушки пиломатериалов заслонки
могут покрыться льдом и не открыться.
В этом случае можно в ПЛК создать программу, обнаруживающую
неисправность приводов заслонок. Одним из решений является исполь-
зование узкополосного фильтра с заданной и известной частотой, соот-
ветствующей частоте открывания и закрывания заслонок.
Рисунок 2.13: Переходные процессы с датчиков температур
Если эти сигналы пропустить через такой фильтр, то можно
увидеть спектральную составляющую процесса изменения температур.
И если есть корреляция, то привода работают исправно, если корре-
ляция отсутствует, то следует бить тревогу о нештатной ситуации.
Передаточная функцией узкополосного фильтра представлена выра-
жением
, A blS 2 /
IV (s)=---------у-, где а0=a>r, ar=(DrIQ; Ь1=а1К.
[a0+a1s+s )
(2.74)
88
В выражении (2.74) а>г — частота фильтра (радиан в секунду), Q —
добротность фильтра. Иногда сложно ориентироваться в выборе
значения добротности, поэтому приведем выражение, где добротность
связана с шириной полосы пропускания
(^тах ^min
(2.75)
где comm и а>тах - минимальные и максимальные значения полосового
фильтра, между которыми коэффициент передачи не ниже уровня
равного 0,707 от коэффициента передачи на частоте со,, который
задается значением К.
Для синтеза разностного уравнения воспользуемся дифференци-
альным уравнением. Дифференциальное уравнивание можно получить
из передаточной функции (2.74)
Ь, зХ = а0У+а, зУ+ s2 У, (2.76)
где дифференциалы представим в виде отношения конечных величин с
заданным временем дискретизации
. (x-*i) (У1-У2) Jy-2yi+y2)
ь1—-----“а03/+а1—;-----+-----2----• (2.77)
*d td
Из (2.77) составим уравнение
Ь1^(х-х1)=ао^У1+а1^(У1-У2)+(У~2У1+У2)> (2-78)
из которого выведем за знак равенства значение выхода у
У = 2У1-У2-ао^У1-а1^(У1-У2)+Ь1^(х-Х1)- (2-79)
В классическом виде выражение (2.79) можно записать в следующей
форме
У=(2~ «I td-а0^)У1+(а1 td- l)y2+b1 td (х-Xi). (2.80)
Выражение (2.80) может понадобится в ПЛК, где имеется реализация
фильтра второго порядка в классическом виде. В этом случае важно
помнить, что погрешность задания коэффициента при yi должна быть на
два порядка меньше чем погрешность задания параметра ао.
К примеру, если точность требуется задание параметра ai с точно-
стью 0.1 % , то отношение максимального возможного значения ai к
89
времени дискретизации td не менее 1000. По касательно параметра «о
отношение должно быть 106.
Использование выражения (2.80) может быть успешным при доста-
точной точности задания параметров и переменных состояния дискрет-
ного уравнения. Поэтому для реализации узкополосного фильтра
воспользуемся выражением (2.79) и напишем код на языке ST.
1. FUNCTION_BLOCK upf
2 . VAR_ INPUT
3. x: REAL;
4 . K: REAL;
5. w: REAL;
6. Q: REAL;
7 . END_ VAR
8 . var’ ’output
9. y: REAL;
10 . END_ VAR
11. var’
12 . yl: REAL;
13. y2: REAL;
14 . aO: REAL;
15. al: REAL;
16. xl: REAL;
17 . bl: REAL;
18. END VAR
19.
20. aO := w*w;
21. al := w/Q;
22. Ы := al*K;
23. у := 2*yl - y2 - a0*tds*tds*yl - (yl - y2)*al*tds +
(x-xl)*tds*bl;
24. у 2 :=yl;
25. yl :=y;
26. xl :=x;
Данный код соответствует выражениям (2.74) и (2.79). В строках
24,25 формируются прошлые и позапрошлые значения выхода, где
порядок инструкций имеет особое значение. Фиксируем в начале самые
ранние значения и в конце последнее значение.
Основная программа для тестирования на языке CFC показана на
рисунке 2.14. Период колебаний составляет чуть более минуты, что
примерно соответствует заданной частоте в радианах на секунду
о)г = 0,1.
90
u2
upf
1
10
0.1
2
Рисунок 2.14.- Программа тестирования узкополосного фильтра
Переходный процесс напоминает импульсную характеристику коле-
бательного звена, так как передаточная функция У ПФ (2.74) содержит
дифференцирующее звено в числителе.
Рисунок 2.15: Переходный процесс узкополосного фильтра
Параметры УПФ могут быть переменными и формироваться в
других подпрограммах ПЛК. На рисунке 2.16 приведен пример исполь-
зования УПФ для оценки скорости вращения двигателя постоянного
тока (ДПТ).
Известно [], что ДПТ имеет вращающиеся контактные группы для
переключения обмоток. Следовательно, ток потребления периодически
прерывается в моменты переключения. Эти моменты непосредственно
связаны частотой оборотов двигателя, которая присутствует в спектре
91
тока потребления. Спектр тока содержит много других составляющих,
мешающих определить период переключения. Если процесс изменения
тока пропустить через фильтр, то на выходе будет наблюдаться синусои-
дальный сигнал, по которому можно определить частоту переключения
обмоток. На рисунке также собрана замкнутая система ПИ-регулиро-
вания оценкой частоты полученной из синусоиды, для формирования
параметра частоты УПФ. Более подробное описание работы системы
управления вращением УПФ можно взять из статьи [].
Рисунок 2.16: Использование УПФ для оценки скорости вращения ДПТ
Рассмотрим процедуру вычисления частоты переключения, при
условии, что фильтр настроен на эту частоту с точностью 10 %. На
рисунке 2.17 показан переходный процесс измеренного тока, по
которому можно увидеть наличие гармонической составляющей
искаженной другими внешними сигналами. После УПФ выделена
гармоническая составляющая тока и с достаточной точностью
соответствует синусоидальному сигналу.
Далее остается написать небольшой алгоритм, вычисляющий коли-
чество моментов-переходов через ноль и разделить на период подсчетов.
92
Рисунок 2.17: Процессы на входе и выходе УПФ
Рассмотренные в главе динамические функциональные блоки могут
составлять базис для всех математических моделей линейных и нели-
нейных динамических систем, как для реализации САУ, так и моделиро-
вания. Все блоки можно компилировать в виде библиотеки и использо-
вать для других проектов.
Вопросы к разделу.
1. Какие элементы системы управления реализуются с помощью
дискретных уравнений?
2. Перечислите основные типовые звенья ТАУ, которые требуются
для реализации ПИД регулятора?
3. Где могут потребоваться узкополосные фильтры (УПФ) при
разработке систем управления.
4. Дайте оценку, преимущества и недостатки трёх методов полу-
чения разностного уравнения.
5. Почему не следует реализовывать разностные уравнения для
передаточных функций 3-го и выше порядков?
93
3. Нелинейные системы
3.1. Гладкие функции
Нелинейные монотонные функции наиболее часто встречаются в
САУ Обычно задачи автоматического управления для таких линейных
объектов решается несложно. Рассмотрим пример нелинейной связи
между какими либо физическими величинами х и у в модели объекта
управления.
Рисунок 3.1: Монотонная нелинейная связь
Как известно из ТАУ любую линейную функцию можно предста-
вить у = Кх относительно точки равновесного состояния, где К - коэф-
фициент передачи пропорционального звена. Следовательно можно
применять ТАУ для линейных систем.
Если функция у =f,,e(x) нелинейная, но при этом монотонная и
гладкая, то можно для произвольной точки равновесного состояния х,
записать выражение для частной производной
----
О X
(3-1)
Тогда для любой х,- можно записать передаточную функцию
W(s,xi) = kne(xz)
(3-2)
94
и в окрестности этой точки, при незначительных отклонениях можно
использовать весь теоретический аппарат линейной ТАУ.
Если определён диапазон изменений точек равновесного состояния,
то имеют место утверждения
У ( Xmjn > X тах) kj ( ^min > к max ) ’ ^min >0. (3.3)
В этом случае также можно пользоваться линейной теорией вместе
с методом D-разбиения определения устойчивости во всем диапазоне
изменения коэффициентов передачи k.
Можно линеаризовать систему последовательным включением
синтезированной компенсирующей функции fcn(x), которая удовлетво-
ряет условиям
VxG(xmin,xmaJ^kne(x)-kcn(x)=kconst. (3.4)
Для этого необходимо решить нелинейное дифференциальное урав-
нение
SfneM Sfcn(x)
дх дх
(3-5)
На примере функции fne(x)=jd, из частной производной
SfneM
дх
= 2х
составим дифференциальное уравнение
£ ( у । /г
'-у / сп\^ / const
дх 2 х
Решение этого уравнения известно
Zz
£ ( \ const 1 I I
= ln|x|.
Однако следует отметить, что не всегда легко и быстро можно
получить из уравнения. Часто это сложная задача.
Если в математической модели объекта имеется нелинейная и не
монотонная функция, то на множестве изменений входных величин,
есть область, где частная производная меняется знак.
Такие случаи встречаются очень редко. Иногда можно использовать
дополнительный нелинейный модуль, исключающий многозначные
95
зоны. На рисунке 3.2 показан пример, где введена компенсирующая
функция х =fcn(u). Эта функция представлена ломаными линиями и
исключает значения х, где функция у =fne(x>) меняет знак частной произ-
водной.
Рисунок 3.2: Компенсация многозначной зоны
В результате обеспечивается условие
ду(и)
ди
При этом обеспечивается только монотонность. Далее можно исследо-
вать диапазон изменения коэффициента передачи по рабочей области,
как это рассматривалось в начале раздела.
Следует отметить, что приведённые методы не являются универ-
сальными для всех случаев с нелинейными гладкими функциями связи
между переменными состояния. По этой причине, решая подобные
задачи важно ориентироваться не только в учебной литературе, но и в
научно-технических публикациях для нахождения оптимальных
решений задач, близких исследуемой проблематики.
96
Далее рассмотрим несколько видов нелинейности, не относящихся
к гладким функциям. Обычно их называют кусочно-линейными функ-
циями (КЛФ).
3.2. Кусочно-линейные функции
3.2.1. Функции с ограничением по выходу
Функция ограничения по выходу настолько популярна, что реализо-
вана в стандартной библиотеки CoDeSys. Вид такой функции пред-
Рисунок З.З: Функция ограничения сигнала по выходу
В области, выделенной серым цветом функция линейная и пред-
ставляет собой обычное пропорциональное звено с коэффициентом
передачи к. Следовательно, если процессы проходят в этой области, то
ТАУ линейных систем может быть применена.
Для приобретения навыка быстрого, корректного и эффективного
созданий простейших нелинейных блоков для моделирования и синтеза
регулятора создадим собственный блок.
1. FUNCTION_BLOCK logr
2 . VAR
3. END_VAR
4. VAR_INPUT
5. x: REAL;
6. Xmx: REAL;
7. Xmn: REAL;
8. END_VAR
9. VAR_OUTPUT
10. y: REAL;
11. END_VAR
12. у := x;
13. IF x > Xmx THEN
97
у := Xmx;
14 .
15.
16.
17 .
END_IF
IF x < Xmn THEN
у := Xmn;
18. END_IF
В код не включён коэффициент передачи, поскольку его можно
учесть предварительно перед блоком добавить функцию или блок умно-
жения. Конкретно в этом блоке коэффициент передачи в линейной части
будет равен единице согласно строки 12. Значения на входе Хтп и Хтх
являются параметрами, определяющими границы ограничения выход-
ного сигнала и учитываются кодом на строках 13-18. Отметим, что
данный функциональный блок не нуждается в сохранении промежу-
точных перченных состояния и может быть реализован как обычная
функция, не требующая экземпляра блока в памяти. Поэтому опытный
программист в данном случае создаст функцию, если её не окажется в
стандартной библиотеке.
Для тестирования работы можно создать проект с генератором
пилообразного сигнала, где амплитуда превышает значение параметров
Хтп и Хтх. Код функционального блока-генератора пилы представлен
ниже.
1. FUNCTION_BLOCK pila
2. VAR_INPUT
3. Т: REAL;
4. Ymx: REAL;
5. Ymn: REAL;
6. END_VAR
7. VAR_OUTPUT
8. y: REAL;
9. END_VAR
10. VAR
11. yl: REAL;
12. sg: REAL := 1;
13. END_VAR
14. у := yl + sg * tds / T;
15. yl :=y;
16. IF у > Ymx THEN
17. у := Ymx;
18. sg := -1;
19. END_IF
20. IF у < Ymn THEN
21. у := Ymn;
22. s g := 1;
23. END_IF
98
Тайкой блок нельзя представить в виде обычной функции,
поскольку имеются переменные для сохранения текущего состояния
выхода -yl и направления - sg. Поскольку это генератор сигнала, то на
входе имеет только параметры Т - время изменения сигнала и его
границы Ymn и Ymx. Логика программы достаточно проста:
• при старте сигнал возрастает (строка 14), поскольку sg = 1;
• возрастает до максимального значения Ymx (сроки 16-17) и меняет
направление (строка 18);
• далее сигнал уменьшается до минимального значения, которое
контролируется в строках 20-23.
Основная программа на CFC показана на рисунке 3.4.
Рисунок 3.4: Тестирование блока ограничения
Амплитуда генератора больше значения ограничения (4 > 3) и (4>1). На
рисунке 3.5 показаны графики входа (генератор пилы) и выхода (сигнал
с ограничением), полученные в результате моделирования.
99
Рисунок 3.5: Результаты моделирования работы блока ограничения
Важно по мере усложнения нелинейных элементов оценивать
результаты моделирования на соответствие полученных сигналов с
ожидаемыми. В этом случае вероятность допустить ошибку в коде
минимальная.
3.2.2. Функция с зоной нечувствительности
Нелинейный элемент с зоной нечувствительности может встре-
титься как в математических моделях технологических объектов, так и в
составе регулятора. В математических моделях обычно элемент описы-
вает механизмы со свойствами трения в исполнительных системах. В
регуляторах искусственно созданные элементы призваны исключить
ложные срабатывания от внешних воздействий шума в технологических
объектах.
Нелинейная функция с зоной нечувствительности показан на
рисунке 3.6.
100
Рисунок 3.6: КЛФ с зоной нечувствительности
Реализация отличается от предыдущего элемента только кодом
1. у := 0;
2. IF х > Xmx THEN
3. у := х - Хтх;
4. END_IF
5. IF х < Xmn THEN
6 . у := x - Xmn;
7. END_IF
Заголовки у этих элементов одинаковые с 1 до 11 строки. Тестирование
работы блока также можно проверить с помощью программы на языке
CFC как показано на рисунке 3.7, а на рисунке 3.8 приведён график
изменения входного и выходного сигнала нелинейного элемента.
Рисунок 3.7: Программа тестирования НЭ с зоной нечувствительности
101
Рисунок 3.8: Результаты тестирования НЭ с зоной нечуветвиетлъсноти
3.2.3. Релейные элементы
Релейные элементы также могут быть отнесены к кусочно-
линейным функциям. На рисунке 3.9 показаны два релейных элемента:
обычный слева и с зоной нечувствительности справа.
Реализацию этих элементов можно объединить в одну, поскольку
обычный релейный элемент является частным случаем элемента с зоной
нечувствительности когда размер зоны равен нулю. Также можно опти-
мизировать библиотеку элементов если реализовать в виде функции,
поскольку тут не требуется запоминать промежуточные значения. В
результате функция предоставлена следующим кодом.
1. FUNCTION RLZ : REAL
2. VAR_INPUT
3. X: REAL;
4. Zn: REAL;
5. END_VAR
6. VAR
7. END_VAR
8. RLZ :=0;
9. IF X > Zn THEN
10. RLZ :=1;
11. END_IF
12. IF X < (-Zn) THEN
13. RLZ :=-l;
14. END_IF
102
Рисунок 3.9: Релейные элементы
Программа для тестирования обоих элементов, также одинаковая
(рисунок 3.10). Для обычного релейного элемента следует установить
сону нечувствительности равной нулю (zn = 0).
Рисунок 3.10: Программа тестирования релейных элементов
Обратите внимание, что функция в отличие от блока не требует
создания экземпляра. По этой причине на блоком-функцией RLZ отсут-
ствует название экземпляра.
Результаты тестирования также объединим в один рисунок 3.11, где
не составит труда увидеть отличие в выходных сигналов, поскольку при
наличии зоны нечувствительности выходной сигнал приобретает
значение ноль при малых значениях входа.
103
Рисунок 3.11: Результаты тестирования релейных элементов
3.2.4. Кусочно-линейные функции с гистерезисом
Эффект гистерезиса встречается на многих исполнительных
элементов, где при смене направления движения наблюдается отсут-
ствие движения на выходе. Примером может послужить механический
редуктор привода штока в запорной арматуре. Иногда значение гистере-
зиса на столько велико, что приходиться учитывать его влияние на
системы управления. По этой причине рассмотрим два типа элементов с
гистерезисом и создадим функциональный блок для каждого.
Обычно редко специально применяется гистерезисный элемент. Но
необходимость отработать замкнутые системы непосредственно на
этапе моделирования возникает достаточно часто.
На рисунке 3.12 показаны кусочно-линейные зависимости гистере-
зисных элементов. У таких элементов по две функции, выбор которых
определяется последним состоянием или направлением движения. Ниже
представлен код, реализующий правый элемент рисунка.
1. FUNCTION_BLOCK ghyst
2. VAR_INPUT
3. х: REAL;
4. gh: REAL;
5. Xmx: REAL;
6. Xmn: REAL;
7. END_VAR
8. VAR_OUTPUT
9. y: REAL;
10. END_VAR
11. VAR
12. ofst: REAL := 0;
13. END_VAR
14. y:=x+ofst;
15. IF у > Xmx THEN
16. ofst :=gh;
104
17. у := Xmx;
18. END_IF
19. IF у < Xmn THEN
20. ofst :=-gh;
21. у := Xmn;
22. END_IF
Ширина гистерезиса задаётся параметром gh, положение на одной
из кривых определяется переменной состояния ofset функционального
блока. Результаты моделирования работы элемента показаны на
Рисунок 3.12: Элементы с гистерезисом
Элемент справа представлен следующим кодом.
1. FUNCTION_BLOCK RIGh
2. VAR_INPUT
3. х: REAL;
4. z n: REAL;
5. END_VAR
6. VAR_OUTPUT
7. y: REAL;
8. END_VAR
9. VAR
10. yl: REAL;
11. END_VAR
12. у :=yl;
13. IF x > zn THEN
14. у :=1;
15. END_IF
16. IF x < (-zn) THEN
17. у :=-l;
18. END_IF
19. yl :=y;
105
На рисунке 3.13 справа показаны результаты моделирования этого
элемента. Сравните эти результаты с релейными элементами на
рисунке 3.11. Можно увидеть, что при наличии гистерезиса наблюдается
Рисунок 3.13: Результаты моделирования элементов с гистерезисом
Рисунок слева также напоминает результаты моделирования на
рисунке 3.5, где также наблюдается эффект запаздывания.
Классификация нелинейных элементов может быть выполнена
согласно несложному алгоритму:
• определяем тип нелинейности, даём название;
• указываем цель реализации такого элемента: это свойство объекта
или искусственно созданный нелинейный элемент в изменяемой части
САУ;
• приводим известные методы нивелирования нелинейности и
анализа устойчивости;
• если нелинейный элемент в ведён в процессе синтеза САУ, то
указываем цели или преимущества использования нелинейного
элемента.
Вопросы к разделу.
1. Какие существуют виды нелинейных элементов в САУ?
2. Перечислите основные типовые нелинейные элементы в
объектах управления и методы компенсации их влияния.
3. Перечислите основные типовые нелинейные элементы которые
специально вводятся в САУ и с какой целью.
4. Приведите процедуру классификации нелинейных элементов
для САУ
5. Что такое гистерезис и какие нелинейные элементы обладают
его свойствами.
6. Как учитываются монотонные нелинейности в САУ?
106
7. Как учитываются немонотонные существенные нелинейности в
САУ?
8. Как реализовать гистерезисный элемент?
9. В чем сходства и отличается работы звена с запаздыванием и
гистерезисного элемента?
10. Опишите метод тестирования нелинейного элемента в CoDeSys.
3.3. Устойчивость нелинейных систем
3.3.1. Линеаризация
Устойчивость нелинейной системы можно исследовать средствами
линейной ТАУ при некоторых условиях. Основная идея заключается в
том, что при малых изменениях вокруг точки равновесного состояния
параметры линейной системы меняются незначительно, поэтому можно
использовать теорию линейных систем. Линеаризация в точках равно-
весного состояния возможна для нелинейной системы
—L=Fi(x1,x2,...,xn),iE(l,2,...,n
at
(3.6)
где функции Ft() могут быть нелинейными, но, при этом, гладкими.
Другими словами на всем множестве изменений переменных состояния
(xi, Xi, ... ,хп) существуют частные производные
dx. Л, dFhvx2,...,xn) А
-----X^V' (3.7)
/ = 1 СЛ( /=1
тогда в каждой точке множества (xi, xi, ... ,хп) систему (3.7) можно
описать в виде линейной формы
*1 а11 °12 : а1п *1
х2 — а21 °22 : а2п х2 9
@п1 ®п2 : Fin
(3-8)
где все ау зависят от выбранного множества (xi, Xi, ... ,х„) точки равно-
весного состояния.
Для того, чтобы ответить на вопрос устойчивости нужно перебрать
все точки области изменения (xi,xi, . ,.,х„) и убедиться в устойчивости
нелинейной САУ Конечно, можно выбрать только характерные точки на
107
границах исследуемой области и оценить устойчивость в нескольких
точках. При этом нужно уметь доказать, что выбранные точки являются
граничными.
Если нелинейными свойствами обладают один или два параметра,
то на основе линейной ТАУ можно воспользоваться методом D-разби-
ения по одному или двум параметрам функций F() (3.6).
В случаях, когда нелинейными свойствами обладают несколько
параметров или функций, тогда всю рутинную работу можно поручить
вычислительным средствам MatLab или SciLab. Поэтому, не смотря на
большое количество вычислений, метод весьма прост. Но, при этом,
необходимо, чтобы все функции F() во всей области исследования
(xi, Xi, ... ,х„) были гладкими. При не соблюдении этого требования
можно использовать оценку устойчивости вторым методом Ляпунова.
3.3.2. Функция Ляпунова
Теорема об устойчивости формулируется следующим образом.
Пусть имеется нелинейная САУ (3.6), удовлетворяющая условиям. Для
всех переменных х, равных нулю все функции F() также равны нулю. В
математическом представлении представлено в виде выражения
Vx_=0 =* (3.9)
Существует знакоопределенная функция
BV(x1,x2,...,xn),
из которой можно получить функцию зависящую от (3.6)
dV y
dt
dV dx, A dV c ( x
ax,dt § ax, i( ’ 2""’ w(x.’x2--F-
(3.10)
(З.П)
Тогда можно сделать один из выводов:
1. САУ будет устойчивой в области изменения (xi,xi, ... реп), если
во всей этой области функции V и W будут иметь противоположный
знак.
2. САУ будет неустойчивой найдется область X=(xi, Xi, ... ,хп)
прилегающая началу координат Х=0, где функции V и W будут иметь тот
же знак.
3. Если условия для вывода 1 и 2 не восполняются, то функция
(3.10) выбрана неудачно вывод об устойчивости нельзя делать.
108
Касательно ограничения (3.9), тут во многих случаях ограничение
можно снять методом замены переменных состояния. Функция (3.10)
при которой возможно ответить на вопрос устойчивости называется
функцией Ляпунова. Поиск этой функции является весьма сложной
научной задачей, поэтому развитию методов поиска функции посвящено
много научных работ [] и диссертаций []. При поиске и выборе функции
Ляпунова нужно чтобы она вместе с полученной функцией W были
знакопостоянными или знакоопределенными по все исследуемой
области (xi, Xi, ... ,х„).
Так как успешное определение функции Ляпунова весьма сложно и
не имеет прямой процедуры поиска, многие исследователи интуитивно
предполагают некую функцию и проверяют на соответствия свойствам.
Однако при таких условиях есть успешные предложения в качестве
функции Ляпунова. Примером может послужить функция Лурье
V=2-^aixi+J 0—<k,k>0. (3.12)
i=l 0
На примере этой функции рассмотрим процедуру анализа устойчи-
вости для нелинейной САУ
dxx
dt
dx2
dt
2 > 2\
ax1 —bx2)
ax1—bx2)
(3-13)
где a, b, a, 0 - положительные числа.
На основе функции Лурье (3.12) предполагаем функцию Ляпунова
V=aX| + 0X2. (3.14)
Поскольку переменные состояния Xi, Х2 зависят от времени возьмём
производные по ним
|^=2ах|+2(’)х2. (3.15)
dx
Затем получим функцию W
109
dV э dxx
IV= = 2ax,
dt dt
dx2
2dT
(3.16)
Используем (3.13) в (3.16)
IV =---= 2 ax. (x. — Bx?)(l—ax2—bx2)-
dt 1 1 2 1 2
-2[;)X2(x2+aX|)( 1 —ax2—bx2) =
г-» f 2.0 2\ ('i 2 j 2\
— 2 l^a^+p х2Д1 — ax1 —bx2).
(3.17)
Для того чтобы функции V и W имели противоположные знаки
sign (v)v sign(IV), (3.18)
Необходимо выполнение условия
(1-ax2—bx2)>0. (3.19)
Границу условия (3.19) представляет эллипс, внутри которого выполня-
ется условия устойчивости.
Тандем САУ (3.13) с функцией Ляпунова (3.14) очень часто исполь-
зуется в учебной литературе [ ], как один из ярких и простых примеров
для анализа устойчивости методом функции Ляпунова. Касательно
других объектов и систем, выполнение подобной работы требует от
инженера весьма хорошей подготовки по курсу высшей математики.
3.3.3. Гармоническая линеаризация
Для САУ, где применяются нелинейные элементы из раздела 3.1,
представленные релейными функциями с разрывами первого рода или
гистерезисом в большинстве случаев возникают автоколебания вокруг
точки равновесного состояния. Такие системы могут рассматриваться
как устойчивые в том смысле, что переменные состояния не покидают
заданной области имея внутри этой области периодический характер
изменения. Для анализа таких систем, целью которых является опреде-
ление частоты и амплитуды автоколебания, чтобы определить область
изменения. Тогда в рамках этих периодических изменений можно рассу-
ждать об устойчивости автоколебательного режима.
Предполагается, что на нелинейный элемент воздействует периоди-
ческий сигнал
ПО
x(t)=xmsin (cot)
(3.20)
с заданной амплитудой xm и частотой co. На выходе нелинейного
элемента также ожидается периодический сигнал у (t) необязательно
синусоидальной формы. Поэтому к этому сигналу применим разло-
жение в ряд Фурье для определения гармонических составляющих
G 001
у (t) =—[ак cos )+bk со sin (co1 к t)),
2 k=i
_2 л . /. „ \
CDi — т , kG(l,2,...,n),
(3.21)
где T - период колебания в замкнутой системе. Коэффициенты ряда
вычисляются по выражениям
2 я/2
ak= — J* у(т)со5(со/ст)с1т
— л/2
л/2
Dk= — J ущ)5пцсокт)ат.
-л/2
(3.22)
Далее полагая, что колебания происходят вкруг точки равновесного
состояния, то постоянной составляющей нет, то есть ао= 0. Более
высокие гармоники значительно подавляются благодаря инерционным
свойствам объекта, поэтому ограничимся первой основной гармоникой
aiC0S(<Dl t)+b| sin((Dlt). (3.23)
Синус и косинус выразим из выражения (3.20)
• / \ \
зпцсоДcos(cD1t)=7—(3 24)
Хт (со1хт)
В выражение (3.23) подставим (3.24) и получим линейное дифференци-
альное уравнение
y(t)=alfX^\+b1x(t) (3.25)
К*™)
для зафиксированной частоты coi.
К выражению (3.25) применим преобразование Лапласа
111
Ш1Хт
z z bl z z
s X (s)h— X(s),
(3-26)
и получим передаточную функцию нелинейного элемента на первой
гармонике coi для амплитуды хт
(3.27)
Автоколебания возникают всегда на границе устойчивости.
Используя критерий Найквиста запишем уравнение разомкнутой
системы для границы устойчивости
Wp(s)=-1 = W^s} Wne(s, хт, wj
(3.28)
Из которого выразим передаточную функцию линейной части системы
W (s)=______-___
1 Wne(S^m^\)
(3.29)
из линеаризованного нелинейного элемента. По сути (3.29) не является
передаточной функцией линейной части, а является функцией, зави-
сящей от параметров нелинейного объекта, которая имеет одинаковое
значение координаты годографа с линейной частью на некой частоте coi.
Тогда если построить годограф с учётом (3.27)
• \ -1
S = J(x)1 ) =------
W (х
rг дп \ т
-qo+jqi
I 2 , 2
Vq0+qi
(3.30)
на одной плоскости вместе с годографом линейной части, то в точке их
пересечения можно определить частоту и амплитуду автоколебания.
Параметры qo и qi получены для большинства релейных и нели-
нейных элементов и доступны в справочной и учебной литературе [].
Некоторые из них представлены в таблицах 3.1 и 3.2.
На примере линейной части САУ
112
10
(l+10s)3
(3.31)
и нелинейного элемента под номером 3 в таблице 3.1 создадим скрипт:
1. clear ();
2. s=poly(0,'s')
3. Wo=syslin( 'с', Ю / ( (l + 10*s) * (l + 10*s) * (l + 10*s) ) ) ;
4. nyquist(Wo, %f);
5. b=0.2; c=l; x = b:0.01:b+4;
6. Q0=4*c./(3.14*x.A2) .*sqrt(x.A2 - bA2);
7. Ql= -4*c*b./(3.14*x.A2);
8. Re=-Q0./ (Q0.л2 + Q1.A2); Im=Ql./(Q0.л2 + Q1.A2);
9 . plot(Re,Im);
Годограф линейной части формируется в 3-ей строке скрипта на осно-
вании выражения (3.31), годограф (3.30) реализован в виде параметриче-
ского графика (8 и 9 строки). Строки 5-7 сформированы на основании
таблицы 3.1 третий элемент.
113
Таблица 3.1.
114
Таблица 3.2.
Результат работы скрипта представлен на рисунке 3.14, где имеется
точка пересечения годографов.
115
Рисунок 3.14: Годографы линейной и гармонической части
Из рисунка видно, что пересечение произошло на частоте
0,02548 Гц, что соответствует периоду автоколебаний 39,3 с. Амплитуду
можно вычислить как расстояние начала координат до точки пересе-
чения
xm~V1.482+0.162=1.83
116
Чтобы проверить результат расчёта воспользуемся математической
моделью САУ на функциональных блоках в среде X-cos, которая пред-
ставлена на рисунке 3.16.
Рисунок 3.16: Математическая модель на функциональных блокахX-cos
Результаты моделирования показаны на рисунке 3.17.
ХП77.000
Y:2.74964
Х:217.327
Y:2.74619
Х:197.100
Y:-1.11824
~1—----—----—I—----—•—•—I---—•—----—I--—•—----—I--—•—•--’—I
50 100 150 200 250 300
Рисунок 3.17: Результаты моделирования
Период колебаний Т=217.327 - 177.0 = 40.327 с незначительно
отличается от результатов гармонической линеаризации 39 с. Амплитуда
хт = ( 2.74+1.11 ) / 2 =1.925 отличается от 1.83 не более чем на 5%.
Конечно, для анализа устойчивости при наличии навыка програм-
мирования гораздо проще использовать результаты моделирования и
численных экспериментов. Поэтому для быстрой и эффективной работы
инженера в области создания САУ важно освоить программирование
скриптов в математических пакетах MatLab или SciLab. Для развития
фундаментальных знаний в области синтеза САУ важно знать известные
аналитические подходы, которые представлены в этом разделе.
Вопросы к разделу.
1. Какие методы исследования устойчивости рассматривались в
курсе?
2. Какие методы линеаризации рассматривались в курсе?
117
3. Сформулируйте основную идею линеаризации гладких
функций?
4. Сформулируйте теорему об устойчивости по Ляпунову
5. Сформулируйте основную идею гармонической линеаризации?
3.4. Реализация ШИМ
Широтно-импульсная модуляция (ШИМ) в проектировании САУ
встречается очень часто, поскольку существует большое количество
исполнительных механизмов, управляемых дискретными сигналами.
Обычно это электромагнитные и твердотельные реле, управляющие
электроприводами, электронагревательными, клапанами с фиксирован-
ными состояниями и т. д. Также встречаются электропривода с посто-
янной скоростью для управления задвижками, положениями механизмов
и т. д. Иногда привода для задвижек называют механизмами электриче-
скими обнооборотными (МЭО), они управляются трех-позиционным
дискретным сигналом имеющим значения: закрывать, не менять состо-
яние открывать в значениях (-1, 0, +1).
3.4.1. Программная реализация ШИМ
Основная цель ШИМ обеспечить аналоговое управление сред-
ствами дискретных сигналов. Идея заключается в том, что аналоговый
сигнал можно представить шириной импульса в рамках периода как
показано на рисунке 3.18.
желаемое напряжение
------соответствующий ШИМ
Рисунок 3.18: Принцип работы ШИМ
Из рисунка видно: чем шире импульс те больше эквивалентный анало-
говый сигнал. Если ширина импульса занимает все время периода, то
118
соответствующий аналоговый сигнал принимает максимальное
значение.
ШИМ обычно реализуется с помощью генератора пилообразного
сигнала, который рассматривался в разделе 3.2. На рисунке 3.19 показан
функциональный блок и графики значений переменных состояния -
пилы на фоне входных значений и выходов.
Г/
Рисунок 3.19: Функциональный блок ШИМ и принцип работы
Выхода формируются по результату сравнения соответствующего
входного сигнала с значением генератора пилы. Код, реализующий
принцип работы ШИМ представлен ниже.
1. FUNCTION_BLOCK pwm
2 . VAR_ _INPUT
3. T: REAL;
4 . xl: REAL;
5. x2: REAL;
6. x3: REAL;
7 . x4: REAL;
8 . END_ _VAR
9. VAR_ _OUTPUT
10 . у: REAL;
11. yl: REAL;
12 . у2: REAL;
119
13. уЗ: REAL;
14. у4: REAL;
15. END_VAR
16. VAR
17. yo: REAL;
18. END_VAR
19. у := yo + 100*tds/T;
20. IF у > 100 THEN y:=0; END_IF
21. yo:=y;
22. IF xl>y THEN yl:=l; ELSE yl:=0; END_IF
23. IF x2>y THEN y2:=l; ELSE y2:=0; END_IF
24. IF x3>y THEN y3:=l; ELSE y3:=0; END_IF
25. IF x4>y THEN y4:=l; ELSE y4:=0; END_IF
Из кода программы видно, что амплитуда пилы ограничена значе-
ниями от нуля до ста (строка 20). Период сигналы пилы соответствует
параметру времени Т. Конечно, можно создать блок с одним входом и
выходом. Но что бы описать принципы аппаратной реализации далее по
тексту имеет смысл показать четырёх канальный ШИМ.
Тестирование блока выполняется простым вызовом в основной
программе так, как показано на рисунке 3.19. А построение графиков
сигналов на выходе ШИМ выполнено с использованием подходов к
созданию проекта, рассмотренных в разделе 1.3.2.
Результаты работы программы показаны на рисунке 3.20, из кото-
рого можно увидеть соответствие работы ШИМ на рисунке 3.19.
Программная реализация ШИМ применима в основном для оцень инер-
ционных объектов, у которых время инерции превышает время дискре-
тизации как минимум в сотни раз. Иначе при передачи дискретного
сигналя ШИМ могут возникнуть автоколебательные процессы с
чувствительной амплитудой.
Основным преимуществом программной реализации ШИМ
являются:
• возможность использования любого дискретного выхода ПЛК для
передачи сигнала;
• использование различных типов широтной модуляции с
переменным периодом или с настраиваемой формой генератора сигнала
для сравнения.
120
1
0 -j-1—I----1----i—*—j----1---[J—I-----1----r—I------1—5-----1----1--------1----1--------1---
12:32:24 12:32:44 12:33:04 12:33:24 12:33:44 12:34:04
Рисунок 3.20: Результаты работы ШИМ в программном исполнении
Чтобы управлять малоинерционными объектами нужно уменьшать
период ШИМ, а вместе с периодом нужно уменьшать время дискрети-
зации. Следует отметить, что бесконечно уменьшать время дискрети-
зации для ПЛК невозможно и в большинстве контроллеров время мини-
мальное время дискретизации составляет миллисекунду
3.4.2. Аппаратная реализация ШИМ
Для управления многими исполнительными устройствами требу-
ется контролировать ширину импульсов с шагом от микросекунды. И
периоды для этих устройств также могут быть весьма короткими -
121
менее секунды. К таким исполнительным устройствам относятся следу-
ющие устройства:
• сервоприводы с дискретным управлением шириной импульса;
• преобразователи дискретный сигнал в аналоговый ток или
напряжения на операционных усилителях, где период ШИМ должен
быть менее миллисекунды;
•циркуляционные насосы с преобразователем частоты с
электроприводом на асинхронном двигателе, где управление
формируется на дискретном входе с ШИМ с малым временем периода.
Поскольку необходимость решения таких задач встречается очень
часто, практически во всех микропроцессорах имеются встроенные
многофункциональные таймеры с возможностью генерации ШИМ
различной формы.
На рисунке 3.21 показан фрагмент структурной схемы таймера с
4-мя каналами для ШИМ. Принцип работы такой же, что и на
рисунке 3.19.
Рисунок 3.21: Аппаратная реализация ШИМ
Роль генератора пилы выполняет счётчик CNT, частоту тактиро-
вания которого можно гибко менять с помощью дополнительного счёт-
чика Prescaler PSC. Значение предварительного счётчика можно зада-
вать в широких пределах от 1 до 65535. В результате максимальная
тактовая частота счётчика может быть равна тактовой частоте ПЛК. На
122
примере микроконтроллера S77V732FIO3 она составляет 72 МГц. Таймер
можно настроить так, чтобы счетчик генератора пилы считал до задан-
ного значения (Auto Reload Register). Таким образом, выбирая только
значение предварительного счётчика-делителя частоты и максимального
значения счета, можно с достаточной точностью задать период ШИМ,
даже если он на много ниже времени дискретизации работы программы.
Сам дискретный сигнал формируется на 4-х выходах, где для
каждого определён регистр сравнения (Compare Register). В результате
на аппаратном уровне выполнен алгоритм, соответствующий коду
программной реализации ШИМ в строках 1-25.
Задача использования аппаратных ШИМ в ПЛК обычно сводится к
инициализации вышеупомянутых регистров. Эти регистры определены
как глобальные переменные и описаны в руководствах пользователя
конкретных ПЛК.
Достоинством аппаратного ШИМ является возможность задавать
период ШИМ и ширину импульса меньшими чем время минимальное
дискретизации ПЛК.
Недостатком перед программной реализацией ШИМ является огра-
ниченность в выборе дискретного выхода для ШИМ. Обычно в руко-
водствах пользователя ПЛК указаны лишь некоторые дискретные
выходы к которым можно подключить ШИМ аппаратных таймеров.
Впрочем, грамотное распределение выходов контроллера при
создании принципиальной схемы позволяет обеспечить практически
всем дискретным выходам ПЛК подключение к многофункциональному
таймеру. К примеру, микроконтроллер STM32F103 содержит в себе до
7-ми таймеров с 4-х канальным ШИМ у каждого. Следовательно, макси-
мально возможное количество аппаратно поддерживаемых ШИМ может
составлять более 25 каналов. Важно внимательно читать характеристики
ПЛК, чтобы определить количество каналов и возможности реализации
аппаратных ШИМ.
3.4.3. Использование релейных элементов для реализации
непериодических ШИМ
Использование релейных регуляторов в системах управления
нелинейными объектами позволяет построить оптимальные алгоритмы
стабилизации, обеспечивающие нечувствительность к параметрическим
и внешним возмущениям. Рассматривая технологию синтеза такого
класса регуляторов, следует отметить эффективность методов теории
систем с переменной структурой при решении различных прикладных
123
задач. В частности, для нелинейных объектов, представленных
математической моделью второго порядка вида
x1(t)=x2(t),
x2(t)=h(x,t)+g(x
(3.32)
где h(x,f) и g(x,t) — нелинейные гладкие положительные функции, при
выполнении условий
a1-x2(t)+h(t)
(3.33)
можно определить движение объекта на траектории скольжения,
описываемого уравнением
s(x,t)=a1-x1(t)+x2(t)=0,a1>0 (3.34)
При этом классическое двухпозиционное релейное управление
u(t)=-k-sign(s) (3.35)
с ограничением k > kl гарантирует приближение фазовой траектории
объекта к траектории скольжения, на которой выполняется равенство
хх(г)= — a1-x1( t) (3.36)
и обеспечивает робастность регулятора по отношению к изменениям и
в определённых пределах. Следует отметить, что реализация данного
управления возможна в том случае, если фазовую координату x^f)
можно непосредственно измерить или вычислить, например, на основе
оценки производной переменной xi(/) состояния объекта.
124
Рисунок 3.22: Траектории притяжения в фазовой плоскости
Введём дополнительную переменную состояния хз, физически
связанную с переменными Xi и х? через управление и, в модель (2.72)
объекта управления второго порядка:
х{ = х2
х,=
*з =
— h-x2+g-u,
—а2-х2, если(н = 0),
— кри, если(н#0),
(3.37)
где h и g - параметры модели объекта, которые в общем случае могут
быть нестационарными или нелинейными, представленными функ-
циями h(x,f) и g(x,f). Динамические параметры переменной х3: аз и кз
большей частью могут быть представлены как некоторые функции
a3(x,f) и k3(x,f).
Определим функцию, обладающую свойством гистерезиса:
у = т](х,5)=.
ecaH(|x|>6)-»y=sign(x),
если((х-х_1)<0)-»у=0,
иначе-» у=У-\,
(3.38)
где обозначение y_i имеет смысл значения, принятого на предыдущем
шаге вычисления, так как гистерезис предполагает запоминание
прошлого состояния. Графически функция представлена на
рисунке 3.23.
125
Рисунок 3.23. Функция с гистерезисом
Предполагается вычислять управление объектом вида (3.37) с
помощью функции (3.38) вместо применяемой в классическом решении
(2.70) по выражению
х3 —*4,6
W = T|
(3.39)
Для объекта, представленного моделью (3.37) с управлением (3.39),
возможно существование траектории скольжения вида
s=as(t ,x(to))-xl+x2=0 , (3.40)
где яД/,х(/0)) >0X7 t G (t > /0) , если выполнены необходимые условия
(/).
a3>as
(3-41)
На рисунке 3.24 показана структурная схема САУ с регулятором с
переменой структурой.
Рисунок 3.24: Регулятор с переменной структурой
126
Реализация алгоритма (3.37) включает переменную структуру, где
она определяется значением управления и. На языке CFC программа,
соответствующая рисунку 3.24 представлена на рисунке 3.25.
Рисунок 3.25: Реализация САУ с регулятором с переменной структурой
Большинство используемых блоков рассматривались в предыдущих
разделах кроме одного с названием strct. Этот функциональный блок
содержит два подблока выбор которых определяются сигналом управ-
ления. Блок реализован на языке ST и представлен ниже.
1. FUNCTION_BLOCK strct
2. VAR_INPUT
3. х: REAL;
4. Tk: REAL;
5. Tob: REAL;
6. END_VAR
7. VAR_OUTPUT
8. у: REAL;
9. END_VAR
10. VAR
11. yl: REAL;
12. END_VAR
13. IF x =0 THEN
14. y:=yl _ yl* tds / Tob;;
15. ELSE
16. y:=yl + x * tds / Tk;
17. END_IF
18. yl:=y;
Из кода видно, что блок работает в зависимости от входа х
(строка 13). Если значение входа равно нулю, то блок работает как инер-
ционное звено (строка 14), иначе - как интегрирующее звено
(строка 16).
Схема на рисунке 3.25, содержит достаточно простой блок с пере-
менной структурой, но при этом характеристики управления могут быть
весьма привлекательны. В частности, на основании выражений
127
(3.32-3.40) можно утверждать, что регулятор с переменной структурой
может работать с объектами, у которых параметры могут меняться в
широких пределах.
На рисунке 3.26 приведены переходные процессы не настроенной
САУ Однако, при этом, замкнутая система устойчивая и управляется
дискретным сигналом. Отличительной особенностью является форма
сигнала: она не периодична и ширина импульсов меняется в очень
широких пределах. В установившемся режиме автоколебания незначи-
тельны либо вовсе отсутствуют.
Рисунок 3.26: Не настроенная САУ с переменной структурой
Интерес представляет переходный процесс и сигнал управления
для настроенной системы (рисунок 3.27). В этом случае количество
импульсов минимально-необходимое, в отличие от ШИМ с заданным
периодом. Минимизация количества управляющих импульсов является
важной характеристикой для исполнительных устройств на электромаг-
нитных реле, поскольку количество срабатываний ограничено десят-
128
ками тысяч. Это совсем не большое число, и при частом срабатывании
Рисунок 3.27: Настроенная САУ с переменной структурой
Конечно, все идеи синтеза и реализации ШИМ описать в рамках
учебного пособия невозможно, поэтому для дальнейшего изучения реко-
мендуется обратиться к другим учебным пособиям [] и научным публи-
кациям [].
Вопросы к разделу.
1. В каких случаях требуется программная реализация
2. ШИМ?
3. В каких случаях требуется аппаратная реализация ШИМ?
4. Сформулируйте основную идею управления в скользящем
режиме? Укажите преимущества регулятора в скользящем режиме.
5. В чем принципиальное отличие регулятора с переменной струк-
турой от традиционных.
6. Какие основные преимущества рассмотренного регулятора с
переменной структурой?
129
4. Современные САУ
4.1. Оптимальные системы управления
В современной ТАУ есть отдельное научное направление опти-
мальных САУ, где можно найти много подходов. В рамках учебного
пособия все известные подходы нет возможности изучать, поэтому
выбраны лишь те, которые хорошо себя зарекомендовали в инженерной
практике и несложно реализуемые на ПЛК.
4.1.1. Классификация
Оптимальные системы можно разделять по критерию оптимизации.
•Модальный регулятор, которые обеспечивает оптимальное
расположение корней на комплексной плоскости замкнутой системы.
• Модульный оптимум, частный случай модельного регулятора,
когда пара самых медленных корней имеют одинаковые значения
вещественной и комплексной частей.
• Симметричный оптимум для систем с астатизмом второго
порядка, где критерий оптимальности определяется частотной
характеристикой разомкнутой системы.
• Оптимум по параметрам качества переходного процесса. Обычно
в качестве параметров выбирают два противоречащих друг другу,
например время регулирования и заданное значение
паре-регулирования.
• Оптимальные системы, минимизирующие функционал.
Функционал может иметь весовые коэффициенты и некоторые вариации
подчёркивающие энергоэффективность или быстродействие.
Методы могут отличаться исходной информацией.
• Прямой метод синтеза оптимальной системы на основе известной
заранее математической модели, построенной на базе описания
физических процессов объекта управления.
• Математическая модель объекта формируется по переходному
процессу на основе результатов эксперимента.
• Математическая модель объекта формируется в течение процесса
управления методами идентификации параметров ОУ.
• Рекурсивные методы оптимальной подстройки по прямым
показателям качества переходного процесса.
• Методы, обеспечивающие робастные свойства САУ для
нестационарных объектов с интервально-определенными параметрами.
130
В пособии приведены только те признаки, которые в нем рассмат-
риваются. Конечно, есть и другие признаки оптимальных систем,
которые не представлены в этом пособии, но более подробную инфор-
мацию можно получить из учебных и справочных пособий [].
4.1.2. Модальное управление
Одним из наиболее популярным и практичным является модальный
метод. Слово во множественном числе «моды» - греческого происхо-
ждения, к которому по смыслу ближе слово корни. В русском языке
слово корни также не однозначно понимаются. Поэтому корректно уста-
новить соответствие: моды - корни алгебраического уравнения. Следо-
вательно, когда говорят о модальном управлении нужно полагать, что
решение связанно с корнями характеристического уравнения замкнутой
системы.
Из курса ТАУ известен метод оптимального распределения корней
на основе коэффициентов Баттерворта для систем 2-7 порядков. Полное
соответствие расположению корней по Баттерворту возможно для
полностью наблюдаемой и управляемой системы управления. Обычно
метод применяется для линейного объекта управления представленного
в матричной форме
dx(t) л / х л / х
----- =Ax(t)+Bu(t),
d t-(4.
y(t)=Cx(t),
где матрица А - описывает динамические свойства объекта, В - столбец
управления объектом, матрица С определяет вектор у(0, доступный
измерению по переменным состояния.
Управление объектом предполагает знание всех переменных состо-
яния x(t) полученный из вектора y(t). Сигнал управления вычисляется
согласно выражению
u(t)=—Kx(t), (4.2)
где К - в общем случае матрица, в частном столбец параметров регуля-
тора, полученный в результате модального синтеза САУ
Замкнутая система в матричном виде получена из (4.1) с учетом
(4.2)
131
----Ax(t)—BKx(t)=Arlx(t),
dt
где Ad=A-BK.
(4-3)
Выражение для матрицы Aci является уравнением относительно
матрицы К, значения которых вычисляются стандартными средствами
MatLab. Коэффициенты матрицы К вычисляются исходя из заданных
собственных чисел матрицы Aci соответствующих корням, которые
могут быть определены из таблицы Баттерворта или, так называемого,
биномиального распределения корней.
Оптимальное управление возможно только если объект управ-
ляемый и наблюдаемый. Управляемость понимается как возможность
перемещения объекта из начального состояния Хо в произвольное состо-
яние X при управляющем воздействии ограниченными свойствами
матриц А и В. Наблюдаемость - это возможность вычислить или
оценить вектор х(?) по доступному для измерения вектору у(0 согласно
возможностям матрицы С.
Для численной оценки этих двух условий используется критерий
Калмана. Согласно критерия вычисляются матрицы управляемости и
наблюдаемо сти
и=[в ав а2в а3в\,
V=|c СА С А2 СА3].
(4-4)
Для того, чтобы объект был управляем и наблюдаем необходимо,
чтобы ранг соответствующих матриц U и V совпадал с рангом
матрицы А. Для вычисления матриц U и Ив среде MatLab реализованы
функции:
19. »V=obsv (А, С) ;
20. »U=Ctrb (А, В) ;
по которым можно вычислить ранг матрицы
21. >>rank(U)
22. >>rank(V) .
Настройка ПИД-регулятора согласно модальному принципу
возможна при использовании динамических объектов третьего порядка
и ниже. При этом потребуется пересчет параметров модального регуля-
132
тора в виде вектора К в классические параметры ПИД-регулятора
(кР, д, тд.
Учитывая тот факт, что время переходного процесса определяет
самый «медленный» корень характеристического уравнения, можно
обеспечить соотношение вещественной и комплексной части только для
этого корня. Из курса ТАУ можно узнать как это достигается приведе-
нием передаточной функции разомкнутой системы к заданному виду
Для системы с астатизмом первого порядка вид передаточной
функции разомкнутой системы представлен выражением
/ \ 1 1
Wbrk S ) = 7--т------7------77---------------7,
“ ' (l+sT„)sgT„ (l+sri)(l+ST2)...(l+sr„)’ (4.5)
где ge(0.3...2...3),max(Т1лТ2,...Т_)<0.1 Т.
Выбор параметров ПИД-регулятора согласно (4.5) часто называют
модульным оптимумом.
Если САУ имеет астатизм второго порядка, то обеспечивается выра-
жение
( х (l+s8TM) 1
IT (s)=—-------------------------------------
“ (l + ST„)S2gT2 (l+sri)(l+Sr2)...(l+Sr„)’ (4.6)
где gg(4...32),max(T15T2,...Tn)<0.1 T...
Выбор параметров ПИД-регулятора согласно (4.6) часто называют
симметричным оптимумом.
Из симметричного оптимума вытекает метод желаемой частотной
характеристики, где синтез управления можно выполнить графо-анали-
тическим методом, с которым можно познакомится учебных пособиях
по ТАУ [].
4.1.3. Практическая реализация модульного оптимума на ПЛК
Как уже отмечалось, реализация настройки выполняется по
известной математической модели или по переходному процессу,
который можно получить из результатов эксперимента.
В среде CoDeSys имеется полезный инструмент для фиксирования
переходных процессов в памяти ПЛК и последующей передачи его на
ПК для дальнейшего анализа. На рисунке 4.1 показаны два диалоговых
окна для настройки Tracer.
133
Рисунок 4.1.- Tracer для сохранения переходных процессов
Tracer можно достаточно гибко настраивать режим запуска и
частоту записи переходного процесса. Частота записи задаётся пара-
метром «шаг сэмпла», который измеряется в миллисекундах. Это
значение должно в целое число раз превышать время дискретизации
выполнения задач. Иначе среда выдаст предупреждение и работать
непредсказуемо касательно формирования переходного процесса.
Работа Tracer показана на рисунке 4.2, где выведен переходный
процесс входного и выходного сигнала. Переходный процесс получен
для объекта представленного передаточной функцией
(l+10s)2(l+5 s)(l+2s)'
(4-7)
После формирования переходного процесса результаты можно
загрузить из ПЛК в нескольких форматах.
134
Рисунок 4.2.- Результаты работы Tracer
Для согласованной работы со стандартным программным обеспече-
нием, таким как Microsoft Excel можно использовать текстовый формат
«.csv». Файл содержит текстовую информацию
1. Zeit .ginp .gout
2. О 6.339901 19.02078
3. 500 6.339901 19.02074
4. 1000 6.339901 19.02071
5. 1500 6.339901 19.02068
6. 2000 6.339901 19.02065
7 .
8. 198000 24.1133 72.3285
9. 198500 24.1133 72.3289
10. 199000 24.1133 72.3294
11. 199500 24.1133 72.32977
со значениями переменных состояния. Если файл переименовать, указав
расширение «.xls», то его можно открыть непосредственно программой
MicroSoft Excel и построить его средствами график переходного
процесса, как показано на рисунке 4.3.
135
Рисунок 4.3: Переходный процесс в программе MicroSoft Excel.
На рисунке показан необходимый минимум анализа переходного
процесса, где вычислена постоянная времени объекта Ti=19c, обоб-
щённое время запаздывания Т- = 14 с. На основании этих данных можно
предположить несколько вариантов передаточной функции для разного
порядка полинома знаменателя. В выражениях
(l+19s)(l+5s)3 ’
2.99
(l+19s)(l+7s)2 ’
(4-8)
представлены передаточные функции 3 и 4 порядка. На примере
функции 3-го порядка для регулятора представленного передаточной
функцией
136
Wr(s)=
(4-9)
выберем параметры регулятора (4.9)
Тг 1 -19; Г, - Гг 2 - 7 ;
Tir = (2.99-2Tj = 41,9.
(4.Ю)
Значения (4.10) выбраны согласно цели приведения разомкнутой
передаточной функции к форме (4.5). Выражение (4.9) можно
преобразовать в классическую форму ПИД-регулятора
, х Гг1+Гг2 1 TrlTr2s
Wr s =——-+---------+ rl r2 . (4.11)
v T sT T v 7
ir ir ir
На практике более удобно настраивать ПИД-регуляторы, где
коэффициент передачи пропорционального звена вынесен за скобки
( . 1
Wr(s)=Kp 1+——+Tds ,
\ S1i
(4-12)
где параметры которого можно вычислить согласно выражений.
Т 1 +Т 2
К , = —---—=0.62;
Р у ’
L ir
T-bib, (4.13)
1 d~ т
1 rl+1 r2
Т,=Тг1+Тг2=2б.
Реализация ПИД-регулятора (4.12) на языке CFC приведена на
рисунке 4.4 с параметрами (4.13).
137
Подключим регулятор в замкнутую цепь САУ совместно с
объектом (4.7), от которого был получен переходный процесс
(рисунок 4.3). Замкнутая цепь САУ с ПИД-регулятором и объектом
показана на рисунке 4.5. Важно обратить внимание, что для синтеза
регулятора использовалась другая передаточная функция третьего
порядка (4.8), которая построена на основании переходного процесса
исходного объекта (4.7).
Рисунок 4.5: Математическая модель замкнутой системы САУ
Результаты моделирования работы настроенного регулятора по
модульному оптимуму для САУ с астатизмом первого порядка показан
на рисунке 4.6.
138
Рисунок 4.6: Результаты моделирования настроенного регулятора
Из рисунка видно, что качество переходного процесса соответ-
ствует хорошему быстродействию с пере-регулированием не более
10 %. На практике настройка выполняется таким же образом за исклю-
чением того, что вместо модели объекта (4.7) используется реальный
объект, подключенный к клеммам ПЛК. В этом случае рисунок 4.6
следует называть результатом работы ПЛК на действующем объекте.
Подобным образом можно настроить регулятор с помощью симмет-
ричного оптимума для системы с астатизмом второго порядка.
4.1.4. Использование Вариационного исчисления для
настройки ПИД-регулятора
В математических средах MatLab и SciLab имеются средства реали-
зации поиска минимума функционала в вариационной задаче. У этих
функций есть ряд ограничений связанных с требованием к поверхности
функционала. Поверхность должна быть гладкой, то есть иметь
конечные значения производных для вычисления градиента изменения
параметров. Также, если пользоваться типовым примером использо-
вания вариационной задачи, то нужно представить замкнутую САУ в
139
матричной форме линейной математической модели (4.1). При этом
исходной информацией на практике, как правило является переходный
процесс (4.2), для которого можно получить передаточную функцию
объекта третьего порядка (4.8). В общем виде рассмотрим на примере
выражения
(1 + T,1s)(l+T2s)(l+T3s)
(4-14)
где к0, Ti, Т2, Тз - параметры объекта, полученные по переходному
процессу.
Для формирования матричной формы представим передаточную
функцию (4.14) в виде полинома в общем виде
т2т2т3
3 2-1 1-1 2+-1 3-G+-1 1-1 3 J-l+J-2+J-3 1
s +s ------------------+s-----------+--------
Т2Т2Т3 ТзТ2Тз ТзТ2Тз
который соответствует выражению
Y _ Ьо
Т Т 3.2 . .
U s +s a2+sa1+a0
(4-15)
(4-16)
Из передаточной функции (4.16) можно запасать уравнение в форме
Коши
y = ub0—a2y—a2y—a0y.
(4-17)
Такую же процедуру следует выполнить с передаточной функцией
регулятора
1 . TdS
Tis Tfs+1 j’
(4.18)
приведя ее к отношению двух полиномов
р
(4-19)
Полином нормируем относительно старшей производной выходного
сигнала
140
(4.20)
Выражение (4.20) запишем в компактной форме
Wr(s)=
2
s c^+sq+Co
s2+sd1
(4-21)
U
— Y
Из которого получим дифференциальное уравнение
(4.22)
Коэффициенты обоих дифференциальных уравнений вычисляются
согласно выражений (4.15) и (4.20)
, ко
Ьп =-------
Т.Т.Тз
(4.23)
Поскольку выражение (4.22) включает в себя значение рассогласо-
вания и ее первую и вторую производную следует использовать матема-
тическую модель третьего и выше порядков, чтобы эти переменные
состояния присутствовали в (4.17). В результате вектор переменных
состояния включает в себя указанные переменные состояния рассогла-
сования и значение управления с его производной. Такое формирование
вектора состояния важно для описания функционала, который может
включать в себя кроме рассогласования и сигнал управления. Учитывая
141
(4.11) и (4.22) составим уравнение замкнутой системы в виде матрич-
ного уравнения.
У 0 10 0 0 У
У 0 0 10 0 У
У — -a0 -Qi ~а2 b0 0 • У (4.24)
й 0 0 0 0 1 и
й —c0 ~c1 ~c2 0 — d1 й
Ниже приведён скрипт для решения вариационной задачи
1. clear;
2. function Y=PZD_Tune(TT)
3. Т1=ТТ(1);Т2=ТТ(2);ТЗ=ТТ(3);Ко=2.99;
4. а0=1/(Т1*Т2*ТЗ);
5. al=(Т1+Т2+ТЗ)*а0;
6. а2=(Т1*Т2+Т2*ТЗ+ТЗ*Т1)*а0;
7. ЬО=Ко*аО;
8. function dx=systl(t,х), dx=A*x,endfunction
9. function J=Jac(t,y),J=A,endfunction
10. function J=fhJt(p)
11. Kp = p(l); Ti=p(2); Td=p(3); Tf=Td/10;
12. cO=Kp/(Tf*Ti) ;
13. cl=Kp*(Ti+Tf)/(Tf*Ti) ;
14. c2=Kp*(Tf+Td)/Tf ;
15. dl=l/Tf;
16. A=[ // yO yl y2 u ul
17. 01000;
18. 00100;
19. -aO -al -a2 bO 0;
20. 00001;
21. -cO -cl -c2 0 -dl
22. ];
23. x0=[-30;0;0;0;0]; t0=0; t=0:0.1:100;
24. y=ode("rk",xO,tO,t, systl, Jac) ;
25. J=( (y(l, :) ) .*t) * (yd,:)') + ((y(4, :) ) . *t) * 47:
(y(4,:)') * 30.3;
26. endfunction
27. function [f,g,ind]=cst(p,ind)
28. f=fhJt(p); g=numderivative (fnk, p) ;
29. endfunction
30 .
31. sTi=Tl+T2; sKp = (T1+T2)/(Ko*2*T3);
32. sTd=Tl*T2/sTi;
33. pO =[sKp;sTi;sTd];
142
[f,xopt]=optim(cst,pO) ;
34 .
35.
36. р = xopt;
37 . Y (8) = р (1) ; Y (9) =
38 . Кр = р(1); Т1=р(2);
39. сО=Кр/(Tf*Т1);
40 . cl=Kp*(Ti+Tf)/(Tf*Ti
41 . с2=Кр*(Tf+Td)/Tf;
42 . dl=l/Tf;
43. A=[ // yO yl y2 u ul
44 . 01000;
45. 00100;
46. -a0 -al -a2 bO 0;
47 . 00001;
48 . -c0 -cl -c2 0 -dl
49. ] ;
50 . x0=[-30;0;0;0;0]; tO
51 . y=ode("stiff",xO,tO,
52 . J=y(l, :) * (y(1, :) ')
53. plot(t,у (1, :));
54 . plot(t,у(4,:));
55. xgrid();
56. endfunction
p(2) ; Y(10) = p(3) ;
Td=p(3); Tf=Td/10;
=0; t=0:0.1:100;
t, systl, Jac) ;
Сама вариационная задача поиска минимума функционала выпол-
няется с помощью функции optim в строке 35. Для этого необходимо
описать функцию cst, которая включает в себя расчёт функционала и
стандартную функцию частных производных в строках 27-29.
Вычисление функционала выполняется в строке 25 согласно
выбранному из выражений
со
f(Kp,T1,p)=f(y2+k„U2|dr
» ° (4.25)
ГДкр,т,,т„)=] (t-(y2+k„u2)|dr,
О
где первый настраивается коэффициентом ки для выбора
энергетического оптимума. Второй из (4.25) соответствует функционалу
для оптимальной системы по быстродействию.
Функция fnk имеет вектор параметров р, включающий в себя пара-
метры ПИД-регулятора (строка 11). Так как параметры подбираются в
процессе оптимизации, необходимо соответствующие элементы
матрицы (4.24) пересчитать коэффициенты (4.23) в строках 12-15.
Остальные коэффициенты из (4.23) рассчитываются при инициализации
143
в строках 3-7. Матрица замкнутой системы (4.24) заполняется коэффи-
циентами в строках 16-22. Начальное состояние САУ должно быть выве-
дено из равновесного заполнением не нулевыми значениями вектора
переменных в строке 23. Для успешного поиска оптимальных пара-
метров замкнутая система должна быть устойчивой, поэтому предвари-
тельно выбираем параметры регулятора согласно модульного оптимума
(4.13) в строках 31-33.
После успешной решения вариационной задачи в переменной xopt
находятся оптимальные параметры ПИД-регулятора, которые изыма-
ются в строке 38. Далее, в строках 39-42 заполняем коэффициенты
матрицы оптимальной САУ, заполняем непосредственно матрицу в
строках 43-49. Устанавливаем начальное состояние в строке 50, и
решаем дифференциальное уравнение в строке 51. В конце получаем
переходные процессы с помощью функций в строках 53-55, которые
показаны на рисунке 4.7.
Рисунок 4.7: Оптимальные процессы по энергопотреблению и по времени
На этом рисунке представлены результаты моделирования в среде
SciLab. Чтобы получить эти же переходные процессы на практике в
ПЛК, установим полученные параметры ПИД-регулятора в проект
CoDeSys (рисунок 4.5). Результаты работы ПЛК представлены на
рисунке 4.8.
144
Рисунок 4.8: Переходный процесс на мнемосхеме проекта CoDeSys на ПЛК
Если сравнить качественные показатели переходных процессов на
рисунках 4.6 и 4.8, то можно увидеть преимущества использования
вариационного исчисления. При этом для настройки необязательно
знать все тонкости этой теории, поскольку большая часть стандартных
задач решена и легко используется грамотными инженерами с помощью
средств MatLab или SciLab. Современное оборудование позволяет загру-
зить переходный процесс в персональный переносной компьютер непо-
средственно на объекте. С помощью заранее подготовленных скриптов
выполнить необходимые расчёты на компьютере и отправить результаты
вычисления параметров ПИД-регулятора в ПЛК.
Использование современных SCADA, как уже отмечалось в
разделе 1.1, позволяет сделать всю работу по настройке удалённой САУ
непосредственно из комфортабельного офиса. Владение инженера
такими технологиями весьма высоко ценится в компаниях с распреде-
ленными объектами управления на больших территориях. Как правило,
такие компании весьма достойные и относятся к нефтегазовому сектору
экономики страны.
145
Вопросы к разделу.
1. Оптимальная система управления - что это и какие критерии
оптимальности вы знаете?
2. Модальный оптимум, его критерии. Вариационная задача и ее
применение в оптимальных системах управления.
3. Опишите метод построения матрицы однородного дифференци-
ального уравнения замкнутой системы
4. Представьте процедуру настройки трейсера CoDeSys для полу-
чения данных переходного процесса.
4.2. Автоподстройка в САУ
В процессе синтеза, проектирования и обслуживания современных
САУ на всех этапах задача вычисления оптимальных параметров ПИД
регулятора и других динамических блоков всегда актуальна. При
эксплуатации САУ нестационарными объектами часто требуется
подстройка параметров регулирования, которая выполняется квалифи-
цированными специалистами с достаточно высокой зарплатой. Тем не
менее изучая материал предыдущего раздела можно формализовать
знания по методам оптимальной настройки так, чтобы разработать авто-
матизированные методы настройки или даже автоматической
подстройки параметров.
Рассмотрим методику работы специалиста по настройке пара-
метров ПИД с целью определения шагов, которые можно поручить
программе или алгоритму. В частности, при практической реализации
модульного оптимума требуется получить переходный процесс, который
автоматически фиксируется средствами ПЛК. Следовательно инфор-
мация о переходном процессе (рисунок 4.2) может быть проанализиро-
вана с целью определения математической модели и ее параметров
согласно формул (4.8). Анализ переходного процесса в разделе 4.1.3
выполнялся вручную обработкой графика (рисунок 4.3).
Далее параметры вычисляются согласно выражениям (4.9—4.13).
Вычисление по формулам даже с витиеватыми логическими конструк-
циями достаточно легко поддаются программированию. Самым
сложным методом в этой цепочке действий является обработка графика
с помощью разработанной программы.
Такую программу можно разработать при обеспечении нескольких
условий:
•Переходный процесс должен закончится, чтобы знать
установившееся состояние, следовательно нужно описать признак
окончания переходного процесса.
146
•По всему переходному процессу нужно оценить производную с
целью определения уравнения прямой, а именно угла и точки
касательной. При вычислении производной важно, чтобы измерения
были достаточно точными и не подвергались внешним возмущениям.
•Внешних возмущений не должно быть. Наличие внешних
возмущений существенно искажает переходный процесс, что делает
невозможным корректное вычисление касательной и, зависящих от нее
параметров времени.
Если поручить программе полностью всю работу по анализу пере-
ходного процесса, то требуется создать дополнительный алгоритм
оценки достоверности самого переходного процесса и отсутствия
внешних возмущений. Этот алгоритм формируется из анализа
случайных процессов с вычислением корреляции и автокорреляции с
типовой формой ПП. В результате подобные методы чаше всего
тщательно исследуются в научных работах, где практическую реали-
зацию нужно проверить, чтобы рекомендовать для создания алгоритма
подстройки по переходному процессу.
В автоматизированном режиме, когда рисунок 4.3 анализируется
человеком, задача определения пригодности переходного процесса
решается легко на интуитивном уровне. Подобно задаче, которую
выполняет охранник без особого образования различая лица прохо-
дящих и принимая решение, пропускать или не пропускать. И лишь
математическая формализация работы его мозга требует серьёзных
знаний теории вероятности и методов распознавания образов. Данное
направление активно развивается в науке, и вопрос качественного опре-
деления пригодности ПП с помощью ПЛК остаётся открытым сложным.
Но даже при успешной реализации данного метода автоматической
настройки имеется существенный недостаток в том, что нужно
дождаться признака окончания переходного процесса. Обычно это
несколько (от 4 до 8) максимального времени из значений постоянных
времени объекта. Поэтому на практике чаще используют идентифи-
кацию кривой разгона, впервые предложенной в статье Зиглера-Нико-
лоса, о настройке ПИД-регулятора [].
Определение. Кривая разгона - это часть переходного процесса до
момента максимальной крутизны графика. На рисунке 4.3 - это точка
соприкосновения касательной. Время кривой разгона обычно в
несколько раз меньше времени ПП, что позволяет принять решение по
настройке гораздо раньше.
147
На рисунке 4.9 показана кривая разгона на переходном процессе,
где видно, что время кривой разгона в 3-4 раза меньше времени переход-
ного процесса.
Из кривой разгона, после определения уравнения касательной
линии, вычисляются всего два параметра сц и ti. По ним можно вычис-
лить параметры регулятора согласно таблиц 4.1-4.3.
Таблица 4.1.
Параметры ПИД при перерегулировании 40 %
Тип регулятора кр Tt Td
Р 1,0 а
PI 0,9 а 3,0т/Кр
PID 1,2 а 0,9 т !КР 0,5 т / Кр
Как показала практика использования метода, вычисленные пара-
метры для разных объектов дают ощутимо разные показатели качества
управления. Это связанно со многими причинами: качество измеренной
кривой разгона сильно зависит от качества АЦП контроллера, расчёт
параметров получен из обобщённых решений для универсального
случая. Тем не менее, метод настройки, как правило, надёжно обеспечи-
вает устойчивость замкнутой системы.
148
Таблица 4.2.
Параметры ПИД при перерегулировании 20 %
Тип регулятора кр Д Td
Р ЪД а
PI 0,6 а 1,0 т /Кр
PID 0,95 а \Дх/Кр 0,47 т /Кр
Особенно если выбрать параметры для меньшего значения пере-регули-
рования (таблица 4.2 20 %) или вовсе без пере-регулирования
(таблица 4.3)
Таблица 4.3.
Параметры ПИД без перерегулирования
Тип регулятора кр Д Td
Р 0,3 а
PI 0,35 а 1,2т/Хр
PID 0,6 а 1,0 т /Кр 0,5 т / Кр
Приведём преимущества и недостатки рассмотренных методов
автоподстройки.
Настройка по кривой разгона объекта.
• Используется в методах подстройки Зиглера-Николоса и их
модификаций;
• При качественном измеренном сигнале может быть достаточно
точным и эффективным;
• Для вычисления параметров ПИД, достаточно дождаться
максимальной крутизны процесса;
• Недостаток заключается в том, что метод требователен к качеству
и шуму в канале измерения.
Настройка по установившемуся переходному процессу объекта.
• Можно использовать модульный и симметричный метод расчёта
параметров регулятора;
• Менее требователен к качеству канала измерения;
• Недостаток: требуется дождаться окончания ПП (время примерно
в 4-6 раз больше чем время кривой разгона).
Настройка по установившемуся переходному замкнутой системы
149
• Используются методы прямой оценки качества переходного
процесса
• Менее требователен к качеству канала измерения;
• Наиболее точный в сравнении с предыдущими;
• Недостатки: предварительно требуется устойчивость системы,
очень медленная итерация, требуется несколько итераций, сложный
расчёт градиента изменения параметров ПИД.
Как уже было отмечено, основной проблемой использования алго-
ритмов автоподстройки параметров ПИД-регуляторов является качество
измеренного с помощью АЦП сигнала. Поэтому на порталах ведущих
производителей ПЛК эти методы предлагают использовать с осторожно-
стью предупреждая о проблемах, которые могу возникнуть.
Если технологический объект позволяет автоколебательный режим
работы в процессе настройки, то можно воспользоваться методом
настройки Зиглера-Николоса по параметрам частотной характеристики.
На рисунке 4.10 показана частотная характеристика, где представ-
ляет интерес всего лишь одна частота сол, при которой фаза равна -л. На
этой частоте нужно определить коэффициент передачи объекта управ-
ления /Д и период Д, соответствующий этой частоте.
Рисунок 4.10: Настройка по параметрам частотной характеристики
Для реализации метода на ПЛК необязательно измерять частотную
характеристику объекта управления, поскольку интересует только одна
частота. Эту частоту также нет необходимости вычислять. Достаточно
вместо ПИД-регулятора использовать обычный релейный модуль с огра-
ничением по амплитуде на выходе. Диапазон изменения сигнала управ -
150
ления обычно уже ограничен технологическими условиями исполни-
тельного элемента. При этом можно в разумных пределах еще умень-
шить диапазон выходных сигналов для уменьшения амплитуды выну-
жденных колебаний. В результате работы замкнутой системы с
релейным модулем должен появится автоколебательный режим, если
объект управления представлен инерционным звеном третьего и выше
порядка.
Автоколебательный режим будет соответствовать частоте ац . Коэф-
фициент передачи объекта можно легко вычислить как отношение
амплитуд колебаний на выходе ко входу. Далее вычислить параметры
ПИД-регулятора по формулам из таблицы 4.4.
Важным преимуществом такого подхода к вычислению параметров
регулятора является отсутствие требования оценивать производную от
измеренного с помощью АЦП сигнала. Следовательно, в этом подходе
нет особых требований к точности АЦП. Также если ссылаться на
форумы производителей ПЛК, этот метод простой, надежный и легкий в
реализации. Не смотря на то, что метод реализован во многих библио-
теках CoDeSys, возможно представлен открытым исходным кодом,
рассмотрим реализацию в качестве примера.
Таблица 4.4.
Вычисление параметров ПИД по частотной характеристике
Тип регулятора кр Д Td
Р 0,5 Кп
PI 0,4 К, 0,8 TJK*
PID 0,6 TJ(2K„) Т„ KJ%
Для реализации автоподстройки добавим блок автоподстройки и
назовём его, на пример - PidTuning. У этого блока на входы и выходе
есть параметры регулирования, которые в обычном режиме просто
ре-транслируются на выход.
Процедура подстройки начинается с появлением активного сигнала
bstart на входе. После этого согласно процедуре следует вместо регуля-
тора подключить релейный элемент. Однако в схеме этого элемента нет.
ПИД регулятор с достаточно большим коэффициентом передачи при
времени интегрирования и дифференцирования равным нулю является
аналогом релейного элемента, где значения Ymn и Ymx являются пара-
метрами ограничения релейного элемента.
151
Рисунок 4.И: Замкнутая система с блоком автоподстройки
Для того чтобы стало возможным установку времени интегриро-
вания равным нулю и избежать деления на ноль в коде интегратора
изменена строка 14 на странице 80 как показано ниже.
14. IF Т>0 THEN Y := Yl + X * tds / Т; END_IF
В результате интегрирующее звено не работает и не влияет на САУ.
Основной информацией об объекте управления является поведение
значений управления IU и сигнала рассогласования 1Егг, которое
представлено на рисунке 4.12.
На рисунке сплошной линией показан выход с объекта управления IY,
который отличается от 1Егг только смещением на gYset. Алгоритм
работы блока авто настройки заключается в следующих шагах:
1. Работа алгоритма начинается с активного сигнала bstart, после
которого параметры регулятора устанавливаются согласно свойствам
релейного элемента. Эти параметры указаны на рисунке 4.12. В
результате замкнутая САУ управляется в автоколебательном режиме.
2. Наблюдается процесс изменения значения рассогласования
1Егг, до момента перехода через ноль. Этот момент Ti фиксируется для
вычисления периода.
3. Наблюдается значение 1Егг до достижения максимального
значения 1Еггтах, которое фиксируется.
4. Наблюдается процесс изменения значения рассогласования
1Егг, до момента перехода через ноль. Этот момент Тз фиксируется для
вычисления периода.
5. Наблюдается значение 1Егг до достижения минимального
значения lErrmin, которое также фиксируется в памяти.
152
6. Наблюдается процесс изменения значения рассогласования
1Егг, до моментов перехода через ноль. Эти момент тз и Т4 фиксируется
для вычисления периода. Таких переходов можно наблюдать от 3 и
более. Большое количество переходов обеспечивает высокую точность
вычисления периода колебаний.
7. На этом этапе можно вычислить параметры регулятора согласно
таблицы 4.4.
где Кя=
\1 max min)
№rrmax-IErrmin)
(4-26)
где п - количество интервалов-полупериодов усреднения.
Рисунок 4.12.- Результаты моделирования работы блока автоподстройки
На рисунке 4.13 показана работа регулятора с учётом ошибок
дискретизации АЦП.
153
Рисунок 4.13: Результаты работы блока автоподстройки с каналом АЦП
Как видно из рисунка процесс и результаты настройки не претерпели
изменений. А воздействие умов дискретизации заметно на переходном
процессе сигнала управления.
Этот метод подстройки наиболее популярен в практических реали-
зациях и имеет некоторые модификации. Приведём достоинства и недо-
статки некоторых их них.
Подключение релейного элемента вместо регулятора.
• Используется свойство замкнутой системы находящейся на
границе устойчивости в методах подстройки Зиглера-Николоса и
модификаций по ЛАЧХ и ЛФЧХ;
• Не требователен к качеству и шуму в канале измерения;
• Простой алгоритм вычисления параметров ПИД;
• Недостаток: не все объекты позволяют автоколебательные режимы
на границе устойчивости.
Использование дополнительного сигнала к управлению объектом.
• Можно контролировать амплитуду вынужденных колебаний на
выходе объекта;
• Менее требователен к качеству канала измерения;
154
• Недостаток: требуется выполнить несколько серий испытательных
сигналов, чтобы оценить параметры объекта.
Подключение релейного элемента вместо регулятора с регулируе-
мыми значениями максимального и минимального значения.
• Используется свойство замкнутой системы находящейся на
границе устойчивости в методах подстройки Зиглера-Николоса и
модификаций по ЛАЧХ и ЛФЧХ;
• Менее требователен к качеству канала измерения;
•Можно контролировать амплитуду вынужденных колебаний на
выходе объекта;
•Недостатки: существуют объекты, которые не позволяют
автоколебательные режимы на границе устойчивости даже с малыми
амплитудами.
4.3. Адаптивные САУ
Адаптивные САУ являются более сложными, как в математическом
описании, так и в построении алгоритмов управления и автоподстройки.
Основная цель алгоритмов автоподстройки является поиск оптимальных
параметров САУ в процессе функционирования технологического
процесса. В отличии от систем с автоподстройкой, рассмотренных в
прошлом разделе 4.2, где процедура автоподстройки запускается в
ручном режиме на этапе первичного запуска САУ, в адаптивных
системах процесс автоподстройки постоянный в течение всего времени
эксплуатации САУ Такая необходимость возникает в системах, где пара-
метры объекта могут изменятся в течение всего процесса в значи-
тельных пределах, так что робастных свойств замкнутой САУ недоста-
точно для качественного функционирования.
Приведём краткую классификацию отличий от оптимальных
систем.
Вычисление параметров регулятора выполняются:
• на этапе проектирования у оптимальной системы;
• на этапе работы у адаптивной системы.
Параметры объекта предполагаются:
• стабильными для оптимальной системы.
•меняющимися в процессе работы так, что требуется подстройка
парамеров регулятора у адаптивных систем.
Реализация САУ:
•достаточно простая, поскольку основные задачи синтеза решены
на этапе проектирования для оптимальной системы.
155
• весьма сложная, поскольку включает в себя дополнительные
алгоритмы вычисления параметров регулятора согласно поведению
объекта.
Область научных направлений синтеза адаптивных систем весьма
широка и имеет множество направлений и методов. Важно ориентиро-
ваться в этих направлениях, поэтому приведём классификацию наиболее
распространённых направлений адаптивных систем.
Для настройки параметров регулятора нужно наблюдать поведение
объекта. Если объект управления находится равновесном состоянии, то
управление и выход объекта не изменяется. В этом случае получить
информацию о параметрах объекта и качестве переходного процесса
невозможно. Адаптивные САУ делятся по способу получения инфор-
мации об объекте. Приведём два способа.
• Реализация алгоритма адаптации происходит постоянно, для этого
необходимо выводить объект из равновесия дополнительным
искусственным возмущением и наблюдать за ним.
• Реализация алгоритма адаптации происходит по событию,
вызванному оператором или автоматически по расписанию или при
обнаружении условий, требующих подстройки.
Исходя из поставленной цели адаптивные САУ можно указать
следующее.
•Стабилизацию качества управления или заданного критерия в
условиях изменения параметров объекта управления. Отметим что, в
отличие от робастного управления тут присутствует подстройка
параметров или включение дополнительного сигнала управления.
•Автоматическая оптимизация качества управления или заданного
критерия. В качестве критерия может быть функционал из
вариационных методов оптимального управления.
Методы адаптивной настройки могут быть:
• самонастраивающиеся, когда изменяются параметры регулятора;
• самоорганизующиеся, когда изменяется структура регулятора (в
отличие от регулятора с переменной структурой, структура меняется на
основании полученных свойств и параметров объекта);
• адаптация при обнаружении особых фазовых состояний (в
качестве одного из примеров можно привести регулятор в скользящем
режиме);
• обучающиеся (самообучающиеся) системы.
Обучающиеся системы включают в себя медленные процессы
накопления информации об объекте управления, которая используется
для настройки параметров или структуры в целом. Такие системы
156
требуют построения грамотно реализованных нейросетей или
экспертных оценок.
Также следует различать адаптивные САУ по способу изучения
объекта.
Поиск методами решения вариационных задач:
• Экстремальные регуляторы, где успешно подобран
быстродействующий явно выраженный функционал, в отличие
среднеквадратичного функционала, способный дать оценки в течение
переходного процесса.
• Рекурсивная подстройка параметров регулятора на основании
показателей полученного переходного процесса.
Без поисковые методы:
• Прямой метод Зиглера-Николоса по кривой разгона.
Системы с эталонной моделью, где на основании сравнения
эталона и объекта:
• формируется дополнительное значение управления (сигнальная
адаптация)
• формируется изменение значений параметров регулятора
(параметрическая адаптация)
Системы с идентификатором параметров объекта (не путаем с
наблюдателем переменных системы):
• Идентификация коэффициентов матрицы разностного уравнения с
помощью обратной матрицы.
• Оценка параметров объекта по измеренной частотной
характеристике с помощью гармонического воздействия.
Далее рассмотрим лишь некоторые из наиболее популярных
подходов в практических реализациях адаптивных САУ
4.3.1. Адаптивная САУ с эталонной моделью с сигнальной
адаптацией
Система управления с эталонной моделью содержит в себе два
замкнутых контура: один с действующим динамическим объектом,
второй настроенный замкнутый контур с эталонной моделью объекта
управления. Идея заключается в том, чтобы на основании рассогласо-
вания работы двух контуров определяется значение корректирующего
сигнала управления так, чтобы поведение обоих контуров были макси-
мально похожи. В этом случае, будем считать, что САУ с действующим
объектом управления скорректирована.
На рисунке 4.14 показана структурная схема САУ с эталонной
моделью с сигнальной адаптацией.
157
Рисунок 4.14.- САУ с эталонной моделью с сигнальной адаптацией
Предполагается, что объект управления представлен математиче-
ской моделью
(4.27)
где параметры объекта Коь, Т, могут быть известны. При этом имеется
один нестабильный параметр с интервально-определённой областью
изменения.
Регуляторы и эталонная модель представлены выражениями
(4.28)
Поскольку параметры регулятора и модели могут быть выбраны
разработчиком, то можно обеспечить соответствие параметров
регулятора параметрам объекта удовлетворяющее условиям
оптимальной настройки. К примеру можно выбрать модульный оптимум
(4.5) (4.11-4.13) для формирования следующих связей
158
(4.29)
Синтезу подлежит передаточная функция Wc(s), которая обычно
соответствует передаточной функции регулятора или содержит неко-
торые его элементы. К сожалению, универсального решения или мето-
дики выбора ПФ Wc(s) и её параметров найти сложно. В основном
решения основываются частично на интуиции разработчиков, которые
следует исследовать во всех возможных режимах чтобы рекомендовать в
качестве готового решения.
4.3.2. Адаптивная САУ с эталонной моделью с
параметрической адаптацией
Идея заключается в том, чтобы на основании рассогласования
работы двух контуров определить направления изменения параметров
регулятора так, чтобы поведение обоих контуров были максимально
похожи. В этом случае, будем считать, что САУ с действующим
объектом управления настроена, поскольку соответствует настроенной с
эталонной моделью. На рисунке 4.15 показана структурная схема адап-
тивной САУ
Рисунок 4.15: САУ с эталонной моделью с параметрической адаптацией
В отличие от рисунка 4.14 направление пересчёта оптимальной системы
изменено. В начале определяются параметры регулятора, по которым
вычисляются параметры эталонной модели регулятора
159
T ml~ f Тт1(т i ’T d) ’
T m2~ f i’T d) ’ (4.30)
К mob f kmob p’ ml > m2 > d) >
из выражений (4.28) (4.29).
Наблюдению и анализу доступны переменные состояния регуля-
торов и эталонной модели вместе с параметрами. Предполагается, что
передаточная функция объекта в общем случае представлена выраже-
нием (4.27) и не все параметры объекта известны. Также доступны для
измерения выходные значения объекта.
Синтезу подлежит программа вычисления параметров регулятора
на основании известных параметров и всех переменных состояния,
доступных измерению или вычислению. Наличие такого большого
числа входных парамеров программы даёт широкие возможности в
выборе алгоритма программы. Однако с математической точки зрения
решений может быть много и все они не имеют обобщённую методику
синтеза. С подобной задачей может справиться специалист сразу в двух
областях: программирования и современной теории автоматических
систем.
В научных изданиях можно найти подходы к синтезу программы с
помощью нейросети или генетических алгоритмов, где алгоритм может
обучаться методом проб и ошибок на основании результатов значитель-
ного количества экспериментов или моделирования. Познакомится с
этим направлением науки можно в дополнительных материалах [], не
входящих в рамки учебного пособия.
4.3.3. Идентификация модели объекта управления
Более строгую математическую форму имеет метод адаптивного
управления с идентификацией параметров математической модели
объекта управления на основании разностного уравнения. Положим, что
все значения выхода объекта на протяжении достаточного количества
шагов можно запомнить вместе со значениями управления. Тогда выход
на каждом шаге можно описать в виде множества разностных уравнений
у0=с1у1+с2у2+с3и0+с4и1+с5и2,
У1 = с1у2+с2у3+с3и1+с4и2+с5и3,
yi=c1y1+i+c2y2+i+c3ui+c4u1+i+c3u2+i.
160
Если предположить, что объект полностью соответствует математи-
ческой модели, представленной разностными уравнениями (4.31) на
каждом шаге, то можно составить систему уравнений для нахождения
коэффициентов разностного уравнения сг. В матричной форме урав-
нение (4.31) может быть записано в следующем виде
То У1 У2 и. и2 С1
У1 У2 Уз U1 и2 из С2
У2 — Уз У4 и2 из и4 * С3
... ... ... ... ... ... С4
Уп Уп+1 У п + 2 Un Un+1 Un + 2 Сз
(4-32)
Для однозначного решения необходимо, чтобы количество уравнений п
совпадало количеством коэффициентов. Касательно уравнений (4.32), их
должно быть пять. При этом квадратная матрица должна иметь
определитель, неравный нулю. Тогда решение можно записать в виде
-1
С1 гч гч Уо
С2 гч гч У1
Сз — Уз у4 и2 и3 и4 У2 (4-33)
с4 ••• ••• ...
С5 Ts+l У5+2 Us us+1 us+2 Уз
На практике измеренные значения у,- подвержены воздействиям и
ошибкам дискретизации АЦП, поэтому для решения уравнения (4.32)
используют псевдо-обратную [гандмахер].
Процедура псведо-обращения матрицы переменных состояния
позволяет иметь количество уравнений большим чем количество коэф-
фициентов. Однозначное решение в процедуре псевдо-обращения
достигается дополнительными условиями, например минимизация сред-
неквадратичного отклонения.
Но даже при использование такой матрицы не гарантирует
успешной идентификации параметров объекта во многих случаях.
Поэтому следует учитывать как минимум два фактора:
• Требуется очень высокая точность измерения переменных
состояния. Высокую точность можно обеспечить применяя АЦП с
высокой разрядностью от 16 до 24 бит. Но даже при качественном АЦП
измеренные значения могут содержать внешние воздействия в виде
шума.
161
от нее как
•Время дискретизации разностного уравнения должно быть не
очень маленьким и не очень большим. Обычно время дискретизации
выбирается раз в 10 меньше чем минимальная постоянная времени из
инерционных объектов математической модели. При этом максимальная
постоянная времени может превышать минимальную в лучшем случае в
10 раз. В итоге для оценки максимальной постоянной времени
необходимо, чтобы время дискретизации отличалась
минимум в 100 раз.
На примере обобщённого объекта 2-го порядка
b0+b1s+b2s2
. . 2
Go+t^s + s
получим разностное уравнение (2.80) в общем виде
W(s
(4-34)
y = ^-a0t2d-a1td)y1+(a1td-l)y2+
(Ь^ + Ь^ + Ь^и-^Ьг + Ь^^Щ+ЬгЩ,
с3 с4 с5
(4-35)
где отмечено содержание коэффициентов сг. Из этого содержания на
примере Ci видно, что искомый параметр объекта аО, в с\ присутствует
дважды умноженным на время дискретизации. В результате, чтобы
оценить значение параметра с погрешностью в 1 %, следует оценить
параметр с\ с погрешностью (t4 1 %). Тогда его множитель переменная
состояния у, должен быть измерен с соответствующей погрешностью.
Если оценить абсолютную погрешность как 1/(100-100-100). Такую
погрешность может обеспечить 20-разрядный АЦП. Это похоже на ситу-
ацию когда оценивают содержимое небольшой тележки взвешивая её с
вагоном в котором она стоит.
В ПЛК чаще всего используют 10 разрядный АЦП. В дорогих
моделях дискретность АЦП может достигать 16 разрядов. Уменьшить
требования к АЦП можно, если поменять разностное уравнение
y^-^-a.t^y.+ia.t.-lb^b^u
на уравнение
У-^У1+У2 = -а0^У1-а1^(У1~У2)+ь0^и- (4.36)
162
На основании дискретного уравнения (4.36) можно составить
матричное уравнение подобное выражению (4.33) вместе с её решением
(4.34).
На примере математической модели объекта
Ьо
(4.37)
с её разностным уравнением (4.36) с помощью (4.34) можно получить
параметры модели (ао, щ, bo), которые содержат в себе постоянные
времени и коэффициент передачи объекта (4.37). Это в иде в выражении
ъ„
J. 1 J. 2
1 ^1+^2 2
——+s ———+S
(4.38)
Далее составим уравнения
=ь, 1
1 2
а1
1 ' -I 2
--------------------------------= <к,-------------------=cl ,
т\т2 °’Т1Т2 0 тгт2 1
из которых запишем
1 а1 Ьо
а0 а0 а0
Чтобы найти постоянные времени составим квадратное уравнение
1+л_=^
a()Ti Gq
а0Т2г— агТ г+1 = 0
о
О
1 -1 2
и решим его
_аг+^а2+^а0 _
J 1 n J 2
2 а0
а^сь+Лао _Ь0
---77----’к о-~
2 а0 ао
(4-39)
В результате для математической модели объекта (4.37) можно
использовать разностное уравнение (4.36) с помощью (4.34) можно
получить параметры модели (ао, ai, bo) и из них с помощью выражений
163
(4.39) вычислить параметры объекта для реализации настройки
ПИД-регулятора используя модульный оптимум (раздел 4.1.3).
Структурная схема адаптивного управления с идентификацией
показана на рисунке 4.16.
ob^!,Г2,Г3Г^1^2^3^4^5
Рисунок 4.16: Структурная схема адаптивного управления с идентификацией
На рисунке присутствуют две программы. Программа справа
фиксирует значения переменных состояния, формирует систему урав-
нений и решает ее относительно коэффициентов (tz0, а\, Ьо), которые
можно пересчитать в параметры передаточной функции (4.37).
Программ слева выполняет расчёт параметров регулятора согласно
методу, рассмотренному в разделе 4.1.3.
Вопросы к разделу.
1. Оптимальная и адаптивная САУ: в чем отличия?
2. По каким признакам формируется классификация адаптивных
САУ.
3. Как применяется вариационная задача в адаптивной управлении
САУ.
4. Опишите поисковые и без поисковые методы адаптивного
управления.
5. Приведите структурные схемы адаптивной САУ с эталонной
моделью для параметрической и сигнальной адаптацией.
6. Приведите пример математической модели объекта и метод
идентификации его параметров.
7. В чем отличие адаптивных систем и систем с автоподстройкой?
8. Дайте классификацию систем с автоподстройкой.
9. Какие методы авто настройки основываются на переходных
процессах, какие переходные процессы используются?
164
10. Опишите методы авто настройки на основе автоколебаний в
САУ.
11. Какие методы авто настройки используются в системах с допол-
нительным воздействием.
4.4. Теория нечётких множеств
Не смотря на весьма странное название этого научного направ-
ления, возможно даже отталкивающая своей нечеткостью, эта теория не
просто имеет право на существование, но хорошо зарекомендовала себя
в научно практических задачах. Изначально понятие нечеткого множе-
ства было предложено профессором Калифорнийского университета
Заде (Zadeh) в 1965 г.. Это была попытка математической формализации
лингвистической информации для описания физических объектов.
Другими словами Заде предложил математическую модель опираю-
щуюся не на доказанные физические законы и дифференциальные урав-
нения, но на обычные объяснения, пояснения, выраженные словами при
описании ситуации.
По началу, теория была воспринята научным сообществом крити-
чески, с точки зрения значимости. Но уже в 1973 году ученые из
Лондонского колледжа Мамдани (Mamdani) и Ассилиан (Assilian) пред-
ставили первое практическое применение теории нечетких множеств
для создания математической модели парового двигателя и лабора-
торной установки на базе вычислительной машины.
В 1983 году выполняя заказ фирмы Fuji El ученный-исследователь
Сугено (Sugeno) разработал систему управления очисткой воды, где
формализовал и использовал первый нечёткий контроллер. Разработка
была на столько успешна, что появилось много идей использования
теории нечетких множеств в различных задачах:
• Для компании Canon впервые использована теория для наведения
и фокусирования фото-камеры на основе лингвистических описаний
решений фотографов.
• В системах управления двигателями внутреннего сгорания
большая часть физических процессов хорошо описана и реализована на
базе традиционной теории. Однако система диагностики и принятия
решения о качестве работы двигателя в значительной мере опиралась на
словесное описание специалистов, работающих и ремонтирующих
двигателей. Наверное опытный водитель по звуку работающего
двигателя легко услышит, что поршень один не работает. Звуку этому
придумал название: «троит» двигатель. Но!!! Не предоставил ни одной
165
формулы и уравнения, по которым можно вычислительной машине
принять решение о выходе из строя поршня. Как ни странно, контроллер
Сугено, справился с этой задачей и успешно применен в системах
диагностики двигателей таких производителей как: Mitsubishi, Honda,
Nissan ....
• Также, нечеткий контроллер успешно использовался в
видеомагнитофонах Toshiba для быстрой и корректной установки
магнитной головке на носитель информации.
• В стиральных машинках фирмы Samsung нечеткая логика
используется в управлении двигателем. У меня дома работает
стиральная машинка с использованием теории нечетких множеств. Об
этом ярко отмечено на лицевой панели. Было всегда интересно, когда
она включает эту самую логику при стирке. Могу засвидетельствовать,
что машинка весьма странно ведет себя, когда обнаруживает, что в
пододеяльник забилось множество мелких вещей: носков, наволочек ... .
При этом, только управлением направлением и скоростью двигателя,
достаточно часто ей удается вытряхнуть обратно мелкие вещи из
пододеяльника. Кто нибудь может предложить передаточную функцию
регулятора скоростью направлением двигателя для решения такой
задачи? И что нужно подавать на вход регулятора? Полагаю есть
специалисты, которые опишут решение в подобном стиле: если звук
машинки «хлоп-хлоп-бряк», то два оборота в противоположную сторону
медленно, и обратно быстро один раз. «Хлоп» и «Бряк» можно легко
отличить с помощью измерения спектра сигнала, поскольку есть спектр
соответствующий звуку «Хлоп» и несколько другой спектр
соответствующий звуку «Бряк». Дальше все лингвистические описания
и, соответствующие им решения, можно формализовать с помощью
теории нечетких множеств и заставить творить стиральную машинку
чудеса, неподдающиеся логике сердобольного ученого-скептика.
В инженерной практике можно встретить большое количество
научных задач или даже проблем, которые могут быть успешно и
быстро решены с помощью теории нечетких множеств. Попытка
описать решения опытного лётчика при посадке самолёта на палубу
авианосца, при условии незнания им высшей математики и динамиче-
ской физики. Так, если потребуется создать контроллер для посадки
крупного дрона на палубу можно выбрать два пути:
1. Разработать очень подробную математическую модель посадки
дрона на палубу, проверить и доказать адекватность модели. Выполнить
синтез регулятора для математической модели нелинейного динамиче-
ского объекта. Реализовать и успешно посадить дрон на палубу.
166
2. Расспросить у опытного лётчика как он принимает решения в
различных ситуациях, представленных словесным описанием. Создать
нечеткое множество состояний и решений, на базе которого реализовать
нечеткий регулятор. Реализовать и успешно посадить дрон на палубу.
Корейские, японские, китайские ученые, истинные поклонники
теории нечетких множеств, утверждают, что первый путь дает лучший
результат при очень больших затратах на исследования, синтез и разра-
ботку. Второй, дает приемлемый результат, при значительно меньших
затратах на разработку САУ.
Полагаю, что эта проповедь о полезности теории нечётких
множеств сняла всякие препятствия, недоверие и скептицизм для непо-
средственного ее изучения и следующий материал будет воспринят
внимательно и с доверием.
Сама процедура формализации лингвистической информации
должна быть знакома, особенно если обучались вождению на автомо-
биле и помните как это было, особенно если инструктор был нервный и
не воздержан в словах. Весь этот поток слов и выкриков всегда был в
ситуациях, которые вы можете описать и привязать «совет» или
«нервную мольбу» инструктора в виде решения вместе со значимостью
необходимого действия. После того как, у вас сформировалось конечное
число ситуации и решений, достаточное для принятие решения во всех
остальных бесконечных ситуациях, вы обучились и сформовали
нечеткий контроллер у вашем сознании. Осталось навести математиче-
ский грамотный порядок для описания вашего решения, что и сделал,
теперь уже великий учёный Заде.
Рассмотрим понятие нечёткое множество. Чтобы постоянно
абстрактно не мыслить, рассмотрим на примере множества из пяти
значений
Хе(х1,х2,х3,х4х5). (4.40)
Давайте придадим лингвистический смысл инструктора по
вождению каждому элементу множества: Хз - нормально, хорошо; Х2 —
аккуратно направо; Х4 - аккуратно налево; Xi - КУДА!! направо ... ,
хорошо; Xs - КУДА!! налево .... Границы разметки множества несложно
сформировать наблюдая за поведением инструктора: вы знаете на каких
направлениях он доволен, на каких направлениях он советует, на каких
направлениях он истошно кричит. Эти границы вполне определены и
оценены математический в виде чисел. Так почему же множество
нечеткое, если значения четко определены? Потому, что мы не знаем о
167
чем думает инструктор, когда ситуация не на границах множества, гдето
между этими точками.
Чтобы рассуждать о всех ситуациях, которые могут быть введем
понятие функции принадлежности. Для этого рассмотрим множе-
ство 4.40 на рисунке 4.17, где к каждому элементу множества приложена
линия-функция принадлежности.
Рисунок 4.17: Нечеткое множество на примере пяти точек
В самой точке значение ее функции равно единице. На удалении от
точки функция уменьшает свое значение. Физический смысл функции -
мера принадлежности произвольной точки на оси х к заданному
элементу множества. В результате, имея все пять функций принадлеж-
ности можно говорить о любой точке множества в формате: на сколько
эта точка принадлежит каждому элементу множества.
Функции принадлежности можно классифицировать по нескольким
признакам:
• Z, П, S - образные функции, касательно рисунка 4.17 xi
принадлежит Z-типу, х5 принадлежит S-типу, остальные П-типу;
• кусочно линейные могут быть представлены в виде трапеции или
треугольника, как показано на рисунке 4.18;
• аналитические функции, обычно это функции распределения
Гауса, применяемые в теории вероятности.
168
Рисунок 4.18: Функции принадлежности
Примером функции распределения может быть выражение
ц.(х) = е 2d
где d - задает дисперсию, ширину распределения функции.
В реализациях нечетких множеств может быть несколько. Важно
понимать, что нечеткое множество представляет:
• переменную состояния объекта, доступную для измерения;
• рассогласование, его первая и вторая производная в одномерных
САУ;
• рассогласования, их первые и вторые производные в многомерных
САУ.
В случае если множество не одно, решение составляется из
наборов элементов из каждого множества. Каждому набору эксперт
привязывает решение или выходное значение. Уже для трех множеств,
достаточно сложно представить набор знаний эксперта. Поэтому для
лучшей иллюстрации решений на рисунках ограничимся двумя множе-
ствами. В качестве примера рассмотрим ПД-регулятор (рисунок 4.19),
реализованный с помощью двух множеств: значений рассогласования и
первой производной. Серой зоной выделен непосредственно сам регу-
лятор, из которого будет формировать Fuzzy-контроллер. Согласно схеме
управление формируется согласно выражению
u=Kpex + Tde2,
(4-41)
из которого с учетом реального дифференцирующего звена можно запи-
сать передаточную функцию
(4.42)
169
Выражение 4.41 можно рассматривать как уравнение плоскости и в
трехмерном пространстве (ei, ez, и). Выйти за рамки плоскости в этом
выражении нельзя.
Рисунок 4.19: ПД-регулятор
В отличии от ПД-регулятора решение Fuzzy-контроллера и может
быть гладкой поверхностью с самой замысловатой формой. И если в
качестве нечетких множеств принять набор значений ei и е?, то можно
построить регулятор с выходным сигналом и в весьма большими
возможностями настройки уже не плоскости, а поверхности управ-
ления и.
Выберем набор из 5-ти элементов для множеств ei и е?, подобно
тому, как показано на рисунке 4.17 и расположим их по координатам
х и у. В результате получим плоскость, показанную на рисунке 4.20.
Поскольку в каждом множестве по пять элементов, то количество
возможных решений будет равно количеству пересечений элементов
двух множеств. На примере управления машиной с лингвистическими
решениями инструктора множество ei(en, еп, еи, ем, ем) можно взять из
значений отклонения направления машины, а множество
62(621, е??, е2з, е24, 625) из значений скорости изменения курса автомобиля.
170
Рисунок 4.20: Плоскость логического вывода
Лингвистический множество бфбп, еп, ем, вы, 615) можно описать
так:
• ев - направление правильное,
• еп - направление стало левее,
• бы - направление стало правое,
• бп - направление совсем левое,
• 615 - направление совсем правое.
Множество 62(621, 622, 623, 624, 625) опишем так:
• 623 - курс не меняется,
• 622 - курс меняется влево,
• 624 - курс меняется вправо,
• 621 - курс катастрофически меняется влево,
• 625 - курс катастрофически меняется вправо.
Имеющие опыт общения с инструктором по вождению, и не только,
могут с уверенностью сказать, что посоветует инструктор, если ситу-
ация соответствует элементам множества бп и 621. Ничего он советовать
не будет, это понятно особенно, если перевести ситуацию в языковую
форму: «направление совсем левое, при этом курс катастрофически
меняется влево». Инструктор будет кричать: «ВСТРЕЧКА!» повора-
чивай на право! И мы принимаем решение Rn - максимально быстро
крутим руль вправо. Набор ситуаций (бв, 623), (бп, 624), (би, 622)
инструктор будет воспринимать спокойно. Очевидно, руль в нормальном
171
положении касательно этих ситуаций. Процедура выбора множества и
назначение решений в точках пересечения элементов этих множеств
называется фазификацией.
В результате на имеющиеся композиции лингвистических
описаний у нас есть решения Ry. Следует отметить, что не обязательно
для всех пересечений нужно иметь решения, но для основополагающих
ситуаций обязательно. Но это всего лишь решения для отдельных ситу-
аций или отдельных точек на плоскости. Рассмотрим произвольную
точку на плоскости на рисунке 4.21.
Рисунок 4.21.- Произвольная точка на плоскости логического вывода
По отношению к имеющимся решениям 7?,,, можно дать оценку: на
сколько (процентов) точка принадлежит к каждому имеющемуся
172
решению. Эта оценка определяется функциями принадлежности, как это
уже рассматривалось выше. Вклад каждого решения в произвольной
точке R(x, у)
(4.43)
зависит от значений двух функций принадлежности касательно решения
Ry.
Какую из функций принадлежности взять для оценки вклада? Тут
четкого решения нет. Есть только несколько, хорошо себя зарекомендо-
вавших, логических конструкций для принятия решений, которые пред-
ставим в виде функции
aSei^ejy)=Lk(^eiX\^Sejy)}- (4.44)
Само логическое решение выбирается из ограниченного множества
решений, реализованных в Fwzzy-контроллере. Обычно в контроллере
они пронумерованы и представлены в документации. В качестве
примера для двух функций принадлежности предлагается ряд логиче-
ских решений:
and
or
noC 1-Д1,
Lk~ A^B д2/д i, (4-45)
B^A / jZ/Z 2 j
mean ^2+^)/2,
gmean У /С Д1 •
Поскольку не обязательно все решения Ry доступны, а только N
решений, то набор существующих решений обозначим как
R(ri, Г2, ... rN). Поскольку известна доля влияния щ (4.44) каждого
решения ук в произвольной точке (х, у), то можно вычислить средневзве-
шенное решение по всем существующим. В математической форме
решение представлено выражением
173
N
Xak(eiX’ejyh
-----------• (4.46)
ak ( @ix ’ ?jy )
k=l
Процедура вычисления управляющего сигнала (4.46) на основе частных
решений (рис. 4.20), функций принадлежности (рис. 4.17 и 4.18), логиче-
ских выводов (4.44) и (4.45) - называется дефазификацией.
Оценим количество настраиваемых параметров полученного
аналога ПД-регулятора на базе Fuzzy-контроллера.
• Выбор точек-элементов множеств еДеп, еп, £1з, ем, eis) и
62(^21,622, б2з, в24,625) включает 10 вещественных чисел. Это не
обязательно равномерное распределение точек, поэтому на рисунке 4.40
отмечено, что точки можно смещать.
• Выбор функций принадлежности к точкам включат 10 целых
чисел с номером функции принадлежности в базе доступных
контроллеру.
• Указание значений управления в точках пересечения включает 25
вещественных чисел Гу.
•Количество логических выводов соответствует количеству точек
пересечения и равно 25 целым числам, где хранится номер логического
вывода из базы доступных в списке (4.45).
В результате требуется указать-настроить 35 параметров в виде
вещественных чисел, и указать 35 номеров решения по выбору из
списков функций принадлежности и логических выводов. В итоге, 70
параметров против двух для ПД-регулятора. Казалось бы, что настроить
ПД-регулятор в таком случае легче. Однако ясное понимание работы
Fuzzy-контроллера и опыт работы с объектом у эксперта часто сводит
процедуру настройки Fuzzy-контроллера в обычное заполнение
типичной анкеты с простыми вопросами и простыми решениями. При
этом все происходит без осмысления частотных характеристик, годо-
графов, дифференциальных уравнений и других средств высшей мате-
матики и ТАУ.
В результате чего Fuzzy-контроллер, каким то чудным образом
имеет вполне приемлемую тактику управления, основанную на вашем
опыте, взятым из анкеты эксперта. Сейчас промышленность предлагает
готовые Fuzzy-контроллеры, построенные на базе принятого в 1997 году
международным инженерным сообществом стандарта (Fuzzy Control
Language) IEC 1131-7. Теперь это устройство, в которое нужно внести
174
результаты анкетирования эксперта, после этого оно в большинстве
случаев работоспособно. Уже известны разработки ученых, где
Fuzzy-контроллер реализован на базе PLIC-микросхем с временем
принятия решений менее микросекунды.
Процедура настройки Fuzzy-контроллера уже сейчас стандартная,
типовая и популярная в инженерной деятельности. Возможно скоро в
анкете принимаемого на работу инженера будет включена опция умения
выполнить фазификацию и дефазификацию Fuzzy-контроллера наравне
с опцией о владении программой MicroSoft-Exell.
Вопросы к разделу.
1. В каких задача применяется Fuzzy? Опишите постановку задачи
аппроксимации с помощью Fuzzy.
2. Что такое нечёткое множество? Какие примеры и виде
множеств применяются в САУ?
3. Что такое функция принадлежности? Каковы её свойства и
виды?
4. Приведите пример альтернативного использования Fuzzy
вместо ПИД-регулятора.
5. Что такое логический вывод в Fuzzy? Как формируется логиче-
ское правило.
6. Опишите принцип реализации фазификации и дефазификации.
175
5. Моделирование и управление
электромеханических объектов
Для исследования динамических свойств непрерывных линейных
электромеханических объектов (ЭО) классическими методами теории
регулирования, после описания дифференциальными уравнениями
отдельных элементов, обычно переходят к передаточным функциям этих
элементов. Далее составляется общая структурная схема, в которой
отдельные блоки представляются звеньями с типовыми передаточными
функциями. В результате структурных преобразований записывается
итоговая передаточная функция объекта и его исследование осуще-
ствляется в операторной или частотной областях. Изучение же характе-
ристик объекта во времени предполагает обратное интегральное преоб-
разование Лапласа.
5.1. Модель ЭО в пространстве переменных
состояний
В основе большинства методов современной теории управления
используются математические модели электромеханических объектов в
функции времени всех составных элементов электромеханического
объекта. При этом совокупность переменных, полностью характеризу-
ющих поведение элементов объекта управления, определяет его
пространство состояний (ПС).
Пусть г-порядок электромеханического объекта, равный количе-
ству его динамических элементов, обладающих физическим свойством
накапливать электрическую, электромагнитную, механическую энергию
и другие виды энергии, тогда перемещение объекта во времени характе-
ризуется траекторией движения ' -мерного вектора переменных состо-
яния в пространстве А’ . Таким образом, в качестве вектора состояния
можно принимать выходные сигналы динамических элементов. В каче-
стве примеров таких переменных, характеризующих состояние ряда
электротехнических и электромеханических элементов, можно рассмат-
ривать:
- угол поворота ! вала электродвигателя или механизма, связан-
ного с угловой скоростью "’(л соотношениями
t/Ц) = | г)(/г, (l.l)
- ток '<••*>, протекающий через индуктивность /. в электрической
цепи и определяющий падение напряжение i:)
176
(1.2)
L dt I
- напряжение 1!> на конденсаторе ( , связанное с током , (t) через
конденсатор
ЦЙ) (Гк/(л.5 '/! ,П_ ’ (1.3)
( •' dt С v 7
Многие элементы электромеханических объектов не являются
идеальными интеграторами и должны рассматриваться с учетом их
диссипативных свойств.
Примерами таких элементов являются:
- электрическая цепь с индуктивностью / и активным сопротивле-
нием Л’:
I <7i-А’ю)-( </) - /Д'’1 -. (1.4)
На основе данного уравнения записывается уравнение в форме
Коши:
t/z(7) R \
—/(/)+ J (/), (1.5)
(И /. /.
где 4/)- ток в электрической цепи, ' Й>- напряжение источника
питания;
- механическая цепь с массой и механическим сопротивлением 5:
dl (/) Z1 Z4
/(/)-5 J (/) + /» . (1.6)
dt
В форме Коши уравнение (1.6) принимает вид:
</J'(7) л .. 1 .
J (/)♦-/(/>, (1.7)
dt т /и
где - (71- скорость движения массы, /(•')- вынуждающая сила переме-
щения.
Для распространенного электромеханического объекта - электро-
двигателя постоянного тока с фиксированным магнитным потоком в
статоре и общепринятыми допущениями, математическая модель может
быть сформирована на основании следующих уравнений:
- уравнения схемы замещения электрической цепи с напряжением
I источника питания постоянного тока, э.д.с. t ,<7> электродвигателя,
активным сопротивлением R , индуктивностью Д. и током <й) в цепи
якоря двигателя
U = ?,(/) + /?Дя (/) + /.„
di^it)
dt ’
(1-8)
177
- уравнения электромеханического равновесия в двигательном
режиме с электромагнитным моментом U) двигателя, частотой
вращения М/> вала двигателя, статическим моментом V. (/) и динами-
ческим моментом нагрузки, приведенным к валу двигателя,
,, ., . dcAt)
\1 .(/)- V/. (/))./ , ; (1.9)
(It
- уравнения электромагнитного момента И (О с конструктивным
коэффициентом А двигателя
Л/,(/) = А.Д„(/); (1.10)
- уравнения статического момента Н. (/), которое, например,
линейным образом зависит от частоты вращения „4/1 и коэффициента /?
механического сопротивления
Л/((/) = М/); (1.11)
- уравнения э.д.с. 1’ > двигателя с конструктивным коэффициентом
к.
еД/) = МХ/). (1.12)
Рассматривая совместно уравнения (1.8) - (1.12), можно записать
систему уравнений в форме Коши:
е/ф(/) /?я . ( Ау ,
= - lud)- М
dt кя кя
d(t)(t) A.. . b
= /,,(/) вэ(1)
dt J,
(1-13)
/.
Для наглядного представления взаимосвязей элементов электродви-
гателя уравнения (1.13) можно представить в виде структурной схемы
(рис. 1.1).
Рисунок 5.1: Вариант структурной схемы электродвигателя постоянного тока в
пространстве переменных тока якоря и скорости вала
178
Принимая обозначения: ,
'Я
I h I
— , ~~г система уравнений
* U ! * I»
(1.13) принимает вид:
dt I'm
d(’j(t) Л„
~dT] Tt
В результате динамическое движение электродвигателя в
пространстве переменных .|/|, записывается векторно-матричным
дифференциальным уравнением вида:
лЦ) 5 (1-15)
хДО а11 Л12 />| 1
где й') = Х2(г) , Л((/)= /;,,(/), луП) = 1 = а2 а,: 9 0 ’ П" ~ А ’
Включая в пространство переменных состояния модели электро-
двигателя угол </(/ > поворота вала, можно включить дифференциальное
da(t)
уравнение . -<'>(/). Тогда, система уравнении (1.13) записывается
(ft
следующим образом:
di„(t)
dt
-R>! + 1 t'
(1-16)
d <>)( ! I
dt
- -^-/.,(7)-----
J . J .
Аналогичным образом, как и в предыдущем случае, взаимосвязь
элементов электродвигателя для системы уравнений (1.16) можно отра-
зить в виде структурной схемы (рис. 1.2).
Матрично-векторная запись системы уравнений (1.16) принимает
вид:
</ф(/)’ dt dojjl) dt da(t) - 1 d, 0 i 1 0 0 0 m{t) tz(/) + A. 0 (1 I (1-17)
dt
179
Рисунок 5.2: Вариант структурной схемы электродвигателя постоянного тока в
пространстве переменных тока якоря, скорости и положения вала.
В этом случае вектор -U/) состояния и матрицы параметров элек-
тродвигателя для уравнения вида (1.15) записываются следующим
образом:
- вектор состояния U7) -
- матрицы параметров
л. (t) = «(/);
= 0. а
= 0
1 к,
Г ’ !
к и 1
=0, = Т
а
В некоторых практических задачах исследования систем регулиро-
вания с электродвигателем постоянного тока используется не система из
трех уравнений первого порядка вида (1.16), а одно дифференциальное
уравнение третьего порядка относительно положения вала:
b Ru .. hR., к.к.. к,.
»(/)-(- ')«(/) + ( )«(/)- I. (] Ш
7; У. / / , 7 / ’ и’В * 10;
где количество точек над символом < i ’ । означает порядок производной.
На основе этого уравнения можно записать математическую модель
в пространстве состояний. Введем вспомогательные переменные:
v,U) «(/), «(/) \ (/) щп л.(О. Тогда уравнение (1.18)
третьего порядка в пространстве новых переменных v,<7>? л<7), т.(7)
записывается следующей системой уравнений в форме Коши:
л, (Z) = л 17),
vjn = .v-j7), (1.19)
180
Х,(/> =
bR„ к t к
. b
I = (I ( I ) = (I
’ -л. А/
A
можно запи-
Обозначая 1 , .
J <L>1
J,L
сать векторно-матричное дифференциальное уравнение в канонической
форме: £,(/) .v,(r) Принимаем следув 0 1 = 0 0 0 а, эщие обозв "л (/)’ 0 Tv,(O' 1 + в2 Л<Й) гачения: 0 1 0 0 0 и 0 ’ (1-20)
х(/) = Л <71 5 .1- х,(7) 0 0 1 0 — а, -а-. 0 (1-21)
В результате уравнение (1.20) записывается в векторно-матричной
форме:
.<(/)=.!л(/)+/?С. (1.22)
Следовательно, при определенных допущениях уравнения (1.15) и
(1.22) являются математическими моделями электродвигателя постоян-
ного тока, которые можно использовать при решении задач построения
автоматизированных систем управления технологическим оборудова-
нием с исполнительными электроприводами постоянного тока.
5.2. Модели взаимосвязанных ЭО в пространстве
состояний
Опыт эксплуатации технологического оборудования с многокоорди-
натными исполнительными электроприводами позволяет заключить, что
необходимо учитывать взаимные связи между отдельными степенями
подвижности многих промышленных механизмов: роботы различного
назначения, манипуляторы, металлообрабатывающие станки с
числовым программным управлением, транспортные механизмы и т.д.
Такие электромеханические объекты целесообразно рассматривать как
многозвенные конструкции с динамически связанными движениями
отдельных механических звеньев. Степень взаимного влияния
отдельных звеньев друг на друга существенно зависит от структуры
механики оборудования и существующих дефектов механических
цепей, проявляющихся в виде неточностей при сборке, неизбежных
люфтов, нелинейностей, зон нечувствительности и т.д. При создании
особо точного оборудования необходимо принимать определенные меры
181
для снижения уровня взаимодействия между отдельными степенями
подвижности технологического оборудования. В ряде случаев в систему
управления электромеханическим объектом вводятся перекрестные
компенсационные связи или используются алгоритмы адаптивного и
робастного управления, позволяющие решить задачу создания незави-
симых степеней подвижности электромеханической конструкции.
В качестве примера для формирования модели в пространстве
состояний рассмотрим двухкоординатный электропривод постоянного
тока с перекрестными связями в механических цепях (рис. 2.1).
Рисунок 5.3: Структурная схема двухкоординатного электропривода с
перекрестными связями в механических цепях
Линейные уравнения этого электромеханического объекта для
динамического режима в форме Коши имеют вид:
'и (')- J 1а1(0+*>(0),
182
L,(0 -----,A. ,rz,(/) + A, j- (7)i
<ц(/) = — (A,, /.,.,(/)A", ('f.(i)-k' , fz,(/))5
о (i) (A,, i,17 )- b.oAt) - A c) \ t)- к (/ (/)),
('z|(/) = A /'>(/),
«,(/) = А ,.рл(/)?
где u>, й), й»й), <> i7), с/й), (/ <и - соответственно, токи, угловые
скорости вращения электродвигателей и положения степеней подвиж-
ности механизма; / ,L , ..R. Л - индуктивности и активные сопротив-
ления схем замещения электродвигателей; J .J - динамические
моменты инерции и коэффициенты механического сопротивления; А ,
А' , А , ,А - коэффициенты, характеризующие взаимные связи по
скорости вращения электродвигателей и положению соответствующих
степеней подвижности механизма; у. , Z - коэффициенты передачи
редукторов; ’’ й) и у .й) - входные задающие воздействия по поло-
жению координат подвижности механизма.
Систему уравнений (2.1) запишем в матричной форме:
R,., А| 0 0 |0 0 * 7 0 0 J 0 Z .А.,
w (/) м (?) г\ (О гл <7) А’„ У о А, 'ЛЧ| 0 О (.')' w 11) : ) ГЛ(/) • 1 0 0 0 0 II 0 0 А,. 0 0 J г (/> г (' 11
о,(/) 0 0 и к 7. 0 Г,, 7. /.у. С- 7 /.„ 0 а,(/1 ! 0
0 О 0 0 Аг. 0
(2.2)
Данное уравнение представляется в компактном виде:
А'Й) . 1л(/) +tfi'.(t), (2.3)
где вектор задающих воздействий v й)~|_г ,(/). г (/)| ; [ - символ
транспонирования; I - разреженная блочная матрица параметров с
наличием нулевых компонент.
183
1 = &Я\ ^Е1 А.,,/ ^Я\ ^Я1 А 0 0 Ар1 0 0 0 1 1 0 -i 1 0 1 0 Li _£L1 ./ 1 ./, ) 0 . (2.4)
0 0 0 А"' к' 0 Л J 0 0 0 Матрицу 1 параметро J ^я? _ ^12 ”/ 12 А\12 0 в можно записать ’ 4, 42' Д. 1 г, к ,А\., t'-- 1/ - > — Я2 ^Я2 0 J2 к\, 0 в блочной форме: (2-5)
где - соответствующие 3-х мерные матрицы, выде-
ленные штрих-пунктирными линиями в матрице I.
Матрица В параметров задающих воздействий имеет вид:
А.. 0 0 0 0 0
0 кУ2 (2-6)
L>i2
0 0
0 0
На этапе предварительной оценки свободного движения двухкоор-
динатного электропривода (при равенстве нулю задающих воздействий
г (М) можно использовать решение характеристического уравнения
вида:
/?(Я) = |х/
(2.7)
184
В результате подстановки элементов матрицы параметров из (2.4) в
(2.7), характеристическое уравнение взаимосвязанного двухкоординат-
ного электропривода записывается на основе следующей матрицы:
All 0 0 0
^Я1
АМ1 ь л + — о 1 °
А Л ./ ।
pU) = 0 -к: Л 0 0 0
л + -^ 0 0 0 /-Я2 () _ А М2 7, 7, 7, 0 000 А1?
. ь. 4 + — 7, 0 2 (2-8)
Решение уравнения (2.8) позволяет получить собственные числа
матрицы 1, распределение которых на комплексной плоскости опреде-
ляет свойства свободного движения взаимосвязанного двухкоординат-
ного электропривода.
Другим примером взаимосвязанных электромеханических объектов
является многодвигательный электропривод поточных линий, обеспечи-
вающий перемещение ленточных материалов (производство бумаги,
полимеров, кабелей и т.д.) с заданным натяжением на определенных
участках движения.
Рассмотрим трех двигательный электропривод перемещения
ленточного полимерного материала (рис. 2.2).
На схеме приняты следующие обозначения: ! (' j, I <7>,
линейные скорости движения материала, определяемые угловыми
скоростями <у(г15 ем:/), гл(п вращения валов исполнительных электро-
двигателей 7, л' , ,/ ; .7/Л, ,/// - датчики натяжения полимерного
материала; ' 1' ', v '1 - величина натяжения полимерного материала,
определяющая его деформацию на участке между валами исполни-
тельных электродвигателей.
185
Рисунок 5.4: Кинематическая схема трехдвигателъного электропривода
перемещения ленточного материала
Стабилизация линейных скоростей '.(/>, I движения мате-
риала на входе и выходе зон деформации обеспечивается электроприво-
дами постоянного тока. Передаточная функция, описывающая функцию
натяжения материала или механическую взаимосвязь исполнительных
двигателей электроприводов через обрабатываемый материал, имеет вид
апериодического звена первого порядка:
где 1 </й, I (/И - линейные скорости движения материала, обуслов-
ленные угловыми скоростями вращения ведущего и ведомого электро-
двигателей (для данного количества двигателей / I.-.3) или линейные
скорости движения материала на выходе и входе зоны деформации; А' ,
Г, - соответственно, коэффициент передачи и постоянная времени,
обусловленные физико-химическими свойствами ленточного материала
в зоне деформации.
Структурная схема каждого электропривода, входящего во взаимо-
связанную электромеханическую систему, представляется следующим
образом (рис. 2.3).
186
Рисунок 5.5: Структурная схема исполнительного электропривода постоянного
тока в системе стабилизации натяжения ленточного материала
Принятые обозначения: г <7 i- величина задания скорости вращения
электропривода; у. (Л, .,</> - токи якоря и нагрузки электродвигателя;
f».i.' ', угловые скорости вращения ведущего / и ведомого । • D
электродвигателей по направлению движения материала; К.., -
коэффициенты передачи интегральной и пропорциональной состав-
ляющих ПИ-регулятора скорости; интегральная составляющая
ПИ-регулятора скорости; < - коэффициент передачи и некомпенси-
рованная постоянная времени замкнутого контура тока; А’ - сопротив-
ление якорной цепи двигателя; - конструктивная постоянная электро-
двигателя; Л - электромеханическая постоянная времени электродвига-
теля; Я, - радиус приведения круговой скорости вращения вала электро-
двигателя к линейной скорости перемещения материала; К. , Л - коэф-
фициент передачи и постоянная времени упругого (упруго-пластичного)
натяжения; А' - коэффициент передачи обратной связи по скорости.
Используя схему (рис. 2.3) и уравнение (2.9) для однодвигательного
электропривода, можно построить структурную схему, например, трех-
двигательного электропривода с взаимной связью электроприводов
через обрабатываемый материал (рис. 2.4).
Влияние статического момента И,(/) нагрузки, создаваемого
расходным барабаном (на котором располагается обрабатываемый поли-
мерный материал) на первый электропривод, можно учесть путем
введения в структурную схему и, соответственно, в математическую
модель многосвязного электропривода тока <Г|, пропорционального
этому моменту нагрузки. Кроме того, с целью постоянного натяжения
полимерного материала между расходным барабаном и валом первого
исполнительного двигателя, значение угловой частоты сл, (/) вращения
187
расходного барабана должно быть меньше, чем частота вращения вала
первого исполнительного двигателя.
Рисунок 5.6: Структурная схема трехдвигателъного электропривода в системе
стабилизации натяжения ленточного материала
Без потери признаков общего подхода к алгоритму формирования
уравнений состояния такого типа объектов, рассмотрим математическую
модель двухдвигательного электропривода с двумя участками натяжения
полимерного материала. При формировании уравнений состояния будем
выделять обобщенные координаты математической модели электропри-
вода, исключая алгебраические уравнения связи между переменными.
Для этого запишем систему уравнений в операторной форме по струк-
турной схеме (рис. 2.4).
188
\n.( I />) ——(г ,(/?) A /•>(/>))
P
1 ЯI (P) A ' , <Xi * P । + A’;, iJ A , P)>,
/ p +1 ’
, Л», ,, , . x R4. x. ,
/ц(р) -— (/;|(/>)-—Л,(/2)-/. (/;.|- ’ .\.(/Ц)
< Г,. p с с,
•\ (/’) Л':''(2.10)
Л',
\и Д р)- ' " < 1 < />)- К -('>,[/>))
Р
i»Ap}~----——(Ап,,-(/>)+ А.. ,» ,(/И— А К
1 " ’
ч . х R‘C к- хх
(оДр) = (/„ •( />)- Л Др))
< Т.,Ур с, ’
Л (/*)- Ц(Л|(/>))
Л:Р + |
Для построения системы стабилизации натяжением полимерного
материала целесообразно минимизировать возмущения, которые влияют
на первый электропривод (т.к. эти возмущения находятся вне замкнутых
контуров по скорости движения и натяжению материала). При опреде-
ленной конструкции расходного барабана можно выполнить следующие
условия: стационарность статического момента V, (7) д А/, 2 ctwo и, соот-
ветственно, гД1\ - i, - const а также стационарность угловой частоты
бэдптгл ico/oi вращения. Таким образом, структурную схему первого
электропривода можно представить в виде следующей структурной
схеме (рис. 2.5).
Тогда, в уравнениях
\ (/<) (сЦ р)-а>. (/>))
Т^р 1
f,)'(Р(/?)"Т"Л|(р} (р}~ v'(р}} (2.11)
системы (2.9) выделяются постоянные составляющие (с/, тсо/м/,
/, . )5 значения которых являются возмущениями для первого элек-
тропривода:
Лл ц) А ' <7.9 ( /П-Л9, )
I
^-Щр)+—^Ар) »;). (2.12)
189
Рисунок 5.1: Структурная схема первого электропривода с постоянными
значениями тока нагрузки и частоты вращения расходного барабана
В итоге, система уравнений (2.10) принимает вид:
V/, (р) = ——,(/?)— А (р))
Р
/)., (р) ———(Д//.,, I р) + К о. г , (р I - А А И1й» (р))
/. р + 1 ’
<Ц(/>) = ШР> — Л',(р) + — Л?(р) if.)
СТч\Р с Г1
\(р) =—(с>(р\ С>.)
Л.р+1
А' ч „
\и.. (р) ——(г , (/>)-А .с>.(рд
р - - - ’
1цЛрС (Ди.,.(р) + A,,,i ,(/>)- А К р)),
(2-13)
с> (/’I (/.. (/>) А .1/ГЦ
к. Z
\ (р) = - — (с> < р) ГЦ( р))
л...р-l
С учетом приведенных рассуждений, на основании системы урав-
нений (2.13), записывается математическая модель двухдвигательного
электропривода в пространстве состояний. Первоначально эту модель
сформируем в операторной форме.
Введем в операторном пространстве вектор переменных << р> состо-
яния электропривода:
190
где ] - символ транспонирования; компоненты вектора состояний:
х,(р) = Д«И|(р)5 х2(р) = 1Я1(р)^ х,(р) = <ц(р), х4(р) = #((/?), х5(р) = ДиЛ2(Р),
хй(р) = 1Я2( р), X (р) = СЛ (р) 5 Xg(р) = N2(р) .
С учетом данных обозначений запишем систему (2.13) уравнений в
пространстве переменных состояния:
х2(р) ------—(х,(р)+Кя Г р)- .. К :(/Й)
, ч Я,., Z ч \
Д’,(р) =-i—(х2(р) — л,(р) I —л;(р) /, )
<Л|/> <i G
-v </й = ’ LV.I р) (!). )
Л, р -I
х5(р) = -^ (тл2(/й К .х. (/й), (2.15)
х6(р) =--——(л..(/й +А',,.г J/И-А’ .А',,..г (р))
R„ R,r
У-(/Й = 7 (.х,Д/Й — гДр|)
сЛ,.-р С.
К..Л„
д-Д/й = ггл/й лД/й)
Т, р । I
Приведенная система уравнений позволяет записать математиче-
скую модель рассматриваемого электропривода в виде матричной пере-
даточной функции.
Для записи математической модели электропривода во временной
области необходимо символ «/ :» заменить на символ « . ». Следова-
<h
тельно, вектор состояния электропривода на основании (2.14) прини-
мает вид:
х(t) = [.v, (t). .v. (/), А-; (/).л, ( I). д .. (/). д„ (I). д-, (t). д; (/)]г, (2.16)
где Х|(О=ДИ/П(О, = ^(0 = <Ц(0, M0 = ^i(0, х5(1) = ЛиИ1(1),
V UI =v (/) = vjn = .V,(/).
Система (2.15) уравнений представляется системой дифференци-
альных уравнений в форме Коши:
\ (/) -А,, А л (/> - A i </1.
191
х,(/)= ,г х,(/) — х4(/)3
£Г WI £’| \1,'1
х.(/) =
*' Д|хД/)—^-i
^’1 Лп
. , v к. я,
х,(/)- -х4(/)~
Л, Л г,
К,.2К , л-(/> I K;,-v ..(/)
(2.17)
л\(/) =
х,,(7) = — л-5(/) - —л-„(/) -
— л-7(/) •
г ,(/)
/?W1 _ R^Rt,
л<7) = у .¥,(/) — . л;(/)
/А K*2RB
/ = —-r—-
г,
, х К. Я»-, /v 1
Х,(Г)--“-Х,(0-— £,(/)
Введем в рассмотрение
вектор задающих воздействии
v..(/> и вектор стационарных возмущающих воздеи-
ствий \1 - if.-f)., . Представим систему (2.17) уравнений в векторно-
матричной форме:
,4л(/)+ + В.М (2.18)
где матрицы 1, В и />’ параметров двухдвигательного электропри-
вода определяются следующим образом: Г 0 0 -Кн 0 0 о 0 0
А’.. 1 Л’ К,,,Л’ 0 0 0 0 0
Г1П Т!Л
0 0 11 Л/1 А 0 0 0 Я,, Л
£i Лп £ । 7^i/i
0 Rh, о м К' Л. 1 л? 0 0 0 0
. I - 0 0 0 0 0 0 -к,гя 0 9
о О О о 1 о
Л:
0 0 0 0 0 сТ}!: 0 r„2rB2 с ;
0 0 л..; 0 0 0 к,я.г TV: 1
(2.19)
192
К/Л 0 0 0
К.. К 0 0
• 1 ’ 0
/?„
0
0 0
0 0 К ,/с
Я = /г 0 -—
1 0 К,г 5 д,
К...К 0 0
0
г„. 0 0
0 0 0 0
0 0 0 0
Матрицы параметров модели многодвигательного электропривода
являются диагональными с большим количеством нулевых состав-
ляющих и прежде чем исследовать его динамические свойства целесо-
образно использовать методы декомпозиции, позволяющие понизить
порядок векторно-матричного уравнения.
5.3. Линеаризация нелинейных моделей ЭО
Динамическое движение многих нелинейных электромеханических
элементов и объектов может быть достаточно адекватно представлено
линейными или линеаризованными моделями. В качестве примера
рассмотрим трехзвенный механизм в пространстве угловых скоростей
<у<7), глй) вращения исполнительных электродвигателей его
звеньев. Угловое ускорение каждого кинематического звена в процессе
его перемещения в пространстве нелинейным образом зависит от
угловых скоростей двух других звеньев механизма. При использовании
электродвигателей постоянного тока, управляемых полупроводни-
ковыми усилителями, и определенных допущениях движение такого
электромеханического объекта можно представить следующими уравне-
ниями:
(!) Ц) = к II /I /1/ГЛ Ц )(> (I )
= к.и \ I />-(?,,(/ кЛР ), (3.1)
w(7) I /I —/>.гц(/)«.(/)?
где ' , У, * - коэффициенты, значение которых определяется динами-
ческими моментами инерции двигателя и нагрузки, конструктивными
параметрами электродвигателя; ",(/|, //.(/), /Н/i - управляющие воздей-
ствия (электромагнитный момент или ток электродвигателя); >’, /', -
193
коэффициенты, определяющие влияние угловых скоростей двух звеньев
механизма на третье звено.
В данных уравнениях вторые слагаемые являются нелинейными
(произведение переменных c/ri, гл(п, глц) состояния) и для исследо-
вания электротехнического объекта инженерными методами целесооб-
разно их линеаризовать и иметь линейную модель, аппроксимирующую
исходную систему (3.1) с определенной точностью. Процедуру линеари-
зации рассмотрим для электропривода с регулятором, стабилизиру-
ющим угловые скорости гл(о, глц) вращения соответствующих
исполнительных электродвигателей.
Систему уравнений (3.1) представим в векторно-матричной форме.
Запишем вектор переменных ЙО состояния и вектор г'й ) управляющих
воздействий в виде:
V, (/) <ц(0 и {if
Ш) = v,(/) = ГЛ (1 ) , «(0= и XI) (3.2)
Х3(О. <У.(П nil)
Обозначим правую часть уравнений (3.1) вектор-функцией / (л.и./):
/. ( &Л . (О .U..I)
U'.l )
Ад (/| [
к.и. 11 - but) {!)<'> I/1
к.и, । /| — (/)&*,(/) I
f(.wu.i) =
(3.3)
Таким образом, систему уравнений (3.1) можно записать векторно-
матричным уравнением вида:
л(0 = l(x.u.l). (3.4)
Предполагается, что нелинейную функцию /Млм), которая
является непрерывной в рабочей области изменения всех переменных
состояния и управляющих воздействий, можно разложить в ряд
Тейлора.
Линеаризуем уравнение (3.4) при условии малости приращений
Дт(П, lv(O, относительно положения равновесия > (|, где
- вектор переменных состояния положения равновесия при фиксиро-
ванном управлении щ. и малых на интервале , гДе _
момент времени, определяющий начальное ,, и конечное состояния
электромеханического объекта.
На основании данных рассуждений можно записать следующее
линеаризованное уравнение:
., v cKx.u.l) А . df(x,ud)
Лл(/) = ----Лг(/) * ----Л//(/)
cv ди
(3-5)
194
cf(X.ll.t) cf(X.U.t)
где частные производные и вычисляются в точке
cv си
г. л равновесного с сх юстояния: C/^x.u.i) с/\(х,и.() d/t(x.u.t) (3.6)
civ, C.V, СЛ\ ('/.i.X.U.I ) ('/,(.V.»./) с /.(x.u.l)
ЙГ] C.V, c?.v, <7;(cfy(x,u,t) cf.(x,u.t)
cf(x,llj) си C.V, C.V, C.V, (7|(.V.»./) (f\(X,U.l) ('/^X.U.t)
Aj A, cv\ с/, (-V.и. 1) c!.(x. u.t} ('!.{x. и.i)
cu{ cu2 cus cf\(x,u,t) cj\(x.u.t) cf.ix.u.t )
A, du, etc
Матрицы (3.6), которые формируются в результате вычисления
частных производных, называются матрицами Якоби.
Для рассматриваемого электромеханического объекта матрицы (3.6)
принимают значения:
с/{x.u.i) _ сх 0 ° , (3.7)
cf(x.u.t) си -byu,(t) A, 0 0 0 к. 0 0 0 A; 0
В результате линеаризованное уравнение (3.5) принимает вид:
0 -btMAt) -/yu.(t)' Amp) Д-, о 0
Av(/) = -b.c>j,(f) 0 Am,(/) + 0 k. 0 Ли. (/) •(3.8)
-/>,(!). (l ) -b./o^t) 0 рЧл I AmJ/) 0 0 A; A«,(/)
Данная математическая модель может быть использована не только
для исследования процессов в электромеханическом объекте, но и для
синтеза регуляторов автоматизированной системы управления манипу-
ляторами с исполнительными электроприводами постоянного тока.
Рассмотрим другой нелинейный электромеханический объект -
асинхронный трехфазный электродвигатель переменного тока, который
195
широко используется в качестве исполнительного двигателя на нижнем
уровне автоматизированных систем. Динамическое вращение ротора
данного двигателя для активной механической нагрузки может быть
записано нелинейным уравнением:
(/). (3.9)
Электромагнитный момент зависит от напряжения
питания статора двигателя, угловой скорости МО, и характеризуется
зависимостью ,(<у. (.) (кривые 1-3). Момент механического сопротив-
ления И, (О зависит от скорости МО и определяется зависимостью
V о?1 (кривые 4, 5). Приведенный к валу двигателя динамический
момент -1 инерции механической нагрузки не изменяется и равен
постоянному значению.
Рисунок 5.8: Графическая линеаризация нелинейной характеристики
асинхронного двигателя
В точке « I» на кривой 2 имеем установившиеся значения
о ) М , , при значениях М/ t,» о, и <7 -1 р- Г 5 где /. -
начальный момент времени рассмотрения динамического процесса в
точке « I», в которой выполняется режим устойчивого равновесия.
Учитывая значительную нелинейность характеристик '/.(О и И
осуществляем их линеаризацию в относительно небольшом диапазоне
изменения угловой скорости \М / >.
196
Функциональные зависимости электромагнитного момента '/,(/) и
момента Ц </) сопротивления в окрестности точки « I» равновесного
состояния можно представить в виде ряда Тейлора:
Л/,(/) = Л/м- । \ С(О(1) ДГ'(/) А( >(!)+ - ~> 1 Г • 1 (г2Л/?(/)) [ cco\t) M>:(t ДГ9 (/)+ -• (3.10) )+•••
' М/д/);
п. м д/ 9 (3.11)
(/)' 1 ( <' XI. (1) |
U, .(/) V, , - ч с (0(1) ДМ/) — 11' fro (t ) J Ar-o (/) + ..., (3 12)
.tfr< Д Л/Д/= /,)),,,
Подставим два первых слагаемых ряда (рассматривается только
линейная часть нелинейных характеристик) в исходное уравнение (3.9),
записанное в отклонениях Н/)и М (/> с учетом равенства 'Л, = ’/ :
. JAM/) (AW.(z)j сМ ,(i) , . , Л ( ЛИ.,(/))
.7 , + ДМ/)“
J/ । ч сМО Д, ( c(o(t) ),,, । ( сМО
В относительных единицах по отношению к значениям М и '
(/). (3.14)
данное уравнение имеет вид:
JAM/)
7 о>л ! рЛ/( (/) ' i сЛ/,(/) j ДМ/) Lr,pA/,(/)j AL’(/)
dt у бМ/) J'-j У бМ/) Л-j <оА (о, \ oU(t) J<v, L't
(3-15)
Для записи данного дифференциального уравнения в общепри-
нятой форме введем дополнительные переменные: относительные пере-
менные --< > приращений частоты вращения и напряжения «(/) питания
двигателя:
Электромеханический объект обладает постоянной i времени и
коэффициентом передачи, которые из уравнения (3.15) определяются
следующими выражениями:
197
J .
cMc(t) \ J cM ,(/)
ca)(l) ,.i, ( Г toll)
Ut I cM ДО
л>Д cU(t)
f cM( (/) ' f с?Л/ ДО
. ГГУ(/) L, С«У(/)
(3.17)
В итоге дифференциальное уравнение (3.15) записывается в
компактной форме:
4/Q(Z)
7, ,f Hh/)-А (3.18)
В операторной форме уравнение (3.18) записывается следующим
выражением:
///',£>(/?) <2(р) = А ,п(/Ц (3.19)
На основании данного уравнения передаточная функция асин-
хронного двигателя по скорости имеет вид:
А,
(3.20)
Передаточная функция асинхронного двигателя по углу </( р > пово-
рота вала будет определяться уравнением:
а(Р}
(3-21)
Следует отметить, что в точке «К» с зависимостью момента И <<л
нагрузки (кривая 5) будет наблюдаться неустойчивый режим работы
электродвигателя.
Рассмотренный алгоритм получения линеаризованных математиче-
ских моделей нелинейных электромеханических объектов на основе
графического представления зависимостей имеет общий характер и
может быть использован в случае аналитического описания характери-
стик.
5.4. Модели ЭО с упругими механическими связями
Синтез регуляторов многих электромеханических систем предпола-
гает предварительный анализ и моделирование таких особенностей
исполнительного привода, как влияние упругих связей механической
части оборудования. Механическая система обычно характеризуется
спектром резонансных частот, который определяется не только много-
массовостью конструкции, приводящейся в действие от вала электро-
двигателя, но и импульсным характером передачи энергии от источника
питания. Примерами таких исполнительных приводов могут служить
электроприводы роботов и манипуляторов, грузоподъемных меха-
198
низмов, механообрабатывающих центров с лазерной и плазменной обра-
боткой материалов, систем высокоточного слежения.
Рассмотрим один из вариантов механической части электропривода
с упругими связями между редуктором и исполнительным элементом
конструкции механизма (рис. 4.1).
Рисунок 5.9: Структурная схема механической части электропривода с упругими
связями
Электродвигатель с динамическим моментом инерции 7 ротора и
электромагнитным моментом 17 н) приводит в действие механическую
нагрузку с динамическим моментом инерции Л. и статическим
моментом И <' > сопротивления. Угловая частота вращения ротора
двигателя передается на выходной вал редуктора с коэффициентом у
его передачи. Выходной вал редуктора вращается с частотой ("О и
приводит в действие нагрузку через упругую механическую связь с
коэффициентом < упругости и коэффициентом демпфирования.
Перемещение исполнительного элемента механической нагрузки можно
представить в пространстве углового ' J'1 положения и угловой
частоты вращения.
Для анализа влияния параметров упругих элементов на динамиче-
ские свойства двухмассовой электромеханической системы, используя
структурную схему (рис. 4.1), составим следующие уравнения в
пространстве состояния:
(() = —[А/!(Г ) - С t ((t) (fj,, (t)) - c, icz, (i) - </„ (t))],
(4-1)
«>н(/) = —(i)tl(I)) + <•, (a (/)-«„(/))- M, (/)].
' H
199
a(t) гуР) ,
где «|(0 = -т—, сц(0 = -7—, М|(/) = А>Л/>(/), J, = А,. ./..
лл
Очевидно, условием отсутствия колебательных движений в элек-
троприводе с упругой связью является равенство скоростей движения
первой cjJ/i и второй <’ Р) механических масс, т.е.
\о»Р) = (('_?,(/) <<л. if )) = О или <-.'Р) = ('/,(/). (4.2)
В этом случае можно записать уравнения, которые гарантируют
отсутствии колебательных движений в электроприводе:
d(<D.(t\-(/)) 1 ... .. . . . . .. .. . .
————----------~ — [ 4/ ,(/)-<• .(«>]</> — гл, p ))-<•, (a (/) - a H (/)) 1 -
dt
, (4-3)
[c ,(л?р)-бэ„р)) + с. (cr,<Z) — rz.,(z)> — Л/, (/)] 0.
Несложные преобразования данных уравнений позволяют записать
равенство, выполнение которого для постоянных и априорно известных
параметров может служить основой алгоритма компенсации возму-
щений в двухмассовой механической системе электропривода:
J.M (И j,.\l р)
с, р/р» »„(/)) = —— -----——. (4.4)
Во многих случаях при синтезе регуляторов электромеханических
систем необходимо обеспечить требуемые (с символом ) значения
углового положения </., (/) и частоты <о;. (/) вращения исполнительного
элемента механической нагрузки, которые удовлетворяют условиям
движения электропривода без упругих колебаний. Обозначая в качестве
необходимых заданий по положению 0), частоте вращения щН) и
моменту -V, (/) можно определить задающие воздействия гр) Р>,
г,р) с.> iti и , р ) I/ р) для следящих электромеханических систем в
режиме позиционирования, с произвольной постоянной скоростью или
постоянным ускорением и т.д. Преобразуя равенства (4.1) и (4.3), можно
записать уравнения:
v (/) = л.‘(0 = «/(/)+ 1 ‘ + (/)],
с. dt
Г -<<(/), (4.5)
, . ,... . ,, . . , , da>,,’(t)
г... (?> = Л/ Р1=И (/)(./ ./,,)—----.
dt
Данные уравнения описывают математическую модель отдельного
задающего устройства или программного блока цифровой системы
200
управления электроприводом, формирующие согласованные задающие
воздействия г,(О (И, г п) (•> (7), »’,.(/) А/ (7).
Таким образом, для полного исключения колебаний нагрузки,
вызванных упругими связями в механической части электропривода,
кроме коэффициента <• упругости и динамического момента 7,
инерции ротора двигателя, необходимо идентифицировать динамиче-
ский момент 7. инерции нагрузки и статический момент V. (/) сопро-
тивления.
Рассматривая более внимательно особенности работы двух-
массовой механической системы с упругими связями, целесообразно
представить глобальное движение такого объекта в виде суммы
локальных движений: первое движение - движение сосредоточенных
масс в ограниченной области по заданной траектории в пространстве,
второе движение - относительное колебательное перемещение двух
масс в окрестности заданной траектории. Такое представление вклады-
вается в идеологию разделения процессов на быстрые и медленные
движения, протекающие в электромеханических системах. Для матема-
тического описания таких процессов необходимо декомпозировать
исходную систему (4.1) уравнений на две системы уравнений. Для такой
декомпозиции введем следующие дополнительные переменные и пара-
метры:
- переменные и параметры, описывающие относительное движение
масс
I I I
лД) = ЛоЦ) =(7'Э,Й) ay(Z))? дЩ) = = (//Ц> aH(t)) — = — + —; (4.6)
»/ «./ | «./ Г1
- переменные и параметры, описывающие движение сосредото-
ченных масс
. _ J,m(i) JAt) A.aAt) J ..a,At)
xAt) = 1 " " .v(/i= 1 ---11 ' J.=A+Jr
J 4 7„ ’ 4 7, 4./, ’ - 1 "
В результате замены переменных исходную систему
нений запишем в виде двух подсистем:
- подсистема относительного движения масс:
I. MAt) MAD
д (0 = —k -v О + с, v. /)] + —!—т—-—
7 J 1 - 7, J„
xAr) = x\t),
- подсистема движения сосредоточенных масс:
л*,(0 = 1 [Л/ (()-Л/, (z)]
л ,
(4-7)
(4.1) урав-
(4-9)
201
Рассматривая подсистему относительного движения масс, можно
записать два варианта уравнений (4.8) в матричной форме:
- первый вариант:
v:(f) 0 c.i 1 V| (t) v-(7) 4- 0 Л/,(/) + 0 ; (4.Ю)
J ./ _ •A •Л,
- второй вариант:
1|(7) r2(/) = 0 c . 1 Cj. Vi(0 A,(/) ‘o' 1 А/, U). (—!— + —! ) (4.И)
— ./ ./. —
Первый вариант записи модели движения механических масс
(уравнение (4.10)) позволяет алгоритмически разделить управляющий
момент формируемый исполнительным двигателем, и возмуща-
ющий момент И О) нагрузки. В том случае, когда имеется достаточно
точная информация о возмущающем моменте И (м нагрузки электро-
привода, то в качестве модели механической подсистемы с упругой
связью используется уравнение вида (4.11).
Для дальнейшего использования уравнений (4.10) и (4.11) в задачах
синтеза регуляторов электромеханических систем можно записать:
- уравнение (4.10) в виде:
x(l) = Ax(t) । • В Л/ДП,
(4-12)
где вектор состояний и матрицы параметров записываются следующим
образом
- уравнение (4.11) в виде:
л(7) = J.v(/) I BM(t),
(4-13)
(4-14)
где вектор состояний и матрицы параметров записываются следующим
образом
г -1 г -I Г 0 I ]
х(О О I
ЦП- . .1 I . , .
в =
о
(4.15)
Уравнения (4.9) подсистемы движения
векторно-матричной форме можно записать:
сосредоточенных масс в
202
(4-16)
.v,(/) О О л\(/) I Mit) Mti)
+ (—!----------!----)
V4(z) I О x4(f) О Л
Данная система уравнений может быть записана одним векторно-
матричным уравнением:
v(z) — Jv(/Wn/(r), (4.17)
где
Таким образом, уравнения (4.12), (4.14) и (4.17) могут служить
достаточно адекватными математическими моделями электромеханиче-
ских объектов с упругими механическими связями, структура которых
имеет вышеприведенный вид (рис. 4.1).
5.5. Нормальная и каноническая формы векторно-
матричных уравнений
Векторно-матричные уравнения электромеханических объектов в
нормальной форме Коши обычно записываются на основе «физики»
электромеханических процессов или в результате преобразования урав-
нения 11 - го порядка, являющегося математической моделью объекта
(путем введения дополнительных переменных).
Общий вид нормальной и канонической форм записи векторно-
матричного дифференциального уравнения Коши, характеризующего
состояние линейных или линеаризованных электромеханических
объектов со стационарными параметрами, записывается следующим
образом:
л(/) Ax(i)+HL (5.1)
где vi/t л, - мерный вектор состояния электромеханического объекта;
I in-in- мерный вектор управляющих воздействий, закон изменения
которых определяется регулятором системы управления; 1 - 11 - мерная
квадратная матрица параметров электромеханического объекта; В -
- матрица параметров управляющих воздействий.
Необходимые измерения, которые обеспечиваются датчиками и
устройствами преобразования сигналов в автоматизированной системе
управления, можно также представить линейным алгебраическим
векторно-матричным уравнением со стационарными параметрами:
г(/) = Сл(/)-/>•(/), (5.2)
где г(/)- - мерный вектор измерения переменных состояния в системе;
( _ гхп . матрица, определяющая включение компонент переменных
состояния системы в состав вектора измерения; /) - 'V'?/ - матрица, опре-
203
деляющая включение компонент управляющих воздействии системы в
состав вектора измерения.
Алгоритм преобразования нормальной формы записи дифференци-
альных уравнений в каноническую форму заключается в следующем.
Рассмотрим свободное движение электромеханического объекта
(при равенстве управляющих воздействий нулю < (О °), которое
описывается однородной линейной системой дифференциальных урав-
нений с постоянными коэффициентами. В этом случае уравнение (5.1)
принимает вид:
-<(/) А(/>. (5.3)
Запишем данное уравнение в виде системы уравнений:
v, (/) = а , ,v, (t) + а, ,д , (г) +.... + aittxn (t).
.............................. (5-4)
а;,, (/) , А', (I) + а,,2 .V, (/) + .... 4- (/).
Известно, что решением дифференциальных уравнений (5.4)
является уравнение следующего вида:
л. (И ,с.г , (5.5)
где постоянные коэффициенты интегрирования дифференциальных
уравнений; - - корни характеристического полинома системы (5.4);
/ - 1./;. После подстановки (5.5) в (5.4), с учетом сокращения множителя
; в правой и левой части преобразованных уравнений, получим:
(ан + — + =0’
«,.е, ч (о,, z)e, i ...<«, ,е =0,
" ; (5.6)
tf.igi + + ...-F Щ,.„ -2)gB =0.
В матричной форме данное уравнение записывается:
(5.7)
где G - 1!- мерный вектор постоянных коэффициентов - интегриро-
вания дифференциальных уравнений (5.4); / - единичная 11 - мерная
матрица.
Уравнение (5.7) будет иметь решение в единственном случае - при
равенстве нулю определителя:
б/н — Л а,, ... а|п
</„ ап2 ... 2
В компактной форме это равенство записывается следующим
образом:
204
= /л| = 0. (5.9)
Уравнение (5.9) называется характеристическим полиномом,
решение которого позволяет получить распределение его корней или
собственных значений матрицы 1.
При рассмотрении электромеханических объектов и систем линей-
ными или линеаризованными моделями используется принцип суперпо-
зиции и общее решение уравнений (5.3) или (5.6) представляется
суммой решений скалярных уравнений. Т.е. общее решение системы
(5.3) и (5.6) уравнений записывается как сумма отдельных решений:
= У г(/) = Уол. у (5 до)
Таким образом, изучение распределения корней характеристиче-
ского полинома (5.9) на комплексной плоскости дает возможность опре-
делить характер свободного движения электромеханического объекта.
Нормальная и каноническая формы векторно-матричных урав-
нений связаны друг с другом линейным преобразованием переменных
состояния, которое для уравнений вида (5.3) не изменяет собственные
значения z исходной матрицы I. Это преобразование записывается
следующим уравнением (для различных характеристических чисел
матрицы 1):
= (5.11)
где Л/ - 11 - мерная квадратная матрица преобразования уравнения (5.3)
к каноническом виду; 1 (/) - вектор переменных электромеханического
объекта в преобразованном пространстве состояния. В дальнейшем,
после вычисления матрицы '/ , значения ' <7) определяются уравне-
нием:
-v.U) М. '.<(/). (5.12)
После подстановки (5.11) в уравнение (5.3) запишем:
\/ .<(/) = .1.1/ л;(/)_ (5.13)
При условии существования обратной матрицы Л/ , возможно
выполнение следующего преобразования на основе умножения левой и
правой частей уравнения (5.13) слева на матрицу V :
М 'Л/ Л й) Л/ И/ ! й), (5.14)
где произведение । Л / ’./ i дает единичную матрицу, т.е. i й \1 > /.
В результате преобразования (5.14) записывается дифференци-
альное уравнение в каноническом виде:
д.Й i = Лд.(/)5 (5.15)
где матрица \ ' / 1 / является диагональной матрицей.
205
Характеристический полином данного уравнения равен характери-
стическому полиному исходного уравнения (5.3). Это утверждение дока-
зывается следующим уравнением:
|2/-Л| |.W - М. :.МЛ| |Л7.‘(л/-ДШ |ЛЛ 'Л-/.|-\/J -,-f| \Л1-.l|.(5.16)
Т.е. матрица 1 и матрица \ V !•' имеют один и тот же характе-
ристический полином, который для преобразованных переменных v u i
состояния электромеханического объекта записывается уравнением:
Р-/-А -(). (5.17)
Так как, матрица \ по определению является диагональной
\ = ;/.. /..z, ; 5 следовательно, из (5.17) запишем равенство:
0 0
0 z - 2, 0 = 0 (5.18)
0 0 2-2„
или в развернутом виде
р(Л I = (2 л )(л - 2,= 0. (5.19)
Следует отметить, что характеристические полиномы (5.17) и (5.19)
записываются для свободного движения электромеханического объекта
независимо от количества управляющих воздействий, формируемых
системой управления.
5.6. Моделирование непрерывных ЭО с
использованием переходной матрицы состояния
Прежде чем рассматривать вычислительные алгоритмы для
решения матричных дифференциальных уравнений, с помощью
которых исследуются многомерные процессы в электромеханических
объектах, рассмотрим достаточно простую задачу. Например, опреде-
ление динамического изменения тока МИ в электрической цепи с индук-
тивностью /. и активным сопротивлением R. При определенных допу-
щениях математической моделью в такой электрической цепи является
скалярное дифференциальное уравнение вида:
ММО R . I,. 1Ч
7-- -<!/)+-< «I, (6.1)
(и /. /.
где '' (/ ) - напряжение источника питания.
При отключении источника питания i it) '* в электрической цепи
будет наблюдаться, так называемое, свободное движение тока - его
изменение от некоторого значения (например, установившегося) до
206
нулевого значения. Дифференциальное уравнение такого состояния
электрической цепи принимает следующий вид:
(6-2)
Предполагается, что в начальный момент времени •' значение
тока 1 1 равно определенной величине i \ f = f ' . При этом возможен
частный случай равенства момента времени • 0. Обозначая </ ,
запишем:
<//(/)
—///(/I, (6.3)
at
где размерность коэффициента а равна 1/сек.
Решение такого уравнения осуществляется следующим образом.
Запишем данное уравнение в виде:
I
<///|= a (It. (6.4)
Выполним операцию интегрирования левой части уравнения в
пределах от начального значения Л до конечного значения - А
(при этом полагается, что • ~ 11) и правой части - в пределах от началь-
ного момента 11 времени до конечного момента / Л . В результате
интегрирования запишем
|/|/ = ;V) t-N
In / /| = -at
/.., О
(6.5)
После подстановки пределов интегрирования:
hi /1t\ — In /’, = - a t + 0 или to
= -a t
(6.6)
Последнее уравнение можно записать в виде равенства:
(/ |/ | '
( *•> 7
Окончательно, решение исходного уравнения для
движения тока 0/1 в электрической цепи имеет вид:
/,/: - /„с
(6.7)
свободного
(6.8)
В данном примере процесс изменения тока ! является монотонно
затухающим, т.к. коэффициент </ является вещественным числом с
отрицательным знаком. В общем случае знак С1 может быть не только
207
отрицательным числом. Рассмотрим все возможные варианты значения
коэффициента Д.
Допустим, а - вещественное число, которое может быть равно
нулю, больше или меньше нуля. При этом процессы будут иметь моно-
тонный характер.
1. Значение а 0. Решение дифференциального уравнения: ' .
С точки зрения устойчивости процесс протекает с нулевой скоростью.
2. Значение и >0. Решение дифференциального уравнения:
г/1 и . Происходит возрастание ' по экспоненте из заданного
начального состояния ' Процесс развивается с определенной скоро-
стью на некотором интервале времени или процесс является неустой-
чивым: процесс изменения тока ‘\> >' при стремлении времени t > ‘
3. Значение </- 0 . Решение дифференциального уравнения:
'Д ='.<’ . Происходит уменьшение ' по экспоненте из заданного
начального состояния ’ Процесс развивается с определенной скоро-
стью на некотором интервале времени или процесс является устой-
чивым: процесс изменения тока ' > ° при стремлении времени I —> < .
В электротехнических элементах и объектах существуют и другие
формы процессов, в частности колебательные. Такие процессы вклю-
чают две составляющие - гармоническую составляющую и экспоненци-
альную. В этом случае коэффициент а является комплексным числом,
т.е. " 7 - ip. Решение дифференциального уравнения будет иметь вид:
/Д। -/ . (6.9)
При этом вещественное значение 7 может быть положительным,
отрицательным или равным нулю и определяет скорость изменения экспо-
ненциальной (/„</' ) составляющей тока 0 и в электрической цепи. Мнимая
часть I : //»! определяет осциллирующую (гармоническую) (
< • ‘' cos /> / г / siп /? /) составляющую тока.
Далее, рассмотрим решение системы двух дифференциальных
уравнений, которые описывают поведение электродвигателя постоян-
ного тока (с определенными допущениями) в пространстве переменных
тока ; й), и скорости М /):
R.. . , v к,. ч 1
/.,(М= /м(/М L
I / / ’
'-я '-я
А(1 . , h
/Д/) г/(7). (6.Ю)
«У • }
208
R, _ A. A,. I
Обозначая коэффициенты: . ' , u , — <6.,
.1
запишем однородные уравнения для свободного движения электродви-
гателя (при равенстве (. 0):
/.,(/) а ц.<7) + и сАГ\, (6.11)
г'Я/) и. ।(/) — </
В таком электромеханическом объекте свободные переходные
процессы тока /..(/) и скорости М/) возможны только при ненулевых
начальных условиях, определяемых в первоначальный момент отклю-
чения электродвигателя от источника энергии с напряжением (
питания. Модель начальных условий определяется следующими выра-
жениями:
17 = ! I = i .
) = (Ц,.
(6.12)
В векторно-матричной форме система уравнений записывается в
виде:
Л I- .1 Л | 115 v<7 =/0) = .V,!,
(6.13)
где вектор состояний и матрица параметров:
v(/)
х>(/)
x2(t) = ai(0, 4 =
ЙП (/12
(,2 °".
(7.14)
X
x,(/) = />y(/)
Дифференциальное векторно-матричное уравнение (6.13) имеет
первый порядок и является линейным относительно искомой функции.
По аналогии с решением скалярного дифференциального уравнения
решение данного уравнения будет определяться экспоненциальной зави-
симостью от времени (так как это система скалярных дифференци-
альных уравнений). Поскольку " является вектором пространства
состояний, то очевидно должно существовать общее решение, которое
можно записать в виде:
л<7) e'z, (6.15)
где скалярный параметр х называется собственным значением (характе-
ристическим числом) матрицы 1 , а вектор - - собственным вектором
матрицы 1 (обозначение собственного значения и собственного
вектора может быть произвольным).
Обязательным условием решения векторно-матричного уравнения
является следующее: значение параметра /. должно быть одним для
всех скалярных уравнений, входящих в векторно-матричное уравнение.
При выполнении этого условия, очевидно, что множитель (t ) будет
являться общим для всех скалярных уравнений. Подставляя уравнение
(6.15) в векторно-матричное уравнение (6.13), запишем равенство:
209
Ле z Ic z. (6.16)
Сокращая скалярный множитель е' ’ в правой и левой частях урав-
нения, получим нелинейное алгебраическое уравнение относительно
значения параметра /. и вектора - (произведение неизвестных
значений параметров л и z):
(6.17)
Для решения этого уравнения - выделим общий сомножитель Z
путем переноса ( • -) в левую часть, что позволяет записать равенство
I 1-х/| z - 0. (6.18)
Прикладное значение для исследования технических систем имеет
только одно решение линейного уравнения, при котором наблюдается
равенство:
I 1-х/| О. (6.19)
Для многомерных систем это равенство возможно только тогда,
когда вычисляются такие значения , при которых существуют нену-
левые собственные векторы - . Другими словами собственные векторы
Z должны находиться в нулевом пространстве матрицы | 1 - z /1.
Запишем ключевое определение собственного значения матрицы:
число л является собственным значением матрицы . I с соответ-
ствующим ненулевым собственным вектором Z тогда и только тогда,
когда характеристическое уравнение для матрицы . I равно нулю:
р-Л/| = 0. (6.20)
Характеристическое уравнение может быть записано в виде харак-
теристического полинома - алгебраического уравнения, содержащего в
качестве слагаемых элементы с параметром /. в степени от 0 до fl .
Максимальное значение степени Z определяется порядком матрицы. В
результате решения такого уравнения определяются собственные
значения матрицы. Для данного примера характеристический полином
равен следующему полиному:
-(<7Ч + a,. )z + z" - аГа,
л' - (а,, + ar )z + (апа;;>
а : -i1.
(6-21)
Таким образом, матрица / имеет два различных собственных
значения: < и < . Каждому из этих значений z соответствует
пространство собственных векторов Z, удовлетворяющих равенству:
а -- - -/-•. (6.22)
Вычислим собственные векторы и " для соответствующих
значений z и z на основе уравнений:
210
| I z;/|_-=0,
|.l 4'1-7 =0. (6.23)
Решениями этих уравнений являются любые векторы, значения
элементов которых кратны значениям элементов , ‘ :
Z,=[z‘‘ ’*2= Z ' (6'24)
Рассмотрим решение 1 - г ' - исходного дифференциального
уравнения. Математически можно записать, что для пар 2 । - и
существуют два решения в виде экспонент (частные решения,
при которых могут не выполняться начальные условия <7 = / ) = (, ,
а>И =!, ) = cj, );
7 , (6.25)
L”2I_
v -I t) =ел'-'г2 = 4'I"”12 "I.
Кроме того, каждое из этих решений не может быть однозначным
решением вследствие множества собственных векторов, кратных и .
Такие математические особенности практически интересуют техниче-
ских специалистов. Наиболее приемлемым вариантом выхода из такой
неопределенной ситуации является следующее рассуждение.
Поскольку исходное уравнение является линейным и однородным,
оно допускает суперпозицию решений, т.е. любая комбинация из двух
его частных решений будет общим решением:
.viz|=ce "7, "г,. (6.26)
В данное уравнение линейным образом входят два произвольных
скалярных параметра <' и <• . Одним из вариантов определения значений
с и < может служить модель начального состояния:
г(/=/ ) = .v =се j, । с ,< - . (6.27)
Принимая в качестве начального момента времени нулевое
значение ' ", на основе данного уравнения можно записать:
•V: = с(6.28)
Раскрывая это уравнение, для рассматриваемого примера, запишем:
211
Вычислить коэффициенты с и < можно не только путем записи из
данного векторно-матричного уравнения системы одномерных урав-
нений, но и на основе следующего равенства:
(6.30)
где - обратная матрица, вычисляемая по известному алгоритму
Таким образом, в явном виде записывается результирующее
решение исходного векторно-матричного уравнения (6.13):
-Vl И = < е г, t <,('' 'г,. (6.31)
Для анализа составляющих компонент вектора ’ , характеризу-
ющих изменение во времени конкретной переменной, целесообразно
представить это уравнение в виде двух уравнений:
Д I /| - с _ е +( _ е ,
Д-,|/| = С1Г,|€/'' +C.Z..C''-' . (6.32)
Начальные условия v, и v по данным уравнениям проверяются
достаточно просто: путем подстановки значения / - 0.
При небольшой размерности матрицы параметров, для которой
вычисляются собственные значения, записать характеристический
многочлен не представляет трудности. В случае большого порядка
матрицы । для записи характеристического многочлена используется
алгоритм Бохера.
Рассмотренные выше алгоритмы решений дифференциальных
уравнений являются достаточно простыми и хорошо работают при
моделировании процессов в стационарных электромеханических
системах, в которых возможны режимы с нулевыми начальными усло-
виями. Более сложные задачи в математическом отношении возникают
при исследовании нестационарных взаимосвязанных электромеханиче-
ских объектов и систем, представленных моделями в форме векторно-
матричных уравнений.
Рассмотрим модель нестационарной электромеханической системы
в 11 - мерном пространстве состояний д(и и многомерным 1,1 - мерным
вектором управляющих । > воздействий:
дц) + (/), (7.33)
где И/i - и - мерная квадратная матрица нестационарных параметров
электромеханического объекта; В - нхт - матрица нестационарных
параметров управляющих воздействий. Модель начальных условий
определяется уравнением:
дй = t, ) = д;|. (6.34)
212
Причем значение момента t времени может принимать различные
значения на всем интервале функционирования системы, и равенство
11 является одним частным случаем.
Модель измерительной системы, обеспечивающая измерение
технически доступных сигналов, можно представить нестационарным
линейным алгебраическим векторно-матричным уравнением:
д/i-Ci/I (6.35)
где г(/) - - мерный вектор измерения переменных состояния в системе;
С(/) - л - матрица, определяющая включение компонент переменных
состояния системы в состав вектора измерения; /ЛИ - , - матрица,
определяющая включение компонент управляющих воздействий
системы в состав вектора измерения.
Поскольку анализируется класс непрерывных электромеханических
систем и объектов, то все элементы матриц предполагаются непрерыв-
ными функциями времени.
Рассмотрим решение дифференциального нестационарного
векторно-матричного уравнения, позволяющее записать в явном виде
переменные состояния в функции времени. Для однородного уравнения,
являющегося моделью свободного состояния электромеханической
системы:
.<(/)- l(/).v(/) (6.36)
можно записать, так называемую, переходную матрицу Ф(/л„> размер-
ности " х" для всех действительных значений :
Ф(/,/о) ехр |л(г)</г =/ +|л(г)г/г+—|л(г)*/г-|л(г)*/г+... (6.37)
Значение первой производной переходной матрицы Ф(м,1 равно
следующему выражению:
</Ф| /./ :
---= Щ|Ф|/л„1 (6.38)
(Il
с начальным условием
ФЦ,Л (6.39)
где / - единичная матрица соответствующей размерности.
Тогда решение однородного уравнения (6.36), которое является
моделью свободного движения электромеханической системы, записы-
вается в виде:
л(/)-Ф> /./„ а„. (6.40)
Примечание 1. Свойства переходной матрицы состояния для неста-
ционарного случая:
213
7) <l>i t л. ।-Ф|=Ф(Гр/,) длялюбых ! <-б;
(6-41)
2) Ф| t,.t = / ;
3) |ф|/,/0|| = ехр| p/-J(rWr
(6-42)
(определитель матрицы Ф|/./ J где
К1 - след матрицы Н • । (сумма ее диагональных элементов); (6.43)
4) <I>| it,i. | - Ф| для любых uh. (6.44)
Переходная матрица состояния для стационарного случая определя-
ется из однородного уравнения при равенстве -4<f I J и может быть
вычислена матричной экспонентой или матричным рядом:
Ф / / - exp . 11 / - ! . Ь I /„ I • 1 • I •' I, । . (6.45)
Для значения начального момента времени равного нулю 11
записывается следующее равенство:
Ф(/) = с" (6-46)
Примечание 1. Свойства переходной матрицы состояния для стаци-
онарного случая:
7)Ф|/-г Ф !. —! । - Ф| I -I, для любых (6.47)
2)Ф(0) = /; (6.48)
3) Ф(/) - невырожденная матрица для конечномерной . I; (6.49)
4) Ф (/I Ф(-0. (6.50)
Наибольший интерес, с практической точки зрения, представляет
решение неоднородного дифференциального уравнения, позволяющего
записать модель изменения переменных состояния замкнутой электро-
механической системы. Рассматривая нестационарный вариант модели
электромеханической системы в виде неоднородного векторно-матрич-
ного уравнения:
л(Л </), (6.51)
для его решения будем использовать достаточно известный математиче-
ский прием. Обозначим правую часть уравнения (6.51) вектор-функцией
</>(/)
ф</1 .</) (6.52)
и введем дополнительный вектор состояния -(/), производная -(/) кото-
рого равна <1/1, т.е. v(/) z(/i. Тогда исходное неоднородное уравнение
можно преобразовать к однородному виду:
.<(/> = Д/) = гД/). (6.53)
Поскольку такое преобразование не изменяет свойств исходной
модели системы, то очевидно, что переходная матрица Ф /./, будет
214
иметь один и тот же вид, как для исходного неоднородного уравнения,
так и для преобразованного уравнения.
Таким образом, общим решением уравнений (6.51) и (6.53)
является следующее равенство (здесь и далее переходная матрица
(й , / л. состояния записывается в общем виде и алгоритм ее определения
приведен в следующем параграфе):
(6.54)
Для записи решения уравнения (6.54), следовательно, модели изме-
нения переменных состояния замкнутой электромеханической системы
предлагается следующий алгоритм. Запишем полную производную
уравнения (6.54)
и/) = Ф\ /./:_-(/) । Ф| и, -(f). (6.55)
Сравнивая данное уравнение с исходным уравнением (6.51), можно
установить следующее равенство:
ФИ./„| Д/)-/Й/)г(/). (6.56)
Используя свойство переходной матрицы для нестационарных
систем: <1>1 -Фил, для любых С и б или для интервала ИД
времени Фи./. Ф1 / ./ ? данное равенство запишем в виде:
Д/)-Ф|/„./1 (6.57)
Решение данного уравнения определяется интегрированием его
правой части на интервале 1 и времени:
t
z(/) = _-(7„) I [ф|/„.’1 5(г)г(гк/г. (6.58)
Используя исходное предположение (6.54), после подстановки
\(/) = Ф /.г | ~(z> в (6.58) (умножения левой и правой частей уравнения
(6.58) на функцию Ф|), запишем для интервала 1'л времени следу-
ющее уравнение (с учетом свойства переходной матрицы состояния
для нестационарных систем: Фылл -Ф / л, = Ф|/,л । для любых РД л.)
или для данного случая if-', -И):
л-(/) = <1>| | л*(Л ) * |(,>| t,i„ । Ф| г,.,. п /?(г)г(г)</г = Ф|/л,,) л-ц, | +
(6-59)
+|ф|/.Г1 /?(rh’(rk/r.
В результате модель изменения переменных состояния замкнутой
электромеханической системы принимает вид следующего уравнения:
215
vp) Ф|ц/ v;z,,i+-|Ф|/.- (6.60)
Данное уравнение называется переходным уравнением состояния
нестационарных систем.
Для стационарных замкнутых электромеханических систем модель
изменения переменных состояния принимает вид:
лП1 Ф/л л(/ I-| Ф I.; I Bvdblp (6.61)
В этом случае уравнение называется переходным уравнением
состояния стационарных систем.
5.7. Способы определения переходной матрицы
состояния электромеханических объектов
Существует несколько способов определения переходной матрицы
состояния, которые можно использовать для исследования электромеха-
нических объектов, представленных как стационарными, так и нестаци-
онарными моделями.
1. Поскольку переходная матрица состояний представляет собой
матричную экспоненту, то одним из вариантов ее вычисления - это
разложение матричной экспоненты в матричный ряд. Однако погреш-
ность такого представления может быть достаточно большой. Это
связано не только с учетом ограниченного числа слагаемых матричного
ряда, но и сходимостью ряда к экспоненциальной зависимости.
Например, для стационарных моделей электромеханических объектов
переходная матрица записывается следующим матричным рядом:
<I>| U = С.\р| .1 I' 11 = / г A\t-t )+ - .1 | i’ - .... (7.1)
В том случае, когда начальный момент времени г 11 это равенство
принимает вид:
Ф(/) = У ' (7.2)
АО Л .
2. Другой вариант вычисления переходной матрицы состояния
основан на свойстве матричной экспоненты для исходной диагональной
матрицы:
0 ••• 0
О 0 ••• а,1П
216
Это свойство заключается в следующем: для такой матрицы экспо-
ненциальная матрица является также диагональной и записывается в
виде:
е"'' 0 0
схр[.1( /-/„)] - 0 с' 0 (7.4)
0 0 ... (> ''
Однако практически всегда матрица параметров электромеханиче-
ских объектов имеет недиагональную форму и поэтому чаще всего
используется следующий вариант вычисления переходной матрицы.
3. Данный вариант предполагает предварительное построение
диагональной матрицы, элементами которой являются собственные
значения исходной матрицы. Очевидно, что для формирования такой
матрицы необходимо предварительно вычислить собственные значения
исходной матрицы и записать промежуточные матрицы вида:
Ч 0 ... О' 0 0
л - 0 0 е' 1 = 0 (7.5)
0 0 ' А О 0 е " ' '
Алгоритм вычисления переходной матрицы заключается в следу-
ющем. Для вычисления переходной матрицы необходимо определить
модальную матрицу '/ , которая, как известно, преобразует исходную
матрицу ,1 в диагональную матрицу \:
Л Л/ 'ЭЛ/.. (7.6)
Из данного уравнения можно записать обратное соотношение:
М 'АЛ/ - .1. (7.7)
Для невырожденной матрицы 1 (невырожденной матрицей называ-
ется матрица, которая имеет обратную матрицу) известно соотношение:
• Г АЛЛА/ '. (7.8)
Тогда для переходной функции или матричной экспоненты записы-
вается равенство:
е':'' \1.е" " Л/. . (7.9)
4. Для получения переходной функции электромеханических
объектов, представленных линейными моделями часто используются
передаточные функции и преобразование Лапласа. Рассмотрим
применение этого способа для уравнения свободного движения при
ненулевых начальных условиях 1 , в начальный момент времени = 0;
217
-v(/i V / = /„ = <> = V . (7.10)
В операторной форме данное уравнение принимает вид:
рл(р) .\„ = Лл(р), (7.11)
где /’ - оператор преобразования Лапласа.
В результате преобразования данного уравнения можно записать
равенство:
/'/ — Л д(/И л, или ц/О - [/>/—/ . (7.12)
С другой стороны для свободного состояния системы, характеризу-
ющегося уравнением (7.10), модель переходного процесса на основе
переходной матрицы состояния описывается следующим выражением:
VI7) = ф| и = () V =(. , . (7.13)
Записывая прямое преобразование Лапласа для данного уравнения
L а(/) - L Ф -()ia„ - L е а , (7.14)
и, сравнивая с уравнением (7.12), можно установить следующее: прямое
преобразование Лапласа переходной матрицы состояния с начальным
моментом времени равным нулю 11 позволяет записать равенство:
/ Ф м. 0 1с р!- < . (7.15)
Таким образом, переходная матрица свободного состояния системы
определяется как обратное преобразование Лапласа характеристической
матрицы р/ ij :
, (7-16)
где / и / - соответственно, символы прямого и обратного
преобразования Лапласа.
Примечание.
В некоторых случаях, для инженерных расчетов процессов в
замкнутых электромеханических системах целесообразно использовать
передаточные функции. Рассмотрим алгоритм преобразования диффе-
ренциального стационарного векторно-матричного уравнения в переда-
точную функцию.
Допустим, имеем уравнения линейного стационарного электроме-
ханического объекта в пространстве состояний:
Л</) (/I,
г(/) Са(/)-/Л (/), (7.17)
\(/ = /, .) = V, .
где vizt - п . мерный вектор состояния; I - _ мерная квадратная
матрица параметров электромеханического объекта; '' й I - м - мерный
вектор управляющих воздействий; Н - 11X111 - матрица параметров управ-
218
ляющих воздействий; f„ - момент времени начального состояния; г(/) - /•
- мерный вектор измерения переменных состояния в системе; С - ' -
матрица, определяющая включение компонент переменных состояния
системы в состав вектора измерения; /) - - матрица, определяющая
включение компонент управляющих воздействий системы в состав
вектора измерения.
При нулевых начальных условиях данные уравнения в операторной
форме принимают вид:
/л\(/Л ,1л(/?) + //((/;),
.(/;) (л(/Ц + /Х(/Ц. (7.18)
После соответствующих преобразований первое уравнение (7.18)
записывается следующим образом:
/>/-.|]а(/о - Bt (/<i или х(р)=[р/-Л]'в(/(р). (7.19)
Уравнение измерительной части или выхода принимает вид:
1</Й-| Cl />/-! Н-Г) (7.20)
В результате записываются соответствующие матричные переда-
точные функции:
- передаточная функция по вектору состояния
И (/»- '1/” -/>/ |]:«; (7.21)
с (/?) '
- передаточная функция по выходу
ч (/>> = =С /’/ । В/>. (7.22)
t ( />) v 7
На основе данных уравнений, с использованием табличных переда-
точных функций, могут быть вычислены модели переходных процессов
в электромеханических объектах и системах.
5.8. Цифровое моделирование непрерывных
процессов в ЭО на основе метода Эйлера
Для примерной оценки на ЭВМ непрерывных процессов в электро-
механических объектах можно использовать достаточно простую
модель в пространстве состояний, использующая аппроксимацию
первой производной переменной величины конечной разностью.
Основой такого подхода является предположение о стационарности
параметров электромеханических объектов на фиксированном интер-
вале дискретности по времени. Одним из вариантов практической
реализации алгоритма моделирования непрерывных процессов является
алгоритм аналого-цифрового преобразования аналоговых сигналов в
219
цифровую форму без учета влияния нелинейности квантования по
уровню.
Рассмотрим алгоритм дискретного моделирования электромехани-
ческих объектов, представленных нестационарными уравнениями в
виде:
л(/)
к/1 С(/)л(/) + М0б'(/), (8.1)
v<7 = /,)=' ,
где - а - мерный вектор состояния; ii.'i - 11 - мерная квадратная
матрица нестационарных параметров электромеханического объекта;
( (/) - т . мерный вектор управляющих воздействий;/Й71 - -
матрица нестационарных параметров управляющих воздействий;
момент начального состояния; г(/) мерный вектор измерения пере-
менных состояния в системе; < 1 1 - - матрица, определяющая вклю-
чение компонент переменных состояния системы в состав вектора изме-
рения; Э(/ I - - матрица, определяющая включение компонент управ-
ляющих воздействий системы в состав вектора измерения; , - вектор
начальных значений переменных состояния.
Для моделирования такой системы на ЭВМ используем дискретную
аппроксимацию в моменты времени ' , где при равномерном интер-
вале дискретности V можно записать ' = t . Тогда производную
т(/1 в дискретный момент времени • t: можно вычислить следующим
соотношением (с учетом обозначений г- ) , Ц/ ) = .v );
Д/js - |д-_ лI. (8.2)
Следовательно, дифференциальное уравнение (8.1) с учетом (8.2)
можно аппроксимировать выражением:
v : • (8.3)
После соответствующих преобразований запишем модель изме-
нения переменных состояния замкнутой электромеханической системы
в дискретной форме:
л , ' / + А/ .1 I л - А/ HI
гЛ = C.v. 4-ZH (8.4)
Данное уравнение может служить основой для моделирования
электромеханических процессов в системах регулирования скорости
движения и положения различных механизмов с исполнительными элек-
троприводами. Существенным ограничением такого подхода является
то, что интервал V дискретности должен быть меньше, как минимум в
220
два раза, значения постоянной времени наиболее быстрой состав-
ляющей переходного процесса.
5.9. Примеры вычисления переходной матрицы и
моделей переходных процессов в ЭО
Пример 1.
Рассмотрим электромеханический объект, структурная схема кото-
рого приведена на рис. 9.1.
Рисунок 5.10: Структурная схема электромеханического объекта
Пространство состояний данного электромеханического объекта
описывается дифференциальными уравнениями:
v,(/l= л, (7)+ {.'(/), \ 2.V.(?) I С(1}_ (9.1)
Управляющее воздействие - U) формируется регулятором системы
управления в соответствии с измеряемыми сигналами, поступающими с
датчиков:
г(П л (z) + 3.v,(z). (9.2)
Данные уравнения в компактной векторно-матричной форме запи-
сываются следующим образом:
дц) . 1х(1 }+И1. (л, (9.3)
117) <'лЦ1,
где матрица параметров
0
имеет диагональную форму; вектор
I
параметров управляющих воздействий />'
; вектор параметров изме-
рительных каналов <
221
Вычислим переходную матрицу (1>i,'.< =о и переходные процессы
переменных ',(/) и 1 электромеханического объекта на единичное
ступенчатое управляющее ' U) Ю> воздействие.
Т. к. матрица I является диагональной матрицей, то переходная
матрица (1’1'-А при начальном моменте времени ' 11 равна следую-
щему выражению:
(9-4)
Используя данное уравнение, определим реакцию системы на
ступенчатое единичное воздействие при нулевых начальных условиях.
Модель переходного процесса записывается выражением:
v(/)~ е' ' л - [г Д| - | (/| г| ч!т .
(9-5)
При нулевых начальных условиях: ' 11 и (1, уравнение прини-
мает вид:
Н7) " 7?! г И (г ></'. (9.6)
В результате, модель переходного процесса каждой переменной
состояния и измеряемой переменной записывается уравнениями:
л,(/1 [е' '11(гк/г < 1-е
х,(/)=р-21'Г)ы(гу/г=|е: ' 5 (9.7)
•,</)-л,(/>Т-Зл-(/)--' е - .
Пример 2.
Рассмотрим электромеханическую систему, структурная схема
которой приведена на рис. 9.2.
Рисунок 5.11: Структурная схема электромеханического объекта
222
Пространство состояний данного электромеханического объекта
описывается дифференциальными уравнениями:
\,(/) -л. I; I л IZ)-2a.(7), (9.8)
Управляющее воздействие ( > формируется регулятором системы
управления в соответствии с измеряемыми сигналами, поступающими с
датчиков:
г(0 = 4а\(г). (8.9)
Данные уравнения в компактной векторно-матричной форме запи-
сываются следующим образом:
л</) .LxiD+Ul. (/I,
(9.Ю)
о
где матрица параметров ।
; вектор параметров управляющих
0
4J
Вычислим переходную матрицу Ф( /,/„ - О и реакцию электромеха-
нической системы на ступенчатое управляющее ’ U) ИО воздействие.
Т.к. матрица I параметров не является диагональной для вычис-
ления переходной функции, воспользуемся алгоритмом, который пред-
полагает построение матрицы
собственные числа матрицы I.
характеристический полином:
воздействий
; вектор параметров измерительных каналов <
собственных чисел. Определим
Для этого составим определитель или
0
о
(9.И)
Собственные числа и соответствующая матрица равны:
’ 1 0 1
(9-12)
(9-13)
Следовательно, матричная экспонента определяется выражением:
... е" <> _____
С =
_ О
Для определения модальной матрицы W определим собственные
векторы матрицы I из следующих уравнений:
(9-14)
где • - собственные векторы матрицы . I.
После подстановки соответствующих значений элементов матрицы
I и собственных чисел этой матрицы в уравнения запишем:
223
о
о
(9-15)
Из данных уравнений получим
запишем собственные векторы:
и - 11
. В результате
(8.16)
Записывая модальную матрицу
в виде:
вычислим обратную матрицу А/ ;
|Л/.
где Ad/M - присоединенная матрица.
В результате запишем переходную матрицу <!>/,/,, -();
моментом ' 11 времени:
(9.17)
с начальным
Л/.еЛ'А/. ' =
(9-18)
Используя ступенчатое единичное воздействие 1(f) КО при
нулевых начальных условиях, определяем модель переходного процесса
каждой переменной состояния и выходной переменной
-V, (/)
= |ф(Цг)Л(г)1(г)</г =
О
О
к
О
д,(/) р •' l(r)Jr = 1-е", (9.19)
х2(0
I) Z X
Г(О 2-4с -2е .
Пример 3.
Рассмотрим электромеханический объект, структурная схема кото-
рого приведена на рис. 9.3.
224
Рисунок 5.12: Структурная схема электромеханического объекта
Пространство состояний данного электромеханического объекта
описывается дифференциальными уравнениями:
Г|(/)= Л'П) I {. (/), л2(0 = 2.v,(/) I I (/i. (9.20)
Управляющее воздействие '' < >) объектом формируется регулятором
системы управления в соответствии с измеряемыми сигналами, поступа-
ющими с датчиков:
ri7) = .v п) । Злу(/). (9.21)
Данные уравнения в компактной векторно-матричной форме запи-
сываются следующим образом:
лЦ) .lxit)+BL (/I,
(9.22)
где матрица параметров ।
-1 0
о
; вектор параметров управляющих
воздействий В
; вектор параметров измерительных каналов
3 '
Рассмотрим общий алгоритм получения передаточной функции
электромеханического объекта на основе моделей в пространстве состо-
яний вида (9.22).
Аналитический вывод передаточной функции можно получить,
используя преобразованную по Лапласу модель в пространстве состо-
яний:
/л\(/Л ,1л1/Ц-/Л (//)?
г(/>) с'х(/>), (9.23)
где /? - оператор преобразования Лапласа; т(/Л, ( (/Л, т( /> i— соответ-
ственно, вектор состояния, скалярное управляющее воздействие и
выходная переменная.
225
Первое уравнение системы (9.23) можно записать в следующем
виде:
। /)/ - .1ш/'i //(.(/Пили н/л-1/)/ .ц HI (/)}. (9.24)
Далее, записывая второе уравнение системы (9.23):
и//) с (/>/ — .() 1//(, (/и, (9.25)
получим передаточную функцию электромеханического объекта по
выходу:
и = (/>/ л1//. (9.26)
Рассмотренный алгоритм целесообразно использовать для аналити-
ческой записи передаточных функций 11 < /’) объектов на основе урав-
нений пространства состояний систем второго и третьего порядков.
Определим передаточную функцию по выходу для данной электро-
механической системы, представленной дифференциальными уравне-
ниями (9.20) в пространстве состояния.
Используя преобразование Лапласа при нулевых начальных усло-
виях, уравнения (9.23) записываем одним уравнением:
г(/>)-< ' /7 - г //( (/И. (9.27)
После соответствующих преобразований передаточная функция
электромеханического объекта по выходу определяется следующим
выражением:
I 3 /, + 1 Г'Ъ—/, + 2t3;,t3- (9.28)
I _lj /7+1 /7 + 2 (/> + !)( /7 + 2)
/? + 2_|
4/7+5 _ 2р + 2.5 _ 2,5(0.85/7-1-1)
(р + 1)(р+2) (/7 + 1ХО,5/7 +1) (р + 1Х0.5/7 +1) ’
Пример 4.
Рассмотрим электромеханический объект, структурная схема кото-
рого приведена на рис. 9.4.
226
Рисунок 5.13: Структурная схема электромеханического объекта
Математическая модель данного объекта описывается дифференци-
альными уравнениями:
.Vj(i) = х.(г), .v,й) = -2.V,(0-Зх2Й) + 91'(t). (9.29)
Управляющее воздействие ' й> формируется регулятором системы
управления в соответствии с измеряемыми сигналами, поступающими с
датчиков:
.гй)= у й). (9.30)
Данные уравнения в компактной векторно-матричной форме запи-
сываются следующим образом:
лй) Ст •/Л й),
(9-31)
О
где матрица параметров 1
3
; вектор параметров управляющих
о
9
воздействий !> -
; вектор параметров измерительных каналов с
0 '
В результате использования преобразования Лапласа второе урав-
нение системы (9.31) запишем:
(9.32)
где матрица р> - ’ \ , .
Вычислим обратную матрицу /й . I :
/>(/>
р
р
(9.33)
227
В результате модель электромеханического объекта в виде переда-
точной функции записывается следующим образом:
И'(р)=[1 0]
9
о
9
(9.34)
Р
а. I
Пример 5.
Рассмотрим нестационарный процесс свободного движения таких
электромеханических объектов, как исполнительных электроприводов,
приводящих в действие маятниковые конструкции. Непосредственно
после отключения исполнительного электропривода от источника
питания, математической моделью, отражающей положение маятни-
ковой конструкции в пространстве, может являться нестационарное
дифференциальное уравнение следующего вида:
a + = (9.35)
<ll
Рассмотрим решение задач вычисления переходной матрицы
<!>(/,/.,) и построения модели переходного процесса движения маятни-
ковой конструкции, предварительно преобразуя данное уравнение в
форму Коши. Алгоритм преобразования предполагает замену пере-
менной . . При этом моделирование переходного процесса будем
производить для конкретных коэффициентов </,, </,, </ , например, 6
, ", - 3, ю =1.
Тогда исходное уравнение (9.35) записывается в виде:
о.
(9-36)
Введем дополнительные переменные -И), для
вания скалярного уравнения в векторно-матричную форму:
преобразо-
.v(r)=’(r), v(r)=~(r) = rjr), .< г» - (г). (9.37)
В пространстве введенных переменных уравнение (9.36) записыва-
ется двумя скалярными уравнениями в форме Коши:
_-(-)= (9.38)
В векторно-матричной форме данная система уравнений принимает
вид:
где вектор состояния -(г) =
, матрица параметров i
(9.39)
0 1 1
228
После вычисления переходной матрицы Ф( г. г„) состояний во
времени ’ одним из методов, приведенных в разделе 6 учебного
пособия, запишем:
(9.40)
Осуществляя обратное преобразование к времени /, путем подста-
новки в данное выражение г - In t, запишем переходную матрицу (/, /(|)
состояний во времени I:
(9-41)
Правильность полученного выражения указывает то, что
значение переходной функции в начальный момент времени равно
единичной матрице, т.е. выполняется условие:
Фи,,./.,)-/. (9.42)
В результате математическая модель переходного процесса свобод-
ного движения маятниковой конструкции после отключения исполни-
тельного электропривода от источника питания записывается в следу-
ющем виде:
Вопросы к разделу.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
229
6. Средства согласования модулей расширения
ПЛК
Современные САУ обычно включают в себя множество контрол-
леров, HMI-панелей, АРМ, которые взаимодействуют между собой
выполняя распределенные задачи управления и наблюдения за
процессом. Для обеспечения такой работы необходимо передавать
данные между устройствами. Для таких целей практический каждый
ПЛК содержит одно или много устройств передачи данных с верхним
уровнем или другим контроллером. Самым популярным средством
является универсальный последовательный порт. Однако кроме самого
средства передачи данных требуется протокол-соглашение, по которому
данные формируются и расшифровываются однозначно.
Это можно сравнить со способностью человека издавать различные
звуки, но чтобы его можно было понять принимаются общие правила
распознавания всякого рода звуков. Такое соглашение между людьми
представляет язык общения. В мире можно насчитать более сотни попу-
лярных языков общения английский, французский, русский и т. д. Пред-
ставители разных языков могут не понимать друг друга. Как хорошо
было бы, если на всей планете был один язык и наречие, тогда бы все
понимали друг друга везде.
Подобно языкам в САУ также в процессе разработки появилось
много языков-протоколов общения между устройствами и ПЛК.
Поскольку контроллеры не обладают тщеславием и не тяготятся к
своему родному языку-протоколу, то в их мире не сложно было создать
единый стандарт общения между устройствами. Но все же, не смотря на
попытки стандартизировать процессы обмена, появились несколько
популярных протоколов. Это связанно с недостатками старых перед
новыми. В учебном пособии рассмотрим три протокола связи из
десятков известных полагая, что этих трёх будет достаточно.
6.1. ModBus протокол обмена
ModBus протокол предложенный компанией Modicon. Протокол
использует последовательный интерфейс микропроцессора и предпола-
гает процедуру общения в виде запрос-ответ. Тут все как в школьном
классе: учитель спрашивает - ученик отвечает. Только во избежание
хаоса излишней болтовни все придерживаются правила: не говорить,
если учитель не спросил именно вас. Следовательно в один момент
времени говорит только один. Такой режим общения будем называть
230
полудуплексный. Дуплексный - означает, что общение может быть в
обоих направлениях, приставка «полу» отмечает, что в любой момент
времени говорит только один.
В персональных компьютерах старого образца присутствовал порт
полнодуплексный, его использовали для клавиатуры, мыши других
устройств. Физический стандарт реализации такого порта имеет
название RS232. В нем сигнал передаётся в виде изменения напряжения.
Передача сигнала напряжением имеет недостатки: сигнал подвержен
электромагнитным полям и ёмкости между сигнальной линией и общим
проводом. В результате передача возможна при отсутствии электромаг-
нитных помех и небольшой длине кабеля между устройствами до
10 метров.
Расстояния между ПЛК в технологических объектах значительно
превышает и может достигать сотни метров, при этом сам технологи-
чески объект может содержать множество источников электромаг-
нитных помех: электродвигатели, преобразователи частоты, пусковые и
силовые устройства и т. д..
На рисунке 6.1 показана схема реализации передачи данных с
помощью токовой петли. Такой способ очень мало подвержен электро-
магнитным помехам и имеет низкое волновое сопротивление 120 Ом.
Рисунок 6.1: Токовая петля RS485 для передачи данных
В этом случае передача данных на расстояние более километра на
скорости 9600 бод достаточно устойчива. В большинстве случаев
расстояние редко превышает километр. Однако если расстояние превы-
шает или между цехами имеется высокое наведённое напряжение на
линии связи, то можно использовать, так называемые, гальванически
развязанные повторители. Схема такой сети показана на рисунке 6.2.
231
Драйвер
RS-48 S Повторитель
Повторитель
Рисунок 6.2: Гальванически развязанные повторители для сети RS485
Иногда контроллеры имеют полнодуплексный канал передачи через
токовую петлю. Такой канал называется А5422 и пример подключения
показан на рисунке 6.3.
Рисунок 6.3: Пример физического подключения устройств по RS422
Важно отметить, что выхода от такого подключения может быть только
тогда, когда в сети два устройства и в любой момент времени оба могут
передавать данные. Касательно протокола ModBus, эти преимущества не
нужны совсем.
Кроме способа подключения проводов очень важно знать сам
протокол, поскольку он прост и легко внедряется даже в контроллеры с
самыми скромными характеристиками. А реализация протокола в ваше
232
простейшем устройстве позволяет ему быть полноценным участником
крупной сложно и современной САУ По этой причине рассмотрим неко-
торые стандарты передачи данных протокола ModBus. На рисунке 6.4
показана структура запроса и ответа в ModBus, рисунок взят из офици-
ального источника [].
Рисунок 6.4: Структура запроса и ответа в ModBus
Согласно протокола запрос отправляет единственное устройство со
статусом Master. В штатном режиме запрос всегда адресован одному
устройству из устройств со статусом Slave. Подчинённым устройствам
присвоен уникальный номер-идентификатор Device Address. Общая
структура всех запросов и ответов протокола ModBus содержит после-
довательность данных в следующем порядке
• Device Address - байт данных в диапазоне от 1 до 127.
• Function code - байт данных с кодом функции из стандартных
значений.
• Data Bytes - набор данных, структура и объем которых зависит от
кода функции.
• Error Check - контрольная сумма из двух байтов известная в
теории передачи и контроля данных как CRC16. В оригинальном
233
руководстве пользователя [] приведён код программы для вычисления
контрольной суммы.
Контрольная сумма необходима, поскольку существует вероятность
повреждения данных в процессе передачи из-за электромагнитных
помех или ненадёжных контактов. Подчинённое устройство формирует
ответ в таком же формате. Иногда запрос может быть неподдержива-
емым или недопустимым. В этом случае к значению кода функции
прибавляется значение 128, на программном уровне просто взводится
старший бит байта. Разумеется, код функции не может превышать
значение 127.
Данные по R5485 могут передаваться в двух режимах:
• RTU mode - Remote Terminal Unit (Блок удаленных терминалов),
• ASCII mode - American standard code for information interchange
(Американский стандартный код для обмена информацией).
К сожалению, переводы этих названий мало что говорят об их
отличиях, поэтому не взирая на текст названия опишем эти отличия.
В начале, когда только появились вычислительные машины, не
было привычного нам графического интерфейса. Дисплей мог отобра-
жать только цифры и буквы англо-американского алфавита и несколько
символов из других языков. Чтобы не было путаницы, утвердили стан-
дарт кодирования этих букв и символов, который в последствии назвали
ASCII. Современные компьютеры имеют графический интерфейс и
пользователь обыватель мало, что знает о взаимодействии с ПК в терми-
нальном режиме. Однако, многие до сих пор пользуются программой
FAR в Windows. К терминальным программам можно также отнести
инструменты: cmd, telnet, putty и т. д.. Сетевые администраторы
довольно часто используют терминальные программы, поскольку они
просты и позволяют работать на нижнем «хардварном» уровне с
компьютером и контроллерами.
В Linux, Unix, Dos, RTOS подобных операционных системах терми-
нальный режим является основным в ядре. Практически большинство
ПЛК построены на выше указанных операционных системах. Исключе-
нием являются ПЛК, построенные на OS Embeded Windows.
Если устройство поддерживает ASCII mode, то к нему можно
подключится стандартными средствами администрирования сетей
(telnet, putty). И в обычном текстовом режиме формировать запросы и
получать ответы. Правда в этом режиме для передачи байта требуется
два символа. К примеру, чтобы передать символ «:» нужно отправить
соответствующий этому символу код из ASCII, который равен 58.
Однако значение кодов могут достигать трёхзначных значений, к
234
примру - 126. По этой причине байт делят на две тетрады по 4 бита и
отправляют символ для каждой тетрады. Тетрада в свою очередь может
принимать значения от 0 до 15. Было принято использовать символы
(А, В, С, D, Е, F) для значений (10, 11, 12, 13, 14, 15) соответственно.
Согласно таких правил число 58 =3-16 + 10=0x3А. Такая форма записи
данных соответствует, так называемому, HEX формату. К сведению,
когда вы нажимаете клавишу «Enter» в компьютер отправляется
код-команда со значением 0D. В результате при использовании
ASCII mode достаточно символов клавиатуры, но при этом объем
данных в терминале увеличивается в два раза.
В RTU mode данные передаются непосредственно без кодирования
в HEX формат. Размер пакетов не увеличивается, но для работы с этим
протоколом нужны специализированные программы. Обычно пакет
жанных формирует устройство или программа и отправляется в шину
RS485 байт за байтом без задержек между байтами. В ASCII mode время
между байтами может быть большим, поскольку пакет набивается в
ручную на клавиатуре. В этой связи принцип определения начала пакета
в этих модификациях отличается. В таблицах 6.1 и 6.2 показан порядок
отправки пакетов. Для ASCII mode признаком начала и конца пакета
являются символы.
Таблица 6.1.
Порядок передачи данных в ASCII mode
Старт Адрес Функция Данные LCR сумма Конец пакета
1 символ «:» 2 символа «06» 2 символа «03» 2- п символов 2 символа «DA» 1 символ «Enter»
Таблица 6.2.
Порядок передачи данных в RTU mode
Старт Адрес Функция Данные CRC16 сумма Конец пакета
время 4-Ть 1 байт 0x06 1 байт 0x03 п байт 2 байта время 4-Тъ
235
Для RTU mode признаком начала и конца пакета являются проме-
жутки времени, равные четырём интервалам времени Тъ, необходимого
для передачи одного байта. Ингода разработчики обеспечивают
поддержку обоих модификаций, в этом случае не рекомендуется исполь-
зовать адрес подчинённого устройства, равный коду символа «:».
На рисунке приведён пример запроса в режимах ASCII и RTU.
QUERY
Field Name Example (Hex) ASCII Characters RTU 8-Bit Field
Header : (colon) None
Slave Address 06 0 6 0000 0110
Function 03 0 3 0000 0011
Starting Address Hi 00 0 0 0000 0000
Starting Address Lo 6B 6 В 01101011
No. of Registers Hi 00 0 0 0000 0000
No. of Registers Lo 03 0 3 0000 0011
Error Check LRC (2 chars.) CRC(16bitS)
Trailer CR LF None
Total Bytes: 17 8
Рисунок 6.5: Промер запроса в режимах ASCII и RTU
Рисунок также взят из оригинального руководства пользователя, где
можно увидеть различия обоих режимов.
Ниже приведён список основных команд, утверждённых стан-
дартом:
• 01 Read Coil Status - Чтение состояния дискретных выходов,
• 02 Read Input Status - Чтение состояния дискретных входов,
• 03 Read Holding Registers - Чтение регистров хранения,
• 04 Read Input Registers - Чтение входных регистров,
• 05 Force Single Coil - Чтение состояния одного дискретного
выхода,
• 06 Preset Single Register - Запись одного регистра хранения,
• 07 Read Exception Status - Чтение флагов исключения,
• 11 Fetch Comm. Event Ctr. - Чтение значения счётчика событий,
• 12 Fetch Comm. Event Log - Чтение журнала событий,
• 15 Force Multiple Coils - Принудительная загрузка дискретных
выходов,
• 16 Preset Multiple Registers - Запись значений нескольких
регистров,
• 17 Report Slave ID - Запрос описания типа и идентификатора
контроллера,
236
• 23 Read/Write 4X Registers - Объединённая команда записи
регистров и чтения регистров в одной транзакции.
Для обеспечения совместимости контроллера с современными
SCADA, достаточно обеспечить две команды 04 - для чтения из
контроллера и 16 - для записи в контроллер. Рассмотрим эти команды
подробнее.
Команды 03 и 04. Запрос включает следующие байты:
1. 11 адрес подчинённого устройства;
2. 04 код команды может быть 03 или 04;
3. 00 старший байт адреса регистра или пара-
метра; 4. 6В младший байт адреса регистра или пара-
метра; 5. 00 старший байт количества запрашиваемых
регистров; 6. 03 младший байт количества регистров;
7 и 8. ... контрольная сумма LCR или CRC.
Ответ включает в себя следующие байты:
1. 11 адрес подчинённого устройства;
2. 04 код команды может быть 03 или 04
3. 06 количество отправляемых байт;
4. dh[107] старший байт 1-го регистра;
5. dl[107] младший байт 1-го регистра;
6. dh[108] старший байт 2-го регистра;
7. dl[108] младший байт 2-го регистра;
8. dh[109] старший байт 3-го регистра;
9. dl[109] младший байт 3-го регистра;
10, 11. ... контрольная сумма LCR или CRC.
Значение 101 соответствует значению 4-го байта в запросе,
6В=6-16+11=107. Обычно в контроллерах, предоставляющих данные по
этим командам в руководствах пользователя принято указывать адреса в
форматах:
•40108, 40109, 40110 для команды 03,
• 30108, 30109, 30110 для команды 04.
Почему принято именно так? Сложно объяснить, поэтому следует
просто запомнить. Также в описании регистров принято нумеровать их
от одного, тогда как программисты нумеруют от нуля. Поэтому в доку-
ментации указанный регистр - 40108, следует читать по адресу 107, на
единицу меньше. Регистр данного протокола представляет собой двух-
237
байтовое целое число в диапазоне от -32768 до 32767. Поэтому для
описания вещественных величин к каждому регистру приводится
описание.
Пример описания:
Номер регистра Название величины Описание
40108 Температура якоря представлена
в 0,01 °C
Так например, если получено число 9645, то оно соответствует темпера-
туре 96,45 °C.
Команда 16. Запрос включает следующие байты:
1. 11 адрес подчинённого устройства;
2. 16 код команды;
3. 00 старший байт адреса регистра или пара-
метра;
4. 6В младший байт адреса регистра или пара-
метра;
5. 00 старший байт количества передаваемых
регистров;
6. 03 младший байт количества регистров;
7. 06 количество отправляемых байт;
8. dh[107] старший байт 1-го регистра;
9. dl[107] младший байт 1-го регистра;
10. dh[108] старший байт 2-го регистра;
11. dl[108] младший байт 2-го регистра;
12. dh[109] старший байт 3-го регистра;
13. dl[109] младший байт 3-го регистра;
7 и 8. ... контрольная сумма LCR или CRC.
Ответ включает в себя следующие байты:
1. 11 адрес подчинённого устройства;
2. 16 код команды может быть 03 или 04;
3. 00 старший байт адреса регистра или пара-
метра;
4. 6В младший байт адреса регистра или пара-
метра;
5. 00 старший байт количества передаваемых
регистров;
6. 03 младший байт количества регистров;
7,8. ... контрольная сумма LCR или CRC.
238
Адресация, нумерация в описании построена по таким же принципам
что в предыдущих командах.
В стандарте предусмотрены команды пользователя с номерами от
40 до 4F, где разработчик может расширить протокол обмена для своих
нужд. В приложении приведён пример контроллера поддерживающую
одновременную передачу данных от мастера к подчинённому устрой-
ству и обратно.
С появлением ПЛК оснащённых TCP - пакет портом встал вопрос
об использовании ModBus в рамках TCP соединения. Чтобы понять
процедуру преобразования ModBus в ModBusTCP отметим два факта:
•TCP - пакет уже содержит в себе 32 разрядную контрольную
сумму всего пакета, гарантирующую целостность данных.
•TCP - пакет может «гулять» по сети Ethernet достаточно
непредсказуемо, вплоть до смены порядка поступления пакетов. К
примеру, отправленный ранее пакет может прийти позже последнего
отправленного пакета. Для этого в самом протоколе TCP есть
идентификация каждого пакета, но она используется на аппаратном
уровне для подтверждения доставки пакета.
Основываясь на этих двух фактах ModBusTCP не содержит своей
контрольной суммы, но в начале добавлены три поля для включения
необходимой информации о пакетах, чтобы их не перепутать. Перепу-
тать пакеты можно при чтении одинакового коилчества данных
командами 03 и 04 по разным адресам. Если пакеты во времени поменя-
ются, то будут приняты некорректно, поскольку ответе нет инфор-
мации, с каких адресов получены данные. На рисунке 6.6 проиллюстри-
рован принцип построения ModBusTCP.
239
ADU
7 байт I байт 6 байт 6 байт 2 байт 46... 1500 байт 4 байт
Рисунок 6.6: Принцип построение ModBus TCP
Таким образом, для использования TCP следует убрать контрольную
сумму и включить идентификаторы пакета на усмотрение разработчика.
ModBusTCP одинаково формируется как для RTU, так и для ANSII
режимов.
Приведём недостатки протокола ModBus.
• Стандарт специфицирует метод передачи только двух типов
данных.
• Стандарт не регламентирует начальную инициализацию системы.
• Длина запроса ограничена, а данные могут быть запрошены
только из последовательно расположенных регистров.
• Не предусмотрена передача сообщений по инициативе
подчинённого устройства (прерываний). Ведущее устройство должно
периодически опрашивать ведомые.
• Не предусмотрен способ, с помощью которого ведомое устройство
могло бы обнаружить потерю связи с ведущим.
Два последних недостатка могут быть устранены при использо-
вании протокола CAN, которому посвящён следующий раздел.
240
Вопросы к разделу.
1. В чем отличие дуплексный полудуплексный канал? Опишите
принцип работы RS485.
2. В чем отличия RTU и ANSII форматов передачи в ModBus.
Опишите преимущества и недостатки каждого.
3. Опишите обобщенный формат запросов и ответов в ModBus.
4. Какими функциями запрашиваются регистры входов и пара-
метров.
5. Как можно передать данные в устройство?
6. Укажите достоинства и недостатки ModBus.
7. С какой целью вводятся в пакет ModBus TCP дополнительные
данные?
6.2. Аппаратный интерфейс CAN
Читателю возможно известна ситуация, когда собрались несколько
очень воспитанных собеседников жаждущих рассказать несколько своих
любимых анекдотов. И вот они судорожно пытаются захватить
внимание остальных собеседников уже не первый раз начиная рассказы-
вать свой анекдот. Но в этот момент начинает также рассказывать свой
анекдот другой воспитанный собеседник. И в силу, своего воспитания
оба останавливаются, выжидая эту глупую паузу, и никак не могут
синхронизироваться. Для этих целей назначают арбитра, который один
решает, кто будет говорить. Это подход, принятый в ModBus.
Ну если ситуация с анекдотами некритичная, можно спокойно
дождаться своей очереди. Хуже когда, собеседнику нужно сообщить
критичную новость, но он вынужден ждать позволения арбитра. А
арбитр пробегая по списку, каждого спрашивает: «У тебя все
нормально?» и получает ответ: «Нормально». А тот у кого пожар, ждёт
когда его спросят, теряя драгоценное время. Эта важная проблема
успешно решена в стандарте протокола связи CAN, на аппаратном
уровне. Поэтому топология шины CAN, показанная на рисунке 6.7,
включает в себя дополнительное устройство CAN Controller.
241
Узел 1
Узел 2
Bus CAN_L Bus
termination termination
Рисунок 6.7: Топология CAN шины
В остальном сеть CAN мало отличается от сети RS485. CAN
контроллер умеет очень надёжно передавать письма размером до 8 байт,
даже если желающих контроллеров передать своё письмо в одно и тоже
время много.
Для организации порядка для «хором кричащих» в шину контрол-
леров был принят стандарт, определяющий структуру пакета, показан-
ного на рисунке 6.8. Как и в ceTH-RS485, в введено понятие активного
сигнала. И в качестве активного сигнала принят логический ноль, логи-
ческая единица передаётся как пассивный сигнал. Это означает, что у
активного сигнала приоритет выше. Другими словами, если хотя бы
один контроллер передаёт 0, а все остальные 1, то на шине будет 0. Это
обеспечивается на аппаратном уровне реализуя на шине логический
элемент «И».
Рисунок 6.8: Структура пакета CAN
242
Письмо-датаграмма начинается после периода молчания большего
чем нескольких тактов передачи одного бита, количество которых
можно настроить, обычно равно 7-ми тактам. Далее рассмотрим саму
датаграмму, пока полагая, что работает один спикер.
• SOF - Start of Frame. Начало сообщения, включает в себя 1 бит,
где передаётся 0, активный сигнал.
•Identifier - Идентификатор стандартного в отличии от ModBus -
передающего контроллера. Идентификатор содержит 11 бит или 29 бит
данных.
• RTR - Remote Transmission Request. Удалённый запрос на
передачу состоит из 1-го бита, передаётся пассивный уровень - 1.
• IDE - Сигнал для указания стандартного - 0 и расширенного - 1
форматов.
• R0 — резервный должен быть (0)
• DLC - Data Length Code. Длина кода данных включает 4 бита.
• Data Field - поле данных до 8 байт, которые передаются.
• CRC - контрольная сумма из 15-ти бит,
• CRC Delimiter - 16-ый бит разделитель, всегда пассивный сигнал.
• АСК Acknowledge - Подтверждение 1 бит, передатчик
отправляет - 1; получатель подтверждает - 0. Важно заметить, что в
формировании письма участвует не только передающий контроллер, но
и принимающий, который именно в это поле даёт активный сигнал. В
результате передающий контроллер установив пассивный сигнал в
момент этого бита ожидает активный ноль, который свидетельствует
ему, что его слушают. Если активного сигнала нет, то контроллер
повторит дата грамму ещё несколько раз, пока не увидит
подтверждения. После заданного числа попыток, не получив ни разу
подтверждения, контроллер выдаёт процессору сигнал, что письмо не
дошло.
• АСК Delimiter - Просто разделитель 1 бит, должен быть
пассивным сигналом
• EOF - End of Frame. Завершение сообщения состоит из 7-ми бит
пассивного сигнала. По сути, это и есть период молчания в сети, равный
семи тактам, после которого можно начинать новую датаграмму.
А что, если несколько контроллеров начали передавать разом. Тогда
они попортят друг другу процесс передачи. Но этой трагедии не проис-
ходит, потому что на аппаратном уровне выполнена процедура отмены
передачи контроллером, если его приоритет ниже чем у остальных пере-
дающих контроллеров. Момент отмены передачи определяется просто,
согласно правилу: если вовремя передачи идентификатора контроллер
243
передавая пассивный сигнал увидел активный, то вместе с ним передаёт
сигнал другой контроллер с большим приоритетом. В результате, при
одновременной передачи датаграммы процесс передачи закончится,
только у того контроллера, у которого значение идентификатора было
минимальное. На рисунке 6.9 показаны моменты отключения,
проигравших «битву» за право передать датаграмму.
Рисунок 6.9: Определение приоритета CAN контроллера
Из рисунка видно, что 1-ый передатчик на 3-м такте обнаруживает О,
хотя передал 1, поэтому дальше в шину активные сигналы не передаёт.
Аналогично отключается второй передатчик на 4-м такте. И только
третий передатчик беспрепятственно отправляет дата грамму с первой
попытки.
А что с остальными? Как только третий отправит свою датаграмму,
процесс начнётся заново для 1-го и 2-го передатчика. Не сложно дога-
даться, что на это раз повезёт 2-му передатчику. В результате, без всяких
задержек, стройно и по порядку и без задержек между пакетами будут
отправлены все датаграммы.
Кроме того, что контроллер способен вовремя замолчать и дождав-
шись своей очереди отправить пакет, он может содержать приёмные и
передающие почтовые ящики. Количество таких ящиков у процессоров
может быть разное в зависимости от сложности контроллера. Но даже у
самых простых контроллеров типа STM32flO3 структура достаточна
богатая. На рисунке 6.10 показана структура почтовых ящиков CAN
процессора STM32F103.
244
Рисунок 6.10: Структура почтовых ящиков CAN процессора STM32F103
В передатчике имеется три почтовых ящика, имеющих статус -
пустой или загруженный. Передатчик «прослушивает» шину и посто-
янно начинает передавать данные, если у него хотя бы один ящик
загружен данными. Соблюдая вышеуказанные правила общения в шине,
в своё время передаёт содержимое заполненного ящика. И, в случае
успеха опустошает ящик и сообщает процессору о том, что имеется
свободный ящик. В результате процессор, если у него есть что отпра-
вить, может заполнить ящик новым письмом. При этом программа
процессора не занимается передачей данных, но всего лишь укладывает
письма ящики по мере их освобождения.
Приёмник устроен несколько сложнее. Дело в том, что в шине CAN
может появляться огромное количество писем, которые не интересны
программе процессора. Но попробуем представить ситуацию, когда вы
ждёте письма, которое вместе со всеми письмами, пришедшими в ваш
город вываливается в общую кучу на центральной площади. Тогда вам
нужно постоянно перебирать все письма, пришедшие в город. Эту
рутинную работу выполняют наши доблестные почтальоны. И чтобы
вам не ковыряться в этой куче писем, вы поручаете почтальону дать вам
уведомление только по тем письмам, которые обладают признаками. Для
этого в CAN контроллере есть 27 отдельно настраиваемых фильтров,
позволяющих из огромного потока пакетов зафиксировать только
245
нужные и интересные. После совпадения с правилами фильтров письмо
попадает в свободный ящик одного из двух приёмников. Как только
пакет скопирован в ящик, процессору приходит уведомление, что ящик
содержит данные, их нужно взять проанализировать в программе и
освободить ящик для следующих писем.
Фильтры CAN приёмника весьма гибкие и, следовательно, доста-
точно сложно настраиваемые. Описание работы фильтров представлено
на сленге администраторов TCP сетей, и достаточно сложно восприни-
маются даже опытными программистами. По этой причине в учебниках
и инструкциях приведены стандартные настройки фильтров на
заданный тип пакета или на группу пакетов.
В этом разделе представлен только принцип работы аппаратной
части CAN сети. Для передачи регистров, архивов и других данных
необходимо реализовать программный протокол, использующий аппа-
ратную часть. На момент написания пособия уже имелись принятые
стандартные протоколы такие как CAN Open, Can Bus, Device Net.
Однако все они на стадии развития и являются собственностью
компании или группы компаний. К сожалению, сложно рекомендовать к
изучению эти программные протоколы, поскольку они не являются
полностью открытыми и не стандартизированны подобно ModBus. Тем
не менее, разработчик может сам определить программный уровень
обмена данными между ПЛК и использовать его.
Вопросы к разделу.
1. Укажите недостатки ModBus и как они устраняются в других
физических протоколах
2. Как работает физический уровень CAN?
3. Понятие почтовых ящиков в CAN.
6.3. ОРС серевер
Рассматривая предыдущие средства передачи данных между ПЛК и
другими устройствами можно заметить, что эти средства связи ничего
не говорят о физических характеристиках значений. Передаются только
значения отличающиеся адресом устройства и адресом в массиве
данных устройства. Для того чтобы разобраться как значения регистров
соответствуют физическим величинам к программе ПЛК поставляется
документация для расшифровки значения регистра. К примеру, регистр
с адресом 0x40003 содержит целое число и значение скорости измеря-
емое в сотых долях от тысячи оборотов в минуту. То есть, целое
значение регистра равное 220 соответствует 2,2 тыс. оборотов в минуту.
246
Чтобы построить SCADA систему нужно пересчитать каждый регистр в
физическую величину и в удобном виде разместить на НМ1-панелях.
Для того, чтобы разработчик не тратил время на скрупулёзную
работу по изучению таблиц, программисты придумали сервер, который
способен с помощью различных протоколов, включая ModBus, собрать
данные. Далее в удобном и автоматизированном виде передать разработ-
чику SCADA системы. Основным типом передаваемых данных является
понятие ТЭГ.
ТЭГ - некая структура данных, привязанных к переменной. Эта
структура, кроме значения переменной, имеет дополнительные поля:
название, описание, имя физической величины, дата и время последнего
считывания, оценка качества значения и т. д.. ТЭГ также может быть
группой, что позволяет строить древовидные структуры данных объекта
управления.
Среди элементов структуры ТЭГ-а есть обязательные свойства,
которые перечислены ниже:
•Текущее значение переменной, ее тип и права доступа (чтение
и/или запись).
• Качество переменной зависит от выхода измеряемой величины за
границы динамического диапазона, отсутствии данных, ошибки связи и
других параметров. Обычно принимает значения: хорошее, плохое,
неопределенное и дополнительная информация.
•Метка времени сообщает о времени, когда переменная получила
данное значение.
•Частота опроса переменной ОРС-сервером задает время
обновления значения переменной.
• Описание переменной, которое содержит информацию для
пользователя о том, что представляет собой эта переменная.
На рисунке 6.11 показано диалоговое окно стандартной SCADA,
где подключён один из ОРС-серверов. Как видно из рисунка, после
соединения на экране появляется древовидная структура данных,
доступных серверу. Для этого в протоколе ОРС имеется несколько стан-
дартных команд для начала общения.
Другими словами, разработчик берет ПЛК-«чёрный ящик» с ОРС
сервером. Открывает окно и подключившись, как бы спрашивает: кто ты
такой и что может показать?
247
Рисунок 6.11: Подключение к ОРС и древовидная структура данных
Кроме команд для знакомства, есть команды для запроса данных.
На рисунке 6.12 показано диалоговое окно с данными из структуры
ТЭГа, где есть значение, описание, качество данных и время последнего
обновления данных.
Как видно, достаточно просто пользоваться ОРС-сервером. Чтобы
подключить значение переменной к HMI-панели достаточно:
• подключится к серверу и увидеть дерево ТЭГов;
• в дереве выбрать интересующий нас ТЭГ из всех, просматривая
их описание;
• указать поле названия и значения ТЭГа для элемента HMI-панели.
Таким образом, ОРС-сервер несмотря на свою сложность весьма
просто использовать, гораздо легче, чем использование низкоуровневых
протоколов типа ModBus. Это стало причиной широкого распростра-
нения ОРС, как основного и самого популярного средства передачи
данных в SCADA системах.
248
Qnlopc Стенд испытател1>ны><пктснд.п1п
Файл Устройства Свойства Помощь
El & NL16HV
S 4* NL8TI
В laboratory}?
Тор
Mddle
Bottom
*+j Ter most at
E ♦+» Compressor
♦X; Pressure
Lt & NL8A1
Hawatrie | Описание | Значение
Датчик справа 71 з
Датчик слева 69.9
| Резу/ътат | Время
/1П4
Vin3
ОС
ОК
18.01.2008- 10:57:21
18.01.2008- 10:57:21
Рисунок 6.12: Панель значений ТЭГ-ов
Передача данных через сервер может быть выполнена в разных
режимах. Приняты четыре стандартных режима чтения данных из
ОРС-сервера:
• синхронный режим: клиент посылает запрос серверу и ждет от
него ответ;
• асинхронный режим: клиент отправляет запрос и сразу же
переходит к выполнению других задач. Сервер после выполнения
функции запроса посылает клиенту уведомление и тот забирает
предоставленные данные;
• режим подписки: клиент сообщает серверу список тегов, значения
которых сервер должен отправлять клиенту только в случае их
изменения. Для того, чтобы шум данных не был принят за их изменение,
вводится понятие "мертвой зоны", которая слегка превышает
максимально возможный размах помехи;
•режим обновления данных: клиент вызывает одновременное
чтение всех активных тегов. Активными называются все теги, кроме
обозначенных как "пассивные". Такое деление тегов уменьшает загрузку
процессора обновлением данных, принимаемых из физического
устройства.
При выборе ПЛК проектирующие инженеры предпочитают те, для
которых разработан и существует в продаже ОРС-сервер, так как его
наличие освобождает от ответственности разработчика в плане обеспе-
чения диспетчеризации и передачи данных.
Однако у технологии разработки и реализации ОРС-сервера есть
существенный недостаток. Чтобы пояснить проблему, рассмотрим
249
структурную схему взаимодействия ОРС-клиентов и серверов, пока-
занную на рисунке 6.13.
ОРС Client
ПК
MES, ERP
Рисунок 6.13: Структура взаимодействия ОРС клиентов и серверов
На персональных компьютерах, связанных с управленческим
персоналом обычно устанавливается следующее ПО:
• ERP (Enterprise Resource Planning) - Планирование ресурсов
предприятия, включающее управление финансами, персоналом и
операциями (логистика, снабжение, сбыт ... );
• MES (Manufacturing Execution System) - Оперативное управление
производством, включающее в себя множество задач для обеспечения
эффективности и качества продукции.
Всё это ПО взаимодействует с программой-ОРС-клиентом.
ОРС-сервера обычно включены в состав ПО SCADA системы,
вместе с драйверами устройств, у которых нет ОРС, но есть свой
протокол или ModBus (на рисунке это две левые ветки). Также
ОРС-сервер и клиент могут быть включены в состав ARM оператора.
Иногда ОРС-сервер установлен на промежуточное устройство,
которое, собственно, и предназначено для того, чтобы простейшие
модули и даже просто датчики были доступны в SCADA.
В результате все устройства и ПК могут передавать и принимать
данные через Ethernet сеть. Однако передача данных происходит не по
250
стандартным открытым TCP протоколам, но по протоколу обмена
DCOM (Distributed Component Object Mode).
DCOM предназначен для обмена объектами программ, запущенных
на различных дистанционно разнесенных компьютерах по сети.
Построенное на OLE-технологии (Object Linking and Embedding) взаи-
модействия программ в среде Windows. Эта технология позволяет
связывать и внедрять компоненты сторонних программ в другие
программы, документы и объекты. Примером из повседневного исполь-
зования может быть редактор формул MatType, поскольку это отдельная
программа, но в word-документах формулы реализуются сторонней
программой. Данная технология, разработана корпорацией Майкрософт,
сейчас называется ActiveX, полностью принадлежит компании и
исходный код до сих пор закрыт и не планируется быть в открытом
доступе. В результате, использование ОРС клиентов и серверов полно-
стью зависит от корпорации Майкрософт. Это позволяет корпорации
зарабатывать на своём ПО везде, где требуется ОРС. Другими словами,
чтобы был ОРС, нужно использовать компьютер и даже ПЛК с операци-
онной системой Windows. Типовое решение обеспечения ОРС-техно-
логии передачи данных для ПЛК, модулей и датчиков показан на
рисунке 6.14.
Рисунок 6.14: Типовое решение обеспечения ОРС для ПЛК, модулей и датчиков
Таким образом, зависимость ОРС технологии от закрытых прото-
колов OLE, ActiveX, DCOM является существенным недостатком.
Возможно по этой причине сложно развивается ПО с открытым
исходным кодом в ОС Linux, Android и т. д.
Прежде чем представить альтернативные решения по поддержке
функций, доступных в ОРС-технологии, рассмотрим исторический
251
сформированные стандарты для ОРС-серверов. Стандарт ОРС состоит
из нескольких частей:
• ОРС DA (ОРС Data Access) - спецификация для обмена данными
между клиентом (например SCADA) и аппаратурой (контроллерами,
модулями ввода-ввода и др.) в реальном времени.
• ОРС Alarms & Events (А&Е) - спецификация для уведомления
клиента о событиях и сигналах тревоги, которые посылаются клиенту
по мере их возникновения. Этот сервер пересылает аварийные сигналы,
действия оператора, информационные сообщения, результаты контроля
состояния системы.
• ОРС HDA (Historical Data Access) - спецификация для доступа к
предыстории процесса (к сохраненным в архиве данным). Сервер
обеспечивает унифицированный способ доступа с помощью DCOM
технологии. Обеспечивает чтение, запись и изменение данных.
• Batch - спецификация для особых процессов, которые не являются
непрерывными. В таких процессах работа выполняется согласно
рецепту. ОРС-сервер выполняет обмен между клиентом и сервером
рецептами, характеристиками технологического оборудования,
условиями и результатами обработки.
• ОРС Data exchange - спецификация для обмена данными между
двумя ОРС DA серверами через сеть Ethernet.
• ОРС Security - спецификация, которая определяет методы доступа
клиентов к серверу, которые обеспечивают защиту важной информации
от несанкционированной модификации.
• ОРС XML-DA - набор гибких, согласующихся друг с другом
правил и форматов для представления первичных данных с помощью
языка XML, веб технологий и сообщений SOAP (см. раздел
"Архитектура автоматизированной системы".).
• ОРС Complex Data - дополнительные спецификации к ОРС DA и
XML-DA, которые позволяют серверам работать со сложными типами
данных, такими как бинарные структуры и XML-документы.
• ОРС Commands - набор программных интерфейсов, который
позволяет ОРС клиентам и серверам идентифицировать, посылать и
контролировать команды, исполняемые в техническом устройстве (в
контроллере, модуле ввода-вывода).
• ОРС Unified Architecture - унифицированная архитектура,
реализующая функциональность и стандарты современной технологии
ОРС. Этот стандарт никак не связан OLE-технологией доступа к
данным. Весь функционал ОРС, перечисленный выше реализован на
открытых протоколах передачи данных в TCP-сетях, включая все
252
современные наработки в области интернет протоколов: Https, ssh, xml и
т. д„
На рисунке 6.15 показана структура ОРС Unified Architecture.
От К От К
ОРС UA ОРС UA ОРС UA ОРС UA
клиента клиенту ▲ клиента клиенту
Рисунок 6.15: Структура OPS UA.
В начале отметим сходства с ОРС-сервером на базе DCOM, которое
можно сформулировать в виде правила. Все что не связано с DCOM
может присутствовать OPS UA. В частности, ПО драйверов для
контроллеров, датчиков, низкоуровневых протоколов остаётся прежним
или доработанным для развития функциональных возможностей. В
остальном, все кардинально отличается.
Во первых? понятие ТЭГ заменено на более внятное понятие
«Узел». Узел содержит практический всю информацию ТЭГ-а и
оснащён новыми функциями, необходимыми для взаимодействия с
современными интернет сетями. Кроме функций доступа к данным ПЛК
и других устройств добавлены функции и события ядра операционной
системы сервера для своевременного оповещения ожидающих клиент-
253
ских программ. Конечно, тем кто не знаком с программированием
сложно понять, что это за функции, события, процедуры обратного
вызова функций и т. д.. По этой причине можно предложить осмыслить
эту всю функциональность на примере взаимодействия владельца
смартфона в социальной сети.
Первое что делает пользователь социальной сети: подключается к
сайту (это запрос) и смотрит материал сайта (это ответ). Такой тип
общения, когда один спрашивает, второй отвечает - так часто и назы-
вают: «Запрос-ответ», см. рисунок 6.15 слева.
Второе, что может сделать пользователь социальной сети, это
подписаться на новость (новая фотография или обновление ленты). Для
этого как минимум нужно оставить номер телефона или адрес элек-
тронной почты для получения уведомления. В результате, клиент не
отслеживает неизменяемые параметры, но получает уведомление о том,
что параметр поменялся, см. рисунок 6.15 справа.
В результате ядро ОРС UA-сервера становится многофункцио-
нальной системой очень похожей на мощный WEB-сервер, способной
регистрировать клиентов, проверять обновления и изменения, рассылать
сообщения ит. д.. На рисунке 6.16 наглядно показано различие режимов
запрос-ответ и подписки.
Клиент - Сервер
Рисунок 6.16: Два типа доставки данных в ОРС
Издатель • Подписчик
ОРС Client
Подписчик
ОРС Client
Подписчик
ОРС Client
Подписчик
В режиме запрос-ответ количество связей гораздо больше и этот
факт является недостатком. Поскольку одна и та же информация пере-
даётся несколько раз и часто, даже при отсутствии изменений и нужды в
обмене данными. В режиме подписки минимизируется количество пере-
даваемых данных, при обсечении своевременного оповещения о измене-
ниях. Это позволяет экономить трафик сети и повышать быстродействие
обмена данных в SCADA системах.
254
На рисунке 6.17 показана структура из рисунка 6.13 на базе
ОРС UA-сервера. Как видно, наследие DCOM полностью исключена,
при этом повышена функциональность сервера.
Рисунок 6.17: Название
Ядро ОРС UA-сервера может быть включена, как в ПО персональ-
ного компьютера, так и в ПЛК различной сложности и даже в простые
датчики. Конечно, сложно представить, что сервер можно установить в
датчик размером со спичечный коробок. Однако, это возможно
поскольку на рынке появилась микросхема ESP8266 и более совер-
шенная ESP32 с поддержкой WiFi и встроенным АЦ,П. Микропроцессор
ESP8266 настолько мелкий, что его сложно паять вручную, поэтому на
базе этого процессора выпускаются устройства типа ESP-O1. Это
255
устройство имеет размер 15 мм длиной и 10 мм шириной. На
рисунке 6.18 показано изображение этого устройства.
Рисунок 6.18: ESP-01 на базе ESP82632
К этому устройству прилагается огромное количество открытых
для изучения и использования разработок для систем умных домов и
устройств из серии интернет вещей IoТ. В результате, ОРС UA пригоден
не только для передачи данных между контроллерами и SCADA
системой, но и на полевом уровне от датчиков и 1оТ устройств к
контроллерам, а также от локальных систем в облачный сервис
хранения данных.
Поскольку стандарт только развивается, разработчики планируют
разбить стандарт ОРС UA на 4 части в зависимости от производитель-
ности устройства и необходимых ему возможностей.
1. Nano Embedded Device Server: подходит для самых маленьких
датчиков;
2. Micro Embedded Device Server: подходит для недорогих ПЛК;
3. Embedded UA Server: подходит для более мощных ПЛК и погра-
ничных шлюзов;
4. Standard UA Server: полноценная реализация, поддерживающая
все функции.
В заключении отметим, что если вы планируете изучать програм-
мирование и заниматься развитием АСУ ТП, то можете стать пионером
в становлении нового направления развития OPC-UA-сервера. Можете
внести свой вклад в становление данного программного продукта,
поскольку проект развивается как свободный с открытым исходным
кодом.
Вопросы к разделу.
1. Что такое ТЭГ?
2. Какие режимы передачи используются в ОРС?
3. Какие расширения протокола ОРС знаете?
4. В чем принципиальное отличие ОРС UA?
256
5. Какие приняты уровни реализации ОРС UA?
Заключение
В пособии представлен материал, позволяющий освоить методы
программирования контроллеров и построения SCADA системы в
задачах, где требуется знание теории автоматического управления.
Основная цель пособия заключается в формировании у обучающихся
связей, навыков и подходов для использования знаний ТАУ в практиче-
ских задачах с использованием средств разработки для ПЛК.
Изучение материалов глав сопровождается практическими приме-
рами, которые можно реализовать и протестировать среде CoDeSys. Это
позволяет студенту достаточно быстро освоить методы создания
программ для ПЛК и уверенно использовать эти навыки на практике.
В пособии не преследовалась цель обучения программированию
контроллеров, поскольку для этого существует достаточно много спра-
вочной литературы и готовых открытых проектов для различных задач
управления технологическими процессами. Поэтому для дальнейшего
изучения рекомендуется посетить обучающие семинары производителей
ПЛК и SACDA систем. Однако возникающие проблемы у инженеров,
проектирующих САУ, связанные с построением и настройкой замкнутых
динамических систем обычно там глубоко не рассматриваются ссылаясь
на материалы ТАУ Данное учебное пособие может быть весьма полезно
именно в свете таких задач, поскольку достаточно подробно описаны
методы реализации замкнутых САУ, включая нелинейные системы.
Учебное пособие может быть полезно как инженерам проектиру-
ющим системы управления замкнутыми динамическими контурами, так
и студентам, освоившим ТАУ, для выполнения первых шагов в области
программирования контроллеров и построения систем управления на
практике.
257
Список условных обозначений и сокращений
• GPIO - General Port Input-Output. Базовый порт ввода вывода.
Обычно это унифицированный порт.
• SPI- Serial Port Interface.
• АСУ ТП - Современные автоматизированные системы
управления технологическими процессами.
• HMI - Human Machine Interface.
• SCADA - Supervisor Control And Data Acquisition.
• ПЛК - программируемый логический контроллер
• ЦП - центральный процессор
• АЛУ - арифметическо-логическое устройство
• ПЗУ - постоянное запоминающее устройство
• ОЗУ - оперативное запоминающее устройство
• АВР - автоматический ввод резерва
• АЧР - автоматическая частотная разгрузка
• АПВ - автоматическое повторное включение
• ЧАПВ - частотное автоматическое повторное включение
• КБ - конденсаторная батарея
• КРМ - компенсация реактивной мощности
• PLC - programmable logic controller
• CodeSys - Controller Development System
• SCADA - Supervisory Control And Data Acquisition
• DDE - Dynamic Data Exchange
• OLE - Object Linking and Embedding
• OPC - OLE for Process Control
• POU - Program Organization Unit
• IL - Instruction List
• ST - Structured Text
• SFC - Sequential Function Chart
• FBD - Function Block Diagram
• LD - Ladder Diagram
• CFC - Continuous Function Chart
Глоссарий
• Pin - контакт.
• Protection diode - защитный диод.
•Next
258
Список литературы
1. Калабеков Б.А. Цифровые устройства и микропроцессорные
системы: Учебник для Техникумов связи / Б.А. Калабеков. - Горячая
линия-Телеком. 2003. - 336 с.
2 Микропроцессорные средства и системы: курс лекций / Д.Н.
Беклемишев , А.Н. Орлов , А.Л Переверзев и др.; М.: МИЭТ, 2013. -
288 с.
3. Микушин А. В. Цифровая схемотехника: монография / А. В.
Микушин, В. И. Сединин. - Сибирский государственный университет
телекоммуникаций и информатики. Новосибирск : СибГУТИ, 2016.
328 с.
4. Димитрова М. И. 33 схемы с логическими элементами И-НЕ:
пер. с болг. / М. И. Димитрова, В. П Пунджев. - Л.: энергоатомиздат.,
1988.- 112 с.
5. Угрюмов Е.П. Цифрова схемотехника. - Спб.: Петербург: БХВ,
2004,- 528 с.
6. http ://www. que s 10. com/p/2 858O/write-a-note-on-different-types-
of-memories-in-emb/
7. Микушин А. В. Программирование микропроцессоров
семейства MCS-51: Монография. / А. В. Микушин, В. И. Сединин. -
Сибирский государственный университет телекоммуникаций и
информатики. Новосибирск, 2016. 177с.
8. Микушин А.В. Программируемые логические матрицы. / 2001-
2019. - Режим доступа: http://digteh.ru/digital/PLA/
9. Каршенбойм И. Микропроцессор своими руками - Ассемблер
и софтсимулятор. // Компоненты и технологии, 2006, No 3. - с. 154-159.
10. Каршенбойм И. Микропроцессор своими руками - Ассемблер
и софтсимулятор. // Компоненты и технологии, 2006, No 4. - с.200-204.
11. Тарасов И. Проектирование конфигурируемых процессоров на
базе ПЛИС. // Компоненты и технологии, 2006, No 2. - с. 78-83.
12. Тарасов И. Проектирование конфигурируемых процессоров на
базе ПЛИС. // Компоненты и технологии, 2006, No 4. - с. 68-73.
13. Довгий П. С.Прикладная архитектура базовой модели
процессора Intel. Учебное пособие по дисциплине «Организация ЭВМ и
систем». /И. С. Довгий, В. И. Поляков. - СПб.: НИУИТМО, 2012. - 115
с.
14. Пономарев В. Новые микроконтроллеры фирмы
STMicroelectronics на базе ядра ARM Cortex-МЗ ЭЛЕКТРОНИКА:
Наука, Технология, Бизнес 6/2007 С. 50- 55.
259
15. Trevor Martin, Insider's The Guide to the STM32 ARM based
micricontroller - Published by Hitex (UK) Ltd - United Kingdom P. 91.
16. Шило В.Л. Функциональные аналоговые интегральные
микросхемы. - М.: радио и связь, 1982. - 128 с.
17. Sigma-Delta ADC Tutorial/Analog Devices, 1995-2019. -Режим
доступа:
https://www.analog.com/en/design-center/interactive-design-tools/sigma-
delta-adc-tutorial.html
18. Kester W. ADC Architectures I: The Flash Converter. Analog
Devices, MT-020 Tutorial. - Режим доступа:
www.analog.com/static/imported- files/tutorials/MT-020.pdf
19. Kester W. ADC Architectures II: Successive Approximation ADC.
Analog Devices, MT-021 Tutorial. - Режим доступа:
www. analog. com/static/imported-files/tutorials/MT-021 .pdf
20. Kester W. ADC Architectures III: Sigma-Delta ADC Basics.
Analog Devices, MT-022 Tutorial. - Режим доступа:
www.analog.com/static/imported-files/tutorials/MT-022.pdf
21. Kester W. ADC Architectures IV: Sigma-Delta ADC Advanced
Concepts and Applications. Analog Devices, MT-023 Tutorial. - Режим
доступа: www.analog.com/static/imported-files/tutorials/MT-023.pdf
22. Аналого-цифровое преобразование для начинающих /
«HABR», 2011. - Режим доступа: https://habr.com/ru/post/125029/
23. Общий принцип работы АЦП / «ФВ», 2016. - Режим доступа:
http://fb.ru/article/250298/obschiy-printsip-rabotyi-atsp
24. RM0008 Rev 20 Reference manual: STM32Flxxx /
STMicroelectronics, 2018. - Режим доступа:
https://www. st.com/resource/en/reference_manual/cdOO 171190.pdf
25. Ишматов 3. Ш. Микропроцессорное управление
электроприводами и технологическими объектами. Полиномиальные
методы, Монография. — Екатеринбург: УГТУ-УПИ, 2008. — 278 с.
26. ГОСТ 34.003-90. Комплекс стандартов на автоматизированные
системы. Термины и определения.
27. Пронин Д.А. Применение протокола Ethernet в системах
АПИС КУЭ Автоматизированная информационно-измерительная
система коммерческого учёта электроэнергии // «ИСУП», № 3(27)_2010
36. С. 50-52.
28. Рушкин Е.И., Семёнов А.С., Саввинов П.В. Анализ
применения протокола MODBUS для управления электроприводом на
горных предприятиях // Фундаментальные исследования. - 2014. - №
11-12. - С. 2615-2619;URL:
260
http://www.fundamental-research.ru/ru/article/view?id=36032 (дата
обращения: 24.02.2019)
29. Сетевые протоколы [Электронный ресурс] - Режим доступа:
http://bourabai.ru/dbt/protocols.htm, (дата обращения: 24.02.2019).
30. Денисенко, В.В. Современные технологии
автоматизации/В.В.Денисенко //Протоколы и сети Modbus и Modbus
ТСР.-2010.-№4.-С. 90-94.
31. Денисенко В.В. Компьютерное управление технологическим
процессом, инструментом, оборудованием. - М.: Горячая линия
Телеком, 2009. - 608 с., ил. ISBN 978-5-9912-0060.
32. Модуль управления драйвером шагового двигателя ZET 7060-S
[Электронный ресурс] - Режим доступа:
http s ://zetlab. com/shop/tsifr ovyie-datchiki/modul-upravleniya- shagovyim-
dvigatelem-zet-7060-s/, (дата обращения: 24.02.2019).
33. Орлов С. «Журнал сетевых решений/LAN», № 09, 2013
Ethernet и промышленные сети Режим доступа:
http ://www. osp.ru/lan/2013/09/13037411/37.
34. Третьяков С.A., CAN на пороге нового столетия, Мир
компьютерной автоматизации №2/99
35. Dmitry Zaitsev, Stanimire Tomov, Jack Dongarra. Solving Linear
Diophantine Systems on Parallel Architectures, IEEE Transactions on
Parallel and Distributed Systems, 05 October 2018. DOI:
10.1109/TPDS.2018.2873354
36. Майк Фарион Применение промышленного Ethernet // Control
engineering Россия, 2013 - выпуск 43 - С. 54-58
37. CANopen Application Layer and Communication Profile, CiA
Draft Standard 301, Version 4.02, Date: 13 February 2002
38. Миниатюрные контроллеры для управления шаговыми
двигателями с возможностью работы в сети CAN-Bus производства
UIRobot [Электронный ресурс] - Режим доступа:
https://electroprivod.ru/driver_cmd.htm, (дата обращения: 24.02.2019).
39. Анучин А.С., Обновление программного обеспечения
встроенных систем управления преобразователей частоты и источников
питания по CAN-сети, Электрооборудование: эксплуатация и ремонт
№3//2012, с.25-29.
Бесекерский В. Теория систем автоматического управления. —
М. :Профессия, 2007. — 752 с.
Ротач В. Теория автоматического управления. — М.:МЭИ, 2004. —
400 с.
261
Кориков А. М. Основы теории управления: учебное пособие. 2-е
изд. — Изд-во НТЛ, 2002. — 392 с.
Востриков А., Французова Г. Теория автоматического управления.
Учебное пособие. — Новосибирск : Изд-во НГТУ, 2006. — 368 с.
Гюнтер М. Теория автоматического управления: Учебное пособие.
— СПб. : Лань, 2016. — 224 с.
Гончарова И. ВИС: Теория управления. Конспект лекций. —
М. :Приор, 2006. — 224 с.
Гапоненко А., Савельева М. Теория управления: Учебник и
практикум для академического бакалавриата. — Люберцы : Юрайт,
2016, —336 с.
Власов К. Теория автоматического управления. Основные
положения. Примеры расчета: Учебное пособие. — Харьков : Туман.
Центр, 2013, —544 с.
Азаров Б., И.В. К. Теория систем управления: Учебное пособие. —
СПб. : Лань, 2013, —424 с.
Агажанов А. Теория автоматического управления: Учебное
пособие. — СПб. : Лань, 2010. — 224 с.
Топчеев Ю. Задачник по теории автоматического регулирования.
Учебное пособие. — М. : Машиностроение, 1977. — 592 с.
Даньков В., Скрипниченко М., Горбачёва Н. Теория
автоматического управления. Задачи и решения: Учебное пособие. —
СПб. : Лань, 2016. — 608 с.
Дьяконов В. П. MatLAB 6/6.1/6.5 + Simulink 4/5: основы
применения. — М : СОЛОН-Пресс, 2002. — 768 с.
Гюнтер Н. Теория автоматического управления (с использованием
MATLAB -SIMULINK): Учебное пособие. — СПб. : Лань, 2016. — 256
с.
Гуревич А., Корнев В.В Хромов А. Теория автоматического
управления в примерах и задачах с решениями в MATLAB: Учебное
пособие. — СПб. : Лань, 2016. — 464 с.
Агравал Г. Системы автоматического управления: теория,
применение, моделирование в MATLAB: Учебное пособие. — СПб. :
Лань, 2013, —208 с.
Башарин А., Новиков В., Соколовский Г. Управление
Электроприводами. — Л. : Энергия, 1982. — 392 с.
Ловчаков В., Сухинин Б., Сурков В. Оптимальное управление
электротехническими объектами. — Тула : Изд-во ТулГТУ, 2004. —149
с.
262
Юревич Е. Теория автоматического управления. 4-е изд., пер. и доп.
— СПб. : BHV, 2016. — 560 с.
Усынин Ю. Теория автоматического управления: учебное пособие
для вузов. — Челябинск : Издательский центр ЮУрГУ, 2010. —176 с.
Тутубалин В. Теория вероятностей и случайных процессов. Основы
математического аппарата и прикладные аспекты. — М.:МГУ, 1992. —
400 с.
Денисенко В. ПИД-регуляторы: вопросы реализации // СТА. —
2007. — № 4. — С. 86—97.
Денисенко В. ПИД-регуляторы: вопросы реализации // СТА. —
2007,—№ 1, —С. 86—99.
Денисенко В. ПИД-регуляторы: принципы построения и
модификации. Часть 1 // СТА. — 2006. — № 4. — С. 45—50.
Денисенко В. ПИД-регуляторы: принципы построения и
модификации. Часть 2 // СТА. — 2007. — № 1. — С. 78—88.
Денисенко В. Разновидности ПИД-регуляторов // Автоматизация в
промышленности. — 2007. — № 6. — С. 45—50.
Денисенко В. Непараметрическая модель объекта управления в
ПИД регуляторах с автоматической настройкой // Приборы и системы.
Управление, контроль, диагностика. — 2009. — № 6. — С. 9—13. —
Глава 5.
Silva G., Datta A., Bhattacharyya S. New results on the synthesis of PID
controllers // IEEE Transactions on Automatic Control. — 2002. — Feb. —
Vol. 47, no. 2, —P. 241-252.
Kristiansson B., Lennartson B. Robust PI and PID controllers including
Smith predictor structure // Proceedings of the 2001 American Control
Conference. — 2001. — Vol. 3. — P. 2197-2202.
Ivanova E., Hadjiski M. Rules based adaptation of Smith predictor. -
Intelligent Systems, 2002. Proceedings // 2002 First International IEEE
Symposium. — 2002. — Vol. 3. — P. 26-30.
Ротач В. Настройка регуляторов модифицированным методом
Циглера-Николса. // Промышленные контроллеры АСУ. — 2008. — Т. 2.
— С. 38^42.
Автоматическая настройка и адаптация в промышленных ПИД
регуляторах. / А. Шубладзе [и др.] // Приборы и системы. Управление,
контроль, диагностика. — 2007. — Т. 13. — С. 26—30.
Оптимальные автоматически настраивающиеся
общепромышленные регуляторы / А. Шубладзе [и др.] // Приборы и
системы. Управление, контроль, диагностика. — 2002. — Т. 10. — С. 30
—33.
263
Silva G., Datta A., Bhattacharyya S. On the Stability and Controller
Robustness of Some Popular PID Tuning Rules // IEEE Trans, on Automatic
Control. — 2003. — Sept. — Vol. 48, no. 9. — P. 1638-1641.
A tuning algorithm for the PID controller utilizing fuzzy theory / H.-S.
Hwang [et al.] // International Joint Conference on Neural Networks. —
1999. — Vol. 4. — P. 2210-2215.
Hemerly E. PC-based packages for identification, optimization, and
adaptive control // IEEE Control Systems Magazine. — 1991. — Feb. — Vol.
11, no. 2, —P. 37^13.
Self-tuning IMC-PID control with interval gain and phase margins
assignment / W. Ho [et al.] // IEEE Transactions on Control Systems
Technology. — 2001. — May. — Vol. 9, no. 3. — P. 535-541.
Ho H., Wong Y, Rad A. Adaptive PID controller for nonlinear system
with tracking performance // Physics and Control. — 2003. —Aug. —Vol. 4.
— P. 1315-1319.
Абдрахманов В., A.B. P. Элементы вариационного исчисления и
оптимального управления. Теория, задачи, индивидуальные задания:
Учебное пособие. — СПб. : Лань, 2014. — 112 с.
Диевский В., Малышева И. Элементы вариационного исчисления и
оптимального управления. Теория, задачи, индивидуальные зада ния:
Учебное пособие. — СПб. : Лань, 2014. — 112 с.
Афанасьев В., В.Б. К. Математическая теория конструирования си
стем управления. — М. : Высшая школа, 2003. — 614 с.
Гайдук А. Теория и методы аналитического синтеза систем
автоматического управления(полиномиальный подход). — М. :
Физматлит, 2012. — 360 с.
Гайдук А. Б. В. Теория автоматического управления в примерах и
задачах с решениями в MATLAB: Учебное пособие. — СПб. : Лань,
2016.—464 с.
Hodel A., Hall С. Variable-Structure PID Control to Prevent Integrator
Windup // IEEE Trans, on Industrial Electronics. — 2001. — Vol. 48, no. 2.
P. 442^151.
Аграчев А., Ю.Л. С. Геометрическая теория управления. — M. :
Физматлит, 2005. — 392 с.
Богословский С. Теория нестацинарного управления: Учебное
пособие. — СПб : ГОУ ВПО СПбГУАП, 2011. — 380 с.
Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети,
генетические алгоритмы и нечеткие системы. — М.:Горячая линия
Телеком, 1006. — 383 с.
264
Усков А., Кузьмин А. Интеллектуальные технологии управления.
Искусственные нейронные сети и нечеткая логика. — М.:’’Горячая
линия-Телеком”, 2004. — 143 с.
Терехов В., Ефимов Д., Тюкин И. Нейросетевые системы
управления. — М.:Изд. журнала ’’Радиотехника”, 2002. — 480 с.
Цыпкин Я. Основы информационной теории идентификации. —
М. Лаука, 1984, —320 с.
Ротач В. К расчету оптимальных параметров реальных
ПИД-регуляторов по экспертным критериям // Промышленные АСУ и
контроллеры. — 2006. — Т. 2. — С. 22—29.
Ким Д. Теория автоматического управления. Том 2. Многомерные,
нелинейные, оптимальные и адаптивные системы. — М. : Физматлит,
2007. — 440 с.
Keel L., Rego J., Bhattacharyya S. A New Approach to Digital PID Con
trailer Design // IEEE Trans, on Automatic Control. — 2003. — Apr. — Vol.
48, no. 4. — P. 687-692.
Karimi A., Garcia D., Longchamp R. PID controller tuning using Bode’s
integrals. - Control Systems Technology // IEEE Transactions on. — 2003. —
Nov. — Vol. 11, no. 6. — P. 812-821.
Изерман P. Цифровые системы управления. — M. : Мир, 1984. —
541 с.
Сергиенко А. Цифровая обработка сигналов. — СПб. Литер. — 608
с.
Петров И. Программируемые контроллеры. Стандартные языки и
приемы прикладного проектирования / под ред. В. Дьяконова. —
М.:СОЛОНПресс, 2004. —256 с.
Ицкович Э. Современные алгоритмы автоматического
регулирования и их использование на предприятиях // Автоматизация в
промышленности. — 2007. — № 6. — С. 39—44.
Богданов С. Умный дом. - Наука и техника. — Санкт-Петербург,
2003, — 112 с.
265
Приложения
1.Первое приложение
Тексты первого приложения
2.Второе приложение
Тексты первого приложения, к примеру подготовленные ссылки:
PolyakovOl : Поляков А.Е. Метод функций Ляпунова для систем со
скользящими режимами высших порядков / А.Е. Поляков, А.С. Позняк //
Автоматика и телемеханика. - 201Е - No 5. - С. 47-68.
266
Учебное издание
ШИЛИН Александр Анатольевич
СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Учебное пособие
Научный редактор доктор технических наук,
профессор В.Г. Букреев
Корректура И.О. Фамилия
Компьютерная верстка М.Д. Марков, Д.В. Сотникова
Дизайн обложки С.М. Семенов
Подписано к печати 15.04.2022. Формат 60x84/16. Бумага «Снегурочка».
Печать CANON. Усл. печ. л. 9,07. Уч.-изд. л. 8,21.
Заказ 00-19. Тираж 100 экз.
Издательство
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
267