ВЫХОДИТ РАЗ В ДВЕ НЕДЕЛИ
Рекомендуемая розничная цена: 279 руб. Розничная цена: 49,90 грн, 990 тенге
ГОЛОВОЛОМКИ
КОЛЛЕКЦИЯ ЛОГИЧЕСКИХ ИГР ОТ D^AGOSTINI
Мозаика
занимательные
«ЗАНИМАТЕЛЬНЫЕ ГОЛОВОЛОМКИ» Издание выходил раз в две недели Выпуск №15,2012 РОССИЯ
ГОЛОВОЛОМКИ
КОЛЛЕКЦИЯ ЛОГИЧЕСКИХ ИГР ОТ D4AC.OS71NI
В этом выпуске:
ИЗДАТЕЛЬ. УЧРЕДИТЕЛЬ. РЕДАКЦИЯ: ООО «Де Агостини-, Россия ЮРИДИЧЕСКИМ АДРЕС? 105 066, г Москва, ул. Александра Лукьрнова,д.З, стр.1 Письма читателей по данному адресу не принимаются.
ГЕНЕРАЛ ЬНЫЙ ДИРЕКТОР: Николаем: Скилакмс ГЛАВНЫЙ РЕДАКТОР: Анастасия Жаркова
ФИНАНСОВЫЙ ДИРЕКТОР: Наталия Василенко КОММЕРЧЕСКИЙ ДИРЕКТОР: Александр Нкутов МЕНЕДЖЕР ПО МАРКЕТИНГУ: Михаил Ткачук МЛАДШИЙ МЕНЕДЖЕР ПО ПРОДУКТУ:
Любовь Мартынова
Свидетельство о регистрации средства массовой информации в федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор) ПИ N* ФС77-4331О ст 28.12 2010 г
Для заказа пропущенных номеров и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ru
по остальным вопросам обращайтесь по телефону бесплатной ।горячей пинии»в России:
С 8-800-200-02-01
Телефон ^горячей линии» для читателей Москвы:
С 8-495-660-02-02
АДРЕС ДЛЯ ПИСЕМ ЧИТАТЕЛЕЙ: Россия. 170100, г. Тверь, Почтамт, а/я 245, *Де Агостини», «Занимательные головоломка
РАСП РОСГРАНЕНИЕ:
ООО «Бурда Дистрибьюшеи Сервисна
УКРАИНА
ИЗДАТЕЛЬ И УЧРЕДИТЕЛЬ: ООО чДе Агостини Паблишинг, Украина ЮРИДИЧЕСКИЙ АДРЕС: 01032. Украина.
г. Киев, ул. Сакса ганс кого, д. 119 ГЕНЕРАЛЬНЫЙ ДИРЕКТОР: Екатерина Клименко
Свидетельство о государственной регистрации печатного СМИ Министерства юстиции Украины
КВ № 17502-6252Рот01 03 2011
АДРЕС ДЛЯ ПИСЕМ ЧИТАТЕЛЕЙ:
Украина. 01033. г. Киев, л/я «Де Агостини», пЗанИмательные головоломка
Укра'|на. 01033, м. Ките, а/с «Де АгоспнЬ
Для заказа пропущенных номеров и по всем вопросам, касающимся информации О коллекции, заходите на сайт www.deagostini ua
ПО остальным вопросам обращайтесь по телефону бесплатной «горячей линии- В Украине:
С 0-800 500-8-40
БЕЛАРУСЬ
ИМПОРТЕР И ДИСТРИБЬЮТОР В РБ: ООО «Росчерк». 220037, г. Минск, уп. Авангардная, д. 48а, литер В/к, тел ./факс: +37517 2-999-260
АДРЕС ДЛЯ ПИСЕМ ЧИТАТЕЛЕЙ: Республика Беларусь, 220040, г. Минск, д/я 224, ООО «Росчерки, лДе Агостини», ^Занимательные голо волом ил-
КАЗАХСТАН
РАСПРОСТРАНЕНИЕ: ТОО «КГП <Бурда- Алатау-Пресс*
РЕКОМЕНДУЕМАЯ РОЗНИЧНАЯ ЦЕНА: 279 руб. РОЗНИЧНАЯ ЦЕНА 49,90 грн, 990 тенге
ОТПЕЧАТАНО В ТИПОГРАФИИ: G. Canale & С 5 р А 5о$. Сетка 47, BuCuresti, Pantehmon - llfov, Romania,
ТИРАЖ: 68 ССОэкз.
Издатель оставляет за собой право изменять последовательность номеров и их содержание.
Издатель оставляет за собой право увеличить рекомендуемую цену выпусков.
Неотъемлемой частью каждого выпуска является приложение
Q ООО чДе Агостини, 2012
6 ЯВА Col^ccionables, 2011
ISSN 2225-1782
ДАТА ВЫХОДА В РОССИИ: 28 00 2012
МатематиЧ' cki is всаленн и
О взаимозависимости Интуитивное знание довольно часто помогает нам разобраться в сложных матсм этических понятиях. Случается, что в математике оно становится важным и необходимым компасом, но все же нс превращается в штурвал корабля: любая концепция, независимо от уровня интуиции, требует точного определения. Это особенно важно в тех областях, где существуют исключения, противоречащие любой интуиции.
Блистательные умы
К ночевия фигура ювреиеннои илинчитн^и Выступления и кни гп Жан-Пьера Серра неизменно восхищали слушателей остроумием, глубиной и удивительным балансом между точностью и доступностью. Се-рр — математик, получивший огромное количество наград в качестве признания св^их научных заслуг. Медаль Филдса, премия Гастона Жюлиа, премия Ьальцана — вот далеко не полный их перечень.
Математика на к’шдый дань
Прекр иный беспокойный аир Одномерный телефонный шг1 р. двумерная поверхность стола, трехмерный диван для отдыха.. Мы слышали и о четырехмерном пространстве, хотя и не сталкивались с подобным в евоей повседневной жизни. А знаете ли вы, как выглядит предмет, имеющий размерность 1,25?
Математически* аадачки
1учшее ош Cjlim ioiifLi Как правильно заказать футбольный мяч; кое-что о важности телосложения при перетягивании каната; как получить премию, придя на школьное занятие» — ответы на эти и другие заковыристые вопросы вы получите, решив задачки величайше-
го американского головоломщика.
Головоломки
Мозаика Сколькими способами четверо друзей могут сесть за круглый стол в ресторане * Если от вс г на этот вопрос для вас нс составляет труда, то и с нашей мозаикой вы справитесь играючи — ведь в ней всего лишь восемь квадратных фишек с четырьмя цветными точками на каждой. Получилось? Тогда попробуйте «найти пару» и сложить «радугу».
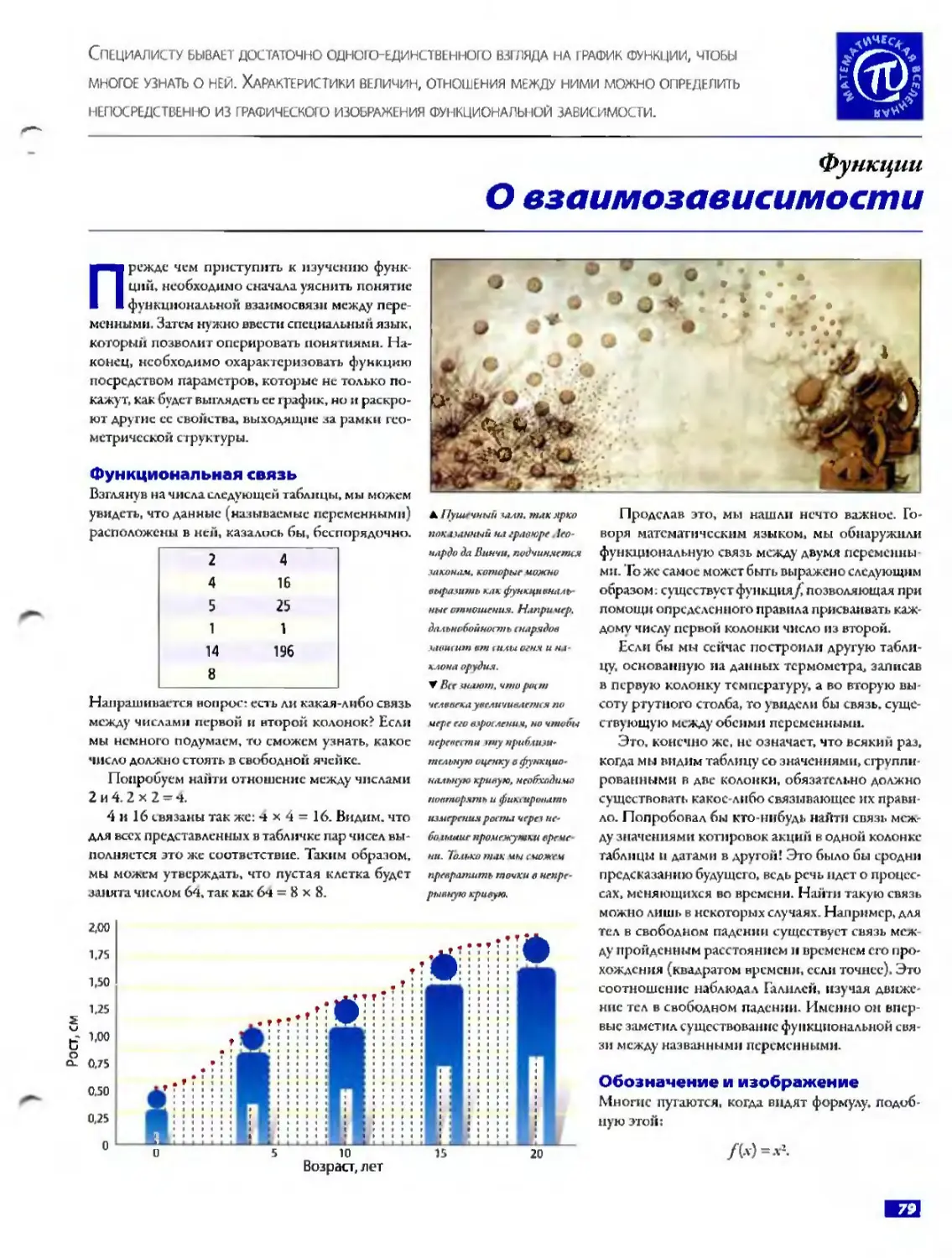
Специалисту бываеп достаточно одного-единственного взгляда на график функции, чтобы многое узнать о ней. Характеристики величин, отношения между ними можно определить непосредственно из графического изображения функциональной зависимости.
о
Функции
взаимозависимости
Прежде чем приступить к изучению функций, необходимо сначала уяснить поня тие функциональной взаимосвязи между переменными. Затем ну жно ввести специальный язык, который позволит оперировать пеня тиями. Наконец, необходимо охарактеризовать функцию посредством параметров, которые нс только покажут. как будет выглядеть ее i рафик, но и раскроют другие ее свойства, выходящие за рамки геометрической структуры.
Функциональная связь
Взглянув на числа следующей таблицы, мы можем увидеть, что данные (называемые переменными) расположены в ней, казалось бы, беспорядочно.
2	4
4	16
5	25
1	1
14	196
8	
Напрашивается вопрос: есть ли какая-либо связь между числами первой и второй колонок? Если мы немного подумаем, то сможем узнать, какое число должно стоять в свободной ячейке.
Попробуем найти отношение между числами 2 и 4.2 х 2 - 4.
4 и 16 связаны так же. 4x4 = 16. Видим, что для всех предс! авленных в табличке пар чисел выполняется это же соответствие. Таким образом, мы м«жем утверждать, что пустая клетка будет занята числом 64, так как 6ч = 8 х 8.
Л Пушечный мля. так ярко показанный ня гравюре. 1ео-нлрдо Лг Винчи, подчиняется законам, которые можно оыразюнъ как функциональные отношения. Напри мер, дальнобойность снарядов зависит от силы огня и агл-jc-mwtj орудия.
V Вес знают, что рен т человекаувеличивается по мере его взросления, но чтобы перевести эту приблизительную оценку в функциональную кривую, необходимо повторять и филировать измерения роста черел но бо мшив промежутки времени. Только так мы сможем превратить точки о непрерывную кривую.
Проделав это, мы нашли нечто важное. Говоря математическим языком, мы обнаружили функциональную связь между двумя переменны ми. То же самое может быть выражено следующим образом: существует функция^ позволяющая при помощи определенного правила присваивать каждому числу первой колонки число из второй.
Если бы мы сейчас построили другую таблицу. основанную на данных термометра, записав в первую колонку температуру, а во вторую высоту ртутного столба, то увидели бы связь, существующую между обеими переменными.
Это, конечно же, не означает, что всякий раз, когда мы видим таблицу со значениями, сгруппированными в две колонки, обязательно должно существовать какое-либо связывающее их правило. Попробовал бы кто ннбудь найти связь меж ду значениями котировок акций в одной колонке таблицы и датами в другой! Это было бы сродни предсказанию будущего, ведь речь идет о процессах. меняющихся во времени Найти такую связь
Рост, CM
можно лишь в некоторых случаях Например, для тел в свободном падении существует связь между пройденным расстоянием и временем его прохождения (квадратом времени, если точнее). Это соотношение наблюдал Гл хилей, изучая движс нис тел в свободном падении. Именно он впервые заметил существование функциональной связи между названными переменными.
Обозначение и изображение
Многие пугаются, когда видят формулу, подоб ную этой:
Ду)=^.
79
И хотя язык математики очень краток, тем нс менее, он одновременно и очень прост, ведь он должен быть нс только точен, но и удобен в применении. Предыдущее выражение означает, что перед нами функция f, которая каждому числу ставит
в соответ! гвие его квадрат:
/(2) -4;	/(5) = 25;	/(138) = 19044.
Можно сказать, что 1 — это образ 2, а 19044 — образ 138, и, обобщая, х1 — это обра х.
А вот эта формула, например.
^(ж) = 2х+1
означает, что для получения образа числа необходимо сначала умножив. его на 2, а татем к результату прибави гг> 1:
g(2) = 2x2 + 1 -5: u?(5) = 2x 5 + 1 = 11 £038) = 2 х 138+1 = 277.
В прсдыд) щем разделе мы видели таблицу значений и искали функцию, чтобы связать «данные числа. А если у нас уже есть функция, го пос троение таблицы — уже чисто механический процесс.
f м = Хг
X	f(x)
1	1
2	4
3	9
-I	1
-2	4
•3	9
х	gW
1	3
2	5
3	7
-1	-1
-2	-3
-3	-5
Графическое изображение
Более гого, мы .акже можем пос троить график функции, если зададим систему координат. Здесь абсцисса представляет собой переменную фу нк-ции,л; а ордината — значение самой функции,у. Таким образом функция также может быть нред-
Из формулы видно, что самый естественный способ описания функции — через значение ординаты графика кривой. Иногда отношение между х и у задается неявно посредством уравнения вида
Л(х,у) = 0, где А — функция с двумя переменными. Например, функции
/(х) = ^ соответствует следующий неявный ви„ у — х'— 0,
который можно записать как F (х,у) —у — лЛ
Самый простой способ начертить график функции — это построить его по точкам, создав таблицу значений. Правда, в большинстве случаев этот метод наименее эффективный. Мы уже видели, что такая тактика может быть результативной в очень простых случаях, как в примере с нзобра жением прямой: ведь чтобы начертить прямую, необходимо знать координаты лишь двух точек.
через которые она проходит.
Но в случае нелинейной формулы, то есть когда переменная х возводится в степень, большую единицы, мы получаем кривую, которая в нскотор! ж случаях может быть гармоничной и даже прекрасной в своей прсдска |усмости, а в других — ужасно капризной и абсолютно неуправляемой. Часто бывает, что нелинейную функцию даже невозможно изобразить. Поэтому для графического изображения функций в очень сложных случаях необходимы аналитические техники, позволяющие узнать форму кривой вслепую. Для тгого изучается целый ряд признаков кривой: возрастание или убывание, максимумы и минимумы, кривизна, во-гнутость-ныпуклос гь. пересечение с осями координат, непрерывность и многие другие Эти методы позволяют из формулы вида/(.х) = sin (1 /х) почти магическим образом получить следующий график:
ставлена в следующем виде-
7 =/*)-
Все эти методы сформировались в результате длительного исторического развития, начавшегося
О взаимозависимости
Конусы и неявные функции
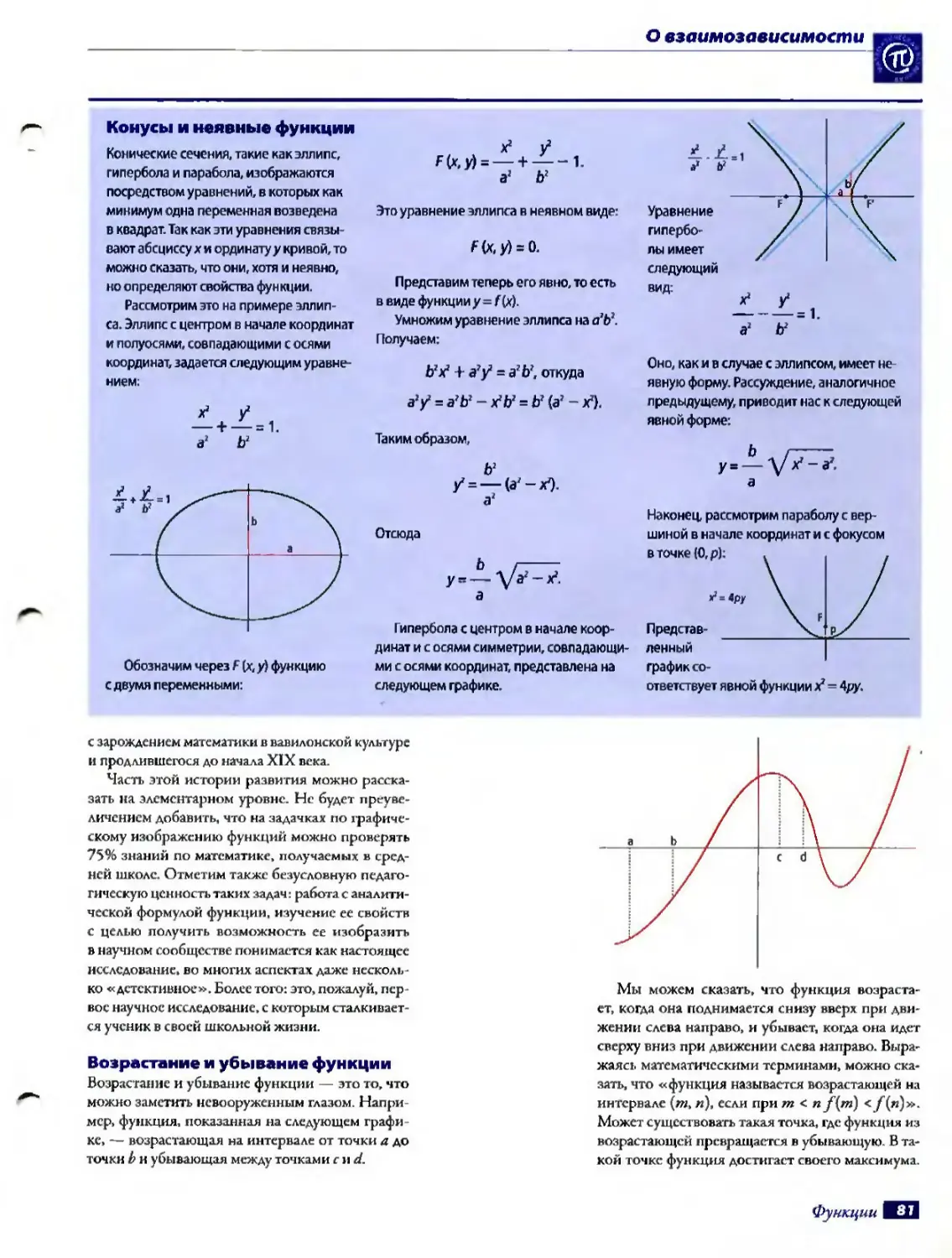
Конические сечения, такие как эллипс, гипербола и парабола, изображаются посредством уравнений, в которых как минимум одна переменная возведена в квадрат. Так как эти уравнения связывают абсциссу х и ординату у кривой, то можно сказать, что они, хотя и неявно, но определяют свойства функции.
Рассмотрим это на примере эллипса. Эллипс с центром в начале координат и полуосями, совпадающими с осями координат, задается следующим уравнением:
Обозначим через F (х,у* функцию с двумя переменными:
X1 у» — +--------1-
а1 Ьг
Это уравнение эллипса в неявном виде:
f(x,y) = o.
Представим теперь его явно, то есть виде функции у=f (х).
Умножим уравнение эллипса на aJb:.
Получаем:
tfx1 + а’/ = агЬг, откуда
a7 = a?b?-/bI = b?(aJ-n
Таким образом,
Ь1
/ = — (а2-^).
а1
Отсюда
у = — \/а2 - х2.
a
Гипербола с центром в начале координат и с осями симметрии, совпадающими с осями координат, представлена на следующем графике.
а1 V
Оно, как и в случае с эллипсом, имег неявную форму. Рассуждение, аналогичное предыдущему, приводит нас к следующей явной форме:
Наконец, рассмотрим параболу г вершиной в начале координат и с фокусом
ответствует явной функции / = 4ру.
с зарождением математики в вавилонской культуре и продлившегося до начала XIX века.
Часть этой истории развития можно рассказать на элементарном уровне. Не будет преувеличением добавить, что на задачках по графическому изображению функций можно проверять 75% знаний по математике, получаемых в средней школе. Отметим также безусловную педагогическую ценность таких задач: работа с аналитической формулой функции, изучение ее свойств с целью получить возможность ее изобразить в научном сообществе понимается как настоящее исследование, во многих аспектах даже несколько ''.детективное». Более того: это, пожалуй, первое научное исследование, с которым сталкивается ученик в своей школьной жизни.
Возрастание и убывание функции Возрастание и убывание функции — это то, чао можно заметить невооруженным глазом. Например, функция, показанная на следующем графике, — возрастающая на интервале от точки а до точки b и убывающая между точками г и d.
Мы можем сказать, что функция возрастает, когда она поднимается снизу вверх при движении слева направо, и убывает, когда она идет сверху вниз при движении слева направо. Выражаясь математическими терминами, можно сказать, что «функция называе гея возрастающей на интервале {т, п), если при т < nf[m) Может существовать такая точка, где функция из возрастающей превращазтея в убывающую. В такой точке функция достигает своего максимума.
Функции
87
Аналогичным образом при переходе из убывающей в возрастающую функция проходит точку минимума.
Максимум и минимум функции
У всех нас есть интуитивное представление о максимуме и минимуме. Любой человек, которому мы покажем график, предоавлснный ниже, не минуты не сомневаясь, обозначит точку Л/ как максимум и точку т как минимум.
Функции в мире физики: синусоиды
Функции как сущности, живущие в платоновском мире математических идей, могут быть сколь угодно сложными и экстравагантными. Чтобы функции были «хорошими» они должны быть четко определенными и непротиворечивыми. В физическом мире с некоторыми простыми математическими функциями мы сталкиваемся постоянно. Например, синусоиды. Мы встречаем их тут и там, в простом движении пружины или маятника, в дрожании гитарной струны, в распространении звука и электромагнитных волн. Даже загадочная волновая функция, одна из нерешенных про блем современной физики, представляет собой синусоиду. Во всех этих случаях математические функции выглядят как
y=asin wr,
где а является постоянной, соответствующей амплитуде колебании; мп — это тоигонеметрическая функция синус, Г — переменная функции; aw — постоянная, называемая пульсацией, связанная с периодом колебаний Т формулой;	2Л
Т = —-. W
Соответствующая кривая выглядит следующим образом:
У
т
Она одна из самых важных в физике
Интуитивное знание в довольно большой степени соответствует математической концепции о максимуме и минимуме. Слу чается, без сомнения, чго в математике ч.ггуиция становится важным и необходимым компасом, но так и не превращается в штурвал корабля: любая концепция, независимо от уровня интуиции, требует точного определения. Это особенно важно в области функций, где существуют определенные исключения, противоречащие люоой интуиции Точное определение локального максимума функции звучало бы так: « Говорят, что функция^х) дос гига-ет локального максимума в точке оси абсцисс Л/ если существует окрестность М. где
Л*) «/(Л*)
для любого х, принадлежащего этой окрестности». Если перевести это определение на более понятный язык, то оно подтвердит то, о чем нам говорила интуиция: «с обеих сторон точки» функция принимает значения меньшие, чем в самой точке. То сеть мак, имум точки - это как пик горы, где любая другая точка всегда будет ниже.
Заметим, что мы говорили об «относительном», локальном максимуме. Но максимумы могут быть также «абсолютными», глобальными Говорят, что функция достигает своего глобального максимума в определенной точке, когда значение функции в этой точке больше других локальных максимумов. Например, следующая функция в точке М достигает глобального максимума, i вточк.гхЛпВ — локальных максимумов.
В графиках, которые использует спортивная пресса для описания зтапов велогонки, обычно показывается несколько локальных максимумов. Перевал 1-й категории (иногда ег<  называют перевалом специальной категории) и представляет собой глобальный максимум.
Все, что было до сих пор сказано о максиму мах функции, такж, можно отнести и к минимумам нужно лишь заменить максимальный предел минимальным. Следовательно, определение
82
О взаимозависимости
минимума функции будет следующим: «Говорят, что функция f(x) достигает локального минимума в точке оси абсцисс т, если существует такая окрестность т, где для всех принадлежащих ей х
/W >/(«)•
Аналогично определению глоба сытого максимума можно дать определение глобального минимума.
Вогнутость и выпуклость функции
Рассмотрим другие характеристики функций — вогнутость и выпуклость. Речь снова идет об интуитивном понятии, ведь все знаю г, когда поверхность вогнута, а когда выпукла. Если на столе мы видим предмет, способный вместить в себя жидкость, мы говорим, что он вогнутый (как, например, миска). Этот же предмет, если его перевер-нутг и снова положить на стол, продемонстрирует нам выпуклую поверхность. То есть вогнутые поверхности дальше от нас, а выпуклые ближе. Но это зависит от точки зрения. Один и тот же предмет может быть вогнутым или выпуклым в зависимое ги от того, с какой стороны на него смотреть.
Когда речь идет о функциях, применяется следующий подход: мы «встаем» на горизонталь ную ось ч смотрим вверх. И это все. Но все же нам нужно более с грогое определение. Для того чтобы его получить, мы сделаем следующее. Возьмем две любые точки на кривой и соединим их хордой. Если функция расположена сверху хорды, то она выпуклая в интервале, определенном точками; а если снизу, то она вогнутая.
Вогнутость и выпуклость — эти характеристики, которые связаны с понятием кривизны, так
как они однозначно определяют направление изгиба графика кривой.
Точка, в которой функция изменяется с вогнутой на выпуклую или наоборот, называется точкой перегиба.
Ч Эти тонкие и сложные геометрические узоры, которыми испещрены банкноты и банковские чеки, на »hs.i-ются гилыпи. Этот орнамент играет роль не только зстетическую, но и защитную, так как он существенно усложняет ф нотификацию. Математически данные функции получаются с помощью  сожения и умножения синусоид с различными периодами.
По касательной
Одним из величайших открытий, сделанных в изучении функций, стало аналитическое определение касательной, то есть определение урав-НСШ.Я касательной прямой в точке на заданной кривой. В общем случае можно сказать, что касательная прямая — это прямая, которая касается кривой в о хной точке, не пересекая ее.
Посмотрим, что происходит с касательной, когда мы приближаемся к максимуму.
Видим, что касательная образует угол меньше 90' с осью ОХ на тех интервалах, где функция возрастает, и угол больше ^0° на интервалах, где функция убывает. Изменяя свой наклон, касательная непременно пройдет через точку касания, где, находясь в горизонтальном положении, составит угол в 0° с осью абсцисс. Это происходит всегда, когда мы встречаемся с максимум^ >м. То же самое происходит и в точках минимума, ведь карательна я, проходящая через них, тоже гори юнтальна. Но горизонтальность касательной в какой-либо точке не является гарантией, не является достаточным условием того, что в этой точке функция проходи, мак; чмум или минимум. Может случиться так, что речь будет идти о точке перегиба — о той точке, которая отделяет в< .гнутую тону от выпуклой. Тем не менее в < итуации, когда угол между карательной н осью абсцисс равен нулю, всегда есть возможность определить аналитическими методами, идет ли речь о пределе (максимуме или минимуме) или же о точке перс гиба.
Функции
S3
4 Божественное, которым окружены девять небес Денте. на известной гравюре Гюстава Доре. Система концентрически х сфер может рас с иатркватыя как своеобразное представление функции хг +у! + гг = г* где х,у, z являются прямоугольной декартовой системой координат, а г, радиус сферы, изменяется при переходе от одной сферы к другой. Гскпм образом, речь идет о функции с тресся переменными.
Непрерывность
Одно из наиболее важных свойств, характеризующих функцию, — непрерывность. Ес определение требует хорошего знания понятия функционального предела, а потому мы нс будем приводить его здесь. Но для практических целей достаточно определить непрерывность следующим образом; «Говорят, что функция непрерывна в том случае, если вы можете прочертить ее без отрыва карандаша от бумаги». Все функции, которые мы рассматривали до настоящего момента, были непрерывными; не было необходимости поднимать карандаш от бумаги для того, чтобы их нарисовать. Когда нужно оторвать карандаш, функция называется разрывной, а точка, о которой идет речь, — точкой разрыва. Одна функция может иметь одну точку разрыва, несколько или бесконечное их количество, как в случае с функцией J (v) = Е (х), где Е означает «целая часть». Например, Е (1,24) = 1; Е (0,235) = 0. В этой функции любому числу соответствует число перед запятой — целое число. Таким образом, всем числам между 1 и 2 (нс включая 2) ставится в соответствие 1, числам в интервале между 2 и 3 (не включая 3) ставится в соответствие 2 и так далее. Графически эта функция выглядит как лесенка И является разрывной с точками разрыва н каждом целом значении переменной: чтобы начертить график функции, необходимо поднять карандаш от бумаги в каждой нз этих точек.
5
4
3
2
1
~0
1	2	3	4	5	6
Мы уже знаем, что Галилей (156ч—16-12) стал первым, кто установил четкое понятие функциональной зависимости — основную идею функции. Если сильно упростить, то под функцией можно понимать некую связь, отношение между переменными. Такое представление о функциях мы можем обнаружить в первых находках, относящихся к вавилонской и египетской культуре. Более детальное и углубленное изучение взаимосвязи переменных началось в XVII веке. Особенное внимание уделялось прикладному изучению кривых. Джеймс Грегори (1638—1675) определил функцию как «количество, полученное из других количеств с помощью последовательных алгебраических операций или любой другой операции, которую вы можете себе представить». Грегори также поднял вопрос о возможности включения в число операций пределов функций. Ньютон (1643—1727) использовал термин «неустойчивость» для определения отношения между переменными, а Лейбниц (16<16—1716) стал первым, кто использовал слово «функция» в своей «Истории...», опубликованной в 1714 году. Здесь же стоит вспомнить и Эйлера (1 “07—1783). К его заслугам можно отнести рассмотрение функций вне их связи с 1еометрисй, а также законченное им систематическое изучение и классификацию всех элементарных функций.
Функции и дыхание
Давление воды, где бы она ни находилась, — в контейнере, в озере или в спокойном море — это очень простая функция глубины В частности, разница между давлением на поверхности и в точке на глубине х равна dgx, где d — плотность воды,ад — ускорение свободного падения. При таком раскладе давление, которому подвергаются легкие водолаза, равно сумме двух слагаемых: атмосферного давления, существующего на поверхности, и гидростатического давления, только что нами упомянутого. Гидростатическое давление равно приблизительно одной атмосфере на каждые 10 метров погружения. Прибавляя
к этому давление на поверхности земли, мы получаем, что давление на глубине 10 метров равно двум атмосферам, на глубине 20 метров — трем атмосферам, а на глубине 30 метров — четырем. Таким образом, нет ничего странного в том, что способ дыхания под водой через трубочку из тростника, столько раз виденный в кино, вскоре перестает работать. Очевидно, что через некоторое время легкие будут настолько сдавлены, что у человека не хватит сил для вдоха. Это происходит уже на нескольких метрах глубины. Дыхательным мускулам становится не под силу сделать легочное давление меньше атмосферного, что является необходимым условием для вдоха.
Характерные для Жан-Пьера Серра остроумие и глубина нашли свое отражение в его выступлениях на математических конференциях, книгах и курсах, восхищая слушателей удивительным балансом МЕЖДУ ТОЧНОСТЬЮ И ДОСТУПНОСТЬЮ.
Ключевая фигура современной математики
Жан-Пьер Серр
4 Жгч-Пьгр Серр на ц,р'мв-нии вручена я первой Апе ив-езеай премии ей чапц иатике 3 гнрг ея 2003 лАт« Or to. С появлением математиче-ктг j .гв. коп np.rчиа» чатечатнки ее его чира, начиная, Серри, гчогж получить вознаграждение за значите зьнме открытия, едеалнные в течение ввей
».изни.
В 1956 году Серр получил место профессора на кафедре алгебры и геометрии в Коллеж де Франс.
•ту должность он занимал вплоть до своего ухода на пенсию в 199ч году. Ныне Жан Пьер Серр — почетный профессор Коллеж де Франс. Эта постоянная должность в престижном неведении позволила ученому совершить много научных поездок в разные страны мира, особенно в США. где он работал в тесном сотрудничестве с Прин-
ж  жан 11ьср Серр родился 15 сентября 1926 года в Даже, Франция. Окончил Я I Переднюю школу в городе Ним, а затем поступил в Парижскую высшую норма тьную школу, где учился в течение трех лет. В 1951 году Серр получил диплом доктора философии в Парижском университете Сорбонна. В течение 1918—195-1 гг. занимал ра тинные посты ч Национальном центре научных исследований, пока нс получил должность доцента На факультете естественных наук в университете города Нанси.
▼ Ко меж де Фране — одно и • .-т грейших и. <	пре-
стижных oSpa юв сше юных учреждений Франции. Поцз-началыео установившем,, я традиции занятия в „ко-роаевеком коллеже*, общедоступны, хотя эмо больше форма зьнаеть, неж, ш реальность, ведь там преио-длитз а чыг таиюи зивые учены, Франции. Напри и р. ми Серр.
Gracfaate Texts it Mathematics
h— wwibm г.
ACawne tn AntbmeiK
• 'i"*»
стонскпм институтом перспективных исследований и с Гарвардским у ниверси те том.
4 Одна «йдект книг, где ученый продсмонс тририя. гл широкий спектр своих интересов и способность передать свой знгпузназм и качество своего оОрахования новым по-холениям u.лтематпков.
Признание труда
Ж т Пьер Серрявляется одним из математиков, получивших наибольшее количество наград в качестве признания своих заслуг. В 195ч году Жан-Пьер стал самым молодым математиком, получившим медаль Филдса (27 летний С. Доналдсон повторил это достижение в 1986 году). Жан Пьер Серр — обладатель премии Гастона Жю-лиа в 1970 году, премии Бахьцана в 1985 м, премии Стила в 1995 м и премии Вольфа в 2000-м. Кульминацией его блестящей карьеры стало получение нм Абслевской премии. 3 апреля 2003 года в Норвежской Академии наук и литературы Сер ра чествовали как первого математика, котором', был вручен этот эквиьалент Нобелевской премии «за ключевую роль в придании современной формы многим отраслям математики, включая топологию, алгебраическую геометрию и теорию чисел». Премия, полученная ученым, составила 6 миллионов норвежских крен (768 тысяч евро).
Математика Серра
Серр является универсальным математиком. Его первые работы в сфере а хгсбраичсскои топологии подарили этой науке новые мощные инструменты исследования.
Жан-Пъер Серр (р. 1926)
27
Нобелевская премия по математике
Когда Альфред Нобель писал свое завещание, в котором распределял
свои средства на ежегодные премии выдающимся ученым, он почему-то не вспомнил о математиках. Об этом ходит большое количество легенд.
Самая популярная из них намекает на возможный роман между шведским математиком Г, Миттаг-Леффлером (1846—1927), который теоретически должен был стать первым обладателем этой премии, и супругой Нобеля.
Хотя эта история и является самой популярной, но она не выдерживает никакой критики уже потому, что Альфред Нобель никогда не был женат. Независимо отличных мотивов, Нобель, скорее всего, просто не очень
интересовался математикой: ведь в течение целого века ни одна награда Норвежской Академии Наук не была вручена математику. Правда, чуть
позже большую часть этого вакуума заполнят медали Филдса. Тем не менее норвежское правительство в августе 2001 года организовало фонд в 200 миллионов норвежских крон (около 23 миллионов долларов) для вручения ежегодной международной премии в математике. Названа эта премия была ь честь великого норвежского математика Нильса Абеля (1802—1829). Предполагается что обе награды — Абелевская премия и медаль Филдса —продолжат существовать наравне, ведь первая —это признание величайших трудов ученого, а вторая — награда за конкретную работу.
Благодаря его исследованиям и достижениям в этой сфере так называемых спектральных сериях), а также за новейшую разработку теории
Ч Нет, это не группа друзей, выехавших на пикник. Это члены секретной группы Бурбаки. Л{атеиатикл с такой фамилией никогда не t ущестпвоволо, но без его вклада невозможно представить себе чатематическую науку XX век.к Жан-Пьер Серр — крайний трава.
функции комплексного переменного Серр и получил медаль Филдса в 1954 году. Стоит упомянуть влияние Серра на теорию чисел, особенно на все, что связано с эллиптическими кривыми и модулярными функциями Не стоит забывать, что его предположение о модульности представлений Галуа с гало ключевым элементом в наборе результатов. коюрые могли бы привести к доказательству последней теоремы Ферма. В 1934 году Серр присоединился к группе Бурбаки, организованной математиками А. Картаном и Л. Вейлом с целью реформирования преподавания математики в вузах. Жан-Пьер Серр участвовал в разработке элементов так называемой «Библии матсмати ков», трактата более чем на семь тысяч страниц, подписанного вымышленным Бурбаки, чьим именем и была названа эта группа.
А Маркл в намцтъ о ее iuko и норвежском математике Нильсе Jfae (JS02—I829). Памятник, изображенный на марке» был создан и 190S году Густавом Веге-лундом н находитсяс/ Огла.
МОТО
Премия Вольфа, которой был награжден Жан-Пьер Серр в 2000 поду, была создана дипломатом и филантропом Рикардо Вольфом (1887— 1981). Каждый год премия вручается в шести номинациях: сельское хозяйство, химия, математика, медицина, физика и искусство. Премия в области искусств п| и суждается поочередно в четырех видах искусства: живопись, музыка, архитектура, скульптура Ежегоднс j премиальный фонд сот тавляет 100 тысяч долларов в каждо 1 номинации.
Мать Жан-Пьера была фармацевтом по специальности и чувствовала необъяснимую тягу к математике. Будучи студенткой фармацевтического курса в Монпелье, она по собственной инициативе прошла обучение на первом курсе по математическим вычислениям и потом с особой нежностью хранила учебник, который помог ей сдать этот первый и единственный курс. Именно этой книгой заинтересовался 14-летний Жан-Пьер и именно в ней впервые прочел о ' производных, интегралах и рядах,
I Часто Серр работал ночью, между двумя снами. «Тот факт что у тебя под рукой нет ничего чем можно было бы писать, заставляет тебя лучше концентрироваться».
Говорят, когда Нобель спросил, кто мог бы быть первым лауреатом премии по математике, ему ответили: «Миттаг-Леффлер». Нобель отреагировал весьма категорично: Не будет премии по математике!»
В ТЕЧЕНИЕ НЕСКОЛЬКИХ ВЕКОВ МЫ БЫЛИ ОЧАРОВАНЫ ОБАЯНИЕМ ЕВКЛИДОВОЙ ГЕОМЕТРИИ.
НО СЕЙЧАС ФРАКТАЛЫ БЛАГОДАРЯ СВОЕЙ БЕСПОКОЙНОЙ КРАСОТЕ ОТКРЫВАЮТ ПЕРЕД НАМИ ДВЕРИ В HOBVtO ГЕОМЕТРИЮ — ФРАКТАЛЬНУЮ.
МАТЕМАТИКА
Фрактальная геометрия
Прекрасный беспокойный мир
Представим себе, что нам необходимо измерить длину средиземноморского побережья от Барселоны до Аликанте. Мы могли бы снять приблизительные замеры с помощью линейки, соединив две точки прямой. I Ьмеряем длин}' от резка, умножаем сто на соответствующий масштаб карты, и вот у нас приблизительная длина побережья Понятно, что это далеко не самое точное измерение. Другой способ — взять циркуль, установить его раствор на 1 см и пройти так по карте весь берег шаг за шагом. Просуммировав все проделанные шаги, мы найдем длину по-берс •кья Эго приближение будет более точным, чем предыдущее. Но так как берег нс является однородной линией, каждый раз, когда мы будем поворачивать чтобы установить циркуль в следующую гоч! у, мы обнаружим- что нс охватили весь контур побережья. Если карта подробная, то, установив раствор циркуля поменьше, мы сможем точнее пройти маленький залив, выступ или мыс. Становится ясно, ч го чем меньше раст вор циркуля тем точнее будет измерение,
► ЦмЮрОЖвНие атЛаИЛШ-ноского побуракья Африки и его увеличенный фрагиент. . 1иния береги миел» ч при-пери ( фрактального объекта в природе. Размерность фрак таы ирриклн. кого побережья .сктавкяет 1,1 против размериоПни 1.25, редиим ноиорекигчпоб.режьч, что покатый сет « шероховаты ть» береги.
▼ Фрагмент работы - Нойер I» Дж- хам i Поллока, наши юной в IV-) 'году бще до открытия фрактал™ многие художники ощутили красоту фрактальных. трук тур. В приведенной работе отражает, ч иатенлшиче-tKoe понятие гамончдооия.
Бесконечная длина и размерность фрактала
Мы находимся в парахоксальной ситуации: чем меньше рас гвор циркуля, тем больше времени нам потребуется, чтобы измерить длину побережья от Барселоны до Аликанте. И эта шра «меньше значит больше» не имеет конца, так как количество отрезков, нд которые мы разбиваем побережье, может увеличивать^ я бесконечно. Если мы лежим на скале у моря и принимаем солнечные ванны, то, глядя на сложную форму скал, мы можем увидеть в ней миниатюрную модель того самого берега, длину которого мы собираемся измерять. Мы привыкли прибегать к евклидовой геометрии, чтобы измерять длину, но тутона нам не помощник: при столкновении с фракталами необходима фрактальная геометрия. В евклидовой геометрии термин «размерность объекта» интуитивно понятен: любая линия одномерна, как электрический кабель; плоскость двумерна,
37
гшя квторрж начинается
с кум, которого выреза'
ютс.ч куры меньшегр размера
Кантореi ю множество
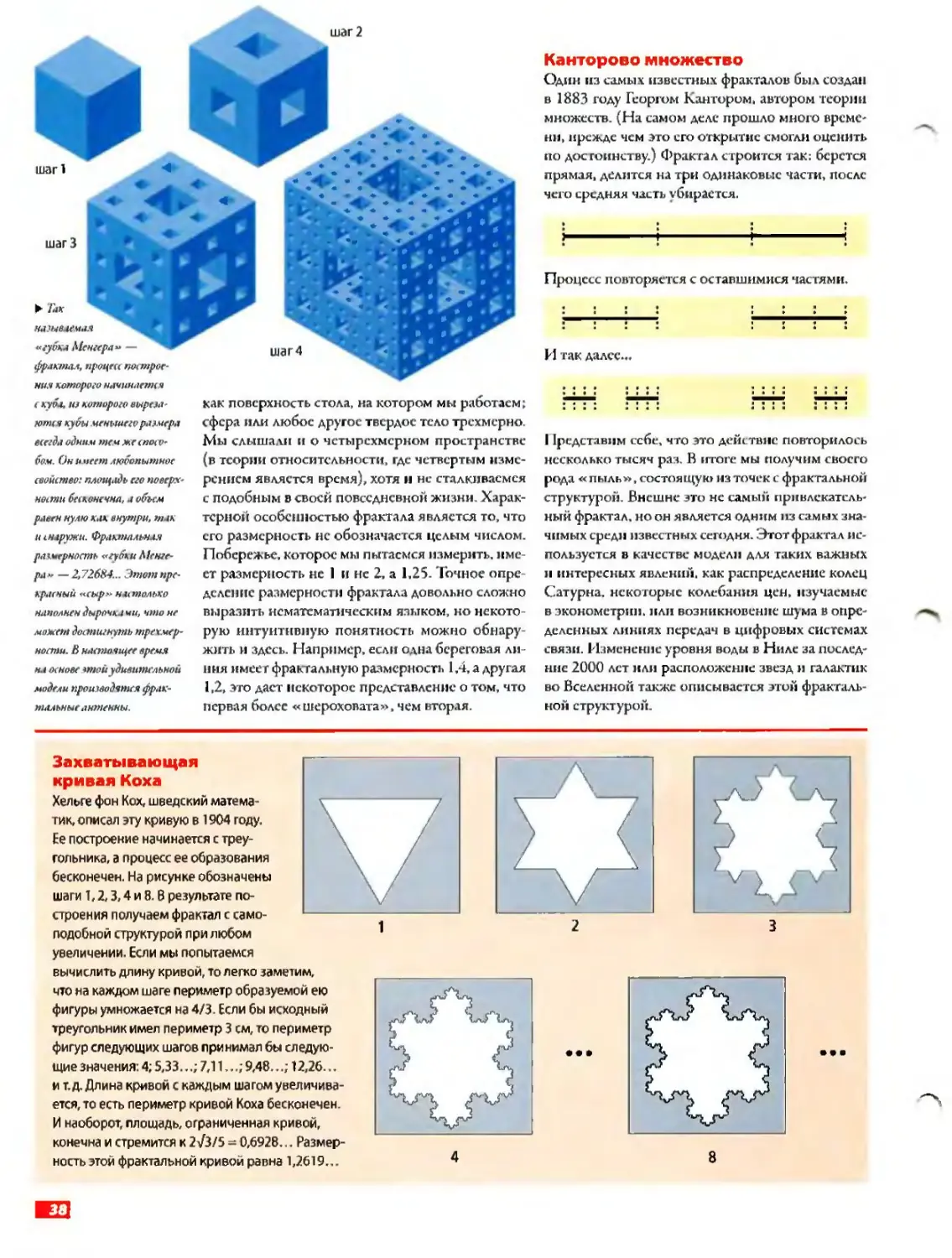
Один из самых известных фракталов бы л создан в 1883 году Георгом Кантором, автором теории множеств. (На самом деле прошло много време ни, прежде чем это его открытие смогли оценить по достоинству.) Фрактал строится так: берется прямая, делится на три одинаковые части, после чего средняя часть vbupae гея.
Процесс повторяется с оставшимися частями.
И так далее...
как поверхность стола, на котором мы работаем; сфера пли любое другое твердое тело трехмерно.
всегда одним mi и же способом. Он и иеет любопытное свойстве: ллещадк его поверх-нести бесконечна, собьем равен нулю км внутри, т ск и сн грчжи. Франта юн ся расмерность «губки Менге-ря» — 2,72684 - Этет пре-
Мы слышали и о четырехмерном пространстве (в теории относительности, где четвертым измерением является время), хотя и не сталкиваемся с подобным в своей повседневной жизни. Характерной особенное гью фрактала является то, что его размерность нс обозначается целым числом. Побережье, которое мы пытаемся измерить, имеет размерность не 1 и не 2, а 1,25. Точное опре-
красный «сыр» н.ипюаркр
деление размерности фрактала довольно сложно
нано^нен дырочками, что не может достигнуть трехмерности. В настоящее время на основе стой удивительной модели производятся фрактальные антенны.
выразить нематематическим языком, но некоторую интуитивную понятность можно обнаружить и здесь. Например, если одна береговая линия имеет фрактальную размерность 1,4. а другая 1,2, это даст некоторое представление о том, что первая более «шероховата», чем вторая.
Представим себе, что это действие повторилось несколько тысяч раз. В итоге мы получим своего рода « пыль», состоящую из точек с фрактальной структурой. Внешне это не самый привлекательный фрактал, но он является одним из самых значимых среди известных сегодня. Этот фрактал используется в качестве модели для таких важных и интересных явлений, как распределение колец Сатурна, некоторые колебания цен, изучаемые в эконометрии, пли возникновение шума в определенных линиях передач в цифровых системах связи. Изменение уровня воды в Ниле за послед ние 2000 лет или расположение звезд и талактнк во Вселенной также описывается этой фрактальной структурой.
Захватывающая кривая Коха
Хельге фон Кох, шведский математик, описал эту кривую в 1904 году Ее построение начинается с треугольника, а процесс ее образования бесконечен. На рисунке обозначены шаги 1,2,3,4 и 8. В результате построения получаем фрактал с самоподобной структурой при любом увеличении. Если мы попытаемся
вычислить длину кривой, то легко заметим, что на каждом шаге периметр образуемой ею фигуры умножается на 4/3. Если бы исходный треугольник имел периметр у см, то периметр фигур следующих шагов принимал бы следующие значения 4; 5,33..7,11..9,48...; 12,26... и т.д. Длина кривой с каждым шагом увеличивается, то есть периметр кривой Коха бесконечен. И наоборот, площадь, ограниченная кривой, конечна и стремится к 2/3/5 = 0,6928... Размерность этой фрактальной кривой равна 1,2619...
Лучшее от Сэма Ло ‘да
Задачи о детях
А Л иывраччцч м п?
1.	Задача о футбольном мяче
У меня нет стальной защиты для носа, а потому я не хочу рисковать этим органом, засовывая его н игру с которой не знаком. Наплечники и флт-больныс щитки не были в моде в мои школьные годы Обычно мы играли в футбол просто ногами, как того и требует название ггого вида спорта. и нмкиуда не пытались калечить своих соперников. Одпаы । моя <адачка ис будет иметь ничего общего ни с «пасами», ни с «дриблингом», ни даже е проспам линками по мячу Это всего лишь воспоминание о тех днях, когда мы, деревенские дети, любмди гонять резиновый мяч по зеленому полю. Мы жили в сельской местности и обычно заказывали мяч по почте. В каталоге о\ного из спортивных магазинов требовалось, чтобы клиенты при заказе «указывали точное количество дюймов». Вот здесь и возникает проблема.
Нас просили указан размер в дюимдх. но мы
не знали, что при этом имелось в виду: площадь поверхности мяча или объем воздуха внутри Поэтому нам приходилось совмещать два этих параметра. Мы заказывали мяч. объем которого в кубических дюймах совпадал бы с площадью его поверхности в квадратных дюймах!
Кго из наших читателей сможет назвать дпа-м< гр заказанного мяча?
2.	Эксцентричный преподаватель
Затронутая в этой задачке проблема возрастов, ч уверен, развлечет молодых и одновременно ласт пищу для размышлений научным работникам, сделавшим статистику своей специальностью.
Одни умный н эксцентричный преподаватель, желая увеличить число старшеклассников в ip\ п-пе, upiанпзацшн которой он занимался, ойъявпл
о ежедневной выдаче премии Она полагалась тон гр.ппе молодых людей или девушек чей общин возраст будет больше.
В первый день на занятие пришло только два человека, ма льчнк и девичка. Так как возраст мальчика был в дьа раза больше возраста девочки, то ему и была отдана премия. На следующий день девочка привела в школу свою старшую сестру. Так как возраст двух девочек был в два раза больше, чем аозрас г мальчика, то в этот день премию поделили они Когда школа открылась па третий день, то оказалось, что мальчик привлек к соревнованию одного из своих братьев. На этот раз возраст мальчиков оказался в два ра га больше возраста обеих девочек, поэтому премия досталась ма лъчпгам
Борьба между ccmi ямм Джонс и Бра; н разгоре лась не на шутку, и па четвертый день две девушки пришли в школу со своей с гаршей сестрой. Та ким обра юм, в этот день в группе оказались три девушки против двух мальчиков. Есгес гвсыно, девушки выиграли премию четвертого дня, так как их общий возраст был вдвое больше общего возраста обоих мальчиков
Битва продо.сжалась до того момента, пока класс нс заполнился под завязку, но мам развивать эту задачу уже необязательно. Мы хотели бы у шатп возраст того самого первого мальчика, пришедшего в группу нашего хитроумного преподавателя, принимая во внимание ту информацию что последняя девушка вош ла в класс в день, когда ей исполнился 21 год.
Это простая,, ио очаровательная задачка для разгадки которой необходимо больше изобретательности. нежели математических знаний. Вы легко се разгадаете, пользуясь типичными для головоломок способами решения.
V Ci~o>f6iw впит реиемж /оспами О'Тул?
3.	Взвешивая ребенка
Госпожа О'Тул — весьма экономная дама. Она пытается взве-сггться сама, взвесить своего ребенка и собаку, и все это за один ценз. Если она весит на 100 фунтов больше, чем собака и ребенок вместе, а собака весит на 60* с меньше ребеи ка. можете ли вы определить вес маленького ангелочка?
27
4.	Умножение и сложение
11реподаватель обьясняетсвоим ученикам: дважды два даст тит же результат, что и два плюс два. Хот я 2 — единственное натуральное число с такими свойствами, есть мною пар чисел, способных заменить а и b в уравнениях, напск 1нных на доске (иллюстрация ниже Можете ли вы найти подобную пару? Конечно, это могут быть и дробные числа, но их произведение должно быть равно их сумме.
< Найдите такие
pas личные точения лиЬ. чтобы
а и. Ь—а + Ь.
5.	Загадка о перетягивании каната
Сила четырех крепких мальчиков равна силе пяти
Две пухлые девочки и один крепким мальчик не уегу-
Стройиые близнецы и три пухлые девочки против ОДНОЙ пухлой девочки и четырех крепких мальчиков. Кто выиграет последний раунд?
Решения
1.	Объем мяча можно рассматривать как совокупность большого количества маленьких пирамид, чьи вершины обра щены к центру мяча, а основания составляют его поверхность.
Мы знаем, что объем пирамиды равен площади поверхности ее основания, умноженной на 1 /3 ее высоты. Таким образом, объем сферы равен сумме оснований пирамид умноженной на треть высоты. В нашем случае это поверхность сферы, умноженная на треть радиуса. Так как этот объем совпадает с площадью поверхности, то получается, что треть радиуса равна единице. Таким образом, радиус равен 3 дюймам, а диаметр мяча составляет 6 дюймов
2.	Первой девочке было 638 дней, а мальчик вдвое ее старше, то есть ему 1276 дней. На следующий день самой младшей девочке было уже 639 дней, а новенькой 1915. Их общий возраст 2 544 дня, что вдвое больше возраста первого мальчика, которому на второй день было 1277 дней. На третий день мальчик 1278 дней от роду привел свое
го старшего брата, которому исполнилось 3 834 дня. Таким образом, на твоих мальчиков приходится 5112 дня, что ровно в два раза больше возраста девочек, которым в этот день 640 и 1916 дней соответственно, то есть всего 2 566 дн₽й
Мы приходим к 7670 дням следующим образом. Девушка пришла в школу в день своего 21-го дня рождения. Умножаем 21 на 365, получаем 7 665. Плюс еще 4 дня за високосные годы, плюс 1 день за первый день после дня рождения.
Те, кто сказал, что мальчику три с половиной года, проигнорировали тот факт, что возраст учеников увеличивался каждый день.
3.	Госпожа О’Тул весит 135 фунтов, ребенок весит 25 фунтов, а собака — 10 фунтов.
(Задача имеет несколько решений.)
4.	Существует бесконечное количество пар чисел, произведение и сумма которых совпадают. Если одно число а, то второе всегд. можно полу-
чить делением а на а-1. Например, 3 х 1,5 = 4.5 и 3 + 1,5 - 4,5.
5.Объединенная сила четырех крепких маг.ьчикоъ равна силе пяти пухлых девочек. Как показывает вторая иллюстрация, стройные близнецы уравнены по сине с одним крепким мальчиком и дьумя пухлыми девочками. Упростим изображение на третьей картинке, поменяв двух стройных близнецов на эквивалентную им силу то есть на одного кре пкого мальчика и двух пухлых цевочек. Благодаря этой замене сейчас на третьей картинке у нас пять пухлых девочек и один крепкий мальчик борются против одной пухлой девочки и четырех крепких мальчиков. Уберем пять пухлых девочек с одной стороны и четырех крепких мальчиков с другой, так как первый рисунок показывает нам, что они равны по силе. После этого у час останутся крепкий мальчик слева и пухлая девочка справа. Это означает, что команда слева с третьей картинки должна выиграть, так как у них на одну пятую больше силы, чем у команды справа.
Чтобы собрать мозаику, необходим повторяющийся мотив. Мотив этой игры —- простейший из ВОЗМОЖНЫХ, ВЕДЬ ЭТО КВАДРАТЫ С ЧЕТЫРЬМЯ РАЗНОЦВсГНЫМИ ТОЧКАМИ. Но НьОБХОДЙМО СОБЛЮСТИ ОДНО УСЛОВИЕ, которое и делает ЭТУ ГОЛОВОЛОМКУ ИНТЕРЕСНОЙ
Четыре цвета для восьми фишек
Мозаика
Об этой шрс мало что известно, хотя существует легенда, утверждающая, чги се привез Марко Поло из Китая в 1295 год', чтобы показать Западу мастерство восточных авторов головоломок. Согласно классификации головоломок Джерри Слокума, эта игра относится к категории edge matching puzzles. то ест ь к классу головоломок, стыкующихся по краям. Суть игры в том, чтобы се детали соприкасались краями, и в этих зонах соприкосновения был<> какое-либо совпадение. по форме, цвету, написанным числам и г.д.
Пестрое семейство
Есть множество вариантов этой идеи. Один из них — Ряаг-it Puzzle (« Наи уи пару»). Эта голово-
Л Критерий, пи которой) гтреитея мпа мозаика, очень пррет:. мгкные точки различных фишек дозжнн быть одного цвета. Изящное умозаключение шаг га шагам приводит к нкхомдению решений
В нашей игре под названием «Мозаика» восемь квадратных фишек. На каждом углу каждой фишки стоит точка определенного цвета. Цветов всего четыре: желтый, красный, зеленый и синий. Также у нас есть рамка интересной геометрической формы, в которой мы должны разместить наши фишки таким образом, чтобы точки на прилегающих друг к другу сторонах разных фишек были одного цвета.
Фишки
Хотя некоторые решения можно найти методом проб и ошибок, тем не менее, интереснее обратиться к логическому анализе, который выдаст нам все существующие решения. Первый шаг — это изучение восьми фишек, входящих в нашу головоломку. Поместим их таким образом, чтобы же стая точка нах уи iaco в левом верхнем углу рамки. Мы увидим, что у нас есть две похожие фишки, у которых в правом верхнем углу стоит красная точка. Дадим каждой фишке свое имя (см. иллюстрацию внизу). Это обозначение не произвольно. Фишки А — похожие. Обозначим одну из них А>, а вторую А,. Можно заметить, что на этих фишках желтый и красный цвета смежные, так же. как синий и зеленый Туже закономерность видим и на фишках группы В, в то время как цвета на фишках в группе С совпадают по диагонали.
На самом деле в силу своей симметрии желтый и красный цвета играют одинаковую роль в головоломке. То же самое происходит с синим и зеленым цветами. Именно поэтому количество решений в игре кратно четырем.
ломка состою из шее ги шест иуголыш ков, размещенных в кру глои рамке. На каждой стороне шестиугольников изображены числа от 1 до 6. Суть игры заключается в расположении фигур таким образом, чтобы соседние шестиугольники соприкасались друг с другом стиронами с одинаковыми числами.
Другая очень нзвеез мая игра из ттого же семейства — Arc-en-Ciel(«Радуга») — состою из девяти фигур кругов, расположенных в три ряда по три кру га в ка адом ряд Каждая и з фигур имеет по четырехконечной звезде; каждый из концов звезды разного цвета. Су гь ш ры в том, чтобы повернуть крут п таким образом, чтооы шесть цветов расположились в соответствии с правилами игры по горизон тали и по вертикали.
49
Центр
В связи с тем, что самое трудное — это понять, какие фишки будут находиться в центре, начнем с того, что узнаем ком >инации четырех фишек, с помощью которых можно создать квадрат 2x2. 11оеле тоги как мы это поймем, гологоломка. моя -но сказать, будет практически решена.
Забудем на время о конкретных цветах на фишках, а сосредоточимся на том, что их всего четыре. Фишка в верхнем левом углу имеет все четыре цвета хотя мы и не знаем, как они расположены. Условно назовем их 1, 2, 3 и 4 — в том порядке, в котором они показаны на иллюстрации. Звездочками обозначим те цвета, которые нам еще предстоит узнать. Чтобы фишки подошли дрхг к другу, четыре центральные точки должны соответствовать цвету ]. Кроме этого, мы знаем номера цветов еще двух точек — 2 и 4.
Теперь у нас есть две возмож
ности в зависимости от того, какой цвет мы поместим в нижний правый угол верхней правой фишки: вариант а соответствует цвету 4, вариант Ь — цвету 3. В случае а цвет, которого нс хватает в верхнем правом углу нижней правой — 4;
Фигура 1 (л)
3 2 4 1	2 * 1 *
4 1 * ft	1 * * *
3 2 4 1	2 3 1 4
4 1 * *	1 4 * *
Открывав гея одновременно две возможности: цвет 2 (<-) или цветЗ (<7) в нижнем левом углу нижней левой фишки.
Фигура 2 (с)	Фигура 3 (J)
3 2 2 3
4 114
4 114
2 3 3 2
3 2 4 1	2 3 1 4
4 1 3 2	1 4 2 3
В случае b расположение цветов в квадрате 2 х 2 уже полностью определено. ( труктура должна быть следующей:
Фигура 4 (£)
3 2 2 4
4 113
Здесь числом, которое должно занимать центральные позиции нижней линии, должно быть 2. Если бы это было 4, то тогда бы оно дважды встре
тилось в нижнем левом квадрате. Таким образом, мы можем написать оставшиеся номера:
Фигура 5
3 2 2 4
4 113
4 113
3 2 2 4
Подведем итоги. Мы получили три возможные основы для нашего кваграта 2x2. Изображены они на фигурах 2,3 и 5.
Уменьшая выбор
Можно увидеть, что на самом деле существует только одна основа, так как фигура 3 нс может быть построена с помощью фишек игры, а фигуры 2 и 5 соответствуют в определенной степени одной основе.
Почему мы не можем построить квадрат 2 х 2 со структурой фиг уры 3? Заметим, что фишки. расположенные по диагонали друг от друга, одинаковы. Учитывая, что фишки, которыми мы располагаем, относятся к группе А, нам обязательно нужно построить квадрат с двумя фишками типа А) и двумя фишками типа Аг. Е^ли у этих фишек мы видим цвета по часовой стрелке, то мы убедимся, что красное идет после желтого у всех четырех. Как мы видим в случае с номерами I и 2, это обязательно должны быть зеленый и синий цвета (в любом порядке). По той же причине не подходят красный и желтый
• • •	• • •
• • •	• • •
Почему мы говорим, что
фигуры 2 и 5 соответствуют одной модели? Так как числа произвольные и направление квадрата 2x2 тоже произвольное, го если взять фигуру 2 и повернуть ее на 90' против часовой стрелки (фигура 6), а в полученной фигуре поменять двойки и четверки местами, то мы получим простое изменение «номенклатуры» (фигура 7). А фигура 7 идентична фигуре 5.
Фигура 2
3 2 4 1	2 3 1 4
4 1 2 3	1 4 3 2
Фигура б
3 4 2 1	4 2 1 3
2 1 3 4	1 3 4 2
Фигура 7
3 2 4 1	2 4 1 3
4 1 3 2	1 3 2 4
Поэтому можно сказать, что любое найденное решение расположения четырех центральных фишек будет соотватс .ъовать структуре, показанной в фигурах 7 или 5- В частности, все эти четыре фишки будут разными.
50
Мозаика
Конкретнее о фишках
Теперь определимся, какие четыре фишки из восьми нам надо выбрать, чтобы сформировать в центре квадрат 2x2.
Можно заметить, что в четыре* фишках цвета 1 и 2 смежные, так же, как и цвета 3 и 4. Та ким образом, для каждого из этих цветов есть дру| ой цвет, который находится рядом с ним на всех четырех фишках. Какой цвет всегда рядом с желтым? Рассмотрим три возможных варианта. Б каждом из этих вариантов существуют четыре определенные фпшил для формирования квадрата 2 х 2:
Цвет, смежный с желтым	Необходимые фишки
Синий	Ар В„ С, иС2
Зеленый	А^г Bjr и Сj
Красный	Ар А> В| и
Выбрав фишки, где рядом с желтым находится синий цвет, мы увидим что завершить головоломку невозможно. Дсйстви гелыю, в этом случае можно
построить квадрат2x2 четырьмя разными tnoco-бамн в зависимости от цвета, который мы захотим поместить в Центр.
Рассмотрим теперь случай, з котором в центре бу-
Учимся считать заново!
Сколькими способами четверо друзей могут сесть за круглый стол в ресторане?
Читатель, наверное, уже узнал в этой головоломке типичную задачу по комбинаторике — разделу математики, который занимается тем, что подсчитывает подмножества, отвечающие определенным условиям. Комбинаторика очень помогает в таких областях как, например, расчет вероятностей, искусственный разум или теория графов
Предположим, что обедающие садятся один за другим. Если вы садитесь первым.
понятно, что неважно, какое именно место вы займете, просто нам нужно знать вашу позицию относительно остальных. Второй человек будет иметь три варианта для выбора места, третий — два, а последнему человеку придется сесть на оставшийся свободный стул.
Таким образом, определяющий выбор делают второй и третий гости, что дает нам шесть различных вариантов действий (см, иллюстра’ (ию).
Какое отношение все это имеет к игре? Мы могли Оы спросить, почему
две фишки повторяются. Ответ прост: если бы в каждой фишке было по одной точке, то можно было бы сделать то> ibko шесть различных фигур. Мы показали это на примере задачи с рестораном, где обедающие г-н Красный, г-н Синий, г-н Зеленый и г-н Желтый представляют собой точки. Так как фишки могут поворачиваться, то единственное, что важно, — это позиция каждого цвета относительно остальных цветов (нетсмысла говорить, что в конкретной фишке «зеленая точка занимает нижний правый угол»).
4-й обедающий
3-й обедающий
1 -й обедающий 2-й обедающий
Четыре цвета для восьми фишек
51
Уже создав центр, мы видим, что нам нужны еще две фишки, в которых желтый и синий цвета были бы смежными. Но у нас есть только одна такая, независимо от того, как мы разместим квадрат 2 х 2 в рамке. Точно так же мы не сможем найти фишки, где бы были смежными желтый и зеленый цвета 'здесьречь идет о симметрии). Очевидно, мы должны разместить центральные фишки так, чтобы смежными оказались желтый и красный цвета. Это фишки Ан А2, В, и В-.
Предположим что в центре находятся желтые точки:
Подходящи» цвета
Рассуждения, подобные предыдущему, приводят нас к с «дующему выводу: ни синий, ни зеленый не могут быть цветами четырех центральных точек. Если мы поместим синий в центр, то нам в< ег-да будет нс хватать одной части для укомплектовки периметра. К примеру, есть только одна из двух необходимых фишек со смежными красным и желтым цветами:
Мы можем разместить фишки Ci и Сг в положении:
Таким образом, цвет центральных точек должен быть желтым или красным. В таком случае головоломка будет завершена без проблем.
И головоломка легко собирается;
Решения
У этой головоломки восемь решений, и топько два из них принципиально различны. Решения, находящиеся в нижнем ряду, получаются из р шений вепхнего ряда заменой красного цвета на желтый и наоборот. Также можно уяидсть, что пары решений 1-2,3-4, 5-6,7-8 идентичны друг другу, если поменять местами синий и зеленый цвета.
12	3	4
5	6	7	8
52
D^AGOSTINI представляет
Пропустили выпуск любимой коллекции?
Q Просто закажите его на сайт
www.deagostini.ru
Для украинских читателей — по телефону горячей линии 0-800-500-8-40
В следующем выпуске через 2 недели
Шарики и отверстия
Симметрии
Менять, не меняя
Гений топологии
Эдвард Виттен
Вселенная Эшера
Математика, ставшая искусствам Спрашивайте в киосках!
Лучшее от Генри Э. Дьюдени
Геометрические задачи