Экспериментальная аэродинамика. Часть II. Индуктивное сопротивление - Юрьев Б.Н.

Автор: Юрьев Б.Н.

Теги: самолетостроение самолеты аэродинамика

Год: 1938

Похожие

Аэродинамический расчет самолетов

Основы авиационной техники

Аэродинамика. Несжимаемая жидкость

Аэродинамика элементов летательных аппаратов

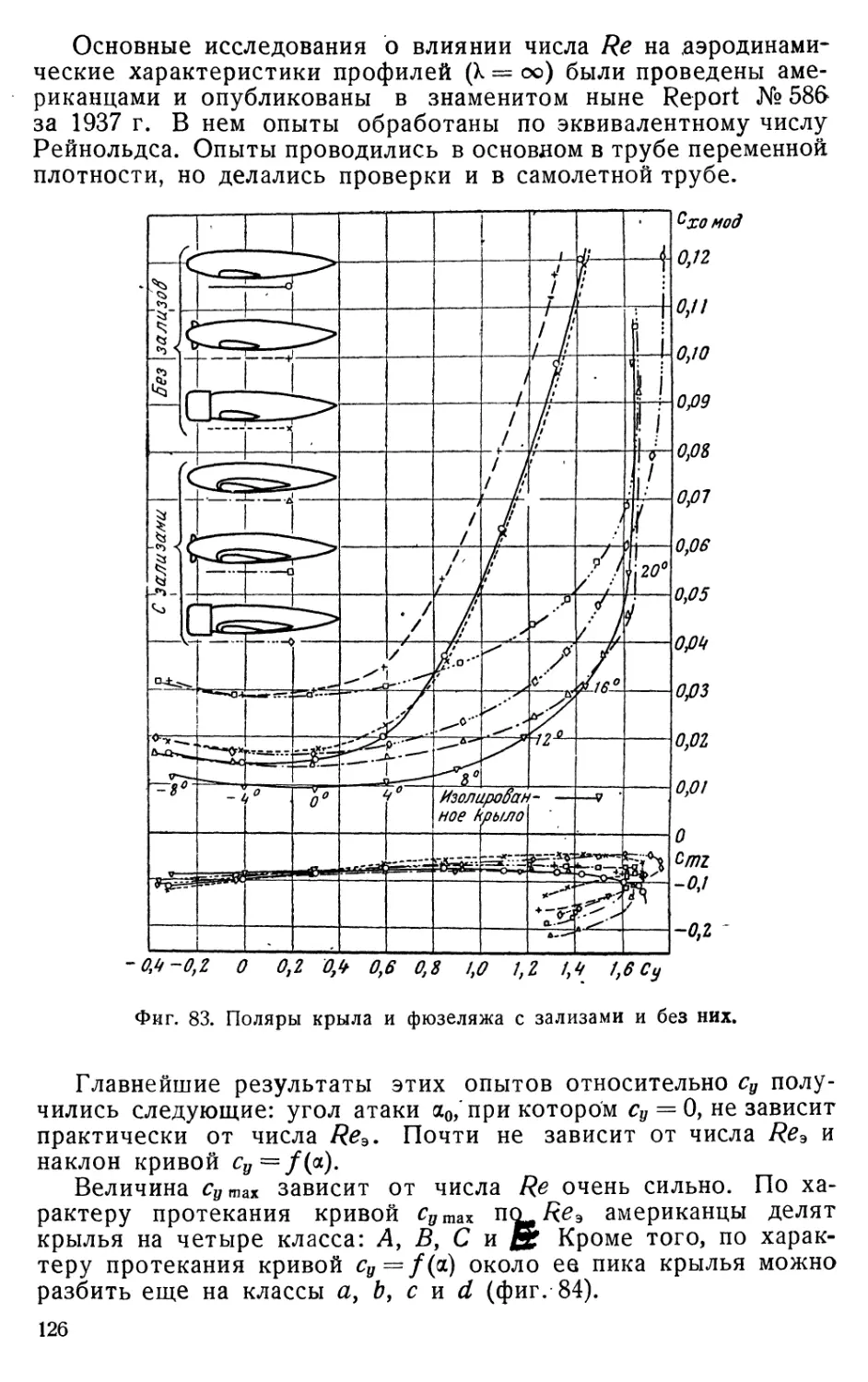
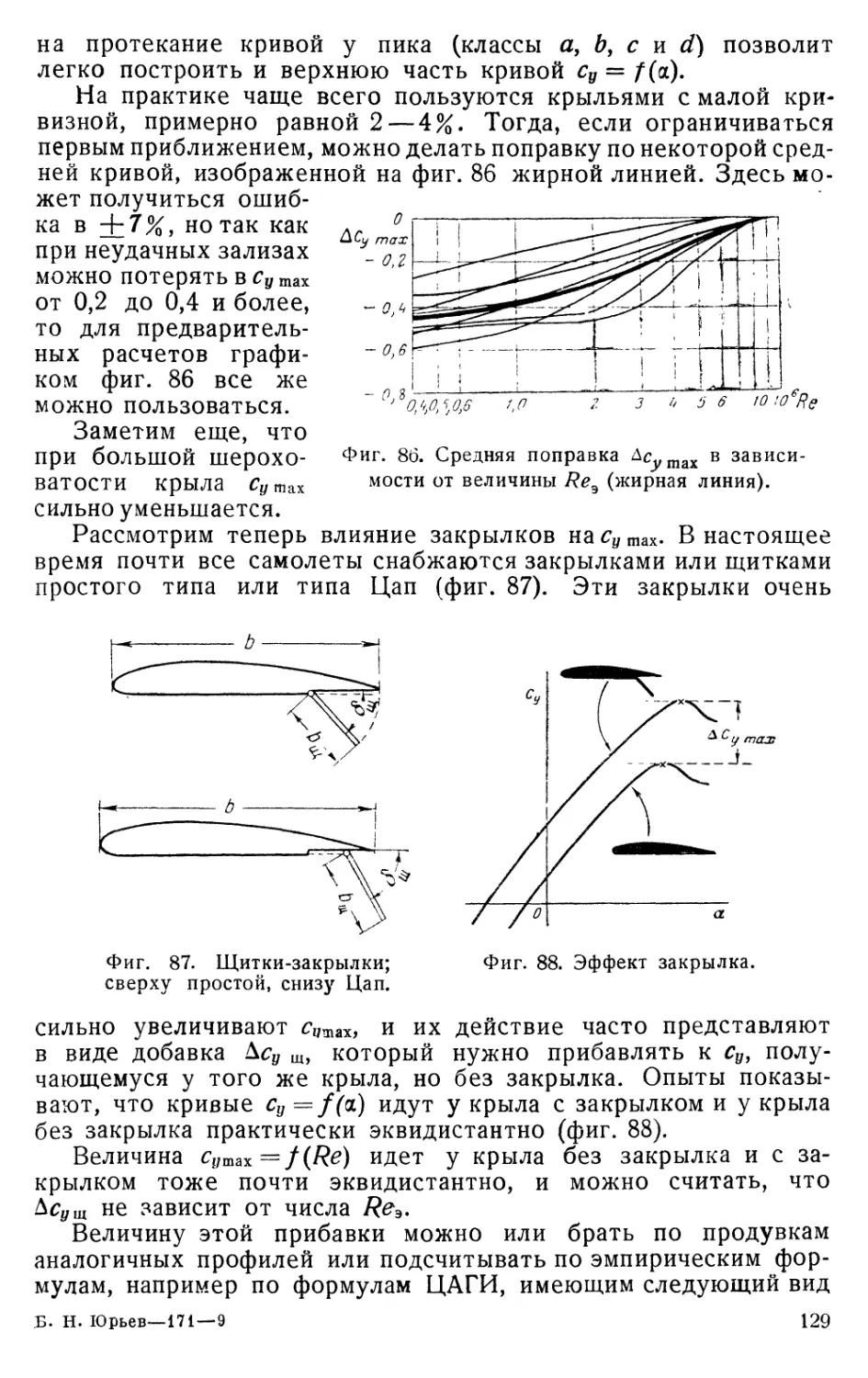
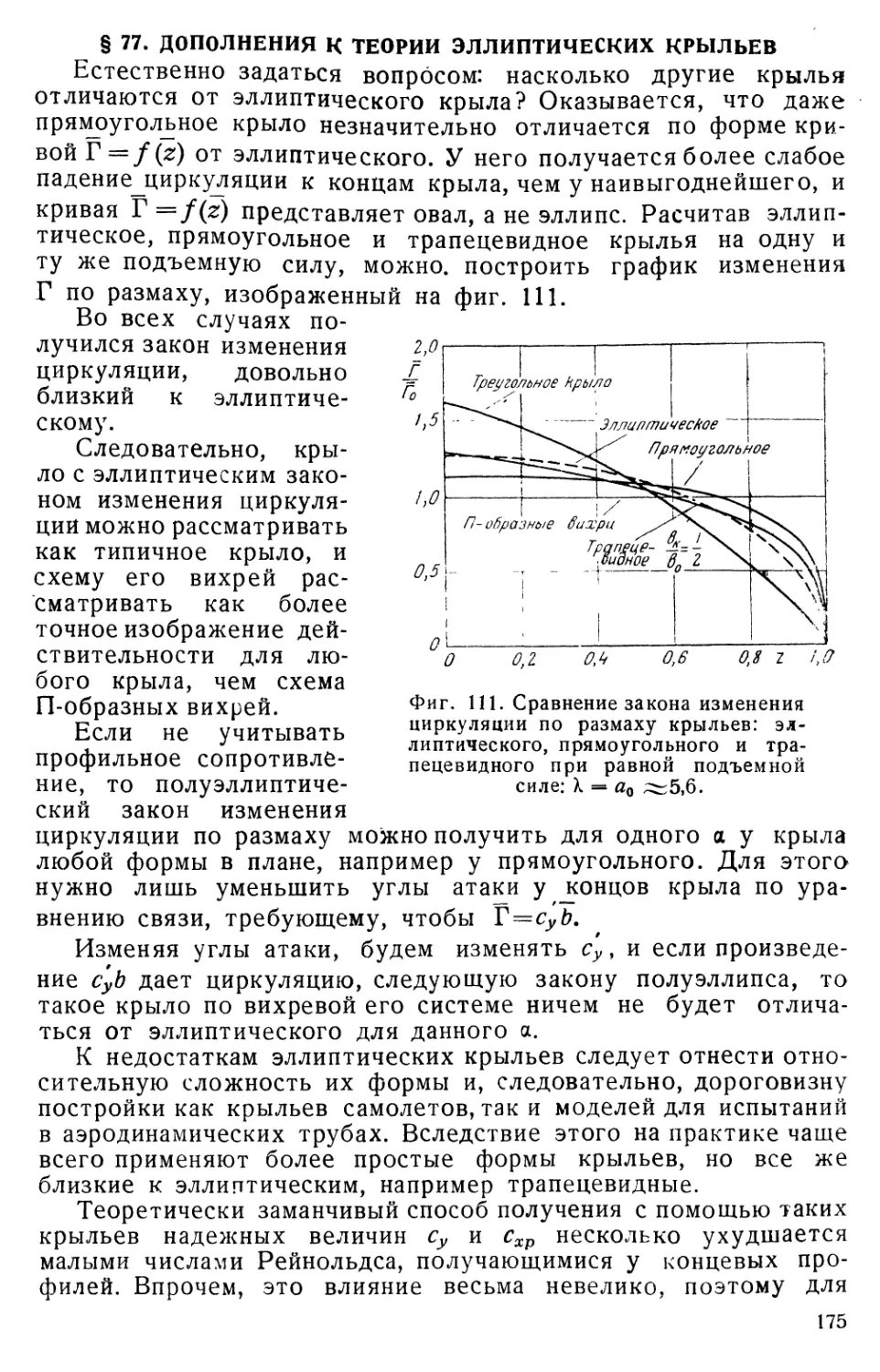
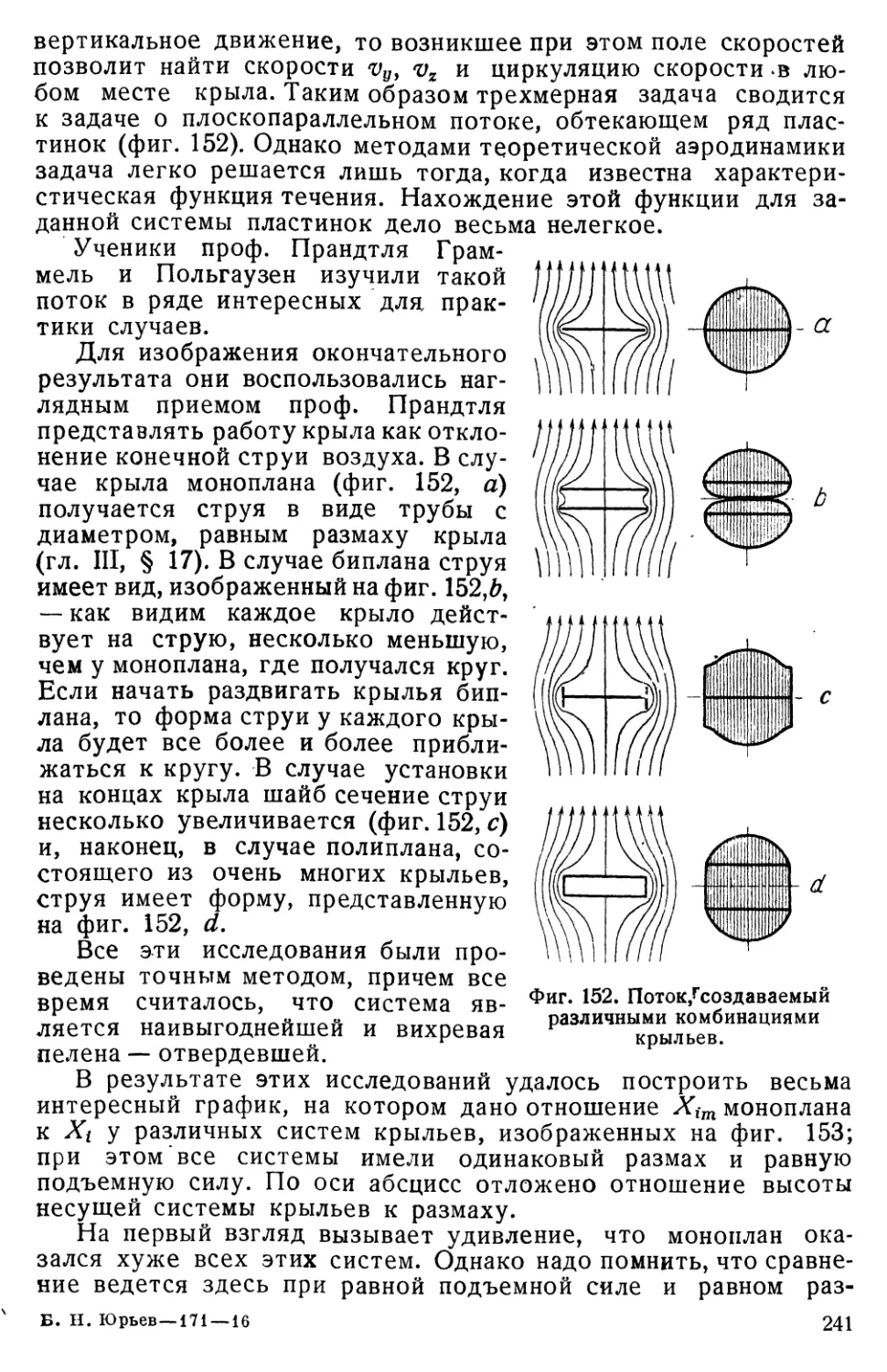
Текст

ЭКСПЕРИМЕНТАЛЬНАЯ
АЭРОДИНАМИКА
Б. Н. ЮРЬЕВ
Профессор Московского авиационного института им. Серго Орджоникидзе
ги Ордена Ленина Военной воздушной академии РККА им. Н. Е. Жуковского
ЭКСПЕРИМЕНТАЛЬНАЯ
АЭРОДИНАМИКА
Часть II
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ
Главным управлением учебных заведений НКОП
утвержден в качестве учебника для втузов НКОП
НКОП СССР
ИЗДАТЕЛЬСТВО НАРКОМАТА ОБОРОННОЙ ПРОМЫШЛЕННОСТИ
МОСКВА 1938 ЛЕНИНГРАД
Книга представляет собой вторую часть курса „Экспери-
ментальная аэродинамика* (ч. I вышла в свет в 1935 г., чч. III и IV
намечены к. изданию в 1939—1940 гг.) и посвящена индуктивному
сопротивлению крыльев. В ней дается вихревая теория крыла,,
являющаяся основой аэродинамического расчета самолета, при-
водятся теории моноплана и биплана и теория влияния крыла на
хвостовое оперение. В книге даются также методы расчета моно-
плана, биплана и хвостового оперения.
В книге использован богатый экспериментальный материал со-
ветских и заграничных экспериментальных исследований.
В основном книга является учебником для авиационных втузов,
однако указания по приложению теории к практическим расчетам
делают «этот учебник ценным руководством для конструкторских
^юро самолетостроительных заводов.
Редактор А. И. Жилина Техн, редактор А. А, Базанова
Сдано в набор 26/VIII—1938 г. Подписано к печ. 28/Х— 1938 г. Издат. Л* 47.
Автор, дог. № 206. Инд. А20-5-2. Тираж 6000. Кол. печ. лист. П1/*
Кол. печ. зн. в листе 47000. Учетно-авт. лист. 18,72 Формат бум. 60х92/1в
Уполн. Главл. Б—52975 Заказ № 171
Киевская типография Оборонгиза. Крещатик, 42
ПРЕДИСЛОВИЕ
Теория индуктивного сопротивления еще очень молода. Да-
той ее возникновения обычно считают 1917 г., когда проф.
Л. Прандтль и его ученики опубликовали ряд основных работ.
Однако проф. Н. Е. Жуковский и проф. С. А. Чаплыгин разра-
ботали основы этой теории еще в 1914—41919 гг. Результаты этих
работ докладывались на заседаниях Математического общества,
но не былй опубликованы, так как проверка этой теории в
устаревшей плоской трубе Высшего московского технического
училища не подтвердила основных ее выводов.
Прошедшие 20 лет ознаменовались весьма большими успе-
хами теории индуктивного сопротивления и в настоящее время
она обратилась в важнейший раздел прикладной аэродинамики.
Ее успех объясняется многими причинами. Во-первых, эта
теория дала четкие ответы на целый ряд фундаментальных во-
просов, интересующих авиаконструктора: какова наивыгодней-
шая форма крыла, как влияют друг на друга крылья биплана,
каково влияние крыльев на хвост самолета, насколько точны
опыты в аэродинамических трубах, как влияют стенки трубы на ре-
зультаты опытов и т. д.
Во-вторых, эта теория дала практические ответы почти на
все аэродинамические вопросы, интересующие расчетчика са-
молета. Проверка теории подтвердила ее точность для многих
случаев расчета.
В-третьих, эта теория привлекает инженеров своей просто-
той и наглядностью. Основной элемент этой теории—вихрь—тра-
ктуется в ней чисто по-инженерному. Вихрь „опирается на
крыло", он „действует" на окружающий воздух, он поддается
графическому изображению.
Все это привело к тому, что теория индуктивного сопро-
тивления стала весьма популярной и в конструкторских бюро,
и в исследовательских институтах.
В настоящее время на всех языках имеется большая лите-
ратура, посвященная вопросам индукции. К сожалению, вслед-
ствие быстрого развития эта теория приняла весьма разно-
образные формы из-за различия в осях координат, в коэ-
фициентах, в обозначениях величин, из-за отсутствия стандар-
тов и общепринятых правил. Это затрудняет изучение ее по
первоисточникам.
Кроме того, теория эта развирается очень неравномерно.
Некоторые вопросы освещены с исчерпывающей ясностью, но
многое остается до настоящего времени темным, и недоработан-
ным.
Последние годы ознаменовались углубленной работой аэро-
динамических лабораторий по проверке теории и по ее углуб-
лению. Советские лаборатории принимают деятельное участие
в этой работе и выдвинули ряд молодых ученых, давших много
ценных исследований.
Во втузах теория индуктивного сопротивления входит в курс
экспериментальной аэродинамики и подготовляет студентов к
слушанию курсов воздушных винтов, динамики самолета и к
дипломному проектированию самолетов. Число отводимых на
нее часов невелико,—г обычно 20—30 час. для самолетчиков, — и
ее приходится проходить весьма сжато. Настоящая книга и
рассчитана преимущественно на студентов-самолетчиков. В ос-
нову ее положены программы, по которым этот курс читался
в течение ряда лет в наших авиавтузах.
Темы, которые на лекциях прорабатываются очень сжато,
часто без детальных выводов, освещены в этом курсе достато-
чно подробно, чтобы студент мог самостоятельно разобраться в
интересующем его вопросе.
При написании курса пришлось учесть наличие в наших вту-
зах и других специальностей, которые нуждаются в более про-
стом изложении аэродинамики. Для этого настоящая книга раз-
бита на два раздела. В первом прорабатываются все вопросы
с точки зрения элементарной теории П-образных вихрей. Во
втором разделе дана углубленная трактовка — циркуляция ско-
рости здесь считается переменной по размаху крыла.
Такое построение курса позволяет удовлетворить потребно-
сти всех специальностей наших авиавтузов. С этой же целью
отдельные, особо важные параграфы изложены так, что они
могут читаться независимо от остальных частей книги. Эта,
правда, вызвало небольшие повторения, но методически оказа-
лось весьма удобным.
Автор, понятно, не задавался целью „исчерпать предмет" в
этом курсе,—для этого пришлось бы написать несколько книг,—
и ограничился минимумом, безусловно необходимым авиацион-
ному инженеру.
Во изменение первоначального плана, изложенного в первой
части курса экспериментальной аэродинамики, настоящая книга
выходит в качестве второй части курса.
Автор заранее благодарит товарищей, которые помогут ему
исправить в дальнейших изданиях недостатки, несомненно име-
ющиеся в этой книге.
Проф. Б. Юрьев
28/VII-38 г.
Основные обозначения
Oxyz — оси поточные.
Ox^Zr — оси связанные.
а —угол атаки крыла, отсчитываемый от центральной хорды.
аа — угол атаки по аэродинамической хорде; когда оговорено, индекс а не
ставится.
а'—текущий угол атаки сечения.
да — угол скоса потока.
Даг. о — угол скоса потока у горизонтального оперения.
аг —истинный угол атаки.
Ф = а' — а — угол закрутки сечения крыла.
S —площадь крыла.
— S
S « .д-а—отвлеченная площадь крыла.
I — размах крыла.
Ь, Ьо и Ък — хорды текущая, центральная и концевая.
h Г s
°ср = —тть== 5— Средняя хорда.
Ь, Ьо, Ьк, — хорды текущая, центральная, концевая и средняя, отнесен-
ные к Z/2.
х, у, z— отвлеченные координаты, отнесенные к Z/2.
L — условная длина самолета — от центра тяжести до шарниров руля высоты.
. Р Z 2 4
1= —$ = у = =— = -^-—удлинение крыла.
X*— эффективное удлинение в присутствии фюзеляжа.
Хэ— удлинение эквивалентного крыла моноплана.
у—стрелка кривизны профиля.
f = -у— относительная стрелка кривизны.
г —толщина профиля.
с
с == ---относительная толщина.
о
h —высота коробки крыльев.,
а
— вынос верхнего крыла по отношению к нижнему и наклон кривой Cjnott
(см. далее).
— консоль крыла.
с
V —скорость полета или потока вдали от тела.
vT — результирующая скорость потока.
Wx, Wy, Wz—компоненты результирующей скорости потока.
v — индуктивная скорость.
Vy, vz — компоненты индуктивной скорости.
vyo —средняя по размаху скорость скоса у моноплана.
- Vr ~ Vy — Vz
Vx, = -у; vy = vz = у—отвлеченные индуктивные скорости.
Vx Vy Vz
= -j—v ,, =------v y *= .----------относительные индуктивные ско-
I I y I 1
рости.
R— результирующая аэродинамических сил.
X У, Z—компоненты полной силы в поточных осях.
V
5
М — полный аэродинамический момент..
Мх, Му, Mz— компоненты полного аэродинамического момента в поточных осях.
су, cZi стх, cmyt cmz — поточные аэродинамические коэфициенты (новые)
отнесенные к скоростному напору.
с rt си, с'* с'„ с' — текущие аэродинамические коэфициенты для
сечения крыла, лежащего на абсциссе z .
а = — наклон кривой су = /(а) для всего крыла в целом.
de
= __у — наклон кривой Су — f(a) для крыла бесконечного ра3маха или для
dcii
сечения.
Ап, Вт, С2к— коэфициенты разложения в ряд Фурье разных функций.
, р—массовая плотность воздуха.
pV2
q == ---скоростной напор потока.
а — площадь вредной эквивалентной пластинки. Прандтлевский коэфициент
индукции биплана.
1,28—условный коэфициент лобового сопротивления для пластинки.
£. £12» e2i —коэфициенты индукции и взаимной индукции крыльев.
Р-125 Р-21 —коэфициенты взаимной индукции для горизонтальной скорости.
12
Р =-у—отношение размахов крыльев в биплане,
п
h
rt = г /---относительная высота коробки биплана.
*1 "Г *2
2
х—отношение индуктивного сопротивления данной коробки к индуктивному
сопротивлению моноплана того же размаха.
Индексы 1, 2, 3 — номер крыла, считая сверху.
(—) — черта над буквой обозначает отвлеченную величину.
(') — штрих сверху употребляется в разных смыслах; при аэродинамических
коэфициентах обозначает местные для данного сечения значения.
ф. к и г. о — в индексе обозначают, что величины относятся к фюзеляжу, концу
крыла и горизонтальному оперению.
РАЗДЕЛ I
КРЫЛО С П-ОБРАЗНЫМИ ВИХРЯМИ
Глава I
ОСНОВЫ ТЕОРИИ ВИХРЕЙ
§ 1. ЦИРКУЛЯЦИЯ СКОРОСТИ
Напомним вкратце основные положения теории вихрей, про-
ходимые в курсе теоретической аэродинамики. Крайне важным
во всей аэродинамике является понятие о ,
циркуляции скорости по любому /уХ.
замкнутому контуру. Если взять в текущей /s
жидкости какой-нибудь замкнутый контур у /
Д2?С(фиг. 1), то можно, разбив контур на ма-
лые элементы длиной ds, написать выра- ''та \
жение: Л gl
dT = Vs ds, } У
где Vs = V cos <р — проекция скорости жидко-
сти на касательную к этому элементу; вели-
чина t/Г называется течением скорости фиг' *• Циркуляция
вдоль элемента ds.
Делая круговой обход этого контура и подсчитывая тече-
ние скорости по всему замкнутому контуру, получим цирку-
ляцию скорости:
(1)
знак у обозначает интеграл по замкнутому контуру.
Циркуляция может быть отрицательной, положительной и
равной нулю. В геометрическом смысле она является скаляром,
а не вектором. Выражение циркуляции формально напоминает
выражение работы силы, однако физический смысл циркуляции
совсем другой. Ее размерность такова: [л/]2 [сек.]-1.
При помощи циркуляции определяется, завихрено ли течение
жидкости или нет. Если циркуляция по любому замкнутому
контуру в какой-нибудь области течения жидкости равна нулю,
то это означает, что движение жидкости в этой области не за-
вихрено; наоборот, если Г не равна нулю, то движение будет
вихревым.
7
§ 2. ПРЯМОЛИНЕЙНЫ» ВИХРЕВОЙ ШНУР
Наиболее простым случаем завихрения является прямо-
линейный вихревой шнур (фиг. 2). В нем жид-
Фиг. 2. Прямолинейный
вихревой шнур.
кость завихрена равномерно. Бли-
жайшее исследование показывает, что
такой шнур просто вращается, как
твердое тело, около своей оси 00'.
Снаружи жидкость может быть и не
завихрена. Однако в последнем слу-
чае, как показывает подробное изуче-
ние, жидкость не будет находиться
в покое, а придет в особое цикли-
ческое движение, причем части-
цы ее хотя и будут бегать по кру-
говым траекториям, однако не будут
иметь угловой скорости вращения.
Далее в гидродинамике доказывается,
что циркуляция скорости по любому
контуру, охватывающему вихревой
шнур, равна постоянной величине. Таким образом силу вихря
можно измерить имеющейся вокруг него циркуляцией.
§ 3. КРИВОЛИНЕЙНЫЕ ВИХРИ. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА И СТОКСА
В общем случае вихри имеют криволинейную форму.
В этом случае вокруг вихря возникает сложное движение жид-
кости, а сам вихрь может при этом все время изменять свою
форму, как бы „извиваться змеей". Несмотря на сложность таких
движений жидкости они все же подчинены сравнительно про-
стым законам, найденным впервые Гельмгольцем. Эти законы
или теоремы Гельмгольца формулируются обычно таким образом:
1) циркуляция скорости вокруг вихревого шнура по всей
его длине остается величиной постоянной, т. е. вихрь не может
внезапно окончиться;
2) вихревой шнур все время остается вихревым шнуром
(теорема о неуничтожаемости вихрей);
3) циркуляция скорости вокруг движущегося в жидкости
вихря во все время его движения постоянна.
Из этих теорем следует, что вихревой шнур должен или
простираться обоими концами, в бесконечность (фиг. 3, а), или
замыкаться сам на себя, образуя вихревое кольцо (Ь), или опи-
раться одним концом (с), или двумя концами (d) на границы
жидкости, т. е. на твердое тело, или на ее свободную поверхность.
Эти теоремы доказываются в курсах гидродинамики и находят
весьма широкое применение в теории индуктивного сопротив-
ления крыльев.
Иногда случается, что через воображаемый в жидкости кон-
тур проходит не один, а несколько вихревых шнуров. Тогда
применима знаменитая теорема Стокса — циркуляция скорости
8
по контуру равна алгебраической сумме циркуляций отдельных
вихрей, проходящих через него. Эта теорема позволяет находить,
скорости в потоке, обусловленные наличием вихрей. Обычно,
в таких случаях говорят, что вихри вызывают в окружающей
жидкости скорости.
Это выражение не
следует понимать
буквально, так как
в идеальной жидко-
сти нет трения и
вихрь не может за-
крутить поток вок-
руг себя. Правиль-
нее говорить, что
вихри и скорости
в окружающей их
жидкости взаим-
но обусловлены. В
дальнейшем мы бу-
Фиг. 3. Возможные формы вихрей.
дем называть скорости, вызванные вихрями, индуктивными
скоростями и будем их обозначать малой буквой V.
§ 4. СКОРОСТИ ОКОЛО ВИХРЕЙ. ТЕОРЕМА БИО-САВАРА
В случае прямолинейного шнура скорость, вызванная им
в какой-нибудь точке А, может быть легко найдена путем сле-
дующего простого рассуждения. Проведем через точку А плос-
кость, перпендикулярную к оси вихря, и начертим на ней окруж-
ность (фиг. 2), проходящую через эту точку, с центром, лежа-
щим на оси вихря. В силу симметрии и вследствие отсут-
ствия в потоке источников и стоков заключаем, что скорость
во всех точках этой окружности будет одинаковой и направ-
ленной по касательным, т. е. всюду vs = v = const. Отсюда цир-
куляция скорости по этой окружности будет такой:
Г = ф vs ds = v$ds — v2itr,
где г — радиус окружности. Сила вихрей задается циркуляцией.
Зная циркуляцию Г, находим:
•V =
Г
2кг*
Эта скорость направлена в ту сторону, в которую вращается
вихревой шнур; Нередко в приложениях приходится вичислять
скорость, вызванную половиной шнура, т. е. отрезком вихря, иду-
щим от плоскости Р вверх или вниз в бесконечность (фиг. 2).
Действие такого вихря на точку А оказывается в два раза
меньшим, чем в случае целого шнура (см. далее), и вызванная
им скорость вычисляется по формуле:
Г
“V — -г- •
4кг
(2>
(3>
9
В случае криволинейного вихря скорость приходится вы-
числять сначала для бесконечно-малого элемента длины шнура dL
и затем ийтегрировать по всей его длине.
Как доказывается в теоретической аэро-
динамике, скорость dv, вызванная эле-
ментом криволинейного шнура,
жается формулой Био-Савара,
щей вид:
выра-
имею-
dv = -т^-ssin
4лг2 *
(4)
Здесь <р — угол между г и осью эле-
мента 00', Г — циркуляция скорости
вокруг вихревого шнура,—величина по
всей его длине постоянная (фиг. 4). Фор-
мула эта имеет полную аналогию с за-
коном действия элемента электриче-
ского тока на магнитный полюс, поме-
щенный в точке А. Чтобы получить
Фиг. 4. К теореме Био- полное действие криволинейного шнура
Савара. на точку А, нужно просуммировать
геометрически все скорости dv от всех
элементов по его длине. Направление скорости dv легко найти:
оно совпадает с той скоростью, с какой вращалась бы точка А
•около оси 00', будучи скрепленной с элементом dL.
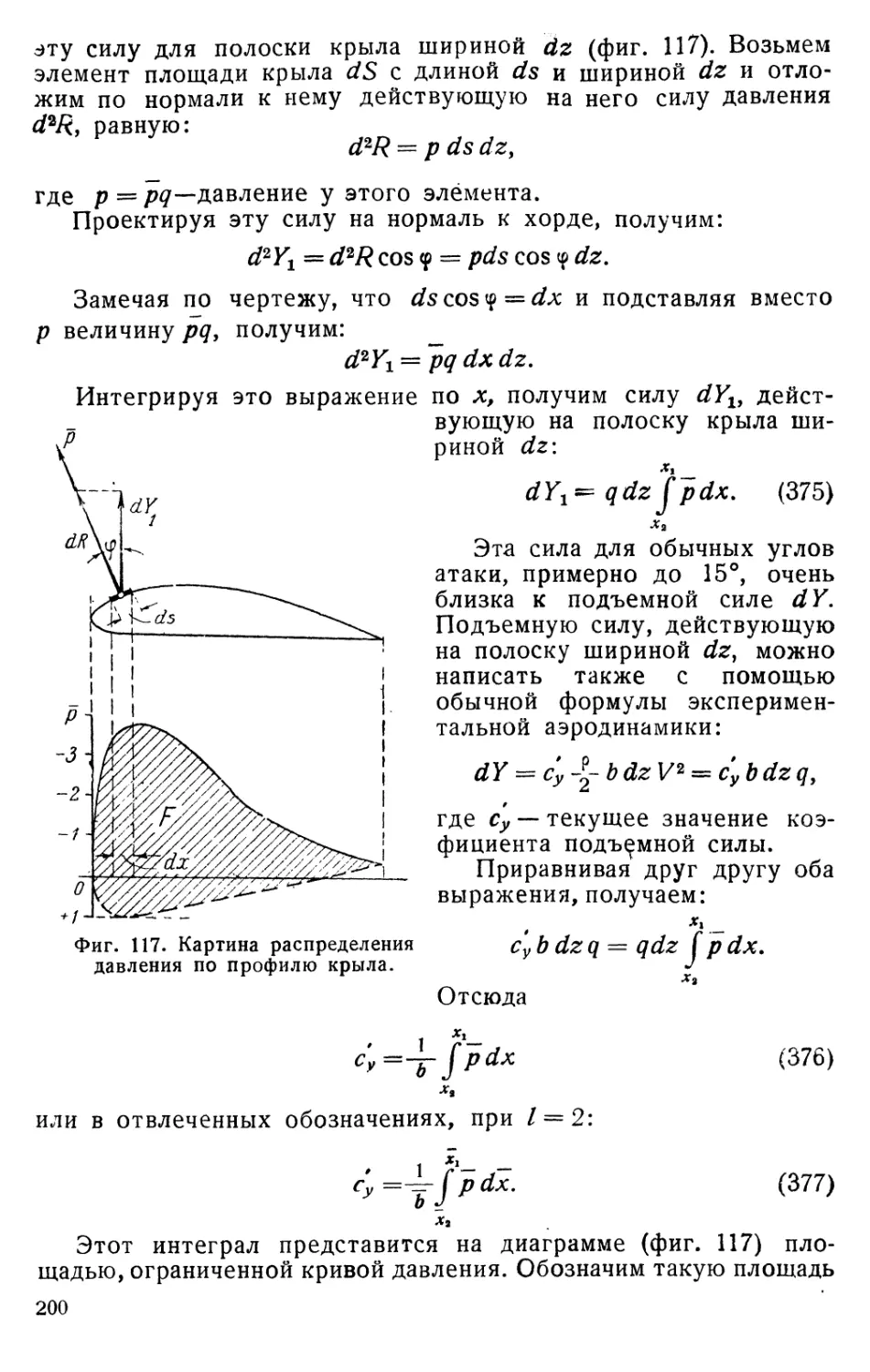
§ 5. ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ ВИХРЕЙ
Формулу Био-Савара следует применять ко всему простран-
ству, занятому жидкостью. Следовательно, при криволинейном
вихре или при наличии нескольких прямолинейных вихрей одни
из элементов вихря будут вызывать скорости у других эле-
ментов и таким образом вихри придут в сложное движение.
Теорема Био-Савара показывает, что скорости, вызываемые от-
дельными элементами, а следовательно, и вихрями, просто сум-
мируются геометрически.
Отсюда получается очень важный для приложений принцип
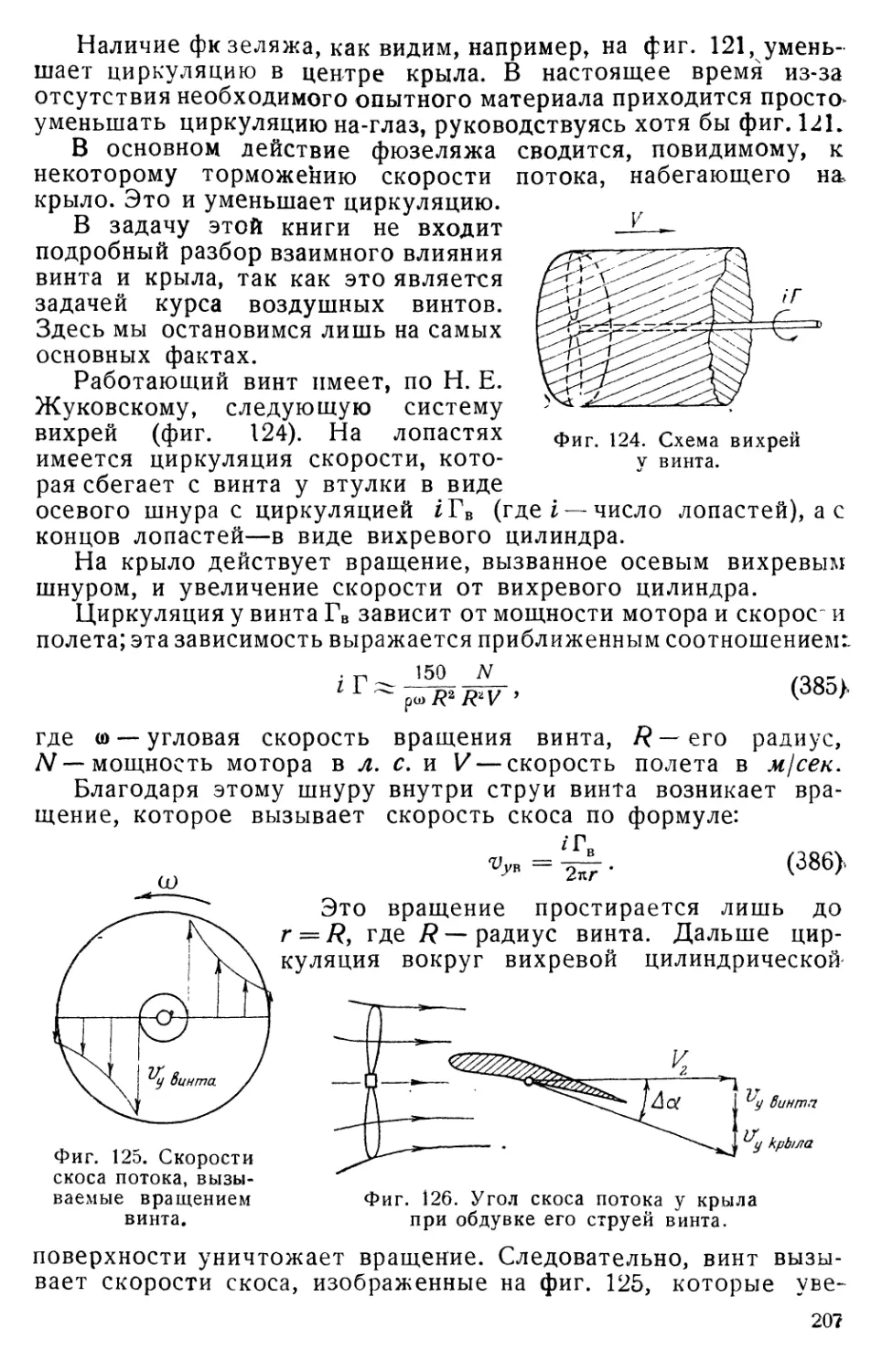
независимости действия вихрей, или принцип наложения, кото-
рый можно сформулировать таким образом: при наличии в жид-
кости нескольких вихрей скорость от каждого вихря в любой
точке может быть найдена так, как будто других вихрей не су-
ществует; геометрическое сложение найденных таким образом
-скоростей дает истинную скорость в этой точке.
Если при этом, как это постоянно имеет место в теории
индукции, на систему вихрей набегает еще поступательный
поток со скоростью V, то эту скорость следует геометрически
•сложить со скоростями, полученными от вихрей.
10
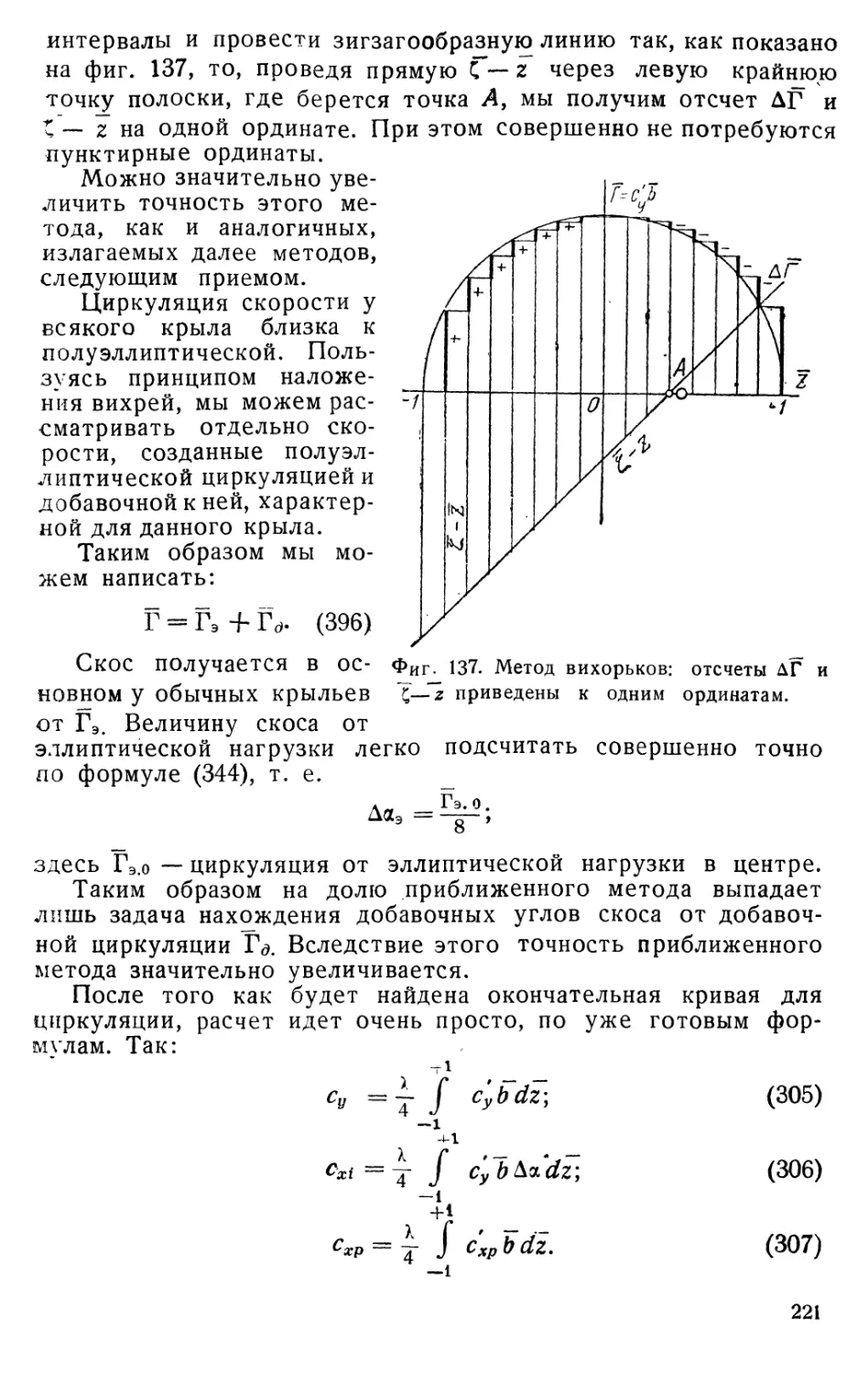
§ 6. ПРЯМОЛИНЕЙНЫЙ ВИХРЕВОЙ ОТРЕЗОК
Как увидим далее, вихри, сбегающие с крыла, имеют прямо-
линейную форму. Пользуясь принципом независимости действия
вихрей, их можно разбивать на прямолинейные отрезки.
Возникает вопрос о величине скорости, вызванной таким
отрезком.
Пусть мы имеем отре-
зок вихря ВС. Найдем ско-
рость, вызванную им в
точке А (фиг. 5). Прове-
дем оси координат,как по-
казано на чертеже. Пусть
точка А лежит на рас-
стоянии от оси вихря,
а концы вихря, т. е. точки
В и С, лежат на расстоя-
ниях хг и х2 от основания
перпендикуляра О, опу-
щенного из точки А на
ось вихря (начала коор-
динат). Все элементы, лежащие на отрезке ВС, будут
вать на точку А, вызывая в ней скорости по
Био-Савара:
Фиг. 5. Действие вихревого отрезка.
действо-
формуле
dv = sin <? dL.
(5)
Возьмем текущий элемент be и применим к нему формулу
Био-Савара.
Заметим сначала, что соединив концы этого элемента с точ-
кой А, мы получим расстояния АЬ и Ас, в пределе совпадающие
и тогда равные г. Описав из точки А дугу радиусом г, получим
бесконечно-малый треугольник abc, причем / acb в пределе
равен <р.
Легко видеть, что
ab — rdy и dL = ——
т sin ср
Далее
г — —V ч
5Ш ср 4
и, следовательно,
dL = -^-df.
Sih2 ср т
г dv
S1U Ср. ‘
(6)
Подставляя найденные величины в формулу Био-Савара,
получаем:
dv =-----5; sin <р - V— = — sin и do. (7)
4лу? S1“2® 4пу! ‘ т к '
11
Для получения полной скорости интегрируем действие всех
элементов шнура в пределах углов от ?х до <р2 и получаем:
t' = 4^/sin'PtZ<₽='4^(COS(?2-COS^- <8>
Формула эта и решает поставленную задачу. Легко убедиться,
что она дает правильный ответ и для прямолинейного шнура
и для полушнура. В первом случае мы должны подставить в нее
<р!= 180° и <р2 = 0°; тогда получим:
Г
'и~'2ку1>
во втором случае, подставив ?1 = 90° и <f2 = 0°, получим:
г
v — 1—,
4V1
т.е. эти формулы совпадают с уже полученными формулами (2) и (3).
Основную формулу (8) удобно для приложений освободить
от тригонометрических выражений, для чего достаточно заме-
тить, что
cos =
V У1+х1
_____Х2_______________
l/" «.2 । у2
И _У1 + *2
и
cos <f 2 =
подставив эти выражения в формулу (8), получим:
Г /'*2*1
О)
Величину лх следует брать со знаком минус, когда концы
шнура лежат по разные стороны от основания перпендикуляра,
опущенного из точки А на ось вихря.
Если один конец шнура уходит в бесконечность (х2=со),
а другой лежит на конечном расстоянии л, от начала коорди-
нат, то формула (9) принимает вид:
и =
У1+х1/
(Ю>
Глава II
ТЕОРЕМА Н. Е. ЖУКОВСКОГО
V § 7. ТЕОРЕМА Н. Е. ЖУКОВСКОГО ДЛЯ КРЫЛА БЕСКОНЕЧНОГО
РАЗМАХА
Теорема Н. Е. Жуковского заняла в настоящее время исклю-
чительное положение в прикладной аэродинамике. Доказана она
была проф. Н. Е. Жуковским еще в 1906 г., но до 1910 г. оставалась
незамеченной. Лишь после развития теории крыльев бесконеч-
ного размаха—теории, в создании которой русские ученые играли
12
руководящую роль, эта теорема получила мировое признание.
Особенно ее роль возросла после разработки теории индуктив-
ного сопротивления крыльев.
Теорема эта относится к плоскопарал-
лельному потоку. Пусть в таком потоке,
текущем вдали с постоянной скоростью И,
находится крылообразный цилиндр, пер-
пендикулярный к потоку и имеющий бес-
конечную длину (фиг. 6). Если выделить
двумя сечениями, перпендикулярными
к размаху крыла, отрезок крыла длиной I,
то на него в общем случае будет дей-
ствовать подъемная сила Y, которая
определяется по теореме Жуковского:
подъемная сила Y, действующая на
выделенный отрезок I крыла бесконеч-
Фиг. 6. К теореме
Н. Е. Жуковского.
ного размаха, равна циркуляции скорости, умноженной на
плотность жидкости, на скорость не возмущенного потока и
на длину отрезка I, т. е.
Г=ГрУ/. (11)
Для того чтобы найти направление подъемной силы, надо
взять вектор невозмущенной скорости V и повернуть его на
прямой угол в сторону, противоположную циркуляции скорости.
Лобовое сопротивление крыла бесконечного размаха равно
нулю, т. е.
Х = 0.
Мы эту теорему вывели в первой части курса эксперимен-
тальной аэродинамики. Подробно она излагается во всех курсах
гидродинамики.
Н. Е. Жуковский показал, что крыло в гидродинамическом
смысле эквивалентно вихрю, так как и вокруг крыла и вокруг
вихря существует циркуляция, скорости. Это поаволяет оамо.
нять_лфыде--тщьюм вихрей, идущих внутри его контура. Такие
вихри, которыми мпжип чямриитк vpmn были названы Н. Е. Жу-
ковским п р и с о е. п и н е н н ы м и в и х р я м и. Если уничтожить
крыло и заменить .его простыми Пвихрями,-то набегающий поток
воздуха унесет их с собой. Присоединенные же вихри несмотря
на набегающий поток стоят неподвижно, поэтому их в боль-
шинстве стран называют также связанными вихрями.
Очевидно, что на связанные вихри при набегании потока по
теореме Жуковского будет действовать подъемная сила, и для
того, чтобы они стлали неподвижно, на них должна действо-
вать сила, обратная подъемной (у самолета — вес). Эта сила
и удерживает вихри на месте и делает их связанными. Таким
образом удерживать вихри бесконечной длины приходится не ло-
бовой силой, которая равна нулю, а поперечной, к потоку, и
направленной обратно развиваемой вихрями подъемной силе
13
§ 8. ТЕОРЕМА Н. Е. ЖУКОВСКОГО ДЛЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
В 1910 г. целый ряд исследователей заинтересовался вопро-
сом, что получается у крыла не бесконечного размаха, а ко-
нечного.
-Если у крыла размах равен I, то заменив это крыло при-
соединенными вихрями, мы получим явное противоречие первой
теореме Гельмгольца: вихревой пучок оканчивается теперь вне-
запно, в точках, где находились торцы крыла. Вихри эти не могут
окончиться внезапно и должны выйти за пределы размаха I.
Но там они, не будучи связанными, так как на них не
действует вес самолета, будут подхвачены общим течением
воздуха и вытянутся в так назы-
фиг. 7. Крыло с П-образными
вихрями.
шелковинку, чтобы обнаружит
ваемые вихревые усы, иду-
щие в бесконечность (фиг. 7).
Следовательно.крыло конечного
размаха~можно_заменить систе-
мЪи'ТГббразных вихрей или. еше
проще, одним вихрем П-образ-
нои формьГУ такого вихря цир-
куляцйя~скорости Г будет всю-
ду одна и та же.
Опыты прекрасно подтверж-
дают эту схему. Достаточно
ввести в поток у концов крыла
ь эти вихри. В стороне от концов
крыла такая шелковинка просто указывает направление потока,
у концов же крыла при попадании ее внутрь вихревого шнура
она начинает быстро вращаться, описывая конус.
Описанная схема П-образных вихрей является простейшей и в
чистом виде, как увидим далее, не существует. Ее можно обобщить
Фиг. 8. Крыло с уступами.
Фиг. 9. Многоступенчатое крыло.
на крылья более сложной формы. Так например, если крыло
имеет уступы, как на фиг. 8, то подъемная сила будет распре-
делена по размаху неравномерно,—обычно она бывает боль-
14
ше в центре; следовательно, циркуляция в средней части Г2.
крыла будет больше, чем циркуляция Г, на концах крыльев.
Если такое крыло заменить присоединенным вихрем, то этот
вихрь будет иметь ступенчатую циркуляцию, и, следова-
тельно, сбегающие вихревые усы должны иметь циркуляцию,
равную разности циркуляций примыкающих участков крыла.
Распространяя это положение на многоступенчатое крыло, при-
дем к картине фиг. 9, а взяв бесчисленное количество ступеней,
перейдем к крылу с непрерывно сбегающими вихревыми усами.
Циркуляция скорости у каждого такого_уса будет бесконечно-
малой; совокупность таких вихрей образует вихревую пе-
лену.
В дальнейшем мы покажем, что в действительности с крыла
всегда сбегает вихревая пелена.
Эту пелену можно представлять как совокупность наложен-
ных друг на друга П-образных вихрей с бесконечно-малыми
циркуляциями (фиг. 10). Исследования этой пелены показали,
что она неустойчива и вскоре после
сбегания с крыла она от действия слу-
и чайных причин сворачивается в два
вихревых уса (фиг. 11).
фиг. 10. Схема вихревой
пелены.
Фиг. 11. Свертывание вихревой
пелены.
У крыльев, по форме близких к прямоугольным, вихри сбе-
гают главным образом у концов, и вихревая пелена в этом слу-
чае довольно близка к П-образной схеме вихрей. Для решения
очень многих задач практики схема с П-образными вихрями ока-
зывается 'достаточно точной. В первом разделе этой книги мы
будем пользоваться лишь этой схемой.
§ 9. УРАВНЕНИЕ СВЯЗИ
Для решения различных задач индукции нужно уметь вы-
числять циркуляцию скорости вокруг крыла. Это удобнее всего
делать с помощью уравнения связи, которое выводится таким
образом. Подъемную силу крыла мы можем найти по формуле
Жуковского:
Г=.ГРИ/.
Эту же силу можно вычислить, зная су крыла, по обычной фор-
муле экспериментальной аэродинамики:
Y = cgSq, (12)
15
.где с» — коэфициент подъемной силы (новый), S — площадь
крыла и q — Ч,--скоростной напор.
У прямоугольного крыла S = Ы, где b — ширина крыла и
/ — размах. Следовательно,
Y^Cy^bl. (13)
Очевидно, подъемная сила Y как по формуле (11) чисто
теоретической, так и по чисто экспериментальной формуле (13)
.должна получиться одна и та же. Следовательно,
ГР И = су ф Ы-
отсюда
V = ^-bV. (14)
Это выражение называется у р а в н ен и ем связ и — оно свя-'
зывает экспериментальную величину су с теоретической величи-
ной Г и таким образом объединяет теоретическую аэродина-
мику с экспериментальной.
Уравнение это находит широкое применение в теории ин-
дукции и в теории винтов.
§ 10. УПРОЩЕННЫЙ ВЫВОД ТЕОРЕМЫ Н. Е. ЖУКОВСКОГО
ДЛЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
Точный вывод теоремы Жуковского для крыла бесконечного
размаха довольно сложен: приходится определять по уравнению
Бернулли давление в струйке жидкости, обтекающей контур, и
затем суммировать давление по всей поверхности профиля.
Однако в случае крыла конечного размаха с вихревыми усами,
как показал сам Н. Е. Жуковский, вывод этой теоремы можно
сделать довольно просто приближенным способом.
Сделаем следующие допущения: 1) вихри за крылом идут
все время горизонтально на расстоянии I друг от* друга и
2) давления не играют заметной роли в точках, далеких от
крыла. На самом деле вихри влияют друг на друга и идут, все
время снижаясь и извиваясь наподобие змей. Давления играют
некоторую роль и в далеких от крыла точках. Однако указан-
ные допущения все же близки к действительности.
Если мы проведем далеко за крылом плоскость, перпенди-
кулярную к направлению скорости потока, то эта плоскость
пересечет вихревые усы, и мы получим картину, изображенную
на фиг. 12. Вихри эти создадут вокруг себя скорости, которые
можно вычислить по формуле (2), т. е.
-и = _L.
2лг
Сразу видно, что между вихрями воздух получает от их
действия скорости, направленные вниз; снаружи же один вихрь
16
гонит воздух вниз, а другой вверх. Протекающий через нашу
плоскость воздух имеет, следовательно, вертикальные скорости
и несет некоторое количество движения, При сделанных нами
предположениях подъемная сила крыла должна равняться се-
кундному приросту количества движения в уходящем от крыла
воздухе. Подсчитаем это количество движения. Сначала найдем’
количество движения, создаваемое одним вихрем в бесконечно
узкой полоске с шириной dz и длиной,
равной единице по направлению у
полета.
Вертикальная составляющая ско-
рости, вызванной в точке А левым
вихрем, будет такой:
= v cos <р = Т- cos <р, >
где — угол, обозначенный на
теже.
Замечая, что
___ g Фиг. 12. Индуктивные скорости
r cos 9 ’ от вихрей за крылом.
получаем:
Р
^ = ^со^<р.
Количество движения, имеющееся в параллелепипеде дли-
ной по направлению полета, равной единице, высотой dy и ши-
риной dz может быть написано в виде:
vy dm = vg р 1 dz dy;
здесь dm — масса этого параллелепипеда и р — массовая плот-
ность воздуха.
Из чертежа видно, что
dy = =
cos ср COS2 ср •
Подставляя это выражение в предыдущую формулу, получаем:
р
Vy dm = р - dz dy.
Обозначим через dM количество движения во всей полоске
шириной dz; тогда
dM = у Vy dm = р dz J dy = рГ dz.
Г. тс
Б. Н. Юрьев—171—2
17
Получилось очень интересное выражение для dM—оно не за-
висит от координаты z. Следовательно, для всех полосок оди-
наковой ширины dz количество движения будет одним и тем
же. Так как у нас имеются два вихря, то в области между ними
их действие суммируется и количество движения каждой по-
лоски удваивается и равно рГ/Zz; снаружи же, где вихри дей-
ствуют в противоположные стороны, количество движения по
вертикали равно нулю. Следовательно, для получения полного
количества движения нам придется суммировать лишь полоски,
лежащие между вихрями.
Итак, находим:
i i
2М= f 2dM=pV f dz = рП.
О о
Это выражение дает количество движения по вертикали
в полосе шириной I и длиной, равной единице, по направлению
полета. Подъемная же сила равна секундному количеству дви-
жения. Через рассматриваемую плоскость в секунду будет про-
ходить воздушная колонна длиной, равной не единице, а V.
Следовательно,
Y = рГУ/,
т. е. мы получили теорему Н. Е. Жуковского.
Доказательство, приведенное здесь, нестрого, но весьма
наглядно. Мы привели его здесь в качестве примера того, как
Н. Е. Жуковский умел давать простые пояснения сложным
вопросам аэродинамики.
Глава Ш
ВЛИЯНИЕ ВИХРЕВЫХ УСОВ НА КРЫЛО
У § 11. СКОРОСТЬ СКОСА У КРЫЛА
Учет сбегающих с концов крыла вихрей позволил построить
теорию, дающую возможность учитывать влияние размаха крыла
на его аэродинамические свойства.
Рассмотрим сперва простейшую схему крыла с П-образными
вихрями.
В этой упрощенной теории принимают, что сбежавшие с
крыла вихри идут на расстоянии Zx, несколько большем раз-
маха I. Тогда оси вихревых усов будут лежать на небольшом
расстоянии е от концов крыла, причем, очевидно:
е=А=±. (15)
Рассмотрим действие вихревых усов на точки, лежащие на
присоединенном вихревом шнуре. На фиг. 13 изображено крыло
моноплана в двух проекциях. Проведем через присоединенный
вихрь плоскость, перпендикулярную к скорости полета V. По-
лушнур 1 действует на точку А, находящуюся на расстоянии z
18 I
от него, вызывая в ней вертикальную скорость ч)д, которую
можно вычислить по формуле (3), т. е.
_ Г
4лг ‘
(16)
Эта скорость направлена вниз и-потому мы ставим у нее
знак минус; называется она скоростью скоса. Скорость эта не
будет постоянной по размаху и,
как это следует из формулы (16),
она будет изменяться по гипер-
болическому закону, как это и
изображено на фиг. 13 внизу.
В этой теории вместо истин-
ных скоростей скоса вычисляют
среднюю скорость скоса по раз-
маху. Обозначим эту скорость
через vgo и определим форму-
лой:
1+е
J Vgdz.
е
Коэфициент 2 взят здесь пото-
му, что у нас имеются два вих-
ревых уса. Интеграл берется
по всему размаху крыла, т. е. в
пределах от едо 1-+-е, и делится
на I для получения среднего результата
Подставляя сюда значение vy по формуле (16), получаем:
l+e 1е
/*
J г
е
L—1
или, подставляя сюда величину е = 1
тельно:
Фиг. 13. Скос потока в плоскости
присоединенного вихря у крыла
моноплана.
(17)

-^1”—
2к/ е
получаем оконча-
Величина
v —_____£_ iq А+_£
^0- 2nZ 1П Zt-Z
(18)
г’уо — 2

1 И “Г *
” lnt=7
(19)
называется коэфициентом влияния крыла самого на себя, или
коэфициентом самоиндукции монопланного крыла.
На основании более строгой теории, а также исходя из
опытов с крыльями, можно принять 1,04/. Тогда
1 Zj 4- Z .
е = In —-r 4.
-- I
1 Здесь получается полная аналогия вычислению среднего давления двига-
теля по индикаторной диаграмм^: находят площадь диаграммы и делят на
длину хода поршня.
19
Подставляя это значение е в формулу (18), получаем:
^-Ъй = -ЧГ- (2°)
Для практических применений удобно заменить циркуляцию
скорости конструктивными величинами; для этого нужно вос-
пользоваться уравнением связи, т. е.
Г = -£рК (14)
После подстановки получаем:
(21)
Величина
X = ЦЬ (22)
называется относительным размахом крыла или его
удлинением. Она играет,огромную роль в теории индукции.
Вводя ее в формулу (21), получаем окончательно:
(23)
§ 12. УГОЛ СКОСА
При обтекании крыла потоком к скорости скоса vyQ приба-
вится еще скорость самого поступательного потока V (фиг. 14)
Фиг. 14. Скоростнойи силовой треугольники
у крыла.
на фиг. 14. Тогда
tg Да = —
и результирующая ско-
рость будет равна W;
она образует со скоро-
стью невозмущенного
воздуха V некоторый
угол, называемый уг-
лом скосапотокаи
обозначаемый у нас че-
рез Да.
Условимся считать по-
ложительным угол скоса
потока, получающийся
при скорости скоса, на-
правленной вниз, т. е.
так, как это изображено
(24)
Знак минус ставим здесь потому, что vy арифметически
является величиной отрицательной; положительная скорость
направлена по оси Оу. Угол же скоса моноплана принято у нас
считать положительным.
20
Угол скоса обычно невелик — он.равен нескольким граду-
сам, вследствие чего в теории индукции обычно принимают*
W = V
и угол Да вычисляют в радианах по формуле:
Да=-^°, (25)
т. е. принимают угол и тангенс малой величины Да равными.
Подставляя сюда величину ‘VIf0 по формуле (23), получим
фундаментальную формулу теории индукции:
Да = —(26)
Для перехода от радианов к углам в градусах пользуются,
как известно, формулой:
а° = ^а = 57,3а. (27)
Следовательно, угол скоса потока в градусах Да° будет
иметь у крыла величину:
Д»х° = 57,3 = 18,23 . (28)
ТСЛ Л
Таким образом влияние вихревых усов вызовет скос потока
и, следовательно, в том месте, где находится присоединенный
вихрь, воздух будет течь не со скоростью V, а со скоростью 117,
образующей угол Да с направлением V.
Если крыло стоит в потоке под углом атаки а, то на самом
деле истинный угол атаки будет иметь меньшую вели-
чину и будет раве^н
а.( = а — Да. (29)
Если бы крыло было бесконечного размаха, т. е. имело бы
к =оо, то Да = 0 и, следовательно, истинный угол атаки равнялся
бы кажущемуся. Чем меньше относительный размах крыла X,
тем больше угол скоса потока и тем меньше истинный угол
атаки при данном су.
|/ § 13. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ КРЫЛА
Вследствие уменьшения истинного угла атаки крыло конеч-
ного размаха разовьет меньшую подъемную силу, чем крыло
бесконечного размаха, если считать длину взятого участка бес-
конечного крыла равной размаху конечного.
Это первый, весьма важный вывод теории индукции: крыло
дает при. заданном угле атаки тем меньшую подъемную силу,
нем меньше его удлинение.
Еще более важный вывод получается из рассмотрения сил,
действующих на конечное крыло. Если бы мы взяли крыло
21
бесконечного размаха, то на него действовали бы, в коэфи-
циентном написании, подъемная сила сдоо и сопротивление сх,
последнее для крыла бесконечного размаха принято писать с
индексом р и называть профильным сопротивлением.
У крыла идеального, не имеющего ни трения, ни срывов по-
тока, схр =0. У действительного крыла в зависимости от со-
вершенства его профиля получается некоторое сопротивление
схрф0. Обе величины сд и схр у крыла бесконечного размаха
являются функцией угла атаки а.
При переходе к крылу конечного размаха поток, набегаю-
щий на профиль, повернется на угол Да и истинный угол атаки
будет уже равен:
аг — а — Да.
Следовательно, мы должны взять у профиля уже другие ве-
личины сд и схр, соответствующие истинному углу атаки ац,
зависящему от А.
Таким образом разница между работой профиля у крыла
бесконечного размаха и конечного будет заключаться лишь в
том, что в последнем случае нужно брать меньший угол атаки
и считать поток повернутым на угол Да, Но при потоке, по-
вернутом на угол Да, повернутся на такой же угол и су и схр
(штрих напоминает здесь о том, что взят истинный угол ата-
ки at, соответствующий данному 1).
При аэродинамическом расчете мы интересуемся силами и
коэфициентами, взятыми по поточным осям всего самолета,
т. е. отнесенными к скорости V в бесконечности, а не к мест-
ной скорости W около профиля. Для получения таких коэфи-
циентов проектируем коэфициенты с'у и с'хр на обычные оси ко-
ординат (формулы перехода см. в части I, § 41) (фиг. 14) и
получаем:
су = су cos Да — с 'Хр §in Да;
сх = с'у sin Да 4- с'хр cos Да.
Считая Да величиной малой, делаем замену:
sin Да = Да;
cos Да = 1
и находим:
с — с’ |
У У , (30)
б\=с;да +J
Получился очень важный вывод: у крыла конечного размаха
коэфициент сопротивления оказывается большим, чем у крыла
бесконечного размаха на величину су Да. Эта величина называется
коэфициентом индуктивного сопротивления и обо-
значается в расчетах через cxi. Штрихи в формулах (30) можно
не ставить, помця всегда, что величины су и схр берутся по
истинному углу атаки.
22
(29)
(26)
(33)
(31)
Сх —
Тогда получим основную формулу теории индукции крыла:
Сх = Су + СХр = Cxi 4" СХр9 (31)
где
cxi = су Да. (32)
Величина угла скоса потока нами уже найдена [формула (26)].
Вводя ее, получаем окончательно:
Cxi = Да = ^ = -^ . (33)
Таким образом коэфициент индуктивного сопротивления
зависит лишь от су и удлинения крыла X. Он не зависит непо-
средственно от формы профиля: какой бы профиль мы не взяли,
при одной и той же величине су и X мы получим одинаковый
коэфициент индуктивного сопротивления cxi.
Подведем теперь итоги.
Основными формулами теории монопланного крыла при гипо-
тезе П-образных вихрей являются:
0-t = а — Да;
Да = -^-;
9
о
СУ .
It). ’
с2
Cxi Схр — Ч- СХр-
Кроме того, постоянно приходится пользоваться формулой:
Да° = 57,3 • Да (27)
для перевода углов, вычисленных в радианах, в градусы.
Изложенные выводы имеют огромное практическое и принци-
пиальное значение. Оказывается, что для получения подъемной
силы от реального крыла конечного размаха необходимо преодо-
левать даже в идеальном случае (схр = 0) некоторое сопротив-
ление 6Xi- В случае же идеального крыла бесконечного размаха
индуктивное сопротивление равнялось нулю и подъемная сила
получалась без затраты работы.
§ 14. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ
Проф. Л. Прандтль предложил наносить на диаграмму
Лилиенталя 1-го рода параболу индуктивного сопро-
тивления, получаемую из формулы (33):
подстановкой в нее такого X, какое было при продувке крыла.
23
Эта кривая представляет собой кривую Лилиенталя идеального
крыла, так как она дает связь между cxi и су. На фиг. 15 дана
обычная диаграмма Лилиенталя длй крыла с нанесенной на ней
параболой индуктивного сопротивления. Эта парабола разби-
вает полное сопротивление крыла сх на две части — профиль-
ное схр и индуктивное cxi.
Огромное количество проведенных в настоящее время испы-
таний самых различных профилей позволяет установить следую-
щие свойства этих кривых.
1. Кривая Лилиенталя у хороших крыльев идет почти экви-
дистантно параболе индуктивного сопротивления на всех летных
углах атаки. Возле посадочного угла атаки и иногда у угла
пикирования (су = 0) наблюдается резкое увеличение профиль-
ного сопротивления, что объясняется наступающим на этих
углах атаки срывом потока (фиг. 16).
Фиг. 15. Парабола ин-
дуктивного сопротив-
ления.
Фиг. 16. Срыв потока на верхней
и нижней поверхностях крыла. .
Крылья симметричные и несимметричные, но двояковыпуклые
дают обычно на малых углах атаки бессрывное обтекание, и схр
у них остается почти постоянным.
2. Величина профильного сопротивления очень мала и у
хороших тонких профилей сравнительно мало зависит от тол-
щины и кривизны профиля, но очень сильно изменяется с изме-
нением числа Рейнольдса и очень близка к величине трения
воздуха, вычисляемого по формулам проф. Прандтля. При
числах Рейнольдса, лежащих в пределах от 0,5 MRe до 1 MRe
(т. е. лабораторных), величина сжр 0,007 — 0,01 у лучших тон-
ких крыльев, а у более толстых она лежит обычно в пределах
от 0,01 до 0,015. Подробнее мы остановимся на этом вопросе
в гл. XII, § 58 „Профильное сопротивление**.
3. На больших углах атаки индуктивное сопротивление в
.несколько раз больше профильного. Вследствие этого на само-
24
летах, летающих на больших углах атаки, как-то: высотные
машины, машины для сверхдальних полетов и т. п. приходится
для уменьшения их полного сопротивления брать крылья с очень
большим удлинением. Рекордная величина к была взята на
советском самолете ЦАГИ-25, где она достигает значения 12,8.
На машинах скоростных, летающих на малых углах атаки, можно
брать малую величину К, например 4.
Обычно у самолетов к лежит в пределах от 5 до 8. У пла-
неров нередко к достигает очень большой величины, напри-
мер 25 и более. У самолета при большом удлинении крыло
получается очень тяжелое и при обычной его форме склонное
к вибрациям. Во всяком случае попытки делать у тяжелых
самолетов крылья с относительным удлинением ббльшим 10
вызвали целый ряд катастроф. Однако усовершенствование
методов расчета крыла на вибрации уже позволяет теперь строить
вполне надежные самолеты с k ss 9 — 10.
§ 15. ПУТИ УЛУЧШЕНИЯ АЭРОДИНАМИКИ КРЫЛА
На первый взгляд теория индукции приводит к довольно
пессимистическим заключениям. Действительно, если индуктив-
ное сопротивление неизбежно и имеется даже у идеального
крыла, а профильное сопротивление близко к трению воздуха
о пластинку, то кажется, что нет никаких средств для даль-
нейшего усовершенствования крыльев.
Однако это не так. Оказывается, что индук-
тивное сопротивление можно уменьшить, напри-
мер, с помощью шайб, поставленных на кон-
цах крыла (фиг. 17); эффект от установки таких
Фиг. 17. Крыло с шай- Фиг. 18. Крыло с подвижным покрытием,
бами на концах.
шайб эквивалентен увеличению размаха крыла приблизительно’
на if5h, где А —высота шайбы. Другими словами, при вычисле-
нии угла скоса потока у таких крыльев нужно вводить в расчет
не I, a Z + -|-A. Грубо объяснить действие шайб можно тем,
что при их наличии сбегающие вихревые усы идут на боль-
шем расстоянии друг от друга, чем в случае отсутствия шайб.
Точно также можно уменьшить, а теоретически даже сделать
равным нулю, и профильное сопротивление крыла.
Для этого нужно покрыть крыло подвижным (на роликах)
полотном, как изображено на фиг. 18; тогда под влиянием
трения это полотно придет в движение и сила трения значи-
тельно уменьшится. Приводя такие полотна в движение от
25
мотора, можно получить не только нулевое сопротивление, а даже
отрицательное, т. е. силу тяги. Давая верхнему полотну большую
скорость, чем нижнему, можно получить увеличение циркуля-
ции скорости около крыла и, следовательно, увеличить его
подъемную силу *.
Построить такие крылья весьма трудно, так как при боль-
шой скорости на полотно во время обегания роликов действует
огромная центробежная сила. Трудно разместить внутри такого
крыла силовые элементы — лонжероны, нервюры и т. д.
Однако, как видим, по крайней мере принципиально, крыло
можно значительно усовершенствовать, и теория индукции сама
указывает на пути, какими это улучшение может быть достиг-
нуто.
§ 16. ВОЛЕЕ ТОЧНЫЕ ФОРМУЛЫ ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ
Основные формулы индукции крыльев выводятся при гипо-
тезе П-образных вихрей с целым рядом упрощений и допуще-
ний. Естественно задать себе вопрос, насколько эта теория
оказывается точной.
В гл. XIII мы сделаем подробное исследование крыла по
значительно более строгой теории, учитывая изменяемость и
циркуляции и скорости скоса по размаху. Оказывается, что
строгая теория дает весьма близкий к этой приближенной тео-
рии конечный результат.
Формулы в строгой теории получаются в таком виде:
(34)
с1 2
(35)
т. е. и там получаются те же самые формулы (26) и (33), но с поправ-
ками т и 8, стоящими в скобках. В табл. 1 приведены эти поправ-
ки для прямоугольного
крыла, вычисленные
Глауэртом (Англия).
Поправки даны
здесь в зависимости
от величин к/л0, где
X — удлинение, а а0 =
^^уоо
= ---производная
от суоо крыла беско-
нечного размаха по ис-
тинному углу атаки.
Таблица 1
Значения т и б для прямоугольного крыла
*•/«» 0,5 0,75 1 1,25 1,5 1,75
X при я0 = 2к 3,14 4,72 6,28 7,87 9,42 10,98
т 0,10 0,14 0,17 0,20 0,22 0,24
6 0,019 0,034 0,049] 0,063 0,076 0,088
1 Такие крылья были впервые предложены автором в книге „Индуктивное
сопротивление крыльевТруды ЦАГИ вып. 20, 1926 г. Они были испытаны
во Франции в 1936 г. и дали весьма интересные результаты.
25
Фиг. 19. Поправки бит для
прямоугольного крыла.
среднее X, определяемое по
Теоретически, как это доказывается в курсе гидродинамики,
эта величина равна 2т:. Мы поэтому дали во второй строке
таблицы значения X, соответствующие а0 = 2тг. Данные этой
таблицы графически изображены на фиг. 19.
Как видим, поправка 8 для cxi весьма мала и при обычных К
равна всего лишь нескольким процентам. Поправка же т для
Да оказывается довольно заметной
и при точных подсчетах ее нужно
обязательно учитывать.
Более строгая теория показала
(см. гл. XIV), что формулы:
Да = -^-
И
с2
С - = -^-
Cxl «X
можно рассматривать как первое
приближение для любых крыльев.
В них только нужно подставлять
формуле:
/2
х = -s- <36)
Строгая теория показала, что вполне точно формулы (26)
и (33) можно прилагать лишь к крылу с эллиптической формой
/2
в плане. Тогда, подставляя в них Х = -^-, мы получим вполне
точный ответ (подробно см. в гл. XIV, § 3).
Фиг. 20. Типичные
формы крыльев.
Эти же формулы с поправками т и В, спе-
циально найденными для данной формы крыла,
делаются вполне точными (с той точностью,
какую вообще может дать теория индукции,
являющаяся по своей сути теорией приближен-
ной).
Поправки т и 8 зависят от формы крыла и
от удлинения X. Если ограничиться удлине-
ниями от 5 до 8 и брать среднее значение
для 8 и т, то для типичных форм крыльев
получатся ошибки всего лишь в 5—7°/0-
В прилагаемой табл. 2, которой можно поль-
зоваться для приближенных подсчетов, мы даем
средние величины угла скоса и коэфициента
индуктивного сопротивления для типичных
крыльев, изображенных на фиг. 20, причем
предполагаем, что крылья эти имеют одинаковые профили по
всему размаху и не имеют закрутки сечений, т. е. что все их
аэродинамические хордц лежат в одной плоскости (см. далее).
27
Таблица 2
Приближенные формулы для величины угла скоса потока И коэфициента инду-
ктивного сопротивления крыльев (см. фиг. 20)
а) Эллиптическое крыло (точно):
2 2
Cv Cv Cv Cv
Да = -У- = 0,318 -Л; cxi = -< = 0,318-У-.
кХ К ’ xt кХ X
к * 1
Ь) Трапецевидное крыло при — = —ч-—-----------как у эллиптического.
VQ 0 2
с) Прямоугольное крыло при Х^5-т-8:
с с%
Да X 0,375 ; cx(Z 0,335 .
Л к
d) Крыло со скошенными концами:
с
Ьа % 0.338 -4-; с,, ~ 0,318 -У- .
е) Крыло с закругленными концами:
с
Да ~ 0,365-^-; с 0,318-^.
X к
f) Ромбовидное крыло:
с
Да ~ 0,363 -У-; сг, ~ 0,363 -Л.
К лг ~ > X.
§ 17. УПРОЩЕННАЯ СХЕМА РАБОТЫ КРЫЛА ПО ПРАНДТЛЮ
Проф. Л. Лрандтль предложил весьма простой и наглядный
вывод формул индуктивного сопротивления, основанный на
искусственной схеме работы крыла.
Крыло отклоняет набегающий на него поток вниз. Действие
крыла распространяется на всю массу обтекающей его жидко-
сти—вплоть до бесконечности.
Однако сильное влияние крыло оказывает лишь на ближай-
шие части воздуха, в далеких точках его влияние ничтожно.
Проф. Прандтль допустил, что это
влияние простирается у обычных
крыльев лишь на круглую струю,
имеющую диаметр, равный размаху
крыла (фиг. 21). Внешний по отноше-
нию к этой трубе воздух тогда сле-
дует считать как бы неподвижным
и имеющим давление, равное- атмо-
сферному. Проведем три сечения: /,
II и III, как показано на чертеже.
л/2
Площадь сечения струи обозначим через F = — • Скорость ско-
са в сечении II обозначим через vy , а в сечении III—через vyi.
28
Напишем для такой упрощенной схемы уравнения импульса
и живой силы, взяв интервал времени, равный единице.
Подъемная сила крыла тогда будет равна лишь секундному
приросту количества движения по вертикали в уходящей струе,
так как давления всюду на границах струи равны атмосферному.
Количество движения напишется так:
Y = mvyi.
Секундная масса воздуха, или расход такой трубы, будет,
очевидно, равен:
т = р FV.
Отсюда
r = PFW/B1. (37)
Кинетическую энергию в уходящей струе (в сечении 111),
принимая осевую скорость неизменной, получим в виде:
т - mv^ - .
1 ~ 2 ~ 2
Работа Т получится за счет возникшей у крыла силы со-
противления которую получим, разделив Т на И, т. е.
Т ?РУУу! «si vB1
V 2V 2V ~ 2V‘
Величину геометрический смысл которой совершенно
ясен, — это угол скоса потока в сечении II, — легко вычислить
по формуле (37), так как
Y
рЛИ ’
отсюда
vyi^ Y
2 V 2?FV* •
Заменяя Y его обычным выражением
г = , получим:
через су и подставляя
__ z
2V 2,4 И
4
Су _ Су
т. е. обычную формулу скоса.
Как видим, угол скоса потока далеко за крылом в два раза боль-
ше, чем скос у присоединенного шнура самого крыла. Этот вывод
совпадает с выводом, получаемым и из рассмотрения вихрей. Дей-
ствительно, на крыло действуют полушнуры, а на далекие от
крыла точки — шнуры. Действие же шнуров в два раза больше
действия полушнуров [формулы (2) и (3)].
Манерой Прандтля заменять действие неограниченного по-
тока условной струей, мы воспользуемся в гл. XXI.
29
§ 18. ФОРМУЛЫ ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ В НАТУРАЛЬНЫХ
ОБОЗНАЧЕНИЯХ
В заключение этой главы заметим, что формулы индуктивно-
го сопротивления иногда пишут не через безразмерные коэфици-
енты, а с помощью натуральных величин. Так, основные формулы:
cxi — ^ и Да = -v>
х -кк яХ
вводя в них:
У Xt . /2
Су — Sq ’ Cxi ~ Sq И * — S ’
пишут иногда в виде:
Xi = = -417-2 ; (38)
1 л/2^ лр/2/2 ’ v 7
Да =-£- = —Fv2^- (39)
л/2# лр/2и2 4 7
Вместо формулы: cxi=cv Да можно написать:
Xi = У Да. (40)
Наконец, циркуляцию скорости для крыла с П-образными
вихрями получим из формулы Н. Е. Жуковского:
Формулы с натуральными величинами менее удобны, чем
безразмерные (26) и (33), и ими пользуются лишь в особых слу-
чаях, например при выводе некоторых теорем. В инженерных
расчетах пользуются исключительно безразмерными формулами.
Глава IV
ПЕРЕСЧЕТ МОНОПЛАННЫХ КРЫЛЬЕВ С ОДНОГО УДЛИНЕНИЯ
НА ДРУГОЕ
/ § 19. ПЕРЕСЧЕТ С Xt НА Х2
Выведенные в предыдущей главе формулы позволяют решить
весьма важную для целей практики задачу определения аэро-
динамических характеристик крыла с любым удлинением Х2 на
основе обдувки крыла того же профиля с каким-нибудь удли-
нением kj. Это обстоятельство позволяет испытывать в аэро-
динамических лабораториях крылья со стандартным удлинением
(в СССР принято брать = 5), а конструктор может пересчи-
тывать эти продувки на нужный ему размах.
Пусть у нас имеются два крыла: № 1 с удлинением испы-
танное в трубе, и № 2 с Х2, характеристики которого требуется
найти (фиг. 22). Будем вести пересчет, ставя условием иметь
равные истинные углы атаки аг в обоих случаях.
30
Тогда все величины, являющиеся функцией истинного угла
атаки, будут в обоих случаях равными, т. е.
СУ1 — СВ2 — Clh |
Схр1 ~ ^ХР2 Схр'г
£/nl — ^т2 — ^ш>
^31 === Сд2 ^д*
(42)
(43)
Однако кажущиеся углы атаки ах и а2 будут у крыльев № 1
и № 2 различными, так как
(44)
— а/ — Да/ = а/ — Aa2°,t
а скосы потока Ла/ и будут при разных к заведомо различ-
ными, так как по формуле (34) для нашего случая получим:
Фиг. 23. Пересчет су и ст на
другое удлинение.
Фиг. 22 Пересчет крыльев.
Профили и углы атаки.
Отсюда условие равенства истинных углов атаки соблюда-
ется тогда, когда мы будем иметь:
ах° — Дах° = а2° — Да2°
или
ах° — а2° = Да/* — Да2°.
Подставляя сюда углы скоса потока [по формулам (45) и
(46)], получим рабочую формулу:
ао_ао = ^('1±21_1+^)57>3. (47)
Если на диаграмме Су = /(а1)., полученной продувкой (фиг. 23),
мы имели угол атаки ах°, то такой же самый су мы получим
у пересчитываемого крыла на угле атаки а2°. Следовательно,
для пересчета нужно лишь перенести точку А по горизонтали
в положение Alf сдвинув ее на величину ах° — а2°.
зг
Сдвиг этот будет различным для различных сд. Для задан-
ного перехода из формулы (47) видно, что
»i° — аа° = cgk*; (48)
здесь ka — const. Таким образом видим, что сдвиг пропорцио-
нален с„. Если вычислить сдвиг для одного какого-нибудь сд,
отложить его в виде отрезка ВВ3 и провести прямую линию
ОВ3 (фиг. 23), то любой отрезок В^В' будет давать нужный
«сдвиг для любого сд. Сдвигая всю первоначальную кривую на
эти отрезки, дающие аг° — а2°, получим изображенную пунктиром
пересчитанную на удлинение )а кривую су по а. От-
резки ВВг откладывают с помощью циркуля.
Вспомогательную прямую, дающую’ — а2°, удобно строить,
беря точку 2?! для сэ = 1.
Рассмотрим теперь сопротивление наших крыльев № 1 и № 2:
Cxi ^xil "Н Cxpi >
Сд?а ^*xia ~1~ Схр2'
Вычитая из первого уравнения второе и помня, что у нас
^xpi= &хр2 = ^xpt получаем:
Cxi Сс2 = ^xil ^xi2’
Величины cxil и cxi2 выражаются для крыльев № 1 и № 2 с по-
мощью формулы (35) таким образом:
с2
(1 + 3,)
и
Отсюда
_ /1 + % \ (49)
« \ >2 /'
Эта формула и решает вопрос о
пересчете кривой Лилиенталя. На
фиг. 24 дана диаграмма Лилиенталя
испытанного крыла. Новое крыло
Фиг. 24. Пересчет поляры и кри- с 12 будет иметь уже сопротивление
вой ст =/(с2,)на^другое удли- не а так как эт0 произойдет
при с91 = сУ2 = Сд, то мы можем от-
ложить по горизонтали из точки, например А, отрезок — схз
и получить точку At новой, пересчитанной поляры крыла.
Сдвиг будет различен для различных сд.
32
Для заданного перехода формула (49) примет вид:
Cxi Х2 — Су
(50)
где kx = const.
Если вычислить величину сдвига для какого-нибудь значения
Су, то отложив отрезок ВВг = сХ1 — cxi и получив точку Blf мы,
проведя через нее квадратную параболу, будем получать сдвиг
для любого су. Откладывая по горизонтали с помощью циркуля
такие отрезки, мы перестроим всю кривую Лилиенталя и по-
лучим новую для Х2, изображенную пунктиром.
Разметка углов атаки на новой кривой получится с помощью
уже перестроенной кривой cy—f{a.). Найдя по ней величину су
для нужных углов атаки, напрймер для а = 0, 2, 4, 6° и т. д.,
мы сможем найти на перестроенной кривой Лилиенталя новую
разметку углов атаки.
Рассмотрим теперь перестроение кривых момента и кривой
центра давления для нового Х2. Заметим, что ст и сз являются
функциями истинного угла атаки а;, так же как и су. Каждому
значению Су соответствуют определенные значения ст и Су и,
следовательно, если при каком-нибудь перестроении по теории ин-
дукции величина Су попадает на другой угол атаки, то и ст и сд
попадают туда же. Запомнить это можно в виде мнемоничес-
кого правила: ст и сз всегда следуют за своим су.
Кривые ст даются лабораториями в двух видах: или на диа-
грамме Лилиенталя как функция си, или на диаграмме подъем-
ной силы как функция а. В первом случае кривая ст = f(cg)
останется неизменной для нового л2, так как су остаются при
пересчете неизменными (фиг. 2 !4). Во втором случае кривая
Gn=/(a) должна быть исправлена на разность Таблица 3
— а2 и примет на фиг. 23 вид кривой, КОЭфИЦИСНТЫ Ка. и кх для перехода (принято aQ — 5,6) от 5 К /-2
обозначенной пункти-
ром. В точке D, т. е. при су = 0, поправка 5 6 7 8 9 10

т 0,165 0,175 0,20 0,22 0,24 0,25
равна нулю, и старая и
новая кривые
пересекутся в этой точке. 0,045 0,050 0,065 0,075 0,080 0,085
Кривые центра дав- 0° 0,700° 1,13° 1,47° 1,75° 1,99°
ления перестраивают-
ся совершенно анало- гично кривым ст. kx 0 0,0108 0,0182 0,0239 0,2830 0,0319
Все указанные здесь
перестроения делаются весьма быстро и наглядно с помощью
счетной линейки и циркуля прямо на диаграммах, полученных
из лаборатории. Для облегчения таких подсчетов мы вычислили
табл. 3, дающую готовые коэфициенты кл и kx для перехода к
>.2 от = 5.
Б. Н. Юрьев—171—з
33
§ 20. ПЕРЕСЧЕТ КРЫЛЬЕВ НА БЕСКОНЕЧНЫЙ РАЗМАХ
Развитая в § 19 теория пересчета крыльев позволяет легко
находить аэродинамические характеристики крыльев бесконеч-
ного размаха. Такие характеристики нужны для расчета винтов
и для определения характеристик крыльев произвольной формй,
о чем изложено во втором разделе этой книги. Кроме того, как
сейчас увидим, переход от крыла бесконечного размаха к крылу
конечного размаха проще, чем описанный в предыдущей главе.
Американцы в последние годы дают результаты продувок
крыльев, уже пересчитанные на Х=со. Рассмотрим такой
пересчет.
Пусть имеется диаграмма испытания крыла с удлине-
нием (фиг. 25). Пересчет ее на к2 = со производится по фор-
мулам (47) и (49), которые для данного случая примут вид:
а1'-я°0О=57,3^ (47')
сх1- сх2 = -у. 1+1>. (49')
к К
Формулы эти показы-
вают, что при переходе к
крылу бесконечного размаха
нужно у крыла конечного
размаха вычесть весь угол
скоса и все индуктивное
сопротивление. Это непо-
средственно следует из
обоих принципов теории
индуктивного сопротивле-
Фиг. 25. Пересчет крыла на X = оо. НИЯ крыльев.
Само перестроение ве-
дется уже описанным приемом. Полученная кривая Лилиенталя,
изображенная на фиг. 25 пунктиром, дает зависимость: cxp—f(cy);
ее называют иногда полярой профильного сопроти-
вления. Кривая Су исправляется на весь угол скоса Да.
§ 21. ПРОВЕРКА ТЕОРИИ ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ
Ввиду громадной практической важности пересчетов крыль-
ев очень многие лаборатории занимались проверкой этой теории
на опыте. Обычно брали несколько крыльев разного удлинения
и испытывали их на одинаковых числах Рейнольдса для сохра-
нения аэродинамического подобия. В опыты вводили поправку
на влияние стенок аэродинамической трубы, на чем мы остано-
вимся подробно .в гл. X.
Все эти опыты блестяще подтверждают теорию индуктив-
ного сопротивления крыльев.
34
В качестве примера такой проверки приводим проведенные еще
в1919г.в лаборатории.проф. Прандтля испытания крыльев про-
филя № 389 с относительными удлинениями X = 1, 2, 3,4,5, 6 и 7
Фиг. 27. Кривые фиг. 26, пересчи-
танные на удлинение Х=5.
и пересчет их аэродинамических характеристик на К = 5. На
фиг. 26 даны кривые су по а, полученные в результате про-
Фиг. 28. Кривая Лилиенталя фиг. 29. Кривые фиг. 28,
крыльев одинакового профиля, пересчитанные на удлине-
но разных удлинений. ние 5.
дувки, а на фиг. 27—пересчитанные на л=5; мы видим, что после
пересчета все точки легли на одну линию.
На фиг. 28 и 29 даны поляры непересчитанных и пересчи-
танных крыльев; и здесь получилось прекрасное совпадение
35
кривых. Лишь точки, относящиеся к X = 1, несколько выпадают,
что объясняется более сложным обтеканием таких квадратных
крыльев, чем это учтено теорией.
На фиг. 30 даны значения
ст полученные продувкой
для этих крыльев. Опытные точки
дают, как видим, общую кривую
Ст = f(cy) ДЛЯ всех что и ДОЛЖНО
было получиться, так как эту кри-
вую, как нам известно, пересчиты-
вать не надо.
Как эти, так и многие другие
исследования данного вопроса
вполне подтвердили теорию индук-
ции для монопланных крыльев и
сделали ее одним из основных ме-
тодов расчета самолета.
§ 22. НАКЛОН КРИВОЙ Cy=f(d)
Очень часто при расчетах не-
обходимо иметь аналитическое
ных углах эта линия близка
пользоваться формулой вида:
выражение кривой гу=/(а); на лет-
к прямой, поэтому весьма удобно
Су = а(а —а0);
(51)
здесь
dcy
а — -~
аа
(52)
— угловой коэфициент прямой и а0 —угол нулевой подъемной
силы, у несимметричных профилей отрицательный.
У крыла бесконечного размаха получится другая, большая
величина для этого коэфициента, который обозначим так:
de
= (53>
Возникает вопрос о связи этих величин между собой.
Мы можем написать для крыла конечного размаха формулу
для сд не только ц виде (51), но и в таком виде:
\си = «о (аг — ао). (54)
где а0 взято по истинному углу атаки at, т. е. такое же, как
у крыла бесконечного размаха.
Но oif = а — Да, следовательно,
= Оо(а — Да — do) = а0[а — (1 + — «о1-
36
Диференцируя это выражение по а, получаем:
da 0 \ як da )'
Замечая, что а = , получаем:
Отсюда
(55)
(56)
Теория крыльев в плоскопараллельном потоке показывает,
den о
что величина = т~ = 2гс.
и dai
Тогда формула (55) примет вид:
п__dcy__X
da А 4- 2 (I
Однако пересчеты крыльев конечного размаха на бесконечный
размах постоянно дают для а0 меньшую чем 2it величину. Это объ-
ясняется трением воздуха о крыло, что уменьшает циркуляцию
вокруг крыла; кроме того, при больших углах атаки происходит
срыв потока. В общем, на основании наиболее надежных аме-
риканских данных, можно принять, что при больших числах
Рейнольдса величина ао^О,9 • 2it~5,6. Она колеблется в пре-
делах от 0,8 • 2it до 0,95 • 2п в зависимости от условий опыта
и профиля крыла.
Если брать углы в градусах, то
й о= rfcy=0 9 2к = 0 098-
° daf 57,3
от 0,094 до 0,115 у разных профи-
Таблица4
Значения а-- при разных К для
прямоугольных крыльев
(принято а0 = 5,6)
Эта величина колеблется
лей и практически для
данного профиля не
зависит от числа Рей-
нольдса.
Если принять для
л = со величину а0 =
= 5,6, то для прямо-
угольных крыльев раз-
личных X получатся
значения а, приведен-
ные в табл. 4.
Таким образом на-
лои кривой £у=/(а)
очень легко определить
Во многие формулы входит, как мы видели, угол атаки при
нулевой подъемной силе, а0. Для упрощения написания формул
; = 5 б 7 j 8 9 10 г
а 3,95 4,15 4,28 4,40 4,50 4,58 5,6
0,0697 0,0723 0,0746 0,0766 0,0783 0,079 0,0980
и без продувок.
37
очень часто в теории индукции отсчитывают углы атаки от так
называемой аэродинамической хорды, т. е. такой хорды,
у которой при а=0 и су = 0. Следовательно, обозначая угол
атаки, отсчитываемый от такой хорды, через аа, получим,
очевидно:
^0?
т. е. она должна быть повернута по
хорде АВ на угол а0 вверх (фиг. 31).
отношению к продувочной
Если условимся отсчиты-
вать углы атаки от та-
кой хорды СВ, то пре-
дыдущие формулы (51) и
(54) перепишутся в более
простом виде:
су = ма; (5 Г)
сУ = aoiia. (54')
В дальнейшем мы ча-
сто не будем ставить
значка а у угла атаки,
Фиг. 31. Продувочная и аэродинамическая
хорды крыла.
делая оговорку в тексте, что отсчет ведется от аэродинамиче-
ской хорды.
§ 23. АМЕРИКАНСКИЕ ДИАГРАММЫ
В настоящее время аэродинамические исследования наиболее
широко поставлены в Американском совещательном авиацион-
ном комитете (NACA). Благодаря большим числам Рейнольдса,
получающимся на мощном американском оборудовании, эти
исследования являются в настоящее время ведущими и широко
используются всеми авиационными конструкторами.
Американцы в последнее время пересчитывают все свои
результаты продувок крыльев на бесконечный размах и дают
диаграммы в виде, приведенном на фиг. 32 и 32а. Коэфициент
су является основным и отложен поэтому по оси абсцисс; ко-
эфициенты схр и ст даются как функции су. Момент берется
у американцев не относительно передней кромки крыла, как
это принято в Европе, а относительно точки, лежащей на хор-
де на расстоянии х/46 от передней кромки (фиг. 33). Знаки мо-
мента противоположны нашим, —плюс берется для момента,
поворачивающего крыло на кабрирование. При таком выборе
точки, относительно которой берутся моменты, коэфициент сП1
почти постоянен. Эта точка близка к так называемому фокусу
большинства крыльев (см. далее).
Кроме этого, американцы дают еще или кривую а как
функцию Су на той же диаграмме^ или приводят обычную допол-
нительную диаграмму подъемной силы, т. е. су = f (а) (фиг. 32а).
Американцы продувают свои прямоугольные крылья с К = 6
и затем тщательно пересчитывают их на Х = оо. При этом
они вводят в пересчет добавочные, чисто эмпирические поправки.
38
Так, если после пересчета результатов испытания прямо-
угольного крыла со слегка округленными концами на X = со полу-
Фиг. 32. Американская диаграмма испытания крыла,
пересчитанная на Л=оо.
чаются величины ^шах, я'-, %' и с'хр, то американцы принимают
за истинные величины следующие:
Сц max = 1,03
^=0,96 а'.;
«о° = < + 0,39 с';
^р= с'хр + 0,0016 с*’ - 3- (Г— 6) 0,002.
Здесь с — максимальная толщина профиля в процентах хорды.
В случае, если крыло имеет прямой обрез крыльев, а не округ-
ленный, то делается поправка для максимальной подъемной
силы еще на 4% и, следовательно, в этом случае гутах = 1,С7 с’утял.
Эти поправки имеют чисто эмпирическйй смысл и делают
результаты продувок более совершенными, так как пересчеты
,0
1,25
2,5
51,°5
10
15
20
25
30
90
50
60
10
80
90
95
100
100
О
1,90 - 0,77
2,89 - 1,15
9,39 -1,70
5,38 -2,18
6,15 -2,62
7,08 — 3,90
7,99 -3},98
7,60 -9,30
7,55 — 9,96
7,11 -9,96
6 52 -9,30
5,61 -3,83
9,98 3,16 -3,19 -2,26
1,70 - 1,25
0,93' (6,12)
%
io*
к)
о
-/я
Е1К.
О W чв во W 1007о
о
5е
3.030 000
2 420 000
1 280 000
665 0001
341 000
172 000
су
2,0
1,8

/, 2
1,0
Ofi
0,6
Чрыло МА С А 2301 2~ 33
ор
0.2
О
0,2
а°
~д,Ч
- О О if 8 12 16 20 гр Z8 32
Фиг. 32а. Американская диаграмма испытания
крыла, пересчитанная на Х= сю.
Находим наш коэфициент ст*.
различных крыльев
одного и того же про-
филя на бесконечное
удлинение, сделанные
с этими поправками,
дают совпадающие ре-
зультаты.
Найдем теперь фор-
мулу для перехода от
американского коэфи-
циента момента к на-
шему (фиг. 33). Обоз-
начим американский
коэфициент через стХ.
Действующие на кры-
ло силы, выраженные в
коэфициентах, сведут-
ся в американской си-
стеме к сп, ct и стА.
Напишем выражение
момента для точки А.
Получим:
М=сп ^SV* bT-
знак минус поставлен
перед стА, так как у
американцев положи-
тельное направление
момента берется на
кабрирование.
сП1 = ТS^T = Т ~СтА = Т cos ’ +Сх sin а) ~ СтА-
Если нужно определить поло-
жение центра давления, то коэ-
фициент центра давления можно
найти по формуле:
которая в нашем случае даст:
Фиг. 33. Пересчет американского
коэфициента ст на коэфициент.
принятый в СССР.
Ст 1 стК
Од = — = ~Г----------
сп 4 сп
(57)
40
Фокусом крыла, как известно, называется такая точка хорды,
относительно которой аэродинамический момент для всех
углов атаки постоянен при постоянной скорости, т. е. ст =
= const.
Американские опыты показали, что при больших числах
Рейнольдса у самых разнообразных крыльев фокус лежит прибли-
зительно на расстоянии Ь/4 от передней кромки крыла. Этим и
объясняется американский выбор точки, относительно которой
берутся моменты.
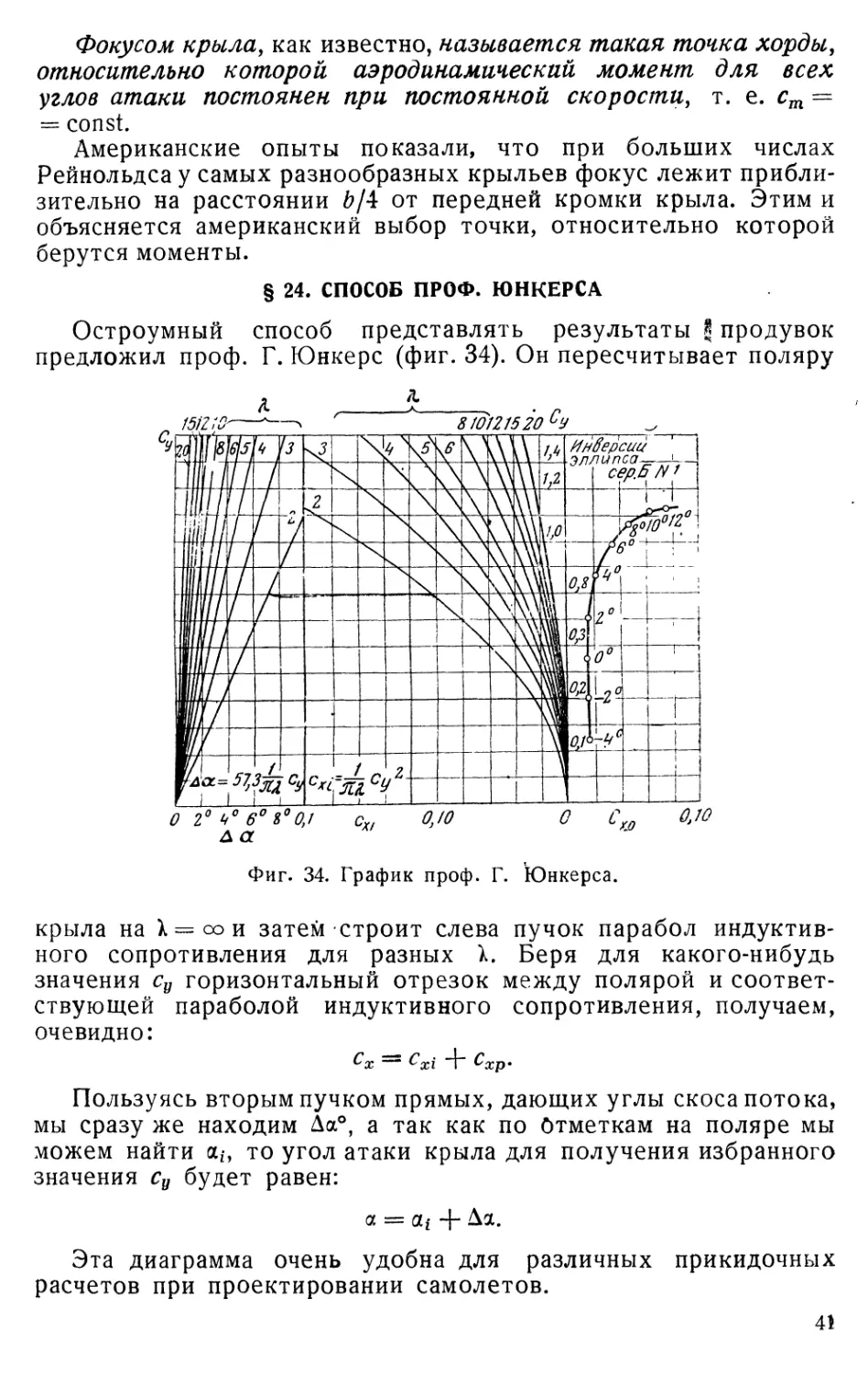
§ 24. СПОСОБ ПРОФ. ЮНКЕРСА
Остроумный способ представлять результаты Я продувок
предложил проф. Г. Юнкере (фиг. 34). Он пересчитывает поляру
Фиг. 34. График проф. Г. Юнкерса.
крыла на Х^оои затем строит слева пучок парабол индуктив-
ного сопротивления для разных к. Беря для какого-нибудь
значения су горизонтальный отрезок между полярой и соответ-
ствующей параболой индуктивного сопротивления, получаем,
очевидно:
Сх Cxi "4“ Схр*
Пользуясь вторым пучком прямых, дающих углы скоса потока,
мы сразу же находим Да°, а так как по Отметкам на поляре мы
можем найти аг-, то угол атаки крыла для получения избранного
значения су будет равен:
а = а/ + Да.
Эта диаграмма очень удобна для различных прикидочных
расчетов при проектировании самолетов.
41
Глава V
ПОЛЕ СКОРОСТЕЙ ОКОЛО КРЫЛА
§ 25. ОБЩИЕ ФОРМУЛЫ ДЛЯ ИНДУКТИВНОЙ СКОРОСТИ
Теория индуктивного сопротивления позволяет вычислить
скорости, вызываемые крылом конечного размаха в окружающем
воздухе. Знание этих скоростей необходимо конструктору для
учета взаимных влияний в сложных коробках крыльев, для на-
хождения скоса потока у хвоста самолета и для решения мно-
гих других вопросов.
Эту задачу решают приближенно, заменяя крыло присоеди-
ненным вихрем и считая вихревые усы направленными по
скорости невозмущенного потока. Следовательно, эти выводы
будут недостаточно точными возле самого крыла, так как там
воздух, очевидно, будет следовать за действительной кривизной
профиля, а не просто обтекать вихревой шнур. Поэтому фор-
мулы, которые мы сейчас выведем, можно применять лишь к
точкам, достаточно удаленным от крыла; примерно они должны
отстоять не менее чем на 23 хорды
от присоединенного вихревого шнура.
Рассмотрим сначала простейшую
схему вихрей, т. е. П-образную, Прове-
дем стандартные поточные оси так, как
это изображено на фиг. 35. Жирными
линиями начерчена система вихрей,
заменяющих крыло. Возьмем какую-
нибудь точку А с координатами л,
V и z и определим скорость по-
тока, вызванную в ней влиянием
П-образного вихря.
Задачу решаем, разбивая вихрь
на три прямолинейных отрезка /,
отыскивая скорость, полученную от каждого такого
отрезка, по известной нам формуле (9), т. е.
2 и 3 и
= —Г- /£1
4“л
Берем сначала присоединенный вихрь ВС и находим вызван-
ную им в точке А скорость vlt для чего подставляем в фор-
мулу (9) вместо ylt и х2 соответствующие величины по
фиг. 35. Определяем длину перпендикуляра, опущенного из
точки А на ось вихря ВС, и расстояния от концов вихря до
основания этого перпендикуляра в таком виде:
(9)
= Z/2 — z\ л2 — Z/2 + z,
42
и, учитывая, что точки В и С лежат по разные стороны от
основания перпендикуляра, получаем:
4л х^+у*
Z/2 + z _______1/2 —г________
V Х^ + у- ± (//2 + Z)* + ]<х2+у! + (//2-г)2
(58)
Этач скорость лежит в плоскости треугольника ADDr и пер-
пендикулярна к АОр Замечая, что
cos(5\; Ох) = cos(D^AD) = —4—r—,
cos (^; Оу) = - sin (D^AD) = -
У хл+уг
и
cos (^j; Oz) — О,
ищем проекции скорости Фг на оси координат; получаем:
фп ~ vi cos (^i’> Ох) — -Г- -Д—а [ Г— ll2 + z —+
1 41 ' 4лх2+_у2 [ /Л2 +_у3 1|- (l/2+z)2
________//2 — 2___] .
+ /х2+У+(//2-7Г2] ’
V,, » », cos(«i; Оу) = -4„— | v +
,______7/2 — 2 1.
"Г р х2+у2+(1/2 — z)2 J ’
• 0 = 0.
Ищем теперь скорость v2, полученную в точке А от
ния вихря СС2. Находим сначала длину перпендикуляра, опущен-
ного из точки А на ось вихря СС2, и расстояния концов вихря
от основания этого перпендикуляра. Получаем:
(59)
(60)
(61)
влия-
Г1=ДСг = /^4-(//2-г)2;
Хг = х- Х.2~ СО,
и, следовательно, учитывая, что концы вихря лежат по разные
стороны перпендикуляра, по формуле (10) находим:
V-2
4 л у у-2-г (7/2- z)2 [ —
(62)
43
Эта' скорость лежит в плоскости ДД£>СХ и перпендику-
лярна к ACV Замечая, что
cos (х»2; Ох) = 0;
cos (-v2; Оу) = - sin(DACJ = - —^2~г -;
у y2+(Z/2 — zy ( (63)
cos (v Oz) = - cos (DAC.) - - y=^=y,
находим проекции скорости v2 на оси координат:
0; (64)
‘l'p2=t'2cos(‘Ua; Оу) =
Г Z/2 - z
4л У + (Z/2 — z)2
1 Ц- ---------... - /
V x2+y2+(l/2 — z)2
(65)
vz2= v2 cos(-y2; Oz)=
L__________у_________ i +_____________________________1.
4л у-г (/(2 —z)2 уЛс2 + у2 + (Z/2 — z)2]
(66)
Наконец, вычисляем скорость ut, полученную в точке А от
влияния вихря ВВ2.
Ищем сперва длину перпендикуляра, опущенного из точки А
на ось вихря ВВ2, и расстояния концов вихря от основания
этого перпендикуляра; получаем:
У1 == АВХ = / у + (//2+ г)2 ;
Х2 = оо.
По формуле (10), учитывая, что концы вихря лежат по раз-
ные стороны от основания перпендикуляра, получаем теперь:
......... — - - 1 + —----------------
4л У y*+(Z/2+z)2 I V х2 + у‘ + (Z/2 + г)2
(67)
Эта скорость лежит в плоскости ^B^AD и перпендикулярна
к АВг. Замечая, что
cos(i/3; Ол) = 0;
cos ^3; Оу) = - sin (5ХДР) =-
V y2 + (ll2 + z)2
I
cos (i/3; Oz) = cos (BfAD) = -7=^==, I
/ j2+(Z/2 + z)2
(68)
находим проекции скорости v2 на оси координат:
44
X
(69)
(70)
А _у | 1 -[ л
— 4я yi + (1/2 + z)2 I y' Jcryy2 + (i/2ysy
(71)
Полная скорость потока получится, по принципу независи-
мости действия вихря, геометрическим сложением скоростей,
вызванных этими тремя шнурами и поступательной скоростью
потока V. Скорости, вызванные вихрями, обычно называются
индуктивными скоростями.
Следовательно, проекции полной индуктивной скорости по-
тока в точке А с координатами х, у, z будут таковы:
^Х -----
“Уу — ®1У + V2B + г'зу',
= f2z + f3z-
(72)
Если сюда подставить найденные величины проекций ско-
рости от трех вихрей, то получатся довольно громоздкие фор-
мулы (73) — (75), решающие поставленную задачу:
Г у Г______________42 +г_________________Z/2 —г________
4и х2+у2 /х24-уа+ (//2+'г)2 ' J^Tr2+y2+(//2 — г)2
_____TJ х
4л | х'~+у2
Z/2+ г____1/2 — 2_________
^^-гу2+(1!2+г^ + V х2Д-у2+(1\2-^
-LI_______1_______ 1 + х..............—
4л | у2 + (//2 + г)2 у х*уу*+(1/2+г')2
______У______Г1 X Х------------------- 11.
У2 + (//2-г)2| у' х2+уг+(1/2-г)2 J (
Отметим еще, что все индуктивные скорости пропорциональны
циркуляции скорости Г.
Общий анализ этих формул затруднителен, и мы разберем
в следующих параграфах лишь частные случаи, имеющие прак-
тическое значение.'
§ 26. ОТВЛЕЧЕННЫЕ ОБОЗНАЧЕНИЯ СКОРОСТЕЙ
Для получения более общих выводов в аэродинамике очень
часто пользуются отвлеченными, безразмерными величинами.
45
В формулы индуктивных скоростей обычно вводят отвле-
ченные длины, считая за единицу полуразмах крыла, т. е. ве-
личину //2. Такие величины мы будем обозначать чертой сверху.
У нас таким образом получатся отвлеченные координаты
точки А:
— х — у — г
* ~Т^ '1 У ~ 7/2 и 2 “ 7/2"
Для получения безразмерных скоростей все скорости выра-
жают в долях скорости полета V или же через абсолютную
величину средней скорости скоса | т)ио | изучаемого крыла.
В первом случае будем применять обозначения:
= и (77)
и называть такие величины отвлеченными скоростями.
Величина vy = — Да, т. е. углу скоса потока. Величина vz — — Ар,
где Д?—-угол бокового скоса; последний обычно не учитывают
ввиду его малости. <ох — дает изменение горизонтальной состав-
ляющей скорости потока. Полная скорость по оси Ох в точке А
будет:
+ (78)
или
Ж = 1 + vx. (79)
Приближенно ее считают обычно равной полной результирующей
скорости потока в точке А, т. е.
Wx. (80)
Точное ее выражение как для равнодействующей скоростей
и будет таким:
W = /(И + vx)* + -Ц2 • (81)
Так как скорости wg и vz очень малы по сравнению со ско-
ростью V, то их обычно отбрасывают; тогда получают:
т. е. формулу (80).
Безразмерные скорости второго рода будем писать в виде:
-- Vt —• V,, —• VM
^=Т7ГТГ; ^=ТГТ и = ТГ7 и т-д-’ (82>
I I I vyo I I Vyo I
т. e. ставить черту co штрихом, и будем называть их относи-
тельными скоростями. Знаки этих величин совпадают со
знаками самих скоростей.
4б
Средняя скорость скоса у крыла с П-образными вихрями
нами была найдена в гл. III. Она оказалась такой:
(ВД
ИЛИ
С помощью безразмерных величин можно написать все фор-
мулы для найденных нами индуктивных скоростей. Для этого
в них нужно подставить вместо размерных величин их выра-
жения через безразмерные, т. е. х = Л-//2; у =_у-//2; z=z4j2\ vx=
= и т. д. Тогда именованные множители сократятся и мы
получим связь лишь между безразмерными величинами.
Например, для индуктивной скорости по оси Ох мы получим
из формулы (73), следующую, более общую формулу:
<UX
1 У 1 + Z____р 1 — Z
4 л2 + у2 [/х2+У + (1 +1)2 Vr X2 + + (1 —7)2
(83)
С помощью формул этого вида мы изучаем уже не какое-либо
заданное крыло с размахом / метров, циркуляцией Г м2/сек
и точку А с координатами х, у и z метров, а исследуем вопрос
с несравненно более общей точки зрения, для всех крыльев,
независимо от их абсолютного размаха I и циркуляции Г.
Связь между отвлеченными и относительными скоростями
найти очень легко. По определению vx = vx | vUQ |; деля обе части
этой формулы на V, получаем:
но -у = vx и —1^а1> следовательно,
^ = 1^1^. (83')
§ 27. СКОРОСТИ В ЛОБОВОЙ ПЛОСКОСТИ КРЫЛА
Рассмотрим индуктивные скорости, получающиеся в плос-
кости (у, z), проходящей через присоединенный вихрь и пер-
пендикулярной к скорости полета V.
Индуктивная скорость по направлению оси Ох [формула (73)]
будет в этом случае (при х — 0) такой:
v = £Г.... Ч2 + 2 +__112~2 1 (84)
х 4-у L Y у2 + (//2 + z)2 /у2+(//2 —z)2 J’
Из этой формулы видно, что скорость потока W — V 4-
над крылом, где у > 0, будет больше скорости полета, так как
vx > 0, а под крылом, где у < 0, она меньше ее, так как vx< 0.
47
Рассмотрим ось Оу (фиг. 36). В таком случае 2 = 0 и фор-
мула примет еще более простой вид:
— г 112 = г 1 _ г 1
'х ~ 2кУ у 7Т(/72у ~ у 2тсу /Г+7’’
Подставив сюда циркуляцию по уравнению связи, т. е. Г =
1 I2ГI
= ~cybV, и заметив, что X = //b и | vgo | = , получим:
c„bV I 1 c..V 1 1
vx = — f—= = —-== = IМ -- Г—=2; (85)
4к-у 1 V 1 + у1 2у V 1 + v2 2у/ 1 +у2
Фиг. 36. Индуктивные
скорости на вертикаль-
ной оси крыла.
отсюда
vx 1
<ОХ = --— = ---— •
1гуо1 2у/ 1+_у2
(86)
Задаваясь различной относительной
высотой точки А, получим относи-
тельную скорость:
v — 1 2 19
У — 1з з 1 z
^-1,42 0,62 0,35 0,11
Из формулы (86) можно полу-
чить отвлеченную скорость
<vx = Для этого пишем согласно
формуле (83'):
(87)
Как видим, отвлеченная индуктивная скорость фх пропорци-
ональна абсолютной величине угла скоса потока.
с
Если для примера мы возьмем крыло с 1 = 6, то Да = ~
^0,05су. На летных углах у современных самолетов сд ^0,2,
следовательно, скос потока у крыла в радианах будет равен
всего лишь 0,01 радиана или в градусах 0,57°.
Изменение горизонтальной скорости в этом примере для
точек, лежащих на высоте у = х/з- т. е. на высоте одной хорды,
будет равно:
Ух = ~ = Да vfx = 0,01 • 1,42 1,5°/о,
т. е. величине сравнительно малой.
При посадочном угле атаки Гдтах~1,2 угол скоса возрастет
в 6 раз и будет равенуже 0,06 радиана или 3,43е. Соответ-
ственно увеличится и ivx и достигнет величины 8°/0. При уста-
48
новке на самолете приборов для измерения скорости полета сле-
дует помнить об этом изменении скоростей потока около крыла
и вводить поправки на индуктивную скорость. Это же измене-
ние скорости приходится учитывать при расчете бипланов.
Рассмотрим теперь скорости vg и vz, для которых формулы
(74) и (75) в данном случае (х=0) примут вид:
_____Г Г Z/2 — z . 7/2 +z 1
— 4n L У2 + J/2 — z)z "* у2 + (1/2 + z)2 J’
<0 = X Г___________у_________________у_______1
- 4ге L У2 -г (7/2 + Z)2 у2 + (Z/2 — z)2 J ’
Приведя дроби к одному знаменателю, получим:
V - Г //2[y2-z2+(7/2)2]
у 2л [у2 + z2 + (Z/2)2]2 — 4z2 (7/2)2 ’
= _£___________— 2-7/2-JZ_________
z 2л [у2 + г2 + (7/2)2]2 — 4z2 (Z/2)2 ’
(88)
(89)
(90)
(91)
12ГI
Подставляя l^irol = Lz и переходя к относительным скоро-
стям, получаем:
_ vy _
Vy —Г^1
I ио I
J_______у2 — z2 + I
2 ( у2 -b z2 4- 1 )2 — 4 z2 ’
(92)
“' = _£z_ _________У г_________
Vz pyo| (у +32 + I)2 — 4?
(93)
Знаменатели этих дробей существенно положительны, и знак
величин Vz и vy зависит от числителя. _
Таким образом сверху крыла боковая скорость потока v'z на.
правлена к центру крыла, а вни-
зу— к концам крыла. Физическое
объяснение этого явления весьма
просто: над крылом получается раз-
режение, и струйки, бегущие по
верхней поверхности крыла, стре-
мятся к его центру; снизу полу-
чается повышенное давление, и Фиг. 37. Индуктивные скорости
струйки стремятся разойтись в v2 вдоль размаха крыла,
стороны (фиг. 37).
Скорость скоса потока vv в пределах крыла, т. е. при
1 > ? > — 1 направлена вниз, так как vv <0; вне крыла, т. е.
при z2 > 1, vy>0, поток течет,_скашиваясь вверх.
Проследим, как изменяется Vy вдоль оси у. Формулы (90) и
(92) примут в этом случае (л = 0 и z = Oj следующий вид:

Г 7/2
2л у2-г (7/2)2
Б. Н. Юрьев—171—4
(94)
49
или для относительных скоростей:
Г - _ + 1 =- _2k-. f95>
vy- 2 (_y»+l)2 7+1
Это дает такую зависимость между vy и у:
у= гз 7з 1 2
= -0,45 -0,35 — 0,25 —0,10
Скорость скоса на расстоянии одной хорды для крыла с
X = 6, т. е. для у = Vs» равна 0,45, т. е. примерно половине ско-
рости скоса на самом крыле. Скос очень быстро убывает с уда-
лением от крыла. Этот скос приходится очень внимательно учи-
тывать при расчете бипланов.
§ 28. СКОРОСТИ В ДАЛЕКИХ ОТ КРЫЛА ТОЧКАХ, ЛЕЖАЩИХ В ЛОБОВОЙ
ПЛОСКОСТИ КРЫЛА
Для очень удаленных от крыла точек в формулах скоростей
скосов (90)—(93) можно пренебречь размахом, величина которого
мала по сравнению с координатами z и у, или в отвлеченных
обозначениях можно считать zuy много большими единицы.
Тогда получим:
v - . П/2 у8 —г8 ,
я 2ic (у3 + г2)2 ’ (96)
Г112 2уг
или для относительных скоростей:
—, 1 у3—г2
= (у2 + г2)2’ (98)
—, у г
Vz~ (у2+г2)2* (99)
Эти скорости не зависят от закона изменения Г по крылу, так
как всякую нагрузку крыла можно представить в виде наложен-
ных друг на друга П-образных элементарных вихрей, мы же
здесь считаем, что расстояние между вихрями исчезающе мало
по сравнению с х, у и г. Формулы эти указывают на быстрое,
уменьшение скоростей по мере удаления от крыла.
Если мы возьмем далекие от крыла точки на оси z, т. е.
при х = у = 0, то получим:
+ (ЮО)
Этой формулой мы воспользуемся впоследствии.
50
Заметим еще, что выведенные нами формулы справедливы
и для точек, лежащих на плоскости, параллельной лобовой-
и находящейся далеко за крылом. В этом случае величина ско-
ростей увеличится в два раза.
§ 29. СКОРОСТИ НА ПРОДОЛЬНОЙ ОСИ КРЫЛА
Изучение этой скорости необходимо главным образом для
расчета хвостового оперения самолета.
На оси Ох, т. е. при у = z = 0, продольная и боковые индук-
тивные скорости обращаются в нули. Остается лишь скорость
vg, которая в нашем случае [формула (74)] будет иметь вид:
Г [ Ч2 , 2_ Г *11
4к I л Гх2+(Z/2)2 + z/2 I 1 + <101)
Переходя к отвлеченным обозначениям, получаем:
’’"-Мт7^г + 1+-/=+~)' (102)
12Г I
Замечая, что I'M = “Ы [формула (20)] получаем:
+ <103)
или, делая приведение в скобках, находим окончательно:
г'»-7Й = -М1+ ;-)• <104>
Скорость v'y по мере приближения к крылу, т. е. при умень-
шении х, стремится к бесконечности. При этом скорость перед
самым крылом положительна, аза крылом — отрицательна. Про-
исходит это от действия присоединенного вихря, заменяющего
крыло. Воспользовавшись формулой (103), можно расчленить
скорость vv на две части; первая vyi будет получаться лишь от
присоединенного шнура и будет зависеть только от первого
члена в скобках, т. е.
= — ~2 х/ГТр ’ <105)
а вторая vyt получится от вихревых усов и будет зависить лишь
от второго и третьего членов в скобках формулы (103), т. е.
^ = “+(1 + 7Йу)- <106)
Первая формула будет давать скорости потока, обтекающего
профиль, являющийся в нашем случае простым вихревым шну-
51
ром. По мере приближения к нему х уменьшается и устреми-
тся к бесконечности.
Вторая формула дает скорость, возникающую от действия
вихревых усов и связанную с конечностью размаха крыла.
В таблице ниже даны обе скорости для различных значений л:
X — х/з 2/з 1 2 со 0 —1 —со
^-—1,32 —0,62 —0,35—0,11 0 oz оо +0,35 0
v' « -0,66 —0,78 —0,86 —0,95 -1,00 — 0,50 —0,15 0
= —1,98 —1,40 —1,21 —1,06 — 1,00 ±оо +0,20 0
На фиг. 38 изображено изменение скорости, скоса на про-
дольной оси крыла. Углы скоса будут пропорциональны скоро-
Фиг. 38. Индуктивные скорости
от усов Vyt и Vy2 от присоединен-
ного шнура; пунктир—резуль-
тирующая скорость (»,,).
стям скоса, так как они получаются
делением этих скоростей на И. Из
таблицы и фиг. 38 видим, что ско-
рость vy2, возникшая от влияния
усов в центре крыла, равна — ^з,
т. е. она составляет половину сред-
него скоса потока у крыла. Вдали
за крылом величина этой скорости
достигает единицы, т. е. равна сред-
нему скосу потока у крыла. Скорости
vyi дают типичное распределение ско-
ростей около вихря. Пунктиром обоз-
начена суммарная скорость скоса.
Глава VI
СКОС ПОТОКА У ХВОСТА САМОЛЕТА
§ 30. ФОРМУЛЫ СКОСА ПОТОКА ДЛЯ КРЫЛА С П-ОБРАЗНЫМИ
ВИХРЯМИ
Угол скоса потока необходимо учитывать при расчете ста-
тической устойчивости самолета. В этом параграфе мы выведем
величину скоса, возникающую у хвоста от действия нз него
вихревой системы крыла.
Заметим, что у горизонтального хвостового оперения будет
существовать еще скос от его собственной самоиндукции. Мы
в этой главе его рассматривать не будем, так как будем счи-
тать аэродинамические характеристики хвостового оперения
уже заданными.
Вообще же хвостовое оперение пересчитывается на другие
удлинения совершенно так же, как и крылья, т. е. по правилам
гл. IV, § 19.
Скорость скоса у горизонтального хвостового оперения мы
можем найти или по общей формуле (74) или непосредственно
из рассмотрения фиг. 39.
52
Фиг. 39. Влияние вихрей крыла
на хвостовое оперение само-
лета.
Обычно считают, что хвост самолета лежит в плоскости
П-образных вихрей. Общая формула (74) позволяет учесть вли-
яние на скос потока высоты располо-
жения хвоста. Для обычных самоле-
тов это влияние очень невелико и им
обычно пренебрегают.
Выведем теперь формулу верти-
кальной скорости потока у хвосто-
вого оперения независимо от пред-
шествовавших исследований скорост-
ного поля около крыла1.
По принципу независимости дей-
ствия вихрей вертикальная скорость
потока получится от влияних трех
отрезков вихря (7, 2 и 3) и будет
равна сумме скоростей, получаемых от каждого отрезка вихря
отдельно, т. е. + 2^У2, так как vy2 = ^Уз.
Действие же отдельного вихря мы можем получить по фор-
муле (9):
*2-У1 \
Г У 1 -Г -*2 г У1 + х1/
=----
4ДУ1
Подставляя в эту формулу для вихря № 1:
Vj = L, х.2 = 1/2, х1 = — //2,
а для вихря № 2:
jy = 1/2, х.2 — со, лу = — L,
получим:
Г 2Z-2 , о Г Г, , L
“Uy =----, . —7=^--— 1" 2 .—. . 1 ---, ------I
у (//2)2+£2 4it//2L ]/\z/2)2+Z2 I
= -izf1 +Vl + (2l/) ]’
Замечая, что
2Г
VU0 ~ id ’
где г'у0 — средняя скорость скоса у крыла, получаем:
Разделив обе части этого уравнения на V, мы получим угол
1 Приводим это доказательство, учитывая потребности моторных и эконо-
мических факультетов, на которых проходится сокращенный курс аэроди-
намики.
53
скоса потока у горизонтального оперения (фиг. 40), обозначаемый
у нас обычно через Даг. о. Итак, __
Даг.0 = д4[1 + + (107)
где Да =—= — угол скоса потока у крыла и Даг. 0 = — —
угол скоса потока у горизонтального оперения хвоста от вли-
яния крыла;
Вводя сюда значение Да, получаем окончательно:
Д*г.о =SH1 + /1 + (108>
Это и есть простейшая формула скоса потока у хвоста са"
молета.
Ее очень часто пишут не для угла Даг. 0, а для скорости
скоса, т. е.
^г.о = - tzglfi + |/ПЦ_у2]. (108')
Это представляет удобство при точном расчете полного
скоса (см. § 32).
Как видим, угол скоса потока у хвоста самолета пропорцио-
нален су крыльев и обрат-
лК но пропорционален отно-
сительному размаху кры-
gl I льев. Формула эта пока-
Г зывает, что скос потока
у \ У самолета очень сильно
----------------------------меняется при различных
скоростях полета, так как
Фиг. 40. Угол атаки и угол установки хвосто- при этом изменяется Сд.
вого оперения самолета. „ „ „ „ „
н У новейших самолетов
на максимальной скорости полета ^^0,2, а при посадочной
скорости он доходит до значения сЭШах= 1,3, т. е. увеличивается
приблизительно в 6 раз; во столько же раз возрастает и угол
скоса потока. Если на самолете имеются закрылки и пред-
крылки, то Суаш может достигнуть значения 2,4, а угол скоса
тогда увеличится в 10—12 раз.
Все это заставляет стремиться к возможно большему уточ-
нению формул скоса. К сожалению, как увидим дальше, в этом
вопросе еще не получена достаточная ясность.
Нетрудно в формулу (108') ввести скорость полета V и врс
самолета G. Для этого достаточно в нее подставить, считая
полет горизонтальным,
тогда получим:
Даг.° = 2 [1 +У 1 + (зг) ]•
Р
54
Эта формула для определенного самолета и заданной высоты по-
лета дает зависимость вида:
(Ю9)
т. е. угол скоса потока у хвоста самолета изменяется обратно
пропорционально квадрату скорости, т. е. очень сильно.
§ 31. БОЛЕЕ ТОЧНЫЕ ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ УГЛА СКОСА
ПОТОКА У ХВОСТА САМОЛЕТА
Точное знание угла скоса потока у хвоста необходимо для
надежного расчета продольной устойчивости самолета. Угол
атаки горизонтального хвостового оперения аг.о в первую оче-
редь зависит от угла скоса потока, так как этот угол, по фиг. 40,
очевидно, таков:
Яг.0 =« + <? —Д’г.о, (Г10)
где а — угол атаки крыльев и <р—деградация стабилизатора,
т. е. угол, образуемый хордой оперения с хордой крыльев.
Ввиду важности формулы угла скоса потока у хвоста, очень
многие лаборатории занимались ее проверкой. Формула (108)
является лишь первым приближением, так как она базируется
на самой грубой схеме крыла — на схеме П-образных вихрей.
В действительности с крыла сбегает вихревая пелена, как
было указано в гл. II, § 8. В дальнейшем мы выведем формулу в
предположении, что циркуляция скорости изменяется по раз-
маху крыла по закону полуэллипса (гл. XXI, § 101). Эта формула,
естественно, оказывается другой и имеет вид:
4“-=S2[i+tG4)']- <ш)
Обычно у самолетов величина 1;тогда rio формуле (108)
для П-образных вихрей получим:
Даг.0 = ^ • 1,22,
ЛА
а для полуэллиптического закона по формуле (111):
Даг.о=^-2,5,
тел
т. е. при полуэллиптическом законе угол скоса потока у хвоста по-
лучается в два раза больше, чем при гипотезе П-образных вихрей.
Многочисленные экспериментальные исследования, проведен-
ные для выяснения этого вопроса, дали весьма пеструю картину.
В общем для обычных соотношений получается некоторая сред-
няя величина угла скоса у хвоста самолета. Проф. Мунк (Америка)
предлагает пользоваться упрощенными формулами следующего
вида:
Даг.о = • 1,8 —для монопланов, (112)
тел х 7
И
Даг.о = 1,5 —для бипланов. (113)
55
Коэфициенты в этих формулах получены из опытов в трубах.
Структура этих формул такова, что они подходят под любую
теорию, так как во всякой теории угол скоса потока должен быть
пропорционален циркуляции скорости, т. е. для данного крыла
коэфициенту си, и обратно пропорционален размаху, т. е. раз-
носу вихрей по ширине. Следовательно, всякую формулу угла
скоса можно' привести к виду:
Даг.о = Л^, (114)
Л
где k — функция высоты расположения хвоста, т. е.~~/, харак-
тера очертания крыла в плане, закрутки крыла и т. д.
Величину k можно брать или из опытов или вычислять по
какой-нибудь теории.
Из многочисленных формул, служащих для вычисления угла
скоса потока у хвостового оперения, упомянем еще о форму-
лах, в которых угол скоса связывается с углом атаки крыла.
Идея эта напрашивается сама собой, так как су крыла почти
пропорционален углу атаки.
Угол скоса потока у крыла самолета выражается формулой:
Л» = ^(1+г).
Угол скоса у хвостового оперения будет в 1,5 — 2 раза
больше. Беря последнюю цифру, получаем:
Д^.о = 2^(1 +т). (115)
Вводим сюда аэродинамический угол атаки крыла, и тогда
пишем по формуле (5Г):
сд - ала.
Величина а нами найдена в гл. V; она дается формулой (55):
~ _____ао_______ 2лХ
~ . а 1 + * ~Х + 2(1 (-?).
1 + йо-^г
Отсюда
2тСа
Сд — а*а — х + 2(1 +т)
Подставляя эту величину в формулу (115), получим:
_ 2.2тсХ(1 Ч- т) 4(1+г)
аг'0-лХ Х + 2(1-Н) " “Х + 2(1 + т)’
и окончательно, пренебрегая в числителе малой величиной т,
получаем американскую формулу:
А“г. о_ 4 /1 1
аа Х + 2(1 + -с)-
56
Такими формулами очень часто пользуются американцы. Так
как Да г. о не вполне точно равно 2Да, то в формулу (116) вво-
дят поправки и тем ее уточняют. Например, по Вуду и Дилю
можно пользоваться достаточно точной формулой:
Даг. о Збср (117)
ад л -f- 2 5
L
где зу- дает поправку на удаление хвостового оперения от
крыла; здесь Ьср — средняя хорда крыла.
В настоящее время имеется весьма много таких формул,
однако они дают хороший результат лишь в нормальных слу-
чаях и в пределах тех опытов, на основе которых они получе-
ны. У необычных самолетов могут быть и весьма большие от-
клонения от таких полуэмпирических формул.
§ 32. ВЛИЯНИЕ ВИНТА И ФЮЗЕЛЯЖА НА УГОЛ СКОСА ПОТОКА
У ХВОСТА САМОЛЕТА
Величина угла скоса Даг.о определяется обычно в лаборатор-
ных условиях при отсутствии фюзеляжа и винта. Эти факторы,
однако, вносят заметное изменение в угол скоса. Будем в даль-
нейшем обозначать угол скоса потока у хвоста самолета через
4а'г. о. Рассмотрим сначала планирующий полет, а затем полет
с работающим мотором.
Расчет оперения на самолете осложняется из-за фюзеляжа,
который, во-первых, тормозит скорость набегающего на опере-
ние потока и, во-вторых, изменяет величину угла скоса.
Обычно считают, что нормальный фюзеляж тормозит посту-
пательную скорость потока до величины
Иг. о = 0,9 И. (118)
Однако проведенные опыты показывают, что встречаются боль-
шие отклонения в этой величине — примерно от 0,95 у очень
хорошо „зализанных* самолетов до 0,75 у самолетов очень пло-
хих форм. Кроме того, это торможение не постоянно по раз-
маху оперения, а сильно изменяется.
Фюзеляж резко изменяет все обтекание крыла. Как увидим
далее, в гл. XI, § 56, эффект фюзеляжа как бы уменьшает удлине-
ние крыла. Поэтому при вычислении угла скоса потока у хвоста
рекомендуется во все формулы подставлять не действительное
удлинение крыльев К, а так называемое эффективное удлине-
ние X*, которое в среднем можно брать по формуле:
к, = 0,85 X. (119)
Взяв такое удлинение, мы получаем уже угол скоса потока
не от изолированного крыла, а от комбинации крыло — фюзеляж.
Таким образом получаемый по всем описанным формулам
угол скоса потока должен вычисляться по эффективному удли-
57
нению X* и затем исправляться в отношении , так как
(1'20)
у г. о v у г. о и г. о
Это при обычном торможении, т. е. при Vr. о~0,9И, дает
увеличение угла скоса на 10%.
Весь этот расчет относился к планированию самолета. При
моторном полете хвостовое оперение полностью или частично
попадает в обдувку струей винта. Струя винта имеет в области
хвостового оперения повышенную скорость и, кроме того, вра-
щается. Добавочная и вращательная скорости учитываются на
основе теории воздушных винтов. В результате левая и правая
половины хвостового оперения работают с различными скосами
потока. Расчеты эти затрудняются тем, что струя винта несколь-
ко тормозится и ее вращение уменьшается фюзеляжем и крыль-
ями. Учет этого торможения очень труден и мало разработан.
Фиг. 41. Скоростные многоугольники правой и левой половин
горизонтального хвостового оперения.
Чаще всего расчет скоростей у хвостового оперения ведут,
не вполне законно применяя принцип независимости, и склады-
вают геометрически векторы скоростей:
V —поступательного потока (скорость полета);
“Ууг.о—скорости скоса от крыльев, вычисленной по 1*,
“Ил в —добавочной скорости от винта,
vyB —добавочной скорости от вращения струи винта,
•Ул-Ф —скорости торможения потока фюзеляжем,
vyr —скорости от изменившегося благодаря работе винта
закона распределения Г по размаху крыла.
Эти скорости вычисляются частично по теории винтов и ча-
стично берутся по всевозможным приближенным формулам или
графикам. В каждом конструкторском бюро имеются свои упро-
щенные приемы. Некоторые такие формулы даны в „Справоч-
нике авиаконструктора"х. По этим скоростям строятся скорост-
ные многоугольники, изображенные на фиг. 41. Скорость вра-
щения струи винта на одной половине оперения увеличивает
угол скоса, а на другой уменьшает. Бывают случаи (на малой
скорости полета), когда одна половина оперения работает с
1 Изд. ЦАГИ, 1938.
58
положительным углом атаки, а другая с отрицательным. Нако-
нец, иногда в струю попадает не все оперение, а лишь его часть.-
Тогда обычно считают, что каждая такая часть оперения работает
независимо от другой и соответственно их и рассчитывают.
Найдя угол атаки оперения со всеми поправками, вычисляют
аэродинамический момент горизонтального хвостового оперения
ТИг.о относительно центра тяжести самолета. При этом сдг. 0
берут по продувкам оперения и считают подъемную силу опе-
рения приблизительно перпендикулярной к оси фюзеляжа.
Тогда
Мг.0 = еуг,0 -pr.o W2L. (121)
Затем находят безразмерный коэфициент аэродинамического
момента оперения относительно центра тяжести самолета:
с _ р (122)
2 sy.iL — Су г.о S \ у)
Подробный анализ этой формулы обычно дается в курсе
динамики самолета, в разделе „Статическая устойчивость".
В заключение заметим, что еще не имеется точной теории
угла скоса потока у хвоста самолета, а все существующие
приемы инженерного расчета очень грубы и приближенны и не
обеспечивают достаточной точности расчета.
В гл. XXI мы снова вернемся к этому вопросу.
Глава VII
ТЕОРИЯ ПОЛИПЛАНОВ ПО БЕТЦУ
§ 33. ПОСТАНОВКА ЗАДАЧИ
Задачей исследования полипланов с точки зрения теорий
индукции является получение формул, позволяющих вычислить
по данным продувки монопланных профилей аэродинамические
характеристики любых комбинаций крыльев, образующих ту
или иную „коробку крыльев". Эта задача была решена проф.
А. Бетцем (Геттинген). Теория эта основывается полностью
на гипотезе П-образных вихрей.
Пусть у нас имеется сложная коробка крыльев. Заменяем
все крылья П-образными вихрями, отмечая крылья, начиная
с верхнего, и все относящиеся к ним величины номерами.
Возьмем поточные оси координат.
Рассмотрим верхнее крыло. Под действием нижних крыльев
у него возникают индуктивные скорости от второго и третьего
крыльев и их усов; условимся применять двойные цифровые
индексы крыльев, причем первая цифра будет давать величину,
относящуюся к рассматриваемому крылу, а вторая — к крылу,
действие которого на рассматриваемое крыло изучается.
Например, у верхнего крыла под влиянием нижних крыльев
возникнут следующие индуктивные скорости: т>В12, T>yj3, vxl2 и vxl3.
59
Скорости от самоиндукции будем писать в виде: т/У11 и ^У22.
Тогда по принципу независимости действия вихрей мы можем
написать:
+ ^12 + vyia‘> (123>
^Х12 “Ь (124)
Скорости эти, вообще говоря, будут величинами перемен-
ными по размаху. В дальнейшем,
_________у при изложении теории Бетца,
’Т’1 у будем, заменять их средними ско-
i/1—2—г У' ростами, как и в теории моно-
' плана.
Фиг. 42. Скоростной треугольник Таким образом результирующая
у верхнего крыла биплана. скорость потока, набегающего на
какое-нибудь крыло, например на
первое, получится векторным сложением скоростей V, фх1 и
vyi (фиг. 42) и будет равна:
1^1 = /(И +vxl)2 + v2yl. (12°)
Тангенс угла скоса получится равным:
(1ВД
Знак минус ставим потому, что положительному углу скоса
соответствует отрицательная скорость <иу.
Индуктивные скорости обычно очень малы по сравнению
со скоростью потока И, поэтому предыдущие формулы упро-
щаем, считая, что в первой из них можно отбросить ^У1; тогда
получим:
V . = V + ъх1. (127)
Во второй формуле тангенс малой дуги заменяют дугой и
тогда
Да = -^
(128)
Другими словами, считают, что скорость набегающего потока
увеличивается на индуктивную скорость vxl, а скорость vgl лишь
поворачивает скорость Ух = V + т>ж1 на угол скоса Да.
Если теперь разделим уравнение (12г>) на V,, то получим:
Vyi__Vyu । Vyi2 । уУхз
Vi “ И1 V. •
Эти величины представляют собой углы скоса, которые обозна-
чим так:
Да! = Дап + Да12 + Да13. (129)
Угол скоса Дап будем называть углом скоса от самоиндук-
ции, величины Дя12, Да13 и т. д. — углами скоса от взаимо-
индукции; так например, Да12 обозначает угол скоса у‘первого
крыла, получившийся от влияния второго.
60
Если теперь умножим формулу (129) на истинный су1, отне-
сенный к скорости полета V, то получим:
СУ1 — СУ1 + СУ\ ^а12 4" СУ\ ^а1з- (130)
Произведения су на соответствующие углы скоса потока
дают индуктивные сопротивления, так как они дают проекцию
повернувшейся подъемной силы на линию полета. Пишем теперь
формулу (130) в таком виде:
— Cxill + Cxi\2 + (131)
где
Л
схИ1 — СУ1 (1 4“ 8)
называется коэфициентом индуктивного сопротив-
ления от самоиндукции и выражения:
Cril2 ^а12> 1
схаз — cyi аа1з f
называются коэфициентом индуктивного сопротив-
ления от взаимоиндукции крыльев.
Такие же выражения можно написать и для остальных крыльев.
Следовательно, мы можем подсчитывать угол скоса и индук-
тивное сопротивление у любого крыла как сумму углов скоса
и индуктивных сопротивлений, возникающих от взаимного влия-
ния отдельных крыльев. Это чрезвычайно упрощает все расчеты.
§ 34. ВЫЧИСЛЕНИЕ СКОРОСТЕЙ И УГЛОВ СКОСА ПОТОКА ОТ
ВЗАИМНОГО влияния
Из изложенного ясно, что, изучая полипланы, мы должны
рассмотреть сначала взаимодействие пары крыльев, так как
всякая коробка может быть разбита на такие пары. Решение
задачи о взаимном влиянии ведется следующим путем. Нужно
взять на верхнем крыле точку и найти индуктивные скорости,
вызванные вихрями нижнего крыла. Для этого надо воспользо-
ваться формулами (73) и (74). Скоростью <uz обычно пренебре-
гают, так как ее влияние на крыло ничтожно. Скорости же <vy
и vx необходимо учитывать; они будут меняться вдоль по
размаху крыла. По предложению проф. А. Бетца в расчетах
пользуются средними по размаху индуктивными скоростями.
Вычисление этих скоростей по формулам (73) и (74) для
сложной коробки крыльев приводит к простым по существу,
но весьма длинным вычислениям. Это происходит из-за слож-
ности, вернее громоздкости формул (73) и (74), которые при
вычислении средних скоростей приходится интегрировать.
Мы здесь не будем делать подробного вывода общей фор-
мулы влияния, а дадим далее готовый результат, найденный
А. Бетцем. Но чтобы иллюстрировать ход рассуждений, при-
61
мененный при выводе этой формулы, сделаем вывод ее для про-
стейшей коробки крыльев, т. е. такой, у которой размахи
верхнего и нижнего крыльев равны друг другу и нет выноса
Фиг. 43. Простейшая бипланная коробка
крыльев.
верхнего крыла по
отношению к ниж-
нему (фиг. 43).
Рассмотрим дей-
ствие левого ниж-
него вихревого уса
на точку А верхнего
крыла, лежащую на
расстоянии z от ле-
вого конца крыла.
Этот полушнур вы-
зовет в точке А индуктивную скорость v, перпендикуляр-
ную к линии О А, образующей с нижним крылом угол <р. Скорость
эта получится по формуле (3), т. е.
v =
4кг*
Проекция этой скорости на вертикаль найдется из уравнения:
Г2
Vy = — Т-1 COS Ф.
у 4кг *
Знак минус ставим потому, что скорость эта направлена вниз,
а ось Оу идет вверх.
Из чертежа видно, что
г -------
cos Ч = .7 2 и г = /?* + Л2 *,
У г2 + A2 r ‘ ’
где А — высота коробки крыльев.
Подставив эти величины в формулу скорости, получим:
7) — __ _2 __
у 4к г2 + Л2 ’
Скорость эта будет иметь в различных точках размаха разную
величину. Пунктирная кривая дает закон изменения vg по раз-
маху верхнего крыла. ,
Ищем среднюю по верхнему крылу скорость от двух нижних
вихревых шнуров, пользуясь тем же приемом, какой мы при-
менили в теории моноплана1. Находим:
1г
2"/Г J '°9d's = ~~M1 J
О_________________о
1г
z dz
Vy 12 —
(133)
1 Здесь мы считаем, что расстояние между вихрями равно размаху крыльев
так как влияние отрезков е на величину vy будет в случае биплана ничтожно
малым.
62
Введем обозначение:
812 " 1П Vх + (4У
(134)
и назовем отвлеченную величину е12 коэфициентом вза-
имоиндукции. Тогда формула (133) перепишется так:
р
^(/12 = £122я/1 ‘ (135)
Если сравним эту формулу с формулой (20), дающей скорость
скоса от самоиндукции верхнего крыла как моноплана, т. е.
‘U»°‘ = — 2л/! ®’
где е — коэфициент самоиндукции, то увидим полную аналогию
этих формул. В дальнейшем коэфициент самоиндукции ess 4
мы будем для однообразия формул писать с двумя индексами, т. е.
8ц = е22 = £33 ~ 4.
Рассуждения, с помощью которых мы получили формулу
(135), можно применить и к нижнему крылу; тогда мы получим
аналогичную формулу, но с измененными индексами.
Таким образом фундаментальными формулами в тео-
рии индукции являются следующие:
^У12 - — 612 2^ >
^1)21 ~ ®21 2п/2 - (136)
Этим скоростям скоса соответствуют углы скоса:
= (137)
Даг1 “ 7^= 6г1 (133)
Циркуляции скоростей Гг и Г2 заменим по уравнению связи
следующими выражениями:
— у су1
Г2 —
(139)
Здесь Cyi и Сцц — коэфициенты подъемной силы крыльев,
отнесенные к истинной скорости набегающего
потока у каждого крыла, т. е. к и H^2ssp'2. Эти
коэфициенты можно брать прямо по продувкам монопланных
крыльев.
63
Введя эти величины в формулы углов скоса, получаем в окон-
чательном виде формулы Бетца:
л„ „ с»п ,
Да‘2 = 612 4777 (И,)
л Cyl bi 1Л
(14!)
Совершенно аналогичным образом определим горизонталь-
ные индуктивные скорости. Горизонтальная скорость получится
в точке А только от действия присоединенного шнура. Вихре-
вые усы не будут вызывать продольных скоростей, так как ско-
рость, вызванная прямым вихрем, всегда к нему перпендикулярна.
Применяя в нашем случае формулу (9), пишем:
v — -X2 [ _z j_____l — z 1
х [|/л24-22 /л2+(/—z)2J
Средняя скорость по размаху найдется по формуле:
’.НА*=
Произведя интегрирование, получим:
^12==^7г4(^2 + ^-А).
Отвлеченный множитель
р-12 = (yr Р -{-А2 — А)
называется коэфициентом горизонтальной индукции
нижнего крыла на верхнее. С его помощью получаем формулу
горизонтальной индуктивной скорости:
^12 = И12 "Й—- (142)
Совершенно аналогичным приемом получим формулу для
нижнего крыла:
Vx2i==^2l~MT’ (ИЗ)
Эти формулы являются основными в теории Бетца. Заменяя
Гх и Г2 по уравнению связи формулами (139), получаем оконча-
тельно:
^12 = pi2 И2; (144)
‘Vxit — P2i C^(bl 1Л- (145)
Мы вычислили здесь значения $12, е21, р12 и р21 для простейшей
коробки.
64
Бетц сделал такие же вычисления для общего случая. Ко-
робка была взята с разными размахами 1Г и Z2 у верхнего и у
нижнего крыльев и
с выносом а у верх-
него крыла по отно-
шению к нижнему
(фиг. 44). Он ввел
вспомогательные ве-
личины:
4
з
Фиг. 44. Общий случай бипланной коробки
крыльев.
—средний размах и
с_______ ~~
С ~ 2
—свес верхнего кры-
ла над нижним или длину консоли. С их помощью были найдены
формулы:
,1!- 10 + (146)
= (147)
Р-12 = — Н21 = а2 + /2 +А2 —•/* а2 + с2 + №). (148)
Этими формулами и приходится постоянно пользоваться при
расчете полипланов.
Заметим, что h и а берутся здесь по вихрям и по потоку,
поэтому при изменении угла атаки они изменяются. Так напри-
мер, при увеличении угла атаки положительный вынос а (фиг. 45)
может сделаться нулевым и да-
же отрицательным. Следовательно,
аэродинамический вынос
нельзя смешивать с конструктив-
ным выносом коробки.
Величины е могут получаться
положительными и отрицатель-
ными, и следовательно, скос по-
тока от взаимоиндукции может быть любого знака.
Из соотношения Н2 = —р-21 следует, что горизонтальные'ин-
дуктивные скорости направлены у пары крыльев в противопо*
ложные стороны.
Фиг. 45. Вынос верхнего крыла
биплана по отношению
к нижнему.
§ 35. УЧЕТ ГОРИЗОНТАЛЬНЫХ ИНДУКТИВНЫХ СКОРОСТЕЙ
Наличие горизонтальных индуктивных скоростей в коробке/
крыльев заставляет различать два рода аэродинамических коэ-
фициентов, которые мы будем обозначать римскими и арабскими
цифрами.
Б. Н. Юрьев—171—5 65
Если мы найдем, например, у первого крыла истинный угол
атаки а, то по продувке монопланного крыла, пересчитанного
на X = оо, получим су., с которым это крыло работает в коробке
крыльев. Его подъемную силу придется вычислить по формуле:
У1 = Syl = су. f St (V + ^12)2,
так как поток воздуха обтекает его со скоростью V\.
Однако мы можем написать для этой же подъемной силы
выражение:
V^c^StV*,
т. е. отнести с,, к скорости полета, а не потока. Такие коэфи-
циенты обычно и применяются в экспериментальной аэродина-
мике. Их можно получить в аэродинамической трубе, испыты-
вая первое крыло в присутствии второго.
Связь между этими коэфициентами получим приравниванием
обоих выражений подъемной силы друг другу. Тогда после со-
кращения получим:
CyiV^Cy.Vl
ИЛИ
„ _ г — о (V + ^12)2 _ / , . Url2\2 .
Cyl — Cyl Cyl р Cyl 1 -j- у J
Развертывая выражение в скобках, получим:
r (l | о I- I ^12? 1
Cyl — Cyl I 1 -j- _ у + у J I
Величина по сравнению с первыми двумя членами очень
мала и ею можно пренебречь. Тогда получаем:
Cyi = Cyi (1 -г 2 Vy~^ • (149)
Подставляя сюда значение 'индуктивной скорости т\.12 по
формуле (144), получаем окончательно:
с — с т (1 4- 2и Су11
С»‘ - Cyi + 2н-12 4ж/1
Второй член, стоящий в скобках, дает поправку, обычно
не превышающую 5%; следовательно, множитель является
здесь поправкой на поправку. Его величина обычно отличается
от единицы не больше чем на 5°/0. Таким образом, заменяя в
этой формуле единицей, мы делаем ничтожную ошибку,
не большую обычно т. е. около
66
Вследствие этого предыдущую формулу следует писать в
таком окончательном виде:
^i=^i (1+2^2^
\ 4*/j
(150)
и аналогично:
Су2 — fyll (1 2 р-1
(151)
Такую же поправку нужно сделать и для коэфициентов сХ:,
и ст, различая и у них римские и арабские индексы. Напри-
мер, для верхнего крыла получим:
_ /-> /1 1 О Гу II Ь2
С.хр1 = C.xpl I 1 + 2u12 -4к/^ -
(152)
Cml = Cml (1 + 2gi2
Найдем теперь полную подъемную силу Y коробки крыльев.
Напишем сначала формулу через коэфициенты с римскими
индексами:
У - Л + у2 = СУ1 + 2u12 ± blil +
+ ^n(l-2p12^Aj-?-&2/2^ =
= су1 ± V* + cVII -j- b2l2 У8 + 2р, 2 ^-С~V2-
— 2u<2 --'7I Cgn Ь1Ьг V2 =
4л 2
= ^i^- ViV2 + Суп-j- b2l2V2,
т. e. члены с у. сократились.
Если бы мы написали формулу подъемной силы через коэ-
фициенты с арабскими индексами, то получили бы:
7=^4- У2 = су1-^ b^V2 + Суг } b2l2V^.
Таким образом при вычислении полной подъемной силы ко-
робки можно пользоваться коэфициентами как- с римскими, так
и с арабскими индексами и совершенно не учитывать измене-
ния горизонтальной скорости потока.
Если же мы интересуемся подъемной силой каждого крыла
отдельно, с чем приходится встречаться в расчетах прочности
и устойчивости, то влиянием горизонтальных индуктивных ско-
ростей пренебрегать нельзя.
67
§ 36. ТЕОРЕМЫ МУНКА
Всякую коробку крыльев можно разбить на пары крыльев.
М. Мунк доказал, что у каждой такой пары имеются некоторые
интересные свойства, облегчающие расчеты.
Обычно эти свойства коробки крыльев формулируют в виде
„трех теорем Мунка".
Теорема первая. Полное индуктивное сопротивление
пары крыльев не зависит от их выноса, если считать cyi и cvu
заданными.
Индуктивное сопротивление состоит из индуктивного со-
противления от самоиндукции крыльев и индуктивного сопро-
тивления от взаимоиндукции. Самоиндукция крыльев не зави-
сит от их выноса, так как она вычисляется по формулам моно-
плана:
с2
г — Cyl
С XI 11 — -у у
о
cv2
Ctz 22 — *
Следовательно, нам нужно доказать, что сумма сХ112+^21 не
зависит от выноса коробки.
Ищем коэфициент индуктивного сопротивления от взаимо-
индукции по формулам:
__ Л СуП^2 V2
Cxi 12 Cyl А<*12 Cyl -pj S12 “4^ ’
__ а „ V2 СУ1Ь1 /х
Cxi 21 — Су2 — Суц -у-2 е21 у-
и вычисляем:
Хг 12 + 21 = схМ4- V2 + сх1 21 &2/2 V- =
= сДг суА Vi Р А > т/г
;/г 12 4к/1 V1 '2 °^liV +C'II I/. 21 4п/2 уг 2 D^V' •
После приведения получим:
ЛХг + Хи.-(•„ + =„) | ^1/, (153)
Вынос а в эту формулу войдет лишь в коэфициентах е12 и е21.
Вычисляем e12 + s2i по формулам Бетца (146), (147); находим:
_ _ь, _ . / я2 + /2 + й2 + я , . fa2 4- Z2 + hX-a
V я2 4- с2 4- й2 + я '/а2 + С2 4-Й2 — а
, (V a2 -t-/2 4-й2 4- а) (/’^ТК+’Л2 — а} _. /; + Л2
( f + я) ( / а2 4- с2 + й2 - а) ~ с2 + й2' (154)
Величина а, как видим, сократилась. Это и доказывает пер-
вую теорему Мунка.
68
Ранее многие конструкторы думали, что, разместив соответ-
ствующим образом крылья в пространстве, можно получить
уменьшение их сопротивления. Иногда строились весьма при-
чудливые коробки крыльев (фиг. 46), от которых ожидали особо
хороших результатов.
Теорема Мунка показывает, что всякую коробку крыльев
можно привести к эквивалентной коробке без выноса, т. е. такой,
у которой несущие вихри будут лежать в одной плоскости, пер-
пендикулярной к линии полета.
Фиг. 47. Крылья тандем н
эквивалентное им моно-
плавное крыло.
Фиг. 46. Коробки с выно-
сом и без выноса, дающие
одинаковое индуктивное
сопротивление.
Эта же теорема позволяет установить правильную точку
зрения на тандемные комбинации крыльев (фиг. 47). Многие
конструкторы думают, что, поместив крылья одно за другим
на достаточном расстоянии, они избавятся от взаимодействия
крыльев и получат хороший результат.
Теорема Мунка доказывает, что этого не будет и скос потока
у такого крыла просто удвоится. Если у каждого крыла было
некоторое К, то, уничтожив вынос, т. е. сдвинув эти крылья,
мы получим у эквивалентного крыла удлинение лишь что
дает двойное индуктивное сопротивление по сравнению с оди-
ночным крылом.
Вторая теорема Мунка. В коробке без выноса у пары
крыльев индуктивные сопротивления от взаимоиндукции равны
друг другу.
Доказываем эту теорему, написав выражения для Лиг и Х21-
Получаем по предыдущему [формула (153)]:
y — е SnМг р ..
Xi 12 - 612-~ у И1И2;
у — е СУ1 СУП 61 &2 Р 17 I/
Лиг-бд-----------%-
Ищем теперь величины е12 и е21, входящие в наши формулы.
69
Формулы Бетца (146) и (147) дают для случая а=0 следующий
результат: ____
! //2 + Л2
S12 = е21 = In _______;
12 21 у
но тогда и
Xii2 — Xi21.
Это и доказывает вторую теорему Мунка.
Физический смысл этой теоремы легко уяснить следующим
примером. Представим коробку крыльев с очень большим верх-
ним крылом и очень малым нижним. Тогда малая подъемная
сила нижнего крыла получит очень большой скос под влиянием
верхнего крыла, и, наоборот, большая подъемная сила верхнего
крыла получит очень малый скос под влиянием нижнего крыла.
Индуктивные сопротивления крыльев получатся как произведе-
ния подъемных сил на скосы. Теорема Мунка и доказывает,
что эти произведения равны. Полное индуктивное сопротивле-
ние биплана можно написать в таком виде:
— Xi и Xi 12 + Xi 2i Xi 22- (155)
В случае коробки без выноса это выражение упрощается и
принимает вид:
(156)
Так как всякую коробку можно привести к коробке без
выноса, то при изучении сопротивления коробки обычно и поль-
зуются последней формулой.
Третья теорема Мунка. Всякую коробку крыльев можно
заменить эквивалентным
Су
С*1
• >y= J г J c
1 =
Лсхе
Эквивалентное
монопланом.
Пусть у нас имеется сложная
коробка крыльев (фиг. 48). Обозна-
чим общую площадь ее крыльев
через S = Sx + S2 + Зз* У каждого
крыла получится некоторая подъ-
емная сила и индуктивное сопро-
тивление. Очевидно:
Фиг. 48.
монопланное крыло.
Каждой силе будет соответст-
вовать некоторый коэфициент
подъемной силы и коэфициент сопротивления.
При аэродинамическом расчете самолета предпочитают поль-
зоваться так называемыми коэфициентами суммарного действия
коробки крыльев, отнесенными к суммарной площади коробки 5.
С помощью таких коэфициентов предыдущие формулы напи-
шутся в таком виде:
Су = cyi | S#2 + cy2 Sy* + cV3 S3V2;
cxi = cxil S, И2 + cxi 2 S2l” + Сиз f S3V2.
70
Отсюда получаем коэфициенты суммарного действия коробки:
____< 4" + суЗ$з
Су s1 + s2 + s3 —
_ слП^1 + cxi2 ^2 4- cxi3S3
4-S2-j-S3
Таким образом на нашу систему крыльев будут действовать
силы, выраженные в коэфициентах cXi и су .
Вообразим теперь монопланное крыло с площадью S = Si +
+ 52-|-S8 и попытаемся получить у него те же самые су и cxi,
как у коробки. Коэфициент су мы получим легко, подобрав
нужный угол атаки, но для получения того же сХ1 нам придется
придать эквивалентному крылу вполне определенное удлинение
Хэ, так как у нас имеется связь:
(157)
су>
с xii
Фиг. 49. Биплан-
ная коробка
крыльев, имею-
щая ПрИ Су == О
Cxi Ф 0.
если, как в нашем случае, су и сХ1 заданы, то, решая это урав-
нение, мы получим ответ:
(158)
Таким образом эквивалентное монопланное
крыло должно иметь площадь S = S1 + 52 + ‘S3 +
4-S4+... и удлинение кэ.
Заметим, что у такого крыла 1, вообще гово-
ря, изменяется с изменением угла атаки. Дело в
том, что в сложной коробке крыльев суммарное
индуктивное сопротивление может и не рав-
няться нулю при нулевой суммарной подъемной
силе. На фиг. 49 изображена такая коробка. Общая
подъемная сила у нее равна нулю, но суммарное
индуктивное сопротивление не равно нулю. Сле-
довательно, для сложных коробок крыльев нельзя
провести простую параболу индуктивного сопро-
тивления.
Все же не будучи вполне строгой, замена той или иной
системы крыльев одним, эквивалентным, крылом оказывается
полезной и часто применяется на практике.
Далее, в гл. IX, § 42 мы укажем как надо располагать хорду
эквивалентного монопланного крыла.
Глава VIII
ПЕРЕСЧЕТ МОНОПЛАНОВ НА БИПЛАН
§ 37. ВЫВОД ОСНОВНЫХ ФОРМУЛ
Теория индукции позволяет делать пересчет монопланных
крыльев на любую комбинацию крыльев, т. е. находить полные
71
аэродинамические характеристики всех крыльев и всей коробки
в целом, имея лишь результаты испытания профилей, из кото-
рых составлена коробка, и чертеж самой коробки. Пересчет
ведется в виде проверочного расчета. Углом атаки коробки
считается угол атаки верхнего крыла.
Как и у моноплана, здесь существует два приема расчета:
приближенный с помощью гипотезы П-образных вихрей и бо-
лее точный с переменной по размаху крыльев циркуляцией. В
настоящее время хорошо разработаны оба эти приема. Однако
во втором, которым мы займемся в дальнейшем, очень трудно
учитывать вынос крыльев. Это гораздо проще делается в пер-
вом способе, основанном на формулах Бетца.
Мы здесь изложим наиболее точный прием, хотя и основан-
ный на гипотезе П-образных вихрей, но учитывающий и вынос
крыльев и горизонтальные индуктивные скорости.
Основной задачей пересчета является нахождение для задан-
ного угла атаки коробки углов скоса потока от взаимоиндук-
ции, т. е. величин:
- я12 - с12 4-Zi (/
(140)
и
. cyl V1
(но
(см. гл. VII).
Входящие сюда скорости Vt и И2 нам известны, так как в
гл. VII, § 35 мы получили формулы (144) и (145), дающие го-
ризонтальные индуктивные скорости. Эти скорости напишутся
так:
V, = V + , = V + И, = V 11 + 4’);
V, - Г + v,n = / +иа = V'fi +л,-^--к’)-
Делаем преобразование вторых членов в скобках, умножив их
В,2 1 ^21 2
соответственно на — -тт и на — -тг, т. е.
£12 М. £21 *2
Нг, />П&2 ^2 — Н12 д_ Vi.
ех. ’12 V ех, 12 V >
(159)
- СУ У г — Да,, У.
г,/21 4пЛ V2~V - 41 V
Дроби и ~ являются поправками на поправку и их можно
принять равными единице.
72
После этого получаем:
и
V. = V (1 +
к2= у(1+ Ь1Да21).
\ £21 /
(160)
Подставляя эти величины в формулы углов скоса, получим:.
Cz-T-W i
Да,, = г,,
12 12 4it/j
. ь 1 + ^Дсм
yll g 21
1 1 + -^Да12
S12
Да — е Cylbl
аа21-621 4я/2
1 +
£J2
1 + Да21
£21
Эти уравнения нужно решить относительно Да12 и Да21. При
этом получаются уравнения второй степени, что усложняет
расчеты. Можно, однако, практически почти не понижая точ-
ности решения, упростить эти два уравнения. Для этого можно»
воспользоваться приемом, хорошо известным в теории прибли-
женных вычислений, а именно: дробь вида
1 4~
1 + u)2’
где сох и со2—малые по
заменить выражением:
сравнению с единицей величины, можно*
1 + — ш2-
Применив это преобразование к нашим формулам, получим:
Д~ _______________ - СуТ1Ь2 (. I Р-21 Д_ Рчг ДЛ \
и
[ дя ).
41 /
\п - - СугЬ' (1 J_
М21 “ '21 -4^- + —
Решая первое уравнение относительно Да12 и второе отно-
сительно Дл21, получим:
ДЯ}2
(162)
Да21
1 + да81
£21_____________.
4*4 j Hia 9
S12CJ/II^2 £12
1 _j--Да12
______gi2_______
4*4_____JJ-21’
£21£у1А e21
Эти выражения, как увидим далее, и являются основными
для всего пересчета.
(161>
73.
Для удобства вычисления выгодно ввести следующие обо-
значения:
А} = ; 1 £12 А — ^21 • 7, (163/ В, = —; £12^2 D 4^2
С помощью этих шутся в таком виде: величин предыдущие формулы перепи- А 1 4“ А 2 Д®!] 4а*"= В, 77 (164) А „ 1 + Дз12 31 ~ я • (16о) Г cio cvl
При заданном угле атаки коэфициенты Аг, А2, Bi и В2 бу-
дут постоянными. Неизвестными в этих уравнениях будут Да12,
их нахождения требуются не два уравне-
^^21, су1 и Суп. Для
Фиг. 50. Характеристики крыльев биплана
без учета взаимного влияния.
ния, а четыре. Для
получения этих недо-
стающих уравнений
пользуемся двумя диа-
граммами фиг. 50,
дающими Cyi =
и G-п = /2 fas) Для верх-
него и нижнего крыль-
ев, пересчитанных как
монопланы на удлине-
ния кх и Х2. Если бы
эти крылья работали
отдельно друг от дру-
га, то их углы атаки были бы Oj и а2. Однако в бипланной
комбинации они вызовут друг у друга углы скоса потока Дах и
Да2 и, следовательно, их углы атаки в биплане будут такими:
ai2 — ai Аа12;
(166)
®21 — ^2
(167)
Диаграммы фиг. 50 дают различные су при различных Да.
Таким образом при заданных углах установки крыльев
<M=/1G42), (168)
=/2(^21), (169)
74
т. е. графики су1 и суц по аг и а2 можно рассматривать как два
недостающих нам уравнения. Следовательно, решить задачу о
скосе потока мы можем с помощью двух уравнений (164) и
(165), написанных аналитически, и двух уравнений (168) и (169),
заданных графически (фиг. 50).
Решать эти уравнения можно самыми различными способа-
ми. Наиболее быстрым оказался следующий способ последо-
вательных приближений. Нужно задаться уулом скоса Да12 верх-
него крыла. При малых углах атаки можно взять Да12 = О, при
больших 2 ~ 3°. По этому скосу находим угол атаки верхнего
крыла в биплане:
а12 = а1 — ^«12-
По графику фиг. 50 находим по а12 величину cyi. Зная cyi и
Да12, по формуле (165) вычисляем Да21; затем находим:
0-21 ~ О-2 Да21
и по графику (фиг. 50) получаем соответствующий
Пользуясь теперь формулой (164), вычисляем по Да21 и су11
угол скоса потока у верхнего крыла, который обозначим через
Дад это будет первое приближение для угла скоса у верхнего
крыла.
Далее находим:
012 — «1-ДО]2
и по графику фиг. 50 получаем с'уГ Затем опять переходим
к нижнему крылу и получаем: а21=а2— Да21 и суц; эти вели-
чины можно рассматривать как первое приближение к истин-
ным. Повторив такой прием еще раз, получим вторые прибли-
жения и найдем Да]2, cyi, Д?21, Суп и т. д.
Произведенные по этому способу подсчеты показали, что
уже первое приближение достаточно точно; повторные опера-
ции обычно не изменяют найденных t
величин. 1"
Быстрая сходимость этого процесса \ /\ /\ А
объясняется тем, что скос потока от \/ \/ \/ \
взаимной индукции является как бы vj'
поправкой к скосу от самоиндукции.
Если МЫ неверно возьмем У первого Фиг. 51. Схема вычисления
крыла угол скоса Да12, то ошибка в этой скосов потока,
величине будет для нижнего крыла уже
поправкой к поправке, которая еще более уменьшится при
возвращении к первому крылу, и т. д.
Ход такого расчета схематически изображен на фиг. 51 Ч
1 Заметим, что несколько лет тому назад под способом последовательных
приближений понимался у нас способ, когда просто задавались сразу углами
скоса у верхнего и нижнего крыльев и повторяли несколько раз расчеты,
исправляя на-глаз получающиеся результаты. Такой способ дает крайне пло-
хую сходимость. Нужно непременно вести расчет так, как здесь указано, т. е.
змейкой.
75
Получив истинные значения Да12 и Да21, мы сможем найти
по диаграммам фиг. 50 величины cyi, cxi, cmi, суц, схц и стп-
Пересчитаем эти величины на обычные, т. е. с арабскими индек-
сами, по формулам^ 50) и (151),введя в них вместо и у21
равные им по формулам (159) величины Да12 и Дая.
Получим для всех коэфициентов, например для сд1 и сд2, сле-
дующие выражения:
ги = ^1 (1 + 2^Да12) =^1(1+2Д1Да12); (170)
^2 = ^ц (1+2^- Да21)=^п(1+2АД«2]). (171)
Индуктивные сопротивления от взаимной индукции най-
дутся по формулам:
Ои'12 ~ Cyi ^#12 >
СХ121 = СУ2
И, наконец, полное сопротивление крыльев будет таким:
Фиг. 52. Аэродинамический момент
коробки биплана.
Аэродинамический момент всех
СхЦ — СXi Т" 5
^х21 ~ 0:2 “Ь 0/21 •
Аэродинамический момент
коробки крыльев при таком
расчете определяют обычно
относительно центра тяжести
самолета. Вычисляют его сле-
дующим приемом.
Возьмем поточные оси ко-
ординат с началом в центре
тяжести самолета (фиг. 52).
Обозначим координаты пе-
редних кромок наших крыльев
через и х2у2, беря их с
соответствующими знаками,
действующих на систему сил
можно определить прямо по чертежу и получить:
м = ст1^- -£-S1V'x1-cxl2-£-S1V*y1 +
+ ст2 S2 V*b2 + cU2 A S2 V2x2 - cx21 ± S2 V2y2.
Отсюда коэфициент полного аэродинамического момента ко-
робки крыльев будет таким:
— м __
Ст ц.т--“ —
-f(S1+52)A/2
__ “b Cm-2^2^2 4" СУ2^2*^2 /Т79\
76
Здесь L—длина, обычно берущаяся от центра тяжести само-
лета до шарниров руля высоты.
Получив величину сти. т для нескольких углов атаки, строят
кривую ст ц.т ==/(«) для всей коробки крыльев. Эта кривая кла-
дется в основу расчета самолета на устойчивость. Результи-
рующий момент получится алгебраическим сложением этого
коэфициента момента с моментом от хвостового оперения
[гл. VI, § 32, формула (122)].
§ 38. ХОД ПЕРЕСЧЕТА
Изложим сжато весь процесс пересчета.
Задание дается в виде чертежа коробки крыльев и резуль-
татов испытания профилей верхнего и нижнего крыльев. Далее
необходимо:
1) Пересчитать крылья на те удлинения и к», с какими
будут эти крылья работать в коробке биплана.
2) Выбрать углы атаки коробки (ак = аД для которых нужно
определить аэродинамические характеристики. Ввиду плавности
этих кривых можно ограничиваться четырьмя углами атаки.
В исключительных случаях приходится брать до шести и более
углов атаки.
3) Определить по чертежу величины, характеризующие ко-
робку, т. е. а, Л, / = с = Следует помнить, что а
и h берутся по потоку и между вихрями. Обычно не учиты-
вают изменения положения присоединенных вихрей при разных
углах атаки и берут их так, как изображено на фиг. 53.
4) Вычислить для каждого угла атаки
по формулам Бетца величины е12, е21 и
и12 = — рь21 и расчетные коэфициенты Alf
Д2, Вг и В2.
5) Найти для каждого угла атаки истин-
ную величину углов скоса потока, пользуясь
формулами (164) и (165) И графиками фиг. 50, фиг. 53. Условная точка
пересчитанными по п. 1. Получив Ла12 и Да21, на профиле, в которой
найти по графикам все коэфициенты: cyi, помещают^ присоединен-
Ctl, С ml, fylb CrII И Стц. Р
6) Исправить коэфициенты на горизонтальные индуктивные
скорости *vxl и г\г2 и получить:
Cyi = Cyi (1 + 2А1 Аа12) 5 Суя = О/П (1 4“ 2Д2 ^^21) >
cxi = сХ1 (1 + 2At Да12); сХ2 — схц (I + 2А2 ^a2i) >
cml ” Cml (1 4" 2ДяЦо) J ^т2== стИ (14* 2Д 2 Ля21) •
7) Найти полное сопротивление крыльев по формулам:
Сг12 ~ СXI 4“ СУ1 ^12» Сг21 = 4" Су2 Д^21*
8) Вычислить полные коэфициенты всей коробки:
_ СУ1$1 Су'S2 . _ CXi2Sl -|- Сх21^2
су- 4- ’ х ~~ $! + $2
77
9) Найти аэродинамический момент коробки относительна
центра тяжести самолета по формуле (172):
Подбор углов скоСа удобно вести по табл. 5.
Таблица 5
Ход пересчета монопланов на биплан
а21 ~ а2 ^Л21
По графику с"п
<\1
ет1
сх11
Cyi
е^12
cmi
Су%
cmi
Ст
Су
Сщ
-^а12
“12 ~ а1 “ Д<Х12
По графику сут
По формуле Дап
®21 == “^^21
По графику суц
По формуле Да12
“12 = “1 — Д“12
По графику су1
По формуле Да21
а21 а2 ^а21
По графику с'у11
По формуле Actj2
“12 = “I —
По графику су1
По формуле Да21
Обычно можно остановиться уже на первом или втором
приближении.
§ 39. СПОСОБ С. Г. КОЗЛОВА
В дополнение к изложенному в предыдущем параграфе спо-
собу последовательных приближений изложим еще графо-ана-
литический способ проф. С. Г. Козлова, довольно часто приме-
няемый на наших заводах. Способ этот заключается в особом
графическом приеме нахождения углов скоса потока от взаи-
моиндукции, т. е. Да12 и Да21.
78
Перед расчетом по этому способу крылья биплана пересчи-
тывают как монопланы на бесконечное удлинение.
Способ этот был разработан по первоначальной теории
Бетца, по которой разницу в скоростях V и Vt учитывали при
вычислении коэфициентов, но уравнение связи писали без этого
учета. Благодаря этому исходные формулы для скоса пишутся
у Козлова в таком виде:
Х = + ^12 = ^^- +е12-^-= 4^-(6п^И+81Л^2); (173)
Да2 = Да22 + Дйм = 822 4" £21 4^ = (e-22^2Cff2~t~S21^1eyi)> (174)
т. е. в них входят cv с арабскими индексами и нет отношения
о V2
скоростей -j/- и
г 1 '2
Связь между коэфициентами с арабскими и римскими индек-
сами такая же, как у нас, т. е.
сп = (1 4* cyi (175)
(176)
здесь р» = |i12 = |л21.
Обозначим углы атаки верхнего крыла через ах, а нижнего —
через а2. Тогда
а2 = ai + <?, (177)
где с?— деградация нижнего крыла биплана.
Так как в способе Козлова крылья пересчитаны на беско-
нечный размах, то важно установить зависимость между ис-
тинными углами атаки у обоих крыльев. Сделать это легко,
так как
a2i = а2 — Да21 = ах Н- — Да21 - afl 4- Да^ + <р — Да21 = а, х +<?+Да,
где
Да = Да12 —Да21. (178)
Очевидно, что если бы мы знали Да, то, задаваясь истинным
углом атаки верхнего крыла, мы легко получали бы истинный
угол у нижнего крыла.
Вычислим эту величину. Пользуясь формулами (173) и
(174), пишем:
Да = Да12 Да21 = (еп brcyl + s12 b2 сУ2)
4п1<> (£22 ^2 ^У2 £21 ^10/1)* (179)
Входящие сюда сУ1 и сУ2 заменяем через сут и сун, для
чего сперва решаем уравнения (1/5) и (176) относительно
7$
<и и и получаем:
1 *" CsI1
С«1 ~ , ^ЬХЬ2 Сп ’
l+4WT CBI Сш
1 нА „
’-•2^ГСИ1
Cai ~,—й^Л т'
1 + 4^лгСу1Суп
(180)
(181)
Подставляя эти выражения в формулу (179), получим после
простых преобразований:
Да = Да12 Д&21 = j xcyj Cyil l/fyi “1" (^и (182)
где для сокращения введены обозначения:
л__________________________Р2 Ьг .
Л — 4л2 1г1£ ’
г snt)l S21 bl .
4я lt ’
e12 ^2 .
41^/, ’
P-61 J
2nl2
4rt /i
f £22 b2
4г.1г
[У Iх b2
A — 2it /.
(183)
Величина А обычно очень мала и потому множитель, сто-
ящий перед квадратными скобками, может быть отброшен. Пе-
реходим от радианов к градусам, умножая все выражение в скоб-
ках на 57,3; и получаем основную формулу С. Г. Козлова:
да° = j>Cyl + ^Су1 - L°) суи. (184)
Здесь J°=57,3J, /<° = 57.3К и £° = 57,ЗА.
С помощью этой формулы и решается задача о биплане.
Ход расчета при этом таков. Имея кривые су по а у обоих
крыльев, пересчитанные на 1 = со, задаемся сУг у верхнего
крыла. Подсчитываем J°cyi и К°сп—L° и находим:
а/2 = а<1 ? "Ь J°cn "Ь {^°сп (185)
В этой формуле три первых члена известны, и следова-
тельно, можно на фиг. 54 отложить от аг1 величины и J°cyl
(точка 714). Четвертый член при заданном су зависит лишь от
су11, причем эта зависимость линейная. Если теперь из точки М
проведем прямую линию MN до пересечения ее с линией си=1
и из точки N отложим величину К°сп — L°, то получим точку
Р. Соединив Р с М прямой, будем иметь линию РМ, показы-
80
вающую изменение Аа2| с изменением сдп. Очевидно, что в точке
пересечения линии РМ. с кривой сд по а для нижнего крыла
мы будем иметь а(2 и ст, соответствующие сУ1 и afl, кото-
рыми мы задались.
Для ускорения процесса вычисления рекомендуется следу-
ющее расположение диаграмм (фиг. 55). Вправо от диаграммы
су по а проводится ось ОВ и от нее по оси абсцисс в мас-
штабе углов откладывается а на линии сд = 1 (горизонталь-
ной линии) откладывается <р+-/° (при сд=1, J°cg = J°). Еще
правее проводится ось О& и от нее откладывается по оси
абсцисс величина — L°, так как при сд = 0 величина К°сд— L° —
=—L°, а по линии сд = 1 — величина К° — La, так какпрису=1
выражение К°сп —La = Ка— L°.
Полученные точки соединяются,
как показано на фиг. 55.
Фиг. 54. Пересчет биплана по
способу С. Г. Козлова.
Фиг. 55. Диаграмма С. Г. Козлова
для решения задачи о биплане.
Теперь для каждого значания сУ1 будем иметь отрезки, да-
ющие величины <р+У°сУ1 и К°сп — La. Отложим, соблюдая
знаки, первый из них от точки afl и получим точку т\ второй
отложим, соблюдая знаки, от точки т и получим точку р',
Затем перенесем точку р' на линию су = 1, получим точку р и,
соединив т и р прямой, получим, как и на фиг. 54, величину
€УП и a i2.
Проделав такое построение для нескольких значений сд1, мы
будем иметь соответствующие величины afl, аг2 и сУ11.
После этого задача уже может считаться решенной. Вычи-
сление всех коэфициентов идет далее уже известным нам по
§ 38 способом.
Способ С. Г. Козлова удобен тем, что он механизирует всю
вычислительную работу. Им выгодно пользоваться тогда, когда
для одной коробки крыльев подбирают различные профили.
В этом случае, построив вспомогательные линии, можно весь-
ма быстро проделать все расчеты для любого числа профилей.
Недостатком способа Козлова является допущение постоян-
ных значений для s12 и «21 и р. Обычно берут средние значе-
ния этих величин, например для угла атаки коробки в 6°. Тем
не менее следует помнить о том, что в этом способе вынос
коробки учитывается не вполне точно.
Б. H. Юпьев—171—6 81
Если расчет преследует цели получения общих характери-
стик всей коробки крыльев, то по первой теореме Мунка вы-
нос роли не играет и получаются вполне точные результаты.
Лишь в тех случаях, когда интересуются работой отдельных
крыльев биплана, здесь получается некоторая ошибка.
Глава IX
ДОПОЛНЕНИЕ К ТЕОРИИ БИПЛАНА
§ 40. НАИВЫГОДНЕЙШИЙ БИПЛАН
Теория индукции позволяет решать очень много интерес-
ных и важных для конструктора задач. Одной из таких задач
является вопрос о наивыгоднейшем биплане.
Задача ставится так: при заданных размахах верхнего и ниж-
него крыльев /х и /2 и высоте коробки h для заданной общей
подъемной силы Y получить минимум индуктивного сопро-
тивления.
Положим, что нижнее крыло несет нагрузку Т2=/Т; тогда
нагрузка верхнего будет равна:
^ = (1-7) Г;
здесь Y—полная подъемная сила, т. е.
Г=ГХ + Г2.
Нам, следовательно, нужно найти у, дающий минимальное
общее индуктивное сопротивление Xt = Х{1 4- Х(2.
Мы имеем по предыдущему:
Xt = Х( п -j- Xi 12 + Xt 21 + Xi 22 =
Cv1 е „ । , Cy‘2 „ о „ । C,J1 о ,
“ кХх ' Sx?+£12 4я/х C,J^ 5^ +
, S3g У2, У,У2 Y.Y Y*
4 : # Hn I-82* 774—'---------H— =
kZ2 S2q Anl^q nl2q
Y V v2 1
+ (^+*21)^ + J]-
размахов, обозначив его через
[Л = А-. (186)
Тогда предыдущая формула примет вид:
= —
itg L 4
Введем сюда отношение
82
Сумма е12 + е21 не зависит (согласно теореме Мунка) от
выноса коробки а. Вводим обозначение:
Подставляем в предыдущую формулу значения К2 = У/ и
Ki = К(1 — у). Тогда получим:
I г
Найдем значение Хь дающее минимум сопротивления. Для
этого диференцируем выражение для Хл по / и приравниваем
результат нулю. Получаем:
-2(1 ~z) + v 0-/)-~ z + >-0-
Решая это уравнение относительно у, получим ответ:
Х = . (188)
V-23 + jx
Таким образом для получения минимального сопротивления
у коробки биплана необходимо иметь вполне определенное от-
ношение подъемных сил у верхнего и нижнего крыльев.
Так например, если оба крыла имеют одинаковый размах,
/о 1
т. е. и = ~~~ = 1, то мы получим:
_ 1 — а ____ 1 — а _ 1
~ 1 — 2а+1 “ 2 —2а — ~2'
Следовательно, при равных размахах обоих крыльев наивы-
годнейшей нагрузкой будет одинаковое нагружение обоих
крыльев, т. е. Yt = Y2.
При разных размахах крыльев приходится прежде чем най-
ти по формуле (188) величину у вычислить, пользуясь форму-
лой Бетца (154), величину
_ е13 + £21 _. 1 1 _
8 8 с2+Л2’
Величина а несколько изменяется при изменении углов атаки.
Подъемная сила крыльев зависит от истинных углов атаки,
которые тоже изменяются при изменении угла атаки коробки.
Таким образом получить наивыгоднейшую раздачу подъемной
силы можно лишь на одном угле атаки. Правда, небольшие
отступления от наивыгоднейшего соотношения мало сказыва-
ются на общем сопротивлении коробки, и коробка, выгодная
83
при среднем угле атаки, будет близка к наивыгоднейшей и при
других углах.
Мы снова вернемся к вопросу о наивыгоднейшем биплане и
полиплане в гл. XXII, § 105, где рассмотрим эту задачу, исходя
из переменной по размаху крыльев циркуляции скорости.
§ 41. ПРИБЛИЖЕННАЯ ФОРМУЛА ПРАНДТЛЯ ДЛЯ ОПРЕДЕЛЕНИЯ
ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ
Сравнительная сложность вычисления индуктивного сопро-
тивления коробки крыльев заставила искать для прикидочных
расчетов более простые формулы. Такие формулы являются,
понятно, грубо приближенными. Наиболее удобна приближен-
ная формула, предложенная проф. Л. Прандтлем. Он прини-
мает, что для любой коробки крыльев индуктивное сопротив-
ление можно вычислять по формуле:
Cxi =
где cxi — коэфициент суммарного индуктивного сопротивления
всей коробки и сд — такой же коэфициент подъемной силы.
Прандтль предложил следующую простую формулу:
Фиг. 56. Условная лобовая
площадь по Прандтлю.
а это дает:
__ 5 2
Cxi rcZ2_j_4F Су> (.189)
где S—общая площадь крыльев ко-
робки, / — наибольший размах и F—
условная лобовая площадь, получен-
ная суммированием всех кусков пло-
щади, заключенных на фиг. 56а между
двумя соседними крыльями и двумя
отвесными линиями, проведенными из
концов меньшего крыла; крылья счи-
таются здесь имеющими одинаковую
ширину.
Прандтль показал, что эта формула оказывается точной для
нескольких частных случаев. Например, для моноплана F=0,
5 2
г • —------- — - --
_ л/2 лХ ’
т. е. обычную формулу индуктивного сопротивления крыла
моноплана.
Подробный анализ показал, что она верна еще для случая
полиплана, состоящего из бесчисленного количества крыльев,
расположенных одно над другим (фиг. 56, с) и для коробки,
составленной из бесчисленного количества крыльев таким об-
разом, что вид спереди на такую коробку представляет собой
круг (фиг. 56,6).
84
Проф. Л. Прандтль произвел проверку этой теории в Гет-
тингенской лаборатории и получил хорошие результаты для
бипланов.
Интересно сравнить моноплан с полипланом, пользуясь та-
кой простой формулой, как формула Прандтля. Для этого пред-
положим, что коробка имеет п крыльев равного размаха Л
Пусть расстояние по высоте между соседними крыльями h
будет равно ширине крыльев. Тогда мы получим:
S = пЫ;
F = (n—V)bl.
Каждое крыло будет иметь удлинение:
Подставляя эти величины в основную формулу Прандтля, по-
лучим:
(190)
В табл. 6 приведены подсчитанные по этой формуле зна-
чения А для разных п и X.
Таблица 6
Величина А для разных К
Л = 4 i5 6 8 10 12 15 20
Моноплан . . 0,080 0,063 0,053 0,040 0,032 0,0266 0,0213 0,0160 1 кк
Биплан .... 0,121 0,101 0,0875 0,068 0,057 0,0477 0,0391 0,0299 2
«1+4
Трехплан . . . 0,146 0,127 0,112 0,0905 0,071 0,066 0,0545 0,0424 3 'лХ+8
Четырехплан. 0,162 0,144 0,130 0,107 0,092 0,080 0,067 0,0504 4
теХ+12
Эта таблица показывает, что если мы возьмем у моноплана
удлинение X = 5, то для получения равного индуктивного со-
противления биплан должен иметь к ^8,7, триплан к = 12
и четырехплан к = 15. Если задаться определенной площадью
крыльев и не стесняться высотой коробки, то во многих слу-
чаях полипланы могут оказаться выгоднее монопланов. Здесь
все зависит от того, компенсирует ли уменьшение индуктивного
сопротивления от увеличения л прирост вредных сопротивлений
от стоек и тросов.
Общепризнанное положение, что биплан аэродинамически
хуже моноплана, справедливо лишь в том случае, когда срав-
8
ниваются крылья одинакового удлинения. Биплан с большим
удлинением может быть сам по себе значительно лучше, чем
моноплан с малым X.
Однако стойки, расчалки и кабанчики делают обычно биплан
как самолет в целом значительно худшим, чем моноплан.
§ 42. СРЕДНЯЯ АЭРОДИНАМИЧЕСКАЯ ХОРДА
В гл. VII, § 36 мы вывели третью теорему Мунка, согласно
которой всякую коробку крыльев можно заменить эквивалент-
ным монопланным крылом. Такое крыло дает при той же пло-
щади, как и площадь всех крыльев коробки, одинаковые с ней
подъемную силу и сопротивление.
Возникает вопрос: как поставить такое эквивалентное крыло
по отношению к самолету? Было бы, конечно, самым правильным
поставить его так, чтобы и аэродинамический момент у него
был равен аэродинамическому моменту всей коробки крыльев.
Сделать это для какого-нибудь заданного угла атаки очень
легко. Найдя по формуле (158) эквивалентное удлинение моно-
плана, т. е.
и вычислив ширину такого крыла:
нужно его поставить таким образом относительно центра тя-
жести самолета, чтобы получился эксцентриситет г полной силы,
дающий такой же момент, какой был у коробки крыльев.
Построение это не вызывает никаких сомнений для одного
угла атаки. Однако при переходе к другому углу атаки мы
получим в общем случае и другое Хэ, другую ширину Ьэ и даже
другой эксцентриситет г.
Надо помнить, что у коробки крыльев индуктивное сопро-
тивление следует другому закону, чем у незакрученного моно-
планного крыла; например, при су = 0 cxi, вообще говоря, мо-
жет и не быть равно нулю (гл. VII, § 36).
Таким образом понятием эквивалентного крыла можно поль-
зоваться, строго говоря, лишь для одного угла атаки.
Однако практическая потребность в упрощенных расчетах
заставляет пользоваться понятием эквивалентного моноплана
как понятием, независящим от угла атаки. Эта потребность
столь велика, что во всех странах установились более или
менее однообразные правила для нахождения этого условного
моноплана и для нанесения на боковой вид самолета его сред-
ней аэродинамической хорды.
Рассмотрим сначала, как строится средняя аэродинамическая
хорда у крыла моноплана сложной формы (фиг. 57).
86
Сначала находят площадь крыла:
"Н/2
S = J b dz
-иъ
и вычисляют длину средней аэродинамической хорды:
h
^ср — Z .
Затем находят координаты х0 и z0 центра тяжести площади
полукрыла, т. е. точку Ог Делают это или графически, раз-
бивая площадь полукрыла на куски, или вычисляя коорди-
наты центра тяжести л0, ?0 аналитически,
т. е. находя сначала статические моменты
площади крыла:
Xi +1/2
uz=J bxdx и их = р bzdz
хг —1ft
и деля их на площадь крыла 3:
U 11 г
-Хо £ И Zq §
По найденным координатам наносят на
чертеж точку О1( проводят через нее сече-
ние крыла АВ и считают получившийся там
угол атаки 4 за угол атаки средней аэродина-
мической хорды; этим учитывается закру-
ченность крыла, так как берется не корне-
вой угол атаки, а угол со средней закруткой.
За профиль эквивалентного крыла при-
нимают профиль, лежащий в сечении АВ;
этим учитывается изменение толщины и
формы Профиля ПО размаху. фиг‘ 5L Построение
т ,, г -г г j средней аэродинами-
Наконец, среднюю аэродинамическую ЧеСКой хорды для
хорду совмещают с хордой сечения АВ крыла моноплана
таким образом, чтобы точка, лежащая на
1/з длины средней аэродинамической хорды, считая от носика,
совпала с точкой Ог. Этим учитывается стреловидность очер-
тания крыла в плане.
Предполагается, что если взять по продувке аэродинами-
ческие характеристики профиля, лежащего на средней хорде,
. \р
и пересчитать их на к = — , то прямоугольное крыло с разма-
хом I и шириной Ьср будет эквивалентно исходному крылу
сложной формы. Таким образом сложное крыло заменится
простым прямоугольным крылом, не имеющим ни закрутки, ни
стреловидности, ни сужения к концам.
Эту хорду наносят на чертеж бокового вида самолета, и тогда
ведутрасчет устойчивости, исходя из этойусловнойхорды(фиг.58).
Можно пользоваться при этом понятием центра давления и т. д.
87
Построение это, не будучи строгим, лает для обычных
монопланных крыльев удовлетворительные результаты и очень
часто применяется в конструкторских бюро.
Довольно часто при взвешивании самолета и определении
его центра тяжести дают координаты последнего в процентах
средней аэродинамической хорды. Для этого проводят связан-
ные со средней аэродинамической хордой оси координат, нахо-
дят xlt yt и вычисляют:
Лц.т % =-Г1 100
ср
И
З'ц.Т % — 100.
ср
Величинами лц.т и уц.т дается так называемая центровка
самолета. _
Обычно расстояние у сухопутных самолетов мало; вели-
чина Лц.т у хороших самолетов близка к 30%. Центровку свыше
35% называют обычно задней, меньшую 28%—передней.
Более сложным и значительно менее строгим является на-
хождение средней аэродинамической хорды у биплана.
Чаще всего поступают таким образом. Находят сперва от-
дельно средние аэродинамические хорды верхнего и нижнего
крыльев. Затем соединяют их концы прямыми АгА2 и BXB2
(фиг. 59) и делят эти прямые точками А и В так, чтобы отно-
шения отрезков
Фиг. 53. Средняя аэродинамическая
хорда и координаты центра тяжести
самолета.
Фиг. 59. Определение
средней аэродинами-
ческой хорды биплана.
Д и получают среднюю аэродинамическую хорду биплана.
Самым слабым местом этого построения является учет отно-
с 1
шения Если находить суг и су2 по методу Бетца, то теряется
88
Таблица 7
Значения
0° 10° 20° । 30°
Cy\jCy2 1,05 1,1 1,2 1 4
весь смысл приближенного построения средней хорды, так как
при производстве точного расчета мы непременно получим
истинный угол атаки крыльев коробки и сможем найти точное
значение аэродинамического момента по формуле (172) (гл. VIII).
С
Вследствие этого при определении отношения — пользуются
су2
упрощенными формулами или таблицами.
У нас часто пользуются табл. 7, дающей — как функцию
с_у2
выноса р верхнего крыла по отношению к нижнему, данному
в градусах. Этот вынос берут не так, как у Бетца, а по фиг. 59,
т. е., соединив точки q и с2, лежащие на передних третях сред-
них хорд крыльев, берут угол р по
отношению к нормали CN верхнего
крыла.
Получив среднюю аэродинамиче-
скую хорду, приводят задачу биплана
к моноплану. Разделив суммарную
площадь крыльев на />ср = АВ, полу-
чают размах этого эквивалентного
монопланного крыла. За форму про-
филя такого крыла приходится брать средний профиль между
верхним и нижним крылом.
Этот способ определения средней аэродинамической хорды
биплана весьма условен и не увязан с теорией индуктивного
сопротивления. Так, если подсчитать эквивалентное Хэ по тео-
рии индукции, то оно не совпадет в общем случае с тем, какое
получается из разобранного построения.
В общем лишь для биплана, составленного из двух одина-
ковых по профилю крыльев и не имеющего деградации, пере-
мещение центра давления по средней хорде несколько напоми-
нает перемещение центра давления у отдельного монопланного
крыла. В случае же деградации при некотором угле атаки одно
крыло может иметь су=0 и не работать вовсе, в то время как
другое будет работать; более того, при некоторых углах атаки
одно крыло может давать положительный с9, а другое — отрица-
тельный. Все это указывает на большую неопределенность по-
нятия средняя аэродинамическая хорда.
Очень часто положение центра тяжести биплана относят к
средней аэродинамической хорде, проводя через точку А свя-
занные оси координат (фиг. 59), и вычисляют его координаты
в процентах:
^и.т°/0 = 100 и J„.T% = фи 100.
^Ср ^ср
Этот способ указания положения центра тяжести самолета
надо признать крайне неудачным, так как сама аэродинамическая
хорда на самолете ничем не зафиксирована. Хуже всего то, что
иногда в расчет средней аэродинамической хорды вводят отно-
89
шения сУ11сУ2 не из условной таблицы, а из точного расчета,
например по Бетцу или из результатов испытаний. Тогда вос-
становить эту хорду, не имея данных, по какому способу она
была рассчитана, совершенно невозможно.
Правильнее всего было бы относить положение центра тя-
жести просто к хорде центроплана верхнего крыла, так как
она существует физически и имеется на любом чертеже само-
лета. Получив же данные о центре тяжести, отнесенном к сред-
ней аэродинамической хорде, нельзя ничего сказать, не зная
метода, каким она была построена.
Во всяком случае было бы гораздо рациональнее строить
среднюю аэродинамическую хорду чисто геометрически, не
вводя в нее отношения сУ1/сУ2. Тогда ее было бы легко нахо-
дить по чертежу коробки крыльев; точность же определения
устойчивости от такого упрощения нисколько бы не пострадала,
так как она все равно получается и при учете сУ1/сУ2 мало удов-
летворительной. Вообще при современном развитии методов
теории индукции понятие средней аэродинамической хорды
нужно считать несколько устаревшим.
§ 43. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ БИПЛАНА
Рассматривавшаяся нами до сих пор теория биплана базиро-
валась на гипотезе П-образных вихрей. Дальнейшим шагом яв-
ляется учет вихревой пелены, т. е. создание теории, учитываю-
щей изменяемость циркуляции верхнего и нижнего крыльев по
их размаху. Такая теория была развита проф. Прандтлем и из-
ложена у нас в гл. XXII. Дальнейшим шагом является учет
сворачивания пелены в два вихря. Эту задачу достаточно
полно еще не удалось решить, хотя такие попытки делались;
на них мы остановимся в гл. XXI.
Еще большую точность приобрела бы теория биплана, если
бы вместо крыльев, замененных простыми „несущими вихре-
выми линиями" или присоединенными вихрями Жуковского,
удалось рассмотреть или сами крылья непосредственно, или
хотя бы „тонкие крылья" по Мунку, заменяющие с большой
точностью действительные крылья.
Однако все такие попытки ведут к необычайно сложным
формулам, мало пригодным для инженерных расчетов.
Как первый шаг к такому уточнению теории следует рассмат-
ривать предложенную проф. Т. Карманом схему вихрей, заме-
няющих крыло. Эту схему подробно разработал в Америке
Милликен (С. В. Millican). Идея эта заключается в том, что
крыло заменяется не одним вихревым шнуром, а тремя. Один
из них дает подъемную силу по Жуковскому, т. е.
Y = РГИ/.
Пара же других вихрей, вращающихся в противоположные сто-
роны, образует вихревой дублет. Один из этих вихрей дает
90
силу Yi —рГдУ1, направленную вверх, а другой — такую же силу,
но направленную вниз. Окончательно получается момент, равный
произведению этих сил на расстояние между вихрями г, т. е.
М = pIW/s = pJVl, (192)
где J — момент дублета; как известно, сила дублетов измеряется
их моментом, так как расстояние между вихрями считается у
них бесконечно-малым: г—»0.
Дублеты, как известно, создают вокруг себя поток, подробно
изучаемый в курсе теоретической аэродинамики.
Для нахождения величины Г и J пользуются двумя уравне-
ниями связи. Первое нам хорошо знакомо; оно получается при-
равниванием друг другу выражений подъемной силы, написан-
ных по формулам теоретической и экспериментальной аэроди-
намики. Вид его таков:
Г = ^сиЬУ.
Второе уравнение связи найдется аналогичным способом,
только вместо сил придется говорить о моментах. Теоретиче-
ская величина аэродинамического момента у нас уже написана —
это формула (192). По правилам экспериментальной аэродина-
мики мы можем написать:
М = ет-^- SV*b = ст ЪЧУ2.
Приравнивая это выражение выражению (192), получаем:

(193)
Далее Милликен заменяет крылья П-образными вихрями
с циркуляцией Г и вихревым дублетом с моментом J. Дублет об-
разует вытянутое вихревое кольцо
(фиг. 60). После этого путем сложных
интегрирований находятся выражения
индуктивных скоростей и углов скосов.
Формулы получаются очень сложные, и
американцы дают для облегчения вычи-
слений целый ряд графиков и таблиц
(см. библиографию).
В общем эта теория дает лишь не-
много более точный результат, чем зна-
чительно более простая теория Бетца.
Однако и она не дает полного совпа-
дения с опытами. В этой теории вихри
берутся всегда в центре крыла.
Если в теории Бетца учитывать
перемещение вихрей по хорде при
разных углах атаки (а это очень легко
сделать описанным в § 38 методом
Фиг. 60. Схема вихрей у
крыла по Карману и
Милликену,
последовательных при-
ближений), то теория Бетца не должна отличаться сколько-ни-
будь заметно от теории Кармана-Милликена. По этой причине
мы в наше^ курсе подробно эту теорию не излагаем.
91
Глава X
ВЛИЯНИЕ ГРАНИЦ ПОТОКА НА АЭРОДИНАМИЧЕСКИЕ
СВОЙСТВА КРЫЛЬЕВ
§ 44. ПОСТАНОВКА ЗАДАЧИ
На практике нередко встречаются случаи, когда крыло рабо-
тает вблизи различных стенок, ограничивающих так или иначе
воздушный поток, набегающий на крыло. Примерами могут
явиться влияние на крыло близости земли при разбеге и пробеге
самолета и влияние стенок аэродинамической трубы при про-
дувке моделей в лабораториях. Эти влияния бывают, как уви-
дим далее, иногда весьма значительными и их необходимо
внимательно учитывать. В настоящее время все продувки, про-
изводимые в аэродинамических лабораториях, обязательно исправ-
ляют на влияние трубы. Раньше этого не делали, вследствие чего
опыты, произведенные в разных лабораториях, не совпадали.
Мы начнем рассмотрение этих взаимных влияний с наиболее
простых случаев. Всюду мы будем пользоваться известным из
курса теоретической аэродинамики методом зеркальных отобра-
жений, при котором эффект стенок заменяется вторым, вообра-
жаемым течением жидкости, создаваемым вихрями, надлежащим
образом выбранными.
§ 45. ВЛИЯНИЕ ВЕРТИКАЛЬНОЙ СТЕНКИ НА САМОЛЕТ
Пусть самолет А летит возле неограниченной вертикальной
стенки (фиг. 61). Спрашивается, как изменится при этом аэро-
динамика самолета, — ухудшится или улучшится?
Решим эту задачу с помощью метода зеркальных отображе-
ний, для чего представим себе, что, удалив стенку, мы поме-
стим в неограниченном теперь потоке второй фиктивный само-
лет Ап расположенный зеркально по отношению к действи-
тельно имеющемуся самолету. Самолеты заменим двумя П-образ-
ными системами вихрей с одинаковой циркуляцией Г.
Пограничным условием на стенке было равенство нулю нор-
мальной составляющей скорости потока на самой стенке, так
как жидкость могла лишь скользить вдоль по стенке, но не
пересекать ее.
При замене стенки фиктивным самолетом это условие для то-
чек, лежащих в плоскости ООхне изменится, так как вихри распо-
ложены симметрично и скорость в любой точке В этой плоскости
не будет иметь нормальной к плоскости составляющей (фиг. 61).
В этом легко убедиться, рассмотрев скорости, создаваемые
парами вихрей 1—4 и 2—3. Скорости г»х и от пары 7—4
будут в силу симметрии равны и направлены под одним углом
к плоскости ООХ; складывая их по правилу параллелограма, полу-
чим скорость W, лежащую в плоскости стенки. То же.г самое
получится и для пары вихрей 2—3 и вообще для любой сим-
92
(^П=О) не нарушит.
Фиг. 61. Влияние вертикальной
стенки на самолет.
метричной пары. Следовательно, какой бы ни был закон изме-
нения циркуляции по размаху, все равно замена стенки зеркаль-
ным самолетом граничного условия
Итак, с точки зрения аэроди-
намики стенка вполне эквивалентна
фиктивному самолету.
Заменив же стенку фиктивным
самолетом, т. е. П-образной систе-
мой вихрей, мы сможем сразу же
подсчитать скорости, вызванные
этими вихрями у действительного
самолета. Таким образом задачу
о влиянии стенки мы сводим к за-
даче о влиянии соседнего самолета.
Решение ведем, вычисляя скос
потока, вызванный фиктивным са-
молетом у действительного.
Назовем расстояние от центра
самолета до стенки через а.
Тогда получим в центре этого самолета скорость скоса:
Г Г _ Г //2 1
Vy ~ 4я(2а — Z/2) 4к(2а + //2) 8те а2 j /_Ц2 ’ (194)
\4а /
Принимаем эту скорость за среднюю по размаху и вычисляем
средний угол скоса потока, возникший от стенки:
— с bV
д _ vy _ Г Z/2 1 _ 2 у Z/2 1 _
Мст ~ ре “ а2 / ZV — 8кИ а2 / Z \2 “
1 Ua ) 1 V 4а )
= с J________________
16 к v а2 1 г / V * (194х)
Формула эта показывает, что получится отрицательный скос,
уменьшающий угол скоса от самоиндукции. Таким образом
работа крыла при наличии стенки улучшится, т. е. у него воз-
растет истинный угол атаки и, следовательно, уменьшится
коэфициент индуктивного сопротивления на величину:
Cxi ст — Су Даст — Су b
Z/2 1
ai
\4а /
(195)
Формула эта показывает, что чем ближе к стенке будет
происходить полет, тем лучше будет аэродинамика самолета.
Формула (195) грубо приближенная (так как скорость в центре
крыла принималась за среднюю скорость), но ее можно в случае
надобности уточнить тем же приемом, как это делается в теории
моноплана и биплана. Здесь мы этого делать не будем.
93
Если самолет летит, касаясь крылом стенки, то его ото-
бражение сольется с ним самим в один самолет двойного раз-
маха, что в два раза уменьшит его индуктивное сопротивление.
С точки зрения индукции было бы выгодно летать группами
самолетов в плотном строю, касаясь друг друга концами крыльев.
Выгоден и строй клина, когда на задние самолеты дей-
Фиг. 62. Строи самолетов, выгодные
с точки зрения индукции.
Фиг. 63. Влияние близости земли
на аэродинамику самолета.
ствуют вихри передних, и можно мыслить такой полет, когда
вихри самолетов сольются в один шнур (по фиг. 62), охваты-
вающий все самолеты. Реально это осуществить трудно вслед-
ствие возникающих при этом больших моментов крена.
§ 46. ВЛИЯНИЕ БЛИЗОСТИ ЗЕМЛИ
Пусть самолет летит над землей на высоте у. По предыду-
щему очевидно, что землю можно заменить фиктивным само-
летом, как бы отраженном в земле, как в зеркале. Этот фиктив-
ный самолет будет лететь в опрокинутом положении. На этом
месте, где ранее была земля при такой комбинации самолетов
получится всюду ^=0, так как оба самолета будут давать
в любой точке плоскости равные и противоположные нормаль-
ные скорости.
Задача, как это видно по фиг. 63, сводится к задаче биплана.
Коробка крыльев будет здесь без выноса, с высотой h = 2у и
с отрицательной циркуляцией у нижнего крыла и, следовательно,
91 = Су 9.
Угол скоса потока получится в этом случае по обычным
формулам Бетца:
где в данном случае
+(^У'
Скорость скоса будет направлена вверх, что улучшит аэроди-
94
намику самолета. Кроме того, получится еще индуктивная го-
ризонтальная скорость ^12 , вычисляемая по формуле Бетца:
^12-—^12
где в данном случае:
^12 = “I-
Скорость набегающего потока 1/^ при этом несколько умень-
шится, что уменьшит все коэфициенты, как это следует из
теории биплана в отношении:
СЛ,.Ь
1 — 2(Х12
Решать эту задачу следует, учитывая различие в cyi и сУ]у
т. е. тем же приемом, как она решалась для биплана в § 38.
В общем же действие земли на крыло сводится как бы
к увеличению удлинения крыла и некоторому уменьшению
скорости, а следовательно, и су .-
Формулы эти применимы лишь для не слишком малых высот
полета. При малых высотах начинает сказываться кривизна про-
филя и грубость гипотезы П-образных вихрей.
Кроме того, особо интересующая конструктора величина
су max при вычислении по методам индукции остается почти
неизменной. Опыты же показывают, что обычно су max возра-
стает при посадке. Объясняется это тем, что при малых высо-
тах полета фиктивное крыло действует на реальное подобно
закрылку и несколько улучшает его обтекание. К сожалению,
до сих пор еще не получены по этому вопросу исчерпывающие
опытные данные. В самое последнее время выяснилось, что
о dd
наличие при посадке самолета угловой скорости —
затягивает срыв потока с крыла; он происходит на больших
углах атаки, чем при статическом (т. е. на фиксированном угле
атаки) испытании крыла в аэродинамической трубе. Это
явление называется эффектом Фаррена. В общем су поса-
дочный у самолета в натуре получается на 10 — 20% больший,
чем у моделей при опытах в аэротрубах.
Указанная схема вихрей позволяет решить обратную задачу—
о действии самолета на землю. Мы можем подсчитать в любой
точке А земли индуктивную скорость, т. е. найти по формулам
(73) и (75) ее компоненты vx и (vy = 0). Вдали от самолета
скорость потока равна /, а давление будет атмосферное, т. е.
равное ра . Применяя теорему Бернулли для далекой точки и
для точки А, где скорость потока равна W, а давление р\у
получаем:
2
Р. + ^-Р^ = Р^(У + «,Г+^-
£ £ £
95
Тогда
(197)
в нее
Отсюда избыточное давление в точке Д будет таким:
Рх-рл = -^[Иа-(Г+ -и,)*-^] =-±_(^ + 2И^ + 4). (196)
Подставив в эту формулу выражения для скоростей vx nvr,
мы сможем вычислить давления в любой точке земли. Они
оказываются положительными, и картина давления самолета на
землю имеет вид, изображенный по способу векторов на фиг. 63.
Эту задачу впервые решил проф. Прандтль.
Мы не будем вычислять давление в любой точке плоскости,
а ограничимся лишь точкой, лежащей прямо под серединой
самолета (z = 0, х = 0, ,vz = 0 и у равен высоте полета),
из формулы (196) получим коэфициент давления:
- _ РА”/’а _ 2'(2Иг'л:+Va) _ Q Vx V2
PV2 pl/2 2 V и2’
Скорость vx вычисляем по основной формуле (73);
придется подставить z = 0, х — 0 и удвоить общий результат,
так как нижнее фиктивное крыло дает такую же индуктивную
скорость, как и действительное. Знак индуктивной скорости
будет отрицательный, следовательно, давление будет положи-
тельным. Таким образом получим:
« —- 1
- = 2^ = — -- г
vvo У Vi + уг
или
ъх = .
У У 1 + у2
Если самолет летит на высоте нескольких сотен метров,
то у делается очень большим по сравнению с единицей и
можно писать:
vx______1_ _15_о|_ = _ Да .
v ~ у v ’
формула (197) после отбрасывания малой величины -р- и подста-
новки в нее найденного значения ~ примет вид:
(198)
Например, если самолет летит на высоте у = 20, т. е. на высоте
10 размахов крыльев, то при Да = 0,02
0,02
Ра ~ 2 202 “ 0,0001.
96
При скорости полета V =* 126 м!сек q = = 1000 кг]м2 и
давление в этой точке будет:
pk=pA q = 0,0001 • 1000 = 0,1 кг/м2-
это величина очень небольшая, практически неуловимая. Однако,
как показал проф. Л. Прандтль, если просуммировать это дав-
ление по всей плоскости, изображающей землю, то равнодей-
ствующая сила будет в точности равна весу самолета.
Таким образом летящий самолет как бы опирается через
промежуточные слои воздуха на землю.
§ 47. КРЫЛО МЕЖДУ ДВУМЯ СТЕНКАМИ
Рассмотрим теперь случаи двух вертикальных и двух горизон
тальных стенок.
Пусть крыло помещено между двумя вертикальными стен
ками, находящимися на расстоянии d одна от другой (фиг. 64)
Применив метод зеркаль-
ных отображений к одной
стенке, получим зеркальное
отображение крыла. От-
ражая полученную систему,
состоящую из двух крыль-
ев, в другой стенке, мы
получим уже четыре крыла.
Продолжая такой процесс,
мы придем, очевидно, к
бесконечной совокупности
Фиг. 64. Влияние вертикальных стенок,
расположенных у концов крыла.
крыльев.
Вычислим угол скоса потока, получающийся в центре нашего
крыла от всего бесконечного ряда отображенных крыльев. Для
этого воспользуемся формулой (194'), полученной при изучении
одной стенки:
Да=т 16яСу b a2 (JX* ’
В этой формуле отбросим в знаменателе как величину
малую по сравнению с единицей. Расстояние d между центрами
самолетов будет у каждой последующей пары вихрей увели-
чиваться по закону:
а
а = ~2 п>
где п принимает значения: л=1, 2, 3,...,оо. Формула полного
скоса получится от двух систем вихрей — левой и правой и
будет равна сумме ряда:
VI 2 2^уЫ/2 су Ы 1
1 1
Б. Н. Юрьев—171—7
97
Ряд сходится и имеет
1
7t2
—. Следовательно,
б
сумму, как известно, равную
Да =
Фиг. 65. Влияние стенок,
расположенных сверху и
снизу крыла.
lai',. (1ЭД
Рассмотрим теперь случай горизонтальных стенок, находя-
щихся одно под другим на расстоянии h.
Из предыдущего видим, что, заменяя
обе стенки зеркальными отображе-
ниями, мы получим бесконечную сово-
купность крыльев, расположенных одно
под другим на расстоянии h, причем
циркуляция у соседних крыльев будет
противоположной. Задача сводится к
вычислению скоса потока в точке А ре-
ального крыла от действия всех вооб-
ражаемых крыльев.
Вертикальную скорость, вызванную
в точке А отображенным соседним кры-
лом, легко найти или по формуле (74)
гл. V, или независимым путем по
фиг. 65.
Возьмем один вихрь, например В, и вычислим скорость, вы-
званную им в точке А Получим:
Получим:
этой скорости будет такой:
... cblV j
V (199')
вертикальная проекция
_ т J/2 _ _Г ;,0_
vyi — V1 г — 4ягг /’ — 4Л [Л2+ (//2)2] — 1блй2
Пренебрегая малой величиной в знаменателе и замечая,
что bl — S — площади крыла, получим:
cySV
Vyl 16lt/l2 '
Взяв четыре вихря В, С, D и Е, расположенных симметрично
и вызывающих в точке А одинаковую скорость Vyt, получим
вызванную ими скорость:
^4== C>SI
у4 16 кА2 “ 4 к/г2
или отсюда
и, = -^ =______LifT.
V 4 к/г2
Взяв следующие четыре вихря, мы получим уже расстоя-
ние не h, a nh, где п = 1, 2, 3,...,оо. При этом знак скорости
98
Vy будет все время меняться. Учитывая это, получаем формулу
для полного угла скоса как сумму воздействий на точку А без-
численной совокупности вйхревых четверок, т. е.
. _ 1 суs v <- О'*
— 4 гсЛ2 2. п2
1
Найдем сумму этого ряда:
У(-1)',__1 , J_____________±ц_2___±4-2-
± п2 ~ 1 + 4 9 + 16 25 + 36
_ 1 it2
Подставляем сюда сумму ряда = -у; получаем:
1)" _ л2 ._1_л2_ *2
п3 ~ 6 2 6 ~ 12‘
Следоват'ельно,
л*=-й4с- (200>
Формулы (199) и (200) показывают, что вертикальные стенки
оказывают в два раза большее действие, чем горизонтальные.
И в том, и в другом случае крыло улучшается, так как доба-
вочный скос у него получается отрицательный.
§ 48. ИНДУКЦИЯ ТРУБЫ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
Рассмотрим теперь'прямоугольную сотой А. Применяя последовательно метод зеркальных отображений, придем в конце концов к схеме трубу ширин ой d i I ВЫ-
вихрей, изображенной на фиг. 66. Вычисление индуктивной ско- 45 &
рости, вызванной всей совокуп- ностью вихрей, делается тем же v ППИАШГНМ к’ЯГ^НЙ IVTkT ПЯЧО^ПЯЛИ R "I ’
iiuridvikjxvXj i\cii\Uri xvxjdi l/cidviv p/avin jd предшествующих параграфах. Центры фиктивных самолетов —- d—. & &
будут иметь координаты у= = + nh и г = md. Их действие
МОЖНО ВЫЧИСЛИТЬ ПО формуле (96), Фиг. 66. Влияние стенок трубы
дающей вертикальную скорость в прямоугольного сечения.
далеких от крыла точках:
______Г 21/2(-/ + z2)
9 4it (у14- г)2
(96)
39
Подставляя сюда и вычисляя Да, получим:
йл~ (у2 + г^^св-
Подставляя сюда значения у = +nh и z = + md, получаем для
угла скоса от трубы Дат следующее выражение:
4-оо 4-оо
д _SCgyy п„ mW-Vh* _
т 8л Li Li ' (пМ + г№)г
4-оо 4-оо
= Sc« V V Г— 11» м2-*-8”2
8na2 Li L.' 1 (т* + XW? •
—со —со
. h ъ
здесь лт = -----относительная высота сечения. Величины т
и п принимают все значения, за исключением нуля, так как
это даст действительное крыло, скос которого в индукцию
трубы входить не должен. Знак угла скоса будет меняться в зави-
симости от п.
Суммирование этого двойного ряда не приводит к простым
формулам. Глауэрт показал, что решить задачу можно таким
искусственным приемом.
Возьмем разложение котангенса:
оо
ctg z — — 2z У
ь 2 Ай г2 —
1
и сделаем подстановку:
z —
где х — временная переменная, аг- мнимая единица.
Тогда получим выражение, в которое войдет гиперболиче-
ский котангенс:
X L. « | 24Х V 1
ctgh Ых = ------|- •-— У------х—.
Преобразуя алгебраически это выражение и диференцируя его
по х, получим:
У------г - -------1--|г — ctgh Xr itx;
Zj -н*-*2 2Х?х2 24х 5
1
\ 1 24х2 'I я , . л8 . .
7--------;= —5— — — ctgh 1т тис-----------a- cosech 4 ях.
Li K/n2 + X2x8)2 к?х2 2ХТ х 6 2
100
Складывая эти выражения, получим:
ОО
VI /и2 — )Лх2
/ —f----.9 ха = ~5-------5" cose ch2 Хт тс.
(т2+1?л2)2 2)2х2 2
Отсюда получаем для двойной суммы;
т2 — ^п2
+ - 4cosech’X. ™ -
к2
241?
1
—2ХТ ппр _
к2
245?
_______
2>.т^ >
окончательное выражение для искомой суммы примет вид:
+ оо+оо оо оо
\'У, A'V ... ,
in_______________________
1 1
2 V 1>”
Х2 Л
Р._____
2ХТ пр *
Последняя формула удобна для расчетов, так как входящий
в нее ряд очень быстро сходится и
ную точность, отбросив все члены,
в формуле р = 1.
Тогда получим окончательно:
можно получить достаточ-
кроме первого, т. е. беря
m2 - к2и2
kl («а + Х2ла)а
-о—|- 8гс---а
3 1 + е4 ”
и угол скоса потока найдем по формуле:
а х, Scy d 1 ♦ S
Л“т “ 8itd2 ~h Т7 k~F~cV'
(201)
где F— площадь сечения трубы и k — коэфициент.
Глауэрт вычислил этот коэфициент для трубы прямоуголь-
ного сечения с различными отношениями сторон и получил сле-
дующий результат:
kT = hjd=.\^
k = 0,262
1/2 1//2 1 2 4
0,137 0,119 0,137 0,262 0,524.
обладает труба с Ат = —~
Наименьшей индукцией
0,707,
т. е. с отношением сторон 1,4:1.
101
§ 49. ИНДУКЦИЯ КРУГЛОЙ ТРУБЫ С ЗАКРЫТОЙ
РАБОЧЕЙ ЧАСТЬЮ
Наиболее часто применяются в аэродинамических лаборато-
риях трубы с круглым сечением струи воздуха в рабочей
части. Эти трубы устраиваются или с закрытой рабочей частью
или со свободной струей.
Мы рассмотрим сначала трубу с закрытой рабочей частью.
Условием на ее границе будет равенство нулю нормальной со-
ставляющей скорости потока.
Если бы трубы не было и крыло обтекалось неограниченным
потоком, то на тех местах, где должна была находиться стенка
трубы, получились бы некоторые нормальные к ним скорости
потока.
Труба, очевидно, накладывает на скоростное поле крыла свое
скоростное поле, причем сложение этих полей и должно дать
на стенке vn = 0. Задача сводится к нахождению таких систем
Фиг. 67. Схема вихрей, заменяющих круглую
аэродинамическую трубу с закрытой рабочей
частью.
вихрей, которые давали бы тот же аэродинамический эффект,
как и труба, и соз-
давали бы на стенках
трубы нормальные ско-
рости, обратные ско-
ростям, создаваемым
самим крылом.
В случае круглой
трубы такую эквива-
лентную систему вих-
рей найти очень легко.
Она сводится к двум
Г-образным вихрям,
расположенным по
обеим сторонам трубы
(фиг. 67) и имеющим
циркуляцию, равную
циркуляции вокруг
крыла.
Найдем расстояние
2, на котором следует
поместить эти отображенные вихри. Для этого возьмем точку А
над серединой крыла на высоте радиуса трубы R.
Крыло вызывает в этой точке направленную вниз индуктив-
ную скорость, которую получим или из общей формулы (74)
или по формуле (199'):
2Г 112
‘V»K— 4 л Z?2-}-(Z/2)2 ’
Вихри Огхг и ОиХц вызовут в той же точке А скорость,
направленную вверх и равную на основании формулы (199'):
_ 2Г г
VffT ~ 4л № + г2 •
102
(202)
Эти вихри должны нейтрализовать скорость, созданную самим
крылом, т. е. обе эти скорости фук и г»9Т должны быть равными.
Отсюда
1/2 _ г
R* + (Z/2)2 — Я2 + г2 •
Решая это уравнение относительно z, получаем:
г=< (203)
//Z
Таким образом доказано, что выбрав z по формуле (203),
мы в точке А получим вертикальную скорость, вызванную че-
тырьмя вихревыми усами, равную нулю. Легко видеть, что будет
равной нулю и скорость, созданная каждой парой вихрей (ССХ;
01X1) и (BBt- О2х2), так как условие нулевой скорости напи-
шется для каждой такой пары в том же самом виде [формула
(202)], как и для четырех вихрей.
В теоретической аэродинамике доказывается, что линии тока
у двух вихревых шнуров, имеющих равные, но направленные
в разные стороны циркуляции, имеют форму окружностей. В на-
шем случае (z = эти окружности будут иметь центр в на-
чале координат, так как в точке А скорость фу = 0 и, следо-
вательно, линия тока имеет здесь горизонтальный элемент.
Складывая потоки, полученные от этих пар вихрей, мы
получим наложение этих окружностей одна на другую, и, следо-
вательно, общей линией тока явится и для четырех вихрей
эта же окружность.
Так как скорости в точках, лежащих на линии'тока, каса-
тельны к последней, то отсюда следует, что по всей нашей
окружности, изображающей аэродинамическую трубу, нормаль-
ные составляющие скоростей потока будут равны нулю.
Таким образом мы можем действие стенок трубы на крыло
заменить действием вихрей OxXi и О2х2.
Действие это сведется к углу скоса потока Дат , возникшему
от двух вихрей О^, О2х2 в центре крыла. Вычисляем
скорость скоса по основной формуле (3) и получаем:
ф — 2 —= 2-^—
сначала
Заменяя выражения циркуляции по уравнению связи и заме-
чая, что bl = S и л/?2 = F — площади трубы, получаем:
_ Cybl р _ CgS у
- 87t/?2 V - 8F V
и находим величину угла скоса потока:
_ _ 1 5 (204)
Дат=------8’7гС»-
Легко убедиться, что полученный угол скоса будет близок
к углу скоса в квадратной трубе. В §48 для квадратной трубы был
найден коэфициент k = 0,137, а теперь он получился равным
i/8 = 0,125.
103
Этот скос будет направлен снизу вверх и будет увеличи-
вать угол атаки крыла. Таким образом, если крыло установлено
в трубе под углом атаки ат, то на самом деле его угол атаки
будет:
а = ат + Дат. (2С5)
Кроме того, от угла скоса потока возникнет добавочное индук-
тивное сопротивление от стенок трубы, равное по общему
правилу:
Сх,т — = -д —р Су . (206)
Это сопротивление имеет знак минус. Измеренный в трубе
схТ получается преуменьшенным; его следует исправить, доба-
вив к нему с11Т. Тогда получим истинный сх модели, равный:
Сх — cxt сх1т = схх -|- р-р Су. (207)
Поправки на индукцию трубы следуют тому же закону, как
и самоиндукция крыла, т. е. угол скоса потока пропорционален
Су, а индуктивное сопротивление с*. Исправление опыта обычно
ведется графически тем же приемом, как и пересчет крыла на
другое удлинение (см. § 19).
Удобно также представлять индуктивное действие трубы
на крыло в виде кажущегося изменения его удлинения. Вычи-
слить это удлинение можно таким путем. Полный угол скоса
потока у крыла в трубе будет равен:
Да 4- Дат = -^ — j-pCy.
Представим эквивалентное крыло вне трубы с Хэ, у которого
угол скоса потока будет Да8 = и величина его будет равна
полному углу скоса первоначального крыла в трубе, т. е.
Су Су 1 S
= la
замечая, что ХУ = Za, получим:
Су __ Су_ /._1 _ Су г.____1 /£у]
icX3 я). к 8 £. [ 8 \RJ J'
Отсюда
i. = 1----(208)
Таким образом крыло, работающее в закрытой трубе, как
бы имеет больший размах Х9, чем в действительности.
Обычно в закрытых, круглых аэродинамических трубах ис-
пытывают модели с размахом 1 = R. Стандартная величина X
104
у нас равна 5. Следовательно, в закрытой трубе крыло как бы
имеет эквивалентное удлинение, равное
1, = X——j1---; V2- = 5-Ц-= 5 4 = 5 • 1,14 = 5,72,
'-т
т. е. удлинение крыла как бы увеличивается на 14%.
Поправка эта, как видим, весьма велика и ее теперь не-
пременно вводят во все продувки, производимые в трубах. До
1925 г. многие лаборатории этой поправки в свои опыты не
вводили, и поэтому все старые исследования необходимо исправ-
лять на индукцию трубы.
Иногда, стремясь получить большие числа Рейнольдса, в ла-
бораториях испытывают очень большие модели в малых трубах^
например, довольно часто берут I 0,65 1,3/?. В этом слу-
чае поправка становится уже равной почти 30% от индуктив-
ного сопротивления крыла, т. е. величиной чрезмерно большой.
Возникает вопрос: насколько точны такие поправки? Проф.
Л. Прандтль исследовал теоретически такую поправку, принян
эллиптический закон изменения циркуляции по размаху. Ока-
залось, что при этом угол скоса потока от трубы будет таким?
<209'
Для обычного соотношения, т. е. Z = /?, получаем очень малое
значение выражения в скобках, а именно: второй член в скобках
будет иметь значение, равное4 ~9,019, т. е. около 2%.
Вся величина Дат является сама поправкой, равной в нормаль-
ных случаях 14%, и поправка в 2% к этой поправке, Д,ает
окончательную погрешность в сх не более О,3°/о, т. е. величину
совершенно неуловимую в обычных аэродинамических опытах.
Вследствие этого можно во всех случаях пользоваться фор-
мулой (204) как достаточно точной.
Опытную проверку этой поправки делали почти все сущест-
вующие аэродинамические.лаборатории. Оказалось, что она дает
прекрасный результат и обеспечивает хорошую сходимость
опытов с моделями разного'размаха в одной и.той же трубе. При
учете же числа Рейнольдса и турбулентности потока эта по-
правка обеспечивает хорошую сходимость и для опытов, про-
веденных в различных трубах.
§ 50. ВЛИЯНИЕ СТЕНОК ТРУБЫ НА РАБОТУ ХВОСТОВОГО ОПЕРЕНИЯ
Из рассмотрения вихревых схем трубы и крыла (фиг. 67)
видно, что у хвостового оперения получится другой скос от
влияния трубы, чем у крыла. Это очень часто забывают в аэро-
динамических лабораториях й дают неисправленные данные
об устойчивости моделей самолетов.
105-
Найдем эту поправку, для чего подсчитаем скос, получаю-
щийся от Г-образных вихрей в точке А хвостового оперения
{фиг. 68). Хвостовое оперение считаем находящимся в плос-
кости вихрей.
Пользуясь формулой (10), получаем для прямолинейных вих-
рей № 1 и № 2 индуктивные скорости vn и vys,; удвоив их,
получим полную скорость о»:
fy = 2‘Vg1 2Vy2 —
•Фиг. 68. Скос потока у
хвоста от действия трубы.
Величина z известна по преды-
дущему параграфу:
Кроме того, Г = свЬУ, где сд и b
берутся для крыла. Отсюда угол скоса
потока у горизонтального хвостового
оперения от действия трубы будет
таким:
ДЯг. о.
___Vv______1_ S_
~ И ~ 8 F в
1 S
Величина Лдт =-----— — су, равна углу скоса от индукции
о Г
•трубы у крыла. Следовательно, предыдущую формулу можно
•написать окончательно в таком виде:
Даг. о. т = Лат
(2Ю)
106
По этой формуле и должна делаться поправка на влияние
трубы на хвостовое оперение.
/?2
В обычных трубах l^R и, следовательно, z = = 2R.
В среднем у самолетов 1st//2 = R/2. В таком случае предыду-
щая формула после вычисления в скобках примет следующий
вид:
Даг.о ~Дат • 1,2, (211)
т. е. угол скоса потока от индукции трубы будет у хвоста
приблизительно в 1,2 раза ббльшим, чем у крыла.
Этот факт вызывает в трубе своеобразную „разверку мо-
дели". Хвостовое оперение модели начинает работать более
эффективно, и общая устойчивость модели повышается. Бывали
случаи, что машины, слегка неустойчивые в полете, при опытах
в трубах оказывались устойчивыми. Найденная в трубе уста-
новка стабилизатора обычно оказывается при полетных испы-
таниях слишком малой и ее приходится увеличивать на1/* — X/2O.
Особенно сильно эти влияния сказываются на больших уг-
лах атаки. Так, при св = 1, мы получим в нормальном случае
(/ = /? и К = 5):
Да; = - 57,3 А * с, = - 57,3 2-Х = - 0,45" - 0,5»,
-а угол скоса у хвоста:
т. е. поправку довольно заметную. В трубе получается такой
же эффект, как если бы при увеличении угла атаки в полете
летчик поворачивал руль высоты вниз, т. е. давал бы ручку
от себя.
Исправить кривую моментов можно таким простым расче-
том. Истинный угол атаки хвостового оперения будет равен:
«г.о. «=<* + <? — Да™, к-Даг.о. т — Д«г. о 5
здесь а — угол атаки крыльев, <р — деградация оперения, Даг. 0. к—
угол скоса потока от действия крыльев, Даг. о.т~ угол скоса
у хвоста от влияния трубы и Даг. о — угол скоса от самоиндукции
хвоста.
У хвоста получится подъемная сила, почти перпендикуляр-
ная к линии полета и равная:
Уг. О = Су г. О Sr. О
Заменяя саг. о аналитическим выражением:
Су г.о = CLqfitt = 4ZQtr. о,
где аг. о = « + <? — Д«г. о. к —Д«г. о. т, получаем:
Хг. О == “2“ Sr. о Д^Г. О. К Д^Г. О. т)"
107
Очевидно, добавочный момент получится у модели самолета
от добавочной подъемной силы у хвоста. Угол скоса Дат учиты-
вается при исправлении всей продувки самолета.
Следовательно, разность сил получится лишь за счет разно-
сти Даг. о. т—Дат=8, т. е.
ДКг.о= - -|-5г.оИ2а8.
Но добавочный угол скоса у хвоста от действия трубы будет
в среднем, как мы видели, равен:
д = 0,2Дат.
Следовательно,
ДУг.о= - а Дат Sr. о У2- 0,2;
Это изменение подъемной силы вызовет момент ДЛ1 =
= ДУг. oL или изменение коэфициента продольной устойчи-
вости
Ьст = -°- = - Дат . 0,2 а. (212)
SV*L SV*L
По этой формуле и можно делать поправку на влияние
трубы на продольную устойчивость модели самолета.
£
Беря для средних соотношений —^ = 0,15 и считая а для
малых удлинений, какие встречаются у обычных хвостовых
оперений, равным 4, получаем:
Дсот = — Дат • 0,12.
Приняв, например, угол скоса у крыла Дат равным—0,01, по-
лучим:
Дст = 0,0012.
О значительной величине этой поправки, которую у закры-
тых труб нужно вычитать, можно судить уже потому, что сама
величина ст на летных углах имеет у обычных самолетов по-
рядок нескольких сотых, а нередко, у мало устойчивых машин,
и тысячных.
Таким образом продувки самолетов в трубах на продольную
устойчивость нужно обязательно исправлять на индукцию трубы,
хотя бы описанным здесь простым приемом.
Как увидим в следующем параграфе, в трубах со свободной
струей получается скос от трубы такой же величины, как и в
трубах закрытых, но с другим знаком. Следовательно, для них
поправка для ст может вычисляться также по формуле (212), но
должна браться с обратным знаком, т. е. с плюсом.
108
§ 51. ПОПРАВКИ У ТРУБ С ОТКРЫТОЙ РАБОЧЕЙ ЧАСТЬЮ
В настоящее время подавляющее большинство труб стро-
ится с открытой рабочей частью, так как открытая рабочая
часть значительно облегчает проведение экспериментов—модель
в этом случае доступна со всех сторон, ее легко подвесить на
проволоках, легко фотографировать, она доступна для различных
насадков и т. д.
Возникает вопрос о влиянии такой трубы или, вернее, ее сво-
бодной струи на аэродинамические свойства испытываемых в ней
моделей.
Основным свойством свободной струи является постоянство
давления на ее границе, равного всюду атмосферному. Это
обстоятельство позволяет получить условие для обеспечения
граничных условий струи. Напишем уравнение Бернулли для
точки, лежащей далеко от модели, например для сечения возле
самого выходного сопла, где скорость равна Й, и для любой точки
границы струи, но уже около модели. Модель вызовет индук-
тивные скорости, которые, сложившись со скоростями, вызван-
ными системой вихрей, заменяющих границы струи, дадут ре-
зультирующие индуктивные скорости vx, vg и -»z. Теорема
Бернулли напишется так:
Ра 4- — Ра -4- + 4- 4-
T + 2g~ Y ' 2g 2g ' 2g'
Отсюда
2Vvx = vt + v2y + v2. (213)
Это и есть основное граничное условие струи. Скорости
Фх, и vz — величины малые по сравнению со скоростью V.
Следовательно, vx должно быть очень малой величиной. Это
станет особенно ясным, если формулу (213) написать в виде
соотношения отвлеченных скоростей:
гтМт-МтУ + бтЛ
Скорости на границе измеряются несколькими процентами
от скорости V, следовательно, их квадраты очень малы и у
имеет второй порядок малости по сравнению с и . Поэто-
му Очень часто формулируют граничное условие для свободной
струи как условие получения на границе полной скорости <их,
равной сумме скоростей от крыла и отображенных вихрей,
равной нулю, т. е.
vx = 0.
Это условие иногда называют условием проф. Л. Прандтля.
Однако легко видеть, что если ч)х = 0, то из уравнения (213)
получим: vg = 0 и = 0. Другими словами, условие vx — 0 по-
109
лучится лишь при отсутствии крыла, в присутствии же крыла
нужно решать уравнение (213) в полном виде.
Оказывается, что круглую свободную струю с атмосферным
давлением на ее границах можно получить с помощью картины
вихпей изображенной на фиг. 69. Получается полная аналогия
с закрытой трубой (фиг. 67), но Г-образ-
ные вихри вращаются теперь в обратную
сторону.
Для соблюдения условия Прандтля,
как можно убедиться, проделав под-
робно вычисление скоростей и под-
ставив их в уравнение (213), необхо-
димо поместить отображенные вихри
на расстоянии
“ Ц2 *
Фиг. 69. Схема вихрей, заме- 1
няюгцих свободную струю
ограниченного сечения.
Следовательно, все выводы, сделан-
ные нами для закрытой трубы, могут
быть перенесены и на открытую трубу с той только разни-
цей, что направление скоса как у крыла, так и у хвоста будет
обратным.
Итак, в трубе с открытой рабочей частью:
— ~з
Д^г.о. т ^^1,2До£у у
. 1 5 2
Cxi 1 ~ 8 7 S”
Я -- tty & tty .
(214)
По этим формулам делаются поправки, так же как и в за-
крытых трубах, но только направлены они в другую сторону. В
открытой трубе аэродинамика крыла ухудшается, а в закрытой
улучшается; поправки приводят опыты к совпадению.
Исследования, произведенные в ЦАГИ В. В. Белостоцким, по-
казали, что за сечение свободной струи нужно брать чистую
струю, и не учитывать пограничный слой, охватывающий та-
кую струю. Таким образом во все формулы следует подставлять,
не площадь F, а несколько меньшую площадь отношение
-рг лучше всего получить экспериментальным путем, испытывая
в трубе крылья одного удлинения к, но разных площадей S и
добиваясь полного совпадения продувок после исправления их
на индукцию трубы.
§ 52. ТРУБЫ СЛОЖНОЙ ФОРМЫ
В настоящее время изучены поправки для самых разнооб-
разных форм струи. Так, японцы Tani, Itiro, Sanuki и Mata с
110
развили точную теорию труб с эллиптическим сечением; от-
крытая прямоугольная труба была изучена теоретически амери-
канцем Т. Theodorsen. Была исследована работа крыльев, поме-
щенных в трубе эксцентрично.
Таким образом по этому вопросу имеется целый ряд серь-
езных монографий. Точные решения этой задачи ведут обычно
к очень сложным математическим выражениям.
Структура окончательных формул для угла скоса получается
одинаковая, а именно:
А , и S
ZjCCj — ~т~ К р
Фиг. 70. Коэфициент k для эллиптических
закрытых труб.
где k находится путем сложных вычислений.
Мы здесь дадим без
вывода величину k для
эллиптических труб, ши-
роко применяющихся в
новейших лабораториях.
На фиг. 70 дана вели-
чина k для закрытых эл-
липтических труб в за-
висимости от двух па-
раметров, — отношения
размаха крыла I к ширине
трубы 2а и отношения
высоты сечения трубы 2Ь
l b
к ее ширине, т. е.^у и - .
На фиг. 71 дан такой
же график для эллипти-
ческой трубы со свободной струей.
Влияние эксцентричности расположения крыла на индукцию
трубы было исследовано Т. Теодорсеном (Report NACA 547,
1935 г.) Влияние это оказалось довольно большим. На фиг. 72
дан график для эллиптической трубы с шириной в два раза
большей высоты. Кривые даны по параметру эксцентриситета,
2х i
равного и по отношению . Это влияние должно сказываться
на продувкйх бипланов и в тех случаях, когда при испытаниях
модели самолета на больших углах атаки ее нарочно подве-
шивают эксцентрично, чтобы ее хвост не выходил из струи.
Очень интересные результаты получил Теодорсен, задавшись
вопросом о форме труб, совершенно не влияющих на модель.
Оказалось, что такими безиндукцйонными трубами являются по-
лузакрытые трубы, у которых стенки охватывают рабочее се-
чение лишь частично.
Теодорсеном намечены следующие варианты таких труб
(фиг. 73): а — квадратная труба с горизонтальными стенками,
b — прямоугольная труба с отношением ширины к высоте не-
111
много меньшим чем 2:1, и снабженная только вертикальными
стенками, и труба с прямоугольным сечением с отношением
Фиг. 72. Влияние эксцентри-
ситета моделей на коэфи-
циент k.
Фиг. 71. Коэфициент k для эллиптических
открытых труб.
ширины к высоте равным 2:1, и имеющая лишь или пол (с) или
потолок (d). Эти трубы представляют большой интерес, и было
бы весьма желательно осуществить их, так как это упростило
бы эксперименты и сделало их более надежными.
Фиг. 74. Отклонение крылом струи
в трубе с открытой рабочей частью.
§ 53. ЭЛЕМЕНТАРНЫЙ ВЫВОД ФОРМУЛ ИНДУКЦИИ
АЭРОДИНАМИЧЕСКИХ ТРУБ
Фиг. 73. Сечения безиндук-
ционных труб Теодорсена.
Как показал М. Мунк, формулы индукции труб можно легко
вывести, хотя и не вполне строго, применяя основные уравнения
механики к струе и делая ряд упрощающих предположений.
Представим свободную струю, вылетающую в неограничен-
ное пространство из сопла (фиг. 74). Пусть сечение ее будет F
и скорость V. Если бы в струе не было крыла, то она пошла
бы прямо, как это показано пунктиром. Если же в потоке на-
ходится крыло, то струя отклонится вниз и окажет на модель
давление, в результате чего и появится подъемная сила Y.
Осевую скорость V будем считать неизменной по длине трубы.
112
По закону действия и противодействия с такой же точно си-
лой Y будет действовать крыле? на воздух по направлению вниз.
На некотором расстоянии за крылом давления внутри струи сра-
вняются с атмосферным, и мы получим у струи скорость т»и1,
направленную вниз; эту скорость будем считать постоянной
по всему сечению.
Теперь, применяя закон импульса и количества движения,
мы пишем, что сила Y равна секундному количеству движения,
уносимому струей, т. е.
Y = —
Секундную массу воздуха т (массовый расход струи) можно
представить так:
т — p/V.
Тогда
Y=-?FVvn. (215)
Отсюда
_ Y
Vn ~ '
v41 является скоростью в далеком от крыла сечении ab. Нас
же интересует скбрость скоса в том сечении струи, где на-
ходится само крыло. Для нахождения этой скорости пишем за-
кон сохранения энергии, считая работу отклоняющей струю
силы, равной Yvg, и приравнивая ее изменению кинетической
энергии струи. Получаем:
Уг; = - £ ( И’ + <) = _ т„к =Y^.
Отсюда
= (216)
Таким образом формула (215) перепишется теперь в виде:
Г = — p/V2<^.
Отсюда скорость скоса потока от ограниченности струи будет
равна:
_ Y
Vy ~ 2?FV *
Заменяя Y по формуле Y = cy-^SV2 и вычисляя угол скоса,
получим:
= Су. (217)
Этот скос вызовет у крыла добавочное индуктивное сопро-
тивление
Cxif = — "д" ~р С2у. (218)
Б. Н. Юрьев—171 —-8
113
В таком виде' формулы применимы лишь для струи, выте-
кающей в неограниченное пространство, что встречается, на-
пример, у сверхзвуковых аэродинамических труб. У обычных
же труб струя течет несколько иначе. Сравнительно близко за
крылом находятся второй коллектор и диффузор, которые от-
клоняют струю вверх и засасывают внутрь трубы (фиг. 75).
Вследствие этого струя поворачивается вверх и скос на крыле
уменьшается.
Теоретически изучить получающийся эффект нелегко. Од-
нако опыты показывают, что в этих случаях получается почти
в точности половинный скос, и, следовательно, для случая
обычной открытой трубы можно пользоваться формулами:
л 1 S „
— g р
1 5 2
Cxi!= 8 РСУ
(219)
Таким образом приближенная теория приводит к тем же
формулам, как и точная, рассмотренная в предыдущих пара-
графах.
Фиг. 75. Отклонение струи мо- Фиг. 76. Решетка, заменяющая
делью у аэродинамических труб стенку трубы.
с открытой рабочей частью.
Получить выводы о закрытой трубе можно с помощью сле-
дующего искусственного рассуждения. Струя скашивается кры-
лом вниз на угол Дат. Если мы вообразим непосредственно
перед крылом установленную решетку (фиг. 76), напоминающую
направляющие колеса турбин, то с ее помощью мы сможем,
поток отклонить вверх на некоторый угол Ла. Берем его рав-
ным Aq.T. Тогда струя после крыла пойдет прямолинейно, т. е.
так, как она идет в закрытой трубе при отсутствии модели.
Отсюда действие трубы равносильно действию этой решетки.
Решетка же давала у нас скос — Дат.
Следовательно, закрытая труба отклоняет поток вверх на
угол — Дат, и мы можем для исправления опытов в трубах при-
менять формулы (219), ставя перед правыми частями знак минус.
Теория эта очень схематична и целый ряд допущений в ней
произволен, как например, постоянство осевой скорости в ра-
бочей части, постоянство по сечениям скоростей г»у и ъУ1, не
совсем точное применение закона сохранения энергии и т. д.
Тем не менее эти рассуждения очень наглядны и быстро
дают расчетные формулы.
114
Глава XI
АЭРОДИНАМИЧЕСКИЕ СВОЙСТВА САМОЛЕТА В ЦЕЛОМ.
ПОДЪЕМНАЯ СИЛА САМОЛЕТА
§ 54. „ПРЕДСКАЗАНИЕ" АЭРОДИНАМИЧЕСКИХ СВОЙСТВ САМОЛЕТА
С самого начала исследований крыльев в аэродинамических
трубах делались попытки научиться „предсказывать" на основа-
нии обработки этих опытов аэродинамические свойства любого
профиля без его продувки.
Идеалом таких „предсказаний" было бы развитие теории крыла
до такой степени, чтобы на основании чертежа крыла можно
было вычертить его аэродинамические характеристики. К сожа-
лению, такого точного метода еще не создано. Долгое время
не удавалось создать и приближенного метода таких „предска-
заний". Это не удавалось потому, что тогда не знали теории
индукции и во всех получаемых результатах не учитывались
такие, теперь хорошо известные, факторы, как влияние трубы,
влияние удлинения, влияние формы крыла в плане и т. д. С разви-
тием теории индуктивного сопротивления крыльев эти „предсказа-
ния" вступили в новую стадию и увенчались большими успехами.
Эти вопросы приходится сейчас очень тесно связывать с воп-
росами влияния числа Рейнольдса и турбулентности потока
в трубах, так как без учета этих факторов нельзя сделать пе-
реход от модели, испытанной в трубе, к самолету в натуру.
И, наконец, надо с самого начала помнить, что крылья в чистом
виде на самолетах не применяются; на самолете имеется фюзе-
ляж и другие детали, сильно влияющие на аэродинамические
характеристики крыла. Кроме того, шероховатость, самолета
больше шероховатости модели.
Для изучения всех этих сложных явлений нам придется
в этой главе пользоваться следующими основными понятиями.
1)Числом Рейнольдса
где V— скорость потока вдали от модели, b — линейный размер—
длина хорды крыла и v — коэфициент кинематической вязкости
воздуха, равный при 15° и 760 мм рт. ст. 1,45- 10~6. (Подроб-
ности о числе Re см. в части I гл. XI.)
2) Начальной турбулентностью потока, равной
е7. = 100,
где у — средняя квадратичная пульсаций потока, получающихся
от заполнения турбулентного потока мелкими беспорядочными
вихрями (см. часть I, гл. XII, § 71). В старых трубах турбу-
лентность была очень большой —от 1,5 до 3%. В новых она
115
лежит в пределах 0,4—0,7%, у самолета в полете она очень
мала и равна 0,1—0,2%.
3) Эквивалентным числом Рейнольдса
Re9 = Re • К,
где К—фактор турбулентности. Понятие это было введено
в практику американцами и сейчас нашло всеобщее признание.
Основано оно на том факте, что все аэродинамические харак-
теристики, построенные графически по числу Re, при увели-
чении начальной турбулентности как бы сжимаются по оси
абсцисс. Для приведения этих кривых, полученных при различ-
ных начальных турбулентностях, к совпадению достаточно по-
строить диаграмму не по числу Re, а по числу Re3. Таким обра-
зом вместо двух критериев подобия получается всего лишь
один.
Величину К чаще всего находят по испытанию в данной
трубе шара (см. часть I, гл. XII, § 71). Построив на основе опы-
тов с шаром график cx=f(Re), определяют критическое значе-
ние ReK при сх — 0,3 и, считая, что в абсолютно нетурбулентном
воздухе эта величина сх получается при /?ек = 385000, находят
фактор турбулентности данной трубы по формуле:
„ 385000
К ««к
Этот фактор изменяется у различных существующих труб
в пределах от 1,1 до 2,6.
Хотя понятие Re3 и нельзя считать строго обоснованным
теоретически, тем не менее оно оказалось весьма полезным на
практике и теперь очень часто применяется при обработке
опытов, проведенных в аэродинамических трубах.
4) Относительной шероховатостью поверх-
ности. Опыты указали на весьма большое влияние степени
шероховатости поверхностей, обтекаемых воздухом, на полу-
чаемое при этом трение (см. часть I, гл. XIII, § 77). Так как
модели, испытываемые в трубах, делаются очень гладкими,
а самолет нередко бывает сильно шероховатым из-за окраски,
гофра, заклепок и т. п., то возникает вопрос об изучении влия-
ния шероховатости на все аэродинамические характеристики
самолета и в связи с этим вопрос о мере шероховатости.
Обычно мерой шероховатости поверхности считают отно-
шение средней высоты ks бугорков шероховатости к длине
рассматриваемой поверхности Ь, т. е.
k
ш = •
b
Мерой гладкости поверхности является обратное отно-
шение
b
г = —
«s
11б
Таким образом переход от модели крыла, испытанной в трубе,
к самолету в натуру—весьма сложная задача, требующая внима-
тельного учета целого ряда факторов. Вопрос этот является
важнейшим вопросом прикладной аэродинамики, так как основ-
ные наши сведения о крыльях, фюзеляжах и о прочих деталях
самолета получаются до сих пор в аэродинамических трубах.
К сожалению, во многие из этих вопросов еще не внесено
полной ясности. Более того, по ряду вопросов имеются про-
тиворечивые результаты, полученные в разных лабораториях.
Мы будем придерживаться в основном американских иссле-
дований, так как несомненно в этих вопросах, благодаря имею-
щемуся в США ряду аэродинамических труб, дающих натураль-
ные числа Re, американцы заняли руководящее положение.
§ 55. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОФИЛЕЙ
Как мы видим, теория индукции позволяет, зная характе-
ристики профиля, т. е. крыла бесконечного размаха, делать
пересчет его на крыло любого удлинения. Отсюда становится
ясной необходимость научиться прежде всего находить аэроди-
намические характеристики профилей разной формы при раз-
ных условиях их обтекания.
Попытки дать чисто теоретическим путем характеристики
профилей, несмотря на то, что задача сводится в этом случае
к плоскопараллельному течению вязкой жидкости, до сих пор
успехом не увенчались. Вследствие этого в конструкторских бюро
развились полуэмпирические методы, основанные на систематиче-
ских опытах с крыльями и на обработке результатов испытаний.
При таком подходе к крылу нужно научиться задавать форму
его профиля простейшим способом. В первой части курса мы
уже указывали некоторые такие приемы. Как мы видели, суще-
ствует несколько различных манер давать геометрические харак-
теристики профилей. Мы здесь остановимся лишь на американ-
ской манере как наиболее простой и распространенной и, самое
главное, основанной на исключительно обширных и надежных
американских опытах.
Американцы принимают за единицу длины хорду крыла и на-
правляют ось х, в данном случае связанную, по хорде с началом
у носика профиля.
Сперва рассматривают симметричные профили. У наилучших
крыльев ординаты профиля, оказывается, можно представить
следующим простым уравнением:
+ у = а0 угх + агх 4- а2х2 + «Зх3 + а4х4. (220)
Постоянные а0, а2, а3 и можно подобрать по лучшим
профилям, пользуясь обычными для них соотношениями. Аме-
риканцы эти условия формулируют для крыла с толщиной
в 2О°/о таким образом:
117
1. Максимальная ордината 0,1 должна лежать на 0,3 хорды,
т. е.
л = 0,3; у = 0,1; (dyfdx)ofi = Q (условие максимума).
2. Ордината конца хвостика профиля лежит в точке
л=1; у = 0,002.
3. Угол у задней кромки крыла определяется из соотно-
шения:
л = 1; dyldx = — 0,234.
4. Форма носика задается координатами:
л = 0,1; у = 0,078.
Очень хорошо удовлетворяет этим условиям следующее
уравнение толщины профиля:
±j/4 = 0,29690/л - 0,12600л —0,35160л2+
+ 0,28430л3- 0, 10150л4. (221)
Получающийся по этому уравнению профиль (фиг. 77) будет
иметь толщину 0,2, т. е. 20% от хорды. В табл. 8 даны его
ординаты в процентах хорды.
Л /- ----а-------------------NA СА
\ Clark К
0 0,1 0.2 0,3 0^ 0,5 0,6 0,1 0,8 0,9 1,0
Фиг. 77. Исходный американский профиль.
Для других крыльев, с другой максимальной толщиной,
ординаты профиля получают простым умножением этих орди-
нат на отношение где с — сь—относительная толщина про-
филя. Радиус кривизны у носика получается по формуле:
1 / ё"
Гн = 4" \^2ао) = 1,10с2. (222)
По американским исследованиям оказывается, что если вы-
прямить лучшие существующие профили и привести их ординаты
к 20% толщине, то эти профили сливаются с основным амери-
канским профилем. На фиг. 77 нанесены точки для крыльев Clark Y
и Gottingen 398; они лежат прямо на американском профиле.
Обычно крылья бывают несимметричными. Для их построе-
ния американцы пользуются средней линией профиля,
называемой иногда скелетом профиля (фиг. 78). Кривая,
изображающая эту линию, составляется из двух отрезков: часть
от носика профиля до максимальной ординаты _ушах этой линии,
118
соответствующей абсциссе х = р, определяется уравнением
средней линии:
где 9 — угол,
зонталью:
= (223)
а задняя часть кривой—уравнением:
Уср=(т”“2 (1 -2р + 2рх - л2). (224)
Заметим, ЧТО Величину фертах
начают через/. Очевидно:
у нас часто обоз-
Сам изогнутый профиль строится таким
образом. Выбрав уравнение для кривизны и
задавшись х, находят ординату средней ли-
нии Уср-Затем вычисляют по уравнению толщины
(221) или берут по табл. 8 ординату yt
выпрямленного профиля и откладывают ее
вверх и вниз от средней линии, по нормали
Фиг. 78. Построение несимметричного профиля по
§ американскому способу.
s
о
® к этой линии (см. фиг. 78). Получают точки:
» верхнюю В и нижнюю Н. Для точного пост-
® роения профиля удобно найти координаты
« точек Ви И относительно обычной, связанной
“ системы координат.
>> Из чертежа видно, что
(£ Хв = х—_ytsin6; x# = х + у( sin 9;
Ув=^ср+3'<СО5 9; Уя=уСр—_y<cos9,
составленный касательной к средней линии с гори-

Задавшись уравнением средней линии, можно вычислить
величину tg 9 и найти координаты точек В и Н.
119
Достаточную точность можно получить и графически, про-
сто вычерчивая профиль, проводя нормали на-глаз.
Уравнения кривизны в противоположность уравнению тол-
щины бывают весьма разнообразными.
Для быстрого распознавания крыльев американцы придер-
живаются следующей, весьма удобной нумерации профилей. Нор-
мально дается четырехзначное число, например 2312. Первая
цифра определяет максимальную ординату средней линии _уср в
процентах от хорды, вторая—положение этой максимальной
ординаты в десятках процентов хорды, а последние две
цифры—толщину профиля в процентах хорды.
В тех случаях, когда нужно более точно указать положение мак-
симальной кривизны профиля, пользуются двумя цифрами, дающи-
ми удвоенную величину абсциссы в процентах хорды. Например,
один из наилучших американских профилей обозначается 23012;
это значит, что профиль имеет наибольшую стрелку кривизны,
30°/
равную 2%, лежащую на расстоянии —= 15°/0 от носика
крыла; толщина профиля равна 12% хорды.
Эти обозначения весьма удобны. В тех случаях, когда
нужны добавочные уточнения, ставятся еще различные услов-
ные цифры, но уже за запятой.
Следовательно, основными характеристиками профиля явля-
ются относительная толщина с и относительная стрелка кри-
визны фертах, часто обозначаемая у нас через f.
Перейдем теперь к вопросу о предсказании аэродинамиче-
ских свойств крыльев по их геометрическим параметрам, рас-
смотрев предварительно вопрос о влиянии фюзеляжа на крыло.
§ 56. ВЗАИМОДЕЙСТВИЕ КРЫЛА И ФЮЗЕЛЯЖА
В предыдущих главах был подробно разобран переход от
одного размаха крыльев к другому. При этом удобнее всего
исходить из крыльев, уже пересчитанных на бесконечное удли-
нение. Американцы такие диаграммы называют характеристи-
ками профилей.
Когда речь идет о самолете, возникает сразу же весьма
важный вопрос о влиянии фюзеляжа на крыло. С точки зре-
ния индукции возникает вопрос: сомкнутся ли присоединенные
вихри обеих половин крыла или же часть их циркуляции обра-
тится в вихревые усы в месте стыка крыльев с фюзеляжем?
Многочисленные опыты, проведенные в разных странах, дают
весьма пеструю картину. В общем все же можно считать дока-
занным, что фюзеляж как бы заполняет вырез в крыле и дает
подъемную силу, близкую к подъемной силе недостающей части
крыла. Области разрежения воздуха над крылом и сжатия под
ним, смыкаясь над и под фюзеляжем, заставляют последний раз-
вивать эту подъемную силу. Поэтому принято за площадь крыла у
самолета брать площадь самих крыльев плюс воображаемый
120
участок крыла на месте фюзеляжа (фиг. 79). Такую площадь
называют иногда аэродинамической или несущей пло-
щадью крыла.
Простейшим предположением при расчете комбинации крыла
и фюзеляжа является допущение, что можно просто суммиро-
вать их сопротивления. Тогда
Х=ХК + = схф^ 5Ф I/2;
здесь схк и Сл-ф—коэфициенты лобового сопротивления крыла и
фюзеляжа, 5—несущая площадь крыла по фиг. 79 и 5ф —миде-
левая площадь фюзеляжа. Коэфициент
сопротивления комбинации крыла и фю- (\
зеляжа получим в таком виде:
=Гхк+Сгф^, (225)
2 s
или, пользуясь формулой теории индук- \ /
с* UU
ции: сх = схр+получим: /"][ \
2 о
„ ,су । „ г,Ф ZOORA Фиг. 79. Аэродинамическая
сх— Сгр-Гя-А-Г^Ф 5- V-W) площадь крыла.
Напомним еще раз, что величина S берется здесь условно
по фиг. 79.
Опыты показывают, что такой простой зависимости не наблю-
дается. Так, при Су = 0 должно было получаться выражение:
но на самом деле сопротивление получается обычно несколько
большее, а иногда и меньшее, чем дает эта формула, и преды-
дущую формулу следует писать в таком виде:
сх — схр -|- схф -~-|-ЛСхфк, (227)
где ДсЛфК—ко эф и ци е н т сопротивления от взаимо-
действия, или интерференции, фюзеляжа'и крыла.
Обычно величина Дс\фК равна 5—15°/0 от схр + схф -у-. Встречают-
ся исключительные случаи, когда ДсЖфК = 0 и даже отрицательно.
В неудачных случаях интерференция может достигать величины
30°/о и более.
Индуктивное сопротивление такой комбинации крыла и фю-
зеляжа оказывается обычно значительно большим, чем это
[2
получилось бы у крыла с удлинением Х=^. Получается уве-
личение сопротивления, изменяющееся, как показывают опыты,
приблизительно пропорционально с2; это обстоятельство и
позволяет считать его индуктивным.
121
Но предложению американцев влияние фюзеляжа на крыло
учитывают на летных углах атаки очень простым приемом,
а'Именно: берут при расчетах фиктивное, так называемое
эффективное удлинение крыла, обозначаемое обычно X*,
и на основании опытов принимают во всех формулах:
sk 0,85 X,
(228)
Заметим, что у плохих комбинаций крыльев и фюзеляжа
получается значительно худший коэфициент перехода—около
0,75—0,8, а у очень хороших он доходит до 0,93 и более.
С помощью этого эффективного X* и делается пересчет
крыла.
122
Фиг. 81. Крыло с зализом и
без него.
Коэфициент сопротивления комбинации крыла и фюзеляжа
«следует писать в таком виде:
с2 S
сх = +Дс^к> (229)
коэфициент же подъемной силы будет равен коэфициенту
крыла Су, но площадь крыла при вычислении подъемной силы
нужно брать по фиг. 79.
Американцы считают более надежным пользоваться величи-
ной Х* и для исправления опытов с моделями самолетов в трубах
на индукцию трубы (см. гл. X). Они же рекомендуют пользо-
ваться 7.* при определении скоса потока у хвоста самолета.
Однако этот способ дает хорошие результаты лишь при летных
углах атаки, т. е. примерно от — 2 до 10°. При углах же атаки,
приближающихся к посадочному (t>max), сопрртивление комбина-
ции крыла и фюзеляжа иногда очень резко возрастает, свиде-
тельствуя о наступающем срыве потока с крыла и фюзеляжа.
Самые обширные исследования этого вопроса были сделаны
в Америке, где в трубе переменной плотности были испытаны
при больших числах Рейнольдса 127 комбинаций модели крыла
и фюзеляжа. Повидимому, срыв потока при больших числах Re
несколько смягчается. Примером
может явиться диаграмма фиг. 80,
на которой даны результаты испы-
тания крыла без фюзеляжа и с
фюзеляжем в американской трубе
переменной плотности. До насто-
ящего времени нет надежных ме-
тодов учета этого срыва. Опыты
показывают, что наименьший срыв
получается в случае примыкания
крыльев к середине фюзеляжа (по
высоте). В случае низкопланов
срыв получается весьма сильный;
случай высокоплана дает средний
результат. Таким образом аэроди-
намически наиболее выгодным яв-
ляется так называемый среднеплан.
Устройство „зализов" может
значительно уменьшить срыв по-
тока у крыла (фиг. 81 и 83). Зализы
заполняют верхний угол между
крылом и фюзеляжем и не позво-
ляют воздушным струйкам сильно
расширяться, как это изображено
сверху. Такое расширение вредно, так как при этом уменьшается
скорость потока в струйке и повышается давление в задней части
крыла. Это вызывает стремление пограничного слоя двигаться
вперед, что и служит причиной срыва потока с крыла и фюзеляжа.
123
Описанное явление называется диффузорным эффектом
стыка крыла и фюзеляжа, так как воздух течет в таком
входящем угле подобно струе воздуха в диффузоре, т. е.
с очень большими потерями на завихрения. Потери в диф-
фузоре (см. часть I, гл. ХШ, § 78) тем больше, чем больше
угол диффузора. Вследствие этого в тех случаях, когда нужно
уменьшить эти потери, например в аэродинамических трубах,
углы диффузора делают очень малыми.. То же самое делают и
у самолета, ставя в образующийся угловой канал заполнитель-
зализ, уменьшающий угол расширения струи.
При правильном зализе
резкого срыва потока не наб-
людается и кривая су у
комбинации крыла и фюзеля-
жа идет, так же как и у кры-
ла, с к*.
§ 57. ПОДЪЕМНАЯ СИЛА
Легче всего „предсказать“
вид кривой су = f(a) на летных
углах атаки. Для этого нужно
сначала определить угол атаки
нулевой подъемной силы а0;
его проще всего находить по
способу Мунка (фиг. 82,а).
В случае очень плавной кри-
вой профиля этот угол полу-
чают таким простым постро-
ением: через середину хорды
Фиг. 82. Способ Мунка для нахожде-
ния а0 и угла атаки при ст = 0.
проводят ординату, находят точку К средней линии и, соединив
К с задней кромкой крыла В, получают прямую линию КВ,
даюшую направление скорости потока при нулевой подъем-
ной силе; найдя угол между линией КВ и хордой АВ, полу-
чают а0-
Более точным является следующее построение, также пред-
ложенное Мунком (фиг. 82,Ь). На средней линии находят две
точки К! и К2, с абсциссами 11 и 89%. Через эти точки и зад-
нюю кромку крыла В проводят две линии: К.В и К2В. Биссек-
триса BD получившегося между ними угла дает обычно очень
точно направление потока при нулевой подъемной силе.
Этим способом можно найти и направление потока V, при
котором ст=0. Для этого нужно отложить по хорде отрезки,
равные 4,25%, как показано на фиг. 82, с, и восставить из их
концов перпендикуляры до пересечения со средней линией.
Соединяя прямой полученные на этой линии точки Кг и К2,
найдем направление потока при сщ= 0.
Легко найти наклон линии сд = /(а) на летных углах атаки..
Эта линия близка к прямой и, как мы знаем [гл. IV, § 22,
124
формула (55)], ее угловой коэфициент имеет величину:
а =(230)
На основании американских и других опытов в эту фор-
мулу нужно подставлять не геометрическое удлинение крыльев
самолета к, а эффективное: л* —0,85м Кроме того, величина
а0, теоретически равная 2к, в действительности, при больших
числах Рейнольдса, близка к 0,9 • 2п = 5,6.
В табл. 4 (стр. 37) были даны величины а для разных
размахов л; беря к*, мы сразу получим величину а для само-
лета и сможем построить кривую су = /(«) для углов атаки
до 10°, просто проведя прямую линию с наклоном а, через
точку а0.
Примерно от угла атаки, равного 10°, начинается все увели-
чивающееся отклонение кривой су — f(<z) от прямолинейного
закона и, наконец, в некоторой точке получается су шах, после
которого подъемная сила крыла падает.
Величина Сушах для конструктора весьма важна, так как обычно
площадь крыльев самолета выбирается из условия получения
требуемой техническими условиями посадочной скорости само-
лета. К сожалению, очень трудно‘заранее указать эту величину
для самолета в целом. Американские опыты показывают, что
влияние фюзеляжа, капота, мотора и зализов весьма велико и
может резко снизить величину СуШах по сравнению с Cj,max
изолированного крыла.
На фиг. 83 дана характерная американская диаграмма, полу-
ченная в трубе высокого давления при числе Рейнольдса рав-
ном 8000000, т. е. близком к натуре.
Оказывается, что поляра крыла (она у американцев ледсит
боком) становится совершенно неузнаваемой при фюзеляжах
без зализов. Прлучается срыв потока, и сопротивление возра-
стает в несколько раз; Су тах при этом может уменьшиться на
20 — 40%.
В случае хороших зализов даже у низкоплана Сушах, отне-
сенный к аэродинамической площади, может быть приблизи-
тельно равен Сутах изолированного крыла. Делалось много по-
пыток определить Су тах у крыла в натуру на основании опытов,
проведенных в обычных трубах при малых числах Рейнольдса.
Обычно при таких исследованиях пользуются в качестве исход-
ного материала американскими опытами, так как до 1936 г.
только американцы имели трубы с натурными числами Рей-
нольдса. Лишь в самые последние годы прибавились немецкие
трубы переменной плотности воздуха, такая же английская
труба и французская самолетнач труба.
При обработке этих оРытов учитывают и турбулентность
труб, пользуясь понятием эффективное число Рей-
нольдса.
125
Основные исследования о влиянии числа Re на аэродинами-
ческие характеристики профилей (X == оо) были проведены аме-
риканцами и опубликованы в знаменитом ныне Report № 586
за 1937 г. В нем опыты обработаны по эквивалентному числу
Рейнольдса. Опыты проводились в основном в трубе переменной
плотности, но делались проверки и в самолетной трубе.
Фиг. 83. Поляры крыла и фюзеляжа с зализами и без них.
Главнейшие результаты этих опытов относительно су полу-
чились следующие: угол атаки а0,'при котором су = 0, не зависит
практически от числа Re3. Почти не зависит от числа Re3 и
наклон кривой cy=f(a).
Величина сутах зависит от числа Re очень сильно. По ха-
рактеру протекания кривой Сршах по^/?еэ американцы делят
крылья на четыре класса: Л, В, С и В? Кроме того, по харак-
теру протекания кривой су — /(а) около ее пика крылья можно
разбить еще на классы а, Ь, с и d (фиг. 84).
126
Обработка огромного экспериментального материала позво-
лила американцам установить ряд весьма важных соотношений.
Прежде всего оказалось, что в зависимости от класса крыла
получаются различные законы изменения сутм по числу Re3,
причем очень сильно сказы-
вается и кривизна средней линии
профилей.
На сводной американской
диаграмме (фиг. 85) дана вели-
чина ДСутах» которую НЭДО ВЫ-
читать из Сушах, полученного
для стандартного числа Re3 =
= 8 200000, к которому амери-
канцы приводили все опыты.
Цифры на кривых дают кривизну
профилей в процентах. Класс
кривых указан на самой диаг-
рамме. фиг 84 цетыре класса крыльев по
По этой же диаграмме мож- виду КрИВой с9-/(а).
но исправлять результаты про-
дувки крыльев, сделанные на малых числах Re3. Для этого
нужно поправку Дсутахне вычитать, а прибавлять к полу-
ченному на малом числе Re коэфициенту Сушах- В случае пе-
рехода не к числу Re3 = 8 200 000, а меньшему, нужно брать
разность этих поправок.
Фиг. 85. Сводная диаграмма для поправки Дсутах для разных типов
крыльев.
Толщина профиля сказывается на величине Дгутах слабо. Труд-
нее всего установить класс, к которому нужно отнести про-
127
филь. У американцев получилась довольно пестрая картина.
Мы приводим основные данные для ряда американских крыльев
с указанием также и классов, к которым они принадлежат.
Таблица 9
Американские крылья
Основные характеристики при Re3 ~ 8 200 000
№ Класс по Re Форма пика Щитки и их углы отклонения -^ = 0,2 ь СУ max г хр mtn Дг» у щит « dcy ао = “7“ 0 аа
0009 В а — 1,39 0,0064 — • 0,098
0012 С а — 1,66 0,0069 — 0,099
0015 D а — 1,66 0,0077 — 0,097
0018 Е а — 1,53 0,0088 — 0,096
2412 С а — 1,72 0,0071 — 0,098
23012 D а — 1,72 0,0070 — 0,100
4409 В а — 1,77 0,0073 — 0,096
4412 С d — 1,74 0,0082 — 0,098
4415 D с — 1,72 0,0090 — 0,097
6412 С d — 1,82 0,0091 — 0,098
6712 С d — 2,05 0,0115 — 0,096
8318 Е d — 1,59 0,0127 — 0,095
0012 С а Отклонение щитков 60° 2,35 0,167 0,69 0,091
23012 D а » » 60° 2,48 0,166 0,76 0,088
23012 D а » » 75° 2,54 0,201 0,82 0,085
23015 D а — 1,73 0,0081 —— 0,098
23015 D а Отклонение щитков 75° 2,70 0,198 0,97 0,086
23021 Е b — 1,50 0,0101 — 0,092
23021 Е а Отклонение щитков 75° 2,74 0,191 1,24 0,094
43012 D а — 1,84 0,0079 — 0,100
43012 D а Отклонение щитков 75° 2,65 0,200 0,81 0,082
Таблица эта позволяет в случае необходимости подобрать
американский профиль близкий к заданному: определив по таблице
класс крыла, можно по графику фиг. 85 найти поправку для пере-
хода от лабораторного числа Рейнольдса к натурному. Указание
.128
Фиг. 86. Средняя поправка дСутах в зависи-
мости от величины Re3 (жирная линия).
на протекание кривой у пика (классы а, Ь, с и d} позволит
легко построить и верхнюю часть кривой су = f(a).
На практике чаще всего пользуются крыльями с малой кри-
визной, примерно равной 2 — 4%. Тогда, если ограничиваться
первым приближением, можно делать поправку по некоторой сред-
ней кривой, изображенной на фиг. 86 жирной линией. Здесь мо-
жет получиться ошиб-
ка в + 7%, но так как
при неудачных зализах
можно потерять в су тах
от 0,2 до 0,4 и более,
то для предваритель-
ных расчетов графи-
ком фиг. 86 все же
можно пользоваться.
Заметим еще, что
при большой шерохо-
ватости Крыла fz/max
сильно уменьшается.
Рассмотрим теперь влияние закрылков нагутах. В настоящее
время почти все самолеты снабжаются закрылками или щитками
простого типа или типа Цап (фиг. 87). Эти закрылки очень
Фиг. 87. Щитки-закрылки; Фиг. 88. Эффект закрылка,
сверху простой, снизу Цап.
сильно увеличивают гушах, и их действие часто представляют
в виде добавка Дгу щ, который нужно прибавлять к су, полу-
чающемуся у того же крыла, но без закрылка. Опыты показы-
вают, что кривые су = f(d) идут у крыла с закрылком и у крыла
без закрылка практически эквидистантно (фиг. 88).
Величина гутах=/(/?г) идет у крыла без закрылка и с за-
крылком тоже почти эквидистантно, и можно считать, что
Дсущ не зависит от числа
Величину этой прибавки можно или брать по продувкам
аналогичных профилей или подсчитывать по эмпирическим фор-
мулам, например по формулам ЦАГИ, имеющим следующий вид
Б. н. Юрьев—171—9
129
для простого закрылка:
Дс9 щ = 2 (0,14 4- 0,0165с) (1,18 - 0,045/), (231)
здесь принято, что bm]b = 0,2 и угол отклонения щитка 8Щ — 60°
(фиг. 87).
В случае закрылка типа Цап, т. е. не только поворачиваю-
щегося, но и сдвигающегося назад, можно пользоваться фор-
мулой: _
Дсвцап = 2(0,12 + 0,028с) (1,135 — 0,045/); (232)
здесь принято, что Ьш/Ь = 0,3, угол 8 = 60° и сдвиг щитка назад
равен 15% хорды.
Формулы эти дают лишь ориентировочную величину. В общем
щиток увеличивает с91ПахВ среднем на Дсрщ=0,8—1,2.
Подведем теперь итоги. Если при испытании в трубе при
числе Re3 мы получили у крыла некоторый сутп, то в натуру
он будет равен:
с9 max = су шах 4- (ДСу тах ДСу тах), (23_)
где Дс"тах — поправка, взятая по графику фиг. 85 для Re3
натуры, и Дс^тах— поправка для Re3 трубы.
Если при этом крыло будет снабжено закрылками, то
с9 шах = су шах 4- (Дг^, шах Ьсу шах) 4- Су Щ. (234)
При пользовании продувками, пересчитанными на X = со,
надо уменьшить этот с9 на 3%(гл. IV, § 23).
Глава XII
АЭРОДИНАМИЧЕСКИЕ СВОЙСТВА САМОЛЕТА В ЦЕЛОМ.
СОПРОТИВЛЕНИЕ И ПОЛЯРА
§ 58. ПРОФИЛЬНОЕ СОПРОТИВЛЕНИЕ
Профильное сопротивление крыла очень сильно зависит от
числа Рейнольдса. Так как крыло с нулевой толщиной пред-
ставляет собой пластинку, то по предложению проф. Л. Пранд-
тля принято схр крыльев наносить на известный график трения
по Прандтлю (см. часть I, гл. XII, § 70). На этом графике
откладывают удвоенное значение коэфициента трения пластинки
(а=0) как функцию числа Рейнольдса (фиг. 89). Берут удвоен-
ный коэфициент потому, что у крыла в схр входит трение,
получающееся с двух сторон крыла.
Как известно, трение воздуха о пластинку представляется
тремя кривыми: /—трение при ламинарном пограничном слое
пластинки, // — трение при турбулентном слое и ///—при сме-
шанном. Длина ламинарной части пластинки (при а = 0) равна
Z, = 485000* (часть j, гл. хп, § б7)
130
Кривые сХр min, нанесенные на этот график для какого-нибудь
профиля, идут несколько выше кривых для пластинки и как бы
копируют эти кривые с некоторыми искажениями. График
Прандтля обычно строится в логарифмических масштабах,
тогда кривые I и II обращаются в прямые.
На фиг. 89 мы приводим характерную диаграмму для четырех
американских крыльев: симметричных 0012 и 0015 и несиммет-
ричных 4412 и 4415. Эта диаграмма показывает, насколько
ненадежны опыты, проводящиеся при малых числах Рейнольдса
в старых трубах. Так, при Re9 = 150000 для крыла 4412 полу-
чается сХр = 0,025, а при натурном числе Рейнольдса, равном
Фиг. 89. Минимальный коэфициент профильного сопротив-
ления сХр по эквивалентному чис^у Re3 у характерных
крыльев. Пунктир—коэфициент сопротивления пластинок по
Прандтлю.
Из диаграммы видно, что более или менее закономерное
течение кривых получается после чисел Рейнольдса порядка
одного — двух миллионов. В этих условиях пограничный слой
крыла становится почти весь турбулентным и схр идет почти
эквидистантно переходной кривой III.
Эта кривая представляется уравнением (часть I, гл. XII, § 70).
2cxf = 0,148/?г-,/‘ - 3400 Re-1 (235)
пли более точным:
^'-«да-3400^- (236)
Кривая эта ассимптотически переходят в прямую турбулент-
ного трения.
131
Величину схр крыла можно представить при больших числах
Re такой формулой:
^хр ~ “I” &Схр' (237)
Добавок Дсжр зависит в свою очередь от числа Re и формы
профиля. Делается очень много попыток найти простые формулы
для нахождения этой величины. Все они основаны на обработке
статистики крыльев, а так как точность опытного нахождения
малой величины &схр мала, то у разных авторов получаются
различные результаты.
Можно, например, пользоваться такой формулой:
Эта формула дает довольно хорошие результаты для Re
в интервале от 2000000 до 10000 000. Впрочем, отдельные
крылья немного выпадают из этой зависимости. Вообще нужно
предостеречь от чрезмерного увлечения такими формулами,—
гораздо надежнее и проще пользоваться прямо продувками.
Очень большое значение имеет гладкость поверхности крыла.
В лабораториях обычно испытывают крылья, полированные до
зеркального блеска. На самолетах этого стали добиваться лишь
в самое последнее время. Раньше очень часто крыло изготов-
лялось из гофрированного листового дуралюмина с выступа-
ющими наружу заклепками. Часто крыло покрывалось матовой
шероховатой краской. У старых самолетов это не вызывало
больших потерь, так как эти машины имели плохую аэродина-
мическую форму и сопротивление от трения играло у них
малую роль. У новейших же самолетов полностью „зализанных",
не имеющих выступающих частей, трение, воздуха об их
поверхность является главной частью всего сопротивления.
К сожалению исследование этого вопроса можно проводить
лишь в трубах, дающих натурные числа Re, или на самолетах
в полете.
При малых же числах Re при испытании в трубах получа-
ются самые пестрые результаты. Дело в том, что, как показал
впервые Никурадзе (в Геттингене), трение ламинарного слоя не
зависит от шероховатости поверхности пока бугорки полностью
погружены в этот слой (см. часть I, гл. XIII, § 77). По этой
причине, по примеру проф. Юнкерса, долгое время во всех
странах строили самолеты с гофрированным покрытием. В ста-
рых трубах не обнаруживалось заметной разницы между крылом
гладким и крылом с мелким гофром, выполненным достаточно
точно, например из гипса.
Однако при искусственном создании очень большой шеро-
ховатости, получаемой в лабораториях или путем обклейки
моделей наждачной бумагой или обсыпкой их по клею песком,
нередко получались неожиданно большие последствия: резко
увеличивалось сопротивление и падала подъемная сила крыла.
132
Объясняется это тем, что высокие выступы, выходящие за
пределы ламинарного пограничного слоя, могут перевести этот
слой в турбулентное состояние, и тогда коэфициент трения
нужно брать уже по кривой II (фиг. 89), а не по кривой 1.
Такой переход почти удваивает величину коэфициента трения.
Следовательно, изучение трения можно вести лишь при
числах Рейнольдса, приближающихся к натурным, т. е. когда
пограничный слой у моделей будет таким же, как и на само-
лете.
Фиг. 90. График Шлихтинга: зависимость коэфициента трения cxf от степени
шероховатости поверхности.
Наиболее надежные данные по вопросу о трении турбулент-
ного слоя о шероховатые поверхности были получены Шлих-
тйнгом. Он характеризует гладкость крыла относительной
величиной где ks—высота бугорков шероховатости и I —
Ks
длина пластинки. По его собственным опытам и произведенной
им обработке опытов Никурадзе он построил график (фиг. 90),
дающий cxf пластинки в зависимости от Re.
На этом графике даны кривые для пластинок с различной
степенью шероховатости, создаваемой посыпанием их по клею
песком или карборундом с зернами разной крупности. На
этом же графике приведены значения числа Res для отдельных
бугорков, вычисленные по формуле: Res — ^. Вместо этого
133
графика можно пользоваться эмпирической формулой Шлих-
тинга:
cxf - (1,89 + 1,621g (269)
Как видно из графика, шероховатость сказывается тем больше,
чем больше число Re, т. е. скорость полета. Кривая сх1 у глад-
кой поверхности идет, все время снижаясь, кривые же сх{ для
шероховатой поверхности идут почти горизонтально.
Насколько важна хорошая полировка крыльев видно из ан-
глийских исследований, проведенных в Национальной физичес-
кой лаборатории (NPL).
Были испытаны два крыла с американским профилем NACA
0012 и английским профилем RAF-34. Оба дали одинаковые ре-
зультаты, и мы приводим лишь две диаграммы для крыла NACA
0012. Крылья испытывались с разной степенью шероховатости.
Кривая А на фиг. 91 дает турбулентное сопротивление глад-
Фиг. 91. Изменение схр Ш1П в зависимости от Re и
шероховатости профиля по опытам NPL.
кой пластинки, кривая В—сопротивление крыла с отполирован-
ной вручную поверхностью, кривая С—крыла, нижняя поверх-
ность которого покрыта карборундовыми зернами диаметром
0,025 мм, и кривая D—крыла, вся поверхность которого пок-
рыта такими же зернами. Как видим, эффект такой шерохова-
тости очень велик.
Такая же картина получается и для коэфициента подъемной
силы (фиг. 92j. На этой диаграмме добавлена еще кривая А соп-
ротивления крыла с хромированной зеркальной поверхностью.
Таким образом на диаграмме cv = /(?) ясно улавливается различие
в аэродинамике крыла с поверхностью, полированной ручным
способом, и с поверхностью наивысшей достижимой гладкости.
Все эти, весьма существенные для самолета особенности вли-
яния шероховатости на аэродинамику крыла, совершенно не
отражаются в опытах при малых числах Re, меньших 1000000.
В качестве примера крыльев, дающих минимальное профильное
сопротивление, приведен график фиг. 92а.
Так как многие конструкторы все еще сохраняют выступаю-
щие наружу заклепки на поверхности крыльев, то во многих
лабораториях занимались вопросом о влиянии их на cXf крыла.
134
Наиболее подробные опыты были проведены в ГерманииШлих-
тингом. Оказалось, что заклепки можно свести в расчете к эк-
вивалентной шероховатости крыла, причем если лобовая пло-
щадь заклепок равна FT и высота h, то в зависимости от от-
ношения -у- можно найти коэфициент а, с помощью которого
найдется эквивалентная гладкость поверхности:
l I
ks ~ ah’ (240)
График Шлихтинга приведен на фиг. 93.
Опыты Шлихтинга относятся
к плоской пластинке, и для пе-
рехода к крылу следует к полу-
ченным таким образом величи-
нам добавлять величину Дслр,
вычисленную хотя бы по фор-
муле (238).
Исследования проф. Б. Т. Го-
рощенко показали, что высту-
пающие „головки заклепок
при нормальной, встречающейся
Gottingen 387
висимости от шероховатости
профилей по опытам NPL
0,01(Г
Схр тщ
0,009
0,006
0,0 ПЬ
о,оог
о
8,3 6 62, 6,4 6,6 6,8 7
Фиг. 92а. Крылья,
ное профильное
дающие минималь-
сопротивление.
обычно, густоте эквивалентны по сопротивлению сплошной ше-
роховатости с высотой бугорков около 0,1 мм, и для самолета
с V =500 км/час они способны понизить скорость на 6,5°/0,
т. е. на 33 км]часи*
* „Приближенный расчет лобового сопротивления, вызываемого заклеп-
ками", Технические заметки ЦАГИ № 175.
135
Отсюда можно сделать единственно правильный вывод: нужно
решительно отказаться от устаревших конструкций крыла с вы-
ступающими наружу заклепками, с помятыми листами, с пло-
хой окраской и перейти на зеркально
Фиг. 93. Учет заклепок по
Шлихтингу методом экви-
валентной шероховатости.
полированные поверхности.
§ 59. ИСПРАВЛЕНИЕ КОЭФИЦИЕНТА
СОПРОТИВЛЕНИЯ ФЮЗЕЛЯЖА
Сопротивление фюзеляжа весьма
сильно зависит от числа Рейнольдса.
Чем лучше форма фюзеляжа, тем бли-
же его полное сопротивление к сопро-
тивлению от трения.
Для грубых подсчетов оказалось
возможным разбивать все сопротивле-
ние фюзеляжа X на две части:
X = Xf+Xb,
гее Xf — сопротивление, зависящее от трения, а Хо — сопротив-
ление от распределения давления по фюзеляжу. Принимая в
первом приближении скорость, с которой воздух трется о бо-
ковую поверхность фюзеляжа S6, равной скорости полета, мо-
жем написать:
X^cxf^SoV2 + cM^S^-
г- Я.О2 Л- о
здесь Зф = -4 площадь миделя фюзеляжа, а 5б — поверх-
ность, по которой происходит трение. Можно положить, что
S6 = &cDL, (241)
где D—диаметр фюзеляжа (при овальном сечении D равновели-
кого круга), L—его длина и s — коэфициент, зависящий от формы
фюзеляжа; этот коэфициент у обычных форм близок к 0,9—0,7.
Коэфициент сопротивления фюзеляжа может быть написан
теперь в виде:
X So .
= ;-----= cxf — + с,о- (242)
5ф V*
Отношение может быть написано таким образом:
оф
== - 4£ 1А
^Ф *’ (243)
4
где — удлинение фюзеляжа, равное Подставив это выра-
жение в предыдущую формулу, получаем окончательно:
схф = 4г1ф cxf + сх0. (244)
136
Учитывая, что скорости на средней части фюзеляжа несколь-
ко больше скорости полета, можно брать в этой формуле
es^l; тогда получается очень удобная формула:
Слф — 4Хф cXf Схо. (245)
Величину Сх/ следует брать по графикам Прандтля или Шлих-
тинга, учитывая когда нужно шероховатость поверхности и
наличие наружных заклепок. Величина схо зависит от формы
фюзеляжа. У наилучших аэродинамических форм, близких к
корпусу дирижабля, величина сх0 очень мала и может быть при-
нята равной нулю. У обычных фюзеляжей очень хорошей формы
она лежит в пределах от 0,01 до 0,02, и лишь в случае грубых
форм эта величина поднимается до значения 0,03 и больше.
Капот NACA с мотором добавляет к сопротивлению фюзе-
ляжа еще от 0,005 до 0,01. Точный расчет капота и охлажде-
ния мотора мы здесь рассматривать не будем.
Заметим, что описанные расчеты носят грубо прикидочный
характер, так как результатов хороших опытов с фюзеляжем,
испытанным на полных числах Re, почти не опубликовано.
Пользоваться же данными продувок, полученными на малых чи-
слах Re, тоже нельзя, так как без поправок здесь возможны
ошибки в 1,5—2 раза.
§ 60. СВОДКА ЛОБОВЫХ СОПРОТИВЛЕНИЙ
Для аэродинамического расчета необходимо иметь полную
поляру всего самолета. В предыдущих параграфах мы разоб-
рали вопрос о взаимном влиянии крыла и фюзеляжа и научи-
лись исправлять опыты на число Рейнольдса.
Осталось учесть сопротивление малых деталей самолета.
Обычно оно учитывается простым суммированием сопротивле-
ния всех не дающих подъемной силы деталей самолета. Такое
сопротивление называется вредным лобовым сопротивлением
самолета и обозначается через ХР. Очевидно:
п
1 2 к
где k обозначает текущий номер детали.
Вредное сопротивление самолета выражают через коэфи-
циент вредного лобового сопротивления в таком
виде:
Сх = 4 i cxhSk teY. (246)
2-SV2 J i \v /
2
Из формулы (246) следует, что для такого расчета нужно знать
Vk z
величину -у- для данной детали, т. е. знать скорость набе-
гающего на нее потока, которую можно определить при про-
дувке схематической модели самолета путем замера маленькой
137
трубкой Пито истинных скоростей потока в точках, где будут
находиться эти детали или же вычислить Vk с помощью формул
индукции.
К сожалению, очень часто этого не делают и считают, что
-£^1. При таком допущении формула принимает вид:
м CxkSk
CXBV=1-^-. (247)
О
Для вычисления этой величины составляют обычно сводку
лобовых сопротивлений по форме табл. 10.
Величину сХВр ненесущих частей самолета иногда для на-
глядности заменяют сопротивлением эквивалентной плас-
тин к и, т. е. такой плоской пластинкой, которая имеет при том же
скоростном напоре сопротивление, равное сопротивлению всех
ценесущих частей самолета. Площадь этой пластинки обозна-
чают через <з и считают ее коэфициент сопротивления равным
1,28. Получают:
Отсюда
1,28 aq = cXBpSq.
__ с XBpS_^CjckSk
Эта величина у новейших самолетов очень мала; иногда у
малых машин она равна лишь 0,2—0,4 мг. У больших самолетов
она растет, достигая значений от одного до нескольких ква-
дратных метров.
Гораздо удобнее пользоваться отвлеченной площадью
вредной пластинки, т. е. величиной
° SCsj-Sfc схвр /^404
S - 1,28 S — Т28 ' V ’
Оказывается, что эта величина почти не зависит от разме-
ров самолета и является очень хорошей характеристикой со-
вершенства его аэродинамической формы.
Наилучшие в аэродинамическом смысле самолеты имеют
o/S = 0,005—0,01, хорошие от 0,01 до 0,02, удовлетворительные
от 0,02 до 0,03 и плохие свыше 0,03.
Величину а/З удобно давать в процентах. Можно пользо-
ваться следующей классификацией самолетов по их аэроди-
намическому совершенству.
Для самолетов первого класса величина а/З* 100% не более 1 %,
для самолетов второго класса эта величина равна от 1 до 2%,
для третьего класса — от 2 до 3% и т. д. Заметим, что хоро-
шая аэродинамика самолета не гарантирует хороших
летных качеств, так как последние зависят еще от веса
конструкции самолета, от его нагрузки, от мощности мотора
и т. д.
138
Таблица 10
Сводка лобовых сопротивлений
Наименование деталей Число Размеры Поправки Мидель Re Схк Vk V С /W CxfcSfcl -у ) %
Фюзеляж .... Радиатор .... Фонарь-кабина . Стойки Концевые крепле- ния стоек . . . Расчалки .... Концевые крепле- ния расчалок.. Ноги шасси * . . Колеса Подкосы .... Выхлопные трубы Головки цилинд- ров Кабанчик управ- ления закрыл- ками Костыль .... Трубка Пито . . Горизонтальное оперение . . . Вертикальное опе- рение
Сумма (при уб- ранном шасси). Сумма (при опу- щенном шасси) Общая добавка на интерференцию, например,4-5% Полная сумма . . 100%
Коэфициент сх для различных деталей берут по справочникам или по
первоисточникам (главным образом из американских и английских репортов).
139
При указанной манере расчета пренебрегают взаимными влия-
ниями, которые оценивают просто как процентную добавку. К
сожалению, до сих пор еще не разработана более строгая ме-
тодика подсчета лобовых сопротивлений самолета.
§ 61. ПОСТРОЕНИЕ ПОЛЯРЫ САМОЛЕТА
После всех описанных исправлений аэродинамических коэ-
фициентов поляру всего самолета строят весьма простым при-
емом. Считают, что
Су ~ Су кр Су оп, (250)
где б’укр — подъемная сила крыльев и су оп — подъемная сила
оперения. Напомним, что фюзеляж уже вошел в вычисление
подъемной силы в неявном виде, так как площадь крыльев
бралась условно, по фиг. 79, и, кроме того, вместо геометри-
ческого удлинения к было взято эффективное X*.
Подъемную силу оперения во многих случаях можно отбра-
сывать из-за ее малости, хотя учет ее очень несложен и описан
у нас в § 62.
Следовательно, в прикидочных расчетах принимают:
Су = Сукр- (251)
Лобовое сопротивление считают суммой индуктивного, про-
фильного и вредного сопротивлений, т. е.
А’ = Xi + Хр + Xap = cXi <fS-[-cxp qS + 1,28 oq
или, в коэфициентах
= А = Cxi+ сх1> + схвр = “L +сХР + 1,28 “• (252)
Q Д/< • Д [J I Д/ i Д>Д^ I z Q
Первый член берут,
подставляя в него
0,8эХ; второй член,
т.е.Сср, исправляют, как
было описано, на число
Re, на турбулентность
потока в трубе и на ше-
роховатость поверхно-
сти модели. Член сХВр
вычисляют по сводке
лобовых сопротивлений,
учитывая интерферен-
цию &сх.
В случае отсутствия
опытных данных испытания модели в трубе величину сХр вы-
числяют по геометрическим характеристикам профиля.
140
Если мы начертим на фиг. 94 сначала поляру только крыла,
то для перехода к поляре самолета следует добавить по гори-
зонтали отрезки г^вр = 1,28-у; пунктирная поляра и будет
полярой самолета. Можно вместо этого просто перенести на-
чало координат влево на ту же величину схвр. Построение, как
видим, очень простое. Поляру самолета можно уточнить, учтя
влияние на нее хвоста самолета. В таком виде поляра, строго
говоря, относится лишь к режиму планирования. При моторном
полете струя винта обдувает различные части самолета и весьма
заметно увеличивает их сопротивление. Однако обычно эту
обдувку учитывают отдельно по методам, излагаемым в курсе
воздушных винтов, и на поляре она не отражается.
Учет сводится к искусственному уменьшению тяги винта,
равному увеличению сопротивления от обдувки. Обозначая истин-
ную тягу винта через Р, а прибавку сопротивления самолета
от обдувки через ДА", пользуются эффективной тягой
РэФф=Р~ДХ. (253)
Этот прием значительно упрощает все расчеты, так как по-
ляра самолета не требует учета обдувки от винта, и в первом
приближении может считаться неизменной.
§ 62. ИСПРАВЛЕНИЕ ПОЛЯРЫ НА ВЛИЯНИЕ ХВОСТОВОГО ОПЕРЕНИЯ
Обычно при аэродинамическом расчете поляру самолета не
исправляют на подъемную силу и сопротивление хвостового
оперения. Это влияние у обычных
самолетов невелико. Однако учет ----— z
влияния хвоста не представляет
никаких трудностей и может быть ( о 7 г0
'легко введен в аэродинамический ,и
расчет (фиг. 95).
Для полета на каком-нибудь фИГ. 95, учет влияния хвостового
угле атаки горизонтальное хвосто- оперения на крыло,
вое оперение должно уравнове-
сить аэродинамический момент, возникающий от крыльев
Этот момент получается по формуле:
Л1к ~ ц.т qSL,
где ст ц.т — коэфициент момента крыльв, отнесенный к
центру тяжести самолета, a L — условная длина от центра тя-
жести до шарниров руля высоты. Летчик, действуя на ручку
управления, отклоняет руль высоты на такой, обычно малый,
угол, что получающаяся на горизонтальном оперении подъем-
ная сила Уг.о, действующая на плече, приблизительно равном L,
дает момент:
^4г.о == Уг.оЛ — ст ц.т qSL = /Ик j
отсюда
Уг.о — гтц.т^5. (254)
141
Знак минус ставим потому, что положительному моменту,
берущемуся у нас на пикирование, соответствует сила Уг.о, на-
правленная вниз (фиг. 95). Эта сила алгебраически прибавится
к подъемной силе крыла. Вместо силы удобнее прибавлять к
коэфициенту подъемной силы величину:
Дсу = = ст ц, г, (25э)
т. е. получается очень простая формула; добавок подъемной
силы, в коэфициентах, равен коэфициенту момента крыльев с
обратным знаком. Момент cmu.T крыльев очень легко подсчи-
тать для нескольких углов атаки (см. часть I, гл. IX, § 51).
Рассмотрим теперь добавочное сопротивление, получаю-
щееся у хвоста. Оно возникает, очевидно, от профильного со-
противления горизонтального оперения и от его индуктивного
сопротивления, связанного с углом скоса потока у хвоста
Даг.о, получившимся от действия крыла, и с углом скоса пото-
ка Да' от самоиндукции хвостового оперения.
Очевидно, полное сопротивление оперения определится те-
перь по формуле:
Х = ХР + Уг.о(Даг.о + Да').
Профильное сопротивление Хр обычно вводится в сводку
лобовых сопротивлений и его учитывать здесь не приходится, —
оно уже было учтено при построении поляры фиг. 94. Нужно
только, подсчитывая его, брать несколько повышенную вели-
чину его коэфициента сопротивления, учитывая среднее откло-
нение руля и интерференцию фюзеляжа. Это обычно и делают,
принимая для хвостового оперения сх^ 0,015.
Подсчитаем поэтому лишь индуктивную часть сопротивления
горизонтального оперения, т. е.
Xi = Гг.о(Даг.о4-Д«').
Разделив обе части этого выражения на qS, получим:
Д^ас = Ст ц.т(Даг.о 4" )• (256)
Угол скоса потока можно найти по формуле: Даг. «~2Да или
cv
^олее точно по формуле (111), в которой Да = Угол скоса
с Y
у оперения от самоиндукции будет Да' =-^— = — =
_ У-.е___S___ _ _ S_________1_ .
5Г 0<лг 0 т щ т Sr 0 лХг 0
После этого основная формула (256) перепишется в таком
виде:
^•сх = — ста. —стц.(257)
По этой формуле очень легко для нескольких углов атаки
подсчитать величину Дсж, дающую- добавок сопротивления
142
к поляре от действия хвоста. Таким образом для каждого угла
атаки можно найти Ьсу и &сх, с помощью которых получится
новая поляра, исправленная на действие горизонтального опе-
рения (фиг. 96).
Ввиду малости поправок их можно вычислять грубо, беря,
как мы здесь сделали, угол скоса у хвоста равным удвоен-
ному углу скоса у самого крыла. Можно здесь с достаточной
точностью применять формулы Мунка
(112) И (ИЗ).
Более точно эти поправки можно найти,
проделав подробный расчет устойчивости
самолета.
Мы этими вопросами здесь заниматься
не будем, так как они проходятся в курсе
динамики самолета.
§ 63. ИСПРАВЛЕНИЕ ПОЛЯРЫ НА ВЛИЯНИЕ
БОЛЬШИХ СКОРОСТЕЙ ПОЛЕТА
Непрерывный рост скоростей полета
Фиг. 96. Исправление
поляры на влияние
хвостового оперения.
самолетов заставляет в настоящее время
очень внимательно относиться к иследо-
ваниям влияния больших скоростей на
аэродинамические свойства крыла и дру-
гих деталей самолета.
В части I, гл. X, § 59 мы подробно рассмотрели число Берстоу
(Ва — как критерий подобия при больших скоростях полета.
Так как при больших скоростях полета увеличивается и число
Рейнольдса \Re = то современная авиация испытывает
крайнюю нужду в получении надежных характеристик аэроплан-
ных деталей в функции этих двух параметров. Как мы знаем,
аэродинамические коэфициенты являются сложной функцией
типа:
сх = fx (формы, а, р, Re, Ва),
су ~fv (формы, а, р, Re, Ва),
cm = fm (формы, а, 8, Re, Ва).
(258)
Конструкторов быстроходных самолетов интересуют числа
Re порядка нескольких миллионов (8 — 20 млн.), и числа Ва
близкие к единице. Это значит, что скорость потока в трубах
должна приближаться к скорости звука, которая в нормальных
условиях равна 340 м/сек = 1220 км/час. К сожалению, имею-
щиеся трубы не дают возможности получать одновременно боль-
шие числа Re и Ва. Большие самолетные и винтовые трубы
дают скорость потока, равную всего лишь 50—70 м1сек, трубы
переменной плотности при больших числах Рейнольдса также
имеют малые скорости, порядка 30—60 м/сек.
143
Лишь в сравнительно малых трубах удается получить боль-
шие числа Ва, но при этом числа Re получаются очень малые,
порядка сотен тысяч.
Вследствие этого приходится пользоваться разными упроща-
ющими гипотезами. Например, заимствуя у артиллеристов,
можно писать для тела данной формы и данного угла атаки
сх = Cxof{.Bd) = (Re)f(Ba),
т. е. считать сх зависящим от чисел Re и Ва как от независи-
мых множителей. Эта гипотеза является простейшей, но суще-
ствуют и другие.
Пользуясь этой гипотезой, сх исправляют таким образом:
сначала находят сх0, учитывая число Re, а затем множат та
функцию скорости f(Ba).
К сожалению, найти эту функцию чисто теоретически удалось
лишь для чисел Ва> Для интересующего же конструктора
интервала: 0,2 < Ba < 1 приходится базироваться на опытных
материалах, которых в настоящее время опубликовано очень
мало. Наилучшими исследованиями являются опыты, проведенные
в Америке Стэком и Денхофом (NACA), которыми были испы-
таны 16 различных профилей на числах Ва от 0,40 до 0,9 при
числах Re от 350000 до 750000.
Во всех этих опытах коэфициент профильного сопротивления
крыла резко повышался уже начиная с Ва^0,7, что соответ-
ствует скорости полета 850 км[час. Лучшими профилями ока-
зались тонкие симметричные и слегка несимметричные.
Мы приводим результаты ис-
пытания трех американских сим-
метричных профилей NACA —
0006, 0009 и 0012. На фиг. 97
Фиг. 97. Влияние числа Ва на с min фиг. 98. Влияние числа Ва на а=~.
r UCL
и 98 представлены зависимости схр „ип и наклона кривой су = /(а)
от Ва. Такие же по характеру зависимости получаются и у
других крыльев.
В общем при числе Ва, лежащем в пределах 0,8 — 0,9, коэфи-
циент профильного сопротивления возрастает скачком в нес-
колько раз. Таким образом при скоростях порядка 900—1000 км[час
сопротивление крыльев возрастает в 4—6 раз. По такому же
приблизительно закону .возрастает и сопротивление фюзеляжа
и прочих частей самолета.
На самолете в целом влияние числа Ва должно сказываться
еще раньше, так как скорость потока, обтекающего крыло и
фюзеляж, в ряде мест будет больше скорости полета, и многие
детали могут начать обтекаться со скоростью потока большей,
чем скорость полета самолета.
Как известно, на спинке крыла у самой передней кромки
наблюдается разрежение воздуха в четыре скоростных напора,
а иногда даже до девяти скоростных напоров. По теореме
Бернулли это означает, что там получаются двойные и даже
тройные скорости по сравнению со скоростью потока вдали.
Вследствие этого ряд мелких деталей (например, заклепки,
фары, стойки) могут обтекаться со скоростью, близкой к ско-
рости звука, хотя самолет летит со скоростью 120—150л//сек.
Подъемная сила изменяется с числом Ва по закону, представ-
ке
ленному на фиг. 98: сначала коэфициент а = растет, дости-
гает максимального значения при Ва^ 0,8 и затем резко падает.
Глауэрт нашел теоретически, что этот закон можно пред-
ставить формулой:
* 1
Су — Су у----------f
у у V1 — Ва*
(259)
где су — опытная величина, полученная при малых числах Ва,
а с'у—исправленная величина. Формулой (259) можно пользо-
ваться до Ва -^0,8. Она дает грубое приближение к действи-
тельности, однако при малых числах Ва, порядка 0,5, ее при-
ближение достаточно.
В общем же обнаруженное в последние годы увеличение
сопротивления деталей самолета при Ва, близком к единице,
было давно известно артиллеристам. Современная наука еще
не открыла способов к его уменьшению. Единственным сред-
ством остается постройка очень тонких крыльев, толщиной
4 — 6°/0 и уменьшение миделя всех деталей самолета.
Для расчета крыльев при больших скоростях в настоящее
время можно рекомендовать пользоваться лишь результатами
американских продувок, опубликованными в репорте NACA 492,
1934 г.
Б. H. Юрьев—171 —to
РАЗДЕЛ II
КРЫЛО С ИЗМЕНЯЮЩЕЙСЯ ПО РАЗМАХУ ЦИРКУЛЯЦИЕЙ
Глава XIII
ТЕОРИЯ КРЫЛА С ИЗМЕНЯЮЩЕЙСЯ ПО РАЗМАХУ
ЦИРКУЛЯЦИЕЙ
§ 64. СКОС ПОТОКА У КРЫЛА С ИЗМЕНЯЮЩЕЙСЯ ПО РАЗМАХУ
ЦИРКУЛЯЦИЕЙ
До сих пор мы рассматривали лишь схему П-образных вих-
рей. В гл. II уже указывалось, что такая схема физически не-
осуществима, и на самом деле циркуляция скорости вокруг
крыла является функцией z, т. е.
г (260)
В этом случае вихревые усы сбегают по всему размаху
крыла, образуя вихревую пелену, неустойчивую и обычно до-
вольно быстро сворачивающуюся за крылом в два вихревых
уса (фиг. 11). Разобранная в предыдущих главах теория оказы-
вается вследствие этого лишь грубо приближенной.
Мы рассмотрим более строгую теорию, основанную на учете
не двух вихревых усов, а целой вихревой пелены,состоящей
из бесчисленного количества вихрей. И в этой теории прихо-
дится прибегать к различным допущениям, так как точные
решения оказываются или слишком громоздкими или просто
недоступными для математического анализа.
Из основных допущений этой теории, которую в дальнейшем
будем называть теорией крыла с изменяющейся по размаху
циркуляцией, можно отметить следующие: 1) вихри считаются
прямолинейными и направленными по скорости невозмущенного
потока, т. е. по скорости V\ 2) обтекание сечений происходит,
как у крыла в плоскопараллельном потоке.
На самом деле пелена обычно сворачивается в два уса,
и обтекание профилей, особенно у концов крыла, происходит не
в одной плоскости, а в пространстве трех измерений.
Тем не менее, несмотря на упрощения, эта теория оказы-
вается гораздо более точной, чем теория с П-образныл и вих-
рями.
Перейдем теперь к выводу основных формул этой теории.
146
Пусть мы имеем крыло (фиг. 99), на которое набегает воздуш-^
ный поток. Возьмем нашу стандартную поточную систему ко-
ординат, у которой ось х направлена по скорости V, ось у
лежит в плоскости симметрии крыла и перпендикулярна к V
и ось z направлена по левому крылу; начало координат поместим у
передней кромки центроплана.
Если мы проведем два бес-
конечно близких сечения это-
го крыла / и //, то циркуляция
вокруг крыла в этих сечениях
будет равна соответственно
и Г2; разность 1\ — Г2 ПРИ
убывающей обычно к концам
крыльев циркуляции равна
—dV, По теореме Гельмгольца,
эта разность не может унич-
тожиться и между сечениями I
и 7 обязательно сбежит вих-
Фиг. 99. Крыло конечного
размаха при Г«=/(4
ревой ус, вращающийся так,
как показано на фиг. 99, и
имеющий циркуляцию — с/Г.
Такие же рассуждения можно привести для любой точки
крыл^, и мы приходим к заключению, что' с крыла сбегает
бесчисленное количество бес-
Фиг. 100. Определение скоса.
конечно слабых вихревых ни-
тей (фиг. 10).
Рассмотрим действие такой
системы вихрей на какую-
нибудь точку А присоединен-
ного вихря. На фиг. 100
показан вид крыла спереди.
Циркуляция скорости у обыч-
ных крыльев имеет вид кри-
вой EDC. Наточку А, которую
зададим ее абсциссой z, будет
действовать любой, беско-
нечно слабый вихрь. Возьмем
вихрь, лежащий на абсциссе
С и сбежавший на участке z/C.
Этот вихрь по формуле полу-
шнура (гл. I, § 6), вызовет в
точке А элементарную ско-
рость
dvg = . ,?Г- .. (261)
у 4л (С — г) v
Полная скорость скоса
получится интегрированием этого выражения по всему размаху
крыла, т. е.
147
e!li г12
vg = -±- -r^— = -r- (262)
y 4л J С — z 4л J Z — z '
—Z/2 —Z/2
Здесь Г рассматривается как функция С, а величина z для вы-
бранной точки А будет постоянной. Скорость %zff будет в общем
случае величиной переменной по размаху, т. е.
=/(*)• (263)
Формула (262) является основной в излагаемой теории. Эта фор-
мула, простая по внешнему виду, в математическом отношении
оказывается довольно неудобной. Дело в том, что для обычных
форм крыльев подинтегральная функция имеет разрыв при С = z,
dr
а на концах крыла получаются бесконечные значения для
dr
На фиг. 100 внизу построены кривые и . Следова-
тельно, мы имеем здесь дело с несобственным интегра-
лом, т. е. с таким, при решении которого необходимо для
каждой функции Г исследовать пределы, к которым этот инте-
грал стремится. Даже в случае простых функций Г решение
этого интеграла представляет немалые затруднения.
В дальнейшем мы снова вернемся к вопросам вычисления
этого интеграла.
Зная скорость скоса, получим угол скоса по формуле:
V
---(264)
здесь величина vg переменна по размаху и, следовательно,
Да = <р (z). (265)
Истинный угол атаки сечения будем попрежнему вычислять
по формуле:
а/ = а' — Да . (266)
Однако теперь все эти величины будут переменными по
размаху, так как даже угол атаки а' в общем случае, у закру-
ченного крыла, будет функцией координаты z.
Углы а( и Да мы будем писать попрежнему, местный же
угол атаки будем отмечать штрихом. Угол а будет у нас далее
обозначать угол атаки центроплана.
Напомним еще раз, что через С мы будем обозначать абс-
циссы вихрей, а через z — абсциссы точек крыла.
§ 65. СИЛЫ, ДЕЙСТВУЮЩИЕ НА КРЫЛО С ИЗМЕНЯЮЩЕЙСЯ
ПО РАЗМАХУ ЦИРКУЛЯЦИЕЙ
Перейдем теперь к вычислению сил, действующих на крыло
с переменной циркуляцией. Найдем сначала подъемную силу
крыла Y.
14S
Выделим у крыла бесконечно-малую полоску шириной dz
(фиг. 101). Допуская, что поток в пределах этой полоски бли-
зок к плоскопараллельному, можно написать формулу Н. Е. Жу-
ковского в таком виде:
dY = fiVdz. (267)
Отсюда видим, что величина
< = РГИ
(268)
дает погонную нагрузку (на 1 м) лонжеронов крыла подъемной
силой. Следовательно, кривая Г=/(?) представляет в некото-
ром масштабе эпюру нагружения крыла. Поэтому крылд с
П-образными вихрями очень часто называют к р ы л о м с по-
стоянной по размахуна^
грузкой, а крыло с перемен-
ной циркуляцией — крылом с
переменной по размаху
нагрузкой.
Подъемную силу Y всего
крыла получим суммированием
всех полосок, на которые раз-
бито крыло. Следовательно,
Фиг. 101. Полоски, на которые
разбивается крыло.
+Z/2
у = рИ j Ydz. (269)
—Z/2
Величина этого интеграла может быть найдена по диаграм-
ме фиг. 100; она равна площади S, ограниченной кривой Г и
осью абсцисс z, т. е.
Г = рИ2. - (270)
Подъемную силу крыла можно вычислить еще следующим
приемом (фиг. 101). Если мы, зная истинный угол атаки крыла
а,, возьмем по характеристике его профиля, т. е. при к=со,
местное значение с', то для полоски шириной dz сможем на-
писать:
dY — c'v^bdz И*,
(271)
а для всего крыла, суммируя все полоски, получим:
-Н/2 +1/2
Г = ф j c’bdz — q J c'ybdz. (272)
—//2 — иг
Найдем теперь индуктивное сопротивление крыла с задан-
ным законом циркуляции. Для этого рассмотрим бесконечно
узкую полоску шириной dz, на которую действует подъемная
сила dY (фиг. 101). Поток в этом месте будет скошен на угол
Да, а так как подъемная сила dY перпендикулярна к скошен-
ному направлению потока, то получится проекция этой силы на
149
ось х, называемая индуктивным сопротивлением полоски, т. е.
dXt=dYhi. (273)
Подставляя сюда значения dY = pVVdz и Да =—полу-
чаем :
dX( = — pTvydz. (274)
Величина
dX,
= - fI4 (275)
дает погонную нагрузку лонжеронов крыла лобовым сопроти-
влением. Полная сила индуктивного сопротивления получится
в результате суммирования элементарных сил, т. е.
+1/2
Xi = -p f Yv„ dz. (276)
—Z/2
Простая по виду формула индуктивного сопротивления на
самом деле очень сложна. Подставим в нее значение <иу и от-
метив значком что производная от Г берется по С, получим:
H-Z/2 +Z/2
Р Г Г 1
Х==-т-- / Гйг I -±-г----------=
1 4л J J +, — z
—1/2 —1/2
-il/2 i Z/2
р г г dVr 1
= -/- I -----------------d^dz. (х77)
4л J J d\ С — г v
—Z/2 —Z/2
Как видим, получилось довольно сложное выражение, при-
чем подинтегральная функция имеет разрыв при г = С, а про-
йГг
изводная обычно обращается в бесконечность на концах крыла.
Это очень сильно затрудняет вычисления по формуле (277).
Найдем теперь величину профильного сопротивления. Зная
истинные углы атаки а;, мы можем по результатам испытаний
профилей (гл. IV, § 20) найти с' ; значок штрих (') будет
указывать, что любая величина, в данном случае с' , берется
для истинного местного угла атаки по характеристике крыла,
пересчитанной на бесконечное удлинение.
Величина с'хр будет в общем случае изменяться по размаху.
Выделив полоску шириной dz, мы сможем написать:
dXp = c'xp^bdzV\ (278)
Полное профильное сопротивление получится как сумма эле-
ментарных сопротивлений, т. е. по формуле:
+ Z/2 -4-Z/2
= J C'Xpbdz~4 f C'XPbdz- (279)
—Z/2 —112
150
Получим теперь уравнение связи для крыла с переменной
по размаху циркуляцией. Взяв опять полоску крыла шириной
dz, напишем для нее оба полученных выражения подъемной
силы — формулы (267) и (271), т. е.
dY = c’yLbdz
Отсюда, приравнивая их, получаем:
(280)
т. е. ту же самую формулу, как и у крыла с П-образными вих-
рями, но только теперь в нее надо подставлять местные
значения величин Г, с' и Ь, так как они изменяются при изме-
нении z.
Уравнение связи также является основным уравнением изла-
гаемой теории.
§ 66. АЭРОДИНАМИЧЕСКИЙ МОМЕНТ У КРЫЛА С ИЗМЕНЯЮЩЕЙСЯ
ПО РАЗМАХУ ЦИРКУЛЯЦИЕЙ
Найдем, наконец, величину аэродинамических моментов крыла.
Будем определять моменты Мх, Мд, Mz относительно осей ко-
ординат. Начало координат выби-
раем у передней кромки центро-
плана (фиг. 102); координаты перед-
них кромок сечений крыла обозна-
чим через хА и уА.
Тогда на полоску шириной dz
будут действовать: подъемная сила
dY, сопротивление dX — dXf + dXp
и аэродинамический момент dM-A, ....
Отнесенный К передней кромке Фиг. 102.' (Жределение""полного
Сечения, Т. е. К точке А. аэродинамического момента
Элементарный момент выделен- относительно начала координат,
ной полоски относительно оси Oz получится из чертежа в
таком виде:
б?7Иг = dMzA + dYxA — dXуА.
Полный момент получится суммированием всех полосок и
будет равен:
+Z/2 т(/а +Z/2
Mz = f dMzA+ J dYxA- fdXyA. (281)
—?/2 ~ —Z/2 —Z/2
Все величины здесь — функции z. Расчет по формуле (281)
можно вести как в поточных осях, так и в связанных. При
расчетах удобнее пользоваться не силами, а аэродинамическими
151
коэфициентами. Замечая, что:
dX = c'xbdzq\
dY = c'ybdzq-,
dMzA = c'mzbdzqb,
подставляем эти значения в формулу момента; получаем :
+Z/2 +Z/2 +Z/2
Mz=q$ cmzbidz^4 j с'уbxAdz-q J c‘xbyAdz.
—1/2 —i/2 —IH
Наконец, коэфициент момента, отнесенный к началу координат
и длине хорды центроплана Ьо, будет таким:
= С С b»dz +
Sqb0 J т~
+U2 +Z/2
+ J c'ybxAdz— j cxbyAdz .
—1/2 —1/2
(282)
В тех случаях, когда рассматривается только симметричная
нагрузка, в этой формуле не ставят индексов z у моментов и
пишут просто 2И, ст и с'т.
В случае крыла с несимметричной нагрузкой получаются
еще моменты относительно осей Ох и Оу, которые легко вы-
числить. Так, момент относительно оси Ох получится от подъ-
емных сил элементарных полосок, равных plVofe, умноженных
на плечо z, на котором они действуют, т. е.
"Н/2
MX = ?V j' Yzdz-,
—1/2
отсюда
Стх= —~ = yot Г Г# dz • (283)
Таким же образом'получится момент Мд, причем он будет
состоять из суммы моментов, возникших от индуктивных со-
противлений Mgi, и момента от профильных сопротивлений Мдр,
т. е.
+Z/2
2ИУ,- = рИ J ГДк z dz
—Z/2
И
1/2 +,/2
= J c'Xpbzdz-
—Z/2
152
Переходя к коэфициентам, получим:
м < о +V2 cmyi j ГДаг dz, (284)
Мпп 1 +г/2 , СтУР — р ~ S&0 J Схр bz dz • %SV4t '-fa (285)
X § 67. ОСНОВНОЕ ИНТЕГРО-ДИФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
ТЕОРИИ КРЫЛА
При расчете крыла большую роль играет уравнение связи:
Если форма крыла задана, то, очевидно, при данном угле
атаки величину Г можно найти по этому уравнению, зная Су.
Однако величина Су зависит от скоса потока и, следовательно,
от искомой циркуляции. Действительно, для величины Су можно
воспользоваться формулой (53'), т. е.
Гу = ;
, А / I vy
здесь а£ = а — Да = а + у-, следовательно,
сэ = а0(а' +
Величина vy нам известна по основной формуле (262); введя ее
в выражение для су, получим:
Если теперь мы подставим найденное значение сд в уравне-
ние связи, то получим уравнение, по которому нужно вычис-
лять Г; оно имеет такой вид:
/ +г/2 \
r=-Wa' + ^ Г <286>
\ —Z/2 /
Это выражение является типичным интегро-диферен-
циальным уравнением. Решение таких уравнений нелегко.
В нашем случае дело еще усложняется тем, что под интегралом
стоит разрывная функция.
Удобнее всего это уравнение решается с помощью рядов
Фурье, с чем мы познакомимся в дальнейших главах.
153
§ 68. ДРУГОЕ ВЫРАЖЕНИЕ ДЛЯ СКОСА ПОТОКА У КРЫЛА
С ИЗМЕНЯЮЩЕЙСЯ ПО РАЗМАХУ ЦИРКУЛЯЦИЕЙ
Глауэрт показал, что рассмотренная выше манера представ-
лять работу крыла ябляется не единственной.
Можно, выделив элемент крыла длиной dz, считать его неза-
висимым крылом с двумя вихревыми усами с циркуляцией,
равной циркуляции вокруг этого участка крыла (фиг. 103). Если
мы теперь рассмотрим действие такого элемента крыла на ка-
кую-нибудь заданную точку крыла А, то индуктивную скбрость
найдем как сумму скоростей от двух вихрей с циркуляцией Г,
т. е. по формуле:
, _ Г Г _
Фиг. 103. Вторая [манера пред-
ставлять работу крыла.
Считая ширину полоски dZ
бесконечно-малой, можем от-
бросить ее в знаменателе и
тогда получим уже знакомую
формулу (100) действия кры-
ла на очень далекую точку оси
Oz. Она будет теперь иметь
вид:
Разбивая все крыло на такие
элементы и суммируя их дей-
ствие, получим:
Г
(С-*)а
Ч- Z/2
dt.
(287)
Формула эта была выведена Глауэртом и кажется на первый
взгляд более простой, чем формула (262), так как в нее не вхо-
дит производная от циркуляции. Однако в приложениях она
оказалась мало пригодной, хотя и представляет большой те-
оретический интерес.
Эта формула должна получаться из основной формулы ско-
рости скоса (262). Действительно, если в основной формуле
скорости скоса:
-4-Z/2
_ 1 С dr
Vy 4к J с — г
—12
154
возьмем интеграл по частям, то получим:
, +Z/2
—Z/2
Первый член в квадратных скобках пропадет при подста-
новке пределов, так как на концах крыльев Г = 0. Останется,
следовательно, выражение, найденное Глауэртом.
§ 69. ПЕРЕХОД К БЕЗРАЗМЕРНЫМ ВЕЛИЧИНАМ
Для того чтобы отчасти упростить формулы и, главное,
сделать выводы более общими, выгодно перейти к безразмер-
ным, отвлеченным обозначениям (см. гл. V, § 26).
Примем за единицу длины полуразмах крыла Z/2. Тогда все
линейные величины станут отвлеченными. Обозначим их теми
же буквами, как и размерные величины, но с чертой сверху.
Таким образом получим:
’ = Z/T’ 2 = //2'5 Ь = 7/2~’ х = 7/2’ У = Ц2 и т’ Д‘ (288)
Размах крыла будет равен / = 2.
Все скорости будем измерять скоростью полета V; получим:
V = 1;
<У9 = = — Да;
V (289)
— Vz
Vz = -у- И Т. Д.
Силы и моменты будем измерять обычными, безразмерными
аэродинамическими коэфициентами сх, cxt, схр, су, ст и т. д.
Текущие значения этих коэфициентов будем отмечать штрихом,
например сх.
Отвлеченную циркуляцию Г определим из формулы:
Г = £* (290)
Введя эти отвлеченные обозначения в расчет, мы сделаем
все выводы более общими, относящимися уже не к одному
какому-нибудь конкретному случаю, а ко всем случаям, обоб-
щением которых являлся тот или иной вывод.
После решения задачи всегда можно вернуться к размерным
величинам, написав: _ _
С = C-Z/2; z =z-Z/2; 6 = Zz-Z/2; х = x«Z/2 и т. д.;
*»» = vgV; vz = vzV-,
Г= Г^;
Г = сX=c±SV* й т. д.
155
Посмотрим, какой вид примут основные формулы, выведен-
ные в предыдущем параграфе, при введении в них этих обо-
значений.
Начнем с геометрических соотношений (фиг. 104). Полураз-
мах крыла будет равен 1, размах равен 2. Ширина крыла
в любом месте b = ~. Площадь крыла представится теперь
так:
+Z/2 +1_
S = J" bdz= (-g-j I b dz •
-HZ —1
Фиг. 104. Крыло с безразмерными обозначениями.
Введем еще одну безразмерную величину S — площадь крыла:
-ы
S = f~bdz. (291)
—1
Здесь за единицу площади принята площадь квадрата со сто-
роной Z/2. Средняя хорда будет получаться по формуле:
которая для безразмерных величин примет вид:
ИЛИ
—1
Удлинение крыла X напишется теперь в виде:
к = — = /3 = _L
S S (Z/2)a S
или
(292)
(293)
(294)
(295)
156
Центральную хорду мы обозначим через Ьо и ее отвлечен,
ную величину — через Ьо. Угол атаки всего крыла будем от-
считывать по углу атаки центральной хорды и обозначим его,
как всегда, через а.
Напишем теперь основные уравнения. Уравнение связи:
Г =-LCybV
после введения в него отвлеченных обозначений примет вид:
Сократив обе части на именованный множитель, найдем весьма
простое соотношение: __ _
Г = <уЬ. (296)
Формула скорости скоса потока имела вид:
, +Z/2
f
—1/2
(/Г
после введения в нее отвлеченных
на общий множитель эта формула
vy = — Да = -
dr
обозначений и сокращения
примет окончательный вид:
1
(297)
1 +;
^dl
— г
Формула подъемной силы:
+ Z/2
r = pV I' V dz
—1/2
после такой же подстановки и сокращения примет вид:
cy = ^-+frdz- (298)
-1
Формула индуктивного сопротивления:
4-Z/2
= — р f ГЧ/у dz
-Z/2
после введения отвлеченных обозначений и сокращений напи-
шется так:
cXi = -~ J*rvgdz= — +fr&«d~z- (299)
—1 —1
157
Формула (279), дающая профильное сопротивление, напи-
шется теперь в таком виде:
41
Ор = 4" / c'xPbdz- (300)
—1
Преобразовав формулы для моментов (282), (284), (283), получим: (285) и
~ -г 1 4 1 _ 4-1 ~ cm2 = -=- f e'mzb2dz+ J'c’ybxAdz- f c'xbyAdz ; ° L —1 —1 —*1 у cmx — /Г" ( Г 3 dz . 4^o Д (301) (302) (303) (304)
Очень часто, особенно при графических методах расчета,,
оказывается выгодным в этих формулах перейти от циркуляции
к аэродинамическим коэфициентам. Сделать это очень легко»
так как циркуляция связана с с'у простым соотношением:
Г = суЬ.
Подставив ее во все наши формулы, получим:
Cy = ^-j'e'ybdz- (305)
—1
41 _
cXi = — l'c'yba.bdz; (306)
—1
—1
-г 1
cmx = -z=- / c'bzdz-,
4b0 J y
—1
+1 _
= -7- f c' \4bzdz-,
4&c J y
—1
(307)
(308)
(309)
158
X +1 -- —
CmVP= 4^ f C'^PbzdS’
—1
£ 4-1 _ , _ f______к —
C"‘z =7T f (С'™ЬЗ+ CybxA — cxbyA)dz.
(310)
(311)
Для удобства обзора всех полученных формул мы приводим
их в табл. 11. Этой таблицей и фиг. 104 следует пользоваться;
пока не приобретется привычка к отвлеченным обозначениям.
Глава XIV
ТЕОРИЯ ТРЕФТЦА-ГЛАУЭРТА
§ 70. ТРИГОНОМЕТРИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ ДЛЯ
ЦИРКУЛЯЦИИ И СКОСА ПОТОКА
Трудность математического анализа основных формул пре-
дыдущих параграфов и неприспособленность их для технических
расчетов заставили искать более удобных приемов расчета.
Наиболее удачное решение дано Трефтцем и Глауэртом. Мы
здесь будем придерживаться в основном манеры Глауэрта. Она
сводится к введению, в расчет крыла тригонометрических
рядов Фурье. У нас основным аргументом была величина г;
для применения рядов Фурье
ее нужно заменить каким-то угло-
вым аргументом 6. Глауэрт заме-
няет г на 6 по формуле:
г = —Z/2-cos9. (312)
Геометрически эту замену мож-
но представить так. На размахе
крыла чертится окружность радиу-
сом Z/2 и с центром в середине крыла
(фиг. 105). Отсчитывая аргумент 9,
Фиг. 105. Связь между гиб
в методе Глауэрта.
как показано на чертеже, мы и полу-
чим ту связь между 6 и z, какую принял Глауэрт. Теперь по-
ложение любой точки крыла мы можем обозначать уже не
абсциссой z, а углом 9. Для величин, характеризующих точки
вихря, напишем формулу (312) в таком виде:
С=- 4 COS 9,.. (313)
Циркуляцию скорости Глауэрт представляет в виде бес-
конечного ряда Фурье такого типа:
r = 2ZV£Ansinn9. (314)
1
159
Основные формулы теории индуктивного Сопротивления моноплана
Таблица 11
Именованные величины Отвлеченные величины
Отвлеченные величины
без циркуляции
Циркуляция
Г «/(г)
Уравнение связи
w
Скорость скоса и угол скоса потока
+02
J С — z
-112
t-z
£Г
- . 1 С «Г If
V* —Да=8'Л J
-1 -1
dP
=0^4^
(.-г
Подъемная сила
+02
У=рУ f Г dz
—1П
Индуктивное сопротивление
Н 1/2
Xi == - р J" Ггу dz
-42
Профильное сопротивление
v,+//2
= S C'xPhdz
—112
у +1-
c»- ~ J Гdz
—1
+1
X ~ Xi + xp
Cx = Cxi +• cxp
. Юрьев—171—11
Аэродинамический момент
C-mz ~ qSb0 c:n:
= Sb J (С'т-.Ь2+СУЬХА-С>УА)^
° -1/2
+ 1
+ Г ( C'nfil +суЪхА- c4> Уа> dz
bo J
6-Ц
Интегро-диференциальное уравнение
( 2
r=^aobV\a' + ^j
T112
/ +1 c
- , i г & -
Г = a0 b I a + 8lt J rf.
—1
Геометрические параметры крыла
площадь
+U2
s= j bdz
—in
средняя хорда
h =A
*cp I
S Г -
S= = I bd
(1/2У _J
1, 3
6cp = Y
удлинение
k=-^=^-
5 Z>cp
^cp
4
S
Множитель 2Z/ вводится для того, чтобы сделать выражение
под знаком 2 безразмерным. Я случае крыла циркуляция на
концах крыла обращается в нуль.
Промежуток, на котором разлагается функция Г в ряд, ле-
жит в пределах: 9 = 0 и 9 = тс. Следовательно, циркуляция ско-
рости в способе Глауэрта представляется рядом Фурье по
синусам кратных дуг на промежутке 0 — тс.
Для обобщения формул перейдем к отвлеченным обозначениям
и получим тогда из формулы (312) очень простое выражение:
z =—cos 9. (315
Вместо формулы (314), получим:
r = 8S^nSinn9. (316)
1
Эти две формулы и будут у нас основными.
Фиг. 106. График отвлеченной циркуляции по г и Н.
Рассмотрим графическую интерпретацию получившихся вы-
ражений (фиг. 106). Закон изменения циркуляции мы можем
представить или в виде Г = f(z) .(черт. 106, а), или в виде Г =
= Ф(9) (черт. 106, Ь). В первом случае величина z должна изме-
няться в пределах размаха крыла, т. е. от — 1 до + 1. Во вто-
ром случае величина 9 будет изменяться от 0 до тс. От диа-
граммы (а) к диаграмме (Ь) переходят или по формуле (315),
или прямо по графику (а).
Ряд Фурье дает разложение функции Г по синусам кратных
дуг и в развернутом виде напишется так:
Т = 8 (A sin 9 -J- А2 sin 26 + А3 sin 39 + At sin 49-НАsin 59+...). (317)
Коэфициенты ряда Фурье Av А2, AZi... быстро убывают.
Функция Г получится как сумма ординат последовательных
синусоид по схеме фиг. 107. Легко видеть, что при симметрич-
ном крыле и при симметричном обтекании члены с четными п
должны пропасть, так как они дают несимметричную суммар-
ную кривую Г. Следовательно, четные члены нужно вводить
1 62
в расчет лишь тогда, когда изучают несимметричные крылья, напри-
мер, крылья с отклоненными элеронами. В обычных случаях рас-
чета крыльев пользуются лишь нечетными членами. У обычных
крыльев члены ряда очень быстро убывают, и для получения вполне
достаточной точности можно брать, всего четыре первых коэ-
фициента, т. е. Лх, А3, А6 и Д7.
Выражение для Г в этом, основном случае получится в та-
ком виде:
Г = 8Д, sin 9 + 843sin39 + 8.Assin 59 + 8Д7зт 79. (318)
Таким образом в способе Глауэрта любой закон изменения
циркуляции по размаху крыла задается четырьмя (или п) чис-
Фиг. 107. Схема суммирования
синусоид ряда Фурье для
Г
получения Д..
циркуляции по раз-
лами Д1( А3, А5 и Аъ ..., Ап. В этом
и заключается огромное удобство
этого способа. Как увидим далее,
целый ряд аэродинамических ха-
рактеристик крыла в конечном
итоге изображается с помощью
этих же чисел. Лишь в исключи-
тельных случаях приходится брать
в расчетах больше четырех чле-
нов, например 6 или 8.
Теоретически любой закон
изменения циркуляции по размаху
может быть представлен бесконеч-
ным числом этих членов типа
Ап sin пб. Следовательно, полагая
в дальнейших выводах число чле-
нов равным бесконечности, мы
получим совершенно точные вы-
воды для любого закона изменения
маху крыла.
Преобразуем теперь основные формулы теории моноплана
с помощью ряда Фурье.
Начнем с угла скоса потока, который выражался ранее фор-
мулой (261):
vg = — Да =
+1 _
/• ЙГ
J <. — Z
—1
Вычислим сначала dr по формуле (316); подучим:
оо оо
ЙГ = 8d У, Ап sin = 8^ пАп cos nfi db.
__ 1 _ 1
Кроме того, z = — cos 9 и Z= — cos9c Пределы интеграла соот-
ветственно будут 0 и я. Следовательно,
ТС ОО
vg = - Ьа. = — — f V пАп с05 «9— (319)
у nJ / . и COS be----cos 6 v 7
о 1
163
Задача сводится к вычислению интеграла:
f-----
J cos6r — cos b •
о 4
Этот интеграл встречается очень часто в теории рядов Фурье.
Он имеет разрывную подинтегральную функцию, поэтому его
вычисляют путем тщательного исследования его пределов. Вы-
числение этого интеграла дано в приложении. Оказывается, что
г cosnb siiinb
। ----------—- аог = тс---—.
J cos — cos 6 Sih b
0
Отсюда
oo
лЛп sin
(320)
(321)
Зная коэфициенты Дх, A3, A5 и т. д. и задавшись какой-
нибудь точкой крыла, т. е. углом 9, получим по этой формуле
угол скоса в данной точке.
§ 71. ТРИГОНОМЕТРИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ ДЛЯ СИЛ
Найдем теперь подъемную силу крыла. Воспользуемся для
этого формулой (298), написанной в отвлеченных обозначениях,
т. е.
+1
Подставим сюда основное выражение для Г по формуле (316) и
dz — — d cos 9 = sin 9 d\ (322)
после чего получим:
n 00 °° к
Су = -j- .f 8 УАпsin n9 sin 9 d9 = 21 У Ап J sin «9 sin 9 d9. (323)
0 1 10
В этой формуле, как и в ряде дальнейших, у нас будут
встречаться под интегралом выражения типа sin пЗ sin/п9. В лю-
бом справочнике1 можно найти готовую общую формулу:
f sin «9 Sin ти9 rf9 = _ ^(^±49 + с. (324)
2(m — n) 2(m + n) ' v '
Она пригодна для n^m.
В нашем случае т—1 и, как легко видеть, при подстановке
Например, см. Hiitte, том I, раздел .Математика*.
164
в нее пределов интегрирования 0 и к мы получим для всех чле-
нов суммы, у которых «> 1, значение этого интеграла, равное
нулю. Остается первый член с индексом п = 1. Для него получим:
к
fsin29d9 = f4-(l-cos20)d9 = 4. (325)
о О 2
Таким образом находим окончательно:
су = •ккА1. (326)
Получился замечательный результат: коэфициент подъемной
силы, крыла зависит только от первого коэфициента разло-
жения Г в ряд Фурье.
Найдем теперь величину коэфициента индуктивного сопро-
тивления крыла, для чего основное для него выражение пре-
образуем, введя в него тригонометрические величины. Итак,
мы имели:
+ 1
cXi=-^ f Tvvdz.
—1
Подставляя сюда:
Г = 8^ j4nsin пв;
1оо
\±пАп siii и в
sin О
И __
dz = — d cos 9 = sin 6
получим:
Тс 00 00
Cxi = -8- J sin «9 ^«An Sin «9 nf9 =
0 1 i
oo TC
= 2k У nAnAm f sin «9 sin /«9 J9.
i о
Для второй суммы мы поставили т вместо п, так как при
почленном перемножении этих сумм мы должны придавать «зна-
чения 1, 2, 3 и т. д. и получим всевозможные сочетания этих
цифр, например: 1x3, 1x5, 3 X 5 и т. д., т. е. произведения
типа п•т.
Рассмотрим интеграл:
тс
J sin «9 sin/«9 d9.
о
По общей формуле (324) видно, что для всех значений тфп
мы получим после подстановки пределов интегрирования нуле-
вые значения.
165
1 + о. (329)
В случае пг = п этот интеграл будет иметь величину:
Jsin2«9aW = J” -^-(1 — cos2«9)d9 =
о о
Следовательно,
cxi = ^nA*. (327)
1
Это тоже весьма интересная формула. Оказывается, что
коэфициент индуктивного сопротивления зависит лить от
суммы, составленной из квадратов коэфициентов ряда Фурье,
помноженных на их порядковые номера. Эта сумма всегда поло-
жительна и, следовательно, никаким распределением циркуляции
по крылу нельзя избавиться от индуктивного сопротивления.
Полученную формулу индуктивного сопротивления можно
написать еще в таком виде:
оо со
= (328)
т. е. мы получим основную формулу индукции, найденную нами
ранее приближенным методом.
Входящую в эту формулу поправочную величину пишут
обычно так:
^пАп
Л31
Тогда основная формула перепишется окончательно в таком,
хорошо нам известном виде:
cxi=-£(l+8). (330)
Следовательно, для нахождения поправки 8 нужно лишь знать
величину коэфициентов ряда Фурье для крыла данной формы.
В гл. III, § 16 приведена таблица 1 значений 8 для прямоуголь-
ных крыльев, найденная с помощью этих коэфициентов.
§ 72. ФОРМУЛЫ ДЛЯ ПЕРЕСЧЕТА НЕЗАКРУЧЕННЫХ КРЫЛЬЕВ
НА X - оо И С ?! НА /,
Для пересчетов крыльев на другое удлинение приходится,
как мы знаем, пользоваться двумя формулами: одной, служащей
для пересчета кривой Лилиенталя, — она нами только что най-
дена — это формула (330), и другой — для пересчета углов атаки.
Найдем вторую формулу.
Угол атаки у сложного крыла отсчитывается по центральной
хорде. Назовем такой угол атаки через а. Крыло в общем слу-
чае будет у нас закрученным и иметь разные профили в раз-
166
ных местах размаха. Таким образом каждое сечение будет иметь
в общем случае свой угол атаки а'.
В расчетах удобно пользоваться аэродинамическим углом
атаки, отсчитываемым от аэродинамической хорды. Как мы знаем:
аа = а — а0,
где а0 — угол нулевой подъемной силы. В дальнейшем, чтобы
не усложнять излишне формулы, мы будем всегда брать
угол атаки по аэродинамической хорде и не будем
ставить индекса а у угла атаки.
Текущий угол атаки а' будет в общем случае связан с углом
атаки формулой:
а' = а + <₽, (331)
где ф =/(z) — закрутка сечения крыла по отношению к цен-
тральной хорде. Этот угол будем отсчитывать в ту же сторону,
что и угол атаки.
Если закрутка крыла равна нулю, то это значит, что аэро-
динамические хорды всех профилей лежат в одной плоскости.
В этом случае при нулевом угле атаки подъемная сила крыла равна
нулю и, следовательно, равно нулю и индуктивное сопротивление.
В случае закрученного крыла этого не будет и индуктивное
сопротивление при су = 0 не будет равно нулю. Величина полу-
чающегося в этом случае индуктивного сопротивления зависит
от величины закрутки и закона ее изменения по размаху.
В этой главе разберем крыло без закрутки.
Для крыла в целом мы можем написать формулу (326), т. е.
су = аа = -Ц.
Отсюда находим:
а=~1 (332)
или отношение:
— = —*. (333)
а0 аоа 4 7
Следовательно, если для крыла известны X, и а, то найти
отношение — не представляет никакого труда. Как находить А±
по форме крыла, мы разберем в гл. XV.
Для перехода от данного крыла к крылу бесконечного раз-
маха для того же значения су можем написать для данного
незакрученного крыла:
cvi = ал
и для крыла бесконечного размаха:
Су2 '== •
Угол атаки крыла бесконечного размаха мы обозначили через
а не через аь чтобы помнить о том, что здесь речь идет не об
167
(334)
(335)
истинном угле данного крыла, а угле ата ки другого, беско-
нечного крыла. Отсюда при сУ1 — сУ2 = су получим:
а Яоо-сД а —
Подставляя сюда величину а по формуле (332), найдем:
/а 1 \ су ( а тс Л \
~ ЛАЛ?
Обозначая:
“J!* = 1+Т)
Л1 я0
получаем уже знакомую нам по гл. III формулу (34), которая
теперь напишется у нас в виде:
а —а« = 4|-(1 + т)- (336)
По этой формуле пересчитывают данное крыло на беско-
нечное удлинение. При переходе от удлинения Хх к Х2 придем
к формуле (47) гл. IV, § 19.
Надо помнить, что формула (336) относится к незакрученным
крыльям. В случае закрутки получается более сложная картина
и ее мы разберем, ознакомившись с методами поверочного
расчета крыльев.
Величина т для незакрученных прямоугольных крыльев при-
ведена в табл. 1 гл. III, § 16.
§ 73. ФОРМУЛЫ ДЛЯ МОМЕНТОВ
Аэродинамические моменты в способе Глауэрта также выра-
жаются через коэфициенты ряда Фурье. Так, формулу:
х +1-- -
стх = f Г z dz
4&0
с помощью известного нам метода, т. е. метода тригонометри-
ческих подстановок и последующего интегрирования, можно
привести к виду:
Стх = ^-~А2. (337)
2 Ьо
Получается интересный результат: момент около оси Ох за-
висит лить от второго коэфициента ряда Фурье, т. е. от А2,
остальные, дающие несимметрию, четные коэфициенты на этом
моменте не сказываются и из формулы выпадают.
Формула:
+1 _ __ _
Cmyi = J ГД 1 z dz (338)
тем же путем по еле подробного рассмотрения интегралов при-
водится к виду:
1 68
cmyi = 4 X? (2« + 1) AnAn и. (339)
2 0O Xad
Моменты cmyp и cmz удобнее вычислять по формулам (310)
и (311), так как они мало упрощаются от введения тригономе-
трических величин. В большинстве случаев нужно рекомендо-
вать графическое интегрирование по размаху крыла.
Для удобства пользования ниже приведены основные фор-
мулы теории Глауэрта в отвлеченных обозначениях.
z = — cos 9; Г = 8 sin п9; (315) (316)
УлЛп sin пЬ Ч)и= — Да = — —2-, ; у Sih 6 ’ (321)
Су =— j (325)
Cxi = У> (327)
ИЛИ г2 У иЛ2 с2 е +8). Cxi icX д* яХ ‘ (330;
V П^п 4 (329)
с - — А А • 1 тх ,, -г- 2 > (337)
2 Ьо cmyi = ^^\\2n+l)AnAnii. (339)
Для незакрученного крыла от 1 кХ2=со переходят по формулам:
а-а=о = ^-(1 -Н); (336)
1 + х= Т’ Л1 «а (335)
а ллЛх «о аоа * (333)
Глава XV
ТРИ ОСНОВНЫХ ЗАДАЧИ ТЕОРИИ М0Н0ПЛАНН0Г0 КРЫЛА
КОНЕЧНОГО РАЗМАХА
§ 74. ПОСТАНОВКА ЗАДАЧ
Полученные в предыдущей главе формулы позволяют решить
три важнейших задачи, интересующие конструктора.
Первая задача заключается в построении крыла с заданным
законом изменения циркуляции по размаху крыла. Вторая задача
160
решает вопрос о наивыгод^ейшем крыле моноплана. Третья
задача решает вопрос об аэродинамических свойствах крыла
произвольной формы; ее можно назвать задачей о проверочном
расчете крыла заданной формы.
Все эти три важнейшие задачи проще всего решаются по
формулам Глауэрта, особенно при пользовании отвлеченными
обозначениями.
Выгодность этого метода особенно ярко проявляется при
решении второй задачи — о наивыгоднейшем крыле. Впервые
эта задача была решена М. Мунком с помощью методов вариа-
ционного исчисления и с тех пор часто называется „Изопери-
метрической задачей теории крыла". Работа Мунка представ-
ляет собой солидную докторскую диссертацию. С помощью же
метода Глауэрта решение этой задачи дается, как увидим,
буквально в нескольких строках.
§ 75. ПЕРВАЯ ЗАДАЧА — ПОСТРОЕНИЕ КРЫЛА С ЗАДАННЫМ ЗАКОНОМ
ИЗМЕНЕНИЯ ЦИРКУЛЯЦИИ ПО РАЗМАХУ КРЫЛА
_ Пусть задано спроектировать крыло с заданным законом
Г = f(z). Здесь могут встретиться два случая. В первом случае
закон изменения циркуляции уже задан коэфициентами ряда
Фурье, т. е. обычно четырьмя величинами: А3, А5 и
Тогда задайа для симметричного крыла решается очень легко,
прямо по выведенным в гл. XIV формулам.
Циркуляция скорости представится рядом:
Г = 8 5} Дп sin п9 = 8 (/^sin 9 + ^3sin 39 Д5 sin 594-Д, sin 79). (318)
Во втором случае закон циркуляции может быть задан или
графически, или аналитически. Тогда с помощью гармониче-
ского анализа разлагают эти функции в ряды Фурье и находят
коэфициенты Д,, А3, Д5 и т. д. На этом вопросе ь ы остановимся
в гл. XVIII.
Зная коэфициенты Alt As, Д5 и т. д., можно вычислить цир-
куляцию для нескольких сечений крыла, задаваемых углом 9 и
соответственно абсциссой z = — cos 9.
Угол скоса потока найдется в любой точке 9 по формуле
(321):
да _ S П^п. sin «9
Siu 6
После этого нужно выбрать подходящий угол атаки профиля
af для заданных сечений, пользуясь продувкой этого профиля
(к == со). Выбор можно делать на основании различных сообра-
жений. С чисто аэродинамической точки зрения выгоднее всего
брать угол, при котором обратное качество = |Г имеет
су
170
минимальное значение; такой угол атаки профиля называется
наивы годнейшим. Приходится иногда брать угол а(Л, исходя
из условий прочности или жесткости крыла.
Зная а,, находим угол атаки сечения крыла:
а' = а,- + Д-х.
По имеющейся продувке этого профиля мы найдем для
угла атаки а, величины с'у, схр и с'т. Если нет результатов про-
дувки этого профиля, то поступаем по правилам § 57 и 58.
По уравнению связи:
Г = с‘у b
находим ширину профиля:
су
Зная профиль, его ширину b и а', можно вычертить крыло
с размахом I = 2. По чертежу крыла с помощью планиметра
или аналитически находим среднюю хорду крыла:
Ьер = Т Г bdz
—i
и вычисляем получившееся у него удлинение:
После этого переходим к вычислению силовых коэфициентов
и находим их прямо по готовым формулам (326) и (327):
су = ккЛх;
Cxi = пАгп
Профильное сопротивление при-
дется вычислять по формуле (307):
J-1
Схр = -J f c'xpb dz.
—1
Фиг. 108. Графическое опре-
деление схр крыла.
Проще всего находить это выражение графически (фиг. 108),
строя на размахе крыла, равном 2, величину схрЬ.
Площадь 2Р, заштрихованная на чертеже, даст величину
интеграла, и мы получим:
^р = |«р- (340)
171
Заметим, что с'хр изменяете^ по размаху обычно несильно и во
многих случаях его можно брать постоянным. Тогда
СхР = Схр‘
Понятно, при точных расчетах величина с'хр должна браться
со всеми поправками, т. е. на число Рейнольдса, на шерохо-
ватость поверхности, на наличие выступающих заклепок и т.д. по
методам гл. XI и XII. Переходим, наконец, к вычислению мо-
мента относительно оси Oz.
Сначала надо найти по чертежу крыла (фиг. 102) координаты
Ха и у а передних кромок крыльев (точнее —точек, относительно
которых брался момент с'т). Затем по формуле (311) найти
величину коэфициента момента, отнесенного к передней кромке
корневой хорды крыла Ьо:
х +1 ____________ _______ __
Cmz = f (cmb2 4- c'yb xA—cxbyA) dz.
Таким образом первая задача решается очень легко, если
заданы коэфициенты Аь А3, Аа, А, и т. д.
§ 76. ВТОРАЯ ЗАДАЧА — О НАИВЫГОДНЕЙШЕМ КРЫЛЕ
Решим теперь задачу Мунка о крыле наивыгоднейшей формы.
Заметим, что крыло тем лучше, чем больше у него удлинение X.
Самые лучшие характеристики будут у крыла с X = со. Для
решения практических вопросов, очевидно, нужно считать X
величиной заданной.
Мы получили для крыла формулы:
су — ttXA,;
cxi = ri£nA2 = як (А* + 3AS2 + 5А*-j-7А* + .. .). (327)
Наивыгоднейшим крылом будет такое, у которого при задан-
ном Су величина cxi наименьшая. При заданном сц будет задано
и At. Для получения минимального cxi нужно обратить все
положительные величины ЗА|, 5Aj, 7А* и т. д. в нули. Следо-
вательно, наивыгоднейшее крыло должно иметь А3 = Аа = А7 =
= Аэ = .. . = 0.
Тогда мы получим для сд и сх1 две весьма простых формулы:
Су = тгХД,; I % ч
f <341>
Последнюю формулу можем написать через су, подставив
в нее величину из верхней формулы:
су
cxt = 9
тел
т. е. мы получим хорошо известную нам формулу (33).
П2
Рассмотрим теперь, как будет изменяться у такого крыла
циркуляция. По формуле (316) получим для нашего случая:
Г = 8£AiSin «6 = 8А, sin 6 = 8АУ1 — cos2 6 = 8Aj/i—Р;
таким образом
Г = 8АХ /Г—?. (342)
Эта зависимость на графике (фиг. 109) представится эллипсом.
Для циркуляции нужно брать
верхнюю часть кривой. Отсюда
получается весьма важный вы-
вод: циркуляция скорости у
наивыгоднейшего крыла изме-
няется вдоль его размаха по
закону полуэллипса.
Наибольшая величина цир-
куляции получится в центре
крыла. Обозначая ее через Го,
найдем:
Го = 8AV (343)
Фиг. 109. Эллиптический закон из-
менения циркуляции и постоянная
скорость скоса потока по размаху.
Найдем теперь по формуле (321) угол скоса у такого крыла:
vy = — Да = —
sin нВ
sin b
1
ИЛИ
Да = Аг = ~.
(344)
Мы пришли к замечательному выводу: наивыгоднейшее крыло
имеет постоянный по размаху угол скоса, равный первому
коэфициенту разложения циркуляции в ряд Фурье или отвле-
ченной циркуляции Го, деленной на 8.
с
Подставив в последнюю формулу значение Ах = -у- по фор-
муле (341), получим:
Да=Чр (345)
т. е. уже найденное ранее приближенным методом выражение
для угла скоса.
Таким образом согласно строгой теории крыла лишь для
крыльев с полуэллиптическим законом изменения циркуляции
по размаху формулы:
Г — У
Cxi ni
173
являются совершенно точными. Для всех других крыльев надо
пользоваться формулами:
'С Z
Да = ^(1+г);
сж1. = ^(1+8).
Посмотрим теперь, какую форму будет иметь наивыгоднейшее
крыло. Угол атаки его должен быть взят всюду наивыгоднейший,
а сечения профиля — наилучшие из известных. При этих усло-
виях истинный угол атаки а; будет одним и тем же во всех
точках размаха крыла. Угол скоса потока в этом случае, будет
также постоянным; отсюда угол атаки сечений
а' = а, + Да = а = const,
а следовательно, все хорды крыла лежат в одной плоскости.
Такие крылья, как мы знаем, называются незакрученными, или
плоскими. Их общий су равен элементарному су, так как
с'у = const. Точно также схр = с'хр, cxt = cxi и cxi — cxi. Это де-
лает эллиптические крылья весьма удобными для получения
надежных характеристик
профилей (Х= со).
Посмотрим теперь, как будет из-
меняться ширина крыла по размаху.
Ее мы найдем по уравнению связи:
8Я, ---=7
= —‘к 1-
Фиг. 110. Возможные формы
наивыгоднейшего крыла.
ь = -4
су
л ^У
поставляя сюда получим:
b
(346)
Следовательно, ширина такого крыла
изменяется также по закону полуэл-
липса (фиг. 110, а). Откладывая от
осевой линии вверх и вниз Ь)2, полу-
чим эллиптическую форму крыла
(110, Ь). В обоих случаях присоеди-
ненный вихрь, который помещается
в центре давления профиля (обычно на х/з хорды от носка),
будет иметь кривизну. Более близкое совпадение аэродинами-
ческих характеристик с теорией будет у крыла, построенного
по схеме фиг. 110, с, т. е. с центрами давления, лежащими на
одной прямой. Так как у обычных крыльев на летных углах
сд то точки, делящие хорды крыльев в отношении 1:3,
должны лежать у наивыгоднейшего крыла также на прямой.
Таким образом наивыгоднейшее крыло обладает рядом заме-
чательных свойств и оказывается во многих отношениях про-
стейшим крылом.
17-1
§ 77. ДОПОЛНЕНИЯ К ТЕОРИИ ЭЛЛИПТИЧЕСКИХ КРЫЛЬЕВ
Естественно задаться вопросом: насколько другие крылья
отличаются от эллиптического крыла? Оказывается, что даже
прямоугольное крыло незначительно отличается по форме кри-
вой Г = f (z) от эллиптического. У него получается более слабое
падение_циркуляции к концам крыла, чем у наивыгоднейшего, и
кривая Г =f(z) представляет овал, а не эллипс. Расчитав эллип-
тическое, прямоугольное и трапецевидное крылья на одну и
ту же подъемную силу, можно, построить график изменения
Г по размаху, изображенный на фиг. 111.
Во всех случаях по-
лучился закон изменения
циркуляции, довольно
близкий к эллиптиче-
скому.
Следовательно, кры-
ло с эллиптическим зако-
ном изменения циркуля-
ций можно рассматривать
как типичное крыло, и
схему его вихрей рас-
сматривать как более
точное изображение дей-
ствительности для лю-
бого крыла, чем схема
П-образных вихрей.
Если не учитывать
профильное сопротивле-
ние, то полуэллиптиче-
ский закон изменения
Фиг. 111. Сравнение закона изменения
циркуляции по размаху крыльев: эл-
липтического, прямоугольного и тра-
пецевидного при равной подъемной
силе: k = aQ ^5,6.
циркуляции по размаху можно получить для одного а у крыла
любой формы в плане, например у прямоугольного. Для этого
нужно лишь уменьшить углы атаки у ^концов крыла по ура-
внению связи, требующему, чтобы Г=суЬ.
Изменяя углы атаки, будем изменять су, и если произведе-
ние суЬ дает циркуляцию, следующую закону полуэллипса, то
такое крыло по вихревой его системе ничем не будет отлича-
ться от эллиптического для данного а.
К недостаткам эллиптических крыльев следует отнести отно-
сительную сложность их формы и, следовательно, дороговизну
постройки как крыльев самолетов, так и моделей для испытаний
в аэродинамических трубах. Вследствие этого на практике чаще
всего применяют более простые формы крыльев, но все же
близкие к эллиптическим, например трапецевидные.
Теоретически заманчивый способ получения с помощью таких
крыльев надежных величин су и схр несколько ухудшается
малыми числами Рейнольдса, получающимися у концевых про-
филей. Впрочем, это влияние весьма невелико, поэтому для
175
проведения особо точных исследований в настоящее время
очень охотно пользуются такими'крыльями.
Полученные нами формулы для эллиптического крыла были
выведены с помощью хзтвлеченных обозначений. Нередко на
практике пользуются также формулами с именованными вели-
чинами.
Из таких формул упомянем о формуле для скорости скоса,
встречающейся во многих работах, которую мы получим из
формулы (344):
vy0 = — Да = — А,. = —
или
- __Г0
fjo- 8--
Переходя от отвлеченных обозначений к именованным, получаем
%_ Го _ Го
V IVQ 21V'
Г8
Отсюда находим окончательно:
^ = —(347)
Выше мы получили среднюю скорость скоса у крыла с посто-
янной циркуляцией в таком виде:
^0=-^°- (348)
Меньшая скорость скоса у эллиптического крыла получается
потому, что в формулу (347) входит Го—циркуляция в центре
крыла. К концам крыльев циркуляция у эллиптического падает,
а у крыла с постоянной циркуляцией остается неизменной. Если
сравнить два таких крыла одного размаха, но с равными в цен-
тре циркуляциями, то получится картина нагружения, изобра-
женная на фиг. 109.
Подъемная сила выразится площадью, ограниченной кривой
циркуляции и размахом крыла.
Для Г = const получим:
е = г0/.
Для полуэллипса же мы получим по обычной формуле площади
эллипса: S = itab такое выражение:
2э=4~пГо4- <349)
Следовательно,
2 _ 4
2Э - л •
176
Подъемная сила у крыла с постоянной циркуляцией будет
в отношении —- больше, чем у эллиптического; отсюда полу-
чится и большая скорость скоса.
Вычислим теперь подъемную силу эллиптического крыла
в натуральных величинах. Эта сила выражается через площадь,
ограниченную кривой циркуляции, формулой* (270), т. е.
+Z/2
Г = РУ/ Гй?г = рИ2э. (350)
—1/2
Площадь полуэллипса мы уже нашли. Следовательно,
Г = -;-рИГ0, (351)
и индуктивное сопротивление выразится формулой:
Х^ГЛа = ^рГ02. (352)
Подставляя в него величину Го по формуле (351), получим:
<352')
Формула (352) интересна в том отношении, что в нее не
входит ни к, ни /. На первый взгляд это противоречит теории
индукции. На самом же деле при изменении размаха в этом
случае возрастает подъемная сила Y. Мы же в обычных фор-
мулах принимали величину подъемной силы заданной.
78. ТРЕТЬЯ ЗАДАЧА —ПОВЕРОЧНЫЙ РАСЧЕТ КРЫЛА
произвольной ФОРМЫ
В этом случае бывает задана форма крыла, т. е. в каждом
сечении дана хорда Ь, угол атаки !' = « + ? и профиль.
Для профилей имеются результаты испытаний, пересчитанные
на Х=оэ. Требуется найти для такого крыла су, сх, ст, закон
распределения циркуляции и угол скоса потока.
Здесь, очевидно, нельзя применить непосредственно тот
метод, которым мы пользовались* до сих пор, т. е., пользуясь
коэфициентами Д3, А5 и А7, вычислить аэродинамику крыла
по готовым формулам. Основной задачей будет в этом случае
получение на основании заданной формы крыла коэфициентов
Аъ А*, А5 и А7. Получив эти коэфициенты, мы сведем третью
задачу к первой.
Для нахождения закона изменения циркуляции по размаху
крыла служит основное интегро-диференциальное уравнение
(286). Однако оно крайне неудобно для применений. В способе
Глауэрта мы будем пользоваться тригонометрической формой
этого уравнения, с безразмерными величинами. Удобнее его
получить непосредственно из формул Глауэрта.
Б. н. Юрьев—171 —12 177
Уравнение связи имеет вид:
Г =су Ь.
Величину коэфициента подъемной силы можно по § 22 пред-
ставить так:
су = a02i = а0(а' — Да).
Следовательно, _
Г =а0Ь(а' — Да).
Напомним еще раз, что углы мы отсчитываем от аэродина-
мической хорды.
Пользуясь формулами Глауэрта с тригонометрическими ряда-
ми, т. е.
r = 8£Ansinn9 и ДЯ = Sill-2L
после подстановки этих выражений в нашу формулу, получим
следующее выражение:
8S sin п 9 =аоЬ («' — ""I",,5;—•
Для сокращения введем следующее обозначение:
= (353)
приводя формулу к одному знаменателю, получаем:
Ап sin «9 sin 9 = р-а' sin 9 — а 5} пАп sin п 9.
Замечая, что стоящие в , суммах левой и правой частей
п=1,3, 5... имеют одно и то же значение, мы можем эту фор-
мулу написать окончательно в таком виде:
У, Ап sin п 9 (sin 9 -|- пр) — ua' sin 9. (354)
Эта формула и является основной в-третьей задаче. С по-
мощью ее мы должны найти значения коэфициентов ряда
Фурье -Aj, А3, Д5, Д7 и т. д. Обычно достаточно знать четыре
члена. Решать это уравнение проще всего по методу Глауэрта-
Трефтца, для чего нужно написать его для стольких сечений
полуразмаха крыла, сколько мы решили искать коэфициентов
ряда Фурье.
Пусть мы выбрали, следуя Глауэрту-Трефтцу, сечения, опре-
деляемые следующими значениями основного аргумента:
9 = 22,5°; 45°; 67,5° и 90°.
Этим сечениям будут соответствовать отвлеченные абсциссы
z = - cos 9 = - 0,924; — 0,707; -0,383 и 0.
Для этих сечений по чертежу крыла нужно найти соответ-
ственные значения j^, у.2) н, р.4, аг', а/ и а/.
178
Для выбранных точек пишем наше основное уравнение (354);
получаем систему линейных уравнений Глауэрта:
I. 0,383 (н+0,383) Дх+0,924 (3^+0,383) Д3+
+0,924 (5^+0,383) Д5+0,383 (7^+0,383) Д7 = 0,383^';
II. (н2+0,707) А,+ (3Иа+0,707) А3 - (5^+0,707) А 5 —
— + 0,707) Д7 = fi2a2';
III. 0,924 (pig + 0,924) Лх —0,383 (3u3+0,924) Д3— (355)
—0,383 (5р.3+ 0,924) А5+0,924 (7р.3+С,924) Д, = 0,924 |i3a3';
IV. (^ + 1) Д, - (Зц4+1) Д3+ (5р4+1) Д5-
—(7щ + 1)Л, =
Решая эти четыре линейные уравнения, получим величину
четырех неизвестных коэфициентов Дъ Д3, Д5 и Д7.
Само решение может вестись любым способом: подстановка-
ми, сравнениями, с помощью детерминантов и т. д. Решив эти
уравнения и найдя Аь А3, А5 и Д7, сводят задачу к простому
применению основных формул. Так, коэфициент подъемной силы
крыла находят по формуле:
Су —• т,ХДх;
Коэфициент индуктивного сопротивления вычисляют по формуле:
cxi — V^/гДд = itk (Д4 +ЗД| + 5Д& +7Дх +...);
находят:
Sn4nsii п9
а, = а' — Да.
Зная истинный угол атаки сечения, находят схр, с'т, c'v и вы-
числяют, обычно графически:
+1 _
J c'^dz
—1
и
+ 1
с = _L f (с’ть2 + c'ybxA — c^byA)dz.
4<’o
В случае отсутствия результатов испытаний крыльев модно
пользоваться эмпирическими зависимостями, изложенными в
гл. XI и XII.
Решение четырех линейных уравнений Глауэрта не пред-
ставляет никаких трудностей. Однако когда берут пять, шесть
179
и более точек размаха и решают такое же число уравнений,
трудности сильно возрастают.
Решение некоторых задач, например, учет вырезов в крыле,
учет работы элерону и закрылков, требует иногда включения
в расчет шести—восьми точек. Это сильно затрудняет вычис-
лительную работу, и поэтому приходится пользоваться другими
способами, изложенными в дальнейших главах.
Глава XVI
СПОСОБ И. ЛОТЦ
§ 79. ОСНОВНЫЕ УРАВНЕНИЯ Ц» ЛФТЦ
Способ Лотц является дальнейшим развитием теории Глау-
эрта. Ей удалось составить весьма удобную систему уравнений
для нахождения коэфициентов разложения циркуляции в три-
генометрический ряд. Вследствие этого способ Лотц нашел
много последователей и часто применяется наравне с основным
методом Глауэрта на авиационных заводах у нас и за гра-
ницей.
Этот способ имеет много модификаций, так как каждый
расчетчик приспособляет его для типа изучаемых им крыльев
или вносит те или иные мелкие усовершенствования в основ-
ной метод.
Здесь мы изложим способ Лотц в основном виде, причем
рассмотрим общий случай, когда крыло симметрично в плане,
но имеет несимметричный закон изменения углов атаки вдоль
размаха. В этом случае можно применить метод Лотц к изуче-
нию действия элеронов, к исследованию авторотации крыла
и т. д.
В основу метода Лотц положено основное уравнение Глау-
эрта [формула (354)]:
^Ап sin п 6 (sin 9 + п^) = рюс' sin 0.
Перепишем это уравнение в таком виде:
пЛ ~ +я) = a'sin 9.
Величина у. = Введем еще величину
(356)
1*0 8
При этом, очевидно,
Но __ __ Ьц
и ~ У ь •
180
Умножим и разделим левую часть уравнения (356) на и0;
тогда получим:
(^-sin9+«fi0 ) = «'sin 9. (357)
И. Лотц предложила входящие в это уравнение величины
-у sin 9 и a'sin 6 разлагать в ряды Фурье, причем для удобства
вычислений первую, симметричную, функцию раскладывать в ряд
четных дуг косинуса, а вторую, несимметричную,—в ряд синуса.
Это и является особенностью метода Лотц. Итак, полагаем:
ySin9 = ^C2fccos269, где 6= 0, 1, 2.. .оо (358)
и
a' sin 9 <= Вт sin mb, где т = 0, 1, 2...со. (359)
Число членов можно брать любое, но на практике ограни-
чиваются лишь несколькими первыми членами.
Левые части этих уравнений при проверочном расчете крыла
будут заданы как функции 9 или z. Следовательно, пользуясь
методом гармонического анализа, мы можем найти входящие
в эти ряды коэфициенты Со, С2, С4, С6..., характеризующие
ширину крыла, и коэфициенты Blt В2, В3, характеризую-
щие изменение угла атаки крыла по размаху.
К вопросу вычисления этих коэфициентов мы вернемся в
дальнейшем. Теперь же подставим эти ряды в основное урав-
нение (357); получим:
— 5} Ап sin nti (У C2fe cos 269 + npt0) = У Вт sin /и9. (357')
Но
Раскрщв скобки, мы получим выражения типа sin a cos р, ко-
торые мож’но преобразовать по известной тригонометрической
формуле:
Sin a cos Р = у [sin (а + Р) 4- Sin (а — Р)].
Делая такое преобразование, мы получим уравнение:
У п Ап sin п9 + У Ап С2к [sin (п4*26) 6 + sin (п — 26) 9] =
Развертывая это уравнение по всем индексам, получим раз-
ложение по синусам кратных дуг. Коэфициенты при синусах
равных дуг в правой и левой частях этого уравнения должны
быть равны друг другу. В эти коэфициенты войдут и коэфи-
циенты разложений наших функций в ряде Фурье, т. е. Aif Д2,
Со, С2, С4, С6,... и В19 В2, Bs,...
181
В результате такого приравнивания коэфициентов получаем
уравнения Лотц:
(Cq — "2 ^2) ^1+ [2“ (^*2 О1)^з4“
4“ ~2 (^4 ^б) 2 ^в) 7 4~ • • • J — Но»! >
2Но^а+ (со — 2~ С4 Л2 + [2"(0г — Q) ^4+
+ у(с4—с8) д6 4--|-(С6 — с10) д8+ • • •] = Л;
Зу«(Лз+ —~2 С6^Л3+у (С2—С4) Д1+
+ [у(Ог~ С*8) Л5+у(С4 — С10)Д7 + . . .j = |ХО£?3;
W4+ (с0-1с8) л4+ |(С2-С6) А2+
+ [у (О — Сто) ^б+ 2 ^4 ~ О2) ^s+-“l = Ро®4;
бр-о^б + (Со — у Сто) ^5+ у 1^2 — Cg) Д> + + 4 (С4 - Св) 4+[4 (С2 - С12) л7+... ] 6М« + (с0 - 4 с12) л6+ 4 (G - С10) д4 + = Но®5*> (360)
+ 4 (с4 - св) А2 +14 (С2- С14) Л8+.. J ?Р-о^7 + (Со — у Ач А~2 — ^’12)^5 + = Р-0®6?
+ ~ СюМз + 4(С6 — С8)Л1 + ... "Ь (Со 2 ^б>) ^8 + у (^*2 С’и) Аб +
+ 4(С4 - С12) л4 + 1-(Св - С1О) л2 +... и т. Д.

§ 80. РЕШЕНИЕ УРАВНЕНИЙ И. ЛОТЦ
Эти уравнения обладают двумя очень важными свойствами.
Во-первых, они распадаются на две системы — четную и нечет-
ную, так как в них входят коэфициенты А или только четные
или только нечетные. Нечетным коэфициентам, как мы знаем
182
(гл. XIV, § 70), соответствует симметричный закон изменения
циркуляции по крылу; четные коэфициенты дают несиммет-
ричную кривую Г =/(z).
Следовательно, можно, разбирая случай сложной нагрузки
(например, крыло с отклоненными элеронами), рассматривать
эти коэфициенты отдельно друг от друга.
Вторым очень важным свойством этих уравнений является
легкость их решения способом итераций.
Способ итераций, или последовательных приближений, за-
ключается в том, что систему линейных уравнений решают
относительно каждого неизвестного отдельно, отсекая малые
члены. Уравнения Лотц чрезвычайно удобны для такого метода
расчета, так как в них члены, которые мы заключили в квад-
ратные скобки, очень малы по сравнению с остальными.
Приспособляя уравнения Лотц для такого метода расчета,
решаем первое уравнение относительно- А,, второе относитель-
но А2, третье — относительно Д8 и т. д.
Группируя отдельно четные и нечетные уравнения, полу-
чим две системы, приведенные на стр. 184. Мы намерен-
но дали эти уравнения с большим числом членов, а именно:
нечетную систему для восьми гармоник и четную — для шести.
Пользуясь методом Лотц, легко допустить ошибку в индексах,
приведенные же подробные формулы должны предохранять от
ошибок.
Обычно довольствуются меньшим числом уравнений, и чаще
всего берут лишь четыре первых.
Для того чтобы получить уравнения с меньшим числом гар-
моник надо просто положить все члены Ап, свыше нужных,
равными нулю. Например, взяв четыре нечетных уравнения,
надо положить в общих формулах Л9 = Ди — Л13 = Д15 = 0.
Решение этих уравнений по методу итераций ведется так.
Возьмем нечетную систему. Решаем первое уравнение, отбросив
малые члены, стоящие в скобках. Получаем первое приближе-
ние At. Во втором уравнении отбрасываем малые члены, стоя-
щие в скобках, и подставляем в него найденное по первому
уравнению значение At. Решаем это уравнение относительно
неизвестного коэфициента и получаем для него первое прибли-
жение Аз- В третьем уравнении отбрасываем малые члены и
подставляем в него А{ и А'з. Решая опять уравнение с одним
неизвестным, находим А$. Продолжаем такое вычисление до
тех пор, пока не получим всех нужных коэфициентов. Получим
первое приближение для всех коэфициентов.
Если теперь подставим в первое уравнение все эти значения,
то мы сможем вычислить уже второе приближение для Ati
затем, подставляя найденное значение At, и значения А5, Ai
и т. д. во второе, получим второе приближение для Аз и т. д.
При этом мы все время решаем уравнения лишь с одним не-
183
Система уравнений Лотц
Нечетная (для симметричного закона изменения циркуляции вдоль размаха крыла)
Л1(ре4-С0—2Q) = Ho^i— И(^2—Q)^3 + (^4—Св)Лб4-(Св—С8)Л74-(С8 ~ С]о)Л94-(С10 “С12)Л114-(С12— СИ)Л]34- (Ci4— С1в)Л]б];’
Л j3p0 +*Q)—2^) = P<A— 2(^2—С4)ЛХ— 2 [(^*2 С8)Ле4”(С4 С10)Л7 4" ((~6 ~~Cy зМ э4 (Cl С\4)Л114~(С10—С} в) А13 4“ (С12 С18)Л16]}
^s(5}xo4“£o—2^io)=H'o^s—2'(С1—С6)Л!—2(С2—CS)A3 — 2 [(С2 С12)Л74-(С4 С14)Л94-(Сб С16)ЛП4-(С8—С18)Л134“(С10—С2о)Л 1б];
Л7(7р0 i-C0—2С14)=|л057—о(Сб—С8)Л,—J(C4—Сю)Лз 2(С2—С12)Л5—2[(С2~Cie)^e4“(С4 С18)Лп4-(Се С20)Л134-(С8— С22)Л18];
Л9(9р0 +• Со—'jCle) —Р0^9 2'(С$—*С1 о)Л| 2(^6—£1гМз 2'(<-’4—{-'иМб 2(^2—^1б)^7 2 [(G“ 2о)Лц4“(С4—С22)Л134~(С6-Со^Л^] ’
Лн(1 1|ЛоН-Со—2С18)=»Ро^11“~2(^10—^*12Mi—2(Q—*С14)Л3 2 (Се—C1G)A5 2(С4—С18)Л7—2(С2—С 0)Л9—2[(С,—С24)Л134-(С4—С26)Л16];
Л1з(13|Лд+С0 зСго^нАз 2(^12““Cn)Ai 2(^10 С1б)Л3 з(С8 С18) '5 j(C6 С2О)Л7-'2(С4 С22)А9—i(C2—С24)Л11—2 [(С2—С28)Л16];
Л16(15р.о4"Со— 2 С82)= Po^is 2 (С14 С16)41 2 (Cj2 С18)Л3 2 (C;o~ С20)Л5 2 (С3 ~ С22)А7 | (Сб С24)Л9 — j (С4—С8б)Л11.1
Система уравнений Лотц
Четная (для несимметричного закона изменения циркуляции вдоль размаха крыла)
Л2(2^о4-Со 2’С4) — Ро^з—2 [(С& Св)Л44-(С4 С8)Л64- (Сб С10)Л84~(С8 С12)Л1О4- (С1о—Cj4)A12 ];
44(4po+Co—lCs) = Ро^4—з(С2—С6)А2—2[(С2—С10)Л64-(С*4—С712)Л 8 4-(С76 -С14).4104-(С’8—С1В)Л12];
Л6(бра +• Со - 2С12)г=Ровб'“2'(С4—С8)А2 —2(С8 - С10)Л4—J [(С2 С14)Д84~(С4 C16M104-(C6—С18)Л12];
Л8(8р-о4"Со—2Cig) = Ро^8—2’(Св -С10)Л2 i(^4 С12)Л4 ^(С2 uMe 2 [(Сз Cj8Mi34-(C4—С20)Л12];
Лю(10ро 4“Со — — р0В10—|(Сз С12)Л2 — 2(С® ~ С14)Л4 (С4 С1б)Л6 z(C2 С]8)Л8 - о [(С2—С22)Л12] ’
Л|2(Г2р04-Со—2С24)— Ро^гз—2 С р СИ)Л2 —^(С8-С]6)Л4 — 2(С6--С18) 1б ^(£4—С20)Л8—1(С2—С22)А1о.
известным. Этот процесс нужно продолжать до тех пор, пока
последующие значения коэфициентов не перестанут изменяться.
Уравнения Лотц обладают очень быстрой сходимостью, и обыч-
но второе приближение можно принимать за точное решение.
Третье приближение вычисляют лишь для крыльев необычной
формы или с целью проверки.
Вычислительная работа при способе итераций сокращается
в несколько десятков раз по сравнению со способом простого
решения системы уравнений^ Особенно большая выгода полу-
чается, когда берут большое количество уравнений.
Уравнения Лотц очень легко написать для любого числа
коэфициентов разложения, так как закон группирования членов
в скобках совершенно ясен. Можно, ничего не вычисляя, просто
формально продолжить эти уравнения до любого их числа.
Все это объясняет ту большую популярность, которую имеет
способ Лотц.
После того как будут найдены коэфициенты Аъ А3, А5, Alf
Д9,.«. или, в случае несимметричного изменения а' по размаху,
еще коэфициенты Д2, Д4, Д6, Д8,.дальнейший расчет ведется
по обычным формулам теории Глауэрта.
Примечание. Мы всюду писали выражение циркуляции в безразмер-
ных величинах, а именно в таком виде:
Г = 8 An sin п и.
Лотц, как и большинство ее последователей, пользуется размерными
величинами и пишет:
Г — sin ’’
ЯД
где р0 = —— ; следовательно, у нее
4Г чг' ♦
г = lv = 8и»^л'»sin
отсюда
Ап =
т. е. у Лотц коэфициенты иные, чем в способе Глауэрта. У Глауэрта коэфи-
циент At имеет простое, легко запоминающееся выражение:
причем эта величина имеет очень простой физический смысл: это средний
>гол скоса потока в радианах. Его величину всегда можно грубо определить,
подставив примерную величину су, получающуюся у крыла. Это позволяет
легко вести контроль при вычислениях.
Вследствие этого мы отказались от введения новых коэфициентов Ап = —
Р* о
так как это никакой пользы при расчетах не приносит и даже затрудняет
контроль. Кроме того, формулы для всех аэродинамических величин и в спо-
собе Глауэрта и в способе Лотц получились у нас одинаковые. У самой же
Лотц во всех формулах стоит величина р.о, добавочная по сравнению с фор-
мулами Глауэрта.
Заметим еще, что многие наши и иностранные авторы иногда вводят и
другие обозначения, например, р0 = , Г = aQbУ^ДП sin пЬ и т. п.
185
Вследствие этого, пользуясь методом Лотц по различным
книгам и с п р а в о чн и’к а м, следует тщательно ознако-
миться с системой обозначений автора иначе можно допустить
грубые ошибки. 4
Мы в нашем курсе все время придерживаемся однообразных безразмер-
ных обозначений.
§ 81. ВЫЧИСЛЕНИЕ КОЭФИЦИЕНТОВ и Вт
Способ Лбтц дает возможность очень быстро и точно ре-
шать задачи о вычислении закона изменения циркуляции ско-
рости по размаху крыла. При этом основное уравнение удовле-
творяется не только в нескольких сечениях, но и на всем раз-
махе крыла, которое, однако, изображается в этом методе
лишь приближенно. Любую форму крыла можно математически
представить лишь бесконечным числом членов ряда Фурье.
Обычно же ряд Фурье берется с весьма ограниченным числом
членов; чаще всего берут четыре члена, соответствующие ко-
эфициентам Аь А3, А5 и А? и полагают все остальные Ап = 0.
Но тогда отпадают и члены C2k и Вт высокого порядка. Оста-
ются, например, при четырех уравнениях лишь Blf B3f В5,В7 и Со,
С2, С4, С6, С8, С1о, С12 и С14. Следовательно, как бы точно мы
не разлагали в ряд величины ~ sin б и «'sin 6, мы можем использо-
вать лишь первые члены.
Таким образом крыло и все его характеристики будут в
этом методе представлены волнистой линией. На фиг. 112
Фиг. 112. Изображение постоянной циркуляции с помощью ряда Фурье.
крыло с постоянной циркуляцией изображено с помощью четы-
рех коэфициентов: Alt А3, А& и А-,. Форма получилась хотя и
волнистая, но все же близкая к исходной.
186
Американцы исследовали вопрос, насколько возрастает точ-
ность расчета по методу Лотц когда берут много точек для
вычисления характеристик крыла или берут больше уравнений.
Оказалось, что влияние числа точек очень невелико. Точность
расчета зависит почти исключительно от числа взятых уравнений
Главную трудность в решении уравнений Лотц представляет
предварительное нахождение коэфициентов разложения:
~^sin9 = £C2ft cos 2&9
и
a'sin 6 = sin mb.
Как известно из теории рядов Фурье, любой коэфициент
разложения может быть вычислен по формулам:
С« = — f 4- sin 9 cos2£9d9;
J V
0
Co = — f -v-sin 6 cos 2kb db;
° Я J Ь
0
Brn = ^ J" a'sin 9 sin mb db.
0
Если форма крыла и его закрутка заданы аналитически, то
нужно вычислить эти интегралы для ряда последовательных
значений индексов k и т. Решение затруднительно и требует
большой вычислительной работы. Кроме того, при расчете
крыльев с острыми концами
приходится учитывать беско-
нечные значения подинтег-
ральной функции и искать
величину несобственных ин-
тегралов. Все же принци-
пиально вычисление всегда
может быть доведено до
конца.
Чаще всего на практике
форма крыла задается черте-
жом. Тогда для определения
Фиг. 113. Характеризующие
крыло функции.
коэфициентов ряда Фурье при-
ходится пользоваться методами гармонического анализа. Для это-
го нужно сначала построить по чертежу крыла закон изменения
-у- sin в = f(z) и a' sin 0 = y(z) (фиг. 113).
187
Быстрее всего этот анализ может быть сделан при помощи
специальных приборов так называемых гармонических
анализаторов. _ _
е Обводя штифтом прибора кривые f(z) и u(z), получают последо-
вательные значения всех коэфициентов разложения. К сожалению,
такие приборы довольно дороги и редко бывают в распоряже-
нии конструктора.
Чаще всего этот анализ ведут арифметически; различные
методы расчета подробно излагаются в курсах математики,
в разделе рядов Фурье. Для производства таких расчетов поль-
зуются специальными формулярами, дающими указания оЗпоследо-
вательности вычислений. К сожалению, обычно такие формуляры
составляются для разложения в интервале 0—2тс и для полного
ряда Фурье. В теории же крыла применяются разложения от О
до я и обычно по синусам. Их приходится вычислять заново,
что требует времени. Мы приводим поэтому здесь удачный фор-
муляр, рекомендуемый Американским авиационным комитетом
(Rep. NACA 585 1937 г.), приспособленный к методу Лотц. Вы-
числение по этому формуляру ведут таким образом.
Формуляр для вычисления коэфициентов разложения ряда Фурье C2k и Вт
для 10 точек полуразмаха крыла
Таблица А
Точки идут через 9°
п 6° | г | =- cos ' । 1 sin b Ь£- sih8=>n a'° a'° . , • , 57jS,n"=^«
10 90 0 1,00
9 81 0,1564 0,9877
8 72 0,3090 0,9511
7 63 0,4540 0,8910
б 54 0,5878 0,8090
5 45 0,7071 0,7071
4 36 0,8090 0,5878
3 27 0,8910 0,4540
2 18 0,9511 0,3090
1 9 0,9877 0,1564
0 0 1,0000 0
Полуразмах крыла разбивают на десять участков, соответ-
ственно приросту 0 на 9° для каждого участка. По табл. А
188
вычисляют для z величины у = -у- sin 6 и у — a' sin 9. Затем по
табл. В находят члены Вт.и по табл. С—коэфициенты C2k .
Ниже приведен формуляр для симметричного крыла. Для
несимметричных разложений рекомендуем обращаться к соот-
ветствующим руководствам и справочникам.
Таблица В
Определение Вт
Ь + Ь — Ь~У7 + У9 = G; У2 — Уь + -у Ьо = G
I II I II I II I II I 11
sin 9° = 0,1564 У1 —У1 —Уз Уз •
sill 18° = 0,3090 sin 27° = 0,4540 Уз Уч У1 Уб -ь Уб —у?
sin 36° = 0,5878 siu 45° = 0,7071 Уб У* Уб —У* Г1 -Уб Уб Уб -ь
sin 54° = 0,8090 sin 63° = 0,8910 У1 Уб —Уб Уч У1 Уч ~~Уз Уб
sin 72° = 0,9511 у8 У* —ь —Уз
sin 81° = 0,9877 Уб Ь Уч У1
sin 90° = 1,000 т5,10 — -у Ьо - у Ьо Т-У^
Сумма I Сумма II
Сумма I -{-сумма II = 56, = 5В3 =5fis = 5В7 = 5В9
Сумма I—сумма 11 = 5В19 =5В„ =5В16 = 5В13 =5ВП
Проверка. Вг В34-Вб В7 + В9—В1г-\-В13—^15 + В17—Bi9=bo*
Примечание. Если а' = const, то = а и остальные Вп =» 0.
Таблица С
Определение C2k
Ординаты 1 У1 У2 Уз У4 Уб V0 Vi V2
'V1O У» Л Уч Уб v5 V4 V3
Сумма ь ^3 Vl ^5 Ро Pl Рч
Разность Wo Wj Wo w3 w4 Ч1 42
189
Продолжение таблицы С
sin 18° = 0,3090
sin 36° = 0,5878
sin 54° = 0,8090
sin 72° - 0,9511
sin 90° = 1,00
Сумма I
Сумма II
Сумма I+сумма II
Сумма I—сумма II
I
—Qi
56*12
II
10 Со — Pq + А +р2; 5С10 « wQ — w2 + ЮС20 = qQ — + q2.
Проверка. Со ^-С2-}-С^С6 + С10 4- С’12 + С’144-С1в-}-С,18+ Сзв^О.
§ 82. СРАВНЕНИЕ И КРИТИКА МЕТОДОВ ГЛАУЭРТА И ЛОТЦ
Теория, как видим, полностью решила задачу о расчете
крыла любой формы. Хотя это и сделано при некоторых упроще-
ниях действительного явления, все же результаты подсчетов
очень близки к опытным.
Однако вычисления при этом получаются сложные и трудо-
емкие, поэтому во всех странах возникла мысль заранее сделать
в исследовательских институтах такие вычисления для типич-
ных крыльев. В последние годы опубликован ряд таких работ
в Америке, Англии и в СССР (см. библиографию). Такие гото-
вые результаты чаще всего даются для трапецевидных крыльев.
В СССР богатый материал по таким крыльям приведен в со-
ставленном ЦАГИ „Справочнике авиаконструктора", т. I, 1937 г.
Здесь для ориентировки мы приводим сводную таблицу зна-
чений коэфициентов Ап для типичных крыльев, не имеющих
закрутки, заимствованную у Глауэрта icm. табл. 12).
Таблица эта вычислена для \ = ай. Считая aQ = 5,6, получим»
следовательно, размах этих крыльев X = 5,6, что близко к сред-
нему размаху у многих самолетов. Угол атаки был условно
принят равным одному радиану, т. е. d = 1. При других углах
атаки у незакрученных крыльев эти коэфициенты изменяются
пропорционально отношению углов атаки; в данном случае
нужно табличные значения коэфициентов Ап умножать на
а0
Я = 57^”
140
Удлинение крыла изменяет форму кривой нагрузки, т. е.
коэфициенты Ап. Однако при малых изменениях X эти кривые
мало отличаются друг от друга.
Таблица 12
Значения коэфициентов Ап
Угол атаки условно принят равным 1 радиану; X = ав
Крыло в плане bk Ьо Аг А, ^5 ^7 а во т
Эллиптическое .... 0,250 0 0 0 0,760 0 0
Прямоугольное .... Трапецевидное .... 1 1 ( 0,232 О',029 0,006 0,001. 0,729 0,17 0,049
>> .... 0,75 0,236 0,020 0,008 0 0,742 0,10 0,026
» .... 0,50 0,240 0,007 0,010 —0,001 0,754 0,03 0,011
>> .... 0,25 0,241 —0,012 0,010 —0,002 0,757 0,01 0,016
» .... Треугольное 0 । 0,232 -0,050 0,002 —0,004 0,729 0,17 0,141
На фиг. 111 приведены полученные в результате расчета
кривые циркуляции для крыльев различной формы; эти крылья
имели одинаковое удлинение X = а0 и развивали равную подъ-
емную силу. Диаграмма показывает, что циркуляция у эллипти-
ческого крыла занимает среднее положение. У прямоугольного
и трапецевидного крыльев кривые циркуляции довольно близки
к эллиптической; лишь треугольное крыло дает большие откло-
нения от эллиптического закона.
Отсюда делаем вывод: у встречающихся на практике форм
крыльев изменение циркуляции по размаху близко к закону по-
луэллипса.
Глава XVII
ЗАКРУЧЕННЫЕ КРЫЛЬЯ
§ 83. ОБЩИЕ СВОЙСТВА ЗАКРУЧЕННЫХ КРЫЛЬЕВ
Незакрученным, или плоским, крылом называется такое крыло,
у которого аэродинамические хорды лежат в одной плоскости.
У такого крыла при су = 0 обязательно и cx-t = 0.
Всякое крыло, у которого аэродинамические хорды не лежат
в одной плоскости, называется закрученным крылом. Заметим,
Что крыло, у которого геометрические хорды его сечений ле-
жат в одной плоскости, но кривизна его профилей различна, в
аэродинамическом смысле будет закрученным, так как угол атаки
нулевой подъемной силы, т. е. а0, будет меняться по размаху
крыла и, следовательно, будет изменяться а'.
191
Местный угол атаки у закрученного крыла, как всегда от-
считываемый от аэродинамической хорды, связан с углом атаки
крыла а соотношением:
а' = а + ф,
(364)
и для истинного угла атаки
az- — а — Да
где (р — угол закручивания сечения по отношению к углу атаки а,
отсчитываемому по центральной хорде крыла.
Возникает вопрос: как сказывается закрутка на аэродинами-
ческих свойствах крыльев?
Оказалось очень удобным, пользуясь принципом независи-
мости действия вихрей, рассматривать циркуляцию у закручен-
ного крыла как бы состоящей
из двух частей — из циркуляции,
этого же крыла, но не закручен-
ного, и отдельно из циркуляции,
связанной с закруткой.
Пусть мы имеем на фиг. 114
циркуляцию закрученного крыла
Г. Если мы подсчитаем цирку-
Фиг. 114. Сложение циркуляции
нззакрученного крыла 1\ с цир-
куляцией от закрутки Г2.
куляцией Г2,
Итак,
ляцию у такого же крыла, но не
закрученного, то мы получим у
него некоторую кривую Гх. Раз-
ница между Г hJ\ и будет цир-
связанной с закруткой крыла.
Г = Г1 + Г2.
(365)
Заменяя выражение для Г по уравнению связи, получим:
-^-CybV = су1 bV + сУ2 bV
или
Су = Су1 4- С V2- (366)
Здесь Cyi и Cyi — местные коэфициенты подъемной силы; пер-
вый соответствует незакрученному крылу, а второй — закручен-
ному при а = 0.
Величина су может вычисляться по истинному углу атаки
крыла по формулам:
Су = д0(а 4- (р— а);
Cyi = (а — Дах);
Су2 == ^оа1*2 “ ^0 (^ Д^г)*
Отметим очень важное обстоятельство: су2 не зависит ст
угла атаки, а зависит лишь от закрутки крыла ф и его формы,
определяющей величину Да.2.
192
Из (366) получаем соотношение:
« 4" ф — Да = а — Aat 4- f — Да2
или
Да = Да* Ла2.
Таким образом угол скоса потока у закрученного крыла можно
рассматривать как бы состоящим из двух независимых углов
скоса: Дах — плоского крыла и Да2—закрученного при а=0.
Этот вывод можно сделать и непосредственно по принципу
независимости действия вихревых систем. Перейдем теперь
к индуктивному сопротивлению таких крыльев.
По общей формуле для любого сечения крыла:
Cxi — Су&%
для рассматриваемого случая напишем:
c'xi = (Cyi + с'у2) (Даг + Да2) =
= CyL Да, + СУ1 Да2 4- Су2 Да, 4- Суг Да2 =
= exil 4“ 4" СУ2 4“ Cxi2 • (367)
Получился интересный результат: индуктивное сопротивление
закрученного крыла равно сумме индуктивных сопротивлений от-
дельных его нагрузок схц и сл,2, плюс индуктивные сопротив-
ления от взаимной индукции Да2 и су2Да2. Здесь получается,
как указал инж. В. Н. Беляев, полная аналогия биплану.
Вопрос о величине cXi у закрученного крыла очень важен,
так как такие крылья очень часто встречаются на практике. Нам
нужно найти связь между сх1 и су и научиться строить кривые
индуктивного сопротивления для закрученных крыльев. Соотно-
шение (д67) написано для местных величин. Полные же вели-
чины, относящиеся к крылу в целом, получатся интегрирова-
нием этих выражений, т. е.
+1/2 +ll2 +Ц2
cxl=-±- f с'хп bdz 4- -у- j c'yi^2bdz + -~ J Cy2^lbdz +
—Z,2 —Z/2 -Z/2
4-Z/2
+ ~S~J c'*ibdz-
—Z/2
Первый член представляет собой обычное индуктивное со-
противление незакрученного крыла:
C.xi ACyi-
Последний член выражает индуктивное сопротивление от за-
крутки, а так как угол скоса потока Да2 и циркуляция Г2 не за-
висят от угла атаки а и, следовательно, от общего су крыла, то
Б. Н. Юрьев—171—13 193
эту величину следует считать постоянной, т. е.
cXi2 = С = const. (368)
Исследуем интегралы, дающие взаимоиндукцию нагрузок, т. е.
+//2 +Z/2
J сУ1 bdz-\—J cyi Дах b dz.
—1/2 —1/2
Легко показать, что оба эти интеграла пропорциональны cyi.
Действительно, первый мы можем переписать в таком виде:
4-Z/2 ,
Величина, стоящая под интегралом, является теперь лишь
функцией формы крыла, так как cyl/cyt не зависит от самого сУ1.
Следовательно, этот интеграл имеет вид произведения cyiBit где
Вг = const.
Рассмотрим теперь второй интеграл, введя в него значение
Дах в развернутом виде:
+ Z/2 + /2
4? "S’ J СпЬ dz f "С=7
— Z/2 —Z/2
Подставив в это выражение по уравнению связи Гх = -~-су1ЬУ,
получим:
аС'-ь
1 +'/2Ч/* , cyi
J cy^b^r^dz.
—1/2 —1/2
Под знаком интеграла стоит выражение, зависящее лишь от
формы крыла, но не зависящее от сУ1. Следовательно, этот
интеграл, как и первый, имеет вид произведения сУ1В2,
где В2 = const; сумма обоих интегралов равна су1(В1 + В2) =
= сУ1В'.
Таким образом индуктивное сопротивление крыла может
быть написано в таком виде:
С»; = Асу1 В'сУ1 + С.
Подставим в это выражение су всего крыла по формуле:
сп =су — сУ2. Получим:
Сн = А (су сУ2)' + В' (су сУ2) -|- С .
Раскрывая скобки и замечая, что сУ2 = const, получаем выра-
жение вида:
cxi = Асу + Всу + С. (369)
194
Это выражение было впервые дано инж. В. Н. Беляевым1.
Итак, полное индуктивное сопротивление закрученного кры-
ла представляется параболой второй степени, но со смещен-
ной вершиной.
Таким образом, если эллиптическое крыло имеет параболу
индуктивного сопротивления, которая изображена на фиг. 115
кривой еОЕ и выражается уравнением: cxt == -г-, то парабола ин-
дуктивного сапротивления плоского крыла произвольной формы
изобразится кривой dOD и выразится уравнением: cxi
= 1 + — Асу. Закрутка крыла вызовет в этой кривой сле-
дующие изменения: во-первых, вер-
шина сместится в точку Ох на рас-
стояние С, и, во-вторых, придется
прибавить величину Всу, дающую ли-
нейную прибавку к величине индук-
тивного сопротивления. В результате
получим параболу JOXF.
Эта парабола может пересечься в
частных случаях с параболой незакру-
ченного крыла в некоторой точке Д
в этом случае закрученное крыло
сравнивается по индукции с незакру-
ченным. Может быть и такой случай,
когда закрученное крыло станет луч-
ше незакрученного. Наконец, пара-
бола закрученного крыла (fO^F) может
коснуться параболы эллиптического
крыла в точке Е. В этот момент за-
кон распределения циркуляции по
закрученному крылу должен быть
эллиптическим. Мы уже отмечали в
§ 77, что у крыла любой формы с
помощью надлежащего закручивания
Фиг. 115. Парабола индук-
тивного сопротивления у
закрученного крыла.
можно получить эллиптический за-
кон циркуляции. В точке £*> следо-
вательно, мы и имеем такой частный
случай. Пересечься с кривой еОЕ
наша парабола индуктивного сопротивления не может, так
как эллиптическое крыло является наивыгоднейшим.
Вообще же парабола закрученного крыла обычно не пересе-
кается с кривой dOD, не касается кривой еОЕ и идет внутри
этих парабол.
Указать общие закономерности относительно влияния за-
крутки на аэродинамику очень трудно, так как конструкторы
1 В. Н. Беляев, Аэродинамическая теория закрученного крыла, „Техника
воздушного флота", № 2, 1933.
195
придают своим крыльям самые разнообразные формы, руковод-
ствуясь при этом вопросами устойчивости, прочности, антишто-
порными свойствами крыльев и т. д.
Определять аэродинамические свойства закрученных крыльев
следует с помощью поверочного расчета по описанным у нас
методам. Формулы Глауэрта, Лотц и другие построены так, что
в них входит местный угол атаки а' или функция а'sin9; пере-
менный угол а' и отражает в этих формулах закрутку.
Теперь выясним, на скольких углах атаки нужно рассчиты-
вать такие крылья.
Очевидно, что для построения параболы закрученного крыла
нужно сделать три расчета, так как в нашу формулу входят
три коэфициента: А, В и С. Получив после расчета три значе-
ния сХ1, cxi и Cxi и соответственно су, су и су , получим три
уравнения:
Cxi = Асу 4- Всу 4- С}
Cxi = Асу 1 2 4" Всу 4- С;
Cxi = Асу 2 4* Всу 4-С.
(370)
Решая эти уравнения, находим А, В и С.
Обычно удобнее решать прямо задачу о закрученном крыле.
Однако, заготовив заранее расчетные таблицы и графики,
выгодно задачу расчленять и определять отдельно аэродинами-
ческие характеристики плоского крыла и его закрутки.
Наиболее подробные исследования таких крыльев были про-
ведены в ЦАГИ В. Н. Беляевым и А. Б. Рисбергом *.
Работы А. Б. Рисберга вошли в „Справочник авиаконструктора"
(т. I, 1937 г.) в виде целого ряда весьма полезных графиков. Поль-
зование этими графиками в „Справочнике" подробно объяснено.
Все эти исследования показывают, что даже небольшая за-
крутка сильно сказывается на аэродинамических свойствах крыла.
Большое значение имеет вопрос о деформации крыльев
в полете, так как у крыльев малой жесткости благодаря за-
крутке во время полета может очень сильно изменяться вся их
нагрузка.
Расчет крыльев с одновременным учетом их аэродинамики
и прочности излагается в курсах прочности и конструкции само-
летов.
Простейший прием заключается в применении метода после-
довательных приближений. Сначала рассчитывают крыло без
учета закрутки, затем, найдя его аэродинамическую нагрузку, вычи-
сляют закрутку по жесткости крыла, затем исходя из получив-
шейся деформированной формы крыла снова повторяют аэро-
динамический расчет. Так поступают до тех пор, пока предпо-
ложенная форма крыла не будет совпадать с получающейся.
1 А. Б. Р и с б е р г, Влияние формы крыла на распределение нагрузки по
размаху и на продольную устойчивость. Труды ЦАГИ № 335, 1937.
196
Этот способ не всегда удобен, так как при крыльях малой
жесткости может возникнуть так называемая дивергенция, когда
крыло закручивается настолько легко, что нарастание аэроди-
намических крутящих моментов не уравновешивается жесткостью
крыла, и оно ломается.
Более строгие способы основаны на решении основного
интегро-диференциального уравнения крыла путем введения
в него закрутки, зависящей от нагрузки. Эти задачи очень труд-
ные, и здесь мы их рассматривать не будем, отсылая читателей
к специальным курсам.
§ 84. ПРЯМОУГОЛЬНОЕ ЗАКРУЧЕННОЕ КРЫЛО
В качестве примера расчета закрученных крыльев рассмотрим
случай прямоугольного крыла с постоянным профилем, но с за-
круткой, следующей закону: _
<? = ¥«?, (371)
где г —абсцисса сечения и закрутка на конце крыла. Пере-
ходим к рядам Фурье. Тогда z =—cos 9 и
= <fK cos 9.
Отсюда угол атаки
а' = а — tpK cos 9. (372)
Основное уравнение Глауэрта теперь примет вид:
Ап sin п 9 (пр + sin 9) = р sin 9 (а — <рк cos 0).
Решение этого уравнения может быть проведено для несколь-
ких первых членов как обычно, но только каждый коэфициент
разлагается теперь на сумму двух членов, один из которых
пропорционален ра, а второй рлрк.
Глауэрт вычислил для X — а0 четыре коэфициента этого урав-
нения. Закрутка крыла считалась отрицательной (<рк < 0) и угол
атаки уменьшался к концам крыла. Получились следующие ве-
личины:
Л! = 0,928 р« — 0,408 р<рк ;
Л3 = 0,115 р<х — 0,242 p.fK ;
Л5 = 0,023 ра 4- 0,010 р<рк ;
Л7 = 0,004ра — 0,023 р<рк.
Коэфициент подъемной силы закрученного крыла имеет
величину:
сд = п\А1 = 4,56а - 2,02<fK, (373)
причем наклон кривой су по а остается таким же, как и в слу-
чае незакрученного прямоугольного крыла; су уменьшается на
постоянную величину.
Коэфициент индуктивного сопротивления всегда можно на-
писать в виде:
с2
197
но только при закрученном крыле коэфициент 8 будет изме-
няться вместе с углом атаки. Вследствие этого сЛ1^0, когда
z^-эО, так как величина 3 при этом стремится к бесконечности.
|Если взять закрутку на конце <рк = 0,1, то характеристики
крыла при различных углах атаки будут такими:
а Су 6
0,10 0,256 0,205
0,15 0,484 0,027
0,20 0,712 0,000
0,25 0,940 0.0J3
Сравнивая эти значения 8 со значением 8 = 0,049, получен-
ным для незакрученного прямоугольного крыла того же размаха,
легко видеть, что закрученное крыло с уменьшающимися к кон-
цам углами атаки дает меньшее индуктивное сопротивление.
При малых же значениях коэфициента су величина 8 растет,
стремясь, как указано, к бесконечности при су = 0, так как
парабола индуктивного сопротивления закрученного крыла через
начало координат не проходит.
Глава XVIII
ПРОВЕРКА И УТОЧНЕНИЕ ТЕОРИИ ИНДУКТИВНОГО
СОПРОТИВЛЕНИЯ
§ 85. КАРТИНА ДАВЛЕНИЯ И ЦИРКУЛЯЦИЯ
Ввиду большого значения этой теории для инженерных рас-
четов были проведены многочисленные исследования по ее про-
верке. Проверка суммарного эффекта, т. е. сравнение расчетных
Су, сх и сП1 с результатами испытаний дает очень хорошие ре-
зультаты, но все же получаются хотя и малые, но заметные
отклонения.
Обычно значение су у прямоугольных и трапецевидных кры-
льев, получающееся при опытах, оказывается приблизительно
на 3% большим, чем по расчету. У эллиптических и трапеце-
видных крыльев, но с закрученными концами, получается более
хорошая сходимость опытов с теорией.
Для углубления этой теории недостаточно пользоваться
суммарной проверкой ее результатов, нужно проверить всю
физическую картину работы крыла в действительности и срав-
нить ее с принятой в теории. В первую очередь нужно прове-
рить самый закон изменения циркуляции по размаху.
Экспериментальная аэродинамика дает для этого прекрасное
средство в виде картины распределения давления по крылу.
Как известно, для изучения этой картины испытывают в трубе
дренированные крылья и определяют избыточное давление р'=
==р —ра в различных точках поверхности крыла.
Для приведения результатов опытов к безразмерным вели-
198
чинам вводят коэфициент давления р, определяемый из соотно-
шения:
Р=Т> (374)
Фиг. 116. Картина распределения
давления по крылу.
где q = ~ скоростной напор потока (см. часть I, гл. VII, § 36)1.
При таких опытах изучают давление в точках, расположен-
ных в ряде поперечных сечений крыла (фиг. 116).
Картину давлений обычно строят на хорде крыла, отклады-
вая в проекциях точек профиля на хорду величину коэфициента
давления. Обычно отрицательные
значения р откладывают вверх,
а положительные вниз; по точкам,
относящимся к верхней поверх-
ности крыла, проводят кривую
сплошной линией, а относящиеся
к нижней поверхности—пункти-
ром. На профиле всегда имеется
точка, где давление достигает
максимально возможной при об-
текании тел величины, равной-J-1.
Соответствующая точка профиля
называется критической.
На верхней поверхности у
носика крыла при больших углах
атаки получается весьма боль-
шое разрежение, достигающее
при больших числах Рейнольдса
огромных значений р= — 8, — 10.
Скорость воздуха, скользящего на поверхности крыла в такой
точке, получается значительно большей, чем скорость полета.
Применение теории Бернулли показывает, что местная скорость
будет в 2—3 раза больше скорости полета, что при современ-
ных скоростях полета, близких к 120 м)сек, дает уже сверх-
звуковую скорость. Обтекание при таких скоростях различных
бугорков, заклепок и выступающих из поверхности носика
крыла деталей должно сопровождаться образованием местных
волн Маха, что вызывает увеличение сопротивления этих дета-
лей в несколько раз. Следовательно, профильное сопротивление
у современных самолетов может заметно увеличиваться при
больших числах Ва.
Переходим теперь к определению подъемной силы и цирку-
ляции скорости по картине давления. При обычных углах атаки
можно считать су = сп, поэтому вместо подъемной силы
можно определить силу, нормальную к крылу. Будем вычислять
1 См. Б. Н. Юрьев, С пределение аэродинамических сил и моментов по
картине распределения давления по крылу. Изд. ВВА, 1933-
199
эту силу для полоски крыла шириной dz (фиг. 117). Возьмем
элемент площади крыла dS с длиной ds и шириной dz и отло-
жим по нормали к нему действующую на него силу давления
d^R, равную:
d2R = р ds dz,
где р = pq—uwsnenite у этого элемента.
Проектируя эту силу на нормаль к хорде, получим:
= d*R cos ф = pds cos <f dz.
Замечая по чертежу, что ds cos <(> = dx и подставляя вместо
р величину pq, получим: _
d2Yy = pg dx dz.
Интегрируя это выражение
Фиг. 117. Картина распределения
давления по профилю крыла.
по х, получим силу dY1} дейст-
вующую на полоску крыла ши-
риной dz:
dYx = qdz$~pdx.
X,
Эта сила для обычных углов
атаки, примерно до 15°, очень
близка к подъемной силе dY.
Подъемную силу, действующую
на полоску шириной dz, можно
написать также с помощью
обычной формулы эксперимен-
тальной аэродинамики:
dY = с'у b dz V2 = с'у b dz q,
где Су — текущее значение коэ-
фициента подъемной силы.
Приравнивая друг другу оба
выражения, получаем:
Ж, _
c'yb dzq = qdz J р dx.
X,
Отсюда
Cy=-^-fpdx (376)
или в отвлеченных обозначениях, при 1 = 2:
cy=±fpdx. (377)
О 4
л»а
Этот интеграл представится на диаграмме (фиг. 117) пло-
щадью, ограниченной кривой давления. Обозначим такую площадь
200
через F—для размерного написания формулы (376) и через
F—для безразмерного. Получим:
с'у = 4 <378>
или
Су = ~, (379)
ь
т. е. площадь диаграмм, давления для какого-нибудь сечения
крыла, деленная на длину хорды, дает местный су крыла в этом
сечении.
Зная су, находим отвлеченную циркуляцию Г в данном сече-
нии z по уравнению связи:
Г= с'уЬ = Л (380)
Получается очень важный результат: площадь диаграммы
давления для какого-нибудь сечения крыла, вычисленная в от-
влеченных единицах, равна отвлеченной циркуляции вокруг этого>
сечения.
Если площадь F была определена в именованных величинах,
то
Vi /7. F 77 _ Fb _2F ,адп
1 — Су b — ь b — . (381}
Циркуляция скорости Г = Г-4, следовательно, равна:
FV
г = —. (382)
Таким образом обработка опытов по изучению распределе-
ния давления позволяет определить для любого сечения крыла
величину местных су или Г. Построив диаграмму изменения этих
величин по размаху, полу-
чим эпюру нагружения крыла
[фиг. 118). Отвлеченная площадь
U, ограниченная этой кривой и
размахом крыла, дает, как мы
знаем [формула (298)], величину
cv для всего крыла:
Су = 4 = (383)
—1
Фиг. 118. Определение площади S2-
§ 86. ОПЫТНАЯ ПРОВЕРКА ТЕОРИИ ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ
С ПОМОЩЬЮ КАРТИНЫ ДАВЛЕНИЯ
Картина давления позволяет очень глубоко заглянуть в ме-
ханизм получения подъемной силы. Она позволяет определить
в любом сечении циркуляцию скорости около крыла и поэтому
20»
может служить прекрасным средством для проверки теории
индукции.
Для получения правильной картины изменения Г по размаху
нужно иметь достаточное число сечений по размаху. Особенно
важно исследовать концы крыльев и места резкого излома
формы крыла в плане.
К сожалению, вследствие кропотливости таких опытов лабо-
ратории стараются брать поменьше сечений, и картина изме-
нения Г на концах крыла изучена пока еще недостаточно. Кроме
того, большинство опытов было проведено на малых числах
Рейнольдса. Имеются хорошие исследования картины давления
на самолете в полете (главным образом американские), но и там
число сечений бралось слишком малое, особенно на концах
крыльев и в стыке крыльев с фюзеляжем.
Тем не менее имеющиеся материалы позволяют сделать ряд
ценных выводов.
а) Теория индуктивного сопротивления дает в общем хоро-
шие результаты. Кривые Г =/(г) как опытные, так щвычислен-
ные в средней части размаха, идут очень близко друг к другу
даже в случаях очертания крыла с изломами; например, полу-
чаются хорошие результаты для крыла с открытыми закрылками
на средней части крыла.
б) Однако у самых концов крыла постоянно наблюдается резкое
расхождение теории с опытами. По теории Г должна падать
у обычных крыльев плавно до нуля. В действительности полу-
чается резкий скачок; Г сначала возрастает, затем снова падает
и лишь на самом конце крыла обращается в нуль.
Это явление особенно резко проявляется у крыльев, кончаю-
щихся хордой конечной длины, т. е. не имеющих в плане округ-
ления на концах; особенно оно сильно на больших углах атаки.
Объяснение этого явления весь-
ма просто. При выводе всех фор-
мул индукции предполагалось, что
-ZEzyiJy-- обтекание каждого сечения про-
/ исходит так же, как в плоско-
параллельном потоке. На самом
деле на конце крыльев этого быть
-Фиг. 119. Циркуляция на конце не может, ТЭК как над крылом по-
крыла. лучается разрежение, а под ним —
сжатие, воздушные струйки стре-
мятся выравнять эту разность давлений, перетекая с нижней
поверхности крыла на верхнюю (фиг. 119). При этом возникает
срыв потока с крыла и создается вихрь конечной циркуляции,
присасывающийся к верхней поверхности крыла. Это создает
добавочное разрежение на концах, вследствие чего подъемная
сила несколько возрастает.
Для наглядности в аэродинамических лабораториях иногда
изготовляют гипсовые модели, у которых на дощечке, изобра-
зи
жающей_план крыла, откладывают по нормали коэфициент да-
вления р. На фиг. 120 даны фотографии таких американских
моделей. На них совершенно ясно видны бугры разрежения,
созданные присосавшимися к концам крыла вихрями.
в) Работающий винт и фюзеляж, пересекающий крыло, вно-
сят резкие изменения в работу крыла. Очень интересны амери-
канские опыты с моделью крыла с вращающимся от моторчика вин-
том. На фиг. 121 приведена одна такая диаграмма (Rep. NACA 569,
Фиг. 120. Концевые бугры разрежения.
1936 г.). Очертание модели крыла было прямоугольное, а
величина X изменялась и была последовательно равна 6, 5,
4 и 3. Опыт велся в самолетной гигантской трубе на боль-
ших числах Рейнольдса, в среднем равных 4 000000 для большой
скорости и 2000000 — для малой. Эти скорости были подобраны
так, что большая соответствовала максимальной скорости само-
лета и малая — взлетной.
Эта диаграмма, а также ряд других, здесь не приводимых,
показывают, что на кривую Г = /(z) оказывают большое вли-
яние факторы, учет которых еще детально не разработан.
Рассмотрим способы, с помощью которых можно улучшить
эту теорию и сделать ее более точной.
§ 87. УЧЕТ ВЛИЯНИЯ КОНЦОВ КРЫЛА
На самом конце крыла, если концевая хорда там не равна
нулю, циркуляция не падает плавно до нуля, а при больших
углах атаки внезапно поднимается и затем уже у самого конца
падает до нуля. На основании крайне недостаточного имеюще-
гося материала весьма трудно установить точно наблюдающиеся
при этом закономерности. В общем все же можно сделать сле-
дующие выводы (фиг. 122): скачок циркуляции наблюдается
обычно на расстоянии от конца, равном приблизительно чет-
верти концевой хорды. При больших углах атаки замечается
большой скачок циркуляции вверх, при средних она идет
почти горизонтально, а при малых углах атаки циркуляция хотя
и падает, но все же близка к постоянной величине.
203
Расстояние от центра 6 дюймах
Фиг. 121. Влияние работы винта и размаха крыла на кривые Г «f(z).
Отсюда вытекает следующее правило для исправления кри-
вой циркуляции: нужно построения делать по теории лишь
до значения z — 1 —далее нужно в первом приближении
считать циркуляцию постоянной. Следовательно, с концов
крыла должна сбегать очень интен-
сивная вихревая пелена, которую можно
рассматривать как конечный вюсревой
шнур, идущий на расстоянии z—\ от
центра крыла.
Таким образом опыты заставляют
ввести существенный корректив в тео-
рию. В действительности система вих-
рей представляет собой нечто среднее
между системой П-образных вихрей и
системой вихрей у крыла с изме-
няющейся по размаху циркуляцией
(фиг. 123).
Вычисляя скорость скоса, мы дол-
жны учитывать концевые вихревые усы.
Фиг. 122. Эксперименталь-
ная кривая циркуляции
на концах крыла.
Их влияние можно наблюдать на ряде американских, английских
и немецких диаграмм; они уменьшают довольно сильно углы
Фиг. 123. Уточненная схема вихрей у крыла
с 6к^0.
атаки у примыкаю-
щих участков крыла
и тем уменьшают
циркуляцию.
По принципу сло-
жения вихревых по-
лей можно рассмат-
ривать отдельно
скорости, вызван-
ные на размахе
крыла П-образными
вихрями и добавоч-
ной циркуляцией
(фиг. 123), лежащей
выше линии АВ.
Скорость, вызван-
ная концевыми вих-
рями, найдется со-
вершенно так же,
как в гл. III, в § 11, только циркуляция будет теперь другой,
концевой Гк. Следовательно, в какой-нибудь точке крыла, на-
ходящейся на расстоянии z от середины, мы получим скорость
скоса по формуле:
_ Г Гк ।_____Гк 1 _ ___ Г к 2
— — L 4я(//2 —г) "Г" 4г. (1/2 + г) J 4n (Z/2)2 - г*
205
(384)
или, переходя к безразмерным величинам:
L_.
У , 8я 1 — z2
Такая зависимость дает резкое изменение скорости по раз-
маху. Так, при к = 5 срыв потока начинается на расстоянии
гк = — = — = 0,1.
4 2\
Этому соответствует скорость в центре (z = 0), равная
Г«
увк= — -g^-, а у концов крыла
„ =_А 1
ак 8л 1 - 0,92
г
— 5,27,
т. е. скорость от вихревых усов изменяется в этом частном случае
в 5 раз. К этим скоростям нужно прибавить скорости, вызван-
ные циркуляцией, лежащей выше линии АВ. Грубо прибли-
женно можем принять верхнюю часть нагрузки за эллиптиче-
скую; тогда получим добавочную скорость по формуле (344):
Принимая Го^Гк, получим:
- - Гк-
^0 Г’
с помощью таких величин может быть построена более точная
кривая циркуляции, чем дает современная теория индуктивного'
сопротивления. Все уравнения этой теории должны соблюдаться
для участка крыла CD, на концах же мы должны считать цир-
куляцию постоянной и брать с'у из уравнения Г = суЬ, не счи-
таясь с получающимися там углами атаки, так как в условиях
концевого срыва потока понятие угла атаки теряет смысл.
Для устранения этого срыва нужно закруглять концы крыльев.
По американским многочисленным опытам, проведенным с
крыльями в натуральную величину, для получения хорошего
эффекта такое закругление должно быть довольно большим;
оно должно быть по длине, не менее Ък и иметь в плане форму,
близкую к эллиптической.
При плавном сходе ширины крыла на-нет, повидимому, те-
ория индуктивного сопротивления дает большую точность.
§ 88. ВЛИЯНИЕ ФЮЗЕЛЯЖА И СТРУИ ВИНТА
НА ЦИРКУЛЯЦИЮ КРЫЛА
До настоящего времени еще не создано общепризнанной те-
ории взаимного влияния крыла и фюзеляжа, и в практических
расчетах приходится пользоваться грубыми эмпирическими ме-
тодами, изложенными в гл. XI, § 56.
206
сводится, невидимому, к
потока, набегающего на,
И
Фиг. 124. Схема вихрей
у винта.
Наличие фк зеляжа, как видим, например, на фиг. 121, умень-
шает циркуляцию в центре крыла. В настоящее время из-за
отсутствия необходимого опытного материала приходится просто
уменьшать циркуляцию на-глаз, руководствуясь хотя бы фиг. 121.
В основном действие фюзеляжа
некоторому торможению скорости
крыло. Это и уменьшает циркуляцию.
В задачу этой книги не входит
подробный разбор взаимного влияния
винта и крыла, так как это является
задачей курса воздушных винтов.
Здесь мы остановимся лишь на самых
основных фактах.
Работающий винт имеет, по Н. Е.
Жуковскому, следующую систему
вихрей (фиг. 124). На лопастях
имеется циркуляция скорости, кото-
рая сбегает с винта у втулки в виде
осевого шнура с циркуляцией /Гв (где I— число лопастей), а с
концов лопастей—в виде вихревого цилиндра.
На крыло действует вращение, вызванное осевым вихревым
шнуром, и увеличение скорости от вихревого цилиндра.
Циркуляция у винта Гв зависит от мощности мотора и скорое и
полета; эта зависимость выражается приближенным соотношением:.
150 W
р<оЯ2Яа1/ ’
(385>
где (о — угловая скорость вращения винта, R— его радиус,
N — мощность мотора в л. с. и V — скорость полета в м)сек.
Благодаря этому шнуру внутри струи винта возникает вра-
щение, которое вызывает скорость скоса по формуле:
= i£jL
2пг
^ув
Фиг. 125. Скорости
скоса потока, вызы-
ваемые вращением
винта.
(386).
Это вращение простирается лишь до
г ==R, где R — радиус винта. Дальше цир-
куляция вокруг вихревой цилиндрической
поверхности уничтожает вращение. Следовательно, винт вызы-
вает скорости скоса, изображенные на фиг. 125, которые уве-
207
личивают углы атаки крыла на одной части и уменьшают на
другой. Это очень хорошо видно на фиг. 121; в тех местах,
где винт вызывает скорость скоса, направленную вверх, сильно
увеличивается циркуляция.
Кроме скорости скоса, винт создает повышенную скорость
в отбрасываемой им струе —это так называемая скорость ухо-
дящего воздуха. Она связана с циркуляцией центрального
шнура следующим приближенным соотношением:
'387)
Применяя принцип наложения индуктивных скоростей, мы
получим следующие скорости у сечений крыла, лежащих в струе
винта (фиг. 126). Скорость потока будет равна теперь И2, ско-
рость вращения в струе равна vyB, и, наконец, скорость скоса
от вихрей крыла-Пук. Учитывая эти скорости, можно определить
угол скоса потока по формуле:
да _ £ Vy____Vy« ±vye
u2 " К
. Расчет этих влияний удобнее всего вести графически.
Заметим, что крыло служит для струи винта как бы контр-
пропеллером, уменьшающим циркуляцию у центрального шнура.
Величину этого уменьшения можно определить после оконча-
тельного расчета крыла, учтя действие струи винта. Для этого
нужно лишь найти изображенную на фиг. 121 разность цирку-
ляций ДГ. Эта циркуляция вычитается из первоначальной цирку-
ляции г Г, и вихревой шнур винта (конечно, воображаемый,
идущий как бы внутри фюзеляжа) имеет за крылом циркуляцию
/Г —ДГ.
Эта остаточная циркуляция вызывает довольно заметное
вращение в струе винта за самолетом, что в свою очередь соз-
дает разницу в углах атаки левой и правой частей горизон-
тального хвостового оперения и может дать одностороннее
нагружение вертикального оперения.
Все указанные вопросы, очень важные для конструктора, без
труда решаются с помощью теории вихрей. Труднее решение
вопроса о расчете крыла с переменной циркуляцией, к кото-
рому мы снова вернемся в гл. XIX.
§ 89. НЕКОТОРЫЕ ПРИНЦИПИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ
ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ
При возникновении теории индуктивного сопротивления
долгое время оставался неясным вопрос: каким образом, рас-
сматривая идеальную жидкость, можно получать в ней вихри?
По известной теории Гельмгольца, вихри, если вначале их не
было, никогда не могут возникнуть.
208
то у задней кромки можно
Фиг. 127. Возникновение циркуляции
около крыла и схема вихрей.
Неясным был также вопрос: почему по контуру, охватываю-
щему крыло, в неподвижном его состоянии циркуляция равна
нулю, а при движении она равна Г? По теореме Томсона, если
контур с самого начала не имел циркуляции, то он никогда не
должен иметь ее.
Проф. Прандтль показал, что здесь никаких противоречий
не имеется. Во-первых, в действительности у крыла образуется
вихревая пелена, а не конечные вихри. Пелена эта по сути
является разрывом сплошности в течении жидкости. Так, если
рассмотреть схему крыла фиг. 37,
наблюдать следующую картину.
Под влиянием разрежения над
крылом струйки сверху бегут,
сближаясь к центру крыла; под
влиянием сжатия под крылом
струйки бегут снизу, разбегаясь
от центра. При их слиянии воз-
никает скачок скоростей,
подробно изучаемый в курсах
теоретической аэро-и гидроди-
намики. Этот скачок скоростей
вызывает разрыв в непрерыв-
ном скоростном поле. Оказы-
вается, что такой скачок скоро-
стей ничем не отличается от
вихревого слоя, кроме того, что
в нем нет совершенно вихревых
нитей и толщина его равна ну-
лю. Следовательно, объем завих-
ренной жидкости равен нулю.
Таким образом вихревую
пелену можно рассматривать
с точки зрения аэродинамики как скачок скоростей, тогда ни-
какие вихри за крылом не будут образовываться.
Теперь рассмотрим возникновение циркуляции около крыла
(фиг. 127). Пусть крыло покоится, и мы очертим около него
контур А, циркуляция по которому, очевидно, равна нулю,
т. е. Гд = 0. Если теперь крыло придет в движение и возникнет
подъемная сила, то, как мы знаем по теореме Жуковского,
вокруг него возникнет циркуляция Г. Для объяснения этого
противоречия проф. Прандтль предположил, что с задней
кромки крыла в момент начала движения сбегает начальный
вихрь с циркуляцией, обратной циркуляции на крыле.
Опыты блестяще подтвердили это предположение. Для про-
ведения их пользуются ванной Прандтля (фиг. 128), в которую
налита вода. Крыло помещают в ванне таким образом, чтобы оно
своим верхним концом лежало немного выше зеркала воды.
Поверхность воды посыпают порошком алюминия, который,
плавая сверху, делает хорошо видимым движение воды.
Б Н. Юрьев—171—14
209
Оказалось, что как только крыло приходит в движение, за
ним тотчас же образуется начальный вихрь, остающийся все
время на месте.
В этой ванне можно продемонстрировать еще более любо-
пытный факт. При движении крыла около него возникает
циркуляция Г, а на его старом месте стоит начальный вихрь
с циркуляцией — Г. Если крыло остановить, продвинув его на
небольшое расстояние, то между двумя вихрями — присоединен-
ным и начальным — возникнет взаимодействие: получится пара
вихрей разного направления вращения. Такая пара должна дви-
гаться поступательно вниз. И действительно, в момент оста-
новки крыла с задней кромки
его сбегает присоединенный
вихрь, который далее, взаимо-
действуя с начальным, бежит
вместе с ним вниз (фиг. 129).
Этот поразительный опыт
показывает как бы реальность
присоединенного вихря.
Фиг. 129. Возникновение на-
чального вихря: 1—начало
движения, 2— остановка,
3—движение вихрей после
остановки.
Вихревые усы, начальный вихрь и присоединенный образуют
один общий вихрь, имеющий форму удлиненного кольца, как
это и показано на фиг. 127, с.
Таким образом теория индуктивного сопротивления в насто-
ящее время может считаться вполне строго обоснованной.
Очень часто непонимание многих положений теории индук-
тивного сопротивления получается от незнания теоремы Томсона,
гласящей, что тело, обтекаемое жидкостью, всегда соприка-
сается с одними и течи же частицами жидкости.
В этой теореме принимается, что тело имеет спереди и
сзади некоторые радиусы закругления г (фиг. 130). Тогда в
некоторой передней точке k получается нулевая скорость
течения — это известная нам критическая точка, давление в
рГ2
которой q = .
Такая же точка будет расположена и сзади. Следовательно,
ни одна внешняя частица не сможет подойти к телу, так как
в точке k скорость равна нулю, точно так же, как и в задней
точке kx ни одна частица, лежащая на поверхности тела, с него
210
не сойдет, так как ее скорость у самой кормы упадет до нуля.
Таким образом критические точки k и как бы „закупори-
вают" струйки, охватывающие наше тело. Если даже вообра-
зить, что сзади тело оканчивается математическим острием, то
и тогда новые частицы не коснутся тела. Лишь к телу, имею-
щему спереди математическое заострение, теорема Томсона
будет неприменима.
Из теоремы Томсона вытекает в частности и такой очень
важный для теории индукции факт: если перед крылом (фиг. 131)
очертить какой-нибудь контур А, то
крыло никогда в него не войдет, оно
будет лишь его неограниченно вытяги-
вать. Очень многие ошибочные рас-
суждения и выводы связаны с незнанием
Фиг. 131. Контур А
не может быть разре-
зан крылоли
Фиг. 130. К теореме Томсона.
этого факта. Если циркуляция по контуру А была равной нулю,
то она и останется всегда равной нулю, и никакого мгновен-
ного создания циркуляции Г у такого контура в момент „вхож-
дения" в него крыла быть не может.
Глава XIX
ПРИБЛИЖЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ЗАКОНА
ИЗМЕНЕНИЯ ЦИРКУЛЯЦИИ ПО РАЗМАХУ КРЫЛА
§ 90. ПРИБЛИЖЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ЦИРКУЛЯЦИИ КРЫЛА
Сложность уравнений Глауэрта и Лотц, требующих боль-
шой затраты времени на их решение, заставила искать более
простых и более наглядных методов решения той^же основной
задачи теории крыла, т. е. нахождение кривой Г = f(z).
Такие методы можно разбить на два типа. Применяя методы
первого типа, кривую циркуляции ищут на основе чисто гео-
метрических построений, почти несвязанных с аэродинам1усой.
По методам второго типа решение дается правильное с точки
зрения аэродинамики, причем широко применяется метод по-
следовательных приближений. При этом можно пользоваться
или тригонометрической формой уравнений, или обычной.
Применение обычных формул дает различные прямые ме-
тоды расчета, которые мы разберем в гл. XX. Сейчас же пе-
рейдем к геометрическому нахождению кривой циркуляции.
Как мы видели, кривая циркуляции скорости Г=/(г)у
большинства крыльев как бы повторяет форму крыла в плане,
211
т. ,е. кривую b = tp ( z ), только в несколько округленном виде,
со сглаживанием резких переходов и крутых переломов.
Основываясь на этом, можно предложить следующий, весьма
простой, способ приближенного определения формы кривой
Г = /(7). _
Вычертив кривую b = <p(z)
Фиг. 132. Пррближенное_построение
кривой Г = f(z).
отсюда
для данного крыла (фиг. 132),
и находят равновеликий эллипс,
т. е. такой, площадь кото-
рого
(389)
(здесь полуось а = 1, Ьэо—•
2 ширина в центре) равна
~ площади крыла. Следова-
тельно,
1 V "с
к b3Q = S ,
(390)
h _ 25
&э° — я
После этого строят хорду такого эллиптического крыла по
формуле: Ьэ = 1 — z2. _Разделив пополам разность ординат
Ьэ ь
кривых, находят кривую —» весьма близкую по форме к
кривой циркуляции, получаемой точными расчетами или путем
испытания.
Для определения величины циркуляции, умножив это выра-
жение на суэ эллиптического крыла, находят:
Г ~ СуЭ
ьэ+ь
2
(391)
Величину суз для эллиптического крыла всегда можно найти
по формулам (5Г) и (56) гл. IV, § 22, приняв т = 0:
а =----и сц3 = аа.
1 + -^
л л
Для применения их нужно предварительно вычислить
х = -4- = -Д
Ь ср <$
212
Зная величину суЭ) находят окончательно:
Г Суз
Ъ э 4- Ь
2
Такое построение Г при проверках неожиданно оказывается
очень точным. В качестве примера приводим на фиг, 133 крыло,
рассчитанное американцами с очень большой точностью (NACA
585, 1937 г.). Американцы вели расчет по способу Лотц и брали
четыре и десять
уравнений, а число
точек, по которым
находились коэ-
фициенты С2к и Вт,
равнялось 10 и 20.
На диаграмме сдела-
ны надписи, из ко-
торых видно, на-
сколько изменяются
кривые при измене-
нии числа точек и
числа уравнений.
Из этой диаграм-
мы следует, что при
четырех уравнениях,
несмотря на то, что
бралось 20 точек для
определения вспо-
могательных коэфи-
циентов, циркуля-
ция все же почти не
отразила резких вы-
резов в центропла-
не. Лишь тогда,
когда число уравне-
ний поднялось до 10,
вырез начал вырисо-
вываться достаточно
ясно на кривой Г.
Напомним, что точ-
ный результат можно
получить только при
числе уравнений,рав-
ном бесконечности;
при этом, несомнен-
но, влияние вырезов
Фиг. 133. Крыло, рассчитанное американцами по
способу Лотц с помощью четырех и десяти
уравнений, и приближенная кривая.
сказывается еще сильнее.
На эту диаграмму нанесена построенная по описанному
методу приближенная кривая; как видим, совпадение в дан-
ном случае получилось очень хорошее. Следует помнить,
213
что для построения кривой по 10 уравнениям Лотц потребова-
лась длительная, многодневная работа, а описанное здесь по-
строение требует около */« часа.
Такие же сравнения и в других случаях дают, как правило,
очень хорошее приближение к точным расчетам. Поэтому мы
рекомендуем при производстве расчетов более точными мето-
дами делать обязательно и описанное здесь построение, так
как оно служит прекрасным контролем для вычислений и дает
правильный порядок величин.
Заметим еще, что при таком построении у крыльев с кон-
цевой хордой не равной нулю концевая циркуляция равна не
нулю, а -|*&ксу,т.е. примерно тому же, что дают опыты (гл. XVIII,
§ 87). Таким образом это приближенное построение е точки
зрения передачи картины срыва потока с концов крыла оказы-
вается более точным, чем построение по точным теориям, ко-
торые совсем его не учитывают.
С помощью приближенного построения очень легко вычер-
тить кривую Г и для случая крыла с закрылком или с откло-
ненными элеронами. Сравнение с точными американскими рас-
четами показывает, что здесь можно поступить так. Участок
крыла, на котором поставлен закрылок, дает повышен-
ный c'v на величину Дсу (см. гл. XI, § 57). Зная среднюю
величину Суз, мы можем считать, пользуясь формулой Г= су Ь,
что здесь ширина крыла как бы увеличилась в отно-
шении Суэ + —. Таким образом мы получаем эквивалентное
крыло ступенчатой формы (фиг. 134). Далее поступаем по-
Фиг. 134. Циркуляция скорости Фиг. 135. Циркуляция скорости
у крыла с закрылками. у крыла с элеронами.
прежнему, — ищем равновеликое эллиптическое крыло и строим
циркуляцию, деля пополам ординаты; получаем:
г = суэ. (392)
Таким же образом можно построить и циркуляцию для крыла
с отклоненными элеронами (фиг. 135) и для закрученного крыла.
Ввиду важности для конструктора уметь быстро находить
циркуляцию, повторяем вкратце ход ее вычисления по при-
ближенному методу.
214
1. Найти />эо = — ; Х= -4г.
л S _
2. Построить кривую с ординатами —
3. Вычислить
„ _ «о 5X5
4. Построит^ кривую
Это и будет первое приближение для кривой Г'=/(г).
Легко убедиться, что полученная этим способом циркуля-
ция, аналитически выразится такой формулой:
тл/ 5,6 ( S г----— \
1 ~ I 5х 1 -Z2 + "2-J • (393)
§ 9 . УТОЧНЕНИЕ КРИВОЙ Г/( г) МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ
ПРИБЛИЖЕНИЙ
Основываясь на близости найденной в § 90 кривой Г' к дей-
ствительной, можно вести точный расчет крыла следующим
способом последовательных приближений. _
Найдя первое приближение, нужно, считая кривую Г'за-
данной, вычислить скорости скоса. Сделать это можно следую-
щим способом. Определим с помощью гармонического анализа
коэфициенты разложения этой кривой в ряд Фурье, т. е. Лъ
А2, Л3, А4, А5, Ав и т. д.
Получить эти коэфициенты можно проще всего с помощью
анализатора, а за неимением его — обычным арифметическим
способом с помощью формуляра. Мы здесь даем (стр. 216)
специально составленный нами формуляр для разложения функ-
ции в промежутке 0 —л по синусам.
Размах‘крыла делится на 12 неравных частей по указанным
в формуляре величинам z . Ход вычисления коэфициентов ука-
зан в самом формуляре. Этот формуляр дает достаточно точные
величины для Лп Л2, Л3, Л4, Л3, Л6, Л7; величины Л8 и Л9 полу-
чаются грубо ориентировочные. Формуляр пригоден, следова-
тельно, и для анализа несимметричных нагрузок крыла.
Анализируя кривую Г’=/(г), следует помнить, что полу-
чаемые непосредственно величины коэфициентов надо разде-
лить на 8, так как основная формула для циркуляции имеет
вид:
Г = 8 У, Ansin nf).
Найдя для первого приближения циркуляции Г' ее разложе-
215
to ормуляр для вычисления ряда Фурье по синусам для 12 ординат в интервале от 0 до я , 1) Разбивка размаха к рыла
№ орди- нат 0 1 2 3 4 5 6 7 8 9 10 11 12
1 N —1 0 —0,9660 —0,8660 2) -0,7071 Нечет —0,5000 н ы е коз -0,2583 ф и ц и е 1 0 иы +0,2583 (с и м м е 1 0,5000 г р И Ч н Ы ( 0,7071 г) 0,8660 0,9660 0 0
0,2588 0,5000 0,7071 1 11 2 10 3 9 1; 3; 9; 11, —5; —7 5; 7 10; 2 —3°; __д° О о О О 7 1 О %”' СМ СО 1 1 о О ~ Ю 1 1°; 3°; 9°; 11°; —5°; —7°
0,8660 0,9660 1,0000 4 8 5 7 6 2; 10 -6 —4°;—8' 1; И 6° 4°; 8° Г;11° -6° 6° —2°; —10°
Сумма An 6Д1 л. 6Д3 6Дб 6Д7 1 А3 1 ^5 1 ^7 3) Четные коэфициенты (несимметричн 6Л. лв ы е)
0,2588 0,5000 0,7071 1; 5; —7; —11
0,8660 0,9660 1,0000 О 7 00 О> 1 1 7 СЧ 00 1; 2°; 3; 7; 8°; —4°; -5; —10°; -11 р. 4о. 7о. 10о. __2°; - 5°; —8°; —11° 1;5;9°; -3°; —7; —11
Сумма An П p a I 6Д2 | 6Л4 I 6/le i 6Л8 1 <^2 1 ^4 1 Ав 1 ^8 вила пользования, а) Снять по чертежу ординаты разлагаемой функции,, отмечая знаки; заполнить табл. 1. б) Умножить ординаты соответствующих номеров на общий для строки табл. 2 ко- эфициент. Величины со знаком (°) были уже вычислены, их нужно прямо переписать, соблюдая знаки. Заполнить табл. 2 и 3. в) Вертикальные суммы табл. 2 и 3 дают величину коэфициентов, умноженную на 6; деля их на 6, получим коэфициенты. г) По 12 ординатам достаточно точно находятся коэфициенты Др А2, А3, А4, Аб и Дб;' коэфициенты А1 и z,8 находятся менее точно, а для коэфициента До определяется лишь порядок истинного значения.
ние,< вычислим угол скоса потока для ряда точек размаха по
формуле:
. __ S пАп sin пв
Я sin 6
Зная углы скоса, получим истинные углы атаки:
а{ = а' — Да.
Затем найдем местные с'уг для чего воспользуемся форму-
лой: су = аоаг или, что точнее, возьмем величину по графику
испытания профиля. Затем вычислим второе приближение для.
циркуляции по формуле:
Г" = с'у b
и построим график Г" = /( z). Эта циркуляция будет очень
близкой к истинной; будем считать ее вторым приближением.
Значение
р„,_ Г'+Г"
2
в большинстве случаев можно считать окончательным. При
необходимости получить особо большую точность нужно кри-
вую Г'" подвергнуть снова гармоническому анализу и найти
новые коэфициенты А{, Д2, А'3, А1, Аъ и т. д.
Приведенный здесь ход расчета значительно проще, чем
способ.решения основного уравнения, и дает достаточно точ-
ный результат. Он позволяет учесть нелинейность кривой св=/(а,)г
так как в этом случае можно пользоваться данными испытаний
профиля в трубе, а также можно без труда учесть концевые
вихри по методу, изложенному в гл. XVIII, § 87; наконец, весь
такой расчет крайне нагляден и, производя его, трудно ошибиться.
Найдя окончательные коэфициенты Ах, Д2, Аа, Д4, Л5, Дв,...,
можно далее вычислить по основным формулам Глауэрта:
cxi = S пА" ’
cv = itkAx
И т. д.
Глава XX
ПРЯМЫЕ МЕТОДЫ РАСЧЕТА КРЫЛА
§ 92. ПОСТАНОВКА ЗАДАЧИ
Разобранные в предыдущих главах методы расчета крыла
произвольной формы оказываются на практике довольно гро-
моздкими. Они требуют большой вычислительной работы и
применения тонких математических приемов. Вместе с тем они
являются, по-существу, методами грубо приближенными, так
217
как все характеристики крыла, в том числе и его аэродинами-
ческие свойства, получаются в виде рядов Фурье с несколькими
удержанными первыми гармониками.
Естественно, что наряду с такими методами возникли зна-
чительно более простые, прямые методы расчета
крыльев. Повидимому, эти методы впервые были разработаны
в СССР и путем постепенных улучшений были окончательно
доработаны в 1930 г. (см. библиографию). Однако вскоре .они
были у нас незаслуженно забыты *.
В последние годы во всех странах велись широко развер-
нутые исследования монопланных крыльев и за границей наряду
с методами Глауэрта и Лотц все чаще и чаще прибегают
к прямым методам расчета, пользуясь иногда и советскими
работами.
Прямые методы оказались более простыми и наглядными,
чем косвенные. Кроме того, они более гибки, так как в них
можйо вводить нелинейный закон изменения су по а, т. е. делать
возможным расчет и при посадочных углах атаки, можно оце-
нивать концевые вихри и т. д.
Характерной чертой всех этих методов является отказ от
решения основного интегро-диференциального уравнения (286).
Вместо этого задача нахождения закона изменения циркуляции
по размаху крыла решается методом последовательных прибли-
жений, с которым мы уже познакомились в §91.
Задача, таким образом, распадается на следующие этапы:
1. Наметка исходной кривой циркуляции. Чем ближе к истин-
ной величине будет взята эта кривая, тем быстрее и точнее
будет получен окончательный результат. Хорошие результаты
дает способ, описанный в § 90.
2. Вычисление углов скоса в ряде точек размаха по задан-
ному закону изменения Г по размаху. Эта задача является
центральной, и излагаемые далее методы отличаются друг от
друга лишь манерой решения данного вопроса.
.3. Вычисление циркуляции, получающейся по истинным
углам атаки сечений, по формуле: Г = суЬ.
4. Построение кривой циркуляции второго приближения как
средней между предположенной и полученной. Если разница
между этими циркуляциями большая, то нужно сделать третье
приближение и т. д.
1 Б. Н. Юрьев, Определение аэродинамических свойств крыльев про-
извольной формы в плане, «Вестник воздушного флота", № 2, 1923 г.
Б. Н. Юрьев, Индуктивное сопротивление крыльев, Труды ЦАГИ №20,
А. В. Ч е с а л о в, Построение поляры Лилиенталя монопланного крыла
произвольной формы, Труды ЦАГИ № 42, 1929.
Ю. А. Победоносцев, Графический метод построения циркуляции
по размаху, Труды ЦАГИ № 42, 1929.
J. R. Grean, The Calculation of Span Loadings Aircraft Engineering, Feb-
ruary 1937.
218
5. После нахождения закона циркуляции и, параллельно,
истинных углов атаки задача нахождения всех аэродинамических
характеристик решается очень просто графическими интегри-
рованиями.
Рассмотрим более подробно эти вычисления на простейшем,
первОхМ способе, который назовем методом вихорьков.
Все выводы будем излагать в безразмерных величинах.
§ 93. МЕТОД ВИХОРЬКОВ
Предположим, что мы задались изображенным на фиг. 136
законом изменения циркуляции по размаху крыла.
Разобьем размах крыла близко расположенными друг к другу
сечениями, которые^ представятся рядом сплошных орди-
нат. Кривая Г (г), пересекаясь с этими ординатами, даст
местные значения циркуляции. Разность двух соседних цирку-
ляций, которую обозначим через ДГ, сбежит между двумя
сечениями в виде вихревого
усика. При малом расстоя-
нии между сечениями мож-
но считать, что эти усики
сбегут на серединах соот-
ветствующих полосок. На
фиг. 136 через середины
этих полосок проведены
пунктирные орди-
наты.
Таким образом при этом
методе непрерывная вихре-
вая пелена заменится боль-
шим числом отдельных ви-
хорьков.
Если мы возьмем точку
Д, в которой хотим вычи-
слить угол скоса потока,
ТО МЫ ДОЛЖНЫ прОСумми- Фиг. 136. Метод вихорьков.
ровать действие на нее
всех вихревых шнурочков. Условимся точку А всегда выбирать
на середине участка, т. е. на пунктирной ординате. Тогда она
будет лежать на оси вихорька, сбежавшего на этом интервале,
и, следовательно, он на нее действовать не будет. Этим мы
избежим необходимости исследовать бесконечно большие
величины.
Скорость скоса вызванная в точке А вихорьком с абсцис-
сой С, найдется по обычной формуле действия полушнура:

ДГ
4тс (: — г) *
219
Переходя к отвлеченным обозначениям, т. е. вводя = VgV’»
z=~z-1/2, С=£.//2и ДГ — ДГ у, и суммируя действие всех вихорь-
ков, получим:
Да = -5>,= -4я2^
или окончательно:
<394>
8” С — z
Вычисляя Да в градусах, получим:
Ы> = — Эт!3у=^= -2,28У=^. (395}
8п г С— г
Величину ДГ очень легко найти графически, проводя гори-
зонтальные линии между соседними ординатами. На чертеже
величины ДГ обозначены жирными отрезками. Условимся счи-
тать прирост циркуляции положительным, если циркуляция
увеличивается при переходе от левой ординаты к правой. На
фиг. 136 знаки при ДГ поставлены согласно этому правилу.
Остается только подсчитать сумму ДГ.
Удобно поступить таким образом. Через точку А провести
прямую линию под углом в 45°, как показано на чертеже.
Пунктирные ординаты этой прямой дадут непосредственно зна-
чение С —z для любой точки размаха. Отсчитывая'длину соот-
ветствующего отрезка ДГ и деля его на. ординату этой прямой,,
будем получать влияния отдельных вихорьков. Откладываем
эти величины на счетах или на арифмометре. Пройдя весь
размах крыла, получим сумму, умножив которую на 2,28, затем,
на отношение масштабов ДГ и С — z, и поставив перед ней минус,
получим угол скоса для взятой точки в градусах.
Следует помнить, что сложение будет алгебраическим, так
какДГиС — z меняют знаки на протяжении размаха крыла.
Точность этого способа зависит главным образом от точно-
сти и аккуратности выполнения работы и от числа взятых
ординат. Размах крыла должен иметь на чертеже длину не
менее 300—500 мм, кривые надо проводить острым и твердым
карандашом, величину ДГ брать с точностью до десятых мил-
лиметра, для чего следует пользоваться лупой, и т. д. Число
ординат брать не менее 20—30. В таких условиях этим спосо-
бом получают почти такие же результаты, как и другими
методами, но обычно в несколько раз быстрее, чем с помощью
рядов Фурье.
Известным неудобством является здесь наличие пунктирных
и сплошных ординат и отсюда возможность ошибки отсчета
ДГ и С— z по разным ординатам. Если разбить крыло на равные
220
интервалы и провести зигзагообразную линию так, как показано
на фиг. 137, то, проведя прямую С—z через левую крайнюю
точку полоски, где берется точка А, мы получим отсчет ДГ и
t — z на одной ординате. При этом совершенно не потребуются
пунктирные ординаты.
Можно значительно уве-
личить точность этого ме-
тода, как и аналогичных,
излагаемых далее методов,
следующим приемом.
Циркуляция скорости у
всякого крыла близка к
полу эллиптической. Поль-
зуясь принципом наложе-
ния вихрей, мы можем рас-
сматривать отдельно ско-
рости, созданные полуэл-
липтической циркуляцией и
добавочной к ней, характер-
ной для данного крыла.
Таким образом мы мо-
жем написать:
Г = Гэ+1%. (396)
Скос получается В ОС- ФИг. 137. Метод вихорьков: отсчеты ДГ и
новном У обычных крыльев "С—*z приведены к одним ординатам,
от Гэ. Величину скоса от
эллиптической нагрузки легко подсчитать совершенно точно
по формуле (344), т. е. _
здесь Гэ.о — циркуляция от эллиптической нагрузки в центре.
Таким образом на долю приближенного метода выпадает
лишь задача нахождения добавочных углов скоса от добавоч-
ной циркуляции Вследствие этого точность приближенного
метода значительно увеличивается.
После того как будет найдена окончательная кривая для
циркуляции, расчет идет очень просто, по уже готовым фор-
мулам. Так:
-rl
су = ~ jf Су b dz; (305)
-1
^f==T / Cyb&zdz-, (306)
Схр — J* cxpbdz. (307)
221
Эти величины выч_иеляют путем графического _интегриро_
вания, строя кривые с'уЬ, суЬ Да и схрЬ как функции z и плани-
метрируя площади, заключенные между этими кривыми и
осью Oz.
Коэфициент момента продольной устойчивости (тангажа}
определится по формуле:
1 ' _ _ '__________ ,________
стг = —=. Г (cm/b2dz + cvbxAdz~ cxb yAdz). (311)
4&0
В случае несимметричной нагрузки, например отклоненных
элеронов, расчет ведется тем же самым методом. По данным
такого расчета можно найти также величину коэфициентов
моментов крена и рыскания по формулам:
етх = -±= 4fzdz- (304)
х +1 _ _ _ н! 1 _____
стУ-= ( j ГДа? dz + J схрв z dz^.
Таким образом теория индуктивного сопротивления позво-
ляет найти путем поверочного расчета все шесть компонентов
аэродинамического воздействия потока на тело.
94. ЗАМЕЧАНИЯ О РАСЧЕТЕ ВРАЩАЮЩИХСЯ КРЫЛЬЕВ
Заметим, что указанный в § 93 прием расчета может быть
с успехом применен и для расчета вращающихся крыльев. Если,
например, крыло вращается около оси Ох с угловой ско-
ростью то это вызывает у элементов крыла добавочные
вертикальные скорости, равньГе &xz. Обычно такие скорости
значительно меньше скорости полета, поэтому можно принять,
что они вызывают лишь добавочный угол скоса Даш от враще-
ния.
Очевидно,
Учет этого угла скоса не представляет никаких затруднений
при графическом решении задачи.
Этим же приемом легко рассчитать и эффект вращения
около оси Оу. Скорость набегающего потока будет в этом
случае с обычной для теории индукции точностью равна:
V1 = V+^
222
Эту скорость нужно вводить во все выражения вместо ско-
рости полета И. При графическом решении это также не пред-
ставляет особого труда.
Вычислять моменты, возникающие при вращении крыла,
приходится при расчете динамической устойчивости самолета,
например при расчете штопора. Очень часто их вычисляют
чисто аналитически, совершенно пренебрегая индуктивными
скоростями, что иногда может привести к очень большим
ошибкам.
Графические приемы позволяют производить такие расчеты
более точно, учитывая вихревую пелену.
Большой интерес для конструктора представляет вопрос о
вычислении изменения момента продольной устойчивости и
подъемной силы при вращении крыла около оси Oz с угло-
вой скоростью 0).
С этими вопросами конструктору приходится встречаться
при расчете динамической устойчивости самолета и при рас-
чете крыльев на вибрацию типа флатер.
Для полноты сообщенных здесь сведений отметим, что вы-
числение изменения момента продольной устойчивости (тангажа)
не может быть сделано такими
простыми методами, как для стх
пстУ. Его приходится вычислять
точными методами аэродина-
мики, рассматривая плоскопа-
раллельное течение воздуха. Од-
нако, если довольствоваться
малой точностью, то можно оп-
ределять величины Су и cmz у вра-
щающегося крыла искусствен-
ным приемом, сводящимся к
замене крыла данной формы
эквивалентным крылом такой же
формы, но с измененной кри-
визной.
Такая искусственная кривиз-
на называется динамиче-
ской.
Фиг. 138. Исходный и эквивалентный
профили при вращении крыла.
Пусть у нас имеется исходный профиль ОВ (фиг. 138),
средняя линия которого задана относительно указанных на
чертеже осей координат уравнением:
У = f (к)-
Этот профиль обтекается потоком со скоростью V и вра-
щается с угловой скоростью «о вниз.
Вообразим эквивалентный профиль OBlt например
с нижней линией, заданной уравнением:
J’» = /1 (•*)•
223
Этот профиль не вращается, а лишь обдувается потоком со
скоростью V.
Возьмем на обоих профилях точки А и Др лежащие на
равных абсциссах х, и рассмотрим относительную скорость
потока у этих точек. У первого профиля эта скорость
получится сложением поступательной скорости V и враща-
тельной о>х; у второго будет иметься лишь скорость по-
тока V.
Угол, образуемый этими скоростями с элементом профиля,
назовем местным углом атаки. Найдем этот угол у первого
профиля. Угол между скоростями W и V, очевидно, найдется
из соотношения: tg(W, V) = ^-. Тангенс наклона самого эле-
мента подучится как производная^. Считая эти тангенсы ма-
а>Х dy
лыми, можем считать — и соответственными углами в ра-
дианах. Тогда по фиг. 138 получим местный угол атаки исход-
ного профиля:
„ — 4У I
m~dxr V •
Местный угол эквивалентного, невращающегося профиля
будет равен углу наклона его элемента, т. е.
• _ ау»
Ят ~ dx •
Если допустить, что при одинаковых местных углах
атаки на равных абсциссах аэродинамические
свойства обоих профилей совпадают, то можно на-
писать условие:
dy3 dy шх
dx ~ dx + V ’
которое и позволит находить эквивалентные профили.
Интегрируя предыдущее уравнение, получим:
У°=У+%£- (397)
Это уравнение показывает, что ординаты любой линии экви-
валентного профиля получаются путем добавления к ордина-
там исходного профиля добавка, величина которого изменяется
по параболе.
Так как профили строят, принимая хорду за основу, то рас-
смотрим, во что обратится хорда первоначального профиля. Она
получится добавлением к ординатам первоначальной хорды вели-
чин следовательно, она обратится в параболу. Если пер-
224
воначально хорда была прямой ОВ (фиг. 139), то после при-
бавления к ней добавочных ординат она обратится в па-
раболу OBY.
Найдем относительную стрелку этой параболы /, беря ее в
центре хорды, т. е. при х = Ь/2. Получим ординату параболы
<1>Ь2 0,62
др- и ординату прямой jp-; их разность и даст стрелку кривизны:
____0>&2
7“ — 8/ ’
Относительная стрелка,
или кривизна, найдется те-
перь по формуле:
(398>
Кроме того, первоначаль-
ный угол атаки увеличится,
так как к нему прибавится у
Полагая тангенс равным углу,
Фиг. 139. Динамическое искривление
хорды при вращении крыла.
ол между линиями ОВ и ОВг.
получаем:
(&Ь2
_ BBt __ 2V __&b
~ ОВ ~ b
(399)
Таким образом вращающееся вниз крыло можно заменить
невращающимся, но с большей кривизной и с ббльшим углом
атаки.
Динамической кривизной называется сумма первоначальной
кривизны профиля и кривизны, вызванной вращением, т. е.
л =/+л~/ + ^.
(400)
Динамическим углом атаки называется величина

(401)
Таким образом, рассчитывая вращающееся крыло, мы должны
взять по продувкам или рассчитать по формулам гл. XI и XII
неподвижное крыло с кривизной fa и с углом атаки а<?.
При вращении крыла вверх знак поправок будет обратным.
§ 95. АМЕРИКАНСКИЙ СПОСОБ РАСЧЕТА КРЫЛА
Мы опишем здесь американский способ расчета крыла, введя
в него отвлеченные обозначения.
Б. Н.. ЮРьев—171—15 225
Основным уравнением в американском способе является урав-
нение (297):
Да =
(297)
Для того чтобы обойти точку разрыва при С — z — 0, аме-
риканцы пишут этот интеграл в таком виде:
т. е. поступают по общему правилу для вычисления несобствен-
ных интегралов. Третий член они получают, заменяя кривую
циркуляции в интервале от z — Д до z + Д параболой вида
су b = а + cz 4- dz2. Решая последний несобственный интеграл,
они получают:
г-д б/г
z-Д
rfc /Г-Д
Таким образом окончательно получается американская рабо-
чая формула:
г~д dT dr
J J £-г^ +
—1 г+ д
При пользовании этой формулой приходится сначала нахо-
ГГ гг
дить производную циркуляции—= по всему размаху крыла. Де-
лают это графически, так как кривая циркуляции предполагается
заданной и вычисление идет методом последовательных прибли-
жений. Как известно, графическое нахождение производных
обычно дает малую точность. В курсах технических вычисле-
ний описывается ряд способов таких вычислений. Самым про-
стым является проведение касательной на-глаз и определение
производной по отношению отрезков, которые она отсекает на
226
осях координат. Для получения более точного результата сна-
чала проводят нормаль к кривой с помощью зеркальной линейки
(фиг. 140), которую устанавливают так, чтобы между кривой и
ее отражением в зеркале не получа-
лось перелома; найдя нормаль, прово-
дят касательную и затем находят про-
изводную. Но чаще всего сначала раз-
бивают кривую Г=/(г) рядом ординат
иа кусочки, как на фиг. 136, и прини-
мают производную
Фиг. 140. Проведение нор-
мали к кривой с помощью
зеркальной динейки.

(эти отрезки надо откладывать очень точно). Полученную тем
или иным способом производную строят на размахе крыла как
функцию z (фиг. 141).
Далее
величину
вычисляют
и
С-г
кривую для
Фиг 141. Американский способ вычисления Да.
строят ее
каждой точки (z), в ко-
торой отыскивается
угол скоса. Эти кривые
планиметрируют в пре-
делах от—1 до z-Д и
от z + Д до + 1.
Выделенные над
точками z участки, ле-
жащие в пределах от
z— Д до z + Д, вызы-
вают угол скоса, вы-
числяемый по фор-
муле:
Д
Этот угол скоса при
малой величине Д
очень мал и в боль-
шинстве случаев его
просто откидывают,
так как
Графическое вычи-
сление угла скоса при-
ходится делать для нескольких точек, следовательно, расчет при-
ходится повторять несколько раз. Если при этом учесть, что под-
бор циркуляции ведется методом последовательных приближений,
227
то становится ясным большой объем вычислительной работы, не-
обходимой при этом способе. К этому недостатку присоединяется
еще неудобство, возникающее от получающихся на концах крыла
больших значений ~=; теоретически эта величина может быть
«С
равна бесконечности. Графическое интегрирование в этих
условиях недостаточно точно.
Этот способ сам по себе очень нагляден, но точность его
вряд ли выше способа вихорьков, так как и здесь трудность в
точном определении ДГ осталась вследствие того, что входя-
др —
щие в формулы величины k = зависят от ДГ и, следова-
тельно, ошибки в определении ДГ одинаково вредны в обоих
случаях.
Американцы этим приемом рассчитывают крылья самых раз-
ных форм, например с закрылками, со щитками, с выступами
и т. п. Способ этот можно уточнить, исправляя на основании
опытов кривую Г у концов крыльев. К сожалению, американцы
этого не делают.
§ 96. СПОСОБ ПРЯМОЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Для повышения точности вычисления угла скоса по пред-
ложению автора у нас с 1923 г. применяют следующий прием.
Кривую предположенной циркуляции разбивают на прямо-
линейные участки и заменяют ее ломаной линией (фиг. 142).
Число участков для полу-
чения достаточной точности
надо брать не слишком ма-
лое, — примерно 12 — 20.
Самую ломаную линию сле-
дует делать не вписанной
или описанной по отноше-
нию к кривой циркуляции,
а проводить ее так, чтобы
она возможно точнее изоб-
ражала заменяемую ее кри-
вую, т. е. ее нужно делать
пересекающейся с кривой
циркуляции в ряде точек.
Она займет некоторое сред-
Фиг. 142. Разбивка кривой циркуляции
на прямолинейные участки.
нее положение между опи-
санным и вписанным многоугольниками.
Точки, в которых вычисляется угол скоса потока, нужно
брать в достаточном количестве, не менее четырех — пяти на
полуразмахе крыла. По причинам, которые укажем далее, эти
точки берем на серединах участков, на которые разбита цир-
куляция.
228
Вычислим теперь: угол скоса в точке А, вызванный ка-
ким-нибудь прямолинейным участком циркуляции. Для этого
воспользуемся формулой (297), которая в нашем случае напи-
шется в таком виде:
A
Да== —J- / JLdi.
8n I С — z
Замечая, что в пределах прямолинейного участка
-S- = £= const, (403)
d£
получаем:
Дзх = —
k Л dC
8л J Т—Т
8л ?2 — г
Полный угол скоса, выраженный в градусах, будет равен
сумме углов скоса, вызванных такими участками и, следова-
тельно,
Да°
. 57,3.
k—-In
8л
57,3.2,3 С2 —г
8л S Cj —7
(404)
Если условиться всегда разбивать ось абсцисс однообразным
способом, то предыдущую формулу можно написать в таком
простом виде:
Да =
где a=f (положения точки А и номера
участка). Вычислив заранее величины а
для разбивки, принятой за нормальную,
мы сможем весьма быстро вычислять ско-
рости скоса.
Поясним теперь, почему мы брали
точки, в которых вычислялся скос (точки А),
на серединах участков, под которыми
они находились. Функция —=^имеет раз-
рыв, когда z = С. Для вычисления дейст-
вия участка на лежащую на нем точку А
(фиг. 143) получается несобственный ин-
теграл. Очень легко доказать, что он
равен нулю, когда точка А лежит сре-
ди участка.
Возьмем две симметричных точки В
Фиг. 143. На точку,
лежащую на середине
участка, сам участок
не действует. ,
и С с абсциссами
229
Cj = z— 8 и C2=z4-8. Подинтегральная функция будет иметь
в них величину:
k ___ k ______ k
7— z~~ ~z — 8 —~z~~ 8
И
k ___ k ______ k_
Z — z z + 8 — z 8 ’
т. e. значения получатся равные, но обратные по знаку. При
интегрировании элементарные полоски k~~ и — k~ попарно
сократятся, а так как мы весь такой интеграл можем разбить
на парные полоски, то и общий итог будет равен нулю. Физи-
ческое объяснение этого факта очень просто: беря симметрич-
ные относительно А вихорьки, мы получаем от них в точке А
равные, но направленные в противоположные стороны индук-
тивные скорости.
Заметим еще, что горизонтальные участки, где k = 0, также
не дадут никаких индуктивных скоростей.
Особенно упрощаются формулы в том случае, когда кривая
циркуляции симметрична. Тогда величина k= у симметрич-
dZ
ных точек размаха получается равной, но с обратным знаком.
Следовательно, можно вычислять сразу действие двух симме-
тричных участков на заданную точку с абсциссой z, т. е.
писать:
Да =
k~i +4-511 4+2^
— г 8it С2 + г /
обозначив:
57,3-2,3 —г
---------1g г = а,
8п s — г1
получаем:
ко. ^ka.
(405)
(406)
(407)
Проф. А. В. Чесалов вычислил эти коэфициенты для приня-
той им нормальной разбивки крыла.
На фиг. 144 размах крыла разбит на 20 элементов равной
длины, кроме того, концевые элементы разбиты еще пополам.
Точки, в которых определялись углы скоса, обозначены на чер-
теже кружками и взяты на серединах элементов. Условимся
обозначать точки номерами соответствующих им элементов.
Таблица, составленная А. В. Чесаловым, содержит величины
коэфициентов а для различных точек и участков (табл. 13).
Пользоваться этой таблицей надо так: сначала нужно в ниж-
230
dV ДГ
нюю строку подставить значения k = -=. = -=; найти эти вели-
dz &z
чины можно теми же приемами, которые указаны в § 95.
Затем умножают а на k и заполняют приводимый ниже фор-
муляр расчета. Предварительно ищут истинную циркуля-
цию Г, для чего приходится сделать два-три приближения.
Фиг. 144. Стандартная разбивка крыла на участки по А. В. Чесалову.
Найдя окончательное значение для циркуляции, получают, как
уже было описано, с', с'т, c'xi, с'хр и путем графического ин-
тегрирования или по способу трапеций вычисляют су, сх и ст
всего крыла.
Этот способ можно еще более уточнить, взяв вместо прямо-
линейных участков параболические, но мы здесь этого делать
не будем.
§ 97. ГРАФИЧЕСКИЙ ПРИЕМ Ю. А. ПОБЕДОНОСЦЕВА
ДЛЯ ВЫЧИСЛЕНИЯ УГЛА СКОСА ПОТОКА
Остроумный прием вычисления угла скоса Да0 предложил
Ю. А. Победоносцев. Полученное в предыдущем параграфе вы-
ражение:
Да° = V ak
он предложил решать графиче-
ски, разбивая кривую Г = /(з)на
стандартные участки по табл. 13
и проводя горизонтальные
линии, как показано на фиг. 145,
интервал между_которыми равен
ДГ. Разделив ДГ на длину соот-
ветствующего участка Дз, най-
дем производную:
k =
Фиг. 145. Горизонтальные линии,
определяющие ДГ.
ДГ
Дг ‘
231
Подставляя ее в основную формулу, получим:
Введем обозначение:
. а
(408)
тогда,
Да° = £Artgf.
(409)
Если взять стандартную разбивку крыла, то для каждой
фиксированной точки и для каждого прямолинейного элемента
циркуляции tgf будет величиной вполне определенной, и его
можно заранее вычислить по формуле (408).
Если взять фиксированные точки, для которых определя-
ется скос потока, н4 серединах участков 3, 5, 7 и И, то для
каждой из них можно построить пучок прямых, идущих так,
что tg 7, который они образуют с вертикалью, будет равен ~
&Z
для участков 1, 2, 3, 4... циркуляции. Будем обозначать фик-
сированные точки номерами участков, на которых они лежат.
Тогда получим по табл. 13 точки 3, 5, 7 и 11 (точку 9 можно
в обычных случаях расчета не брать).
На фиг. 146 мы приводим пучок прямых для'точки № 5;
номера на прямых дают участки, действующие на точку № 5,
причем подразумеваются парные участки, т. е. цифра 1 дает
действие участков 1 и 22, и т. д.
Фиг. 146. Пучок прямых,
определяющих tg 7 для точ-
ки №5.
угла скоса потока гра-
фическим путем для
точки №5/
Имея такой
пучок, очень легко вычислить
выражение:
Да° = ДГ tg х.
Для этого на горизонталях, полученных по фиг. 145, строят
многоугольник, начиная построение в точке 0 нулевой линии
(фиг. 147). Проведя через О линию, параллельную линии 01
232
Таблица 13
Коэфициенты а к способу Ю. А. Победоносцева и А. В. Чесалова
(Разбивка крыла по фиг. 144)
5S - S Э л е м е н т ы (У ч а с т к И) К р ИВО й ц и Р к у л я ц и и
5 « * 55* tT О £ Е-* о 1—22 2—21 3—20 4—19 5—18 6—17 7—16 8-15 9—14 10-13 11-12
3 - 1,000 — 1,650 — 0,136 2,360 1,010 0,603 0,394 0,264 0,193 0,099 0,0315
5 — 0,424 — 0,491 — 1,315 — 2,660 -0,180 2,310 0,956 0,538 0,321 0,193 0,0545
7 — 0,302 — 0,325 — 0,753 - 0,958 — 1,375 — 2,730 — 0,252 2,215 0,837 0,384 0,117
9 — 0,250 — 0,270 — 0,592 — 0,685 — 0,828 — 1,050 — 1,492 — 2,870 — 0,456 1,930 0,398
11 — 0,235 — 0,246 — 0,536 — 0,612 — 0,709 — 0,832 — 1,030 — 1,340 — 1,930 — 0,369 — 2,510

233
Формуляр хода расчета крыла
Точки сечений b а' а • k Да° = ^ak о О Д 1 а о 8 с'у Г = Су У Cxib — су ЛаЬ с'хр схр b т
1—22 2—21^3—20 4-195—18 6—17 7—16 8—15 9—14 10-13 11—12
3
5
7
9

(фиг. 146) до пересечения с горизонталью се, получают отре-
зок cd, длина которого равна Octg-(. Но Ос по построению
равен ДГХ; следовательно,
crf = Aritg .
Фиг. 148. Расположение диаграмм по способу Ю. А. Победоносцева.
Далее от точки d проводим линию, параллельную линии 02
(фиг. 146), и получаем точку h в пересечении со следующей
горизонталью. Отрезок
= tgf2AT2tg.
Продолжая так далее, получаем в результате полную сумму
^Artg^f, т. е. Да5.
Построение это выполняется очень быстро, если заранее
составлены пучки для точек 3, 5, 7 и 11. Располагать построе-
ние удобнее так, как это изображено на фиг. 148. В тех слу-
чаях, когда приходится часто рассчитывать крылья, рекомен-
дуется вычертить заранее эту диаграмму в большом масштабе.
234
_Пучки прямых очень легко строить по табл. 13, беря
ДГ = 0,1 и откладывая значения а по оси абсцисс в градусах.
При этом надо помнить, что на концах крыла для точности
взяты половинные интервалы, и tg у для интервалов 1—22 и
2—21 нужно увеличивать в 2 раза. На фиг. 148 пучки прямых
даны с тремя масштабами для разных величин Г и Да°.
Глава XXI
СКОРОСТНОЕ ПОЛЕ У КРЫЛА С ИЗМЕНЯЮЩЕЙСЯ
ПО РАЗМАХУ ЦИРКУЛЯЦИЕЙ
§ 98. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
Как мы видели в предыдущих главах, вычисление скоростей,
возникающих около крыла, является основной задачей всей
теории индуктивного сопротивления. Зная скорости скоса у при-
соединенного вихря, мы получим в случае монопланного крыла
скорость скоса от самоиндукции; учитывая скорости скоса у
соседних крыльев, мы получим теорию биплана; скос потока у
хвоста дает возможность рассчитать статическую устойчи-
вость самолета и т. д.
До сих пор мы занимались этим вопросом, исходя из про-
стейшей П-образной схемы вихрей, сбегающих с крыла. Эта
схема очень груба и получаемые с ее помощью результаты
можно рассматривать лишь как первое приближение.
Теперь мы рассмотрим более строгую теорию, исходящую
из произвольного закона изменения циркуляции скорости по
размаху, выражаемому формулой:
Т=/(7).
В этом случае за крылом получается вихревая пелена, кото-
рая, как мы уже указывали, на небольшом сравнительно рас-
стоянии от крыла сворачивается в два вихревых шнура. Отсюда
возникают два варианта этой теории. По первому считают
элементарные вихорьки прямолинейными и направленными по
скорости невозмущенного потока (горизонтально); по второму
более строгому варианту пытаются ввести в расчеты свертывание
вихревой пелены в два вихря конечной циркуляции. Промежуточ-
ное положение занимают теории, в которых учитывают наклон
вихревой пелены от скоса потока, но пренебрегают сворачиванием
пелены. Принципиально эта задача в первом варианте теории сво-
дится к уже разобранной нами в гл. V, § 25 задаче о скоро-
стях, возбуждаемых простым П-образным вихрем, так как вих-
ревую пелену можно рассматривать как совокупность бесконеч-
ного числа бесконечно слабых П-образных вихрей.
В случае симметричного крыла мы получим, таким образом,
для координаты крыла z элементарный П-образный вихрь с цир-
235
куляцией d£— ^=dz, причем расстояние между этими вихрями
будет равно 2z. Следовательно, любой компонент скорости
потока мы сможем вычислить по формулам_ (73), (74) и (75),
подставляя в них вместо размаха I величину 2z и вместо цирку-
ляции Г —величину йГ и интегрируя затем это выражение
в пределах от — Z/2 до + Z/2.
К сожалению, это вычисление даже в простейших случаях
оказывается очень трудным и, главное, получающиеся формулы
чрезмерно громоздки и неудобны для вычислений. Пользоваться
такими теориями в конструкторских бюро можно будет лишь
после того, как будут составлены специальные таблицы и гра-
фики для типичных случаев. Мы рассмотрим скорости в лобо-
вой плоскости, проходящей через несущий вихрь крыла, з
далеком от крыла сечении и у хвоста самолета.
§ 99. Эллиптический закон изменения циркуляции
по РАЗМАХУ
Для большинства крыльев кривая Г = /(z) весьма сильно
приближается к полуэллипсу. Естественно поэтому в качестве
второго приближения брать крыло не с П-образными вихрями,
а с вихрями, распределенными по закону полуэллипса.
У такого крыла скос потока по самому крылу постоянен и,
как мы знаем, равен _
= — Да = • (344)
Для расчета бипланов представляет большой интерес скос
потока, получающийся у такого крыла выше и ниже его оси.
Если ограничиться плоскостью, проходящей через несущий
вихрь крыла и перпендикулярной к скорости полета, то для
этого случая имеется решение, найденное Польгаузеном. Ско-
рость скоса оказывается в этом случае можно брать из обте-
кания потоком бесконечной пластинки шириной I, движущейся
вниз со скоростью vy (фиг. 149). Действительно у нашего крыла
скорость Vyo постоянна по размаху I, так же как и у пластинки.
Следовательно, граничные условия в обоих случаях одинаковы,
а это однозначно определяет потенциальный поток. Правда, у
крыла имеется еще наложение поля поступательного горизон-
тального потока, но при обычных допущениях это никакого
изменения в скорости vy и не вносит; скорость И лишь приба-
вится к vx. Задача же об обтекании этой пластинки приводится
к двухразмерному течению, где можно пользоваться методом
аналитических функций.
Эта задача была изучена еще в 1877 г. Г. Ламбом. Вычисле-
ние скоростей потока при таком движении пластинки излага-
ется в курсах теоретической аэродинамики. Линии тока абсо-
лютного движения изображены на фиг. 149. Скорости vy были
вычислены Польгаузеном и приведены у нас в табл. 14 в без-
236
размерном виде. За единицу скоростей была взята скорость vur>
на самом эллиптическом крыле. Эта скорость нам хорошо из-
вестна и всегда может быть вычислена по условиям работы
крыла, так как она связана с основными характеристиками
эллиптического крыла следующими со-
отношениями:
41 V’=-‘g- (410)
Скорость vy В/любой точке в виде
относительной скорости может быть
выражена так:
___________, и __ _
z). (411)
Ж
Эту скорость можно найти по фиг. 149 поток у движу-
табл. 14 или по графику Польгаузена щейся вниз пластинки
(фиг. 150), составленному по этой же бесконечной длины,
таблице.
Таким образом для вычисления скорости скоса в какой-нибудь
Фиг. 150. График Польгаузена.
точке с координатами у, z ил=0 нужно сначала вычислить
— у — z —’ —’
У — ц2> z==Tj2 11 затем найти vy и вычислить ^=0у|^о'.
237
238
Таблица Польгаузена*
Таблица 14
Скорость — У как функция у = — //2 11 1 N S ; для эллиптической циркуляции
__ \У z 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0,00 - 1,0000 — 0,9005 — 0,8039 — 0,7126 — 0,6286 — 0,5528 — 0,4855 — 0,4265 — 0,3753 — 0,3310 — 0,2929
0,05 - 1,0000 — 0,9001 — 0,8032 — 0,7117 — 0,6276 — 0,5517 — 0,4845 — 0,4256 — 0,3744 — 0,3303 — 0,2922
0,20 — 1,0000 — 0,8943 — 0,7925 — 0,6976 -0,6116 — 0,5352 — 0,4686 - 0,4109 — 0,3613 — 0,3188 — 0,2823
0,40 - 1,0000 — 0,8716 — 0,7514 — 0,6449 — 0,5541 - 0,4782 — 0,4152 — 0,3629 — 0,3192 — 0,2825 — 0,2543
0,60 — 1,0000 - 0,8102 — 0,6486 — 0,5251 — 0,4351 - 0,3692 — 0,3197 — 0,2811 - 0,2500 — 0,2243 — 0,2025
0,70 — 1,0000 — 0,7398 — 0,5446 — 0,4198 — 0,3421 -0,2915 — 0,2557 — 0.2281 — 0,2070 — 0,1880 — 0,1731
0,80 — 1,0000 — 0,5904 - 0,3663 - 0,2686 - 0,2245 — 0,1994 — 0,1835 — 0,1712 — 0,1606 — 0,1510 — 0,1419
0,90 — 1,0000 — 0,1984 — 0,0701 — 0,0719 — 0,0874 — 0,1001 — 0,1081 — 0,1122 — 0,1134 -0,1126 — 0,1103
0,95 — 1,0000 4- 0,2092 + 0,1158 + 0,0328 — 0,0191 - 0,0514 — 0,0714 — 0,0835 — 0,0904 - 0,0938 -0,0947
1,00 0,7022 0,2922 0,1296 + 0,0444 — 0,0057 — 0,0366 — 0,0561 — 0,0683 — 0,0756 — 0,0796
1,10 + 1,4004 0,9191 0,4856 0,2658 0,1442 + 0,0708 -4- 0,0293 - 0,0071 0,0273 — 0,0418 — 0,0511
1,20 0,8091 0,6909 0,4821 0,3148 0,2000 0,1224 0,0692 + 0,0321 + 0,0059 — 0,0127 - 0,0259
1,30 0,5650 0,5193 0,4171 0,3092 0,2175 0,1505 0,0990 0,0607 0,0323 + 0,0112 — 0,0045
1,40 0,4289 0,4068 0,3509 0,2826 0,2171 0,1610 0 1156 0,0796 0,0516 0,0298 + 0,0129
1,50 0,3416 0,3289 0,2958 0,2514 0,2044 0,1607 0,1226 0,0907 0,0646 0,0434 0,0265
* Взято из Durand, Aerodynamic Theory. Vol. II, стр. 150.
График Польгаузена приносит большую пользу при расчете
бипланов, так как позволяет получать истинный угол скоса от
взаимоиндукции в любой точке крыла.
Если считать вихревую пелену не сворачивающейся, то в
очень далеком от крыла сечении, перпендикулярном к скорости
полета, можно получить ту же самую картину скоростей, но
только действие бесконечно слабых вихорьков увеличится в два
раза, так как в разобранном случае мы имели вихревые полу-
шнуры, а при далеком сечении мы получим уже шнуры; послед-
ние вызывают скорости, в два раза большие.
При эллиптическом законе изменения циркуляции скорость
скоса в пределах размаха постоянна. Следовательно, и скорость
vg в далеких за крылом точках в пределах пелены будет посто-
янна и направлена вниз. Так как свободные вихри не могут
пересекаться потоком, то это указывает, что вихревая пелена
за крылом в действительности медленно опускается вниз со
скоростью 2Vy0, сохраняя свою форму, т. е. оставаясь в сече-
нии прямой линией.
§ 100. ПРИНЦИП ОТВЕРДЕВАНИЯ ВИХРЕВОЙ ПЕЛЕНЫ
У НАИВЫГОДНЕЙШИХ НЕСУЩИХ СИСТЕМ
Указанное в конце предыдущего параграфа свойство вихре-
вой пелены было обобщено Бетцем в виде следующей теоремы:
у всякой, несущей системы, имеющей наивыгоднейшее распреде-
ление подъемной силы по крыльям, вихревые пелены, сходящие
с крыльев, движутся в далеких от крыльев точках с постоян-
ной вертикальной скоро-
стью, как одна затверде-
вшая система поверхностей.
Предложенное им дока-
зательство этой важной
теоремы весьма просто.
Представим себе какую-
нибудь сложную несущую
систему, например крыло
с каким-либо законом изме-
нения циркуляции (фиг. 151).
Если закон будет наивы-
годнейшим, то всякое малое
изменение этой циркуля-
ции не повлияет на индук-
Фиг. 151. К доказательству теоремы
Бетца о постоянстве угла скоса
вдали от наивыгоднейшей несущей
системы.
тивное сопротивление, так как всякая функция у своего макси-
мума или минимума при бесконечно-малом изменении ее аргу-
ментов не изменяется. Если же закон изменения циркуляции
будет не наивыгоднейшим, то всякое изменение распределения
подъемной силы вызовет изменение индуктивного сопротивления.
Представим, что, не меняя подъемной силы, мы в одном
месте убавим, а в другом увеличим на ту же величину нагрузку
239
крыла. Это можно представить как наложение на крыло
двух малых П-образных систем вихрей, имеющих циркуляции
—dT и 4-оТ. По первой теореме Мунка индуктивное сопротив-
ление системы не изменится, если мы разместим эти вихри с
выносом,— в данном случае мы отодвинем эти П-образные вих-
ревые системы настолько далеко от крыла, что скорость скоса
можно будет считать там не зависящей от присоединенных
вихрей самой несущей системы.
Эти П-образные вихорьки можно представить в виде малень-
ких крылышек с размахом dz и циркуляцией и — dr. По-
ток вдали от крыла будет иметь от действия пелены углы
скоса, равные -р- и где ч)У1 — вертикальная скорость потока
у первого крылышка и vy2— у второго. Следовательно, наши
крылышки дадут подъемные силы б/ГрКйг и —что
вызовет у каждого крылышка индуктивное сопротивление
dXir = — dr р Vdz у- =- p^i dr dz
И
dXi2 = drP1/dz = ?vy2drdz.
Полное изменение индуктивного сопротивления будет равно:
dXn + dXft = pdVdz (vy2 — ^yi).
Если система—наивыгоднейшая, то малое изменение закона
распределения Г по размаху не должно изменить общего ин-
дуктивного сопротивления. Следовательно,
что и доказывает теорему.
Эти вихорьки мы могли бы взять и на разных крыльях; сле-
довательно, теорема является совершенно общей.
Если скорость скоса потока постоянна в далеких точках
пелены, то, возвращаясь к крыльям, мы получим лишь умень-
шение этой скорости в два раза; отсюда: скорость скоса в наи-
выгоднейшей несущей системе без выноса одинакова у всех
крыльев и постоянна по их размахам.
Этой теоремой часто пользуются при решении различных
задач для комбинации крыльев. К сожалению, конструктору
обычно задают форму несущей системы, и для решения задач
об углах атаки, ширине крыльев и т. д., связанных с приданием
этой системе свойств, близких к наивыгоднейшим, нужно знать
закон изменения циркуляции по крыльям. Решение же этой
задачи весьма нелегко. Принципиально ее следует решать так.
Представим, что заданная коробка крыльев вытянулась вперед
и назад до бесконечности и обратилась в совокупность беско-
нечно длинных пластинок. Если мы сообщим этой системе
240
Фиг. 152. Поток,^создаваемый
различными комбинациями
вертикальное движение, то возникшее при этом поле скоростей
позволит найти скорости vy, vz и циркуляцию скорости в лю-
бом месте крыла. Таким образом трехмерная задача сводится
к задаче о плоскопараллельном потоке, обтекающем ряд плас-
тинок (фиг. 152). Однако методами теоретической аэродинамики
задача легко решается лишь тогда, когда известна характери-
стическая функция течения. Нахождение этой функции для за-
данной системы пластинок дело весьма нелегкое.
Ученики проф. Прандтля Грам-
мель и Польгаузен изучили такой
поток в ряде интересных для прак-
тики случаев.
Для изображения окончательного
результата они воспользовались наг-
лядным приемом проф. Прандтля
представлять работу крыла как откло-
нение конечной струи воздуха. В слу-
чае крыла моноплана (фиг. 152, а)
получается струя в виде трубы с
диаметром, равным размаху крыла
(гл. III, § 17). В случае биплана струя
имеет вид, изображенный на фиг. 152,Ь,
— как видим каждое крыло дейст-
вует на струю, несколько меньшую,
чем у моноплана, где получался круг.
Если начать раздвигать крылья бип-
лана, то форма струи у каждого кры-
ла будет все более и более прибли-
жаться к кругу. В случае установки
на концах крыла шайб сечение струи
несколько увеличивается (фиг. 152, с)
и, наконец, в случае полиплана, со-
стоящего из очень многих крыльев,
струя имеет форму, представленную
на фиг. 152, d.
Все эти исследования были про-
ведены точным методом, причем все
время считалось, что система яв-
ляется наивыгоднейшей и вихревая
пелена — отвердевшей.
В результате этих исследований удалось построить весьма
интересный график, на котором дано отношение Xim моноплана
к Xt у различных систем крыльев, изображенных на фиг. 153;
при этом все системы имели одинаковый размах и равную
подъемную силу. По оси абсцисс отложено отношение высоты
несущей системы крыльев к размаху.
На первый взгляд вызывает удивление, что моноплан ока-
зался хуже всех этих систем. Однако надо помнить, что сравне-
ние ведется здесь при равной подъемной силе и равном раз-
Б. И. Юрьев—171 —16
241
махе, и при- реальном осуществлении такой схемы мы в биплане
получим у каждого крыла удлинение 1 приблизительно в два
раза большее, чем у моноплана, что и уменьшит очень сильно
индуктивное сопротивление всей коробки.
Этим же методом удалось изучить влияние на индуктивное
сопротивление щелей, пересекающих крыло поперек. Такие
щели встречались ранее довольно часто на самолетах в местах
Фиг. 153.. Сравнение различных несущих
систем.
стыка центроплана с кон-
солями. Нередко они бы-
вают в месте стыка кры-
ла и фюзеляжа.
Теоретическое иссле-
дование неожиданно вы-
явило огромное влия-
---1+S——
Фиг. 154. Крыло со
щелью.
ние этих щелей, на величину индуктивного сопротивления.
Поток, найденный приемом отвердения пелены, изображен
у нас на фиг. 154; здесь же дан чертеж крыла. Если обозначить
величину щели через s, а размах крыла через I ф- s, то в за-
висимости от отношения j-^~s получается следующее увеличе-
ние индуктивного сопротивления по сравнению с монопланом,
имеющим размах Z:
о 0,001 0,01 0,1 1
x'i
k= v" = 1 1,312 1,480 1,763 2
A;
§ 101. ОПРЕДЕЛЕНИЕ УГЛА СКОСА ПОТОКА У ХВОСТА ПРИ Г=/(г)
ПО ТЕОРИИ ГЛАУЭРТА
Вычислим теперь угол скоса в точках, лежащих на продоль-
ной оси координат Ох, принимая сначала эллиптический закон
изменения Г по размаху крыла. Формула эта дает также скос
потока у хвоста самолета при подстановке в нее х = L.
2А2
В случае П-образного вихря мы уже вывели в гл. VI форму-
лу, учитывавшую действие как присоединенного шнура, так и
вихревых усов. Она имела вид:
Да = _ТГ
nlV [
Разобьем вихревую пе-
лену на отдельные П-образ-
ные вихри (фиг. 155). Раз-
махом таких вихрей будет
являться уже не I, a 2z;
вместо циркуляции Г надо
брать dT, и для получения
окончательного результата
нужно проинтегрировать
полученное выражение от
О до //2; тогда мы учтем
все П-образные вихри. Та-
ким образом мы следуем
порядку, указанному в § 98,
Фиг. 155. Действие вихревой пелены
на горизонтальное хвостовое оперение.
и получаем:
В случае эллиптической циркуляции
Г = Го
а следовательно,
— — z dz
dr = </Г0
VI—г2
Замечая, что Г = Г-^, получаем в правой части лишь отвле-
ченные обозначения:
Удобно ввести сюда угол скоса потока у самого крыла, ко-
торый в случае эллиптической нагрузки будет иметь весьма
простое выражение:
Да = (344)
О
Тогда предыдущая формула примет вид:
243
Этот интеграл приводится к эллиптическому при помощи под-
становки:
А Г 9 1 -
z = cos 9, Р = --7,2 >
что приводит его к виду:
_2
(412)
О
Величина л
•Т
Е = //1 - k2 sin2 6Т/0
о
находится по имеющимся в справочниках таблицам значений
эллиптических интегралов.
Таким способом Глауэрт вычислил величину угла скоса у
эллиптического крыла для разных расстояний оперения от кры-
ла, и получил таблицу:
А. - ± 2 1 о
Z/2 “ 3 3 1 z
^2-= 3,23 2,43 2,22 2,06
Лот 1 1 9
Фиг. 156. Эквивалентный
размах крыла по Глауэрту.
При обычных расстояниях от крыла до хвостового опере-
ния угол скоса, у хвоста примерно в два раза больше угла
скоса у самого крыла. Если сравнить этот результат с тем, что
дает картина П-образныхв ихрей, то получится примерно удво-
ение угла скоса.
Опыт показывает, что обе картины не вполне верны. Угол
скоса, вычисленный как по формуле (412), так и по формуле
(108), сильно отличается от истинного.
Причина неточности обеих теорий
для этого случая вполне ясна. Вихре-
вая пелена в действительности неустой-
чива и сворачивается за крылом в два
вихревых уса, идущих на некотором
расстоянии друга от друга (фиг. 156).
Действие же таких вихрей сильно от-
личается от действия эллиптической
циркуляции.
Глауэрт предложил поэтому рассчи-
тывать угол скоса потока, заменяя вих-
ревую пелену П-образным эквивалент-
ным вихрем. Циркуляция скорости у
такого вихря будет равна Го, так как
в него войдут все сбежавшие с половины крыла вихревые нити;
расстояние между вихрями можно найти из условия, что подъ-
244
емные силы как у первоначальной системы вихрей, так и у
эквивалентной будут одинаковы.
У первоначальной системы вихрей подъемную силу можно
вычислить по обычной формуле:•
где су, по Глауэрту, выражается формулой:
Су = n\At;
следовательно,
Г = пХА15ф = ^-р/1И2А1. (413)
Циркуляция скорости в общем случае представляется рядом:
Г = 2/Г An sin п 6. (414)
В центре крыла она представится рядом:
Го = 2/У (А, — А3 4-Аб—...). (415)
В случае постоянной циркуляции при расстоянии между
вихрями, равном /„ выражение для подъемной силы напишется
по формуле Жуковского таким образом:
У = рГ0П.
Подставив сюда выражение циркуляции по формуле (415),
получим:
Y = pVli 21V (Aj - А3 + А6 - ...) =
= 2p//1V2(A1-A3 + A6- ...).
Приравнивая оба выражения (413) и (416), получим:
А = в__________А_________.
I 4 — Лз + 4s — 4? + • • •
Найдя расстояние между вихрями 1Ь далее можно
зоваться обычной формулой для П-образного вихря, подставив
в нее вместо I величину lt:
4”-° = <418>
Как видим, получается очень удобный способ расчета скоса
у хвоста, причем учитывается и характер нагружения крыла.
Здесь опять видно преимущество метода Глауэрта.
Для оценки величины угла скоса переходим к отвлеченным
— iv Г
обозначениям, замечая, что Г0 = Г0— и Да0=-^-; подставив
(416)
(417)
восполь-
245
эти значения в уравнение (418), получим окончательно:
(419)
Если величину L сделать очень большой, то в пределе по
лучится:
(420)
В табл. 15 приведены значения /х// для разных крыльев, вы-
численные с помощью коэфициентов Alt А3, А5 и А,.
Таблица 15
Угол скоса потока у хвоста по теории Глауэрта
Крыло к 4/z ( Ааг.о\ \ Да JL=oo / Ааг.о\ V Д1 JL^l/2
Эллиптическое Независимо от X 0,785 1,62 1,84
Прямоугольное — =0,5 а0 1 1,5 1,75 0,844 0,875 0,896 0,903 1,40 1,31 1,25 1,23 1,62 1,52 1,46 1,44
Угол скоса очень сильно
---- Пелена
Фиг. 157. Сравнение углов скоса
потока у разных крыльев.
возрастает при приближении к
крылу. На фиг. 157 представ-
лена вычисленная Глауэртом
Даг.о
зависимость между —для
разных отвлеченных длин хво-
ста —. Удлинения крыльев
были взяты равными о^^б.
Пунктирные линии изобра-
жают скос для П-образных
вихрей и эллиптического за-
кона с несвертывающейся пе-
леной; сплошные линии дают
эффект эквивалентного П-об-
разного вихря.
В общем теория Глауэрта
дает значительно более точ-
ный результат, чем более
простые теории. Однако вблизи крыла точность ее все же
246
получается небольшая, и проверки этой теории указывают на
систематические отклонения вычисленных величин от опытных.
§ 102. попытки УТОЧНИТЬ ФОРМУЛЫ ДЛЯ СКОСА ПОТОКА У ХВОСТА
Дальнейшим уточнением вихревой схемы является учет уча-
стка, на котором происходит сворачивание вихревой пелены в
два отдельных вихря (фиг. 156).
Попытки в этом направлении делались у нас И. Осто-
славским, М. П. Могилевским и С. Я. Финкель Ч Однако ими полу-
чены чрезвычайно сложные, неудобные для расчетов выражения,
пользоваться которыми можно будет на практике лишь после
составления ряда таблиц и графиков.
Вследствие этого многие авторы у нас и за границей начали
применять весьма упрощенную схему (фиг. 158), допуская, что
присоединенный вихрь имеет перемен-
ную циркуляцию, такую, как она полу-
чается у крыла данной формы. Вихре-
вые же усы считаются начинающимися
у самого крыла. При этом обычно рас-
суждают следующим образом: вихревая
пелена сворачивается очень быстро и,
следовательно, ее можно заменить от-
дельным вихрем, идущим до самого
крыла. Действие же присоединенного
вихря очень сильно зависит от закона
изменения его циркуляции, поэтому его
нужно учитывать точно.
Однако такая схема полностью про-
тиворечит основным теориям Гельмголь-
Фиг. 158. Упрощенная схема
вихрей.
ца о вихрях — здесь вихри внезапно кон-
чаются. Следовательно, все выводимые таким путем формулы
являются недопустимыми с точки зрения теоретической аэро-
динамики. Их можно рассматривать только как чисто эмпири-
ческие формулы, оправданием которых служит лишь получение
хороших числовых результатов.
Примером наиболее удачных таких формул является фор-
мула, разработанная М. П. Могилевским и И. В. Остославским.
Она дает, как показали ее авторы, очень хорошие числовые
результаты и потому ею часто пользуются в конструкторских
бюро.
Рассмотрим действие вихревого отрезка, вдоль которого
циркуляция изменяется по закону полуэллипса, на точку А с
координатами хи у (фиг. 159). Длина этого отрезка пусть будет/
и расстояние точки А от вихря = л2-Jr у2.
1 М. П. Могилевский и И. В. Остославский, Исследование скоса
у оперения, «Техника воздушного флота*, № 10, 1930 г.
И. В. Остославский, Новый метод аэродинамического расчета би-
планной коробки, «Техника воздушного флота", № 12“, 1931 г.
247
Выделим на этом отрезке вихря элемент длиной dz. Угол»
образуемый этим элементом с линией, соединяющей его с точ-
кой А, обозначим через <р. Тогда мы можем написать для дей-
ствия этого элемента вихря формулу (7), выведенную нами в
гл. I, § 6, а именно:
^1 = 4^- sin <рй-
Скорость d4)lt получаемая по этой формуле, будет перпен-
дикулярна к плоскости, проходящей через вихрь и точку А. Мы
будем интересоваться скосом потока и, следовательно, нам
Фиг. 159. Действие присоединенного
вихря на точку А.
нужно вычислить вертикаль-
ную проекцию скорости, ко-
торая, как видно из чертежа,
будет:
=- -L -^-sin <₽ d<f.
Входящая в эту формулу
циркуляция скорости будет
уже не постоянной, а изме-
няющейся по закону полуэл-
липса, т. е.
г=г"|/ ’-иг
Для удобства интегрирования удобно привести формулу
скорости к тригонометрическому виду. Для этого заметим, что
z = r0 ctg <р.
Тогда _________ ___________________
= .b-'L|/ - , V,^sin4-1
sin ф Z/2 I/ ( r0 \2
F V/2/
и, следовательно,
ton sin’»-1
» 0 f r о
Здесь мы ввели величину r0 = —. Очевидно, что
~ ~2 I —2
>о к лс 4“ У •
248
Интегрируя выражение dvn в пределах от <р до у, мы по-
лучим действие полукрыла на точку А; удваивая, получим пол-
ное действие всего крыла, т. е.
2
= р. ^Sin"f-1 df.
О'' Г 'о
Угол <р, очевидно, равен arc tg= arc tg г0, следовательно,,
входящий в эту формулу интеграл будет функцией только г0.
Его нельзя взять в конечном виде, так как он приводится к
эллиптическим интегралам, и при вычислениях по этой формуле
нужно пользоваться уже готовыми таблицами или вычислять
этот интеграл графически.
Обозначим этот интеграл через у., т. е.
V-=f(r0) =f{x, у).
Тогда формула для скорости скоса примет вид:
г0 х _ г х
Vn ~ ~ 2к х2 + у2
Найдем теперь скорость, полученную в точке А от действия
вихревых усов, идущих на расстоянии /х друг от друга.
Пользуясь основной формулой (9):
v = Г /—~ ,
^Vxl+yl / xl+yV
получим в нашем случае (фиг. 159а):
Г = Го;
Л= /j/2+(4/2)2.
Х2 = оо ;
Хг = — Л,
чт;о дает для двух усов:
Фиг. 159а. Действие вихревых
усов на точку А.
V — ------ - ....
2 4лГ>2+(/1/2)2
1 +
VУг + (4/2)2 + X2
249*
Скорость эта перпендикулярна к плоскости, проходящей через
вихревой ус и точку А. Проектируя ее на вертикаль, получим:
V = - _г° h + _ * .] fi/2 =
92 к У2 + Ui/2)2 L Vy2 + (4/2)2+ ха] V(Z,/2)a+ у2
____Го {1/2 _ Г. — х. ... (421)
— 2кУ2+(1112)3 [I + /x24-y2+(Z1/2)2J ’ ' '
Здесь мы ввели в формулу:
cos (v, Ox) = .
Уу2+(11!^
Величину Zx вычисляют по принципу Глауэрта, т. е. исходя из
условия равной подъемной силы у крыла с заданным законом
циркуляции и у крыла с Го — const. Для случая эллиптической на-
грузки это сводится к условию равенства площади прямоуголь-
ника Г0(х и площади полуэллипса 4-лГ04-, откуда
= = (422)
Заменяем в выражении (421) Zx на I по формуле (422) и получаем:
Введя безразмерные величины:
Л==7Г2И У = -ТГ2’
‘получим окончательно:
_ г» 0.406 _ / j , х
I 14-1,62уа( /о,616 + ла+уа
Полная скорость скоса будет равна сумме скоростей скоса
от присоединенного вихря и вихревых усов. Следовательно,

0,406 / j ।___________х_________
1 + 1,62уа \ у/~0,616 4-х 2 4-у2
Вводим сюда вместо циркуляции Го ее значение через суммар-
250
ный су &ля эллиптического крыла; по уравнению связи можно
написать:
Го = “2” •
Величину &0 — центральную хорду эллиптического крыла —
можно вычислить по площади крыла:
«-44-=т«
откуда
(423)
Теперь можно написать для циркуляции Го следующее вы-
ражение:
r0=4-w = 5»'.
Пользуясь найденными соотношениями, вычисляем угол скоса
потока и получаем:
Да°=— -^-57,3 = 57,3 § и +
j 0,406 / J ।______х______
l + l,62ya \ Z0,616 + х8 + у*
Это и есть формула И. В. Остославского и М. П. Могилев-
ского.
Обозначив выражение, стоящее в квадратных скобках, через х,
получим:
Да° = 57,3~х. (424)
Ttk
Величина х должна быть вычислена заранее. Остославский
и Могилевский дают для нее следующую таблицу:
Таблица 16
у)
х у 0,4 0,6 1 0,8 1,0 1,2 1,4 1,6
0 1,296 1,059 0,964 0,913 0,887 0,864 0,855
0,1 1,233 1,038 0,949 0,902 0,876 0,855 0,845
0,2 1,076 0,966 0,899 0,859 0,834 0,815 0,804
Напомним, что величина х вычислена здесь при условной
схеме вихрей. Формулу (424) можно считать универсальной,
так как это, в сущности, формула Мунка (гл. VI). Величину х
251
можно находить по любой теории или из опытов; структура
формулы для угла скоса останется при этом неизменной. Сле-
довательно, поскольку получаемые величины /. в описанном
расчете дают хорошее совпадение с опытами, этой формулой
можно пользоваться на практике. _
Табл. 16 показывает, что высота установки оперения у
мало сказывается на скосе потока. При обычных длинах опере-
ния х. 1; тогда можно считать х^0,9 при всех обычных вы-
сотах хвоста у. В общем формула Остославского и Могилев-
ского дает средний результат между теорией П-образных ви-
хрей и эллиптической циркуляцией.
При расчете хвоста биплана нужно рассчитывать скос от-
дельно от верхнего и нижнего крыльев, определив, хотя бы грубо,
распределение подъемной силы между крыльями, т. е. отношение
сУ11сп- Грубость определения этого отношения скажется очень
мало на окончательном результате, так как координата у мало
влияет на угол скоса.
В последнее время Остославский и Могилевский стараются
уточнить эту формулу, вводя в нее члены, учитывающие кри-
визну вихрей. Поправки получаются очень небольшие, и их
можно в расчет не вводить, тем более, что основная схема
вихрей, впервые предложенная Helmboldt, теоретически не
вполне закономерна.
Глава ХХП
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ У ПОЛИПЛАНОВ
С ИЗМЕНЯЮЩЕЙСЯ ПО РАЗМАХУ ЦИРКУЛЯЦИЕЙ
§ 103. ПУТИ РЕШЕНИЯ ЗАДАЧИ О ПОЛИПЛАНЕ
К решению задачи о сложных коробках крыльев можно
притти несколькими путями. Самый простой путь — использо-
вание схемы П-образных вихрей. Мы с ним подробно познако-
мились в гл. VII, посвященной теории биплана по Бетцу. Эта
теория дает сравнительно не плохие результаты, но все же
расчеты, сделанные с ее помощью, не вполне совпадают с опы-
тами. Опыты дают хотя и небольшие, но все заметные откло-
нения, которые желательно уничтожить.
Вторым приближением, обычно очень хорошим, является спо-
соб, предложенный Л. Прандтлем, и заключающийся в том, что
принимают нагрузку крыльев всегда эллиптической, учитывая,,
что такая нагрузка гораздо ближе к действительной, чем пред-
полагаемая в гипотезе П-образных вихрей, постоянная нагрузка.
Наконец, можно представить теорию, учитывающую действи-
тельную нагрузку всех крыльев по размаху. Подсчет по такой
теории был бы самым точным, однако мы видели, какие труд-
ности он представляет даже в случае моноплана. Тем не менее
такая попытка была сделана С. Г. Нужиным *, который пытался
1 См. Труды Казанского авиационного института, № 3, 1935.
252
обобщить метод Трефтца-Глауэрта на случай полиплана. Полу-
ченные им интересные результаты, к сожалению, мало при-
годны для практики из-за сложности вычислений и громоздко-
сти формул.
Можно еще более уточнить теорию биплана, учитывая
свертывание вихревой пелены, наподобие того, как это делается
при расчете скоса потока у хвоста самолета. Такую попытку
сделали у нас Могилевский и Остославский.
Наконец, целый ряд задач нерасчетного порядка удается ре-
шить приемом отвердевания вихревой пелены, о чем мы гово-
рили в гл. XXI, § 100.
В общем же в теории полипланов получаются довольно гро-
моздкие формулы, причем выводятся они с целым рядом допу-
щений и упрощений и точность их не намного выше точности обы-
чной теории Бетца. Большинство конструкторов предпочитает по-
этому вести расчет коробки по Бетцу и затем вводить уточ-
нения путем продувки модели коробки крыльев в аэродинами-
ческой трубе или с помощью более строгих теорий.
Здесь мы остановимся лишь на основных методах, находящих
применение в конструкторских бюро.
§ 104. ПОЛИПЛАНЫ С ЭЛЛИПТИЧЕСКИМ ЗАКОНОМ ИЗМЕНЕНИЯ
ЦИРКУЛЯЦИИ ПО РАЗМАХУ
Всякую коробку крыльев можно без изменения ее индуктив-
ного сопротивления привести к коробке без выноса согласно
первой теореме Мунка. Теория Прандтля в современном виде
не учитывает выноса верхнего крыла по отношению к нижнему.
Это, следовательно, ограничивает ее применение при расчете
устойчивости, где продольное размещение крыльев играет
большую роль; кроме того, это .вносит в нее небольшую не-
точность, так как коробка может не иметь выноса лишь при
каком-либо одном угле атаки; при других углах атаки вынос
непременно получится. Таким образом расчет коробки по теории
Прандтля может быть проведен только для одного угла атаки.
Пусть мы имеем сложную коробку крыльев (фиг. 160). Будем
нумеровать крылья сверху вниз. У верхнего крыла под дей-
ствием нижних получатся скорости скоса:
“°yi ~ ^ВП + Яи12 + f»13 + • • •
Для вычисления этих скоростей предположим, что закон
изменения циркуляции у всех крыльев, полуэллиптический
и воспользуемся графиком Польгаузена (гл. XXI, § 99, фиг. 150).
Изучим действие крыла 2 на крыло /. Взяв какую-нибудь точку
А крыла 1, определим ее отвлеченные координаты по отноше-
нию к крылу 2, т. е.
— г ТУ
Z~~ 1212> У ~ ~Щ2>
253
По графику Польгаузена найдем vv и затем, задавшись цир-
куляцией Го у крыла 2, получим:
Подставив индексы 1.2, найдем:
^01.2= ^у I^ikbI-
Такой расчет мы можем сделать для всех точек размаха
верхнего крыла. При ра-
счете сложной коробки при-
ходится, как видим, зада-
ваться или циркуляциями,
или подъемными силами
отдельных крыльев и итти
методом последовательных
приближений, на чем мы
остановимся дальше.
Совершенно таким же
путем мы найдем и влияние
крыла 3. Отвлеченные ко-
ординаты здесь будут:
2 = 4/2; =
И fH03=— 2^-
Таким образом мы можем
определить скорость скоса
от взаимоиндукции у всех
крыльев. К этой скорости
следует прибавить скосы
от самоиндукции, равные
соответственно
Гох Г0о
^01=-^^<В=-2/2ИТ-Д-
Полный скос получится
суммированием всех этих
скосов, как это и изображено на фиг. 160.
Найдя скорости скоса, подсчитаем индуктивное сопротивление
крыльев, которое, например для верхнего крыла, получится в йиде:
4-Z,/2 -> /1/2
X1.2+3=-J
-/7/2 -/./2
+ /./2
= pJ" Гх t/j, j 2+8 ^2.
-/1/2
254
Строим на размахе каждого крыла соответствующую величину
—Fty и, планиметрируя заштрихованные на чертеже площади,
находим интегралы 2а, Si2 и 2i3, после чего
= p2ix и т. д.
Для получения эллиптической нагрузки необходимо для каж-
дого крыла соблюсти условие, налагаемое уравнением связи.
Для п-го крыла получим:
Г'г 2~ суп Ьп V,
а так как в любой точке крыльев нам заданы Гп и V, то можно
лишь комбинировать величины сВп и Ьп так, чтобы всегда
, 2ГП
сУп Ьп--
т. е. для каждого сечения нужно или подбирать ширину крыла,
задавшись истинным углом атаки ain, или, задавшись шириной
крыла, определить угол атаки. При проектировании крыла мы
можем наметить эти величины наиболее удобным для нас спо-
собом, например, взять истинный угол атаки наивыгоднейший
для всех сечений и т. д.
Угол атаки сечения найдется тогда по формуле:
а'п = а«п + Д“п-
Зная истинные углы атаки, можно подсчитать профильное
сопротивление и аэродинамический момент теми же самымй
приемами, как это делается у моноплана. При таком проекти-
ровании мы получим вполне определенную коробку крыльев.
Однако для инженера гораздо важнее уметь производить
аэродинамический поверочный расчет, так как обычно размеры
коробки намечаются по конструктивным соображениям. К сожа-
лению, разработанных методов такого расчета еще не имеется.
Можно рекомендовать следующий путь. Задавшись подходящей
нагрузкой крыльев, например, исходя из вероятных Су, делают
допущение о эллиптической нагрузке крыльев и производят
расчет по фиг. 160. В каждом сечении и у каждого крыла нахо-
дят угол скоса потока и, зная для него угол атаки а, получают
истинный угол атаки:
а, = а' — Да.
По этому углу находят сд и затем Г =-^сдЬУ. Строят кри-
вую Г = f(z), которая теперь уже не будет изменяться по за-
кону полуэллипса и для вычисления индуктивных скоростей ее
заменяют эквивалентной полуэллиптической нагрузкой. По
этой нагрузке снова вычисляют индуктивные скорости и по
ним находят циркуляцию, уже более близкую к окончатель-
ной. Затем процесс повторяют до тех пор, пока кривые не пе-
рестанут изменяться.
255
Способ этот довольно громоздок и не вполне точен, так
как помимо упрощения кривой циркуляции пренебрегают ско-
ростями vxli и х»Ж21, которые учитывали в способе Бетца.
Для того чтобы не подсчитывать каждый раз площади 211(
&i2 и т. д., проф. Л. Прандтль предложил заранее вычислять
особые, безразмерные коэфициенты индуктивного сопротивле-
ния для типичных коробок. Прандтль пишет для биплана:
Хг = Лг11 + 2^(.12 + Х32.
Величину Х112 для типичных коробок легко подсчитать по
предыдущему графическим способом. Для этого заметим, что
+ Ц/2 + г,/2
Х12 = / dY^=-f dY^,
— Z./2 — Zi/2
НО
dYt = tf\Vdzlt
а так как у Прандтля предполагается для всех крыльев эллип-
тический закон изменения циркуляции, то
rfr1 = pl/<Z21raj/l-(A)\
Скорость скоса получится по способу Польгаузена:
— — 2I7
Отсюда индуктивное сопротивление равно:
+ '1/2 ______ _
%„=/ p№,r,j/l-(Ay^=
- '1/2
получим:
Н- Z/2
Замечая, что у крыльев с эллиптической нагрузкой
л рИ/л
01 ~~
и Гог =
-Ь z/2
• = С
"2 « /х/3 р/2 J
-112
= AAAJ_a.
тр pV2 ’
л pV’Z2’
— ^[/12
ТС
(1гг
(425)
Г
здесь о — коэфициент взаимоиндукции крыльев биплана по Пран-
дтлю. Его приходится вычислять графически с помощью диа-
граммы Польгаузена (фиг. 150) по последней формуле.
256
В качестве аргументов величин о у Прандтля взяты безраз-
мерные характеристики коробки крыльев:
(426)
т. е. отношение размахов крыльев, и
<426')
2
т. е. отношение высоты коробки к ее среднему размаху. Тог-
да а будет функцией лишь этих двух величин:
° = <? (н» Ч)-
Таблица 17
Величина а = (р., ц)
H \ ° ; 1 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,50
1,0 1,000 0,780 0,655 0,561 0,685 0,420 I 0,370 0,327 0,290 0,258 0,230
0,8 0,800 0,690 0,600 0,523 0,459 0,401 I 0,355 0,315 0,282 0,252 0,225
0,6 0,600 0,540 0,485 0,437 0,394 0,351 0,315 0,285 0,255 0,231 0,210
табл. 17 даны
В
результаты вычисления
&
V
as
0,6
0,1
0J6
0.5
о.з
0.1
0.1
0 0,1 0.2 0,3 0,4 0.5 Д
. Фиг. 161. График Прандтля для
расчета бипланов.
величины а для
различных значений р и т;. На фиг. 161 полученная зависимость
изображена графически.
В таблице приведены величины р<1. В тех случаях, когда
[л > 1, следует брать р'= Т-. Это следует из теоремы Мунка,
согласно которой A"(12 = Xtn,
а следовательно, и для верх-
него и для нижнего крыльев
мы можем брать р = Z2/Z< или
р' = Zx/Z2, и пользоваться тем
из них, который меньше еди-
ницы. В частном случае, до-
вольно часто встречающемся
на практике, р = 1 и 4 = 4-
Тогда вместо таблицы или
графика можно пользоваться
приближенными формулами
проф. Прандтля. Если
Л
7» = -
лежит в пределах:
то можно брать:
~ 1
° ~ 1 4- 5,3rf
(427)
Б. H. Юрьев—171—17
257
Можно пользоваться и более точной формулой:
1 — 0,66г,
1,055 + 3,71)’
(428)
Эта формула применима для -»), лежащей в пределах от Vis
до Va- В случае, когда [х ф 0, надо пользоваться графиком.
Таким образом полное индуктивное сопротивление коробки
биплана напишется по Прандтлю в таком виде:
— Хц 1 + 2x¥i]2 + ^V/22-
§ 105. НАИВЫГОДНЕЙШИЙ БИПЛАН
Мы уже имели формулу (352'), дающую индуктивное сопро-
тивление крыла с эллиптической нагрузкой; в нашем случае
2
\7 _ 2______1 .
111 “ яри* Z2’
У 2
^!'22 ярИ2 /2-
По формуле взаимоиндукции (425) получаем:
У - 2 Г1Г2 г
Л'12 лрУ2 ///2
Следовательно,
г2
2 /У,2 YY Y-
—— I — +- 2а ~±1Д2_ j----------:
крр \ /2 + 2 />/2 1‘
(429)
Формула эта полностью совпадает с аналогичной формулой
гл. IX, § 40.
Вся разница заключается в том лишь, что раньше мы нахо-
дили о по теории Бетца, а здесь она вычисляется более точно,
на основе эллиптической нагрузки крыльев.
Этой формулой можно воспользоваться для нахождения наи-
выгоднейшего распределения силы между крыльями.
гт Ь Y«
Полагая и = -у- и считая отношение подъемных сил-у —/,
где, как и ранее, + К2 = Y, мы сведем задачу к уже разоб-
ранной в гл. IX и получим тот же самый ответ, т. е.
U —- 5
'/- =—г—-
Р- Н-------2s
Р-
Подставляя это значение / в формулу (429) в ее разверну-
том виде, получим:
9 V2 1 _ д2 9 V2
*imin = = (430>
где х, как легко видеть, есть коэфициент уменьшения индуктив-
ного сопротивления по сравнению с монопланом той же грузо-
258
подъемности Кис размахом /х. Это видно из того, что у такого
моноплана индуктивное сопротивление:
iмоноплана —
Следовательно,
2 К8
крК2/* *
х Xi биплана
Xi моноплана >
(431)
Если ввести суммарные аэродинамические коэфициенты, т. е.
написать — су$Я и Л) = cxlSq, где S — площадь всех крыльев,
то формула (430) примет вид:
^imin = х - --с2. (432)
Величина % зависит
т. е> = 1, то, как мы
уже знаем, у — и
Величина х была
подсчитана проф. Л.
Прандтлем, который
составил таблицы и
графики, представляю-
щие х как функцию
безразмерных характе-
ристик коробки ц и 7]
(фиг. 162 и табл. 18
и 19). Этими графи-
ками очень удобно
пользоваться при ре-
шении различных част-
ных вопросов по проек-
тированию бипланов.
Например, задав-
шись размахами вер-
хнего и нижнего
от формы коробки. Так, если =/2 =/,
Фиг. 162. График Прандтля для определения ин-
дуктивного сопротивления наивыгоднейших би-
планов с эллиптическим распределением нагрузки.
о
крыльев и расстоянием между ними, легко наити -г- и ,п=т-гг и
*1 *1<»2
по графику фиг. 162 получить /их. Если при этом оба крыла
имеют одинаковую нагрузку на единицу поверхности, то, как
легко убедиться на частных примерах, у нижнего крыла с мень-
шим размахом получится и меньшая ширина.
Проверкой этих формул занимались многие лаборатории
и в настоящее время по этому вопросу опубликован весьма
обширный материал.
259
Совпадение опытов с этой теорией оказалось достаточно
хорошим, и в настоящее время теорией Прандтля весьма охотно
У Таблица 18
Величина / = (-у = f (р., т()
X. п н X. 0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5
0,6 0 0,060 0,104 0,134 0,157 0,176 0,191 0,202 0,211 0,218 0,224
0,7 0 0,105 0,164 0,202 0,228 0,248 0,262 0,272 0.281 0,288 0.294
0,8 0 0,172 0,246 0,285 0,310 0,327 0,338 0,347 0,355 0,361 0,361
0,9 0 0,303 0,359 0,387 0,402 0,412 0,419 0,425 0,429 0,431 0,433
1,0 — 0,500 0,500 0,500 0,500 0,500 0,500 0,500 0,500 0,500 0,500
V
i биплан а
Таблица 19
Величина (у., -rj
Л i моноплана
\ ‘G X 0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5
0,6 1,000 0,990 0,974 0,954 0,932 0,911 0,892 0,875 0,861 0,848 0,839
07 1,000 0,982 0,956 0,926 0,897 0,871 0,849 0,830 0,812 0,797 0,783
0,8 1,000 0,974 0,932 0,892 0,855 0,825 0,800 0,778 0,758 0,740 0,728
0,9 1,000 0,950 0,893 0,847 0,807 0,773 0,744 0,719 0,699 0,683 0,671
1,0 1.000 0,890 0,827 0,779 0,742 0,710 0,684 0,662 0,645 0,629 0,615
пользуются все
конструкторы. Диаграммы Прандтля
ются во всех . авиационных справочниках.
встреча-
Фиг. 163. Коэфициент х по теории Бетца-
пунктир и по теории Прандтля—сплошная
линия.
в величинах х равно всего лишь
При оценке этого расхождения
Результаты сравнитель-
ного вычисления коэфи-
циентов х по формулам
Бетца и по теории с эллип-
тическим законом циркуля-
ции изображены на фиг. 163.
Коробка была взята с 4 =
= 4 = I и Р* = 1; величина
h
4 = -j- менялась в широких
пределах. Из этой диаг-
раммы видно, что расхож-
дение этих теорий не слиш-
ком велико. Для наиболее
часто встречающихся вы-
сот биплана, т. е. для =
= 0,06—0,15, расхождение
7-16%.
следует помнить, что ин-
дуктивное сопротивление составляет лишь часть полного со-
противления коробки крыльев. На малых углах атаки оно при-
близительно равно профильному сопротивлению коробки кры-
260
льев. Следовательно, окончательное расхождение обеих теорий
не превосходит для обычных случаев 4—8% от полного сопро-
тивления коробки крыльев. Эта величина уже близка к степени
точности обычных измерений лобового сопротивления в аэро-
динамических трубах. Кроме того, у крыльев обычно получа-
ется промежуточный (между Г = const и Г, изменяющейся по по-
луэллипсу) закон циркуляции.
Таким образом на практике можно без особенно большой
ошибки пользоваться и более простой теорией Бетца. Она имеет
еще одно большое преимущество — с ее помощью легко учи-
тывать вынос крыльев, что по описанной теории еще сделать
не удалось.
§ 106. НАИВЫГОДНЕЙШИЕ ТРИПЛАН И ПОЛИПЛАН
Совершенно аналогичным путем можно исследовать индук-
тивное сопротивление трипланов. Ограничим задачу, взяв у всех
крыльев триплана равные размахи. Комбинируя крылья попарно,
получим по предыдущему параграфу:
(У? + =х гх У2 + а2 Y, Г8);
X* = + °*(Г1Гз +
= +о1Г2Г3 + о2Г1Г3).
В этих формулах соответствует расстоянию между крыльями,
равному/г/2, и а2— расстоянию h (здесь h — полная высота ко-
робки).
Если задаться вопросом о наивыгоднейшем распределении
подъемных сил у триплана, то сразу же, на основании принципа
независимости действия вихрей, можно сказать, что при равных
размахах подъемные силы верхнего крыла Y\ и нижнего У3 дол-
жны быть равны друг другу, так как они представляют собой
бипланную коробку, обладающую, как уже доказано, этим свой-
ством. Влияние среднего крыла не отразится на наивыгодней-
шем распределении подъемных сил у крайних крыльев, так
как эти влияния будут одинаковыми как для верхнего, так и
для нижнего крыльев, нагрузку же среднего крыла нам придет-
ся вычислить. Считая Уг = Y3 и обозначив У2 — У/, где ¥ —
= Yt + У2 + У3, мы можем написать:
А) — А’ц 4- 4- Х,з =
= +°2-2x(l+ в2-2о1)4-Хг(3 4-э2-4а1)]. (433)
Это выражение имеет минимум при
1 4~ g2 —
3 -J-
(434)
261
В табл. 20 приведены значения у. для разных величин =-у- •
Оказывается, что для наивыгоднейшего триплана величина /
всегда будет меньше х/3. Другими словами, среднее крыло в
Таблица 20
Величина / =-уН Для наивыгоднейшего триплана
h Ч--Г 0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 j 0,50
X 0 0,161 0,177 0,190 0,202 0,212 0,222 0,231 0,238 0,244 0,251
триплане должно быть нагружено меньше, чем другие крылья.
Для вычисления Индуктивного сопротивления пользуемся
такой же, как и для биплана, формулой:
2 У2
KpV2/2
или
2
- су £.
Cvimki — р
(435)
(436)
Здесь 5—полная площадь крыльев и- cxt и cv — суммарные
коэфициенты. Коэфициент х получается подстановкой в основ-
ную формулу (433) наивыгоднейшего значения у по формуле
(434). Этот коэфициент показывает уменьшение индуктивного
сопротивления данной комбинации крыльев по сравнению с мо-
нопланом, имеющим величины S, I и су (или Y).
Таблица 21
Коэфициент уменьшения индуктивного сопротивления к
h ^ = ~Г 0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50
Биплан . . 1 0,890^0,827 0,8890.824 0,779 , 0,742 0,710 0,684 0,662 0,645 0,629 0,615
Триплан. . 1 0,774 0,732 0,695 0,663 0,637 0,612 0,591 0,571
Наивыгод- нейший триплан. 1 0,885 0,819 0,767 0,724 0,687 0,656 0,630 0,507 0,585 0,565
Наивыгод- нейший полиплан 1 0,865 0,787 0,728 0,678 0,637 0,601 0,572 0,545 0,521 0,500
В табл. 21 для сравнения приведены также данные для би-
плана и триплана с равными подъемными силами на всех кры-
льях, т. е. у биплана у = х/а;, а у триплана у = х/з- В той же таб-
лице приведены значения х для наивыгоднейшего полиплана,
состоящего из очень большого числа крыльев равного раз-
262
маха, с высотой коробки h. По подробным исследованиям
Л. Прандтля, которые, здесь не приводим, у такого полиплана'
закон изменения циркуляции близок к эллиптическому лишь у
внешних крыльев, у средних же крыльев ой близок к закону
постоянной циркуляции, причем крайние крылья оказываются
нагруженными сильнее, чем средние.
Результаты всех этих исследований представлены графически
на фиг. 164. Из диаграммы легко усмотреть, что разница между
трипланом с наивы-
годнейшим распреде-
лением подъемной си-
лы по крыльям и
трипланом с равно-
мерно распределенной
подъемной силой очень
невелика.
Наивыгоднейший по-
липлан является мерой
совершенства той или
иной коробки крыльев,
позволяя сравнивать
ее индуктивное сопро-
тивление с наимень-
шим возможным соп-
ротивлением при за-
данных Z и h.
Для наивыгодней-
шего полиплана можно
пользоваться также
приближенной форму-
лой Л. Прандтля:
Фиг. 164. Сравнение индуктивного сопротивле-
ния моноплана, триплана и полиплана по
Прандтлю.
1 — 0,45?)
1,04 + 2,81т, ’
(437)
Ко всему изложенному следует прибавить еще следующие
замечания. Эллиптический закон циркуляции может быть полу-
чен, вообще говоря, лишь для определенного угла атаки, при
других углах он может заметно нарушаться. Точно так же и
наивыгоднейшее распределение подъемной силы по крыльям
может быть осуществлено лишь для заданного угла атаки.
Полипланы, таким образом, оказываются с точки зрения
индуктивного сопротивления более выгодными, чем монопланы.
Однако в этой теории совершенно не учитывается вредное
сопротивление стоек, расчалок , и т. п., наличие которых делает
полипланы менее совершенными, чем монопланы.
263
ПРИЛОЖЕНИЕ
г /1 \ Г cos nft d6 *
ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ ВИДА: /п(ф) = J —- fl _ со^
О
Подинтегральная функция этого интеграла обращается в
бесконечность при 9 = 6 и этот интеграл является не собствен-
ным; при его вычислении необходимо исследовать пределы,
к которым стремится его величина.
Как известно по Коши, под таким значением интеграла
понимают выражение:
ф—Д к "1
г ,,ч _Р (* cosnBrfO . Г cQsn^dft______________I
n ‘ 2To J cos b cos "Г" J cos Ь — cos
Lo ‘ <р4-д
Вычисление начнем с нахождения интеграла /0(ф):
Так как
* Вывод заимствуем у проф. В. В. Голубева, Теория крыла аэроплана
конечного размаха, Труды ЦАГИ № 108, 1931.
264
Таким же образом можно получить интеграл еще в виде:
Отсюда
Sin-2-
6 — ф
—2 .
+ С.
sin
(2)
1в (ф) = Ит
Д->0
—Ц- In
SH1 ф
о
— lim Дт
Д—>0 81ПФ
In
г . * + Ф
sin —
+ 1п --------~
1 тс — 6
Sin—г—
ИЛИ
/0 (Ф) = lim —Ц-
A_»osin4'
1- 1 .
= lim—г In
д о Sin ф
т. е.
/о(ф)=О.
(3)
Переходим к вычислению А(Ф);
А (Ф) =
/cos н d1
cos в — cos ф
о
cos 0 — COS ф
cos 6 — cos Ф
о
cos ф 46
siu 6 — cos ф’
т.
е.
А (ф) = к + cos ф 4, (ф) = я.
Для вычисления всех остальных/п (ф) выведем рекуррентную
формулу. Так как
г —Г cos(n
п 1 J cos 0 —cos Ф
о
и
I _____ Г cos (п — 1)6
л~'1 J cos О — cos Ф’
265
то
I л Г _ /cos(« + 1)6 +COS (я— 1)9 ,fi о /• cos «8 cos 6 ,ft
/n+l+A-i -/ ---------cos6-cosФ------M = 2 J cosb-c^^
о c
или
, , , _ с, r cos «9 (cos 8 — cos Ф) , Q Г cos rf) cos Ф ,c
In+1 + /л-i - 2 J —c-0-s-B-_C0s(p +2J ^-co-^ db, T. e.
о 0
7C П
/я+14-/л-1=2 f cos nb cZO 4- 2 cos ф f = 2 cos ф/„ (ф).
о о
Итак,
/л+i (ф) + 4-1 (ф) = 2 совф/п(ф). (4)
Отсюда
4 (Ф) + /о (Ф) = 2 cos ф/х (ф);
подставляя значения /0(ф) [и (ф), получаем:
/2 (Ф) = 2п cos ф = п• (5)
Величины:
4(Ф) = 0; /1(ф) = П; /3(ф) = к^ -
представляют собой значения:
<6>
при n = 0, 1 и 2. Далее, применяя метод математической индук-
ции, доказываем справедливость этой формулы при переходе
от п к п -Ь 1.
Предположим, что
т /|Ч sin (и — 1)ф г /1\ sin лф
Л-1 (Ф) == Я--7-7-— И 1п (Ф) = ТС —7х
VT' Sill Ф п V * / Sin ф
и по (4) найдем Лч ь Получим:
. /|Ч Л 1 sin лф sin (л — 1) ф
1п+1 (ф) = 2 cos фк-р- — к —- г-— =
VT/ * Sin ф sin ф
__ 2созф8шлф — sin лф cos ф 4-cos лф sin ф _
__ sin лф cos ф -j- cos лф sin ф
Siu Ф
Окончательно
266
Доказав справедливость формулы для п = 0, 1, 2, мы можем
по формуле (7) получить:
И т. д.
г sin Зф
Таким образом при всяком целом положительном п
/cos nO sin лф
,т~ ----- — - - —
cos t) — cos ф sin ф ‘
о
Литература
W. М. К u 11 a, Auftriebskrafte in stromenden Fliissigkeiten. Ill aeron. Mitteilun-
gen, 1902.
H. E. Жуковский, О присоединенных вихрях (сообщено в Математическом
об-ве 15 ноября 1905 г.). Университетская типография, 1906. Поли. собр.
соч. т. V, 1938.
Г. W. Lanch ester, Aerodynamics, Vol, II, 1907.
F. W. Lanchester, Aerodonetics, Vol. II, 1908.
IN. Joukowsky, Uber die Konturen der Tragflachen der Drachenflieger. «Zeit-
schriftfiir Flugtechnik und Motorluftschiffahrt» (сокращенно2ЕМ) 1910, Heft 22.
Поли. coop. соч. т. V, 1938.
N. Joukowsky, Geometrische Untersuchungen fiber die Kutta’scheStromung.
Moskau I—1910, II —1911. Поли. собр. соч. т. V, 1938.
С. А. Ч а п л ы г и н, О давлении плоскопараллельного потока на преграждаю-
щие тела (к теории аэроплана). Университетская типография, 1910.
Н. Е. Жуковский, Определение давления плоскопараллельного потока
жидкости на контур, который в пределе переходит в отрезок прямой. (Сооб-
щено в Математическом об-ве 15 марта 1911 г.). Труды Отделения физич.
наук О. Л. Е., вып. 15. Поли. собр. соч..т. V, 1935.
Н. Е. Ж у к о в с к и й, Теоретические основы воздухоплавания. Студенческое
издат. об-во при МВТУ, 1911 г., 2-е изд., 1925. Поли. собр. соч., лекции,
вып. 1.
Н. Е. Ж у к о в с к и й, О поддерживающих планах типа Антуанет. (Сообщено
в Математическом об-ве 25 апреля 1911 г.). Труды Физич. отд. об-ва Л. Е.
в Москве, I, XV, вып. II. Поли. собр. соч. т. V, 1938. Эта работа была
переведена в 1913 г. на немецкий язык.
С. А. Чаплыгин, Теория решетчатого крыла. Москва, 1914.
С. А. Ч а п л ыг и н, К общей теории крыла моноплана. Высший военный редак-
ционный совет, 1922.
С. А. Ч а п л ы г и н, Схематическая теория разрезного крыла аэроплана. «Научно-
технический вестник», № 4 и 5.
Л. Прандтль, Подъемная сила и лобовое сопротивление несущих поверхно-
стей в теории. Перевод ЦАГИ под ред. В. П. Ветчинкина.
А. А. С а т к е в и ч, Аэродинамика как теоретическая основа авиации. Петро-
град, 1923.
I. Prandtl, Ergebnisse und Ziele der Gottingen Modell Versuchanstalt. «ZFM»
1912.
L. Prandtl, Tragfliigeltheorie, I Mitteilung, 1918.
L. Prandtl, Tragfliigeltheorie, II Mittelung, 1919.
L. Prandtl, Naherungsformel fiir den Widerstand von Tragwerken. «Technische
Berichte Flugzeugmeisterei» (сокращенно «ТВ»), т. II.
L. Prandtl, Der induzierte Widerstand von Mehrdeckern. «ТВ», III.
L. Prandtl. Die neueren Forschritte der flugtechnischen Stromungslehre. «Z. des
Vereines Deutscher Ingineure» (сокращенно «ZVDI»), 1921.
L. Prandtl, Ergebnisse der Aerodynamischen Versuchsanstalt zu Gottingen.
I Lieferung 1919, 11—1923.
L. Prandtl, Applications of modern Hidrodynamics to Aeronautics. Report
№ 116, National Advisory Committee for Aeronautics (сокращенно «NACA»).
Washington, 1921.
'258
A. Betz, Beitrage zur Tragfliigeltheorie mit besonderer Beriicksichtigung des
einfachen rechteckigen Fidgels. Doktor. Dissertation, 1919.
A. Betz, Tragfliigeltheorie, 1920.
A. Betz, Die gegenseitige Beeinflussung zweier Tragflachen, «ZFM», 1914.
A. Betz, Berechnung der Luftkrafte auf eine Doppeldeckerzelle aus den entspre-
«Fl chenden Werten fur Eindeckertragflachen, «ТВ», I Bd.
A. Betz, Einfiihrung in die Theorie der Flugzeug Tragfliigel. «Die Naturwissen-
schaften», 1918. . ,
A. Betz, Wirbel und im Zusammenhang damit stehenden Begriffe der Hydrody-
namik, «ZFM» 1920.
H. Bader, Grundlagen der Flugtechnik, 1920.
H. Bader, Flugzeugbaukunde, Berlin, 1924.
R. Gramme 1, Die Hydrodynamischen Grundlagen des Fluges. Sammlung Vieweg.
M. Munk, Spanweite und Luftwiderstand, «ТВ», I.
M. Munk, Beitrag zur Aerodynamik der Flugzeugtragorgane, «ТВ», II.
M. Munk, Isoperimetrische Aufgaben aus der Theorie des Fluges. Dissertation,
1919.
H. G 1 a u e r t, Calculation of the characteristics of Tapered Wings. R. a. M. № 767,
1921.
H. G 1 a u e r t, Some Applications of the Vortex Theory of Aerofoils R. a. M.
№ 752, 1921.
H. G 1 a u e r t, Theoretical Relationships for a biplane. R. a. M. № 901, 1924.
H.^G 1 a u e r t, Experimental Tests of the Vortex Theory of Aerofoils R. a.M.
№ 889, 1924.*
H. G 1 a u e r t, Aerofoil Theory. R. a. M. № 723, 1923.
H. G 1 a u e r t, A method of calculating the characteristics of a tapered Wing.
R. a. M. 824, 1922,
A. F a g e, On the theory of tapered aerofoils. R. a. M. № 806, 1923.
A. F a g e, The prediction on the Prandtl theory of the lift and drag for infinite
span from measurement on Aerofoils of finite span. R. a. M. № 903, 1923.
W. С о w 1 e у u L. Jones, An experimental test of the Prandtl correction for
tunnel wall interference, R. a. M. № 898, 1924.
H. G lauert, The interference of wind channel walls on the aerodynamic charac-
teristics of an Aerofoils R. a. M. № 867, 1923.
L. S i m m о n s, Note on the applications of the vortex theory of aerofoils to the
prediction of downwash. R. a. M. № 914, 1924.
L. Simmons and E. Owner, An investigation of downwash in the slipstream.
R. a. M. № 882, 1924.
M. Munk, General biplan theory in four parts. NACA 151, 1922.
N. F 1 о r i n e, Trainee induite des ailes d’avions. Bulletin duLaboratoire Aerotech-
nique de Belgique. Bruxelles. 1922.
M. R о y, Sur la Theorie des Surfaces portantes. Scientia, 1922.
Fuchs-Hopf, Aerodynamik, Berlin, 1922.
Сборник. Vortrage ausdem Gebiete der Hydro-und Aerodynamik (Innsbruck 1922).
Статьи E. Trefftz, C. Wieselsberger, L. Prandtl и др.
О. T и т ь e н с, Гидро- и аэромеханика. По лекциям проф. Л. Прандтля, т. I и II.
ОНТИ, 1935.
Н. Glauert, The elements of airfoils and airscrew theory, Cambridge, 1926.
Handbuch der Physik, Band VII. Mechanik der Fliissigen und Gasfor-
migen Korper. Springer, 1927.
C. Eberhardt, Einfiihrung in die theoretische Aerodynamik. Oldenbourg, 1927,
ГНТИ, 1931.
W. F. Durand, Aerodynamic theory, vol. II, Springer, 1935.
I. Lotz, Berechnung der Auftriebsverteilung beliebig geformter Flugel. «ZFM»,
vol. 22, № 7, April 14, 1931.
I. Parsons, Span Load Distribution on a tapered Wing as Affected by Partial
Spane Flaps from Tests in the Full-Scale Tunnel. Journ. Aero Sciences, vol.3,
№ 5 March 1936.
H. A. Pearson, Span Load Distribution for tapered Wing with partialspan
Flaps. NACA 585, 1937.
269
A. SJ 1 v e r s t e i n and S. Katz off, Experimental investigation of wind-tunnel
. * * interference on the downwash behind an airfoil. NACA 609, 1937.
R. G. Robinson and W. H. Л/errnstein, Wing-nacelle-propeller inter-
ference for Wings of various Spans force and Pressure-Distribution Tests»
NACA 569.
E. J а с о b s and W. Kenneth, Interference of Wing and Fuselage from Tests
of 209 Combinations in the NACA Variable-Density Tunnel. NACA 540,
1935.
A. S h e r m a n, Interference of Wing an Fuselage from Tests of 28 Combinations
in the NACA Variable - Density Tunnel. NACA 575, 1936.
E. Jacobs and A. Sherman, Airfoil section characteristics as affected by
variations of the Reynolds number NACA 586, 1927.
Tarti, Itiro, Sanuki, Ma t a o, The wall interference of a wind tunnel
of Elliptic crossection. Proceedings of the Physics-Math. Soc. of Japan, vol. 14,
№ 10, 1932.
H. G 1 a u e r t, Interference on characteristics of aerofoils in windtunnel of Rectan-
gular Section. R & M. .1459, 1932.
T. Theodorsen, Interference on an Airfoil of finite spane in an open rectangu-
lar wind tunnel. NACA 461, 1933.
T. Theodorsen, The theory of wind-tunnel wall interference, NACA 410,
1931.
Б. H. Ю р ь e в, Определение аэродинамических свойств крыльев произвольного
очертания в плане. «Вестник воздушного флота» № 2, 1923.
Б. Н. Юрьев, Индуктивное сопротивление крыльев аэроплана, Труды ЦАГИ
№ 20, 1926.
Б. Н. Юрьеви Н. П. Лесникова, Аэродинамические исследования,
Труды ЦАГИ № 33, 1928.
Б. Н. Юрьев, Пересчет монопланов на биплан, Труды ВВА № 5, 1933.
Б. Н. Юрьев, Экспериментальная аэродинамика, ч. 1, ОНТИ, 1936.
В. В. Голубев, Теория крыла конечного размаха, Труды ЦАГИ № 108, 1931.
Ю. А. Победоносцев, Графический метод построения циркуляции по
размаху, Труды ЦАГИ № 42, 1929.
А. В. Чесало в, Построение поляры Лилиенталя монопланного крыла произ-
вольной формы, Труды ЦАГИ № 42, 1929.
Е. В. Красноперов, Приближенное определение коэфициентов Вп и С2&
при расчете крыла по методу Лотц. «Техника воздушного флота» № 9, 1937.
Е. Е. Сол о д к и н, Влияние формы монопланного крыла на его аэродинами-
ческие характеристики, Труды ЦАГИ № 234, 1935.
А. Б. Р и с б е р г, Влияние формы крыла на распределение нагрузки по раз-
маху и продольную устойчивость, Труды ЦАГИ № 335, 1937.
В. Н. Беляев, Аэродинамическая теория закрученного крыла. «Техника
воздушного флота» № 2, 1933.
С. Г. Ко з л о в, Аэродинамический расчет бипланной коробки. «Техника воз-
душного флота» № 3, 1927.
М. П. Могилевский и И. В. Остославский, Исследование скоса
потока у оперения самолета. «Техника воздушного флота» № 10, 1930.
И. В. Остославский, Новый метод аэродинамического расчета бипланной
коробки. «Техника воздушного флота» № 12, 1931.
И. В. Остославский и М. П. Могилевский, Скос потока у оперения
самолета при крыле произвольной формы в плане, Труды ЦАГИ № 312,
1937.
С. Г. Н у ж и н, Обобщение метода Трефтца на полиплан, Труды Казанского
авиационного института № 3, 1935.
Е. Е. С о л о д к и н, К методике исследований крыла с элеронами, Технические
заметки ЦАГИ № 146, 1937.
Я. М. Серебрийский, Крыло наивыгоднейшей формы в плане, Техни-
ческие заметки ЦАГИ № 159, 1937.
Я. М. С ер ебрийский, Аэродинамика упругого крыла, Труды ЦАГИ
№ 329, 1937.
К. К. Федяевский, .Турбулентный пограничный слой крыла, ч. II, Труды
ЦАГИ № 316, 1937.
270
Б. Т. Горощенко, Приближенный расчет лобового сопротивления, вызы-
ваемого заклепками. Технические заметки ЦАГИ № 174, 1938.
Ф. Г. Гласс, Юпределение сильна крыле по скосу потока за крылом, Труды
ЦАГИ № 117, 1935.
Е. М. Минский, Изучение piacn ре деления циркуляции по стреловидному
крылу, Труды ЦАГИ № 117, 1935.
Т. R. Grean, The calculation of span loadings. «Aircraft Engineering», February
1937.
Я. M. Серебрийский, Влияние близости земли на аэродинамические
характеристики самолета, Труды ЦАГИ № 267,z 1936.
А. А. Космодемьянский, Новые экспериментальные исследования со-
противления трения. «Техника воздушного флота» № 4, 1938.
Б. Т. Горощенко, Современный подход к выбору основных размеров и аэро-
динамическому расчету самолета (В пбмощь к дипломному проектированию).
Изд. ВВА, 1938.
И. В. Остос л а в с к и й и В. М. Титов, Аэродинамический расчет само-
летов, ОНТИ, 1938.
Справочник авиаконструктора, ЦАГИ, 137.
Н. С. Уханов, Задачник по экспериментальной аэродинамике. ОБОРОНГИЗ,
1938.
R. Т. Anderson, The experimental and calculated characteristics of 22 tapered
wings. NACA 627, 1938.
Л. E. Калихман, Влияние формы профиля, на сопротивление трения.
Исследование пограничного слоя в области отрыва. Труды ЦАГИ № 333,
1937.
ОГЛАВЛЕНИЕ
Стр.
Предисловие.......................................................... 3
Раздел I
Крыло с П-образными вихрями
Глава' I. Основы теории вихрей
§ 1. Циркуляция скорости...................................... 7
§ 2. Прямолинейный вихревой шнур.............................. 8
§ 3. Криволинейные вихри. Теоремы Гельмгольца и Стокса ... 8
§ 4. Скорости около вихрей. Теорема Био-Савара ................ 9
§ 5. Принцип независимости действия вихрей................... 10
§ 6. Прямолинейный вихревой отрезок........................... 11
Глава II. Теорема Н. Е. Жуковского
§ 7. Теорема Н. Е. Жуковского для крыла бесконечного размаха . 12
§ 8. Теорема Н. Е. Жуковского для крыла конечного размаха . . 14
§ 9. Уравнение связи ...................................... 15
§ 10. Упрощённый вывод теоремы Н. Е. Жуковского для крыла
конечного размаха ........................................ 16
Глава III. Влияние вихревых усов на крыло
§ 11. Скорость скоса у крыла.................................. 18
§ 12. Угол скоса.............................................. 20
§ 13. Индуктивное сопротивление крыла . .......................21
§ 14. Парабола индуктивного сопротивления..........• . . 23
§ 15. Пути улучшения аэродинамики крыла . . •.................. 25
§ 16. Более точные формулы индуктивного сопротивления .... 26
§ 17. Упрощенная схема работы крыла по Прандтлю............... 28
§ 18. Формулы индуктивного сопротивления в натуральных обо-
значениях . .............................................. 30
Глава IV; Пересчет монопланных крыльев с одного удлинения на другое
§ 19. Пересчет с на д2.............’.......................... 30
§ 20. Пересчет крыльев на бесконечный размах.................. 34
§ 21. Проверка теории индуктивного сопротивления.............. 34
§ 22. Наклон кривой су = f(a)............................. 36
§ 23. Американские диаграммы ................................. 38
§ 24. Способ проф. Юнкерса.................................... 41
Глава V. Поле скоростей около крыла
§ 25. Общие формулы для индуктивной скорости.................. 42
§ 26. Отвлеченные обозначения скоростей....................... 45
272
§ 27. Скорости в лобовой плоскости крыла...................... 47
§ 28. Скорости в далеки^ от крыла точках, лежащих в лобовой ।
плоскости крыла.............................................. 50
§ 29. Скорости на продольной оси крыла........................ 51
Глава VI. Скос потока у хвоста самолета
§ 30. Формулы скоса потока для крыла с П-образными вихрями . . 52
§ 31. Более точные формулы для определения угла скоса потока
у хвоста самолета ........................................... 55
§ 32. Влияние винта и фюзеляжа на угол скора потока у хвоста
самолета..................................................... 57
Глава VII. Теория полипланов по Бетцу
§ 33. Постановка задачи...................................... 59
§ 34. Вычисление скоростей и углов скоса потока от взаимного
влияния...................................................... 61
§ 35. Учет горизонтальных индуктивных скоростей........... . 65
§ 36. Теоремы Мунка ......................................... 68
Глава VIII. Пересчет монопланов на биплан
§ 37. Вывод основных формул................................... 71
§ 38. Ход пересчета . . . . •................................. 77
§ 39. Способ С. Г. Козлова..................•................. 78
Глава IX. Дополнения к теории биплана
§ 40. Наи вы годнейший биплан................................. 82
§ 41. Приближенная формула Прандтля для определения индуктив-
ного сопротивления ......................................... 84
§ 42. Средняя аэродинамическая хорда....................' . .. 86
§ 43. Дальнейшее развитие теории биплана.......................90
Глава X. Влияние границ потока на аэродинамические свойства крыльев
§ 44. Постановка задачи..................................... 92
§ 45. Влияние вертикальной стенки на самолет ............• . . 92
§ 46. Влияние близости земли ................................ 94
§ 47. Крыло между двумя стенками...............................97
§ 48. Индукция трубы прямоугольного сечения ................. 99
§ 49. Индукция круглой трубы с закрытой рабочей частью .... 102
§ 50. Влияние стенок трубы на работу хвостового оперения .... 105
§ 51. Поправки у труб с открытой рабочей частью...............109
§ 52. Трубы сложной формы . ...................................ПО
§ 53. Элементарный вывод формул индукции аэродинамических
труб......................................................... П2
Глава XI. Аэродинамические свойства самолета в целом.
Подъемная сила самолета
§ 54. „Предсказание* аэродинамических свойств самолета . . • . . 115
§ 55. Геометрические характеристики профилей.................117
§ 56. Взаимодействие крыла и фюзеляжа........................124
§ 57. Подъемная сила ’..................................... 124
Глава XII. Аэродинамические свойства самолета в целом.
Сопротивление и поляра
§ 58. Профильное сопротивление...............................130
§ 59. Исправление коэфициента сопротивления фюзеляжа.........136
273
§ 60. Сводка лобовых сопротивлений........................ 137
§ 61. Построение поляры самолета........................... 140
§ 62. Исправление поляры на влияние хвостового оперения .... 141
§ 63. Исправление поляры 6az влияние больших скоростей полета . 143
Раздел II
Крыло с изменяющейся по размаху циркуляцией
Глава XIII. Теория крыла с изменяющейся по размаху циркуляцией
§ 64. Скос потока у крыла с изменяющейся по размаху цирку-
ляцией .................................................146
§ 65. Силы, действующие на крыло с изменяющейся по размаху цир-
куляцией ............................................. 148
§ 66. Аэродинамический момент у крыла с изменяющейся по раз-
маху циркуляцией....................................... 151
§ 67. Основное интегро-диференциальное уравнение теории крыла 153
§ 68. Другое выражение для скоса потока у крыла с изменяющейся
по размаху циркуляцией..................................154
§ 69. Переход к безразмерным величинам . . . • •...• . . 155
Глава XIV. Теория Тррфтца-Глауэрта
§ 70. Тригонометрическое преобразование выражений для цирку-
ляции и скоса потока.........................................159
§ 71. Тригонометрическое преобразование выражений для сил ... 164
§ 72. Формулы для пересчета незакрученных крыльев на к = оо и
с kj на к2.................................................. 166
§ 73. Формулы для моментов .... .............................168
Глава XV. Три основных задачи теории монопданного крыла
конечного размаха
§ 74. Постановка задач..................................... 169
§ 75. Первая Задача — построение} крыла с заданным законом
изменения циркуляции по размаху крыла.......................* 170
§ 76. Вторая задача — о наивыгоднейшем крыле . . ............172
§ 77. Дополнения к теории эллиптических крыльев . j. ...... 175
§ 78. Третья задача — поверочный расчет крыла произвольной
формы...................................................... 177
Глава XVI. Способ И. Лотц
§ 79. Основные уравнения И. Лотц........................• . . . 180
§ 80. Решение уравнений И. Лотц..............................182
§ 81. Вычисление коэфициентов С2к и Вт.......................186
§ 82. Сравнение и критика методов Глауэрта и Лотц............190
Глава XVII. Закрученные крыльц
§ 83. Общие свойства закрученных крыльев.....................191
§ 84. Прямоугольное закрученное крыло........................197
Глава XVIII. Проверка и уточнение теории индуктивного
сопротивления
§ 85. Картина давления и циркуляция........... . . . •.......198
§ 86. Опытная проверка теории индуктивного сопротивления с по-
мощью картины давления.......................................201
§ 87. Учет влияния концов крыла..............................203
274
§ 88. Влияние фюзеляжа и струи винта на циркуляцию крыла . . 206
§ 89. Некоторые принципиальные вопросы теории индуктивного
сопротивления . . . .....................................208
Глава XIX. Приближенные методы определения закона изменения
циркуляции по размаху крыла
§ 90. Приближенные методы определения циркуляции крыла . . . 211
§ 91. Уточнение кривой Г =/(7) методом последовательных при-
ближений . . . •..............................•..........215
Глава XX. Прямые методы расчета крыла
§ 92. Постановка задачи.......• . • . .................. 217
§ 93. Метод, вихорьков.................................. 219
§ 94. Замечания о расчете вращающихся крыльев.............222
§ 95. Американский способ расчета крыла...................225
§ 96. Способ прямолинейных элементов* ....................228
§ 97. Графический прием ГО. А. Победоносцева для вычисления
угла скоса потока .... . . •.............................231
Глава XXI. Скоростное поле у крыла с изменяющейся по размаху
циркуляцией
§ 98. Общая постановка задачи............................235
§ 99. Эллиптический закон изменения циркуляции по размаху . . 236
§ 100. Принцип отвердевания вихревой пелены у наивыгоднейших
несущих систем...........................................239
§ 101. Определение угла скоса потока у хвоста при Г =/(2) по
теории Глауэрта......................................... 242
§ 102. Попытки уточнить формулы для скоса потока у хвоста . . 247
Глава XXII. Индуктивное сопротивление у полипланов
с изменяющейся по размаху циркуляцией
§ 103. Пути решения задачи о полиплане •..................252
§ 104. Полипланы с эллиптическим законом изменения циркуляции
по размаху.............................•............... . . 253
§ 105. Наивыгоднейший биплан..............................258
§ 106. Наивыгоднейшие триплан и полиплан..................261
Приложение. Вычисление интегралов главы XIV...........264
Литература. . . ;.........................................268